Introduction
Plugins
katex
\[
\text{MSE}(q) = \mathbb{E}_X \left[ d(q(x), x)^2 \right] = \int p(x) d(q(x), x)^2 dx,
\]
admonish
```admonish success
```
reading-time
全文字数: **{{ #没有空格word_count }}**
阅读时间: **{{ #没有空格reading_time }}**
全文字数: 433 字
阅读时间: 3 分钟
alert
> [!CAUTION]
> Negative potential consequences of an action.
note
Highlights information that users should take into account, even when skimming.
tip
Optional information to help a user be more successful.
important
Crucial information necessary for users to succeed.
warning
Critical content demanding immediate user attention due to potential risks.
caution
Negative potential consequences of an action. >
repl
这不是 jupyter notebook,所以请把代码写在一个 codeblock 中。(你可以编辑 codeblock )
class Greeter:
def __init__(self, name):
self.name = name
def greet(self):
return "Hello, " + self.name
g = Greeter("world")
print(g.greet())
mermaid
graph TD;
A-->B;
A-->C;
B-->D;
C-->D;
graph TD;
A-->B;
A-->C;
B-->D;
C-->D;
embedify
{%这是一个空格embed bilibili id="BV1uT4y1P7CX" loading="lazy" %}
vector db
全文字数: 1021 字
阅读时间: 7 分钟
Index
| 索引算法 | 介质 | 优点 | 缺点 |
|---|---|---|---|
| Flat | 内存 | 精确 | 速度慢 |
Brute-force
Flat
暴力搜索
- 保证精确度
- 效率低
适合在小型、百万级数据集上寻求完全精确的搜索结果。
IVF
IVF_FLAT
使用倒排索引方法,结合聚类算法(如k-means),将高维空间中的向量划分为多个簇。每个簇包含相似向量,并且选取簇的中心作为代表向量。为每个簇创建倒排索引,并将每个向量映射到所属的簇。
查询时,系统只需关注相似簇,避免了遍历整个高维空间,从而显著降低了搜索复杂度。通过参数nprobe控制搜索时考虑的簇数,平衡查询精度与速度。
- IVF_FLAT将查询向量分配到距离最近的簇中心
- 然后在该簇内执行线性搜索,查找与查询向量相似的向量。
IVF_FLAT适用于需要在精度和查询速度之间取得平衡的场景,特别是在大规模高维数据集上,能够显著降低查询时间。它非常适合那些对精度要求较高,但可以容忍一定查询延迟的应用。
IVF_SQ8
IVF_SQ8 在 IVF_FLAT 基础上增加了量化步骤。IVF_SQ8通过标量量化(Scalar Quantization)将每个维度的 4 字节浮点数表示压缩为 1 字节整数表示。量化的过程是将原始的浮点数值映射到一个较小的整数范围。
- 通过量化将存储和计算资源的消耗大大降低
- 核心思想与 IVF_FLAT 类似
IVF_PQ
IVF_PQ 在 IVF_FLAT 基础上增加了 Product Quantization 步骤。将向量空间划分为更小的子空间并进行量化。
通过将向量划分为多个子空间,并对每个子空间进行独立的量化,生成一个代码本(codebook)。这样,原始的高维向量可以由多个子空间的量化表示组合而成,从而降低存储需求并加速检索。
在IVF_PQ中,乘积量化应用于IVF的聚类过程。每个簇的中心点会被进一步量化,原始的查询向量和数据向量在计算距离时,不是直接与每个簇中心进行计算,而是与每个子空间的量化中心进行计算。这种方法不仅降低了存储开销,还减少了计算距离时的运算量。
Graph-based
HNSW
HNSW(Hierarchical Navigable Small World Graph)是一种图索引算法,基于分层结构和小世界图理论,用于高效的近似最近邻搜索。它构建一个多层图结构,逐层精细化,提高高维数据集的搜索效率。
HNSW结合了跳表(Skip List)和小世界图(NSW)的技术:
- 跳表:底层为有序链表,逐层稀疏化,查询从最上层开始,逐层向下查找。
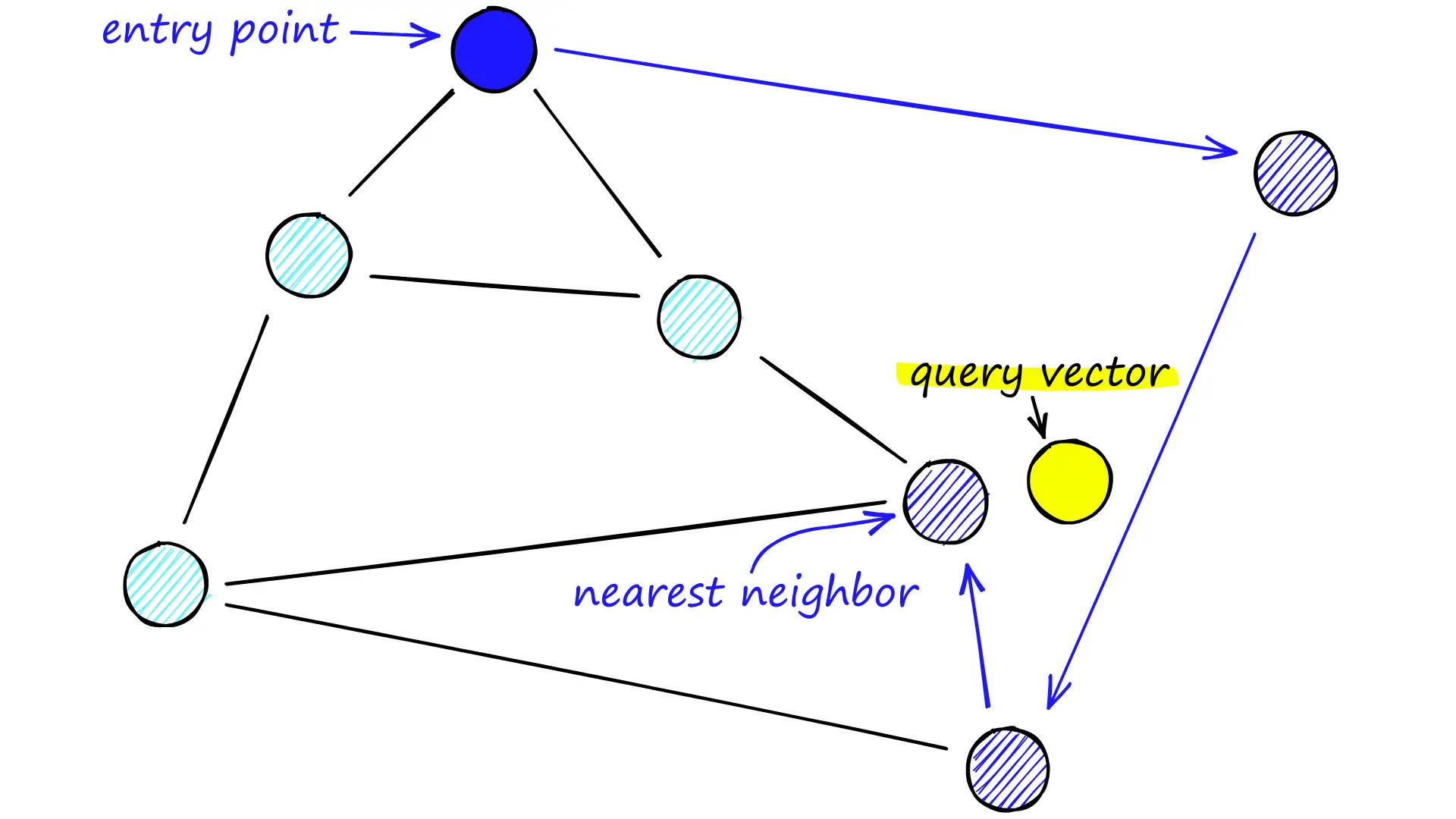
- NSW图:每个节点连接若干相似节点,使用邻接列表,从入口节点开始通过边查找最接近查询向量的节点。
HNSW工作分为两个主要阶段:索引构建和查询过程:
- 索引构建:HNSW构建多层图,每层提供不同精度和速度的搜索。最上层图提供粗粒度搜索,底层则提供更精细搜索。每个新节点连接若干近邻,形成局部小世界结构,保证图的稀疏性和高效性。
- 查询过程:查询从最上层开始,逐层向下,通过图的边接近目标。到达底层后,HNSW使用局部搜索找到最接近查询向量的结果。
DiskANN
Cluster-based
SPANN
Strategy
Graph
Graph Structure
Delaunay Graphs
Relative Neighborhood Graphs (RNG)
Navigable Small-World Networks (NSW)
Randomized Neighborhood Graphs
Dataset
Product Quantization for Nearest Neighbor Search
全文字数: 5526 字
阅读时间: 35 分钟
Notations
Vector quantization
量化是一种破坏性(destructive)过程,其目的是减少表示空间的基数。形式上,一个量化器(quantizer) 是一个函数 ,它将一个 维向量 映射到一个向量 ,其中索引集合 现在假设是有限的,即 。再现值(reproduction values) 被称为质心(centroids) 。再现值的集合 被称为码本(codebook) ,其大小为 。
映射到给定索引 的向量集合 被称为 (Voronoi)单元(cell),定义如下: 量化器的 个单元构成了 的一个划分。根据定义,所有位于同一单元 内的向量都由同一个质心 重构。量化器的质量通常通过输入向量 与其重构值 之间的均方误差(MSE, Mean Squared Error) 来衡量:
- 表示 和 之间的欧几里得距离
- 是对应于随机变量 的概率分布函数。
对于任意概率分布函数,通常使用蒙特卡洛采样(Monte-Carlo sampling) 进行数值计算,即在大量样本上计算 的平均值。
为了使量化器达到最优,它必须满足Lloyd 最优条件(Lloyd optimality conditions) 中的两个性质。
- 向量 必须被量化为最近的码本质心,即在欧几里得距离意义下: 因此,单元(cells)由超平面(hyperplanes) 划定。
- 重构值必须是 Voronoi 单元内向量的期望值,即:
Lloyd 量化器(Lloyd quantizer) 对应于 k-means 聚类算法,它通过迭代的方式寻找近似最优的码本,不断地将训练集中向量分配给质心,并从这些分配的向量中重新估计质心。需要注意的是,k-means 只能找到局部最优解,而非全局最优解(就量化误差而言)。
均方畸变(mean squared distortion) ,描述了当一个向量被重构到所属单元 的质心 时的误差。令: 表示一个向量被分配到质心 的概率,则该误差的计算公式如下: 均方误差(MSE)可以由这些量计算得到:
Product quantizers
乘积量化(Product quantization) 输入向量 被划分为 个不同的子向量 ,其中 ,每个子向量的维度为:
其中 是 的整数倍。这些子向量分别使用 个不同的量化器进行量化。因此,给定的向量 被映射如下:
其中 是与第 个子向量相关的低复杂度量化器。对于子量化器 ,关联索引集合 、码本 以及对应的重构值 。
乘积量化器的重构值由 乘积索引集合 的一个元素唯一标识:
因此,码本定义为笛卡尔积:
该集合的质心是 个子量化器的质心的串联。假设所有的子量化器都有相同的有限重构值数量 ,因此,总质心数为:
在极端情况下(当 ),向量 的每个分量都会被单独量化,此时 乘积量化器退化为标量量化器,其中每个分量的量化函数可能不同。
乘积量化器的优势在于可以通过多个小型质心集(子量化器的质心集合)来生成大规模质心集合。当使用 Lloyd 算法学习子量化器时,使用的样本数量有限,但码本仍然可以适应数据分布。
乘积量化器的学习复杂度是 倍于在 维度上进行 质心的 k-means 聚类的复杂度。
显式存储码本 并不高效,因此只存储所有子量化器的 个质心,即:
个浮点值。量化一个元素需要 次浮点运算。下表总结了 k-means、HKM 和乘积 k-means 的计算资源需求。乘积量化器 是唯一能在大 值时被索引存储于内存的方法。
| Method | Memory Usage | Assignment Complexity |
|---|---|---|
| k-means | ||
| HKM | ||
| Product k-means |
为了保证良好的量化性能,在 取常数时,每个子向量应具有相近的能量。一种方法是在量化前用随机正交矩阵变换向量,但对于大多数向量类型来说,这并不需要,也不推荐,因为相邻分量通常由于构造上的相关性而更适合使用相同的子量化器量化。
由于子空间正交,乘积量化器的平方畸变(Squared Distortion) 可计算为:
其中 是与子量化器 相关的畸变。
下图 显示了 MSE 随代码长度变化的曲线,其中代码长度为: ,是2的幂
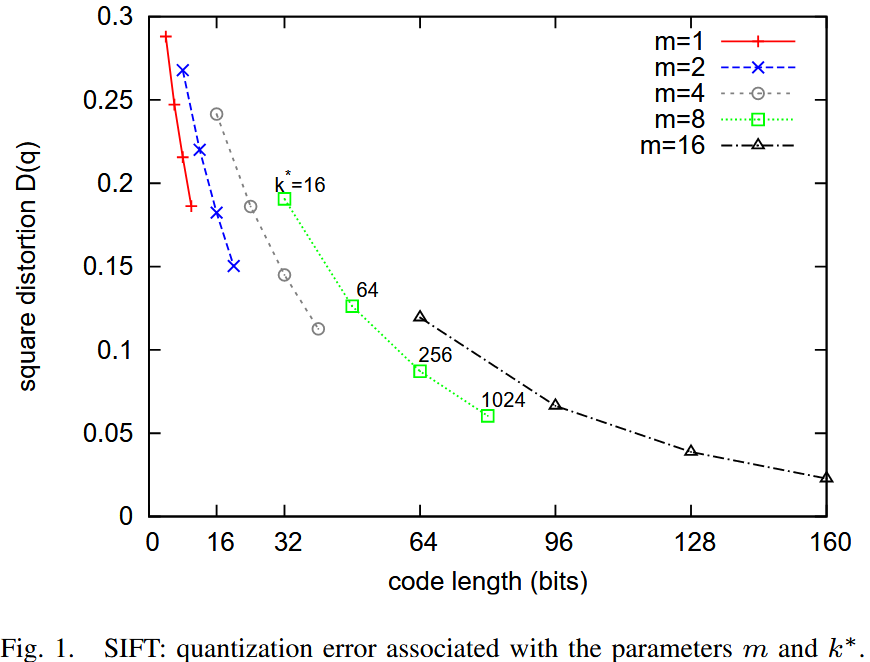
可以观察到,在给定比特数的情况下,使用少量子量化器,但每个子量化器有更多质心,比使用多个子量化器但每个子量化器比特数较少要更好。
在极端情况下(当 ),乘积量化器退化为标准 k-means 码本。
高 值 会增加量化器的计算成本(如表 I 所示),同时也增加了存储质心的内存开销(即 个浮点数)。如果质心查找表无法适应缓存,则效率会降低。
在 的情况下,为了保证计算开销可控,无法使用超过 16 位的编码。通常,选择 且 是一个合理的选择。
Search
Computing distances using quantized codes
假设有一个查询向量 和一个数据库向量 。有两种方法来计算这些向量之间的近似欧几里得距离:对称距离计算(SDC) 和 非对称距离计算(ADC)。
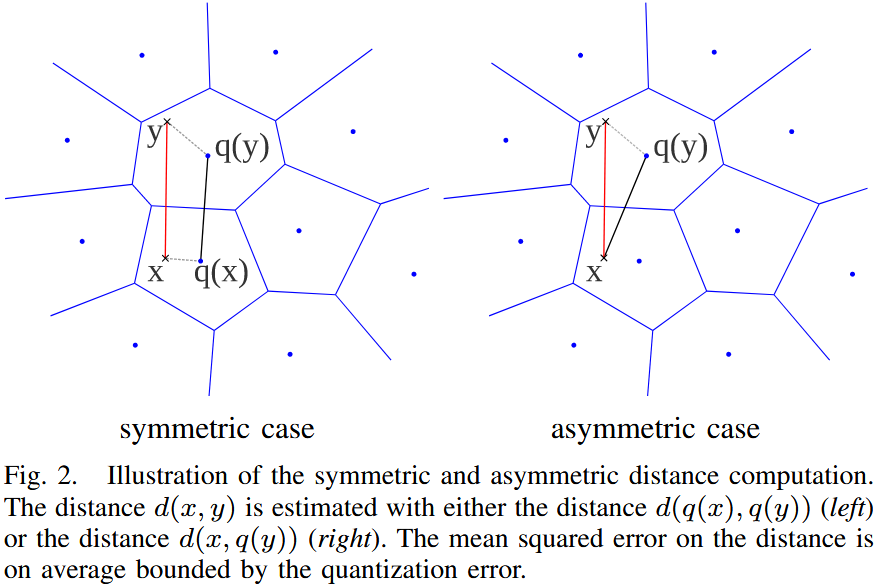
对称距离计算(Symmetric Distance Computation, SDC):
在 SDC 方法中,查询向量 和数据库向量 均由其对应的质心 和 表示。因此,距离 近似为:
利用 乘积量化器,这个距离可以高效地计算为:
其中,距离项 从查找表中读取,该查找表与第 个子量化器相关。每个查找表包含所有质心对 之间的平方距离,即存储了 个平方距离。
非对称距离计算(Asymmetric Distance Computation, ADC):
在 ADC 方法中,数据库向量 仍由其质心 表示,但查询向量 不经过编码。因此,距离 近似为:
其计算方式如下:
其中,平方距离 在搜索之前已经计算,其中 ,。
在最近邻搜索中,实际上不会计算平方根,直接使用平方距离进行排序。
下表 总结了在数据集中搜索最近邻所涉及的不同步骤的复杂度。假设数据集 的大小为 ,可以看到 SDC 和 ADC 的查询准备成本是相同的,并且不依赖于数据集大小 。
| SDC | ADC | |
|---|---|---|
| Encoding | ||
| Compute | ||
| Compute or | ||
| Find |
当 很大()时,计算量主要由求和运算决定。而搜索 个最小元素的复杂度 是对 的元素进行无序比较的平均复杂度。
SDC 与 ADC 的对比
| Pros | Cons | |
|---|---|---|
| SDC | 减少查询向量的内存开销 | 更高的距离畸变 |
| ADC | 更低的距离畸变 | 相对较高的查询向量内存开销 |
在本文的剩余部分,将重点讨论 ADC 方法。
Analysis of the distance error
分析使用 代替 所带来的距离误差。这一分析不依赖于乘积量化器,对满足 Lloyd 最优条件的任何量化器都适用。
在重构的均方误差(MSE)准则的基础上,距离畸变(distance distortion) 通过均方距离误差(MSDE) 来衡量:
根据三角不等式有:
同样地,可以写成:
可得:
最终得到:
其中, 是与量化器 相关的均方误差。
该不等式适用于任何量化器,表明本方法的距离误差在统计意义上受量化器的 MSE 约束。
对于 对称版本(SDC),类似的推导表明其误差在统计上受 约束。因此,最小化量化误差(MSE)是重要的,因为它可以作为距离误差的统计上界。
如果在最高排名的向量上执行精确距离计算(如 局部敏感哈希(LSH)),那么量化误差可以用作动态选择需要后处理的向量集合的标准,而不是随意选择某一部分向量。
Estimator of the squared distance
分析使用 或 进行估算时,如何在平均意义上低估描述符之间的距离。
该图显示了在 1000 个 SIFT 向量数据集中查询一个 SIFT 描述符所得的距离估计。该图比较了真实距离与SDC与ADC计算出的估计值。可以清楚地看到,这些距离估计方法存在偏差(bias),且对称版本(SDC)更容易受到偏差的影响。
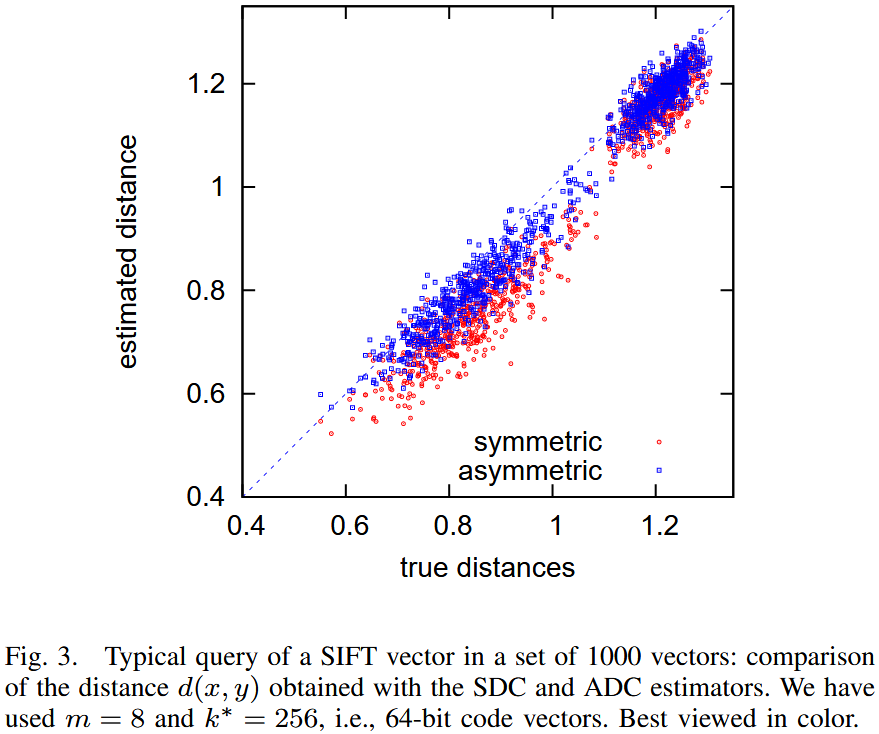
为了消除偏差,计算平方距离的期望值。在乘积量化方法中,一个给定向量 的近似值 由其子量化索引 (其中 )获得。
量化索引标识了向量 所处的单元 。因此,可以计算期望平方距离 作为修正项:
根据Lloyd 最优条件有:
因此可简化为:
其中, 代表了重构误差(distortion),即 由其重构值 近似时的误差。
在乘积量化框架下,向量 与 之间的期望平方距离可以通过修正方程 (13) 计算:
其中,修正项 为第 个子量化器的平均畸变(distortion):
这些畸变值可以预先学习,并存储在查找表中,供量化索引 使用。
对于 对称版本(SDC),即 和 均经过量化,类似的推导可以得到修正后的平方距离估计公式:
Discussion 该图显示了真实距离与估计距离之间的概率分布。该实验基于大规模 SIFT 描述符数据集。
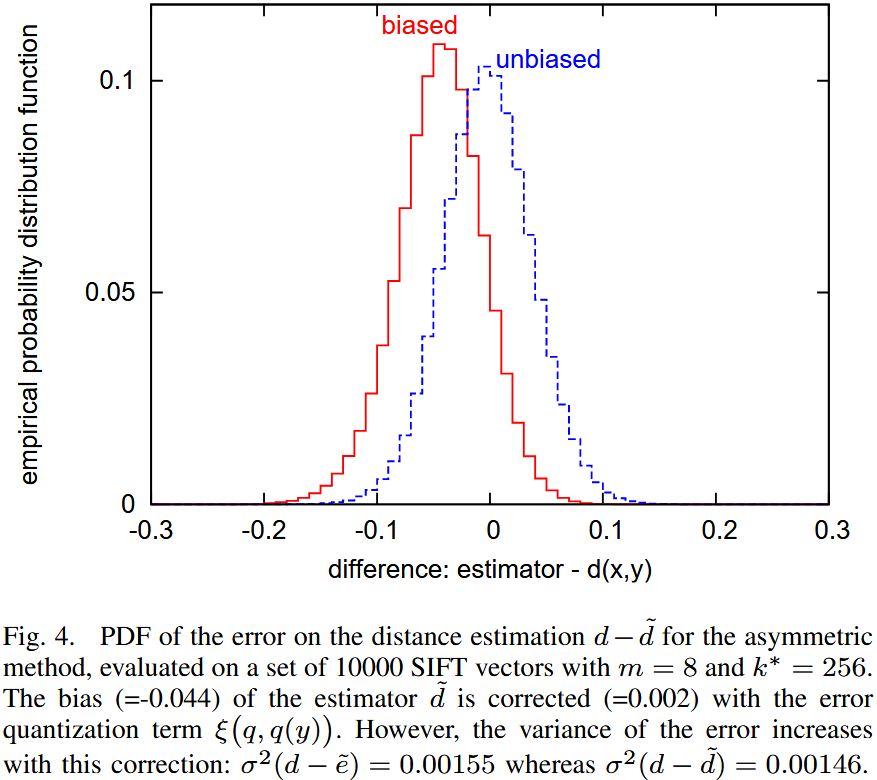
- 进行距离估计时,存在明显偏差。
- 采用 修正版本(,距离估计的偏差显著减少。
然而,修正偏差 会导致估计方差增大,这在统计学上是一个常见现象。此外,对于最近邻搜索而言:
- 修正项往往估计值更大,这可能会惩罚具有罕见索引的向量。
- 在 非对称版本(ADC) 中,修正项与查询 无关,只依赖于数据库向量 。
在实验中,修正方法在整体上效果较差,因此建议在最近邻搜索任务中使用原始版本,而修正版本仅在需要精准距离估计的任务中适用。
Avoid exhaustive search
使用乘积量化器进行近似最近邻搜索非常高效(每次距离计算仅需 次加法运算),并且大大减少了存储描述符所需的内存。然而,标准搜索方法是穷举式(Exhaustive)的。
为了避免穷举搜索:
- 倒排文件系统(Inverted File System, IVF)
- 非对称距离计算(ADC)
该方法称为 IVFADC。
传统倒排文件仅存储图像索引,而本文在此基础上增加了额外的编码,以便对每个描述符进行更精细的存储。使用乘积量化器对向量与其对应的粗质心之间的残差进行编码。
- 显著加速搜索过程,代价仅是每个描述符存储额外的少量比特/字节。
- 提高搜索精度,因为对残差进行编码比直接编码向量本身更加精确。
Coarse quantizer, locally defined product quantizer
码本(codebook)是通过 k-means 学习得到的,并生成了一个量化器 ,在后续内容中称为 粗量化器(coarse quantizer)。对于 SIFT 描述符,与 相关的质心(centroid)数量 通常在 1000 到 1000000 之间。因此,与 乘积量化器相比,粗量化器的规模较小。
除了粗量化器,还使用乘积量化器对向量的描述进行细化。具体来说,粗量化器 生成的质心可以提供全局信息,但仍需进一步编码残差信息,因此使用 乘积量化器 对残差向量进行编码:
其中,残差向量 表示 Voronoi 单元中的偏移量。由于残差向量的能量相比原始向量要小,因此存储其量化信息的代价也较低。
向量 可被近似表示为:
它可以用元组 来表示。
类比于二进制表示的概念:
- 粗量化器() 提供的是最高有效位(MSB),用于大致定位向量。
- 乘积量化器() 提供的是最低有效位(LSB),用于精细校正残差信息。
查询向量 和数据库向量 之间的距离可以近似计算为 :
令 表示第 个子量化器(Subquantizer),则可分解计算该距离:
类似于 ADC(Asymmetric Distance Computation) 策略,对于每个子量化器 ,预计算部分残差向量 与所有质心 之间的距离,并存储这些值。
乘积量化器是在一个学习集合中通过残差向量训练得到的。虽然向量最初由粗量化器映射到不同的索引,但最终的残差向量被用于训练一个统一的乘积量化器。
假设当残差在所有 Voronoi 单元上进行边际化(Marginalization)时,相同的乘积量化器仍然有效。然而,这种方法的效果可能不如为每个 Voronoi 单元单独训练一个独立的乘积量化器,但后者的计算成本极高。如果要为每个 Voronoi 单元分别训练乘积量化器,则需要存储 个乘积量化码本,即:
个浮点值。这对于典型的 值来说,将会导致极高的存储需求,在实际应用中难以承受。
Indexing structure
使用粗量化器(coarse quantizer)来实现一种倒排文件结构(inverted file structure),它被组织成一个包含列表的数组 。如果 是要索引的向量数据集,那么与质心 相关联的列表 将存储集合 。
在倒排列表 中,与 相关的条目包含一个向量标识符(vector identifier)和编码后的残差 :
| field | length(bits) |
|---|---|
| identifier | 8–32 |
| code |
标识符字段是倒排文件结构带来的开销。根据存储向量的不同特性,标识符不一定是唯一的。例如,在使用局部描述符(local descriptors)表示图像时,图像标识符可以替代向量标识符,即同一张图像的所有向量都可以使用相同的标识符。因此,20 位的标识符字段足以在一个包含一百万张图像的数据集中唯一标识一张图像。
通过索引压缩(index compression)可以进一步降低存储开销,使存储标识符的平均成本降低到约 8 比特,具体取决于参数。
Search algorithm
倒排文件(inverted file)是非穷尽(non-exhaustive)的关键。当搜索向量 的最近邻时,倒排文件提供了一个 的子集,用于计算距离:仅扫描与 对应的倒排列表 。
然而, 及其最近邻通常不会被量化到同一个质心,而是被量化到相邻的质心。为了解决这个问题,采用 多重分配(multiple assignment) 策略 。查询向量 被分配到 个索引,而不是仅仅一个索引,这些索引对应于 代码本 中 的 个最近邻。然后,扫描所有相应的倒排列表。多重分配不会用于数据库向量,因为这会增加内存占用。
下图概述了数据库的索引和搜索过程。
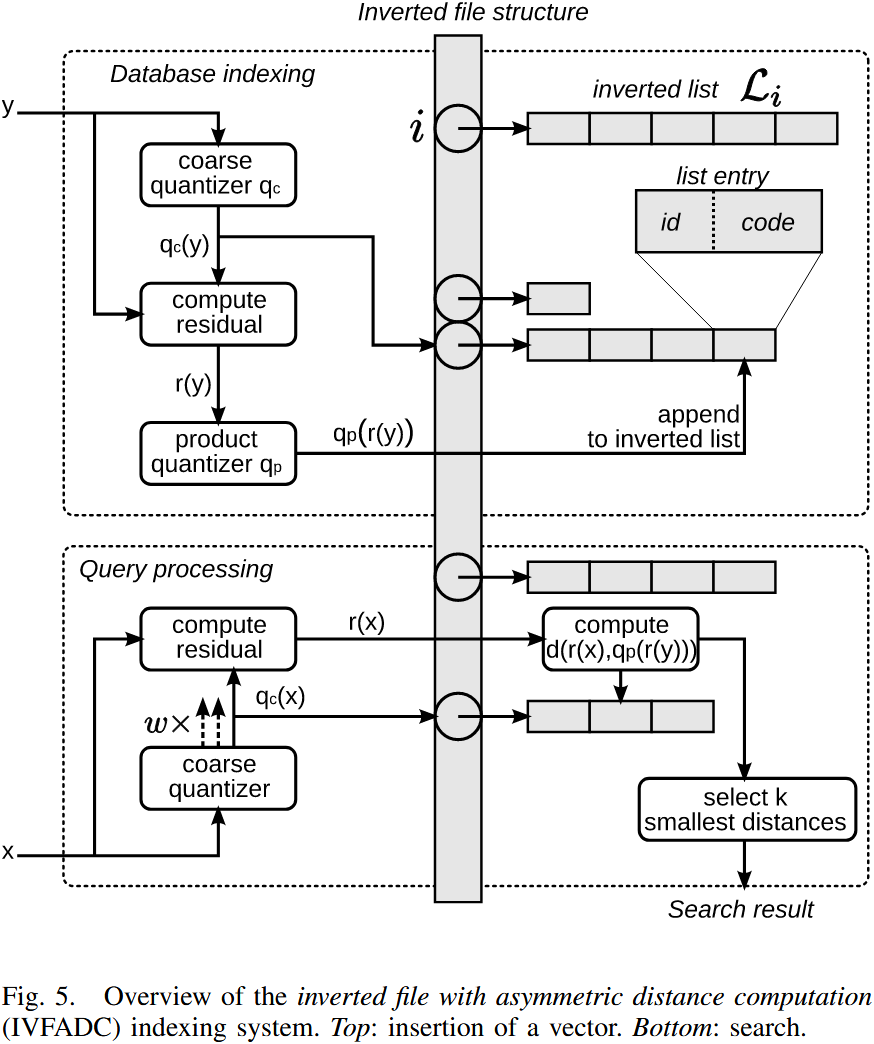
索引(Indexing)向量 的过程如下:
- 对 进行量化,得到 ;
- 计算残差(residual):;
- 对残差 进行量化,得到 ,对于乘积量化器(product quantizer),这意味着将 映射到 ,其中 ;
- 向倒排列表 添加新条目,该条目包含 向量(或图像)标识符 和 二进制编码(即乘积量化器的索引)。
查询(Searching)最近邻 的过程如下:
-
将 量化到代码本 中最近的 个质心;
为了便于表述,接下来的两步中简单地用 来表示与这些 个分配相关的残差。这两个步骤适用于所有 个分配。
-
计算平方距离 ,对于每个子量化器 以及其所有质心 ;
-
计算 与倒排列表中所有索引向量的平方距离;
使用上一步计算的子向量到质心距离,最终得到总距离。这一过程涉及查找 个预计算值(见公式 31)。
-
根据估计距离选择 个最近邻:
- 这一过程使用 最大堆(Maxheap) 结构(固定容量)来存储 当前已找到的 个最小距离;
- 每次计算距离后,仅当该点的距离小于最大堆中当前的最大距离时,才将其插入数据结构。
只有第 3 步 依赖于数据库的大小。与 ADC(Asymmetric Distance Computation,非对称距离计算) 相比,额外的 量化 到 仅涉及计算 个 D 维向量的距离。假设倒排列表是均衡的,则需要解析 个条目。因此,该搜索方法比 ADC 显著更快。
Characterizing the Dilemma of Performance and Index Size in Billion-Scale Vector Search and Breaking It with Second-Tier Memory
全文字数: 2670 字
阅读时间: 17 分钟
Background
Second-tier memory(如通过 RDMA 或 CXL 连接的远程 DRAM/NVM)具有 细粒度的访问能力,能够有效解决 搜索粒度与访问粒度不匹配 的问题。
然而:
- 现有索引主要针对 SSD 设计,在 second-tier memory 上表现不佳。
- Second-tier memory 的行为更类似于存储,使其像 DRAM 那样使用时效率较低。
为此,本文提出了一种专为 second-tier memory 性能特性优化的 图索引与簇索引 方案,具有以下优势:
- 最优性能
- 数量级更小的索引放大
High Performance and Low Index Size Dilemma
增大索引大小可以提升性能:
- 对于 图索引(graph indexes),增加更多的边可以减少跳数(I/O 操作)。
- 对于 簇索引(cluster indexes),在簇之间复制相邻向量可以减少搜索的簇数量。
相反,缩小索引大小会导致性能下降。一种在不改变算法的情况下减少索引大小的替代方案是 复制地址而不是重复存储向量。然而,这种方法会引入额外的小随机读操作,在 SSD 上会显著降低性能。
根本原因:工作负载模式与 SSD 要求不匹配
- SSD 的页面通常为 4KB,而 second-tier memory 支持 更细粒度的 256B 访问。
- 图索引和簇索引 的读取操作通常仅涉及 几百字节的数据。
Graph Index
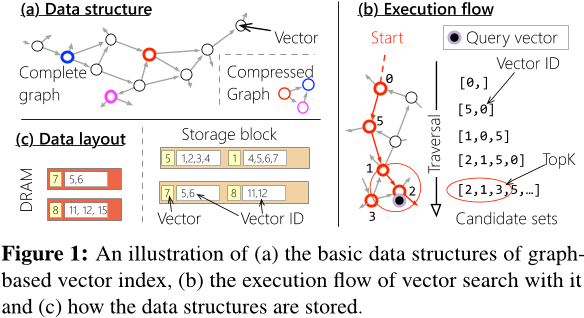
- 图索引(Graph indexes) 能够捕捉向量之间的细粒度关系,使得在访问 top-k 以外的少量额外向量时,保持较低的读取放大(read amplification)。
- 然而,其 指针跳转(pointer-chasing) 访问模式导致 高延迟,并且 带宽利用率较低。
在 DiskANN 中,每个向量默认分配 32 条边,每条边由 4B 向量 ID 表示。这意味着边列表的大小可能会超过原始数据的大小。例如,在 SPACEV 中,一个大小为 100B 的顶点需要 128B 来存储其边信息。
理想情况下,边所引起的空间放大应尽可能减少。然而,减少边的数量会增加查询向量的 遍历距离(traversal distance)。
即使增加边的数量,每次图遍历的加载量仍然受限于 SSD 的访问粒度(4KB)。如果超出此限制,索引大小将急剧膨胀,甚至可能达到原始数据集大小的 39 倍。例如,一个 100B 的节点若使用 3,996B 存储边信息,将导致 极高的空间占用。
Cluster Index
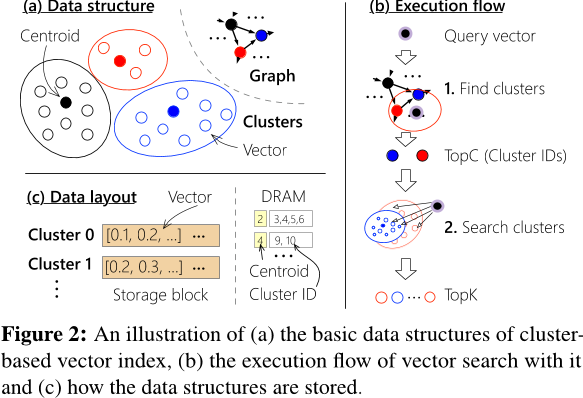
- 存储效率高,支持 大批量读取(large bulk reads) 簇数据。
- 由于簇内存在冗余向量读取,导致 高读取放大(read amplification)。
- 向量复制 造成 高空间放大(space amplification)。
理想情况下,簇索引的大小应尽可能小:
- 簇的索引数据 远小于整个数据集的规模,通常相差数个数量级。
- 每个簇可能跨越多个块,因此不需要填充(padding)。
为了 解决边界问题导致的准确率下降,相邻簇之间会复制 边界向量(boundary vectors),这需要 额外的索引存储空间。
为 减少过多的向量复制,一种替代方案是 增加每次查询搜索的簇数量。但 额外的簇搜索 会导致 额外的向量读取,从而 降低性能。
经验上来看,增加索引大小仍然可以提升吞吐量(throughput)。
Workloads Mismatch SSD Requirements
-
图索引(Graph index) 需要 细粒度的存储读取 以保持可接受的索引大小。然而,这与 使用足够大的 I/O 负载(4 KB) 来高效利用 SSD 等传统存储设备 的需求相冲突。
-
簇索引(Cluster index) 需要 不规则 I/O 来进行 去重(deduplication)。与其在其他簇中存储重复的向量数据,不如 存储一个指向原始簇的地址。向量地址(8B) 远小于实际数据(128–384B)。然而,这意味着每个被复制的向量都需要 单独的小随机读(100–384B) 来获取原始向量,进而影响读取性能。
Power of Second-tier Memory
-
细粒度块大小(Fine-grained block sizes)
- 更高效地利用设备带宽
-
对不规则 I/O 具有更强的适应性(Robust to irregular I/O)
- 将(部分)顺序访问 替换为 随机访问
Improvement
Graph Index
Software Pipeline
在发出second-tier memory请求后,立即调度下一个未完成的查询执行,从而在软件层面以流水线方式高效处理不同的查询。
Compressed Layout
DiskANN 采用填充方式进行存储,这种填充设计会浪费索引空间。在 second-tier memory 上,由于其能够有效适应 跨块大小的不规则 I/O,填充设计已无必要。因此直接选择 压缩稀疏行(Compressed Sparse Row,CSR) ,以减少存储空间占用,同时保持性能稳定。
Cluster Index
Decoupled Layout
向量数据采用独立存储,而每个簇仅存储对应向量的地址(b)。这样,对于需要复制的向量,仅复制地址,而无需复制向量本身,从而有效减少存储开销。
尽管decoupled Layout有助于缩小索引大小,但它将原本0.1–2.2 MB 的顺序 I/O 拆分为 60–68 次小随机 I/O(每次读取 100–384B)。更具体而言,工作负载中的 98% I/O 变成了小随机读取,而在 second-tier memory 上,这些 I/O 操作的效率同样不高。
Vector Grouping
为减少工作负载中的 小 I/O 操作,在 decoupled design 之上提出了 向量分组(vector grouping) 方法,以尽量减少 小随机 I/O。通过 将同一簇的向量分组存储在相邻的存储位置,可以使用 一次大 I/O 操作 读取整个分组的向量数据(见 图 11(c))。分组操作 在 索引构建后(post index build) 进行。
由于 不复制向量,必然会存在某些簇无法通过一次 I/O 读取其所有向量。因此,分组的性能 主要取决于 向量如何被分组。
向量分组的目标是 确定哪些向量应该被分组,以减少给定工作负载中的小 I/O。这等价于 向特定簇分配向量 的问题。假设在一个向量数据库中,向量集合为 V,簇集合为 C,使用 $P_{i,j}$ 表示 第 i 个向量是否被分配到某个分组。
采用 整数线性规划(Integer Linear Programming, ILP) 来找到 $P_{i,j}$ 的最优分组,目标是 最小化发往存储管理节点(MN)的 I/O 请求。由于 I/O 数量取决于 每个簇的访问频率,我们使用 $h_{j}$ 来表示 簇 j 的访问频率。
这些频率可以通过 后台监控工作负载 获得,并可以根据 访问频率的变化 动态调整布局。
综合以上内容,问题可被公式化如下:
$$ \text{min} \sum_{j}^{|C|} h_j \cdot \left(1 + \sum_{i}^{|V|} P_{i,j}\right) $$
约束条件:
-
簇约束(Cluster constraints)
根据簇索引设计,每个向量必须 分配到一个簇,但可以 复制到多个相邻簇。约束条件如下:$$ \begin{cases} 0 \leq A_{i,j} \leq 1, \quad i \in [0, |V|], j \in [0, |C|] \ \sum_{j}^{|C|} A_{i,j} \geq 1, \quad i \in [0, |V|] \end{cases} $$
-
分组约束(Group constraints)
分组算法必须将 一个向量分配给唯一的簇组,约束如下:$$ \begin{cases} 0 \leq P_{i,j} \leq 1, \quad i \in [0, |V|], j \in [0, |C|] \ \sum_{j}^{|C|} P_{i,j} = 1, \quad i \in [0, |V|] \end{cases} $$
Conclusion
Second-tier memory is a promising storage medium for vector indexes.
NSG
Introduction
单调相对邻近图(MRNG,Monotonic Relative Neighborhood Graph)
- 保证连通性
- 降低平均出度
- 缩短搜索路径
- 减少索引大小
设计了 MRNG 的近似结构,称为 导航扩展图(NSG)
DiskANN
全文字数: 12807 字
阅读时间: 1 小时 21 分钟
Background
DiskANN系列主要包含三篇论文:
- DiskANN: Fast Accurate Billion-point Nearest Neighbor Search on a Single Node
- FreshDiskANN: A Fast and Accurate Graph-Based ANN Index for Streaming Similarity Search
- Filtered − DiskANN: Graph Algorithms for Approximate Nearest Neighbor Search with Filters
SNG
DiskANN: Fast Accurate Billion-point Nearest Neighbor Search on a Single Node
Algorithm
GreedySearch
大多数基于图的近似最近邻搜索(ANN)算法的工作方式如下:在索引构建过程中,它们根据数据集 的几何属性构建图 。在搜索时,对于查询向量 ,搜索采用自然的贪心或最优优先遍历,如算法1中的方式,在图 上进行。从某个指定的点 开始,它们遍历图以逐步接近 。
在SNG中,每个点 的外部邻居通过以下方式确定:初始化一个集合 。只要 ,从 到 添加一条有向边,其中 是离 最近的点,从集合 中移除所有使得 的点 。因此,贪心搜索(GreedySearch(s, , 1))从任何 开始都将收敛到 ,对于所有基点 都成立。

RobustPrune
满足SNG性质的图都是适合贪心搜索搜索过程的良好候选图。然而,图的直径可能会相当大。例如,如果点在实数线的一维空间上线性排列,图的直径是 ,其中每个点连接到两个邻居(一个在两端),这样的图满足SNG性质。搜索此类存储在磁盘上的图将导致在搜索路径中访问的顶点的邻居需要大量的顺序读取。
为了解决这个问题,希望确保查询距离在搜索路径的每个节点上按乘法因子 递减,而不仅仅是像SNG性质那样递减。

Vamana Indexing
Vamana 以迭代的方式构建有向图 。
- 图 被初始化,使得每个顶点都有 个随机选择的外部邻居(在 时连接良好)。
- 让 表示数据集 的中心点,它将作为搜索算法的起始节点。
- 算法按随机顺序遍历 的所有点,并在每一步更新图,使其更加适合贪心搜索(GreedySearch(s, , 1, L))收敛到 。
实际上,在对应点 的迭代中,
- Vamana 在当前图 上运行 GreedySearch(s, , 1, L),并将 设置为贪心搜索路径中所有访问过的点的集合。
- 算法通过运行 RobustPrune(p, , , ) 来更新图 ,以确定 的新外部邻居。
- Vamana 更新图 ,通过为所有 添加反向边()。这确保了在搜索路径和 之间的顶点连接,从而确保更新后的图会更适合贪心搜索(GreedySearch(s, , 1, L))收敛到 。
- 添加这种形式的反向边()可能会导致 的度数超过阈值,因此每当某个顶点 的外度超过 的度数阈值时,图通过运行 RobustPrune(, , , ) 来修改,其中 是 的现有外部邻居集合。
算法对数据集进行两次遍历,第一次遍历使用 ,第二次使用用户定义的 。


Design
Index Design
在数据集 上运行 Vamana,并将结果存储在 SSD 上。在搜索时,每当算法1需要某个点 的外部邻居时, 从 SSD 中获取该点的信息。
然而,单纯存储包含十亿个100维空间中的向量数据远超过工作站的RAM!这引出了两个问题:
- 如何构建一个包含十亿个点的图?
- 如果不能在内存中存储向量数据,如何在算法1的搜索时执行查询点与候选点之间的距离比较?
问题一
通过聚类技术(如k-means)将数据划分成多个较小的分片,为每个分片建立一个单独的索引,并仅在查询时将查询路由到几个分片。然而,这种方法会因为查询需要路由到多个分片而导致搜索延迟增加和吞吐量减少。
与其在查询时将查询路由到多个分片,不如将每个基础点发送到多个相邻的中心以获得重叠的聚类。事实上,我们将一个十亿点的数据集通过k-means划分为k个聚类(k=40,通常ℓ=2就足够),然后将每个基础点分配给ℓ个最近的中心。接着,我们为分配给每个聚类的点建立Vamana索引(这些点现在只有约Nℓ/k个点,可以在内存中建立索引),最后通过简单的边缘合并将所有不同的图合并为一个单一的图。
问题二
将每个数据库点 的压缩向量 存储在主存中,同时将图存储在SSD上。使用Product Quantization将数据和查询点编码为短代码在查询时高效地计算近似距离 。尽管在搜索时只使用压缩数据,但是Vamana在构建图索引时使用的是“全精度坐标”,因此能够高效地引导搜索到图的正确区域,
Index Layout
将所有数据点的压缩向量存储在内存中,并将图以及全精度向量存储在SSD上。在磁盘中,对于每个点 ,我们存储其全精度向量 ,并跟随其 个邻居的标识。如果一个节点的度小于 ,我们用零填充,以便计算数据在磁盘中对应点 的偏移量变得简单,并且不需要在内存中存储偏移量。
Beam Search
运行算法1,按需从SSD获取邻居信息 。这需要很多次SSD的往返(每次往返仅需几百微秒),从而导致更高的延迟。为了减少往返SSD的次数(以便顺序地获取邻居),而不过多的增加计算量,一次性获取一个较小数量 (例如4、8)最近的点的邻居,并将 更新为这一小步中的前 个最优点。从SSD获取少量随机扇区的时间几乎与获取一个扇区的时间相同。
- 如果 ,这种搜索类似于正常的贪婪搜索。
- 如果 太大,比如16或更多,则计算和SSD带宽可能会浪费。
Caching Frequently Visited Vertices
为了进一步减少每个查询的磁盘访问次数,缓存与一部分顶点相关的数据,这些顶点可以基于已知的查询分布来选择,或者通过缓存所有距离起始点 为 或 跳的顶点来选择。
由于索引图中与距离 相关的节点数量随着 增加呈指数增长,因此较大的 值会导致过大的内存占用。
Implicit Re-Ranking Using Full-Precision Vectors
由于PQ是一种有损压缩方法,因此使用基于PQ的近似距离计算出的与查询最接近的 个候选点之间存在差距。为了解决这个问题,使用存储在磁盘上与每个点相邻的全精度坐标。
事实上,在搜索过程中检索一个点的邻域时,也可以在不增加额外磁盘读取的情况下获取该点的全精度坐标。这是因为读取4KB对齐的磁盘地址到内存的成本不高于读取512B,而顶点的邻域(对于度为128的图,邻域大小为 字节)和全精度坐标可以存储在同一磁盘扇区中。
因此,随着BeamSearch加载搜索前沿的邻域,它还会缓存在搜索过程中访问的所有节点的全精度坐标,而不需要额外的SSD读取操作。这使得我们能够基于全精度向量返回前 个候选点。
Evaluation
(具体实验条件参见论文)
- 内存搜索性能比较
- NSG和Vamana在所有情况下recall@100都优于HNSW
- Vamana的索引构建时间优于HNSW和NSG
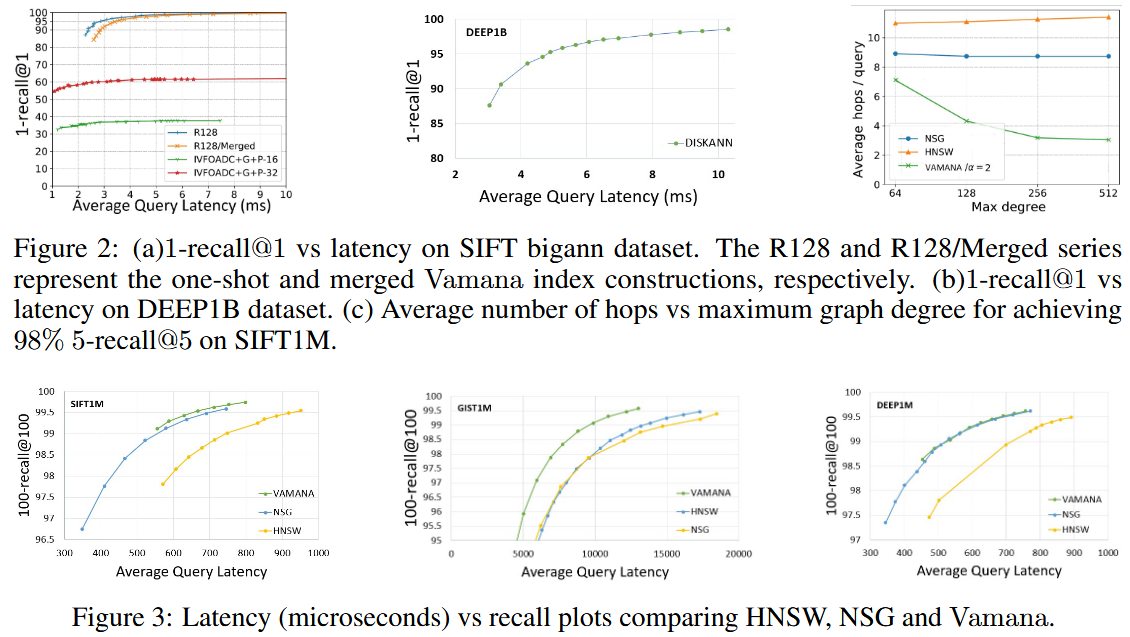
- 跳数(搜索中基于图的跳跃次数)比较
- Vamana更适合用于基于SSD的搜索,其在大型数据集上比HNSW和NSG要快2到3倍。
- 随着最大度数的增加,HNSW和NSG跳数出现了停滞趋势,而Vamana跳数有所减少,因为它能够增加更多的长距离边缘。推测Vamana在 时,比HNSW和NSG更好地利用了SSD提供的高带宽(在BeamSearch中,通过最大化𝑊来扩展搜索进行更大的磁盘读取)。
- One-Shot Vamana 和 Merged Vamana
- Single:2 days, degree=113.9, peek memory usage=1100GB
- Merged:5 days, degree=92.1, peek memory usage<64GB
- 单一索引优于合并索引,合并索引的延迟更高
- 合并索引仍是十亿规模k-ANN索引和单节点服务的一个非常好的选择:相比单一索引,目标召回时只需增加不到20%的额外延迟
FreshDiskANN: A Fast and Accurate Graph-Based ANN Index for Streaming Similarity Search
Introduction
在许多重要的现实场景中,用户与系统的交互会创建并销毁数据,并导致 的更新。针对这种应用的ANN系统需要能够托管包含数万亿个实时更新点的索引,这些更新可以反映数据集中的变化,理想情况下是实时进行的。
形式上定义 fresh-ANNs 问题如下:给定一个随时间变化的数据集 (在时间 时的状态为 ),目标是维护一个动态索引,该索引计算任何查询 在时间 时,仅在活动数据集 上的近似最近邻。这样的系统必须支持三种操作:
- (a)插入新点,
- (b)删除现有点,以及
- (c)给定查询点进行最近邻搜索。
一个 fresh-ANNs 系统的总体质量由以下几个方面来衡量:
- 搜索查询的召回率与延迟之间的权衡,以及随着数据集 演变其对时间的鲁棒性。
- 插入和删除操作的吞吐量与延迟。
- 构建和维护此类索引所需的整体硬件成本(CPU、RAM 和 SSD 占用)。
freshDiskANN 注重于 quiescent consistency 的概念
Quote
Quote
quiescent consistency: the results of search operations executed at any time t are consistent with some total ordering of all insert and delete operations completed before t.
quiescent consistency(静默一致性)是指在系统中执行的操作(如搜索、插入和删除)的结果,在某个时刻(如时间 𝑡)前的所有操作都已经完成,并且这些操作的结果与已执行的操作的顺序保持一致。如果一个查询需要依赖于之前的插入或删除操作,那么在查询时,插入和删除操作应已完成,并且查询结果应该基于这些已完成的操作。
删除操作为什么难以实现?
HNSW算法通过将删除的点添加到黑名单并将其从搜索结果中省略来处理删除请求,因为缺乏能够在保持原始搜索质量的同时修改可导航图的方法。考虑三种流行的静态ANNS算法,分别是HNSW、NSG和Vamana,并尝试了以下自然更新策略,看看在面对插入和删除操作时它们的表现。
- 插入策略。 对于插入一个新点 ,运行相应算法使用的候选生成算法,并添加选定的入边和出边;如果任何顶点的度数超过预算,则运行相应的修剪过程。
-
- 删除策略A。 当删除一个点 时,简单地删除与 相关的所有入边和出边,而不添加任何新边以弥补潜在的可导航性丧失。
- 删除策略B。 当删除一个点 时,移除所有与 相关的入边和出边,并在 的局部邻域中添加边:对于图中的每对有向边 和 ,在更新的图中添加边 。如果任何顶点的度数超过限制,则运行相应算法的修剪过程来控制度数。
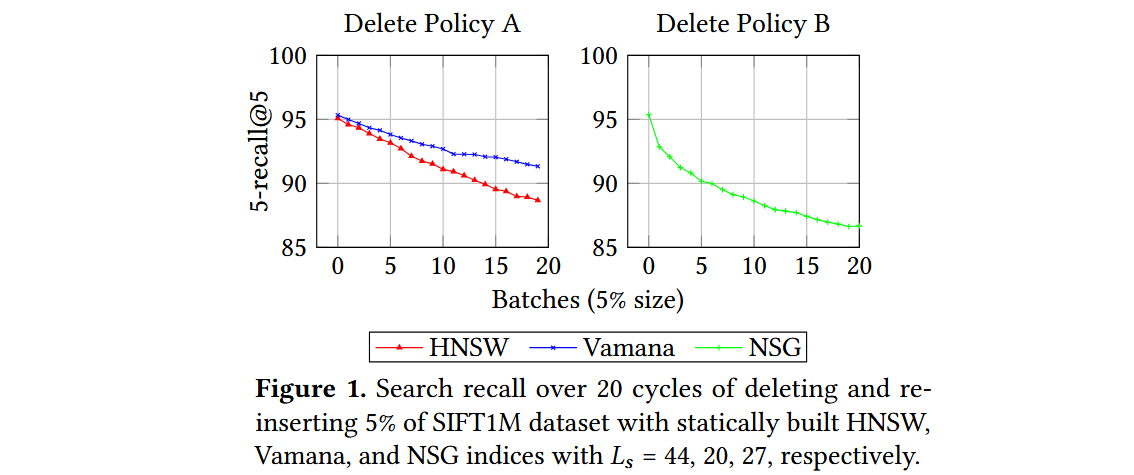
一个稳定的更新策略应该在每个周期之后产生相似的搜索性能,因为索引是建立在相同的数据集上的。然而,所有算法都表现出搜索性能持续下降的趋势。
FreshVamana
随着图的更新,图变得稀疏(平均度数较小),因此变得不那么可导航。怀疑这是由于现有算法(如HNSW和NSG)使用非常激进的修剪策略来偏向稀疏图所导致的。
α-RNG Property. DiskANN中构建的图的关键思想是采用更为宽松的剪枝过程,它仅在存在一条边 且 必须比 更接近 时才移除边 ,即 ,其中 。使用 生成这样的图直观地确保了查询向量到目标向量的距离在算法 1 中以几何方式逐步减小,因为只移除那些存在绕道边,使得s'yu显著朝目标方向推进的边。因此,随着 的增加,图变得更加密集。利用α-RNG属性,确保图的持续可导航性,并保持多个插入和删除操作过程中的稳定召回率。
Algorithms
GreedySearch 与 DiskANN中的算法1相同
Index Build
构建一个可导航图。图的构建通常有两个对立的目标,以最小化搜索复杂度:
- 使应用到每个基点 上的贪心搜索算法在最少的迭代中收敛到
- 使所有 的最大出度 不超过
从初始图开始,经过以下两步构建算法逐步精炼G,以提高可导航性。
- 生成候选 : 对于每个基点 ,在图 上运行算法1(从固定的起始点s开始)来获得 ,其中 包含最接近 的节点,将它们添加到 和 的良好候选,从而提高更新图G中对 的可导航性。
- 边修剪 : 当节点 的出度超过 时,修剪算法(如算法3,)会从邻接列表中过滤出类似的(或冗余的)边,以确保 。过程会按距离 的增大顺序对其邻居进行排序,如果算法1能够通过 从 到达 ,则可以安全地移除边 )。
Insertion
- 对于新插入的点 ,从起始点 开始运行,将访问过的点保存在中。
- 将后的结果集合作为的邻居。
- 对的每一个邻居进行剪枝,确保其加入新邻居后的度数不超过。


Deletion
- 对于删除后的图中剩余的每一个点,检查其出边是否包含已删除的点,若有则继续
- 将出边中包含的已删除点的邻居加入到集合中
- 将出边中其余的点加入到集合中
- 对于集合中的每一个点,将其邻居加入到集合中
- 在集合中排除那些已经被删除的点()
- 运行来更新其出边

算法 4 参考了上文中的 删除策略B,关键特性是使用宽松的 -剪枝算法来保持修改后图的稠密性。具体而言,如果删除点 ,则在图中添加边 ,其中 和 是有向边。在此过程中,如果 超过最大出度 ,我们使用算法 3 对其进行剪枝,以保持 -RNG 性质。
然而,由于该操作涉及编辑 的所有入邻居的邻域,代价可能很大,无法在删除到达时立即处理。FreshVamana 采用了懒删除策略 —— 当一个点 被删除时,我们将 添加到 DeleteList 中而不改变图。DeleteList 包含所有已删除但仍存在于图中的点。在搜索时,修改后的算法 1 会使用 DeleteList 中的节点进行导航,但会从结果集中筛选掉它们。
删除合并。在累积了大量删除操作(例如,索引大小的 1%-10%)后,使用算法 4 批量更新图,以更新有出边的点的邻居,从而将这些删除的节点更新到图中。
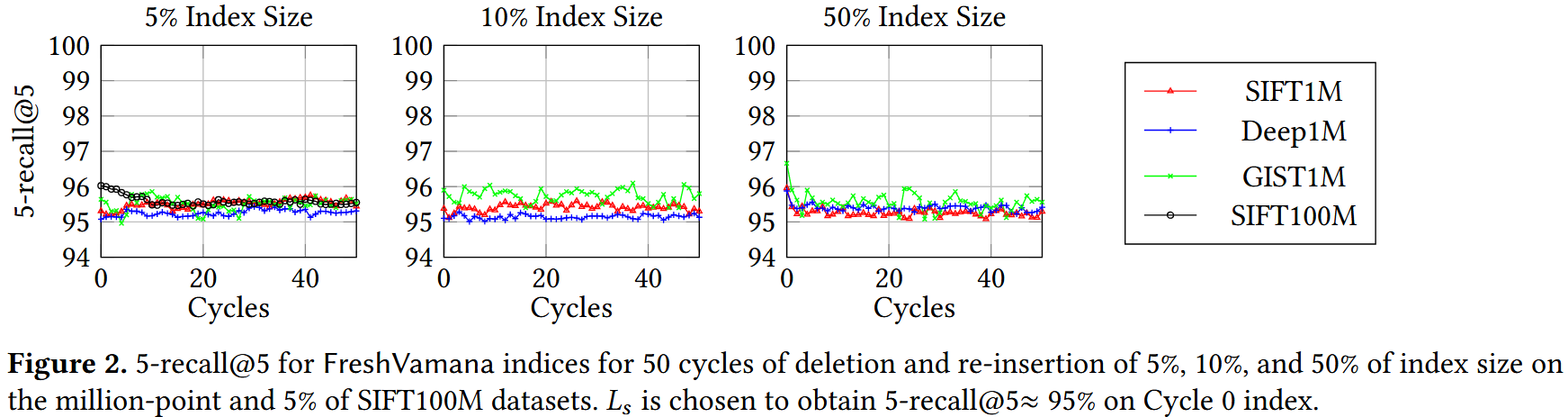
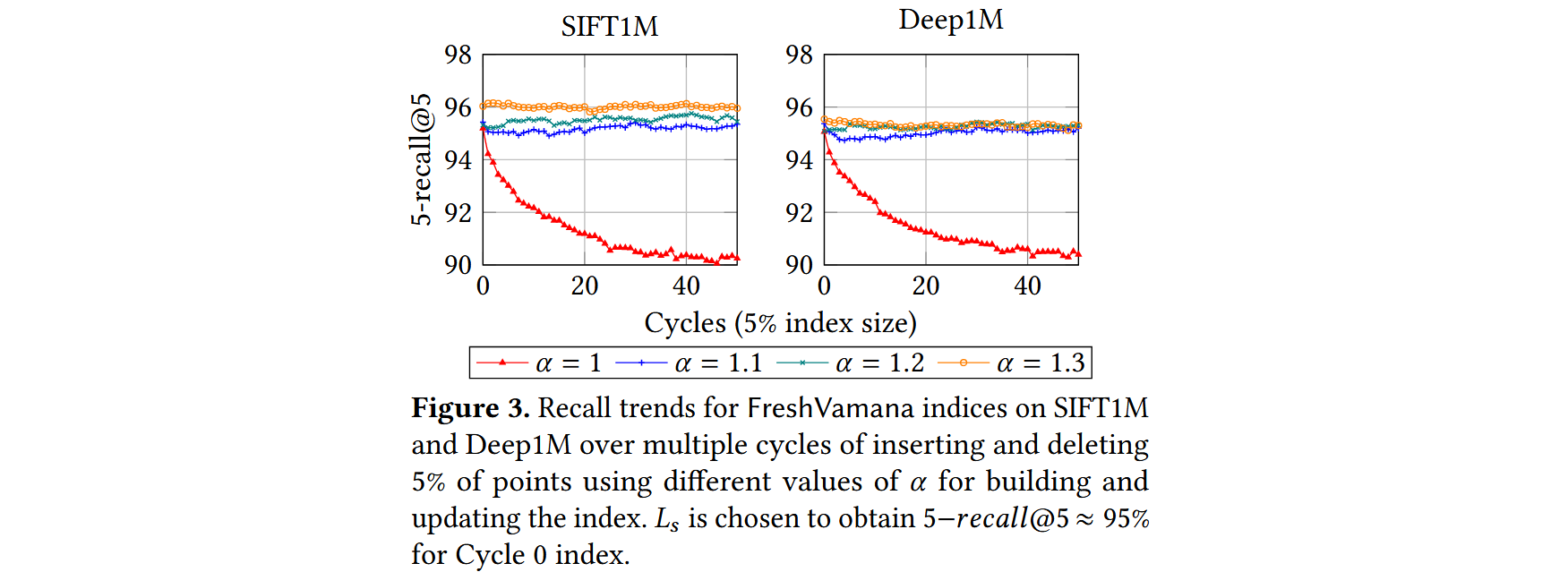
- 一组良好的更新规则应能保持召回率在这些循环中稳定。
- 除 𝛼 = 1 外,所有索引的召回率都是稳定的,这验证了使用 𝛼 > 1的重要性。
FreshDiskANN system
FreshDiskANN 系统的主要思想是将大部分图索引存储在 SSD 上,仅将最近的更改保存在 RAM 中。
为了进一步减少内存占用,可以仅存储压缩向量来表示所有数据向量。使用 -RNG 图并仅存储压缩向量的思想构成了基于 SSD 的 DiskANN 静态 ANNS 索引的核心。
由于无法直接在 SSD 驻留的 FreshVamana 索引上运行插入和删除算法。插入一个新点 需要更新至多 个邻居以向 添加边,这将触发最多 次随机写入 SSD。意味着每次插入都需要进行同等数量的随机 SSD 写入。这将严重限制插入吞吐量,并降低搜索吞吐量(SSD 上的高写入负载会影响其读取性能)。如果每次删除操作都立即执行,则会导致 次写入。
FreshDiskANN 系统规避了这些问题,并通过拆分索引为两部分,将基于 SSD 的系统的效率与基于内存系统的交互式低延迟结合起来:
- 内存中的 FreshVamana 组件:用于存储最近的更新;
- 驻留在 SSD 上的索引:用于存储长期数据。
Components
系统维护两种索引:长期索引(Long-Term Index,LTI)和一个或多个临时索引(Temporary Index,TempIndex),以及删除列表(DeleteList)。
- LTI 是驻留在 SSD 上的索引,用于支持搜索请求。它的内存占用很小,每个点的存储仅包含约 25-32 字节的压缩表示。其关联的图索引和完整精度数据存储在 SSD 上。插入和删除操作不会实时影响 LTI。
- 、TempIndex,完全存储在DRAM 中的 FreshVamana 索引实例(包括数据和相关图结构)。TempIndex 存储了最近插入的点 。内存占用仅占整个索引的一小部分。
- DeleteList 其中的点存在于 LTI 或 TempIndex 中,但已被用户请求删除。此列表用于过滤搜索结果中已删除的点。
- RO- 和 RW-TempIndex 为了支持崩溃恢复,FreshDiskANN 使用两种类型的 TempIndex。在任何时候,FreshDiskANN 都会维护一个可变的可读写 TempIndex(称为 RW-TempIndex),它可以接受插入请求。定期将 RW-TempIndex 转换为 只读的内存索引(RO-TempIndex),并将其快照存储到持久化存储。随后创建一个新的空 RW-TempIndex 以接收新的插入点。
API
- Insert(xₚ):将一个新点插入索引中,路由到RW-TempIndex的唯一实例,该实例使用算法2来处理该点。
- Delete(p):删除请求,将已存在的点p添加到DeleteList中。
- Search(xq, K, L):搜索K个最近的候选项,使用大小为L的候选列表,通过查询LTI、RW-TempIndex和所有RO-TempIndex实例来执行,参数为K和L,聚合结果并移除DeleteList中的已删除条目。
StreamingMerge
每当各个RO-TempIndex的总内存占用超过预定的阈值时,系统就会调用一个后台合并过程,修改驻留在SSD上的LTI,以反映来自不同RO-TempIndex实例的插入,并同时处理来自DeleteList的删除请求。为了方便记法,假设数据集P表示LTI中的点,N表示当前阶段的点,它们存在于不同的RO-TempIndex实例中,D表示标记为删除的点。
删除点之后,StreamingMerge的期望结果是一个驻留在SSD上的LTI,数据集为(P ∪ N) \ D。合并过程完成后,系统清除RO-TempIndex实例,从而保持总内存占用在可控范围内。该过程必须遵循以下两个重要约束:
- 内存占用应与变化的大小|D|和|N|成比例,而不是与整个索引|P|的大小成比例。因为LTI的内存占用可能远大于机器的内存。
- 有效使用SSD I/O,以便在后台进行合并时,仍然可以执行搜索操作,这样合并过程本身可以快速完成。
从高层次来看,StreamingMerge首先运行算法4来处理来自D的删除操作,以获得P \ D点的中间LTI索引。然后,StreamingMerge运行算法2,将N中的每个点插入到中间LTI中以获得最终的LTI。然而,算法2和算法4假设LTI图以及所有数据点的全精度向量都存储在内存中。StreamingMerge的关键挑战之一是以内存和SSD高效的方式模拟这些算法调用。该过程分为以下三个阶段:
-
删除阶段:该阶段处理输入的LTI实例,并通过运行算法4处理删除操作D,生成中间LTI。为了以内存高效的方式完成此操作,我们按块从SSD中加载LTI中的点及其邻居,并使用多线程执行算法4来处理块中的节点,然后将修改后的块写回到SSD中的中间LTI。此外,每当算法4或算法3进行距离比较时,我们使用已存储的压缩PQ向量来计算近似距离,而不是使用准确的距离。请注意,这一做法替代了精确的距离计算,通过使用压缩向量来计算近似距离,这将在StreamingMerge的后续阶段中继续使用。
-
插入阶段:该阶段将所有新点N添加到中间LTI中,模拟算法2的过程。作为第一步,我们在SSD驻留的中间LTI上运行GreedySearch(s, p, 1, L)来获取搜索路径上访问的顶点集V。由于图存储在SSD中,任何由搜索算法请求的邻居Nout(p′)都将从SSD中获取。α-RNG属性确保了邻居请求的数量较小,从而保证了每个点的总体延迟是有界的。然后,我们运行RobustPrune(p, V, α, R)程序来确定p的候选邻居集。然而,与算法2不同,我们不会立即尝试将p插入到Nout(p′)中(即反向边),因为这可能导致大量随机的读取和写入操作,从而影响效率。
-
修补阶段:在处理完所有插入后,我们将Δ数据结构修补到输出的SSD驻留LTI索引中。为此,我们按块从SSD中获取中间LTI中的所有点p,添加每个节点p的相关出边,并检查新的度数|Nout(p) ∪ Δ(p)|是否超过R。如果超过,则通过设置Nout(p) = RobustPrune(p, Nout(p) ∪ Δ(p), ·, ·)来修剪邻居。此操作可以以数据并行的方式应用于每个节点。随后,更新后的块将写回到SSD中,之后再加载新的块。
Complexity
- I/O成本:该过程在删除和修补阶段分别对SSD驻留的数据结构进行了两次顺序遍历。由于中间LTI的-RNG属性,插入算法每插入一个点都会执行少量的随机4KB读取(每个插入点大约100次磁盘读取,比候选列表大小参数(我们通常设为75)多一点)。请注意,如果没有-RNG属性,这个数字会大得多,因为可能存在非常长的导航路径。
- 内存占用:在整个StreamingMerge过程中,数据结构的大小为,其中是索引的最大度数,通常是一个较小的常数。例如,如果,且,则内存占用大约为7GB。此外,为了计算近似距离,我们还会保留PQ坐标的副本,用于索引中的所有点(大约32GB用于一个十亿点的索引)。
- 计算需求:插入阶段和修补阶段的复杂度与要插入的新点的大小基本成线性关系,因为插入阶段仅使用算法1对中的新点进行搜索,并更新数据结构;修补阶段则以块为单位添加反向边。
删除阶段的固定成本较小,仅需扫描每个点的,并检查是否有已删除的点,同时存在一个较大的变量成本,与删除集大小成线性关系,我们会将其上界为(假设随机删除)。有关这一计算的详细信息,请参见附录D。
Recall Stability
尽管我们已经证明了我们的更新算法算法2和4在第4.3节中的长时间更新流中确保了召回稳定性,但这些算法在我们StreamingMerge过程中的实际实现形式是不同的,特别是使用了用于距离计算的近似压缩向量。实际上,随着我们处理更多的StreamingMerge过程周期,我们预计初始图将被完全基于近似距离构建的图所替代。因此,我们预计初期会有小幅下降,但随后召回率将稳定。
在图4中的实验中,我们首先使用从SIFT100M数据集中随机采样的80M点构建了静态SSD索引。然后,在每个周期中,我们使用StreamingMerge更新索引,以反映8M个删除和来自20M点备用池的等量插入。我们总共运行了40个周期的实验,并在图4中跟踪了每个周期后索引的召回率。请注意,索引的稳定值低于静态索引的初始召回率,这是因为在StreamingMerge过程中使用了近似距离。我们观察到,在删除和插入大约10%索引大小的20个周期后,召回率稳定,此时我们预计大部分图是通过近似距离确定的。图4(右)展示了SIFT1B的800M点子集的相似图。我们已经通过实验证明,FreshDiskANN索引能够在更新流的稳态中保持稳定的召回率。
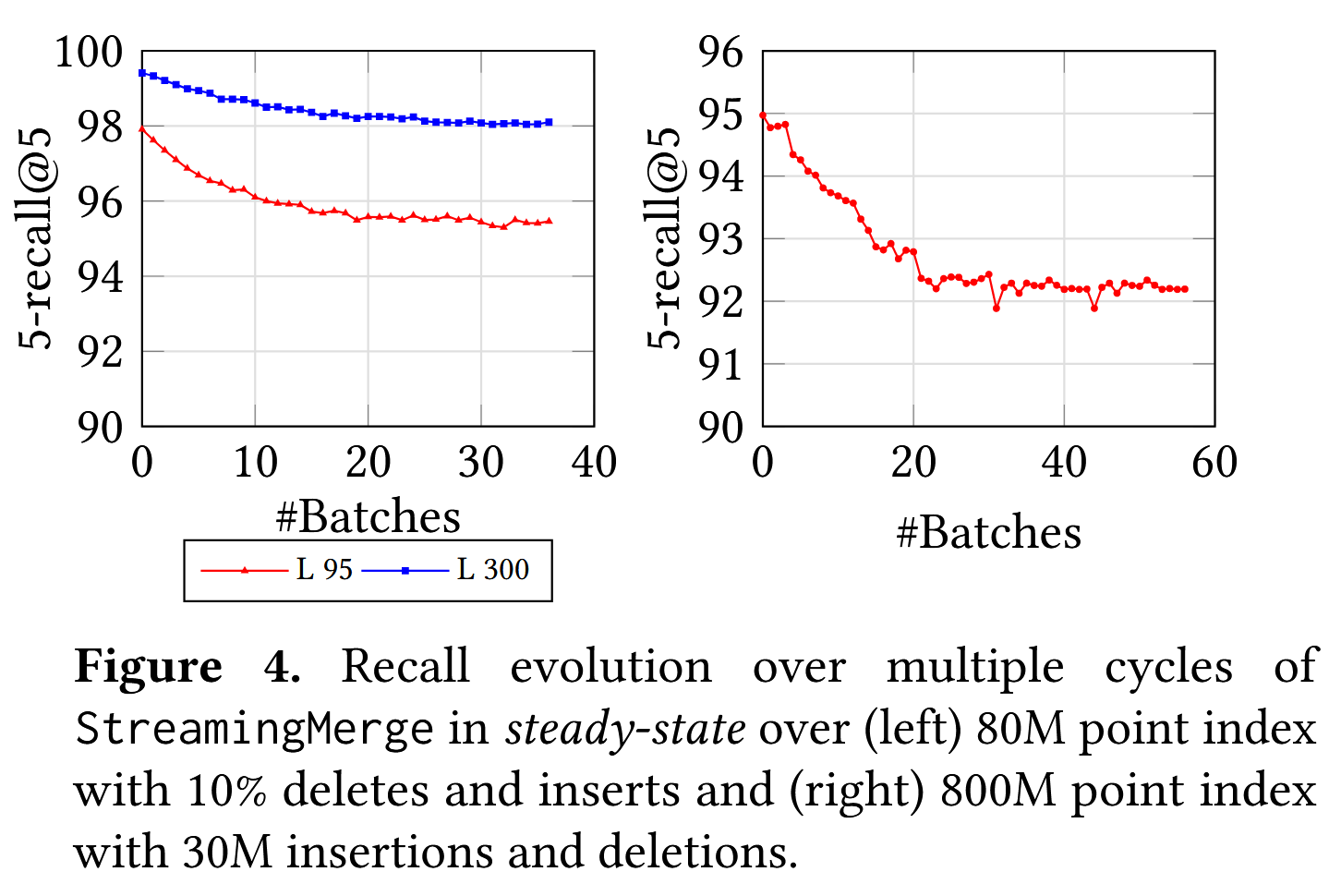
Crash Recovery
为了支持崩溃恢复,所有索引更新操作都会写入重做日志。当崩溃导致单个RW-TempIndex实例和DeleteList丢失时,它们通过从最近的快照回放重做日志中的更新来重建。由于RO-TempIndex和LTI实例是只读的并且定期快照到磁盘,它们可以简单地从磁盘重新加载。
RW-TempIndex被快照到RO-TempIndex的频率取决于预期的恢复时间。更多的快照会导致RW-TempIndex的重建时间较短,但会创建多个RO-TempIndex实例,所有这些实例必须在每个查询中进行搜索。虽然搜索几个额外的小型内存索引不会成为查询的限制步骤(因为搜索大型LTI很耗时),但是创建太多索引可能导致低效的搜索。对于一个十亿点的索引,通常会在每次合并到LTI之间保留最多30M个点的TempIndex。在内存中限制每个索引为500万个点会导致最多6个TempIndex实例可以在0.77毫秒内完成搜索,相比之下,搜索单个30M大小的索引需要0.89毫秒,且候选列表大小为100。
Filtered − DiskANN: Graph Algorithms for Approximate Nearest Neighbor Search with Filters
FreshDiskANN Introduction
随着基于近似最近邻搜索(ANNS)的稠密检索在搜索和推荐场景中的广泛应用,有效回答过滤后的ANNS查询已成为一个关键需求。过滤后的ANNS查询要求从索引中的点中找到与查询的标签(如日期、价格范围、语言)匹配的最近邻。当前的索引具有较高的搜索延迟或较低的召回率。
本文提出了两种具有原生支持的算法,以便更快速、更准确地回答过滤后的ANNS查询:一种支持流处理,另一种基于批量构建。算法的核心是构建一个图结构索引,该索引不仅基于向量数据的几何形状形成连接,还包括相关的标签集。
大多数当前针对过滤后的 ANNS 方法的共同点是,它们只修改了搜索步骤,而没有修改索引构建步骤。
Drawback of Existing Methods
一种直接的方法来回答混合查询是后处理方法:构建一个标准的 ANNS 索引,像往常一样查询,并通过选择仅那些与查询过滤器匹配的索引返回结果来进行后处理。虽然这种方法容易实现,但在实践中效果不佳。事实上,对于一个低特异性的标签过滤器 f,我们可能需要检索大量候选项才能找到一个符合过滤器的结果。
相反,可以考虑一种简单的预处理方法,即为每个可能的可过滤标签 f ∈ F 构建一个单独的索引,以便将查询路由到与查询过滤器关联的索引。然而,这种方法在过滤器数量庞大或每个点可能有多个关联过滤器的情况下,将很快变得代价高昂。
Tip
Tip
ANNS 索引需要从 中找到与 最近的邻居,条件是这些邻居的标签与 匹配,即从集合 中选择点。索引应最大化 ,但它是相对于使用集合 计算的真实值,而不是 。在实际使用中通常无法事先确定满足结果的top-k需要多少个候选项,因为中的top-k很有可能大部分都不在 中。
Related Work
已有大量的研究致力于 ANN(近似最近邻搜索)算法的研究 。见最近的基准测试 ,对最先进的 ANN 算法的比较。大多数现有的研究从提高召回率 、规模和成本效率 、分布式索引 、启用实时索引更新 和设计具有理论保证的算法 等角度解决标准的 ANN 问题。随着 ANN 在语义搜索/密集检索中的日益重要的角色,许多应用关键需求在研究文献中未得到充分关注,其中之一就是过滤或过滤查询(这两个术语可互换使用)。
最近有两项关于过滤 ANN 的研究工作。Analytic DB-V ,阿里巴巴的实际系统集成了过滤 ANN 查询,并在 SQL 引擎上进行了优化。它支持并优化了基于查询计划的复杂过滤器,查询计划根据过滤器的特异性来处理:
- 高特异性:后处理索引
- 中等特异性:内联处理 IVF-PQ 索引
- 低特异性:内联处理蛮力索引
在这项工作中,我们限制为更简单的过滤器——与一个过滤器的精确匹配。为了在交互延迟和高召回率下支持此类搜索,我们开发了新的基于图的索引,这些索引可以更新。我们可以通过简单地找到对应每个单独过滤器的答案,并按查询的距离对这些结果进行聚合和排序,轻松扩展到多个过滤器的并(OR)操作。我们将多个过滤器的合取(AND)和其他更复杂的表达式留作未来工作中的挑战。请注意,当可能的谓词集合已知且不太大(几千个)时,我们可以为每个向量标注谓词,以标识它所满足的条件,并构建图来支持通过这些标签进行过滤。
另一个支持过滤查询的近期算法是 NHQ 算法 。它与我们的工作相关,因为它是基于图的,并且实际上修改了索引步骤:它们将过滤器标签编码为向量,并将其附加到真实向量和使用 ANN 算法(如 NSW 或 kNN-graph )的索引中。然而,这篇论文考虑的是每个数据点有效地只与一个过滤器标签相关的情况——即集合 是完全不交集的,这种情况可以通过为每个过滤器分别使用标准的 ANN 索引来处理。此外,这种技术在扩展到多个过滤器/标签时可能会无效,因为每个点的过滤器/标签的数量越多,召回率的显著性影响越大。如果索引中的某一点有三个过滤器标签,而查询只有一个,那么索引中其他两个标签坐标的距离会对候选点产生不利影响,相比之下,只有相同查询标签的数据点将受到更少的影响。我们证明了我们的方法优于 NHQ,并在附录中进一步证明,这比 Analytic DB-V 的表现要好得多。
FilteredVamana
基于图的ANNS索引是这样构造的,使得贪婪搜索能够快速收敛到查询向量 的最近邻。我们首先描述了过滤查询的贪婪搜索的自然适应,称为FilteredGreedySearch(算法1),以及一个索引构建过程(算法4),该过程允许搜索通过相对较少的距离比较收敛到正确的答案。
FilteredGreedySearch
给定一个查询 和一组标签 ,我们要求输出 个近似最近邻,其中输出的每个点至少与 共享一个标签。搜索过程还接收一组起始节点 。对于具有标签集 的查询,集合 通常是 ,其中 是在索引构建期间为标签 计算的指定起始节点。
在本文中,我们基准测试了标签集 是单元素集合的查询,但该算法也可以用于具有 的查询。
该算法维护一个最多包含 个元素的优先队列 。每次迭代时,它会寻找 中最近的未访问邻居 。然后将 添加到已访问节点的集合 中,这是本文稍后引用的一个有用不变式。接着,我们仅将那些从 出发且至少拥有 中一个标签的外邻添加到队列 。最后,如果 ,我们将 截断为包含距离 最近的 个点。搜索在所有 中的节点都已被访问时终止。输出由 中的 个最近邻和已访问节点集合 组成,后者对索引构建有用(但在用户查询中无用)。

Index Construction
起始点选择。我们要求每个过滤器的起始节点满足两个条件:
- 对于带有单一过滤器 的查询,起始点 应与该过滤器相关联,即 ;
- 不应有点在 中作为过多过滤标签的起始点。使用不同过滤器的查询应该跨越许多点来共享,以便我们可以构建一个具有小度数的图,该图适用于所有过滤标签。
实际上,如果一个单一节点作为许多标签的起始点,则从该起始点出发,可能很少有邻接节点带有某个标签,从而导致搜索效果差。我们通过使用算法2中描述的简单随机化负载平衡算法来实现这一点。

增量图构建。FilteredVamana图构建是一个增量算法。我们首先为每个过滤标签识别起始节点 ,并初始化一个空图 。然后,对于每个数据点 ,与之关联的过滤器/标签 ,我们运行FilteredGreedySearch(, , , ),并以集合 为起始点。这将返回一组在搜索中访问到的节点 。所有已访问的节点都具有标签 。
接着,我们通过调用算法3中的过滤感知剪枝过程,以参数 (, , , ) 来修剪候选集 。这确保了图节点对应的 至多有 个外邻。

外邻剪枝,同时消除冗余的近邻向量。剪枝过程依赖于以下原则:对于顶点三元组 ,, 和常数 ,如果满足下列条件,则可以将有向边 从图中剪除:
- 边 存在,
- 向量 比 更接近 ,即 ,
- 包含 和 所有共同的过滤标签,即 。
最后,我们从 到 添加反向边,其中 ,并且,如果任何此类 的度数超过 ,我们在 上运行FilteredRobustPrune过程。

StitchedVamana
我们现在提出一个用于构建索引的不同算法,称为 StitchedVamana(算法 5),该算法只能在已知点集的情况下使用。对于每个 ,我们使用 Vamana 算法 [39] 在带有标签 的点集 上构建图索引 ,其参数为 和 。这些参数比前一个算法中的参数更小,从而加速了索引构建。接下来,由于顶点可能属于多个图(即一个点 可能属于多个 ),我们将各个图 “拼接”到图 中,图 的边是每个 的边集的并集。图 可能会有较大的度数。我们通过使用 FilteredRobustPrune 程序将其最大外度数减少到 。最终的图与 FilteredGreedySearch 程序兼容。

Summary
Comparison of Vamana with HNSW and NSG
Vamana 与 HNSW 和 NSG 非常相似。这三种算法都在数据集 上进行迭代,并使用 GreedySearch(s, , 1, L) 和 RobustPrune(p, , , ) 的结果来确定 的邻居。这些算法之间存在一些重要的差异。
- 最关键的是,HNSW 和 NSG 都没有可调参数 ,而且隐式使用 。(这是使 Vamana 在图的度数和直径之间实现更好折衷的主要因素)
- 虽然 HNSW 将候选集 设置为贪心搜索(GreedySearch(s, , 1, L))的修剪过程的最终候选结果集,Vamana 和 NSG 将 设置为贪心搜索(GreedySearch(s, , 1, L))访问的所有顶点的集合。从直觉上讲,这个特征有助于 Vamana 和 NSG 添加长距离边,而 HNSW 仅通过添加局部边来构建图的层次结构,进而构建嵌套的图序列。
- NSG 将数据集上的图初始化为近似 -最近邻图,这是一个时间和内存密集型的步骤,而 HNSW 和 Vamana 则有更简单的初始化过程,前者从一个空图开始,Vamana 从一个随机图开始。
- Vamana 进行两次遍历数据集,而 HNSW 和 NSG 只进行一次遍历,动机是基于我们观察到的第二次遍历能提高图的质量。
SPANN
SPANN: Highly-efficient Billion-scale Approximate Nearest Neighborhood Search
Faiss
Faiss的使用说明和相关知识。
Composite Indexes
一个复合索引可由以下部分组合而成:
- Vector transform:在索引之前应用于向量的预处理步骤
- PCA:主成分分析,尽可能减少信息损失,将向量投影到低维空间
- OPQ:通过旋转变换优化向量分布,避免信息分布不均匀,以提高量化效果
- Coarse quantizer:用于限制搜索范围
- IVF:
- IMI:
- HNSW:
- Fine quantizer:用于压缩索引大小
- PQ:
- Refinement: 搜索结果排序方式
- RFlat:在原始向量上计算距离
| Vector transform | Coarse quantizer | Fine quantizer | Refinement |
|---|---|---|---|
| PCA, OPQ, RR, L2norm, ITQ, Pad | IVF, Flat, IMI, IVF-HNSW, IVF-PQ, IVF-RCQ, HNSW-Flat, HNSW-SQ, HNSW-PQ | Flat, PQ, SQ, Residual, RQ, LSQ, ZnLattice, LSH | RFlat, Refine* |
Hierarchy
The CPU Faiss class hierarchy looks like this:faiss_class_hierarchy.pdf
Getting Started
全文字数: 1772 字
阅读时间: 12 分钟
Installing Faiss
# 新建一个干净的环境
conda create -n faiss_env python=3.9 -y
# 切换
conda activate faiss_env
根据需要安装CPU或GPU版本的Faiss
# CPU-only version
conda install -c pytorch faiss-cpu=1.10.0
# GPU(+CPU) version
conda install -c pytorch -c nvidia faiss-gpu=1.10.0
# GPU(+CPU) version with NVIDIA cuVS
conda install -c pytorch -c nvidia -c rapidsai -c conda-forge libnvjitlink faiss-gpu-cuvs=1.10.0
# GPU(+CPU) version using AMD ROCm not yet available
Basic Usage
import numpy as np
d = 64 # dimension
nb = 100000 # database size
nq = 10000 # nb of queries
np.random.seed(1234) # make reproducible
xb = np.random.random((nb, d)).astype('float32')
xb[:, 0] += np.arange(nb) / 1000.
xq = np.random.random((nq, d)).astype('float32')
xq[:, 0] += np.arange(nq) / 1000.
import faiss # make faiss available
index = faiss.IndexFlatL2(d) # build the index
print(index.is_trained)
index.add(xb) # add vectors to the index
print(index.ntotal)
k = 4 # we want to see 4 nearest neighbors
D, I = index.search(xb[:5], k) # sanity check
print(I)
print(D)
D, I = index.search(xq, k) # actual search
print(I[:5]) # neighbors of the 5 first queries
print(I[-5:]) # neighbors of the 5 last queries
Getting some data
import numpy as np
d = 64 # dimension
nb = 100000 # database size
nq = 10000 # nb of queries
np.random.seed(1234) # make reproducible
xb = np.random.random((nb, d)).astype('float32')
xb[:, 0] += np.arange(nb) / 1000.
xq = np.random.random((nq, d)).astype('float32')
xq[:, 0] += np.arange(nq) / 1000.
d:向量的维度nb:数据库的大小nq:查询的数量xb:数据库向量xq:查询向量
xb[:, 0] += np.arange(nb) / 1000.:构造具有一定分布规律的数据,使与i号查询相近的向量就在数据库中i号附近。
Building an index and adding the vectors to it
import faiss # make faiss available
index = faiss.IndexFlatL2(d) # build the index
print(index.is_trained)
index.add(xb) # add vectors to the index
print(index.ntotal)
Faiss 是围绕 Index 对象构建的。它封装数据库向量集,并选择性地对它们进行预处理以提高搜索效率。
所有索引在构建时都需要知道它们操作的向量的维度。大多数索引还需要一个训练阶段,以分析向量的分布。对于 IndexFlatL2可以跳过这个操作。
当索引构建并训练完成后,可以对索引执行两个操作:add 和 search 。
要向索引中添加元素,调用 add 并传入 xb。还可以查看索引的两个状态变量:is_trained(指示是否需要训练)和 ntotal(索引中存储的向量数量)。
Searching
k = 4 # we want to see 4 nearest neighbors
D, I = index.search(xb[:5], k) # sanity check
print(I)
print(D)
D, I = index.search(xq, k) # actual search
print(I[:5]) # neighbors of the 5 first queries
print(I[-5:]) # neighbors of the 5 last queries
为了检查正确性,可以先搜索数据库中的前5个向量,查看其最近邻居是否是自身。
[[ 0 393 363 78]
[ 1 555 277 364]
[ 2 304 101 13]
[ 3 173 18 182]
[ 4 288 370 531]]
[[ 0. 7.17517328 7.2076292 7.25116253]
[ 0. 6.32356453 6.6845808 6.79994535]
[ 0. 5.79640865 6.39173603 7.28151226]
[ 0. 7.27790546 7.52798653 7.66284657]
[ 0. 6.76380348 7.29512024 7.36881447]]
实际搜索输出的结果类似于
[[ 381 207 210 477]
[ 526 911 142 72]
[ 838 527 1290 425]
[ 196 184 164 359]
[ 526 377 120 425]]
[[ 9900 10500 9309 9831]
[11055 10895 10812 11321]
[11353 11103 10164 9787]
[10571 10664 10632 9638]
[ 9628 9554 10036 9582]]
由于向量的第一个分量增加了附加值,数据集在 d 维空间的第一轴上被扩散。所以,前几个向量的邻居位于数据集的开头,而大约在 10000 附近的向量的邻居也在数据集的 10000 索引附近。
Faster search (IVF)
...
import faiss
nlist = 100
k = 4
quantizer = faiss.IndexFlatL2(d) # the other index
# here we specify METRIC_L2, by default it performs inner-product search
index = faiss.IndexIVFFlat(quantizer, d, nlist, faiss.METRIC_L2)
index.train(xb)
index.add(xb) # add may be a bit slower as well
D, I = index.search(xq, k) # actual search
print(I[-5:]) # neighbors of the 5 last queries
index.nprobe = 10 # default nprobe is 1, try a few more
D, I = index.search(xq, k)
print(I[-5:]) # neighbors of the 5 last queries
为了加快搜索速度,可以将数据集划分为多个片段。在 维空间中定义 Voronoi cells,每个数据库向量都会归属于其中一个细胞。
在搜索时,仅比较查询向量 所落入的细胞及其附近的一些相邻细胞中的数据库向量 。
这一过程是通过 IndexIVFFlat 索引实现的。这种类型的索引需要一个训练阶段,该阶段可以在与数据库向量具有相同分布的任何向量集合上执行。在本例中,我们直接使用数据库向量进行训练。
IndexIVFFlat 还需要一个额外的索引,即 quantizer,用于将向量分配到 Voronoi 细胞中。每个细胞由一个centroid定义,确定一个向量属于哪个 Voronoi 细胞的过程,本质上是找到该向量在所有中心点中的最近邻居。这个任务通常由IndexFlatL2索引来完成。
搜索方法有两个关键参数:
- nlist:细胞的总数。
- nprobe:搜索时访问的细胞数量。
搜索时间大致与探测的细胞数量成线性关系,同时还会有一部分由量化过程带来的额外开销。
当nprobe=1时,结果类似于:
[[ 9900 10500 9831 10808]
[11055 10812 11321 10260]
[11353 10164 10719 11013]
[10571 10203 10793 10952]
[ 9582 10304 9622 9229]]
当nprobe=10时,结果类似于:
[[ 9900 10500 9309 9831]
[11055 10895 10812 11321]
[11353 11103 10164 9787]
[10571 10664 10632 9638]
[ 9628 9554 10036 9582]]
得到了正确的结果。但是获得完美的结果只是因为该数据有很规律的分布,它在 x 轴上具有很强的分量,这使得它更容易处理。该参数始终是调整结果的速度和准确性之间的权衡的一种方式。设置 nprobe = nlist 给出的结果与暴力搜索相同。
Lower memory footprint (PQ)
...
nlist = 100
m = 8
k = 4
quantizer = faiss.IndexFlatL2(d) # this remains the same
# 8 specifies that each sub-vector is encoded as 8 bits
index = faiss.IndexIVFPQ(quantizer, d, nlist, m, 8)
index.train(xb)
index.add(xb)
D, I = index.search(xb[:5], k) # sanity check
print(I)
print(D)
index.nprobe = 10 # make comparable with experiment above
D, I = index.search(xq, k) # search
print(I[-5:])
之前看到的索引,IndexFlatL2 和 IndexIVFFlat,都会存储完整的向量。为了扩展到非常大的数据集,Faiss 提供了基于**乘积量化(Product Quantizer)**的有损压缩变体,以压缩存储的向量。
这些向量仍然存储在Voronoi 单元中,但其大小被减少到可配置的字节数 m(维度 d 必须是 m 的倍数)。
由于向量并不是以完全精确的形式存储的,因此搜索方法返回的距离值也是近似的。
运行结果如下:
[[ 0 608 220 228]
[ 1 1063 277 617]
[ 2 46 114 304]
[ 3 791 527 316]
[ 4 159 288 393]]
[[ 1.40704751 6.19361687 6.34912491 6.35771513]
[ 1.49901485 5.66632462 5.94188499 6.29570007]
[ 1.63260388 6.04126883 6.18447495 6.26815748]
[ 1.5356375 6.33165455 6.64519501 6.86594009]
[ 1.46203303 6.5022912 6.62621975 6.63154221]]
可以看到最近邻被正确找到(即向量本身),但向量与自身的估算距离并不为 0(明显小于它与其他邻居的距离),这是由于有损压缩导致的。
这里将64 个 32 位浮点数压缩到8 字节,压缩比为32。
Simplifying index construction
构建索引可能会变得复杂,Faiss 提供了工厂函数根据字符串来构造索引。
index = faiss.index_factory(d, "IVF100,PQ8")
将 PQ8 替换为 Flat,即可获得 IndexFlat。当对输入向量进行**预处理(如 PCA)**时,工厂函数特别有用。例如,使用字符串 "PCA32,IVF100,Flat" 可以通过 PCA 投影将向量维度降至 32D。
Basics
全文字数: 1555 字
阅读时间: 10 分钟
MetricType and distances
METRIC_L2
平方欧几里得(L2)距离(由于平方根是单调的,没有做平方根运算),此度量对数据的旋转不变(正交矩阵变换)。
METRIC_INNER_PRODUCT
查询向量的范数不会影响结果的排名(数据库向量的范数确实重要)。其本身不是余弦相似度,除非向量已经归一化。
**如何对余弦相似度进行向量索引?**向量x和y之间的余弦相似度定义为:
它是相似度,而不是距离,因此通常会搜索相似度较大的向量。
通过预先归一化查询和数据库向量,可以将问题映射回最大内积搜索。执行此操作的方法:
- 使用METRIC_INNER_PRODUCT构建索引
- 在将向量添加到索引之前先归一化向量(在Python中使用faiss.normalize_L2)
- 在搜索之前先归一化向量
Clustering, PCA, Quantization
Faiss 具有非常高效的k-means 聚类、PCA、PQ 编解码实现:。
Clustering
Faiss 提供了一个高效的 k-means 实现。将存储在给定 2D 张量 中的一组向量进行聚类,操作如下:
ncentroids = 1024
niter = 20
verbose = True
d = x.shape[1]
kmeans = faiss.Kmeans(d, ncentroids, niter=niter, verbose=verbose)
kmeans.train(x)
最终的质心保存在 kmeans.centroids 中。
目标函数的值(在 k-means 中是总平方误差)在每次迭代中的变化存储在变量 kmeans.obj 中,更详细的统计信息存储在 kmeans.iteration_stats 中。
要在 GPU 上运行,在 Kmeans 构造函数中添加选项 gpu=True。(使用所有 GPU)或 gpu=3(使用 3 个 GPU)。
Kmeans 对象主要是 C++ 中 Clustering 对象的一层,所有该对象的字段可以通过构造函数进行设置。字段包括:
nredo:运行聚类的次数,并保留最佳质心(根据聚类目标选择)verbose:使聚类过程更加详细spherical:执行球形 k-means —— 每次迭代后,质心会进行 L2 归一化int_centroids:将质心坐标四舍五入为整数update_index:每次迭代后是否重新训练索引?min_points_per_centroid/max_points_per_centroid:收到警告,表示训练集已被子采样seed:随机数生成器的种子
Asignment
要计算从一组向量 到聚类质心的映射,在 k-means 训练完成后,可以使用:
D, I = kmeans.index.search(x, 1)
将返回 中每个行向量的最近质心, 包含这些质心的索引, 包含平方的 L2 距离。
对于反向操作,例如查找 中距离已计算质心最近的 15 个点,必须使用新的索引:
index = faiss.IndexFlatL2(d)
index.add(x)
D, I = index.search(kmeans.centroids, 15)
其中,大小为 的 包含每个质心的最近邻。
PCA
将 40D 向量降维到 10D。
# 随机训练数据
mt = np.random.rand(1000, 40).astype('float32')
mat = faiss.PCAMatrix(40, 10)
mat.train(mt)
assert mat.is_trained
tr = mat.apply(mt)
# 打印此结果以展示 tr 的列的幅度在减少
print((tr ** 2).sum())
Quantizers
量化器对象继承自 Quantizer,提供了三种常见的方法(见 impl/Quantizer.h):
- train:在一组向量矩阵上训练量化器。
- compute_codes 和 decode:编码器和解码器。编码器通常是有损的,并返回每个输入向量的 uint8 类型代码矩阵。
- get_DistanceComputer:这是一个返回 DistanceComputer 对象的方法。
Quantizer 对象的状态是训练的结果(代码书表或归一化系数)。字段 code_size 表示量化器生成的每个代码的字节数。
支持的量化器类型有:
- ScalarQuantizer:将每个向量分量单独量化为线性范围内的值。
- ProductQuantizer:对子向量进行向量量化。
- AdditiveQuantizer:将一个向量编码为代码书条目的和,详情见 Additive Quantizers。Additive 量化器可以通过多种方式进行训练,因此有子类 ResidualQuantizer、LocalSearchQuantizer 和 ProductAdditiveQuantizer。
有趣的是,每个量化器都是前一个量化器的超集。
每个量化器都有一个对应的索引类型,它还存储一组量化向量。
| 量化器类 | 平面索引类 | IVF 索引类 |
|---|---|---|
| ScalarQuantizer | IndexScalarQuantizer | IndexIVFScalarQuantizer |
| ProductQuantizer | IndexPQ | IndexIVFPQ |
| AdditiveQuantizer | IndexAdditiveQuantizer | IndexIVFAdditiveQuantizer |
| ResidualQuantizer | IndexResidualQuantizer | IndexIVFResidualQuantizer |
| LocalSearchQuantizer | IndexLocalSearchQuantizer | IndexIVFLocalSearchQuantizer |
另外,除了 ScalarQuantizer 的索引,所有索引都有 FastScan 版本
一些量化器返回一个 DistanceComputer 对象。它的目的是在一个向量与许多代码进行比较时,高效地计算向量与代码之间的距离。在这种情况下,通常可以预先计算一组表,以便在压缩域中直接计算距离。
因此,DistanceComputer 提供以下方法:
- set_query:设置当前未压缩的向量进行比较。
- distance_to_code:计算与给定代码的实际距离。
ProductQuantizer 对象可用于将向量编码或解码为代码:
d = 32 # 数据维度
cs = 4 # 代码大小(字节)
# 训练集
nt = 10000
xt = np.random.rand(nt, d).astype('float32')
# 编码数据集(可以与训练集相同)
n = 20000
x = np.random.rand(n, d).astype('float32')
pq = faiss.ProductQuantizer(d, cs, 8)
pq.train(xt)
# 编码
codes = pq.compute_codes(x)
# 解码
x2 = pq.decode(codes)
# 计算重建误差
avg_relative_error = ((x - x2)**2).sum() / (x ** 2).sum()
标量量化器的工作方式类似:
d = 32 # 数据维度
# 训练集
nt = 10000
xt = np.random.rand(nt, d).astype('float32')
# 编码数据集(可以与训练集相同)
n = 20000
x = np.random.rand(n, d).astype('float32')
# QT_8bit 为每个维度分配 8 位(QT_4bit 也可以使用)
sq = faiss.ScalarQuantizer(d, faiss.ScalarQuantizer.QT_8bit)
sq.train(xt)
# 编码
codes = sq.compute_codes(x)
# 解码
x2 = sq.decode(codes)
# 计算重建误差
avg_relative_error = ((x - x2)**2).sum() / (x ** 2).sum()
Guidelines to choose an index
- 少量搜索?
- 只进行少量搜索(例如 1000-10000 次),那么索引构建时间将无法通过搜索时间来摊销。此时,直接计算是最有效的选择。通过 "Flat" 索引来完成的。如果整个数据集无法放入 RAM 中,可以一个接一个地构建小的索引,并组合搜索结果。
- 需要精确的结果?
- 唯一可以保证精确结果的索引是 IndexFlatL2 或 IndexFlatIP。它为其他索引提供了结果的基准。它不支持
add_with_ids,只支持顺序添加.
- 唯一可以保证精确结果的索引是 IndexFlatL2 或 IndexFlatIP。它为其他索引提供了结果的基准。它不支持
Index
| Index | Quality | Speed | Memory | When to Use |
|---|---|---|---|---|
| Flat | 🟢🟢🟢🟢🟢 | 🔴 | 🟡🟡🟡 | |
| IVF | ||||
| HNSW |
Flat
Introduction
不对数据进行任何修改
- 没有近似
- 没有聚类
完美的搜索质量,显著的搜索时间。
Implementation
import shutil
import urllib.request as request
from contextlib import closing
# first we download the Sift1M dataset
with closing(request.urlopen('ftp://ftp.irisa.fr/local/texmex/corpus/sift.tar.gz')) as r:
with open('sift.tar.gz', 'wb') as f:
shutil.copyfileobj(r, f)
import tarfile
# the download leaves us with a tar.gz file, we unzip it
tar = tarfile.open('sift.tar.gz', "r:gz")
tar.extractall()
import numpy as np
# now define a function to read the fvecs file format of Sift1M dataset
def read_fvecs(fp):
a = np.fromfile(fp, dtype='int32')
d = a[0]
return a.reshape(-1, d + 1)[:, 1:].copy().view('float32')
# data we will search through
xb = read_fvecs('sift_base.fvecs') # 1M samples
# also get some query vectors to search with
xq = read_fvecs('./sift/sift_query.fvecs')
# take just one query (there are many in sift_learn.fvecs)
xq = xq[0].reshape(1, xq.shape[1])
xq.shape
(1, 128)
xb.shape
(1000000, 128)
xq
array([[ 1., 3., 11., 110., 62., 22., 4., 0., 43., 21., 22.,
18., 6., 28., 64., 9., 11., 1., 0., 0., 1., 40.,
101., 21., 20., 2., 4., 2., 2., 9., 18., 35., 1.,
1., 7., 25., 108., 116., 63., 2., 0., 0., 11., 74.,
40., 101., 116., 3., 33., 1., 1., 11., 14., 18., 116.,
116., 68., 12., 5., 4., 2., 2., 9., 102., 17., 3.,
10., 18., 8., 15., 67., 63., 15., 0., 14., 116., 80.,
0., 2., 22., 96., 37., 28., 88., 43., 1., 4., 18.,
116., 51., 5., 11., 32., 14., 8., 23., 44., 17., 12.,
9., 0., 0., 19., 37., 85., 18., 16., 104., 22., 6.,
2., 26., 12., 58., 67., 82., 25., 12., 2., 2., 25.,
18., 8., 2., 19., 42., 48., 11.]], dtype=float32)
Flat 索引无需训练,直接搜索。
d = 128 # dimensionality of Sift1M data
k = 10 # number of nearest neighbors to return
index = faiss.IndexFlatIP(d)
index.add(data)
D, I = index.search(xq, k)
Flat 索引非常准确,但是速度非常慢,在相似搜索中,搜索速度和搜索质量间总是存在着权衡。
Inverted File Index
Introduction
IVF索引通过聚类来缩小搜索范围。它基于 Voronoi 图的概念,
note
Voronoi:想象将高维向量放入二维空间。然后在二维空间中放置一些额外的点,这些点将成为我们的“簇”质心,这些簇就是Voronoi。
从每个质心向外延伸相等的半径。在某个时刻,每个cell的圆周将与另一个cell相撞——形成边缘。每个数据点都包含在一个cell内,并分配给相应的质心。
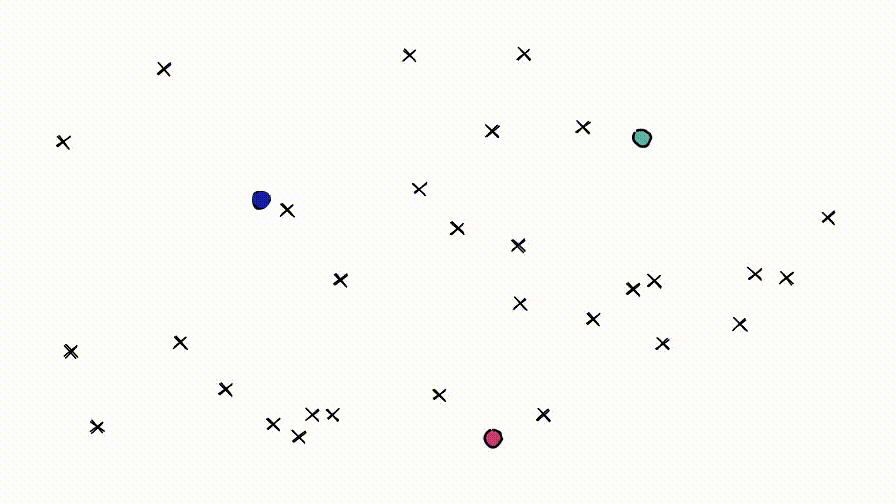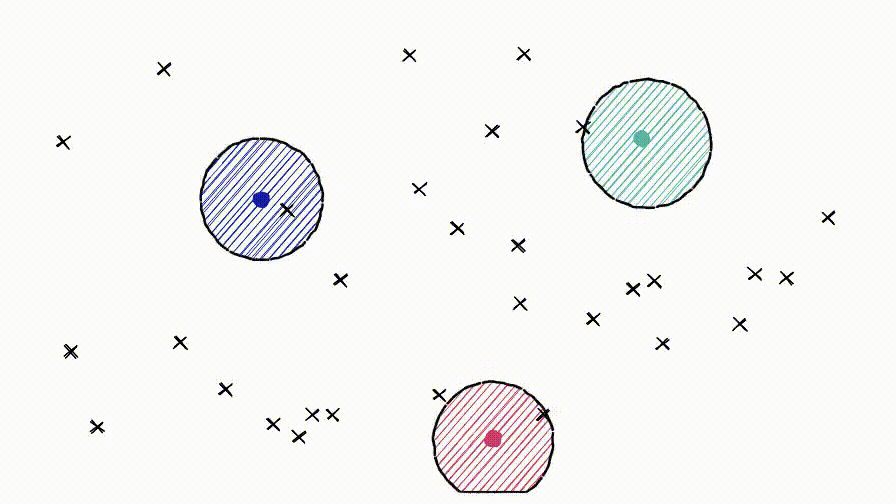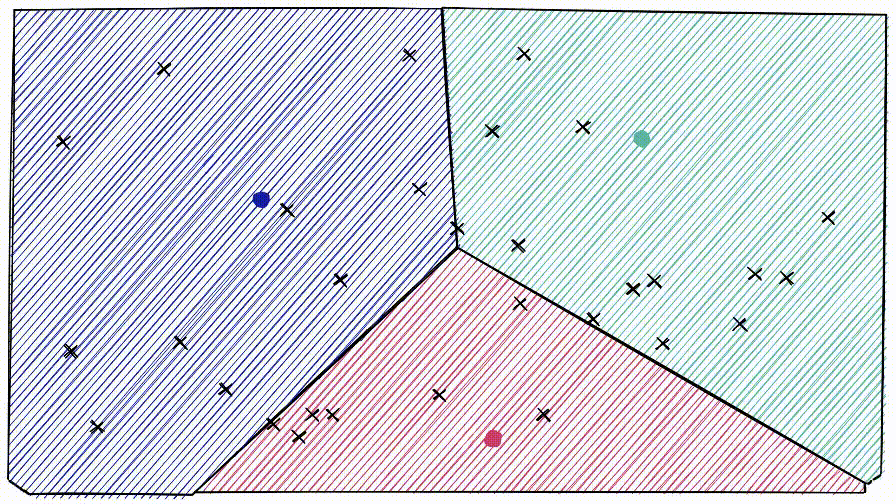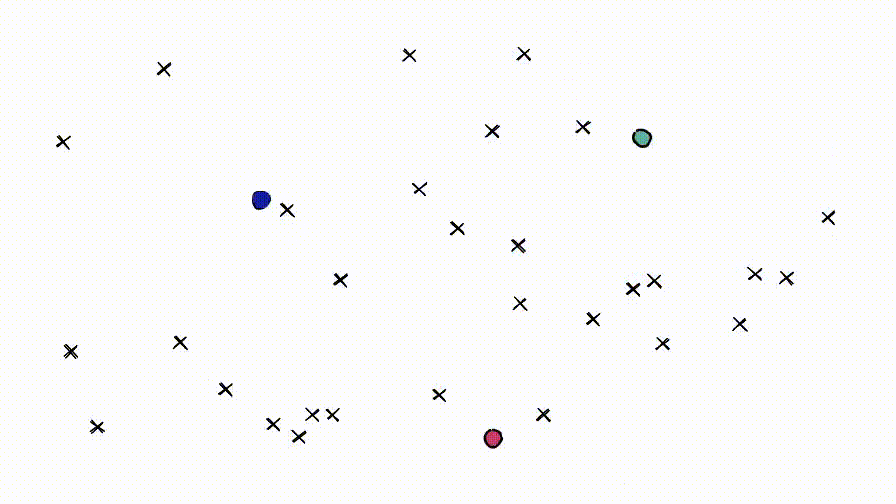
查询向量xq也落在其中一个cell内,此时将搜索范围限制在该单个cell。
但是,如果查询向量落在cell的边缘附近,就会出现问题,很有可能其最近的数据点落在在相邻的cell。称之为 edge problem。
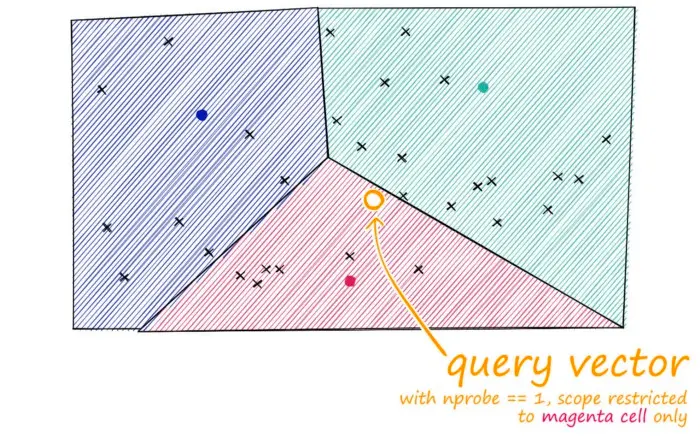
可以通过设置参数 nprobe 来设置需要搜索的cell的数量。
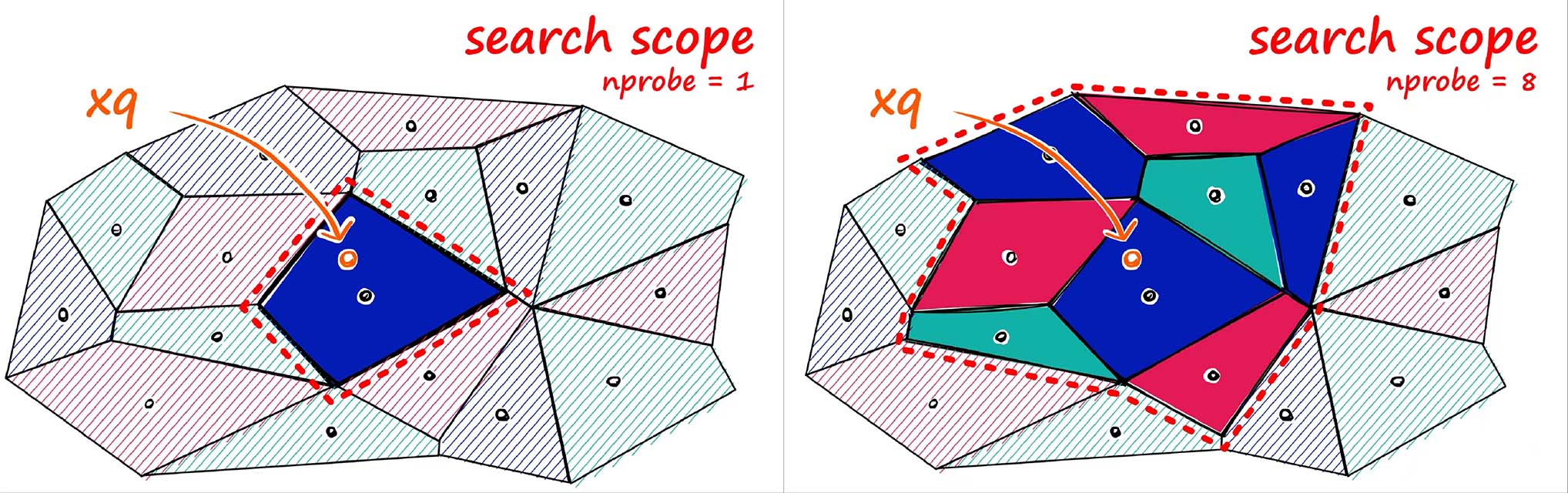
设置参数nlist来设置Voronoi的数量。
Implementation
nlist = 128 # number of cells/clusters to partition data into
quantizer = faiss.IndexFlatIP(d) # how the vectors will be stored/compared
index = faiss.IndexIVFFlat(quantizer, d, nlist)
index.train(data) # we must train the index to cluster into cells
index.add(data)
index.nprobe = 8 # set how many of nearest cells to search
D, I = index.search(xq, k)
Hierarchical Navigable Small World Graphs
Introduction
important
HNSW是ANNS最佳索引之一。
note
NSW 是一种所有顶点都与最近的一些邻居相连的图。
一张可视化的NSW图。(但是不清楚“所有顶点都与最近的一些邻居相连”如何理解)
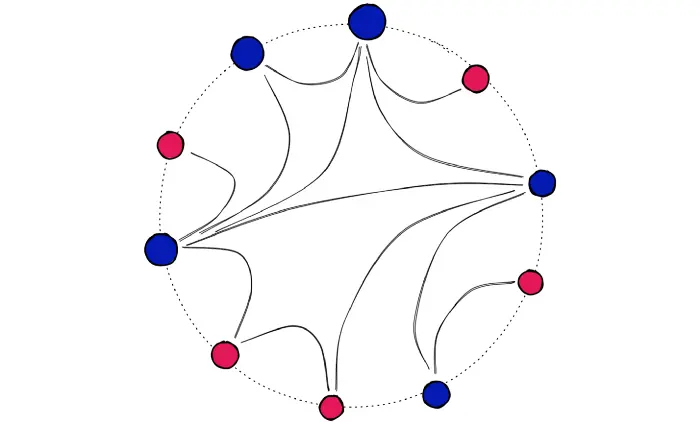
HNSW将NSW分解成多层来构建,每个新增的层都消除了一些顶点到顶点的中间连接。
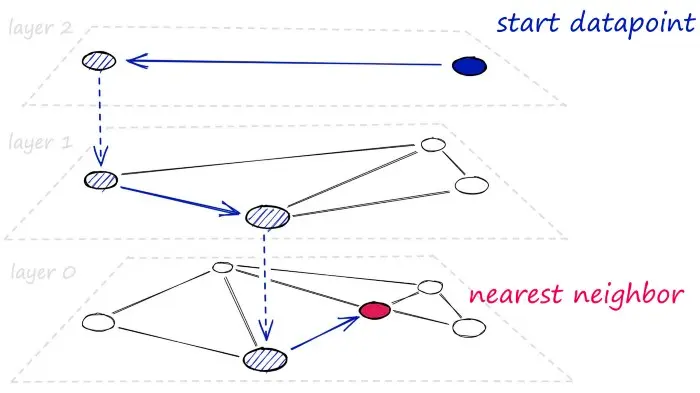
Probability Skip List
Probability Skip List
跳表能像排序数组一样快速进行搜索,同时也能使用链表结构快速插入新元素。
跳表的实现方式是构建多层次的链表,在第一层找到跳过很多中间节点的连接,随着向下移动层,每个链接跳过的节点会减少。
搜索时,从具有最长跳跃长度的最高层开始,沿着边朝右(下)方移动,如果下一跳的值大于我们要搜索的值,那么就向下移动一层再进行搜索。
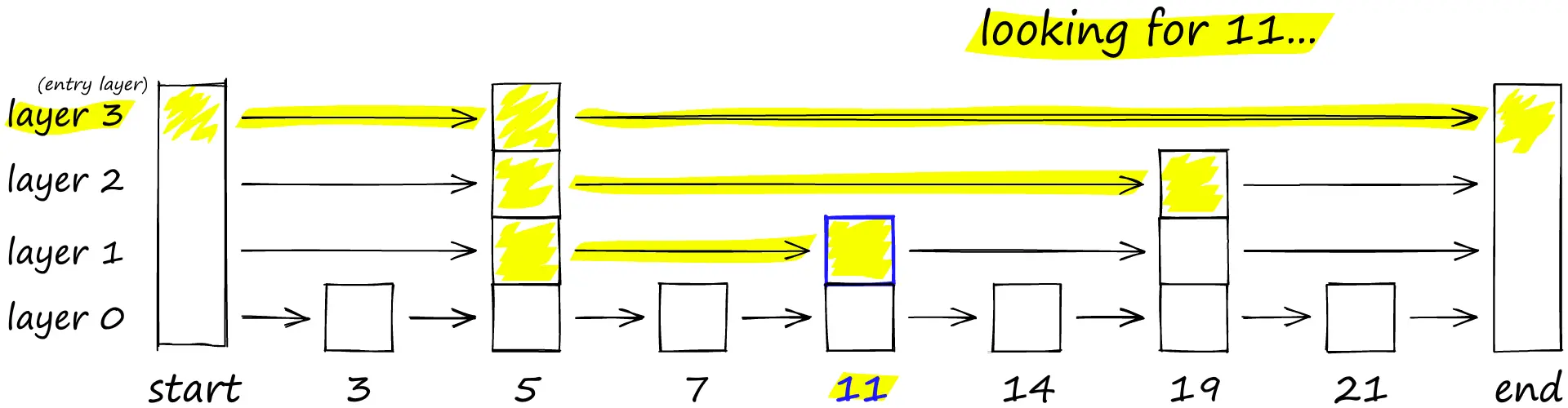
HNSW 继承了相同的分层设计格式,高层的边较长(用于快速搜索),低层的边较短(用于准确搜索)。
HNSW是NSW的自然演进,为NSW添加层次结构生成的图结构其中的链接分散在不同层上
- 在顶层,有最长的链接
- 在底层,有最短的链接
搜索时总是从顶层出发,这里链接最长,而且这些顶点往往是高度数的顶点(链接分散在每一层上),这意味着HNSW默认从NSW描述中的zoom-in阶段开始。
Algorithm
Construction
在构建图的过程中,向量会逐个插入。层数由参数L表示。
向量插入到哪一层是由m_L(level mutilplier)决定的,当m_L为0时表示向量仅插入到第0层,向量会被插入到该层及其以下所有层。
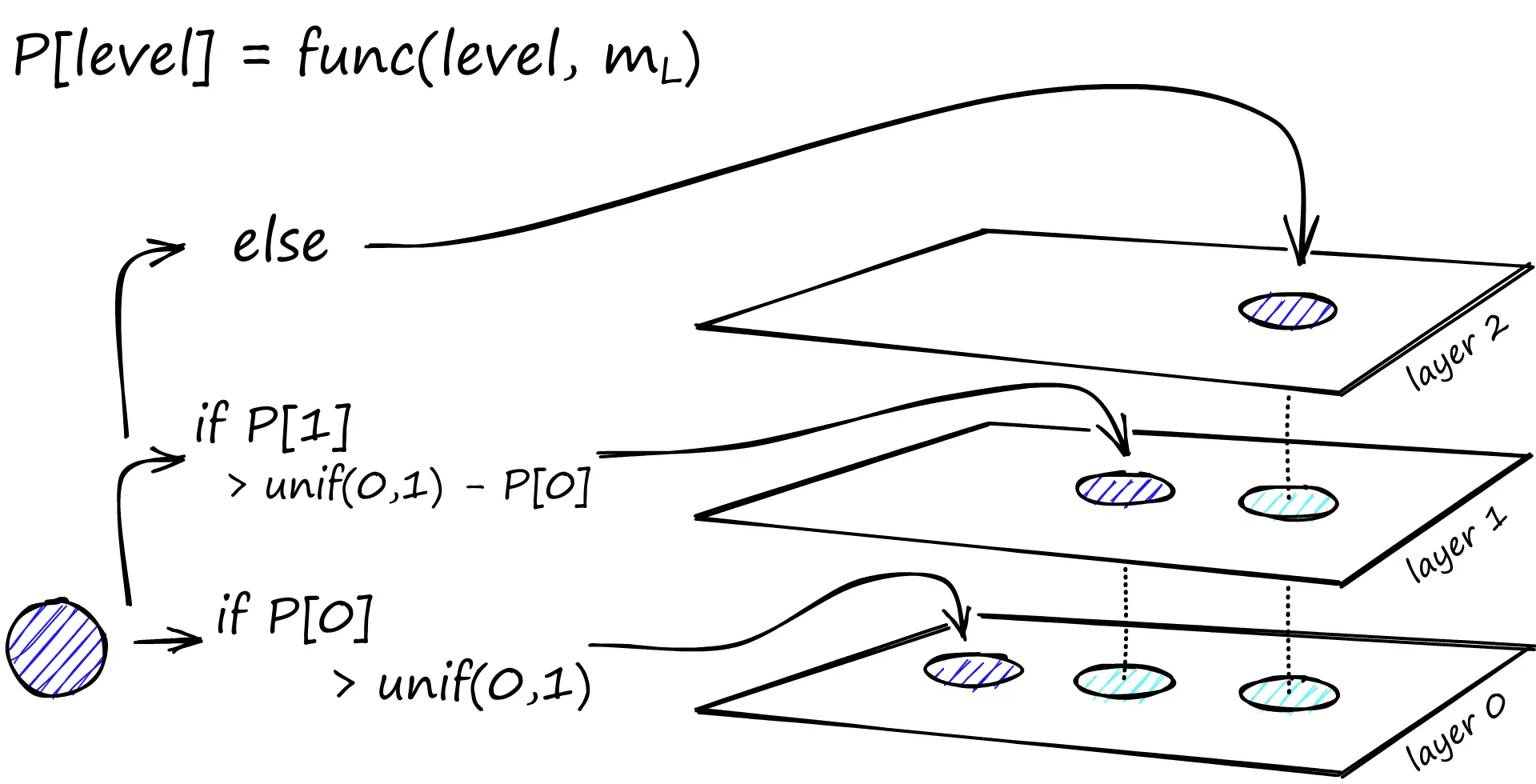
note
当最小化重复跨层共享的邻居(每一个顶点都会出现在下面的层,但是边(邻居关系)不是,这条规则的目的是减少跨层重复的边),可以获得最佳性能。
减少m_L可以帮助最小化重叠(将更多的向量推送到0层),但这会增加搜索期间遍历的次数。
因此需要权衡m_L的值。一个经验值是
- 第一阶段:在待插入的层级之上:
- 从顶层开始,找到距待插入向量q最近的点(W,ef = 1),作为下一层的入口点
- 第二阶段:在待插入的层级及以下:
- 将上一层的候选列表作为这一层的入口点。(入口点即预先放入这一层候选列表中的点)
- 搜索据插入点q最近的ef=ef_construction个点,产生候选列表W
- 从W中为插入点q选择M个邻居(最近 or 启发式)
- 为q和邻居添加双向边,检查邻居的连接数是否超过Mmax(第0层则为Mmax0),若超过则重新选择Mmax个邻居
- 如果为插入点分配的层级大于当前顶层,则将HNSW图的入口点设置为q
Search nearest neighbors
- 将已访问集合v,候选集合C,最近邻集合W初始化为入口点ep
- 当候选集不为空时:
- 若候选集C中距插入点q最近的元素c的距离大于最近邻集中距插入点最远的元素f的距离,则停止。
- 对于候选集C中的每一个点,访问它们的邻居e,如果邻居e未被访问:
- 添加到已访问集v
- 若e距q的距离比最近邻集中最远的点f还要近,或者最近邻集W未满(ef)则将e添加到候选集和最近邻集中。
- 保持最近邻集元素不超过ef个
Implementation
# set HNSW index parameters
M = 64 # number of connections each vertex will have
ef_search = 32 # depth of layers explored during search
ef_construction = 64 # depth of layers explored during index construction
# initialize index (d == 128)
index = faiss.IndexHNSWFlat(d, M)
# set efConstruction and efSearch parameters
index.hnsw.efConstruction = ef_construction
index.hnsw.efSearch = ef_search
# add data to index
index.add(wb)
# search as usual
D, I = index.search(wb, k)
| M | efSearch | efConstruction | |
|---|---|---|---|
| 含义 | 每个顶点的连接数 | 搜索时队列的长度 | 构建时队列的长度 |
分析
初始化HNSW
# setup our HNSW parameters
d = 128 # vector size
M = 32
index = faiss.IndexHNSWFlat(d, M)
print(index.hnsw) #<faiss.swigfaiss.HNSW; proxy of <Swig Object of type 'faiss::HNSW *' at 0x7f91183ef120> >
M_max 值默认设置为M , M_max0设置为M*2
在使用index.add(xb)构建index之前,我们会发现层数(或 Faiss 中的级别)尚未设置:
# the HNSW index starts with no levels
index.hnsw.max_level # -1
# and levels (or layers) are empty too
levels = faiss.vector_to_array(index.hnsw.levels)
np.bincount(levels) # array([], dtype=int64)
如果我们继续建立索引,我们会发现这两个参数现在都已设置。
index.add(xb)
# after adding our data we will find that the level
# has been set automatically
index.hnsw.max_level # 4
# and levels (or layers) are now populated
levels = faiss.vector_to_array(index.hnsw.levels)
np.bincount(levels) # array([ 0, 968746, 30276, 951, 26, 1], dtype=int64)
甚至可以找到哪个向量是我们的入口点:
index.hnsw.entry_point # 118295
HNSW不同参数下性能表现部分将放在Comparison中讨论。
Product Quantization
PQ并不是一种索引,而是创建复合索引中的一种Fine quantizer。
Introduction
向量相似性搜索可能需要大量内存,随着数据集大小的不断增加,内存占用会变得难以承受。PQ可以大幅压缩高维向量,甚至能减少97%的内存占用。(But at what cost?)
Quantization & Dimensionality-reduction
量化与降维不同,降维的目的是得到一个低维向量,而量化的目的是得到一个低精度向量。
tip
比如我有一个128维的FP32向量,我可以将其降维到64维(不是简单的裁切,比如使用PCA主成分分析),也可以将其量化为INT8向量。毫无疑问这两种方法都减少了向量的占用,而且都损失了信息。
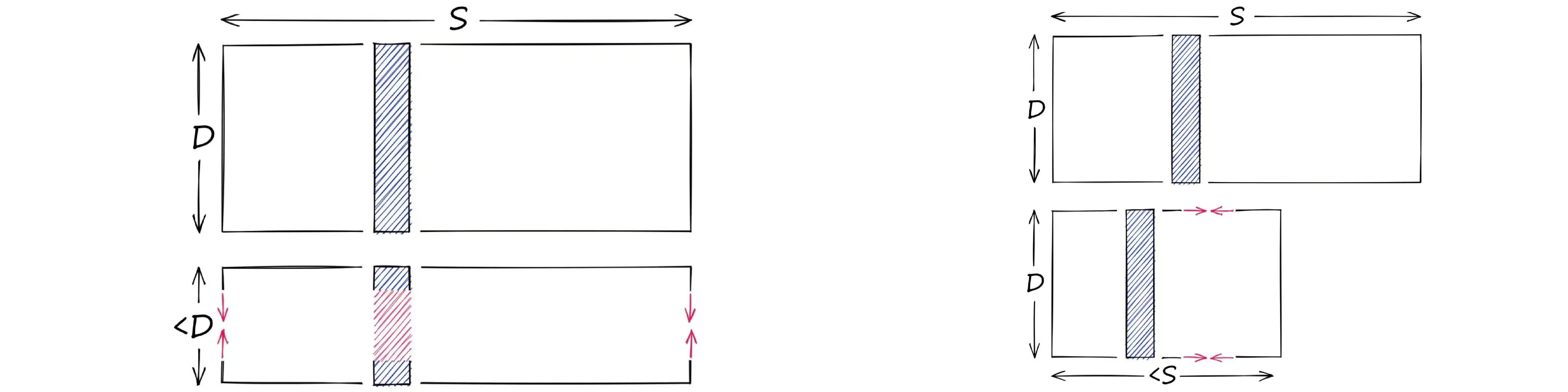 降维缩小了向量的维度,量化缩小了能表示的范围。
但是PQ并不是简单的将每个维度的信息量化成更低精度的表示。粗略地说,PQ先将向量分成几个子向量,每个子向量用它们所在的簇的ID来表示。
降维缩小了向量的维度,量化缩小了能表示的范围。
但是PQ并不是简单的将每个维度的信息量化成更低精度的表示。粗略地说,PQ先将向量分成几个子向量,每个子向量用它们所在的簇的ID来表示。
How PQ works
- 我有一些128维的向量。
- 按32维切分成4个子向量。
- 对所有128维向量的相同位置上的32维子向量进行聚类,例如得到128个簇。
- 用每个子向量所在簇的ID来表示这个子向量。(这样我们就能用2字节表示一个子向量)
- 最终128维的向量可以用8字节表示。
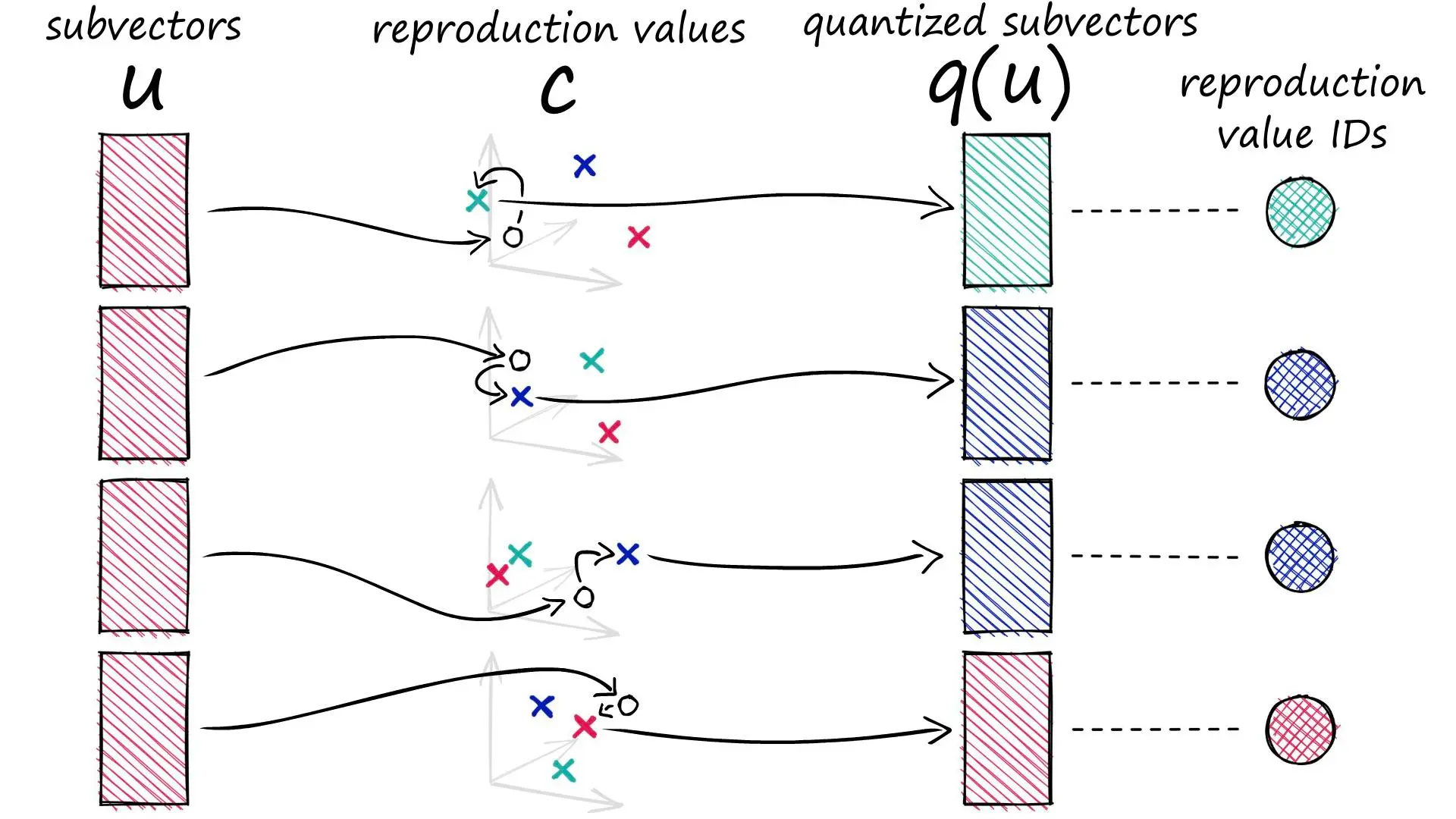
切分向量
x = [1, 8, 3, 9, 1, 2, 9, 4, 5, 4, 6, 2]
m = 4
D = len(x)
# ensure D is divisable by m
assert D % m == 0
# length of each subvector will be D / m (D* in notation)
D_ = int(D / m)
# now create the subvectors
u = [x[row:row+D_] for row in range(0, D, D_)]
print(u)
创建聚类 为方便起见,这里随机生成聚类中心。 再现值(reproduction values):用表示第个子向量的第个所选质心。
k = 2**5
assert k % m == 0
k_ = int(k/m)
print(f"{k=}, {k_=}")
from random import randint
c = [] # our overall list of reproduction values
for j in range(m):
# each j represents a subvector (and therefore subquantizer) position
c_j = []
for i in range(k_):
# each i represents a cluster/reproduction value position *inside* each subspace j
c_ji = [randint(0, 9) for _ in range(D_)]
c_j.append(c_ji) # add cluster centroid to subspace list
# add subspace list of centroids to overall list
c.append(c_j)
定义函数计算L2距离和寻找最近邻居
`ids`记录距离每个子向量最近的质心的标识符。
def euclidean(v, u):
distance = sum((x - y) ** 2 for x, y in zip(v, u)) ** .5
return distance
def nearest(c_j, u_j):
distance = 9e9
for i in range(k_):
new_dist = euclidean(c_j[i], u_j)
if new_dist < distance:
nearest_idx = i
distance = new_dist
return nearest_idx
ids = []
for j in range(m):
i = nearest(c[j], u[j])
ids.append(i)
print(ids)
q是用质心坐标表示的向量。
q = []
for j in range(m):
c_ji = c[j][ids[j]]
q.extend(c_ji)
print(q)
Example
Example
假设:
u = [[1, 8, 3], [9, 1, 2], [9, 4, 5], [4, 6, 2]]
我们有 m=4 个子空间,每个 u[j] 都有 k_=8 个可选的簇心 c[j]。
代码执行 nearest(c[j], u[j]),找到 u[j] 在 c[j] 里的最近簇心:
ids = [7, 1, 5, 3]
这意味着:
u[0] = [1, 8, 3]在c[0]里最接近c[0][7]u[1] = [9, 1, 2]在c[1]里最接近c[1][1]u[2] = [9, 4, 5]在c[2]里最接近c[2][5]u[3] = [4, 6, 2]在c[3]里最接近c[3][3]
然后 q 通过 ids 找到这些簇心,并拼接:
q = []
for j in range(m):
c_ji = c[j][ids[j]] # 取出最近的簇心
q.extend(c_ji) # 展开并拼接
最终:
q = c[0][7] + c[1][1] + c[2][5] + c[3][3]
Success
Success
x = [1, 8, 3, 9, 1, 2, 9, 4, 5, 4, 6, 2]
m = 4
D = len(x)
# ensure D is divisable by m
assert D % m == 0
# length of each subvector will be D / m (D* in notation)
D_ = int(D / m)
# now create the subvectors
u = [x[row:row+D_] for row in range(0, D, D_)]
print(u)
k = 2**5
assert k % m == 0
k_ = int(k/m)
print(f"{k=}, {k_=}")
from random import randint
c = [] # our overall list of reproduction values
for j in range(m):
# each j represents a subvector (and therefore subquantizer) position
c_j = []
for i in range(k_):
# each i represents a cluster/reproduction value position *inside* each subspace j
c_ji = [randint(0, 9) for _ in range(D_)]
c_j.append(c_ji) # add cluster centroid to subspace list
# add subspace list of centroids to overall list
c.append(c_j)
def euclidean(v, u):
distance = sum((x - y) ** 2 for x, y in zip(v, u)) ** .5
return distance
def nearest(c_j, u_j):
distance = 9e9
for i in range(k_):
new_dist = euclidean(c_j[i], u_j)
if new_dist < distance:
nearest_idx = i
distance = new_dist
return nearest_idx
ids = []
for j in range(m):
i = nearest(c[j], u[j])
ids.append(i)
print(ids)
q = []
for j in range(m):
c_ji = c[j][ids[j]]
q.extend(c_ji)
print(q)
Implementation in Faiss
在开始之前,我们需要获取数据。我们将使用 Sift1M 数据集。
import shutil
import urllib.request as request
from contextlib import closing
# first we download the Sift1M dataset
with closing(request.urlopen('ftp://ftp.irisa.fr/local/texmex/corpus/sift.tar.gz')) as r:
with open('sift.tar.gz', 'wb') as f:
shutil.copyfileobj(r, f)
import tarfile
# the download leaves us with a tar.gz file, we unzip it
tar = tarfile.open('sift.tar.gz', "r:gz")
tar.extractall()
import numpy as np
# now define a function to read the fvecs file format of Sift1M dataset
def read_fvecs(fp):
a = np.fromfile(fp, dtype='int32')
d = a[0]
return a.reshape(-1, d + 1)[:, 1:].copy().view('float32')
# data we will search through
wb = read_fvecs('./sift/sift_base.fvecs') # 1M samples
# also get some query vectors to search with
xq = read_fvecs('./sift/sift_query.fvecs')
# take just one query (there are many in sift_learn.fvecs)
xq = xq[0].reshape(1, xq.shape[1])
xq.shape # (1, 128)
wb.shape # (1000000, 128)
IndexPQ
import faiss
D = xb.shape[1]
m = 8
assert D % m == 0
nbits = 8 # number of bits per subquantizer, k* = 2**nbits
index = faiss.IndexPQ(D, m, nbits)
索引需要3个参数:
D:向量的维度m:子向量的数量nbits:每个子向量的位数
tip
nbits 定义了每个子量化器可以使用的位数,例如 nbits 为 11,每个子空间有2048质心。
因为使用的是使用聚类的 PQ,所以必须预先训练我们的索引。(这里直接使用 xb 进行训练),然后再将向量添加到索引中进行搜索
index.is_trained # False
index.train(xb) # PQ training can take some time when using large nbits
index.is_trained # True
index.add(xb)
dist, I = index.search(xq, k) # 在dist中返回距离,在I中返回索引。
%%timeit
index.search(xq, k) # 1.49 ms ± 49.1 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
使用L2索引作为基准,计算召回率
l2_index = faiss.IndexFlatL2(D)
l2_index.add(xb)
%%time
l2_dist, l2_I = l2_index.search(xq, k) # CPU times: user 46.1 ms, sys: 15.1 ms, total: 61.2 ms, Wall time: 15 ms
sum([1 for i in I[0] if i in l2_I]) # 50
搜索表现部分将放在Comparison中讨论。
IndexIVFPQ
为了进一步加快搜索时间,我们可以添加另一个步骤——使用 IVF 索引,它将减少搜索中比较的向量。
首先初始化IVFPQ索引:
vecs = faiss.IndexFlatL2(D)
nlist = 2048 # how many Voronoi cells (must be >= k* which is 2**nbits)
nbits = 8 # when using IVF+PQ, higher nbits values are not supported
index = faiss.IndexIVFPQ(vecs, D, nlist, m, nbits)
训练,添加,搜索...
index.train(xb)
index.add(xb)
dist, I = index.search(xq, k)
%%timeit
index.search(xq, k) # 86.3 µs ± 15 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
sum([1 for i in I[0] if i in l2_I]) # 34
搜索速度从1.49ms降低到86.3µs,但是召回率从50%降低到34%。在给定等效参数的情况下,IndexPQ 和 IndexIVFPQ 都应该能够获得相同的召回率性能。
在这种情况下,提高召回率的办法是提高nprobe参数。(当nprobe=nlist时,IndexIVFPQ退化为IndexPQ)
| nprobe | 召回率 | 时延 |
|---|---|---|
| 1 | 34 | 86.3µs |
| 2 | 39 | |
| 48 | 50 | |
| 2048 | 50 | 1.49ms |
Conclusion
| Index | 高召回 | 低时延 | 低内存 |
|---|---|---|---|
| Flat | 🟢🟢🟢🟢🟢 | 🔴 | 🔴 |
| PQ | 🟡🟡🟡🟡 | 🟡🟡🟡 | 🟢🟢🟢🟢🟢 |
| IVFPQ | 🟡🟡🟡🟡 | 🟢🟢🟢🟢🟢 | 🟡🟡🟡🟡 |
Comparison
Project
Faiss
bench
HNSW
faiss/benchs/bench_hnsw.py
本程序用于对比不同索引算法在 SIFT1M 数据集上的性能表现,帮助用户评估搜索速度与准确率。测试方法包括 HNSW、IVF 等多种常见索引类型。
使用步骤
-
基本命令格式
python 程序名.py [k值] [测试方法1] [测试方法2]... -
参数说明
- k值 (必需): 指定每个查询要返回的最近邻数量
- 测试方法 (可选): 指定要运行的算法测试,支持以下选项:
- hnsw (HNSW 平面索引)
- hnsw_sq (量化HNSW)
- ivf (IVF 平面索引)
- ivf_hnsw_quantizer (HNSW量化的IVF)
- kmeans (K均值基准测试)
- kmeans_hnsw (HNSW辅助的K均值)
- nsg (NSG 图索引)
若不指定测试方法,默认运行所有测试
-
运行示例
# 返回10个最近邻,测试HNSW和IVF python demo.py 10 hnsw ivf # 返回5个最近邻,测试所有方法 python demo.py 5 -
输出说明 程序运行后会显示每个测试方法的以下指标:
- ms per query: 每个查询的平均耗时(毫秒)
- R@1: 前1个结果的召回率(准确率)
- missing rate: 无效结果比例(-1表示未找到)
示例输出:
Testing HNSW Flat add... search... efSearch 16 bounded_queue True 0.153 ms per query, R@1 0.9210, missing rate 0.0000 efSearch 16 bounded_queue False 0.162 ms per query, R@1 0.9210, missing rate 0.0000 ...
Note
Note
在代码中,missing rate 是通过以下方式计算的:
missing_rate = (I == -1).sum() / float(k * nq)
I: 是搜索结果的索引矩阵,形状为(nq, k),其中nq是查询的数量,k是每个查询返回的最近邻数量。- 如果某个查询的某个最近邻未被找到,
I中对应的值会被设置为-1。
- 如果某个查询的某个最近邻未被找到,
(I == -1).sum(): 统计所有查询结果中未找到的最近邻数量(即I中值为-1的元素总数)。k * nq: 表示理论上应该返回的总结果数量(每个查询返回k个结果,共有nq个查询)。missing_rate: 未找到的结果占总结果的比例。
直观上看,missing rate表现了要搜索k个最近邻但是并没有找到那么多的最近邻的情况。
运行结果
以下是对实验结果的详细分析,按测试方法分类总结性能指标(搜索速度、召回率、缺失率)和参数影响:
HNSW Flat (分层可导航小世界图)
| efSearch | Bounded Queue | 耗时/查询 | R@1 | 缺失率 |
|---|---|---|---|---|
| 16 | True | 0.006ms | 0.9125 | 0% |
| 16 | False | 0.006ms | 0.9124 | 0% |
| 32 | True | 0.010ms | 0.9620 | 0% |
| 32 | False | 0.010ms | 0.9620 | 0% |
| 64 | True | 0.017ms | 0.9868 | 0% |
| 128 | True | 0.029ms | 0.9966 | 0% |
| 256 | True | 0.055ms | 0.9992 | 0% |
- 速度与召回率的权衡:
efSearch增大时,召回率显著提升(从 0.9125 到 0.9992),但搜索耗时线性增加(从 0.006ms 到 0.055ms)。- 推荐参数:
- 高精度场景:
efSearch=256(R@1=99.92%),耗时 0.055ms/查询。 - 平衡场景:
efSearch=64(R@1=98.68%),耗时 0.017ms/查询。
- 高精度场景:
- Bounded Queue 影响:
- Bounded Queue 开启与否对召回率和速度几乎无影响,可默认开启以节省内存。
HNSW with Scalar Quantizer (标量量化)
| efSearch | 耗时/查询 | R@1 | 缺失率 |
|---|---|---|---|
| 16 | 0.002ms | 0.7993 | 0% |
| 32 | 0.003ms | 0.8877 | 0% |
| 64 | 0.006ms | 0.9453 | 0% |
| 128 | 0.010ms | 0.9780 | 0% |
| 256 | 0.017ms | 0.9932 | 0% |
- 量化对性能的影响:
- 相比 HNSW Flat,量化后搜索速度更快(
efSearch=256时 0.017ms vs 0.055ms),但召回率下降(99.32% vs 99.92%)。 - 适用场景:
- 内存敏感场景:量化可减少内存占用,但需接受轻微精度损失。
- 相比 HNSW Flat,量化后搜索速度更快(
- 参数选择:
- 若需接近原始精度,选择
efSearch=256(R@1=99.32%)。
- 若需接近原始精度,选择
IVF Flat (倒排文件索引)
| nprobe | 耗时/查询 | R@1 | 缺失率 |
|---|---|---|---|
| 1 | 0.004ms | 0.4139 | 3.0% |
| 4 | 0.005ms | 0.6368 | 0% |
| 16 | 0.014ms | 0.8322 | 0% |
| 64 | 0.046ms | 0.9562 | 0% |
| 256 | 0.132ms | 0.9961 | 0% |
- nprobe 的重要性:
nprobe=1时缺失率 3%,召回率仅 41.39%,表明搜索覆盖的聚类中心不足。nprobe=16时召回率 83.22%,耗时 0.014ms,性价比最高。
- 与 HNSW 对比:
- 相同召回率下(如 99%),IVF 耗时更高(0.132ms vs HNSW 的 0.055ms)。
IVF with HNSW Quantizer
| nprobe | 耗时/查询 | R@1 | 缺失率 |
|---|---|---|---|
| 1 | 0.003ms | 0.4095 | 3.16% |
| 4 | 0.005ms | 0.6324 | 0% |
| 16 | 0.013ms | 0.8291 | 0% |
| 64 | 0.041ms | 0.9540 | 0% |
| 256 | 0.136ms | 0.9922 | 0% |
- HNSW Quantizer 的影响:
- 性能与传统 IVF 几乎一致,但训练速度可能更快(代码中未展示具体时间)。
- 仍需设置
nprobe≥16以避免高缺失率。
KMeans 聚类测试
-
Baseline KMeans:
- 目标函数值
3.8508e+10,聚类不均衡度1.227。
- 目标函数值
-
HNSW-Assisted KMeans:
- 目标函数值略高(
3.85126e+10),但训练时间显著减少(24.75s vs 53.52s)。
- 目标函数值略高(
-
HNSW 加速效果:
- HNSW 辅助的 KMeans 将训练时间减少 50%+,适合大规模数据聚类。
NSG (导航小世界图)
| search_L | 耗时/查询 | R@1 | 缺失率 |
|---|---|---|---|
| -1 | 0.004ms | 0.8150 | 0% |
| 16 | 0.006ms | 0.8852 | 0% |
| 32 | 0.009ms | 0.9533 | 0% |
| 64 | 0.015ms | 0.9832 | 0% |
| 128 | 0.027ms | 0.9959 | 0% |
| 256 | 0.050ms | 0.9994 | 0% |
- search_L 的影响:
search_L=256时召回率 99.94%,与 HNSW Flat(99.92%)相当,但耗时稍高(0.050ms vs 0.055ms)。- 优势:NSG 在中等参数下(如
search_L=64)即可达到 98.32% 召回率,适合对精度和速度均衡要求较高的场景。
综合对比与推荐
| 索引类型 | 最佳参数 | 耗时/查询 | R@1 | 适用场景 |
|---|---|---|---|---|
| HNSW Flat | efSearch=64 | 0.017ms | 98.68% | 高精度实时搜索 |
| HNSW SQ | efSearch=256 | 0.017ms | 99.32% | 内存敏感场景 |
| IVF Flat | nprobe=64 | 0.046ms | 95.62% | 高吞吐量批量查询 |
| NSG | search_L=64 | 0.015ms | 98.32% | 均衡精度与速度 |
| IVF+HNSQ Quant | nprobe=64 | 0.041ms | 95.40% | 需要快速训练的 IVF 场景 |
- 精度优先:选择 HNSW Flat(efSearch=256) 或 NSG(search_L=256)。
- 速度优先:选择 HNSW SQ(efSearch=16) 或 IVF Flat(nprobe=16)。
- 内存敏感:使用 HNSW SQ 或 IVF 索引。
- 训练时间敏感:尝试 HNSW-Assisted KMeans 加速聚类。
实验输出
实验输出
(faiss_env) gpu@gpu-node:~/faiss/faiss/benchs$ python bench_hnsw.py 10
load data
Testing HNSW Flat
add
hnsw_add_vertices: adding 1000000 elements on top of 0 (preset_levels=0)
max_level = 4
Adding 1 elements at level 4
Adding 26 elements at level 3
Adding 951 elements at level 2
Adding 30276 elements at level 1
Adding 968746 elements at level 0
Done in 10194.740 ms
search
efSearch 16 bounded queue True 0.006 ms per query, R@1 0.9125, missing rate 0.0000
efSearch 16 bounded queue False 0.006 ms per query, R@1 0.9124, missing rate 0.0000
efSearch 32 bounded queue True 0.010 ms per query, R@1 0.9620, missing rate 0.0000
efSearch 32 bounded queue False 0.010 ms per query, R@1 0.9620, missing rate 0.0000
efSearch 64 bounded queue True 0.017 ms per query, R@1 0.9868, missing rate 0.0000
efSearch 64 bounded queue False 0.017 ms per query, R@1 0.9868, missing rate 0.0000
efSearch 128 bounded queue True 0.029 ms per query, R@1 0.9966, missing rate 0.0000
efSearch 128 bounded queue False 0.030 ms per query, R@1 0.9966, missing rate 0.0000
efSearch 256 bounded queue True 0.055 ms per query, R@1 0.9992, missing rate 0.0000
efSearch 256 bounded queue False 0.055 ms per query, R@1 0.9992, missing rate 0.0000
Testing HNSW with a scalar quantizer
training
add
hnsw_add_vertices: adding 1000000 elements on top of 0 (preset_levels=0)
max_level = 5
Adding 1 elements at level 5
Adding 15 elements at level 4
Adding 194 elements at level 3
Adding 3693 elements at level 2
Adding 58500 elements at level 1
Adding 937597 elements at level 0
Done in 3322.349 ms
search
efSearch 16 0.002 ms per query, R@1 0.7993, missing rate 0.0000
efSearch 32 0.003 ms per query, R@1 0.8877, missing rate 0.0000
efSearch 64 0.006 ms per query, R@1 0.9453, missing rate 0.0000
efSearch 128 0.010 ms per query, R@1 0.9780, missing rate 0.0000
efSearch 256 0.017 ms per query, R@1 0.9932, missing rate 0.0000
Testing IVF Flat (baseline)
training
Training level-1 quantizer
Training level-1 quantizer on 100000 vectors in 128D
Training IVF residual
IndexIVF: no residual training
add
IndexIVFFlat::add_core: added 1000000 / 1000000 vectors
search
nprobe 1 0.004 ms per query, R@1 0.4139, missing rate 0.0300
nprobe 4 0.005 ms per query, R@1 0.6368, missing rate 0.0000
nprobe 16 0.014 ms per query, R@1 0.8322, missing rate 0.0000
nprobe 64 0.046 ms per query, R@1 0.9562, missing rate 0.0000
nprobe 256 0.132 ms per query, R@1 0.9961, missing rate 0.0000
Testing IVF Flat with HNSW quantizer
training
Training level-1 quantizer
Training L2 quantizer on 100000 vectors in 128D
Adding centroids to quantizer
Training IVF residual
IndexIVF: no residual training
add
IndexIVFFlat::add_core: added 1000000 / 1000000 vectors
search
nprobe 1 0.003 ms per query, R@1 0.4095, missing rate 0.0316
nprobe 4 0.005 ms per query, R@1 0.6324, missing rate 0.0000
nprobe 16 0.013 ms per query, R@1 0.8291, missing rate 0.0000
nprobe 64 0.041 ms per query, R@1 0.9540, missing rate 0.0000
nprobe 256 0.136 ms per query, R@1 0.9922, missing rate 0.0000
Performing kmeans on sift1M database vectors (baseline)
Clustering 1000000 points in 128D to 16384 clusters, redo 1 times, 10 iterations
Preprocessing in 0.15 s
Iteration 9 (53.52 s, search 53.23 s): objective=3.8508e+10 imbalance=1.227 nsplit=0
Performing kmeans on sift1M using HNSW assignment
Clustering 1000000 points in 128D to 16384 clusters, redo 1 times, 10 iterations
Preprocessing in 0.15 s
Iteration 9 (24.75 s, search 24.04 s): objective=3.85126e+10 imbalance=1.227 nsplit=0
Testing NSG Flat
add
IndexNSG::add 1000000 vectors
Build knn graph with NNdescent S=10 R=100 L=114 niter=10
Parameters: K=64, S=10, R=100, L=114, iter=10
Iter: 0, recall@64: 0.000000
Iter: 1, recall@64: 0.002813
Iter: 2, recall@64: 0.024688
Iter: 3, recall@64: 0.117656
Iter: 4, recall@64: 0.334219
Iter: 5, recall@64: 0.579063
Iter: 6, recall@64: 0.759375
Iter: 7, recall@64: 0.867188
Iter: 8, recall@64: 0.928594
Iter: 9, recall@64: 0.959063
Added 1000000 points into the index
Check the knn graph
nsg building
NSG::build R=32, L=64, C=132
Degree Statistics: Max = 32, Min = 1, Avg = 20.055180
Attached nodes: 0
search
search_L -1 0.004 ms per query, R@1 0.8150, missing rate 0.0000
search_L 16 0.006 ms per query, R@1 0.8852, missing rate 0.0000
search_L 32 0.009 ms per query, R@1 0.9533, missing rate 0.0000
search_L 64 0.015 ms per query, R@1 0.9832, missing rate 0.0000
search_L 128 0.027 ms per query, R@1 0.9959, missing rate 0.0000
search_L 256 0.050 ms per query, R@1 0.9994, missing rate 0.0000
运行结果(WSL)
HNSW Flat 性能
| 参数 | 构建时间 (ms) | 搜索时间 (ms/query) | R@1 | 缺失率 |
|---|---|---|---|---|
| efSearch=16 (bounded) | 28,095.8 | 0.015 | 0.9069 | 0.0000 |
| efSearch=16 (unbounded) | 28,095.8 | 0.015 | 0.9069 | 0.0000 |
| efSearch=32 (bounded) | 28,095.8 | 0.023 | 0.9614 | 0.0000 |
| efSearch=32 (unbounded) | 28,095.8 | 0.025 | 0.9614 | 0.0000 |
| efSearch=64 (bounded) | 28,095.8 | 0.043 | 0.9868 | 0.0000 |
| efSearch=64 (unbounded) | 28,095.8 | 0.041 | 0.9868 | 0.0000 |
| efSearch=128 (bounded) | 28,095.8 | 0.069 | 0.9964 | 0.0000 |
| efSearch=256 (bounded) | 28,095.8 | 0.126 | 0.9995 | 0.0000 |
- 搜索效率与召回率正相关:
efSearch值越大,搜索时间增加,但召回率显著提升(如efSearch=256时 R@1 达 0.9995)。 - 队列类型影响小:
bounded与unbounded队列对搜索性能无明显差异。
HNSW 标量量化(SQ)性能
| 参数 | 构建时间 (ms) | 搜索时间 (ms/query) | R@1 | 缺失率 |
|---|---|---|---|---|
| efSearch=16 | 12,376.8 | 0.007 | 0.7884 | 0.0000 |
| efSearch=32 | 12,376.8 | 0.011 | 0.8827 | 0.0000 |
| efSearch=64 | 12,376.8 | 0.020 | 0.9419 | 0.0000 |
| efSearch=128 | 12,376.8 | 0.033 | 0.9751 | 0.0000 |
| efSearch=256 | 12,376.8 | 0.055 | 0.9912 | 0.0000 |
- 量化显著加速构建:构建时间缩短至 12,376.8 ms(相比 HNSW Flat 的 28,095.8 ms)。
- 召回率略降:相同
efSearch下,量化后 R@1 低于原始 HNSW(如efSearch=256时 R@1=0.9912 vs. 0.9995)。
IVF Flat 基准性能
| 参数 | 搜索时间 (ms/query) | R@1 | 缺失率 |
|---|---|---|---|
| nprobe=1 | 0.022 | 0.4139 | 0.0300 |
| nprobe=4 | 0.018 | 0.6368 | 0.0000 |
| nprobe=16 | 0.035 | 0.8322 | 0.0000 |
| nprobe=64 | 0.103 | 0.9562 | 0.0000 |
| nprobe=256 | 0.332 | 0.9961 | 0.0000 |
- 需高
nprobe保证召回率:nprobe=256时 R@1 接近 HNSW,但搜索时间显著增加(0.332 ms vs. HNSW 的 0.126 ms)。
NSG Flat 性能
| 参数 | 搜索时间 (ms/query) | R@1 | 缺失率 |
|---|---|---|---|
| search_L=-1 | 0.008 | 0.8152 | 0.0000 |
| search_L=16 | 0.011 | 0.8849 | 0.0000 |
| search_L=32 | 0.017 | 0.9528 | 0.0000 |
| search_L=64 | 0.032 | 0.9843 | 0.0000 |
| search_L=128 | 0.051 | 0.9959 | 0.0000 |
| search_L=256 | 0.086 | 0.9993 | 0.0000 |
- 高效搜索与高召回率:在
search_L=256时,R@1 达 0.9993,且搜索时间(0.086 ms)优于 HNSW Flat 的 0.126 ms。
综合对比
| 索引类型 | 构建时间 (ms) | 最佳 R@1 | 对应搜索时间 (ms) |
|---|---|---|---|
| HNSW Flat | 28,095.8 | 0.9995 | 0.126 |
| HNSW SQ | 12,376.8 | 0.9912 | 0.055 |
| IVF Flat | - | 0.9961 | 0.332 |
| NSG Flat | - | 0.9993 | 0.086 |
- HNSW 系列:
- 适合高召回率场景,但构建时间较长;量化版本(HNSW SQ)可显著加速构建,但牺牲少量召回率。
- IVF Flat:
- 需要高
nprobe达到高召回率,但搜索效率较低。
- 需要高
- NSG Flat:
- 在搜索速度与召回率间取得最佳平衡(
search_L=256时 R@1=0.9993,搜索时间仅 0.086 ms)。
- 在搜索速度与召回率间取得最佳平衡(
- 实时搜索:优先选择 HNSW SQ 或 NSG Flat;
- 高精度需求:选择 HNSW Flat 或 NSG Flat;
- 快速构建:选择 HNSW SQ。
实验输出
实验输出
(faiss_env) root@Quaternijkon:~/faiss/benchs# python bench_hnsw.py 10
load data
Testing HNSW Flat
add
hnsw_add_vertices: adding 1000000 elements on top of 0 (preset_levels=0)
max_level = 4
Adding 1 elements at level 4
Adding 26 elements at level 3
Adding 951 elements at level 2
Adding 30276 elements at level 1
Adding 968746 elements at level 0
Done in 28095.800 ms
search
efSearch 16 bounded queue True 0.015 ms per query, R@1 0.9069, missing rate 0.0000
efSearch 16 bounded queue False 0.015 ms per query, R@1 0.9069, missing rate 0.0000
efSearch 32 bounded queue True 0.023 ms per query, R@1 0.9614, missing rate 0.0000
efSearch 32 bounded queue False 0.025 ms per query, R@1 0.9614, missing rate 0.0000
efSearch 64 bounded queue True 0.043 ms per query, R@1 0.9868, missing rate 0.0000
efSearch 64 bounded queue False 0.041 ms per query, R@1 0.9868, missing rate 0.0000
efSearch 128 bounded queue True 0.069 ms per query, R@1 0.9964, missing rate 0.0000
efSearch 128 bounded queue False 0.069 ms per query, R@1 0.9964, missing rate 0.0000
efSearch 256 bounded queue True 0.126 ms per query, R@1 0.9995, missing rate 0.0000
efSearch 256 bounded queue False 0.122 ms per query, R@1 0.9995, missing rate 0.0000
Testing HNSW with a scalar quantizer
training
add
hnsw_add_vertices: adding 1000000 elements on top of 0 (preset_levels=0)
max_level = 5
Adding 1 elements at level 5
Adding 15 elements at level 4
Adding 194 elements at level 3
Adding 3693 elements at level 2
Adding 58500 elements at level 1
Adding 937597 elements at level 0
Done in 12376.822 ms
search
efSearch 16 0.007 ms per query, R@1 0.7884, missing rate 0.0000
efSearch 32 0.011 ms per query, R@1 0.8827, missing rate 0.0000
efSearch 64 0.020 ms per query, R@1 0.9419, missing rate 0.0000
efSearch 128 0.033 ms per query, R@1 0.9751, missing rate 0.0000
efSearch 256 0.055 ms per query, R@1 0.9912, missing rate 0.0000
Testing IVF Flat (baseline)
training
Training level-1 quantizer
Training level-1 quantizer on 100000 vectors in 128D
Training IVF residual
IndexIVF: no residual training
add
IndexIVFFlat::add_core: added 1000000 / 1000000 vectors
search
nprobe 1 0.022 ms per query, R@1 0.4139, missing rate 0.0300
nprobe 4 0.018 ms per query, R@1 0.6368, missing rate 0.0000
nprobe 16 0.035 ms per query, R@1 0.8322, missing rate 0.0000
nprobe 64 0.103 ms per query, R@1 0.9562, missing rate 0.0000
nprobe 256 0.332 ms per query, R@1 0.9961, missing rate 0.0000
Testing IVF Flat with HNSW quantizer
training
Training level-1 quantizer
Training L2 quantizer on 100000 vectors in 128D
Adding centroids to quantizer
Training IVF residual
IndexIVF: no residual training
add
IndexIVFFlat::add_core: added 1000000 / 1000000 vectors
search
nprobe 1 0.009 ms per query, R@1 0.4102, missing rate 0.0323
nprobe 4 0.014 ms per query, R@1 0.6327, missing rate 0.0000
nprobe 16 0.030 ms per query, R@1 0.8288, missing rate 0.0000
nprobe 64 0.094 ms per query, R@1 0.9545, missing rate 0.0000
nprobe 256 0.332 ms per query, R@1 0.9925, missing rate 0.0000
Performing kmeans on sift1M database vectors (baseline)
Clustering 1000000 points in 128D to 16384 clusters, redo 1 times, 10 iterations
Preprocessing in 0.07 s
Iteration 0 (36.15 s, search 36.12 s): objective=5.58803e+10 imbalance=1.737 nsplit=5 Iteration 1 (71.32 s, search 71.25 s): objective=4.11771e+10 imbalance=1.378 nsplit=0 Iteration 2 (107.25 s, search 107.15 s): objective=3.9914e+10 imbalance=1.301 nsplit= Iteration 3 (142.60 s, search 142.47 s): objective=3.93716e+10 imbalance=1.269 nsplit Iteration 4 (178.17 s, search 178.01 s): objective=3.9066e+10 imbalance=1.253 nsplit= Iteration 5 (214.30 s, search 214.11 s): objective=3.8872e+10 imbalance=1.243 nsplit= Iteration 6 (250.13 s, search 249.92 s): objective=3.87377e+10 imbalance=1.237 nsplit Iteration 7 (285.57 s, search 285.33 s): objective=3.86397e+10 imbalance=1.232 nsplit Iteration 8 (321.46 s, search 321.19 s): objective=3.85653e+10 imbalance=1.229 nsplit Iteration 9 (357.11 s, search 356.81 s): objective=3.8508e+10 imbalance=1.227 nsplit=0
Performing kmeans on sift1M using HNSW assignment
Clustering 1000000 points in 128D to 16384 clusters, redo 1 times, 10 iterations
Preprocessing in 0.07 s
Iteration 0 (11.13 s, search 10.96 s): objective=5.58887e+10 imbalance=1.737 nsplit=0 Iteration 1 (21.37 s, search 21.07 s): objective=4.11817e+10 imbalance=1.379 nsplit=2 Iteration 2 (31.33 s, search 30.89 s): objective=3.99504e+10 imbalance=1.301 nsplit=0 Iteration 3 (41.08 s, search 40.47 s): objective=3.93767e+10 imbalance=1.269 nsplit=2 Iteration 4 (50.91 s, search 50.17 s): objective=3.90675e+10 imbalance=1.253 nsplit=1 Iteration 5 (60.60 s, search 59.72 s): objective=3.88936e+10 imbalance=1.243 nsplit=0 Iteration 6 (70.48 s, search 69.46 s): objective=3.87889e+10 imbalance=1.236 nsplit=0 Iteration 7 (80.54 s, search 79.37 s): objective=3.8648e+10 imbalance=1.232 nsplit=1 Iteration 8 (90.33 s, search 89.03 s): objective=3.85683e+10 imbalance=1.229 nsplit=3 Iteration 9 (100.14 s, search 98.69 s): objective=3.85264e+10 imbalance=1.227 nsplit=1
Testing NSG Flat
add
IndexNSG::add 1000000 vectors
Build knn graph with NNdescent S=10 R=100 L=114 niter=10
Parameters: K=64, S=10, R=100, L=114, iter=10
Iter: 0, recall@64: 0.000000
Iter: 1, recall@64: 0.002969
Iter: 2, recall@64: 0.024531
Iter: 3, recall@64: 0.110781
Iter: 4, recall@64: 0.332656
Iter: 5, recall@64: 0.559375
Iter: 6, recall@64: 0.751094
Iter: 7, recall@64: 0.862188
Iter: 8, recall@64: 0.922656
Iter: 9, recall@64: 0.953906
Added 1000000 points into the index
Check the knn graph
nsg building
NSG::build R=32, L=64, C=132
Degree Statistics: Max = 32, Min = 1, Avg = 20.056442
Attached nodes: 0
search
search_L -1 0.008 ms per query, R@1 0.8152, missing rate 0.0000
search_L 16 0.011 ms per query, R@1 0.8849, missing rate 0.0000
search_L 32 0.017 ms per query, R@1 0.9528, missing rate 0.0000
search_L 64 0.032 ms per query, R@1 0.9843, missing rate 0.0000
search_L 128 0.051 ms per query, R@1 0.9959, missing rate 0.0000
search_L 256 0.086 ms per query, R@1 0.9993, missing rate 0.0000
hnswlib
Presentation
The Vamana Graph Construction Algorithm in DiskANN
<!doctype html>
<meta name="description" content="Simple example touying slide show" />
<meta name="author" content="OrangeX4" />
<!-- This file contains common styles for example presentations. -->
<style>
/* impress.js doesn't require any particular CSS file.
Each author should create their own, to achieve the visual style they want.
Yet in practice many plugins will not do anything useful without CSS. (See for example mouse-timeout plugin.)
This file contains sample CSS that you may want to use in your presentation.
It is focused on plugin functionality, not the visual style of your presentation. */
/* Using the substep plugin, hide bullet points at first, then show them one by one. */
#impress .step .substep {
opacity: 0;
}
#impress .step .substep.substep-visible {
opacity: 1;
transition: opacity 1s;
}
/*
Speaker notes allow you to write comments within the steps, that will not
be displayed as part of the presentation. However, they will be picked up
and displayed by impressConsole.js when you press P.
*/
.notes {
display: none;
}
/* Toolbar plugin */
.impress-enabled div#impress-toolbar {
position: fixed;
right: 1px;
bottom: 1px;
opacity: 0.6;
z-index: 10;
}
.impress-enabled div#impress-toolbar > span {
margin-right: 10px;
}
.impress-enabled div#impress-toolbar.impress-toolbar-show {
display: block;
}
.impress-enabled div#impress-toolbar.impress-toolbar-hide {
display: none;
}
/* Progress bar */
.impress-progress {
position: absolute;
left: 59px;
bottom: 1px;
text-align: left;
font-size: 10pt;
opacity: 0.6;
}
.impress-enabled .impress-progressbar {
position: absolute;
right: 318px;
bottom: 1px;
left: 118px;
border-radius: 7px;
border: 2px solid rgba(100, 100, 100, 0.2);
}
.impress-progressbar {
right: 118px;
}
.impress-progressbar DIV {
width: 0;
height: 2px;
border-radius: 5px;
background: rgba(75, 75, 75, 0.4);
transition: width 1s linear;
}
.impress-enabled .impress-progress {
position: absolute;
left: 59px;
bottom: 1px;
text-align: left;
opacity: 0.6;
}
.impress-enabled #impress-help {
background: none repeat scroll 0 0 rgba(0, 0, 0, 0.5);
color: #EEEEEE;
font-size: 80%;
position: fixed;
left: 2em;
bottom: 2em;
width: 24em;
border-radius: 1em;
padding: 1em;
text-align: center;
z-index: 100;
font-family: Verdana, Arial, Sans;
}
.impress-enabled #impress-help td {
padding-left: 1em;
padding-right: 1em;
}
/*
We might want to hide the help, toolbar, progress and progress bar in the
preView window of the impressConsole that is displayed when you press P.
*/
.impress-console.preView .impress-progress,
.impress-console.preView .impress-progressbar,
.impress-console.preView #impress-toolbar,
.impress-console.preView #impress-help {
display: none;
}
/*
Hide the help in the slideView as well.
*/
.impress-console.slideView #impress-help {
display: none;
}
/*
With help from the mouse-timeout plugin, we can hide the toolbar and
have it show only when you move/click/touch the mouse.
*/
body.impress-mouse-timeout div#impress-toolbar {
display: none;
}
/*
In fact, we can hide the mouse cursor itself too, when mouse isn't used.
*/
body.impress-mouse-timeout {
cursor: none;
}
/*
And as the last thing there is a workaround for quite strange bug.
It happens a lot in Chrome. I don't remember if I've seen it in Firefox.
Sometimes the element positioned in 3D (especially when it's moved back
along Z axis) is not clickable, because it falls 'behind' the <body>
element.
To prevent this, I decided to make <body> non clickable by setting
pointer-events property to `none` value.
Value if this property is inherited, so to make everything else clickable
I bring it back on the #impress element.
If you want to know more about `pointer-events` here are some docs:
https://developer.mozilla.org/en/CSS/pointer-events
There is one very important thing to notice about this workaround - it makes
everything 'unclickable' except what's in #impress element.
So use it wisely ... or don't use at all.
*/
.impress-enabled { pointer-events: none }
.impress-enabled #impress { pointer-events: auto }
/*If you disable pointer-events, you need to re-enable them for the toolbar.
And the speaker console while at it.*/
.impress-enabled #impress-toolbar { pointer-events: auto }
.impress-enabled #impress-console-button { pointer-events: auto }
/*
There is one funny thing I just realized.
Thanks to this workaround above everything except #impress element is invisible
for click events. That means that the hint element is also not clickable.
So basically all of this transforms and delayed transitions trickery was probably
not needed at all...
But it was fun to learn about it, wasn't it?
*/
</style>
<!--
This file contains styles specific for this example presentation.
-->
<style>
/*
We display a fallback message for users with browsers that don't support
all the features required by it. All of the content will be still fully
accessible for them, but some more advanced effects would be missing.
When impress.js detects that browser supports all necessary CSS3 features,
the fallback-message style is hidden.
*/
.fallback-message {
font-family: sans-serif;
line-height: 1.3;
width: 780px;
padding: 10px 10px 0;
margin: 20px auto;
border: 1px solid #E4C652;
border-radius: 10px;
background: #EEDC94;
}
.fallback-message p {
margin-bottom: 10px;
}
.impress-supported .fallback-message {
display: none;
}
/*
The body background is the bacgkround of "everything". Many
impress.js tools call it the "surface". It could also be a
picture or pattern, but we leave it as light gray.
*/
body {
min-height: 740px;
background: #525659;
}
/*
Now let's style the presentation steps.
*/
.step {
position: relative;
width: 1920px;
height: 1080px;
padding: 0px;
}
/*
Make inactive steps a little bit transparent.
*/
.impress-enabled .step {
margin: 0;
opacity: 0.0;
transition: opacity 0.0s;
}
.impress-enabled .step.active { opacity: 1 }
/*
These 'slide' step styles were heavily inspired by HTML5 Slides:
http://html5slides.googlecode.com/svn/trunk/styles.css
Note that we also use a background image, again just to facilitate a common
feature from PowerPoint and LibreOffice worlds. In this case the background
image is just the impress.js favicon - as if it were a company logo or something.
*/
.slide {
display: block;
}
/*
Fade-in/out is a straightforward fade. Give it enough seconds that all browsers render it clearly.
*/
.future .fade-in {
opacity: 0.0;
}
.present .fade-in {
opacity: 1.0;
transition: 3s;
}
.past .fade-out {
opacity: 0.0;
transition: 3s;
}
/*
Zoom-in.
*/
.future .zoom-in {
transform: scale(10);
opacity: 0.0;
}
.present .zoom-in {
transform: scale(1);
opacity: 1.0;
transition: 3s;
}
.past .zoom-out {
transform: scale(10);
opacity: 0.0;
}
/*
And as the last thing there is a workaround for quite strange bug.
It happens a lot in Chrome. I don't remember if I've seen it in Firefox.
Sometimes the element positioned in 3D (especially when it's moved back
along Z axis) is not clickable, because it falls 'behind' the <body>
element.
To prevent this, I decided to make <body> non clickable by setting
pointer-events property to `none` value.
Value if this property is inherited, so to make everything else clickable
I bring it back on the #impress element.
If you want to know more about `pointer-events` here are some docs:
https://developer.mozilla.org/en/CSS/pointer-events
There is one very important thing to notice about this workaround - it makes
everything 'unclickable' except what's in #impress element.
So use it wisely ... or don't use at all.
*/
.impress-enabled { pointer-events: none }
.impress-enabled #impress { pointer-events: auto }
.impress-enabled #impress-toolbar { pointer-events: auto }
.impress-enabled #impress-console-button { pointer-events: auto }
</style>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g/>
</g>
</g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 101.25229606299213)">
<g class="typst-group">
<g>
<g transform="translate(60 60)">
<g class="typst-group">
<g>
<g transform="translate(-0 -0)">
<path class="typst-shape" fill="#f3f3f3" fill-rule="nonzero" d="M 0 4 C 0 1.790861 1.790861 0 4 0 L 717.8898 0 C 720.0989 0 721.8898 1.790861 721.8898 4 L 721.8898 53.108 C 721.8898 55.31714 720.0989 57.108 717.8898 57.108 L 4 57.108 C 1.790861 57.108 0 55.31714 0 53.108 Z "/>
</g>
<g transform="translate(136.36988188976386 37.108000000000004)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAA04F5A758CD25067AB4970D92BD8D48" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gBF7003968C37118C38C261089BC07E3E" x="18.98" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g95CE2BC5509AF8D30239EF1BC4EFF519" x="26.026000000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g85343A6F33712521F311CF4CB0AC0F62" x="37.648" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA51F6CED3EFDFEC9262BEAC693E60869" x="47.32000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g85343A6F33712521F311CF4CB0AC0F62" x="59.20200000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB1EAA71230153002555C13CC154E2F78" x="68.66600000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gF006044D2EF809484FA4F0971EB12F31" x="79.79400000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gBF7003968C37118C38C261089BC07E3E" x="93.78200000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB1EAA71230153002555C13CC154E2F78" x="100.82800000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA51F6CED3EFDFEC9262BEAC693E60869" x="111.95600000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1F9E5392163967BC76397AFAED7B547D" x="123.83800000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCAC2C7C1DFDFBEEBC3DF952A591B36B2" x="137.20200000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA51F6CED3EFDFEC9262BEAC693E60869" x="155.37600000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC6442A1633CE18C286B5485AEC3656D6" x="167.25800000000004" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gBF7003968C37118C38C261089BC07E3E" x="180.18000000000004" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g6AD8C97DF7CDF2ED1EF2147DE12AFD11" x="187.22600000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA51F6CED3EFDFEC9262BEAC693E60869" x="200.22600000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFEF3271F57AEF3982EEF5E8106A85D5B" x="212.10800000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1F9E5392163967BC76397AFAED7B547D" x="224.92600000000004" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g95CE2BC5509AF8D30239EF1BC4EFF519" x="231.79000000000005" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8E7FE75B66DB12942F4A6EDE903CB302" x="249.91200000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g843DCCBE2350EDDDD327871E3E5456B4" x="262.52200000000005" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA51F6CED3EFDFEC9262BEAC693E60869" x="283.06200000000007" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1F9E5392163967BC76397AFAED7B547D" x="294.9440000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1F9E5392163967BC76397AFAED7B547D" x="301.80800000000005" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g208DDDB1ED04A26500BFF1AFCA3248F0" x="315.172" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD4E6C16CC26FC4313B4D4244D59D0C2E" x="337.81800000000004" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g85343A6F33712521F311CF4CB0AC0F62" x="350.922" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1F9E5392163967BC76397AFAED7B547D" x="360.59400000000005" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gBFCF8059DB7AB71C743804964FB38D58" x="367.458" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g6AD8C97DF7CDF2ED1EF2147DE12AFD11" x="387.11400000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g85343A6F33712521F311CF4CB0AC0F62" x="400.11400000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA51F6CED3EFDFEC9262BEAC693E60869" x="409.78600000000006" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gEFA3682D52D5362AA411E0366F57089" x="421.66800000000006" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gF006044D2EF809484FA4F0971EB12F31" x="435.16200000000003" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(396.9448818897638 133.108)">
<g class="typst-group">
<g>
<g transform="translate(0 11)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g4C316C137CA4A8A5853884E7C7170709" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g9C80E5943281B4667476E9F1C710542A" x="16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF3917F4B6EE4083CE066418D1068DA5B" x="32" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(385.77688188976373 176.108)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g54C180954D544D3C78C9AD9E4F48A6CA" x="7.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="14.88" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g58626FCFBD19425464A4FA7F304374C4" x="22.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g6F04C7AFA6F8271B5D0FF4DA7BA6C29F" x="29.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g54C180954D544D3C78C9AD9E4F48A6CA" x="35.168" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gEF535BAC325E1F03037EDB94EE368989" x="42.608" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g6F04C7AFA6F8271B5D0FF4DA7BA6C29F" x="50.047999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="55.455999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="62.895999999999994" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(387.2616818897638 202.636)">
<g class="typst-group">
<g>
<g transform="translate(0 8.4224)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g2CBC2880522141B53B47B0A6499DB080" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g839D86CB47DDAAE73A261EBDB55D4DA7" x="8.895999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g83A6AA7A836EACB3652229F4716CDAF" x="17.8688" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3AA24D70F4F015B80CBB2E3D4341ADF1" x="24.0768" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g62FB493C725E8111415666ED52983E5C" x="30.8352" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1F6C3165F1EEE020BF61921E6B80BD99" x="36.851200000000006" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g83A6AA7A836EACB3652229F4716CDAF" x="45.312000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g821DF1C680AAF98A6D3A41D44CE1EAAB" x="51.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gC140EDAFC6E31AC0B50ADAF04BA4A77" x="59.0976" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 473.56299212598424)">
<g class="typst-group">
<g/>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="gAA04F5A758CD25067AB4970D92BD8D48" overflow="visible">
<path d="M 16.068 3.1720002 L 16.068 13.598001 C 16.068 15.7560005 16.51 15.886001 18.33 15.964001 C 18.486 16.12 18.486 16.666 18.33 16.822 C 17.264 16.796 15.938001 16.77 14.950001 16.77 C 13.988 16.77 12.740001 16.796 11.596001 16.822 C 11.440001 16.666 11.440001 16.12 11.596001 15.964001 C 13.416 15.886001 13.858001 15.7560005 13.858001 13.598001 L 13.858001 9.438 L 4.966 9.438 L 4.966 13.598001 C 4.966 15.7560005 5.408 15.886001 7.228 15.964001 C 7.3840003 16.12 7.3840003 16.666 7.228 16.822 C 6.2400002 16.796 5.1740003 16.77 3.848 16.77 C 2.548 16.77 1.482 16.796 0.49400002 16.822 C 0.338 16.666 0.338 16.12 0.49400002 15.964001 C 2.3140001 15.886001 2.756 15.7560005 2.756 13.598001 L 2.756 3.1720002 C 2.756 1.014 2.3140001 0.884 0.49400002 0.806 C 0.338 0.65000004 0.338 0.104 0.49400002 -0.052 C 1.638 -0.026 2.8860002 0 3.874 0 C 4.81 0 6.084 -0.026 7.228 -0.052 C 7.3840003 0.104 7.3840003 0.65000004 7.228 0.806 C 5.408 0.884 4.966 1.014 4.966 3.1720002 L 4.966 8.346 L 13.858001 8.346 L 13.858001 3.1720002 C 13.858001 1.014 13.416 0.884 11.596001 0.806 C 11.440001 0.65000004 11.440001 0.104 11.596001 -0.052 C 12.766 -0.026 14.014 0 14.976 0 C 15.938001 0 17.186 -0.026 18.33 -0.052 C 18.486 0.104 18.486 0.65000004 18.33 0.806 C 16.51 0.884 16.068 1.014 16.068 3.1720002 Z "/>
</symbol>
<symbol id="gBF7003968C37118C38C261089BC07E3E" overflow="visible">
<path d="M 4.7060003 3.1720002 L 4.7060003 8.346 C 4.7060003 9.646 4.81 11.31 4.81 11.31 C 4.81 11.4140005 4.6800003 11.492001 4.472 11.492001 C 3.744 11.206 2.704 10.972 0.91 10.738 C 0.85800004 10.582 0.91 10.166 0.962 10.01 C 2.392 9.88 2.652 9.724 2.652 8.242001 L 2.652 3.1720002 C 2.652 1.014 2.366 0.936 0.78000003 0.806 C 0.624 0.65000004 0.624 0.104 0.78000003 -0.052 C 1.638 -0.026 2.652 0 3.6920002 0 C 4.732 0 5.7200003 -0.026 6.578 -0.052 C 6.734 0.104 6.734 0.65000004 6.578 0.806 C 4.992 0.91 4.7060003 1.014 4.7060003 3.1720002 Z M 2.3400002 15.574 C 2.3400002 14.898001 2.964 14.222 3.588 14.222 C 4.316 14.222 4.94 14.924001 4.94 15.47 C 4.94 16.094 4.394 16.822 3.6920002 16.822 C 3.068 16.822 2.3400002 16.198 2.3400002 15.574 Z "/>
</symbol>
<symbol id="g95CE2BC5509AF8D30239EF1BC4EFF519" overflow="visible">
<path d="M 10.036 2.418 C 9.074 1.4300001 8.32 1.014 6.8120003 1.014 C 5.876 1.014 4.784 1.5600001 3.9780002 2.8860002 C 3.4580002 3.744 3.1460001 4.94 3.1460001 6.448 L 10.062 6.396 C 10.374001 6.396 10.556 6.552 10.556 6.8380003 C 10.556 9.022 9.776 11.362 6.162 11.362 C 3.9 11.362 0.962 9.204 0.962 5.2520003 C 0.962 3.796 1.326 2.392 2.184 1.404 C 3.068 0.36400002 4.29 -0.26 6.162 -0.26 C 8.1380005 -0.26 9.542 0.65000004 10.582 2.002 C 10.504001 2.262 10.348001 2.392 10.036 2.418 Z M 3.224 7.3320003 C 3.7180002 10.27 5.538 10.504001 6.162 10.504001 C 7.15 10.504001 8.32 9.958 8.32 7.774 C 8.32 7.54 8.216001 7.4100003 7.9300003 7.4100003 Z "/>
</symbol>
<symbol id="g85343A6F33712521F311CF4CB0AC0F62" overflow="visible">
<path d="M 4.576 9.308001 C 4.524 10.348001 4.498 11.024 4.368 11.284 C 4.316 11.4140005 4.264 11.492001 4.056 11.492001 C 3.328 11.206 2.652 10.972 0.85800004 10.738 C 0.806 10.582 0.85800004 10.166 0.91 10.01 C 2.3140001 9.88 2.6000001 9.75 2.6000001 8.242001 L 2.6000001 3.1720002 C 2.6000001 1.014 2.288 0.91 0.676 0.806 C 0.52 0.65000004 0.52 0.104 0.676 -0.052 C 1.5860001 -0.026 2.6000001 0 3.64 0 C 4.6800003 0 5.876 -0.026 6.7860003 -0.052 C 6.942 0.104 6.942 0.65000004 6.7860003 0.806 C 4.966 0.936 4.6540003 1.014 4.6540003 3.1720002 L 4.6540003 6.7860003 C 4.6540003 7.4620004 4.966 8.06 5.278 8.528 C 5.564 8.944 6.162 9.802 6.474 9.802 C 6.708 9.802 6.942 9.75 7.15 9.464 C 7.3320003 9.204 7.644 8.866 8.086 8.866 C 8.71 8.866 9.308001 9.516 9.308001 10.166 C 9.308001 10.66 8.84 11.4140005 7.748 11.4140005 C 6.526 11.4140005 5.46 10.27 4.862 9.2560005 C 4.7060003 8.97 4.576 9.178 4.576 9.308001 Z "/>
</symbol>
<symbol id="gA51F6CED3EFDFEC9262BEAC693E60869" overflow="visible">
<path d="M 7.618 1.248 C 7.774 0.442 8.06 -0.26 9.360001 -0.26 C 10.348001 -0.26 11.284 0.18200001 11.83 0.702 C 11.778 1.014 11.674 1.248 11.3880005 1.404 C 11.206 1.248 10.764 0.98800004 10.426001 0.98800004 C 9.672 0.98800004 9.646 2.002 9.646 3.198 L 9.646 7.02 C 9.646 10.712 7.618 11.4140005 5.7200003 11.4140005 C 3.588 11.4140005 1.4300001 10.01 1.4300001 8.528 C 1.4300001 7.9040003 1.742 7.592 2.3400002 7.592 C 3.094 7.592 3.562 8.1380005 3.562 8.476 C 3.562 8.658 3.536 8.84 3.484 8.944 C 3.4580002 9.022 3.4320002 9.178 3.4320002 9.464 C 3.4320002 10.27 4.524 10.556 5.512 10.556 C 6.396 10.556 7.618 10.114 7.618 7.176 C 7.618 6.994 7.54 6.8900003 7.4620004 6.8640003 L 5.2260003 6.3180003 C 2.73 5.6940002 0.936 4.316 0.936 2.548 C 0.936 0.416 2.392 -0.26 4.212 -0.26 C 5.122 -0.26 5.902 -0.052 7.046 0.832 L 7.566 1.248 Z M 7.618 6.058 L 7.618 2.6260002 C 7.618 2.288 7.4620004 2.106 7.254 1.95 C 6.578 1.404 5.6940002 0.806 4.966 0.806 C 3.6660001 0.806 3.094 1.8460001 3.094 2.652 C 3.094 3.822 3.64 5.018 5.564 5.512 Z "/>
</symbol>
<symbol id="gB1EAA71230153002555C13CC154E2F78" overflow="visible">
<path d="M 10.348001 2.366 C 10.244 2.6000001 10.036 2.704 9.802 2.73 C 8.918 1.5860001 7.8 1.014 6.682 1.014 C 4.784 1.014 3.198 2.938 3.198 5.98 C 3.198 8.84 4.446 10.556 6.162 10.556 C 7.696 10.556 7.9040003 9.646 8.008 8.736 C 8.086 8.034 8.45 7.8 8.996 7.8 C 9.542 7.8 10.27 8.1380005 10.27 8.944 C 10.27 10.374001 8.788 11.4140005 6.2920003 11.4140005 C 3.7180002 11.4140005 0.962 9.1 0.962 5.408 C 0.962 2.0540001 2.834 -0.26 6.11 -0.26 C 7.67 -0.26 9.048 0.234 10.348001 2.366 Z "/>
</symbol>
<symbol id="gF006044D2EF809484FA4F0971EB12F31" overflow="visible">
<path d="M 4.342 7.4360003 C 4.342 7.9820004 4.576 8.294001 4.784 8.528 C 5.7720003 9.49 7.098 10.062 8.112 10.062 C 8.632 10.062 9.178 9.724 9.49 9.126 C 9.75 8.606 9.802 7.9040003 9.802 7.124 L 9.802 3.1720002 C 9.802 1.04 9.542 0.936 8.190001 0.806 C 8.06 0.65000004 8.06 0.104 8.190001 -0.052 C 8.918 -0.026 9.802 0 10.842 0 C 11.882 0 12.740001 -0.026 13.598001 -0.052 C 13.728001 0.104 13.728001 0.65000004 13.598001 0.806 C 12.142 0.936 11.856 1.04 11.856 3.1720002 L 11.856 7.046 C 11.856 8.476 11.752 9.75 11.154 10.530001 C 10.712 11.102 9.906 11.4140005 8.996 11.4140005 C 7.722 11.4140005 6.162 11.076 4.576 9.308001 C 4.576 9.282001 4.55 9.282001 4.524 9.2560005 C 4.446 9.152 4.316 8.996 4.316 9.308001 L 4.342 15.158 C 4.342 16.848 4.446 17.888 4.446 17.888 C 4.446 18.07 4.342 18.148 4.1080003 18.148 C 3.4580002 17.888 1.508 17.524 0.468 17.446001 C 0.416 17.238 0.468 16.822 0.624 16.666 C 0.702 16.666 0.78000003 16.666 0.85800004 16.666 C 2.002 16.588001 2.288 16.588001 2.288 14.534 L 2.288 3.1720002 C 2.288 1.014 1.9760001 0.91 0.468 0.806 C 0.312 0.65000004 0.312 0.104 0.468 -0.052 C 1.326 -0.026 2.288 0 3.328 0 C 4.316 0 5.1740003 -0.026 5.902 -0.052 C 6.058 0.104 6.058 0.65000004 5.902 0.806 C 4.576 0.91 4.342 1.014 4.342 3.1720002 Z "/>
</symbol>
<symbol id="g1F9E5392163967BC76397AFAED7B547D" overflow="visible">
<path d="M 2.47 3.1720002 C 2.47 1.014 2.184 0.884 0.598 0.806 C 0.442 0.65000004 0.442 0.104 0.598 -0.052 C 1.508 -0.026 2.47 0 3.51 0 C 4.55 0 5.538 -0.026 6.396 -0.052 C 6.552 0.104 6.552 0.65000004 6.396 0.806 C 4.81 0.884 4.524 1.014 4.524 3.1720002 L 4.524 15.158 C 4.524 16.848 4.6280003 17.888 4.6280003 17.888 C 4.6280003 18.07 4.524 18.148 4.29 18.148 C 3.64 17.888 1.69 17.524 0.65000004 17.446001 C 0.598 17.238 0.65000004 16.822 0.806 16.666 C 2.3140001 16.562 2.47 16.484001 2.47 14.534 Z "/>
</symbol>
<symbol id="gCAC2C7C1DFDFBEEBC3DF952A591B36B2" overflow="visible">
<path d="M 14.456 13.312 L 14.456 4.81 C 14.456 4.316 14.456 4.03 14.274 4.03 C 14.17 4.03 13.780001 4.498 13.026 5.46 L 4.1080003 16.77 L 0.598 16.822 C 0.442 16.666 0.442 16.12 0.598 15.964001 C 1.7160001 15.886001 2.496 14.976 2.652 14.3 L 2.652 3.4580002 C 2.652 1.144 2.21 0.98800004 0.39000002 0.806 C 0.234 0.65000004 0.234 0.104 0.39000002 -0.052 C 1.508 -0.026 2.678 0 3.302 0 C 3.9 0 5.096 -0.026 6.188 -0.052 C 6.3440003 0.104 6.3440003 0.65000004 6.188 0.806 C 4.368 0.98800004 3.926 1.092 3.926 3.4580002 L 3.926 11.4140005 C 3.926 12.298 3.926 12.688001 4.1340003 12.688001 C 4.29 12.688001 4.576 12.402 5.018 11.83 L 14.092 0.36400002 C 14.378 -0.026 14.716001 -0.26 15.132 -0.26 C 15.496 -0.26 15.7300005 0.052 15.7300005 0.546 L 15.7300005 13.312 C 15.7300005 15.626 16.172 15.782001 17.992 15.964001 C 18.148 16.12 18.148 16.666 17.992 16.822 C 16.926 16.796 15.704 16.77 15.08 16.77 C 14.534 16.77 13.338 16.796 12.194 16.822 C 12.038 16.666 12.038 16.12 12.194 15.964001 C 14.014 15.782001 14.456 15.678 14.456 13.312 Z "/>
</symbol>
<symbol id="gC6442A1633CE18C286B5485AEC3656D6" overflow="visible">
<path d="M 8.45 10.348001 C 9.854 10.244 10.01 9.932 9.464 8.606 L 7.3580003 3.51 C 6.942 2.496 6.8120003 2.496 6.396 3.588 L 4.524 8.606 C 4.056 9.854 3.9520001 10.166 5.33 10.348001 C 5.486 10.504001 5.486 11.05 5.33 11.206 C 4.472 11.18 3.562 11.154 2.704 11.154 C 1.8460001 11.154 1.066 11.18 0.286 11.206 C 0.13 11.05 0.13 10.504001 0.286 10.348001 C 1.664 10.192 1.8460001 9.776 2.366 8.45 L 5.6940002 0.234 C 5.85 -0.156 6.006 -0.312 6.3440003 -0.312 C 6.604 -0.312 6.7860003 -0.156 6.968 0.286 L 10.426001 8.424 C 10.92 9.568 11.206 10.218 12.662001 10.348001 C 12.818 10.504001 12.818 11.05 12.662001 11.206 C 12.142 11.18 11.518001 11.154 10.842 11.154 C 9.984 11.154 9.1 11.18 8.45 11.206 C 8.294001 11.05 8.294001 10.504001 8.45 10.348001 Z "/>
</symbol>
<symbol id="g6AD8C97DF7CDF2ED1EF2147DE12AFD11" overflow="visible">
<path d="M 11.544001 10.062 C 12.038 10.062 12.5060005 10.530001 12.5060005 11.05 C 12.5060005 11.596001 12.012 12.012 11.31 12.012 C 10.634 12.012 9.386001 11.570001 8.71 10.686 C 8.398 10.894 7.54 11.4140005 6.006 11.4140005 C 3.6920002 11.4140005 1.5600001 9.854 1.5600001 7.4620004 C 1.5600001 6.058 2.184 5.2520003 2.9120002 4.55 C 2.184 3.926 1.768 2.808 1.768 1.924 C 1.768 0.98800004 2.288 0.26 2.964 -0.078 C 1.5600001 -0.91 0.832 -2.106 0.832 -3.224 C 0.832 -5.486 2.964 -6.188 4.966 -6.188 C 8.476 -6.188 12.272 -4.498 12.272 -1.69 C 12.272 -0.85800004 11.882 -0.208 11.128 0.416 C 10.114 1.248 8.294001 1.274 7.3320003 1.274 C 6.8640003 1.274 6.214 1.222 5.59 1.144 C 5.2000003 1.118 4.94 1.092 4.81 1.092 C 4.056 1.092 3.1460001 1.4560001 3.1460001 2.5740001 C 3.1460001 3.094 3.302 3.64 3.614 4.0820003 C 4.238 3.7180002 4.966 3.536 5.98 3.536 C 8.268001 3.536 10.374001 4.966 10.374001 7.514 C 10.374001 8.736 10.01 9.438 9.2560005 10.218 C 9.438 10.478001 9.958 10.842 10.2960005 10.842 C 10.478001 10.842 10.66 10.764 10.816 10.530001 C 10.92 10.3220005 11.258 10.062 11.544001 10.062 Z M 3.4320002 -0.26 C 3.7180002 -0.338 4.1340003 -0.39000002 4.472 -0.39000002 C 5.278 -0.39000002 6.006 -0.312 6.3700004 -0.312 C 7.67 -0.312 8.762 -0.338 9.516 -0.754 C 10.530001 -1.326 10.842 -1.69 10.842 -2.366 C 10.842 -4.238 8.086 -5.2260003 5.7460003 -5.2260003 C 4.81 -5.2260003 2.6260002 -4.472 2.6260002 -2.704 C 2.6260002 -1.82 2.678 -1.1700001 3.4320002 -0.26 Z M 8.294001 7.254 C 8.294001 4.836 7.072 4.342 6.11 4.342 C 3.926 4.342 3.6920002 6.188 3.6920002 7.852 C 3.6920002 9.672 4.342 10.608 5.7720003 10.608 C 7.4100003 10.608 8.294001 9.412001 8.294001 7.254 Z "/>
</symbol>
<symbol id="gFEF3271F57AEF3982EEF5E8106A85D5B" overflow="visible">
<path d="M 4.342 10.244 C 4.186 10.088 4.0820003 10.14 4.0820003 10.374001 L 4.0820003 15.158 C 4.0820003 16.848 4.186 17.888 4.186 17.888 C 4.186 18.07 4.0820003 18.148 3.848 18.148 C 3.198 17.888 1.248 17.524 0.208 17.446001 C 0.156 17.238 0.208 16.822 0.36400002 16.666 C 0.442 16.666 0.52 16.666 0.598 16.666 C 1.742 16.588001 2.028 16.588001 2.028 14.534 L 2.028 1.8460001 C 2.028 0.832 2.002 0.36400002 1.924 0 C 2.0540001 -0.208 2.184 -0.312 2.496 -0.312 C 2.652 -0.156 2.9120002 0.078 3.1200001 0.312 C 3.38 0.624 3.536 0.624 3.822 0.39000002 C 4.42 -0.104 5.2000003 -0.26 6.11 -0.26 C 8.762 -0.26 11.856 2.158 11.856 6.2920003 C 11.856 9.464 9.516 11.4140005 7.254 11.4140005 C 6.136 11.4140005 5.1480002 10.972 4.342 10.244 Z M 4.524 9.438 C 5.2000003 10.036 5.98 10.27 6.734 10.27 C 8.32 10.27 9.62 8.346 9.62 5.8240004 C 9.62 2.8600001 8.424 0.624 5.954 0.624 C 5.1480002 0.624 4.602 1.196 4.0820003 1.8460001 L 4.0820003 8.346 C 4.0820003 8.892 4.186 9.152 4.524 9.438 Z "/>
</symbol>
<symbol id="g8E7FE75B66DB12942F4A6EDE903CB302" overflow="visible">
<path d="M 10.27 16.406 C 8.762 16.614 8.814 17.108 6.2660003 17.108 C 3.64 17.108 1.326 15.366 1.326 12.610001 C 1.326 9.88 3.588 8.632 5.876 7.748 C 7.4360003 7.15 9.360001 6.422 9.360001 3.874 C 9.360001 1.768 8.190001 0.676 6.11 0.676 C 3.6920002 0.676 2.132 1.794 1.5600001 4.368 C 1.222 4.472 0.962 4.42 0.702 4.29 C 0.806 2.288 0.91 1.612 1.222 0.338 C 2.8600001 0.338 3.588 -0.26 5.902 -0.26 C 7.072 -0.26 8.190001 0.026 9.1 0.598 C 10.608 1.534 11.544001 3.1200001 11.544001 4.784 C 11.544001 7.54 9.464 8.762 7.3320003 9.568 C 5.7720003 10.14 3.1720002 11.128 3.1720002 13.312 C 3.1720002 14.768001 4.498 16.224 6.032 16.224 C 8.554 16.224 9.360001 14.612 9.88 12.896 C 10.166 12.844 10.504001 12.87 10.738 13.052 C 10.634 14.3 10.530001 15.028 10.27 16.406 Z "/>
</symbol>
<symbol id="g843DCCBE2350EDDDD327871E3E5456B4" overflow="visible">
<path d="M 4.42 9.308001 C 4.394 10.088 4.342 11.024 4.212 11.284 C 4.16 11.4140005 4.1080003 11.492001 3.9 11.492001 C 3.1720002 11.206 2.496 10.972 0.702 10.738 C 0.65000004 10.582 0.702 10.166 0.754 10.01 C 2.158 9.88 2.444 9.75 2.444 8.242001 L 2.444 3.1720002 C 2.444 1.04 2.106 0.91 0.676 0.806 C 0.52 0.65000004 0.52 0.104 0.676 -0.052 C 1.4560001 -0.026 2.444 0 3.484 0 C 4.524 0 5.33 -0.026 6.11 -0.052 C 6.2660003 0.104 6.2660003 0.65000004 6.11 0.806 C 4.784 0.936 4.498 1.04 4.498 3.1720002 L 4.498 7.4360003 C 4.498 7.9820004 4.732 8.294001 4.94 8.528 C 5.98 9.542 6.942 10.062 7.748 10.062 C 8.736 10.062 9.464 9.438 9.464 7.696 L 9.464 3.1720002 C 9.464 1.04 9.2560005 0.91 7.852 0.806 C 7.722 0.65000004 7.722 0.104 7.852 -0.052 C 8.502 -0.026 9.464 0 10.504001 0 C 11.544001 0 12.402 -0.026 13.052 -0.052 C 13.182 0.104 13.182 0.65000004 13.052 0.806 C 11.752 0.91 11.518001 1.04 11.518001 3.1720002 L 11.518001 7.306 C 11.518001 7.67 11.518001 8.034 11.492001 8.346 C 12.740001 9.724 13.91 10.062 14.924001 10.062 C 15.912001 10.062 16.484001 9.49 16.484001 7.748 L 16.484001 3.1720002 C 16.484001 1.04 16.224 0.91 14.872001 0.806 C 14.742001 0.65000004 14.742001 0.104 14.872001 -0.052 C 15.522 -0.026 16.484001 0 17.524 0 C 18.564001 0 19.474 -0.026 20.202 -0.052 C 20.332 0.104 20.332 0.65000004 20.202 0.806 C 18.772001 0.91 18.538 1.04 18.538 3.1720002 L 18.538 7.28 C 18.538 9.594 18.148 11.4140005 15.860001 11.4140005 C 14.534 11.4140005 12.922 10.92 11.570001 9.49 C 11.492001 9.412001 11.336 9.282001 11.284 9.516 C 11.05 10.582 10.036 11.4140005 8.684 11.4140005 C 7.176 11.4140005 5.8240004 10.530001 4.732 9.308001 C 4.602 9.178 4.446 8.996 4.42 9.308001 Z "/>
</symbol>
<symbol id="g208DDDB1ED04A26500BFF1AFCA3248F0" overflow="visible">
<path d="M 21.060001 14.690001 L 17.004 3.4060001 L 16.926 3.4320002 L 13.338 14.404 C 12.896 15.808001 13.806001 15.886001 14.690001 15.964001 C 14.846001 16.12 14.846001 16.666 14.690001 16.822 C 13.624001 16.796 12.4800005 16.77 11.440001 16.77 C 10.582 16.77 9.672 16.796 8.84 16.822 C 8.684 16.666 8.684 16.12 8.84 15.964001 C 10.218 15.886001 10.79 15.08 11.024 14.404 L 11.622001 12.688001 C 11.726 12.376 11.804 12.116 11.804 11.882 C 11.804 11.622001 11.778 11.4140005 11.570001 10.972 L 8.216001 3.354 L 8.086 3.38 L 4.29 14.872001 C 3.9780002 15.782001 4.6800003 15.912001 5.59 15.964001 C 5.7460003 16.12 5.7460003 16.666 5.59 16.822 C 4.732 16.796 3.588 16.77 2.5740001 16.77 C 1.664 16.77 0.91 16.796 0.156 16.822 C 0 16.666 0 16.12 0.156 15.964001 C 1.326 15.886001 1.508 15.860001 2.002 14.456 L 6.8900003 0.39000002 C 7.02 -0.026 7.176 -0.312 7.4620004 -0.312 C 7.8 -0.312 7.9560003 -0.052 8.1380005 0.39000002 L 12.012 9.1 C 12.246 9.62 12.324 9.75 12.454 9.75 C 12.558001 9.75 12.662001 9.464 12.818 9.022 L 15.808001 0.39000002 C 15.964001 -0.052 16.094 -0.312 16.406 -0.312 C 16.692 -0.312 16.874 -0.026 17.004 0.36400002 L 22.23 14.378 C 22.568 15.288 23.036001 15.886001 24.466 15.964001 C 24.622 16.12 24.622 16.666 24.466 16.822 C 23.712 16.796 22.880001 16.77 22.204 16.77 C 21.528 16.77 20.384 16.796 19.344 16.822 C 19.188 16.666 19.188 16.12 19.344 15.964001 C 20.41 15.886001 21.45 15.808001 21.060001 14.690001 Z "/>
</symbol>
<symbol id="gD4E6C16CC26FC4313B4D4244D59D0C2E" overflow="visible">
<path d="M 1.066 5.33 C 1.066 2.678 2.834 -0.26 6.526 -0.26 C 8.190001 -0.26 9.464 0.338 10.348001 1.196 C 11.518001 2.3400002 12.038 3.9780002 12.038 5.564 C 12.038 8.268001 10.556 11.4140005 6.578 11.4140005 C 4.862 11.4140005 3.4580002 10.712 2.496 9.594 C 1.5600001 8.476 1.066 6.968 1.066 5.33 Z M 6.188 10.504001 C 8.424 10.504001 9.802 8.476 9.802 4.732 C 9.802 1.4560001 8.112 0.65000004 6.8900003 0.65000004 C 4.186 0.65000004 3.302 3.926 3.302 5.928 C 3.302 8.190001 3.848 10.504001 6.188 10.504001 Z "/>
</symbol>
<symbol id="gBFCF8059DB7AB71C743804964FB38D58" overflow="visible">
<path d="M 8.684 1.3000001 C 8.814 1.404 9.048 1.4560001 9.074 1.274 C 9.152 0.65000004 9.360001 -0.26 9.360001 -0.26 C 9.568 -0.338 9.698 -0.312 9.854 -0.26 C 10.426001 0.208 11.336 0.598 12.922 0.78000003 C 13.078 0.936 13.078 1.326 12.922 1.482 C 11.258 1.612 11.024 2.106 11.024 3.38 L 11.024 15.158 C 11.024 16.848 11.128 17.888 11.128 17.888 C 11.128 18.07 11.024 18.148 10.79 18.148 C 10.14 17.888 8.190001 17.524 7.15 17.446001 C 7.098 17.238 7.15 16.822 7.306 16.666 C 7.3840003 16.666 7.4620004 16.666 7.54 16.666 C 8.684 16.588001 8.97 16.588001 8.97 14.534 L 8.97 11.206 C 8.97 11.024 8.918 10.972 8.736 10.972 C 8.632 10.972 7.566 11.4140005 6.708 11.4140005 C 4.992 11.4140005 3.848 10.842 2.808 9.854 C 1.69 8.736 1.014 7.202 1.014 5.278 C 1.014 2.08 2.6260002 -0.26 5.434 -0.26 C 6.448 -0.26 7.4100003 0.26 8.684 1.3000001 Z M 8.97 3.224 C 8.97 2.73 8.918 2.522 8.554 2.21 C 7.592 1.378 6.76 0.962 6.11 0.962 C 4.7060003 0.962 3.25 2.496 3.25 5.7460003 C 3.25 7.618 3.614 8.658 4.004 9.204 C 4.81 10.426001 5.902 10.504001 6.422 10.504001 C 7.3580003 10.504001 8.008 10.166 8.528 9.568 C 8.892 9.152 8.97 8.97 8.97 8.1640005 Z "/>
</symbol>
<symbol id="gEFA3682D52D5362AA411E0366F57089" overflow="visible">
<path d="M 4.056 9.568 C 4.03 10.348001 3.9780002 11.024 3.848 11.284 C 3.796 11.4140005 3.744 11.492001 3.536 11.492001 C 2.808 11.206 2.132 10.972 0.338 10.738 C 0.286 10.582 0.338 10.166 0.39000002 10.01 C 1.794 9.88 2.08 9.75 2.08 8.242001 L 2.08 -2.8600001 C 2.08 -5.018 1.794 -5.1480002 0.208 -5.2260003 C 0.052 -5.382 0.052 -5.928 0.208 -6.084 C 1.118 -6.058 2.08 -6.032 3.1200001 -6.032 C 4.16 -6.032 5.408 -6.058 6.2660003 -6.084 C 6.422 -5.928 6.422 -5.382 6.2660003 -5.2260003 C 4.42 -5.122 4.1340003 -5.018 4.1340003 -2.8600001 L 4.1340003 -0.052 C 4.1340003 0.286 4.238 0.26 4.498 0.156 C 5.1480002 -0.104 5.928 -0.26 6.76 -0.26 C 8.216001 -0.26 9.516 0.18200001 10.582 1.196 C 11.804 2.392 12.5060005 4.004 12.5060005 6.11 C 12.5060005 8.866 10.556 11.4140005 7.9040003 11.4140005 C 6.708 11.4140005 5.382 10.634 4.342 9.464 C 4.186 9.308001 4.0820003 9.308001 4.056 9.568 Z M 4.55 8.606 C 5.2260003 9.438 6.422 10.218 7.176 10.218 C 8.84 10.218 10.27 8.346 10.27 5.408 C 10.27 3.276 9.516 0.624 6.604 0.624 C 6.136 0.624 5.2260003 0.754 4.758 1.1700001 C 4.238 1.638 4.1340003 1.794 4.1340003 2.73 L 4.1340003 7.4620004 C 4.1340003 8.008 4.238 8.242001 4.55 8.606 Z "/>
</symbol>
<symbol id="g4C316C137CA4A8A5853884E7C7170709" overflow="visible">
<path d="M 8.1875 7.8125 Q 8.3125 7.6875 8.25 7.3125 Q 11.625 7.5625 12.65625 7.71875 Q 13.6875 7.875 14.28125 7.5625 Q 14.875 7.25 14.875 7 Q 14.875 6.8125 13.40625 6.875 Q 11.9375 6.9375 8.25 6.75 L 8.1875 5.75 Q 9.875 5.9375 10.3125 6.03125 Q 10.75 6.125 11.15625 5.96875 Q 11.5625 5.8125 11.90625 5.5 Q 12.25 5.1875 11.90625 4.90625 Q 11.5625 4.625 11.1875 3.875 Q 10.8125 3.125 10.46875 2.75 Q 10.125 2.375 10 2.875 Q 8.6875 2.75 8.125 2.75 L 8.0625 1.625 Q 9.3125 1.875 9.625 1.875 Q 10 1.875 10.3125 1.59375 Q 10.625 1.3125 10 1.1875 Q 9.375 1.0625 8.0625 1 L 8 -0.0625 Q 10.8125 0.1875 11.625 0.28125 Q 12.4375 0.375 13.09375 -0.125 Q 13.75 -0.625 13.21875 -0.65625 Q 12.6875 -0.6875 11.5625 -0.625 Q 10.4375 -0.5625 8.65625 -0.625 Q 6.875 -0.6875 5.4375 -0.8125 Q 4 -0.9375 3.34375 -1.03125 Q 2.6875 -1.125 2.34375 -0.96875 Q 2 -0.8125 1.75 -0.59375 Q 1.5 -0.375 2.28125 -0.40625 Q 3.0625 -0.4375 7.375 -0.125 L 7.375 0.9375 Q 5.9375 0.75 5.40625 0.96875 Q 4.875 1.1875 5.53125 1.28125 Q 6.1875 1.375 7.375 1.5 L 7.375 2.6875 Q 6.625 2.625 5.6875 2.5 Q 5.4375 1.875 5.21875 2.34375 Q 5 2.8125 4.65625 3.71875 Q 4.3125 4.625 3.96875 5.03125 Q 3.625 5.4375 3.9375 5.4375 Q 4.3125 5.4375 4.59375 5.375 Q 4.875 5.3125 7.375 5.625 L 7.375 6.6875 Q 6.3125 6.5625 4.90625 6.375 Q 3.5 6.1875 2.90625 6.125 Q 2.3125 6.0625 1.96875 6.125 Q 1.625 6.1875 1.28125 6.5 Q 0.9375 6.8125 1.875 6.78125 Q 2.8125 6.75 4.21875 6.875 Q 5.625 7 7.375 7.1875 Q 7.375 7.625 7.125 7.9375 Q 6.125 7.75 5.5 7.8125 Q 4.875 7.875 5.90625 8.125 Q 6.9375 8.375 7.78125 8.75 Q 8.625 9.125 8.84375 9.375 Q 9.0625 9.625 9.4375 9.46875 Q 9.8125 9.3125 10.09375 8.96875 Q 10.375 8.625 10.03125 8.5625 Q 9.6875 8.5 7.75 8 Q 8.0625 7.9375 8.1875 7.8125 Z M 9.375 11.0625 Q 9.6875 12.1875 9.46875 12.625 Q 9.25 13.0625 10.15625 12.6875 Q 11.0625 12.3125 10.8125 12 Q 10.5625 11.6875 10.1875 11.1875 Q 11.75 11.375 12.34375 11.46875 Q 12.9375 11.5625 13.46875 11.09375 Q 14 10.625 13.125 10.6875 Q 12.25 10.75 9.875 10.5625 Q 9.1875 9.625 9 9.625 Q 8.875 9.625 9.1875 10.5 L 6.375 10.25 Q 6.4375 9.5 6.28125 9.125 Q 6.125 8.75 5.6875 10.125 Q 4.3125 9.9375 3.59375 9.8125 Q 2.875 9.6875 2.3125 10.0625 Q 1.75 10.4375 2.5 10.4375 Q 3.3125 10.4375 5.5625 10.625 Q 5.1875 11.5 4.875 11.84375 Q 4.5625 12.1875 5.25 12.125 Q 6.3125 11.9375 6.3125 11.625 L 6.3125 10.75 L 9.375 11.0625 Z M 9.25 4.65625 Q 9.5625 4.6875 9.75 4.4375 Q 9.9375 4.1875 9.4375 4.125 Q 8.9375 4.0625 8.1875 4 L 8.125 3.1875 Q 9.3125 3.375 10.0625 3.375 Q 10.625 4.625 10.53125 5.0625 Q 10.4375 5.5 9.8125 5.46875 Q 9.1875 5.4375 8.1875 5.3125 L 8.1875 4.5625 Q 8.9375 4.625 9.25 4.65625 Z M 5.6875 2.875 Q 6.6875 3 7.375 3.0625 L 7.375 3.9375 Q 6.4375 3.8125 6.03125 4.03125 Q 5.625 4.25 6.0625 4.3125 L 7.375 4.5 L 7.375 5.1875 Q 6.25 5.125 5.125 4.875 Q 5.3125 4.1875 5.6875 2.875 Z "/>
</symbol>
<symbol id="g9C80E5943281B4667476E9F1C710542A" overflow="visible">
<path d="M 10.3125 6.3125 Q 11.5 6.4375 12.375 6.59375 Q 13.25 6.75 13.96875 6.59375 Q 14.6875 6.4375 14.9375 5.9375 Q 15.1875 5.4375 13.625 5.59375 Q 12.0625 5.75 7.6875 5.5 Q 6.9375 4.125 6.375 3.125 Q 8 3.375 8.90625 3.53125 Q 9.8125 3.6875 10.09375 3.84375 Q 10.375 4 10.84375 3.8125 Q 11.3125 3.625 11.90625 3.1875 Q 12.5 2.75 12 2.40625 Q 11.5 2.0625 11.0625 0.75 Q 11.625 0.5 11.59375 0.3125 Q 11.5625 0.125 10.625 0.09375 Q 9.6875 0.0625 7 -0.25 Q 6.75 -1.0625 6.53125 -0.53125 Q 6.3125 0 6.1875 0.65625 Q 6.0625 1.3125 5.8125 2.4375 Q 4.9375 1.5 4.15625 0.90625 Q 3.375 0.3125 2.46875 -0.0625 Q 1.5625 -0.4375 2.5 0.28125 Q 3.4375 1 3.90625 1.4375 Q 4.375 1.875 5.4375 3.0625 Q 5.25 3.5 5.75 3.5 Q 6.25 4.25 6.75 5.375 Q 3.875 5.125 3.15625 4.9375 Q 2.4375 4.75 1.78125 5.21875 Q 1.125 5.6875 1.5 5.6875 Q 1.9375 5.6875 3.15625 5.71875 Q 4.375 5.75 6.9375 6 Q 7.375 7.0625 7.21875 7.6875 Q 7.0625 8.3125 7.875 7.84375 Q 8.6875 7.375 8.46875 7.125 Q 8.25 6.875 8 6.125 Q 9.125 6.1875 10.3125 6.3125 Z M 9.5625 10.125 Q 10 11.375 9.75 11.96875 Q 9.5 12.5625 10.4375 12.09375 Q 11.375 11.625 11.1875 11.34375 Q 11 11.0625 10.5625 10.25 Q 11.3125 10.3125 12.125 10.4375 Q 12.9375 10.5625 13.5 10.3125 Q 14.0625 10.0625 14.09375 9.78125 Q 14.125 9.5 13.46875 9.53125 Q 12.8125 9.5625 12 9.5625 L 10.25 9.5625 Q 9.875 8.8125 9.4375 8.21875 Q 9 7.625 9.09375 8.15625 Q 9.1875 8.6875 9.4375 9.5 Q 8.1875 9.375 7 9.3125 Q 7 8.625 6.9375 8.21875 Q 6.875 7.8125 6.6875 7.8125 Q 6.5 7.8125 6.3125 9.1875 Q 4.4375 8.9375 3.84375 8.8125 Q 3.25 8.6875 2.6875 9.09375 Q 2.125 9.5 2.90625 9.46875 Q 3.6875 9.4375 6.1875 9.6875 Q 6.125 10.6875 5.65625 11.25 Q 5.1875 11.8125 6.125 11.5 Q 7.0625 11.1875 7.03125 10.9375 Q 7 10.6875 7 9.8125 Q 8 9.875 9.5625 10.125 Z M 10.3125 0.6875 Q 10.5625 1.9375 10.625 2.53125 Q 10.6875 3.125 10.25 3.0625 Q 9.8125 3 9.40625 2.96875 Q 9 2.9375 6.625 2.6875 Q 6.8125 1.3125 6.9375 0.375 Q 9.25 0.5625 10.3125 0.6875 Z "/>
</symbol>
<symbol id="gF3917F4B6EE4083CE066418D1068DA5B" overflow="visible">
<path d="M 10.65625 6.84375 Q 12.25 7.1875 12.71875 7.375 Q 13.1875 7.5625 13.59375 7.40625 Q 14 7.25 14.5 6.9375 Q 15 6.625 14.6875 6.28125 Q 14.375 5.9375 14.25 5 Q 14.125 4.0625 13.90625 3 Q 13.6875 1.9375 13.40625 1 Q 13.125 0.0625 12.375 -0.625 Q 11.625 -1.3125 11.46875 -0.78125 Q 11.3125 -0.25 10.6875 0.40625 Q 10.0625 1.0625 10.9375 0.71875 Q 11.8125 0.375 12.09375 0.65625 Q 12.375 0.9375 12.65625 1.75 Q 12.9375 2.5625 13.15625 3.65625 Q 13.375 4.75 13.40625 5.71875 Q 13.4375 6.6875 13 6.71875 Q 12.5625 6.75 11.4375 6.5 Q 11.9375 6.25 12.125 6.0625 Q 12.3125 5.875 12.125 5.75 Q 11.9375 5.625 11.40625 4.25 Q 10.875 2.875 9.9375 1.8125 Q 9 0.75 7.78125 0.25 Q 6.5625 -0.25 7.5 0.4375 Q 8.4375 1.125 9.21875 2.03125 Q 10 2.9375 10.40625 3.78125 Q 10.8125 4.625 11 5.34375 Q 11.1875 6.0625 11.125 6.4375 Q 10.5625 6.375 9.5625 6.1875 Q 10.25 5.75 10.0625 5.5625 Q 9.875 5.375 9.625 5 Q 9.375 4.625 8.65625 3.6875 Q 7.9375 2.75 7.09375 2.375 Q 6.25 2 6.90625 2.5625 Q 7.5625 3.125 8.28125 4.21875 Q 9 5.3125 9.25 6.125 Q 8.5 6 8.15625 5.875 Q 7.8125 5.75 7.6875 5.71875 Q 7.5625 5.6875 7.53125 6.1875 Q 7.5 6.6875 7.90625 6.71875 Q 8.3125 6.75 9.3125 7.84375 Q 10.3125 8.9375 10.71875 9.46875 Q 11.125 10 11.0625 10.125 Q 9.625 9.75 9 9.65625 Q 8.375 9.5625 7.875 9.90625 Q 7.375 10.25 8.25 10.25 Q 9.125 10.25 10.0625 10.53125 Q 11 10.8125 11.1875 11 Q 11.375 11.1875 11.90625 10.96875 Q 12.4375 10.75 12.6875 10.53125 Q 12.9375 10.3125 12.65625 10.15625 Q 12.375 10 11.84375 9.5625 Q 11.3125 9.125 10.46875 8.1875 Q 9.625 7.25 9 6.6875 Q 9.0625 6.5 10.65625 6.84375 Z M 6.03125 8.90625 Q 6.25 9 6.5625 8.875 Q 6.875 8.75 6.59375 8.4375 Q 6.3125 8.125 5.4375 7.9375 L 5.4375 6.4375 Q 6.625 7.125 6.4375 6.8125 Q 6.25 6.5 5.4375 5.8125 L 5.4375 3.3125 Q 5.4375 2.625 5.53125 1.8125 Q 5.625 1 5.21875 0.15625 Q 4.8125 -0.6875 4.46875 -0.0625 Q 4.125 0.5625 3.53125 1.1875 Q 2.9375 1.8125 3.5 1.59375 Q 4.0625 1.375 4.4375 1.375 Q 4.625 1.5 4.6875 2.75 Q 4.75 4 4.8125 5.375 Q 2.625 3.75 2.21875 3.25 Q 1.8125 2.75 1.53125 3.0625 Q 1.25 3.375 1.0625 3.5625 Q 0.875 3.75 0.90625 3.8125 Q 0.9375 3.875 1.4375 4 Q 1.9375 4.125 2.6875 4.65625 Q 3.4375 5.1875 4.8125 6.0625 L 4.8125 7.75 Q 4.25 7.6875 3.71875 7.59375 Q 3.1875 7.5 2.65625 7.6875 Q 2.125 7.875 2.75 8 Q 3.375 8.125 4.8125 8.5625 Q 4.8125 9.6875 4.75 10.6875 Q 4.6875 11.6875 4.4375 12.0625 Q 4.1875 12.4375 4.4375 12.46875 Q 4.6875 12.5 5.34375 12.1875 Q 6 11.875 5.78125 11.5 Q 5.5625 11.125 5.4375 8.75 Q 5.8125 8.8125 6.03125 8.90625 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
<symbol id="g54C180954D544D3C78C9AD9E4F48A6CA" overflow="visible">
<path d="M 3.6480002 -0.16000001 C 4.88 -0.16000001 6.7520003 1.088 6.7520003 4.848 C 6.7520003 6.432 6.3680005 7.7920003 5.664 8.72 C 5.248 9.280001 4.576 9.76 3.7120001 9.76 C 2.128 9.76 0.624 7.872 0.624 4.704 C 0.624 2.992 1.1520001 1.3920001 2.032 0.512 C 2.48 0.064 3.0240002 -0.16000001 3.6480002 -0.16000001 Z M 3.7120001 9.200001 C 3.9840002 9.200001 4.2400002 9.104 4.432 8.928 C 4.9280005 8.512 5.36 7.2960005 5.36 5.1520004 C 5.36 3.68 5.3120003 2.6720002 5.0880003 1.8560001 C 4.736 0.544 3.9520001 0.4 3.6640003 0.4 C 2.176 0.4 2.016 3.1360002 2.016 4.5280004 C 2.016 8.464001 2.992 9.200001 3.7120001 9.200001 Z "/>
</symbol>
<symbol id="g58626FCFBD19425464A4FA7F304374C4" overflow="visible">
<path d="M 5.104 3.0240002 C 5.104 1.5040001 4.3040004 0.384 3.344 0.384 C 2.736 0.384 2.528 0.78400004 2.288 1.1040001 C 2.0800002 1.376 1.8080001 1.616 1.4720001 1.616 C 1.1680001 1.616 0.864 1.3440001 0.864 1.024 C 0.864 0.36800003 2.2240002 -0.17600001 3.1360002 -0.17600001 C 5.1200004 -0.17600001 6.5280004 1.296 6.5280004 3.3120003 C 6.5280004 4.8640003 5.4560003 6.2560005 3.6640003 6.2560005 C 2.976 6.2560005 2.384 6.1120005 2.0960002 6.0000005 L 2.4160001 8.672001 C 3.0080001 8.608001 3.5200002 8.528001 4.288 8.528001 C 4.768 8.528001 5.3120003 8.56 5.9680004 8.624001 L 6.2240005 9.712001 L 6.1120005 9.776 C 5.2000003 9.68 4.3360004 9.6 3.4880002 9.6 C 2.8960001 9.6 2.3200002 9.632001 1.7600001 9.68 L 1.2160001 5.072 C 2.0640001 5.392 2.6720002 5.4560003 3.2480001 5.4560003 C 4.288 5.4560003 5.104 4.768 5.104 3.0240002 Z "/>
</symbol>
<symbol id="g6F04C7AFA6F8271B5D0FF4DA7BA6C29F" overflow="visible">
<path d="M 4.3360004 3.568 C 4.544 3.568 4.768 4.0160003 4.768 4.208 C 4.768 4.368 4.704 4.5280004 4.544 4.5280004 L 1.0400001 4.5280004 C 0.84800005 4.5280004 0.64000005 4.1600003 0.64000005 3.8720002 C 0.64000005 3.7120001 0.73600006 3.568 0.88000005 3.568 Z "/>
</symbol>
<symbol id="gEF535BAC325E1F03037EDB94EE368989" overflow="visible">
<path d="M 6.88 3.5040002 L 5.552 3.5040002 L 5.552 8.176001 C 5.552 8.976001 5.552 9.6 5.584 9.728001 L 5.552 9.76 L 5.0400004 9.76 C 4.9280005 9.76 4.848 9.6640005 4.7840004 9.584001 C 3.7760003 8.352 1.9200001 5.7120004 0.448 3.4240003 C 0.49600002 3.1840003 0.592 2.752 1.072 2.752 L 4.3360004 2.752 L 4.3360004 1.2800001 C 4.3360004 0.544 3.7280002 0.544 3.0400002 0.49600002 C 2.9440002 0.4 2.9440002 0.064 3.0400002 -0.032 C 3.5520003 -0.016 4.1920004 0 4.9280005 0 C 5.552 0 6.1600003 -0.016 6.6720004 -0.032 C 6.768 0.064 6.768 0.4 6.6720004 0.49600002 C 5.8880005 0.56 5.552 0.528 5.552 1.2800001 L 5.552 2.752 L 6.656 2.752 C 6.88 2.752 7.1200004 3.0560002 7.1200004 3.2480001 C 7.1200004 3.4080002 7.056 3.5040002 6.88 3.5040002 Z M 4.3360004 8.112 L 4.3360004 3.5040002 L 1.2800001 3.5040002 C 2.0960002 4.8160005 3.232 6.6080003 4.3360004 8.112 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
<symbol id="g2CBC2880522141B53B47B0A6499DB080" overflow="visible">
<path d="M 1.984 1.0112 L 2.688 2.8672 C 2.7519999 3.0335999 2.8288 3.0848 3.136 3.0848 L 5.8367996 3.0848 L 6.5792 0.9216 C 6.7328 0.48639998 6.2464 0.43519998 5.632 0.39679998 C 5.5551996 0.32 5.5551996 0.0512 5.632 -0.0256 C 6.1056 -0.0128 6.8096 0 7.3087997 0 C 7.8335996 0 8.32 -0.0128 8.768 -0.0256 C 8.8448 0.0512 8.8448 0.32 8.768 0.39679998 C 8.2688 0.44799998 7.8335996 0.48639998 7.6159997 1.1007999 L 4.9792 8.4223995 C 4.7872 8.3071995 4.4416 8.1664 4.2752 8.1664 L 1.3695999 1.3055999 C 1.0368 0.51199996 0.65279996 0.43519998 0.0896 0.39679998 C 0.0128 0.32 0.0128 0.0512 0.0896 -0.0256 C 0.4224 -0.0128 0.8448 0 1.2287999 0 C 1.7536 0 2.3936 -0.0128 2.8672 -0.0256 C 2.944 0.0512 2.944 0.32 2.8672 0.39679998 C 2.3808 0.43519998 1.7792 0.48639998 1.984 1.0112 Z M 3.3664 3.6223998 C 3.0848 3.6223998 2.9952 3.6608 3.0463998 3.7888 L 4.3519998 7.1039996 L 4.4288 7.1039996 L 5.632 3.6223998 Z "/>
</symbol>
<symbol id="g839D86CB47DDAAE73A261EBDB55D4DA7" overflow="visible">
<path d="M 1.8944 8.256 C 1.4336 8.256 0.75519997 8.2688 0.24319999 8.2816 C 0.1664 8.2048 0.1664 7.936 0.24319999 7.8592 C 1.1392 7.8208 1.3568 7.7567997 1.3568 6.6944 L 1.3568 1.5616 C 1.3568 0.4992 1.1392 0.43519998 0.24319999 0.39679998 C 0.1664 0.32 0.1664 0.0512 0.24319999 -0.0256 C 0.7424 -0.0128 1.4208 0 1.9072 0 C 2.3808 0 2.9183998 -0.0256 4.2367997 -0.0256 C 6.0415998 -0.0256 8.4223995 0.79359996 8.4223995 3.9424 C 8.4223995 6.3231997 6.4639997 8.2816 4.0064 8.2816 C 3.0976 8.2816 2.3936 8.256 1.8944 8.256 Z M 2.4448 1.0752 L 2.4448 7.2191997 C 2.4448 7.6671996 2.8927999 7.8464 3.52 7.8464 C 6.2848 7.8464 7.1935997 5.6064 7.1935997 3.6352 C 7.1935997 1.0496 5.6447997 0.4096 3.84 0.4096 C 2.5856 0.4096 2.4448 0.6656 2.4448 1.0752 Z "/>
</symbol>
<symbol id="g83A6AA7A836EACB3652229F4716CDAF" overflow="visible">
<path d="M 5.0559998 8.076799 C 4.3136 8.1792 4.3392 8.4223995 3.0848 8.4223995 C 1.7919999 8.4223995 0.65279996 7.5648 0.65279996 6.2079997 C 0.65279996 4.864 1.7664 4.2496 2.8927999 3.8144 C 3.6608 3.52 4.608 3.1615999 4.608 1.9072 C 4.608 0.87039995 4.032 0.3328 3.008 0.3328 C 1.8176 0.3328 1.0496 0.8832 0.768 2.1504 C 0.6016 2.2015998 0.4736 2.1759999 0.34559998 2.112 C 0.39679998 1.1264 0.44799998 0.79359996 0.6016 0.1664 C 1.408 0.1664 1.7664 -0.12799999 2.9055998 -0.12799999 C 3.4815998 -0.12799999 4.032 0.0128 4.48 0.2944 C 5.2223997 0.75519997 5.6832 1.536 5.6832 2.3552 C 5.6832 3.712 4.6591997 4.3136 3.6095998 4.7104 C 2.8416 4.992 1.5616 5.4783998 1.5616 6.5536 C 1.5616 7.2704 2.2144 7.9872 2.9696 7.9872 C 4.2111998 7.9872 4.608 7.1935997 4.864 6.3487997 C 5.0048 6.3231997 5.1712 6.336 5.2864 6.4256 C 5.2352 7.04 5.184 7.3984 5.0559998 8.076799 Z "/>
</symbol>
<symbol id="g3AA24D70F4F015B80CBB2E3D4341ADF1" overflow="visible">
<path d="M 1.9072 0 L 4.6335998 0 C 4.9792 0 6.1568 -0.0256 6.1568 -0.0256 C 6.2848 0.61439997 6.4128 1.4463999 6.4895997 2.112 C 6.3616 2.1759999 6.2208 2.2015998 6.0671997 2.1759999 C 5.8111997 1.2544 5.3375998 0.4992 3.9808 0.4992 L 3.1743999 0.4992 C 2.6752 0.4992 2.4448 0.7424 2.4448 1.3952 L 2.4448 6.6944 C 2.4448 7.7567997 2.6624 7.8208 3.5584 7.8592 C 3.6352 7.936 3.6352 8.2048 3.5584 8.2816 C 2.9824 8.2688 2.3808 8.256 1.8944 8.256 C 1.4336 8.256 0.83199996 8.2688 0.24319999 8.2816 C 0.1664 8.2048 0.1664 7.936 0.24319999 7.8592 C 1.1392 7.8208 1.3568 7.7567997 1.3568 6.6944 L 1.3568 1.5616 C 1.3568 0.4992 1.1392 0.43519998 0.24319999 0.39679998 C 0.1664 0.32 0.1664 0.0512 0.24319999 -0.0256 C 0.7424 -0.0128 1.472 0 1.9072 0 Z "/>
</symbol>
<symbol id="g62FB493C725E8111415666ED52983E5C" overflow="visible">
<path d="M 1.3312 1.216 C 0.93439996 1.216 0.65279996 0.9472 0.65279996 0.5888 C 0.65279996 0.192 0.9856 0.063999996 1.216 0.0256 C 1.4591999 0 1.6768 -0.076799996 1.6768 -0.3712 C 1.6768 -0.64 1.216 -1.2287999 0.55039996 -1.3952 C 0.55039996 -1.5231999 0.576 -1.6128 0.6656 -1.7024 C 1.4336 -1.5616 2.1759999 -0.9472 2.1759999 -0.0512 C 2.1759999 0.7168 1.8432 1.216 1.3312 1.216 Z "/>
</symbol>
<symbol id="g1F6C3165F1EEE020BF61921E6B80BD99" overflow="visible">
<path d="M 2.2015998 6.6944 C 2.2015998 7.7567997 2.3936 7.8208 3.3792 7.8592 C 3.4559999 7.936 3.4559999 8.2048 3.3792 8.2816 C 2.7775998 8.2688 2.1504 8.256 1.6511999 8.256 C 1.152 8.256 0.6272 8.2688 0.12799999 8.2816 C 0.0512 8.2048 0.0512 7.936 0.12799999 7.8592 C 0.89599997 7.8208 1.1136 7.7567997 1.1136 6.6944 L 1.1136 2.9824 C 1.1136 0.3712 2.8032 -0.12799999 4.1088 -0.12799999 C 6.7328 -0.12799999 7.3599997 1.4976 7.3599997 3.776 L 7.3599997 6.6944 C 7.3599997 7.7184 7.5776 7.7696 8.3456 7.8592 C 8.4223995 7.936 8.4223995 8.2048 8.3456 8.2816 C 7.8592 8.2688 7.3343997 8.256 7.04 8.256 C 6.7711997 8.256 6.144 8.2688 5.5551996 8.2816 C 5.4783998 8.2048 5.4783998 7.936 5.5551996 7.8592 C 6.5151997 7.7696 6.7328 7.7311997 6.7328 6.6944 L 6.7328 3.5456 C 6.7328 2.112 6.5407996 0.39679998 4.3775997 0.39679998 C 3.7631998 0.39679998 3.2384 0.6272 2.8544 0.9984 C 2.2272 1.5999999 2.2015998 2.5728 2.2015998 3.4048 Z "/>
</symbol>
<symbol id="g821DF1C680AAF98A6D3A41D44CE1EAAB" overflow="visible">
<path d="M 4.48 1.5616 L 4.48 6.4512 C 4.48 7.2704 4.608 7.7567997 5.0688 7.7567997 L 5.3504 7.7567997 C 6.3104 7.7567997 6.9119997 7.424 7.1296 6.4384 C 7.2704 6.4384 7.4495997 6.4512 7.5648 6.5024 C 7.4751997 7.0912 7.4112 7.744 7.3984 8.32 C 7.3984 8.3328 7.3728 8.358399 7.3599997 8.358399 C 6.9248 8.32 5.5039997 8.256 4.4927998 8.256 L 3.392 8.256 C 2.4064 8.256 0.89599997 8.32 0.4096 8.358399 C 0.384 8.358399 0.3584 8.3328 0.3584 8.32 C 0.30719998 7.744 0.1792 7.0783997 0.038399998 6.4639997 C 0.1664 6.4128 0.32 6.3999996 0.4736 6.3999996 C 0.72959995 7.424 1.3184 7.7567997 2.1632 7.7567997 L 2.7904 7.7567997 C 3.264 7.7567997 3.392 7.2704 3.392 6.4895997 L 3.392 1.5616 C 3.392 0.4992 3.1743999 0.43519998 2.1504 0.39679998 C 2.0736 0.32 2.0736 0.0512 2.1504 -0.0256 C 2.7775998 -0.0128 3.4304 0 3.9424 0 C 4.4288 0 5.0815997 -0.0128 5.7216 -0.0256 C 5.7984 0.0512 5.7984 0.32 5.7216 0.39679998 C 4.6976 0.43519998 4.48 0.4992 4.48 1.5616 Z "/>
</symbol>
<symbol id="gC140EDAFC6E31AC0B50ADAF04BA4A77" overflow="visible">
<path d="M 4.5696 -0.12799999 C 5.8111997 -0.12799999 6.9504 0.4608 7.8208 1.5999999 C 7.7567997 1.7152 7.6671996 1.7919999 7.5263996 1.7919999 C 6.6176 0.79359996 5.7472 0.39679998 4.5568 0.39679998 C 2.8288 0.39679998 1.6384 2.3423998 1.6384 4.2111998 C 1.6384 5.312 1.9327999 6.2335997 2.3936 6.8096 C 3.0335999 7.5903997 3.776 7.9487996 4.4416 7.9487996 C 6.2079997 7.9487996 6.9119997 6.8992 7.2447996 5.7984 C 7.3984 5.7472 7.5263996 5.7855997 7.6671996 5.8624 C 7.6032 6.528 7.5136 7.1424 7.3855996 7.8464 C 6.7328 7.9104 6.1568 8.4223995 4.5824 8.4223995 C 3.4944 8.4223995 2.5856 8.0255995 1.8304 7.3343997 C 0.9856 6.5536 0.4736 5.2992 0.4736 3.968 C 0.4736 1.7407999 1.8176 -0.12799999 4.5696 -0.12799999 Z "/>
</symbol>
</defs>
</div>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g/>
</g>
</g>
<g transform="translate(40 30)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(624.3697637795275 25.8)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6E7B5CC2B72AC8CDDEB63FB023F45240" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gAF2E61F9C5EC3B2D9B048D1511B1060D" x="29.2" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g385ED71BD3F10D2170A1311D8F1A15B" x="53.12" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g2192B3D4CEA94ECF87445F8EE62E404B" x="67.44" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g8F4F96B13A9D8B27A4F3C34609AEF61C" x="80.44" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9BEF8AB47349CEAA320776726D3DB3DB" x="93.32" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g5CEF84A95ABDCAB0EDEF87161576AC77" x="117.96" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 47.800000000000004)">
<g class="typst-group">
<g>
<g transform="translate(0 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g89D0CDE21020452133A6A28D357E8121" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g14B71EE4190EC9CF4EC86C87E0E47E9A" x="8.074" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD56DD9CEC6529211EE0EE20264633A82" x="22.418" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g6724C1A826126332467C6264F812F404" x="35.134" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFFAD8ECF2B9E19A17BA2A700D6B3A275" x="48.07" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCAF57F9C910E8D30AE93F639B069896D" x="61.028" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g57ADA767123831952CB5EB6096864EC8" x="75.174" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g828464FD2C7A0947CAB01825239D7F1" x="88.506" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD56DD9CEC6529211EE0EE20264633A82" x="100.034" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1707CF3A32B022CA2D70483E817BB0E1" x="112.75" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFFAD8ECF2B9E19A17BA2A700D6B3A275" x="120.758" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g14B71EE4190EC9CF4EC86C87E0E47E9A" x="133.716" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(148.06 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(153.56 0)">
<g class="typst-group">
<g>
<g transform="translate(0 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(8.74856363850041 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.49712727700082 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(26.245690915501232 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(34.99425455400164 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(43.74281819250206 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(52.491381831002464 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(61.23994546950288 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(69.98850910800329 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(78.7370727465037 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(87.48563638500411 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(96.23420002350451 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(104.98276366200493 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(113.73132730050534 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(122.47989093900576 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(131.22845457750617 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(139.97701821600657 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(148.72558185450697 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(157.4741454930074 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.2227091315078 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(174.97127277000823 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(183.71983640850863 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.46840004700903 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(201.21696368550946 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(209.96552732400986 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.71409096251026 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(227.46265460101068 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(236.21121823951108 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.9597818780115 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(253.7083455165119 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(262.45690915501234 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(271.2054727935127 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(279.95403643201314 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(288.7026000705136 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(297.451163709014 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.19972734751445 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(314.9482909860149 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(323.69685462451537 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.44541826301577 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(341.1939819015162 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(349.9425455400167 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.6911091785171 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(367.43967281701754 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(376.188236455518 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.9368000940184 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(393.68536373251885 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(402.4339273710193 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(411.1824910095197 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(419.93105464802017 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(428.6796182865206 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(437.4281819250211 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(446.1767455635215 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(454.92530920202194 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(463.6738728405224 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(472.4224364790228 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(481.17100011752325 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(489.9195637560237 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(498.6681273945241 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(507.41669103302456 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(516.165254671525 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(524.9138183100255 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(533.6623819485259 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(542.4109455870263 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(551.1595092255268 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(559.9080728640272 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(568.6566365025276 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(577.4052001410281 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(586.1537637795285 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(745.0817637795275 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(750.5817637795275 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g9395E96C48DADE2CF7A23A407777B6BB" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 74.99)">
<g class="typst-group">
<g>
<g transform="translate(16 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8F5620C85403271F8A8A2AC29AB7F075" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g5EE22C3CF302EFF7E29425466980B287" x="11.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1741EC601D45A91DF6927753AEFC05FD" x="22.863999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1068D2C5F0B4CD106582F955D1D295A8" x="30.623999999999995" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.84 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.92251968503937 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.84503937007874 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.767559055118113 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.69007874015748 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.61259842519685 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.53511811023622 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.45763779527559 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.380157480314956 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.302677165354325 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.225196850393694 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.14771653543308 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.07023622047244 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(76.99275590551181 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(82.91527559055118 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.83779527559055 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(94.76031496062991 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(100.68283464566929 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(106.60535433070865 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(112.52787401574803 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(118.45039370078739 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.37291338582676 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.29543307086615 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(136.21795275590551 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(142.14047244094488 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(148.06299212598427 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(153.98551181102363 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(159.908031496063 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(165.83055118110235 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.75307086614174 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(177.6755905511811 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(183.59811023622046 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(189.52062992125983 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(195.44314960629922 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(201.36566929133858 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.28818897637794 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.2107086614173 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(219.1332283464567 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(225.05574803149605 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(230.9782677165354 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(236.90078740157477 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(242.82330708661416 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(248.74582677165353 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.6683464566929 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(260.5908661417323 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(266.5133858267717 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(272.4359055118111 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(278.3584251968505 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(284.28094488188987 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(290.20346456692926 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.1259842519687 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(302.0485039370081 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(307.9710236220475 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(313.8935433070869 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(319.81606299212626 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(325.73858267716565 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(331.66110236220504 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.58362204724443 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(343.5061417322839 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(349.42866141732327 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(355.35118110236266 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(361.27370078740205 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(367.19622047244144 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(373.11874015748083 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(379.0412598425202 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.96377952755967 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(390.88629921259906 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(396.80881889763845 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(402.73133858267784 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(408.6538582677172 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(414.5763779527566 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(420.498897637796 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.4214173228354 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(432.34393700787484 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(438.26645669291423 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(444.1889763779536 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(450.111496062993 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(456.0340157480324 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(461.9565354330718 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(467.8790551181112 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(473.80157480315063 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(479.72409448819 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(485.6466141732294 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(491.5691338582688 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(497.4916535433082 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(503.4141732283476 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.33669291338697 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(515.2592125984264 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(521.1817322834657 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(527.1042519685051 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(533.0267716535445 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(538.949291338584 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(544.8718110236233 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(550.7943307086628 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(556.7168503937021 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(562.6393700787415 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(568.5618897637809 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(574.4844094488203 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(580.4069291338596 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(586.3294488188991 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(592.2519685039385 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(598.1744881889779 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(604.0970078740173 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(610.0195275590567 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(615.9420472440961 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(621.8645669291354 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(627.7870866141749 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(633.7096062992143 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(639.6321259842537 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(645.5546456692931 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(651.4771653543324 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(657.3996850393719 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(663.3222047244112 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(669.2447244094507 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(675.1672440944901 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(681.0897637795294 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(750.4497637795275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="4" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 98.518)">
<g class="typst-group">
<g>
<g transform="translate(16 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5EE22C3CF302EFF7E29425466980B287" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1741EC601D45A91DF6927753AEFC05FD" x="11.184" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1068D2C5F0B4CD106582F955D1D295A8" x="18.944" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(54.16 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.921109092132714 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.842218184265429 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.763327276398144 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.684436368530857 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.60554546066357 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.52665455279629 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.447763644929005 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.368872737061714 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.289981829194424 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.211090921327134 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.13220001345985 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.05330910559256 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(76.97441819772527 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(82.89552728985798 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.81663638199069 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(94.7377454741234 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(100.65885456625611 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(106.57996365838882 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(112.50107275052153 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(118.42218184265424 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.34329093478695 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.26440002691967 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(136.18550911905237 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(142.1066182111851 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(148.0277273033178 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(153.9488363954505 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(159.8699454875832 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(165.79105457971593 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.71216367184863 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(177.63327276398135 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(183.55438185611405 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(189.47549094824677 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(195.39660004037947 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(201.3177091325122 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.2388182246449 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.1599273167776 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(219.08103640891034 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(225.00214550104303 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(230.92325459317576 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(236.84436368530845 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(242.76547277744118 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(248.68658186957387 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.6076909617066 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(260.52880005383935 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(266.4499091459721 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(272.3710182381048 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(278.2921273302375 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(284.2132364223703 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(290.134345514503 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.05545460663575 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(301.9765636987685 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(307.89767279090125 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(313.818781883034 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(319.7398909751667 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(325.6610000672995 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(331.5821091594322 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.50321825156493 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(343.42432734369766 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(349.34543643583044 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(355.26654552796316 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(361.1876546200959 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(367.1087637122286 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(373.0298728043614 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(378.9509818964941 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.87209098862684 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(390.7932000807596 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(396.71430917289234 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(402.63541826502507 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(408.5565273571578 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(414.47763644929057 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(420.3987455414233 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.319854633556 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(432.24096372568874 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(438.1620728178215 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(444.08318190995425 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(450.004291002087 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(455.9254000942197 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(461.8465091863525 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(467.7676182784852 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(473.6887273706179 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(479.6098364627507 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(485.53094555488343 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(491.45205464701615 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(497.3731637391489 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(503.29427283128166 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.2153819234144 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(515.1364910155471 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(521.0576001076798 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(526.9787091998126 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(532.8998182919453 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(538.820927384078 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(544.7420364762107 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(550.6631455683435 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(556.5842546604762 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(562.505363752609 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(568.4264728447417 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(574.3475819368745 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(580.2686910290072 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(586.1898001211399 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(592.1109092132726 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(598.0320183054054 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(603.9531273975382 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(609.8742364896709 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(615.7953455818036 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(621.7164546739364 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(627.6375637660691 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(633.5586728582018 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(639.4797819503345 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(645.4008910424674 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(651.3220001346001 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(657.2431092267328 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(663.1642183188656 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(669.0853274109983 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(675.006436503131 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(680.9275455952637 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(686.8486546873964 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(692.7697637795293 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(750.4497637795275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1B31FFD796CA2E900A884ECD4210CED3" x="4" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 122.046)">
<g class="typst-group">
<g>
<g transform="translate(16 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g49CDBE81A8A431C9159130967B9EC9E" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7079AB3C3D467A375535C421787E42DB" x="8.656" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9A2E3AAC6CC7A3D99F4D7199A710CE2" x="14.48" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD032B844D751F1F27806C7004D4F5D2F" x="22.544" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8F0641061D7822251E2A1C9000154920" x="30.432000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD032B844D751F1F27806C7004D4F5D2F" x="37.744" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8EC8620411AE7F46663E6890D2DD9166" x="45.632" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g776E4106C35A60F8D71A42812632C381" x="49.967999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8EC8620411AE7F46663E6890D2DD9166" x="54.19199999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g94C24BD726F4D930F93182C299232222" x="58.52799999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE500E45C96D97FD9DA8792F5A18C8416" x="63.58399999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1741EC601D45A91DF6927753AEFC05FD" x="75.82399999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g618B2D8299EA06ECBEE324E5599CA8A3" x="83.58399999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8EC8620411AE7F46663E6890D2DD9166" x="91.77599999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g37CC7CC101B9B1BA56FE179E8D4E6231" x="96.11199999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1FAB015722B609C2ED5D2F86E1044EFF" x="108.41599999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8EC8620411AE7F46663E6890D2DD9166" x="116.86399999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7E49B8D69C443145BC38CA6BB9F62850" x="121.19999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g94C24BD726F4D930F93182C299232222" x="127.43999999999997" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(152.49599999999998 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.944337637795275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.88867527559055 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.83301291338583 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.7773505511811 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.721688188976376 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.66602582677166 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.61036346456693 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.5547011023622 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.49903874015748 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.44337637795275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.38771401574803 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.33205165354332 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.27638929133859 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.22072692913386 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(89.16506456692913 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(95.1094022047244 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(101.05373984251969 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(106.99807748031496 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(112.94241511811023 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(118.8867527559055 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.83109039370078 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.77542803149606 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(136.71976566929135 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(142.66410330708663 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(148.6084409448819 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(154.55277858267718 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(160.49711622047244 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.44145385826772 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(172.385791496063 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(178.33012913385826 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(184.27446677165355 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(190.2188044094488 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(196.1631420472441 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.10747968503938 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(208.05181732283464 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.99615496062992 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(219.94049259842518 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(225.88483023622047 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(231.82916787401575 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(237.773505511811 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(243.7178431496063 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.66218078740155 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(255.60651842519684 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(261.5508560629921 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(267.4951937007874 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(273.4395313385827 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(279.383868976378 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.32820661417327 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(291.2725442519685 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(297.2168818897638 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(303.16121952755907 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(309.10555716535436 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(315.04989480314964 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(320.99423244094487 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(326.93857007874016 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.88290771653544 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(338.8272453543307 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(344.771582992126 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(350.71592062992124 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(356.66025826771653 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(362.6045959055118 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(368.5489335433071 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.4932711811024 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(380.4376088188976 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(386.3819464566929 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(392.3262840944882 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(398.2706217322835 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(404.21495937007876 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.159297007874 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(416.1036346456693 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(422.04797228346456 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(427.99230992125985 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(433.93664755905513 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(439.88098519685036 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(445.82532283464565 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(451.76966047244093 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.7139981102362 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(463.6583357480315 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(469.60267338582673 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(475.547011023622 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(481.4913486614173 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(487.4356862992126 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(493.3800239370079 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(499.3243615748031 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(505.2686992125984 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(511.2130368503937 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(517.157374488189 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(523.1017121259842 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(529.0460497637796 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(534.9903874015748 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.9347250393702 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(546.8790626771654 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(552.8234003149606 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(558.767737952756 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(564.7120755905512 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(570.6564132283465 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(576.6007508661418 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(582.545088503937 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(588.4894261417323 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(594.4337637795276 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(750.4497637795275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g58626FCFBD19425464A4FA7F304374C4" x="4" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 148.574)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g41BD02C814E5F1F9CC57CE5A8E90AFBE" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g48ABC493FE7862658825720022C8179D" x="11.12" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g31FD4B68C132D0D1A1E4FD30ACE8848" x="18.016" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA95D2B4A225624CA202B59CBD1BF487" x="26.671999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE307093CF7EFBC8D676E62CB78C07836" x="35.67999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDBEAA3BAB7923CD0435518D325CA6C53" x="43.855999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAACD21C62EEBAEA5F571EAFD70656C36" x="48.831999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g99884B2AD96AC7B048FEEB28FC8E4747" x="57.29599999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g20DDE86F15DD9C8B9599512790FC45E4" x="67.07199999999999" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.74399999999999 10.528)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(81.74399999999999 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.939158605174353 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.878317210348706 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.81747581552306 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.756634420697413 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.695793025871765 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.63495163104612 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.57411023622048 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.513268841394826 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.452427446569175 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.39158605174352 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.33074465691787 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.26990326209223 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.20906186726657 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.14822047244093 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(89.08737907761527 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(95.02653768278962 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(100.96569628796397 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(106.90485489313832 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(112.84401349831266 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(118.78317210348702 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.72233070866136 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.66148931383572 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(136.60064791901007 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(142.53980652418443 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(148.47896512935876 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(154.4181237345331 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(160.35728233970747 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.29644094488182 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(172.23559955005615 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(178.1747581552305 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(184.11391676040486 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(190.05307536557922 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(195.99223397075355 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(201.9313925759279 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.87055118110226 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.8097097862766 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(219.74886839145097 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(225.6880269966253 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(231.62718560179965 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(237.566344206974 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(243.50550281214836 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.4446614173227 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(255.38382002249705 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(261.32297862767143 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(267.26213723284576 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(273.20129583802014 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(279.14045444319447 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.07961304836886 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(291.0187716535432 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.9579302587175 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(302.8970888638919 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(308.8362474690662 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(314.77540607424055 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(320.71456467941493 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(326.65372328458926 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.59288188976365 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(338.532040494938 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(344.4711991001123 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(350.4103577052867 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(356.349516310461 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(362.2886749156354 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(368.2278335208097 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.16699212598405 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(380.10615073115844 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(386.04530933633276 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(391.9844679415071 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(397.9236265466815 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(403.8627851518558 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(409.8019437570302 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(415.7411023622045 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(421.68026096737884 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(427.6194195725532 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(433.55857817772755 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(439.49773678290194 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(445.43689538807627 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(451.3760539932506 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.315212598425 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(463.2543712035993 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(469.19352980877363 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(475.132688413948 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(481.07184701912234 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(487.01100562429673 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(492.95016422947106 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(498.8893228346454 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(504.82848143981977 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(510.7676400449941 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(516.7067986501685 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(522.6459572553429 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(528.5851158605172 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(534.5242744656915 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.4634330708659 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(546.4025916760403 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(552.3417502812146 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(558.2809088863889 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(564.2200674915633 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(570.1592260967377 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(576.098384701912 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(582.0375433070864 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(587.9767019122608 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(593.915860517435 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(599.8550191226094 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(605.7941777277838 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(611.7333363329581 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(617.6724949381324 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(623.6116535433068 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(629.5508121484811 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(635.4899707536555 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(641.4291293588299 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(647.3682879640043 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(653.3074465691785 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(659.2466051743529 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(665.1857637795273 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(750.4497637795275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gB81772063B54F81148CB0F3810A30A3E" x="4" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 172.102)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g54625A295C6156FB7E0CA1A81FF5B54D" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gCA97BC07D124B95C474D25CFC2493057" x="4.648000000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gBBFA548D7BC5ACA0036C5BF286E59830" x="14.378" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEABB154513753541217365D535D0C073" x="18.074" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="25.074" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gD8D2A5E78EA4643EEAAC69DB934A336F" x="28.154000000000003" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g202FAE631B7A80A660AEE76AD2161E37" x="34.664" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g176D627313BEF56D87624592E290FFD2" x="43.148" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="52.19200000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g77113E0CAAA23E0B77E89A338ACC30A4" x="59.248000000000005" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g2027E4E303C701A0DF6BD0919BBDE7B4" x="66.836" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g88B62CE1F53AC1AE1D938018DA31319" x="72.29599999999999" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9AE4831982D6CA553E49B4F41E9A233F" x="76.72" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9928BAA4F6AD9C2CD04BDE4A0594D984" x="81.928" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g5D527560B31964E4713419A527341CBD" x="89.362" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g88B62CE1F53AC1AE1D938018DA31319" x="95.354" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="99.77799999999999" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="103.57199999999999" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g77113E0CAAA23E0B77E89A338ACC30A4" x="110.62799999999999" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.71599999999995 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.195625116775658 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.391250233551316 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.586875350326974 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.782500467102633 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.978125583878292 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.173750700653947 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.36937581742961 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.565000934205266 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.760626050980925 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(51.956251167756584 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.15187628453224 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.347501401307895 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.54312651808355 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(72.73875163485921 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.93437675163487 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.13000186841053 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.32562698518619 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.52125210196185 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.71687721873751 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(103.91250233551317 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(109.10812745228883 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.30375256906449 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.49937768584014 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.69500280261579 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(129.89062791939145 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.0862530361671 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.28187815294277 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(145.47750326971843 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(150.67312838649408 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.86875350326974 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.0643786200454 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.26000373682106 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.45562885359672 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.65125397037238 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(181.84687908714804 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(187.0425042039237 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.23812932069936 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.43375443747502 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.62937955425068 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.82500467102633 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.020629787802 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.21625490457765 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(223.4118800213533 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.60750513812897 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(233.80313025490463 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(238.9987553716803 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.19438048845595 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.39000560523158 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.58563072200724 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(259.7812558387829 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(264.97688095555856 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(270.1725060723342 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.36813118910993 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.5637563058856 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.7593814226613 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(290.95500653943697 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.1506316562127 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(301.34625677298834 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.54188188976406 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(311.7375070065397 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(316.93313212331543 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.1287572400911 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(327.3243823568668 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.52000747364247 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.7156325904182 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(342.91125770719384 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(348.10688282396956 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(353.3025079407452 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.4981330575209 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(363.6937581742966 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(368.88938329107225 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.08500840784797 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(379.2806335246236 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.47625864139934 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(389.671883758175 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(394.8675088749507 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(400.0631339917264 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.2587591085021 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.45438422527775 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(415.65000934205347 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(420.8456344588291 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.04125957560484 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(431.2368846923805 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(436.4325098091562 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.6281349259319 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(446.8237600427076 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(452.01938515948325 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.21501027625897 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(462.4106353930346 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(467.60626050981034 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(472.801885626586 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(477.9975107433617 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.1931358601374 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(488.3887609769131 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(493.58438609368875 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(498.78001121046447 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(503.9756363272401 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.17126144401584 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(514.3668865607915 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(519.5625116775672 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(524.7581367943429 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(529.9537619111186 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.1493870278942 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.3450121446699 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(545.5406372614457 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(550.7362623782213 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(555.931887494997 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.1275126117727 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(566.3231377285484 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(571.5187628453241 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(576.7143879620997 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(581.9100130788754 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(587.1056381956511 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(592.3012633124268 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(597.4968884292025 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(602.6925135459782 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(607.8881386627538 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(613.0837637795296 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(751.8797637795276 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g68885674EB6A8B1A6039D4F45B463C56" x="3.5" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 194.314)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g54625A295C6156FB7E0CA1A81FF5B54D" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gCA97BC07D124B95C474D25CFC2493057" x="4.648000000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gBBFA548D7BC5ACA0036C5BF286E59830" x="14.378" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEABB154513753541217365D535D0C073" x="18.074" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="25.074" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9696EE00168B299790D79B47B78C5F18" x="28.154000000000003" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g202FAE631B7A80A660AEE76AD2161E37" x="34.664" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gF73CF51A640CD9E8903A9C4D4B743CCF" x="43.148" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g634FF9E9D0A0144E2AFDD807D5ECB7D0" x="49.938" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g3649D621BC998C9216AD40BBEFAC3AB1" x="56.196000000000005" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9AE4831982D6CA553E49B4F41E9A233F" x="62.59400000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g5D527560B31964E4713419A527341CBD" x="67.69000000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gD0DD0C2B056F25673B3EED0135505F92" x="73.68200000000002" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.71399999999998 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.20068611023622 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.40137222047244 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.60205833070866 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.80274444094488 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(26.0034305511811 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.204116661417316 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.404802771653536 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.605488881889755 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.806174992125975 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(52.006861102362194 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.207547212598406 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.408233322834626 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.60891943307085 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(72.80960554330707 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(78.01029165354329 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.21097776377951 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.41166387401573 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.61234998425195 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.81303609448817 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(104.01372220472439 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(109.21440831496061 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.41509442519681 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.61578053543303 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.81646664566925 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.0171527559055 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.2178388661417 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.41852497637794 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(145.61921108661414 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(150.81989719685035 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(156.02058330708658 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.2212694173228 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.42195552755902 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.62264163779523 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.82332774803146 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(182.02401385826767 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(187.2246999685039 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.4253860787401 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.62607218897634 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.82675829921254 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(208.02744440944878 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.22813051968498 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.42881662992122 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(223.62950274015742 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.83018885039363 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(234.03087496062986 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(239.23156107086606 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.4322471811023 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.6329332913385 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.83361940157474 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(260.034305511811 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(265.23499162204723 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(270.43567773228347 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.6363638425197 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.837049952756 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(286.0377360629922 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(291.23842217322846 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.4391082834647 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(301.639794393701 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.8404805039372 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(312.04116661417345 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(317.2418527244097 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.4425388346459 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(327.6432249448822 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.84391105511844 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(338.0445971653547 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(343.2452832755909 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(348.4459693858272 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(353.64665549606343 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.84734160629966 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(364.0480277165359 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(369.2487138267722 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.4493999370084 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(379.65008604724466 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.8507721574809 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(390.0514582677172 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(395.2521443779534 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(400.45283048818965 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.6535165984259 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.8542027086621 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(416.0548888188984 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(421.25557492913464 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.4562610393709 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(431.6569471496071 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(436.8576332598434 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(442.05831937007963 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(447.25900548031586 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(452.4596915905521 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.6603777007884 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(462.8610638110246 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(468.06174992126085 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(473.2624360314971 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(478.4631221417334 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.6638082519696 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(488.86449436220585 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(494.0651804724421 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(499.2658665826783 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(504.4665526929146 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.66723880315084 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(514.8679249133871 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(520.0686110236234 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(525.2692971338595 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(530.4699832440957 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.670669354332 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.8713554645681 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(546.0720415748043 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(551.2727276850404 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(556.4734137952767 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.6740999055129 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(566.874786015749 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(572.0754721259852 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(577.2761582362214 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(582.4768443464576 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(587.6775304566938 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(592.87821656693 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(598.0789026771662 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(603.2795887874024 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(608.4802748976385 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(613.6809610078748 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(618.8816471181109 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(624.0823332283471 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(629.2830193385834 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(634.4837054488195 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(639.6843915590557 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(644.8850776692918 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(650.0857637795281 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(751.8797637795275 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gB1BEBEB6281B0C94AE56C4BB0BF6ED0C" x="3.5" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 216.526)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g54625A295C6156FB7E0CA1A81FF5B54D" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gCA97BC07D124B95C474D25CFC2493057" x="4.648000000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gBBFA548D7BC5ACA0036C5BF286E59830" x="14.378" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEABB154513753541217365D535D0C073" x="18.074" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="25.074" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gD0485EF23018DAF4BFC69AAD15075193" x="28.154000000000003" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g202FAE631B7A80A660AEE76AD2161E37" x="34.664" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g176D627313BEF56D87624592E290FFD2" x="43.148" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gD0DD0C2B056F25673B3EED0135505F92" x="52.19200000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="59.72400000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="66.87800000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g2027E4E303C701A0DF6BD0919BBDE7B4" x="73.93400000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="79.394" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g77113E0CAAA23E0B77E89A338ACC30A4" x="83.188" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEABB154513753541217365D535D0C073" x="90.776" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g77113E0CAAA23E0B77E89A338ACC30A4" x="101.276" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g634FF9E9D0A0144E2AFDD807D5ECB7D0" x="108.86399999999999" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="115.12199999999999" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEABB154513753541217365D535D0C073" x="118.91599999999998" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gD0DD0C2B056F25673B3EED0135505F92" x="125.91599999999998" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gC80234271A0A022352A099322F0FCD32" x="133.44799999999998" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="140.48999999999998" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9AE4831982D6CA553E49B4F41E9A233F" x="147.546" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g2027E4E303C701A0DF6BD0919BBDE7B4" x="152.754" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(175.714 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.1979427869681425 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.395885573936285 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.593828360904427 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.79177114787257 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.98971393484071 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.18765672180885 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.38559950877699 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.58354229574513 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.781485082713274 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(51.979427869681416 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.17737065664955 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.37531344361769 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.57325623058584 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(72.77119901755398 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.96914180452212 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.16708459149027 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.36502737845841 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.56297016542655 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.76091295239469 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(103.95885573936283 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(109.15679852633097 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.3547413132991 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.55268410026724 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.75062688723538 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(129.94856967420355 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.14651246117168 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.34445524813984 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(145.54239803510796 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(150.7403408220761 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.93828360904425 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.13622639601238 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.33416918298053 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.53211196994866 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.73005475691681 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(181.92799754388494 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(187.1259403308531 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.32388311782123 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.52182590478938 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.7197686917575 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.91771147872566 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.1156542656938 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.31359705266195 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(223.51153983963007 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.7094826265982 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(233.90742541356636 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(239.10536820053449 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.30331098750264 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.50125377447077 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.69919656143892 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(259.8971393484071 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(265.09508213537526 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(270.2930249223434 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.4909677093116 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.6889104962798 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.88685328324794 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(291.0847960702161 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.28273885718426 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(301.48068164415247 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.6786244311206 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(311.8765672180888 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(317.07451000505694 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.2724527920251 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(327.4703955789933 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.66833836596146 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.8662811529296 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(343.0642239398978 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(348.262166726866 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(353.46010951383414 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.6580523008023 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(363.85599508777045 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(369.05393787473866 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.2518806617068 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(379.449823448675 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.64776623564313 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(389.84570902261135 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(395.0436518095795 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(400.24159459654766 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.4395373835158 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.63748017048397 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(415.8354229574522 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(421.03336574442034 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.2313085313885 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(431.42925131835665 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(436.62719410532486 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.825136892293 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(447.0230796792612 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(452.22102246622933 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.41896525319754 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(462.6169080401657 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(467.81485082713385 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(473.012793614102 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(478.2107364010702 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.4086791880384 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(488.60662197500653 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(493.8045647619747 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(499.00250754894284 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(504.20045033591106 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.3983931228792 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(514.5963359098474 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(519.7942786968156 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(524.9922214837837 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(530.1901642707519 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.38810705772 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.5860498446882 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(545.7839926316564 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(550.9819354186245 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(556.1798782055928 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.3778209925609 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(566.5757637795291 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(745.3697637795276 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD8D2A5E78EA4643EEAAC69DB934A336F" x="3.5" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gC9680074409574DDF948104B0C55D755" x="10.010000000000002" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 241.738)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g985B950D50769631420A9A59AEA7CEFC" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g20DDE86F15DD9C8B9599512790FC45E4" x="4.752" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3E944C953D169E97A30360D928248E70" x="15.424" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE307093CF7EFBC8D676E62CB78C07836" x="22.8" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA95D2B4A225624CA202B59CBD1BF487" x="30.976" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gBAC0ED7F2DB725071CE720AF8BC15D72" x="39.824" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDA675C10B642A458CD97A11D372FF5DA" x="48.592" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g20DDE86F15DD9C8B9599512790FC45E4" x="56.224" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDA675C10B642A458CD97A11D372FF5DA" x="66.896" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2F3EA0F52D7EBFDBD1E9205C07C62175" x="74.528" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAACD21C62EEBAEA5F571EAFD70656C36" x="84.16000000000001" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(92.62400000000001 10.528)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(96.62400000000001 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.952460775736366 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.904921551472732 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.8573823272091 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.809843102945464 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.762303878681834 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.7147646544182 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.667225430154566 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.61968620589093 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.5721469816273 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.52460775736367 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.47706853310004 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.4295293088364 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.38199008457275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.33445086030912 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(89.28691163604547 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(95.23937241178183 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(101.1918331875182 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(107.14429396325455 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(113.09675473899091 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.04921551472728 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(125.00167629046364 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.95413706620002 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(136.90659784193636 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(142.85905861767273 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(148.8115193934091 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(154.76398016914544 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(160.7164409448818 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.66890172061818 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(172.62136249635452 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(178.5738232720909 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(184.52628404782726 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(190.4787448235636 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(196.43120559929997 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.38366637503634 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(208.33612715077268 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(214.28858792650905 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(220.24104870224542 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(226.19350947798176 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(232.14597025371813 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(238.0984310294545 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.05089180519084 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(250.0033525809272 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(255.95581335666358 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(261.9082741324 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(267.86073490813635 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(273.8131956838727 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(279.76565645960915 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.7181172353455 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(291.6705780110819 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(297.6230387868183 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(303.5754995625547 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(309.52796033829105 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(315.4804211140275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(321.43288188976385 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(327.3853426655002 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(333.33780344123664 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(339.290264216973 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(345.2427249927094 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(351.1951857684458 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(357.1476465441822 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(363.10010731991855 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(369.052568095655 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(375.00502887139135 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(380.9574896471278 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(386.90995042286414 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(392.8624111986005 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(398.81487197433694 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(404.7673327500733 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.7197935258097 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(416.6722543015461 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(422.6247150772825 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(428.57717585301884 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(434.52963662875527 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(440.48209740449164 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(446.434558180228 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(452.38701895596444 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(458.3394797317008 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(464.2919405074372 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(470.2444012831736 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(476.19686205890997 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(482.14932283464634 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(488.10178361038277 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(494.05424438611914 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(500.0067051618555 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(505.95916593759193 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(511.9116267133283 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(517.8640874890647 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(523.816548264801 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(529.7690090405373 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.7214698162736 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(541.6739305920099 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(547.6263913677462 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(553.5788521434827 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(559.531312919219 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(565.4837736949553 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(571.4362344706916 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(577.3886952464279 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(583.3411560221642 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(589.2936167979007 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(595.246077573637 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(601.1985383493733 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(607.1509991251096 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(613.1034599008459 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(619.0559206765822 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(625.0083814523186 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(630.960842228055 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(636.9133030037913 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(642.8657637795276 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(743.0097637795276 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="4" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="11.440000000000001" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 265.266)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g176D627313BEF56D87624592E290FFD2" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="9.044" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g6D1F08816BC4457F813BBA2B6CEC4900" x="16.1" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gC80234271A0A022352A099322F0FCD32" x="27.160000000000004" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="34.062000000000005" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g77113E0CAAA23E0B77E89A338ACC30A4" x="37.856" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g634FF9E9D0A0144E2AFDD807D5ECB7D0" x="45.444" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEF9FD20106DF1BE872ABEE235642DEFC" x="51.800000000000004" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g3B79D8E86480C20827A395F926C73BE1" x="62.384" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="72.842" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g88B62CE1F53AC1AE1D938018DA31319" x="76.636" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gD0DD0C2B056F25673B3EED0135505F92" x="81.06" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gE0345006C183149AF583AF5DE80FA9FE" x="92.092" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g7E303FA8E2D87EE13FB94A41DEF3418E" x="96.586" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gBB75D665A04FFE2A82A14DE003A19CAC" x="105.714" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.00400000000002 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.188862404911251 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.377724809822501 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.566587214733753 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.755449619645002 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.944312024556258 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.13317442946751 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.322036834378764 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.51089923929001 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.69976164420127 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(51.88862404911252 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.07748645402377 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.266348858935025 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.45521126384628 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(72.64407366875753 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.83293607366876 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.02179847858001 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.21066088349126 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.3995232884025 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.58838569331375 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(103.777248098225 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(108.96611050313624 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.15497290804748 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.34383531295873 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.53269771786998 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(129.72156012278123 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(134.9104225276925 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.09928493260375 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(145.28814733751503 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(150.47700974242628 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.66587214733752 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(160.8547345522488 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.04359695716005 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.23245936207132 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.42132176698257 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(181.61018417189385 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(186.7990465768051 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(191.98790898171634 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.17677138662762 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.36563379153887 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.55449619645015 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(212.7433586013614 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(217.93222100627264 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(223.12108341118392 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.30994581609517 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(233.49880822100644 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(238.6876706259177 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(243.87653303082897 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.06539543574021 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.25425784065146 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(259.4431202455627 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(264.63198265047396 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(269.8208450553852 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.0097074602964 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.1985698652076 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.38743227011884 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(290.5762946750301 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(295.76515707994133 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(300.95401948485255 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.14288188976377 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(311.331744294675 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(316.52060669958627 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(321.7094691044975 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(326.8983315094087 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.0871939143199 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.27605631923115 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(342.4649187241424 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(347.65378112905364 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(352.84264353396486 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.0315059388761 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(363.2203683437873 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(368.4092307486986 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(373.5980931536098 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(378.786955558521 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(383.97581796343223 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(389.1646803683435 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(394.35354277325473 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(399.54240517816595 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(404.73126758307717 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(409.9201299879884 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(415.10899239289967 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(420.2978547978109 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(425.4867172027221 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(430.6755796076333 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(435.86444201254454 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.0533044174558 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(446.24216682236704 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(451.43102922727826 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(456.6198916321895 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(461.8087540371007 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(466.997616442012 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(472.1864788469232 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(477.3753412518344 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(482.56420365674563 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(487.75306606165685 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(492.94192846656813 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(498.13079087147935 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(503.31965327639057 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(508.5085156813018 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(513.697378086213 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(518.8862404911242 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(524.0751028960356 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(529.2639653009469 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(534.4528277058581 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(539.6416901107694 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(544.8305525156807 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(550.019414920592 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(555.2082773255033 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(560.3971397304146 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(565.5860021353259 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(570.7748645402371 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(575.9637269451484 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(581.1525893500598 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(586.341451754971 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(591.5303141598823 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(596.7191765647935 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(601.9080389697049 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(607.0969013746162 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(612.2857637795274 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(745.3697637795276 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD8D2A5E78EA4643EEAAC69DB934A336F" x="3.5" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9696EE00168B299790D79B47B78C5F18" x="10.010000000000002" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 443.56299212598424)">
<g class="typst-group">
<g/>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="g6E7B5CC2B72AC8CDDEB63FB023F45240" overflow="visible">
<path d="M 27.76 13.16 C 27.76 21.119999 21.84 26.32 14.5199995 26.32 C 10.5199995 26.32 7.04 24.6 4.72 21.84 C 2.6399999 19.359999 1.48 16.039999 1.48 12.36 C 1.48 4.44 7.7599998 -0.39999998 14.559999 -0.39999998 C 18.68 -0.39999998 22.039999 1.0799999 24.32 3.56 C 26.519999 5.96 27.76 9.24 27.76 13.16 Z M 14.04 24.64 C 18.32 24.64 21.72 20.439999 21.72 12.32 C 21.72 5.68 19.4 1.28 15.36 1.28 C 10.96 1.28 7.52 5.64 7.52 13.16 C 7.52 21.32 10.48 24.64 14.04 24.64 Z "/>
</symbol>
<symbol id="gAF2E61F9C5EC3B2D9B048D1511B1060D" overflow="visible">
<path d="M 20.4 5.3199997 L 20.4 12.24 C 20.4 15.599999 20.48 15.12 20.48 16.08 C 20.48 16.76 20.32 17.199999 20.08 17.44 C 19.359999 17.4 18.56 17.359999 17.8 17.359999 C 16.68 17.359999 14.08 17.4 12.5199995 17.44 C 12.28 17.199999 12.28 16.32 12.5199995 16.08 C 14.559999 15.88 15.2 15.599999 15.2 12.24 L 15.2 4.8399997 C 15.2 4.44 15.2 4.04 15.24 3.6399999 C 13.599999 2.6399999 12.28 2.56 11.559999 2.56 C 9.96 2.56 8.76 2.76 8.76 5.56 L 8.76 12.24 C 8.76 15.599999 8.84 15.12 8.84 16.08 C 8.84 16.76 8.679999 17.199999 8.44 17.44 C 7.72 17.4 6.8799996 17.359999 6.16 17.359999 C 4.12 17.359999 2.6 17.4 0.88 17.44 C 0.64 17.199999 0.64 16.32 0.88 16.08 C 2.72 16 3.56 15.599999 3.56 12.24 L 3.56 6 C 3.56 1.76 5.24 -0.39999998 8.679999 -0.39999998 C 10.12 -0.39999998 13.04 0.76 15.36 2.04 C 15.44 1.04 15.5199995 0.28 15.5199995 0.28 C 15.559999 -0.19999999 15.88 -0.39999998 16.44 -0.39999998 C 17.92 0 20.32 0.56 23.08 0.91999996 C 23.16 1.16 23.08 1.9599999 23 2.2 C 20.84 2.3999999 20.4 3.04 20.4 5.3199997 Z "/>
</symbol>
<symbol id="g385ED71BD3F10D2170A1311D8F1A15B" overflow="visible">
<path d="M 2.52 17.359999 C 1.9599999 17.359999 1.36 17.199999 0.84 16.76 L 0.84 15.599999 C 0.84 15.4 0.88 15.36 1.04 15.36 L 3.6399999 15.36 C 3.56 11.32 3.52 6.2 3.52 4.2 C 3.52 2.8 3.8799999 1.4399999 4.72 0.71999997 C 5.64 -0.04 7.08 -0.39999998 8.04 -0.39999998 C 10.24 -0.39999998 12.679999 0.71999997 13.48 1.8399999 C 13.48 2.32 13.24 2.56 12.759999 2.96 C 12.24 2.56 11.24 2.3999999 10.48 2.3999999 C 9.599999 2.3999999 8.72 3.08 8.72 5.08 C 8.72 7.08 8.679999 11.36 8.679999 15.36 L 12.719999 15.36 C 13.12 15.36 13.679999 15.5199995 13.679999 15.88 L 13.679999 17.119999 C 13.679999 17.279999 13.559999 17.359999 13.36 17.359999 L 8.679999 17.359999 L 8.72 18.72 C 8.8 21.4 8.92 23.24 8.92 23.24 C 8.92 23.48 8.8 23.6 8.599999 23.6 C 8.32 23.6 6.8399997 23.16 6.2 22.88 C 5.52 22.6 4.36 22.359999 4.08 22 C 3.8 21.64 3.6399999 20.56 3.6399999 17.359999 Z "/>
</symbol>
<symbol id="g2192B3D4CEA94ECF87445F8EE62E404B" overflow="visible">
<path d="M 4 5.08 C 4 1.76 3.36 1.4 0.91999996 1.28 C 0.68 1.04 0.68 0.16 0.91999996 -0.08 C 2.6 -0.04 4.4 0 6.6 0 C 8.8 0 10.559999 -0.04 12.28 -0.08 C 12.5199995 0.16 12.5199995 1.04 12.28 1.28 C 9.84 1.4 9.2 1.76 9.2 5.08 L 9.2 23.32 C 9.2 25.92 9.32 27.4 9.32 27.4 C 9.32 27.76 9.04 27.92 8.679999 27.92 C 7.2 27.439999 4 27 1.16 26.88 C 1.04 26.4 1.0799999 25.96 1.28 25.599998 C 3.8 25.4 4 25.359999 4 22.6 Z "/>
</symbol>
<symbol id="g8F4F96B13A9D8B27A4F3C34609AEF61C" overflow="visible">
<path d="M 9.28 4.88 L 9.28 12.84 C 9.28 14.839999 9.44 17.08 9.44 17.08 C 9.44 17.52 9.08 17.76 8.5199995 17.76 C 7.3999996 17.32 4.16 17 1.4 16.64 C 1.3199999 16.4 1.4 15.599999 1.48 15.36 C 3.6799998 15.16 4.08 14.839999 4.08 12.559999 L 4.08 4.88 C 4.08 1.56 3.6399999 1.48 1.1999999 1.28 C 0.96 1.04 0.96 0.16 1.1999999 -0.08 C 2.8799999 -0.04 4.56 0 6.68 0 C 8.8 0 10.44 -0.04 12.16 -0.08 C 12.4 0.16 12.4 1.04 12.16 1.28 C 9.719999 1.4399999 9.28 1.56 9.28 4.88 Z M 3.8799999 23.84 C 3.8799999 22.519999 4.8399997 21.199999 6.44 21.199999 C 8.24 21.199999 9.28 22.64 9.28 23.68 C 9.28 24.88 8.36 26.32 6.68 26.32 C 4.7999997 26.32 3.8799999 25.039999 3.8799999 23.84 Z "/>
</symbol>
<symbol id="g9BEF8AB47349CEAA320776726D3DB3DB" overflow="visible">
<path d="M 9.12 4.88 L 9.12 12.92 C 10.719999 14 12.32 14.799999 13.04 14.799999 C 14.639999 14.799999 15.839999 14.08 15.839999 11.8 L 15.839999 5.12 C 15.839999 1.76 15.2 1.4 13.559999 1.28 C 13.32 1.04 13.32 0.16 13.559999 -0.08 C 15.24 -0.04 16.52 0 18.44 0 C 20.64 0 22.4 -0.04 24.119999 -0.08 C 24.359999 0.16 24.359999 1.04 24.119999 1.28 C 21.68 1.4 21.039999 1.76 21.039999 5.12 L 21.039999 11.36 C 21.039999 15.759999 19.16 17.76 15.719999 17.76 C 14.12 17.76 11.28 16 9.08 14.48 C 8.96 15.88 8.8 17.08 8.8 17.08 C 8.76 17.56 8.44 17.76 7.8799996 17.76 C 6.3999996 17.359999 4 16.8 1.24 16.44 C 1.16 16.199999 1.24 15.4 1.3199999 15.16 C 3.52 14.96 3.9199998 14.639999 3.9199998 12.36 L 3.9199998 4.88 C 3.9199998 1.56 3.48 1.48 1.04 1.28 C 0.79999995 1.04 0.79999995 0.16 1.04 -0.08 C 2.72 -0.04 4.4 0 6.52 0 C 8.36 0 9.48 -0.04 11.2 -0.08 C 11.44 0.16 11.44 1.04 11.2 1.28 C 9.5199995 1.4399999 9.12 1.56 9.12 4.88 Z "/>
</symbol>
<symbol id="g5CEF84A95ABDCAB0EDEF87161576AC77" overflow="visible">
<path d="M 17.24 5.16 C 15.599999 3.48 13.44 3.04 11.92 3.04 C 8.8 3.04 6.8799996 4.8399997 6.8799996 8.76 C 6.8799996 9.04 6.92 9.2 6.92 9.4 L 16.52 9.4 C 17.48 9.4 17.68 10.08 17.68 10.639999 C 17.68 14.04 16.359999 17.76 10.48 17.76 C 6.2799997 17.76 1.48 14.04 1.48 7.9199996 C 1.48 5.6 2.32 3.1599998 4.04 1.5999999 C 5.56 0.24 7.52 -0.39999998 10.36 -0.39999998 C 13.12 -0.39999998 15.839999 1 17.84 3.9199998 C 17.84 4.44 17.64 5.16 17.24 5.16 Z M 7.08 11 C 7.12 12.4 7.3199997 13.92 7.8799996 14.719999 C 8.5199995 15.679999 9.599999 16.08 10.04 16.08 C 11.12 16.08 12.599999 15.04 12.599999 11.84 C 12.599999 11.599999 12.599999 11.08 12.5199995 11 Z "/>
</symbol>
<symbol id="g89D0CDE21020452133A6A28D357E8121" overflow="visible">
<path d="M 2.508 11.506 L 2.508 2.684 C 2.508 0.858 1.892 0.77 0.682 0.704 C 0.462 0.572 0.462 0.088 0.682 -0.044 C 1.562 -0.022 3.19 0 4.07 0 C 4.95 0 6.534 -0.022 7.414 -0.044 C 7.634 0.088 7.634 0.572 7.414 0.704 C 6.204 0.77 5.588 0.858 5.588 2.684 L 5.588 11.506 C 5.588 13.332 6.204 13.42 7.414 13.486 C 7.634 13.618 7.634 14.102 7.414 14.234 C 6.534 14.212 4.95 14.19 4.07 14.19 C 3.19 14.19 1.562 14.212 0.682 14.234 C 0.462 14.102 0.462 13.618 0.682 13.486 C 1.892 13.42 2.508 13.332 2.508 11.506 Z "/>
</symbol>
<symbol id="g14B71EE4190EC9CF4EC86C87E0E47E9A" overflow="visible">
<path d="M 8.976 0.704 C 9.394 0.154 9.856 -0.264 9.856 -0.264 C 10.626 -0.264 11.682 -0.198 12.078 0 C 12.078 0 11.968 1.562 11.968 2.244 L 11.968 7.436 C 11.968 9.262 12.21 9.306 13.552 9.416 C 13.684 9.548 13.684 10.032 13.552 10.164 C 12.892 10.142 12.1 10.12 11.44 10.12 C 10.78 10.12 9.79 10.142 9.13 10.164 C 8.998 10.032 8.998 9.548 9.13 9.416 C 10.472 9.328 10.714 9.262 10.714 7.436 L 10.714 3.322 C 10.714 2.992 10.626 2.97 10.406 3.2779999 L 5.368 10.12 L 0.924 10.164 C 0.792 10.01 0.792 9.57 0.924 9.416 C 1.782 9.394 2.112 9.042 2.376 8.712 L 2.376 2.684 C 2.376 0.858 2.134 0.792 0.792 0.704 C 0.65999997 0.572 0.65999997 0.088 0.792 -0.044 C 1.452 -0.022 2.442 0 3.102 0 C 3.762 0 4.554 -0.022 5.2139997 -0.044 C 5.346 0.088 5.346 0.572 5.2139997 0.704 C 3.872 0.814 3.6299999 0.858 3.6299999 2.684 L 3.6299999 6.864 C 3.6299999 7.876 3.696 7.788 4.114 7.216 C 4.136 7.194 4.18 7.15 4.202 7.106 Z "/>
</symbol>
<symbol id="gD56DD9CEC6529211EE0EE20264633A82" overflow="visible">
<path d="M 7.876 2.9259999 L 7.876 7.15 C 7.876 8.998 7.9639997 9.24 8.932 9.24 C 10.604 9.24 10.868 8.69 11.242 6.974 C 11.484 6.974 11.901999 6.996 12.1 7.084 C 11.946 8.096 11.8359995 9.24 11.814 10.23 C 11.814 10.252 11.7699995 10.296 11.748 10.296 C 11 10.23 9.24 10.12 7.502 10.12 L 5.2799997 10.12 C 3.586 10.12 2.09 10.23 1.254 10.296 C 1.21 10.296 1.166 10.252 1.166 10.23 C 1.078 9.24 0.858 8.074 0.616 7.018 C 0.83599997 6.93 1.21 6.908 1.474 6.908 C 1.914 8.668 2.156 9.24 3.608 9.24 C 4.906 9.24 5.104 8.888 5.104 7.216 L 5.104 2.9259999 C 5.104 1.1 4.906 0.77 3.146 0.704 C 3.014 0.572 3.014 0.088 3.146 -0.044 C 4.224 -0.022 5.302 0 6.446 0 C 7.612 0 8.734 -0.022 9.834 -0.044 C 9.966 0.088 9.966 0.572 9.834 0.704 C 8.074 0.77 7.876 1.1 7.876 2.9259999 Z "/>
</symbol>
<symbol id="g6724C1A826126332467C6264F812F404" overflow="visible">
<path d="M 5.368 2.794 L 5.368 4.554 C 5.588 4.576 5.9179997 4.554 6.292 4.356 C 6.402 4.29 6.5559998 4.092 6.71 3.85 L 8.118 1.606 C 8.734 0.682 9.834 -0.198 11.066 -0.198 C 11.88 -0.198 12.518 -0.154 12.716 -0.044 C 12.782 0.088 12.782 0.506 12.694 0.65999997 C 12.1 0.792 11.44 1.3199999 11 2.002 L 9.35 4.532 C 9.284 4.642 9.196 4.752 9.174 4.84 C 10.846 5.368 11.572 6.468 11.572 7.59 C 11.572 8.734 10.714 10.274 7.59 10.274 C 6.776 10.274 4.62 10.12 4.004 10.12 C 2.794 10.12 1.826 10.142 0.88 10.164 C 0.748 10.032 0.748 9.548 0.88 9.416 C 2.222 9.35 2.574 9.152 2.574 7.3259997 L 2.574 2.794 C 2.574 0.968 2.222 0.77 0.88 0.704 C 0.748 0.572 0.748 0.088 0.88 -0.044 C 1.804 -0.022 2.794 0 4.004 0 C 5.148 0 5.962 -0.022 6.6879997 -0.044 C 6.82 0.088 6.82 0.572 6.6879997 0.704 C 5.786 0.792 5.368 0.968 5.368 2.794 Z M 5.368 9.306 C 5.72 9.394 6.424 9.416 6.732 9.416 C 7.942 9.416 8.492 8.602 8.492 7.216 C 8.492 5.39 7.172 5.2799997 5.368 5.2799997 Z "/>
</symbol>
<symbol id="gFFAD8ECF2B9E19A17BA2A700D6B3A275" overflow="visible">
<path d="M 12.122 5.17 C 12.122 8.712 9.702 10.4279995 6.402 10.4279995 C 3.322 10.4279995 0.83599997 8.382 0.83599997 4.884 C 0.83599997 1.3199999 3.454 -0.22 6.424 -0.22 C 9.68 -0.22 12.122 1.562 12.122 5.17 Z M 6.358 9.548 C 8.514 9.548 9.042 8.14 9.042 4.862 C 9.042 2.068 8.316 0.65999997 6.534 0.65999997 C 4.62 0.65999997 3.916 2.112 3.916 5.148 C 3.916 8.448 4.708 9.548 6.358 9.548 Z "/>
</symbol>
<symbol id="gCAF57F9C910E8D30AE93F639B069896D" overflow="visible">
<path d="M 4.004 0 C 5.082 0 6.094 -0.044 7.854 -0.044 C 10.78 -0.044 13.1779995 0.99 13.1779995 4.84 C 13.1779995 6.512 12.496 8.074 11.22 9.042 C 10.23 9.79 8.888 10.164 7.3259997 10.164 C 6.732 10.164 5.17 10.142 4.004 10.12 C 2.794 10.12 1.826 10.142 0.88 10.164 C 0.748 10.032 0.748 9.548 0.88 9.416 C 2.222 9.35 2.574 9.152 2.574 7.3259997 L 2.574 2.794 C 2.574 0.968 2.222 0.77 0.88 0.704 C 0.748 0.572 0.748 0.088 0.88 -0.044 C 1.804 -0.022 2.904 0 4.004 0 Z M 5.434 1.914 L 5.434 8.558 C 5.434 9.108 5.83 9.284 6.6879997 9.284 C 9.988 9.284 10.098 6.886 10.098 4.466 C 10.098 1.298 9.284 0.83599997 7.3259997 0.83599997 C 5.654 0.83599997 5.434 1.298 5.434 1.914 Z "/>
</symbol>
<symbol id="g57ADA767123831952CB5EB6096864EC8" overflow="visible">
<path d="M 10.076 7.304 L 10.076 4.268 C 10.076 2.508 9.878 0.704 7.3259997 0.704 C 5.544 0.704 4.884 2.112 4.884 3.9819999 L 4.884 7.304 C 4.884 9.152 5.236 9.35 6.578 9.416 C 6.71 9.548 6.71 10.032 6.578 10.164 C 5.654 10.142 4.664 10.12 3.454 10.12 C 2.244 10.12 1.276 10.142 0.32999998 10.164 C 0.198 10.032 0.198 9.548 0.32999998 9.416 C 1.6719999 9.35 2.024 9.152 2.024 7.304 L 2.024 3.41 C 2.024 0.198 4.62 -0.22 6.952 -0.22 C 10.4939995 -0.22 11.176 1.65 11.176 4.444 L 11.176 7.304 C 11.176 9.152 11.66 9.35 13.002 9.416 C 13.134 9.548 13.134 10.032 13.002 10.164 C 12.408 10.142 11.132 10.12 10.67 10.12 C 10.142 10.12 9.196 10.142 8.25 10.164 C 8.118 10.032 8.118 9.548 8.25 9.416 C 9.592 9.35 10.076 9.152 10.076 7.304 Z "/>
</symbol>
<symbol id="g828464FD2C7A0947CAB01825239D7F1" overflow="visible">
<path d="M 6.798 10.4279995 C 3.74 10.4279995 1.012 8.844 1.012 4.928 C 1.012 2.112 2.662 -0.22 6.71 -0.22 C 8.448 -0.22 9.878 0.506 10.758 1.76 C 10.692 1.98 10.4939995 2.156 10.296 2.244 C 9.24 1.144 7.986 0.924 6.842 0.924 C 5.742 0.924 4.092 1.584 4.092 5.148 C 4.092 8.646 5.39 9.548 6.5559998 9.548 C 8.844 9.548 9.218 8.646 9.746 6.886 C 9.988 6.798 10.384 6.864 10.626 6.996 C 10.516 8.052 10.384 9.042 10.164 10.164 C 9.13 10.23 8.118 10.4279995 6.798 10.4279995 Z "/>
</symbol>
<symbol id="g1707CF3A32B022CA2D70483E817BB0E1" overflow="visible">
<path d="M 2.574 7.3259997 L 2.574 2.794 C 2.574 0.968 2.222 0.77 0.88 0.704 C 0.748 0.572 0.748 0.088 0.88 -0.044 C 1.804 -0.022 2.794 0 4.004 0 C 5.2139997 0 6.182 -0.022 7.128 -0.044 C 7.2599998 0.088 7.2599998 0.572 7.128 0.704 C 5.786 0.77 5.434 0.968 5.434 2.794 L 5.434 7.3259997 C 5.434 9.152 5.786 9.35 7.128 9.416 C 7.2599998 9.548 7.2599998 10.032 7.128 10.164 C 6.204 10.142 5.2139997 10.12 4.004 10.12 C 2.794 10.12 1.826 10.142 0.88 10.164 C 0.748 10.032 0.748 9.548 0.88 9.416 C 2.222 9.35 2.574 9.152 2.574 7.3259997 Z "/>
</symbol>
<symbol id="gDC78B3846EDAB84D21B8DADC57D4B72" overflow="visible">
<path d="M 1.078 1.276 C 1.078 0.44 1.782 -0.22 2.662 -0.22 C 3.542 -0.22 4.29 0.484 4.29 1.3199999 C 4.29 2.178 3.586 2.838 2.706 2.838 C 1.826 2.838 1.078 2.134 1.078 1.276 Z "/>
</symbol>
<symbol id="g9395E96C48DADE2CF7A23A407777B6BB" overflow="visible">
<path d="M 8.074 2.684 L 8.074 10.626 C 8.074 11.792 8.25 13.046 8.25 13.046 C 8.25 13.332 8.074 13.42 7.876 13.42 C 7.656 13.42 7.282 13.332 6.776 13.09 C 5.434 12.474 3.938 11.946 2.024 11.154 C 2.046 10.78 2.2 10.4279995 2.508 10.208 C 3.696 10.714 4.488 10.758 4.796 10.758 C 5.082 10.758 5.2139997 10.67 5.2139997 9.57 L 5.2139997 2.684 C 5.2139997 0.858 4.158 0.77 2.948 0.704 C 2.728 0.572 2.728 0.088 2.948 -0.044 C 4.752 -0.022 5.786 0 6.666 0 C 7.546 0 8.536 -0.022 10.34 -0.044 C 10.559999 0.088 10.559999 0.572 10.34 0.704 C 9.13 0.77 8.074 0.858 8.074 2.684 Z "/>
</symbol>
<symbol id="g8F5620C85403271F8A8A2AC29AB7F075" overflow="visible">
<path d="M 9.8880005 1.9520001 L 9.8880005 8.368 C 9.8880005 9.696 10.160001 9.776 11.280001 9.824 C 11.376 9.92 11.376 10.2560005 11.280001 10.352 C 10.624001 10.336 9.808001 10.320001 9.200001 10.320001 C 8.608001 10.320001 7.84 10.336 7.136 10.352 C 7.0400004 10.2560005 7.0400004 9.92 7.136 9.824 C 8.2560005 9.776 8.528001 9.696 8.528001 8.368 L 8.528001 5.808 L 3.0560002 5.808 L 3.0560002 8.368 C 3.0560002 9.696 3.328 9.776 4.4480004 9.824 C 4.544 9.92 4.544 10.2560005 4.4480004 10.352 C 3.8400002 10.336 3.1840003 10.320001 2.368 10.320001 C 1.5680001 10.320001 0.91200006 10.336 0.30400002 10.352 C 0.208 10.2560005 0.208 9.92 0.30400002 9.824 C 1.424 9.776 1.6960001 9.696 1.6960001 8.368 L 1.6960001 1.9520001 C 1.6960001 0.624 1.424 0.544 0.30400002 0.49600002 C 0.208 0.4 0.208 0.064 0.30400002 -0.032 C 1.008 -0.016 1.7760001 0 2.384 0 C 2.96 0 3.7440002 -0.016 4.4480004 -0.032 C 4.544 0.064 4.544 0.4 4.4480004 0.49600002 C 3.328 0.544 3.0560002 0.624 3.0560002 1.9520001 L 3.0560002 5.136 L 8.528001 5.136 L 8.528001 1.9520001 C 8.528001 0.624 8.2560005 0.544 7.136 0.49600002 C 7.0400004 0.4 7.0400004 0.064 7.136 -0.032 C 7.8560004 -0.016 8.624001 0 9.216001 0 C 9.808001 0 10.576 -0.016 11.280001 -0.032 C 11.376 0.064 11.376 0.4 11.280001 0.49600002 C 10.160001 0.544 9.8880005 0.624 9.8880005 1.9520001 Z "/>
</symbol>
<symbol id="g5EE22C3CF302EFF7E29425466980B287" overflow="visible">
<path d="M 8.896001 8.192 L 8.896001 2.96 C 8.896001 2.6560001 8.896001 2.48 8.784 2.48 C 8.72 2.48 8.4800005 2.7680001 8.016001 3.3600001 L 2.528 10.320001 L 0.36800003 10.352 C 0.272 10.2560005 0.272 9.92 0.36800003 9.824 C 1.056 9.776 1.536 9.216001 1.6320001 8.8 L 1.6320001 2.128 C 1.6320001 0.70400006 1.36 0.60800004 0.24000001 0.49600002 C 0.14400001 0.4 0.14400001 0.064 0.24000001 -0.032 C 0.92800003 -0.016 1.6480001 0 2.032 0 C 2.4 0 3.1360002 -0.016 3.808 -0.032 C 3.9040003 0.064 3.9040003 0.4 3.808 0.49600002 C 2.6880002 0.60800004 2.4160001 0.67200005 2.4160001 2.128 L 2.4160001 7.024 C 2.4160001 7.5680003 2.4160001 7.8080006 2.5440001 7.8080006 C 2.64 7.8080006 2.8160002 7.6320004 3.088 7.28 L 8.672001 0.224 C 8.848001 -0.016 9.056001 -0.16000001 9.312 -0.16000001 C 9.536 -0.16000001 9.68 0.032 9.68 0.33600003 L 9.68 8.192 C 9.68 9.616 9.952001 9.712001 11.0720005 9.824 C 11.168 9.92 11.168 10.2560005 11.0720005 10.352 C 10.416 10.336 9.6640005 10.320001 9.280001 10.320001 C 8.944 10.320001 8.208 10.336 7.504 10.352 C 7.4080005 10.2560005 7.4080005 9.92 7.504 9.824 C 8.624001 9.712001 8.896001 9.648001 8.896001 8.192 Z "/>
</symbol>
<symbol id="g1741EC601D45A91DF6927753AEFC05FD" overflow="visible">
<path d="M 6.32 10.096001 C 5.392 10.224001 5.4240003 10.528001 3.8560002 10.528001 C 2.24 10.528001 0.81600004 9.456 0.81600004 7.76 C 0.81600004 6.0800004 2.2080002 5.3120003 3.6160002 4.768 C 4.576 4.4 5.76 3.9520001 5.76 2.384 C 5.76 1.088 5.0400004 0.416 3.7600002 0.416 C 2.272 0.416 1.312 1.1040001 0.96000004 2.6880002 C 0.75200003 2.752 0.592 2.72 0.432 2.64 C 0.49600002 1.4080001 0.56 0.99200004 0.75200003 0.208 C 1.7600001 0.208 2.2080002 -0.16000001 3.6320002 -0.16000001 C 4.352 -0.16000001 5.0400004 0.016 5.6000004 0.36800003 C 6.5280004 0.94400007 7.1040006 1.9200001 7.1040006 2.9440002 C 7.1040006 4.6400003 5.8240004 5.392 4.512 5.8880005 C 3.5520003 6.2400002 1.9520001 6.8480005 1.9520001 8.192 C 1.9520001 9.088 2.7680001 9.984 3.7120001 9.984 C 5.2640004 9.984 5.76 8.992001 6.0800004 7.9360003 C 6.2560005 7.9040003 6.464 7.9200006 6.6080003 8.032001 C 6.544 8.8 6.4800005 9.248 6.32 10.096001 Z "/>
</symbol>
<symbol id="g1068D2C5F0B4CD106582F955D1D295A8" overflow="visible">
<path d="M 12.960001 9.04 L 10.464001 2.0960002 L 10.416 2.112 L 8.208 8.864 C 7.9360003 9.728001 8.496 9.776 9.04 9.824 C 9.136001 9.92 9.136001 10.2560005 9.04 10.352 C 8.384001 10.336 7.6800003 10.320001 7.0400004 10.320001 C 6.512 10.320001 5.952 10.336 5.44 10.352 C 5.3440003 10.2560005 5.3440003 9.92 5.44 9.824 C 6.288 9.776 6.6400003 9.280001 6.7840004 8.864 L 7.1520004 7.8080006 C 7.2160006 7.616 7.2640004 7.4560003 7.2640004 7.3120003 C 7.2640004 7.1520004 7.248 7.024 7.1200004 6.7520003 L 5.056 2.0640001 L 4.9760003 2.0800002 L 2.64 9.152 C 2.4480002 9.712001 2.88 9.792001 3.44 9.824 C 3.5360003 9.92 3.5360003 10.2560005 3.44 10.352 C 2.9120002 10.336 2.2080002 10.320001 1.5840001 10.320001 C 1.024 10.320001 0.56 10.336 0.096 10.352 C 0 10.2560005 0 9.92 0.096 9.824 C 0.81600004 9.776 0.92800003 9.76 1.2320001 8.896001 L 4.2400002 0.24000001 C 4.32 -0.016 4.4160004 -0.192 4.592 -0.192 C 4.8 -0.192 4.8960004 -0.032 5.0080004 0.24000001 L 7.392 5.6000004 C 7.5360003 5.92 7.5840006 6.0000005 7.6640005 6.0000005 C 7.728 6.0000005 7.7920003 5.8240004 7.8880005 5.552 L 9.728001 0.24000001 C 9.824 -0.032 9.904 -0.192 10.096001 -0.192 C 10.272 -0.192 10.384001 -0.016 10.464001 0.224 L 13.68 8.848001 C 13.8880005 9.408 14.176001 9.776 15.056001 9.824 C 15.152 9.92 15.152 10.2560005 15.056001 10.352 C 14.592001 10.336 14.080001 10.320001 13.6640005 10.320001 C 13.248001 10.320001 12.544001 10.336 11.904 10.352 C 11.808001 10.2560005 11.808001 9.92 11.904 9.824 C 12.56 9.776 13.200001 9.728001 12.960001 9.04 Z "/>
</symbol>
<symbol id="gD91DF12E6685C776523A4EFE671EF7FE" overflow="visible">
<path d="M 0.91200006 0.688 C 0.91200006 0.224 1.296 -0.16000001 1.7600001 -0.16000001 C 2.2240002 -0.16000001 2.608 0.224 2.608 0.688 C 2.608 1.1520001 2.2240002 1.536 1.7600001 1.536 C 1.296 1.536 0.91200006 1.1520001 0.91200006 0.688 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
<symbol id="g1B31FFD796CA2E900A884ECD4210CED3" overflow="visible">
<path d="M 3.44 9.200001 C 4.1280003 9.200001 4.768 8.784 4.768 7.76 C 4.768 6.9600005 3.8400002 5.728 2.256 5.504 L 2.3360002 4.992 C 2.608 5.024 2.8960001 5.024 3.104 5.024 C 4.0160003 5.024 5.2000003 4.768 5.2000003 2.96 C 5.2000003 0.832 3.7760003 0.4 3.216 0.4 C 2.4 0.4 2.256 0.768 2.0640001 1.056 C 1.904 1.2800001 1.6960001 1.4720001 1.376 1.4720001 C 1.0400001 1.4720001 0.70400006 1.1680001 0.70400006 0.91200006 C 0.70400006 0.272 2.048 -0.16000001 3.0080001 -0.16000001 C 4.912 -0.16000001 6.6080003 1.072 6.6080003 3.1840003 C 6.6080003 4.9280005 5.2960005 5.552 4.352 5.7120004 L 4.3360004 5.7440004 C 5.6480002 6.3680005 6.0160003 7.024 6.0160003 7.872 C 6.0160003 8.352 5.9040003 8.736 5.5200005 9.136001 C 5.168 9.488001 4.6080003 9.76 3.7760003 9.76 C 1.424 9.76 0.75200003 8.224 0.75200003 7.6960006 C 0.75200003 7.472 0.91200006 7.1520004 1.296 7.1520004 C 1.8560001 7.1520004 1.9200001 7.6800003 1.9200001 7.984 C 1.9200001 9.008 3.0240002 9.200001 3.44 9.200001 Z "/>
</symbol>
<symbol id="g49CDBE81A8A431C9159130967B9EC9E" overflow="visible">
<path d="M 1.664 8.368 L 1.664 1.9520001 C 1.664 0.624 1.3920001 0.544 0.272 0.49600002 C 0.17600001 0.4 0.17600001 0.064 0.272 -0.032 C 0.99200004 -0.016 1.7760001 0 2.352 0 C 2.9120002 0 3.8560002 -0.016 4.656 -0.032 C 4.7520003 0.064 4.7520003 0.4 4.656 0.49600002 C 3.4080002 0.56 3.0240002 0.624 3.0240002 1.9520001 L 3.0240002 4.6720004 C 3.3760002 4.5600004 3.7600002 4.512 4.32 4.512 C 7.2320004 4.512 8.112 6.4160004 8.112 7.7760005 C 8.112 8.72 7.4880004 10.432 4.5280004 10.432 C 3.92 10.432 2.976 10.320001 2.3360002 10.320001 C 1.7440001 10.320001 0.91200006 10.336 0.272 10.352 C 0.17600001 10.2560005 0.17600001 9.92 0.272 9.824 C 1.3920001 9.776 1.664 9.696 1.664 8.368 Z M 3.0240002 8.864 C 3.0240002 9.328 3.2640002 9.8880005 4.4160004 9.8880005 C 5.5200005 9.8880005 6.6240005 9.52 6.6240005 7.4880004 C 6.6240005 5.76 5.7920003 5.056 4.2400002 5.056 C 3.8400002 5.056 3.2 5.0880003 3.0240002 5.136 Z "/>
</symbol>
<symbol id="g7079AB3C3D467A375535C421787E42DB" overflow="visible">
<path d="M 2.8160002 5.728 C 2.7840002 6.3680005 2.7680001 6.7840004 2.6880002 6.9440002 C 2.6560001 7.024 2.624 7.0720005 2.496 7.0720005 C 2.048 6.8960004 1.6320001 6.7520003 0.528 6.6080003 C 0.49600002 6.512 0.528 6.2560005 0.56 6.1600003 C 1.424 6.0800004 1.6 6.0000005 1.6 5.072 L 1.6 1.9520001 C 1.6 0.624 1.4080001 0.56 0.416 0.49600002 C 0.32000002 0.4 0.32000002 0.064 0.416 -0.032 C 0.9760001 -0.016 1.6 0 2.24 0 C 2.88 0 3.6160002 -0.016 4.176 -0.032 C 4.2720003 0.064 4.2720003 0.4 4.176 0.49600002 C 3.0560002 0.57600003 2.864 0.624 2.864 1.9520001 L 2.864 4.176 C 2.864 4.592 3.0560002 4.96 3.2480001 5.248 C 3.4240003 5.504 3.7920003 6.032 3.9840002 6.032 C 4.1280003 6.032 4.2720003 6.0000005 4.4 5.8240004 C 4.512 5.664 4.704 5.4560003 4.9760003 5.4560003 C 5.36 5.4560003 5.728 5.8560004 5.728 6.2560005 C 5.728 6.5600004 5.44 7.024 4.768 7.024 C 4.0160003 7.024 3.3600001 6.32 2.992 5.696 C 2.8960001 5.5200005 2.8160002 5.6480002 2.8160002 5.728 Z "/>
</symbol>
<symbol id="gB9A2E3AAC6CC7A3D99F4D7199A710CE2" overflow="visible">
<path d="M 0.656 3.2800002 C 0.656 1.6480001 1.7440001 -0.16000001 4.0160003 -0.16000001 C 5.0400004 -0.16000001 5.8240004 0.208 6.3680005 0.73600006 C 7.0880003 1.44 7.4080005 2.4480002 7.4080005 3.4240003 C 7.4080005 5.0880003 6.4960003 7.024 4.0480003 7.024 C 2.992 7.024 2.128 6.5920005 1.536 5.9040003 C 0.96000004 5.216 0.656 4.288 0.656 3.2800002 Z M 3.808 6.464 C 5.184 6.464 6.032 5.216 6.032 2.9120002 C 6.032 0.896 4.992 0.4 4.2400002 0.4 C 2.5760002 0.4 2.032 2.4160001 2.032 3.6480002 C 2.032 5.0400004 2.368 6.464 3.808 6.464 Z "/>
</symbol>
<symbol id="gD032B844D751F1F27806C7004D4F5D2F" overflow="visible">
<path d="M 2.6720002 6.3040004 C 2.5760002 6.208 2.512 6.2400002 2.512 6.3840003 L 2.512 9.328 C 2.512 10.368 2.5760002 11.008 2.5760002 11.008 C 2.5760002 11.120001 2.512 11.168 2.368 11.168 C 1.968 11.008 0.768 10.784 0.128 10.736 C 0.096 10.608001 0.128 10.352 0.224 10.2560005 C 0.272 10.2560005 0.32000002 10.2560005 0.36800003 10.2560005 C 1.072 10.208 1.248 10.208 1.248 8.944 L 1.248 1.136 C 1.248 0.512 1.2320001 0.224 1.184 0 C 1.264 -0.128 1.3440001 -0.192 1.536 -0.192 C 1.6320001 -0.096 1.792 0.048 1.9200001 0.192 C 2.0800002 0.384 2.176 0.384 2.352 0.24000001 C 2.72 -0.064 3.2 -0.16000001 3.7600002 -0.16000001 C 5.392 -0.16000001 7.2960005 1.3280001 7.2960005 3.8720002 C 7.2960005 5.8240004 5.8560004 7.024 4.464 7.024 C 3.7760003 7.024 3.1680002 6.7520003 2.6720002 6.3040004 Z M 2.7840002 5.808 C 3.2 6.176 3.68 6.32 4.144 6.32 C 5.1200004 6.32 5.92 5.136 5.92 3.584 C 5.92 1.7600001 5.184 0.384 3.6640003 0.384 C 3.1680002 0.384 2.832 0.73600006 2.512 1.136 L 2.512 5.136 C 2.512 5.472 2.5760002 5.6320004 2.7840002 5.808 Z "/>
</symbol>
<symbol id="g8F0641061D7822251E2A1C9000154920" overflow="visible">
<path d="M 4.688 0.768 C 4.7840004 0.272 4.96 -0.16000001 5.76 -0.16000001 C 6.3680005 -0.16000001 6.9440002 0.112 7.28 0.432 C 7.248 0.624 7.1840005 0.768 7.0080004 0.864 C 6.8960004 0.768 6.6240005 0.60800004 6.4160004 0.60800004 C 5.952 0.60800004 5.9360003 1.2320001 5.9360003 1.968 L 5.9360003 4.32 C 5.9360003 6.5920005 4.688 7.024 3.5200002 7.024 C 2.2080002 7.024 0.88000005 6.1600003 0.88000005 5.248 C 0.88000005 4.8640003 1.072 4.6720004 1.44 4.6720004 C 1.904 4.6720004 2.1920002 5.0080004 2.1920002 5.216 C 2.1920002 5.328 2.176 5.44 2.144 5.504 C 2.128 5.552 2.112 5.6480002 2.112 5.8240004 C 2.112 6.32 2.7840002 6.4960003 3.3920002 6.4960003 C 3.936 6.4960003 4.688 6.2240005 4.688 4.4160004 C 4.688 4.3040004 4.6400003 4.2400002 4.592 4.224 L 3.216 3.8880002 C 1.6800001 3.5040002 0.57600003 2.6560001 0.57600003 1.5680001 C 0.57600003 0.256 1.4720001 -0.16000001 2.592 -0.16000001 C 3.1520002 -0.16000001 3.6320002 -0.032 4.3360004 0.512 L 4.656 0.768 Z M 4.688 3.7280002 L 4.688 1.616 C 4.688 1.4080001 4.592 1.296 4.464 1.2 C 4.0480003 0.864 3.5040002 0.49600002 3.0560002 0.49600002 C 2.256 0.49600002 1.904 1.136 1.904 1.6320001 C 1.904 2.352 2.24 3.088 3.4240003 3.3920002 Z "/>
</symbol>
<symbol id="g8EC8620411AE7F46663E6890D2DD9166" overflow="visible">
<path d="M 2.8960001 1.9520001 L 2.8960001 5.136 C 2.8960001 5.9360003 2.96 6.9600005 2.96 6.9600005 C 2.96 7.024 2.88 7.0720005 2.752 7.0720005 C 2.3040001 6.8960004 1.664 6.7520003 0.56 6.6080003 C 0.528 6.512 0.56 6.2560005 0.592 6.1600003 C 1.4720001 6.0800004 1.6320001 5.984 1.6320001 5.072 L 1.6320001 1.9520001 C 1.6320001 0.624 1.4560001 0.57600003 0.48000002 0.49600002 C 0.384 0.4 0.384 0.064 0.48000002 -0.032 C 1.008 -0.016 1.6320001 0 2.272 0 C 2.9120002 0 3.5200002 -0.016 4.0480003 -0.032 C 4.144 0.064 4.144 0.4 4.0480003 0.49600002 C 3.072 0.56 2.8960001 0.624 2.8960001 1.9520001 Z M 1.44 9.584001 C 1.44 9.168 1.8240001 8.752001 2.2080002 8.752001 C 2.6560001 8.752001 3.0400002 9.184 3.0400002 9.52 C 3.0400002 9.904 2.7040002 10.352 2.272 10.352 C 1.8880001 10.352 1.44 9.968 1.44 9.584001 Z "/>
</symbol>
<symbol id="g776E4106C35A60F8D71A42812632C381" overflow="visible">
<path d="M 1.5200001 1.9520001 C 1.5200001 0.624 1.3440001 0.544 0.36800003 0.49600002 C 0.272 0.4 0.272 0.064 0.36800003 -0.032 C 0.92800003 -0.016 1.5200001 0 2.16 0 C 2.8000002 0 3.4080002 -0.016 3.936 -0.032 C 4.032 0.064 4.032 0.4 3.936 0.49600002 C 2.96 0.544 2.7840002 0.624 2.7840002 1.9520001 L 2.7840002 9.328 C 2.7840002 10.368 2.848 11.008 2.848 11.008 C 2.848 11.120001 2.7840002 11.168 2.64 11.168 C 2.24 11.008 1.0400001 10.784 0.4 10.736 C 0.36800003 10.608001 0.4 10.352 0.49600002 10.2560005 C 1.424 10.192 1.5200001 10.144 1.5200001 8.944 Z "/>
</symbol>
<symbol id="g94C24BD726F4D930F93182C299232222" overflow="visible">
<path d="M 0.688 6.8640003 C 0.46400002 6.8640003 0.4 6.6720004 0.4 6.544 L 0.4 6.3360004 C 0.4 6.2560005 0.416 6.2400002 0.48000002 6.2400002 L 1.424 6.2400002 L 1.424 1.424 C 1.424 0.28800002 1.9200001 -0.16000001 2.6560001 -0.16000001 C 3.3920002 -0.16000001 4.1920004 0.192 4.8160005 0.896 C 4.7840004 1.056 4.688 1.1520001 4.5280004 1.1680001 C 4.112 0.84800005 3.6320002 0.72 3.216 0.72 C 2.7840002 0.72 2.6880002 1.2 2.6880002 2.1920002 L 2.6880002 6.2400002 L 4.352 6.2400002 C 4.512 6.2400002 4.736 6.3040004 4.736 6.4480004 L 4.736 6.768 C 4.736 6.8320003 4.688 6.8640003 4.6080003 6.8640003 L 2.6880002 6.8640003 L 2.6880002 7.4880004 C 2.6880002 8.528001 2.752 9.168 2.752 9.168 C 2.752 9.264001 2.7040002 9.312 2.624 9.312 C 2.5600002 9.312 2.4160001 9.248 2.272 9.168 C 2.0960002 9.0720005 1.9360001 8.992001 1.728 8.944 C 1.536 8.88 1.376 8.832001 1.376 8.72 C 1.376 8.528001 1.424 8.64 1.424 6.8640003 Z "/>
</symbol>
<symbol id="gE500E45C96D97FD9DA8792F5A18C8416" overflow="visible">
<path d="M 3.2640002 -2.5600002 C 3.5200002 -2.112 3.7280002 -1.664 3.92 -1.184 C 5.2000003 1.904 5.92 3.5520003 6.7520003 5.3440003 C 7.0720005 6.0160003 7.2960005 6.2720003 8.048 6.3680005 C 8.144 6.464 8.144 6.8 8.048 6.8960004 C 7.728 6.88 7.36 6.8640003 6.912 6.8640003 C 6.432 6.8640003 5.9360003 6.88 5.4560003 6.8960004 C 5.36 6.8 5.36 6.464 5.4560003 6.3680005 C 5.9680004 6.32 6.4800005 6.2240005 6.2240005 5.6480002 L 4.6400003 1.9840001 C 4.5280004 1.728 4.3840003 1.6800001 4.256 2 L 2.832 5.328 C 2.5440001 6.0000005 2.4640002 6.3040004 3.3600001 6.3680005 C 3.456 6.464 3.456 6.8 3.3600001 6.8960004 C 2.7680001 6.88 2.128 6.8640003 1.552 6.8640003 C 1.008 6.8640003 0.57600003 6.88 0.256 6.8960004 C 0.16000001 6.8 0.16000001 6.464 0.256 6.3680005 C 0.896 6.288 1.1040001 6.144 1.5200001 5.168 L 3.328 0.96000004 C 3.4720001 0.64000005 3.7120001 -0.096 3.5520003 -0.544 C 3.3600001 -1.072 3.1680002 -1.5200001 2.9280002 -2.016 C 2.752 -2.3360002 2.528 -2.48 2.128 -2.48 C 1.904 -2.48 1.84 -2.4320002 1.664 -2.4320002 C 1.2 -2.4320002 0.96000004 -2.9120002 0.96000004 -3.1200001 C 0.96000004 -3.456 1.2800001 -3.7120001 1.7120001 -3.7120001 C 2.048 -3.7120001 2.6880002 -3.584 3.2640002 -2.5600002 Z "/>
</symbol>
<symbol id="g618B2D8299EA06ECBEE324E5599CA8A3" overflow="visible">
<path d="M 1.376 1.9520001 C 1.376 0.624 1.2 0.56 0.30400002 0.49600002 C 0.208 0.4 0.208 0.064 0.30400002 -0.032 C 0.832 -0.016 1.376 0 2.016 0 C 2.5760002 0 3.104 -0.016 3.4720001 -0.032 C 3.568 0.064 3.568 0.4 3.4720001 0.49600002 C 2.8160002 0.56 2.64 0.624 2.64 1.9520001 L 2.64 3.344 C 2.9440002 3.328 3.1680002 3.3120003 3.328 3.2640002 C 3.5040002 3.1360002 3.6480002 2.992 3.8400002 2.736 L 5.0080004 1.1680001 C 5.472 0.544 5.664 0.24000001 5.6800003 0.048 C 5.6800003 0 5.696 -0.032 5.7440004 -0.032 C 6.064 -0.016 6.4160004 0 6.7360005 0 C 7.2320004 0 7.728 -0.016 8.048 -0.032 C 8.144 0.064 8.144 0.4 8.048 0.49600002 C 7.504 0.56 7.1040006 0.624 6.6720004 1.1680001 L 4.5600004 3.8240001 C 4.4960003 3.9040003 4.4480004 3.9680002 4.4480004 4.0480003 C 4.4480004 4.112 4.4480004 4.144 4.512 4.208 L 5.92 5.664 C 6.4 6.176 6.9600005 6.3040004 7.6000004 6.3680005 C 7.6960006 6.464 7.6960006 6.8 7.6000004 6.8960004 C 7.2320004 6.88 6.7840004 6.8640003 6.208 6.8640003 C 5.6000004 6.8640003 5.0080004 6.88 4.6400003 6.8960004 C 4.544 6.8 4.544 6.464 4.6400003 6.3680005 C 5.5360003 6.3040004 5.1520004 5.7440004 5.0080004 5.552 C 4.6400003 5.0880003 4.144 4.544 3.7280002 4.2400002 C 3.3760002 3.9840002 2.9440002 3.7920003 2.64 3.7440002 L 2.64 9.328 C 2.64 10.368 2.7040002 11.008 2.7040002 11.008 C 2.7040002 11.120001 2.64 11.168 2.496 11.168 C 2.0960002 11.008 0.896 10.784 0.256 10.736 C 0.224 10.608001 0.256 10.352 0.35200003 10.2560005 C 0.4 10.2560005 0.448 10.2560005 0.49600002 10.2560005 C 1.2 10.208 1.376 10.208 1.376 8.944 Z "/>
</symbol>
<symbol id="g37CC7CC101B9B1BA56FE179E8D4E6231" overflow="visible">
<path d="M 2.496 5.8880005 C 2.48 6.3680005 2.4480002 6.7840004 2.368 6.9440002 C 2.3360002 7.024 2.3040001 7.0720005 2.176 7.0720005 C 1.728 6.8960004 1.312 6.7520003 0.208 6.6080003 C 0.17600001 6.512 0.208 6.2560005 0.24000001 6.1600003 C 1.1040001 6.0800004 1.2800001 6.0000005 1.2800001 5.072 L 1.2800001 -1.7600001 C 1.2800001 -3.088 1.1040001 -3.1680002 0.128 -3.216 C 0.032 -3.3120003 0.032 -3.6480002 0.128 -3.7440002 C 0.688 -3.7280002 1.2800001 -3.7120001 1.9200001 -3.7120001 C 2.5600002 -3.7120001 3.328 -3.7280002 3.8560002 -3.7440002 C 3.9520001 -3.6480002 3.9520001 -3.3120003 3.8560002 -3.216 C 2.72 -3.1520002 2.5440001 -3.088 2.5440001 -1.7600001 L 2.5440001 -0.032 C 2.5440001 0.17600001 2.608 0.16000001 2.7680001 0.096 C 3.1680002 -0.064 3.6480002 -0.16000001 4.1600003 -0.16000001 C 5.056 -0.16000001 5.8560004 0.112 6.512 0.73600006 C 7.2640004 1.4720001 7.6960006 2.4640002 7.6960006 3.7600002 C 7.6960006 5.4560003 6.4960003 7.024 4.8640003 7.024 C 4.1280003 7.024 3.3120003 6.544 2.6720002 5.8240004 C 2.5760002 5.728 2.512 5.728 2.496 5.8880005 Z M 2.8000002 5.2960005 C 3.216 5.808 3.9520001 6.288 4.4160004 6.288 C 5.44 6.288 6.32 5.136 6.32 3.328 C 6.32 2.016 5.8560004 0.384 4.064 0.384 C 3.7760003 0.384 3.216 0.46400002 2.9280002 0.72 C 2.608 1.008 2.5440001 1.1040001 2.5440001 1.6800001 L 2.5440001 4.592 C 2.5440001 4.9280005 2.608 5.072 2.8000002 5.2960005 Z "/>
</symbol>
<symbol id="g1FAB015722B609C2ED5D2F86E1044EFF" overflow="visible">
<path d="M 2.384 0 L 5.7920003 0 C 6.2240005 0 7.6960006 -0.032 7.6960006 -0.032 C 7.8560004 0.768 8.016001 1.8080001 8.112 2.64 C 7.952 2.72 7.7760005 2.752 7.5840006 2.72 C 7.2640004 1.5680001 6.6720004 0.624 4.9760003 0.624 L 3.9680002 0.624 C 3.344 0.624 3.0560002 0.92800003 3.0560002 1.7440001 L 3.0560002 8.368 C 3.0560002 9.696 3.328 9.776 4.4480004 9.824 C 4.544 9.92 4.544 10.2560005 4.4480004 10.352 C 3.7280002 10.336 2.976 10.320001 2.368 10.320001 C 1.792 10.320001 1.0400001 10.336 0.30400002 10.352 C 0.208 10.2560005 0.208 9.92 0.30400002 9.824 C 1.424 9.776 1.6960001 9.696 1.6960001 8.368 L 1.6960001 1.9520001 C 1.6960001 0.624 1.424 0.544 0.30400002 0.49600002 C 0.208 0.4 0.208 0.064 0.30400002 -0.032 C 0.92800003 -0.016 1.84 0 2.384 0 Z "/>
</symbol>
<symbol id="g7E49B8D69C443145BC38CA6BB9F62850" overflow="visible">
<path d="M 0.768 2.2080002 C 0.832 1.424 0.88000005 0.67200005 0.88000005 0 C 1.0400001 0.032 1.2 0.048 1.2800001 0.048 C 1.3920001 0.048 1.488 0.048 1.6 0.016 C 2.032 -0.096 2.4640002 -0.16000001 3.0560002 -0.16000001 C 3.9520001 -0.16000001 5.6000004 0.272 5.6000004 1.8560001 C 5.6000004 2.9440002 4.8160005 3.584 3.7280002 3.9840002 C 2.7680001 4.352 2.128 4.592 2.128 5.472 C 2.128 6.1280003 2.7040002 6.4960003 3.2480001 6.4960003 C 3.6000001 6.4960003 4.5280004 6.3680005 4.736 5.0080004 C 4.8320003 4.912 5.1520004 4.9280005 5.248 5.024 C 5.2960005 5.6000004 5.328 6.1920004 5.3440003 6.7200003 C 4.848 6.8 4.0800004 7.024 3.2480001 7.024 C 2.0640001 7.024 0.99200004 6.2560005 0.99200004 5.2320004 C 0.99200004 4.064 1.5200001 3.568 2.752 3.0560002 C 4.0800004 2.512 4.3840003 2.176 4.3840003 1.488 C 4.3840003 0.70400006 3.6160002 0.36800003 3.0240002 0.36800003 C 2.4 0.36800003 2.048 0.57600003 1.8880001 0.75200003 C 1.536 1.12 1.36 1.8240001 1.264 2.2240002 C 1.1680001 2.3200002 0.864 2.3040001 0.768 2.2080002 Z "/>
</symbol>
<symbol id="g58626FCFBD19425464A4FA7F304374C4" overflow="visible">
<path d="M 5.104 3.0240002 C 5.104 1.5040001 4.3040004 0.384 3.344 0.384 C 2.736 0.384 2.528 0.78400004 2.288 1.1040001 C 2.0800002 1.376 1.8080001 1.616 1.4720001 1.616 C 1.1680001 1.616 0.864 1.3440001 0.864 1.024 C 0.864 0.36800003 2.2240002 -0.17600001 3.1360002 -0.17600001 C 5.1200004 -0.17600001 6.5280004 1.296 6.5280004 3.3120003 C 6.5280004 4.8640003 5.4560003 6.2560005 3.6640003 6.2560005 C 2.976 6.2560005 2.384 6.1120005 2.0960002 6.0000005 L 2.4160001 8.672001 C 3.0080001 8.608001 3.5200002 8.528001 4.288 8.528001 C 4.768 8.528001 5.3120003 8.56 5.9680004 8.624001 L 6.2240005 9.712001 L 6.1120005 9.776 C 5.2000003 9.68 4.3360004 9.6 3.4880002 9.6 C 2.8960001 9.6 2.3200002 9.632001 1.7600001 9.68 L 1.2160001 5.072 C 2.0640001 5.392 2.6720002 5.4560003 3.2480001 5.4560003 C 4.288 5.4560003 5.104 4.768 5.104 3.0240002 Z "/>
</symbol>
<symbol id="g41BD02C814E5F1F9CC57CE5A8E90AFBE" overflow="visible">
<path d="M 2.48 1.264 L 3.3600001 3.584 C 3.44 3.7920003 3.5360003 3.8560002 3.92 3.8560002 L 7.2960005 3.8560002 L 8.224 1.1520001 C 8.416 0.60800004 7.8080006 0.544 7.0400004 0.49600002 C 6.9440002 0.4 6.9440002 0.064 7.0400004 -0.032 C 7.6320004 -0.016 8.512 0 9.136001 0 C 9.792001 0 10.400001 -0.016 10.960001 -0.032 C 11.056001 0.064 11.056001 0.4 10.960001 0.49600002 C 10.336 0.56 9.792001 0.60800004 9.52 1.376 L 6.2240005 10.528001 C 5.984 10.384001 5.552 10.208 5.3440003 10.208 L 1.7120001 1.6320001 C 1.296 0.64000005 0.81600004 0.544 0.112 0.49600002 C 0.016 0.4 0.016 0.064 0.112 -0.032 C 0.528 -0.016 1.056 0 1.536 0 C 2.1920002 0 2.992 -0.016 3.584 -0.032 C 3.68 0.064 3.68 0.4 3.584 0.49600002 C 2.976 0.544 2.2240002 0.60800004 2.48 1.264 Z M 4.208 4.5280004 C 3.8560002 4.5280004 3.7440002 4.576 3.808 4.736 L 5.44 8.88 L 5.5360003 8.88 L 7.0400004 4.5280004 Z "/>
</symbol>
<symbol id="g48ABC493FE7862658825720022C8179D" overflow="visible">
<path d="M 6.064 0 C 6.064 0 6.432 1.536 6.544 2.2080002 C 6.4 2.288 6.2720003 2.3200002 6.096 2.272 C 5.84 1.3280001 5.3760004 0.544 4.368 0.544 L 3.6480002 0.544 C 3.2800002 0.544 3.0560002 0.8 3.0560002 1.1040001 L 3.0560002 5.4080005 C 3.0560002 6.7360005 3.232 6.7840004 4.208 6.8640003 C 4.3040004 6.9600005 4.3040004 7.2960005 4.208 7.392 C 3.6160002 7.3760004 2.96 7.36 2.4160001 7.36 C 1.9200001 7.36 1.2320001 7.3760004 0.64000005 7.392 C 0.544 7.2960005 0.544 6.9600005 0.64000005 6.8640003 C 1.616 6.8 1.792 6.7360005 1.792 5.4080005 L 1.792 1.9520001 C 1.792 0.624 1.7600001 0.544 0.64000005 0.49600002 C 0.544 0.4 0.544 0.064 0.64000005 -0.032 C 1.424 -0.016 2.48 0 2.48 0 Z "/>
</symbol>
<symbol id="g31FD4B68C132D0D1A1E4FD30ACE8848" overflow="visible">
<path d="M 7.5520005 1.4560001 C 7.5520005 2.7840002 7.6480002 2.832 8.144 2.9120002 C 8.240001 3.0080001 8.240001 3.344 8.144 3.44 C 7.8560004 3.4240003 7.4080005 3.4080002 6.912 3.4080002 C 6.432 3.4080002 5.696 3.4240003 5.2320004 3.44 C 5.136 3.344 5.136 3.0080001 5.2320004 2.9120002 C 6.208 2.848 6.288 2.7840002 6.288 1.4560001 L 6.288 0.592 C 5.7760005 0.448 5.248 0.36800003 4.688 0.36800003 C 2.6880002 0.36800003 2.032 2.4160001 2.032 3.7280002 C 2.032 5.664 2.96 6.992 4.4960003 6.992 C 6.0800004 6.992 6.7520003 6.1920004 6.992 5.168 C 7.1520004 5.1200004 7.3120003 5.1200004 7.472 5.216 C 7.4560003 5.872 7.4080005 6.544 7.2640004 7.2640004 C 6.7840004 7.2640004 5.6000004 7.5200005 4.704 7.5200005 C 2.4160001 7.5200005 0.592 6.0480003 0.592 3.5200002 C 0.592 1.488 2.112 -0.16000001 4.4 -0.16000001 C 5.4880004 -0.16000001 6.6720004 0 7.728 0.57600003 C 7.616 0.688 7.5520005 0.832 7.5520005 0.94400007 Z "/>
</symbol>
<symbol id="gAA95D2B4A225624CA202B59CBD1BF487" overflow="visible">
<path d="M 8.432 3.7600002 C 8.432 6.032 6.6080003 7.5200005 4.5280004 7.5200005 C 2.3040001 7.5200005 0.592 5.9040003 0.592 3.5520003 C 0.592 1.376 2.24 -0.16000001 4.4 -0.16000001 C 7.024 -0.16000001 8.432 1.6800001 8.432 3.7600002 Z M 4.3840003 6.992 C 5.808 6.992 7.0400004 5.6800003 7.0400004 3.5360003 C 7.0400004 1.5680001 6.064 0.36800003 4.6400003 0.36800003 C 3.088 0.36800003 1.9840001 1.7760001 1.9840001 3.7440002 C 1.9840001 5.9040003 3.1840003 6.992 4.3840003 6.992 Z "/>
</symbol>
<symbol id="gE307093CF7EFBC8D676E62CB78C07836" overflow="visible">
<path d="M 3.0560002 1.9520001 L 3.0560002 3.344 L 3.936 3.344 C 4.544 3.344 4.768 2.8160002 4.9760003 2.2240002 L 5.328 1.264 C 5.696 0.272 6.2400002 -0.112 6.9280005 -0.112 C 7.168 -0.112 7.6640005 -0.064 7.9360003 0 C 7.984 0.16000001 7.952 0.32000002 7.84 0.448 C 7.2640004 0.448 6.9600005 0.544 6.6400003 1.376 L 6.176 2.5760002 C 5.984 3.072 5.7920003 3.344 5.584 3.5520003 L 5.584 3.584 C 6.1280003 3.7760003 6.9440002 4.432 6.9440002 5.5360003 C 6.9440002 6.8640003 6.1120005 7.4240003 4.208 7.4240003 C 3.808 7.4240003 2.8960001 7.36 2.4160001 7.36 C 1.9520001 7.36 1.2800001 7.3760004 0.64000005 7.392 C 0.544 7.2960005 0.544 6.9600005 0.64000005 6.8640003 C 1.616 6.8 1.792 6.7360005 1.792 5.4080005 L 1.792 1.9520001 C 1.792 0.624 1.616 0.57600003 0.64000005 0.49600002 C 0.544 0.4 0.544 0.064 0.64000005 -0.032 C 1.248 -0.016 1.904 0 2.4320002 0 C 2.9280002 0 3.456 -0.016 3.9680002 -0.032 C 4.064 0.064 4.064 0.4 3.9680002 0.49600002 C 3.216 0.544 3.0560002 0.624 3.0560002 1.9520001 Z M 5.552 5.5360003 C 5.552 4.2720003 5.184 3.808 3.7600002 3.808 L 3.0560002 3.808 L 3.0560002 5.8880005 C 3.0560002 6.7360005 3.216 6.8960004 4.112 6.8960004 C 5.2320004 6.8960004 5.552 6.4960003 5.552 5.5360003 Z "/>
</symbol>
<symbol id="gDBEAA3BAB7923CD0435518D325CA6C53" overflow="visible">
<path d="M 3.1200001 5.4080005 C 3.1200001 6.7360005 3.2960002 6.7840004 4.2720003 6.8640003 C 4.368 6.9600005 4.368 7.2960005 4.2720003 7.392 C 3.6640003 7.3760004 2.976 7.36 2.48 7.36 C 2 7.36 1.3280001 7.3760004 0.70400006 7.392 C 0.60800004 7.2960005 0.60800004 6.9600005 0.70400006 6.8640003 C 1.6800001 6.8 1.8560001 6.7360005 1.8560001 5.4080005 L 1.8560001 1.9520001 C 1.8560001 0.624 1.6800001 0.57600003 0.70400006 0.49600002 C 0.60800004 0.4 0.60800004 0.064 0.70400006 -0.032 C 1.296 -0.016 1.9520001 0 2.496 0 C 3.0080001 0 3.7120001 -0.016 4.2720003 -0.032 C 4.368 0.064 4.368 0.4 4.2720003 0.49600002 C 3.2960002 0.56 3.1200001 0.624 3.1200001 1.9520001 Z "/>
</symbol>
<symbol id="gAACD21C62EEBAEA5F571EAFD70656C36" overflow="visible">
<path d="M 4.8640003 1.9520001 L 4.8640003 5.984 C 4.8640003 6.576 5.024 6.8160005 5.5360003 6.8160005 L 5.952 6.8160005 C 6.9600005 6.8160005 7.168 6.4960003 7.4880004 5.3440003 C 7.6480002 5.3120003 7.7920003 5.3120003 7.9200006 5.392 C 7.84 6.176 7.8240004 6.768 7.7920003 7.5200005 C 7.2320004 7.4560003 6.208 7.36 4.8640003 7.36 L 3.6000001 7.36 C 2.032 7.36 1.1040001 7.4400005 0.67200005 7.5200005 C 0.67200005 6.768 0.656 6.144 0.56 5.392 C 0.70400006 5.3440003 0.84800005 5.328 0.99200004 5.3440003 C 1.312 6.4960003 1.488 6.8160005 2.528 6.8160005 L 2.9120002 6.8160005 C 3.4080002 6.8160005 3.6000001 6.6240005 3.6000001 6.0000005 L 3.6000001 1.9520001 C 3.6000001 0.624 3.4240003 0.57600003 2.4480002 0.49600002 C 2.352 0.4 2.352 0.064 2.4480002 -0.032 C 3.0400002 -0.016 3.696 0 4.2400002 0 C 4.8 0 5.4240003 -0.016 6.0160003 -0.032 C 6.1120005 0.064 6.1120005 0.4 6.0160003 0.49600002 C 5.0400004 0.56 4.8640003 0.624 4.8640003 1.9520001 Z "/>
</symbol>
<symbol id="g99884B2AD96AC7B048FEEB28FC8E4747" overflow="visible">
<path d="M 8 5.4080005 C 8 6.7360005 8.176001 6.7840004 9.152 6.8640003 C 9.248 6.9600005 9.248 7.2960005 9.152 7.392 C 8.592 7.36 7.8880005 7.36 7.36 7.36 C 6.912 7.36 6.208 7.3760004 5.584 7.392 C 5.4880004 7.2960005 5.4880004 6.9600005 5.584 6.8640003 C 6.5600004 6.8 6.7360005 6.7360005 6.7360005 5.4080005 L 6.7360005 4.032 L 3.0400002 4.032 L 3.0400002 5.4080005 C 3.0400002 6.7360005 3.216 6.7840004 4.1920004 6.8640003 C 4.288 6.9600005 4.288 7.2960005 4.1920004 7.392 C 3.584 7.3760004 2.9120002 7.36 2.4 7.36 C 1.9200001 7.36 1.264 7.3760004 0.624 7.392 C 0.528 7.2960005 0.528 6.9600005 0.624 6.8640003 C 1.6 6.8 1.7760001 6.7360005 1.7760001 5.4080005 L 1.7760001 1.9520001 C 1.7760001 0.624 1.6 0.57600003 0.624 0.49600002 C 0.528 0.4 0.528 0.064 0.624 -0.032 C 1.264 -0.016 1.904 0 2.4160001 0 C 2.9280002 0 3.568 -0.016 4.1920004 -0.032 C 4.288 0.064 4.288 0.4 4.1920004 0.49600002 C 3.216 0.56 3.0400002 0.624 3.0400002 1.9520001 L 3.0400002 3.5040002 L 6.7360005 3.5040002 L 6.7360005 1.9520001 C 6.7360005 0.624 6.5600004 0.57600003 5.584 0.49600002 C 5.4880004 0.4 5.4880004 0.064 5.584 -0.032 C 6.176 -0.016 6.8160005 0 7.3760004 0 C 7.8560004 0 8.528001 -0.016 9.152 -0.032 C 9.248 0.064 9.248 0.4 9.152 0.49600002 C 8.176001 0.56 8 0.624 8 1.9520001 Z "/>
</symbol>
<symbol id="g20DDE86F15DD9C8B9599512790FC45E4" overflow="visible">
<path d="M 7.728 6.1120005 L 7.84 6.1120005 L 8.048 1.968 C 8.112 0.64000005 8.096001 0.57600003 7.2320004 0.49600002 C 7.136 0.4 7.136 0.064 7.2320004 -0.032 C 7.7920003 -0.016 8.384001 0 8.832001 0 C 9.312 0 9.776 -0.016 10.208 -0.032 C 10.304001 0.064 10.304001 0.4 10.208 0.49600002 C 9.392 0.57600003 9.376 0.67200005 9.280001 1.968 L 8.96 6.096 C 8.912001 6.7360005 9.056001 6.8 9.856001 6.8640003 C 9.952001 6.9600005 9.952001 7.2960005 9.856001 7.392 L 7.6960006 7.36 L 5.2960005 1.6320001 L 3.2480001 7.36 L 1.024 7.392 C 0.92800003 7.2960005 0.92800003 6.9600005 1.024 6.8640003 C 1.8080001 6.8160005 1.9520001 6.7360005 1.9200001 6.432 L 1.4080001 1.9360001 C 1.264 0.60800004 1.056 0.544 0.448 0.49600002 C 0.35200003 0.4 0.35200003 0.064 0.448 -0.032 C 0.768 -0.016 1.248 0 1.5040001 0 C 1.8240001 0 2.4160001 -0.016 2.736 -0.032 C 2.832 0.064 2.832 0.4 2.736 0.49600002 C 1.8240001 0.56 1.84 0.75200003 1.968 1.9360001 L 2.4320002 6.0000005 L 2.4640002 6.0000005 L 4.736 -0.064 C 4.768 -0.14400001 4.848 -0.192 4.9280005 -0.192 C 4.992 -0.192 5.072 -0.14400001 5.104 -0.064 Z "/>
</symbol>
<symbol id="gB81772063B54F81148CB0F3810A30A3E" overflow="visible">
<path d="M 2.3040001 5.4880004 C 2.736 6.9440002 3.7600002 8.56 5.8880005 9.360001 C 5.8880005 9.552 5.8240004 9.696 5.696 9.776 C 4.0800004 9.2960005 3.088 8.624001 2.1920002 7.5840006 C 1.2 6.432 0.70400006 4.9760003 0.70400006 3.7120001 C 0.70400006 0.46400002 2.5440001 -0.17600001 3.7760003 -0.17600001 C 5.872 -0.17600001 6.7360005 1.8560001 6.7360005 3.232 C 6.7360005 4.6080003 6.0000005 5.84 3.8240001 5.84 C 3.4080002 5.84 2.7840002 5.7120004 2.3040001 5.4880004 Z M 2.16 4.912 C 2.6880002 5.2640004 3.216 5.28 3.4880002 5.28 C 5.056 5.28 5.4080005 3.7440002 5.4080005 2.9440002 C 5.4080005 1.184 4.736 0.384 3.9520001 0.384 C 2.9440002 0.384 2.032 0.92800003 2.032 3.6640003 C 2.032 4.032 2.0640001 4.4480004 2.16 4.912 Z "/>
</symbol>
<symbol id="g54625A295C6156FB7E0CA1A81FF5B54D" overflow="visible">
<path d="M 1.5120001 -2.7020001 L 4.48 -2.7020001 C 4.564 -2.618 4.564 -2.3660002 4.48 -2.282 C 2.548 -2.128 2.45 -1.9180001 2.45 -0.70000005 L 2.45 7.854 C 2.45 9.0720005 2.562 9.282001 4.48 9.422 C 4.564 9.5060005 4.564 9.758 4.48 9.842 L 1.5120001 9.842 Z "/>
</symbol>
<symbol id="gCA97BC07D124B95C474D25CFC2493057" overflow="visible">
<path d="M 2.17 1.1060001 L 2.94 3.1360002 C 3.01 3.318 3.094 3.374 3.43 3.374 L 6.3840003 3.374 L 7.196 1.008 C 7.3640003 0.532 6.8320003 0.476 6.1600003 0.43400002 C 6.076 0.35000002 6.076 0.056 6.1600003 -0.028 C 6.678 -0.014 7.4480004 0 7.9940004 0 C 8.568 0 9.1 -0.014 9.59 -0.028 C 9.674001 0.056 9.674001 0.35000002 9.59 0.43400002 C 9.044001 0.49 8.568 0.532 8.33 1.204 L 5.446 9.212 C 5.236 9.086 4.8580003 8.932 4.676 8.932 L 1.498 1.4280001 C 1.1340001 0.56 0.71400005 0.476 0.098000005 0.43400002 C 0.014 0.35000002 0.014 0.056 0.098000005 -0.028 C 0.462 -0.014 0.924 0 1.3440001 0 C 1.9180001 0 2.618 -0.014 3.1360002 -0.028 C 3.22 0.056 3.22 0.35000002 3.1360002 0.43400002 C 2.604 0.476 1.9460001 0.532 2.17 1.1060001 Z M 3.6820002 3.9620001 C 3.374 3.9620001 3.276 4.004 3.332 4.144 L 4.76 7.7700005 L 4.8440003 7.7700005 L 6.1600003 3.9620001 Z "/>
</symbol>
<symbol id="gBBFA548D7BC5ACA0036C5BF286E59830" overflow="visible">
<path d="M 1.33 1.7080001 C 1.33 0.546 1.176 0.476 0.322 0.43400002 C 0.238 0.35000002 0.238 0.056 0.322 -0.028 C 0.81200004 -0.014 1.33 0 1.8900001 0 C 2.45 0 2.982 -0.014 3.444 -0.028 C 3.528 0.056 3.528 0.35000002 3.444 0.43400002 C 2.5900002 0.476 2.436 0.546 2.436 1.7080001 L 2.436 8.162001 C 2.436 9.0720005 2.492 9.632 2.492 9.632 C 2.492 9.7300005 2.436 9.772 2.3100002 9.772 C 1.96 9.632 0.91 9.436 0.35000002 9.394 C 0.322 9.282001 0.35000002 9.058001 0.43400002 8.974 C 1.246 8.918 1.33 8.876 1.33 7.826 Z "/>
</symbol>
<symbol id="gEABB154513753541217365D535D0C073" overflow="visible">
<path d="M 6.216 5.418 C 6.4820004 5.418 6.734 5.67 6.734 5.9500003 C 6.734 6.244 6.4680004 6.4680004 6.09 6.4680004 C 5.7260003 6.4680004 5.0540004 6.23 4.69 5.754 C 4.5220003 5.866 4.06 6.1460004 3.2340002 6.1460004 C 1.988 6.1460004 0.84000003 5.306 0.84000003 4.018 C 0.84000003 3.262 1.176 2.828 1.5680001 2.45 C 1.176 2.114 0.952 1.5120001 0.952 1.036 C 0.952 0.532 1.232 0.14 1.5960001 -0.042000003 C 0.84000003 -0.49 0.448 -1.1340001 0.448 -1.7360001 C 0.448 -2.954 1.5960001 -3.332 2.674 -3.332 C 4.564 -3.332 6.6080003 -2.4220002 6.6080003 -0.91 C 6.6080003 -0.462 6.3980002 -0.112 5.992 0.224 C 5.446 0.67200005 4.466 0.68600005 3.9480002 0.68600005 C 3.696 0.68600005 3.3460002 0.658 3.01 0.616 C 2.8000002 0.602 2.66 0.588 2.5900002 0.588 C 2.184 0.588 1.694 0.78400004 1.694 1.386 C 1.694 1.666 1.778 1.96 1.9460001 2.198 C 2.282 2.002 2.674 1.904 3.22 1.904 C 4.452 1.904 5.586 2.674 5.586 4.046 C 5.586 4.704 5.3900003 5.0820003 4.984 5.5020003 C 5.0820003 5.642 5.362 5.8380003 5.544 5.8380003 C 5.642 5.8380003 5.7400002 5.796 5.8240004 5.67 C 5.88 5.558 6.0620003 5.418 6.216 5.418 Z M 1.848 -0.14 C 2.002 -0.18200001 2.226 -0.21000001 2.408 -0.21000001 C 2.842 -0.21000001 3.2340002 -0.16800001 3.43 -0.16800001 C 4.13 -0.16800001 4.718 -0.18200001 5.124 -0.40600002 C 5.67 -0.71400005 5.8380003 -0.91 5.8380003 -1.274 C 5.8380003 -2.282 4.354 -2.8140001 3.094 -2.8140001 C 2.5900002 -2.8140001 1.414 -2.408 1.414 -1.4560001 C 1.414 -0.98 1.442 -0.63 1.848 -0.14 Z M 4.466 3.9060001 C 4.466 2.604 3.808 2.338 3.2900002 2.338 C 2.114 2.338 1.988 3.332 1.988 4.228 C 1.988 5.208 2.338 5.7120004 3.108 5.7120004 C 3.99 5.7120004 4.466 5.0680003 4.466 3.9060001 Z "/>
</symbol>
<symbol id="g47288CF7D8F788F93B1406172900DCDE" overflow="visible">
<path d="M 0.79800004 0.602 C 0.79800004 0.19600001 1.1340001 -0.14 1.5400001 -0.14 C 1.9460001 -0.14 2.282 0.19600001 2.282 0.602 C 2.282 1.008 1.9460001 1.3440001 1.5400001 1.3440001 C 1.1340001 1.3440001 0.79800004 1.008 0.79800004 0.602 Z "/>
</symbol>
<symbol id="gD8D2A5E78EA4643EEAAC69DB934A336F" overflow="visible">
<path d="M 4.032 1.7080001 L 4.032 6.566 C 4.032 7.406 4.046 8.26 4.0740004 8.442 C 4.0740004 8.512 4.046 8.512 3.99 8.512 C 3.22 8.036 2.4780002 7.6860003 1.246 7.112 C 1.274 6.958 1.33 6.8180003 1.4560001 6.734 C 2.1000001 7 2.408 7.084 2.674 7.084 C 2.9120002 7.084 2.954 6.748 2.954 6.2720003 L 2.954 1.7080001 C 2.954 0.546 2.576 0.476 1.5960001 0.43400002 C 1.5120001 0.35000002 1.5120001 0.056 1.5960001 -0.028 C 2.282 -0.014 2.786 0 3.542 0 C 4.214 0 4.55 -0.014 5.25 -0.028 C 5.334 0.056 5.334 0.35000002 5.25 0.43400002 C 4.27 0.476 4.032 0.546 4.032 1.7080001 Z "/>
</symbol>
<symbol id="g202FAE631B7A80A660AEE76AD2161E37" overflow="visible">
<path d="M 3.4720001 9.856 L 0.504 9.856 C 0.42000002 9.772 0.42000002 9.52 0.504 9.436 C 2.436 9.282001 2.5340002 9.0720005 2.5340002 7.854 L 2.5340002 -0.70000005 C 2.5340002 -1.9180001 2.4220002 -2.128 0.504 -2.2680001 C 0.42000002 -2.352 0.42000002 -2.604 0.504 -2.6880002 L 3.4720001 -2.6880002 Z "/>
</symbol>
<symbol id="g176D627313BEF56D87624592E290FFD2" overflow="visible">
<path d="M 4.998 -0.14 C 6.3560004 -0.14 7.602 0.504 8.554 1.75 C 8.484 1.876 8.386001 1.96 8.232 1.96 C 7.2380004 0.86800003 6.2860003 0.43400002 4.984 0.43400002 C 3.094 0.43400002 1.792 2.562 1.792 4.606 C 1.792 5.81 2.114 6.8180003 2.618 7.4480004 C 3.318 8.302 4.13 8.694 4.8580003 8.694 C 6.7900004 8.694 7.5600004 7.546 7.9240003 6.342 C 8.092 6.2860003 8.232 6.328 8.386001 6.412 C 8.316 7.1400003 8.218 7.8120003 8.078 8.582001 C 7.3640003 8.652 6.734 9.212 5.012 9.212 C 3.822 9.212 2.828 8.778 2.002 8.022 C 1.0780001 7.168 0.518 5.796 0.518 4.34 C 0.518 1.904 1.988 -0.14 4.998 -0.14 Z "/>
</symbol>
<symbol id="gA4DE3951E8A0322DEC5E3569D1D30666" overflow="visible">
<path d="M 0.574 2.8700001 C 0.574 1.442 1.526 -0.14 3.5140002 -0.14 C 4.4100003 -0.14 5.096 0.18200001 5.572 0.644 C 6.202 1.26 6.4820004 2.142 6.4820004 2.996 C 6.4820004 4.452 5.684 6.1460004 3.542 6.1460004 C 2.618 6.1460004 1.8620001 5.768 1.3440001 5.1660004 C 0.84000003 4.564 0.574 3.752 0.574 2.8700001 Z M 3.332 5.656 C 4.5360003 5.656 5.2780004 4.564 5.2780004 2.548 C 5.2780004 0.78400004 4.368 0.35000002 3.71 0.35000002 C 2.2540002 0.35000002 1.778 2.114 1.778 3.1920002 C 1.778 4.4100003 2.072 5.656 3.332 5.656 Z "/>
</symbol>
<symbol id="g77113E0CAAA23E0B77E89A338ACC30A4" overflow="visible">
<path d="M 2.576 5.012 C 2.492 4.914 2.408 4.886 2.408 5.012 C 2.394 5.3900003 2.3660002 5.9360003 2.296 6.076 C 2.2680001 6.1460004 2.24 6.188 2.128 6.188 C 1.7360001 6.0340004 1.3720001 5.908 0.40600002 5.782 C 0.37800002 5.698 0.40600002 5.474 0.43400002 5.3900003 C 1.19 5.32 1.3440001 5.25 1.3440001 4.438 L 1.3440001 1.7080001 C 1.3440001 0.56 1.204 0.504 0.36400002 0.43400002 C 0.28 0.35000002 0.28 0.056 0.36400002 -0.028 C 0.78400004 -0.014 1.3440001 0 1.904 0 C 2.464 0 2.884 -0.014 3.3040001 -0.028 C 3.388 0.056 3.388 0.35000002 3.3040001 0.43400002 C 2.5900002 0.504 2.45 0.56 2.45 1.7080001 L 2.45 4.004 C 2.45 4.2980003 2.576 4.466 2.6880002 4.592 C 3.22 5.11 3.8500001 5.418 4.396 5.418 C 4.676 5.418 4.9700003 5.236 5.138 4.914 C 5.2780004 4.6340003 5.306 4.256 5.306 3.8360002 L 5.306 1.7080001 C 5.306 0.56 5.1660004 0.504 4.438 0.43400002 C 4.368 0.35000002 4.368 0.056 4.438 -0.028 C 4.8580003 -0.014 5.306 0 5.866 0 C 6.426 0 6.9300003 -0.014 7.3500004 -0.028 C 7.42 0.056 7.42 0.35000002 7.3500004 0.43400002 C 6.566 0.504 6.412 0.56 6.412 1.7080001 L 6.412 3.7940001 C 6.412 4.564 6.3560004 5.236 6.0340004 5.67 C 5.796 5.978 5.362 6.1460004 4.872 6.1460004 C 4.1860003 6.1460004 3.4020002 5.964 2.576 5.012 Z "/>
</symbol>
<symbol id="g2027E4E303C701A0DF6BD0919BBDE7B4" overflow="visible">
<path d="M 0.67200005 1.932 C 0.72800004 1.246 0.77000004 0.588 0.77000004 0 C 0.91 0.028 1.0500001 0.042000003 1.12 0.042000003 C 1.218 0.042000003 1.302 0.042000003 1.4000001 0.014 C 1.778 -0.08400001 2.1560001 -0.14 2.674 -0.14 C 3.4580002 -0.14 4.9 0.238 4.9 1.6240001 C 4.9 2.576 4.214 3.1360002 3.262 3.486 C 2.4220002 3.808 1.8620001 4.018 1.8620001 4.788 C 1.8620001 5.362 2.3660002 5.684 2.842 5.684 C 3.15 5.684 3.9620001 5.572 4.144 4.382 C 4.228 4.2980003 4.5080004 4.3120003 4.592 4.396 C 4.6340003 4.9 4.662 5.418 4.676 5.88 C 4.242 5.9500003 3.5700002 6.1460004 2.842 6.1460004 C 1.8060001 6.1460004 0.86800003 5.474 0.86800003 4.578 C 0.86800003 3.556 1.33 3.122 2.408 2.674 C 3.5700002 2.198 3.8360002 1.904 3.8360002 1.302 C 3.8360002 0.616 3.164 0.322 2.6460001 0.322 C 2.1000001 0.322 1.792 0.504 1.6520001 0.658 C 1.3440001 0.98 1.19 1.5960001 1.1060001 1.9460001 C 1.0220001 2.03 0.75600004 2.016 0.67200005 1.932 Z "/>
</symbol>
<symbol id="g88B62CE1F53AC1AE1D938018DA31319" overflow="visible">
<path d="M 0.602 6.006 C 0.40600002 6.006 0.35000002 5.8380003 0.35000002 5.7260003 L 0.35000002 5.544 C 0.35000002 5.474 0.36400002 5.46 0.42000002 5.46 L 1.246 5.46 L 1.246 1.246 C 1.246 0.252 1.6800001 -0.14 2.3240001 -0.14 C 2.9680002 -0.14 3.6680002 0.16800001 4.214 0.78400004 C 4.1860003 0.924 4.102 1.008 3.9620001 1.0220001 C 3.598 0.74200004 3.1780002 0.63 2.8140001 0.63 C 2.436 0.63 2.352 1.0500001 2.352 1.9180001 L 2.352 5.46 L 3.808 5.46 C 3.9480002 5.46 4.144 5.5160003 4.144 5.642 L 4.144 5.9220004 C 4.144 5.978 4.102 6.006 4.032 6.006 L 2.352 6.006 L 2.352 6.552 C 2.352 7.4620004 2.408 8.022 2.408 8.022 C 2.408 8.106 2.3660002 8.148001 2.296 8.148001 C 2.24 8.148001 2.114 8.092 1.988 8.022 C 1.8340001 7.938 1.694 7.868 1.5120001 7.826 C 1.3440001 7.7700005 1.204 7.728 1.204 7.63 C 1.204 7.4620004 1.246 7.5600004 1.246 6.006 Z "/>
</symbol>
<symbol id="g9AE4831982D6CA553E49B4F41E9A233F" overflow="visible">
<path d="M 2.464 5.012 C 2.436 5.572 2.4220002 5.9360003 2.352 6.076 C 2.3240001 6.1460004 2.296 6.188 2.184 6.188 C 1.792 6.0340004 1.4280001 5.908 0.462 5.782 C 0.43400002 5.698 0.462 5.474 0.49 5.3900003 C 1.246 5.32 1.4000001 5.25 1.4000001 4.438 L 1.4000001 1.7080001 C 1.4000001 0.546 1.232 0.49 0.36400002 0.43400002 C 0.28 0.35000002 0.28 0.056 0.36400002 -0.028 C 0.85400003 -0.014 1.4000001 0 1.96 0 C 2.52 0 3.164 -0.014 3.654 -0.028 C 3.7380002 0.056 3.7380002 0.35000002 3.654 0.43400002 C 2.674 0.504 2.506 0.546 2.506 1.7080001 L 2.506 3.654 C 2.506 4.018 2.674 4.34 2.842 4.592 C 2.996 4.816 3.318 5.2780004 3.486 5.2780004 C 3.6120002 5.2780004 3.7380002 5.25 3.8500001 5.096 C 3.9480002 4.9560003 4.116 4.774 4.354 4.774 C 4.69 4.774 5.012 5.124 5.012 5.474 C 5.012 5.7400002 4.76 6.1460004 4.172 6.1460004 C 3.5140002 6.1460004 2.94 5.53 2.618 4.984 C 2.5340002 4.83 2.464 4.9420004 2.464 5.012 Z "/>
</symbol>
<symbol id="g9928BAA4F6AD9C2CD04BDE4A0594D984" overflow="visible">
<path d="M 3.038 -0.14 C 3.584 -0.14 4.242 0.14 4.928 0.70000005 C 4.998 0.75600004 5.124 0.78400004 5.138 0.68600005 C 5.1800003 0.33600003 5.2920003 -0.14 5.2920003 -0.14 C 5.4040003 -0.18200001 5.474 -0.16800001 5.558 -0.14 C 5.866 0.112 6.3560004 0.322 7.21 0.42000002 C 7.294 0.504 7.294 0.71400005 7.21 0.79800004 C 6.314 0.86800003 6.188 1.1340001 6.188 1.82 L 6.188 4.5080004 C 6.188 4.928 6.244 5.9500003 6.244 5.9500003 C 6.244 5.992 6.202 6.0340004 6.132 6.0340004 C 6.0620003 6.02 5.852 6.006 5.642 6.006 C 5.1940002 6.006 4.69 6.02 4.214 6.0340004 C 4.13 5.9500003 4.13 5.656 4.214 5.572 C 4.9 5.53 5.0820003 5.362 5.0820003 4.438 L 5.0820003 1.7360001 C 5.0820003 1.47 5.0540004 1.358 4.8580003 1.19 C 4.34 0.74200004 3.808 0.518 3.4580002 0.518 C 3.038 0.518 2.338 0.71400005 2.338 1.96 L 2.338 4.5080004 C 2.338 4.928 2.394 5.9500003 2.394 5.9500003 C 2.394 5.992 2.352 6.0340004 2.282 6.0340004 C 2.2120001 6.02 2.002 6.006 1.792 6.006 C 1.3440001 6.006 0.84000003 6.02 0.36400002 6.0340004 C 0.28 5.9500003 0.28 5.656 0.36400002 5.572 C 1.036 5.5160003 1.232 5.362 1.232 4.452 L 1.232 1.764 C 1.232 0.79800004 1.6520001 -0.14 3.038 -0.14 Z "/>
</symbol>
<symbol id="g5D527560B31964E4713419A527341CBD" overflow="visible">
<path d="M 5.572 1.274 C 5.5160003 1.4000001 5.4040003 1.4560001 5.2780004 1.47 C 4.802 0.85400003 4.2000003 0.546 3.598 0.546 C 2.576 0.546 1.722 1.582 1.722 3.22 C 1.722 4.76 2.394 5.684 3.318 5.684 C 4.144 5.684 4.256 5.1940002 4.3120003 4.704 C 4.354 4.326 4.55 4.2000003 4.8440003 4.2000003 C 5.138 4.2000003 5.53 4.382 5.53 4.816 C 5.53 5.586 4.7320004 6.1460004 3.388 6.1460004 C 2.002 6.1460004 0.518 4.9 0.518 2.9120002 C 0.518 1.1060001 1.526 -0.14 3.2900002 -0.14 C 4.13 -0.14 4.872 0.126 5.572 1.274 Z "/>
</symbol>
<symbol id="gAAC2A4387B1619C03EEEB0968B96165F" overflow="visible">
<path d="M 2.5340002 1.7080001 L 2.5340002 4.494 C 2.5340002 5.1940002 2.5900002 6.09 2.5900002 6.09 C 2.5900002 6.1460004 2.52 6.188 2.408 6.188 C 2.016 6.0340004 1.4560001 5.908 0.49 5.782 C 0.462 5.698 0.49 5.474 0.518 5.3900003 C 1.288 5.32 1.4280001 5.236 1.4280001 4.438 L 1.4280001 1.7080001 C 1.4280001 0.546 1.274 0.504 0.42000002 0.43400002 C 0.33600003 0.35000002 0.33600003 0.056 0.42000002 -0.028 C 0.882 -0.014 1.4280001 0 1.988 0 C 2.548 0 3.0800002 -0.014 3.542 -0.028 C 3.6260002 0.056 3.6260002 0.35000002 3.542 0.43400002 C 2.6880002 0.49 2.5340002 0.546 2.5340002 1.7080001 Z M 1.26 8.386001 C 1.26 8.022 1.5960001 7.6580005 1.932 7.6580005 C 2.3240001 7.6580005 2.66 8.036 2.66 8.33 C 2.66 8.666 2.3660002 9.058001 1.988 9.058001 C 1.6520001 9.058001 1.26 8.722 1.26 8.386001 Z "/>
</symbol>
<symbol id="g68885674EB6A8B1A6039D4F45B463C56" overflow="visible">
<path d="M 2.38 7.4900002 L 4.886 7.4900002 C 3.7940001 4.774 2.6880002 2.0440001 1.7360001 -0.08400001 L 1.848 -0.18200001 L 2.8000002 -0.14 C 3.598 2.24 4.368 4.564 5.9360003 8.386001 L 5.7120004 8.554 C 5.474 8.484 5.1660004 8.400001 4.6340003 8.400001 L 1.75 8.400001 C 1.274 8.400001 1.302 8.54 1.0500001 8.596001 C 1.008 8.596001 0.994 8.596001 0.994 8.554 C 0.98 7.8820004 0.82600003 7.0420003 0.71400005 6.314 C 0.86800003 6.2720003 1.008 6.2580004 1.1620001 6.2720003 C 1.47 7.392 1.932 7.4900002 2.38 7.4900002 Z "/>
</symbol>
<symbol id="g9696EE00168B299790D79B47B78C5F18" overflow="visible">
<path d="M 0.85400003 6.552 C 0.85400003 6.2580004 1.12 6.006 1.414 6.006 C 1.6520001 6.006 2.072 6.2580004 2.072 6.566 C 2.072 6.678 2.0440001 6.762 2.016 6.86 C 1.988 6.958 1.904 7.084 1.904 7.196 C 1.904 7.546 2.2680001 8.05 3.2900002 8.05 C 3.7940001 8.05 4.5080004 7.7000003 4.5080004 6.3560004 C 4.5080004 5.46 4.1860003 4.7320004 3.3600001 3.8920002 L 2.3240001 2.8700001 C 0.952 1.47 0.72800004 0.79800004 0.72800004 -0.028 C 0.72800004 -0.028 1.442 0 1.8900001 0 L 4.34 0 C 4.788 0 5.432 -0.028 5.432 -0.028 C 5.6140003 0.71400005 5.754 1.764 5.768 2.184 C 5.684 2.2540002 5.5020003 2.282 5.362 2.2540002 C 5.124 1.26 4.886 0.91 4.382 0.91 L 1.8900001 0.91 C 1.8900001 1.582 2.8560002 2.5340002 2.926 2.604 L 4.34 3.9620001 C 5.138 4.7320004 5.7400002 5.348 5.7400002 6.412 C 5.7400002 7.9240003 4.5080004 8.54 3.374 8.54 C 1.82 8.54 0.85400003 7.392 0.85400003 6.552 Z "/>
</symbol>
<symbol id="gF73CF51A640CD9E8903A9C4D4B743CCF" overflow="visible">
<path d="M 5.53 8.834001 C 4.718 8.946 4.7460003 9.212 3.374 9.212 C 1.96 9.212 0.71400005 8.274 0.71400005 6.7900004 C 0.71400005 5.32 1.932 4.6480002 3.164 4.172 C 4.004 3.8500001 5.04 3.4580002 5.04 2.086 C 5.04 0.952 4.4100003 0.36400002 3.2900002 0.36400002 C 1.988 0.36400002 1.148 0.966 0.84000003 2.352 C 0.658 2.408 0.518 2.38 0.37800002 2.3100002 C 0.43400002 1.232 0.49 0.86800003 0.658 0.18200001 C 1.5400001 0.18200001 1.932 -0.14 3.1780002 -0.14 C 3.808 -0.14 4.4100003 0.014 4.9 0.322 C 5.7120004 0.82600003 6.216 1.6800001 6.216 2.576 C 6.216 4.06 5.096 4.718 3.9480002 5.152 C 3.108 5.46 1.7080001 5.992 1.7080001 7.168 C 1.7080001 7.952 2.4220002 8.736 3.2480001 8.736 C 4.606 8.736 5.04 7.868 5.32 6.9440002 C 5.474 6.9160004 5.656 6.9300003 5.782 7.0280004 C 5.7260003 7.7000003 5.67 8.092 5.53 8.834001 Z "/>
</symbol>
<symbol id="g634FF9E9D0A0144E2AFDD807D5ECB7D0" overflow="visible">
<path d="M 5.4040003 1.302 C 4.886 0.77000004 4.48 0.546 3.6680002 0.546 C 3.164 0.546 2.576 0.84000003 2.142 1.554 C 1.8620001 2.016 1.694 2.66 1.694 3.4720001 L 5.418 3.444 C 5.586 3.444 5.684 3.528 5.684 3.6820002 C 5.684 4.8580003 5.264 6.118 3.318 6.118 C 2.1000001 6.118 0.518 4.9560003 0.518 2.828 C 0.518 2.0440001 0.71400005 1.288 1.176 0.75600004 C 1.6520001 0.19600001 2.3100002 -0.14 3.318 -0.14 C 4.382 -0.14 5.138 0.35000002 5.698 1.0780001 C 5.656 1.218 5.572 1.288 5.4040003 1.302 Z M 1.7360001 3.9480002 C 2.002 5.53 2.982 5.656 3.318 5.656 C 3.8500001 5.656 4.48 5.362 4.48 4.1860003 C 4.48 4.06 4.4240003 3.99 4.27 3.99 Z "/>
</symbol>
<symbol id="g3649D621BC998C9216AD40BBEFAC3AB1" overflow="visible">
<path d="M 4.102 0.67200005 C 4.1860003 0.238 4.34 -0.14 5.04 -0.14 C 5.572 -0.14 6.076 0.098000005 6.3700004 0.37800002 C 6.342 0.546 6.2860003 0.67200005 6.132 0.75600004 C 6.0340004 0.67200005 5.796 0.532 5.6140003 0.532 C 5.208 0.532 5.1940002 1.0780001 5.1940002 1.722 L 5.1940002 3.7800002 C 5.1940002 5.768 4.102 6.1460004 3.0800002 6.1460004 C 1.932 6.1460004 0.77000004 5.3900003 0.77000004 4.592 C 0.77000004 4.256 0.938 4.0880003 1.26 4.0880003 C 1.666 4.0880003 1.9180001 4.382 1.9180001 4.564 C 1.9180001 4.662 1.904 4.76 1.876 4.816 C 1.8620001 4.8580003 1.848 4.9420004 1.848 5.096 C 1.848 5.53 2.436 5.684 2.9680002 5.684 C 3.444 5.684 4.102 5.446 4.102 3.864 C 4.102 3.766 4.06 3.71 4.018 3.696 L 2.8140001 3.4020002 C 1.47 3.066 0.504 2.3240001 0.504 1.3720001 C 0.504 0.224 1.288 -0.14 2.2680001 -0.14 C 2.7580001 -0.14 3.1780002 -0.028 3.7940001 0.448 L 4.0740004 0.67200005 Z M 4.102 3.262 L 4.102 1.414 C 4.102 1.232 4.018 1.1340001 3.9060001 1.0500001 C 3.542 0.75600004 3.066 0.43400002 2.674 0.43400002 C 1.9740001 0.43400002 1.666 0.994 1.666 1.4280001 C 1.666 2.058 1.96 2.7020001 2.996 2.9680002 Z "/>
</symbol>
<symbol id="gD0DD0C2B056F25673B3EED0135505F92" overflow="visible">
<path d="M 2.338 4.004 C 2.338 4.2980003 2.464 4.466 2.576 4.592 C 3.108 5.11 3.822 5.418 4.368 5.418 C 4.6480002 5.418 4.9420004 5.236 5.11 4.914 C 5.25 4.6340003 5.2780004 4.256 5.2780004 3.8360002 L 5.2780004 1.7080001 C 5.2780004 0.56 5.138 0.504 4.4100003 0.43400002 C 4.34 0.35000002 4.34 0.056 4.4100003 -0.028 C 4.802 -0.014 5.2780004 0 5.8380003 0 C 6.3980002 0 6.86 -0.014 7.322 -0.028 C 7.392 0.056 7.392 0.35000002 7.322 0.43400002 C 6.538 0.504 6.3840003 0.56 6.3840003 1.7080001 L 6.3840003 3.7940001 C 6.3840003 4.564 6.328 5.25 6.006 5.67 C 5.768 5.978 5.334 6.1460004 4.8440003 6.1460004 C 4.158 6.1460004 3.318 5.964 2.464 5.012 C 2.464 4.998 2.45 4.998 2.436 4.984 C 2.394 4.928 2.3240001 4.8440003 2.3240001 5.012 L 2.338 8.162001 C 2.338 9.0720005 2.394 9.632 2.394 9.632 C 2.394 9.7300005 2.338 9.772 2.2120001 9.772 C 1.8620001 9.632 0.81200004 9.436 0.252 9.394 C 0.224 9.282001 0.252 9.058001 0.33600003 8.974 C 0.37800002 8.974 0.42000002 8.974 0.462 8.974 C 1.0780001 8.932 1.232 8.932 1.232 7.826 L 1.232 1.7080001 C 1.232 0.546 1.064 0.49 0.252 0.43400002 C 0.16800001 0.35000002 0.16800001 0.056 0.252 -0.028 C 0.71400005 -0.014 1.232 0 1.792 0 C 2.3240001 0 2.786 -0.014 3.1780002 -0.028 C 3.262 0.056 3.262 0.35000002 3.1780002 0.43400002 C 2.464 0.49 2.338 0.546 2.338 1.7080001 Z "/>
</symbol>
<symbol id="gB1BEBEB6281B0C94AE56C4BB0BF6ED0C" overflow="visible">
<path d="M 4.578 3.584 C 4.2000003 2.3100002 3.3040001 0.896 1.442 0.19600001 C 1.442 0.028 1.498 -0.098000005 1.61 -0.16800001 C 3.0240002 0.252 3.8920002 0.84000003 4.676 1.75 C 5.544 2.7580001 5.978 4.032 5.978 5.138 C 5.978 7.98 4.368 8.54 3.2900002 8.54 C 1.4560001 8.54 0.70000005 6.762 0.70000005 5.558 C 0.70000005 4.354 1.3440001 3.276 3.2480001 3.276 C 3.6120002 3.276 4.158 3.388 4.578 3.584 Z M 4.704 4.0880003 C 4.242 3.7800002 3.7800002 3.766 3.542 3.766 C 2.17 3.766 1.8620001 5.11 1.8620001 5.81 C 1.8620001 7.3500004 2.45 8.05 3.1360002 8.05 C 4.018 8.05 4.816 7.5740004 4.816 5.1800003 C 4.816 4.872 4.788 4.494 4.704 4.0880003 Z "/>
</symbol>
<symbol id="gD0485EF23018DAF4BFC69AAD15075193" overflow="visible">
<path d="M 3.01 8.05 C 3.6120002 8.05 4.172 7.6860003 4.172 6.7900004 C 4.172 6.09 3.3600001 5.012 1.9740001 4.816 L 2.0440001 4.368 C 2.282 4.396 2.5340002 4.396 2.716 4.396 C 3.5140002 4.396 4.55 4.172 4.55 2.5900002 C 4.55 0.72800004 3.3040001 0.35000002 2.8140001 0.35000002 C 2.1000001 0.35000002 1.9740001 0.67200005 1.8060001 0.924 C 1.666 1.12 1.4840001 1.288 1.204 1.288 C 0.91 1.288 0.616 1.0220001 0.616 0.79800004 C 0.616 0.238 1.792 -0.14 2.632 -0.14 C 4.2980003 -0.14 5.782 0.938 5.782 2.786 C 5.782 4.3120003 4.6340003 4.8580003 3.808 4.998 L 3.7940001 5.026 C 4.9420004 5.572 5.264 6.1460004 5.264 6.888 C 5.264 7.308 5.1660004 7.644 4.83 7.9940004 C 4.5220003 8.302 4.032 8.54 3.3040001 8.54 C 1.246 8.54 0.658 7.196 0.658 6.734 C 0.658 6.538 0.79800004 6.2580004 1.1340001 6.2580004 C 1.6240001 6.2580004 1.6800001 6.7200003 1.6800001 6.986 C 1.6800001 7.8820004 2.6460001 8.05 3.01 8.05 Z "/>
</symbol>
<symbol id="gC80234271A0A022352A099322F0FCD32" overflow="visible">
<path d="M 2.338 5.5160003 C 2.2540002 5.432 2.198 5.46 2.198 5.586 L 2.198 8.162001 C 2.198 9.0720005 2.2540002 9.632 2.2540002 9.632 C 2.2540002 9.7300005 2.198 9.772 2.072 9.772 C 1.722 9.632 0.67200005 9.436 0.112 9.394 C 0.08400001 9.282001 0.112 9.058001 0.19600001 8.974 C 0.238 8.974 0.28 8.974 0.322 8.974 C 0.938 8.932 1.092 8.932 1.092 7.826 L 1.092 0.994 C 1.092 0.448 1.0780001 0.19600001 1.036 0 C 1.1060001 -0.112 1.176 -0.16800001 1.3440001 -0.16800001 C 1.4280001 -0.08400001 1.5680001 0.042000003 1.6800001 0.16800001 C 1.82 0.33600003 1.904 0.33600003 2.058 0.21000001 C 2.38 -0.056 2.8000002 -0.14 3.2900002 -0.14 C 4.718 -0.14 6.3840003 1.1620001 6.3840003 3.388 C 6.3840003 5.096 5.124 6.1460004 3.9060001 6.1460004 C 3.3040001 6.1460004 2.772 5.908 2.338 5.5160003 Z M 2.436 5.0820003 C 2.8000002 5.4040003 3.22 5.53 3.6260002 5.53 C 4.48 5.53 5.1800003 4.494 5.1800003 3.1360002 C 5.1800003 1.5400001 4.5360003 0.33600003 3.206 0.33600003 C 2.772 0.33600003 2.4780002 0.644 2.198 0.994 L 2.198 4.494 C 2.198 4.788 2.2540002 4.928 2.436 5.0820003 Z "/>
</symbol>
<symbol id="gC9680074409574DDF948104B0C55D755" overflow="visible">
<path d="M 3.1920002 -0.14 C 4.27 -0.14 5.908 0.952 5.908 4.242 C 5.908 5.6280003 5.572 6.8180003 4.9560003 7.63 C 4.592 8.12 4.004 8.54 3.2480001 8.54 C 1.8620001 8.54 0.546 6.888 0.546 4.116 C 0.546 2.618 1.008 1.218 1.778 0.448 C 2.17 0.056 2.6460001 -0.14 3.1920002 -0.14 Z M 3.2480001 8.05 C 3.486 8.05 3.71 7.966 3.878 7.8120003 C 4.3120003 7.4480004 4.69 6.3840003 4.69 4.5080004 C 4.69 3.22 4.6480002 2.338 4.452 1.6240001 C 4.144 0.476 3.4580002 0.35000002 3.206 0.35000002 C 1.904 0.35000002 1.764 2.7440002 1.764 3.9620001 C 1.764 7.406 2.618 8.05 3.2480001 8.05 Z "/>
</symbol>
<symbol id="g985B950D50769631420A9A59AEA7CEFC" overflow="visible">
<path d="M 3.0560002 1.9520001 L 3.0560002 8.368 C 3.0560002 9.696 3.328 9.776 4.4480004 9.824 C 4.544 9.92 4.544 10.2560005 4.4480004 10.352 C 3.7440002 10.336 2.992 10.320001 2.368 10.320001 C 1.84 10.320001 1.056 10.336 0.30400002 10.352 C 0.208 10.2560005 0.208 9.92 0.30400002 9.824 C 1.424 9.776 1.6960001 9.696 1.6960001 8.368 L 1.6960001 1.9520001 C 1.6960001 0.624 1.424 0.544 0.30400002 0.49600002 C 0.208 0.4 0.208 0.064 0.30400002 -0.032 C 1.024 -0.016 1.8080001 0 2.384 0 C 2.96 0 3.7280002 -0.016 4.4480004 -0.032 C 4.544 0.064 4.544 0.4 4.4480004 0.49600002 C 3.328 0.544 3.0560002 0.624 3.0560002 1.9520001 Z "/>
</symbol>
<symbol id="g3E944C953D169E97A30360D928248E70" overflow="visible">
<path d="M 3.0240002 1.9520001 L 3.0240002 3.1360002 C 3.3120003 3.0080001 3.6320002 2.9440002 4.032 2.9440002 C 6.176 2.9440002 6.8320003 4.48 6.8320003 5.44 C 6.8320003 6.2720003 6.352 7.392 4.0800004 7.392 C 3.4880002 7.392 2.8160002 7.36 2.384 7.36 C 1.9200001 7.36 1.248 7.3760004 0.60800004 7.392 C 0.512 7.2960005 0.512 6.9600005 0.60800004 6.8640003 C 1.5840001 6.8 1.7600001 6.7360005 1.7600001 5.4080005 L 1.7600001 1.9520001 C 1.7600001 0.624 1.5840001 0.57600003 0.60800004 0.49600002 C 0.512 0.4 0.512 0.064 0.60800004 -0.032 C 1.136 -0.016 1.6960001 0 2.4 0 C 3.088 0 3.6480002 -0.016 4.176 -0.032 C 4.2720003 0.064 4.2720003 0.4 4.176 0.49600002 C 3.2 0.56 3.0240002 0.624 3.0240002 1.9520001 Z M 3.0240002 6.144 C 3.0240002 6.656 3.216 6.8640003 3.9840002 6.8640003 C 4.9280005 6.8640003 5.44 6.3680005 5.44 5.248 C 5.44 4.096 5.024 3.4720001 4.064 3.4720001 C 3.7440002 3.4720001 3.344 3.5200002 3.0240002 3.6480002 Z "/>
</symbol>
<symbol id="gBAC0ED7F2DB725071CE720AF8BC15D72" overflow="visible">
<path d="M 2.9280002 5.7920003 C 2.5440001 6.7040005 2.5600002 6.7840004 3.4240003 6.8640003 C 3.5200002 6.9600005 3.5200002 7.2960005 3.4240003 7.392 C 2.9280002 7.3760004 2.384 7.36 1.728 7.36 C 1.2160001 7.36 0.73600006 7.3760004 0.32000002 7.392 C 0.224 7.2960005 0.224 6.9600005 0.32000002 6.8640003 C 1.1040001 6.7840004 1.2160001 6.6080003 1.6 5.696 L 3.8720002 0.448 C 4.0800004 -0.016 4.1600003 -0.192 4.3360004 -0.192 C 4.4480004 -0.192 4.512 -0.064 4.736 0.448 L 7.0720005 5.6800003 C 7.4080005 6.4160004 7.5840006 6.8 8.448 6.8640003 C 8.544001 6.9600005 8.544001 7.2960005 8.448 7.392 C 8.096001 7.3760004 7.7120004 7.36 7.2960005 7.36 C 6.7040005 7.36 6.2560005 7.3760004 5.8240004 7.392 C 5.728 7.2960005 5.728 6.9600005 5.8240004 6.8640003 C 6.688 6.8 6.768 6.6080003 6.4480004 5.7920003 L 4.704 1.8080001 C 4.656 1.7600001 4.6400003 1.7600001 4.592 1.8080001 Z "/>
</symbol>
<symbol id="gDA675C10B642A458CD97A11D372FF5DA" overflow="visible">
<path d="M 3.9680002 3.6000001 C 5.024 3.6000001 5.0400004 3.2960002 5.072 2.7040002 C 5.1520004 2.624 5.44 2.624 5.5200005 2.7040002 C 5.504 3.072 5.4880004 3.6160002 5.4880004 3.8720002 C 5.4880004 4.096 5.504 4.6080003 5.5200005 5.0080004 C 5.44 5.0880003 5.1520004 5.0880003 5.072 5.0080004 C 5.0400004 4.288 5.0080004 4.112 3.9680002 4.112 L 3.0560002 4.112 L 3.0560002 6.3840003 C 3.0560002 6.656 3.2640002 6.8320003 3.568 6.8320003 L 4.48 6.8320003 C 5.7920003 6.8320003 6.0000005 6.3040004 6.288 5.392 C 6.4480004 5.3760004 6.5920005 5.4080005 6.7200003 5.472 C 6.656 6.0160003 6.464 7.2640004 6.432 7.3760004 C 6.432 7.4080005 6.4160004 7.4240003 6.3840003 7.4240003 C 6.1600003 7.3760004 6.0000005 7.36 5.728 7.36 L 2.4160001 7.36 C 1.9520001 7.36 1.2160001 7.3760004 0.64000005 7.392 C 0.544 7.2960005 0.544 6.9600005 0.64000005 6.8640003 C 1.616 6.8 1.792 6.7360005 1.792 5.4080005 L 1.792 1.9520001 C 1.792 0.624 1.616 0.57600003 0.64000005 0.49600002 C 0.544 0.4 0.544 0.064 0.64000005 -0.032 C 1.2160001 -0.016 1.9200001 0 2.4320002 0 L 4.8960004 0 C 5.5360003 0 6.5920005 -0.032 6.5920005 -0.032 C 6.7840004 0.624 6.9600005 1.5040001 7.0720005 2.176 C 6.9280005 2.256 6.8 2.288 6.6240005 2.24 C 6.3680005 1.296 5.9040003 0.49600002 4.576 0.49600002 L 3.8880002 0.49600002 C 3.216 0.49600002 3.0560002 0.67200005 3.0560002 1.2 L 3.0560002 3.6000001 Z "/>
</symbol>
<symbol id="g2F3EA0F52D7EBFDBD1E9205C07C62175" overflow="visible">
<path d="M 2.48 1.9520001 L 2.48 4.992 C 2.48 5.7760005 2.6880002 5.6320004 3.0560002 5.168 L 6.8160005 0.16000001 C 7.056 -0.096 7.3120003 -0.192 7.5520005 -0.192 C 7.7440004 -0.192 7.9040003 -0.080000006 7.9040003 0.24000001 L 7.9040003 5.4080005 C 7.9040003 6.7360005 8.08 6.7840004 9.056001 6.8640003 C 9.152 6.9600005 9.152 7.2960005 9.056001 7.392 C 8.576 7.3760004 8 7.36 7.5200005 7.36 C 7.0400004 7.36 6.4800005 7.3760004 6.0000005 7.392 C 5.9040003 7.2960005 5.9040003 6.9600005 6.0000005 6.8640003 C 6.9760003 6.8 7.1520004 6.7360005 7.1520004 5.4080005 L 7.1520004 2.4160001 C 7.1520004 1.9840001 7.1040006 1.7120001 6.6080003 2.384 L 2.9440002 7.36 L 0.67200005 7.392 L 0.64000005 7.3440003 L 0.64000005 6.9600005 C 0.64000005 6.8960004 0.73600006 6.8640003 0.78400004 6.8640003 C 1.3920001 6.8160005 1.5680001 6.6240005 1.728 6.3360004 L 1.728 1.9520001 C 1.728 0.624 1.552 0.56 0.57600003 0.49600002 C 0.48000002 0.4 0.48000002 0.064 0.57600003 -0.032 C 1.056 -0.016 1.616 0 2.0960002 0 C 2.5760002 0 3.1520002 -0.016 3.6320002 -0.032 C 3.7280002 0.064 3.7280002 0.4 3.6320002 0.49600002 C 2.6560001 0.57600003 2.48 0.624 2.48 1.9520001 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
<symbol id="g6D1F08816BC4457F813BBA2B6CEC4900" overflow="visible">
<path d="M 2.38 5.012 C 2.3660002 5.432 2.338 5.9360003 2.2680001 6.076 C 2.24 6.1460004 2.2120001 6.188 2.1000001 6.188 C 1.7080001 6.0340004 1.3440001 5.908 0.37800002 5.782 C 0.35000002 5.698 0.37800002 5.474 0.40600002 5.3900003 C 1.1620001 5.32 1.316 5.25 1.316 4.438 L 1.316 1.7080001 C 1.316 0.56 1.1340001 0.49 0.36400002 0.43400002 C 0.28 0.35000002 0.28 0.056 0.36400002 -0.028 C 0.78400004 -0.014 1.316 0 1.876 0 C 2.436 0 2.8700001 -0.014 3.2900002 -0.028 C 3.374 0.056 3.374 0.35000002 3.2900002 0.43400002 C 2.576 0.504 2.4220002 0.56 2.4220002 1.7080001 L 2.4220002 4.004 C 2.4220002 4.2980003 2.548 4.466 2.66 4.592 C 3.22 5.138 3.7380002 5.418 4.172 5.418 C 4.704 5.418 5.096 5.0820003 5.096 4.144 L 5.096 1.7080001 C 5.096 0.56 4.984 0.49 4.228 0.43400002 C 4.158 0.35000002 4.158 0.056 4.228 -0.028 C 4.578 -0.014 5.096 0 5.656 0 C 6.216 0 6.678 -0.014 7.0280004 -0.028 C 7.098 0.056 7.098 0.35000002 7.0280004 0.43400002 C 6.328 0.49 6.202 0.56 6.202 1.7080001 L 6.202 3.934 C 6.202 4.13 6.202 4.326 6.188 4.494 C 6.86 5.236 7.4900002 5.418 8.036 5.418 C 8.568 5.418 8.876 5.11 8.876 4.172 L 8.876 1.7080001 C 8.876 0.56 8.736 0.49 8.008 0.43400002 C 7.938 0.35000002 7.938 0.056 8.008 -0.028 C 8.358 -0.014 8.876 0 9.436 0 C 9.996 0 10.486 -0.014 10.878 -0.028 C 10.948 0.056 10.948 0.35000002 10.878 0.43400002 C 10.108001 0.49 9.982 0.56 9.982 1.7080001 L 9.982 3.92 C 9.982 5.1660004 9.772 6.1460004 8.54 6.1460004 C 7.826 6.1460004 6.958 5.88 6.23 5.11 C 6.188 5.0680003 6.104 4.998 6.076 5.124 C 5.9500003 5.698 5.4040003 6.1460004 4.676 6.1460004 C 3.864 6.1460004 3.1360002 5.67 2.548 5.012 C 2.4780002 4.9420004 2.394 4.8440003 2.38 5.012 Z "/>
</symbol>
<symbol id="gEF9FD20106DF1BE872ABEE235642DEFC" overflow="visible">
<path d="M 4.676 0.70000005 C 4.7460003 0.75600004 4.872 0.78400004 4.886 0.68600005 C 4.928 0.35000002 5.04 -0.14 5.04 -0.14 C 5.152 -0.18200001 5.222 -0.16800001 5.306 -0.14 C 5.6140003 0.112 6.104 0.322 6.958 0.42000002 C 7.0420003 0.504 7.0420003 0.71400005 6.958 0.79800004 C 6.0620003 0.86800003 5.9360003 1.1340001 5.9360003 1.82 L 5.9360003 8.162001 C 5.9360003 9.0720005 5.992 9.632 5.992 9.632 C 5.992 9.7300005 5.9360003 9.772 5.81 9.772 C 5.46 9.632 4.4100003 9.436 3.8500001 9.394 C 3.822 9.282001 3.8500001 9.058001 3.934 8.974 C 3.976 8.974 4.018 8.974 4.06 8.974 C 4.676 8.932 4.83 8.932 4.83 7.826 L 4.83 6.0340004 C 4.83 5.9360003 4.802 5.908 4.704 5.908 C 4.6480002 5.908 4.0740004 6.1460004 3.6120002 6.1460004 C 2.6880002 6.1460004 2.072 5.8380003 1.5120001 5.306 C 0.91 4.704 0.546 3.878 0.546 2.842 C 0.546 1.12 1.414 -0.14 2.926 -0.14 C 3.4720001 -0.14 3.99 0.14 4.676 0.70000005 Z M 4.83 1.7360001 C 4.83 1.47 4.802 1.358 4.606 1.19 C 4.0880003 0.74200004 3.64 0.518 3.2900002 0.518 C 2.5340002 0.518 1.75 1.3440001 1.75 3.094 C 1.75 4.102 1.9460001 4.662 2.1560001 4.9560003 C 2.5900002 5.6140003 3.1780002 5.656 3.4580002 5.656 C 3.9620001 5.656 4.3120003 5.474 4.592 5.152 C 4.788 4.928 4.83 4.83 4.83 4.396 Z "/>
</symbol>
<symbol id="g3B79D8E86480C20827A395F926C73BE1" overflow="visible">
<path d="M 2.842 5.572 C 2.926 5.656 2.926 5.9500003 2.842 6.0340004 C 2.4220002 6.02 1.932 6.006 1.4280001 6.006 C 0.896 6.006 0.518 6.02 0.154 6.0340004 C 0.07 5.9500003 0.07 5.656 0.154 5.572 C 0.81200004 5.5020003 0.966 5.362 1.26 4.6340003 L 3.094 0.112 C 3.1780002 -0.08400001 3.2900002 -0.16800001 3.43 -0.16800001 C 3.556 -0.16800001 3.6680002 -0.08400001 3.766 0.14 L 5.1800003 3.584 L 6.622 0.112 C 6.7060003 -0.08400001 6.8180003 -0.16800001 6.958 -0.16800001 C 7.084 -0.16800001 7.196 -0.08400001 7.28 0.126 L 9.114 4.564 C 9.338 5.138 9.576 5.53 10.29 5.572 C 10.374001 5.656 10.374001 5.9500003 10.29 6.0340004 C 10.01 6.02 9.702001 6.006 9.282001 6.006 C 8.862 6.006 8.274 6.02 7.854 6.0340004 C 7.7700005 5.9500003 7.7700005 5.656 7.854 5.572 C 8.904 5.5160003 8.764 5.11 8.568 4.6200004 L 7.392 1.7080001 C 7.2520003 1.358 7.196 1.358 7.084 1.6520001 L 5.88 4.718 C 5.6140003 5.3760004 5.642 5.5160003 6.3840003 5.572 C 6.4680004 5.656 6.4680004 5.9500003 6.3840003 6.0340004 C 5.964 6.02 5.4040003 6.006 4.984 6.006 C 4.6340003 6.006 4.172 6.02 3.752 6.0340004 C 3.6680002 5.9500003 3.6680002 5.656 3.752 5.572 C 4.4100003 5.5160003 4.578 5.11 4.83 4.48 L 4.914 4.256 L 3.934 1.778 C 3.752 1.316 3.7240002 1.302 3.542 1.75 L 2.4220002 4.6340003 C 2.1560001 5.306 2.17 5.53 2.842 5.572 Z "/>
</symbol>
<symbol id="gE0345006C183149AF583AF5DE80FA9FE" overflow="visible">
<path d="M 2.674 1.7080001 L 2.674 7.322 C 2.674 8.484 2.9120002 8.554 3.8920002 8.596001 C 3.976 8.68 3.976 8.974 3.8920002 9.058001 C 3.276 9.044001 2.618 9.030001 2.072 9.030001 C 1.61 9.030001 0.924 9.044001 0.266 9.058001 C 0.18200001 8.974 0.18200001 8.68 0.266 8.596001 C 1.246 8.554 1.4840001 8.484 1.4840001 7.322 L 1.4840001 1.7080001 C 1.4840001 0.546 1.246 0.476 0.266 0.43400002 C 0.18200001 0.35000002 0.18200001 0.056 0.266 -0.028 C 0.896 -0.014 1.582 0 2.086 0 C 2.5900002 0 3.262 -0.014 3.8920002 -0.028 C 3.976 0.056 3.976 0.35000002 3.8920002 0.43400002 C 2.9120002 0.476 2.674 0.546 2.674 1.7080001 Z "/>
</symbol>
<symbol id="g7E303FA8E2D87EE13FB94A41DEF3418E" overflow="visible">
<path d="M 6.2720003 8.596001 C 7.308 8.526 7.308 8.148001 7.0140004 7.392 L 4.802 1.778 L 4.7460003 1.778 L 2.506 7.4760003 C 2.184 8.316 2.2680001 8.498 3.22 8.596001 C 3.3040001 8.68 3.3040001 8.974 3.22 9.058001 C 2.66 9.044001 2.03 9.030001 1.526 9.030001 C 1.0220001 9.030001 0.532 9.044001 0.07 9.058001 C -0.014 8.974 0 8.68 0.08400001 8.596001 C 0.85400003 8.526 0.966 8.288 1.3440001 7.322 L 4.102 0.154 C 4.1860003 -0.07 4.284 -0.16800001 4.4240003 -0.16800001 C 4.578 -0.16800001 4.676 -0.042000003 4.76 0.154 L 7.6580005 7.294 C 7.9240003 7.952 8.148001 8.498 9.030001 8.596001 C 9.114 8.68 9.114 8.974 9.030001 9.058001 C 8.610001 9.044001 8.12 9.030001 7.7980003 9.030001 C 7.4760003 9.030001 6.846 9.044001 6.2720003 9.058001 C 6.188 8.974 6.188 8.68 6.2720003 8.596001 Z "/>
</symbol>
<symbol id="gBB75D665A04FFE2A82A14DE003A19CAC" overflow="visible">
<path d="M 3.9620001 4.5220003 C 5.152 4.5220003 5.1940002 4.2000003 5.236 3.5700002 C 5.32 3.486 5.6140003 3.486 5.698 3.5700002 C 5.684 3.92 5.67 4.326 5.67 4.802 C 5.67 5.2780004 5.684 5.642 5.698 6.006 C 5.6140003 6.09 5.32 6.09 5.236 6.006 C 5.1940002 5.236 5.152 5.0540004 3.9620001 5.0540004 L 2.66 5.0540004 L 2.66 7.5740004 C 2.66 8.33 2.828 8.47 3.444 8.47 L 4.0740004 8.47 C 5.558 8.47 5.908 7.9100003 6.216 6.9440002 C 6.3840003 6.9440002 6.538 6.972 6.65 7.0140004 C 6.5800004 7.5880003 6.3700004 8.932 6.342 9.044001 C 6.342 9.0720005 6.328 9.086 6.2860003 9.086 C 6.0480003 9.044001 5.978 9.030001 5.6280003 9.030001 L 2.058 9.030001 C 1.61 9.030001 0.81200004 9.044001 0.252 9.058001 C 0.16800001 8.974 0.16800001 8.68 0.252 8.596001 C 1.232 8.554 1.47 8.484 1.47 7.322 L 1.47 1.7080001 C 1.47 0.546 1.232 0.476 0.252 0.43400002 C 0.16800001 0.35000002 0.16800001 0.056 0.252 -0.028 C 0.74200004 -0.014 1.442 0 2.072 0 C 2.7020001 0 3.388 -0.014 3.878 -0.028 C 3.9620001 0.056 3.9620001 0.35000002 3.878 0.43400002 C 2.898 0.476 2.66 0.546 2.66 1.7080001 L 2.66 4.5220003 Z "/>
</symbol>
</defs>
</div>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(40 17.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gF74D1E4498220F56E34936C81B24ED2C" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g46E28FC12585DA626130081849FE40B4" x="3.564" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="10.788" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g48BCA4F06942DA5990D42018985FC781" x="17.136" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="23.268" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE1B486BBD379D5D210F28624A61384AE" x="30.024" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g9FB16590C6D64699AE0CE54876927A05" x="36.804" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g6799D348D26A0968EEDA80A0E5D50B73" x="43.716" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="49.620000000000005" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g45E4C10E27056C5AE488FE2D8290DF06" x="55.968" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="59.7" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g46E28FC12585DA626130081849FE40B4" x="66.456" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 28.192)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5ABA589ED074A65FC8C929AB4EB2344C" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 30.592000000000002)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(6.768 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 48.784)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(404.54488188976376 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6F0940D406D545443F0C3F5AB20F1452" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g6D72A0AB4EFB019D977FFECF4A1600A9" x="6.95" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7035BD9A81EA6DB089327941BB80DFF8" x="11.26" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="16.67" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="22.3" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g5503E15E5E4E70E9E217A15BD1ECD752" x="27.41" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="30.52" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFF65128B49BB3276E17D04989ECB7ACE" x="35.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="41.92" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 8.579999999999998)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.64 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 23.739999999999995)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 32.31999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(743.9997637795276 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g97A8E46F7A64F11D13C6F357868587EE" x="9.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.25" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.36" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gB844DCFB76B4CC44608DB013C9764E9C" x="24.89" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="30.37" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="35.14" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="41.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="46.58" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="52.599999999999994" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 15.16)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 60)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g72A3AE02AE43C077271D415C6766410E" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g14F95E5F274105B73EC9103738D4C7FD" x="19.608" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFC5C8D23DE5E426807758A924FDBA2FC" x="37.368" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g47EDFEA5ED41C2BE4D53DD4DC8C28ED" x="49.464" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 39.48)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gB8789F2F5F06048D4163694E4C0F3B6C" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="14.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="20.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="28.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="36.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="45.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="52.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="61.379999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="72.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="77.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="86.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="95.26" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="105.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="119.52000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g17AD34DB90B05275C6F1422A9B4B5274" x="128.66000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="138.60000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="144.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="154.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="163.16000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="173.02000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="178.30000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="192.24000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="201.94000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="217.74000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="226.88000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="232.16000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="242.44000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="259.86000000000007" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="269.94000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="277.38000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="282.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g757CB60871AF468909C575234729D90A" x="297.78000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB8789F2F5F06048D4163694E4C0F3B6C" x="303.74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="318.34000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="332.32000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="342.02000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF5D967C73B153E080367AE40708278EE" x="361.04" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 26.16)">
<g class="typst-group">
<g>
<g transform="translate(8 6.160000000000001)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 109.9 0 "/>
</g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="9.7" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="16.02" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="25.16" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="31.48" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="40.42" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="47.18" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="57.26" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="63.46" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="70.22" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="76.53999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="87.3" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="96.24" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="103" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="112.14" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="119.58" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(125.89999999999999 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="3.421509388249549" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="19.22150938824955" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="28.161509388249552" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="34.48150938824955" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="45.24150938824955" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="55.461509388249546" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="69.00301877649909" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="75.20301877649909" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="85.28301877649909" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(230.04452816474867 6.160000000000001)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 75.68 0 "/>
</g>
<g transform="translate(222.04452816474867 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="5.42" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="16.259999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="23.02" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="38.82" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="47.760000000000005" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="63.56" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="73.64" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="81.38" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(313.7245281647487 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(325.1460375529982 6.160000000000001)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 31.72 0 "/>
</g>
<g transform="translate(317.1460375529982 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="10" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="17.44" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="26.580000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="36.96" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(364.86603755299825 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="3.421509388249549" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="8.841509388249548" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="19.681509388249548" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="29.80150938824955" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g5925E4E4FE8F59A76637BD462660B390" x="38.601509388249546" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="48.40150938824954" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="53.821509388249545" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="64.66150938824954" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 76.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD5ADBDB4F1D8E002AEFDDEC4CBF7721F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="14.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="22.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="30.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="36.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="46.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="62.019999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="67.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="78.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="86.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="96.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="101.88" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="109.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="118.24" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="133.35999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="143.21999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="153.51999999999998" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 102.64)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 102.64)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="13.979999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="23.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g757CB60871AF468909C575234729D90A" x="47.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="53.660000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="67.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g17AD34DB90B05275C6F1422A9B4B5274" x="76.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="86.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="92.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="102.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="111.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="121.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="126.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="140.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="150.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="165.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="175" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="180.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="190.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="207.98000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="218.06000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="225.50000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="230.78000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF5D967C73B153E080367AE40708278EE" x="240.90000000000003" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 128.8)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 128.8)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDACA5EBB44D5F3DB530A1F5F650BFBAB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="10.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="18.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="28.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="38.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="47.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="57.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="62.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="67.74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="73.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="79.47999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="94.77999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="104.47999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="114.71999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="120.13999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g607CD744DAB7515984E0B3F495F7DE81" x="135.51999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="146.07999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="151.49999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="159.29999999999998" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(476.5475469412478 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<image xlink:href="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAArwAAAGJCAIAAADnh3eXAAAgAElEQVR4AexdB3xUxdaPXekhAdJDEnqxoViwPXzWZ3v2jiiiICBVqtJBQRQLqNjLU3z2Z8OOWLAXhABppC1bs+Xu3l7O9505u5ObTTbU91S89ze/zWTuzJmZc++d858zZ86kgXM5HHA44HDA4cBfkgMmmDsMAGbLgZItACvOuxT5ePmW62qZOJhgscBL70RTd9gXe4aU9dpqtOexl7XH7XmaxFPwp6UXrRnniKs23jYvZW+DPd6kDfa+pGhPs7rBTi0RbySU1rwpTorDAYcDDgccDvwVOJAQCS2Lc7q7N4QQiZyWa0lJ3wENDmj4K3yETh8dDjgccDjwZ+GAAxpSQpbGqXV8Kp6KVykppJjZt/RuNJvtO5qGltjkpDkccDjgcMDhwO/JgVSC0J6+q0KxmQDk4tfRNCArWrqa8cwBDS2xyUlzOOBwwOGAw4HfkwN2cJAqviegoWnfGkWjva6U9JssTyClxvKJeOIv3iGaBpg8UErzPM3T7XlSxe1ttsdT5Y83t9UlBjQHQYsQ1rPm8VbL2ttgj+98e5rzM5GSDO/sz9GxabBzw4k7HHA44HDgL8QBu7BJFd8TIdSUlQmRlBDwVGNK+g5ocEBD0xfI+c/hgMMBhwMOB35PDqQCCvb01EKdzZITWycS8+Um+oCmfWsdNOgAesq6GKHG8ol8Cfp4xwQwMJgaC6RvMLE5dDWW3gFYadIDeyk9wZYm+wsSbWnMGU8hkd+q4E+0zf6X0UlZtrEWW2OS2pPc3+T2JGprpNXYB7uOgRiBKYkS+NfRNNi54cQdDjgccDjwF+KAAVaTYHGB2Sg8GgUKv0mRZuKwuRBqysrG+wZoPFigWZbBEMOugQYbcaRMoEED4MFgTU9ka6x9J0ADIRjeHh1ANTHoCSo7zZ9mXEq0J9VfVsMug4bGZ9OUbqK9uIW1cXMs5bHdixdv8jKwd4PlcUBDU6Y6/zkccDjgcOCvxgGLXYYFjcEEIxFIVCTmsjsWkHbx05ST9jsU1xElgGJaogExFhQOIJoClEZKzangPUpNqDp0E0TVUCzwR2UJIKoZiTuMjk1kpu4XxwoqAAaGEnQTZBNEFlRbSxrZwgkm2mTLlQJgNfat5VgzCo2oIH7LniMqqpqBhDS9ST5G256xhbKUlPwaWHE3GfSe2NvoaBrs3HDiDgccDjgc+EtwgISBnpCKugEUCDcwQdKCUOTSkSJcRtrlUlP22e9QHEGDacmGKepAQdYtleEGUg3wIo2UeBJF8AZPYtCA5sIBQRUN8AShql4KyxCK6aQrwPy7Aho4V1glJgMN0d8DNLS2ZMMZYALEohBsACECkgRmo7qIGGjPGI83TyLQ0Pg+mHGDUgc0NL6FTszhgMMBhwN/WQ4kg4a4nDRJQc0wQXwJn29GaB5hq90ogOxgwibPm8smTLEswzRNQ7eYiDJ1S2egwTBQ02En1QgMkgjhU2uqwDcBdReKCdvq4MZb7jv7/OnbvagoYOgi/gfJsYSmtVCNJC4pTrYR+JuolysbdqBp4JQbi3IajRFqBmtKinyJZK754BFqEZVN8MoEMQJffhrbugl8bsZBLK8n1lMS2ZrwNjnRAOS/bqm6paqg40MxTd0049aojU12bBpsvHCiDgccDjgc+ItwAEGDGdcuJOaXKL9ppSAx1UbRQliBWxdShP9LuIELSw4jEmIvIXYbRSbKIVMHA0UTCyZgvbRQguvoHDrYyjQlh8+oCWhAgwZJ0zWA3zZD96LrO6aft60W/GGIaaCjOExYTWDJZHnJGo88YD1FrNBoFUEdi8tgmYlh3qoW6TQmNm2ynQ+Nr5g91R5PlOVYgUcoF+sG74gJY0c+XZIzrGfBZaUbFF1DvGCAxJZ+NBs/G9tmf14UTwINKuiq5YCGxiflxBwOOBxwOPCX54CF2mwAFKqqxowbUGZrBigMNDQ6PLADBQ1MNRG0xLTWLoQSAs8uBFmcb6E0wVBAjWHVYhSX4TXDiJtT7CRosFgliBtMsOJLEJKmx1RY+cjWkpJJxx4/3ReEkIjQgoMGtLY0ET6QgLS3mUAS23yBrQpEIapCWAJFAVUGVWVcihtvoulo07LJwtjg4pwDDHvEtlCCdFviVyKNYwUeaQQNlAdbYsIxA0f2yr+xV+Hl7jrQVNAMiy39RGnRp/XWJu5iEyVFs5g1h4QU+CvRxDjEsWmgp+b8OhxwOOBw4E/PAbtIoc40T8F0kgImKBI89fiH55w1vLpaQLFtAROoOD1FZTX+4g5GjhIoIoNJYbdBgybBEyvWnnfWtG3loGmoFjd1pn5gDbCLMWp/0i+23yRlA+5rYP9gt6Iy3Dbq46xuE4fd9LQ3hAqDmG6Ssp3oM9ltEG5I1GJyTT7pGHRAuCBbsPKxD889+/b6GlAVBqqQG8SZ1kADX8Th9BMIINGJHYEG9uAoM8cKPELp9Gzjv6YJI4Yt6dH98ltH3h+LYGtxa4op60DGIs3XfUx6vk2VEMgbRYYnnvrPmedeU1EbVtmGFlquste3a6DBspogDjshJ+5wwOGAwwGHA78jBxKOCnD0pyspJS5wEhLXtMDnhb69LispOuedtzYYOk7aSR3AREUT0EAogUCDCKbIcMOugQYmsVGCmhDYDkf2vrYo54p336gxVDA1y9IAA+rVd7A8EV+YINCAiEEm0BCKxurdcNLxK/v1XvKf92saJMwYlsXECj0utDArQVyZ4doCVpaW/1UCDWEZiTYIcNxJNw3sd+XHa6pDQVQ5EKJKMAm1CxwfcNVCIgWNShPaC8zZBDekAA2Jh5Z4dHElCsIFEz1YUGgBNIAFP/1Su/zhl31BiEmoF9F0MDRsn27G8UESgiHQwNZs4m3DDBYEPNC31xXdS/7xxju/4NYRxHC4YGRvmwMa7Nxw4g4HHA44HPizcsBkgkVjv9gHHPFR/oksyGypHvEEigl26rQBm36DgrzruhddtnGjrpMen4lTJvFM1cLJOollTkQGiLEg4i00JrAsQ8dNiSqTTFxCktIe/01cVDEKs00/Qd+SW3K7XFW2EZcqTEIMKUED1/8jJSb7WS9wDhuniX4eTNheD53a3V6YP9sXxkZqAFFdwuV50KlHlsXUDBaJw8amAqpVNOpsgwj1PvjiGzM754qSoiu3lqI+BtUhbO1GB0PBvR46y6+zhZu4DUR8mybokhXTgfaR6iprb2JBgx4Om8OzPQ5xAEQwohFM6AxAxVGCHfkRMy0bTxkGg5BiKOxJ6QAyIQYVaaDtSKPyhp4FQyForqDjc2PcJACkAWzaAAV5wwuKLvu1VMUnaiFUMbCVjddOgQaVLemY7CKbW/ptJOPEHA44HHA44HDg9+aAAiAxYUn7J02AsAUeE6pN+DUAbgGN/SxVw4V6tJeDxx6r7JIz+qTTZoWiKCFQCLNfmiarJigWEgwbWoOuCwBRjEMEQGBAhBYGTFNXraBoBERNojlpnBTjRkzDPyq2SpdMLRwDbwBWPVKXnzXulJPmRsIsEyk/WLQlQ0V0wWAi+GGYR8dK1JhC2aMKtgohkQJvv1aalT7h1JMfbxAxRQJTMhXFUlXLRN9MFnjD9Rboig6CCIrOJu/Ua4a0VLRmQOK1XnjkkYbsrDtOOWmuLIGskPhURCOogiybMQ03i6I9SEAUgqrmlyGgQ8BAtshghOQGxRIlI6pioyCKaAQgEAaFoFdUMUKKDjER4QgAyDHMZ+q0bIRy3zJFTQ0L0QDgCgt2PqzHuROJaJpmKRKzs0CDFHxkMvOGSbhQMVE+I6viBOMyX9J0ISayVImZoZqWYRq6oeqabKkSaCLAcy+HOnUbdcRxt3kjIOm43BNjhh2GbRtnStDAVyI0TRMEAdum4z4ZBzTEH53zx+GAwwGHA38YDpgoaqygZUaYWNAsCAsQFOD517eccdXiNn2vzj5m+OL739I1sCQwY6AKEA7CP698vVPurAmzvq7ygTcKggrbvSjANA2DoqPkoLXtKEBtED791vP0yz/UCVAVgjCDAqhpQHmMIi+monB1h9HE0WDwJaZBnQ+2B2F7GEV70ETgUuOFSy57r1v23CnTvq2rx3bi1NkAOcoiNivChFJdNSFiIoG4NQZOjy3we9SYDBENQgAuGUX7/NnvFBZMHzP+m5BK6hBLxCV+XUFnUhgaJNkTVgURvv8J/vOe241CGcWryObuYRFNGQDAG4HzL3gvv+DBmXM2NUTBFwZ3A4gGSuHEvg0sENW0sIYVVfjglY9D762XtrN6Q6oU0yIxLSKB6VXglbfXX3PxGNkNpmiApYm6IAPU+WHNJ+Gly754+dVt27ezZjDtDz09AF3R9AbBimlQ44MfSqE+DPUhkEyQVTR1RDNFdskxUHVkjVtBVKfFORS/S3jBAIgoUkwDSYGYhAjG1A1TNwzdUgwQLYhY4Ddhuwz/uPKt9l3uvH3aWl8QLTgAENZ4vU18P6QEDQZDc6ZpBgIBr9drmqaqqnbEwFFFonXOX4cDDgccDjgc+B04QBpsFcAraRKbdte74beN8Le/LckpmJJdPCW376jOuRcOPfW20HaI+sBTB5sr4LtNkNHjvrb5S68b//38h6tHTf3g5vGvXnP90zNnvqPIoKhx0OCN6r4YrHxmU3GfCe073TTgqEVnXfxUmQfqYygvaUbrb4DX39p61OBhb72/uUHDaXdQh7J6uO329YUldxf1njf/vk1lPtjohh+q4evN0LXo4fSclTeO2rjoPu+EyV9dcvHTl/7z6emT30LDy5ZAA6B2Q0S3RUy6m2zeLhlQ7YOnXq0av/Dr+Ssqqjxw/qWrOudMfG8tzvgxWAYzv0AdRdSCqAENIjz0+I89+07MKZjSvdfsq258tdKDuhPJws2Z/jBs2irXeeGzryGv5MGu3VeNubN23orwqOmllw5775+XPz533lto38DUA4oIogSeBpg2+4tuxTMP6Tors8fc2+d87lNQXRGMhnTQJAtCGuT1uqpH71tX/7vWL4ArDF4JPvnBHHLuIxlFc9plzW+bNev6297zi7QQQLAJV3rcQfh+A1x4xQuF/edkFs3oWjzz2lvervFCjQutFmIRyTJx84vPBzNnP/nxN6UhJvslCyQNvvu+8vvvK2UVXF7UcpgAIRkCERCZesICXDuRLUO0QDDAq8C2CGzwwHeV0Dn//vRuj906umL5fdpdU93DLvts2KVvzrrjXTTfYHTMVs6eoCUJTdNq2aUoyh8KNOAuE+dyOOBwwOGAwwE2mpMRn8wmqoEYrPsasnNv7tVn1oAj7x5z+ycbtsBrr5eW/hhrqIV/nD7pxBMmFx0+pUOPWQflLTsof3mbkrkdek0uOuaOLsU3tO10ybHH3S4xnbysgqSCNwSjJjzfOfua9Oxbh5z6SJ/+i7v3XnTsqfe8u67KG1NJmERjcNSxE3oPHHXX3e9HAaoj8G0p9Bk0rWPXWelZd3ctWJTVa0bO4aOyBg7v2GPkYXlTDsl6sF324x3zl2QU3tnvyIVZuaNzs0cPOnKMqtP2jfiuSDKKZG6nJdPUdQNUJuDDOtSG4J6VX6aX/LNd96s6lUzK6rvw6NOeKeh3d0bRlF9rUPcQTqyhRNmqimCCoMM5l9xT0HN0Ud9pJ5/xTMmAZXk97xx0yox1P8fCKuKGM84dcdTg64r6DO+af3ubLgsP7LIkLW/moT3vbNtz3n6dx5T0n3TqaZMRMRgghkAR0Iz0zDOXZhVO6nXkA8f+/bX8AQ+2zZl43lUry+tUxbQkXdYBvvkNeh89vUv3SSue87tkaAC4+9ENeYdP6VAytfeQJwuPeb5LvxXti2Y89Vqg1s8MDi00BI3o8NiLG3scNSOr56ycvrOzes8u6Htveu60405fVOeN6wBQDaDB9Dv/3Tn7zKHnjQgpEFRQHbLdA737nN+779kuX9yCMSDC2vXBMRNePPOcRe++J3oCENUgYuph02zQ4YihVxUNHtax5w0HdBubnv94TvHq3MIHMzrfWZK/JKfzzH7Fd55z+rydBQ2qqmqaVlpaGgwGFUXRaGHmv/OJch3GzpCPRqP2xqCTkoS9BRV3tCA7w0Ynj8MBhwP7DAe4skEEqNwOfY6c3a1g4i1j3yuvh5CE0sUgg0YJJt2+4vBjRhYfOzUte3xaxpyMI57455i14+7+etVb5R987yvbDpWu+Da5mAKiDKNGv5+eefPRJ9/x4XrRG4N31soFfeel50985o1NLrJIAJwW5/W6seeRY978VNwuwg9lMOTsh7oVTz3z4mdeeNs8+m/3dCgaPuicmR1Krsg9Ylpm78UHd7uvcOCLV9z69Zz7Nz/9SvWn34Qr66C2nh32gA6mGkEDM120LGbch7p0E2ojSq0I193+4iF513fuN2zKPWvf/BxuuH19m64PprVbOGDIwlqBIQYLlfZRgIACfhE8Alw57KGeA8cefsLUdT+BS4C310Juz8ldC2965d3tYRXqG2DcpKXFvS/o3vPWrgXTs3o9VHLC0xeMe3fcQ98++Hbdi2tdn//q9QoQkWSU1jKIApxx2souGRNOPXPJTxVQ1QALHqrqWrQgI2f8xq2WYkFEQYCxuR4yeoxr333co69LG32w+MktHYtG7df16oVPbamQoVSAopMWH5h928jJH4omWlcCM9V4b53cvvuNGb1unbho3QY3+HR49X2t16C7uvaYsOD+74UoiIJsMsuMy4Y9np577eXXzkVn0iqaWqz9PNyx87lZBReUbgOvjPQefc6VkTO+94B7i3sszuwy8fMv8JUIaXqDrgc0GH3nyv6njMs7YmaX3vd2K36me7+nr7nl/WUrf3ntP+6PPg6UloLHjeCDh9aWJzRNi0aj5eXlgiCoqrp3J/ccJSRFdvgNm6apsYvaY1kWtTMUCkWjUUWJW8fskI6TweGAwwGHA/sMB0h7rAJEVFi2srxTzh1n/fMVVwSNCVASmZahWyhAdAg1QLUbtvjh8LNXHZg/e84q5Wcv+ABn51EmsywATyAEAA1hWHT3V9m5k4p7T/9yg1kng1uFigZonzOpU/4d73wZ9InxJfRvf4MuPW7q2md4qRu2NcBp5606LHPUXUtKywPg0aAqDB/+oHgN+KUeNeF9T3zw4C4zH34OakIQMtGeMG5QGVeZoINpCoQecJrLTAplHdXpAsDZw5Z06HPrkCse+dkD2zXslicCR534UZuuD59z6WNBHRcjYgnQILJOzVm4Jr3bxUcOnvjjZgjgPBt+3gKds28r6j3xi28gKKI1QEiCbW7YXANHnvhwZtGiB180f22AKgshiMwMP1GxzwwbggpcfNXyrOw7Lrjo31uqISjjFP/bXyG7cFF+8bzybbhGEJG1sA6btkN6z/EH5Y19/ydY/Sm07T4yu/+4tRugXoWyMNSpcOGN/0rPHz/1zq81k5mSiFBTDYefOCO957hpy77wsw0sAQMCMVi+akPH7hN6HjNL1UGRjXBICovQ69i7OheNf+XVSoV5slI0WPOhnNFtWFHfkZtdEAD46Aczr9fUw49ded7F7x/UdmJhj2Wjxq0NRUGQjIiiBBUrqMH3ZVDph/4nPN6227zHXoS6GLgVZGBMQyMV2tWxY9DAfIMbPp+vpqZGURQycdiLHxgJfgNtMdC+kptY7mQVBB0URXG73fX19XV1dbW1tTU1NX6/nxZWdpKOk83hgMMBhwP7BgdoyVZQ4MobX22XM/XyWz+rCkFQxSmviH4Q2MUyhQUorYasvlPaF47/7FeoF8EtQ4OCQgK3+KORnR6T4N13wz17TcktHPX+WikECCy2SbCuFNrkTs0onvFrLYpwXUIg8p+P9Y4lo4uOHb9NgMlzy9LajLxk+L+2i+BRwa+DX4agBiEm738og15HT87tPXrdD1AfRAksG4ZqxDRDMPSYqbP/bJoGAwzUHKu4M1PSIaTDoy97Dise0/PsxT+FwWVByEL7voYADB7yUmbukllzPpU0FOGSxfaaWiBo8Opb5f0Hju7d5+ZvfhQjKsp4yYAP1kDXzhP69piB7psM3Ccisk2q35VCRtGUzIJp324En4pYSmAQRAPMYwB25K6HPz+saFjRUdN/3IxWk5EwxPyw+pnanIIFvQ9fur0BtzyEFC1owCYPpPca3bnHwpfWQP8hqzKKx769LuISkScWgL8Brrz0Xz3ypj61sgZ3PJgghGH+otfbZF5yzpUraiOYJ6IzQBOMbK3SDuw26tCcsRW1+Ch1AwIidOh5R/djl2+rAUPC4pIMr70hd82b1P+4u7b64VcvDP7H3PTCm+59ZJtHgkdXhzO7z+s7cIEUAk2w1FhMktAwUtDAFYLc3lO7loxbtwH8zIQkKIOMzkEtRZM13H0SVzak1DTQdom6ujqXy0XWDDv/XdHqQOtrBLLtsisbmtfSoobDNE1FUaLRaE1NjcfjIV1IbW2t2+0OBoO4JcV2Naf5O6a0zpbfsWF/nKptj46ZMv9PWuY8l/8Jm51K/pscsHCqKmkwc+HXnYunFA5avGhVTV0s7qdBYUoBy8DtBKYJn38L2T3G9jxm0vYY+JX4nj2UUcxpkqgpnjCcdNpd3XuMmzH3XYM5ZvABlIZgwuIvu/S+N6fvfLeMpaQIivOX39fb95w05OIV6zZDft8Fx5/+6MY6CDKrAr+ERvX+sBFWUTit+9HqVnz9gEG3RHXcC8A2IwgAQTAjYIqWqaJKJOHpmbxSov8IQ1U13EoQUiC/97TsPne9/o0RZGIsIKI55ubfoFPGnZnZC1e/UCdHcD8pzpLZtogKDxw5eGJOzvX3LF4biuAeCgnAHYDpd/xSlLugR/4EJYZbEnSwYpZW3WB+8B1k9JjY95hZftw1GL9oQdwXlgUNtrghe8DoTj1vWfFCqQSAeyEARD+MvfnN7MIFh5/wQFBGOBXS9ICKmoaMHhMHnPjShdf+lJ4/febir2j1xGL+K7fVQo+i6X0Lp376dgydJgD8Uqbn9bmyfe7Fb33qb1CgQdQjshWKiACwtUZM7zXlwNwx3hAIUUR2v1TC/t0nZQ1eWlqOD06OgRCFZ16QM/PvOuLk+7f6YMGqujaFwy8dsao+gvqS9ZVwcN7kwgHzYyH2RCVdjUmaAqEofPk9dO8/+chT7qiNoj5JBNS+0CVKQXKFyfCk0Rpo0DStqqrK4/HEiyb+hEKhqqqqysrK6upqr9eLZ3gzIQ0A4XA4EAhw0CAIgtvtdrlcVFSWZcuyampqtm7d6nK56uvrZVkmywlZluvr630+n2VZiqKEw2Gfz1dWVuZ2u+3mC4km4P7PYDDocrnC4TBpQajSioqK8vJyu9RJinMKrURIC0K/sizzBnAdRirtCNVl6AwaM7ZwUlQdZaC4pmmtLKYkybCkf/FLS3jn5Os1SXXZ8yTFm/c9iUv8X1I42RVCXCfEG9Ccmr2z9ED5G2LPzGvhVimt65yI7ZwCL55UHafGM+xkU6mzzdtgp2O/S+n22nnbkiL2nEm3nH8dDuwdDjAlMo1R1V4YfvtbB3a7pW2P6QPPe/Txj2L1JvjQPRE7WMJAQ/pHnq47LGPYOZctcUfRQpBtk2QOkkxd0wyPAiv+/VWn/H8cddLogAzboyhoQwA/uSCj7+z07g8f+7dnAzLOgFUBQcPSx2sOLbrjgpvXXDfx8+x+d7zyoexW8a5ggKyx0xBUkBQjGINnXt7WJvOyy65d4Q8jvtFMEUAzFR8yIe6tAY/BtJk14NKEDnrEMCUD5i/4rChv4qib3hQE3AIgSIas4o6Da655Iad4VWb28i0bQAvj1sMYU9fHTJj9wJacvnOPHnSXrqE36EAU/BpsdkHvASsLCpZfctEqVUSHj7KhxCAWtGD+Y6Vti0ZfOPx+0UIi2A0TQMU9ihEJahvg5nEv5ReMuvySB1QGF6JsK+jPG6F4wKLsXkuGjf0soKJyImyiScG6XyCj+4KM3BUduiw4458P10aQjQET9zGETbj3eX+7oilHDZouCqgviVqw6t26w3oP6z90XJ2AmAx1G2xDRECFdZv1dn3GFQ6eGdMgFsM2f7hePqT/1HPHvROQ0fOUHINoFB59Su6Yu/icy97eUAN5Ry0vPnb+T5VW2MJlnc0CdDp2QVrOmJ9LUUVkMa8NhopPf9nK8vbdRv7jivvcEexuXC8FYDBbRtPE0y91dk5Ia6BBUZSamppAgG1lZVLK0I1AIOBhVyAQcLvdtHiBhiGKIklSXV2dx+Mh3YBpmoIgVFRUkJsHVVVlWa6rq6usrFRVlUCDqqokYklnEAwGAcDtdldUVHg8nrq6ukAgwEW1/dMydCMajQaDQUM3JEki6SvLcnV1dW1tLRfqqYZ4OymKc7miaRrJSPolSUxxLuMVRbELEtpaQpVSd0gRYq/FnofSCTRQC+nXnp/EvKEbSe3h7eSZ0TsHYyNvsMIuKkjZaMcspdvvEjV7X+ztaV1IUwt3SRzaK+Jx3hEesT81nmiP8LI7rL05uzidJCKWZam2i2fj3bSnNI83p9Y8pXkpJ8XhwN7hQFxDYGqK4G8IRlVU4z/7dsOR5yw/qNfkNgOm9B0648tNig64GwIA6r1wy5gPM/MnzVj8rlfGnZNh5tAA33YpFhXVBoDep40pPuaG+55YKwK4RahpgP+fN19263sdiu8+oMP9l133VYz8FrDzKh94LrB/7vTTLnuva5/Zl458rsyPIipogmRYOKNUDEtBrwCSCjfc+q/cXuPuvv+rhijEDJDNGDNpAFWQBX8YcQM6KWwCGmRUoFhBE2o9cPjAyT1yx/3wOUT9KM9wM4UBj63anJU3rVvxc53zHtj0G2gCWCpIMaS1PQi9hyzP6n/3Uy/VRyXUPYRMXGe5bPTr+3ec277rPdcOX42nUqmgGopkCUELzh/x6kF5t93/3PoIearSE7jBQgCEFg/HzRzYb/K7b7iUGEhRWRLR5/SQs588OOeutE5TFz3i2epF6xAB0HjilfchI29ZZtbKnPYLf3EAACAASURBVO73fLcZPAp49XCUbYAo80HJ6Uu6DJo5b9mn6HBC1N0xuOj2lw/rf/tl4x71qBAzscGyhhsmawSYet8XB3YfcdHIZ1GDwqxJ7lnxXVrxqNHLfwgYoKimKiOYmDqnpmPug0tXwOx7I517LJ6+9LcGDRpUQQKolKH4vEfSSqa880U4EIZwA7JIkCwV4KpRb7QvGHPnko+DMsNI5DvKRGedDT4/riAZeJKFCmpK0EDCuK6uLhKJ0Lgpy7IgCFVVVT6fTxRFTdPsoCEajQYCgcrKynA4bAcN5eXlpGAg3cDWrVtJdUGggU9Aw+EwwQtCDzU1NaIohkIhURRbNKdA5+FMoHK8YuiG1+t1u92BQEBRFLvwa0Vy8C/W7pei0nZt3ry5rq4uysAk9cvQDWptReLyer3BYJDMMHnfA4FAle3y+XzUHVrrMXRDlmVRFOtsV319vdfrJYtOWh6SJCkSidiy1NnzkI5BkiRifiBxUXtEUSSUQ4hBkiS/7QoEApFIRJZlQjlcwoVtVzAYpHUf4jbHUlHbZc9j57ktS5RQXRL64dR4xF6cx3nDLMuSJIlUU4Rm+C2emSI83R6xAybaCmQvxV8De8RevMW4nQLPQOoK3ll7k+zEnbjDgb3Jgfgcnf2xdBxeDJTxVVGYu+rL3GPGpxdNLh4w/bfNCBoEtqI/9OznD02fuPr97T4DQUNQEdHtYpjNqgF+rIL2PUd07nF9dQPiD/L9cPcDm/L6Lyoc+FR+z9cuvvxbPHWaLXTrGixd5d4/a07fE1Yf3GXsu1+FghbUhQUNLHSeaAig4v4NQ8W5ap+jpuf1nfzuF4GAChFQoibO1uUYmLpq6DG2Y5Q7jcYIM4I0I6AFdfjsK+jS5ebjB98ZakDm+SNKnQC/bINeA2cfedwLnXs+07bonh+3QFRCVwo6m3xv2qIWD5rbrd+M6gDaS7p1cAPMfXJT2mE3Fhz94kHdFl8+4m2PgGsZsqHIlhAyoPDope2K5nz4g+RVoa4B/UehI2XFkkV0Pv3qe2KH3BEDT5zkiaFfKcmAim1w6/jP2ufN69pv1QFZCyfML20w0fkBOc1cstLfOffebvkP3zr+x6AK22OoWhEAd3P848qHsgdPKT5loieGGgVBlWtD0Pvkxe16TZu94usGE+1RmBdnbHldA/Q6dk5Gz9EvrvGgz2wdtSaXD38srfjWJa97g+i6ytIUECJw/mWfdMh+7N6H4fDjnys6al6FH0IMAUgAdQqcNuLNg3rfOf+RnzxR8IRx5ShoSn6AHqfOP6j72DfXBWLMK5fAdhSEg4ibNAmXhwxT1HEZR04JGmRZjkaj9fX1Ejs81dANQRD8fn91dbUgCCSu7MsTsiwHAoH6+noEisyJAmkaampqotEoKRtqa2tdLpemabSy4Ha7SdeNHjYDgbKyMlEUKysr/X4/iXka3FsX+XSXBDkHNARTaBynxrT4fVIGukX6DPJLkRC++Nfj8fAVEMopy7K36eVyuQKBgCRJJCEIY7ndblLJ0K89D2UgTUN908vv93OcZOhGJBIhW9Qa2+XxeCKRCFmnqqoqiqIgCJW2q6qqihZuiA+qqkqSJAiCHXzU1tZ6vV7avMoFnmVZ1baroqKClD3RKAp+fpHrDvqlukKhECEDLptt7cXVqNra2nA4zEUpAYVy20XvUiQSobeLy2Mb7qoqKysjFJsEdBLgDf/W1NT4fD5BEKLRqL1fPttFyEwURft7YllW0HbxzkqSZKdDYEi0XZSTN9g0Tdl22cva4/QuNf/dW3maU97tFN6kVBR4hh1+qpQzFZ29lb6T7dlb1f1R6HD7H03VFMEEXWQLCgrAL3XQ6+gH26VPHj3mX4qGk/lQDDKyZnYtuPulD6Jeprj2K3ogCC+v/tazXQiEYc16SO8xuecxd9UEwc9cIq56pjqr++1HnvjwxJme3ILnTz/rw5iKB04YJprLzVhUeli3Bdk9Hh5y+mMR5tXYGw0HY37VCmpmANcwFEWTLFmBvF5T2mSNfvuriEeDgIXekV3b4aUXv/F5g4oqpAAN0KCjx8nHnqrr2XvaTaNeCTJDjaAJv/mh/9Bp7buN/M8nkN5nZZuS+d+UoUWnEGWOkmPw7fpguy6jBpx873YJtglWjQ5zn15/QPdhhScuHzXX27Hn0r9f8+9SL0QMUMBUjZigQdcei3IGrnz/e3O7ivs+JACXB15/7UuXS9QsmDHv5+zeMy8a+fyWIGyXwB2Bu+Z/fUj6iDMvf/ecYV917PHAiDt+rIsgDqOtKBPv2tyuy93tMxa/+jYK76CGaxbbfDBj3roO2cOzB474qQ4dYemoHFHcAgz62/J2OVMXPvyrW4AAOzorauGW0Wtvejkjd/QFV66s8ePWylDE8vnglLNmpw+Y8tj7kSBzkq0p6OVzwOBnDs586LxLf2rfdfoDT5a7BTzqU9Rigma5RLh8wpo2fWZefttrAkBYA68kCQCbwtDxqKlpOaPf+0EnHYk3Aq46eOetjfU1MUMDw1C1HYIGxHF+f0VFBaltAcDn81VVVYXDYVLO0+JFbW0tX2Korq72+Xwau6hUMBisqqqKRCKWZZHQ8nq9LperpqYmGAzSbkmaUnu93srKSlI/iKh5wYsG4h0ONKZpRiIRWs4glxJUtvUhjNOnBtMvN4+wjzs8nmp0UNlFFAhO0dScQ6IWCxJZu7DhFVHLufUA0adf+ySblyUZnCSSOX0esRso2IUiT9c0TVVVEvyyLBNooxpbzJOUgecxdCNkuyKRCNrososaQ79+vz8QCPh8Pr7m5ff7SfnB1Q92oFNeXu5yuQgN2Flqz7N582YOUDh/TNO0YarKTZs2VVdX06tib0+F7aqsrKyvrw8Gg6Io2unYQQwBpmAwGIlE7HmqbdfGjRup2YFAIFWeqqoqysNxJ+X0+XykzKPGEGbibwW1HIFt4iKjYAKU9n4JtovW9aLRaBLwsuEcjNI7wF85/oLxV5Esmcjcx14XvRL2p0MQ2Z6H7hJoptGD+mvPY+eVPT2JMq0D0otHb05Sdejrl9acAWQZJ7XNNZctDhT2Su3fY1ID+L8tEuF3KUI07XFeS1LO3fmXQIMJsmSKsko6dcFC54xeBSbPqOjQafKIm55AUwAdFyP6Hf5AevayZ9/CybfPgo01cOGl9/Tpd8MHayvcEVj+pC+j+4LBf3uhvB4ECWbMWpeXN75n71m/bIFX/wNdc5d1L7m/shYaJJwKWwCLl9V2ylqYXXD3+Ds+FzSQLEk1FE2X7KDBUKDeBT0Ov/PQrPHvfwc+E/5fhpXWwFnnLOvVc/i6LzarusE2jjbRNDAFORO3Kjy0quKAtldfOeLF2gj6PP54Q6zrUaM79xv52IulDQr0OuHh/bInPfdeyCfDp1/4fvslqoXg0WWfd8udOvCEFdUhqBTguqnvpw+ckHnEyM+2wLxHPIcUTMo+ZvbGINoZSAD+gLu62izsu6RT93tf+RQ8AFsE+G4bnH7uvJzcC6tq1P/fvnH7lF/S8+8+8Z8v/eiG6iDccMsTh3W44LSzlv5aC+MX/dq5571Dzltdh9p5XAdxi3DhNR+06bwkr/jR5Su1zeUQjML2ANx82+pueRMKekx88Z1tFQE9pEq4PwQUQYFzL3i0fadxF1/xfOk2BBMRgK1uGD3plZyCW08+bdHWckQwqPwAKC+HE0+b2bHotpc/QZCISh8Vd5G07Tp9v44L22TOOen0RwQVz69SLFWx5IAgB2R44i1v26IxaR2um7Xo2/MvnfHtRlcMYKsAh/SekpY37aVP0SeEKwrfbYC/n/ZAYc5N67+pkxRDM1XNlCmk1DTYQQN9Zh6Ph4ZjPCyEGSXU1NSkAg00S65hlyzLpml6PJ6amhq32+31emnSiVqpxGfMQQONrfTlNx9KkFWJi+zdVFUNBoOktNc0jYqQfGpFx0A0aIGDZK3P5/N4PEnTU/5J27/2RP0t/7UXaTkHsw6xZ/vd48Q0LhgIOnAs2LwXXKLbEUxSL+yDPo+ToOIEKd2yLHoN+JIThylEk+cngdQ6FEtawuBV8+Zxu1Ea5Xk6N5+kIqmWXUK2KxwOR6NRErd2noRtl33pyp7HZ7tcLhctq0mSZM/j8Xj4jmKXy1VVVUWaP94p0zTtiipStHg8HjJG5l2rsV1kKUwKG57Bsiw78Nq6dStZQJPNEG+SHTCVlZVt3bq1pqYmFArZ2yMIQnV1dXl5OQ0XlIdGAJ6NvrW6ujpqFw0IgiDY20PLo8Fg0MOuYDBIRKDpRSo0WZZpIY/UorwiGgFCoRA9o0gkYugGn5M0pYRTFG5C1PzdAABaB6Svg0YY+/vPqe1w2OE57fjGnrh7cRS3Fh5DUF4lffpl+cZyaUO59uVPwtx71xw1ZGpm/oSSvndsLYe6etRI13mh/6D7Duo058TzXn32fbj7yY29T7iloPeNSx74Cue1Grz3JbTLntytePHQc1Yfdez84uJbz/j7/VvK8XCKb3+GbrlTM7tNeXa1L6AiYgjo8OBKb1bOvMwuE99+X5R1wB16mmXqhsb2UuJZSKphKCDE4OSz7+9YOHXIBU89/oZ05wM/FB1+W9f8m+5Ztp5Oum4RNNBZnQrAG2vCnfNHHn7KogmLvj77xgcP7XlxxwEjl72w2R3ByfcF17zQpef0rr1vOvWCu/JLLnxkxYegwK9fBNLTb2mTOeGk8+4ZMPSOQ4tGdj9h1trfwKvBN5shre2V3Y6Y8+ibQa8JPhG9Qxsa9DliYXr+otMvX/34u/LIRR91G3RLVo8b73vom1AMIjKsfLKhfc7stK6T/3bVy/2OGZ/Z7dzrrl2xtQIXcV58L5jVZ1n7nNnPvVpZH2QbTXUYePyTGbkP5ZUsL+m/5NIr/n3zLW8U9xjdo9eYgUfehf4hFBT27LIENaBb8K/nqrvnTsjNGnfv8rL1pXDf07+ce/XDHbOvPua4Gb/+DGoMD72KinI4ajYEoc+A20r6T5l/33cxcvOsgz8AWb1mtCuYn1k87YPP2YneaG0qK5asAfhEqA5BTt8bu3W/NbvgpuOH3FxVh+dU+QBKTpl3cMnM48576vHXYnOWf1c0YHSnTiPuWfST14+wQzOMXQAN9A1omkbbL2luQQv2qUBDMBik7Q9VVVU1NTU0p6+tra2srPR6vTTpJC2u3+9P0jTwT5ojAPtQwj8nWuGmWmpqalwuFw1wtH7PZ8mtw3/+5Uej0aqqKrfbnaSLtlfdOinesJ2JJJH9I/zLx1lqzA570UqbU5VNRZljBXocHBnwJvG5NaecRIo3hmcgAcALJj07wgc0+tsn3Lx4EkH+b5JtB5emFOGKFnvLuVzhmi26y+si6ExfGUdLlIfgLDWe5uX09fGKqAukFZAkSRRFWiRK8vhOSyr06/f7vV4vLRfa+2VTRggej4cLad41OoYmodTAhcja2lpyi5JEJxVo4NnsoKGysrKurs7r9ZI+kuchuFBVVbWVXdXV1dQqO9+CwWBdXR1hKYrU1dWRCpPTiUQiVVVVNPiQOocUonY6oVDI5/MRBQ68aJGU01EUxe/3u1wuj8djX5y006HtYz6fL9L0SspDrLYjhqT3Myn/zvzL3UFWuWHQKeMyi67L6TU6q3h8h6xRHXNvy+0z4fSL7vn8J0FkpxzhBsgoLLivrPioRzoUL+rUa+4B2cNzjxy5aOXnpfXgN8ALsLkBTr/ivs5F4zvnjivpdcuYsU9VVaPvI29UDytw0qlz8rqPK+x9yzvr/D526OWzLwmZXcZ3zbq+dDPzPok+DTBoKmga26+nWqYGkRhMXbC2S+8ZaV3HtSuedkC3G7v1GTl32dqN2ywm9vDoCQM3hDYJBvOt5I2BR4aegydmD5h1SPeJBxbfXHz6lPte+6UmhiYRagg+/EDumn9TVsmwvF5X3LnwlWAIZ7dmyLzw/Pt7Hzk/rd3F+ceMnrD0jS1B3NMhKVBTA4NPXNQ+e3rn4knfVGh+xQwFYqDCvEXfF/ZfvH/mHR36LEgrvDnjhDFzH/+0PoZ7GQQN6iMw+KwlbQunZRRP63/kzSuWr4l5IeqFSBBcfsjqsbRd1tySATdWuHAloj4MnfMWFfR64o45ZT2OmNkh/cbMjOHHHXfndcNWVblwx2nMgIgaM9D7Flldgt8N113xWEne+K5dxhf2m5deNLF94ciTz128YRPuUsHLwm0HwYjuccPxx03NLbxt+qyP6HRRywSvH/IHjmtfMu7Wmf/ZHkanWOz8clNBY0dUCykAH35VM+LWR8aOeaK2wrKYH/CICSNmPt+5//hDc6Z1KLjzoG7XFw64efmjX3mCeNAlqhUNC3dPsLBjTQMNZ7QxgTZYRiKR8vLyQCDAQQONznx5YuvWrbR/0u1219aiHwpZlknTQKZ5hBvC4TDtxjRNk2saqLodahpM0wyHwx6Pp7Kysra2lswM6VcQBJpuEuxo5ZOjyTSZbpARANXOR4qkSCukdulWEtk/zr8734sdtpkLtubaYKqFJDcfLrmAt0tcOxESqM1bSHRItnEUSGTtjWxekDeDZ2sxD79LEWqePdH+rtobz7vWYgZqKv3ynBwoEx27UzXqPu2USaqFN4b3iDOTbiX1i5YYqFW8bPOIvRaKJ9Gh6XsSnV1dniC1ZTQaTQI6RJx+CRXRr70NZEdFYIJWuAKBQJKdCp5YyK66OjQiDoVCZMpjp8Mth8rKykpLSysrKz0eTygUsvOERomysrLy8nK7xsVOR5blqqqqjRs3Vje97Hmi0SgZAyUpNe15diPOQUPMhBvHPF40YGTbrtd07zPlxKH3z1r489rvUNRtF5gJAltNQLZEYc7STaecv2rIuSuuGfvyx98rAY0Z6KmiAFAvg1eHf7/re+E1d2k5npbJDkfEp60DbKmE8y6cN2biM34RV+5DBmytguOOn3rRxbNCIbTRQ09STFzhcrjGdh/ouNGAuUOA2fd9e+TQxX+75PGxsz74YgPUC2hSENbY4lFTuEDoAUGDZYWYW4hNdXDDhDcvvPGl2Y9u+MGFU2TBAkXQ0YgA4KuvlSee+bG0CkWjNyChLwJZqa+HN96NvP5h5KtNZnkIb4Ui6AQ6FoZPPhT+ftbKMVM+cIvQIOOc35BwYj1h5geDTr1/wKn3Xz/zvTWlBrnLDCroskkw4OsN8rOvhd9bCxWVIEewpxozzAxH4Nl/x4ac/dDihz5kB3PDj1ugfdbcgt4rfVF49W3XpClv3n/ftz/8iK42PUEgY8OIjL64Q9GYpMuSYpgqSCF44J71Q46f1++I2Zdcv/rRf1VVeiCmJEADdtRCrZIK9y796OijRn/yWVBhkMMywRewPv4u+uqngcoGRCT0IPAIbNySicdyCpoR1XDzhangNhNAg0qmhFBh9gOfnHjOQ6ecu2rkpNe/3ogaiBBb3ZDUnQMNlmW5XC7avqhpmiiKtbW1BMPJgVI0GvV4PBUVFW63mywYvF4vgXqXy0XggKYjNJnz+/21tbW0jkD7LFwuF23NME2Ttlnat3cmDUb2D8nQjdraWoImdvUsqXld7OKr0XxEpiGA6FBckqRQKORhl32IpLv2/Pba9704Z9He6trOEGw9D38Ee9ik1mvZSeK8Ma1Ta/1uK++zvRk7U9cOK7IT3Cvx1r+FnWmzvft7pUmtENnJ9rRCYfdu2eu1gx57Os12ampqSO1KYyOtquxepVQKdWBg6SY7l1LDLRKSgl4O0TOxCf9vvqcl3PmRMhwdNlh4S7XigSQ7dxVM/2IeVpYXZ5oApKYx/wE8v8EsIg2LnaGMTYnXh3oDtPVnwWLr7mz1vrHeJm1DE/qEuj7OD0rhFSEaYW2WmfpBZfXgGomBJU0TvRoYCZpYK3OzaCSYQB0xabMJ5ScuUb0s3WSZVQuPyRYTtRBDVOYRkrqv0ZGbCVJ40JaJRcgEMmqhxH3pLaF91uzTzno5piAWkTUMCrpZxFM2GDWL7S/Fx4fBQp8TFkNdhoZPEAPlpIOz2SoU+rGwcCuHaqFfSN3EOIMS2AZqOd6ykPmWjr/sr0VHaiOLTAYiGNPo5cG9nRbatMqJGmUG/PBJWqCbJvftnVLTYFmW3+/3eDw0xVEUxefz0SoATQvI2I0ABI1iiqKQWo6U/KqqlpWVEQXLsiKRiMvl4jpA2iZAM3vTNIPBoNvtJq0p/3jsHxtPJB0g6QltNuwYJQVDKjUDUSM6FKddiB62P8IBDXYO/+7xvSUX9yId+/vTIn92pi7+SrdIwS5Zd4ZaKiJ7Pb31vvNOtd5mnm2vNy+JIK+o9fYkldrzf+31poqTEoj819EkKhQKcQcwe9KGVDXaaZIApum7Pb2VOOkwmHBBcW4PzUuRvEe2m/HmxPMwUcfiSZCgkUYqyqnSG0s2i9nb3Oxmqwl0ykKKLNSSFDcpGXetaoCWeiLbmzBhxme5vZZedeP7Mk7WDcU0ZMvAbRqWiWLYjLMpjhgYbkj1HJumox8LnaELA/38IdpAo5BmV1yuJUAD+tZsIVezYoRBE/RZ8xoPBGkNNESjUftuQ5LQ3D6OPP3RGipfUyCbavo3GAyWl5eT8RFtlDB0Q1EUURRJwUBsJqxNvqHsdFoZQEOhUDgcJuu5Vh9hnD2Ux84YYqWqqrQ3r7lfB565dfrOXYcDDgccDhAH+KDRSoQPceS3hgxOyVTlf8DG/40Atnc/3imTqSB2q4c7IapboLt7pVogtGtJpomqBHQUKTLDkWNPWZTTa8GC+yo4aFBMQ0Vf2YgY+DLiroMGplhKCHVSFbQIGvizIE2Dvgu4JK78SFAwuJvO1kCDpml8FxOZKybKx/9yfpJVI/1LFlu0lOhyuYgCQX7uyokXbH1vpL06exFa66UF7ziSSjyAJKhBFKisnRp9uvaJSBIdntlerxN3OOBwwOFAKg7wQaP1CM2dyG0an7ekorl303cDNOAQTar7PWlKqzP41gnvhdpbr2Bv3jVNdLmkE2iodENOydi22WNXvyPLGu71JWUDRwx7AhoIKHC1AcGOHbx4u4IYmpHaEWigAiRHW3ddwEn7fD6uZNM0LRKJ1NfXl5eX8zO17RI66TG1cispJ8cEdhnP47wxSZHmRJqnJBXh/zbP6aQ4HHA44HBgVznAh5Skzb00fFmWRd7GiCzti+HDHZXd1Rr3Vv69ILb3ADTsrV78b+gwF5ZoAyoCfPIVZBbe1j7/lnW/oB2DydYjaFWCL0zsyZO1Pxd7PFVPdyZPqrL29JY1DdQTDhrsr3uqeE1NDe2eoPUL2qVN2yDtRex18/j/DDTwPfpcSWhvg72dPM4zOBGHAw4HHA7sNgf4kNIiaKBdJLT3hJ+2Yy+yS4PkbjeyxYJ7Qdj8hUADOxWMGRXOmPdlZsHYw7Kv3Rb8i4EGrkJJeoOT/lVVlTs8rqys3Lx5s9vtptUHjpdbfCN3NZHq5doFeySpSfxfexW0QYv2fNrTeeakiD2PE3c44HDA4cDuccA+sNhHLYoTTVVVI5GI3+8nr7u0nssL7l69Tqn/JQfIBlNjoGH4La937zsjd+Aot4LbJZIeOn+svyMc3D3O7FjTsJOggaqnTRbkJs++rtF8Zr97zeX4I+kB0L/2x2CP2+sqLy+vr68Ph8McztNde3573F7WiTsccDjgcGD3OGAfVZoPX0RT0zQ+9fL5fHbfFXtxCN299juldoYDpJVBF5YWrFtv9T3i9qde2RzUcNtk0kO3vw87Q/mPk6dl0MBls71jrcd5lygbZ5C9FM+zhxE7zZ2JU3V0EIbL5aI9Ts5HuIdPwSnucMDhwK5yoJXxio+Zfr+f3OLRSStUhTNe7Sqrf5f8HDSgYwnmuyLu4sJqeafj79LIPaz0LwEayKFKXV1dZWUlIYY/nUZoDx+zU9zhgMOBPwIHUoEGjhgIHMiyHAqFyK8uDVbOkPVHeHw7bAMHDUn+KFI99x0S/ANm+EuABkM3PB4PHb5Mi4V/wCfhNMnhgMOBfZ4DqYRHEmigbZnhcJgcY+/zbNlnOkiggX7tnUr13O15/izxfRY0cFMMQu7cuyWH7Q5y/7O8o047HQ7sMxxIJTzsoIH2XpJNmKqqsiyTccM+w4R9uCN/adCwJ8811YexJzR3tSxfAmx+6BHHE/Z27ir93ze//dVsjmp/37Y5tTsccDiwqxxoPhbZUzikcKY6u8rYP3h++1P+s8RTahr2hNepOr8nNHepLO2EpiLoh0vT+CnG/PNLgg7c9nOXKvq9Mjug4ffivFOvw4H/BgfsYybRt6fQqCVJUn19fV1dXSQS4ZOi/0ZjHJr/Mw7Yn/KfJb5vggZyei2xi44b3iFoSDww+8ks9Ob8AWby5BqF/VI77b7K/wDt+599Yk5FDgf2TQ4kxh/8Sz20pxBokGW5rq6uoqLC4/EIgsBxgz3nvsmdfbdX9mf3Z4nvy6AhxC67moFO7OTKhqSHxNJ1PN8rfpKrfT6f8rXlH3nKHHt+g4MGPEcdgwMa9pypDgWHA38cDtjHImqVPYWGLPIaGQqFPB6Pz+cj3EAH/vHMf5weOS3ZGQ7wB/cnivxXQMPOMOu/mseyrNraWpfLFYlE6PALDhTsEf6cbIm6YaiqJmq6xM5kRwzBYATustXYxVtOx2xyvM/Tdz8Sd7bKwQoeFYMX6RjYee2495dOsseT3ekgMjwm1dE37D7bnZIOB/6oHOBjVFKkrKysvLycTvyxDV+JE6lZ7j9qn5x2/bk5sK+BBsuyaIszd+KUpF1o8QOjRFzCQMQgq5qs6YphqExcN3nApmmq7KL1Drq315QNyaDBRDdiiVPmyFVII2JoBA0IHRzQ0OQ5Of84HNgnOJCEFfi/0Wg0GAyScUOLY9peG5T2CTY6ndiLHNjXQIMsy3RWViQSURSF1AD2j8oeT3yBhmmiggGDbuAeJ0kVY6oQkWRJNQ080lQQhEAg4Pf7Q6GQIAjRaFSSJMuyknxR78UHw06k0P+1ZwAAIABJREFUJdCgm6AboOug6WCooNPJquy0NNATigeOLVA5wZcz/oyRvctEh5rDgT8zBxJjVPJfMtym0wFpAtN8ZPsz99tp+x+XA/sUaLAsKxQK1dbWVldXK4pCG53p0Cz7F8XjiQ8xDho0XWHrD9amjZVvvv7hjGkLLrvkuqOPOr5P7wFZWTkdO3bs1KlTQUHBoEGDhg4d+sgjj/z222+BQKAVRJ+g3/h3J18EQgB4mCouQOgaCypoKhiKBYqFnswxWAw0sEWKfQc0xO3AdpJVTjaHA/syBxrHDluMTuulcYxstsjcO2lk25f54vTt9+PAPgUaoraLfz+tRDjbJUnQdCkYDCxcsDgnq3i/tI5paR3zc47o2K6wY/vsDu0z27Rpd9hhhx1yyCEHHHBAGrv233//Qw89dMiQIa+99lowGAQAQRDol/4NBoNUte1jj0d5vUkRvsRgAmhgsmCpABJA1DDDqh5W0MrBG4SQCGEZS5totGkw40iMJ/kuTaLf+r922NFkEYSbULQUsZf6b8Rbb7Nz1+HAX5ADtF2chhfuA4pOuiJDq78gT5wu/884sE+BBpldiqKoqkoAvBXEQGidjBx9/u1337Pg0MMOTktLO/jATiWFx37/dd07b/w6efwyUQCfN1xeVrlhw4YnnnhqyJCThw4dWlJS0qlTp7S0tDZt2nTq1CkrK+u5556TJEkURQCQZZm+5F1VG3KhawDIYEhgxABiAAEFNIQRiBU+WRu54aaVV1y7YNT4pT9trPUEwyooKp68Gjdr2G3cwGtnp7uSieWOf+2l/hvx/9mX4FTkcGAPOEDv/h4Q2JWiNPmwz0noTG2fz1dWVsaPx9wVkk5ehwM7y4F9BzTYP6TWsQK7y0wCTF0UhY8+/eic887e78C0dp3aHHvckGnTFvrc8NH7laefclvAA9EoxCRNUjRF09d+vn7BonslRQOA7V7Pa2+8sWTZvWefe05Ofs6hbQ/JK8j/ZO1nOlouQiQqREXRDhqoPgMadzqkGmbQVAL0CMQCIDaYRoMOUQuq3LDyyV/PPGdJcfHEwu639+03aurMlyQLGiRZ0BsANBPDHpkwMKNLsqJAQ46dDPZSezVOipOmOGSP+reLph47+wX99fK1/hQYP5o+tt1RgDWnkOp7oQewq/kT5sXNy9kfqP2uPT0pzvR9uE+bIXbiT1KWPfzXRtOE+OepWzr3UEdTIEVRKioqKisrfT5fNBrdmxu79rD9TvF9iAP7DmiwP5RWAISmK4oimaZqmurX69eecOKgtP3TOmW0n7dwzrfffy8quKL+/ntb+/e65LuvYrKEVFUTwlHTG1CuvPqWcFQPRiOyoUiaHpMhLMDCux+edde8h1auaNu+Y6fOGXPnz/P4faIi43xdN/jejQRoaNzpkHIQxG0R4FHUOhVcEriicM+Kb045Z2F67tX5PW4tKBzTs+e46294/Iv1kZAMMi5PaDrE0HfDLoAGPLi1WUCLSwoGaM2DBVrzkPBpoe9hpAnl+DZX+5C9h4hoV3hjG6DtL1Ur8aYNJbjT+m8cnDWDWa2X2vt3W+lUyltx/rTWaVu/4m1OSS3FjVTUU2RPyZnU4CBVDanSm9fMc+qA9kWKBZpp6pahg2nht4iNin8XPGuLEZa5KX1issVokG8WyzRNpMbMojW0z2aggXADL2zohtfrraysrK2ttTuA4hm461saJO3pTtzhwM5w4M8KGmgNgnpI+xroY6AU+h6a/aLHBU2XorEQAKz54D+5eRn7H5g2eMgAt79GNjRJQ0G6aUvwxBNvmjf7NSmGH70g43jg9cP5F4z/4OONggwNkk8BUUdlA7z4r9Iz/z5elCEsilvKay698rq0tP0v/OdFkagQEtDVKzqxNgzdpMmBpQMGSVUQi+gGAATDgqLpOLqYYGigKqApEI5CZQOs/th31ehXeh4zt23OqE6Ft/Y+YcKlIx54a822sioIi+APg2xh2+i8dpzj0EBjsDp0MDXLwskPG7+SrQv5mGSPNA5o5J0i6RdnOBQsDXhIDItsfFQBditYCliKZcqAkQRxqovEgb2Zux1v7F+rosTGq+Yl7B8VF40JvpAZSpNffqtphBu36mrC0JWZu3IW2yP4WtL6FDGX4vTbHPpRyk7mt3UwGcfYe4qvli0rE3IoKZMCM89thJ4MgHKySKDxSv0Q7fVQX+wp9ji98PaUlvLrZDRsYmvt0NZezp6eKt6k+QlAoOJCIogAogWSacmGKZq6jCbL2G9FU/zBYJVmRdDaScaH+FuZ55MvNzzz0rv3Ln/qyedef+zx1csffHLJ0pUzZy28ftit1183YuvmbbjEGZHBADkYwbVHVQVNtDTBtEQDJBNkA1SG6Y3mgp/GHFEUyWukLMt2n/qqqtK2Lz42Nj4RJ+ZwYOc48GcFDaqqKgpudqivr6+urg4EAkkImn8VSREAS5ZFf8B91NH99zsg7cKLT99c+Y1iNIiqphrww8/u886/fcSI+xUFZBUiIigG+IIw4ubFjz+xVkCLBZBBVAERxgcfVh137OjSTZiTxsCQYIwZO2G/A/a/5PLLmoMGHQwakCwAPSGZFBMCETMcQ8q+AEQEqNoGd859Y/DQ6YUDJ3TIHlPQd87oKd88/5ZYI0BtDLxRNkpZUN9gyBbDDUyixP050OBOPi35CEp1URP5UGlYjSAAx/MmYiEJLqDlh12K2eOJaVDcV+UO/iXU1OzX1NhmUhl/cVepjgFrSSCe1DImzvodZuAdbz3C6LSSJemz4jntopoLdUrkzyGRmdhHuEHVgAfcWMsD1/owdTQWSdjGNkbsT4UjGJa/EWfwxhC45E1KNIaDAZRyTaGBra+cvZQF3yjTjhi4YG4W4RiC6NtopojaG9GMdU2aSAR2lN8OGuy4wV6Ox1MhhsTSQ2ObSYvAQYOMEt2MakZMM2KWyVy8WDqYombE3AHf6+9+fuNtCzMLhh7YYVDaoYenpfVMSytOS+u934F99z+o30EH9WvTrn9aWu5BBxVcf+3kr9dt2V4jCH4VUYaigq4AKOwrVwyIqThjUVoEDYQPaHGW6zgJRvCG8zz2gZHfdSIOB3bIgT8laKDPQJKkQCCwdevW2traaDS6Y9DAbAU1zVIV8+GHVh562MH9B5bImhcgFFG3B4VorUu/+ebll1w8b8tWlN+SBjENpfLMOY+MnXhPWELxFFYgEFMaYvDThvDxQ4Y/+fSnJkA4hpkDDbCx1HPu+Zdcfs3VbTu0f+b553TT1AymabC4lwUU+TEdJAuCIkQ0CKsQ1aHGB9/8BA8+Vn7GPx7uln9b+843Dh6y9PoR/3n1TdXlg1ovCBpOZ6IWm9QANKhQG4SQjiFsIEGc29DAouGEykr8WhqYKgZDAU2yWDA0yVAkVZFkCroqM81nfOhsbs1gwxAWCnJ7IHHCR93WI1z2JEVM1I6QagRVMYZpGSaYFtp27sJlr5tGfz4V1pFMUqUt/UskuGRlkThESkhllFupLire5K69FrpNKZjJJGSQmAHz1iZFZDadxV+TBf5vswgVpL5jM3eqPfFWkSktL0up7DcBcJv0K06cFAmNWCcBelQ2G278TYAJxBCJ/rYcSSyQNaeJKTYsFS++i/lt/UrqD3siCZ7ZszWPU0meji2xQNNMUTViqiloRoxGpF83VsxbvKJr/vFpaSVpB5yUdsDZafudd0DHG7KLJ/U5en5Jv1m53cd3SL/xoEOvOLTNRWlpQ9LS+qftf+wBBx2ZnXPqCSdccd/Sp7xujyoFARRJDhogGfgCaDbQEPdXy0e/JMTAoQMZhnOgwI0hKKUFTjhJDgdScOBPCRo0TbMsKxqN1tXVud1uQRDIWQL/JFqOsFFRkS0xqh95xDGHHHLI9z98FQjWRpV6yYhYAPMXvnDiCaN++hG1AA0CRCTUKD79wsen/P2aGo8kmnF5j9BBhMuvuuuqa+dIGniDSkREdWF5uXzhRbdsLqsWNWXwCccPOHxgKtDgi4I3DA889tH9j65b/ND64WPfOO70hwr7LsoomJ9ZeHd+7/v/efXaZ1+EZ1+A514SV78Wfu3t4OvvN7z6XuDl/3heXeN//SP/mi9jn/9kfb0Bvt4AX22Eb36DH3+FX34xf9sAG3+D0lLYvBm2bMFQX4/B5QLXdtjuBo8XfH4WAgiM/A3gD2JnwyKbwmiIPwSthRBTMQMFSQEeZBUVLbKyc0EFWcOg6BhIpGgWRhS9MV2i0ZG5o0CFSCKgCG9p2ycmNjPQaCElVVmezojYFfskhPlk3U6TJEYciLB/eDubTIe5ZGGbUrChlMIkcZwIfpz2fAlpistLTQAEid6kxCb/YhGaFjcFDRy72OtJijfuv0m6QciAfltkdRxX2TUfCfQQl/3NhX0q6GAHAeShxE6qOZ0d5W9sfIoxcOeTOVtaKIJLn6aqGpJqSLKhPf3Cm6eecW3agT3SDj32wI7/SGtzyUGZYw7LnpXZ84FOhcvb59zbJuueDtn3pmcv69R1aYfMRR0y5nbsOqtD50lpaVekpZ2dlnZ8Wtox+x185H4Hdb1u+M3rvl4v6aqoSZKpqGhvpCc0DSlBAxlUcdBAjulEUSSXdw5oaOEROkk7x4E/JWgwTVMQhPr6+vLycv5t8M+DsHYLuIGBBiGiREJqRnr2RRddGolEo7GIaqC546efVJ359/E//yLFZIjIeJSDDvDKa9+dePIVHj+O6CpqCMyYivLy2uvmDj19lL8BBMWUDJS73/0QPGnIdWs+2KAYoJjGE089mbb/ft//9COetwmWosm6paKe0cLNkYICP/8WOvPcsd17X9M2e2xW34fSOizqkPdkt5LVB2c+kNZm1mHZi9MLHuxa/GCXkvnpBVM75k5Oz5/ZKWdep5x56fnTO+VP7pg3Mb1gSkbR1HjoPj2zYEaX/FldCu/sUnhn1+53ZRXPzu05N6/XvLxe8/J7zy3oO6+w34LigRTmFQ+c13/w0v7H3cPC4mOGPnjM0AcH/W35kafed+I/VvFwxuUv8HDJjW/xMHzsJyx8NHzsRxPu/B7DXd9OuOvbufdt5WHZKhcPT7wci4d/B1e/L6xeE2Qh8PaXMg+f/QI8/FgFP23DsGEbbN4GFdVWRbVVVQs1LqjdDvVuDC4PBrcPPH7wBhj0CUNDBIIChrAIggRROYGEVIgqCAEpRJU4+hE1EDWQ9HgQNUwnzBTRIaJDyISIAWEdfyMGxFgQLVzBxmCghknW44EWnJWm02Eusgy2wGCooGm4SC1rIKnxmaNqm30TKtIMS0XnpGi1KyqyqDCnHAxZ6AzZ8AUeOn+EpBme6ioqoqxKiiYbhmJaCoBkWJJmSlq8qaqGE1VNR7FDS0mIe5pciC9MMNlqmkG/CqrI40ECPRHQCEUGdCWiMt2WijYpIFsWBXQ+xr4j8kKmGZZdUUBtblIzVcy6SfhMZ0p5foIcR0NUltpPccqvEYDCr8ySDUNGPZ/F6yVo03wBzZ4eR4GsWQYaNVqNgIhtjOJzelK/scbi+GAwNjZEYi+/9mZGTp/92wxIO3TIYZlX5PSd1j5/1mF5dx+ct/ygvEcPzn324Jx/HZzzr0Ny/nVY9r/aZmFo1+2ltl3+3T5zddvMZ9tlPtou8972mfPbZc5q33V02v6D0g4pSTsgd8b8hxpEXPYAAFGL6ZaOeyfY1cJYZ0uiPIFAgKwjo9GoZVkKu5KY7/zrcGBnOPCnBA2iKAqCEIlEQqHQLoMGIbZ1S+XBB7V74flXIyHV0ECU4NdfXGf+fczWzfjx13tlFXUJ5hdf1xaXnPHeml9CUQhLKo1f4RjMmffswMMv3VgqRmU0mI4q8O33vqFDb3vskY9lGYWBqCkv/fvl/Q884IOPPjTYkByTY7ql6pZONtaCjKaONW7rqhuWZRRPyB2wskvJM/u1f7j7gLdPPve7s6/8eugla4b+84MTznn1xHOfOf2S54447b6j/rbi6JOfPGLI4wOH3N9v8KJ+gxf1P25xyRGz4+Hw+cUDFhX3X1LY/56Cfnfn912Q22d+IszN7TM3v++8/L7zMounsXBHRtHUzoXT0gvwN6P79IziGZklMzNLZmYUz+hYNI1Ch8KpHQqnti+4g0KH/DswFExunz+xYx6GTvmT0wsnde4+OaNoSmbx5IyiSemFEzrmj+uYP6597tj2uWPb5Yxpnzu2Y/649MIJnbtPxFA0rnPJiM49bkgvHpZePCy7/y0UsvqOzOo7slufEUkhq+/1fY8eNuCoqw4fdDWFAYOuHXjMdQOPGTb4pDGDTxp3/MnjeTjh1NtPOPX2v5817e9n33HGOVNZmHLGOVPOPPeOM/8x+bKr51929fzLr1l4xbWLrr7+7mtuuOfa4UuuHb5kzITHeZiz8I3Zi96Yvei1Oxe9sWzl5/c+8vm9j3625NHPVr34I4VHX/r+pTXlLGx9ac3Wd75wvbcuHtZvlNZvlL7ZJH+/Sf15s/7rVnNjOZRWYNjyf+x9CZwUxfX/IsgRD5Rr2YMb5TIRb5AfKMpluNS/gAqICiiIJuIJEhKMByYcMYhHoqAoKoIICElEI4eJQgQFRSGwh3MyJ3P0TN9H/VP9dt7WzuzMzh7AAN2f+uy+qX71qup1ddW3X1W9KiOHy0lpOYU4ngANR4PEFSDOIHEdqwzuEPGEyNFjFcETpIAGQlylpilPtCLwhMQNGnhzZgpQDoWzKl0jJ5qL5UI8CYrkmERDSCYRhYaoTOfXICCEipvTcLxqYiCdLrTjNVOyTvfkVCKkxNQYTwhnQiiKpcwAWKrir0qNVXQCTqElQXtSxRZeWPpvwiZJIjQIFUEW6UJgClVMHrA8AZ4DuxT8Te3UdIPODchmxWndAQLKJiaDMZZNAxCj6l9ZMhcgg8tVJVEMk1AUAwKgB2YsNkm66IBCJjqjZ5Zh0ZI3zmpakNfk4rzmN7bIn9my04LmhYuaFr3WuGhlXvHbecXv5RWvzyvekFe8oVHRhsaFG5oU0NC0/eam+VubtdvaLH9zi/z157R//5yCVecWvH5+0aI23R/Paz40r9m1jc67fPa8FzmNcCo1NtQWNOi6HolEnE6ny+UKBAKKQveNo89cVkMWbWkgswZOSdAAWyeSTAtJBrfk17viN92w4HCWNm/+s9/NX0g0EvKRLZu+Hzli1v59UcOgQz7tfSTy7bfB/v2mvPfuLtq3SrpkkHCczotv/vveX/S95Yt/OzmB2gziMtn1taN//7sffXRl0E9X78nm3sfZjz7SrEXz/+zZk7A0UMRggga68CCm6UFeEAlxHNPf21I26JdLWhY83q7DH89r94drBm9Y+FJo1wFyxEscEXI0Tv86osQVJ64osYfoAOCLEz9HgjxxBSuD00+c5uoHm5f85CHlR0mp0wwuUuoiJQ4avi/RKsIR4+vvjK/3Ewiff8l//iX/z3/HPtkZ+fjzwKZ/+iF8sMWB4bW39r321r5X3/z2lZXfvPzXb5b/Ze+y175e9truZ/6wFcOc+RvnzN/45G8+enze+kfnrHvkybWzn/hg9hMf3H3fa1Omv3rX1Fcm3/vy5KkvTbr3xYn3LL3j7iVjxz03dtxzY257dvStz/zy5gU3jf3dsLG/HTLqNzeOfGrwTXOuG/HkoOGPXTfswYFDZ/7fkBkDbry//+Dp1wy+3wwzf3H1/b+4auYvrpr58ytn/PzKGZdccT+E7r3ugtCt5+RuPaZ0vfiubj2mJMI9F/Waaobp3XtO695zWrceU7v1mNr1ons7d7+7U7cpbQvGtS0Y16pwXKvCCYXdZxZ2m1XQfVb7bg+06zKrTaeZrTvOaNlp2s+6TDu7y9Qmne9t1mVqi24zzuv+AISW3R5o2e2BVt1nteo+q3W3WW27zsrv/lB+94cKzFB08cPFPWZ37vVol96PdLnk0S4/n92n//w+/ef1unZez/5P9e73VK9r5pph3tWDn8cwdOzyoWOXD6HhldF3rhp956qRE2mYOGPDpJkbJ83cOHnWprtnfXzPg1vueXDLvQ/97aln9jz1zJ45z+yZ8+yuxa8fXPzG94tWHli08sDSlT/86c0fX1x18MVVB9//WwDDJ/9SPvmXsvXf2tYvlU+/Uj/9Sv5st/TZbmHXD2T3j2TPj2TvIRq++S/59gjZV0LDd0fI92b4yUt+8tLVNg4fbXjOBB4CVESnvY6RYIiGSIREo4SPEYGvxAeySCBoEqy2ITJPpDgRYyQOgSdx3rQVSeYGAma9qKzQGJgRE0QiiCQuUYgQV+gSQQgwCyaas2CKWrHWVDNxQOpfxdyyBPG6SoEL/XqAkDDDUNuLuRmK9jOmzZL2KHR9YtggIZUuNSDr1m9v/rNeLVpcnpfX/+xWD53bcen5nd5q1PadRgUf5hV9lNdhbV7HNXmd19HQyQwd1+V1MEPx+kZFJowoWt+4aF2Twg+aFr5PrRFFbxb0fjPv/MfOK/p13tlD8/Iu+nKfLU4Mgxi43zK7fo/u14QpXZfLVVpaCu5rM48N1l1LA9Vq4JQEDViTCvNc4l8aoGBGV7znmqREolygb9++l/S5cu9/SqfeNe/yX9zy4Zq9gkCOelT6yWCQkhL1+uvue2T2K9EoNWhHRSUQpVMY337nuXbghNdXfEptywrt0crt8uVX/r+7pjzDx2jHxMVJlFcP/PdgsxbNJ0+5C6zK8LcCNJg2XtGQeSLHDSmian6eOPzkq2/Ib3//7WVX/KGw+JHO3X/VqcfMh+Z8vGlH5GicBGXCmZu6YqZ3SIFUfF/CGguc8YYDKVTzqwtMtTCHTj/CEovQqBk88Vkmq0xfbC5ag287+O6EvzGZxBJ9Mf1k1KmjBtmcUIWOG/tu6MGpZ0q5ooMGWpKJIBCeJ/F4ReA4wnEVAwPP04FEFGgQTDoukLhAhwFBpOqFEJVIWKDrRo/FSIAjPo54IuRoiLjhex2gkoeUu2n4yUlDqY2U/ESOlJPDZeS/JTQcLq0M335HMGz/Qtj+hbBtZ/zzHbF/buc+3Rb95PPI3z+Pr90Y+mAjB2HVmiCElR8E/7ii7PmVFWHOkm/mLNk3Z8m+J/+494k/7Hl84ddPmOGhedt/nQjTHv4bhvFT3h0/5Z3/N+XtW+966+ZJb4ye9Pov7/jLTbe/OmLCK8NvWz70luVDbl425OZlN4798w2jX7xu5IsDhy3+v6GLBgyj4dJrf/fzAb+75Nrf9uk/v3e/3/S+el7PK+Zg6HH5kxdf9kSPvk9cfOnj3fs+3u3SR7pe9qsufWd1umxWh0vv6/Dz6UV9phb1mVrY697CHncXXDyl4OIp7bpPzu86qV2Xifld78zvemf77hPbd7+jsNsd7bve3q7zuLYdb2vT8Za2HW7p3GNi5553YOja445uF9/Rrce4Pn3v7HPZ+F9cNuEXl0249PLb+15xx5VXTbzq6slXXT35mmvu6tdvyrUDpgwYeNeggVMGDZw8aODkXw6f8cvh90G4Y8KjGB6Y/vsHpv9+1n3PVIYZz86asXDOnNfmzHntSTM8/czbv3/2nWeeW/3c8+899/x7z7/w/sI/rHnhjx8sf/kfEJa98o9V73711ntfrXp/19trdq9et+f9D/et+Wj/Bxv2fbhx74ZNNGz8+JvPtx9mQunn2yvCV7vdX+127/rP0V3/Obp7j/vrr9179hzds+fod9/5K8L3R72+eIyjx9fpiWkdEzQo5urkiKLzGiGjxtzf6KxLWzQb0brtQwXdXmuW/2bjNu+26Pj3vIIteYVb8oo/zuuwMa/ThrxO6ytCx/V5HdfndTADtUCsz+uwrlHxusZFFaFJ4Qdn5b/VJH/5OcUvnN32gcYXjPxFv4meiBqVJJybyBI0IEoQRdFut5eXl2MMdqcWYWkgGw2cGqABtgkpigL+oVlPZ+mAQnLlcSEYIXxc3L7tX82bnd+10y9eXLryhYVvcFHCRemGyHCYhEPk3rtfuH38vNJSSVLo7ENUNKIC3XjZf8DtS19c7w0qMZHOCv/0E+nfb8rEO+e73YSP07lqQsg3+/a3a5/fqUuXMBdlp04ANGh0l4PMzhbTyWmDRskSiRwjf9t09J5JL3fpMrVtp1+16fpY50ufmjxrw18/cH1TTvY76NaJYzHC8dQiQndjmZ9B4Tg984LuOaBT0ZXfSKABNiaZTiwwxBV81ROMzGQJSbeyFFhLNnb5YSWNqxerErhoMS1hUAM4BHBWhcALfibdRYdWsGxT0AivVyxuoAZ50xSP8whIVHzpmqs+09H4Wcybi0DTsWE8CqfrMCQSF0lMoI0hGqezXcciJBimazt8YeIBOOUjNh+1B/zkJmUJa1OZXS+z66U2rdSmfbv/WHUhvOML+/adtm3b7ds+t33+z/J/flb22aelWz8p2fDR/g0f7V+/Yf+HH+378KNv1q3fC2Hlis/feOOfr//1s7/+Zetf/7L1L6998tqr/3j1lS1Llqz70+KK8Phjyx5//MXHHvvTI48ufXT2kkd+vWj2r/44+1d/vGfKPAzjb/nV+Ft+Ne7WX4275ZGbhv/qpmEPDx/+8NARDw8YOAPDJb+4HUKfn0/o1ef2nr0n9Ogz4aLe4y/qdXu3XhO69bqjixk697yjQ4/biy++o7jbpKKuk9t3mdSu0x2ti8a3Khx3YfH4Vh0mtO18hwmYJuV3ndS+Cw2FXScXdp1c1H1ScbdJHbtP7th9cnE3Shd3m9S52619+tz09IKXNGqprNjCAaM1XeKgE1lVwpzSrEXPc84Zlt/m4fx2f7qw7Tvntlvfov0HTQs/aFy0Pq9oc17hZ3lFn+cVbc0r+kdeIQ2NCv9mhs2NijaZYUMjammgxobGRevyitY2KlzTqOi9xkVvNSt49ZzChXlNJ+blXbFo+WbeXAaZ+FaiJgS8kvu9mn4nLSGvid26b2mAnBqgwdydpgcCATgLin1u+LYkESxPxeKmxFY3Pi7Lkv7uux8UFXSR4/OuAAAgAElEQVRrlHfOO+985HJFVZX4vXo8Rmb/+tUhN8x0O6mAaJxOkUYF4jgq3jbhoTlPveo/RmNiEikrI5PuXDJ54sLyMl3g6cKIGC8ve3l5sxbNr7jqyv+WHOHisWpBAyx7phYNQzPdIAp02ZZmGkUJXUgW9hJ7OfnNc3uuGvLnlh0eaNd99oWdH2rf47Frhr105/T1f/zT7i93CS4P+W+JGI4RTqD9WGI1tQIryRNDeaLCVXRR5x8AGNjF+akQos7CGyxhapkyx1SiEHOBYYbtlNDAoKdmn+xJoc3jWCmGBoclsK4NJuzo0khzOwk+MM08DRVAD3WBoVGAS4Nplk/9KwtEFogiVgmyUDF9wMepWYh6ITP9UinmUgA5sToBLEZ8nMJooCv+mtYjsEixawiAhr8wVSGLdBaDj5M4RyJRCoYoEgqSo4HK4PITp484PMR+lE7G/eQh3x5Uvv1Rg7D3oLHnB33PD/rXB8jX35Fd+2n48luyYw/Z/nVF2LJDxPDhP8IYVqyxVYb3yleY4a33f1j1zo5dX/3XPJFOh+WcFDSYKjZMo104Si5s1a9JkxGtWs7tULCqdasN57f+2znt1jcr+KBJ4bpGhZvzCj7PK9iZV/BZo4KtjduboeAfjWn4W+OCzTQUbmpcSBc6mLhhfV7hh3mFHzYqXNu48L1m7Vf8rGBJ81YPNjln5EW/GB0391zWHzQYhgENifqgUxT2Y6zBXkhL0GmngVMGNESjUafTGQgE6vUIzE9zSVJ02m8a+/f/cN2goWc3bTng/4b+6U9vuJzC2vf/de01tx/YH42GyLEg/aAPRIW4Qp7/w6rJU37jDdB18nGF2N3C1Gkv9O8/reQI4WLE61V27Nhzw5AR55zXcvhNI5xul6TQJVjscAKWBsbhAYIGc0eFrisyEeNEiBKJo8Z5QsgBN1m7NTDu3rc7XvRkfvFvOnRe3KXL0j49F3Usnt2x4/S+l92/7qPv6LpLyRDMeRWNWh/YQf1MBA21bR5JkCJDchaVYn9dI8G2geNH41cvlp9uzTCXRtLVkYzBAz1JyYkJfpjFh79wQBm1ViXm8tndBGDFoo6+VLpaEOACPa/dFMUeblZh78LSmIAM/FpqhMTieiyux3kjzhu8QAG3JNFZLVwIqYGTB3NoFM1lCnS9grk8UzCXaorU/yJdp0kXBqYPcXN1J2++szGZ7lqKiPTUN3pIrEBDxW4acw4OdxpH1Yp1oyGZLiGiy0hNP2889eNKBKliDwiCBl2hc3BRjpx7fv/mLUZf1HVhUf6K1q02nd/qs3Pa/q1Z/qYmBRsoaCj8BzUzFP6jUQVQ+JsJFxKIoRI3bDLRw6ZGBRsbFWxsnP9x0/y1zfNfP6/guSbn35nX7Mpz23Z3HQtKOvUzCxfbMhmVZ0VqqiaKYiQSCYVCsBszq2QW0xmsgVMGNJSXl3u93liMfr7X53kJPP2slyQlEqZWfULIO6vXtG5b9LNz2jVu3Lp1qx5zn1x61K0RnR7ZRN08c/x7H26+d9rTx8LmFLtE14QvXPTGdYPv+vKro0eO8IsWv92p06Utfta6dduC9z9YBzLhLztIZAQNFOPruIPfdIQoJdYx+OLkyz3k+T+U3nD9270vXnpx92cn3/nx0qWHVq44bHNSA7WkwtZ5LQEacBy0QAP7NOpLs11zoruu+T/bBhqQTh0taPFMZ5DwHSyba1nUhMkBmgIiAfALQYyKXZdJuxABQMBuy8T2AU1RKgKbNbP/kOafpGIwhMiqomiabOjmDBq0VQowKo6M03V0ZwJbHNnyo//spMkm2Zyb4w0S1w3eMHh6JCz13gx+HRS6IpmeF5/0AuDGyErTo7lVUtWp6wO6WZo6CDGExN7amErXLEOo2PZpWqLMElI1UL1Rp2QUNHAxMuymR/POGnzueTOat3j6wjbrzm/9DxM0bG5SQGcf6AxF8ea8os2NCk27AqCE9H8btf+4cf7HZ7fb0rzd2vPav3JBwbxGPxuWl1ec17R5kA8outwgoEHXdUEQAoGAy+UKh8OIG9jWnvRYrZ9nuAZOAdAQi8XsdrvP5+M4Dtw61fOZVRjlVElR6SHasqzS2YrV63v1uOKss85v3abTWWed36pV5xtvvGXu3Gdf/suK/7tu+LZtpT/+yO/9xv7JZ7tXrf7owtadb7hxQkFh37ObtW/T7qIrrhi0du1mzSD+4DG2K6w6pFTeqWJvgFOgDI32+OZJEbrZ0cu0E1TBF6C5BZS6KDhcQp574fPRY35/5dVTX/nLtmiUSErFuZnmfv2KfW311E+a5IhFkog07KdpNNuZZkMfbzXgUI0E+3hg8oWNqWt5qIyKdptyblnCvgVWLvZvxeRPwv8SeIiomERj3TQBDYeW4fxd4hAVOLGlwoaWNJ2EP03HFbivk3rHSEzSmTVOgg/oMx3BVALwgJ8Mtg6yeZaLZh4mQfcs0KWQGl0/ZAJ9sLvIMv2i2Lrd1bj5wHNb3XFOq8datf/r+e0+aNH2w6b5HzVuv5GChuINeR0qN1uCOSHD3yYFm5q239Qsf9O57d+5sHBR+06z8/J65zVqXdytEycEcPdEUiOsw/PVVI3n+WAw6HA4AoGAJFGLSpJY/FkH+VaS00wDOQ0aDMPgOM5ms5WUlNQPMWAPUknAQZfmX1XXSCQsPPbo/P8eKZ/z1Lz+A/7v/Jat89t3yctrnpd3Vl5ek6bNOufldWjTtk9eo1bNfta2SbOW7Qq6j7550p+Xrzxc6qJroxLmD/PoKfrxhN8BCehQE2ignpMrujqzKzQ9PtAlktTJn6iRcIw6MlINOsX7k1PyBhjEQHGGge6fj08bxdIlEccnt1yVir1nlsSJrwf7eGBMNWPQy1QlkWhubAqgodSp8RDDDqk10yw4AN+ObAxLA/hIxNByVnUxWQkEkkpWvZJZQMDSbGI2PoEbktxzmuyq6cCb7ljS6f4hhYIGKJwJHeg5szJ1szH9V8ubnH9dXvOxLdrMbd5mSbN2f23afjVd01BEd0bQYO6urFi7ACsY2L8VCyHpcsgmheubFqw7t2BNy/Z/uTB/7gXt78xr2rNR0wuWvfwiLwSxg0lqh9WroqZYwA2BQMDtdns8nkAgkOi16H82i5okWfdPfw3kNGiAY15dLpff76+rjQF7iNTeDVfNy4To4RAviYYgCOZqaPXAwQOr31137YAbB1034qKLLrv4on4XXtCjZ8+h7dtftuCZpf/csbPURrECXHHB3DiRMHWCfZV+klS50oAG8xho+MbCLzaz36xYuAYr/TWiy4ZO3fxpJC7SqQy6ZkJPuFVmEINGDcDH40JNJhHHIy9LZt01kDgjo3LQNWOwVVYS2N4SBD7ZuueemhKFwh5gnIVj44GGtKnxWKMEyknJJM3Yn8RXnWQKRDJfZiqVkCgxHYSavq8SoIGuiYzpJKoasmSQAKf7YmTQ2Pvzzro479xf5l047ez2v2vW4eUmxasadXg/r8P7eR0/MEFDxaoFZtkj7LH8oHHx+2Z4t3ExDc0KV11Y/GardgvPvWBqs3MH/+y8HuMnTJFlVVMkOJ+FHc6BzlyXDHc1VZMkKRgMut1ur9cLWAE6MDaXDBKsW2eIBnIXNBiGAYt0NLWaE2CzfjzYUWQCDQahSyM1ldDjHM35TVmTJFlX1ArvsITQ3ZgTJ85d/vKHvKzE5ZioSaEYPfEWMoDywKRphYWzLqABcUxlz266GIYpXY0QIxw7JmsSF6cHdIELYTQwIJG1cmrFiJpMImolxGI+7hrAIRZWOFT1ap3UrlJfCrY5N0RRjSrmAcbyUSW+IlfzWz+peZk/KQBKvGppCBY3VC14mgTVS6yalP4yk6uExKqCBs0cUFWKGOixcbxMVLrGwiDHNHLPwwvyml6Ud/6gFu3vadn5N+cWL2pR/FKz4lebFq9oYu7ANK0I65sWUFtC04Qrp6ZF71An08VvNi1e0bT49abFr7cofim/4+LW7R5ufs4vz2pyyS9HTg4GI5oiEV1rcNAAUxIAHURRBNAA+3Es0JDaKs7kmNwCDSxYZumGeEKpXQfbY5rfGxX2SbDfYp8iEtNHbDCo3Tnx13QTphYlFf77Yba1ineExEBOl3pVvcztEmBXqPZvwiWt+dmXVFqcukU3/FDIyr9Vu9TsFZaUUdJPkAORqXT2uVicJ1oDLHRg6artJOlxp/7MUGxghpeITVh9EpaDpavnTl/KavhZuJBKV5MgU1Rq2cwYOI+UekczQ2UXYU5VUKfOsnkeNqL+1eu2FHa+iq5bbNS/8dmjzz9vWseO88+/4Onz8t9o1u7ds9uubtr6neZtE2dPFK4+r3jVecVvntfh9XOKXm5RuOz8zstadll2foen85qPa9Lihjb5g/+w+D36DaOJuh4mhDPnVSssmWw/k6luGe+BELSNshgC05mGWPxlEWeoBnILNFBcr+uw6fy4bRpmuwWWrmwBbKxOffmIqk44Tt+777Cg6JwclOi3hYKHBrH8dQcN1MiR2gWDbLYvrMQ66QeDyrrURLFlT6UhNcSn0jXJtu6fPA2wbYOl0w/HqU+ffe5sTSAe2iGMkpVtsqr8ylTZS4c0teBnX45UurIIWVFsvulLwoIGZidIxZJJGkMIcbr8c+e8UNj+6ry8i85vdn2zvMFdO84+/8K5P2v1/LltX7ig/eLWxX9qXbykdfGSNh0X53de0qbT8xcU/fbc9nN+1u6R5m1nNWp5d17TkXmNLx9w3ZRv9nuJaQIF0KDr4RMDGhRFkSQpHA6LogioIislWkyntQZyETSEzOu4gYaanyd2HKZxUqcbxnTqN5q6dhEFQeNlTYL1iYAbkN+ctaVdBgT2C6DKjolqLQ0UNLCSWJrtCys76PSDQc11ZPKqFJhALRDDFgBnfiEyG/kWz8nUQNLDw58NUSYQBo0kB0BDQ1QJZaCisiTwZU8iQhFOVih0sNkif1723qhR93fudF2zZn2bN7u+WfNfNm8x8uymwxs1GdqoyY2NmtzYuNnQJs2HnNX0+ry8q/Lyfp6X1zMvr1fXS26efN8zn/7rkGiQQEShTtzpFKqmaTLtkMwFmGAYYPsZrEhtiVRLA3iakSTJbrfDhkw45qq2ki3+00wDuQgaPOaVI6CBAnyV+snhJSLRQb3iSoy0dIaC7V/YvoN9mU8gaEgUsYb/bNefqE2FqQN/sjUDcZUaqEG8dfukaoB9cizdEIXK3HKqz42NZel05WF5WDodf0PFs3llQ7PvexKtaEaMp27aeJGedXcsxH/yyZfz5708csTM1hdc1qJpj7y8zhiaNO7WocOAG2+8a9Lkx9586+NdXx/yhYSoqIiG4QoEeEXiRAmO+a5yYLeJGth+ps56yAwaSkpK7HZ7OBwG+bi/t87ZWQlPXQ3kBGiIxeiyPkKIKIpu84pGo7Bd+KRolu0siOnAjhASPEYXHXCiEIuZ2xYSTu4y2AeqFp6VWluatTSko6vmVvOv2pahZokWx5mhAbblAL5kY1j61NMHW/r60TCFoZpbNAWDmMHQgoF40K8EvLLvqOh18kftnPunmPunWNhHhAjRJWIopsMougmKumszz+kUTN+Yirn/quo+1IYDDUm+GeAnLIeMxWLBYNDpdJaWlgYCAZiqOPUerVXiBtJAToAGqAvP8z6f7/Dhw7BLuIEqWBcxbGdhGNTTbUmJ+sGa/0RFI0YPzTL9KVmgoS6qtdKcBhpg3w8LNFQ7p4gLJ0WdwKYKziAchQ7mcbvgh1uTTDeWgqEIRBPNuUE6VtNgGBo4qDQPRONMH5WCasjo0wkmJhpweiIJNKDhAQhZljmOC4fDfr9fkiTL0nAavMZ1rkKugAZZlv1+v9PpdLlcHMedxLmJxCYr6AuoryYupi7702d9et/p9CgCNTTSi93PwHaiLF3BWvGPvVNbOp11gY2vmlvNv2pbhpolWhxnhgbYlmOBhlTQUGljMJ1BidQ5NXVRTdckVJ3CoN0Iq03ofMwV0Yp5zrwgmwepJhxbxzWwWBDJnO5k5yUq6Pq0wGrEMa7B4ahhcJmTLhdWQjoeK/5U10CugIZIJOLxeADGShL17gzenE4KpMXXmBBdEEOEkKV//KIof/x/y2QpMaePnmqSXntMm2DEFsLeqS3NgoN0NGaUJVHbMmQp1mI77TXAthwLNFQZ9U3VsKBBTniQRLhAfV2Ds0s4HSOpuZgdi67S48AkwA0qxRyVwZzpkKg7OLqeOvlKklarn8myEr/pmsuEsxw4TwTupApPpKD/U+9aMaeHBk4aaBBF8yRHcx1DOiNbDrQ8XeApaPjjwt2F7accOCTJiXeh9qChoRoM22XXXyYrLZWuv3xLwumqgdTWAjGna32zrxfooRJOmbucKrEFCEqnvkQ8II8qf6tbTH3ch2fshBEQgMcndBkJDOCLD3mQyF5rFuepooGTBhpkWYaGJcvm9qEc9XCuS2LUUMmfFn3bvu2U736QJNNzM3UnwcxQJN7zyn4BYo5PI2Bzq38OrLRUuv7yLQmnqwZSWwvEnK71zb5erGZoquTf2UuqmhZHYpMAZ3GUrI28uvOyucNnXiwW83g8sBsTunGWB+i652elzFUNnDTQYBgGa+nC1pZjitJVmRfj5JXl37Rpe9s3P0QFlSiaRj2r0FXMFSsb2E6BpY9PXRo2B1ZaKn18amBJPR00kNpaIOZ0qFuu1SEXNItdNCxu0HU9Go36fD6Hw2G324PBIOAGnMiwQEOutaKGKs8JBQ1JoFg0r6RVuw1VsYaSo6syFzHeeH1Pq7Yj9hzwxWRDVkRN5y3Q0FAatuScmhqwQMOJe265CRpgilmSpPLychY3sPDixOnIyulEaeDEgQZoSbgtQlGU8vJym80WiURyv5GVlZPfPrPGEyFxVVdUQTfEpHlK7EFP1IOz8rE0YGnA0sCJ1gDbV7PbPt1ut91u9/l8HMexPCe6fFZ+x18DJw400Lk9cxUu+DP3+XwATmFBDbaz41/l2uRgEDkuxDhVlMmxOD3PjqfWEokQEZY1IFZAojbSLV5LA5YGLA2cShrAjhonKQA6aKoWCoWCwSCeUgGcp1LdrLJmp4ETChqoS2ZFicVi4XDYbrcHAoGT6PYxK/2Ya4w0hXASiRPCUbBgECJboCEr7VlMlgYsDZxeGkgHGqCWoiiC6ydkO71qb9WGauBEgwY4M83r9fr9fp7nFfPK3UdhEOo72lzwGBQpbpDpUmh6SI/psq3iYCo0M6T4ZsjdmlklszRgacDSQG01gGggydKAn3/oXwdMyLWVb/HnvgZOKGiQZVlTNZfL5fV62caXu2oyiBJX+Zh56oRG5yTCCkeIpilCtZ5VklZ65m69rJJZGrA0YGmgfhpg+3CWBgChqZrdbuc4DjJBxzz1y9NKffI1cEJBA1SXNy+2kZ18NaQvgaFSV/DeIHnlzW0hlSjE4HnOXJ5RuQzoVKlL+lpadywNWBqwNFA7DbD9HkvDCdqaqgUCgfLycr/fH4vFYENm7TKwuHNSAycaNMC3+Km1l1fiydZ/2gs6Dt24dXdEVjVVE/k4+5KwdE4+ZatQlgYsDVgaaGANsP1eEg0b6fFEIYfDEQqFZFlu4BJY4k6GBk4oaNBUDU7BRneQ0NRORsWzzlMnkWNk+7Zg24Lh73/0ZTiuaqpB9Gq8vp8Cdcm60hajpQFLA5YGMmsgCSiwHSA7UQvHartcLlEUcct9ZsnW3VzWwHEHDdFo1DAMmNmqNOjnqNPoap6UJhvEINs/5/ILb317zW665pEeUVUFNMBpthV/q5FhRVkasDRgaeAM0gCCBkASkiTBXjmMPxXHgjPo+WWs6nEHDaIogqvRWCx2KjYUQyWKRP61U2/b7va3Vn+rGERWDF2tODijAlyzB09mVLd109KApQFLA2eIBnCHBRLpKo5Gi3QMVnzuaOC4g4ZIJFJWVuZ2uzmOOxVBAyEkHiNf7yJtWk18863vJYUIkiYrvHmUTOI5WqAhoQnrv6UBSwOWBvBwAOjz4WBMNDPgXcQKSFiqy30NHHfQYDMvPE0VcQO2ErYl5aa+QiFj/z7SqtXIFW/uikuEF2VJjlugITcfllUqSwOWBnJBA9DDY4ePnn+hbDHmOoXGglxQ7Ekvw3EBDbDOkeO4Q4cOeTwenufZpgN0LjcUxlmTLslxzSD+EFm5+pMyVzQmE0EWNL2qpeGkP0arAJYGLA1YGsg9DaTr5wOBgN28AoEAIcTakJl7jy5tiY4LaKAuFFXN5/OVlpZWixgQdUKTSlu6k3SDBQ2EKIISj4iiN8pHZD2uqqpBPUJWsTScpHJa2VoasDRgaSCXNZAONEiSFAqF3G63y+XC3ZjW3opcfpRYtuMFGgRBiEQiSYsfWXtDusaEJTuJRFXQoPESH1M0mZC4QiSDmOdbqhZoOIkPyMra0oClgVNCA+n6eV3XFUXhOM7n89lstnA4LJvXKVGpM7yQxwU0iKIITsHgZEsWKyCdrjHlwvNgQAPhJZ7WgpCYRCSd0O2WNFinTOTCg7LKYGnA0kBOayBdPy8IApRbEISysjKbzRYKhXK6JlbhEhpoGNCQtJiR/ck2mnR0ojC58p8FDZp50GU0To5FiUC3ThDNhAwsT66U2yqHpQFLA5YGcl4DMBDgB6Smahiw7MCDPy0idzTQMKABFjFI5qWpGlu9dECBjWf5c4FmAQEvqscikqaTjZv/Y3cpOiGiQiRZZ3lyocxWGSwNWBqwNHBKaCAJNCB6sNY0nBKPr8FAgyiKAfNKOs2MBQfp6FzTFAsIVEIklRz1qIWFVyz90xouTn8aFZMUMFWRa8W3ymNpwNKApYHc1UAG0KCpmqIokiQljSO5W5kzr2QNBhp4nneYF8/TRQB4pQMKbDwyZ0nUJy2bRTo5LGgQVYMXicOpXXzR0McfW+7zU8QAqxwq2UyonE4a5Ah32dzT0ezkTjqe7OMbVlr2+abjrLE8NTKkk1yH+GzyypInG7YaS1hjI8kylxrlgHedbMpTIw8wZC5Y5rtZZoEegWrkh+wyZJrhVo3CTxZDA5Y5c091AioIBWANDCzNcZzL5SopKYGDirJsqyeg2FYWoIH6ggZFUbxeb0lJice8wO2jYRhwSInH47ExF9tYdV3ned7n89ntdkAb8Jd9MLquC4IQDAbdbrefudgWRghRFCUSifiqXklyZFmOxWKRSCTIXKwcTdUkSeI4LhwOc/FYIvAVoMFBLu42+rln1sdjJBjSQxwfjsbCXBQCTshlINi8dF0Hb1fAr5iXLMs8z0uSlK53YN80SAh1hHXIrPssLIaiKBCfuiIVYiRJQpDHymGfFOTCbqRm6yIIAjDjyqYMcjAhlhxjcOUsTm8ZhgGagVpgBdknCzQ6qdV1XZIkiAQCYgRBwIxwu2+WctBkCh9AoNtUaWwZUHvIhuWEh4sM1RKYCu9CDJwNm3oX2JAHKohdLXsXGx6WB6WxBLYfrDsO2MgGM5J4biF8IEIkJmcfH2o7qTxYWmSAvKCoIArlZCgPvL/QCLGamqrBmnz4i3KwjUGmyCNJkiAIkiQBA7ZJRVEE5uISF1seQoiYuIAX5bDvSIKF/qddDcdJkqTrOlsGURRBAm9esK7cMIxYLAbtB/oKuMvzfDQa5XkeS4uPhvGfFPN6vbBDAdULj5LlYcsDmoE272cur9cbDAaxJPCSiqLIsFAyGo2y5UmV43A4fD4fx3GyLGOD0VTNyVyHDh1yOByRSCTpebFNxaJPvAbqBRqgHbtcriNHjng8HkAMhBBBEEKhkMe8mDbgxE4QEsI+3QygIRKJBAIBt9ttt9tZOWwji0ajgCpY5OFwOFhViqIYiUTcbndZWZmduVg5giCEw2GXy1VaWlr2U3ki2KK8HI6S0hKjc4ebfjXr1aNuYndyNpentPyn0vIyCNgZKYoSjUYDgYDT6SyrerF5sTwlzAWgAXoijuOCwaDL5SqvekWjUTTcGYYBwMtms7H6YXkAnPn9flvVi80L5Hi93iQ5oVAoFovBG8vmxajQHgwGceSojxyv14s9PjQhAJRJeXEcB52Rpmo8zweDQY/Hw9bd7XbDRl9gk2UZ8CvbPILBYDZyoF7wODRVC4fDbrc7nRxwUBONRv1+P1sev98PkAUYCCGSJLFCHA4HW550chwOB8AgURSBkGWZzcjpdPr9/kgkgrBJUzVoRWx2Pp8PywMNSZKkOshxOp3s9nrDMARB8Hq9SXmFw2FRFGGoq7Y8DocjHA4LgqAoCihcURSXy8U+d5/PV6Mcu90Oqka0RAjx+/2lzJVODvMKlpSVlXk8HmhCxLwkSfL7/Wx5MC+ol67rsVgsFApVfcNsoGoQAo81EAiwPKWlpS6XC6oGxYad6qwODx8+7HK5EJFD+3G73Uy1SsvLyz0eTzQalWUZcE80Gg2FQizPkSNHXC4XfLsj8tNUja17UnngeyypuYJ+sIdB0MCW2eFweDyeUCgE5xRWK8flcvl8vkgkwvM82ze6mMvhcECxk8AZqtQiTooG6gUawBIQCARcLhciBrYa8P2B34jQWI3EBZ+ksHxSMS/ghPvwFoEEWZZZhM42MuhrEJsDQmffMSiPpmqCIAAkR4SOLw80SkVReJ6n1ohQKBEiGiGyRjwe0rvXmIdmvcjFSFwgwUjsWDh6LBKGgIXHDxSABQHmYvOCwoRCIa/X62cudiDXdR2+RaoaUHz4uoJ+sgENsRj9zkh6q9m86jPYn66gAQdpeKZ1Bg0ejwc+NOFLFPCQvep1IkGD2+3meR5Gu/qABvhMhBcHrAV1Aw1lZWWhUAiQUH1Ag9vtDofDiqKAmQEMad6qVzrQwL5iDocDzmPEfkyW5UAgAJ9A8Nfv97PdHYKGMHNBedhPZJDDsIShO0IeAF6RqhdrZgMcDF9crJxYLIbIDIqNYzl2mzBCowToQqHjks1LkqSk8uDyduwwgYDHhBlpqiaKIssDT1aQQNMAACAASURBVBNKDmxgB2J5WAtTUt+I3XskEnG5XOAyEuRYf3NBA/UCDVABsOqzYBA/haGNsvU0EhfP84IgYGeB4y40JujU2IRIgx0YGxYkZJtdIgf6H1LBdwxKQIJNxfM8eL+mrwoxKoJBeFnjeGKzi926XXf//b8XJeqqIRIXQYhuMqMczBGzQAJ50HqPCAl5cCA3DAMrmIGoKIPpJoVFZpAEcgRtYBYsAab7U3R6glU1OzWA39lA1Hl6AvSJ5gF4arIs44wPPlDQMP7EBoyaB/szO9sCjZYdDzBVtXIgkn3EyA+5oAaQB3NPKp5hGKIoIhubHdLY5OClBlUnyZEkSVEUfAp1np6AT2fUNrTPat9xAATYgJPKA+8OzuBgBbGE8L2L/QxrkECZADXwJ/ZjoiiicmAqge3ukJ99ClASuMVOT7By4K4sy4IgwMiNDQPbBvCAZBitAeKznMADgzfyowagqWA8FgAUyOoHeKA8KBMmWbBJ4JwLCgRAgAXGlonoDXozVg5qDzWWWiqcY4KMrL+5o4G6g4aklxabYBKRrqosG8uDjTiDfGhhwMCmTUenywtbahLBggaQKWvkpZff++fn+ySFSBoNmlGJLdjk6UrF8gCdVCr4ibdS+VNjWAkszXKy8agfNi98yVlOoJE/iWA5k27hz3Q8+Hyh12bZ4BZ2KCgqlUBOtqYszQqH5EkZ4U9WOEayfRnb+bJZJOkt6SeKgiQgECLZHJNolg0lAMFmnXQLf2bPk6FSrBCgWWViXkjAXaw+JMG78KTYh54kjc2OTZVODiuK5Wc1CfFQJIzHSBiNsGCsQGRGgs2iWho5k+qF8Wy+bGWRZsVCqtQYQDOpzQNzqRVRrfzU8mN2WNRqiaS2hPqE5PAUkp5FUmlZsWzZkE7it36eXA1YoIFtsRV0EmigPp1kciyiSCqFC7JOZIOoOlF1HThZEdDQUx8qywM0vhJs/5XKliGGlcDSbBI2HksFkcjG8rA08icRx4MnG5lYDGDG8qcSqdLYGJZGmUmdZqrM1BhWTjoaUrF32RxTaZaTpdnc2XiWri0Py5+OZuVnQ4McljNzHdl82VS1lcPmwsrBeIjE7KrlQWYkWLZqaeRMaj8Yn5QvFgAJViykSo1B4QjOgAdzqRVRrXzMgr2LQz6WNpWoETRAEgQTqUVlZbK5s3RqKivmZGmgvqCBfa7V0ukqxjKzPNi2WIYMNJs2Hc0mZ3nYeJbGuQmNnjRBZyhgPgJsDLKBoKHC2IBvBQphcwEab7EAHCPxjWXfnxppTJ5EsAnZW1gqiEQ2loelkT+JOB482cjEYgAzlj+VSJXGxrA0ysRHUKNwzI6Vk44GZvYum2MqzXKyNGaaNGzUh4eVmY5m5WdDZ1NfVg6bb2o8G5NZV+zdalNBJGZXLQ8rBGiWrVqaTcIyYDwbWSOdmmlmOXi3VgRbDDYhG18fGmSmSmDzYulUztQYlt+iT64GLNCQ2j4rFzSAD2lCSDjOqUSTDFnSNQs0sCpL13xry5MNP+YFzDgApBKp0tgYlkaZFmhIVWMGgMLqkKVBCBvDahho9i6baWo8G5NZDnu32lQQidlVy8MKSS0qmwRpNglG4pdPUqNiGaqlUzNF+Rn4kSdLghXFJmHj60ODzFQJbF4sncqZGsPyW/TJ1UDdQQOUG5/ucapGtfIhsmFzxIzYF54QOgcBGWlEiokhRadLIFVdTxfSyWFLm46HjT8edLoypMuL5c81Ol2Z2fj6lJmV01B0rpWnoeqVTk429U2Xlo3PRk42PKxMls4mbT152OyS6FpJTuqdapW2zsxJBc78k80FOdlIiz7VNWCBhooniO076bWUVSUa4zRi7P/+e6fbhTDCAg0nt+mzzysdXZ8SppNZn/hcK0996pJN2mzq21By6pNXNmnryZOhmrWSnNQ71SptnZkzFD71FpsL3mUjLfpU10B9QcOpXv9syq+oxO8Xr+1/08033x2PE0UhslJl9wQLIPA9yfB6p+Nh448HzVY2G/ksf67Rx7v82civLU99dFjbvHKBP5v6ZlPObORkw5Mur2zSWjyWBiwNgAYs0JCxJRhEkggFChIZ0H/cmJH3yyLheRLnLdCQUW/H/2a6AYCNr08pWDkNRedaeRqqXunkZFPfdGnZ+GzkZMPDymTpbNJaPJYGLA2ABizQkLElGEQ3iCAQiSdXXTZh6A33x6NE4IksVwENlVs0CdsXVbiWypiBddPSgKUBSwOWBiwNnDIasEBDDY9Kp0dpmKCh78Shg2dR0CAkT09YoKEGJVq3LQ1YGrA0YGngtNCABRpqeIwUNIhgabhj6OCZFDSIRFa1ynOxWbfTlqWhBnVaty0NWBqwNGBp4BTWgAUaanh4GjEEyRB4ctUVY4feOCUeI4JkyKpigYYaFGfdtjRwnDXAzgWmywp40t214i0NWBqorQYs0FCDxlSdyIohiORf/963evWGUFhSNJqEnZJg6Ww6shqytG5bGrA0QKjVLp0a2LcMaDxRKYlgOdNJyxwPZ57VX07mXKy7lgZOFQ1YoCHtk6LdBD1gggZZ1XhRDhwLyaomSAovyixQYGmrc0mrUOuGpYEUDbDvS2YanTnCiVN45AGkShFcEQF3MQl7OCTS6LcR2DAeCEmSkk65ZMuZLl8r3tLA6aoBCzSkfbJm16CphqoaqqLLsqqAd0hZk2ICpxHNDAmf04nTtK0OJa1CrRuWBhIawLE8dTgHUwG6o04ayBMC6H/2XWMhBUsjDxuJNN5FAm7BSd8AGpAZYQrEQBK2PBZtaeBM0IAFGtI+ZcPQDENTiagRRdE0RTNk1ZyZoIdYKRrRdFJxyuVJtzRkMOSmrV79btSYY40M9cv/JKfOXDscgTKz1ViHbOScSJ4aC5w0kKfjZ8ssprnS8USYi+Xh0lwsjzfNxfJ4mMtms7lcLp/PFwqFBOZi+dPV0Yq3NHC6asACDZmfrK4SUTXkKK/KGonE6DkUMpHDfJCQyglXPXEahcZEwoAhiqIsy0l5yLKsVeCPKnfgAEz40qpyI+MP7MJYLoxEmYqipDKwMWyPD/HsN5Ysy4qi4CjIEsjGSoMCsDFAp1bcMIxoNMrahKEksiwLggCpFEWRJAkzAhVhGUDDhmHwPJ/5KxDkSMzFlpAtAzs1zsZjLSRJQiVDppgE47GEkCo1HsrDyo8xF8vPjFlCOBzmOA4UwvIEmSsUCgGPpmrpeJxOp9/v53k+icdV9XI6naFQKOnwKgdzOZ1Om83m9/uTvsVtzFVSUuJwOAKBAMdxbHnszHXkyBG73Q48mJ2u6wyLHeQEg8FYLMbKcTJXaWkplJnneZaHwQMeRAPhcJjlYXEFgIZAIBCNRjVVi0ajTqfzyJEjPM9LkpT0QsEjtv5aGjjtNWCBhsyPmKIEQVIkhfgDZPuOw7JGJL0CLrBYATZTUJODqkEXnCQXOyaMhxj4iedl411FUdiuHOJh2IaEuq7DYAPdKzCgsReKAWOSLMvYBaMcHID1xIlcKAHHbBwFoccUBAGY8a8kSZAKxSbVHQopy7IkSbJ5YZlhfRkmZMsTjUZhJEPhUJEoc0GvDSWB7lvX9Vgs5mcur9cL34iIVBRFkWWZHRhcLlcgEIjFYojtRFGE4QGHIYfD4fV6o9GoKNLjygzDAECDDED4fD4cy7E6duYqKytzOp3BYJDjOKy4LMvlzOVyufx+P5QHhei6zozRjtLSUpfLFQ6Hk+ba2bE+Gx4cFCORCJuXm7k8Hg9gC1EUsQ0bhsHW3eFwAA/HcWybYR6FPxgMRqNRFvlBjswjjQYCgUgkIooigA9s5ywPgiFs0sDGYK0Y8MiyzBYY0TM79ZCEcliZ0HTx7TAMQxCEQCDgcrlsNhvP84QQCzfgG2oRZ44GLNBQw7PWDHrYRDxGFvx2Tb+r7/b56OQE4AZV1+OCEIpG4oKAIRKJCIKAoxTdZ6FqsVgMO1MYtxRFwcFeUzVRFDmOg85OEARRFMPhMH4CgjRd14PBYKTqFYvFsOfSdR3lhBKX3+/nOA76PlYOO8C43W6/3x+JRHieB2maqgUCAXZg8Hq9kUgE7sL4qiiK3++3MVfA7PQFQcAiSZIUi8XYAe/gwYMOhwM+E0H1uq6HQqGyqhcOisADoIEtT2lpqdvthk9J4JEkye12lzAXDPbwRIBHUzVZltmsjjdoYAdOj8cTDAbZ5gHlSTwr+t/n84XDYTBj6MzFDpwsqGJY6NPHK4kHQSQAOFjcB0guaYRmBUKzQcMYjsFJ6wwAu0BTZ5ODzvEJskMyomRWJgso2XiWBvms5FQ6HY/MXGwqtsz4niKegFIRQnRdFwSB4ziHw+HxeMDegGVDgpVs0ZYGTj8NWKAh0zOFU7ElkcgSefihlV06jAkFSTRGojydcZBVJRSNuD0ep9uFwWazRSIRHFZ1Xec4zm6325irvLzc6/WytvdoNOr3+w8dOlRSUgLff0eOHPF6vWAkQGkOh4P5KKVCwuEw3IVOjeO4QCBQylwHDx50uVzwiczKsVe94EsazPa0arKcVGawG4MEMDDIsgxFRfwBn5ssjhEEakv3MZfH4wmHwwhNQPuiKEaYKxwO46c2MABowBERzAwYidBBlmXkSSLAQgBfmTBIYC+PkwgwPMBfHDzgJww3CIYA5+Fgg0MyEBiPhh9WCIiCekF5gGb/QtlYOSwNnGDtYONTa5SBh80OlMMmR53A9zQ8d5aBzRdaFyEEp4fgLuozSZlJ6AHyAhgBkJqd+oFMsbSswYAtJDIAgZqvlgdkslXAqiXJQWlAGHSVk8bzvMPhAHsDJkSiWglWpKWB00YDFmio8ihZl006dcZAL1mj5008Pvvtnt3HHXXRUyfoCE1IXBK9Ab/N6fAG/BhwwMOPRVmWo1FqesULrAgweMC3Jox2giDwPA+z16IowhCu6zr7dQg8vHkJggBfgdjtQmWU+l2GYWQQgGbbDDwn8RaOT0jA2IDjBDvpgx19lgR8ecO4lSFJtaNREj+M0zC2Jd06rj+hhaT+hUxT42sbwxY+Xdps8qp2sE8nsA7xbDmzKQ+bBUAHjuM8Hg/buliZLL9FWxo4nTRggYYqT5MFDVoCNGiE/M/YMPeJd7t3udnpIJJKEYNKDF6RQtGIN+AXZEmQJUmRJYWuFoTlCLhyEBcf4DCGBJpLMRV8hMEHaBKqgJ/AmcRfpQ5n9g+2406l03XxqZzHOwZBQ+pn93HNOl3rgEzT3c0+ni18hlQ1YoIaGTIIz+YWW8661R2gQ7oWlU0ZLB5LA6eiBizQUOWppYIG2dAljagqWfC797p2HmGzqbxEZEOXDV3UFIALiqapuq7qdAcmDgaIDKrtknBOl+102KIgAxLAyf493h0rW55TncZB4gQP0phvOuIEl+dUf44NVf7Ux1EHyfBu4uqHdO9yHSRbSSwN5KwG0oKG1AEpNSZna1XngqWCBl6RJI0ekP3cc2936vh/5eU8J2iipki6JhsUJeiE8JKIgc0aJ1aBQCMBy4M09GLsqjS8ZRH110DqIHFmxtRfk6eHhNSnX4d6QZfIggYUWwdpVhJLA6eEBtKCBjCqE0Ki0ajX6wVMfUpUqT6FTAUNXJynlgadfPej96nf/tnlo5vuooIIxgY0MKB/JzZ3NBJgVwIEy8PSCMuQYO9atKUBSwM5qAFFUUKhkNvtLi8vhw1KsVgsB8tpFcnSQINoIBNogI3Ofr8fQAO7jbBB8s5BIUmgQTZ0RTNUncQVEhVIOEYkgzp7ivB89qAhCTFYgCAHn7tVJEsD1WoAX95q70Ik7KkG3ODz+QAxnAm9ZQadWLdOYw2kBQ2EENjMbbfbz1jQQNdCGkRS1JiixVQS14ig0fkIuqXCXNZQo6UBOx2WOI3bk1U1SwOnkwbwtc1QKVgRqShKLBaD7cccx+FG6AwJrVuWBk5FDWQCDeDJBBwGnIHTE2B1IITEeD4iyAohYUmTzc2WskLND7JBFz/C+sd00xPY6bDEqdhQrDJbGjjVNVCHdxCTsHXHyFSrYSQSKSsrO3DgAHhYYVNZtKWB00MDaUEDIOVAIGCz2dDXCjp9Y98WfIWSnAqjgsDNAPwEHwDgiQh8wmS24wFPqmS2AOBCMRAIuN1ucHuAWdeboGdTEaJyEolIJMQTQSGSRHSVWiAQKLBEvXO0BFgasDTQ8BqAbgo3H6G/c+xJwK+U2+2ORCKQPXq6BL9VEBmNRlEI7HxB11jQrUUiEZvNBi5fG74alkRLAydbA2lBA/ix8fl8DocD3yssLVrk0B0y69sOYQRABDzcBZ0HAyJBJ7VAABuYNOAFBjwBdzFrdk+jLMvBYBDOnjl8+PDxAQ2arPCSuaxh67YDsk40magi3TXBYgWk2XJatKUBSwM5ogHoWHAjNDt9wPO8LMtOp3PHjh233377kiVL4BANcDkKDlIJITDpAF7A2R0TuGkWaqrreiQSQVCSI9W3imFpoKE0kBY0gFHB5XJ5PB42MzitJxaLhcPhSCSCPoPhJREEAc0SAB3Q2T6cJwSuD0OhkN1udzqd4AEJYEEoFMI1RIIgRKNROBAPffeyxQBnrpFIpLy83OFw+P3+gwcPNhRowIkJQnRJjBKicyJ5Z93OXpeO/tdXDjFOdMUCDezTsGhLA7mugSTQQAjx+/2ff/75iy++OGzYsMsvv/yKK64YMWLEwIEDBw0adO21115//fXz58+fO3fuzJkzP/3009LSUuis4DytakEDflydIZO5uf7IrfIdHw1kAg2SJNntdr/fz2bN83woFHI6naWlpXD2AcwdgFUAjlxiLQ1OpxMMDDD2cxzncrkcDofb7Xa5XIIgxGIxOIWhrKzM6/XCqTBwmpzXvMDBIlsG8IcfiUR8Pp/L5QJc73K5ADRUCzKSkmf+yYIGTY1Lisxr5L0Pdxd1vumrr44pdNOlNT2RWYXWXUsDuaWBJNDwwgsv9O3b9+yzz+7ateuCBQv27t0L3yE8z8MZpE6nc/fu3QsWLOjZs2ffvn1Hjx597733ulwu1vkKzlOwPV5uVdsqjaWBhtZAJtAQCoXKy8vBJRFMCvA8Dwcb+nw+Qojb7bbZbLDswDAMjuNKSkpCoRBYI+B8hJKSknA4jMUuKSk5fPgwrDR2Op1wJhMhJBwO22y2UChECAkEAiUlJYIgwP6lVNDAOnCF6UZBEEpLS6PRaCozZl0TUQkVKinqMNoQJEXQyUebDxYU3fLxJqcBZgaDepJOCuARsqaMrPuWBiwNnAQNwMHcO3fu7N27d6dOnR588MGvvvoqnRtH6MR0XQ+Hw9u3b588efLEiRPHjBmzcOFCWKQFc6+sNzaEDkl1g0+v1IVZSWzWT0sDp4QGagYNeDCuLMuhUKi0tDQQCMDXPIAGsBPAAcd2ux2++zVVkyQpGo2Wl5dHIhGA58FgEI0TDocjGAzCGmM4ZNnpdEqSBIc0hsNhnM5IfS0R4MNsoizLHMeVlZXBdCMaCWv5ACqhQiVlihAkjVfJR5uPFBRM3LgxAG4gtRTEoBLDAg211LnFbmngxGnA7/eXlpb27Nlz/vz5R44cgY8ZQRCSegwc+zmOwwM8NVXbtm3bhAkTBg0a9Nhjj6E5E3o2TFIt4ff7S0pK7Ha7hRtO3MO2cjpuGqgBNNhsNlgxZBhGLBZzOp0OhwNQgqZqLGhQFMXtdoNtALdFhEIhl8sVi8XgKOGysjK/3w/HQKMccD3p9/sBNJSVlblcLnj3AK+wnwIQz4IGWEsRDAbrvWK5EipUUqbeecmgoOHj8oL292zcEKWgwaD4gDEzEJUeYVVxAOZxe1iWYEsDlgZqpwF2FJdl+c4771yzZk2SqRIkspwwl8GCCehnRFGcN2/ehRdeuHfvXsMw8ChwuJskAX/CPG9JSYnf70cUUrtqWNyWBnJGAzWDBlyyEA6HS0tLJUkC6xzP8yxokCTJZrOFw2E4uxkqCN4kYXEyx3E2m83pdJaXl5eUlMRiMUmScM9FOBx2OByhUKisrAzSwoIjxAf4BsL7jPEA+X0+n91uh1cXdcu+8xiZnqiACuYJlvRQbM10yUAIEVXCa+Sjzf8tKLxj40YfoZstNTjoMoEbKLOoGpgkfS7WHUsDlgZOnAbYfkOW5UsvvZS+0aK5LomQzHYC+J4RRREOrA8Gg+DybvHixU888YQsy9CzYV+E2yjYTKEXkiTJ7/fb7fZAICCKYi27phOnLisnSwM1aiATaABMAKBBURSbzeZ2uwExcBzn9XoPHz7scrlgdzIhpLS0VFEUsEPA9gq73V5eXg6vls/nKy0tdTgcYBWE1xX2TYiiCKDBbrfD3mhYSJH6NqbWB/Z8ejwer9cLCy8URRHNK3WvZmpyM4bCBUngFVVSFIUXZeooWpBFQnxcXKXOHwlvEIdPvv+Bpfu+i8jgEpIQkYIEIpsMhnkgBYAGQB8JrjR5WtGWBs4wDQiCAGZLURQz+D7CU2/gdU7146LruizLgiAoiuLz+fbv379jx44NGzYsXbr0ueeemzZt2j333DNq1KgDBw7A1AMO4TzPX3755TBzCr0WboJAHiSg88EtmrAeArZfBgKBUaNGQUcH/Q8wY9okAioiimIgEIhGo/WbRT3DGo1V3dzTQM2gAVC5LMsAGiRJAsTg8XgOHz4MGzJ1Xed5vqSkhOd5wA12u93tdpeUlJSWloJRwePxACZAz07RaDQQCMDkRSAQgCTQZbCvYuoLiWoEWGAYhsPhsNlsHvPyer1utxsMFciZkaCrHQkxDHrAtU6Hf1GJyKTMExYJiSmKRHSZUB/SEZHEJBLhoxL9L8dVVTbI2+9v9ofiOiGcKMkGXTmJIWOm1k1LA6e5BtixEwyQYBdMejcBBIAJE0dxURThqDy73f7tt99u3759zZo1r7766oMPPjht2rQ777zz1ltuHTly5E033TR8+PBhw4b169fvmmuuGTJkyA033DBq1Khx48aNHz+e53m2DLIs9+7d+8iRIyxiYBlYOgk0gG0Adl1u2LBh2rRp8PCALbWPYkVBWsMwRFGEnu00f/BW9U5rDdQAGnCYR9CAiCEWi9ntdtw9IctySUnJjz/+ePDgQdhUGY1GS0pKHA4HgPRgMOh0OuFrA+CCz7x4noeNGDDnl2pjSH0hgQdWTQaDwXA4fOjQocOHD4PPBo/H4/P52I6JfYGreZoUMNDoOHUMETcI4ST94TlP97xiSEAgMU2OaZxARNmcsBBUohFq2wzynriqH/WS3n3GHjrsVQnhFYlXJEQMlqWhGlVbUWeGBnB/I3hpAwMDfHDjd0U0Gg0GgxzHeTyeH3/88T//+c/atWuXL1/+6KOPTp48edSoUUOGDOnXr1/fvn379evXv3//AQMGDBw48Morrxw4cODw4cPHjh07derUJ5544sUXX3znnXf27t1bXl7u8/k0VfN4POwEBI7riqIsWLBg2rRpPM+nLq9mewmcA0VLgyzLsHVc1/XBgwd//vnnAAJQeLq5CRQL1T8znr9Vy9NZA2lBg2EYbrfbbreDFQ5Bg9fr9Xg88P54PB6wLsAb6PP5ysvL/X4/vrRlZWWwOZOe4BCLwWqGI0eOgGHA6/Xiu+1wOA4dOhQKhVJtDKmgQZIk2JBZXl7+ww8/lJeXHzhwoKysjOM4XJ8MoAExPvvq4vOsmFk0QYMiCQ6b3W5z85IRV/Wlr71d0PW6bw9xPi4uGPE4iXOqxMnUp7RIYpzilYnwPydxj8x+p6hgzH++Lpc0IqhyXOYt0IDqtYgzXAOw6Rr+Hjp06MCBA5999tnKlSsfffTRe++9d+TIkf3797/kkksuvfRS8K10/fXXDxgw4Oqrr77sssuuvfbaMWPGzJw5c968eevWrdu6deu+ffvKy8tDoRBY+KXEJZtXNBqlZ9abf9mtDeygTgj5/vvvW7ZsuWfPnhrHeEiIoAEepdfrveGGG55++mn4mdRZYSeTjkhqDxX9T1Ks9dPSQG5rIC1o0HU9EAiAtyWoAnzZwzYkQAkwcvt8PpzewzEbZiJtNhvHcTzPwywmOGuCv/DBgcoBOwQcxp3ulcN4sGfGYjG/389xHMxuJvUCuMQpKR5zBOBP31uDSILoczmPOl2RMIUChJB/f3Okc49b3/7gu5hCBKLy1Hk0icn0VlTmJMKrhNjcet++s0bd9NyxY0SSdVmTZE3QiY64AURZfy0N5JoG4FWCUuGbkq6Q6DM+aQCGyUFJkmKxWCQS2b9//zfffLNly5aVK1f+9re/nTFjxrBhwwYMGNCnT59OnTpddNFFvXr1+vnPf963b9/+/ftfe+21Y8eOveeee5588snFixevXbt2+/bt5eXlrE8XKA++9VkSuLbaMAxYPYDFBgnLli0rLCzcuXMn+J8F22c4HAafTpApzpLghnNRFJctW9azZ0/YfAGikvqWbErIKllRlFAoBDvS2XiLtjSQyxrIBBrgICgcyGHlMLxOUCVwb4K4nt28ANY8mN3IsOgJsTa86oDcs3n3EDewc4RsQuwpkl7s1IfBx2JHnS6P0yFGeV0mgkjXMbgDavceU+69b6Wfo0sdBYOeVvX1vkAoRiKyHpaUYzHy9LMfdO929983HxMEIsmELoggqgUaUjVsxeSIBlJ3EgJiwFeYNcvjyQvgii0UCtlstn379n3yySdr1qxZuHDhgw8+eNdddw0ZMqR3796XXHJJfn5+YWFhcXFxz549+/XrN3To0AkTJsyYMWPBggXLli3buHHjtm3bDhw4YLfbwTYAbyhMNcKbm6Ql9nWuLY3LJ3HBNUAc2DqxevXqoqKiefPm7d27NxgMwv4I+OAxDAPPytFUTRCEnTt3zps37/LLL589e3ZZWRn2h7UtUmodFUXBpeJY4CQlWD8tDeSaBtKCBlgrhA0dCfxAx/EeqhQOh3HmEt5MOLcCxmxMhWN5UnLUS/avInYHmBZzwb4PsmNlsswAg9wO50+lZbFQqMtLBgAAIABJREFUhG6TUEmcpyscAlFy1VVP9rt2QcTcnHUsTvZ+H+nQZcyiF/8RFumiBu8xcu3A2QMHPuawE0EgqgqCrZUMSQq2fuacBmCtMczxiaKIm6g5joOjYrdv375u3bqlS5fOnTv39ttvHzFiRN++fTt16tSyZcsLLrigdevWbdq0gRmEe+65Z9asWc8+++yqVas+/vjj/fv3O53OYDDIDoFgqAA7P7yPsAMLYlJduLJva91o+LCRJClpoxbP87FYDHqkvXv3Dh8+/Nxzz+3Xr9+MGTPmzp27aNGiZcuWLV26dPHixfPnz3/ggQeGDh3arVu366+/ftGiRQ6Hg+d5dCFTt4IldXqaqnm9XpvNBu5tWKXlXKOxCmRpIKGBTKABeLChp74nMCtBCBEEAZYU4MnXgiCUlJQEg0E2VSLTrP6zCTPQSbKQE9FJkqUBGaBewWDQYbMfddKNo6qgSXGiG3QvpULIrx/eUNxhxtffGZxKJEJ+8pA2+be9sOTfMiGhOPnkU75rt3tf+MMnikZUpWIpZVJhrJ+WBjJoAN+sDDwNfsvv95eVle3du3fHjh2vvPLKvHnzxo8fP3DgwEsuuaRbt275+fktW7YsLi7u3r37pZdees0119x7771PPfXUihUr/v73v+/cuXPfvn1utxsmHNGeD4YKjuPQYsEWG6c/wDEzLmNieVi4z76hdaNhccPatWtvu+22ffv24V4JzBF2MciyvGPHjmnTpsHKyqFDh1599dUdO3a84IIL+vXr97vf/W7btm1w8g7Mv/xvImPu3LnPP/983UoFqbAMUCrwgm+z2fx+P+wjS1IFy2/RlgZyQQM1g4YMpWRfHtgw6ff7wQuk2+0Gj9EsD0tnEFvjrWzksDxAs1aHKpBCM2cVVEIU6uVR14ioSaJBvvoPKe547/NLv3CH6PrHfYdI14sfmf34do0QZ4BMnbq2qOgem5NwPPX1ZPpr0M2dmxaAqPEBWgwVGtBUDe1z0EphzGCPhk9VFjg+wXiwGYAcRVEi5kFue/bs+fTTT995553ly5dPnz795ptvvvzyy4vNq715de3atV+/fsOHD3/wwQeff/75v/71r5988slB84IBDMuDGSHBvlCZQXlSEjYh0BlywbTVEpgQkApgEZ7ny8vL58yZc999961YsWL79u0zZsz4n8kET4vATNkewMlckUgE1Au7K3FxA9hFAoHA6NGjZ82aBR5yYT04ysyGYOvC8ttsNjh7Lwk0sDxsWou2NHCyNNBgoAEOsw4Ggz6fD+AC7F9gX86GegGykcPyAM2WBI2lRgVi0MERNAUNui5qUkwingC54ppH+17zcFgkPCFfHyBdL5rzxJy9xwTiOkYuu2LuxDtWcjH64HQ6XxGjjqRh96a5gfNkPVEr31NOA9Aa2dVCWAX4OhfMC1YTK4oSjUadTue+ffv+d/bS2rVrYeHhxIkT+/Xr16tXrzZt2jRt2rSoqKhXr17XXXfdmDFjpk2bNm/evBUrVmzZsmX//v2wtxkWCcKSApgjgOEfQQCWIWcJXKYA84ybN2+ePXv2Aw88sMm8Zs6ceddddx05cgSOwUs3GEO3gGuqkhSCnQa4dRIEIRAIDBky5OGHHwbPE5kdSKf2Qqwy2bswdRIzL8wUnwVwsmkt2tLAydJAw4AGKD0cMAEuV3F+jn0xWLo+Fc5GDssDNPsqZgYNqqHGFeqj6ZEnP+x00d0792qeONlzSOvQ9dHZT+x2hcmajw8WdLjjo4980Rh1Mk23YZKYaaawzAz1ebBnXFrW+yH4RWUXHDgcjn379m3ZsuXtt99+7rnnHnzwwVGjRl155ZX5+fntzKtt27aDBg0aMWLEzJkzlyxZsnr16k8//RSOYsLBr9opg3SKhjcl3d1ci0ffjuvXrx83btzTTz+9a9eut99+e+zYscuXL3c6nYQQqD7Ai2r7BDD2SJKEyzvQuoA9BnQXgBs0VQsEAhdffPHcuXNh8Vaq2AwxrA6RDTMihGDXBJHIc1Ims9jSWrSlAdBAw4AGWOtUbbNmGz1L1+cBZCOH5QEa30yYZMWugTU2gKVBI4pByDGObP8y2rnH3U8s2OwXyfflpH2nGdMe+LsnSm6ZuKBP36nf/0C8AaiHTAhPDJkY5gxFfepmpT1jNCDLstfrLSkp+fvf/75q1apnn3324YcfHjFiBGxT7NixY35+fp8+fYYPHz5x4sT58+e/9NJLmzZt2rVrV2lpKSws+J+nEPBNgtMZ2MihebOvJPtG4Ccsa+RgmU+Jh3Do0KEFCxbcesut77777u7du+fPnz9+/Ph169Zx5kVNhuYZE1BHOPGBVQLSqLQMBPiDgkGdEBIIBAoLC6dNm4b+YFBaZoJVLHJiJC7uxpIgzyn3dLBSFnGaaaBeoAF1UWODhqaP/CeR8Pv9DocD3E/Bm2loOuIGWNOgmTsoJY16Y7jhpvl9+/+6zEc4g0yctnLjJ6I7TLr0Hjfqljli5UnYABpEihuohcK6TkkNsOZuwMHgQAhGndR1/mAVgPlyrDB8uULvLwiCy+U6ePDgF198sWXLloULFz7yyCO33XbboEGDwJ3RFeY1cuTI6dOnL1q06N133wUvRuDVFAABDhvQXHGYBwJHlwwESkgi2CTsLazLySWCwSC4ScDuBYwBuq7v2rVr2rRpM2bM+PTTT7dt2zZp0qQZM2Z88cUX6N+pViVn656BxpkImOk4fPhwly5dHn300Wg0Ck5vM6TFW9kUzDCMqHlhKiCySWvxWBo43hpoGNBQYylzodHDoRhw9Db4dYFOMwEaVKLqcNy1bogykSWD8Dp57a19rYtve+ODgz8dIyGNOMLk3Q3urr0nLfrzBrnSrKCaMxQ8MUQLNNTYGHKKIalfRisUCxGSvv9wDIN1PD6fz+l0grvD119//dlnn505c+bNN998/fXXDx48+Jprrhk8ePDNN988ceLEBQsWvPrqq1u3bt2/f395ebnH44lEInBCG8ypS5IEs3t4KDzkBQ01CS6k/mRBAEsn1RF/puPJnQcE7ylAN8MwAoHAW2+9NXr06Pvuu+/7779ftWrVxIkTFy5c6PP50K1cHQqPCsmSgHkKQsiePXvatWu3dOlSv98vSVI2ybMpnq7rkUjE4/G4XC7WQJJNWovH0sDx1sAJAg3Huxo1ylcUJRwOe71e8ETL9sUMaFArQIMuy0SUiMobxMuRjr3uGTDime/t5KhMjhEy/eG1xd0mfX84Elforgnz0unuCYoYLNBQ46PICQbo3wENwPQ/rJZn3Yvh8oJYLOZyub799tsdO3asXbv2pZdemj179p133jls2LAhQ4YMHjz4+uuvHzNmzPTp059//vkVK1bs3LnzyJEjgUAABjPWgJFUeXSPBvMFSXdhVx47tGemsxm0suFJLcaJj4lEIrC8EbIuKSl5+umnhw0btnz58q+++urZZ5+99ZZbV69eDbMG4HYWd4DXtrTZ6ITlQfmSJH3xxRcXXHDBCy+80ICgAbbDBAIBOE0DcQPmaxGWBk6iBs4U0CAIgtfrLSsr8/v9uEcLuuBqQYNKT6iSBYMcjZI5z25p33Pau58ED4aIQyRXDJpz5YDZnETCPM+J9IQquvqRwg16SrZlaahza8Yv+DpLqENC9nyEkpKS3bt3r1+//vXXX3/sscdmzJgxYcKEkSNHXnfddWPHjp0+ffoTTzzx0ksvrVmzBhYWuFyuYDCIngTZ3FlDBbgaA8MArk8Ed+xQ5SSvpkkmhMxAgb3LDmz1odmKnEQaVobu3bt30qRJU6dO3bFjx+bNm8ePH//II4/s378fpoHAWyUueMQtErUqdm11pakanJ8Jh+1t3LixefPmCxYsyEZONgWLRqMgKhqNulwuOH4vm4QWj6WBE6CBMwU0wMeix+OB2UfcY0a/8Mw1DYam0qCaeyB0VTVkmagCIRGD/NdDCvpMvX7cErtE/n3E6NTn7ofnvhcWSFiISbpWsYSBLoE0E1ecjH0Cnt1pmAWsh4fjAKB64IeHrSqsNmB9k+OojEvlFUWBbhcSwk84DXXXrl0bN2584403FixY8OCDD05hrjlz5ixevPj9997funXrnj17SktLg8FgIBBgz1vJZmBgediS141mpdWNTpcvKy0dz4mJBycTrN+nYDD46quvTp48eeHChbt27Vq6dOmoUaNWrlx5YsqTfS7QDtetW1dcXPzcc8+Bgya0DbAaBjp7ycDJ8zy4cKhtQovf0sBx0sCZAhrggxKWlLOIoSpoqAAQOgUNqmzoEvUrTcKE3PHQiuYd73h9k++pxTsvvnz6pq1lIZ6ehV2xFLLCPYNOd09YoKHhmir2ueySQzgaABcBwHFlgiCEQiGv11taWvr9999v2rRpyZIlTzzxxOTJk0ePHj1mzJjhw4ePGzdu1qxZTz311Kuvvrp27dovv/zy0KFDcA4C/IU9COBWGb7gIYads2i4ymUrCZVQZyJdTqzAdDzHNR7wH0wSAW4IBoMlJSXz5s0bOXLk22+//T+fjA888MD/Z+864Ksotn4EFUQREBGRJvVJsYA+EBSBSJUWCCmPNEkCUkJJwNAkBKQEaZEijxYpIkWQIi8ICAhSpUonQMhNIbfllr13e5nvmz1hXG9ISKgJ7P72l5w7OzvlTPvvmTPn9OrVa/fu3TRNw57FQy1SURMHWRHLskuWLGnYsOGUKVPyO94J3C5q+qDfACKNor6rx9c58DA48FSABq34F2S//xDq5koaiMgBPxTVm1cQraDrZnT8Bnq10aBK9WOefy20wXuhN28hBy1z8m2VBmLTiRAPo62egjQBHGiPC4JiIKjNC4JgsVguXbp09OjR3bt3JyUljR07NiQkpF27dm3btm3Tpk3r1q379u0bGhoaHx+/Zs2akydPZmZmgtkcIrhWFIWmaRA4EQPDWts+kLuW2TDdQ5/RLrSFobXp6PQdOQAt4nA4jh07NmrUqLCwsD179iQnJ/v4+ERFRV29ehVUmHmeJ4ar75jOYwmE/SYwSzNt2rRatWotWrSogI5xD4XUOgK8h9f1V3QOPFgOPBWgAYY0zE2wJBQAGuARAQ0IoRwOmQQUPX1fzbe/fqP+l//5fKaMEM0pkipYyG0PAheAeLCt9HSkRuwWnD59es+ePatWrZo7d25MTAy4UmzWrFnDhg1btmzZs2fP0NDQCRMmLFy48Ndffz137lx6errFYgHhNrHKDCgB1BuJwiOZf0EDkZgKJjAFHBs6nU5tD9HSBawHd3z0dDTdvdfS6XS6XK5t27b5+PjExsYeP3581qxZHTt2XL58uclkQgiB3wfIoACV0nsvwf296XA4JFFyOp1wpGLKlCk1a9ZcvHjxHTvD/Wjt5Kcqe3/F19/WOVBkDjyxoAEMt4GbO+0A1i4ABdMqbsCbDXiHQkYnr6PqDWJr1B2xb/9NXkCChLci/nGVfLhAGPWPev3zh8fER/QJwFwBaA+QN8hqDYcJKYpKS0s7d+7cvn37tm7dumDBgri4uLCwsK5du7Zq1aply5bvv//+u+++261bt9DQ0LFjx3733Xfbt28/efJkdnZ2VlaW0+mEzQiyX0AyumeCVLmQxD1npL8IHGAYBlxR22y2CxcuTJo0KSAgYNWqVVu3bo2IiOjXr9+vv/4K2xZ3VAiFZiq2zOR5fsyYMfXq1Vu1ahWxxantWvdWcjLKQP2TnMjVkcS98VN/63448ASCBliorFZrVlaWxWIhJllg6BYMFLRPxdwfoqSepLTLqLX3lBatY1kOMxw/9GB8yQcNHhWCnzzPw8E2AhfAbYE2MhEgOxyOjIyMlJSUw4cPb968GRQL4AxCq1atmjZt2qBBg/feew+MH0dHRyckJGzcuBHOKBIrh5CydkKEVYSIgklJtGV4sLR2otfSDzaXpyc1EOEghKxWK0VRZ8+eDQwMjI2N3aheffv2HTVqVGpqKjGB4IEYiIAQ2qJ48o04zYqMjKxZs2ZiYiKU80H1H1mWwflFRkYGRVEePCnOnCme7aWX6t448KSBBrAdS1FURkZGdnY2yJm1g1YLCwpBi4pMy8jFI55FaNuuq3v2p0kCclP4ELnmAv1HTUBJJiVRcrlcxM0P7PeDIIFhGJfLlZGRcenSpUOHDu3cuXP+/Pljx4718/P76KOPGjduXL9+/f8Xz4L9Y29v74iICHCsvG3bttOnT6enp1utVmJBjzAJdo7yGv8nByXAvI+HGIO8/jAIbZ/R0g8jr6chTcDYFotl586dffv2jYqKOnjw4IwZM3r06LFkyZLMzEz4egZWgCSJDE+tHlJxXhplWYYNL4vFEhAQ0Lhx4/Xr13vYb7ifttaChqysLIIb9P55P1zV3y0qB5400CCJEkVRFosF/MzCJ6l2UJGZqHAEgAYnh5w84nNo2ZDldNipPFwW1U0M+OspgMgTOd8AUs58Yzz8BzRNW61Wg8Fw+fJlsGU0c+bMUaNGdejQ4cMPP2zYsGH16tWrVq1aq1atRo0aNWvWzMfHZ8SIEeBY+dixYxcvXoTpDKTQMIdCqUEakV8N8goPZFm+HzN/+WVUyHDSFh5EIV/Xo3lw4PLly1OnTu3evfsPP/zw+++/BwUFBQcHnzp1CrQBtJFBK0U7PEsKaCDKtgghu90eFBTUvn37FStWaLuQtqaFp2F7gpwh4nk+S70AN9x/+oUviR5T58CTBhooijIYDFevXtVOOtpBlR8NXQH2MmDjkHQOlnNxkh0LThHPS/ij15GD9Z4EHnEctgegIgbwjk0rKNdCQN5VkCR4RwIKBsUm78I0AfHJyQLyusvlIssqHEQkLxJ5Pgj5IXEwSmOxWDIyMlJTU48fP75p06bFixfHx8cPHTq0R48eLVu2rFOnTo0aNapWrVq5cuXGjRs3b968T+8+gwYNmjBhwqJFi/bs2XPx4kUQ4ZCpPC9LoRZaCTOpFykhqUXJIvJWtuCQklW7ey4tKJaCwFx7WMlisezatSsoKCgqKmrnzp2rVq3q16/ftGnTLJZcV2/ajgGchDJAuPavls/3XM5H9iLLsi6Xy9fXt3379hs3bgQ8QbQc7qEYWlYAbTAYLl68aDabSxZn7qHu+ivFigNPGmigadpsNlutVu0Y0w6q/GhZlrUOKaCRQNdRkZEg0wgxCDEytvmI4QLjVngOsYyomrClBMmNvWPjE5r3DhpAG4Mc/7uD1oRaekAPHrJ6QRBYlqUoyqFeWVlZFy9eBFjw3XffjRkzpn///p07d/7www/r1atXpUqVl19+uUqVKrVr127YsKG3t3e/fv3Gjx+/YMGCHTt2HD58+MaNGzabDXil1S2Aua8AuJAfe0s6ViCDtoAK3vERefEJJsDBEtgSIPIhiqIWLlwYEhISFxe3devW6OjokJCQpKQksvWAEKJpGsaplnXAKO34zS9OcWYpRVFG9erRo8f777+/Y8cOKO09DwRgEWGLoig29fIwJFWceaKX7cngwJMGGliWBTU9Mrq0n9raucmDhk92q83G8NgyNC8KgoTNMAgivp1u2y1zWlpmyi1Tps3B5Nh4XkBuWmI4SZRxZJqjac7FS4yiSOqNky9SF9EqSEPhQeChNZMHCQqCQFGU1WpNT08/efLkpk2bFi1aNHr06PDw8M6dO3/wwQf16tWrXbs27CNUrVq1YcOGH330UdeuXYcMGRIfH79y5crk5OQzZ86kpqYCToKMwKgRsIW4WiZyUXIo0YNvhf9ZJG4U28iFry/ELLYVeYAFEwSBpmmn00nTNEVRly5dmjFjRs+ePZcsWbJhw4agoKDBgwcfOXKEYRgQgMFBSvBICV1dy1UomDYkvzgPsAoPL6lr16699957bdu23bRpEwyie8sLGEJYAfoTYI9Sy6t7S1x/S+dA4TlQgkGDx6qsKAqI6AElwOgiY0w7ru5Ig9p2jsN+PfXGxPhJn/Xo/m7zZm3afvrBB+1aterQ5O2mr1WrXPr5Z16q8HK1NxrUqNGoSZMWjRq/HxwS8cPan/46fzkzy8RwEs3yauISZFH4ZoAveCJpkETJZDJdv379xIkT+/fvX7NmTUJCQkRERJcuXby9vVu3bv3uu+82aNCgXr16DRs2bNy4cdOmTZs3b96pU6fw8PDY2Ng1a9bs2LHj1KlT4GvD6XQSSxUeBSNcgnAQV2hNHZAqsCzL87h2EALxi/SXJFWiiSJVmbCrRFf5roWH3uVyuc6dOxcYGBgeHr5169bZs2d37dp18eLFZrMZXElB/wExFXCGYZi8IxSy0/I5vzh3LdjjjQBs4Xk+Ozu7U6dO3t7ee/fuhXrdQ8HgRe2A9WAUzCH3kLL+is6BInGgZIMGcuiIfAeTymsnnfxo8HMjIYXmWIbnDh098lmP7qWeLe3l5fVsmedffLn8Cy9WKFumas0aTWvWql+nXoOatd+s/ea/GjVq5es74LNu/q1aedeo0eC11+q8VP71V155098/YvPPu24ZzbwokGIQNAB7CjDmKfUCVaYTJ04kJycvWbJk6tSpERERgYGBXbt2bdeuXaNGjRo3btykSZOmTZuCbkHbtm07d+7s7+8/bNiwuXPn/vDDDwcOHLh06ZLVarXZbB7HID2mmLzTbn48yRsT6pJf/KKGazmj0yWLA8SNpKIo5Hih2Wx2uVzLli0LDg6ePHnyrl27Bg8eHBAQsO7HddCX8vtLhFgkQmH6UknhmLYuCKELFy506dKlffv2u3fvhjPMeTVA71o1jzRJfCKMJHJW8kgndA48cA6UYNAAyzDLskaj0Ww2A64nDNIOsPxohJAkSnbK6WaYifGTSj/3nJd61a5Tr6dP77jJ8cf//OvbxDWREWP27/9TkpHdybpciOfQ5k0H5s1byqkGG7Ky6J83/97/8y9fqfTWSy/VevudfyetXOlmGEGSPJQSDAbD6NGjBwwY0Kd3n08++aRDhw7vvfde06ZNP/jgg08++aSjenXv3t3Pzy84ODg2NjYxMRH2ETIyMkwmk9PpJLMDnEQgTjS0X7RQWTIRa4n8+KANh/jaEGCpNuR+aNJAOlFCOQAAneM4lmXPnDkzffr0Pr37LF68eOvWrYMHDx41atSJEyeK6tQ7b6/Lr4+VFKZpyw9fDgcOHOjatWtgYOCBAwcURbkHk9geaXqwQhIls9lsMBi02I684hFZ/6lz4J45UOJBg81mS09PN5lMHis0GS0FEKC6lXkrq0PnTl5eXpVerTRo2NBf9+5lRYViBQmhQ8dONX//s82bj9idCjincrrR+QtWP/9ht0wuN4vZLsnISaE//kj194+Nm7S4UeP3X3y5/KedOmZlZ0tirjBfknin0zljxoyuXbu2adOmZ8+egwcPHjZsWEJCwtatW/fv33/x4sWMjAw4pgjTMRgt0G61aNvY43wHPMr76UYQQwFMuOsjkvhdYxYmgrYWOl18OKBtu7uWimGY3bt3R0dHDxgwYNu2bQkJCX5+frNmzcrMzCRmCViWLaQ6kTbru9J3LVsxiaCtCPABIbRlyxZfX9/Dhw97fOEUsszaNOEVCAEaQMP169dNJhPR6yKvFDILPZrOgbtyoMSDhuzsbJvNBirE2tqS0VIAIcuyxWJp8nbTsuVeiJ8yOSMrU0bIzYk0h0QFXU5J+7ht19VrdufYkINCNItkBdlsKDJyyl9/mXPsEifiEMqFjhw2t/no88XfJdM0cjpQVNTYZ597udobdU6fOocQ4jjGYsVW9NPS0gAWwHeY+ojTGlrmOM5jNtHiAHJmgag+EExwV6IAJtz1EXD1rtEKGUHbRjpdfDigbb4CSmU2m5OSkrp27Tpt2rRNmzYNHTo0ODj4yJEjNE0LgqD1O69N8AHSBZStWD3yqDJ80kiidOTIEaDvwXGlR5rkJxFAsixrsViuX78O8gYtaCtWzNELU6I5UCJBA+g8WiyWtLQ0u90O3zSFbAYy0hRFYRimS5cuL1csv3bdOpPNykmIFZDJyjnc6OJV82c9++/ae9bmwIhBUrBEISUF9e4z/tRph8WGXBxy88jFoPPnhebvRI798gebHXECcjvRkIGz/H1jvLwq1qn7do7dyUt4G4P4zCaEhLDLK7jyrvracuZ9WpgQbQpAF4ZFhY9ZmNT0OCWCA9DopFNBmRmG4XkeZN0URV27di06OjogIGDJkiUJCQk+Pj4JCQmnTp3ygLke9c3bCQsI8Xi3RP+ErUNQr4aphjAKQAP4vHbcvgwGw4kTJzp27Ojt7T1mzJhly5Zt3rwZZjY4g01gB5xyIlpc5LsCCI7j7Ha7wWC4dOmSDhpKdBcqtoUvqaCBoqjs7OzMzMwiIQbYXCTT1vLly0uVKuUX0NfpoiTsuBLZsdEmdP6SdXBU/B/HrlAsEmUMF2ga5VhQ/8/nrl59Kkc1Ie1ikdGCLl52/7tF2LDBy1kaiRKiGbQm6cjXcT8FB05s9FZ7L68yCTPn4PPoHC0j7KtCe+ugodiOiqetYHlBA03TcDzSarXu3r07LCwsKChoy5Yt48aN8/Hx2bp1K1kCC/5iJmOtMMQTxnY4hQRiAJ7nb9y4cejQoTVr1sydO3fgwIG9evVqr7k++eQTPz+/7t279+rVKzg4+LXXXqtYseInn3yyYsWKGzdugMo2/NVazPRoOAAWgiA4HA6j0aiDhiesRxWT6pRI0CAIgt1ut1gs4FqiqKwk81eLFi28vLzWrluHEHKzGDEIEjp+wtypy4C/LpvtnCAgxIgoMxuZjKhvn2nfzt9DC8hCIQslO1h05Qbb8qPgwH4TzFZktqIcB7pymY38fHrk59Ozs9CXo2dWrFijXv23jBazKmmQPXDDowQNRWWRHv+p4gB8pML+lyRK4HbE4XCsXbu2W7duM2bM2LBhQ0hISEBAwOHDhymKAsWFOxoZe6r4VkBlib9sWZZ37doVFhb21ltvtWzZMiIiYvny5YcPH4bNSkZzEXuRcEpz7969ISEhr75C7BZSAAAgAElEQVT6aoMGDQYMGHDmzBloJlq9wEIDEQ4RAooEitJaX30FFFV/pHOgSBwokaCBpmmXy8WyrIdVxELWHM4aKIpSqVLlZ54pffT4nzk2muGQ0SRn3kI+fUbdMMhWCrFIcSv48OStbBQaMm/0qLU2F3KwSED4vnKDbvlRv4CgCVYHYkV0yyI6KTRq1PKePYefO2t22tHevaeeKVXutarVKbdLBw2FbBo92mPhgAdoSElJiY+PDwwMTEpKmjlzpq+v75QpUwwGA3w031EJ97EUu7hlCh/62qNMly9f7tatW/fu3ZcuXZqVlWW324lghljGhPUeIURUE8A9G9TObDavXLmycePGZcuWHTNmTEZGhtaSJsEKQBCUoDXOBt9IxY1XenlKLgdKDGggMNxji6GorCdD+lrKDS+v0qVLl93+yy5JRpyIsk2Cr3/UXxesNjdiFGTnOZeILFYUPTKpffshThdyCSiHFnkFXU9TOn02bPCwRJMN0SJyskoOpfyw9sRHH0X+uuuczYH1KLOMjhderFCl6utGi5kTWAlJ6o31GLSbFETs8ZCIovJHj/9kcwDWKvgOhjWG1Jdl2eTk5JCQkLFjxy5dujQmJiY8PHzfvn3E3ymJqRN35ADMUeBoFyG0a9euZs2a7dmzRxs5v2FecByTybR27dr69eu/++67p0+fBqNY5BUCHaBxSRba7QlyDvOOpttIUjqhc+CuHCgxoEFRFJ7niV1CMjDuWkOPCPA1gBDKysouVer5ihVeGzBwGMehmwZHtx6hS5M2ZhjdFkqWEGIRynGhwYPnd+kyymhGDjdy8MjBoSwT6thl5H+Cp1psWOQgIsQrWHGySVOfRd/txiqTasgtc85zZV6o9WZthudERdRBg0dD6D8fFwfI+gH7Cwghm802Z86cvn37Tp8+fcmSJQMGDIiOjj5y5AixJQDLz+MqcAnKl0gLNmzY4OPj43CoClCaCpCJy4PQRLmtHa0oHmzPyMjw9fWtV69eamoqSCagKQloIOddPRJXFOXatWtmsxkQg/apNl+d1jlQGA6UGNBAPFHBlgTp94WpJIkDYljQ8KJpun79hmXKvFCh4qvnL9zoHx77xaDxNzIzeaSICLEKMlrRqC9XdOo07I8j6byC8YGVQhY7+jxi1tBhiy05yMViMQPFIUOm1Kv38KjhcygamW1uJ0txsvTbgf1lXig7YeJETpZ4RRZxsrm3hDCwkFS9SNBs0Oo3kKrdkShqfFJ3ndA5AKd8EUKwk44QOn78eHR0dJcuXZYsWTJ9+vS+ffvOnTuXYRiHwwELEuyOE3ih87BgDtjtdkmUrl+/3qlTJ4PBALuo2lfuOKiJ+BNiesQBNxPEn21iYmKrVq0sFgtFUWCZG6Y1aCOtdEGbzvXr19PS0sCktzZcWzad1jlQGA4Ua9CgHUsZGRnXrl0zmbDBg3vu9DC6eJ4HQeLEiROrV69eo1ZN/4Cg6zetTjeiODer8C4eZdxS4idt7twpdueuC/hoJa+CBhsaMuTb6JjvWA6ZzOiWCQfaXWjh4i3BoeNumZHRzPKqPac/z5x4tVqVsi+WYXgmx+ngZAkQA48UHp+0zAUNKoE3LET1YwHXS8a7F2oFJewwE/vMBA9YuX6wdNBQmG6tx8mPA5IoWa1WhNC+ffv8/f0HDBiwfv36qKiokJCQ5ORk+FAGAQPoRfI8T+QN+aWphwMHBEEAs639+/dPTk4GcyxE9gBxtHOXltbykITDXCeJksvlgk0iEBWMGjUqMTGRtAuRNGjPYZJEgBAEwWQypaampqenk28n7QSrLYBO6xwogAPFGjTAYOA4zmg0GgwGcHh9z6ABBo/WMpLJZKpevforVV71esYrdtxYN8PYnS4FoRy7snTpzuD/JMydncxLiBY4UUF2B4qLWzZ79oYcGzKaRWwGikUKQn+eOt+5m+/lq5kUg705SUhZu/6HCq+8/MyzXiNiRtAczcmSk6HtjJN4vZSwUai/L6zlgIuVK4jASeDRzEjIrd6MhDj1Fm7vcUiFl0z8nY1OPTUcIF2d1Jic00tNTV24cCHsRMyYMcPf33/atGkZGRnwCvwlb+lEUTnAcVxWVlbLli3BmgKZrIqaDnkRxKIA4MB8liRK2dnZrVq1QggBbiBtBxMm+aklQNPCYrGkp6enpaXBV5PHdsY9FFJ/5SnkQLEGDQCxDQbD1atX74gYioSUPYYQyPF27NhR4ZWXSz3nVbqM18TJExhOupVNrf1h57AhM78au9p8C1msbrvLzUto7rwfJ078TpQQwyGHm0cIZVusWSZzH/+AoydPcTJWb7xuSO/YpbNXqWe8vLy69exmc9oQQg4an55gsNkorBjBSlhx0iVIvKr9QJQiRaSakFLUvwiDBuU2aFBp7p+CB21tCqKfwj6tV1nLAfjStdlsp0+fjomJ6dGjx5w5c6ZNm+bv7798+XLwja5dooo0prQZ6TTsI1y6dMnX1xfEmR5KCUViEYxqwAEAGrKysiAFiqIaNWpE1CHJ+M9vb4IkBSYjzWYzgIb72eotUl30yE8SB4o1aFAUBTxEZ2RkkONMZIQAUfjG0L4IQxE+v65cu9Khc4fSzz/jVcqrYcO3Zn+z0N93YHBgzNXzNJKRKGCrTN/MTJqZsMJmQ4KAzT0hhERsqwmNm/DVT5t/djPc5i3bPuve06tU6WdKl3qlyqsDBw1yuiheFEQsQcCIYd6cg19G/2/zJuOVayjTgkxO5BSwrqVbRgxCnKp3SSPkxrfCIrwZgWQh91YERG5ZQvjW1qYguvD80WM+SRyALXBZls1m8+7du/39/UeOHLlhw4agoCAfH5/du3fDiWVwUuDRgZ4kPjzKugA+u379eo8ePVwuF2CIey4ANIoWNECTURR1+vTpkJAQlmXBxJZH8xXwE+QNYO0bdk+0ke+5qPqLTxUHijVokGXZbrcTC07a/k3owrcWeUWrN2Q0GnmJs9jMv+3/bXj08IoVX6lU8fVnvCpUfbVRt079Z8/44fe9V+fOXturZ/i5c5mZmfaU6+k3DRnnLl44dPTIuAnj33632ceftHvp5YovvVyxbLkXG/zrrfgpky9fvYoQslNOhudkhLcw3BxaNP9kk7eia9XuX71mQLMWgwPDvkn87287D2Sdu4bSLMguISfCt1293aofLHwwA8sfEN7NwLsXKnS4DRoAN8CcUsAXRuH5o8d8kjgA6njz5s3r0KFDQkLCxIkTvb29p06dCt6MQJzA8zysOuC6hQyQJ4kP91MXwpDCSF9g3xOMKDRq1MhgMMABh7zvkmQLLhtE04IGaCxZlgcOHPjLL7/AsRdim4EkWzBBjo9BwbSRCy6P/lTnAHCg2IEG7dlxsiI+wEVRO0i06QM7sNn2tKzF330fGjykYb2WFcvXrfhyQy+vyq9VafDc85XKvlDhpZcrvlm3vlep0mXLvVi23IvPlH72rcZNff0C4iZPOXXmrKRgCYTHzSsyL2MFiP/9en3w8MUfe4+uXS+kdv2BdRoMq9NwdJ0G41u0+XZIzN4lazL3n0YXMlEGg0wMcriQxCGJRy6nqkWpKJLEMgylgpDc3qstv5bW1vFhdHSypaLKXB5GDnqaheUAfN2CzAysBLIse+TIkaFDhwYFBc2ZM2fEiBF9evfZtm0bOEsDnwjQQx5lnylsfYpNPA8WgQlnOFECxxbgSx180nIcBwJ/KP78+fM/+eQTp9NJLDiBimIBiooe9YYPG6LKQKxrSKK0du3a4OBgi8UCjnCLChq0IIZ8PmkDPUqi/9Q54MGBYgcatOXLb1K7n0VR+y5JXx0zMl6XRYnneZeLxkpGTuHkn5cS563euGHXjBmJ369am/DNrMT5381L/O/EuBmfduy6/8BBq82Ro/qroFmeZrGigwdiEGUZgwZV75FXdRPSTOjKTfTLLmry9CNB/Tc2eieuVr3YKjWHVKk5oPq/hjT5MLZX2JIvJ/+6bYcx5Spy01hKYXPlOq1wshJkwXEc+BOCaQUmI211SDW1/HxQtA4aHhQn7zMdSZRguQIrJjRNJycnDx06NDIyMiEhIUy9jh07BtGIoyPtJ+Yj6zP3WdNH/7p22YaPFp7nwQ8twQdas1fEXhZCyGw2x8TEREREmEwmeAVszDAMQ2CEx4fQHSsoiRKrXmRR37NnT/PmzcE6J+wykJFeeEKbl91uz8zMtFgs2kCd1jlQAAeKF2iAgQpKwtrR5THAtMOjgLrd8ZH2XUKDHzlV+ocXREHkWJaWJAwC8CKNV2okYcdVyOkUsm/Jn4fFnjt/neEEQVJU6QLiRfyUgAbtwUgRSazEMSLPIay+4BCRTUSUjGj1pyEHHfnLvXTN6di47U3eH1mzYVTV2lE1648tX3HIq6+PaPnx7M8Hb1m61nDgFMp0oiwH4vGWRe4RTXIS5EGCBkWVZWj/qvXS/tFBg5Ybj53Ozs62WCwzZ8708fGZNGnSlClTunTpMn/+fLCExjCMy+WCVUcrmiZfmYAbyFgg69Njr9fjLYAWNMBcRMoD0hqGYWw226lTp1JTU0GfFP7CJgLP84sXL27evHlSUlJ2djaIgkA4USSgBqkBEJk5c2bz5s3BstM9IwaP9rVarampqWlpaU6nk+RFaqoTOgfycqBYgAZtP7ZarUaj0Wq1enhk0U5qWjpvlQoO0b5LaPKKIHKyLCIkSxJLMzaOYwATqKBBcNG0yy2Pjvnm4IErOTZWUpDT5ZYR4gRRUrAwQJRzJQ1a0KCek8SaCIzIuiWWRzKDREpiHAJt55lbdodLQG4BGW3IwaArN9C6TTkTJ5/o+NnSd9+fXq3O8FdqDixfLbTSm/3rNhv+aa+pE6es2/bLaaMZOd3YkXfuLWJkI4u5t8bYg+ZopycOwOVVby0GkLEKhsdNuHOb0L5wO0z//3g4cOrUqSFDhgQFBc2ePTssLKxv37779++32WwwpkDPkZTMA3yT1csjnMR/mgktaJBEyWQyXbt2LTk5ed68ef/vuKtjx45du3aNjIxctmzZ4cOHnU4nmcScTtVVrupL4ty5c40bN65evfrgwYMPHDgA2pGE7WT+Ie/mZbjT6bx8+fKcOXMaNGjQtm1bkrhHk2mTuiutzYWmaZvNlpmZeePGDYfDoeMGLXN0+o4cKBagAWyZsSzrdDrT0tIyMzPh2+iuvb+AwXbH2noEkvQ9wsGFtWpVKdfakjrORSxjZPiUq2n4i0FCZPADAanlHczgbOKfBp0wwsgFFuoZS1HCzi84AbE8Ynh8qjPbinKc6MhJxzff/uYbNO/DdhPrvDWkeu3BFSr0r1gxssabw5u+Pz7ki/XfLPrr1yPy+RvIRiGORjyLGAbxPD63CRfH8CInYyOXYIESFnycP4uQC2F5B4uw/EIVYWAYoYEEgB403NE8y42neaiTD5gDWrtAxCAgdDCLxbJ161YfH5/w8PD4+Pg+vftMmDDhxo0bsKgQQ9EeBYIuSgJJ//cgSISSS1AUZbfbFUUhG/+yLFMU5bEogkIAfJ+AGSvwoHv16tXDhw8vXLgwJibG39+/T+8+4eHhcXFxSUlJW7duXbVq1cSJE0NCQvz9/f38/CZNmkREOHk55nQ6k5KSWrRoUaFChcaNG/v4+EydOvXXX389ffp0RkaG0+nkOM7lckHuNpvN4XA4nc6zZ8+uXr168uTJzZs3L1euXKNGjVasWOEx4ZCf2ubLW4CCQ2BDlqIos9l8/vx5s9l8n5NqwdnpT58ADhQL0ADdlKbp1NRUo9Fos9lgitQOhvzo+2kDkmYhEwEFAqPR6CFm1IIGkiYhCGggK27B2akSC5mVBJAD0AK2VJ2Rjfb/Ia5YmTEgIvnjjxbVqTeuToOxlaoNrFA1vFr9oe98OKHzZzMnT975v2Tjn38y6RnIZEEUjcUPLI94dXsFMs3FDPiHB2i4LXXwEDPcBh/a10lFdEXIgpvyPp+S0w1E+q0oyvXr1+fMmRMUFBQTEzNhwoQ+vfusWLECRNZgbgF6aWGmftJFPYj7LPZjf50ArLwloWmaoigAXnC6IT09/fjx46tXr46Lixs5cmTXrl1DQkJGjx49ZcqUlStXbtq0KSkpadKkSREREYGBgSEhIVFRUStWrDhx4oTVarXZbDRN5wfRtLkzDHPo0KHJkycHBAQ0adLkpZdeKl++fJUqVSpXrlyrVq333nvvgw8+aN26dbNmzWrVqlWmTBnwiN28efOYmJhffvmFYRiP7SSCGDy+UrSZFkxDo0M6AB3S0tK0OykFv64/fWo5UFxAA8dxFoslLS3N5XIRPSOPueyOPx99y8H25B0Lc8eZuqhLLFnXZdUHN/bNbRFdDF7+HU5sNILn0eUr6KefbsZ++UvvXvPfafJlzRpR1WvH1qg7oWqtmIqvDWzaPO4/YT9+l5R26AS6cQsZcpCRRjkCNgJBBAsylhSocgWCErQFBfq2pEH7RCuw0EHDw+5+YPJZURSr1Xr+/PkxY8b06d1n3Lhxkep1+PBhQRBAqizLMk3ToHZ3x36Yt6iF78N53y3mISzL0jQtqBcoMIKGh8ViOXz48PLly6OiogIDA318fPz9/SdMmLBs2bLk5OQ9e/YkJSVFR0f36tWrZ8+eERERkyZN2rRp0+nTpy0WC4gTAJOBJjKxlABWkvLjCXj6oNULzCtdunTp8OHDGzZsSExMnDBhQmxs7MSJE8eMGRMfH79w4cLNmzcfOXIEPk5gOYes88MN2nbMrwx5w+EtAhokUaIoimGYAiBX3kT0kKeQA48NNGg7OhhGTU9PJzt20BLaOPnRj6vNCl8e7YpbmNJCfJAOiAg5GRb7GeJlu5N10wrDYtwgCoiyYyNQnAOlXUL790gLlqT3Dt1U5+0JVetHV6g+uEK1IeWrDnrptYi67w7r6Dszdlrykg3nf/+LvWxENtWElKDgdPCtFHjf3q7A6hq3lSCwJ09Vh0MHDYVp0HuOw7Ksy+ViGCYpKSkwMDAqKmr06NF+fn7Tpk0j2nBEJkdygaWlMLih8H2YJF4iCLCObLVaz5w589NPP4G2R/v27YOCgkaOHLlw4cLt27fv3r177dq18fHx/fv3b9euna+v7+jRoxcsWLB9+/arV68SvUVBEIhnXThdCV/2giCAs6j/t/AGkbV7SR5cIl9BgGPgKaRMYpKPJe1OB7xIznNqpQtaWtuOJMG7EvCWFjSQPkMkMXdNRI/wFHLg8YAGbX+FQQKOXkpQA2gHqpbOrwoABfJ7qg2/DRokVYNSEBVeRKwk05LskiRW4JHAIYlVbxpJbqS4EMfgzYZMAf11Cx26zC/ecHlk/K8fdp5eseagCtVGVaw2oXLNca/WGlu7SXyjD2b07LcxZsKBX393X7iGzBRycogSsEaDS0DZDqzXSYmCnRN4hDgFO71gBHxj7xdKruIDgAYtdCh87bQ11WnCATJfkxBZlrOzs8ePH9+lS5cJEyYMHjzY19d3+/btsDH/WI7akrI9QIKMHbJ6EVaAnAAMJPDqBccWeJ6nadrlcoGCAlg5vHbt2smTJ5OSkoYNG9avXz8fH5+IiIhp06b9/xGG7du3b9u2bdGiRaAx6uvrGxAQsGDBgrVr1546dSorK0u7AOdHE4Z7ENr4pC6kCnkZdcc4EHjHjQZt/MLQeXMsOOSOaUJJdOhQMOue2qePDTSQ44IwNcBfLcou5k1yx8FWwGRR+GVVjSlLSFBvTsT+t2lJdqo3LQiSavRJkXhF4SR884Ik8S7E5yDegmSzjLJFlO5GKRZ0IR2t3MiMm5LSofvamg3iq9QcW+n1L1+rNeGNeuPKvhZcvdFg7z6zB4/5edXWm0cvyukOlOFAOSx2ekGJ6JYNa08KSPWBISBGUlgZm7vmsQErfOug4YF0UVh1tEmxLHvs2LHQ0FBvb+8xY8b06NFj6NChJ06cgNURFkuydBV10dJm9Hhp7QjKuz4RRQEQmIP8X5ZljuOcTue1a9cOHTo0e/bsESNGBAYG+vv7BwYGTpo0aePGjfv379+wYcOCBQtGjBjho16hoaGzZs3as2fPtWvXbDYb7FaAQgMICbQ8vB9aW6P8eHvHOBBYfEADCKssFovZbAaxTX7V0cOfQg48ftAANhKIauFT2AYeVYZNg9uIAR+q4BErKrwgY3QgSIp6S5iWeUFmBZnlRNolUS6ZdiOeQQqDkFvBSgwWFusx2Hh0y4HSTOiX3baEb0/0+c+yJi3jqr09vkytaK8qQ0u9Hv18jdjnq4+t02LRZ4G/zF+aves3+XoasjhVvxgKti3Bg2sMRXlgoIEoUtxWm8Ad4E53LnM00f7Jridnh4Tn+fT09O3bt/v6+g4cOHDo0KHNmzdfvnx5VlYWkZaDfDu/he2OC9I/2VWMfmlLS2oEW/gcx4G6Ihx5OHfu3NatW+Pj40NDQ3v16tW9e/eoqKikpKQd6rVq1arp06cPGDCgq3pFRkauXLny2LFjVqsVNDxA/0B7+hT2dLSfKKQA90Noa5Qfo+8YBwKLFWhQFMVsNmdkZNjtdh035NeaT2d4sQANBWwHPoWtkgc0CDwSeUXmZImT74AYADeICs8jnhbcFIdNTStI5BHHIpYSOQcv21lko5Hdjew0yqGwx6wdh9Gi9e6wmIPveS+u8faMinUmvVh9UqVaWBpRtVZM/aZjWrSbHBW7KWnDpUs3UYYFW5KgBfVcqISPY/ASEhV8e+hFahZ+TKrHVrHzLXLfCRjgmFqv37mJqMoWWqMRuX4+kYBTQ4KC5SAQt/h2kzsuEh7F5TguJSVl/vz5nTt3Dg8PDwkJ8fPzS05OBqwAts7gFdjkzm9hK0xeHlk/xp/a0kKNwF/G1q1bExMTIyMjg9QrMjJy0qRJy5cv37lz5y+//LJo0aKRI0f6+fn17ds3Ojp61qxZO3fuvHbtmtPpBHuLsJEBOxcg+dOKMQgzCWLIj5n3EK6tUX6MvWMcCCxWoAHrUXGc3W43Go0Oh0PHDfk16FMY/khBA5yHBqFCSkpKZmYmfE88hXwvsMp4IQToIOeuptgEpPYWJGzxWpJ4uGVZVBRJVES4VQmEKpn4WziBBBHxt41BMSxyschB595Xb6Cft6VFf7nm08/im7WJf/2tkeVrDH6t/qhX646uVOvLqvUnNnwnoUe3dV9POrd3D7pxA2VmIKyPibBJCRYrPYhOhrW73Nifp8jzWGMSyUgSZCwgIbe6zGM1CdWaNnNbhIHtQyjqXgxob4iK6GYEtxsd3HeVdqjmJVRm0TQlI5eM7AoWo2BhirpzwmF3oPisoeYukLmP7KF2eYAViCjNwdlI0LDbt29fZGRk//79Q0JCevbsOWHChPPnzyNse9QJb2nTgcJr1zPtUy39yKpJ3GprcwT5NgmBpVq7eedyuTIzM69fv7527drp06f379+/e/fu4eHhEyZMWLx48bof123ZsmXp0qXjx48fMGBAv379QkJC4uPjV69efeDAgWvXroFX6Pz4kB/fSHk8CI/VWsvGe6Y9srjrT21Gd438aCLAZpDD4bh+/fqNGzfsdjtpayjtoymGnktx48AjBQ2A7jmOy1Qv8LminUqKG3ceU3m0oCHXBpQWMWB326IKGm7/1c6ehaLBfKTqeRtrLsjYBTfHYCuTJy4pO4+KXy843cV/aaN/f1255pcvvx5bs35CrTenV6067vVqo+s2iG3Tfuag4ZtWrks9eIy7ZUMmClkZZGeRg881FMUgROO9DFlECqfwHEAHxGKNTlW3UsKaEgyxK6WatmIFmca3JOXY+BvX2JbNwyKD52beQCyFi4eVOWSXpNhV6OBSFKeiuDAEIaABPIr+07DEY2pBnC1MrNAc0F4URdE0dmvCsqzJZFq/fr2Pj09oaKifn1+f3n02bdqUnp4OBQYThPktftom1i42WvqRVVxRFFBI0rqag9x5nodTBgzDGAyGc+fOrV+/fvz48X169+nZs2doaOjYsWOXLl267sd169evX758+ZAhQ/r169e3b9/g4OD58+dv2LDhxIkT6enpsJvAcRxN0yBI4NRLa2leW/f8+JYfT7TvPig6v7zyC9fmm1+cRx9OcENmZqbRaAR5Aynqoy+PnmNx4MAjBQ1kukxJSaEoimVZIiQsDrwoVmXIFdGr8netUWrtgnGvtIhflFSjlvBXU3NGxocpKB5vRqRmoWOnlXkLT/Tpt6h5+7ia731Zuc6o1+pOeL3+lIrVvyr/xpeVa46p3Xhq5z7r4udc2ZDMnE1FV4zIyGEf3w4RUSo0wLIFhDi8XcJi5QwkwS0hQdWn5GXEi1hm4eKQk1NoTsISkauXULvWX73/1pjOH886fRhzgeMQVuaQ8VkSWaHVm8XSCwIa8tV70FQvH1LL7cLT+SSWGwxzK7QRgAbYbjAYDDNmzHj33XdBtNCnd5/z589brVZyMA809bSidY9pmvwsgCi4bPf5FLSYCVYgdYQqOBwOOMuwYcOGMWPG9OzZs0uXLgEBAePHj//hhx/27dsHxpj79+/fsWPHzp07h4aGzp8//+DBgzAtQNkULDqTAHNQFAX4gOh2yLIMiIQMAS0rIFAbUnB9tTEfFF1wjnmfavPN+/QxhsAU7XA4QEek2JbzMbLoacv6kYIGWZYzMzNTUlLgmJMuYyigt2mXrocAGrD3TbgVxMkIr9yqDAB/zzOcxLBIFPFiLqurtdGGUu3ojyto/trrX4zZ27LTotpNvy7/xqgK1cc1bD7/zaazX28QV7ludM2mo9/+ZFJEzObFa68eOClcSUcOTsUft71zgWyBmK0W8OkMWVDVL3jEcgrNIpaVkdmGTEbUu/vUGlVCa1Qe2LDWF3t3Gx0ObGabE9XjG+pGDHgJgV6U627jXtUitdwuPF1A891R0rBv376IiIhOnTr5+vp27959zpw5sBNPLCsIggDuCeCcYX6Ln3bizo/Or2wPatCBwSL4e+rUqc2bN0+ZMiUiIoJYB5cAACAASURBVAJECKNHj542bdqKFSuSkpJmz54dHR3t6+vbuXPnwMDA8ePHb9++PSUlhaZpp9PpcDgIFAChRd4SwvcuMVpAvjQIYvDYX8iPbwXwJD823nN4fnnlF67NKL84jzEcIBrp1VDax1gePevHyIFHChp4njeqF5kmHmPNS2jW2sml6PRthUSsRahVL3CDogAGEFh3QpVDiEgSkMQjQRURuAXkFLD8wCFgs5IX0tD67RkzF5zo4juncctRNd4aWvftMTXeGlu36fS6TWbXrD/9hUpD6zeZ6BOwMvar39ZuSj15Scp2oEwb1kpQBQ84ETdCTpmnsfgh96J4llV4VlFcPLI60MFDWaNifmjccECDOpFzZx3lOAxtGAErQQA8ABceKh9uVw0rXSoAs24v/6Ag8vfpDC0Iw3oGoiAhxUXjnZG/Lpy/dOUyeCs9f+nyqdPnLFbKSXEumledmmJfpthSpyRxAi/KMs2xoozL4nRRgoS1K+DjGHs4Uz+UWZbNzs7evHlz375927dv37Fjx6FDh27YsEG74Glp7caTNryobX2bo57/4QueHFmCx7IsE7tqFEWRQKJCCF/2LMsaDIY9e/YsX7584sSJ/fv379ev39ChQ6dNmzZz5szExMRFixbFxcWNHj06LCysX79+0dHRiYmJe/fuhbOOWlvIBfhlhZpqy5237h6rV94IJESbjk4/EA4QZdIHkpqeSInjwCMFDQgh+DQpcWwqPgUms+E9EbdX1juABkaFEcLfoEFSNxIEDB0EUb0lpJ7gkFgZuSXk4pGDxUjCxqJDp5k5i//s139Nq/Zz67wVV7tBfO1/TX6nxdxmLWfXazy+QtXwmg2HtOkwPXjA9wtWnN3xm+laFkYMGDRI2FG4U8SpKQg5WYlTvYDSiKcVLKXIodCFqyhm9LaatT7v0Hn87v0mN4cY9fiGIOZajFDLzMsKK8s8HNO4E2jI1S1VFSZxewLgoDnWTjkNmRnzvk38qE2bqtVef+HFcv/+sGWtN2uXLffic2XKV329TouW7bw//axPX//Qz8PmJn67bsNPJ06fysrOVi1gYXsVdqcLwEeufUYsnhEkUWJZNi4urnXr1t7e3h06dJg+ffrVq1ehL2kBgZZ+BKABbBGCTziy0QB7IvA1D/4UwGnyzp07ly1bNnLkyB7qNWDAgKlTp3733XdLliyZOXPmiBEj/P39e/ToERERMXXq1KVLl+7ZsyclJQXSAWSQKwpSFMiLVFBb67ydWTvi8j4tfIg2HZ2+fw6AtXK7enl4/7r/xPUUSgQHHjVogNFeIlhTPAtZ+OmywJgqesi1HwVWpITbhx7xZ7qo3rwiww1qmKAGIYnqiQ71S19BKMfBWJycg8ZnMk127Jzz1AXnxh0pwUOXte7+dd33Ymo1iW3w3oxmrVe0/Hh98w/XvNlgWpVqI+s0jG3Xec6YSb9tSjanZOAjoBSLD11YnMjGIJckuhUBiyJUbckcHllpNH/JoXr/6l//XwMHRq27cAXl5Kh2MBmZ41Sgo9xWdFAlJVhXFCn/lDRg69twqy2rMDxnp5wbN23u8lm3ci+XL1v+Ja/Szzzz/HNlXir3XLmypcs8X7pM2efLVShTroqXV1mvUmXwzxdf9PIq5VXquWdfKFPmpbItW7eMHTf24KFjNocbvKKrOyaQPP577tzZgIAAX1/fLVu2gAokoAoPt+/a5ZOsqXf9Fi+wfe+sDkr2QaBvg8wZMkpXr99//33BggWRkZFdunSB85+JiYkrV65c9+O6xYsXh4eH9+jRo2fPnpGRkYmJibt27UpLS7NYLCBcIUoGkAtBDFqsoK1p4ctfcMyCn0JN9b8PigOAOK1Wq8Fg0F1pPyiulqx0Hh1oALkozBp5Fa1LFtceY2kLniKL8hTjhttAAYhcqT4gBhEp2D6Eeou5Rz6xi218kIGRBBarwcmyKMg8wzMgmZcRonmB5gUWIZuMrVL+dRPtPY7Gfn3iM98fGzaZ9Wb9mXXqTW/Zaql3xx8+aruk2b+/qf2v2NoNopu+P/4/od8nrUk5cxFl25HZhY9jOATkUBCFUI6IjCyycCh5P93g7RH1GsW82WDgug2XbhmR3YlvbKRSEVUFSVaWxVyIo8oSVIkCyBhEVXWDxQ6/JObX3Tv7hQS//kaNF8pVev31+u0+9Umcv6JN+w5t2nvfzMg8/OefB48cvXj1xvU047mLNy9fzTzy57mft/8vafWamNivAoP6N2vxQZU3XivzwvNepZ559rmXKr1SLWLAwD+OHKZpLNvHJrhl5HK5Zs9OOHP2FFH+J7v1WrV/7TqqXV8fBmiAfkvTdFpa2rlz55YvXz558uTg4GBvb++AgICYmJjExMTVq1fPnz9/xIgRfuoVFBQUHx+/7sd1Z86cMZvNoE+g3V6E8pMRwbK4Z5CfcL6aICFtZQvuq9oUCo5Z8FNtOjr9oDhAUVRqampmZqaOGx4US0tQOg8LNMiyTESdWs972hFegtj0NBQVvsu1+/2E/rvVZPX7vRDsUJUcsSlJXjW1YGewv82zl9HXMw6HRWxu0Sqhdp0xTd6Z1bpNUsfPtnTpvqWV99LG/06o3SS+ZqMJn/ZYFjvlyP8Oyn9excgjzYWsMjLzyCqg4xdRu67zXnq1/wuVgnsHJSX/7rIyKAcfY0ScjD+vVcSQa+UaionPk8osL1OcZHcLOWs2Jn34ScsKVSrVrFsnLGLgwUN/OSmUnYWWLd3fuOnHew8ccQlYNcElSBQn37LSv+49zkp4L8PFK5yCHC758LGzFMvZXPbL168kLlzUs0+/ajUaenk94+Xl1eqj1t+vWmu3ioqIz1UyrAMb0hClwi+W2phaGk4eEUEF4A8AGVo1QFikifdnsM9z8eLFHTt2zJs3b9y4cQHqFRERER0dnZCQMGPGjOnTp0+bNs3f379v376DBw8Gi8spKSlgSLEQTV2EKH93pH9SRUhCj/qYOKBtMeiZRqPxxo0b4I1T+/QxFVDP9hFx4KGABvgcEQTBbrenp6dbLBaY7PSO9Yha9Z6yAdCgbaM70kVK+zYQQVhTQRZyD3PyKNOE/jyNFi/LHDRkX6s2i+u/Pe2NJuOad1zwqd+m9r239ok4+F7bxeWqf/F642FN233VP3bjtCVHd5/mbzpQlhudvo56hiSXrxlXo+msWu9OmTTnr0sGlMPkOuEkhq55UeIEkRclCStLSBJy37Jc//yLAK9nvd55/+25C+bfyslx0DLDIrMZrVxxolvXmN/2nmEFbPDKSom3LOzWHX8MHvbVf1f8xAj4PCjWdqTRf5duGDlqopvjsQkKWaJYjubQmh+3hfUf0Oqjj71Klfby8vqktc/RQxex32SJfVCgQesimXzow1ELkBhT6uV0Oi9fvvzLL79MmzZt6NChAQEB/v7+YWFhY8aMAXwwbty48PDwwMDAyMjIkSNHzps3D5wyQLMS/QPYcYBhW6QWLzjyHXsUEcAU/K7+9PFyQNt2ABqcTmdmZmZGRobNZtM+fbzl1HN/2Bx4KKABDnA7HA6DwaCDhofdhMU5fVn99GclgZUEDjv0xku7ncUeNRHCNq0pHmWa0dELKGl36hcztr3vM7NGywkv/SumyafzPuq7vF/Mb32HHGzWaU2Dj+eXemNonRbf/Lvr6qjJhvnrUbfwv8q9uajZpweqvZXUtudPu48jgwNl0zStKKyigL1tXpQYTnDRtNNtO33u6AcfNilXsfSkaV8ZbqU7GdbJSlYntgmxfduF0M8nZ2Yji0Ng1IMc2VZ09ITp43Zh3y3banFiYYnNjW6Z0fKkPV17fD4w6kujzYEV+BFyc+K5izf9AiNuZdtEGZ0+c7lfvyHly9YrU7ra0CEjrDlmkMxrZQba6TUvrY2ppR0Oh4fYn2VZq9V64cKFbdu2xcXFBQQEdOvWrXv37gMGDJg5c2Z8fHxcXNygQYO6d+/etm3bvn37TpkyZevWradOnbJarXDKA3oOiCvAbgqxvqzdTIRCFuduppftEXBA21ehZ0qi5HK5bDab1WrVPn0EhdGzeIwceCigAa8HdrvBYEhNTaVp+o7bE4+xznrWj4wDtyUNCq/IjMi6eZeTdfDYZwQW+NMy9oiRQ2PHWgYR3VTQTQldodD242jKkvPe/5lX7+OxFRt9Vffj/77bdfWnIb9GjL/aJez3eh9//+o7i0vXml+m9vflam/6qMelt1r+VL5mzNiE/2VQWHeSU1UrBAnvVgiScstkvJxysVadapWqvJj82y8U53ZzvIRQpsnFCihpxd7Zs34yWZHV+bcriz+OmN97P2Te/J2sjFjVIbjJjhZ891v9f322eNnPbgFZKZaRsKJl+i2Lf7/wjGy7yy06nQJoM2xaf7h1i55lnqvw0UdtHhRooGnabDYfP3583Y/rRowY0atXrw4dOvTp3WfKlCmzZ8+eNWtWdHS0j49Pjx49+vTuExISsnPnzsOHD6elpWkdu8COA6AEmqbJiUo4wQi9AtYDsgY8sq6iZ1TMOUC6hIc6LXQejz2yYl4XvXj3w4GHAhpomgZlbJiYyAeTttvdT6H1d0scB9Tzjbl6l6pFSGy9Gt+q1ykWIUpGThk5JGQXkJ3Hf3N4ZOTRz39SX6++6Dty84e+S974YGqlxpPf8l7hM/RM18hLLXufrNNid6UGP5SvsfCNhvMqvTGsW99vLqba3aLICLmmH3gFpWVltPH+xMvLK2nNClbi1D0DzL9MI79iZfLX01db7dj2A69gyYGA0J79qd4dh4yOXWW0YLOYbvX+8afDTd/tu/C/ewxZWEoiIGwQ2+IQBg0bfeDoSYQQzSmsgNwUOv2nLSRwTJZBmPTVnDLPVYiKGm6xWEDVAKT9cIwCDBaBWyDwtETaFGxInzt3bvv27YsWLRo6dGiPHj06dOgQGBg4bNiwsWPHjh49euTIkaGhoQEBAREREVOmTNmyZcvp06dNJpPLhQ9/EvNHZEInY5DoJIKpBkHAR0PJ7YEY9I0D0ig6ARzIbw4n9j+gz+inMZ/gDvNQQAPLshb1AkPRZMLKr8M9wfzVq5aXAyB+0P6VVFG/k8HWGtKzkY1CdpfqUktCBhaly+iyHe2/hJJ+QZ+PPlXz/VleVcc+V2POi28uqdxwdfXGq5+r+HX1unPKVxj5VpMRK1bvsqjmiThZAYnC8lUrn32hjF+/QIR3E3hWRBaHZHWg9T8dmBD3ndONskyCleJdHDLmoItX+NZtQgP6Tcy2IJrH4ofsHLT793P/bt3nz9M5rIRyXJKLVxw01nKIm/LtL78edLKCnabNNjdC6PJ5vp9/fEjgOKsRWY1ozOhpXl6l/fz8srOzyUIO0AGUBgRBsNlsZrP57NmzP/30U2Ji4rBhw0JCQnx9fUEtcdy4cbGxsWFhYX169/Hz8xs6dGhCQsLx48cNBgPLsi6Xi+M4nse6ljC48qpGagddATQZpNpPRh005O29T3mItgtpWQGa7xRFmUwm/UiFljNPHv1QQIMkSuBRhsxl2q4G9JPHSr1G+XLgbi4oZfWQhUNEpy6yrdqO+KjthPYdpn3WY66P36KQL35s02Ve/be/rttoZqWqE8q/Nq5ijbGv1Z9apsrUclXnvlLj26q15r5SeUKzd+e833zKpQsoy4QdiHOyoqiSDF5BdRrWr/LG69cNaQ6aphiJE5HFjlav3RMcOs6cgywOLPNQfXWiGzdR125j/xMSl27E+yYUh2gR/XbgaofPwg4cvSog5BZRDi3aWYVV0Mofdy1astHJYKmD2YkdAFqtKKL/nJ5dxv912i6LyGZFdhsqU/bldt7tOYHHJiMFgWEYmqYNBsPatWtnzZoVHh7ep3ef7t27+/n5RUREREVFBQcH+6pXSEjI6NGj169ff/HixYyMDLLLABYbtbYQYL4GRaICZAZ5x2BhQvJtU/3BU8kBbZ/RMgCUc1mWzczMTE9Pdzqd0BW1cXT6yeDAQwENWtZoO5mW1sbR6SecA/mBhlwXU9gOs4CwWadMM2rX4cvKVXrVqBnWuMmw9z+I7eU7L+TzVYOH7Bw6dO/AgbtHjjo4cfLxyQlnvlth//5H6eft6Nc96OhRdPIYOnUcOR3YzrSMQYDkoGlWkpJ37/Hy8uo/MFIVM4j4cASFNm09PHT4dIsN5Tgx4402SlDQpStsUL+E7t3GXbjkEhHKsrh5BV24bPHxizp+JoNVkIMX3bJEK0hC6Kdtf4waO8fqQA4sX0CMiCgaRQ2f17bN4L17Mi1GbHhKYNGpE5mVX61ZqXLltIx0UZanTZvWoUOHLl26BAcHR0ZG+vj4dOrUqWvXrkFBQWPHjl21atW+ffvS0tIcDgd4dITxAn1DEiWwpkp0FWF/AaZmsOdIjDWRQ57aEXdv9BPeM/XqFZED2l6kfRX2xfBZZZcrLS0tPT3d4cDKwvr15HHgAYAGkIjmJ8nMr5M9eazUa1RkDmjAhMuFGBadOmXybh8WEfH19u3nUq7yZjM+3YD9VGlvEbutYtQbwnkB+9YSBexki5OwqgQrYXmDgtDwmFFezz7709YtoHrJS2jL1kPhEeMYFtkc2KolJ2OPETkW9HnwPO+2g7dt+4vhMOxwuGSjmfUPjDpy/CZCWOrglrG6gIDQqb/SB0fFZ5kUAWFRhIQQxaAZ05P//cEX6zecoBlsJUJGKPWG3LnzgHIvvlrq2dLnL13kBN5kMvn7+w8aNGjatGkbN248fvy42Wy2Wq3g8Vk7grSjBmgtb7VPSTgEkl0GbZz7oUn6OqFzoAAOaPuY2WxOSUkBLXiiJUO25wpIRH9UIjhwv6BBURSO41wul8lkApMyHtXWdiaPR/rPp50DBDTIWKmBcSGBQ8YsN1Lwl7op2+m086KE8E1MQGMCW4rO74a9CfjLCGLn7j28vLzOXrjIq3aZFi7a2LVreNYtIeOWy2Szcgrv5kSnCyXO3uvXe8aPaw9LMrJTEsUoRjMb8vmIPw5fsDtVpxgcxyjurJxb6dn2fqHDLQ7FlKOYHBi7iAra9HPKx61jJsdvFxUMIFge2R0ovP/0nj2H16n7dqXKlc/8dZbhObC1QNO0y+XCVhxEbEVKO6t60PmNnTuGQ6AOGp72MfWY6q/tk4Ig0DSdlZUFvs6JtQ9tnMdUTD3bB8CB+wUNkig5nU6z2Zyenm6323Wl2QfQJk9dEnilk0T19MLtujO0ak0p18JjvhAhL3TwAA3enTp7PVNq5+6D23856dsnxrt9f6MJuRnk5lgJOR2shWHRksX7encfN3vmz1aLQrl4jkdms+vzsJirVy3YqSXWjcCnK3OcDpqXxk6cefr8TQYv99hThtWBDh/h+vrNDB8wS0IoPROHUy404avVnTqMPPRH1itVar9arSqY2ZaQYqfUHZHb1YT/RPO8AI0E7Rt3nHx10KBlkU4/Yg7k7ZMMw6SmplIUpYOGR9wWDzu7+wUNgiBYrdaMjAyQsuoyqIfdYE9c+nCKAh+95LGPKnxUkqYdLjdWLXS57aLCY78ScOcvYCDoQQsaeAWFf/HFixUqjhw1cd26g2GhcVlZKNsocRKiBc5oNzAiv33blc4dxgwb/G1WhgoQEHIzwugv43b8cgRcKOQ4cmjBbXXg8sRNnrV7/wlORkabw2ijeISuXEOBgd/69v0m5Sbv5hDlRi4X+vHHC83eCdu1M2Pjxj+ff6FyYHCQnXICbuAEfNIBRA787ctDh/GOGgnads87QcPRStCOJOIKbbR7prX56rTOgfw4oO1g2kO/pDfqp3LyY12JC78v0MAwTGZmZlpamtVq9ThrXuIYoRf4cXAgFzGohyfATwWrIEZBjKzQ2NW1woqIVXFD4aHDP/YyDvxx6LkyL7zy6utHj54zm2msIcFh5QmOQ06ncvGcrfdnkyNDvstIU3geSTKiWTFuUkJS0kZO3XdQBRIitu6gKLO/Xbps5SYF5TrkFBA6f9XRu+/4zz6bfOUqPrVhcShuF9qVnFW3Vt+kpaes2aiDd+jr1epeuZaCsAMORZAkQcr1QwGTLCz2RMBA4AKZaslcXJjWIZEfIFGYfPU4Ogfy4wB0RWJGDHo4wbjwNL939fDiyYH7Ag1GozE1NdVsNnvocBXPquqlKn4cIKBBvI0b8oAGLGmAu5Dyhr9BA9R30JCoCpVeaf1xG6PFDB6tEEI5OXLqNeHz4OmhAYknjrA8iyiXKCto1aotU6YkMqqfbqvDnkPZZIQonv9x07bERatSUs0yQma7yIooy4jCIqaGhX+zI9kAGZms6M9jOR+3+uKb6btMt9DsmZu8vCot+m45POVFIT/QQM5P6qCh+HVRvUT3xQEtfgXnrjzPUxSlDb+vDPSXHzkH7gs0WCwWs9lMDtsQ6aiOHx95O5boDImdp1wTkQoSZJlX79tAQcl1eE22IfIn/gYNLpqVEco2WSIGDCzzQrnPenTPuJVqd+XwgpJjRcOHJPbzm3pgj4WyIZsNa+Ps/vXsuNj5drwRgdyCM8dlxC6pGGn3/uORg79089hqJP5IQigrGw0b/t3wkSuWJR1y86pnChO6kYrafTJo5LClN2+guInfP1e65hdfjMk25eADpZLECTyUWStFIJ9cEOjxt6gTqzb+g6JLdMfSC//YOaDthxkZGUajESyiasMfeyH1AhSJA/cIGohoATzsEfmqx4RYpKLokZ9uDuRCB0WRFEUi2gv5g4P8tCNzQYOkIElBvCi5aJYTxLmJ377wYrlXqlRcmvTfzFvZ48cnhAaNT1r6uzkbu8FgWHTlamZI0JcWIzb2QDOyhHgZCRSNTp0xRI2cnJKawwiqHSe7aLKisWO/HzZsadxk7ABTQnhD5dQZa6dOw4ZHfbvl57MtWvg+91ytjz/qCQ1KcyzNsQzP6aDh6e7hT2PtteDAbrenpKQYDFgyB+Fa7YenkTsls873AhrI95C2Q2jpkskKvdTFhQPavlRUWkIKuYkEA4jjJ074Bfh7lXrm9TdqfPDvjxMSFtE0wvYgZWQxO317B2VnuigKCQJiBWxowUmLx0/e6h8+NT1LFBRsN5qTsOPsJSv2DR3+bez4FUYTstiw34qDRy/29hvUuo1vX7+oChX/9Wzp13v2CHO5cFKQNXA2P0hdmDoWl7bRy6Fz4F45AEbTDQZDdnY27FDooOFeefk43ysCaAAjTgzDgHFo3UT042y3Jzrvwiyi+cUhiEFSz0kS3AAM4wRx46bNTd95t2y5FytUfNXPv9+2rf+7cd0weNCIs2cuKTJy2Di7Q8RmrRWUlU359BmVehO5GIwM8K6ESVq2ct/I0YuHxyy4mYkcLhyevPvYJ949K1ap4/VcJS+vF156ufqMGQspClua4nkdNDzRPVWvXBE5QHCDwWBwOp1EYl3EZPToj5MDhQUNsiyzLAv+SMDMOMdx+U3cj7NCet4lnwP59avChOcHGjjstRq5aBYhNHtuYvKvu/38+1V57Q0vL68a1d9s2KBp/KTp+/YeSr2RSTOI5lBaZna/kC+O/ZntorHgweHG/im27jg8fNSc3n6jDxy5uWvf+fFx8z7t0rdcxWqlylbw8ir3XLnKbb27X7ySkZlpx2IGEXH/BA2KjIEM1ELbSoWplza+TuscKLkcILhBBw0ltBELCxokUaIoymKxpKamgu8chmHym+xKKC/0YhcTDuTXrwoTnh9okLEBBgYsS2Jr0JIiSCjH7lq0cEmbj9s3b/bhc6VfLF2q3AtlK1R7o17jt/9du+5bvn7hCbPWzE3cPHlqUvDno3r0CS1bvlq12s2fe/HNFyvVf+HlGl7PlC39wst132rcqXuvhHnfGrLMFCMxHLYEZbbkGnHSbk/ooKGYdDC9GI+XA4Ig5Lc9oR3jj7eQeu75caCwoMHhcBjUi+zLehjr0Bs7Pxbr4cWBA7n9U/3WlyUkiQrPyRwrMbRAu3nKyTkd7Kafts+ZvSA0bFCbdl3adujeoHGL0mXeeKlSk1eqvu/1bPVXa/zrlTfqNGjc4qN23fuFDRoZO37ztu2nL5x1MHY7bXPQLjfDMZzEC4osIXLnAgWNjAFKUhx4opdB58Dj4gAZBVp7gDzPa9cRLf24yqnnm5cDhQINLpcrVb3Au4SuCJmXj3pIMedA7gR0GzSouAFJIhIERRAwgOA5WRLxYi/JuQqPVqecmkUZsqVl3/8+ePg3n38x6uiZ85yCWBkxkuKWeDfvongbxVsp3kZzLl4UQJJBEIOsKlb8jRs0s2AxZ5dePJ0DD5UDmqGggPtWQbXAShYXj4/Sh1oYPfEicaBQoMFoNGZkZFgsFmKJgcgbtG1P6CKVQI+sc+ARcCC3c2pAA6zl2qxV684iw0luVuYUrAtpcgq//XF+UNSc0PApO/ed5LGhJ9ElCG6JZRQ3h5wcyuGQiUM5gswKkgLnPP8BGsio+CehzVendQ48bRzQjgZQlbPZbFrEoIOGYtsl7gIaoGnNZjMoPxZgsU7bCYptbfWCPbUcyO2ft0ED1jtQLTXdZgjoHigIyZwgUozEI+TiEYPQifPXfQNjLl51uQRkd2PXGApCrCK5JZpDLhG5ReQQkVtCEiAGSfl7bwJLGvK5buer/9c58DRyQDsseJ4HdwQOh0OLG7RxnkYeFdc65wsa4IAlNFvBcgVt0wJdXCurl0vnAOYA7qWgZJDro0pGiEOIkZELIZYTeJrLBRQCQobsbLODdTL49AQj4r9YCCHjGxuwRNiEFLlJsn8TeYeHGqK3hM4BnQPAAVmWGYYxmUxZWVnZ2dnwgapLGopt97gDaAC4oEV8Omgotu2nF+weOJC7jgNuwEfFBQVRCN9OXnTicxYssrtlikMOluWQKCCZQ/jgJcOpoEFGvIRvUcG3JKu3Ch3+xgq3QUk+mOEfUo57qIL+is6BJ4kDBDekp6dnZWU5nfjwkXbsPEmVLel18QQNxB4Dx3GAFQow4qRtVC1d0pmil//J5kBuX801sBUn1AAAIABJREFUmSApWHZAKciBECPJtCijnbuPrN+020EjB8MLSMbOIxDWjuRExMkaSQMBDbeFDRg0FO56sjms107nQFE5ALjBaDQaDAabzaaDhqIy8JHF99JOcdiB7217DA6Hg+AGbZyCaZApFab0hbEFVpg4BedFSltwtMI8haTuGrMwZS5MnLtmVPgIhSx54RMsKTFBbzcvt3N7hbrAy7KoAQ00Qshi4fwDo9p9GmSxIx6h/2PvveOkKrLF8fd5f7zP+73ve7tvV3cN6xowgcCqyKrIImFZhCXMEAaQIYjASFyXsPrUFURBcUVxFRdBQXJGouQgiAgOScLgTE83Hek4nW7fHM7PumemKG5PDz06A4P2/fRnprr63FOnToVz6tSpUzGBU8kxC+IFoUHlxkTl9gSaGao0hswODLQbXkzUNw8vlmRktGqkcyadqizxULB0DJhDAWootKHBZKoLm9/QaM6GHpb+BpXWdZ3neUEQJElKX6w2KFJ/ysT8G7sNAQCSJHm93pKSkmQyKUmSoijU+RGnYLybqlrlAH9CbsqyjEdoqmUu9mz2hG46GAtD03SjJB2ezaGkUmMJ/moYhlT1IIWKosiyjNEtLRiwUFR40/HQX9m3KDPZTExTbtBImpiPm0GUq5qqIUmWuZVygEJiHREJuaKReSgSSZJkWcYWtCDEI9GUBkzIskyrgK2DHON5XhRFxKYwDxKD+EnEJPPQFPYi+hPSRvEYhoGXnHEcJ1c9FCUWSqtjCSCGRGqqJooii4fSzPCAJNmNNkv18Vfzrl5UGlIGpEhba5CMQ6+eE9v8YXAkQrYkzMfQQdFNDwaR3FepSoqqaESNIK/opCDzITdSaZqsabIJQgARRNNkUeSrwMh/M//iH8MwZFkWBAGzFEWRJHz3IgxyGOuO/cFSKdrtaYtn6qXYx5AeiorFRump9lekqWYYfJF2b3aL+pIqmVZorHumsigSdi5iqU1HSFHRn2qgh+UDhcdEOh7MR4ssx3GZ2pT2YcuKmYXHnkwHiKUsFgMtlH2dptmhR5FQ/hiGgQIYR7eFHgDAHoUDFsephQm0dFmWRVGkw9xSFo7iat9lC6UA6fDYoxCALcWiQFAMucRV4cC/sZO7JEk+nw+tQ5Yui/MR7YjYCWivxQRel06bnIorCsa+jhMBTl50LrDoIiwMlfFUj7Fgo+IftQIEo7VDqtgJl1JF+Y6jC1/BX80zeESyIYWUJ6IoUszY9Wm3Zmlm64XzCwCgtNZ1HQmmpdNxRXOQHrYilM+iKPLmg8A42KpEcCW19CfUIaiygkMdgZF4Kqs0VavSqSr/p4s3WkF8N5lM8jyPvkscx2Gj6LpOiUGdzIIHRT4Lg3hwpqC8stCTTCaxBVkWKYqC57wFQeB5PplMchyHixWkEPmMZGCtUCGuQmKYlgbBAElRNIGDWAR65/+99aPDgwFIcARKB0UGXtA4XhF4SUwJAsfzyRSXEgRBJoq12S6oMYiywkuSIAgpnk8Scri4KPKGQbQ62uV0XU8yTyKR4Hme9i6UASxzZFlOJpOCICAb2ck6wTyo2NEBQoujRVk4w3Z1tt1ZeiiSGmjGLoHdjHJbFEVBEERRxJGbJR4KRmnGjkEblB1TLIyl7lg17ADIyRroEZknGAzGYjF2okBuc8wTi8VQ5WVnDLTRUpJQz8Y2ZflD+yHSk0gkcPTRiiNwIpGIRCKJREKSpLj54OKbTjsMySS6PwKzSJBsHEFIDHYhOs8gAAAkEgk6n4iiiP4EVaPD7P/mZCUIQjKZjMfjHMfhepLth7hUiMfj2HlwdsJbsCkq7BtYcUVRkKNUOcABgvxBehKJBJZFZ1dKM8WZS1x5DlRaGrAvhkIhu93udrtx8kVLEU5VKAyonJZlmef5+KUPXRuhhiGKYjQajTGPIAiKolBUOBVGo1EWDWqytCDsW7FYLMo8PM/jEMI5VFEUJCbCPBzHsbMnSutIJOJnnkAgEIlEsF/i1owgCIlEwsc8sVgsmUxSSU/xuJknHo+zkz6l2cs8oVAIZyIcJJRmF/MEg8FoNEplsKZqSI+Hefx+fywWYwWMKIp+v9/OPJZ64eqB47jyS59AIIDCHsxHFEWv18uQ4/J6veFwmC73aXtdiqbc5/OxYlgURZ/Px7DHzeLBNTTHcfF4nMVjt9v9fj/P83QSURQlGAyWMI/D4fD7/YlEAuWQJEmIp5R5/H5/OBzGOZ3OsJqqsfWy2WxerzeRSJi9UTMdISXD0Mptbntpwv4t/Kn98w+3GOHzQEWURGuQDF6ChGgkRT3lcDkcTid+vrWVnXe7QqFAPB417/KWdZ18XK7z9OM4X+73+xKJmKyI7JzuZB673e71elFWYVugtsryx+Fw+Hw+3DQ0mIdpdjJy/X5/NBq1BGFjinKWlJS43W4M4svSY2Melh4WhsWTCYZBY6P0JBKJ2uJhy3K5XD6fL10usjAOh8Pj8YRCoVgsxpaVDT3MMCVG1vLycuyxBvNY+o/b7cahypbF0uN2k24fDAYjkQiDxmDL8ng8SHY0GmVhgsGgw+EoKyvDRscm9vl8bFksHqfTicChUIjFE4lE8EgCEuN0Oj0eTywWY2Hi8bjD4fB6vThgvV6vw+Gw6A2hUMjv93s8HqfTabfbsTkCgQCLh+M4n89nt9sdDgc79rE/499IJBIIBNxuNw52DBjo9/spjGEYkUgEC/L5fGVlZVic1+tly6LwucRV4cAlSoPL5fJ4PD6fLxAI2Gy28vJy7K+hUAgXf9hyoihGIhHsInTO8vl8eCcF9mzDMFAIUQDsKNFoFFUHTdV4ng+Hw16v1wKDsycKD1mWY7FYIBBgJ1CcQVB10HVdkiSkh+2swWCQ4zhcl6AKwvO8heZAIBCLxajg1FQtkUiEQiF2QOIsjDAsHifzBIPBeDxOBTmlmaXH4/HgVI5giqLE43Ec0lRFQTxUalJ6XMyDigXloWGQeGrBYJCl2VIvABAEIRaLhZjH6/VGIhHU83CtLIoiznGRqgcVJtTPsHdKkpRIJMLMEwgEotGoKBKJiPyRJCkcDscufVCroCxC1SHKPKFQKB6P07ZAHS4WiyUufbDidKggHhbE7/fTtmCVhqo6kf+4vKsyfugGiclEdNmgPxEOQTIKgwrfaPngILcLQhFNVA3JEEUjzmtRQUtwQjKZ4hJcMpZM+Pz+aCJeZUWo1Bh0XU5ycfpJJGKCkDL3Kdg5X2dppivXKpKIaxGqlXTFhoop6twG87BsDoVCiUQCmcwWxpaFC3eqc1MwjnlYeiiArmekmYVh0HBID/ZnFoalJ5uyssFDFVO2IF3Xs6Enaj7Iybj5IIUMmw1qQkgmk9FoFFfnVUamyjLZeuEQwMU9iwfLwr8oRCORiMWwoShKLBYLh8PxeFwURSQMh1hlSbrO4onH4whs6R5oG0BU0WgUR3e6xRGHMI7paDQaCAToFIQDDVVzVEH8fj9qZnjdFK1aMpnE2SWZTCLB+JcOVbSfcRwXDAbdbncsFsPlWywWozBoMUW24FSMcQVdLhctiK4n6Vu5xBXmwEWfBlzcSJKEpiGO4+g4wQZjdyXR05UOSDR/0eU4QuKUTc1x1EpJsdEBwJracOONdhFqmKLm03Q8FIa+RRNYBP1aQwKNY5kA2LpfFqZmerDTU4Q1tHe1wyNT6Znya8Bf7U+Z8GTKrxZJDZksHtoBkBv0LRbmh6Qt+C+iouchdbh4wZVhXkppgN8v/2Xcq23bFYQilZ4iqrk9oQOvAq8asgYa0TPIBx/6FY0WStWvLEwV7OX+042/GnrR5XBk9TvtgVlB1wMQtg7OEor5sEoebTsKUO2v6UjY7Tx2LyMbPLTQ9OrSzmlJsJCWn+jXhgZDCWvgCewV+LeBk/qTIq9SaaAuVNSkb5FYbL/HNDtc6YI+Heyq51z1ybFmDtS2t9WMLf3XhoY/G3rSa/H9cqgMsPYBVmmgZx/MQwaqeffEuW9du/d9JevAS0Y0yZn3T8k6uXRC1EC5jNJQqU9QTaJ2tFOlwUpz7dBck9Bse12tdCbGZeq3LPy1ApOJzgaVj4y1jIIGReFPlpjKI5fZ1J8dHrl0XXEgG86zMLUtl303m3R9468PGmpLMxuCiQZz1EylIcVr4UgqxRuyDknBUA0SNLoWSsMlFoha08W+YJku2Z9y6SvPgWz6bQ4mx4GfAgeyUhqu/BD96ZRY205WW840NPzZ0FPbOtYaPoOlAQ+uqhpIEvAShKICuWZC066K0lDrSuVeqE8OZNNvczA5DvwUOHAxuBNb2/ocfTncl3CAZXs26UtezuJLNjhZmCxQXgLCvnstpvGiKhK4ybQ0SPIllUA1QidXUEkaCBq5wUolZzArPywwzbTGYGCBcukcB3IcyHHgmubARaXhElGQ+3KlOFDb3lNbuhoa/trSU9/w6aIegyolEookgaoBLxLPx5zSUN8NkcOf40COA9cEB3JKQ22lcB3D17aX1Lb4hoa/tvTUNzyrNKimjYAX4OviM+/Pnh+NSYoKvKiaJyyUnKWhvtsihz/HgRwHGj4HckpDbaVwHcPXtovUtviGhr+29NQ3PKs0pARFUYl1YfKUmbff9nA4SJwbSMQIEl0ajQ1S1cYEvsdSx2Ji83PpHAdyHMhx4MfDAestlz+eml0jNbnWlYD6pr8+m5GIeXJxROWHuDXICigqvDF9wb139Cs5AYpEMsmH6A3kU5/05HDnOJDjQI4DDZ0DOaXhKrdQfQvdax1/fTYPuYKqSmMgV0hdVBqmLb73tqElx0GVq5SGqnAO9UlPDneOAzkO5DjQ0DmQUxqucgtd60K9vumvz+ZBpUHViepAtIeLSsP0Bffe/mTJCVAV0HRGb8hZGuqzPXK4cxzIcaDhcyCnNFzlNqpvoXut46/P5qlBafj43kY9S74xiNJQZWPIbU/UZ1tcgtsSjvaS33JfchzIceCqciCnNFxV9gNc60K9tvQ3JHhyVYQZFlrC4NAYYEE3YMvmQ4+07He8OEy8IA0aloF4PxD6mdhQF9MNqWINnJbLDjmk3xITE99iq5Yp1DR9nb2T2nIJE0sDeyUbXvnB/ppL5ziQ4wDLgZzSwHLjKqTZSTCbdG1JzAYnC5MJP1380QRCsu9ea2lyPQSrNKQESTMVB6czvn3riWSC7E2Qm8wqP7oOKqljTmn4vi2dqXdln48lXxaeEnhZSLzsg4LhNTr0ay6R40COAxYO5JQGC0Ou9Fc6u1kS9OKi9Pxakciuxiyoqv2aCTnVFWgCIVkktCw286qnLQtWhh6iNKiGrIJI/hqqrGqyQo5cmleegqJALJkQZKFKaVB1kMnr1SkNtO6Zi2NK/gknkVHslZX0LkrkSg39qla8ZQtSFEU2H3pZLu3nBukEmizLoijiDfKiKNJfc4kcB3IcsHAgpzRYGHKlv2YSHw1NadDJ8QLy0AR+ZenPRnBmA8PirDmN2DLBXK4ssj1BNIYqpQGAfOdSuqJURmiorHKlpYH4S5KyckpDJo5nl4/yO/0vchv/cubDM49gPmwJCJP+l4WJM0+IediyEolENBoNBAJer9dut/v9fo7jNFQeWbhcOseBHAcAckrDVegFskxuONB1PRaLORwOjuOQCEmS2J1XXAOJosgKPzYtCIIsk7Uv2XpXNfphYdg0AmAOTqyomhA5qJu79VXTLdJT9Y38p3Oopmp0uSZJksg8tCxculEwURQxLcsy3r2OlFhex1okEgl2K1qWZXxXFEVN1RRFkcyIS+lloVChf0VRpPe841uUUo/HE4lEJEkA0C1KAwBRF6i84IQ4gFYVqoHsZUSZx+fzRaNRbDJKj67rEeZBIZRMJnGznLKUQRN1mE8oFLK0QjweD4fDfr/f7XZ7PB632x2JROi6HEv0Mo/LfEKhkCzLLD3BYNDn87ndbizIZrP5fD5BECgxhmHE4/FgMOhwOM6dO2e3210ul9frDQQCLEwikfB4PKWlpWVlZTabrayszOv1JpNJtqxIJOLz+crLy8+ePXvq1KnS0lKPxxMKhSgeXdcDgYDb7bbb7aWlpZT8QCCAvQ7/IgwS7HA4bDab2+2Ox+MsDMdxkUjE4/GUl5dTPF6vl6VHFEW/319eXu50Or1er818vF4vpccwDEVRgsGg0+lEJns8nmAwmEwm2cHIlptL5zjwU+ZATmm4Oq2vKET8OJ3O0tJSh8PhcrkcDgdd5eBqnioNPuahMxrKTsMw0LLKTpqlpaUoFVA1oXMoC+P1esPhMMdxFgHjYh673Y7ylZ1AFUWxM4/L5fL7/fF4XBAEWpCmagwIkUAUhmo2mqpRkeBwOEpKSkpLS0OhkIVmnOXxL/InHo/zPE/L0nWdhSktLXW5XOFwGOU0ilhLWWVlZU6nMxC4EI0GWaUhJUh4YZWiwIULAlEgVF7ReXJugsR30jTQ3Mxjs9lcLlcwGIzFYiw9DAtdKIN9Ph8rOA3DYNCQpMPh8Pv9FkEeCoWCwaDf7/f5fE6ns7y83OPxxONxtiyma/g8Hg+ymuM4FiYcDgcCAfzV5XK53e5gMJhIJFjBGY1Gg8EgpSQYDEajUQuMKIqhUMjj8fj9flyXh8NhSZLYsmRZ5nk+FouFQqFAIBCJRJLJpCiKtCxd13meTyQS8Xg8FoslEolkMslxnGVTQJIkQRDi8XgkEuF5nuM4LIgdrtj5k8lkNBrlmIelB7sTbj1Q3Rr1bEqSqSlKSfMRBCEajSLD4/F4Tm9gGZ5L5zgAOUvD1eoEgiAEg0FczLndbqfTiWsvNI3WodLACulslIYQ8/j9/kgkIggCLvGRV4qihJnH5/OFw2Ge5+myHktkQMIWGEpSgnkURaGSg53041VPNBqNRCKxWAwn92ph4vF4KBTCtS+VEFgcU1SC4zie50WRlxWiE5gfUdHllCBxKRUAPO7kG9M/drmIBUg1ZM0wIzkYqqLLyAo0XfA8LwiCJEmyTPLxg9vn1DqC5g0EoFIKkchVDwotlE8UxjAMihmlI5KNZiG2+mwa6aEGJMRGGy7dlEWLw1eQMFEUqQWLAmCC5/lkMom/Ihir5FF/FyTS4lSIGKgZCYHxK1JY7V9UaulPtAg2BznP8oGmFUXBIrAb41v4K60aRYXmNFEU0V7i8/lyegNlTi6R4wBy4PKWBssotXzN8TEbDqQzTRAEnHxRYOBslT6na6r2A7cnqDCjCXbGpNKFTuVU8lHfMRRtdMlFE1hxOvPSadqCny2iBhie5xEhNb8j5kzspeUib+lfKlMz1ReFHNlAUUSL0gAAPPF6hIMHS+64te3WLSeJl4NWuT1hxo5UgYnvhKYgxXywOFr3dLIpwek/YR/ApTYFMwwD1+jUiYSqbrQUCkxx4pLass2Bv+q6zgpgFPwUA76CkCwYbT7kMHsi0UIPpYoSQxO0FGwdVKFoWYqipA8Q+q6u64JArD4AQBNUxaG9he3AbDfDrUDUIKkxg7V8oHKG+LHPIz2aqoVCoZzegJzJ/c1xgHIgK6WBzkHszEJR5BKX5QBOmgjGpi0vWuZWnAfZGZA2BAtZc9ryOv2a6S0EYH9FIqnoogkL8TiPUwrTf8UcC2YqKdF3AYWHruuSJJnGAGLWpqiSySSWYkFFAVgJR7WH9BpVMUHVdVnR8eiErOqVESFlBQ5+8e2dt3Zeu/JkKkX8GzAoZJXSUOkQaqEBpZeldixhNafZF2k60ysUgGWOBTgbGMsr3/trNmWxMDRNe3gNRSNwVZNVet5UC0/RsgkWks3PlKYFsQlUj6g+XQPb2eJy6RwHfpQcuLzS8KOsdsOsFDuR4ZzFLqQwh4XJJs3OfWw607vppSCvWPhM3EM5jZA1wFBULAy6KWiqlkwmbTZbMBhEz0dUHagbJuoTdPsmvSyKPEulwTxsSc5bVikNhqk0lN352x5rl5elktkqDZn4xtaxhjRLNk1ngqcANUivbGAy4a9tfjZlsTA0TZlWQ4kITLsufq0WnqJlEywkm58pTQtiE4gEX2ER5tI5DvwEOZCt0oB7tD9BBtVhlXEzvgaE7ETGzllsmoXJJs2+y6YzvYsw7K9IcHpOekW+H4wsy8Fg8PDhw4WFhbfeeuvDDz/83//933fccUfjxo1vvfXW3r175+XldevWrXPnzjNmzEAfe0mSMpXF5meqb1U+sTRYlAZFIxddHvyi7M5bCtYuc6YSoKrU0kDiNJinLy9WnRaXiW8XQWtMUTxsItMb2cBkerc+8rOhh4WhaWRazSQhcFWTXR1LAyqp6GpZM7W5X3Mc+NFzICulAbf3QqEQXfD96PlS5xXkOI54ybvdHMfRSdOyUmTz6SxpSbAw2aQtr9Ovmd5FAPZXZEV6TjqLvgeMYRgOh6NNmza9evaaNGnStGnTnnvuuddff33WrFlTpkwZOHBg165dCwsLx48fP3Xq1Oeff75NmzZz5861bEOwlLA00MrSTRP8tSq/WqXBkBWDbE/ckr92WTmXYC0Nck5pYFlN0yzPaaYlwcJY0hZIy9dLm+yqKQ2yLHvMhzpJWOjMfc1x4CfCgayUBsMwvF6v0+m0TL4NkEd0PmJpo5kWIc3C1EeaHhKjM04sFrM4oLG0ZZOuLZ3Z4MwEU9uyagsfj8dFUWzWrNmGDRtqeDeZTJ45c2bv3r0ffPDByy+//Pjjj7dp02bBggXoD5FIJNC3EaM+oDMpbWiMKpHuaoc+jLIipsSUBhovETdM8y4KQ1a18+crGt/157Urj3Jc5Q2YZPMCBA0Ew9AocpZmlodsfi79wznA8pZN/3DM6RhY/GwaABKJhNfrRdfIGjx70nHmcnIc+DFxICulQZZlt9sdCAQsAWoaAiPYgV21giT/MR8pZGGuJM3o58VxHJ5uR43B4qbA0pZNurb0Z4MzE0xty6otvCiKAwcOXLRoUaYpGEU79TFE/3lRFPv27ZuXl3f27NloNAoAx44dGz169AMPPNC2bdsBAwaMHz/+vffeW7Vq1dmzZ0OhEPpUUiTo60DDTwGArEmyJmG4aEUzFM2IVAhrVx/wuAVF02QthTdnm7dUKDmlobat/MPhr2T/zFQWXmrF87zP57PZbNivMvXbH17lHIYcBxosB7JSGpLJpN1u53m+4SgNOLZRS6BezWygm0QiYTlYha9c4ZbgOM7n83m93mo1BqrcZJqq0vNrS386huxzaltWbeHnz5/fqFGjRCLBHqVjkdDQVRjnUZZlDDdUUlLyH//xH2fPnkVVIBKJOJ3OnTt3zp49e8SIEXl5effff/8NN9zw85///D//8z//93//t1GjRk2bNs3Ly5s6deqyZctOnjxZVlaG8RxVMzy2aqi8xOsAGhiqrguSluRB0kADSTE4TTX0Ks8GEkOaOdBBqWW5SjNziTrhAMtbNl0nyC1IWPxsGicTTdUSiURZWZnD4YjH47ntWgv3cl9/ChzISmmIRCI2mw3XzexAuiyDqp1eL/tWrQBobGBRFNngRRhQKF11qBXy7wHM8gdd/DCCE43/w5pDfuJKQ8uWLYcMGYJBpqtlNd1cwF9xP4Ln+UAgcPfdd8uyjJEMeJ6nwYh0XadBozHE4cmTJ/ft2/fee++9+OKL/fv3b9euXePGjRs1anTzzTdff/31t9z628f+0PqPnf60fec2RSO3Wqq6rupEYxBVQzESBqQURatUGvDWifpRGq7AYKmWyQ0/kx1TbLo+KGfxs2kAoB01EokEAoFoNIrjtz7IyOHMcaDBciArpQHDttMj8jTAC8/zHo/H6/ViSGNFUWi4VnrgDfebQ6EQjfdHAuYoCgDEYjG/3x8Oh2n0XEEQ8Ogdz/M4hyYSCYxEm4mDGKAQg+wGAgEa5D8cJoEInU4nRV7fkzI7xbAmEEzjrxYPPvaVLNOZ+NCQ8zG8P865iqJglD1d1wcMGDBt2jSU/eiRkN5GqKpi1B00SHwXj3ny5MlFRUVYZbQ9iKKIdxtpqiYIAhulp1qe8zwfDAZdLtfO3XuWLl8x6bnnTnxzksRxAoNcd2mAChDjRRU4AF5MSQBwwZ/cuevg2bPnHA4HBsrEqzSojRrDEGGcRAxESBu9htYxDIPneXR/Sa9+DS/mfrqSHGCHJy0XM2kHoPm5RI4DP2IOZKU0uFwuPOpGh4csy6FQCG+1wfjHNLisrus+n8+8EIhMtagi+M3rCaiJj+M4m83mNx+bzUbluiAIXq83GAziZjZKfbvd7nQ62TZg59ZkMul0OvHaJ6rNoMoSj8ddLhfqH+wrLKo6TNMZBOVcpoiE7OzzPdJ1SPAVQ8UGkcQ0sujcuXN33333qlWriGOBeYmXoiixWIyFZxdzaLmZP3/+LbfcUlJSAgDxeHzz5s1DhgxZs2YNhnbAaIaIDS/0otXEXkF7At5uIJuXU+EmBe5NqIYqalogIpm7FZJu8HySBw0cDvcdd9573S9/9dvf/rZp06YPP/xwr569Ro0a9eabby5atGjjxo2nTp2KRqOCIKD1C7dUUJ8GAFSa0U8TxxF2clpZ2hkowblEw+EAbR1Lgiq1NRwDbji1yFGS48AP50BGpYHOrQDgcrnwej2c4AzDiMVi5eXliUQCl4lutzsWi+ErsiyXl5fj7TtoZhAEAe89QhM9XrvgdrtxVsUEDkVBEPBdWZbxBkiv1+v3+71eL1tVBMacQCDgcDjC4TB+pa5zGB0W7y5ixzmLp27TWAprY7CEFqYsZempbbpuab4y2Gj4XgzpSOWoIAhbtmy55ZZbioqKUK2kHYYegkDLAV5evG/fvu7du//sZz+bN28eZaYgCD169MjLy+vUqVO3bt2mTp1aUlKCtzbQuxtYL0hLlRXN4HjRPHypKJpG9iYMVVBg5nsrDh8nqqokJ3VVqwiFZYXHIA3JZLKsrOzw4cPbtm1buHDhlClTRo4c2blz5wceeOC35tOsWbPHHnssPz9/yJAhc+fO3bx589mzZ/HiRFp3JAmJQeMEVXktFObAxDtvAAAgAElEQVS+NgQOZBqnuCjiOA4nQAtYQ6A8R0OOA3XLgayUBrzcFm9T1FQtGo3irgT6qcXjcaoiAABe5huNRnF+RK0ChTeacxOJhNvtRve3SCRit9uppYHn+fLyckEQwuGwy+WKRqPoakRXY1h5dvVZXl6OCg1d2WMCr87zeDw+n48dyXXLPhYblpJTGlieYBp7QjKZPHv2bOfOnTt27Lhv3z7sDLIs+3y+WbNmtWzZcsKECdu3b08mk7hVgXcvOZ3OdevWFRUVPfzww48++miHDh3WrVunqRreVYGYw+Hwjh07hg0b1rp1a4zr0KpVq6effnrTpk2lpaWW7Ql0eqDbB8kUOWyp6jovieQ2SzAUXeYluK1Rp4nPkYAQipQCRSbHMQESHLmaGTFQJxUcF3hflyRJeDDvzJkze/bsWbt27bRp0/r16/foo4+2atWqadOmDz30ULt27Tp37jx8+PBp06Zt2LDh+PHjeEN0Jm/QdH7mcq48B9g5xJJG85jlGnGEufJ05krMcaC+OXAZpQFvzfF4PBxHbvxDbyBqDMDVPF5XT2/Gw8sbWbpjsRiaIjCsZDgcdjgcNHQBDZZiGEYikbDb7eFwuLy8HHepccan2yKIlvoPut1un8+HkeHZTQGMQByLxVwul+VKYpawOkzThWMymfR4PIFAALUH+tcy0dCvdUjDVUdV7UQZiUQ8Hs/mzZs7dep088039+7de/v27Xh4khoAJEmKx+Pbtm0rKipq3rx5q1atOnTo0L59+1atWt1zzz2//vWvn3jiiVGjRm3fvj0QCKCigJaG9BJPnTo1adKkjh07Dhw4cPDgwR07duzVs9eMGTNOnTqVTCbRZZIqMQCQEiRelAVZQocG3TyByQtw971PDxuxUBBBVzWiNChgyKAroGtEaaDNRw0elPn0SCdtetp7eZ7Hgx7nzp1bv379Bx988Ne//rVv3749evRo06bNQw891LJlyz59+owePfrNN99cuHDh559/fvz4cY/Hg/68dGsDb9e0eFRQAvBiKtwKpJnUiY+9jCqdexQ+l8iSA7hEQe8uNL7iizX0kCwx58ByHGiYHMhKacA4hliBaDRqt9vj8ThOhTzPu1wu3GDG2crhcPh8Plpb3Id2u93JZFJRFHR9d7vdHo+HnkLESVzX9UQigU6XHo8Hbct07FGEeGEd5lerNMiyjBf4BoPBUCgkCAI7y7N46jYtSVIwGHQ6nZFIBDUhVmzQilgSdUvDVceGy26sOPoczJgxo1WrVnfccceIESNKSkqo0QgdDnCBjmofXqeJbHQ4HHa7HU369FJjNDshby1spF/xV0VRgsHgO++807lz5969excVFfUwn3Hjxu3cuRN3SSiviKKgKpJC7qxCpSHJw133jB02bDW5XlGHSqVBAl0GXb2M0kDRVpvQVI3jOLTDoRKADBFFMR6PJxIJm8128ODBJUuWvPXWW4MHDy4oKOjUqVPr1q0feOCBJ554YuTIkVOmTJk3bx66UASDQVQdUP3iOA6HEir3SICiKIlEAkcrZT7VsNOVnmrJzmVm4gB2dUEQotGo3+93u92hUIidcHIczsS6XP41yoGMSgPOMmhpYJUGDA1J702ORCIOh6O8vJwejohEIn6/H0V7IpHA5b7T6URbRTwexzhRHo+HSlb0mlQUBZfpDocDjzNVa2ZAzDgsq1UaRFGMxWKBQIAaSHBgU7lSH8NY1/VoNGqz2VwuF7Uz/zSVBhTt586de+mll2644Yb77rtv1qxZLpcLRwjuLOBRSYywRFfMtIFwCwDxoCaKx2pQI2G1RvoKm8CCaCuUl5fv2LHj6aefLigoyMvLGzt2bN++fbt16zZjxozS0tKUIEmKqlVdeK2BIWtSkoe77x03bMQaUTSvwlZVUHRDMTWGKksDlvID+xKSjfsduB2DWzPIE8oxdArhOO706dO7du1avXr1+++/P2HChMLCwscff/xPf/pTjx49CgoKJk6cOHPmzHXr1h06dMjv99OTRMhJAEC2o7GBnm9KZx2Wm/ubJQfwiC8632CoeFyo5FSHLBmYA7u2OFBrpcHhcOBJimg0GggEfD6f3+/HCNNoqfN4PH6/Hw+SYbQlm83mcDhwExr3JsLhMM5cKBI8Hg/aIfBUhd1up1vOOKNZeIpRgQ3DSFca0MwQCAScTifuEaAEqtcBrKlaJBJB8wluyePK76emNKBeuH///v79+994443dunVbvXp1OBymt51R6UW3J7DPYOtQXSGTJNZ1PR4nXgUWT/X0ToKHPFHxxWPAhmFEo9FTp0699dZb3bt379+//5gxY4qKijp26vy351/YvW9vRTyGzg2yJnEi3NnkmWFFK0TJtDRICui6oZFQ0rhGpxTShKWLVvvVAkz1IQSmvYWV4umvIMdQUKFiJAgCbhEeO3bswIEDmzZtWrF8xQsvvNC/f/8uXboUFBQMGDBg8ODBEyZMePPNN/ft21dcXFxeXh4MBq+AMl0tH35kmWgxwkolk8lwOIymHbYd6fzzI6t7rjo/QQ5kVBqQF2g1tdlsdOnvcrmC5uNyuTCmXjQa9fl8aPmUZRmX+F6v1+PxuFwuzEEvIZy+A4FAJBLBGTMSiSBCNCoEg8HS0lK/389Kl/RWQT9zPJ9ps9lQLGHABr/f7/F4wuEwXcvS4ZouWtIxf78cWZbx+Ch7r4SlXHYGYdPfr8QG8haV4slkMhaLbdq0qU2bNrfccsvzzz+Ph2AzCXjkAMsiWiP6E4o0ACguLrbZbIgK9UXUKdnXWZbSNBXD1BqPElcURZfLtWjRokGDBnXtnjdm3F/G/mUcOkKquq7osqDAnc0Kh476iCgNBoBIYkOaXVRD/0cLtRbRTn/NlKB1pKRSDGxOpjSiZX+l4p/+xFY5FAo5HI5jx47t37//nXfeeemll4YOHdqjR48OHTr06NFj0KBBI0eOnD59+vz58/ft21dSUmKz2Xw+H2r5FGF6XVAzQ3shjl8MmGh5Be1DFCwdz48jB5vD0hBYNXYJwbbaj6PiuVr81DhwGaUB4/ajRwKOB4/HYzMfj8eDBlXcgPD7/RzHybLMcVxpaanb7cbriFilAZeS6AsWCoXwLGU4HMblI26BO53OcDiMa8RMjYEDD7chysvLcYmPf8PhMO7sUic7dpTSqTkT5u+dj5GFcOq0lFjz1+9d4tV6Ec3abOkcx61YvqJZs2Z33HHHvHnz6EY7Wtott3pauMHiwTQCUHl/+PDho0ePjhgxAs+2odS3IMn0lSKxJGRZpiEcYglux67d4559tiIeM2NBkiOXkgFLNhz/dFepIJtEqUBuqlJJGp0wKNm0aJqTTYLWkb5Oeyabkyl92SKoMyZ7jBMzaUEYG4NejFJcXLxy5crnnnuuV89e7du3b926dYsWLZo2bdq1a9eioqJ33nln9erVO3bsOHLkiMvlQsdM6iGBTtBIVSKRwHzDMGikCtb7EsFo1S5bl2sFAGuEPY0yme4BsXoDVXavlarl6MxxgOVARqUBuzv6LlDPPtyETpoPDdwrSVIoFPJ6vfF4HN9C2Ynjx6I0oF0a9w68Xi9G1qOzD/qvWfzUWHJpGilBTwLcBKHqAp2Pqk1QDHWbwMr+FJQG5Bt1V5w+fXqjRo26dOny+eef44WTdD+I1fyybwt28tV1vXfv3gAwePDgEydO1EpjoPO1RWNAqgRBwM0USVF5kbhASoosq0plnAaAKEDYgKQskvoKADIYCqR4Q5ZVKhLY5q5Vd6J1ZNmCGNicTOnLlmWpO6s60Ju68AYmNEiwLYUmQBqfyuv1Hj58eNGiRdOnTx8+fHifPn3atGnTrFmze+6557HHHuvTp09RUdGsWbMWL168Z8+eEydOoBsTjejKsgiLtmjzl63LtQJA25SdCiRJwqWUpRMi8LVStfqgU8eYJ/WBut5w1gvNhmnLrDea6wNx9UoDhkjCjm4YBi4W0QGNbhygxzvSpJgPNc7jTEFd4v1+P7pB4N42RtvFVxRFoQ5riAoXMZetKmslxgmOnZ4yzbbsdH/ZItIBMr1Oj+xTZ4saCLD8lF7KNZGzb9++4cOH33XXXTNmzMB4nSiEUG/AToLih7rdWSqeiZkIRifZOXPmLFmy5NixY5MnT0bhl44nUw5Fkp5A0YVHLjWDnJDgeJ5aGnjQ/CBfMFJxLWaAYvCgc/DVl6dfnvxGScm3VMSy5daq1Wgd0zGwOZnSly3LojQgPL39i+romI/MoWlsF9x6wBNM7AkXKvI1VfP7/cXFxdu2bZs9e/Yrr7wyfPjw/Pz8Bx98sEmTJs2bN3/88cfx3MrUqVNnz569b9++c+fOoUrB1uuydblWALBStKfhdIQuDvF4HEeBpQNfK1WrDzpZAayRO+AM0M1PfRRWRzhZmqtFSW6uMT+aAQZC65fTCVilwSA35oFifnRSAh2MdMhUW+4VzqxeaUAi0qf19ByWXDzcZRHeGOsJNQMcUbT+NWNjMTeENJ0UkBj09sDVKkvetVUplvL0ND3egkoAtu/WrVs7d+78xBNPLFu2DAN+0walGCiv6BxKYdgEhbckWJhYLDZgwABZlgsLC51OpyRJyWQySyazeDKl6dDGKy7N+E4aD3IExAoQkxCXFV5JgcLB0eJTEyb9bfz48V27dv3rX/+6Z88e3LZD4lFDoqEULDVK/8rSk/7rD89h9QYWWzblsjC0BbNMoCnR5/OVlpbu2rVr1apV6EXRoUOHu+6668Ybb7z77rtbt27dsWPHHj169O3b95VXXvnoo48+//xzm80WDAaj0SjG0qDnb3F1ge5QqJRjdSiR+FXXdZ7naexRXPYgMXgnDiJEDIFA4KOPPpo8eXLnzp3btGnTsWPH/Pz8v/71r7Nmzdq5c6fNZlu3bt2BAwewfVHeo05MY4TQ0jMlkCo8YWuz2SKRCKWTvoI5P8G/5lgj8rHyXlnzallQDfIxY6BcdZ6QU1SqwkuirCqyqmhgXAgGMPgb/mXnDaTW0InGIJgf4gpl7mZCSpcSPKlntY9hssBctFSCRGQ47ROKy42YiG7XeLdOg+ozNSkN1VazhkxFUQKBQCgUQjMy/sUrqaj4oft5yIUasDXAn9CWi47rbrcb3TgaIJ11RRKqepqqiaLo8Xjmz5+PQZMOHTqEa1DL5eO0XGxcKmZoj7ckKLwlwYLxPD916tTi4uKtW7dOmzaN7pdbXqn2K4snU1ozSLBHdjrQQBPBCIDu0UUZZFPtJ39Ky20fzp9b0K9vXl7ehAkTJk+enJeX16dPn1WrVp07dy4ajVJuUFNEtVRhJktPDWDf+6erpTRguSjpLXxAL4dwOOx0Oo8ePbp+/fp58+YVFhZ26tSpcePGv/jFL37961/feuut991334MPPpiXlzdmzJj3339//fr1Bw4cKCsrCwaDfr8fN0zpiRjax6ijJT3LYBgG1SFINE8z5v13nljPPffc448//vTTTz9oPq+//rrdbj9x4sT69evffvvtXj17tWzZ8uc///l//dd/3XLLLV27dh03btyK5SvOnj2LqiotERNsO1rS2HaaqmGoe5/PZzn1870b91p/kVUaCNM0HWQNZJ18NJJx1SuISoMuSBCXIMxDQgJB1lUSZr5mpYEH8447wwDZgIhilEfIFCKaJoT0WqHSgPoCCRED4OY3FL44v8cY8Cc1shFKHIPSe1o6piuZU2dKA2oDeLckOhngX4wYzY43dmhdyarWSVmKomCcebvdHgqFRFG0zIx1UkrDQYLXj73wwgutW7eeNWsWXgJC52KLkyMlG5uYTq9si7NpCm9JsDA8z58+fXr06NGJRKJPnz54Q6YFPtNXFk+mdAalATYesq/cfyYs8xokJSkmCnFFFyuSUVlVQqHQkSNHRo8e3aZNm4EDB06dOjU/P79Lly5vvPHGd/mhUCgTPWw+Sw+bX1fpTPgz5bPlsjC0EbNPsKionk2FerpxjtomeZ73+XwnT57cv3//d9eLTJ48uW/fvo899tidd955/fXX//znP7/xxht/85vftGjRonfv3mPGjFmxfMXWrVuLi4vLysqcTmcikaDBYdlAF3jyi+f5I0eONGnSpEWLFt27d9+0aROe4TIMIx6P48YB2ipEUeQ4rqysbNOmTa+//vrDDz/8b//2b+3atRs1alQwGKTUslzKlEZWoF8XRr1DpQrhWUb9pNKs0kAMDiJAygAehSvhzVXnBm7PQVQUVx/8pNPw7X9/FzwxUAhtqDSkU2gQhYeoChKQD9EA7HHPot2rnnpJ3X/OzEp/ydy8wF0NCcDHa5tPrmjUc2mTArCFJYncBU3HHdvHqkN05fLqTGlAQYIxHz3MEwgEeJ6nm9zXtKUBw2Zj5Ch0DrWsZq5cu12Rkg4cODBs2LBOnTpt3LgxmUzSq0DYUV1tV8bMart7tfCW2rAwsixLkjR8+PCDBw9u3rx51qxZ9KyN5a30ryyeTOnqlQYDmrcd0/3pty6kBNxj1PWYjscuAbAz4yLgzJkzs2fPLiwsHDJkyLPPPjtixIjOnTuPGDFi0aJFbEi0mmlL//WH57D1ZbFlys8EQxsxmwQix50avO2T+k9gZHfqd0mxYbm6rqPPIF5rjkZK6vaEhzaj0ajb7d6+ffvixYunTZs2bty4bt26tW7d+q677rr++uv//d///X/+53+aNm3apUuXiRMnTpgwYcGCBXa7neJfu3btzTffPGrUqFOnTmEoBdy8QHMa9YuimxH4IsaWXblyZYcOHd57771JkyZRzy2WkzWkKWPj8Th7oy87iCjMjzvBcgnN+2TjXwaIA0QMSJqWfXN5fdX5UKk0hMXV7YavaVH4cfeR8G0ApMrdExoLjqXT0Ikfg66BqpsagghwJjqvzdAlrYaee20xpMivlRwwIS++i0pDEqA8eWTk21t+2X3z7X3gzAWx8uxWpd7Acu/iu1cjVTdKA9YHJwLLgEfPKVTk6UxxjaoOuq7TsFE4CWLAgKvRcD+0THbOoqtAtOLyPL9kyZJBgwY9//zzxcXFbKyF7Etlu3imdDbYOI5TFOWrr74aP368ruvt2rVDp9ps3s0Ght2brErrMkDLjpObtpkUV0CFhA4VOsQ00FRiZSS1QcxsvTwez9atW5977rnOnTsPHTq0qKho6NChvXr2QvMDKjqodLJuxZIk4VjIhtSrAsPWMZt0pjHO5mOaxWapGv6U/gqbgzB4xhsv3d2/f//8+fNfffXVl19+uUePHo899lj37t2nT58eCoWOHj3avn374uJiVEosgp9Fm4k2v9/fvXv3++67z2JpsFBe7Ve2prQs2osQYbUv/pgyCRNMmUrs+6Z7oKGComgQFaEsIX12HGwRSGoZt/+vLC8M3aQtJK98/Om5d3TZPmoanI9RpSGTiwKJ6WLOEaoOkAL44sLcRj1X39v/wuTlkCD6BCoW7F+CigSqB4gB2NUdXZ7b84v8U60nQnmcMMd8LumTFoXjyrIFS6t7pYGOipoT7EC6GhX/PmXineDRaBT9ya9djQGtXuicgbEHcN3s9Xo/+OCDxx9//P3336d7EMgpbK/suca2b6Z0NtiQSMMwevfubbPZli5dumL5CsuJm2zwZIKpUhTIyK36mErDH19t+of/i8ugAq9DQjd4VSdrCPROumQYm9XjOA7Dlsiy/OWXX7744ov5+fmDBw+eMmXKs88+m5+fX1RUtH37djSJox7GksSKEDb/qqcztV2mfHbUszBsfjr3LNXEF9NfSc/BY5zsWSpq0UWceGKrffv2ZWVl2G3QI7Jm2tILwmAkv/71ry0npCyUV/u12rKo49dVb3pCgG5UBVKvtga1zGRPBFS9SnQGoncbZKsezxjIBrHAh/nEon1z2z217x8LIFEZRa3qpYv/M8rpiyCXSeHovgxQ1c+VSkNUPvTC++v7ToKvbGTtULU9kZEYVBpUMktAAmDFiQ33Dlx2Yzf45y6IkYqT2aPqg9sZRC/AQxMVGhxwr3l4+PpfdIWXPwWfedjbPEDBjhd8nWhddfrQLpoN1rpUGmjBtU1kQ2hDgEHJihbXa1pjoMyMxWIYFePw4cOFhYVPPPHEqlWrMKQ3xvWiW0vYpvTFyyay6QOXRYIKDYLt37//ueeeCwQChYWF2byYJUyVokA1BtDJvVTQ8k8vNm0zgSgNZMiqxOpoflBpSK9denGSJIXD4Q0bNgwYMODRRx995ZVXpkyZ0qdPn/z8/MWLF+PFZnjrBL5bK+FBCUgvt25zaEFZJlhxy77C5rOTIMJYaMbM9FdoDh6OQPslfRfdBagVk54JP3LkyIgRI3iepzfm0BcvWxBb4pEjR+655x6Kv1rKKTFsAiHZsvBwbyKRoJexsfBEilQndy+BqfEL9mp2RVsTuG46A1/2cGBNKJjfqHPfpZ4JVqVBAUPSBF6BgLB70Kv/vCevdN4WCEtVe4AMwspDFmSE0odN08z0BOWDZlQehszyReKdoGpaSoZAXHUEQDRUcgii0qEBbSV06rikXM30eVSJ5UB/e8emOwcsvSUP1p6CeEaloVJviCiwvXRtuzEbWhXBxjNks8Z82B5oGAZdulwslPYWS6I2DUq76EW0mVM5paEa3lQ7feOUxF4qWC1YNegaahaG7Fy1alWHDh2KiopsNhvP83imPBYjFzHQ65WpOTf7qtBeWEMiG2zRaBQAcJOiT58+paWlM2fOXLlyZTbvZgNDRz6T0BWARztOuv8PY5NSlXWhSmkgxoZLr8bGClrKEgQB3fUVRYlGo7IsnzhxYsqUKd26dfvuBOkLL7yQn59fUFDw8ssvb9myhZ7Hy75HUa5ayq3zr7SgLBN0jrNwic3HNIvQQjb+lP4KzcHBiM4l1b5LMwVBmD179pw5czRVwyM/1CWFbjRQtJYENVqgbrdo0aK8vDz6FhJJC6ohwdYUi0ClIRQKcfGEIRN/t4tKK55ExBmfkbukb2BEkUohav6GLoWS6UIomg54pkmbCkuCFsUYJlTTEo4LfdwjwMMLim4ed0wLKoAagGZa3U15S6mrXB8rZqGS6ZqgVtVC0Um5KMPQ9o6ujhwAb+i8QiwNMgCvQUyB8/z8Jn2W3dcf9tnAJxB3ANPCX8mQKuVJoecPTNwWbpPKUZHJjORKMNOkTytdyRNkhWxSgtgruUZe0gyyPSEKxKEKXd3NpQPZYVCBqA5Yu0oVBPmDBahVloMIqH//dPV13dc0HwS7HZAwnSQVUjsDTRE6yBIxSVRWLSRGZm//qPmTa3pOgjMVlY6TqkFOlEjmx7TQaKqhaORT2RdoaAc85oXNU8U0wmSWG7RF2EzsBlpl37cwttqvdaM0IGp2bFw2XS01DSQz04GITJVqIGRnIoP6qOIkiObZEydO4Nmz559/3u12szCZ8FzhfOQ29mW05e7bt2/27Nlut7tPnz5ohLDsodQVhboOeT3+/sc/jhfNMNK6Luu6qulAPub5zPSekKloCyQAoO9knz59Ro0aNW7cuMGDB2Oo5o8//tjhcODSE30JWU8gxG9ZTKcjz0TGFcu3kHTZr5kIy+bFanUsfJGKf8Mw8J5xDDuGQ5u6Z9ZcCkbaRo8fURS7du26ePFinucpcotilKkulfnmlI3u96bgMMpKyz3lzoQ3TMSkaMgVnB6XIaWT0wQSES2SrIuCTCIFIQpTwhHLuakkcLwoV3BwPgL2JOwugaMX4LgHghxCE1mAigLKRRVUT4Vx7gK4OXBUQFQGTtFEVVfMNTiqHebqHwMMVNrnNYCkDP4U+DgQgU/yEU3G6+KJQPJzxAh/1A1HzsM3PogahHLZgJQiVnB8SiT14jQ4ewF2nA2+t8n+j1XkHEFUVCXViJGdP/CrsKVk3W96f/n7cXDwAvGITAFENbJPkVJIPVG8oTcyWvJZRUoFiVxpr+G9cqTiknl6wYSUggkwoLKCGikNg8JrokrojGnGSTecCxPKbREIp4A383nDkDRZxjALIKYkVVJBg3hFAp0cZVRQyKJKi0SihqRBhQhRlbAoIhHMqAL6DHfvGbt+0/fTx0dCKW+yQoekSkjiNZ2w2hA4uVJp0AG8omv8/OX3FR586UOwV2hJidQdT5SURcDHQ4TXUrIhaUSb0YEnE5GpYMVUuCCAMwXuFHCGKmgcL5PIEioYKdNHJE4Oc4AMFZ4gwWmY3ASQvBUEC6+Ru3VMhY+6amJ3y/Q3pzRUwxmqNEiSFAgEYrEYThyZpphqUDSMLLTi4gILXcBEUdy4cWOvnr1atWr17rvv4hFKXEhJklSHvgI/nAHs7I9KQyKR6NatWzgcnjx58tGjR9EIQWNX//ASL2LQYd/O0oN7nao5Kxm6bH6+j9JwEadpuUELOcanikajGzduHD16dH5+/vDhw8eMGdO7d++CgoKZM2eePHlSURS09+CdLKjwYZwiy7Y67ZZsWVcrTYnJMpGJzsu+XvOLVK4DgNPpbNKkSXFxMZ6XtsSQqKEgLAId6b+7m6Nx48bxePwHKQ3mOlMGQwRDBkOV1LgnJNmD8jkfBFKkOBEgqhCpGRQhIBCZgZISSVHI1I9BhEh/iPIQ1aTdp3aOfH32gwULH+i/qe//gTdFFqnmxjlRGlTTEpACCCngEvnVh7aPeG3lgOdOvLUUyiqICEmpRNDyBpHTYSX69bfB46XkqwIQ4IiR/GxY23z83D/XKF/ZwE+M5gJR2AEiMhx27nrm9Y/bDV3557H/emwg7DoLMTXmC+txU11QgdTihHfH6Dfeb5q/4MH+81oN/KD7M2QPIiaDT4bSFByN+Ud9ePimQr7LP2B3CI4n4FgYjvrEEy4ImILW1LTwjAUR+VUaQ6VdQQSoEOVwkje1eyIUQykivyMKcGAEkoRO4kBUyTdyHlJS9EgKXEk4FTo9Y+nyPhMWdx/7j46DT6/fQ2S/2QhE7xENcMfBFiK2EABDUAVOxK0BUrRqKjeeBOFPafDMvA2x5fsDH9jPoEsAACAASURBVH4G5TwEie80+ThV959f3XNjn6+LZoKDh7AiOCMEP2mIJGlcU5CjXkfgHXzpgJlzfvEn+NxOukFIBFsYDpV//fLcz558cePgv8NJH1QokFI1UZUVQxE0iKsk3P2XjrMzV20pmm6fvUncfQZsUZBAS6lyQiYVr5DBHol+ccYoC5JmlQEqVAiocMxXsepAbMNh9Ws7wSMRRxNiSDEf7G6Z/tal0pCpjGsuH1cwaFh2OBzBYLDmSHANvILotRAOh998883777+/ffv2W7duDQaDuEyn+7sNrRbYfensj5rcypUrFyxYUFZWNmjQILperHPKiY+SApJA9iaIk50ime5bF3c0v3eJ7OIYL/TCS+RPnz49a9asXj17de/efdSoUcOGDWvbtm1RUdG2bdtoOHZRFHmep3dGIGdYmfe9qarDF1l6sklnKrrmdzO9ReZ386HdBs+t4OmJTp06HT16FBcACEDxVFscWrPwBte77777wIEDGMIBVVhaBLU3UGyZEhqRNQZnfkQUgFEJTl849PqCTf/3DpElnBkbKKyDS4Riv7L5JJwOEr96NICjzQDlTISHEv+F2ZsWths2//GntncZv/t3Ty25M//4rOVE2EvARZNEFMmmeIsAHL5wvOitxb/rt6vN6LnX/3FN0/7StHVwwA0RjciSlAFBVVm4f3HbYYv7TYQTPqJSnI7AnH372oxZcFPnRXf3XPSHp4KLd0MK1AgHPl7fdHzRA/1X3VOws+2Ylc36b2857Iv+U4j7HinRFJzHfaF3NmxuP/pft//5X03y9wyZumbwi3MHToQLcmrbcdfLS/3PzBGe/ujz6wvO/X8FnuuecjYet+WXeetu7/vPu/JmdX7GseNrICt88kHLSqXSYG4JkNU/p9m3Hlo17rXU3lMgEg8JwvYLKfjaCfu/1U57IGlASiMqAmcyQTZluQLgTcL2M6u7jH2vec+t3SYse3jwnEcL3ysYK5V4TbFqKLwMArhnrPqk9ZBv3lsNSSBqkKktycSYAURXOM/BEd+h0W/Nvb/g00eGfnJzly035+96eAScihLrCwdQltpzZ+Fn1+Wpyw/DBZHofyERjnmklYeOjZ8NB1wQNqnCgNMywLfJ7b8fuet3w2G/C1wqHA2F3ly74L4+y2/L23hT3tLfdN095DVwihBTiZ6X0qFCA5sYnr52W+sxy+/uv+KhoctaPLWq+aDzkz4BW4rQkNRIoS7xs7Fvvv1gn5OvLiL6aJCH0pRrwtzlN/553XVd1tySt+WJv4A9gRXX1CqlLFMPNvNzSkNG9giC4Pf7g8EgDShU7czCioGMuOrnB5aeTCUYhnH27NmCgoJmzZp9F0Xg8OHDABAOh9H0ypoWWKe8TNiuZD7Wjp2aMXR3jx49ZFkeO3ZsaWmpJcReHbaFpsmSJCjEJxJ3M1XD0DTQMoV2yYYz7NFWhMeNdnSqlWWZ53mPx/NdVIwJEyZ06dKlqKho1KhR/fv3LywsnD9/fnFxMRvvBDlTQx+gP2VDW13B0EKzTGQqt+bXM72VrjSgN8m2bds4jlu7du0jjzzSvHnzd955x+PxUL0hU1l4Ann27Nl33HHH/PnzafzyH6I0cGDEqpQGRVTIsr3YN/P3Ba+2yIOTQTLXR3TYW/rlM28te2jwlnZj9w1+DY4Rq7IaFfGKdrLSNWMbxBbt+bBFv41PjIPNZ2CLLdr3rZU3dfXO3QL+VMoXqdQYePPutQuwKW/ix80L9nT/G8zZD9M/+7JFUfGjY78Z9AZ4JFO6GHBBiU38ZEeLoV+MeAPKJTgahOVHtrUYuu6WvB2PjFh+/5Mft3xy2zPTSEAFTwo2fbP4ocKV9/WDt3bAVg+8unHRzzqUDJoBXskUaSrEQf7XzpX39VvapMA56SPY8S2p3fkkeDjwS7v+/q859/dbd3uf/Tf0P3ndgFP/++SJ6wecvPeZk4+MP9B2Qtn4j868+ykESVhmdGCkjgek3U1rAeGAJ7Fw2IvvtOhT8dEOYtJQAILqmbdXLO5Y9EnrIW+3KVQ+LyFSMyYBZ+5ZYBSpChVOBdd0HvvP2zp7XvgEdrph0YmlDzy5ZMDfoIwJy+ZOfd3thRW/6X5w3NsQ1shukaktEK4mAYLg+uenC9sN++ih/l/2fRne3KyO++T4Df3W/7+OwqIDEFCIteNsbNtt/fbfNRhOxsArEI2wNLZj+GvLWw7a1vypLa2egXNJNGyQ/SAe4Jv4ipt7Hm4xBg4E4GjFwf5TFjfru7fzBPWlVfDc2s8a9Z3TuBcUByGskNPfFRp4tBNPv7Xp/qe2PzLqwl/mC29tdY/7aOX13TfcO/DC+1vIboVoqlClyQVdxix69Kng2xvAyYE9cWbiv1Y37rvv3kGlj03YfnvfD+/q4d50EHjVkDSylZPFk1MaqmdSPB53OBx2ux3d2RCohsmleiz1mYvEUJkKAGg4pdbseDy+adOmLl26tGjRYtKkSU6nMx6PY1BStHXTd1HWIsL6JPn74GarqalaOByeNWvWsmXLjh8/PnHiRF3XM0Wl/D6FMe8IQkrXiVOTpskkzq1OlAbzQyhiAL9nEutFeU6riXYF3MU4evTopEmTunXrNmrUqNGjR3ft2rVDhw5Tpkw5deoUXu2N1he84CAcDuP5Q0oQWwRN019/fAnsDPT4pSAIxcXFw4YNGzp06Jo1azASpWEY27Zta9u27V133fXSSy8dP36cHrJAhUMQhFAo5HA4tmzZUlBQcPPNNzdp0uTAgQNoa8QDnKg0ZFIdaJumc9i0NBChI5qrZ+IFF1Vhw4klrYYsbF8E+89DBOBE6PiT0zfc3HP/XYNX/lfHJf/vj8KUtXCOOCYLnCiai1jZH4fi8LLHnl7RaSxsPAVOFU6n9jw4Yv6vOsPhCxAwHSOIYkGEN3wT/WLUzFkP9ds95i04FyV2i/0Xvur+0trbejtH/QvO80RiyQBe6UjHiWt+08P2+jL4NglrT6x4ZMiyhwcHZ6yBYxfgmwu7ps658OkXRPCfqjjV+YW1N3WHBQegTIZD4aN9X9nechi8v5PIV14jekN5YskdeVsaPwmbviEG8wAPcYVUWzKDPybgwppDxocHLnR6bff/9jz0h/GwJwBfXiDlelQIYSjmKjZh5AOTxkovDVz1n/LP6zxyecshMGcv+HXw6xUzNy2+q/eW5kOW3dht2z2FWzs+C14FeEOVKh0WCettwr6h0z9p2u/CpE/gRBKKY/DSup2PjDw69RNidDGdKAxBB5fyebOnt93YCxbsh6AKsuloCUC2P75ylPx9/tzf9Zv/2FOpT78Gt0Jo3m7fe32vvTf1hV02wv+QAscCm27pffKRZ+E0B2cicDy6s89LKx8cvOnO/l/d0G/TDfnEzBM3+wj2hs0lX9w3PNbtH7Cq5NjwmYsffPLLp6bBmTB4ZDh4YV+vFxY9+hR87oSgRqLGnInGP9i19q4ndz06hlgmzsUgCFAqw6tbljUqWNb1L/C1i1Q2CXA6PKvT8LfbDoZt5+CIz/Pm6rVtRuzsOhG2nIWTUVhxeP2YabIvKqsa2ZRBL870jntpTk5puJQfVd98Pp/H48lGY6gTEVJVbC3+UwdyOoWh3mAYRiAQePXVV2+77bbGjRvjoiqZTOI9QHQzgrrUUeNqDZNdLciqa1CkCvUbjDfqcDiGDRsWDocLCgrKy8upAkTlYp20iCxBrELkU6IZncy8MZsp4IfXkkFWqYKwNaUCCS3kwWDw3XffHTBgAG5eFBYWtmvXbsyYMQsWLHC73ay5CAmzBF5ML+uH098wMaDNRhCEffv2DRgwYODAgR9//PGAAQNGjx79nSsMeifEYjFd171e71tvvdW6detHHnlk2LBhr7/++syZMydMmNCuXbumTZted911991336BBgzZv3ow1Xbt27Z49ezBNRxxGrmOVb8rqavmDe/N4EQHxN9CBWJs/PbHykSGfPD4cjgThZNT37pbVd/fz/fk1mH8qkD9j+8+62Xu8BiVJSGgcxwumiR1c0ZOD39zcdLB38jI4GoGvLxwYN+vDO7qfLXoXygWImiEJJYCYDufirv9buKrV8NUDXpQO2yEkEHl2NnWo79T19xVGJ68Er+k6oAG4xYMPjthza19Yfhi+dO/sOnHZQwOjc7dDWZwsiIMc+Vvih1Oh4Our1/+yC1/4TziVgm8qEu9s+rBpr3VPjIXjIWI40QAqePjSvvH2PicfHQc7zxEzQErTRBV9AoiCIgBUGHAkGOw+Y+9N/W0TPiZ6T1glKoXpt0FgMBpzlZEBTQ6Vt0eS22kBjvkXdxy59HcDYM4BsGvxxfs/vrf3/Ju7yi+vhde2Hrip347Gg+EMUbYkGbc0ADwiLDy0sFHPrW3HwjYnHKmAJUeWNOq1rtUI+CYMCqiCJqYUUvrJyMaben72q3zYbSfLepF4R0JSgfMJz5ur3779iZVtnyH6gU+BoEysL9tLD97z1MGmw6HYT+ADsvLp0dU35X3b8SUokcGhlvzlX8vvLzw+5E1YcMLefNyhRoOTH+4iHglk1gaIgPjBnk9/1hWGLZXHL11w/5MHBr9KPFtDKQiLUJJc03nsnIcLYb8Twgap+07npy2Hr7qrv/H+XvBKXJgnLA0BbLB92nL43MeGwDE/yXHF4SvXzD8UftTrWfiGg3n7Fzfru6vH32DjSWIOCYlwPg4hUVG0FJDjGFk+OaWhGkbpuh43H3qmi84F1SaqQVH/WRalASMLHTt2bPDgwdddd12nTp02b94ciUQQDKMJ4SKMznE0wVaq/gmvXQkW2vCi9ldeeeXIkSN79+6dOXNmvSgNOnxzvGLlskMcR6hVDVk1iBO7Zp7dqhOlxFKvdLu6pmp4wR3yS5IkNBQdP3580qRJ+fn5Q4cOHT9+fN++fTt37vxdLKmTJ08iKxAzbdwGrhTWrjfUCI0OH7t27erevXurVq169+49aNCgefPmeb1eVDcFQUDnWUSTSCREUQwGgydPnly4cOH06dNnzZq1cOHCAwcOlJSU4ClfxPniiy/u2LGjV89eeM/q91YaKsnHc4xo7k4QpWHFI0MWdCqCL3ywzbHi90/t6TQR1n8LZ3lY+82qX3TZ9buniSoggCoRJzjQIPXp4c/vG3qo0WDYG4Cdjm/H/Wt2k167hk4DhwJhvdJyIJqxmXeWrby15+YHhmr7vpV9cSKJXXHY59rZ8a9rHhxiLD0EYZ5IVA2gnNt/W//jN/WHzQ7flKVLmvfzvbwEys1wATIApxAjfwTgS9+KBwrXNOoFsw/ChlLH+A/XtRq2KW+iccQuuc09EQVipR5hU/GG23rtuKUPrDwOTons8YuVoY2ISBZNl8bjF47+bvT6/3wClheTNbFmZopEiGoSiCqRerJBTgGAUun+SYwOKNuSAF/7l3cY+XHLQlhzBnZ69/R6ac6D/WHdCaJ/HAp83azo0191h92lBK1oGhBiKhwLfP7omL2Nh8DSY/B1HD78ctOjRQseHiyvKyZuB5x5IIGc+ADYa1v2m7yv2o4nhgTePJTBKeCKJ9ceWvHQoE8fGQoHnFASJvpZithyKl5Zteeewc5BbxO9hNPBJ5a8tnTNHX2kUQvgSExZfHDe/f33DpgKZTyUKdKoBct/2cX9+ipwmhdgpgDKhbJn5+38ZS94cv76m/J39XgebAlCBtmFScLW0hW/H7zoz2OJKhAx4Gxcfnbpxht7fzlgOtlIUon3FVG2wgCnpSWPDlvU4Rlt6ylwxuGCrC88uLb9qKV/HgeHKo63nbDzwaHaki/AJxHmmu3OcXwKjISphmW6V6uy31b9yykNVZww/9MJF+dfXJez83u16UtQ1MOXaqWURWn46KOPHnnkkZtvvnnkyJEnT55MJpOyLOMalOM4NK7SIBO1XSHVQ52yRckyHM8OAIDL5Ro+fHg8Hu/WrVsikUABSSGzRV0DnAaTnl3wUPMhdhuXEpRKpcE8comnkmp4NcufKLW0cTGHFfYsKgqGMTM4jnM6nXPmzOnTp0+/fv2GDBkycuTI7t27jx49ev369Rh3kqJKL4vF/ONIx2Kx9evXt2/f/re//e0TTzzxnVfpqVOnqKWQqs7odspWGTf18IoTHDK4kYFHVHCkeDyeP/3pTx9//HFBQYHD4fj+SgMNfGSefCPSukKGNSc+/f1TB4dOg52O4/lTNrQYanx8AA46wc2DQ9nZ9Kmt9xbCsQDxYpMNIrz90um/zdnyn52gz7/gzR2b8v4293f9HFOWQmmSGK6JhMNdAIBT0a1dJ225txBe2wQe2UgoxDHCr8Ksnatv773y/kHwuVOP8sTHTzagJP75r3qWXtcfVpav+v3gHb3/j/hS+FNkM18mwRWI9HUkxRkbPmtSeObPL8GcQ/u6TFzwYP+vhr4O++1EvJnreQLJqeBIftXjhaU3dFnxQGHgH2vhdAXxhMB9kMoLnQBOBQ80K/rs5gLYe54ISAM0wQykmARZgSRWpUppIPHbzbunyVFIzbyu4iv/6nYjl7R+GnZd0F9cs7z5gNOTPyHnFJIAZyJlXaes/GWX1JIvyHEGUxEBvwh7HVt/3fPsfSNh5ZmjI2eteuTpzZ3/CltPQ0gnNpgkOXmolIfBHhdWHvrkjnz7qNkQ0kAwTfcxBb5yftCy3+a2I2MzN4AjRVbqAR5scVh7+vNHx6y47s/w7i5SugTg5HcPf/3T3w2GWQdgvW3V48+semIcfOE049GD8caWtXf12104FZzmAQcO4GTFlwVTd/6y17Fbn9r9+2fgs2/BRawQSpyH83H5jQ1rfldIdpfKzfMshwM7byzY/IsesPVbSIDIGbwEGqdDBcCx+KI2w99t2R92fwt+Ac4G9be3Lftt/rlhs4w3tqz+TY/IXz6C8xLEFEMgjMT+mDI1hqRp8jC9SdnxUU06pzRUMkUURbyrhp1hs0xXw9c6zWKPgFLE0Wg0HA6fPn362Wefbdy4cZMmTSZPnlxaWoprVoy+TLUEutykgsQiaGlNKf4GmKBEfrcFM3LkyNOnT69evfrdd9/FKtcVweRkuA6jn17wUNMx5x2GSpYfCvmYlgY2LEpdlcjiwTpie7H5bJrlA1rFNmzYMGzYsIKCgpEjRw4fPrxr166FhYVz5871er1Ud6SYWVR1kmZ5kildWRCGl2H/1oYCdiMGzWaGYXg8ns2bNz9sPuPGjTt37hwaCRAxy6tM6XRIyzDRdd3v93fo0GH27NmDBg3CExl4+IiFZPFXXy2qNGBCA+IY+N72Xc0Hwd/XwKKT25sM/OLPf4NynjtaXnGyHOz80dZ/WXNDVzh4HkJiwltBjNUng58+PvLAz/MDTZ/dfM/A3f1fiS49SHa+IyTMADmab57lI3bsT45saDpoxx+fha8rwC0QoX5BhK8uHGzy9O6fdd/yu6eID3+UnCQEQYVTkf2/yPNcNxD6zd7SukjYdoJcCU0OhpJQB8RnEwDOJ490ee7zW/oee+CZT+/tt7rjSNu7a6HcPHnIaZUmhKQZDSGmwEF7cdE/Vj04cOHtPbY8PCzx1gb4tipmkQ4Q1+HzssW/zfuq49/gPDmtIPFmaAQRUkGCImVqMsTtA08wmmGRcJNCUQziDfDZucXNn9ze/i+w1rb3/uHrHxoKdvOQggbgE4Nj5q29rffZVxaR1XzC1EXcgu3lRZ//qveFe8fuvGfQ2rYjj7z8EXxzAQIiUcgSGKQByOZCefLrlz/6uFk/Ze5eQodkKg2elG3Mvxbclnf8+blg48iuBG/qSaV8+ZMzN1+X9+nNvWHNWUKYTJxPl3QZu7zFYFha8k3bvy28PR+2nCa+Hf8/e98BHlW1tZ3vu/+n3nsVC9IhSJXeRQSpUoKUBFJJgAABpErz0hQRLiiIEFQEQUXpvXeQEnrvSQgppE2SmUymn17W7z4r2RwmhQChSeaZJ1lzzj67rLPLu9deRTuakRYeWFsz4FTo13DFTECGHeCadVOrYQfL+u8u5yf9GpGt1aG5V4CrhojO43c07m9ceYSIMUygLD+xv5TviYbDwEBgllMCm6SpWWUKcCh+ZcvQOe/5QbxDMdiIRGHhn8feCbIFLTjVejRRgz2XRtxpuDS7lJzzCDTHQb9Q5C3T4Zl3J4Zi0ECU42VJRgtstOLTD/7C0Pnwtigv040mZsowTERERO9evUuVKtW4ceNFixYx2gedAqFjBgyQQeFCYRriVkpRNqAo8tI34eLFiyNGjOB5PigoiGEY9NZQJEaYCBo+G72+fo0hCXHAkS2W/EyBBj0v9RYZsiTfvHlzzpw5nTp1Cg4OHjp0aLdu3Zo0abJw4cLr169TdyMoRWNZtqhetx4ooI1c7r+YRl/zwtOyJLMsiycFCBBZ7ZOamjpnzpzOnTuHhYXFxsaiTRBtlL63FExjTfRp9FAAaUEQEhISOnfuPHXq1EmTJhkMBhq3kybW55B36yhoQHYIZBlmxy8/804QTN6R1O2rVZV7woE4MAqKhXElmeBU3Pl24zaW/lhec5LIpe0ycSx4Onll/T4HyvQ+XNYvZkA4nEonC5UIkk1SXSqXlAVpToIPUiTL8GU7qwTGTl4OsSzxi5DKwS3XzcHhh9/0Ofiy175mQ+BcBkEhggp2AS6bTpf2SykRdKViyI2Qr4lRpebsgbgg1HwjkhbdsV/sMGHXyx8dqNU3+dMlcOgW2YgLAHaRLH6ZIqQ6Ic3hMtmIMCCd4BvYcCm675yt7wZuahCyyXscXEohgnGnCFa489OurXVDzvX8AhKJI0iekRRGJvVxaiIYlst2HEk9LWrGFJqvRpWsfL+f3lo14I7PbBi/bunrHWzfbCNrKvqDSuMg/ODKyj5HBswiJztOTSXwtuPMwDknSvmde733Ta8vYPNVSNDsF+wySZDigngLqVs6CxnqzsH//a6WN2y/pkkOVOKi6rLhQL0Ba8v1IJt4u2Y/aRTUK2kZP+zdUMb7ULmAXfUHwokMomfqICBgXcvBOxqEwoy9Oyr5pn66DCKzyNrOq5DGwOarmxuHrm/cH44mE3yQBXDBtKpF2K+vdbz08TRIEEgOxHcCQBofs2DjugZ9LvWZSbQd79ggVUqYvnpX6d4pfvPACLwArAgsrwpOEVKYlJlr/niv75FJ34OBETIdkC7A9K2XKoUY3puwp3qguPI40VS1al6zqGtPdPdEgYKeyLsTv/CgQVEUjuMcDkd6errFYinYH4N+UtDT+fC2yC6jpEEURYfDYTKZFixY0LBhw9dff71Tp05btmxBaSqVRtDgwvoaFp4usko/hoz0reB5PjQ0NDY2dunSpWvWrClC15AIGmZ+ua2qp19cnOggimKyBCLOXfoF8jE0MSd4rtbUQuaPUiW03qSPZGZm7tixIzAwsGfPnmi32b59+7CwsO3btxsMBtSZRYNV+shDEMSnds43JxAPmbdzvooI93wxDX1EI8gCh9/8KqD3ksnzfGxsbHh4eIcOHTw9PRcuXIhuSKj7NQRD+q5yXxrL1SejOIASmCYmJgY9cS1atAhNlGkCN3Sed1soaEAfxqwIic64LlOuvtkb+v1yqv7AU4NmQbwV7MSJg2R1Kmdv3+47d0uV3rfGLyG7WxNHFuaIO0vq+W1oEgrLTkC8QLwZiqDaRbJdjrdE/bL3536TyTqUDEeaDzvScDCcN0OaTBazZClm1OLVpT42dp65q3zvVQ2CiQmfkSM2+mYezqcfe6Pn7X/13vvvLrDoMAmdkBdo2FKld0SVPmL4HrhqgngbWCXJ5AAzB5Embtel77wGkpN+4lOI16T0FmLSeckIvx6L6DFxXfXe5/rPIsYIaXZI406MC99dLcDQfwFkEOQhuwQ+zQJpAtzKzD5xx24k3T2YuKsImanAl9tOvd4LgpbtLd3rUNfP4FoWYQ4yNk2EbVEb6ods/WgUnEknBz1WgGjrvt6TN7zUAQb9BpcdBGHImiJqhkA8Uuy6ubTrMOlmmqbGCCt8x4U38oPD8cQVEgdk9d1+9VyDT250mAQGTRUxlYXTiZfGLdrWfLAw4vddtfttaPMJ3HQQxYJkCdbf2Fs15E7TcVFNPj3VZSLJx6zF05Y1M8i9URsa9d9RoTesuEoccmRwcDZ5UYuQxdW9YeNVokdilogkI8bmWLz/92Yh61oOhL1RBPNZFTDJJ8b/sKdigDV0MaSDymoyGbtWw8PRS2t47/xouHI6BmwcEcsZWXnS2otv+19+2/9i85Fw2Qg2Layo3lF3MWjIe6zmf1WWZIfDkZmZmZiYSP0d6aePwtD5Z19kdxiG2bdv36hRo6pWrVqjRo2xY8dGRUUxDHqMA5Mp28K4kEoYBTSqyGr8GDLSVxsATp8+PXXqVKvVGhISgsipSMpE0PDdtzsrlO10O57JcsrEHyRImutfcrRKw9UUSXFumbi10e1u7p8YUQyDbuMuHM0CMXQIOig7c+bMjBkzgoODe/fqHRgY6O3tHRQUNHv2bOroIne2hb6SveJTHHCvjAHXHfe/NDGCBiyLot7cReOt+Pj4VatWeXt7V6lS5YMPPpg3b57FYnE4HE6nU+8V9DGBBhxZTqfz6tWrAQEBHTp0OHbsGB5oUtyAmhMFvMFs93/o/VcEcPFwx3muTui1f/Y4VaJ7RIuhcCkVGCJWcfGc7OIg1WmZtXFH4/4HvcbBoVjhUiLEmOFo/NL3Qta2Ggx/JsJtFzG+twLZg15Ivjhn9U/dR16ZvxHSJLhgPPXB6LVveMG2KLjFQAxzafLSLR8Mudn9S1gfu/+9oeEVOsOxZOKOySIQ0HAhfdtL7S//2/t8o6FwnngowtfGsQLL8E4nQzz/3DIdaDJwR+kesPU6XEmHNJ6s02kuiLdl/fHn3Ca9joydD3c4smU3a74KGO2c3ATEzuKPC+vLdYvwmgCRJiLzv20+NvSbDa9+BKNWwi0XaYJRgOuGP8K+OPvTJjBqenpooqnpcrCaycVdzdo/aQAAIABJREFU0JAhCSN+P/dKj1tl+u0q2UNdd04DWxKBq2SNl+DPhN1dxpLgTxuvqSdiyYob5zoQNG1v6V4w+De4xRG+WVSizZABsOPG2laDN3lPIODALEE8s8pnLLFnORADJi2GVioj/35izb8+uv7BODiRCmmKa/uF1b3G/dosxDBqKSy/trxSj40+EyDaRiQH8QJ8d/jA277nXut14C1v5vt9kOBULOhfWmtGOmzrMGpPed/YXrPgtpMcUZ1KmPde4M6PRsOfBkiUCea7YWGXHfqjWciqD0KldacJFmG0Z+1wcsqSwzUHJHz8X0jUpBQmIBanxxP+6Djk96aBcf9dARmMwvIkrkW6U/p8w5ES3fa/1FEYtZyc1EjAZTkJtKJQvRg05J5xCr6iqqrZbL5586bJZKICW/2wLwxdcBEPdJcKV3EvyHGc1Wrdu3dv+/btmzRpUqtWrTlz5ly/fh0AHA4Hna3cdjmFqXN+aR6otk8xMe4sAwICbDbbXzLq06dPU1OXR6wVGU0qfPfdusqeba5eSyEhY4j3VQQN2U4hccQ9YkGP+Lj+Dep7AtJud9F8Jjo6+ocffujXr1/r1q19fHz69evn7e09fPjwiIgI9PFAz3cwk3xqqJ9vCC2LvMth49lsCCty5DCWZzmOcdmtFpFnRaLeDSpxicCDIgsiJ0q85gZD051TQdZ8OwOoDiearpOSHU4bWjesW7tuyJAhnTp18vPza9OmzdKlSxEl4yJdANrIp/4FXdbzzY1GnoiiiPoNtWrViouLw17nplnsNh5peaJ2fk1cFWe7IuYhwflnhd5nX/baX7pH4rjFYFPsToddERiQFUkm+8IDUZs+HPxr5W5/NAhc0v0T+WgU/Bm97MP+G+qHZI5YBgdS4ZILzlnh11NHuk5a3qTfxqGzyAJj4OA2d6BW/z3/7CyPXA7hh0+2H7O95eBdgVPgtAHOZ+3oMGJtZW+YvxfSZaK7YBHggmFXWe+TZfwifWcQ0wDNbkhViN9ljhU4ViDhGDLl4+0+3fJa51u+M+FYGlwywXUzRNy5Om7Rr836bPEeB+eSyYKXock/EhxkPY52QBQPv5277TNjXfXeEX2mE1+TmnOqi58uPFiyp7XtF7AvBQ4n2r7evLJt2KLOYdLZOOCBhNVA0CBpCqCaTQMGjCL8NAknPhp3olTvXf9of6XzRLhJdk0Sq1lLEgNREaKyNnmP+6NSt831+vzcNjR26U6INB0ZPmfra51jmo6Gg4lwwwKHb8GhGOP0NX80CtrWfQy3/TzRbHBIcD7xh1YhvzTwJ16zrNrJv4ljdlxcW85731u9zrQee6TThF/qB67o8EnG0kNwjYW5f25rOPDMZ4vhtoP45opjrBNWHCzru+d/P4pqNwmikJVkpSYfASBDvjL1l1UVeuxsOMC2+SykixDnSPp++67a/WDSVtgcBb+eTA1dsLlO0PqPPjEs20N8YzAEwxHRyB2LtPH8Tk+/feV9YVcs3BbhmgNWnz3ae8rSZgEHxs2FmDRwsBLHkrGWwbLTN558t/+Wkl3Ju86SWF4kHpwKAArFxxP4mvL7y3FcRkZGUlKSwWB4aMSgX+bzK6iQ1x3aB4WxsiQbjca5c+e2bdu2cePG7dq1W7x4sd1uR9/DOLnrlwq3Ce6hfxayqs9CMp7nd+/ePXv2bIPBMHjwYAy08egVwyXxRmTa0mVbzRaJk4BXVF6RBZAEEh/78UoaCl9//SvW9wSk9Xep+Qy6oAYAq9V68ODBESNGdO3aFQNetGjRIigoaP369QaDARX90B8imuHcW6t7QQOZzLS1X0ukOlgmLdMYm3h0x95P+oS0adSkfdPmsyZOvnn6nDUpBVwsMBw56uF4lWEVlpV5QZFkVVaIAy1FYlmypPIsY84ynTlzatCgQX5+fj/99NPcuXN79OixevVq6tWKuim7t26P+kvPtzxpVBtKSEhop31MJhMK/KhJhf5dYA60Tu6gQQGINe9tFrqxZOc9bYfChVSwMiT6IyicqoEGlwwWODdl8YoPByxvPeDkV0vJMXyC8/h/vl/fuP/Wd/sc6TD+jM/0Pz+eFF7ea0vTsAtDFpDwB2aZ7I/NEBkyd1Opj7dW919XtdfGmv5xYxZDpJngiXjnuf8sWlc7YGvLwVEr9pCV0i7AtbQ1nj03vt3V8d0OYhqgbfUxbJUgSKJI4iSBVeYW7d9Rv+/aKj473w/b4/PZio+GLG0WtOy9Pgf7fAE3bGR5kyBm/aFfB00+MGH+uUk/nR4xb3vnUWvrBq5r0OdQyDQ4m0yEEyxAGhP33cY9VQN2vNblfKfP9n00amOz/j/U75X2x0Gy82ZVYlxKok8RzC7KKm6zSRAm4mkJwCH/2f+rpW9/tKdBf6KdkCkwLo7AGmJgopIzhXTetvXML40D138wYPegr0hUrVgTRNw61HDA9pIfb31/4AavkZu8x/3aqv+K9/tt8hpFDEBis8jCLgMkOpd2Hbq4gR+sP0sqo4UTg1uZp/t9s7NO6O4GA7a/P+Rc2LdEIyTOBfESzNq7oWafqzNXQYZWdIzlkM/kA/UGHK4zAFZfhZtGNPhAdQuSm0WB03d2+0xc1qL/qfC1REMijeEO3tjWdODWir23Ne6/qpbf7yU7nv94MnGokKh5yNDgEMGaTgADnOj02eKXP1xbP/h44PRDgdPCG/guaRxweNhsuJkENpfKsCrHqRwHZkH66eDq6r1W1PKDY3fAIRJ/DNgd9eAgP5p23HuJF1oR0m63oxMnhmFw7c9zmrjvxXtZ+qi/MjMzT548GRAQ0KZNm8aNGwcGBu7atQvF7zg9MQxTsOb2fStcQIJHrf0TfB71Pf39/U0m08iRI69evarXrn/oiuCSSFZWh6gAODgRjyeeZdBQwAvVd2zEmth5OI7DPXpUVNRPP/3UqVMnb2/v4ODg7t27+/j4zJ49++LFi3a7Hd0l4dY5h6V60ICaHkS3Mikp/sievVMHDfugfNXKHq94erxczuMfZTw8Knj8vxqvvPaWh0elf7zSpnqtAV27zxgx+vdvv7uw90BaVAzRiNA+iiLZ7VYAReLYowcPdOnUccGC727evPnjjz/27Nlz9erVTqeT1rxIXnROc+75XzAn8S4+cP369UaNGgUFBSGOQWsOvciBZkULcD+eAIB027X5q/8cM1c6HQ1ORXAwLpaVFAKhiO8nTiYHB5miGp2Wdf4WiRBh44lUIIU59cm8je8NXF4n4LcGQYsaB27xn2RffwpuGJU7NjbNQVZlK0Ck9cS48I2B/zk6Zj4ciCTqBUanZGVs0cmuiMg13UaFt+xzdsUOUj2JrFt/fjxh9wdDlN1XINlONBK0jyiSkI/ZoIGRIZ2/MPO31e2HrGkcsqFx3zVN+271GW9ZcwxisogWpJ1sp3dOnL+o48B1PmN+bhHye5M+K97re3rYt66tZzFUo2B1yS6BrM1p/L6AKRubh/72Xkj4ewGHxs5TT8ZABg8CWfqJKwdUUNACKWV7aNAAqlMUQYGrq/dsHTXrzi+7IV0kehVE5KVp02Qf85OYVXAzTTgdQwKAkRhOAqTYnIv2HmgzYnkNn81th85vHrC429DrC9ZBghPSGVIkxgxLcy0KHrOgTV9u6zlib8KqBKYIAPEMv/s6nEggCp7pCgnkbRYg3mUesWxNBe+MZQfALDuIhoewe9jXv7QMTfzvOrhJXGORqJTa9p70dezvaSwkM8JNAzBaqAvN12TWuoiD/b9a3nno/v7T1d+OwckU8srMAqlYzoGC7BCJIGdv9DHfL3a3GraqQfDPH/T/1Xds/Po/SXutDAiyyrDA88AR00o4ELW4Zd/f/cZAklOWVIfGoewhlx9WoNexB+T6+0KDBk77OJ1OnD3pIH9QIhdX875wX/l5dHT0smXLgoKCWrZs2aZNm7CwsKtXr9LTepwxUd/NLWqRmzj0QeuvT5931Z+9q8gWURSXL18eHh5++/btKVOmUCWPR6kvLolER8rJS+Svi4IGSX1GJQ36N5ibxr2vnifocRk3x2QbpJknxMXFHTp0aMyYMV5eXj169GjXrl23bt0mTpy4efNmk8mkOwXQgQZikCfdOHVqfP8BtUq8Vfsf/27k8XJHj7f9SlT70ONfXTxKenm81f1/y/i9+o7Pa5V7lqj80ctl3vd4tYHHS3U9/q+Wx/+r7PG/Q3oHrPzlF1NGOgk+LgvkjENR7CZT3O2YSZP+4+vru2nTJgz+YrPZcElGHKNvThHSubmX+wr2PbRVqVOnzsiRI/EYEflJJQ30wXuqh7qQVBNNUMDMQqqFrJPahwA7RSWIQVKAF4mTACDRmHiWrFwpKYb05DSyGMS6yIn7livEFcGJO5AqkbVE886jsuAwM2RXapch3kyCJWZo7pU0q0kHx2dvx88nwKVkLimTKF1iPMw917iVEdk+IjVhupukQeVlycqQWIvXjeLak8SN9K5IuGbSvEdr/gkkLbZkpNG07ljikp3cupOw4Rw57LjDgE0LsQia7TI21SmTsE9/RnG7LsHZBBKfkyWZcHYibnGBml0rjCOu+VUjUEMBRiAtIXGz0h2kyTw57pEUDTRgVE8eWIt2KMCpktmJ4aY4Wdtjx9nhTCpsvsyvOg7HoiHaBCaBeGggjiC1hZ1IAnj7xVjm6E2iQSKQZZaVVRa9Stm19dtKlCfELFZ0iJDMXe72xZ7a/eBIrJpCDtdEl+Q6GwvnkiCJ+N+Us1iy5GtnUgqAKKpEa9WlkCNPVuR50haHJJIoWRkMMZKMMRPN0ESGaH5YZdJAUZN/aMcTikikLOQEKsoJW6/BuvPSvutwLYUYxzI8CILWeSRCCAK4BLhtytpznrkY50w0Ei2aYtCAfe+h/9Iz0UdcdAtZAUEQcLqhmz+qSHXjxo1p06Z169atY8eO3t7es2bNMpvNeBjhVjd9WXRWKkJCn/8zS2N76ezs4+PjcDhCQkLoGbPT6dTbIhbQEN0CeI9uEJmVtCjzhFAlDS6QaFUFZPUUb+XuALQy2NnoT0q48ZAyU1EUhmHOnTs3f/78QYMGdenSpUWLFj169Ojdq/fKlSujoqJ4nlWJjFOWRdZlzPhq6Mh6Hq809fhHO4+XJ5Rq9HsDn21Ngg60CN3XqM/Bhn0O1+9ztE7Qn/WCdtbz2/9B6K5WoSub+X1Vsfnw12v6eLzR1ON/Grz0+r88PFo0abhixW9Wa6YicSKRN8CZ48fPnDnldNk5jkgB8/zQtjx5AiNWqKp6+/bt8uXLr1ixAg2vsCZ0zOZdMWpDQYnsrV92cvLKFO2rQYecsxtFVcBqscfdjk+PTyFWjrilxhCOnLYVRiyit6ajfg40kRAJ30rdJXEY3AEPhhQQFbKSORXgCV4hhWof6pKcIDZJc1nCa0usXSTYxSYS+0lGBF5UBXKGQYAOI4JLJmaKmCGjRZrOHdeAetVGd0+4NGrH7SiSIZEmcr7EqZpGq0r2Xp38w9ahK0nITkAu4hU9ezU8QIYvCX6hCfldml6hFjWbLOqUaTSgKDEN1YAXBzLxTJmTRlv+OVYSeIUs5/GuXfVDDzQcBGeSSOZYYXSDjXE1UYFAe7d3t/iYTJtOkCT5Y1RS9JyNFcNa0a0/Tj/IN3z7LnyJWrnkLmamKJKgyhJRxOI15mtHI8gwzJJUh2abdzfN9+qLJWnAY2+6Z3rCoIFO37ie4cK2d+/e4OBgPz+/IUOGtG/ffvXq1egtGM8gqAcbOmnq3yS9WISEPv9nlsb20nVu0aJFO3fuPHr06Oeff44n8VSh775NyB5kdLTlEDwHPEeGoKAqOaCBaDPcN8OnkiB3B3iUamCMBpZlnU5nSkrKypUrQ0ND/7IXaNeuXRvy+fDsudPGjNSs1JTOdRrW9fi/jzz+NeH1Omvre1/tNPps435nagad8Ox13tP3WuXAaM+g25WCblUKulLB98jbXQ+U7nq4uu+xpn231++9vErHryu1bOvxSmOPf5f28Hjdw6O/b282y6zasnUhZZl4GSRak2R3lsfnUdpYJM+i7PD69euenp6RkZGoC0KHOSUeoiyKG/RzlCypLMNnpJtSUgwpKQbGxakKsIyIZg64rGYvrg9R5P0e0b8AOvQKIPTp75d33vcpUAB0357zN+/UGmigTChMGpo4N5ENRzgNNFhlYphqVQmGwOAfCnCaR0VwgX0j8R15sttk4owSDxHyX4yz8UF+lSv8dVqE+4SUAxryD7B3F7jQTApfrpbyxQINqAJGo0Hqe7y+iz8ofV+e66cPjuN4njcajT/++GPLli3HjRvXpUuXHj16HD9+nGVZq9VKFSxQbowiWVolfVn0YhES+vyfWRrbS1+fxWLx8vJKTU0NCgpKSUmhBzqFqX9+oCEjXd265WSWjQgPNedOWlBs9yFamBKevzR4SE87Lc/z6Ezp4sWLkyZNOn7imCzyUVcvN69ctb7HS14eJX6p+/Heen5nawWeLN/jbEXvCxV9rlTqfb1i76gKfrEV/O+UD0iuEGjwDLn1tndkKe/4qiGxdUIjG4Readj/ROO+W98P+u3DgNFVmtXz8Kj1v//ybt4SsqwgCIzdJsuCIGKUgnvcV+Dbf0bYikDh8uXLzZo1S0hIKMJa5R7UskTCN3CsYDKZ4+ISDIZ0luFZhtjWEbMCXFO1x4qwGjSr3PUpzBX6+DNC5MYH+V0huEEgZhrzgsfs+3QeHIohliAGhdhHOICoW96xwQ3bkT7TFlXrZvthN/G+xd1rmPD42kzXe/cZKXs+ywnJm631mEdF8s0hj7Rul1440JCeno5h7ogoR/cpzADIL42ep3Sq1V+kdGZm5pUrVyZOnOjr6zty5EhfX9/JkydHR0ejRRwmw32entaXS7Mi4qXH8NHn/8zS2G769gBgzpw5+/fvX7Vq1dKlS5Ezhax83qBBhUP7o2tW67hj1ymGRzPLFwg04O6Was+oqor+yDGAFsu6bl27Vv2tkrX/51+9/1lh44chB2v1vlC5d3S53rdL94os532znHd0eZ+Y8r3vIoZygbGvdUsrG5hWNvBWiW7X3/j4RlmfW1WDImv1PVc3cE9dnx2tQ37vEDKqdqtG/3ht+6Kl4HJpB9SggYY8+nkhX+4TSIbauDab7eTJk927d09ISKC2J1i6m+uUwlcp9+CWJZWI6Mm5uGw2W9LTjJYsG89nSxqycYPuscKXVZiUuowfgCxMzk8yTX4QIc/r5PTBxMWtP/JTh0GLGgc6Fu6HsxaIZoknhptZWpyqdSsba7amUST8N5/pIMJJuh4/vobRIvIBDTkC03vPvfT1yTcHfaK86RcFNAiCYLVaU1NTMzMzqer1A/T9ApNS1uIyhj9p3Adcw5xO55YtW3x9fcPCwqZMmdKtW7dvvvkmPT0d1RowDT6uLwqRDc2/mKAccONSenp6v3797Ha7n5+fzWYrGLrRTO6eAeoGGYERCpw7lVWx9Ee7d152OMgxMFpaPrPHE/oWFS2t5zPCWbvd2vOjDqU8PNr/483f3u+9q5bP9WqB0W/0sFTom/q6T1JJ7/hS3ndK+9wp55tcITCpUlBKxaDkCoEp5QOTywUklwtILB8QV94/toL/Lc+AW54B0ZUDrlQLOFEncGfTwC0+Izu9UrZ77UayOYuoq2vuHBjGQQdsIfVUipYD980N2cJx3K5du7p06ZKRkQEAqLyJmwE3HtKf982ZJsBHqKoEmn1qfrVFFD/cFTbQ3O8laFZFQtybd0G/iqS4IsykoLoSsJwjsNEIkIG1MJAppK09sbLNJ5ur99n9Tp9E32/FSeuFaZuvBcz8uXyXja0Hq39GEufQZh4YmYCGR/3gRuYhcslzB/QQ+dznkRcCNGBQn5SUlPj4eDqYi3Cn7sZjqjPB8zzDMPHx8TNmzOjevfvs2bOnTJni6+u7Zs0aOg9iNRBh5Aka3DIv/okc0A9+be8lDh8+PCoqKjw8fMuWLXqttII5luc4UxQ4e9zxTnmfbZuvuJwkIvYLCxr03EP7nXPnz/w/D49aHv83pdaH+z8MPV61V0LFwKR/93CW65v+mo/hTW9DSZ+00r5p5fzTKvZJrRySWjkksWIg+ZYniCGxfMCdcv4J5fzjKwTc0X7GVQy4Xi3wWL3AbW0HdPF448O3KgDLycQKWlZVWZYFXCxxNFFLUX3FngUa9aU+//zz999/PyUlRRRFFDnojTDpqo+9t/DVxvT0cQQNmsJTdrxpejxBxW808YOWVZha6UdfwXRhcnuSaQqurRtoUBWwO1iizmkEOBh3ufd/N5TxXvV2t5Vlu617139H66GrWg2w/v4nsTexS0ShgSuSbcXDgYa8Z7LHwdsXAjSwLJuenp6SkmI2m+lq7Tao7tOZCrytfzGYrSAINpvt0KFDI0eODAsLW7JkSf/+/YODgy9cuCAIAk6+uAspwLy78NtlfQVeEFr/QtA5ptFoHDZsWGpqar9+/R4dNJw84nj3nZD1qy+yxDkfChtkmZxz/o0+Dy6itNvtf/zxW/mX/9n+lTLLWvideD/0ejVNivBaz6yKfVPe8Ml408f8lm9maf+0cv6pFQOSPQOT3+mT6BmQUMn/TgW/xPJE2JBcxj+5jH9q2RzBQ8WAyCqBp2sH7n6/n4/Hm31qNQNBTrtzp127NmFhA7/5ZvaVK1dwAdb8RoqC9qHQ/Nl5HxgibtiwYR07dkxKSkJFEOro4tG3BLTPU9sNvYQSobMeo9D0xTPJw3QSNLggbM323wwpCpxNj5mx+vz4RYc/C49buR8MDmJvYs42qmSFHO8W9y8vzzUeH9ODhsILLvLMsPCP37/GNMULARrwYILOO9lvRhvE+nH10DTlJhIOh2PTpk3+/v7ffPPN9OnTe/fqPWnSpKioKCpcxVA3qOdYDBrcuFfIn/qXxXEcKj8OGTIkISFh2rRpEREReUqScmee91BT4MRha70a/Vf/cVbgNNtLImwgoAHLzZ3P83Iley9FmkGNzIjnmXs/eq7cvWM2WwBgy5Ytpf/vX21eLv9H676nmw+Krt7HUC4w8bWeGZX7JpX1N77tbyrpm1HaD0FDUqWApEoBiRX9yVdDDKllA9LKBqaWJt+0soGGcoEJFQM1SUOfzW1Ce/1f+Xlho4ATZOLBjBn96chhw4ZisG9/f//p06cfO3YsPj5eFAl0uFuzZ4NyOMhJCs/zrVu37tSpE1VuKKrdP+3zuDPBRuNFvIJiGFocTV8MGh6ug8gq8QZLXGGiAWSWSMw1LQCxVmJPQeJpyU6bnZiYcjIr8MSPZ6FK0o8vPY0P45XcdMFZ6/PR0wU/9TB3/7aggSpzoSIS5Q2OHxxO1BeQKIoYHBKPJ9HEi5yqCkJsbOz27dsvXLhgMBhwR4vX0R8OPoiZq6pqsViWLFnSsmXLhQsXLliwICQkJDw8PC4uzk3pko5qJLCG9CKtajFRSA4oioJRmqKiokaPHh0bGzts2DD9ZKqfPd0mUP3wukurcCuSr/FOtzUrTzCubNCAhpf6rApZvaefDCUKiqaaobnKIUfgiqAqjKowikLk//iRFLQvFSSVfiVyUXM15GJFSYZUQ1a7pm1qebz+ZX2vrbV8z5fvFVeyd8IbvWIrBCZ4BqeVD0ovHZBamggSUssGpJQncghDucCkkr3Mnv3MnqFJb/lmlAtOLt0nqUyfpFIBia/53Hijx9nawRvfCxpd7YNqHi9dP3lalgWWdSmKZDQaN2/ePHz48L59+4aFhU2dOrVnz549evQIDg4ODw8/depUcnIyihyoBBHNINHbun5xdQORj+mlyJLMcSTAYJ06dcLCwjiOw/6G3g4eU6G4/bBarYmJienp6dQ67Lnsq4+PRw+Vs6xqKrnU3QUPwGruKjkVBOK4gvQ3USY+KiRZynFvmn9ROMfkf//unbuzkZvCle4nptbnqafv5lW01N8WNCCbBEGgyACv5DmQ0KENRswTBCEmJiYiImLp0qWfffZZkyZNlixZMmPGDG9v70GDBn3zzTdRUVExMTF0G4HoBDNPTU09cuTI/PnzfX19t23bZjabMe4UDuOcmdn9fzFoePQ+TXHD0KFDjUbjXxEdr1+/Tv3SUI7j29cXl9/QNGUovy7bdeN6usNBQiWIsoqgAbPKnY8+z2eO1oEGjFQtS6qsMLJi176MqAiiLOOXV4WcL4cEp8rkqwCnEL95JL7o0Qs1Xi3X6ZXKv9b33V/NN6He0Gule516u9uNyoF33umDmo93yvnfKZctXUguF2D07JvwVu+Et3pneA6ILxNkeveTjFqfxJQLuvRqt0vVgvY17ze58getX6swIjDEZMrgVIEnxpZk22Y0GtGjSVxc3JYtWyZOnBgYGOjv7x8WFubn59epU6egoKBZs2adPHkyKSmJ4zg8/kMkQTuAfqvwBN6dLMnXr1+vVq1a7169rVYr6lHZ7fb7+oR96J6DMxhG0rFYLHr16ifQ3oeu9rP/oJuWA1ZYkYkTVbdv9syAGpT5Nqzwi3p+M5P+enZ1cKRoPwqff75VvO+Nvy1owLU8txgThxD+lSXZYiESVwQKP/30U7du3WrUqFGmTJm2bdt27dq1cePGU6dOnTBhwrhx44YPH96iRYtXX321bNmyb7zxRqtWrXbv3p2RkUF3NqIo4lG60WikAaUQW1DPj3T1ciP0tbrvOytOkCcHEDccPHjw888/P3fu3KhRo+iaQbmdewLVD0E9LUrgYmRBVAVJFiRRkMTnGDRo/CJtV0CRiOCEoASFEVU7+SoMr+rxgYr4gFNVTpUZEBjgGJAZVeUAjHYx0yGZrdyu9dureLz68UuV5tX02tko+GAN/yNVe5+s3Pt6Bb+4ikF33umT4BkUXymQflOqhUaX8Y8s43+netiNisEnXu9+/I3uZ6sG763uu7PlgCGv1nrf4zWv2o2tKQZtZ6dq+o/E+y4qGNLlFiV8ZrP59OnT3333XXBwcOvWrdG11VdzAAAgAElEQVSPKobu/PLLL6OiooxGI32QHvM/yVGmqurq1as7duw4bNgwhmGopnOeXbdILiJuMBqNBoPBYrFgzHQqXymSIl7YTPQ9B2k6peAkc7eP5Qsa9LOLns6PqZgGY7vk+VefCT0VwYv55Vk01/+2oMFmI3F1czNJ//rxADIyMtLb27tkyZKVK1f28fGZN2/ezp07d+/effTo0YsXL549e/bcuXNxcXF/hVJMTU2NjY2NiYlJSEhYsWJF+/bty5Qp06ZNmwULFiQnJ+OBoiAIKCmlilq4+9F3sty0vla561x8pZAcQNwQEhKSnJzs5+f3oKBBc5BDtrfaVxEVAV3WSqokKkJu0PB8vTWyiGou+gXtpJZXZJ0gQWVUYFQSEcklg0siEgXylYife/LVIganmkkaowMYhSCP3eu31v1Xqfc8Xhv475qrWwQfajN0b02CGy5V9CXOnaoE3KgamPPtc6mif1TtgTfqhJ18J/BM/YFn3xt66v2he5oPnFW5bWePN1u+VCqsQzfGkAGSJLhIoEsSfkgmGo84jmRJZhiGnkGgQB7fb2ZmZmRk5KZNm8aMGdOhQ4f22qdly5YYOOPAgQO3b9/GTeGTfF+qqv5V2+nTpwcHB/fr149hGCqbLGRnfohk2P+NRmNSUlJ6errT6aRSzCfZ9oeo+TP+iJ57SOvncH3MEZRM5NUcnFdw+c+ZYwoy0NSnzxM05MSwyp6xsEyKHvKqQhFd+1uBBpxEWJY1Go1xcXFms9ntABuZhrsWdFmzYcOGkiVLNm3adN++fUlJSVQ5ERWh6Zko1ZBA0QXuG5xO58GDB/38/OrVq9e0adOJEyempKTo30vurlbwFf2zxfTDccDhcGzfvn3BggW7du1auHAhVZfTc16fswwqLwou4gSRp3aVGiGLSraqnagIgszjFx160i6kz5bS+vyfLq2fnNDzvJ0RzA7OJYKdBVYkhuUMEJsyi0B0wDMZMDrhRhycvAiHT8DJ87B6k2v+D4nT/3u7T9/977w7rf/QXQNHrf/hl5MmF1gd9sO797WqUqeex6vvebwyseqHq1sE76vtd7Z+v4uNBpxv0P9wlV5Hq/meeDfwVO0+h6v4Hq4VdKTpoIj2o1Y0CfyudrchJep+6PHqB//zdtdqjbb+/AdIKoMRQ0icIgLctGDZZHLWT8o4WVNWUwKVCWw2W2Zm5saNG8eMGdO1a9f27ds3b968cePGXl5ec+fOPXv2bHx8vMPhwKUURzGJa5izu8A4cHlOGg/6HkVRdGqf0NDQzz//fMyYMXhSiYrPmBstSO/1nPZYTINTEG0mJfKrD85ULMtmZmaisYl+eaOPPwSRX4kv4HXknp6xd19TEUsa3EZwAT+f3Hv4W4EGNGI0mUyJiYkZGRlu2gzIVDxEsNvtHMedOXOmRIkSc+fOpVIBCg4oXMjvVaC6Pio6Xb58OSQkpGPHju3btz916hSqMlDBYOHHZ35lFV9/IA6kpqb2798/IyPDx8eHHg/p34I+N168q4RPQYMEwPDEokAGsDtd5HhCAw2iREyqEDe4Kbfml7++rCdPu80xMkCGnbmVZJ7wxcId+6+dOJe+/2jchp3nl68/MubzRSHD5rTr/p+6zUd7vjumrOekEm9N+sdLY6vV+KHE6/8tXfrHf7/2bany31at883rlUInf7053SZZXQ6r1SranCvm/ejbuHV1j//3ocdr/h6vjfd45/sKbX599+PfanX7uWqnBRVazy39weIaXv8t12roSzW9PN5o6/FGNQ+P2h4vd6/RZPeSFRjIEQBcPCdIJOox+WpSEcQN9wUNlLFol4QyP6vVmpSUdOzYsVmzZnXu3Llhw4Y1a9asXr16z549582bFxUVZTab0fcDPfvAd0rFEjTbRyGioqL8/PzCw8NxT4IzjCAIPM/TaQfVNrEU9CKPpzConU0Xp8L3MSwFQQM2R89DfT6Fpx+FCX+/Z5HD9NUUg4bn9RWj/QIiBirJpHAeW6WqKm4s0tPTq1WrtnPnTjz7RHMpPeS/LxesVhKODz8Oh2P//v2dOnX6K6DwhQsX8GLhBySmzMms+P+jcmDZsmWbNm1at3bd9u3bcSXQvwt97i6W4AAJwGyzYhoJSKAkUYV9B6/fjM7kRCBqDTIvSqwosYgFFc1fA7EqyPnml7++rKdLk7C8ADYZfttypEqDnu/U9q36bmCNuiF1GgfXaxbwXvvgFp3CPvz4P227z+nmt6an/75WbbdV8Pz55X99/fI/v6vkuf6Nt5d4/N/4Nz1HrT4Qn8SCUwvlLLs4wjuXADLE37j5w7SZbd+q1Op/36zp4VHHw6O69reRxytN/+e1qh4eNTxequ7xT0+Pl+r+q9S4Xn3PbtglJ5mIMZsWONjBsS6ey9Y/FxUQiX0raKEWcWrWc9iNpudQyGE65FGZAMcpwzDHjx8PDw/v3at33bp1//nPf1apUsXX13fmzJmXL19GoE+F+TRDmtXDvTsUG1y5cgVdxdvtdpPJdObMmcWLF0+YMKFfv37oH3bRokU7duy4ePGifr/h5uDh7rKkNf6+9cEmoMSU4ob7ctKNsfqf9y3xhUqg58w9dLGk4fnqBzabLV776Ie6niaRyx0O1Hz09fX9448/cFQ/kONh5AnHkeB7iD8wIiUAXL58uV27dh07drRYLPmF5runh9374/ni9rNZW3SW53A4+vXrl5yc3L17d4fDgQIhymx9zV2sqABk2IQzl6NJkAmixUA0/pIzoHpt32kzVjpYEFTi0piYVwnq7l2H426niiKRQ2iIQdBMFgXNfWF2Cfr8nxEad+8ikFA7Bg7O3nIdOW8/e1W5EgW3kiDBCMk2SLZDkg2SLbD3CAT1P1mq/JxS5Ra89sZ3dRtsbtPu6Julvvmgw8/Hr4IJwAySg+MlliciAUFRWF7keFbiiCTGxWbdur3l52VffDK8Y8MmHeo3bF2n3vu1a3du+eHg4JCFX889smd/VpKBxF+2EQRGgIxE+JZuNvFKjpm7qIVgzg7OrBZmqcNNOXJblog2BA5zN8kQmuYqinLz5s3NmzePHj26devWlStXrlq1ardu3WbNmnXs2LGEhAS3faTbHFLId4rihKSkpPXr10+dOtXHx6dhw4YlSpQoWbJk2bJlK1WqVLNmzX/+85+enp7BwcEffPBBlSpVKlas2KhRo8mTJ+/YscNqtbIsm8deVutl961DMWi4L4seJQGdTNyJYtDwKGx98s+iz0c3b4B5Dvjo6OiePXvq3/cD1RYfpONZn8++ffvatGkzc+bMwsx0+gfzrOcD1ao4MXJAFMXMzMwlS5bs3bt37ty5hw4dQn06ym09o3gBMq3w7Y87GzUPiothZIHse20iJKTBW2X9xv5nucWphbsTOUUAZxZ81Krf2WMJqkR0/AlcUDnyVZ4aaHA7gMj1U1FIJA3yFUDmQHUC2ACyAMwy2CQSxs+ukqi/Rg5SrHD6OgSG7nmz1BdvvP15lepfNXnvh2kzjD8ugcbNFrb3+v5aDPGWa5NFjqhCaoF5cs4RFEkmW2FZAUkiJqqSePcriyCLGr+0aIwYJoE4ytK+GOAHTySokymFyBhQzEDfmp7Qv8GC6cI8lZCQsGvXrkmTJnXv3r1EiRLVqlVDz2yXLl0ym82KojidTgxMhQcKVO2AOnShdWC0j8ViiY6OHj9+/Pvvv9++fftp06YdPHgwKioqNTXVYDCYTCar1WqxWMxms81mQ8eR6M/xypUry5Yta968+T/+8Y+6detOnTrVZDKh/MPtuJOWWDChKIrD4cjMzIyPj6dWXW5Z6Vl0X7rg4l7Mu8i0wrUdB2jh0pJUuQb0PVcKn09Rpvxb6TSYzWaHw+F2xOC2GOM49/PzO336tH6EPBBT8UEKGvREenp6q1at2rZtiwer+iLuSz9QHYoT58kBamlmMBh8fHxMJhPayuulu24PKgAbdsWU9ex+cG8CawenKPIAcWlQpnLoyHG/ObXttEj8DcGRvTE1K3pdOkXcb5DoggQ0MM8kaFA0b0yCAne/EvAcyIwmbLABWBTIEsEigVFQMiU4fws+nXrw9XIjylSaWKbCpMbvfTtj9vmrN2HxkqwKlSa0bf9NZCw4ROAAeJUB8l/7qECWdllRJFmVCWhQiQsICVTR/YtYIfdft5dBf2LO+YwZmqqoCLQ7YBjGbrffuHFjzpw5bdq0qVixYvny5b28vObPn3/p0iX0m2S1WtGLMwIIrCBWg+d5k8mUmZk5duzYl19+uVWrVngqQaEGFWDQ8wJUO0BEgpngkcrly5c/++yzsmXLVqhQYdmyZShy0DOjkA3H01in02k0GhMSEgwGA50e9bkVni5kuS9UMn0fuF/Di0HD/Tj0JO+jDhTdU+ZXNMoh6tati0cSdLTklz7P6/iUHitQGsM016tXz2az6RcqWlABRJ5lFV98OA4IgjB79uzTp0+PHDny0qVL+ndBM0T7JBHgeqz8zrs+A/rNBQUcouwAiE2FqrUHDB75A6v5kJVVsJth7PAfGtbyjb8lyAIIgpQtaSAeFTUJe86rpfk/ASKfnYikEJ/4du3rVIhggJOJwqEoqAoPCgOyC4iAIdECV+Jh0Nh1b1Ua/Gb50SVKj2vdafHi32MTjHA7Bb5fer5ajeFhYRsjbwHDg4Mj/p0k4GVgNS/UKGwgoIF+syUKRF7j9s2npk+ARwUWgS+NJsEzBUEQVFV1OBy3b99esWLF8OHDa9as6enp2alTp5kzZ165ciUhIQH9wyIOoDsTu93u7e0dEBAwY8YMnBPQIItlWTw0oSmxRHqIQIUWOI/h0s4wzA8//FC/fv2AgACe53P6F/lPK3xfAmsoiqLBYEhISDAajVRSos+wkPR9iytOUCAHikFDgex5kjf1o4j2/vwqYLFYmjRpYrfbaUr94/k9pb+OD1KgoCcAYPPmzRUrViyWNOg59sRonHNZlkWvur6+vmfOnJkyZQoFDSjsxTcoa3NvukU22eEjr9G1awUZTeCUIM3iupMK9RqFDhr6DYlWI5OzdmMGfNB0SB//aVYTOGyo04AKDeT9P3RfekTO5LkUy2Rdt0iQIUGWRKADpxDFDFFVVUkmLhZ4CRgJrsWJ//nv1jc9+3jWG/tq+f5tP/5h9RYmMp4cW7gU+Dr8YNVa/n6B39ld4GQg3QycRM4PJFVIMyVnVztH0pALNCj3goY8q/mgE+gjsqqgx3FlxXUd3bfQ1Ki6xHFcSkrK5s2bx48f37Rp08qVK3t5eS1ZsiQ1NZXihr/0aaZMmRISEvL555/zPG+z2axWK4oZUPnprgsgXXfBwwIsGu046F9MZTabQ0NDe/TooXvoAUCDviFGozE+Pt5kMrnhBkyjzz8/muZWTDwUBx60zxcwcJ6ES4Y82/hcHk9gj1cUBRcGh8OBq75+8dZ3en3L0UtM7dq18RARb9FTQ33Kgml9/nSXgFqWhw4dGjRoEM4FmAkdonjRbY2hWRVcYvHdgjmAbMQ+gOJfh8MxevTomJiYQYMGxcbG4uN0xyaDKml6eE4BLDb4bfmxchW9V627qRB7S8jIgEYNew0cOFXRQtxxKmzecucdz6CVf5y1WgDtNDUVSIlI3CWiQflU3mOek4qGCrJESBchU1TtGJxTVYBnyVcRITYapkzeU6veZ2Uqj6hQ89NOft//tP5SooOoSRpdkG6BaTOOVfDs13/gUjsLdj7b0ROnZYTKCNnvIsdBNdFmQEUEGjnznsNXLSYWvaUnCn6pT/wufYluhH5uEUURQ9IsXLgwKCjIarWi/aTJZKpbt27fvn3RqxKFCPisW4ZuG5Xcd/EKhvQEgJ9++qlr164Mw6CsVJ++MExCZIM1oROm24P6PPOj3R4p/vkCcuC5BA0o8bNarcnJyUajEUeRflS7rcr694qDp0yZMvPmzaPrOhomuQ1j/VO5af2gwqIRhZhMpnbt2q1buw4fwZyRxmhY1KGsPgekc5dSfKXwHEAe4rtA0MBx3IULF8aNG3f48GEUNnAcR6dycrqgKia71cVLsgiRkc5KVfv0HbiYk8jyZ8+CP37Ze/TIVaLdD8QDUtiIVXUbjD59JtPlIjJ4PMknxUnPHGiQVIGHLA5MnGrjZJ6XgROAYYFxwZ1YWPT9pWZNJlWtMsqz8iifwOWHz0KqHe44iHZkBgt3TNA/7OeqNQYNG7EyzQR2gYheXORsQ+UVVVBJ0++GCC8ANGiymLuaXHqgoKcL/4KfvZQ4Y6AvEFEUN23a9Morr2RkZGA3oz0N+2TB4z33XbyCUgf0LtO8efOQkBB0Y6VPXxjG6EEDVRXPPePps82TLkxZxWn+3hx4LkEDyhiSk5Pj4+OpByc3s2Z9j9e/QpZl7Xb7smXL3nzzzfDwcHyKekHJPYr0z+ppff4oYAAAi8WC0SvQWwuagaFjab0vF+pDpgBwoy+rmC4MB/CN4ASNf3met1gsfn5+qampAQEBiYmJVNKDCYibBS1rnlPNJujq/W3V2oNSjWS5413AO8k9ViKuBIwcVG0wpqf/UrMFiJ5ktr2lJmYQyd79cUsaciQKaArhtosn9h26QNcggMSBk1VdrCKyEtxJ4Z0cXLspzpt/olHDqRUrjqroOTgkdOmfRy1ZDsh0EbNHF4CRhdRMGD7m1xr1Ar/9YbdNgCxOcam8C1wcMBwBHpJEEAP56t4I0YS8J9A2qZ0eFyCte+I5J9G7F3UoiT7lFEWZOHHi0KFDzWYz1XPU90b9jIG0ng2579L+TH1Wrl69unbt2tHR0SzL6tPr88mPprnhnIPJaHiOguv5oGXlV4fi638PDjyXoAFlDPHx8QaDgS7zhQQN+NpYll2+fHnJkiV79+p96tQpFDA+kLxBP5AQFqxfv75x48bVqlU7duwYPZVMTk5euHBhixYtJk2atGXLlvT0dPRDhycaxaChCEeRflrESRDd6p05c2bkyJFbtmxZtWqVm2NdVuDtgkszjyBb4vXb0irWCA3/YZ/Fmo0MZAArRxDDjhPJr1ce8N3PMXanJldQVc1Jg0LOJp4CaCChqjXlBCmnfLLwU9xAgl6D7FBIzAgXD0YzfDlze71GodVq9atYdfCgTzaevQLpVmBEsrbbOZVVIdNJXFOM+HR5Bc9e332/16YxhQXOBQ4WbBw4eZURSKHyvaCBgJkXCjSgvBBnG3QFgVoLADBu3Lh9+/bhio64oeDFWN/59fOJnqYzCcMwcXFxlStXPnfuHGJfmkyfT340TYwEHSBoCULHBdXPcEtPf+aXf/H1F4cDzyVowLDxGJIKezPu3WnPdiPye51Go3H06NFly5bt2LHjsmXL/hJl2+32vwa/3W6nhkn6Z6lXVxxjZBvKsunp6fv370cBw8yZM5OTk9HDNCbmef7SpUtTpkzp2bNnzZo1S5UqVa1atZEjR65evTomJgZ1HTCYLwozsTh0UE/xkL4OxXTBHMBXT+dEfJu+vr6RkZHdu3fneR6hIYFrxLOAIoDEa/4dJRHiUqBZywktWkxLM5BCVCBn+ZkMMTEIGL6wVO2hl+PIGoxChez1IMf1wOOTNOTIGMj+XStNkknICKeoHR1wJASlxAHxuEC0EgFYhpdVcp6SwRDJwZxvTzVqPLZq9f7vfTBkwPBvz0dZkyxEdmKXINNOZCaCCi4WjEYYM3Z1laoBi5ecZASi88irwINColSrApExEICEMgZSI+r+gZhT3PPV1TeXiEF3L1tYUvDbfL7uzpgxY93adSzLOp1ONIvAQe02HdGfhWwdWl7Ikmy1WitVqpSamlrIB92S6ecTSicnJ2dkZDidTnpFURQ3Z2i0wjSNW87FP18oDjyXoMFoNGLsV7SM0vfpPOn83igebfxlTLFz587Q0NCGDRvWrVs3ODh48eLF27dvv3LlSkpKCnprwb8cx7Esm5SUdPLkye3bt3/11Vddu3atV69eYGBgREQEiXmk+aGjdaA4AK2z7Hb7uXPnfv31Vy8vr4oVK7766qu1a9cODQ1dt3ZdSkoKOi6kxyV60+386l98PTcHkPm4omNMMgDYtWvXjBkz5s2bd+TIEQRkFDSgI2hFJpL3DAtM/mr3O1XG7N1LpPoiEFPFTIY4SWzWafK7H4yzgmZBQBZM9w996UU+seoXWgoaRLCLYBXAyZHQ1cRtgqAt3cTWgyfOGVKzYNnqi63aTXrtDe8mzcd/NnXz+as2K6c1CsAqCVaBdwiCg+MZTsowCSF9/lu9mv/y5efMNuBEYqBJ/GCqRO2DwAWV+HTOCzQQmUcxaMB+uG3btu7du6PgoahAAz1+VVV11qxZkyZNwviZuXv+fa/k2TMZhjEYDMnJyRjgyq1b63s10vctpTjB354DzyVowAUV19fc3Tr3lfzeoqqqPM9TuQLLshjepk6dOhUqVKhevXr79u29dZ/Q0NB+/fr5+vp6eXm9+uqrnTt3Xrd2HWpKoxYkWmdRYwqMa+dmwYXVM5vNFy5c2LVr14gRI9CbbLVq1bp37x4eHh4ZGUmVITiO028C8mtI8XXKAf3bp4fBsiT36NEjPj5+0KBBKI8l9jKadwEyS2pLsaAd1J+9IlZ4J6xP/xUGM1y6mXUtJjOLhRUbkyvUGvpl+DGTQJZSvU4ZnWTdyqX1KZjQAwKkc6fH66i1oB1GSCIIIjlbcMog4HVRMwPhAO4YiS/LRb9ertvs04pVB9SsO2jGN3viUolcgVEhi5PssuKUJYckOgSBI36xIcvG/vjTyrdL1V+2bA/KVzgZOFVzRUHyJ0EgsFY5NST/NedR5IhEI+4KHnQAIsdiQnsYn8VIm5R2I3K3/fm64nA4SpQosX79ejS3picU+r6hpwvTOnQXoSjKnDlzXnnllejoaBRkFubZQqZxOp0GgyEpKSkzMxNr7nb88aB1LmS5xcmeUw48l6CB8lrfmwugafrcBG4L8OAQzzhwJ2o0Gg8cODBnzpy+uo+vr+9f7gXHjBmzbNkyg8GAh5eiKNJ4Fvr8cWlBQw+n04nnHaqqostCVEEym80oLElOTt69e/eQIUOaNWtWunTpSpUqdenSZf78+TExMRiuM89dgr64Yho5QLsBbvWos6/t27cvXrx4+vTpp0+fzlZe0awEVYlYXioy2Z0TVVYWQgb/WqX2sOgkaPXRZx/1GJvFwKQvT5auFHb4osPgAEnNQ8zw0LopbqtmnpbXmEarpiqAKpB4WrKo6TSQ9DJZphWFRNi6Y4RVW6+17DShat2wVu1mzv/+UmQMOcmwa7oLZoalAglJO8ggoEoiKo17D0Ss37RHC91FRBGcKvMqp51RcHrQoOtj2aABoYPuqELvniEP0OCmsOnWfF3+zys5cODAsmXLXrhwoagkDTiBzJkzp3379oMHDy5yvuDEoihKSkpKfHw8yhv0oAFhMR1WRV6B4gyfOw4866CBSuntdjsu8LT7Fp7I863g43SnqCeo8rOb0ZQ+TX40Zoujjq4lmJhmS4016BV8CsGHyWTauXPnsGHDmjVr9vbbb5cpU+YvwcZ333135coVk8nkdDoR1lDTTWxdAWZUeTb/b39RP2srisIwTM+ePS9cuDBkyBD0tEM4oBDEQEADMb+EO6k2lwo7/kx70zNw/LQzLdp+16brNyYHNG+xoHHTzxPTyBNEFp/Xu9f3xoJ567ZSuv3M/ay2DpNq8kCcOfJkUVedoozrPWMHUxpkGGDHjtvtvSaUr+bTrN2wWfP32ljikcmluVhgZZWVVSI/kImmgqDe1ScQJBmDQ+FfXlF5osTAiQojkaMYElaD+rvU1S271ggaNATi1g7tp06nIa/b2dWgt3T5P6+k0Wh8//33mzVrZjKZULmBrsrUWQsKOKneA417h5MGbmBQsYBhmOTk5EmTJnXq1Mnf3x83HrnPZB+FWfpp0KZ5o6K2YLixoZ2dzmyPUlzxs38DDjzroIEqG1IvZnqPfvqZugA6z/ekHy10YBQtUUCVct/ColmWvbukAaSkpBw+fHjSpEktWrR4/fXXS5cuHRQUNGfOnLNnz+KxCMMwKPCgbaRn9vTKi0m4vV+e58PDw9etXRcSEhIbG0t8fDmdiqjqQINCIkcLcDsd2nSf2eCD75t++Hvdpgv2HoDqVb+aPfsCy4PJasvWgcjVUfQvtGCG0zVST6C6wL2mjNnZIGjQdBJlTlWJfqJKDEFZTdrgcMLpUxndu016913/j3tOXfL7qdQsYgrhEoAVUDtB5FWOV2Rec/mkaSog9CFHC6Ks5nxlUZY1xCCICicqnKRKkprdXGxdth0lqVd23fFsgv50J1480CAIQkRERIsWLapXrx4fH48HZHREOxwOqhqJt6jCdTaHtXdOcYbdbvfz86tcufK0adOwN+DZhBtuyO4oD/XPbZjgNgY9StFNGnb2wvfwh6pI8UPPDQeeOdCg75oY5thkMkVHR2dkZFAnTvo0haHzfBuFefAJp8FRiuoRVEpBj07MZvOlS5cWL14cHBxcvXr1UqVKdenSZcaMGQgg9F6ksL1UDTPP5rtdpC11u/78/sQW0cUdANLT07t3737p0qXZs2eTdY+EupZzQIOkhbcEh0zsDr7+6dwb5T6vUXf1O9V+GTv2TtV3vjp3VnNTQLwwU1Zlh2x+0ClVL8zXzhawCuQvzTzbu6LG/RzQIHEqAQ2cQgABCeedCcdPJ3f+eOI7NQO8/b7YsOXy7TjOzmhqCCIIPAgCCJIsyHw2CCBGojn6jJpiI4kDnqOVgLoJ2ZBCwwKo/HiPVchdEEBBA9FmuLeT6LDQ3fQ5KMMdVtxz/d58ntdfgiAYjcZZs2bVqVNnzJgxu3fvjouLQ7Ms/SGjLMkYpxtVoFBpF73ImEwmAIiIiGjcuLGXl1dERATDMKIooqwCccPdXvggcShy81Q/TOhdlIVQWWZ+dpg0fTHxQnHgmQYNPM8bjcZE7YOH0yjY1w+YwtB5vtHCPPiE01B8gO5isL0sb3UAACAASURBVNp6JEEPaxwOR2xs7KZNm/r371+jRo1q1aq1b99+8uTJx44di4+PpyoUeTY8z4u0pXnefR4vYosoaMD+M3v27G3btgUHB2dmZhLcoEkaiCKkou2qNRsEgwMiDfBu44Uly/xYperadm33N24wJzU72IKk+STI5hbNnCI8vFEwu+4FDYoEJChkjp2CtqiiOYJMbCjRzFI7myABJMgRg0TsIzZtPevX5z/v1u3ew++LdVujWZncZbTYk6q2iJN41CRrWZYFScVvttkkqaSiGY4WABpkkDWEkZ1Sa1hekgaECPoWU9CQ4+FJu0mvFkDoc3nuaD0gIF1LURITE7/88stSpUoNGTLE19e3W7duPXv2DAgIGD58+KxZsxYvXnz8+PHo6GiLxZKenm61Wk0mU1JS0o0bN+bPn9+2bVtfX98DBw5YrVb9WSfiBjdp66PwCnssdmDMByECYhSccKh0BBPTv49SbvGzzy8HniHQQPsi9lpFUUwmU3JyMkakxY5L/S/RxI/IeprPs0AUpi1u9RQEweFwWCyWgwcPjhw5smHDhrVq1WrXrt2ECRNOnjxptVqdTic6tcVJjT7uNk3Q63qiMPV5ltPo28KyLAAkJSX1799/+fLlq1ev5nmeYRg0nSChnbXFWwRwAqQ6IPSTve/WXvbGG+ElXv3yi8lnXMR/B5Eo60GDPn89XTBPEDTkuGaSJBLIQtJAA9n3E9NJEn9aM4fQln+LM0sA2c4SAJGUDJs3R3boMKZO7cCQkJn7D8Y4id8l4k+ClYgup6zhDLJo5TiQoMiG1FDDCiQjNRs0UEGCdj4iY1wJ6sGJHpq4CRN0DdQwAEoUdHIFXYJ7SGy7Ttxwz92/0w+cxJxO54ULF8aMGdOlS5evvvpq1apV+/fvP3bs2L59+9atXTd16tRRo0YFBQV169atYcOG1apVK1my5MsvvxwYGHjkyBE8mc2PJ24YJb9k972u77d6Gm3L4+Li0KSC4gY3fEwfuW9BxQn+Nhx4pkGDHjHQGPa0myLxiG/CLbfH8fO+NaSF3jdlngmovhLubxwOx9GjR7/++msvL6+aNWt279596tSphw8fRpmnoigoFEV+oknn33UioIzVz7ATJ048fvx4ly5d0N2vJmYgCyuCBgFUDsCpwubdbPmK08qXm1fV8+vD+2W7BUSRWB4WKWgQNMEBLwDRPeRVgYiaEDSg1wUAp1PzMcWDzQ5r1lz17f3Vu+/6BwTMOHw4VVHBwZBwlkR7UfPRhAcKuJWnsgQ3Ivs8QPMDlX1LY1MOXNCrRSJNXEBinnl1Pw1OPDxoyB+N5FXYc3QNQQP+5ThOEISoqKjdu3dPmTJlxIgRISEhPXv27NGjh4+Pj5+fX2Bg4IQJE5YuXXr58mWn9kFZAlWGeHwN148RPY3eVI1GoxtuQAyqT4n046thcc7PGgeeOdCAnRL1caiMIT/EoF8MnjXOPu760FkJC8IwNlT1mh5kXL9+fdWqVYMGDWratGnHjh3Hjx+/e/fulJQUp9NJHVxiVrmng8fdhMedv35qQ4UYhmEiIyOHDh26cOHCY8eO2Ww2bLUGGohWgWbTSHBDbAq0bD2vfIXJ7zX5JiUpu6Yi7yC75JzAC/r89XTB7dJJGjiRBNR0csRXtZWHLFF1ksibgmbQIRG9BEsW3IqG35ZFeXdb8G71sAD/2REnUpOSWbuLwAUXp9D1GpdfKvzPdseUo7uAZxakYvQBSmjVzTk0Qd0G/d+70S7ybRfNKocz+aXMJWn4O4MGOqz02o6osURtndCikhpWUL6pqsppH3rlMRH6fqunsTiUN1AXDgXIGx5T9YqzfQY58EyDBnRpgJHm/6674UfpE2goUUAOFFSh1lVkZOSGDRtGjhzZtm3bLl26jB8//q8D/tu3b9OF043JBeeMU0wBaZ76rdyTIPr0HDJkSEREhJ+fH8pmKFrSgmUT6MABMUD4ZNSq0mX7jxi5iXGRiNISn+OpOWdp1OevpwtuuLZwEpGCTIwbGA7sHFhZsHCQxYOTiA20e4IE6WmwZvXNzh1mvFttpE/3H/buymI5yLQS1wyMyLoERsrBL7hqY7kUN+QtHtAv8PrH7nqG1iMGKQdMFNgmfZ4FJnwxQQNGY0dzCTwmQ+hAWYVTHFVpompMucEEfaSoCH2/1dOYP8ob3Fw/0e1K7vRFVavifJ5lDjxzoMGNWfp+mSftlv6F+kknl0K2Ws/ApKSkvXv3YlCMv4IyTJ48ee/evcnJyRaLJfdU9VcEP/RriToluOGgay3NtpDVeCrJED9hVc+dOzd48OBRo0bdvHmT4gZyyqPZL2jyBki3wa6DUQ2a9D10JJnhQCZOkDS9QUUlEZoK/BTcQNQ+lIlXR04AliO+qiWn5HLILhnAJqlGB6Rkwuw5W5s0HVytSlD7thM3bUhwuUiECJcALkkh0a5VQQtUTcwmSRNyiqSIIeeC9l+/qOdHawlzIILewyPN8h5nTXlILHLnfE8l8Icut+yTkjwS/T0u6bucHpdTusBOdPfmU+EGLZ7WVr+jQN1M/Ispn0oliwt9Khx4VkADOjNxOp0MwwiCQLV2ad/Nj3gqXPt7FIpWXhzH2Wy2iIiI6dOn+/j4tGjRAoP1YdwNNDrA0yK93EKPG+hs8iyzRd9/BEEICQk5fPhw//79ceeHM6MONKhWgbdJapzBxRCHSIICnAqiqjmRLBLQgIiBIZIGlQSMUImbZx4gJkOeOmdVzUb+VWv5tus4YcWqy6kGSDFku2lySYpLFjiFRdcLWmAIzYoyx18TXZPveRe5l/PcV7QHikHDPXx7tB9FAhoerQoP/7R+vCBN86LtKgYNlCcvFPFMgAY8wDObzampqWazGSM/oUwvd991u/JCva0ibKzD4UB8hg7pqIWF0+k0Go2bN28eNGhQjx49Bg4c+Ouvv8bFxdlsNjwtwpniuQYNoiieOXNm4sSJoaGhx48fdxM2aAaPqgCMU7WqxF5C4CFLBovmG/F+Qgatd+pfE67ibldkkASixWh1AO9QwOQgzpvPXZfHTdvi2XBQ5UZhLTqNXfT7sUwGLEy2D0dOFrWvzMmyJmlgeC1glaRKev3HhwENuso9MGjAZ/UQRJdbXiStICXySvX3uqafsvLcuOsTuNFPixNu1aD6Gfr6I40pn1Y9i8t98hx4JkCDoigOhyM1NfX27dvofhUZkbvj5r7y5Fn29ysRBQnU+JsG/pYlOTExcc2aNaNGjerQocPgwYMXL168f/9+s9mMJhv0kWd/4tD3HFRDCwwMXLd23bRp0/TCBtIuEs5REcBllUzpjnSXYpfBrECmCiw1ndBPl/qc3fhA/DJpzo/o8QEqIcgg88A5VNGuBYY4dYH/9D+bq9cf8panf+O2E39afTMhCzJFyOSyrSNtbBanOjiFzcENIq8iaLAXg4Znfzzqe4h+0dVfz49+Wq1zqw9WGycKnB/c4gU+rXoWl/vkOfD0QQMKyVNSUhISEsxm8/MyqJ78q3p8JbpNEPSnW4kpKSnr1q5Do/OuXbvOnDnzyJEjDoeDuoKg4R5QpYvneTcX124ZPsWfLMsePHhw3LhxQ4aGpRqSNaMCRVVl0v20amkqDLhmKwAsgF0Fq6o6Ud6g76VIU6bRQxxFM4PkZRLjCj8Sh8Eoed7JOEUw2ODoGan/oHVVa44vWzGs0fufLlp+0qGCA7K/DClY4YlYQhJknnwlUZBEUZZFJdtlEzlSyTmbyIufuSUdeaXSeU64i2+yE1KRgBuRdz7FV/PkgL57PBCdZ25P8SKqN5nNZoPBkJmZiSM9txbUU6xhcdGPmwNPHzSIomgwGBISEjBupH46LszoetwMehHyLzyfMfITANhstjVr1owbN65ly5Zt27YdO3bsjh07jEYjTiLo9faZZZ3NZpNlQZR4r66d5377zcmTx1QQecFFBP8yx4scKwm8SgI05Cy5sgouBayyaiVpJBm/+fVVbLgGGhROJkEfRCCaB5JIJAxADDFg+774bn5z3iwd9PK//d+tO+HbBRfvpJHiGPJVnNpXQwwKOosUiWfHnD2eTOJEYFgI/dlEXgzPaUFe9/TX9IhAfz2HB/r7hc3z3nxe6F+FGWJ5pnnWuMYwDAAIgpCamooxeDmOw8OLZ62qxfV5TBx4yqBBVVW73W4wGIxGI/pUz28iznNE0V3dY+LOC5JtfrzVX+c4DnUg0HIMOY/qqw6HIyIiYsaMGXXr1q1Tp05wcPBvv/12/fp1i8WCTuyfJTaSBY/4f5Q5AOnI/2/vSuCkKs58cwzMcMxwOOBiRCMmWQPsml0xRo1RBEGjUREv1FxKdFVWIUoCisETiUDULIjmEIWNmmiiiRdh1RUPLgENwgjMDH09+vUx7+x3H7Vb75suiu7pmZ5hphmYqt/8eqqrv1f11b+u/6vjq/f+/uk/NuuGlDWFrClYnrSn8fPPdm6NJMImCjYTeNgcgm6Zup01HdW0FNsx8ZUVAW+AYRs+aaxIfvEyhG9kXU20zLSGkjKK8Ojp3zadcfbyEcfPrhnxgwlnzV20dG04ibIOZgyiiec0DOTr+NgnNhoBN2LjT3xzRLOjKUtx0lA4zOcP9m1L4JwUk8LhuT0QB4RI3pmnRQToelKKv8VIDmMg9NIIIVEUo9FoJBLheR52RB1GrVjS5USgrKQBGgmdPddxOY4zDCM3K4yvA8r1je3edEbHzPylI1Bi5wUmtiBa2AcAexrgXjEtcPF4/LXXXps3b97kyZO/+tWvfuc73/nFL36xbt06uPGvdJW6TBIPda5r+chWsyJCrucbtpt1kPbm31+98eYZx35pSP/q3udM+vbmbds3b/ts89YdW7Z/vqtub5xLyoquZDU8YLdFGig8XQcZiq3yqr4vjR5d/tFp5/2yYujskSc+ctJXF6z8TfiLeiRbSLXxVITuo7Rq6YFtJ7AxdYAxdJw0wD0W9MB/AFo6lPYfkMA++pd8PyMNB2PV9jeqbpTkbTvGskiArtAzk1bvOm46neY4ThAEYveJ5KoserFEDgMC5SMNpNrBexL9qkrqWQc8hwEzlmSAAF1YZDdDbgLdRghxHPfaa68tWLBgypQpxx133KRJk+67775169ZFIhHLsmBWEyEEExLASOBO3k6/YQTOR8A1YLquu65lmvgqinQm8eLLf7ji6ssHVleFQqFQn1CvvqHKgRW9+uJvVQOGVvSrqaqqDYUGVVbW1lSP/tKXvjZ1ysXLli1bv359JpNRsqqSVenq4CGU1XXCeoN7JR0bobfe2/G1U68ZctyVw78889SJj81btCUpoCYRyQo+RKGYHra+4AVzGwgBV3ARIlc/YKtT1EwDxN+MP1wnQSvR7M8f4HPD/wHRtiXwURnqr4BAMNJwAM2e4aNbPbzgmaYJpCFvWzRI9gxUelYuy0oa6KEFahh90jevOpb4tWcVV3fKLV1A1DCJvfDaQZQ1TVNRlLVr186bN2/cuHEjR44cO3bs9ddfv2bNmnA4DJNMcHcwWNXt9FUnMn1lmqbr+KZpv/Xm2ltuvnX06BNDodCAQdX9qwZMnHTB3J/PP/ucc4cMG1Ez5JjqmtrTJpz9z6ecNmTIiaHQwKFDvlbR5/iBA06o6DMwFAoNHjy4urr6tlm376zbhVcNggHZtC3NNCzHBlqMaZCLr6swPLRtB3/muTO/cfrNv3zioy/i2HJUNosMDZmGq1umaRuWq9uehe0uBEsScN1DHmnIA7kZf0YaSD1jnq5HgG71xE86drqKwq9drxFLodwIlI80wHgAL5SqqoLVIBgeSOXrgKfcgLH0cgi0Ulhwry4YffI8z7ZtKGjYJikIwrp16xYtWjRx4sShQ4eOHj36kksuWb58+ZYtW6TAaZoGd/wQZplLs+3/tFY5aTym+76vaVqSTz/++H+NH/fvVZVDK/sN69O7urb2xOee/9PO3RFFwy/VGcGLxtWzvn3xg488jvC0AdJ0tH8/qtuVPfusG84/74aFCxdPOOObw0fUVg0c0KeiIhQKff1fx6/679VcIuEEBy/wZdaO7zq+7fqm57sI8YKguyi2X86kfUsLXtzhNksH+Z6GN1f6Ta7f5CHVxTsoXKAgeQsDkC9UaI+SkYZcMbP/ZUCAbl/ED1zhiLPdUga4jsokyk0abNtWVZXneUVR8k76kirYLs9RWSpHRKZaKSaYPIA7+oAoEMoYvOvj92+EkCzLsVhs69atS5cunThx4vHHHz969OjJkycvWbJk7dq1iUQimUy2Fwpaq9yzeBSWJGnpkl+NqB1V2b+6etCxZ33rwl8tefbhh5c//vjvZdn3EUqmXVFCTU3o1tseuuPOhyTVSQm6FWgqSWj27Ccu/u6scNhSdHyAMhyNv7t+w8/veXTg4FGDh44I9e37zTO/tWr1KlERZVVxHWQHf5gCBEqIWQUvjuiB4QUP+WowNYFZioaQ7KEmD4kevlyTkYZcobH/3RIBun0RP7weMNLQLUus85UqE2mA+WHXcTOZTCQSicViMHiQakc8nZ9FFmPXI0CKDzwdSNB1XEVRNmzY8OSTT06aNOmEE06ora0dO3bswoUL33777XQ6Ta4KJEtasFNBkiRyg7AkSbQmuakO569/e3XMmDGhUKi6pvZHP54VDksIoW1b991y67woJyOElCzeXiDLaOHC33/vsln7U15TNisZWlKwdQut+cMH3zrrmvp9WkZGWbv5KKYgofvuXTP5/Nu3bo/Nvnv+Kf8yrmJg37Hjx73+5tuptCzLeFeHpmPS4AJDAFCI/YdmjFy8hwHfh+1gM9V4YgI7mGygP5vFg3/tAZlMW9ARdNQP+xs6+jR77qhHwHXcVCq1Z88e2Kh01Oe3Z2awHKQBGINlWbquh8PhSCSiaRq5sIDu5Tt9MbtnFmr5c33ohUhu/5NlGSw2btmyZf78+eecc05tbe3gwYPHjh07b968V155JRqNEsYJOQWzELCwSmsCOx/nzJnTp0+f/49k6ZInRAnbofE8FAlrN86c94/PY/uTquXi0d0w0Lat0gWTb+FTyPKQ7voWQrqNPt2Rnjjlhxs+iVgIiYavBdc2yRp68aVNZ5xx46dbDVlBkupF9ycXL102qHpYr96Vky64ePeemKahrNY8/LdRIsFgTFMBmi4UDvu0ZBsxl5Z+W5HkfmekIYcE+98iApZlwRH6aDSaTCa7rW23FpVngSUi0OWkgTAGRVG4wEmSBIvcdP9O/CXqzcSOJgRgTZTOETFljd/XNW3jxo3PPPPMhRdeCDMQp5566nXXXffUU0/t3LlTFEWwBgFMgt6KlUqlpk+fPnLkyFmz7rBMzzKRoniqikwD3fXTR996e5ukYFpgukhS0eZPhBkz7t9V5zg+UoNjkKKOdu/LTp9xx0uvrldtpLpeNN3ENWmqiT7aqJx59k/e/3CP5SMZW7vBtps++OgfZ3976vBjjh9UfcywY47dsasO5gzoiQY6j634WycNrTxY8FMh5SgQKT2AkYbSsep5knDRoG3buq4nk8loNMpxnKZp7FXwKKsL5SANtm0ripJOp3ft2gUvkaqqEpaQ5znK8GXZKQUBct+mZVnQxRDSAIcwYbkU3mM2bdr09NNPT5069aSTTho+fPjJJ5986aWXLlmypKGhgZySAOowd+7cqqqBSx5bZuiOkMFnLBW8tQD9atlzq559XZTw1dSWh5cPUhk0e86KnbvcjBBYb0RIc/BKxMxbf/Hn1zfwktOkWU26pgdrDR9vTU357vw310YUAy8tZC2kGijGWRdMvfbXv179zrubqmuG9+rT+5Rxp9iekVtqKAWGAzKMNBzAgvmOBARgozGZL/R9XxCEPXv2JBIJxhuOhAJsh47lIA1kJUJRFNhL3+KJXmAP7dCdiR4tCEDRk0kCmkeSwDwPzFft3LlzxYoVU6ZMGT9+/KhRo/74xz/CfINlWdFodPCgmutm3KCqRrAJEYOl6+jDD3fNmX3/vn0iPgxp4VFfyqK7f/7kM79ZB5dE7M8gxUT7OHvJky88/9JayQwsLwX7DnjJ2b5DnDT1ttff3i2oeIoC70fwUXS/cdNPfv7X1z+GayCefe6/+1dVhkKh//3gnY6RhqOlYFk+egQCee0X8mzbdiaTUVWVbIXOw4I087xw9rWbI9CFpIH08qRytMkY2ERWN68uXaReXqdDKkzezAGpUUBDDcOAiSvYI7lhwwZQD/ZFTp8+vaZmaDrd5HvINpFtIDGNvqgTfjJzfipp6RbeeWhYSJTR/Q+umn3XklRTQCCCyYOMgp5/8Z17H1guwNJDYK5R91Ek4V517fxVaz5CwfZFWcNzDKKMbrlt4TvvbTNsZNhIt1BWc8+ffGEoFLpx5k2BSgWXQHURjixahsDhQKCw/YIWYKWNaES3a9pPBJjniECgq0gDuZWAVA5iAISEtOg5IlBjSnYuAlATCCegKwYJzPMQfkm/x+AdkY6JkM/z+ysrK6+YdqUsq5btmyZSJJRKoB/c8LO6LzKgvKgZoopWr/7koot/tntfVsd3Urlp3eIltOblDy69cqZkItXBBxskE6VllJHRjO8vePp3/yNqOKRJs7IW4lPohu8/8PKft4LtRITQ/iS2EblgwWO9elUvW/Z05wLFYmMIdEME8tovcPpCPWHNkb45BR4slGQh3RmBriINcIIunU6TAQA6ffK1mKc7g8V06yIEoDIQWkDXDRJIe4iAZVlw7R7ZA+Ej2/Os99e/V1HR54ppV7oOUlRD01A8gr479ba//GWj5aL9Gc0OlhXefb/uOxNvX7supgVHHfmsJFju2vfrzr/oRi5jwFFI3UdNWWzsed49K59Y8VcujQyEElI2LZuyhm6c+cBzz22UVSTIhoN8KWsJkvfs7187f+KVvXsPW758FbbFwBxD4KhGIK/9kq4+L9MG5UgTJuw/T5h97bYIdBVpMAwjHo/v3buXVA6ys4GEtOjptkgxxboUgRYrQyuBLXEI18fbD/DSwR//9If+/StOn3CG6yDd9MNh5aor59/905WmjVTLNwMeENmPTj/zhocXvyhqqEnzNB8bWvpgS8OkKbPWf5zQ/Ga7TKqJN0suWbp66bLVooqPMNoIyTre0HD3XU8uX/6GpiE5uIDC8vGeiRdf/Ps1V//niuUv9K0Y8qeXX+1S0FjkDIFugkCxpkqrl0gkIpEIbI0k4bT9FRLIPN0Zgc4nDTD7xPN8LBajje0w0tCd68Fh161Yp1MsvBhpsGwVIXfH59v7968YM+Yr6ZQsiOYPvj/7ogtva6zHBywdhBQbcWnn6uvumXP3iqSEr6XGBysstOWz+OlnXf3cmk8kDUmW5yMkZr0mAa18+pVFi39nuUjKWpKmOgilBG/2nMfuu+83hoE0A+9jEGTHdNCGj/ececZlDXvViROn1Qwdtnnr5sMOLFOAIVAGBIq1UzppSZJ4nocLtfXgXjf6V+Y/UhDoZNLgOq6qqul0urGxMZVKEeN9JTIGNlV1pNSbTtezWKdTLLwYadANyUemrKSvunpa//5VL734l6uv+dFNN8/dsDES44IrJTWUzKCfzX/ykstuSTQhw0eShRIi2hM2zp96038tfwMhbLbB8pGoogTvPvf8mw8+sNxxkJr1TAtppq9oaNHi391773Jdw1MLsmI2CZrjos8/Vyb82+UbPgy//rePQ6Feo0aPUPR0B4w0dDq2LEKGQFcjUKyd0unatm0YRiaTCYfDHMfBYTpagPmPCAQ6kzQAYxAEYffu3YlEAuadoDIx0nBE1IbDqGSxTqdYeDHSgJBju1lZSX+8YX119ZDTTzv7r39b98BDTySStuUi3UCmhV7+8/aLLvmPJhkvNIjBcYnP92bPPOf6+x9YI8nIdLC9JtVAhole+fOHd85+WFHwRVFNgiGIpuuj59e8cefsRXwSYTtRZjNm+xrd6dPmr1n14c4dmZqaL1X0r3rltRc0uyk4ZnEYcWVJMwTKgUCxdtpi2rIsRyIRjuOIXYcWxVhg90SgM0kDGOaTZZnnecMwYNqgWGUqFt49YWJadTcEWqo/eE8DvvMJ70/A9zisWLGyf7/B3zzjvO3b91ouNuosK+iTT7QZMx78Yo+TNZFqIl70Gvbbky+++Wf3/LZhn58WMF3Alhx9tGlz49y5j3KcmtV8ODRpGngBYtbtD2bS2KykaSLLxrdSKjL60fcf/OXDr76zbvfJYyZUDRg644brBTmTd+9Ed8OQ6cMQKCcCdJtNJpOwhRlsvYMacIK6nCqxtDqAQGeSBoSQbdtwrzFZaKArSin+DuSBPdIDEWipLrm+38wbgDSIgjxr1uxevSvHjBm3ZeuerIae+c07F198944d+LBE1kQZCfECuvzqn97yn0sUHVkunmZwgisnIrHstdfdynEyvqk64BC6jv7xGT/rtodjUR2f4cR7G7BranIWL3rurjtXLnn01eHDTqmsHD7pgqnhWNR28e3YIMM+GQIMAbrNEsbAYDniEGg3aaALvjC3MNlAGAPZ00A/1bq/ME4WwhAoRKClWkRIgw2kwbZdPpG56uobQqGKUGjQ+PGTpk2744U/bORieC+Cj/AWhx/PfOyOOSu/aLCSElIMpAXLDbv3pq648qZtn9XLajarY/vTpoE+/mDf5d+7I5PCEwyyggMRwisUf3ll06iRZ445YWIodEwoNODSy6Ynkmn41TQQO3IJULBPhgDdZvPQgO3zeYHsa/dEoJNJA0w20FmlK0opfvpZ5mcIFEOgpbqUTxrwDIGLVxAWLlw8cPCoUGjgwEEnLrx/5c5dTdnA1OOqVWtvve1XkSjSA65gudikYyJp3nTz3P95d6ucRZrhWI5rO2jHDu7y783a+FHcNBBce61q2rbtOxYseOzYEf8WCtX0Cv1TTfWJ9y18hEsknWBywsJWphhpKFaALLzHIUDabF7OTdMUAseWJ/KQ6Z5f20EaSJET476wRfMgwgAADrtJREFU1dGyLDgoAfMKpe95pCMk/u4JE9PqSEAArnlygr2HudsdfWxZwXHRzl31l0+7tmb4cYOHHBsKDZh8wRUPPvjE5Vf8mE96jovtSbs+EiTEp6xbb7/vnnuXWSbSNIQHfoT21O2fOvmq1c++Yekosi/99lvvzplz1+kTzghh16tf3yFDqkdNmXzph+s3a1kLgPJc5NqoeSvEkYAd05EhcLgQ8DxPURSw66MoCpmoJoMCCTlcGrJ0aQQOiTR4npdOp6PRaCKRgEiBT9CF3V4/rRzzMwTag0AeaWh+FEJVzfAQinD7f/3UymnTrwmF+lRWDe1bUX3ahHNuvuWnv/3tC2+89SGX0B965KlLLv1hOKpqwXHKWDT78Ud1k86bNvaUb9704zvHnjJh0IBjQqF+oVDvfhWVvXr1qakZ+qMf3vjee+9LIr5AU9dMQ7dcx2d0oT0Fx2R7OgJwFJMLHOEN9NjR0wHqTvlvN2mAo26wBCXLckNDQ2NjowJXDiPESEN3KtyepgvQA/LZnH34bjl48yPZnPj3dev/9vq6RY8um3j+RSed+PXhQ48LhSor+g0dMODY/v1GfPnL3xg27KTevYeFQgOrqkb26zNs8MCR/foO6d1rQFVlzZCaEf/8tXHnnTv54YcWp1OioVs6bIVAyIWLMoOUfY/NNPS0Gsjy20EEfN83DENV1UQiASYcaMbAZho6CGvXPNZu0uD7PjAG13HDgRNFfMswOEYackiw/+VHgNAF8DQrAF9c5FuOrRl4+cBDeDEC/mzb17Punt3h1c+/NGXKZedPuuTcc7/7la98o7b2xGOPPbm2dvSgwSPGfv3fx4+bcMXl1y56ZOlbb76za+ceVTV8D+maLUuaaWLb1V5wewVeoQu4AvksPwosRYbAEYoArFMw3tDNi68dpIHkxHVcWZZTqVQ4HBYEwbZtz8Nbv/K4Yce+klSYhyHQIQQOYgwkBqiNLvKb/3KkwffweG/bviRm8bZHG5/ahJOSkTD38EOLN23a6jqI/Hkuloc/wgzYYgTBmXkYAu1FgGySg2ls27YVRUkmk81t1nFN06Qvs21v/Ey+cxHoIGnQdV2WZcIYXMftGEUofKpzs8di63kIlEYacuwB18BgbgBvXcwxCWJe4c033nYdn/4jjMFzD5pU6Hk4sxwzBDoBARgCgC7Qn67jep7nOq5lWSS8E9JjURwyAh0hDbBCAZcRQ7lCARcygA6EHHKOWAQMgRYQOLgqBoczffJ58I/Bt8AGg2pZeDmDrMdBPSddGP1YC0myIIYAQ6AtBKARkTZFPLCPwfM80zQNw7Asi0xptxUl+71rEWg3aaD3pBDGwEhD15YSi/2QEaAHeGw4sq0/z3MCGwuermcPJg2O5zX/0XEesoIsAoZAT0SgGGmAJW/btkVRjMViqqqS19SeCFN3ynPHSQMpbOhS6Q70UPzdCRymS09AAJYz8j89zyHEgrCEnMfyPCsQOFDTewJSLI8Mga5A4EArKvDZtq3rejqdbmhoSKVSMPNHv7h2hT4sztYRKJU0mKaZTCaj0SiJDsqXnk0qKPGOBJD4mYchUBYE8ulCcLrCI4zB990cV4AJBmAMQBoObOUpi6osEYbAUYhAi+MEPY2t6zrHcfF4XBRFy7IYaTi8laAk0uB5XjKZbGxsjMViRF1GGggUzHP0IUB3ZAeTBnp54sAyx9GHAMsRQ6A8CNBtjfiBNNi2DTPZmqalUql4PJ5KpUCmPLqxVAoRKIk0AGPgeZ5+HkqulJmGdp3GpJNor59UuEOkoqXEw2QAgfaWUXeWp8uU9reXNBytRzFpTLq6HMuZVmflpbN07qx4oOPtlNxBjwqKdUqEdCR0foEiwLACmxiANyCENE3jOK6hocEwjEPs4enUmb+9CLRGGjzPMwyDMAZd18kBGEiG3C9CPC0mTwrYolyLkpCiYRgm5aDq0JXJoJxOOVL5PM+zbRtSg823RArStW0bwklaIEynArHJlBNFUVEU0zTz7tegRORiMiLlUqmULMtwcwfR2ff9DOVisVgqldI0Le84KyWSSSaTHMdJkpRHy2iZeDwei8UEQcjTmadcPB5Pp9O6rufJJCnHcdzevXs5jqMV9n0/TrloNBoOh5PJpG3btBhYh4VPnufr6+vB7jgtk0gk4vF4OByur6/neb6hoaFQJpVKJRKJWCwGYrt3747FYpqm0fHQae3atSscDqfT6TyZVM7xPM9xXCKREARBlmU6HpKtWCwWjYbjXDSdSYpik+ta5E8QMqkUH+eikci+urq6cDicyWQ0TaOPZaqqCkb16+vrGxoaIpEIx3F5/NuyrEgkUldXFz3Y0W3Esqx0Oh2JRMBqeyLn8mRIPLnf8f9iMnRqtIyu66BzY2MjHQ95Q4BNahzHQWEVi6eUfNm2DRZfYrFYhHJ0WsRcPcdxlEiELi9d10VR5DiusbGxFX3AAAAtQC+5YkPghxAPrbNpmrIs8zxPKxyJRBDl4OA6vEDTKhWLh9TJeDxO5933fU3TEolEfX19jHLQU0GCtD656o//58VjGIYgCIlEgpah7TrDlYS6riuKIlBOVVU44wDJga0F6nfsNQwDOj3or2zb1jRNlmVFUVRV1TRN13UrcEAUPM+zLAvSkiRJzDlFUaAGUlgyb/kQaI00+L6v6zrP859++mljYyMMPzAq6MF9waCm67iCIEQo19DQEIvFMpkMmJd2HVdVVUEQ6ikXDoc5jhNFUdM0y7IMw1AURZKkhoMdHQ++odg0FUWhkorQaXmUa6QcpCUIArnE3Q0MhlDtK1ZfXx+NRtPptCzLVDRemHL19fWwrmYYRntlKHVwpwYDFdR+EhXdKYTDYRjLJUkiAp7n0TLQ0SSTyTydaZlIBEMUj8fz4qE7KUgrlUqJokinRfEKPLg2NjZyHAfcgojRgzStj085euBJJBLhcDiRSMDrApECAhSNRhsbG6Gr5XneNE0iAKQqmUzG43FgJxCPKIq0DJ33vXv3RiKRZDIpCAItQ/LFcVwsFgOc8/JO6kY0ijlBLBZJpXhByBDG4LpWpimVTCZisUg43EjSEkWRtusgyzIZyaAvBoICbQc+NU2Lx+MNDQ00mBzH5cnwPB+NRoFzkCzkyZB4iEAeQSklLRjtgoxH6LIDSg2fvu/D6CKKIo15MX3orNEyiqKkUilAm46HTkvTtEwmAzGQconFYnSZyrIMMpFIhI6HTktVVVEUoQoVkzmUeGidYUzleZ5WmF7ehdFXUZREIgGdGJEsFk+YcnTeLcuSZRlaFt3P0DaRIO+gT4RydDxAYtLpNFBzog8ZpGEUJ2ntpZwoioZhANqWZUmSFI/Hqf4eeyVJUhQFqAOQmEQi0djYuJtyds6BNSdVVcPhMAxAJGtEH7pwmb9sCLRGGmCQ5nmeMAZ4yUsmk4WkIU05nueBVwIfJKQhdbCTJImeooDpAfotGWgHbQsMSINIORjm6bd2GM/oeARBUFWVJqdAGmTKpVIpSZJgdy4ZEcGsqZJzsizDq3/em33ud/y/mAzdEei6Tp88Ju3WoJxpmpZlkbOs8DhMn8AsjGEYMPcDuJFIwIo7iQkQw6+/nkdkXMclMzGWZeWlBWJkTTHXivHcDOBDBGigYJYI5kXyZkdIumDhA/KVhyG2xBycyQZSQs5k089Cq4DpLuAT8BQtAypBBkFzOuMgSVoXQEdXMDoq8GMcXMv3m81Ek6WKXIhnO6Zp6qZpgs7YWFTOZCTYlgaEoVxgDoYoQDyFhUjm54gMcGtixx1y2mKOSpShM0tSgXKBr3A4nlSAvOLG2dZxxmlNiulTLC0AHyoPHT9tEoNAATWH/okuXMCQvKQWS5G2P1goA79ClknrI2J5KNEKQ3shISAJgdB4aZTgV1LJ86KlNSTx0G0/j0yDjOu40CfoOUfPNJB4XMfN/Y7/k6wByKSFkolYeJ0jv0L1ME1TVbEVE+LI5gPXcTVNA2ZAR15Y/6HQFUWB/rDFSV+6pyKzz2Tmg8aN+cuGQFHSALVH0zSgq6TjAPtcoB8Z8kGGjIukAhW2E5KxwoYBSwb0I1DnyOhCGiRdF0kg3X2QXgaSI4qR4QHGJzotohhJLi8SIgAzZrQO5CfiKZQhOhCFSVdCR0WyTKICfchTecIglrccQMvACw092APydPy0nzwLXTDpFKC/tm07b4aAVpi8aqiqSofT8UNGgLSRtAjUED901tBfFMr4vg+1EaLN0wdQJTUQGAbsuKajAj/8SqZM6aIn5YU7a9tw3dyd1weMNLgI4UMWlm2Ypg4p5gabA7wB8IeKR7cdggloQr4W83ieB30rMTaVV3vz4iG1i7QLkrtiSZBwqC1AyEjDhxGO1EOagpMHaU+ePvRPtF9VVfhKKk9ehYeMgwxRDL5CEvCZQx6fZ6HjJ34Qa11tUrWA9ZJnaU+xeOgOjXAFWkPw01GREqF/IvGTlkJ6rRafJYHQYMlXeOUj+SUEKC9RWkMYtul3FfiVDNK+79OzF6SNFGpIK9+imGEYhU+RvIO2xRg20YfOLPOXDYGipKFsGnRiQlDnSomQtKVShFuUoRtbiwJ5jfMQZYo9TsLbpQ95qtBTejyFz3ZFSLExoDCt1ku/xHhI9gvjh5A2BUos92Lxd+dwkvfWoe6sLJDk2oywlMItRabNhKBwWxErXedSIjl0nQ89BtAT4ilPuQPIrXfRnZWvVkqB/VQMgR5KGg69zpHeoZWoSpGhx5hihdRKEuSRUtIiMuSpQg+RaSVRkCl89vCGdIpWJPvF8tKmADxYolixVLpnOMlUK3WjEzUnyXVinF0dFeh8iKl0YsY7q6Qgnk7JXYngtK5567+WmAQT6xgCRxVpKB0CVudKx4pJMgQYAgyBMiPAuugyA156cj2UNJQOEJNkCDAEGAIMAYYAQwAQYKSB1QSGAEOAIcAQYAgwBEpCgJGGkmBiQgwBhgBDgCHAEGAIMNLA6gBDgCHAEGAIMAQYAiUhwEhDSTAxIYYAQ4AhwBBgCDAEGGlgdYAhwBBgCDAEGAIMgZIQ+D+47EvbOpyohQAAAABJRU5ErkJggg==" width="285.34221683827985" height="160.19927316777714" preserveAspectRatio="none"/>
</g>
<g transform="translate(76.03110841913993 173.19927316777714)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="15.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="25.119999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="35.739999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="43.019999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g13CAD87D675A42FC6A129543D89F948C" x="56.959999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="66.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB8789F2F5F06048D4163694E4C0F3B6C" x="75.97999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="90.57999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="104.55999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="114.25999999999999" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 297.0829921259843)">
<g class="typst-group">
<g>
<g transform="translate(280.90000000000015 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="0" fill="url(#g8BF286A751A64D04318FAE9D5808AE03)" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="9.7" fill="url(#g11BB493CF5D400C3E11CA69FA1CC67B8)" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="19.78" fill="url(#gE0948157D48E5C62CE3ECFC0AC3AE29A)" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="35.58" fill="url(#gC8C7957CBD1EB68E7F4389559EB4F205)" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="49.519999999999996" fill="url(#gC2C3DF145E9D150521FAB824EFA788B3)" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="54.94" fill="url(#g71857523B25144D53E22586A9DCD08D3)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="70.74" fill="url(#gA89D841A70C642F4FC683A0FDAE46559)" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="79.88" fill="url(#gCC92CA1EB330BF9FC4B80C8636A2FCE0)" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="89.88" fill="url(#g83AD37751272D20BA8B46F72C45E8340)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="98.82" fill="url(#g510C684A996A65B4A8E4BBA8BCA0EA3)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="111.61999999999999" fill="url(#gA3A7ABE42C73D65B3ECF9DEFD397AC1F)" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="119.41999999999999" fill="url(#g8293AEEDE3E503405F50CA6094393521)" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="129.5" fill="url(#gA10FD8777B830FD3FAD141AB130D4E97)" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="140.12" fill="url(#g7F4B8BF8910A5EA1AA85B2CF4E924DD2)" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="147.4" fill="url(#g41D277A0316896AC373DFC417CCA2AF2)" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="155.96" fill="url(#g8D189FECA823958010EA96AFE1B7FB37)" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="165.04000000000002" fill="url(#g46BE48E7652E6F2D774DEA78692D27F6)" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="180.16000000000003" fill="url(#g1AED89B7EE7618AF617249B24B59FA66)" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="186.36" fill="url(#g96A1E38A9703EA0AF1F04B7B1128CAA9)" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="193.64000000000001" fill="url(#gFEC5145352DF50898A59363463DD451E)" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="203.72000000000003" fill="url(#g818DC020A045126E122CCEC62AEF635F)" fill-rule="nonzero"/>
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="224.52000000000004" fill="url(#gDB7DBEF21119702BD7CE5C94EA64E7AA)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="234.22000000000003" fill="url(#g15EF886B7CD7CA26BB37EEC3F5AB6FF4)" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="243.36" fill="url(#g88CD5C624948E3DAC117EA3520D42146)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="248.78" fill="url(#g1619F3D1FE50B3EA91C76459F70DE91E)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="256.58" fill="url(#g8163C9E5CCD07611B0D3DB525072CCB2)" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="264.38" fill="url(#gE6DBA2CE4A2C0616DFF9ECCAF76570BA)" fill-rule="nonzero"/>
<use xlink:href="#gB2E338F181D915F0996F60E92302C895" x="274.1" fill="url(#gDCB943C619B2C8AF401FA74DE8E3A6DA)" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="286.04" fill="url(#g11EE8FB2ADA714058BFF795517CB9DD4)" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="296.8" fill="url(#g127B7482475120E5C4C87E0C43026304)" fill-rule="nonzero"/>
<use xlink:href="#gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" x="310.74" fill="url(#gF3E4E7E87E59AF74295E016D66F83ACB)" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="327.52" fill="url(#g1998F6B3F913C3A60FCE5F3731A97E34)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="332.94" fill="url(#g5BA69C97F761DBB4A9BAF83B7FBAB76D)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="340.74" fill="url(#gED460B2A719CC9438E21939C79896C84)" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="348.54" fill="url(#g8CABE8CEBC5A9D0C379F40AFEC33375F)" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="353.96000000000004" fill="url(#gE2A346E8248C50A04B25C47DC0738DFC)" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="364.8" fill="url(#gC393462E41F9C8ADC4F9F1EB967CB260)" fill-rule="nonzero"/>
<use xlink:href="#gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" x="379.8" fill="url(#g3714DAB417D0B22B15932651A8D4A0F4)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="396.58000000000004" fill="url(#g9ACAE960B8430625BFCEE398DC65B3B5)" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="405.72" fill="url(#g8A3FF624D919E6F7B060A76E1D45EFC9)" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="416.56" fill="url(#gCF2AD80F3C19FA4EC204837E2FF60EC)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="427.18" fill="url(#gF804B2C4065942A8ADD2D5CD29A3B62A)" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="436.32" fill="url(#g5FD38B0F68E66334612629A8DF6BE7E6)" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.90000000000015 14.72)">
<path class="typst-shape" fill="none" stroke="url(#g139AD8AE4C4940AA9BA27DD05E0E4E8C)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 79.128395 0 "/>
</g>
<g transform="translate(371.8056376333327 14.72)">
<path class="typst-shape" fill="none" stroke="url(#g4BB9C564F901612DB3DC9A919AFEEA28)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 273.14276 0 "/>
</g>
<g transform="translate(656.7256376333327 14.72)">
<path class="typst-shape" fill="none" stroke="url(#g6164E4B94969A626222C332FC8AB6A9A)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 65.77436 0 "/>
</g>
<g transform="translate(0 37.16)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g757CB60871AF468909C575234729D90A" x="0" fill="url(#gF37D02089003EBADFDA5BC88F9156EB6)" fill-rule="nonzero"/>
<use xlink:href="#g8934F85724FE2A1B73A1C811C5B32995" x="5.96" fill="url(#g185B6AD298AC34516663A207FE304BF5)" fill-rule="nonzero"/>
<use xlink:href="#g98926218EB374AD77A2D864C6D10734B" x="11.9" fill="url(#g48798496EF573D47FA23B24B66A2178E)" fill-rule="nonzero"/>
<use xlink:href="#g98926218EB374AD77A2D864C6D10734B" x="23.040000000000003" fill="url(#gF6DA7E5B16EE1DC48CB27130157BACB4)" fill-rule="nonzero"/>
<use xlink:href="#g98926218EB374AD77A2D864C6D10734B" x="34.18000000000001" fill="url(#gD5E7B3915A537EBA85D6C475734C2EAC)" fill-rule="nonzero"/>
<use xlink:href="#gB2E338F181D915F0996F60E92302C895" x="50.32000000000001" fill="url(#g6C99B24EEC33AEEC0963706D93B1F51D)" fill-rule="nonzero"/>
<use xlink:href="#gDACA5EBB44D5F3DB530A1F5F650BFBAB" x="62.260000000000005" fill="url(#g1135455F9AEC68AC20210472C40510E0)" fill-rule="nonzero"/>
<use xlink:href="#g844C4CEA683BD523227FE7A466FBF8A3" x="71.9" fill="url(#gEBFCD1DC7850F1F6F024F260B282CB76)" fill-rule="nonzero"/>
<use xlink:href="#gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" x="85.80000000000001" fill="url(#gDE4F4A649C6D2B43EB33F01712A52A05)" fill-rule="nonzero"/>
<use xlink:href="#g8934F85724FE2A1B73A1C811C5B32995" x="102.58000000000001" fill="url(#g2A936134EFC773FCCDCBC1244E9382B5)" fill-rule="nonzero"/>
<use xlink:href="#gCAFB20A65E8FBEFE071D9C4C8EE95E49" x="113.52000000000001" fill="url(#gD034569FFA5BF443C8BFF427679B48E0)" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="122.82000000000001" fill="url(#gCCA47087E4C1F5485D1EA42FB43E1F5F)" fill-rule="nonzero"/>
<use xlink:href="#g13CAD87D675A42FC6A129543D89F948C" x="132.12" fill="url(#gDFBB6E40E58C00BC282E5117D341B149)" fill-rule="nonzero"/>
<use xlink:href="#g18D1F1E967E0B15C3E9466BFBC921865" x="141.42000000000002" fill="url(#gD824C4DE65816E9A60386E9A54ACCA71)" fill-rule="nonzero"/>
<use xlink:href="#gF5D967C73B153E080367AE40708278EE" x="150.72000000000003" fill="url(#g6C40DB9DAD1FCD6EF99B6A17130F3B61)" fill-rule="nonzero"/>
<use xlink:href="#gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" x="161.68000000000004" fill="url(#g5D31022486B36F3824DE5AAB04A1602C)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="178.46000000000004" fill="url(#g9211C663B53F4CB9E502E05E1A61A98A)" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="187.60000000000002" fill="url(#g8B0DC45C04739D6DD2DC775A009B38CB)" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="192.88000000000002" fill="url(#gFAFD1614275AD9571289C2B05D15312A)" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="203.12000000000003" fill="url(#gAAF7892BB383B0A28DB7D16974FB0EBB)" fill-rule="nonzero"/>
<use xlink:href="#g17AD34DB90B05275C6F1422A9B4B5274" x="213.06000000000003" fill="url(#g2B6C9CD8A9C4101F3D0D3071A8CA5AD1)" fill-rule="nonzero"/>
<use xlink:href="#gAF2FD2F3D3B2E5808B8997943B6FD5DF" x="228.00000000000003" fill="url(#g2AFF153A54E5856A79B012D5E4D7E2F2)" fill-rule="nonzero"/>
<use xlink:href="#g844C4CEA683BD523227FE7A466FBF8A3" x="244.50000000000003" fill="url(#g66752D63E5B1F46492FA8D9ED20F1341)" fill-rule="nonzero"/>
<use xlink:href="#gB91E67CF1B63A9F4CC30BB03AE35508D" x="258.40000000000003" fill="url(#gF238A49A6BC94E30D4528FDF8F8A475E)" fill-rule="nonzero"/>
<use xlink:href="#gAF2FD2F3D3B2E5808B8997943B6FD5DF" x="267.8" fill="url(#g168F5E6F617C7CD777699418942A0CF4)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="278.1" fill="url(#g90E429D1E4D49620C732CDB6D046620E)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="287.24" fill="url(#g2DEAEBDB310EA818EE8591872A3C31D)" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="295.04" fill="url(#g3BC5E9ED8B2AA7DAEB7500F2CEDDB463)" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="305.8" fill="url(#g609438E0D4B4BB2B3EC56AEC845B7E19)" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="316.42" fill="url(#g2A460FCA572950AAF74D3E3BBB8B745B)" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="327.26" fill="url(#g3ED4A90D3858A91C9D535D86DCE760C)" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="332.68" fill="url(#gAC9620A9D162A5C04A13CA64E318EAFA)" fill-rule="nonzero"/>
<use xlink:href="#gD5ADBDB4F1D8E002AEFDDEC4CBF7721F" x="348.52" fill="url(#gEE6773694D33A3FD2BE553F976B39F28)" fill-rule="nonzero"/>
<use xlink:href="#g844C4CEA683BD523227FE7A466FBF8A3" x="367.53999999999996" fill="url(#g226E89C3FF1CD7BFD495640F7F4AC27A)" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="381.43999999999994" fill="url(#gF9B60F1E4674667C8F9AA21E365D5405)" fill-rule="nonzero"/>
<use xlink:href="#g98926218EB374AD77A2D864C6D10734B" x="390.8399999999999" fill="url(#gCC0356E15436C6C281A32D718B989B46)" fill-rule="nonzero"/>
<use xlink:href="#gD8A8B32586FC3285A065621F1BC44F0" x="401.9799999999999" fill="url(#g82C8CBD63B7C316C1BC0DAAE272FB79F)" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="418.5599999999999" fill="url(#gE559B38C6B24D24703708DDA21E0964F)" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="427.1199999999999" fill="url(#g952D62BE015F6EB801BDBA7A59416D2D)" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="432.5399999999999" fill="url(#g8D4AB1BF3E0CA31585FFB00FB87B8693)" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="441.4799999999999" fill="url(#gA5F5C4CB9C4AADC5AAE0496E448998E3)" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="452.3199999999999" fill="url(#g46D8F077DEDDC5E945394FB28C0121D8)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="463.6399999999999" fill="url(#g938CAE98CCEC6B4687D0CAAB9A69C48)" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="472.77999999999986" fill="url(#g846586F961FE141F66D9BF19A6D4B9CE)" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="483.61999999999983" fill="url(#gDBD6993D97AF840DFCC30699D5B3707D)" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="498.73999999999984" fill="url(#g89C797AC3848E3524AB9B5CEF2B2B489)" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="506.0199999999998" fill="url(#g7D8E6B5D4CE2D44FCA3FA727FFA1D6F7)" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="516.0999999999998" fill="url(#g2E44E69D70A4D57F9FACE6352C515660)" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="525.9599999999998" fill="url(#g7F544F60455463EF2885F4A29860323C)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="536.5799999999998" fill="url(#g396882AA7B0302E4EE21BAC147AD7427)" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="544.3799999999998" fill="url(#g3B406D1E144A2C799A1F71D518000E4E)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="555.6999999999998" fill="url(#g7FCB957C688F9C8C3754BB86F108A873)" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="564.8399999999998" fill="url(#g51950441F4C3A6CA7D7C4BA504A60205)" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="575.2199999999998" fill="url(#gB4A49DE8F22C3936633EB2DD7D199204)" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="585.5999999999998" fill="url(#gCA648D5D0453971201F1061881F63F45)" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="592.8799999999998" fill="url(#g6F5B47E8FEFB9C44E6A2E87D15F22D6)" fill-rule="nonzero"/>
<use xlink:href="#g5925E4E4FE8F59A76637BD462660B390" x="602.8199999999998" fill="url(#g63564D798D4B4B240E7ABADF492C59EF)" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="612.6199999999998" fill="url(#g394E6CB4D73E2FFF18C71CFD97EFE3B8)" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="618.0399999999997" fill="url(#g194E45EE8F41D488C726858F35A83AC7)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="633.8399999999997" fill="url(#g67AE0F03C7992A6E3792E6753E624113)" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="642.9799999999997" fill="url(#g289F9E69EFC07B287BC035097591C843)" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="649.2999999999997" fill="url(#gA096D1637514ED48B311AC55C26EEBE3)" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="663.2399999999998" fill="url(#g97EE2ABAFF7124311766D7F7A41C46AA)" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="674.0799999999998" fill="url(#gD0B9B01D801537946B4F92252F2A8E16)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="683.0199999999999" fill="url(#gEAF30E3EF18C3CF6877DBE2B93F87A79)" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="692.1599999999999" fill="url(#gEA1744A579244FDCDCC6E78CCDDAD27F)" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="699.4399999999998" fill="url(#gB2269652CAB28ACB1818BE84B6A819E3)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="708.3799999999999" fill="url(#g7E71706D09E591653269799F6D5E96BF)" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="716.1799999999998" fill="url(#g7B62EBE8E0969DDD6003CBBE953E16EE)" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.6497786313264715 14.72)">
<path class="typst-shape" fill="none" stroke="url(#gCC97456F13F0455A65A95CF9BE40EE1C)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 145.36835 0 "/>
</g>
<g transform="translate(155.35759723552235 14.72)">
<path class="typst-shape" fill="none" stroke="url(#g639F7A28502247E3FB2D950556196FB4)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 103.44672 0 "/>
</g>
<g transform="translate(262.89176489868066 14.72)">
<path class="typst-shape" fill="none" stroke="url(#gD78770B435D3CD67F040D6744757530E)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 301.94824 0 "/>
</g>
<g transform="translate(569.62 14.72)">
<path class="typst-shape" fill="none" stroke="url(#gC1BCAB05EFF4F26E1A38413BCC5D11E7)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 5.6 0 "/>
</g>
<g transform="translate(579.9999999999999 14.72)">
<path class="typst-shape" fill="none" stroke="url(#g7C4B1B6AAEA4F171D861C20A467F69E8)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 142.5 0 "/>
</g>
</g>
</g>
</g>
<g transform="translate(0 63.31999999999999)">
<g class="typst-group">
<g>
<g transform="translate(194.14000000000016 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="0" fill="url(#g435F4A12C98DC039A0BE205E3A19FA9D)" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="10.84" fill="url(#gFB64FAE4AA1EA0A26DC85722A5E7F9A9)" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="19.78" fill="url(#g2C2F67E99CF03FFA7C0A421A915D5E83)" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="25.200000000000003" fill="url(#g4BBAFBE0C7E0F07F25AC36B1B23DE1F1)" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="35.2" fill="url(#g2AB596A08E8EF4332CA03B45154EB6A1)" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="45.96" fill="url(#gB02D7DE48CCBF1E9E858333FF5D9DC25)" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="56.02" fill="url(#g18325D88782360F3502F5C58E75432CB)" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="66.10000000000001" fill="url(#g1D962147EA3BEB991ACF121DB1C31E66)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="78.54" fill="url(#g4C4D715FC3F74B9F778B8604D059F6C2)" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="86.34" fill="url(#gCE418398A76CE75FE060A0C2BEFB7AE6)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="95.28" fill="url(#g17E6C0673CC68E91E58FCE647E9708B8)" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="104.42" fill="url(#g827961D68AEC62A0BF20DCF3DC431921)" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="111.7" fill="url(#gF24BC925B962674C01621C0EE3CC4112)" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="120.26" fill="url(#gDCED89F017767316FD8D03DAD9D87E3E)" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="136.02" fill="url(#gE5BDC981A6E6F3D2A2C1A6C67AB421A4)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="146.64000000000001" fill="url(#g1061F4E961BAE606664B5D937FD73A22)" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="154.44000000000003" fill="url(#g3E5771806410E56C6E6A39E3DEBC988)" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="159.86" fill="url(#g46609CD97B4EF0705DC6307B79521F0C)" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="170.70000000000002" fill="url(#gABE02A447D8700E801064AF94C5F9921)" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="185.70000000000002" fill="url(#g6B65AFBD3C33263B302EDB3653798396)" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="196.46" fill="url(#gA1558A64511168A8B7D0DAE4A3998729)" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="201.88" fill="url(#gF17CEA6DBBA645C5DC456A57240A197B)" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="210.82" fill="url(#g952D9EAB08F4B05F9BCEFD17865025D)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="218.26" fill="url(#g425DF789F61723458B8F9A25A03A1D61)" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="227.39999999999998" fill="url(#g4DE0979B5E5AA4F3E5E0202DA27F6E1A)" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="234.67999999999998" fill="url(#g192BACF3059B760BD6B3A4A3B3DFB84E)" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="243.23999999999998" fill="url(#g446307A53418D14F621B34087790ABC8)" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="253.99999999999997" fill="url(#gACBE62ADDF3FD1A2383D0F0B6CA9423)" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="259.41999999999996" fill="url(#g627E16906D0C729E9B218E8D88DB3C75)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="267.97999999999996" fill="url(#g524BC9DB9301C79B4865CEE22A96FBA4)" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="277.11999999999995" fill="url(#g9334E61ABEEA9B5B3D7E8C99C21210E2)" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="287.3999999999999" fill="url(#gBA6437C1F30853423BF20F6521DDAC44)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="298.2399999999999" fill="url(#g52AE2E80F30CADB79BEC14FEDF6421AA)" fill-rule="nonzero"/>
<use xlink:href="#g17AD34DB90B05275C6F1422A9B4B5274" x="307.3799999999999" fill="url(#g611F93CD2FEB63AA2811C70061D42CC)" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="317.3199999999999" fill="url(#gFF44DC305974D4C37ADBEE9F83612E5)" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="322.7399999999999" fill="url(#gB4E8B051EF2A93C1022F8A7A75357D67)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="332.7399999999999" fill="url(#g7F0559A2EC23376633F8F91F3ABE72F3)" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="341.8799999999999" fill="url(#g640939A3642AE83201B5C357462F50C4)" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="351.7399999999999" fill="url(#g558B8A36DF1478852821734EE9F437A)" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="357.01999999999987" fill="url(#g62F53387E9F92208DF20DEB66AE134F8)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="370.95999999999987" fill="url(#g223D9BE11162DC0AA7F852957D57633F)" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="378.7599999999999" fill="url(#g87D833280F4B77513F184CB077A9EBD9)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="394.5599999999999" fill="url(#gB5B3979762E395A14D5F38D94F430955)" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="403.6999999999999" fill="url(#gD589B0AE3B9522F533376EE601927EB3)" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="408.97999999999985" fill="url(#gF3A12E5102DCD30B76E9032F0698424C)" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="419.2599999999998" fill="url(#gD76980CCA0CB52459A7DBD0B86933356)" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="434.0399999999998" fill="url(#g6A078BFA393F2FFA8563DB03EBC5DEA6)" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="444.1199999999998" fill="url(#g5D650DCC4CD2FB23414AD90403FF2650)" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="451.5599999999998" fill="url(#gC922D2D12E8D43E1F75BCEDD6ADFE1D3)" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="456.83999999999975" fill="url(#g502678CA81DBD6EF4784061087A4FB9C)" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="471.95999999999975" fill="url(#g2A7D07B8301EFC2C031D6BB165146CDD)" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="481.95999999999975" fill="url(#gCE559C856730CDF1201D3FAB516DB20F)" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="489.39999999999975" fill="url(#gC9F0E529049448FB3C27D72DC854E58)" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="498.53999999999974" fill="url(#gC088E640106A57D2A3CD992401346A70)" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="508.91999999999973" fill="url(#gC9D9DF57F8DF0B98EB08BEDC6E22F301)" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="519.6799999999997" fill="url(#g5733AD992C8564482C8B68F5AA25AB51)" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="527.4799999999997" fill="url(#gD05F59AB2E1B0EC9A3C1BA2F6DD8A61D)" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(194.14000000000016 14.72)">
<path class="typst-shape" fill="none" stroke="url(#g878CBF76947C930B1164A6659D123B64)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 24.448395 0 "/>
</g>
<g transform="translate(230.3656376333327 14.72)">
<path class="typst-shape" fill="none" stroke="url(#gCDADC4CB4002CC19E4EABB69767C0B26)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 133.72276 0 "/>
</g>
<g transform="translate(375.8656376333327 14.72)">
<path class="typst-shape" fill="none" stroke="url(#g2B1A4CD2C24971590727FA17ED4AF27C)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 140.26276 0 "/>
</g>
<g transform="translate(527.9056376333325 14.72)">
<path class="typst-shape" fill="none" stroke="url(#g6C8CEF8565CF7938AB1FEFDC0EFCE2E0)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 137.44276 0 "/>
</g>
<g transform="translate(677.1256376333325 14.72)">
<path class="typst-shape" fill="none" stroke="url(#g9BCF0BB7D30B3A930894C652F97CF435)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 15.554362 0 "/>
</g>
<g transform="translate(697.4599999999999 14.72)">
<path class="typst-shape" fill="none" stroke="url(#gB17002E36788F5753A766FAC06F44384)" stroke-width="0.8" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 28.56 0 "/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 433.56299212598424)">
<g class="typst-group">
<g>
<g transform="translate(8 18.5)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAA14E57E2DCC57A3F7809273EECD3C51" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="9.344000000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="12.812800000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="18.5344" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="23.296000000000003" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="29.1456" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="33.8048" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="39.2832" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="46.1696" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="49.638400000000004" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="55.116800000000005" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="60.96640000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g1CB3EC9D05726EBFDE8ADABEC8504FCD" x="67.54560000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="76.4928" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD62975B7DE3250BE5F195D0E8335F60D" x="82.3424" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="88.704" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="92.1728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="98.5728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD5EEFB9760BC9A91B84F628EDDA52971" x="104.4224" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="110.7328" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="114.112" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g83A6AA7A836EACB3652229F4716CDAF" x="123.03359999999999" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gDB4862E33098F259EEBBA99A57E5AFA" x="129.2416" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="139.3536" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="145.2032" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="148.5824" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g793DBE65A5AEC1A16A65955B6C0E046" x="155.1616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gA11612CECC8CBEF18835767DAB11B2F7" x="166.3104" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="172.7616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="177.52319999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gCEFEF3D67F35C6E83CC3757B1DD21B13" x="180.90239999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="190.57919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="196.97919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="201.74079999999995" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g645CA8FA3D9155E2CBD9F8EED3C1540D" x="207.59039999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="214.23359999999997" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(798.4017637795276 8)">
<g class="typst-group">
<g>
<g transform="translate(0 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" x="11.440000000000001" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.608 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="7.44" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="gF74D1E4498220F56E34936C81B24ED2C" overflow="visible">
<path d="M 2.292 1.464 L 2.292 6.276 C 2.292 7.272 2.496 7.3320003 3.336 7.368 C 3.408 7.44 3.408 7.692 3.336 7.764 C 2.808 7.752 2.244 7.7400002 1.776 7.7400002 C 1.38 7.7400002 0.792 7.752 0.228 7.764 C 0.156 7.692 0.156 7.44 0.228 7.368 C 1.068 7.3320003 1.272 7.272 1.272 6.276 L 1.272 1.464 C 1.272 0.468 1.068 0.408 0.228 0.372 C 0.156 0.3 0.156 0.048 0.228 -0.024 C 0.768 -0.012 1.3560001 0 1.788 0 C 2.22 0 2.796 -0.012 3.336 -0.024 C 3.408 0.048 3.408 0.3 3.336 0.372 C 2.496 0.408 2.292 0.468 2.292 1.464 Z "/>
</symbol>
<symbol id="g46E28FC12585DA626130081849FE40B4" overflow="visible">
<path d="M 1.86 1.464 L 1.86 3.744 C 1.86 4.3320003 2.016 4.224 2.292 3.876 L 5.112 0.120000005 C 5.292 -0.072 5.484 -0.144 5.664 -0.144 C 5.808 -0.144 5.928 -0.060000002 5.928 0.18 L 5.928 4.056 C 5.928 5.052 6.06 5.088 6.7920003 5.1480002 C 6.864 5.2200003 6.864 5.472 6.7920003 5.544 C 6.432 5.532 6 5.52 5.64 5.52 C 5.28 5.52 4.86 5.532 4.5 5.544 C 4.428 5.472 4.428 5.2200003 4.5 5.1480002 C 5.232 5.1 5.364 5.052 5.364 4.056 L 5.364 1.812 C 5.364 1.488 5.328 1.284 4.956 1.788 L 2.208 5.52 L 0.504 5.544 L 0.48000002 5.508 L 0.48000002 5.2200003 C 0.48000002 5.172 0.552 5.1480002 0.588 5.1480002 C 1.044 5.112 1.176 4.968 1.296 4.752 L 1.296 1.464 C 1.296 0.468 1.164 0.42000002 0.432 0.372 C 0.36 0.3 0.36 0.048 0.432 -0.024 C 0.792 -0.012 1.212 0 1.572 0 C 1.932 0 2.364 -0.012 2.724 -0.024 C 2.796 0.048 2.796 0.3 2.724 0.372 C 1.992 0.432 1.86 0.468 1.86 1.464 Z "/>
</symbol>
<symbol id="gA2769E14ED9B16297025579DD26D23A1" overflow="visible">
<path d="M 3.648 1.464 L 3.648 4.488 C 3.648 4.932 3.7680001 5.112 4.152 5.112 L 4.464 5.112 C 5.2200003 5.112 5.376 4.872 5.616 4.008 C 5.736 3.984 5.844 3.984 5.94 4.044 C 5.88 4.632 5.868 5.076 5.844 5.64 C 5.4240003 5.592 4.656 5.52 3.648 5.52 L 2.7 5.52 C 1.524 5.52 0.828 5.58 0.504 5.64 C 0.504 5.076 0.492 4.608 0.42000002 4.044 C 0.528 4.008 0.636 3.996 0.744 4.008 C 0.984 4.872 1.116 5.112 1.896 5.112 L 2.184 5.112 C 2.556 5.112 2.7 4.968 2.7 4.5 L 2.7 1.464 C 2.7 0.468 2.568 0.432 1.836 0.372 C 1.764 0.3 1.764 0.048 1.836 -0.024 C 2.28 -0.012 2.772 0 3.18 0 C 3.6000001 0 4.068 -0.012 4.512 -0.024 C 4.584 0.048 4.584 0.3 4.512 0.372 C 3.78 0.42000002 3.648 0.468 3.648 1.464 Z "/>
</symbol>
<symbol id="g48BCA4F06942DA5990D42018985FC781" overflow="visible">
<path d="M 2.292 1.464 L 2.292 2.5080001 L 2.9520001 2.5080001 C 3.408 2.5080001 3.576 2.112 3.732 1.668 L 3.996 0.948 C 4.272 0.204 4.68 -0.084 5.196 -0.084 C 5.376 -0.084 5.748 -0.048 5.952 0 C 5.988 0.120000005 5.964 0.24000001 5.88 0.336 C 5.448 0.336 5.2200003 0.408 4.98 1.0320001 L 4.632 1.932 C 4.488 2.304 4.344 2.5080001 4.188 2.664 L 4.188 2.688 C 4.596 2.832 5.208 3.3240001 5.208 4.152 C 5.208 5.1480002 4.584 5.568 3.1560001 5.568 C 2.856 5.568 2.172 5.52 1.812 5.52 C 1.464 5.52 0.96000004 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.212 0.432 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 0.936 -0.012 1.428 0 1.824 0 C 2.196 0 2.592 -0.012 2.976 -0.024 C 3.048 0.048 3.048 0.3 2.976 0.372 C 2.412 0.408 2.292 0.468 2.292 1.464 Z M 4.164 4.152 C 4.164 3.204 3.888 2.856 2.82 2.856 L 2.292 2.856 L 2.292 4.416 C 2.292 5.052 2.412 5.172 3.084 5.172 C 3.924 5.172 4.164 4.872 4.164 4.152 Z "/>
</symbol>
<symbol id="g4C6038BE04CA3E1481E54A97A0E34303" overflow="visible">
<path d="M 6.324 2.82 C 6.324 4.524 4.956 5.64 3.3960001 5.64 C 1.728 5.64 0.444 4.428 0.444 2.664 C 0.444 1.0320001 1.6800001 -0.120000005 3.3 -0.120000005 C 5.268 -0.120000005 6.324 1.26 6.324 2.82 Z M 3.288 5.244 C 4.356 5.244 5.28 4.26 5.28 2.652 C 5.28 1.176 4.548 0.276 3.48 0.276 C 2.316 0.276 1.488 1.332 1.488 2.808 C 1.488 4.428 2.388 5.244 3.288 5.244 Z "/>
</symbol>
<symbol id="gE1B486BBD379D5D210F28624A61384AE" overflow="visible">
<path d="M 1.776 5.52 C 1.452 5.52 0.912 5.532 0.444 5.544 C 0.372 5.472 0.372 5.2200003 0.444 5.1480002 C 1.176 5.1 1.308 5.052 1.308 4.056 L 1.308 1.464 C 1.308 0.468 1.176 0.432 0.444 0.372 C 0.372 0.3 0.372 0.048 0.444 -0.024 C 0.90000004 -0.012 1.44 0 1.788 0 C 2.1 0 2.58 -0.024 3.54 -0.024 C 4.872 -0.024 6.36 0.6 6.36 2.7 C 6.36 4.296 5.376 5.544 3.372 5.544 C 2.556 5.544 2.124 5.52 1.776 5.52 Z M 2.256 0.912 L 2.256 4.776 C 2.256 5.076 2.556 5.1480002 3.024 5.1480002 C 5.04 5.1480002 5.316 3.744 5.316 2.496 C 5.316 0.816 4.572 0.372 3.252 0.372 C 2.34 0.372 2.256 0.576 2.256 0.912 Z "/>
</symbol>
<symbol id="g9FB16590C6D64699AE0CE54876927A05" overflow="visible">
<path d="M 5.2200003 4.056 L 5.2200003 2.532 C 5.2200003 1.5 5.2200003 0.372 3.636 0.372 C 2.448 0.372 2.196 1.308 2.196 2.424 L 2.196 4.056 C 2.196 5.052 2.328 5.088 3.06 5.1480002 C 3.132 5.2200003 3.132 5.472 3.06 5.544 C 2.592 5.532 2.112 5.52 1.716 5.52 C 1.284 5.52 0.816 5.532 0.384 5.544 C 0.312 5.472 0.312 5.2200003 0.384 5.1480002 C 1.116 5.1 1.248 5.052 1.248 4.056 L 1.248 2.172 C 1.248 0.372 2.124 -0.120000005 3.432 -0.120000005 C 5.292 -0.120000005 5.784 0.936 5.784 2.688 L 5.784 4.056 C 5.784 5.052 5.916 5.088 6.6480002 5.1480002 C 6.7200003 5.2200003 6.7200003 5.472 6.6480002 5.544 C 6.288 5.532 5.856 5.52 5.496 5.52 C 5.136 5.52 4.716 5.532 4.356 5.544 C 4.284 5.472 4.284 5.2200003 4.356 5.1480002 C 5.088 5.1 5.2200003 5.052 5.2200003 4.056 Z "/>
</symbol>
<symbol id="g6799D348D26A0968EEDA80A0E5D50B73" overflow="visible">
<path d="M 3.312 -0.120000005 C 4.248 -0.120000005 4.824 0.228 5.388 0.984 C 5.364 1.068 5.244 1.2 5.1480002 1.224 C 4.596 0.576 4.176 0.336 3.372 0.336 C 2.184 0.336 1.488 1.62 1.488 2.808 C 1.488 4.824 2.424 5.244 3.3240001 5.244 C 4.284 5.244 4.848 4.716 4.992 3.876 C 5.112 3.8400002 5.232 3.8400002 5.352 3.912 C 5.352 4.404 5.328 4.908 5.208 5.448 C 4.752 5.448 4.212 5.64 3.252 5.64 C 1.668 5.64 0.444 4.44 0.444 2.688 C 0.444 1.932 0.684 1.104 1.272 0.564 C 1.752 0.120000005 2.424 -0.120000005 3.312 -0.120000005 Z "/>
</symbol>
<symbol id="g45E4C10E27056C5AE488FE2D8290DF06" overflow="visible">
<path d="M 2.34 4.056 C 2.34 5.052 2.4720001 5.088 3.204 5.1480002 C 3.276 5.2200003 3.276 5.472 3.204 5.544 C 2.748 5.532 2.232 5.52 1.86 5.52 C 1.5 5.52 0.996 5.532 0.528 5.544 C 0.456 5.472 0.456 5.2200003 0.528 5.1480002 C 1.26 5.1 1.392 5.052 1.392 4.056 L 1.392 1.464 C 1.392 0.468 1.26 0.432 0.528 0.372 C 0.456 0.3 0.456 0.048 0.528 -0.024 C 0.972 -0.012 1.464 0 1.872 0 C 2.256 0 2.784 -0.012 3.204 -0.024 C 3.276 0.048 3.276 0.3 3.204 0.372 C 2.4720001 0.42000002 2.34 0.468 2.34 1.464 Z "/>
</symbol>
<symbol id="g5ABA589ED074A65FC8C929AB4EB2344C" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z "/>
</symbol>
<symbol id="gD77922058D8F1A3A631DDE5946887BDC" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z M 3.384 5.112 C 4.764 5.112 5.88 4.008 5.88 2.628 C 5.88 1.248 4.752 0.132 3.384 0.132 C 2.004 0.132 0.90000004 1.248 0.90000004 2.628 C 0.90000004 3.996 2.004 5.112 3.384 5.112 Z "/>
</symbol>
<symbol id="g6F0940D406D545443F0C3F5AB20F1452" overflow="visible">
<path d="M 1.55 0.78999996 L 2.1 2.24 C 2.1499999 2.37 2.21 2.4099998 2.45 2.4099998 L 4.56 2.4099998 L 5.14 0.71999997 C 5.2599998 0.38 4.88 0.34 4.4 0.31 C 4.3399997 0.25 4.3399997 0.04 4.4 -0.02 C 4.77 -0.01 5.3199997 0 5.71 0 C 6.12 0 6.5 -0.01 6.85 -0.02 C 6.91 0.04 6.91 0.25 6.85 0.31 C 6.46 0.35 6.12 0.38 5.95 0.85999995 L 3.8899999 6.58 C 3.74 6.49 3.47 6.3799996 3.34 6.3799996 L 1.0699999 1.02 C 0.81 0.39999998 0.51 0.34 0.07 0.31 C 0.01 0.25 0.01 0.04 0.07 -0.02 C 0.32999998 -0.01 0.65999997 0 0.96 0 C 1.37 0 1.87 -0.01 2.24 -0.02 C 2.3 0.04 2.3 0.25 2.24 0.31 C 1.86 0.34 1.39 0.38 1.55 0.78999996 Z M 2.6299999 2.83 C 2.4099998 2.83 2.34 2.86 2.3799999 2.96 L 3.3999999 5.5499997 L 3.46 5.5499997 L 4.4 2.83 Z "/>
</symbol>
<symbol id="g6D72A0AB4EFB019D977FFECF4A1600A9" overflow="visible">
<path d="M 3.79 0 C 3.79 0 4.02 0.96 4.0899997 1.38 C 4 1.43 3.9199998 1.4499999 3.81 1.42 C 3.6499999 0.83 3.36 0.34 2.73 0.34 L 2.28 0.34 C 2.05 0.34 1.91 0.5 1.91 0.69 L 1.91 3.3799999 C 1.91 4.21 2.02 4.24 2.6299999 4.29 C 2.69 4.35 2.69 4.56 2.6299999 4.62 C 2.26 4.61 1.8499999 4.6 1.51 4.6 C 1.1999999 4.6 0.77 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.1 0.34 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.89 -0.01 1.55 0 1.55 0 Z "/>
</symbol>
<symbol id="g7035BD9A81EA6DB089327941BB80DFF8" overflow="visible">
<path d="M 4.72 0.90999997 C 4.72 1.74 4.7799997 1.77 5.0899997 1.8199999 C 5.15 1.88 5.15 2.09 5.0899997 2.1499999 C 4.91 2.1399999 4.63 2.1299999 4.3199997 2.1299999 C 4.02 2.1299999 3.56 2.1399999 3.27 2.1499999 C 3.21 2.09 3.21 1.88 3.27 1.8199999 C 3.8799999 1.78 3.9299998 1.74 3.9299998 0.90999997 L 3.9299998 0.37 C 3.61 0.28 3.28 0.22999999 2.9299998 0.22999999 C 1.68 0.22999999 1.27 1.51 1.27 2.33 C 1.27 3.54 1.8499999 4.37 2.81 4.37 C 3.8 4.37 4.22 3.87 4.37 3.23 C 4.47 3.1999998 4.5699997 3.1999998 4.67 3.26 C 4.66 3.6699998 4.63 4.0899997 4.54 4.54 C 4.24 4.54 3.5 4.7 2.9399998 4.7 C 1.51 4.7 0.37 3.78 0.37 2.2 C 0.37 0.93 1.3199999 -0.099999994 2.75 -0.099999994 C 3.4299998 -0.099999994 4.17 0 4.83 0.35999998 C 4.7599998 0.42999998 4.72 0.52 4.72 0.59 Z "/>
</symbol>
<symbol id="g7FD6A8241485CEBC032BD9E4CE659816" overflow="visible">
<path d="M 5.27 2.35 C 5.27 3.77 4.13 4.7 2.83 4.7 C 1.4399999 4.7 0.37 3.6899998 0.37 2.22 C 0.37 0.85999995 1.4 -0.099999994 2.75 -0.099999994 C 4.39 -0.099999994 5.27 1.05 5.27 2.35 Z M 2.74 4.37 C 3.6299999 4.37 4.4 3.55 4.4 2.21 C 4.4 0.97999996 3.79 0.22999999 2.8999999 0.22999999 C 1.93 0.22999999 1.24 1.11 1.24 2.34 C 1.24 3.6899998 1.99 4.37 2.74 4.37 Z "/>
</symbol>
<symbol id="gFAD9169AC3141E7FC4EA568E3BBD2E9B" overflow="visible">
<path d="M 1.91 1.22 L 1.91 2.09 L 2.46 2.09 C 2.84 2.09 2.98 1.76 3.11 1.39 L 3.33 0.78999996 C 3.56 0.17 3.8999999 -0.07 4.33 -0.07 C 4.48 -0.07 4.79 -0.04 4.96 0 C 4.99 0.099999994 4.97 0.19999999 4.9 0.28 C 4.54 0.28 4.35 0.34 4.15 0.85999995 L 3.86 1.61 C 3.74 1.92 3.62 2.09 3.49 2.22 L 3.49 2.24 C 3.83 2.36 4.3399997 2.77 4.3399997 3.46 C 4.3399997 4.29 3.82 4.64 2.6299999 4.64 C 2.3799999 4.64 1.81 4.6 1.51 4.6 C 1.22 4.6 0.79999995 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.78 -0.01 1.1899999 0 1.52 0 C 1.8299999 0 2.1599998 -0.01 2.48 -0.02 C 2.54 0.04 2.54 0.25 2.48 0.31 C 2.01 0.34 1.91 0.39 1.91 1.22 Z M 3.47 3.46 C 3.47 2.6699998 3.24 2.3799999 2.35 2.3799999 L 1.91 2.3799999 L 1.91 3.6799998 C 1.91 4.21 2.01 4.31 2.57 4.31 C 3.27 4.31 3.47 4.06 3.47 3.46 Z "/>
</symbol>
<symbol id="g5503E15E5E4E70E9E217A15BD1ECD752" overflow="visible">
<path d="M 1.9499999 3.3799999 C 1.9499999 4.21 2.06 4.24 2.6699998 4.29 C 2.73 4.35 2.73 4.56 2.6699998 4.62 C 2.29 4.61 1.86 4.6 1.55 4.6 C 1.25 4.6 0.83 4.61 0.44 4.62 C 0.38 4.56 0.38 4.35 0.44 4.29 C 1.05 4.25 1.16 4.21 1.16 3.3799999 L 1.16 1.22 C 1.16 0.39 1.05 0.35999998 0.44 0.31 C 0.38 0.25 0.38 0.04 0.44 -0.02 C 0.81 -0.01 1.22 0 1.56 0 C 1.88 0 2.32 -0.01 2.6699998 -0.02 C 2.73 0.04 2.73 0.25 2.6699998 0.31 C 2.06 0.35 1.9499999 0.39 1.9499999 1.22 Z "/>
</symbol>
<symbol id="gA419F36517085793EDBF3FE4736A2E59" overflow="visible">
<path d="M 3.04 1.22 L 3.04 3.74 C 3.04 4.11 3.1399999 4.2599998 3.46 4.2599998 L 3.72 4.2599998 C 4.35 4.2599998 4.48 4.06 4.68 3.34 C 4.7799997 3.32 4.87 3.32 4.95 3.37 C 4.9 3.86 4.89 4.23 4.87 4.7 C 4.52 4.66 3.8799999 4.6 3.04 4.6 L 2.25 4.6 C 1.27 4.6 0.69 4.65 0.42 4.7 C 0.42 4.23 0.41 3.84 0.35 3.37 C 0.44 3.34 0.53 3.33 0.62 3.34 C 0.82 4.06 0.93 4.2599998 1.5799999 4.2599998 L 1.8199999 4.2599998 C 2.1299999 4.2599998 2.25 4.14 2.25 3.75 L 2.25 1.22 C 2.25 0.39 2.1399999 0.35999998 1.53 0.31 C 1.4699999 0.25 1.4699999 0.04 1.53 -0.02 C 1.9 -0.01 2.31 0 2.6499999 0 C 3 0 3.3899999 -0.01 3.76 -0.02 C 3.82 0.04 3.82 0.25 3.76 0.31 C 3.1499999 0.35 3.04 0.39 3.04 1.22 Z "/>
</symbol>
<symbol id="gFF65128B49BB3276E17D04989ECB7ACE" overflow="visible">
<path d="M 5 3.3799999 C 5 4.21 5.1099997 4.24 5.72 4.29 C 5.7799997 4.35 5.7799997 4.56 5.72 4.62 C 5.37 4.6 4.93 4.6 4.6 4.6 C 4.3199997 4.6 3.8799999 4.61 3.49 4.62 C 3.4299998 4.56 3.4299998 4.35 3.49 4.29 C 4.1 4.25 4.21 4.21 4.21 3.3799999 L 4.21 2.52 L 1.9 2.52 L 1.9 3.3799999 C 1.9 4.21 2.01 4.24 2.62 4.29 C 2.6799998 4.35 2.6799998 4.56 2.62 4.62 C 2.24 4.61 1.8199999 4.6 1.5 4.6 C 1.1999999 4.6 0.78999996 4.61 0.39 4.62 C 0.32999998 4.56 0.32999998 4.35 0.39 4.29 C 1 4.25 1.11 4.21 1.11 3.3799999 L 1.11 1.22 C 1.11 0.39 1 0.35999998 0.39 0.31 C 0.32999998 0.25 0.32999998 0.04 0.39 -0.02 C 0.78999996 -0.01 1.1899999 0 1.51 0 C 1.8299999 0 2.23 -0.01 2.62 -0.02 C 2.6799998 0.04 2.6799998 0.25 2.62 0.31 C 2.01 0.35 1.9 0.39 1.9 1.22 L 1.9 2.19 L 4.21 2.19 L 4.21 1.22 C 4.21 0.39 4.1 0.35999998 3.49 0.31 C 3.4299998 0.25 3.4299998 0.04 3.49 -0.02 C 3.86 -0.01 4.2599998 0 4.61 0 C 4.91 0 5.33 -0.01 5.72 -0.02 C 5.7799997 0.04 5.7799997 0.25 5.72 0.31 C 5.1099997 0.35 5 0.39 5 1.22 Z "/>
</symbol>
<symbol id="gEDADDD9BA25BBB833C1F4B684DC50419" overflow="visible">
<path d="M 4.83 3.82 L 4.9 3.82 L 5.0299997 1.23 C 5.0699997 0.39999998 5.06 0.35999998 4.52 0.31 C 4.46 0.25 4.46 0.04 4.52 -0.02 C 4.87 -0.01 5.24 0 5.52 0 C 5.8199997 0 6.1099997 -0.01 6.3799996 -0.02 C 6.44 0.04 6.44 0.25 6.3799996 0.31 C 5.87 0.35999998 5.8599997 0.42 5.7999997 1.23 L 5.6 3.81 C 5.5699997 4.21 5.66 4.25 6.16 4.29 C 6.22 4.35 6.22 4.56 6.16 4.62 L 4.81 4.6 L 3.31 1.02 L 2.03 4.6 L 0.64 4.62 C 0.58 4.56 0.58 4.35 0.64 4.29 C 1.13 4.2599998 1.22 4.21 1.1999999 4.02 L 0.88 1.2099999 C 0.78999996 0.38 0.65999997 0.34 0.28 0.31 C 0.22 0.25 0.22 0.04 0.28 -0.02 C 0.48 -0.01 0.78 0 0.94 0 C 1.14 0 1.51 -0.01 1.7099999 -0.02 C 1.77 0.04 1.77 0.25 1.7099999 0.31 C 1.14 0.35 1.15 0.47 1.23 1.2099999 L 1.52 3.75 L 1.54 3.75 L 2.96 -0.04 C 2.98 -0.089999996 3.03 -0.12 3.08 -0.12 C 3.12 -0.12 3.1699998 -0.089999996 3.1899998 -0.04 Z "/>
</symbol>
<symbol id="g1E8994F5C297EC73FA26D93D22635023" overflow="visible">
<path d="M 2.82 -0.14999999 C 4.11 -0.14999999 5.16 0.9 5.16 2.19 C 5.16 3.48 4.11 4.52 2.82 4.52 C 1.53 4.52 0.48999998 3.48 0.48999998 2.19 C 0.48999998 0.9 1.53 -0.14999999 2.82 -0.14999999 Z M 2.82 4.2599998 C 3.97 4.2599998 4.9 3.34 4.9 2.19 C 4.9 1.04 3.9599998 0.11 2.82 0.11 C 1.67 0.11 0.75 1.04 0.75 2.19 C 0.75 3.33 1.67 4.2599998 2.82 4.2599998 Z "/>
</symbol>
<symbol id="g5396A27CA60B9808846A090320835A9F" overflow="visible">
<path d="M 1.91 1.22 L 1.91 5.23 C 1.91 6.06 2.08 6.1099997 2.78 6.14 C 2.84 6.2 2.84 6.41 2.78 6.47 C 2.34 6.46 1.87 6.45 1.48 6.45 C 1.15 6.45 0.65999997 6.46 0.19 6.47 C 0.13 6.41 0.13 6.2 0.19 6.14 C 0.89 6.1099997 1.06 6.06 1.06 5.23 L 1.06 1.22 C 1.06 0.39 0.89 0.34 0.19 0.31 C 0.13 0.25 0.13 0.04 0.19 -0.02 C 0.64 -0.01 1.13 0 1.49 0 C 1.8499999 0 2.33 -0.01 2.78 -0.02 C 2.84 0.04 2.84 0.25 2.78 0.31 C 2.08 0.34 1.91 0.39 1.91 1.22 Z "/>
</symbol>
<symbol id="g97A8E46F7A64F11D13C6F357868587EE" overflow="visible">
<path d="M 1.89 1.22 L 1.89 1.9599999 C 2.07 1.88 2.27 1.8399999 2.52 1.8399999 C 3.86 1.8399999 4.27 2.8 4.27 3.3999999 C 4.27 3.9199998 3.97 4.62 2.55 4.62 C 2.18 4.62 1.76 4.6 1.49 4.6 C 1.1999999 4.6 0.78 4.61 0.38 4.62 C 0.32 4.56 0.32 4.35 0.38 4.29 C 0.98999995 4.25 1.1 4.21 1.1 3.3799999 L 1.1 1.22 C 1.1 0.39 0.98999995 0.35999998 0.38 0.31 C 0.32 0.25 0.32 0.04 0.38 -0.02 C 0.71 -0.01 1.06 0 1.5 0 C 1.93 0 2.28 -0.01 2.61 -0.02 C 2.6699998 0.04 2.6699998 0.25 2.61 0.31 C 2 0.35 1.89 0.39 1.89 1.22 Z M 1.89 3.84 C 1.89 4.16 2.01 4.29 2.49 4.29 C 3.08 4.29 3.3999999 3.98 3.3999999 3.28 C 3.3999999 2.56 3.1399999 2.1699998 2.54 2.1699998 C 2.34 2.1699998 2.09 2.2 1.89 2.28 Z "/>
</symbol>
<symbol id="gB844DCFB76B4CC44608DB013C9764E9C" overflow="visible">
<path d="M 1.8299999 3.62 C 1.5899999 4.19 1.5999999 4.24 2.1399999 4.29 C 2.2 4.35 2.2 4.56 2.1399999 4.62 C 1.8299999 4.61 1.49 4.6 1.0799999 4.6 C 0.76 4.6 0.45999998 4.61 0.19999999 4.62 C 0.14 4.56 0.14 4.35 0.19999999 4.29 C 0.69 4.24 0.76 4.13 1 3.56 L 2.4199998 0.28 C 2.55 -0.01 2.6 -0.12 2.71 -0.12 C 2.78 -0.12 2.82 -0.04 2.96 0.28 L 4.42 3.55 C 4.63 4.0099998 4.74 4.25 5.2799997 4.29 C 5.3399997 4.35 5.3399997 4.56 5.2799997 4.62 C 5.06 4.61 4.8199997 4.6 4.56 4.6 C 4.19 4.6 3.9099998 4.61 3.6399999 4.62 C 3.58 4.56 3.58 4.35 3.6399999 4.29 C 4.18 4.25 4.23 4.13 4.0299997 3.62 L 2.9399998 1.13 C 2.9099998 1.1 2.8999999 1.1 2.87 1.13 Z "/>
</symbol>
<symbol id="gDAA1267270512376F631C9A10449D5F4" overflow="visible">
<path d="M 2.48 2.25 C 3.1399999 2.25 3.1499999 2.06 3.1699998 1.6899999 C 3.22 1.64 3.3999999 1.64 3.4499998 1.6899999 C 3.4399998 1.92 3.4299998 2.26 3.4299998 2.4199998 C 3.4299998 2.56 3.4399998 2.8799999 3.4499998 3.1299999 C 3.3999999 3.1799998 3.22 3.1799998 3.1699998 3.1299999 C 3.1499999 2.6799998 3.1299999 2.57 2.48 2.57 L 1.91 2.57 L 1.91 3.99 C 1.91 4.16 2.04 4.27 2.23 4.27 L 2.8 4.27 C 3.62 4.27 3.75 3.9399998 3.9299998 3.37 C 4.0299997 3.36 4.12 3.3799999 4.2 3.4199998 C 4.16 3.76 4.04 4.54 4.02 4.61 C 4.02 4.63 4.0099998 4.64 3.99 4.64 C 3.85 4.61 3.75 4.6 3.58 4.6 L 1.51 4.6 C 1.22 4.6 0.76 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.76 -0.01 1.1999999 0 1.52 0 L 3.06 0 C 3.46 0 4.12 -0.02 4.12 -0.02 C 4.24 0.39 4.35 0.94 4.42 1.36 C 4.33 1.41 4.25 1.43 4.14 1.4 C 3.98 0.81 3.6899998 0.31 2.86 0.31 L 2.4299998 0.31 C 2.01 0.31 1.91 0.42 1.91 0.75 L 1.91 2.25 Z "/>
</symbol>
<symbol id="gEEE4EC0F13100E99C1017169F912BE3E" overflow="visible">
<path d="M 1.55 1.22 L 1.55 3.12 C 1.55 3.61 1.68 3.52 1.91 3.23 L 4.2599998 0.099999994 C 4.41 -0.06 4.5699997 -0.12 4.72 -0.12 C 4.8399997 -0.12 4.94 -0.049999997 4.94 0.14999999 L 4.94 3.3799999 C 4.94 4.21 5.0499997 4.24 5.66 4.29 C 5.72 4.35 5.72 4.56 5.66 4.62 C 5.3599997 4.61 5 4.6 4.7 4.6 C 4.4 4.6 4.0499997 4.61 3.75 4.62 C 3.6899998 4.56 3.6899998 4.35 3.75 4.29 C 4.36 4.25 4.47 4.21 4.47 3.3799999 L 4.47 1.51 C 4.47 1.24 4.44 1.0699999 4.13 1.49 L 1.8399999 4.6 L 0.42 4.62 L 0.39999998 4.5899997 L 0.39999998 4.35 C 0.39999998 4.31 0.45999998 4.29 0.48999998 4.29 C 0.87 4.2599998 0.97999996 4.14 1.0799999 3.9599998 L 1.0799999 1.22 C 1.0799999 0.39 0.96999997 0.35 0.35999998 0.31 C 0.29999998 0.25 0.29999998 0.04 0.35999998 -0.02 C 0.65999997 -0.01 1.01 0 1.31 0 C 1.61 0 1.9699999 -0.01 2.27 -0.02 C 2.33 0.04 2.33 0.25 2.27 0.31 C 1.66 0.35999998 1.55 0.39 1.55 1.22 Z "/>
</symbol>
<symbol id="g72A3AE02AE43C077271D415C6766410E" overflow="visible">
<path d="M 13.536 12.552 L 13.536 8.808 L 6.096 8.808 L 6.096 12.552 C 6.096 14.544 6.768 14.64 8.088 14.712 C 8.328 14.856 8.328 15.384 8.088 15.528 C 7.1280003 15.504 5.4 15.4800005 4.44 15.4800005 C 3.48 15.4800005 1.704 15.504 0.744 15.528 C 0.504 15.384 0.504 14.856 0.744 14.712 C 2.0640001 14.64 2.736 14.544 2.736 12.552 L 2.736 2.928 C 2.736 0.936 2.0640001 0.84000003 0.744 0.768 C 0.504 0.624 0.504 0.096 0.744 -0.048 C 1.704 -0.024 3.48 0 4.44 0 C 5.4 0 7.1280003 -0.024 8.088 -0.048 C 8.328 0.096 8.328 0.624 8.088 0.768 C 6.768 0.84000003 6.096 0.936 6.096 2.928 L 6.096 7.656 L 13.536 7.656 L 13.536 2.928 C 13.536 0.936 12.864 0.84000003 11.544 0.768 C 11.304 0.624 11.304 0.096 11.544 -0.048 C 12.504 -0.024 14.28 0 15.24 0 C 16.2 0 17.928 -0.024 18.888 -0.048 C 19.128 0.096 19.128 0.624 18.888 0.768 C 17.568 0.84000003 16.896 0.936 16.896 2.928 L 16.896 12.552 C 16.896 14.544 17.568 14.64 18.888 14.712 C 19.128 14.856 19.128 15.384 18.888 15.528 C 17.928 15.504 16.2 15.4800005 15.24 15.4800005 C 14.28 15.4800005 12.504 15.504 11.544 15.528 C 11.304 15.384 11.304 14.856 11.544 14.712 C 12.864 14.64 13.536 14.544 13.536 12.552 Z "/>
</symbol>
<symbol id="g14F95E5F274105B73EC9103738D4C7FD" overflow="visible">
<path d="M 15.144 0 C 15.144 0 15.024 1.704 15.024 2.448 L 15.024 12.288 C 15.024 14.424 15.432 14.544 17.112 14.712 C 17.256 14.856 17.256 15.384 17.112 15.528 C 15.936 15.504 15.528 15.4800005 14.52 15.4800005 C 13.440001 15.4800005 12.936 15.504 11.736 15.528 C 11.592 15.384 11.592 14.856 11.736 14.712 C 13.416 14.544 13.824 14.472 13.824 12.288 L 13.824 5.544 C 13.824 4.9440002 13.512 5.064 13.176 5.472 L 6.816 12.96 L 4.68 15.4800005 L 0.768 15.528 C 0.624 15.384 0.624 14.856 0.768 14.712 C 1.8000001 14.64 2.52 13.824 2.664 13.2 L 2.664 3.192 C 2.664 1.056 2.256 0.936 0.576 0.768 C 0.432 0.624 0.432 0.096 0.576 -0.048 C 1.752 -0.024 2.208 0 3.264 0 C 4.32 0 4.752 -0.024 5.952 -0.048 C 6.096 0.096 6.096 0.624 5.952 0.768 C 4.272 0.936 3.864 1.008 3.864 3.192 L 3.864 10.32 C 3.864 10.56 3.912 10.8 4.056 10.8 C 4.176 10.8 4.368 10.632 4.632 10.32 L 12.672 0.768 C 13.152 0.168 13.632 -0.288 13.632 -0.288 C 14.472 -0.288 14.712 -0.216 15.144 0 Z "/>
</symbol>
<symbol id="gFC5C8D23DE5E426807758A924FDBA2FC" overflow="visible">
<path d="M 10.104 15.144 C 8.784 15.336 8.28 15.792 6.048 15.792 C 4.968 15.792 3.552 15.456 2.544 14.64 C 1.656 13.92 0.984 12.816 0.984 11.64 C 0.984 10.728 1.224 9.576 1.776 8.856 C 2.88 7.368 4.872 6.552 5.9040003 5.8320003 C 7.008 5.064 8.088 4.104 8.088 2.76 C 8.088 1.584 7.056 0.768 5.592 0.768 C 3.984 0.768 2.328 2.088 1.848 4.272 C 1.464 4.416 1.08 4.32 0.72 4.224 C 0.696 4.224 0.672 4.2 0.648 4.2 C 0.648 2.4 0.84000003 1.128 1.104 0.24000001 C 2.4720001 0.24000001 2.544 -0.24000001 5.856 -0.24000001 C 7.32 -0.24000001 8.496 0.192 9.4800005 1.08 C 10.344 1.824 11.112 2.928 11.112 4.416 C 11.112 5.664 10.584 6.504 9.864 7.296 C 8.928 8.328 7.584 9.0720005 6.6480002 9.552 C 5.688 10.032001 3.984 11.28 3.984 12.648 C 3.984 13.992001 4.8 14.808001 6.024 14.808001 C 8.064 14.808001 8.736 12.96 9.168 11.376 C 9.504 11.28 10.104 11.28 10.368 11.496 C 10.368 12.768 10.272 13.752 10.104 15.144 Z "/>
</symbol>
<symbol id="g47EDFEA5ED41C2BE4D53DD4DC8C28ED" overflow="visible">
<path d="M 13.8 14.712 C 13.344 14.616 12.672 14.616 12.36 14.712 L 8.928 5.04 L 8.76 4.416 L 8.52 5.184 L 5.9040003 13.752 C 5.664 14.544 6.528 14.64 7.6800003 14.712 C 7.824 14.856 7.824 15.384 7.6800003 15.528 C 6.7920003 15.504 4.392 15.4800005 3.456 15.4800005 C 2.4720001 15.4800005 1.128 15.504 0.24000001 15.528 C 0.096 15.384 0.096 14.856 0.24000001 14.712 C 1.176 14.616 2.04 14.448 2.4 13.416 L 6.912 0.264 C 7.08 -0.24000001 7.44 -0.288 7.704 -0.288 C 7.9440002 -0.288 8.328 -0.24000001 8.52 0.264 L 12.12 9.84 L 15.792 0.264 C 15.96 -0.192 16.224 -0.288 16.584 -0.288 C 16.896 -0.288 17.232 -0.168 17.4 0.264 L 21.912 12.552 C 22.416 13.968 23.376 14.64 24.432001 14.712 C 24.576 14.856 24.576 15.384 24.432001 15.528 C 23.64 15.504 22.824 15.4800005 21.984 15.4800005 C 21 15.4800005 19.872 15.504 18.984 15.528 C 18.84 15.384 18.84 14.856 18.984 14.712 C 20.352 14.496 20.808 13.992001 20.52 13.104 L 17.808 5.04 L 17.52 4.176 L 17.16 5.184 Z "/>
</symbol>
<symbol id="gB8789F2F5F06048D4163694E4C0F3B6C" overflow="visible">
<path d="M 12.36 2.44 L 12.36 10.46 C 12.36 12.12 12.7 12.219999 14.099999 12.28 C 14.219999 12.4 14.219999 12.82 14.099999 12.94 C 13.28 12.92 12.259999 12.9 11.5 12.9 C 10.76 12.9 9.8 12.92 8.92 12.94 C 8.8 12.82 8.8 12.4 8.92 12.28 C 10.32 12.219999 10.66 12.12 10.66 10.46 L 10.66 7.2599998 L 3.82 7.2599998 L 3.82 10.46 C 3.82 12.12 4.16 12.219999 5.56 12.28 C 5.68 12.4 5.68 12.82 5.56 12.94 C 4.7999997 12.92 3.98 12.9 2.96 12.9 C 1.9599999 12.9 1.14 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.26 -0.02 2.22 0 2.98 0 C 3.6999998 0 4.68 -0.02 5.56 -0.04 C 5.68 0.08 5.68 0.5 5.56 0.62 C 4.16 0.68 3.82 0.78 3.82 2.44 L 3.82 6.42 L 10.66 6.42 L 10.66 2.44 C 10.66 0.78 10.32 0.68 8.92 0.62 C 8.8 0.5 8.8 0.08 8.92 -0.04 C 9.82 -0.02 10.78 0 11.5199995 0 C 12.259999 0 13.219999 -0.02 14.099999 -0.04 C 14.219999 0.08 14.219999 0.5 14.099999 0.62 C 12.7 0.68 12.36 0.78 12.36 2.44 Z "/>
</symbol>
<symbol id="gE68C39294AA7FBA9B91EA2F8E9CC3997" overflow="visible">
<path d="M 3.62 2.44 L 3.62 6.42 C 3.62 7.4199996 3.6999998 8.7 3.6999998 8.7 C 3.6999998 8.78 3.6 8.84 3.4399998 8.84 C 2.8799999 8.62 2.08 8.44 0.7 8.26 C 0.65999997 8.139999 0.7 7.8199997 0.74 7.7 C 1.8399999 7.6 2.04 7.48 2.04 6.3399997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.71999997 0.59999996 0.62 C 0.48 0.5 0.48 0.08 0.59999996 -0.04 C 1.26 -0.02 2.04 0 2.84 0 C 3.6399999 0 4.4 -0.02 5.06 -0.04 C 5.18 0.08 5.18 0.5 5.06 0.62 C 3.84 0.7 3.62 0.78 3.62 2.44 Z M 1.8 11.98 C 1.8 11.46 2.28 10.94 2.76 10.94 C 3.32 10.94 3.8 11.48 3.8 11.9 C 3.8 12.38 3.3799999 12.94 2.84 12.94 C 2.36 12.94 1.8 12.46 1.8 11.98 Z "/>
</symbol>
<symbol id="g7FBC39AA6D9FB89D8B638A3651405A80" overflow="visible">
<path d="M 7.72 1.86 C 6.98 1.1 6.3999996 0.78 5.24 0.78 C 4.52 0.78 3.6799998 1.1999999 3.06 2.22 C 2.6599998 2.8799999 2.4199998 3.8 2.4199998 4.96 L 7.74 4.92 C 7.98 4.92 8.12 5.04 8.12 5.2599998 C 8.12 6.94 7.52 8.74 4.74 8.74 C 3 8.74 0.74 7.08 0.74 4.04 C 0.74 2.9199998 1.02 1.8399999 1.68 1.0799999 C 2.36 0.28 3.3 -0.19999999 4.74 -0.19999999 C 6.2599998 -0.19999999 7.3399997 0.5 8.139999 1.54 C 8.08 1.74 7.96 1.8399999 7.72 1.86 Z M 2.48 5.64 C 2.86 7.8999996 4.2599998 8.08 4.74 8.08 C 5.5 8.08 6.3999996 7.66 6.3999996 5.98 C 6.3999996 5.7999997 6.3199997 5.7 6.1 5.7 Z "/>
</symbol>
<symbol id="gB9C04FB79CAD4691AB5EC7F01BE2AD7F" overflow="visible">
<path d="M 3.52 7.16 C 3.48 7.96 3.46 8.48 3.36 8.679999 C 3.32 8.78 3.28 8.84 3.12 8.84 C 2.56 8.62 2.04 8.44 0.65999997 8.26 C 0.62 8.139999 0.65999997 7.8199997 0.7 7.7 C 1.78 7.6 2 7.5 2 6.3399997 L 2 2.44 C 2 0.78 1.76 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 2 0 2.8 0 C 3.6 0 4.52 -0.02 5.22 -0.04 C 5.3399997 0.08 5.3399997 0.5 5.22 0.62 C 3.82 0.71999997 3.58 0.78 3.58 2.44 L 3.58 5.22 C 3.58 5.74 3.82 6.2 4.06 6.56 C 4.2799997 6.8799996 4.74 7.54 4.98 7.54 C 5.16 7.54 5.3399997 7.5 5.5 7.2799997 C 5.64 7.08 5.8799996 6.8199997 6.22 6.8199997 C 6.7 6.8199997 7.16 7.3199997 7.16 7.8199997 C 7.16 8.2 6.7999997 8.78 5.96 8.78 C 5.02 8.78 4.2 7.8999996 3.74 7.12 C 3.62 6.8999996 3.52 7.06 3.52 7.16 Z "/>
</symbol>
<symbol id="gAA212A9DBB5FA7333A767E41B2F6A3B3" overflow="visible">
<path d="M 5.8599997 0.96 C 5.98 0.34 6.2 -0.19999999 7.2 -0.19999999 C 7.96 -0.19999999 8.679999 0.14 9.099999 0.53999996 C 9.059999 0.78 8.98 0.96 8.76 1.0799999 C 8.62 0.96 8.28 0.76 8.0199995 0.76 C 7.44 0.76 7.4199996 1.54 7.4199996 2.46 L 7.4199996 5.4 C 7.4199996 8.24 5.8599997 8.78 4.4 8.78 C 2.76 8.78 1.1 7.7 1.1 6.56 C 1.1 6.08 1.3399999 5.8399997 1.8 5.8399997 C 2.3799999 5.8399997 2.74 6.2599998 2.74 6.52 C 2.74 6.66 2.72 6.7999997 2.6799998 6.8799996 C 2.6599998 6.94 2.6399999 7.06 2.6399999 7.2799997 C 2.6399999 7.8999996 3.48 8.12 4.24 8.12 C 4.92 8.12 5.8599997 7.7799997 5.8599997 5.52 C 5.8599997 5.38 5.7999997 5.2999997 5.74 5.2799997 L 4.02 4.8599997 C 2.1 4.38 0.71999997 3.32 0.71999997 1.9599999 C 0.71999997 0.32 1.8399999 -0.19999999 3.24 -0.19999999 C 3.9399998 -0.19999999 4.54 -0.04 5.42 0.64 L 5.8199997 0.96 Z M 5.8599997 4.66 L 5.8599997 2.02 C 5.8599997 1.76 5.74 1.62 5.58 1.5 C 5.06 1.0799999 4.38 0.62 3.82 0.62 C 2.82 0.62 2.3799999 1.42 2.3799999 2.04 C 2.3799999 2.9399998 2.8 3.86 4.2799997 4.24 Z "/>
</symbol>
<symbol id="g713198A7DA4F5CD7D462D4529B1D64BD" overflow="visible">
<path d="M 7.96 1.8199999 C 7.8799996 2 7.72 2.08 7.54 2.1 C 6.8599997 1.22 6 0.78 5.14 0.78 C 3.6799998 0.78 2.46 2.26 2.46 4.6 C 2.46 6.7999997 3.4199998 8.12 4.74 8.12 C 5.92 8.12 6.08 7.4199996 6.16 6.72 C 6.22 6.18 6.5 6 6.92 6 C 7.3399997 6 7.8999996 6.2599998 7.8999996 6.8799996 C 7.8999996 7.98 6.7599998 8.78 4.8399997 8.78 C 2.86 8.78 0.74 7 0.74 4.16 C 0.74 1.5799999 2.18 -0.19999999 4.7 -0.19999999 C 5.9 -0.19999999 6.96 0.17999999 7.96 1.8199999 Z "/>
</symbol>
<symbol id="g3C2FFF86BC828E66F78F8A687CE12C70" overflow="visible">
<path d="M 3.34 5.72 C 3.34 6.14 3.52 6.3799996 3.6799998 6.56 C 4.44 7.2999997 5.46 7.74 6.24 7.74 C 6.64 7.74 7.06 7.48 7.2999997 7.02 C 7.5 6.62 7.54 6.08 7.54 5.48 L 7.54 2.44 C 7.54 0.79999995 7.3399997 0.71999997 6.2999997 0.62 C 6.2 0.5 6.2 0.08 6.2999997 -0.04 C 6.8599997 -0.02 7.54 0 8.34 0 C 9.139999 0 9.8 -0.02 10.46 -0.04 C 10.559999 0.08 10.559999 0.5 10.46 0.62 C 9.34 0.71999997 9.12 0.79999995 9.12 2.44 L 9.12 5.42 C 9.12 6.52 9.04 7.5 8.58 8.099999 C 8.24 8.54 7.62 8.78 6.92 8.78 C 5.94 8.78 4.74 8.5199995 3.52 7.16 C 3.52 7.14 3.5 7.14 3.48 7.12 C 3.4199998 7.04 3.32 6.92 3.32 7.16 L 3.34 11.66 C 3.34 12.96 3.4199998 13.759999 3.4199998 13.759999 C 3.4199998 13.9 3.34 13.96 3.1599998 13.96 C 2.6599998 13.759999 1.16 13.48 0.35999998 13.42 C 0.32 13.259999 0.35999998 12.94 0.48 12.82 C 0.53999996 12.82 0.59999996 12.82 0.65999997 12.82 C 1.54 12.759999 1.76 12.759999 1.76 11.179999 L 1.76 2.44 C 1.76 0.78 1.52 0.7 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.02 -0.02 1.76 0 2.56 0 C 3.32 0 3.98 -0.02 4.54 -0.04 C 4.66 0.08 4.66 0.5 4.54 0.62 C 3.52 0.7 3.34 0.78 3.34 2.44 Z "/>
</symbol>
<symbol id="g1788914935A6D7BFA016214155630E72" overflow="visible">
<path d="M 1.9 2.44 C 1.9 0.78 1.68 0.68 0.45999998 0.62 C 0.34 0.5 0.34 0.08 0.45999998 -0.04 C 1.16 -0.02 1.9 0 2.7 0 C 3.5 0 4.2599998 -0.02 4.92 -0.04 C 5.04 0.08 5.04 0.5 4.92 0.62 C 3.6999998 0.68 3.48 0.78 3.48 2.44 L 3.48 11.66 C 3.48 12.96 3.56 13.759999 3.56 13.759999 C 3.56 13.9 3.48 13.96 3.3 13.96 C 2.8 13.759999 1.3 13.48 0.5 13.42 C 0.45999998 13.259999 0.5 12.94 0.62 12.82 C 1.78 12.74 1.9 12.679999 1.9 11.179999 Z "/>
</symbol>
<symbol id="g560AC22EF992EFD90E66808483D7B3BA" overflow="visible">
<path d="M 11.12 10.24 L 11.12 3.6999998 C 11.12 3.32 11.12 3.1 10.98 3.1 C 10.9 3.1 10.599999 3.46 10.0199995 4.2 L 3.1599998 12.9 L 0.45999998 12.94 C 0.34 12.82 0.34 12.4 0.45999998 12.28 C 1.3199999 12.219999 1.92 11.5199995 2.04 11 L 2.04 2.6599998 C 2.04 0.88 1.6999999 0.76 0.29999998 0.62 C 0.17999999 0.5 0.17999999 0.08 0.29999998 -0.04 C 1.16 -0.02 2.06 0 2.54 0 C 3 0 3.9199998 -0.02 4.7599998 -0.04 C 4.88 0.08 4.88 0.5 4.7599998 0.62 C 3.36 0.76 3.02 0.84 3.02 2.6599998 L 3.02 8.78 C 3.02 9.46 3.02 9.76 3.1799998 9.76 C 3.3 9.76 3.52 9.54 3.86 9.099999 L 10.84 0.28 C 11.059999 -0.02 11.32 -0.19999999 11.639999 -0.19999999 C 11.92 -0.19999999 12.099999 0.04 12.099999 0.42 L 12.099999 10.24 C 12.099999 12.0199995 12.44 12.139999 13.84 12.28 C 13.96 12.4 13.96 12.82 13.84 12.94 C 13.0199995 12.92 12.08 12.9 11.599999 12.9 C 11.179999 12.9 10.26 12.92 9.38 12.94 C 9.26 12.82 9.26 12.4 9.38 12.28 C 10.78 12.139999 11.12 12.059999 11.12 10.24 Z "/>
</symbol>
<symbol id="g17AD34DB90B05275C6F1422A9B4B5274" overflow="visible">
<path d="M 6.5 7.96 C 7.58 7.8799996 7.7 7.64 7.2799997 6.62 L 5.66 2.7 C 5.3399997 1.92 5.24 1.92 4.92 2.76 L 3.48 6.62 C 3.12 7.58 3.04 7.8199997 4.1 7.96 C 4.22 8.08 4.22 8.5 4.1 8.62 C 3.4399998 8.599999 2.74 8.58 2.08 8.58 C 1.42 8.58 0.82 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.28 7.8399997 1.42 7.52 1.8199999 6.5 L 4.38 0.17999999 C 4.5 -0.12 4.62 -0.24 4.88 -0.24 C 5.08 -0.24 5.22 -0.12 5.3599997 0.22 L 8.0199995 6.48 C 8.4 7.3599997 8.62 7.8599997 9.74 7.96 C 9.86 8.08 9.86 8.5 9.74 8.62 C 9.34 8.599999 8.86 8.58 8.34 8.58 C 7.68 8.58 7 8.599999 6.5 8.62 C 6.3799996 8.5 6.3799996 8.08 6.5 7.96 Z "/>
</symbol>
<symbol id="gFB54B84572F46C3C9CB2B1A90182D6B2" overflow="visible">
<path d="M 8.88 7.74 C 9.26 7.74 9.62 8.099999 9.62 8.5 C 9.62 8.92 9.24 9.24 8.7 9.24 C 8.179999 9.24 7.22 8.9 6.7 8.22 C 6.46 8.38 5.7999997 8.78 4.62 8.78 C 2.84 8.78 1.1999999 7.58 1.1999999 5.74 C 1.1999999 4.66 1.68 4.04 2.24 3.5 C 1.68 3.02 1.36 2.1599998 1.36 1.48 C 1.36 0.76 1.76 0.19999999 2.28 -0.06 C 1.1999999 -0.7 0.64 -1.62 0.64 -2.48 C 0.64 -4.22 2.28 -4.7599998 3.82 -4.7599998 C 6.52 -4.7599998 9.44 -3.46 9.44 -1.3 C 9.44 -0.65999997 9.139999 -0.16 8.559999 0.32 C 7.7799997 0.96 6.3799996 0.97999996 5.64 0.97999996 C 5.2799997 0.97999996 4.7799997 0.94 4.2999997 0.88 C 4 0.85999995 3.8 0.84 3.6999998 0.84 C 3.12 0.84 2.4199998 1.12 2.4199998 1.9799999 C 2.4199998 2.3799999 2.54 2.8 2.78 3.1399999 C 3.26 2.86 3.82 2.72 4.6 2.72 C 6.3599997 2.72 7.98 3.82 7.98 5.7799997 C 7.98 6.72 7.7 7.2599998 7.12 7.8599997 C 7.2599998 8.059999 7.66 8.34 7.9199996 8.34 C 8.059999 8.34 8.2 8.28 8.32 8.099999 C 8.4 7.94 8.66 7.74 8.88 7.74 Z M 2.6399999 -0.19999999 C 2.86 -0.26 3.1799998 -0.29999998 3.4399998 -0.29999998 C 4.06 -0.29999998 4.62 -0.24 4.9 -0.24 C 5.9 -0.24 6.74 -0.26 7.3199997 -0.58 C 8.099999 -1.02 8.34 -1.3 8.34 -1.8199999 C 8.34 -3.26 6.22 -4.02 4.42 -4.02 C 3.6999998 -4.02 2.02 -3.4399998 2.02 -2.08 C 2.02 -1.4 2.06 -0.9 2.6399999 -0.19999999 Z M 6.3799996 5.58 C 6.3799996 3.72 5.44 3.34 4.7 3.34 C 3.02 3.34 2.84 4.7599998 2.84 6.04 C 2.84 7.44 3.34 8.16 4.44 8.16 C 5.7 8.16 6.3799996 7.24 6.3799996 5.58 Z "/>
</symbol>
<symbol id="g733371913480EE84B3609C9E9CD62F8C" overflow="visible">
<path d="M 3.34 7.8799996 C 3.22 7.7599998 3.1399999 7.7999997 3.1399999 7.98 L 3.1399999 11.66 C 3.1399999 12.96 3.22 13.759999 3.22 13.759999 C 3.22 13.9 3.1399999 13.96 2.96 13.96 C 2.46 13.759999 0.96 13.48 0.16 13.42 C 0.12 13.259999 0.16 12.94 0.28 12.82 C 0.34 12.82 0.39999998 12.82 0.45999998 12.82 C 1.3399999 12.759999 1.56 12.759999 1.56 11.179999 L 1.56 1.42 C 1.56 0.64 1.54 0.28 1.48 0 C 1.5799999 -0.16 1.68 -0.24 1.92 -0.24 C 2.04 -0.12 2.24 0.06 2.3999999 0.24 C 2.6 0.48 2.72 0.48 2.9399998 0.29999998 C 3.3999999 -0.08 4 -0.19999999 4.7 -0.19999999 C 6.74 -0.19999999 9.12 1.66 9.12 4.8399997 C 9.12 7.2799997 7.3199997 8.78 5.58 8.78 C 4.72 8.78 3.9599998 8.44 3.34 7.8799996 Z M 3.48 7.2599998 C 4 7.72 4.6 7.8999996 5.18 7.8999996 C 6.3999996 7.8999996 7.3999996 6.42 7.3999996 4.48 C 7.3999996 2.2 6.48 0.48 4.58 0.48 C 3.9599998 0.48 3.54 0.91999996 3.1399999 1.42 L 3.1399999 6.42 C 3.1399999 6.8399997 3.22 7.04 3.48 7.2599998 Z "/>
</symbol>
<symbol id="g3BBBD96D467CC564123619D79E97B4D6" overflow="visible">
<path d="M 7.8999996 12.62 C 6.74 12.78 6.7799997 13.16 4.8199997 13.16 C 2.8 13.16 1.02 11.82 1.02 9.7 C 1.02 7.6 2.76 6.64 4.52 5.96 C 5.72 5.5 7.2 4.94 7.2 2.98 C 7.2 1.36 6.2999997 0.52 4.7 0.52 C 2.84 0.52 1.64 1.38 1.1999999 3.36 C 0.94 3.4399998 0.74 3.3999999 0.53999996 3.3 C 0.62 1.76 0.7 1.24 0.94 0.26 C 2.2 0.26 2.76 -0.19999999 4.54 -0.19999999 C 5.44 -0.19999999 6.2999997 0.02 7 0.45999998 C 8.16 1.18 8.88 2.3999999 8.88 3.6799998 C 8.88 5.7999997 7.2799997 6.74 5.64 7.3599997 C 4.44 7.7999997 2.44 8.559999 2.44 10.24 C 2.44 11.36 3.46 12.48 4.64 12.48 C 6.58 12.48 7.2 11.24 7.6 9.92 C 7.8199997 9.88 8.08 9.9 8.26 10.04 C 8.179999 11 8.099999 11.559999 7.8999996 12.62 Z "/>
</symbol>
<symbol id="gD3761FB0B01B207797C607CDFB6E3A0B" overflow="visible">
<path d="M 3.3999999 7.16 C 3.3799999 7.7599998 3.34 8.48 3.24 8.679999 C 3.1999998 8.78 3.1599998 8.84 3 8.84 C 2.44 8.62 1.92 8.44 0.53999996 8.26 C 0.5 8.139999 0.53999996 7.8199997 0.58 7.7 C 1.66 7.6 1.88 7.5 1.88 6.3399997 L 1.88 2.44 C 1.88 0.79999995 1.62 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.88 0 2.6799998 0 C 3.48 0 4.1 -0.02 4.7 -0.04 C 4.8199997 0.08 4.8199997 0.5 4.7 0.62 C 3.6799998 0.71999997 3.46 0.79999995 3.46 2.44 L 3.46 5.72 C 3.46 6.14 3.6399999 6.3799996 3.8 6.56 C 4.6 7.3399997 5.3399997 7.74 5.96 7.74 C 6.72 7.74 7.2799997 7.2599998 7.2799997 5.92 L 7.2799997 2.44 C 7.2799997 0.79999995 7.12 0.7 6.04 0.62 C 5.94 0.5 5.94 0.08 6.04 -0.04 C 6.54 -0.02 7.2799997 0 8.08 0 C 8.88 0 9.54 -0.02 10.04 -0.04 C 10.139999 0.08 10.139999 0.5 10.04 0.62 C 9.04 0.7 8.86 0.79999995 8.86 2.44 L 8.86 5.62 C 8.86 5.9 8.86 6.18 8.84 6.42 C 9.8 7.48 10.7 7.74 11.48 7.74 C 12.24 7.74 12.679999 7.2999997 12.679999 5.96 L 12.679999 2.44 C 12.679999 0.79999995 12.48 0.7 11.44 0.62 C 11.34 0.5 11.34 0.08 11.44 -0.04 C 11.94 -0.02 12.679999 0 13.48 0 C 14.28 0 14.98 -0.02 15.54 -0.04 C 15.639999 0.08 15.639999 0.5 15.54 0.62 C 14.44 0.7 14.259999 0.79999995 14.259999 2.44 L 14.259999 5.6 C 14.259999 7.3799996 13.96 8.78 12.2 8.78 C 11.179999 8.78 9.94 8.4 8.9 7.2999997 C 8.84 7.24 8.72 7.14 8.679999 7.3199997 C 8.5 8.139999 7.72 8.78 6.68 8.78 C 5.52 8.78 4.48 8.099999 3.6399999 7.16 C 3.54 7.06 3.4199998 6.92 3.3999999 7.16 Z "/>
</symbol>
<symbol id="g87DD77732F07A5C65A64D31E4C3C918D" overflow="visible">
<path d="M 16.199999 11.3 L 13.08 2.62 L 13.0199995 2.6399999 L 10.26 11.08 C 9.92 12.16 10.62 12.219999 11.3 12.28 C 11.42 12.4 11.42 12.82 11.3 12.94 C 10.48 12.92 9.599999 12.9 8.8 12.9 C 8.139999 12.9 7.44 12.92 6.7999997 12.94 C 6.68 12.82 6.68 12.4 6.7999997 12.28 C 7.8599997 12.219999 8.3 11.599999 8.48 11.08 L 8.94 9.76 C 9.0199995 9.5199995 9.08 9.32 9.08 9.139999 C 9.08 8.94 9.059999 8.78 8.9 8.44 L 6.3199997 2.58 L 6.22 2.6 L 3.3 11.44 C 3.06 12.139999 3.6 12.24 4.2999997 12.28 C 4.42 12.4 4.42 12.82 4.2999997 12.94 C 3.6399999 12.92 2.76 12.9 1.9799999 12.9 C 1.28 12.9 0.7 12.92 0.12 12.94 C 0 12.82 0 12.4 0.12 12.28 C 1.02 12.219999 1.16 12.2 1.54 11.12 L 5.2999997 0.29999998 C 5.4 -0.02 5.52 -0.24 5.74 -0.24 C 6 -0.24 6.12 -0.04 6.2599998 0.29999998 L 9.24 7 C 9.42 7.3999996 9.48 7.5 9.58 7.5 C 9.66 7.5 9.74 7.2799997 9.86 6.94 L 12.16 0.29999998 C 12.28 -0.04 12.38 -0.24 12.62 -0.24 C 12.84 -0.24 12.98 -0.02 13.08 0.28 L 17.1 11.059999 C 17.359999 11.759999 17.72 12.219999 18.82 12.28 C 18.939999 12.4 18.939999 12.82 18.82 12.94 C 18.24 12.92 17.6 12.9 17.08 12.9 C 16.56 12.9 15.679999 12.92 14.88 12.94 C 14.759999 12.82 14.759999 12.4 14.88 12.28 C 15.7 12.219999 16.5 12.16 16.199999 11.3 Z "/>
</symbol>
<symbol id="gFB78EB03C35D4F852337F4EC6AC104AC" overflow="visible">
<path d="M 0.82 4.1 C 0.82 2.06 2.18 -0.19999999 5.02 -0.19999999 C 6.2999997 -0.19999999 7.2799997 0.26 7.96 0.91999996 C 8.86 1.8 9.26 3.06 9.26 4.2799997 C 9.26 6.3599997 8.12 8.78 5.06 8.78 C 3.74 8.78 2.6599998 8.24 1.92 7.3799996 C 1.1999999 6.52 0.82 5.3599997 0.82 4.1 Z M 4.7599998 8.08 C 6.48 8.08 7.54 6.52 7.54 3.6399999 C 7.54 1.12 6.24 0.5 5.2999997 0.5 C 3.22 0.5 2.54 3.02 2.54 4.56 C 2.54 6.2999997 2.96 8.08 4.7599998 8.08 Z "/>
</symbol>
<symbol id="g42587C4E387B2C5F870DA01C2914651F" overflow="visible">
<path d="M 6.68 1 C 6.7799997 1.0799999 6.96 1.12 6.98 0.97999996 C 7.04 0.5 7.2 -0.19999999 7.2 -0.19999999 C 7.3599997 -0.26 7.46 -0.24 7.58 -0.19999999 C 8.0199995 0.16 8.72 0.45999998 9.94 0.59999996 C 10.059999 0.71999997 10.059999 1.02 9.94 1.14 C 8.66 1.24 8.48 1.62 8.48 2.6 L 8.48 11.66 C 8.48 12.96 8.559999 13.759999 8.559999 13.759999 C 8.559999 13.9 8.48 13.96 8.3 13.96 C 7.7999997 13.759999 6.2999997 13.48 5.5 13.42 C 5.46 13.259999 5.5 12.94 5.62 12.82 C 5.68 12.82 5.74 12.82 5.7999997 12.82 C 6.68 12.759999 6.8999996 12.759999 6.8999996 11.179999 L 6.8999996 8.62 C 6.8999996 8.48 6.8599997 8.44 6.72 8.44 C 6.64 8.44 5.8199997 8.78 5.16 8.78 C 3.84 8.78 2.96 8.34 2.1599998 7.58 C 1.3 6.72 0.78 5.54 0.78 4.06 C 0.78 1.5999999 2.02 -0.19999999 4.18 -0.19999999 C 4.96 -0.19999999 5.7 0.19999999 6.68 1 Z M 6.8999996 2.48 C 6.8999996 2.1 6.8599997 1.9399999 6.58 1.6999999 C 5.8399997 1.06 5.2 0.74 4.7 0.74 C 3.62 0.74 2.5 1.92 2.5 4.42 C 2.5 5.8599997 2.78 6.66 3.08 7.08 C 3.6999998 8.0199995 4.54 8.08 4.94 8.08 C 5.66 8.08 6.16 7.8199997 6.56 7.3599997 C 6.8399997 7.04 6.8999996 6.8999996 6.8999996 6.2799997 Z "/>
</symbol>
<symbol id="g757CB60871AF468909C575234729D90A" overflow="visible">
<path d="M 0.88 5.04 C 0.88 4.14 0.96 -0.48 5.12 -4.08 C 5.3199997 -4.04 5.48 -3.8999999 5.54 -3.74 C 4.88 -2.98 2.54 -0.22 2.54 5.04 C 2.54 10.3 4.9 13.059999 5.54 13.78 C 5.48 13.98 5.3399997 14.12 5.12 14.139999 C 2.74 12.099999 0.88 8.76 0.88 5.04 Z "/>
</symbol>
<symbol id="gF5D967C73B153E080367AE40708278EE" overflow="visible">
<path d="M 5.08 5.04 C 5.08 5.94 5 10.559999 0.84 14.16 C 0.64 14.12 0.48 13.98 0.42 13.82 C 1.0799999 13.059999 3.4199998 10.3 3.4199998 5.04 C 3.4199998 -0.22 1.06 -2.98 0.42 -3.6999998 C 0.48 -3.8999999 0.62 -4.04 0.84 -4.06 C 3.22 -2.02 5.08 1.3199999 5.08 5.04 Z "/>
</symbol>
<symbol id="gC1513612DA0E34F2B247DB2830CD7DFD" overflow="visible">
<path d="M 1.24 4.6 C 1.24 3.34 2.26 2.32 3.52 2.32 C 4.7799997 2.32 5.7999997 3.34 5.7999997 4.6 C 5.7999997 5.8599997 4.7799997 6.8799996 3.52 6.8799996 C 2.26 6.8799996 1.24 5.8599997 1.24 4.6 Z "/>
</symbol>
<symbol id="g22D858CFD6AD86697C1391C74FD687D1" overflow="visible">
<path d="M 0.85999995 8.58 C 0.58 8.58 0.5 8.34 0.5 8.179999 L 0.5 7.9199996 C 0.5 7.8199997 0.52 7.7999997 0.59999996 7.7999997 L 1.78 7.7999997 L 1.78 1.78 C 1.78 0.35999998 2.3999999 -0.19999999 3.32 -0.19999999 C 4.24 -0.19999999 5.24 0.24 6.02 1.12 C 5.98 1.3199999 5.8599997 1.4399999 5.66 1.4599999 C 5.14 1.06 4.54 0.9 4.02 0.9 C 3.48 0.9 3.36 1.5 3.36 2.74 L 3.36 7.7999997 L 5.44 7.7999997 C 5.64 7.7999997 5.92 7.8799996 5.92 8.059999 L 5.92 8.46 C 5.92 8.54 5.8599997 8.58 5.7599998 8.58 L 3.36 8.58 L 3.36 9.36 C 3.36 10.66 3.4399998 11.46 3.4399998 11.46 C 3.4399998 11.58 3.3799999 11.639999 3.28 11.639999 C 3.1999998 11.639999 3.02 11.559999 2.84 11.46 C 2.62 11.34 2.4199998 11.24 2.1599998 11.179999 C 1.92 11.099999 1.7199999 11.04 1.7199999 10.9 C 1.7199999 10.66 1.78 10.8 1.78 8.58 Z "/>
</symbol>
<symbol id="gE8171CD7697771DDE124968BDB3EF0D7" overflow="visible">
<path d="M 5.42 4.46 C 5.68 4.46 5.96 5.02 5.96 5.2599998 C 5.96 5.46 5.8799996 5.66 5.68 5.66 L 1.3 5.66 C 1.06 5.66 0.79999995 5.2 0.79999995 4.8399997 C 0.79999995 4.64 0.91999996 4.46 1.1 4.46 Z "/>
</symbol>
<symbol id="gCDF8B867C9AAFA36255BC29C36465E90" overflow="visible">
<path d="M 3.5 2.44 L 3.5 7.7999997 L 5.3599997 7.7999997 C 5.54 7.7999997 5.8199997 7.8799996 5.8199997 8.059999 L 5.8199997 8.46 C 5.8199997 8.54 5.7599998 8.58 5.66 8.58 L 3.5 8.58 L 3.5 9.719999 C 3.5 12.799999 4.42 13.28 5.08 13.28 C 5.68 13.28 6 13.04 6.2799997 12.34 C 6.44 11.98 6.66 11.7 7.08 11.7 C 7.4199996 11.7 7.8999996 12.12 7.8999996 12.5199995 C 7.8999996 12.86 7.68 13.219999 7.2599998 13.54 C 6.74 13.9 6.22 13.96 5.46 13.96 C 3.78 13.96 1.92 12.5 1.92 9.38 L 1.92 8.58 L 0.9 8.58 C 0.53999996 8.58 0.44 8.34 0.44 8.179999 L 0.44 7.9199996 C 0.44 7.8199997 0.45999998 7.7999997 0.53999996 7.7999997 L 1.92 7.7999997 L 1.92 2.44 C 1.92 0.78 1.5999999 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 1.92 0 2.72 0 C 3.52 0 4.48 -0.02 5.18 -0.04 C 5.2999997 0.08 5.2999997 0.5 5.18 0.62 C 3.62 0.7 3.5 0.78 3.5 2.44 Z "/>
</symbol>
<symbol id="g35631D62198EF939061DC90C9391724A" overflow="visible">
<path d="M 3.6799998 7.16 C 3.56 7.02 3.4399998 6.98 3.4399998 7.16 C 3.4199998 7.7 3.3799999 8.48 3.28 8.679999 C 3.24 8.78 3.1999998 8.84 3.04 8.84 C 2.48 8.62 1.9599999 8.44 0.58 8.26 C 0.53999996 8.139999 0.58 7.8199997 0.62 7.7 C 1.6999999 7.6 1.92 7.5 1.92 6.3399997 L 1.92 2.44 C 1.92 0.79999995 1.7199999 0.71999997 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.92 0 2.72 0 C 3.52 0 4.12 -0.02 4.72 -0.04 C 4.8399997 0.08 4.8399997 0.5 4.72 0.62 C 3.6999998 0.71999997 3.5 0.79999995 3.5 2.44 L 3.5 5.72 C 3.5 6.14 3.6799998 6.3799996 3.84 6.56 C 4.6 7.2999997 5.5 7.74 6.2799997 7.74 C 6.68 7.74 7.1 7.48 7.3399997 7.02 C 7.54 6.62 7.58 6.08 7.58 5.48 L 7.58 2.44 C 7.58 0.79999995 7.3799996 0.71999997 6.3399997 0.62 C 6.24 0.5 6.24 0.08 6.3399997 -0.04 C 6.94 -0.02 7.58 0 8.38 0 C 9.179999 0 9.9 -0.02 10.5 -0.04 C 10.599999 0.08 10.599999 0.5 10.5 0.62 C 9.38 0.71999997 9.16 0.79999995 9.16 2.44 L 9.16 5.42 C 9.16 6.52 9.08 7.48 8.62 8.099999 C 8.28 8.54 7.66 8.78 6.96 8.78 C 5.98 8.78 4.8599997 8.5199995 3.6799998 7.16 Z "/>
</symbol>
<symbol id="g21D1E528F66DB45787699F71DA377CC5" overflow="visible">
<path d="M 4.08 -3.1999998 C 4.4 -2.6399999 4.66 -2.08 4.9 -1.48 C 6.5 2.3799999 7.3999996 4.44 8.44 6.68 C 8.84 7.52 9.12 7.8399997 10.059999 7.96 C 10.179999 8.08 10.179999 8.5 10.059999 8.62 C 9.66 8.599999 9.2 8.58 8.639999 8.58 C 8.04 8.58 7.4199996 8.599999 6.8199997 8.62 C 6.7 8.5 6.7 8.08 6.8199997 7.96 C 7.46 7.8999996 8.099999 7.7799997 7.7799997 7.06 L 5.7999997 2.48 C 5.66 2.1599998 5.48 2.1 5.3199997 2.5 L 3.54 6.66 C 3.1799998 7.5 3.08 7.8799996 4.2 7.96 C 4.3199997 8.08 4.3199997 8.5 4.2 8.62 C 3.46 8.599999 2.6599998 8.58 1.9399999 8.58 C 1.26 8.58 0.71999997 8.599999 0.32 8.62 C 0.19999999 8.5 0.19999999 8.08 0.32 7.96 C 1.12 7.8599997 1.38 7.68 1.9 6.46 L 4.16 1.1999999 C 4.3399997 0.79999995 4.64 -0.12 4.44 -0.68 C 4.2 -1.3399999 3.9599998 -1.9 3.6599998 -2.52 C 3.4399998 -2.9199998 3.1599998 -3.1 2.6599998 -3.1 C 2.3799999 -3.1 2.3 -3.04 2.08 -3.04 C 1.5 -3.04 1.1999999 -3.6399999 1.1999999 -3.8999999 C 1.1999999 -4.3199997 1.5999999 -4.64 2.1399999 -4.64 C 2.56 -4.64 3.36 -4.48 4.08 -3.1999998 Z "/>
</symbol>
<symbol id="gAC7FD886AB12F72ED3B61B0327264BE7" overflow="visible">
<path d="M 3.12 7.3599997 C 3.1 7.96 3.06 8.48 2.96 8.679999 C 2.9199998 8.78 2.8799999 8.84 2.72 8.84 C 2.1599998 8.62 1.64 8.44 0.26 8.26 C 0.22 8.139999 0.26 7.8199997 0.29999998 7.7 C 1.38 7.6 1.5999999 7.5 1.5999999 6.3399997 L 1.5999999 -2.2 C 1.5999999 -3.86 1.38 -3.9599998 0.16 -4.02 C 0.04 -4.14 0.04 -4.56 0.16 -4.68 C 0.85999995 -4.66 1.5999999 -4.64 2.3999999 -4.64 C 3.1999998 -4.64 4.16 -4.66 4.8199997 -4.68 C 4.94 -4.56 4.94 -4.14 4.8199997 -4.02 C 3.3999999 -3.9399998 3.1799998 -3.86 3.1799998 -2.2 L 3.1799998 -0.04 C 3.1799998 0.22 3.26 0.19999999 3.46 0.12 C 3.9599998 -0.08 4.56 -0.19999999 5.2 -0.19999999 C 6.3199997 -0.19999999 7.3199997 0.14 8.139999 0.91999996 C 9.08 1.8399999 9.62 3.08 9.62 4.7 C 9.62 6.8199997 8.12 8.78 6.08 8.78 C 5.16 8.78 4.14 8.179999 3.34 7.2799997 C 3.22 7.16 3.1399999 7.16 3.12 7.3599997 Z M 3.5 6.62 C 4.02 7.2599998 4.94 7.8599997 5.52 7.8599997 C 6.7999997 7.8599997 7.8999996 6.42 7.8999996 4.16 C 7.8999996 2.52 7.3199997 0.48 5.08 0.48 C 4.72 0.48 4.02 0.58 3.6599998 0.9 C 3.26 1.26 3.1799998 1.38 3.1799998 2.1 L 3.1799998 5.74 C 3.1799998 6.16 3.26 6.3399997 3.5 6.62 Z "/>
</symbol>
<symbol id="g5925E4E4FE8F59A76637BD462660B390" overflow="visible">
<path d="M 3.6399999 7.16 C 3.1799998 7.8399997 3.32 7.8599997 4.22 7.96 C 4.3399997 8.08 4.3399997 8.5 4.22 8.62 C 3.6799998 8.599999 2.8 8.58 2.2 8.58 C 1.5999999 8.58 1 8.599999 0.48 8.62 C 0.35999998 8.5 0.35999998 8.08 0.48 7.96 C 1.16 7.8999996 1.7199999 7.56 2.28 6.74 L 4.02 4.2 C 4.12 4.06 4.12 4 4.04 3.8999999 L 2.36 1.74 C 1.56 0.71999997 1.12 0.65999997 0.42 0.62 C 0.29999998 0.5 0.29999998 0.08 0.42 -0.04 C 0.82 -0.02 1.26 0 1.86 0 C 2.46 0 3.02 -0.02 3.54 -0.04 C 3.6599998 0.08 3.6599998 0.5 3.54 0.62 C 2.82 0.7 2.6599998 0.78 3.1 1.42 L 4.36 3.24 C 4.52 3.48 4.6 3.46 4.72 3.28 L 5.8799996 1.68 C 6.58 0.71999997 6.2599998 0.68 5.62 0.62 C 5.5 0.5 5.5 0.08 5.62 -0.04 C 6.22 -0.02 6.8799996 0 7.6 0 C 8.36 0 8.9 -0.02 9.38 -0.04 C 9.5 0.08 9.5 0.5 9.38 0.62 C 8.48 0.68 8.179999 0.74 7.3799996 1.88 L 5.58 4.42 C 5.5 4.54 5.48 4.6 5.58 4.72 L 7.2599998 6.8599997 C 8 7.7999997 8.48 7.8999996 9.2 7.96 C 9.32 8.08 9.32 8.5 9.2 8.62 C 8.8 8.599999 8.34 8.58 7.74 8.58 C 7.14 8.58 6.58 8.599999 6.06 8.62 C 5.94 8.5 5.94 8.08 6.06 7.96 C 6.7999997 7.8799996 7.02 7.8199997 6.54 7.14 L 5.24 5.3199997 C 5.1 5.12 5.02 5.14 4.8599997 5.3599997 Z "/>
</symbol>
<symbol id="gD5ADBDB4F1D8E002AEFDDEC4CBF7721F" overflow="visible">
<path d="M 2.96 12.9 C 2.24 12.9 1.18 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.16 -0.02 2.22 0 2.98 0 C 3.72 0 4.56 -0.04 6.62 -0.04 C 9.44 -0.04 13.16 1.24 13.16 6.16 C 13.16 9.88 10.099999 12.94 6.2599998 12.94 C 4.8399997 12.94 3.74 12.9 2.96 12.9 Z M 3.82 1.68 L 3.82 11.28 C 3.82 11.98 4.52 12.259999 5.5 12.259999 C 9.82 12.259999 11.24 8.76 11.24 5.68 C 11.24 1.64 8.82 0.64 6 0.64 C 4.04 0.64 3.82 1.04 3.82 1.68 Z "/>
</symbol>
<symbol id="g67483374C2628B9150A7D3585AC4A61B" overflow="visible">
<path d="M 0.96 2.76 C 1.04 1.78 1.1 0.84 1.1 0 C 1.3 0.04 1.5 0.06 1.5999999 0.06 C 1.74 0.06 1.86 0.06 2 0.02 C 2.54 -0.12 3.08 -0.19999999 3.82 -0.19999999 C 4.94 -0.19999999 7 0.34 7 2.32 C 7 3.6799998 6.02 4.48 4.66 4.98 C 3.46 5.44 2.6599998 5.74 2.6599998 6.8399997 C 2.6599998 7.66 3.3799999 8.12 4.06 8.12 C 4.5 8.12 5.66 7.96 5.92 6.2599998 C 6.04 6.14 6.44 6.16 6.56 6.2799997 C 6.62 7 6.66 7.74 6.68 8.4 C 6.06 8.5 5.1 8.78 4.06 8.78 C 2.58 8.78 1.24 7.8199997 1.24 6.54 C 1.24 5.08 1.9 4.46 3.4399998 3.82 C 5.1 3.1399999 5.48 2.72 5.48 1.86 C 5.48 0.88 4.52 0.45999998 3.78 0.45999998 C 3 0.45999998 2.56 0.71999997 2.36 0.94 C 1.92 1.4 1.6999999 2.28 1.5799999 2.78 C 1.4599999 2.8999999 1.0799999 2.8799999 0.96 2.76 Z "/>
</symbol>
<symbol id="g8C7315D77A5D71E18736DE61553C419F" overflow="visible">
<path d="M 1.4 1.1999999 C 1.4 0.62 1.88 0.14 2.46 0.14 C 3.04 0.14 3.52 0.62 3.52 1.1999999 C 3.52 1.78 3.04 2.26 2.46 2.26 C 1.88 2.26 1.4 1.78 1.4 1.1999999 Z M 1.4 7.16 C 1.4 6.58 1.88 6.1 2.46 6.1 C 3.04 6.1 3.52 6.58 3.52 7.16 C 3.52 7.74 3.04 8.22 2.46 8.22 C 1.88 8.22 1.4 7.74 1.4 7.16 Z "/>
</symbol>
<symbol id="gDACA5EBB44D5F3DB530A1F5F650BFBAB" overflow="visible">
<path d="M 2.08 10.46 L 2.08 2.44 C 2.08 0.78 1.74 0.68 0.34 0.62 C 0.22 0.5 0.22 0.08 0.34 -0.04 C 1.24 -0.02 2.22 0 2.9399998 0 C 3.6399999 0 4.8199997 -0.02 5.8199997 -0.04 C 5.94 0.08 5.94 0.5 5.8199997 0.62 C 4.2599998 0.7 3.78 0.78 3.78 2.44 L 3.78 5.8399997 C 4.22 5.7 4.7 5.64 5.4 5.64 C 9.04 5.64 10.139999 8.0199995 10.139999 9.719999 C 10.139999 10.9 9.36 13.04 5.66 13.04 C 4.9 13.04 3.72 12.9 2.9199998 12.9 C 2.18 12.9 1.14 12.92 0.34 12.94 C 0.22 12.82 0.22 12.4 0.34 12.28 C 1.74 12.219999 2.08 12.12 2.08 10.46 Z M 3.78 11.08 C 3.78 11.66 4.08 12.36 5.52 12.36 C 6.8999996 12.36 8.28 11.9 8.28 9.36 C 8.28 7.2 7.24 6.3199997 5.2999997 6.3199997 C 4.7999997 6.3199997 4 6.3599997 3.78 6.42 Z "/>
</symbol>
<symbol id="gF9DE6E66E5D3ACB0B17DC7988DD660B8" overflow="visible">
<path d="M 1.7199999 2.44 C 1.7199999 0.78 1.5 0.7 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.04 -0.02 1.7199999 0 2.52 0 C 3.22 0 3.8799999 -0.02 4.3399997 -0.04 C 4.46 0.08 4.46 0.5 4.3399997 0.62 C 3.52 0.7 3.3 0.78 3.3 2.44 L 3.3 4.18 C 3.6799998 4.16 3.9599998 4.14 4.16 4.08 C 4.38 3.9199998 4.56 3.74 4.7999997 3.4199998 L 6.2599998 1.4599999 C 6.8399997 0.68 7.08 0.29999998 7.1 0.06 C 7.1 0 7.12 -0.04 7.18 -0.04 C 7.58 -0.02 8.0199995 0 8.42 0 C 9.04 0 9.66 -0.02 10.059999 -0.04 C 10.179999 0.08 10.179999 0.5 10.059999 0.62 C 9.38 0.7 8.88 0.78 8.34 1.4599999 L 5.7 4.7799997 C 5.62 4.88 5.56 4.96 5.56 5.06 C 5.56 5.14 5.56 5.18 5.64 5.2599998 L 7.3999996 7.08 C 8 7.72 8.7 7.8799996 9.5 7.96 C 9.62 8.08 9.62 8.5 9.5 8.62 C 9.04 8.599999 8.48 8.58 7.7599998 8.58 C 7 8.58 6.2599998 8.599999 5.7999997 8.62 C 5.68 8.5 5.68 8.08 5.7999997 7.96 C 6.92 7.8799996 6.44 7.18 6.2599998 6.94 C 5.7999997 6.3599997 5.18 5.68 4.66 5.2999997 C 4.22 4.98 3.6799998 4.74 3.3 4.68 L 3.3 11.66 C 3.3 12.96 3.3799999 13.759999 3.3799999 13.759999 C 3.3799999 13.9 3.3 13.96 3.12 13.96 C 2.62 13.759999 1.12 13.48 0.32 13.42 C 0.28 13.259999 0.32 12.94 0.44 12.82 C 0.5 12.82 0.56 12.82 0.62 12.82 C 1.5 12.759999 1.7199999 12.759999 1.7199999 11.179999 Z "/>
</symbol>
<symbol id="g607CD744DAB7515984E0B3F495F7DE81" overflow="visible">
<path d="M 2.98 0 L 7.24 0 C 7.7799997 0 9.62 -0.04 9.62 -0.04 C 9.82 0.96 10.0199995 2.26 10.139999 3.3 C 9.94 3.3999999 9.719999 3.4399998 9.48 3.3999999 C 9.08 1.9599999 8.34 0.78 6.22 0.78 L 4.96 0.78 C 4.18 0.78 3.82 1.16 3.82 2.18 L 3.82 10.46 C 3.82 12.12 4.16 12.219999 5.56 12.28 C 5.68 12.4 5.68 12.82 5.56 12.94 C 4.66 12.92 3.72 12.9 2.96 12.9 C 2.24 12.9 1.3 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.16 -0.02 2.3 0 2.98 0 Z "/>
</symbol>
<symbol id="g8D44D9C01F9AF6C3B1D634FDF54DE6FB" overflow="visible">
<path d="M 5.66 6.46 C 7.3599997 6.46 7.4199996 6 7.48 5.1 C 7.6 4.98 8.0199995 4.98 8.139999 5.1 C 8.12 5.6 8.099999 6.18 8.099999 6.8599997 C 8.099999 7.54 8.12 8.059999 8.139999 8.58 C 8.0199995 8.7 7.6 8.7 7.48 8.58 C 7.4199996 7.48 7.3599997 7.22 5.66 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.9 4.04 12.099999 4.92 12.099999 L 5.8199997 12.099999 C 7.94 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.92 9.34 9.96 9.5 10.0199995 C 9.4 10.84 9.099999 12.759999 9.059999 12.92 C 9.059999 12.96 9.04 12.98 8.98 12.98 C 8.639999 12.92 8.54 12.9 8.04 12.9 L 2.9399998 12.9 C 2.3 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.06 -0.02 2.06 0 2.96 0 C 3.86 0 4.8399997 -0.02 5.54 -0.04 C 5.66 0.08 5.66 0.5 5.54 0.62 C 4.14 0.68 3.8 0.78 3.8 2.44 L 3.8 6.46 Z "/>
</symbol>
<symbol id="gD8CB364949770E6EB9E57283C62D30EB" overflow="visible">
<path d="M 4.3399997 -0.19999999 C 5.12 -0.19999999 6.06 0.19999999 7.04 1 C 7.14 1.0799999 7.3199997 1.12 7.3399997 0.97999996 C 7.3999996 0.48 7.56 -0.19999999 7.56 -0.19999999 C 7.72 -0.26 7.8199997 -0.24 7.94 -0.19999999 C 8.38 0.16 9.08 0.45999998 10.3 0.59999996 C 10.42 0.71999997 10.42 1.02 10.3 1.14 C 9.0199995 1.24 8.84 1.62 8.84 2.6 L 8.84 6.44 C 8.84 7.04 8.92 8.5 8.92 8.5 C 8.92 8.559999 8.86 8.62 8.76 8.62 C 8.66 8.599999 8.36 8.58 8.059999 8.58 C 7.4199996 8.58 6.7 8.599999 6.02 8.62 C 5.9 8.5 5.9 8.08 6.02 7.96 C 7 7.8999996 7.2599998 7.66 7.2599998 6.3399997 L 7.2599998 2.48 C 7.2599998 2.1 7.22 1.9399999 6.94 1.6999999 C 6.2 1.06 5.44 0.74 4.94 0.74 C 4.3399997 0.74 3.34 1.02 3.34 2.8 L 3.34 6.44 C 3.34 7.04 3.4199998 8.5 3.4199998 8.5 C 3.4199998 8.559999 3.36 8.62 3.26 8.62 C 3.1599998 8.599999 2.86 8.58 2.56 8.58 C 1.92 8.58 1.1999999 8.599999 0.52 8.62 C 0.39999998 8.5 0.39999998 8.08 0.52 7.96 C 1.48 7.8799996 1.76 7.66 1.76 6.3599997 L 1.76 2.52 C 1.76 1.14 2.36 -0.19999999 4.3399997 -0.19999999 Z "/>
</symbol>
<symbol id="g13CAD87D675A42FC6A129543D89F948C" overflow="visible">
<path d="M 5.7599998 2.44 L 5.7599998 9.38 C 5.7599998 10.58 5.7799997 11.8 5.8199997 12.059999 C 5.8199997 12.16 5.7799997 12.16 5.7 12.16 C 4.6 11.48 3.54 10.98 1.78 10.16 C 1.8199999 9.94 1.9 9.74 2.08 9.62 C 3 10 3.4399998 10.12 3.82 10.12 C 4.16 10.12 4.22 9.639999 4.22 8.96 L 4.22 2.44 C 4.22 0.78 3.6799998 0.68 2.28 0.62 C 2.1599998 0.5 2.1599998 0.08 2.28 -0.04 C 3.26 -0.02 3.98 0 5.06 0 C 6.02 0 6.5 -0.02 7.5 -0.04 C 7.62 0.08 7.62 0.5 7.5 0.62 C 6.1 0.68 5.7599998 0.78 5.7599998 2.44 Z "/>
</symbol>
<symbol id="gB2E338F181D915F0996F60E92302C895" overflow="visible">
<path d="M 7 2.44 L 7 10.08 C 7 11.36 7.2 12.12 7.9199996 12.12 L 8.36 12.12 C 9.86 12.12 10.8 11.599999 11.139999 10.059999 C 11.36 10.059999 11.639999 10.08 11.82 10.16 C 11.679999 11.08 11.58 12.099999 11.559999 13 C 11.559999 13.0199995 11.5199995 13.059999 11.5 13.059999 C 10.82 13 8.599999 12.9 7.02 12.9 L 5.2999997 12.9 C 3.76 12.9 1.4 13 0.64 13.059999 C 0.59999996 13.059999 0.56 13.0199995 0.56 13 C 0.48 12.099999 0.28 11.059999 0.06 10.099999 C 0.26 10.0199995 0.5 10 0.74 10 C 1.14 11.599999 2.06 12.12 3.3799999 12.12 L 4.36 12.12 C 5.1 12.12 5.2999997 11.36 5.2999997 10.139999 L 5.2999997 2.44 C 5.2999997 0.78 4.96 0.68 3.36 0.62 C 3.24 0.5 3.24 0.08 3.36 -0.04 C 4.3399997 -0.02 5.3599997 0 6.16 0 C 6.92 0 7.94 -0.02 8.94 -0.04 C 9.059999 0.08 9.059999 0.5 8.94 0.62 C 7.3399997 0.68 7 0.78 7 2.44 Z "/>
</symbol>
<symbol id="gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" overflow="visible">
<path d="M 13.259999 2.32 C 13.36 0.7 13.28 0.68 11.98 0.62 C 11.86 0.5 11.86 0.08 11.98 -0.04 C 12.719999 -0.02 13.5199995 0 14.12 0 C 14.719999 0 15.639999 -0.02 16.3 -0.04 C 16.42 0.08 16.42 0.5 16.3 0.62 C 14.94 0.68 14.88 0.76 14.759999 2.4199998 L 14.16 10.84 C 14.08 11.92 14.179999 12.2 15.54 12.28 C 15.66 12.4 15.66 12.82 15.54 12.94 L 12.92 12.9 L 8.679999 2.76 C 8.599999 2.56 8.54 2.48 8.5 2.48 C 8.46 2.48 8.4 2.58 8.34 2.74 L 4.24 12.9 L 1.3399999 12.94 C 1.22 12.82 1.22 12.4 1.3399999 12.28 C 2.72 12.2 2.84 12.16 2.7 10.66 L 1.9 2.4199998 C 1.78 1.22 1.54 0.71999997 0.39999998 0.62 C 0.28 0.5 0.28 0.08 0.39999998 -0.04 C 1 -0.02 1.64 0 2.12 0 C 2.6 0 3.3999999 -0.02 4 -0.04 C 4.12 0.08 4.12 0.5 4 0.62 C 2.6799998 0.71999997 2.58 1.3399999 2.6799998 2.46 L 3.4399998 10.48 L 3.48 10.48 L 7.62 0.099999994 C 7.68 -0.04 7.7999997 -0.19999999 7.9199996 -0.19999999 C 8.04 -0.19999999 8.12 -0.06 8.2 0.099999994 L 12.7 10.679999 L 12.74 10.679999 Z "/>
</symbol>
<symbol id="g8934F85724FE2A1B73A1C811C5B32995" overflow="visible">
<path d="M 3.82 2.44 L 3.82 10.46 C 3.82 12.12 4.16 12.219999 5.56 12.28 C 5.68 12.4 5.68 12.82 5.56 12.94 C 4.68 12.92 3.74 12.9 2.96 12.9 C 2.3 12.9 1.3199999 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.28 -0.02 2.26 0 2.98 0 C 3.6999998 0 4.66 -0.02 5.56 -0.04 C 5.68 0.08 5.68 0.5 5.56 0.62 C 4.16 0.68 3.82 0.78 3.82 2.44 Z "/>
</symbol>
<symbol id="g98926218EB374AD77A2D864C6D10734B" overflow="visible">
<path d="M 5.62 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.7 4.04 12.099999 5.12 12.099999 L 6.62 12.099999 C 8.12 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.88 9.34 9.92 9.54 10.0199995 C 9.44 10.84 9.139999 12.759999 9.099999 12.92 C 9.099999 12.96 9.08 12.98 9.0199995 12.98 C 8.679999 12.92 8.5199995 12.9 8.04 12.9 L 2.9399998 12.9 C 2.34 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.1 -0.02 2.3 0 2.96 0 L 7.2599998 0 C 8.22 0 9.82 -0.04 9.82 -0.04 C 10.099999 0.96 10.4 2.28 10.559999 3.3 C 10.36 3.4199998 10.12 3.46 9.86 3.3999999 C 9.46 1.9599999 8.76 0.78 7.24 0.78 L 4.92 0.78 C 4.08 0.78 3.8 1.1 3.8 2.04 L 3.8 6.46 L 5.62 6.46 C 7.3199997 6.46 7.3799996 6 7.44 5.1 C 7.56 4.98 7.98 4.98 8.099999 5.1 C 8.08 5.62 8.059999 6.18 8.059999 6.8599997 C 8.059999 7.4199996 8.08 8.099999 8.099999 8.58 C 7.98 8.7 7.56 8.7 7.44 8.58 C 7.3799996 7.48 7.3199997 7.22 5.62 7.22 Z "/>
</symbol>
<symbol id="g844C4CEA683BD523227FE7A466FBF8A3" overflow="visible">
<path d="M 3.1 1.5799999 L 4.2 4.48 C 4.2999997 4.74 4.42 4.8199997 4.9 4.8199997 L 9.12 4.8199997 L 10.28 1.4399999 C 10.5199995 0.76 9.76 0.68 8.8 0.62 C 8.679999 0.5 8.679999 0.08 8.8 -0.04 C 9.54 -0.02 10.639999 0 11.42 0 C 12.24 0 13 -0.02 13.7 -0.04 C 13.82 0.08 13.82 0.5 13.7 0.62 C 12.92 0.7 12.24 0.76 11.9 1.7199999 L 7.7799997 13.16 C 7.48 12.98 6.94 12.759999 6.68 12.759999 L 2.1399999 2.04 C 1.62 0.79999995 1.02 0.68 0.14 0.62 C 0.02 0.5 0.02 0.08 0.14 -0.04 C 0.65999997 -0.02 1.3199999 0 1.92 0 C 2.74 0 3.74 -0.02 4.48 -0.04 C 4.6 0.08 4.6 0.5 4.48 0.62 C 3.72 0.68 2.78 0.76 3.1 1.5799999 Z M 5.2599998 5.66 C 4.8199997 5.66 4.68 5.72 4.7599998 5.92 L 6.7999997 11.099999 L 6.92 11.099999 L 8.8 5.66 Z "/>
</symbol>
<symbol id="gCAFB20A65E8FBEFE071D9C4C8EE95E49" overflow="visible">
<path d="M 1.22 9.36 C 1.22 8.94 1.5999999 8.58 2.02 8.58 C 2.36 8.58 2.96 8.94 2.96 9.38 C 2.96 9.54 2.9199998 9.66 2.8799999 9.8 C 2.84 9.94 2.72 10.12 2.72 10.28 C 2.72 10.78 3.24 11.5 4.7 11.5 C 5.42 11.5 6.44 11 6.44 9.08 C 6.44 7.7999997 5.98 6.7599998 4.7999997 5.56 L 3.32 4.1 C 1.36 2.1 1.04 1.14 1.04 -0.04 C 1.04 -0.04 2.06 0 2.7 0 L 6.2 0 C 6.8399997 0 7.7599998 -0.04 7.7599998 -0.04 C 8.0199995 1.02 8.22 2.52 8.24 3.12 C 8.12 3.22 7.8599997 3.26 7.66 3.22 C 7.3199997 1.8 6.98 1.3 6.2599998 1.3 L 2.7 1.3 C 2.7 2.26 4.08 3.62 4.18 3.72 L 6.2 5.66 C 7.3399997 6.7599998 8.2 7.64 8.2 9.16 C 8.2 11.32 6.44 12.2 4.8199997 12.2 C 2.6 12.2 1.22 10.559999 1.22 9.36 Z "/>
</symbol>
<symbol id="g616EA0B06482AD9EB82F211B94D5D49E" overflow="visible">
<path d="M 4.56 -0.19999999 C 6.1 -0.19999999 8.44 1.36 8.44 6.06 C 8.44 8.04 7.96 9.74 7.08 10.9 C 6.56 11.599999 5.72 12.2 4.64 12.2 C 2.6599998 12.2 0.78 9.84 0.78 5.8799996 C 0.78 3.74 1.4399999 1.74 2.54 0.64 C 3.1 0.08 3.78 -0.19999999 4.56 -0.19999999 Z M 4.64 11.5 C 4.98 11.5 5.2999997 11.38 5.54 11.16 C 6.16 10.639999 6.7 9.12 6.7 6.44 C 6.7 4.6 6.64 3.34 6.3599997 2.32 C 5.92 0.68 4.94 0.5 4.58 0.5 C 2.72 0.5 2.52 3.9199998 2.52 5.66 C 2.52 10.58 3.74 11.5 4.64 11.5 Z "/>
</symbol>
<symbol id="g18D1F1E967E0B15C3E9466BFBC921865" overflow="visible">
<path d="M 7.8599997 9.7 C 7.8599997 11.139999 6.74 12.2 4.7799997 12.2 C 2.74 12.2 1.42 10.98 1.42 9.44 C 1.42 8.32 1.9599999 7.5 3.1799998 6.74 L 3.6999998 6.42 C 3.12 6.12 2.58 5.7599998 2.08 5.3199997 C 1.26 4.6 0.91999996 3.6999998 0.91999996 2.9199998 C 0.91999996 0.88 2.36 -0.19999999 4.48 -0.19999999 C 7.1 -0.19999999 8.38 1.7199999 8.38 3.24 C 8.38 4.4 7.8799996 5.42 6.8199997 6.06 L 5.4 6.92 C 6.3399997 7.3799996 7.8599997 8.42 7.8599997 9.7 Z M 4.52 0.5 C 3.62 0.5 2.26 1.12 2.26 2.9199998 C 2.26 3.52 2.52 4.92 4.24 6.06 L 5.18 5.5 C 6.42 4.74 6.92 3.8 6.92 2.84 C 6.92 0.84 5.42 0.5 4.52 0.5 Z M 4.68 11.5 C 5.98 11.5 6.46 10.639999 6.46 9.719999 C 6.46 8.639999 5.4 7.74 4.8599997 7.3399997 L 4.24 7.72 C 2.98 8.54 2.84 9.2 2.84 9.82 C 2.84 10.74 3.48 11.5 4.68 11.5 Z "/>
</symbol>
<symbol id="gAF2FD2F3D3B2E5808B8997943B6FD5DF" overflow="visible">
<path d="M 6.74 2.44 L 6.74 5.16 C 6.74 5.7599998 6.7599998 6.08 7.1 6.68 L 9.48 11 C 10.04 12.0199995 10.48 12.2 11.38 12.28 C 11.5 12.4 11.5 12.82 11.38 12.94 C 10.82 12.92 10.179999 12.9 9.719999 12.9 C 9.26 12.9 8.54 12.92 7.8999996 12.94 C 7.7799997 12.82 7.7799997 12.4 7.8999996 12.28 C 8.78 12.219999 9.099999 12.0199995 8.679999 11.219999 L 6.46 7.04 C 6.2999997 6.74 6.2 6.7599998 6.02 7.08 L 3.6999998 11.179999 C 3.22 12.0199995 3.3 12.219999 4.42 12.28 C 4.54 12.4 4.54 12.82 4.42 12.94 C 3.6999998 12.92 2.9399998 12.9 2.1399999 12.9 C 1.36 12.9 0.7 12.92 0.099999994 12.94 C -0.02 12.82 0 12.4 0.12 12.28 C 0.96 12.219999 1.3 12.099999 2 10.94 L 4.62 6.52 C 4.98 5.94 5.04 5.72 5.04 4.98 L 5.04 2.44 C 5.04 0.78 4.7 0.68 3.1 0.62 C 2.98 0.5 2.98 0.08 3.1 -0.04 C 4.08 -0.02 5.12 0 5.9 0 C 6.68 0 7.68 -0.02 8.679999 -0.04 C 8.8 0.08 8.8 0.5 8.679999 0.62 C 7.08 0.68 6.74 0.78 6.74 2.44 Z "/>
</symbol>
<symbol id="gB91E67CF1B63A9F4CC30BB03AE35508D" overflow="visible">
<path d="M 2.08 1.9 C 1.4599999 1.9 1.02 1.48 1.02 0.91999996 C 1.02 0.29999998 1.54 0.099999994 1.9 0.04 C 2.28 0 2.62 -0.12 2.62 -0.58 C 2.62 -1 1.9 -1.92 0.85999995 -2.18 C 0.85999995 -2.3799999 0.9 -2.52 1.04 -2.6599998 C 2.24 -2.44 3.3999999 -1.48 3.3999999 -0.08 C 3.3999999 1.12 2.8799999 1.9 2.08 1.9 Z "/>
</symbol>
<symbol id="g316778D5069ED68A0C52C06F0AD18D23" overflow="visible">
<path d="M 1.14 0.85999995 C 1.14 0.28 1.62 -0.19999999 2.2 -0.19999999 C 2.78 -0.19999999 3.26 0.28 3.26 0.85999995 C 3.26 1.4399999 2.78 1.92 2.2 1.92 C 1.62 1.92 1.14 1.4399999 1.14 0.85999995 Z "/>
</symbol>
<symbol id="gD8A8B32586FC3285A065621F1BC44F0" overflow="visible">
<path d="M 13.2 2.44 C 13.2 0.78 13.0199995 0.68 12.0199995 0.62 C 11.9 0.5 11.9 0.08 12.0199995 -0.04 C 12.66 -0.02 13.32 0 14 0 C 14.679999 0 15.46 -0.02 16.18 -0.04 C 16.3 0.08 16.3 0.5 16.18 0.62 C 15.059999 0.7 14.78 0.78 14.78 2.44 L 14.78 7 C 14.78 7.6 14.82 8.78 14.82 8.78 C 14.82 8.82 14.799999 8.84 14.74 8.84 C 14.139999 8.599999 13.54 8.58 12.84 8.58 L 8.96 8.58 L 8.96 9.719999 C 8.96 12.799999 10.24 13.299999 10.9 13.299999 C 11.559999 13.299999 12.38 13.059999 12.5199995 12.2 C 12.7 11.12 13.059999 10.62 13.7 10.62 C 14.12 10.62 14.54 10.98 14.54 11.4 C 14.54 12.139999 13.84 12.92 13.099999 13.42 C 12.599999 13.759999 11.88 13.96 11.139999 13.96 C 9.82 13.96 8.66 13.16 8.12 12.46 C 7.8599997 12.96 7 13.62 5.4 13.62 C 4.8599997 13.62 4.16 13.5 3.74 13.24 C 2.36 12.44 1.8399999 11.0199995 1.8399999 8.58 L 0.82 8.58 C 0.45999998 8.58 0.35999998 8.34 0.35999998 8.179999 L 0.35999998 7.9199996 C 0.35999998 7.8199997 0.38 7.7999997 0.45999998 7.7999997 L 1.8 7.7999997 L 1.8 2.44 C 1.8 0.78 1.5799999 0.7 0.5 0.62 C 0.38 0.5 0.38 0.08 0.5 -0.04 C 1.22 -0.02 1.9399999 0 2.6 0 C 3.28 0 3.9399998 -0.02 4.56 -0.04 C 4.68 0.08 4.68 0.5 4.56 0.62 C 3.6399999 0.7 3.3799999 0.78 3.3799999 2.44 L 3.3799999 7.7999997 L 7.3799996 7.7999997 L 7.3799996 2.44 C 7.3799996 0.78 7.16 0.7 6.2799997 0.62 C 6.16 0.5 6.16 0.08 6.2799997 -0.04 C 6.8599997 -0.02 7.5 0 8.179999 0 C 8.84 0 9.559999 -0.02 10.24 -0.04 C 10.36 0.08 10.36 0.5 10.24 0.62 C 9.139999 0.7 8.96 0.78 8.96 2.44 L 8.96 7.7999997 L 12.639999 7.7999997 C 13.16 7.7999997 13.2 7.58 13.2 6.7799997 Z M 7.6 11.3 C 7.4199996 10.58 7.3799996 9.82 7.3799996 9.38 L 7.3799996 8.58 L 3.34 8.58 L 3.34 8.82 C 3.34 10.179999 3.4399998 10.84 3.56 11.219999 C 3.98 12.82 5.06 13.059999 5.3599997 13.059999 C 5.8599997 13.059999 6.3599997 12.74 6.6 12.04 C 6.7599998 11.62 6.94 11.259999 7.46 11.259999 C 7.5 11.259999 7.56 11.259999 7.6 11.3 Z "/>
</symbol>
<symbol id="gA1481BA28623480CC7E6165783E2A864" overflow="visible">
<path d="M 4.06 7.96 C 4.18 8.08 4.18 8.5 4.06 8.62 C 3.46 8.599999 2.76 8.58 2.04 8.58 C 1.28 8.58 0.74 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.16 7.8599997 1.38 7.66 1.8 6.62 L 4.42 0.16 C 4.54 -0.12 4.7 -0.24 4.9 -0.24 C 5.08 -0.24 5.24 -0.12 5.38 0.19999999 L 7.3999996 5.12 L 9.46 0.16 C 9.58 -0.12 9.74 -0.24 9.94 -0.24 C 10.12 -0.24 10.28 -0.12 10.4 0.17999999 L 13.0199995 6.52 C 13.34 7.3399997 13.679999 7.8999996 14.7 7.96 C 14.82 8.08 14.82 8.5 14.7 8.62 C 14.299999 8.599999 13.86 8.58 13.259999 8.58 C 12.66 8.58 11.82 8.599999 11.219999 8.62 C 11.099999 8.5 11.099999 8.08 11.219999 7.96 C 12.719999 7.8799996 12.5199995 7.2999997 12.24 6.6 L 10.559999 2.44 C 10.36 1.9399999 10.28 1.9399999 10.12 2.36 L 8.4 6.74 C 8.0199995 7.68 8.059999 7.8799996 9.12 7.96 C 9.24 8.08 9.24 8.5 9.12 8.62 C 8.5199995 8.599999 7.72 8.58 7.12 8.58 C 6.62 8.58 5.96 8.599999 5.3599997 8.62 C 5.24 8.5 5.24 8.08 5.3599997 7.96 C 6.2999997 7.8799996 6.54 7.2999997 6.8999996 6.3999996 L 7.02 6.08 L 5.62 2.54 C 5.3599997 1.88 5.3199997 1.86 5.06 2.5 L 3.46 6.62 C 3.08 7.58 3.1 7.8999996 4.06 7.96 Z "/>
</symbol>
<symbol id="gAA14E57E2DCC57A3F7809273EECD3C51" overflow="visible">
<path d="M 7.9104 1.5616 L 7.9104 6.6944 C 7.9104 7.7567997 8.128 7.8208 9.024 7.8592 C 9.1008 7.936 9.1008 8.2048 9.024 8.2816 C 8.4992 8.2688 7.8464 8.256 7.3599997 8.256 C 6.8863997 8.256 6.272 8.2688 5.7088 8.2816 C 5.632 8.2048 5.632 7.936 5.7088 7.8592 C 6.6047997 7.8208 6.8223996 7.7567997 6.8223996 6.6944 L 6.8223996 4.6464 L 2.4448 4.6464 L 2.4448 6.6944 C 2.4448 7.7567997 2.6624 7.8208 3.5584 7.8592 C 3.6352 7.936 3.6352 8.2048 3.5584 8.2816 C 3.072 8.2688 2.5472 8.256 1.8944 8.256 C 1.2544 8.256 0.72959995 8.2688 0.24319999 8.2816 C 0.1664 8.2048 0.1664 7.936 0.24319999 7.8592 C 1.1392 7.8208 1.3568 7.7567997 1.3568 6.6944 L 1.3568 1.5616 C 1.3568 0.4992 1.1392 0.43519998 0.24319999 0.39679998 C 0.1664 0.32 0.1664 0.0512 0.24319999 -0.0256 C 0.8064 -0.0128 1.4208 0 1.9072 0 C 2.368 0 2.9952 -0.0128 3.5584 -0.0256 C 3.6352 0.0512 3.6352 0.32 3.5584 0.39679998 C 2.6624 0.43519998 2.4448 0.4992 2.4448 1.5616 L 2.4448 4.1088 L 6.8223996 4.1088 L 6.8223996 1.5616 C 6.8223996 0.4992 6.6047997 0.43519998 5.7088 0.39679998 C 5.632 0.32 5.632 0.0512 5.7088 -0.0256 C 6.2848 -0.0128 6.8992 0 7.3728 0 C 7.8464 0 8.4608 -0.0128 9.024 -0.0256 C 9.1008 0.0512 9.1008 0.32 9.024 0.39679998 C 8.128 0.43519998 7.9104 0.4992 7.9104 1.5616 Z "/>
</symbol>
<symbol id="gF5F8064101DBF0FCB4BCFDA7012527FE" overflow="visible">
<path d="M 2.3167999 1.5616 L 2.3167999 4.1088 C 2.3167999 4.7488 2.368 5.568 2.368 5.568 C 2.368 5.6191998 2.304 5.6576 2.2015998 5.6576 C 1.8432 5.5168 1.3312 5.4016 0.44799998 5.2864 C 0.4224 5.2096 0.44799998 5.0048 0.4736 4.928 C 1.1776 4.864 1.3055999 4.7872 1.3055999 4.0576 L 1.3055999 1.5616 C 1.3055999 0.4992 1.1647999 0.4608 0.384 0.39679998 C 0.30719998 0.32 0.30719998 0.0512 0.384 -0.0256 C 0.8064 -0.0128 1.3055999 0 1.8176 0 C 2.3295999 0 2.816 -0.0128 3.2384 -0.0256 C 3.3151999 0.0512 3.3151999 0.32 3.2384 0.39679998 C 2.4575999 0.44799998 2.3167999 0.4992 2.3167999 1.5616 Z M 1.152 7.6671996 C 1.152 7.3343997 1.4591999 7.0016 1.7664 7.0016 C 2.1248 7.0016 2.432 7.3472 2.432 7.6159997 C 2.432 7.9231997 2.1632 8.2816 1.8176 8.2816 C 1.5103999 8.2816 1.152 7.9743996 1.152 7.6671996 Z "/>
</symbol>
<symbol id="g3976D55F213F07C6469FD06EC16139AA" overflow="visible">
<path d="M 4.9407997 1.1904 C 4.4672 0.704 4.0959997 0.4992 3.3536 0.4992 C 2.8927999 0.4992 2.3552 0.768 1.9583999 1.4208 C 1.7024 1.8432 1.5488 2.432 1.5488 3.1743999 L 4.9536 3.1488 C 5.1071997 3.1488 5.1967998 3.2256 5.1967998 3.3664 C 5.1967998 4.4416 4.8128 5.5936 3.0335999 5.5936 C 1.92 5.5936 0.4736 4.5312 0.4736 2.5856 C 0.4736 1.8687999 0.65279996 1.1776 1.0752 0.69119996 C 1.5103999 0.1792 2.112 -0.12799999 3.0335999 -0.12799999 C 4.0064 -0.12799999 4.6976 0.32 5.2096 0.9856 C 5.1712 1.1136 5.0944 1.1776 4.9407997 1.1904 Z M 1.5871999 3.6095998 C 1.8304 5.0559998 2.7264 5.1712 3.0335999 5.1712 C 3.52 5.1712 4.0959997 4.9024 4.0959997 3.8272 C 4.0959997 3.712 4.0448 3.648 3.9039998 3.648 Z "/>
</symbol>
<symbol id="gB7BB853387AAC07ADB7DDEF96856059B" overflow="visible">
<path d="M 2.2528 4.5824 C 2.2272 5.0944 2.2144 5.4272 2.1504 5.5551996 C 2.1248 5.6191998 2.0992 5.6576 1.9968 5.6576 C 1.6384 5.5168 1.3055999 5.4016 0.4224 5.2864 C 0.39679998 5.2096 0.4224 5.0048 0.44799998 4.928 C 1.1392 4.864 1.28 4.7999997 1.28 4.0576 L 1.28 1.5616 C 1.28 0.4992 1.1264 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7808 -0.0128 1.28 0 1.7919999 0 C 2.304 0 2.8927999 -0.0128 3.3407998 -0.0256 C 3.4176 0.0512 3.4176 0.32 3.3407998 0.39679998 C 2.4448 0.4608 2.2912 0.4992 2.2912 1.5616 L 2.2912 3.3407998 C 2.2912 3.6736 2.4448 3.968 2.5983999 4.1984 C 2.7391999 4.4031997 3.0335999 4.8255997 3.1871998 4.8255997 C 3.3023999 4.8255997 3.4176 4.7999997 3.52 4.6591997 C 3.6095998 4.5312 3.7631998 4.3648 3.9808 4.3648 C 4.288 4.3648 4.5824 4.6847997 4.5824 5.0048 C 4.5824 5.2479997 4.3519998 5.6191998 3.8144 5.6191998 C 3.2128 5.6191998 2.688 5.0559998 2.3936 4.5568 C 2.3167999 4.416 2.2528 4.5183997 2.2528 4.5824 Z "/>
</symbol>
<symbol id="gF8EC31AC53CF59E01ED9143906F6DA7B" overflow="visible">
<path d="M 3.7503998 0.61439997 C 3.8272 0.21759999 3.968 -0.12799999 4.608 -0.12799999 C 5.0944 -0.12799999 5.5551996 0.0896 5.824 0.34559998 C 5.7984 0.4992 5.7472 0.61439997 5.6064 0.69119996 C 5.5168 0.61439997 5.2992 0.48639998 5.1328 0.48639998 C 4.7616 0.48639998 4.7488 0.9856 4.7488 1.5744 L 4.7488 3.4559999 C 4.7488 5.2736 3.7503998 5.6191998 2.816 5.6191998 C 1.7664 5.6191998 0.704 4.928 0.704 4.1984 C 0.704 3.8911998 0.8576 3.7375998 1.152 3.7375998 C 1.5231999 3.7375998 1.7536 4.0064 1.7536 4.1728 C 1.7536 4.2623997 1.7407999 4.3519998 1.7152 4.4031997 C 1.7024 4.4416 1.6896 4.5183997 1.6896 4.6591997 C 1.6896 5.0559998 2.2272 5.1967998 2.7136 5.1967998 C 3.1488 5.1967998 3.7503998 4.9792 3.7503998 3.5328 C 3.7503998 3.4431999 3.712 3.392 3.6736 3.3792 L 2.5728 3.1104 C 1.344 2.8032 0.4608 2.1248 0.4608 1.2544 C 0.4608 0.2048 1.1776 -0.12799999 2.0736 -0.12799999 C 2.5216 -0.12799999 2.9055998 -0.0256 3.4687998 0.4096 L 3.7247999 0.61439997 Z M 3.7503998 2.9824 L 3.7503998 1.2928 C 3.7503998 1.1264 3.6736 1.0368 3.5712 0.96 C 3.2384 0.69119996 2.8032 0.39679998 2.4448 0.39679998 C 1.8047999 0.39679998 1.5231999 0.9088 1.5231999 1.3055999 C 1.5231999 1.8815999 1.7919999 2.4703999 2.7391999 2.7136 Z "/>
</symbol>
<symbol id="g68DDE7C8FDC8A226B6C32EAD39AF7364" overflow="visible">
<path d="M 5.0944 1.1647999 C 5.0432 1.28 4.9407997 1.3312 4.8255997 1.344 C 4.3904 0.7808 3.84 0.4992 3.2896 0.4992 C 2.3552 0.4992 1.5744 1.4463999 1.5744 2.944 C 1.5744 4.3519998 2.1887999 5.1967998 3.0335999 5.1967998 C 3.7888 5.1967998 3.8911998 4.7488 3.9424 4.3008 C 3.9808 3.9552 4.16 3.84 4.4288 3.84 C 4.6976 3.84 5.0559998 4.0064 5.0559998 4.4031997 C 5.0559998 5.1071997 4.3264 5.6191998 3.0976 5.6191998 C 1.8304 5.6191998 0.4736 4.48 0.4736 2.6624 C 0.4736 1.0112 1.3952 -0.12799999 3.008 -0.12799999 C 3.776 -0.12799999 4.4544 0.1152 5.0944 1.1647999 Z "/>
</symbol>
<symbol id="g570B752173035444311A253BD2376AD" overflow="visible">
<path d="M 2.1376 3.6608 C 2.1376 3.9296 2.2528 4.0832 2.3552 4.1984 C 2.8416 4.672 3.4944 4.9536 3.9936 4.9536 C 4.2496 4.9536 4.5183997 4.7872 4.672 4.4927998 C 4.7999997 4.2367997 4.8255997 3.8911998 4.8255997 3.5072 L 4.8255997 1.5616 C 4.8255997 0.51199996 4.6976 0.4608 4.032 0.39679998 C 3.968 0.32 3.968 0.0512 4.032 -0.0256 C 4.3904 -0.0128 4.8255997 0 5.3375998 0 C 5.8496 0 6.272 -0.0128 6.6944 -0.0256 C 6.7584 0.0512 6.7584 0.32 6.6944 0.39679998 C 5.9775996 0.4608 5.8367996 0.51199996 5.8367996 1.5616 L 5.8367996 3.4687998 C 5.8367996 4.1728 5.7855997 4.7999997 5.4912 5.184 C 5.2736 5.4656 4.8768 5.6191998 4.4288 5.6191998 C 3.8016 5.6191998 3.0335999 5.4528 2.2528 4.5824 C 2.2528 4.5696 2.24 4.5696 2.2272 4.5568 C 2.1887999 4.5056 2.1248 4.4288 2.1248 4.5824 L 2.1376 7.4624 C 2.1376 8.2944 2.1887999 8.806399 2.1887999 8.806399 C 2.1887999 8.896 2.1376 8.9344 2.0224 8.9344 C 1.7024 8.806399 0.7424 8.6272 0.2304 8.588799 C 0.2048 8.4864 0.2304 8.2816 0.30719998 8.2048 C 0.34559998 8.2048 0.384 8.2048 0.4224 8.2048 C 0.9856 8.1664 1.1264 8.1664 1.1264 7.1552 L 1.1264 1.5616 C 1.1264 0.4992 0.97279996 0.44799998 0.2304 0.39679998 C 0.15359999 0.32 0.15359999 0.0512 0.2304 -0.0256 C 0.65279996 -0.0128 1.1264 0 1.6384 0 C 2.1248 0 2.5472 -0.0128 2.9055998 -0.0256 C 2.9824 0.0512 2.9824 0.32 2.9055998 0.39679998 C 2.2528 0.44799998 2.1376 0.4992 2.1376 1.5616 Z "/>
</symbol>
<symbol id="g9662C1D9A80FEB5040A57FD9DFCA7985" overflow="visible">
<path d="M 1.216 1.5616 C 1.216 0.4992 1.0752 0.43519998 0.2944 0.39679998 C 0.21759999 0.32 0.21759999 0.0512 0.2944 -0.0256 C 0.7424 -0.0128 1.216 0 1.7279999 0 C 2.24 0 2.7264 -0.0128 3.1488 -0.0256 C 3.2256 0.0512 3.2256 0.32 3.1488 0.39679998 C 2.368 0.43519998 2.2272 0.4992 2.2272 1.5616 L 2.2272 7.4624 C 2.2272 8.2944 2.2784 8.806399 2.2784 8.806399 C 2.2784 8.896 2.2272 8.9344 2.112 8.9344 C 1.7919999 8.806399 0.83199996 8.6272 0.32 8.588799 C 0.2944 8.4864 0.32 8.2816 0.39679998 8.2048 C 1.1392 8.1536 1.216 8.1152 1.216 7.1552 Z "/>
</symbol>
<symbol id="g1CB3EC9D05726EBFDE8ADABEC8504FCD" overflow="visible">
<path d="M 7.1168 6.5536 L 7.1168 2.368 C 7.1168 2.1248 7.1168 1.984 7.0271997 1.984 C 6.976 1.984 6.784 2.2144 6.4128 2.688 L 2.0224 8.256 L 0.2944 8.2816 C 0.21759999 8.2048 0.21759999 7.936 0.2944 7.8592 C 0.8448 7.8208 1.2287999 7.3728 1.3055999 7.04 L 1.3055999 1.7024 C 1.3055999 0.5632 1.0879999 0.48639998 0.192 0.39679998 C 0.1152 0.32 0.1152 0.0512 0.192 -0.0256 C 0.7424 -0.0128 1.3184 0 1.6256 0 C 1.92 0 2.5088 -0.0128 3.0463998 -0.0256 C 3.1232 0.0512 3.1232 0.32 3.0463998 0.39679998 C 2.1504 0.48639998 1.9327999 0.5376 1.9327999 1.7024 L 1.9327999 5.6191998 C 1.9327999 6.0544 1.9327999 6.2464 2.0351999 6.2464 C 2.112 6.2464 2.2528 6.1056 2.4703999 5.824 L 6.9375997 0.1792 C 7.0783997 -0.0128 7.2447996 -0.12799999 7.4495997 -0.12799999 C 7.6288 -0.12799999 7.744 0.0256 7.744 0.2688 L 7.744 6.5536 C 7.744 7.6927996 7.9616 7.7696 8.8576 7.8592 C 8.9344 7.936 8.9344 8.2048 8.8576 8.2816 C 8.3328 8.2688 7.7311997 8.256 7.424 8.256 C 7.1552 8.256 6.5664 8.2688 6.0032 8.2816 C 5.9263997 8.2048 5.9263997 7.936 6.0032 7.8592 C 6.8992 7.7696 7.1168 7.7184 7.1168 6.5536 Z "/>
</symbol>
<symbol id="gD62975B7DE3250BE5F195D0E8335F60D" overflow="visible">
<path d="M 4.16 5.0944 C 4.8512 5.0432 4.928 4.8896 4.6591997 4.2367997 L 3.6223998 1.7279999 C 3.4176 1.2287999 3.3536 1.2287999 3.1488 1.7664 L 2.2272 4.2367997 C 1.9968 4.8512 1.9455999 5.0048 2.6239998 5.0944 C 2.7008 5.1712 2.7008 5.44 2.6239998 5.5168 C 2.2015998 5.5039997 1.7536 5.4912 1.3312 5.4912 C 0.9088 5.4912 0.5248 5.5039997 0.1408 5.5168 C 0.063999996 5.44 0.063999996 5.1712 0.1408 5.0944 C 0.8192 5.0176 0.9088 4.8128 1.1647999 4.16 L 2.8032 0.1152 C 2.8799999 -0.076799996 2.9568 -0.15359999 3.1232 -0.15359999 C 3.2512 -0.15359999 3.3407998 -0.076799996 3.4304 0.1408 L 5.1328 4.1472 C 5.376 4.7104 5.5168 5.0304 6.2335997 5.0944 C 6.3104 5.1712 6.3104 5.44 6.2335997 5.5168 C 5.9775996 5.5039997 5.6703997 5.4912 5.3375998 5.4912 C 4.9151998 5.4912 4.48 5.5039997 4.16 5.5168 C 4.0832 5.44 4.0832 5.1712 4.16 5.0944 Z "/>
</symbol>
<symbol id="gEFCBD5CCFA072E8B49E2065B449FDBBF" overflow="visible">
<path d="M 5.6832 4.9536 C 5.9263997 4.9536 6.1568 5.184 6.1568 5.44 C 6.1568 5.7088 5.9136 5.9136 5.568 5.9136 C 5.2352 5.9136 4.6208 5.6959996 4.288 5.2608 C 4.1344 5.3631997 3.712 5.6191998 2.9568 5.6191998 C 1.8176 5.6191998 0.768 4.8512 0.768 3.6736 C 0.768 2.9824 1.0752 2.5856 1.4336 2.24 C 1.0752 1.9327999 0.87039995 1.3823999 0.87039995 0.9472 C 0.87039995 0.48639998 1.1264 0.12799999 1.4591999 -0.038399998 C 0.768 -0.44799998 0.4096 -1.0368 0.4096 -1.5871999 C 0.4096 -2.7008 1.4591999 -3.0463998 2.4448 -3.0463998 C 4.1728 -3.0463998 6.0415998 -2.2144 6.0415998 -0.83199996 C 6.0415998 -0.4224 5.8496 -0.1024 5.4783998 0.2048 C 4.9792 0.61439997 4.0832 0.6272 3.6095998 0.6272 C 3.3792 0.6272 3.0591998 0.6016 2.7519999 0.5632 C 2.56 0.55039996 2.432 0.5376 2.368 0.5376 C 1.9968 0.5376 1.5488 0.7168 1.5488 1.2672 C 1.5488 1.5231999 1.6256 1.7919999 1.7792 2.0096 C 2.0864 1.8304 2.4448 1.7407999 2.944 1.7407999 C 4.0703998 1.7407999 5.1071997 2.4448 5.1071997 3.6992 C 5.1071997 4.3008 4.928 4.6464 4.5568 5.0304 C 4.6464 5.1584 4.9024 5.3375998 5.0688 5.3375998 C 5.1584 5.3375998 5.2479997 5.2992 5.3248 5.184 C 5.376 5.0815997 5.5424 4.9536 5.6832 4.9536 Z M 1.6896 -0.12799999 C 1.8304 -0.1664 2.0351999 -0.192 2.2015998 -0.192 C 2.5983999 -0.192 2.9568 -0.15359999 3.136 -0.15359999 C 3.776 -0.15359999 4.3136 -0.1664 4.6847997 -0.3712 C 5.184 -0.65279996 5.3375998 -0.83199996 5.3375998 -1.1647999 C 5.3375998 -2.0864 3.9808 -2.5728 2.8288 -2.5728 C 2.368 -2.5728 1.2928 -2.2015998 1.2928 -1.3312 C 1.2928 -0.89599997 1.3184 -0.576 1.6896 -0.12799999 Z M 4.0832 3.5712 C 4.0832 2.3808 3.4815998 2.1376 3.008 2.1376 C 1.9327999 2.1376 1.8176 3.0463998 1.8176 3.8655999 C 1.8176 4.7616 2.1376 5.2223997 2.8416 5.2223997 C 3.648 5.2223997 4.0832 4.6335998 4.0832 3.5712 Z "/>
</symbol>
<symbol id="gD5EEFB9760BC9A91B84F628EDDA52971" overflow="visible">
<path d="M 2.1376 5.0432 C 2.0607998 4.9663997 2.0096 4.992 2.0096 5.1071997 L 2.0096 7.4624 C 2.0096 8.2944 2.0607998 8.806399 2.0607998 8.806399 C 2.0607998 8.896 2.0096 8.9344 1.8944 8.9344 C 1.5744 8.806399 0.61439997 8.6272 0.1024 8.588799 C 0.076799996 8.4864 0.1024 8.2816 0.1792 8.2048 C 0.21759999 8.2048 0.25599998 8.2048 0.2944 8.2048 C 0.8576 8.1664 0.9984 8.1664 0.9984 7.1552 L 0.9984 0.9088 C 0.9984 0.4096 0.9856 0.1792 0.9472 0 C 1.0112 -0.1024 1.0752 -0.15359999 1.2287999 -0.15359999 C 1.3055999 -0.076799996 1.4336 0.038399998 1.536 0.15359999 C 1.6639999 0.30719998 1.7407999 0.30719998 1.8815999 0.192 C 2.1759999 -0.0512 2.56 -0.12799999 3.008 -0.12799999 C 4.3136 -0.12799999 5.8367996 1.0624 5.8367996 3.0976 C 5.8367996 4.6591997 4.6847997 5.6191998 3.5712 5.6191998 C 3.0207999 5.6191998 2.5344 5.4016 2.1376 5.0432 Z M 2.2272 4.6464 C 2.56 4.9407997 2.944 5.0559998 3.3151999 5.0559998 C 4.0959997 5.0559998 4.736 4.1088 4.736 2.8672 C 4.736 1.408 4.1472 0.30719998 2.9312 0.30719998 C 2.5344 0.30719998 2.2656 0.5888 2.0096 0.9088 L 2.0096 4.1088 C 2.0096 4.3775997 2.0607998 4.5056 2.2272 4.6464 Z "/>
</symbol>
<symbol id="g83A6AA7A836EACB3652229F4716CDAF" overflow="visible">
<path d="M 5.0559998 8.076799 C 4.3136 8.1792 4.3392 8.4223995 3.0848 8.4223995 C 1.7919999 8.4223995 0.65279996 7.5648 0.65279996 6.2079997 C 0.65279996 4.864 1.7664 4.2496 2.8927999 3.8144 C 3.6608 3.52 4.608 3.1615999 4.608 1.9072 C 4.608 0.87039995 4.032 0.3328 3.008 0.3328 C 1.8176 0.3328 1.0496 0.8832 0.768 2.1504 C 0.6016 2.2015998 0.4736 2.1759999 0.34559998 2.112 C 0.39679998 1.1264 0.44799998 0.79359996 0.6016 0.1664 C 1.408 0.1664 1.7664 -0.12799999 2.9055998 -0.12799999 C 3.4815998 -0.12799999 4.032 0.0128 4.48 0.2944 C 5.2223997 0.75519997 5.6832 1.536 5.6832 2.3552 C 5.6832 3.712 4.6591997 4.3136 3.6095998 4.7104 C 2.8416 4.992 1.5616 5.4783998 1.5616 6.5536 C 1.5616 7.2704 2.2144 7.9872 2.9696 7.9872 C 4.2111998 7.9872 4.608 7.1935997 4.864 6.3487997 C 5.0048 6.3231997 5.1712 6.336 5.2864 6.4256 C 5.2352 7.04 5.184 7.3984 5.0559998 8.076799 Z "/>
</symbol>
<symbol id="gDB4862E33098F259EEBBA99A57E5AFA" overflow="visible">
<path d="M 2.1759999 4.5824 C 2.1632 4.9663997 2.1376 5.4272 2.0736 5.5551996 C 2.0479999 5.6191998 2.0224 5.6576 1.92 5.6576 C 1.5616 5.5168 1.2287999 5.4016 0.34559998 5.2864 C 0.32 5.2096 0.34559998 5.0048 0.3712 4.928 C 1.0624 4.864 1.2032 4.7999997 1.2032 4.0576 L 1.2032 1.5616 C 1.2032 0.51199996 1.0368 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7168 -0.0128 1.2032 0 1.7152 0 C 2.2272 0 2.6239998 -0.0128 3.008 -0.0256 C 3.0848 0.0512 3.0848 0.32 3.008 0.39679998 C 2.3552 0.4608 2.2144 0.51199996 2.2144 1.5616 L 2.2144 3.6608 C 2.2144 3.9296 2.3295999 4.0832 2.432 4.1984 C 2.944 4.6976 3.4176 4.9536 3.8144 4.9536 C 4.3008 4.9536 4.6591997 4.6464 4.6591997 3.7888 L 4.6591997 1.5616 C 4.6591997 0.51199996 4.5568 0.44799998 3.8655999 0.39679998 C 3.8016 0.32 3.8016 0.0512 3.8655999 -0.0256 C 4.1856 -0.0128 4.6591997 0 5.1712 0 C 5.6832 0 6.1056 -0.0128 6.4256 -0.0256 C 6.4895997 0.0512 6.4895997 0.32 6.4256 0.39679998 C 5.7855997 0.44799998 5.6703997 0.51199996 5.6703997 1.5616 L 5.6703997 3.5967999 C 5.6703997 3.776 5.6703997 3.9552 5.6576 4.1088 C 6.272 4.7872 6.848 4.9536 7.3472 4.9536 C 7.8335996 4.9536 8.1152 4.672 8.1152 3.8144 L 8.1152 1.5616 C 8.1152 0.51199996 7.9872 0.44799998 7.3216 0.39679998 C 7.2576 0.32 7.2576 0.0512 7.3216 -0.0256 C 7.6415997 -0.0128 8.1152 0 8.6272 0 C 9.1392 0 9.5872 -0.0128 9.9456 -0.0256 C 10.0096 0.0512 10.0096 0.32 9.9456 0.39679998 C 9.2416 0.44799998 9.1264 0.51199996 9.1264 1.5616 L 9.1264 3.5839999 C 9.1264 4.7232 8.9344 5.6191998 7.8079996 5.6191998 C 7.1552 5.6191998 6.3616 5.376 5.6959996 4.672 C 5.6576 4.6335998 5.5808 4.5696 5.5551996 4.6847997 C 5.44 5.2096 4.9407997 5.6191998 4.2752 5.6191998 C 3.5328 5.6191998 2.8672 5.184 2.3295999 4.5824 C 2.2656 4.5183997 2.1887999 4.4288 2.1759999 4.5824 Z "/>
</symbol>
<symbol id="g793DBE65A5AEC1A16A65955B6C0E046" overflow="visible">
<path d="M 10.368 7.232 L 8.3712 1.6768 L 8.3328 1.6896 L 6.5664 7.0912 C 6.3487997 7.7823997 6.7967997 7.8208 7.232 7.8592 C 7.3087997 7.936 7.3087997 8.2048 7.232 8.2816 C 6.7072 8.2688 6.144 8.256 5.632 8.256 C 5.2096 8.256 4.7616 8.2688 4.3519998 8.2816 C 4.2752 8.2048 4.2752 7.936 4.3519998 7.8592 C 5.0304 7.8208 5.312 7.424 5.4272 7.0912 L 5.7216 6.2464 C 5.7728 6.0927997 5.8111997 5.9648 5.8111997 5.8496 C 5.8111997 5.7216 5.7984 5.6191998 5.6959996 5.4016 L 4.0448 1.6511999 L 3.9808 1.6639999 L 2.112 7.3216 C 1.9583999 7.7696 2.304 7.8335996 2.7519999 7.8592 C 2.8288 7.936 2.8288 8.2048 2.7519999 8.2816 C 2.3295999 8.2688 1.7664 8.256 1.2672 8.256 C 0.8192 8.256 0.44799998 8.2688 0.076799996 8.2816 C 0 8.2048 0 7.936 0.076799996 7.8592 C 0.65279996 7.8208 0.7424 7.8079996 0.9856 7.1168 L 3.392 0.192 C 3.4559999 -0.0128 3.5328 -0.15359999 3.6736 -0.15359999 C 3.84 -0.15359999 3.9167998 -0.0256 4.0064 0.192 L 5.9136 4.48 C 6.0288 4.736 6.0671997 4.7999997 6.1312 4.7999997 C 6.1823997 4.7999997 6.2335997 4.6591997 6.3104 4.4416 L 7.7823997 0.192 C 7.8592 -0.0256 7.9231997 -0.15359999 8.076799 -0.15359999 C 8.2176 -0.15359999 8.3071995 -0.0128 8.3712 0.1792 L 10.943999 7.0783997 C 11.110399 7.5263996 11.340799 7.8208 12.0448 7.8592 C 12.1216 7.936 12.1216 8.2048 12.0448 8.2816 C 11.673599 8.2688 11.264 8.256 10.9312 8.256 C 10.5984 8.256 10.0352 8.2688 9.5232 8.2816 C 9.4464 8.2048 9.4464 7.936 9.5232 7.8592 C 10.047999 7.8208 10.559999 7.7823997 10.368 7.232 Z "/>
</symbol>
<symbol id="gA11612CECC8CBEF18835767DAB11B2F7" overflow="visible">
<path d="M 0.5248 2.6239998 C 0.5248 1.3184 1.3952 -0.12799999 3.2128 -0.12799999 C 4.032 -0.12799999 4.6591997 0.1664 5.0944 0.5888 C 5.6703997 1.152 5.9263997 1.9583999 5.9263997 2.7391999 C 5.9263997 4.0703998 5.1967998 5.6191998 3.2384 5.6191998 C 2.3936 5.6191998 1.7024 5.2736 1.2287999 4.7232 C 0.768 4.1728 0.5248 3.4304 0.5248 2.6239998 Z M 3.0463998 5.1712 C 4.1472 5.1712 4.8255997 4.1728 4.8255997 2.3295999 C 4.8255997 0.7168 3.9936 0.32 3.392 0.32 C 2.0607998 0.32 1.6256 1.9327999 1.6256 2.9183998 C 1.6256 4.032 1.8944 5.1712 3.0463998 5.1712 Z "/>
</symbol>
<symbol id="gCEFEF3D67F35C6E83CC3757B1DD21B13" overflow="visible">
<path d="M 4.2752 0.64 C 4.3392 0.69119996 4.4544 0.7168 4.4672 0.6272 C 4.5056 0.32 4.608 -0.12799999 4.608 -0.12799999 C 4.7104 -0.1664 4.7743998 -0.15359999 4.8512 -0.12799999 C 5.1328 0.1024 5.5808 0.2944 6.3616 0.384 C 6.4384 0.4608 6.4384 0.65279996 6.3616 0.72959995 C 5.5424 0.79359996 5.4272 1.0368 5.4272 1.6639999 L 5.4272 7.4624 C 5.4272 8.2944 5.4783998 8.806399 5.4783998 8.806399 C 5.4783998 8.896 5.4272 8.9344 5.312 8.9344 C 4.992 8.806399 4.032 8.6272 3.52 8.588799 C 3.4944 8.4864 3.52 8.2816 3.5967999 8.2048 C 3.6352 8.2048 3.6736 8.2048 3.712 8.2048 C 4.2752 8.1664 4.416 8.1664 4.416 7.1552 L 4.416 5.5168 C 4.416 5.4272 4.3904 5.4016 4.3008 5.4016 C 4.2496 5.4016 3.7247999 5.6191998 3.3023999 5.6191998 C 2.4575999 5.6191998 1.8944 5.3375998 1.3823999 4.8512 C 0.83199996 4.3008 0.4992 3.5456 0.4992 2.5983999 C 0.4992 1.0239999 1.2928 -0.12799999 2.6752 -0.12799999 C 3.1743999 -0.12799999 3.648 0.12799999 4.2752 0.64 Z M 4.416 1.5871999 C 4.416 1.344 4.3904 1.2415999 4.2111998 1.0879999 C 3.7375998 0.6784 3.3279998 0.4736 3.008 0.4736 C 2.3167999 0.4736 1.5999999 1.2287999 1.5999999 2.8288 C 1.5999999 3.7503998 1.7792 4.2623997 1.9712 4.5312 C 2.368 5.1328 2.9055998 5.1712 3.1615999 5.1712 C 3.6223998 5.1712 3.9424 5.0048 4.1984 4.7104 C 4.3775997 4.5056 4.416 4.416 4.416 4.0192 Z "/>
</symbol>
<symbol id="g645CA8FA3D9155E2CBD9F8EED3C1540D" overflow="visible">
<path d="M 1.9968 4.7104 C 1.984 5.0944 1.9583999 5.4272 1.8944 5.5551996 C 1.8687999 5.6191998 1.8432 5.6576 1.7407999 5.6576 C 1.3823999 5.5168 1.0496 5.4016 0.1664 5.2864 C 0.1408 5.2096 0.1664 5.0048 0.192 4.928 C 0.8832 4.864 1.0239999 4.7999997 1.0239999 4.0576 L 1.0239999 -1.408 C 1.0239999 -2.4703999 0.8832 -2.5344 0.1024 -2.5728 C 0.0256 -2.6496 0.0256 -2.9183998 0.1024 -2.9952 C 0.55039996 -2.9824 1.0239999 -2.9696 1.536 -2.9696 C 2.0479999 -2.9696 2.6624 -2.9824 3.0848 -2.9952 C 3.1615999 -2.9183998 3.1615999 -2.6496 3.0848 -2.5728 C 2.1759999 -2.5216 2.0351999 -2.4703999 2.0351999 -1.408 L 2.0351999 -0.0256 C 2.0351999 0.1408 2.0864 0.12799999 2.2144 0.076799996 C 2.5344 -0.0512 2.9183998 -0.12799999 3.3279998 -0.12799999 C 4.0448 -0.12799999 4.6847997 0.0896 5.2096 0.5888 C 5.8111997 1.1776 6.1568 1.9712 6.1568 3.008 C 6.1568 4.3648 5.1967998 5.6191998 3.8911998 5.6191998 C 3.3023999 5.6191998 2.6496 5.2352 2.1376 4.6591997 C 2.0607998 4.5824 2.0096 4.5824 1.9968 4.7104 Z M 2.24 4.2367997 C 2.5728 4.6464 3.1615999 5.0304 3.5328 5.0304 C 4.3519998 5.0304 5.0559998 4.1088 5.0559998 2.6624 C 5.0559998 1.6128 4.6847997 0.30719998 3.2512 0.30719998 C 3.0207999 0.30719998 2.5728 0.3712 2.3423998 0.576 C 2.0864 0.8064 2.0351999 0.8832 2.0351999 1.344 L 2.0351999 3.6736 C 2.0351999 3.9424 2.0864 4.0576 2.24 4.2367997 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
<symbol id="g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" overflow="visible">
<path d="M 4.688 10.336 L 4.032 10.336 L 0.24000001 -0.94400007 L 0.896 -0.94400007 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
</defs>
<defs id="gradients">
<linearGradient id="fD7C012D2AF80355F4C7C5ACE2CA2D57C" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="f363FA645F4DDF880CAFE55377689608C" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="fD1DE6F2D42B356B963F3EFEDF9B8AED6" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="fBD7F84C29550CE3656482B9B477C45F3" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="fAD566D6795458FC9E5F2C77BE78CA351" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="f30325C9099C45C4D355E9F01DBC44059" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="f366D3893095F02AFC8E7B807FB7435F8" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="fC6191A7A22B881E0085E6748EBA27194" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="fE006BF89422BA632EB208DEC2513AD77" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="f4499ABC3C72D241D8C7C361D7CD322FC" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="fC56F2EF7D9EE84A815C802518E760D80" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="fDD0C4B7A171DA606DB46C35BBACC6B00" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="f171022186BBCE2AE36D566478FB1BBC7" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="f85C4DCB91F6EADACAA4255BB643ED944" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="f25AD22204B4E367C5BE1BDA4A18D6AC9" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="f62DDAA6B091DEDA07FAC654B5159FDA0" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="f1C4EAA78D3204BE173079491818E2EC8" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="fDEF5A249E4AF9665C4581E12C3B3A587" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="f282C2CF828FBBE97A71E7F0675382158" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="fCBC04A8E62AC78F0CD8D7E772F6C608C" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="f91CF3CEA929A916FA73B5E0A0C2FBE99" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#edb081"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.39%" stop-color="#edaf80"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="0.78%" stop-color="#edae7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.18%" stop-color="#edad7f"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.57%" stop-color="#edac7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="1.96%" stop-color="#edab7e"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.35%" stop-color="#ecaa7d"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="2.75%" stop-color="#eca97c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.14%" stop-color="#eca87c"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.53%" stop-color="#eca77b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="3.92%" stop-color="#eca67b"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.31%" stop-color="#eca57a"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="4.71%" stop-color="#eca479"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.1%" stop-color="#eca379"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.49%" stop-color="#eca278"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="5.88%" stop-color="#eca178"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.27%" stop-color="#eca077"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="6.67%" stop-color="#ec9f76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.06%" stop-color="#eb9e76"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.45%" stop-color="#eb9d75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="7.84%" stop-color="#eb9c75"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.24%" stop-color="#eb9b74"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="8.63%" stop-color="#eb9a73"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.02%" stop-color="#eb9973"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.41%" stop-color="#eb9972"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="9.8%" stop-color="#eb9872"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.2%" stop-color="#eb9771"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.59%" stop-color="#ea9671"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="10.98%" stop-color="#ea9570"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.37%" stop-color="#ea946f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="11.76%" stop-color="#ea936f"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.16%" stop-color="#ea926e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.55%" stop-color="#ea916e"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="12.94%" stop-color="#ea906d"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.33%" stop-color="#ea8f6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="13.73%" stop-color="#ea8e6c"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.12%" stop-color="#e98d6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.51%" stop-color="#e98c6b"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="14.9%" stop-color="#e98b6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.29%" stop-color="#e98a6a"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="15.69%" stop-color="#e98969"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.08%" stop-color="#e98868"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.47%" stop-color="#e98768"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="16.86%" stop-color="#e98667"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.25%" stop-color="#e88567"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="17.65%" stop-color="#e88466"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.04%" stop-color="#e88366"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.43%" stop-color="#e88265"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="18.82%" stop-color="#e88165"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.22%" stop-color="#e88064"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="19.61%" stop-color="#e87f64"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20%" stop-color="#e77e63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.39%" stop-color="#e77d63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="20.78%" stop-color="#e77c63"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.18%" stop-color="#e77b62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.57%" stop-color="#e77a62"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="21.96%" stop-color="#e67961"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.35%" stop-color="#e67861"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="22.75%" stop-color="#e67760"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.14%" stop-color="#e67660"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.53%" stop-color="#e67560"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="23.92%" stop-color="#e5745f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.31%" stop-color="#e5735f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="24.71%" stop-color="#e5725f"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.1%" stop-color="#e5715e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.49%" stop-color="#e5705e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="25.88%" stop-color="#e46f5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.27%" stop-color="#e46e5e"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="26.67%" stop-color="#e46d5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.06%" stop-color="#e46c5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.45%" stop-color="#e36b5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="27.84%" stop-color="#e36a5d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.24%" stop-color="#e3695d"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="28.63%" stop-color="#e3685c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.02%" stop-color="#e2675c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.41%" stop-color="#e2665c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="29.8%" stop-color="#e2655c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.2%" stop-color="#e1645c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.59%" stop-color="#e1635c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="30.98%" stop-color="#e1625c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.37%" stop-color="#e0615c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="31.76%" stop-color="#e0605c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.16%" stop-color="#e05f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.55%" stop-color="#df5f5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="32.94%" stop-color="#df5e5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.33%" stop-color="#de5d5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="33.73%" stop-color="#de5c5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.12%" stop-color="#de5b5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.51%" stop-color="#dd5a5c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="34.9%" stop-color="#dd595c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.29%" stop-color="#dc585c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="35.69%" stop-color="#dc575c"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.08%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.47%" stop-color="#db565d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="36.86%" stop-color="#da555d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.25%" stop-color="#da545d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="37.65%" stop-color="#d9535d"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.04%" stop-color="#d9525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.43%" stop-color="#d8525e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="38.82%" stop-color="#d7515e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.22%" stop-color="#d7505e"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="39.61%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40%" stop-color="#d64f5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.39%" stop-color="#d54e5f"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="40.78%" stop-color="#d44d60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.18%" stop-color="#d44c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.57%" stop-color="#d34c60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="41.96%" stop-color="#d24b60"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.35%" stop-color="#d24a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="42.75%" stop-color="#d14a61"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.14%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.53%" stop-color="#d04962"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="43.92%" stop-color="#cf4862"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.31%" stop-color="#ce4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="44.71%" stop-color="#cd4763"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.1%" stop-color="#cc4663"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.49%" stop-color="#cc4664"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="45.88%" stop-color="#cb4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.27%" stop-color="#ca4564"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="46.67%" stop-color="#c94465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.06%" stop-color="#c84465"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.45%" stop-color="#c84365"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="47.84%" stop-color="#c74366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.24%" stop-color="#c64366"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="48.63%" stop-color="#c54266"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.02%" stop-color="#c44267"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.41%" stop-color="#c34167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="49.8%" stop-color="#c24167"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.2%" stop-color="#c14168"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.59%" stop-color="#c14068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="50.98%" stop-color="#c04068"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.37%" stop-color="#bf4069"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="51.76%" stop-color="#be3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.16%" stop-color="#bd3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.55%" stop-color="#bc3f69"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="52.94%" stop-color="#bb3f6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.33%" stop-color="#ba3e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="53.73%" stop-color="#b93e6a"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.12%" stop-color="#b83e6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.51%" stop-color="#b73d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="54.9%" stop-color="#b63d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.29%" stop-color="#b53d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="55.69%" stop-color="#b43d6b"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.08%" stop-color="#b33c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.47%" stop-color="#b23c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="56.86%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.25%" stop-color="#b13c6c"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="57.65%" stop-color="#b03b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.04%" stop-color="#af3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.43%" stop-color="#ae3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="58.82%" stop-color="#ad3b6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.22%" stop-color="#ac3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="59.61%" stop-color="#ab3a6d"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60%" stop-color="#aa3a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.39%" stop-color="#a93a6e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="60.78%" stop-color="#a8396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.18%" stop-color="#a7396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.57%" stop-color="#a6396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="61.96%" stop-color="#a5396e"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.35%" stop-color="#a4386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="62.75%" stop-color="#a3386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.14%" stop-color="#a2386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.53%" stop-color="#a1386f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="63.92%" stop-color="#a1376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.31%" stop-color="#a0376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="64.71%" stop-color="#9f376f"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.1%" stop-color="#9e3770"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.49%" stop-color="#9d3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="65.88%" stop-color="#9c3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.27%" stop-color="#9b3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="66.67%" stop-color="#9a3670"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.06%" stop-color="#993570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.45%" stop-color="#983570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="67.84%" stop-color="#973570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.24%" stop-color="#963570"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="68.63%" stop-color="#953470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.02%" stop-color="#943470"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.41%" stop-color="#943471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="69.8%" stop-color="#933471"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.2%" stop-color="#923371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.59%" stop-color="#913371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="70.98%" stop-color="#903371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.37%" stop-color="#8f3371"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="71.76%" stop-color="#8e3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.16%" stop-color="#8d3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.55%" stop-color="#8c3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="72.94%" stop-color="#8b3271"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.33%" stop-color="#8a3171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="73.73%" stop-color="#893171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.12%" stop-color="#883171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.51%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="74.9%" stop-color="#873171"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.29%" stop-color="#863071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="75.69%" stop-color="#853071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.08%" stop-color="#843071"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.47%" stop-color="#833070"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="76.86%" stop-color="#822f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.25%" stop-color="#812f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="77.65%" stop-color="#802f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.04%" stop-color="#7f2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.43%" stop-color="#7e2f70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="78.82%" stop-color="#7d2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.22%" stop-color="#7c2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="79.61%" stop-color="#7b2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80%" stop-color="#7a2e70"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.39%" stop-color="#792e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="80.78%" stop-color="#782e6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.18%" stop-color="#772d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.57%" stop-color="#762d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="81.96%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.35%" stop-color="#752d6f"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="82.75%" stop-color="#742d6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.14%" stop-color="#732c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.53%" stop-color="#722c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="83.92%" stop-color="#712c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.31%" stop-color="#702c6e"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="84.71%" stop-color="#6f2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.1%" stop-color="#6e2c6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.49%" stop-color="#6d2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="85.88%" stop-color="#6c2b6d"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.27%" stop-color="#6b2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="86.67%" stop-color="#6a2b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.06%" stop-color="#692b6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.45%" stop-color="#682a6c"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="87.84%" stop-color="#672a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.24%" stop-color="#662a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="88.63%" stop-color="#652a6b"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.02%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.41%" stop-color="#642a6a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="89.8%" stop-color="#63296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.2%" stop-color="#62296a"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.59%" stop-color="#612969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="90.98%" stop-color="#602969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.37%" stop-color="#5f2969"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="91.76%" stop-color="#5e2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.16%" stop-color="#5d2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.55%" stop-color="#5c2868"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="92.94%" stop-color="#5b2867"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.33%" stop-color="#5a2767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="93.73%" stop-color="#592767"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.12%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.51%" stop-color="#582766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="94.9%" stop-color="#572766"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.29%" stop-color="#562666"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="95.69%" stop-color="#552665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.08%" stop-color="#542665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.47%" stop-color="#532665"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="96.86%" stop-color="#522564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.25%" stop-color="#512564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="97.65%" stop-color="#502564"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.04%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.43%" stop-color="#4f2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="98.82%" stop-color="#4e2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.22%" stop-color="#4d2463"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="99.61%" stop-color="#4c2362"/>
<stop offset="100%" stop-color="#4b2362"/>
</linearGradient>
<linearGradient id="f33E03C75571CB473EEA4DB0D986DF9AA" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fE186731572801AD70C450F793EBEC591" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fEB756D53E496EF388D77A9FC4FADF98B" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f64E810A2B0301B3AFE31F0083C2435EE" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fA544A357A483A8A3AF5578997F22F0A3" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fD7087123C09B6772C7F2CF671F56DB63" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f30EDC632E0E689E1E4032E5187F00E6C" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f7710571C89B2BD7DF9F67F66C9CF062" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f124498C8722594BC84D3DE83E1D46B5D" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fBD2AE68E6F0F8329CA1878286515665A" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f1AAA3A0AFBE423B107F2B850809F00C7" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fD8E9D71C813711217F1BF86793E87A81" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fCC8581D2E55103DD9CA35019887FF2E3" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f25978294C782F8D9A3DE32B6961F8CBD" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f41DF624984D130456C441D06B0FA8D74" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fCA62F9C34FD4B4F29ACA26A49A514B81" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fD43D71A7992AE2B86B5D81EB000787C8" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fFB9DC6CDFE951412AF6B4B19B75FCF2E" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fBA29C4CBEE0B5362118A04DD58CD81F8" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f1AA1F0063E906525BE1703D5AD8989B4" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fFC19A2481BDD18CFFD031F73916C83DD" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fC22102A8F4B325C3451F66BD68CF3AB5" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fB4D1BB231EEA0FFE3FBA0000F1107622" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fB4D40DD3986F9B84780D20DA4213A2F7" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f35B2DA2DA46577085A97D87CED860140" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f48B1B6B68EF3F19E52FEDD3DEE9200BE" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f30F1023381C693524939E7F4CF8AA101" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f76171BC9D9B6A1F74C6089979E7AB9E4" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f32218FBEA8E29C084BAF753778DB4994" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fCDE10BECEEC846D9ACFF80B8B5870348" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f23E45BA991A59ABBB74F553B5F42C08E" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fDEAB44B206FF6EE16248A189944B0B57" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fBC7E1BE44AD3C7AEC7D6A9E33B858D3E" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fA41B7B4CB827AC614E03EE8C61914E28" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f8A132A93F5E14EF8B4BE33F7586EDEB0" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="fB6A7370788ABD55AFF119F7D63BF935" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f918C16FDCB8EC70D1A0509598F87777" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
<linearGradient id="f2817556A795F8EDD0C1D32EB581EFBD2" spreadMethod="pad" gradientUnits="userSpaceOnUse" x1="0" y1="0" x2="1" y2="0">
<stop offset="0%" stop-color="#a5cd90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.39%" stop-color="#a4cc90"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="0.78%" stop-color="#a3cc91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.18%" stop-color="#a2cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.57%" stop-color="#a0cb91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="1.96%" stop-color="#9fca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.35%" stop-color="#9eca91"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="2.75%" stop-color="#9dc991"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.14%" stop-color="#9cc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.53%" stop-color="#9bc891"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="3.92%" stop-color="#9ac791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.31%" stop-color="#99c791"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="4.71%" stop-color="#98c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.1%" stop-color="#96c691"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.49%" stop-color="#95c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="5.88%" stop-color="#94c591"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.27%" stop-color="#93c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="6.67%" stop-color="#92c491"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.06%" stop-color="#91c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.45%" stop-color="#90c391"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="7.84%" stop-color="#8fc291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.24%" stop-color="#8ec291"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="8.63%" stop-color="#8dc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.02%" stop-color="#8bc191"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.41%" stop-color="#8ac091"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="9.8%" stop-color="#89bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.2%" stop-color="#88bf91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.59%" stop-color="#87be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="10.98%" stop-color="#86be91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.37%" stop-color="#85bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="11.76%" stop-color="#84bd91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.16%" stop-color="#82bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.55%" stop-color="#81bc91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="12.94%" stop-color="#80bb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.33%" stop-color="#7fbb91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="13.73%" stop-color="#7eba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.12%" stop-color="#7dba91"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.51%" stop-color="#7cb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="14.9%" stop-color="#7bb991"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.29%" stop-color="#79b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="15.69%" stop-color="#78b891"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.08%" stop-color="#77b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.47%" stop-color="#76b791"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="16.86%" stop-color="#75b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.25%" stop-color="#74b690"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="17.65%" stop-color="#73b590"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.04%" stop-color="#72b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.43%" stop-color="#71b490"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="18.82%" stop-color="#70b390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.22%" stop-color="#6fb390"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="19.61%" stop-color="#6eb290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20%" stop-color="#6db290"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.39%" stop-color="#6cb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="20.78%" stop-color="#6bb190"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.18%" stop-color="#6ab090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.57%" stop-color="#69b090"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="21.96%" stop-color="#68af90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.35%" stop-color="#67ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="22.75%" stop-color="#66ae90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.14%" stop-color="#65ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.53%" stop-color="#64ad90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="23.92%" stop-color="#63ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.31%" stop-color="#62ac90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="24.71%" stop-color="#62ab90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.1%" stop-color="#61aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.49%" stop-color="#60aa90"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="25.88%" stop-color="#5fa990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.27%" stop-color="#5ea990"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="26.67%" stop-color="#5da890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.06%" stop-color="#5ca890"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.45%" stop-color="#5ba790"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="27.84%" stop-color="#5ba690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.24%" stop-color="#5aa690"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="28.63%" stop-color="#59a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.02%" stop-color="#58a590"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.41%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="29.8%" stop-color="#57a490"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.2%" stop-color="#56a390"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.59%" stop-color="#55a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="30.98%" stop-color="#54a290"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.37%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="31.76%" stop-color="#53a190"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.16%" stop-color="#52a090"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.55%" stop-color="#519f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="32.94%" stop-color="#509f90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.33%" stop-color="#509e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="33.73%" stop-color="#4f9e90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.12%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.51%" stop-color="#4e9d90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="34.9%" stop-color="#4d9c90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.29%" stop-color="#4c9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="35.69%" stop-color="#4b9b90"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.08%" stop-color="#4b9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.47%" stop-color="#4a9a8f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="36.86%" stop-color="#49998f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.25%" stop-color="#49988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="37.65%" stop-color="#48988f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.04%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.43%" stop-color="#47978f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="38.82%" stop-color="#46968f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.22%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="39.61%" stop-color="#45958f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40%" stop-color="#44948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.39%" stop-color="#43948f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="40.78%" stop-color="#43938f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.18%" stop-color="#42928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.57%" stop-color="#41928f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="41.96%" stop-color="#41918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.35%" stop-color="#40918f"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="42.75%" stop-color="#40908e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.14%" stop-color="#3f8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.53%" stop-color="#3e8f8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="43.92%" stop-color="#3e8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.31%" stop-color="#3d8e8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="44.71%" stop-color="#3c8d8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.1%" stop-color="#3c8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.49%" stop-color="#3b8c8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="45.88%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.27%" stop-color="#3a8b8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="46.67%" stop-color="#398a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.06%" stop-color="#388a8e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.45%" stop-color="#38898e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="47.84%" stop-color="#37888e"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.24%" stop-color="#37888d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="48.63%" stop-color="#36878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.02%" stop-color="#35878d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.41%" stop-color="#35868d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="49.8%" stop-color="#34858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.2%" stop-color="#33858d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.59%" stop-color="#33848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="50.98%" stop-color="#32848d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.37%" stop-color="#31838d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="51.76%" stop-color="#31828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.16%" stop-color="#30828d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.55%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="52.94%" stop-color="#2f818d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.33%" stop-color="#2e808d"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="53.73%" stop-color="#2d808c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.12%" stop-color="#2d7f8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.51%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="54.9%" stop-color="#2c7e8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.29%" stop-color="#2b7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="55.69%" stop-color="#2a7d8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.08%" stop-color="#2a7c8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.47%" stop-color="#297b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="56.86%" stop-color="#287b8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.25%" stop-color="#287a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="57.65%" stop-color="#277a8c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.04%" stop-color="#27798c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.43%" stop-color="#26788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="58.82%" stop-color="#25788c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.22%" stop-color="#25778c"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="59.61%" stop-color="#24778b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60%" stop-color="#24768b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.39%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="60.78%" stop-color="#23758b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.18%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.57%" stop-color="#22748b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="61.96%" stop-color="#21738b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.35%" stop-color="#21728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="62.75%" stop-color="#20728b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.14%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.53%" stop-color="#20718b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="63.92%" stop-color="#1f708b"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.31%" stop-color="#1f6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="64.71%" stop-color="#1e6f8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.1%" stop-color="#1e6e8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.49%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="65.88%" stop-color="#1e6d8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.27%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="66.67%" stop-color="#1d6c8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.06%" stop-color="#1d6b8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.45%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="67.84%" stop-color="#1d6a8a"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.24%" stop-color="#1c6989"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="68.63%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.02%" stop-color="#1c6889"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.41%" stop-color="#1c6789"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="69.8%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.2%" stop-color="#1c6689"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.59%" stop-color="#1c6589"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="70.98%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.37%" stop-color="#1c6488"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="71.76%" stop-color="#1c6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.16%" stop-color="#1d6388"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.55%" stop-color="#1d6288"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="72.94%" stop-color="#1d6188"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.33%" stop-color="#1d6187"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="73.73%" stop-color="#1d6087"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.12%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.51%" stop-color="#1d5f87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="74.9%" stop-color="#1e5e87"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.29%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="75.69%" stop-color="#1e5d86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.08%" stop-color="#1e5c86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.47%" stop-color="#1e5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="76.86%" stop-color="#1f5b86"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.25%" stop-color="#1f5a85"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="77.65%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.04%" stop-color="#1f5985"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.43%" stop-color="#205885"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="78.82%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.22%" stop-color="#205784"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="79.61%" stop-color="#205684"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80%" stop-color="#215584"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.39%" stop-color="#215583"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="80.78%" stop-color="#215483"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.18%" stop-color="#225383"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.57%" stop-color="#225283"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="81.96%" stop-color="#225282"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.35%" stop-color="#225182"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="82.75%" stop-color="#235082"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.14%" stop-color="#235081"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.53%" stop-color="#234f81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="83.92%" stop-color="#244e81"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.31%" stop-color="#244e80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="84.71%" stop-color="#244d80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.1%" stop-color="#254c80"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.49%" stop-color="#254c7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="85.88%" stop-color="#254b7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.27%" stop-color="#254a7f"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="86.67%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.06%" stop-color="#26497e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.45%" stop-color="#26487e"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="87.84%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.24%" stop-color="#27477d"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="88.63%" stop-color="#27467c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.02%" stop-color="#27457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.41%" stop-color="#28457c"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="89.8%" stop-color="#28447b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.2%" stop-color="#28437b"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.59%" stop-color="#28427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="90.98%" stop-color="#29427a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.37%" stop-color="#29417a"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="91.76%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.16%" stop-color="#294079"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.55%" stop-color="#2a3f78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="92.94%" stop-color="#2a3e78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.33%" stop-color="#2a3d78"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="93.73%" stop-color="#2a3d77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.12%" stop-color="#2a3c77"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.51%" stop-color="#2a3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="94.9%" stop-color="#2b3b76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.29%" stop-color="#2b3a76"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="95.69%" stop-color="#2b3975"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.08%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.47%" stop-color="#2b3875"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="96.86%" stop-color="#2b3774"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.25%" stop-color="#2b3674"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="97.65%" stop-color="#2c3574"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.04%" stop-color="#2c3573"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.43%" stop-color="#2c3473"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="98.82%" stop-color="#2c3373"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.22%" stop-color="#2c3272"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="99.61%" stop-color="#2c3172"/>
<stop offset="100%" stop-color="#2c3172"/>
</linearGradient>
</defs>
<defs id="gradient-refs">
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -320.90000000000015 370.24299212598424)" id="g8BF286A751A64D04318FAE9D5808AE03" href="#fD7C012D2AF80355F4C7C5ACE2CA2D57C" xlink:href="#fD7C012D2AF80355F4C7C5ACE2CA2D57C"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -330.60000000000014 370.24299212598424)" id="g11BB493CF5D400C3E11CA69FA1CC67B8" href="#f363FA645F4DDF880CAFE55377689608C" xlink:href="#f363FA645F4DDF880CAFE55377689608C"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -340.6800000000001 370.24299212598424)" id="gE0948157D48E5C62CE3ECFC0AC3AE29A" href="#fD1DE6F2D42B356B963F3EFEDF9B8AED6" xlink:href="#fD1DE6F2D42B356B963F3EFEDF9B8AED6"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -356.4800000000002 370.24299212598424)" id="gC8C7957CBD1EB68E7F4389559EB4F205" href="#fBD7F84C29550CE3656482B9B477C45F3" xlink:href="#fBD7F84C29550CE3656482B9B477C45F3"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -370.42000000000013 370.24299212598424)" id="gC2C3DF145E9D150521FAB824EFA788B3" href="#fAD566D6795458FC9E5F2C77BE78CA351" xlink:href="#fAD566D6795458FC9E5F2C77BE78CA351"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -375.8400000000001 370.24299212598424)" id="g71857523B25144D53E22586A9DCD08D3" href="#fD1DE6F2D42B356B963F3EFEDF9B8AED6" xlink:href="#fD1DE6F2D42B356B963F3EFEDF9B8AED6"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -391.6400000000001 370.24299212598424)" id="gA89D841A70C642F4FC683A0FDAE46559" href="#f30325C9099C45C4D355E9F01DBC44059" xlink:href="#f30325C9099C45C4D355E9F01DBC44059"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -400.78000000000014 370.24299212598424)" id="gCC92CA1EB330BF9FC4B80C8636A2FCE0" href="#f366D3893095F02AFC8E7B807FB7435F8" xlink:href="#f366D3893095F02AFC8E7B807FB7435F8"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -410.78000000000014 370.24299212598424)" id="g83AD37751272D20BA8B46F72C45E8340" href="#fBD7F84C29550CE3656482B9B477C45F3" xlink:href="#fBD7F84C29550CE3656482B9B477C45F3"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -419.72000000000014 370.24299212598424)" id="g510C684A996A65B4A8E4BBA8BCA0EA3" href="#fC6191A7A22B881E0085E6748EBA27194" xlink:href="#fC6191A7A22B881E0085E6748EBA27194"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -432.5200000000001 370.24299212598424)" id="gA3A7ABE42C73D65B3ECF9DEFD397AC1F" href="#fC6191A7A22B881E0085E6748EBA27194" xlink:href="#fC6191A7A22B881E0085E6748EBA27194"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -440.3200000000001 370.24299212598424)" id="g8293AEEDE3E503405F50CA6094393521" href="#f363FA645F4DDF880CAFE55377689608C" xlink:href="#f363FA645F4DDF880CAFE55377689608C"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -450.40000000000015 370.24299212598424)" id="gA10FD8777B830FD3FAD141AB130D4E97" href="#fE006BF89422BA632EB208DEC2513AD77" xlink:href="#fE006BF89422BA632EB208DEC2513AD77"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -461.02000000000015 370.24299212598424)" id="g7F4B8BF8910A5EA1AA85B2CF4E924DD2" href="#f4499ABC3C72D241D8C7C361D7CD322FC" xlink:href="#f4499ABC3C72D241D8C7C361D7CD322FC"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -468.3000000000002 370.24299212598424)" id="g41D277A0316896AC373DFC417CCA2AF2" href="#fC56F2EF7D9EE84A815C802518E760D80" xlink:href="#fC56F2EF7D9EE84A815C802518E760D80"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -476.8600000000001 370.24299212598424)" id="g8D189FECA823958010EA96AFE1B7FB37" href="#fBD7F84C29550CE3656482B9B477C45F3" xlink:href="#fBD7F84C29550CE3656482B9B477C45F3"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -485.94000000000017 370.24299212598424)" id="g46BE48E7652E6F2D774DEA78692D27F6" href="#fDD0C4B7A171DA606DB46C35BBACC6B00" xlink:href="#fDD0C4B7A171DA606DB46C35BBACC6B00"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -501.0600000000002 370.24299212598424)" id="g1AED89B7EE7618AF617249B24B59FA66" href="#f171022186BBCE2AE36D566478FB1BBC7" xlink:href="#f171022186BBCE2AE36D566478FB1BBC7"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -507.26000000000016 370.24299212598424)" id="g96A1E38A9703EA0AF1F04B7B1128CAA9" href="#f4499ABC3C72D241D8C7C361D7CD322FC" xlink:href="#f4499ABC3C72D241D8C7C361D7CD322FC"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -514.5400000000001 370.24299212598424)" id="gFEC5145352DF50898A59363463DD451E" href="#f363FA645F4DDF880CAFE55377689608C" xlink:href="#f363FA645F4DDF880CAFE55377689608C"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -524.6200000000001 370.24299212598424)" id="g818DC020A045126E122CCEC62AEF635F" href="#fD1DE6F2D42B356B963F3EFEDF9B8AED6" xlink:href="#fD1DE6F2D42B356B963F3EFEDF9B8AED6"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -545.4200000000002 370.24299212598424)" id="gDB7DBEF21119702BD7CE5C94EA64E7AA" href="#f85C4DCB91F6EADACAA4255BB643ED944" xlink:href="#f85C4DCB91F6EADACAA4255BB643ED944"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -555.1200000000001 370.24299212598424)" id="g15EF886B7CD7CA26BB37EEC3F5AB6FF4" href="#f30325C9099C45C4D355E9F01DBC44059" xlink:href="#f30325C9099C45C4D355E9F01DBC44059"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -564.2600000000001 370.24299212598424)" id="g88CD5C624948E3DAC117EA3520D42146" href="#fAD566D6795458FC9E5F2C77BE78CA351" xlink:href="#fAD566D6795458FC9E5F2C77BE78CA351"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -569.6800000000001 370.24299212598424)" id="g1619F3D1FE50B3EA91C76459F70DE91E" href="#fC6191A7A22B881E0085E6748EBA27194" xlink:href="#fC6191A7A22B881E0085E6748EBA27194"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -577.4800000000001 370.24299212598424)" id="g8163C9E5CCD07611B0D3DB525072CCB2" href="#fC6191A7A22B881E0085E6748EBA27194" xlink:href="#fC6191A7A22B881E0085E6748EBA27194"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -585.2800000000002 370.24299212598424)" id="gE6DBA2CE4A2C0616DFF9ECCAF76570BA" href="#f25AD22204B4E367C5BE1BDA4A18D6AC9" xlink:href="#f25AD22204B4E367C5BE1BDA4A18D6AC9"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -595.0000000000002 370.24299212598424)" id="gDCB943C619B2C8AF401FA74DE8E3A6DA" href="#f62DDAA6B091DEDA07FAC654B5159FDA0" xlink:href="#f62DDAA6B091DEDA07FAC654B5159FDA0"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -606.9400000000002 370.24299212598424)" id="g11EE8FB2ADA714058BFF795517CB9DD4" href="#f1C4EAA78D3204BE173079491818E2EC8" xlink:href="#f1C4EAA78D3204BE173079491818E2EC8"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -617.7000000000002 370.24299212598424)" id="g127B7482475120E5C4C87E0C43026304" href="#fBD7F84C29550CE3656482B9B477C45F3" xlink:href="#fBD7F84C29550CE3656482B9B477C45F3"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -631.6400000000002 370.24299212598424)" id="gF3E4E7E87E59AF74295E016D66F83ACB" href="#fDEF5A249E4AF9665C4581E12C3B3A587" xlink:href="#fDEF5A249E4AF9665C4581E12C3B3A587"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -648.4200000000002 370.24299212598424)" id="g1998F6B3F913C3A60FCE5F3731A97E34" href="#fAD566D6795458FC9E5F2C77BE78CA351" xlink:href="#fAD566D6795458FC9E5F2C77BE78CA351"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -653.8400000000001 370.24299212598424)" id="g5BA69C97F761DBB4A9BAF83B7FBAB76D" href="#fC6191A7A22B881E0085E6748EBA27194" xlink:href="#fC6191A7A22B881E0085E6748EBA27194"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -661.6400000000002 370.24299212598424)" id="gED460B2A719CC9438E21939C79896C84" href="#fC6191A7A22B881E0085E6748EBA27194" xlink:href="#fC6191A7A22B881E0085E6748EBA27194"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -669.4400000000002 370.24299212598424)" id="g8CABE8CEBC5A9D0C379F40AFEC33375F" href="#fAD566D6795458FC9E5F2C77BE78CA351" xlink:href="#fAD566D6795458FC9E5F2C77BE78CA351"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -674.8600000000002 370.24299212598424)" id="gE2A346E8248C50A04B25C47DC0738DFC" href="#f282C2CF828FBBE97A71E7F0675382158" xlink:href="#f282C2CF828FBBE97A71E7F0675382158"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -685.7000000000002 370.24299212598424)" id="gC393462E41F9C8ADC4F9F1EB967CB260" href="#f366D3893095F02AFC8E7B807FB7435F8" xlink:href="#f366D3893095F02AFC8E7B807FB7435F8"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -700.7000000000002 370.24299212598424)" id="g3714DAB417D0B22B15932651A8D4A0F4" href="#fDEF5A249E4AF9665C4581E12C3B3A587" xlink:href="#fDEF5A249E4AF9665C4581E12C3B3A587"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -717.4800000000001 370.24299212598424)" id="g9ACAE960B8430625BFCEE398DC65B3B5" href="#f30325C9099C45C4D355E9F01DBC44059" xlink:href="#f30325C9099C45C4D355E9F01DBC44059"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -726.6200000000001 370.24299212598424)" id="g8A3FF624D919E6F7B060A76E1D45EFC9" href="#f282C2CF828FBBE97A71E7F0675382158" xlink:href="#f282C2CF828FBBE97A71E7F0675382158"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -737.4600000000002 370.24299212598424)" id="gCF2AD80F3C19FA4EC204837E2FF60EC" href="#fE006BF89422BA632EB208DEC2513AD77" xlink:href="#fE006BF89422BA632EB208DEC2513AD77"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -748.0800000000002 370.24299212598424)" id="gF804B2C4065942A8ADD2D5CD29A3B62A" href="#f30325C9099C45C4D355E9F01DBC44059" xlink:href="#f30325C9099C45C4D355E9F01DBC44059"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -757.2200000000001 370.24299212598424)" id="g5FD38B0F68E66334612629A8DF6BE7E6" href="#fCBC04A8E62AC78F0CD8D7E772F6C608C" xlink:href="#fCBC04A8E62AC78F0CD8D7E772F6C608C"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -320.90000000000015 -371.8029921259843)" id="g139AD8AE4C4940AA9BA27DD05E0E4E8C" href="#f91CF3CEA929A916FA73B5E0A0C2FBE99" xlink:href="#f91CF3CEA929A916FA73B5E0A0C2FBE99"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -411.8056376333327 -371.8029921259843)" id="g4BB9C564F901612DB3DC9A919AFEEA28" href="#f91CF3CEA929A916FA73B5E0A0C2FBE99" xlink:href="#f91CF3CEA929A916FA73B5E0A0C2FBE99"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -696.7256376333327 -371.8029921259843)" id="g6164E4B94969A626222C332FC8AB6A9A" href="#f91CF3CEA929A916FA73B5E0A0C2FBE99" xlink:href="#f91CF3CEA929A916FA73B5E0A0C2FBE99"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -40 407.40299212598427)" id="gF37D02089003EBADFDA5BC88F9156EB6" href="#f33E03C75571CB473EEA4DB0D986DF9AA" xlink:href="#f33E03C75571CB473EEA4DB0D986DF9AA"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -45.96 407.40299212598427)" id="g185B6AD298AC34516663A207FE304BF5" href="#fE186731572801AD70C450F793EBEC591" xlink:href="#fE186731572801AD70C450F793EBEC591"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -51.9 407.40299212598427)" id="g48798496EF573D47FA23B24B66A2178E" href="#fEB756D53E496EF388D77A9FC4FADF98B" xlink:href="#fEB756D53E496EF388D77A9FC4FADF98B"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -63.04 407.40299212598427)" id="gF6DA7E5B16EE1DC48CB27130157BACB4" href="#fEB756D53E496EF388D77A9FC4FADF98B" xlink:href="#fEB756D53E496EF388D77A9FC4FADF98B"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -74.18 407.40299212598427)" id="gD5E7B3915A537EBA85D6C475734C2EAC" href="#fEB756D53E496EF388D77A9FC4FADF98B" xlink:href="#fEB756D53E496EF388D77A9FC4FADF98B"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -90.32000000000001 407.40299212598427)" id="g6C99B24EEC33AEEC0963706D93B1F51D" href="#f64E810A2B0301B3AFE31F0083C2435EE" xlink:href="#f64E810A2B0301B3AFE31F0083C2435EE"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -102.26 407.40299212598427)" id="g1135455F9AEC68AC20210472C40510E0" href="#fA544A357A483A8A3AF5578997F22F0A3" xlink:href="#fA544A357A483A8A3AF5578997F22F0A3"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -111.9 407.40299212598427)" id="gEBFCD1DC7850F1F6F024F260B282CB76" href="#fD7087123C09B6772C7F2CF671F56DB63" xlink:href="#fD7087123C09B6772C7F2CF671F56DB63"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -125.80000000000001 407.40299212598427)" id="gDE4F4A649C6D2B43EB33F01712A52A05" href="#f30EDC632E0E689E1E4032E5187F00E6C" xlink:href="#f30EDC632E0E689E1E4032E5187F00E6C"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -142.58000000000004 407.40299212598427)" id="g2A936134EFC773FCCDCBC1244E9382B5" href="#fE186731572801AD70C450F793EBEC591" xlink:href="#fE186731572801AD70C450F793EBEC591"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -153.52 407.40299212598427)" id="gD034569FFA5BF443C8BFF427679B48E0" href="#f7710571C89B2BD7DF9F67F66C9CF062" xlink:href="#f7710571C89B2BD7DF9F67F66C9CF062"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -162.82 407.40299212598427)" id="gCCA47087E4C1F5485D1EA42FB43E1F5F" href="#f124498C8722594BC84D3DE83E1D46B5D" xlink:href="#f124498C8722594BC84D3DE83E1D46B5D"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -172.12 407.40299212598427)" id="gDFBB6E40E58C00BC282E5117D341B149" href="#fBD2AE68E6F0F8329CA1878286515665A" xlink:href="#fBD2AE68E6F0F8329CA1878286515665A"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -181.42000000000002 407.40299212598427)" id="gD824C4DE65816E9A60386E9A54ACCA71" href="#f1AAA3A0AFBE423B107F2B850809F00C7" xlink:href="#f1AAA3A0AFBE423B107F2B850809F00C7"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -190.72000000000003 407.40299212598427)" id="g6C40DB9DAD1FCD6EF99B6A17130F3B61" href="#f33E03C75571CB473EEA4DB0D986DF9AA" xlink:href="#f33E03C75571CB473EEA4DB0D986DF9AA"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -201.68000000000004 407.40299212598427)" id="g5D31022486B36F3824DE5AAB04A1602C" href="#f30EDC632E0E689E1E4032E5187F00E6C" xlink:href="#f30EDC632E0E689E1E4032E5187F00E6C"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -218.46000000000004 407.40299212598427)" id="g9211C663B53F4CB9E502E05E1A61A98A" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -227.60000000000002 407.40299212598427)" id="g8B0DC45C04739D6DD2DC775A009B38CB" href="#fCC8581D2E55103DD9CA35019887FF2E3" xlink:href="#fCC8581D2E55103DD9CA35019887FF2E3"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -232.88000000000002 407.40299212598427)" id="gFAFD1614275AD9571289C2B05D15312A" href="#f25978294C782F8D9A3DE32B6961F8CBD" xlink:href="#f25978294C782F8D9A3DE32B6961F8CBD"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -243.12000000000003 407.40299212598427)" id="gAAF7892BB383B0A28DB7D16974FB0EBB" href="#f41DF624984D130456C441D06B0FA8D74" xlink:href="#f41DF624984D130456C441D06B0FA8D74"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -253.06000000000003 407.40299212598427)" id="g2B6C9CD8A9C4101F3D0D3071A8CA5AD1" href="#fCA62F9C34FD4B4F29ACA26A49A514B81" xlink:href="#fCA62F9C34FD4B4F29ACA26A49A514B81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -268 407.40299212598427)" id="g2AFF153A54E5856A79B012D5E4D7E2F2" href="#fD43D71A7992AE2B86B5D81EB000787C8" xlink:href="#fD43D71A7992AE2B86B5D81EB000787C8"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -284.5 407.40299212598427)" id="g66752D63E5B1F46492FA8D9ED20F1341" href="#fD7087123C09B6772C7F2CF671F56DB63" xlink:href="#fD7087123C09B6772C7F2CF671F56DB63"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -298.40000000000003 407.40299212598427)" id="gF238A49A6BC94E30D4528FDF8F8A475E" href="#fFB9DC6CDFE951412AF6B4B19B75FCF2E" xlink:href="#fFB9DC6CDFE951412AF6B4B19B75FCF2E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -307.8 407.40299212598427)" id="g168F5E6F617C7CD777699418942A0CF4" href="#fD43D71A7992AE2B86B5D81EB000787C8" xlink:href="#fD43D71A7992AE2B86B5D81EB000787C8"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -318.1 407.40299212598427)" id="g90E429D1E4D49620C732CDB6D046620E" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -327.24 407.40299212598427)" id="g2DEAEBDB310EA818EE8591872A3C31D" href="#fBA29C4CBEE0B5362118A04DD58CD81F8" xlink:href="#fBA29C4CBEE0B5362118A04DD58CD81F8"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -335.04 407.40299212598427)" id="g3BC5E9ED8B2AA7DAEB7500F2CEDDB463" href="#f1AA1F0063E906525BE1703D5AD8989B4" xlink:href="#f1AA1F0063E906525BE1703D5AD8989B4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -345.8 407.40299212598427)" id="g609438E0D4B4BB2B3EC56AEC845B7E19" href="#fFC19A2481BDD18CFFD031F73916C83DD" xlink:href="#fFC19A2481BDD18CFFD031F73916C83DD"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -356.42 407.40299212598427)" id="g2A460FCA572950AAF74D3E3BBB8B745B" href="#fC22102A8F4B325C3451F66BD68CF3AB5" xlink:href="#fC22102A8F4B325C3451F66BD68CF3AB5"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -367.26 407.40299212598427)" id="g3ED4A90D3858A91C9D535D86DCE760C" href="#fB4D1BB231EEA0FFE3FBA0000F1107622" xlink:href="#fB4D1BB231EEA0FFE3FBA0000F1107622"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -372.68 407.40299212598427)" id="gAC9620A9D162A5C04A13CA64E318EAFA" href="#fC22102A8F4B325C3451F66BD68CF3AB5" xlink:href="#fC22102A8F4B325C3451F66BD68CF3AB5"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -388.52 407.40299212598427)" id="gEE6773694D33A3FD2BE553F976B39F28" href="#fB4D40DD3986F9B84780D20DA4213A2F7" xlink:href="#fB4D40DD3986F9B84780D20DA4213A2F7"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -407.53999999999996 407.40299212598427)" id="g226E89C3FF1CD7BFD495640F7F4AC27A" href="#fD7087123C09B6772C7F2CF671F56DB63" xlink:href="#fD7087123C09B6772C7F2CF671F56DB63"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -421.43999999999994 407.40299212598427)" id="gF9B60F1E4674667C8F9AA21E365D5405" href="#f35B2DA2DA46577085A97D87CED860140" xlink:href="#f35B2DA2DA46577085A97D87CED860140"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -430.8399999999999 407.40299212598427)" id="gCC0356E15436C6C281A32D718B989B46" href="#fEB756D53E496EF388D77A9FC4FADF98B" xlink:href="#fEB756D53E496EF388D77A9FC4FADF98B"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -441.9799999999999 407.40299212598427)" id="g82C8CBD63B7C316C1BC0DAAE272FB79F" href="#f48B1B6B68EF3F19E52FEDD3DEE9200BE" xlink:href="#f48B1B6B68EF3F19E52FEDD3DEE9200BE"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -458.5599999999999 407.40299212598427)" id="gE559B38C6B24D24703708DDA21E0964F" href="#f30F1023381C693524939E7F4CF8AA101" xlink:href="#f30F1023381C693524939E7F4CF8AA101"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -467.1199999999999 407.40299212598427)" id="g952D62BE015F6EB801BDBA7A59416D2D" href="#fB4D1BB231EEA0FFE3FBA0000F1107622" xlink:href="#fB4D1BB231EEA0FFE3FBA0000F1107622"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -472.5399999999999 407.40299212598427)" id="g8D4AB1BF3E0CA31585FFB00FB87B8693" href="#f76171BC9D9B6A1F74C6089979E7AB9E4" xlink:href="#f76171BC9D9B6A1F74C6089979E7AB9E4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -481.4799999999999 407.40299212598427)" id="gA5F5C4CB9C4AADC5AAE0496E448998E3" href="#fC22102A8F4B325C3451F66BD68CF3AB5" xlink:href="#fC22102A8F4B325C3451F66BD68CF3AB5"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -492.3199999999999 407.40299212598427)" id="g46D8F077DEDDC5E945394FB28C0121D8" href="#f32218FBEA8E29C084BAF753778DB4994" xlink:href="#f32218FBEA8E29C084BAF753778DB4994"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -503.6399999999999 407.40299212598427)" id="g938CAE98CCEC6B4687D0CAAB9A69C48" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -512.7799999999999 407.40299212598427)" id="g846586F961FE141F66D9BF19A6D4B9CE" href="#fC22102A8F4B325C3451F66BD68CF3AB5" xlink:href="#fC22102A8F4B325C3451F66BD68CF3AB5"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -523.6199999999998 407.40299212598427)" id="gDBD6993D97AF840DFCC30699D5B3707D" href="#fCDE10BECEEC846D9ACFF80B8B5870348" xlink:href="#fCDE10BECEEC846D9ACFF80B8B5870348"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -538.7399999999999 407.40299212598427)" id="g89C797AC3848E3524AB9B5CEF2B2B489" href="#f23E45BA991A59ABBB74F553B5F42C08E" xlink:href="#f23E45BA991A59ABBB74F553B5F42C08E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -546.0199999999999 407.40299212598427)" id="g7D8E6B5D4CE2D44FCA3FA727FFA1D6F7" href="#f41DF624984D130456C441D06B0FA8D74" xlink:href="#f41DF624984D130456C441D06B0FA8D74"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -556.0999999999998 407.40299212598427)" id="g2E44E69D70A4D57F9FACE6352C515660" href="#fDEAB44B206FF6EE16248A189944B0B57" xlink:href="#fDEAB44B206FF6EE16248A189944B0B57"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -565.9599999999998 407.40299212598427)" id="g7F544F60455463EF2885F4A29860323C" href="#fFC19A2481BDD18CFFD031F73916C83DD" xlink:href="#fFC19A2481BDD18CFFD031F73916C83DD"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -576.5799999999998 407.40299212598427)" id="g396882AA7B0302E4EE21BAC147AD7427" href="#fBA29C4CBEE0B5362118A04DD58CD81F8" xlink:href="#fBA29C4CBEE0B5362118A04DD58CD81F8"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -584.3799999999998 407.40299212598427)" id="g3B406D1E144A2C799A1F71D518000E4E" href="#f32218FBEA8E29C084BAF753778DB4994" xlink:href="#f32218FBEA8E29C084BAF753778DB4994"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -595.6999999999998 407.40299212598427)" id="g7FCB957C688F9C8C3754BB86F108A873" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -604.8399999999998 407.40299212598427)" id="g51950441F4C3A6CA7D7C4BA504A60205" href="#fBC7E1BE44AD3C7AEC7D6A9E33B858D3E" xlink:href="#fBC7E1BE44AD3C7AEC7D6A9E33B858D3E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -615.2199999999998 407.40299212598427)" id="gB4A49DE8F22C3936633EB2DD7D199204" href="#fBC7E1BE44AD3C7AEC7D6A9E33B858D3E" xlink:href="#fBC7E1BE44AD3C7AEC7D6A9E33B858D3E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -625.5999999999998 407.40299212598427)" id="gCA648D5D0453971201F1061881F63F45" href="#f23E45BA991A59ABBB74F553B5F42C08E" xlink:href="#f23E45BA991A59ABBB74F553B5F42C08E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -632.8799999999998 407.40299212598427)" id="g6F5B47E8FEFB9C44E6A2E87D15F22D6" href="#f41DF624984D130456C441D06B0FA8D74" xlink:href="#f41DF624984D130456C441D06B0FA8D74"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -642.8199999999998 407.40299212598427)" id="g63564D798D4B4B240E7ABADF492C59EF" href="#fA41B7B4CB827AC614E03EE8C61914E28" xlink:href="#fA41B7B4CB827AC614E03EE8C61914E28"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -652.6199999999998 407.40299212598427)" id="g394E6CB4D73E2FFF18C71CFD97EFE3B8" href="#fB4D1BB231EEA0FFE3FBA0000F1107622" xlink:href="#fB4D1BB231EEA0FFE3FBA0000F1107622"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -658.0399999999997 407.40299212598427)" id="g194E45EE8F41D488C726858F35A83AC7" href="#f8A132A93F5E14EF8B4BE33F7586EDEB0" xlink:href="#f8A132A93F5E14EF8B4BE33F7586EDEB0"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -673.8399999999997 407.40299212598427)" id="g67AE0F03C7992A6E3792E6753E624113" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -682.9799999999997 407.40299212598427)" id="g289F9E69EFC07B287BC035097591C843" href="#f32218FBEA8E29C084BAF753778DB4994" xlink:href="#f32218FBEA8E29C084BAF753778DB4994"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -689.2999999999997 407.40299212598427)" id="gA096D1637514ED48B311AC55C26EEBE3" href="#f76171BC9D9B6A1F74C6089979E7AB9E4" xlink:href="#f76171BC9D9B6A1F74C6089979E7AB9E4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -703.2399999999998 407.40299212598427)" id="g97EE2ABAFF7124311766D7F7A41C46AA" href="#fC22102A8F4B325C3451F66BD68CF3AB5" xlink:href="#fC22102A8F4B325C3451F66BD68CF3AB5"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -714.0799999999998 407.40299212598427)" id="gD0B9B01D801537946B4F92252F2A8E16" href="#f76171BC9D9B6A1F74C6089979E7AB9E4" xlink:href="#f76171BC9D9B6A1F74C6089979E7AB9E4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -723.0199999999999 407.40299212598427)" id="gEAF30E3EF18C3CF6877DBE2B93F87A79" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -732.1599999999999 407.40299212598427)" id="gEA1744A579244FDCDCC6E78CCDDAD27F" href="#f23E45BA991A59ABBB74F553B5F42C08E" xlink:href="#f23E45BA991A59ABBB74F553B5F42C08E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -739.4399999999998 407.40299212598427)" id="gB2269652CAB28ACB1818BE84B6A819E3" href="#f76171BC9D9B6A1F74C6089979E7AB9E4" xlink:href="#f76171BC9D9B6A1F74C6089979E7AB9E4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -748.3799999999999 407.40299212598427)" id="g7E71706D09E591653269799F6D5E96BF" href="#fBA29C4CBEE0B5362118A04DD58CD81F8" xlink:href="#fBA29C4CBEE0B5362118A04DD58CD81F8"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -756.1799999999998 407.40299212598427)" id="g7B62EBE8E0969DDD6003CBBE953E16EE" href="#f32218FBEA8E29C084BAF753778DB4994" xlink:href="#f32218FBEA8E29C084BAF753778DB4994"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -45.64977863132647 -408.9629921259843)" id="gCC97456F13F0455A65A95CF9BE40EE1C" href="#fB6A7370788ABD55AFF119F7D63BF935" xlink:href="#fB6A7370788ABD55AFF119F7D63BF935"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -195.35759723552235 -408.9629921259843)" id="g639F7A28502247E3FB2D950556196FB4" href="#fB6A7370788ABD55AFF119F7D63BF935" xlink:href="#fB6A7370788ABD55AFF119F7D63BF935"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -302.89176489868066 -408.9629921259843)" id="gD78770B435D3CD67F040D6744757530E" href="#fB6A7370788ABD55AFF119F7D63BF935" xlink:href="#fB6A7370788ABD55AFF119F7D63BF935"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -609.62 -408.9629921259843)" id="gC1BCAB05EFF4F26E1A38413BCC5D11E7" href="#fB6A7370788ABD55AFF119F7D63BF935" xlink:href="#fB6A7370788ABD55AFF119F7D63BF935"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -619.9999999999999 -408.9629921259843)" id="g7C4B1B6AAEA4F171D861C20A467F69E8" href="#fB6A7370788ABD55AFF119F7D63BF935" xlink:href="#fB6A7370788ABD55AFF119F7D63BF935"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -234.14000000000016 433.56299212598424)" id="g435F4A12C98DC039A0BE205E3A19FA9D" href="#fC22102A8F4B325C3451F66BD68CF3AB5" xlink:href="#fC22102A8F4B325C3451F66BD68CF3AB5"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -244.98000000000016 433.56299212598424)" id="gFB64FAE4AA1EA0A26DC85722A5E7F9A9" href="#f76171BC9D9B6A1F74C6089979E7AB9E4" xlink:href="#f76171BC9D9B6A1F74C6089979E7AB9E4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -253.9200000000002 433.56299212598424)" id="g2C2F67E99CF03FFA7C0A421A915D5E83" href="#fB4D1BB231EEA0FFE3FBA0000F1107622" xlink:href="#fB4D1BB231EEA0FFE3FBA0000F1107622"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -259.3400000000002 433.56299212598424)" id="g4BBAFBE0C7E0F07F25AC36B1B23DE1F1" href="#f918C16FDCB8EC70D1A0509598F87777" xlink:href="#f918C16FDCB8EC70D1A0509598F87777"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -269.3400000000002 433.56299212598424)" id="g2AB596A08E8EF4332CA03B45154EB6A1" href="#f1AA1F0063E906525BE1703D5AD8989B4" xlink:href="#f1AA1F0063E906525BE1703D5AD8989B4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -280.10000000000014 433.56299212598424)" id="gB02D7DE48CCBF1E9E858333FF5D9DC25" href="#fDEAB44B206FF6EE16248A189944B0B57" xlink:href="#fDEAB44B206FF6EE16248A189944B0B57"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -290.1600000000002 433.56299212598424)" id="g18325D88782360F3502F5C58E75432CB" href="#f41DF624984D130456C441D06B0FA8D74" xlink:href="#f41DF624984D130456C441D06B0FA8D74"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -300.2400000000002 433.56299212598424)" id="g1D962147EA3BEB991ACF121DB1C31E66" href="#f23E45BA991A59ABBB74F553B5F42C08E" xlink:href="#f23E45BA991A59ABBB74F553B5F42C08E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -312.6800000000002 433.56299212598424)" id="g4C4D715FC3F74B9F778B8604D059F6C2" href="#fBA29C4CBEE0B5362118A04DD58CD81F8" xlink:href="#fBA29C4CBEE0B5362118A04DD58CD81F8"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -320.4800000000002 433.56299212598424)" id="gCE418398A76CE75FE060A0C2BEFB7AE6" href="#f76171BC9D9B6A1F74C6089979E7AB9E4" xlink:href="#f76171BC9D9B6A1F74C6089979E7AB9E4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -329.42000000000013 433.56299212598424)" id="g17E6C0673CC68E91E58FCE647E9708B8" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -338.5600000000002 433.56299212598424)" id="g827961D68AEC62A0BF20DCF3DC431921" href="#f23E45BA991A59ABBB74F553B5F42C08E" xlink:href="#f23E45BA991A59ABBB74F553B5F42C08E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -345.8400000000002 433.56299212598424)" id="gF24BC925B962674C01621C0EE3CC4112" href="#f30F1023381C693524939E7F4CF8AA101" xlink:href="#f30F1023381C693524939E7F4CF8AA101"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -354.40000000000015 433.56299212598424)" id="gDCED89F017767316FD8D03DAD9D87E3E" href="#f1AA1F0063E906525BE1703D5AD8989B4" xlink:href="#f1AA1F0063E906525BE1703D5AD8989B4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -370.1600000000002 433.56299212598424)" id="gE5BDC981A6E6F3D2A2C1A6C67AB421A4" href="#fFC19A2481BDD18CFFD031F73916C83DD" xlink:href="#fFC19A2481BDD18CFFD031F73916C83DD"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -380.7800000000002 433.56299212598424)" id="g1061F4E961BAE606664B5D937FD73A22" href="#fBA29C4CBEE0B5362118A04DD58CD81F8" xlink:href="#fBA29C4CBEE0B5362118A04DD58CD81F8"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -388.5800000000002 433.56299212598424)" id="g3E5771806410E56C6E6A39E3DEBC988" href="#fB4D1BB231EEA0FFE3FBA0000F1107622" xlink:href="#fB4D1BB231EEA0FFE3FBA0000F1107622"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -394.00000000000017 433.56299212598424)" id="g46609CD97B4EF0705DC6307B79521F0C" href="#fC22102A8F4B325C3451F66BD68CF3AB5" xlink:href="#fC22102A8F4B325C3451F66BD68CF3AB5"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -404.8400000000002 433.56299212598424)" id="gABE02A447D8700E801064AF94C5F9921" href="#f918C16FDCB8EC70D1A0509598F87777" xlink:href="#f918C16FDCB8EC70D1A0509598F87777"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -419.8400000000002 433.56299212598424)" id="g6B65AFBD3C33263B302EDB3653798396" href="#f1AA1F0063E906525BE1703D5AD8989B4" xlink:href="#f1AA1F0063E906525BE1703D5AD8989B4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -430.6000000000002 433.56299212598424)" id="gA1558A64511168A8B7D0DAE4A3998729" href="#fB4D1BB231EEA0FFE3FBA0000F1107622" xlink:href="#fB4D1BB231EEA0FFE3FBA0000F1107622"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -436.02000000000015 433.56299212598424)" id="gF17CEA6DBBA645C5DC456A57240A197B" href="#f76171BC9D9B6A1F74C6089979E7AB9E4" xlink:href="#f76171BC9D9B6A1F74C6089979E7AB9E4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -444.96000000000015 433.56299212598424)" id="g952D9EAB08F4B05F9BCEFD17865025D" href="#f23E45BA991A59ABBB74F553B5F42C08E" xlink:href="#f23E45BA991A59ABBB74F553B5F42C08E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -452.40000000000015 433.56299212598424)" id="g425DF789F61723458B8F9A25A03A1D61" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -461.54000000000013 433.56299212598424)" id="g4DE0979B5E5AA4F3E5E0202DA27F6E1A" href="#f23E45BA991A59ABBB74F553B5F42C08E" xlink:href="#f23E45BA991A59ABBB74F553B5F42C08E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -468.8200000000001 433.56299212598424)" id="g192BACF3059B760BD6B3A4A3B3DFB84E" href="#f30F1023381C693524939E7F4CF8AA101" xlink:href="#f30F1023381C693524939E7F4CF8AA101"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -477.3800000000001 433.56299212598424)" id="g446307A53418D14F621B34087790ABC8" href="#f1AA1F0063E906525BE1703D5AD8989B4" xlink:href="#f1AA1F0063E906525BE1703D5AD8989B4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -488.1400000000001 433.56299212598424)" id="gACBE62ADDF3FD1A2383D0F0B6CA9423" href="#fB4D1BB231EEA0FFE3FBA0000F1107622" xlink:href="#fB4D1BB231EEA0FFE3FBA0000F1107622"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -493.5600000000001 433.56299212598424)" id="g627E16906D0C729E9B218E8D88DB3C75" href="#f30F1023381C693524939E7F4CF8AA101" xlink:href="#f30F1023381C693524939E7F4CF8AA101"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -502.1200000000001 433.56299212598424)" id="g524BC9DB9301C79B4865CEE22A96FBA4" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -511.2600000000001 433.56299212598424)" id="g9334E61ABEEA9B5B3D7E8C99C21210E2" href="#fCC8581D2E55103DD9CA35019887FF2E3" xlink:href="#fCC8581D2E55103DD9CA35019887FF2E3"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -521.5400000000001 433.56299212598424)" id="gBA6437C1F30853423BF20F6521DDAC44" href="#fC22102A8F4B325C3451F66BD68CF3AB5" xlink:href="#fC22102A8F4B325C3451F66BD68CF3AB5"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -532.3800000000001 433.56299212598424)" id="g52AE2E80F30CADB79BEC14FEDF6421AA" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -541.5200000000001 433.56299212598424)" id="g611F93CD2FEB63AA2811C70061D42CC" href="#fCA62F9C34FD4B4F29ACA26A49A514B81" xlink:href="#fCA62F9C34FD4B4F29ACA26A49A514B81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -551.4600000000002 433.56299212598424)" id="gFF44DC305974D4C37ADBEE9F83612E5" href="#fB4D1BB231EEA0FFE3FBA0000F1107622" xlink:href="#fB4D1BB231EEA0FFE3FBA0000F1107622"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -556.8800000000001 433.56299212598424)" id="gB4E8B051EF2A93C1022F8A7A75357D67" href="#f918C16FDCB8EC70D1A0509598F87777" xlink:href="#f918C16FDCB8EC70D1A0509598F87777"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -566.8800000000001 433.56299212598424)" id="g7F0559A2EC23376633F8F91F3ABE72F3" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -576.0200000000001 433.56299212598424)" id="g640939A3642AE83201B5C357462F50C4" href="#fDEAB44B206FF6EE16248A189944B0B57" xlink:href="#fDEAB44B206FF6EE16248A189944B0B57"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -585.8800000000001 433.56299212598424)" id="g558B8A36DF1478852821734EE9F437A" href="#fCC8581D2E55103DD9CA35019887FF2E3" xlink:href="#fCC8581D2E55103DD9CA35019887FF2E3"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -591.1600000000001 433.56299212598424)" id="g62F53387E9F92208DF20DEB66AE134F8" href="#f76171BC9D9B6A1F74C6089979E7AB9E4" xlink:href="#f76171BC9D9B6A1F74C6089979E7AB9E4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -605.1000000000001 433.56299212598424)" id="g223D9BE11162DC0AA7F852957D57633F" href="#fBA29C4CBEE0B5362118A04DD58CD81F8" xlink:href="#fBA29C4CBEE0B5362118A04DD58CD81F8"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -612.9 433.56299212598424)" id="g87D833280F4B77513F184CB077A9EBD9" href="#f8A132A93F5E14EF8B4BE33F7586EDEB0" xlink:href="#f8A132A93F5E14EF8B4BE33F7586EDEB0"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -628.7 433.56299212598424)" id="gB5B3979762E395A14D5F38D94F430955" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -637.84 433.56299212598424)" id="gD589B0AE3B9522F533376EE601927EB3" href="#fCC8581D2E55103DD9CA35019887FF2E3" xlink:href="#fCC8581D2E55103DD9CA35019887FF2E3"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -643.1199999999999 433.56299212598424)" id="gF3A12E5102DCD30B76E9032F0698424C" href="#fCC8581D2E55103DD9CA35019887FF2E3" xlink:href="#fCC8581D2E55103DD9CA35019887FF2E3"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -653.3999999999999 433.56299212598424)" id="gD76980CCA0CB52459A7DBD0B86933356" href="#f2817556A795F8EDD0C1D32EB581EFBD2" xlink:href="#f2817556A795F8EDD0C1D32EB581EFBD2"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -668.1799999999998 433.56299212598424)" id="g6A078BFA393F2FFA8563DB03EBC5DEA6" href="#f41DF624984D130456C441D06B0FA8D74" xlink:href="#f41DF624984D130456C441D06B0FA8D74"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -678.2599999999999 433.56299212598424)" id="g5D650DCC4CD2FB23414AD90403FF2650" href="#f23E45BA991A59ABBB74F553B5F42C08E" xlink:href="#f23E45BA991A59ABBB74F553B5F42C08E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -685.6999999999999 433.56299212598424)" id="gC922D2D12E8D43E1F75BCEDD6ADFE1D3" href="#fCC8581D2E55103DD9CA35019887FF2E3" xlink:href="#fCC8581D2E55103DD9CA35019887FF2E3"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -690.9799999999999 433.56299212598424)" id="g502678CA81DBD6EF4784061087A4FB9C" href="#fCDE10BECEEC846D9ACFF80B8B5870348" xlink:href="#fCDE10BECEEC846D9ACFF80B8B5870348"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -706.0999999999999 433.56299212598424)" id="g2A7D07B8301EFC2C031D6BB165146CDD" href="#f918C16FDCB8EC70D1A0509598F87777" xlink:href="#f918C16FDCB8EC70D1A0509598F87777"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -716.0999999999999 433.56299212598424)" id="gCE559C856730CDF1201D3FAB516DB20F" href="#f23E45BA991A59ABBB74F553B5F42C08E" xlink:href="#f23E45BA991A59ABBB74F553B5F42C08E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -723.5399999999998 433.56299212598424)" id="gC9F0E529049448FB3C27D72DC854E58" href="#fD8E9D71C813711217F1BF86793E87A81" xlink:href="#fD8E9D71C813711217F1BF86793E87A81"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -732.6799999999998 433.56299212598424)" id="gC088E640106A57D2A3CD992401346A70" href="#fBC7E1BE44AD3C7AEC7D6A9E33B858D3E" xlink:href="#fBC7E1BE44AD3C7AEC7D6A9E33B858D3E"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -743.06 433.56299212598424)" id="gC9D9DF57F8DF0B98EB08BEDC6E22F301" href="#f1AA1F0063E906525BE1703D5AD8989B4" xlink:href="#f1AA1F0063E906525BE1703D5AD8989B4"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -753.8199999999999 433.56299212598424)" id="g5733AD992C8564482C8B68F5AA25AB51" href="#fBA29C4CBEE0B5362118A04DD58CD81F8" xlink:href="#fBA29C4CBEE0B5362118A04DD58CD81F8"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 -473.56299212598424 -761.6199999999999 433.56299212598424)" id="gD05F59AB2E1B0EC9A3C1BA2F6DD8A61D" href="#f35B2DA2DA46577085A97D87CED860140" xlink:href="#f35B2DA2DA46577085A97D87CED860140"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -234.14000000000016 -435.1229921259843)" id="g878CBF76947C930B1164A6659D123B64" href="#fB6A7370788ABD55AFF119F7D63BF935" xlink:href="#fB6A7370788ABD55AFF119F7D63BF935"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -270.3656376333327 -435.1229921259843)" id="gCDADC4CB4002CC19E4EABB69767C0B26" href="#fB6A7370788ABD55AFF119F7D63BF935" xlink:href="#fB6A7370788ABD55AFF119F7D63BF935"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -415.8656376333327 -435.1229921259843)" id="g2B1A4CD2C24971590727FA17ED4AF27C" href="#fB6A7370788ABD55AFF119F7D63BF935" xlink:href="#fB6A7370788ABD55AFF119F7D63BF935"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -567.9056376333325 -435.1229921259843)" id="g6C8CEF8565CF7938AB1FEFDC0EFCE2E0" href="#fB6A7370788ABD55AFF119F7D63BF935" xlink:href="#fB6A7370788ABD55AFF119F7D63BF935"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -717.1256376333325 -435.1229921259843)" id="g9BCF0BB7D30B3A930894C652F97CF435" href="#fB6A7370788ABD55AFF119F7D63BF935" xlink:href="#fB6A7370788ABD55AFF119F7D63BF935"/>
<linearGradient gradientTransform="matrix(841.8897637795276 0 0 473.56299212598424 -737.4599999999999 -435.1229921259843)" id="gB17002E36788F5753A766FAC06F44384" href="#fB6A7370788ABD55AFF119F7D63BF935" xlink:href="#fB6A7370788ABD55AFF119F7D63BF935"/>
</defs>
</div>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(40 17.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gF74D1E4498220F56E34936C81B24ED2C" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g46E28FC12585DA626130081849FE40B4" x="3.564" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="10.788" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g48BCA4F06942DA5990D42018985FC781" x="17.136" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="23.268" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE1B486BBD379D5D210F28624A61384AE" x="30.024" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g9FB16590C6D64699AE0CE54876927A05" x="36.804" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g6799D348D26A0968EEDA80A0E5D50B73" x="43.716" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="49.620000000000005" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g45E4C10E27056C5AE488FE2D8290DF06" x="55.968" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="59.7" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g46E28FC12585DA626130081849FE40B4" x="66.456" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 28.192)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 30.592000000000002)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5ABA589ED074A65FC8C929AB4EB2344C" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(6.768 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 48.784)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(404.54488188976376 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6F0940D406D545443F0C3F5AB20F1452" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g6D72A0AB4EFB019D977FFECF4A1600A9" x="6.95" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7035BD9A81EA6DB089327941BB80DFF8" x="11.26" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="16.67" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="22.3" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g5503E15E5E4E70E9E217A15BD1ECD752" x="27.41" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="30.52" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFF65128B49BB3276E17D04989ECB7ACE" x="35.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="41.92" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 8.579999999999998)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.64 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 23.739999999999995)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 32.31999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(743.9997637795276 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g97A8E46F7A64F11D13C6F357868587EE" x="9.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.25" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.36" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gB844DCFB76B4CC44608DB013C9764E9C" x="24.89" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="30.37" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="35.14" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="41.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="46.58" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="52.599999999999994" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 15.16)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 60)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g14F95E5F274105B73EC9103738D4C7FD" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFC5C8D23DE5E426807758A924FDBA2FC" x="17.76" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g47EDFEA5ED41C2BE4D53DD4DC8C28ED" x="29.856" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 39.48)">
<g class="typst-group">
<g>
<g transform="translate(0 12.9)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gF7DAC8BB30649014016B28F6AD7EC048" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8F63AAB7FFA6B186E1B4BC124750174B" x="14.799999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1E298373CF470F56F03EC97C7DE8EA04" x="24.88" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g73F93EFBB215913414E078CF4300A07" x="50.44" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="64.75999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAFD7B3D7EB6599FB514B70015F312425" x="74.39999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1E934D63EFC0D2D779AEFC9122E70AE4" x="90.55999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g5A467C6F5424E9C7BB01147ABA438205" x="97.89999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="109.11999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g50FEF586148C287DB923CFE895D558DC" x="118.89999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gED653E9CCAB5F6C6237350979071A74F" x="129.01999999999998" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.06000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 39.06000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g187DB76C80CD961C20BAB3AF6259527" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="13.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="21.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="29.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="42.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="53.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="60.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g5925E4E4FE8F59A76637BD462660B390" x="70.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="80.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="85.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="101.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="106.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="113.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="128.42000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="138.42000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="145.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="155" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="165.38" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 65.22)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 65.22)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gFE29E79896646B3825DA2D41961151C9" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="11.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="22.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="27.799999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="33.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="43.199999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="55.99999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="63.79999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="74.55999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="84.63999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="92.07999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="103.39999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="112.53999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="123.37999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="138.49999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="143.77999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="153.85999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="164.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="174.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="181.45999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="191.57999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="196.99999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="204.79999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="211.11999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="220.26" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="231.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="239.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="253.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="258.88" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="264.3" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="275.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="285.38" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 102.12)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8F63AAB7FFA6B186E1B4BC124750174B" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="10.08" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g50FEF586148C287DB923CFE895D558DC" x="19.86" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g936880EEF467D45CE0F64A721CAEDAB8" x="29.979999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7B316FC97C7634445DBF19AF1976B5C8" x="38.379999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g37DC97609493A252C8A67743647C955" x="47.49999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gF418DD62CA77762FBF8DB07ECAE6BC0" x="64.88" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g936880EEF467D45CE0F64A721CAEDAB8" x="77.16" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g814D257E196F777517493FCE505E18DF" x="85.56" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7B316FC97C7634445DBF19AF1976B5C8" x="96.72" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="105.84" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCD50B0C5537328D0484BBB5C5B7C30A" x="115.62" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCD50B0C5537328D0484BBB5C5B7C30A" x="124.16" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gED653E9CCAB5F6C6237350979071A74F" x="132.7" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 128.28)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 128.28)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="16.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="25.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="32.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="38.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="51.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="60.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="72.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="86.32000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="96.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="103.98" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="112.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="120.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="129.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="140.98" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="149.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="160.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="167.07999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="174.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="190.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="200.64000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="210.72000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="216.14000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="226.98000000000002" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 154.44)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 154.44)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="16.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g17AD34DB90B05275C6F1422A9B4B5274" x="26.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="36.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="45.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="58.239999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="64.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="79.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="90.48" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="100.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="110.82000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="119.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="132.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="141.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="146.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="156.48000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="164.28000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="173.22000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="185.66000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="191.98000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="207.06000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="213.38000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="224.14000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE7450862BF743B056E90C8779357A05F" x="238.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="248.14000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="258.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="267.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="275.44" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 191.34)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gCF24A1AE12C8178F68C1BA3421208D44" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g936880EEF467D45CE0F64A721CAEDAB8" x="14.68" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g50FEF586148C287DB923CFE895D558DC" x="23.24" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD5518A84533F4D2E67DB7AABF1806BFD" x="33.36" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB1351C61B7F6B471ABB1B8F64AC9D816" x="48.9" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g50FEF586148C287DB923CFE895D558DC" x="59.739999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7B316FC97C7634445DBF19AF1976B5C8" x="69.86" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB591690011940384999C1B007F794058" x="78.98" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCD50B0C5537328D0484BBB5C5B7C30A" x="91.24000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gED653E9CCAB5F6C6237350979071A74F" x="99.78" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 217.5)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 217.5)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gB8789F2F5F06048D4163694E4C0F3B6C" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="14.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="20.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="30.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="45.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="53.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="62.519999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="71.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="78.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="87.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="103.26" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="111.82000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="121.9" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="137.70000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="148.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="153.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g5925E4E4FE8F59A76637BD462660B390" x="162.16000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="171.96000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="177.38000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="183.70000000000002" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 243.66)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 243.66)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g54DD1A53056317C9D72B591A0D7293A0" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="13.700000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="22.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="33.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="41.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="48.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="58.699999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="67.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="82.49999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="87.91999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="103.75999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="109.03999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="119.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="127.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="136.95999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="147.23999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="163.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="168.45999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="179.29999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="184.71999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="200.51999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="214.65999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="223.79999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="235.11999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="240.39999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="250.33999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="265.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="272.03999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="282.15999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="291.09999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="301.09999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="308.37999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="317.4599999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="331.3999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="342.2399999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="352.4599999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="362.5799999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="371.5199999999999" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(465.13385826771656 0)">
<g class="typst-group">
<g>
<g transform="translate(40.062047244094494 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<image xlink:href="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAB4AAAAQ4CAIAAABnsVYUAAAgAElEQVR4AeydB5xdRdn/z9YkpGy5vZ3b79YUQkDBTrGgomLhBQv6qijq+2Iv2F5FeUVUBEVRLPAqgoglGjoJqSQhCell05PdZPvefk8/z///zJx77rl77667lCTA3M987s6ZM/PMzG/mbD75nmef4YB9mAJMAabAaVJAA+3fprKh6QBm0gC04iWpRE2RUnqv/NtsOC5T1kHpYuKBYbeVqdQSiqMa15FeVmUi+2WVrBeV1miJtY4lz+wbW8WiiTV7uvSZqN/nq9w6x9LDohe3rGXPVO7hqZQ8X/ar2KFFlhHSgspRGW0rn4gyo+yCKcAUYAowBZgCTAGmAFOAKcAUYAowBc4UBbgzZSBsHEwBpsDLT4GpQLcyVazIiXIpC66i1oqkrQJbWdta82UdlC4mHlsV+qyV2pGc1b41b6k2kX1LlfKs1Y41X17LvGL2GYBmANp8HFiGKcAUYAowBZgCTAGmAFOAKcAUYAowBU6jAgxAn0bxWddMgZe7AhNBUmt5mUZW8MoANFWjTKDShVVDa75UY1zOqq01P65a8dJq05ov3q/4abVpzVdUpAVWm9b8BNWn5HVubWu1ac1b65TlrWO25ssqlS6sNk9lvjSCcZ74VZ6X6q9SKl7dlFV7vuxXsUOLqLaW25XjMW5aV6GilcUAyzIFmAJMAaYAU4ApwBRgCjAFmAJMAabAaVaAAejTvACse6bAy1mBqYC5Mn2syKkKUMOAHhN4QD9vgLJqB2WDHAf+rGO21Jto7pYq5VmrHWu+vJZ5xey/9DygVVAnWlaz3NwAmLHukyrPy4RPS9VNTgufF/tlRsxx0lI6ZkuNysEYN62zq2hlMcCyTAGmAFOAKcAUYAowBZgCTAGmAFOAKXCaFWAA+jQvAOueKfByVsCkZpNkyvSxIqcKoFYFPVvrT5Qv66B0UT6k6qiuVLsqRKvs0dLAat9SXJ6ttFBZUt7CvGL2pw6gTdHGZyrVriwZ38a4tuo/lTxtls6mAEDRFTPRchVUSRU1TdF1VQVM1WziLi37WEdb8bxMCHbLTOCFtWbZzedin7al5ibKk7u0d1rRmi/D61YLZUNkF0wBpgBTgCnAFGAKMAWYAkwBpgBTgClw+hVgAPr0rwEbAVPgZatANYg2/ljCMnEmBV7loIygKmv9ifJlHZQuysdWxuBMHleqzQB0mRbFi4k0t5YX6477adV/3K3SpdXORPlS7bLcqbRv7WuifF7ME9SLDFnWJJoUXSFO/ebINQagS5C9csVNnViGKcAUYAowBZgCTAGmAFOAKcAUYAowBc4kBRiAPpNWg42FKfAyU6AI4yjeHY+e6d3qkoxjT0Ylkwybmeqty3wnJ6hSHBsd1bMC0BNYpsVW+5NWrHbTOv1q9ynKNLuYoMrExcz+xNrgnWnqYy7EJBkAyIt5SRVFWajoQNdAU0HV9VKqfN1CN331gVcbsPmQmJnqbct7ql7nWdinTag5a756B0bpZHOctCG7yRRgCjAFmAJMAaYAU4ApwBRgCjAFmAKnUQEGoE+j+KxrpsDLRwELODJZFYKtSfCuwaMn1Mi0o5tVTJJmZsxb5ZkqbcsrlMY2yQjLm1ghmjVfXsu8Ks4d7ZuFU81Mc/xTNWvWY/ZNKapmpqmPuR2LGWNvFy9xByi6snrdylVrV2zcvHH5yidpevLJJ5ctW7Z+/fre3l5BEHTyAU1HHD3+nYhxbY4X61p3VsWetPZO82bbcRlrzXG3SpfTtW+tb82XLFbJTT7OKg1YEVOAKcAUYAowBZgCTAGmAFOAKcAUYAqcAQowAH0GLAIbAlPgJa6ABiCRpKHrqAaga5gIMSty2CJO0wleG89/q8HoMmg1JUQ2BZlLdkq5ctQ3oRE6nrJRja9rtTn+Hrt+aSlQ3Niasei68bJFkksvTNDruQBbtx7gambUNnC1jZi4Oo7jasmPOpKpJd/1HFffkeh+yyVv/ernv3zHz27fuG41aLIi5FS5oKqSpmmqDooGsqqLsiLKiqzqmmo8amUkurSf6cuPCXZlxU621qP5iVbMWnOiOlPxIp+ordW+NT9RfVbOFGAKMAWYAkwBpgBTgCnAFGAKMAWYAqdXAQagT6/+rHemwMtBgSKApkiLEiNEYgogMaOpyOk0BqBfDlvipT/HMgBdpM902oiJtTyADAA7du3nuLq6BgTQXD1BzRzHcTUcV19TlhpruRn1JDVw9fVcTR3HRYO+3/7qF+vWrKZmcwVxNJk2gSxGj35JA2gVYJwf+Et/V7EZMgWYAkwBpgBTgCnAFGAKMAWYAkyBF6cCDEC/ONeNjZop8OJSwOpNqVNnZ00DSQNJJd+E1pFy464ZncMMVlCWKTlxFj2nLSUlaUwYNy5TrDGuuOyy7KKqdbQyWa2J7tHy4hgm+2mBmOOmP1mrqd9j9ifX6rnoY2lL3qkUN7ai0j4VgIwKhR/c/H0EznWEOWMOPzUIomstqb4WoXNDHdfYyM2cyZ01q2bWrPqZtPKcWXPOOmvOm9741t/89u59+w+LkkYPLqQvdlQdaCrfjeZ2Uibfw1Z9yi1MuPXHVbNaKMvT3wmW3wzTeS6w90oAbe26rC92wRRgCjAFmAJMAaYAU4ApwBRgCjAFmAKnVQEGoE+r/KxzpsDLRIEiW9IAZN1AzpIOqoYUSdEoDhuHtExGVj0zFXBmBVLWfFF1a9n4/PjrYn/FtvTnZLUmukfLy+1Uv7JAzDIRqteefimzP7lmz0UfS1sCoIk/sqZCIYd99g/1L3vkgU9+5mMzZ2PEjXGfGq62hkPobE0moq7hauu5htkzZ89qnEUa1lubB8PxL3/1G/sPHgUw0PPEABoZdXFfV+7W8dpU1phKyXgr5jUD0KYULMMUYAowBZgCTAGmAFOAKcAUYAowBV7qCjAA/VJfYTY/psBpV4DGvFXQXzgrwlgOjvfDmvXw2HLIJXFwkoTfiMk08o1xa8t4a9XLsmlZ/CiN2LKW25WYzLhpbWUUleqWcuWIzmLYzFbWxVuVpdYSszFmrCOx5kmlyukbbStqltm0XlhrWvOnxL51IGX5ipGU3Z3GhVVXmp9GY6xqHYk1T8w8O/0LUkHRcdMDQCGP37s3w9XvvXtB4mOu1tdxnI3jGorguI6raajBoBpcTU3dzBlzyK2G8m8zHnSxUW1NMUdjRtOw0dyMmXM4rmbGzDkXXvzm3931x4JoeFxjvGlBkhQ5LwrFGU0KoKvoMH5L09lVflvXo/KuUTKB/anUt9qfKD+hHXaDKcAUYAowBZgCTAGmAFOAKcAUYAowBU65AgxAn3LJWYdMgZeZAkjhRAx4q6qQk+Ce++AVF6yKda6PRldc+trlj/8DZJH8QX0xVoBaitExGYYuU9EKs6x5UqkSURltK2qWQ2Oj1rjmZf1Wr6LR4nENx12W2bGOxJonlYq4sKSG0baiZplN64W1pjV/SuxbB1KWrxhJ2d1pXIyT1tB/GgasI7HmiYlnob+u6yrud5W0xW11150buiOfml3zjnruAo5r4zgHx81saLDV17lruDCHaXYdx8/g5nOYzuW48y3pFRz3Co5bzHHdHNfBcV21dW0c5+K4uVzN3Dkt7rrGOZwRQ7p+1uymuoZZ6C5d08DVNDS3Oj//ha+kMwVTDUmRizNiANpUhWWYAkwBpgBTgCnAFGAKMAWYAkwBpgBT4AVUgAHoF1BcZrqKAhVwp+h7OH1mVMU6KzojFdBBFUAtgCLD0n+A2/5gNDLoCY7wgZNt9s1XXLRRE3HYFRCxxFuLvKyspGyq1n1lzZNKFZaLTStqlo+i3DG2eK/Y2Pqzeg+VpdYSa/viU0DKKkZVOX2jbUXNMpvWC2tNa57UeaHtWwdSlq8YSdndaVxYdaX5aTTGqtaRWPPEzHT0KetdVsRkcrT/xOh73/2p2TM7OM5Zy/EEHLdw3AySmjkuVsu9uY57dw13Ccdd1sp9p9O5tJvf2MFv7eC3dgZKqcP/TJt7c8j2uGvu75pn/w/HvY3jXknIdStXP6+ucQ7B0DOKbtF4jCFX14hgugYPN/zg1R/ef/Aw/qlB6S8MqgBoXVdpqlRw6ipba1baMUqq6Iy/BCb8WOpb7U+Un9AOu8EUYAowBZgCTAGmAFOAKcAUYAowBZgCp1wBBqBPueQv5w71EsOj1ADF0AB5yKTk4eWs2Uth7iQEhyyAKsPbL121qGM4xoPNIYf8cpfjxOeuyqrEO5NsAs2Ck8pw84QQkApkgVNlMJHctdg0MLehqrWVsTdxAPgx9yruT5JI8QSArHoPlaXWEtqP8W3pwtodvTvh3K2tysxVXFhrWvOk4gttv2I0xYKKkRRvTPenVVean6YF60iseWJmcn10nYaYof0qUIyqLIqFfyx94M1vuZgQ4SaOO6u2bg4eLsi1EAYd4LjOGu7iuY2fDrb+ujuwdFH0gSWxxxf59iRaToRt+aBNMVO4VQm3KhGbHrVBwqV0BIe7Y7vaI/9KJH5td3ye4y4mztELuJrzCZKmjtJtHBfkOEfDLAdHQkXXzWjkOO4jH/1ENi+RsSr0FFAASdMkAE2WZZM+owN3xWfqKltrVpgpFlTRedJ/Biz1rfYnyhe7YT+ZAkwBpgBTgCnAFGAKMAWYAkwBpgBT4PQrwAD06V+Dl9EIirGAx9IpijcUDU+gowC6Kkd4GYnzEp0qXdaRsTFNB0WBjrZ7FnePBr1gtwke22iXfd//3Qxyxpy8SqJ1iOimaYBYumnMCi9gRsVeNdqfVCBDoL2JKnlNUrXrqtvWitEN5E3rVTXxUi60QMOyadLyie6SqlbsS9vSkqIdoqjVzgTWrCtUbPu8/iQ7RtckWczoGGtGKgip3/z2F+1toTlzkfnWNnK19XU1tY1cTS3HzeG4WAP3mpncfzTV/U88uDLi74l4eyPeE/jt6Y+40iGXwLu0gAvMxDsh5Comtx72SmF/Oh4cjPBHfJ4dc2b9o6b+h3Obbgv4Hm4Lrw+7H3c1/X5W/Zc47p0cd15Nfbxm1lwOB4KfmvqmULj7wUceJvtb0SGjQV7W8pIiF0RZVVS9/KOCTjymS9t4Qu0q9LcqP/n+r6w5eX06hqnUmXC07AZTgCnAFGAKMAWYAkwBpgBTgCnAFGAKnEIFGIA+hWKzrnQActycIiHnUzRIp4koqgB46FyJcZh5ptmLXQGylFpWGMPFV+HK921aED/BuxSPXYh4+ru9q7YuB7EEoHWAHEAGI0afWgCNr0JIlwXcjKDlQEnjWLQcWQG6I6vAcHOrlmXKLiwb+8W+mtMefwWUNCxYwfEERl80AJqOX5cL+bFUeui73/uGw9k0d96suvqaunqkzw2zKfudwXFujjub497ZVPvNuO2v3b7dIXfa54apJL8HzMR7gfdCyAcRPwQ94HaMBfwHA/6ekGc07MyEHaNR1+GYb20kcL/bcSPHXc5xXfWzE1zdPK7+LK52Xk19E8dxb33bhYPDR3R83HQN9z5Isq5pWjl/RvrMAPQEO5QVMwWYAkwBpgBTgCnAFGAKMAWYAkwBpsBUFWAAeqpKsXrPgwKE38lZ+OQH95/btfKaq4/t3QGFLICeZAD6eZD3zDWhaJClTPa3d0pt/F6+VeDdQlfsyGc/ekDPgixYh54HyJ4uAK3q8IMbBs+JPvH2V+5+6I9IwoVhMjY6egagrQs1lfzLA0BrJHDLA3+9z+Fs4Wq5uoYGgpxr8SRA4zOrtq7trIYrWxpubHes7Wg50j53hJ+ZCjm1qdBnn7tEn/0epM+8F9GzwaC9EA/qEb8YdBa885IhWzLuTHb6R7tDA0HbM1HvKnfz/3HcNfWzLuRmRbiZzRgFpA4DRNtsTffd9ye6jKoOsqqqiqppikY+FD0zAD2Vbc7qMAWYAkwBpgBTgCnAFGAKMAWYAkwBpsDkCjAAPbk+7O7zqgCheD/4xq5zE3s6vUNB++ZPfOQg6UBWQVV1oMnqPfq8ds+MnS4FMDCuRrzft26BhO/BoGNnIrR9yaLH9u9G92BVBlmWi4MTTguAVkCXdXjiMYj7Hl0cSC7xjbwmsbp3JyhZkPMSC8FRXJ1p/jz1ALriJcHz+/uEsmarCqqiPvToI4uXnI0BLupqaahlgnhnY7jnGr6mbn7jjDc2zbmOt9/T7t4ebxpJzIOOZmizYVSN5wKgKYMOeoB3QsChh11qyCWFHWLYJoRahLBNiLkKUftQ1HU44Fzhcv54VtMHudolHOfEwCANNY0NM2trG698/9XmdAz2rGmqok4PQFdzabcqT/NmR+MylTUnr0+bT6XOuI7YJVOAKcAUYAowBZgCTAGmAFOAKcAUYAqcFgUYgD4tsr9cO1VAHIXXLX58Ybg/7hXj/rELljwtq5AWMiZ9Hpd5uSpVfd5lwGUitFe96ekrpaf5YTwNFSOwaHD1lQ+98fXLrr9+76GjkC3gW4fiMW50kAoJ1DLBaX8vwDyEAsaFUTRIjsEnPp6MenpjrepiLwRmrljxdxBpCI4J+q0GzujZiVXiyZy6KU0w2tNQbOWSE+UnGJY1BIdV57LqVpu0kuW5sLai+bK207/QNDypj7aTJNw2I2Nj133+c4aXc309V1PPNTbWza5vnDunZoarpq6L4y6e1fCFNv+TcffBmOtkzDEWs4kRmx5phbCNgGNLrGcz6PNEVNqMwuH3oAe0kbwQ8oghTyHkkUNOLeTUwnY1bJeRRDvEiCMXcY5FXCfb+KNB79qm5jvqG/6T4xx0zHV1MzmOe9e7r0im8c8QVB0KIk4QSTQJHUMCo5dt5jLZJtW/rCa5qFyR52VdKjtiJUwBpgBTgCnAFGAKMAWYAkwBpgBTgClwRinAAPQZtRzP32AsFOb5M/pcLWkybFwB53Vsb/cnQx4xwo9c/cGcoEJW0hUNCSBNVgb9XLt8abUvgzVn5BKP15vSZxM7QU7XQMxjklQQiFO0pFeC2cqS8Yaf32tZJodiarCgc1PAno45IOFILwhtGj4KQgEjQk/UnTkzS4YBaItaVkA5Ud5S3Zo90wC0pmmiKKoqCWNPBrp06VK311sMssFxjY1c/Uyu9iyOm028jF89Y9ZHbc0/8dqeiDhShDjrQYccdIgkyQGHip7LzwOA1kLeHCaPjMcVOiBog6AdgnY96FBJkgM2wdNU8LaOBn098fBDTQ2fnsm9juPCHDeXjL/G4wvu23/Yqj8wAD1ODnbJFGAKMAWYAkwBpgBTgCnAFGAKMAWYAs9WAQagn61yZ3I7k/qZxKditBZehnyNpIkxW0XzSQqo5aoVNAl+/F2Yz/eEvSmfeyia2HP7ryGvgqiCquFJWJWpqh1L4SS9WWqNy1rRrSmRmTG8/ca1OVWX5jCKkQSsM7TmjZPtrPVp/lSNdFw/1XcR3YoqOeBPBTzPzPLRiMflhHDXUvOFzorE6/PQIXDaHgp7Mrx9NObdffWVe3QVRHGy54KuSPl36WkyHyuzwgs9kdNl35zgVFfTum/LBl2yVNxRVj0nXotqBku2jKelrKdpXVDfZ1WVFCmfTo0MDfS/+12X19fWUvrccNZMrrGOmzkDAXS9j6t7Ncd9pKXp1x7byojncNg1hhTYDgGnGHDlAu4UJlfG7yoEXNrzAaCB94q8t8B71JALeAfwdiMF7ECTrxXczQWvPRX2JzuCg932XbGz/uxs/HQjt7imZh7Ooo6zOW1/+cffi7948A8WzGRVsrpuVv1NExVVrXas+YqKrIApwBRgCjAFmAJMAaYAU4ApwBRgCjAFXlIKMAD94llO43/19L/txrCt/4dH9EPr0FKdOG6WVS9N1tJQI57Hxh9cl2og6sHQvSRZqpsIqAruxCYUGxE7pgVCpXSQRbj6iuGI94TfVfB4BqKdq5evg7wOMkwNQFsZRxUBLGMvZekYLFjMNELrmJfGdMrHXLJTnrO2Kr/znK6oWQ2QxBOd6RqaGEjSEQlZ1rW4LmZDugfGAyDD2vTHpuGOqpqKPZMtRxFhCRSWdURjbyiEZuHAdDGvEOdKbTSdUnWcp2V5yppWuxg/t2p1xpVV7IHSfXoLB6Co8NvfDHQldndHwdvc3x3f+tNbhlJZ3NCTfEwZLJmSDkWEasxxUkuTdPIiuGWZvrmaSvWFrdxOZfMrWSqqZ9XTNF7Wxrigli13SrbIUJ6N/uZoi2bTqaGdO55x2R21XO3smbM5jpsx6ywEuDVzOM7Lcd1c/Xvn2X/o9T8a9B0MujIBhxqwg98Bfqfud4l+d87vzvg9Kfx2FXxuPISwkkFPNwQH75FJ0nl3GYDGfh3gR/YNET9yarc9452Xbm9WO+f1xVr+YT/rOo7r5Oqb8bzEBo6bwT204iGNBMExg2+QZ1c3Q0IXlaj4aWo18TNauSK0pMIWK2AKMAWYAkwBpgBTgCnAFGAKMAWYAkyBl5QCDECf4cuJ/z03/tOug4a0Dg9zI2gG0pmCQohkpoDAEtEkRSwIAnQAGb/L/n9vEgJj1uQm5QzjmAFpDgWAHOC3iNYw0QypTI2V6ScXK6OzKxlRAaBAT5/L5yGVgkhkk88nI17xjZ7/hvVDAuQB8lolVy1yT7RPeYhizIXOqDReExnTqkW5ig017AHDmxog1bRCnXPpLEo2aV8SdlrqAlsXP6Sc1i+R4meDtooGiz+tzsK6RBCQQT91gBxZScEQSiIzonUEI2IybQ6gy5BJYixXURZUY1xacc+UxBk/YlMBagdvEymsrzHMWatkL0jkG2tKGggqItxq9q064zpLoOmaphnHTtJ9C6KG+2Tc2tCCoj7YFl9VkIU0C81lNUtM4E03hgiQARgBSJk1MINrB+S0w1Gz/OqrNvta9/ItSrAlwztW7u9B33wiVLWtQHaOZczm4GnGCuVLebOvl0zGqoAKGkn0jyryGgZZKcmCUy7tLroG1vvj8+OvLabMWxPJaFYYl5mofpVyHSejFo/GJEFadADld7/9+awZdY1cYz13Vn1NY01dPdLn2lZuxgKOuzwcWRoMbA/4D/q9AwQxy16X7nWCkVy616WSJPudqt+p4m/CaiE4KJKuxNDWGNC8F8wU9AImDyCALifatAu/BwJuhffIAbfEu5SwXY3ZxJhzKO5fN2/eF7m6V3E1Aa5uJjeTq2viNuzYjE81EUUDEDVdVsvOJKwOo63/IljzVcSdtIi2fS4WJjXPbjIFmAJMAaYAU4ApwBRgCjAFmAJMAabAqVeAAehTr/m0ekR+YjAUAyZrhPSVjCgqZMg5abICUhGXEFJcQGBHGxvVTVdaA6iRmxP9d18lRsTiNwXQlAASc2a70lgooTZ7oTyaDAOgkIVVyyEY7vH4wesFPth/7ZeODYqItCntJoMpG27RMCWJFsdfOvwSFTRaUQuUzpO8pCHczhIGXRwzKiKhW7e1kQlJjbsTAWgyElqZuCITiGkYKo722f6kZg1PYYHIjoGSZcLvRYCcBgUyZZUAXzILSqIF4qWO/eoqaCJoMqgKvq6QZCgIIOmajnTYmDEdbnUAbd4z+Czxfzfna5pQyXsQuegcT+I5y/iN7sJmMoQogaQiGtZlTcOZqThMXQFZhqQMabOhhvycut5bxaSvQ8jSmK8T6DhLOwHPUQOQdNxW1IJEKPMQwJjVFo4SW2UBkgCiAiAW4NVLnmr3J6MOCNmSS7qfyQtoougEXtYaL0inljGXJk4KS9DZ6slbYeVFX2BVwATQJCOo+FoC14Mm3HJ0Lxmbz9q0Sr5KkWV30bsTyTdR24nqVym3biojr33t+i/V1nANdVx9DQLo2pqZXE0riaR8bsPMjwWD9we9x/1OiphVRM8u3eMmyQUeVxFDEx5NfZMnoc8BF0wDQBcPJEQA7dFJZA8t4NKIh7XxHXArpYQhQfSwTY+4BnjPw3PnfoOrvYSr8dXMa+Bmc/VNjb+8624AXD9BxYdUBV3RNJpM+qzSZ8DUrvSkk4W2CmjWmUrG/JflWVuYSi+sDlOAKcAUYAowBZgCTAGmAFOAKcAUYAqcQgUYgD6FYk+vK2SdFnSlqATwUS9QhMEqjI6ApoCQhSM9sHs7DA2AYvyPXST+nini+1kg/If2bbZG19jypGuIOksAe3qDxdpW/ABFbF1ECBLoSbjhK6PB0BFPAPw+CEZ2/205jKjonEwBqkmUigNDhFcyTEqJD3hx5IZLOHEMJ3SecC4qFB5xp0JWhbQMWcJGkYJRG4b7sDFe2r8ViZlRR8o1wKkQd0BQcBh0bUi/Rr3iXMubTfnK5Lz4xgFHlSvImo6M9m9/g5/coh46AskCZGWRTsSygAqAoKOjunE8mq7gKX+5NIg54pKKVdGoFQUWRS4OzySD5iwMfUhFkjcAIopAwLcuYRYVwJciRGTDN79olP6kXZW2h4rAN69AToGMAikJxgiAxsAcxaRr5l42bAnEi3mEKGMsVvmOM73CkdjT0w2LXB49yEky51a2W1FuBdathah/dcybDTvEiPv4p65JiRooxWAoplw0QwalavgUalVVLT659FjNEoy2rFpxFuViveiuqCCmCOQ9lSbjSxDqr274RBefPvoM0kepuNrmslPgb1Qpvngrl2zcQkz3clryqgqIgmqekfmb3/yaqyHuzhxXX8vV1tZztfM4rovj3m9v+l0s+EzQ0+d356iPs8c9JQBNPZ15J5jJGo5j6gDadIXmveD36GaaDEA75LCjEHGkYs6hoOOpeXO+wdWfz81oxBnOqeNq6g4eHxTJX9gIqmjSZwX/dqEUjsPUf7ywpcd9/J1/f03bPhcL/74PVoMpwBRgCjAFmAJMAaYAU4ApwBRgCjAFTqkCDECfUrmn01kZgCZezwLFOpIKkgRCAW6/RX7fZdsWJB5b0rnBb1+2sGPpTT84JhgQskDoc4ZwN7HYr+mhbDAeE7WS8//EqQPoCniGf5xe7IX+pME6COkDEpljFN578d4gP4gAOiAFo1v39sGQBGMC9A4S+K2BomCSFQR7MmEfButf1qwAACAASURBVGQkPE/W0bUV4SL503hNIRSYsuAigJZBk4yElBRjQ5DwENQbUyLxpgmdzCPXwlaSRryDTYJGSBnCr/EfA0DL6GGrgiCDIKKLMbJ8CjYteHN826lcG9hFQ59gHLWGk1Xh+i+PdcdXh71rrr1mMJVDzCwTJEdNFvEfOjgLAr6QeOZp+MF3eq/9yL7L37L+E1fv/s0dwrFeKKjU69uk8NUGRBk0AcpoVkNruBAyBu+WCyAJIInkkhwaSd8PWHRTqAf0ONO6efAgQeCqimhZwi2clyAjwRhJOQmXHfcQBZd0XkVTOgnkktQgTdh35eLopDxPvmmMGhqfxNyT1Pm6aK/8JwJoFb53A0T8B1pmDjibk4nI8Tt/Q47HBNyHODG6M+lbGkLHyWiNWN0mhrNkStC5CKOpYJYq5cN4kV6Z86E7gS6fTFaCxmihf7FRDqBpozMdQKMLcAF/n0qS8pe//GXGjBm1dYhnm5qaamrP4jgfx53DcVfwrn96W3YH7Ol4EEz6fEYDaJcWcOgBhxp0FpBB21Rk0O6H5837PMc5uIYaDudZ3zC7aeX69QU1n5dziq6YTtBVAfT4Z/K54GMGoF+kvwvYsJkCTAGmAFOAKcAUYAowBZgCTAGmwMQKMAA9sTZnwB2KruhAEEkC5GXI5eD2n0J78JGF4YPtnr52/4C/9WDUeyTi3T0/uuPjHzqayyERzebzpCFhcASSqlq2oBiBCHJ5EGXyF/KGYyx1HB6PEdACjYWqIqglhwWKBOpSX9dSxGRd11VV0HTqiouMVNd1nYBtAJAzsGc1nBvZ53Emw3FwutKvvyh9IgnDOUjlIJ+FbBr6j8G2TbDqCXj8Edi+DQaHCdfFEaHHsazjZR5g2aNw0w+F396e1rOEVlp8r3Xid41RFTRICvD00/DzW+ADVxx688WbP/d58fd/hJE8uhYTN28MPU38yDGuBUW61H9cRhyJlNkka5UbYWAEPvDB7d0dj77r7et3bcPoDQaDrqw67RLsVkOHYhjNwq9/k2kPru0KJOeH5I7gxp5DkJFLAJquFv0uyPDQ3+HDl4+2ezeeE+2d7+9v9/TF3Lvi/vUR/z/uvx8BdJZgemNEVQkRYeiyImp01xTgsYfg+i/DBYv3dAZ3tAe2zY9vfMslWz9z7cH16xDL5smeKMaCpoKVhMulC1QWjLKRAzENahYjhMgK7iQJdAFkAVQBM4YjPB0bJfkCWad0Crex6b5Nd3WhkMNBaoog4F1RLGSzdLfTEBzUCRq9j8nuNt4M0OMEM9lUKj1CFgwlUMk+GJPgta856LENe116a1OG548/vQXGcpCTkLkrIowNwZH98PR6ePwx2LIZtm2FVB4lVYvra+6W8gzF0Na9ZL1fbPzi/0n/NEFFx2fcjzmydsjuiUQK+vHjuwwSugX/sKO4SyoZtHnr9HtAk0Hi7nvs8Udqamrq6gh+xtP6muu4zpn17/W03NEd2RZxHw+4Mhh5wwkk4IbqcWOiITiMbzMMdDFDQ3BUekBTV+jpxoC2ekDzPjCT6Qrt9+i8mehBhQ4IObWIU4o6hJgjFXcMJHwrOe5tXF0bxzm5GjxZcWbzrLQwpoIi4S8kyOYxmL6ql1JptcbtYStEtubHVfu3l8+l7b81ziowBZgCTAGmAFOAKcAUYAowBZgCTAGmwKlSgAHoU6X0NPsp/seeQjTIilAQIZeHvT3wjsvWvWLBzg7fsbgzHbZlvc29bcHRkCfZwcsRR25+dM+f/mRgsUwua0SxIDxVVjMUlA71wr139S/7azKTgZxIvWKNv5QfN0yVICUspJgTCa+gQEaFHI3hS/AdOeKv2FLIgSph5AIVj5nDJBHE+J3rIOE6EQlCMAIeT+Hb/wPXXJu96v273nTRpgsWr10QXd4dXNPm3Rh3r+8OP9Ude6i7/Xf33ZshhA/JoaRjnOBb7hyOdjwaCa09J7bsu5/vARX5oPmhtCsH8Mxe+MjHtndG1yd8hxPeo/OjQ+2JgUhs83uu3HawF7khcYLOAihZCSN0PPwI3HzTgW9/6+mREQxmQSlmcQlM80ZG1+C7N0jh8NNe596u+IZbbz6gCiV9xtee/rWGiFyTADIFuOKKTSHXgUgrhJthQezoEyvQLZfG4cbhESg/nIETw/C5z/YEbU8u8KW7PRBthmgTxFog6pAi7mTMP7howY6/PgxDebKMVqZjsFm6wGSNyZeUhh1r4J0XreRdy72OQ7wjG/dCmx9CrnzQezwe3hUKPP7xaw4PZWC4YDB9gypS40XtFNHYN3/+vXTx+Q8vDC/94rUnBk5CMou6ZBTZRM/0LMWCAj0H4JZb9v/rbwin6eLiXiJOx4ZzP4CI3tLEUxxAIgHQQYZCHvKirmBd+o6EehwbnvgYL0MBWQIpC4U0SVnI5pEjpyS4568Qjx/2e/RQGGzOQvdC7Zpr4YNXj1x++Y7XXbBxUfuGhH9TzLsh6Hk84F7WFl7D++/57y+tzyhI4sxPcdIlvFr0fS6VkI1iVjSbvugzRQCNnvi5PCz7p3D7bUN/ulsaGYCxYcTQ5Jmih2HSV1lUhDMZQBuh5zdv2eAPuGfMaKira+S4Wo6b0VCfaODexzt+3xXcG3GOBJ0Fv1P3kCjPJoAmrtAYA/qMBtAGgxbiDiHRCm2Ovqj3D8iguYUc18yR4xUXv3KRiI+p8ckVRAagi2Kwn0wBpgBTgCnAFGAKMAWYAkwBpgBTgCkwVQUYgJ6qUqeynunvSf6QXZBVkAqgZGHVo9AWfTQW3Ou3H1ncJkdcA238UbdzeTzyTMtZB0NOrcMPMc/ez35mH7qFoi+iTkirgo6oRVKWPgmfumLPK8LrzvY/9u0vHZQKSOwsPRoTpeBQysPxHnh6JaxfASePIQ0WVCDRe1NFAG11A5U0GTatgE9/YN/bL9l/6cUnL72k79KLT77tjUOXv03rCA5H/WrAB81N0NEO3R0Q5/vi3p6oc2/Uti/hONzpHl7g0Rb6Ie4YsTWuC3se/s7XTyItpnFINXj0SYh2LXUEngmF+qIt2975qo0YkAI/9LxEGZ2XAR58HLo61s2P9UWcI2FbPtSS97XmHI5cKCxE+N5PfTyXyxE1MIQHTvwPf4KI58GEe3Onf/X1XxwRNbRqcFNDjNIPGo3hoosOd7TlWpqORYPb/vOqtQqJ51Gq9BxydCEwnrGOeLQ9/ggSrmaI2GBB7Pjf/o5TNQG0qqH/+Kq1cOmb9iUCuwLNR0LNmVgLoudYC0RsetSph9xq2KvEo0PR9lUnBknEYtwJxaP1jF1heLIjFFRATcJPviad79+8xD8QdqZ8HoX3gd+DKcxDJAS8X3K0DkYjRy59e0/PEchhSA2qJTn6EANXkwSgFNBxcqQPLuh+uNPdk2jt7fZv/9J1PQCQEmFMwHcTxBUaFw4ABgfh/e/e3Ol/tN296uvXpeQCZLNZCqBJTA01I40UVKTXyKZVSB2HzY/DrjWQ6QONbAbizI7nNRYXoRR2Bpso8M1Pj3zojSeuvOTQFZcces+bjrzrTb1ve/Pogu5en3s0ENB9QbC5pEQHuJwjYb437D0YtB/1NZ3wN40FW8bCnr6o/2g8MBAJbupe8vuhLDrmmx+TK1syLxsPaPLIYJx6FR74A8wPLFsc3tXt3XFB4uk/3A6pUciTF13k/EwKoCvRMy0piVfKEePPy6W5WFPIIIAeGevr6AxzHFdTy9U3zuS4GTX1LbbmS9t9f/eetdU/71BnSAg4Ra8LXZ5dHkxF92fV79T9zhcQQNNHstp3KQb0hB7QTuAdELJDyAERhxZ1KIlWaLdn2z09Uc+9HHchV+/j6jiukauf1fDRj31SFGUzFjYD0FPYPKwKU4ApwBRgCjAFmAJMAaYAU4ApwBRgCpQpwAB0mRxnzgWlLWb8XCELqx6BjtBjrpYdbZFsPNQfC+2++ipp6d/heB9s2gKJUK+tIRVzQtzd+953rCuQ4AeKrmhGbAMCHAHSKfjxDUqne9MCT/Lc4NA58X9KGfzzeOJ1S7yNacwNEgPi0QfhEx/e2hl4MOZc3hV84vyFy35yc/9YEp2RFXQypR8a9BXzBSEFGnz14z2LPGsX8gOdfKGTL3Twor9lNOgsOFtyjlbF6SQnEPog4tPb/EqXP9/pHelwn+xwDXTah6NNI6E5/XH7oXbflpD7/of/hc7UGMEDMNrDXX+EaHyr03/c5Ryaz4/95ztG5DQZgy5Td1hBhV/dCd2d24Ouk11BiLm1qEsOOzM+RzoSBpcT4l6Iubdt3lAKNixK8MrzVwVbjyRsUrTl5OuXbKcYjM6t8lvTYXAIvM619tac3yeGfXvfd9k6lK8oR2WTaZWUALSGh0x2xtZ0+IWIDboDEPMffPAR7IeGNxYAD/K7/6/Q2b4mETzhbRrkm/u6AqMLogPtvv3t/h0J/76wd4z3qLwX4lHd5d59223Il8nkyYhLryVw/bFrDdQCfOO/U4v82+a3Js/xg695zOfqD/FHI+GDft+eePQk7x2e23iiMwru5lyIP/r2d/RkFNxkGAJYlcihh+RkPjycj3Slw9/+OJZwrwu3ZIOzZf+c3R/8j03o/iwYwU+MyOYAkgI//2ky0PRQovXYOT7pDQv25ZNowwTQAug5HZ2f8wI88hB87AN7z+t4vItf3eVf0RW6/3e/wPjUKvapWgA0jf5MBqPBo3+Dxe61C5oGFtkHFjhOdjmH2l1jAdtIWwi8bnHevGSLM9viyDvdituZD3jTEV866EqFbMkFAej2Sh3eEzHP3rBrZ9j/6Cf/65mMhD2Zn2qE9GUFoDUVJFmFH39PiNvXddqTZ/uAn9nbbt950flP/+h/RyURf9XQ111ENBKIxdjOigUyG/lqehqP2rO+ZS7WFDIIoF/72gvmzG2srePqGhpqauZxnGdG/Wu9thvijt0JPMQv52lN+pwSBdAUPZPgG6rfeQYDaI9OA30ggLZDxAFRO8RtELcr7c5Mu3d7NPAzjjuPq53JzUD2/v9PJfzRzT8VRXyZJKv4j4rJoK0LUSYp/d1S9bus3r+7sFr4d3XZfaYAU4ApwBRgCjAFmAJMAaYAU4ApwBQ4YxVgAPoMXRr6/25FBTGHcVX37IaOrg2h0Em/a9Rt6+H5h3/5K8gKiCCzCp7mdsE5hwJN2XYnRG0nvnjdCYxKrIEo4yF8xC3YANAA8MpztoQ8o3EeeMeJ7tDyk4eMuK0UJA+PDagKJAfgtv+F7uCqTn9Pm3e4zZOcHxoNtGw5O7rpq9cNp8YgZzqYIj+yRMEA+MEXk+e4N7/CP7zAke22S/O90BXA6A0BJ4R8EOIRQKNHrSMfdgzF3EejjmcittWRlifbXCsWBJ9cnHj4gsV/ve5T2x5/GNJJEsQDgzGIORU+/0Uh4Nkd5Ie9joHFsZFf3AgFCihljMKsKHDfnyDqO8DbpXYe4n456B6Kh3q9nk2LFvQH3SPelux5bTCf77njlhwOWQQlA3+5H9rbdvtaBmI2+dywem7HBotLa5W9oemwbx+4Hat4jxr0QMR77N2XbsB6FhBZpdlUikjHFEDjGW4qDA9AIriig08GW8B7FkS9h9ZuwGgGWQ1PmhxU4M8PQXvHnogvHfOJftuJzlDP6y/Y9vOfqYcOQy4LDy4Dr3dNS0ufxy37/YrHc+ydl/UQLEwP6xvnBI0u8kMn4DMfPRawrUkEklG/3hYQwrbNl71h74++J/3+19pDS+H3v4S3vnZXp393zFUItGphr9Tese+u+yBDgizIBVXXVRKvWwZdVtElHXffrd8bXZw43uaDcKvEt27+2lf20kMmTTaMbt0qnnN4TsffFoeOLfbCfDss8u06cZC4bBPgJZJoLzkNg8b8+CbwOjb7/Yc9gT5XYMDjPxmL9wX8K274TrogUEZJui6XPZOG9cthoWtN+8z+rnnDna1j3Y58l0dM+MUYrwR9SlPTmNcr+AOCw55MRMVoqD8SPBQMbA+5Nrfbnlnk2HR+eNWrO5ddc8Xm235wFB3vyWGMNNC56R9a3ie9smK6ifLV2p2KsudlPHiOo4bhYfKyDisfh4XxR2KO4+e1Af5NhluJOcZirn1vfOXuW/9XTg5AehRGxwTy2qKQl0dJTHkMs0MSPUMS40QXS6zQmQJ989t6a0r5qSiaN6Lnw7e+8c1Zs+ai93NDTX3DvMYZHRz3Fs+c38Udu6PObMgBvEsLuDSvS/e5oZg0n1ujEZyt38W7ZjUjY60z3Tzvhn+bym3iaIsJDAaNHtCYQhiOQ4m4sglvX9y3ydN6G8cluBo7x82urW3muMblT6ySyGtHTcV3QjRZ16hMWys4tlayltO8pZm14nP/hWoxzLJMAaYAU4ApwBRgCjAFmAJMAaYAU4ApcJoVYAD6NC/ABN3rGmJhdDSTBBg5AW+8cEPn/JTDnXY5jyTaNvz8TkiKRmRVADjZD2HXumiT0O2ESMuhB+5FlqPLxBsVATEJUUz+ty8I0NW+x+vRgiHwuE90htacPGgCaOyR/rf/u18WIq1rO92DbS4p4YSoA8J2OerMR1qGFke2bFiNuLAICBTioEzngRjywCY4x//AQufKV8UOXBA71ubYl/CcjHoyET+4bGrz3HQkkvMFdrz1bWPXfRq++3W441a47y5YsQx2boDRE8iF06NQyKE3q07Go4AoQCGrwofePxx0Hw35xkLe/qBzy6N/R2dX9H5WMbDv02vhvPk7wjb0F+7gxYi/513vGvvrUnhqM9zyM2iPbgq7dic8h7oDq3/3s6RGYhBDAT70/kHe3xtySb656Q738euvwylUgZfFddIAduwA3rc+4JTDboj6Tn74it0G+irWeZY/DRyDcE0tAuh2/ol231CoWfPOhTb+8M59GFoiq+D3sqfAHno4GEiH3ZDg8yHP1v/6VDqdws4FHf2LMwL8/JfQ6tjp9kluDKAx9vpX7SQe5dJ4J2ga5CQPP/shLEnsTwTSAU++1XEkENz0658C5DC6hZzHhNQ+CTd+RV/SNsy3CkEPBAK9HQv+fHKYTBqZtqyDSFJxN+Xgq58+0RU8HvMAnnjm3fzAAzpGYTDP7yNN8UjDJMyPPNbtHeh2wHwbLPTv6T1EAbSq6EqBAOiMBJ/+1EjU1+exgcMNrV5o8eutPtUdkDs7UlH+sRWP4nOhoEN3lVcJmgj/+a59i1ybXh0/dE64p9OzM+LYwztO8J60z5V1OUdc7uMO57YLXtN35Qey138LfvgT+P0f4Z9LoXcbpPYCDAKN7SGQNx9yvkTiGIDGNyN4SCrkc/Bf1/R18scSXgjYwd8KwWaMCRNvPdHt2/zaxQ8tewBG+40A35IGkm71E58WgK4KqScj0VN8NnVdf2rtmgY8dbCGxH2u4Tgfx10a8dwVbtkTbRVCDihnu9ZLzXqQIK12BgLogKvEoBGmOyHgVnh3HqPGe0bivo0t877McR0c5+c4PJDQYfdkswL9w4ZTA6CL/8RMcdFYNaYAU4ApwBRgCjAFmAJMAaYAU4ApwBQ4cxVgAPqMWxviBaYJ6NaMBC01Al//ghp27Y761Wgo29W98c7/Qwg2XMDD0zSAbBpuuREW8kMLXBCfJ50d3jM6hJPCwMTkZwlAAwwPAe/b6PPqoQj4vMe7IysHDlMArcjYI1q7/cfQ7l3X5jze4U62uYSYWws5tZAD2ryQaIVI097PXnMY7ZcDRHQI1bKCIIgZSPbB7382+uMbBm7+3slf3ga33waxyCa/53gspAY8+UTHwWOjkNRhOIdHwBVEBMxCHg+RkyRQivRXB6AnMEroGqtmFXjN+dvD7oGQJ9kZ7e+Mr+rvw+lhzGIBho7DRUt2hJuOzg9AJ1/oSuy+9WdwZAiOpmFIhbQGjy2Hyy5d3xb842c+ul3MgUgBtA5tsdV+12jEBcGWsVct2r31aSpZxdyIlPTr6Y3QHtnpaxEjLoj5jn/u2uNqyR/cUm+6WVxt/Kt/ymZlBSFdR3BFp3co1KwEbdAROzgwZvgab9oKwcSTrY4jIZ+e4KX5if2/+gVkspAjoZRFkQTT0OHEEMQ6tvBhxeWCoFdbMn8PDlUjIbCN7hDy0MMMVz4GC0O7Fgeh3Q3u1mOdZ6//8z/Rr1zMgyyiSzUusQwK8Xf/yFXZoOt40Cc5bL0e7+P/XIYLp2t5Tc8rICi6pOjEKVpHfv2+t2wNuw+GnErco3ZFt50YQEZM3aNNkTQVkoOQ8P0rYT+eaJa6HbAwsK33MGiaputZBdDpu28YfvxjiAX3NjeO+lrB40QGjckDAT8E3KmQc8eHrthNAHSBHEWIsVnMLkQVI7bkU/D3e7Rbb+r/+U/Td96h/PZO+NBVEPCMYETvyGA0vuXu+2CwAAMiDEkwqkKaRBchk8e5iGOgoUM+sapazZv9VGbGeXZWvaxsdWpKqg7m2aE/hQJoALj6qs1R186YU+ZtWtAG4VaItEKHU2l3jJ7N90Wa17zjNUf/dAekBvCXT0Ei8VvwXQOGWC+mqnDZ9H02M5Ph5sq5TVHTZDLZ3Nzc2Fhf18CRT11NzSvm1f+8O3g85hwItI4R3+cSdKbEuer3CwegJybgpYGV1zHdnw0fbdMJmvJ0n0cJePK8Ox9yCTFv38LEk7Xc1RwX5Li6uoZZHFfzxksuzaTxl53pBG1VuExbq6eztZK13HjlVmpnrUjzpXssxxRgCjAFmAJMAaYAU4ApwBRgCjAFmAIvZgUYgD7jVo/8x1sT9IxAfDj/+TcI2FZFHJmoS40Fjr3/6h0qwCiB0xi4V4b1KyFiWxFvGY7MTS8M9n3jC6ATfFoVQB89BrbWlV6PwofAH+zrjD4xcITGBQYZFEGH1Ssg4V3d4T7e6R3r8Pa2BXoSwZ1tkcMJPh+26eF5cHZAjrn+mh5CNEnO8CsJqCMYl4WCosvIjJEn6ZApwIFDsGjRBj5wKBJMO1t7r7gynSRutWLZEW6GHYzgoGBSSHwDcrygIgBkJUiEVkfcyZA73RXv++CVxwoUAgJkRuHjV26d7+yJzxub7xts92/8xa14Ol8BIANaEkTiFgzJJJw8DlIe0jRyNMCKR6A9sj3slYKt0BkY/NJ/pzIpkP4dfFu7GrriB3wtYsgBUe+Rb35pSDJYf0mKZ5MziDC6J+PKEgDdGX6ywzMYapF4m9bd3iNokCpALg1vvviZaPRENKJ57SdCni2//AXoGJjb+OQzgixBQYCcCpGO5W3dutMOIRe89ryTao7wVGOO5IeGGyCXhTdf+NTZ4WzCBh0YoXv7n5dCBiCnkNEQwxphuXlBEkVY+SQE/Zs9rkGfN9uVGPzMtWOIpbRkEUArJQCdhdcufCpgO8Q78h1+aXHnM5kcQkOJRPcuDhldiYf7IOZZGm09Gp6X7bAXFgY39OKbDgTQGkD/KKzdAD7XCt4+yrdCZxj8vpP+wEFv4LDXN9A8e8w5J+WZfWRR+wpyyB2GgdbR95+cYml0gw8GxiBWUS5Jh5wMySy8/z8gFsz7HKNu555I9J+H+9AFPg0wrOFrkiwJMYNKKYouiUrBEnDm320Vc3aE+lfiNWuJpe4pzVrHYM0/m0FoIOFBoDI8+ii87oL17cFdEdfJsCMXtsuRVnSCTrSCt3EseNbIAne2w77/9Yu3/vC7YiGLb6EkDWWnB2xiPPHqkpnc2cw8/wBaVdQLLriAguf6mRxXP7Omrqux7pMdgb3us4bDzgzvyJJAFgbnrcqdzUITAVd1gjbvnpLMhAAa3Z9d4HNrXq/g80gBF4RcwpKOEb/zbo5bMmO2l+Nmzpwxh+Pqf3H7r6kTNA3OPuGOsYJmayVrOQPQz+YhY22YAkwBpgBTgCnAFGAKMAWYAkwBpsCLUgEGoM/MZUNyqwFkUvD6Vz0ddh+MuPLtvsKrzz187AQyQQFgIAljaXh6A7zu3H3nxFKR5pGE59BbL9mEhwQS5qYaIRBkDAONIT1wpj37wefb4HGrbq8Sjg6+YvEqOWsAaADoH4K3XHSg3X8yah/1zt7THV59y81w6Bhs2gpnL9gX82aj8+BcHs6LHnjofvT91JB50ngOVEYMHYHgSMcArhjIGDAu7IOPQpBfEXD1dsblUKDnhzdDfwryBDBhM3Js3LhlIBFgNQ0JtlbAs+1g/xFI8JujLpF35xPhA9/7RlYifscFFX7yv9J878aOub0LbP0LA2t+fjM6U+ukd3Jen0aZriSjMkjIyEdV4ZvXpyP+A11haPPI3eE9O7fi3cmhYiEP//oHdIQPBu0636LEPD0/vCGlilP0hB03y/LLCgC9bwd0R1a2uwdCLULAlr/oDSMyQDINN38bOnxHXPbBaHw0wq+65/8I6BdABxH0AsV4GE4F4GQSQh2PtDj7XE6I+NS3XpxGAK3Q0RZdg8mRb7f8CM7u7gvZhkO2ZNx76Ac3GLWotzQZKOIiGplXVnHvvevyk21tyTAP9jmD583fphRAVVI6iCrIOvnIWh5UGD4IS8KbQvb+oDPX5h+48VuGyBRnmxJoKuzfA1H33+POvuDcsUjLyfO61uMGIv6WkoDnZ77pks1RX1+bD1oaBgOuPb+6Ew73wbrNsGDRmrZwim/RgvPy3cFt//oX7n3F2IAZApDLFojOXAHI6FjplUtORH0YgiDsOXrVVfuzIhamVYNeS0hFJRVIRBvcHQrZskVGagVq5mQmy1gbWPOTtXkh71nHYM0/uz6NSCRZFTbvge9879jCrjVt/kNh27CjMZlwgH82dHjBNycfa9XjrXKbLdXmPHzhuQduvQmS5O82qL4FVRcUXVRRawu9pNCZhoc2AbQ1Y61cPV91Vrqua5omkw8A3HzzzQ0N6Pk8Y9ZMcgJfgOOuaQ+ujXpOhFwS71L8Th1xrWtKAJqSaMqXKxn0KeHOEzlEY7kJyn1u8Ho0t1dxezWvC0P2J/zQFtrV0vwljuusaXBzHGrSavPu78H3QpPGnKkqMym0bjGat9S1rLWx4L7kygAAIABJREFUfJabLMsUYAowBZgCTAGmAFOAKcAUYAowBZgCL2IFGIA+MxcPXWAB4M7boSve42k9Gfam/PYd9/wf0lr6yWTgsYfh1Us2tAeO8s0nAy094cDDy1dDXkNaptJDonSVHPA1HkC7nJrDqYUi/Ze9lXDDIpP9+tf620MHws5M0NbXGXrmn3/FrkbzMJyGO36Jh+AlHBBrgnOCIz+7kQKIIsQ0BoVhM0jCP583AfTPboe22A53S6+r+ZjftXrLFoy8YXxovbJICRRuKHTkGsgYURhg0zOQ8O+JOiHkkaP8rn/8GUNFqwBPrIKO4MpFnuGFLSfPD+y66atJSi1HkkKREYIKKjImFVG7GTkkJ8CFr9s6P57yNKf8rUevuwbDgIybT3GUpZ+CCH+4G2L+/Rg1tVWKeXffcZtIaW+p0rPLYd/oGWyG4Ni3A+ZHV8Xd/aHWbMQ/es3HoH8Abv9p7tzIwWhLMhwYdvnX/OIOGCQ6SPoIwBjoGXKcH46gIMKug+AJP+j09vp8YiSQ+swnQM0XnUtpiAyA9Ak4vhe8jicjfCHoEBO+/ledu0Ugbr50WYgmxjpp1Dtbg2QBrv3vwWi0PxIE91xpUXxPfgx0VdF1PJkPQ8TqugJ5VYZNj8E5gX0xVy7kynuaNj26FGQJg36M+ygaAuiId2nCczLYPBq0Hbjs4l0yjZRC4snc9F3oju7zt4xG3bmIb/tf7oeTw+Q1gw5/ugf89h2+uXK4Bdp9+2/7aVbWqCe7iE7wNGxzeY90PlmAnuMQi+wIONSAAyK+Qzd8dzBXdHFWyeGHxBVXooGtiy81zJ2l4wjMNG5K1S/N2uMy1Wu/8KXjhmFePsueVQzVraV1fUSBgQwMj8DPfgKL2jd0Rw52BlNBR9rTnHLPyweaINKMv0zizRCzJcOtO87rfvqGbxYO7oc0WXQ8o1DGtxmKpqkY0ZtyZwxQU3w7ZUXPNF8dOlux5uSzkmV527ZtLS0t8+bN4ziupmE2V+fmat7Eu/8Rch4JeZK8Swq4NOTILxUATRk0cX8GtwdcPs3hA5cHvC4IuiHmGw0HHpwz95NcTYTj6qlX+HvfcyXoQA8knFzPKnfN/WVmLJWsK0XzlpssyxRgCjAFmAJMAaYAU4ApwBRgCjAFmAIvYgUYgD4jF4/CMgHedvE+V9N+j204FDh+2WUHsoSQpjOgCPCH30BHcHXU0dMdyMW8fQHfw7//A4YLyJGQzwoiV4xmoSGRrgTQYLOB29N73X8NaCKec6hJsPIRmB9ZxzuTUb9qn/fkb++AfAEE4oTYP4ZUKBZe2eGXQvP0RQHh4/+RlUi44XL56KmBiA40EswZPaBl+PCHBrrifbxryDF3z8L2NapEAvpiSzLPKh7QOsFMeByZqAt4rJkKDz0CCd/hqANCbjUWfGbjamyfFeCSN68O2g6d7VHfEOv73JW9ahqjSagaJNN54vWNDs3orKeCrmBSSGATGWDbTuD9a/zuAd45GuN3PLIMWxXHRKc13hkavaoV+NGPUkHPft4GUafeHtz3t3uN49Rom2f/jWJoAIIhnQJ7dkJ3fG3UPcjbRxPRw//zbdi1DeaHVywJ5jvwxLw1X/uOMJRF5E9IcYEA6DFAV2QRQBvLwv0PgDew2h864Q8Oh0OH7vylGWKbRjsgg03BNz47EOb3BQK6Y54yv23gl79W0hLkdV2EbBHbEgVRIRIeRIe0Ajfdqvv9h0N+8DWr7f4do71ozYqNNMgXsvC7H8Jib2+wueCzjXVGN504WpKLOkrTVrIO+/ZC2PuvmHcg0DIccu/+zDUj6VHDQX7HBgjbn0q4hXavHAvs+cUviVI6ZAksLqShLbjFNTsVd0PCe/TjHz6kSCBiZGESwYW8yxm3LqJCQnAAPPAgBIPr/J5UwC1F+K1PPI6WSx+KyRCY53RIAT5hAhlTqco0cyZ4G5eZppnnrfq4YZiX0+nAfO7x7ZOYh2wWBBr9BHm0js/pr+6UL3zDep97dTQy6HfnAg49aCMMuhm63NDhFMJNhxeGDnvnLf/k1eKa5fgbSVJxjSR85pIq8awv/lqoRM/PGUAXX4lcfOGF6Ps8YwZxgp7T0PCW1uab2vidvpYB3p0PeAQfJsnnRgxN/ZdNJ2IayMJ0arb6Pp+xHtDmaL1uAqC94PBh8njB74aAUw44jvOeB7i6VxAAXc9xDTW1jSuWr5ZlVRoXRmcqW8bcX2bG0ooBaIsYLMsUYAowBZgCTAGmAFOAKcAUYAowBV5SCjAAfUYupwZKBlYsg3Z+c8Ax6nfneH7v3fdBVsGD5qQ8fOsLqcWxLQnHYb75+PxIbyL65J/uJycTijCmFQQSRVnFWNCqikBTQPJKuFpPDwQDW70uaG0Fh/3QjTcWdBVjImsyvP/yQ3HvAb41H/MNX/fpzFjK+Pt3AMTYIyl45zu3tgdGFwSg3S1f+IqD2aJ3KsXI5Tpqio6nCSI7FuHSS44n+NGYTwx7D77/ip2pMRwf+ZAIHlZmaVihoR7Q1TEvizJAQYF774WE93jUAbxLiYW37NuNGPAXd4DbvaIzqC3w5i9sX39yK3FRBVAlVZUo2FZweKQLjPyroBN0ShCyKtz9R4jHD3YkxKD36CvPXTM2ZniyFvljaVjmH5ujf7IKX/960m8/5J6nxrx6Z3j38keABgMpV2D6VwRAa4T5YyBdBXbtgK7Y5ohzJOjM8YEDd98Fn/oIdPoOxJtGzg4PXfG+/VkVRoruuiSYRA49oFURlx3QE/r6rwLP7+WD/aHw8Wj4qSceMx3ACwAiqixBbgDa/Mt43wlbczbqLlx4/tFkGpce0R/uKaqHCaCJbzuJjHz3n8Ht2RPyQ6BViro3DhzBKZdUw2whnYLrP610uAbsjVn3vJOXv/1ALo0nGdKPTqOVk1ayDnv3QjjwcNg9wNtHg75t3/m2NjqA8TOUUfjwO3bM50fCDrHNd+JjH8rkBETLOD6ZBALX4KMfEHz2gTZeb+f7L3zNNkXAMCwkWK1OeHERpGPHGCUGHxIdX87cfFsmENwU8Cb9nlQ4sHr7Vqyhq4qGgcfJywoiAAHQGfTuxeZWa8ZcJvlBNUFESrafJpNjP63fCg7VSFb/Xp24ipuHRk6v24lGZJK/STITtZ243BibTgKeYBR3fPmEv8ZSGcgVAH93jeVg5VPw+kueibU9E/AdDbpSYTs6rYebIW6DmE3mZ6fjdmVhQDg7fuS9b++7717YtgMZtKzhqw8U0NhgVtyM/tEUT5Nfd/iwTpKqT4AeeArwq9tvq6vhOK6W4xrr6ufW1S06a8b10eBTftuxgC0bcEuInimDfskBaJ8LTAbt8mluD4kx4gD3XMFr2zhr1gdrGyNcbXNdI0aC5gMRXdcLhemfvlq56SxLUrlwlpssyxRgCjAFmAJMAaYAU4ApwBRgCjAFmAIvYgUYgD4TF09Vkdm88x3bo/7DQWfBZ8+Hw7sPnMDQyWuehMsvOdDp3tvuHEw4h2PenW94/eq1myGlYqyBLECakDOMeqxjwj9hLwLobAYeWgax0FHeBw47+Hz7//I3nL6iwL+WQjj0ZGdktNs1uijw9P49hIOSc+3Q7VeFvAQ//7nczvfHHBBu0SLutTkMOjzhR5J1CYNEQ18fdMd2hR1i2A1B7547fjWUzJgNScRXiiTQUhU4kSnooowTufkmYUn7GAXQHR27jvVDSoRExxN+z9GAPZlw7Xr0XtDHaPyP4rfJM3TA0BA6InnKPDMKfPbLmtt3wOHsj4R3fvyT6zFuCaIr8wxCGXQSEFoFWURncPrJ5OGyt/Z47Sccc+S4D7rCW59+akIRpn9DowAa4Z0CjzwIXeH9vC0dcmoBz8hdd0LUeTTaerTN1reAX3egB1ICBiehOJfE4ybAlIJ3gk2XLNrpbDoa9idj4f2veuVyRSQOzDgsEaCggpzMwE9+Cp0dJ1225OJ2iDue+ePt1GKB0GfzXEMaWcVYcIxQrsMPbkv5+d0hXg/Yk52RtaMncQGp5GTimgKCIMN733OS9yQjHvC2HLnpRgEhbDGOjEkMZdAEHR55BGLh1QHHYMidnd916Le/hdQYjmLFfXCOf6e/6UDQsX9hfM2B3RhFmoxMIv7IuFC33AyR4IGwP9keSXZGN+ZSkM8QEjnBGuQFSQcYzsB7rtwVjRzjvQW/d+g1r9qVGSOtZIwjYkzG2J84MxoCu5rJyq1Lj9PDugJ5CfLgP+GGb+Vu/RHcerORbrkJMw8vhccehFUrYMsWOHoYRkfwhVA6g6+a8G2TCrkcZnIF5KyCDIKIx0uKMgJ0I94NGTIJf6OL+NcFokbAdfHNCx2vTiLZ0PjfMih5uZAWMkl8+GlYC1nVJVkRJVmWVUWlZerUIv2qGkiKLGuChoOSSPAcVcYXDaqM56RiDHeB/HFGRoX+MfjHMvj4tUM+fk08fCzqQb/1sA3afBCxQ7QFYjaIOdWYZ6g9uO+VZ+/9/vdQlrEh4tZffJlANjrOS9dVTRfIfszoeOwkiT9eQtXjYXS1tcN9K+dyeiHjbJnRWEvjTMzlOE9t7dsj/KqAZyTgFP1OlcapIL7PWtFx2HqsH81XD7hcGf2ZlhTtVG91au5aPbVJJGjAMNAenKPfrvntStB9OB65l+Mu4epiXO1sFKim4e6779Y08/dDdV2rlFY+KMbzVaUuK2IKMAWYAkwBpgBTgCnAFGAKMAWYAkyBl4wCDECfiUspq7B9N/DBFed0KxE3xL3wlS/AgaPwpa8NdQbX8XO2nxcTFoaG2/nNn7p28GAv9KYpfZbyhBrSP35HhIQAWtNAQo6kQj4L9/4BYvxAyAMBLzidz2zdhaC5kIcPXbUrFNgb948s9O78w09BLMBQMqXqSOFUArIFFeM5JAJHIk4ItEA8sOXgYYQ7E30kAsg0gCefgM7ggbBN5x0QD+1buVrL4TDxgw6wCCNNTmx19TSwhCAhcVN1+P538wuiAxE7hD3awoW9KQFu+7XQ1r43FkoHPfs+cXVaz4CWIYDKao/mUQdZIR3qCog6hpZ409uPhKKjLudQKLTxR7fuIbgc2RkdEKHPBEBriNDop6DAgw9CLPT0gnZwz9MTBEDv32Xcfe4/NJQD4SoNXfLne6CNPx60CUE7hDzieQvgVV0Qbjra5t5872+QS5ohtxVcYOKoTaGjgq7NS/8K7aEDiYDWHpL8zg03fT+DLxsMhiwTBq0LKrztXSfntRxz2wr+lr5zQsvlAQqg6dl9FBXTk+Ho4Xs4S0WHMQE+84VjfPCgHx3bRy5YshlkEAt5qjeRQsuLQk6ARedsCgULQQ/wrgP330fvUKkwJgp9I4AAWoM//xm15Z3JgDvl9a9duwExq5SB972+v73paNxzrD28+bYfglZ0+ib+yBgIRlPg3nsgEd0e8AzEQsm28I4De4H6RtOeKr8FIY+zyMCS89YH+UGfRwj4jn/8P1Po90wnau6i4msWs6DSWrV3J0XKTmr39MA585dGvU9HfDsj3h6aFsRPtPGHO8JHI76difCm9viazvZVC7pWvPvyA+++fO+737P9ve/ZctWVW77whd4bv5+68caRm28eveNXhb/cD488DGvWkrQO1jwFooLxKUSydwV82vFVCgDkBMTW+Tzk8oiw02koFFArfODMx04x3LFVCTPmI42YWyK8u2ic/kFD1W9KtXV8ZhQJHzSVWNXJOxxcZRoOXiAYWgA9r+ILkM174fNfFSPxJz2upxd2prz2Xt6Rj9ohagP8dkCbW20LoGN7Z/Tw+9524K5fwmAfWR0SCYeeJkq2Zl6DJElZhNE6Cfhe/mtl0rUjjvuq/OH/eA96PxsfN8fN9zluCnsP+x1AE437XA6OXzoA2sTQZIKa16UGHKrfriCAdg7E+admNHyFqz2Hq5nHcWfV1M50Op3kd3jx8aj2VFQpYwC6iiisiCnAFGAKMAWYAkwBpgBTgCnAFGAKvPQVYAD6TFxjWYHf3QW8f7OveSTcCr658p/uhIteDX7bvrBtMO4Yijr3RgP/uvsePFKOxCCAHMIluWAgHlFCfGSgKMM3VsXbP/1xJuzp4x0Q8kA8unukgGcM3vtH6AhuibqS7f6BN792HYZxLUBeFCjUpL7Dso4emgH3Dt4BvlatPbz70UfRPXOiD2JrwIjDN33v/7F3JmByVOX67yTsS5KZXqprr+p1tgxJQEEQ0SAKioIgIKAsl4sKguj1isqiIvzdEJBFVLgoAsoVF1AQwxayh+x7JstMMpmZzD49M73VXt/f75zuns4kgbB4DfH0U09PdXV11an3nO48+Z233s9MS23JKMRFaG7c0tsLFiYU44PUBkQSVkkdIHHN1YgCd8Mb7G249aahlNCu1HgJGU58j9W5C045dZkit4nc5uOOe7l7FwFOGK6wtwUbg1wMeaeDgR5d/ZBsWhRPFXkuJ8uL5r+GSSX0UQbQLnIz3/E8x/T8nAOjNuQd+MwF3XGxi68xuCmQ5KFB3TDQCb41xkRLR3lLf8oA2kO7qAP33wtxvlPnXH6qx0/NohW6plAvdH79+iJGWpNTkFxrrCdIqSmtjue60NMBF32yU+W6xRpTCY+m1GVtm/ADZbshYkjHh119oCXmalqOD1mxaNeVn2p1hyoOaOrhrXbZUmxddAB6huAjZ25Q5aFo2IjJPdf8B9LtYqGM6knbCkXYug2i/GxNLSq8H1c2t7RUdEG5K822wCt48MD9oIprdL4ohHvrGhb1j2DXP/MUHCeubAzvioc2nPvR1swAHsFxoVjMkwFu4UW5sHQxJGJLFbFH5gcTasuLz5Wd4ZUT7r7i+65hwYpVoGqvyuIAHx3V1K2//CVJU6nAWTqWiNClCJIy2x13sLKuJflL71KtPZzgeeCnu45LLK+ThuP8iM5nNQEXITSoizmFH03HCro8oEndaOePtqlCuy516FJHXGpPaZ1SuEUXtkxv6BFqV8qR1bqwJqGsq9M31sc3kWWDJizRxAWaNE+TXm1uWH7qyZvPO2fgysvNu34Id/0Il7t/DD/6kfe3Z2HZa/DKyzD7OVi6CDq2Q24YjCxZcnjhCI8tMIoIrA0LZ0JMu+y5NjFLJ29C3kLnfNFFh/7Y4qLBuYyhS+koJpnioA596oAukBkD+pM14GGaSUcO1nfCd+/a+f4Pv5xMLVLFLTqf1znQOQxY10NucwwaVYhHCqlIn16zuV7Y/NlPGs//Abp3jmls4+0ZOQtDPkZdjOpGEzR9e88fg907jrzCfb0dmzcdc9iEQyYEjj5qwgQstqccEfhSnTxf44f2YUMuo+eoI3PldaxPWL3AvozPle37OPj/qSG6OsNaqVwLluV0laCjBB01PBrjWyXuiQmHfigQmEKWQwOBwJ+efroi9V6EfcNN43/p3/ADbAemAFOAKcAUYAowBZgCTAGmAFOAKcAUeLcqwAD0gdhztg03fcuLKTtjYScVBaXGqxcgzUED7zcp2QZl02UXdW3egi7CDMnT9ZEt5w2wyx7DvAFZC3zqhcT70YlX1jHge7cOK5FOOQhK0PngqQOjLgwW4f0nbjg+aSTDhemxbX9+CgoEabuuVQLQpPyXA9DVDdHwIjFoKRGoj2197NGCZZNb/fchIRbHM+A/P7u9Ue1J8n6dDiccv3FwcAxAE95aCnctM2g8ZxnnlSmSD0UTvvH1nkR0u3isnVbhlPfBPfcAzy3TpY7muo2/ehRG8vih/ChJ99gTOxEAbYGLRyeOztdWgKQvisUdnjMUZXHfEBTRIY0HIfiR8kZMnwZwi6Qhgzn43vcH6uMb1FBOE0AOQ50Ex+mbvTw45uvGPexDnz03E0EcCwiAduGO20DluhKCH5lsaZzVpIM0tT/GvbZyOensEmm3yTUh/jNJDjS6TW147GFIiWtTsqNwTkNs6KpLR8AA1yjx+ZLJOQcvvwK89Koi56JBs0HvfvhuMqGBKJHS53KONvkc8a3ayMZ92NkBDen1Ml+I1GRVcd0vHsDac1Uc3gcfgeYLsyESeVkURxXBTMXXV+0wBqCpPbbgwu3fAynckhBcMdz1sU+0mA7ksvCxWUuTwU3asVua9aV/fwanWcqzHh65CnTt+h60t0MqPk+TesXoUEza8puHiTrU7VsaR+P1tkz45S8gEVsX5QYEYVCPr5w3j+Q8VDDyfgHo6uFa+SQ5Fzkvnde468ddzfFlUk2HHOwXgxkhhIsUGa2LuXxwIKEa4am90dp+iRtWogWNt3XO1Tlf54CfbOocJHjQwkBvhkjLkJbxrohYtLzwXowsCcFPipAQXI0rYHZ8cJcU3CmFdkjhlubGbQI3JxJ6KZVYKUbmqsLCuLI0oS3TxEUyP08WXpHFF+LK8zOb551x+toLzm+94rM7rvjctis/13LlZWt/+hPnp3cVf3pX9qf3DD75pDt/ASxaBIsW77bMfhGWLIXWHdA/RBzZDiHXlF/bWIm0QOZv8g5kXVxyJC9oBGDAgYwHGROemw1XXgG62KvzRT2KCtQcMiweayciUB8F+VgvzYF0VPE4zYlHNjbor1z6mZV/fga6B3GazfCQiZM5GJs6oGln7/lLMG4QID/FbvLO/PCHDp8UOOqIiZMOmxQ45IhAoLlB/asWbNc4Yx+MmEDnqCMfdABa4TzE0GFXLQNoJVyQanumpVYfevjlgUD8mGOSgcAxkw45+iNnnMkA9LgRxV4yBZgCTAGmAFOAKcAUYAowBZgCTAGmwF4VYAB6r7L8izfaFpx91nY53IehqGGIhUy9djjNGfHQjvc2LXvycRgtwqiF5IV6SAnC8whgRCvisJ1BbIrvl261R35oQXEYrrlyZ1odjhzrJKLZr98AuzLwyJOQ1HckeCstDHzlatcsApp+fcfxHdcjERxoxs07AKMFmNa0hq8dTkiQktvu/P6Aa2G5u0qNvnGq/aNen1OE9zUvmKYNxTlbjPRd+yUsSeagYRd9q2XoTKuLIcgjORLVRI/sBwigr7+2LS3tFI6xkhp87EyY1gAJfWhG3cCsU9cYJkbPlsFxFb6mRyLBHrTGGx7OQ1/ns38DLbEhFgM+YsViy00Xiv9wWRNeRSCiV8AIYTBhNOvYGQNGivC9O0ARlwiTd8bCnspDzVFWowKz3ttRHAKrmAEPb/wn1/XWnwj29giA9vIuXH8NxPiBlAQaB3rUTkojcnjjT36AmcJ2ues9rNBWGgaYHgKQy8Py1yClzE8ro+kYiNxwSl++eink+0g1SSTwLgXQo6Nw001b0qkNMd3mao2Y0LJiAWm8SzQcu47SGVwSN1007XwO7rsL6vV+PmRNawBde2lbK8b9Yhk9An7xyQXHhId/4QiRxbIwqinZ953Yms3RDG6fNgBHL4HmNPP6is9mpZqOlAAxYed/fW2gvQt+/gA0J7fX8fk6of3i89YV8jRVJkuM/nT447V4HgyPwLTGuZrUrYj5mLjjru+jKH6eSFNJcy43rnRlPnz3FlD4VrQ/6wNq7IWeHmwzylO9kEFZmZEo4++KOtXDddy6CxiMgUC2vR1OnPm3pLI0LrXExB0xcYcubFe4bQq3LSbuSMg741JHTOiM8T1qpF8ODirBXCzsJDiIHpNPcJDggDumKNd6agj0CPJocaqrR/A5xoEaLC1aCPQwaCEMyRGmWtPikJI9OTQamdwdE0eTyqgmZiRuSOGHFX6YD/VFanr4UJ8Y6ZOivUq0S+W7NLGTOK876vVBsaYtOrklEW1PRFsT/JYE35IQNqrh1U2x1jp1sx5dnZI3JKX1CWFtnF8TF1bFhRVkWRYXyov42kXneBed65DFuujc0nLBeYWLLyxeemnhBz+AH98Jd/wA7vg+WW6H674ASmQoOmWoOYnMXQuBFoRYEGJhLxYx4pwZj+YT0UxC6E1JO1PKtlRs4wnHr7/pW96KlTCQwfkwI49p7iRziAa87FaWsNJtlRXf9+fNmzdpQmDCxEBg4gTMOD4kcfSxV6uRlU0qtkGJlPzIShTGFt5X9rYcBA5oCqApg5aJD1oNu9LUQkLaLnA/DwQ+HgjEA4EpEwJHTggcOueVuSbWm2QPpgBTgCnAFGAKMAWYAkwBpgBTgCnAFGAKvJ4CDEC/njr/qvdsE947fYMSLuhBUGs9taanTmidllj949uxIB71VJKAViykRlN/bUz9tS3wMb2BBCEsXZnJEbso7o8YDO28H5+1SgruSkug1u78+T3Q2Qsnf3BDOol+yUZ99crFtLxbzvEtx/MwABqBYdZBP7U7WoTTTmsRwr0JGeLCjhu+0GrmMWTDI7inBI9p41A4D7nbFjg+taxBGo5zpsBtv+12DKWldLOaPpOaYdSdjImxVSZojOfwAZHx9de21ckd0mQnLsP73wcxFRR+uEHf+MBdeNkUqRL+STqtmgSWADTugw8XLAsefxxkZUtMh2jYSCVWDmUw7YHSU4oaCwZSFcOHwTxs74Yrr+pQ5dW6MKiGR+sliNa6DQmoV9xPfbTHGgW7OOq7jud5ftWDnu1NPdNTEwBt5T24+go7JeXUsB0+Ni/W5sVga0PdvN5+bFUVgEa+RuchLJ/UGLThnI8ul8It4amjDQ0giq3fvs0jRnnAuQWMryDpLB4Uc3DdNVsTsU0x2RWDVkJZt20jaS/N4t6t6TTQhYyjAvR3wsnNm2NcTuYgyrV/+jObshjFDJU+xVUHrDzc/u2swq9XpZyqDJx55k7DIBnEWAgSxyitk1lyQNtwzln9ak0mzrkpqfP7d0BmEE6a2V2v5uXazIy61hf+hqcgYzJfBaDRZ+/5kCvABz6wXFd6VNGICbu+fDXatb0cOY9DJ1LKieYlWywOh0vOz6TUUU2xU6n+02YtGcmR+G2qZiXTpDQNUxlju+myx3RHZeTRa8x7YGYNTBYfzMCTv4P774b77yot9/wQvnczfOXa/FWf673swu7PXtBz6fn9F38qc+Jxa2fUrW7QViSkpY2t/A6oAAAgAElEQVTxVXFxsS4sqdPWqNEVurAmLm1MKS26sE4ILp/RsKte365xWzRumxZpi0W7UmJfSuyLcd1aeKca3q5F2nRhe1zqSGkD9fGRlDYs871CpEvkdsl8L1n6pWivzPf/o8qlxg/pwogujepiLiYYaqQY4616DWIRKxZ2yOIFD8soNQ5GupNn/HWiS9BR97JYatDSa3FRg3Qx1KCB012yFeezKSmnc/0xYVdS6UhqW5Naa1odik7tUSN5JWRQAK2EQAmDwjlK1FCiBSVqaBGn9FYYVAGikZwQ2RJX//rk74YxsYckzO8/gAaAWbNmBSZOCgQmBiZNCkzgAoHTo9Gfp7UBjZ6aAeiQr9R4enhI5+ZNOeKWQKC5AqCv+I//HPd9YC+ZAkwBpgBTgCnAFGAKMAWYAkwBpgBTgCmwpwIMQO+pyb9+i22CLizSIo4S9PRwfkaq+8JPdaxdhw0bGikBaLSYot2ZkD8EfraLd717WEzPgdtuGpwWf+jp36FDuQKgnRE4oX6eWNPdFIPp8a4/PArfvRU4blttbXeUW/f1rw54FhJMF0xae5DQZ9tF+3M25+dGLLj4M72a0KPxdkLsOPO0V0cH9gagS/gyb7nwwtPQJK+Mh4YSvMFzLY/9DptYfnhYhJBAXwIuabEyCqDpLuTeeA9djaYF11+7I8nvUGs9nYd0ArioMWVyywnTlg3tIlXUyhAWP1lhgBU875PT0KO6qM89dzk836bIwIcLKX351q30PXo3P4GjAFk0g8MTT8BJ71kvRjfVJwuaOCLWdqiR3pgESR2SSvfnLx/0i5gB7bveOwSgPQssAwp5H875WHdSKKphOzq1qHFGQtv4tRvbaQE3ykgrtN8jhSIxnLcIN12XaZLW18VNUXSDXOaUWd1DBSJJFqDgY6I3CS3AsoxFuOi81Zq8ReFthfMa4+syGaID1Y1KUno2fMzsRWQ82g8/vtVNRbY2SMDVFkKRlU8/X9m1SGrgkeQLG8xRuOrStqTaHpPyktjxucszbqnFSI3HA2gLTpreFgs7cq0VF7tf/Avcfyek5W6dz8e1vi9+HoYzkM/ihAReDD6ccga0iyPEhYsuaoup3WLEiAv9p79vI4ajF8oA2vNxGNGFTJX4lpkfgpOO24yAVYN4ov2qL+4s2Fg+D79Y1UsZQNP6e2QaY9wI2+tLOhBND2d+yE0E5NkpF/3zbHRbY9h6FrLDeEaPTiKZkBvFPBP6Pc8XwPXQ27tqDcxbAAsXYvDFktcwBGPOHLj33t4f/2jXA/dlH7i3+MBP7Qfu8a+5quXzV2y56nMbr7ik5bOfaTnvE6s+fNr8k06YU5ec3Ziek0q8pMrPNTbNT9fNicdfVLXZsjxbll6Wxfmy8Foq1pLS25JaZ1Lfqamb4/EtutbGR7bpcp8uDetiIS7bSdXXBUcMFfjanBDMS2GjvFhSuLyQynWkfp2nBEuEWsHYH1CCuEWutfSQXS9BOgrTddBrHT1o6MGcHhqVpmSSgi3X5MXaYsl9HAG5hIC9ct4F2RIGPgTBCHCip0p+XGp538zHsOMAzKKFA71U4nKfDmjXwbsW1q9ff/iRRwUmHh4IHBKYdHggkD70kG+q/OK62KgUtjSuyvX8b+yA1oO+OjVfx2WUqc8EAicHAsdOCBw+YcKkiYdMyoyO4LfRw68mezAFmAJMAaYAU4ApwBRgCjAFmAJMAaYAU2CvCjAAvVdZ/sUbEUBLixUefamx6HBzanM2Q9EKFN0yxMM2GoSxUWZGbKUuFhP70n8MJbm5ddIrjz2EwQj4IA7o/nZoji1ISiNJ3lVrtq6aC1o0J3N5XR5I6PNXLENrMMZugI8Amq4gwTYdKA7bI3kXrvlSJqF2SOFCQhyoi/2tpwu9yRaxllIHNAW9SGPBcDz41X3QKGzWa4eTQjEaXfHCHGI0Ji0iARwlrylN88UIYxcNumWQQQA0YceWDddfszPObY2FMZ+UD1nxOMjSlq/eMIAXSCI96LHw2ON4IEGWpfQFn7BFD267tU8MbdajINTk0sr6lUvLKvkYaWG5kC3AwAB852ZIKaumHrGRr+1StZ2RyKqHHwRdaFWEYly1dLHl618ZRcBoW+8QgPZM3yA1IIt5D049aYsaytVroPPAT80m9XWtnQhuMfaYtLfyhEEWLozm4Hvf6U5FF0WP2Bad3B9XhyV5xV9nQ6Hk/aazFSSNBQOhwSrAWbPmK/xGjTdjUWjQ1yKhpQfdPU3Ex5Rdq+AhgH7+aZiuLa3n+hOhvC72XnYFZoCg797CKnAerhIAbYExBB+fta5O6YnLpihuv+4Gyykd3aFJHI6PExIUJBdMSMnrEhyINWacz6xbBMcnt9WJZkrK1adXzpkD2REwcqXuI22kn8O8anrUa7+0Q9PbQ7VZWRiV+XnFEQx09hzAiQGa7eJBKSaFRKJvWQfTUxuSImiKz4vrv/HtvpyNw72KPqMcvotU2nbgH8nsNt0BT0/3GzfUKi8rPVPyetOQgkJJVbpbZZ9xL0vbXQ8sx7XcokMQdmXvygotAWra+JXBhdw7gIPfQ5btmDiPYVHAPQrZUcx2HxmFvn7IZqGjE5avwATwBQtgwXxYMA8WzIV774J7fgJ3k+XHP4Ef3wXfvMm6/PLec8/Zce4nes79xMC5Zw+fe/bwjGnrpOgrUvQVXZ6vSwvJslgXl6niqvKyRhXXqOI6VdigCptUfqsa3a5yHUq0iywdKtfBT25tkIYiR2xNcgPx2j5cgj3x4C491JkWBmoPbUuJthZxZA7E6iXqCZyLFfw4ECO4xDRcV2qhTuo6+4y/024xCsX9AdDYi457ySWXoP15wpGBwJGBSccGAidFav4QndqmRUeTKsnZqObOlfW95W8ovH9wRnCEfD2IpQj0GtBDawOBcwMBMRA4OhCYEAgEHn38MdO2CmaljGtlhLIVpgBTgCnAFGAKMAWYAkwBpgBTgCnAFGAKlBRgAPpAHAqWBQ3Nq6JiQYr405Lu6e/fVcjBSAGdqzbSUYNkVlAKZuet/u7+jnwBYVNuAC77VG8jv7VBam9IL1q4qAx8PSxst2g2xLh5segQd0wxHfEuPAO4I606wa+Ltn3jWsMqlAE0pc/kHJTbuug1tU2Anz0A9cnNScmO1g5ykUV/fAYyNuTAy+Gb5QfhX5i768I9t0MDvysZsupjZpifO3cJEkx8kOO6rkFoKnK5YhEe/xV8/IPLLjt/oYfAlKJi20OwhgTw4vNXxaObY2FHDflSBMFQOrn5L8+XuDxJGKF188rN2NdfD22nT/8etNpl9WFPPdYSj9l42zeLo4PYYGy2j9T+zu/D8Q1r45H2esmKcblUrP3DH1v1yiI0n6rSCpEbjimmxK1+6EGs7Oc7GfDtSvzGvs78hts98PI2umGL4G3vgLS2FNMPeDR9y7WWxq/uy8BwyfLugmcSbfCoFmJW+Pa37LiwLKH0h4/uStf2TpdXzXket1uU9yKhdzECmjqgPTDycNF5i4PHzI8JhaQASWltRxeGRZAH5hcDmJaF7NQHd9gybYBN22DmjLUN+rA+pa+O65yRWjH/Vcg5WKvRQfGKPn6q5IAGA2YkFsSjA3HJFcXtN34LCth4UtiQFH/zPKymSO3QCxZiA+KcK4UNjStc/HGITc00CVAv7vzvG3Zhk8ojpwzf6Qgp01sXHnk4ywnL5QQcGzHCyvo//RWrMmJ2ebFE4CtsGaNOTNi4Ahpjy2OCoSluVFxz8//r6suR8YkjYIzxm0XMElm7CK67vOfEaU8umkPfqvihy83BJpbSPcY+jPLjcKZL9a5U5f14xiNUH3dsvWzpxmmDSvoJXaGR5+Vn10Ww7jr7Xmwc8y4h7JSz7/ZMwn1sE38CqhfLwJd9PbB6BSxdCK8twGXxQrj/p7vuvReXn97bf+ddmZtv6bv689svunDz1VcNXvKZrrM/vu7Dpy1NKM836K+kpeea9L83x19q0l86bfqaafr8pPhCUlqU4Fv0SLfGGUoUpCiIfHkRfD5qc5wj8KBIkBAgfiykjoHpYWiMrFq/HC8TA3lci14xfa7WZpzgnZ2dgUBg0qFHBiYeQ4jqlCOPuSQprY2FHY2zFM6SOW8fRQhpMDQpRciVQqJfd8933z5KBPOvlQgGYeu1mDMuhUAWuqeEfhoIvPeQQ8UAeZx9zidtnLcpz12Nk5i9ZAowBZgCTAGmAFOAKcAUYAowBZgCTAGmAAAD0AfiKDBs4LUXaiMDcRlUbiStrxkZRmqYcz0KoF3CpIiPs/TfftuEl/8Gnz6jZ5rQ0cQNpaMtN95oGg4amfFBAPQfH4V4ZIXODcq1TqwGGgXQJoM+ZejE5Or2tYgNPZr7PC4sl+AzGnkwfx7wtS8poSGFs1R11xVXu0MWul57MvDrR9d1tpNzkRJ2poV884c3Q12kLxGxhWBfmJ8/dwkB4rv7RC0DAwd+9D2Ynlx5crqrWX3WQdc2xYsmOqkBGd7F569K8Fv0kKuGfDns6oKViC3tw0qB4GHawghGXKM5eHfvLmnR2BM5tWnBs0/7ydCCJs5MBZ0GIVMnz3/6KVi8CB79NVx7TfuHP7A6Ja5XazrTnKHW9qe1zVdcMdTSCYMWvPAyyMJiic8oYlaVVjz/HPqIwRt6RwA0gFN0MgB+0YclSyGtrk5EvRjvxaKQ4uHD77eGhvBSiq5PjMalK8VSkBZ85ZouYfJiuaZPiuQS4sAp6W0P3oYM2SexEoidEeST/BEcShaGtljwhf9clVJa5GBBmmLEpZYFC2HEoCOKWndt2zNGi0bBhbwLK9fCaR+aH6pdl5Dy8dCOBmHBw/fiIfM+BdBAMlXomTCKI9sDzfrSWCQT4x1F6vzGTZjUTNrhYC8RbFowsV2OD3/8AySl9bGwo3CY8NsggHRUkT+yL8bNo8nUxijpRjQl0xiOyjBCHRwDXlsIUWG+FIcaEY7ldp593qbRImZfdGfgqT8MZIbxu0DpLSZUF2HjcmjUV+pRU+QNVd/y1W/t9IHY+cGldwCgX9sHMwvPPA4z1eXv0backHjpsV+QIo4lpFwFqrF1Y3B4bMiVt1ZveTevj10j6W68aqPouCbOxFA8bRhgGFg41DDBsHAlW0B7fq6AMxCWg0HbjoGh9WYBzdr93bB4Hix5GV79Gyx+GRa9BPf9P/jIKVh4U+NA4pFB4zMPkuBKoplOueFIz9SpOxS+fabSMTO8vjm45MkHsE8tG2zsPXt/ALTneTfffDOlqIFJRwQCkwOBpmDtrUl+RywEmIDEOQxAVwNoIQy8MBKR/x6YdEUgoJekCwSy+Rwd/e/mgc3azhRgCjAFmAJMAaYAU4ApwBRgCjAFmAL/RAUYgP4nivuWD23ZcOoHW0Kh3oQC0SnDYm3LE4/BQA5GPM8g/lVat406fk0fRrLwkx9CdMoL9XxfXWi4LrL9oyev6+nC8xP+TGyYFtz5bUiGN6qR/oTgx8IgHGWnQ9AsDdz/QyjS8F/CtcvV+MbjNNuFvl1Qr86Ra3fJQSOu5CRp+wfPGDj7nJGG9Mb62Es3fXPTSJaekdhcHbj7u9AsjqailsplJWn7zx9BU2rJ0UlaNtQP65fCZ8/ZdXxiRzLUlgqvv/LTO9DzjA9k0B4yJQqgVySFtlgY7XgKZ4nh7mu+4GdMKILvl6JILHK5ewXQPmHTJXPvaMHr6sTqiDM0Qw8NizW9Mb5P5zti0ra4sikV21intdVJo9MUIyW0N6WW3HOfPeoARigD/PZJECMrVKkgRvvTqWVtrQRAlwAsbfbbeXYAca5vePDkk25a2VgB0PJUNyF2vDoHWR6FuGiqdaGvC7aug8+c3ZeKbE6GRoRjMmp4aGb9tntut9xRklkByKB9GlSCXeuhCZoGNXjws/sK02K75CnATzYTyo4v39AzUqx4mLErLXANH4NWli+FU45vaVB2yTU9zYmhGPfqt78+ahE7dp6wf8enWRgEQCPKhe3roVFenOJG1LAdU3u/dTOySPJwsNOobxdrCGKj7vxBMSluROdpCLQgJMLQKENK2HLnHYg1wSPXUrIQV6Pn0rpjFTL90NywOhIxRBUE2YmJbed8NHvZFeb0E5Y0pRdd/4UOTGuhaS8W+HkCoLX1Oudzobyq7fzYJ1qKDgXQJc9ydhSsHPzk25CqWaEftTUdWtUce3zT2tKXiozPcYNtDM5WD4IS9a7e9C5eH3eNpS7Z1wW5Nik7Sd7OjHjEAo8vDAulzpMAH/Tk2+Bb0LYBfv8wXH4uNIpD9ZITj/g6B1rUxYxynjwLpiJlUuluSVt+yuktN96c3boRZ1ncHGR6wTLB9iwX6fP+AuhoNFqiqIdMDASmBgIX6PyfktEe/J1hDuhqB3QQHdBCBHi+qMZajp3640AgVpJu4oQXXnqRJm7vaxiw7UwBpgBTgCnAFGAKMAWYAkwBpgBTgCnwb64AA9AH4gD4B4759ndAErbHeEusLcaiQ6e8d/vytZAlRtSCi6m+GBVsw9AwPPUHOO+8dQllnRbqiQdz05TB6bFX1y/F2+3zxSKhZQ7GGtvwtS9mU5Gteri/XoN6GeoEv54rnHVy/yBNOPBgeKSPJgZUQya6XjRtw4D8MJx/5pok1x4+fEgJF6I1GVUqyHwuLrnR4MqbbunKFNDQaiJcQsh53/dhht4r1wzUaZ7ED376QiNvYoYI3uBPqOKvfgaN0pxpUmdDNJ8IdyWjL65ajKX/yg88DNpRXbj408tKzsQwja7e9IMf4SkMzMygsRJjHyt/vPLXJYy0hD9d8AomfOPLRlLYJgV3aZxRr+MN8lLIE0M5PtwpBrcLx7amhJZPndU2ezZkbejMEMjtwS9+DkJwY1y2+XDntOaFlglmnrLy1zl7pRlvuIL0FrGvCz+9eyQptsTCTozHJS1Cgu+fllr029+gGgAwMAxtO+C6z7ceF1+cCnUkg8X6iJEId6WUVY/8HLwiOlLpA4EzzQn3iAMa5yNwXOQNWDQf9OjaeBjkMMTV4WRq0frNUHDAICZSm8wEjGTh/p+CHn21Pjo6TYBkpDvOLbz0gpWWBQUL+kbtIgXQgBkcYwZnC1YvhCQ3N8WNKCFLk/pvugUtseRh0wxoj/BbTIew4b+/3EOu19OCoNXCNAXUYNcZp63t7oTRkXLMM5LhvdBn9Oj7pmvAWR/eWHP0Vj5icTVWinOOiwHP99cENx/f3Pvdb/ooiEPyqosAeYzgmKat1TlfjBiS0CsLizeuR+uu5SAPtQyY9yJcdVH3TLmrOZprCPekI3N/eFsnVlyrxs7V61TW0nNJfDoJ9I4MjrEj/ivXqn8bwDSLhUK2guRJu7C4KFbkHF+UjgbW00QXNOGbgADacCFfhD8+Bdd/vmtG3cJpOmZDNwhmHQ8pDuKcG4/m48JgXOyKy61xZUNcX3zTLbBkFc75DGOSOT5M8sd2xwoP7ssB7ft+pWEbNmyoeHgDkwKBQOzoibfUS+uSkeFY2GMO6EoEhxIBNYQ/EQigo7aq9GnKs4HAewKBwycdevg/NPzu925zPM/d7Yvxrxyj7NxMAaYAU4ApwBRgCjAFmAJMAaYAU4ApcKApwAD0gdYjxKPpYFkwjZ8f54aTUdA4gw+2NzVsvfFG+P1TMG8evDgbHvo5fPdmOPG41Tq/PC7sTMtGo+bXK0MfPW3n6pV4UR5A0c77yG9tLCRowTWX9TZJ7bHIYJ3mpWVLqm0/sWnHn38LpoHU0/Mszy9Q8yBNi6URstSwTGXyTHj2KWgWNzZHIRa01bAbE6AhBXFtIJF4Zfk66CcAuujns3bBcuFvf4IT6jbUK0MaZ8gRsz4xeNXl+Wf+CEtehV/eA2eeNHSC3qdPbU2G+/Wa3HHJnb99ArLG+CJ7eAEmfPnabcloZyyIDmiNH0gnVz35R1rwzsFyiW/APlwkjsisEF8WLExzeG0xNCUWS8Fd0WOt6GRf5aH22GxCs7nIjpi88fjkqicfhvwoFAgzNT3ImSjp9V/wxNr2mOiKkfZPX7gFTdpmpQze2x9LmE7sAGRG4Bv/3adHtqhBa3odBI/uTklFNdgbOXJzItpaH99Qn1zRkFpeH1+nhlvlmr7j49Ao5BqEHdP0uY//ChwbF9cl3NZH2Evq9NGgkgIpzIfjo1CEfB4+8N4NUm2PKoIQBS68a9aHBv/+IvT2YdG/tSvhkZ/BR07talR2HKcUUlOt+DH9DcLqa6/cUTCg6JLFQ1kNrNKHJLkEoAGjFVYvhFjo5UQ4o4dcOZq59NIcSSsmBTF9g3QFZHMWmqFtuOwzaxvUbQkOFCx0BnrITevrHvofzFhB4I4E1wDIlVNWxmFoorwPjz0M09OrGpR8PATxGicR9rmQKSndDY0vz3kFkx/Qbl0kVnaAbC/MTKxsVDyJs2WuGI/21Qnr//wkLHwVfvsIXHGBPV3vVI/ZOUP268JDqeiqr12X6e1Dgl0aaxQ97wag9z4AKLLd+3vvvq27AejxzafdsvvWYs7KZzOOnQPPxYkQ8nA8aNkCv3wQrrrMTIirE9HWBNcRj/Yk+P44PxKLGLGQGQ8bKS6b4LoS0XUzGpZ87pK2p/4A/cMYq1IgWeNm+XYQei8I3hNAbfWklib54Rofju37vmmaIyMjlmXdcMMNYwB64qGBQAN/9BP1XG8qYhLzta9F/YMs1vmtXQ5N4VAipPZj1OOCwxI3PxA485CJUiBwRGDihAsuurBgGgxA7z7w2SumAFOAKcAUYAowBZgCTAGmAFOAKcAUGFOAAegxLQ6QNWSQLpb2+soX+8XJK2OhYloCjCLlC3F9OBXfHpPXa/zqmLAxxm9Xg10JviDXZhrVgly7/tLzc90keQMQ1NkmNbP6pAKZCR95/zx1ymo93K9xhXo13xDf+tnPtDg2mA44vuP5xr4BNHpmXRPrHHoF+NpVw83i+ia1470N2fpYd0xZ+/6T185+EQbzUEB+ag4X+imlG+yB9x33SkpoV0KGGLSUaCGpdKXVrdP07e9JjChHjCRr3DpxMCZsSWubnv0L5Gy0RtKkBAIdkTt6AEYRfvDdkRS3qwSgxV319a+2tEHOhwLkvDegz7TwHfXpIqrOGRnTg6EMPPorkCMvS+EtKtdRr/cnlDZVWjFrVtudPwZ7BO/rd2wooknTLdqeQwrJXfjJETnYj7nM4o7//voAFuZ7Jx+e7RkWscue/dFlerhNr7VwqiDYecmnIBFtbxS8VATSMsQVT1NcTfE1EZSQEY/2JfgVn/74utYt6C6n0Nb1kDvj4vs+ipolSdkFpHYEFLo+ViV85k+QjK3hornaEATDNhfeJYqL04m5TaklaXUtP7mVP7q/QYTjRKgL9dZzy2768nB2CD2nWKPQw8UAnwBojD4gSBApo2fD1tVQF52XCA4hDpbND5za6nlgmibujnEmaIbFPQki//Cpf4pF1ughOyVAvQpxseuqKwZtgKGCg8Zq5LwFgNF9AmgPHd9mFm766s5GeXE9vz3NtSaFNkna8N5T1j3xexjM4jjHXjQIysZpA7j9Rjip2VSiBYXzkiGnLjxUL7fo4eWxYGuTaDRyUB+G+uhQo772lhtty0LH7liHVxg4vYx9P/9bAGiixhicpgUSSbYGFcYs4g9Ifgh2tMAdt+44+6yljQ3LwlNWSbV9etDHGnchUEKWEBqUw306N5gQupPClqb4qg+dtPJXP4e2bTRAHOc8aNVKWgWy8ky+nW8MoHEYFQoufpmhvr4eKxBOmnTEkceSAOgPacGX6sP5VNiNR0DjcHlrxPbg+5QSBiVMATTwIUOOrK456suHBqYFAsdOOvTQdEM9+ZHdj9mYfX9N2DtMAaYAU4ApwBRgCjAFmAJMAaYAU4ApcBArwAD0gdi5GCrhwbatMCP10nHxYTkEKg+86NZyfbLUU3P05tCxnXWaU6d5jTEQgxk13NqkznvwTsiO4i3tZonVFXIw4kDR912MUjbhv7/YMz2+Ra7pkWtHpGDntIbFq9cDZv66CCI9Dxm0iwSZZjb4JaaDCNjzXcfIjroWudfdgV8+MHjlxWs+dvqC669t++VDRr6c9gBg+J7h+UbO7DUc33bhq9e31KmbhZqcFLYUztKEfJzPxoPD6uTBBs5ORQfT+roPnr589hxs9kAB8h7mFWMNO6SNOcfHNI9iAZ58FOqi/fEg6BzocvusM1bmHBh1oehn9yPfgGZAl0oU2q5vElQynIely+DmmzrP++TiSz+9+pZvDMx9BUMYRkZhNEO8vAAmVlGzbRczGYa64aSmLUowp3N+fbzjid+W7v1/B8eQaRuWC6OjUBf/S5zfFQ874uSBM0+FV2dDTHi5UcvFOIiJIIgQFSEquVNDA03Nw3UNS++826EWxDxWRcRCbGX6jA5yBNBoPybZzMQ4XhHN9uC6/+rRGjuODg/XRoqCWEjHRzVxp8K16dFenfNTAihToU7InFS/9Hf/g9wWQyo8AqDBM7GYnG+RMVNxQOMkig1922GGvqw+MhKfCnUqpFPLenswzruMkgsliQmD/ur1yxrVljjnJkVIqgPve9+6LTvQ6EpnD8rZGXhphEZX6G9lBff0bLAL8JtfZv/j0pVnnv78pZcsuO/nPSZAXw4KHhg+DiY0++MoR2/17L9CU3KlIgwonJcKeunafL3Q0xzrn6bmEqFsKmI2KgMK99zd99gjRQzAGfXo/EhVrUt6/ndwBBzohxqDzONaip1etVSj4ewobNsMv/8NnHfWlqTwkh5ZklC2Raa2yqHhmelSvAP60PmCJA/K8k5FXKdKL37zxpE1a3D+yQfIlsJbwPAogHZIegf+HlWW6paR9fH2ZxI9A5aFMx9tbW3U/jxp0qRjjo0GAtIRh13apK6qCxcTEVePgBYBhQBoMcowNNJnueSABkUwtej6pPxgIPD+QGDqpEMPPfSIw20X77gYNyTYS6YAU4ApwBRgCjAFmAJMAaYAU4ApwBRgCgUREUkAACAASURBVFAFGIA+EEcCZS5FA155Hs48bbMwtSWtmvV1I5rWJYXatPDOOnloRqog1GyMSy0NyXVXXzG8cgEMdgIt35e1MapgGIp5yFUAtGPC+lVw4dlrleBzsej8U9+7au48ZIgYn1wC0J6HJbz2DqBxR9cixeygaCDcHBkBo4Drjg95EzEQgOn7OXAMz0EzdcEumi4Mj8BlF7XXqRtS0s60OpQShqTJO2PB9vck+5q1zdPrXrvzThjMEZsz6QpyN73jod11GGDUcosYvmDA3BehUdhcF3JT3EhKWXXt9S3DBu5EPNP704mUFI6FdRi+lXfxvIMZcEysJWgVyTLmccXDVkDtUAaWvwZq+LVY0I6Fnen1O5//O3ESo4LvDHnBcArP9QCWLwdVeCEuDGo1hZkJ857vQfdOeOAeSCnzda5Fl7drynZJ3yzF1px46tZbvgdbd6KGJKWiq+h24zSA71a8zz6WfrQxhQM7iaYgU5s1+nl7MzCQh6u/kok3bRCULTG1tzmVn1mXb9K6ldrNKbGvXhmqk9sv+3R2/QqUA3O3vaLl40VbOK9hEfqMxyUECtEfMl4XcoNwcuNL08T2ZE1fvdo3re6llctoTxEvtm/6OMeBD8eFVSvg9FMWntC4SY3OO/OM9c+/BJkCpmXYeDSa8W0R0/TrAGjbKGbwql0Y6MMxYzj4SdIw18YAagdd23gUx3ZHAGAkA/fcDXF1cVzYWRfpS9V2xmpbEtENjUrbcfE2Jbj4vLN3rFiJshkA/WYu641YaCQ3qZTYdAagaReS3neJQd0ichV8vP+iNwOP/c4779wlcfW5Bn39zPqRGN/XqNvRKcN8TUGPQlqChOCqXEYW22VlrSDPOe/Crsd+B63teNwCiewYNXuL3pCFv2am6RsOBqlYHplToAFBZfSMQ6W8ToudjmfQ5cbCww8/fNhhh02cODEQCEyeLAYCqdpjv/KedBvmb3CuxiF9VriS5/fgczS/2SuqBtAx2VWiLfXxPwUCnwwEpgQmTjj0iMO7+3rfBoDGKKOqZbdZpUqXsRWmAFOAKcAUYAowBZgCTAGmAFOAKcAUePcqwAD0gdl3HgYbEBtpfxc8cj988vSVyejTTfLc42PrG6LL46HZevh3p5/87J3f79u6GYpFzLd1HWJyJf+PJ75U18H0Zxsd0MT4CQCDg7BiGTz/7IBlIp4zEMaRAnU+ILLEsI6xQl5VKIeSWLoB73N3SHoDJdeOhy9d8DHHw3N8lxgNcQtCawegox0euHvwAzNn13GzZ6rLpyuvzUy+clLzXx75Baxcjm2u8EWHAD0P0LGNFBVMG5m4b3q+WYCLz9hyWqpnBr/+hMRfN61D9zFxolYQ8Rt2pU/QYZFER9j0YhB7kPO5hMK7LnEJI0/GWoCEpZYY9LAND/5PIaW0JCJuPGy9t7G1fwDxo1eOtX3D07/hDgigfbRn/vYJUKMrkkJRmjxyQqL36ceRjzsWLJkLN311w5eueu17t2z5za+HZ8/2MIvZRJu2RWCrW8rGsGhvlhPAcRi4NIqjhGSR01Xs0EUPuvrh2b/B1Ze1zkwtiNW8OkNbNTMxLxH9faP+v7d8daBlFSqHY8zF3scKbz4ZBgTvUsiLnLeUvQseGvGJb/03/onpecfHVzcrsx+80+7tpBpkMQ+EDDVSt5AMJwcjGl592Xz15aJt0YGL/YvWfOyBykkqcGqv0B8r35W60qNNxXFIoDR6ryk3d7BCnmWTMp6FIvzxf+HiT6xpEl+aqS49Lr6Qm/z48Y1//ep1O16YDVvasA20Yh5Z8Ux8RWHZG/bnQblD9a9C9bpvYRo6SlPwYcSCeYvguhsMPbZQ0zYpSpciZRQ+h2kn/KjGF7WIJ9eAONXVw8XQUZuk4IIZzXOu/0rrivXQMYRHGLah6BOvPh7TdnzL8S3Mqfcs6ugn0yqkkimRmTSlgpv3Tp+pAxonykzz2muvnTBhAgLoCQGkqIGmmPLDBLcpxUGM93Qe6bMUBYnH5c3i2oNuf0/hLDlqiVEQoxCTQIzu0BMvBgIXBwIyETDw9F//8jaGOy0Smy8n9ZtkImNssvBtHJl9lCnAFGAKMAWYAkwBpgBTgCnAFGAKMAUOCAUYgD4gumGPRjg0JBcjEwjsKg7BxtfglT/DM7+B2b+HpS/D5lWQz2AuBEIfQgMpiPXRVopL+VGNlfFg9EGQHiYnlMMT8HOvC6DLn8QW4fFpUkc1sEb87Hk0+QHzHhD8YUowttDCVOXWlbD0BdiwBPp3YnYDUiLSeAoXKc0iWNElplePtMdF9gQF24LMdnj0x/Cz2/xNS0j0AwGL+xEAPdZywjVocHEJQFcjNCojcll8UB+n6YGPNnKCRi7/woaYtC3BmUlu6LPn5dBSu//0u7oV+1inANoFuP02kEJtKQn0YC4dXdaykswS0E/RymvldvskUMIj9SJp+0m/l2I3KKoj9NlGaoz9X/ok9UNTUzENY0Zum4f2DTDnGfj9w/D8U7B9AxQz4OYx2sJ3KM/F+QwyVkqjDvuOTCFUd6IHBRcFhHwO5v4d7v2+sfQVAv89MIqW7+d8P+dhIjOh/+X5DNcm9RHRhI8XQVqIV0aGSfmCS5bj8cbjytt0RFWhcLxgOp9AAXRllLoEYRq0gF0RMh2waSXMmQ1tW8AhXyuKvckkzVj0BvkGjT/7PvrzoNxcrXT1OlgkWHk4B7v64LIr1qbr5sbj2yRpRBR8kQdcMNHCIww6p3GGGh6WarfzUxd94KRVv3oIU+8HR3CAmgBZ3x9x3LyHszHUWU9mthzfs3xMfMFIGbpUxjP13e+18GD1RtolpmmeddZZE8gjMHFCIFATCJwQk+5LRFpTEQTQquAhemYAmqZgRx0lWpD5ghj1KIDmo51Kcm4gcHkgoEyYNPHIo4+69bvfeRvDHWOWyvQZJwjLAJox6LchKvsoU4ApwBRgCjAFmAJMAaYAU4ApwBQ4kBRgAPpA6o2xtlQsn4jPHAeTDkogDUoWZQDI5qBQBNMuYUWM/d33w8XYDOJTJpgYMRyhzxUAXY2S6Xo1Xqpe33NPuoWgPcIlMTS6YsdGUyp9uBaiPbuI8QiWjcEL1EON5JRcX9nUiliVkFV6Pa4DBYzuNcErgpUDM1fyHdNWlQ+/v3+rr6V6fXcATbvAdcDNONkiwM4BSKaf0/mOWHgkLW+77yd4FeVLK//d3ybsfT8E0ODlbbjg/EG+ZjAWgTRvnnrcMmOIpBtb+IxuXhvNwth/lD57HgXQ5dBnyofHIF01gK6OLKDGcwcN4X7RdpAjOxgjTnzd6F13bIxyJhHgJDoZzackzYPgYZ9ajMnkB5WO9iOZMTFIsT+8TAzwHYXcMMHNNtiO6XsF3yugC5n6qX3E0Hsq+I4DaDr+x5qKESK4YBFOm3zFCEzPF7HenUlyritBxpWVyhQO7cLq8bP3Tj3YtlZfcWW99K0HgO2tcPopy49Lten8JiHcpohZSbAl3ld4X+EcjTO0aC7GD8SFHXJ47gXntfz5zzCag6KFoNnwceKi4EPO9XKuZ3jUAo9jA6fVcJTbZDLExu8AXfDN0lINmve5Tn6NbNuWJKkKQIcDgQ/o0iOJaHuCA70MoEVif2YOaDnqyPwYgNZEEPkuAqCvCEyIBQKBI446cvrxM9/2SK/c3EDvMKDP/86TPW9bUXYApgBTgCnAFGAKMAWYAkwBpgBTgClwwCjAAPQB0xXjGzIGVgCgaGEUMoV0hKMhsXV8TEKl/lOK1fbNn/Gd6ozOEjImRuZ9AeXqFlSv72t/6i2lLaneH8A3nYJpj1UqNG2naNqW49qu7xCOSfcnuBKJw3gATW7ABwDbtpGcv/kHjXqgn6tuW/U6bXnZAV1yzTrg9hgDOYBfPQ66skQJ9+iRrobYwhf+hjERpEeoTb0Mz9982yqf8DBeGUYL8J7pW4VaW6qBernwhUvanSxS++qH50KxYOZyBSLImwLQZVxXlWrhgE9KF+IZ8lYhb2QdjNc20Lnu2KbtkNKIec/HUBR0ntKA6dcD0AgLLZxf8IZGsxVpPM+xnaLvkUqVaJdHvzzKTlJQCrlSzxbKRS3pMKgQRrJSoVSVo2Kz9+zH6i2VHUpDtwzNiWsbj0O/GqMFq2ToJjMi1Risen23jqg6dfX2g3e9WtfKOpmf8HHWaO0qmJ5cPjNRTAkDUm2fHjW1qKtFXZ0vxvi+uNAWl1cn1blf+nxh4TychRoiruciiRSvHI6uUG86XX+nALRt267juo4bCASqADQfCJytC7+P850x3tOirsL7EnVtk9CJgy5S402GiuwOoFWhCkBPjNNajkccdWRlzPv+bt/Nyvb9Xqn+jjMAvd+ysR2ZAkwBpgBTgCnAFGAKMAWYAkwBpsABrAAD0Ads51Dw8nrNG8dr9vSQVn+YAuh9seO9bt/z+K+/pXwQ1y1VCUM8XnZsl4JBKOSlzxgeXYGYBDpXAHSFQQNgEAc6btG6SJfqy9rfdcvB4n6VRzWPrmwsHX034oFJIwWAURcuuLC9PtYtTOlLSTvff+Js08TY5XccQOcs2LYDdHGjEgYlCNO04R99N1MYId5nRON03sEmYbjEQ+z41P7sEYt7qfAgSVOhmSo0xoTmb7hIendjtVUvDQ9yHoyS5wLJ0Mi7UCSL6YBhe4VK7gHtkZLhutKD5RwYPCZhyg6N1aY7QN7F8n0YaEFTFNDB6pFKiR72fXWWCF5L6YGxMLs3uRpOVbput5Wqi9rrdpoUXNaBWvXH0qvL5v09t5fbUX3QfZ2rep+Da736isfWSzdY+Ggkv+4/83LNRjXY2yhDXRTSEUhH/VS0PyG8NuuUhQ/8LD80AjmSQT+ua2kueQVejh19zAFNfNDlrit3SGnHfbqeye0UpXc9zzCMpUuXHnHEEZRBkwgONTz1xlj0hZTYkxBchfNkUn5QIPRZjL5JXEtjKw6m590jOBTeF/kuOTEnECAO6AmBCZMmTpg0sa+vjw511yETOpVv6ht8AejPGngYfOMAeIXcKP2E73q2Ybr27mVh3+Bo7G2mAFOAKcAUYAowBZgCTAGmAFOAKcAUOBAVYAD6QOyVcpsqBKbyX/nKCu5SebuyUv7g3v+WAXGZBVfVG9zrW5XD7udK+SAUQBse2nmRQeP2sue0tEIcr2OA0itVpCs7XvEyCZ0mhlTit8UScvRBNSi/2s+/eF5Ci8eOs8cn6WUi5q0wMFJE0QfY1gGNdUul2p6kYMrBFT+4A1ELpeflftjjcG9+g+dDzoDn/w663K5HIBaBRrXj0YeMYq7SJJsEFRQ936hw58rKbhEcVQy6Qp/3A0DnPCjQjiPBHSZl0KQEHAlmxp40cSGzAvSM1Z1bil7xSOA06Xt0N6OhuOhCngLosfyEfyWAJhMa4ynz2CxH6ULKSTLVX4Hqjt3X9up9Dq716iseW6drmLJtw68fgqSwNhHp16aOpCL54+PFOr7l47Panvg1jAyjGDTZt/KRsj4lEFn9G1c5AZ1NISkce1Lr0l77A6BpBcJnn3328MMPrwLQ8fCxd8Qii9JSf0Kw5bAvhUGIAE8wNAPQMgHQGAPNYQY0PlcAdECn9HnCpIlLly6lXYmThZVeHPstLffz+L/Y7y65xcMxLYybp9Z3C6OWxh5vfJyxfd/5td3+Uaj82/vOn4cdkSnAFGAKMAWYAkwBpgBTgCnAFGAKHKwKMAB9IPcsjSG2SIGmLMAIWbLkpU0Q7XgG/foXUwbE/2QAXe2ELUc5VzPK0jph0FgXzyGwEhklRgGTNGD87355HekS4qcKr6Irr3+pe7yLUrow1AuP/0/PL+7eihyqCKZV7YouiVkFoH0AG8tBunDLbTt1eXlaK2q1uZS0elMLnsDBNvvvJID2MNT7O98ZTii9ShhiHCTE1fNfBitPToLn9NFBDCbmeJMifhUb8tgKSVuhwI4+7x+ArmKv5GyEGuNcAg4b0lk4bpAs5X2sEjdmXh7rXNpnLnFAE3HIqcn0AzkC6RYHfBMXBOdYanDvyz/dAV0FoPF6HQ+GPBggHnCDvCx/uarN0ZV+KA+wEvvcY3v5/YPvb/UVV9ZLWiGAduGRX0JCeC0t7VRDLVpozifPWPXqK5AvQN6AEYIUK98Z/PqVwCJGkZOlMtE0TrrKufa5sp8AGgDuv//+ww47rApAp8NH3x0Pr6mThxiA3kveSAVARx0xClLElYRe4oC+MlAFoB955JGx8I03AaBJR/ulyp/ogXbIP3G0EKgJjmmhCfptAujq9ryFdTroSm2g/y6jWfvf6Hs/7uvIXjIFmAJMAaYAU4ApwBRgCjAFmAJMgTepAAPQb1Kw/9PdKwA6DxhfUAHQecDqXCUkW81jXr91/woAjRXs9uKALsf+IoCmyz4BNNrNSO4wAYEV++PrX+oe75qe6zjw2jxoUn/xnvTv//gbyGdxp2qEMLZeAg2IRm2AwQycfNKCVGwXX9PfpGau/MxowYYi4SQuujnHPrfHaV9nw7hPYV9jsnMOLrmwLSEPirWghl0lsnDrJrDNCqej3NvG9I29Augqblth0BWNX9cBTS6j4gimjnXqkS93VhWAzr8egCYlKMlgswm/dpFQjwFoIirJ3/jXA+hy5xGr/oAHfR4Mlz3gDu2hPZ+rO7X63ertB+969RVX1kvfAawS6MHwINz0tdyVl/Rdf3Vm5RIYGICCifww52CQOfpd6eQT5YCoFP2h+78D0DfffPOhhx5aBaCbQkc9pIfbUlIuJrrU/ixE0AQtcsAc0DLnKVFD5g0xig5oKeLLfK8WmxMI7Aagb731VhKURMZ+NeTdvy8D1pg14d4frbvyghcuO3/hDVe3/ui2/id+3bd0Cf4q+i5OBtIfFIcGsdBc9nG5LaXhVBmZVSu0SZ6PQ/BNLXgKj5RLoHVbrdKdHCQwZP8uju3FFGAKMAWYAkwBpgBTgCnAFGAKMAX+3RVgAPoAHwH0/8/UFWYBSbQg9szxftUD/DL22jxqfS2xgL3uMbaxHLZMwcHY9v1c8w2vaJrwqwfcJvXF4/TNcWHBkiUwXMCUkIFcBsAnFfNoKjVqTq18RRuGMnDvj2BG3XCMd3Q+G+eX/PkppM42CTN2sP4fUhFCe0tTAvvRJiw3SJaKBdsByHkuDHZBvbZIFzLRKbZYYzbFVxA+lyOQrgTMS2S54h0uQedxFsEq8rIPRL7nHnQL9sjuj1JPlTbS0bj7HvTVeLOwV0Heu/dy6TzjDkHPgs9vt4jZuAPv9WVFefquB4BciYbGlL20JeHGCbXXw7GNleKoOKVkg2uCa5HvBslgKWuIP1zgk9mzimQ43srv7zn4KrvhSmW3yspub+/Pi39M3tx6662UPpfqEAamR4LPyVw2LttadDcAvRc78MEU7rzf16JEMAi7AqB1rr9OmTMxcHkgoFYiOG677TbsW/rlrSa8+9MrAH4RVs+HZu3pabHNSa1TVraJ8gZNWRvXVsRjC+Pxl8/51PYbvpb7n9/Aq/NgdBCKQ2CNglvAaqeuSe5oMfE2GvJFNskzJuZXnXzcmKm8LP8UVG+oTCxS+ow/DlgLAGCYLKPkpVX+Wa46CVtlCjAFmAJMAaYAU4ApwBRgCjAFmAJMgb0pwAD03lQ5gLdV/x+5ev0AbvI+m0bB6T7ffiff8F28wR+e+yM0SH+v4zum6QNxae4jj8BoAU9DKYVDsDL11fnU4OzDonkg1yyPh52UCFKo7dyPrXFsyNuQtXOWj3EYNCv5TQJoDPYgS4WPIIB2XVj0CtRJG7ToaHRqUQ4WPvKBdsLrBsu0Gvu8BKBLKc9l/Dwe2laPDro+XtA999j7fgQq7ScUHndMWpuuDHjGN2Dc6xKAJhc07q1/wsu9X+u49u/15T+hMQfJIffUdM8te7nU3WaV9pj92O0De3bIbm/vz4tCoXDHHXfsDqBPEKPzFdFTBU/mPOp9ps8MQFMFygAa/eASpgP1NsqzDw1cOqEKQH/kIx+xKwUD3zyAzvXDE7+AOv6lhNArRx2ON8OCLUZB4X1FMBVxRFV6FLVVVjeqytKk/OoH37Piios6v/WVzEMPwN/+Atu3gIUOe5yjME0oGhhHbptgW+A4YFn4svIgw4gWIy1N5eJb1dEwFWM1/ipR4zMF0EMAQ4REFwjj3s/ftsqZ2QpTgCnAFGAKMAWYAkwBpgBTgCnAFPg3VYAB6HdZx+8JYPYL8bzLrvKdb65lWcgmbLj43PlpYaU6paNB7G3U1n/1uuyqFVAk5ILCC7Q2k/MXDVi/Ek6dsaZJGm2IghYcbkqsm/080uq85xtQoE7gdwhAA8bn2nDv9yHBb4kJBSGY14WRL16J3JzwDuq2w96uBtD7VmrPkTJ+3z33ePtj6Z9xzPHt/me+3lf7q7f/M8//7j722x8/b3T91f3wVs5Gfwe+9KUvHXbYYdT+PGHChEDghJi6VJNB4V0p4jIAvSd23wNAdzeqfz00cP6EgFhxQM+aNQsAbNvOZrOlOx52m1p4/b7FiYfOVmhOPKbxi2WuU+RyUsTVONA40DnQIp4cLMjBnBTJ6Xw2JY/GhX4puJObujmttKfV1pSyJaWuv/g856vXwb33wFP/C6tXQYHML2bzkDUgW4CiA7aPP+BklpFWb6Xr+Fw9tsgryp3pzzx9NsisYY48G2SOkgHo1+9W9i5TgCnAFGAKMAWYAkwBpgBTgCnAFCgpwAD0u2woVP8nuXr9XXYZ/+fN9Wykz56NTPmcM1akIiuPV40ZmhHnVjfoL11+Scujv4I1a2FXH+IJ04VtO+DRX8OJ01ZMk3bFJheTtWajsuOaq/qKJhR8yLrZEoB+iw7oSgQHVrKizl8AvJH82s+NJrgurITGFVNqz+23YJoBsT9XvNJ4k3vlsW8hq0cHXR+/75577H2/8Z97vdf/jGO+3vne6ff21f7q7e/0OQ+e47398fNGWlT3w1s5Gw0p/trXvjZx4sRqAJ2ILVdEtD9LEZ8B6L0AaM4jERwkFDsEsWhHo/6/hwbOmhDgKwD6rLPOwp8qg1QPfPMOaATAPixZAN/8ev/FF/bMmLYuXLMwrmxKSFsT0nad2y4Hd8q1u3Quo/N5jTPEUEGoLXK1RlqHuABSEPipjhQ2NHFEV3Yl9M2R8N9V5ZnTZy3+8ld23Xe/88xfYOMGGM2CYZYM0ZaDNTNx8fBeFtvHYCW6kJRp3OzhdGSl3mCl/CCF2Iw+v9H3lb3PFGAKMAWYAkwBpgBTgCnAFGAKMAXKCjAAXVaC/T2IFaCBGsTb7JrQuR2uuGhtvGbdDNVLCwPNsX6dW9+c2lynr0rjsi6tbYhJK1VuQ5IbmqHCezWITek7vm7uxvUk+hnyFuRdsBBCeNQ3t1sk934ISROHMdSbAmikzD4UR6BJXZTisjrvaUJe5db9/jdgoYmPkY79EJXt8q9W4K0g4X9Fm2+66aZxERwIoHmXAmgpjCkTdNkTxf5bbvEUzlE4D0syciCFvBjfGhcfmBR4/4RAaByA3s+snupup79uPimW6rhgOFC0IW9CzoCFS+C3v4Nv3LjjM59eMbN59oyGBdPSy+vjmxLyzoTSn44V0glPjFhSGJQIKByoghdXHU3O81yfzPemtIGYvCupdNWpnXXK9pS0KSUtP3XmxovP7fvON+HhB2HtahgcAsOGTBZGijBqQ87HArMG+Wkm4dKO4RXzVq5o523PshzXdsdSYtzSbGDFP119WWydKcAUYAowBZgCTAGmAFOAKcAUYAowBcYUYAB6TAu2dtAq4JObrsv2NtcGx4D7fwgN8moxuCom7lCiHXKkR+fzCcGOib7COWLI0CJOIurpNaPSUTvqhCUvPw/5HN6p7UDWhYIHrutXAPS427ffUEjqpNsdQLuwbT00SWtTHOg86NJoSls59wW0RTP+/IaCsh0OBAXevQA6pS+Xo44UcaWIX6HPUhgr77FF5iiAdioAWuc3SZHbDwkcPyEwtQKgZ82a9Rboc2l6jdSlJAjadsHFwAsf7cdFBxfDAdMGx4WuTnj1VfjfJ+GO2+ELV9vvf3+Lqi3ghaWKsiUZ761PDdWlepPxblnsCE3dHldyumgkZEhLkIhCLARq0IlHCjPjbpOaSfI71fDapuRKOfrX46a9cNFFG77xzY4HH8ovXAadAzBi4Bxj5a4Tx4eiCaYztoV+3VyfEmgGoA+Enx/WBqYAU4ApwBRgCjAFmAJMAaYAU+CAVoAB6AO6e1jj3iEFPPAcBBiEQVsG3oVtGtDRCd/5fk5KPBviFkUirZpc1ERflW1VtkXeidRmorU7NGH5uR9bs3wJ1rNyXcQiDtgekme/FAfgg+e/WQBNqQvNGEX/n0ca9vwfoVnYlg6BHgVdGjqhec2OLUSANxGl+g4Jxg7DFDh4FdiLA1pbxgD0vlG7p3CWHC0BaIXzNH5tzZT/CgTqAxMnVwA0jeB4C6MGfwEJgKbp9vhj6mLlP8/Fg9HbVwwPciYUbLxnxAUwPLwPJWchKV68Ev78HPzk/tzXb+r+xLnL6hv+KkSfrk+vlKPrVK5DDg4KNaNysKBxVoy3koKZFIpxPquEBuTgYIwrJHhDCQ1Fp+4Qa7fo/OaU0tKQ3NCYXnn2mR033wiP/BzmvwID3eCbMJLBk2ZtyDqQdzCpyfEOWAD9bpkMegvjhX2EKcAUYAowBZgCTAGmAFOAKcAUeFcqwAD0u7LbWKPfpAIe+BY4NhrYiKvNBd8FyNvQm4dNO+HuB+A/rson468l4ysSiddwia9Q5Fc/8YnWBx+E4QwUC2DZmBzqeJVyVW8fQFMfNMEvLvg2PHxfT7PQUh+GRNRLKDtOPfnFQr58oWO3fZe3sL9MAabAW1JgTwAdV5ZKnI32Z7qwCI7drN/ogJbLERxa1Je55UcffUUgEApMPKoCoC+99FKaAY1FCN/MoxTBUQ62x19YcqdJ5RilG0Z8zwHbgqIFpokziqWHA1B03yd89AAAIABJREFUkU1nTcgb+Cu9qwsWzofbbvZuvhHO/3hfWl+S1pam1f/P3pvAyVGX+f/f6Z4rk0kyR3fXffQ5RxIIhyIo6CIouqwiKh4giHiLiyir/jiUxQUFQXA5vNBlVzlUXGSRM0DICSE3OYdMJpM7c09PH3XX8/9/q7p7eiaTEELuPP360l1dXV3Hu2o6L9799OdZ1qKsalXWTY92Tle72+VtCa5XCZu0ySELUgjkJjqkRhAaTbk5o0R6Y+zWJN9xevuGGdF575654BMXLrv++o7f/L5n0RLY1UdrojUdNINusdBjwP/3pVQPvbcP7fKA7L1NF49uosfCV597/DSmfD4K6InI4TwkgASQABJAAkgACSABJIAEjhwBFNBHjj1u+XAS8Dv9eX2u/M36/4NuOKDZNANUMyCvwa5dsHoNLFhgdW6Enl5aJZ3P08Jn2ytzBteb8P6/33v7aPTzAR2K4yVIu36oqGHCM08OSpP/3t7Um5i2JcW99Ps/9AzSAGh68x1N4Qk+IAEkcEAEDMMAgFdeeYWMuZ0aaXpRiphS2KUjonvTVEruvSj4RHlJYP0j9ZoQRkAKQ4sEMWkxCXyQVE8hgSAJVPjj/91wvWHRlqk2rVp+e7dydbrPd5Z87dilHO9nKA4N76AJSyZYBtgG1dWmDoYOnW/Cgrnw8EP6XbcNfOHipe8/dfas6DOntS5LRN9UojtluU8Uh4VILjwtJ4eBb3TZKVpScFOCKTT0Sk074tyONmVXW7S7RV6fklemlNdT6oJZJ7160cc33/Qj+O8/wOI50LMJtAEY2Q1GGswcWHqhgnvMjtLj9H4vQ/ObipQcr+Whf1/+71Tphy9jfmHjOPRr0NKg/4j4w/ty1Y91KnVNHLNxfIIEkAASQAJIAAkgASSABJAAEjiCBFBAH0H4uOnDSKAkLor/1/+W23Zd1zRNwzAsh4pm/1YuSor/53/gdtgT0HTFpcZWf/hPmMH/Yzr31Jc+t3QwAzlwdHAMq/R6cT/wEQkggQMlMG/evClTppQp6FmRpuckJi+FbTqYPHXQYRTQVD0LLB0FER8GOQxJXudCTxEyi1QHSLBgn0mg4o677ixEC41+Xu7vGRr7ufr2P1H9bxZLH/Jlm6V5Hi6NX7JMqqQdHYZ20Q6Deh+88To88me45Wdwyed3v+uMVSz7clvrmwL3xqy2vrbobraxo3nyOqGpW2neGQ33Rpn+JJ9PMU4iYicYPcWlE3JvQtkeVTfF5TWnt66Jh56ZoTz9ifOWXvfNLffdmZ87G7Z1wsgg5DNejr9Na7bNPBh5sDUaMDJ6kH65N6379oNICp1t6QL+KP6b5T3bU0D7S/ll4n4Ndvnay1jgJBJAAkgACSABJIAEkAASQAJI4MgRQAF95Njjlo8mAo7jmN6t1EfLdV3bsm3LdhynNLPkBMZNHNih+F67dK+ZNPF0zSqY/VzO8ubmwMlallEUEAe2FXwXEkAC4wiU2WdCyEls898VZlCNWErIlRmDRh4zIEWK4nVMHsWJNXNUQHvlz2rEaZV7Gup/TUiUMgxWkMqAXwG9ZPky77s02y7l45dZ1nH8xz0d93Fa+sJv3GJ7fbpPAb3nuyyHpmcYXptBmuBhwHAG+gdh0SJ45jm45+7sN7+25YLzlk5PPRsXZs9Mrp4R65yubJ0uDbWydioEqbAdj+TU5gE53KMwO+XwDqV5dyLcn2L74+HtSvNGNbwhJb45XVl/auu6fzl/1/e+Db+4A556Ajo3QCZNM50sL+Ha8vot2ib9kY1redSoTLZoBbkXhF3IjLK9JOzCkxKqPQ7L8+/+y3u8hjOQABJAAkgACSABJIAEkAASQAJHmAAK6CN8AnDzRw8Bx3EMw8jn8/vIMC393/+4iQM7ipJ69n63DnmT5prmdNrqUPMacGUdW0f7fGBw8V1IYO8Empubyxx0Oxt+ROF2qowmN1uegLYwfMMnUC6g5TCoTE7lljXU30IITwEGCBXQFYQEKkrW2EvYL0bk7/0UlL8y7uO0tKryZfY1vU8BbTlOTtfyRt73uA4YeXNYt9M26JZrmLZNk/2Lm7S8vAvLBNeF3Ah0d8HCOXDvL+Arl/dd9fl8m7i8VVzXKq5L8WsT/NqUuKE93jU9tqtNyrXL0CJClLGjDCQYiIchFoZYxIhzIwmxJyFvVrjXJf6ld52y+JMXb/zG17tuu3Xwb3+FJa+BlgEtB0YODI3WaNtmIVHab5lL7wsC2vBCNkrxGsU9LtV9+3tO2+QWaqn3RQxfQwJIAAkgASSABJAAEkACSAAJHF4CKKAPL2/cGhIoI+ArhD3liz/Hor8Up8VwqKDLmOEkEnhHBGyLfrdz7rnnEkIqvBshqck1dyrchjg3IocMmbH8nnslBy1HQMZq6AjN34hxfa2JFwn5FO1A6N0ClUFSQThRKApRmgFdXgT9js7WQXiza4Pp0BAO3aXDdBwaqlS4efHLhZ6HfvNAr/rYD+4wXdBN+o1gNg/ZHGQzoGmwpQteeQn+/DD8+Kahq67ofO97XlKEp1qUVSlpc1zYLkV2sA09ckhLcKCGQQ5pKpOL8bmklG9Rs0l5KCrsltmtbdHemLA5Ib4Z55dLzXPeM+uNKz+bufE6+K9fwQtPw9ZOWhCdGYZsFrQ83QcHIGcWBDrQwzFsyHv23C2pc/otJrXPtJbahmJLRxf/9TgI1xCuAgkgASSABJAAEkACSAAJIIF3TgAF9DtniGtAAgdIYC8C2vEK8golhCigDxAuvg0J7IXA/9+K8Mc//nGZgE7U1/5HlF8e5wblJk2NWDLjSIVBAzdQQEuefVbDEOe2ScJvCHkPIVNp+TMhvoD+5CWf9mHv+XXaXk7CYZvt+i37PAFtuq5d3vPPn6YCumSfC/tlO6B5ntfxX7Rc2vjP8GaZXoCGbYOuw0gGBgbhjRXw5P/CLTfDlV8cOf/c7vaWVRK3NC6vS0U3JeRNMWGzHNkihXYKoV6+aYBvzPCNdniqJYVdtmFEjgzJTK8c3iFFOtvi3e2JdW3J19pTz3/yU6u+851ND/xGf+ppWL4K0nkYzILuQFqDnFX4blLTaJdF2nHRLnQ3NL2vLVFAH7bLCzeEBJAAEkACSAAJIAEkgASQwH4SQAG9n6BwMSRw8AmMFdBOsash7eE1bhz8beMakcCJSiCfz69cubJMQMfqJ90YFRclhD65SYsytsq6MgsiV4h7RgEte+0HqYAWNjZOu4EQhZB6EhwV0I/+5c/+1VRe++x/iB3xq8zfDb8u23ZpmbDtfcU3eu/NLFVw+zs8+gnsem7XhVJvRf+Tmipqk4ZH7x6g77AB8ha1wy5AJg/LVsEfH3Zu+cnwN76247z3L26LzU6KC5Pi6pTQlRB7klGnoWFElkGSbIHTBD4ni5ooZAUhLQgDotQvyjtluVuNdbWkNrdP71Tkxbww5yMf2X75F4du+Qk8+BDMfw22bANLA8framjpYOige2Kahna4oyXQ+8W/LMej8KObvc3Z5+pGoe1zMXwRCSABJIAEkAASQAJIAAkggROQAAroE/Ck4yEfLQTeSkC7jt+Y6mjZX9wPJHBsE3A8iWgYxuDgIK3eDXhFvESun3xdXHwlwe+WGrMl+4wCejSEJEwDJeKMGZdWTJp8OSGNJBgklTQDmlZAByq27dgOe3xtdnQJaF897/2+KKALmRX0qS9hi1bVtanktWlQP73ppmFYpukYpqPZkLVpXbLpv+QCaC6YLi1MtkygdjgHyxbB//0F7rgFrv6aedHHh+ToYklZEo2tFoRVstwRj21JJvuaI1sjbJ8gjUiyLoqWINgC6/CMzTbnVdHkQj2R5s0C1yGLKxV5cUx56ezTX7n0ohW3/HDg9/fBa3OhqwOyI5DLgZGnbtryi6MtuhvUtruFUm+/2ts7LOrSC60iS8Z59NvPIoEJXipCGV3Y1/Kjz30UeI8EkAASQAJIAAkgASSABJAAEvAJoIDGKwEJHBUE9lb+fFTsHO4EEjiOCLheMO6ZZ55ZFNDCtPpr4vJzCX672JApCGgWRBbktzlKxvYYnfBrvcvv6YFEQI14ApobntEyn5BTadfBam8QUlFJUi0Jx7E8WzmBlxxrMQ/BZeTr0f1ecaEIumiiadTRW968Tex9SQdoPoflfYaPGljHe5fjlU4Xcj8s2mDQMqkRHhyAjnWwZBH86m79hmt3XvLRJe8++eWYOk+SV4jCOp7p4sO7JSYvhW2uwRIaTanJUMJ6lNUTgp7gclFmUA3tmi72xJs71WkdJys7k6GNsWlrT5G3X3BG+qrPuj/+ATzyEMybA8ODkB6BXB40C3SAPEDaghHTzdGWh6YOmu5qJQC5TNrUs46dK36b4I4WRNMjs/zhp5oU72kwSXF6VEMX11kU3MXn+IgEkAASQAJIAAkgASSABJDAiUkABfSJed7xqI86AkUBXeYvCpVpR92u4g4hgeOAwLXXXltRUeE10ovU1n4+Kj6S4rcqzQYK6HECWvTyN2KcE+c3SeKDhKjUPlfRMam+sqKSXH/DD3U9X1SWezroUgHtoWmI93YFtNejz0/k8Fv1HeaL2XVoGbVtesBsoFY4R8Wwm4VNG+Gll+HXv4Ibr4dLPjFw1mkbk+KKOPdGSu6I8R1K+E2xqVNp3qk296nNQ9HmXLzRSDQ40XorMQ2SDRCfAieF4TQZTo5BizKgcBv4yAI2/MR7zpz71a9t+ekd2Xt/O/jE8+76zZCxoT8LQwat1PYNfD4LepaSsE1wvAzpPbA4Xr60BjQde9zwBXQppKT01vKLoTQTJ5AAEkACSAAJIAEkgASQABI4EQmggD4Rzzoe81FIoPz/1PecPgp3GHcJCRzTBObMmePZZ0LIZBI4U+DvbBE3J1lQGVr4LGIFdIR2X/QroPkGaJEMVZwzecq/koomKqCDNH+DEBKsDnZ2vmla+rEioI+Gi9Z1wDRAy0EmDa5XFm3rtBrZjzExTMhrNO4jn4Mtm2HBfPjjw3Db7ekrvrjuvA++nlCeTymvtyobWsXtbWy6Nay3Ray2sJNshtZmSDVBoslVwroYyUSa+kONOyOhnQK3W1X6Y9FdUbVDVpdJ6kIl+tI5566+/Kreu34JT/4frF8B2V6qwq0c6HnQNMjrNOHacEZTO2xa4q05kHMgA5D2RsZz55pXFu15bLd4FYwGmfhF0/6/aUcDe9wHJIAEkAASQAJIAAkgASSABI4MARTQR4Y7bhUJjCOwp3QunzNuYXyKBJDAOySQz+eLAjpIiMrx/9aqrJkuQbQooAWO9iF8Wykcx2jyRmm3y2ufy6eFBrc9NiAp/0OC55NgLRXQAUIqSG3dpJmzZnr5G+UfV+Omj64K6Hd42Ry0t7s04H/vsR50O/4CfqL0iAnDGgxlYGgY1qyGJ/4K9/0Crrp05LwzO5PcXKVprtT06nRlY7uwiZm8KqX2JdR0TMnIosYzJhtymCYIN0BLHKIycEwuHO7j2B2i2C3Jm6LKmiQ/55TEixec/erll6y687ah/30M3lwPlkElOB0mGBYYNpi2F2ztZUn759ijUTrde0tb8fK0/WrzsfcHDSauCAkgASSABJAAEkACSAAJIIGjngAK6KP+FOEOIgEkgASQwCEgcPbZZxdSOCaxhJyTEp+bqWTijK0ytALaF9Bvy0GXTO4xOlEunVWv8aB/TytqmWXN/PWkIk6qgjR/I1hBKqpqamruvPNO13VNs9B/r3iWSlLS2ZuVLC55Aj/6Zt5H5XcGpDD8uTbQ4mPTG47pZTfnXci7kLOLw2uHqFnQ0webN8OLL8KDv7G/8603P/bRxa0ts5Px12PRVZLYwbHbuMiQzNkSA2yTzTbZCgcJGbiQllAgITt801CKS6fY/kR4e7u4fYbS3S52tHCrUuzS88/cednFuZuuo7J7wSuwrQtGhqGvF0ZykNNAN8DyKp1tgLyZzWiDWS1rWLZ/RmkEdvHm2GBbrlN2Gyui6bPisviIBJAAEkACSAAJIAEkgASQwPFJAAX08Xle8aiQABJAAkhg3wSuvfbaYDBI66Ar6wiZHqq/c7rSkWDyagREBgSWVkCfUAJaYmjshj989RwLQSxsKZFeVXyJBC4gtREqoCsJCVSQQLCioqK3t9cwDGd8/C8K6L1dentEVpdiKwrtEMvVs+5FRBu2l75sgGvQzoG6AVkDRgwY1iFtgO47fv9ttOeh53K7u2m2xj2/hB/8EC79vHbaKW9GmubH5XUxsSMmbFKFLSm1TwjvlJne6TEnztgJBpIspDhIhCHaCGqDEw9BImKmItkk05Ngu05p6ZbC81qi8//5/HXfvnrXL+42X3gJNm2mu5K16MhbtFba0ukwNTosA1zTE+kuzZW2Lbs0fBddrqH3xgvnIwEkgASQABJAAkgACSABJHB8EEABfXycRzwKJIAEkAASeHsEZs+eXVVVRQJBQkMlFEIua4/OTrDD0RDIYeqgPQHtytweg504muMYLXzec7flCJQEdDySi7Kd4aY/EDKT1NSTYA0JVJEAqQiQr3/9q3uoZ/8UoIDe26VYXvZcolRa2NfI/n2hKNhfyKJh0a5F+xeaFuj+6E/3pfM5v+RYs2hqc96gtcmFc+CAZtA5mgE5A7IazF8AjzwMN12/9YtfeOP89y+c1f5yXHoxIa9MyQNxRheasuzUDN9gKCE3ytALQG4y1MZctDknN6fl5qEoN5IQR1Suj2e6OX6jEu2Ip9bEWl49+/yNX/62cevP4M//BUufh5Gt3vZ1z5qbowHRjuP4ArpUCX2kBLSPtAS9OLHn6Si+go9IAAkgASSABJAAEkACSAAJvGMCKKDfMUJcARJAAkgACRyDBIaHh6urq4NVNZ6AZgg5RRHuTfHdVL2FQYrQImiBdSSGjjEa+ngU0PRgvbpv30erYYiHIR6CJNMjM/8g5IqKSW3UOgfrSKDGF9Bdmzs1jfpOwzDGnv+Sy8MIjrFgCgkbRatMO/tZDjjesLxq4TH22W9L6NAXXBvssWOCBGkbdMPOmlbetjXLtUzbNe1CUAYApEdAy4Nh0NrkfAZ6tsOiufDQ7+E/74KvXgnvOmVdQlmakNfE5Q1xqTOlbpkZ3z091pPgdyrMzig/nFTsuOiqrKtwoAggC44g6LyQjnC7GkKbmhtXxRpfm8nOPz328lntz132saU3XLvpzw/Ba/OgdydYeXAMMPJgaN7w0qUtT6jbFj0wWrtdbGFYmhjHbi9PS4uXJvayYHG2v1zxmf9Yem+hEH3sq/gMCSABJIAEkAASQAJIAAkggXdKAAX0OyWI70cCSAAJIIFjlMCFF15YW1vnCegGQqTa2sukyMtKeEAO58SwITKmyJgSa9Hhaeh9y+g9S4mPlTkCCzxHhxc84sosxBhIRKCVg1ZxTW3NF0lVkgSmkIoKEqyuCFQTQj7ykY/kcrlSr7yJLgBf6vk1v3tET0z0hhNmXjmTUvxx+cwDI+GvgWJ3XduvL/YVtu0CHQ4dlgWWCbY3LJNOGyboOuQ1yOdgzRvw3DPwy1/o1127/UPnvdLe+jdZ+GsqPieuLlWl9QrfLTM7hVC/0DwohdJiJCOEMi0qJBVXaB5UQz1q8/YoszUlbkmInXFxfVxcnRRXnNa+9rwzuy79eN83rxj55e3w5/+BJQtg6yZID0E2Dfk85HWa4OGD0IGGW/vBJJbjGJZp2rYfje26hYDpMjquF5PtZ5Xo3rS/cNki+zWJ1+d+YcKFkAASQAJIAAkgASSABJDAARNAAX3A6PCNSAAJIAEkcGwTeOihhwghwUAdIXWE1JPAGeGmeyVmmRzeJTXnpIjuO2iqoU8MAc1zjsBR4Z7kqX1uYdNy6P9I4F0kGCSBgBdXQuqnNlRUBBcueHWf9rlUvPvOveqxfY1NtPeHXHeW0i38rZeeuu6YZoBeGobhQNqBDLW9BuRyoGm03BoABtJgurCrF16aA/f/Cm76sX3ZF3acf94GMfK0yr/SEl0+Pdkxq3VHlOliGzYqkd0JPh1jMnI4LYczSiSvMoYasZSwKTflouFsih9KCbviwsYou0zlFin88+ec+drnLln37zdlfv8gPDcbOrsgnYOhERoYYpi0ILqw88WJ0pziDN9U215Sdt67L2ZOly2xH5OlS3Q/lsVFkAASQAJIAAkgASSABJAAEjggAiigDwgbvgkJIAEkgASOZQJ+EG06nWYYrjo4qYJU0fJeEq6q/YzEPyJHtklNlhQxPQdNNXShDtqrht5bHMexUu+8536WKqA9AW1InJYS7FZxqFXYMKXqdkLaafhGIFgYhFx51Vfyuuk6MEEMxOhVgRXQoywO81TJOPvbLT2dSEA7jmPR/2yazpHXqIA2bep/DQDN9QqSAfpzMGyC5qVk7BqAlWvgiX/Ar35rXfOvWz/2zytPnvFSSl1wUrJrhrq7TR5I8UPxSCYetmIhiEYgxoPK2lJEl5h8VMilZK1FzbdGMzK7NSp1p2Ld7clNfGQR2zTn5NZVn7iw7xtXGbf+GB5/FF6bD/k05LNUi+c0yJug2ZB3IO/SffNCsX1P7Zall4zPMPGrp70FTE9SjyuXLpRXH+YThJtDAkgACSABJIAEkAASQAInGgEU0CfaGcfjRQJIAAkgAfC755mm+Y2vf2tS1eRgMEiChNBs42SY+X8Ss0RuTiuRfFFA6yeGgKblzwKnyWwuJZht/DY5/JdKchkhIqmsLNnnyurajo2brLewz1gBfST/ykrG2d+J0tMJBLQNjg2OVQjoGLfTnpHO6WCM2NkhIzts62nbyQHkXMiakNZo50PLhuEh2PgmvPgs3P1TuPJzA1/4dC4lLU4Jq5J8R4zrlLj1orAhqmyJx/qS0ZGomOZDg6Ep/THBjXKgsq7MOAnelZo1uSmX5PPRyM4E25UU1rbKr8eEZ845Y8FXrtj24xvTv/sdPPs8bOoG3YWcDTmH7obueH0OreJ96VuPwpH41c22l86BAnrc6cWnSAAJIAEkgASQABJAAkjg8BFAAX34WOOWkAASQAJI4Ogi4ELH+vVBEgxWVpAgCdYTUllDqs+aMvU+PrRSjgxMKKBFzhU5t1AHXdaQcM/K4mNljt9uUeAMgc9JfFplM1J95t0tuxrqryGkhZDJhAQCldV19VODVTU3/uhmB0A3Lb8Ceu910CUXiBEHR8VVX66hC9PetwiFMzhRLoj/LUNxKdvxwjlsoI0NTaABHaZN4zIMm5rovEHrlLMajGRpnHRXF7z4EvzpUfjpHSNf/daG95z9HMP/KZGcF4sti8obFG67EsnHGJo2LjeD0gSxEO17mWAgwVrxSE5p6hem7RAbt6aEnpS4o03dEeXWRPmVMXFFQln+4Q/2XHWleccd8NjDXp/DLV7Btgm5YdpfUcuDboLhguUapmN4KdJek8OJA6KPiuvT/2spvz8qLhrcCSSABJAAEkACSAAJIAEkcJAIoIA+SCBxNUgACSABJHDMEfDU079+6+r6OtpYjwQIqSUkwJDAJfVTHpTYTSeagJa4nMylY+xArHFnPPL8pJqPksBUSoaQ2rrJgcrqk085bVdPn+XF8aKAPrau9wkENK2Ipjkq+4xS8aOWyyytS5d33LLhRXN4q7Etv9jYpVbadKkF1l0a5aF7tnrOXHjsMfjpbXDt1cbFHxl8d3u30rxcblw5K7Z7utyT4nYmIrtjTK8S6ZVDfXLzUCxipDhIMiA1OUrYjjJ2goMY50hMVmB28UynwK1MKa/FhGfee9rCL1229d++u+uX92jPPwdr1sLACA2Vzpvga2cbwLDAtGgDRtqG0abDF77FmI4jeT7L1XNxr47k/uC2kQASQAJIAAkgASSABJDAwSWAAvrg8sS1IQEkgASQwDFEgKoe29Traj0BXUVIJSE19SQokeBnmeZFckjzHbSXTWH598dpBTR49dqOzGoxflurMq++6gcVgdNIYGp9Q9hrPxiomVT3zHMv2C5YDpj2qLvci770NVpJXLrH0GVxXO7qxALatV2vlLmYYeGfJv+slZIryiqH/bNqFZTzWFB7nGIXHIdGfNg2WBZNl85nwdTL3mRB73ZYvgju/Vn2+9/addEHl5za8mJcejkqL1bltVGpOyEOyyFNboKkSLOkY4KrCIbM5yUuI7IjAp/huWGRGxS5foHZwYY7OWa9KK6JqWtTyTdYZvZppy2/9PP93/+Bc+8DsGAx9A7SJoeGBo5Ba7npvhWOw3bA9J6V7dtbTh6kS7u4D6WdKWlx/5W33A9cAAkgASSABJAAEkACSAAJHAMEUEAfAycJdxEJIAEkgAQODQEXwHEs42e33zapvpbGQFcSUlVBamsJmVE/5Zcyt1Zh+0VGp+qZdbyoCjjGBbQjsQYdjFNKCBEYEBgQwyBHQGUzcWlVKn4fIWdUBGMk2FBZVU8IqZlUd933fwgAA0Np3aQ10KXiWRTQh+biPMhrnUhA225BQOtehoXl1QKXSp7HCuiSlKYZHF5XP3oR+GHf/muFHXYdME3Xscfuvw2u7RS7BXpNBMExTdfQ6TxbAysD5jDkB2FzF8ybB7/9Hdz8I7jwgq0zkkv40ML2eGdC7YxF6VDlTknoksQdMXVIVXRVgpgMUQlkHhQBFBEU3lF4J8pbUUGLyYNJdVtMXSuI89pmLPrQh1Z96bI1d9828sJTMPsZMPJgGrQs2rTBNGlxtG15xdGOF4rtVXlTH1zumsunR6Vx2dTY4y4+m9Az0xfHvkCtuD+KrxRXgI9IAAkgASSABJAAEkACSOBYJoAC+lg+e7jvSAAJIAEkcBAIOL29u3mJJ4QEJ9eS6iAJBgiZRsi7m0K3KsIbbOOwxDgCA7w3RK7goH0TXbqXy/Kg92e65H8P6wRrSPwQHdRBe1XPEZAiIIToUFm7LT6ciD9HyPtIMEKCTSRIIzimTW2ORVNDgxnasI6qOnsv0vkgnAxcxWEkMFZ+Uhdafit/dSIJW74PbE5OAAAgAElEQVRs2fQ+rw1/nX7TQD/JxROtvtS2vHaIXlCGaVIj7FJtDf09sGIF3P9r7Qc39n7iU0vffcbsttYXWpMLU/EVCbVLCvckZUhIwDfpMuOIIYdvtOUmmi4dY0AJuXKTFo2MJPh0nO9P8DvbhC1t/JttwrpWfpXc+Mp7Zq794qf1G74LTz4Oi+bD9q00PzprwLAO/TkYzoGdA8iCNezkB4zRo3TAtHTLNYrKngZ9+IMeoVvQysXlaatEBwwHNO/ecOhTyxPN5QLa8WYa3jITF5kXV4iPSAAJIAEkgASQABJAAkjgGCOAAvoYO2G4u0gACSABJHBwCbgurdX82xNPEEIqJ9WQqiANgyZBUhkh5KyaqjsVfp0Yzh0vAtqSuAwdrEUFtGef/XuZhZg8KHCza+uvJUGZ1FSQyrpAMQN66ZKVtFrTE9BvVft8cM8Pru3QEfB18KFb/0Fbs27RqmvND5h2oKcPli2DRx+F22+Hz36q/wNnbm6PLYsKS1V2tcp0xNitcbYnwQ7HI7l4WIuF9FizGQ3ZsTCkIpAKQbKZjlYG2nhoYW21KSM0bBOalyvSolRq/vSZL37ui5uuu6n/wUfhpbmQHwB7AJwhsIfAGAYn5xWAu2DZoNk029ov57YKfRDLTLSnoT0EVEB7r2vevVG8p5a5XPOXyp+L6SAHDSCuCAkgASSABJAAEkACSAAJHFkCKKCPLH/cOhJAAkgACRxhApqm+Xvw3eu+R+1zVdDruldBAg2EsISc1RS6XYh0y2GaU0GjKo7pCuiSdC4rf6YCmoHWmMuxi8ikq0hVC6mpIzWEVNYGgvUVpOaee+6jiQouCugjfK2eOJvfU4379cW+u9UB8g6kdRjKUeELAD274dVF8NST8Mu7zCsvX3vu++alxOdahIWt4hvtUlcL3xNn0tFmLdbsxpvBH4kIJFhaJS02gxTRY3K/Gt3K8RvDbEeYf5OROlmhQ+A6UkLXe6f3ffJD+lc+p9/3c3jqb9C9iW4xk4cRje5D2oRsQTA7Xr40VdJmMaSkrKrcOybXAjoMOuiChlcBXlYH7Xd39HNQTpzzjUeKBJAAEkACSAAJIAEkcLwTQAF9vJ9hPD4kgASQABLYJwFfQGfzeQdAVpUKmr9BCKmgI9Dg10HL/BMyu1VmNYkKaHfCsT+xG+XLHNbkDV83+/dhr/CZZkA7XBNI3lOZy6jqmmDdraTqZFJdSah2JoHKYDBY+7F/udjQaVyv6zWUc+y3TH/eJ258EQnsB4GSgDZtO0+Dogs3hypbVwfLoInNlkm7G+qW45gWGKaX5mzQWGdLBz0HHavhr4/AXbfCpZ/c+U9ndrSoS5LiqqSwPslvivNb4tyOON+vsml68fNZRRpSpAGeH2TCw8kkyApEIhBqBLYB5DCkRGiRM0mlK6WuaIkvaG15/vwPL/rq1zvu/bXz1PPQvRNGLFqgnQfImaCZdGcML0vE9n40MK7OmdY9UwHtF0RTR02P11fPLo2ftko/NfCiu4tHj49IAAkgASSABJAAEkACSOBYJYAC+lg9c7jfSAAJIAEkcNAJ9A8OplpbCSFVlTWehg6SyjpSwZHq8zjhHiH8RpS3ZM6WJ3LQ5XJ5f6aPmICmGtqRuJzEGmwDnJSChAgtqS3V035Cqv+JVDOkNlA5LVA5mQI47fRT/JJNP3wDIzgO+iWHK9wfAn4dsW+lx92PNuvzBa7fP9ABy6XD9O51m1Yr7x6Erbvg8f+FBx7Qvnfdlss+v6G95emWxLxEbElMWqvwW2PCkCoM86FBkdFlgXY1lHloqM+EGvMSayiCpkrZqDikCv1RqScR62lN7GpNbmlNbZSFxTPaV33w/d2f/HjPz2+FP/4BFs2BTR0w3A+ZIchlQM+DrkE2A9ksGDoYhmWYOZf6atN2QdchnTZ7BkZ8FLZL51oO/a7HH+UNJPcHFy6DBJAAEkACSAAJIAEkgASONgIooI+2M4L7gwSQABJAAkeMQE7X1q9fz7NsTVW1J6C9SuhgLanlCHmvIv9JZFbJXPq4EdCy134wGe+tb/4DqT6f1IRIbSWpI8H6QEUlEaXIuvVrUEAfscsRN1wgUHDOftc+Os/1huPd0+ejUrrY38/wIpo1mxYi2358hwaQcyFr0SLlvAk5A0wbOjrgr4/DnbfDddfAv5y/oz3+qsotkJjFirAyEX0zFeuOqdslfrvI7ow07w419Ecas1yzwzXT1BqZBZV1ZcYSwzmJycb4TEoaalW2tUY7WtWVbdH555698tJPb7rxB/n77naXLoHt2yE9An0DkM3RKmnfqtOejX6MSPF0Ww7YLtjgWq5lOY7lOCigi2zwEQkgASSABJAAEkACSOBYJYAC+lg9c7jfSAAJIAEkcCgI2Ja95o3VTVOn1QQqfAcdqKwlZGrV5JmEvJcTfiEwGyTGkTl3nIben6rn8mUOfQU0DdmYYCthGrshR0BmnDgPkaZtzdyjhFxIagRSR0g9ofeVpDnMzZu3gBL25B5tPOi6jndDHXYoLjxc5wQEfNHs349a5qKALr6h2LvPcsD3zjkbMk5h5CzQ83Yub2kGWGWJzFRi+ypb12lhsmXSp0YetnTCS8/DHx+yb76p+2tfXt+e+ntrfF5rfFlC6ZDZ7VIoLTU5Uoj+BUkRk9ZK83pcseKqpkhpieuXIjskZpvCbI8LO1vUXS3yVpXZyDetSCmrVWH+zPbXzj9vw1e/OvSLX8Kzs+HFl8AYAStN740c2BoND7FML4WDqnRqn48aAV2y/EXu+IgEkAASQAJIAAkgASSABPabAAro/UaFCyIBJIAEkMAJQMBxnGx6ZMmrr02uqS4YaFIZCEwlZBpVtDXnNjX9XuDeUPldKp+lcRxsoS2hF81B0znKLfM+pidQw+VJze902pFYqyCgqSnzc5+pNRObaKatGnFUbigqdSeTL5OqTxMSJpOqqX2uJ2QSqaiuefxvzwCApTsFAe1ZZxTQJ8BfwNF0iBMLaKdQAe3taVGLOp6GNhzQHMiVDc0G3XQ0m/YFpLd0tj9nDDk0f9m0wTZt2684Nk3TMCx/Gb842bHA1MHMUSX98nM0WOO6a+DiC4dPbdt4auvmlLI2paxNKOtj4nqJWSNx61VxU0LZroq7hUhPZOrOhpodMc6KMq4aBrkZpLAdF+24nJH4nWxkQzy+UZKXJeOvtceeP/+sBV++dOON1+3+n9/Ba/NgeABGhiGfh7xOh67TRGk/7ppmQzvFtOjywm9vurDzow/lvn10bvFLJZ9YIZ56zMsTP7G8VotWYVOlUzPxwjgXCSABJIAEkAASQAJIAAmMIYACegwOfIIEkAASQAJIgAoay35j+bKT2tsIIVPqphJCOxMGaqcEa1VCTp88+RqZezql7IhxhsqATDsTgszn6fCU9D68c+mlwyKgvR6DIeq/5BAteVYjltTkzFBgRsxQ+SXhyB2TGj9BJkm01rs2SOqCdKKC/O6//mcorflXgl/77Pln23VHB14nSOCIESjURO+5fV9Hl1QptaX+Retp072+bc8VjRZI+10ELdru0DLBNGmTQ1OHxQvgqcfhP+/I3Pjdnos/vOyM6S+2Cc+cnFiSim6MKTuj4oDEjAghTWiiX/mITRANQ4qHJA9qxIpxRkzMxqThmNwfFbcrQpcidEb5jqiwPiqsjQmrY+KySy5Kf/ubzi/uhEcfhtVrYGiYdiakEdImLeR2/fptb79LKtjyojws7zujnJ4rHRRtbzjWVnvHZNm0YNzvdzh+AX/50hq8Cb9rYpmAHo1AGbsgPkMCSAAJIAEkgASQABJAAnsQQAG9BxKcgQSQABJAAkgAwNTzfTt3fuwj/1xfV1eKhK6qmURNbfVJTQ3fU7gnEkJ3wUGzIPN6QUDvXxH0IRbQXqdBZlRAqyHPfEU0qTGb4PpblGU8ey+pPo9URUiQ0FFZEZhcHxGV1R0bB0dG7VUxcGNUPReNHl4lSOAIEXhbJrlc1h7E/XWLTteCbD+ABgNbYO6zcNft8N1r4eKLes5810aJWRzj17cq26ZHB/ipWxLsYJuUS4l5uXlIahrmG9NcU1pgMiKT94YuRmwx4ko0JMcWmSGJ2SYwG3huycwZyxX1H6ef/tIXvrDhJ/8+8OBvzZdnw9o1VIjnNRgagb5+KqYBoGcAMjnQLcjq1Ckbnnq2gJZ/+8OPw7bB8YuqzT0E9KiKLh1ggTYK6IN49eCqkAASQAJIAAkgASRwwhFAAX3CnXI8YCSABJAAEtgfApnhNLi0FPorX7qq0JDQewgESbCqobK2bcrUSyX20YT4ZozP0TpoLxV69J6lPcpkrz66VPVcPnHoBTTtk+YPOUIzN2IRI8bk1KbdUvP8cOimQM05hMiETKb2uYYEJtXMPOX0nGGO7YjmoyoUlo6tgC6vqtwforgMEjg+CIwpP3ZokAfNbgYvwGNgAIbTNDrDsKCnB1atgCcehwf+0/7Mx9d87EObzj51bZuyrE3sSPFb42xPlOlXmEGFGZTYYYkZkZi8FDGpfQ4bYjgnRtISO6gK/XG1JxHbJUubJXZjlNsaZbr5plWR+vmntL9xwQe6v/El65Yb4IWnYd4rMDgIugY5HQwHRvI0jkQHMDz7bBQnxprognCmJ8Y3zr6u9ovIfV3t/6G7pbpyLwLFL38uI3F8nFo8CiSABJAAEkACSAAJIIFDRAAF9CECi6tFAkgACSCBY5xAscrStZ2//+8ThBC/DroyQAI0qSJAiDS1/kqJ/6+EvDIm9qkszYP2R8n8SkxhTuml0kT5ModiWgiBGKZbVwWQGUNl0yrfExc6ktzcqbU3EzKTkNraKUJwUgOprCSEXHjRJ7Zs22XaeyqlkpeyUEAf49c07v7BIWA5Tt7QDb9xYXGVxRaHY/6CbBsMDXIZcE0aJz20G7o7YO5zcN8d8NUv5K+6zEjIL8WUOTF5flReHBVXKeJ6ReiMSTtaosMJNSNx/WzTbq65T+XyUd6QGYcGuDeD0gxysxUNZ2ORwQTXm2C7EsKKluirUenZtsRTn//M+ptvHvnVA/DyHNjZAzkTdBs0CzST3hsWjd4wbTAd2u3QdmmodCFW2ynmPO8poGmgNFXRru2nUAMN59lrynQRCj4iASSABJAAEkACSAAJIAGPAApovBCQABJAAkgACbw1gaWvL3nPaac31k+tKpZDBwP1hEQCle8Ph3/SlloU5QfjPC15ZhpGm/6NM8sl+yyzo+XJ45Y5KE+5kMU22VwTqCwkRGBDWTbcKUgLY4mHp029vK7mXYVug/RYagmZfPfdD9qeTtpDKpWXOe9j+q0B4hJI4FgnsOcfQPGIXADbc7cGQN4buld27BbErus1D7RHg6QNkwZl5EzIO9C9E15eCI89Drfc1vfVr2/8wPvnJGP/F1cWxYRVUW6dEn5TCm+NsUMqk+MbM0KjqYahRYQ2BVoEiDN6NJyNhobibF9K6EmJO1LilpTQmRTWJ8XVSXFFlFt8SvsbH37/5k9/fNt//AgeehBemw/bukHLgabREI/SV075Quq7d0z+t07Fwys90nJvy7atcYE8hZye0mI4gQSQABJAAkgACSABJIAExhFAAT0OCD5FAkgACSABJDARAcft27n7e1dfU+sJ6CpC6qqraibVVlSxJHBmReBbscRCNtzJhvtlzhbDtPpYjLhixJYYxxvUOJcE9EGxzPtYiRhxuZAlRlyFg5isN4VWyslXwrH/JBUX1Na1BElNVcA/DhIJ86tXbnGtQj3jWAG9p3Db25yJiOE8JHB8EZjo6ne8nn9+wbCfkqwXBbTvoEvxyzrQPAzTU9VUV5teJoavqzWAnAsZg1Yo+7c5L8Njf4Kf3QLf+Ub+iksGzj51bZyfH40sTnJr48ybcaYzynTHw9ujzbvioYFoaCgazsYZPcEZcUaPRbRYKB8LZ+NhLcHosXBWad4tNG5qVza3KuvalGWt6iunn/zyRR9b+sPv7773Xu3vT8DCRZDN0fAQGiGtU10O4GWJ5MAphfKUfhTi2o5jOK7muFrxVxHUQR9fZxuPBgkgASSABJAAEkACSOBgEkABfTBp4rqQABJAAkjgeCVAf3huu6Drzz7xZzUyNTK5tj5YOblmWrCqiVSECImRqoum8L/glDnhcIfI6J6AtkXGLNnncQJaYGHCsQ+tPO4lOQJyZEwldWmFIueqoi0Lw6LYxSlzm5Rfk8YvkdqTSWWIkMqairpKUjW5pvbab39Nyw/T9Fdfi1HB5v0gv2CaJhJuo03Kyl89Xk87HhcSGCVQdsU7DlgOTVo2vAkqbMfGUZSWLUUn+xPeUl5vQMctVE37qcuaDVkD8l5JsmVDLgf5vCd/XSqqnRxs64R5z8Gffgs/vTH7hU+u+8DpC9uFl6bzS04W180Ut7WKQ14YfU5lNJUxomE9GjKVZkNpNmJhKyXY7YqjhDLRyEiMSXvZ09tj/JaUurk9uUlkFqWiS+LKgo+c133l5UM/uh7+9D8wZw709MHgMIzkqBb39bJjgW25tu3ZZ8g4bs4Fs9in9LAK6BLfsdgLOSGj5wynkAASQAJIAAkgASSABI4OAiigj47zgHuBBJAAEkACRzkBmpMKlpYHsLWhnmu+RjsTVlXUVZBJxUyOMCHvqay7Jhp9PCYuiXFdMWZnlBlUI5ZvimknwGJXQDFMxbHgj7Em2rPMtGia5r2+1SitsOimHYnTJD4dU3a3JTe0Jueq0Yc55TZC3kdInFTW0uTqiipCKiZX1/3vX/4Kjm4bGSqgLT/fFQX0UX4V4u4dSQJF6UmrnicU0MUFyjr7jfnCprjz3hc8VEA7oBs0jrl0c2grQ7+GOgOQ84qkSy/SCSMN5gjYWXCzYA/BxqXw5H/DXTfDFZcMnfu+rvb44hZlWUJYkeBXJ7j1UfZNObJFiuyQwj1yZEiJ5GOc0yLCdJV+dyUzjhQxxbDGNaWFcDohW3QZbrcidKny2mh0qSA8ferp8z95ycZvX7P1jjs2L5gHm7tgaJi2WMx7rlw3wDLANmgbRtv06qZ9BAUXXc7DP4o954w5uj2flL9hb9Peu8a9uOeacA4SQAJIAAkgASSABJDAkSSAAvpI0sdtIwEkgASQwLFHwLK8JFdr3eo1Hz7/AkICtbW1ldV1XlvCBkJEQk5tnvzlJHv/qcrLraG1MyWnXYQUDwmWtg4Tm+iQQiCHx0dFC6wjsL56tmTGUiOWyhhlQ/NrG+mcCF2ALsO6CRHiAlXbKgMxwZSFHklay3B/mVJ/1aSacwg5mZBkdW2cBBqKopxc/vkvZtPZIvli3WLx9/XF+aVawnKzU/YiTiKBE5RA+V+EP01BjE7tN5aJmvj5qynVTZcV+Pq5zF7WtGODY4FjgmN4Q6ebd23o74HVy+G5J+H392k//HbH5y5aOuvkudNnLEvEl6vyWknoFtndYiQthnN0MHmZMxXBEiIG06TFRFA4kMJ2XHTjki4yAxLXK3G76RC2KuJq2iZRmR9VZ1/4L11XfWXoJz+FP/wB3ngdhneAnYaRPq+ToUNNtGWDl0yiewLdoKkjjm0ZWj4/UtbucBQaPebyXojFzyTHyyux97j3GZXd0+8Div0T/dn7fQ5wQSSABJAAEkACSAAJIIHDQgAF9GHBjBtBAkgACSCB44mA4zreDRz30YcfPuWUUyZNmkxIpW94qyonVRCOkFk15HJ1ym9TzKsJtjPJ7ohF+qPhvNLkKM2gNHmjmWpoOgpJGo7EWhJryYxRGKwmj46czOboU/qqRYujIyCGLK5hmGvslSI7FKFT5BaK4lNTm+4h5GISiFYEqr1650AwWEtIoLqqLhZNzX9l4cSnAgX0xFxwLhIYR2BixTnx3HFvPVRPHU+/0rWbujdZjJ7OadDZDbNfhocfgR/fDF++Kn/O+9bHlQUtyeUJdZUirJSYNYrQJUS6W9SRpKonVFdkTC5kyKwXZB8GMVSciNgik5f4tCL3KcoOWelSpfUz42vi4dmnt829/FMbf/zD3t8/kJ8/BzZvos0XLZvmSo+kIZ+jVdLUmDvefADNhrwFuhdFUvLLvoMuaeWS0y8t4E+MLuAXkhfUf2l2mbI/VLRxvUgACSABJIAEkAASQAJvmwAK6LeNDN+ABJAAEkACSIDGVriuaZoAkMlk/vuhP4abparg5Nq6Up1xDSEKIScR8k+1Vd+MKw/OapuXFNYmwv3RRog1QLyRjlgzHWoY1IgjM5bEGhKnCeMGnxNKg75k0Thpz1yrYYixQzFhtao8KUfvaua+TMi7CYmSyhipmOIVZdP9oSaaBG679Y7enkHXAdsCwyg2Oxt/Lss9zp7T45fG50gACRxpAvTv1LTympbzP5Ho/nhG2rFpYbDtPfN30gHQbZqhsWwpPPl3uONnfd/5VucXP7fx5Nano+yTKeU1SVqvRgdiss6FDBpkH6I/1xgdYaA/vOD0mJiPy/mklEnwQwmuVwlt5RvWi6E1SniFwiyWmXmnzVz6z+dv+NbX0rfcDLOfg+Wvw87ttL0hVeQu5AwYztOmi8YYW053tTS8GupCZDb11qVRnmpSrJU+0qcAt48EkAASQAJIAAkgASTwFgRQQL8FIHwZCSABJIAEkMDeCAwNDZVe2rF94J8/+nESIMEaEizmQldUNgaqJBKYQcjZhFwannqXHPp7q7AiyXam2G0pZlcq0pNk+pLMQJwZirFDKpuWubTEZSQuI/BlQ0gLwpAgDAhijyTukoUdqrBNFbbEpLUS+49pU24n5FOEtBDSRLcdqCGkoiTCCSHnnnfBG2s2AICu2ZmMBkA7iU308/9S0eGe6tmfUzpcnEACSOAoIVD423QcyzDpX7d/c2ywLdo41YW8aWdNO2u5tGWip3LBsEDTIJ+FXJpKXz0NfdtgyQL46W3wox/D5z+TO/Ndm2PCqhi/Nsavj3GdMWZnLNIfi/Qn2MEUPxRnhoSG3sjkXZEp/VKzJoYNrjHXqkKCt4WmLDttgG/qoz/L4Lcq/DpFWB5XFrUm509vf/Fzn9103b/1/f4P8MILsHUbpLOgmdSJayZtdWhYYNheb0fa3LAsVNqX6FQ3+7XexY6OvoAuuWn00cWzj49IAAkgASSABJAAEjjaCKCAPtrOCO4PEkACSAAJHCoCjlP4dXYul/NLmA/mljz38dLLz06fGfeqjgkhgUCwLhCYSkgNIVNpG0ByqtcP8DxCLgpN/YHK3NMee6Rd+ccpqeXtyho1vIFv2BjjemLsgMqNjig/GBV6o+LOqNwZi66KJebKsUebmTtq66+tqvs8qTyTVMQJCRMyjZA6QqoIqa6omuxNkKZm/u57HqCJsWOH68AeAnpv0nlUPWtamd4qwqROyHEMw/C8dlk/tYMJF9eFBJDAWxLw/1T9omc/g8OihcPFv2zXdlzb8j8LCp8A3quuBa5JB20naICtg2nQKI++XbBiCfz5T+5dt2Y+97E1F7x31ZnTXz89tWK6sLKVW59kuqKR7XKoTw6nZTancvmYYPpDYvJs4zDXlI4KWkK24pIpcxmRGVK5gZjYk5C2pOSNLfLa9tiK957a8akLB79yhfaz/4An/gIvPg9bumF4BDI50HQa4kE/phywTLCLHy2u6yUgUb0OWt7JjNBPHvopZNMfdpim6boFD+2W3d6SHS6ABJAAEkACSAAJIAEkcEgJoIA+pHhx5UgACSABJHB0EXj11VenT59eV1enKMrw8DCtECy7vZN9dRxH03K53HB6pO/Rxx6KJ6TaScVU6JpJwaoaaqUDdSRQT6iSDhMSI+Q0Qs4h5JOEfKWG3BCafB/f9Ceu4c9Mw19LIzLt8VD9X5rrH22oe2ja5PunTL61fsr3CLmQkDMISRISorXOhXLnACG1FYG6mpqGSXWNk+oaf3Tzbdmcncla4+yz42kd30CVZM2opir5qjETlI3/A38f2m9/+1uWZWtqaq655hpUz+/kysH3IoGDRKAkoP0CYS/fokxAj6ZYUEM7buFiEz9/edpE0PX7HLo6OBqM7AZ9EIa2wfql8Ph/w723w3e/kf3cJ3bw4f9ThBcTscVtyTVMeDHPrFbFzTFpV5TvV5hhOZwRw5rKulEWYhyoEZodpDIQZdwYZ8XZfDQyIjX28dM2p6RN05MdcXFBa/yV885dedmlm350Y+6B+2D5UujshHSGEsrmIavR+A7NBEMDK09dOU2X1mknRqrRva/ZbMse98Fe9il3kEjjapAAEkACSAAJIAEkgATeJgEU0G8TGC6OBJAAEkACxyyBNWvWNDc319bW+vEUd999t67rZf75nf5+eyQznM+PFPFojzx6T2tbZFJd1bRp0+rq6yurawOV1d4IkqrqmsmNJFhPyCRPIqueTW4hpJWQNkKml42TvCDpWV719Cne/BghLCH1XmF1KWqj2it/rieESFLr1d/+fs9uGg9imq6u2QXX7FU9+zKazinc/B+3F4skx0jnPWcWDq63t7e+vr6mpibo3RYuXKjrum0VaxSLCPARCSCBQ09g3N+pt8FSKoX3zF+iFK/sTxT7FEJxgn42jFZMl38cetOmBnqWrm5kmPYVtLzfk+g2bN4OL82DRx5zr79h55e+2HnO+15LRV9W2deizNo482aU6Y4xvTEmk+CMGOeorCtzrsraYljjmoa45gGFGY4J6ajQKzHb2qL9CXHHjGRfS3RHlO8Swmu4yEpJWBaNvp5MLbzoU9uv/NrA9f/u3n0PLHwONi6GzDaAPIAONEzaLDRiLJRI+41iHcf/nDv0Z2HiLfjkJ34N5yIBJIAEkAASQAJI4EQigAL6RDrbeKxIAAkggROYwOLFi3meJ4TUeLeqqqpnn33W/712UcWWG5cDJOW6tudCNICM7ewEGHll7gtXXnllVa1XAV0ezLy36QDtHVjhj4qKAL1VBoPVVZWTqqvqq6vqq4KTA7SpYKXXYzDglT8HCKkmpDYYbLzppp93b+nP5s4aY4AAACAASURBVMqOxaU/Yy+NgoAu2mdvh8cJrL0+1f0mYgDXXnttTc3oEbW2tg4PD/vC5wDB4duQABI4QAKlP9ji+z377Lilb5NoXM4+7LPhfWYZ3jJ0FeXrc+iXWFreMM3Rr5dsP0ba25pfME0VtksLk/N5qqeH+2DBbPjrH+GOW+C6b1r/cl7XWSevTIivJKUlCWlDXOyKi90xfovMbJYjW9TwNoXZeVKbzUZ6W6JWc31fUoaECHGe1kqzTTYT0nk2z3EDoUhXiF3HSWtUZcV06bVT5XlnJF4+q/25qy/v+skP+v70W3jhKdi4Dvp2g2XQEmlDB8MAwywkeNgO0OGOoihEMpVkPf3U9A++mDFdZOG6Nk2lph/v+3UrIZxwYr9WgQshASSABJAAEkACSOD4IoAC+vg6n3g0SAAJIAEkMBGB1157za/V9e8JIc3NzTt27KC+oVgid1B/pl1eYkh3aNOmTffff/8HP/BPhJDKAHXPNTVVlTWVwepgRWUpQ2O8kw4Gg4QQ/76igk4HAjTWo7a2btyi55z9gccefXyiQ/fmlTvokm6nMmVCPTJu5uhaNU3zc7QvvPBCb2cCFd5t0qRJl156qQ/woGIc3TROIQEk8LYI+H/GpbeM+6ve29PS8oW8DvC+u6LmlQ7LcSyHRvj44cwlqV1Ym9c20LbA9uKkTdNTwDpdpZaDrZth1XK49+fZm747+IWLNnzojKUny3NPFpecxL3RwnSowrZ4ItPSYkZVS+ZcmQGFATUMUjOIzSCFXSliyqym8tm4nGmNZpJSb4zdrkY2x7juhNCdkmiIR0re2B7vmp7ceMnHjM9cPHj3z+G//wDPPw9Ll9IOh0M5yFowYkEO6PD2yzvcgoemh2qZGdsaAdCoUXdytpOjcx3DpY0Sszbkqb8uiuwyho5DOyaWxqjjLiEqnyh74+hH8Ch5nEICSAAJIAEkgASQwPFIAAX08XhW8ZiQABJAAkigSMBxnHXr1kmSNE5AB4PBSZMm3X///YdGQBc3X/ZomubQwOC2LVt/95vffvTDF0ybNm3SpEkkQDM06utpdIavdMeZZf/VYDBYSg4pX+D8D573wAMPbNy48S16Kk4goO39rn0uOwZv0rbsLVu2nHnmmb599ovKCSH/+Mc/xi+Kz5EAEjhCBHzLebA2XmZXaT31/o/SDjhAexvqI6APgTkE5gBkt8O6BfDY/XDrD+DyLwy87/3rWtpebW1dLfGrolJ3W3z4pBZDaNwph3ti7FCcG4kxuRiTS/Kml+ZhRFkzyppK2JbCrhwBKQJSGNgGCE8BVQBVGI5Hd6jqOkl8lROenvXu2Rd+6vWPf2bu1d9f89Nfbn/uFdgxTB30yBDow2DnwM6DkQM95x1baadpqoeru4YBmkHTp42CffYcdBmEknr2Jygf3zj7y5TZ59KS4xmWbRMnkQASQAJIAAkgASRwHBJAAX0cnlQ8JCSABJAAEvAJaJqWz+clSaqtrS0X0BVetAUhZNasWYdaQDuOY5qmvyf+XhmG4dcRd3d3P/bYYzfffPM3v/nNU045paqqqqKiwk8I8e9ra2urqqoIIaUdvuCCC84+++xbb711zpw5AJDL5fL5/H4VHRczObwCaGqfXZqZWqZQxkz7e+q/OuZqKqVwrFmzJhwOl9vwxsbGdDr9Fip8zMrwCRJAAscGgQMW0JYDuuHohmM59CMGXHDsQom0Y9EugvkRL7UjS1/VTdi+E556Ch78jXvDD3uuuqLrtJNempGcF+NeERoWzoztmKEMzpS1VlaPh4142EoxkAhDLARqiLY3lMIQFSGuAhMBgXenNfQ3h/o5YVBU+hius75habJtKye/EU9u4IWlqrLsXad1XfxR80ufgx9eAz+7Gf74IKxZCZk0DAxBzoKMTQ217qVMF4qmvfLnQjW4UxZEMv4cln2u+vkehU9Xw6utznn3pbrr8W/G50gACSABJIAEkAASOC4JoIA+Lk8rHhQSQAJIAAlQAsPDw2eddVZFBa0yLhfQfqgFIeTDH/7woRbQtmUbhlFyxH5Qsm3Z/nb982QYBgDYlr1o0aI5ZTf/6bx581zX9Vv8+ff+8qVzbHq30tN9T1D17OeZvn0B7fds9HNLAOAvf/lLIBDwvXl1dXUgEDj//PNLR7rv3cBXkQASOIYIHLCALj9G03ZN2hK1cCso6dGnjp/XTOuNc5DNwEiaSt6eHfD6Anjyr3D7zfDFzwyeMXP56a1vzFBWtopvJLnVKW5jkt0WZ3ti7IDKpkU2294GPK+1zwCGMxnOZnnHv4+qIIqOqoAsgyqBIoLEOCoDMc6KRoZlZnNrtEPi5rYn55537tIbfzT0s7v6nn0RNm6FYYOOEQNyGlgauHlwNXD1YttDy6t29n108Xs+77s9y8vW9uOk/emxArqUPV0kgI9IAAkgASSABJAAEjiOCaCAPo5PLh4aEkACSOBEJJBOp31L29vb+973vpfGXHi3qqqqWu9Wirw47bTTNm3a5Bth/340HtkdFQnvEOJbCll/o6XdKN+H8ul3uBtlby+rzhtT9Vw+v2zxssny/fFLoa+++uqSzSeEVFdX33333X59d6lWumwFOIkEkMAxSeCdCOjyTxZv2p9R7mQtGjldmm2Ba4JjgWPSmmhdB00HTYO8DnmN9jnM52BzF8yfCw/+JnfzjTs/f8nKs898ZWb7i6eevDIRXaEqGyR5Eyd0s+wuhhsSBF0UHZ5zBNYROVcUoKEhK/BuVIWoDCIHMgtRDlTOVPmsyg2pXJ/K71LFzTFxY1x6My6vS0SXnfnu9Z/+1O6rvz78u3tgxQJ45RkY6QUjA2aeNjx0bDC9+u4RDbJm6fz6DWkN0x5xaSF1WQNDF97y34XSWnACCSABJIAEkAASQALHBwEU0MfHecSjQAJIAAkggQIB3z6n0+mZM2f6tc9++bOfoTxlyhQ/avnTn/70yMiIX8w7ofw9bECPUQFdqoOeNWtWTU1NdXU1IaSurq62tnbNmjWO4/h4DxtG3BASQAKHjsABC+g97bMDflGw4RUIa15HQGNUQNM3uK5juI7mOjnHzVmQs2gKs2W4QIcf5eEdKs330KCvlyrgkRFYsQL++Ee44+fwjW8NXnTxZoZ7SpLmJhMrWpJvxpRNCWX79OTQydM1me9T5WFZGOEiaSFiqAz4I8rSCTlMmx9GI97wpuWQITQP8qEtYmhNq7Ty5NjrKf756erT7z7p2U989PUffnf3ffeYTz8Nc+dDJkd3a2AEhvOQt+hx+oXRep42KASg+R4AkM/SMnB/eMeBd0gACSABJIAEkAASOP4JoIA+/s8xHiESQAJI4EQjkE6nZ82aVR5P7DfKmzJliq+hr7rqqlIBWsk+l2dxlF49DOjKy4r3MX3w9qSkPvYxMfHWynfPX8I0zZ6enqlTp5ZoV1dXn3baaRO/H+ciASRwbBI4uALaARq/MdEHEA2I9oZpg25Dvmzo3nyaH+SHeFg2ZHMwOEgri22HLm3Y0D8IQxlaK205MJKDjZvghZfgj3+CH/zbrisv2/xPZ77aGn2hTX11ZnL9zPjmlLgjFh6OhvOxiBFn7HgE4mFIePfxooNWw6BGHCVMGx5GuXxMSCuR3W3qcELsEZq7pHBXjN+WlLfK7Pr25GY2vDARW/KpTw5f8x24/1c0zPqFZyAzAPkMLYA2vTpu+tWdW2hRaBc1dCmW5EhdHeXn4kjtA24XCSABJIAEkAASOL4JoIA+vs8vHh0SQAJI4IQj0NvbO3PmzJIP9QMiAoFAac5ll12maZppFn4pjQK6zIGULMTEl025gPYB+qZ+zpw5Jbx+gfm111478SpwLhJAAscggYMqoJ292WcHLBvMsQ6aamgXdG+YXoQ9/RyyLdexaZCFN2noVsaws17LQHNM2IXXKdBxqfzVM5BLQ3YQFr8Cz/wN7rsDrvumddF52957ckcLv7iFW9HKdbTy3a3c9hTbm2CH49xIlB+OciMz4tAig8q6QrMVFyApQWSqxjXQ0mna+TAEYjO0ynRajkB46rAQHhDZ3RK/XZXWN095ckb8uaT42Gc/seqqy1f85j7tz4/Apk4vVMQEwxumCaYFtj9sWs3tA3I81V76UN7bxFtdTePeN3HvxPKF3mqF+DoSQAJIAAkgASSABA6EAAroA6GG70ECSAAJIIGjikAu5/3yGUDX9YsuuqiU+0wI8Uueg8GgH8fx4IMPjtvzcqlaPj1usUP9tLTpQ72h4vp94VB89o4fb7jhhqqqKl9DV1VVNTQ0LFy40JfUjuOM65r4jreGK0ACSOCYJ1AuPYslwIXPJe/z0GuX6jdNHb0vfFKOPfhxa6IrG53lehXHtmd4TbAN2kjQ0MHQwMjT5bKDsHk9rHoV/vRr+On1mS99cv15ZyxuTyxMxJfHoqtjykaJ2ZKU062qkxQgJUKLSHVzmwKtEqSEQlhHkqPzkzwtl1YjVowzYrwW54YT/O4ktyXJbU7ym5L8xhTfkeLXp4TV06Mrzj2r66rLtOv/De6+HR75I7y2gAZbp4dp98W8BppZKPTOmmCA62WUQN4pfnFaPH7dps5+9OY3Nhw9fMcrNjccmlyiedOUxp5q249AKdAfXV2J4ugsnEICSAAJIAEkgASQwIERQAF9YNzwXUgACSABJHB0EchkMn19fVdcccU4+xwIBPx44oqKigceeMC3F+W7XjK/4ybKlzkM06WtH4ZteZvYQzW8sw07jnPOOef4Arq6urqiokIQhJGREduysRvhO0OL70YCxyeB/4+9N4GToyr3/mt6mC1OkpnMdNde3dXd07NkAUIAARX1KqgoILuARDb/cH1xX1AuuFxZFFS84AKIF+KGvCLiwk4gCQkJkz2ZJJN9m0wye2+1Vz3/99TprulMQkgwCZPMU5/z6TldderUOd9TkO5fPf17AnWzqD4PTzP4/+F+K8PtDrq2336I34cNnkPDpAF08HIAWXBzsGcPvLkE/vBH+NE9MPPq/ve/t0MV5wiT5jbH1iXEDdHwemnSxmapL8Wnk2xObciK4wfF8YOx+nwz5zVzkGRJSUS8BGvFI2Y8YhJh2neUpq8q66i8FuN7E9L2pti6VGJZc2JBKvnChz80/6orV9x+254HHsi/8QYsfBPSOcjoZJ6DWWLcsWcAbK/goh2kyjUdsCziQ1KqvDskFNx1iBkJVZ/zfmVYgCai876lgLR0cfZdn4Pmjg2RABJAAkgACSABJFAkgAJ0kQT+RQJIAAkggWOWgGmaju1cccUVpUYQgRgaCoXq6uqefvppYhW6V7QYmfB+hYmj6QH9LlE/zAI0AOTz+QkTJlRUVASi/6WXXvouzQ4viwSQABIYJrCf/8+74PnFtcHQfJtm2tzXZD0gOq9mkryCpkl8qfv7YPVq+Mc/4Re/hi9+ueviizqbYi+mom82K2tT4uYkt7WJ65osp6fIRhvvpSIFL2mV9RTWlFlX5EBkh4vAegJrSaIhiTmJH5D4PkXuicV2NSV3phKbo1KHGFkc45ecPGVDUlp06omrrp+Z+dFd8MsH4ZWXoLMTdu6EdIYoznmd+HhYfhw08dX2Y58dcC2AYnF9c2zdhbwLeSDatb+VKsxEyXb9QzQ/JM2eiLpzARX+QQJIAAkgASSABA4LARSgDwtG7AQJIAEkgATeZQKXXHJJYAERyNDU+rmurq69vZ18wyZZryBwf6Yj3o8w4e96l+dzxC9/OAVoy7Io25deemmE6fasWbN0XR8Dgv4RXzC8ABJAAu+YwL7/n3+rrizL0nU/5LikheeCZXm2CwZAzoGsSTIc6gZs2gDP/h0e+SXc/i24+tKuM09+c0br4lZlWau8tlnakpC2q9JOReyWxV5RyAqCKfAgcCBLEFPIayRi1tXlmuIQlYALm5Mm5hIqxGOQUCAuAVeXi7wno7JetDHfJPWpwubJyU3N8cUy9/fTp8+58vLOb3y1+957MrNfhFXLYesmyAyRIVkOWC7oDnHc0D3QAUxfjPYDogu2HmRmXtGno+DaQQVo02+OAnTJ2mMVCSABJIAEkAASOEwEUIA+TCCxGySABJAAEng3CLiu69jORZ++qKqqimEY+sowDHV8Zhimrq5u7ty578bQxtw1qQZ966230gcAoVCotrZ2woQJIxT/MccFJ4wEkMAxQaAYP0ysLhyqz3p+TkA/pNgjscMWMeooKZ4v8nq+2usQ42bdgJdnw69/3ffje3dfe8OqU099bcqURdHoG5HIYkXZKYv9EqvxjSbf4MoRSCrQGgdukqNwEOVJJTzBjkx0RJa8jQmgcsXCeipnqbymCkNJsTcldaXkLc3SpmZpS6u0oVXuaFOWvH96x8XnbfvGF+1774JXX4HN2yBrQEYD3QbTd+1w/CBnojGXBDebpp3NFpIoWJaja6Zpmq5re8SaxPWzPjpUvj8m1hAHiQSQABJAAkgACYxaAihAj9qlwYEhASSABJDA2xDwPM+xnWuvvTbQnSsrK2kcdG1t7bhx4+rq6hYuXIgC6NtwPKyHXde96NMXUQ2a2nGcccYZ+0YUHtZrYmdIAAkggUMlsM+vQIKgYHpk2B+56NZB1OhhawuLuF/kLUj7Je+/JeHGORsG80SYTvuB1Ht6YdFi+Oe/4N574T9vdj9wVqfMz0tIHXGhMyFsSghbEvyOBNcdjewW63fLk4aiYSMadmKsLz2zoLJ+nkNaYSHOQpzzC28nOTfJQioCKRZSnJ5ih5q47iS3NcGvnNa2TJb+MW3aC5dc1nHLl7bfdffgn56EV+cSXd2wIZ0n1tKaRWKliX+0A44FnuVr7h64Nji2Z9mG65ooQB/qXYXtkQASQAJIAAkggbcigAL0W5HB/UgACSABJDCqCdDY52uuuSZw3igrKyutt7S0zJ07l7pD0ODcUT2f42hwmUympaWlNCD9jjvuwCU4jlYYp4IEjgMCI2VmX3/de16+Bk3aecXix0b7yf1Ifj9qr+xA3i+6A6ZN5FwSYJyzXWq37Hqg6TA0RHq2bdA1yKZhSyfMfQEeud+54yt7rrqg471tL0+Jvnj2ieumqxvahG3J8M5keCjR6CYboFDCEI/46rMvQKs8qLyr8i4Vo5OcG4+YUl1arOuTJvUKdTsaJ3bybGc8trU5sb0pvikurRUjS8P1ryviolNnrLvsssFbvmz99AF48hlY3kn0aD0DTgasLFg5YiDtOuC6puvlXdd2XXe0RkDv8whh79XDd0gACSABJIAEkMCoIoAC9KhaDhwMEkACSAAJHCwBx3ZmzpxJFeeqqioa+1xRUUHr06dP7+vro31RqRptiA+W7OFot3z5coZhyv2NVjZs2HA4OsY+kAASQAKHhUCpAE1MN1wgafz8UsjmR1sU1GfX16CJSk3b0FfbP8t0ia0FcV12QU/ne4AEGmf3HiXJa+jHT/u6NLVc9i+Q6wE3AwPbYPk8ePJR+N5XjEvOWfepD2xuU5a0SZ2t4rZmobtZ6E6Je5Jib1Lsj4uDcTGtillV1H0ZGlQeEiI0KZCQQGzMhycMTJrYw0fSiqDJfF7hdJIIMWJIYV2M6BKXkcVeRdk+eeqO5ikdidaFyabnzj9n4c2fXf6j73Y//lDmzfmwfQuYBhgG2LSYYJvg2CQ42temAxSloPaDrpRA0Ya7YG7iy/0jch6WOIOUnlmoF1bDP7E0ZeKBz9pPR7gLCSABJIAEkAASeFcIoAD9rmDHiyIBJIAEkMA7JODYDj3zhhtuGDduHMMw1dXV48ePp6bPNAPeiSeemM8XTC1pY1Sf3yHuQz+NLpBpmrNmzaqqqgqFQnRpZFnGtTh0nHgGEkACR5TAsNGGn5jvUK814vR93+7boUd2UbsPajYd6NK+17RrEdnX9JXf9evgqSe1++7puuTTCz589uvTT3x1WuuClNqeVFbHpQ0xYU9UAIkDPgxsg8M2OFyjLUUcmbNlzhQjekyymhPQpEJMMhSOKNEx3ojxll/8PXxW4dMxvjchbU9K65PymqSyPCm9wU16/sTUos9c1POjH8Csh2Huy7ChA4wc5NPgOWBZYFiQM4jnNfWVNjxTd3Oak9dtL9CDNcu2/cS/JAMwEa4dv1gOGH7RHMi5kPeL7iv45AFAAQ4F6fqgCLAgR2KpBbfpa/pBysTgyvsyxz1IAAkgASSABJDAu08ABeh3fw1wBEgACSABJHCQBKibs6Zpt9xyS2VlJcMwNAK6rKyMSs8Mw1x11VWDg4PkC2vxq+9Bdo7NDhcBx3Yc2zFN86JPX0TXpaampqqq6rrrrjMMI5sdERh4uC6L/SABJIAEDpUAVToP9azD074YFEzSGXhgeWB4oHmgOWDYnq1Zrmb6iQ1NyOSJu8dAGtatgxdegId/DV+4eegTH9syuW1tc3KrGtsgiet4tlPkNyVi3c2J/qZor9C4g63bJjbubpK1JslIyXZSsFTOIMkMWU+NgBIuKRGQWVfmbD6cZydl5YihCmaMSxNhOro2GV3aFJ3bFP3Xeecsv/zSjttv6330t8b8hdA/SIK6+9IwpIFmk9HnfNtrD6A/Q2LCraJCbIJXjKU2bWJDrdmQCwRoP60jVZOLIvJ+lHwXiMN2FiDtv+b9vovtC6HYh2ddsBckgASQABJAAkjgSBBAAfpIUMU+kQASQAJI4IgQMAwDAJ588snKykoaV0vtHWjKu4kTJ86cOTOfz2uaRn4B7Tc+IuPATg9IgArQALBnzx5VVenq0ESRS5cuxXU5IDw8iASQwNgiUJShqQZtecRF2nKAhBI71NrD/9mPBUScppsNxHZ6SCeWH7v7YFUHvL4A7rvP/vpXhy65cN0H3vtmS+I1VZin8u1NQmeK35XkMi2C18x5KU5PslqCNRKsEwtDjGrQRH0G0S8CBwIHrc3QlIBJ9TrPDQriblnqjkm7JrcO8GxnMrG9oW7p5OZuVVmfSq459dQNF1zQ84VbnJ8/CH99BvbshswQ5HKQyUFeh7wJOYsozXkXNKDFNcExwTKJDG0QTdkbYcRB35YabgT3g+2rz4P+q+6HRQch0kEbrCABJIAEkAASQAKjlAAK0KN0YXBYSAAJIAEksC8B0zSffvrpysrKmpqaUChUXV1NxU0aZjtz5kwAcGzHdV1d9wOx9u0C9xxhAoFHCg2C/tvf/ha4cIRCobq6usCb+wgPBLtHAkgACRwDBIoCtB8H7TmeR6wqgshey/HylqE7Fp0JtaKgQrTnhwSbXiH6l7h6OGDrYORh1zaYPwd+9yj87Edw9SV7Pnz6+mZhUYu8vEVeSl6l1SlpfULYFue743xvjEsrnE6MO1iXa3QbJ0G4EXgeJAmiKiiqzXLZhsYBJeo0JUDk9ZgM7CRPZEFgvYb6QZ7vF8TdorxDUdam4vMV/i8nTXn2kouW3n7bnl//2pj9GnRugqwGWR2yBmRN0CwS4635GRsLttjUioQabpBdhWjoot02maBvHe26hQjovN+m6GRSOPEYWGscIhJAAkgACSCBsUwABeixvPo4dySABJDAsUHANE2qLP/2t7+tra2lojPDMDU1NdQDmmGYr3zlK5lMhlhrlmzHxvSO91HeeeedwaMChmEuu+wyukxok3K8rzzODwkggSNNoBgUTa/jEXNpzyOFhBB7YHtgWpDNwp5e2LETXnkJfv3g0I/vHrz+cx2nTX9uSurFaa0LU7EVCXFnUkirfE6OGHyjzdUD10AKG3FF0VGijqp6sZgtSlo4MtTYmI5EdJ5zeM5heYflLVoEPhfld8X5zXGhMy50JIUVSXFJUlqUlN6IRl479+wdV1869MPvwqO/guf+CZs3gmMAiYHWwMoRg2m7oLGDSQRostEoaGqXbYKjg246OYecQzbPHS5k2rghASSABJAAEkACo5sACtCje31wdEgACSCBMU/ANE1d1x3b+c1vfhMYPVP/jUDWnDVrFlUzXdct0Z/xK+mouHt279595plnlhpxzJkzB9NCjoq1wUEgASQwegiUGh+TUVEBlibZ80dJtdi9Bmz5Iq4BxG+5dCOh0r7+7Hq+WbLhge4Qj+Z0mkjSuSzoGhGm35gPc1+FB+6Dr34BPvq+bUQs5pYmpfVtia5pbf2yuFkSNnL8ep7fpMi7orEeRekVxUGezfIRU2AdnvN4FkiJgBABYh4dzhWLFm8slnCuWcjJk7qS7PYWZWNzdEUq+maL8vLln1r95c9v/p8f5//8O5j3KnTtIMYceQPSeWLfYRQtpA2AnA0ZP+2hTd1JvGH1eTjvYSkArCMBJIAEkAASQAKjjAAK0KNsQXA4SAAJIAEksA8Bx3Yee+wxaiIciM6BoHn//fe7rmtZluu6pmk6thNo0Pv0hDveBQKGYXR0dEiSFAqFaOrI0047bWBgAADQKeVdWA+8JBJAAqOTQCBAFzwlaNo9HSDv68u+FXQQFVx4wOoAWC5YNnHtIEpssXiuv8cDSGt6zrB12zNdcpQkSLBIxXagd4CEDg9lSMS0ZUIuDYP9sHUjvDEPnvgd/Oxe83NXr/7UJ9qnn/RCTPq7Kr8Wl9rjckdC3KnyWjTsyJNMqdGWw06hRCw5YkTDtFjRsKM2eGoDkNewIdUPNgmaGsnEw0MJdjDJDSX5viauK8ltTvKdCX5lQlgcZeefNnX1ZRcOXv+5of+6HWb9AWbPg+4B6M9B3vJ9SQJEVIAmyRsNjyjVgWfJwS0t7WfftiX9+8Hk6DG9LyPcgwSQABJAAkjgHRJAAfodgsPTkAASQAJI4OgQcGznkUceqaqqCrIO1tTUVFRU1NTUVFVV/eY3vwlMhy2LhIAF6jPG2B6dBXrbq9AVWbZsGX1mQNfxyiuv9DyPmqugF8fbMsQGSAAJHP8EAvVzPwI0jXH2VeegGSFChGbbLyMEaF86JbqsYdmWr10DQF63AcB2iVybyQ/aoBtO2o+hthxis0xOIkbSFhga6HnQMpAZhD3dsGs7UaX/9DjcoCdR+gAAIABJREFU+rX8Zz6948OnbT6lZUOLtLJJWNHEdzRxnUluY5zfGuV3ynyPzA3IbIYo0Y1etAGijSA35Btr97TGQOWsSO0QP8FQGkCNQGsMkhIoERDq9BaFHFU5qyVmx5WeRHxbMrm+qXm1Ep87fcbiT35q4+c+t/Und6afmuWtXAQD3WBrYBtg+zkNXQsKxSbjd3336KIoHWjypXdQcWexUeFYQZguPVpaL+0B60gACSABJIAEkMChEUAB+tB4YWskgASQABI4CgSy2WxwFZp1kGqX9fX1DMOUl5dXVlZOnDjxySefDBTMoH2pBl26E+vvLgHTNH/wgx9UVFTQpZw4ceLDDz/s+jqIZVn7Xcd3d8B4dSSABJDAUSUQKMuF6GYqfdq+EYVfL8ijew2qmKlv/yHAB3wQWyqtFk/3XT5cr6DhEjHXAZIV0QbH8ovpezcDpPuhYxnMfRF++6D3g2/2ffaCFWefMjepvhaLtUflFVFxoxDZKUXSzVFQWFuKZPmGflXUJVYL12WliKdwIIVBlSEqArHyiJgCZ4iiIwqewLt8xORZXeA0UcgrMimSko3K6RTX18rtauM624Qll3y0+/rLe269JX/P7eYLT8PSBdC7k6AysmBq4JgkcaFrgWNmi8kKfW6ELRX4XdPRNCtnuWZx8vQBtgOeBZ4BoJeUQl7EQlh0QK50yYL6XuuDb5AAEkACSAAJIIECARSg8VZAAkgACSCBUUegt7eXfm1+6KGHKioqJkyYECQbpPJlbW3tokWLHNuhCmYwgdLw5wN+8Q7OwMrRI6Dr+pVXXkkfIdAFbW9vp5cPwtiP3mjwSkgACSCB0U7AHaVGEIHY6oKZBisNzhCp7NoFbyyCx2fBXT+Em2+yLvn0YHP8zcmpVXFlSVtqbbhuocyvbY7vTqr9itDPN/QmomYiascUJyo7kkDUZ1EAgQc+4vJhYiotsiBGQGCB5YCLgNIA8XpINEC8wUqGB5q4rjZpa6u8tklc1BJ9/aTmeadOfeWy85d/48u7fv9bmP8apHuJ+JwfJMvs0iByP1zctEC3wXDALGj9JPzbcD3b9TVoCATovO9/kgcwwbNJuHkgPQeV/T0VOGRLkNF+H+L4kAASQAJIAAkcBgIoQB8GiNgFEkACSAAJHAkCf/nLXwLbDao70ySE48aNW7VqVWC4QSulgc+BDH0kRoV9vjMC1O55YGAg5G/U0Xv69Ol0v+u6mqa9s57xLCSABJAAEjiaBEhYtAWWQUKMiXbr+uHGDsl7aLqQM2AoS5TzvAG6Cas74M034LHfwr13azdes/HTn1g7tflVqeH5JnlJXOhICNsS/ECcN1XWi7EQ4zyFNaVwnhTWkDlbZkFmfSXaf/XfujJnK5xOA6sj9Xta40aTklbY3VLDNpXd3izvnBzvnt7c3RbrnBJfeekns5dd0HPP9+ChB+GZv8K810gmxqEMDGRhSIOcS0Kd8y7kHOInbXvgeESG9gPPTSI90+LaUCjU9cN/W7Ddtl0yb90l3eT9/mjE9NFcE7wWEkACSAAJIIHRTgAF6NG+Qjg+JIAEkMDYJPDQQw9xHEcV5yDxYGVlZW1t7apVqwYHSURToF3uV33GCOhRdefQ5wSu6y5fvry6upp6cZSVlV111VUAgBHQo2qxcDBIAAkggbciQNRnm1pMF5q4DhiGkc9nfNGWCtKF0GLTJrkZbIsEEGtpMLOgD0K2DzqXw3NPw6/uh9u+Dhd/suu9J65OKYtT8sqksjIhrVKFlSq/RhU2xoUdcX5PnBuMcVmF02XOFjlX5G2BtQTWkXhPVSARg6QCcREUFuQIxCKgsqCEQW4AsZ5UGscPcPVdfON6hV+RiC1taZqfTP7j/e9/9ZqZa7/+rW0/+8XAi6/BngHIm6AZoBtgGsRdmmjrlj8h2xfZizo7SYZIlGgTvII2XVSfSwVoG4Og3+r+wf1IAAkgASQwZgmgAD1mlx4njgSQABIYXQQ8zwtimR999NHAqGH8+PFBffLkyStXrjQMY9+ho9y8L5PRtodGpgPA3XffHQqFKisraWD7rFmzMPx5tC0WjgcJIAEkcFAEAg8K3z+6YLA87FVRNLmgnhV2IVsgcZQ2wbLAssG0iSGG6cCq1fDyK/DLB3M3X7/20k8tO+3El1XumbboohZpdZOwSY3sirFmUiJ5C2lYtMIBLTGBCNBR31eanwRiYyFiWmBB4EDgXZE3RTEtiv2y2CtL3TFpV0zeqUrbVXmzqqyLKSvi0fZE9PXPXWXc+jV45Bfwj6dg9VIY6gFPh+wgGaqfsMDn4U/INmiMM3XotlwSB04OBM4cQeWgGGIjJIAEkAASQAJjgAAK0GNgkXGKSAAJIIFjgUAmkzFNM5/Pb9iwgSYbpNIzNQsOhUKJRKKnp4cGOx8LE8Ix7p8AfVRw/vnn1/hbWVlZTU1Ne3s7jWff/zm4FwkgASSABEYFAaqsFocSiM577fb8mOGS9InkX+5CoQ1pPLEv2FLzCpIJ0LBJt65LApDNLAmU7uuCxfPgqVlw+zecqy7efe4HuqY2rY3xS1LRDoVfFZc2NKvbm2N7EkJPlB2IcdkYm1c5S2FdmSXatFgQoIkGLQhmofC26B8iBtMsiBwQow/OVPisKvSRmGuhMyEsPTG1JMo/M2PKy1ddtva/vz/4yEPmSy/C6pVg22SEfX0wMFSAYBiQyxXqjk1UddvZS4kuwsK/SAAJIAEkgATGNAEUoMf08uPkkQASQAKjjcCf//znUChU7m+B73MoFJoxY0ZfXx8dbRAoPdoGj+M5SAKe5/X19VFnlcrKyoqKijPPPHNoqPht/iB7wWZIAAkgASRw9AgEQb0jKsEIXCjYKRMfZIfENNtO0b6CGlrQV2pdURBpSzP7AXG2cEwwNbC0oomFSzwx8lkYGoK+XsikoWsHtC+CR36V+8F3d33uqmXnnj2nSfhbSpzdprRPi607Kb57Wiw3WbGbJVBZj3pGi7wt8nqxmMTHg2rTfny0wNtEm+Y0rnFIaByQw/1RdijG96tCnxzp4hu2y5EuJbKDrVvdMGF+PNp+9VX2J87bds9d8MffwGv/hG1rwKD/fDlg66DlQbfAT1k4LEMHjA5npajp+7HXB+q4dMGK7fa3r3gM/yIBJIAEkAASOBIEUIA+ElSxTySABJAAEngnBF5//fWGhoaamhoqPdfV1VEP6EQi0dfXNzAw4NiOpmmWv72TC+A5o4aA53kbN26kC00TEn784x8fNaPDgSABJIAEkMAIAqWS5ci66wcu+yn4si7knYIA7VIBel/12QS3IEAHPfnWFkZG94hNh0e02+HNoWbMDhh5I5/XXCJse8RX2jJAzxDde/s6ePYp+NV98NUbBi/92NYzpiw9rW1Nk7QiIa2NS50xaUNM2qRI2xSxi7hwCGmZz4u8HsREC7wtSa4ighRxIhP0hnH58HhDDhMLabERpEaQwyCFfesPXuf5/nhiSFV2pKR1bfKyqbEF0xIvXXLeyi/etO3XP/f+/jRs2wb5PLGTtqjNiEVyNroW8Y4GWgKj7KJDyfBch1XrvRCUNNjb6iOwQNm7RakdiL86Ln0t3V+sjzwT3yMBJIAEkAASOBIEUIA+ElSxTySABJAAEnh7Ap7nObZDi6Zpzz777MSJE6kiWVtbyzBMXV0dwzAnnXRSV1dXkMLOdV3HdlzXRdPnt0c8WlsEjs933HEHwzChUIhhmLKysscffxwATNMcrQPHcSEBJIAEkECpAFqg4cvIblFetYuK515iaiA1BxVychDGW1oPdhb02ZHvyQg8onmT4hB51zHBMUhx/VfLAFOHBa/DX5+C++7Nff1rPed+dPHU1jmq/Fpr0+qo1BEVN0v8donbrYi5mOjFJIgJfhrDRoiFQY1AkodmGZKCJzbmpbAe462E5MRFKyrqkqiJQl4Sc+RcIRMTh2LiQFzqjUt7klJ3St6iCktPblt57tlbrrhw5/0/hj/PgvbXYedGMAbBzoCTA/AdpA0NcnkwLY8qzZZDZHXbMw07a3lZAFczHMu3JaGUXWp4QsR52w82pz7U/tlFQkW2xMjEz45IHU50FwqleGJwbvEMvK+RABJAAkgACRxhAihAH2HA2D0SQAJIAAkckEA6nQaAxYsXNzQ0UPONiooKKkMzDDN16tSurq6enh7XdfP5vOtvNJddkNHugN3jwVFKIHB8vuCCC4IkkzU1NStXrnRIbBvgKo/SlcNhIQEkgAQKwvIwCKpiDr//N2tFOXVYnqZ7Drpbl7pQe2B7JD+g5UJPDxga7NwOL78Ej8+CH3wfLrlkx4yT28P1LwiRBarYkZA2R7nNKr+zRe6dlsgKdTuikd3RyG65Ybcc7iWmHFxa5XOqYKqCrfCOxHuiACLvFw4klhQlDNIk4CY4XF1ObhxMCD0t0W2T1XVt8WVT1Lnvmz7v0vOWfuuW7p/cmX3lOdi4FoYGiLVIXoP+QTI3yyPSsuWB6VdKqdIZ0T0OmH6wue5LzHbBrKQYTF08K3geQC1Pgle9qEHTE2nzA0RbHzR0bIgEkAASQAJI4IAEUIA+IB48iASQABJAAkeewOrVq6urqysqKqj5BhWgKyoqZs6cSWOf3eH088O65JEfF17hCBII1jSbzY4bN45GQDMMk0qlstlsPp9HAfoI0seukQASQALHNQGqqlK7C9MDzYacAVmd+FJTndYB4tScyxP9d+06eP55+N//hR98d+jmG3ec+x/tJ7XNVrgXUsri5tiapLQ5wfUm2LQayajhXDxiJiJekgeVhygPigAK7xeOpD1UOLIz6u8UIsA3mmLElFlN4bNxMd2k9CfEnVJ4AzdxRUtsi9ywVOVWnDZ5/dWX9f3w+/DwL2Hua7ByFWRzZJADWTCAFB1A80jMtAngm5nYFphWweTE9MVoerAoKAeScmllWMGnwnRpBPRxfSvg5JAAEkACSGDUEEABetQsBQ4ECSABJDD2CGia1tnZGQ6HGYaprKycOHFiYAA9c+bMgEc+n6d1FCUDJsd6xbIsx3aos0pnZydNSDjO3y655BIUoI/19cXxIwEkgATeRQIukCDinO7mSD7AwmYSPde1iV2HbbgOiTL2wHFJqkTDIIUad+SzJNXhhrUw5xV48Gfw5ZuNT39s21mndLREF6Sk9pS4qklcmxA3JKTtqrQrJvXExCFFzCm8QwRoFuQIiCyRpFUZmmKkxETgwxBu8NgICBwIEeAaXbEREgK0SNAkQpzfI7NrmmNrEsoiVX6uuekf537kjS/855Z7fjzw+yegfSl090LehLwFuk2EZ90jxfRVacuP9S4EMFOVuVR3Lq2XaNAeCbO2PM9BN7Pi3YF/kQASQAJI4IgTQAH6iCPGCyABJIAEkMC+BKjyuGzZMuq8Qe2ey8rKqB3wF77whX1PQVuG/TI5FneWPkigJuB33nlneXk5zUbIMMwjjzwCAPTQsThBHDMSQAJIAAm8iwR8wwrPIQbRNGp42I165KhonkSb6LiODbYNpk0CjE2TZBGkZZBYhcFQBl5+Gf72FPzqQfObX99+zdXrTzlpdkvTnLaWZQlldVzZlpQHVFGPcQ4JjiZB0J7IuQJribwty54SgwkTM5MadUGCaAwmTsxERRJA3TghJ7GGzOZkNhNlB6Jcj8rtUvntKr9V5bfG+Y1xoSMpLmlSFpx/zq4brtHuvRtefhG6usA0YE8vCeLOZImGblpkkM7eXhok2YZjWrbmumbBqQM8mkWj9B/ioy1DD0vhI1ej1F88EM/306hkV9AsqJQcxCoSQAJIAAmMIgIoQI+ixcChIAEkgATGDoFsNktjnwPNsaKiorKykmGYO+64AwBonjpqB1yKJfjKVLoT68cWgWARPc/Tdd0wDF3Xr7jiisD7m2GY9vZ2+pSCvh5bE8TRIgEkgASQwLtIoJie0HbAtsClYcJUah6WKfeNF/btOQoN/CSHjm8hTdL++ekSDZeYeNh+6LQNMJiB3gF4ZQ68+BLcdQ986Ytw/ie7Tz91rSLNj0WXNCVWtaQ2JJMbo+oGKbZZim5X4r2xeFqJZUUpJ4h5SbIl3muo0wXWE1hPCoMUBrnRL2GINgwXtdFJ8mabYsQjfS3SzpNb1qnSSyn1n2ec+srlF7ffcfvuXzyQnf0yrF8HQ76XtOMQVTpvEPNrADB0EtztWCT823NJITqvL8+Tt/52VBcLBeijihsvhgSQABIYLQRQgB4tK4HjQAJIAAmMEQKWZWWz2cWLF0+cODEQHMvKymj9l7/8JQqOx/2dEAjQNA6Lztd13erq6pqaGnozzJgxI5PJHO2wrOMePU4QCSABJDAGCPgiMpVY3RECNJWhg9e9I4aLaDw/XNjvxXHBtJ2cnjMskwqnju/vQUwwAHqyxOKjX4e+PGRsYtnsAGzuhgXL4HdPWj++v/eaa9vPO3/BSTP+KUf/Ek/OiSeXJhKdiURXTBngI2kxbEd5kFiLlIgjRQoy9LAS3QhyGKKNXpwDtdFqlaCZc1pEI8EOquHdKru9Rd4eC685fXLXiYkNTcKyKcnVH/tQ9003eHf/EB5/HBYugl1dvnt0kIPQAo/K0MG/xAcvQNP5H/i1iPBAf9+qB/+c4AlBUDlQV8ML9dZB7gc+H48iASSABJDA0SKAAvTRIo3XQQJIAAkggSKBzs5Oqj6Xl5czDEOzDpaXlz/++OPFJkBl6Gw2G+zBynFDoPRrL52UYRgAsGbNGmoCXlVVVVlZedVVVxmGEUTBB3kLjxsOOBEkgASQABI4EgSodunH+BIXjgOUosrpugUBszgceoBKpcV9hp037KxDdGay5RydiNF+fPSglRmy0xknkwNT9zMH5mxI66SZB6BZJCT5tbnw5JNwzz3wlS8ZF57fNa1tiRiZO7mpU5VWqGKHKnQS2w1ul8r2qZGhKJvxfTk0mdXkiKGyDjdePykOKQ7iDSBNgGg9TJZBrXeTYU+akIvVm2oEEiLEeINv7BbYzQK/WhSXqfLc950y5+rzl/7gm32PPmC/OQ+2rwczB2aemHiQYhL7DscGx/GLC44HLi0l8i6dMplMUIrsCuRoesdCuwP+CXoo4KUd0ZyRtgu2H8BeIigfsOcRo9j/E4UDDgcPIgEkgASQwNEhgAL00eGMV0ECSAAJIIECgYGBgfr6+urq6gkTJgT+G6FQ6OGHH+7r66POv1SgpKbPCG7sEDBN8/bbb6ex8PTeeOSRR6g2bVmWaZpjBwXOFAkgASSABN4xgX1Fybfac4iXKHRDLT727pNI2K7vOj2sd/tJDh23oO1aDlg2WBYpdGdvD6xYBn98HP7nXvtbX+y5/ortbcrzbdLcFr49xa5UuLWqtJ1v2KqwPWLDgNygK74vhzjeaWKhWQC1wUuxcGIM+HED0bAjRIDnQRZB4F2B0wQ+J3EZmRtQud1JdmeS3Z5k16eEtVOjHae2dJ51UsdN1xrfvQ0eexSeew727IH+AcjmIGeQbIeaDbpLMhXavgbtlGAigeVBYsdgP2Wxt7JM9gWx5PRQgGx4v0tCskEHyNLiQt4lweW+krx3h0T7LrlQ0NmISjAorCABJIAEkMCoIoAC9KhaDhwMEkACSOD4JEClw4GBgaVLl9J8g4H5BsMwoVDoiSeeoOoz8SV03X0jZI9PLjirvQmQdEm2c/nll9PQ+AkTJjAMs2rVKtoqCIXe+yR8hwSQABJAAkhgLwIjFMng7V6NRscbi1ozW75RhkFyJu7eBHP+BX94CO67B667bvCT521JJebElfnN6sqpTVtPbulNid2xcFe0YVeSG2gRMpOjeoJNN0mOwAHLgsiDJIDAgRAhptKBm0e0AeR6kCbYcp3lm0rrzepQU3JnMrm+KblMFJ6bMu3Vc85ddsVVq375iP3Xv8PS1dDdSyRf24GcRiK4dR1sk8RKUxdpzyOh04ZJGvhZH0mk+TDqQCwOdrkl0dOlR0l3JkB+bwF678aBEk1789+WdlxaHx0Li6NAAkgACSCBkQRQgB5JBN8jASSABJDAYScwODjoum46nZYkqbq6mmEY+krV5z/84Q8jrogC9AggY+St53mu6/b19Y0fP76srKyqqioUCp100kn0AYbrujQ15RihgdNEAkgACSCBd0bgWJQjqcTq//aL2GJoOo0BhsE0EXnXrYXX58Af/+A9eL91zWWbzvlAR1tsTjwyr1XuaOI6p8R2N0kDcdGRWZAinswCrRBT6WKRw16MhbhEisR7AmvxfE4Q06I8JEX7JblHUnZFo13x+LZE00Y1vkoQF7KROaedvumC84e+9kW49054+VlY9ibs2QG2by3ieqAZkNEgZ4FFlHOiIvv5HontCQlgLlWZC8IxzYHo7ucQWWnX998gFhzkXSA6B2iCnf5tUbrKpXX/IL4gASSABJDAqCOAAvSoWxIcEBJAAkjguCSwdOnSyZMnMwxDw1oZhqmsrKSxz3S+ju0EJr8oQB+X98DBTMr1t5UrV1ZUVFA/aIZhrrzySurNcjA9YBskgASQABIY4wSOCTnSchzNJHbSGd3QLJuaFxueaYJtg0UMrD0iPZMYZCrYumSvaUAuTYReLQ0dS+Glf8Ev7oPbvwGXnr9n+rTVzerSuLJElZZFpY6o2BkVN8riVlnYKfO7Zb4vJmRikiVzdkOdXvuetBIDXvQmNeq1E9KSDJzghhuNxgY9EjFZ1mQbc1wkHxXNpGI3K06bOqiE30yIr7TFX5iaevozly75+tc2PvIb89nnYcsOGNIg74DuF9MB0/EnUHB1hoKRB4mAdotv/Du0KDGXrhetO8VDBRk6uKFLxOh9z6J7grZYQQJIAAkggVFFAAXoUbUcOBgkgASQwHFIoK+vb3BwcPr06VX+RrMOhkKhioqKxx9/XNO0gYGB43DaOKV3RCB49nD33XfTAHnq1vL73/8eLTjeEVE8CQkgASSABEYdgVLxtHRwJfoqDfd1/EjgkiaebzVNQ4V9ndeywLCIcbPpQVcvLFoC/3oRfvrzzI03rb7w04taWp9qbXm5tWlhKrGiKbqZm7SNrxsS6h1+EvBhaJhkyBLwnBOJmLEo1NXlBN7lwqbEQ5MKqTgkJIhyoLKg8qDyWoIfSgg9CWl7St6UUtamoqtSsRVtyXVnzNh2/nl911ydvuuH8NtHYc6r0LkWMmkYGiCuHbpGYrqJlFyyGQA5g4RS+3HSwy7Thg15g9h6EJtsPyNiyUnFsGh/V0Gq9pNMlvIsre91Lr5BAkgACSCBd5UACtDvKn68OBJAAkjg+CXgeV5g/dzS0lJWVkaVRGrvW1tbu3Llynw+T757+NvxSwJndggEAgFa07QLLrhgwoQJZWVloVCopqZmyZIlQYz8IfSITZEAEkACSAAJjDICRZG0kLrQT2BIjCdoAkPXC0wofE8LsntkSHCxB3LM8uOKS7Vqw/VlXADdgC2bYcF8+NPv4Kf3wlWX9H/8w70ntW5R+FWRhsWtqe0i33ni1EGB3Vw/fm1c6eMbu8VwWpyUE+p0sc6JNUI8UiixCCgsKBzEOC/GOTHeiPGazGp8vc7X56VIOib1qPLmmLJCVd5QlRenn/TC5ZevvPHGjvvuG/r7MzBvPmzcAv0ZyNskXDrngOYUK/4UdAtyOmgm0dMdFKBH2R2Lw0ECSAAJ/PsEUID+9xliD0gACSABJPCWBCzLmjFjRm1t7fjx4xmGqa2tDYVCtbW1HR0d9BzP2zsk5i17wgNjgkAgQGez2b6+PurCUelvZ555ZiaTGRMUcJJIAAkgASRwXBMI5GO/EsjQBQG6IEMXcvoFR+2iRTJxSS7tgdgnE1xUiyY+F47/3jRIALJtDUcfk3jkLAz2Q88eeOlF+OUDxj13atdds/6D71swtfmVk1sXyQ3zEuFNqYbdzQ0DqcZ8a9htDUNrI6TCEIuAxIHEEwtpSbAk0ZBETRINkbf5iM02ag316Yb6wXBjPxvp4bjuaSflxeimtsldHLs8pnTElFWJ6MpkfNH5n9p28xcG/ucBeOpvsHw1ZAwy+N4h4jRiu0R6JuHPIwXo0ukW6j4El3iVFILCA1CkQ1oO201Uqv8ftk6xIySABJDA2CKAAvTYWm+cLRJAAkjgqBFwbGf37t2tra0Mw9Ag1rKysokTJ1ZUVCxfvhwANE2zLAsAhoaGaCj0URsbXmjUEggEaADIZrMrV66kgfNVVVUMw3z84x8ftSPHgSEBJIAEkAASOEgCgULqVwLllKTvKy0lzYIEfVSnLQjQ5HJ+uLRLPlZlTCvrBxMXRmFoOnhgWRZJszHsckHkad0kthieA5khIkmDB/lBeP0VeO4p+Mn34Jufh8s+2nX21I4TpfYTxRUnCh1t4gZV3ipFdyryLkXeJSm7Sd5CuY/nBsMN2fAkXWA9SQRFBpEnzh4TxmdFAWIKhBsNkXMVgWRHZOvt8ISh5sRgU3xTVFkiSq9NmTqvqeXvp572/MWXLvrh9/c8+rA2+0VYsxLMPJgamDrxvHYsv9hElR4Wm4uzLor1wwxLoFFlnhpPU0fq4OB+Fyo4SislbUiwRHC0ZD9WkQASQAJI4KAJoAB90KiwIRJAAkgACbwdAerSS1/7+vpaWlpqa2srKirK/Y1hmPr6+tmzZ9NuLMuiGefoa6A8Ykz022EeE8cDt4377rsvFApRGZphmMceewwTEo6JOwAniQSQABIYGwQCXXPfyt4ASo/vfaTw7m0bFM/y1VvisExjje2iyGuCY4BrgKuDq4Gbh53rYclceGpW/uf39lx/07pPXLxiyoyXeeUfavINJb5cVjolcWdcsZpiEBOhcVKOpi6UWE2M6GIjKGFolmFyHIR6R2p04wIkZYhLOVXqV+VeVd4Tk3bF5J2qtDMh7kyJ3c1iV6u0qVXumBxv//BZ62+8Ovtf34A/Pw6vvQQ7NoOtQzoN6SzkdWLTYRYldZrA0Z+86xABn2wuuLZn255pQ97y0paXdiGQgDchAAAgAElEQVQPYPgCfalbSZEJMTkJxH/qfBIcCvy4aYO9nbpLW2EdCSABJIAE3poACtBvzQaPIAEkgASQwKET0HWSUiabzba0tASiIRUQa2pqFi5cWNolCtClNLBeSsCxHU3TAEDX9Ys+fVGZvzEMU1lZuXz5cnxKUcoK60gACSABJHDsEiiVjUvr78aMguuTmGjPAdcC1wTPAsuGjAM9Guzohy3dMGcRzPoTfPPbzqWX9Zz53k3NydVxZdnk5vUSu0SVVrUlNk9N7pocy7aIWpOgxdm80pBVJuVjrBljTZUz4rypCrbKuyS3IecXFtQIKcRymoOkYDWJuaTYn5C2t6obk9HFUf4lgX3yM5/p/NIXt957X+axWdYbC6Gnl0CiVm62R2yvcxroejGHoUcU5aI5ieOB6YLlkn0jzN+ooByoz4HKHKzAiAYoQAdksIIEkAASOAQCKEAfAixsigSQABJAAgcmQGOfTdM8/fTTa2trqQBdWVlZVlZWU1OzZs0a6rkRdOJ5XqBBYwR0gAUrlICu61SDzmQy1EOc3lGJRCKTydBHHcgKCSABJIAEkMAxTSAQfX2p9N2dSjCWkcOwADQAvajd2gA5F9I69Gchb0HehG1b4bVX4Kc/GvzWl7df9qn2D576akr8R0qc3SS9kRI6msUdLcJAs6AlWSMZsVKsm2QhyULcLyoLKgtRDhQeFIEUifezHYoQl724YkTlQZHfKbAbW1K7muIbovIKgW+XuHYuPG/a1BUXXLjrttvgpz+HJ5+GOfOIcYetgeXbdwwOQc4A258N9eCwR1pp0MBna3+R0dRTe988kCPh4PvDRYDef4erN+znrQgE/50HlbdqifuRwOElgAL04eWJvSEBJIAExjqBTCZz+umnMwxTUVFB41UrKirq6+sXLlxI1ecRGjQK0GP9jjng/IeGhmiw89q1a2lCwurq6v8XBH3hhRdms9kDnooHkQASQAJIAAkcAwQCDWi0CdCuA3nd1gxiauH5Am2QzrA0itgGTzMcQwfXl3hdDewMWIPQsx1WtsPf/gy/uh9u/aJz6Sd3ndKy5MTkqlZlWauyqlVe2yxtaha7UkJvUuyPi+moqCuSqYh2LAqJGKgyCBForHN8PdqTBEfkbZmzZc6UWEOMmHER+EabD2fjsUGOX89Ly8Towmjs1eboM++f/uJnLlz8fz7f8cBPh159BQb6QTeIa4dhk1Buy89zSDM5uiOCofe6X0gotEsKyetIy17H8c3hJoCQDzfR/fcX3M9BZf/t3m4vBg+9HSE8PpIACtAjieB7JIAEkAASOCQCPT09rus6tkPDn2+66abKysog8SDDMI2NjcuXL3dshwa00g8rwSVKP7sE9eAoVpAA+d7rR8rfeeedFRUVNBthdXX1L37xi6GhIcuy0I4DbxIkgASQABJAAoedgOc5QKKHbSDmFSSMeH8SeZDiz7++5zeiJhY2yRloO2BT2dcCwyT+GOvWwmuvwv/+1rrnhwOfuXTZWe99dXLL8ydPW55SNzVF98SVPlVKJ2NOSoWEDNwki603pYiTkCHlO03HRIiKJEo6JgHX6IqcO6luiIukObafY3vFyJ5EeFeqcWcqvDUV3piKrGvmOpr5FS3ikvedvOaKC3Z/75vwyAPw6vPQuRr0NGSHiNPIiK10mp4/fxogTWOhbXLGsCRd2nhEP/j2UAmgAH1gYvQTr+d5+Xw++PRLk6YEh2hkT/C9LOiwp6envb390UcfveOOO75923f++5673vehs8/95Hkf+8THZ5x2Gi+JFdVVFdUk4/eH/uPDp53x3g9/5CP/+X++8Ls//P7NJYuDm9wBzzA0wyAWeZqmBV/cRlSCi2IFCYwggAL0CCD4FgkgASSABA6NQJAsTtO0iy++mEY9B469tbW1CxYsoNp08FFpxMeUfd8e2giw9fFOwPI3wzCuuOIKmtBy/PjxoVBo8eLFVJ6mN9jxjgHnhwSQABJAAkjgqBGgyrIOkAVIA8ng5wdCUwNkGjhMXm0/Ntoo5vcr9Ucerrt+gj/Lb03FLNrBnl5wXchkYNlSeOZpePgXcOvX4XNXGaefsiYuvyFzb7Qm1qSUtUlpfUreEhd2RNldSqRf5TOqqMsRS+WBnaRLEUcM235xpUZXrYfkxEJpqoOmSaSkGqGZNZv5wRZuV0rojIffaJZendb08vVX7rjlpo333Nnzt7/A4jchMwj5PImSNl3QTFJsf9IZE/IOmP4s/LkQDTooR21Jju8L0ZukaNt9fM/1cM6Oas2GYdBON27cOGfOnEceeeR73/veaaed9sEPfjD4WWqQm4fECVVWMGUMU0V+rlrYyshuUvdfaKWsPBQ6obx1yuQvffUrS5Yt9f/jdf1HU+Rqwc9YXdct/TZ3OKeHfR1fBFCAPr7WE2eDBJAAEjjyBOgnjOA6VPvr6ek5+eST6ScYar7BMExtbe3q1asNw9B1PVCfqWJY+jFl33rQOVaQQCkBz/NqamoqKipoWssZM2b09voZiEobYR0JIAEkgASQABL4dwm4QBTXLMAgQL//mvf3+BoUjXQevoTrEiW54FNRjJcMgqMLp1A/C9sD2yNuGKZHnD1ofLXpgGmRiGm6ZdOQS8OmjfDKizDrt/aPfzhw87XrLjh3SZJ/plmYO0VZOTW2vYndE60faOaNeESPR0xSwnY8bCfCdlOjXxrcpgZI+EWtg1gdRCc6ar2rNujNgibV7ZqsDor1m6LhzSq3MaVsmKyu4ye9MmPayisvzXzza3D/z+Cvf4HVq2EwTUyuMwYM5EnRDKK70U+zwwBGY+0YiycOnlIMa9DB047SymhEfZTGFHyZCr5YDQwMLF269Lvf/e6HPvShs88+m2GY6urq4IsY/UEqwzDUxY5hmFCICMpMyP/GRl/pl7fh1xNItYwJnVBeVh4KxOiy8lBZeSiWiN/zo7sMQ6OGiihAH6WFP44ugwL0cbSYOBUkgASQwFEhEOjF9GqO7WiaNn36dPqxJvis09jYuGDBAvpAnqaSA4BMJhOcfoDKUZkHXuQYI0AfdaxcuZJ+SB43bhzDMFdeeaWmaaZpHmOTweEiASSABJAAEhjVBKgAnffDnwf916yfhtBP40cFaD+MuVR3Lq37cnRJ5j+/seeCYdmWU1SawTHsrOVl/TBq2yU20mRzHdA12zB95doGj6YOdMAchC0dMPsZ+P2v4KH74JqL0tdebrbIr7dIi1rEJS3ispS4qknY0MRvaeJ2JLjuBNufiGQTYV1tdNQGiDdAioM2CaQJdhMHcp2l1LtqGGKNEG0ApcGWJ2XkSQNKY6/K74xLnYno8mR8UXPytY9+ZPUll3Xe9IXu7/zXzmf/4a5ZDVoWzDw4BjimX4LobreYqLG4uD4TKtC7Lth+IZYmRZmetCeOHjQmvHjW2/3dm/Rw69L9tD58bLTWCuP0BWjXAtf074bi4wxKpnReo3UeR35c+Tz5IYKu6+3t7Z///OenTJlSVhaEKw9LyGVlZaFQiB6iERvBsfITysr9JD3MCWVEZR43gWHqGCZaxjRVhBLVVSzDVJSV+xq0f84JVSeM87PKh04g/orjamurqioibOM111zT19e3XwH6yGPAKxzDBFCAPoYXD4eOBJAAEjj6BKhqHJg+W5ZlmiaNfQ4+4lRVVbW0tHR2do4wIDuA4jzi0NGfF17xWCHguu59991HP0mHQqGamppZs2Y5tkNjMUpvpGNlRjhOJIAEkAASQAKjjwCV/Aoe0H6kMpWBh4XTgxhzoBsW2gYhnMVzgwa0Utwd/A1CX4OGRWNq1wbX8iVgDTJ9sG45PPOE+8B9QzfdsPWiT3WeMnWezD6flNqTQofKbYyzu+NsOh7RY6wZ5+2k4DUJkBKhWQKh1pYnQrwRmjhIsM6UGETG98XYfFzIxsV0XBxMir1JqTsp70jK21LKhmZlVWt0SWvsjTb11asv2XPrV93HHoLZz4I2BGYWXA08E2wDtBLPEt+8xHHBtCGjeb0G9AIQF10XQNMhr/n5G+kEg/nSSsChKMf6keZUyDbdgjd3gIaGnJv+cwKzxO+kpJdRVSWau+uPVi/UvIwFJOvloKnZkHfsTHG8JFC+OK9DugOLHRxTfx3boVqz53k0lIcG3T/77LM333wzy7IMw9CcKMHn4dra2vLy8kBophWqRDMMc0IoVFFeVlFRbFBeyZSVnTCx8vT3X5SUv/Ie5mvvYb6hRr5xxns/O74+QjqvJUEeTDkRqf3tBKasigRBn8DQEjqhPHRC+cyZM9P+RulalpXP59EW75i61472YFGAPtrE8XpIAAkggWOdAM0I57ouDTv97Gc/Sz8G0c891dXVqVSqu7ubfv6gz8apLHgw5htBy2OdEo7/iBKgbuP0l4YMwyxfvpxeLoi1P6JXx86RABJAAkgACRzvBN5CER4t06YB2iaA67lgGWDp4Ohg6iSSOJuH3Xtg6xaY/zr8+Y/ww+/C56/Xrv2srkqvpGIL4vIbk5s6W2IbktJmld06WR1sVdLN4lCSG0qw6WZBUxrSSc6OcxBn/cIBqXMQ591ChYMkbzbLeps62BzrjgudSmTBlMTLH3nf/Buv2XjHt/Y89KA++yVoXwRDacLLBsiZMJAjdd2DrA05C3IG6AYYFknSaNvgevsUX7f2eQcScxBRbvqCbFFlHlarA9sT+rRgtKzW/sdREKDpXFwH3H6tTwfIWAXrbatgawy++fYYEqCp+kxEeddNp9OO7cyaNSuVSlExOHgNLOmIVry3+iwIwvvf//6PfvSjN910063f/NYd/3X7Ky++8uLzzy5qn7Ote2POtnMOgdzZCSer//dEbs5k9m+fu/i1XBp+/JMHyquqK8ZVM2VFh44yhimrICXEMOUMeSWljBSG4Thu9uzZpes7NDRU+hbrSKCUAArQpTSwjgSQABJAAgdFwLEdqj5ff/319GPQhAkTQqFQVVVVKpWinzwc2wnyEx689IwC9EEtwNhupGmaruu1/k8C6e13yimn0JgLXdcx8mJs3x04eySABJAAEhhDBKg0azt+5kALdItou3kLcr7IS1Rqj+QSzGhEmHZ9m4vXXoMXnoX/fQi+9dUdV1+6ekr8H23qK23R+W3KkpTQEW9c3yb1prh8KgLJcIkGzbtx3lYFW+VdlXejghsTvZjkKIIhhtPcpN1TUplmtSvOb5TDq05MbZEmLWqLrmbHv3TBub03ztTv+j787yPwysuwq4u4Xff3g2WRYtpEg9YtcHyRdcSrP7vSuGa9EC/smSRq2nNJCdTpoBKEUY/yG4GOs2A/QmzADQ96BuAnd9tXXLj2J3f16mnyRMGyqCk0Fd+P//Dn0kWzLGvJkiXJZDIQnYMK/eEp/S3g+PHjI5HIWWed9Z3vfOeFF17YsGEDtaczTTOTyWT9xyBahqIzM9ZuC+ycRZJ/Xn7Bm++NbTyZX/vpD863syQDZ9eenhtuvikiceRCIaasqrwQB13uq8/0tUSALi8vr66uPu+884aGhnTdj2T3g49KZ4F1JBAQQAE6QIEVJIAEkAASOBCBUl2P2h1cd9119GNQeXk5NRpraWnp7u4mgQo2cfcLkrSUGiMcTP1A48BjY5tAEIC/ZMkSGvFBP4JffPHF+PRibN8aOHskgASQABIYMwSKGisV1Xz7YGInnTEK0ZfUV7nUWll3c7Zn2i5YJpgmmBroedDSoGdh+0Z4fTb87Qn4+Y/hP6/tu+STO6YkFzYrq5qlTSl5U1LZkpS3JeUdcbkrLu1RpUFVzEZFXeEtmbOliCeGXTHsyqwrc7YcsaJhKyl4k6MQD7sJ1oo2ZuWG3Sq7WRVWpqILZfbp1uQzHzl79uev7fjud7Y+9mjmuX95uSzx4iCjosUXpk0HLAccmt6xNFjYs4n6TGylh405iIBN3/oVqk6P9rshEKDJKpoOECH+r3+xTk4tnqZsPTGx4Cf/7boG2BY4XkGg9xeaOGYfZzr0PtY05DuUZVk333zzvtHNdE9VVVVlZeVZZ5119913r1mzhn41oyse9JbNZske/7mL/+3Ms2DQI09AoHsPfOHGTVPkuVO5FedMX71xJaQHgvvF02y9f0h76aWVn7n0rkkTzmYYnmHeQ0Ke946ADnIblpeXRyKRn/zkJ8F3wGAkwWCC3rEylgmgAD2WVx/njgSQABI4BAL0k41jO9SP7IYbbigrKxs/fnx1dXVlJUlMIYri8uXL02nya8N9DXkPRncO2hzCsLDpWCXw/z6af+c73wns7UKh0J/++Kd8Po+fdMfqHYHzRgJIAAkggTFDgGZBHBaYHYC8B0MOZPxgaM8GxwbHl3AtmvrPz2xXTH5IE965JNshccCggm/xVfdjqLd1w4I34bHf2z+4q/+GGzf9x4faW5tnNycWtjVtaI3vTKl7mpT+uJhuVhx+UlZsMNlJuhRxEjK0qhAen2PH55KCR8ymRS8u6EpkUGF7ouyuOLc9zm9OchubhA0twsYWcX2ruKZFap+izv3MRdv+5z548Kfw4r9gwevQ3wO5tJ/t0CDCtG0VFndYfy0Ki8Or7pFpG4bl2OQz9fD+0VkrPkWgCqnjEqH5qstfnRztPD0Jp0T1k6Obr75wx7yXyehdf/0M3ziCxokH8vvonNwhjcrzvNJAHwB4/vnnRVGkgT5l/kZijcfV1E6cUF5R0RAJ33///QsXLgx+Y/p2lyOKfTbfm871EW4O/Pdt/SeqiydLi8856+Wlb4Afu0z68Ii3i6F7juvBnh3wqTOWnRZ/sVX+zve+8+Qp0z/KhMon1E0MnVBeXlFRVVM9wveDYZhzzjln+/btNALJ9Le3GxgeH1sEUIAeW+uNs0UCSAAJ/PsE8vn8DTfcQEXnCppJmWEmTpy4aNEiwzBo4sFMJhOoye+g8u8PEnsYCwQsy7rssstC/kZ+KRgKtbe3U3OYsTB9nCMSQAJIAAkggbFLgMqXZP40kV0WYBAgDWD70iTVJwPTZPp2JC0/vNh2wXaIKEfCbK1itrs8QBYg50HegaxOrtHfT2ydn/4L/OoBuPWrcO2V+ZNb21V2ztSmVfykhQl5Y1zYFhO7VHG3KvSJjbtj/KDYMCA3ZGO8lZA8Yt/BWSrr0JLwLT4SDZCsB7VOT4YHEuxmpWFlgls9Ob5GFean1Nkfel/7lZeuu+1b6f/5mbmkHXr7SPh2f78/CxcMDXQNHJMM2tJIKHewEUNld/9TDtq8+5XCChbG6bigm/CTH6VT4qpkg6bWmeqEwRZuy7T4nId/YWbSZAlyJslFaBXtSkb9DA+NcRDFfPXVVwdWG6WV0AnlE+vr/vjEE7Rf8qNAh7iwHMTmARgOuVfI9sjP4eT43Mni0inqC+2LQLNgMGdnfctt//53sybs3AyXf2zJDH7NtPDCR3+qg0MegazfuPWKK/2x0eSERSfoYJA1NTXRaPSZZ56xLCvIoHgQw8MmY4UACtBjZaVxnkgACSCBf5NA8GT+xhtvpIYb9NPGuHHjqqqqli9fToXm4CrvQHcOTgk6wQoSODCBwcFB+iyEJiScPn16JhPkTD/wqXgUCSABJIAEkAASOBYJlAqP1CKZysVpXzTW/bR/fpvSGFuPKJh7F5cGR/uvBb2WytC2T8WPkyankCyCOskoODgImTSx7yB7AfQMMfFYvAAWvQ4P3gff+lL2k+eunto6pyW+MC4taVU3J8Sd0UiPEk7LbC7GGzHOiXGewkGMhVgY4o2gNnjxBidSPdAqupMVVxi/OxrpESftTEp74sKOhETCpcVJa8Pjl7QlNsvsorZU+8fP2XrbbfDAg/DPZ2HJEn8kBngZcDLg6YWBjeJFLZFLS1fHfwCgGfDkn/UZbQta+J0JdrBN8qbK0ML2xcPtF56zdvVy6OknzwOsogZdeh+Q2N39llHMYsTQNE2bP3/+jBkzGhsbaVwF/apVVVXDMExFRcXHzztvV+8eG7yhfNZ2XeftYtxL73bTdggfHRa8CKcoq6dw609ufm7eHHJj9+fo7UzAbu3J5AAGM/D5y3adGGk/Lfb67bf0On7+TMuCvE7+y9i2c8cnzv9UeRX5/StxiPazEQYaNK1885vf9DwvkNRHzBTfjlkCKECP2aXHiSMBJIAEDopA8As+z/Oy2eyNN97IMMz48eOD2OdEItHb20t/AkZ79JNPkJdAUD7UykGNDBshAZ/AsmXLGIYJHopceOGFAZjSNJjBTqwgASSABJAAEkACxzKBQFijAc5mITUf0Bx9ZlGA9hVJatPhkgyEwWnFCvFRLpaRRz0/zFZ3rJxBVDfDHY40JYlOqDhNLG8LIB0dXB08i1y8ewcsmg9/fQJ+di9cfenAB85Yp8pzVWmhKq1QxbVRcWNU2K5yu+JsT5ztiTXuURr7E5zWLEGrBCclQZyUaYlC43t6Vc6KsabSaKosJARQIqBw+WQsrUa3KNEVsfibyeSrbdG/f+yseV+8ftuPv5f902PQvgCyQ2TilkHCpR0THKtgR+L4Yd5kwt5eNIbvhP0KuCN2juRUIigPd7TfGlXyKXu/QeCjQt6RuHXDJf7Ev3sUPvTeZVH+zcnqYIvgqRPt1ojZImxVwn+9715tIAOaDaYLlr+g5NRghMV1Hd5DRntsbOl0eunSpTU1NVVVVWVlZRUVFcEn29r3TJAk5Ykn/5I3Lc+/uYkVScltvvcMKQ6yb/je9kj8sqvDjrXwyTNWTWM3TxNX/fUJYrrtAmR8exfN7xmAJPD8xlfXt06a/97o2m/f3G2kh2/ynFYwgrE9eO7Fpc1tFzFME3GILhtfXTOeWoWMGzeusrJy3LhxM2fOHBEUUvp9cO8x47uxQgAF6LGy0jhPJIAEkMA7I0BdyVzXNQzj+uuvp3Gm9INRZWXljBkzArn531GcSz+RBJL3OxswnjXWCHie9+1vf5thmKqqKhp28fjjj1MjcmpZHtxdY40MzhcJIAEkgASQwHFNgGqaVIYO1Me9Jc63ixLdL5/SvhzwHPBIwCl4hZjTffuke3xFlQjVHnh+GkTPlwAtByyLxE0vmAd/mAW3fm3n5RetOGPGPFV6QY68PCWxplXd2hYdaJGy8XBOmZRXJuXVsKaGNSWcjUZI6LTCmkqDHQ07TQq0xiGpGlG5X+R38vwWhd+oChujYmdUWqsoa2OxNWp0dVxZ8plLsl+9xXvwp/DUn2DTOpJijhheWySxoe1rttS7pCD9+jKuZ/gjN4h1tp4hOV2GN0qEzM32TUqI6O8SHdj0pzgsSxPxdz8btUnR/XN9UThQjYvtadfEAsKBvAF33+NFxdfE+k3yxGxzBLiqPjWys0ladeapy37zMPEeyWv+ZYoPAAppCkv9ocmg7NEcE15qUvHQQw9VVFQEH2XpB9qKUGVlec1ll165aeMOkqjRnwz10fjrY3Bq6sGVS4rW4MPMyVJRui5YNlhUg88NwY5OuPrcrlPkFWc2L/u/syCTLTw98e9N0wNIW5C14AffA6Vx7llNaz/zkdXb1gX8iusEYPvS/+Ag3PL/beciv2SY/2DKm/0Q7Qo6bGJXXV09fvz4RCKxe/duwzA0jaxW8IF8RGV47Fg73gmgAH28rzDODwkgASTwTgkEHw5oB9ddd924cePoL8Jo0okpU6Z0dXWhAP1OAeN575BA6Z1JH1cYhnH++edXVVUFgfnr16+nd2bQGB9svEPceBoSQAJIAAkggdFLoERu3neQw8Gg+x47qD2lSvQBr/RWvTk0rpcETDtENtXyoOchn4d0GgwTtm2Ff/wd7vohfPWLcOF5PadOWyuxrxP7jsSayU0bUmpnQl6vCOtlbpPK7VbZ/5+98wCPozrX8GhlFTuSi6TtvanbkgvG2KFDAEPoNUAKJdwkEPolkEBIISEJaTiEgB0ChtBJQgsGG/cmS5asZrnKcpHVV9uml//e/5zVWjjA5eKCLZ155pHGu7NnznnP6PHsN998fz8WMzQn3FbB71CDHvA6VY9D8DgEl1NyORSnw3DYwWEDh1VzWQc8lt1ey2a3taY0uLK85L2TT1p6xeW1v/1t7NmF0pJl0NgMcR56+7HnCpU2AYQB0AUwJFB5IkYraf2RDvCAAK2nBGj1YwToA1rl8E/xAPyQiEokcAp02M7UVq6RnaICrK2BG78ZLfW2BM3dnvx4mQP8ZqHMF6kIb73myq5liyEegWSUHCJtpk7HpmCzMlmPXQ1akiRqmHjuueeysrLo9yx6KZuRkZHJZXIc97cFaKrQVUxqjolKhMfxtm+FL5evnRX+97ZmShh/kpM9dZKmT3xRSyn08iBcfub6E3wNFbaVzz2JSTKROD4yIIPCAy9i/AZEkvDMX8E+cV2FZ+eVZ2/evy3tfaa6Ph4lyadKYt53Z3vQujrgXuco/n2O9atcpoUjNYGoBo3hHESGnjVr1u7du2kWxyd9ZzwwBrY10gkwAXqkzzAbHyPACDACh0CA5j5rqnb99den72lzHJednV1ZWdnV1YWXRMOW4WLfoWwfQpfZR0cdAaos9/f3pyPzTCbTnDlzent7DzoJRx0aNmBGgBFgBBgBRoAROOoEhmRrmu8hk4zplEdYI55hUUftj9cgrkJUxZ8i0foMgG27YeV6ePYl9de/H7zp262XXrpp5okfBgP/dtk+dFtrvZbNrqJdzom97kmCrwj8FsBoaUfSZxc8DsltU10Ww1kE9iLVbubtlpjLOui295aFYw7rDnNhq8exJRzY6fO0Ouw1VvOS4uJVF17UeePNyd/9Fj54C9Yuhng3KAmQk6ArkExgIIZspOr+qankZSxwqKXKNqaCsw/kXBycc0JTtqkQTANShuRgKpGmhVIyR5RbuhQkpmxr8M5bMLtqk79gp39SYmoQ3EWDfke/vWhH0Lvp+mv3dXai8MorqcqEB3qC3uf/iGQ56mfCZzngU089NfwxvvTDpjlZ2auWr1JElIZ5nleJXzkug5iEy89r/HJJy7gOy2AAACAASURBVPN/ACUV34yGdAOtyQfSRyhM2UDPuy7Cw9+H6e7G06c0PHR3VCZFNbGupiAmdU0BiBtafwJefwmmljZOK9l26oya9i14RkoyyAq5F5FqGCdeFuCtl8H+pUUBc5PHurKk/NnnXu5/+R+rbC4n/baYDg+h/5w8eXIkEpEkadhXxo/kNH4WSmyfkUGACdAjYx7ZKBgBRoAROCIEaITu9ddfn52dnZubazKZ6BXSjBkz9u3bRw/5SRcTB2l//69/HpHBsEZHIoFY7MAjonV1dePHj8/KyqJlCS+44AJagzt97o1EAGxMjAAjwAgwAowAI3BsEfioAJ0qdUi0QZTxZENPamJc4WNyPGkIEhhUoE1HWScBEhrEZYgkoHsAdu+DnTth0b/hub/Bww/CLTeJp83eOaV4s7uw3mtt8Tvqvc56r7PJ49jisbd7bPs81l6fMxryigGP5LTGzJMGCsb3e52qz2lYJgpeO3hs4LbJLlvSZuk2F+52u/c67JsrAi0zSjdNCa2cUbnk69dse+Sn4tNPwcpVsK0d9vdDQsZwBl4DXkdRGCOYddDImgqVJlbptIWZOmZp6LSG+c64/p+BGEPcQAM1quwHkBKaruqwtx0euR/KXChDl3sE+8Soo0AqDWgOa6vXt+iBB3s2b8U4Y1nDYGjNoGkcqJIPLzJ5jJwiwx/IUxTlscceS1uGqfc5kyzhcHhrWxufSOiqbGgYmkK1dQPg1z+DKZ411Z71tYvpmFSACEC/DoKOo8dzjJKMEbt0PAJ//jVUWjbMDm578K6ILAAvI6LdPVGaYgIAvTF45VUoda8OW5pPmrKmfgPJ5AaqPoOu09QWjfZhw2qYEW4LF+6t9LYXe5f8aZ6WECEqQld/7znnnUuToOnP9NDC4XAkEvmk74zHyNSwbhwFAkyAPgqQ2SEYAUaAETj+CCiKIssYMnbdddeZTKaxY7H+MsdxeXl5J5100vALiOHbaaXvEDeOP16sx180AXpB/4tf/CJ9sZubm7tgwQIAEASBleH+oueHHZ8RYAQYAUaAERgtBNJCKtlIC9AKia1A97NOxFINYznShmKVyLmplGUq1io0ZVnDvWUVlV9RBV5FjLEkbNsFtfXw0ivwuz8kb/v+ziuvbAz6Xve73/M6l/scNX5na9jbURbqrwjxIY/ssyuuItVeqDvNustiOKya3SLbLbLHqTpsgtcp+u3xgG2w1DVY4R8s8/YUu3YHnduDrraAq6GqfPNpJ3d89fw9jz0Gzy6EJcuhuQWDGxQBzbCyBKIMcQHiEkioMRsqFj7EondDBSCp7A4JXqRnAPmaoBkGrgdlfNAddMQiqCAhB6J6ygKsXAw3f61nsnun40vd/iLNW2TgoGzdlsINZcVrb/5W3weL8NOKhp1JL0QK1+lh6Lyk3zr6G7qu06dLJUlSFOXVV189yCxMQw6nTp0aj8dViaY9YzcNw+AFlJWXL4WZZRurfC1TvG+/geEcaBPXoUuHLg1vW8g6lnJExRpXA/q64MWnYGZwU4Vlw903JXUd7yKIBprDBYAkQL8mR1VY9iGcOqO91NJeZlv/4XsQpcEmKFMboGu6KopSQsNphO2tUBWq8UzYFSra7zevvv8utIJoAALpbDwep5L62LFjJ0yYYDKZMrNSwdCnnXZafz8GvgiCwIqE05kbhT+ZAD0KJ50NmRFgBBiB/4MAz5M75gD33HMPLSKRkZFhMpkmTJgwderU/v7+4aLz8O1D1J3TH/8/+sfeZgT+gwDN0RNF8bLLLqMpMVSJXr16tSjiFx52sfsfzNgLjAAjwAgwAowAI3D4CXysAD1Usg/V549mE9PdU5ohtQkfaCHl56WuXgyaUElYh0YCJngd0ycEGT2togySAnv2wMrl8OpL8JtfwB3fTc49o6UyvNJvXRGwbgjaWnzWNodlq92y0+Xc5/X0hQLJcEB2WhNOi4i2aCt4LGQ1g4esbjN4rLrfIYe8YjgQdTl2OJ2NDud6l3Nx2P/GeWcsv+/Ozj/Pk1asgJ27ICGiOJ5QQCJBHAAwkICYiK5kg4Rp8BKR13UgyjuWZtRSAxqWnDE0G1Sepl8NgCRoKzzEuuH91+ArJ+4rtu0KmSMlTgjZwW/VXAU9zoK2kHvVNZe3frAIs61lA7vRF8UDKEPEvnABGnOpib9HkqS//vWvNDQ5Ozs7Pz8/rUTPmTMnHo/LsmykDMeKAYJKkpx7u+CM2Ssmu5umBRsf/u8eXYREHIik3K1Bt4baskp+ylR9Bg3aW2Cad12Fpe78UzZ1bKNnkUGjSdBoDxAHWF0Ds6qbii3bpgda/7EQJ4DMhzGUCkMd1ahF9+yBC87o8BbuDJn7pxd3/uB2KdqXmjBFQ5VcUZRIJPL+++9n5eZwGRxnysB1aLn44oupI4RCGJpq9nsUEWAC9CiabDZURoARYAQ+IwFZliVJuv/+++kFA9bByMzMzs6eOnUqXg8Zhq4fiO5iAvRnpMp2O6IE0vpyJBKhQRz0Ur6qqmpwcPCIHpo1zggwAowAI8AIMAKMQJrAkHxMM6BTDuh0sb6h3dJ7DSUmUMNwKj5hSJMlkQrpXXXQZVAFRRUUXTJQZk0qEBchymMFuUgCbcgyCWEwNNAlQE+yCIOdsHkD/PN5mPdo/M47uq66tn3OyRuKS5YFfGvD/s0uS6vTutdu5e02w5mqYQh2C1mtYLdLVnusyNJXZOmzWfscjn6nc8Dr6Qt494e8e4LuHQFns8u61utYeUJV8yUX9Nx8Q/InD8LLf4eVK6GnDwYiKAfzCq4qQEI2JB0t0sTdLKiYGjGUCj1URw/latQ80XsLhmLoskFFd1Ku0BBAjsATv4STyjb5xu/0fCkRyDdKzBC2axV+wVW4pTLUdMHcLX97DvZ2QV88FWBNI0GOBQGaPrFXW1trsWDVvnT17PHjJ3Icd9VVV8ViMUlSdA2ikUEiAScFMSKrEB2E73970Dlh6bRA2yVnbY5GIJkEQUIoGkTJqqbjuVGAVqFzG8wuWV1StGpm2bJ9nXhiUU+1DIaIWd/JQYD19XDy7Noyd+tk74aXn4VoZOj0TP1GcvRcNAbh7ht4n3mzx9xV7tn9zasisZRRGk3vhg7pxw0TPN/V31s8pYIbg+GNw5d77rlHRnmcLaOUABOgR+nEs2EzAowAI/ApBBKJxM0333xQepfT6ezs7ASARCKRtipTMTqtQQ9//VC2P6Vv7C1G4FMIyGSpq6ujF/Q0Ouaqq65KXxN/ymfZW4wAI8AIMAKMACPACBw6geF6MdGdqRKdkpZJkgHRWOkLQ3sPU56HXqJSbKpD+KKOOxEhlrwoKsBLGH9MX1IAbb9YLVAzZFnV5AN7ggJGAoQI6rqY4yGifLlyOfzrdfRK33sXnHtOV/W0HS53ndvT6Ha3uZ3tbucel73D5txude9wevd5An1+f8Lj5m2WROGkGA2VDrog5AZ3YcJvF4I2wW+JBm09Je59pb7t5YEGt/XfM6auuPKKrbfdtut3j+1+712lrhYSCRBJnzG1WUEpWhuWRYIeXTJ6Q0dN00D/NFbhSy1DAzKSsL0BLj6tbVZ4d2lh7ww/BMzgnKjZ8mXXxFjA0el3155xRu28PymiiOkl6LUe8pIPBVIPtXngN8V+4N9HYkvX9Z6enuLiYpq2kZ+fT/XZjIzMr5w9l0+KGpYSTC8KgBCJCrwALz4P5b66WeWd58xu6twJiSTERYXOMEl0kYj6jPHZGsktUXm49rzdJ/g2zipbumE19CVRfU4SJ7UMmoinAwyqcP55rVWh1urwxjv/q5veAgDM906kMqeH1GcxAb/7EVRaGosd+4r9O79y2uaBPpwr/IgKWNVQSXVbUUlijAar1sRzx87kuPEcl5XBZWWNycnMzM7IyHz4xz9PD49tjDYCTIAebTPOxssIMAKMwMcT6O/vp89DCYKwcOFCjuNMJhMt5paVleX3+9evX08/+RmV5Y8/DHuVETjyBHRd/+Uvf5mugpKTk/PMM8+kLdJH/vjsCIwAI8AIMAKMACPACHwqASouf+zPT/3c8DeHhOoD2vXBGmq6IB2tD6gTYzEVxWn+tAq6gm7ZCHGzxmOwegWsWAxPzxN//sOeay9vmHbCsvKqteGymkBok9+33e/p9Dn73baI2xq3FwwG7LLXLLkL+aIvDboLZNcE0fqlqHNCNGhLlnuSIUe339rhs26dVtJZ6dtR7m4udW4sda8+Z862r1/W9+N74c+/g9Ufwu4dMNgP3V0giiCQFEDFwMDrJFGeh6zggNHSmjYkjIKQBDkJ8/8onVq9Zop3W9gZd0zSSl3gKwRvIQStUsjVXuypO31m2x9/BQPdKN4bJMBEwUqKAjWk40sHVH6VWITTBxxO+lC3dV2nD5hqqnbqqafm5eVlZWVRDZoK0DNmzIxF+XhsWHw1BjVLmmr090BDLUwr3+AurJ8zbeuuraAoeAtBNjBlm7rDSfQ2WssBNFEFJQl33tAz3VMz3b+4dRPuEyOBGzy5g0GF4879cOF5tTNKtpxUsfnuWzuifSS0GwdK/eK4RYkNJOCN18FduGKyt7vU23LeOU2RQbyNQW4WoIEdyyTqmsgLQhJl6Hgcdu6A6vA/Kz2vcNxZHOfiuFwyzDEcl8lx2evW1ioK7cWhgmWfP74IMAH6+Jov1ltGgBFgBI4IAZqfS5t+4IEHcnPxKiErK8tkwienzGbz9u3b6bufUX0eXuL5iPSYNcoIfDIBevpdffXV9Jo+JyeH47j6+nr6ieFn+ye3wd5hBBgBRoARYAQYAUbgiBE4oHsesUP8Pxqmgb/4AU0GTQAphvEdcgJrAHb1Q2MLrFgJv/k1/OBeuO6q2Dmn7ykP1kyv3OyxrA15Wkp9OysCXZa8LSF7b7knWe4Ryj1SqVMqtolBqxS0KoFCLTQJwgVQbDZKrHK5PV7u6C9zdJU6dkwtaXVZ3g373znvK7W33Lzjt4/xT8+Xlq6CvX1YU2//AKqwMtFEqfe7tw8EAYVRiZp5JWjfCvOfhPLSjWUlfSE3eArAWwB+MwRtQsgWKbMNlNq2nzGz9fe/gt4+iMQxDCSp4MeHy/cElUyCtY9IQIQsy9QJ8fOf/5x+veI4jlol8vLyPB5PLBb7qPcZHzrFXhkQ74NTZzZVFe+cUrLp5RfxFgIWpUT1GYtYEukZJWa6ygZK8/d9p3uqe9k036LmdXhrgQrQMTo8g3ikAe69LR6yLCuxr73ynLbuPQRAysSsGSApuigTN70KsGo1VE1eHHJtC7m2zahe0ttDdkarOhXA1eGufADo2A4XnVUfLtoUmPThNRe9dP653+M4Ljd3HBm4ieNMU6tPSCR4lgSd4jiafjEBejTNNhsrI8AIMAKfSkBRlD/84Q/p6yEq3s2ePbumpoZ+zjAMTdUURRluJv0kSfpTD8XeZASOIAFN1WRZFkWR3kqhZzItKU7PYXaD5AjSZ00zAowAI8AIMAKMwPFEALVwTRMlSdBotTtiAlZEDGFWdRLZIUE8CYNRiMfQp6wq+NbmZlixBJ76E//H3xo3f33Hhec2Tg6/X+xaUuqqKfM0l7l2Ftu7Q7Z4sVUPmSFURFYzBM2qryDmKxz0mgc9RX2uwk6Pdb/P0eO176so7rMVtYZ8OyZMXFVatqWssvGyK+JXXt3145/BM8/B+lro7MZQaUlG760MaGOOSqhT8wBLN8C5l9ZPmdJRGhR8dslvU/w2KWgTvJOinvH95jE7w9aO02fsfuwR2NwEgggiRnvo1OurofdXJVUiRbKBzuLDa4TWdV2SpMWLF+fl5dFa2YWFhdQhMWnSpNramli8D0CXDhigMTEb9WcBHn0Ayhzbip2NT/4F+hMg6iAQ9ZykbaAWrYJCYrWJsmzAb38aLS74oNK25NXnQJYgKoBA2koACCDJBogJuP/73ZWemqmBhvNOXtq7B+80aEp6zBqAIoGY1CAuw8ZGmFyybHJwl9/WOLNqzXrypTAuGJKCJb6pfxyLA0GSytC6BFd9Zd8U+66SwpaLT28d7IHubmnG9Nk5OVkcis8cbnDc9dd/w9BTJRmPp78V1tdDI8AE6EPjxz7NCDACjMAIIvDII4+kSzDTh8Kqq6v7+vokSUpXHVQURRAOXBzhhccnLCMIDBvK8UdAlmVBEOrq6miYDD2xL7744tQ3q+NvQKzHjAAjwAgwAowAI8AIHAkCHzFjp8tm0GJx6cgLPLCBhlu6ol6pAZ8AhUfzrS5BIorRwjvaYN1yePFZ+P0v4OoLe0+duTPsaih2bSl27ih2todc7aXevZOD3RWBnqBzn8ey12vrDzlRMnYUCCEXlPnBbQWfC/w+CIXAYY97PT2B4E5/oNHnX+3xvD9t2oorLt/84I8iv/19dOUaaNsB/QL08tAjQK8AD/0cps+I+Zz9PrsQsOtes+YtVINmCEwCV55W7pAceU0zKzc/9SeIxTHlQzRQyJYBxWgSSS0fCQGaIu3r6/N4PNQVkS4/aDKZWltbZSrmopr70UWF91+DKldNoGD1g/+NbxHRl/ZZ0XAEvEbCMFTia1YFeOEvcGL4gynOD55+DJJxlNFFgLgOMaIQCwCCAr9/VJkWWhEqXH1S5cq2TanCg4aS9jEbOir8KOvv3g83fHOHp6DOO2nLzMq6TRtJg5oma5Kuq6mcbmKEpv2ODcJD9+6vsm+fZuubXbqxeT1ImMGt9ff3T5tWzWVwpjFpANz111+fSCTS59tHR87+NTIJMAF6ZM4rGxUjwAgwAp+dgCiKgiDMmzePJj6nrwsmTpyYSCSGPx5FSw5+9pbZnozAF0vgf+XmH//4x+nbKhzHPf3008NP6S+2e+zojAAjwAgwAowAI8AIHDMEqBKNReyGrfRF8tMYihrWiXtY1fEFBcvQacSOqyqk3B+VciUsNpgUISFCgofVq2H+0/CLX0jXX9t2/jn1UyuWhbzvV4ZrS/1t5f59Yc9+r6XbXRCx5UX9VrAXgtcBVjO4XWC3yOaiAbu1x+vpCfq6igOdYW9H0LndZ2sN2pvcRWvLww2nn9Zx8aW9D/0M/vo8/PkpuPYqqCqBoAPcReAzH1j9ZilgjgesvSHbjopg/YP3Q2cPSKg+QxyMAT0R1ePEW3yYJ0QURU3VbrzxxqysrOzs7PR1aU5OzlNPPUUOpqM7GZS03I9uHx02rYdqd31Z0cZbvr4JjedkVohirstYezKhQUxDSzTGkmgi/GMhnBioqbB+eN9tTYoE8pC8LhCRPSKgo/nZhVAeXF7u2Tit+P3WjaDKpM4gtXwbqC9T63dUg4QC990tV4e2hc1bTyje/Prf0fxO3kWhHNVnQ9N1WdFJBxT0xf/xESg1r6yy7ZoTbm1aC3wcGzewNKZiGFrVlKkcN4Z6wGkOCa1vf5hxs+aOYQJMgD6GJ4d1jRFgBBiBo0JAluXHH3+c6s70aiAzM3PixInNzc2yLDPH6FGZBHaQI0VAU7XLL788fXqbTKZly5YdqYOxdhkBRoARYAQYAUaAETheCaQF6KFoilQ9OuJ2TuVeUP1TQs+zJhs6WYnsrJGfqUhiA9VPkayCgVkZg0kYTJDABgNiUXRP9/XAyqXwxO/gpw/A16/cf/qsRvv4tyf7GjyFG6pK9vlde9yOfaWhaDgYC3giHseA09Jjm9hjy484xyd9k+RAoREoNPwFaokLppeBw7y9pHhXqGRLQVG90zbgLJTDLvBbwWMmqwU8Vt1nUcmKGwErH3Lvdjne/t4d7Tv3Q6+Iht9+GdT/cCEf+mTKsvzee++NGzcu7fKhG9/+9rejUSz+aBiaAYIBEgIayv4QInDunFXVnsavzGru3ou9oCUBJUznVhVIqhAnAjR+QOZhVzPMDP3j9Mq2H35P1Un9Rmrupj9pqwuegcnli3z21cXeJa/+HSQhJRCnj0t3MwCiCrz0Bvgda6oD+6f4Nr64AGL9aRIaGChAE/WZV0EzAOI8vP4yVLjXhwsa5xQ3bq8FNUn6jLF3Eo7OMJqbehy2aaaMFIfs7DEXX3xxulG2MRoIMAF6NMwyGyMjwAgwAp9IYLj3OTc3NzMzMyMjY+LEiQ0NDenP/Gfuc/ottsEIHPsEenp6srIwb47juMzMzPz8/OGn97Hff9ZDRoARYAQYAUaAEWAEjhiBYR5nVCIPWjQUPNElrKHkiCtqpBoYZNWI7iypINBVw/J+ioauaBRzVQPlSUnBoGIALKBH9FaQ5VTgQ2IQrbvYvAxiH2xaAysXwfzHoz97cO+3vtFwxmlLg75/hPwrg+6GgGNrwNpbYoGSIggVGP6Jsr9ALrVDiQv85qS9oNtp6fG7Yh5n3OeSwj4S5eEArx033FbdbZNTq1V3W3W/HQrG9nhtvSFfu8P2wcM/g83tOM4kDbk4iMGh/VNTNZfLRS9Ex40bR6Ofy8vLAUBRSC3FVBg1YUQQaSJ8+4ruKs+G8vBr69ZCnNQjRIDEKS2ArEBUh4iO6Rog8cjtK9PWz/Qtv+SsFcIggUxczyKJ4BBJmx++D1772z7HuoD/7Wefw5GSGoI4g0MCdKoAY1KGZ16AAvMir7WpOtTw1muQjJLgb2wYb07gCYCTK0sGTqykwoY1MLOyLmxpnB7cuGktaDyuqd11zYCkZoCYhB/94I3cHCdFQW1P77zzDtmP/RgVBJgAPSqmmQ2SEWAEGAFytYdpzWkUoijKspxO3jCZTGn1ubm5Ob0bXmioWiIxdOEz/A22zQgc8wREEb9JNDQ0pDVojuOmTp16zHecdZARYAQYAUaAEWAEGIGjQCAtQH/ssbAk3TABGlVLqj8epEFrWBtPGBKgNXyXqM+4s05csgCylPL3aqqmyqKuipi9jAtJi6D6p0QOoIOQBF6A3l7YuRVWfgh/+wv8/AG49GzhrJmxKv8WX8H6oLWhqnhnRWino6i+OLDH79rns/cF3HGXPVpRAtYCPuCi6jO4barbLuJqk1GMtoI5X/LbwDFJcxaJPvuAw9JWXFz/vVv3CAKWt/lYEP+vF4cXbJ8/fz7HcRMnTqTCa25urtNpb2raRBtEqR4PSAsrosAvC/Dk7wanuFZWulcu+RCzOQAgloxQAZo6oHXgdUjqYOg6RLtg7uxFpUWvX3b6RjkGSR4nSCQKME+inEUFalfDyVOXV4d2eK1r7rmvsycKCRUSWlQEDe8FUMv70O2HtevghKlNZaFtVcU1v3kEIv2ogAsSPU9SGHQAWVVUHdNXNm2EEypqq0JtZZ7Vr78APLq6ceGjSZoboumoX7/xEkwrnzch/yKOs2RmTjKRQOhAIJDam/0aBQSYAD0KJpkNkRFgBBgBQsAwDE3V0pEaiqIsWLCA3oTnOI7mkZnN5jVr1hx04XXQPxlORuD4IiAIgq7r1157LS07znFcbm7uHXfcwW6uHF/zyHrLCDACjAAjwAgwAkedQFqePliWTZchTwnGKWk6HSP8qT1NiZl0ZzTR4t4qEbp1FGR1A1QdZB3d05IEvIhitCyBqoLAQ3c37NoJa1bBr37V89NH9l//jfoZJywuKV1eVlLr9zWFvHuC3kGPjfdYVUzesBk+u+KzS36b5LdqfiumQnvM4DYDVik0S2GX5Db3eay9k0vXbKjBYSqKIklSeoCf46uQoig8jx5gSZIyUktmRgY+h8dx3BNPzFNUMmTAEG0i/BJhGVB2f+ZxCFnfqAr8+/lnoCeGaESsN5gEzLJQZdBJ1UTEDQA9e+GKs2on2984c/rz8W6QRYQmgyGAGMcikRgtsmY1zCmrr7TtKLU1Xv7V7XEREkh8UIJBATApRSO534YCmgTRXrj4nNZK1/pp/mX33NqM2dNK6hbCkPk9lcyCoxOhuwNmT24MWDaV+dYtXAiRGE4cjkqXQNewYCK5r7D8AyhxLnEXrCkufZ/L/DbH2bOzxuXmYhzHgw8+OFSGkWrsqbsUn3oCsTePSwJMgD4up411mhFgBBiBz0eAqs/U+7xgwQJ6Hz5dCiM/P7++vl7XdVmWRVH8HBdbn69X7FOMwBElQKsOGoYxffp0es7TOy7vv/8+/Y5xRI/OGmcEGAFGgBFgBBgBRmDkEUjrs59naGlZG3VUmQjQxgFdk7SY9lCjf1ZD6VnSQNSUpKomZYiLEIkDr0BCgH2dMBiFyACsXAErlsI1V8C5p0NVMbjNhs8KHytA+8zgLQKvWXEXxB0TehwTO/3W3snFq+rrDowmPcDP8Z1IUzX6qYceemhIgMbf2dnZs2bNlCRqayaafkrYV/r70TncuQ1OCK8ocyx54L/3KRgLDUk0K8eplZnI8qjoRnmU40GAW65uqHK+fUb1oi0NeCMAQRE3uQgwoOFjgINJOPPLS0uLWovHb5lVsaJ3P/Aq8Fghsk/AN9FhjZka1Imuw4VnNkz1b6h2Lvrhd/YaMoZ9UAN7ajqIVZta4hUNBvvgmrn9k507Qs7Vd3y/XzSwNZIKncTKjkSAFgZhz1Yod7/pymstcUYczjpP6K8cFzaNyeU4zmQaU1RU1NHRPsT9s93AGNqb/T6+CDAB+viaL9ZbRoARYAQOlQBNJHj99dfT3ufcXPzvPz8/f8eOHbR1URTpbf9DPRj7PCPwRROQJDSYyLIsCALP836/P61Bjx07tqOjI/1MwBfdU3Z8RoARYAQYAUaAEWAERhUBkkKMAjSNQiZeagSAoqyBARMkajpV2ZDkT5NdaK0+VQPDwHSI9u3wr5fhB3fC5ReC174/7JICDqxA6LWCxwoeG7gcmssp0dVjV9AWbQZ/IWAlQ3MyYN3vKKytKK299KKV6BkmC8/zhyJA0wiOjo6OrKysAwK0ibNYi3bv3gUAosiTYaYitkVRFOKwdQOcVLym2rvyluvbExJqwkkYEKHXAJ6UdZSJNRw1e1WDaA/88GYon7RuVsk/9u8AIQFJ3sDcbR0/SIO1u/rgioubZpa2VrvbZpetGezHUpBYFhJ0AUQe0z5wT0wBrX5+XgAAIABJREFUUUCPw0O375/urQ9MWva9b7RKMTQ44/OCJEFFBUXFdG+cKhSgDSxLeMfN+6pd28Pm+vvv2du+F93W1MiuYeZK0iC6dvcuqPIunuxst2Tt9BW1V1XWfe/Wtj8/tTQjeyzHmcZk4/fQX/36l8MmljmgCceR+IMJ0CNxVtmYGAFGgBH4ZAKyLB+kPufl5ZnN5vr6+vSHdF3/HLf60x9nG4zAsUNAlmWqQdMY9JaWlrTlPy8vr6qqqre399jpLesJI8AIMAKMACPACDACI54AtbkSodHQhgobDhv1kABNqhkaChgSpkNQmRp0SMSgdz+89xbc8d3Wqy9pLPV+4JrUELL3B6yxsAtDNtyFELBC0A4+B3jshstuoAbtUDzOpMcV8Th7AvaukK0jbGsLO2tOrFrz2KPQthkiEZDkAxnQhyJAy7Ksqdrtt99On7pLadAm7pe/fIRckaLgbqSil9EqoevQvxcumrN7uqfl8nM2de6GJBYHjAuwX4V+HRQdxXY1ZRw3UDP+w0+Tvuyl1dbaN54DPg48j6IvjedWdHQuRyJw7517qoINk11bTqpYu6UJAVO3OTFP6wLoKhGgZQNUEZ59HGaXrqxybvzKifW9nTBIihmiAI3edEPFWoOShq5mVJ8VCe66uX1WaG2Fpe7BOzB4WiaNY/vEgi2DJmsw0A2XnbOlwtYx1a1UuLrCrnU/fVDr6kED+8w5J6RNIYUF5liUytc0hWPYucA2RxABJkCPoMlkQ2EEGAFG4BMI0EgNmSwLFy4kjzuZ0rnPRUVFra2t9KPDK2Z8QmPsZUbgeCWg63oikXjsscc4jks/AfCNb3yD+FBEZoU+XueV9ZsRYAQYAUaAEWAEjisCwwRoEIkOLaMHVyMrGnI10CUdyxhScVaRMFJYE6F2BfzXdT3XzO0ttq4rtbaVWPaELftC5v6gWQyY9YBZD1mh2A7FDghYwG8BzH12yEEHBB0QsEHANui1b/E5V1UWf3DLjbteeA6WfgiyDLIGspFKoThcIHmeN5vNaY3VZDKFw+G9e/cS4zMqyYqCsRcyyb5IDsJtN7S7c5d/ubxJjIGogIxxzwkZ8zdSvuNBHusQxpMgJeBfz8Jk27tT7G+9/DTJfSYRJSpJW04S23IyBvd+NznF2+ibsPWk8i0f/BuSxFJN7M9AcGJIM3bAQMP5B4sgbH0vMGnFJac3dLenzOYUhY7/kjH+BERBSwgSHvHhe/ZX2zdNc2y5+crtUpxI0qSgJG+QxBAdIgpEeLjh+t6wtaPcqpXbklOL6199AZvkyZBb29fmjOfG5OB3Uo7LvuVb921p2j9UB/FwTQJr59giwAToY2s+WG8YAUaAETjsBKjuTJtduHBhZmYmx3H0J8dx48aNW7t27WE/KGuQETgGCaTvr5xxxhnUB03D+BYuXEhNLjSg5hjsOesSI8AIMAKMACPACDACI4MAVZ/VVHU6jCTuH8RoiKRCVgml0mgSxxrnYcmH8O478NvH+GuurJ1e+V7Ytc5bsDlsHQgWiMGJEJqEa6AAAkVkNQMK0A4ocUHYoZQ4o6WeHSWe1rBja8jWUulvuey8/l/9FN58HS3DaOUlZl4V0x9kHZVwmaZ/HDpnRVGefPLJtN0BFdas3AULnhlqGaMsDB0EmgWtwv3f318V+HeF+4NNa7HoomIkVBRyEyqIqq6rOqnsNxTU/OICmBOqPdGz/uE7OlBBxlJ/qqpitUDqH45G4Of38778daXmPVXeza8uhKSIcdKCTvM3MIJDAh0TPUiHWlpgzsy3i53LTyhfva0RVNorWhkS4Yg68Boeh7SvwFsvw2TXm4Fxay85ZXe0h+REI05eIxp0VMUih30i/OChHr+z1VMY8xUOFjva/vI4jlcQSZa3EQdIfvfOGzNyMseOm8RxpvFjnd+67lYmQBPGI/YHE6BH7NSygTECjAAjQAlQTU0QhGeffZbehM/IyDCZ8G7zuHHjWlpa6O13hosRGD0Eenp6gsEg/SvgOC4rK6u5uXn0DJ+NlBFgBBgBRoARYAQYgS+KQFqAVkiohqDAd25qvfDsXX7bMr9lnddS67bW+t0bi4ONPm+DpWitw7bR7Wj0utrctp1O8/6AIxFyChUBKHUYgUIlUKjhatZ9Vtln5T2WAXfRPo9lt9e+I+SqPXf2mjtuaHpxvlK7EjQe5CSIcRBiIPGop9JEC8KBplFjGPJh0aBFUfR6vePH56H0nJ2dNSanqKhoWNsSqbsIsQEQoqjnljmWTC9e+upL2BdJA01P6JBaUYMm6RuDSV1W4JXnoMy2eEphza2X9wCR6WUdXcwoQ2sYIQIavLwAfF9aW5LfNd279wd39EQGifoMRH0e0qAxKEODZAyi3XDeaXUBx6LpU99sqP+Y0esQ02FQA1XTscNb6qDM8uaJwXUXnb6qdy92mJd4HXgdEhqam3WsfyjDy2+A2bIu4BKc5oFJ45c8+QSmdSeJtC2pKZ25Y18XSYLOys7KnTThS/fcdStJgv6iTkx23CNOgAnQRxwxOwAjwAgwAkeZAI1vTps9ZVkGAKo+m4YWjuOKiorWrl1L1ef0zjyfjt86yr1mh2MEjjiBdEVyRVGamprSAnRGRkY4HB5MZ90d8Y6wAzACjAAjwAgwAowAIzBKCaS1XoVIon94fEelf21wYm9pkVFcCKEi8BaCqxBcZrAV6eO/FPW5NI9DcNsTbnvCZR20F3SHPQMBR6ff2h6ykdW+NehuDHpqgt7VQd/Sqy7r/dH98Na/YMdmMHgAUmjPkInjeij7Q1EURRU+WvOGvndYBGh98YfvmjI5Ez53ymVk4K9Hf/WLRGKoxCFN+zAgEYWli6A8+O600KonH8OM57gsKpqmq7Khi4aR0CFGBWgqlzfUQYlrUbm95urTt8faQUuCKIqoPusg6SApWIrwtYVQ5WwondARymv+ztdifIIYn7HqIJYcxAgOsqIALQPfB9+8uK7Mvnx62brGJhAUEkWixYefmipK4SJ6tiXYthG+XLqkwvb+3Nnre/aALGFCNFlEDQQNeJox/eIbEAw32G2dXm/E7Wmc9xdI0KQREcsnok2bhqtocOnF93McwcRxTuf4IVv88OOz7ZFDgAnQI2cu2UgYAUaAEaBl1gzD0FQtrbUBwPz58/Pz82nmwIQJE8aOHZuXl9fUREpREGo6WWgKAcPICIwSAg899ND/1t0eO3ZsVlYWx3FXXnkl/QsaJcNnw2QEGAFGgBFgBBgBRuAoE9BJjgQtWCcCltr79aN9k927qmwQyDcwVcMMITuUeVCDLsiHwglyUUHUZu3z+vrDwd6AfUfY3lrhb6wMbqgsXnranA3XXd1x5+27588fXLUWoglUQEWZxDrLoCgkEoJESmPYBNWW/w+FmcrQh0jF+NbNF2DmIV5g4pKVldmxu40MN0GDNGQsPQh1G2H6rEab8/1bbtyUKrEImIStKwCqirUXQVF09BJFBmHtMgg735sc2jj3tEaIk+qBJPQZhqR1DWDLJpgZqiuduGNOeO/Vc+tj/Shqy6g+82RFDZpIwXj0eAx+eEt8TrCxyrPi1ecgEkWpOp3LQdM8dACJqMW6Bj274Oqz+ssK1p0x453tLaDIoOkoJdMcD1XH34ICzU1QUVpjKdpqt+/0htc8Og8d1Fi6EAOvDSo9o19bgh/euS9k/wXHBXJzxo8dl5Uzluvq6qRFWaiD6hCngX38WCPABOhjbUZYfxgBRoAROJwEdF1/+umnhy59ssaPH28ymQoLCxsaGuhh0g5oXdfTtZ4PZw9YW4zAMUmAXt3OnDkzLy8vndA3b968Y7KzrFOMACPACDACjAAjwAiMBAIHCdCCBv9185IKV12lLVpq6y13dk/2d1UV97qKdlUEI6WhTru1zuNZO3NW2/Xf5O+/H/74G/jzY1C/Fho3YCk8SQJRQufvYBKSMlYvBBLrgXZdYrOl8mhKVP5P6fk/X8EGqKD6eWjTy0tN5yeZia+XFNjLysq68KK5AAlF7wWsL0iLBUJDHUyZ/I4nvPyiq7fv2oV6LgAkEgmdFGREZddQeD6Oj6ca0LwRJvuXlzhqZ01b37OfKNRkVJRnX1xXAWrWw+zJDZW2HZWW1jkVq2O9kExAfzQWU3pFGBQgJkBCQGwQFyHBw8t/U2e4V1ZZ1739dxBjiFEy0jJ4CoROSBo6JnV8be6G8oK66Z7aLZvwXYWUbaSoKfZYAlasgOqSFWW+PR57eyBU/517OqPE7JwAbFwdhvZv8+XqwOJq32tOy0Ucl5Wfn5+dPea2225jVcE/z5l3nHyGCdDHyUSxbjICjAAj8P8hQB8oEwThtddey8/PpwI0NXsWFhZu3rxZkvC2Oz59pihUdx4uQH/0ebT/z4HZvozAcUWgr6/P5XLRGGgqQ9fW1rJShMfVHLLOMgKMACPACDACjMDxQYAKwdQMi35Y4uLd1wU/vKtjWvF7J1QuOuvLq665tOk7N2791S8G/vyn+NLF0NONkm1SRs00LmDggwEoo/IyJCRIyFj5DgvkEeWUtj/850dcz6mwiCPFKv346QeL/52VzXFEfc7Nzc3JyXnppYWApmVcVIDeQVi1DsrDDSX+pjlffqc/iq9HB+MAejQyaKD9GeVzw6Bl/2BHE5x1QmuwcP3k4KqmTYQDfoKHVCVFJNnSAjOr1gWLWoKTNp06fXVLLYrUAwOoyUsQk2BQggEBV3FQQLG7fhWUOd4+IbDiDz9OmaJlFfFSeqSnqW3NQHn6xks6yiYtn+r5sHENqETrV7DqIU9+4u4DcejugtNmfeCbVB+0dDgty++9T9g9AHvjIJK5FjQcD52EDxdBhf+fVb6VV57XsLEGTKaJVLCfNGlSOhmS9oH9HEkEmAA9kmaTjYURYAQYgQMEdF3/05/+lJmZmZGRQRMGOI7Ly8traGiQyEJ3NQxDkqThERwsiOMARLY1cgmIokiT+FpbW9N3aEwm0+TJk7u7u+ntmZE7ejYyRoARYAQYAUaAEWAEjjaBtDRMbbMaeoGjMqBU2tcJhgqajAZdWcAYCjTVKujhjfPAy5qkaypGPhhRPoZRD6pIeq9JBp+UeVE1JBkEyeAFkgQxPG0jvX2Eh9vf34/2aV2/6aab0teWtAghjkVNKqIkkV63bIHTz2zyubZXlW9u24zdkpWUmCwJsiah69jQQSN6bc8+uOzM7grH5lkVda+/hCUKSaaITIr+qQrJ9eiLwtxztvms9SH7Vp/5g+WL0cata5AUJJLgoeggEBP0IKkCiH7q2WU1xZOW3H1zp8rjgUTlgPqMs0MzmomLXEzAHTdtOCm4vsq24o2FMNCDwrSCK69ATMHIExgUscbg3DNXlbrWhs1tlZ6mB+4Ruvswf1sGrJVIs6FpGkpjA8ysWlLiWnb+GfUD+3Gwc+d+jeNyTBm5WWNynnjiiSM8Uaz5L4wAE6C/MPTswIwAI8AIHHYChmGIoihJkmEY8+bNo7rz2LFjabE1s9nc3Nwcj6duv6eF5nTyRvqVw94x1iAjcCwTuP/++zmOS9ckvOiii8j3BI09CnAszxrrGyPACDACjAAjwAgcpwSGlGhZhz4NYhpJPFZlUCSSLCyhJG0oKEkbKugqFuXTNFHTeV2XdV1WDVXVdbJiqoOqg6KS6GTcGaVbEsDx0dDnI2x/Tk8Ez/Mul4fjMtIa9ElzZosCOpGTpAZh0yaYUd1oKdwQCqxbuxqixP6c7jCOV0n1VZUh0gWXnrWryt1Zamt4/hno6qXqMwZayCAaAEkdYjzMndsc9NUHXG0lvppnngJJBV5EEVvTRAMUHaloIogJI2EARLvg4tM2neCvueiUBjWJNmZVQ4YacZGTewNIEQsbktsA834G1c5/T/W8+c6LZGfiz1bJTxyUIcRVFNDvuLW3xLGx0tVe4V7/wJ0xVcXChdT7LOq4EVV4XoOO3XDFxS3lvvqK0Iq62hS25xe+hUq9aUKWKfer51+Arm3ytG6aKtsYGQSYAD0y5pGNghFgBEY7gYOUsnfeeWfSpEk5OTlp9Tk/P3/jxo2CINDHmtLJGwepzwe1M9qxsvGPGgLnnnsu/Z6QmZmZm5v75z//med59gzgqJl/NlBGgBFgBBgBRoAROPoE0Dur4yqS5GWqapKfqfBmA328ugYGBg7jamhkNVAtHbYaOurOKek5bXk+WqIzBUfzDPfs3kcLv6cF6N/89o9psmvXQXHojYC71Wure/Iv+DJ6mGmCMsZupAKoEzHcGOyDy8/bEbTUhS2N990KXV1UfY5pMKCCwBvQk4D+JHzrhm6fr9Zhawj61991b0wgDapolRYMDF5WdF2VSfE/XkWWN1y6s9q58szpKwY7hwRlIuIP2dKROO2wEIc3X4TQhDdKC976x7OgS9gBFdV+uoH7CYBG6J//VC/31VW4uiZ7tl92Xh0WUST6v2bgnjRrBaNXDLhwbo2z8G2/6/1XX4GogC3IGNcNJm5cJjc2y5Rt4rje3l4mQNMpGGE/mQA9wiaUDYcRYARGLwGqHQuCsHjxYnrFk5ubSwOg8/Pzt23bJsvy8KoO/yk9Mwf06D17Rv3IeZ63WCy5ubnpbwutra2yLLNbMqP+1GAAGAFGgBFgBBgBRuCwEjhYIEYRksRBi0M/aTXBlB47ZJf+2H/qOnxkHRJxh1W7O6x9/5TG6DepF154IXUxmZGyQbdt2a0poCWgtR7CJSvCpdtLg7U/uFuMRrCxlEieZkIPoEP/XrjmgvZA0cZppVsefECKxlC9JZnQog6JXrFfA4hIcMfdfX5fvd3a6vHXfP2mfRJAj4ByvqDFDJDQRq6jZE9bFRLw4J2JKfaaCtt7DTVooqbGZ9UAlVQUVEh1QxrPHY/Doleg2vlBhfVfP7unRyT2bTIXBhWgAWBPnxaX4PkXIORa5zfvLHW0nzxjY18ftiZJ5H6ADgZJ6BY0iMfhu9/urPRt8NremzdfEEh4CO2YphqXXXx5VmYmx3GZYzLmz58v4PtsGWkEmAA90maUjYcRYARGMwFZlleuXElFNJq/MW7cOLPZXFdXpyj09noKzyepz0xuG83nzygf+7Jly9IpHCaTye12Dw4OMhP0KD8r2PAZAUaAEWAEGAFG4DATSIut6Q20yabVZxlQF/0YuXnIoos6LHHNYtAxMe/SHI7Uz2H23HQzh3kEn9Lcddddd5AAjSqzAlvqYPbUZW53azC87YpL26ieS9tJycOoReu6gXEWg/1wzQUd04NbKgNN/3XjYEzE9zAmOuUY1nskGDTgV78Hf2C1z73V720554LmiIh1CVXcE6vN44JNaoYOMtGin38CpvtXhwvefvMFjN9G4zWK2oZG8rdpOUGZ3A0wAHZvgznhNVMsK7977WZhEEQJNKSNLnNyCGw7LsFbb0PQs8hn3lLu2Xvp3N7OPSCqMJhIAkBiUASSoyJrkJTgL/OgIriu1LHmvttjPYM433FJ5yU0swPAXxc8R+oQIrwrrriCfScl8zfSfjABeqTNKBsPI8AIjCoCokjrbwD9T3rZsmV5eXk5OTn0uicvL2/cuHFvv/02fYhpuP0ZL0iMo/tY2qiaGDbY44oAvT0jiuLTTz/NcVxGRkYmsWCcddZZuq6zZwCPq8lknWUEGAFGgBFgBBiB445AWilOb3zMENLvfXQDHdBUr6Zu6I/Trod/4mNaPowvnfLlkzHOeEwWx3Hjx4+/4IKv9fZi0b9TprSWO3YF7ZuuuHjXQD9K7GmTtjZsGwB6e+Ds01YFLa2VgfYrL98kkv3iGiSVGAwpy3ED/vE+hEIbrIXNtqKastJFG5pIGgbKxwkVU6CV9Hc9WQAlAf9cCJXW1ScGNr73Bh6CLlTR1oHXULuG7kjUAKwq2LYRZoTemulb/dU56+QEauKqgtEbioZfIHViXh5IQE0dTCmtC9t3lXv2XnMx39UJcQHd7Aq5QwAG6Koo8pDk4a8LoNS72jNp6WVz1w90Eg2b6uMG6AYWl6xv2M+ZLBw3JjMry2q1HsYZYU0dOwSYAH3szAXrCSPACDACn4dAWlZubW11u93jx4/Pzs7Ozc3NysrKzs7evHnzQSL15zkG+wwjMNIJKIqi67ooiiefjF8bLBYLfYbg1ltvTV++j3QGbHyMACPACDACjAAjwAh8cQSoIfpTjz9cSB6+TT9EX/miBGhqWZiYPz4ni0a65eRmWf777r8tfJqvDr0bLOgoMe+fXrp8xxbsrIC+5NSiA0iGLJNygXv2wDWXtlT4N4YdO08+cfvufVhmkDdA0KhPWqMVFt9eDJPM/3DYtjmtW+zWf/x7ESQ0FKBlFIpFDT3KwxYV2jfByaUfTHOuefR+fB2Nz+nDoxgu6kSABgBeho4dMKts6TTPynNOWB7tBFkG2cBChemF6svbd8Cps2uKXdt85m3TKxraWjDNOS6h+kx30AHN1YoAG2vgyzOXzqis/+pXNvd1kmZU0gncI9Xq/KfqOW4Kx6Fwz3HcsmXL0odjGyOGABOgR8xUsoEwAozAqCawfv36wsJC+h92dna2yWQaP378unXrRjUUNnhG4DMTkGWZ+qAHBwfHjh2LCXTEBM1x3BtvvCHL8mduie3ICDACjAAjwAgwAowAI/AFEhguTX/S9hHp3s6dO8floPqcPSYrL9fMce4Lz3qmpODDKlt/aWH/zPItLc14XAVA0LGUH+2cCkZcickAySTcdP22qcEd/sK2WdVNm+pxZ4lItP3RWEyMSgbEeGhoguopLQF3p9fREfCs+vtL0DWAGjHVptNBJYKCORgAMLAHLp7VNsW87I4bWkAHUUF9WgNN1XVMh04ZyHVeiyQVGOiGc+bUFxd+eFLp4o421LNlHWSiQssgx+Q4vSbe3wXnnrplsr/dNXFDddnqxgYUtWWypgVozQAlCV07YHblhkrPuqqKl5o20R4NRagQ+VkQYMd2OHnW/Jwx12VmBXLyxnEc99RTTw3tyn6PHAJMgB45c8lGwggwAqOHQNqSSTdqamrcbjetN0htmyaT6Z133hEEQVEUTdVYju3oOTfYSD8HgbS+rCiKIAjr1q2j93Lw+0N2diAQ6Ojo+BzNso8wAowAI8AIMAKMACPACBx1Ap8kOg9//Yh0qqamJn0NyXETxmbM9BX8vNrSPs0hlNo3vvI8xEVI6sb+SJ9oaJh1PZSnrAEMROGO7+4p86z1TWjzTlrz7puQTGB2s6alEheTCuq1W7bCSSdsKPEOlHgSJf76++6NyDq+PhhHi3JqhKRcoaxhEjTfBzddsulEz4YT/R8M7MUoZ5l4nw0MdMZFVzEEQx9yIt9wZWeZbe2ssuVvvZxCpIKmgiIZvARyXMU2IzH4+jWbTyzbFyjYWu5bsWoZdj4uQV9UE9SUAxplaA2SA3Dt+S2+/CWV3g9WLAOB1CRKf5Mlh4dkDG65qT7gfnYMdxvHBceMxTDJn/zkJ6nDs18jiAAToEfQZLKhMAKMwKghkBaUDcNoaWmZOHFiVlYWrZ+Wl5fHcdzrr7/OagePmtOBDfQwE5Ak6bHHHuM4jsapm0ymk046KX0M9peVRsE2GAFGgBFgBBgBRoAROPYIDBeaP2n7iPR63rx5RIDOID8nctz0qcEngvnLpgcb/vJntA4LWGzRkEmWs0z8v3QbAL529foZxdvK7B3Tw/XPzwdFwtWQiKhM4pI1gN4+uODcjopAT4VH9Vo233N3b0JAnXcoHkMj7mos4UgTM6ID8OjdRpVl+TnVSzsaQIjhqIlFGtVnKkArmiZImiqjWHzPd3eV29eVWJe8+Jw8EMGd6T5YI9IweAMjqHticPdtiaClrsq9p9Sy7pXncDdBQ6e2pIOgYgJI+oM3XNFR7Vlb4Xjt+Sf1wQEcMCljqOnDQkIe/xX47Ksvu6T3ksuX5+RWmsZkchx34YUXYitsGVkEmAA9suaTjYYRYARGOgHDMHRdN8gCADU1NePHj6c1LujPoqKilpaWtEb2kTvMIx0OGx8jcFgI0MKDM2fOpB4WemvnrrvuwotpYhZJ/wEelsOxRhgBRoARYAQYAUaAEWAEDh+BTxKdh79++I42rKUf/vCHmVwGh2sWxzlM3OnTwo9PC/zrvts6VYCepEgEaBAxrBmFYGo77o/CjTe0VZasKXPuqnRvfvTHOlWUZT6Ou1J1WYWBPvjvu2N+x1Z3YW91Sc9Fc7fv2gO8gtkX2BC2pQJGOfOoSBsgJOHNF2GabeXJwaa3iEyskvgMDbOaZY3sraForCsSRHvhZ/cMTHa+e0Lx+t//AnqH1GeZdFHUsMO0auATT+oe8/Jyx65i25qnfgtSgsRz6KhNUw06KWM/kkn4wT2tgcK3qzzLfnrvTiVOMUkqaApoEoiDkiYZ0NUNs6fucxa233o75OT9iOO8tB74KaecMowr2xwhBJgAPUImkg2DEWAERhUBKis3NzfT2A0qk2VlZeXk5Dz55JNpFFSqTv+TbTACjMBnJ9DW1jZ+/HiTyZRJFo7jnnuOXLwDMAH6s2NkezICjAAjwAgwAowAI3B0CQwXmj9p+4j06Nprrx2Xk5vJZWIxEc6bw10wtfhXF579vIExypAEXkQHNF0NkYjGugG336YGXa3F7l0Vwfo7b40kYhDpJ90TNdxVwQ9og/Doj6GqtN08cb/Tvn3GjLd7+iBOEi3QpEzjn3GLB0ioBrqrNy6Dk0vXVNs+fOInIJEGdR0LDmoQU3ClyrYiEGn5p3d3z3CvrLC9f+u3MHlaIx5tNaWQY7hzHCBmwBv/BEfRB9XBjqrgxh/ds9/QIUZc1aqWCoCWSBQ1z8NP7o96Cl+bEl561UXrQQE+RruoKKRlaqyOC3DdtdsrwvsqQnwg1GZ1/SUzewqtwpKbm3tEZog1+oUSYAL0F4qfHZwRYAQYgc9LoKmpKSsrKyMjIzs7O4MsHMc988wzeGvawFvVVCNjDujPC5h9bpQSUBRFFDFrL5FILFptLBcBAAAgAElEQVS0iKrPGRn4KOWECRNaWloSiQQToEfpycGGzQgwAowAI8AIMALHAYFPEp2Hv35EhnHWWWfljcMaeplcpomzjuVOO//03w50Y0pGVOHjekQeEqCpFbpnEG6/VfdaNgft0Wnl/TfesC+eSHXMkDQjqaGXmEjXy/8NQevaEkefz7x3zglbN2xMvSPj20TOpYMDEXMyDGirh9Mq15wcbv7Z7ZLUl2pT00FSVBH6FYiJgFqwAaBK8NYL4P/Sa7N8DZed1qiSyoUiQAJ0tGnroBCFuicGS1aAo3CJp2Db5GDTzd/cLUnoo6ZSMtXAZR0kFaIx+OerUOldFbCsOvOUD/ftwwzp6GAPVl6ElAdcBhhIwLIV4LQv99v3hVxdTvviu+/ZxXEO6oDmONQq6TfZdPjkEZkz1uhRJMAE6KMImx2KEWAEGIFDIKCpmqZqiqIYhtHc3DxhwoT8/Pxx5BKHOqBfeeUVKpwpeDnBTJqHwJp9lBEYInDrrbfSv6/c3NysrKzp06fHqNNjKI5jaEf2mxFgBBgBRoARYAQYAUZgVBM4++yzaUH4zCy8fiwNntLaKOpERlaJTqySGGiBqMr7euHe+6TK4s5ij+gxd55/7v7+RMrUjBBlXCUJ6/ttqAeX491yd0+ppavKuub5P0JsEGsJYuQFkYB1rCioEpu1Eoloahxu+3rzVNcH13ylrW9XekZEAF3RZVFPCsAnQe5NGrIMa5bAFMvaqqLWk0uWKtR5TVRynnivdQ10DdM8tm+ByuKlxZaekLnj0q/WawYenQ6KHoCmToMGWxpQfS63t5b7lzVtRoWaiNSarPXJkOB1iPDAyxCJQvWUJo91f9gVnRzYdumZS/Q4mLgieuHNcdzKlSt1smipptMDYRvHKwEmQB+vM8f6zQgwAqONABWXRVHcuXNndXX1cOmZ47i///3vdAd8ZkrVmENztJ0ebLxHgoCmajzPl5aWZmRk0L84k8n0ta99jf6VAYAkYSlwtjACjAAjwAgwAowAI8AIMALTp0+nj81lZHKciTv9tLMVBeVXKtQqoEugJlQM1eiPwl13xvzu2lJ/IuTun1a1fd/+j/IbEm5rGmHqrFU2W52rYEeFrfmdBSDtA01G97FqYFYGWVUNi/+ptInn5sFU7xuXn7m+px1Nzgq+TL3X+L4GetJQePLBbS0wp/zD4nH10+zNzaswHUMRcB+aE4KeJlLXUByE2ZPX2cetCxa0X3L2QG8P7O3BUQwXoGNRVKxrlsFJZZsqHJtDlmXvvYk70H100FWICfogT+oP9vXBnd9PBF0dYbdQ5ttz6dnbpf1ouiYlwHPGjx+fkZHxz3/+U9d1pj5/9LQ4vv/FBOjje/5Y7xkBRmCUEKCmZkmS6uvri4qKJk6cmL45zHHc888/P/zRJKY+j5Kzgg3z6BCgf3Tpv7js7OxnnnlGFEWmPh8d/uwojAAjwAgwAowAI8AIHBcEnE4nx3GmTLxszBzDnX/++TSbQgdDBUEFIapixEZPFB5/HEKumhJXd4mvpzzcsHY9ji8mYU1AsmDlQV2Drv0wpXKRw7Gqomx7ia/mkQcwSRqrDSop9VkBXQFZAZGskIzBA7fvmOr58Iypa9ctw3p/qCEPix7RSVFBFWBAgA0bYE75hunOrSf6G/71N2J4JseOJTBcWqLasQbxLvjaubssmSvDRU0zK5e1NOKhgeyu4LhQYZd0Q+ChaxtcfvqOk4p3V3k2vPQCjkUiu9GChypIcYnGVsObr0PQ2mDP7/Bb2+fMXLdrKwjEfD0260vp4it/+tOfDMOg34JJv9iP454AE6CP+ylkA2AEGIERTGC4rIxFJXh+7NixNBiLPt5Fvc90N0VRmPd5BJ8MbGhHn4Cu6/Sq91//+ld2dnZubi7HcdnZ2VlZWatXr2ZFPo/+jLAjMgKMACPACDACjAAjcMwSoN/UsrPHmDK5DBN36qknywrWGtQxBllSwOhLoqX45VegomSpa2KbZ9KOMt+avy/EJA1ewVSN9KIboEhwxYXtHnNdeXBbRXj9N77WFu1HVVrXUVMm1mRdIVq0QuVgBRb8US+3vxoufO2Df6AYjY/ryTomWBANWlcAmyXH2LMHzjx5RWhSfWlh/UN3CWCAxOMbNPF5SF/GPtx7i1Bp3zzFvqvcsWLDGuAlbIwc3dBQ4kaDdV8Eov1w7fktJwQ2Fhctfvg+MRIFnhwLtWwNBAWl70FeVgzYWAdzpm33TOoode0Lu1e0NGLEB12qq6uzs7NRvs/MfPjhh9G5LZMI6tT77NfxTYAJ0Mf3/LHeMwKMwMgmIIpiPB5XFEWSpJ6enlAoNNyGyXHcggULKIH0/83M/jyyTwk2uqNPgMbPfetb35owYUK67Kfb7eZ5Pv13d/R7xY7ICDACjAAjwAgwAowAI3DsEIhGo/Sb2tixY7OyskyZ3KxZM2n3YoKoAyRJ+Mb8+eBzLC917av2RacE6l9+nui5OpWIgURViCqAKMK3b9hREd5a4t7vtzWcf1aDwGOJP1kH2dBJbUJDBkkGJUkU5UQC1i2DaveiCtu7f/lDVNdwTxWVYkPVgSe1DTViXVY02LMbzjutdbK3tdRV+9P7QeZBEIlRmmZu6CBIKERH4vCDe/vLXVtP8EcrXWtffw57JWrpgA60OAvAR0TgBfj+t7eUOZZUeZb96O7dYiLlkpZJSIhsgKhJxDYNvd0w98x6x4Qmb+HOqWW1Sxahgj4kvBuzTz6JM2WYTKb/9VpRAfrYmV/Wk0MnwAToQ2fIWmAEGAFG4IgQMAxDEEgKF0AkEjn11FPpNU1mZua4ceMyMzNffvlleuBEYqheMvk3rRd8RPrEGmUERiuBSCQSDAY5Ek1H/xIvu+wyWZYPekxhtOJh42YEGAFGgBFgBBgBRmBUE5BlmeO4vC+N57gMmiNx3txzJElK8lo8CQZAZw88/RT4HEtLXN3Ftl5/0fq//A4MDdDja5AVCwmmxNiXXgC/e6XDvL04sGfGlLWNGzFoQ0b/MS+BKKNTWZFBkMEYjCP2xjqYWfH3E0NLb71+TzQCSRlkUiRQQ2F5SODF+iXQ0wXnnLJkRnG739zwnZu6VA3LCSZRBVaxEwZGb+g6JAX49aNSdUldsW13oKjhkR9qUgJklRZHRBu1DpoEWlQBXoUf3L1vavGH5e6ll3ylVohBLI6uZ7qopF2UwnVQRPjlg1Adai7xtFeUNL7zFu5CU0F00AxQx+WP4ziOPunLBOgUwRH0iwnQI2gy2VAYAUZgZBGIRCK0rmAkEqmqqkp7n//3iSSavJGuycDzPIujHVmTz0ZzLBLYvn17Xl4e/UvMyMCvFr/5zW9YMt2xOFWsT4wAI8AIMAKMACPACBx1AkVFRfn5+SQvEb+vnXjiiehVJstgFJ5fCD7b+hJnpNgWKfM03/Zf2zAiQwRZIJEWOsq/ug68CPV1UJD3VkV4wOHa4wmtXroc1Wei5CYkEIkAjYnSRIDG1/fvhUvPaZhW/O7Xr1ghCpAgFiYUoNGAbCi6TL828jyIAlxx/qZyZ03AsumsUxr39UBUhRiRlXVUlUnehY6e6Hf+CWH7imJne7m/8bZbBgzaGjYoyWCIAAJAUkO9+o+/V50TllQHt1aV/KupASM50uozho/o2A1VhXgUGmtgirMxMGl7cbjm/ocHBxIYjE0XWq4QE7RNJlrIkQnQKTQj6BcToEfQZLKhMAKMwPFP4CDz8v+wdybwUZT3/392N3uFnOQkByH3DYRgOBSs9wH1Qqt/FQ88autdrWcBD8Sj9ai1Wtt6gi2KViuteKACcgQICYQ7BAiQi5x7zT3PfP995tks69FfqYpNlu+89rWZzM7OPM/7yWZnPvOZz1fXdFmWa2pqbDYbv5mLi1933313qK+of4VQ4AwSOKoEFEV5/vnnHQ4HPyyOjo6OjY3ds2cPmqCPKnbcOBJAAkgACSABJIAEBj8BSun48eP5yZrVGkUIcbvdvNm+bnhrAVTkriob4StKlUuzdp93VqNv4BZWw7QTcxO0rkJLM0wctyYraWdmasuowro/vMaiMHSmTWvUkBQmQAsa+EwB2pB06D4EF06vG1OwrGbM370895myoAwzrCOYwsGUbhkkAe665WBh6qqS9M1VBcu2bWatk8EngRowRAn8FFQWFq3DrgaYWP5BWdauvJTG009ZE5BYGzQwVN1DwSsbzLQtmPEaHy6F3Iy/5ySvr8hd88WK4Cjxqoe6rlCqMGOzDooMvm6YPObTmryDJRlbZv10b7/OU0dk/h7NjLF2Rbujo5kJ2mq1zp07N7g5/BEpBFCAjpSRxH4gASQQEQT41emQpuzxeMaOHcuPY1wul81mczqdc+fODVUdNAwDCw9GxMhjJwY7gdANB7NmzeL3BvIaKSkpKa2traFXB3s3sH1IAAkgASSABJAAEkACR4GArumTJk1icW12R5SFCdAWK2Eiqwqv/BZKUxsL43tGOpT8xPZpp9T19TAjsaIza7DB0ipoX18PAKsceN5pnRUjPekx+zJT1tx22x4Wo8zik6mhgaGBxsRfvwb9GjDpVlHgxivVspEbJ4xfurGBLVIAZJYTHRSgFVYC0Uz50OHOG5Wx+Tuqcg4cX7Jux2pQ+0FjgR7dEvgE8ArgN5NCYN9umFy6rmT41pKUjeee3ugTWHq1rIOi+lXaJ6t9GqWiyjTu5mYYX1ZbltNYmLPklZfZriWzAWaVQl3VRHMBk9b7e+GaS1oqRq4tTFt+zrS6Xg36TA+1pKu87KFssLcTYuFnvoSQOXPmcG/WVxxaR2HocJM/EAEUoH8g0LgbJIAEkMCREJAkKfQV6/F4qqurXS5X6GuYEPL000/rmi4IQkik5lUHQ+86kr3gOkgACfy3BAzDEARWHbyvr6+6ujr8U1leXs5f+m+3iesjASSABJAAEkACSAAJRAyBadOmEUKiLFFRFoeD3b8aa+jw2u9gQt6eqnRlbAoUx3VV5zds38Sq+Skaswazx+GIZrj2iu0VOT2jEoXinOa7fiFpOhOGez29kuijKhOgKVWYaqz5fQHQFJg/RypKr8tNW/3O+0z8FUxVV4HDArQKoBos4mPevUJF9s7SjLaClC/efRXEgwCqbEC/Ar0yeEUQVIAAQJ+f+alLknbXjOw5uXrtzi3sBclQVCrpVABQvN5+Pl779kB5wYLC9LXjSzY9/FA3z3wOUJ1r0KauHoyf9nvg2cel/JRP8tJWnDdtfdNe8AD4WBwIk98VTe/t9wuKrjMB+vA0e/ZsSqlhGHivYcR8QFCAjpihxI4gASQQCQQUdj8TGIbh8Xguv/xyQki4AH333Xd7zRuruPrs8/lC6jMK0JEw/NiHQUyAf/R4A5ubm0eOHMkPkKOjoy0Wy3333TeI245NQwJIAAkgASSABJAAEjjqBPh9cswEHRVNiJsQ972/+LR8xLJxmZ4xqeKYEe3HFa/cXg+aCL19XHqmmulWlg0QFHjzNRiTvyc/yV82qmfa2Q2H+pmm3OPtZf5nTeIOaCZAG1pAhN4u+OsfIT+ptiJ3zbyHNMEsOegf8CCHNGgVWGbH6y9CYWrthCJf8YiGR+b0se1SYC3QJWoICtOCqW6al6+6fF/xiIbKjPYTSrfv2MTMyxIF2ZBY7IamirLhE1ggta8Pzjl585jc+uKsD+fe2++XoZf5NFiMtBTWBgogBWDpYhiXt6EwZf3kcat2tzCbtp8J5boCssaipFn/AJSPP/0nM0APPFCAPup/rz/4DlCA/sGR4w6RABJAAkdAYNq0abzYIDuCcToJITfffDO/CBxSn1VVRQH6CFjiKkjg+yHAL/OIoihJ0m9+8xueT8dlaLvdvnjx4tBu+Acz9CvOIAEkgASQABJAAkgACUQ8gTvuuIMfGdqInZBhsc7K3NQ7SpJrx6Z7R6d11BRtXLIYRDP6mRqg6rqZp6Ew9VmDunqozG/MT+7KTz1QM3brlh0sZFkB8IsenbmK2WQ6oDVNY2nOi16HkXFrSzOarrtqf48nqOOKZnlApj6bJmiVMrF422Y4vnJnSdr+khE77vipbKhAzVqDzH+sCZQqikFFynThOQ8crCzcljt8T97wNe8uDA6XqT4LsqFIlCVKazpQGc47/aPJRbtGxa6ecfYajye4pgRGwFB5fUL+rAPs3AJTKnaWpe84fkx98y6WXd2niiJroaGxGoQ+AOqTOjSQln2+LKQ+EwuZPXs2tz+jAzrId+j/QAF66I8h9gAJIIHIIqBr+hVXXOF2uwkhvIwyIeSiiy4K9ZKrYOHSM6pdITg4gwR+AAKSxE4DLrnkEkIIT4K2WCwxMTEtLS1+PzurwEjoH2AUcBdIAAkgASSABJAAEhg8BCilzz33XIxZQ4+QKELi7aQ4Jfpn4zI3TcjpLc9cuXgBq8Wn6mZFQZaKIfcJHQYzAsOu3TC2/ONRKTvLczpyM5Zs3coSlvtFltCssgSN4ESppuosqnnDaqjMW1aYuvnkidt9AQjoLD1DMI3MMoBssAefViyDqoLVRekHK7P3X37ePl+XKU6brxpUorRfp+zYVZThr29A6ajVZdkdhSO2vf0XCPjYBkQVvFIfAHiVgGBGhVAKc+6USlO/mJC37+wJ27taQTO3xhI89AHRXFd6ZUkFaDkA005tGJVYV561/rNlLOlDMl3SKphaNhOgPQCyT+hVVPjtsy8RSxSxBk3QDzzwALNGU7bX8DPfYMfwxxAkgAL0EBw0bDISQAIRR4DrWVy0uuKKK3jx31hzIoTccMMN7FvfDN8QBCH8Czh8PuKoYIeQwCAlwCt/ejye8vJyi4UVS3E4HBaLZeLEiaqqCoKAAvQgHTlsFhJAAkgACSABJIAEjg4BSZJWrlxJCLERG3si8VaSE2O7cGLBmjFZG+6/vVNXWWFAlUnPwYmZiSm0d8Npp65LTViVk9JUUdiwaBELvvArTERWNXNNytzCTA4OMK130wYoHrm0Mn9recGKz5ZBQGXSswSCzMI0BIWp3KxmIAC0H4BJ5bUl6XtGpTRNrdm5f7epPutm4gV7XVeoRzYLIS54GYoyVpZm7htd2HzX7dRr2rQN0+9stgD8OmX2Z4C7f7G/Or+hYsT20Zmf7d8CimnOZlEbhsEabK7jpZpszlxz9b7y/NWjUj5e8jZ4A0x91syds/wP9mAOaIkGFAoBP4wdcz4h0eECNL/xF+/65UMQAc8oQEfAIGIXkAASiBACiqJwT+Xh4guEzJo16+tiVrjuHJqPEArYDSQwdAjs3r07ZILmH9vLL78cA9mHzgBiS5EAEkACSAAJIAEk8P0QUBTF4/E4ouxWpqE6mJZKYixkTFn2C/fe2K1r4JOZPquyEAuWeQzAIpAphfvv6sweUZeZurcgp/6uO7ySzgI0RKpqQTlXo1Qxvc+GLEHXPrh42p4xhW3lhTv+utj0PhsggV8Cvwr9FLopKyqoiCp0tcOJVXUjXdurRvVMmLCxcRfIMggeU/rVAYxgG3wirF8J44u2FKV15KZtueOONh7JHKqMGBDVgMpaK8rw1kIoy15enrG9NOOz1/+giX5QzZdUKmmGppjpzwaAj0JHH7z2OmSlfFSSs+qlP7H3SgN75LgpE+J5X0FW4a47l9rIiYQkEZuFWNnjtddeQwGas4qYZxSgI2YosSNIAAkMYQK6pnP1mec+c08l9z7rms5v6hcEs7LDl29BCqnPqHkN4eHHpg8pAvxDx28JlGX51Vdf5WHQPIuDEBI6XB5S3cLGIgEkgASQABJAAkgACXxXAiNS09iRIXGZGrTVQkbMmPai7AO/CB7JpzLJVdJNEzQF8Pvh1RehMPOj4ty24oKWmZe1yjqzCYvMyCz1eDpYCUBDoODVDK3XA50H4azj1xem1BVkb7/xRq1PYtX8TPuzVzYFaIBugwqyDkIArphxKD+xsTq7u3Jk/aefsfgLMEAPSEx4VvkTs1o3NEB1cUNJ2sHCtL2XXdR9sBsEAC/VFCMoQasas2z7VVj8DowuWFWWsbloxOd/eBp8A9HPBog6FXTQNTN4WgFmyl65CnKz3irPX/2za7pZp4Lqs7lNygR4U4DWWNFCBRa83peZcQchUwhh9LgAvWLFCozg+K5/joPs/ShAD7IBweYgASRwTBIQBOH+++/nDkpecjAmJubaa689JmFgp5HAYCcQfuFHVdULzr+Af3j5BaTY2Nhdu3YN9j5g+5AAEkACSAAJIAEkgAS+VwK6pvP7WS3EyQVoQty7dvkMpv2CBroOim46oDUAjwC1tVCW/dnY3IOZyevPOGN7vw88IisnKLPVVMpqBSqK1g9gCrUyXH/V7ryE+sKUHWef1bCvk2m4lKnVksxUXIEaAo/3UPxwzWX7cpI25SU3jc1dvXQxGH7TnKwAMxtrVNcMn2ooAG1tcOZJHaOSWgrSmydUf9rZCx4FAmaSRsgBDQABGdZtgVEFyyeWd40a/vk9v9ij6aBoLP2ZtdPcr26wXw1gTW+og5ryxuqibZddtNHnC0WO8PiNAfXdZCKqsOITqCh8r6L8t4RUEZLID6rdbveWLVu+18HBjf3vCaAA/b8fA2wBEkACxxoBSqmqqqFgDVmWn3vuudCN/Nz+PGvWLHajkygahuHzmTUgjjVM2F8kMFgJhAvQANDT01NVVcULh7pcLrvdXl1d3dHRwe6slOXB2glsFxJAAkgACSABJIAEkMD3TODxxx8nxGIhdguxMye01fL+0g9CYi4FqpsZGAqFQ11wwY/ry7J2jM3dXz36885DTL1lR48GKAZolD10MHhgtAYw7wFvdcmG0Tl7x5VuajnIfMrcKy2z0GeFCdD/qg9oAPTDL3/aXV20LSdpd1FWw+0/bxZ6mUoNMjUjqBWqSRSgT2ae6FN/dLA4q7Mg80B22oebtoIM0G8euvLoabY1HagCG+tg8glbs7IaRybVXnd5Z0AAnwQSZe3UWdx0gENUzLd1HIDx5R9V5++8ZHqvzwsBCfp9qqKbujpLfg5OksJm2luhqri2aOQqd8zNhFQS5hwPToZhUEpFUeR1CAfehz+HMAEUoIfw4GHTkQASGKIEDMPgmRuqqvp8vpdffpkQwtUr/n17/fXX866F61wYsjFEhxubHXkEwj+YrICLptfW1g4cLRN+Demyyy4LfYojjwD2CAkgASSABJAAEkACSCCcgKIwSbW+vt5ut1ssNovFxg4OrZY5Dz8YVnWQx0DDvgNw0fRt44uai9K2ThnfULeBbckTMFVdykzE/AEAHT0gSLD4r1A0Yn1JZlNe1nuffw4BDboF8CiaKT3rXIDWNBAPwYvzoDChtiq7p2zkzrNPqadc/GbFATXQFYO5qtnU74Nbb5GKcw9kpzbn53786Wd8MXsWVc1Uss0lCjTVQ03ppyNT1lcUbJ1+xvqeHuj1MSFZMoVyhQVZezQIyJTp56oAV8/oOaFs96TKZfXrwTDA6zVTopkNmhm6Tfl9YF8UzjmtLit+RX7WRwnJl0XFFxDmHGeT0+nk+RuSJKEAPcBryP9EAXrIDyF2AAkggaFCICRahRrc09Pz9ttvh0vPDodj+vTpra2tfB2fz4e6cwgXziCBQUIg9FkO/3g+//zzLtdh1wYh5KmnnuKnIoOk2dgMJIAEkAASQAJIAAkggaNEIHTU53a7LeZECLHZbJfOvJznKVNTf2Wpxzr8/nfecflbytNb8lM+/dtfQFFZiULFDEpmq5kCtKyDqAI14O1FMLZodVVuV1nWtpdfgvZu6PIydzLblKGzXA3DfIsI7y+Eqow1Y1IPlSbt/X/nHujt4n3VDEOnmk6pplGW5iyo8PvnoCCnviD7YNGozU88yVTpfj/oBitUGJooBSrARafsrkzfXFOwa3zZJxs3gGhGQkumAM2eQVWYHs7e5umFO2/cXZKyakr5tk3r2AsAoKg8GITbu7kGzZZrGtx8XU9u6qdlOWsvv2RHXvHFJMrtiI3h6vOUKVO8Xm+oJTgTGQRQgI6MccReIAEkMHgJcK2KUspvIwq/hLtgwQJ+jZcQwqWrCy+8UBRFSZJC/QlXuEILcQYJIIFBSCAUBk0IsdvthJB169ZRc+LnJOEf7UHYfmwSEkACSAAJIAEkgASQwLcjwM/aBEG49NJLrVYrr+vjcrnSMzK8Iismb1YBBK8Cn3wI40u/KEhoHJe97Y0X2d5YMjTwSGVmFeZuYgOgqw/WrIL8tDXVeYeKUhuu/X9tsgJ+hRmJmafZlJ5V8+0+H6xeDjVFG8pT99dke6aWNjauA25/ZjHNQFXd8Il6v8CSN/74Cowp25qbsTc9cfV997CUDEEFVQWqmcHMZv81Azz9MPOi3eNGHqhM2Tex+OM1y8DjZTtVzPQPU30GCQwJaK/COvj0fKjMXDmlYuP7b4AWPJ3VWZVEJk+rotAXAivrsOBVyIz/rCi9/pzTaxs3wUD5weDJ8fXXXx8S9EPvwpmhTgAF6KE+gth+JIAEBjuBkABNKQ3lPgPA559/zi/wWq1W/k07YcIEjHse7MOJ7UMC/55AV1fXhAkTQleV+Afc7/eHf/C/0T397zeJryABJIAEkAASQAJIAAkMGQKyLC9cuDB0NMg9Rus31rHMCgCvxkzNp0/dUp7ZODqj7rG7QfGAt59Jz1yA1gwIyMw5bAAIFOrqYWJ1w7h8X2HSvnNO3tJ3iHmlWf4bUJVVJmTFCSmwKoTbGmFyVW1u0o6yEW158Z9t/MzUidmaukol2WC5z9QMgq5dDyXFHxXnHygc1Tz97J1t7Sz6Q+Hp1Ia5EnsP/Cu++c5b+/JHrC1Obi5OXLV0oakksw1KCsim7swkdSm4H3hzEZRnLytPX/WXF0Hzgym5a6ZOLvMIagBDkiTe/vXroSD3nZKRdWOLVnd1wKsL1pEoF3EQSxSx2Nip8TPPPDNkhhwbesQEUIA+YlS4IhJAAkjgWxH4ugCtKEpDQ4Pb7U5ISEaxqlAAACAASURBVOBHJ3FxcWeddVZXF7tLShTFb7UffBMSQAL/ewLNzc1Op9Nisdhstri4OJvNdtppp4WapSgKCtAhGjiDBJAAEkACSAAJIIHII+D3+9PT0/lZnsPhsFqtTz3zNAD4VOjqgVlX7KzI2VSVu/UnZ6/T/az3ssyyL3ReeNAI+os1gA4PHDeuflTqvoqRnilVu7dtAoOCz8d0ZDMmWlJBUgH8EqxdDScftzsnoSU/oysrbc2i103PMZO0WSVDBTSf7DHMZRsaYOzotbkZu4ry2iZP2uUVWHyHqLLVmObNcz1koCJcf/W28rytJdktYwrWPvWAjzXUNDVrLFpDlUCXwBBNUVoC+PgDKMn5sDJv2UN3CawD5iSbIjSfBRApaKpZgzDQBxNrNueM3FBR9vddO0GU4dKZP2VxJS7idNkcDofdbq+rqwtuBX9EEAEUoCNoMLErSAAJDD4CPHmDt0tVVX5nVnNzc1pamt1udzgchJVJtpSXl/f19akqL9EAoZnB1yFsERJAAv+WABeXX375ZbvdbrVaeQrHv04/HnjgAV6rkP9DCGnQ/3ZD+AISQAJIAAkgASSABJDA0CSgquqPp59rtUbxEz1CyLnnXagbLOPiD09D+ciVVblbTzmuvreDCcl+M+hYN9OfNVN97pfVbgFae+D8C+uKRu3LTm4ty91cuwo0ncnEBi8qyN5KWfiGAYcOwQnH/bMweU9ZhpyWvPHxJyDA7Uwqy8FQdUMGzadICkBLB1x0ydYRifXF2e1Tj2tetTLoidZ0UFWd6qb9WWGi8sI/QGXe6qKMA/kjGq+/ZqcU4OqzYICqga6BrIAssoqDTJTevBkmj95emFo746y6/k72MgD0dpvd475rFiuiygCyCu0H4JzTP60s3FZaWPfxx3Col3XB6XbY7MTpJu5op9vtjo6Oxti6ofm3/x9ajQL0fwCELyMBJIAEvgsBRVHCQ59VVa2vr4+Pj+eXxK1Wq81mKy8v7+npCd9L+FvCl+M8EkACg5mAYk4AcNppp/HLS0lJSfzDXltby4wjkhRSnzHefTAPJbYNCSABJIAEkAASQALfmsDf3/3IPAK08OPAmNh02Q+rP4LRGXXFSVunT9na3AhSABTZjF2m0NvHMpR1c38eFXr8cOop63MyG5NjdpTkbXnwoX6fxMTiwwnNALrO/MpeL1x2/v7xJR15iV1FmXvv/ZXcJ0Ovn62s6rpf9IhGgPdCMeCMs9aXFu5MGbajLGPjPxYAeIEqTNc2KFsZQPWJrAmrPoXsuGVlI9pykhrPPnmrXzTdy+Cl0K2DqjOFOaCw4GhFMODAAZhctX5MzvaJpev6O1iPNDNL2qAKGFrQVW0mcSgAogG33H6oKHdZScaS998AQ2XBI4sWv+V02VhynS14c/D06dO/NXl842AmgAL0YB4dbBsSQAJDmwCvOhguM23fvt3pdHJlKjU11WazTZw4saenp7OzM3y1od1tbD0SOFYJcLOGLMt9fX381ku7ORFCoqOj+/v7uQ86pEEfq5yw30gACSABJIAEkAASiGQCiqLwrEWLWevHZk3747NbLzhlWenwdeOzt37wJvR2sOBmlrxssAefFACfDDKFa6+rzxi+Ji+9NWfE+p9ctCNgCrWmAK1zmdowXcbdnfDzq/cVpTaNy9Urclunn9W0twO6ZFb1zywVqAlqIGDILIqDws9u2DIiaWXeiJbCrIYn5gxkZ2hg6JSa3mpRNwQNGjbD1Em1xal7R2d3/GTawUMdIGggMmG5V4F+HQwWFcIEaD2gQU8fTD91Z3H6+ors5Y21THDWzXRqVsyQ6uaD9U41pWcd4LEnu0cVfJCa/LcXfg0Sy55k0+Uzf2K3WwiJiiJBAXrJkiV4Q3CQTmT9QAE6ssYTe4MEkMCgJGAYhq7p9fX12dnZbrebEMK9z5WVlbzqIKrPg3LcsFFI4FsSUBRlw4YNiYmJNhszdPBCo+PHjxdFUdd0FKC/JVZ8GxJAAkgACSABJIAEhgABlUL3jbde5I4hXIB22QsKRtwwqeSlmoL3fvcwUIFpswpllmdWfpBJuoYC0NGnyhrcd2dfcebassz2ouytF124rrOXhUfzeAyz6zIH0NMBt13XX5nVVJEm5ybuH1/14abt7JVWD1OceW1ADUDQoasXHv6VXpa9OWf4vpzUjXPv62briQCixEI6dIlSquig6LBpE4wt/mJM3v7SjObynGVbNrP9ipStK4OigDbQWlGhIHrhojNbxuXuKU5d9fZr4O0J+rOZ71lj89QUy1lOCECfAAteherK1YW5/7j/7n5Qwd/PXt7dtG+Y22mq9EyD5oZxzN/gQxx5zyhAR96YYo+QABIYdAR0TZckqbCwkNshXS4X9z5z9XnQNRcbhASQwLclIEmSLAdPDB588EF+GM3ve7BYLA888AClNKRBf9ud4PuQABJAAkgACSABJIAEBi0BGcCzZedHdichFuJ0RxOSYiVTJ5Q/9ui9u0FmwRe6zrRdBXTFYCHIrEShAv9Sjufe31Gcvr4spaMwaefxY2u3bmcyrl9hURY8TpmCzpb44OfX7KjM3jomUyxN9ZRm132xmonOXgqyKfv6dcprAUoq/HMJ5KfWVmT35iZtO/+Mpp4uFqKhyRR0FagMmkY15nA+0AIXnLVtZFzjyJidlbkrV33GlHGWmzHwkM1feYMlGW6a2X9CUWtR4vo/PXF4ICjVDJ010UzqYHHQEkBAg89XwPFVDceVbvv5rFbBD16zqCEYcN/d9/GjZUaKmTaizjnnHADw+836jIc3jHORQAAF6EgYRewDEkACg5mAYRgdHR35+fkDX67MDllZWdnf3y+KvELEYG4+tg0JIIEjJRCyNvMZSumMGTMIIbwAusWc3nnnnSPdHK6HBJAAEkACSAAJIAEkMPQI6H6xTZDar7zqMocjaljcMIs1mpC0qy59qq+NycM6i7xgHmgFVMXUi/tkQwV44RmoyNw2cZSe69pzXP66FR8woVkz9VxeelA03cQ9AVj0FxiV8nFFRldRUvu4/M1vLgBBAa/OxGLJDFwOUMOjsDet+BRGF6zKT9tbkdNyYs0K0cx9DorZJlhVAEWA/k6YeV57XvyWysxDFTn1i9+E7n6mjEsD6rNohnYEQBcM6PPCI3Nax2RtqM7a9sCtEtO8zUgQM8ZaZTEdrFZhnwI+zVTPd+2E4yo/rcxZf/HZBz3d0NkZHFFvf19iXLyN2GzEZiVWKyEul2vJkiW8bsrQG3Zs8X8igAL0fyKEryMBJIAEvgMBwzDa2tqqqqoIIXFxcVyDnjBhAk+D/Q4bxrciASQw6AiEC9C8cT09PTk5OVyDJoTY7faEhIS9e/diodFBN3jYICSABJAAEkACSAAJfD8EWCk/v9C9a9cuQqxRLhLljHI6Uv/fJbeyMoKmVtsv9CgsAkNVWboFc0O/thBKshpHp8tF0T1FcfUv/Rp0Pxj8NTPOQgXoFkEw4OPlkJ+7LCupqXhEf2nGzofvE/xe1m6VKdrMsywNyNDd3TBl/MbM2M05KU0FIz/f1giCz9SnaTAuQxaoaiZG33Nj2+iM3aWpPaXZO+bNga5+cyNGMH+Dq89+YBq3ArDkXchNXpQX++GNl/Rp/QPebNYEg9U+ZE7ugAI9Eug9fti2CyaN/6Iw49PTJq3vbIGAh+nvPGTjkYcfIoRwAdpGbI4o+/HHH69qMpq0vp8/w8G3FRSgB9+YYIuQABKIIAIh9ZlHwbrd7vT09NbWVkFglY7xyzWChhq7ggQgXID2+/08i+OTTz7hye82my02NpYQUlNTg/cV4p8LEkACSAAJIAEkgAQilIAuqz0AoqJop55yZpQreB+sOzqpYeNuXWWd9koeBWQJdAXAr8PSpVBZtDE36VBhgrcyddc9s3xar+k95gZpU4AWDOgVYOmnkJz0Xkl+d05Kf1xU4zmnHaQa6AaIqk9ncjHPzTAkCl1dMO3U2oqs5tyUfWWVm/7wCpOHA32mW1kHCpQCVUXDEOB3D0PVyKaKVG9+UvPtNwvth1gZQ2amNthDNB8CgJ+yMJDXX4VxeTsqRmz/2aUtgS4QPOFjqAOroSjoIKigSAa07INJ1WsrC9dNqfli6xbm5hZl9qzK0HbQGzcsiRASZYmyEVuUJcppd7311lvhm8P5CCOAAnSEDSh2Bwkggf89gfCKggUFBey6rlmIzOVy5eTkNDc3c/X5f99QbAESQALfK4FwAZr5UMwJAGbPnh1K4ImOjnY4HLNmzdI15o7BCQkgASSABJAAEkACSCCyCBimp1kCgLa2Q4QQSxSx2i02m+3mm281b4Njqc+K6W8WALbuhOOqtmYm7C9KDYyM3Xr2pDp/+0CohWwalgd+27gZRo/ekDOiNStFKBzpPWVqe0cbk5XN11W+qkZZOUFRhpuvb63M3ViV11sysum2O/o1YJnPbFLNGBDQmPlahIV/MqpyGvNjW0tHtMw4u83jY3bsABegTSd1UICm4Jdh1RdQlP1BSWrzGTXt3oEkDXr4kFY2axZKOoBKQRJhxrQ9pTnrJoxZsa3RrGeoagBUZrkjcME5s9z2eJb7TKzM/mxzO6OiWYiHpguCEH5CHVl/G8d0b1CAPqaHHzuPBJDAUSXwwgsvhFQnQojT6WxsbGT3JhnmccJR3TduHAkggUFDwDCMadOm/asIIf+H4DCnxYsXD5oGYkOQABJAAkgACSABJIAEvkcC1DB0Zk2gMHfubKuNHQNarKzSXlNzfZ+/NaB6ZYO5hbduh3Fj60alHCzJFPPTmiZWrpS8oPOwZ9kMdebFBAEkAaZMbsjL2J+R5CvIUDNT6zduYmZjMx46lKzBuuD3wL2/6M9PrS3O2l9Z2HL5T3p074CfWmWJGarKygMKADt3Q37OqrLsQ2VZLaNL3uvuZQkbhpkKwtM8FKABFk8NkgzNO+D0SU0lIzZMrlzdupvVLdQoM1/rBnNT60zWFnTw++QAk9f9cOWMrSMTPqrM/ax+I3gFEBW2DoCmgfTeu/8wqw4Gj41thAH684uvfI8DgJsahARQgB6Eg4JNQgJIIEIInHbaaVxvio+PT09Pb2xslCRJ13R0PkbIAGM3kMARE/D5fPn5+fxmCP4cHx9fV1fHL0epLAAQJySABJAAEkACSAAJIIEIIRC6MU7X9NjYWLvNFu2KckaTCy8+FUAXTVm5cTNUFK4syjqYndjNgjIKPv5iJZN6dc2gusAqFErM3NzXCx1tcPkFLfnpOzPjPTnJQmHO3tcXMKW4X2F6sqkuBx1OighPPgRVeY2Fqa35GXuqj1uzu9m0NEtmPrSZQO1jYZCwcStUVNZljWgpGnVwTNm62nUQ0KFPZoo2d1MroCmg9ct6rweat8GpNavG5mw8ady2TWvBUJnPWmOJ1qrGUp25AO3XQaIGeLvhoTvlcbkrJpXXvreI7Us0WJ1C3usdu7fEx8cTYo2NSXTYo3kKx8Tjjufp2BEy/NiNbyKAAvQ3UcFlSAAJIIHvTECSpDfffJML0HFxcRs2bOC3FH3nDeMGkAASGJIEGhoanE5nTEyMzZx4GLTX68UrUkNyOLHRSAAJIAEkgASQABL49wRCAjQAzJs3z26zxUQ7rHZisZGVq2oVCZoamaE4d/ieUYk9o5JaKgvXLlygUgBJ5ZquorOAaBD8IPXBpefsKUypT3PuLUoxCtPb5s8DlnMB4FE0yoRo8xcD5AAsWQz5ySsLkw6WZ3WXFKz9eC0TsZn6qxo8fIMCiBocOAjn//hgXuaenMy9leUra9fzKA+2Ta8smsqyrpo1EjUATy9cce7+ihFfTB27vK0ZFAFkhXmlFaaRs4cpWGs6K1IIkg9m39I2dkTdcaMaXn3BfM2UvkO3AOcX5llsUSx7gxCr1cEF6F3bd/17lvhKhBBAATpCBhK7gQSQwKAiwAv7Goaxe/fupUuX+ny+f+XAUkpRaRpUw4SNQQI/DAFFUVRVlSTp2WefZTdgmhO/OjVjxgwsRvrDjALuBQkgASSABJAAEkACPxiBkABtGEZrayshJNoVRawkNs45Krdi2yY4/5TG8vS95SPkwpSuE6p2PvsUZTkVBlOWRQ0kw2AzEoh+uO1aIT9x0+RCbVK+UZnec+EZXX7TwqyZwrLBQjXYQ9NhSz1Ul6wsStmb7t41MnnlG2+Az1yHhTlrEujMqxxQoaMbTj5xc/Kw+uNGS6UFm95YBL0+JlCHJsqszSx6QwXoaIUrL6obl7uiPOODv/+V7ckAUAyWYa0wIVpVzHBpM1maFVW8/dotVdkflqeu+NMT4OuDgMy2yrdtAFx57VU2RzB5w0Ls/Hj48fmPh3aNMxFMAAXoCB5c7BoSQAJIAAkgASQwuAhceOGFPIKDH3AnJiY+++yzg6uJ2BokgASQABJAAkgACSCB75XAlZfPtNss0S5m+yXEObrkZwXJ79QUdJeld5dlb57/YAcAyCqIKjMs+yj0mVkZHYfg+qvaSzI2Fw/vPHcCjE7rOK7ws307gGpB0ZlruwpAvwSt7TBx3JqqgraxuT0VeZueeVr2SSAz7VmloBmGLmpKn5/16tpr9xXnNBVkdheM3Dp/HrdPA+UiMQVq5kpLGkga+LwwfWrdhMKNuckvvbsIVDlopDa1aUVldm1FNQ3OrLqhAI/e763KXFea/Pm9t+wxVDBdWBCQJQ1URVMfeHg2ieKHwMz3TEiUhdgz0jJ0RZe4UP29MseNDTYCKEAPthHB9iABJIAEkAASQAIRS+DgwYPR0Sztzm4Pmj6Sk5PXrVvHO6woA4VmIhYAdgwJIAEkgASQABJAAscQAVmWKaU7tm6LdjmGue1uh5MQByFlsy7eWVO4OT951YwzGzvbmJTLvcws8kJnwrEO8PzzUFm0uTx7/13XQklCR3nq+rrlpqXZrDxorvKvMods5W4PXDCjLju1IS+jLX/khrvu7O/1QZ/Etqmzd7DVdGBlD++/vzcr/dPslAOFIw/ceIMoSCxMIziF3NQAgQAEvHD/Hc3VuavG5iz/y6vQ3RNSnzVTd5ZCAjQL+ZDg/YVQnvZJWfKa267sN8zuDGwXDND+/MoLFrtZetCUoNPTswix2myODbUsqVLm+dChN+BMJBJAAToSRxX7hASQABJAAkgACQxWAh999JHL5bKak8PhsNlsLpers7OTB/UM1lZju5AAEkACSAAJIAEkgAT+awKUMrXY0OktN94U9D877YQkxzhmTBz752mnfHiolW2zq7fNVJIVHaAfoD0Ar70JebnLy/P3z7sbSjK2FKeseeUZoGb4BvM/M21ZBDNjubMfLrl4T/7IndmpHdkZm08+e+mBbrbN/oDG0zkogELBK8Any6Akf2VO6s7you4fT+/ZexC6Ayz3IzhxlVpnARyBfnjnZShIWjK+6O/v/AVUnenXPOtZBc18KAMyNMgCvP8XmFrcVJ687qYrm709TE/XAAIyE7cp6K/99c/uWGKxE7ubRMe6TOnZRQhZsmSJrqp+j1cWWVQ1TpFNAAXoyB5f7B0SQAJIAAkgASQw6AjMnTvXauXnIMTtdjudzhNPPNHr9Q66hmKDkAASQAJIAAkgASSABL4DAS5AgwHtB1uzMjJZGPQwh9OZQEhxeup59etBDAY6ewH6DRB4BMcX6yE3/938UfW3/wwuOxdKslf+8sYeb9dAmnIwVlmm5oJf/1oszmtOSejMTN9fVbOxvpkp0x6FqdQqryQI0OuFrY1QU/VpadbukuwDk6q3dvWyXpn+aKYvU30gTFqF/k5493UYm7nq+NJNv/uNjxosGKRf9QxIz1yApjwkWlVh0xooTX+rMm3dhSc3BfqDVm6FxVmzYI9X33iFEOKOtdqcofwNNvP8888riqLJykD8x3egjG8dCgRQgB4Ko4RtRAJIAAkgASSABCKCAC9Jqmt6RUUFIYQ7oPnB+COPPBIRXcROIAEkgASQABJAAkgACQQJGIZBB6bfPft7ftRnjXIQ4iQk4dbb5vX2spdZigWYCc0Am7bAxOqG7LSNv7wNHp0LuSkbp9bUBfwgaMxWHD4pCix+A8pyt+SP8BXn+ceM27Lwb8xAfUgGldmkDWaBBhBkaGuDs09qyhu+oyy9e2rFvi0b2XLFNDVrAIrOahgGJxkWvcDU53GjVt99U7cis9X4I6g4s3dRnyKxqol+2FwL4/M/nFi48uaZu8Q+th3ZkCQa8EoeA2DeY4+bnSUx8XGEkJAD46677vqy7myEiesDLcGfkUUABejIGk/sDRJAAkgACSABJDDoCRiG4ff7ExISgichphvaYrE0NjYO+rZjA5EAEkACSAAJIAEkgASOlEC4AC0EpOnTzhnQoG2uaLd7WPSrr75KNRZVYeggi7CvCSaM/bQir/GkCd4lb0PuiKWFWX9vbICACgJIEvhlqus6ePtY8EVjHUwu35WbdKg8Vx2VvWP2I1o/5UEZ4FMkVQ+Kyh1tMOOczUWpTfmJ7eNymv7+OlO7ed5GSFOWdfAFgKrwz7egKnvF2Iz1v7rNK/lZdsc3CdCsPQCwvQ4mFL9fnfvJOSeu8R5iSwwAj9wGoPuE/p9cdjkTnaNchNjMh4UQEhMTc911130NHwrQX0MScQtQgI64IcUOIQEkgASQABJAAoOYgCiKlFJd0+vr653mRAix2WyEkMTExKampkHcdmwaEkACSAAJIAEkgASQwH9BwAibAKCtrS01NTXcC2wl5LVXXpX8oPrB2w7TJu0vSGo4dcqOll1QmbsxJ23x4rc1QYUAhQAoAktyFgIqqyro6YTqwtU1+Z6xOWJu2rYf/ahBNKDVw2oSek2vtKQwOdjXB/feCiPjNpWmeiozmxf+gUVtKCIIssRjnbm+7FOgpwe21MIJFcsmFq685aoDosBCNBTj6wI0C98AgOZtMD5vWeWIz6++cH1Xq5kcLZjx1KAf7GgqrcwndpsrJsFmd9vsbovVwZX3F1980Qz7MHRVNqgyYHzmAjR/5snV/wVkXHVIEEABekgMEzYSCSABJIAEkAASiBAChhEq9QJz5sxxOp28ICE/KK+uro6QfmI3kAASQAJIAAkgASRwzBMI058NVVX9fv9HH33kdDrtdrvFYrGbFgS30/7mwg+79sH5Jy8dN3JjTdH+XY1w8w1KWe7nP5+126zjx1KYJYAACAFmlQbBD1ec1zcqdse4LCErZvPkcSs7OsFvOp5lM1iDg/d5YcFLUDFya25ca0VWyy9vYGtoKvT09Kkai5BWzXgNtmURtjTAxKJlozM/u/D0LwyJeZ95TEfIAS0bQXu1qsP+Jjhp/N/HZa85rXp9WwvIEni8rPagoukrVn0WNzyU9xwV5Yg27c9R0TFxL7zwgmEYohiQJIEFUBsqCtDHzkcEBehjZ6yxp0gACSABJIAEkMDgIkApPf7448ODOOLi4mbOnMlbqSjsfkyckAASQAJIAAkgASSABIYugZAGzbsgiuK7777LD/+irNZol8OsTO0877Rfj8577OSatzd8Dq+/ABX59Wef8oXXA/0CqBBM05AAOvzQ54E7blJK0veNTpePy/WNzV3RvBv8MlOouVgsmXuSdXj/b1CRu7Iwvbm6ZN9PZx1kgrLMYpoprzoI0ONTNFMD3rkZTqj4eHJh47lTtikBUDQWDK2EFGdTqpYo2wsAtLbA5WftmTiqYWLhB7s3sWQQPima/tC8+czfbSN2u4VYiM3utFqjCLEkDU9ZvnylJEmGYWiKZBY95Ikd3JmBDuggwwj+gQJ0BA8udg0JIAEkgASQABIY1AQ8Hk93d3dMTIzdbufnIYQQi8XyySefAIAsy6EzlnDf9KDuEjYOCSABJIAEkAASQAJIIIxA6HAutEwUxbfeeosf+0W7HA47ibYPt5FxGcOvWrcK9uyAstw1Y4rXfv4pe4cG4Nc9PPXCACYBv/4K5Kc15Mf3jYxurynYtvg1tpqoCzoEdBBZUUGDvau5GSqLvkiJrh1f3jL97J3tXeBTzHqDlMm/GgVZZ4kePgnW18JJ1cvHZi0fn/dx82ZQVFPINr4qQMsURAkCXrjkx8tGpy0/sXTT1loIeEDSDAC5q+/g5CkTLDZTTg8d17LCg1E1x030elmJRVEUBUEw1WdWIzEExJwPadAYwREGJoJmUYCOoMHEriABJIAEkAASQAJDhwCveA4AH3/8sdPpdLlcPBDQarU6nc7m5mZmCwmbhk7PsKVIAAkgASSABJAAEkACXyLAS4CELAWU0tdee81pd8REu4YnRpuCbSIho66d9eI1V/+jqPDlp58GWYMAy3FWA0avaLqbPRL8859QVdKQk9AyJguK05qfeEgM+JipWdVEAA+ARwdZ0aGjFSbXrEyJ3ZgzYufEyav2tIIOIALVKFBKNUPTKIvY0Cg0rIfJo1ccl9dwQvnKfdtBEtlCzVSfFdP4HCpUKKmginD1+c2lyZ9UjXx39Yegy6AbTEhe/P4biSluYiWWAf3Z5YyJiUuOssdcPvNqDsLvFwaIcPU5pDh/ZQYF6AFOkfUTBejIGk/sDRJAAkgACSABJDCkCKjm9Nxzz/E0QO4XsVqtlZWVlNIw/TncJDKkeoiNRQJIAAkgASSABJDAMU+AUsqP+jgJWWZhFkv/+UHssGibhbijnS5nHCEuQrJcrhOm/fgPghB0CAe0bgqiTMHjhy2NMLZkTVV+d0laX2nGwemnNu3bGyRrUIkJ0IZo6KAJcNOsQ5kJX+Rl7a4et7V+M8iUBXR45U4NBA0kBRS+wfoNcMrExgmFO4uSl775UjAYQzNt119Rn1Ud/B6479a9lemry1O/WPpWcL8ffLJ03MRx1oF7+RxOpkDbbC5CbOkjRr308kKeYR0af50ngLDO/bsHCtAhWhE1gwJ0RA0ndgYJIAEkgASQABIYigQEQaipqeFBHKE4jiuuuIKboENe6aHYNWwzEkACSAAJIAEkgASQgGEYuqbr9onTtAAAIABJREFUms7tBRyIoigHDx5MSIwbiKxwRDkTCXGkpo399eMLgNUGVJlx2Zw62+C8UzryEw8UDw/kD987peaL9nZmkdZYOT8dIKBKvayqnwQLn4fi5PX5qdsqKr94fQFQ2VSUgQIIAEz4FswSg2tWwuTRG8oztpemr3njz9DbBdSAAPNPs82ZKR0GBVZaUBCZqH3/z7yT8uomjFo799Z+Q4G9+7y3//I+Z0zMQOPZT+6AjotLuHDGJVxIDn/mHRmwgXMB2lwWNsvXwefII4ACdOSNKfYICSABJIAEkAASGGIEVFWVJMntdhNC4uPjQ8fxzz77LAAwqwhOSAAJIAEkgASQABJAAkOZQOjOtvBOqKrq83uOP2ESIcQ9jGdxBI8ET5xyRlNzi0885BckWYKbrtlckry5Mi1Qltw9vmhzfR2TnlUzmkMD3TDY4aLQC8vehvGj1hQP356buu7l11nKM0t01igYCoDgFQ9IzAEN6+tg4piNI+PrSrPqn5gL3YdYo3Rggc6m+kx1kHS2B+jqAl2Cl3+rTMpff0r57p9f2mSI8MADLyempBNiYW212niLrVar1UZycnLee+89SVTCpedvcjWHqc5hs+FwcD6SCKAAHUmjiX1BAkgACSABJIAEhjCBNWvWOJ1Oq5Xduuh0Os0bGG0NDQ1DuEvYdCSABJAAEkACSAAJIAGTQEiA5nnQ4be4ybL87LPPJiYl2aNd1iim50ZZori8e/nMn3i96r7dUJLzZHnGxvz4LRNLN7y1gIUvS2awhsQVZh1UAXZugAmjNpQl7KzO3TH3LujnqcvMI62Z9me/DoIOsKkBqis2lGS1jinad88vu/q8oBpMy2ax0OZEWbVCQQdN1kAR4LN34bhRnxQlvPeT09c++5v6rKyJhEQTMowQm/mwWqNsdrvdarU++OCDXq9XURSevPEVDXpg8wM7AfqlHI4vv4y/RRgBFKAjbECxO0gACRwmMHBrz+ElOIcEkAASGLQERFFUVXXOnDkOh4PnQUdHMxdMYWHhoUOH8B/aoB04bBgSQAJIAAkgASSABI6EQEiANgxDFMXQLW4+nw8AVFXdv3//1JN+FJcQP8zF7orjU2K822aNvv6aJ++8eeVZJ6yqLvng9pu2+r1MLPbILNmZCdAUFBna9sLl03dWpe0ZndZ83skNnt5QoygYEoCfAvXL0N4Bo0trM4fvSI9vuHhGZzfbOXgkEJloHJwoq2vIBOiACPUbjBPHvVac+qechEcyk66x2/NsjhhLVGJ0zAjCsp6ZCdpqtV577bVtbW2CEKo0yFr4lcfA5vlP80XufUYH9JfRRORvKEBH5LBip5AAEoDwaK0QDn6Te+hXnEECSAAJDCoChmGoqjplyhSr1ZqQkGCzBe9nvOD8CwzDkCRpULUWG4MEkAASQAJIAAkgASTwrQl8xV6gazr3RD///PNpySlmtgVxWJjH2JxcxJrrcJwUM+yslgNBq/Ihj0cFqprRGUDhhsu8k4tbK0bsPP+kpu4O1i4ZqAY+lXaZQdIqBehohzNP3V2S3Z2T3nLij9a09QZjoUWNeZ6pzkoDUsqzp0FUA3v39hQXnuS0ljmtFTZSSEimzZpGSAwhDhb4HGUjVjJz5syOjg7B75fFLx2shqvPnBJf8iViKEB/CUck/4ICdCSPLvYNCSABJIAEkAASGHIEurq6kpOTeR40q+Visbjd7nvuuUdVVVEUec30IdcpbDASQAJIAAkgASSABJDAkRCglHr6eh97+GEuPFsJGZ7Is6EthMQTS2JeWdXM66/7aPlyw9ycT4I+L7z0R7EgdUVZ+o4Tx61ftxK8PvBKPlHrA/DJRodEA4IG23bAWac1lRe254zoHFfVvG4z9GjgMz3UsgEa3xzA/gPdy1d+8ct77pg8ZRIhLkJinC5WadBmt9vsbpstkRCn25VYUFD08PyH9x3YE+56Du8gCtDhNHAeBWj8G0ACSGAIEfj6V9j/2XjKrt/ihASQABIYcgRWrlwZioF2uVyEkLS0tF27dvGOoAY95AYUG4wEkAASQAJIAAkggSMhYNqiDa+nB4D2tLdee8VlriiL2+EkFjshdjNwmRAXs0dbnDEjcoouveqq1xZ98Lf3944adW9hxvtVRR8t/5ztR2blAw9PBkBLE0yuqi0Z2Vac35s+8rPFS1noc5cGfnOt3oC4dNmym2796YRJlUz4thCrnbiiWRKI0xVnsUXZ7Kw8iTXKRYj15FPOfv3113VdEWRBN0+5mXX6a9PXz97DHdChvOmvvQ8XRCYBFKAjc1yxV0ggIglQdjOQBvxhaMAfwduPvqHHmqx1tHZsqN2w9J8ffP7psk2b63t6O837k/DL7htw4SIkgAQGCQFd03khGm574UnQhJDU1NSQBj1ImorNQAJIAAkgASSABJAAEvh+CYhiwKBKMFpDV7Ztarxu1nWJSWnRcYkWh5Op0E5ColidQmJxkSgHscYRkkPIcVZy/fjqp5atbHn/k4/XbNjQdaiPN8zvF1r2wVWXfjQq7Y2Kwg3HVdc9+ET/kuXKUy+/M+PaK7Ir8pjL2cIzP/jhJw92HpgP+1kz8YSPP/lcUZi8TalCKZVV5RvV568UIeQt+YoAjafl3+9fziDfGgrQg3yAsHlIIGIJGIYRXvaX91OSJFEUw8OweGUGWRY1QxOAlUVYsfKTzRtW1X724VMP3f/43LuffPSBu+78xRlnnFFTU3PWWWdNrJkQZbXaiCXGHWO3uoKXiAlxmtFZGRkxO7ZvADB0VdU13e/nl3vh3900FLH0sWNIAAkMegKqqp5xxhlhB/xsdurUqYqiqKo66JuPDUQCSAAJIAEkgASQABL4NgTMakZmHjPlzwZQONTZPW/+YzGJ8cGDQ4eF2B3EwnRoJh5HJVqiMoglj5BMYh1GoizB0oDEaiVWcx03IVmElBAylpAKQkYSMpzYHEzI5g++loU4o805a9D+zHeXn5/7+9//nlIabBGlhm4+2Fl9sNLg17v6dQc0Xyd8efj817eASyKJAArQkTSa2BckMMQIKEqwzi6lVFEUSZIUReE1uAzD2LFjx5///Of77rtvxowZU6eekJI+nDiINdZqiSLDXMFvUQchTguJiXbZbDaLxWK32+2saJd5jxL/qmRfvMFrudYo4ooh6xtWMkz0G7I5woXvIYYSm4sEkEBkEeD/DH0+X0pKCo/giImJsZjOlEceeSSy+oq9QQJIAAkgASSABJAAEggSMNXn4BOrCUgN83GYz6J3Fp99zo9ZMkZMtCs2xkzG4OJx8AQ4dB5ssViirGxix5AWwk6hraGTY3PGZqrPA1UOrXaL1R48d45LiOXbmTHj/CX/eJfvngnQA1NQgKaAAvThscG5/5MACtD/Jx58EQkggaNMQJZlSZK4G7q1tXXBggUzZ8489dRTk5KSeP6pw+GIj2eXea028/uSzZlfhU7iihvQoQmx2WwOh4OJz4RER0dHDVwKDl7PtZjXfV0sNWt4VvLPb/rZvHkPPfTQQx9++KEoigDAv+GPcl9x80gACSCB/0yAOUs0lqLHn99//332b89qtdlssbHsTMBisbz//vtfv4PkP28a10ACSAAJIAEkgASQABIY3ATCBejQWWrIKcUDlxVN3bm76Zbbb4tPTLDZ7cRqYQ8+cf+VJXj0aLfbgwK0Ges8YM0yV7WYdwvzs+xwYdp8MT0z/alnnmza09Tf36tqMoBBqTYgPrOfhx3QzAP9b03QoSCOcOp8fX0gHDP09vCZ8PVxPjIIoAAdGeOIvUACQ5KAJEmU0oaGhscffzwvL4+7/LiROfj1OfDDbrcFvywdTFKOindYop32+DgmN8ck2J2sNkJo4tsxheoowlzTTmKNYg9iJfYo+7Bh1iimUzudrIrCuHHjGhsbudlwSELERiMBJBC5BFRVpZQ+8sgjoQtsXIzOzMzs7u6O3H5jz5AAEkACSAAJIAEkcIwS+EYBOpyFZirBACAqskbppsbGX82dk5ObG+V0sBuCvzYdFqBDJ8x8JtwTbSE2BztHLq8su/2O2xq3NWqGmfJs1luSJEEQfKYGfViC/kYB+hsznb++EAXo8AE9duZRgD52xhp7igT+9wQ8Hg8A8OQNURQXL15cU1NDCOHaCv9q5PeYc5HF4XAEvxxtVovTYnExPZk4iNPtcrnjo+wJhMTZbIlmKV5mgo6Li3M4HDExMXanO8rlZoqz1Uns0eZGrKYb2m2zxtitjtBNSjab7fTTT5dlGQAkSQo1738PC1uABJAAEjDvzwCAM8880263JyQkcAe02+0++eSTeRI05kHjnwkSQAJIAAkgASSABI5xArqmi6K4aNGiiy++ODk52W63E0Li4uLcbmbVcgxMPLHS4XBYreyE2Gq3JKUmnXbmaffNvvfVBa9ubKgL6c4UKH8Yhh56DOSB8FQQ9synI3IuGwADKZjh6/+7+WN8QCOy+yhAR+SwYqeQwOAiwPWR0A3jgiDU1dVNmTIlKC6bqaYWczIjqqwOu8s5YGrm4c58TWIh5eOLzpp++glTfzT5xLOOP/MnhT86L3PCySXjJk790cmnn3bmlClTpk6deuqpp0750Ykn/OikM889n91WZI8m7gRijSWuFBKdTuzDidVpszkGsjyYFXr27NmKwmr4hm57H1wEsTVIAAkcqwRCd1wO3NvB/h3yC3VXX301XjM7Vv8usN9IAAkgASSABJAAEjhMwDAMnt7GF7W2tq5YseJfZQNnz5796KOPzgmb5plhlC+88MIHH3ywdt0an+A13zKgDZu/hNRnyjRmFKAPc8a570IABejvQg/fiwSQwJESkGWZVxpctWrV5MmTg4LywA+LxWK1sZRnU4COcjnjLMTpcsacd955c+b86qWX/7Rhw7rOvg4VVJ4u5ZVUGWALwIu+wG8PHly1t93rYeZlpsWoEoCh64qq63WbNpMo0wHtjiOlo3/++qJb3l8af9p0MjyVWO2mbzrohHY67dXjqzZs2MC1ck0OVkc80u7hekgACSCBo0nAMIyGhgZCSExMDP/HGR0dbbVaFy1axG/gOJo7x20jASSABJAAEkACSAAJDEYCvJZSyK/Afw0VFOEtNgxDDZt8Pl9ouaLLsiqp9Esnv5qh6aCHNGgUoAfjwA/NNqEAPTTHDVuNBIYUAVajwDA8Hs8111wzoDmbVRGIZRgLyiBRVmuUlS0hUVbicNw2/4l1re3beg/t9R0OOdVA94E/ALJiQJcGGwF+3xW4te3Qb3VjP0A/gKizy7aawb8+mZfZJ8kkPok44okj8aznXpm7+8DTqvrY/paxF15sj002fdAu7oNOTh5ui2IK+CMPz/P3ecyoqzDEX7oeHLYcZ5EAEkACR5kApVQURV3TZVm+7777+L/QxMTE0P/S2trao9wE3DwSQAJIAAkgASSABJDAYCRAKVVVNeR9FkUx1Eq/3x9aHlrI7/eVJCmU4ca1ZrNUIFWpIquSossoQIcTw/nviwAK0N8XSdwOEkAChwmErsHyRaIoPvnkk2lpaTYbq2xgs9lCCRtxTneUldUXtBCSk5X94sIFm3yeLQDPHNj+/L6Nq2lXD6gSexgC6H4qCAAKQAvA831wZzvc0wVP+OG5g51bAAQAryxqoOogA9WBGoKiturw6y92XPzmqjkdcEuXPqu35/bWlg87erbu7ayqmUqIze0eFryx3TRDJ8fGZiQmf7b0Ix0MA0ASRF1WQmFVh3uIc0gACSCBo08gGKs3UO4FAPgdJOFxHEVFRTxYHwDQDX30xwT3gASQABJAAkgACSCBwULgKw7o76tZXzmd/+bNhmU68xV4mvM3r/xNS//b9b9pG7hsKBFAAXoojRa2FQkMLQL863D16tVjxozhujOL2rBaHQ6HxcKU6NA06+qZy5Z+5NfpfoAX9+9+0tv+pP/giz3bmwF6QJZAVUzdWTHAA9CkwXse+FUn3NzNBOg5+8UFXqURoA/AYygKyAaoQA3NgG6AbQB/7oF7D8C9AbiqXbqhv+tFUNoARGBxHrXrGiorxzii7I6ow+1xE4uLWB546EGZ6lTTGXN0QA+tvzxsLRKIFAJfF6D9fn98fDwhJFyDvu666yKlx9gPJIAEkAASQAJIAAkggf8xARSg/8cDEKG7RwE6QgcWu4UEBgeBP/7xj2lpaazArllmNyRD22y22GExw2yOG66+sqH+C1H1AIAf4Dmv946uztmejt/1HWhimrKugGoYOugAGuvSAQUW9MHD3fCIBLMDcGen/ES7soHCISZVQx9ofH2DMj26HuBFAX7Vpl29s/d2AW7r6vuT2LcdoN3clKSDQmHpPz4mhMRbHEyBdtotLoedEBex2Oz20tEVLXv3KgERBejB8deErUACxxyBrwvQALB69eovVWc1L+W9+OKL7GIZu3MDJySABJAAEkACSAAJIAEkcJQJoAP6KAOOvM2jAB15Y4o9QgKDgoDf7z/vvPO4x5knb4T8zryOVllZ2d7mJlY2UPMaAL0ASwPiHd29twQCj/YfWgnQBrpXCehceNZA19k6n/Sq87vU+wLwDMBDHuXJXvkzgC4AyYyBDrDoDU0DwwuwG2AhwK2d3ntluEeEm9u6nvX1N7A0DzjkC2ZjqaYSvWPzzg0r1u1r3nfdfb8kw2zBuoRmc2NiYh57ZD7KOoPiTwobgQSOPQJfEaB5FIeu6XfffXdycrLFYgn5oB0Ox6ZNm74x6e/Yw4Y9RgJIAAkgASSABJAAEjjKBFCAPsqAI2/zKEBH3phij5DA/4xAKH50z549sbGxTqeTi87R0dEh9dlqtaakpPzxj3+QVcmMt2CtDQCsBfh1d9dN7b3zBHU5wAEAH1AVdD8YGoAoM3/0ZxQeafPc3db7G4Bf9OiP99C1Cis/KJv2aHNruigGAKAJ4E9e3y1tvXfocCfAHf3+P3kDG8HwAFX1ANN0KIAO7BkgoEKvRPuYZq3/Zf3yvNIinscREx/HoqkJmTZtWk9PTwir3+8PzeMMEkACSOCoEuAadOh5IA6annvuufzantvtjo6O5v9aw/9THdVW4caRABJAAkgACSABJIAEkAASQAJHTgAF6CNnhWsiASRwRAQ2btzI1We73W6xMAXXYrFER0c7HA6bzXbzzTcfONCi64qq67zsgB9gO8Af/f77Ozse7Rc+ANhvVhQ0Tc9GH9BeU6H+rAcea5Xu74e7+9R7u5UHD+l/k1nyRtikU9BVgIMA74H6q0Mdd2vGHTrc4vPP6+mtNU3WuiqCJjJlmxrMWq0x9bkPYAfAJ0Lv8zvXfdSz54Cn+/iaiVwxtw5kQ8fHx7/99tt8XzpGcoRBx1kkgASOKoGQ9Bw+Qynt6urKy8uz2+0848hiThecfwGlNLwA+lFtG24cCSABJIAEkAASQAJIAAkgASRwJARQgD4SSrgOEkACR0rgzTff5Iozf7bb7U6n0+1wWglJSIybP38ey9xQJVEMSJIEzObM3Mqv9cHDvYEn+ryfaHoXsDKCZuE/3QDdC8Z+gHUAT+73PNCmP6rA/Qrc2aK852HVCL9sRVb9oO4HeBe88/taf9lz6FcAd/b3P9PrWU6hHUBkQdIGy/IADQwVFFatsFdi6vOb4J/vaXp475q/e/YoZl+vvnKm08mUnWEJMVyMjh0W/fCDcwHAI/h1A3wB4Uih4HpIAAkggW9LIFx3Dp8HgK1bt4ZuLrHb7XFxcYSQefPYv1n+D/bb7hPfhwSQABJAAkgACSABJIAEkAAS+D4JoAD9fdLEbSGBY5zA/PnzedpGKHPD6XTGxsZaCamurq6vrzOlZ59JiYVfSGbUxj8B7mnu/43HeEuEvaECWmYpLQ2gG2ArwG/7/L/qEX+tw2MKPNwPT+6RtkrQL7MtmCkaQMGQwegA+BxgnrftjraD8yi909M7r6d7OWVeZy81AzdY8oYGoOi6xKobmsL0+7Iyx9d+r2ffo01r97BKhoquK5QqV1x9GRd3LDZrtNMV7bA77VGXXDUz1MZjfLix+0gACfwABMJF56/MA8D8+fP5vymHwxESo5csWfIDNAx3gQSQABJAAkgACSABJIAEkAASOEICKEAfIShcDQkggW8mwH12lNIbb7yR3wPOn10uF88ntRHLFVdeziRdM7lCVgKaIoAmaKzMIGwCeKBbebBP/5vEgjhM97EK3KKsggqwGeAVP9zV7plLYS6FX7V5X9vv2Wdap2WDeaUlltehe8A4BLAeYPaB7jkSPKqwEoX3d7a9BXq7KVJzXzPbMBUBJFFn5mkKsBzg/taOO3oDv/YKe9mmqAIapaw6oUqVBx6ZFxOX4HQMG+Ya5o4y9R2HdfrFl/R6VIo69Df/ReBSJIAEflAC06ZN40EcXIB2Op1JSUkHDhzgjTAMAysT/qDjgTtDAkgACSABJIAEkAASQAJI4GsEUID+GhJcgASQwH9JgFJ6ySWX8MyNkAZts9lcLldKUvLChQtVqoiapAH0Kj5Zlf4/e28CJldVp//f7uotgQQQBUQCBEFBVFzmLy6zOI6MOpvz/ESdR0dnXFG2QMi+7/tKwg6yRnZZZZNNCIQ1gZCQkL2X6trr7vs55/3/vud2d3pQmR8akk7yraee7puqW+ee8zmVqr7vfc/7VYISMGzgZWBpQcwy08s9+Tr68jRI2fXJiUzhGDeWMatKsRvTgXG2vaxYXusE5GFGmqo0VrSnBdEF9RJwXS0cX0tG+5hiYk7RuzVON+xuVsd6yAgIJQIPSSZYL6xa09xkdoUqH9ZJ+U6VoHuSRnFMqvUtq+7MDTq87dD35YzckCGHkMTT0nLaxz9fKYVQUEpZlkVNa8v2uyTHuzMBJsAE/hwCIhVhGMZxnCRJGIbHHHOMYRhtbW2ZBp3L5T7zmc/0VYUNw5BTof8cyvwaJsAEmAATYAJMgAkwASbABPYQARag9xBIboYJHKwElFI/+9nPDMMYMmRIn/qc1R489NBDt2zZLCAkJS6TvtyTmizhRenmWP3Kkosq6VX5+uta/CXXsb5JvefrwA21ZEE1HdntLgJG1CoL8h1Px0GF8qFFDDeFn6o0oNeKtYiutLxJNW+ilGOjaKaXXueoN4GqRCqoUQXyUyslBBIJUQGekGp5xR7RUVzi42EHpo4EgRT63tMT6PiOFbf+xmhsy7UOJnEnZzQOPdQwWj99xpdcl2Ks+6Tnvo3eF/NvJsAEmMB7RUCkQkqKIEqS5Mknn+yTnrMNwzDGjBkTRZFSKkkSx8myj96rznC7TIAJMAEmwASYABNgAkyACTCBdyDAAvQ7wOGnmAAT+N8JrFq1qqGhoaWlpbGxsb8APXjw4PXr1yslEkk+4lrsuECk2/OBLZF6PBBLS97SbnsHUNXirxaKaQ83RTtwZ5pOKpSmueJS4JxSaWIxf1e1lNe5GSm8mCKgXR+yQjke0U314qSaNTqRY9Jwgl270o+eB/IJAk9lKdEU/gwIHdlRIcFaXhWGF+8sTCt41xbCDl2iMCUxWehChXSYOKRIkDLweGdt3DU3GYdSgS+jiX40NpDT8PNnftF1/0cdRNag//d3DO/BBJjAX0xASpkkSSZAZyUHL7/88paWliz46Igjjshk6AcffDDzPvNH01+MnBtgAkyACTABJsAEmAATYAJM4M8nwAL0n8+OX8kEDmYCUsowDFetWtXnttPRFD1VsM4444xeOJJil0n7pYiKBAiATuBeYE5n5812/JIuMxgAXk8ANPmlu4FnFRba9kWV8mJgmp9Ot63lpa6tmYsZUQorhFmD0w1sBpZUSpeUu35pFyYDP+0sLjHDVxUdKNZqtdQ/qT+6XqEDrAOusAsjugsz68lvqtiewiHV20upLqGg/qZkmbZ0SvVD5ejyzV2POMnyO+7JBtt2SK7BMBqNBsMwTj/99FKpFOsbJYf4vm3bWaGwXgL8mwkwASbwnhDok5WzLP7vf7+nbmpra6thGK2trYMGDVq3bh2ALFDoPekEN8oEmAATYAJMgAkwASbwPwnsPgP9n4/zv5jAwUyABeiDefZ57EzgzySQ2X7vv//+wYN1KkU/Ebq5uflzn/tcb/2r7Ju3R4Amm55Wn+920hn5yuxCMVOfs+SNUD8rAUfhpVhe2tU9zbRmAlO9aIEXX2lb67RIresTBjFcVzi2LlF4XRxeXK7+3DbHAb+0apPy5u8oFRph6ANSguoJauWZBusCG4AbZXxJvn1EoXpdgjeinmAQRbp2oJCQ+izJrF0EbjfV0pK3sOTd7qs3Q3H9bbe2HZIbPIgGfEQbqe25XO7f//3f+zgqpXzfl/qWydAsRvfB4Q0mwATeUwLFYnHYsGF9SdDZRcHPfOYzu3btek+Py40zASbABJgAE2ACTOBgJaBPeP+gOj0L0Afr+4HH/U4EWIB+Jzr8HBNgAn+KwIsvvjh0qI6k6Kc+G4bxV5/7nOmYOhlZKEV3ilQm67NItaR7LzAjX5m5q35PgErWutIJzdqwbJOjOb2qWppdq8/z44WhmlX3rrS8N4GSVqhjXX4wVjIAdgGrJMaaznl1dzLwIzuZ6OHeGHndnueWs1dIkqHp5mrv8w1pMsb1flmyFtlite6SQ/ulCpGi+oQpJAnlXcBTwLiKc77pn5evT93asUHBTOPZcya35YxBhjGk0RjU3EilFxuN733vP6h9vyfjOpUylZIF6D/15uHHmQAT2LMEwjC0bTuO48cee6y1tXXIkCGZAzr7eP7BD36QJMmePSK3xgSYABNgAkyACTCBg56AXuyrUihJFYf0LZOeWYA+6N8bDOCPEGAB+o9A4YeYABN4ZwJRFJ166qlZ2Ohu/bnB+OSnP7Wzo50Sn526QEJu4qymH0Siw5Q3AtPzhWnF+t0+KbwUDp3VB9QhHTVgG3BPbE3u7pgr1fxIzSyaS7trL2uZOLNIR4J0Yld7nH9bTadWvNEJpgHnVZMJHn6VkPocUYRGoqQPqTeOimhTAAAgAElEQVSRJrqq4SbgxliNq9kjQjElUg9qCZuaEokrHCCSWoBOdCb1GmBhJbgkxvl+ukTgZidsB+ph6Hu1X/z3fwzJGUOajRYK4TCam3NDhhyyYPGibDRRkrIAnaHgn0yACewFAv2XWSilrrjiitbW1swHffjhh9NFsoaGZcuW7YWe8CGYABNgAkyACTABJnAwEZD6jDYmAVqSB6q/+ty3BvdgAsJjZQLvRIAF6Heiw88xASbQR0ApFUVRZqP71re+deihh1IGslZgSYVtbBjyvsNfXf9apidLqF4BOlJIUmAn8Ftg6o76rO7wNh9be/M0svazWn8bgZui+OIdu6YF8WyJ8TV7cnv30zq1w9UmakoyTZNAwgZ+52DuVndUMZkAXGjJyaa4NcJ6UJqzTKFI/o6EoqqDArEL0Q48DMzyMcLCLIE7tNjtamE6FEmcZCUShQTqwJvApSV3dMEaaYlJBXetDoN2gFQi8TxA/vK//2sQBUEbhw6maoTNbc2GYTz0u0cBeFGYCdCC/hLhGxNgAkxgbxP45je/ufvSYO/WCy+8EARBf7V6b3eLj8cEmAATYAJMgAkwgQOGAK3ilVAxVEjnnxJCu6u8EHXHZQf0ATPPPJA9SIAF6D0Ik5tiAgc4gSiKpJSXXnopqc9kq6N7rpm017bBg158+eXe8dMlYAEdwYEkADqANcC47d1jd9Vu8/AGSEEmrVdnZaRATdcSvNGyx3XXJ/iYoTC6uza3aD3Wqz77QKhikXqBECVgLbCyG1NLGGNjtIMp9eSWhNTnOiATug6tkAgtfKf0L1mCejhxl9reyDJGlUh93qCl6ihCrBAjVTJUMvR9JwWJ47cHycTO0tSaP7vTfAZUFNHX5RNj1ZMnva2947QzzugVdnp+H/WhY3flO1OoVMpMfWYBuvctwb+ZABPYSwTCMAyC4FOf+tTbFql85CMfyefzXJBwL00DH4YJMAEmwASYABM4gAlkZ4U9AnScCdBxTxwjDVv0q0J0AGPgoTGBd0WABeh3hYt3ZgIHLwHHcQC8/PLLjY0UfNx3GzJkSEtLy+LFC0V2zRfkOlZxIlKVSgTaO/w7YGK+OrVuLi9VNmn1OdKOZh2aRYHL24E7fHdyZ35cJZ0hMKbmzymYz7gUtRHrPX2SgClY2QSeUFjpiqnlaFqI0W40sWrfpr3PFSCMegI4BJKYgqfpuz8ENgFXmrWJ3d0TC7VrXLFFq89hQjuFEr5SqaLcjIrrdwB3AxNrlemV+uL2/AZForY+OhU2dPX8K8AEntyxLTfsQ8bhh2Uomge3GY3GX535V1WzKkhdZ/H54P3PwiNnAvuQQBRFQRC88sorLS1UKLX/7dvf/vY+7BgfmgkwASbABJgAE2ACBwiBTIAmn7OuN6RSOu0ESl148mHk2yEEnw0eIFPNw9iDBFiA3oMwuSkmcGASkD01/GBZ1oc//OH+cka2/Y1vfAOAbdZ18JVEmKhAxgnJtWWQMXmmK0fb4VLbegqpCSgqTajlYS0XdwC/T+KJm9+a6sQzFcaaGNteejTL6FAkIaeCRGSXkp3xFnCl5Z3X3nWR6U0IklmRv7xa2aC9z0Gom4sAoWIkofZYh9q//IAt5tfq06vFa+36m73e5ySmPRJQqHSsSGXuAp5WckHkjKrm53XmXwVcId1aLVbS1a9yqW3qyQ7gIc++4IZfGYMHGW2tDUMOaWxuaMwZuWZjytRxkrI6WIA+MP878KiYwMAnIHUR1DvvvPNtH9etra0rV65UqrdKzsAfCfeQCTABJsAEmAATYAIDk0CmQQuolPonU2xchy/91UOf/PDvvvDpO6gCEqnTfEo4MCePe7VvCLAAvW+481GZwP5CQEqZ5T4DGDlyZLMO3MiqWrW0tORyuWHDhlWrVT2clPIvhK4SGNEDNvA68KtAXFD3p0Xy97pyIOVjkZKsqFJwTFtrgEX5wuSSNd6X51nJmJr/gE7toK9yfek41kbmRMu+93iYWw3GBvEFaXiBVbrcLW/W0jC1JrRfWkBABUg8XYq4DPzWw+KiM7FYuCpy39S7+JQPTbqz/sOA1kfFMcnKrwKXVvOza/nrYtqzBiiRQoQOYguSdGoBN6ZEjlvcaKlZvbpc/N7lK43Bg422toZGo7XBaMkZTTnjmdWPU7qIEnHcU2dxf5lu7icTYAIHDAGl1Le//e1Mg27QN8MwWlpaXnjhBT4jOmBmmQfCBJgAE2ACTIAJ7EMCSiKIVM0KXB+rrsfJx77wseFdw46+54rLe/7c8v1+wRz7sKN8aCYwAAiwAD0AJoG7wAQGKgEpZRRFIqUFRZ2dna2trYZh9M8VbW7OtbfvBKTjWiDtOSFzc0oG4ACU9Xyjq6ZXnMluuEpnceiB6lhmpYsEA29GWFG0LmovTvDkyHowpu7e2FseMAF5nyNFInUMdErcZSZzut2x9Whsqi4KrblRbTXCLBajJ2dLG49jCA+iro/4uIMlBW9KZ/Vy21vdk6GhEhmSrqy9z5lTuQqsCeSSQsdCu/uK2q6tQJFCn6maYKpSB7EDSZ0R6FB40MTCSrAMeAK4vHPXUX//ZZJ1GozBDUZrjjTov/7SZ2yrKkQcRRGbDQfqu5v7xQQOfAKmaX784x9vaOgrF0tydEtLy6ZNm+I4ZlfOgf8O4BEyASbABJgAE2AC7zEB25e+RKIwYQyGf7DjlGHBJ0597Y7bdmYn0e/xwbl5JrA/EWABen+aLe4rE9ibBDLvs0jJxmtZ1llnndXY2Di0N/I4c9Wdc+7PdJd61haFiAPKVSY38RbgVkuNr/qTLe+uONmkReTd/dey8pvAlVU5ppxc5OE8Kxlfde8S6i1tnfYpgkNR6b+EnNB1qKcta/rO4gVF/3w/vSSMZtvm40CFfM99LmNtV0bqQ3qQeeA3EeaXonFdtaUl55WI0pwTUrMT0pZVFCOlCoQxqsCzQl5RL4/t2j6vtH0bRTxHDswAgaeTQIIsWTqlw90fY1anPbssLpWYUquutMo3bXqj8QNHtDYYQw1jcM5obTKaDOPWm2/KBhunye6VV1QreTcD3mICTIAJvNcE1q5d23fVsK2tLfvo/uxnP5sdNwiC97oD3D4TYAJMgAkwASbABA48ApT/rEcVJGSFem0TTj7pxeEfck84zv3IKWtKZXpOpCKK9NLgA2/8PCIm8O4JsAD97pnxK5jAQUbAsqz169dnskVTa09Vq6bWxo9+/COh9KLUBVSSBgpJStZjZesw5d/UxKIub1otWWGnb0g4/zN1NNXRzNc4GFsTo2NMBUbV/Zt1xLOppeqUYjRSD8KOohjYDFxVqZyXr/7cERe6ycSqfaeftOtvfZE6gNK5HiqBCiEdnT29CZhTCUZ3e/Or3n1OUoqRBkKnf1DsM0QoZRposfv5UF5Rs+ab5vxq9/PUsagY7vJR8eDVdb3BSJERu667MafiXZg3FwWYW4yn7Nhxa1ArAHc//nBLIzmgW5qNpmajrdH4+Kkf7a5XnnzpeTeJ0kx1ztRnFqAPsv8+PFwmsM8JXHXVVY2NjX0BStn22WefzWdE+3xquANMgAkwASbABJjAfkpAq89ZtiRZnBYvD04/deeJw7xhw9p/ca5HFYE4AHo/nVru9ntGgAXo9wwtN8wE9n8CmTlOSvm1r32tIddI9yYSolsPbTOajV/fdbOfWjH8FK4i2TmCFqF3AE8Bs7rDafnk+lK6Q9uH9QVikmBjL0p1mvO9wGg7/rmT/LJkXbSz4zYh12pHM+UyKy0UpzJOk0CbqS+t1Eaa1o+88Od+PMtM7wmoDKBLUnUaw08gddnhHuI14DVgeSG5oKM2pqP0kJPG2QVq2WdAlkrGkKIO9XuomR1dUwrRnE7vVaAAVCnWI3Dgm/BMJDZIO3eA5yWWl/0Jlji36E0sBfN2FjcBJVD1QglccvF5Go3R8r7mTKy/eOGMB998uRA5cRZ4vfvo+/87g0fABJjAfkXghz/8oWEYgwYN6ovjaG5uvuWWW3Ravco+6tkNvV9NKXeWCTABJsAEmAAT2OcEUsCPI3guPn/my8cdu+Ok4YXhpzy1diPipEeA5jzGfT5J3IGBQ4AF6IEzF9wTJjDgCMRxnCTJxo0bW1pa+gRo0qDbGr789b8DItevSOVD+hAu0hCK1NgnBBYUqpOL3kpTbgMqgS4PSApxTwJFFXhAYKaLn3nRz7xgdLG6slxbq8Vfj5RnHc8RAYlwoN4E7ojisaY3IsXP/XCCF98RYauWfXU2dJIgSXqKDxNAob3V11YxqSuZVLCvdfztPeL07vyLWMkAqgy1JglWePUJlfqMfPJkTwdiD0kIoYcUuYhMKFdXU1xpOiO7yyMq7hQrWdhVe1n7rONs6ZW+An76pz9htBlGzhjURD7xoWecnAd2BSZxyaoks/15wL3HuUNM4EAmEMdxVvrG9/0zzzyzpaVnCcugQYMMwzjqqKPa29szDbqv2OyBjIPHxgSYABNgAkyACTCBPUkgVcqVCa66DB87Zfthh2w5/sTN/+d7rwFUu1713vbkAbktJrA/E2ABen+ePe47E9grBL73ve8ZhtGY3XIGCdBNxtpNL5P0TN+uMd2jWKXaJgwsCNIR3fnL7NoGIJ9AJIASUAmlYGmB+NUEC6v4ZTH4Uc26oFq9zA6fFujSaRi2Tt5ALBFLV6QdwI2pN6LY9ZOaP05gtknq82YdixEryt1IISIkUY8ATcfYCjwCjM8nE4vRKjPYoEOcdapHIBElUJFOl26Huh/R0tgeX68sDeWddXQDNSAERTZLnekh9MuqwFrgGl+OKlcusuqzgmBlubJNN+vRDr2rr4D773uIvM8NRoNhNDTkjEHG77av3xWYQRbBwQ7ovfJ25YMwASbQR6B/yMbLL7986KGHZusz+srJfupTn8qC/pXq8UH3vZY3mAATYAJMgAkwASbABP6QQF/6c/ZU5OOsv9101JDtJ36ofuLwtdfelKZAqliA/kNy/MjBToAF6IP9HcDjZwLvQCAIAsdxPvShD2UCNP3UAvT3z/mepNJ/MQIfoURImw6wEbjcikeVzal1cjRvh+9DkDgsXar7p4sKbgFWORhdxPk1/Lyza65V+x3tSS8PAIuCNSRSGUnVATwJXFzc9Z2u9p/Z6RQPdwekL5uAL7RCTHZpkYLitVKdAFIG7oswvcOdYWOpmbyYUkwH2aKVKWAl1B96+U6ox+DNl+a42JpuOTd6YptWn7X/eneYR6JV5nbghhiTzWis7U6slK+0KluzJI9E6ACQ3QI0gP8eNdFoaB162JGk8hw55Bs/+o9dgen1dPYdSPNTTIAJMIE9TyBJkjjuK9OKG2+8MROg+6zQhmGcffbZWZV2XiK65yeAW2QCTIAJMAEmwAQOOAK7BWgF28SzT2P4B1886Vj3Q8e0f+mv1zsRTBeCBegDbt55QH85ARag/3KG3AITOJAJXH311b2OuUbaaDByrcbGba8JBIhDhAIOKbCuwk5gYdUZ3V25zE6fBXYhtFEXJE5HPqm+pBFbwBX1eFQ5vqCISTYW2/ZvVbJFP54qCAlPJztDp1s8DIyr5M+rVH5aNi+sJzO67A362Z6QaB1nIenLnW6ukJsRP4pkZt0aW7RX1pKnFYqU1KFSBClMocwYYagLJN6vwlnVjvPLHZNc69aIAqOLWmvWFYxllkAtJWztp34BmO5RXPXcsnmH63bp9A/IFDIW5P2m+OkEPUN9ouQbxww3mnvWuR9+/LHbzFJNhAfyW4THxgSYwP5AIKuEc9555/VVI2xubs7lcoZh3Hzzzf116v1hNNxHJsAEmAATYAJMgAnsGwJ9ArSUkAkuunDX8Udv/dgp4uMf27b8UgqEBCgAWomeO6Tafd83XeajMoEBQYAF6AExDdwJJjBgCXzlK1/pFaCNTLb4zx98R8CTwiU5VyurpsIu4Pqyf1F793TLewrIU56GpyXcIEUUQZSQ1IBHA4yq+P9ZcH/RFc2pit9K9RZQ12uUSJ8WZKu2tRn5dWBCPv+zUvkiKxxnxhPaq4/rEoUp+tuJKdZZgpRrC3hUpbMKuy7O5+fWnCcjlHvUaiURSfhShZ4ufvg4ML1aHe95Ez1nsWmt1WK3Qx7uVCvJCYVqaCl8m8KLwLJKNLWaziqHd9nxNtoNpD4nMQR5wBPIWNu3LeAN4IoO81+WX23kmoxm0usbB7U+v2l9HXGq12AN2FnmjjEBJnCQECgWi2eccUZWirC1tTX7eB88ePCGDRsOEgI8TCbABJgAE2ACTIAJ/CUE+gRokWLLmxh2zP0nD6u+b+iW40+8r2bSqWTgV5VIWYD+SyDzaw9IAixAH5DTyoNiAnuGQD6f71Ofs43Gxsat2zZJaSK1dfozeZ93AddWw7nVYGbR/o12DXvkCY5Bym+kbcV4C3gQmFoJfl6Lflj2xtaT60NSnx0ScBW5iIX2SAsyS78CzMu7Y2viZ3l3oofJu6rPaOeylomVjt0Q2qhMAnSq9d9XUyyvxRdv75rT3f1gEJDjevetp/ZfJ/AbYFaCc0rBGBeXpXgwEd2U+0zdpUBpUOnD7LJ1u6BuzLWSKZXosvbw0RI69B4U+JHG9AK6uh0LqsCIEvAqcL2nJtrB1HzJOOF4o9HIJJ4fnPdzChUB4pSs23xjAkyACewrAlmlwbVr1x5xxBF99ufss/2EE05w3SyyaF/1jo/LBJgAE2ACTIAJMIEBToDE590CdIzlC3HqiTuPO7p8yinbRo5rz4LPYt9iAXqATyR3b58QYAF6n2DngzKBgU6AwkAVrrrs8iFtgwzDaG5rNZqajIbGfzzr63pJkQ1hI4kjhU7gppI7r2JdGom7I6rXV9HSsxZohYTwoSrAc8CUfOWXVW9EhDGeuibBC9rRHFNVwDRGqrOiKQa6HbjcEWNr4oJCPMnC1F3mI6AKgZk/WZLiLBLan1RdqW3OW4BfFfyJOysz8pW7HXNHJiGHMYVpaPE5AarA08CcGL9wkot9zLBxT0qJ0uThJhe1zpFWoa6XCB/YAFxWCibUnWkF69ESijE1qndMoUgz1y2nsfZrbwMuy9fHdpZHuMH47uJf/+IcwzDacs2ZsrN+x5ZYyUTsTpce6NPP/WMCTODAIqCUoqWgvbdVq1ZRolJDQy6Xa2xszFa3nHXWWQfWoHk0TIAJMAEmwASYABPYswQodSMFndcJhTjAaSeu+cypOGmYc/rpr7+sl5NJgTT0+uzPSsjd+Ruyxxe1Z/vErTGB/YUAC9D7y0xxP5nAXicQqx/889mthtHcqBONm5oMw7hi5RUqJidvKAOQWCweBSZ17ppXKdwVR3mdj6yNvpn0SzKtBWwCroc9plY/t+yPrCWXB3hdC8eWNi87VKMwDpFWIbYCN7rueTvyY2JcXLHnVJ3HYnRkMjGU1px7OfSEP1PcxxU1Z3qptsw1b6kXt8IPyHmtayRSiUJSrjuBe4BxNfuHBfM8R84JcYckidnOoqkjhTRBGtI9iQNBjua7FKYX3QWlymPAzhiJItOz9nXLWKdfxzpYwwF1704zWehjjBlN89PlpcryBx7QcdnGoKY2qvH1/e/3dpp/MwEmwAT2DYH+AjSAESNGZBp0/2UuK1euBGDb9NHINybABJgAE2ACTIAJMIEeS1OPdJwtho2tCBUbt9+Bk4dtPvFo//ijav/89W4z0CeMSYJEkACdknOKlutmZqc+4zQzZQIHKwEWoA/WmedxM4E/TYB8vvo27LCjcoYxaNAhmUJx3PDh1e4aInLy2oi6gd/LYL6ZXxTUrq+VtmcysdSm417rsQ9sB25StRlBcZxtT6oGV/l4RscuC61W+/RTOogd7X2+wa9Ns6oXOu55VWtivnx3Inf2qc8QZELu7Ru0xXobcHeUTC7VZ9nuNYX2XbRzBPgCYYpEIgm0+vw4MMY0fxqEP/fSiyv2HYrymqv6wnWPrkyRHjJJkrpCF3BTsbrMDhfXnfsCd6fup5R08EyADkmA9n3EkR7InVawsOqMr3vT/Xhpub5OJ3IcffTRbbnWQU1tDQ1U46tcrv5p3vwME2ACTOA9J9DrfqbflmVFUfTFL36xv/pMi12amx955JH3vCt8ACbABJgAE2ACTIAJ7C8EshPbXvlYIJVIU6BQxVe/uu6U47s/Oiw++oj1v16FUJBJS6SiT3pmAXp/mWTu594hwAL03uHMR2EC+w0BJUGJzMDWLdszbSI3eLDRlDNaW3/0k58BSCxXJU4V8dPA4nppVrVjZZmUXx2jTOozScSKjMdSR2f8FsnkSnGsY8+0rF/Z/gagqAsP2kgiFSuRIk0jyF3Ao8DoWuEcuzIyDscUy9eXnC2gSOiIZGf9zd+ja/cEMHcC1wZiTNWZE2JF0dqmzc76KnOoYzoUICvAw8A8of6zVPlpEI4W/jLf2gR4WYezvyQUicuhFo53AEscZ2w5v8zsfkS4eX30OAt8zo5OV78lEPu61uLvgQnV8gVWaXpgL60U3gSVQ6y67o/+678OaTuk0WhsNKga4fIly/ebdwB3lAkwgQORQH8Bmj7Jk6RUKg0dOrS/Bt3S0jJo0KCNGzceiAB4TEyACTABJsAEmAATePcE3i5Ay4QCJPH44/joSa+cPjw4asj2z3/u1UjASRCpWOpkyf4aNJ079t3f/fH5FUzggCHAAvQBM5U8ECawZwj4HqUiA/jVDTcZzS2koDblBr3vCMMwnnl+DYAgjipxrQv4le9O6ui4xi6+AlULtfore79bSfuFC7wGLK3XRxbMCbXgWsd/Lkki3biNyBJBIjyIGIl0gNXA7Hr54iQ8J/RGu7WlldLrkqTnKJOV6VUUS013uuasbOBhNxlT8c4puCtcytOgfgcqy56OdLhHBViDZFGanBvGPwniX5rmkrC6ui95Q0DoqI5Q69FVYCdwdSUYUa1dVO683esu6K5KKbM4Dxpbb6VEqaOfnwcWVoKxsTfKLy2qt7+m1Wcv9ILAu+mGG3tlnQbDMM74+Bm657pFgCK2+cYEmAAT2IsE+gvQIu2JpL/jjjt6P6nod4O+/d3f/Z3v+3uxa3woJsAEmAATYAJMgAkMVAJvF6DprM4LMeZiefyRb35yeHzSsRuXr4QvaRFujDTVdi4WoAfqdHK/9iUBFqD3JX0+NhMYgASShISJVGLc5MlUeLCpycjljOam9w87IdSqbhF4C/KRuH5Fvb50R/sOrbpSuFVmVJZUxi9WsCSFb1xWsabW7am2XFaL3yDjs4ooHMNPZBglpBjHSViPVCdwWc0cZZo/9exzbXNFYK2GcjI6Wssm8VmpTP5VklzGzwNLa855XdaUSpLVM5Rpj0ZtIqlIyoZ+HMk8t3hOrfbTKPllEC1OkjVITF1KELoaRCY9x3oIeeDKcjix257sxpdaVnuPYExXq0OQBk0PpNSnJEVNqp3AnHz9kmJ9fL10RVTdTJJ0GlOgiA9Iq2a3NlMAtGEYjUZjzsg9+/SzABzHoYH0qj8D8A3AXWICTOBgIJCVJfy/H2xTpkzJPqkMw2htbc3lckOHDv3ud797MEDgMTIBJsAEmAATYAJM4H8h8McE6J3bccYpr5/8geqJH8ifdMJTZZtWA2tHViKgeircU6VCfe+zP/cPq2Q/0v/CnZ8+AAmwAH0ATioPiQnsEQKf/5u/yQTohhzJ0N/58Y9tUD7yTuC+NLi6Vr50x9ZXdS1BCluOezM4JKm0gaI6fquq6fSie/6W/GWWfB7o1PHNKXylXKSpEjKOKcjiLeCBCNPK5oi6ea5tzgzsp6DKPV5n3WxP6QZSuQMFB9gMXF53platBba4X/cqyMRp/apEp3w8D8xzqiMT9+dh9MNKfZ5QD+vIZupf9keAol67wC5gK3BD2Z7YZU0qxfPztY36sLRnStnQuupgTKZuQepzoPd/QKbju6vjKtbVgfOKVp+l8iFcpGHik7b+waM+aBhkf9ZVHBtGjxydLXuXUlI0WL/bHpkvboQJMAEm8G4JZKsxvvCFL2QadC6Xa2yk1KDBgwfffffdFLWvP6zebbO8PxNgAkyACTABJsAEDhACfQK0jpoU+kRyxSJ1zCHrTvqAd+oJ7Rdd7GfLdmOqlRQpRSd6PWtnWYA+QN4EPIw9Q4AF6D3DkVthAgcegba2wU0NTS1GU6vR1NjYdMO990gtFt+emMvNYH574SUkFVpmFCNMlZZqIRR5hGMKbn4UmNptT65jRoe9OiSdt6KTLlIVZ7EbSGAH2AbcJTHdCkZV7VHV2hzPfABpuY+motbIWy3oW1wmsBSJxbd5mNxpLaj5jwSipP3LaXY9Wb8w80dfGYXnlc1zAnFOFE90vceBDl1OkFqUKaVvCLpSvRNYCywyC+Nqxam2XJAPNmtVmrzOFPVMV60ThCF8IKbkDam2Ar9FtNQsTqtUrvaijSBJmrzPwkUcI5LCI8P0WV/9mq5AmGtpHmwYxkknfDjwaFW71Ld++jNf/u6bb95gAkxgHxBwXfewww7L5XINDXTNLLsNGTLkzTfflLJf4dd90DU+JBNgAkyACTABJsAE9imBTIDWZ2yUriHg1vGZjz5+ygfKww6vnXby2pdepe6FCGMEguxSpEFD9tOg2QG9TyeQDz5wCLAAPXDmgnvCBAYEAd8LRaoqlZouoGe0GLlBRktDY9uOON0A/AbB/ELnrHbzcW0cFhBack1TKSP6Pg4FVAi0AzM7umeFcmFNPZxSYkYgRAjU44RWJCUSiZIpSdKP+JhuRhfb0aiqPd9x70G6OQu6oJRkfY/pSxyxgKJrynngSWB2Z7KgO/5NiB1aLA61VkzJIfqfa9x0abkyyrTP9dR/l7xJTnSv7m3Y49JOexZIKdhafV7YXbio3Dnecxab8eu6hSggrZkE6JTuAnGCUCLNCg8+ksaX1rvn17qu85yXtapOMyd9JD6iFDFEqiKBi0aNJQd0rq0xN7i5adAhbYc89cTTSpD9mfI8+nWt7fcAACAASURBVN0GxMRzJ5gAEzgoCSRJopR67rnnDMNoaWnp1Z/p96c//ekkSQ5KKjxoJsAEmAATYAJMgAloAn0OaF3uKE6x6gZ85Lh1px0Xnzqs8m//+npWgygToFPSoCOFhAVofvcwgT8kwAL0HzLhR5jAwU5ApOKZZ57JFmIbhtFmDP7UmWd1AHfGuNTHvKL7mKB8Z1P7g6WUSqQRibOxAycCCsDtnjvdrM6pO08E8LTcK7ScG2VJHTHVEZTAeopRDsfYuNhOFvvpvcBGqBrlRCsJqtyQ5XCQ8ByTp9gGfh9h0s7SzIL/iIXtMWrkPiY9NwFsgSqwCbi6hHPbaz+u++dY8fiqf3vFz2uZONG7Jdqt7CO0gLUxFlfCaRGmemJGZ+llbdMOM935bVeqdVds4Alg2tYdl1YqN9XK20FHpJ5RrEcEESGly911IcpCzl15pWE0G42thlbwDSM3Y8asKCI1hyM4Dvb/Yzx+JjDwCMyaNStTnzMrdCZG//SnP02SJIqiLKyj34Uz2hx4g+AeMQEmwASYABNgAkxgTxPI1oP59JeP5eGsr24eflz3R46PTzpu3YMPo+DAkWRbSuhUMNabsudEttdS9cf/uae7ye0xgQFOgAXoAT5B3D0msLcJKKWCIJg9e/agwa2ZGNFoHPqP3zv/TlPMajeX1OTNFuVmWFrSpegJhVSlMdIAaR1+B/A7YLFTmVbN309VB3s05MxPTFqxzlKOobYB19TkhIoa6aQXd1XuBd7Q+q+vBegEKqEvaiBVKoxjRUL2q8DcLZ1zasGvXOyMECUIaecoQuKAUqfXA9dXMb2CkRHOj3BR2bq0bBc0wr4iEDGVUozzSF8UuLocjTPTC8revIpzvxdXgUQoiprui+vq1cCFzo+msI7u8qKavapsbevzPpNTWlc7ForM0lqaf9Gxp119vWG0kgZt5HQYdMPf/8NX+6azv47T9yBvMAEmwAT2MoEoihzHCUNKrv/6178+ZMiQhoaGxsbG5ubmXC5nGMaSJUuyRRtvW7rBAvRenik+HBNgAkyACTABJrBvCEjASilTUuHZ5zFs2HMnDKud8MHilz6/vlBD1fccJRJyJFH0htR36uc7q898HX/fzCUfdV8SYAF6X9LnYzOBAUtgxowZrTljsFZPjcbDfrbkhvld9pitXbcU3Y1aYPV0VEUmQJNiG5NjuS6xDlgWVaeYHTd65uZseJme25sjqgLyPm8B7oqT8btqE+rpeNNa4VpvalHb1XbpSFuVdavkfg600XgtML9SnWkGK7u9LUConcxAkMAzkZSAl4CbXEwuRFMlRilcYtlLSuXXgW4tZAtK8aDwi1BLyashFjjRhWZ0kY8plnOfV29HIlJFedN9HZa9ZYuhTOBl4IqaN7Grc2l3d1c2tMxTrYdG4rO2TttaKL+lWFz5+LNG81CjoYUqETbRfejhQ/okGxagB+ybnzvGBA4qAtmHkuM4ZOqxrCFDhjQ3N2dXH1taWhoaGo477rhXXnmF1qDYdhzH/Nl1UL09eLBMgAkwASbABA5yAnSqp1M2pAnPwZix7cd+cM1xH9x1/LGvzp8PJ+yJmswW+marfntPfP83DfogJ8vDP/gIsAB98M05j5gJvCOBrETeV7/61cMGNR1uGIc0GEbu8Mn3/X5uzZtTqL0UUMRzqMvuBVnxPQUpSDCOJHYBvzGDqe07ljvFdUCnSONU+5i1RVjQNWHYYWIBTwFzXH9CLZheC+YX8q+CwjR03jL9zOoI68vI1NcIeA24tlyaVK3NNL1ntbGa2pIK8CIEZe19vsnH6F3ViTEmA2MCZ2qh/RlQZnQKVP1SAj9G7Gst+0WJK2rOBVb0iwCXlN1b0vQtBJ4yEad0sOzAWVVD8jTTAzt0scRLNmyb07FjLVAPtf850oZuLVinioRyW+dfX12qrsgXHuqqG4ccRQJ0o2G00L35kKZisShSEQQBizjv+DbkJ5kAE9h7BJRSURRlx8vCoFtbWzP7s2EYhx566Ic//OFSqdT/Uyvb3ntd5CMxASbABJgAE2ACTGBfEOhRk0M679u+CZ/99OMnHbfp6PevG37ivd16pS1VONL3vjW0LEDvi4niY+4HBFiA3g8mibvIBPYmgUwe/cIXvtBkGIcZxqAmw2gZctWGHcst5x4dkUERxlCUvKG1XbLFKZQFuoBba2JZu33drlIWjhxAxKRLp9R/vb+jE6LXAFPr9kjXn2TaVzneWi0Ku/prO1upFAG+1p31KynH47YwmWdbS3zvfmCrtmDrwlgJENhQ64BbPEyrhmN9OQk4v9w9s9L+e1CXfBKKvZCUYeFCbE6Sl4BlVW9kt/3LmhhTlbf5eF2hDEvChKASgj0CtJaeqXCi9muvMkvza9ai7upLsSxL8l2TAp6VnIhIkvdNet0G4Nq8uaLmXl1xugCj9X2UAZ3TURw6jWP16tVc1Gtvvp/5WEyACbxbAitWrGhubm5paWlra8vlcs3NzY2Njd/61reSJAnDsL8M/W5b5v2ZABNgAkyACTABJrC/EOgrCURhkgliFwtn4oQPvD78mO7hH3pl5KjNfgyhkzT6S8/Zq3rG+M4pHPsLCO4nE9hDBFiA3kMguRkmcGAR+OpXv2po2y4txD7i8Gs2b3kQ8g3tfYaMBBIBqranJKnPFS283p+KBQV/SYe7QQvEIcnTUYggoJ9UDDhL0ngJmLGz64KKNdL1V/jOar2z7JOb9Td2og+U/SwDT9uYUzAnFUoPAZt1gIZL0c9JhMSG2KjUKldNq8RjfUwQGOtFc8zKbxHtpKxnhEJEKhSIQ4guKdYDS4r10ZY8p6ZG1eTKmtiQwpagNGlKmZZkeM6UdUUPlbT5+hbPWVKpzOpqfxwoSyQxPRVmijlkZtgOBLmk70wwo7OyrLuyTsvWn/6HfyUButcB3dBkrF69WlAQCN+YABNgAgOOQN+n03e+852+DGjDMLKatEuXLqUTMCn7NOgBNwDuEBNgAkyACTABJsAE9hCBPgGaPM4JraU98+PrzxgenvzB8nFHPfzCSwhiOnfsv1vfdk8XWIDeQ3PBzRwYBFiAPjDmkUfBBPYYAZEKKWVvAGiT0WQ0fvykBwo7dumUjJDUVz9EQFkVKanQZSE3AKsQzvBKC2rhPQnKOh46JTtx4pFGnNQRWpAesFFgYcG+uGJPFJhQqq2GLGc2au2PpsVKWfAFVLZwyQIeA0m6k9vtG12K+HBIeg5SeAmCOsQ6qFv8cIIZXxxitMRYH3OrweNAB+nUkSMRUh/pXrKTDuCyqjvKTH7i4XwbSyviuQierlisY6LJLk11uDINWmdSv4rkBlkf3VVeFKh7E3snlKOEkLQnqdu0L9U4DoFtCnebmFlNZtWjV7TR2wY+9rm/MZrajFyL0dxoNDU25JpWP/s8JU3zjQkwASYw8Aj0rc+wbfu0007LUjja2toyE3RDQ8Ojjz7KAvTAmzfuERNgAkyACTABJrDnCWRqcnYuCeCG65yTj3ntlA+4Hz2u/ex/3QpdlKhPcX7bRk9vWIDe89PCLe7HBFiA3o8nj7vOBN47Am1tg0mDbmoyDGPIpz/6+/xbujygiMhK7PuUpxxBJqmOubhPiElBZbRXuiaIs3wMreKSAB1CeVAW4iqwQeFOU02uhaOceFLB/q0OaNYR0ZRlkX1n6xFRsIXU8m4ncJWVTO6o3ODgTa1ra3nYk/BsRBsR3er5k4q1iyOMBEYHmFK07k8oeYPimGMvUpSoEepo5o0C17Rb4+vBiBjne5hiqTsrkQmtf8e7E0K8rMqElpjfBG6U9bHd22Y78haF7UBBOanum6f90gktxiJhPQ/cZ6tZW0sTO8xfS7whqUhyBHzyc180cm363tLQ2NLY2LL62ReShB3Q7907l1tmAkzgzycgUpGFQYtUrF271jCMrCBhS0sLrYlpaRkyZIhlWX0a9J9/JH4lE2ACTIAJMAEmwAQGJoFMNdbOKFDyc5qAytn/yzee/sixHccfVjzluDW330J5jKL3HPZt6jNnQA/MieVe7XMCLEDv8yngDjCBgUVAKSVSkS24bsg1Gobxua/8rS3jGCqVMlVppGIfYaiTnR1dTnBih3lB3Z0ZBi9n5QH1gAQ5oAWt1NbfwEXgLmB81R1lBXOc+NGYTMp+75KlrNBfQv/UscppmgJvAVdtLlzTGdxrUu6zk3Gi1lQI2Q08EPnTOosX5mszgRFmZWzX1juCWtasK+JQxTGSAGgP5VpgQV1c5OAXEX5cLC+w6/f5/s4sQ0P/vZBlgMSZHVtr1luAu4EpdjSpYt+fYpOO4/C15VkgDRHr1A6SrruB36XJwqozeVf51qrfpQsTCh19/Q9f+6eGxjZ9J/XZMIynnnw2SQRr0APrTc+9YQJM4I8RuPzyyw3DGDxYX4/U62IaGhpOOumkvn37sjiU4oUdfVR4gwkwASbABJgAE9ifCPyhfNynIAuoUFkJ8OLzOO3ENacea512bP5L/9+jIqYBBn7S/7X705i5r0xgXxBgAXpfUOdjMoEBTECkIhOgGxoacrlcQ0PD3/7t38ZxLPWN5GmoGNLXKRPPAQuq6biSGN/tPqxLFPaIEJJ2E7ryoNB24Idq6cSqOcL3p/vxb4B2Lf5mX+2yN/Qiy15OtNZcAn7VVVj8VsdDVUq3oGSMzJusX1gAnlDRvHz3Jd32fGB8HE4z87f6xU2IYqRp7IdCBGRSTroQbwaW5c1RIX6S4hcxxpbN+wJ7J2RPm/qvBrqsTfK3VNq5vA14FJhninHF8NJ6srFfmUSd8xVrh7QP3dVHI2tRcdeYHduvdv1NvRI29CXxr339XxoaWxoa2xq1/XnIoUf8/unnOIJjAL/9uWtMgAnsJiClPPvssw3DaGho6M1lajnrrLOkpA/vJElYgN4Ni7eYABNgAkyACTCB/ZNAfxG5/zYAPxaJHtTsqTj56C0fPtI86ajXliy0oohSobP8yL6X7J+j514zgb1HgAXovceaj8QE9gsC7yBAZ1qDDlWm6nwPI1rie+e212bVcXc1LWfDE5TfnIJWJClJIrQJPJ5QFcGfFbrHeM7dIDexpYXarGgDva53oVMm6W4FruqsLisVrysWt2k/spaqSdwOdd7FsxDTOrdP9vyZEtMSjCmXVslgFxAqJaJQxVT20AbekvYbwNKaM87yx4hkZOBNsaNr7XRLX5uq14Pde5k70uL4Qy5WhJjYbV9RclYLFHT6R9gjUuvYDkl6dQKsTsT0SuGS0s5llR0vIIx65zjWO2sHdE/4hnZAN9IQAn3FvHdP/s0EmAATGIAEwjCMoqher3/5y1/O1sQ0NzcfffTRL774In2OhWF/9Zkd0ANwBrlLTIAJMAEmwASYwP8LgT4F+W0bdGbqI1VY/zo+efIznxxe/8Qw769OXb91CxIFx/NB57t0WT67/78ci/dhAgczARagD+bZ57EzgT9CQKQiSZJMbujvgO7TGkKoAHgB0TLfGl1zxtTi5eXwrRgi0ubkiKKwUkXScypJfX4LmFUwx9r+BMeZVy2/ro3SCX1bxwnVMdTqs5aipQ7l6ATuFpjTZS3v7HwRimKakeg7HaEIvARcJezx9colZjgpwAwLSyr11zMbte2LKBSKwj1KwKvApYWd42x7lFAzgClWfXmh+lJPlnSv6p39vaCVYwF0Ao85WJlPZhWjuR3mo7ZvaptzZpEmWTmLFFFkoF4PXG1646r1WVZlDeIu+Cl1lVKhXR0S/aV/+JqR6xGgmxpajnzfByhHLE7/CHd+iAkwASYwkAhkQc9xHL/xxhtHHnmkYRjf/e534ziuVqv6cyz2fb/ve4EF6IE0ddwXJsAEmAATYAJM4F0Q6FOQ37YRhIgihB4WzfZPO/6NYUN2fubk4rk/cf0AsUKUuolwUpX2vepdHJJ3ZQIHJQEWoA/KaedBM4E/TSBzQGeFpwzDGDp0aGMj+Xb7hIYAlMh8Q+JOqDtTXSyrpa9q8Vf4PoQg7TkTa3WWxRqBZTVngpAX1mqXV83XtL/YhKKdVCx0SQeyP0t4EcqK1Or7A0zuqM0v1FcnSY2MzF5M+c+h0Mr1BmBeWJsg/fH1YI6PyTXMaHdf1BEZcSpEFIZKZPpvB3BtyZxaLIyoF2YAE31xqZM+l8paNva+vxQUPCuKQrJXV7SmfGmd1OeV+eQxh/RoT1caFPridgoViJ72twPzuivTrWBxt/0sUKbxBkAkICuQVa1Bf/Eb/2w0kwDd1NDSYrT86z/9G+dv/Om3Hj/DBJjAgCNAMf5Ssr484CaGO8QEmAATYAJMgAnsIQJ954Vv26B1rwKhhS9+Ys3HPpj/7MneGSeveWkNghQxfAFPIZAypojKHg90/wb2UOe4GSZwABFgAfoAmkweChPYEwSyWM8TTjghS/zM5XKtra19q62hpd6rSp3TrPoYR0wqxXeH2JkdNw4UEvoCzuIngLcErqzFo4vVsVE0LwqfV2SIrpOBWuvUKcnVia47mICe2gjc5pP3eXpX6e4kLVKzKoYbw5aIPWALcL0fnVcsjANmRJicjxeWxRM6jdqjaOoIUoTaerwduLcULco7k+v+fOD8ru4lLh7RBuoe+3H250GM0BOWR417wOvAso7K1Eowt5o85FJQtUfW61AglDQqeqmnu7oe6Q318rju6kStPneT+pzFR1NMWEnft6Zhy7DjjJYWI9cjQM+fMz8rPxjHaZ+gz8rOnnjbchtMgAkwASbABJgAE2ACTIAJMIF3TaC/bNy3LQAnRBzjlivw16fmTxpaOeGILeef052S6pwJ0IFC1HP+ywL0u6bOLzgYCbAAfTDOOo+ZCbwDgTimhOJ//Md/NAxj8ODBmRX6ySefzARTAFujZNaOrhFFe5SpFrsUc1HtSbNIQiQhhJIIFbYBt1qYXAxGlewlvvd7kp4R0VXkhEr96YKDosdcTKpuJ/CbFKMq/ohC+Q7f3QpJ6Ryk6oYJwhhpHrgVGFvyJ9YxxcXEOuaVkocF8roDoRBQCciAjbzEg268tMtaXFXXACPywfh25wlBh/BJRe4JC6G2Y0ShcrUwvQ5YYkeTKsnSAJflrW1aa46pG34Cl6oOyhS6oOJ6pNelpUmVHbPL/k0mJUTrruor3/oQBeA1hI9s32I0GCRANzU1NjY1NTQ98shjWfGuIAhYgH6HNyE/xQSYABNgAkyACTABJsAEmAAT2AsE+kRnvUGZzkLfIwnPxTf/ftfH3l8741iccOTae+6jpwJFqYyCIieFUnRnB/RemCY+xAFAgAXoA2ASeQhMYE8SyAToH//4x5kDOvt57733ZkZdKeWznd3XSlxUjccWgoe11TfokV4RQwZat+0G7nGxuJxOKcXTO83HJCVUUJZzGpFMLEmkFhKCMjsoTLkEPAMsNcXIqjvPdddCWCKCSukVEDbQBawDxuet8S4uB0bvCKZ0OA9r4bgi4CS0q9ClBavAAyVrSXd5RYIbgGkFObVTXlsm9TmifooEcai3s+gPCjPVyRu3yGRC3ZliJSu6rVe1zZninBFrzTkQFMVBVQd3AjfUi2Nru+ZK/yYr2arlbxpbb0VFS0eU3NbdedUzzxitzcYhbUaD0ZAjDTpjG0WRSAUL0HvyXcttMQEmwASYABNgAkyACTABJsAE3j2BPxCgpbZJIUiwZjVOfv+LnzgmOfHQylc+tyMScCTZnmOVncmyAP3ucfMrDmICLEAfxJPPQ2cCf4xAkiT/9+GpU6caZN5tMQyjsbHxggsuyPaNoqgA3AxMsaMr6+4WymjuV/ZXkajbDjzoYGFBTO1ILm33fudStrKk8n0UkBxDBIgDhJHypfBjERUkRT8vs9NpJXdpvvym9kpnDukASTfETuB+YHxH9aId4ZwIU3xMK9d+C+wAPAkVwvOVR85qckOvCjG14k2q2NeB9pxaTm6xqVqgpzVihUTqyodS9nTbBTZKXF3z59rBdLN6pWu9kqKmtWxBPm1fDzGUyo90SPSqML6ko3tUyV5QtN/Q9QnDfhgTpB3AlaX6so7ajHseNAYNNoa2kYjfYHz7u9+R+vY29ZkjOPrx400mwASYABNgAkyACTABJsAEmMA+ISCBVEJXKlJUtmjymOTYwevO/DD+5hPO8gVwAjqFjMjAlAp4OgZaR1D2OyHeJ/3mgzKB/YIAC9D7xTRxJ5nA3iOQCdCrVq0yDCPL32hsbPzyl79M/mV9qwE315w523au0ZX3KLCjJ4KDNirAwxEWFs2J3e787uBJp8f7rFL6lk4pe0PFiGJ4KYI4CSuJ2AJcWa1Mq5kzC+WXtfU4BoRCCFGF2gU8CMzykwsryawI0yqYXjJv9OztgAXosn+IE4qQ3gI8EGBGKRpnJ1cBM1M1qRpc65N12oS2U6fQGjjlTpMXWqvSBeB3MWZXkknV4ErXWg2qfCgo+lkmCHUpQUcp10HQATwNTDbN0XY4Ix88l3WgV8iOSOGmNJKHg+pc059b8r8371Kj7VCjqSFzka+48vJEiD9Un1mA1u8g/sEEmAATYAJMgAkwASbABJgAE9i3BMinRA5ogW1v4iPHPnPy+4vHtG097YRnKkU4PszAjVUmQFsCFsVA747g2Lc956MzgYFOgAXogT5D3D8msJcJiJQCjbdu3Tpo0KBcLmcYRi6XO/LII+M4zrRpXxf9qwB5EWchFVl1vljrvE8LzHHiEbXK1Hr3vWlEyRuKgjaoVUrU0D8peCNSSpkhOoAllj26Vphrdf5GmDonGlmiVgjVDTwGLHCdUeVwrI9xIaaU4vtstVXAUUiyaoeC9OK3gBtCzK3J+V32HcDkKBxvWje6ah3IzkzVA/WhU9K+I2SObB398RRFPwejLTnHxfOKdtaDolyOkHpNFQh9hO0Q98hoQeiNSeIxVecpBaqRmJBWLfVvywtNUqjTedXOsX4wq+6d9q3vN7QOzRlGi2G0tQ0u1euJ+B/JG30pHHt5ivlwTIAJMAEmwASYABNgAkyACTABJvB2AorKFQmQw+mKJTj1mJ2nfiA6fVh+3MiyH8IXCGQUK6RSClgCdUFLfIVEtrz27Y3xv5kAE+hPgAXo/jR4mwkwAWQCNIAjjjiirY3iI5qbm4888shSqZQJ0NCV/gIK6oCAryikgmzQLvACcKUtRtX9iaH3a1ibte1Y+tRkTOuZ9I6ZaixVoIXsm7v8sWVzjFW60e3s0oZmap9iOlQJeBOYsWvH2GJtooc5CmNq8TUeNkk6NInfujxErI3YD4VithlPNpO7gMudZEq9PKl9ZxblTOpzJn9LFSIJEEmksXYrbwJmlfKXVCozY9ysKCe6r4REojub6AyOCvAsxCLfPK/QNcl0bwfe0C7qHj1d71ME1iBZGdqj6+WRnr3QdFo/9tm21sOHNDQf0Tzo+//x3yTFS/SJzv03+G3HBJgAE2ACTIAJMAEmwASYABNgAvuSgCKbktTFiuIAnzn51dOPdT89HJ/56JZXXqE8SS9NaWGtoJwOAUdr0CxA78sZ42PvXwRYgN6/5ot7ywTecwJZzgaAb37zm1l2REtLy9ChQ1etWlWtVsk7rD2/OsQiTOE4cVVChhIFYEXBmVB2FgTyKsfZiNCCGyOUMg6QRpA9AjQgIpiJ7AJutdS8YjizHi3s6t5FDaus6HCqo7VeBObmOyZ0FGdY6QpgUsG9PsAa7WiOASfVYdU6rPnREIs7itN3dl8NXAtM7KjN3LH1dyKoZeEgmfZNx1ceEk87oD3gOaRL6/lLnMIF5dJKU+7SDu40K32oQ0Uy1hbwCjC/1HVRuXNMZ+dDHt5KeozSZH4meRt14CVgRnnXWMe+yHZHlSsLd+4yhr6/tenQwUbLUYPe98LvX8/27K87922/55PKB2ACTIAJMAEmwASYABNgAkyACTCBdyQQBaRBBy7uvBknHPb6SYc5px9fOfvfdpVr8JUKEaYQqcwEaCpTL5CwA/odifKTTGA3ARagd7PgLSbABPoTWLRoERXPa2hobm5ubW396U9/SuqzlCIlmVjf4wRhBFmGKgC35+sTuirTnfDKirmD8pEpmTmEGyIKsuALQYUCRUTJytuBh2Ixq+xPr6sl7dU3dYP66OSMDoBNwEovuLi7PNmNVwDz6/6KorVGlxl0yZusQp3gXAFeVViwvXNu0bo+wu3AnKpYUHQfjqPtWkqmjpKrWaX0EuEiMSFC3f5V9eK4ws4xVmlpFL6lWw5JT44iCG3vpu7YoAjpRd31uX46sVK+zqzvjJCmJCZTUommkADbgGVe5UK3cq4f/KJQnd1d/uWv7zAaWw0j19w0qLlhMNm6A2qwT3Tuv9EfO28zASbABJgAE2ACTIAJMAEmwASYwN4n4Hu6wHyIf//KuuFDu07/YHLC0c/deRe8GDFEShmQaa8ATSe3gsImOYJj708UH3G/JMAC9H45bdxpJvBeE4jjeNu2ba2trc3NzQ0NVEZv+PDhrutKSfkXVEuQsrFUANWlxdwras6sijul6i0uVnbozkkZC+kHSFxEHn1le5ARpDITuR34rfQXmKXxbjKt4G3psxvrjI5YoR24oarGFcNLIswCJvnugh3bX9aRHTbpziqkq86UwvyEiq6xqgvL9fnV4AFgZR2LdtSekNilEzao6CDiFFFIxufEhbAhCsB64GbXnVoszDKt5cXyFl07Ue8cgaojRnqb1OcXgWvDaGRXOrGEa/Nmh66L3CM/a10bQDfwKHBBvvucMPiFF88O5DPASf/wT5RecsgQI5f7p7O/R0h0ckh/3blv+72eTW6fCTABJsAEmAATYAJMgAkwASbABN6RgD5hA9Y8jo8c+cxHj7SOHbrlr//6iQgIBIVOUvlBJVMpKYJDQugzYhag3xEpP8kEdhNgAXo3C95iAkwgs+hmTucwDIcMGdLa2poJ0I2NjevWrcsQ0XetpLwMT3uZr67WJ5nu3AQL2iuv6/QMkqZFrJQIITwkDhUIfWVTJQAAIABJREFUDqGSUIvIj0bJ4nppar02ueg905v7rLViciDXgYdDzMgnY2qYAVxg2jPN8hpgl0pdSlsWMWIPsUOpF8l1VnFOMb8ywZ3A3CoWtAd3lcJduk29fEoqMl8HMcIYoYekCrUVuDGNZlrOHDe82hPPJWgnMzN0mAfZryWSSMc6rweuib1xdfO8zmiZia3acw2V6CvfmQWaROoXgKWxON8JL/DTcRXvKeCKJ9cYuUHkHx88yBg6ePZll/shye/sgM5A808mwASYABNgAkyACTABJsAEmMAAIqAyvxD8EOMuFJ84Ln/6sXL40ZtWrPAlEEqqI6QFaKpASEUId2vQ7IAeQNPIXRnIBFiAHsizw31jAvuYwHe+852sCGFjY6NhGCtWrADg+z7FNQuFlOTX22vm7EptnBUuNZONUU8Rv1SltDpJB05AJXFqgyRrsg4/CSyqOLM8NaecPK/Tk/sGmQC7BJmOZ3ZFEy0sBuZ4am6x+mBCtuXsFiorVvUEeA241rVXlEqXmf7dwPRSMqa9dqUZb9DlECmZWSpdJFBpOdqFcLzE3gTvt0jH2PWRdjC/23sJKGnhOUsUERQbkqYQvu7YAykme2psiJWBWq1d0pL+LAkpAqTn6jjWRGqq7fw88C8MxMU7S7cVQxP49Ff+qfGQQw3DaBzUahjG65s3pwKSSlb0DoN/MwEmwASYABNgAkyACTABJsAEmMC+JJBFS+rTNF1+0I2wYQs++tH1wz8Ufmiod/Ixr5ndiAPEAhHZn2kdbo8AreiEOFvSui9HwMdmAvsPARag95+54p4ygb1O4NZf39ra2trW1pbJ0GeeeWYYhqGvwzREAoEKcGl3flq9tsBJHpW0LgkJlJAxWaAlBVlQVIcAYlv5LvC8wMydhSmVYFp3dJ8gs3PPTSuz3cBaYF6nNS3GxBSzPMzcWXooxluZ9Zg8x5EHx4G/Cf5lZn5OrbyyZD8NLHIw38KiTvsFLRNHtKcilTxbKEWx0g6E7eL/Z+9NwKMo07X/6u50dxISFnFhZNxQXMbZXMYFPhY9gDo445zjp853HD1zdHDcZZOEhCQQE8KWACpuLC64ooiKgoABEkMQEUEQEcKSrZPeu6trX5///3nfpOwJ6rigBnnr6qtTXV3L23dVqrt+db/3Y66zUmXhlkmCmB+W3wU4CCDbYJOyijoYClgSAcztGO4B8+LKhHa5MCTXADSTNpCKxxr5cQICWXxpQr8zGrs5kXgwKr4oQwBg0bPLvVlIn3Fwc337nWiQ4oqYnM0GpgBTgCnAFGAKMAWYAkwBpgBTgCnAFOgWCnQCaJKXaJrol5pSljjnV8ET+grnnJEc+0+sYk/zH0n4Rgd9NmzDxIvIjkjFbvFRWCOYAt1eAQagu/0uYg1kCvykCuTk5Hi9XkpTPR5PU9MhbI6h2SYW1WsEmBU9NEeMVhvQisZgpM4aMlxbI1/JCKAtTLjYD8p7ALN56R8HA8UR+YWQ0koM0bg2C+dKAOwDmN0uTIxIeSYUGDAtLj4VTDYTR7OE/NfkQY6BvR20Z5LNRe27iiONqwALD04KJWbH1QMAERO5sIAz2wboWPjPEAFEGRe0NoNaKUXGtTXNjogvJTFpOgYEjxsIrBXQJbBTWD4RPrahKiGURJNzGmNvRvUgoc8pfLZ0wBhsGaBBh2UpqIhrD0T5ieHE4pSOGR02nH3GQCoXh65x7v/dSgKgMYvaKW34k+5RtnGmAFOAKcAUYAowBZgCTAGmAFOAKXBMK0B75yKAtm2TXJhqOulAe9a5q44/7sAp/SMXXrC97n28VjV1ND53pj/TDGiLAehj+vBhH/47KcAA9HeSjS3EFDg2FDAN8+abb3a5XB6Ph+M4j8dTUVGOPZQMw7CNJLEAL4o3vw16EwBvopuY0OcOAE0jOGSwQwCbAMrj4UlJsUSG2SFxN1qlMcfCItkcPCAOfiqsFkT1CSqM17QH49E5raGORGmSyNxmKC2g7AJzmSGWBRqmtn/6OsBLALNbE8WtwQ2EO5sGBmSIZFwBHfQ4WCkD5CjYOwEe50MTo4GSeOyZAHLtBIBhknYQAC2DnSSFDRsAlvFGcShamRTeiUk8mcXsZNA6WXmDAe+k4KF2qUSwZ0mwWDQaSNnDRU8t7uX15eRkU/rMebinnl4oahJawy00iLOBKcAUYAowBZgCTAGmAFOAKcAUYAowBX5SBb4A0BZGJRoAimbBsy/BgIGfDDglecH54Vv//omoQoLHKMm08oMMQP+k+41t/GhWgAHoo3nvsbYzBX5gBVRVXb9+vVOHMDs7+7zzzovH46apKbYWAysA0ALQBhgGjfX7SH6FToitTgzRKglZ/gCgSos+GImVpuyHw+aHxGUcNeS4KgkGMuggwKMxdWJcmWzAFICJqejDYvwjslqJrFbCEA20SC83+dL25oeCbRsB3gWY095WcahlA8Ahsk4Sz4wQnLTEVM0EgCmD3QbwsBQuEMMzVOXJaGqPiTOgk9noANC2bYsAYYDdAAsiydLW9vlxfqVmtpBZLLsjUFoDSJk420aAoiZ+YkzLj4gLAtjUVoDWWLxPTs/ePsx9xgqEGVyf4/u0BJpJcrRt2BhMzQamAFOAKcAUYAowBZgCTAGmAFOAKcAU6AYKoCHKNNEnpKmWrsPV1x3sf0pLn+yDp55Uu3yFJpnomsJ3MQC6Az13ZECzCI5usP9YE44uBRiAPrr2F2stU+AnUKB///65ubkej8fr9fbt23fjxo0UQCfBioMlENqLYcvkYZBvYgMTMNCJHAX4AIw5erTIlEpEc3pAWkWyLxQkuaJo4OJNACtFyI8q92r2WB3yFKVKjm8kZQANAMlGU3MCoAHgPbBnthwobQ28BLAS4OlwdEFr+1uyHiB4WiD4G+sRk0VkTF424pbcDrBClvKFUIGarGoLf064NtYDpLe6//+gLxO7XgkEcD8TM8t4YXJr8xuGvg9AJQkhGCht41wiadXHAFPb5LERY0JYqAgmtwK0k03feMstuTl9MPiZ4zw+9IzfPuY2EhiNRRsJhv4Jdh/bJFOAKcAUYAowBZgCTAGmAFOAKcAUYAp8oUBHcXi8INR1XcEOq7BtK/zqt3tO7Bf59Vn8NcP3JpI4Ma7aTdGEigyaAegv9GNjTIHvoAAD0N9BNLYIU+BYUUCS8Kt43rx5WVlZbrfb5/NxHDfmttstwzQNUwNDJSnLKkZZmJj1bJkY52xgNQaV0OdtID2tBSfGIvkyzBLghbjZRJI6VLBVtD5DmwkvpKAgqueZcJ9u3SMmyqVYDUG6AoBkgagjBW4FeI+XHwkE5raHXtesNwGmh+KVoWS1CI0GzkDTPLDQn4kPhWBxADioGSsssygSnGapZZHgpyTNQ8dZTPLAplK6HAd4S4Mpreo0SZknRnaTqA1sIlm1SRBzO8BHANPj4tgU/LNdKQ/z75O2AUDtJx9xfh+X1YfzdFYg5LiPd2yzUBSkzygRG5gCTAGmAFOAKcAUYAowBZgCTAGmAFPgJ1TAJpd4NligWaCYnf1Ux9554JzzW08+TTjlhD1PVuI8BjEkSeSZGp+dZ5YB/RPuQLbpo1QBBqCP0h3Hms0U+DEUQI6sqi0tLTk5CFV79+7NcVyG2w26CbppGZpuqBpoGvZJ0rE+H1YORgBt2piYsQNgqRKuEKIFsp0f1Ran7B3kux47MYEpkdCM6iQUR9QxcTkP4EFFmy4mlptCiOBjEeyEbsRVDMfYCfBMOz9t5963AKoBFgSiJU2RF3RosIDHNA2T2K8RFyMvJqyXupU3a1DY2vJgPFyVSm0jRmm0aptYGtEglRINLD8IceKwnhOGmQrMFaRqUp+wgz4To7RJXNh7AebyqULFuiuiT4lZ67G4InqpZU2+9D+GcH1yOH9PLus4LiOjZ+/c83/zq0Qq4dBnUt3ix9hr33MblmV1lHMmf77n2tjiTAGmAFOAKcAUYAowBZgCTAGmAFOgGylAADTp4aqZoGCHWB3a9sFZ/Vb+sl/bgNP4i87dqiXIZR5Bz/Jh9mfDYkUIu9H+ZE05WhRgAPpo2VOsnUyBn0CBeDwOAKqq/s///I/b7fb7O9KNZ1XMUGXFUDVVlQ1bM2zNsgybhkwg/7U1gGYSlDwlrNzdKhal4EkFthKqqyIsxiECsExVSqLx++LSPYp5tySXi1KdboodH9RUwVIA2g17P8Ds5vjssL5SgfcB5svGhIam13QE3Ng+HLDuIEHg6GZGBm3j/erNFswPymMPNT/UHtxGZsZ8L8NGy7SKWSG0LGCjBW+ZUB5SpkT0hyXYTDI6FMqyaVFFDQwDAgCvJBCXP9AuzYjD2yR4OgGmbOlzH67C4A03x2V4OJ+PViCcPr1MlkXSGlpbmfDxjgZ/lz+6rqNf+1+Hw6ekv2/btmmYh8+jk8GyLNMwZVlOpVJ0KTp/Fwbt8Oj0NbNxpgBTgCnwQyhgYTw/Dl1OXPREZH3jga5EluUu66HT2TNTgCnAFGAKMAWYAseyAljjB21LFunUa0sWzK2A03rtOv8k+PXJbVPzWgwVrystMDScB2jOJHU9pz8fyxqyz84U+LYKMAD9bRVj8zMFji0FdB3rLgSDQZfL1bt3bw/n8nCuX517nmWYmqbZtm11ZGGRP51J0GGATQClgcT4qDk+bDypQB1J5EAyTNhCGKAWoDgWvYvn71H1cYpZxKdeNYxoh7qmbWk64cr7ARY3h0tb+YcCYj3A6yI81B6eEQh+TGoGYkYzDgoB0Aa2laxfAzgA8HhILgkIc2LC2xqiahN7UZnoRNYIgLawFGECYDvA1HYxP2LMl2ENSf8gq7GwrWROII7s12P27LB+X3NsalR5U4dGgGYRI0rao8G+/Y7nXNwXD5IBrRsqzycwXtrGkOmOlnU0+Fv/0TSk5aqq0j1yOFamMzjrpbCGvhQEgY5QvkyXdTDO4XSG7NaO9x36fPhszrbYCFOAKcAUOFIK0FMNDYD6nuuUZdlZQ/o5k53NHFnYCFOAKcAUYAowBY5NBWhwo06uXqMk0XHQRTvP6Rv/3fH2Bb/Y/fFmVIXU8tFM7OfLAPSxeZiwT32EFWAA+ggLylbHFPg5KeBATEVR/va3v3Ec53a7M8nw3HPPybKs67rDMTXbksFMEGvzFoCHgomJCb7YNIoDrVsJ50UyTOhwCssJwkxeeyCm3CfDvZpdIqorUtoh0sUJQNdAoXbmfQBVTdHSVn5+W3IjwAsmPNqefDGafF9Rg4Q6p/mBSfYz2KCgw/oAwOuaVdDcNiOUWJ2yg6RysYUB0JaI97FpALQeB6gHmNEaLU1ARVDZAtBGqLcGigYiRknblmUjpN4CUBRK3pdITAqHlmr6QVLCkKZDDxsx3Jvt+4I+uzh/lu8f/7wdAHSDxFOj6ZvMa3f05PoOBwmNQ6ELrly5cvz48SNHjhw1atTll18+bNiwUaNGjR49ujRtePnll1etWrV169Z9+/ZRR7Ou6w6JTm8Axc2Ou9A0TGefdrFCpy/FxpkCTAGmwA+hgKZpqVRq6dKl11577XAyDCPDUDIM+cbD8OHDBw0aNHTI8MmTCzdt2rRv3754PC4IAs/z9O7pD9F4tk6mAFOAKcAUYAowBY4GBSwLixgZOulxK5jw7PMw8ORtZ/Rsu7B//K4bJUMCnsfuvRYYFFWnu57Tx4+GD8vayBToLgowAN1d9gRrB1Ogeyqg67ppINJtamri0obs7GxBENJhpQpWAuxWgE8BnlHh7rboPYlIfmj/OyDH6GczEMMaAPsAntDhH62JsQJMEKFQshdKxl4T/cgaJmmkFDBEMttbgjEjLE9tF2sBNgDMbI8/GU19rJnUl5xGn+kG0GCtymgV3gIwPyk+1B58WdH3aiAoaH+mluoUMmhTBJ0H9SDArHDogcb2gv3hVSaQQseggaLYcRUSOhZBBB7gQ4CqoJ6vqhPF2BMa/yGpT2iomgnmwmcWeTIzMrK8CKDdnSZojmto2NuxQx36jEFh3x1AI84mERyPPPIIx3Eej8fn87nd7rR90nXU5XL5fL7MzEyPx8NxXK9evS6++OLLLrts9OjRd9xxRwEZqqqqli1bVl1dvXLlys2bN7e0tMiyzAB09/xnZK1iChwLCsyYMWPAgAHZ2dn0ROfxeNxkcJGh62nu3732ZmByFD1VDhw48K677qquruZ5/lhQkn1GpgBTgCnAFGAKMAW+QgELaw9iKSNbsSEpwnXXfvLr0xoH9m357S+3rXsd+DjoBjUQYTQYyZiEdO7sjH/F+tlkpgBT4EsUYAD6S0Rhk5gCTIHDFZAk6cYbb8zKynIu5svLy6lDls6soL8YozbmRJX7Q/I/eOH+RGAJf7AVmbOJ9FfHsV0AT6VgbFAdEzPzdBjfIj8VVptIeUBShpjXQAhbykGAFQAPBVKPxtQ3AZMxHg7EHouJa0zAmA50UnflzyYJyogDfGrD48FEeVPb67q2k8BiDK8g1maFdLOiVQd3g/q81n5vsGlSnH9DhUOk/RaGfIkqJDTgFUvUiSd6blTP5/WHdG1OLLAV9DbQBUsC0MLRUE6vnhzHuTxut9fl9ro4juvRs8ewYUOIJsTvTX+60GcKoL8fhh44cGAX5EL5sjPR6/X6/f4uE513v8lInz59hg0b9pe//GXIkCGjR4++9dZbCwoKKisr0yG1aZjOg8JxVVVNw0z3WTsz0BsVhx9UqtqZodL5nqZpgiBYlqXruqJgELeiKE4mbOdc7C9TgClw1Ctg27amafQGp67rmqatXr26Z8+ePp/POU1lZ2e7XHhepUNWVpZz183r9dI5c3JyvGSgzNrr9brd7tzcXFq0IKdHT583kyJs+uzxeLKzs2+99daWlhbaiYe2gZ5tjnpZ2QdgCjAFmAJMAaYAU+DfK2CRpEXiT1KhrgZ+c+bOs05oPuekvaOHbpEToKkg44XIF5ecFEMf/vzvN8XmYAowBToVYAC6Uwn2lynAFPh3CjQ0NFAWQC/svV5vIBBwFpIANtv24wlhbEi8P2UXSuY8IfYZGFGMX9bxljHAARsWJ6EkBfdLMF6FByPmYgVrCSZICQhCgAURjGaAtQAzwnJhc+IdEie9ICxW7GtZY8J+UkQQfyzg+mjsBjZBs7EQYQTgI4BH9h54tD25uD25k5Q9pC3UOrI1MC5aRnu1vVRoK2r5fHI8tARgL9k2rtIyTQwAkRRLNABaAF6Pq5Mi4iRJn9Hevh2Dp03VVtBqbSvXXHs1Gp85LqsHmvUy/BnIoN3c2nXvanrHb5aO8I3vDaCd6Oe//vWvFLtQ2tKzZ8+vYc0ul8vj8aQTnA6Q8w3+0KXcbveXLu52uz2dw/XXXz916tSHH364uLi4qKjo3XffXbdu3apVq5xjo8uIU03RIctO8cN0VE0/MqXbmqZRX7YTC9NlnewlU4ApcJQqQG9ETZ482YHLX3p+ouecLm/5/X632+3z+ZzvJpfL5ff7nbOW39eD4zwuF54GnYl415AM55133quvvqqSS0xJkug5xzkvHaV6smYzBZgCTAGmAFOAKfBNFDCJnUnTofhBOP+XobNPjAzst2X+zKStg2lgQgcZOjxPh6NnOuWbbIjNwxRgClAFGIBmRwJTgCnwLRQYP348x3E9e/Z2uVw5OdnDhg0xwdZN2zQw/fnhSOz+SPyfcXUKb78ct1oBDkI0hXgZ+etugKUSTArI4wUYr0F+Sq0MiltIxoWG6FcBUCywQgDrAOby1vy25MsavA+wMKk/KcGTgWQzmYmy3E5HtUjRsUxY8zaAudHEzFjykc8Dn1pIvtNt0gaCcEgRU/MbYqr4UMuU5rbXDXNPBwEn7mgV6yRaZM4WgBWyXRpOTkgIea1tHxGETcQy4gL/2OLF2EPc6+XcruycHCQaGchG7r73LuKkw/qE4ORvfG8ATTksAESj0aqqqsGDBw8dOnT48OHUkP41DLoLr/kmL7OysiipOZwHuVyur0LS6W3IIYKkb+uss8664IILRowYcd11182YMWPq1KkLFixYu3bt6tWrt27dGggE0osoppcIc8yJ6RO/xSHLZmUKMAW6pQL0X9uyjF27Phk2bEiv3rnpZwzas4Tz+jgXBg11nl7wjhqdzd3x94uFnDujHOfyZiCDJvkbbo7LcAA05c64jNvl9XrxL8f9+pzzFj3+pMinsNp9x/D9Oqp0roX9ZQowBZgCTAGmAFOgeypgm2AY2LRPdsKpfT84+0T13P7Rgf3XNB5Mb+8XvwcYgE7XhY0zBb6bAgxAfzfd2FJMgWNUgVQq9YsTT8rKyPS7sJe0K4NbtORpIGR2RYh/MBi/W9QnyOaMEP+ZBhrxNQeMNgOgCWCpDBNDwl0RfYIC+bz+4OeNa2Ro7Cg8aAIIJmg8iX5+VIaH4vprFtqZnxXseQF+UVhsoGEapJ6fZdNID4tsWdRI8cNtAC8IUNgcmxuRthOm3MkSbFIy0DQArctBgPWgzw+1lrdGngil9hMkTTKiSf1jGS3WGjFTr4iLpSFxCq9POti0lkxx9vqWbR/3PukXlIxwbpfL487sgUmjx51wXEugWVVlRZEMTbEM7V8Y9PeI4FBVVdf19MwKmlMhSUi6o9HoOjK88sorlZWVkydPvvfee6+88sqLL7747LPP/oLQfOOxzMzMnJyczMzM9KRpJ06a4zja550+07U6zJrmtFAynt7zPd1+SNfvLOj4qc8880xaU3HUqFFTp04tKysrLi5+7rnn6urqNm7cuGHDBoahnYOQjTAFjlIFHMdQa1tg8uQ8cj5x+TORKLs5rgMsZ7g5bwbnQUbco2fuFVcOKy8vf+nFV9auXfvW2yvfq9kQTeKtzUQK05y37dyxev26rdt3vLt23aba+uLCklkVM274y3WXXvoHDOb39+B82fjwZ3OZmbi5nCzOzWXn5PgycP1+zu3iuP6/OHnps8/wSQx56uxe0/kdcpQKzZrNFGAKMAWYAkwBpsBXKCCnLKxOZMKjD8NZ/ZvPOEE974zGsfem6I8AGqRIvEwdPwYYgP4KIdlkpsC3UIAB6G8hFpuVKcAUAID319e6Oa4nR+y+HHfq6Wc0qfCWBAXN0n1x+35eK03xKzU1Tjo1ySCFQWwHqAXIbw/elVQmWXBvu1x0KPmuBm2UH4NtYNBWRAJjF8AjjXxlRJkbE7cBvGrCnGbhhQQ0EO+zSDzKaa5mG0A3QQtY0qcAzwMUtSQXR6BegzCNie7YYaaFqRqyCEYI7AaA+XzLrGTg+XDoc9IADUwe35Wx2IRqWIYWBFgNxixJeCCsFraI2wHrE8pkbRbpjnX+b36L8NRFHm4XDeJwuVxFRUWOYxdTQsjQHQ4bQRD27t27adOm2trapUuXVlRUTJs27frrr7/88ssvvvji/v37U1+h4y7Mzc2l9kBa7TAdXFMLYTpNptUOaTAINU3TGFZnKepMpGEgXczRztqot7oLsE5/l45Tuj1q1KjBgwdfddVVN998c15e3uzZs9emDem7ID2mnMLrw/vX0wCQr0Lbtm07VRlpUi3+MDVMWcYjQtM0mlVtGibd3d1np3eHA4+1gSnQRQFZUz/6ZPs948deee0ozvdFvjNmGfnxZUdl1V/2P+tPf3r0tRUfNxywwBbkpIOtTZrWBHbSVEVbJ+4lCJmqTLAx9jbBcCYLpCSAnQBzc3Pr1CUv31RQnnnRpVwWEmcu08XlZHIuhN00cNop5zp80KVbNq43hZTCxwGAF5Ky1hFV/1WniC4fkL1kCjAFmAJMAaYAU6C7K0CpsgmaBBf/7uNzB/C/HigPOGPjpnrAKvNfRChaFnQUIWQAurvvU9a+o0EBBqCPhr3E2sgU6FYKWHD7f97s49D+6/K7PF7/7/944+x9ibyAPTaolyatN230NWPms20mQDkEdjWIc4LNxZp6r6hOEMwpAeG1GBb9E0mgswa2CHocxADAolBiVlvqGUGrBXgZoCoQXRzTtpA5qc/aSVamsR4W8S8fAFhpGWXB2LSD0Tod2imn7hTNBkMFWQK1DfQDAM+EArP4lrmxQ/tIaodtAdi6CLIMsm2hZzkJ9g6wqoRwXjJeHDdf0RFng02szADxWPJvf7vV7Sb8nQJo+sxxZ511Vuc2u/VfJ2fZgacoJv64gpqamm3bttXX1xcXF1dWVo4fP37YsGFXXXXVBRdcQCOnOY7z+XyZmZk0etVBzNQTTekz5dH0rUziN6RuaOc5fanDEfPXTHEiQdLxN10bTbumqdR0Sm5u7hVkuOGGG8aNG1dWVjZv3rw1a9asXr26sbGR7iHTMBVFocXQ0sG0aZiO2dw0TJpA7QRVU+95Ouama2MAulsf96xx3UABVVVvv/12l8ft65GVfRxmbri9nD87g/Ny9J7mb357Xl5R0ZI1a574fM/CAwc/U2zeBg1MWRd106TXfib5RogBNIP9iZZqIGH9ewHe52M8vfWIANoAOwUgpsi7nwM8eTC0MBBaD/DUzvqBfx6OW+S4Hh5frsvr0Gd6K5HjuJH/Z9hby5dLKvYvYS7obnDgsCYwBZgCTAGmAFPgyCpgaVIKdFj6FFx8fqzfccFzBgZuuOkzixQWSgPQhgXGV6Fn59b4kW0ZWxtT4GesAAPQP+Odyz4aU+CHUsBW7dNPOf0LjJjT7w/3PrSgzSo/lFouo6+ZDgJmQKP3eU48MqE9VAFQJGiTg5FlOtA0Z41EY9gWkuhGgGfagk/w8YVSajNg9HNRY3ROVKkFu7UTKCsdeR24epUkciTIJtYCLAiLCxsj78WNALEqk6IRtEqhBqAaoIfAbAB4JBEpCwUWJQI7ARrAUgHQqG3ZNjqpdcWSY2DvA3hJEqa0B8pjyXdsDA8RCM3QdVuW9JKSaRznPhxAu93unTt3Um9spwDd+q/DW6mtTxAE27ZpDS5d19PpqsNbLcsKBoMfffTRu+++++STT86ZM6egoOC+++677rrrhg1nx6/+AAAgAElEQVQbdsYZZ1ATNDoZyUD91F6v15nuwGLn4Pka3Hz4W3Qpx6btrMQZoYs4GSAUizu0mhqxnZn9fv+ZZ5556aWXjho16sILLxwxYsS4ceMKCgqqqqpeeeWV6urqjRs3fvrpp8lkku5WRzFnv1qWRe3PdAoD0I4ybIQp8KUKPPXUU/Qf0O925Xi9fhK3kdMnN6ff8ZVPPr7v4KEUwC6AeYfaSyPRGS2BTzUQbfQ065ai2ZZO+DIGNpEONO9A6lG+rao19A5AcThYETh4iNYEwFtqOum4kkqSWKcZgWBZUloCMD0YWMQfWKu27FPib61ede9tY3pnYCgHDhmct09uph8D/TM4v9/X4/j+/aZML8WODuTi80s/EZvIFGAKMAWYAkwBpsBRqYAJhgzXXhk47YTYmafo5wzc9/TzGCCp2+kOaAagj8p9yxrdbRVgALrb7hrWMKZAt1ZgXW0tvWKnV+4c1+em2UuWtSo7LfzOxop5AAGAbQALDe3+1nCxDgUxcVZSXJIS9tFPZuF3vEAebQBrTVgQkp+IRjaQcoWLwqHSg8G3AA6AJdo0/QIMEsRhEGytkpTnAxjoDI/wMD8g1yVsiaBqG2yCLAwLJIKjdQHQcL0kFHooFJkZiW4FaCXbValdjmREmzbEwTxASiBWhILTWtpe1ZE+2wCiDrKkq4q5fPlbHo/P580k0RudERzEAV1WVkahbTfspi3LslPiTxAE58CiDXaiJGigBHVDU9hqWRbFr6SsYrr73FnHv4xQGrtr1676+vrt27fPnTt38uTJJSUll19++aBBg0aOHEnZdOcxg38Pp8xfPyU3N9ftdtN4kJycHL8fS411WaFjlKbrT3+Xsmkn6MPj8dBVpc/zpeP9+vW77LLLxowZM3369LKysueff37jxo319fWbN2+mEmia1p0BdHdu278cQ+zFz1qBoqIiD+fyu125Ph/NevZ6XFf/cXQgkoxq+HXwCcCspliZaI8NR6c0HPhUAY04kE0wFdvUyRleBOzmssmw5grBccHGSoBKgJKkXBWJHyAndpTQ0g0tbIO5H+CFZLIgFCkns01pbn6ebzlEvj5wNlXXk8LLL79434Nje5zUl8vK5Di/x9M3I+N4ztOT83hc2f5Tzz5j+uyKQHv7z3rPsA/HFGAKMAWYAkyBY0kBC0wdttbDqcd/fEY/vf+JoeHDDqgWxEWS4/VFBIfGHNDH0mHBPusPrgAD0D+4xGwDTIGfmQK0JoMC9uTpRVy22+Vxu9Ay5ua4rGdX12PoJnkkiZFtsW4U8mKRCnkxsyQmPBqO0OQNtLSR9IwmgA8B3jTgiQQs5KGeMOtHpfisSMuLwbYAYc2YxUVQsU4WEQmGBoCgBSsByhKpyqj5hgjtBsXJKoHOhg26ZfG6LRjYUxteBr2kLTA/mPqA1CFEXzRZD7XU2SZGPO/UzLcNPT/YPDkUeCEm7aUhIZ37r7a2nqBJJ3eDy85GrxzHcTfccFPnXD/Pv+n4Mn28y6elbzmJyV/F4ltbW6urq9esWfPaa6/Rkom33nrr6NGjR4wYcdZZZ2VmZtI86C9Fw04mtcOdaeyG2+2mS3k8HsfpTANA0v3XdLbDwTTdj9/z+ZJLLhk0aNAVV1wxatSoadOmFRYWlpSUrF27dt26dbW1tQcPYlFtmuORHn5Cub9pmNR+nkph8RM6Jx1xbgbQJBAaP51uUXfmp3PS9TixKs676TvOGafvsmemwA+kgKqqPM/ruh6JRG688UaO47Kzsz3knlEPf4bfm1ExcwbmIBl4P7LGgFmhSAGvPxBTpiT45QBR7KCCTVMt2wDbJF8u7QDvgD093JbXFii37XzNKknqy1Kwn5SKxcBmjIG2dUtpBfM1PVUeD1foMAtgSkKa3YpfKxrJdbdNC9dudfw3mGA+8/xLA88f3OO48zl3fy7jeEwI8WCHF44kLC1YsMBRCf8ZnRdshCnAFGAKMAWYAkyBo0EBJzTDIikb4+4Ln3ZS68l9xd/9OlhZCTIp+vCvgRtfAOij4fOxNjIFursCDEB39z3E2scU6G4KYDYW2BpYSV36vzff6M32cV4P5/VxvmzOlbnouVcMgDjYnwEsk6TihPhgCvJiMEeB+ZHEZhK7jNftxCidAEQGy8Ge1tJaGdDeJfa3t3SYEWl/LNnWDCDaKmZjKCaoJpiWDpZIGDQPEDawp/a0llhJTFqmwB6S2AWGTuizSKpQ2ZahaOihhrdEpTKRrEoI6zUIUahNIkJFy0watkBgdAhgtQJF+5uLU8m5Ar+TdOVW0Mpta4Z58GBz3+NOIoDSAdAdxtuzzjo7EGDmuG9xnNq27SRX0LgPSk5pBggd371799q1a1evXr1o0aKKioqJEyf+9a9/HTly5ODBg88//3xqZPaSIT332ev1Uujs8XgyMzO9Xq/f73cSOZxAagc00+Roh2U707/niNvt9vv9FKC7XC7Hpu31en//+99ffPHFgwcPvuKKK8rLy4uKisrKyhYsWLBly5aNGzfW1NQ4+NghyLqu27ZNreumYUqSZNt2KpWiDNoh0bquS5Lk0GpZlh2WTVO/028MMAD9LY5XNuu3V4D2q6DL2bZdU1PTq1cvmiBPnjM4F3f+b8/9cPtWzEAilHmPDI8npElxfmxMmJIQlpGuMCLN3yddagB5tLEfYAtAabStQBYqTChKGfnxxGMpdQ+ZR6BzEjYcBtgMMF8W7w60zgYobEvMjYmbyTcI6MTPZOD/hGFZmo0PwO812Bmzhv1vAdfjLC7rl855IIPc38Js6JEjd+/eTT+XcxH77eVhSzAFmAJMAaYAU4Ap8KMp4CBl8pODbNY0oOUg/Oacraf340/vnzzzzPXBEKgqWAb2+HQWsIAB6B9tN7ENHRMKMAB9TOxm9iGZAkdMAWJG68CFALyS+u1Fv8OrdDfH+ThXps/bK2f+Mwv3grZUDxengpNSZkEKSkPwaFD5jPSbThHfsUYoQACznu0qNflg48FVCna+fgmgIph8KprcgxSbeJRNEQO6LB0dzWCYhAu3A6y3YeahWEUM5rXJ+wh1JszB0EHT0UvXUTiq1YRXEsKc1sjCkFRPul1jIQnM6JBN0DWAdklJkYZt0KCoJVXCQ1U4tQW3jsnUIkDEFOu3bjm+zwl+f1aX9GG3292nT58dO3YcMXmPpRVZluUEg3T53A5UpSOKojhT0vns3r17t2zZsmrVqpdefKm8vHzcuHE33HDDlVdeefXVVw8YMMDn8zn7yxnxer1ZWVl+vz83N5fWUaRxHEeEQR++EseL7fP5/H6/x+OhsSEUbPl8vp49e9J56LJOm30+34ABAy655JJrrrlm2LBh5eXlBQUFRUVFixcvXrNmzYYNGz744APK+NIzVbrISB3olFk79NmyOg2fBEJ3WYS9ZAocEQUsy3LKeC56aqHb7fZkuGiJv6xsv8vN/X3M/4qgpgAv80yAD2VYHJGm8VoeL5XGIivAaCZpG3gNSKIYNXI2jgNsAqsq1vJgsKXMhukAU9qFJyORD8HmyUlf7UhhwvSlTwDmt6XyQ0KRBvlJpTIq1Jl4Yo+Qbx/NtmwTH4ZlCWClwMKvA4BlMbmqmc//qIG7dDiXlUX/VbOy/bQjRWZmps/nmzBxHM8n8KYokOKtR0QythKmAFOAKcAUYAowBY68AqSbFeY4GlhzncBl/O2hwqxSOKHH7vPOsE/rv7+wKCkpYKPtSGcA+sjvBLZGpkCnAgxAdyrB/jIFmALfRAGar2GZuqFKkgQAgXDbub85z5XR6RXDzsrcFf+85ZHw51NTrQWSMi1pzQ9LHwCEyfoVsCRy/R8C2AGwOBApaWpckEptB6gDeDRlF+9v+4RkNCNCNgUweRtkDWGxSczX2Cn7M4CZsWRxNDWvTV0nAE9/KeBPCksjHIGGUEcB1ia1mW2hkoMtayWI0Q+ommDrNqg2qBqYCcKatwDMa+KLW4V5SetDkl4toy3ajpjiR5/v7NO3rxsRe9ehV69eTgTwNxGPzUMVoOTUsiwnd4JOj8fjDjOllQ8PV0xRFF3XZVnWdZ2uQVEUB8LaNulab1m6rquqqijKgQMHamtrq6urn3322QkTJkyfPn3cuHFXXHHFiBEjzj33XAdMcxzn8Xic+Omue/qbvaZEm85LsbLP56NkOTMzMz2Zukv2dHpIyOHBI7SR6UZvh1PTbf3ud7+79NJLR4wYce21186YMWPixInTp09fuXJlfX39+vXrd+7cqSgKA9CHH0tsyg+nAI1El0Xphuv/L8dxuT1yEEBznCuDO+HEPn/723/LhiLh1R+eluMAj7TGikKpB3mjIJ5aAdYBen1ILgSBJPqLJNx5EygPp9omhRpLwZ4sGflBaX5Y2mQa7Z33IHXSnYUnVW0Xxc0ZApSo6JKe2hapAfymUMnm4ngjE13PpmFiSUPSDAlgZTg6oyVUGk6VNDRvBpix9FmOfrVlcF6vN9uf7XX7qIP7zLNOq91USxg0+qTYwBRgCjAFmAJMAaZAt1SAXj4qQLzMJmD2hmmDJsOlv9l7fFZ7v96R00/e8uke9C7h7xIdb2gzB3S33JWsUT8HBRiA/jnsRfYZmAI/sgJO/33kfQCSrv799r/jZXkPP8dxXo+Ly8rsO+SyWZ9umae1lbTt2gTQ1hF8ASZYvK2EQGsFWJqE8s+jzzfxW0gS9LzmyIw9BzfaWCGQ5uDapqGALoEhgUVL4IXQNA0zwrF7ou3T+GSdjHOK1CvXYXrGNGfBQK7xqmCVt0VL20IvqnpjR+KzZWItK4z+NDHpy9DICmfHoaTVeHRv6weS2mghj1BJLcXtH2375cn9Mz1eh0C6PVxOTnZ2j8zefXpu377dSfVN1+RH3h0/s81RJb/qQzmIuYuT90v1pxMd9vpVmdTBYPDjjz/eunXrG2+8MXny5Dlz5uTl5V199dVXXnnl73//++OPP96xNtPIjqysrPQpzrGRm5uLnQFIYqwzkY6gA5QUPHSQd/ps6eNdFjyCL3Nzc88777whQ4aMHDnyr3/968SJEysqKmbMmFFbW1tXV7du3Tqe52VZpv0bHP27xFVT2Z136e4wDdPJVHGSQ5x5HPc6vXlgGqbjfKe3GdK3+KX70VkVG+nmCjiuZwDYtm3b6aecmuF2Z7i5LD+eQr2Z+DzvkSoAUzHxFJsgof9LRMhvN8ZGrDwBprcn9tEYDfyoHTc8gfDlzwDmRgKTwu15qj4NYHyUn94eW2NBkHxfJMAWSUh0wobPAZ5O6RPaEvmyncdLU5pbN3ZG/5vk6lJC6IzGZ8HUqKQ8QC3AnJZEUWPwsXhqnaAlAWRL3/rRpoF/OIfLxn/EbG8PH+fLwH9mJOmci3t4waPEwY3fPY6pqpvvI9Y8pgBTgCnAFGAKHCsKdHw/KzRY0cI+stj3KhCBF16Cc09vOOsXyvmnKTf+Oa7q5HYyVoZAbRwATS4xDZzUeZnZIR39hUKfjxU12edkChwBBRiAPgIislUwBY41BToQIenK32k+hr/ffhvaSL1eD2VwmZnc6Sflr39pI8QbQCFFHTp0UtDCbK0QhGn7oo+F4GOABoDndJjTGnonIbUQmqCRftk6gcsp8qtBJAWp9gDMCAQnBNsnJSLP2XqQrBJvapPfCgbxsgkATQDrVSgPxIvaYy+o9idknTrOJtmgYq9u/Hlh8QAfgPGUJE8Km6UBfTMWLATRxt8Yumxv2/TRL3qdkOPxdYQ9Exbo93uxLJWHW7Fiefp+Z+AsXY3vM95xdH3FKr4VgP6KdXSdTJ3UdKogCBSYUmztMOvGxsZdu3bV1NS8/fbb+fn5M2fOnDRp0qhRowYPHnzuuedS9MxxHA26pdTY4/HQuA/6kiZW03FqYXYCOuhESrfp+BF/dpJG3G63jwxer5fScGrTpuO0DT6f76qrrrrwwgtHjBgxbty4ysrKgoKCuXPnbtiwobq6eseOHdFo1BFR0zRJktKjUehbdHr6bMlkkr50gr8deel00zDZ/5Gj2NE10mVXLly48KSTTqJHeJbfi3clOS7DzS1c+KQkpTQde8/wpFDtIgkKIvZ9UWuSAFNDUk3n3UewyVmaXAeKAHsBFrS3lqdSE+KpcoAH4sJDydTbpK8MzX0WwERTM2DK/zO8XhRT7okL9ydTZYnkq7IaIN5nE3RMezYtC6vOGhIYoq0bxP68VYOqdnHSgfbK5uhaxT6g41cFgCXrqZgeve2Bf7gzfL1zjvdxmRmuDKTPXs7tdXFu199vvw2/NWRZN01Bkpgb+ug6bllrmQJMAaYAU+DnrMC/AGjNxJxGRQJIqHDNNTtPP/HA+adpA09ueP1lzHnsMD8TORiA/jkfFeyz/aQKMAD9k8rPNs4UODoV+FJIJGvqcy+9gODM6+Z8HhzJ9HC5GbdNuieiJ2MK5mQA6f7UBLDMgLJA6Mk26X2A7QCr0NomvGZgwcAu6JmUAcTuUAmS6VkViReKyXFtTS9JwmfEFkdXi0ZsMJNgt4L1OcCbAFVxozQQeUG1GwjRMAHQ+GyrYKuUldgAn+v6gkRLQay5NBZ5XlAPWCBaoBKEsH3rbo7zuDlXttefDqApGVy69Fmsm2UTmzRpwZdqQtvGnr+VAv8WQKdL/aXj32pzzsyyLFP/Jo2vdXy7zgx0JB20WZZFw0DoW5FIpL6+vq6ubvXq1UVFRbNnz37ggQcGDRp05ZVXXnDBBSeccAL+c3g73PSUAlMn9Y/jgO4CtV0ul9vtphUaaTNo4UTH3E3np1UcqYM7OzvbaT/1ep944okXXnjhqFGjrrrqKmqpHj9+/PLly1euXLl27doNGzYgwzssJteJT9F1Pd0N7UD/rz8GuuwR9rKbKOAUHpwzZw76hbPRNuzzdcQz9fBnLn7sSWwquVsYJ97nRRIUR9SJSXWCrBfGYu8DtJDbjSa5CsSTtoK3Aw8AvK5LJYH2SdFUFUBxQn4oFFkB0Jn+T4M3dJ0svh5gUlC4Iybfk0rlR0Kvifp+Artl3DKWG8Q+uJoBlmTZikUiodcYMDsiT2hum94eqU6YUQDZBsWwFeqDIvouf+3t0075VQaX43ZlYi6Hj+tI5+C4P1x2aSQWxWgnE3Oi2MAUYAowBZgCTAGmQLdQoANAa+THh2FiDDQIFmyohf4nrT85p7F/j4ZRQ3ebKhg4Z+dlHfE1d3Zs0jo68eIMaQNzQKeJwUaZAt9cAQagv7lWbE6mAFOgQwGH+nVRRORT69at+8UZp3J+D0f6XCOA4LizB5y2YMEjooxVHUIWVMdhXkyrTGj1gH2lVwJUBeLPi/bHxL+M9jTyMyHVaVvWbfTKHQBYJJvFqdSEaGCuEN5hmzz+UKC8Gn9QJMEOkNlWWjAzCWVRe6nW4X02ZLANwNQvUwULmyED7FNhWXukKHwwP3HwaTX6MckGpb8uFi9+2evJ9Xlz0NPNuTy0eBYBctk9Mnfu3KEbaOk2O7tvp4Sko0k6oOyiD3v5TRT4eviYrvNXjX+TrRw+DyWhjpNX0zRVVbvAUxpanZ4zkB5J4SxLV07N2ukbsiwrFAqtX79+xYoVmzZtqq+vf/XVVysrK4uKigoLC2+++ebBZDjllFN69uzZhRd/n5eUNTtrcGJAnCl0c+kZ1g6GzszM7OLUdpbCSF9CsWl8dvp0Z5zGW3s8ngsuuGDUqFFDhgz5r//8r7y8vMLCwqqqqmXLlq1fv762trahoYGqmr5P06XrVuPsfzx9d6SrYRrmmDFj6N7PysoiHmFM3shwc4sWPA4G2BIIPKQ02K3BEhEmx8yJSXUin5ocD70L0Ey+AhTSPVYkzykFE5bqAeYI8amCXglQFJeKDzSvtnHmFEAM+7GQerG2KWGJQqgICeMkuFOwilRpsSzsMPBt7CVjg2EbYGqgGqAYYCiWpRmEYi9Q4J8Hg9MS8VcUtdHsoM42MU0nTAHIZakA8Nb23Zy/N+fN4XwZnJc4ujsP9Iv+cHEkFhVl2VGGkmjHQsXAtKMMG2EKMAWYAkwBpsCPpEBHREYHTMb0Z4BICsY9IJ/zywOn5LSe02/X4sdBlCh7NjqivxiA/pF2D9vMsagAA9DH4l5nn5kp8IMoYGNkJqiQiMX/Y/TVXJYvu2dulsfTy+32c1wWxw0b+h8vrqnZpMITTbH5beIrPMY07wWojPJzIsntxONMkzEUsCgy0AEkEWHxboCHw3yRKN3f3jI/GdpOOk2TJC+JMGiI6noT6HsAXgGzPJYsCZkVh4QdxN2GRQcNMCwLAbSuYuEJgHaARTG+LJEsleJlgYadOCdONxTImziFUAUvwmeCnr2ZmG2NpbRye+zcudMx+qVFhDG88IMcU1+6UodRfum7P9BEZ6PpuO3bbiudVn/DZT/++ONNmzatWbPmjTfeKCwsLC0tLS4uHjFixFVXXXXRRRf169fP6/VSyOugXgcZu1yudMNyl4gPLKpGPKr02Ha5XJmZmXQ8/dmxSDuFEymtdgi1s/g3LOH49bP5/f5LL7302muvvfzyy8eOHZufn19eXl5VVVVfX//mm2/W1dXxPO+QfUmSVFXVNO2rMj0OF9kJuaY+d03T6E6hMSxYks7o9L90LszzHb03qJtbVVUWFdKpDf61bds0TCrjHXfckR6D7slweXz4WLDgEbxJqIGu4/m8EeBtGYqD1n1R696EUJSMrALYT+iz2UmfBXJHMEnClMrC4bsDrbMBCiPS1FD46WgkRK4hRbA1vAcpWBZvkZTnFy0oFOGOOIzjzadMrQ70hE2sSzrpAWOR4kN6R8i0QTbxalTODwlTeP0VVdsJtkA+m04WMvAZ+7mkCAR/Xko+tmt3j4su4zKIrduDERwdD477/UUXtoVoKBSYuFTXR7pobJwpwBRgCjAFmAJMgR9cgXSfso2U2QRoOAQnH7/27H7RAcc1n9VvdVMz3qImF3Kkixb1InXWISSXmV+WAZ3e9PStpE9n40wBpsBhCjAAfZgkbAJTgCnw3RSg1/kAqqyIprZs1VtZvXv2zOnBcVxPj5vkDri43n36jBx1+/PLqg1Ez3sBXm8KzW5te9Uwwkh/ycMCCawUQQS6DRJxqM0PK2WKMTEWmcVHN4KSwHc17J5tamAZKUXlyWzLRK08lizn1aqg/j7hEYpto/cZo2WxhzRYhkViQ1+MyGWyOi4aWaApH+AUxNKJWPy+2+45Lrev2+0j9NnDuVyIoDHXmsOqgzu2OdoIgsAAtKPGjznisOCfZKM/JoCmpNXZIkWf9FOnI1fq3V6/fv0HH3ywYcOGJUuWlJWVFRUVFRQUjB49+tJLL7366qsvueQSamT+Usrsdrv9fn86j87KyvKQwZlIgXV2djZdj8fjobnSTrq0Q5b/7Ug64D58/HCDdvo8ND6bTrnkkksuu+yya6+99s477ywsLCwpKXnkkUdWrFhRS4bPPvsslaLVTFEzVVUpsO5y2Ni2raoYy+MMjsI029rR33G4O/uFLtJlhcfOyy6KjRkzhh4b9OaEJ8Pl82WcfPKJdR/UYmcRDW8EygAHAd5UoSKo5CXgnpCSFwo9IyUofaYOJQW7s+AjTGI6pjeH7gwEZwFMiguVgrIoHvmMlgLS8axtAKg2xjW3ACyPqOVJ886wcndIK48bNWC3gY1ndgUwWUm1QDfQzUyuMk1iuH5HsKsC8akxYYkF28FOdBYZot9mBmY24XfQXoClIM+Itz7d0l7dGud6n8BleLh/BdAcxw0eMkSUZVlTDdJ1wrAs3TQNTJzGr59j/Gg5dv4v2CdlCjAFmAJMge6iAEXD9OeFDboNig7TShPnnXHw3JNTFwxoHndXLCmACpqJ4VsyuVQkRgQGoLvLLmTt+LkpwAD0z22Pss/DFPgpFTBsQ1ZVXZMtHV1jhvrn6/8Le2Fj/SmO6+Hjevi5LC/Xt8+AK4cXv/RSNS++cKj1tQjfhHekddAVDHs20dImEQDNE+/z/LAyRYcJoloRba8GBVE1FqiSwNAQP5jAK3YrwFsAZWGtJGRWBfXthEckkU8riJ5NE613JvqfDwI8Z8CEttgkSZ7GJ2uJGzoCyvoP111+4cU5nO/4nL4Eb3lI/AYC6Jw+vc7/za8/+ujDTjqBsbYES7EO1j/l4fZjbtthbQ6O/A5b/w4EKj1jmm6xSyqIbds8z5uGSSMs0u261J3qzE/nMQ1zx44da9aseeyxx0pKSgoLC++8884//elPl19++eDBg2k1xZycHGp8ppyXep9pGDSdQin2vwXNh89AF/+a5w526fHQNjgwmtZOTA/LprkfmZmZzjxfGiHCcZzf7+/fv/8ll1xyzTXX/PnPfy4sLKysrJw8efKKFSucrGolbXD2bLp0jvjU/ky1/Q471Fn5jzNyRI7br2kqNYybhnnLLbfQ3er2cK4MzpOBp31Phmvp0md5EUtWmiokNWiw4Q0ZipP6P6PCfTFtWlheLih7SYgGnkxtPPmLxHEskZN/RSg8UVYnABQBPBiPPp6MtJEZTCBJGQRAK8RS/bpgPhRI3R9R7wlJM+L2OzpWIzTBxBuQ+I1igWSAYmEANLnR2WzD23Eobk5OjQkv6toukhPdeYa3wcZrVlp74DOAlbo4Tww9HAnt1EEF+GBXg79nTwKgOc5NHl6Ph8S733TTTa2trfReBSXRDEB/zfHD3mIKMAWYAkwBpsAPqIBNzEImebZBNzFt4+wB7556Yst5p/KDf7fnwzr0RKvAm1iEXsaMRvzyx58D9BqPOaB/wL3DVn1MKsAA9DG529mHZgr8AAo4YI4EaAGvyoptKqb+9ntrco/v5epBPNBelysrw5dLevr37cX1P3nUpPw3du3DXs+2ArqEQJkka6QAoqRT9sMhYZpsj5XM6Qa8xifbnZbbGv1poBCCvDJhlIeUUh5Km+SNAE3U9AYK3tC2TXS9qTh7AGA1QF4kkq/oxZHIct1oRpxhjysb3+vkHm6O6+XukcllEl5O7bHYkUcAACAASURBVM8IoP/0X3/Z39QIAApWTkb6rJOBFCF0GLTTMjbyM1TgiIC8b8srnY1SQdNTqjVNc/7j6HT6TMGoswMchIoEkEBqxzrtzEMX0XWdOqxpNsWePXu2bt1aU1OzcePGGTNmlJSUTJgw4e6777788suHDx8+ePDgr4HI3/Mtiq1pkkOXoA9S1M7nRFrn5ORQIzad4nixv6oBLpeLBpXQGaiZmm7C7XZ7O4dLLrlk6NCho0ePvv7668vKyoqLi6dNm1ZdXb158+bq6updu3Y5++Xb7tB0zX+c8fSm/hBbpAfYLbfc4vP5MtwIn90eLisbM4s8Gdwjj8wHMHRTTEo8NTWvSEJpm3h7TLpbNSfH+KUpCU+sOOCJVCfnbYHYnxtMWJHQHgxGHzDsiRbkCeY8IfERSWoisxODkoW3LIPofRbLA8n8hDaOV0tS2gobWkl6Bgl6tpBByxYyaIx+xqylFhtWxWDOQW1ym/CIZmwBK0oimEhLSF8ZA68/JXIj81UhPD/U+Gi05U1Jol9Aog679u7lMlyY0kTvVPo6iovm5OS88sor9J+RAWiiJ3tiCjAFmAJMAabAT6SAA6BNvMmtGLDsZTh7wO7fng0DT237200NhgqyDoqd6nBAMwD9E+0ottljRwEGoI+dfc0+KVPgp1Sgat7cnn17cRyXnZOT4fe5fF7Om8FlZSEJ8vguGjSocvasbZvraBMpKf4Q4GFBGxdK3h9OVUjWM1Ex0vkJ4ikpZUFIwW7aEYCXUlAeUfMjqelxcZUFDSTZUyO2Z+xuZaNNzpQhAbCUt0qiycJYqKR5f42N5GLDe7WDfn+B7zgPYme3Q67cmPLp9mT36bPqvfdoZBglzenJnp3NYX+ZAt9IAQcZf6O5j4aZJEnau3dvfX396tWra2tri4qKKioqpk6d+r//+78jR44cSgaaGU291ekBwc4/W/qIx+NJZ8Rut5s6nR0zNfU7p4NpipWdqBCKoek6/WSgMztcO31ztI6is3K32/1Vs3VZCjN5evf+9a9/PXz48JEjRw4aNGjatGl5eXnTp08vLCysqalZvXp1TU3N7t27u3jSD9+r6TcJqOHduZdAZ04veknvH9DpiqKkZ1hbnQMWWSXV8GhHDYdBH77p7zPFtm3amKVLl2IXF3fH2ZPGLrkyuCcXPY7l+yxFVxISGPsBXjPgwcbwON68T4Z722IvqMJneGKmg2aBooAmANYSbAV4TYD8/bGCJBSbMJmH8kBqK7krieVfKa8mV5UCwGaAKgEeDEv3tcfLVOVFgM+QU1uGrYGpqWDhIhopKWgoQPrW7DBgZkAtCopLJLsWb0ySLCe6Znw2wNJ1Qp/XyWJlIvCIGK4BM0K+WUQwFbxfar/3QS3SZ47jMj2cz+WiudAcZqknEglRllVdMyyLOaC/0JWNMQWYAkwBpgBT4EdWIK1MT0qCi/+w5Ze/aB7QXx9wyu53VoPcWfjDxHwOFR9Y+uELBzTpOYX5jWmr+ZE/ANscU+BnpQAD0D+r3ck+DFOgeypACcvevXv+MeY2h0NlZ2dTuuT1emmPfrfbfeKJJ06anL/u/Y37VGm5qk7ct78gkqxIqouiwiHSbxo5AprYoE3DHtYNAK/J8FBUzQ/LsyPiGzpOiRFTswE6TfKyLYwADViwUYDyZmlKO18ZDr7GR5+v2XTLrf/ol9UbHWyEhCMdy/B1cmj3H/98XVKSZB2rktHOWxaOfFFaqnuqzVrVbRX4OQHodKzpGIHTWSrdC9RYTacnEomampo33nhj06ZNFWkD5dT0meO4rKysnJwcmiZMTckO/PV6vTQbxOv10hKL6STa5/M5ZxJnkX874tBnaqP+JgCalnOk5mvKx7uAdadVzojb7T7hhBMuuOCCkWS46aabJkyYUFFRUVJSsmLFirq6ujfffHPTpk30CFEUhfrQSa8LHO9ySKuq6sRbm4aZVhYVZ3R2xw9aLJEGYa9Zs8YpdOn1II7t4ff1yPI/9dQTtL8Iyd5QAmC/YcrTEvHbguE7U/qDKXg4ZXyCVQct0snVsEDTQJFAiYLdBLA8JJS18EUCTNVhUlifG9VrCfy16LcAuTLEXG+SzvyMDZNT9sS4VBCJvwjwEekTI4Ci4TqNFKkogPWFMLbDFEkI9eJma3Zcf6gpuIl0i1FJ9IZB2DSRGisQYXeZlPRYe2ha68GnxfgeYojmQRVBNvDuJs4zd+HjHLU+uzmvx+VzIYb3ZXj/+7//G28DkDBoBqC7HL3sJVOAKcAUYAowBX48BchvKCthaSp8tB0GDtx2/nnGGb/khw09KKg0yhFUXTNNzbZN8iBVCDsjOBiA/vH2FNvSsaEAA9DHxn5mn5Ip0D0UUBTl4MGDt912GzU5er1eWujMgUSeDFeW35vFcX369Rt47R/ve/WVh/d+/nRT0+cAbRgMapsGSQkllHk3wHNYmaptUiw6J5LayENAxZ7WBqkioYEOBrmfbUM7wNPtwYrW9vKDoTl7AlcVlZ78f4ZyLi/n8vtdPmfrXAY18bl7H9f3yYWLHc2clA0GoB1N2AhTwLIs0zBpHA3lnjSghuYC0+J+jkqKguZTapv9tyBekqRAILBixYr6+vp33323qqqqrKxs5syZ99xzz9ChQ6+++uohQ4b069fPSX92/oXTATRF2G63Oysry4GkzpzOyHcA0OnL0nHaksPbQ9+l+R4OjP769vTp04c2aciQIcOHDx80aFB6bvWbb765atWq6urq2traSCSSTCYVRaGCO1I7Bmrqjz7iPuh4PE5N2eFw+NRTT8Uysz1zfD5iAOaQx84sKe0ItCBBza0Aq/T4Q4ngvcnYnSn53qg8LwX1JGfDBsPC07ShgCUij7ZbAF6WYWqAL44lZwKMk+1pvLZRwWBoiuE7XEg23lY8APCCLk6NixPjUnEq+YSS3Enoc4ykSAvkOQZGHAwBLJnA6wMmlH7eNiuuL25P7ibfI85qVUK0KePmATbKxvRovCAUWRRLfEAqIkZAFkE1QMXvGA31lnX4zwfuol1nfByX7XL5qRncxW2o2YhWauaAdo5LNsIUYAowBZgCTIEfXwE0IikggKbAvfcFzjh974nHN58zcP8TT2BTDICUoopyWjFqi9yUZgD6x99TbIvHhgIMQB8b+5l9SqZAt1HANEzTMHfu3DlmzBiHyFBwQ7vquziuJ+dBKuzluL49uCz3CZf87oa7x1Qtevz9ndsU9B/j7wUVYC0vPBRqLOBbKxKhlZrZphJ7W0cZQ9MAE8mGCaoJBwyzZEvdH59eeNr//JPLPIHr8wuydux/n+HL9ngxsZRze1yeDI/X//fb/rG34YBpg6obaLLTOzpesQiObnMQsYZ0CwUEQVBV/MmOCQcaAXKkXYlEgraPWndVVaWWXjqxCy3t8kkcNq3rukYGZwZN09KtvpR9A4AgCJ999lldXd2aNWvWrl07lQzFZBgxYsTIkSOvvPLKs88+m/Johx07I98BQDvBIHQlTklGjuNyc3MpbqbhHs5WaLgHNUp7vV6fz+fcfqNubjonBeVOrUUaSPJVLadroAsOShvmzZvX2tpKd0pnLActmupoeQRGdF0fM2YMnqe9Xo/P46ZhFBx32//7my2SSrLk4i0BsEZJVUabxyZCd8vig7r1UEpfZWHEP55eQTOw+KytkBqAbQB1ABMPhR+UoAygRFfyIpG3CEd2IpqpT1kloHktQHEqODYYyQtF5iWCtWC2k5klwGL2EhmPgxUDI0kM1O0AbyegtD1ZGRe3KHZAVInNCdtBbluaEmlJDGArwEJRLUhIJZHUR4SV8wBhLaHQzrmksKFG+PWy5obcoX/gMrPdHJfFcT3cnr59erkzPKefOUAzdAqgLQDdNA93sh+B3cBWwRRgCjAFmAJMAabA1yiAdetlkGHvbjhn4Hun9G88/7z4eb+qDmGBZLzKE2VM6rKtLx74k4MB6K+RlL3FFPgeCjAA/T3EY4syBZgC30+BnTt3PvDAA9QN7ff7sSYY53FznJ9cyXcUdcIuzRzGa3qxNKCnh++8c8//83U3TJg2Y9Sd9w7Lm3zHiy/MrH1/6eat62o+rFmzqe79D2rr6urqauvqate/V718xYp7xk086exfcZm5XGYvztuLy+jJZWS73D5SPcqFgRsZpCiiyz/yqtGr3l1LoIhp2uA80h3Q6ePf79OzpZkCP1sFnIAOB4AecR8u1c7ZkEOuv15T27YPHDhQU1Ozbt269evXL1mypLS0tKioqLCw8Nprr73sssuuueaaIUOG0HtjlPDm5OQ4HNnj8fj9fnrDjHLn9Lc4jqMzU45MxylNptFDFEPTFBG6oHMTzoHOdDpl3HRzfr+ftsSZ2VnWoedOMyjjHjZsWEtLC03J+HpBvsO7FKTu2bOHbpR+WJ8fu48MGTKYkmLTxHuErQBrJHvKvn0lIp9nWXcnhQod3iYhGEmMZTYMUGQSA21hmVhYDzC5sXFsVMoHuFMz7zh0YC2oHXczyA0OJLkEK+8HqAXIjwXvSbZPioUfE1P1oLciZbYkwDuPNklg0iygJQ0Vkte0JGkUNYZnNbbXGFgSwEQfM1Y+NAE0Us9QBWgE+BCgXEhOiCdnCfBSEjvfSPgwUmYK+9SQ7wCZNKCytXFm+ODtK17gMnw9PJlZHNfT4+7dMxuTZHpkP7looSOvpGIPADYwBZgCTAGmAFOAKfCjKmBDPJTQeJg/C07sXfeLvs2nn7r77rv3KyqmPuumcyc6rVEEQNPXLIIjTRc2yhQ4AgowAH0ERGSrYAowBb6PAk1NTZMnTz755JMpzuiZ2cvHZfu5zGyO6+nmcpA/c24XwcUdnbyxcCHnyURS7c/l+pyIC/q8Hq8f05w9HrfX5fa6XIiyyeB2cS4Px/k8nN/Heb0YtOF2edze7MzMXr04zsV5s++4a1zt+x/Jqi0phm7ahvUFfTa/uAeOfcDTH9/nU7NlmQI/VwXSofAPDaC/g4am0eFFpTnL1LtNs6odd7ZT98+yrJqamvXr19fV1b399tsVFRWTJk2aOXNmWVnZ1VdfPXLkyNGjRw8ZMgRPSR4Pjaimd9TcbrfP56PmZZfLlZ2dTXk0vdPmTOc4jvJlaiXOzMx0/M5OunTHeeywPw597jLScdpzu//yl79QH7Qsy0fWfivL8h//dK0rg8MUpQwX3eLpZ54qyyI1NkdNLPFaDVAeSJaktELNzlMgLyQtNTGjmUfns64hfVZSYMUJU/5Yg7nRxAOhyDjZfkCBiYL0hCwSf5JhJRWM9CcRGQrxPtcAlLdF70/xY8Kt85X4BjBbMcEDJLA0G2ziUAYdc59l4lNuAHgjaZWGxPKoWG0iGTcAVBl9+woB0LQKURBgO0BFKHx3NJInqktimASdwiQN0DBUWkFmjjUG4FOABbJeJCXyWhteFOO35hV48MuF8xMxsnORQffp21cz9JQoAIBzaH2HI5YtwhRgCjAFmAJMAabAd1TAxq95Q4XLL9py6kkHzugfPr7Xmu3bcWWHldjo3AID0J1KsL9MgSOuAAPQR1xStkKmAFPgWyhA6Q/Nh928efMtt9yCWDmjH8cdx3EuF/E9I0h2kUcGSdnM9HW8dmcRqzShHz7O3cOFRmk6ZCCj9nuptdmd1bs35/Z4OMx7xrVRV3UPb3bP3PvHTvx01z5ZwWJYWG2QDFiMIq3YYDp0Th//Fp+TzcoUOGYU6OYAmu4H2kg6ruu6s3OcUBFd1xVFoW/F43FnBkpyqeGa53lnOmXWlmWtX79+06ZNmzdvrq6uLisrKy0tnTlz5uTJk4cNGzZ06NBRo0YNHTqUwmXHQ01pNT110bd8Pp/jd/4qEt2FOzsv3WSgHHz37t20wUcEQNOzn6zJNXUbe/bthfcGyUAZ9I6dH2q6ZOkgGugjXmVCuQR3J5Q8E/IlqBDgaRE+ACweiyhZS8kgCAigEfLWAcyN8PmR5GQd7ub1ieHEq7J6iNzw01IkAZrYkJOAzuXtBsxLCbc1td6fMkuScg2orWDGAVmzaZMutLh3TctWDNuQLWgBWJI0pgWFyji8riN9lsE0LLAMTHKm2TEWGWkEqEjy90Tjk2LS/LByiEBtGY3ShgaSZUsg4+xYJlGGgqRQKMvzguFPSEZH/36/5DguMysDA0kyMJHEm+l/9sXnNUNH8S2bdul1Dhg2whRgCjAFmAJMAabAEVSg8xoNv3Q7x/HrFwCWPpc6o3/NGf2CA04O3H6rLvCgyuRHBmXNXWzQDEAfwb3CVsUU+FcFGID+Vz3YK6YAU+AnUsDpQf/+hx/PePSla268s1fvE72UF1MA7eG4HE/28Tne/4+99wCTozrT/WtmNEFCYLAROZq4xgmv9y4264DXNrvXu8u914/tff7e6/VeB0yWQDmMMpJAQkIIASZYBAEyIIKxSSZYgBBZCBRQGE3q6Rwqp3PO+9/vVM+oR0gYhBAj6eun6anurnDqV42qzlvveb+hFNl84CGHGg2De2M0jMEH1LUc3Nw0tKGhzqjT+rLR0jC4afDgep3vnKgkdSSYNNQbTZ9p+e6Pf3D38mX5YkGEdNHh2jLW9bJiCS8M3MBnAfoT+iHwZvd6AgNZgHZdt4+vZVl90wCS1Om+T2y7alxNJvo+TyaklLWrSm6hRZGWGntnTe6uJe9qNe6+f+voXx7XffXVVx977LEXX3zxueeeW7BgweTJk2fNmjVlypTzzjvve9/73jnnnHPWWWcde+yxfXp0VfSlG3Q7fiSZGA0NDYcddlhbW1uijNc2oLeBH+4vmdl7KwF+63vfbDhgEN0X7NWg586dHUnXF0EpFEVQjcEp7fn/15UeDVxUicZmwqUm1mvzcnKbTwrbU5aFMAesA26WamTZHGUHrRJXlCqLTPMdbUySlI6h26kznbPAmgj3FO2Lu7svc/2J2fBBYCtZqgNK3tAuJwglEMVUj9YOIPPAWmDC1uKUgv9ghNU6DLoS2xTtr9ed3HzwgTxwR96nZvjhnB4rmZMs3WR/DmO4MXzHixyd0bGgGI8reZO6Cy9qkVoCzz33HN3cbDSaGwdpNCRAf/FvzyTHtKl/aTUd2g+HnudmAkyACTABJsAE/hoBfZWSqM9VDTqGihTyRfz7j145/vA1px9bPP34dx5+gO5A06O33mCSHrZt9TXna47g2IaFp5jA7iDAAvTuoMjrYAJMYHcQSHSZrV3d67d2aXEAm9u2PPHnxy8fOeI7/3zuP/+vfyPncoNhDKIAjbqGQdTXr282GrZZBY16GhLeJ9C0tLScfuqpXzv761896+9Hjxs9a9bMVStfoEITdGNckCdN109LrkCkds8JqFjKUAQsQO+OQ8rr2N8J1IrRtdN7C5ekzQOqtfl8fvXq1U8//fSzzz57//33L1iwoLW1dcyYMdOmTTv77LPPPffcb37zm9/WjxdffLGPeZLB/VF2JBIipnQi9ZeXXzDqjfoD66sDUwYb3/juVwERIrBAyRvPA7OKVqsXzpDxNUBr2bk9xLsKvo4zStogZawoLQPvAjflixdt7RjhB+OAMZXSDUHlRYjk5oASkrqFFIpE/cQ08JCPcZ2FC8rmuJLzSInyMXKUkiGqBYNiBSliBCECxypVdDnBOVtK07da99jYqNMzyjpVIwSdA3wd6yF0sxelratjjC7Zk1PZV6DLJCrdO5VKylgK10VYBJ4KcVURk/KYm5crtfqsb1XAC70f/fTHhmEcYNQdQAUL6nR0lPHGG29oabxXvP8ox4CXZQJMgAkwASbABN5DoNfvTLqzrkGf2IqoboQT4pk/4wunvnnMwT1fOKF4zjdeTuRm39UJXL1L9ltljQCtb1VruXqHLul+c/ZbB79hAkxghwRYgN4hFv6QCTCBT4AAlcwCSrbpySi5HgihAkhPRiF9A18Ea9a/fduSJeMmjJ86fcbU6TOmTZsxY/qV06ZNmzx58qRJk6ZMmTJ7zpX33HPXU39+4smnHk9sibqoYBTFVOO49yFJUKBnVYNONpeIzrGKY0VVrPqefRcn2030ro3/MgEmsGMCfQLodhM7nnvgfToABegdQkoMzknQcK0Ruxb7Dhf8IB9KKcOYjMJu4DrC/ckvf6qD+Y26oRSYdNQJw9KFrVZYcnW8xvPAtRVnbN6aCcyJ48mp9JIIL2vll7YlY7rH19vpSwMPBsGEnu6RnjcqjkeblSszqechMloXptkFkhhxT5Ei/EhPOHlrYXTRn+TJ681QJ0RThUCfepOCFGWyP6sQwoGydUXBORs7Jm7ovM/Eaomi7kdaujFCC8KR/mQLcF/Jn27LkVY4JVO6z45TOtBDwxGQQsakvpvAM6G4vmCP7nEm9oT3W2jTc0iHMAcq7OjpbjAahhKYukSAbh7c8vP/+zPSzpP7nPovvzABJsAEmAATYAK7kUBvB01KylOkusJKn98FEAhMGoPTjk4dfWD5tGO2LFogohgicUAnlwLJwrWt6Scrh7pshI4Pe+88/eas/ZqnmQAT2DEBFqB3zIU/ZQJM4BMhIHoHQcX6bE/WN33Gp8xQKQKytm13A7raTIr87I1wDsNQqWqcc1JnrK+kWCLNCFIT6NlfgJYCYofP3suafhUIE0nhE6HEG2UCewuBWgG0dnrvav+AbS3dtJOy75++pJ19AztotEfN46PshZRS389TISLj4AajsW+ciXHLjYsUBWBQDcDXgGvKamxezg9wbYBZtpjZVV4Jil2mf7jpP/rXVGgJOAc85njTc+kRZnEc1EizMreQfzIil3GgawMGOlUjFvAUGav/4GLy1sLFWzOtZe/mSrAZKFTPBkn0BvUCk8SOUPuX1wLz2vNze3I3dfdsAcoKFRU7ED7IEqVt1dSSNmBphIkl/wrXG1cs31XyN+jF/WqPM4YKaPeB9TFuzFqt3ZnWnvSNeXMtYGmLtIyU9mnTSi+5YEST0dCk81ESB/Shn/4MfH0+4nPGR/kJ8rJMgAkwASbABHZCIOmp0R1jEqD9CGEI4SkaHrV6DU49YeWZp4anHeH+/ee3dGylUUm2o0/JtR282jX3k5WTLikL0LWAeJoJ7DoBFqB3nR0vyQSYwG4kkIgmlIChRYRkzaFWLEIlncAPSCvo96jtzotYhPrh+76OKlVCUHRoEAR96kwyT6LXJOqzFqCFUjvWnfvE6Nrrk9rpfq3hN0yACbyHQI3+2W/yPTMO0A+SRg+cxnme15fmbNt2X8nEJJB6u0qD/Yj3xg3t8r6Eka8QTZw2jtTnRsqYMAzju//wrWSFNrAuxh1pZ0paTvNxCzCz25vdYT7oUg1AX8+khIxkGOoEjJTOiZ7bkxuezY5R8Qi7MiWffSwOvao6TMnPPhAqOEAP8DYwqb0wtuBPML2rssUXQopspofsHamiTxZC1yos6GSPReV4Ssq8JVt8WxuugdiH71NUCPVIJWQI8kQvL7rjy+FE4LJycb5ZWaczPZzeMbcSiGToAhsjPFjArKw9KZO9sZh61rNp8K7u7AoIF2EppIJGnTnbaGg0GhqMQXVUq+DAAw3DuOvGW+hWau0ZK2k8vzIBJsAEmAATYAIfmUCtAB2RAO2XAivU9ufrFuLEw9/+7GGlzx+fu/gXURjQNUAYR0GkO4x9/braNuxQgK6dIbmnnsy2Y2fUdnPzWybABKoEWIDmnwITYAIDgkAiQG93GZCM1O4bIJUoDX3z/NXu/A7Fo2RDfV8pRQJ04svTRZOrPuhkuvd1e+9z0oYBAY4bwQSYwH5GoFZZThIqaj+phVHrhq79fJempRD+EccNI+l5cNUB/cJzL0daKV4d4fYe+5pOe2FO3A1MLWFWDn+y0a6zLJIRKbGKfShHq8MrgWty1tisebkd/jpdmFwq369EJ8nH1X/XpTYgewJdihI8rnWjSY4anqvMLpSe0w7l6i7EIUVuUPqGXjIiwfp1YLHttZa9RY5cI0jI1mnPLnmZtb266Pmurmr4Bz+cVbYvKAUXO9EC4T+tY6ar2rfWoJMKiJ3AQx7m5MSlHemFvv0aPK/Xbq1LFJI/Oi2itK5keMq3v200DzJatlUj+Mm//htZsriPuks/O16ICTABJsAEmMD7E0iuAfRN4TCCG8K1hAfA8/GVz79w5knWyUeUPn/Km6+/ilBQUQlJxSXi7a6R+jqY/bfV64DeTnTuU5+3m+i/ML9jAkxgOwIsQG8HhN8yASbwSRLoO/f3TYjetNC+T2ondkdbt104sAC9O3jyOpgAE/h4CdTKze8vQO/WdsiVL60wDKPhUxT9fEDzoNNP+hvLR1eENcC167uv6SwvyEfLgau73Fk53BtSugXJybrvppQIyTGMTu19npHJTypHV5TkGAtjM+4yhXXkjI4lJXlUB7v4Ws9dDyxw1ciyPd6JZ1e8h6OoO9mrRKImVTcCokQHtxXZpW+uBDMr9kIvfibJnqZq9y5lhFACNenRBWCzLic4q2xflM//plCebNuPg6oUmrrNZI9S5MI2dUbHo4GaVYhGZ+wrC9bjtAuOo4rJfum8aXJVF7Xw/VApP/H+e7YFlBjGoQceePShh0rPYwF6t/4aeWVMgAkwASbABKoEdN+wL3/DDuEqwBV4eDlOOuqNYS3pzx1fOv/XxUjRyV0L0FSusBbfznuXLEDXcuJpJvBRCbAA/VEJ8vJMgAnsRgK1p/9k+uMXoLdts9fvTBcl/Z90kfLe527ccV4VE2ACTOADEqgVoN87/QFX8qFmSyI+xowZZRhG80GGUU8S6933LPeADcDszvy4rT0LC9ZyYEbant1lPeKRmEs1fvQwFqEQI/IQ2cAmYLqV/lUpf4WDMUXMLOC2Etbq4IuQ9N5SUoAw0p+8DNwNXJizL8hWrqo4T+kPq13GpEtIb0SsBehEAr65EsyPMTNVekXLx9QIP6S8DRXSv+vUEhLBl0aYUInOLwXnF8vTndID8CknWseDJIEhUBRFnQbuFXKy6Vyas1pzyGt7JgAAIABJREFU9hM+5Vl7iCrIJEWMHEQmIkfr1PfE0eye9lu63jnw618wGiilpKnOqDOMAwYNevbJJ1iA/lA/OZ6ZCTABJsAEmMAHJKD7aFKQv9mNYIZwY8AO8U//+M5pR6VPGhaffnzHA4/oaK8aY1Ptymt7ebWf9/b/9GfbPEu9FYre+0n/hfkdE2AC2xFgAXo7IPyWCTCBT5JA7ek/mWYB+pM8HrxtJsAEBh6B94rOtZ98TO2VUh533HGJt3fI0PqDBg8R2ke8xIymW94Uz78bmNOTnt1dWFKgOn520o5Y6Pqw0ocoASngllL2UrPwm1hMAqYWcX2neBvIaosyyb/KBNWvJ8fyVuB+YHTRHW7HY3Lmci/M6XVSzUOlC9hL6gGSwqyF463AjZYzvWJNS1fuc1UyM9mYI12HSOvWkU6Ufk5hVohfVeT5rhrn+b+H30ZqtYypRGGk8yFJLi7q7OnplcqlxeLYonl9zurWPdEAjo2iR6HScGi/RBfwZODNN635ZuXxsDD13puMQw8wDKOloaHOIBl6wrgxSU3Ij+no8GqZABNgAkyACey3BPoL0LYPGQAvrMJpJ750+lHW6cO8vzt9fawzwSJAKv2s1kauMqvtgfbHmHyjP3uv3PzeT/ovzO+YABPYjgAL0NsB4bdMgAl8kgRqT/87m/4k28fbZgJMgAkMJAKJ9LwHWrRq1apEfR48pLmxsfH//vT8EnBT1h3XU5hYKN4ITPZKV5mFZbnKBp1x4QMUry8DJf0Yoqyl5Rt85/Jy6UInGuFjsq1uttTqmDzPDtmlFWSkgxkRCErJWAfMt/yJJX9GJbwule2s2qkpdVnAl4hkb/SzDawH7nPVDNOeWTEf8aLN2s7s6DWTozlOgj1UGXgGmNRljSyri0vhODe8FfINiIy2Ses0DwfwBOIC8BJwk++OL+RmmOaSgvWOXptAHKDiwgyAWMd05IE3gHnd7TO7iksrcR4oh47RXM2ArjeM5vq6c7/33SiKtqsSuQeOGm+CCTABJsAEmMD+QEBSVWJfO6B9X5/zLx9eOGbY6jNP8L95WuWG6RABYajKyTWq8nv7m/1x1cza/wt+xwSYwC4QYAF6F6DxIkyACXxcBN57EfDeTz6ubfN6mQATYAJ7G4E9JkAvXLgwEaDrGuqNlqGPv9H2aMqf3VNutZxbgdZ89yw7d30h06aNw7b2GVGlHxUBMJWfBf6gcHm59Gs/uCTEmEr4W1ut0okbOqBDaQGauoxBTPbnN4FbKtaMQnlOyb2hK7tJa8OgWn6BRBTTM4gRRFBJrMf9jpqft+eUzaUi2qiVYk+/mom3WpLdqQDxJjC34I4uxOMdOT5fuQPyJaAbyiXbdVJ90IKuMfgmcJ1rjc5lZ1bM67PFzTrQQ7uowwimD9vX+2jq5Oibsl3XlYq3pOw2oCQUVPSLX/xXw6C6IU2NLQ2kRB95+LDkl8Ua9N72fxi3lwkwASbABPYKAlRaUCCOEPsK697G5z77wpEHbT5i8Lt/f8JLlc1QHgK3eq1Bo5x6KwP/tZ4mC9B7xdHnRu41BFiA3msOFTeUCewPBN57EfDeT/YHDryPTIAJMIGBQ0Ap9d3vfre+vr6uob5uSPNnvvyVO7sqc9pyi01nOTDTLF6ZSd1bKGwBumKqCWhr8TcmEzT18HoQPwFMzBQvtYOLY3mZV57rmq8o8j7HCoqkX+FDCUlhGjngNeD6CCNz5Zlm+bqejg6QNhySuSnQriaRdByl3tB64H5HzayYM83yA0GwVivFMYTQBulYL6u0KftViCXlyqitmclWPNOuLInst4GMXkkIpciHXYGyI4SbgdsD89JC5vyensUV/x2gKzkYlAlFJQ0j+A5UXoeQPBbLWVu3Xt+dbddit+tTPMi6t9c0DWpInolwv3njJvJexdUSiwPn4HJLmAATYAJMgAnsAwR01Qm6CPEFrr0anz+x86hP5U85cuvky4rw9EiruM8CnZihaaf/Wk+TBeh94KfBuzCACLAAPYAOBjeFCTCB914EvPcTpsQEmAATYAJ7koCU8sADD2xoaDCamowDh3711+df1Z6+uuI/Aiy0ytcUUr8rZtdqkZc6flqHDQElSDjOQL0OXFkuXZgvjwhwue1e5ef/iCgHCEHqs6D6gCLUYnRZJ28stsSIbDSyGM7LpjZoBRkIY0rmoLkS1xLJwDpUerlN3ueZZvlGv7JWh0GH8KiCoKAGCCgHogK8A9wnxciNm8dny3Nsb3EpvYHEbpUkaSjyNgeAJRBmgUcRTXcKF+Wzl7WnXtSlCElHV7qfGsaQQYS4pAsP/gX4re3O29S1Sm+6tyNLvu8Tjz0mkZ4H1RtDWppu/92SpOWB5ye6/J48grwtJsAEmAATYAL7NgGpSH2m0UwBzjztlRM+3XPmqTj9hNVrVtHpW4/I0udxOqMnt6fp3P/XeposQO/bvxreuz1NgAXoPU2ct8cEmAATYAJMgAkwgb2IwIoVK+r0o+mwIwzDmPjc8ws6u+8Dplru2PbOu/KpdxDltfWYwjcUKb+JabkCrATmwxpumhdU/IuL9uR09s+BmU18x9rSHFA/ECIihTcA7ogxtuBf2uHNTrmJqB0iVtIP4Ib0vYQijbsIbAL+GGNmvjw5lb41k9lSTckItTRNErDSwR1F4F3g91CtlcrlxfJU2/xd5L+hKx9WKNBZyiQhWmvMbRAvABNLXZeX0leWqJhhSvdT6WDpwocqEJEgF3MWeCzyJqc7pqZS63XktEzMV3GsQg+Qv/qvnxmGMbi5kQoRGsaFvzk/6fgqEbMAvRf9+LmpTIAJMAEmsFcQ8AKqUGy7WHY3zjh+02eHWV84vXTev26wysktZDrNk95Mf0mmllR3ggXoveLYciP3HQIsQO87x5L3hAkwASbABJgAE2ACu53AokWLDMOoq6szPvUZ46QzburKPQjMyudHt/csLllrdI1BKt6nn7Gqqs+xwFZgkfAu9kq/tN0LSvbwLR33u0GBzM5xLCh32SMJOBa0DMrASzFas+GIXHBNUT4tKR8jEKB8aBEHcAO4SqlQe403APdFmFs0Z+aL87q61+kPSdCWHmRAy+g+ZlKfcBnURKd0WckeU3Zujf1VWj52tec5lrq1Wtm2FN4G5pbyI4vpUT3t97tBVyI71/ifAgFTyAywCljYkxrf3XZHHKeAKPFHS6gwSATo++9dahhG06BqNcIf/PO5up8LSMFJ0Lv9J8orZAJMgAkwgf2ZgARMz1egEVU/+MdXTj08fcbx4fHHv/jbJVSzWN+PVr3qM5LBWhJ0CfDeZ3+MNVcA/b/gd0yACewCARagdwEaL8IEmAATYAJMgAkwgf2FwA9/+EPDMCiCY9Dg0//3fzwPzAnEyFTmloL9hvYdk4VZJ2pQprMgZTcWlJv8JDCu4P7KDH9uWpeXS7dl81s0syhwSFam9OcwJCMSqc8rIizMhFdsDa4q4EUgrzXlWCd0qAgxohBerKsOpoCHgQm2NzKXv7G9axPQI1xFIrBD6rNOjE58Tu3Aw6GaVHEuLrsji/G15WC1jgqxdUFDclT7WocOYbrU4BuLfmu+PKdYuc8LtmizFPVNKc1ax0rqne0R6iU/vK5oTuroudO21+nGJ8N+I0BKKQKX7FWOM6Spqj7XG8YxxxylCA092AGdcOBXJsAEmAATYAK7SkAXBu5dWNLZmh4vPYvjD3ny1MMrRxzy7jf/aUVFVscv0Xfbag9+cAd0slZ+ZQJMYPcQYAF693DktTABJsAEmAATYAJMYJ8hIKXs00lPPvlkMvM2NRlG/S8XL7mtJMZ05Kd25l7XURiJTpsMaq3KtSEJyquAq7z44lL867K4tOLMK1mpRO/1XJ24IZUSkXS1YIw3IizMmZN63Jmd6o+SAi4oxkNCxpCRfpUUA+0A3cALwPUBRtjW2EzPn0tWSVATRFwRVEhQC9o6LiMHPOWKOd3mZUV/hCmuKavHw6TyYRwmcZBu1aztAm0Cd7X7M3rcKWlrmavatSsqNl3queqqhxHVKCRZfA1wT9lpTeXnW/5LWiX3tbcq1K+A9JxKktjxhTO/MpQeQ5IwaB32QT+QPrD7zK+Fd4QJMAEmwASYwMdPYKd+5UR+dgKMusw/9aj2L52IL38uveiW0K8OPqpVn5NTdPzBIjg+/n3iLTCB/YkAC9D709HmfWUCTIAJMAEmwASYwAcgEEVRopN2d3dTlvHgweSAHvqp3zz1/LiN2Ru6vXe081dQFUEhtKJM/t6YVFgvwBZglhNcFEW/dONfdJWuyZL12NFOaYjEVCwEwkhYLuTbkHda7ri8P6rb/VNITmQtJJOaLRSVHSTplqKa0QG8BMzK2mMy5XmO/ZSuBEhfxAqUvIwQcajdTpZWiuf3FCeWwpGmvMrF0yF6gFBRI6nfKQCHmhyScRoPlDG3K5pViOb3mNVdo32huWgm6vMKB+FWYIkdT+qqXBOGj2g1PNAzaO9VTBkkkvbSAtqBf/n5r4yGlkHNTeQfH1S3atUq3/eDIGAB+gP8AHkWJsAEmAATYAK1BJKLh2SUky5K3Ot6prO0ghtjcyc+d9pbhx6UOfUYnHLUm1aB7mEn5Y6FoisK/ZBaeq46pjlioxYxTzOBj5sAC9AfN2FePxNgAkyACTABJsAE9jICfQL0M888kwjQZOM9+NAF7YXZHeYG7WWmanwxBCKdj0EisBBUhHCLwpJsOFqo/8+yL6oEV5nqLwq5RH0O0StARyFpxqITWGoWZuXzreXgRhebe7Okg77xtCQok8hcBt4AZmdSI1Lp1mzh4Ygymm0tUtP3klIybEhbW5VfgVqcSc0yvdE9lXmOfFiRIhxAp0PHUspQyRAOadY28IQrruxyrsyJBR3mm6CmuoIU6iQgmgoa6vCMHNRfEFxTJpf0w8A6vSx0qqRuLA3pDawi9FePWOVxt91tGC2J/bm+vv7RRx8VsQjDkAXovex/Bm4uE2ACTIAJDAgCiQadXBXoE3+vBq1vh2PmVd7nz8gePDT3mSEbxo9AZFKjdyRA9y6W3F8eELvGjWAC+wUBFqD3i8PMO8kEmAATYAJMgAkwgQ9OIBFJpZRz5szR4Rukox55+hcfT/sbgA7KbdaRE3GSzhxAkWPa0yblpT4uT5cvjPHLSjC3ol4EmZrztp5fxyTr5AuqFZgHnhDRxEzHhExqqRmu0yHLDuAqBFIr1eSCpk3ZwAZgRrlyUSE1odxxZ1TcovuNZJHWCY9JCURLb+slYKHnj0ilp1RKs7tSzwUkc5cAlyKiZaxCCBvClbHIgvKmp3YVx2fM6R2FVwWp2G6MUFA6tJvo7NrZbQPPAdcW0wvz2YejoF3bnBNztNB7Vh3/64oUcC/i2fnUqAf/aDR/euinjmyuaxlUN+imm24iZhEJ2vxgAkyACTABJsAEPjSBbTnO5HtOvMwSiARdLHz+i08fOazjuMMzp570l7feQOTShUIylIrqGZMWTdJzreu5dvpDN4YXYAJM4EMSYAH6QwLj2ZkAE2ACTIAJMAEmsK8TSARoEYtf/OIXiYfXMIxzzv2XrDYIeyEKPQGJtRI+hE/eYi8G6blvAGNy5Usi/LxgTnHlYwJpLR9bpvYx64J+ibnZBt4CrimkW0uZuaX8i07oaPuzL0h99rWzOukmBjrR4vpyeHnJGuNVlqD0JmhmFUZU9E+RWExmZp3dQeqzVb4kXxnlx5M72n+f6+mBovbRU2oNOqTWqtDVVuU5We/y7sq4rszToOxpP0BMtm5Sn91ezdzSTb26Jz1u08ZlZrZD7xEpzr09YaE7tL6ucPi4J6aU09NK6eWZkmEMNYwDmoyWBqNh5syZOqtaC+r7+u+H948JMAEmwASYwG4mkJxzt2nGiQBNVwphhNuX4otf2PT5U4IvnNz94x+vkgqeB9OMtF+aKh/r4sc7EKB3cyN5dUyACeycAAvQO2fD3zCB/ZKAiKlvHEWR5+k8zTCMoigIgv0SBu80E2ACTGA/JZD8sx9F0fe+9736+vpEg57cOp2U1r4hsBQATbZiV7uQba3nTutIXVixf2HZ4y1naYw2wFJwfVAlIF3NT2hbsQm8rrDALk8o9Cyyik/FUVJ4MJaU6BFTPjT8iCRuU1J6xpwea0TGmurIhWVrNcJCIhSrOCT5m9I/Yu1Afhe4wfMuLGR/7YYj8uYDpl2hFsZShvSflqoTX3MSEn1TzpxakWO6zUeBjUBFkfocaYd2lHivY+RirIBaYGYnp7O/C/x1iMqIKEpEy9OJnEz9WkHRzw8DrcXK+Epmfj71lhMl6nOL0Xhg8wGJAM1FCPfT/6N4t5kAE2ACTOCjE1D67KszspKb2XRZopBK42tnv33YoZuOOjh18lErH3lYFi3amOmLUIFSt/RTUBng6qNfWxJpu/emcr+v+A0TYAK7jwAL0LuPJa+JCewTBFzXTTToZG9MU6dn7RO7xjvBBJgAE2ACH5CAbdvJnMcdd1yiPg9pblnx7Ipt3iFFCmxIpmNp6oDmDmBRLn95T+6XufJYy1sGvKMdwXaogmpfsSraloHXJW4t2BPymZlW/gkRdZIqTdHMsaKEZkRQWn3OgFKhb8kWL+kujarIa3LOOqBIijPNKSBiiBAq1oUEC8CDZTU2XxktxKUF8zZdotDVM0OEKqa5Y7JsU8rzauDmSjDHjkZ05hZV/PV6tYH2VSXKciJDmxLvAlNTG8eWOm+K/ZXkklYhPIlQIq6K1JpUBVilMKo7NzYIZuR7niKVHCcec8KwlkMOqms5oLnl29/+NoBKpcIZ0B/wR8izMQEmwASYABPoR0BVEzT06TquuC4VNgaefgaHDHv+c6eJL5xQ/v7X34kCulrxgKLnB1RtmAToWMpe8Zn+br/aPg263xf8hgkwgd1JgAXo3UmT18UE9g0Ctm0HQbBmzZpnnnmGvc/7xjHlvWACTIAJfCgCQRCIWNi23Ze/MWTIEM9zkshFARnqOAsH0tJ67rvA/Z5zSVvH8LIzqqu01CfvswMUlWch1C5pUn59rVmngEXlcGzemVMuL4/cRH32yCTtBvClDEndDVGSpD5fV06Pq+QuK/qtae8t3Z+kgToRpToK6LqHQoWgoI9HQ0zvqVzWY80OcI8dbtYxzZVYqJjmp6KCMaRDIvgG4C4fwzPeODdeUCy9kojaiZkqSZ2m7aOgNfSF6a7JlfS0ctdKHTBt0jDeSO+KL6vGa+rlvgRcbxaHZ/KtFesVoJO2Hnz5a6cfOLSpwTCaBjV897vf8X2/zwG9bQzxhzowPDMTYAJMgAkwgf2ZgJaO9W3gkFRmny4yRo/KnnDylqOOKp1xbMfcVogAodL1i+mqIxmkRBnQtY9+CPvU5/66dL95+A0TYAIfmQAL0B8ZIa+ACexbBJIbwi+++OLBBx9sGMawYcNELLa/S7xv7TLvDRNgAkyACWxHgLKVY/Haa6/1CdCGYYDqAoYCYYhYa8qiAt8CUsCTSo3bsuXiUnmU5V5fcF+RsCkg2Q9g+whcPX9S1q+okzrG55yJdvz7WK7VOnWsSH124HjKoiKBEW2mA7g5nx9fzk2R0YSu/HNaJg5jXSiQih+SBg2d6VjS65zcmRqTK0/Oe9elrIyuZ1gSIhA6e1p3QKMYtk1BGSuAmSWMLGBSxnk1+T4xVSUG7yCEJPV8K3CXcua4hdlWYbmKuqipytO2696UDpKz81KtBZaG3vRcek7ZfEoDCWhm++v//NXGoVWE5/zjd3Q5Q62bUymkpHpiUrxwO/z8lgkwASbABJgAE9gZASnhCoQW3dVFIYUvnPz0MUf0nHB04dRj/uzk4JiQdKccVhyEuvyg0K8sQO8MKH/OBPYMARag9wxn3goT2GsIiFh4nnfooYfW1dU1NDS0tLS8/vrrYRju9IS91+wZN5QJMAEmwAQ+KAHKwQCefPLJ5ubmxsbGREN13YquDhiGWn8ViGxFMU3vSCwoWmNMd3QUj8tk3wLyNENEfuPYo5AMKaj6fKQ84DVg+qbiLCdYoiv7FXVBv4A6iqEvHS+quJEjgR7gjhgTLW9Ezp7aVV4VUvJGQHkasVK0NkGeJrIi54A3gRtz7qh8eXypcrcVrNUf2tD+ZJJ5Yx3tLD2hctqqPKVsXdpVuKGIV/TWk0hJjSYE3DgoQYvdj7rF1tLWyXb6YaHa9bZAsdeSihQKRWK1fryN+J6gOK0nPacnv15XMrR0ooiA+uq3vmoMIngNg+rO/ta3Xe3gtsJQQgjYZpCRVYdWdVX8hwkwASbABJgAE/hrBKS+GokpB8zFNdNwxuHdxw91vnhsavRla1FN6QgFJWVJXaOh2pHtt9pa13PtdL+Z+A0TYAK7kwAL0LuTJq+LCewDBEQsHn300bq6upaWFsMwWlpaHn300WTIcJ8GvQ/sJu8CE2ACTIAJvA+BZODLsmXLGhsb6+rqEg0aJJv6ERUIJOVXwnPgp4E/uphUsscF8cSe/FM6p8KhKkEBpIcoQBRBCCXhCHQD1211Z3T6SwVWapnYU3CpTiACxCFCN/IqwCZguSsn2M5wx51RjB7xUKbyuFpKlkIp/dRpzhlgPbCgszgjb08sVm6IgjVaO66Q1CuVkIikErGUcRSJgpaqr8kWWiulSV2pl7X6TBBENZxaB2vYAm4e8XORdX2+a2ph662x+44WjkkrjslURbNH2jitw6/v84pXFzqvK5qPRZTaoeHIiKoi4e++cZbRUHVA/83Z//CS5a1yvY7Ic0kR9x1VZgH6fX6E/BUTYAJMgAkwgR0RkFJfitgBoPCDr2e+fHjw5WH4yrFvP/8sza4DOnxBt6Flrfe536pqRefa6X4z8RsmwAR2JwEWoHcnTV4XE9gHCPi+/9Of/tQwjCFDhjQ1NTU0NHz5y18OgqBPfeY4jn3gKPMuMAEmwAQ+CIEFCxYk6mlTU9OwYcNAAq3vwg3hC/gKgQM8A0wveGMjf1w2/ZqWdB3tj1YIoIJELIYMPKhNwOK2nsV5/7ZCvBrI6Jl9AVuHNffK0BTQfLMbjzXti8rFSWbpj0ps1Qq1NjIrxDrWkQI4aMG3tPo82fVGFfK/87zXtQG5gtBGHIDqGUopA72hAtAO/NaUcytqzqbuZwVKiYYsqfsakvzt6iG9lNO8wjfnlFMzKtk7zdLrikzWYa+linzPSr8P0Q35jPBndacWFCsrBLm2naoATTK0FqC/XhWg64yjvvf9a9OF60rlF6Wd1j1nHR/yQY4Dz8MEmAATYAJMgAlsI5DUAQ4EHvg9/sepW049JHvCkPU/Obc9OUUnArSEHsy1baH+U7Wic+10/7n4HRNgAruRAAvQuxEmr4oJ7K0EkqHWSeszmczhhx9e9WsZRkNDw+GHH84O6L310HK7mQATYAK7SiCKosmTJ/edDs466yyQEJwI0HYE35EiByz2MLISjMynHwUqeltKUqEfqEgh8rUm6yDqBn4fBfNyhZtT+Ve099lV8PTT1gKxC1KEu4GHLYwv+xdb7hW5zF0y2EjyNNUTIhtTrBKDsYpJ/+4Gbsm4M/L2qEJ+lpl/Xa+2TC30PUQeYl34HoEiY/JmrZXPLMlZefWSIvk71KN0SSeGjOC5FFftF4F3gZutwphCeoHnvRLKfAhXb5YSnHUTKHwjhhfjBYhrs51XdWceiZDV+554w5PXqgA9qI4YDj3g+B/+eEZ3eXbWXOGbOYhEoe6N8djVg8TLMQEmwASYABPYzwgk1YIjCdfGz/9960mHrDnlkLYzjl657HcIfBqtpKsshCxA72e/C97dvYAAC9B7wUHiJjKBj5tApB/JVpYuXVpXp3vLWnVobGycOXPmx90AXj8TYAJMgAkMNAK+7//oRz/qE6C/9rWvhSIIEfvk3vVtyDLweElNTJlX9BQfAjZqHZkUVar7p0hilcLXqRaboe4obZlpZa8P/ZW+LGrLc2J8trUQrMMtqJjhgw4mtftjy3JsT+nhGKshMwg9+DEJzxTATD1LRUp3Cri/HM00gwmF8rWZzJtVSzU1z4fvkDtbeHrlgU3G5GeBOY4zx8cDQGciPRNxAZUYnwIfQQriBYRX+dmRpdTkdPYlXckQEQVOC314nJi838kjC0zfsnV6OvNYGPWtUNQ4oAH8/TfPNhIBurnpf46acGuX/yebjNuJnTqqron/MAEmwASYABNgAh+IQBB4YUznz4qNVS/g+M889eXj8587etM3v/pE6NIaLD8SSJ6KihXXPmqdzjubrp2fp5kAE9itBFiA3q04eWVMYO8kIOLe/jTwwx/+sL6+3jCM+vr65uZmwzC6urr2zt3iVjMBJsAEmMCuE4ii6LzzzusToM8++2zKs6ABrVRZvgy8HmHxZmvi5p7FprUe5DKukNysqEBfLCBFDOEAbcAf4spV6Y3zneL9QvTE1KRARz9bvZp1qOXj5zxM68KEIkZtrdwTYIvWqUMqNhjq3A1B1mNJpQgzwLKymptzWvPl+XrrWyXFbiQG5YhU8sBD5Oj1+8BaiWvL3shUZpmOgSYJuNopVaQuk7pNe/QSxHVOboSdHl7o/qOOoo6TtA19kowBR6ISU4nFdcCd6fS8Yvm3Fau9b2VaIe8zQZuB983vfcdIbuk2Nvzg/EtXFNAm9NzUJ1ZxbyN2/SDxkkyACTABJsAE9j8CbqD+uyDy5LE4augbpx6WP/WIN+bNLngu/IDOrIJKVgihr0f6sdmZ6Fz7eb8F+A0TYAK7kwAL0LuTJq+LCezVBJRSGzdubG5ubmjoLZlkGD/72c+o8lPEPq29+thy45kAE2ACu0Lg3HPPTQTourq6b33rW7QK7UEOBToV7kxjQVd8d670CvwsCbhRWcu+ApFSIoQoQ6SAP0Wlefme60rlFUC7oIL0CKGUCBAnuc+xFpSfiNVCK76oC5NM3JKP12nzMmKqI5gMpyXzs6TcjJS2M4/POWNy5uJUbhM5mkUZvk86tZZ3IygZJgH1TVbxAAAgAElEQVQgWeBV4Ka8N6WjsrhCqy1qU3aoVWcd6Kz7qjp5Y2FUGW5mxlUKt3lBO1AStDkh9VPP7wLpEC+5uDpXmm1W7ijm3knUZ0XKeHVQcK8JGkD94GZjUP2gwc2Ng4dMnTPPShI3KMBagDI8PA10Vw4NL8MEmAATYAJMYP8kQKWJgFwBJx/z3GlHmKcdYX/1jHUb1iMQqNh0l1vQeZsCoLfPuWKhef/8xfBeDxgCLEAPmEPBDWECnyiBpLTgokWLDMNoaWlpamoaPHiwYRirVq0CEP73LWZ+MAEmwASYwH5DIDkpnHPOOcmAmLq6unPOOYf2PiDHcB54soKr3nXvjyhbuTdSI7JJgA6kDAWECXQAKxBfW9hyVS79sM539qVWf6k0vR+rOFCwgDTwnI8Fjj/eiUeVMa9MpQVzMeD59NThz4mgHOptvQzMz3hT7GhGofwWidpxGcJHFCCOIFVUDfVQksIu2oDFJWt8Z+7GElZpj3YE5WhvtVt1LtMSaeBBNxxr5Uc6xQXFylrASjxUWn1WWgS3dUr12wpLS2JMvjgpn3kXKMS6e6tt3VqAJkN1qKsmZkLZ8OnDjPpBRn1dfX394396QsYILJ0mImLA1mUUt41A2m9+XLyjTIAJMAEmwAR2jQCdc0VAy96w2D7ioFVHH5Q/+ajuS34Tmg4NrvIi6UWxgErUZxagd40yL8UEPiYCLEB/TGB5tUxgbyKQRHCEYXjWWWf9d+hzY2NjojgcffTRtekce9MucVuZABNgAkzgIxCoFaCbmpoMXZNW34+MC8BTwNye3M093us6eSMdK08hkHAhqVpgHEtBKRkrgNludmx60zK32KUzLiKyJSkyKYUeFRUEeYAfddSsgndBwbnUDK/38bxWmcnLHAr4roqcSDgIrSj20kJsAm7IejO7zHs91abd0GWd1Gzr9A8yLGszsmtKpbOe7874M3PuQhcrdYnCiIxRsgzKobZ7rVFF4I/AzJw9tlCakcm+puVp8l2HJLhrFzTFidjAVuCOEFNz3jzPeUxvnbZIzziidGgvWWUhRofEzAeeNgYfadQPSVzklUolCCIR6iAR6hrHVW/3RzhMvCgTYAJMgAkwgf2JgERMMVqVNL7ztTVfOqV0/OHdp372+RdepHNwqOtE9EnPO3VA1/DabubtBeuaOXmSCTCBj06ABeiPzpDXwAT2egKJ0LB27dq+rM8kheO3v/0th2/s9UeXd4AJMAEm8OEJUNqzrgqQSM/J2cF2XS+K13nObWZufj79mBm3a622KLSkTPorAi3B2sALAotLlQnF7CJhvaoFXwtRpNOWSbJV5By2gTUKc3POxZnKL/POpIr3p1B1acmXmhwpkEnaieF5sZ+No3eBW3LZGW3dSz35rvYjl3UDHO04TrTgpL6fBwoJebCE2W2FRY58XIvFZFNWFONhwTd1ocJQe59XADPy5kwXc1LF5xT5u0kfjoRWwLUGHSlfV1l8GGpmwZnQlX9cv3X08N4Q0qUAEDuET+WPFLnC79zU8aubfm8ccKxRf6BhGEOaW3yfqiNJKWnssFKCrOTbVUf68MeJl2ACTIAJMAEmsB8RoNu3CLHsVpxx3JYTDy8ce/i6n/zknVj1FYuo3lvuU5b7sUkiOGo+6putb6LmS55kAkxgNxNgAXo3A+XVMYG9l8CYMWP60p/r6+sPPfTQRIDYe/eIW84EmAATYAK7RiAIaIDrhRdemJSlraujUnpbtmz57w9zSj1WyDzreV0CtiLN1dZG5kBLtUmq8RqFa8ru2FzxRst5HmgHsojcJEs51g4lkM77gsBtNq7IWBdmK1Mte7lEmx5XWxVmqaaf8BGYUB2K6v5dUzGn5NO3FHveAhwd5uFAOlQUUbupkzBnQSJ3HlheVJM6zDkl/xndANKGSS+OJVyJsoAZQ+S0m3texb68XGrNF9/W0R8eQLUHpaI/UdUEXQIehZyR65qTTi13gm699YStD2khduBbiE3tkp6fz07v2PpPE1qNwZ82jCEtxpCzzzo7GVHUJ0AnMvSuHR1eigkwASbABJjA/kMgUYdpfxViL/KL+OWP3S+d6H/xZHX8Ea8tWUKic1S9uHhfKjUCdJ/iLPS95L63tRPvuy7+kgkwgQ9NgAXoD42MF2AC+yqB4447rs8BXVdX96tf/SqJfvb9pNu+r+437xcTYAJMgAlsT8D3faXUhAkTklCm5Pbkm2++mcxX0ikZNK0L/YQkQEuXnqT8bgSWuphU9GeUgsc91a5nzinXQxRDafszycevQd3sxpOK4RWlcFLFWwbRpgvzJTOQUVmr2w5UGngHWJy3J+bNKen0mxQn7XoxnZt8+C6Nu42VSLKVqR9ZBignOmVPS1fuFiR/a1lb6lCPUMAFTAnbA9YDt4a4tCM1tpxfDnTp3aOqgwo0Nog0aFLNTWC1xPxiflJqy4OhlU082lRLkBbQuw8LsqB91r8r5EeVM9PN7N/+8j+NlsH1RsuBgw6+YvgVoX5EUZRIzyxAJ78lfmUCTIAJMAEm8P4EtgnQOiNj7Ws4/ai3vnQiTj2u+NUvveYHqFh0y/ivF1V4jwCtQ7RIv97h8/1bxd8yASbwYQmwAP1hifH8TGDfJPDGG280NjbW19c3NDTU19e3tLR0d3crpRKv1r65z7xXTIAJMAEmsBMCkX4sWrSoTj8SAXrWrFnJ7L4KY9KeteMoosCKEMoDekD1A6cVi1fkygts3FdCh9JyLyJTuQFiylVW6PSxFrgXUasZXJpzxmbcOwQZnN2qoksbCRVcLUCXtH/5Fk+Nbs8tzPpvkpmadOckmzmk4Aud/xz5IlSxDnreBMzrsecVvYd8ryuxKktAUWlAAT8ixTjygDUyuqtcnlI0J+RK90Ou1kJ5lORvUJeU0jqgP3wOmJ83Z2SyS0PvXQr90B1VSinRzmuNoSDI/vxIEE/PZoebuQmZzY1fPMWoN5oHUQb0vUuXJYOKRCxYgN7Jj44/ZgJMgAkwASawAwKJOkzDmLRgPHZ49iunVI4/1P7s0W8vuLpaUFio6nn7/XKc3yNA71B37vtwB03hj5gAE/gIBFiA/gjweFEmsA8R+K//+q8++3NjY+PZZ9NgYVaf96EjzLvCBJgAE/gQBEQsRCz+8Ic/1J4ahg8frlchlHShHEifJGU96lUC7bHcAiwJcH42f7np3dQVdQOehNaFIxKs9aMMvA4sCeOJpdIF6fIlncWlEd7UOq9ORI60nEtSsqsV7S7g7lR2ald5Vl48o0h9dmg9IWQMFQoK09AFBRWp2xngXWBJpji/x7yt6KSTAbnVobkSKpRULZC08s3Acs+flc2My6bnlvKrtXfbStRqoTM4BCnWOWA1MDWVas3n7wxF0s5QeCRnV9dG1QoLoSgBLwBXF6xJJXtEd9vCzJYE3cEHfGpww5C3V7+T1FSoVZ+TAgwJFn5lAkyACTABJsAEdkhgmwAdodiDL578wslHlE46qvC5U54uF7R7GTS6KNGgqRbxzh4sQO+MDH/OBPYIARag9whm3ggTGNgEwjA85JBDkq5yYnO77bbbWH0e2AeNW8cEmAAT+BgJJIHFHR0dfRnQ9fX1//C1r9MmY1+hEiMvUCLBVivGZkT5FTea0UwfYyrhzJS1QSKIIQJtJU5m0lHRbwN3KYysBD9PmxemSnNzzhatKWt92tezeEAktZq8Cbi50HFVpntup/uUQofOm46SOoMxSIMm9TkLCsmIs1p9vq6cvyrTszxT6QFKQq9V+RAxeaYD6qaGWn1+wERrvjyykFrgpv8ML0NfqhBkT6bihxE5qQo6IXpytrPVzM0t5dfosocuea0CCIeeKhAgI3Qn8AzEnEr2oh5zuotbcuk5f1puDG5qamoaVF9/2CGfoWWCwPd9zoD+GH+1vGomwASYABPYdwj0GZH1gCO9XyLE7Mn40snZIw7KHP7pNyZNKsg+TVkqJWlIFpUR3tmjb+adZG5s22Qia+9sPfw5E2ACu0SABehdwsYLMYF9hUBiv7rhhhv6PG6GYRx77LEAEq/WvrKjvB9MgAkwASbwIQj0nQIaGhpaWlqampoMw2hubKLygDKKYYYohahI+BTFoShn+QETV/oYawWzsvZKXc3PLVGGMpTSpmbhA20KDwq0lqLzK/LXxeDKordSf0cti4HAE7EDHRVtaZn4tlz6ykL7da71QJk24ff2GCkDg8oGSS09F6HsCLINuCWXn5HvudGuvCNJI+99uOSY1kK50mLxgxVM7bQvSpXG5wuPwM6Srq1iUp0DyAgxpYs4wCbgykrqCis1y8w+BlUEBOV3xAIelAXpSOGGlMiBNcCMQuevO7eM6Cnd7NHbn10xvG7wAXVG45Dmlv/zb+dRXLXvW5bFAnTvQeG/TIAJMAEmwATeh0CiBseSTrtxkowV+vjm320+9Ujzs0ebZ35p3YoX9eIx3FIJLEC/D0v+igkMDAIsQA+M48CtYAJ7nEDibksE6PPOO88wjJaWFsMwGhoa+lI+93ijeINMgAkwASYwIAgIEZLPWMb/9M/fT04N9GoYzz7yBCR8EcSQvghMz/W0Cfnm7srkHnOMac+smCsEOiRyMvaV6C3rowRVDsRzEteYuDSjLinGk7LWSh2yQcUESX0mI7Tyqq7md4EbitaE9tRVpfLtFXNL1b6sBfB+hGK9MNU/vMc1p3R3LiwWntHuaTJK04NEYx9hRIkhFKnxF4jZleDilN1axn268GCg86R1SIhPwRqxsHTyxu2ud3lu6xQ/84ReIW2bqigGEdwIbgjPi8NUTAUPfxuqUZY7vmIv7ux5U1ASyKEnnmQYjYZhDDIaFs1fQMvqB8duVEHwHybABJgAE2ACOyRQ9SlLfX4PJXxPmCFQ8bDsPpx+4tqjDk5/9sjsud/f7EsqFazP4VE/y3Kyhhq/8w63k4yneh/D9M6W4s+ZABPYNQIsQO8aN16KCewLBJKCSIVCIbE/NzZSV3nIkCGpVAqA67r7wk7yPjABJsAEmMCHJ+D7dAoIAm/EiMv6hsg0GMZVrdPIAyxJUDUdsiRvBR7yg8l56/KC3WpZd4R+G1AJYwd+SHEX1UcJeNyKriv4V3T7F2y1ZuaDZ4E23V8kUVcqmjckvbpD4B3gNt8b3ZW62o1vyBRf03nQyYpqh8fSJ5IyH23tQb6ye+usQvqJmJRuu7pZ6n2GkA5iC6IbeBHid4E71rRH5t1lOrLDA2VqkJ2aNk61DUNgg8LvKuGUTGlKOX0Pgs2JTZu0bglFArQP10aUU3gbuN1Tk4vuiIw1K1d+wfYi4C+r19QNPtAwBjXWtzTXtWzd2NYnQFfbxX+YABNgAkyACTCBHRLok4/pvBwK+GZUCAEzwP/53+tOPXbrKceUDjvk5dvvSIK1HH2HmgXoHaLkD5nAwCLAAvTAOh7cGiawJwkkAvRNN93U0tKSqM8tLS2/+MUvkjb0jb/ek03ibTEBJsAEmMBAICBlrJSI4mDlyhdqBehz/u7vpU2ysgJFPHcCy4AxlnmRY15RKV9XKr8FpCR8UnOFpDANSoE2QULtomIwJlMc3t0ztavn6ZACpItShIh8eCFlX1SL/r0FzCz7451wmlVelE9tANKCIqH7nEp9GjQghWcWRPgysLBSmdbedp/jdif4aKZe17HWlfPAq8CtQrWWnbGFws1e2KFNU71rJo+VRJhUPnzIDCemzfE5637fXwuU9f5W3dwU/BEqhGWodcDyCDNy7rhUaX46/3DF7AQqwHW33W4YjQd96jOGUXfcsZ8V4baWDISDy21gAkyACTABJjBwCfQJ0HTyjAXdG6aBUs+twIlHP3vykbkjDt70d19d6UWJAB0lp2i6Ltnh8333M7mieN9Z+EsmwAR2GwEWoHcbSl4RE9i7CARBQCOTY/GNb3wjERdaWlqam5uffvrpvWtHuLVMgAkwASbwcRAII4pcjuKgT4CuN4zBDQ2+SeZoGygAj9gYX/Yv8LzfOIVJlfQjjlvRcq2Ov1ASlPucBzYC94dorUSXF4uzCl1/iK08YEUqQmyLUgjbhxfrEn9rgBsCjHEwvBQs9syXIXqUJyi/maoKbfcUkEW3tB7BXcC4rp6llcom3UdVtnYsJz5tCq2mzutm4M7AH1/2h6fNq9K5t7Rjqk9T1uUESX1OA08Di0rOlFKwoBiuESgJUsZl0gJd1DDpCaeB54HJ3eXJRX921ny0XG5TsgQUnOALf3tWXfPQhuYhdU2DL7zoskQ6/ziOEa+TCTABJsAEmMC+RqBWR9YB0AAqLsaOCk49ZsMZx7snHvnOvPnCjuniQI/I0gBql6qdfl86LEC/Lx7+kgnsZgIsQO9moLw6JrAXEVBKbdq0qU9ZMAzj9NNPT9rPIZV70XHkpjIBJsAEPgYCUsdAk3z7b//2L0OHDjEMY/CQZsMw7rrvPk+rzHdFcq7EGFdekMlP9nP3wE7qBPrVuoIqBtJKbgB+a2KaiYuL9mSn/Gd4m+FYQKhkCN9BKYJrx44VUZrHbQJTIowuYmqXuV6nS0fkaBJVf5Pezz4ZuqTiNuDeSmZie8eistWuZfFYgQKnaSbKhqTuqU5wXhaEY4u5/+zMTC66qxQ8mkXQ16STK8TSV6oDWAHM9uzxFXN+yn1XW6dpDQJSUIx0oAVopQsPvgPMyplji+6UrL1cUO5HCGFa3pur1x30qWF0bq0fZBjGE8+uoNu9ukUfw2HiVTIBJsAEmAAT2LcI9MnHdC6n8oNeiFIRnztx5alH5E4cljn2yGfbUqhEiQDdu+9kl+67QKiZ6FsbD0bqRcV/mcAnRYAF6E+KPG+XCXzyBIIgaG1tbWxsrK+vT2Toe++995NvFreACTABJsAEPnkC2zpvb65+va7eqKueKIwf/t//sIEVnjs1tfnK0LouVguKpfthv6NlWaGdxYF2IlvAeuCOkj/TxcVpb0zGvN13N8H34MeSHgFNk/oc6BKFy0vRTB+X5LxZhegJSQUDewsJ9sORtCwSoluKR+NodnfntYXs89pALQViRU9F9Q8jEo4lhUu/JDDX8S8vV8bkyg9oU7bup0aSxu9WxW0HeEFgbk9houVMyZVfTYKkScKOECsVk/ocKtK0HVBK9eJ0aVLFG54pLqq4L0i4kIh9SPz0339eZzTXD6K6vp86/EhLKZ8F6H4HkN8wASbABJgAE9g5gUQy1uqzpAxoOk1fPz86/jOrjz24ePpxqYsuisshSlUHtF7PtkW2Xb1U9WgWoHdOmr9hAnuYAAvQexg4b44JDCACURSdeOKJ9fX1Q4YMaWpqOuyww0ql0gBqHzeFCTABJsAEPjEC27pwIhZnnXVWcquy3jAampte39rWBjzkZP4CuRnoAFJQFV3uL4byQRkYDrAFWCYxOl0abWJSOngoJ9skbKryZ5O0HEBKGSpYEdmH/yAxLRuMy2N6Hn/04s7Ezpyow9tcS9sMTkEUbgzFvIx1Zcn5M7wsFSqUsSRrM6VFShKgQyALPAXMt/yReXua6T8UxJtB81CJRSiXnnD1tt6WWFzG5ZvS83Ph4zYJzdp4HdHsqqqER3rOrcCSghq5JT/W8iaXio+GQQetT8B3rEz+0KGfOaDlwPpBTUZDw4//388VUAx8dkB/Yj9k3jATYAJMgAnsXQSqp/oQVJvBFxJWCd/52kvHHLjx6IOynzt5w8qVNDaqFIptlQffR4Deu/adW8sE9mkCLEDv04eXd44J7JyA53nr1q2rq6szDKOhocEwjJ/85Cc7n52/YQJMgAkwgf2KwDYBGsDtt99uGMag3uEyI6e35qBSQDuiCoSvRNibeyG0/lsENgFPABPz5TG2GNtdvsdCUfPz4Qt4pO+GpBLbJF7j4WIwLetMtjClPfhTjC6K+IiqHUsd4tyHXvaufyvwZMW9Pu/fK7GRSh3KAGGopK9LCyYlDbPAW0BrNvebzp4rUvYtFayXKEdxqMhYFWo1uaIDOrYAd2Qxtq00M+vfn42TpmpROYjhKTJKU4fYBeWEvAhM3GpNMjE+W74jiFfH0qH2xfDtURddNojM4nX1lL9R9+KbbyQ6NgvQfUeQJ5gAE2ACTIAJvB+BRE2WEiqWkKHA8t/jjBPfPOlw87OHZ877l42xHr5UDMK4JnRDr7D20qVv+v02xd8xASawJwmwAL0nafO2mMDAIjBy5Mi6urqmpibDMBobGzdu3Diw2setYQJMgAkwgU+MQF/PrTrxhS+e0dhIdyvr6+tP/pvTC65lqYjSkAMnEXNjpXM3BGm73cAfgTHd5sVFe3y+srzgt8cIqC9JwRg6T9kvO5ajUAKeUGjtKowuicm54GkXKXJJ9w92rIEQ6+KH64Brc9l5mezTXrRVR3/4ZKwOpQylpHgPgBI8VgJXV8KLit5lhfCaDn8tkIsQ05fVh0cWadkGXFd0J6bKV5e8JTmzXWvTMe1NHELEEAJehDDreV26ROHUfOWC9ty4HvvOChUtJDO1F4rY6Wxbd1Bzc5NRR5gM40tfOdONAnJScwC0hsAvTIAJMAEmwAQ+EIHkwkKHYLkRfvKj3GEHbz5+WHDysRv+9Djc3nFRukbDtuBnvWYpKXxr2/MDbY5nYgJMYI8QYAF6j2DmjTCBAUngoIMOMgwjMUF///vf930/CHQa5oBsLTeKCTABJsAE9iCBbQJ0FAdh5N9xx5KkWkBzM5UivOOOJb1VCqlRsSKZFhG9WjpMedRW6woLo/PObU7YJqmKkBJSCSljhBI5v2QCncBDljsplWkN1BUpe353qROo6sc72VULeBVqSaUwKdV9m+91aG1XQMYqjlUsZaxkGOjkjbXAlenyiJx9uSOmlsTLQCpOsiQp10Mbq8guvQF4EHJ0JtNarCzuzLVrFV0HdAQOPB9Ca9Ceg6gHeBloLRZGesEVXcXFhahDF2MUFPkBzy2NHnPpIMNoopFF9JgzZ46kYI7ejvJO9og/ZgJMgAkwASbABPoRkDrJq4zQxeq3cMLxrx8xrHDcYcXTT3nRjWgAUwCSoYPeEgvbLllqpOdEhu63Wn7DBJjAJ0qABehPFD9vnAl8cgSeeOIJwzCam5vr6uoaGhpuvvnmxDL2ybWIt8wEmAATYAIDh8C23pyUcRj5URyc/Q9f+9TBBw4e0twwqG7o0CGmWfZ9l+KWYxEJCEXPMvA6cGVHeVQZI3PhnWa4TiddRLEXww2p6qC0KPXC3wB1L6KxufyltndZpjxrY9dqhcoOzMJVAVdqW3QnsMQ1p6Y2314urK7GPSf6N9UJpGG5irzPr2j1eaTpXJgvzg/VH3TORjlM8CqJIEZki7ANuBMY7/pTHGd+Or8xie/QwdOC1GfHgefBCxGUoV4H5mR7Lg/DSyredWlvE5BN1GWKHRHrN641KHWDpOdB9caQlqZiPkv5G6K61YFzaLklTIAJMAEmwAQGLAEap6T0Cd6kiRGXZU88buPRh6dPOm7dvLnU6giwIlEJ48QBLbQM3ftKJSBqHdDbrmYG7A5zw5jAfkOABej95lDzjjKBXgJKUWf+P//zPxOLlmEYJ510EnWSYxGG3E/uxcR/mQATYAL7NYF+XbYg8JQSL7/yUnNzY1290dQ0yDCMf/3XHyRyse/7KiZHUglqE7Cw7M0KMbYsZ6Wd1fQhAuULacYwfdhafUY7sDTKjCmkSX22gql5a5UOzdBm4h1zD/QMr2gV+JpCaoN2H1M3NVaIFCLImPxQeWAdsKAYjsjZ5xeL06Pwvjju0TEdkaDTnyT7c+RDFIHHYjnODS9zwvmmtVbbrZSfeKoFZKC0+mwiKEG1Addk2lutyiUV50pHrQG6XVTjJ0P4lv2D//U/DbKG02NIS9OoK0bQiTUKRMRDi3Z8QPlTJsAEmAATYALvJVANyhIQFWQ68MXPvXDssLbjj2o//bSn1qyh2QMBR8dp9YrOVDO497md+kyZXH3P926LP2ECTGBPEmABek/S5m0xgQFBQEqZz+eHDRuWRD8PHjx45MiRvv8+vf4B0WxuBBNgAkyACexBAn39NeoJUnAGpBDhT/79R1WRVf959tmnw8iPgxCSvM9rgRuD3CjbHFkJfmtRYEWKlF8ZwI1hKuhafTr1YinKY8ttFxULIyvBPBOPAZsBkwKid/CQJGHDBN4EFqezN+Rzz+ok6OqsUlFJw5gsURlgI3C7IyZauKjojS6Xbw6dzVpZ1rtAgcwB4MmoCDwHTO5J/TpdGps1X9FCeajF6RhKKYEoQBQIyAzUOuBWv3xFITXSrEzrsf6s0BWAkjcSc7bCypUrDaqnYBj19DJ06JBSqaCUECLUDuhqb3oH+8YfMQEmwASYABNgAppA35VHcnr1yph/JU45ev3Jx2RPOPLNSy7d4ocUpRVIFUgV7yB/A72xG31rYgGaf1tMYAARYAF6AB0MbgoT+LgJJN5nEYuHHnpId5SNhgYqlfTss88mm46iHfb9P+528fqZABNgAkxgoBHY1nmrMQ+pd99dn5w+6rTSevLJn81mqQ6f1LHLv3MKkyrpS0v52Za/igRlyoP2IEP4MVxQnjIJzb8PwiuVfaGTG266M8rx48C7enEbUbyjxORIK8htwPytW+d1d/5ZqS202uSh26kFXleHSt9pq+mlYIyPK4rejZ63RrdBiZgM0lDJqhKt/KYwmOI4Y1L5+yWylD1Nec2SWisEIsQUaB3odd7q2ZPM0gXZ9KjuzDOKSizSeKFQ77ZuxRf/9kvGIOPAYQcajUbj4IbxE8YKESol+p4D7ehye5gAE2ACTIAJDDQCtVceAKwCvvM/2s48yfub48rHDHvi+RfgBzTqSd90ptfa+XunyQFd+03tm4G2v9weJrC/EWABen874ry/+zWBJOVZxOI//uM/EgXBMIwzzzyzDwpHcPSh4In/n73zAJOiyt7+6arO05OZAckZJAgqAgYMa0DMrq6RXRV1V9ecWTNrDhhZs66Y4/pfF9dVFseHIDIAACAASURBVAUVE7qiEkSQPEzuXDmc7zv3dhc9MKMiIDNw+7lPz+0Kt279qrpr6r2n3iMICAKCwI5NoPCWrbCOJ570u9KyYu7CEY4EJ006vdEwViLOQrx2XfOV9Ym7Gpres5wMw+cyZwxKP0jBx+TO/JKFlzUkLtTtczPGjYrzrM5jnzGJLhOgW6GuMNn6kaW1DzXXP58hp+ZmFsjMbkFdCx2XfVyL+D7i1Q3ZC+LaXzL24xZ+y3TqnPrMRGrNcrlL9TMq3hjP3pxIv5RI1nI527FtMtXQuaOHhWYCySpkJuIVjakLm1LX16WfbdBSXG6nbpoWaqqrTnv6MShm8c80pAulFSWqmqV0iEKAbuVgikmCgCAgCAgCgkDrBPh/G9xMAxFffBaH9Fg2ZCd3aM/G449YZduUwEEI0K2zE1MFgY5AQAjQHeEoiT4KAluIgG3ZdMdsmn379g2yFwDccccdfPoW2ohoRhAQBAQBQWA7IFAoOhfW3cam+qqqSm8Us7i4aPq///0h4tS6xlubzDtrsu+o5iqeQcilVEGuia6Fqkuq8YeI1yX0P6bN80z7SkV/MK19zaKbEVFBV0G70KuCZx1Mshjk6WtSD6xseD4VX0i2HpbiUiyzRVHIlk4WH9T4J4h3N6iTVbw0bd3SkPqGPZyrpRS0LSrMLkNjWvYzCl6xOn1Ds3bfusY1bDHy3EDLImNJCnxGx86gu4rZdNzeoF6lOFcl1CebjWWIZhYpmSK9bNXNNhvJ8t47QYRpzwzKtTdcy+aSj4dXtoMTQuyCICAICAKCgCCwVQmw/zYcmx5BwnQWzz79h96Va/uUKzv3WPjyM6grFNts/1QEdGH4M39SyfsnZqt2XjQuCAgCP0lACNA/iUgsIAhsPwR4gPPLL78cDoej0ajP5+vTp8/2s3tiTwQBQUAQEAS2MgHbslVVnTZtGhegJYmcOHxdu10558Obl699cm3qCwubSE0mgwqDa8QuVdYhvoN4ydrm81J4Tta6wor/DZs/Y87LJA07ZM2s8DvF/C4YaCURP0d8SnFvWrnmmVR6MVOrs4iG69iUcMh0MZs2U82ISxEfzRiTm5WzazKT1yW/YC2TTYfj5gRotE2kFIUzHZzcmL0soTyWcb9EZJHaGlOKXXZrS9HUrkWmHEsQ725M35ixr0+pdzfFv0NMInPf0MjM2nIc3bEnHHmEL8zCn5knSb8BfdnDvzTc6zjWRnHQ/C44v4firyAgCAgCgoAgsOMR8BThDSpZurzaFiazJi76Bvt0njuiF44ZaI0bPddUCJOadTdYxfvYgqLLkjTw9xYzxAdBQBDYlgSEAL0t6YttCwLbhMBxxx3nCQcPPvigsN3YJkdBbFQQEAQEgQ5NYPDgwaFQyOfzRaNR8Pthn3GPrVz737rkOhc1Jj0rTFDW0VKY+vwe4tUJ7eyMebGF5zUlp2HzHFRrueLMrDQsZqPBmPDUfph27dWIz9v4l5WNT2bUT1niQScnbbsuJR00ND2jIVltPJFMX9PcfGFj041x9Q0mNKvMfpoapFtQ10G3EfF9E+9cnb1JNac0NH7KFjNJddYopIo/9MvCqjMmrkJ8Mp6+Lp65qLbhnkTmY8RapMRHaCpo0H2wg/jk35/OXU/9LALaL/33/f+yDZqGqQgBukOf4aLzgoAgIAgIAluJgKcab1Bh11bbQl3R8aqLne7F3w+sMrsVfz31dk3NoqFRdzZYxfvYoqtCgG6BQ3wQBNoLASFAt5cjIfohCPwKBFzXXbp0KQAEAgGKWfP5li5d+itsV2xCEBAEBAFBYHsiYJrm3LlzufYKkgyBIMSKh4yfUMdCnhUSdJ0sWhol9nPiLPb5Vg3/UJu60MFLFfXObPITdGtpMfbit4+58GebCdEqot2E+G7KvWudcn+DtoD5R6smWjatpdKGyDVDQfwO8VHTujDeeHbt2utTTf9B/IGFKqvoKOtFbQpenod4U23TbRnzvlXr5lpOgnXARMo8SAHYlFTQttFVTQqUfrzZui6hX9BQf2O8+V2HptDyrms7imOTAL1k6Q+xkjIA8AfDHMUVV09GdFOZJKKlqmkhQG9P57zYF0FAEBAEBIEtRcBTjVmF0gbygohZnVJG1NVhz8p/D+mWGrqTOaznN0sWoW5iOkOzWq67/mOLvgkBugUO8UEQaC8EhADdXo6E6Icg8CsQyGQykyZN4vfJPp/vhBNO0HVdGED/CuTFJgQBQUAQ2G4I6LquqqppmrfffjsAhCI5+RUApj31OHlUoKNRsbJMff7Mce9UrXMz1llZvFxzbqyt+Swfy8zNN3K3jzlAJpOXswq6CxAfXN50z8r4h4gpds9p2WTSrOaDrDOIaxFfaDAvaUyck0lf1rDuZXS+R6xDJUPe0CRP66xZnsbweU2Z3NR0fX3DhzblSCTBmblJUuwzE6Bd180yO+lXa9NTmuxLk/YFa1e+griG9cmgCGjbdDTT0Wx0dxu1B7ue+gAgGisZMWq3hkTcdAzdJF3dtjUhQG8357zYEUFAEBAEBIEtSKBARHYcGqvmhdJAuIiGjo//DQd3X9SrpGFIt7prLsVMGg0bVUPXNKVg3TbUZy8LhbDg2ILHTDQlCGwJAkKA3hIURRuCQEcg4LpuJpPp2bMnAHDXzunTp5um2RH6LvooCAgCgoAgsO0JuOzl5F+2ZR966KGSXwZmfxwtjYAf/jPrnaxOCqxpuxriO446NZu6IKmekbLPbFamxNPzuO2yyTRfe6NYJpYJUEFjIRq3N9b8ZeXq19elG5mUTI4bLGbZS1SoIL6LeM0q5fIGbfK6plcd+3/cVJqilY0MC8cms2bKW4iP1TddX7P6tnT8H4grWTsahVM7PJUhGhQHnTXp02uKft3q+svW6ZMb9GeQfKIppJlcnemVVFKKqf7h9NNkWZb8wdLyCmD7/96Hc5gztWszyw+bUhmuL7mVxR9BQBAQBAQBQWCHJ1AgInMB2nDQYBkU0LCwuRbHjfx4VN90/8rmkf2/njub1GcLXculx6o4PN5CC5CFUc9t1VusID4IAoLAr01ACNC/NnGxPUFgmxDgqsFTTz0VDLJcSQDl5eUkEAgBepscD7FRQUAQEAQ6IIENBGhEXLly5eChg0MhsnWi0U0AGeRZ/52j2ZhycAXifenMBan0mSn9T0nrpozzDx3rEE1FIy1ZZ9qwhTnzZYcFPjFpeD5qj9WvuHjFwgey8e9YvntKOMhmGYgKy0SkIH6o4TUrjVtMvKXRfD5rfZvzdEYDzQxZNZOXtEUB0fharXpXU/qqNateQ+sbZqbBtGyHVGXmQI2IjTY2I75v4M2Nqauzxk0p946a5i9Y+HOGkiLlFWjE5155ASQKfAZJ9gfDPp98/XU3ImJKVWwyBnELpWde74BHW3RZEBAEBAFBQBDYKgRaCtBcfWYiM2JGwRefwCGdvx7R1e4aXXb8UYvoySr6T4CP7+b64w1Fr+9fW6Jz4fT1S4uaICAIbAMCQoDeBtDFJgWBX58AVw3GjBnDNQIAOO+881zXFRYcv/6xEFsUBAQBQaCDEthAgE6lUo7jpNPpvcfuKQNEwB8FuSpU1bXzwNnzf/gO8clG7YpG86yEfVbauCFr/8ekSGSDgogzOqLuMvNlOy8Bs7gmGyn736OacsmqpXfXL5+Daopg2Ww9y2QytG6Rt8aniHfUxi9oxMlxfLbRbkRM00K2abNHeSn62HEQa218y8Ipqxtuj7uPZ+yFJFLb2byWTaKyS4vpzEv6XcSb1urXG3hxffqWFWu+ZMbTabTSqGmoOZaG6C5duoSnUpDl3IDuIQcfqqkGP6ZCgO6g57botiAgCAgCgsCvRmAjAVqzUbPRylpWIolnHNc0vEvTkE44tMeql1/BRJb+c6AA6VyK4oJucnGZT9i4XjilYCVRFQQEgW1FQAjQ24q82K4g8OsR4JLBxx9/zBMPkmVnKLRgwYLCeK5frzdiS4KAICAICAIdk8AGArS3E2pW2WPkqCAJ0IEwRCgSOlJ1/StvPVyTvLw+dUFcuUFRX0KsZSswwdlV0VUQrbwG7ZikMWcRlzv4voN3Wu5VjY2zKZ2glUXFQe7YTM/eGkyv/hbxkXT2knVNF9eZD+vkBJ2hxh0mUPN+UWbBWgdnK3h3Y/Ju1X0yhZ8zf2cDDaMg6hrR1dBZhvgB4s0J59xa86Ik3pRyX0umk2T9YemukqWoawXR/vKzudGiMLmOALN+jsZKS8vT6SwiqqrKlHIRAe2dF6IiCAgCgoAgIAi0QqClAG055LFhcF/IpUuwd/nckd1wZDccPeS7VAYbsiwCemP12fN65lsolJt5vXBKK70QkwQBQeDXJiAE6F+buNieILBNCDiOM3HixFgsxjXo0aNHb5NuiI0KAoKAICAIdGgCXIPm74U7oqvaEROOBLLg8PukKPhj4A8ffc3kO1YvuK3p+8frlq7gTsoOWq5luZaNZOXIPJjJeUOzbRX1DOIcxBuX1F29uuFlxKUs96DrcvsN20XTQUNBnI/OgzW1f4mrF62Lv2i6i1jL7MbVYV7NrotoaWrcodbuaMj+tT77VMZZyERnemjXu/F1WZ0lGPwYnXsxcbaSPiNlXhZ3njEoENtFTOtZ7gxCm84kenffyccMr0OhCACUxEr/+cabLjlT5priZPJx0FyMbvHUcCE0URcEBAFBQBAQBHZ0Ai5dlm10TCYxT75IHdEjPrBMG9x51dRbSZnW+DNQ9NCUxp5fYvYbhRKzEJp39HNI7H+HISAE6A5zqERHBYFfRsChZ4tx2bJlnvkGADz11FO/rDWxliAgCAgCgsCOTKAtARoRE4nExIkT+bVG8od9sh9CUHLY6AcXz15FUcaoI09faLm2xW0yHEoCSC+FrJbVL9G5ryl7S73xYE36W8R6dqPpkp5su2jr5OxsLUf38Ya1tzQ1Xriy/gkHF7N1LWb3zGKhHB0dhSnXSxFvX9d4dX3iccX5iE2hLXHHD1KqWWGbWIz4mFN/obpiotZ4djY7zcAvciHVuUOdUZOrVv0woF+vaJhsN3zsBQBT77oHnbz6zORsIUDnkIk/goAgIAgIAoLATxJgl07HZQK0jfE6HNb70/4VmcHV2eF9P2ms4+kH6Ypt038CSZdlBaZWhQD9k2zFAoJA+yMgBOj2d0xEjwSBLU3AcZxbbrklFosFAgGfj54aTiQSW3ojoj1BQBAQBASB7Z9AWwK0oih8vPOZZ56JFZX4g2EIyBCUoDwM3cqffP0lijx2HNd2HAp+ZqbLBjqOZdB9JcYR56L1eLrpuoaGu+rTixCbEDWXPDpUdFU0bTRSqK9C/JeuXLFm2ZRU/MmmzKKcTMyCpvIP56pMuZ6P+Le61FQ1fU9T7f9YckLyfXZtOxdpxawkyTODMiW+blqTm9f9KV1zdrb+r2bqY+YWorGDqZuajXZGTY8aM4riu2WZK+yRSOS0006zTZPugXn6RBZYLQTo7f87IPZQEBAEBAFBYEsRWC9AG4aDd9xkD++5pEc03r34++smJ438KHX+KaNUPotwmwK094yTV9lSPRXtCAKCwOYTEAL05jMULQgC7ZqAptFNdFVVlSzLkkRPDp9zzjm6rvOb5HbdddE5QUAQEAQEgXZGoC0BmpLUk7UymqY5Y8YM7vgEAdkXDFDIsCwdffTRrp0ToNFkgcc62XEoaCXRXY74imlOXrH8pobafyOuIVGa0ghaLhlDZ9BNu2YNuh8h3rRm+TXx2nuzie8RG3n4NEVIs+KSmJ0k52h8UsO7ksa0ZNNnLDmhTRvUsramsyd5+fO8WQVVlszwzox6YXPzhan4LUbin2guQytpq/y2N6tlP//y891H7yb5c9dQWZYDgcCwYcNMk/tVstvg/J2uEKDb2QkruiMICAKCgCDQjgmsF6DJBHq/PeYO6LxyUJfM7oOXzplD3TZcbE432SxNMRt0TuUeX2ojAjp/NV7vttWOd150TRDY4QgIAXqHO+Rih3c0ArZlv/TSS8EgPTXMX2+88YamaT8iIuxoiMT+CgKCgCAgCGxZAjNmzOhSVf3/TSqKg+H8xQeqKjs9O/0Z1zDNjE5GjuTm6K519bWIbynqX1fWTllb/y8756rB7KNIIDZZSSDZYtxcX3N57cpHzexHiHU512WH1GeTPtguNjD1+aVm/S8rG2+vT8wxjXp0U6gYmHFRdxxLY5YdWaZTpxE/NPHm2sTFzalzGlM3q/obmdRSNBswa1OL9Jo1853yilJJkvhlNByOAsCIXXblYjp/X3+b65BFpct6YrP8ivwj5UMUL0FAEBAEBAFBQBDYmAC7RCpZfP7p7Ih+X/atWDu4x+ojxy9JK3R11V2Ni89sKX4NZ2PUQoDemKSYIgi0ewJCgG73h0h0UBDYPAKu644fP97n8/Hw5wEDBtiWres6d+IUMvTm0RVrCwKCgCAgCLRGwMV4Q+OuQ4ZVhGNB8HnOFcXFxeP23GvO2++iZiOLYlqHOBvxsUT2xtXxhxq1xfmAZcdCzXJVk245VaY+37+6/mYtfZsa/wBxNenIzMjZtdBmGjSZdeA6xFcb7QfXpO5dl3jLwkYKjHYVzBiYodBn1zFY+2lmyvGBiQ81mVdnncs15/Km1CPJdB1iytVUasn9/3kMr7zwkkgoUFxc5GnokuQvK6v46quvhQDd2lEX0wQBQUAQEAQEgU0mYBloZPDkoz4f3mPF8B7pHlUfPP88GmSc5Zlw0CWfjTvn3TiEAL3JmMUKgsC2JyAE6G1/DEQPBIGtSuCbb77hd86hUEiSpLvuusvz3yhUn1mWp63aEdG4ICAICAKCwA5BgFs/ubaTSabOOO00ugYVhehdBghI0UAoIssTxh/w9nvvpBE/tvFvqn19Q+bOVer7BqYYIQoZttFO62hSKPK3tnt7TWqK6t6ZSX+UV58NLkAzWZme0kWsISNpvG1F6o4fmj5RnXyuA8eg53pJfUbbNdgTvBriYgfvqGn+i+JcZuBlceP+RPN3iOsswzDJt+rbBV+NHrVbJBgKhUKRSIQL6NFoLBqNffThx5T9iJ4HdvOF3RSz535FBPQOcYqLnRQEBAFBQBDYogQWf4F9St8Z3jXVq2LFnqM/0B3MGvlnkVrfEL/oFphBs8WEBUfrtMRUQaB9EBACdPs4DqIXgsBWIzBx4kQAKCkpCYfpOejly5fTnXNrr63WBdGwICAICAKCwI5FgBs98Qdupj5wHwR9UByCYroMlRUVA0AwBBDxDdv/oHve+ejWJStvW1X/epOzhjk5o2NaLE8hR7YC8fm1dTesaLg7ZX6MuIp5aPA4KJZQkB7FNVjiwbmID67J3FOvP7K8Mb6et2MjFR49lUFsRvzewdeTxlUNiUsM55KEdWNN4jOWCBERVy5bes4fz6ooK/Gitr3w5+JY6ZLvllISRUcI0Ov5ipogIAgIAoKAIPCzCXCJOCcc8w/pFN5wBY7q17BrHxzYbfkD96HloOFQlt+2X0KAbpuNmCMItFcCQoBur0dG9EsQ2AwCmUyGr11TU8PvnGOxmCRJ48ePd13XtujBZy5Bb8ZGxKqCgCAgCAgCgkArBAqHOPnsd96b1Wdgf7oe+cAPvqBP8kvg8wP4gxCMyj17n3vrnas0x0W0DApATqGZQGxCXIZ4X03i7nVNb9anl9g0RclZP3v3pSRA1yDOsvCOBvfWBv2JNfH5FqYRPacpG12bXfQ0xATid4ivuHhtXfN5Dc03GM5ddYl5iLWI73364eGHHxKQQQKQfSBJks/ni0QiJJcHgyNGjFi2bBki6uzlXUbp+SH+IHArJMQkQUAQEAQEAUFAEGAEcnKyRlmBWe5BGhp2UDUxo2OPHnN77pToVhbvUzUvUUNX+h9Vn/Pr09iyVwRnQUAQaO8EhADd3o+Q6J8g8AsI2Jbtuq7jOPfeey/d77MXADz88MMUNcZSOwkB+heAFasIAoKAICAI/CSBQgGaD3k6jqMoysSJE0Mh8uII+gN+SfJLuReZc8hyWVnZZZdctHTx10jByPZaxHkuPromfmNt8pGEscwku4tWX82Isxz8WwJvbLRuXZtchNjA/KAtx+GFC9C2Sz7QPyD+n6be0dh0fWPimpqmW1bUvJ3Wpr72xtEnncjHa4MBn18iAdrn8/ELKAAMHjyY+4oUdsDbTSFAF2IRdUFAEBAEBAFBoBUCuYu4sl6AdimJg2Li9bdkK6sX9u5p9+lWd9EfWeYHZvncxmWfj/p6urNXaWWbYpIgIAi0KwJCgG5Xh0N0RhDYYgR0XUfEHj16BAIBLkAHAoGmpqYttgHRkCAgCAgCgoAg0BoBT5l1Xdc0TVVV+SXJdd333ntv5MiRPCcBl58DgUAwGJRlORwJhiPByvLiobsOv+fZp/65eum1C+bd3lhz83dLv6SY6FZeDmIS8RPTmapo16Sy9zRkv0RcbZgUSZ1Xny2HPDN4iSO+j/hYPDV1ydppi9ZOvO/v/Y/4HZSUQSAAAKGgFAz4QkEpIPukvO9GOByeNGkSInI7kVY6QbHQrLQ+T0wVBAQBQUAQEAQEAU7AYaZZ9OgSe9EF20Qcd8BXA/pl+vbU+/X59LNP2BwhQOcQiT+CwHZFQAjQ29XhFDsjCHACmqbZlv32229Ho1EewxUIBE455RTBRxAQBAQBQUAQ2NoENhCgvc3pum4YBiI++OCD+ehn+ssjoLnkWxwORYuj4JegJATjxx3+1MP/qG1YQeFSrTyNqyPOV43nmxqmJBtuaG6Yhbgcke5rLcW2DU+D9gToBOKFL79y0J33lB50FIQqIVgVqujtC5ax9IhQFAkEZAjIFPjsvZ544gneZ26+wfclHi+wmBYCtHeARUUQEAQEgR2JgEjhvolH2wtVZuoyWWcYhoMz/osDhy7o0Tndp8u6CRM+9aKe2x7bFRHQmwheLC4ItBsCQoBuN4dCdEQQ2HIETNNExN/85jcBFtXFb6Tnz5/vGWLyf5g8jWDLbVm0JAgIAoKAICAI/DSBZDJ56623RqPRSCTi8/n41Sogy2E+asqvW3IAwlGIVQSqe57+50vvf/iphUtWIGJWoftTw8T5a+seW/TNI7XLX1RS7xrWGhYoTRc420ylm5evWv7JZ5++9Z+373vggauvvWaPsWNAliASgqIIFIUgEgF/DKAMoFqGCiDnZ3LeAAA/08SHD9150bffuLbj2iyBIb9f/uk9K1iC3yO3fQ9dsOimVR3H4UHl/H3TVhZLCwKCgCAgCGwiAS+JDl+P32oJAXoTKa5f3HVt7gmpanjsSavLKxd1LmkYNWTtv97E+gSqTIRu++IpBOj1JEVNEOhYBIQA3bGOl+itIPCzCNiW3dTUFA6HvRiuAQMGcPdnrkE7juOpz+Kfp5/FVCwkCAgCgoAgsKUJOI5zzz33VFdX86tVLBoFrgSzzxL4AlLYF4xAqAikIIAfIAi+kOwv3mXE2H32G7/T8JGBcXuEDtmn24Txww47fPT4w/b5zfiD9jvwkP0OyF3+fACSDySfT/ZMNSQy3Aj7qAQC4CuWoXMQqkK+aEmsKBbNXTenXH+Driqakm2fAjQizp0795NPPjFNU1zEt/RZKdoTBAQBQaBNAvyZGEVR2lxCzPgZBExLRxcdHb+dj70H/K93X6U6tmr3wfMaGzCuUrZhbtLhRUO3bFII0C15iE+CQMchIATojnOsRE8FgU0hcPnll/MwMlmWg8HgQw89JAToTeEnlhUEBAFBQBDYigR4Tj9FUXiWws8++2zq1Kl77r0X5f0LByFIochBHxT5/eFIEAIykC2zzEpQ9hcBBAB84A9AyEdVvwSSn2nXMkCANGYpyM09vIFYqviDIJeAXExNB0nNBtknQ5Efiv0+fzQcDAX8k04/LRlP2KZp6iq5a+QioN3WciB6TxO3AYrfI7cdxNXGaj8xubGxcdiwYTxmfOzYsTfeeONPrCBmCwKCgCAgCGweAZ7gfcKECcFgcL/99vv22283r70dcm12NeQXTn7pRwuvvrS5d781O/VQd+69+t6bUddQz7tEt6E+e75X3iXYq+yQVMVOCwIdioAQoDvU4RKdFQR+igCPhGpoaCgrK/PuuoPBIE8/6IU/iwjonwIp5gsCgoAgIAhsRQLpdJpfsDKZDN+M4ziKrq2oXfviP18/5qTjqjp3IsWY5QaMFuUf6JH9EC5iJUyiswwQkgPhQNAvk3ezJIMv4IOIH6J+HxOgpXxAtZy/JPqKwVcMfi5bk6DtI3k71LlT1dlnnrFy+TIy3EC0mZMVIj0lzCw4NhagvTvetr05toIA7bru008/7fmU+Hw+SZJOPPHErXioRNPtmUArwxv5E7KFeJM/XQvPyR+pr9/l/Irk1ipegsCOS8AwjHPPPVeSpEgkAgBHH320beVMJHZcKJu65w6N5NqINjo2OrqO2Toc1mtO16qGHl0TnYtfXZZT9V2LRUC3+A1rsS3+41X468TrLRYSHwQBQaAdEhACdDs8KKJLgsAvJ8CV5enTp/ObUn7DPWnSJETkD+oWOm949V++PbGmICAICAKCgCDwSwl4lyGv4mUOdBzr+yULX3x++s03//WYY47p338gBP1QzJToTjHm2AwQDoLfJwVapA3MK8301xeCYIkUKvP7wjzRIHN49jPxGqC8U/nYsWMvuOCiBx/4m23ZXE2gy6iFdPvrMNGZbpPzhTS4Vksb+18o8LWxyC+YPGfOnMK0jTzQu0+fPvPmzcvFlBU0Kgw6CmBsd1W34HzkJxudnxbl63RI48mdrTTLYok8DXTzhuYbnMiF0wtXpOfgjXw8otCgt7tTSOzQzyZgW3ZJSYmXXKe6uprfW/3sBsSCuR8km35QHBXNrI3T7sYBVUt6FmUGVi276uIF+VzDti0EaHG+CALbKQEhQG+nB1bs1o5HgGfD4DefgwcPBoBQKMTvS2fMmKGqKn92zLvJL6zseLTEHgsCgoAgRY1plgAAIABJREFUIAhsewKFV6IN6qxzrm0buXhkix7LfSdee/or08/+vxfHXnH+gEMP3P3A/UuqKrniLAVADspU2IvCmsNBiAWhJAylUSiJ+EqjpVXlBxxwwIknnnjXPVNnfzBng/3vEAI0F5SnT5/eqRNFiJNlNkuZyGWR22+/3dsp0zSFS6lHY/useEKzFyhIFSYTe/pyTpg2mACt0dzCcZH1sjWbztfyBGiixgVoGpDZPhmKvRIEfh6Bjz76iKfM5T+8RxxxBF2bLPvnrS2WIgJ8XMxkI1rNNiYNPGTf5UM6J0ZUmcM7z/t4NqdEP1YuOg7m5ehW4PFfLu9nzqu0sqiYJAgIAu2KgBCg29XhEJ0RBH45AZ5K2HXd2bNnR1keJ/4f0rBhw7xGN7i99z56C4iKICAICAKCgCDwqxHwLkMbVHjSghbdUDBr4tOJ9EXr1py3evlNq1Z8lIm7iFnb0E1t5ZqVcz6aPfO9mbz85/2Zb34865E5718685OJMz6dOOPT6z75ZubaVbVmysjf0iq65rXvOqQj/JgA7Zromuz22bvRLax4LbWsFCp9Lef84k+6rruuq6pqfX39qFGj+IXeyzkcCoX23nvv1atX25adSqV+8VbEih2GQKFIkz/f6NTk4ft5xcdGy0aDFYvVvaj+XMVhcg+txc9rJmQ7aLVxlnuT2+CU70n+29ZyMT63cFrhlMI6X6awtcJ6YQubWm9rKz+/ncKebNzaz2+nfS65/e3RZnO+8sorZZm8nHzs9eijj/I7r81u+Kca2MbHgn/Zf6qTP2u+49APkWWioyEmTXz6GRza+9tBnRp6RxeeNH45WmjTLw8fLXO8YbXW2uZQvB8ir9LasmKaICAItCcCQoBuT0dD9EUQ2BIETjvtNP7vEX+/8cYbvfH5De7wvY9bYrOiDUFAEBAEBAFBYNMIeJehDSqUY8h1+cWLP9+DKqYR70qk/5zMXFjT/JyLPyBNIccB17LJbgAddEzHMB1DQSON7jeO/WyjfesP+r3r8IUEfus62dYiqhwbTZPU5w4hQHMynHIymTz33HO5Bl34Xl5e/uqrr258JIQdx8ZMOvyUApHG02BaVrjEzHVn731jAdpar0HnBC/DQaOwqU1gtYE3yAZr8vYLek5fY66keysWzvWW36CyQbOb9DG3jwXrbDylYGYr1Q06U9jhVpbuaJM2lUZH27+f31/vZ3O//fbjP7OSJMmy/L///c+7vfr5rf3kkt7m1i+5jY8F/3Ku785m1BwHNRsNk0U4r6vHP5y6slfFgl17x4d0nTvzDVQzmFE0RBPpeacfDy3nUAp/n7ZgPzdjF8WqgoAg8FMEhAD9U4TEfEGggxDg/7L88MMPPDlGMBgEgPLy8kwmo+s63wmRhLCDHEzRTUFAEBAEBIEWBFzEb128Vcmeu6b+FRUXIDYyTwHmC0D3okw+c2y0bbQttFV0U4j1iGtZqUdMIapkhUsL2Oja6LoOrcaLbbmeJpeTw9qrB3QhF8dx3njjjW7duvHQPK6PhEIhWZYnTZrU2NjI5XvTND0brsLVRb3DE+C6p0vnLBucINXGtHTTTpt2kr2nTTtLxVJpOnvZllt4wjuO5biK4yq2bdiWp6TmbKRdN/fVYIYD9H1hFdcwyB4HEVVV5RX+DyepcvTdoaEhKg6NLvEFcu9cZS6c9iMCdKEkzUWnjVdv0frP+OC4pqJRsKXjaprWQkYs7NVGLXlyF83xOuZ1ni2/nchgW0j0NNircNhsI6j5CRttkTLBEmRXU3InWH7RTfhLZ6/jeD+AfE0+Mf+YAHtYoO0meZizpmmSJPH8OpIk9enTh++Upq1/koba2Ggv2m649Tmu63p3bbklNrvN1rf0c6fSGb2Fzmr6SckaGQfRcPHTj3B4v2/6Vq7cuev3B42ZlYljNoPxZDovQP/oVzEHmver8P3n7pVYThAQBLYVASFAbyvyYruCwBYmwG8A/vrXvxaGQZ1wwgm6TvcbXnCZp0F7Uza8MdjC/RLNCQKCgCAgCAgCm0XAYVrze81199SufTihLECMIyrsPrVVAZpp0JR2jRQw5iNAFZadjSvUGwvQnvrseAa47V6A5sqIoiiLFy8eOXIkv/oHAgGJvQBg4MCB8+fP534muUDyzToOYuV2SCDn6UwBxK5tunWIC238wMWZiO8izkJ8H/FDxLmInyP+D2nsZhHid4jfIy5lZRmrL0ZcjLiETVnJRm3qEOtcrLOx3nabbSdlO4pp6fysS8RT9E1hHri6npuYo8OVWa4+byxAe7ptoazGFSQ+xavz5rzlNwiRLvQe2RKHxVJZrMaPql6e0EUb5B3jfeZrsXe+zJbo0TZto/DobEZHPJOKn/79YVt0bcfSDZKG6eU6lu1sCZPlwjsd/mwNDcjZjms7ORm67X3k4xMzZ87kv6v8/dRTT+XJdbwdzDWw2dy8u7P1PSo8x9ZP/XVqNI7ELqGkQW+pV0pF3cC/Tsah3ev7d6ob1HXe3bfWWjqqKqqGzh68yD170fYWORTvG+lV2l5DzBEEBIH2QUAI0O3jOIheCAKbTcBxKMikvLwcAGRZ5vmInn32We/O0zAM/nyx98+NV9nsjYsGBAFBQBAQBASBrUWAqxE1prZY0xsRE0yPtlsoUC0ioHmMM4Vq8gxqBtOeHWS6c+sR0F4oNK2VK9xG10ZPnM7P8JbIV9rYcU844DvQxlK/ePIGgXLcgIu7bxUGRE+bNs2LQ/zF2xIrtlcC6wVo1sOF9XjxWne/JmvvhLl3wtgvoR+IeDLi7xHPQDwX8QrEvyBejXgt4vWs3IB4E+IjiE+w98cQn0V8A/EDxHmIn7H3BYjLEGsQ4w6mTDfjOBYivvLKK1dfffVpp5227777nnXWWbNmzcpJhxTiaKPZWgS0JygXSnX8G1eoKXlfGW/59V/M/NfOW6a1Y1O4eO4/YZt+M2zMxW6vWbZ85fLlLVbVWchti0n5D2xbXps01fvg/RAVLJNf7cf+FjawqfW22m2rnY2Xb2vJvM7I59N662sbt+JNKfytK6jz0GMeLOwtS5WCZQrrXG52LDuTSnz91TxdVVqsxT78SM9bncVbSGczq9auUVV1vWScG2Lkv/MudaO1F1/+nHPOKRSg33zzTcMw1jflrcj3y/v4sysb35HlD0TLoY42Gizc8dYW+bFj2NY8Np1cm7egAK2raOj027B6Nfbt/MWAKm1gl4ZBPWYuX4a2Q6o0O9/4FunEa/vFQRfud1v70XYbYo4gIAhsCwJCgN4W1MU2BYGtQEDX9UcffZQbk0mSBADV1dX8AUnXpf+2NU3jIrX3X45X2QrdEU0KAoKAICAICAJbhoCDqDIHAfKpZd6QpH610At2UAGa5yTkgaiI+NBDD5WUlHD1mftxhUIhABg+fPjq1au3zMEQrbQjAnyMJfeAPCliOHetu18DRtMY1qjENCxR3ErF6aw4Oyl2L8UYqhgjNHOkZo5U7d0Ua6RqjVKMvbLK+EzmsEz2oHTmQM34rab9QVcuVtW/pMxrE/aUpH1r3Loviy+pOKsp88V3P3xxxhmndarsEvCT2QsABAPhULBIApg561kWXv0ZC8Gey/TrrxC/RvyWvX+NuJAFWdeyZxj4AFGKSdsrkHzdVyCuYmUFq69BrKUhJzLUaWYlg66GroGOQZnMXIXeHQuZ58dGclROPsurqO7q2jX3TXtwzJg9yqLBsAQBWY4VlVx6yZVKWqFfFjIPaUMbzavMeZWLeffYOfU/91vU4heJLejJrK2dMxv1ljZeUNbLcAUTcwsUtlcw1+FORBu8t2i1YM2CFddvl81nc2hQDum5SfaTy58MobneTv2MSiaZ+oY9hJHbrLfKBu3Q9i1E59npzx1z5DHlJaVFEfrhAoDjjjl+wdeL1/eK7CA2KC06T8YqLXf4P+/Mmvj7M8orqyQ/natnnHHGN199o2V1ljSAgqypce/Jl/U9pGZcNPlYy7ChIyUpGJCLfBCQpGB9XWNuj/gfby2vwhot6AhfjneN1fmS+R1HRPYkAV3Z2OlK+0irewMwuTFSfuEjXI5lsPZpOTtXaLCUT2TnJK+zh38YXt54wTst0ELnzfWKFsm3ScbxjHnBer+46qCWoe/Zg/fj4J41vSq1QT2XX3pRmnbfRpOlIMwfX9qTH315aPhu5nf8R9cRMwUBQWCbExAC9DY/BKIDgsCWIaDr+pgxYyKRiCRJgUDA5/NddNFFfHCeP25mmmahAL1ltipaEQQEAUFAEBAEtjIB7pjh3Y5ueKPZQvchVYHdurM+eXJAfpkN18333BuRLXxYOz8zr18VfG631dra2t12241rN/ydK9FlZWX33Xef123viXjPydebJSodhwCX7Xi2QC5dzW3Q925CyKKkUvFTcYOqG2YlqjolqlPWotgVqtUla/XMmr2zVves1TVrd8laXVWze9bsnTIHp3BkIw5ZqQ+rxaPXGVdcfuNeLMpeBpABKNyhKFwMANFABQBMODawrPGPNea4JI6K41jFnWBaf3DMP6FzNuJZiGe7eLGBNyO+OeeDZx55+O55X/3bxfmI77Dg66cQn0Z8gZWnEZ9BfA3xv2jOZeYh81380LYWsuSjTI92atBeg8Y6yjlqUlilbqPuuLpj645tOobtKIi2bsYdxFQme9V1l/tyqiaURaj3sWgYIAgQOvbIE/MiMvvJoPEsGy0LDQN1HbVcJhVEvPe+aeec9+cnn3rU0ZKkBbqkfXOpjEx/HBLDyYZbz77xjxfPOu3M3YeP3nP3vU458feffvQ/e30zuVNMN2npTDYnOyLzps9LqIqD5JZLhQXpmiatpWi08BGHH9OzR9/d9xj95Vf/ywuF1GObMPDzwUDkxdMfeSXXJG+Yd339r6JDO3Tt1ZP323vMn848HS3LNihs3GTDBRSf6q4XJnNS58btOWjrxrLFiyccfJAffABw0H4HGxlu6Mw3SO+WypTf/K4/++wjw4cOAICAL+qXJJnOLAiFSTIG8P+wfClD5qYzcSZVF+5UbgCGM+Ue5owrWmj/6fw/ByOVABGfFAZJDgRkSYae3bov/nYJaawqdZV2y9EYLt4blzmdG4iaojYgagsWLAKIAoRCUrUEsTG77587fpT31rVNM97QuGThgs8//XjGP9/8dO7HqURcyaTyD+CwlnPCLu82XY20NJoKvjXj9QsvmDSgX4/y0mJ2NkKvPp1/f9rvZs15m7mrp01dzXM26NziB5uOrGIbfBPUl9f+9a8Lr7zklqlTDPKmYiciCdYWuio7dCTwGqaiquqCb7+75OKrDth//G67jTru+MPve+B20zRVxXRMHgmePy9c2pRJxWLfrZY6dW7/N/EPQaCLczaB48Yu7tu9sX+PeNed/jPrPXbWusyVPb/9jU8rvrH15+omblwsLggIAu2EgBCg28mBEN0QBDaXwOzZs/mtJn8PhUKrVq1q1fGZ32Zv7vbE+oKAICAICAKCwK9CwJOeW9la7sZ+/ZwWAvT6yblaW7ev240AzffzzDPPJPmGhT/7fKQB8fHpyy+/vKmpiS9jmqZQnzc6QTrWBE+A1hzSpBDx42Ztz5QDKoL+c4or6a5fJ4U6ykqYada0uoqgUQmnsbwJO9Xh4E+X7jJsb5CLwB8ACaRosKQkKoWDwOJKIeQLkmYYhBlzRq+zd1WwRwMGFCy13T6ONcCx+ul2b83pnbJ2rVePv+K6imAAZAkCEbhr2pEJ87yUeZiWPVjLjE+ohyfUw7XMeDM1wUgen01OSmSvUp074sYNKWtaWn0b3a/QmY32m2i9jOYLaL6M9tuInzv4tYNfuPiJS4bXHyLOYc7XC1xc+c23nw8YNDBa4meCOYCP/vpz/zQHJSjxQ+DBO65FY4VjLHHMxa71HdpL0OE22cvQXY7uaj276qijDwUAKeALBOGNVx9iEdkNTBAnSdE1SCE2DXzt1TcHD+4fjjANlYn0oUAwGIidfdYFTY0U7MlHtBCRDG8RX3/t3xdfOPmcP16YySh5VweH6YbMgMIL9ERuU+BcP+WvAX8EwCcHQhdefKkXAMt++ihuemOJlmQ9HkLrCXvUZe8D7xS9T7l+SjRAOr3fB2efcTrJkG5OgKZ0e54A7a26UcXWrAVfzd+pU3XQlyMQkaP33nFfTqlny5P6bKOrUydsUz/5pGNZ6nSQoUiCksqyyqJIAADCET8f5Dj88EN4Fx1byQvrnry+/vpAYnn+9eln34zYdXfJL8v+IoAIO9rUH58Efkk6bPxhSlozVZtSHaLluhlEVVOTtDbfI8JoGFaisanm7LPPBYgBRP1QEfRVXnfNbaecNOnQ8UftOnKPPj37RIKhoF+W6VeWXn6JTq1nnnyM6b88xj8fKc/aRHS1rPnhe1+N2e03uXUAikJ+yh3PXoEgxMrCRx17OOuKp/hraBvUAOn2FrOhotyM6axyyRWTaT0/ffvOOuf3bJZGDwqgglYC0VTVdYj6/G8+P+WUkyIRNlwUqQxIYb8MkZDvsPGHLlu62LTWIa5BXIdumhPgAw8mGltMgKZ2bTuLLzyFg3qurCpb16/vquN+t0A1KSfh+uQL+SOwwZnFD2zu4OSPsvgrCAgCHY6AEKA73CETHRYEWidwzjnneJ6PsiwfeeSRPDUz16B/6ta69TbFVEFAEBAEBAFBoKMR2Bq3qFujza3FNZPJGIbx1FNPdenShYc/B4NBLkPLsty1a9cZM2YoimJbthcHvbW6ItrdugQ2W4BG0JkGzaKkg/ROQdM5ATqLkMESC4etjo9654MxPXtDZTkEZZLYZIDiMJSUUBh0MAqxYgj4oDgIncpICjtgPLzwfxWrU9UKFjlYgliS1QIZPZQ0Io3qgMUrJ0ghaicSovjW7oOg0TmsVq2w3T622yuLVGy3l+v0sZ0BBg5MYb+1dv8694C16dOfnH7U9X/d/ZOvj2rMHm1aE2xrX9vY0zD2Shv7Npv7NRr7Nhh7Npi719kj6uwRNcbB67QrX55xdnU3ruxBcZQqsShEg2wvSDSkPlSUhi4+7wCkzI2vIk5nLtjPIT7PYrFfRHwd8a1bbjskyFbnbV155ZEsLvtjendXo5OisFZNu/zKyb5gyB8JyWE/BH2s+dzWAeDhRx9lZ4TFw1ER8dG/PVkUqpShUoKKc868jM9lGmuh/QLJoqlUnUph17jbbqNYiySnjtv7wJxg6sl1fEyOv3sTPZW6UJ0mcZnsunOSJVq2lR3Sf3B5jILZAaBTcZGZUbm9iZ0PUG3zjM5v9/vFS7tUdS0KF4dDMSYfE+Vbb709tyJpzvQi5dchr+fDDj2IxztLdDAqA9BVzunFEAoEo6FwJBSoKIvZRgbRNdVUSwE6L0Nz8wkWQ66kcd5nC/v2HgYQlCR/OCIFQ1IkXMqi9bkSDZIMb7/9luuS7GnaadNpyOjrZr7/9jG/PX7Y8N2HDd9j2PBdh+0yYpeRuw0fsStACCBUWdaLJPFweaykkz8Q8wejciAi+Ulml2QIhiAaAckHoRCEZPj9yScwuZVpxfkYdaasUnjy5ZdeHAmQEMxEY+Bx+PQYgc9XEonGIpybfNCBh5BVCCnkiJaBtkUh9kyrZdHjhPG9D78MRCsDRUW0eqxk550HsaGLBGIjK02mXptVVv531ivlZQEu69MIDPvi+iHA60cdOdpw/4P4NuJ/yPPdUmij1F3HRM1Ezd7AqYMdwV/wlk2piQY8+ajUwO6Z/j2toTv/MP0F1Fmo9U8K0IXn8i/YtFhFEBAE2gkBIUC3kwMhuiEIbC4B7vvMNWhZlp977jneohCgN5esWF8QEAQEAUGgIxHYGmLx1mhzazHlxtC6ricSiVGjRvGkxN4/CeFw+P9LS9OmTVMUiq8UGvTWOgy/RrtbQoBmGnTOrIPUZ0lDWXGBqc9hDfulnAPvf6hzERPuigCqSyAsU3js8b+LvP6vCavq/vz9qtPuf3h4950g4iMprViC8ghUV8MXi6sVjOmuhCib6DPRr2Ew7Q7+auHRFCqdi46FTr2g3h7dYEPW9GdNqQmBLEQsUE3ImlLCgRqEZiyts/Y57ESQg+CTYf/DYFV8WNbpYbhFJkomgoE+HWUN10dwZzGawBFPvNY71pnWIpWZ9fzQg+G1Vw/8fulZ7885I5ITlP1FUTjoQKhruDCln5qyjk6aRyX0I5u1w5vUw5qzExozv6ttOu+QIyhem8WPgj8Ejz99hIF3Id6KeLeDLxj27FRy8W9/eyRJe6FgKBYNFEm+CEhh0mClEBSV+XwyVFYD4mrEzwycZZM1dm2PzqT2hqAiANHq8gCb+zXil8w1ezHiEsTFrP4l4ieIi7Lqshi5bQP/Ro/bczTTGdew8NU1eQdt7qPtvXtz1zC77Zr8+xpmtL2Ub8LFea67sFMphR77gbTJbpXFZroWsZ5tguVyxQxiwmGFpYNNFLxnSBp2cfxBh/l9wWgoBzcQgspqafHSTxBTBQvHEc1Uat3YMSMCfoqF56+qyk5/e/ChlSsWKemG3580MUgGKfQqi4GprUKHW4dzadV7r2e7w2c5Ria5ZMH3QwfswtaTisKRohh06+E7Y9LRA/rTQEQ0HOTRysf/7mDTXom4SsMvEL9CXHLMCePYWkGAMPgCpCv7Aj4IRcKlki8s+cLBQMwHgVD+vKF46gDIIZADPFCbD2dAURE8N/2qlp7mq9gBqkdMnX3WqfRISjAUknxRH7P2IOkZYjLtrQz0/WKR2uFgIHrgb/ZGXMuc03lGUG6n/iVzV/8WceEDD94W8FPEOh9i3HfvAWxf3kV8E/HfiB87zjdT774knI+vlthXryTMnothe1scpO/izDknNyrnIk5GfADxI8SVFApN7s+ajRoLrt/sXzSHVPSF87E6NrdXld6ne2L8IWttxIxB4c9CgN5svqIBQaBjEBACdMc4TqKXgsCPEFBV9bbbbisuLuYP2wJAaWlpbW0tPSrnukKA/hF0YpYgIAgIAoKAILAdE9A07dJLL5UkKRqN+nw+SZKCwSAfqz7ggAPmzZuXf+Sfgje3Yw7b6a7lBGibRKJfZMGRt+nwop5VlBQMZNxAQoOk1anZGXv/ExVBP0ljEeaDW+KHcXvCu7OHLF47KOHusia9U53WU8dj7n9gaAAg5iOrghKA0iA88wJoWJ1S5eY0mCjrFE8NSWvwG28eUBQiqVpmjhiDdoV6a6yCRYoVUqxAAn0JBMUBzYas40s6gWYM1Ro7T7mzJBKl0M2yYorabEgclzF66Q4YpD7nCncdcREcjMSz3b9eNKakM0RYOC/3Er71ZtkwjqhPDEqawxq0E/oPgXCUlFx/ECaeCTXxMUlrcMrpvkFJmiMz9pmdujK5Lh/S/O5no5K4R6O7k45D1qp7/NBw2km/70cWxmEScOklgxyDCMXdQjQMoQArEfjgs7NrjWNrtN/UK2c9+fcDyIqa9F5CV1kOLt6n4YUanqXhHzU8R8fzWfmzjn9GvMzCW5cuf7i4GEpKAixeGA4fPxCt19F9GN170L0b8cl8+TuiV6azsG7+/iyL7+bvz7Mo72fZ3CcRpyG+XBKhYx1j5s0lAWhY/R4zM5mZzyc5jyJkWynLLGcRYnLiiSdUFldzAIEQKe8jRsOnX02zSD2f7xWXzFIWnXTSfhVlOSXUH4TfnjAgnp6D+L1FivCyW66/tiRYWuwPRSlYHpgo/zXip+h+kivOJ+h8gu6HLHR9Jrqz0flST3yz1679O4WjYfD7QY4AXDP5t5b1AeL8VavfpGMRKArLpNjuMarUxVmI/0B8nFmQv3TJlXtGoxQaz+OCJT+UlhXHIjG/JAVkOSBxETcvltPBph30BcEfgVg5VOwEu46BU0+H9+cejfigjTfZOMXG60y8zsAbUs6dJr511h/34XD4GEwAYNxouOXmkqf/vtN/Z+7x2KP9Ro+AovwZRPI2wF0PjvmhfqKJp5h4VFqfkNYPTltjM9aotL53ff3JZ/++Z5h3l4nXV1w5VLPPy7r7x+0hNendm5Xz775/78pyqIjRN4DGFSSIRaA0BrEwVBeFi32BGEBxCG68SdLwqJS1a8YZbeHvEO8k1dsls2lW8l7dm/5L6g3eOja6Jl52YePAno3dq7RB/Vfecw9myUdkwyB+L9h507cm1hAEBIH2TkAI0O39CIn+CQI/TsA0Tdd1+/btGwqFeO5BADj//PP5naQQoH+cnpgrCAgCgoAgIAhs9wTefffd0lJSwmRZ5gHRPvaKRqOPP/44330RCt0BTwOWZ4wyeFGUIjPo3UQP6I0EaMWFjBswMIbYycaRr73bB/wQYbGZYYDKEBx1KNSsm5CyBqYwmkIpjtDgQBr7pzLnl0chJkEMpBIIl/rh+RfltFmuWCEHQ4ZDzh4ZhLg9+M47B0f9FC4dZFkM/3B+qMHcPYsRLkAnnUASQXFBcyHrQNIJZbFrTXrfPffOGVqURKB/P6hvOE7RWxegVRKgO6eTh+4/DoorKLrYHyDzjfvujWjqnogDsloAse+KpnG+EMVTh8I+KQDX3AIGDs5gLIvSBiVl91xRP6GsigfqxmQ/VHSFhbUj6zCQQkhiaK05/MLrSIsECpmF0kqS+s74Y9nsT058fcbBxx1Hjh+VJVBSBNEoLF45YZValcVeJh43aRIFwAYBigFKZJh0FjQo+zfZw5rc3s3Yqxl7JXBgAgcncVASB2m4S8KZMPfTM4IBiLCA9JAMxx/TKZu+zFCPtdSDjOy4dHqfptRedQWlIbmPVxoT+xaU/RsS+9cl969L7VvLShaP0u3L+3SDYhaW6wco9sMP3/1N124wzQts7RpTnaJrNyjGdVnzurRFJWmzYt5i4vTa+Ev3338lxfbKsbAckGUIhGH8EZB1bmhWJzdkrlBxCi9Z517N+cf5F1C4MbN6pgN07Km+FE7V8M64e3OTfkfG+McRh+4hk7pLwxTjxoFi3mw6t2fUKZpbUtBmAAAgAElEQVR+k6bfpGs36Rr1R9ev0Y2rNOM6Q3sg0/zc5ece0D1GVCtk0vSvvmyfrPKoat2WMq/OmtPOnrSXBFDkJ8W/pAgWL/vLOuV36yhn5qEJ99R3PzjcJ4Psg4pSqCgnPw1Jzom7MvMNp8DzEOy1P5w2qfrSK3rcee8uj08f9cZbe3342YE/1Pw2pZ+a0I9UnMNT1kE1id2T1l4JZ3TCGdXsjE3g+FXp3189ZXgJG5AgE5sQ7djjj+ziWudo5oH1iUE27mm745vrT7zgfL9Ejhrg80MkBlW9YEXi0Bqtm4IVCnbSsExHiY21RNOZ0cdPYO7UTFwGgH/8c/96ZXiKHgWQNOz3wv/1CMfIHicWgE7F5NY+em945KlR//nvby+/vFvnMrLcLmXDSzffASoOUrBEIdv3yoy1v+M+ihSkX88cWgrctTfxh9IToG0L4/U4qM/crhWNfXukhw37pLYOvXFPT3QurGzipsTigoAg0AEICAG6Axwk0UVBoC0Cuq5rmjZr1iz+RK3P5wsEAqFQaNGiRZTwWNc3CH9uqx0xXRAQBAQBQUAQEAS2PwK2RWahmqatXr166NChXvAdD4Xm/zyceuqp3I7Di4be/jhsp3u0gQBtI37UrI/ZhCSEGwnQKkKzDjZWIHb+amF1r4FQXkVnTbEMlRG47ELIantnnE5NqtRsQIKkZ56usE9T4g8DepONgBcB/d6cymYtZKLfRpbnEP0phCZn8PG/g7CPwjzDUQqWfmX2LvVm37QT0CxZMwNpO5J2ZAVBQWo84QbiTt9/vNstVkxiZQCgKAx/OB2aUvuqRmfdBsOldIsK+rJslQzLnZi2B116AYRZrGqoBIrL4c67u2e1caZeaSvgqJGMOuKCy6CknHZNkiBaDItXDDexs4YBlnqREjB6UeEpu+cHn48Nl0CIZN+IFIAJv4W1+pga15/AoIVjH54+CAKQyyIXIFORl97olNJHK+ZuijkqqY65/kbo2wP694Jrr4dmdXQCK9dkKtfU/nZQb6gKkFraiemb8xcPSWLXuFsZx6Ik+pMYTGKnpNslgeUJLMpitMkY/M8394xGWLArQFEU/jAxmMkcZui9UatwjRLFKk065UmnMu5WJh1eqpJOVdpmxeqctjpnWElbOyWdqqRbnMSiOJbGnaomo3vWPP6AvSjMvMQXLvX7yqPw1fxzm7P7JI2eijJQyQ7Oqn3TWu+k3jth9G42ezdZvRvs3nXGbvXmxP9+drpPpkGCsFQkA1RUwol/gJR2YFLvnXH7p51+KadfEvsnsX+zOeGZZymdYzE7QOUR2GtfqHePa8RRK7H/MmNQAo/95/sHkK8F01WLwvDQ3wNN9rCks0uTMSRlDc8Ve+eU2yfl9ko5gxLGuJrakx+cOqpTgAybq3xQ5oMjDoXm1MlZPGitOqAJd45bRzz7/PiSCJQHoDwIFTH4Yfk5TeaoJuyUxF5NZv+UM3rFupF33A1XX03l1ttC9z+8jxyBilI68IEg+IphYfMpy7Kjm41dM8awrDk0YwxJagOTet+M1VvFXgZ2jxvFzXpMw+qEWRK3qDSYPRM4/sl/0M8vc56RyBMmBi++tUdKPyCe7aq4lQoWIXbWsSpj9HLw5L0PZ7q7BNEY+b08Mn1QszN8TRYyWMFKNINRBctV68CRg+nRhCIyDaFBjjVrT2/SemTQb2D50uWDBg2GSJi+NTLQ4Md1t3ZZo+wfx6G1Zv+UO+6d2YOGD4cuVXDKyVCX7KxjIJ96VFKwi46/cfAm0qAd8q2mHJK5SOWf82vqyc7r17F1vP8O3LlXfVmoplvn7665LplIMXtr1l6h7uzVf86WxDKCgCDQsQgIAbpjHS/RW0GgFQIHH3wwd/7iKe+Li4vpfwTHUVVVCNCt8BKTBAFBQBAQBASBHYCA67q2ZXuysm3Zp556Kv+HQZKkQCDABWgA6NGjx8yZM3cAJNvXLlLaN9JqbLRsylNmI37wywRoPa+3ZlFqNv0W9q9r2uWY45lw5aOn9SuicMwESDQeoOmlugsuyhaLFE4ymTjl9mpo/n1FKQnQRSx+tjQCy9cOTlo+FSGuguoEVDeYQmi0dxm2CylikSDESiBYCfXWwc1Wd9WNkgBtyVkrkrVJgM5ScDE0u5EGbfTxp4JfhrIiicJXgzD1fshag3QrYtpAsdVuUEE5zSKs0xhssru8/EYswGKKg4GwHIaTT4P65oOzarWaBsQqRxn6r3/3K6qAUAzCRRAtgT/+GTLOaMRKg+yqgRcubZNziNX31X+N8IUgGpPIvkaCKXcNXK0Mb8DKtVqP9+btXME8J/x+iJVB751h9rwDmjK9bIymVJ/uRE2MqlYXNbuPph7s4h4Zp4uOxU167zfeGFUegJ2CUCWRgHjZBUEFd3OxRMOIgQHuK6JhTMMyA4MGSgb6EmbP518azBLOkThbVARnnQWKMdrCMLrg2qC6BM0raRe8knUoojzr+HhJOz6aVbBwswkG7nvmKWRB4WeuxCEZ3p11aNIanCWjcL/lSLYDtgsWG7fgIe00qIDda5QT9zuSonp9QCn4AOCwY6FROV7Hbg5CyoYUcxXPYjCDFSnnwN1G0C5X+IMRgC6V8M3iQ5qwXyMGVyAss6oXNe+1x/7g80GEIpWhb19YGR+UxHAWoxmKzw3xkkWflhuoCDS7O3/x7aFVnej0C5O6CyP6whdfDk/a/RF71bugYsma9E5LVx7dqZQE6AoZulXBurqjFeytYWBtFjQsi1sBEzul9TLT7mla/ROp/ZatvSCat3CRfDDuEFhpjvjBIEsZi31lFIfGP1QXsjakDUibkLHIEMZGn0GUZBVDKey3PH7M8LG5YGpu5PHijDGrUmMzThfVAcSQxaL+dYSUBilz8DufHiKVMP09QCMuRx4DtcouaXrmoDhNpSiNxSpW63h0dTmJyzyZ4f7jQDNOtWmPylKZXS+5gPRuP5OySyJw79961aT3rXdjKfadzWJJk95bcfepadg9nhnqYjnSWBGd/Cob0VEo1PpQNF9Cew0FQZMAzVNY/uSvKLcGItcOhz2XQRbPDhoqTti/cWB3tc9O6V2HLXr7XcwalOUQdcp46InOhZWf3JJYQBAQBDocASFAd7hDJjosCLQg8P3338uyHA6HPQPoqVOncgHae5zWzb9arCk+CAKCgCAgCAgCgsD2SyB/8c/95Zkhnn322VgsxpOYeWI0H8CeNGmSYRiu6yaTye2Xyna0Z25OtuEpvJjUM7tZ32OTIqANNxdEzAN+s+wBfAePuOj8oogfAgEIhSj0+NjDQE8f5GrVqIXRBMcllU1DXwb9q9MQt4csX3VacZSMNYp8pHkdfBA060OSSKKnYvtUBzQMJLDo8+V9KKyVLRMEuHIyxNP9FWMnFzvpRkg3Zc3yZS3I5uKaoc4sW7j8IJZljcx5fQDVneDr7/o7WK67YLqg26A6crMGiNF6A5rN3kn9pD32IBUyAsFoWNqpB9TW74/Yw1J8jlJsJEZ8OGe3qv7M01oCKQKDRsLqpv2b1S4mhk2UbdfnFZY70aeYO0+5oxPIFAEtMT3vzf/+Joljlqc6NyrHjz+CfBIiMQhFoWsPmPPR7qY9VjHKNcun2wFeVDuiW9W61alZBQvlBEKT3v+cP0qlEnTyyTJA13JYvXpC0uged0Alv2wf97PWMGii3yFTEbAxqNojH39iQICFBgcjEA7DlVcXp50hGumGQd0NZh0fKcv54snNWcen2KxYsmLJWZsVEqOZQs0USQ1Bdwb9fVr/qrwHcSQIDz22y+pE3xQJx0HKJ2kDWoBMhlZNsDCadnwOjrv+9p4ScwVh5hbQeyB8u3pcBodmMcIiyn1ZlLMYXNwEcdzziuugJMw0boDyMDzzTEVjqq9iF9Wloc6tXp7Z64BDyXajhHloBHww7ZFYs90vQ7pzMI2BbL5Q5kkNLBvqdakZ9//d2RK5mTCP4wjA049VG+4oAyvSGEjT+EQk7XZryow49SSokKBnKVx2KSS0IRksiTs02sGLipJKAft+w/FnjCH/eHtfCNPgR0SiQOP7pvaOG0MbbVrYC5BXmACtukAnpAOmDbpDknTKptyYcdr0ntfe3CMSI8+ZoiDt8nV/qc5aByL2Ud2w4Uq576BDK+o2ZMxuzZkj99oXqqqBMjQCdN4JatK711vAd5/F6Rdp2GX+4mHl5fSloB9wGf58PiT1sY1G1MQht90dLY7RrCBAVTncfEssoY5M2yH+bEGGjdZkMJpxyxS3SnNLNZQNBIuShZIGrdO3WzJxCFqXoD0DsY79bnIBmtlx0OhXa7+luUDpnFTNnTtMJl0/9xwO6fd9n85NA7vVH3fkGt1GB01ElXJXFgjQrTVaKErzemtLiWmCgCDQEQgIAbojHCXRR0GgDQKmaZ533nnc1TEajUaYJ1w8HucCtLeSdwvqTREVQUAQEAQEAUFAENjuCXj/ALguCQPcuevLL788/PDDg0EeikfihSzLEkWXwp577rly5Uru2rHdw+nwO+iyoGeHIp/JaYUEoc0SoLMkS5XUpvs/8mR5BQvABIDycqjqBMu+P8bSeqIJqEqokwRpMrMLJizGmo0Rcz46urSY1K6oRJLZeef7ms2+FB/tyFk7YJCoWtSM3Z77dwn4IBSg0NbyCLwzo0xTOulGleVU5AVoykCIWGywoOYkDrr9ni6RMJ2lsRjl8evVBxrTu2Rt6oDlMrHPCSDGXCyKm5Gss/dNt3QuiUJ5UC4O+MpK4N77ezU0V6PrN7MVZnLUBzN369aNGRb4WPq/MnjprdJ6pUfaKnIwwgRo2XZbFMUYccmV/4+9MwGToyrX/1dVXUvv3bMmk0wymZksk32ZhGwkISsEwx42ARcUBUFZLoqgXK8CAoqKooAicgG5yCIgXESRxZVdUOEiq4GQZWZ6r339/vc71dOZhIB/Ba+GVD3n6dT0Un3qPdWV7t956/0yVHEuBkIM4jn406ajtxmLys6aT59Dczlh99J5uOu/F1bVWbqumI7IALRgefVm+7EQ7YXs0sFlUyZRWEReEDiAEz8INX2RHjTXiLwLrIk2ihbyLgKy5iOv2zMu/epYCiYGmhtQ4nDBJa0V7FaJn4pqINeGDc4j0fMO+hwyaHZbf4InkC2a2ZMp8ETL/unxZVmOxlEWlRx5w1OvladUUKoipXgTfXaAMDSSC15z49squec3LSFP+/Ci5OBXTy96TZugUaAwhZmwgBRxIOAK2PO7Z/eRUnSQyABZAdavhqHqgqrdZJqjLGf6a5Vlq48g8JoWIAuURv35z8FgZY6O7SrGakSxqems0fSAAZ4lWjjlmjty5Klm0cm8BEcfCZ63f8mkDrAm6BjXMWti259f7Dh0HaxfCRWt38PRBYemLho0OeT+FitrqTq9l1w+lhNBjkFCgJwIv3lgJWJ/48nhCgFocogzAO2B69YZdMUFC0UXO594cUpMIhaciVP4zNReUCvHDtWaPQzRM88YNG95RJ9pQsVpLpTnnXQSy82QExxAMgUvbp2+3YIqXXZAM0a2p+h++4O/HZ/OA8eSTOIKfOVyqHrTBrUxN9xKx0aSUX6Jh9PPgk0D/TUvboZzNgHxcZ1c4dRMMpJzNmsOxlirM2gbm9Fbg8EliK+ys+UOazOdbHabC70DQNPDHkPPJQt1D484YvPUCW+Mb3l9yvhnr/8BsWfEEmIN0aILd4cZ9O5Oy40HGyu7e1Z0X6RApMCeoEAEoPeEUYr6GCnwFgq88cYbYVkhKuvMlsMPP9xzvbD24Fu8KLo7UiBSIFIgUiBSIFJgr1BgJIAO86Atywph9NVXX03sjE1dK4oS8ujQE33llVcahhE+ba+QaQ/dyV0d0Ij465K1uOZzRr1MGTkZ376NdEBrCNWgrWocO3MGZTQzSyvEE3DLHeNcnGt7CSKPNkOQAXh1AA0WZorevDP+LZ2QydaqsOqC1904lczIBKBFzZVdlG1sGfSmnfp5SOapthsHMHcG2MZay8yaZsowZNOKOa7IHKBQcclkqmOm4i+bO5+4MxVQA0inYM06sHFx1SD6TADaA8OTSwZUHNHB0SVzxeReyLC5FQlg3jx47Y1+y8sZZqY2tPr735qYSwDNvPCs8F8aLv8hbLHHvl4F3Rd9jLsYazSH4jioafaco44HgckhCNA9HcruyVsrh/3sF0uaUsRqySouwRcvkzVcunmQmLjpAgPQdaTIsqqJNiLzGlvY/PzmGbJEEDYTo9u7fjLO8Ptsyt8Alr8RtzFrY9oZAaBdhKrRffan05IIgkAVEdNpuPoHvRXsCg2tNVa2UQuI4P//No89k+HIkgVVXUbnqJk9VLZOimUSMkycAn8pzSxRIDXBSvQ5dDn06hb4giUX9VUbjwmLIpITN9MM538NhnCmih2DDtHnMCVDQ1HH7Far76zzYk15Ei3JQXsT3HPfvJI1y8TpgXfYU0+s718BxLI5qn+YBjjjY4C41nZzJuVv7EDPJgrMscshguM1F9T9ZyxmXl+gYYrJ8OgT0yyvq+pQDgYDrPR8k8g+b2Gqoo1C7CvZyRr1StTpIcqKGflJsQNetWYecQx1Ji7SETWhA8qFYxCnsW3Wdy3MCg+BtU2dYc0V6DCmsY7XcOYnzyF9JI483VkJLvtKwvYXa0EGUWSfvjcD6HxJnXbhl+mAT8TSMmQEHp59pa/sxZiMzKQcyDV71E23JtJZkGQi0Okc3Pvrlpo/vVA5cMUyUNhHLJ+GAw+CVwf7S35rzRdMj3m0mdXa8MEKeCvgbfI+15tDruewEYN2UPGxG/EkxOeG/c4uMyz79ciMN5ug687oMDOaAHTF0T3Ex57EUc0PjG95fVLHpjlT70Of4jwQNUaf2fTZ7gF0gzizHOooqGMP/a8q6nakwAgFIgA9QoxoNVJgT1PgxhtvpDS6Ecsf//hH3/ejH4172khG/Y0UiBSIFIgUiBR49xUYCaDJj8ZqEoZv4zjOiy++2NvbG8ZxSJKkKArP8xzHybK8YcMG26Yro6PlX1oBhnuGHdCI+NuStazmC38fgFYRqs7Uz5+ba4oTAYwBtOThzH+TBrR5ZVexA8r/JQbNDLA+A3YaclutRDVYP66Lns8BxAWQFXjkyeVFZxwBaE+uebKLKQM7t5nkb5XS9LU1mYBjjoUgWOp5SdOSdIM3TI4BaMHwCUAjtm/TOm69pyORACXGZbNZQQRRgdPOzOvOXM0B16cWAmjNE2xsqbq9N9/ePLqFqG4cICXBJV+FweoM3Z5WLC37+InQ0UyVCTMpSt6I5Yg+l7BviwUmxvRAcFBxqahgnUGPANDzVh9YB9DAweLVsF374BvbT12zClLM7i0DfOykZEFb6eI4xFTNehsAzZkoVYMJV13Pt7ZAQiQu2ZSDv2xd9FqBtzFBsRIESRWLEngzDvL+sAPadKFYnfiRkyRFpjAHDiCXh1vumFHDLmZdp0Bn8jL/TQA6RNUMQBcMcDARuPt+7EPh7wqZhikFfyksKWGqwobbCzj0BC8QmTiihn3X3tAti5BRiD7Hk3Dk8VAMlm21pSE2heAwK7FJBu14BVv+UtwnnaWeJzk5pxAb1fwPD2jLy9ahP/j+dJGHHEvTVmSQeTj7VEkrHIhOm21RlkXoemawuE6TbRQQM7o58TvfHRtLgJBgx58Ax38IKua8sgmE1N261ZdhaKLGAxqR9AD5gk2THCbyOtv9BkTWfQp1sd2Mpi+dPYekSEvk1l+/Dmq1NQ6OYq96E4BmUTYjADTlqGwzUy9snZ9rh1gMkjHoyPA9Y+CNbfsWjXSACRKHXrUbAK07cy/7uiLRZ1DOKm0SD//zMs1PjADQYklvu+K7kM6CEicAnW2F/9k8p+ov/sLnaOASLL99Sh+8+Mb+BXdciU1O6CwehEJCwrYbAB06oCWHZb849HFI28H+iL8N0BkuJ2CSrTmc/XorAD0c0OEhbq+qFQNPPUWd0vWX6eNq45of/ebXzTBzg9HnHZvYnaM6BNCN6I8Gjx658i99ho46FykQKbCLAhGA3kWQ6M9IgX91BarVavibMAiCRCIhhlFwALIsd3d3G4YRhjz+q+9G1L9IgUiBSIFIgUiBSIF/tgK6rvf394fAqVHQGACam5sB4L777guxdYgewkusoknuf/agNd7fZ25EN4Qx7N4nytYq1U9Sju3Ojs63/xMxaWJMxbbHfj+pOUH0NgYgczB5KpSNAwfUDguTZPBkYcQhEvUpMRYGDBgwpn3l8ngmSdZVHiAuw7SZUDSOqLidaiCrflL1kzamK07P65XDKZuZJzbW3A633TXTdCZ6AUdEzAXLCQG0aPiCHkDFbdHcgw5YT8hYghQHMieQPfaK787Q3ZmIYuBR2T3bp8TesgEWjlGNDfutgKxC9C0bg9HNMFjeWHXW33bHnH36IZ+hnNyUBJIIM/vhzgfaX9PHvFCAKiZ02v2kHcRD7tZg0OGK6izsnQ7ccMrEMR+GreUTv/+9VTGAXAyaZZg4Dra+sV7Xpph20nQFwwHDIQc080EPwz7G/hAVHXPbarM+dDIkEpTtIPJw5NFQtOYxNy5ZdJlrWLAwsxOAJvd0++DAgrlzSWGJJzO4IMAvfrW4xiI4mN+W2cYZTg2h6l+/HQGgyzaoNnhBz513tocpHxR7koRvXSOUcbyDyZAmO+SWJTuzgT1vFFf3TSHPOxXBE6BzAryybe2A1VmmyO/QQku3JnIaZkvepPO/DGmFDoEMp8QAvvfD7terB79WOuXoEziRmdYp5ESEttFw2dfzhrrCM8eS457FrewCoJlpV/awZaiyeOp0dgLjIZOnlz/5p/0rdgdBeRc0lyI4GqEZodOZBT2H0RzsoQDIDsxYuY2gOmB4ccfpfPH5uQliuZBiERxf/BIU1Uk6xocBNCVXNKzT4ZUE4a3rUYS0g+KAPuZzF4CSoDmPbJxyPL56cc9Aucdknx16xxEAegeJdlsK5Tmf+QxFcHDA88C3ZGFLoR+xVUeZxWUQka8YYz7zOepeIk6fKV6GanDs9vL+E9rIU58AUGS48/4J28zuop+v+CKlsftgetQobJoFVVN0deNEQSg8bgf0QbCDpEPzHykHJd3rR7zZwU2+p7KTjEmnnbeJ4AjpMwPLHjtD1Qyc0v27nlEDMydUxrf89JW/oGqTOZr5qBtns+GVYXjN/h4Jmt9qffiF0b+RApECe4ICEYDeE0Yp6mOkwO4UeOihh0RRDEMbw5+Ol112WfgTMfpxuDvBovsiBSIFIgUiBSIFIgV2VcA0zbPOOiv8IjHyluM4URTPPPPMcrnceI3PloaxunF/tPLPUMBHNBHNEQD6qbK5TvWyRiDt4EoNwPTWKz4Zb7NmsPC882BUkhBxaCe97gbRCCab2MRyIajwICUv10k0FcpD7Bssb+yaQHAtKyoi8PE4HHoklMyVNXeM6sdDAG1ismL33f+7FSATKYvJkGqBP76w2PTbPSqvR831eccVLFc2qFSaHOD8q68em08Rr4xBlucUjqA4/PD2ft2b6iNPecQuuB4B6ABlFyc//fu1iRgz2AqQFODoQzu2DXzivC/A6A4y5woSJTgn43DwQfDSa8tUf5KJubIPRJ+DtEWOVCXMwH0zgB43kT4ZEk+FEE84CQar/7ZsEfHBFAdNcfjRDVlTnerpLb4phnUUG/TZdEcAaA98FGtuu4UbFywBSSa4KCvwuS80F93JNeKksZCNsmRe0UTZITs2YADoZlx9+j0/HpeIQVIGJUYWclmG3/9x/5o3scaSPSi05G+izzt7pVUXajZYfupPz/fGM5QsLIuxZBI+cBKUnX1KnhIGOrNIDaEWdNb89519rpRO0nSFApDPwnevbyo6M8puykTOHR5WBqAFLRhdcZatXEvTA0nadS4Rg+2l/7j02+0dPZSeIWXq555Ro+CWO7pVe7HltgRhzUNWzW8kgA4jI8wgawd9116vNLfQa0VRlGT42Cdga2HfmpumrG1GlsMYaMagY0agUGPTM/TocLOCGAujoCOcALSbtc1Jd/94NIF12juafbjnvtaykxumzzAcAyLUgyzqRmZiyiGAtlGycZ8FC2nCQ4pBSqEojy1bjq6YzY3PJj3Z512/boKuh0E7Ha57yCkfoxBnnnVg/FioOYtNmr2IDwNoqNkTzjibDiFJgkQa8m1Q1E/9jwuhVYE8fVDg6GNhiz53EJPFIF4JKOybAHQjHOZtADSKNspOkGMMWlL9STqeb+KDAQ6xs9wwgN7hXR5x8qvjYzon+eg7LAb6m5dbY5sfWTDFm9u7/ZMf0yoq6kHAAPSIFzZWIwDdkCJaiRR4LyoQAej34qhG+7QXKOA4zlFHHRV+WeN5nr51SdLIn4h7gQbRLkYKRApECkQKRApECrxTBRyHykE99NBDI8sSAkBoiJZlubOz86mnngovsQojpCMA/U5Ff3de7yKqiKqPZIJmyzMVa4PmN/2tANqkUIKev7y2f89YSLEYXhlg1VJQ9WUBNntUmgxC6ucgZ3qgE0uNk+vWmXXyKWReTXKQ4lIyxOIyXPw1qWjMVb0Ow09pmNAowFequjO+/LUOkIBnrW8eFI39LD8R0mfyU4fkzlOMIKFiysf1k7oZ9iWnb5wTyAgtZeHBR1cZwWSLquHx6MRcT7F8BTFVrPZcftnY9iz1BACaUnDxl47rmwjZYbIJCWjqgEu+mto+sLimd2lWKsBs1eFMTFqYsFBi2RdhAG4YRBDe8qqzsK2TthmXiF9/4gzp5ltXxoGq5LUk4ehDwa4t04YU1EQ0wLE53WPeZ2Y1bbhNyXPqgYdSzRk/WD0y30qp1hxH9ti7frpfye1RCZgmrOGZA5sZci0C0Ap6CTR60Tr+kFVUvi8lQVqJx2VIJGHztuOrzhSVFWysA+jQ1LzzbYO07maFEicodEJzoWqSa9jw5688gPaX50FRqOrjQPkQF7stNvFgUWTpiVoAACAASURBVKVKqATTb759EbtMgk1XSPCBD0LRXGJim8mitL1ADJsTEEnXvAkvbVqdz0OaZYvLIByyZuXSxVmyPCdByoMymlK5Tz4NBodmau7Yqi3YbKrD9cnkbg4XHmQRHFSe0UHB9NvL2uJlqwjipzMi8BCT4FePzfFxtu5mDV80PNmgOBqyORPz9RXLy1l+qs5/aUTCEpEiPRRIoeYGlfhrNmsz//0zkE+ABIICYlMSthb3CUF/UDd3U06Fi5ITiPWGwggHtGSi9NLmHlmmiHBJgJZm2HclbCv360FzmJ9u0aQLeB7veTsYtBXwht1V2H7U8sWQT1JCiwhw4Howg4U1nzNHAGjdn3TyqeSjFwT6TI3vge2Fr6QTNHU0SoHu8fDIUysHnakFlMvIUT44MgDtyKadtNy45YkkkS/SITfcyPtMDvdwqinBAHRCxXHb3YMNvBpxc+CFaRh2eO3FbgoREpUOr8wwfbSdACsVXLzgwdGZpye0vja9+5lHfkknKpfAtM/qptbPXDv+iQD0Di2itUiB96ACEYB+Dw5qtEvveQU819u+fXsjfEMUxUQisW7dOt/3TdPUdf09r0C0g5ECkQKRApECkQKRAu+uAoZhLFmyhMgTWxoAGgAURTn//PMtywpjviIA/e4q//du7c0A+tmieUzFH6tRiHC9yBg5NN/a+xw+ZKOwvTzum18b26zQ2LdIUpMC1141x3Zn2wGYQQikBOaLJPw3qIOJo4pO31XXpRT2EgX4JHlzeUmC2386umSN0/wWI0gYgaJhjPI9/LkfPAkoRgMoguOYj0DJmmN7DECz6nyU6YySEUhq0FT1J3/5MiqkFiPXMieKHC+SF1RugqdfOsjGSYYN6Iroyp6XtINkSYNiecYHjoIMBwqIST4VBmakBfIpyynKKFi0Du5/ZDHi6prW5HlpH6VSBRDjFiomSmY9+wIsKsJG6JmZvmlnVXtxngJpqDBjLgGfPWfa0kVk+5WBooqfeWYV4j7oxNEAtChLRB9GzyPjDsLQgwDjht/3u8dWJxK0QQ4glYHnXz225HUyAE0Y1KLqiyS4WR+1nOP2OuqBZ50EzRI0yfS+ikDZEJIEhfJxNXtizefqJuidTc2NUoS74c6h+XeYPlPsiUsMWnWh6nZf8LUxco6GKSYR4vzVr1ZvHWrzkcrfmeS2bio6ByxkpwqKok5DVxdo1lFlq6NogIsxLxB8T/Y92fNlG8nPXnP7fv7zhZR5zdJd4pSGQo72+hKH5m644vreUm0WYiuiEh5yNlPACKSwVCAzQYsWOYsZgHbHl6obW0ZR7IYgQa4JVu0PqrPS8HOGm6w3XyT6HCZdeIrtZmxPqcN9HxxXoNhxVyYq7VPKOc2CIG96o6uV5YcfTIHmlAEtCtMmQUGfo7H+kFufLN6SS6HhCSeIe77MaDtdE0DBGn7M9hI1N339f5GLOSOlYxzk8/CNq+GNUrsZUG1J1ivec6XAkRiDhgAlos8Imt37q4dXZWU63tLMBH3e59MFfaJNR2mcVV+kCA7Dm33iRykjhQeIiTBnXvzCC1ZmJGjiYXwTXHBhouKuLXgdRRQoip1iuHcG0OxSA8OTCb6HjRC8GIrDrnWIOeyyAB3btlGhyM8jvuC5nk/W5rAUYVgYcOezVx1A+xjQrJjt4X//BMeP+nXPqIGu1hcP2v8PloVhbYEIQO8sXPRXpMDeokAEoPeWkY728z2mwBlnnNFwJwlsue+++8Jfhu+xPY12J1IgUiBSIFIgUiBS4P9MgSuuuEKWCW81qhyHXzMAYMmSJc8//3zYE1UN80D/z/oVvdGbFWhEcDQc0C9U8TPbnJlVKvrHIh0CiQU77IjBbeTh1m2hIadGqVSb9f4j+JAJZgTISFAaOtEwx1O9soCSN4hMBbyDgmqDjlIRp97+4L6QBEEmmqgAJIGTAOIJeK0wv8SMzMxYSkzNRn5zccLylVSNjb6+inDBZaC5k127hQCcDyxXOuNiouzzJb/ryecX5FvJ/ilBLCaCkmK+aRmkJthcOc7BiQSgPQm9hO9nHMwg5kx93yVzmP0zNQ4o84BYZ4p6Bb3j4VvfUar2kpo/wQzyRAxdRv0YWDcRhkwo+VAOYLsGFRtqVGUxaZMnWjRQrFlL8nG2gxzVZvz82YdmGJeMA5zyKdhW6/VwnOUrFG7gEeNrJO2+GUC7KBre7JtuInbb3tTGAaTzsKV0VAXbKDKCuGQMkXIe9Dp9BsRJBfPgj57Gp9OUtkwcHASZUyQJ+hfAQGV9zR2tMleyyl71lqx5OG5ipyfUATQLQQ748CHVG/vUS8tae0BKEdlMKXDeZzuGCr0+CpYHNadluz7/4subBcb4ydvbBL/65RjdHKVZguWDF3A+ax7VdaSCgRqKVXfGZ89L59KMltLQSGlIJwBaEuRVP+tMeHnToq2DfYY5wbHzxIV9drzVReAtlCsBZ5O3OmmhUgfQdt9/37NYlIFs1GwW5KKvthS1bsQEszaLxJp9qY6Vfd71YpR3QYiZtQA8MiCD60kMQCfCZyKKmjdhW+WYdBPhY2DE/NBDYUifpiJvo2yjQAEjgeB5Sc/Lem6e5jN80Qs/IwhOELe91prZfdoZkE9BIpaWOEhn4JeP91g43qQ5D2bKDqTAakIrF3jUE0S55kEZYUt1zGc/G29KUbL2KJYu8sTTqwycXKBqmbLJGLEZpA172cYjaZKGA+AFmDu3aUwbjEpDuwxd7bBpYN9BfxSzP0MdQLPJiTCCg3neQ+f7TtNUNnIjAHQ4E8NbmNH9Xh9PQfwDJTCxbA3KgN5tBAdNUbIzlY2Wh6UqHn7Ilp4xW8dmatO7Xr7zTtxWotig4WcNbyX898239XPeiJCh+j3RP5ECkQJ7qgIRgN5TRy7q996sQBAE2WyWeR+k8Fdia2urZVlhdSCanfaHr8Xcm2WK9j1SIFIgUiBSIFIgUuBvVMD3/SeeeGLOnDnA6hsTgBleRFFsbW297LLL/sZNRk//BykQXupuI0Vw+L7vBviygZcXcG0Vc8MAWjGIQb8lgLYDsIJYxYpVtOXzphGxjTOOfNCBUKsdYNnNDgN2dSwV8IYv1uzUG9WWx1+c1zWTTLIggShwCY6yLyQepkyHN2rTS4StJaoQyN5aQyhZs7p7KMKC50BOwJXfh5rdwQB0wvNAc6Dmgo0tGnYXnFX7rYG4QuhT4OHszx4sJkCUIZkBIQV/KRxpYo9uAjoxtBOum7L8lGFLrrVqfDOkCDsTGc3Fid8lAS46b4xWObJcmWgGaZMhQgc5jyE/l/2JVIQwVXLa1KD3x/dCxWivORKLepB0lGooF7WleRGywKdYNPb7VvQLABmA5iT86CdQwYyBaTUQa8GwzzQAc7ja204RHKzSnWbP+s63F/DkySa6mc3DG4WjKkGHyjyqmk86WBgr21BxuYFa84tb5q49FIQ0cdCkLDXzibZYVgJJVmC/dVDUVqhus/4OATRj0w2bvOq3qLhy3UZyjgs8ffhnT4ehoXmGpSB2atbUR59e2dJB9/MMiH/4Q6BrUywLHMoYAT+oNwZkOR25Ggplb9bJp8phqDE5dtkppTkN+6+Bx343E3G5prVaVtqymy0nS/iYaTV88MTKdpPq9D7/cpNmTzH9ZofyPQTTmnXBF8fSryEZMs2gNMGvHl/gYLfpUU8cVyD67EvkrPcpl7lOn3cDoGPDAJrwtI+C7k967NmDYmmKbxZZXc3PnpstGNNU5kEOwzooOsaXPS9NDNpLhw7o0LdOPmKvXbPnnPABouwyl1AEOZWGp/7co2MqvCKBOaBjaOXQzAQeOa8thAEVVMy9tG3G2LEQ52m+QeBgxRp4ect8H3s9TO0A0H6rbq/duJGUZEMEc2aPTvAwJg0tCnz5P9oGrb5tHhSRiDbZn4et8eGkyMhJiMa4N8owhh92p540ApSN7nUgnoD4OMvXYD8ywyKEu2XQjCNrRdRNfPJpnD39lTG5wfG5Yv+UZ7YNYNk2DELY4TKMnIf/rXPtxp/1p0UA+h/0P0i02UiBf4ICEYD+J4gevWWkwDtRwHGcW265peFLCn8Vnn766eFVsRZb3sn2o9dGCkQKRApECkQKRArstQqEV1Nt2rTptNNOS6fT4dcMjuMURUkkEmH818EHH/zKK6/stRL9y+y4z8JU6UL4YQC9CfEWDT9YDdoYdOaJPlPhtd0zaEJOBKClkqa8+tqCvAxZTsnGuP91NF98CWj2FMMjt2aYhECgKohVbVl1Jj334oo58+sckRcpJkMRIBEDWYIjj4OCNbPkQGhTtZFjoQ0wqM5MpyCbVKSYkM7AbXdLFSvtOEnXEayA+HiF7K7dBh523IdBESEdpyJ7+y6Xb737o5xMNs90KgTQx5o4cRhAKwxAJwybLxXmNlOBOyUlpGUBsmk4aAM8+eScmjbbdMcjZRNTT2yWIxEitpBvFnwoOuM8PO7ED0NrE1z3fdheTrsoayiWA7HgyoOVZfkYZEHJkCeYMHQ2BrkYHHEIbKvMtrFJRUlFIbQh6wy4vxWA1gMoG5P/4wsTYgzdUq50HJ585siKM11FRUVJR1kN5KIpm9immgtuuqFvYhc05UCRIZMiKJlhVJ0HkONw9PFUm071sn8VQI+EjG+/bhDLTlVw0reuo8sg4rKQVmiW4Z67szW1ww3ai5X+4z8giMwDHotB6yj4w5+Wqnq76+1Az35AJJrldXAaclXkiv6sI46iEO0Yw6UiB9kcfPf6XMleUHFGlTQwXY6mK/wEK0FJBnAKo2BgvRq0DFUWfucKJSXAMYeBbfWFANo25xx1OB0YYgziWRjdA7XgUMQui5WmdD2izwSgvRhrtBJmNFNEhh+jjGlWA9D2JctPWH6C1QMEi1zhfTfcNh1iZKRPSqBIcN31C0r2DJ2VATR8SkkewWcFlgEts7Tr8BgD28+a7r4H7E+7zENM4ePpDGwamlJiYN1me2chhFUWPebEL1tQNHMFs//Mz9AlBWkxhP/wn7fFVZzoYLuNSXZJAZvU8VpUa83GjTTfwgMkFV4RYXQ2no3BhA546eV1KnYW2GeqxjQkPcNpBp/t4Ag7/MjjoWF/3nkHJSdoQTwS8RE210XTXRTg/BYZzgSRvcCjuCb8+Me3d495Zeo4Y2Lrc9d9G00HDVaZcPcvbXDnxkr9VBsB6H+Z/3OijkQKvGMFIgD9jiWMNhAp8H+uwNy5czmO43n6Ehf+FBwYGEBE27ajFI7/89GI3jBSIFIgUiBSIFLgPaJA4woq3/cLhcIVV1wRAujGtLfCEn8TiUQqlbr77rvfI7u9B+9GiGZCAG37+EaAD3j4+arbzRI2JN0XGYAOGXSMhTzs5IZmWFmqmunf/G68Qg5fKcFDPg3XXAe6P1oPqIabzpqJsuq2l7UZL7+6atFCSMTJlRxPUfxuLEbIOC6DnITPnJ+ouFM1HxwUGiEMKsLzr01IpiAhxuNiMpmA+381umikWfwuoTEVhQGzueKuvfiysekkJAQyU+da4NFnPnbP/RtTWTKiJiUQE/CXoROMYKLhQuDGAkeyPcpN9lF47tm29iyhUspjkKF9FJS1s2ycOVCDkglVFxiA5sIaayF0Y3wzMWh3Fa1D162Dlgy0JuDySyTE2SUXSh6UA3nITQ6WV+aI/MZTtH9iCiiPOs7BbbcvqTjTDULVsV1CMEKf6a4RHAG5mwtq5xlnJ2MSbSVMQb7l9vUla2kF26pBS9XvUP2pBXVORd//jE9S0nQSyCnNA2SzcOnFhyUp5Jr+lBPwsU+CEczTveS7CKAtwr6She3bjZV1ozKzAH/0I6Drqyxn4f0PdssiEVKBJwj+b+eCavZbTrZhfA5X3gSgZ6w6gEixxMg1L8C1P9xn0JlnItFzEymDpWaDHghhQcUQm1ZRqvqjKubSyy7NNSmQA1i9EGxjnufLvi/Yxvx1K+sEFgDmLodBa7kVtCHG6+HOnmh5outJYbMDvj6V4jZZ9jjL6rXsLstts/1sWP4xBNCmB6o/9cJvUPhFMkFHXUsz3PWTdRVnpsamB8IPxTCrFW2v1bZ7bGO+ac3QMRu67O0grVtLFy2kUpMCCDFOSmegaM0bslggNQPQBuV4QOAz+3PAl91UxZl98x3diRRlT1OaTQzWHQihSlU3NlijuSIrqAPoqr5y40YKBOeBVwQhjMFpUuD9x0LFXLrNknTmfQ6DWd4ZgI45mEI8CPGhAA0f7TqA9obTNt7i/LlpE3aPfyCnPDe5Y2Ba5y9eY+lN9RPWbl/a4M6NlfqWIwD9FhJHd0cK7IEKRAB6Dxy0qMt7pQKe64X7/fDDD4e/Bhu3CxYsQETP9cJC9nulPNFORwpECkQKRApECkQKvFMFgmDXa6offfTRRYsWNSKhM5lM4+sHAJxwwgmFQsFxnMa3FMMw3mknotf/PQr4vm/7OBTgnxCvGarNNPyUjUnNE9hl+zIrXyablMnLjWws9VXW/KZb76CEYRGElAiZJPz0wVEudhUsqHhQ8cWCkzRxXNVc/Iv71/RNhGyKjgKZWUR/et+lkkwF8SQFhCTc89D8itdro+hjDIOYS+UQEyWXe2nL1GQKJEGWhKQiwt0/HV/QRluYqjjgoaxip4PHXXRpl8RBTqaoZQHgsivjBeOIx548Kp+GjABZCWJxePJ/DtVxsoMCetQcFGzkAoRXXh0VHpmZhJTJw8w5UFQ/UbG6yhaUWXiuhYkwwcBEjkVOiz42b652vbrlyH0WUTG3tAwdKXj4vn4Hp6hIALqGyYKXevWN+TkBMoSexRQILVIixZOzdaB8TDUYr4XRGY0QjBE+07Dw4I5bZnQtaO1fuXwUiMDJwMuEOE/7ZI+GhxSC7u1m36C+Ynvx2PPPz4wfS/Q5xkoddrbAlElw3wP7/OJX65IK3SnwICXgkm9CwRzDJhig7r8e4Wx9q5iFkY7Xt1qvIQwYfcd/iE+mKLyY56G7GyrFM4YGPzJ7LskcEygjZb+VYAXvc7HN9WJvA6Br5ICesWINkVyZJUfLcXjokUNqOKdIcxvkGjYRqh5UAq6CYg0TFVS2OFDG0VuLqz9/bibHkxqtCpx9Gjj2TD9IYKA45sIp3TQzwWKQYe1hBKArRiZAIQTQjis6rjhYAsRUzaBc7xpCgDEX+0rFlVdclnv/RnjgYdEMxhKADg3RNEZCzZ1x5nmSmKI5lbhIuP8nd+9fdWeR1T2ozzfUEApk8+9VtZXXXtWysh8OWQua2xcWkHQwo2qLDlhHWnGs8mY2C5sH52me6LDAjXBex6bym4qP8aKVGNAmPPLM3PbRhLyzcUnkKCr9/sdmF7GzVldJGC6MCXrQWtH2W7eOUHUMBIHlzoSFN2+6JVfxuwxUPOTDXJd6As+IY+Otxn2YqtNFDyMs3ryLombNR/xpgGUXNQ8d9NjVF7v+d0FnrjBeQzPxyxdh56g/TmgtThn10mc+tsWv7hSwsZuTXIM7N1bYkxrMurGym9dGd0UKRArsIQpEAHoPGaiom3u3AtVqNUzYsG37/e9/P8/z8Xg8/J4tiuINN9xgmmbjt9/eLVW095ECkQKRApECkQKRAu+CAr7vB0HgOE6hUDjrrLN4nue44eCA8CsIu21ra3vhhRfC9wsvw3ozxX4XehNtYrcKhKSGHgoBdNXHNxD/27A3WP5YM8gbgWKiyLizOLyyK4A2qa5ayy138C1ZYm3h98sb/qulak8ve/kBO17yu3xcrroHXPaNdGcbOXBzGYJe+Txce+3R3/vu0bJCbmiQIZaHlwc3VL0uG0VEHgPJDVIWZgYMKFlLk2mKdADgkwp8+6r2ijHfw66yk6lh92uFRWedm4grRJmblFhbDj5xKrepMKPozX/syfUpqV5OUFLgpjtnGTjDwRirdDeMyQJQq315hXCkJIIgQlMrvD5wSsnsrgVENjUKT0g2motNFa+9ZC94+JH5/Qshk4VkkhKNjz8S9PIG3R9dIPrJGZgq+MqrW+ZkBEgzM3KCxUBnFTj8SKh666rYHBYMDMMiVBT0gJrBgg52oOfwzwAGKlC2W/7ztjo3Jf8qUKG/b/9g7O0/b7vi2vRxH4bWVkjJRJnzCpWCzCdg/f7w5xcPKZvrfnxvtyRDQib+q6Tgpjulst1kBTFmIScXuT4CMv59AJoiWRBUHwZqzTffQUHwqRyZbLNZuOZ7h1zwhUXZFL07BUDH4ObbFw1VexHjrPDgjggOykceEcFRQ67szdhwCCgKId1EnEj0lddOH/SmmZjW6pMiFFVc8KGCiSq2bPNGbTbGbS6v+MhJkJJgbJLLAHQ0waZXVzturx8oGEiO2b/PHBpx6g8P+70PVDwMsatcA8vhLEcIW0WDABOaxZU0KJEvePKP70iuXAqj03SwffHLUAs6membJXJQQrRctWeeeV5CTFLsicBRn+/9+UEldyaD47JGnndAHGXirEL1gI9/lCJZWgXqiWbPqwPoIKebi445GuJJQtAA0JSHe3/WiTjdMZOeFzMwprPxKpig+m1Vd879v524ZD+akMimeCkGQhwuuiL+hjmrzLg52yxHWR8040IAulBbvm4d5d6I1Ef65EoAXePg+b/MMLGtilD0KcMkpM+UNjPi2PgbATTVbNScGYh3+bjNxYqL1tsDaN2lx5ctfb6nY/usCfbUjqd/+98YFh/cmS3vfFJrPNZYYY83uHNjZeeXRX9FCkQK7EkKRAB6TxqtqK97rQLhj0BENAxDlmVJkhoWpLa2tlqtFv3Y22uPjWjHIwUiBSIFIgUiBf5xCjhsQcQHHnggnU6HpY8b/DlM5PjfQLALL7wwvBjrH9eTaMu7UWAHgEZEN0DLD0zEpxA/adkza2abh01h9nFoMh3pfQ7XmQNaNIP0w7/Jd7QQRCO3O8C/nZUsVQ/frs+xcdlmbfE9D0478mgKIw5RF0G1JHzn+13F6qmf+lSnopCZF2LQ0w81PMLBHssThgF0zsSmohNT/X27eqleHAC0ZOGUj8eq1SNNf+nrg1Ofe/GA4z4EokT5DNl4LCHCuvWg+weq2FPFaS9tOnhUCzRzlMAQT8CnzgUT5xgYC6Fn3afpgq3PXLGA4DjRSBY0fNFXJm9Tp6moVDFWQaFKFQWTNczXgk4HF6j24Wefk4nHIRWHVIpeNrYXnnu5v6g1B5ivseptOspFFF7dOjkjEoAO6XOag7QC193c8obeVcV4CKB1otUxlrgt0a2/g/c1MLTjAxK4HP/zx/qkVhKQLZTeG09COguZBCg8JGOEnpuS0JSBmAynnwOD1QOK+kLEYy6/Mh9PQiYj8DFI5+GpP0+seEmCiT7RZzUQ3zmADiO/NQ+qVrKoH5lpp+jrcFmxojfBMCsdITKsPhi2VNfaOBEx7QVcCJ0b6Nlh0eEmUgZ0CKDP/kwT0XYeEgqV5jvoYCj5K17TCZKyjBdRRaWM3GYPNln5bdbi790wYcIEyCcJE6cAmiS47bbxhjfXCZp85BHBsaduWE9WdOAoB6ZzEgzWji/VWgwbLDdk0JzlcIhpwyKjMeLEwcK6k08hoi2wiZbWLDz0ePugn1IZqCX/bx1Azz7z3IyYoBRyDkCJw8VfmzDkzSyiWKWo7kwJs1tqPY8+vWL9/jAmRwdGEmD1vlCrO6BFxx9lO/0XXcxlc3UAnc/CB06ASnmZo43znJQWpNgBCTXMVf3FDz+yqKeX6HMI9yEGx58KQ7jfIOarzGLPkj3I798A0EPVZevW0bUCIgPcdEWCBBuPgq2lObUg6WMGyfJPXubQzlzPvw5Y7Dvlre+mNZ7sIEHnkU1zJyLeEuAbLpZ2AOjhYoIjT00eohngj27Hvkl/HN9a7M5vPXLVUFCuW6N355ke+erdrDe4c2NlN0+K7ooUiBTYQxSIAPQeMlBRNyMFmAIXXnihIAiKooQB0KlU6owzzkDEWq0WKRQpECkQKRApECkQKRAp8G4pYBhGOP9tWZZt277vDw0NzZ3LrsCvIyn6J/xCIgjCgQce+OqrryKiaZrvVh+i7fwVBXYB0IHnU2Dbq4hXavbBZbvbw+YQQoVAkOFFjkHnkbeC7oqbNk/NJSAn0ZjKMbr96jdm3PjjaZd+O3nA4VR9T2RlBsORH9sFd923VnXXbRlccehBkFIoLgB4OPA42G4t8HGSHcR9jPkoOZgyMeNgZlt16opV4asp35nn4IKLer9//fjzvySls5TgES75NOy3ArYWV1jYUw7kAad1S3Xt+C7IMwopx2H/w8DENaqXp0p0zGZrE9XlywNdZ3xcFAGUGKVDAA/jeuDRZ5aWnX1UnFf2p1Fz55Xt5UXj4K9fHZ+5gErMCUDANwbQ2QMPPbrcw5mIGReVEllxQUW+jPDy9p6kQsZwGSDJUxhISxM888o0G8dXURjmp7sAaDJBjyz7ZvkQAmjLTW4pzzvyRIZNRTkpZ2Pk2Ia0BE3xRJ6iF2hpbYJl+8HPfrNws7ZYxfEVb/RQbfGnz4OmZqKisRhZvAfUfSqBEAJowxcp73v4TUfaXQ1mat4tcNztnWSC9sDHppI17/iTgU+wPZcgk08CiEkxR5BUhIeemrlF7SzryYA5oMOxGJHbQPUeTRR0kkio+pP/86a+Ol0F0nB0M1x9XauD62vOLM2ZVrPnV535m2sTt9n9dz3UdvxJIPLQliFXbzZGhPXSi9uH1PllJ2eh4rLMaMftPf4YyMTpUUGgTJLvXDNPtddWjXGaOZa1cbrRZRiTfa+/Vp55zVUwsw/ac5DkICdSeMXpp4ODK8oY3xlAi6o9/dPnJBIKDYQcA46H5athu374kDOn6M0pewu36cvP+SJND7TmIRMjAB0X4Cd39Wn+eGZVlh2v2XJ777uvUxHp6EqKkJQhqcCvH16rldYben/FmVnypiAu2mYsuvhrSjxJyRuExZOQaYeFq2C7ccCranYbTS0Qo2cQWfACLvwg60FzQd133TryyIeTRgCgFccN2AAAIABJREFUJOC8f8+YONdFxcEYZV4HfMisHeTqAJptarfj3jg5OFSok3ORH250nYHq9CLeiPiyiyUbPTdAb3eVBH10HcSKiUcd/fv2/DNdLQNTOp67+0bUtiM6dDKLAPRfOaVHD0cKvNcViAD0e32Eo/17rygQXtY6ZcqU8At6eCtJ0rPPPtvYxWB4adwTrUQKRApECkQKRApECkQK/B0KBEHgDy+e6zXaBRdcILAltD+LophgS/jN5Nxzz0XEMBW6UdLw73j36CV/qwJB4LEWIJYQn7Dxa1Xsr2DMZE7GwIeAhc/awXBsxY6YV8GwY9XaPqv3hawMiiByQixMh8g0A8fR1f0iR7nPokDQbZ/F8MIf91HLUxF7Le+AsS3kUSV4JsElV8I2s8vE8RpmNYzrKOoUsCAgplWz79tfH9MwUNPRIgIXBzFOEQe5JCRE2saGDbBp83zVHq8GIstkkAaDeQefAEICYrIkJyCZhTvu67Gx3wzyjJRRcgJiHL0Zv/n53AyjeBJzQFN8RBqOPTb2vR/M+dlD6666duJXvt518in5ZI7V9WP+1jBkefFs+M0D3b432/AzGjlDhSoDfyoShi5Ys3PthDh5gLRI5QfHjIaiN38Aocqin8MYaFbgkaIVDIxZAd9oIQe0A576SV0VDLv10ccnZVPQlBJZ1URiiBJzWKd5Wp/QDd+4StqqLy4E08rYWqNqcnLFXXj2uSSbwBHQXLkCBvQZZR+sIBaGHTuuaHlADPpN7a2A427vtwMe/USATSq2/eedZBXmEuGHu36bTMPZn28b8uZWUDKQH3lEhRba4VvORFknk7hYC8bUzA2d7eRlHiVJDO1CToHDN3CXXjDtzls33HnrwRdf2Hf2pztmz6J3UTjIx6BZhBxPJugf3BDfVuvVcXTZi5ksg8JGMN0JP75lcmsacnEamuZ07H+d+F+8uO9PLx05pB63rXTo9sLGSvmj992z7yknQlcbQefmJOkcav6Vr4uvF6cbOK7CspJZ0U4yBXsYq+ndP/rBxCwbC4VNxvAcvO994pXXLL717jWfu2hs/wrmoOaJfccF6GiFb307NViZo/ktBsZsP+YEcReztrN83hQa0AQ74kZlYe5MuOmmg6vGha8NfOTxPx544Veap86gAp5pGeICJ3AQS8KBG6GgL6vZo1Q/TpZ2ZlWm48fnGzMuOuaL2tIPfIhmjCgFm6dElFQObr1zlo29ZLT3AB3e9+KOn3SCuBOIw4NS90SzSyJohoAl88hhUrxNaTxymDTtUlh22Kh4Y82arJuXID7rYk1DrCKqSDkbtLBpMEMnwOyiVnPw6T/gpAmPTR2n9U/WVi95LAjrAlj1U1ojYCMYDoyuP/CmfxqW511W3vTE6I5IgUiBPUaBCEDvMUMVdXRvViD8CXfnnXfuculrX19faDVyHGcYPtO/e7NW0b5HCkQKRApECkQKRAq8cwVGAuhhEE3/Wpb19NNPt7a2NgC0QEWwaAnzwZYvX/7666+bpqnr+jvvRrSF/08FGgA6QMvDQQ8fsPETKs7WscVFBYkqghdwrg9ho9gE1hwUKDbXnn39tZPHtIeJtWw4mRlXJrRFiwDAxeCs86Gg7o9Wd2Cma1ry2eemtqUgFYvzInApuPfXTQUnW8WciikWlSuE2bW2L5XKo2vFI/pnEciOJyi5FyAFUj2HQgLIKLD/GnjxpU43GG25ScujZIYaCtud0Rd/j2FQibyezU3QOxmef2mh7nXaLJHA8SBwJLTHOtqaw95HXW3KQI6gOLlK4zFQJPJEJxJEurMhS2VB14kUwbs1S2HrK2vQ70OMWztXFFSpA1CwZk6axfpLDmiCsStXQNHpKwwXHhwG0MAYNG/gDvpsMRdqyKA9n2FBYtCibkz75jc6W/L1yIVsklBmKgbTJsFXvjZme/kQDeeaOKbK8n81poOJq5buR97nuEi+1xM/CNv1SeUArEByXNF1RNcR3h0A7cfUKm9YioPJ57aMy3ewfefJBy2IkExBUxv8/oW1JewIjcPW8EzGLojTJriZ1CnlWa5h1sBpV15Vz/JuBj7OmLvCyGxKoH2X2PsoLM4iBZAFGJ2EpjjceP34beo4DzMGKjVmqTaRIwDtjdFqR0wYA21pil6J0wZATNBcRedEmNkPs+dC1wRoa4LWDGRFZmCX6JDoHA033jT11YFeG0fXUGFW93pcskVu+rQbjKlt2zA+R8dojNX3y8gyzz4ZXIwqYZLfH8iKLolk3v/uNeM2D84pGm2Gn7ICAtCuRwZkXe++4aqOHAcZxqABqKtxkQ5FJQ6yQoEkRNuHE5wB4EOfgFcKyyvOKH3EXILlgevFdgbQ2Yq14NPn0FREDCChxGIyfZieeX6FjZ1UY9MFdIRhAB0yZRItbA36zFizbAdxO0iOaHEbZYcuX4g5yDvIa8iXrSm6dSHiMy4aKpvjKiPaIUEecR2Gi0HNxnP+LejIPd/VVO1uffZbl1mWjr694zS2C4DeXYxH/cm7cOfGnzu2Fa1FCkQK7GkKRAB6TxuxqL97pQLhT7iDDz648RuPvrAAXHvttZ7rhXg6AtB75aER7XSkQKRApECkQKTAP0SBkd8rRgJoxyGn2+Dg4KJFi8JvIyJbwiwOxmXkfD5/ww032PYI6vAP6WO00R0K7BgvdDysBbgJ8YEAv+biYS72uUGGZWLEfF/wPN7zeN8XwuYFYkkDB7tUZ/XHTqPqdnKKwTaWUEEhFUDBBWvWwS13tRScSSUvoVqi67f4OOPun4xPCaBwkhiHdCtsKU2veVDzyEnKgj6Y2zoQA2yqaW0Vc8qPftyUzbKiaYy4AlAVtbYktS99ARx7uuspgQeBmQzMtOsIhi+q2PTK4AKIQYbB6pRM1Li/n6qimSg7gey4AmIMMVOttT/6yITmJpYWEidinpQIz7Wk+QRf970S7wvnS3hI5eH8C6GmLfGC8apGdfOoVtubGHTJnrH/IcQIYxQ1TG7Wz57dVDJ7ayPsz41qb6zm284A2q8TSc+DIKDmkTjNNX/m3Q81ffBUWLIK1q6HD30Yfnhz62BtzaA5o+B01LC5HMg1FvHBAHR2W2VtvhkSEmQVCqH+xuWdW9TxNaw7oF0XXJeiM95sf6aKiLsL/N3tnXYAPhWQzLiYrqG4XZu5ah3wrMqfkmQV+RS49Fty0Z5VxRyZcwPJ9qVwrAkK79REM8jq5IWXayjWUB5QJx61EVqTNBYKCGFgd33yirmew5TtFE1NUFDGcUfBn1+do+NkHfMGlZGUNPLUh0U1BTPIa9bUn/90Qmuc4LIMEOdF4uRxqusYLpJAx0CYaiIKkG+Gw4+BR57tLuLEop8uBWHQCtFnNoI0eTBYA8T80LZxp58M7VnarAiQiyVyIp9XKElD4CChSDGeojnmLYRb700Z2F+yuiwcTfMNyGCxJ1H2t9uk1/b9yPuhVYZ2KRH6oBXW1aYU8fKcDHmqIFhf/v0CsHBZCVsqvlgLQGeNhs8D1+ddv17akYoQYrbmT/3ONQmBzQylJUUSoXcqFNS1NnY4SJc7hBNOFL5BWShhqwNohqE5mr8JRPoE+UnHT9tB2vazZpA1g7RJkzGShbzFBrSKUHAmafaFiM+56BjM/qwyAO0xBh1CZI1lL23djuPbfzZ1bHFuTzB13FMvvYCWTa2xvBWAbvDlv7rS2FS0EikQKbDHKRAB6D1uyKIO76UKbNq0afj7yY5/y+VyKIfnejt+eEQO6L30GIl2O1IgUiBSIFIgUuBdU2Dk94oGgA7vbJDlSy65pK2tbcf3kuE1QRAkSTrrrLMKhcK71qFoQ2+rwIjx8jy0AqwhFlhBwisQT/bxfU6wxHb2ta1lprlUN5aEzdSXmOZSw16mWqtUb+PW4mmf+nS/FCfnpxyHXAJGZeGI9e0/uv6gcuWTDm4YNJptbFL9Uao9tVBZef6/KzIHMi/IcWgZDVuL88uGrNmK5SfIVhkCYj+Nfme5lC1piu7OvOuu/im9dKAkFYoOyKbg+I3wq18sLBa6WKU4VqnPlNFIu45seWLZ51Wc84UvZbJpaMtDSiYS3dwGNXeaGRI0j+KVTQ8Qx2jOjJ8/PH3m7LptOymzeJBhV3dLgrIaEiK0tcDhR8MdP+us2HNVL8uQa4K4MItLDhm0OmxwLjmTTzyFIGycGDTh+Ou/P6Goj9WGnxA+k6Fn4tcMy+5g0PYIAO0FFBjCyK+sYWowaNtiTH2tvM/2yoqCuqRg9BStjI6KhpyO4utFqHiEdMmIHXQ+9vsVmTSh54QIqQTcec+UzWq7Sm7rmOMK7yKAtjwwXcHyFRMVE+ed/Rk5zWzjFDchw7SZULZWFc2cESjM6iu5nsQo5y70GVi8Q8MBzb2uwaslvmJteP/7oTkNrSlK35YBJI7VgUxQCcrQCzw6CcvnwzVXdVS0VRW3RUOu7JMXPqTPDECLJop2kEQca5kLv3SemOJgTAYSPMWRhwvPbMU038DixUUFlqyAm388ZXNpiYmdf1HhtRpsM4A4L8HZcOBihi9oPmgeGGaqVp2/fi0FgISDnhnO7mjOUWhGvgk+cgq3rXp4BbvKKHjYYftZos/DANqhoOp4TWuxjPXnfDLXGocURwfP+LyUYq7nvETB4hmO7l++CH752xk1b7aKqTILfqkFNO4UwbEbAM3pmFSx8/afpsNLExICYfEjj4OC2W9iy0hPulmv8cjpdFDVMXQ4T2BTmIlM3Nlrtr120+3U3Qm6O1FzJ2tun+5O192ZujtbdeeWnP7t6mEV/QeIm1y0TEQD0WSpziMBdEAFAPDqb+PEjj+Mz2/r69h89mmoaWFSR8ASO+gi3QhAv+2JPHowUuA9rkAEoN/jAxzt3ntDgVqt9sUvfnH4Zx1wHCeK4sknn9xIVwx90I3fHu+NvY72IlIgUiBSIFIgUiBS4J+oQON7xciVXfrz4IMP9vT0hCbo8DotkUrB0cLz/IQJE+69915EtCzLMMIoUIyywnbR8F3/k+I40EHfw6CG+DLiY4j3I/4M8ZeIj7yp/Zbd/xDiA4i/tJzfbtn24O9//+MHH7jypT9fV9x+A9q3+dZ3C0NnFsonFNS1BX3Z5tK+ZeOYsvaZ/ddTsbi4GFNEWL1GLqof1N2lTrDIwTmq212zR+lus22P8syJaHchEcNcpdhpmyuv/R73zcvhtrtyT/ypp6DN19zJlpdzfaCsap+ykn2KBxFtig+GkpsZ1Pc56VQYNZqymNcdBD/9zbgajnKQ81EwAlBdqLhQsvkhOzXojnqtPOX8i6F3EuHIpECYTwFojlPS7vSpVHru/l+OeWHzWAt7HGxxqKid4ntNnkuFDUMbb2iJDSM4St6Yhx+bpiSJljZJsHAW1CprXZxQ1KjMoD6MoUO/anjbCIAmSywD0PVblg1tBJJGyQ/JEqZLGC9huuK01ew2zU3qHqf70GhVm8CoiXzFmnbhha35BOUmKwK0joKiuaHoj64DaIpooMYc0ILhh22HG3pkf3ZrfN7pzoC3fMXwZBNF1e268jtyc5J83xkOWpvh/ocnGN5sxPGU++GC75Dz2g12sPudTdAUMczqEJIDuorZajC+7Cz6xrf4FctpIkHhqRphPkNIN8ZB32TYeDjccXvettdo1lTNa9PI9QwapUDENAo0J/RM9BnJultRAXGCrs2/5cbc+lUwtoW81WmFphnIqy5BJg1d3XDCiXDPQx2D5sKSPa3ija5ijNguucJjRiCxGIqwJqdMwxQa4QPQvXShOvlLF0FPF3TkoT1O3u32PIzugC98Ge75ZW67M33AaVVRodAVP2H7EtFnZG5lT/LZuoOc6TdXtP4bb8ysWg7NCcjzFC2SZ+fIUTk45SR4/InJW4qThoxRFS+p056ywoM+aD6EQRyWBw5rpDPrnoaxAUcctOYeuIHy2VuyFE1z+735kttjYs4cNrwbtJuCinwVuQrj2uHtcHa5oGGaJpPcbtWeqpr9NWNVVT+4WjuuXP144H8Z8RrEOxB/ivgw4tOI2xBVH1UPTWdn+uwj5f5oOlaLuH6/P08bOzSlozRnyh/u/xkaDvqEoMNXvN2p7s3G57d7dvRYpECkwJ6pQASg98xxi3q9lylgGEZLS0voJ6LJfIXm9zdt2hTKEBapf5sfh3uZWtHuRgpECkQKRApECkQKvAsKjPxq0VjfZbu+7w8MDJx00kmNafIQPXPcjkvLTz/9dNNkl2cj2rat63rEoHeR8d39Mwg89APCPi4ShvY1xApiDX0v8DHw0QuohevsD4eeExQQX0d8EfEVxCHEQcTnGK1+GPHnDEX9F+L3Ea9mt7ch/qJ3MqUYJ2ROjsHJJy9DvBHxUsQvIX4W8ZM+nujiMT4e7dnHBubGwFzuGgt8e4WprjNrxyB+YqB8UMHYv+qvUt2lmrFA02ab6lRTm2QYE3Vzomr1aO5EI5hYtCdV/cVvlDY8/dzHn/6f018aOG6rvl/F71K9bMVIVYyM4TVZ2K7jeBU7N1W5oj+6ZC2uGic8cP/+d99+8E3Xrrrm2/Nu+MH0p3+/tlQ+2PGXm8FYk4qtcS7ZVGN+kPC9NsdrtlEOHaM7AWjMblOn3XBz6lOfgC//R3Lra4sNva+mJU1XMD2CxVpAUdF/FUBbQcwKqEShRgBUqqBcQaGe40GokTMZQbaGb02PaGPFAQ9ziGuPPoKyICg6WYDV66HgLCxhSz2CowGgqfzguwGgWVetgDfctuLg/B9+f/SkUVQV8Ob/klR7qu601nTOd4TAAXQgcMDz3wpAAwt/EHWUWSY43daw1caFVW3975/e97Zb+q76Ts/11836yY/3efAXsxxvnevNcHGCEzTZKIdYPEw1Cas7GoxBM/osOlTcMoaYROwYGhqt1t53//1zL724+Zyz0586JfGFz7VffWXvbbf2FKoHlI25KnapQU4NZAN5sx5azbuouEHKDVKsTB/FuVBaN+WKEPfX6Wk5F2da9lFPPb76gXuXPP7bA159ZWNFO6js9xUxW0AoBDT6dkDQ2WMRGR4BaErhoIB19kY2FTbM1OwJpfLKPz6z3z239V93Ve+dt0z587NrC4MbKupS3R+jYYw5lFkYSFBHz7r3NgAaNDqEJry6ff2ZZ8NFF3b85jdrhmpLTZxa9TvKfrqCQgWFEmaLQfuQ3znkTxjyJg85Mwru3II7t+jNKXrzKu7iir0G8QTEjyN+EvEcxCsQr0O8jX3en6C5K387BlX0TQxcsi6jj1j1qfnDvJhW6tUIEX94Le4zbcukNm1s9qWNhz3vIdp+CKBDq/TbneeGN0jvEba3e3b0WKRApMCeqUAEoPfMcYt6vZcpcP3114e/68KfcxzHjRs3LgxhfDN9jn7U7WVHR7S7kQKRApECkQKRAv9YBRr0+W2+Y1x//fXpNF0S3viuwvM8xxYAGDt27CuvvOI4js2Wf2x3o60TdA7QxcAjv3mADitRGITEeZdbokcEpD30LUStXmDM1dE1ES3WwjSPbQxPb0J8FXEL4sDLm35H8boC1WGTZfjudy8N8PUAXw7wzwH+D+IfWADIY4i/ZRT7t4i/ZuvPofske/QPiI+ze36J+AtiXsEdGNyA3vfQ/a7rfs3Gzxr+6arxacSLbfz3rZXTyu7nNlc/9Yb+sSH7ONVeb9grLXO1pq2s1FaWa6uLtbUlbVXJ3Geo2q8aG8qVQwrFQ0qlQyvVQyu1A0q1fcvanIHi2GI1rxqSbYHvC+gJ6Im+J/tBwsUEq5vH6Qw+Nhh0FaUatrxezlXt6ao5zdTHGXoWMVWrUe7H/yeAHoGeyd8aeqtD+mz4YLqc5YLj1o2uZHd1wHIpjaRqQYCtr74+l+J+AfJSPqnARd+AQWdSBXOVMAOaMoKpWe8YQDeCRAj+BjHbSwVBh6qOt43527dOcP1Ow4u7CKUKoA1osdu/DqCTJib/H3tnAqdFcaf/ervnvYY5nYGBYTgGhhsEhXglnvEM8ci6UTeaZCOJiURXcyyCrkcSTdbVGNZ4rPFYEzQx67KJun9jdAExeEUUAiJeICLINczxvvP2Xf37W13vWzQzzIDAMPO+79Of+rxTb73d1VXf6obup3/9VC4yOjCGtoekjAbLbiCaZPNGx22yzImZzKgOo9xy44atpQxmuELYlaYouQhuoeDnwp+jYqq9XSlhU03aGdJmNXXYUzvMaRljkmWNcr16okFEtUSVHo+7XOPikYNMMc4rOK+Swe+eV+750Wwod4Ax8JCpsf1hljfJ5kdY7vi0NbrNGtXOG9JUlco9PLB9ob/LyH1h8B24rLicCXtlMUmmOEjaLdbh6SavMdx6wx5pOmOE04UzynKbbH+ETTU2Jc3AhzoVGIB0uMxwmOmKJB9IZCOgg1kE5VSZrrDVrvrYGdFKx1v0pR3tp9j+qTadlLZObjNPaLWPb7WP3+mc2Gyfsd28YFvHd3z6hU+/Jvoj0TNEi4Og5mVELwWvRywPApz/RvSmeP7krydvE3nNxNOB9GwHfhvKxTlDFMwuG8x5HyjRXArQ7Wm66JztE+tbGqvsyY0bH/8f2tERPALbt3+Qle6sMvu2HdYCARDIJwIQoPNptNDWoiVw0kknqbl9pBL9y1/+Uhoyhu8JVb5oQaHjIAACIAACIAACB52AusDoQYAmohUrVowePToWi+m6Lq9bpBhdKubfYrFY7J577lH+0aqRyk9MlSBzoAQCATob7CxUaE+GPIcDn8MytAg4zK7hkJcmN022J8VnbgeB0tkjwMvpTUJxenzhfwuzA8b0KIsnIkuWLFLN5kQu5w63HW46ftrj7R5P+9z2HMe3grXETJYUTGMWTGnG28lpJ3s7uRvIW0f8AxIS9tJAKXs10MiWET0RxGb+nmiB5f8yiNb8d6J7iP4jCMr+VeAYcDfRHbZ3HdHdRP9K9GOifzbsb6fNr7v0daJLHfpSxj61vf3YVPvRmfZjjNSxRsfnzMzxwhfbPiZlT293p8rU5hze4orURtPSNLWVJrbySe325O07mzx+pE/TTGd0xhzcYdemHJHS7sCMk02GO0glyx1kBV87eK0IwqXSdoq1kybUZz+a8QYYbqVpl1t23MqpjUJzdIVw6ZEIhrVpzG9+k6xNsLporFqL15SzZ54fvs0Z2EEVrZwZVCIsGrhIhh+OgN4VCp0VcHPODLsZbnRfaPua4TDDZr6INS6VKWUJ2df2ROCz0KB3j4AOJp8Mz3QX5AM38GDiOyY0WT/p8AGtYq6/GBHzAznY8ZjlREyXZWzRa6KoH1hy79KghSAunLUD52Jd1CNm+ROSvVSiuQg0zk4j6VAJJ83xRON3tkmdOhFSq0VJEPleJjVoz60OBGjdFbHMok7Li1puMp0p9WmIT3UpM0bi+QRrcURKC8/oiMTokHAg8aT0HOSDNmtCv/YHBJ/JDE+mnIRLFUQNhl9q+uUGr2ozqogmcBpj2CPbjbo2o6LdLE/ZFSnrsJQ5OGU0dBijOoymjDEhY0zKZKZmMlM7zMPT9uR2Z2KbM3lj+9iddFyavmDRha541eByoh8S3UB0G9F8on8P0i98utunR3xho7Gc/PfJ30meGZzsMszYI+6QZ4uHTzJ5DnFXpOy5TuL8J1uc0MEWMp81chYl3CPXITJcWr2Sjpn04cQ6Z3yNeczkd0yHdmSEAL2Pi9KdVWYfN8RqIAACeUQAAnQeDRaaWnQELEtcpL/11ltSdFafmqZt3ry56HCgwyAAAiAAAiAAAv2VAOc8kxGRcT/84Q/D/huMsWg0quu6jIY+/vjjlYcYETnB0l/7VEztklODCdtoYduxa6aw7hnMmzdPXZrqJZENGzYImTqw+BB/gyWIvBaG1MIVROjcoTnIxBehVIeSjLWUIZbpwAZkG9HOIG0LLGg/Ivowl9YFViHy8wMimdYRvUf0TvD5HtHawEVkDdHqIOZ6RRCU/VqgaEtdW32+HIjd/+PTbzk96tEjDi2w6TcW/dqi+yy63aKfGnSzQT/poJ908BvT3g0G/35b+5fSqdNSQUp3nNqRFuHYHR2nZDInB+nETOZE0zxhx47pbW2fcfzPGnzKjlQD0VSDRmf4qAxvsvg4i4+z/XEuNbpUb9Fhpl+e4fEOT5hfE5XsNOMdxslfOlP4b8QYq2Hs2CmsJXV8i5do4SVtvi5UbF8PG4AYpBlUImaAFPbWSZfiHsU8KvFIU8mliCPDaX2hdO+WODNlCpVbvjCmsANPicC3JCv7BkquyGftj0VGC1KnkvBXuU6nkv35motlzm7rZL01sl/Vr91nNPJLyI+RnwhSiXAeD/xMPC4C5Llf5vuVnMpFdLyvCX3fDyYGDKKVZaR84DEipjHMJTGBZJonU255u10lHk7Y9SljfCpzeNqYmjaC6GzriA7zyJa2Iy3z9EzHGemO01Op09o6TpappeMMy/2qZX/bsK4yjGsCNfkBov8iejJ4UeD5IHj5eaIXcu8WvJaLX14dHO3q4FcnwofBubOTKB3EMgcneNblInz2qbxSgIN/B4LzVHluZP894MGJnBWgbYdo506ae3Vq/JBNk+v52PL377slu2L2TxAuvXtR5285gbtz+a4a1PSF3ayCYhAAgf5PAAJ0/x8jtLCoCViWdeWVV6rre5mZNWuW7/ueqxy3ihoROg8CIAACIAACINAfCMj4aNM0n3jiiaqqKhn1LC2hVUw0Y6ympmbBggVyZc/1eo6q7g/9KpY2KH1nb2qRDFo/66yzNE2TIxuNRh3HCUfK5wToXWUHAWNWJQ+E67018tPvzg4k782Bwchmnzb5tInTRk7vclrO6SWZfHrZFxM5vhoI1v9F9FCQHiC6P0j3BeHY/xGEZt8ThGnf7Ps/CmKx/5VonkuXc7qC6AdE3wvS1URXkyj5DtEsoq+3WWe1OZ9vc05uc4/7sGX0h9uOfXP1V2tKWXmgPlcwdt3VM3a2X7zT+sxO6zNt1lHt9tEiOZ/+tdj1AAAgAElEQVRJ2dNTztSUOyXlTulwpggnCnuqyDiTMt7EjDdeJD42w8ea3lghfPujbRpi00CXBsnk0aAekuPX2l6N5R6WS7WWq5KI8s4mZ7DlDM59lSuoTfphptZ2Btl2vW03OPYIx250nSbXHsudCY490bEPN60pHZawXkkZE1szE4I0qdWY1moc2WJNV2mnNT1In9lpHd1ifa7VOrnNOqvdPidtfylt/QPRPxNdn0s3EN1EdIPnXR8cKvcT/SrI3BdkfkXCKONxoqcDufmV4NnJuuCY3Bl4XyiZuPcyIQE6OIs6f5dPjvzgxQkxvaBp+7T1Ixo3bNHURnNMbdvkumVb3iQvkxWp9/FMhAC9j6CwGgjkNQEI0Hk9fGh8IROQF/eO41RXV4cF6Gg0+uyzz+JurZDHHn0DARAAARAAgfwkIK9PHMd5//33jznmmGQyKaOhZRC0jIaW7hznnXfe9u3bHceBBUfeDbXv+5ZlDR48OBKJRKPReDw+bNgwEdwcWnpFgJYB1FKpOvgCtLQaMIMo0fBnmqg10KabiZpzEdk7g0kaNwRzNr4ThFq/TfR24BzyVpBZE4SjriJaFVjrrvHc1378o3N/fvtXg5XfDITF1bnPlURv5CyzXwkiW18MQlz/4jhLrrvm76tL2QAtEmWsOpFY+7dnAzftJwJPkieJnsqlPxAJf5JAwXzQsP/VsG82nB8bzo8t9yfhZDs/sZ2fuN4/p4wvpezPp61sypif7yGlMyelOk5sS50QpJPaUioJD+5saj+1TaVsoVxNbtX3n63pE3ZPJ7WmTrHcL5nOhab9VdP8NvnXEf+J793muLfazk8M5ybD+XHG+WnwLOE/gmcMCwLyfwrMlJ/Z/fPZQDVeSrQseETxOtHK4ABYmwvJf0/M7Ccm+Xw/KNlAtCEI3l8fZKTB+gaiTUQfE20Njrc0+dIHR74uYAcmGL33Gda1lfLc5Z+o4FGQnH7QobTt0y/+zR09+LWRNTsnNmy69opmayd50myny6bdFUCA7o4MykGgkAhAgC6k0URfCo0A5/y+++4Lq8+MseHDhxuGwTlHBHShjTf6AwIgAAIgAAL5TECqz+l0OpVKEZFhGD/60Y+i0agKgmaMJRIJeWGj63plZeVjjz0mJ1XO534XY9s//PBDNT2JpmknnXRSJpMJ6c/KgmNX2UHDJOOgD1p13VWk1LddGc5dz7Md1/I8m3M35ysSbpBcWZaI6R1l7enMzjVv/S0a1ROJ0t/8+hHyA2dtaVeSMy0JSHmcu5zbMqXSLbZjVlZWR0uSjGkV5YedcPxJRK5PbT41+1k1vCWYN7IlJIi/HWjffwtE7eXC/Jdez6UVgV2D/FxK9NvAQfs/9uFTRnb/KlBgH8jFfcvo718Hkrf8XBAo4PJTlqgI8QcCk+5++PlQEID8nwGNJ4mWBHNjymcD0rNlRW7OzDWBu8uHAfCOIB5Z2sXITzPrjxy4yvi+HEo3GFD5OEZ8CkflwFfZsrI+6N0cf34Q558zw8laXuw6FLO/Zp00eq+8+9btioDmpkefP/7FgYlXRw7c3NTw6l/+L7uV46jHRL46F7qpMduT7n7dZQqkqux2VfwAAiDQfwlAgO6/Y4OWgQARHXfccWpCeXnDduONNyL8GccGCIAACIAACIBAfyMgr0+kS5jnejI999xz9fX1UoMWE9bpuryekTMTlpeXX3nllVK77G/dQXu6I+D7/lNPPaUsViKRyDnnnNMpAnqX8OwfbMUorPd218RPUa7Eu3Dsp5uLMw0XqjW5zHligkffDZIUm+VnWFiWDXHJ+/d77hRHfkTT44n/e34pEWWEd67w2zZc0/AyGacj43RIWBknGz76/WvmxMsScrJHxthvfrfA9CxPzPyWTSFTbSsQRrcGSnRLELWdzomkaaL2IKUDI2D5uTOItJVBuPvxuZFIpU1BVfLz4yB6V+blCvtR+aHZZD3R+lxI8geBt/gmou0+tXI/41LGpQ6XUrZIbTa1uNQcpBaXUq6Ydc9wyQolxyVv9+S4JJMnD5LQwSQOG9vnNrnhTeSwBmPqCXMLkVQwvi2tL+Sxt5sgK8+IQ/4ZaOmUNui3j7aMGvzcuKGbR9S/9XfnvdveKo56IbXvOlVld3o6LbP9Cq+yLz0Kr488CIBAvycAAbrfDxEaWKwEMpnMunXr5E1aLBaTMnR5efm7774ro4pM0yxWNug3CIAACIAACIBA/yIQFhzDeSLauHHjmWeeqQJmGWPJZFJGRktTjilTpjz11FP9qz9oTY8E7rrrLum/EYlEdF2/6KKLCkWA7mpuoGTDXQJ0WAoMS89d83YQ8pqxnTvvuZeVJBjTmR6LJsvu/8/fWEF4dLuZ4mQRGcFkjNzwMm4QN2159PyyV8Qzm0RJvDwWK9OPPn6GyY1AoxRr5GZ1DI+TRdQRVOUEyvZewmSzM0bm9PJspV37sC8lCpLK7MtWh3ydTl3O/UvleeQEyfN88nwRZC6Pg5z665vk2GTlkmOLr56de/ygOh3KeIH6LBVqqU2L+T1zST636CRYy02kZm1JjdujDBcpzcnc7fjbF3H24K4jD7RcnbIxlkemSV8+b+nY+jXjh28ZO+6VRx8Xscy+kM7Di0PiIO9pgQDdEx38BgKFQgACdKGMJPpRcARs27700ktVdEkymWSMyet7GCYW3GijQyAAAiAAAiCQ3wRyUk7nv7JXnuvdcccdjLF4PK6ioeVFjnzKXlpaevPNN8MPOl8Ogssuu0z6euu6HovFZs+eLeeT7Dz8wfd86JSUv6Q8qDTonFoYNjqQAlzXLuWEud1CU7NHv/jju3TMZ44vS1QPiFczFi2NHjb7sh+8ufI9z3GCyOVt0tjByDR7jmF0ZF7/68qhg4dXldUyFheyNWML/+vxQFF2xS7CYqTMZxsgw7I94q5IHheysupHOMOF0qq6anezVniLnvKBaOuGPw+wwkOxuVCBA16eRzL5QoDmIom+CIlZas3iMxeqHKwTNlHpSlg+HOAe+Q75lvjMBqz7xDsnecrkhk3J1jLC2vDI9sgNUjbuvuuh11slPR7qSi9++280qPT3TXWbRjdsGHP4H3wSLe6y7FcEdLiW8PkVLkceBEAgrwhAgM6r4UJji4OAfIO1vb29srJS3qfJOGhx6blwIQKfi+MoQC9BAARAAARAIJ8I7FF59H2/vb1ddqOlpWX58uUNDQ1lZWWMsfLycl3XNU2TodDygmfixImvvvpqPnW7WNt6+umnx2IxTdN0XY/H43PmzLEsq7tjIB8gKUE3rLKqwlBmN1Vu9/LQt6xALIJpg967QjL+22tvTp1wpCYE5UhpSWUiUqmz0tNPOvWBX/3bKy8/kenYaHZsIfK3fLTxtp/9a2k0GWGazmI6K2UseuoJZ/lWzsxEKp7h3clWKdMD388K0D1o0LsEaDHJ3adPu4nXYSG7S34/Ku/FTXJuGMo7xd9NfQ4ioIUG7VMQE214ZGWDo6VanZOeO8v60jDDyQnnQoP2iDu5lDNNkSHW6jOnR4vQbOEpLhvj5Jw9nNxm2YB36XpxyE+o8KGW3bmcErG9g/5ljj926PuTRtiDa1Z875oNraZAJ5bdzhQZ695Tw+U+ul0DAnS3aPADCOQTAQjQ+TRaaGuREJCzC/7ut7/r5P7c1NRUJATQTRAAARAAARAAgYIk0NraesEFF2jBop6vR0JLPB6fP38+EZmmaRiGbQvnUyz9jcCgQYNkAHsikYjH4zfccEN/a+H+tmcPWtu+VhXWyLKKsN8pIPqt1W+dcdqZJZGSmB6P6clkdMCARLI0UaIx4fOcjOuDB9XK86KirLw0XhqPJmJ68rDK2nRb2jJsUZuw/wgmgJMtDe9UNVSsptTooDSnXXdqT7i3xZlXzPaUCSPZ0+/hMrXubiOSKw0XhvPhGnblOSeVdgt237XKIcrxwAxdOpHIKPmsBs59Mhxqbqe6gYvHjTJH1mWmjn7n3VXErcD9WbRaLTkIqmBPGbWSyuxpLZSBAAjkNwEI0Pk9fmh9gRGwLGGPJe+1pk2bJi9AI5FIaWmpruuzZ88usP6iOyAAAiAAAiAAAkVFQF7q/PnPfx44cCBjLJFIVFZWhvTniLz4OfPMM9va2uxgKSo+edHZLVu2SGs4OViapt15551yZPOi/X3VSNM0PddzHOeaa66R6OSnjCIPm6Truh6JROS7AvF4XL4Bads251yGmauM/Nq1R77vdxoRy7IcYfeBJT8IKB1WZfqi3TLQOSxAy1cEuMepw6bb51PTqM0Tx1Dj4K3/fAUZ28lLiWcfPjky7W4W01MPVDdVpqe18RsIgEB+EoAAnZ/jhlYXKAF5Xei53vLly9U1fTKZlJek77zzDuKACnTk0S0QAAEQAAEQKAoCyuX5ww8/nDBhgvTfCAvQui7sbhljdXV1ixcvJiL5ZlhR0MmTTnLOq6ur1UhJjzjpIJcnPeibZhqGoY7/DRs2XHrppdJ5JhqNapr2Sex/VVWVdEiPRqPyp9GjRytTGs65bdtSR96rAE1E0hRl1apVDQ0NjLHq6uq1a9f2Tc+x10IgIMRoTnaQXIfTjjY69rjlYxo76iqap01a88oyES3tGSJC/6AI0EqJ7pQpBJboAwgUKwEI0MU68uh3fyUgNejZs2fLuy95Y6Zp2mmnnWbbNgyg++u4oV0gAAIgAAIgAAJ7IeD7fiqVkitlMhnP9a644gppOKY0aHn9Iz91Xb/qqqv2Uil+PuQEPnkkcOONN2qaJkftiCOOQGjtvgyC53qWZaXTaXk97zjOunXrfvrTn5555plSeq6oqJCZRCLR1NQ0f/78lpaWdDotA1B837dtu729nQdL2HG7696l0v3Jjm688cbS0lJ5Qp144olyTTwt6EoMJXsmIGe8zFq4SAHaFcYcLv15MTWOfGP4wHTTkO1nnf6qZZFpkuMEB6aMgPazszHm4qD3vAdZ2kll7uFrT7XgNxAAgf5NAAJ0/x4ftK4oCXiuV11dLaOe5fw8mqYtWLCgEwxcO3YCgq8gAAIgAAIgAAL5RcD3/UWLFlVWVkoXgvDsF1LcZIyNGjVq2bJlRASVs/8MbiaT+fnPf/7Nb37zZz/7WVghVapo/2lqP2yJpCR1ZKkUc863bt36zjvvLFq0aM2aNel0Otxsec0vJqlzPUVYZsKrhfPyZLFt+7zzzlNBLclkcvv27XI1FYsd3gp5EOhMQArQwtJZyM48O6smNbfSpZfZ9XXr6yt2Tmlc/8f/FpbQlkcZ2wvsn5WA3Lm+7r6rDfaa6a4GlIMACPR/AhCg+/8YoYVFRMC27VQqtWDBgtLSUhlXImfpqaqq6koBAnRXJigBARAAARAAARDICwK2bUuNzPf9bdu2HXvssZFIRD53DwdBy1fBGGM///nP0+k0NOj+MLicc6WQGoYh3R5s2w5ro/2hnXnXBmmsEW627/ud3DbCkHu4F5BB05zz+fPnyxNK07RoNLpgwQJ42oQJI78XArsEaJeT6ZLX3iFmSFz1Nxo2/PWmRquxZsfnpq7ZsYUcog6PrGCCzFzIc3gqwr3sZ6+6s1phLxXhZxAAgX5MAAJ0Px4cNK0oCZimeeyxx0oDOKk+a5r2zW9+k3NumqaKVug56qEoyaHTIAACIAACIAACeUPAcz3DMJSg/MmcaXPnzi0vL5fTr0nJLBaLMcai0WgikWCMzZw5s7m5OW96WLgNlQqmaZpSfZZhudJxWMmjhdv7g9wz6ewsJxiUVUunDtM01dkhyxXbcKa71ijXvg0bNkiPaXlOfeMb3xCxrJxnMpnutkU5CHQhwIkynEyfqMMUP/7wex9PGLdt7CiaNmrrv/2LKDFd3yYyA+0ZAnQXgCgAARAQBCBA4zgAgX5EIJ1Or127VsUpKAF6+fLl6jpSNhcCdD8aNjQFBEAABEAABEDg0xPwXE9KbI7jeK6XSqWWLl2aSCSkCxljLJlMMsbUZHdylrZHH3200656iAPttCa+HkQCMipCwQ+roqrwIO6uGKryXE+9GdC1v50I93wvENaXk8mkepOgvr5ehbN03QVKQGBPBIT5hhSgg6cXtGkdHTH+hcoB60fWp4YN/PPmdZRqpQ6z4xNhusPlsODYE0OUgQAICAIQoHEcgED/InDJJZcoAToWi2maNm3aNGUS1+ktvP7VdLQGBEAABEAABEAABPaXgAwF3bRp09VXXy2vhRhjMvZZSdLy2fwPfvADy7LkNIYynHN/94ntQKDwCcyaNUudUNFodOXKlYXfZ/TwoBAQcw9yEr7PIriZk2s4rmnRPbfR5OFb6qvbx4z86DvfepuIPE62k/Z8cjzC86eDwh6VgEBBEoAAXZDDik7lK4GWlhZ1gSjfOdV1/f7774cAna8jinaDAAiAAAiAAAh8SgK2bf/xj3+sq6uTF0XxeFy9EyZnyIjH49OnT1+3bp2sGBGdnxIwVi8uAgsXLlQvFkSj0Xvuuae4+o/e7jeBrAAtrTVcL6jH6KCzj/94TG3b8Jr0lHFvL/kLdTjkkeeT5XPyP4Xt8343CxuCAAjkKwEI0Pk6cmh3QRK46667NE2LB4sM+Rk0aFBzc/Me37nD4+WCPAbQKRAAARAAARAAASLauHHj0UcfHYlEZBy0lJ6lJJ1MJiORSH19/dy5c+UMeCAGAiDQHYEdO3YwxmKxWDQajcVip5xySndrohwEdiOQFaDNIAJaaMxE9Nz/o6aBL4+pbRlZu+Xkz73dGlhCu+T4vkceiYQFBEAABLohAAG6GzAoBoG+INDU1KQcDxljpaWll19+OZF4lWmPS1+0EfsEARAAARAAARAAgV4koB6x27Z92223hW2g1Yti8XicMRaPx08++eTW1tZ0Oi1nxpPNQkx0Lw4Pqs43Ap7rnXbaadIGWoa5qFMs37qC9h5aAoEA7fMMkU8+eR41b6VLv/K3w0e8O6Jy48i6lQ8/TCmPLLICAdoX6rMr1sUCAiAAAnskAAF6j1hQCAKHjoDjOKlUioief/75SGiRt1iLFy+2bTusPh+6lmFPIAACIAACIAACINCnBDjnf/zjH4cNG1ZRUVFeXs4YU37Q8qKJMTZo0KBly5apZra2tkKAVjSQAQHf97///e8nEgk1FeGf//xnFeACPiDQLYFAgOZemojSKbujndatoTH1T44d/EFD1ZppU5d+tI0yRDutHTbZXKrPrgiChhFHt0jxAwgUNwEI0MU9/uh9PyDgOI5lWZ7rXXbZZSH9OZJMJkeMGBGWnmW+HzQZTQABEAABEAABEACBXicg4zTb29tXrVp19NFHS+lZ6c6MsUgkEovF5DP7W265xXEcOHL0+qhgB3lI4LnnnpPnizS0ueqqq+TsnZjePA8H8xA2ORCgiSwizwvMnX92PQ2vWtZY+1Fj/cp5N25v9aiDKM1N2+dKgIYT9CEcIewKBPKMAAToPBswNLcgCfi+39zcLM0NlQZdWlr68MMPE1EmkynIXqNTIAACIAACIAACILAvBGRE87x583Rdj0ajYT9oZcoRiUROP/30HTt27EuFWAcEioqAaZqDBg1SLxBMmjQJAnRRHQD72VklQPvi2V7LTho/4pmpo3eOHdI+Zfyq198hmyjtk0Nk+yT+lQ48oCFA7ydtbAYCRUAAAnQRDDK62O8JGIZx9913x2IxpT5HIpGBAwdmMhnHcWDT1u8HEA0EARAAARAAARDoXQKWZRHRG2+80djYWFpaKjVoLVhUaKemabW1tU8++SQsOHp3MFB7HhI444wzIpGIcrBZt24dD5bw25Z52C00uTcJBAK0Y7aKxxUe/b8naGzD6xOHdzQO/vj8v/vYJuG/YXBh+8wpEKB51n8DFhy9OSqoGwTymAAE6DwePDS9MAg4wTJ27Fg5z3t5eXk8Ho/FYrNnz4b0XBhDjF6AAAiAAAiAAAgcFAK+7xuGcdVVV5WWlqrY59LS0srKyng8nkgk5IyFc+fOJSLpyHFQ9otKQCB/CcjnMffee69SnxljDzzwABGZpgnXmvwd2UPS8sB6I9jT545a3Fi3fuyI9PChrz38UHbGQU+qz0S+7xH3hRS9l0WI1bunvWyAn0EABAqGAAToghlKdCSPCTz77LPhGd51XWeMvfDCC7Zt494pj8cVTQcBEAABEAABEOgdAk899dSwYcPKysqUDK0yerBMmTJl2bJljuPAyqx3RgC15g0BeTexevVqZZjOGLvwwgvxkCZvhrCvG+p00PPP0vTJb42oa6mteO/zp7yZMYnntGYeqM85AVpETfe4dFKfc7X0uA1+BAEQKAwCEKALYxzRizwmYFnW+eefzxiLxWLqPmrEiBFEZNt2Op3Ga6R5PLpoOgiAAAiAAAiAQO8Q2Lp16xlnnCH9N+QVVHl5uZKh4/F4bW3tvHnzDMPApVTvjABqzQ8CKpxlzJgxKuSlsrJStj6Tydi2nR89QSsPFQElEosd+mRlaPY3W0cMeb+x3h41/MO77yXbI9fLtsajsI9LDwK0qjVr2rF7HLT89VD1EPsBARDoCwIQoPuCOvYJAiEC69evlw6GMvBZXhfeeuutvu97rodbphAqZEEABEAABEAABEBAqB2SgmEY8+fPHzhwoJxdrbS0VGrQyWRSKtG6rn/2s5+V/tEABwLFSUAJ0LNmzYpEIjIOWtf1V155BbcbxXlI7LXXSirmRI5Fa/5Gk5r+2tTQ1jg0c8yMzRs3iwp48M+wtH0OK9DdVy5rdSnnGg0BuntW+AUECpMABOjCHFf0qv8TkPdOlmVdd9110WhUBezEYrFoNLp+/Xrf9znn6har//cILQQBEAABEAABEACBQ0/g+eefnzBhgryUSiaTSl+Ts2swxsrLyxcuXOjlAvakVnLo24k9gkCfEFABztL0T910fOc73+m5PZZl2batTpyeV8avhUQgkJWFy7PjUzpN116zdfK4j4bVpUbUb5zzA9FRKxQ0v8//ooZl7e7yhUQRfQEBEOhMAAJ0ZyL4DgK9TYBz7rme/K/ac70JEybIOyUpQ2ua9vd///cy9hnqc2+PBeoHARAAARAAARDIdwKZTKatre2CCy5gjEWjUaU7y7fK1Nfbb79d9pRzblmWnH4t3/uO9oPAXgnICGjf91tbW6PRqKZpiUQiEolMnjyZiPbdowY3JntFXRgrcOIeBeozkc2ppYWmTPy/kfVbRg9P1w9a9t47wpQjF8Wc7fG+HRvdic7h8sJAiF6AAAjsmQAE6D1zQSkI9CoBx3FkNEF4+sF4PJ5MJqPR6NNPPw0Bulf5o3IQAAEQAAEQAIFCImBZlmEYCxcubGhoYIzF43FN01Skp1SidV0/5ZRTtm7dSkSpVGrfFJNCgoS+FDsBz/VOPvlkeV5I67/Nm4WZQneOf7ZtG4YhqSEOumiOHs6FvTN3iBwi06NfP0RDa5ePHNo8fNgHX/vatlRKkfi08weGhebu8qpyZEAABAqQAAToAhxUdCkvCEg7wosuuqiysjISicjbJE3TxowZI9uP+6K8GEc0EgRAAARAAARAoA8JqOslwzAcx9mxY8dpp52WTCYTiUQsFuskQzPGampqnn32WTGxVs5Iug8bj12DwCEmcP311yeTSU3TdF3XNO3hhx82TbOTAC1vUmzbXrNmzeuvvy41aOXjcYgbjN0dOgJZa32Xk+2S5xDZRBmHzjp1/aghW4bXbR098o2HfyOaY3SQbxuBg/Onal13onO4/FNViJVBAATyjAAE6DwbMDS3kAh89NFH8j24SCQirwLj8fj1119fSH1EX0AABEAABEAABEDgkBGQUtp1110n7TjCQdAyL33PLrvsMjnTRifp7ZC1EzsCgT4h8MorryQSCeVOM3PmzK7NkJL0F7/4Rfn8ZsmSJURk2/a+TTTXtT6U9HsCfuCqwbPeGpxMyzcNooxHL75CI4f+pWnozhF1m44/9m8dtlClfbLIzwrQUjzutoey5vAnBVvsVtLt1vgBBECgwAhAgC6wAUV38obAJ8EFN954o7b7ouv6li1bPNdT01XnTX/QUBAAARAAARAAARDoOwJy9mYikhdRixYtGj58eDKZVB7QUoCWsZ+RSGTKlCnvvffe9u3bEQ3dd4OGPR9qApZlDR48OJlMqucxLS0t4UZwzufPn59IJOQ60Wh0+vTp8rSCAB0GVVB5JUALUw3ukWmR2eEJq+cr/+md0Q2rGwd9PLT2r3f8nAxOLrX51EG+JQlAgC6oIwGdAYFeJgABupcBo3oQ2BMB+Wrb0KFDGWNhCfqiiy7CXdCegKEMBEAABEAABEAABPaVgIxrbm1tvemmmzoJ0JFIRE3+XFNT87vf/g6XXvuKFevlPwHbts866yxd1+PxuLSBXrx4cdgSfd26deFTRtf1U089VbpwQIDO//Hvpgd+YKchZx4U0w+6DmWI6MNNNHr4H8YN+3jggDVTJy/avIVMn1wyfHJ835N1QYDuhimKQQAE9kAAAvQeoKAIBHqbgOM4CxYsYIxJd0KlQf/pT39Sc330dhtQPwiAAAiAAAiAAAgUEoFUMD2WVJ+lYwAR3XvvvVJoUxHQjDE5A0c0Gk0kEuedd57csJBQoC8gsEcChmE8+OCD8ozQNC0Wi82ePZuIZHBMOp1+5plnZHxMaWmpVKJvvfVWWHDsEWbhFIYFaJ+8YPpBIpp/O40dvnLiiLZxI9+eO2/Tjnayxa+OeBSRm4AQAnThHAboCQj0PgEI0L3PGHsAgT0ROO2009S7b5FgGTp06J5WRBkIgAAIgAAIgAAIgMDeCch5BaW5c3jttWvXnnXWWYyxSCQSj8flBZj8jEQi0Wi0vr7+ueeesywrkxFxf1hAIK8J2LYdNjd3HCedTisReePGjdJeQ54LU6dONQxDHvme691yyy3yxkR+app2//33C18GzhEBnddHRU+NVxYcngiF9nzh02zaNKlp6fiGrcMO+2jE0MVvrCE3EKazynN2xqC6A1YAACAASURBVMI91Rr2d96X/J7qQBkIgEBBEoAAXZDDik71dwLvv/9+NBqVk1DL+594PC7jC/p709E+EAABEAABEAABEOiXBMICWThv2zYR3XXXXaWlpfL9s64y9NChQ6XQJlful/1Do0CgJwLh1yht254zZ84xxxxzxRVXhLexbduyrAkTJsjwf/k2wIYNGyzLki7qV155ZViAjkQizz33XPhskvlwncjnPQElQHPinByPUgb99lFqrFs9fqjRNOzDf/iHjzNcuHIEAnUwVyEE6LwfdXQABPqAAAToPoCOXYLA5Zdfruu6vAuSU1HH4/HW1laQAQEQAAEQAAEQAAEQ2D8CXWWysFiWSqWWLFkyYsSISCSSTCalDZqKho7FYpFI5OKLL25vb8dc0PvHH1v1LQHf9z1XOPO+/vrr5557rozu13X9sccekw1Lp9NyhdmzZ+u6Hg0Wxlg4xvnss88OC9CMsa1bt8qt+rZ32HsvEsjGKXPyhQBtu9TSRmec9kZ95QfDa1obG1b8z5Ni54YSoPevKd1FQ+9fbdgKBEAgDwlAgM7DQUOT859ATU0NY0xG38hboFmzZuV/t9ADEAABEAABEAABEOgzAj0I0JlMRhp0bN++/ZJLLikrKwtPBK1kaMZYY2PjkiVLumrQcvM+6xt2DAL7QMD3/W3btjHGZKSLmmlQatBSR7Zt+7HHHlPHfywWO+ecc4hI/nr00Ud3EqCJqOvpsA9twSr5Q0CEM3PiFvnCf8N06KWXaOig50fVpYeUb/jcca9YnDrE9IO5COj96xkE6P3jhq1AoIAIQIAuoMFEV/KEwP333x++z5Gvgr711lu4scmTAUQzQQAEQAAEQAAE8olAJ2Hatu1HHnmkvLw8EonEYjHGWDQaDU9UyBibO3euNDQwTVNOUYjrtHwa8qJsq5SJb731VsZYWVlZPB7XNE3edDQ0NKxcudI0TQmmra1NOgFqmqYHiyw3TbPTTcoZZ5whrTmKkmhRdZqTJ6yKDI/SFl104Zahde9PGOaPHLTq/v9oc4KZCcVTCiFU55awoJwr29e/B7Ltvu4D64EACPQ7AhCg+92QoEGFTcC27ZNPPrnTtd20adMKu9foHQiAAAiAAAiAAAj0FYGwAG1ZlmzGtm3bjjnmmE5m0OoKLZFInH/++YZhqKDRvmo89gsC+07Ac721a9dWV1fLI1ka/SUSiXg83tDQsHXrVhXpfMIJJ0jpWX4uXLiQiFKpVCQSUWcBY+z4449Xp8y+NwNr5iEB7tsGdynj0qp3aOTIV4cO/HjCsPTnj33nvXdEbyyidsuCAJ2HI4smg0A/IgABuh8NBppS2ATS6bRt21u2bFEhNvIKT9O0xx57DGE1hT366B0IgAAIgAAIgEBfEQgL0LINlmW1tLR8Eu43Z84cLVjCols0GpXB0U1NTa+88oq8SIMNbl8NH/a7jwSUUcbq1aurq6t1XY/H4/J2Q9o9f+UrX1FzbF577bVhAXrevHmc80WLFjHGwhYcN998szx99rENWC0fCQRBzdwnixM5RFfP2T64bmXTsOYRg16fc8XOjnay+K45BztHQMsOy4jmUOd5ECsd/sz+GI597rJVqAJkQQAECpAABOgCHFR0qX8SkBODzJ49W70NJzN1dXXyhTjEF/TPgUOrQAAEQAAEQAAE8pqAEqA79UJqysuWLZOTc3TSoKUSF4vF5s6d22lDIlJ1IoagKxyU9BUBJRY///zzKuQlfGD/9Kc/lUHQK1eu1HVd07RIJKLr+ujRoz3Xe+aZZzoJ0PPmzZO6Nh7A9NWYHoL9BjJxVlheu47GT15cX/d+45AN40c8/faq7P45ke0L/w0I0IdgRLALEChUAhCgC3Vk0a9+R0Bet9XW1qqXPeV14Q9+8AMVsNDvGo0GgQAIgAAIgAAIgEChE0ilUpdcckldXZ2S6qQwl0wm4/F4LBY777zzWlpabNuWl3O2bUOALvSDIi/7F34c8sADD8jjORKJSK9nGQ394osvEpFpmoMHD5YrRKNRxtjq1atvvfVWeeSrIOiXXnrJcRwVN52XUNDo7gmoCGWPqNW2HKJ77qfGUX8bMeTjccPXzrtqk7DekAHSQSW71Ofu65S/qJpVJrsFIqD3hg6/g0ABE4AAXcCDi671LwLt7e0PP/xwNBrVNE1q0PJq791335X3MPJV0P7VaLQGBEAABEAABEAABIqDwIMPPjho0CAZAVpeXq4ioKV4l0wmn3nmGc6zCgwPFsjQxXFo5GsvL774Yl3XpZqsrGYmTJgg59U899xzpQAtvThuvfXWefPmdYqAfvnlly3L8n0fGnS+HgQ9tlupww5RB1G7R0d+5qUhde80NWyrr3hu9avkZz3ze6xlTz+qmlUmuxYE6D3hQhkIFAkBCNBFMtDoZt8TSKfTRxxxhLzOk1Ou67p+7LHHEhEu6fp+eNACEAABEAABEACB4ibg+/6KFSvOOussxlg8Hi8vL5duabquy6ABTdNuuOGGTCZDRBCgi/tg6e+9dxxHqsZf/vKXpae5fI4i70HOP/98InrwwQdViDRjbObMmccdd1wikZBStfzcvn27jPfH+5r9fcj3q31SHfaI7GCawXt/vaN+2OJBNR+MG/bxOaesF7HPzn7V28UAelfoNATo/SSKzUCgEAhAgC6EUUQf8oLAihUrGGPyso8xJu9k7r//ftl4GKvlxSCikSAAAiAAAiAAAoVNgHM+d+5cGQfKGAsb6UoHgzPPPLOtra2TAF3YTNC7/CVgGEZDQ4MKgpaKM2Ns4cKFb775pvoqD/iJEyfKA14acWiaJp+1QH3O3wOg55YHAjT3yLWJdmTowq+9MXLY2rHDd46pf/2xh8huJ9o1+2DPNXX+VQU+q0x2DQjQnVHhOwgUEQEI0EU02OjqoScg5xWUcwzOmjVLXtLFgoUxNnz4cExic+gHBXsEARAAARAAARAAgZ4JPPPMM9ISOhwKrdS66urq1157reca8CsI9BMCqVRq2rRp8mlKOLq5ubl54sSJ4fgYdYTLe5YJEyaoYP9+0hc0Y/8IKBW4U6bD7CDyXGpLufTyKzRsyF+mjeXj6rd89sjn7ZTYlSve9xBHQS7Jr10+pazcpRgFIAACIBAmAAE6TAN5EDjIBAzDkDWmUqmBAweqqzoZ/nzrrbdCgD7IxFEdCIAACIAACIAACBwwAdu229raZs6cqWQ7dRWnMt/73vc4562trQe8N1QAAr1LYM2aNdXV1bquhwXo7373u9L0WR3SKiNvVU499VQpQPdu41B77xNQ+nGnTCAtey5ZHTb98GpvcPk7h4+gaaM+vv2WjJEib5cBtNqum7ZCgO4GDIpBAATCBCBAh2kgDwK9ReC+++6T777FYrFEIiFjDT766CMI0L1FHPWCAAiAAAiAAAiAwIERsCzr3nvvrampkVduYTsOTdNisdhRRx3V3Nws33U7sF1haxDoRQKc89dee40xFhagGWPXXnutNJZR0rP0CZSegbNnz/Zcz/f314WhFzuEqj8dAaUfBxnOKZuIqMNyiWjrVpo2/q/Tm9xxdebk4aveepNsh4wOOfThrbvZLwTobsCgGARAIEwAAnSYBvIgcPAJOI5jWVZjY6OMoEkmkzKm4Jxzzkmn05xzzJ9+8KGjRhAAARAAARAAARDYXwLh2aEty1qxYoWcRzoSiciZ3BhjiURC1/VYLFZdXf3cc89Bg95f2Niu1wmkUsJMwTTNRx55pJMAPXHixEgkIoNjlAadSCTi8fgnSvQtt9zC+a7Z43q9odhBrxEIScick5tLYnB9Itui+++mhopXR1fvnNSw7XvfoVQ72R7ZruO4hu97Of+N7g8GCNC9NnaoGAQKiQAE6EIaTfSlnxJ45ZVXZMSBevGNMfbcc8+Fb2/6adPRLBAAARAAARAAARAobgJSXL7qqqvUVNKxWEy+2SY/dV3/xS9+ISGl0+nipoXe90cCnuvJCc/vvPNONbVmJzFaCdCMsWQyyRj7xS9+gfDn/jicn75NXQRom5PNhbMzZTqoo5mmjnpm4uBt42tbpzS+/uf/pQ6TLO7ZnsW5HVKflQAt6/v07cAWIAACxU0AAnRxjz963/sEDMO45JJLlPQsL/VGjBjhOE4qlcJVXe+PAPYAAiAAAiAAAiAAAvtJwPf9TCY7D9eSJUtGjBghX2XrJEAzxqZPn7569WonWOQ01Pu5S2wGAr1DQMrQl19+ufTZ6E6AlpH+mqYtWrSodxqCWg81gd0FaKk+25zcjO1YFj18Nx0x/O3RZS0T6rb/41c2dhiUccj0HMfzgoaGts42HAL0oR5B7A8ECoMABOjCGEf0op8S4Jzbti0DCsIXeXfddZfjOHiprZ8OG5oFAiAAAiAAAiAAArsT8FzPcZy2trazzz5b0zQlQGuaFo1G9WApLS198cUXebDsvjW+gUB/IeA4zvHHH19bWxu+N1HHcyQSkY9YotHoihUr+kuj0Y4DIxCSkLkn3DVMLpIryl0698S3x1VuOmYEHTF80+O/J5so45LpkOsFMdJi16oC2Y6wAK3Cog+sidgaBECgCAhAgC6CQUYX+46A4zg/+9nPYrGYvMJTAQXSi42I5NtwfddA7BkEQAAEQAAEQAAEQKAnAtIzzQ4Wud5DDz0UFuyUNYdU7u644w5YQvcEFL/1HQHHcYho+/bt48eP706AVjcszz77bN+1FHs+mASUfsyJi+DmQICWO1j5Go0a9OLUYe6MYfzM4zYTUasl1rA94rumn1QVyI06CdDQoA/mYKEuEChgAhCgC3hw0bW+J2AYxoQJEzRNk5PVyGmmL7jgAuX+DAuOvh8ktAAEQAAEQAAEQAAE9oFAeOLoN99884wzzlC2uUqDlua5p5122ubNQsqRV3owht4HuljlUBCQx7DjOEuWLJFHb1lZWTiiPxKJqINZvqypDvtD0T7so5cJBAK07ZBJZJMrPi77+odD694eNbS1oWr5z39ChkNpjztE0n0jmKSwuzYpVbpTprv1UQ4CIFDsBCBAF/sRgP73KoEXX3wxmUzKiaQZY1KAfuONN5TurDK92gxUDgIgAAIgAAIgAAIgcHAJ2LZ91VVXyTiDaDSaSCRkXtO0qqqqxsbGN954QwacHtz9ojYQOBACSoN+/PHHGWM9C9BKfcY9y4Ew7z/bciKHeGCtwblD2z+gxkGLBtZ8NGrkjhOOeWPnFuH+rBw3AhXaCfw39tiDTrqz+rrHlVEIAiAAAgQBGgcBCPQigW9+85uMMXk3IjPTpk1T+8OVnEKBDAiAAAiAAAiAAAjkI4EnnnhC2umWlZXJkFJd12XMAWPstttucxxHTWOYjx1EmwuPgJSVP4nQv+GGG+RBu0dLGc45BOgCG30eiMpeICp7Ft30fZrYsHFgRcuQuneum7fZ84UBtEV2zlPDI3I48W6kZVnskgilVqt0yhQYP3QHBEDggAhAgD4gfNgYBHomoOu6eotN1/V4PH7XXXepTSBAKxTIgAAIgAAIgAAIgEA+EuCct7S0nH766UrIky+9JYOFMTZ9+vSNGzfmY9fQ5gIm4Pt+JpPxXG/q1Kk9WHBAgC60Y8AnL1CUPU5OhqaO+uvEoelJo+jIqevWviP6agkJWi0+BGjFAhkQAIEDJwAB+sAZogYQ6ExAxrncdddd8lZEfSaTyZaWFsuyOm+A7yAAAiAAAiAAAiAAAvlJQE45eN9990kDaF3X5XtverBEIpFEIrF48WLpqNve3o45qPNznAuz1a2trUOHDlVWgeo5SiwWkybmSoMuzP4XX698h8y06PZ//Y7G178/ZEDzqMGb/vEr21pTROR4lOnk+xwOad6dVviX7vK7b4FvIAACxU0AAnRxjz9635sEJkyYoKRnOQnhrFmzfN/HXUdvUkfdIAACIAACIAACIHCoCaRSQrxZsWLFjBkzEolE2IVD0zRd10tLS2+88UbZLMdxcDV4qEcI++tCwLZtzrlhGCtWrJBvairrGPnsxHM9pT7jxc0u/PKzwM96cNgWHXfM0oFl60fUpscOX/7iUjId8injk+0LP41dS1ha3lUqcuFfusvvvgW+gQAIFDcBCNDFPf7ofS8QaG5uJqJly5aF1WcpQK9duxZz0fQCclQJAiAAAiAAAiAAAn1DoKswd8011zDGotFop0tBxtiZZ56ZTqc559Cg+2a0sNfdCcijt729XZpBx+PxSCQSj8eTyaSmaaZpQoDeHVg+fpPScK7lPieznTL07NM0YthLTSPMxiGbTj95mWOSn5ttcJf87Itg6LC0nKtF/g3/0l1+9y3wDQRAoLgJQIAu7vFH73uBgJSYL7nkkk53HSeccEI6Hbzv1As7RZUgAAIgAAIgAAIgAAJ9SCDssbZ06VIp4amrwVgsJsNLa2pqnn/+eWjQfThS2LUiYNu2Co455ZRT1OEqMxs3bjwoAnTXhzSqAXvNHMi2e628wFfwZf9yAnTuq28bdgf9w0UfDBq4pq5258QxHzz2iFgzUJt3ydCqKCwt704s/Et3+d23wDcQAIHiJgABurjHH73vHQLvvvtupws4xtgjjzyCOdB7hzdqBQEQAAEQAAEQAIH+RSCdTn/5y1+WF4SapqlZqaVP9C233EJEmUwG+lr/GrZibY1t23fccYfyLpfH7VtvvaUE6AMBwzk3TVM9oZG+H+orEXXnSNMpBBsny6cYBRnPLIKZOZErNgwEaB78fecDGj7y/2oHbmxqNKaMX9m6gzznU9S9+6o5gXv3UnwDARAAga4EIEB3ZYISEDggApzz22+/XU44wxiLx+NlZWWDBg3KZDKcc9/3bTs8ufAB7QsbgwAIgAAIgAAIgAAI9FsC9913X21trZTzYrFYPB6Xs71Fo9Fzzz233zYbDSs2AqZpbt26deDAgSqGJhqNvvDCCwdFgBYiKOee6zmOI6fiVG8AqPjrtrY2tS+5cngI1E/hQuR7IrBLgKasAC3Wdj0Skwxeec1bI0atGdNkDal757ZbyTZ6qmlvv0GA3hsh/A4CIJAjAAE6RwJ/QeDgEWhoaKiqqlIxL4yxm2++WU4kLaf7OHi7Qk0gAAIgAAIgAAIgAAL9kYDnerZtb926dcaMGfF4PBqNyjhoZccxatSotWvXyqYjurM/DmGRtWnVqlU33XRTdXV1JBL5zne+I29eDvqRaRhZvXP9+vULFy6cP3/+dcFyc2h58803OeepVMpxHKU+H/SWFPjwSk8N0Unp6uwStTtEb62nYU1PNAz9eHj9jsmTX93wAfH9D39WUxEWOEt0DwRA4KAQgAB9UDCiEhDYReCFF15QsQPyRTbG2IYNG4gI6vMuTMiBAAiAAAiAAAiAQKETME2TiNLp9MUXXyzDn2OxWDKZlHlN0xhj8+fP3759e6GTQP/yg4Byw5BqrxR/D7zpTz/99EMPPXTDDTdcdtllTU1NiURCvgrAGJNnRKdJOzVNO/nkk9euXdvJhePAW1J8NagIZZcoY3P6t3+n4Y2rGoemJ4z6eN61bZZL2w7onx9Vf/GhRY9BAAQ+JQEI0J8SGFYHge4JyHfKvva1r0l3P3Uhdc4556gIgoN1Gdd9K/ALCIAACIAACIAACIBAHxOQl3w8tziO89prr02bNk36sylLaCnDnXfeeZs3b3YcB8EKfTxs2H2OQDjuuIf7F6lTW5b14osv/ulPf7r55ptvuOGGOXPmXH311TNmzCgrK5NPWSJ7WsIhO3vMV1dXX3jhhQsWLFixYgXnXNoYKjNDzO6eG6vu/kr3Zxn+7PvB33SKph/7+uAhHw0buLNxyKtr3qI2kwxPxEjL9bqrC+UgAAIgcOAEIEAfOEPUAAKCgHybbN26dYwxXdflROfRaFTTtEWLFtm2Hb6MAzIQAAEQAAEQAAEQAIECJtBJgJY9TafT3/rWt+LxeCQSKSsrY4zJqIVEItHY2Pjuu++mUilpmIvrxgI+NvKia+EjUOZlPI1q/PLly++8887TTz996NChyVh8QCL5ietgSRDUH1aTo9HonsRnURZerYe8ruuMscbGxvvuu0/OWCjn1PFcDxq0Go4uGak+u4GwzB3HsQzyLfr9ozR24lujmjJjhm2fecp7qRQZRDaRAwG6C0EUgAAIHHQCEKAPOlJUWLwEPNe76aabZCSLDGzRNG306NHyXbbwZVzxMkLPQQAEQAAEQAAEQKAICMgLv1wAtJiGWsaKGobxwAMPqJkJZXyoVN/i8fh9991nmqZhGHJ9tVURAEMX+xeB8BHoke+Rn7GEn8yKv6287vrrp0yZEovFNMY0xmIlUcZYRbJU6MS7L/KGSA+WrjL07uvu5ZseFXvRNO2cc875w5NP7GxrbU21SwdiN3gLVcbwIow3dBgJDZqTzUkSosxWOvvUZUNHrhnUsHHkkBV//C1ZNnFyLXIs8oAuhA5ZEACBXiEAAbpXsKLSIiQgVeahQ4fKGWbk7URZWdm9994rg6PDl3FFyAddBgEQAAEQAAEQAIHiISAv/JQATUTSD9owDNM0m5ubL7jggnAQaCwWq6ysjMfjM2fOhABdPMdJv+1p+M5FCtD/+6f/nXnOTCE5B0s0CEwuK0nGGasqjQlvmZwCnYizigoWjbKaGrFqRSWLxVkitnuKspjOYhqLMpFKRAhPLmX3sOuPvLHSSyJlZaXJ0ngsFjtyxvR/+/nt4iVUy8mYrlKfoaKGjyhO5JHrkUtEHSl66c80rn7xuKZtdYPXnnDUX6028kXgc4clksHFNywgAAIg0IsEIED3IlxUXWwEnnzyyfCNhHytMpVKSW/oYqOB/oIACIAACIAACIBAMRMIS3i+7ysxWl4Zcs7vvfdeacSh67qaOyQej5eXl7/xxhvFjA5970MCah5C6bkhI2nO+uKZwmYwFokIqVhoxZpQjWNxFi1lrJSxmPDfYDXVbMZn2KxvsZtvKf2X69mNP2L/8i/sRzexH/+I3ZxL11/LvnYxm3k6m/l5dvx0dngjqy8TmyfKZC1MS7JoPKs+a1qJzoSwrUdYVUWiRBd70XSRGGODB9ff/NPb0+k+pNV/d8194j55gcOGTdSWoe9/xxhZubaxcufogatuv2WbbcnGGw6lHAjQ/Xck0TIQKBwCEKALZyzRkz4k4Lke5/z888+X10pqcvNvfOMbnezS+rCR2DUIgAAIgAAIgAAIgMAhIxAWoJX6LI04ZBs458uWLZs0aZJ8f07auEWj0Xg8nkwmb7vttkPWVOwIBLoScByHiDKZzMC6QVJ3FqpzLgK6hLFEkBqHsHO/wObPP/z5pV/Y0Taruf285tTJzanPtHZMTVuHt6UndFiTTWuKTK53hE8zbGeGkTnGNs50Oy602r6e2fGtlm1X/vP1yTk3D/rCBUwvF3sZUM0qa4TQHNWF3i0MphmLRVg8Ij5LNK2qvCoRL9MipSOGj3/8v54iIssWFupwMxYMcuqzEwjQbT6t30xHjH99XG3zqNKPjxz21/bt5HlyzC1OHS4EaAkDnyAAAr1JAAJ0b9JF3cVEYO3atVJ9ZozFYrHS0tJEIvHSSy9BgC6mowB9BQEQAAEQAAEQAIEsgT0K0Jzz1tbWMKNMJnPFFVdomhaPx+WMbeqScs6cOdK4I7w+8iBwyAjccMMNZWVlJXHhsCEXXWPlZay6nJ10PPvxT9gfnqrasHXKlvbxKX64TVPT/qg0DTeo3qbBO4xYmx3fkdHanGjKicnUZpW0GtGMV275tR32oJRR32GOzLhjDD6pxZnQ7h+53Zq2vnni1vQJTy6u/pefscuuZFOnscOqhOhcVcpKIyLaOslYnGkxFisRGnh2+cY3zl/79tKW9vcCxfWQEeq/Owr8N8gh1yRKO3T99c1jh64ec9jmqfXrb7iSZ3b9I+SQUJ8NIVpjAQEQAIHeJAABujfpou6CJsC5mE9GdtFxnB/96Efy8ke6cCQSiUmTJnEuJh0Ov8hW0EjQORAAARAAARAAARAAgSyB7gRopUErl7Z0Ov3yyy+Xl5fH4znrgZysNn369FdffRVMQeCQEZAPSBYtWjR9+nQZlV8SjyUSQuodUMqmHsm+cglb8/aFGzad2GZMdmhYixtp5yxNrJ2znY5IaWIdQbJynzYxlTLEiBIe6ds7GKekTdGMz9pdluLMJt2mWIqirW5phgYaNKzNnWj7f7d1x1cfXTD1S+ewygSriLGyKJMzHpbHSspjomF64AryiQ/1z356lRCgfaipJAVomzzTp63b6IhJS8cO/nDaiB2TGhav+Wv4aPKIrCBBgA5jQR4EQODgE4AAffCZosYiIWDbtrpt8FyvsrKSMRaNRjVNkxr0o48+6rme4zhKpy4SMugmCIAACIAACIAACIBAmEBXMVq5QqvV2tvbv/jFLzLG5FWlvLBkjNXW1j755JNElE6ncVWpcCFzcAlIww1Z5y233JJMJuVDEE3TdDHfoFZaUnlYFXtx+bkbW2bsMBranTLDL7X8mEXM9plDu5LSmnvOWMQMn2V8ZpBIVpDsXMYgzaCSDirt4LVpryHtNLVbMyx+3pK/HH7199nRR7PqUuEcrTNWN0DchSWYflhZVGOsMhm74tuXb/lok2MGJsc5WbUIzx1OZAbTMj58P00e+W5j1eZxg9d++5K3g1kJ1eHjEzlBUiXIgAAIgECvEIAA3StYUWnBE5D3DOo6ZuHChbFYLBqNJhIJOU3z4MGDiUh6Qxc8DXQQBEAABEAABEAABECgBwJdBWjlCi0zatv58+cPHDgwkPxEZMMnQZ3xeDwWi11xxRXNzc3yDTwVA6G2QgYEDpyA7/sbN2488sgj5cOPiooKNb96SWD+XFvDHn86utMfkCaWCYKaXZ+5PvNk4szj4qvri3hnKSjv9XOPIrXaSmrTRhBJnSa9za1us8eknOPSxgW/fXTypV8rGd3AagawyhJWGwjmsaCdco7Ey2Z9c/vWbRJLEZ4yliUsvDsCEX7myR82JL45EAAAIABJREFU1X48flBqyojVi54h7pLriCkKg8UnMVVh1hD6wI8i1AACIAAC3RGAAN0dGZSDwD4R8H3fc72zzz5bWj/L99RisdicOXMMwwiHEuxTdVgJBEAABEAABEAABECg4AjsVYBWAhnnfN26daeccgpjrKysTCmAsVhs2rRpr7/+esGxQYcOPQEezNSnPsm2bcfxnnrq/1VUVInAZy3CIkwr0cXUf5oWi2jJKKuuZIPq2aa2+lQQsGwTc0lIz75MnPmeSJ6nuV6JzUssX+uqI+cEZRHdbPgxw09YXCSRFyHPWe+O3GrZr9LQwyTNplKbKjJU0c4Ht1rjU85xH+/8zGP/PeDii9ngKmEPPSDnXROLaFFdLy0t/eU9d0u+KnLo0OPukz06NnGPTJNeeJ4mjlg1ti41uqZ15kmbPZdsj1w33ChYloRpIA8CINBbBCBA9xZZ1FskBDzXM00zbNgnY1Xef//9TCaj7iWKhAa6CQIgAAIgAAIgAAIg0JXAXgVoqY5ZlqVes7vllltyYhorLS0VRre6XlFR8cQTT3StHyUg8GkISOnZJeHFIPN07733R0uSpaWVJfES8fCjskwvyTorHzGdLfzjxQufnL7+4xkO1Um7DCVAexRo0IEA7XnM9UpcL7ZvAnTC8EtV6qBYh/Dc0KTc3PVT7dcR2rfuUlkbj/s0cKdRu7PtyA/em3nTNYMPi7OExuJCOWc6i0b1AYzFZhx1zKuvvVZcAnQQ3exkyDHp619Z2zj43YbqnRNGbn7ofuowyHDtT3O0YF0QAAEQODgEIEAfHI6opTgJyOuYm2++Wd0eyMwll1xiGEZxMkGvQQAEQAAEQAAEQAAEeiAQFqO7y5um6bneypUrO0U5RKPRSCRy7bXX9lA/fgKBvRHggfQsRErPMy3L+P73f1heVsNYpLSsimmMCQmaxUtZLMFGT2LPvDi62Z3W4o5OeQPTftTwhelzNqnZBXMlIvBZpsCFQ8Uyd8lo0uU5MHou6aCS4KsIgu4hyZBquUKwl5IgkjpBVO96o1PpSTu2n370Z1hlmWi/xpKMlcVjgxlL1Ayse/J/n3J9l8jnXMnuWfF9b7jy8HdOvikeLry9iiaOWTpi8PbG+uYjj3xtWzPZnGxfPHag3MMHFQm/x0wedh5NBgEQ6KcEIED304FBs/KFgGEYdXV1nQToP/zhD5glJl9GEO0EARAAARAAARAAgUNJoDvROVxOJFwRbNt+9dVXGxsb5aWmnGgkmUxGo9Gzzz47lUoRkWVZeOXuUA5fQexLCtBCfybyLr30H8vLqhnTNb1MyLaB+sx0VhJnoyayF1YevYMPcyiRIpYOpg3cTYD2d/N6zkrDIQPoHtRk9ZMMdlZfe8goTw8586Ed7N2hCCfN8yMWZylzUMb++5t+fFjtYSyI5GbJeE08Wcoi4hz6p+/9ExH5vre79FoQQ9qpE1JgJrr62y2Dq14fPjgzauSm71+zxSGyg1Hfo9a8x8JOFeMrCIAACOw3AQjQ+40OGxY7AdM0iejpp5/upD5PnjyZc27beLOp2I8Q9B8EQAAEQAAEQAAEuhIIC83d5UVwIhcaEud8+/btl19+ua7rZWVlyWQw1RpjkUikpqbm97//PWYc6UoYJXsjIJRGzzOJvMsv/7a8l9G10pJoBWMlJQlWWcNKoqxJxD437vBGt1HFVmOX+mzx3UTnsCgc1o7D0crh8gPJh/elorBFe1zmeMyhiEvlKbs+5R6z6u2Tjvksq6xiiRhLlrH4AFYS1wZUDLj66n8i4rtr0HujlY+/++Rk6IO36Yixbwyvaa0/zKofvOK9jWQSORCg83FA0WYQKAgCEKALYhjRib4gkMlkLMu64IILxBtemqZk6Pnz5/dFc7BPEAABEAABEAABEACBPCDQnejcqVz1hHPu+/6SJUvq6+vDl53RaLSsrGzu3Lnt7e1qZWRAYN8IcMsyLr30H+UtTNmAChH7zEri8SgLDJTLa9nilz/bzMfbVLnVZFvameEzIfXKFIpxDovCYXH5oAvQ4R2pCGgpQ2dMoUG7pBEliJIO1X6cGrG1/Qtf/YYQ0+USTzK9RARCf/eKywtYgM5aXXPKtNOdt7VOGrm+qd4bWP3ht77lG5w6vCDoffcI8D0GPqvCfTucsBYIgAAI7J0ABOi9M8IaINAdgU2bNiUSCcaYnHhQmvRt3bq1u/VRDgIgAAIgAAIgAAIgAAL7QcD3/ZaWlu9+97tSTZMXn4yxioqKCRMmrF69ej/qxCZFRUA+4VBd/uEP5ySTA4Jg+og6nMTRpbEjjmUr3z92hzcuRQMzpJtdjZ73QYAOi9HhfCcdWX0NrxPOqxWU6CxLVAS0MOIIIqA9P+IQc0TbSkyqSvOxKf6Fq+eKqRT1QFXPStGMnXve2YEGHUzVp4gURMYj37IsK0NOmj7/2RVDD9swanjL+ImvPvUnSmeopdVSynKnTEH0Hp0AARDo1wQgQPfr4UHj+jmBq6++WqnPkWD5yle+0s/bjOaBAAiAAAiAAAiAAAjkL4Hly5erCUgSiYQeLHV1dXfffbfjOJZl5W/X0PJDQCCTyXCPfnXfQ8lkeTJZHmHRSESPRnU9sH6OaKx+FPvzS4c386Y2ikn12SHmEXN95vLs3INhUTicDwvH3eXD64fz+7K+FJ3lVmEB2uWibSL5ItnBTIYdwre6oc099Vf/OSGWYBXlrKqiLBK8thqPR797xeUB7cLRoH2hqe/qzuO/piPHbR5Vn24Y+u4XvvSi4dHO5iDyOZiBsJP6nLOMPgQHIHYBAiBQvAQgQBfv2KPnB0igpaWlrExMsSyDoOUTdYSfHCBVbA4CIAACIAACIAACINAdAc/1iKitre28886TF5+xWIwFUazRaPTHP/5xMMfaLhGqu3pQXswE3nrrbREVzOIRJizFA/8Ndlh1okRjjU3s1bemuTQlTdU7XWYGAcWeFKADhTcsAYflY5nvTkQOl3fdqudtw+uH967ySonOydCa0qDbfH27VbslM/mehw87rFqcMVUV4vZNLBp76NcPOrwApu2RYrI4og07+/xp51a6cGZ6RHVqSGVH44g3H/3v3L8JNhEE6GI++dF3EOhTAhCg+xQ/dp5vBMLTvCxcuFBevch31iKRyIwZMzALeb4NKdoLAiAAAiAAAiAAAvlEQF6Ocs4XLlxYXS1ENT3wFygvL49Go+eeey4uR/NpOA95Wzdv3jyqsSl4aCFsKcpLqzTGknEWi7JpR7J3Nly62RhGVNHisRQXocRSfeY86nKtH0ZAS3k6pEFrrlcilOggCDojPpPb3di6HWOee+HvqmpYRYW4gZNx0HpMf+2N1w75CBzcHXIil8gmMjnZhmsS0c4Wev45Gj/03cEDjOrkxiMOX27wYPrBDCKgDy581AYCIPDpCECA/nS8sHaREzAMQxLwXO+oo45KJpORiJjLQk4Ic++99xY5H3QfBEAABEAABEAABEDgkBFobW098cQT5YVoJBKR02IPGjToqaeesm1bTkcGPfqQDUc/3FEn3+d0On3UUUeVxBKaMN5gJSWsPBEtT7Cozj53Alvx7gyDDk9ReYYiJkUsFf7sRzxf98RnxCGR7FAKRyiHI53D+fA64byKYlaFciv1tVNGCc3C9znsQ+1rVpBsXwuE8iAI2meWr3VQSZpibXRYK036v+Xjph8r79zkDRyrGzK4NdWesUz5bkE/HMGemiTCmqUAnSHawWmnRXbKpFSGrv6n5rENH00bQ0MO++tt/0qWJ5LvBmJ1aAbCPVUOc449UUEZCIDAwSAAAfpgUEQdRUPAtm3TNFOp1IcffhiLxSKRiHztkTE2dOhQ0zSz8w4XDRB0FARAAARAAARAAARAoE8I2HbWPeCOO+6QcpoMhZb5WbNmbdu2Ta3TJy3ETvucAA8W1YxLL72UMRZPloqHFlFxpMQ0Vp5gnz2Obfj4nDbekCJm5sRlqTVL3Vl99nMB2vI1pUHbvmbzEssvCTRorZXYDhr+0qqTG0az8gom5l8Mli+c/UXFJ88yuwnQ2zyhQfMMp/Ubqb7uTw3VG0cN3jSu6U87W8h0yfGIPCFA+1yI1rtsOzr3Wf2oMp3XwHcQAAEQ2D8CEKD3jxu2KnYCV1xxhXTe0HU9Ho8zxq699loI0MV+WKD/IAACIAACIAACINAXBJ599tnRo0dnFbXgj6ZpEyZMWLp0qWmKt/LzLg5aqV8q0xdcC2GfKj5m6dKlMnQmmRTWzwMSWkxnA+Js+pHsg02ncZrhUJUn1GcmVeYePvtPBHQ2YjoXAa3ioIX6nBOgpQa9YSdrocpmf9Ti5aMPGyJOkkRgBx1NRH/14ANho8W8GXVfGDoHYrJN1OpRu03UbtIvf0n1Na81VH3cWLf6e1et83wyHRLu8TIF3ZOn1e49VaeamxOoVYnK7L4FvoEACIDApyEAAfrT0MK6IJAjUFVVpS7xZbDJ+++/n/sRf0EABEAABEAABEAABECgdwnI6GYV49za2vr/2TsPOCvKc/+/58yp22Ur2zvLNpYmICJiwxK7iYmmXDUxMYaLETX2mERTbnKvSf5qoiZeG4olMZaoWBFh6b1Jh6Uu206bXp7/fd737OEIYkFZduGZz3x2X+bMmXnn+87o7G9+83suu+wy9Ldyb4TX6/X5fJIkTZkyxTAMEqCP7GD0763rur5z5866urrE3y8pAXd6MK4+b9txiQkjIoYvZmHos9FfBejk/I1EBMcnCtBChkY3tO3BGbw6eDUIKOAPgxSGmvcXjBk0mKVnMh6fjlR2bG9zLLt/D+NBvRMCdFyDVi0wexRUpE8cvrSyYGdFzq7S3HcWL0HZWTPBtriq3LuNQwvQIqcjoTgf0Oj9Pv0mAkSACHxxAiRAf3Fm9I3jmICIUXvyySczMjICgYC4v2eMTZ48OWEuOI7x0KETASJABIgAESACRIAIHAUCQl82DOPvf/97QUFBIiNONKqqqpYvX26Zlm3bR9TpqfBJHL/jOAafxE2ypmnJXBKRu+JTy7QS99IYamvbpm0blmVYlm4aYgYAzYinjhyQLJH4bvIuqC0IGKpmm9YNN9yQ+MslKx0r8bkYO20Sa9t7TkQbqjqZRqLeoMMSWc+HMkH3pQM6WXfG6oI2Ozg5OqE4f2KDu6ExM1rF2GivDCd0OuX/nl0cwCQSNuiEFK8k/fLn93A3MRiGkTg5+/splBCguQZt8e4+Mx0aKjYMrzSGFm++4rJNEXz/AXQH+DWyX2E/tAB9gOJ8wD/7OxLqHxEgAv2ZAAnQ/Xl0qG/9joDjOD09PePHj8/OzhYRHKII4csvv6zreqJEYb/rN3WICBABIkAEiAARIAJE4NglIGRlx3EURdmyZUtLS0tGRoa4TRWyo8/n+/Wvf92XAAzDSOjCB5i1RTc6Ozvvueee++677+c///n3/uM7l1568aRJk0aNGjVu/Enjxp900snjx0+YMOHUiadMOvXU0yadetqkUyadeu75X5swYcKDDz749ttvJ6zfiR1Fo9EBZ/TumxFZvXJVwvvswuqDLq/Eho9kq9ZP0qFFhVQDmA0M+Gw7zE6qN/iJGvRAFKB1QH+3Ah4ZvDtVFoHmSy9nPg/ze5CNh7nWLF+pKWqiemffDM2X2sv+CA7bBjBs6GiHMSPeH1Edq8nrKcub/fTjEMXnPpYOOvc/G+DEr0oSoL8UefoyESACh0WABOjDwkZfOo4JrFu3TtzAiTrjkiQ1NTUBgKIosiwPmAfmx/EI0qETASJABIgAESACROAYIyDsxkLwFWL0FVdcgYXm3O6E8sgYq66uXrJkyQFm5K8QhbA8iw0md8kyrc7OzpkzZz744IPXXXddfX09OnDdTPK4AoGAaCf66fZIbo/EPG4muRILUSL0BbwBrLzCGEtJQfPqyJEjr7nmmtf+/YqmKbqh2rap6zpp0AcMaDTcc8ZppwrOGRkZEnMNysgsLGQzPyzv0PO7Ta8DkiUEaIcBqs/HpADt5u5pt277FMfXYTAVqtr2fMPFWFDCM8rN2OiWESjWmpZucNswOqLRWtx/p/0B0KYNoJsw9wOoKV5RlRdtqgxNHNu6rx1MAANUHVSsPwgKgOI4aJUmAbr/Div1jAgcuwRIgD52x5aO7AgQUFV16tSp4sbX5XKJe/p77rlH+E3ELcsR2C1tkggQASJABIgAESACRIAIfDYBYYZwHEfTtOnTp+fk5LhcrmAwGAgEhCGaMXbttdeKDSUcyp+93YPW+ESd90w+JW6Jo9Ho8uXL77rrrosuuigtjVd8E7fRScq4xP2nmAdxwOTmErXLjUK1W8KZMX8Q1eoDpqwTcMuTJ5/5wAN/3r59O2rQIozgoD4fnwtmPPO05GKBVMnFUbslVljAZn3wjS5jqA6+Tp0pPPfZhrj0/Jn2ZwMLFe6fNcy1iM8ikfngn4kVDmgcHKYRz3Tu3aAG8cANseaXiOBwm7bbtDy67dMcj4qHnN8RPnHazSzVw8RZJTF29513hULdGPaix7j6PBAEaFsDnvCsanDjT6CupKMwo6ehfNujj4Bi4CnvgGmjA1pzIMYLEWIQBwnQx+d/DeioicDRJUAC9NHlT3sfAATErbnjOLIs27adkYGhaYlkPcaYquK7WsJsYtv2l7mVHwA4qItEgAgQASJABIgAESAC/ZiAqFkifra2tp544ok+n09kx4nS2YyxWbNmoTLlHKa+lsiSFmbqaDQKADNnzvT7/YWFhS+//PKTTz551VVX5eXlcbHYxQOHXWgz5ToyYy7J63V7cbE/lUkBJvmZJ8Xl8ktM6NFCY3Z7mdsr+VPwM28qc3mTpWd0SUt8w1yp7tWo2QUXXDB79mxZlsUQqaqaaPfjQfvqu6Yoim3bqiq3DGvw+jFjgqUxlFpdbPacsQ6cEnUGRcEdA3fMjtcetDB5QzJtNw9NFj8/pv8m4pgP0JET/zxYej54SWLlAxrJax7wkfhnYu/JjYPX/Nh2HLdIhU46IjwuDZji+BQrJxo9OyvAMvh7ApkpKRlpqWvXrZblkAUG12oP8wL56ofzUFt0AEwTuL15wyaoq1pWMTgyvBZqSxdva0OVmWvNDj8WA+I+6E8/qE+Spg+1d1pOBIgAEfgiBEiA/iK0aN3jnsBTTz2VfOPLGPvmN78JgNUqxF3+J5pBjntsBIAIEAEiQASIABEgAkTgKBCwTGvPnj0XXnjhAXewr7/+urhrPQwN2rZtTdOE1doyreXLlzc1NSVeDUxUukvaY0KAFj7nj6WCSCmM+XF2+ZkryJgPFVLJl8HYCYyVMlbqYkMY80reQV5/uktyo1fazZjbhWq2lzFpv0PazSfhFBk1atRjjz0mjq6zs/N4u0UXx2uZ1pzZswZl+l0SF6C9jHnZr/802IGJOmTGwBcDTww8Cnh0kMRsgPRxrbYfCdAHuKGFDP05BWjNcX+ibB3TGu+8ZZDEz0E8c1zsxFEYxMHtz1Z/j+AQ3bQtBR8AwS/vVcuLN5fmRqsG77j9ZhC9N7n23Hs4VsIBfej/GJEAfWg29AkRIAJfjgAJ0F+OH337OCCQuC9XVfWcc85J2J9dLpfP53vvvfcSYXPH263tcTD4dIhEgAgQASJABIgAERjYBBzHUVX1D3/4g/Aj+3y+CRMmCPn4MO5dhfcZc3J1PRQKLVq0KDs7OxAIBIPBhP4rSZIwXPdq0AkBOuGAZh6/z+P3MDdD1zPjP3t16YxBeUWF44dUTg2yKWnsjoL0O0eP+OkPr73X78/CrF6PLzUj3Rvk9meJuSS32+1xuz0ul5TIGMGQ6FSMVSgYnPfwww9rmnZ8lgp3HOf0SRPio8DxXvkjtjM83obGbtkXg0BCgFZBErMOkrAM9xqHjx0BOlmqTojXilHatv28YuHUZyw9EJSY64knnhg417wNYFkW7NoFDQ2tg3Pas1N31lW2bt6AArRQn4UPmmvQnyfVmgTogTP41FMiMNAIkAA90EaM+tvnBMRbe6qqLlq0qPc2Gn+7XK6amhrRncSrjn3eO9ohESACRIAIEAEiQASIABH4AgRs2w6Hw0J9VhQlYbb4ApsACIVCK1euTElJ8fv9khQXf9PT0xljCfXZ7/dj9jTGPMc16NT0TFzBHzzp5AmTTj/j4ku/PnXaTbfd/fN3Zn2weMWyLbu3dkU1AOjcCRNb3mgseGdk+Qfjm1569aVYJAaz5yz74XXXn37m5HHjTy4oKvAGvBjo4fK6mJ/PXtSguczqllhaui8l1SeMI8OHD08cb/IxHt6BJ2+h37ZVFcvo/f3vf/f0yvoBHxtaz9ZsOzEC5V1KumwEFWe/AzohQKvHmwBtDdrVXnfLzei8z/J7fS7m83jz8vKspJiKw3hO08cnRlSG3/wGKss2FueqQ8u7f/Afm1XlAPX58/eIBOjPz4rWJAJE4IsRIAH6i/GitY9PAiLfecqUKa6kKT09/bHHHhNAhAB9fMKhoyYCRIAIEAEiQASIABEYQATEjWvCBC1KmHzm3WxCrlUURdO0ZcuWBQLoMna5XIloaVGg2+/3p6enB4NBxpgQoFtGjLrxppsff/LpFavW7Gnv6LVkxpmZACqaOEF3QOh+V563tjZ91ZiSPWNq3pr+NzB5LbVkwibfxPIVG+6//5Erv/UDnyeLMZfPm4ImETfzB1kghfn8TFQ4TEnB5TfeeGNPT484CmGIThxR8paPpXZFRQVjLCstNehhfjf75z+GdkeqI4ZPNv2aHcAQZJ6/kRzB8RU6oJMdx8nt5Izm5HbyOsnt5OiMQ7WT1z+4LfaSvHy/A9oJmFC2cevojCALSiyAdnws9vPHP/4xcSaIvwQT/+wPjYRIbANEFOzRuLFrC7J3l+VqxYMWzX4XdAVs5xMrDfaH7lMfiAAROE4JkAB9nA48HfYXIqCqqmVaGRkZSfqzKz09PRQKJQdAf6Ft0spEgAgQASJABIgAESACRKDvCQit2e6dxD8/XYAWWq1lWqKxefNmYXYW0c+J7IusrCxRqbusrOyqq6568skn//3mG7ppGZZj2mA5IH4mH7IFmg6q7thxVdqEO6fERpSsKvdtaspd9ej9YGoQiiR/A9vRbli3HHZsBFsDR4doGP7+6LPTbvxZekZQQt8zxkN7fcznd0seETyNCxsaGl555RWxLU3TjmEB2jCMRx55xO/3uzElm6V52b13B1V5oqqmGQbTbR8K0L3qswLuRAb0cSdAg1uD1I7YsG9+k2UEWUYKC/JSlyUlRbppyBoayfvhlBCgLQfCCjz/T2hu3F5fDUNK5fHDV2g8EpqXHyQNuh+OHnWJCBy/BEiAPn7Hno788xNwHOeRRx4RFo+EBv3Tn/5UbEFUIPz8W6M1iQARIAJEgAgQASJABIjA0SJwGAI0AAjHNACsXr06OzsbBV3GRPiGx+9LSUsTS7wB//MvvtAV6tG5b9mwLAypdcCwHM0wNcMU5mUsn2aDbZsGtGvQboLmAOgxmPE3qMtprc78aHTV2l/cpAlHtOmgOVoHSwdDB8s0YHUrjK99/7KJG75/yeJ/PL0JDDC5D/SRRx+YdMZIKYV5U7Hsntvr8vk8bm5r5bUL0dz67W9/u6OjQ/i+j9YQ9MF+r7ziOyILJTXAassZ6FfEQhmgMbCYaQU0O40L0G4F3AowHVyJ+WCncMIvnPxRop3sYk5uJ1Y4oJG8TnL7gNU+85/JbuhPX1nsRayjAEteWQF31PHrMOqll0dyQz9WuBTTE08/YcUd+X0wXJ9/Fyg+7xegbYiqcPGlKyvLt5XmdTVX7fzXdFBDYGkyoPhMExEgAkSgHxEgAbofDQZ1pd8SsG172LBhQnp2u92i0dbWJu7FI5HIMWyg6LeDQh0jAkSACBABIkAEiAAROAwChydAi9vdhx56SHgyRK6FkOpS0tKGNjaI9o233sStl6g7i7knLMuqLvppWI5hOY6N6jNWMjSiXIDuUrjUt2oxVOe/VHXCyqaStdOu61aicf1P1mTV0mJ2NGbpMQ1iPfC1sRuG524bU7ylpegfN3z/Kcy7NcDC+GjHgsi+0PqnZjwwpKGCuZnkQQ06LS1N5ISIkJCioqKlS5cegO7zOMEP+Eq/+ucBknpubr7LhdJ7Zgr78Q+CYJ8MkAImCtC67dEwfwOlZzEn1GcdXMn67OcReRMbOaCRvJ3k9gGrJf6ZvM7naX+evontiF0cou2O2K4eo3TH3q8NbWBZ6ZhWjikcfjZsWBMA9KfylTYvK2jaYFv84jIBdAuWLIWKsg/qKnuqinaPGbZEDeO14BgxEqD71eVJnSECRAAASICm04AIfDaBvXv3CgeBxCfG2AUXXCCKExqGkfCDfPaGaA0iQASIABEgAkSACBABInC0CSSLrcntT+mXqqrXX3+9l09CaxY/r7/++m072qJK5M9/vf+BR++3QLdBjxldMV3WDNSgnV4l+uOGTPyXbnVF5B4TQDGgowMmjV9VW7y2vmzlJed9hDF3tvBwqni7bYPmyJoN3V1w723RhpzVIwvah+XPvf3a7RAB0PiMUdE2gKE6mNlhgfLCP58pGJyXKIqY6HYg6MvNzZ0xY0bieIWhJBlFop1Yp583dN1EYZJPz814AZ8TYPIzy8tkG1ZfpBpVqMDaTHNQdJZ7pWchy+pogu6dHZas7erOAZbhuGadEI6TG2Jrff8zucOH2ntyP5PbMrAwDNrVM+zOX7hdjKX4XUHMNsdJPKXo6ek5ykOPyeg2gA6gAqg22JoJBoCCJzlc/2OoKNhdPKi9vnzdXx4wLQ0cA8BS8StJpRSP8iHQ7okAESACJEDTOUAEPpOAoihTp06N34bwNw1TUlJef/11kYJH6vNnAqQViAARIAJEgAgQASJABPoVgYS6ekAjuZO2bauqavNw5s7OzhNPPDEYDIrCg8IEPW7cuOXLl6NLVNcUXdEcOWaEbSwZqHNlDDdm2ihIm8K6ybM4LAftz4638cNdAAAgAElEQVRjcc2YB2cAtG2Db166srJ4yZDytV+/aPOmjSDrQn02UUfjVmrdAk2F/75XHztk8dDsNWMrPvrzL7giJ3NpTgfHjHffTNLddA3uu/c36RnBlFSfJElut0dURxT39lOnTk24SXozsfF3MpZkJv227TiObSFYMd166+2MMa8n6HGz4fWsu+s0E4o6dSY7kuyg+kwCdEKDVoH1ON52uejVt8oCPuZjLJUL0MEU/2WXXdYvRvzjArTFIzgUGwXoLXvghNR3SrJ6yrN3NlfPWdAKlskvBNsgAbpfjB11gggQgSQC5IBOgkFNInAIAunp6W4+iVrepaWlYsXEDeshvkeLiQARIAJEgAgQASJABIhAvyOQLLAmt5M7qqpYgc0wjJUrV5aUlAjFVkRYuFyukSNHdnR0iDw6Hg3gmFz/jOiq6jg9cjxzQ3UcjG/unS0H86BxxpVRLjUBurrhhh901RUtaaxcOW7UhyomaYBicvtmwj5tYvLGqzNgROmykWW7GkvmPPb/QOfF1tDvaaDUbdu2ZqNWt6cNvnH+zDGNv+/aCZiFC7B1x/pTTjtJ8qQzlpqSluWSeNIvT1v4zve+297eLsvyQBage4VnnqxtmU5NzRAxXv4Am3YjAzjFgkEoQNte2Q4KGVoosMIvbABLzMluYtEW6yQU2xiw5Dmx/IB45UM5kb/o8uTtJ7eTt5Pc5+TlyW3x3QN6Ljss4rBu09VjZXbJZ9bVILYgr2PJGEtLS0u+Io5a2+HvEeD1go9yLDBNANkBxYH/+m+9LH91dW7n8JqtU37QbahgWeJJDH9yk/Qk5qh1nnZMBIgAEeglQAJ0Lwn6TQQOQeDVV19NFFpBK4HX++CDD4rC2WR/PgQzWkwEiAARIAJEgAgQASLQfwkki87J7YN7PGPGjIKCAnEPnMiyGDduXEdHh/hi4ismQFRDKTgUhXnzQmGuDmPNQC6ICRN0QoBOeKL3tMOv7t46vHz5sKJNY4bOXrsStxdSuWzME50xZcACW4Mtq2F8w+zRlZtGVCx7/Z9xYzRmE/BAXNtCZc4B6OiEW6cqzeUzJ458Zuu6uBU7onQAOL+697/d7izJG0SVkavPktfr9khXX321ZVoDXICOa9CWCapi+v1+LBHpY/5U9uG8agsqZZA0YLLtl610nG2/EGSFRJtQnw04MH8jEcFxsIArxNxDicLJ4u+XaSdvP7mdvM3DFqBjNgtZrNtiUfDF7HGXXMxSvCw9hfm8IguavfXWW4kz/Kg1hADdK0NbYEdNxQQIRaC54b3a4h1DCvc0V895fyaYQoDGc4Hnb5AAfdTGjHZMBIjAJxAgAfoToNAiIpAgoKrq+PHjXS68BRGlSxhj0WjUMIwDCn0kvkINIkAEiAARIAJEgAgQASIwQAlYpiXLshBkFy1aJG6AE7fBkiSNHTtWluVIBHOWRZlBSxg0ATp70JV829TVI4b+/t03IBL7WAC0qJxmOaJkIP5UTHj+KRhesXB8VVfL4MWrF0C0GyyUzgyRJmHboGOyM+zeDmeMXF2e/uGYhjffeh1UA13VBoBmgdEbfKyYEFXh7p+3V+TNqyuZs2wBhPaH9+JKimYtWrIqr6iYeSXJ72Nu5vZgmb601IzLL/9WYrw0TRNi9KdL84n1+0fD5tG/aCz/w//82efzuSTm8rH8MtYeHqlBSly6tb2KmS6bJ8hWuua4ExquAa7EnCzmfqIDOlkFPqCd2KD2SUJ28taS1xTt5E+T2+LTA3aUcFuLNT/956G2ILYZARblnu6QVf3o34akoHTPUoN+8QfgT37yk6NvORLSs7jY+CMVAyCiw7NPQ2nu4qGl4eaqnVdevkbTwDLw8uETCdD947qkXhABIpBEgAToJBjUJAK9BAwDb3UNw9iwYYO4+fB6vYFAQJLQIiHKD4pEvN5v0G8iQASIABEgAkSACBABIjCwCRiGoSjxXOann35aWJ69Xm9CgB41apQsy47jCFUuIUBbgOKvqcOf7jNH1750+dfe7tgNCg/TEOvYXDizeIiAyMzokqF1AVQWzBxdsW1o9ocv/JVXVROWZtvCkA6ewqHrIEfgWxe31g+eN7J60bszkTDWYuPJz1ydRplbNN56B6pKX2+u2nvNFdC1DzQD/dN8sjVTVjRDd2De0sVjThmPKqPXzTw8iyOuQV/uOHHL6IAUoPmx2hac+7WLcMR8jHnZ2ReyqNWo8pKDmPuMAnSqbGbKVioJ0EKAFj7uKLCwXbByzWQvPpJAf7xXklwuV0tLS+KsiJ9Kff/rYw5oHGbVAd2Cy87fW567q77EaKza8OqrEFFRfSYBuu/Hh/ZIBIjA5yRAAvTnBEWrHXcExF31PffcI145xDsRnr8haq0AwNG/FznuxoQOmAgQASJABIgAESACROAIEjAMQ9ziPv74416v1+fziaqDkiT5/X5JkhYvXhyJxCzTCYfDwo0RV5ZtUGIweyaMKH9z7JA3N64GEeWsgiocmQkBWufCccSAhUthxPB5tcXLRtfO/8cTXEK2wIkZPNAZhWrHRHezrsP3vrGztmjWsLp/v/gcxFTokPcL0JguDdCjgwawdRuMqF84OGNVZUHbic2LMZ/aQYu0DY5qKyE5LBtcEQfY2r6rbsQwvLnvFaAZcwUCgQceeCBhNEmUIjyCuL/KTduOrWIeiQm1dY2Sx+ULogD9uz+XR+wqhVcdlB2m2EyxJZ4E7SUBOlmAjgGLOoN6lPMGF4k/+5jEuBTN2N69e7/KgTqMbfHHIr0GaLAdfC3gww+hJHdOaXa4KL3njJM7I1F8pcByeLC62EU8suMw9kdfIQJEgAgcEQIkQB8RrLTRgU5AOKABoKysTJIkcecdDAYbGhoG+qFR/4kAESACRIAIEAEiQASIwAEEEu/2qar66quv+nxYiM3r9Yp3ARljOTk5y5fzhGZe6Q6Tl/kUV5ZNWDIHTh3xWnPZ8y89BZFQYvO9nmKe16GDowNoDixbAcOHza8uXVlfOfvF6VyTFt/Q7bi32cQ8gVgUbrtpR33Z3NK8N999B6VpBUDGqFtdmKCxTiLXrrfthAvOWVKVt25o4Z7qkg+fn4HLLVHoEEA2FBEAYvDqbTrAzj2QOWgMc+cxd4rL7ZMkn9/v93q98+fP13U94YBOYBG968c/MYLDcaw97V3M5XW5mT/ImIe9PfvUsFUqA5MdnBU+i3ZyCEYif8MA18FxFp8eYZEcjpG8zYO3I5Ykr5PcTv40uX2ovYvlh9pL8vJDbeEgATprZ2fzhEnM72VuFojr0Iy1trYe5XHn15DOU2lswFPS1uGn1++oKFxfOKhrSOGe+38N7d38hOdXGS/fyWNx4hffUe4+7Z4IEAEiIAiQAE1nAhH4BAKahv6IV155Rdx5iHrfjLGXX35ZBN59wndoEREgAkSACBABIkAEiAARGIAEbNs2+AQAy5YtE94LxljiHjgtM2Ph4qUmT2ROODETB6qZEOqE752/blT563+4b72u8ygAQKtmPJAWdTHLBKNLxVTm7m445/SNRTmLK0vm/dfvIrYDFlYadMB00Mms44YdA0wZpv1wd3PV+xVFLz77LOztAZkL0Dq6oqNCgxZLVBt+dScMLVrdVLh7RNWq52eAYsTjp4UNVOc9sQA3L7r0/FMwtOxhxsYzludypTHmcrvdEnPl5+R2tu+zTau7sxPjQMxeoT1xtP244djwzrtz/MEUxlgwwDwuJivfj5mFqMA6bs3xCCn2y/xMlptF+8tsre+/m9x/jSeT9JZSdMfsnG696c5fsYwM5vcgQzHddtttR33MbYzdwFMxonTIMdiyDhor36up7CzMaztl1KpQO9qfdf7agOVgDriIUD/q3aYOEAEiQASSCZAAnUyD2kRgPwFN08455xyJT4wxn8+Xl5cXiUQS5uj9q1KLCBABIkAEiAARIAJEgAgMWAKi7B4A7Nq1KzMzU+jOidznYDC4cMliodvKip3IdBZLIrzQ313TltTnPz/lyu2qAgoGOONsO71yL/42TM4nFIGvnfFRQ9m66uIFP/j+XllHXzMG12LusxXPclbAisDv7to2cdiSmoJ3nn4awhrEAGcV1WeVz6aKbmjoUeCRR2Fo8dLa7I1Dcxc88GvMntZ76yIm6reZ3CitAYRVeHsm1BfObchvHdPwWIrndDcrYMzjdfs8/Mgnn3mWZXABe2AJ0DYe8/Rn/uH2oHs96GVDKpkuf10xC1DndTwkQAvFOaFBC/lb4RUIFccXsweF9Jo/PuxOTWN+b0AEoPt8vnvvvfeoX9k2D0/nEeqYdv67u5ySExZVloXLyzbccQs+KQGAkCqb4JAAfdQHizpABIjAoQiQAH0oMrT8eCfQ2dnZ+9gbf7vd7v7w9Pt4HxU6fiJABIgAESACRIAIEIGvmoBlWoZh7Nq1q6mpSdz3ChN0IBDIzMxctWqVibIzTsnqs+2ApqFP+cFfQ0vJi6Nq/ibHpbC4AM1TLzCig6vPmgHQ1Qnf+fq6IYWL6ksXfffKpYDhGKCLymm4aQ1laECj8m9utMfXrmgsevv2adGOLuiMCfUZdJC5+owSMwrQNrTOhZrStxtLNuQH3vzZ9ZvAgkgP9jNRuU2Idya3P6sOrF4GE4ZtqM1Zf9lEOKXuo6GFD/rdzV5PkDEmMVdqABvPz3hOHO8A+mnzOoz3/voP4k8Yr5tddjFTY+crZh4J0AmrdUJ9VoB9TIAGj2JnROyyF1/L8XiZTwq6XFiEkDE2YcKEo3saiItOeJwdwLcN6otn1+aHqsrVuvrVq1fjZahYeMKTAH10R4r2TgSIwKcTIAH60/nQp8cvgYceekgYn0UEniRJmzdvPn5x0JETASJABIgAESACRIAIHIsEdB0zL3p6er73ve8J7TJReDAYDE6fPh0AdNOIKYoQoUWusrAsGzF44TGzpfi104fNXbUQTB2V36hhWQ5q0AbYBqgmGIZwH5tw43XtDUWzGwoXfOfibZEIzw3ojbjA3ADHwtRmDf75BNRkflidseC67242DdyU7MSjoXvtz1yAdkBW4bSTFlfkLagtnHPrf4bDvQq40LETcnnC/qxq0FzVOrws1FTYM7xkX3Ph0uuv3PT3v8wTB+7mv9yMZaSld7bvQ0lv4EyWjt2d8p83M8wTYZKL3TyNyfIkxRpEAvSnC9AoRjtuxUmJQe6sBeXMzbyulPS0THwmIUlnn3320T0LxGkcU208jS3497+grnBT6SC1IGfbN6/osAHCsq6Dozm6BY4FjpiObp9p70SACBCBgwmQAH0wE1pCBJBAdXW1uBNNvvNI/O9c1AcnUkSACBABIkAEiAARIAJEYEATsG07Eon8/ve/F1UHMb0hGJQk6f8C6B566CFVxTp/+5VcG5MyxPHKYVg1F84ZvWhIzvQnHoBwD2Y46w7KykJx1rFUoKyDLQN0heG+u7sbi+c35i+5eNKSbWvAVMA0cBY6r82/BQDTH4aG/NbmgrWTRrR+9BHuWmzN4Cm3OhZg0zvlSEwHVYbJp75fX7qormTO5Ze0qjKYJkZJY/gHD8xNeJ+jOsR06OqAc06fV5A2r2pQe21uT13BqovOmNu2AZQYPPjAwx6Xx+fxJu7/v/n1bwwsAdo28Mgnnn42k3ySB4/jZ7eymDJKszKwIp/twdlhuhN3/iY0WS5Pu3lINP/Zaw3+2ArH7sL9SdaOJwL+sDXZ62ceLEKIzyNcLtekSZP6yQVumdDTDSOaX6/K76opcmqr1z77HL5DoEFUw3PfscDCpziYZdP7YKefdJ26QQSIABEAIAGazgIi8AkE5s1DH4QkSYEA5n95vd7W1lbbtuMPlPmvT/gaLSICRIAIEAEiQASIABEgAgOKQCQSWbJkCWMsMxMtn0J0Y4xdccUVmqZZJs9n/rgGDYBm5842uOSUtU157941dbsWBSxRiH5n4X0WERm6DLaK6bTw4gwYWvxac+HisTVztqxAQI4Kjo4eadOErh5ehhDgjTehIndOXd6msUOXbFmL6rMFYQtU3kjo2vh13YQ7booNKX6/puT9s0+bs6sdV+Z7F0q1Kb5i8oWGAzEZbprSVVO0YHh1qK6wuyp3/SXnbNNjuFw4u6+55gfi8IUPOsUfWLZ4yYAZSYdXcewVoJmLpaayW25jmtmi2WkkQH+KmL5fgAYWcVjUnujzMQ9L4RGMeC70CwHaAT3i6FH45/NQX7uktlQvzN17znmbOkKgGmDy606c/A5oXIAeUO79AXOZUUeJABH4UgRIgP5S+OjLxyqBa665RmR+BYNBv99fXV0djUYNwyAB+lgdcTouIkAEiAARIAJEgAgcnwQ0Taurq0vYn4UIe8bkswQN045XHRR1BS1Aj7NtgxmFW3+8ZWjOS987fw2YGPPMvc9oPObhGzygGfQYQEcMHn0YhlW1NhQumDT8/Y8Wgh3jeraKqcwOF6BVB7qisHgJDKuf11ixszJ3wbNP4/55irTOrc8mOHE3tA7o8JzxBNQVLyrNmXPZpfN38rQMA6ImV9/41oV4ze3YDshRuH1atLZkQXnOluqCUF1J24XnbuzuQt1Os/hsmBY4w4YNE4cvCtBdcsmFuqH2au/9++zAeo9oeo07oL0sK4v97r9ZTK9WnBTucf5qihB+ipI7QD8SArQOTAcWARaFMVyATmNM1KTsLwI0KJh6/v0rOgqz11VXKBUV6x5/Bjoj/IznKepYfhAUB2IYxNGrP8ez2/v3yUu9IwJE4DghQAL0cTLQdJhfjIC49RQmaJfL9fDDD4vvkwD9xTjS2kSACBABIkAEiAARIAL9m8DUqVODwaCLT+IeOJAS3NfZIXod03SuKdsWFzjFi/2mDL+5rWtI7v+OHfK8FcYVLVEAjdtwhQNZBSwbGLPg2elQV/ZWc9mq6kH/fnkGaBFcXwtHwQBHAdsE3ULxevEyGD18ZUvdjhObt/ziDjAtMHiQNO+GKMAW35FhwKY10Fj+fnPF6jHN86IKOqNVCDvQCSjHce2Nq9W8V6AZ8NTfoKlq9ZDCPXXFPZWDNzXUzu7oAJXnFOgOyBqEo6hy//j7DzI2iDEMsPD4fW6va/mq5QkBun9H8NloJu8VoFNSfV4fe+KZQFcsX3ECJEB/ijgeF6CdhAA9+igL0KJ6Jj/v8VwWsw2GDG3roaZo0ZASNT9ra1PTwn0hXMkU6rON4TNcgFYwgT1JgCYNWrCkn0SACBx1AiRAH/UhoA70FwKapomuPP7448Eg1r8OBoNerzcvL0+WZVGepb/0lfpBBIgAESACRIAIEAEiQAS+BAHHcTRNW7lypZCeEwK03+9fsGgRCluAmc6q6RjY1rqUfXElS4enHoK6nBfH172xZG68ByIkGqVqR8jBqJvpAB+8BxNaPhpVtb2x8P1H/htMDb3SKFfzycGChqiVdXXBBefsyEtfXVe+8fLLce9CQLNscHDTFmrVuGEId8PurTC8bGV9/ua6sn+0zkWNm3tDYzZEbDCxmKH4Ft9FKAzPPwP1Jctq8npqC/Ta4h3jx81Ztgq7EBfTAXQDQvvg5qvklpJ/5Z1wkceXmzCjfO/q7yTidOPSdrzv/e0Xr94IzsTTz2KSj9to2OtvF6t2qeL4uMbqUcAjdNjk0AmxRGRDHzIh+tgNgNaAKeBWwKPbPt32HGUHdEJu7pWP8TLg14uF5z786MftxSe01Q2GYeXtv7oTLyWTa82Jc95xMAMaLVO8VGgiur2/nazUHyJABI5PAiRAH5/jTkf9aQRqa2vFTafPh3dv3/72txPa9Kd9jT4jAkSACBABIkAEiAARIAIDh4CmaQ0NDckCtNvtvvfeewEgKqumw4sKct3XRBuxHZbBMWHpLBhd+eqIspdffhp1YiGRcakLMyB6SwVCew/MnwMnNS8aUb6jetDCO6d2giGKoymokXGBDAA6wvDRJjjvnHXNtdsrCjade+bOrTtRuQ6pMsrQNhZW4wK0ZhkKAHTvhh98Y2Nz4cbG4lXTn4TuiFCfLR00kb8h1DeMBDFxJBbOgeE1Hwwt6KrIUpsqlNHD1gj1uSMGHVFcxbTQlH3PjbtPLF47rOCDGU/sraweiUHYvI5fakZw245tsqYalmViGEm/nXoF6DPO4AK0S3KjAC1DcQxIgP6kuotCVXfcKNA7Ad1K0a0ACtDO+KOWAZ0sQCfaXIDWDdjVAUPqFxWf0FOeFanKmb1tHUSiYDpm8hu6ye2E+tyfz9p+ezlRx4gAETgSBEiAPhJUaZsDmEBra6vwPgv12e12L1iwQLxwZ5m9bo0BfHzUdSJABIgAESACRIAIEAEiAJZpTZ8+PRAIJAvQZ511lrjjVU0Hiwo6opagpTpxT+b6JTB5xMbK9NfumLasvR3VZxHTbINsYaaFaoCuc7oL5sNZo9pHFIUaB6+9Y4pmqbjUAsNCy3LMBHz1ULFAVeHSi1bWFK2pKto4omXhhk2JoXG6uzvj1k7u6wQHg6dvuVobXrhizNDWF6eDqmHSNI+I1kzUxh2LO7BxLxaK44vmQHPlh01FHWWpWnFaZ2PNkhdeRGd3hwwxbinVDFAj8OtbYGTponG18/5wTzQag9ZFC9CM4mZSAEXo2+64PaYo/Vt9BjTK2hqAM/GTBOgYsBigA1p4n8kBvT+Rw0H7834B2nZhEUI/87h8R68IIVeM+YOdhIisG/Cn/weD85fWFWmlWetvuG4nXk0W5m8I0RlsB+xk/Zm/OcAvzwP+gk1sk4TpxH9rqEEEiEDfECABum84014GBgFFUa666qpEDRa3233KKacYhsGLr+Bt+sA4DOolESACRIAIEAEiQASIABH4VALhcLikpMTLp4QGraqqYRgxRVEtS+cpHAqYKlYKBF2FvZvhjBHvNRXMu/LczY4Fqi2CLGwbZBuiXH02UQ52oG0bnDpmdmPe3qGDdl848SPQ0WjMFTPFBtmEiA6GDRBR4SfXdTdWr67K3zSkbMlzz0FXBAVlDIk2VNu2UUUDlNgsC3QFnvqL3ZA7b1jRivvvUywTQ6IVE0wUtTXMvU2sbIOpQ8dOmDBicXnmxqoTwnV5kZbqDY89BiEV+9wRCzsAkQj0dMDPb2obUby0MnX2nVM7dRl0vpFvfe8bqVkpTHIxxlIz0j/auOFTWfaHD21wNABr4hmnHeyAJgF6v+J8QJxIXID26RaaoCOWP2qdjgK0252IYZk0aVIfDrAdL7kp3ikAMCzHdkDXYMLJy4vyN1UP7qwrXThvPvYI425M/paAg+ozCdB9OEy0KyJABA6HAAnQh0ONvnNMEtA0raOjIzMzkzHm8/n8fj9j7NlnnsUQLTv+QPmYPHA6KCJABIgAESACRIAIEIHjjcC9997r9Xp9Pp/X6xX2i+eee07jk24aOphRKwLgqKhxQSgK+3bAd8/aVZc5++yxc/Qwir7c0Rx3QFugh/VYFOVg2LQezj55WXX2sqbiDWeftE4Jg6ZhpUHDckxHt3mUMwD0qHDPL7orCueV524YVr3mV3dBeyd0R3FNFN94gIYYFE23TR3WLIbRdf9qKHz9l7foqopKsWnj7izQHDAcCy3QIjpaVWBPG1x4anfT4GhTkVWTt3Nk3YKXX8SNW1iuMN6DcDc89ieoynx5TMWKK87erEUwZ0RzQAN5X6g9kJGSkCB/8atf8iCERDRvPzxZbP68AE49bRLvtsvtYm+8W2pAxeeJ4EjWZ4+3POj9GdBWStTKXLF+iMeLjx5SUgPiBLjjjjv6cLxNgCjgwx2UlPEtAR0UGR7/e6S2bGFFwe4hJRvPnDhP1vENArwELBGSHhegk2XoQzmdD7W8D4+RdkUEiMBxSoAE6ON04OmwDyZgmdZjjz2WkpLi9/tdLvQ7lJWV6bqe/C7Twd+iJUSACBABIkAEiAARIAJEYMARyMvLE64LVJ8lafKZZ8myrGmaYRgmvv0n8pzRjxxRoX0XXHXpvJEFi8eVLpk7E0wDNeJeAdq2UTQ2dQcXbt0El5wzr7Fw5fCyLRNHzduwFhU0ja9h8YKDJtd/ZQsefxoqy2di8kbd9v+4YovKvcmag5qabfLZAlGIRVVg6Xw4qeXVitxnfvQf6yJhvj9MIOD36aBhqDTP4DAMsAyIdMHNP47UF3YOL4Xq3M6yvFk/v2NHVwjVaR0/txUDYlF4+lFnaN7LzYWzL560RA+hSq7ZqOtpeCz21Gk3MbeEURweKWvQCbvb95q9lpR46EH/GnJ0QMtK90knjxeyqeRmb75X1hE54fMUISQBGosQWmkRI+e9uUXBFCa5mc/HU8AZu//++/twqIUALQsBOqIamoHPWM477Z2qgtUNFV1lebOeeBzfONBA1m3+nAZDcEiA7sMhol0RASJwuARIgD5ccvS9Y5HAxIkThQFEkvB28+677xYv/SU06GPxoOmYiAARIAJEgAgQASJABI4vAo8++qioeiLszxJjm9ZttHTL4tFzFjg6RjlHTLC7ZDRg3vzD9obct06qnDvjIbAViMSE1Rh4jUDdgrAFdkiGrn1wyZnrm4tWDSvacFLTvNWrkapmcb3YQmUZQwNs/O76j6C+bklBzrrmoTtGDHu3bS/X1BwIy7qNk8ln27BAjmK2xPmnz68pfOXyi1a27YR9GNPhmJglbTiOBTaWNHRMsEwsPKgpcPcNXScOWV9fGqvI39fSsO6maft4TjSomOSBzuruTljwDoytnj+85MOLT1uwazsoQn12uAbNe7hjT4cnkMqYi6Evhf3y3ntlTU38USAqxPSnk8aWY10AMOHUiW4P1lH3etitdzPVKSYBOlleP7i93wFtZoTVgiefk7JOYB6JuXpDOF544YU+HGgTQE44oDEI2oYF70FVzpsVuZtLs1dPGNuq61h4E6tuOrxEJwnQfTg8tCsiQAS+DAESoL8MPfruMUVgw4YNovCg3+/Pysryer1btmxJvsvsfzeaxxR/OhgiQASIABEgAkSACBCBvkMgYLgAACAASURBVCFQVFTEGMtIS0cZ2hP42dSb5K6IIaumLgO3IOvoLzZCBsgq3DJla33O7HGly+6/3QANDAX7aDm8RKFjG2BjQrQD27bA5AlzhpdsGVfdM65+6Zx3IKZDSI3o3NRschkaALp6YOk8OHlUa27G6ori3ePHrl60BDMxIpYiXNWY+WyrtiObNsgy+qWnfr+7oey9k0a91d0DYSNeddACBZM3eHVEx8YAaNOE9n3w7OPQXDq3JmdzxeCdRfnzp93UubcrLpdrYCo66tQr56P63JS35KT6NyP7UJNWsaKhjfkbNirmloPlFG+46WfCTcwYyzwhSzPib0b2z8IwGFMCcNsdt/M+u9Mz2F33sQ61IgYpvOogFiEU8uvBRQiTZdnjN4LDzAorlf/z/1h2DsNYGv7gweVyzZo1q2+uSr6XeAY0j3yBnii+bfCz68ymom11BfuGlK7560N4ivLamwpW3XQogqMPB4d2RQSIwJcjQAL0l+NH3z5WCBiGMW3aNHGLmZWVFQgErr32WlF78Fg5RDoOIkAEiAARIAJEgAgQgeOXQHd3N6Ch0n777bfT0tKCPr+weGYFsnp2oXkWZWWr24aoCVa3Jht8yV3TlNHl60bkr//2GW1qBy90h9G0OrqkHVB4XnOPDGvXwbkT1w3J3dCY2zmyYv2rL0BnF66EsrBjcj+z2APs64CTGhdWnrB5SPHeytK5jz2BRQllC2U1jBSIr6UbVkRT8R/TH4HyQe8OLXtv9hy0ZHPpTdZ7pTdRpRAAOiMYm/v8dKgZ/MHIyo6yrC3FeQtPP2O+bEM3L2so92588ypoLvlXS+HCsbWz5s0CTRe5z3qyAK2ZYDrwv089E0jPEH8g+IOB+//0R0RkWrouCiXG+9pffnF2N91yq+iwL5WdewVrN06OOoNQX3Y8OB9Qgo/+mShCaPt0I6+rZ/gPf8hSghjBwfNXkKVh4HOOxNQ3w40CtIOPRlYsg5ayRZVpeyoyu0pz5uzahU9TVLD4CwoRC2Ii+/tQvRKJz4f6lJYTASJABPqSAAnQfUmb9tW/CPD3+3rvcgGamppEEJ7I33j//ffxnUFN61+dpt4QASJABIgAESACRIAIEIEvTsAwUFKWZfkHP/gB1h6UJA9zeZjr2iu/j7JufFIVu0fhOnDIgP/6/e7m8iVjK/ZeMGa73IbpyHySef0zFMgUC7pl2LkbLrlgRU3umqaCziHZyx/9I3R2cB8xro1rcd0Yg2r/z6R83dUrq7LWNheqhRlz/nw/uqQjBq6hmaKuYLyYntjT2y/B0KLXG0pnPfU3iOggg61DWMcmCsSWmPmqDsDChdBSs6g2f09tXkdT1dZLL1n/0VaIOijYxSzMtO7qhu0b4MJTVgwZ9O7wspn/ms5zn/GwVA1kDUwMgHaw55EYqCqEuoGxSo83Ky0zze2RaobUij8NhCIpetiPfvKyjb/73e+FAM0Ym3gR261fELYLSIA+pPKeLEDrhdHw5IkTkF9q0Ct50AJdXFxsmVZCfe6zN2JtAMOBUAh+f68yvGRTU57SWNxz/fcxkJ17pA0dYiaELIiQAN2PrkHqChEgAp9KgAToT8VDHx43BF555RVxrybU5+HDh4tDF3fqxw0GOlAiQASIABEgAkSACBCBY5mAZVridldiroDkT/ME57w1WxywqaGEqXFBqyMCj/0dGqrmNZeuOblh8ap5uIoWA8uMof9SRHBws3TbXvj6JVuGlK6qL25rLlt2w/WbVA0UA1M10CqNZdLCJkTRpNwJv73THlO9qbmwq6loy4+v3u0AhFWIGShkKxaKv5g9bUdEf5bPhTOHr6nLm3XP7XvCMeF9DqtoaI6JTGcTfaCOwcXo+XOgqeqDxpL2sqz26oJN37ho565OVJ/bI5guHbXMqAZ6FL557prqzHeG5L786gsQi/HADZSeu/gcRQ2aC9DhMHTtha+d8q9MaQpjed6A3xvwM8beeOMN4SLvhy9KOiaGoTz99DMiO4J5Gctg3c41YbuYBOhPE6Adn+L4dNuja6Wde782OBv/KPR5JLfbLUnSOeecY/dp8UkRwYEvAxgWbNsEZ41f3ly0pzxt6/Ahq+Z+iNeUgTNG31gYEP0ZEzmgPwMQfUwEiEAfEiABug9h0676JQEhMU+cONHv98dvxyVp+vTpjuP0wzvLfomQOkUEiAARIAJEgAgQASIwMAi89NJLLhdPt2Us6AtmpaY7qmrxtItIWAnJqGh1ROC556F88Jz6kk31Je/M+F8IdQJaiHGyeE4y2jNVE+Xjyy5fUTp4RW3ZnuriBT++dpesoydaB/RpcnXM0iGMNQIdePUfMDR30Zgyoy5749cn7+zpjBPrVlB91gFLq2mgaw4GXPTshotOm9M0+P1LzlgdCUMUo59N7n2O6aAZqGuDDoYKKHaHuuH0ceuHlXcMK5Xri3eObJy3YgXGF/QYcYFONqG7C/7zqo5hxQuai956+6W4Os5dz9GPCdA2hnKADTf/aEV93otlGX/ysHrhU3FJ7muvvVZVsRRhP4yBtg1HkbU333yTubGAXmYOY2nsg6Wnh61yIUDr4D2kDnvcZnE4bl6k0YPJ11r5ptVfCzKWhs8amNvt9vv91113Xd86oE0AxQbVAjB0eOkZaCxeNapMbize9vWLVisGhtWIhy4WvyJJgI7/R4R+EQEiMBAIkAA9EEaJ+njECPT09Fim1dbWJm4yxM+8vLw9e/b02QtWR+zgaMNEgAgQASJABIgAESACRCBOwLbtcDh8xRVXMMZS0tKEqHrfvfdw0zM6lBUTRVsN4JnpkHfCrKrCzQ3Vi//yF912sCKhY6LZ2DLAsFXFckJcDL7q6n1lxaua65zqqrZJk9/r5OEdwsPJBTLbAl2FcEiBLetgRPmHNak7mgd1jCqfs3UN6DqamlXAzGmDq9UGQMjQIzp6Oy87a2193jvnnzJL7cZShLojFGfUqbn6bDhgyKCqDuzeDV87c1t98c7G4ujw8s6JI1YtXggxFWsUAkBIw2QPx4LHH4SGvKUN+fPvuWXb/+nLsoKKuo4eak0HRUcdW4+Z6AEPd8GdP46dWD5nTNXMB34T8bprGGMuyZ2akZ6SkrJv3z7DMPqhAK0oMUWJdXZ2er2SS8R7B9gDjw2NGrUAkgMBE3wGuHSHJcvQoiChAu7EnPzpsd8WERzg1oHpauVzjzVk+5jErw2XyyVJ0qOPPqppWh9GcNj8QQw+7bENOKlpWV3entrsfbWD5y9ZhkkyPAPdssQDHkc846H/xBEBIkAEBgYBEqAHxjhRL48cgXA4fMMNN6SkpIgAaLfbPWXKFFKfjxxw2jIRIAJEgAgQASJABIhA3xMQ7/aVlJQI6Zm5XS6Xa/v2zYD5GGbENLpU2NMD//NHKC1cUlO6Ozvz/bvuslXAiAx81Z/PtgNR3QlpWA/whz/ZUFayrKSofVDOutPO3bapE/aa0GVB2LJVG3TM08DZBCw8eOUFO/OlBbUp25tzlr79IugxMLnrmQvKuG0zbkpGMHffumtY2fzxQxcvn4v/1A0nqoQsG3OfxQYdMCyACHeKnjv5o/qKncXpu4vS1k0csWLtclB1CMv4RQtA5TL0v1+AIXkzhwxacOu1lsOTrE2RDxLXoC2dG7x1G5Qo/M+vIsMLW0cVLb7nhm4tDKNHnp+akS55vZLXyxh74oknRApH34/gp+4Rq9YZpgIA6empYohdfvat/2A2jNJsFoox3faYNjMdlqxBH+cCtALuGHiUuABd/aub8wa5mSd+heCvjRs36rrehwI0OqDFQM96E1oqN9blxVrKIxNGrohp+IGBZ3XiciQB+lOvCfqQCBCBfkaABOh+NiDUnaNBYP+NOGN+v3/Tpk1Hoxe0TyJABIgAESACRIAIEAEicKQI6LquaZrQ1oKp6L049bRJfGdOBMvvYVTzf/0ehlStzcvaUFy88vLvrN0TRkO05mD9QCFAWw56iiMW/PD6bTU1iwbnbi0p3Vze/Npby2AvwC7UhyFkhlF6dtCtiVUKe+Da7+6ozV1VN2hzdeZbb7+AtudwD7qqLRu/oHL12eaNbhWeehwqC2Y2lr0163XsnabblqVrmuLYGP/Bc5+NmKNEbOhR4L7fQk3F2oLM7QXpG+vK5rz+KugGr3bIswnQi23CornQXNTamL/kigtWRjtBjoDO40RkI6aDw13YlorebpxeegKaC2c35b17x3VRO4ZL7rjjN5JPmGKZ1yudd97Z/yeR9z+3Ch6wg/oknHrqqdyyzSQ/KyhhneEhismiKlMMZlgkQB9gAEcBOgaMO6BrLzyFZTFMzxZTWVkZPv/oIwFaPOQxVS2Mp50N37l0bWXOhprcaFn2xv/9q8hVt+PeZ/zctsG08cHNZ+Zw8DObfhABIkAEjjYBEqCP9gjQ/o8qAV3XW1tbGWOBQIAxlpaWNm7cuKPaI9o5ESACRIAIEAEiQASIABH46gnIMXXevAWBQMDtkdIHZTG/d8ZLL2qA7/V3qdBtwo/+c1V97brK/N1DSjaedvLK9Zuw4pmIvBDaGGZW2FgB8Ic/2VBbvagof0Nx4abmEcvfXYImahmt1I6GgRk9quPoDmbZxlR44H+gtmDp8JLO5sJ1t/54H2qk3H3scAGaRzk7PSYWNuzW4I23oTT/taaKRX+9Hwl09YguoK4t8qdNsERwh+rAb34DQ2tW15b35GRsri5f+OKLIONmUNe2uChn2hDpgtNOnDk078Mrz9vTsw80DRQFj8LCRGlVx605Cs7QE4VX/wmn1C9uKVx4301mVxsqezEFpj/7Qko66vWiuJ/XK+3c1Sa6w4XoeDY2X8JF4N5W3/62bVvHQ7fte+65xy2xQNDtkpgvhbUuLpDNTIDBquE1HRSgk4M1yAGtgi9iu1RgMXVEdQFLZXEHtNvt/u53v6vyqU8c0OI1ALMn2qEosGUNtNQsqcrdO7Q03Fi7oGMfPtGx8MwVT4KAq886f4JDAnTfXmq0NyJABA6XAAnQh0uOvndMEPi/AOirr75aPOKWJMnr9T7//PPHxJHRQRABIkAEiAARIAJEgAgQAU5A+JctuPGnt8RlVMZ8gzLaYp27FcyoCKnwp79A3dBlZflt9cXbzmiZs20JOBGhFFsWyKqtCJVLseCWn0FF8arKkj2lhRvKyt/8F/cpO4BlCW2MCNB1iCpYoRDV53Wr4MQhu4YVKSPKdl15wc7N6/aPiONYFhgm5i8bMvdZL1oIw+vfqRr8zp032aEQbhAjmVGx5r8ddECLtGjVgBdfgIbqrY1VUFcG9TVb7/8TdEa4U9tBE7SY9u2Bc8cvay5qPf+0D3ZtA8NA6dtEIc8xbNXE1OsYgBPDjGh4ZQYMLXy1If/t26+P6WHQNXRP6zZs37ErNSNdCNB+P9anmzHjaUXtjsT2GlZEmI57j0poiEdFEBQ7tTVNW7ZsGWPM63UxFwums+tuZrsj9RGtFCDfciSLu31VYCq4VJAOnpPl6WO7zcV3twmpHYYnBIUfLKkMBFB9llxYxdEb8D/9zHQRXJMQoHsH+qv47SSFzuD28OSx8fKRIzGYch1kBzcVDYoU5626/a493TE8+Q+ahBx90GJaQASIABHolwRIgO6Xw0Kd6isCkUhEqM/Z2dmMscrKyr7aM+2HCBABIkAEiAARIAJEgAj0CQEhQAOMG30aY6I+nfu7102JiPhngFtuC5eVLqip2ltdsmN03dJ1cwC6uPkZ3b2aBbJQN3t0+NNDqD7nZ+4tyNpcVtL6xNPQEUZVd39GB5gG6ArYMQM2b4Txw5ZWZOyuz+k6fdTqjh0YtBw3U6MKrFkQM9FRjct374FLzt5YXzb3wrOWde4DWcPsaZ747FgoEDsYcgwQ0WBPO/zzBSgr+LAyN1Iz2Kop23brrdARg6iNYnZi0qJw97StpalvjCifu2whdlLRcJcW7jqufbdHt0YtXXNg7mxoKZs9sXHzZWcs6djB1Wc0l5o4m1ZqeiZzMY9fhAN7fjr1NmHiNnictKIovYeV2HlfNxzHsW3TQSEdJ/EHDtZX97LCarat4+yQWqebGSRAJ0vqCrAYuE1I67QyOqzmXz/olYIoPYuZMaboOMCRSKQPBWhbc6AzDNWVqyuLITdrb2nJ+9v24HWC16C4kA9Urvv6ZKP9EQEiQAQOjwAJ0IfHjb51jBB44IEHfD5fIBDwer1+v/+3v/2teMp9jBweHQYRIAJEgAgQASJABIgAEeC6Vfde8LHBjAW5Ohl85MnXIgBdOtxwo1Nfs7Uob0tzXfvY4etmPA4Y/KxyTRVNl6YBdocMIR2efR5qqlsrS/YUZG2uKl0ybVoopGIygKKCpfP1MZfWFv7jDiw82NOY31GfHW4uW7VoPg6Dyf3MopCgye3PJmi6Bfv2wrcuXD6k6K2Thr8f6kadDeM+uC0aV+ZW6KgVEnUFFy+EluplNbl76wuNouxVU6a27eyCTl6iLcoVYQBQeuDuKaGaQa+2VLz14Uz0RCf7R4UGbaIl2jQcWNwKY+vnTazfdfqIVRtWQSSGxmce0NGjY7gIjBg5hjGWkuGTJF/AWzBp/DW/vvOt6779gtYFTlzyFsUUuUSYvKc+PPcURTGMuPf78ssvZ4xJkpSaxgJp7KXXRvcolQa4LAdn/ZOMzwkrdLJEeyy19Y9XX9SACQHagNQwFO2OnTJhMqZmu1wuJjEmsQsvucCwUNA3DEMI0EduMPlTGcx0tgBiGvzxAbO8dFtZiVFWsfHa6zv24YnPp0QAh9CgSYnuBUO/iQARGBAESIAeEMNEnTxSBAoLCyUpXlSEMdbd3U0C9JFiTdslAkSACBABIkAEiAAROBoEHMsGG15/eS5jfhcLevyZzJO9ZjOEdfjJjR1lxWtKcturCvdWDF5wx8/CoW70/1omZlMIwVfUCZzxT6ipmV2St6GsYFtZ0dJp0yJYb1BBpRjjA1CAtniGABg2dHXCrT/dVZe9fnih1li07uUZceOzDqYKhsrFZR0MHTAqWtXgFzcrjaXvnXXSou0bcWvC+4yVDHtlaKxnCCBbsGwZtAx9c1Rld31+uPyEpd+6dOPmHfiVsAWyAz0x2waIdMNf74+MLJs7unLZE38BGTVkUEHtjoY1w7RNdFNb4JgOas3bN8Po2tbGwWtHVy1a3oqaNJYu5EEiOurzYVk1f/TjG7BmTKrk9QQZy2WsqbFsakvFnesWgR4FFeNJVC7bHzUB+gCL7v333+/1elFL5dO11/pCcosDAXRAO5IOXhXnT8jfUEE6lkTn5GM5QIDm6jM6oHUIxqBue+clwQzm8TGXSxIC9N8eexTPGz71lQBtGzbs2gOTz1lbXLIvJ2dvQfEbH87vfXYi7M9CgyYBundo6DcRIAIDiAAJ0ANosKirXw2BhDXg3XffFdYAxlhWVtbVV18dieCdNE1EgAgQASJABIgAESACROAYINDT04MiMjfG3vTTW9zM43JJaVnZBSUNsg63/gzyTlhdMnhvedGuuvKNX79gixIDzQDdQiumyQ3IFtdW//EvKCt/syj/o5L8rQ1DNlx6ybqd7bgC1vqL107jRmUe1aEp8NAfoLl4zrDBO4cVr/3bQ9DDLZyKZenolo6pYChgRUALccPus49DU+GC+pzWV2bg1gwu5WoOqs/toZCDHYhL4bv3wqXn7qgv3Dq8SGkp3nzh5FltbVjqUAPQbJSnFQv27IHH/wr1xW/UF73/2ztA5x5tLnlbpsP15XhMBQ5vtAMuPm3tiRV76guWvfYi9tPk++XhG7IOsg66acGv7v19SobPG3RJUoCxPC8bPaz6h2+93C53c+s3bglh9J8Tpq2tLZHCkerF5qpVTbpeAHaKbUvCAa0DNg6ek0XbY6MtpOfET3FQCQEaIHevXPu/0xuDaSzAWYmHDbvbd4sB5dkvmAAj5iM0yqqFF5Osw/P/gLLKNfmDwzkFm8+5eEGPnNjhIaz1JEYnCFGDCBCB/k2ABOj+PT7UuyNGQNf1a665RhQSESboBQsW8PQ0kXF3xHZMGyYCRIAIEAEiQASIABEgAn1CwMJ3+oWVGZob63htOolJGWPHfefO2zdW5K+pHGxWVYSLilacP3njpo/i2ceaDQpPvQibGD77+NNQVvpeRcm20qI9NZXrL7lk455OVIdxww6vDIgZGY6taCjRASxrhSE5/67JXHhi5eqfXtvdE8IM6ZgllGoUoBWwFP51E+ClF2Bk3WvNg+c8+EsIdeBS00aPsvA+C8nNAYjYsLMdLjhv3dCirUWBLQ356y8+bXWkE/NBTAfrtmkOlhSUVZjfCkMK3xtdu/br567t2AUq36+KbmsjrpgDyFFbjsG+XfDdC7bUDmodmrPslh8ZPT2ofes2atm6Y3MTtKqDadnwyN8e9wYlT4D5/UE3G8RY7cN/+kDuAYcXR+SHIlJDeLN//DjllFO8XtRTPYwFGPvdL71KaCSYOTZGcGAFwoOlZ7Hk2BCdk48iIT0nGr35GywK7hB4u41R557H/F7mc7mzMwsZY5PPPU0M4wHq81f0h+LHntvg6wn8Go0ZGIg+duyK7Jwd5VWQW7xyxis8Ih0vNgscEqD7x6VFvSACROBwCZAAfbjk6HsDloBlWoZhhEIhfguOt2U+n6+lpUUcEN5G00QEiAARIAJEgAgQASJABI4hAuGeblF8UMJCejmZgW+PqP133eC2lhrIL95y+nnbd++FcA+YJphcfY4ChAD2KbBwMdRULS7K3Vk6uKe5vmPUifPa9qLjOKwpmhXG2A30FVs4cx9waCec0jC3MWfl2Iq1l03+oKMdF0dAiXDNmTugDQUgxtkuWAR1JW8MyZt1x9RdADz6w5b55jAfQ3Pi3uceGyIWnP+1LbXF26tzO+sGrz9r/DudO3ETmmw7tmpCVANZNmHBXBhZt6ihbN2YpqVd+7A0opD6UFlGATqCiroNlgaxdrjum+3NBUtGlS298qIl2HcH86w1XhtRRx+0yWOgVRvgrXfexvcmfZho4XYFGEt987WFSeozP5j+5IA2DOORRx4RERxByZXiYvmpbPfG822j1AJmANNxFhq0VwdvshidLN0eG22hO5s2M20m2skCtAnZq7ZWud2o1EssxefOZIy9/f6/MViG674J7/NX54AWbw3EM2aEAK3xE769E/Lz3y8pNbILoiW1y0Mmmvrj+S4mP5vFuZb8kxzQyTSoTQSIQD8mQAJ0Px4c6tqRIWCZlmVaf/nLXxIvpnm93j//+c979uwRAdAUA31kwNNWiQARIAJEgAgQASJABA6HwJd8S882rdde+Zffx1xchHaxisKMm4aVvXv2KKO+uG1Yy8qlqzEXAxU329QdW6jPW7thzhJoGLq0cnBHSbZcW9px4qhFi1ag+mwDKJYcD50wLLAwsEONgtwJV5y1qTJlfkv+R5NHL9u6AbcZsy0TEypAx7wKDIBGAdqC3e1w4XlvlGfP/PrkNlsDBU3RWEPQwQ/Rrcx7BFEbZeObftZZXbY+L6WtZvD2pup31yyDcCfIPRY4gAK0YyoORFX41sW7mkvXDStrXTkflBjIqu44jgUWt1QbOlZS1GQZrBj8fAo0ZK+oSV90+ZmbtQjoJlefHbQ/qxb6oHkStKnz4N0Vy9pRevaKSGX8efttdx80kP3IxaJpWigUys7OZjz228tzQ356jWSqIyzH1StACw06IUCjM1oHdmyIzslHERegHWbyOoS6wzTHHQNPFDxhSNsRzf7NH+PhGx52godl1NXVWpjsYluYFh5/hpFoHDTuh7EgIUBjNowNZk8sYvLygzfdvLKidFNVKeTmb7/6R5psgSZc9sqhI15IgD6MEaCvEAEicDQIkAB9NKjTPo82gVAo1NLSIrzPjLHMzMxEdeMveX9/tI+M9k8EiAARIAJEgAj8f/bOA0yq6vz/Z2Z22u4Cu7BlZvvM9sLC0gWlSRGVqDEYQxITa0RNjEoUQZrBGPM30SSWaIw/e2+oMSKwS29L7yAdlmX79Ln9/ec9Z+YyLEWlLubMc5/ZMzP3nnvu9967z8znfu/35QpwBb4PCqiqGgnQAGD+idPeKkmS7r5nAjESI9bejiMkLzXh9pn3qb2cG3o6ls37GAKYFI38V9L8IQ1JcH0IPpsLfXpvy884UuAUi5z+EteqhUuQDcsUyemDETVoE6SwBuEg/PrmA8VdNpZ23l3cbc6GZWgh1gBzLVT6LEWyQNAqHArD1cOXOhPeGNL3q5AH/dMU+XoBmjRoVpA5C0rUKD3r95CRusLtrC/I3Jfj+GjpYiTK2KlydChNzXDN2JWl2at6ZC/98g0AL+B2qH5QJU1TKIM+mtH8t8dgQM6R8i51Iyu3bVmBOdEhBQ3XbEIAHYXJggCBRpj02wWEdDPGmczWToQYiNH0yLQZx6cxnD2HrK7uGTVuvfmWTgnxZkKshCQSkkTI1g09AHJEsMoREzSh3mfmgGa2aN0cbaAW6W9+jkW9HbMdC6AZg27xE4x+DpNGKavBNybXTRJsxG60do13ObsVv/DC84BB6OzSCh48Kqj6dEa7JLKwDqDRBK3SyzO+MFbL7Fn6ZX66t8IFlSVr9+4CgV3tYedP9Jg8GwPgfXAFuAJcgQugAAfQF0B0vsoLq4Aoilu2bGG3pNlsNkLItGnTBEHQi0fzFI4Lu4P42rkCXAGuAFeAK8AV4ApwBZgC4TD6gE/7/jz9a+3AQQOIAdkpBdCOn/zoL0u/gjt/uO3L10BqYmBYkcEbUvxeBa3Hm/dAn95bSvMDBc5wXkp9We76t15F3huQvBGMHMVhShQxv/sW9C5aVZK8fUDezk9ex3fbvBotZwiSFpkAsPFfT/IjD2ytyv3PJcU1m2sx+kNBmOxXoU2FFgUaFWhlALrZC//v/wkluZvd6Y1u5z5X1vyPP2YzU0c1Y9AAnjaYeK+nzL2kb3ntlF+3QAt1WYsiZk0rmiYDcnMVCQAAIABJREFUZYi4XS1++OezUOxc1stZX+XY8fnrIPsxqSMkhzF/Izq1+vyYfBCGsAcef1Ary/iHgZSTOBsxWAmJM5riH5z0CMPNzCSLTmwKw4+n0hfwSD548CAatwkxYww0svMxQ0kgMBigGMDG/M6UMjMT9PcdQAORgZmgjQCpCqQ1SvEe6PPsS9k2G7FjNA0xkoTU5Dw8ShXfOQbQ7PCRgdb7FDAABv78B6mqYLsrOdgjxz/5t8GAB1Rmf8a5oldvLuDxxFfNFeAKcAXOTAEOoM9MP770xanALbfcYqAPQkinTp3279/PiqjoDPri3Cw+aq4AV4ArwBXgCnAFuAJcge+DAqIohsNh5oDWfdDsm+ppbJ4oyl26YLJthEEbyMQHZ4aCSLXCbRRsYcnBsAhBn6Y0BGDRcqiqWuXKOlTgDBZltJS71i2qQWqsMA8xTaWgxDWSTuBTYP4iKM9f2tP9dVlmzSP3NmsSfh4SJBWrFWoMUksaBn3IInz4KmTZXxxU9uEX70UszAxAK+BXwCtDqwgeBTRBg7dehazkueWZLWVZTS7H/I8/xHyMoIIMGpfUkNA1N8Dv7j3Ss3B7SfbaRyY1eJswyUPzYIozThKu3idg6LQGsG49lLtXFju2FaTOeeN5CLYA/QQkVQwris6gmchKEKbcXdc/Z/OlRSviyGWEWFiCnymuy113PcQCgnUArcc1nMYOOuuLiPShquqIEcN1Bh1PSFIcee2fpd5AaVDTcbOBZkBb6XPsm9/sfWYW6Y7peo4dFTqgKX1WNBoDrVpaA6RVsAmQ0SgMys2P5DKaKax/8R8vYBq55KFh4BETtG5/ZnnNZ7q/jg3NYGdVIAgDKucVp+3L7dRa7Ni2YgldCZtTpGb/6CWfM107X54rwBXgClwgBTiAvkDC89VeOAUkSercuTOrQGi326+99lo2Fp0+61aRCzdGvmauAFeAK8AV4ApwBbgCXIH/XQVUVV2zZs2cOXNqa2sPHDggiiKgIZelIn9nWTZt2mQ0shqElEEbyeRpDwRFr6KEFUkCAAVprRgCrPW3+xCMHn0gveuOggxvXmpduWvDK89DOARBTOagD+bdpDhMAXQN79oLl/RbVOHele+o/d2vD8phELFXfKgQVjFkAFchKeD3wpxPoFfOnF45c/72h2bm6wwJQI3SQQXCEtqOfRJ1fG7dCgO7b+iecahHZlOVa+uU37VqAH4RRETKKjJrBdMzXnoWSnKqy3I3Xztyr9+D70QiP0RKokWcLahCQIV1m6Gy+6dVRYcKHBunP9Qa9uEI/X58ljUZQ5+jDmg29NlvQK+c//RIXzrtbmlQv99S8zjCSrOly623/kbRQFYxJlifOlQER4iGai9bsZRdeIgzIj6PJyQvjezZN7g16AiDnZqgTVEAzRi06Vsmb+izxaLejtkWafqzopEogI4LSHEhSG+RSt/4sFtSMiqUaCWdE8jlQwe0thyiFy60cw6go4eLAtDmhU9nqxU5y7tntFVmtVw1ZI8iQ5Cd7go9GRTugMaTkj+4AlyBi1oBDqAv6t3HB/8dFJDo12sAeOGFF+x2O1aypo9FixZ9h174rFwBrgBXgCvAFeAKcAW4AlwBqkAsEdbb7DunSh+iiEXwBEFgb8Y6mvVUjRUrVqxZs+aZZ56ZOXPm+PHjR44cmZOT07lzZ4sl4rclhCxcuFCf/ztpz9Y756v/WCxx0QgOxG3TZs6Q0M8cMVUi3gY0Hm/5Gq4euyvTuTs7pc2V3ti7dMeUBxsDXtAwASAEqnA0zpmGTagA/hDcfnNLZeHOkpyd4390RFbQpCyjZVPSwKeBT5AR8QaCoAgQaoRBpZ91d/x7xr1BNUyDdSkuVjFmV5JBkUBrk4MeEdavgUsq1lc4D/bObhlS8fV9tx6UAyDLGFWAiRo0ykMQ4KP3wJW23J22tk/Z3B2baIlDJpAGbY1IwVmGAQDMXwaXDFiVm7E5K2XzD0YfOFQXsW8zc2mss9UvgBCGz99XBxXV9MtbMu23h8IeGHzZzwkxWe3xCKBt1ivHXi2rKgPQDCTqz99pB53TmWVVFVSle1XPOLvJZCFWM+Z/x5vI1VeQxsZrPAGXDF0E1dbmI6IaRycLPsN3Y9AdEzrHjgoBtGpUlDicVEzhUMEa1PL2H74yL5d0smBKCSEYA71q+XxN81MAfS4zoJmvmR0xGj30RbhuTE1x+q7eueHeRds+egsvxYhYAZEenvQGAXqyxnqn9fY5PYh451wBrgBX4KwpwAH0WZOSd9TxFRCwjgOMHDnSaDQaDAar1VpYWMjsJNz13PF3Hx8hV4ArwBXgCnAFuAJcgQ6rgA6XGYlmda2Zc5lFvS1YsKC6unr69OkzZ84cPnz40KFDWUkSDMYwYDbzyR4mk2nKlClYIpB+lf1OCrCvuO+88xaWHzSyDGgjIZZp0/8oUTSLtl/AcGQsPOiBMT/Ykpa2Oi874M72VeRv/e2djS1NEPADYKaGBxQRga5EJwCN4uvpUw7mZywudG66+op9/iAI+KEoo+2YAWjMvggEsERhqAV+Mnpdz6xP7xq/E2T0MOvQVkXErUloWcbBHGmBkYN25XfZU9a1sTJ904Sf7MB3BYRxWFFQwwKFbT748gvoUbbSnbEtP2vJvz+h24DIDksTMnbHYjf8KhxogOt+tDY7c11JQd2oy/fvPYBb7ZM0TPGgmdKapsgUQmO+iAKfvC31LfpXueOj6b/xawIaui8dfBVmWcRh/RhiIj8e/0NZk/XYjZgN+U7759zOzCKy5yxYQCwmYiQmM16DMBPSxUru+7UNtGsUzRWSkkXFJmpGWqnPiA34tuEbF1EEBwJo2YKTgjDaJ1k0GHb/vVYzIfEGlMVujrvmqitACdNrFjL162P5QTadkwgOetBgfUEFPv0I+pbXFqW2lWe2DOu/TJEggCE20Ys87PDCg0WHzrGNc3sU8d65AlwBrsDZUoAD6LOlJO+nQyvQ2trKfCg7d+6M/XL/z3/+k/0k6NCj54PjCnAFuAJcAa4AV4ArwBXoYAro9gVVVRlo1pBiKtXV1XPnzp06der06dOHDh06ePBgduMdISQ+Pt5isZjNZoPBkJiYyKphm81m/dupyWTS23rDaDR+8cUX+uq+qwyapj311FPYm5FO6IJNnDbtaUGKuJm91PO5fT+MuHJ9Zua63LzGTp32Z2Zuuv6alSGkx/ShCmhgZsXQVJmRsXAQ3n8dqopWl2WvG9Rr+dJViIi9NHxDxmAKBMUa4mr6EOHm6zb0yf3qR5evaDkMshTpjH2oUuzH6HNjK4wZtdndbVf3dF95yvafjfkagnQuiQZ5aIKiQigMq5ZD3x6byov2FJfUfvgJeAKAmROUuWKiiBap3+aVIaTByNErHGk1GRnre1StnbcUE6YZaKSEjw0BBOoDl0LwwaswuGxRVfZnD/96i6cJRAU8Qf/IMT8ghFhtiUYzAsv7H7ybFTaMRc9HOWGkywv8R6VBJX5JuOHnPzXYLAYLHml2M16MyM8gi+f39Hu6q+BWIImlJEfLEpLvxKBjvcYdsU3ZuqwSRSGabFSkeFFKA6icW+3uYiEmLM+Ij27JXZYuWoY7LHpM6PSZ7mhVZ9BnYacyeowXSnBtogS3/LQhu/OOolQpP3XHy//EewjCJ058juXOevssjIh3wRXgCnAFzoMCHECfB5H5KjqKAqIo3n///brNJCUlRbel6NVdOspY+Ti4AlwBrgBXgCvAFeAKcAU6qgJHjhxZuHDh+++//9hjj917772jR4/u1atXfDzmM1gsFnannf5ss9kYZWZ8mfmd2bPVakUyTAOajUZjYmKizp31xiuvvMJyPE5PjP+WOZk2bRr2FgHQRkJsU2f8KawgGw4CeAGaRPjpzUdycjc50g7n5bQ6s9bd8BOs0S1TeqzKImZjyAqt6adRpzIC5pq5UOSscaesqSqY9/VWpM8+AAaBqa9Y0TRFU2knMjw5ReuVPXdQyb+XzcXtCCiiRIM92EahD5QOxifDL3/ZUJCxKSvhQFna/uuHbW7dS03aACCKGMBBO9y6ESqKviov2OvK2nD7PQ1+DSOeQ5IPCxPKiLZZqEiQViz83cONeZlLi3K2lRRUv/MuHAnguvwUeUdhY0TatkbYtBx65s7uk73osYloEcdkaNAE8A8dOSq+c3KcxcbyGmbOeoQSSQSI7abT203nYikKoBHEN3q9xIIJhBRAJxBi6BRH+laSA7tHAQzyq50YOP7eAmg1TlKIIhGQjIqYJITL/L6r+/UhXeOJlSTZ6FWfK664AncB25eRfHNWdxNN0Dp9jo1qOf1dxtAxXZeiYup5Wd5qd6qvyBEsc685dBiDzkMytHjZ9R8dRevEuV3j9AfCl+QKcAW4AudTAQ6gz6fafF0XTAGJPhRZcTgc7Fu+2Wy+7bbb9AGdtqlE74E3uAJcAa4AV4ArwBXgCnAFOpQCrA6bJEmswb7vsTBlVn2aRSSLohgOh3XIq88AAKFQaOXKlR9++OHMmTMnT55cVVXVvXt33bNsiD4Y2mMuB7PZbLFYGGtmc+rzWywWo9HIwp31j0wm09EKgXpHhAwfPnz8+PFvv/X2mUs6fSoF0DGd9x9aFQCvH6BZg8MBuOv+UGb2+uzMlhxHsNC1/5ofr2kVQFJj7vinbk1QRZwkkH1waCf0KKjuXbC7PHvJO69BKIjVBkOU/NKMZkVBIo30WfLDuy/BZYUbKtOrP30HPK2IsmmMR0iGACXPigaqBNAsw00TmnIz1xc66rK7bOtdskhmn4t0LimshBEK790JN46tL8nc6XJuvXzY9iYBWhFeyzLWUJRoQUWM1Wjxg8cPb70N2RkrslO3VeQsf+cfEgi46jAyZeTUgTCGGkRAnwobl0L/wq8GlS79wdAv6nYDNYlj3jQADBkxnBhoVrCBJHROeHjKpHbcWX955vvrLPagAghYrxGmznyU7X+jMc5sRC+03UQm3NnZr4xslRMDYAwBEdAsfPFHcGjGY4zYWpyoJMqiXQkS0UukUHIoMPjmn5MueLXIREgyIcak5M679uyOlT16ZULfq7GN2BlPt62BIoQFP9LnmVP93QsPZHVtyE3d+bsHMHwjDBDWMJQmSsTZ2ttxZ/3l6Y6BL8cV4ApwBc6vAhxAn1+9+dounALhcPj1119nNhMsHmI2794d+Z7B6fOF2y18zVwBrgBXgCvAFeAKcAXOrQIsOvmE973pXwI1TaupqZk/f/706dOnTJkyePDgQYMG6dEZDBAzz7LuYjYYDCcExyaTiX3hNJvNrMECN0wmk91u1+Oe9bSNnJycq6+++p577pk5c+ann35aW1urD1WSJH2Ep6eRqqqapl05+go7pt1GH0ZSNajYizkW0KTBhPulisrD2RltGSmtGam7+/ddva8B0VekfB9jXwxAQxBouHL9Drjxiv3dszfmpsx54RkMeqCpF+g7ppMgIovGR8ADq+ZDufOdAe7lf5oEnmY0MSvYuSZBQEbPNLqswwo0+2HyLEjJWOV2NpVl1/cpW7FlA6JqgMBRS7MIwVa44cqV7qS1vQqaq8pX1x2BVhU8CKCDAnhlDNLALGkRcNkP3oNc54qsbjsdSQvuv6MefKB4EdtJ6OiOuF1FBXw+0ETYXgv9Cj7o4/7qx1esaTyICdeeoFdFRI6PoSNHoH04Id5ssxrjTJMfmRKLJGPbbP6O86zgzoTDDUdcBfnsCDAYDCbMPSZpKWTGE8QP/T1alwCQkGYRNMv3rQihZhQVm6zYQCYgJYE64LOPCrom4PabzF0N1lSDxf7YHx+L7i88PNjejB4gsfs2+kl07jP8KwZg39fQvWRxXkZ9TvrhzPR5K1dBCO80UGQ6qXjoy9GR6MS5XeMMR8EX5wpwBbgC50kBDqDPk9B8NRdcAUmSxowZk5iYaKKPkSNHsl8jZ/i1/oJvFx8AV4ArwBXgCnAFuAJcAa5AOwU0TdNzmfWCH8zazIoBzpgx49FHHx0xYsSwYcN0D7Ldbo91KzPEbLPZGDtmDgYWsnFC9Mw+slqtDC6bTCa9N4wPtlp79OgxZMiQKVOmPP300/Pnz1+/fj2LjRZFMZaS6wC63UZ9i5eMTB2dUZIkURT79emTGB9vJDTpA8EbGThicJ0Xjvhg6mOQmbU92xnOS4fstPp+vZfs3oNI2McyLPRQAnRDqxhcoSAQ/svDUOnYWpy6YuJ9O/ANmtGsUJZMATQST0bymvfBoMLlvbIWT7xjK6ZnKNiBiu5qQQZBxVegaiCJ8Pe/QmH+qlzn4aykxkFVh7Ztxc8U7IfGRbPxyHDHDYcqnFtLUg9UuNcvWQYeyrD9oAYhHIKwCBoLdxZU2LgGhvTZVZ5bV5yz6cqRc0IR1o3isMhpGcATpD5wBTavggFF1ZVZX44d+kXdPjRuU0ruA1BVRIHapcOG4AFgs5ptmJryl6efOh5MnmU8eXQ3nlHL4/Gw3zufffYZc98fvbJiIHFm8t7sPi1yoReMAbCEogBaAiObvjEP+hi7MZAO+JJFi4RkIsl5wdbb8jPR+Wxn9SQJuXTEkLAi0IqYkcM26vw/+3tY75Ht0aAPXngGit27HF2b8zIPjh+/S5TxToIYAB2bPd2OO+svz+jw4AtzBbgCXIHzpgAH0OdNar6iC6xAXV2dzWYzGo3sefbs2Rd4QHz1XAGuAFeAK8AV4ApwBbgC50YBSZI2bdpUXV393HPP6aCZUWP2rDNihpV1Y7JOmXWHMmN2FoslPj6exTpHjcQn+MuW6tKlS58+fW6//fZHH330X//619y5c4PBoM/nQ/Sp4s39LPqjXQ0S9jI2AEQQhO9olWgPoBVZ0TRt7FVX2y12I4kzEiM6P42EWLuKKnz4EZSX7M9xBDO6CtkpbZVFW5csAZFGzoqKQHkyZi7jREkwNgT4/BXonlLd37Xh/ttaZBnNyyyvAMupxUy+ADTsgx9dvrGs68IbR+wMeyAYYkwZw6QRsuErXFYW4aP3wJ3xZUbylqyue4oyN7z1f2ippp8qCmgKzX3WJPj9w8393HuLux0udqye/QE0+dCf7Kfh0SGQQyCHo/bnbdvh0qrN3XMPZyWturTX4rYWUHBtFC3Sv4oWsXirMmyuhWuGLq9wfjWsqmbLOvxYAQgpfhl8ArTR2eHy0aNwfxuQQROj4d9f/keHie0abP6O88wOIXbIsZKYuCFGdEBjYUwbycgiuw9fiQxaSwmALQwmEQzfMwBNsXi3oDj8ypG41QYsxpiAtQczEncd2KWAGpRCgiZG0TM7j9rtWP3l6e9bvQsMPZdwbcMv21mQ3ezs1uLO3vTll2jjF/HI1B3QHECfvtp8Sa4AV6CjKcABdEfbI3w850QBURSffPJJlrtHCMnPz2fBf+dkZbxTrgBXgCvAFeAKcAW4AlyBkyvAbL+Mjepzqaoq0ociKyw4QhTFUCike5l1I3MskxVFkYHm559/ftasWTfeeOOgQYOSkpJ0fMwo28mede5st9ttNhuLdGZ3y53Q42w0GmN9zRaLpaqq6pJLLpk0adLkyZPnzJmzcuVKtkUej0fftFM0zvY30vYAmmHHe+65x2K2GYnFSOJo9EIcIXlvv63lOZflOwJup1qQ0Taoz+55X0JbG8udFQHBawBJbDSHVg4hkd65Bvpkrq5MXXXdsNneBiRo0c9FGW3TAWTQlB031MH40ft7OteO6be0ZX+E/IqY1CwpoGlY1k0NBqHhCHz+Kbid1YWOg0WO5krXxrdfAw+lvkGR1kAECKrQ5IHPP4Ei5/wemW1VuQceneoPY8Q0eCSsoxjSMPIjBGqb5NEA6o/AdVduK8o40Keo7bI+S2qXIZlWZVBVBOYAmk9Ah7eoQiAATQdhSPelZWnzRvWfc2AnCAJ4AgyUgwKigvNDQAhfMvgyYiS2eLvBZDTbrDULF8TCxNj2KXb3Bf/I5/PhBZUIfWYM2pQQjwx63uLLvVqvQ34SBLMMcTKYdAZ9skasOboDGp8FIArEiWACSPIKaQ3+S39xB+kUT6wmYorgd/J/b7zsEwKiLEmKQq+j6LbikzdiP/k2ezTmpGTHCbtXQAN49VUozt+e4/S7s5ouG7AlFAS/Hy+9KHi55JjKh7T4YeyKY9vfZhB8Hq4AV4ArcOEV4AD6wu8DPoLzo4DL5WI/LYxG47Rp0xRZaec6OT/D4GvhCnAFuAJcAa4AV4Ar8D+uwAkBdCxWZjCaqRQMBlVV9fl8X3755fz582fNmjV9+vShQ4cyLycjyBaLxWAwsLyLb4meWVwGpvrSXGY9tZmhapPJZLPZEhMT9ZcWi2XIkCE//elPZ86c+dJLL9XU1Ozfv59FZ7DEDIZ69ecziNE4k6MjhnXRbth4pkyZYjIhfUYHND5sJlNlQe7jZdl78ruGUxN2lLhWfT4bPB4MPqYYzgtY2C90FDDT3g7vgLGDlpd2XTq4YrGv8eg4qUE5IEJLGDwiYO2+hsPw0D1be2asGliwef1irEMIAEFRESEog19WEQcLHvRTr1oGPcvmpXbemJl0MCtp1cxJkqc10nNYRpLtEaFNgPWboEfx8pzkTYWp2ybcFAyHob4FgbegRiYKoHHBQAgm3Ly/MLM2N3VniWv1G69gfUNVBE0GGTM6/LRWIo2VliDUBjddu74yY8Gg0qVfzcYUD8D4EYyephOatQVM9YDMvCyDxWyMM7FDYve+XbHQObYdGX2H/KPIyrvvvksIibPZaQk+MyHxhJhMBmTQcxaVeKHcJyeEwSBejABaMwo4xeEzDQMBiG/1xwWCGRpc+Y/Xco0JxBpPLGbEz0az4Y477wSAGPrcLoIjFvLGtGOa32onx5yU7F4CzCjXEDTfdmtdYV59WQGmcLz8Avg8EA6HGX3mAPpbactn4gpwBS4qBTiAvqh2Fx/s6Srwzjvv6D8wCCHBIE2qO93e+HJcAa4AV4ArwBXgCnAFuAJnS4FY9FxXV7dy5co33njjj3/84z333DNq1KiePXsyD4EeXMsIoNVqjQ3TYG8e/w57/9TPug+azeZ2uy+77LJbb7112rRp77777pIlSxobkbaGQiFRFGNHq2kaI7wqLZbHzA3BYPAsGB1iIVds+xtEj2FddE422qeffhrrzhnQ+GkwEoOhMyE93M4/DSxpqchoLMr74qOPkBr7gow+I0PGSWOhFdS8rIK/Ga4fsqW7Y+mIS2q2bzpmHDKoAlb/84oQEjXkaNN/669wzOuZ/dUCGnrnp45mXyAoQ4sMLSKIqoQG66+XQa+ipflZ+/KcLaX5eyY91Orzsp4j3mcfpcXzaqC4YHNe1yMVOfXXj90i0jxov4Cj9fhVkSZ6CCCHVPB44Zm/gDttaVbSalfe/Of/ibkfaOuWKIDWZAHCfsXT7EOm3FQHVw5cUZk5rypv9hsvYBpIM7WthzWM66ATOqCDsk8GyZJoNsdbML3BZDSaDSEpgB5uGiHS7vkYaTrki5t++Qs81E1mQsyEJBCC22VPIBm5pGZJ3wZfekAlYTDIEMe8zzIY5WgkdNQNTSQwUgc05nWIYDivDmgGmk+YN63FCWqioNpY7rNfNBw+khjyDnnpH2no/Y+j1N1oIsRQXFouKZooK1HvM9tVsSfbSdqxb3+r/Xv0ANEBdFiFNWuhIG9Zfm5LTmZ9eeliEQ9JfGh4+LW3P3MHdEQd/ocrwBW4mBXgAPpi3nt87N9agdtuu03/4XHDDTfE/nL41n3wGbkCXAGuAFeAK8AV4ApwBc6OArt37160aNG//vWvWbNm3X777WPGjMnPz2fl/oxGo06E9RwM5mtm9f1YKDPzOxuNxvj4eP1rHptNX0p//2SNSy65ZPjw4dOnT3/88cdramqWLVuG+b/RDJCTbWr7b5IqGnVDfpAEEEUIBKlvNxBm2OlknZzkfbaQDOjQjU7fAXjpsx7T/SuvvIK8kRhMxEABdGK8tXd65/vKHUsKUxZ/8h54A5hHQR8yjX6W6NppSC1NYhb98PBv1vV31/YuqP38MwjJx/QvIoCWwyCIGghhWDYPemUvK+22+I1ncTaNZmVg8rUsyNAkQgvibQGadsGV/VYXph1wdj2SnbXj+nH7WdC0JIQUMcKhRYC6JujX96Arw1OQ1jjykkMtLdinn0bl+mj1Q0XFpAxBhaAILz0P3d3LSzN2OrvW3HnvrgBAG7WdaHTAODwaDxIIQ8gDE362tSxtXmXmvH/8RQr7aSfUAB7WRFFTFVBpBIcoaGJDa6Ml0Wywov3ZGGeqrKpQUbCLD0CHQujx9vp9eYX5pvh4YrQSYifE3KVrIjGQOAvJyiHvf5zY4M32yClBsAvInYkEhMJoiwQ2KUqlKYA2iTQwuuMAaFEzynK8rFhEiqdbQ0ktnn4vv5iV1pVY6P0MicldrAldyiqrPIFwqyfg9QciB37kiNbPoJM3Yj855jw40Qs83o4B0Gh/BrwR4M47AimdNpTni6X5+574I5bixCqdIYED6BPpyN/jCnAFvg8KcAD9fdiLfBtOpgDzoezcuRPdCga82cpgMGzZsuVk8/P3uQJcAa4AV4ArwBXgCnAFdAVUVZUkifFWn893fHyZXjGPNfQF9caOHTuqq6tfeOGFqVOnXnvttT179kxKSurcubPVatUpM6PDLH+ZPRvpw263szvYzGaz0WhkKRlIAI0sRwK/17GHzpcZldbZtD5zZmbmsGHDfv7znz/88MMvvvji8uXLjxw5EgwGmX+ZjZbFMbP4adZuD5r1rTquEfYhsBX9EAhCSEHApDMnSQHpWFyLMRHhAN77rwiBUEiQ5GjBPVUBScNAY1Zazw/gpQX2VAxaZtNxqz7ujWNmZXBt0aJFtPBagoHYDUZiMlniTBldE8d0z37+/Zdo8b4IhKOWZ+xAAcw+9omhZg2hGLz2HFzafeElFYveexN8NHZZBtBUHBVWEUS/tCICeL3wzj+he8bcspQlj/7Bt1JPAAAgAElEQVQGgs0Q9lEAzRTRBBW3CLdw/2G4/uq6jKQdpXmQ49x3zbhtB1owzRkABNHn9TQD7bapBUaP3JeRvi/Xeah/5fI1K0CUEX+LmipDWAWvSvMxNA1CAfjqC8h3LMpP3dGjYMvPf7anVcaVRX2lR3WSaP23SXc1lqb+p49r0VOPYhXEsAz4PsJBScQ9hhJQBg0hEeZWL7Ek2E22ODzSjIZb77gJy0lehABaVVVFVmRVXbRkiTUxkcTFYUlKswXdwQaMhjbFEYeT/OkvXT3S5T4t0w/Ep5GgSkQwy1qSpCRLml3SzMwTTaOi42KToM97mzCns/6sAAHVGPQTABKExCax99//lZacToxmYqB7z2yPT051bNy6Dc3I9GqEfqoeS6KPHjCn32LnIp4m+kqwMxlg737oXrw5yVxXnKX2KtuxZy+e+QoNiokl1iddtX6W00046Wz8A64AV4Ar0JEU4AC6I+0NPpazrYAgoOPi8ccfZz9LOnfuXFZWdrZXwvvjCnAFuAJcAa4AV4Ar8P1UILZEnk6f9QYzC7Mtr6urW7Zs2QsvvDBp0qQbb7xx8ODB6enpLDTDZDJZLBYGkXVS/O0bzO+sOwkYU9YZtN4Pe8doNA4cOHDMmDGTJk1ipua1a9ey6oUMvTG+3G5v6ehZjXnoDPpbYujXng+98LT2lz8feelV72fzYMlaDC8OiBCWQFZwCovg8UMzrfLHIDV+qiCNYoX7ROrBVSIV9cIUPQcjBFXnTccMnb0b+5Y+X4RLCZIoKUpra6vJZDOQTgaSgAA6zmAwxtvMRU89tq71EMWuOLtGW6w3JZLCQYn0lx9Dn8L/9HTP/+PvQ/4g+DUIYqgyxgQwWMZMnT4f1PwH+hcs7p295qax+zBBGtBFjO5jdFSrqoqhziqAPwTjxq135+4uzJOcqfvHXNlwoBnqA1Dv82sgCbJflDQNQJRg8kTITduekbK/2LX+vbexgqEM4BM8siaqGgXQKtJ9JQx7t8OAivm93fWubtsG9F3YEsAqin4qn6gxYB0Rqq0VHpm4uyjlk6rshZPuakTkrIGAOwp93CKGkegZ0BjEAQBPPPEGiaNGe1q+74k/P0q3/uJzQOMeUVVJQQb95tvvJnTqgidUnIkBaDyb6MUdi4388g4S0q71yLkSJAF00iAhAqDVBEmzymBh9FnGKn8YwXHep/bomTFoBNBAQDFr4Gz0V/z15UR0eGP4RjwhBltiUnKqY8OW7SwKgx0QOhs+hwAau2brAUGBoABPPxXIS//alaK40w9PegAPPkHBYHQ8vqOznmo87U90tin8mSvAFeAKdGgFOIDu0LuHD+5MFNCdONnZ2ezHicViee21186kT74sV4ArwBXgCnAFuAJcge+9AozVSpLEeGy77a2trV2xYsUTTzwxZcqUwYMHDxo0KJYCWywWq9VqNpvbGZz1eb59w2azMS8z64ohZpPJZLfbExMTMzMzhw4d+otf/GLy5Mmvvvrq/Pnz/X4sdRcOo+fV5/Nh1btvKvuhU+YY8hxp6h99I4D2B2D+l9C3ZG2F61Cha2t+4Yb84o35xetLyzddetm+G25omzAh9PTf4J33YOUaOFCH9cdkgCYvtPihJQQByqCpj1ih7l5JiTFMxtKxY4GUgiHK4AOQVETBrBofax/1WwqSqCBZhn59BxiIGYOgjcRsZpX0rG2NgOnMEVgt0dxjtrcjbSkAW5bD5b0XF6S++cA9+zx+NBQHaXVCZtZUKDFDhi7ClhXQ1720NKVmwo0NLfWgyCCrIEgeWfKDImINQAUEGSHyr25pzU7dkudscecdKq+oXrsVvCrUe3HHyRg/jSNSNZg2xVORt6s4oyk1YdHMaRhRHcBoaEnSvIoiairSbVkCRYCWOrjhirqcTrXds/cP6rNp3WYcpJ+OM8z4PiDrFyTwNsPvJ0Klc1mFo3rShGZZQPrcFvK2hI/4FQ+lzxhPHc2ARpOstwUG9LmHZiVj5TpCyPyFcxCoX4QOaLZ3ZcqgQ4L09NN/O+ZaDvVB4xmKW0n69SMLl/TQ4DIJUo740ARN7c92SbPLYKMM2igDOe/o2aD7nds19LQQUc4OhsY8+DuSglfB8GGw2cwJnZJTHWs2bMYrFvSYVwEkRcMrI1Hm2+5/3Zm+ZJiY9Y5rjJzBBw9A7/I5mUkH3en+wtxFW7fglSpRpZdqaNjzN4+HA+gz3Td8ea4AV+ACKMAB9AUQna/y/Cjg8Xg0TVu+fDlz31it1qysLPab5PwMgK+FK8AV4ApwBbgCXAGuwMWrQH19/YIFC958882pU6eOGzdu6NChDocjgnOi4WZ65IXFYjGZTLHxzVj1zmSyWq0Wi+X0YDQLdDYYDJdddtmQIUOmTZs2Y8aM6urqFStWsG90kiS1y2tmkRoMGTMvQmyKSOy+YJhZp8ynDaAZvJ34wPqyvB2uFCnHKaU7wskpvqSu/tQ0MStbdLsDhYVN+fk73AWrC4uWFpXOKy77/Ppxm381Yddfn1We+UfbnAWwcTscbsKoh7AIYhjEEEjh6CTQSAgJJAmDIZiZGp9VkCnIjgZFSzJSLEGOUKyI35IZeAVJvPvuuyN5JUasQ0h3nOHfn/4bY5nxoVHoGkHROonesRYGFFXndHp//LXLgoj0EUCHaJIyLVOIa0F/swzNdTCkfEOvzM2DymoO7MA5/YiIFRWXCKuqLCssIBt+c/eeyqKDydb9aUnbS0uWL15F1x8hgAGf4MEIkjC89SZUlS0vz2qoym8aO2orlgUEaPW30BUKaKZWkWWLYZD8cPfNR/K6rCtO21eau+itNxDrS0iftTDmcsu0ZiEOtbEePn0bemWuL+xU++PRW47sR+dpmCZ/hLRAGIISAm1cFgG0ClgMToTrxjzXyTKWkCQ8+KlB+FD9XvViBtC411Q1FBRUBR544AH9pI74oI3EGEdsZmIxkdxs8u//lCowzC+ni5pdApOkmSXNSiezBAbpAnifTwqgRSBhsAL0rW8Y+qMfkrQUYjUTo4mY7KRTSpcuaWkbtmzHAJwQXsdg9FmkgSTfDHwjB+l3/MMwMbuaQeGzDIovCG+/BrldF1fmSiU5dT/58Xq/iLk9sha5oKEP5tgLTseumgPoY/Xgr7gCXIGLQgEOoC+K3cQHefoK/OxnP2O/XgghDz744Ol3xJfkCnAFuAJcAa4AV4Ar0JEUUFVVEARWVQx5Ck13jR0gI7CMxmqaJooI4vRbxNicDLwuoI8nn3zyvvvuu+qqq3r27BlNVz7m71FQFdNic7CgDBbTrJNog8GgI2nGo9lHzHTJ4DVbkBCSmJhYUFAwZMiQ8ePHz5gx46WXXqqtrT148CALzdBBs46MT92I1eEU7VN38o3eZ4axRIAFi6GieGFhVnNOhpDhhBQHJKVpKU5wZIIzU8nMCmXleHNyWnJyG3Jz69x5hwry9hXk7Sp0bS10ry9y1RbnrSzNW16Wu7widymbbhjT9KufSjMmwl8fh+ovoPrLyFQzB/Rp7r+h5is4sJfevA/QEK7zYw4zEmGdYTG6rID26WefRPEp7jxLHJqgf3X7zaBJujGTZpUokiwINLW6rQ6G96nJS/rghjFrwv5ISoBAC/Oh3Tpa0C8kgOcwXDdkZa+stZf33LBzI+rNsDjNiMaXQQFzOMIivP4K5OesLMhsysusKypauHgFot4gNWmLEfaLg1+1Ggb12ZCTtK0i48iPRnpam7CTKB1nUSGY/xEKoaP5sUekyrzayuyGStfGZ//ur2/CHvyKGAafiDkoaKmmyBHeegH6ulb2ydp501XNjYcQc4s4VE2k0Jk9MwAdkpD+iV6YeGftqEEvGsgwQlLM8TZCSHFZIYAiqeGL1wGtnxHsgs0dd9wROaGp8RmDoeOQQVviiN1CunQit99CFPWnChQoEAdgE1QianRS40Q1TtCMAq34J5xXN/QxERwamBq9RAFzcyBz567r+vQineKRPpsicfGkoMwtairefEAvHcgqmqAlRZMUDe8XOEePdgCaVssUBRjWd2NRen1O0uGKwnVzasAr4XGoUNc/LWiKo2Gn8DHjioXOJ2sfswB/wRXgCnAFOpYCHEB3rP3BR3MWFVBV1e/3OxwO/YfNjh3Uj3EW18G74gpwBbgCXAGuAFeAK9DxFNA0TZGV2Bu/GGmqqalZuXLlc889N2XKlHHjxg0cODAtLc1ut+tJF0aj0UQfDBwfg59pPecY8hxlVpQyH/++/g6rHxgfjxG6BoPBYrHY7fZRo0YNHDhw5syZDz300JIlSzZv3nx8XAajw7q63wiLY2fQl/rGRuxSx7e/cXE2gwawdD64HOvynb4cB2Q4IN0B6QxAZ4AzU8vKUrOy5KwsOSdTzs1QczNUl1N1ZciuzLA7I1zgDBc5wsXpYnG6WJomlqaFS9P9hanNruSDuck73WnrC5yr2VSYsSY6beju2pPvqC0vnDtl8t5WEcM4miUpSFkqo1cscJm21W07t8XHx1vNFkuc2UiI1RxnNcdVVpRhjAXCrgjdFYQQVt8DaGuAscNX9ypafEmPL3ZvQ/osqWGcFEWkHA0ZNLVtNtbD9cOXV2UuGFK2fM867EmkoSI6B9cAozO8QXj5Zc2VU12Ud9CRsq24eM0/X8H32YpbWmmxQFUJBuDAIagoe68oa2dZ5pFLyrduqgVa1UXfFRj4IYgBVQU5CF98CJWupfnpG3JTVzzyoFLfCH4ZAjLDjAigNboGWYI5n0Dv3MXFSauuH7Kv7SD25hVCjD4LGrqeY6cQDbB+eEJ93/z381InEtKDGFOY/fmmm38KIIck38UOoMPhcCgUYpHuf/7znyNZHGYLMcWTOBsyaBMCaBMhKZ1I/95k66aemtZDVjL8oThBIYJKBMWM04UB0Cx1mmFoQ4vPpEBBUOj92uudszKJ1RL592M0GuOsln6X9KlvPkyjwI8CaMagFQ3zbs4Vg2ZnILsaQ33QmgoL50NpxvaitFBZdv3QQas9Ah6gEQAdcy3oBFT8ZNA59n39LOENrgBXgCvQ8RTgALrj7RM+orOkgCRJf/7znwkhNhu6Fa655hpBEGLL5pyl9fBuuAJcAa4AV4ArwBXgClxIBRRZ0cMoEB22ta1YseLDDz+8//77p02b1r9//+HDh6P71YhuQKSQVqt+fxhDz4wO68iYNdrR55PFaOjv6w19cZPJ5Ha7Bw8efNttt02fPv2dd95ZtGhRQ0MDE0sURUVWfD6fSB+6NVtvtNP0eDp8infaLfuNL0/W1TcuiFkTrdRnLMOQniu7OxuLUiA/DXLSIMcBWU7IcWo5TiknS2RTLgJoyHVGpwyKoTNkt1MucMgFDrXAoeanaQWpWrEDyrOgPBuKnVJ+WpBNBemhgvRQvgOnogwtNf5IUbY3I23umx+pIYBWDD7GSmZHiXJ0AxTQxl59Dds1ljiz2WTqFN+ZEOuObftp6qxEqw4qmMghQ91uGNa/ujKvtmfxwo8+QrOziHEXbaoWljWZOUnRAS1C40H43a+a+mSuLkuZO/cDwEFoGN/MCLiM4Rzopm72w6KlUFrylaPbuoz0Ld17Ln/zQ2j0gVdkAFpRZMqAFRCOwDWj1pXl7yx01Pco2PbGa1ixUMIUD4qEcXMw0wP/yrBtNfTIW9TTtb80Z8PEB5pbfLjegCL6FZ+KxmdJRl8pSApsXQMDSpaVdl06tHzl+iUYU0JVkkXQjqfPkgqeI/D7B7zdUxcOrVie57iVkHSsYkfttO9/9J4K4YDQerEDaABgBduZ0/+1116j0c9GYkokxs74HBdvpOUJTYR0MZL0OPLkw52E1rGa1EOQOgmKSZCtOH1HAB0Ggz6x/Gj28mRZ0if/1CSCCZdSkwEG790y/LbrSReaX23rEoeHepyRGM2XDh7e5g0GQpLufZZVlU0KaApETv3oiXJW/8YCaBpZHvDAL2/YkZt8sCRD6122943XwSNhBMzxADoyDgaX2Yvj27HvnNWB8864AlwBrsC5UIAD6HOhKu+zQyigaVrnzp1ZJRybzfbSSy99m/soO8TQ+SC4AlwBrgBXgCvAFeAKnFIBVVUPHDgwd+7cV199dcaMGbfffvuQIUMKCgoYYWTPjDhHjI3R1GZGok0mk9ls1u8Si3BJi0WfmbmV2zHo2M71NpsnOTl58ODB48eP/8Mf/vDss89+/vnnBw+iyzT225ciK3qShv5Ru+QQFglywk0/GSM+4fsn7OEUb56wk9jBn2jZCP4JeCQlCKoPFn8OPxtzuEf2+tKstUU5a/NzN+bnbHXlbnXlbHfn7nbl7nXlHHRlN7iyvK7MoCtDpJOMPmicRHRDO0V3OrjTwZUGBXQqTI80Ii8dUOCEAge4nZCRrJTmgSsVcpz7Csr/EaDlAVn8RTSt4uioVYC//+1Zm4360I2E2txtRmPSU0+9SK2ZIgXQSMJ8R+C3tzbnp87Pd857/f+g2Qsh/MwvQ5usobVYBFnUMG1aCMATk6E8bWFVxpK570C4BVcnUwatUKotYwQztApQuwn69lnmSKnNSNuRnb104iP19T5mi0ajZ9jnxSURHsNdP9/eJW5OXtruivydjzwkhBWkzwHVryCjYzMFcVYJgs3woysOuLttKnBs/MGYnS1e8Cnglxj7Dohaq8a83AC7v4Z+JUuLU1f0ds3dtpJ2A+AVPTIidIwgOWZSQQrB289BedqXfbIXPTyhcdTwBw3mToQQc7yFGE37Dx1UQPCFmi52AK1pWigUio1Nnzt/fmJSMjqgGYMmNmJAimuPsyUQZLtdCRk1iOzZOcYX7O+Tsn1qsl+1C5pF1Ix0IiwVOhoMzQBxFBNH06IpUDaFASdKkFmbOZrbP4cx1pkBa5MI5uhkCoM5AJ18kO5TCn3hYS/9Iy07maQQkmyg6NlgInFxnbqlTZ05q83PEmV073OEPsuqep4ANAu5UUGRoLEOuiV86E4N5HZtHnZp7YHDeCGEZr+oSrSmZeQAZX9iEfPx7dh3jlmMv+AKcAW4Ah1RAQ6gO+Je4WM6EwX0u01ffvll3YnTpUsXRVbYRf4z6ZwvyxXgCnAFuAJcAa4AV+DbKxBbAc/n8x1/JxZz+7I0Z8ycpTHNjHtKksSSNKqrq7/66qupU6fOmjVr4MCB/fr1S0xMbIeG2UsdCh/fsNvt7XCzPg+L3bDQh5k+WP4Ge9+MZlmsLsjmt1qtPXr0GDly5H+L2s2cOXPBggVLliz5loLEQt5vuciFn40hnpjn6K3xLImYoUvKe6nDURVAFpBrhkVYshxefxsmTvp63I+X3XDDptKyTzMzPqiqXJufva44d1dZfl15fmtRdlt219b0zq2Z3Tx5WY15mZ6sbpDVFXJSEUPrMNqVDq50zeWQ3BlhRNVOyM2ATvaDuZlicTZkp9VX9ZvtVSLe4OgI24vX5vPaE+Kpy5UYTEZjnIXE2dwlZT5RjgBrGaQ2+P3Epl45a4qdy+64dSurYRhGAC0id6YB0CEJ5w8H4L2XYVDhtp7O1f/3V4qvsRxhJIJaUyEoSm20/t++IzDmyj0FefvKC9tc2Wt+c69foqwcK8ExYbEFXj/8bqrmzFmf3mVnZeGuX/xsncePWySCGtYw8ZletFAkqTnoAdkDd/6sCdM8uu0Y0HuJ1wNBWpIxHFm/R4ImFupycA8M77+mPHN9T9fi6i9AoeZp6kyVZRDYeKOFHHGvtR2BN5+D/jlby1MWzHpoHwDk5vUxWfF+ysTkTkUlJRLatUXA2AaVGb3bPbfXvaO+bnc+sv9FG7ds7jPgErM9kRjNeMobMDYnzmi0mUw2I7Ebic1EbHbyizvJ9sYRDVDsh25B2erzEkk0KIpR0Qx0MkkIl5EXhyOTgaJkRpMRH4fBGgarSCf60hQFzQbGpulLEl3KROdP8IpmgFSvZADI2BfudlgZ+NRLXUoqid2Kg40jxESMNjteLXCXlC1aWavX/1MBQ58ZcVZodUn9+dzuH1xxJFnjv0fXvb8NFBbuc2XIjq4bHnt8d4DeO6HQIHI1cjLEBOdAzHvHX1M6t+PmvXMFuAJcgbOvAAfQZ19T3uMFV4Ax6DFjxuh3m/73xk+0TOC3RP7gCnAFuAJcAa4AV4ArcJ4UYIiHrUynz3oDAPR2OByura39+OOPH3300V//+tejR4+uqqqKj49n1Dj2WU/POJ5B60z5+IbRaGSWZ4vFwpgy8zgb6aPd/OwSfnp6+uDBg2+88cYHH3zw2WefXbRoETM169+pGC5nDkrmaGb+5ZMZh9sBr/O0D85wNTHomQEiRhspOmV0S6HtY1ajUhIblCAgoic3IGK9O7T6ivD11/DZR/DOa/Dc0/DkLLjnZrhlHNx4FVx/BYy9CoYMhp4lkO8ElwNcTkDu7IA8h5bnUPKcUp4zRN3T/txMOSs95Exvysn0IYx27Bv3k7VBGnxxzDiOezH+5z8zWUzEaEAMHRdHLCZiMW3dg1VSfEGQwvDAr3ZXOL+ocKy8ftSuw0egxY+24qCmhZCrq5HcZ9rtZ+/CJSVzy9NqHr1XEz30rSh9RhMyfXhF2NcAP7h2ryN1bWFOS2HunptuamjyRIgczsWUwjKB8OprkF2yKbOoJbnT6sv6r6hvxDdFCqBZxwrbF5ipAb+b0Nw9d0tO2sGq7vtW10IwDM1+/JzODzKOWlLCILTAdZfvLHasKkif+84r4GujgSB0h9FadBhXok+CBJ5meHSiUJZa3SNt5ZQ7g6oAn/57kcFip2EOeJY8Mn0ahZi4079nAFoQBPZbqbm19ZHp047+T6CVCfX/NoQYMRbaSnJ7kr+8Yz0k9fOFSgSfE8AJkKxoJgqgzZJmlbSjhmUar6GXDTRQ47P+qZn5oKNxHBFzdDsAHYROQS31wJEEESrCau828bLF23r0GEGsKcRgxXwhqznZZu1MCDGZ7fc/8FB9U6t+frJz9oT0WaEhLexwPSfPWCsTj8ugF+rqIdX5n6Tkr9OSG0oLV63bCkEQfUpIwisZsf9oYq5oxL59TsbHO+UKcAW4AudPAQ6gz5/WfE3nQQH2Ky4YDC5cuNBut7NvTomJiUuXLj0Pa+er4ApwBbgCXAGuAFeAK8D4LMtlPmGgRG1t7YoVK5544okpU6YMHjx40KBB7BsLo8wslNlqpY4++gEjzuyZoeETVgjUb/w6So5O0oqdk1meR4wYMWrUqMmTJz/77LNz587dunVrOBzWyTLbpywrQ9O02PcZa2abqarqqRHzqT+9KI4cZKY6Bm034ohFUadekY8VDWQF6/UJMoRE8PqgzYMkNOiBcBt46jG22bMPls2BfzwD0x6Bn98IIy8DLFHIMDQCaCXPKVAALWB2R6Y/NyvozhHcOUKO0+tKby52r3709/u8IWSpp35s27EjclAYESSiD9pMnn7+cQ0gKMLTf4ZK1/ryjM0Dyub5aFJ3iHqT9zUdDEOITliB0OeBRV9Cn7wVRcnzpvx2v7cJMyvwwcKnsRXRorkV7rnLm5+7sWvnDe6sbWOu2FnfCGEV2vyYy4xzMdQWhg1LIKvrguyMQ2npWysq527cwoKnWTqBbiEFWQK/D2rmQUlWbXaXbe7U5R+8gWUU2fqafIEogNZkGV3Sd48/UNJtbUG3JX+a1ezzRbShIdUyW7NOn2WAYAv87vb9lWmLqjKWTLxjOwAE/PCruyaiUkZCzCaT1bJ77x6GzRVAU/YJp8hqOvwf/XxkI5UkSWfQADBnzpz09HT91oeY/yV4M4Q9kRALTj37kXffdIPwQ9D6+ENdqOvZIGp2SU2QNLMEaIWmuRxEgm+cDDjzMdg64oAOgjkIyQG5UFJGH9g/9o2XK64YQZJSiC0Jbc/2eJPJZLFT4/OQIUNWrVnd0uYN0GM3dgfplme8OBFjgj52N57t3cas1/T60x/+IBS4tqckHypy1909IaDRM8YnBWU8lo4jzbFvxPzPid0i1j7bI+b9cQW4AlyBc6UAB9DnSlne7wVRgN3cqqrq7bffbjAYWPnBnJycECtlfUHGxFfKFeAKcAW4AlwBrsD/pAL19fULFix48803p06dOm7cuKFDhzocDp3jMArMcLPZbI6Fwvo8esNisRgMBt37fMKA5lP3QAixWq35+fn9+/efMGHCzJkzX3/99blz53q9GL/LwgoYQY7dV5qmtXtTkiQfJXmMXqGrNxz+XwDQ7bhPrEpH2zozilqAQQNFhFAAAl7kpKBhcsWBfbCkBl78e3jyA/U/v37nwB7Li5w1hZm1Oc5N2Zn7XFkt7qyQO1NyOdXsVMhLB1eGjADaoeQ5FATTmf7cvP0u9yZ3wdq+fbbeerP0j2eQYHl8GJMhiiel0F4/ItgxY6+O+Hmps9VoIuU9s1SAjz+BQtcXWV1rB3TfVrsEVBH7FFRNBCkAgSCajDG+IizBumXQJ/+Lgs7V1w7Z3EZ9yhHeHPkT0SMgwNSHtYKc9UV5+7uX7hnQZ+mhQ3CE5kRHFYuUP1T80MtdW5TWkJeyJz9vUc0iaAlCUAGf1B5Ae9tg43oY1HdNhetA74L9f54BagC3Go9DFScBBw6iDLIfHrnLV5L8Vd+8NX+cghZTv4CpIComMci6eTkCoDU0eD96f3PPzC/65Cx49L6ARk3ZIQG6pmZiLLKRmKyWvMJ8QWJR1CBIYrtDQn8Z3bqO/lcH0Ow0jx2uKIqapvl8vtGjR5+IQZMuXboQQixWkmAnyQlk+CDy7ttprd5hPrl7QHEF1OygliqCVY+E/i4MmvmjraKWENaSg6ozIBcGxCpfeIjPf8OsmbbSApJiJ8mYiRJ52O0JhJCSkpIPPnyPBX/7AkHcx8ei5Sh0ls4rgNboRSs/NByCwYPWFuY2FOf5SgtXz50DR1ojF06Opc/Rs0j/Z6I36B5qt1H6f5rY3cfbXAGuAFegYyrAAXTH3C98VKepAPv5dODAAbwObrHYbDa73T5x4kT9N9Jp9ssX4wpwBbgCXN5L3vAAACAASURBVAGuAFfg+6WASB+x2xQMBmPtve0q5ukBzWwR5gJmt16Fw+GamprZs2c/9thjd91114gRI0pLS/U71mMbUWByzN8TgmODwWCxWPTbudrRara8wWBg5Fqn2Cx8jM08cuTIH//4x9OmTXvmmWfmzp27Z8+e1tbWWOR0fDtWjdh27Jyx7+ttBrC+0QGtz39xNRTQRJk6galnV9RUUVMlUBko0kCVNL+k+dlGKQJIQdCQ1ILQCpIfGg7AqkXw/isw62H4weVNJZlrCjPWlWRtLcnZWZK3tzSvrii3viCrPi+jISu9MdPRUuz2O7oddmcJGd0CWSlydqrSuwKcXf2FOVh1MCcVyou04orFL7wFLTK0qRCQISQB5hkHQaHlAo8aho8TWgHts39/jvkbLIWDEIORmOPJq68vqCx7rShvUUXJ/I8+QEArKCBqWG9QgGAI0W4Elm3fBD2zv+yZuWTsZfMP7qKF3Sjma7eqkAD/78lA9+LNvUp8+Vnbyou/2rwNZ5FVQESosYHKoEFbPTx8D5Q568ozWyryVr35Cq6aRWvTTGmVtRloazgMPYpqXal7y3N3PDoJ6xAGW2nGLj6pEsiHW+tFBUJt8NCvPBUp63tlrf3NL9eDAIrMqr1JMkhqTOwGADrTPY3w+wf9Vc4VVZmL7rt9TaANvG042ldffxcdtkYs2fnfIoSP/fFxORroJ8qSgikc7SnnxQgET5iZo/96WrFixYABA4ymyH+txASjiQbCm4zEbjV36xRnJaSLnThTSHYWefzJ7P2N49q0y1tVdwDiRSAAXYIqEYC0hQlAZxXMdDKpgJMIxCuQkIYfhTS0SHtVrGQYhsSglhOS+wVDP9yw7trHZ+T07U6yupJ4QmyEJMaReEtkPPGJcZlZ3R6d9Qjdq+wYU2UasCLTqw0ni36O8miW0KzvyXYH8pm/VDHaRoDZ70BZ3rbsbs0F2QdHDVuk0chy+j8k+o/kqAn6VCvVB6o3TjU3/4wrwBXgCnQkBTiA7kh7g4/ljBVgyWWTJ0/Wf8tZrdbdu3d/4w+nM14z74ArwBXgCnAFuAJcgYtJAZZfzIoEsnEzCsOsf+22RJEV9h1j8+bNNTU1Tz311IwZM8aMGTNw4EDmLDYYDCw0w2AwsFTlE6ZkHAOeoy/0Ly3RNyJ/WVesWz2RgzV0MG02mzMzMwcMGHDbbbfNmDHjgw8+qK6uFgRBj5bW85rZd6F2jDj2C9KZt9t13k7Di/Qlo88IShEpQ0iNOHNZDoOgAQY9Cxjx7A9gOsRXX8D7b8Jzfwk/NtV3xy/2DqiqcWX8uyx3fWnm/qJ0T2E31d0VitKgxAGlGVDoVAqcYZfTl5vempN+xJ17xJW7Ny1ttSvv6/zcluz0gMupluUjfc7o5svPUpzdWrLSG7NyVi3dCM0AbQA+OiqsiKeAJtFKgAKrBEgDoRnaikofFDAIQFbVS4cMRgDNGLQREWtFj9G3/GLJVaOWPv+82EwDnbGMooaGYgqgsepgKAzrVkOvwnd7Za8YXL58zRJQJKS6LKCZrUQBCEjQ6od33oVs50c56V/nOneVFM3/ejf4BAgpOEwcqOoDBT3Ggh9+/xBUZO8sy2gsydj04N2NLQ3Ypwwae5bQco1JzaKM06gR1eU5e/NTd/9i3JFAa5R8U+irYD4H2p81gOefhMrMZWXpG64dvLWlDoemqaCAJGIIiihFOscVhemLKb9pqsqsvrRg/S9/sD2EtwRASMThDbpsCCFxVnu8Mc5kT4jfd/AA48uyirEfOgFs14jqfXH/Zf8QFFlh/p7XX381OyfdGHf0v5Q5jsTbLPEWxNFxBpJoMXRJJAkJJCmdXP4D8vf/Iwdb+njFyqZAgV8tCkKuV0sTwRGGrjKkKNFJ0roGhER/OCEodwuomSHIbxPzDnvzwzB6/qL8O+8mFWUk0ULsGDqN6NlISJKdxMcRixGP3wS7+c4JtzS3HhaloC63Tp87BoDGcQU9cP2VBzOT9hdmCGV52959E8IsteYodNZ9zseetPpWRRvtDraL8YJHdFP4X64AV+B/TgEOoP/ndvn/wgaz6jrsZ1u/fv0EQYj9TfW/oADfRq4AV4ArwBXgCnAFvlGB2OrEOrEVRVGSpIMHDy5cuPCVV1557LHHbrrpphEjRpSUlJjNZsZ/ExMTCSEs6Yvdn86eWUrGCdEz80EfhTcxreMBNEPYbBG2Fha+MXjw4LFjx86aNevvf//73Llzd+/erccx6/UAdTMjc3ALAnI0BtBjvw6d0/Y3Kn+KGWLxyilmO28fibIkgxZWpJag7JXAIyJI9YaxZN+27TD7Y3ju7xhzPP7GQ8MHb+pVsaY8f31x3nZ3xo5c5y5X9p4Cd12hu7Ugy1fgkIucUOyEMieUOqEkDUrT5KJUf0HKYVfq3gLHrsKsda7cLy8dsvzu+7yTZ8ILL8EProKMrqHMbmJhrpafE8pIPVxYtPOaG3fs94IfwEPpc5CW3UMzNjJaCoMZD5ZPAKAZq5IU5at5c7skJ1EGTQ2+CYSYjXO+2qWp0EKdvyzPGXOrMdRCZqxs3Wq4vP9mV5cFvdz/2VILIer5ZgCamZRpdUAQANZtBnfe3MLcfYV5dcVFK95+HyF1QNVCih/tz6qCvuowhJrgnZehMH1NcWZdSfbaa0bXKrTPGIeyIoFXQts0NDTB/RMh07m2wLHx9nHNniMgM5asMQcr2r5FwOsBc76AwpTPq/LWjhu74cghpNdBvx9UhQJoMYwAGtNQ2Jhbm2DKb5t7pC8e5F593dAvIQytzbg+UQnM/vwDeppabPEJJrN13I9vYPkbiPqVkwZAf2+AoP6fhMXsUMLrf/7Fx0ePGWS2EJOZEAM+I5KmhmjMBYo2UDcTSU4h1/+EPP188eK1oxpCP2zRhh8SSpvVkkC4Ugj2FII9Q4EeQX+lJPRSpL6BwOBm//hX3iqd/nvn8JEkIZ7YLLRGpgGzpuNwbZGHnXqf83Idr7/20patGxRZo5eHQAjhZRhRwIyV9hO9QKNbnts1jnWxn61/Lew/WeQayYK5kN11eV5XvzvVM2bYQbxZIXKgxHJnvX2qMcT+h4yu41Tz88+4AlwBrkDHUYAD6I6zL/hIzo4Cb7/1Nqvzbjab//v7cMaMGe1+Yp2d1fBeuAJcAa4AV4ArwBW4yBVg0La6uvrNN9+cNm3ahAkThg0bNmDAAMaXjUajyWRiNJmRD92GHCUh+JeZkVn9QJvNxtIw2Ayx4RvfCUC7XK5BgwbdcsstU6dOnT179pIlS1hSM6PkOitXZEUUxViM3m6HiKLIFmz3Xehcv2w3jG96eQxRiX3xTQuezc8j69UwLFhVkFqqMuZasIJ6LS2wfhN8+gU88yL85v76H16/oyh/flHemoLs7QXZB4vzmopz21wZrS5noDBTK8oClwOy06HIDYVuMTfLn5Zcn53alJvWWOBoLcpsKM7aW5q9pSyntiJ38bgxB6fcB5+8DZvX47oON0FbGP70FDgyNubm+PKysZ/sbs3ZKTvKCtc9OCncKsJhAUI0diKIhl9kqQjgIlZkDYuryZTAMZx1rEj+IBpFJUW5+pofIIA2GRjbMyUaf3nLbfq8rDN0QNPyiSERtm+ByuJ3c5MWVeSs/PB1EIMQCiHDZUX/gtR7DQCtAVi6Cqp6f1GSuz8zab/bseyVl9BlHFQhJIcF2S9rMoZWyAAh2LISerhXlWUeKcvde8XIVUcO6+vHz6MOaD8OJgyffwSZaWtznTt7FMxbvZDNGQN7adhCWIZVq6Ci8O0q97LL+63esYORSdAU3KkKZlirYSodA9CCBDMnhbpnVg9wrbnjuv0tB3FFbR6ZqiRdPmqYMc5GiJkYzIQY59VUs7We2v4cM6ajm3Mxtth/CTbyyH8erYXx1Bde/FvPPpVGTCWhj1jujKDYZCBWvBpnJGYrsXYinVNJUhbpN4qM/QWZNItMm0FmTotMf/g9mTGV3HYzGTqEWO3E1glzpa1mYjUarAab1YAU2kJsccTMIkD69Kqc/fFHe3ftpgNDsZWYzHNNQQzdnj5roJwfAH30jDv6b0xV8Yz83X1NRRmHCrqFBpQ3PvcUjoaetDpxbtc41fFytOsoOD/V3PwzrgBXgCvQkRTgALoj7Q0+lrOhgMvlin4bwr+x1ZzPRve8D64AV4ArwBXgCnAFLowCiqwwP+8JV89oMnPtqaqqyIpEH2xmv9+/efPmpUuXPv7447NmzRo1atSAAQMi8MR4DD6J/RZxwja7xUr/iPmXY+t0xbb12fSGCeNkzTrX7t+//8CBAx9++OG//e1vc+bMWbt27f9I5eQoRlFpWKtIC8iJtI0hu2w64Y4+FtycZBYAxuVDQVpLTp8rSgdVGsBKU4Mx6TiMeBRCAvhD4PPB3t2wYjG8/To8/Sf4yXV1g/tsKXQuLHCudmfscDn3uTP2u5yHXI4j+c7/z955wEdR5v9/dje7KQRCSN9sstk00gARVASph6i/O9HzznaiHqKeWM52ZwGpB6LnT6/5U+/0OBueenJ2RVoIhtCkN+k1kJC2dfrM9///Ps/uMNkkFEEN8MxrX5NnZp6ZeZ7PMztJ3vOdz9dfmgPFLshLg/wMKM7GeX4aftxpak5KKDv1aG76fnfWt/muNa6sBZ68z34yfPX99x3617+gaikcrIXD9RiOS1lUkAdZhz374X+uasrJ2Ot2hTLStZQMyM2B/JR9A0pXv/M6iHI4bpdEOesKukBEXtjXAcEbriDJ1wyiZfQ9UqDa7tmzB69Jq42LQVcFR5cuHGfdv+dw0IuK+Xld0TFlH0+at3Y5DKioKXetGnTBqsmPtcghNN9QtXBjRIBmkHY3NodU2LkbbrzhcK+edXnJR/u69029v1ZuAF1EBqdqCMYBIECOuXEr9M5fW5LuzUrcPeTib5fVYPeNyRQErdfXQ82X0DtrfXnG9kvL1q5fATwmU0T2SC6GCH/XYf06GNBndS/P6ovKPtu6DkISXkiqho4buoZEm1hzkz1l7MIj9x3tmbmiJGPZ2GvWQgBaGtHYW9VBUtQPPvggNjbWasVo28Ru3UeMHIUu8AoBh5GriDbifJq3+l6uWrPqZ9f8rEdaj4QucVarlchF76VWi4XgYrQaJ3c+hNKcLZbjHFxMHCLmOEf4YyOBzfGxXGxsuKY1EurssMXGO+Jj7XGx9rjuXbvfP/7eqqWV4YjisOiRkTCuHFKgXwI6b290WvWivQrfdd0xAK1omiTJIX+gkRdhy1YoKlhV6hKKMuov6r2gpQGdZ1RZxrsUedqlYoF+l/EQHbWPrm87/67NZfsxBZgCTIEfWgEGoH9oxdn5vlcFGhoaHA4H/cfPZrPddtttUSmDvtezs4MzBZgCTAGmAFOAKfC9KmCE7lLE7PP5zFSamm7V19cvWLDgjTfemDBhwu233z506NCMjAzq1GwYZXAc17VrVwqFqccFLZ9wTgOZqUWGw+GIJZONTPgGusViPprZrzkjI2PIkCE33XTTk08++Y9//GP58uV1dXWGb4YhmhHdbKw5VwsRjEIBtEAANJ2HMXQHHaeMRz0GHzuoR1eLIsgyKCqiW0HEoF2Bx4KiElsHgNqjsGgpvDmHnzaj9q7ffDtk6ML8/A/z3ZUFuWsKc7YWOPd60g8XpPgKegj5KXpBCuSnQH4qIuaCVK0gTSnM1Iqy1CKnXOTk8zObXD32OZO3uFI35mdv6Jm3etDFG8bceOjZWfDee7BxMwQIDG/0gl8CXkd6SwONBRV8AbQO+PwzuLDXfE/GnlIXZPfQXNmQ6QZXbt3IAdu+qYSQD5sdmQwFqCBETgyGJgW6js4jOxg/qfI8z0+dOhVzEdqora+d4+xjb73bqObnEYQFvfDxOzCovLpf/q7ijOVPPtqEAdSEPlP6qxEnkCCBwC1BuPn6dZnd15S4fL3yDjx5r4oe1SRGWieuB4qGHQ/pENTg5zdszUs7WOGSe7rXVC4C0WCIBCoeA9A6NB6GSwvXXZJz8EJX1XuvkpEPtzK8jx4EuRm8tXD9z7YUOldUeKoXfoE1NHJyhRoukEcOAoCkQSgAahBmTVbLc5eWZK2+rM+yvZuRkoMGoozxtM1ef25uHtpI2OKQ0sc4PvjvR6gGL3aMNQ3lzotCkOcVTQvy/L6DB/75z3/+4he/oDdA46ZqfsxGV9Lbr2GRTwuGnX1CQoLVanWQib7MSvf62c9+9uabb/r94WcOJyPujw2g6cULghDCb6QOz78Azswd+elCTvcNkyYcUBRMl4lR+QxAn8xwsjpMAabAOaQAA9Dn0GCyrgAcOnTI7XbbbDaHw/Hoo4/SbO9MGKYAU4ApwBRgCjAFzl4FDOjctgtffvnl0qVLJ06cOGvWrFGjRg0aNCgxMZFSYLMVBiIkq9Ucqky9NWgdarhxQvRsVDDSDBoezWYT57i4uP79+w8ePPixxx6bOXPmggULvvnmm1AoJAiCqqi0L7Isi6IoCJgRzpg0DJmTMBhWN1CcsfEcLFAMqiGCQcddAqBDGpobmz88sXaQI7jZAKsGfkVlIocCjUTl0sUgD35iKCyrGHLrlyAgQUiA6mp46y34/aPaL6473Lf32t6lm3oWbizO31JcsKswb19e9v4c5+G8bK8nO5SXJeaki65UxZ2qY4wzcmetIFUrTIPiNL00XSjNbCrN3lvi2lzorMno/mF50Ve/uHbj9CneN96EdRvQjKLeC40hTMonRWCoSJEoWaSD6pUgJEKwGf44BYozVl5czLu6eEsyITcFMlJ87vwDV129+zBJo9fmIqAE2NDEJAOtelwATUM0Cgo8tphIxCkXZ7MmHjpYJykyCRdGu4rP5kBB4tdFXbf18az95U83+n3Q4keVMbKYBDQjgNbQEqQhCOPv9HlSN3hSGoqzdw0f9HnLUdJb6ietkshiHb04QjI89ntwZ+4pdPpKPNveeBPzOh5r7DEAjXkI5QBcf/mGi1wbeqUv+svM+iBNkBiJfKUR0EIDhA7BmKvqLsjdUOr5/OOPMJCZ0mek3zo2VAFVAhXLEkAQHr9n7wXu6vLsmgtL5m5aSw+DqqGhMMDEiZOM73t8fJeK3n1U8qUMCRJSeTYBGESYvpWiaZrX6/3HP/5x++23V1RUGOqdTCEhIcGoZrPZLr300scee+z555+vq6ujd05Db5oO0Vj8rgX6Tfmuex9nv/BFTC89kElI/57tcGGftYV5LSXZYrFrzYZ1xv74BIpFQBtysAJTgClwPijAAPT5MMrnUR9VRfV6vTQFPCaw5sMJhs8jCVhXmQJMAaYAU4ApcM4psH///mXLls2ePXvGjBnXX3/9wIEDU1NTjYA7yn+pC7OZBRtQwyjQELz4+HgDPVsslqSkJKPCyReSkpLKy8uHDBly//33T5s2bc6cOQsWLPD7/aIoBgIBSZIoR46iybqua2Qyr6d2YbIsG37N59wARncIdQiDY3wJ3cygAUImBm0AaJJnTDsGCsPcmbJFFWT60UDWsCwqcPgw1CyDr5fA66/DpOne2+/cd+ll1Tl5n+fkfJ3rWu/O3uXOOuzO8OdmKHmZal6mmpuh5WZoeRmQnaakJwfTk/05WSG3K5CX3ZjnPJKXfTA/e29R9rbi7E3F2RtKsteMvGT3nTf7/vIsfPwftG9uasS44GAQvAGSolBGtwcFJBXxbEADQQGR1/1BCAro/YDhzyL5BHn46ku4esT2Ctee4h4tfbKhIhNKMtW81COFuZufmABBBZ0mqN9EJMLZ0NOgz3orDk+3H2O6Rn0shJXXNF3XKysXOWKtVhtnt9vtjiSrLfGqn15Da0sh+PhtuCR/dXnyoQEFDT+/fCMfAAEfkVC8q2no7YzPTBSAxiDMeg7ysjZ4Uo4UZ+7tU7hQww5HzktMMNDaQoNGP8x5B4pz9uZ0byrI3n7fA95mAZpkbFV4Is2mjVRkeOSOxsKkhSXJ8/7wqM+oJBJFwrtoEGqECb85XJH2Tc+UZU89tk+QgDqH0Nhr6lItgY4FBZQg/Oc16J31SWnqggFl879ZET5tSAh7Ca9fv5FkvLMmdunGcVxCQuKbb7wtypgIEZ8PHWtoeMfz8wdNf0rnoihSNGy8wNHS0lJZWTmNTFOmTJk8efKUKVOmTZtG53S9sXXatGlPP/30/Pnzd+/eHfVSiEauUgA4o56KPwyAJpeTDO+8BgU5G3KyGvMzD4y9GVN8htB2RyN+MAxAn5/fHtZrpsD5qwAD0Ofv2LOeMwWYAkwBpgBTgCnAFDiDCmiaRnkEIipSpjG/9BTmlFbGSSmQNdPYFStW1NTUPPPMM4888sgVV1xRVlZGQXPbhH7HYc0UNHMcYjXKlCmepqHQBmWmW+lxOjqaxWJxu90jR4689dZbn3jiiddff33+/PkHDx7sKBbPiNc2d8ro73EK33nH4xyzM29SQVc0TdYkWUOoKWtSUAhisKyuNLY0AuAL7Koq0fhKRSW2DwpyG50gZkEGXkDgq6sQDMC2zfD5J/DXF+DRBwKXD1lTmPtFibu6JGdtz9wt+c5t7qwduVl7PK7D+blHC9wtBbm+gly+IEf2OBXKnXPS1AIX5KQIOSmCJ4vPcx7Jde7Iy91Q4KnJc3986YCFN/9q0yOPHPjT8/yC+dBwFGOr0ceDOAsjQSfxtjJ11SBWDzSBHqHiogKyglRcUkk2PgkEr9qCqQABjtTBqy9ChefbXjne4vRgz8xQYQ9ffvfmotTdxc4v33kTgiGkzzQCXCWotxWDx2OYGbRRPvHIS5JEr+HHH/+9w0FdOMg3wxI777MtQjP88SnolbkuP3FbP/fBYReuk4JkCIhbLfGd1jTsEVI2DeCVV8CVuTo/60hB9vaL+ny5dQNptBHKr2FGR0HGz5oVMKT/lt4ef5+ChtFXr+FJALWA1VHIcIdItwQ/vDjLPyh/U++0VXffsNncVcOJBLMgyvDSc1CU+tlFnpVP3edVQmhUIqno6YEhzyBTAC1qSJ9Bgw/egLL0+WVpiwf3+s+eTXhCUQwDa0qgS0vKHfa4GEtMQixG5l7c72JMShn5nMje4cTKn6s1zHew0y+flSqFH/koJPKf3Aj8MPyCqkLnodKCYG7G0qqF+AxGC1uR820joKkTdEeAPPzoiHzjzOWzUivWaKYAU+C8VIAB6PNy2FmnmQJMAaYAU4ApwBRgCpxpBTpCrmYwTdk0ANTX1y9duvTdd9+dNWvW3XffPXDgQKfTaabANhumsaLzdumzubLBlI2CzWaLi4szADQtOBwOs0czdYKmp7BarW63e9iwYWPHjp04ceKbb765aNGiPXv20Fx2NC4PERiZ2lWObqIhewZ/abdmuyuNXTqSsd29zpmVqgoKyU3nbwY5BBqxS/a2QGMjsW6QkTIfPggb1sCSxbBwPtpo/GGa777xtQP6Ly7xzMvLnl/sXlWcvanEuatn9sGS7KPFWb6CNMHTQ3KnKPlpmidDzc+S8p2hXGdTTladM2OfM213SUF9ofuAO+vb7LT1+a517qwV/ftsv/E674MPSLNmwb/fg8oqNI+WFKSckgrNLeAPYa68SBSsTjG6CqIGggo8+YiEOxO7lQhPwsHF/UQVeAnUZgXDvDduhTvvaCp3Hyl1QrkLSp1Q5hTzU/aVubYMKK9aXQ31h3B4eYknfhdIogl4pZHTxsgb0NlcMLYer0AfF/kD3l69S+12W7du3W22OKstwZk5fMrv9vXJrbzE01jQ/ds+hQtrqhCiow0FbQT2H+PWZQC/DDWr4eK+Oz2ZdSlJG0uKKzdvjhAyPLmu6yqNGg4EoeEI/GLUjorsLb08+64fXX+gDnWo9UtNokAhOzkw7iYHYOnnMKDoiwsya341ao+3Ds27zT3kJQgIyJo3r4eS3IW981aPHloNCsY563oAc8DpmoJq8xj7rGPkuaLAki+hT/5nfdwrKnI+3r+VtE8DUQmIZEhFTf/dY0/ExsZznMXKWe1Wh5WzLltaY9BnTcXnH8bneOKef9vMd7DTL5+V+oWfuEg0ulkX4T+vQEV6TblbyM08MGJojSDRuwfNhUnekSDPXYwkhJGLy7jDtJLBDJ3N5VaV2AJTgCnAFOjECjAA3YkHhzWNKcAUYAowBZgCTAGmQCdWgFIG6ilBg51VRZXIJMsyLe/Zs2fevHn//Oc/Z82adf/9948aNaq8vDw+Pt7hcJgJslGmODgqNpk6OLfF0AZujioYEdB0fUJCQmxsbFxcXGxsrMViSUlJGThw4HU/v+7JJ5984YUXvvjii/3799NIW4OPU9VphkNRFGVZNl4GbzsghrGGYa9h8Je2lTtaY+zS2QG0mQJ21JkTrdc0TZQl4jVMQCZPiI0ASguE6mHZl7D8S3jxGXjhWfj5NYfH/VovKVjTq3hXmedQsas2L22/K+Vbd/q3xa795fn1+ZkHspN35mce6l8qlLlaSpzenpm+onRfQYrPk+xzJ/ncyX5PSsid1pKbVpuT8W1J/qZCT7Xb9UWO8/3/uWrdr2/dOWliw1/+ElixAhow8JpE95L2SzpG7IoKqCrGONOJch+8TnS00lAVUBVV0yRNFxAx68e4c5jVklhoLGOYNIbRqgp4BXjvE7jwwm8Lc4/2dEGJC5JimvPTpUHlUOLccs1VXx85hK7QOiHyxKhDMxg0yfnnJSujPKBPbWAMw3FVlbZsW9O1WyzHcXGx3Wz2eI5zxnK3lWbP7V+4s3dh9ebNgH0jVBnBGPUBQfarSTrUHoH+fatK3Q2Z3fcWl1S/+R5uj0wq2i3jByffUbjj+gN9c7/NTqi6+IJ53+6A+iAafqMbNUiiTg5MPHHlIHy7Gvq751/srhnca+7R/VjH6B7ZAxdVEQ5ugysH7shJWXXphWuOUKdsDHMWdRy3kArNCvgRShPzlvqDcElpTS/3qrLCuV9+is85Ai2SLPqJQQp4FX1B5VJyx7DiyxNWR3K3kPZMOAAAIABJREFU5FtuGqPJ6BfT7oe2hM3DI2K+hZ12+WxUNXJzoHwZtBDcdc2Ovhl70+y1+c5tc97FKzz8PcIvUvhDbaBbX2IMQJ+N48/azBRgCpxYAQagT6wRq8EUYAowBZgCTAGmAFOAKXB8BY4cObJkyZI5c+ZMnTr1rrvuGjp0aGFhoZH6z/BrjiLF7S4aYcs0WjkuLq4teqZr2t2d2Lbiu/OJiYmDBg266qqrJkyY8PLLL1dWVm7ZssVsnWE4lpLkYyZuFol0lmVZEASK6iiGNkSgrLnduZm9GPVPWPhue53wsGe+AqLYY/SElgl4bSVgqxo6CfOLGDTLCjFDAAgEYMcOWFkDLz7vnzHBd+P/rC1xvt83f2m5c+UFOdtKsrYXuPYV5Te6MutyswKuVCUrCdISIK0LZHfX3WlqXoZUkBlMid/jyTxc7KrNSd1ekXe4zLWvMGOrJ22dJ221J325J2OZJ6Oqf8XGa6448tiD8Ofn4c1/wfx5sGcXRtQG/RAKoZkG2jcLYcQp6wEZmhRokvRGBQEp9ksUZT4ky7KO9g4SMaOQ0dwhAqBJxG0UfVbIrnROA4dl0EWQgvDgoy15PddlZdXlZEBeOv0o5Xk+V3L1tVeuCfhQLjQhCcohf2PEKxbbQSQOApwBAE2Dk8kTF4kXG19/42WbzcFxMTGOOI7rbuFGPPW7vfeNPfzRBxAiJtQEkBEMjDBXARLRHZLghl/uLc7dXph1tLxo57Rn+CYJvCIEeJIrEKE7ml+HdBT5T9OhsHtVb+e2IX3Wbd6EodNeDSTkwD4Fs7FhhDXacEhQtwuuG/p1z+5fDi2v2rERuT0OgR4i28OXWYhg7XvHCK6kZX17bdywCc0NUCtC+QmA9qngxZh0DRMPHjkAt/x8c5lzTWH6on//G326eRJlT78gXlXeuHtfclqm+ZbSI6lH0IenaZc+MzPoqHuL+Q52+uWog3f+RdMjIgxt5gOweS30zV1UlLzHk3JkQN9tTX5o4g0AHb6LEgd8vGQNAE1txskNILrTrW6qprtwdD22zBRgCjAFOqsCDEB31pFh7WIKMAWYAkwBpgBTgClwRhVoa4XRNtiWBvPSHHo8z9PIX1VRZVmmHPbIkSNVVVUUNN95550UNJupzXcrW61Wyp1jY2NtNhsNiKbGzXQNx3F00WzNYQDukSNHDh8+fOrUqdOnT6+qqtq1a5cgCMRHGOfGZMYixsqOCrRyu4j5ZFae0rk6asOPud6IOI0E/0YaoxEvYhrZi/OI+4So6Aq6NEQmatigqBhBrJN5SxA2fAvvfwgv/AWu/+XhARdtc2XU5GSsKS/c2zN3jydzV07KXk9aXalLcKcG8p2hvNzm3JyjOdlN2Rktrgw+3wUF2ZCD6Fkoygm4Uvd6srdlp1W7sxcWeeaVF3/5k8tWXv+zLfeO2/fU7w7PnHZg3RpYsQIkAXmxLKNhhEL9mDFsGVulKBjHq9KPhgBUJZYRxyKaKS+inSKCUBZJuHPEFzh8NSjhEaekloqkgq/RS1yIURQ+BEsWwv+M2ufK3ZLlqstyep2ZfFaqlJsqZXdv7Fe+89GH12nouYHgNpKlES0sKKyKAGhjYCJCHwsObrvJqHOcAhJlHcQ7xt4ZH9+Vs3DxCSkJCUW2mIq6egiJxObZFBhODoTstvEo3HP3fmfq+sKc5oLczY/8LtSiIrCnzgI0ayK9SgIyQv+e6UtKUjfkdv3PnNfQc1nEmoqCPF8h5szQ4kWuDQBT7+P7pC/unf3+1/MgFETfb+LqHJKBnoG0RoUZ0/g8T3XvC9dXLsNoZ8zrqARQN5XicV7TBVXB9JVKCMaPqa3IXlXmqn5+JuZ1DIVpfliW+oC/qHcfmz3WZnPEx3exWmO6xHX5aO7HdLMZQId3aPWjLRhstZktnA8KaCS6mQQ447MsIQAPjt9c7Fntzt7Tq3Dnn55Fmx70uA9rQe+Oxhc2qnA8wdjVdjx12DamAFOgcyvAAHTnHh/WOqYAU4ApwBRgCjAFmAJnSAGDqJqBMgmBxOSBlDXTU0mStGnTpsWLF7/00kuPP/74mDFjLr744uzsbBrIbCUTBc1GbPJ34840K6DNZrPb7ZQvG14c1EaD4mbj4AMGDBg6dOjkyZOnTp26ePHiJUuWYFSqjtSKmjVHIXXaZUO/U4LChlwng5vb1jmlcxkt7EQFMxJp1SwKQBQN0TMaAasQ0oAnZXQ4FSQIikhR0TdZgYMHYdF8eGZG7e1j1hWVfJRbsNDpqk5PX5vZY78z2ZfTQ8tJhpweUm5ayJ3O52WEslOa8zJ96d0OOVP35+fvyHGvTs+s7tFjUVHRGk/usl4V60eNPPKrG4VbbvbPnAnPPgMvvQIffwrbvsXEgM3NEPSBLCBrRrtewJbokVBB2gnaelo2j5G5TEeTrgnTXcMDQjNX1M01zRuIQ4euCoibdMKcRB4+mQsD+m7p21twOpuzsoJZWbwzk3el+zK77/Zkrnn0t00agE9Ex+dAAEGq8aFtjgDoVoNBFsxDRctt6xxnDR4+FMKY5b59++F3zcJxlhguJqG4tK8K0BLgQ7IY5YGhBWHGU77CvBU9PV63c9/EibD3CPjQboMXAGvTRxFBHQI67N4Hl/Wv7l+4vTy7Zs6r4G3BxgggShCQIUTdn432vfxsU0n3TytSvvp4DoR8GGyvQgsaNeM1VUe8R7Du3HehT68FFf2WfrII/AiZaU18BKJqQHC0pCoq70eDj+enHemds7h3zvIH76prakb6LBAAjdCQNHToqFHkJmOxx8TGx3exx8Q++tCjeBodZEE2BqKDqGc6Pua50RtWOF8UMAFoSVPh0C7oU/JltnObK3tHSdG8vXugKYD0mT5rIVcfvfDbfnlND/HaE898ndFye7XYOqYAU4Ap0BkVYAC6M44KaxNTgCnAFGAKMAWYAkyB01eAEjHKyKhHc5ipRQ4tSdLu3bvnzZv32muvTZs2bezYsf369UtNTbXb7V27dqW42W63G1DYAMFnpEDhNcXZNJY5MTGRIun8/PzBgwePHz9+5syZH3/8cWVlJY1oNpIBUvcMmkWNOCRgSKYoirquUzfnKBJNe9wKEUZE6OinWb22fPmEa07pXB21obOsJ2n3osAH5aEyWiYIAog8AK9jlJ+owM7d8PmnMGUi3PzzZk/WykLnluLsXaV5teUFjcV5TZ6Mo64eDe7uQU+ylt8D8nuAp4eUl9LiTjmck7rTmbyqLH9dRfHygZcsv+H6tQ88uO2Fv3j//Z62eTs0E4ITlKExiMDRK6E8GEirQ1BFS4eAgEkCfQHwEmthUQFFhxZfqCMZzWNkLpuxctS+5mrHKSOAJhO1j5AFmPBwS3HOyqKcunxX0Olsdmb5Xel6TppakFl/QfH6d94Er5fEPpO98EUElURk68SYIsLQ230x34SGDZgV1eqTWhQEIRAIXNDvQjSDTsBEfBzH/WrMHf4AERr9P3jiQI0pIj/+N3jSlhRmH/Dk7rr88p3b9kKTiGbPPAJoUSbUPaQiFBZ0GH3lnqL0Db09yyc83CLw4cZI6IHRJEPAAOtyEBa8B8N6fnNhzoL/ncRr5LTk8UbYRTqkHAEAbwi+WghDBm7tVVbzj3+BX8JrgCiDmkcSJSoaSKoOYgA+fxvKMz7plfPFQ3fvC18wCKXDlibN/sDPr78hJi6es2LWU9rrwsJiX4ufNpQ+P+hAQeM7QbmisWgudLArW31uKUAtOAhU1lQZXnkeKnI3l7ml4ry9E5860ujH+5XaCkDjY5r2vrwMQJ9bVwbrDVOAKWBSgAFokxisyBRgCjAFmAJMAaYAU+AcVcDwaJ48efK4ceMGDx7s8XgMCwsDKFssFqvVSuOOqfcFBcQ2m81BJiMk2eFwROX6Mw5ySoXBgwffeOONkydP/vvf/15VVVVbW0tjmTVNEwQBYxh5RFYUPcuyHAqhFy/P82YHZ2PQDO5MgbuxnhbMxDBqU9tFWvmEoLmjCqd0rrZn7zxrKEujlNCYy+R9cwnQeFfQMQRaVGHlKnj66bobrl9bmPd5Uc7qQteuntnNPV3Q0wnFmVCQBp6UkCetqTCtsSitrij9UFHGvqKMPUWZ24qzNwzut/vWGwKPPai/9wbUVMHeXYgwqUGzJBNLCgBJB4l4J0igCsSYguSvk2VshYK55oghiFk6JewYbF53rGweI3P59AG0cR36A9DSAHfdtr7csy6nR21xjpLnEnOym1xZje50Pj/jaIm75v050NKC1DYc+6zrmMhTUTGY9/sH0EZT6TOeNevWJiV3tzlscV0wLaE1xjFmzF1EMpmkE+Q1Dbath4vLl1XkHinK2j9k8Ia9h8CrINLl8TlEUCBB0DqAoOEDgAmP7+qVt6E0e/MfJslBH4bNS2joDBImcQyoaJ6BMcuKAHs2wqD8VRdnb3j2CUXyh43CNXyoIVPyzstBUYXNO6Bn6Tu5uQvGja0LkAh3XpFUPCpOetgJgZJ/+OojKM/4qDxjwV9mat5mtOlQCX2mBRXgvoce5iyYdZCLieE4Lr5LojPLtXHDZkVUFBFj1+mcHrzNnH45jMBWM3c2ym12YivORQUMD2gZ0PZnYO/V5a6GkkzR2aN69TrssAAQVNGoPPKwhEVAn4vXAesTU4ApcFwFGIA+rjxsI1OAKcAUYAowBZgCTIHvXwF8417XDaKqEwJF099p2rF3/qMaYpAj8/ra2lojGaDh0WwYZZxkwYhKpoXYWERRRhx0QkKCGT3TY0ZBZwqyrVZrXFyc1WqNj4+/6qqrhg4dOnPmzAkTJsyfP3/Xrl3UN0NVVPoxemrujrlsRoTmsrmOudyuPuYKJyybz3I65ROeqFNVMMgZLaighWReIabEgq5qAEENbQvq/eieEAzCZ5/Afb9pKcldXJK9psi1qdi5r9jZUpgRzE/z5qa05PYIuXtAQTIUpkJRRkNR5raizJVFmfMHVCy49Zcb//a/6rzPYO9uaGpCCimpICvIkuWITTNJKUeoYVgjdPptbULdflgw2igr5EPicI1OnYzU5rE+mfrt1lE1dFb2NsPNP99R4dlanH0k3xlwZwtuV6hnUSgjeWdpXu3AfhsrF6I/NQB2Ga0edLT1UBVVoZ7UpwCg223FSa2M+qasXb8uOSWFI1S2e0pXjnPcdPOvAR0zBEGFYAhGX7G9OGtnn7yGi8o2LFkCPhnhmoAA2stDowB+AeQQieP86F3oW7is3LXququ2+EgAe/jRhYpsGuORZQTHIT9srIYhpQsudq2+cdgOxU8Mu3VQQK1v8uoAooYPHAQFGr3Qv9+XRcULr/3FigZi0GHuoY5XRjgOOijA8kq4rFdlcdqn146oFkPEE0bFhxWSDoKq+njhnff/Q5IuWmMccdYYB8dZExK7zZ79Oh7T8DIhg2I+S6RsXFPHL0Sqs5/nogLmsZckSdPwMvvvB1CQubk4nS9zNY2+co9PABFUEW9vlD5TIYz3FdoWSIUOVp+LKrI+MQWYAueLAgxAny8jzfrJFGAKMAWYAkwBpkBnVoCG/bbbQorD6CZVUanFxNGjR6urq997770ZM2aMHz9+xIgRJSUlFBNTakyJMAXBJ8mdjWpmAB0fH29wZHpMSp/NDNqgz1artaioaNiwYXffffe0adM++OCDBQsWBALEEAEznbV6uVjXdcN72tzHdkX4UVaaQeTplH+Uxn/nk5qRikYy7enEfCGoI/rFqGeAphAsrYEHH9g9sP+Kkpy1xZn7S1J9JSlSUarUM10ry4RyJ5S5WspyjpS7D5S595Zm7y/O3jTm2qMznoR5H8G+7SAFQOZBU5DS0iR7ColdpYzG3IZjKBBLKqlFY04N34P2+kpS1+kk/2Gro7VXN2qdeayjNp3kIoZDEmPi+8avdKeuyk8L5jsFd7aQ6xJycwJZafuz09eOuGzzNyuQO9NJlVSM9I48bzLCn9XW/iftNcBgpe1tPPV1iqatWLXSHme32MPfeJs9/sZfXceTQOTfPbytZ+FmZ4+dFQVrP58LQR5tbUn4s0oAdDOJgAZBhQ1r4JKSFZ6kpT+/aqOvBW1SJBAogFb1MIAmIcawbxtckv/J4MK1I3t/3bQbo6HRYpzQZHrLkAGpdn0LDB/53/KyxVddsbHBh+YbTUFeVCK3F0L3JFC9Em7auR0uKll4Sck31/5kpbce46kVEPCwJCheB/jby69wFkTPsfEJxh1s5qxnJYkMiRn/taOh+Zo6frmdndmqc0YBY+xpjyQeFAlGDl1dkFmfnxYscq57/128bfL4tE5r71mZ+TozyuRgxpJROGdUYx1hCjAFzlcFGIA+X0ee9ZspwBRgCjAFmAJMgc6hQBSWVRWVxgLT1vl8vtWrV3/00UfPPffcQw89dNVVV/Xp08dsf2Eu2+12m81G8bGdTGaUbPDlExaMvSiXobYb1Ayapgq0Wq1paWkXX3zxuHHjpk+f/vrrr8+fP3///v00ltnQ1WzcHNVNGv5s+FcYu3SqghlEnk65U3UqujEG3Wj1dOBYLRXAq0GAMGi/DAsXw+SJ6mUD1vct3VqYsaMg5ciFbihKVkuSAT89lOLUUGl6Y5lzby/3pj6FS+4bV/vX58Tl1dDcCEII42f9AQgFMU6QhjxHuCvGBpo/ht0HKRgOq8Z760YLKZWm3TBWYkHXVfohCRKR/rQHgFrtQhfMY93O5pNYhc3FVHhw2cD3e3nqezrB7dRcOZLLpeTmBJxpO6/8ye49e9CuIjxpxDW5EwDoQCgUJKY3cz+aa7VjMsLY+AR7bDxn4yY88ecXZuzrVfBFhnNrWvbK19/A+HdQkatJGAGtCpgAUsZoaAXqDsIvr1xbmrlicJ9V1dWofAiZPMgkQyRJEomjIckQqoMxo7YOzFszvGzZ0d2ohyqDSkKkRU0XMKul1ixgnPXlV2/qWb5y+NDKrZuxWksAzXlIvkEcW50APoX4exw4BLffvLvEtWj0iA11teg2rYBPgwM6NOh6QBT512b/y2JDzw2O47p0TSK2113GjrsryIuBADENP8H3wnypHr8cGWL281xTAMfdGHu84aha0AuLF4A7a1Vums+dcWjYZdWKBrxxjRoKHLvZmq8zo0zqGUtGwdidFZgCTAGmwNmpAAPQZ+e4sVYzBZgCTAGmAFOAKXAOKUBB7fz582tqambOnHnvvfeOHDmytLSU0mTKi21koq7N1KbZjJhP6NF8QuhsrmAAaHq6oUOHDh8+fOrUqS+//HJlZeWWLVvaxmu35ct0fOh6Oqd7hUIdJoXrbENqBpGnU+5s/Yq0RzN5WWhho+UIGdF0glBVDB091ASbdsNfX9F+MnJFoac6L3NLXuqRwgyxNA36OsEdxxd085elNpWl7y/L2lLmqhk/JvjCDFi2ABoOghwCScTAV0EGSVFlTZIwCFUDNJzQZFWVVVXHJfIJt0yjkdcqib+m80jsM03bFekB/jTwTKTpkYPoIOvoNiz/OABaR6uH9z+AivxdOUmh/CzF7Qq5c5o8eTuvuHxPYwPGCKPzhqrKiqgroMk01Dl8of0oEdBouS5hPk9ijiHMeffN2ASktDZ7rAV/drNz1+Wkvpjl/vi+37fwVG8SY04AtC6ATumzEIT7bjtQkf3VxcVLd2+GgAgyUjgcZxnjm0MyCQj1B6H+IFx7WU158oKRvVbXfA4KT646DecK+kSDDGqzAgEFHvzdtsKimt69V2/ZBHW1pIWSX0XITyg0jrVCo8m9fnjg3pb87C/6FP531xayHS/0Oh0BdJ2u+179+yv2GLQVookHaQT09TfeFOTFkCCpiq4qZCyMKyt8DPMPAzyesGDei5XPCQXCdxqM0cfhj7yjIPIgheCWG2pTum0uconFudvfeA1EES9N4ypp03/jIjMXSC3zClpuszNbwRRgCjAFzi4FGIA+u8aLtZYpwBRgCjAFmAJMgR9BAZm6tAJQ+wtMKCRg7KKxKEmSLMvm4GVjk7m5NOB3CZkmTpz49NNPDxs27Kc//SkNxGs7bwuFzWvM9R0OR1xcHF1jtVppnLJRwWKx2O34Or3h42xs4jjOqDxkyBAKmqdMmbJ48eIlS5aYG28uR9FY8yZW7qQKmHEGNlEjtr0BwODmAJooKJoa0OSgphGTAswlJ0JzCyxYAHePg74VBzzOPSnxu9xpvqIstdip56fIGTZvz+6h3s76XrnrRw5cM+H3dR//FyQeZBF9jTGOVcFQVmSpraObDRzTttBWvUjYslG3bZWO1hi70EJH1c78ehqwLRC7kL+/CL3yDhX0aChKq3OnrXjkwaA3CEEJeA3pODp1oPEzMYBu09UfuN2GDzv9ggPo//7328a9whHTzcJlcZxn5OWPe0MQECDEa7oGooA5IXUyxLwAmgDTfqf2di3tX7hg6VfAhzD1n4yJKqmrBgTVkA6ioECwEX597dpBhStLUv778TvQVE+uFpyJCqA5NA0QDwC8/HfwOD+u8Hz42fvGYKmgEfNsXBHOQMgrSK6feiLoya7sVbLg60riJU2wtCD6AHhVCT737EzaI3tsvM2OGNoeGz/urruDvCiKeBdvN38pOWvU5RS1aDSMFc5BBaIGmyxi7lMsRB5waRrs3g3FBZU9PY0FzqP9StaIjaDzeKs94Q2wQ8nM922GoTuUiW1gCjAFzg4FGIA+O8aJtZIpwBRgCjAFmAJMgR9dAXOQL0XSbQOBMRiPeGgAwObNmysrK19++eWJEyfecMMNAwcOTE5OdjgclAIbxsrx8fEG4okqmHEzjUo2rzFXpl7P5jW0bLfbDTCdmJhos9lSU1MHDRp07bXXPvHEE3/+85+rqqpWrlwpSRIl5pKEKIf2y9xfis6juLOx+KMPDWvAiRUwgwysraApAqJnH5kLGEkc5njQ4oOWADzzXOjC/l/nutZmp9aldwm6U8DZRctICGZ3b85Nq81J21aavXlE/92/HRtY/TUEAuD14140HvWEwKU9oIOkptVkBi7mcqtKJ7NAz3YyNc9MHYKcNAXUoA6VS6BP8Rc9s6oLUuc9PUkRAiQAWNfRUBvz7BFnCnJajBBuj9SfmTad3FGML7Xx1sKHH36Yn59vtVoTyURvLEOHDt20NRxdrCpqQBa9El5B9bXw+3u8Fxeuykl8/5M5GBDKY/izopKAb8qgRdJrkYfpD/GDClf3d89/YWqwqR5DnlWkz7wCQQV4AdkdeCX4aiEU588vdS9+5xUI1BOJNB9h+ySyFMPpwy9VKDK8+DwU5X5V7Fn43rsYfBp+TKiFY1Z/c+ddxk3SYY/jOAvHcQ88+HBIkDA6G+kzCmCSynzldHTNmuuYdmXFc0iB9sY+AqDRuR2ffMgK/Pa3G53pNTnptfnOba/8L0AQyJMXBqDPoUuBdYUpwBQ4DQUYgD4N8diuTAGmAFOAKcAUYAqcHwrwPG9QCVEUQ6GQpmmiKAqCIIri/v37KysrX3/99ZkzZ952220jR44sKSmx2+2xsRhel5iYGBcXRw2UExIw21VycjL108B32202A4i0LZhxc7sAmnJnapQRtbvH4xk0aNAdd9wxadKkl156afHixZs2baLcnIZvtx06yp3N9BlDMzWNOjtTsB4VI0lxVdtDsTWdXAESuydpINCPiqGiIKsg8LCsGqZOgQsuWFVctDnHtT3PVefJ8hdl6zndxcIMsczV4E5fM6DvqnF3bP/wE/AS4hwUMZjXF+HX35k+nxKAbouEOoPmRqtU0AKqlzpErF4BL/25fvY/GgQRRBlZrNAaQBt7tVv4IftlBtDGaxw+n++mm26ib1HQOb2n3XvvvZqmBUIhXpGCIvA+ePy+PRXOyj65VX+YeFgWMKxbQi9sTSWxolQNHd8ggZlPNl6St60ifdXv79kSbEFErWDEPNJniXhJ8yAGNVizGgb0XVvg+vKBuw+1HMWslaqii4JPUyJXG3JvvApDPHzxEfQpqC7Imv/XP6t+HkQ18pKKpge8vv59L+Q4Lt4RG++Ij0X6zCV26fbc83+SMXobJ6TP0ZcgHRC6vd3BMVbSOmx+bipgDLOpQEOfqb2GJOtQ3wQVZZ+X5nk9aU0Xlq2t3w+Yf5AE4Jv2ovWj5x2qZn5weFoP4To8A9vAFGAKMAV+MAUYgP7BpGYnYgowBZgCTAGmAFPgbFWAghie52tqat57773p06fff//9o0aNuuSSSxITE9FK1Go1/JopCKb02QyFLRaLzWajc7rearVyHEeptLmmUT4hgOY4zgyaZ8+e/dVXXxnJAM3JDKOkl2XZiHCkUdt0URAEWZYpg+Z53kDPtNBRHHTUwdli51TADEEi9soYmifrIKkgiDBvHoz9dW3PnjUVpQec6Yc82YGC3IDH2ZjvPNi3pMGdtqFP4aYJD8OH/4GD+yEoIkPxKgjveEJaWgQsC0o0WzGf94TlVtKZgYu5TCq1PVSrfX+kBaNVKmiC7qdgFAPONfAHURxFJ2BU0yViEo0+su1FPRvHiSai33O/zADayCmqaVptbe2UKVNKS0vp7Y6+txEbG5uenv7H5/+3vrkRAObOgd7udy4tXv7bsQ2KhJcBOhSQKWxWQHoa8ME7r8HgijWFiSvGXHX4yD6sQXQQFRAJfcbY5yCgeXS/0uUXFGwbffk39YcRUqO1C3V6xlhxek0g1uYV2LgGehd92suz9Ld3N/kD4Cf+HXgr0/Q1K1Z2S+yaEBs2KXLYYjnOktil29y5H/Ei+njwohwICW3osxGPHunE8S5tWofNz00FzN9Hc5le4RookgbTZ/pcWctLnHKZs/H+O+s1EVRMk4mTeZd2y+F6bX/Qa9w8b1uHrWEKMAWYAmeJAgxAnyUDxZrJFGAKMAWYAkwBpkDHClB4qus6TXCnEhNbg6tS2KrruiiKuq5Ts2Z6MF3XaWWKXOlKv9+/efPmJUuWTJ8+ferUqSNGjBg5cmRboGxg4hMWrFZrbGzscUAzPQLl0R0yUd3PAAAgAElEQVQdrby8fNSoUQ888MAzzzzzySef1NTUHDhwgOcj/+C2EccMktpsbGeFub5RpsS53ahno44RG97OQdmqTqCAwTtUYkWqAoRkEaNQNUwM2NgEigSbNsB9dwtlhd/mZh5wptXlZPg9mWJxtlycGSrLre3lWXn1yDV/fUHZtwcDeDGwVKfGvpQb4lwCTSKmvCT82WyLeixOsCMxjBZGcGWkohk6m8tkO90rUtX00wxr2uxlqvf9FokxLA0wx/uRopMPTa9HcKxC5uZkg6fSoA57fyoHOUFd83c8EAiEQiFZlu+55x76AkfXrl3puxcWm9UW67jrN08PvvBvfdz/GnXpp94jaMniF/DCCApBzAOpSZpGYpZ1+OQ96ONa3S9nx/C+lS2HQSFGGQRA69T3OUDcYXgJrhr5dUXOmhuuaKw/iCH6GvqVAFYiodSaHlLBq4Mi6LD/AFzae1lO0rzRoyqFIEHTpHON9Ud/O/6+GGK1EWt3dEvsSm6wlpKikoaGJiSDkUcxGkmSiGbcZIpIY742OypH6rKf564CHY29qIUdW3gRBl62OqPHdndSS8/0zdvW4X1VpRdqBwC6Q7Xa3sGOv6bDA7ENTAGmAFOgcynAAHTnGg/WGqYAU4ApwBRgCjAFTlMBs5exQaJ1XZckyYynKXFesmTJokWLpkyZMmnSpCFDhowYMSI7O9tmsyUkJFAcTP2aU1JSToYRd8SOqVGGnUw0Q6DVau3WrZvNZqNcm77VTncfOHDg6NGjx48fP2nSpDlz5ixZsuTIkSNRmpidMRj/jRKHLUYpQNEJpc8y8XnmdXR79osY9bxwPvzi6i1p3b4o8xzOyxCKnFDo1HNSGj1pe/sW7Lm4ZNPj9+qrlwJPrDYaW44R59ahu7pM8r2pxEqBkNUoBo0xgB1NZrjTqo4ZH5vLpBLdq1V9utAW1rRT6QdYpQH6TwgaBDQIqcCjwfFZC6Bp5lV6I3377bcLCwupKRDetazopMxZnRw3NNFy24sv7JQE7DkN/ESkq2pCUMYrQIWahdCv4MNemZvKM6tXkCynigq8RJ9hYNZBGvvsl+Hh37ZUeJZecenWI7vxUPisDUE+6DLoImiyDqCEFH9Qhrp6uPG6miLnoqtHbG8+ipegqsE333wz5le3dEvsGu9AKyRMNmizxdodHMfddcddLY1ejcJBBqB/gK/C2X8K8z3KKOPrIyT6HgD+/S6UVWztmR8qTq+/ZsgehdiS08ycRv2oQoeqtL2DHX9NhwdiG5gCTAGmQOdSgAHozjUerDVMAaYAU4ApwBRgCnwHBQwI2667sa7r1dXVVVVVM2bMmDZt2ogRI4YNG4Y8wm43go4NL2bDKIMyCzo/Sctm8y60TI9G3TlsNhsFzRRqX3nllUOGDJkxY8aTTz65bNmy+fPnE8gSjmiWJInneUmSjK61jsv7DiKxXc5ZBaK4hrFIO0wXKSuhAFoH8IZg71549H6hT+GWYucBT/qhYhffMxsK0pSezoZ+Rdt/Onj1rIkHvYfCHqaRQ+kqokXZOIVRIIAbrX6J2++xqGejwncB0KczYmZkczrHOdV92zmvBBDSgddBRhqrtYq6PRMR0MeR9lRb36o+vefQOU1ParwyAgCvvvpqUVFR+OGZlbPHdbfbczkuzx6bl5CUc/0tv373g4/Dh6MXAcCWZTC450p3/IIBpUs+fR83SjoIquoNhRRiSGI4b8yZA/kZVb3yqr9eCBKPwePI+nTCoGWc6xrwInpmCAL8dNi3zm5f9S35cN8uOHwY3prz+YBLLoshBkd2m80Rg/d5amdUXl6+Zs0a2irjrZdj73mQ0Wl9pzVfvx2VW4nGFs5JBVqNPc06SC5Gidwgg14YMXSpK2d7gaclP231p++QmGd03JEV0DvyxD9locz3FnP5lA/EdmAKMAWYAj+OAgxA/zi6s7OejgKt/y48nSOxfZkCTAGmAFPgHFGAhjYLgrB69eqqqipqnTF8+PArr7ySgmYaaGwOajZgMd3kcGBkHLU3pdXoPD4+nhIW8xGMfU+mkJ+fP3jw4HHjxk2ePPmjjz6qqalpaWnB2EANsRGdU8pMMwS2OyQ05NmA0bSOpmmUCrW7C1t5/igQgSNG0HHYcjTy5jcqQcJP8ZVwSYaDtTDrmUBhzrx+xfWeZF9ON6Egw1fuaemVd6C3Z/1vbg5++T4E69HXWQmCKpJYPjyGHOKPRgyfW6kbPjgSGbQ0IO4TeH1HfVrtY1owVzOtPr3ijwVozOelZZRBCgNo/CZ/HwD6e2HQZgCNwy+jXbIsy6IoGs/GXnzxRY/Hw3Gco0t8l6TunMXq6BLPcVxsNzTH57jUywZdN/u197dsaDi0Ay6/5PULXJ9cUjzvpRcCqopeLoBXWUDUBYk8u8AIaAWWV0NpwdwKd9ULM9DHQNOhJdBAkR5Q9Uh3BRnTZk54vKosd27f4gW33PTJkGEPWGwZ9LaM/vocR+eYezA+/rHHHvP7/YFAwPxmjEGf0WioHQBNvzrmK7Rt+fQuVLb32aBAq1EnNzj6SM8rC34RFn4GBVnLinKb8rL3/+TSVSp5XwQd8oEnF2k7N8Pv8o1te28J32HOBgVZG5kCTAGmAAAD0Owq+CEU0HWd53n6bzM134z6F9rcCHOFtrEJqqJGOVGa92VlpgBTgCnAFDgrFKDklPoXH+c3Au2L2aPZ+L2waNGiZcuWzZo1a8aMGTQZIIUO1NeCls1zI5ufeWVU2RwNTSPm4uIwaRUNjqYOznFxcZRHGxHTRoXMzMxhw4Zdf/31kyZNevPNNxctWnTw4MGTHA72bPUkhWLVDAVaAZEw85U0zCaIjsM05g5Ak4N+MRCinrnou+GDj96AC4uXFWRuzks+WpwKhd2hOB2Ks+uLcipvv3HJqq/xDL5GEtdHHpEA+iLQOD/quqECRqIebzK37Xj12tt2Ovtiu9r9tHeiH3ad0S08bRh0UtxpmrdqkrkjrTaYF4zDRhXMdc582Qxt/X5MtFhVVfU/V//MGmOz2KyczWJx2G2xDltsAmdN4Lg4jrNzXLzNkt098cKUpMuHXPbw0Yaw7YaCbhlBDZ9tgMijjcuGNTCw99zeeXMfGb+N94Ubj+kHSXLL8KMUHebNX/Du+x/ceNPYbknFVmsfjuvFcVkc15Xj7FZrjI2aPsei+UbXrl3H3jlu975dAR6bKqmYCcCYov6tMNa3p1qUyN8FIbZ3WLburFIArV/wGVLYfwPUI80w8SEoTKrNT/KXZG3787NNCnE7JwlZeQVE8hU3Hgqeoc6e1P3hDJ2LHYYpwBRgCpwhBRiAPkNCssMcVwHKCw4dOpScnJyamnrXXXcdt3o4wgL/RiR+naFQSJIkip6NHY/7B6JRixWYAkwBpgBT4CxQQFVUWZapewadq4pKI+wWL15cWVk5derUyZMnDyWT3W6nFhYUBJvnBkE2k2UDPdOCedPxy127YroqGvhsxs12u33kyJGjRo2aOXPm9OnTq6qqqqur6e8s+sCVxgnSmGVKN044BvSX2gmrsQpMAUMBEwzTiOcy0mcCoNHbFj/oP0pCTOk+KuxYA3dcs6ckdUVpRl25UyvPgILugZ7OBnfauttvCXxdCboCqgSqDLKsapjxjeaEIwBaVzAE9QTkOdw6U9uM9p5s4XT2bZ8+n1ybT7Z9Z6Le2QugjT+/jfub2Thoy7atf3nxbxdc1A/fO4lP6JLU3R6fELnNxnAECuNNtWsPzp7gSEy6aPDAiwZffMngCy8Z3P/W2+6e9NRfJj7x9/KCsc6uTyTHPPjYw/+dMuXVhx/6/e23337FFddddNFPRowcVd67JKErPheMHCxyeEurNUbg89ChQ7d+u03GZHBI7GhsPj4DONHU3jibr01abq8WW3duK0B8YDQtDKD9KuzaAxf33NkvG4oSm/p71vgaQQk/m1A04DUGoM/t64H1jinAFDgVBRiAPhW1WN3TUEAUxauvvpr+kZiQkHB5x9OwYcPKy8uHDBly3333Pf74488//3x1dTXNKEWN56KCoE+jUWxXpgBTgCnAFPiRFaAOEoFAYP369UuXLn3ppZcmTJgwevToUaNGORyO+Pj4uLg4ipvj4uIMI2Z83Zs4ZlDiTOkwJdERGsFFcWdj0ahgFMxg2mKxOBwO41BlZWXDhg27//77n3jiiblz5y5atIiG+xm4mYZvi6JIH7Uab3Ybv6pOUl8GoE9SKFbNUMAEwzQVBPIJxz7LJDWWwV0lEVMIvvIXGNDrQIX7aEUOX56tlKQHK5x1/Yo33X7zxiU0F5wGvGAcnkaa0pDnSLpBGnNnrtJB2dS2Dmp0vNq8r7nc8R6mLeaoQHPZVKUzFM2+z2YY3aptJ9V+qlBkgKItT+jWVkc9zYW22JY+PjReZJFVVVbVb3fuuPPu35RW9OI4rkvXJC4mDs0wLDFYiInjrCQroNXGxWC4NH6sNkTKVkd6usfCpcbaSjiuO8d1sdnC93+Oc3Ac1uEsnC3Oau8Swzkslhg8pOUY2cbtNPY5JTl56OAhH374IQAEQiFBlZt9zUEhKGsSpoI0fXRdNX2O9a89oczX45nXtr0zsnWdUgENv2kqCBIx03/s0cMVrn29MsV+7tqpD0OQhO2Tr28YQNNXRk7+iml7nbWz70ndHzqleqxRTAGmwHmsAAPQ5/Hg/1BdFwRh586d48ePz87OphZsxv/8HRWMELb4eHSRs9lsBQUFY8eO/dOf/rRx48aosIUfqh/sPEwBpgBTgClwZhSorKx8++23J0+ePG7cuOHDh3s8nri4OAqUKfl1kIniZofDQQG08SuD4mbjN0VUgcZHG7i5bcE4jrmQnp4+ePDgG2+8ceLEia+99lpVVdX27duN3hpYWZZl6hMFAMZK+luJzqmpCMXT5grGoToqMADdkTJsfUcKmCCFAaAx4JnSZ5yTTFkAsGQxjLl5V1b39YVOObO7P98Z6OWp7+vZfM8tLZ/OBV0HEtscNipWCFuJmAuYTmLwjo4aZFpv2s209uSK5n3N5ZPa22hkVOGkdv7hKp1LANqsmihLRxsbAEDRNFnVZVXftn3ns889f80vb+yRnoW33Ji4Lt1SbY5EApIdnIVGKts4zhIbj3HNCYndiG+zhdrxG3dpi8VmscWEFy1YJSbebmw1F6wcN+ZXt1QvXaqIYR8Eo4UqqLImyZqk6IrBoE30WT2Gn3Xj8Y2xd7tm0OatrHy+KIAWNKBJEJAAag9B/7Iad9KBoh5H+rhrtq4Oi0DuQBoJfxYZgD5frgzWT6YAU+BECjAAfSKF2PbvpACNBfP7g//4+2u/+tWvOI6Liw8nd6LJoMx/KdIyZc2UI1gsFrvdbrPZaLyblUz0VWi73Z6Tk3P33Xe/9dZbPp+PRkYblqD0fcDv1GS2E1OAKcAUYAqEFRAEgRof6bpOrZDwP2+SMY9CVeOu265k9M6sKmp1dfUXX3wxefLkhx56aOjQoQUFBbGxsTabLQoot2XEUSHJ9FeD3W6nbhj0t4bVajUHQdM6Boxu+1vGYrHQXzSXX375wIEDJ0yY8H//938LFizYunVru71gK5kCnUsBSlRNbTLBWY34PqP7swK6HLFBVjTYuwce+S3fM2+lO21Hj4RaZ0qwMD9YVLDt4t6ff/A2SCEQeNxH0UDR0bJDRWcCDAg1nYcUzTw3etupLJuPYy6bjmHqV6uAXlOV1kXzcToqt97jR18y97FVYzpqv3l9qx3MR+qo3GqHM7LQEag1fDk0TcOLKvIBgGavv+rr6jfe+veNN9/aq/dF8QkpVluiLaYrx1m6dE1G9NwlNaFLKsfFcpbYpG4p5B5usVkTbFyslWsd5Nzm/k459ohhQ+b+573t27Y1HW0Im7GYekserOgGd47kyYwSzbQDKzIF2lNAVSUN4+hlURf8IXjjNSjL2VWU6i1M33XHzdsUPmofBUAmF1v4btZqM/1e01XmMlkTdWlGHgpG7u8d3hNanYEtMAWYAkyBTqUAA9CdajjO7sbQ16ip8aXX633rrTllpb05zmqx4BtzDgeGLdhiMKKBTmbiQMMcKEqw2WyxsbHG68+R6uGfVquVbrLb7V3i4n8++ppXX31VVkRNU0SRV0l67rNbR9Z6pgBTgCnQmRSgNJne4aPCfo1m7tu3b9myZbNnz54xY8bo0aOvvPJKwzE5NjbWYrHEkslYGXVjx5eq25vaVqNrKMI2fk3QgvkpJsdxSUlJ5eXlQ4cOvfvuu6dNm/buu+9WV1drmkafj9JOGe1nBabAWaCAGTdEojMNQqGi2bNC5piFUFKguQn+/Ly/pHhRXs52V496d2ogP73Rlbq5b+/1zz0DRw+CvwHtnmVZVhU97AKBNgoi+chhBm2cVDNRj9MRyzhgVMF0TKNTUQVTldbFqEO1u9h6jx99ydy1Vo1pt/FRK1vtYD5SR+VWO5yRhVMC0LKqi7IiyoqkqLKq+/yI6EI8bNi4c+6Hn06cNG3a9D/2qhielHBRcteL+vcfmZXtpo8qY2PJe5CcvSMA7crNvvKnV9xz3z1ffvl5ff0R/A0li23RM+2yQZyjCuhsfuxzRuRhBzm3FUATaFkRVQBfAH5y6faC1KNlTrHIuebryrYdZwC6rSZsDVOAKXD+KsAA9Pk79me05/inG0XABw/uHzt2bHp6OrHOiEtISKLppznyjl1cvMNGEHRaWsYQ08Rx3CWXXLJo0aLPPvusqurruXM/evbZZ++77z6Xy0WZAo2Jxkhogh/i4h1duyTEWgnb5rjUtO6PP/Ho3t3b6StOgj9wRnvHDsYUYAowBZgCGBgJAFVVVZWVldOmTbvnnnuuvPJK6q1EYQGlw/Hx8dQ6w4hiNkhxR0D5+ADaYrGQ12CMnFKtDpOUlDR48OBrrrlm1qxZkyZNWrp06bx58+hoSZLE87zhzmwM4fHDt41qrMAU6FwKGBSS4rJoBo2vhKP/hg7BIGzdAGOuPVrm3llWGsx2BnJSAiXZR0ucyx4cV3twG8ksGOkbHwyBLgLwGDmNhSBAEBk0DYI2n9QoR/b9Lj+Ng0QVTMcy40Bz2VSldTHqUO0utt7jR1/qsF/tNj5qZavWm4/UUbnVDmdkoSPLIDOYNtuM0JMa7VM0UEk8p6zjX+yKDKuq5YHlf73hqneCPtDQEkZYv6l62fKvVq6urP564ddVlUuWLF24eOmCRZULFi1aWLlw0ZJFCmbFjHwNIr3SVQW06JWRs+N3pO3HRJ+PxZhGjsd+MgXaV0CVQZJg4VdQ5FxTki160o4OvxRtu1pffCRfIV7s+AYZ/bQ6HP1q01XmMllj7GIUwvtG3RBan7LV8dkCU4ApwBToZAowAN3JBuRsbQ7+ZlxcOf+yoQPjE+M4KzJme0x8OFsIyStiOLVZSaRb3779In1VZNBEgAZNp79feVFWdUxTLcv4ZyQAHGk8+sbbb7ldOXE2u4XjuifGx1q4OMIiLGjuEWOPtzlIOpObr7tu+/oN+B6pwn4bRwRmP5kCTAGmwKkrUFtbO2/evJdffnnGjBmXX375iBEjaPwynbdlyhQTR8U4U+sk+hyxFTZus9BeAHT4jRmLxWKz2fLz8y+//PJbb7116tSps2fPrqqq2rNnj7lbPM+risrzfLt82TBoEkVRVVSfzxcKhdqyafMBWZkp0LkUoNDBQBHIyhRNkwy0oQImVpMF+Otz4qW9vilJr81KaM7LkvOc/mLX/t6F1e/8E8Jmzyph0ColIjrSZwgifWYA+oca8lbDaD5pW7TUdo25/rHQXfMho8qtdjgjC6cEoNtiXVUHGV1edABNUnlNg7dnbxx3/ZcHiR9SUPSqmi8k1AH4AUJGQk1M+0aMYsgBdfLEBT2dJVUkrgiKruInCgEa/W2LnumaCBikohnVWYEp0IECeNniJm8j/Pae/QWZ33oymnu6d73+GjT5oTlAUhAe2xW/wOYv5LEt9Btg/MNKv+mmzea9Wl2dJ7gnmA7BikwBpgBToJMpwAB0JxuQs6o5oVAIf/s2N7311htDhw3C3NQxhDlbbZzFHsPFxXCm9CB2zuXO6HthOcdxGRkZK1euBB1EPqRDUAbYCLASwIcJhfGfIwXwYbGuoC9hUMa/PdF+NCgojb6Fn3/6yPi7+hcWJHNcUgxJh420m0uIi3FwXLIjNoHjbvzp1Ts2bETHLcB3S/3BAC+JZ5W0rLFMAaYAU+B4ClCKaq5h4ABN02iostkug9ZXFZXm0KM7GqFqS8n0zDPP3H///VdccUVFRUW7ONi8krohReFm4rbkoOkEI++rtCLNUdbP5m3U3NlisQwdOnTEiBHTpk2bMGFCdXX16tWr6e8ac2dZmSlwPipAqYfxdxIhIDK0KLpEiiiJ6IN7xuzrmbmqKK2uMDVYnC6WO32elG9uunbLrh0giujOgc/4I1NERi1Cps3Eg2w0k45wbXOd45Qjx2Y/fwgFWuGpH+KEHZ8jcnEd+xlVt/VFgzkvcY0WyZ6JVzO9IOk/BEaCTDyMad9wSGnUwdtd7ETqtNs+tvLsUoDcFeUgfFMDfYpXulJ3lxc3FBYtqG8EXgEJaXPYT59ceBh0f3b1j7WWKcAUYAp8fwowAP39aXsuH5k4BqqCILz7ztuJCZi0GicrGj5zGO8cw3EOjrNZuPj4hGTOGuPomjDxD08dbjwIAJ99/tHufTuoOpoiiRBqAHjFW/+q37uL/PEpUACtYuoSHeCAqG8WgocRTRuTDnxw/ZLKpx59xOPJCZ898iPJEtOVs8Rz3KP3Pxjw+mi+LF4SFfxLlU1MAaYAU+BcUIDG81KgbO6PKIo0fyBl0PQGKAiCLMs02nfBggWvv/76jBkzbrvtthEjRqSmpsbFxbWFxWbW3G6ZemKYdzRHQFOaHBsbGx8fT839I3do9Hq22+0ej2fw4MHjxo2bPHnySy+9VFNTs27dOgAwcglginly0243nNncZVZmCpwvClAAHYFyugKS5tWA90tCUMSXwTevgcF9FvXO3pJl31eYIhdm8Dnddw+7YOfcN6C5AQICiBj3HFBAVjBUGj+RCNCOJTQA9LEqJgZo5oHR5WM7sNL3r0AnQqzHwHOkFNX9ji6gqGrtLkb2pU4aJwv2OpE67faKrTy7FNBBFTTZB7+9K1Di3l9WJKakrPzDLNErAK+BhF78Ov2QC48B6LNrdFlrmQJMge9XAQagv199z8mjS5KkadqTTz6e63bFJ8TaYjgHiURGSMHZbVysjYtPsJM01nEJXfLyJs96trb+qIb/9hBDDcx5w/ulZpX3aZpSB9oy0CfUHpze0EiDoIMY+qyrGr4RWg+wwNv8XlPDN6D7QdIEb9iVAzRVCQKoAYWfV1N1xS+uwTBoq8POWbpwtm5WR6LNkWCPTUlOfv311+lLqrwkMpBxTl6QrFNMgfNcAVVRjahnepdrbGxctmzZF198MWnSpKlTp15xxRWDBw+mPssGCKYF6qSRmJgYtb4jU2YDRhv1jVDodqObBw4cOHr06PHjx0+aNOn999+vqalpbGzE9FOhkCAIlI/T9huDSNG5eU6rGRVYgSlwnipgBtDkkboEilfGN7x4ET54A4b02lmYtKMg8WjvTCjsEahwNw8bsGPnDtxKJwkUCV8tI++ZISI5CQDdvtYRDBgNnc3r29+Trf1+FDibEKv5KjGXT0aZSH0GoE9GLVbne1Rg+yYozVmVkXg03yUWFqzffQhkwBSuiq7Qx3sn+5Dve2wjOzRTgCnAFOh0CjAA3emGpPM3aMqUKS6XKzbW3iU+1spxjlhr9+RuGPhsjeWsXThrVy4miUtMT7no0gf/9td1zUcP+/wA4FfEFj5Aw5B1kIJiM3JhgFUArzQ2zfQGXmgJrAZoRCdCTQVd0bG8FPSXDu77Z13dJoB9oGLabJLuUJJDCghBNaQA+FQMk1t95PAtjzxsccTbSLpDC8fZbWjQERcXd9nQIes2rFc0jdl9dv6ri7WQKcAUOEkFVEXdt2/fN99888Ybbzz99NO33377yJEj+/btm5ycTOmww+GIj4+3WCwOh8Nut1N23DZm2WDNNHOgQZYN1txRwThLYmLiwIEDr7/++okTJ7700kvLly+vqqqi92qDjOu6riqqmZWbuxkV7Ezv1bIsm+uwMlPgfFeABiNH3uaijgVeCQIy/O6RPb3cm0p6ePtmgSfR38vpK8ve+eg9sHs7eEMgUatd/KNLl3T80wuNzhiAPqeuJwagjzecZ5M6x+sH29Y5FNDA3wx//ENtz5ydpXmQ56p79Hf4oi7GWjEA3TmGiLWCKcAU6LQKMADdaYfmx29YIICZqelEA9Deeustt9tN37yOsXIOkiCKpBjkOKudS0jmumTYCvp4brj11/M/nbV367JQ4KCqBUkCkSBmGozkWVAE6va2WYPn6+onHDryT7+6RIc9AHhKSQd8gwn2A/yx7vD/NtZvAzgAsAxgE0CtSCi0JuogChEk3QKwGOC/YsuahqPP/+2luK7dOI5LMMX02Wy2hx9+uLm5mfqfiqJoNkKN9JL9ZAowBZgCZ0wBjTz04nn64Aw0TZNlORAIiGI4HNFwaqanNPNWc/wvz/M7d+5cvnz5yy+/PGnSpBtuuGHQoEFutzspKcmAxVEFMzKmd2yjgs1ms9vtNpvNarW2G7McFxdxVeI4ui9NIZiQkODxeIYPH37rrbfOmDFj9uzZa9asqa2tjerFceSLvI2NP49TjW1iCjAFOlaA0mOhJehVAfwq8Do89pjoca7t5fG7k1o83Vr65DT3dK58Ziq04MsG+NeUTD6YolAjHx3pszkhW8en62hLJA71ZC0QOjoOW88UYAowBc4OBYzHGJoCQguMGrqhKPdwRWnInVe5fBUEQsCL1HlD1XX8tHIsPzu6yFrJFGAKMAW+dwUYgP7eJT6rT0BBiaZpK1asKCsro+QCkYSNowA6Kd7BcZwtsQuX0M1WesHoP08jkWYAACAASURBVDz/1MIVfz1c/+ThHf+CwC6CngUAAfNYKyFMC0jyU5M1mzX45/7av/qE54+0VKtwiCQhlGiGEYBdAP9p5F846n8XYDNAVSA4u+Ho+y2NTVRQ/f//z8XzoLcAeAHWSvBqMPh/jXX7SCp3GeD+3z/CWbmYWIfNZqNupBzHFRUVffbZZ+ED6LooigyInNXXJ2s8U+AcUEBVVIlMALB48eKVK1dOmjRp1qxZw4cP/9nPfmaA41MqRAFoY5HaZdjtdnMcNI2Apl4c9CwUNI8ZM2b69OmzZ8+urKysq6vDbO0EHBv206dqasTut+fA5cq68GMroAKENOCDmhrQsPTk5OaeRd/mprc4k329CtSc5G0Dem16/21oboT6JuBlpM+InulHp6mxVBX/HqMmBt8tPwYD0D/2hcDOzxRgCvywChwD0DL8+zXwZGxyph4sLd1/wy1b9h4iWTTJn0mY55UB6B92aNjZmAJMgbNIAQagz6LB+tGa+vjjj5vZh8VK/DZsGAHdlePibZYb7xr3amXVCoBn9x6e3hiYVt/yISib/x97XwJYVXGvf5OYBJBFZMm+EXa0ru1TfELhgdbX/l9f2/dv+7dga1dFRUR2BJIYNiWgoOJSrVRbqfsKAhoIsikgyiI7ZF/uvp79nO//fjM3h0tYDJAggTnGy9xzz5kz882558588833A8Js8hckaCYCOgBZQcCE6gM2M+3z4oD8t8OhPWyvTjodQ4KlMPb5VRXza6UVEewA3rWwpKHhydry94OeMKBoOiDrkAKwqoHPgFf8yksNykch1DETjwBdzthXUf6TnzFv6IS45EQiyjnn8qc/3+3zEY8tRRTLJBUQp0W+M3zFhQUCAoGLGgFVVXng1v91z1dVtbKysqys7PXXX587d+79999/2223DRo0yOFwJCcnJyYmcl1zQkJCXFxcx44dbbVyE8o49pl8YtpmnHlgQC5kPlHvnJSUNHjw4F/+8pczZsxYunTpqlWrduzYYQu3VVXljLMkSbIsc7r5VB4azWlAQUA3ByVxjEDgVAgw+sMMhL1hQ632KmEdEycr/frsy8muy8kOp3QLpHY7mJ/z/hdfIBiBny29sGzqmczNVANh9icZUEyK9Ezsc6Olx6kue9L9goA+KSxip0BAIHBRIkBPPPtpacgYcVN1XrdQXmYgJ2fza2/bK3z5iFIQ0BflPSAqJRAQCLQMAoKAbhkcL8pcAoHAoUOHfvCDH3DzUM5xdGqXTG7P7O+yeMfvf/Ob8uoaJ/Avl3t+vbPYHyn0SH+T8BXgZUs+TYut/zQgQw8SAa16gA3A34LS9Oq6ktrATpV4assEY56VEIwa0j6HixuCTyn4GkRAL3SG5zY4X/O7K4hZRkRWDagyNB/IteM1BUucyodB0lAfBNZ53Kv276+SZRmIqNqb77zRM7VHx44dk5KIg6ZYhe3jMvLS127aQB6IliCgL8qbV1RKIPAdI2CaZmVl5Zo1a5YtW1ZQUPCnP/1p6NChvXv35k+hk77GEsQJzMKev/LJs2S22XtOmoO980QCOtajuaysbPfu3V4vGfHbzLgtZ7YdQmIRtE0zJEmyienYA5qTFgR0c1ASxwgEjkOA+z6zV5v+UHTIKsbefygv/avMFF9OtpSR4emTX3v9dV9v+QLeMLlCa9ADclA2NH6WAd1AxCDTDvLtYAR0lE8RBPRxgIs3AgGBgECgKQK0XoSvIzEt7NqBa/Kqcq40s1Orhw3/piHACGgdWkSFSQEvhAK6KX7ivUBAICAQaERAENCNSIh/GQKWZfn9fs41FBYWZmVl2Yu14xyOdg7H5YzhSM3oOW9+UXlVpSdkVAMvukOT6z3jJOmBmvoXyj1OJkMOA7rVaD2oQVOCITPiAbYC85yu8eVHn3OHP9NIsywxhQ7zBDVkYDPweHX1kjrnCmAl8IQPc+uCz9X59jO3DVpPqhkGRdChEze6MWeX59l6HACx3suC5pMVnn9+U3s4TFbShgUZhgzt+7fe5EiKS+oUl9DewYIUOhyXJ0+eV0z2iCqz/Ti7RajithEICATaMgJsoupYBbjZPfdi5hHzeDQ8RVH4g6LJAZzA3bVrV2lp6dKlS+fPnz969Ohhw4b16NEj1tHC5oVPk2jXrp19Srt27Wyime/kz2HOUNszglwTbSujk5OTY4MBLl26dPPmzRUVFRrbuHLZPGGLJYWbuRbEPuUYcCIlEBAItBIC1jEfUU4lmxbFv5p2n/mDvq6B2UpeitH9ynDvXg0337hx51fwh8n0WaGp/5AKCtdswODxBg1oBpTGP+3Mpc/R65/5ia0EjchWICAQEAi0GgL25B9dgQhoHZYGBIK46/99c21fb99MaWDfvUufRVgnAtrUKIiRZZiWoQsCutVaRWQsEBAItHkEBAHd5puwZSugaZqqqk6n88477+Syu44dO3ZIbpcU50hyOFIua3dDr74vPf+cpEoWLAkoB94LodCnPKxaf/EHZvtDR4Ag0b4U6IZYYpW9slKGgC9NLK0IzfEGC2tq1hkUWjBEftBkuxFhf4dgzq/8prjuyEZgE7AgiIVhLK2LbGOSakWBoROtrDJ/j0MW3quyntonva8S+/ye13q8KrSkVtkNVAZpyAWDbD1kskDES8v/7ugS72jPeHQuhu6QOPr3dwcCAS7osyV+LQupyE0gIBBoEwhwchmAnbBdjznRvGbNmlWrVk2bNm3GjBlDhgy55ZZbuHuyw+FISkqyieBYlvlU3hexx/A01ywnsM3hcPBIgO3atevUqRM3buYeHfYVf/SjH916663FxcVTp05dtWrVV199FQwGbZy5TfPpqecTuGjS7TTnMSgIaBtnkRAItDoCnARh3K9pkQbP0vD3Z/Dvfdz5HY2+3dE3w+iX7+s/8POvd6C+AS4fgioU6Ix9tglog9HQx72eeckFAX3mmIkzBAICgTaKgE1Ac4UUm3kLyzh8CHmZq/JT63J7Hr3pxo3hCFSTeeurTBzFHtOCgG6jbS6KLRAQCJwHBAQBfR5AbmOXUFX12muvjeVHLmOcbfblXV7/6zIryGwFGf+7H/irO1LoUyYqxmRJnVld+yVQy0TPpH3Wedh1K6RpMlADrAeeqFKfrLUWH6rbDFQAPsrHUmGpuuEDqZj/FXIvcO77G4KfAv8C5tf5l9ZFygGXhrAKQ4uyzwoz33g3gmergmuC+Bz4h4yF9cHFR73bgaPEOzPuW4NlUbAdHtqwtPKAIyfdkXx5giMhOSmeGPYEx4033lhZWRnLNLWxBhPFFQgIBM4KAZts5dbM9kOgrKxs7dq1hYWFxcXFI0eOHD58uK1NTkpKso0ykpOTeVxWThbzY7hymQuWOZscHx9vnxL7XG1mesSIETfffHNBQcGkSZM2bdq0Zs0azoYzQQ4tnZek6DOZl58Lt08kl5uzRxDQZ3UfiZMEAucBAfqykwZPwdZSXJVaem2q75pUZF9uDMoNDByw5osd8IaIfQagWLQCTKf5ekuHxeTPFieg7dkj++l36qLH0s0npk99nvhEICAQEAhcBAicQEADtMTkwTENeanbc7rV9s8+UFDoNhgxrRkwVBbySBDQF0HTiyoIBAQCrYmAIKBbE902mLff77/uuus4h8IFfe07JMc7HEtmzw2UV0XjqVvkfbEXeE2OTGrwPKxaExR1Sn3tCtXYH134aVkGI6BpMtiqh1kJrAYerXBOOuibf0TarsFN2mdLgiZT4EH4VOKjPwUW1dcsCVR8AvwD1mKP9/la3zbGPpsGFJ1oZZWJpj1AWchaUu1aFtb2Mmq78EjVQqd/A7CXmUprbAEqMc8mSX5kw/AAHymBBTu+6HbtjZz6uayRAUpNTd2yZUszyZc22KqiyAIBgUBTBOrr68vKyt54443Zs2dPmDBh8ODBQ4cO5U7x/DU5OTkuLo6/2v4YnGWO9b6Ij4/v0KFD47Mkqlzm3PQZEdBDhgz5+c9+/sADDxQUFGzcuHHdunVci83l2Pw1EolomiZJEvdr5hSSZVmhUEiWZa535m4h9kfN4Z3tY5r5DLQ5rKaYivcCAYFAqyDAVpNZtMTbCOEn/77ve6k1fTqFB3bHVRmRq3tv37YD7gj1jkj7bNFicN4F03lHzALnoJkoz/76MlHf6Up7Iukcu+d0Z4rPBAICAYFAm0fgBAI6LKOuFrdcvzWv58Gc7pW9s8sOl9OD1wA0wyKLaGKfaaGKUEC3+dYXFRAICARaDQFBQLcatG0tY+5wevfddzscDs6bdO7c2eFw3PLvNztdtaYuQ2MjGxm6hAoDr6nqBFfdg4r2R7d3ms+9ggUAjJCfBlTLJPmzTgMhN7APeMc0FoTU2RHMdWsrDDQwgw4mz1F0kPZ5LzPceOxQ3WJ3sBR4H1axs+IpV8MXCpzMsFA14I8qpkk3/RXw1yrvon0HPwPeBkrK6x4/euQjWa5jPh4GFzyzIIMGjAijrcs0faarckLVNwu/3t5v5LDEy8hUhNuMdOjQoUePHtu3b1dVVdO0QCDQ1lpPlFcgcLEhEAqFbDeMk3picAmwaZJxxGkqHwqF1q5d+84770ybNm38+PG33377wIEDuZFFbKS+E9NNlMt8Ws62ZrYTtieGzUHzpwpXPcdac3Tp0uXqq68ePnz46NGji4uLX3755U2bNpWXl6tsk2WZP3++tUYnVpYbbhwjlhoBid1zpukTryL2CAQEAt8FAmRnZpGrMwVxvu/O8mtyywem4qoU5Hf19c/a8MZr3PGZJtyZ5JmFw2K9LINFwuC0cbTkx1Mqp61OLN18Yvq0p4oPBQICAYFAW0eAPy0RfYIaJlQFzz2NgdnfDMz0ZHT76k9/rNdp1MnWmlg6U0If97ht6wCI8gsEBAICgdZAQBDQrYFqG8vTpm/uuuuudu3adenShYv+EhISFj1RAliSFNRMWTNVQ6cY6lUGPvDphf7gQ4p0XzA4xev5h6EcAILstzfq+axTsAYvc9V4XZHn+wIT3eHCgPo245ppxbhOkhwdlmqhHigDHq8LPFrhfgd4C3giUDen5uCHulILCtxuMu2zF8RcO4H9wPN1noVVnrXAJ8DTLnlpQ3BFOHCYsc809oradZG5RwS6E9hk4AVveKKzckrDkXcV/wFL+uWo/+GEEZc0dujQoVu3brt377aXt7exVhTFFQhcdAjwYIBcn2unOZGqaVqT+IHl5eUbN2586aWXiouL77rrrhEjRmRlZcXHxycnJ7dv357bKHNps+2ncSLpfOKe+Ph47rPBHxcdOnSw3ZmTk5Nt7XPHjh25LJo/PG+77bY77rijqKho5syZK1euXLt2bV1dnWVZikIsUuzGq2PohqZpXNcc+2kz04KAbiZQ4jCBQBtEgBgNLhF48zncnL8n/fLa1MuVvK5m37TDf3seXj91eYKGS6dQWIpNFRP7TLEwNJOsOxo3QUA3IiH+FQgIBAQCp0OAxpImkzCpJnSNeW0Mu2lHn57V/TPcffM2f/hxdLhpQDVoHlBmf8cet6fLXHwmEBAICAQuVQQEAX2ptvzx9ZZlefny5TbPkpR0WadOl3+zdzf76aXQvoYZkSF7gMMg7XOhP3ivxzs2GJpSX7tcVw4x5lclopicB1n4QVOGdRj4CChs8D1Y653gUZ9R9AOwQlBUmi4mHw8JkDUcMfCchIfrgy8Ay4FZemRqQ9Wbkr+cZWuaFHRHZs4bdUxP/T4C86sOvgqsAJ7y4MnywKcycdPk9AwTFo21mFOH4YPhgrkbeMqnznJJC9zeNyKBKiAAuCX/7XfcxoN9ccNWh8OR0oM4aFXVj4dHvBMICAS+SwRibSj2799fWlq6dOnSGTNm3H333SNHjszJyUlISOCuF5wmjk07HI727dvbEfxs9wwucD6RcT5xT6y0OTExMS4uLoltqampI0aM+PnPfj516tSFCxeuWLGC+2ZwpDhjbqNm6AYXONt7WjBxorqZZ37i/ubvacHiiawEAgKBM0eAx3Gm3ghxyhqq9mJo/lfX91T6ZSC9Wzi3R8XP76j0enjGhoIGE2GT6OaoYI/xzgETPpNCZDVugoBuREL8ewkjwL8llzAAourNQYAIaCZxRsiErBr427Pon7Evv5svP63qZz874FPoYxojQzYRYct0A+yU5uQujhEICAQEApcoAoKAvkQbPrbamqatWbOGFpInUFw+R7yjV6/cXbu+Ji2wrgCWZqqqIflgHQI2AJOcDQ/Jyv1BeczRmmfdnm/Yj61BP8CGYUE3iYMOw6oCVgLzvfK4hvC4hnBJmGygvaTHCapk/YwwyFWjFtggocRtPabjVWCBqk/zB5439DomqVZp5ammk0+0FQKqgY3AU3LtkwH3e8CCCIqOhP5ZI1Wx+hiREAl9iIA2IzDdMKqYMcibEeVRnzTbJ78vKeVsetonBZyBQFjXf/3b39rsUmICJbt167Z9+45YfERaICAQOP8IfPzxxxs2bJgxY8bcuXNvvvnmESNG8Oki+wtr22jE7jlpmpPOXPhs65c5lXwi3Ry7x+FwdOrUacCAAbfeeuu4ceMKCwuXL1/+8ccf19TU8IUjnGW2F5HEks5czqyqahNdM7fasE9pEWBPpJV5tifub/6eFimYyEQgIBA4WwT4TLpuMjMNjwf3/G7PoNTK/t2Qfnk4p3v5kH/bWXXE1jZzQk0zmQCgkYPWTQgC+mzhF+ddbAgwI/Xo7Ax3Rz82L3Ox1VXUp0UQiCqgKaaQAcgKfvwfVX1T3QOztNyUL19bjoYgghTrSDNokk9m6qaQIKBbBHuRiUBAIHARIyAI6Iu4cb+laqqqSpKkqurhw4czMjKixE27hHY9u27+fJNlGUw+Y5rQVegaUAm8bWBKQ2BcyPyLS57kUp7x619FaWIYFiwaJ9FriHw2rH+ozkfcrnFeaZxfXyCTV0YF+3GWSc5syLD8KpljrLTM2QfKX6gzNwPzQph4tP5tg2yjvcRQayqxz5oKIwx4mPz5ifqK+SHP68ASBUXu0JJ6/17GKcPSYGg0GW1SB1OG6YR+GHjLxMzDnkcbGv6hBA4TS068Oh3MtgZd6/P96x2JVPsE9sdwiK+pqXM63S1LEn1Le4iPBQIXNgK0FkFnXyBWTlmWY99yZtOuAf/u2HSnzcza+wFYllVfX79mzZply5ZNmzbtt7/97Q033JCZmck96BMSEuLZFssIc2PlJixzx44d7f0dOnTgKznsPbbSOfYsniffw9M9evS47rrrRo4cOWnSpIKCgnXr1m3dutWuzoWfEA+rC7+NRAkFAmeCgEXWz4auWgjIeOWfyMz+ukOXo6k9Q1enhb6fu33LOlpNdqothoNmvaJTHSf2CwQuegRM7ssXYgJVmfGD3CxQENAXfdufcwW5o6OCUATbtyOzx7asK73X9A4Ov2WfrECzaLmtRkNLGiyzWyt6UzU+ge31KOdcEpGBQEAgIBC4WBAQBPTF0pJnXg8uxANwyy23RE1RmQZ43bYtsiybOhlpUGBfmGHGPq81Mdcrj6kP/skZnhbC4w3hbaw3R/04ZrtB8RmYUcYh4BXVN0fzjg14/1Jb/5iKD4Cj7KMws91Q6dXyAVthlPidU8qry4CX61BcFVpQ49/Hsg2RjYZmUSBDRYcVYO4frzpds2qrngdKdCyO4Kk6//bGMlimzLlnMuAgCTZpqz8BFjYoj+xvWC5FvibWG4DCohIaKlCro9Tjf/mr7Y7O7TgBzYhoEoHfcsutfl+QFlbFeCeeOcbiDIHARYUA56A1thm6wZ2LuTkpBchSVdvjmH9kWRYnqdeuXbtq1aolS5bMnDnzl7/85dChQ3v27NkkfF9cXBw3XOa8s00cfysBHcssc12zzSzbH8XHx3MD6NTU1KFDh955553Tpk1bvHjxxx9/vHv3bu6hzGtkN1jbonTbVmltkEVCICAQOA0Cmkb8hyuA635woHuGL6Fb/ZXptf26f7lomgULksLYkZOdH0t/nOxzsU8gcMkgEP2WBJiOhRPQx3GFlwwQoqJnjgC7eYJeKArGPxTJTq1Mv9KTn7lrySJoGh8jk/0jc4c+LvPYJzBPH/exeCMQEAgIBC5hBAQBfYk2vh2/a8GCBVGOJt6R3D5p/sLHSKvIZ3At+lmNMOOLN0086pMmuEIPugMPBQKPer1fg4IHSox9tgxa9hlmQQJ3A+/BnO7xjPUHHwr5C33uTxrZZ42bPoN+qyUWS7Ck5tC02orngZc0lBwJPbG/ZhNQxzhl3QLJqo0wEeCm5QY+VIzCmrr5wOPAxFBggctfzbTP4agDtcpmodmKVJPk0muAJ0KBJ2pdb/vCh9mRzKvLULUIWFE/CWgl3vDsWveYl19xdO7icDAldJzDERcflxD/i1/84hK9OUS1BQInQ4CztKZp2rrmJkc5nc5169a9++67BQUFU6ZM+dGPfjRkyBCaz4knb5+EhIROnTrxpw0nl+10LNccm25CPcfKlvm5SUlJ3N+ZXyL6KHM4OnTokJ+fP3LkyNGjR8+ePfvll1/etGlTRUWFpmk2USuxjYf+48Q6r1ckQs8HAPZDskk1xVuBgEBAIHAeENAt8t8A8OQSZGbuTEkPd0oN9BlUP3Lweu/Rb7l+LP3xLYeKjwUCFzMC3Eudx5EJMYN0bqsuVgZczK3egnWj9cAWdu1ETtaG7NRI905V11y1tqGODCWZSEsQ0C0ItshKICAQuCQQEAT0JdHMJ62kpmm7d++OFSFedfXAY0ey4YvKiNodwASn725X4AFvaHx9Q4ns38jYZ4O7P5ukgA4z4vhr4G3gcUUZ51X+UuMr9Hnfg3mU2T0bFtHaEkvLLNslFUdKZP+zwFPAtEP1876p3geUA252jMV/2I0ITCkM7ASecYWKI9oCYILPVxh0lbHDKEIEWwMlk1UIOWyojL8+ACzyhIvq3G/LkYbjHbmCsqIAu4AlnshYn1Js4sXK+p/c86DDcVkSMVjxjrg4RxyliouLjwEiUgIBgQAQCAT27NlTVlZWUlIyderU0aNH//jHP05JSbEtLxyM/+W8s73TTkQXW9hUscPRrl272J0nJZ1jd8acSkTztddeO3LkyDFjxsydO/edd97ZuHGj2+3mDcX115wxt/fYIm67MW1KmqbGmKybq7ntA0RCICAQEAicZwRMwBukybC9e9Ev/9P0lCO5OUpajjs1e13pKppRV8LMWCBqL8A7TMfKKAjoY1iI1CWNAPdSl5kKRbUJaIvGGGITCHwbAhZpn/0BTJ+K7PQDWT2Vq/u6x409pGqku+ILhbn8uYmfS+wTmKe/7Uric4GAQEAgcKkgIAjoS6WlT6ynqqo333wzyX4TyXkiKemybdu+oECCsMjNWSfLDB341MK4w0fvjRj3Ag+qUqG/fqUWOmQw70EWTl23yPS5hhk0v6Ja013uB9zeexvCjzgj7wRlD5lEWzqZQ1PHzyuZQUZVv+2JzKmoXqjozwKPyepCp7+U7Y8wdw4yNuTxQizyzfgGWHS0YX6DUuTXJ3m8c3yuUqCKdSfp559R2xozqgazmd4MLA76ZjtDy1Ts4Xrq4+vvBJ7ySpPCxp/D5riG4N/rvTu9kUEDr2G0cyzB5bB9YJtY3B6fn3gnELggELAsS5KkWGvmE21kOMdqs65NDrarEQqFvvnmm7KyshdeeKGgoODOO+8cOnSobY7RRKd8qv084h8XKfPvlS1V5oYYXBnND0tISOA77fCA9tMpISFh2LBhI0eOLC4utolml8tlss1WZNuVsmvRJNGcI5tzTJNsxVuBgEBAINCCCHBeg9xFLYz5s39A3pF+uVKPK6pzen8zfnJIkalTBZN1faJrvxU2v39KR44WLJvISiDQ5hBQFIVHgKEekSUDlmGo4re+zbXjeSuwTRmbFrk/7z+IQQO+zMv05aWFB+XvrC6n2ET2A9gmoO2zzls5xYUEAgIBgUBbREAQ0G2x1VqgzKZp/utf/2K8c1JycrLD4ZgxYzpIQWzosFRAZgOZrwN4rMo7psF7j4Lf+UIzZP8K5sjBvCyYksAgxXEtsJ18n61Cb/gBV3C8X3s0YLzokWvJQhrEPtO/9L/MqOoVBgoPVj8p4VVgeo2zuKpmFXCIOWmAAgrTH3RYzKmjHHjOHS72mUU+zKgPz/e63oVaS17O9EcaBioqhYCIAH6Wz/yG2gKv62UNXzBSOwhT5UexVwlYrWCiMzTBxL11vrn13n3sxM/WlZECOj6BM2XJyckJCQkDBw6sq6s7FUnXAi0hshAItCgCmqapKo2s7Fx52rIsRVFsWwnbnVlRlEOHDq1Zs+b555+fNWvWr3/96yFDhqSkpHTp0iVWmMy/FNymmdPNsarkkxLQts+GTTrz9Ra2Grpz5848zV/5N44TzUVFRQUFBWvXri0rK+PhCu3q8AQ3Z28NArrJhcRbgYBAQCBwPhGw2We/iopaXNX388yu1V2TanqlVw343ic1bqg6LDPC+must0TdIJl1oI499s9ngcW1BAIXLgL8O8FGISaZBlJJmRmXIQjoC7fVvuuS2VQyBTfSseQZZKTt7J0T+V7f4P1/UNz1MJk7fxMFtH3Wd118cX2BgEBAIHBBIyAI6Au6eVqvcKZpDh482Nb6XtG1s9NZL8sRg6Z1De6nsRlYVC9NrfDPDOMeV2iyL/gmzCONxhfUjWPscpD5Y7wJTHO5H3AF73cZs/34pytcC3hjliRFABdz3vgceNzpfrC87hlganXwmYC13BtkIQpNrrw2GmMJh5j2+S0VM+qUWQbGu61ir/SRKR8mmTbfdBICmTpMIqCdwGbg8YaG4kCoxB3YwdhnJ1NAh6I+0fBS5EPMd/rv9Wjjg+ai8ppv6DAWS95UfvOLn/XsmepwJCQlUlhCTsDNnj3bpu1ar0VEzgKB1kOA07X19fWlpaUvvvhiUVHRqFGjhg0b1qtXrw4dOsTOuNjPBDsR67x8RgQ0p5UTEmhGGp+l2wAAIABJREFUh3+VuBQ6MTGxa9eut9xyy3//93+PHz++pKRk06ZNZWVlhk4DQm6+bFthSJLEjZsVRbEsS5ZlQzf499HQDUFAt949I3IWCAgEzg8CnLaIfeWz9S4Zk6YfzM/aMSBTze8h98/Zt+RpJaCQ7RgZCNgn0FNTZX/np7ziKgKBtoOASUMVI4CV/8Q7L6JmH2QfSVFMU7UsxkGbYB0PQR62nTZt/ZLad4NhwOfHHT86cGXnr9O7Vw3qtfuz1exZS4tQjj2D7YdxzKi39UspriAQEAgIBNomAoKAbpvtds6lfvPttzp07NixI+Oe4hzPPfcU+Z8aqgorwDTOXwNz670zfMocBUVBa/zRqn8xk40GGDL/zTVYLEGLlMvvAQst7c8+75iwNiOEJ2qlL8OqxAtpsK4eY4Ergc+BvwZDD1XVFpl4VEFhlec1r1JPbh8mhTw0SPWsWyTmCcGqAlYAhc5wgYLJQRR6jTeBA8SAM/6ZrA9Nijlo0C9+gH20OOAu8rgWuQJrotpnBBn1HGYa5wYW+fAF3ZzgCk2J4OEDdVs11GuqCjOi+wGt/uiRqP6ZrGk7xMfHJyYmJicnV1dXnzPkIgOBwHlCoKamZtOmTS+99FJxcfHo0aOHDx+elZXFFzoksS0xMTEhIYHLlpOSkmyFMueXE9hm65S5MNnmo22x87cqoOPi4rp37z506NBRo0bNnTt30aJFn3766fbt2xVFsfllVaW5H3uFQaxw+0SwKD4q2/hZ3F0kNiji6U/nSmpb9HRi/mKPQEAgIBA4/wjEkhdcUqdBjwD7KnDdDR9mXLmnX2pkUKbrP27eE5Lgk8h2jJ51/DTmhMaEndGVaee//OKKAoELFgFy3jAx7k87rs1afVVq6cjvr1s4u0pjpoDcb9A6RkCLsIQXbDOe14JxX302xiX58wfvIyfzi+zU6uv6e4betEUKsMKQnN5s8ujmb89rWcXFBAICAYFAG0RAENBtsNHOrcgKReDDrbcP54xSu4SElB5dFTkEqIFQUAE8wKfAo7X+cQfrHo1YsxRtprP+LT2ym0mYw8zwQiLxM4Xw2GVY76nWvIh6rz/yF+CPocgcj7SR0c1UTB78g2ygUQ8cBp72qZMbQpNC0pRQ8NGA6zUtwp03DHKIpgllHiLECziBTcAiAxMljHNHHqn1fKhiP+ORDfarz02lYdI6VD/wNfCSyyyoqFnidn9hER8dJucNVSOBNBUkwLTPiwOhiSHjAbdZEkCpRYJoOSqRjq5dnTz2ocsccYnxSQkJRMxxMu4Pf/jDt3Jb59Ys4uxLAgH7LrIsS9M0LkxuYjGhKIqqqjZFa58iyzK30eDEq6EbVVVVZWVlb731VklJyd133/3DH/4wJyfniiuusJ0uYjliOx0fH9+xY0fbgpk/B7gq2WaiY1lpm3rmCa5o5q82YZ2TkzN48OC77757xowZy5YtW7NmTWVlpWVZNlPcSq1rs8k2Sq10IZGtQEAgIBBocQRi+QvOdxiApMtezSkDTywm4qNXT2/fVG9Ot08/ehsyTdNTf4a24wjoKA992hLGXk1QJaeFSnx4sSBgGPD60Dv3g7ye+3OvrL0qt7Z/nxV7Kih0DcljTPZHS6946BvxvbhYGv6M6sHbPxrQlYaVACKWFQJcEfzf/6nNSyvvm+67ute+15YhwBT0bDCq24/UU16NP5ib83g+ZRbiA4GAQEAgcLEhIAjoi61FT1OfSIQiqgPY+uX2hE7JjnjHZQ5HO4ejuGAWTENTpDCIkC21UOLRHg3h0QhmBpQZTuczPuceIqZNGZYCM2hpASgao3Q/UI2SkPqAN/KHgPKAhRmy+qZhRdXC3PnZRIQdeRD4UMW0+tD4sDExLE33uP5uRr5m3DRXP0O3DJJXk7q5BtgFzHXXTJT1cRGj0C+9GtH3sh98rXHYRT/8FhHWHqAceNGJBfV42hku1U03q6ZGgzWZEdTkFu0E3gLGVdf+xRmc6TdW6MSJqxbppwOMg5YtKywpR+pqL+/eLf4yIqA5++xwODp16lReXi5ILn7/iNezQ4DbLtuks80ja5rm9/sjkYimaYZuxBLT/EKcaF65cuXjjz/+4IMPDh8+/JprrunUqZODdPrtuJbZFizbRPNJE2RyHh+fnJzMT+Q8sk0x87ex3DSnpLl6ulu3brfddtvgwYMLCwsnT568fPny9evXNzQ0nAaN1v7KCAL6NOCLjwQCAoELHAGbv7C9RAGENEWCGtQxbMi2XqnVuV0jgzIb/nP45yZbARKWw9FKnTG1EXs1nr7A4RHFEwicKwKajnmP6VmZm3NSvL3TkJuiZmVs/+ty6vaTjobJn8nQJjqfI74X5wp4mzzfJqAZ92wwY8e6SMRj4YvduPaqXf0yvDlXHr2u/yYvG16aRoSW6cYooE9Z6zN+Sp8yJ/GBQEAgIBC4aBAQBPRF05TNqkgwGAQwZsw9HdpRvL3Ojvj09l0aKmotEyHVagDWAiU+77z60BIDMxVjitv911Bgs2V4WFBAjfXYAhGy1/AB24DFAXm8O/JnvzQ2IM8Lyh8BFSwWO8mTNfolNwG/jiPA+wbm+gMTw+HxUniC3/OcKu1mmbAV+BYUi4mVwwYkk5HFxX7vvZHAX4KB6YHw6woJnOuZ/TSXSFP+tALV9AFfAi94zCclzK6QtxhoYKJmxmUrEiPKI4xYXw8sUDDB7StoqH1LUeo4YEx0JLOcJXbdrUb49ocfcBCvFyWguUnu6NGjmwWxOEggcGoEQqEQX4JAnp1ss5XOgUBgz54969evX7BgwdSpU0ePHn3HHXf06dOnc+fOnDV2OBzcQ/mk3PHpVc+xZLQtc+b8Naeb4+LiEhIS2rdvHxcXN3DgwBEjRowePbqwsPCFF1748ssvd+/ebbtk8MpxmXYsmW5XmpPCXNZ90gPsI889IQjoc8dQ5CAQEAh8VwhwusvWPvP5dZ0FWF67Ef3zNwzICqV3cKd32vbB22i0IKKH6xkW2Kae+Xow+21s4gyzFIcLBNoCApqGt99FWtqO3Ax/Wle5V4aVnnLkups+86k0RrEsw4BmsOEKW1ggvhFtoVFbvIwxCnjmGa5L8PvZktx77q8YlF+RfUXlLd87ung+RUnSol5Hxy1EOWWJBAF9SmjEBwIBgcCli4AgoC+htrcsyzRNn8/TtUuneIejPSOgx476CyxIEtzADmB2fWVR2L/ExAIJkzzeBSH/BhghHji60XKQx7vZAzzncU9uCN3nUcYG5EdcvvfCOhdDqoZCvhjkjkUGF05gtYT53sjEYGi87J8QaHhGlzaz/brFVsFxrbRuQJcMKCHgI1m+t941DrjP43xO0XYxDXWY5cZHaGyBFJlsHAWe98mPurUZNfI/wlQLi5VWsWQJsgrSDHmYPfTTLnV6bagkpL4Vch0CC2Ass0OZ63SIOV9XAM+5a2ZsXue4vKNNQNs6aD91SGhrbVrtEropL7GqGrpRXV29fv36N954o6Cg4IEHHvj5z34+ZMgQ25TZZoptv4vk5GQewY+/2prluLi4xMREW/jcfAKa55yZmXnrrbf+9Kc/LSwsnDp16ooVK8rKygDY/HiTllEUhYf+O+nNz+MB8lNOVHA3yaoF3woCugXBFFkJBAQC5xkBTndxAppP8IdpVTckDdOnH76m78FePfxX54T+c2i1jynvmHXtWRPQOuvxxFJssenzXHVxOYHA+UBA07CgBL1yK1OvdF/TD3lp6HFFbV7e3iVPQ1NIAc0IaIV/E4QO+nw0yQV4DU4TMx08I6BVBUEdOFKN/r1Ls7seybvy8A0DPjmwBxQyiJXfMkyLpfjbU9ZJENCnhEZ8IBAQCFy6CAgC+pJr+3/96zWHw3FZvCPB4eh4WfvVb63mnoJbgMfq64v9rscsfR6IfX4yIpWCKF1G6prE7DZGFDwKPBvw31NV/mBYfcArT69zvezxc01x449xlCj2AeuB4mrPmArXTOBP1fvnBKo+MfRyJjqmX3I+6uI/0jpZbpUaarGrfoKsjw1GlhrqJqZfJr2zzYCzkoQVyuQ1xTOuunqqV3opCFtSLZGVB1ld66zUMrDcwMzqQElt5FOdbEYsSERNE0tO8Xw4S/4VsNTrnVhftTjo++HvftexCylPExITidpLiHc4HBOnTOaetnYwtEvu7rl4KxxrFsENmmPryvW/J+Ve7cOaHLNu3brS0tKCgoKZM2f+6le/Gj58eEZGhm120SRh885NCGX7sMTExKQkkuTzA+Li4tq1a2d/etIEVzoPGTLkhhtuGDNmzOzZs994441NmzZVV1fzlRB2yUVCICAQEAgIBM4/Ao0ENEVK410hFZANeN0Ye4+3T9rRXj29g/IOzJiiB4NQDNB/vB9m8xrNKnQs0XyqdLMyOouDTrzeWWQiThEInB0CmoqFJUjvWZ2VIuVnIDfVyE3TctPDvXO2uargcyOiGjpsAvrsLiLOauMI8Mcpe1QZFD1I95ghp4y5czEo70Dfnp6rsw5Pm1grKzSoNGBwORcnoKM15znwN7HpWGDsh/aZrmCJzUSkBQICAYFA20dAENBtvw3PpAaqqj6z9ClOV3Xs0O7GG29yUqgbVOgoKXfNleTHDO1lYIrbPbW8spSJgmm0Y0boF5kpmk2gDnjDo46trRvtcd4bCD3iCy2PqHt5MUzoFo2jANIzB4A9wEs6Jrgi47yYLqE4UPcuQoeZexYdZrA1TuTERlx02MQuEyUez/RwcExVTUkosgGoZQMzcO0OXz/KyGg38FpD3QJP3dT6hvnu4G5WsAg7WIauQtUpqCFZhWyhPLX5HvWdACmmye5ND8NULFpKZUnMWroCeA94NBS+3+ubH4jMfeMtR3xcFKgunZPbE9k36OqruES0tUOrnUmTimNbAAFZlk/fprG6YEmS7BmIysrKzZs3L1u2bM6cOQ8//PDtt98+aNAgLka2SWFOBJ8mrF+seNk+66SJhISExMRE7sjMrTO4oXNOTs6IESNGjRo1adKkxYsXf/zxx7t27aKvl06O6k249di3HDvbNKMFoBRZCAQEAgIBgUDzEGgkZ2kyXGMLtoIqPbVry3FV3qbMzhV5PasH9ll75AhCEnWC2GZxC7Loa7Mu1Hgd6med6q9ZGZ3FQSde7ywyEacIBM4OAU3BhIeQ0dOV2UPOTbWIgE61clPQO732gbtq0Chojcb2PBV1eHbXFme1FQR4u5N+yjSYypncKoFrBn3WN622T3dvv/Stmz6jPbrFCGhozDc8pnqxd05sOuaQM39ux54s0gIBgYBA4OJBQBDQF09bfmtNLMuSZfnGG29MTEzo0O6y/7WUnf/E4lqLwv2VlLsec6vzZfwdmFhZ+VSD75MI1z5TRBxyWtYjnCPeb+A1VZ/s8vwxEPqjJI/1ul5U5Qp+bWZ+wUMzRDTJY4V3An9XI4V+aVoY430ocGOlZR6A4eacMjfL0KI+GG6TPECe8mjjnP6p4fCi+poNluaOfsgGTSpzRtSJ4K4HPtMwd3/D3HLP83Wer4FytnCVDXVMjfykVYuxz+tMPO0MLnCrbxo4BAQt1m+wyPRNhSHB8gFVwBfAY5HIwxFprF+f55TWV9Xn5vci193LO3AqMLl9u8R2yZ9//nkTRu9bYRcHXOAIWJalqirnoA2dpA2xBVZVNRAIlJaWbtmypaioqKSk5I477vjBD36Qnp6ezDbbE8N2auYiZb6fe2twyjj2yCb8sq2Ajo+PT2QbDy0YGw/wiiuuGD58+IgRIyZPnjx79uyysrLVq1d7vd7Y0samFUXhVTMbt5MSzbEuFk3qHpubSAsEBAICAYFAyyLAeywm6epozl4DhcPQDUwZG7gqa19mp9qBvSp/e/dudxARjegL6n6YoLl1znEc92N1mqKdSAKfuOc0p5/TR+fvSk2KaUPUXJSanH/qt40Z8qpFj2vceerTxCfnB4HjmkVT8F8/dmakBNK6q2nd9ew0LTvNyE5B75Twv+Xu+motwhJUsoFulNiY7Mt1fkoqrnKBIEBfXv5glQ2EZHYLvLIcOamf5feoH5ju/c1/BQIBpoMiAtqyIFkIs3FpYwViSefYdOPn9G/rPZFiryLSAgGBgEDggkdAENAXfBO1aAHLysrIVsIRR44SDocfZFuxoNY5o8Ff2KC8ADwalp+MSKtkihBNk8GkOFZhRXjf7LBmvRWIzPL6xkSke1RjomYuCvu22r01cnSmwMA+oE6V90F+G8ZET81Yf/ghL2Y48TcfDtCnFrlj8B9jrmgG/Ab2A28A9x12TQubhQ2eLcz3mQ5jk9I06pIMaPTODWwBltQFH3cacw+6t+io1Nm1+QCNxNS6TBPV2GaZS9ze2bXuf/j1fUxsLWl+5vhm6IyADsNyMofoF/zSWJf3/rA2zYMny0N1wJJnnrZdOOIS4rkLx/jx43nZxetFhoCiKIcOHVq9evXLL788derUu+66a+jQoQMGDOjYsaPD4Yj1X7b9mk8kkW3tM+eg7WiBnTp1anJwk7c2AR0XF9e3b9/hw4ffc889xcXFr7766qpVqw4fPsw115Ik8eiFhm5wyXYkEuENYZqmzZ7z5YF2A8XKt+2dTXhn+619gEgIBAQCAgGBQKsi0GhZRpSZQSu3ENBQXYsbr95yfZ9gryvcAzJ3fvAhIhZU5icWJaA5R3YqmuMkJT6RBD5xz0lOa/auGMqPUzlRnTVl0LJXOqFIJuvZNarD+cfHET329U849ex3sEldkIGbYcDU2WK+xrY8+1zFmS2AgMnGLXQ/mAY0zdIUXH/NzoyUUFp3NaWrahPQeSnW1aneX91WCxM+iXQtJILmwehaoBgiizaFwDECWrIQkZlG6gffX52XsvfqLH+v7jvefBU+JopuVEAHLQQFAd2m2lgUViAgELiAEBAE9AXUGK1dFEVR7rnnHs58dU3u8LP/d/c24NkGvaDcNT9oLAfm+qyZ1fXLQvIuZrtMFhnmsY61E3g/pM866pzk0yZpeFgyZtS7tgJRAowZW2iwNEZAHwE+BKaE/L/xeX4fUaYr+JufpNZB6huSgocqa1mwTBOmn7lnrAYeDWqTPJElAfNTEy4Oh8El0Dq5OkshsNCFa3RtUSg0zeWdXtVQBhxhh8AyYLBOZ9jiS1W3A0/76gpd3oX1/v1MPK1CVc2gQUw2/enMJ7oSeM0XnlbtGhvBFBlP1WKnRRx6ZV1NlCWMYx7QcQ5HnCMzO4tBwsrf2g0m8mcIcB8JTrwCsO0vVFU1dEOWZW7NzPdrbOP8rCRJnKW1c6AJklBoz549paWlS5cuLSoqGjVq1A033JCVlcUdluPj42NdmGNp4nbt2nE9cocOJIpv3769bZ1h22twtw2a40lIsNM8E5tijo+P504aI0aM+NWvfvXwww/PnTt38+bNGzdu5HXkemWbET5vCXG7CQQEAgIBgcB3gAAjlA2YMusjPbow1P/qitw06bp05bbvHYYJhU29n3O3I4YmbslKNlJ+jYS4Locpe7bazIBlsB6ZTQM3SZxzQVTW5fRRb7WRd7ZU6r1KITng81Of1FLolXy2W2Sj+qqarAERBWE/Du5mAbKjaokWuYTI5KwRiE5IsEgelhSGFEDfvM8zekbSuqsZPUySP6cZmWnITkFWV/TPrF26GIEgJIUR0HQbiZmEswa/jZ9I0w+WBcMr45PV6Je9K7+7c0B61fCbNwbYUkN2b+k6QhaCpIAm56TjDZEan4FtHAhRfIGAQEAg0LoICAK6dfG90HLnXFjiZcn/myh49uWnj7gf91iFlaH3gLl+Y059cFmQgv7VsFGQzPQdJCcGPMBKZ3BOhWuqR5mqYpxXmu2PrObhATmVTKtCLRlGEOph6J8AC8Lyn73+Ub7gBAPzQ8oexh0zmYo9SqCOXgDWEeAT4Em3Pt0VmueXPjWpAHQkZ5/Jo0OHKZvQKqBsAxb5nFN93odq6t4GvuFCaQpLqDItCumxFWAv8Kyn5gnZX9Lg38BZcl0mFttSLFrkKlmQVBguYLVfnl3d8GCde6xPmdkgb2WW0AE2VBl4zdUJyUkORj3z14TExNqGepVWyortO0CAe0TwVy4H5q7ctt8xDTuZTNjQjV27dq1bt+6pp56aMmXKT37yk2HDhqWnp8fHx7dr146zw8nJyQkJCTb1HEs3N0nHxcUlJSUlJibGxcXFOmlwbw2HwxEbEjCBbZyGvv7664cNGzZq1KiioqIXX3xx3bp1u3fv9vv9HDsuVeb8ON+pqipnnM8buDbBfd6uKC4kEBAICAQEAlEEeHhnxnvJgN/EVTe9l5ZXmZ0u9blif9GYWEKMhYHm8/dnA1/rEdAyyZBZz04Nhw2FZAmaphnMLITH72jCO9tvz6Yex52jMwI6QPuOZ+hVhe2h6NUGo6GjkbGPO/ts3hBBqSmQVRQW7u2T9eq/X7Pq4T9s0b2823o2OYpzWg4BTkCrlmUYGuQQ9u1BdsbmtB6hzBQtO81iBLSVmYbMFKR0RnZ3+eZrDpbvRyhCAwNmxKEep2xtuZKJnC5oBDiV3Lie4uf/VZvTvXJgutSr+46XX4SswBMk1RKFFyICWqKBpiCgL+gWFYUTCAgELlwEBAF94bZNi5fs448/jtJniUmO9h0f/Wjlkoa6xZJeCixyWVPKKxfU1W5n7LOTsboqI6BNkywv1pkoqQ9OrHZPCkkPy+FZQdcKk9hbimAY0+uXSY9srQVKNG1CUL7fE5roDC2NGF8Ch5nBGqsUqaQV1sWTmf/yJqDEbRXU6YtckffCag37lEVPAy1uNFSQoEWvAz4Hil21s9TwZFfDC4pWwcpJowFaO6ezlZCU/Ap4yeUsdtUubHAeBHwWM4Q2ZJgKuSwaBvlzmFYA+CSCBc7wQ27PfS7XXF/k9TANImh0wV6nzpxBBHR83LE/h+PVf/5DN01FU9kh4qXVEZBldpc1Xofrnfkrm/uwNmzYsG7duqKiolmzZg0bNmzkyJFdu3a1GWQuW05KSuIkMhcy8zSXMDeRKtsnxiaaHBPryMGJ5qFDh952222zZs2aNm3ahx9+WFZWRo5xgN/vj9Vf80qYpnmqmIe2vruxuuJfgYBAQCAgELh4EeCr/hnPrJqQTeTkL89IL89LrR2Q/sGuz5qwYQbr7hxPtTYXm1YioHU2xR9h/Ct1xyigdMTQLepn0V/jB0QF8z92TAuUJgoDk6wy+pu5aRMvZIsESBlB/UPGQXOVdHPhOt1xhor33kTf3PU5PXb167lzUMq7ezc3dhxPd5747DwgoDMWkUlTVbz/JrIztqanSpnpRmaa1fiHzFT0zkTGFUa/9IY/jwp4vUQv0p0iFNDnoYkuxEuYUMnjTjOx7SsM6r2tX4Y3r3vNDf23e1zQLDR4rJBqqZapWzrpNuj5xR5njZIqPgMXMyC+ECspyiQQEAgIBC4EBAQBfSG0QquXgbN1M2fOTGKbIyEh8Xvfe/KbXbMr9r9H5K8xa7/zeb93M1DLtM+BqGEF8bABYJuBJ93mowqmSdoDrrpJ7qPvMetkjfrbFo/dwUYAJJT+HHgJ1kRVGysZM13SkrrgVqD6WBXpt5oT0Bpzc94BvGKZjzSo87x4J4zdmskcojldbcKUYMkmdA+wDXjcWTPR654SCJT4vLuYVJlnTF0B1h0IAQeBf6pSQWXFwgb3BsY+04jI1GkZpq7x8ZBlEHVeBTzjUaYFtPv9gYfr65ZH5CpQXAm+RTRpVemnxEIeT0Df9bvfgpZeHseKNp4k/m15BDhXK8vy5s2b169fP3v27MLCwhFsi2WQuXWGbaDBKWauVm5CH3NmOVazHMs1nyodFxeXmZl566233nHHHRMmTFi0aNHq1atXrVrFSXDTNNmST5q5sCXMmqZxnxCeUFWVO4Soqhrry2zohs0728R6y+MochQICAQEAgKBCw2BRgKauA/GqN71u039e3+Sl/7B6F/Q7wtjRYgVY72sC5aAJgU0d7k4chirVhsHDkFVoRpQDOKgo3RNDPXcWKNzaA+b+jE5y0xXMUzUN+Dvfw+uK0NEok4fcdBUAiPKEJ3DBelU7vts4Me3V6RecTS7WyCvW92Anps//5j1m88xc3H6uSBwbEKC23LTZM0zC+W8zK8zM5TMdK2RgwYpoFPRszPSOhsD04y87ps2rUc4QrcrH8ucSynEuW0SAQtqMKgTBY1ZM1w5KTvzejgHZh2YV8QeYiYCssEfZbrJfCT580tYcLTJxhaFFggIBL5jBAQB/R03wPm5PGe17rjjDq7cdHTqeNVdo5+trlgJvAjMdPme8AT3ABILISgxGYcJeAN6iKmJXwxiUp023cA0Sy9UXJ/A2gcjEp3nNUw26OCL1qqAV2HcW3P0AVkZ547MPVS7g9HEfPihE/Vs6I0TxAqzb37S55rkqpnmDP5VIpNoct6g8Rj9q1u6aUVA8anJ6Hmus3pK0DMjEFzkCW9j5DVptJn2JgxLUpWAqdcA7yJS5K5d4PVtVuA2KUoMTBg0slOY9pkmrX2ME3/Do06sCdzvlmaEI08HPOWcfaZFVRr3k5Yto1tqT8dl8cf+HI7effucn1Zrc1fhTDGX9yqKomka98qw/TH4fciJWvsjztjasfUArFq1av369cXFxZxovv7660/KIHOmOJZx5mJkm0Hm0QK5AprvtC2e+VnJycmxOfOdHTt27N+//+DBg8eMGVNUVPTKK6+sXr36yJEjPp/PbhHbtqI5Ce7pzF8N3TjpX6zvs30VkRAICAQEAgKBVkXglDQoJzdb9dq8t2OzqNBNIKSgpgG7dmPzJqhs0pzm1ht528Z/z0/hmll5E3pIDStqGLu2Y/QvKq/v/03//B0D8le++ldE/JBkxguTv4HFwm+EozplVplmXuPkh3HunnHyBlNDBH2oOIIf/58v0zPW3njNtqKZktsFVWY9S+KNTp7NGe01QfZtGzchveeG3Ewjs6cxICfcN2Xzu681CxWDAAAgAElEQVRQxG6xfZcIHPsqNdLIEkb/fFt+9r4TCeiMFGT1RF4q8nvIva7c+/3+qzUWZa7xzO+yHuLa3wECFrQgKUg8dbjxe5v6Z7myrqwamF9aW0PSeBmyapmqRc9om4COak3su85OsNJHCerGR7a4r76DNhWXFAgIBC5UBAQBfaG2TMuVy9ZUcjUoCT+7df3js8+sAv4KudhdPb++fh1jn8NqhC+WNMjNGSEQI/xyENPrtWlhTAiqs4LeZapnHwwfiVqYsITMLciNIgAKG/ihjFlu74Ne38SwVFDr2WCgnv/qsmWYClHbBrHBFg1IfMBbQb3A5//TkYNLNWkd0GDXmo8raLRADPRe4F+y8ojfM7au5gl3+ItG9lkjDxArwI7RWAHegzI/UDep+vBSl7vWdpGmS5L1M3QKlSizmIfLfeo8Z3hsgzTJIy+oq496SfOlm4YhkX0gbbf9nx8fY58vi7+MOXIQOX7MUcQu9CWa4DcYNy+OhSASidhGE9xGw/ZuliSpurp669aty5cvLywsvO+++0aOHDl8+PD27dsnJibaNDFnjaOzJo28MreRiWebHdmPBwbkr5xxtp2aOcXM7ZttujkuLq5Lly433njj8OHD58yZM3369LKyspUrV/IOpWmasb4ZXN3Mq9Ycxvkcj4nFUKQFAgIBgYBAoPUQuKAIaGYdYJiApkPT6FU3omo7w2Kz6a0HxNnnTJ08PYSKfRj2b5/0SSnP6Cxlpaq5mYcH5r6y/2soCiIKhSI0SALgN8jmmqj2UyLf/JLwjiLLSFE0k1mnLSlxZ2Z9mZUT7tPLf1W/z9aVsR4qoIaVliGgTYo9+NeXkJayJzMD6T2Rnx0Y1Gvrxk/AC9D84osjWxiBYwygaZghbqgx5LrV+VmHTiSgM9OQ0UNPvSKYeUWgb0/XoPR9Sx4llz6xuLGFG6WtZGfCCtMY9am56J+xL79npFda+UNjaxSNRo8qQir0YwQ0kzRZlkGDGvuusxOsyvYjzk60FSREOQUCAgGBQGsjIAjo1kb4u8+fU2kHDx6Mdzg6JLfjPN5rR/auAGZ73XNqazfregOg6KQ15ssUdVhepn1+ORx51K1McpsTfNqMOs8bgeA+pjg2oKm6oao6aUsMTWfc8TqgxBt+2BmYHtQW+iIfyOSnLJPbMomag1HHDItEMBb8wMdAgdNTEDHnuL2fQ6+BGgJFdghxa2mdFQeoMvF8JDwl4JsRCD7hCW5RKCuZFjtqKi3x1P1mWGbW1WugzI74JjbUz606ulbTfWwxJmmq6YIUeBAmEevVQCkwpcF3nzcwLWw+Vh/Yw4xHSMmta4SBTkUGEDbUeYtKHIlJ7C/BkZjgiHPEJcSvLVv33bfrhVSCWDmzXS5VVWtqaj7//POVK1dOmjSpoKBg8ODBI0eO7NatGyeC27dvHxcX1759e35P8kR8fHzHjh0b2WYHVyVzDppTzwkJCVzazHnquLi4+Ph4voeflZCQYBPNycnJffv2HTFixB/+8IeioqIXXnhh5cqVmzZtsmXX3ApD0zTTNEOhkF14O8HjBJ4jp3xGp9uXFgmBgEBAICAQaFUETkmDcjbh3FW63156kwt0YTGzCAWGFI2ERX2lRgLaYuu+vz2z83+ExYovoWSG2T91V99UuU8OUjPU3Lzyq/u8GXZBkqhDRdID4qDDBlpMAU39NJIpUNw5zQgbBvULb73+4z4Dwum9kJMt9cnf8sxSkiIQRS5pLUJAGybCMv7w5/LU9MOpaUhPQ06W5/prvqyuoPV9YvsOEYjeD+yWiEhOw0CwCldnv5+fWX4yAtoa+u/okxdOu8LfN8Xsf2Xwe+nbKvdFHW9OXovGZ8LJPxV72zQCLMKrWov/uL48Nbkmo2Mkt+fOss+oSgp0FRHdNLn8WbdUC172p5x07MNhsHlnO9Gm4RGFFwgIBAQCLYiAIKBbEMwLMatIJMICkVuLlz7dPim5c8dORNL16PoZML/8yLQ9+z8D6vmyROZ6wZU3AWZ58XLEN93lfNirFmqYWul+zhnYaZCkgG26quqarEFVLRNe4Btgvss7U9JnyiisD73jl32cQDZYlAbG8LL1bXS2DBwFppZXFkjqU2F8xrhpAxQ6PWCSkTT5K5tRr4wVPuMRv+9+r+txH2mfI6B1qaBxmWowAtoL1UWcslFYc2iSs2GON7hK0bzMT4PIZ84lU2AJIsrdoMvNcQcfUjA2pCwMSDtB5ae6kEO0ZmoWX0Z5UMPamtpnVqxwJHd0xCc6Lrss/rIE8oN2OJ5/8a9RGMQ/LNj9unXrNm7cuGDBguLi4nvuuWfYsGF9+/a1hcxcp2z7YyQmJvJIgNzB2eFwcHmynbDpY1vFzKXNiTEbZ5ltBXTnzp1/+MMfDh069KGHHpozZ86qVas++OADr5dHlCRTZuYDHr0VeKPZfiAnfmTohqIo3L6ZO2bEWmScEZt8FgeLe0ogIBAQCAgEzgMCRIySyJhxoyap2hqjkDFTMdY1Ou5no1XKdIyAPsaQ2vsa/UaJgGY/ZMeOaZXCnFWmFnXaJt+rX5frTe0YzMvCFd2lXn0rf/2LzyM+wlfS9EYCWjOgmKAVZKek/ptdhMam4Qv2woaJ7RtwTb/NHTrXpGQiN4uiz5UsqpMVZtYWZaubnfspDjQMhCX8+5Dt6VkNaelEQOdmVQ8ZvMHSuHXcKU4Tu1sfAbofohyxGZG8loWyFbim15a8DGd2mpGdZuSkm+wVWSnITZOmPIz/GKLkpPhzeyD3CrN/StUvf7KDdQhjy8pzZD4v9CWM/Uik2zQCx55AdOfoUFz4+J/o1+PAtVm4Olv+4U37/CFESP5MbvZR9tmEbqmGIKDbdMuLwgsEBALfNQKCgP6uW6CVry+pigKzIuj+2e9+43A4yJ0gKSF96C1PNNTPr3evixAhS5vV2EGHHIa8B/IHpjqzwT1VMSfomOCK/CuCncy5wsfELiQW1mTy9mNi4e3A3LrgZA1/8asTXJEltf4aLkyhvhrP2jBZ7EGfSuvb9gLP1egTq/wLQ+ZWUiZzswwjyHw5gmxJE1lxAe+ZmFzuGVfvmVpV+xkrgM7lNtRzMGHqqmV6gU3A3Fpptt960htapVtOLokhFZEhR1eyagrzCdkJPGVY93pDo2qChV6De0kHLYOFv9Z1yCE97ARV9nmXuUjWF1bXODpc6XAkOxzx8ZclcEp0xowZHLYL9pULey3LkmXZNE075F0wGJ0F4Lr4WKMJ26n5VJXauXNnaWnpK6+8smjRovHjx992220DBw60pcqxCc4L2y4Z/CMuVU5OTu7SpUtSUlITYw1+DN/PCWj+mpSUFB8fz1XPSUlJ11577YgRI37729+OHz9+2bJla9asqaqq4iJlmyM+VfnPaD8njnme3ILjLKjkszvljMopDhYICAQEAgKB5iLA2SS2KotbgZGfFusweMPwqWzym97yefBoP6O5mZ/9cawIJ3BbF67qubGmHDr+7rlFtHS9b5aZk46ePdFvQEVJyWFuZqZoKrcQYZLuRhlDYyZn/W+UcITKHONCLj/+8Rr69PsmM9OfmYZeacjPOvD3VxBgvR6KQ9gSm6GjvBzZOaXZWZHsTGSkmnlpuwsmVtKt02I1a4mCXnp5NE5IRL9NhoX589E3/0heupqXirw05KYaPbsEemVYuSnokvRNwXgsfx75GbW9s5GRjq6d6/r1OlRUQM1oASrNTPGxicYELRJboXDpwXpx1rhxio9NhhlggqYwfjq8OqfT4f6pzu8P2PPa36GyVROkZGI2ktyjksU01QxSNUUXyzZBiO8/8bXJYeKtQEAgIBC4ZBEQBPRF3vSKpkowq5XADbf/kAtOEy5vd8d99y6urn3HQn1s7dngR4XmhLUakaKaow/WOWcAj5gocga3sw4+15mo5KJhQlMtg2Ku7ANeCONBV+iPQXmCgXmu4Ods/SjrxFkgzU6Ug9YZv0y+0m5rTpVU4tE+ZPEAqRTsMJkJnHnAmHpgPfBwlWtyBIUNgbdkVLE+IAUVtMyoeMYg7+lNBp6oCRR68Ui1tMJAJe8TaNRjUMmmQ5IhGbA8TKb9umo8omr3BJVZfrytEQKyobFIP8RnS1CdkL4BXlXwSIM+yR+e53R1vWaww9GBCOj4eK7SHTVqVCxyZ5c+zdKts8vwxLO4yPekXLMkMdofCAaDNg0dCoUOHz5cWlr6+uuvL1y4cPr06bfffvsNN9yQkpJi88WcR+ZEvC1VjmWfY9O2CJrvjM3EPiw+Pj45Obl9+/Z2tMCuXbsOHz781ltvLSoqmj59+qeffrpjxw6Xy3ViBTn1bOhGrE3ziYedxR5BQJ8FaOIUgYBAQCBwQSNgE9CMHmCeDWZEw4IS9+DBHw3/z5X/fFt1Bdiqa3LvooMaWa3vplrnoZ9wLhVjEnJCSjaxZSOu7rsx48rK3AwrPc3fb8BGlxeaYXj8HuKdmYc19xQ5lyvGnmvy1mQEtIWgL4LHFiG/95HsDH9uqpHXE70zD3zwPoKR2JPONa3pKCtFTuYX2Zlybgby0vXr+u59axkt2zs5HXWuFxTnNxeBxq8q/+ZCVvGne/ReuZ68NOSlEAGd01PK6ObPTVPyM5CfVvXrO3aqLvzqv5GSUt89PXJlSjgzNfhvNx7dvgP+CMLMUpyt5FQoSo6lMDv25hZGHHcBI2Czz3SrkOc+jQSx8kN8r8+RPj3cA9KO/PCmUp1kz1QJ/uzSj+OgG38eTlbJE6lnvudkx4p9AgGBgEDgUkRAENAXc6ubjF01yGJC7ZKV2qFzp/aXd3DEO+4vKPgiKFcek2uoXNYsAeUw1iG0WHWNrT1SBIytdRU5/RuZ9Jj37ciRkLkzW4YZZOzzSyFM9YYfjETGBDwFfudXIKaYem4Wc39mC9f4b7UMHABe8Jgz6l1PhMOrJK2C3LV4pz1KUnPJNFlqWCjxyQ+GwuPqXS9WBwJMvyxFGWru1kxG0oeBZ33q+IrqQn9wscd7iB1gGVSh6JJVU4Ol6VDKYb4DTHD7HvAr053qChl1jBBXoMuwVGLJyd+jHHgXcpHb94gnPKfO835I/+ndDyY4Lnc44hIcxEB36NBh2LBh537ftOrAMhKJxFpM8GCA9qtpmjt37vz000+feeaZwsLCO++8c/jw4b169bIJYi6Wt92Z4+PjuTbZNr6w6WPu0Wy/jU1w3wxu0BwrbXY4HO3bt09ISOjbt+/tt9/++9//ft68ea+++uqWLVvq6uoktnFbDMuybO22qqqSJCmKomkat8WwzTFaA0lBQJ/7HS5yEAgIBAQCFxYCsQQ0o0RlBZs24Hu9N/ROPZKduj87/Z3KClZkppI+z8RBI4N2QWDWnLozAtqUoVHfTMUv/+8X+Zm7slMOp6WvWfIspCiFR9VhR0ZNrVuqejEEdMSEKmm4b6zSq1dNbnowL1XLTzH6Z+7csoWIyHPfbFJJ07BkIfIyd+Vm+DNTlMwrXdf03mr4WCzsC6r9zr3ObS2HxjuW6EULRCL/2837cjO1vBT0SkGvNL1fljwoT+qdGc5LMfpn1916/WojjHVrkd939xXdj6Zn6b1y0Du7/hc/328BnjDCmocFaNf47SsmGNraHXHS8pJlPJsy05kXkG6ApFQRA/f9OZJ5xd7+Pf29un7xwtOW3mgaHyWg2Ti5UQR9jIC2nwzfmjhpacROgYBAQCBwCSIgCOiLudE5Ac3c+eCIdzgS4+PaJTmS4l9+43UfFylT7WXWwaKJXhd5WRglwSPjnYcLLGWGJM3zhz8CahlRa2jsHJV4a1MnrrYKeA+Y4VHv9fnGRXyF/tpPyDzaIotm4nOZnyLjgukUwAmsBh5zm3N83uVW5CD0oKUppqGbJoUJpEM0MKeOA8DfZIwtd01X5Mf8/l2NpZSZCDrMmGI3cAj4CHjEE54hhee5Kz6BFA082HhRypIx0W7on8NcaBm/rayfXK++5COiWWc1l8mmg4ITmsyKeitQWHdwuqdhkaK+2hA4CswofirZ0ZkR0AnJye3j4+MHDx587vdNa9CmdqlkmfQ4kUhk48aN69atKyoqmjVr1rBhw0aMGBEXF2drjWP5Ym7NbHPQtnFzrOSZi+j56ZyebtcuGtYyNiue5vroTp063XTTTT/96U+LioqKi4tXrlxZWlrK+WW7tHaCe4bYimx7f2zCNE1ZlkOhkCRJmhYzwI096JzTgoA+ZwhFBgIBgYBA4AJDoAkBbcLUMP6+ozfk1/TraaZ3CqVesf6Tj2FEJ8ajVsXnpw6N9Nn5udq3X6U55eEKaBkGMTrAsy9WXjVw+a9+cfiDj0gT7fZDUhXNMMiCg8VTbB0FtM4W0Fu6hf/5H2d+ni83PdwrTc3vGeqf/cX+fVBbghfWKMQhBbTWVEy43+ibWZWd7knvVjcwr37sH1VfNfRwVEzx7ciKI1oHgcY7lv41QLdfasr67FRk9yACOj813Dfd9V8jMKhXMKtrOPPK8qvzP/Q6EQjjzt9VZuccys01+/VBdrqUl7X1mWcpXGaElmYyQw4+pmiJG6l1qi5ybT4COhtBRkwyXzJNFgOACGgF1/bbdm1usF+P6qtyymqroOhQLdMXcfMFHLHUM0/z+635r80vojhSICAQEAhc3AgIAvqibV8+MOA/jXsPHki4vJ2jfeL/Z+874Nwqrq/XOIZQXHZXvXdpiyuGUAKEEkJIIPwDCUlICKSTEEIxGGNsbDCYbnqP6T1UU1ywcVn37rW32NuLdlddT3q93O+7M5JWLhhTAoZIP6326WnelDvz3sycOXPukcbKsrKyjdu3s4i9Uhg5A8BKMidSNrEQuw0yM0G8KtJ/Hye8D7CLoM/IIMFtljnGMg/QC7CAk+5MKJNY7a+Z+FUDLYuB7wY1iz06pT3nAWjS27dK8DELM3ZEbm1PvCmJTSjxLKLioqpoMm5xokM7mo3XU8KMsHBVZ+oxgV9C0soQN4ZZunJNkOImgBd5uKGPv46VbhXSC7RED3AykF1StPAo3IU86CTAVoC5bObqvvi0BDzcLW0n1a5pmowaHTh3YonGyBaAR7KJmZneG8KtL3DsDhUyGrz4/DuHogTH0EO+891h3zls6FBUJf6C7YZlcVMoJSlnMpk99JcVWaEe8AqpaJomSdIemHXha09Pz8cff/zWW2/dfvvtV1999U9/+tOqqqojjjhib3SYoslUnblYQIO6ARw6dGiBtkx9Bh522GEFT4AFiJmynilUfdhhh5URVnggEDj++OP//ve/33zzzc8///zChQvb2tqSyWShCF/6AdXfKBjhvxH/5xNx/oJXfekFKUVYskDJAvuxQPEEcj/BSj99JgtQq36mS76KwMUANPFRzGfh+PHvV5nb7EclR3vB76hjUtTRsQgEuszTbP8ruStue/89i+2dyoGkVXzVfgqvkIEhSwZRAqCHQUlBw0n5Qd1+rv2CP+GgEbeuYU45CXgBams2+l2Cyyz4bZJLNzA2uDqZwqHrgbyKyzuINOaFuQWJjoLx+8TR64KOjMuctOjbQ+5NLz0DXDzPYjiQlPYThrbP/QT45J/2yP9gET75km/ZL9QC2B404ER47Q3NYdti04O9EnxIgo78/nz4xyVQ44669ZxtVNhjXrJ+PcRY6I6C37c56AWvBzxu0Fd2HvO9+rYwZFWc9KAladT5xvAts9v/WHFkFVjyRgBa0HhOxr0at9wcDVmbJvpkj27jXy/pyGSxznktJUOGOk2l09q977IDP/M/ZudScUsWKFmgZIFPtEAJgP5E03zTf6AYLCWILly4EMU3ysoOKT9qyHcPTWayogYy6ubymsqKLKMCSie/ms7exCRuAHEaK8wcSL5PFDbIDjRRAYVqKqNfPw050Ut5/tFE4sa0cllf8sZk5C0Qu5FLhOgzAaAlRH8JBCwR7vMiFe5tjd/dEns1ITYQPQ0WeCRSo2thOmLEbVHtAPMV7d5IakpX4tbe1FKAToKAZwn3mScc6TThPr+rwE0x8fLe9GxWfgO0NuBYSGsgIKKN2CThPiuQIRj681lu+kDiX53xuwa0VQJqdwAAl4pquMgtKQR9bgV4Lp2d3Nc9qa/jOTGznqQLGix5f9khZcMQfh0ytAyZ5EPKyr6EG6eAnFJwGQAkSRJFkUpMUBBTkRVBEChaDQA9PT11dXXPPffc7NmzL7300jPPPNPpdFJcuJi5THnKFEEuRo0LuDM9oD9RiYwCyjxkyJBhw4ZRdnMxQj1kyJDDDz/cbrcff/zx55577k033TRlypSPP/74ww8/pHcKzXDhrvnSRZkLMX9lB18QR/7cl39lBSwlVLJAyQIFbCEPXpRM8uVYoDAt/3Ki+1Jioehe4RNURYHNa2BCYEXIFHaOTFa70z8/N5zJ0LVhFrdpa/A/AUDvjnvSuisGXPZj/gIAzYMsgixRwA4v+O9DoLlsE8BRgP5+qAns8DvAYZQRgNZ3/+KcLqEAP38aelhosYOPgiKzSIpCtu5r/VEYG9gYtMkeC++xtnud73JpEDO5XX/7MdQB/VRonEVJH9CFeYy0uBQHeOG3JhgpOxn6q5DJwKxbYi57o1WvOvTgN4FL3znjOrhzJoQcbX6L4NDFPbbNb7yJrkdjWZh0FZj1nTaH5g1CMAhO967fXNzSl4Is+pLJN+VPa0LfGkt+qwuiqrg9A0V7yBwVN952dMCE0Uu8lb0hYyxgm79lM7KZZJweplWcROKEsvh5WHyXHfjxt9qqpcKVLFCyQMkCn8ECXwKO9hlSKwX9ai1Ah/9ZRfzwww8LQGRZWZkgSFTHGb34SqrEaQmAt1S4fiA5WVWvTLMzwtzrGeQ+x5HVIsrAiNgdo18/SijeosIDvR3TouF/JpM3RpMLGSFBumcAhW5NynXWxFlgH8AygLt5uK6jf1FG7paRU4CMak1WVRnVN8iURQVo1+DtlHoHk5kaj94XT7yvyBR9ThNyDRZHw2s7iPTHbVnpqgg3LZxZwiMgzgDLQ5IHgTCa0eMNSAhudwEsAbg1KlzTy97Sx7+vIncbRwyyogkZVclogEJfcYAXstnp8cSVkcSMcJw6XcRcKtC9q2dI2WFlww5F5Pk73xmCMPSXeePs4SRQEITGxsalS5c+/vjj06ZNu/DCC0888USHw0G5xnvAysXVWtDWoAzlYkx5D+i54BuQws3UByCFm+m1p5xyyqmnnjpjxozbbrtt7ty5S5cubW5uLjTePdSl9/YBqKqqIuMyQOGSb+LB50aQv+CF30RblfJcssA3xgLFEA/JdPEEcrdS7BaShtrt9wP8ksPhDgRR2i3FA4x+H8F2yyuqWxEYFZHUA3gV5yFnGnJ58fkDKMveVv0kO+TO54W7qHwXYbYeQG4/JUiRJWieUdmZaoAiMKmI8MidEDBu8xvSHj0TcnY+OAeXssmLxw1XFICmJ3KlLorzU1L/9J+LrZQHONB7Rd4mB2DoT0+EDHg+CaAsmIVoXlPYmOaEkAhy1+avpokVWYDQnCn9WUTdA+KzsYDWHFiL+9QSFKVXwHkRdM69CeNVlKF+GwRdDT4zOCpln5n1mTrumoX5z+Vi8GjfCRbXRd7+hXN4CR3crl4HAdt6nxECNqj29l32124mkxv+5lPaM/59559ke89LCoWi1+QNuFsMe0af+17IKyVs5ouQX2L7hKZUPFzZR8TFV+Uzs49gB8UpVUXmPdm4oKAe37k/3uxxNZv1GZ8VAhZw6Xe+9QIsfBuC9uagXfRYeJ+r7dbZkJLQTXlTAwR8G4+oDDurwGiVPd6U27P1gYcgJQBHqn6vKtjrxEFhhFImPtUCtJ3wCso+87ymZHl4/EHw6psDOr7WPnDp7xpTabzZBY1wpLBFlQDoT7VqKUDJAiULlCzwGSzwZeJonyHZUtCvxAKFAeijjz6KSOWRh5UNQ/auIhJJZgWnVyLhCC/hYXpf9kaA6zW4tj8xd0CoJ+gzh+NqTgGGgywHkqJBltCiX+PlSe2t1yXj1/T0vklCYndN5NJQjQ9H/AIdkjMAGwAejHDXhuMPZYRuWnDCUQBVQ/YzkeDSAHpleDcBszqT10bTNyWS7wroJpEhuzt5wq0GQq4OA6wAuF1UrmaFG5L8k3E5TOZGErrASWdAyhKPgoqGQ4YEwHqAx7LalLBwewLeU5H7nMSBBagqmU1oSH/mAbaqcENbx6RI8q4kvEP8E6LgnwYCKyu8OvQ7R5YdfmTZsKFfFgBNfestWrRo9erV06dPv/3220877bRzzjnniCOOKAg0F2BiymgeOnRosce/gpjGsGHDKHY8dOjQo446qgBJU8B6b+i5cCYUCp1yyimXXnrp5MmTn3322Q8++GDnzp1UPJpi4p8VQZYkSS160YnNV9LS/yuJFE/Mvsrj/0phSpGWLFCyAAXTChAPecLnURuVykGSNdNc/5SDtwbDF3rUAzJlPmZMFV8I35BzhQiLDnBJmAJkhZPFiQxCaCSy3ZEglDvNvXKaxSQZVLfESBF9Jr0x0TLNh9zt/26PepoBBTtdJH3likGdNBDUr4AUF8VBYyjgpvmi7sYaywfPG4F8z0VPfyuGCPcoYyEjpEj5aiKX0axRkVaJbJKiLNxBo+WD0ZAI8PKgCriti4d//E6wD2/36GWvmQk4NixfDMSBAhD0GZ2P5XH7POKJkX22lkALt8/PQvELVUTQZyWfGIWCC22CKtLSQhZqfXdL7SuZ4lQKxxiQRlw4RQ9wTZ7AeAR3o00gb/5C7IVrcBs7FYAmG+BIzRSccHx61goRkuzQ1o1epAfbeSElbB3oxZDkTiPOPXINBhNVVahbBm5zg9sA1grOa074rY1vv47e6CjPcc/bmZa9KP3ihHIVjPkvnEazyABvvi16LRt8eghaYHzVwJP/xpOKTO4XWt7CJznIX49PGBIBIqToyxvbIX0sFGWCplgoXb6h5SMpCrn7YSEAOaBPs/zFtAiFRpTLBn3ikHEjMaUAACAASURBVFyQNld88w6WunBVXgyZJEtLuHsOvv5vqoy7KjkiFAhsAkKuJT5Xh1EXDzkhaJOdxrWbVsPOegg41/ltKZ9D9jj7//Z3jhHRIpIAV/8rVWFoNjnBZFMcTsnlSPk8axt2IvuGkKCJhQaLTk3+9Re7lIPPaAHsGQn9mSePLJBlOLZ6e41Z8o4Ua20tHy3MPf1EoiREn0VFz2d6O32ez8+Yz1LwkgVKFihZ4FtrgRIA/a2t2sIkSQZtxowZiEsi+IwvWmZkASnoGHARwJS22HQWrsvAtBT3RIbdIiNKy6PTmNxMRCBezmXCPr63Z+D6eOaqtHLDAPe2iJ4Ac4QhjFdTcSguKGpGUlkeYCfA/ZHMrZHMk5HkBkBEGGfaPI1dFTVVVlUeIAawFuDmvsT1SfnmNLwqQxuZSObnWCKiygARGcnUd6aYy9Lpy5LJ2wfSjUTNA1MFjodsknylA3yOqFrfl5anxeDuqPyhAn1Ex4MFmUW1QArDY+Y3S/DMAH99T3J2VFs4gANYHlBpRNFAFGWJFdF4hx4+BB3ufTkSHPPnz7dYLMUQM62aYgCaUpiLdTBoGKrXTI8LKs+HHHIIRajpVQW6tE6nO+mkk84777zLL798xowZdXV1y5cv7+7OLQRgheVfBeg4fwL/f5tvj1LZShYoWeBbbIFi6ASLibwnAgDRMhOsNu+nQEFPRDlKFJH9RPkFnHnmcdd9QEX7NR2dr+aQwvxzVFVYjJOXMG76mwyaoIkZCVdsKSKk5h7Ag9HnYFPqMZgvzlIyjf4DRKK0JUg8QZxxYiyCIuG0OitpGUUREQbOeU3SNE3RNAU1tXabQZPUVCWbZrCDBkRoJcrrpKAZgtccvvNdMjFoQd0AFb1EWcGNR7u/6NVJLpNk2d1/JLYl+FuKZ9F5A4DEFcsGF+AzzKhCDEZ6dlXCyiIr3iiKkHuhCzgBhCjKaUlJyMSJbwf8MQ9WFyA6TQNFwf6fRFrrWBswyi4DuG3J0aEFXIaspJPLNE0TBBA40DChouzj4ReBn0i2SfukseS5zxhpvqz0XPGnRJA1hgyjUsSDMi07WVg4oOzQWyJnMSxCoUwUXqRWliHCYHukXqHzYHDhKnpA06PuM9DJH3kT+gH9gs1oULpgj4vx6163J443cvUpslyCzagS8WddHJa0gjRxAoK1ko+W3AAqzLk7Y63Y4dKDxyCOD2YcxqWN23GbXyFcLtF8dnOrM3R7QL5G6Y+Yk9yCTe7OoVUOADOnd/utOwJGNWABU/nqjm68m2XibgTjL0Sez5wMWlbhSStEz9CEApHGAS1tU4UqoOHRLMRJmsZjBlRIpzNU/YMl5pAUDZkge72KG4qCVHTKBaYGlfEEbT54oQrASGoMHyicSPn29BMHvWhWRQGJ4aJpJi5Sl+IC0aHINQXaVvbKwdd9QlFEUckKGktqDl5+GqqcGz226KgjY+Zy3m+PnHziJi4D2TRUB993GFuDLtVqTZ9zXiRFnqmCAK1N4NTXOQ1Zs0E2mzS7SXabO844ZWM2i1WRFVms28F7KNdSvu5yl9L/zBYgy1W4XUNCD0jw/jwIGJrGWSFYwf3kpAiThQSLa0QKiEhVIk/Jwm1dfPCZEy5dULJAyQIlC5QsQCxQAqC//Q1ByQPQQw4dNuTQYW6fV0SZPuQyDxB68qx+bgoPNyrwr+7ME4y8RkP0mcxROQVdFeJ8lQctTsSU53HqlHj6sgR3TUx5KIEyHVkyJ8jbkShfgMQDHwfYDNrLmdTsgcicvoFGgH5CPc6Ng1GrGSc5HMlGnSbMCXfdxHLXx9lXFNhBZv/5obwKiFGLKUK+viuSmJxm/5lmpsSTK0icKOihahoC0AIFoGXC1G4FeD7ZPysl3hjm31NRuANn/QInAMsCy4GcIalvk+CJfubWXuaWPva1NOYOWDIGB9TxQGhbVA4/9PBh30GligKKny/v5/x/7LHHFuPIFE0ufFJ2c+FrQd956NChBWSZ/lqAp0888cQTTjjhsssuu/nmm999992VK1fGYjEyf87N4SiqgaYi+hgF6LmAOxcOSgD056zU0mUlC5QscPBYYE+EC+h+m/wEUi5wmgh2MwhAK0QgkkBFFIsliM0+MJ/9FbWAmVIacQEC0zi8Sk1BuAnCjaCkEVTkU5iEIhE2IiF5KmTSO5hALnUCi+fxaBWA5TGHkoRdWiYNqSRkssAJ6FKJYLWQkRRBkhE+oRg0otuIPu8OQGM6mopeiemLTasSB7JA2dMK4VArAAxo6JhJkwhERoKKAgg8ehNW8gBbLor8vwIAjbkVNIYh0LgAEgt8BsJhaNqJUBktXzpJ8DJkdO8J7lAwlBZKJMAB1fZVOEj0wevPw9V/2/W92g/GuheeVLv5zONXvTSXkJcp/lYMC5KI1WSS2mTLWqhy1PuM4DCB0zHwxz/ukAiYmZVAxjINvujSOnoCRuibonjFvw+GPNAjmhNS1Dx6SEmy+W+YxUIjptgwh7WA+7iKh115ALrQyPaRgwJ1uhAIy4BemAm5QOFASgEThr5GaNkKMeIlI8oCS9jQWM5CRgYBOEolyODAikDH9P7Khcw1wE8w0T5iy4UcRJUBq1mWQCAKCZxGrI5F4wYtkLsvUEVNleD6a8J2XbPXADVO8Fo6T/remsgAuvjYLRMUbqYQFG3g9EyuCPnAuQZI22+OLIyLPTz89dKWgLUlYBIDNuHk4zqyInAq8qzxRcpF6cdpHEbjuSyLDvGyAmR51JQluwO5XAMfNCa5PBeDTJySsPms5MLSNsekgUnj3Uo5FDQCFe9ovG3yb1UhbtbykcqaImO7RZ9ruXOSkqVHOQBaIc5bCOtCQQ8xBeI/3qqDLywRTYScy9l/8Pev8Qidqagi8WiOubj5BvBbdnmsaY8NLBWc19b21z93sDzu5fzxWcvsxgavA2wWacIxTRkROI1jeVHmYeY12lh3n03Pm3Vg14Fbn631tE27Dh8KcQZLXtSW9nxGfY1lLyX9mSxAemd0WSQCdpcX/7rBW9kXqgRvZctrz0KaxeVNkShUUgCa1vTen58p0VLgkgVKFihZoGSBggVKAHTBFN/aA03LMaCHDhs2dNgwr9crSZKsyRENNgI8nobJ/fJ0Ba5MZ2YnUusURJ+RYKEikVkEQSO0sTSo9aA8B/LUDPcvRro2Jvyb0darKJ1MtyXmhmXYseNEIQOwBuAunrkh3vNUtLsZoFPikPAhkwvIYFdWkA0SISoZD6Uzk7r7bmEzj6WYVopo48iabO4k6DMDsAXgoWTiFhku70/dGWfflfBaHOTj1BoBaBH1N3B2ohDxjdc5YVp725xE6sU030ZCZiRFVIQsztZ5jvCIGgDmJoTJ0fi0ZPrp/mwYUPGaDrCRCUIAaNDA7XAfOuy7Q4Z+58tiQE+YMKHYE2ABa977gELM1CugXq8/9dRT//znP0+fPv2ZZ56ZP3/++vXrKaZMm69EZs9UQKO4QVPV5uIziEPISgF0Lj4oAdDFhiodlyxQssA33gKD6BKiQwSsQRYtRfWKUBvKrhUJBs0TV0UipRWjBT4H2kLSVQhHWQPYtgUeu1/71c92HRuqd45Y5x6+6bjgjsfuBjaNfNwUz5KdPrj9nuzPL4AdKlk8zaiQIVnKAVIUSiz4WBNSsHoxPHE/3DMLwZclC4En1Gd0tKSSGBGBGgSgCxAc5W7mqlgFjgBTiiIqKvpfom9Ny9FOsU8mWLbI4U4i7CvJiwJhBMrD1PIwDV2QxkCckAu6sx6eewIuPLfFZXgv5Kyr9tR9f+Kqe25HQijLEr6nwGAa+7J2AdbH/VAAba3wwF0wLrDNa9ngNm93GzsClmSVTax2xZzWj+65m1UImjwIZxeQaMBRiirCXbOyQUej26zaLOB0tT7+71RKwCENozASQutaVoKMgCAFUlxpUfM4I0a7N4BYCLPvgzxoRUtCsNH8oUxY2YjGk0CDqZGYChTl3S2Ov+UB6LzR90oZ6ZsAjIpaAjkvHfQgk0Xcdv1ymHyZ+INxjccFdtWY6p0VK87+Yc8rr0FSQCAm51SQZny3pQGkP6u4byB3H+UlWwpAzV4ZKZwYLBzdDo+Ap0JaDxnPAMeBkAWZA5l4NgSAGAORLOaHlFciAz0hb3+0oyrChedtCVq7fUYIGsGpa5w8OZzmQCL3IK28QiGQ6quSXW654V4OW6QByH6BDEGB6Z4JtCzNcmQATj9ppc/U5jVkqhzxSVdChkdmQ8Ew9P7AzXMCZn7rWnjwLpg5lb3y7x2PPSB1tpH7q5CPvdsPniEMaORBqHi7kaRlQORUZCHeB8lesjuB7BpApVrIiMBIKGiLFUHfxMcaQY4x3wijcyKufcX6QRFw1aHwos9B2vhkDZF0mSLyEggs7nxUxVxF5C8hlshbKn/yYPlP9d1ZFs44fofPEPFZOd3IlE0vuq2NT/0bdfp4Ca6b3OmxtrssYDYpXv/GrgHIEIuwWTTvycdschjitgpwVoBHByGT4DWs++BtNC6pZboKll+so1glfn7i7XewmKaUj7wFyCNXlbCHhC1bwKF72zk8Yf3uwMnHbE0lUXSSbE+inhPwziB9Za7bpQ3/YG3++RKW/pcsULJAyQIHtwVKAPTBXT9fRu4KAHQB3NQAUrKyi7jyu6qTmczAtWlxUl/HQkIopkQJDSQRpxaqouLcZRcobyjJKWzqck68JiY9kER8mSU7QunwNjdCJx27BNAIMJeTrk4mro/2rgc+AlkJFJRdlrBvVwhhRFRQkaMB4BlRvqY/dTMPD8QTq1QFx8bIpyKTZiRsiCxAJ8CzKjtLFv6ZyExPCq/HxShR20CSEkLGiobkEkXWEIBOELL2rZ39dzPcc/HIDoo+C8ApCotsMzYFMgPQDfAfCe5glKkcdweT3gzQw6o49CATOirBQTc7jh9/9HcO/S6hP385EhwMw5x44okF/nKhaoYMGaLX68ePH3/GGWfMnDlzypQpdXV1ixYtSiQSxa7/KOhM4WacGhGtDCrfTNWlacMRBKEARquqKgiCqqoceRUjznsclwDoL+O2K8VRskDJAgeFBXCuSPwHKBLCb2SbOSiIq0gS4m8UUMV1TIJH4xlyUiWADkWrByefn1qknHKRShibBMpRVESgb5vdYzE/U+3fbKtoCVggYISQAapNELLu/NMfumjPQ93efQIAjWAfIZlSjAm3D0sE9OAYePZJ4Vc/qR/nWu0YsbLG3jnGnary7LzuOi7BEAFTQmlEqiO+cgzoIgAa2ZSqApvXwh0zW+c+3Ef7dBHSctFbgyxSIyXEnTfUwa1TIhf+dM3F52+++m/Nb76C2DH10qYRBQuEgXIodA4wzcQRonni/mS1681q57bR3sgYv2IYHrOOSlQ54j5r3RV/3f6pGA6OLzSQZJRpfvhh8Lo/qvb26Y7qC7nBawObTjaNUII2cOnBMGrnxRcP8HnyN2IJdOVBQqK3SDLFpuGs07e5LS12k2i3gdfb29QC8SzEMgTMA4iloXEXrFkHHy2GDeuhqxsyLI5N8rjn5wOgCVRFUWciHKySERFpe7KEIraDjW1/YMcghktg9f0hIsheVyElI5kYFZQF8uZVaG2FSf9MBq2r/brWKlM6aJADBggYVb8tMbpq3dPP8jzBYrCV0fjz6CbxzcgCQjOI8LIKZGXczD4YvgDZ7vOGyWUetaMJVIrxKBpS+AEgHYNF78HkK9ov+WXjScd85He++OMfrb762tYlqyDBUwyawNC4TEMyRgjYMgunHldX4xjw6MF8eDbo2PH621ibOdZqbgmKCkgTerZGVCrQDzcWoVAyUlCVjC6JEF1eqIS24/Y2qPYs8Bo6PIZEtbftycdwaEulRuiDBUXrULoNFr4Hl/yy0aP/wK1bE7Jt91o21HjWnnTswqULgWMKejt5YLtgpRxenHeAqUAsBpEozJsHf/1T40kTl04ILDvav/KUCWt+e/7Wpx7ju8Noc5GsExBpGqwoUmTqGDIXPwVHU1l45JHIXbN733wpi9cApBlOVkEg0KqgoXMUUUHonGfh7Vfgqr/1/N9ZKy7+9eabp8c/fA/Q12LhlTPrXvkvBPj6DngJElFw61Z59bzXpph0jMPEO6zrV6zEJioo8NDDWa+tw2GEygrBF9q+ZiMWHOntAhbnvrvlkLPTWQ5ePXjKwXmUOs7FnHzMpo4WovRNAhIaOy0hT2ZCgwsVX1+5Syl/BgvQtWdegRuvT1U7t5sPj07wM/fcLiYZvDPSAuFL4dNFKgHQn8GspaAlC5QsULLAgVmgBEAfmJ2+yaH2BqAFgB6AJSLMaE/fmIbpANcnkk+zkV15SJewYwTcfKkCj5tu4XU2OSvd989k+uqo+FAYVskYQyonlkisQxgldJg7APCsCJO7I7fFmBWI8woCZIgzQ4nSinEOQahJfQAvA9yYZSfx6j0irJZwcylSrtFHkIwJk782gGeTsRuSkb9E+6Zz8otKTiGacJ+R/kzoSQJuGuQQFl8NMKOt5ZZw6pmM3FCk5iGCwgCfRIlIlK5eCzCjj5maEm4biC0kNiFqHiLIIpnRYNq0RCec8H0qvjH8qJFDhgwdOvTQL94iRFF85plnpk6dOnPmzKeeemr58uVtbW1fMNpi7LhwTOMsfNU0bQ/EeY+vxSG/YH5Kl5csULJAyQJfiwXo05vCMQDQ2QZzH9Leey3H8BURgyMYLumLRFQMRuoupezSxz7tfgQNMSaKOlLUpRBzIVhxATVNY1mWwtCSjKjNxnXwwx8sq/Gv8VhbncaUxwIeM9gqwDwCLCPAUSn7PA13PZZO50VzC/3OYLSEKVk4LyCNDxNn0rDkQ/jZaU011m2+8uZacyxkSXn0TMAGVl1/baj53XnIY9UAkiwCTnmBV4pBU2xdlTRIJuGeW9PVlhXByu01lo23TJFEDYUVMhqqU0sgMVImIwm8AO3NcM3fstWWlSFDc0gXDunC46yd3orlP/9hY6wX0VMKLfKaklUQVaQvkYGmjXDBmQ3WIxf7DC2mkT3mynhNACqO4q161VqRtVe2+20r5z6ev6DwP4dU4vcMKUKWg3Wr4ZwzO0POTquu31TZY7ekgx5w6MFlUtxGxW+BoBUso3p/fl5fgoM0yYRIMGuexfEMx0Iqgyjha6+A37PFrO+2GQWXHfwe8e9/gYsv4s8+s+PEY+tDnjUh15ags8XvCAfsSatuZ41vw3XXhKniNtKU8V3I6IEdUKyYEuoAhAysXwovPCGsXIKQZYrDOqKSw/QTBRwUPKkCLiRwxMkasbGkaqyqEZnyXMqUmFkweXF+kEWgIkSM8GtCFKimwtwnwap7a5y3w6ePBQycqzI62gvWUYplpGypSHoszRPHLunpKZKwoGhvHqkV5TSmocHWTfDDH9VbbKvO/nH0w/dxrSWnk0vvmeKMFI6J3Qi5PknwO/wBqYYZeOFROP3opqNdrSFD23hXzHLUNsvI7bX+uLFiw7gxq6fc0JcV86RsSoamJVaAGYCQfUGNPe4q592V/ISa+oZ2Ei1CjoJCeMXoR4RjBHLLI2eY0FjTDMRT2HRTPCNoPJYPK5bqw5FRKCkIWcuAj+ZDwFFnOLKl2pmq8q9rbsYkGHo3ktIxEmzdCn/8bWS0Y5e3PGw7ssdbmfSasrbyeJWdDdkaTpz4QSICbDGYSy4s+kDroEIQQCIO/34Ijh/TaRm1xWfqCFi6qi0Rb3myxiy4R3Z59VsmBFbce4ciomIMci/I8godtVKSeG75R9agJwz/9/M1fv9am3FV0PDqgleQCp3JogmoZDwqQ4sQiyP0fO6p3SFTfdDQ4TN1eMxtQUebRb/41lkSbhCkSwu8JqTZz9z+iwr5XzpEb+kSPPsUVFvaA3rwWMBtEX02Zkz1RobFGucVWL4c7PpGjwn0Osnq2PT8K1L+PsYtE+1tcGzNNp8+hdxnveguVz06rsYXufSipJhF4SDcO6jx+V0eacJv2a/c+X+pqKVoP68FcH1UBYaFSARGe5f5jGHLyAGrvm5nc85Bg5if2+Zlu3CLBn2Th3FhCPB5c1C6rmSBkgVKFvjftkAJgP721/8eAPSwYcMAYCmjPdwnzlFghgBTYuwzslIPWopMgHHzILKJkYic5dAR0VoJ7oolJsXikyL8nASsV1H7gnjqk3Lbk3PTCVTeaAX4UIUZfalZEf49DVnGDMiqxoIm5KjFZI4lqqiesZiFWSnx6jR3uwLvEjkOQlZDUgw5wJF0GOBdFW6Oxv7U2zFNYB9k+EayNxJ/y+0YVFBXUpU0TcuK0AVwV0/P1HDPYym+juhZYx2T0TwPYhrELEA7aJsA7u0KT+5JTulNfESyncb85bHvolEGAJz5w7MJSfmQIUOGlpWV6SoN+dHn52w/LCWMofN0nCEUY745At3niniPeOhXGlPxT3sgznt8LQ75uXJRuqhkgZIFShb4mi1QmCMqKgK1v/rZ4irLwhr7/FkzWkgfl1sGpZttZUJsRXKoBCwPyTSsWYvvZAqxqwyPmBcVQShEW4CD9ygnSpGiVDB2ipwEixbD+JqPveZtHnOH19Lvdw54XF0OR6PN0uY2KpYRYB8FLmvnlTeEEzIyMffxosAf2YxPeFsip2CvwbJw1yyuxrak2tDrGZ4O6bmxbt5e2Wo1dFQc2W/VZWym/tN+0Peft6GxDVldFNOkAtDkMw9Aq/DBPPBa3x5r5Wp14Dyy/+dn9RMRZMyLDApHOm8AWPABTKxaVmVp8etS/nItOAKCI8B7uOQ5MjrW3PXHCyOJBLIv6QvFAUhxNAU++gDG+z8e5+odbc/6jQM+e7fZvNnhanJ5BsympM2gecyqq7LjuisgkQKGp911PqKi/4IGL70OTutHPtuAvUL0WsHviXncbW5bl9vSfNpJfZOvgZO+F3ZbVtf61z//AvQykFQhkoR//GPxBT9bcsFPN1zw0y3nnbPt9B/WHX/SWo93m9vRZzak7UbVZQWvA/wuyW/PeM2Mx8j6TKrfCD4jeIygGw5+F9gt4bGjF3CINhKJlP0ArEV53u2wAEATM81/I/U93yvf8y46JvTywnmIgTJqijqnpJ9kmQTrjhUhnUFkc2UdNGxH6JslzIBMNk2J7WRExuUGOrslieMLFQQViePYjBkRxYgfvhdGu9cHTO1VpnjAFKtx9rmsK6uD9W5rpPKIiNskeYz9IceaeW/iZXlUmzT5fGsUREYireqayztCNQNmu+qwZkeHNrEicpnxmk+xj6wiLwFdU2Z49PT44lzt9GM3+HXbQpWJmkrpaDvUWmT7qHi1A3w28DvAZe0N+pbPuKUrnx9yT9LBpwI7t0HIXheyRtyVGZ8p8aPTWhIiZCEjQ0oBRsFy4D2Z1CCpQFKGF16Bf1zefNaZdRdesPbN19FkIkBGzsqES6Hhvchh86dlQYo08uaffAx8lq0+S9qmaz/xuHWxBApAa+S5wYkwEIfHnoz5Xe+MdvV4R/KuEZp9VNqpTzsNnGlU9qghceuoyDh/0y3TuIEojl7381IV6OmCC85dFbA0uspZZ4VafljCMjJqHZVwjtCqTOArhwkO8FYMBEwbZkzhOBZvHJ7g7MQ+Bc0WHKsKKtw4PenyrNMZe12O1ARXw/P3oo6HJONKDD6pFIUj2//mzEm4DYv8hrCvUvBUgLsSnDrNZtBMhrDdWvfM02SZDnnvCggCcc65n0J8DT/F08Ck4A+/aakyR316cJsQgPbYBn758950FjgNkix0dYCjcnvQCg4LeHzN996XzVeFJoPCKzDndghZtvp04TEufAI4KmWbKVsTbJlzKwr0KBJIMtHyxyaeBFQiJHzyr6G4pSQ/swXI7YCro5IED83R3Lr6sR7w2Pv+8XcVVdrJfoLdt6FQ6DmHQecfbZ/U/3/m/JQuKFmgZIGSBf4HLVACoL/9lV4AoKn/ukMPPbQ9q87tFG6JwG0AU1nlmbTQQEbyOE9BHT6FsJVxgBVRYD3AfX2payPspIh8fxwWy4gyo+gFDtkk4hs7TxIhMO5LGn9bamBWd/o9BXUz8kJ6hMGVU7XAHjwOsICDORFxakSeFZcWAQLHZBCHinMskZdkyODuYwJSX5HKTorF74nHW3N8A9TcIJMEsqkUd7FKPOE1P9zae2cic1+cWSaqPSR/lCjDg8qga0Q+DloLwL3Rrik9XbMGUs8mxTApEflA1ZG8lCHxvaShv0K9wXbUiFGIQR8ypKys7IQTTvji7YbqY6iqKpHXlwL7FkdSOKZZLXwtMaC/eN2VYihZoGSBb4oFFAlunyEGLKuO8SVClh0Tqt9mUkiFo5twCdLHSyCjJzEFli6AP/2mPeRY4tDVOSpXhRxL7pylptMos5pVMwrSoPb1Iv0bAlF5JAMZuxy88T64AmssxpZxATFoD/tsay+5tGXhUti6C9ZuhDHeHl+F4hyeCtm2X/a3rbRDpfPawmcuMfKdsLnVJJfOiMAycOPV7BhLc62eD4zgQ5W8t7LbbV5/yinrjv7eSo+7zapPOq1i5YhOS8XGiWOXPPZ4OJVFzIuQoDWi+5yjdEkKvPQiBFyrHCMSY2xgH9553tldjIxgZVSOcehcAWmDTz8OtfaGgGEgaBR9lZKvQvOPgupKqNUDZqA8W23ZvHljzqo02yJJ7O3/gNe1odovuC2pGne0xrvlkov75y+FnjQsWQP+qvqKIxKWEeCq6P/9L5NiXhY5V/Aie6YycO8j4AhutdqiupEpn0Wy63psxjqf883pUxNLFkM8jdUaZ2DFWli8AquCjlVee0WdWDuv1r652tKOvEhLh8vV76/Kut2swyY6zeA0gdUIZp1orGAtFZxdr7mMyFL3mPDttMCISmW4ecAe2HTRn7dmcSUgP+Ypyt6+msWe5wrVqsqQ6oZfnFI3pnJ1zaiGWt22WyblWhYBuHIqGRQyTmbh4QfhR6d0V1m320auHONYed6p6z78D1K5ydgG8qcb7wAAIABJREFUVUnwXey/b7eUEYskimYYTuHh/luhxlQf0vUHKyJBXdtY3/o7ZsG6jfjrIw+Az9YWsgpufb/TuPg/LxOdGoyNCpGniVERc9VAEDgQIjDa966zqm+4OWswZkbXbEcAmganPhR3ywn9glGpqNvBS4BqD2uXwr8uYWvNDcc4pVCFfIwTgpUpT0Wj19TgMHQ6jSmzjq8JQG214rBtcbteTqfy6xzUoIQ9Pf9tqLJvCFqiIVvaa9w59QZswAk5IUNMgZiGBHD0u9cvwsrN8H/ndxnK17pNYaexxzJqU41zyX+ex7yJBMBViByIhvvxCACdk+8QsypcflnMbdoZcslW3c4/XtKdJYslnEJ2TvBw+wyodqyvtnV59f3OUVGvvj9gb/XYGu3mRpu5J+RGKNNZEZs4el0ksQ+75E5pkE3BltXw05Mb/fodIUvi6BB4bJxR32cytXldfX5HUnd4r88omA6Pe3RCyJKosm3790M5KJmuM+UfU5TPjffvry7qC9UkKp1pmzsx2ln/2qOAqjjkhdITgJpEl1/e4fOucFsbg46Mu1JzV4BTBzaDUmnidZa03x899ui6NAuiTIbJVK0vF8fB8A9bQzyNJGW38f2AOe0xgNuIALTX3nL3HZDM4BQjlsJNMEcHOz0msJpln7/jsst2irj5EV8ywsuQZuDMU5aM9w44Rwl+CzitstGctNtagqYPWjfl9tDQR7KKWyySKtGiyUVR+nfQWSB/N5CMIQCt4Vwz0Q/jfSsCRsZrlKqqWjfWo6dQmUhnDT6oB/HmEgP6oKvXUoZKFihZ4JtrgRIA/c2tuwPNeQGAHjoU2btlZWVPL1j6QFv2QQ0mp/lpveEGJCmTGYPE4+hLkzXAowGAJoCHk+w14fiVMX42AwtVVN5AAUFGBpluxiNadaR/jwB8oMFMJnptuOv5pEJ9CXLovwRnAjQFHAAqkAZoBrg7nrkxnp0dVZ6LyF1kHybBAlQW1DQhFfQCbAZ4tE+5vI+5OiPem+bW5ljSQIQsJRmFqgURHQeia50owJs8e2d//9090Y8AWhQlld8ySHYmKlkQYyD3AjwX6blxoG96KjU3JTYBJHLDDZxo86BSB/PIFSKaJPPXbi4bOgwNRz7KhpSdf/75Xwr1g2VZQRAKdDlqpC/yWYwyF45phIWvJQD6i1i4dG3JAiULfCMsUNhKoghw0sTNPlPCV8lVWyJB++LWnZBisVfKv0VKYJtzd2ZizXK/eUe1NeOpVHwVSo0lPca95e5ZMhL+cjjUXqXfF/oMAOE+qBm3zWyNWY3pkCdpqfzovrsR/qC7tdMi/OIcyV2ecQwfONq3/YartvMs4l57qHxgYvnZMPIOAXE7BeCSSzr8lq3eEdnxRgiWx13lm/71V9ixHZI8ZBWYMRM8zla7OaMbwbkMasjZdPWVWzgiMpJfBUZeJH2LCtw4jTVUrgtYtKAJ/Ob26TcgVTADkEQ/gwjsznsbPIZNE9zgqZRclUmPuc1n2eE31wcNbce4wXN4ZoIZ/Lptc+5iVcAlW5ZTUSVEg5ZdMKZ2vr6ir2KU6PclPa5VTz2BigcZ0uP3M3DiSY1+m+AzQI01ftnFaZ74ACwGDOhuIYaFDxaAzbPMaIuZDBm7KeG2bJk4ZtVtNynhDkgRKI2OSJIi+mVEj3tEfUsGWFUHY71vB/RbA+V9gVFRd3naYwOHA1wu0JVzVR4IWMGpT9srut3GNo+5za5rtpTXBx1tQefOoKvB593irtn4w593zn4QIhxaBiHoPDF2r9awvxPU4AgKSrB2EVTpFh/riB3nUgLlA78+N/L/BUkJURcHM1SpOalAYwdc+MumsSH0euetBH8FBHS8v6LlaO9HyxaieDdZVFBo/76ftGnj4SW4/y7w6rd5R8Z8w+MTnL0/Or5pw1JgEuhokRehYSvUeBp8+phb113rXv7RBwSARpxdJtBzkoyJqNKKLAjQ1QQh19IKa0eFjXO5+eqqtaxE0GHiqRJbGL6opw5KK6RfsZ0oCvq4e+RuONq32l/eMdaiVOmzIcNArbX51z9lHn8A3nodHn8Uxo3pNlTErHrVZRN8zi6z7p1FCyHB5OOmscvw9GMQsjUETJEx3rSlculb7+A2urjCisAQEjQnapCU4IW3wOF+z2VrDznAVQn2cvAapbHO+I++v5XlsXIJq1tQIEUAaKxoKuOjgJYU4Sdn7bLrepwGLuDqvOsuKZXBwqKysADXXxWb6Gsd7xCsR3SOdUUDto2/OHfgkYdgRR3UrYLvHdcW8HGWcgWXNIyrtzXk7EINRGUtKHYsqdDTCWecsLHW2uMeifx0t7nJ51n7578o9z0A782DN9+AW2ZAyLPVa+kc7QbLUWKNWahyrOruwfzv5hUcc6eJoLEK1FSv87glvU12+hi/bWXTOlSAoS+ByM5NvhZZ8AF3n8va63P0u21ht7nDbWlx2NvNjoTJlnbb4iHv0ngKOLmgOFF8pxaK8nUdqNFEmBfgvXeg1tvgsbBuI64tua0Zr2Ptu/NwaUoGSLPo4vL8H7NOHWusyHjd3T8+c20iRoBnXEBEAJqTYdUKGB/cYTqiz6ZnXQ7FbM9azeHxzq7TxtT1tpG7HxuGTNDnEgD9ddX4/tOlDinp5p9CSPR6KoM2kIBXngfT8E3OUcJor/KLCyIsh3tQCo/oQv+YPygB0AUblg5KFihZoGSBL2qBEgD9RS14kF9P1RXmzJlzyCGHFADou19+7dmkeGskM6O1YxlAB3KKFRnhVoYKJqOqHXEP+BgH/wxnr0pLNybTrxKSMp12YalxDZlO8XAM2g+wEOCWRGJyf/yu/uROglOjPxbEiGXSrefIQjygA8MHktwUkZ+aZZ7rT3URUnMWPbVrLKDbwSiIPaB1ADySVKcnlGtj2em90eUAfWSygaNI4rcHndSDlAUlTTKwGeBhKT0r0vnOQDyam3xqPGoSCjJmFV8pgHckYWpn9zX9qdui3Ea6fS7nUEVVQGSAZwi4zhBC97xE4tW2lrKK4WXfKSs78hD8LCu75pprcuMUMlH8Bu2+K4ahD+SYGq30WbJAyQIlC3yzLEABaE3TogPgdax1GFWXHrzGpEO/ZOMGCjPlCpQhbOgrLouEXNuc1maXLWIpT7t1ik+v1VhU94hwyLhi+SLimnBvvCWHPpNZap4PqwFEo3D2Wdu9rgFDORPyZk2GxXP/DZE4IoYMj6nv6gardZVhVDxkkULm9f+ZSxBxorNBZ7yD1lY1dJRGnPqpAP1puPpGzhVsGjGiK6QXvEe1nzJu2/x56B8vIwGjoeJAjAG36227taNiRMJn0cYE2m+8cYdAtBHy0+lcD4ZzdAnOPa/V74mZR2aDdtFpXL1yObIpM4QErWiw4B3w6pf69F1BU8Ze3jeuuvXXv6lfvBS21yOaOdHTXV2ePcaqeEateOoxHpevCaESAGJJ+MHpax2uJrORtZlTbk/d/Q9jUZABqyFsF4lAdWCjs7InaErXWpufeQhE0lHnDZmzAZY6BcHaeSF/u9MUGetjQo51113Z3NWG69vpGGob4+Z5Dd/oAo74lxM04DWREVFe+dLfLjmman5QvypUuavWHPPqw4aRHTZbymTIGEbw1RbBP3z9j8ZuvvLSvpnXRp+YI7/+HKyrg/ZdkElDlkVVFpYIb4vKIOBLpI4Ha+lAjqiKqAK4Zv7a81Dt3Ba0xay6WMiXOvmUTQkOWDmFRHhJE2Sk4+1ohJ/8uMNrQ0ZqwAL2UUqNA6wjuKBZspc3nnPajmwCqw/pzcjB3bt1DmaK47F5vDEPnI6NTiMz2g3V9oHTTqyrX098Yog4/OJiMPcBcFWs8el7xrp7jxm9eGcDAnIkXhQCIbvUci1IUUSGhdf+AwH/NkNlv9XMmw27fv/7fur4Ea+hwyqsSz6/Fy5HNJVUwhzOwOS/QLWle6wTnOVMtS3qqPzgTxc3rVuF0jcMi8IRcQ6efAasxm5bBbjN4LJ224zvrFtHNt/hGgq+EFuX4ZYbIGBu9ZqiTv3OoP+jXe2QkCGhIJqPJgVI8fDCi2C31vmcXbU+yaFn3UbNY4GADbwVvKuybs0azHIegOZQBprc3RS7p/HUBDfaRqWDTnDadsybB2kOZXZkGX77u96aQEe1KT7GlKk1d/pNH730PDBZ6Ilg6nEO5r4INmuTWcdbdazbuu6d90m2ij5QsoYsnDAyXHRRv9PQELRknaMGLCNWnX36po8XE9+AHMhCjnaxrR5+clazaUR/wAjOEdrR/uhVV/SlMmgZgvQrJD7MtaBBZx94nPgMtBrAbkmeMHFNlvh7xCFxRk5kYcZssDk3ei39HkMMRc+9W6++Vl60FN5bABf/vqPK2xAwh/2m7nGhJYkkCOi3lb721+TyYb7S/7E4zJwObkeLw5q1mcFhArctPHH8xwxxu0jByBQDk68AjzFirWACzj6/6x2VSN2TZQCJin3zIvzh4rDH0uiyplwOzWwTDBWJ0QahalT9FZd2iBm8+4kqS1SBKGVA7/nc/krLXUpsbwuIhJVE54L0V7r3gufIPteJR9e7LFmfGSb4IvNexju/0K736CXzUe9x+qBr/Pl8lv6XLFCyQMkCB7sFSgD0wV5DXzB/Anldf/31hx122He/+12KQU++777He/pvb+teRdDnGE49BB7nregGSSPzjAaAx1m4IQNXMNrVscxLAPUElc6P+enoVgAyCesH+EiGmanIdCFz+0B6FZltkJ9QzULNvXEOIAE0AjzGCJMi0es45gEx2wMQFWQe5ygUTZbQZTug9MczIn9Dmru8PzU7nl1AnAQi1Eul7WSkz5BpjZIhIPIaDR7r7b8l2vmskmohdB0yWFBkgj4TeB2j3ajBPZHY9BgzK8yuJLA1MrmJWCHd4MyDyOIcExIAL7CpObHum1cvLxt1RNlhZWXfLSs7FHnQTz3xJJ2GAuGblADoL9hKS5eXLFCyQMkCX64FVKKWoWnawAB4HJvtBvRT5zGmvba6pkYEQLGjwd4G2dC3z+6qcW8NWTmPLauv6CsfvstljjvLmdE2CIxUfSNa/nlJv8YNTlAHs4r42iDBk05J0xm47RYYG+oIWDS/VfO5djz4EPTFsfsTiaYTw8PsOwSPp8nvEd3GxATf+s76XKdVmOMOJlF0lM7AHfeCzbPF5EzZ7HzIFj6hZtvWtRAdQNYei323yqqI/J5/wWaPs9VjVdxGLehquP+BTk7IQYKFJOiBKMApJ7d4HJylgqtypUK+j6JR3FKeEVCTpLcVTh/XWmOIjHez9vJml7nujjsJUoZO2yCRgEVvwRkTmmqtiy77XbvIA0cwRlVCGYEbp8T8gaZKfTjgFWpC7XfMgQghrqI7PABZgntmg9e41a/vd47YcVyorm0byDzia8UvhskqAA88AXbXVmtFh6uy4+iq5ntvJSvVABILAqsqItEWIX4B5SK/UYh9Koj2xuPw+ovw0J1w93R4eDY8/SCc/1PwOuN+N7h1UsjY/cYjBKzgcFVdyYLAgJDFnBB1C0HTchRjDXUu0IXjpzKOi4tQOFaxBaHGFy/Dyy+A39XksadM+pjHFzn7Z02MBJKWoTIuPI+4+YXnR6zlu1yVca9RsJXHnfp0jQeqXOAzg70iMdbb+vYrhARNtNP2A0DLClqA4eFHZ+/yeuIeu+YyJ/2OVZs3kqxRIkEGB2EX/rTLZ24OmcJu3ZpLLtqcZbG0WFu5Rk7Ck6+CJKY5mPMQeHy7LLqUx5LxODbffRcaHG8qiofj/YCceMKbJgkQ5x6ygM6gLz23v1rX4y1XnRWqw9BZFVh1370ST1BfKh+dJTT2zdvBaW1DANoEHkv3hLGLwn14z5JGhGxyhG5l+PsfRL+p12OIeW2Np52xPE70SbJkMImfIsz7EJzmVR5T0m1I+W0pt7kn6EyaRqQdFeCpAFv51vvmZBkRR5UyKhyjx2wsBWFAU0J6RxhC7h2WUbxNLwY8O3rCRK9chmuu7PR7G53GBNK3zU0/O6WhYVNueQLHqBpkNdi0HTyeBp8TEIC2b1yyrNAo8ADlYgSIZpG5P/3WlMddb9VFQhYpaOu85Nf94W4MIwsi2pJYVgXEvne2QMjVajyCr7LAOJ9krXyntxfhZjKklVS8TXHzIQ+wZTt47ZtdenDowGOOXvK7XdmcfguW8933wRnY5AuIPjNrHt543MTmhQuhYwD6Waw5XoY7b4Hja1YdV7tqzp1qhiO52C37B8cXDdeKJBF+dOZOhz1stWWtVsVh1ry2jot+vSNLtlZwoPIADAcP3QMBS4fXlA3aIn7Hou4OfEoQ4yoyLmegnPfOXXD8Mevcth6HWTKbBUtl1nVEulbXNt79xs56FGNSsLHHFYiXAOiDowXskYu9AWjcxkE6BJi/AqqrO4wVbNDBHjd6h0J1vPOQ8h5dZD7ePU7nQ+d/Lv0vWaBkgZIFShY4QAuUAOgDNNQ3NZgiK4qs3HPPPcOGDTvssMMOPfTQYcOGnfenvzzZ1DKPUxMIPSNpiGhuZHn8JrIA2wFeYuGqXuZfjDSd5x9KJ1vJBIIjLk7o3krqUVAjTgI/0OAOJnNFom9aaqCeqGTwOEymfpsGTZchGs0vsjApFb8yHbk/HWvGy2WRyBdqOOzLiqg4qXYAPAvwz3Tqbxlmapr5QECGNVXGIFC1QqT6kPOUJb4TNwE8khWva2t/molvyofMJ0ylPoUkaCs0eCSWvoURZvWl1wHEAB3I4H5aMsfA8Pl9tVmAjQBT422TEy2Xv/5i2WGHIfp8SFnZoUOOOOKIpi31OPKkyPV+pn35HBw8/w+E9Vwc5uDJeSknJQuULFCywIFbgALQCuwOQJviY4OrB8IISNHZpAyw5CMION72Gdpq7OAx8E5z2GJdZtQvqXZkq/UQGA6+I2MTnGtTvYh17TnpHMTmRJW4KZNUWPoxOI0LQpaE9UjZY4hNuoZPcugHjSEqvRrAW2/A949rdVn6rLqI8ajNt0wmSNE+NXMpw5oUO5WA118Fn2NL0C3brJzd2jU6tGLzupxJBAScVHzLkEnBn3/f7bX2jPagDz2fdfOHH8oy6eZ2m0Nr2PeJPNRUbXFaRadeCtg6f3bOWmQxE79qfBIm/1mtKm83H9IbqOyv9W7699PQl0BYKqvi1n7aZ6aSkExANIY5ocBWuAvefhG8hg0ea7I6qNRWt/35skSWeDnLSW9LsGAeTAw2eEb2ekfGqgxbZlzbg0zVvRzpZTOYzA/P6rCaw1UOpcbZe9GvmpMJgjti+sCzWVwXz1HRczxouu4tktpC7VcFGeKo5c2g6DDHwQXn95oqWqucMN4LtbatEbJqzSURd9Yk0qkTOJscyQSAHsSgC11kzvQH/O+TAGivu/sPf4wSbrgo8DllhFk3sTXORmSdH5W0jYq4jI1BV5Pb0uazxn0WyWviTCMa/3QxwwlI2lX2bJeDeVIBVwVECW6YDC5bq6Gy320fcNuXvvQcCCmEJ9UUgYg1uOs2yWreYtYN2Ea0j/asnL8AIylGk2njIdUOvKIICvzratblaXOYM0FnsqZq5dq1aGrMS67d4tqMiorPRKuNSKgrMrRsg4vObq4x1Y+1pH0VGbuu+ZQfrFq6ClJZiKbRDxgtDasghrq5HtyWZlsltmSvpXXq1DiKabA0DN4zMqCY9Fk/6AiYIl5dZLS/8YYbu2gWCMoKfQwsWwG1gbUha8xXyfmNcZe+6bjxjTXebWNcYD0KPDqw6xsvuGCFoOLSFKE3KAUAmtKieYB35oPbusNaLrjNXG11fYpF55C33ST5zcvsla0ha2S8u+EfF/dk06hngliXgOPEBGLlsLMdPK5Gmw4cBgg4Grdvp1bMVZMGECdlX7UWbLYPHea2Kofg0vWdelxnd9cezxwNNEEBjZUhmYWbbwK/o8tjZL3mlNey7qXnKQCNnikJ8wONowAsXAR+22aPXvVUgtfS+fCjcoY8ygQJWppgdGCjx5EwjWL8tsTJx7VtrocBBrIEwKZqMFmy1CTK6J1VyLOfd3uSDDa3r++IPA16u8HjXGyxxMz2rNkmOUzgtXU8eD8uUfAacKrEaxonwLKFELDsqHHyPnMs4KhbthibEIkA7YZPFQlSHDz+BIz2d9greZuet+uSVZa+asuKs099K0vUPCQMhVLmClmazN0dX58BSikXWYCuCpP5IrmBSO2g41MRIJKF3/5xm9/X4zAknaZNTz0ECn1SFK7fva/Mn96jyX/yMzd/Qel/yQIlC5QsULLAPi1QAqD3aZZv28nly5cT8eeyIUPQh974k3/wbmtnN+GG4JBLBU1ReeITO0WUN17iYWZMmpRUro1kHk7Hl2sokampSN3BzzzkKhEG8ccS3JPKTIpEb0rEPwQgXA2QcMhNBqpkTEf91/QCvCHA7SnueiZ+Syq8GaANxAyODAUSWNFwoiT0g/oBx98kSFcDXJbofxnQmSFLZuhU9YNDlgNH3lKCgNpPpzNTusN3JtINhMaUIbsO0U0iFdUjWiFNSKkWJ7X13h7hFgC0iwh4IyCQH2rg8JMMWiSAZgXm9nbezPfMSrb/46nHy4YMLfsuKkAPGzascuQoEMiGPWqIIoDg4G83hZnzAR4c/CUq5bBkgZIFShbY2wIUgFYBCAN6o8MALj14zAPHjluRYSFJeHx9KUik4KxTN1TZG6tMcfvwzhp3y6wZ0NUDa9fBxOpW2xFh/wh5rEmuNTe890rBIVtRaqSDAwQgJAVFdFHg+OfnbnXpG7yVGefI5PeP7u8OQ0aFNBHHYBWoWw0TRq8d7e2368Iu/c6J1av4FDJ5lbxyRVHsuUMuq8gC7GxAh28TgoKzUp5Qo7gdq99/H10dZgnpWEDJAFnUVFEClYOzT93srOwZ44FaJwRd6xsbMSoqAVHowZEjrqHqhc201mZQXAbVY9lxw41d0RTBD1X49xxwH7lxnFEIVSbGOLc+ch9O39My9qsSIo08kcxFEwjILJNkBU0EgLIY55wc9VdmjwmAx9J73HErWjogzmNPj9IGMmxeD2MDy5wjGquNyVpL+xnf2xjrATYDQk4rK28DMsdXJAiFtjosnNeo+C2ts2+TB6LIzmZpycnghOQYi5MTudZymCzDKYyAsVBUWQHI8JBk4KST1jjNYbdRc44aOP+MHpX6K8wnS//nZcTVLxGAltDZG6JWL76IDGiXNWEzxr32lklXDZZc5mDh++DQvesc0Vxry1Tbus45PfnBOxAbgKcehRr/rmoX67dIHkOixr8qS1BOmbiV3D37OJyhg6AMC0uXQMBb77IwdiPjcuz41xVdQmFJn4V0GJ57CjzupXpT2GZjqr1tV/8d1xOIzw4SC2k0hZaDLgjJEvyvfjPgsnc5jakaX//RE97LcjmJlUJ1EMYzryAGjasdqPvMwt9+EzvW01ljDI+2DvhM23/3q4HuAWwedHsbZU3zCoLqWQFefQ0BaLcRPHrZb9u6Zh02Oz5332GJ0XeHCOOrt/lMjMeQOLqq8eWXcUmCLPmg+Nq2XXDs0Zvdxq4JbqXWEvGalr/8LCRisGY5VFl6veWqu1z1WtrP+OHS/gRwpFy0FdGcUAA6q8H9jwioiVwhVrvYS3+LRNrX3wSb7r0Jvn5PZZu7ct3fL+nNoIYKZKUkKyG9gRUQAo4mYclSGB3qCtrAbQCvrb61jaxWYYnxhlHJPowMD7+6cMBpbnIY+33W6NjArhefh0Q2V6tYJHzjOJneZykO1m6AKv8aj7nPoYuO8fdOvwF1S2Qcp+dqn0ccHV59BbyWDR6d4MXUdyxehgsC6OaEgYvOz/jMsbEBMAxvn1CzdVUdcqsZIuSdksSMktuPkOTxrhfI+J+C+/tQq9+j/X3FX8nyzhuvSuPH7LSYGZOdM9sEh1nxOhrmL8BmKaiQVcSMJHEidO6EoHXleC/nNca9lk0vP49NiLYp3OJAjjISDMTgF+e1u8xbbcatTvOqadfDA/fKKPBHrCfhsg6q8pQA6K+4qj9HcqQn0RRcb4UdbeD2z/c5+q3lu6q8H0b7IZvXQ8/FnJ8V0vsonxz9VvyZ/6X0v2SBkgVKFihZ4LNYoARAfxZrfTPDKrKycuVKCkCTzyEWh5d2oSky1MZhpQYpie8FpRFgriJcG01fGRNnROW5CWmDJCXJED/viSU/tiUKc4tY6f5o/LpI3+xUerkMYYIUC6gPLVIeAR3T9avQBvAuD7M5cVo69VQmvVpTwrjqLAq401SUcxsWcYL6Mcg393Zfm+avZdjnCRM5QqLNEhyZANuShgy2LAPqDoD7kuEpPR2PMMJqQmqmIDWr4agQqUwiUqfbAV6F7NR4/O6MuohF9DmNPBfcZYkE8BzXCedUjIjODN8ThTl9HU/FezYC/PXmm3PWO+SQsrKyX194oSIjti6iY6qiaVDR4TezpZRyXbJAyQIlC3x7LECfzz3d4LGvtes1p07zmLrO+1k9S1BU9FGWgdmzxXH+Jp8uPM6RHOve9NECiCTQjx8rwkvPwFjvNp++Z5yTC9k77r5tXwB03loUPRYB5twLQccOe/lA0JQO2bY/PxfdXsVFiIoo0LxgIRx3TLvD3OazxwKWLo9p0ZplwHPoS1fKie2SGIvWNXGDDoESr/pLaoyzxVuZtgzvH1/decftSLHk8uRSERSyqKrIEqgZGONZ5tTHLSNl41Gxo0dvIJgRrwJLdosTdRICDYIK61cjr9OmR4Debdv69EvoYziehAXvQa11x9E2zXNk1Fe5cc4dXE8PripnFfT6S/iVCHJRVCxvBgQrVQXuv0fyG8KBCrAfyXpN6597VmIEDCwSJ2CLP4LjxzWP9Sb9xniVrXV88P1Nq1EFTCbehKniNcJoJG6Fh6YG8Li3Br3g1nP28h03TUX08P9TeiVZkHhJlXAPF+aEGG0QgCYqK6jRQN5UAQzBRAW2b4eAZ4VdH7VXss7K5lunkNFMrixNm7QAAAAgAElEQVRUJ5auoH/JnTpZxEcjsAo89SQC0FZD1G1JBOzbH7uXmJCs2isZOPGY9T5zc7Cyp8qw7dfnbkeJFQHlfRMJ+O2vByyjmn0Gqcomj69qWLcBV+NFsikMraDmFpdZgRc1tVCA8362w6LfZTfzhoreKv+a7h4i1U3qT8nAPbNli3GJ1x93uFV/IHHuz5pjxK8jr5EoKJKNXGaqa4N1Tpmw48atc1gHHIZkyL1j6vROhmSSlIRAlWSBX8HFibSAwgYgpOFvv20b62pzV8QD+rSzcsv559RHojjwo1LLElEpURCmFymB/Q+/7/A7evxWzVUZP2HC9kgit5ZAUsEPXoWt22BiTQcCrKasz7JqG9kWgDoVIkQz8Ke/xk2GBrclVW3uDRo+XEnkLzTAEeQ/LoaAIe6r5EK2HpvpufYulLLBuifDQtIAURgWJbJluH5KMmDt81QqbmPHzdNgy2ao1L3otG7x2dqcunW//2WXyGMdkfbGy3gFJ4MgajjQfPYZcJt2uvQQsGgB5zqWpQZE9ja2Cg11xh99DHz2Br+Fs1ckXKb6mTOVgQT1i0gUzjWCc2qShtFylJucFuD00zdYKhtt5fFqZ+LS36TpwsCgcRSsthnTupzGtU592meRfK51AwPAZFCBfcY0bYy/z65LmyvCE0dvX7EUhXHoi6yooSAy5Wnk/bWSGy0f+8EFxZG9FZf/cbPVsMliEqwuzeLgTYb/x955gMdVXH1f9O4ibe93u1bFBYeWhAQIhNBCJwReSgLBhN4hYEwxJYApMRBKwBBagIAxYDC49yZbtuWm3rW9397O956ZXVkmQEj5XmKy++wj7Up37945M/femd/8539i4xs3FjkckBBTeJVVFEEELgshx8fumk6fOc+YWm+7QRFpZk28isi6Jmmaomi4miSagMm/XXP62fNenMkXiOCZJyybrASlFn+I5YdDUY5N5fd/SgRo1dAbFUrWFbjuVs7j2eIyDjZ42x57sIjpB1Xg5PJUz1ce+HAlD7/4yk0r/6hEoBKBSgQqEfiaCFQA9NcE57vwL03TVEXdtm0b1T4TkLrnqNE1m7Z00OQkEtFB0+WRA0hp4bZCfnKyeFdefzmtrxMxWz0ZvqGzIjo6A3B5HEhwACvy6tPx7F3RwQfy6Q90DQcsZLhDZMcqWW6LvdUc4cLvSTAtlpySz/1B4Fbpagz1XjjSk9D1EVUWPElFuAlg2kD/NJG7PZp4NJZcTyTVWfJfngwDcGCA0JjlQGgD5T0ufVv31t/nkssA4kTxDBoadPCAAFqVUfUwCPCuJk9Nx67vjz2TUdpkYGWQ8J+cgGIsmShzcDzAoSgbFgna4929z8YGV6uYTmn8D47a96CDRlVbqvbaf+9995/18YfEYASKoLGgFmWRE4kCbXio911oOJUyVCJQiUAlArt3BOgwcccOBNBuo8oYVK+1Y/KVfTIgEeYAFi8HxjFvUlA8zK+7R6987QXkMkURbxCsBP29MCH8kde4JezI+2yxiy8oorj4b0KCFgMykl2OiC5P/lmfsybmM6uMaeCYI9fwRcgWUW+YEWDGc4rLvoZxZF2OjNvewVg/fXMman5FBSER5aSl/ZcBNFI5HYWKjz/C17s3TvIrQYPgHtt23lndyTQqIcm9G/kUyfeLwEiSYdln0Mhs9pqL9rGibUz/ySe2k7U9BQ3yGqqxkexR0wZNgfmfAmPrcNaAuwYB9KJV0JuCYhHOO60tbBoMVbONrr4Lzuge6EfHW16holi8v5N5211uewKHY3iBhx8dtc5ySIoZC+Ocws9+2IawmKxq13R44zWo8y8KOWJhOx909Id8C959B+kqBkHFZHpEXMur2CNAiKnLKJf2edYGvIqrJusa2zU+uHHLBshlSLLgcnV8CYAmC5wItEOGSIkywkQFZv0VnUxcJrQDtoxZvGAOrv8ivRe6cJu6a32pJUr5+/6p3yMB9OPTwe/ebjclfbZUg7tpzpsEwUogpuHNP0HIsyPiLoSMbfW2j5vXlJy1kXwpMPsD8Fl2+IxKyKLWebe8/z669GoyoZg4WYEhVDQNtfDEnkIB+GQO2E1LGUfWbs667a333UucnamMU4Hf3RKz2z4zW3o8jGBz9vzoJ507urC+aBtEho2VTFGpUoozafO9g1Af2YRZ2qxZh2XxOx9IGQ6bMXkQiweikkW2AxJaNasw7ebCeHeza3TMVVMMOwZOOb4rHkMriYygCMip0ayDeBpgn4qTYd1KCLjm+R1xD7pM9N92vSaW7L7xi+jJIqjw4QfQ6O9janS/Vfj+xPZiDBQWOJIhcMazUGNYZjD3e5mo3/zZuzOJ5AE7nzjlM/0eiFhag8Zs0DbA2GY3N2O2SYXI51FFjGCRAGhiB33iCevDjmzIDD5Tz+y34NL/Abt1Q8DTH/LsOHz8oq4deEoQPSyooBFGXEBbOR27uTddm44wsbH7xAOOzOmn9AvYNcWmTlq7LimQy8KPv9/U6CuO94HTMOR1L+oagCxJny1htYvoi4PZNmWyhECUiAg3r8Bxxy+t9aELh9+SO/PEmEydosvtE887AW64ut1lXO21pD22wmETt9LArVgEjH1twCH6XVJjXfuLz+2kz5oiaSpHDk9WyaWCXJ0wFCMfwxyOVsTIf30LrxVI9cLPj2lymtpsZtliB5tLcHu6L744xokk0NShiOjl+SycdPSagLnLZyp6avou+kVOKgNobFaqgF76OicpKiuhcT9dSSDgwAcbiEjOBzrSUbDaMaL0+S0UvPKVXxkBvJ6TpAB4GVPI+qRoEsL1a0OhbMAcb/Cs3NqMFZf7QuaBL9/hcCUPv/jy7Sp/rUSgEoFKBCoR+PoIVAD018dnt/+vJEmapmWz2X333XeECHrPadOfoEIHRYeshEO9OMACgPt59YqkcFNKfEWFJkKfyXhDJIlMBHIjxwEzB7BKh8f6em6Lx6cVsnM0oYeGSiRKItIbpQBaIEh3GcAUlrsmPvQCm18J6hCKbyj0xhSAAuHaMYBlAH8oaLflhZviicc62taDHiNUOg86DkeIBlshGFoGrQ+kd/j0I/G+p4b6FmhqjPwfhSsIoFUcvCo4lEkCrAKYks1PHkzc159eqKNMm8e+u8RDvoArmHlk0Qpqn7sAPgJ1Rjoxozs2n4Mo2fLA0QdVYfZBNIF2+v0COaQkQBTUFCXdpOzl5bq7fZupFKASgUoEKhHYPSOwEwJQJiJq6ooVutexjgBo2WvbPu1BMSchf8pKcOklOY+xv9YGAWPsd9dzfA54DkQiZpZkSKfg8ks2Oceu8VlYl0VorG8RSgB657fQ+1JBUuj86J/fBbttrbU677WBz9H18osYRU1H79R778bF7x5r2mNjLZYuj3f+vIWYQQ6ZMTGuoGS3dPNE8orgD4GpBu07wGudw9S0hk2FWnPRa1zV2op7RraFmBWfRKuIGbQkCW66qjDeO+SqybuMRZel9bqrcgTbcSpkyJNXQZdID0AW4C+vaYytqwygW1q6EFH/4UkI2Nf4jT317p4JtQs3b8Ij4WVF0MjNExWrrIYp03YaR5AGgwF69w1wmNaaRg0wtpzbtO6dNyCXI97QMky5VTxyfKu9envAkfE7eyPhRW++ix0AOh2uUKStqyqidRJRHRdJsUWYMGFVXaTY4JMZYzpgjp99Ird+NdHwks/SuiYvd5IgUknDKQk1CqA1HQ287rhV8tpbPNaszz5UF5gXGwA+R/gE3cUXf+5MqPfF//yD76nIlyqg77hd9Dq3uqxZl6l/kndFx2rS2xCgcz1EHJ/5bKk6Rhznanrzj/gdnISuADxhZLEo1DFtAQug869tw4MPpkqTAIqCgFJDr+qy+YYugF4QYfLlvNcZdVqLPm/S7pjV2Y37lDjYvhZOP769Ltxtd6UOGpXweAdPP6t9SyvkZJyhySooziU7p1weXc7JnAByWV6Ejz9FWw/GLrjNGa97wfZeyCmYs5A8FGyS5MPIxgnBfvdFmGBfExw76KkuWsa0T2xcsnIVTvxnSgasJRM0DclzkYVcpghTbpWZmq01Bw14rNm6QOtHsyh3xsaLgldZxQrV4P77oyFHr9cAPrN40Zk43aFmQSzCooXAuFZZbQNGd0+wcd0zM/KgQz4vS1qB7AAWzIZ6x+qAJcqY+wKehZ9+gqqELwXQLA/hwFy3Mes3QL0j/+5L4DT32s39AXc8yKxavQILTbKJlMSw5JSUUQGtQjIK44MrnDW9ATvrNm+Z/ggePCcWaXJLlTTy116Cw+u7vaaMbXTca2+5ZyrEWcjpClkdwSs4D1UG0DqqkksAWobjjl9e6x3ymgQE0D9NyUKpzohyREahdxEuPHeD27Qu6MzazdHTT0rpBYzPr8/LBxwpl1W3mjpvvz3P0fMQJFWUVEFD2TbafeD3UoRHZ8hK1Ut+DXO4kSfgyA3+T19LMNACh3qaGMuQzaxa7WC05A2WRVMfyPC4ngK1JrRFSiRF6m3XJhqYHq+x4DOkj/5eG/po0Gk5vPDymBNd53VdxYsSoGUTlE5QvHcoJNMjdfijs1XDofg/LXLly74uAtT6sUjnXCWtdF4/9nje499it6QDpoFLzoiV7uA4p/B3H8OVPPzi736kskElApUIVCJQicCXRKACoL8kKN+lP0no3oyPAw44YCeA3qPq9PN/QQeOuoZZnBNofAH39A5ek5auiHJPFmANwazY80KdCV07i2MPgXTCNurwx3Tulp6+aTnuLwBtBArj/LJIXqFjNPZ+ZZKQcB3AtGj2Oj4/VSosARjEzp1U3k6RNLTI4Ij39EyAK/uSt+SlhxLZ9QA0RyJJSo9MGYsh4ZcUAQYA5mazv48PPJQa/FSSu4iLCG6ASeYxSb1CErVkAHYAvFTQr+yP35LMfyAhZ88i8tZFKLJ6OocdSxF0XB2aBFggaE9mY9OTQwtUTHuY0WDjjq3luO25d9X+F156KQfQB7AOlDcHu+bkExtAjpHCVAA0aWiVH5UIVCJQicC3EoFh+Sp+O2UivARzP1MCjmaUPxsVr71l9hw0hxUAPp4Htb5tIavMGPJ1zKatzSjdxQ8qeOtCsCXDA/cMBGybAlbVYVD8TLMg4hQngK6qJVpDvgj5Gq/DUA5OPWejxdLhMKkOM18X6kjFcW+L5sEvz4z5jAPO0ZzLkLabd5xw0tCK9ZAjrhQ6YtyihCpJlJ2S+xxhHmTXMtGB3nMnuGq2NDjZsDkVsrQ8+zjk8nioZD0Q2k+QzFnoNotybB6OnLCpzi04awS3Oed1tjz0IE6vSmj8gL64KkI/HSWUhEI+/weesfa4DOBCBXRLgoWBFHx/0qY6Z79zTMuE8Pq/vIVHxZa6EojLie3HlwDobDoFEpx6fFvInXaYsyFvIuhbwuUhn4HF8+DcU7p9piafqc9t6KkLdZzw0x0rmpB1At7T02jGRR2ckVyKBEALlArLKtxzX9HtXuE29znH5L01coMn3ehb8MwTah+Z+kZviLICcdcXCmGmEvpT02zDGsgCnH1aH2Pt81lQgn3iCSsTSeIMigfyt49SH6jcoP52g3/gL9THjALoqyYn3bZtTkvGbew6MjCf60HjFI2HO64uRBytfjsf8sQvv6BHZRH1ChrLIsnEiojHYWJ4S9Cmu415t3nj1ZO7SkeAqIwoZHWckKAr11gNUjlwWFfYDUWnVfB5e++4Uy8WsTSvPQth8+f1jh6nMW4YO2A2t15wMStIRIFM9siBlGLTKkLnki0JCSYugNM0TOr49NO8z9nmt6n26oHvHbo6zmJGwxKARl8zBVCvjNpCQYOeNjiidrH/oNY6A+8aMzAu3PLOX9FuWAcQdAKqS8VAn1YJgwEbW8Fh/azWzdd6wetKBJmFPV3YAyTeuxgKlcy6yDL8+tIWxtzjNYLXkr3lKpDT2HCkIpx3emtdIB0KCK7Qpl9csk2QUfot4Vq+kvly12YY51rkM/UwpoEwg17AJQBdsuDA1kQngTraoLF2tWVUgqmGcU7piLDqtXE2U5/FtOiVmSPaQDmRNUHuugSqIMPbr0Ktc3udW4i4czbD55/PxVJwUlbTJBoviYdzTur1Gbrto5J+25DfO3/jVsipWEYezzwWATTWammCgUJPESAvwjE/abJVtzrGZutduV+dL1AATRNrk+kiTEl66gnLfLYNdb6c3dJ7yYUgZJG8hyxbg2bF72AnjduKyynImajLBZkjE3TY89fJckOZTjzQM2tEUXc56Ub+/dt5LUH3RpjkWV7n6mYsQyZDeyDcfNzPFkczeLUnjiglAK3quMLj2aeEBl+n1yAGDFLQsV4hiWswbuiiIlAATZtzjlz7qPYF5/zok1ybKIMeec35dspe+dYviQAdLOY1vPFhd0CQIZuCH31/BePu9boyhwbaNy3HK6Gs50nlf8kudv3TyHr+27Nh120r7yoRqESgEoFKBL46AhUA/dWx+U78h7oVA8AJJ5xQBqn4e6+D9h/WLLAAKzWYluAuG8hemxWnS6hEjhFhcqmXTtP3kBFYCmADwO8H07cMCHf08B+KsI0gXdwb9t1U8lMja9QQR7cC/JHTr+1P3ZbLvEsSBqI5Bu6XPlVBV9MAnQDvKIXb07FrYrE/FJSFOjJxXDxIeDc/rKURdVlFML1Uh4c7o3cPDrzMcVsJkib7ox6SmESEdhzjAH/KwNQYKqDfJN/CkX1KoMhqQZQznFjkFUQJeYLgH+ruvr+r/ZVUNEZGehLAI88+idJnIh/f96D9li1ZJCJ9hscGo3fFk7cMDj0Yi/4llUgDWTtM3Be/Ew2nUohKBCoRqERgN4jAiEGhRgHZ8NCQesi+9boUdGzzGcBnlOzG5auaIatBmoXTT2+dECr6LbmQZ92T03FlD0pIVQWtC8hD02D2exBxdoQt4DPpYc/Gjla0icChLKoXUWiKhIZAaVaGLR3gYD53uwoOq2639Vz8P5BJwIN3wXimlxmVD4yFBjvUetvOObcjK2ISArL0RyG+zEUJF8qX7C3wTlsmcgrxCXGYVnuq8yGz4DdvO/+sDcV8CUDjsJpSyeHbOcA9d2Z8tk7GCk4DeCx5P7P+o48xlRmvFsmtETkWyjPJRxQW7ryxb0Ikw1jBZeQOHdeXF+DJGRpjaY7YEHZfeUlcIGSKMq9SZPAXJbOlA6W3cw2gpxs81qVem+CxigFPdPJvtOgQ3HEjjPe3BYwJpjobsmfC3pbLr2jb3AFxDnXOLOaly5MMiqBomqIrJD2DqAOPM8WAds+8CDfdNOg2bprgA8eYYsjGuse2+UxNxx3WNf0+NAymIA8XVBHvaEkkPREkpeh8rYBAy4ubqVDrXuczy34TBO3RG67rpOiN1jkt4K4/FTqjvusf/5l3tLpk0AQVfnVRzGNutxtSfkvXWT9aDTkQWFi/EcL+NX5nKuRhJzbu2LGFTIegALVUwTjHIsPNv4WQPeMypH321rNO2xQfxCaDcyKqpGuCpml0e0zEJ8FLL4Pb1uMwgsss+RxdH74PS+fBr87MHcl0TjTHJpqz9ZZBd82iP86AaBwLhfFCTQCK+onVgKiCSNMwEiUsAdAqKtNvvj4xqV5yViuOmt7bb8GWuEvSQkUCLY+6eUCDmrvvgfHhfscB/fWmbKO75aarUbjNEzJEmvtwC9ZFTc0KqEu48tbusbaNRpvo9YLH1XXSSWsU4vwybOeNrVDCsv/wiKWMaYAx8j5Hz6svYHYRnYXp9+G0TcBZdFo6a/2zd2xBnxr01CBdWdoe8oOoN2eqO32WZNjVdv8UdDtBBTRt1+Qn6tYVmD8XIp4myyEpbw2ELap7TLqeAb9n6xNPF1LEPFalJu7l81HDkuPUlA5w1s+ifmMqZBUZc9f3D1uRSiELk7QcWuKQmm1aDQ2uDRELH7KKIXfHb67oBEDL+CJ2gEUJte8EQBOBBVqskNbHA57X9fWrapmY5eBey8Gbb78B64Wak6D+UxV1AK4AR0z4IOzeVu/Pe129116L5iTn/LwtaMx6R7N+46q/zMTTh5dI37y89mL4EkSitbP5jbje/jOnwP/HzyggZeHcEz6exCz1jP7gLzOhrwenE6h9DJE/ozCFzOsh0V+yAiKe7X4D+A04PbCJWDFoGs5qELZMJl1KlzfcyfD05t9C5+E7zv/H0lV2/Q9HgAJojl51cZGNDO/MhIizzXBQe9DTffJxTWIB61XD8V/p0vUVXzKy1Y98/RWbV/5ciUAlApUIVCLwtRGoAOivDc/u/0/auwWAq666aiSArqqq+mjOx7KMXsmbdXghyV8ZLf46UXxMhs+J7TLJkU06WuQHdqaJTccKgAdj0Wk83B2Fl9PQquM4gfaGSU8bpWA0oY8CsBXgbVG6L5Wdli++rslNRNRMe3K0P6vhX7ROgFlS7rH04E3x7ruTA/OJxBgZgILDAHyCiosOBVURkIyvA3g8yj5ZgGeHcmuIyJoMkDUd8xihATQoiAZSAO+ni48lYEqv/LYOmwFw1SXmD9F5lVNRYcMrEicR2r5cl59Ix6fn0zOjsTaAmCzh6AiU439+UtUh+1btXbXHqH1842t1VHDDW5xyy0Ds5mLxukT8KZ5tAqgA6N3/XKmUoBKBSgR2vwiMGA5SAI3YmY45RXJnem4GG7Bu9ZtUn4mb2LgN8+Bp8NwL4DSvcYyJ+cxdJxy3XJSJ6lIFXUP3TwpfFA3Wr0EAHTJDyKJH3JuXL0YYikNZqTACQKPjASvBex+D09NsNOXMZsXjib38PBwxrrvR3RE0CBETOA5M1Hs6/vAEpAp4J2JLQ94SIR0G0GT3ZFRMMLgKcNPNqaB70DlGDNt5p2HBokWlOtJFopAsWUugCFoSoXkVBO0LPdas0wQuIwJoH7N66XJc6YN3PWJuS++qeAvWQGXhzhtidf4YY9Xc5szh30uk89DQMDfkHKp3Z46s39DTDoIOBczRhVH9qscwgP4UHaU3MmadMat248Brr8Lhh+7w2/saPHLQwjHmPr9zxbPPQE6ArEqMPEBm0QhLwNVT+jCARkROHXIBIFeEAouEfsYT4DSvc5nbA45MvVOst0n1lkKdbccRDZ++8rySJXnzEFhTExU0w6XhLaKzsIIwSZWgvQVCru1+E/iNELIPvvY6SnzJtAK1Cf1CEVGvTDD/F/7+z7wtA2ik5Gef1uM29NhrMn5r693XDOo5yGThnPM3eD09HnuOsW+dehdq8GlljfwyRYYH7oagrcdrSYfd/UdMWIJtVkDHCVAUXeO0kgE0nxMxl+Zvr4w7rQmHAVwm8JqHnn0U6p2Lf+DPTTBkx1cPRsY0n3rU9lXzIEXoM+2e8ejPgTySAGgZATQBoDsBtIJJPM48eYfPmgs5wGVuf+Jx7PmVtAolzxK6BB6iaaJl9i6yW2MhC+c+eMtxhy+PD+KkAq+WSC+iZF1XZVFVUA7NyvDy62D1zh/jiBo94HDpDseW31y5FaXsxJemvFYAz6KBHjhiQlPInfZY0zWjPl+3GqPRtQ0C5vVhm+w2pgPO9TP/CFyOOGWXATT1QC/E4cj6pV5DW9Cci9iHrv61jBNBIwE0yW8pK/CnZ6Ge2WYblXWMAmaM1OCSPMbeM07rTeVJdOgSftqCiHl4gczb5Hh4fxY0BtqYGi5kFYOu7dOm5XmJyo1FgCIt/5svQ72zLWJWwxYx5Nky83WscDINAAJKyMsWHCMANEZJg+WroDawxWdL1Lry1jEr/vwyWpyPANBoTyywcMT4j8PuHUFXOujtu+M2mP0hNNZush4Q9xw0cPvkgkoyvXB86mtP8VIbHHG9Hdkq/wNel49s3VxoXQV6ydcFD4zYoaAjjIKXSbyOCQA7uiHo2YSzUEaotXd/NgenrMoOMrQid04E0uLRqTu6t/K34d7o8z8gBJVDGBkBWs/YH6DzQOksnPPTXNCUrnUWXablf55Zmk4mg1a6yciPj3w9XMlfeDFym8rrSgQqEahEoBKBbxqBCoD+ppHaTbdTFTQEBIBXX311JIDed9+9z/jlBVGAVSK8nIU74/xvMrkporCQ0OcC9uoFAdcFcySZH/7qBfgU4FGhcFUy/rs0+6chrZ+IZbC3u1MmoOMiQfLoBHilqDyYzTyWHfwIhFbQExoufSR2HiS/CyHXfUR6fF8scftg/LFU/AOx0Ed63mjjQSUHmASFx+GOoOYU+FSF6ax2Rzr7TB6Np5PEkFrADiVmYVKwA4k5CrMA81j94R0DTw7xr6bkDpILEdc442pGhUOVAw6rAH2c1QWi8kw6Oy0Xn5GOJculUUErcHkatP32PWifAw6+68lnOgDel2FaPn9zLnlHNvpXgHbk1yrmcNfK6ecrOujd9GypHHYlApUI7G4RGDEi3AVAi5quaqj1nXZ33FW9IWQWvKbUWT8vFBXIS/CDI7fXupMRez7s2TjrA7yJYYJBooCmk5iYo0yDRAwi7i1hsx62qBHXtjdmqngPw0fpF31D1I5w+126w9Ph8Ss11XzIQyx6a/K15qL9wF6/ZeNvLu1raiYuGMTAQigRbxRAqkjGUP5M5n1LPENgEYoO9oPX8xljTwQcstvYcf5ZQzxJWojfS8wI8Iaq46wrAK4vvuwXxYBl0GXhnOYSgGYcy7e30ry7ykgAjR9A+wME0D5Hj9Mkeh3pH/9AfnYGMI5mryPtMGx+5glioIAgEgWj5EncPmixR/wcNh6YenfU7+hwG3SvVTEeOMQYE86xcaam6LPEa31bfnFea/M24MjRijjuF1n0ciCsUydeDzpmzyuZ8OKdvBTnbB54CXXr65rhlxf01/q2ucdGfWO4QA0bsaTH2brGOTec+ZPu91/HpMbxOAglfK+QvHYcCTkersqSFH/Odr+ZAGhHZ2cngm8eSV3JPWJEsSQyuZz9QnWP2OAfe7kTQMvwoyM2Ocb2uU2s27jp5ackEGHtSvA4FnnteZuh/4dHLO/rQZhI1ddlWS1WgQgy8CYAACAASURBVCLDzD+Cx7Q56MzWuqMR38JCCnGbipxcIgCa5nYuKgAFHurqP6YA2l0DfpMcsUbD1Z0TzcXI6K5JnpVPTpMVEb9o+CECx6E3BkdmBSTaUyq7cpcwjaZCIQWT6pY6quNBBzq3vD8LTdWJHLkM5Mrh5AS45sb2YG2H21FkapKN7ubXX1TFL5iHk68XeJzoUHT45FNw2hebzTGHFxxeqDHxdnvz9KcKrIgaAnR/JrWFZ7gECz+FxtDGCJP12Hs97tmZNP7v8gtjflPMtH/GPrb9wnOiRWJZg/y2nO0Tv1AHNgun/mR9xNkRMGXrbMWTfzxIAfROxS8F0DJcfXm01tHO1HDuseAzaHVMNuBe/NFs3I2gAJmgIackqTANNF6TMxwkU/DDo9ZPrM2h/NmY/sFhbdva8bSjizPwN0Gd11/RVu/oKAFoZkNHP5ZRJD1h0rOlSQjRLI76Misg86DnJPj9IxBw9fmtUp2bm1C3dstWbMykzeOFRVARs/MFOGLc3JCj01kT87r6H34ATv2ZXOtti9gyQdP6zi1kKgzLQcE1qYmv/lG+DmBT/I96lNAyvTCSUEkiHqOqSgpR4gwfOV27kRMhyKzxWzQCoHufn4G4uXx5pxfHLy/f8H6+8OLLt6789duMAFYRBdC8CosX4aRU0FgMWmNHHbohnRs+MnKS00nU4b/t8uILVT38dpeNKm8qEahEoBKBSgS+YQQqAPobBmp33UyWZQqgV61aVVVVtccee+zE0KPHbgF4PqHem4Lbs9L9svQWaD1kDCzh8C0vQFaAogyYrqUbUBn9iIj0+apY/ClWbSdIl4yHyuMNmviGZOeIA3ych0cT4oOpzFtCtJVYLMqCqOFiWVw0SRc5swDNAM9KxRsHU3fHCrNEkdBn1DKXlhzKpKsuiqBgNpXtOjyZ0y7vGLo7mVxCnTeI3IM4dagCinRw5ynChR/ujD+RkF6J5jcR7TMat6kgybpQdjQUSG7DDUrhuWR2al/0D/nEUsDcO/TBidxLz71wwB4H7IEGHAdXVR2ymYXXsvKDqcLduczDbHo26JvxGHQ08sM1rxUAvbueJpXjrkSgEoHdNALDY0Eidy2lvMdpTkqORLjl6kHbIU1hK+sz9V15OUqVX3sTvLatERdfzwyce0YPpXs0hRuCVnyFwZB1RJn17qaQhQuZpQZX+/QHs2r5BkFueyRmqNtFBe/ZZw26XdEDDuq122WPEYz7pe0H9jNjt31//Nb33sK9sjLe+AoqK0Bexkxr6OcxDCVLAJq+15BJs1l4cQY4Tc12Q2JcWK0Lbp31Hh4aAixhxG0XUOtbzMGjD6puY0vAJjqtnN0qOEyq25Jy2xdGYwizZJI7C/ndSIGniADaad5hq2GD7vzxP4ZjjgS7caA2UPz+4W2FPHoFEI01DuPJU9RwZzvnnGmzoQBaVeH8c7cE3VGPEeoZYIys7eCMpyYZcnUdPmnzM89C1xA6XqPps16UQOSI9pmny6Z0kPAGjU9FJfWADicqyyOqpJ62VGPLK/DSi3BYw5agtd01pn2cozDBJk6w856D271jFz39CCYnpPYOiOtwr/Sej8esFuCemxNBe1fAAj4DhFxbkymUeOd5GlBaGoqfqPY5Swy6dplvGN7oH32Bk+mkIgQRxoeaHGMSHrNkq16/ahF2iS76RS7iGwx7FK9t61NPFGgQ6Cy8qGIt0CpQFJj9DrhqVgZdab8jPiHU0ryK9KiwnnYCaA2kaBbWbAC7Y5bDPuQ0AQLoaj0wZihiaq03N0/+BbtpJQqfRUKKKTsWgWP1LIf0WeJBEUmvScHDFjU0hCjFQVOgYzuE3ct9FtY+JuNzrVu1GjICiqCxeumBUgCtQyoFodDHRkO7y856LX1n/rSbzREs9GXh03WIx+DE4zYHPcmID1xO8PmhemzRZm965330p6anDAXQqsyDDH9+nngpODM20/afHL+myME770CY2Rq0CBN9asSzZEszfhPL6ei/MQJAo7cxDxees7ne0xEwFuus8qTQNoHDtleiqyTFJ4X+55/eU+9MNrggaIWgXXWbN/7ifNwvP5y9TCUAmnxSJTlOUwV45GEIezrdpphldO+4UN8TjwGrYjLB0v5JQ9MFOPlHS+vtfWGL6jezYe/qDIeLJGhGlTKAxrScVIeOfjKEPmdYuPhC0WtJ17nAWdN95mktRZJfRcU0onjC4qmk4WXkiMb5AWu36eBBj33wD4+Dw9geYYYYQ8uUG0Ao/O3Z/GUVU/5b+TpQDlH57/8Jv1WltPoB46pBPo/SbjRVKjfJkS84BYK+JX4rhwtc7IP33llEO+Dh2vzq8ozcycjXX/2Jyn++zQhgblZyv5o6JRtx9NgPGJzg733s9+gLVJp3ozMSu0ipvnDAI+t55OsvbFZ5W4lAJQKVCFQi8I0iUAHQ3yhMu+9GlIrS47fZbPvui2bGe+5Vdcio/ar22/P8t967qTd1e1a5N1mYoyodpZGWIkBRQDlLnuigMefeO6pwV2Lwt4MDd+bZ6SluJUnZF5c0lBADDvQ1WddFnSQ7x2HKUoBHe9nHo/wHMiYM5HDcrYCCHXvSpceBSpFw7Rd57n6ueGs09bKMCQOJwEYEnSU5iMgCVLrEmEiwX0oV744Ldw/k55O3NJE5NeKUSEIaVdFzACtBe57N3zGYeSYHm8hwGcfeZIw2PI5UVPT9agHt+aGO++PxB3oHthM3D5aMgQWBA009esIRo/cYjfR5T+NZN92/WIO7elI39cUeHYquJAeQR0bBgsZiD6f82H1bS+XIKxGoRKASgd0rArsOB0vv6K9cHrJJOOP45pCpixkdH+ePPvl7iCVg/LhFo/feah89GPGvWLgIQQ+raKgVRLhF5MiEDyk6rgM68YddQVM6ZBYaXT3X/6YHM6CVIAXZiPBgNHLmIBJawTiyjEew2zjUJDriAcv8h6aKXB51xJJCFb7kTkRsBChKSyTQppQV8Ms/mUtEWdRkFEAqwK/PK7prhjxmzu8aOuLwNdkC2ubiLZFO91LYh3ANZr0FdUyzy4jyZ4YpVlcPOK2cxzHEuObni7hzlFqOsODAjxJt2OSLWhjrDoeRC7qLp54ALoPkNOTttu2PPIoGDlQzOmItOjFt/goAzbJw+IQVdV7Wb4WQQzMd3FvHZN2WZVOmpHhyIyb0DQ+GPulsNFnAhJnoEBNIsPQzxEWIX5E2luARaqGJHFomYE5UQeBg5gvww4kbvDWbak2ZiFEKVbOBmn5v9cpzT9vY3YOBok5ilGaT7wQxBWccu8Zv6QnZgakRTv8Zm2eRRLDiFwA00kRNF0ivYSct/BdPDVHSELKrsHULBOzrmBqBMesO4/ZtG+Gzj6Ex1O53Zry2wROPbUM9PHnQqRQiay1xXUWF1cuRv/sdUcacqnO3z3qdFA57OQqogqZJEn6JmuLh07kQDC5zufpcNjHshJBZqrNtOeaw5TgjIqPFh6xhpwsn+vGpCyAIOuqh+fIUQzYKm9fRYynSGFIgu3guMKY1XjNnGTUU8i6KJ1Ddz6pE2ktPPwKgszF461WwmZb7GdFsSLotTW+/MVJnWpKa0nNKIykWzz4p6RjdXusSPWbJY9c9TjAa+VB4+9KVpQjsFOsqHGjw0F1Q74kxVtZu7rjiilzvIPzkp7LDmgo6xIB5/ay3gScezXQaY7jtoVULyUt5w9XtEdeOgJGrNSm1js2LP4dCAcuL0g3i2qDpmNPkqIbm8S650Q0hByD6ZxZvakUt/87GoekaAVoSQKKIXdyV68FhXu+xFE2jBmp9XbWRD/M8Bra0YIEENZWAfBxCtvcbHUl/jei35M75eSZL1h6WU3rrEgoyWAWKaJCu64ou5Ti8YvzpJfSUZ4y8e2yhjtkxYwYXxSSgoGDbRxs6dKVWUKsecX/sM/X5zGKtjz3rVIh4uKCtx2f7ZEszrYtyZdN63m1/juD6eL3TSQvUlFKzGXmnUIlu/Ve/yjP2RMgOQUvilBM2FHNoE0weXxcQup/dNkj/RQdeKOB0Jy4FUGD7NmgMft7gyoQtifrA0qEoCqxEHIaWl1SUrP5HNpO/+/q/KJiVolYiUIlAJQL/xghUAPS/MZj/6bs6/fTT99tvPwqgq/asqtqzav8zzrx3IH5PLPMqx+8AhSWjWsC1wBzx30BtRB/AQoBHJO3qdP6aWOrRnDC7gPLnPEBakXgcVgs47JFBlXG8NwSwRIInYuLTRZiZENqJ+hhnmlEipes43sEOAUsSEr6SYu/PsrfEEs+K0gqiXCZDCxmzD6Hth4BiLTLC75VhZrL4QDJ7b3/6I+ITwhKxNnb4iaBLQZ8OtH1r0bVnCvG7U9FHsvwcsoCWVAwuHKYYmo54UgDNKvwpEZ+eTj4Q6/tA5RNEMFLQUKICABuWr9irqmrsPsaqqgOrRvmfXN/9dEy4pzf3RJxtBmiTRQFHbSzoBUxdr6HVCX38p7eDyvFVIlCJQCUC35UIjBwjlsuESkcFMFOfJsDhtUtDxoE6G++3bv/gXXjyUYj42rzGnM/WfemvOgVywS/I6I9MQIVMnGKRX2BGOxEuPi/pNw4ETXytvffkH69Gb1bU1Y0wCSWaYpaF+sA6xi74vEokJNtrOi67AJpW4hHlclDgEP7Sp1p2oaVHruL6ffhfTeiU2zcHXQ+8/Wce0QnhIFwWjpnUGzQrYTfYDBsnXzmQylOARaymFCjk8ThEET78AOr9K62j2tyWhMuZuPpaYAIJjycfCafCgSXROG6Gt0qNPMsKaATQCky+qKUx2O93aW5zYVwQdbLWsSlvYHWaxRu6Bjz5EA0tGs+S55cAGk2HTAomRppq3TxjgolBmBDO/s95/MZNeMwCWtaW/bkIeqfaXqr7FgAnvVMJuP3KgaMb35nzXloleJQA9pL4GtFhiUFjmsgMMa4d6oWHp0LQtvSwcCpsKtTbNO+YlKtm5W+v2iaRLyVyapp5DjsLhQH46ffW+W1DQQd4jblLz1fyHDoRS1jbX/ag0xJfUtwv2/jv/Q1tv2Q0/1o4D/OeeWt0rwXqfLnkIJz2s7aAq89S3R32rX/7deys8FxG1zHr8rD2mTYYRYXBPmBsc4LuqNecDztij99LJ9hV4gEtUQAtg1pQYNaHUBts9jJRp7VYc2DCaWi9fwrkMtgU6cp0Sp8JgJYlnCgpSfxlHdIZ6NwGF5yycVLwuRzOjJRYKwXQb80Er3ELY+RdxsFI6NNkGo+TVQVsasPnJJn2v+G3MmPrcjtlqzU26fANeC5QcTQJlyiTPHGk35lKwtmntfpq+oMmMejov/AcqPMptmre4wS7c03PEC5roHun36CjdwtceEas0cv5bWrAlZ46BX7/GHjCOX8dMLau807uFHMERJZrcBhA42QH6V0+NC0admwLGIWgSay1b3nswawkogKcp9xaw3NNKMKh/i31VgiawWvO+xzb77xL705hF7AMoBFfaURTyWoQK0DHEJx4SlvIl7dWF13Wnrq6lZ8thGgWu7aY74wWACCXhWQv1NoWOg/pdh6cDzvyl10iFBQUbdCVghI6F8sKrhzgyu0Byaoswg+PbPFbU36Taj2484eHbSryJdE0pc+6SjzEJcjGIOKa6x7bH7ZCHSPWMbxx/0G3seX6awZ4gXb6y9H5ew14d/o/AdA04+pwexz5QpLhrnvAYesIWNWgJXNoZBl6l8hA7Hq+LiDlqtudgvFfeax4oZLwNMLHA/dq9jHLgpZMyNF9640pVsQRpogDWXI/ppO+5cvLiEvYyCbzt6//K+NaKXQlApUIVCLwL0egAqD/5RDuPjt4+eWX99lnHwTQwzYce+89Y/nKjxKJbaBnQMrpGexN40BMwUTthD5/AvCYCDexcE0G7k7ys3Ro1zE9N4uEWMMJZLWIOjEB++EdAH/R8w8U4lOGin9MQw/hvzTbUjnHMJFSqZi1b5YKN/cM3JLipyXzy0Cl1s//m3OpSNgzSQGIQ3EAaFXhzQxc1dI3LcO/y4s9pQ2IfEUla0RVTG+dImkPX+HSd6YG7s8mPpHUrtKWVDEjDg+kWYAmgBdZ9vre2GOS9q6Y6gA5D6qg6Fkd8jqIxcKpPzr2gKo996w6uOogt+GUS+4bYh9Iym9GtQGAGCblkTDPul4AnSaIL+Nn4ri9+zSKypFWIlCJQCUCu3EERg4KS5wVpb2apKNIMDEIEefiBmsxaOBC7ramVeA09rmN2Vo363EsWbsZijoqN+k8JjF6EPG2pqF+ENWkMky9HXzGzrCVZ6o7G/1zhnqHBZXlJbuE5xIAvd5rlbxO1W7rm3ToVp5HiSU/vOimNFWKFJXcZRG6It6Ugc3ANZfEAjWfhExzXnwMJIJWAaBtK4Rs64Nmrdape6zNf3weMhySXAlUVS3ly+JFmDsH/K5PGFN7hClaTZvPOBvueQiqLS01ph6nqzMQWNi0Ad0/KMckC5ZK1IyS3ckXtYS8HWEG7NW8bYxQ54IgEz//Vz1FojXWynPGpImoxC2DJ/z9i21G0yHaD3X+Jp+1YB+jOqsLkxo7eRnJGeoNy6AO35QRjkLsq9ELS0MrgBsu6/KPnjvBOfe1Z4dkbpjt4db0E2rJUoMjk91oEMarmKpi42a48Pw2t2G7YxRrP0Su9fJe/5L5yxB8q0TnSvaFuDG+Aw4Prgq5s4xNCdqyt14HRRbTM1Jt78gi6dRim3qXjPzHv/ZakBC/vvS83OAZcI/Sg3Y4+jCY8Qg4DSsNo7f7XNvOOWsTajZF0EVOVdAGe2QLxw6aBsUC1AU+q2ViLvQzzV9yNhHcKoquKpqmKDhvIvBowABvvwX1oW67PR0KQsCXuHIytvU0BwUZz5UyfVZk4BTIKFAgImgkpJwAqxbBj8ZvrjWsj1g+6O/eWWyce1Hg4buBMXZibj1HLBJ+L5XDBsZrxHYX5fka6BqCUg2OOnQDY09YTHlPYPDMC7ZnRPxe0oRQXCCoKnWxWPgJ/OwH6Yle1nFAyl3dfcet8OYb6CzB1OhBD3g86wQVBL0wLDwgB6TJLBxWvzbklBwG8Nvkxx8Cq7mpmklWMz0M8+maJaRiFdB0QdUw498wgBZUVCRoAG+9CUHHDr9J9VsKYceWE4+dLxB/akHM0jJLImQTUG/fHhyLHiZec8zvWrR2A+6KwnaymUC7zgUBo6cB/Gpy1h/sCgYku3XI7197/4N6lse0gQI5hlKDBhB56N8O9fYm58EDBEBnL7s0z+FES07GMGNUiQ13jpx6wBPhQzID902BsDPtM6GQP+zY9s5buCWnEw/octI9VLjLkIlCxPW5a8yAt0YPORSfteCuTrnMSz/9HGt9eOJFHX5Fi71b/iyDY0ISaRZTHbH88NVnZ6kkBV5/GwyGJreJ9ZmzAeeSZJxGu6T037lp5dVuGQE8dUQJlz8MDMD48GrGNOS35CLe5jXrsKKJZQ4RzdNZxtL9/AuX269/u1vGpXLQlQhUIlCJwLcegQqA/tar4P/uALZu3brnngif99qjaj/iBb3HIQddcOMNcVRYQAGynJxEOQRZsFYAxMfzAR4XtWuz4hUJ5fYMvFhU20j3X0VtkS7hOKIASh5X6kqY9+8zXbmPjV+T6LunL7MKIEO0HqUFttQ+UEPHDon4Vzwcz04pSvf1C+/k9W7cC0uHQyzuFDSd8G2AXhneyMKdvcUbO5PPZLkOFEqTOW2aqlzD9bW6hrqSfoD3QX2Ezz7I5v9UKLYComSyIJHmjBI1IizjMG0gzAa4M52cmuRfLKodRNPFa7KgQFbHAfPyBYtGV+0xpmq/PfYdU7X/mAvf/eDOgehLAkRR40OqDK1EOKp9Rr3JiMf/XY1WvqkSgUoEKhH4747A8AARw1DiD9TrCaWmy+bBocGthv17Qg7NZe057sfgMSleo+K1dl13Lc1UhzAOP4o7Ugl9lqn1gwJ4R3juKVR6Bs052yFdEWb1x7MQ76EOk1q+qqgaxTU9RWjwr/eZZcamuKw9Pz2hLZsjvBizEhDpLrovkBy5eJRE10iMnrva4IqLByb4uupt3fWW+esX4J0S2RjAZx9CwLQpaFR9Jm5SQ/df3kXAxOMtWER5rwJ5DubNJ0NrY2cDw/vtPZG6hS2tMP1ZMNib7e6Y2dpRH2levhwpcgmWlYEmFoHEbvJFLaax63wO1W2UbWM4v0UJebbN+gSyuK4JkCPu5DfUwXgEU8fDLD00Hfq7IehZ6TQmbaMV51j2lBPTPEBOlziqs6TgnQ79iYWIQniZoCJWu+yC1nHe1f6aTd/zr9i4DBRiTcsVcYk0MbTFuiH2FZwKeQ37COjXRYl4QcU+yPVXgN9S8BjBYRSqDU0vvoJ4miZkKx2iAn0bocG2vNbH2k1c0JV+cCq6lyg4670LfqNzBKsXwx3Xdx33g2c2b0Qxcrmg/+xvsgMel0vBg/fEGzwDzkO0oB1O/QkEbcmQcyDiixpr3v/0c0zLiIcjivquYnlaEYoOqTSc+rPmENNnHpXxW4UfTuwVstghQ+sNGVeliRrqzQHgtVegMRx1u1ifX2XcvffcS7EL8jikLqUycRpkVUgpaJCOQctzMOdjGO9vDht7IsaO4yat3XlukZNMUeC6KxS/ecBTXYx4EnUEQKvYO+Jw17jb0nxHIQc+x2KbIWWsKZrs7ZfflMkRNxUMoo5Vy3PoafPwPeA1rgtWZ137p4LGjpuvwcmg6Y9D0N7hGSswVm3SxFZBBeLjQn1RSid7dyvUela5jJzHDIwVGpmC3zE41jLoDG393V3JVLJUWZouyHqR+r9RBs3LmFdTB1i0GILOzT6z7DezQXvXhMiyDU2QZ4FIz/HjggTxAQhbmgNjdX+1GrQN/PKcvgKx9Sit2sdY4mnOCmh9Es/AVdf3eH2b7Y64yTro9Gw6/4IdiRykWJzrQm/6YZE4EjLo3ATjXE31ds5bI3st2XNOj3Hoi8KRlNoYR/KCJUmzIZ9HOfQbf4awq8NvBsYMAWfsrNPaZQUSxDlEIZJtnRS1BKCHIOJc6KmOuUerzrGs25h1jO074tDmLLHGGxZxy/IIXfo/28a/1c9RjkgOAVugpuMMFEsumV8CoGUFli+DsaM+dxmSnppkY3DLkkX08Nm/nY76VstV+fJ/LgI4hYiDW4A3X4MJoS5PTdJ0yJYzf45ZH3JkBq50axs+H0mzIZdG+p+/+/OfO7DKpyoRqESgEoH/9ghUAPR/UQuQZXncuHEUQO9fVYVa6H32NPmZJOYzIg9i4awpQk7R+wBeV+COpHBtonCXqP+uUHhZ01pI4kEOR36aAiKRQedAzYOksirM4+THE7mb++PTksVFxIuDJWNEgpU1YkqIRpiioPcCvJ4Ub+5LP5hSP4+XODVZL4i9eCo5UrEzLycAFikwJV64LZF/JS82A2SxAy/j2JNIunii1JYABhTYAPBgPDM1lXu9oEap9hkH2zhqVYBX0EcPR+9RgDkK3JZl78gWZhfkbsK7ORKAgqhlBT3HSo3e8OiqvdCv5MADqk498pHktreyg91EnV3uyZaXYJdi94/94nme5OUGSZL+DSPbf+zLK1tXIlCJQCUC37kI0PR8BH5pCHaQr732IoQ821yupM0lOBya2wqmQxSvOe+xLu3pgaKCdwReVRXMd6fjvUIrJR7QkV2qkgKLPwdnzTLGNGQ+ZMhl6r3ol1p/DHIcqn3/+hoUs+iDIekI0Sb6m/01ss+oWEd1BDwLsxm8l/HoaaBoqMMVVUKpEI2wHOSQWa1fAhecmnAbttuNaZuh5brL2/Az9KHBB3+BWltH0KjaDoqF3M3vvg9JDvIoakRiyqvw+VyYVN/hNSe8RjZgidYyyxYsgawIz84Eo2OVw5Oz2fMhX99fyza4NJVfadQ9AkAz9q0uC+c2FxhTzmfOHtawhRMRlg2Llct3vZEcsnyc5d+ajhS+MbLcbUnZx+gRJ4yLbMuwmE1i+IHeGWXMpWlQ4JH/blgH554+MD7SGfR0h4Odv72iiImPWcoBMLkCJwqshEkLiT2KpCItTQuQFLECSwepAkT7wGfZxphydkPK7+t5+lnk9TKWo5RVTpNh2YcQMKyw1AwZDVm/K3HDb8U06lwLwBepWF3VSmnlXnwGgq4NDvP6gO+vn80dUoltBP05XJx/7AW2TPRvkQX45Vkrah3tnrGCzyy7TbzfKgRtSca24ZKLWnnSsUF6RhR5w+I8WmtUlv2/fPfO2+ONwV63gQs6IODqe+aPkEyjLcPGtTDvExTps+jfDe+9BRMjMcabd3lExpE97ZRoW99wDYCUZbHONLIYHZQCr+Yl/OBLL8AR43prrUmfoXeCb92fXwQWgWzpgV0fFS49P11ri/pqimFH7OgjmrBREgBdlmwriIsBtm4Dp3WRtTprNWlmW+wHJ3f1pHEeJp/EJ6jwzqtwwlHb/NVbGyy5SU6t3t56y/VDLIvzK9fdEPXbWjw1SWdN4vxz+UKpo0qFCqWDWbwYQswGu0FwWxFAh8xCxJxnxgzW+1f3DxASTjb8QhiHk5Qi55chxCwLOYUGF7jHZqyjNl1+abqIk1BYAJwsUkHm4aiGlkO96gQPhBzdb70G2Rxa3+AsFD5KTVziYfN6OOfn/R7rprA373am/XX9h/5g5brNaOEsEAOZ0tlXPglVBeQC+M2zai3poAl8ZjnIoOV2kSTSpIctqCKvCJJGUo4U4e0/Q8S5iakp1rrBao76a5evaSb7J9Sf+rxT6wlZIQroQYg4lvsMCfdo2V0juY3ZkKvv1hvQpKiAGRGxpOQ8Qh85Wp7d9ucXjp+u6Bxx9RpRME2G5AB4rXMY05B9VDzs3vbWa3hFIqOW4cY+4gOVl7tXBGhb0EHMw7HfX24ds7nOl/G6lixZiqb/dMFCaZaM3tZ2th16cn6Tn7tXRCpHW4lAJQKVCPynRKACoP9TauL/4DhkWX766acPOOCAPauq9q+qIukIq6r2sf3cDwAAIABJREFU3fPFN/6MsmTS41JxmAddAB+LcEdSuioPN2S038XyMzVl3S6KZoUIi4oayqTYLOjrOOWpeOa2vugjUW6ODoNk/EhSANF+vKThTR+76QWAtxOF3w+mH0qJL8akNOYRJ10+XeZBz4KaU3BBrAAIkRer8HBX5r4892g2t5aYRKMMBO0hUbYtkW9B+gywBeCZrtR9/elnslI3tX4udfEFFYepLPHRgyTAZxI8MJi7Jp69J5bqID1vUUc+zaL7G443nnjy2b2rqqr3PXDfqr2rDtr7kg+ffS7f0kNGIyNVUuURxL+n6nb/rv+/Jw6VvVQiUIlAJQL/cAQofaZXcASOCKBFFZ56CLy2XiuTNnkkmx1cVrCMFj3m9oemIbDj8XaiSbqmaJquE4mtRrAr0Q8igFahrwcC7k+9tl67Me91iE57zzEnbj//4v4JDZsb/PPuun0zK0BewNvnT4/qCtcI/hrZPSbus2589WVI5pDvkPugXlB5uhxHkkDL4lTqS49ArfEz/9j2eidbG8wee2xnXwcptw7ZNK4vmvEo7xq10TNadI/hvbbWR6ZDjIWeLDLqtASPPQV2QxNTUwxZ9IA5GXatnjMbIaoCMOsTcHqX25xJp0u0W3rvuQsJGs8RLXFZ3zVSAc3YtzssrNOSY8yJgKnv4nMSvECkmuWNvxzh7FpJCHtkOOHYtQ2BnHWUypjAadz69ruQpY4iGt6yVXLjxq+WgC1ANgtPTud99nmWQzZ4LX3m6qajf7RxWyu6W2EhFUnXSFI78kUyqLRHIQMno/2GQPWnGuDtmxfg7VeAMWyyjx60jOkO+TfP/RxdPiXcsgRDNRVaVkDIutJiihkMRa8jfebJgwLNUFfAfoiYQxonsKhQDjo3hzysxzPUOH7R5i1AJ4z/dQAtcCAW4ORjlgYsHV6DyBhFt1Fs9IHfNhDyzZs/D2cqMAPzVwNoBSDPw+xZUOdpsR6UqPdCzSGD4XDXyafkzj4lVc/Mchkf+OQDBQ0rFOTRbvOKgDfjccheq3bkxGR3T6naFFpwqv4jPZtiEdZvgssu73RbNrhrYkFzLuLacfM1STa/S01TAH3WyZ1hy1DQwAVMQ4c1rGZJLQuo20XJPNGq405TOagLrPbaOEu17HTz/saOG++E+fPhkw9g6u3cD7+3qta5Nmhqa7BkAqN7xzs233sLH4sjBOckuOiiTsa6xWtKeYz9V08GtmTJRmX42FeTRJj5sup1bHeYdJcNAXStUWs0ZWsNm95+ATLk7KOHPnx5+AJVQgCtwo3X8rWevnFucBzINrr0Os/W9z+APLEKIbkwcZXD8zPAU73aUx0L2nou/1U0jT1XJP64vkEGRUApxCvPw/jw/HqmJ+RIjT1gh9fdfsTRG5c2QYF0VksXJ3JOYUdTxyUaqLAuwDGHf15rjQeN4DdD0NX+17fRgBvXB6hQ4EvO6SqgLnvmS9Dg3uo6OBk2Qa1DCAab3p4NObJ/mkkSUbKOdaCSKS9ZgQwqoBf7jDFmrOauUdymRMjV8qcXSP+Z+KST6xKend/kNKfx/A781BRgE3DMYct9ph7b6HjQ1T79EeCwQmlj+Q4U8b+7CBQoczDrTajzrgs4Ew7j9mOPXSIS+iyV1VF0nmnXSH3hIvE1b3f9XOVdJQKVCFQiUInAN4tABUB/szh9V7YSBKGqqmr/vfbZt2qPvar2QDOOvarqvzcxnsvQImaIb/JsFR5IwzUx7oascncaZsT1FkKf6dJHroR9FQkkFtgB4Odrwh9ymRsGB+9LZRcoO+nziBTy6MkJRH28VIcp/YN3DAy8U9S6AOJkyId9YU3Ng5wCeUjAESsmM5SVhwdSj6S5J/sGlunIozHBDQ7M0KCTpB7EsX0aoBVgeqwwpSf1wiA6bwzRxZOkZ0HSitBDxo03iDAtXrg+lrwvFXsrl0kCCrl5FZ8KQLoo5gX1kLGGPfbYC42y999rH7/tw1TreiimCUcY2UH/FwE0Jc4yFQ59VxpYpRyVCFQiUInAtxABCg1Ko0lUHKMuUYTbrgFnTcrmVMwucNjBbVeC7uLRR3TwMiSLiHhUtHHAJ1FAEztnouHUEUjLKG2W4Zyzmn3ONqeVs1p5mz1vtvcFQjGXrc3rXnTnXShZ5clYd+rNUGtO+KtVnwE8Ncnjf5jduLEUibwMOaKS1AHSMXjrJTjv+M5x1u2B0b3hsYOHeXuPOWx5ywaycfkeo2nw9huy17TRb4CABTwWNRDc8eFcWNkMz7wERx3dEfD3uY1iwAJ+UyLoWr5kPohEIprNw9YdUN+42mrvcbpZnzcZ9C3pbgeVCDaHRdA7AfTFmxBAm0WnmfWaYwFTyzOPIuyjsRwefP/dOqVccsqd8Qb/gH2MGrKDy5CuD6xbuQyyKfQkZlkoFDFRYWIIba///DycfWrCbV7jrmmvtQ02ODsn+OevwyyPhD4jFVPQiZu4POdVlESL5C5M2QG1x5WIfceGNXD71UqdbUvQFA+aWJ+t+8fHruBViv55MveM2k5Fh3gPRJhFDmvGbAKXWZoQ6tm6gUhAyUS4lofFH8IvTmqtd60JW/s85vZw7br7HywUKaslh/YvThUrMrApOKx2UcA04K1RmRrdbZTdxmyEabnrjlSBxckTVMpSnwjil0JfDlcEnQXfsR3qnMuZ0cmwFTxGCDmhzqPX2fKNru2HBv/66QdouiJpkE7B9w9bE3RHAzYImCFkyV9zmcJmUL0riGjmoBDCqsiweRNM/z3UBtZGfIN+W95nzTV4+399YSZbckIGUSxZr9CK/vFhq4OGvohFZMb21nrmZxLI7Yj/h1o2S5Go5cWZJ/fWenJ2Q9Fm4Y22qNM75HR12qzbHPYdQU93g3+gwdMXqNl2KLN89l9AwJyQkOEhV4Tjj21hzH0hGx+y9z98D8JBUnYaD6w1sQA3XhWzGbvtZpxbYixQa4RGS+8vTtqajRHBfJkmDkdv+AVtPwigdZg3Fxp8ywLmroluqDMBMzp50tGdQ30IiEl4JFlHyfPky3rqPF2MachhbLrrTtw/QmEBevrh1ZfgvDO4kGeLaUwzY+kIu7rqPC3HHrW2aR3OCdFsh397BtFzXRLhsQe4WntvyABBI4RsyUt/GReKUChgSKlPkKrCQD9ccXneZ2sKWjI1e0UnOPWIteWZp1CEXZrZKr+gfWNVR7Yuq5CJQcT9ic/Ux1RLqIA2DwXcS1s2oSKb+PnQj5cAdPny87cH+137C041sjD5ol7G1O6qyXrt3b+dnCdZLr9rJf2vKg89wbHIRP6uFeGis/pq9l8XcnGMbeNzz4lZFhv8FwD0zk/tDNbwpeJrXuzcuvKqEoFKBCoRqETgm0egAqC/eax2+y3pwOnKKybvv9c+++25FwLoPfeo2nuPqn32eH/BXOKMjOYYn4rwUAZuzsJdPNwxJD4ThZVKySWDKiw44m4hEC1zH8gL9ezjbOzm1ODUTHoWyVtIPDpQ+UW7xaWFTRoOIJdr8OhA/r5U9qGBwXYUgZEH3VTTiwRAZ0EvAqwDeLI/emc0/mg2t0JVdhQyPILn8qpg9ACRFVRMQy/Ay4nC1KHso3G2BaCXI8qoUocCrT8E7GmjIG4bB28MKXel2VvTqVfYRPewplvDMQ8Oe3X49ZVXV+2zfylN40F7/eaB37UCLv3MaKJAjTnLDeHLuizl/32D39OnT3/00UenTp26YMGCnp6yKukbfLCySSUClQhUIlCJwC4R+AoA/ZsLdPuopMuO9NllB68973O0vPUaUiEdEdZO836c2iSzmzi3qalEnogAWlDh6WdzjHuJ1dJvsiRdjGJ18nZH3GJaGw5/tKYJYRmKcEWY/zGEHesCprzfCCEzMMZYmFl7043sJ3Nh3QZ4fza8+hpcNTlZ518Sdmyud0Vrjez3PGJgzOozjl6/o6l8v0QFnqxoWq6otLZBLbMs5FAMB2p2AwQDksvT72I6rY4OtzvjtBbdJt5niR79vba1S/E+hx4IhZwmQz4HRxy2wGLd4fLwLlfSZFx6+UUdUhGlmmioTLBmCUDrMPniZgKgZadJ9JqHAualCz7GvML/KIBG4q/CnI/AaVwcsMkeM9QyEGGyQffae++Ezz6GxfNg/lx4/mluym2FQ2tXBawtYWe6wSP6jQMRa8upR29tWox2BPgQMRq6hMJSSYDmTbC+BWWkLFmoxEnIIju74NNP4b57uy48d0Oda6nPsGUSw3qrB/zmtrrAglVNECvibmS03pKpulMDkDkYF/zQx2RNBrAblVpP5qc/6n//dVizBN74E1z0897x7mb/2NaIdfCwcMJnX3D1tZ0U+O7S2P7ZN2jprAAbhbD585Ah5q3RmRpgjGzI1RMJfhaNY9dFpW4wIwA09WEYSUEwQjxc9+v4od6uBgcfNINzlOQcXWTGRMO2Nddetp0vYLElQDfnW26MBh1tETuEjRAyQtjSecIPOmc8CbM/ggXL4M2/wrTfC9dex3k9S13WrSFX0WsuuozRkGfHHTeDyJJUhruWlwLoCcHPfNU9jVbFM6rbZ/4oPognFPF+HgbQmG/vf0t01+25CNNS52UNh2S8HvB6weMCq0W2mpOMs8daszRg/+xX50ZjXehPAgB5OSXpkE7DpMbNXlMq4lRDztbnZiCKJXVBTlzQQQEhA2f8rNU8ptdSgwDaa4GIOT/OsWbeRxBPUEsVPDfpU0e2v/MtdWegliaFIky+tMVvWuQ+qGOcBQKHFHzVS199DhT8RlkBXLuQ4+Gv7wHjWG03xEKeAuPprG9c/ctLhn58fJM/uNhkbHHZ0vV+udaT8bu2hJzzLjl3e2/rroH7ineqCk2rIeJaHzILQTMELRxj2XTN5VJ/F7b/2BCsXwf3ThHG1y732dt95nTEJjbY0t7Rq2ZMA5XHIg2XhcqfRwJoVYFiCuo87wQt3V6D6K4RGHNPwDNblv4fe98BJ0WRtt8zw8zsLhk27+zMbF6SCQ/1PMXDQ07PcMk7P/Xu+/7qZzq985QTE4IIKCpBjBxmPcOpJ4IKiIBkkJwzbM47eTp3v//vrZrp7Y2ALMou1b/5zdRUV1dXPVUzXfXUW8+L/2x0fwYdqFPT9TOHgMY/OAWmPBrMSdvtTQ97Mip+fV0pmQe0004suisgQH/jWFINpdt3b4KCjFX5GQ2e1JohBevr6uk6GfZ8Kj5jXt5rXr8W/xZtfm1+BfvGEGAIMAQYAseHACOgjw+nbpRq69atHMf1sFptnAV9EtptnI37ya9+4QPYoIqv+eWpYRgb1CYD3FMizaiETWEUzRDIlJAoYyAWoo77WhsBVoA6tebQOKH68UjtlxocIvbIJuWN2MhYIpqVOwAmldc/XNbwZn14B5GTVnRFAkHUo7hlGu+Cw+kIwBpennykYmxJ2eMN1f+SQ0di8w4RBTplopqBcys03ygBmF1fO7G27uWAspLkieOL+FBBQ3VDnHcLRKbjzfLws1XRp+si70ryVlDriPYhnc2EBFnSYP5X3yD1bLNxNivXMzHv4uEHow20+jhYRZ9NnXP885//TEpKcjqJynRSEsdxvXv3vuSSS8aOHfvee++tXbtWEJBO0HVd0zRj22+btleSJBkJOqdwLBeGAEOAIdC1EKAEdGz2Sa0b0cZz9CXbvSnlxV7Nlax4UlTXgEN33doYDaP1Iv2DjfHOmo4PDvqK8zmU+KOqxbf879Gzz9mTnX3Um1Pvdlekp6286Gdff/Y5PplkpMKoeCjcdeve3JRdOQOknAGKZ6CUm+7Pd1UXZh8elHOo2HvQk7ontc/+9L4VWf0aclIi+Sm+nIHf3fWnbYd3xS17UZeV1zWBcEqoLPGnm3e7M7cOLlDdGXpGmpCeGkxPa8zK8mdnNWakHs5xbb3rtmBtLdoX40Z9SqcR3vaJxysz07emJPu9OUJqctm5hVX/dV1Z2RFUyaBOEcN8ACnjCDzxcJk7Y3dWiuJN1VIT91w4bGV1GbpNkPTv+cC75abawqxqb7ruzYQ8j1Lgbix0lQ9yHRyatX9o1t7MnhsHu0qGeuo8/Stz+oc9fWq8/dbdcv0RyY8GibqoY9ugfgpIUZj7kjAs74vBOd8V5X5XlLf+5v+Sfn2V7+LzDw/N35GTsfGsggND8/Zl9tuS3bfU278hI6l8iOfgWcWf/Gce4kiUGtCuk5C66G9P1VAvbPLEoCvzUN8+EU+mlp0WKsz252dW5KcfKkg7ktLjYF5//6BUIXfgkdz0hZMm1Nb5cKjTWYeioh36zjUw3Lv+rCx/zgAlqw+fNaBsUOHal+fEboIEdHwAQ6NindpUCJ64Qt6+AUaeM39Y9q5zvb5zcmsGe3Z5Uhb89fYDUZ7IjRPFYQlg33746bBDw9LVc7JgcAoUp8iF6b48V4nXs69335We3L35BRVpaYcH9jnqSfO5kxsHeWoLPeunT0MLXBS+pgsRsb0FWAhKQI++cNNFBZFh6fKwrPqi9K9WLUUDcyKgG3MXSXch0FL/5qpN5w+qc/UL5mYoBW5wp0O+WynIKfW6lv7PzXsWfQlilEjEEKcdaJCgQ301eFI35qdFhnikvKz1Xy0AgSwakQzJqE0B0QfDi78tzg0m95NTBkiDcsWijK3TxqsysU2m1qxxLGXiwDBmDkHtI+kpqgPr98F1l688K3PL2SmNI9wNZ2XP//ANEQloXVJAkHSUfSkph8zUJUMLRFd6JCM1mJZal55e7cpuSEutK8qDjAH+vs6DORl7cjMWPPZgiSoQhejWjUcqEI/Gka+io4DMzGngSd8yJDc02KNl9WnMT/EN89QMLyrPTduU3X9DTtruoqzKwtTI4Ey+OK00d+CXn79HFGOImo1O+ozBOxsBiSw4CSEY/bNFg7MP5KfxeWliXtbB/7l5TygcU0Y3aLg4UMbwGQPd+SAzhTmzI3kZ24blgye9ITdnWY0P/0S7ecW7c6PGei/+wFUUt/nr7Yfy0ve5kxtzMw49NxX/vFQNHaUaf2xtdnvSAdo7Y47v1lCyyjEEGAIMgVOGACOgTxm0p1/GoihSwYcbbriBWvg6nc6kPr0x7OQ+2r3284hvRhQeFeApgPt88sRKdUEY6khFFNBFoNLMyD4rVCJD0J+urJuqiPf7y571lR8k3DExXUIHgWT6gc9xnyRHAPYBvNNY9+Dhyml1kU0qijMquqJrURHCPPX3TRiAKMAegNdq/eNrAw/V1b+lhdZANICjBbQLwzGFooOi65glynR8IfETyo8+40PpjwY6cIyRCOhAXgIlCmojwEGAD8v90+uFh4/UfMjrWwHqQIsgg42zKXqUVzdecPGlnMVqcyY4evfiEhPenPfvqijunKZj9E4cld5zzz0xI2uOozS00SKJiYkcx1kslsLCwmuvvXbq1KmffvppSUmJKMa8U6mKKstyC9LZOBuvDftkCDAEGAJnDALNCGicIkakaESAu+84ku/ZNHyYLyejoshVev7g77ZsJOa9KoRCoSb2uQ0CGqUQqEEcr0JlIzw/B/54Y9llP995w/UVz89AXlMh1GaYUDmCgsTpjh0wpPDL3Mz9+ZlBd7LkSdZz0iE3DUUSvClQmAlFbsjJ0Aqy+ZyMkmGF25+fjntz1JgcgEaWUP0ASEA3RkMSwNqNkFfwfm7u1nx3jTuzPs/j79trT1bm7kGDdpx73qrXXof6BrT05EVi1azolLoFDVavgMHFKzzuam+OlJUl5meJxe5Nr86uoFVCq07yDBXD8NYcLTt9R1p/KT8Dil1VI87+XOaReUTPECd2oMhtyAcHdsNZg9bm5ZRnZAZSM4MZaWFPipw/QB+UjATokAwY7NLzMgKZfQ4UJu8flr7q+YnAN6BrPlXmdUnURXJnFWU6Rpz9ebH7UEGmmJ8p52bJ+Vl8bmY0NxWVBHJTpSKXku8KZKeVF3rr0wdsH1a84y931q5dj24HyVNborgSOVwVlQpUZOqXfQNDhmzPzGzwuuXsdMmVqman6K5kzZWseVO1omxpcE5NsWfl9KeF+kYQO/GpTxhwAGgshwuHLMpL2VbkqivIrslKX33L7QfDChZbIGUlBDRxiUnwp4SHuSl0BU25VR7K98P4+33XX7nv91dveeQfVV8uwEUXQYaQJDWtR2jw4RswJGN70cAqd4KvMBnyUsCbrrsydFcWGiO7MyFtQLjQHc3PKsvP3H716CNLvsK7CUQ8GxkdiiNxikiHTJoK112+p2hgWXH/yNlZjSOK17w9V+ZRIkMmozSN6H9IvCQGg/gbaqiFsffyw/I3F3o3ezM3ZA9Yc9l5Byc9DCuWAB9Aa25FBlnVdRQOQV/YggIb1oE3dUdhujAoO5qXvWzDWoyM98gYAV15EIbkfJbcb3daciQrM+rO3Dd65LqID1caiAg1dvY4XdQuAU0cEmIzN5TDhL813jym8jeX7HzrRRxuqRKoqiSrKvUfKqrw6Hg5J2dTVnppRqrflSa60uT05EhBrpI84Gh2xu5B3nV33FTz7Vc4XCarN+1az5NSaSp6AQxJIPEKVNXA6Cu+y8/Zmp/d4ElR89BWHV9F6foQtzYkRx7s8p+dVT88e9/l525c+QW6VqOHqqAknaFKZ7DPuORCjkgIbv7DqsKs7flpkcIseUjOvqen1EUFHEo3MXFk+0ccKwO0WA7d9kOFhfMgL33jILfqTQ8X5H23bRf+dXTqj77bgnd6Vsz4t9RkCNXDucWr89Jri9zBopx1tRW0yBG0Jmr6Z2jq7ebIY5037nN6wsBKxRBgCDAETmsEGAF9WjdP5xaOss+qou7fv3/gwIE2clgcdnRH6OqX9POzX6s++GJE+yfA2AA8Uit+HILdRKRCwVmBqKFsoCoCevSrAvhGVWb5g48GYWydNKWsZD1oDTgfl+ljWcaZVBQZYF2rFvhDAO9D+JHKAzNK65YJSGpjMj2qoa9vSQIJ51JkuLxHhLlheUKAnxCQX4kI20CqhUgUNEHXRTouVGRQZJ6P+ACWA8ysr55dUbWYl+tjYOlAiirjBE2KgBIGtQTgX0Hp0cMNj9UHn6mt3wkQRE5Z0rCQeFcdICqp45+YzFntnN3BWVEAesSFP1VEtLM2dil2niEUzJ8/HyWmE2JaHw6HIykpKSEhgbLPBjfNcZzD4ejVqxfHccnJyaNHjx47duwbb7yxc+dOSkBLkiQIAvWP1Lm9heXGEGAIMAS6DAL4R67FDInJo0TDJwts2wlX/WpNcdGSswZ/e/mlS79ZhBVCfkrRg/4A/vW39yJPMlVHASZ8qAD4FPAJ0BiASJh4NGi2W1tVdCUgoFu8DVth1OWrhxQd8qT5PFmCJ1PzZIA3E1+uFHClSLmuelfGqjvvrFm/Bap90BiGII+7hsJ8JdlB5Ad8NuFNJYAGHlZthiuvWpmTvTA3faVr4NfnDll+9VWrXnm9sTaI+rPIDeqgor1lFBQe5aaIFocmw2MTq8/6yY6E3ge8uVCQF/VkLVu4AKsvSxDlNbL/HvgwbFkHw8+qyUoGbzIMy6l94J4jFErT4uwJ9AItjNLbK9fBxaM39nev6+c+nOEN5mQJhWlaYSoSagUZanZKfWryXm/msifurSndiGJeKg+aIqhaVFZQO4ISnsEA/OTshUXZFbkEPU8GuDNUTybku5DHz3dr3qwGb+6RoqHbh12w4o4HjixeB9VEulqmQ4V421L3h6KmohovmrPCUzNgQPqa3LxQnz7+tDQpPVPJzJZc7qAnpyo9c+UNf967dA3KLojt8ocnAEjrpKoEz08vOX/YVxmpX5x1zqp77q/2K7jPTCIO8VBZDJtfxBc5OqA6cMsYkQnmiTiZkR71N3RNxiEZWsbzIrz3Ovxs8LaC/kcKUyM5aaorQ8/OguwscKVDngvOLVLPzt872DvvxRlSOIDGyP4AWYSgNvXo7VEmRaJ3QAW0p8bBkJTKwr7BYRl1g7IWTXwY9SYENBRGC2hCQCsCH0NQBghHobYR1m6G3Xugei/xKE113AAkoiNBeh1KUuOIS4XX5kJO+lY02k2vH5z3TVkJyhmTXWh001pMje2Sn3xSkLc3NzeSkVmRlr54yTdIwVPzxuZGjqqGQzny1xCrRNMHRViR0EAe/x+iZE0IsCHQ5kHFnkD8jOL+vBmvhi762daigkMZKfs8GYcyk7dlZ60ePOSbO+/Y/8VHxJM1D0FiDdFE7zbdKhYid1RU8KnQIKERBoQ1OFQNN/y5bPDgIwU5kTwX5KTpuelQ4FK96UFPRtUQz97z3Qtm/KNKrAIZdy/ggcsquibFtevN7LNBQAs8PP9cozt5dU5K4yC3PHzIwWXLiP4G2nLEsEJlHrLtgkJhvMdu000/VAkO74Pc9LU5Kbw3TRpcuPeT+XpUYQR0l2tv2mGx2EZIlWDGVBgxpMGdUpvSZ9u4sUKE6jthKkZAd7kmZgVmCDAEuhUCjIDuVs15nJXRNO3+sQ80cZ02jrNxXIrj9g9fnwcwLQgT65VnykKbVKjUIYjTVUGHqIbbBFFzuQZgqaRPD9U/Fg49GoSnGuT1JFLESTrOfVFpER/wAhAX9mUAizR+YqD04ZojC3jtEJHj0HAKE5ViBLRCJl9wOAr/rpAmN8oP1gRnNfDrcWaqq+i7SApoWoTao6GMpeonItFzhOi0mpovgmIprTluAZU13LjMi8BHQPKDXgmwDNTxFQ2P+KXx1Y3zNDSUJhZWqGUdEdCSOirJy1ev5nokcJyVsztsdlTGmPfp54ROJ0N8Ur5OJKBFUdy8efPw4cM5jkMhFHLYbMTzYZyYtlhQI8VutzscDjMlTcO9evUaNGjQLbfcMmnSpI0bN0pItrCDIcAQYAickQg0J6DRHpDIbAQFXJBcuQo+nw91ZJUyhB4DVVUWNUVql32O6zipGhKRYVULakoUbTNR0iGGLxptUn8HxIaS7KcRyAItL8O0p+GCn2zLz92AJo3e3fmevWcNLvVkbbvs4rqJj8HqFBroAAAgAElEQVTa1dDggwBhigNClBBJIaIp5SePR5weRwjxrQBEyNrv/P/AJ+/DmqWwdzuECHMe1SEkR3VQVA1zwC09Co9WvuRRIBJq8v6Hj2Z5F2Zlrxl1+cH33kOmD8m+2IEVEXkI1MPvfl06KHdf9sAteZlfrFkBZOGVSsvG0x7PJ6XMCY0VEKAiCA9NDY/4xXd5w9YNLtw8LG/XsLw9+CrcOmbUkUmTYMVSkmkAcKVA8WtaUNYkyvQJZHE4ysOrL0Jx7toid0mBu6zAXZHnKvFkHHKl7M8csNWbueH887fefW/ojfchoEAD0QQjTCY2PvWtZ3hc1ED3R0K8jB7bdID6EGofjx5T4c7+Lid3qyd/syd/g6dwxf/c4Z+3EEn/KEBYQiEIUaYP1raJy+NBpUUamTDgPA9Hj8Ly5bD2O6iLQBigOqKFJJTOiElwdEBA086J5KgY0yPTNRG3kZH+RCyX6U1VpBlxMYOXcby1+DOY9AAMcq8udG/J8W7zevdkpO3PTN173tCS319TM2Mq1JdTX9E41MMFCpl0dcroIBve1HV0FdYvh5HnbhnqWj8oa9Efr17dWIcDP+KHkEpwoLiELKvEdSEysUQNAhOgeSn6/iNr+/GCGiiRTqQKKox/RC3KPugd6PemlA4btCAcwa7NY/elxHJMyPzbb+CXv1zn8X418rLtny+ACCHt2yKg0Uo4viRh3A0DiqbxEgKvgi6rqDkeDWuiHNAhpOsqJaAVHX9VIRVLHdSgohq++RrmvATPToH/fATr10IgBPV1pF4It0QqiW9EB4Z+a3ZTAqqiQkAFHxkGo9hJA4+97sVX4Jyz1g0u2JqbvcGVtjrPs9aVsfjKMUdengnVu0CrxmExEGUZWVUl1KlW0dljWxx0KKTJBJD1a8A18LXc9NXnFO762YhlFVVEOEjHzhGj6c9IC2hJRO2X3PTV2QNCOeny0OLDL70ajYq4MYYdXQqBGO1sLPmoOv6Qzy3clJ/uy033F3q3r1iBcvYKT/93cH9Cx69jnY/dsUuhxArLEGAIMAROFwQYAX26tMQPXI5gODRs2DBHD0Ju9rByFmQ1rUOKp5dXPRsQZlf4NwFUkoGugGNoHHsrIAQBDgC8HZEfqW28o77urw01r0SDK8mQmJCzuA+QOhQ0TJB8AOtBe7rswOMlpa+FhM0A1TiPwS2kIm6HjfL4jnO8coCPo/qzdfLkavk1H2yV0U6ZBz8PjSGQ6OycmtNQmY5XqoTJlfVvBqL7ydyAjCZwgkFG1DydLJUBfAbKI/WV91TXTvRFPiceC8mEEif4ABFFxyyD4UjP3n2RfeYsFlsPm91+wQUXUEoXJyCmkX0nNpPh/erbb7998cUXr7/++kGDBlFymfLOBjFtZp8tFkuvXr3apKT79es3cuTIJ554Yt68eTt27BBFkWpGm9U5RFFsod2BBuA6G253YsOyrBgCDIEfA4EYB023tSB/itwKWgcjQ2MoAZPt1cgstc1HGSQVCeDlhCiL0TSUPospN5F973T3OyHWYndEehuVCGQRtm9FKYwFn+kfvBtZtxIO70cTy0gQV0d5gUgc4OOK2lnSJyf1B4bTY0qVxqg0pFQJh0eYRGT4CP9G6hKfR+tKkxEjKSHafKpQWoZcJ4YVo/S0dZAMVGXM9tB+eHnW0ZdnHT60n6o/I0Nosqk9rtbE5wgpFk7+4+olCsCqNcqShdpnH0U++3doyULlyEFobIjVGZ/8MX0rXVVUlXh8kxVAZk3DBQRegK3rYdJDZXf8eduff7fxrv/eO/6Bmjmz9E/fg8N7oaEOrVOjIuFZVbwpMZ1GMk4hjQMxlhLhwHVxFd/Rv6SCpLcsou7H+jWwdi3s3w/BMMajBgTByVBv6JCJOC5kzIliFEm8W8oqUoHUI1Zzpa8mgiPewHEe0+iisZLSeFxWiVc6xvMSS2TTw11Bfrm2HHZvg4VfwL/e9v3nk/B361EfIxJCvkYR0fxYJz0S+zUV0jasClsJE6xaJb/97uF5C2poLdBOOgYWZXvpT6dp4Z704oCGBCoZptGKmNEhYRm0iAg3/q5hSHbQ1ddXmHXoj7/bqCD7DFGROiKJLR1pWuy3JsnILknEqt+A0YwbCcfMfJuQJbdrOf6JAUaVR8iAMv4nYDQT1lfGF2p0kF8QdbwYaxBTvcxlaFVRjXg6pU4yCdik30oirjAdOQirvoV5n9Tv3gFV5bhQhNw7Vbgj7ULszDVFw5dKGs0YUsYCcekZRcGW/eZLadJjW16ZVd1QgwYaEtlnocR7e4flbFXw7hJBB/nXXx32JIdzM4VBeUce/EdtNIJ/tuzoGgjEfmux3zTO60QpqqJx0wfvQ6Frj6d/oDAj+IdrQwJdV8CEMSmf2DXt1tP8m2gv3O7F7ARDgCHAEGAIdIAAI6A7AKc7n1JBP3DgAGU2LRZCPyMDbcm+9ZZnDx9erUEZYZ9xRqehWLOK7LO2D+A/ABME/fYAf4c//FhD47egVNOdonRbJJlW4NCW2EJTwvqV2qMv+GtfLav/DjBbPzq3R8MNHgWapTBIjQCHAeZHhKcaQ49VNb7RqG8iO1LRRRIEefBH0EwB55YyKdVugDeD+ssheKXMvxkzJAdOG+gETAXgNRCplfS46vJ7fI0PNfjeUVGHOm7DgwMVDTloXVb1ERf+1O5E5eUYIDbrmjVrqK6FIAiUYYjxDJ3XKYzZgpElpYZ37dr10ksv3XXXXddcc01aWlq8UPGyWfCgdtNWq7Wp7Zqn69WrV0JCwsiRI+++++4ZM2YsWrRIkiRd10VRlCSptYS0UQYWYAgwBBgCXRWBVtSPuSLNJpw0pSl9LGXzeMOiqhX5Zs6YEG9xnrLpBGXjFBSuUkWiRyXjO5ohi+haVtM0dDNLLmy6Kh5qLz5+3vTZvMymE82CrZSaNF1X8TFEqUZyP5U6WUD2WT9RApqsZaq6Tgh/nTJjMc5bV+LG13EccQVAU8zP1tgiAS4V6JqmKBrun0IVZyDOgkXQ6Cp0FHQeNOp0MZ4bJZhpbnTBuFnNCd1NlgewbKpO6DoFCVYsmIA6JFLMepgw94RHbK5JQEVBaHVoyxjvzW91HN/abNkOeppxp6bqtu63ze8bMzSORRr9g3yn2ZE4TcGuKPCKJBIWM05gx0Y75lWXVoWW0BO1GlY1IT42oxiZSosjMUKaGoVTicp5gCyvGJFNAY2sOuhEVOTi8w4Xpoo5A8PDB5WPe7BUUtG6WUIROAFftPzNfztmDE3FiNHCJIZy0JSyb7pvG6E4wrpOCfm4pXAbSY8d1Qq82CV0EBijj+PrWVg106EpyJghaRZPQAPUzlwjR0cEtIYrLrEVLRUH67IY81GJ8fF/LXPAdPNuHpRk1DD6622Qm+73pocLvUdv/MPhgA+Va9jRNRAw/tvIr4au2kZl3PNx2SUrc1IOD3EreWkHPv2AiNMDoZ7pTo14z2+/mubfRHvh9q9mZxgCDAGGAEOgfQQYAd0+Nt39zP9NRydMmGDIPiCBabVyrtSPD+2tITMKNMlAL0uSpikhWd+vwgciPB6Q7xHhjoDyWL38TkCtINMLnBc1jf3xm0Ak/g4CfCXL08qOvtbQUAJQKeJWUwF0OmhGOWmiMX0E4F+iPtnHP1RdM72mdpsc00OM6OgMiZhIC6gTDbgxdivAB5I0ucH/ciNfARDgkZWOTXPReknUCPscAB0tr2tKHxLFv9YF3onCdjL1MVpVJ5ZeKmj/eGicmbxNSkq69tprUShTRssdVUGjKeNlXN4pAZz7Ew6idW66rlPrjLKysk8++WTSpEk33nhjQUEBVeSw2+02m6099tkwnW5hKF1cXHzdddc9+uijS5YsqampoTfVNKRCWheAxTAEGAIMgS6GQJw2Mqw2T7j8zSe0TY+148iITlKbJWzOJekqClrJEtpmt7S7bHYZfmkjt1ZpTiii9R2bLCVlZGAlAU2AKY14MgQ04bWbnin06RkrKnGtRwYAlKHGYGtCjZh1arj4rZLFZyDSEAbBSVCVUXqA0IPE7jZGpmOVkASP4xerjUZW0lW0CJdVaPuZThQnDI979EIqDkaX1Om7EW8EWnATx26TNlu2g55mvsGxc2+ZonmH1pHKlEVsayrSQpPLsqqiglnsMAY8uDzS1kFLq5OhF0/Ge3QYZoBC+FJUnyYjxKacCfUc92bYKmdZ1XmyQ+279VDs2pXXX8lPE88qOPD+e9hsAipbaGQYGP2+BHQT5drq5u1GUPwNNr7ddCd+ok0Cmm6IwN0Asi7LOuprtGoFTGM6Yj/kZh+4toS/YrKBD03+SYurEu5SUONjZnPXMsInXo+ueoUiCWIUZj4FeVlVWckNhZ7K4cNW1VQQGfKuWqczrNzmvzfSsdGjjwwrV0BB9gp3v4q8lKoxl+2XRLq1hWx7iv+aaIdvHy/jB9FBoP2r2RmGAEOAIcAQaB8BRkC3j023PhMKoTsGXdeHDh1KOWhkM+1WzsENu/ziWNVxMop2SCGAXQL8xyc/WR29pzpybxQe9OlzKpU91N1RfNdlEwcNqJ5xBGAFwAuNdTNLyrYQy2Vdw8mtRPln4tolRGyivwN4LCj/rT78dF39Z34fde4tqHJEU6M6zmDQYgy3V0KJon0iCDNCgclVlWuobrSA1md01kiczIgy2j7rBwFe5Osm8IGx/vCLPGzSoa5pNy7Wj+xG1d5+/x3OwtkTnDa7nbNaevbpzXFcaWlMU5ricMzJWKf3lDaJaU3TwuFwMBhcvHjx7Nmzb7jhhnPPPdegzi0WS8yrZNyenXo4tNls1IehzWZzkMNYcujdu/fFF1/8+OOPf/zxx/X1cSeOnV4ZliFDgCHAEPhhEOhsAvqEiOD2JrSqosqyTA2QKUd0PGC0l9vxXNs6jVmIyTgbI6zIhFyWVar5S1RHCHXVwhTTuKz9gMGAaZomkSO2kYjSigACj/tvKBp08dV8iYmYjhlQa5pGS0WKFxNzUFVJQOFsDSWaFT4aDVDSOZ7VcRDQhKSmV4XDYVohFNSNDSUMHtVMPZ9aArqDnmbmP9rHvr0zBkMTS8BHRUmMczBxP3u4ItIU17Tibo5scQNFQ+cZ1FQ0zj4TowVCbhKbAEo0m9nnFnm0/OoLNqASjQyTx9cXZx7JH6DmJPtdKUvXrkW1YlSzxoOqcOCX1r8RM1Ydh1veu/3v5nzaT/V9ztAe28ICWlNBkpQOzAJwREpsFwwKOt7zzZ+xvQhE2xrlrYlRRdNv3FypFuHvU5OueY2mSGIY3n8bCt37s1Nq8911af2+Kj8MYtN+iK5ZsTOn1MbfGwnQfxwN4JabKwoydrv7VZ1dUPrOWzh7JD45mxHQ9A+kfaha/Cza/Nr+1ewMQ4AhwBBgCLSPACOg28emW5+h41cA2LNnDyUoLRYLmtU6UN7hpZnPIT0toQ+aEMAegOcqq6cE1GfC8HQEJgVhZoVQQfExHsoGDU1Y6RqAJbrwUNneJ+sqlwro9w8PFJNG5Q10naOCHoFaHpYCPBkN/yUsPBoWvwgLlWjqhF6V0EmUCqJO3AGBFkThDlgVFZ6pqHq2rmElkajGUSK9b2yOg2MQHdDYeWag4r5g1d/89c9UBXYRmQ50Bk8VJ0lZZIAVWzcaBC6H8s/I4U6Z8iTPo2fC0+poMd8wJh6yLK9bt+6tt9665557Lr744qSkJLvdnpSUxHGcnRxGBalLw6SkJKcTXSxyHGd4oaSW1ImJiRdccMG999777rvvrly50qg+2tEoqiRJgiBQHQ/zqfYsuI00LMAQYAgwBH54BOij6eTve/z5xFMaD8VmgeaWueZTbZcxnlvbZzsvlt7HoFxjGgUnmT8lNOPPKcomS3EEMG+kykyMZyzGTKARjhh1ODRJ0wVNj2oQ1iFivDBGj8pqBKU8SG5NS8XxfEgtzFAb4fbqZyRoAUsTPnHa00jZXlbtxtMrW59uL751ypOIoQOmWHXixD1ay55onm0BJKOAioZq2t/vUHQJy6HCLy/dnDew0ts/6k0pvWrMgdoGHLvFXSISCQ4kn9sloL/f3Tu+6tS1Touc421Bo1ucbCpjvI8f85PIzhClcT3+TllpemVTjmdiSBejsHUjnD1kmzez1pvRWOTeu3Y5EL+wZyIcXa/OLQhosmlm324Y7Fk3PD+S3vPA2YM31vrwj4L8exAJDuOSY9T2GD/AY1zNTjMEGAIMAYZA+wgwArp9bLr1GfPQc9OmTf3790/qmcBx3IB+vTiOy0pOPrD3oELY582a8mrp0ScbQ88CzNJhSg3MLOO3AYQ0kILxx3n8Sa2RzZhVABsAphzaPTVQ+Y4qlANEVeAjKvKYIBPdZ+S1a6KwF2BKVcNYf/DhCP+mCkfJKEHWoqoSQiZZB0XHlD6AEnRmCHNra56trP1cRweJMQfwplkInVSVALynSA/WV94Xrh9fV7eeXI5ORQz/LYSIXr5tK5eUwFH3i4SQdTqdbrdbRnr8hCdjp7qztElA05vS6YqmaYIgaJq2bdu2+fPnjxs3bsyYMampqZR3/j9inap2WMlBdTwoDW1+p9odFould+/eVqv1kksu+ctf/vLiiy9u2rQpHA5TNqF1TY0JUOtTLIYhwBBgCPwoCLTL3JxgaY4/n1Yp48/FGFHW3te2C9Qqt7aTnXSsRp6HUSKIFY17JjvZXCkXTP2kEQYZyWIdF5QN/8Qtb2E8R+IBNOHUQW4ioDGHlgQ0ctPNtaSbaOjmBHfL+/1439tr2fbiO6+k1FOHRIyIwwCxFokvDLTXP83xBnkTC5j0w4G4kERZ7S8/821ci9opchTNDVSTHEvHgyte4hUNli2EoZ4t7r51uSmhfPeu6c/iAJL0m9gmOtJj0ca6NWKtYzoLvR8qZzPadEhrjmkKx38m7X/GteOonA5hn0UdeB34mBANubSz8Ol6+aCCjCLzEPLD4MIl3qzK7GR/UXbVv+aiKDw7ugYC9H8IYi6F8a9GgXF/qzrLcyQ/xTckr/zeewJk04SE5k/4asf5cBu1bfqttXGSRTEEGAIMAYbASSDACOiTAK8rXyoIgizLlNYEgBUrVlB9Bmci0tCcpUfe8Av8AN9EI08f2P/EkfJFAB8APBmBf+yvXi1CI0B92Ic6yWS7pWGGLABUgbYG5Gfqqp/y+V731R4mchx+UQ1I6PJPADkMko8obywFmFrdOCEgP1rZ8Ikg7SfktaaoMQpYR7UOUdMDABUAawGmR4JPNNR9yOv7CJlMGOq4+gaZ4YRJtp/wMKE+9LAv8mxD6IuQglbSpJQ6ca8kEKuZVZt3Wvr053r2MhPQdrt9/fr16JYQOWh6nEZMtDHPiJuV4WfcWCZeXgCe5w075WAweODAgWXLls2cOfOaa65xu91mutkwhaaRiYmJVLXDnIaGnU5nr169iouLf//737/wwgvffvstdWNovjstXlM5WIghwBBgCDAEugACEtkj1EjeqbvfeKFb8o2EP+wg0riOkF9xP2mSBkEN/IQ+FskTOJ4OP2PzfJM1LqGe4yoZ+JxTUTWbWlWTBw0miBPTHRLQRlHNN2wdjrEYrU90sxhKQEeN5sYlgTjORkN0GDAAjQUMkpMy0YoKm5aDp+ebQ9LmP3Z3qHwPdhhNAR7HYdQnIU8GZO0CGwnBXf/tz+i997wCcPUvG1S4euUaam0gEwm3mO12vJDt5tMFT5gJL6OaLQJNaYwBYbsBLe5sk+irYDK0gEYCGgPxowsC1UlF1gFkSZNAleHCEUuz0g5lDQgNyg4/eC/wqFBo/DXRMO3wFH8aw95PAwRwikbXUFENSJWh4jAMy/1mcGZdXnLdWYO27z1A53+iSp2XIgcdN5xqo/hNv6/4Pwxr8TZgYlEMAYYAQ+AkEWAE9EkC2FUvD4fDkiQZDKYoiu+88w7V4nD27MtxNs7i/K/xj7++a9e7Pt8CgEUAL/nhab/8H0IHE3c1IhA3NkjW0m2doDUiUyy/wfufqK+eHfJvIdbHPOiCrkYACWgRlBBAOcBmgCfDoft9oYcqI/9sQPY5AqApKggycUGtg6gqvMwDVANsA/iXAk/4Ai/L6loNainq6EuFvMiqtkxSLgV4qjb695rQ0zy8WydgSuooRwFVw6EHD7Bq83YusRfXs481RkCj6gjHcf/7v/8bb07DdOo0mpjG5wsxF45me+RQKCSKoqqoVHATR2SaJoqiwURTDQ1RFH0+37p162bOnHnnnXeef/75lINOjB9Op9NwYGgEqA01FfQwIu12e35+/m9/89v7779/8eLFhw4dikPHPhkCDAGGAEOgCyGg0GVi8k4JaOMJeCzG2UxImmrcZAGtAnoUhLAGQcJ8nSgBrcfYZwV5zCbrZtTARQcV5KVgPFXSjROiNCU+/Vu8TIVsCrb5nG9xofG16bKuGFKJ+XOQcNDBkyegiYi0rqGLL5RUURTYuwHOd387eMC24a6dV1605rN/ga8K1KZml4n9QFtL+zrUBWD5Chicu7UoM5LZx5+TfuDOu6r8USSgZRAIAd2CIeqKTdBemc1Va8E7G1+b0hgDwnYDrQlo3FIgxhs9dl17pTkD4onvGB1qauH6P2zJTj2UPUAqzFKvvzoYiRHQqB0Ux0ElCyeMjozjcZp8xghoAdDNLMrHz34Wzs45VDAwMszb+Mff76ftJ+ADiEr3CE120G1Uoen3xQjoNuBhUQwBhgBDoJMQYAR0JwHZ1bLRdd1wBMTzPC4dK+oH73/Qr18/ysaiabCz95x/f1YPsBNgrgyT68PvBpUDhCkGTdchJEGEuoMhNkwar0fKAD4GeCrIv8H7V4NUTma0Igo+yxLIoi7pGjRosBE9BMJttcF7GsTXoyjZXIvmz5RNVnAVW5VBkmQZdZ+/0+D5QGhKo++9qLJahar49ssY5HFxryrQtwJMqws93Cg+6AtPKq/dTmZamEzVpQhPnbzPffMdzmbnetjx3WrnOC4hIclms11wwQXmcXzzwYd5UPKjtbS5eEa4g9IYacwW0+YwtWLesmXLjBkzbr/99jFjxiSQI94BOKvV6iQH5Z0NzWibzZaYmEj1phMSEiiL7Xa7//CHP0yePHn+/PmVlZW0Rxkm0oatPS0wVQsxzhq1MMpsxLAAQ4AhwBBgCJxKBKgTX2Iahn6CO4dkMZPFhvhsWxIcJrIbK9nyaYsPhea0svGYoBod+N4iQfxrM/b5VCLYdfKmRtCUTVMJ2p1Wdmw5Hb18PPTX3RcWfVcwYPuwrENDs7f+6dc1W1YS2hmNEUDjeV2QtKisE1ZaDGrY5uSoi8KlV+0uyq/NHhh29QsWerd/uwbqwmjD2E5ZO6evdhoEnZCRuf93HD6Om7WxatL9EDsOHNpOoqH/UgBRg8cnVOdklHiTIT8Dijyb0XBFA02TVNVwR4gGNzEl4bZzY7E/FgIaaLFNqxEJLrvkiHdgo6e3NDjr4L6dWCRc8tIlsnxlOJKl/zgn/fv6sWrM7ssQYAgwBLo4AoyA7uIN+H2Lb9YUNshBVVHnzJlD3fFRFjLblffyS//cUFE142jp0+XVOwCqqTdhVVaRgEbf9uiZXsPpQQ1oy9Tosz5+ak1gFWjloPvR4lhTdLRUEkGKAjQqqOb8Ui3/WFC9vTY4RYA1APXEGkfCvZoqktWKoquKrmphgCMAHzbyU2tq5wjC2jj73LrSYUA56ZlVVQ/7IvfW+p9qDH1DSG1c/UbrbFkWeV3Xn31mOtbLSqhnq52zIAFt7+FMTEwMBoOmaS216G5zdNL65j9QjLl4RriDextpzKRzizC9XBRx9EbfN2zY8M9//vPvf//7RRdd1L9/f4OMpk4LHQ4HVZE2d5I2hTv69u07evToBx544IsvvigvL6cW90ZpW3h4N4pqBIyULMAQYAgwBBgCPyACnUNRNSOFY//sKJ3RqiJx9jF2wvzYxSjjodBOgOh1xBnnZjelGbdp3dyqEGdMRFumx51UedpyogQ1ZXDTNd8NyVo7OLMuZ2B9QdqR4sx199/SsPQzkP2gh3HEqPEghvBFvYOBCPW18NubajJyD2SkB1P71ee5Sh4eB41RdDfSrnA4lrxF/+mkyvxo2Zj7f8fhH62I3eXGsZ4TVeDlOXxh9tHcVMhJh0Lv9pCPTGpUuiZHq8uT/ZOt/766CxhduB4aTvNUnOp9/Dnke/Z6BkoFKdHrxwTwf4aoRJLlqxa/phaLnS3OdrN/lS7cuqzoDAGGQLdEgBHQ3bJZj10pYy5HRRtEUTTUGx555BEzvchx3DU33/rRgSOrZb2OZowPc1khBHTs8a6BH+BrgBca616qqvkyGqlAB4aaiFIQmq7g5qgwMtSwA+DVGn5yVP17vf+pIP8V8S5I1TkkUNF+RkM/6FHi/7Ac4JOIPKOs5r2ami1E+iOmT0lVNXCEIMvEw00NwPP1wfvqfH+JBB8LhxaraFJNtQYF0DFngGeffZbjrDabg7Pa6MtisZGa2nbt2kNNHnD6Sg4yq6FDF8Mi7HQZoBht19qC2NzwRrIWpDPVXaHXGo1ODZZ5npdR1hsPXddFUSwrK/viiy8efPDBK6+80uVy2e1I2ffq1cvQ4rDZbFar1W63WyyoZELfOY5LSkoyk9f9+vW78MIL77vvvldeeYUIbYMgoGkJynsqqkwOo2Ad18tcRxZmCDAEGAIMgdMQAeMB1CJwokVtcXm7XykH3fz0id6Lpf9eCFCr6hi1rcgQCUBtGdz1P4eGFJYM6FU1rEAfmhdNTdpR7NpzxU+rJz8Ma5Yi3azq4AtAlMfwe2/BVVfUezzlXrdclANZKRVXjNlaWQ9hkmvM/PkY5HnrEVrrmO9VP3ZR90QApxDoawZg+UoodO/NTYOcDCj07N65GWcAsmymm3my+dMc0z1B6Vq1MvPEYQGu+tWazIF7c1MC5+aWffoWTkFRprHl/gnz34IhbkMD5lNdCwlWWoYAQ4Ah0JUQYAR0V2qtTiyrMd5jp2wAACAASURBVE3TNI1SgUD811Hmcdy4cZRJdNgTEpy9OM5eOHLUXn9UARCjGig66KIAEQFEfLYrqK1VCjC7IfBUbd2iSIjoaWioniaj7rKixtjnfQBvBmByI7LPU6P8AoB9gP4MRSSLVQmpZNSokzQIEGJ6C8D0mvoXquvWh6PRmHAXwSBOQGughkBvAHi/zvdoffR+Af7qq/03KUyY7PUlos+6AOrv/vA7wodaHfYEQpPaLBZ8JSb2fO21NwS05I7rSxJozgQC2sw+065lGCbruk5loyVJMiIlSQoGg8uXL58wYYLh0pDKdFCumdLTFovFZkNm3+Fw2Gw2i+mgyai7y9GjR992223//ve/d+zYIUmSKIpGn2QEdCf+0llWDAGGAEPgh0fA/H9uDp9oSczXnmj4RO/F0n8vBNCbW9ySuSkDiYcHxsku78ai/Np8j5CfqeemQ1rvwLnFYlHenmzX14OGLBw1evPwn6wtLFrvzd7vzWoYWgRFuZCdUluYu2b+QsxKAYjKkRhTeAxjdjN51F64qXgsdMYjoIX5APEgAzv2QJFna0GG6k3Xi70HlyzA7iwZzsiRpqYW0IYk9BkP3ukBAP2dy6oqybD0GyjMW1GcXV+YUfXTYWvorFLXYq6CmpeXXteCfW5hbNT8CvaNIcAQYAgwBDoPAUZAdx6WXS0n81zOMJKVJKRiAWDOnDnUytVudVDeMCU18/OP59GzQbEhAhEFqHNz1GX+sKb++cboRxqUIJGrgCKASJhpCQduFQB7AN4JyE/UyvccaZjYGPyKiGYEkVZG3Q0BZB5Qbg3dG4rQoMJCgMdKjz4fDCxSkWImB13Jjn2hno9LAP4tRseVlY/1yw/5pWm1Vd8Rb4QyikqDX5HWfLe+sLiYsKDIOHOclVaHqj/fe+/fYtm1TUC3N42h8calp3XA3NAtwt+73NRQWtf1lStXzpo166677jr33HMNkWjKORs4GwHKUDudTrq84XQ6qXyH0+kcPnz47bffPmPGjHXr1vn9/hYFM7xlSuRgDHULfNhXhgBDgCHAEGAI/BgIUAvoJg5aJaSPoINPgJfeDJ1z3rKM1G2ulGhWMuRmwaACGFTsKygs9+aUuN0lyQP3u7Nr8nL82emB3EzITq32uhcsWAi+CO6vIwYMsV1Zx6pax6O1rjRmO1ZN2flOQUDT0GumioscEpxbvLkok3cnS8Xeo6/OkPlGNIrh+QiSz9gTqQs7s8Vtp5SBZXJSCFAfQPiuw53/K+akleQkB8/yHHp1hggCaHLbCk5xA6OO/zFOqmDsYoYAQ4AhwBDoAAFGQHcATjc/ZeYiKQHdgtf7P0KwT58+TjsS0Ak2W5IDzVp/cfnP9h3ZKQAfBj6E/mZQ7GKppL9cVvUfGbZRv3+KCIKAAtECju+CRMr5nYA6pS46tjzyRK34bwVtn4M4CkCZCxVkBUTCQQOV4zgK8Gxd4PHaus8BDpHBAppa6woxtJEBPdnErKQXhMTHamv/HvTfW14zR9a3kfQyQEhHDzfTX3zRYkPGmdo703dqAc1x3LPPTAeAYDCsKno4HI3JRxJcutMAxdzQRvgkO7csy0ZvMWQ0JEmaN2/erFmzbr311lGjRvXt2zcxMdEQ5WhTKtrgpqknQxTotlptNlt2dvbVV189ffr0JUuWVFdX03URelPDcFtVVFEUDc2Qk6wRu5whwBBgCDAEGAIMgRNHgHLQIjLGOtog0EEdurcGiAow8XHI8+woyKvzuKtdWRUZGUezMircWQF3RjgrxZ+VWpvjLi/IOZrrOvirX1Z9tRiiKlV3i+q4QU5BEvAY+hvHVHRlBPSJt2o3vwIJaBVZShBkGHPZwaIsnztZyHcdue/Wg3x9vPKaCrqsg0i6IiOg47CcHp+UgOZ1qKiGwQW7BmfLQ7MjxVkrfBUgBEFTiAokmd8acx8yc+mYemb/FadH67JSMAQYAt0XAUZAd9+2Pb6amZ/Kuq5HUesidqiK+vOf/9wStxi2OTmuB8ehCDD3t0n312gNVSAcAVgY4Wc1Bl72BQ4SIwFkigUFCWhBAgnFN44ALAF4tCr495rIo1Xhj0WMIb6lNdAVlOjC2YUMuiwRh4Q7AV6oCswMwms+tZQ6OSSTC6IDiNyyBhEfwC6AD3mY2iDfWR8ey4vP+epX4r20aojWg7hx945fjBrVg7P0SEjEEltjmhtEH8LhsCdQ9ploHzfNbFppQHc8TIkjdXp/tmhigzg+yVLruh4Oh1vIN5vzlGV5586dc+fOvf/++0eMGGG326lNvcPhsNvtNnI4HI7ExESHAxc5DKqahs1f+/fv/6tf/WrChAnz588/fPiwLMvUZaJADvNNWZghwBBgCDAEGAIMgR8cgRBAGAlolQia6bGRla8BImHYtRsmTRYuHrly8OBVBTl78rIqPKk1noFVxe5qb8b2QYVrL/7Zt8/O5BvCUE6cjSgqEJeVEiW1GQH9g7dm97+hRvZfyqAICtx1azQ/s8abFs1O3v+na3eiMrQOoVAIkzAC+nTtCxqArENEhscfr8/N3JuTUlfs2vPkg0SBUUAdldbTH0ZAn66NycrFEGAInEEIMAL6DGrsNqva4vGM5iqEg6bWpvX19T8fNdLWg7M6uJ4DeiD73IvjenNcApfk6jtu5lMb/b439+2fVVa2UIcQKvbpOG4TVBAlkLUoQDnAtwDP1IQfDssPNYbn1PO7qUWzqIOKwz+FbJ7CC1UU6ygBeE+G8SU10w437KY8NZnFIK0ds4SJyCDuB/hQkJ/0iQ9G9Puj4rja6q9BOop75sAvh+6f8JAlsQcabhM3g5zTaSag+/UbsHnzVkmKqbmFQhGKzJljAd1mTzihSCoMbchDA6BTwWAwSK2hqaazKIqSJMmyTJPpur558+b33nvv7rvvvuiii6gch2EBTWWjOY5zOp29e/e2Wq1mAppqSVNi2m63ezyeUaNG3XfffXPmzDl8+PAJlZwlZggwBBgCDAGGAEOgsxGIIAENSECjIQK1FiXvkoi2psEwVNXB11/DlIkw7m9wy38Jv7uq8o7/8T/6YPSrL4GXISzj+FEFEFWijICmCQojoDu7mVh+MQSo/awMmqDCxPGQ7zriTQ+m9dt3VsECtLynh6oTDppZQMcBOQ0+dbJ0gBI9uiZpUFUNF56/zpt61DuwZFj+0j2biGQ3kXRuMcOlX7vTDtfToDVYERgCDAGGwAkjwAjoE4asW15gPKTNtYtGo6Io+v2NQ4cNNojCHok2tIOOvSxpuQVX/+nWpfsORuPTDcyBUMYaYZOXAjxZEnikJvykLL0QDuxCr4QkKVmaVoiYBjLBIm6EKwdYFIFp1YEXGqObNfAT82dqhCyTEQXVAtQB1gJMj2j31Nb9paHyiUjtl6BVAByqLXn7w3czPVlJfXtyFixyUlKStQcqh3AWrofTYe1hO2f4eXv27AEAqiZsrm9smyfd7Bnb8klu3iym2RXsy/dGQFVUQRDmzZv3xBNPXHbZZf3796eW0dRKmvY3qiVtUNXUUJrS0JShNhwcXnnllXfdddcrr7yycCFxXQS4886szkHDhpb09y42u5AhwBBgCDAEGAIMgVYIUKdeJLrFqEkHTUOTA5Uwy+hyWjS9ZKSb8RTaISBxHVM6wJGkaQzW6n4sgiFwMgjECWjctPneu5Dv2eLNaBxSEMzLW7ZzJ4SCoEoq+sFUFNCRgNZ1tbN2EJ5Msc/Ia/F/QIu9QCHiKaoGoqaGIvDO6zDYc7gg1V+Qvv/Wm3boMU9GABr6U6evOGhN/y7mf5r4WfbJEGAIMAQYAj8EAoyA/iFQPv3v0SYBHS+27vc3XnrppZQZRA9yVi72slgc9iSHPYnjrDfccMPq1auRSRbRcqCOD1UAfI1SzurY8tCj9eEpNSXbqUUznaSgp0I0aqa+pTWAGhUW+dTZR2pfbgh+C8g+Ux/o1FBZIxpsUUCR6AMAz5X7H6z2Peyrfy7SMA8iO0B4YtZTBXnZth5IPFvtlqTeSc7EBAz3sFl72OwJTo7j/vHQuHil2vo0T5kYAd0WQp0Yp+u6oeZMs62srFy4cOGDDz44ZsyYhIQEg3emjLPNZjN0ommMwT4bqyMWi4X20uLi4jvvvPPFF19cuXIltb82vGuaq6AqqizLLYphTsDCDAGGAEOAIcAQYAicGAKxEdSJXdRGavOorI3TLIoh8P0RMBPQ33wD+Tmrc7Lq8r1Bd86Ghd8AzxN9aJywaIyA/v4od86VlIBG5tnQ4ZYkXLIKh+AXPz2Qn9IwJEsqztq6bDFIEsi8TujnGPtMxHxoORgB3TntwXJhCDAEGAIngwAjoE8Gve5/LSXvRFEMBoMXXXSR2S6V0n9JSb0M+s9ms51zzjmzZ8/etndvBGBFOPK8X54QgnE+eXxpxXcghahptIRSGmAioP3Ek+HXPEwua5xcXr0K9OqY2kbcFoaOExXwAawH5eVI1T/KSh6prHzuSMmr23f8Yew/kj3eXr2SHHYLZ+HsCUSmmhTLZo+F+/Tru+jrxdScpk0uEtvSPNVhBPSp6d2Ud25hRWK4MVQV1TBSLi0t/fjjj6dOnXrZZZdlZ2c7HA6n09lCmoN2QqvVaieHodRhWElTPjo3N/faa6+dNGnS8uXLqcIM8154apqX5coQYAgwBBgCDAGGAEPgdEegiYBW4dBRyPUuzHfXZaf7st1bX5lDdMyJAAzIGpGBlpkF9I/aopoGEnlplIOWRZBEWLoIirO2Ds0SClLqrrjoAADwAghCVNeIamNsEmmw1oyA/lHbkN2cIcAQYAgQBBgBzTrCsRHgeXRmLknSnXfeaTY+pUapKHNhtSYmJlLR3oSEhKQ+/X/2q9/8+ennH99+8Mma4BMVtUsBqkGTIIrbLFsR0LVEUuPl+vDU2oZ3hGgFCnKgDCCALBOyGocQKgoLVuqwQG147PB3k0sO3P75grP+9P+4fmlcDyTBqa/EhJ5N7DPHcZSAHj9xQoPP5w8F0UBbRu0NWudwGPUKmw5GQDdhcQpDkiSZjY4NMjquzoa35nlekiR6ijZTXV3d8uXLx48ff/PNN5999tl9+vQxLKCt8cNYC+E4zm63JyQkOBwOQ9ODBux2u8vluuaaax5++OFFixZVVFScwqqyrBkCDAGGAEOAIcAQYAgwBE4zBCgZKQPymlEB8ryfFHhqs1L8GWl7J0zEsuoy0QFkBPRp0XDNCGhVxTIF6+D+2yuLUw8VJ/uHZR9+7zUU6eBl9Ouja1JcZKM90tlgpU+L6rFCMAQYAgyBMwcBRkCfOW3dCTWVJGnZsmX9+/c35BGoLC/9arVabTYbofkcdksaxyVz/V09Rlz4y/EPfV19NALAK5IWlRV/VA6L6FqGjA4aRWE/wLPlNRPKyz8K1x0iohxkw5QCIDaAQtliPqJHAZYcPjj2X69fcOetXJ9+XFI/ztGH69ErIbE3x3GOnk6L04Y8tI3IP1s4zmr5+eWj1q5fJymyoTFiWODG6E5Nb8PwuTUTbcR0AopnehaGjfNJArFkyZK5c+f+7W9/u/baa83Us0FM22y2RHIYHDQuVMR7aZy1tiYnJ48aNWrKlCkLFiyoqKgwXCbS4mnkMFhyAAiHw8YaxklWgV3OEGAIMAQYAgwBhgBDgCHwwyMQ46A18Pvht9dtLvRU56Sp6QMr/vh7n6aCLBECWlFAo2IOOG/44QvJ7kgQ0DQQyAtVOFDrUYMdq+Ec91pvz9KigVU//8mO0sO4liDrwbitOm3e9ghohitDgCHAEGAI/DgIMAL6x8G9K96VunGTJKm0tHTUqFG9evUyaGiO43r16kXZZ9RDsCak9PT2tGdwlkSuT0/0WGjlsgcPvfLq37716pvb1m5UI8gqKxoaOSsAXx89Mr207C1J2A1qAKijQYhG6hUQaxRBBti7r/Spp2Zdet3vLC4X53RwCU7OkWSzJditCXarg5KPlsQeHMcl9O7F2SwWmzXDlTXntblo76xghi0IaMqB4lBSIy+DXz5moCu2XHcvs67rkiTt3bv3ww8/nDp16pgxY/r37x/rFXFVaDNDTcOUgLbFD2q/b7FY+vXrd8UVV0yaNOntt9/etm0btf0PBoOCILQAkk1FWgDCvjIEGAIMAYYAQ4AhwBDoKgjgBksNQiG46479eZml+RmQncZfeP5BTQU+QiYqikTc2cWmEV2lXt2unJSAjhIVDlToDjXCpL9DUd/9Z6eI3j47p00WeQl32KrA6xpumSWijwYHTfEwk9HdDiFWIYYAQ4Ah0EUQYAR0F2mo06CYmqZRDpqW5e23305PT6eKHImJiVT0ANm8HmiBGuP7rBauRw/OmcAl9OYsCRxn7ZvYz871SOyRkJmWOebKq8Y/MWnitKcnvPzSm5s3bpAi5RDZfHjTp4v/NXnaY3/9yz0jLx2dnpXDIYHN9emdzHF2zubketi5XklcosNqtzitlgSLpY/T6bRjGqSeHfZzfjJ8xaqVsqqKaL2AmhsdENAxO+jW8LbHRLdOyWJ+DATQubWiGprRZi6YmjBXVFR8+umnEyZMGD169MCBA82LJdRXISWgWxPTLWIsFsull176wAMPzJ07d+fOnbKMGi7UdaH5pj8GBuyeDAGGAEOAIcAQYAgwBBgC3wOBGB2paRCOwjPTQq6B+3LTIC8T8t07aqqJCKCqoy9CTdeZYMP3ALjzLtFAU0FQoYmAri2Doalrc+y1g/oKw3P27tuLN0MCWgddwdexCGjWop3XPCwnhgBDgCFwIggwAvpE0DpT07Yg2qj+AM/z9fX1H7z/QVpaWmLPJHtSAme3cQ4b57Rx9rgkMyXzLHbOloTqB5YEG2dPtCUl2Jw2zma1UtbYhqn69MHLOcI2J3A9eiKzbeN6clwPp6NnYmJvK9fDwll7WByYtYUkc+AVCVYu0UYutFp+ceWYzTvQZFXRNJkqhAHIqiqrMdd2lG42RBUMs+g2GpYR0G2AchpFtbdyQP0Z0iamDDUtdCgUWr58+axZs6677rqcnBxDf8OszkF7awtimro3dDqdDoeD2viPGjXq7rvvfueddzZs2HAaIcKKwhBgCDAEGAIMAYYAQ4AhcGwENLIDE9UANR0EEd59G1L7bPGmQG4GFLr3r6fjO+SoGQF9bDRPdQoNm0FQgFchogE01sNzU2rPz68YnKKcleEfdzeIRBVaAV1Fn5FEvxvlUjqwgGbW0Ke60Vj+DAGGAEOgbQQYAd02Liz2+BGIisJXS7/+f/fexSXZuUQr2is7qNUyJfSa3h32hCRnrx7IT1vIy/AdSAI2m8VhtxC9DnKNlaSxccg793Ai9cwl9kjgrIRudto5C5LZHMcNGlQ0fuKEgyVHAPde4YsOKwx+2bCTpYIbRnwLYr3dKpvJ6HYTsROnIwJGW5spaVVRJUnauHHj008/fdNNNw0fPpxKRRs91UaXNOLfLRZLQkKCQVWbyWuHw/HTn/70lltueemll1auXMnzvKqoPM/TvQJtdjCqQk775OkIGSsTQ4AhwBBgCDAEGAIMge6MgKahBKCCdrIaSBIsXwaulE3ZKXpuGnjT9n70AVYe2UwgXmSYveyP2hk00HgkoAUV/IEwRHxwyU/WFRY2eD0NeWmrv/0KfOhmPjYBjE0F29XrNljpFoEftYbs5gwBhgBD4IxBgBHQZ0xTn5qK0n1OGkC9wpcr4ZmfvDP8+jG9CrOQYSYO36xWq8VicTgclL/r7ezJcYRBpuxeD2IEbbFynNVmczidifYeTmoZbbGRU5zVZnfGw5zdmWixWUnW3E9/PvLuv/1l9YY1EVGgYl+ipkq61pqANlhIRkCfml7QxXLVdV0mByWIQ6EQAHz99ddz5869/fbbR40aFWee2/40E9BUecZ45zju/PPPv+mmm5577rkVK1bgaFghVhkEIXpfVVHpfWm37GLYseIyBBgCDAGGAEOAIcAQ6NoINCOgeR5KS8CbuS43S/Ukgyd13zPTAoKMvmpUwDEbk+D4cVub2qvzIGqA7lg+eAOyk9cPTC1z5R6+8Y/76ytxHUFQ1ZhVc8wKqb0it+Cdja/tpWfxDAGGAEOAIdCZCDACujPRPNPyUkAXdDUKWgigEbR90fp5u9Zv5msiAEeqK5YvXz5t2rTbbrvtsssuo2rRPaxWtFvmOK6nhevfg0uwoUdBC8fZbMgz93AmJCQ57Ak2mwP1N/CdS0hKRO2NvgmJOenZI4ZddPUVjzw5cfnqlRoONWRiuID2zioxYyBsOHqeiI09DOK5ecBMQ9MmM0YfRiDWlGbbZxo+09q4m9aXmiHLsiyiL+2mQ9O0cDjM8/yOHTs+eP+Dhx566IILLkhISGhBRRscNLWVNr9TW+nExESqhD5ixIg//vGPU6dOXb9+veHGkJpjN3nCbLo/CzEEGAIMAYYAQ4AhwBBgCJxSBJoR0CIPigwX/mRvriuSk6bnZ5feecf+qACyHjeqPaVlYZl3iABhn3WJaKZIAH4/XH7R3pzUqoEDK1MzV79PbNUBgFckYxLXocE6TUXs35s0OsyXdnh1h0VlJxkCDAGGAEPgmAgwAvqYELEEx0BAAVyPDoNeqYRL9agfoFyLyq0uEgRBivAAUBsIfF65540D6ytBjgAENSWq67LatFdKx91wiq6BKMr+EO6qqpWjn6z8et2h3fUKL4DeGAxIuhaIhhXQdTLmIJvo8JZ6fAeWBtCcdm76xgjoVo1zpkdIkkTFoykQhnQGdXUoSdKWLVs+eP+De++994orrjDYZ0OUo2/fvtQPJ+WpzWGDubZarTabzePxXHvttbNmzVq+fLnP5zM65fdrAONyo8DfLx92FUOAIcAQYAgwBBgCDIEzBoE4AU2JRx10DW68IZidUVOQpZ9V5Lv++h2iDBIjoE+DDkGbKBCNAoAvDAu/hGL3gfwssWfP7ReP3FxVD5KGLUUPg0huv+A0CSOg20eInWEIMAQYAqcSAUZAn0p0u33eZgNh3Kemi6AJoAsQM0M2AKBMGTonBqior/9P+a6vQiUNAFFCXkvEZrkpsYYDQfpSiLEoyBqOLxQdVF0l/o0lXSNqG/iVvuiAorXLiVi25qKaw+S0MV4xAu1eZZSSBc5UBCRJ2r9//8cff/zcc8+NHDkyOzubMtF2u53SzVar1W63U4+FBgFtBJxOZ58+fRwOR58+fXr37n3xxRc/+uijn3zyyaZNmwxEDZ1oyizj4o0kybKsaTG7DJrATEDHfmJGFizAEGAIMAQYAgwBhgBDgCHQFgIatX7VcfZC5Z7//nfVnX0018Xnu6vy8v4jqyACyHSGEuc328qJxf0QCKAdtA6yCvf8pXFwTtCbwRcU7XrrXxCIgkJ0OY67EMZUr4PAcWfGEjIEGAIMAYbACSLACOgTBIwlNyNARbnkuCtpVUczUsII06e6kTbGjmk4gtMASkFtBAgCSOQVG97FUxvsMxkW6miwrOi4ui1hQNd1BfT2CGjzaCKeH/k0k87mMDlpvqpZyc0pabhZpuzLmYuAQQEDQHl5+aJFi8aPHz9mzJjU1FSHw5GYmGh4MnQ6nXa7nYqhU7XohIQEOzksFovNZqMW01To46KLLrr77rtnz569YcOGUChEJUHwV6NpoihS34YUdFoAQ8eDEdBnbl9kNWcIMAQYAgwBhgBD4EQQIOv5GmjkBSCJMO0ZyPHuz8kKezKqcr0LD5eAqDMC+kQwPcVpRR6OHAZX1lJ3hj89uey8ESsjKoQl9CIZv/PxTNVaz/lax8TzY58MAYYAQ4Ah0NkIMAK6sxE9o/KjGsxx0eUYNUwslJvRuHE1DFWWpYgoy2pIV0Uil9EiGQWvBQEdM3kGXSKvuNBzk+2zmfI2DyKaNUVrKtk0SjFf1axIra9qlin7whBoiYAoigcPHvzss8+mTp167bXXFhYWGmbRlGum5tJUx8PhcBh20xzHORwOqhxNeeqkpKThw4ffeuutU6ZM+eKLL8LhcAvFako6m99bloZ9ZwgwBBgCDAGGAEOAIcAQaI5AfEMZdaauh8Lw0SeQm7cr3xNNH1Canbl00WIQVUJAm+YLzfNg304dAq2EmDUQwvDXeyP5eUdcmTVuz/aHJ1WGdRCVpjJooBCb9aaYtkKt53ytY9q6jsUxBBgCDAGGQGcgwAjozkDxTM7DGJahUBqxTW6fgEZFXYlsddNBEYlus8HwmjBsQUCjq0PQefISCAdtyG6YA8cYPhg3ahEg92332haJ2RY8UzOdmUGqCq0q6BWdIqDrukSOcDisKqqmaYIgGGcBIBAIrFixYuLEib/9zW8HDhxI+WiLxWL4NjRIZ4cDHW9aLBYqGG2325OSkgztDo7j3G73b3/z27Fjxy5evPjQoUNGAQwO+sxsFFZrhgBDgCHAEGAIMAQYAsePQBMBTexngwFYswoK8zcXeUNp/Uo9GWtff50R0McPZyemNOZkxFKJjrV1JJYP7YXBRRuyM2q83ipP7uK9h0DQqLgj3p00qAyom9LxYeTfQaDjHNhZhgBDgCHAEPj+CDAC+vtjx65El3/Gi8ChonRzk1Phk4eI5qYS14L0ncZQxs18Lxo+rjvSMh9XUpaIIdCZCMiyrCrqli1bpk+f/stf/rKgoMBMOlPlaMpHtychTfno3r17cxzXt2/fkSNHPvDAA3Pnzt25c6csy4Z4tEwOM1HemdVgeTEEGAIMAYYAQ4AhwBDougjE5i8K0QIEiQfFDwUZi4bkBbKSa/Kyt098XKYW0HSfZ9etaJcqOdV2jFs1G/M1DfgQzJ7uc6Vs8WaG3Jn77r3bDyoEG3zNa3c8BDS94gRmjc1vwb4xBBgCDAGGwEkhwAjok4KPXdwCAcPws7Me7K3zoTGMgG6BPPvaJRAwfiCGmnNdXd2SJUsmTpx4ww035OTkmO2drVargxxmMppqdyQlJVEpD4vFYrfbHQ6H0+lMSEj4xS9+cdttt82ePXv+/PnRaNS4zsfIUgAAIABJREFUCwCEQiEgYjhdAihWSIYAQ4AhwBBgCDAEGAKnCoEYuRkjoEEBzQc/P2dVoavcndpYmH30pj8eFRSU4GAE9Klqgjby1eLO6eMWTpgG/QvxQbj84m9Tex3IS48U521evpgkEMKkfYwNqjKR4DC+tnGDeFTr+WX8DPtkCDAEGAIMgVOJACOgTyW6LO+TRqDjAQI9a34/rhsaK+rHlZolYgh0JgJUpqPNHEVRDIVCy5Ytmzlz5jXXXON2uykfTZloQy2auje02+2JiYlOp9NQ8DDkO+hVSUlJ5513HnVpuH79ekmSVAUFcKLRqCQZDlvaLAiLZAgwBBgCDAGGAEOAIdB9EYjNBajJLW7eVP1wy+/2e1L3ZQ305aXXnn/WWoOA7r4onG41UwCihIM2CGgNQFJV+PQjKHZv8g4I5qbVXX/dAY0nJY+ZSqvx1HSvLG3ajmeHHc8vTzdYWHkYAgwBhkD3QYAR0N2nLbtlTToeIJgHFx2nbAYOI6CbwcG+/HAImJnf1kw0teunpaFiGlQ/esKECb/+9a/z8vKoXgd9pyyzmX1uEU9tpQ2TarvdPmLEiD//+c8zZ85cvXq1YYv9w1We3YkhwBBgCDAEGAIMAYbA6YAAnQugsaxGrGhBDcLD91QPKyhJ79uYlxodPnh7VIaorosqaMdjU3s6VKrLlyFuAU293MerI0tw/a9L8zOritKksz1lH72LDglBAjmCKTRQ6CtOQzMCOg4c+2QIMAQYAqcfAoyAPv3ahJWIIcAQYAi0hUBdXd2yZctef/31W2+9dcSIEb169TL4ZY7jrFarWUXaYrHYbDaDoXY6nZSSptodSUlJw4YNu+mmm6ZNm7Zp0yazWAflvs0Mtaa1ckfeVvFYHEOAIcAQYAgwBBgCDIEug0CMgMbyalF4/QUtz7Uze2A4N0UrcG3dvgcCIkSP6dauy9T29C8o2jsDEDf1poHniq9hcP6+IpeS07f2okE7xCDIIqgiaAo6IVRB1UBr8Tr9q8pKyBBgCDAEzkwEGAF9ZrY7qzVDgCHQVREwqGFRFHft2vXKK6/cd999F154Yb9+/cx8NFXkSEhISEpKovEGH02Vo61Wq9PpdDgcNH7o0KE33njjnDlz1qxZEwqFRLFpykW1O8x4GWUwR7IwQ4AhwBBgCDAEGAIMgS6DQGxPJEo5aAJ88QnkZW/3pireFMhz7f5yEQQliApdpjbdoqCEeCbbWgP+kCaB0ACTHowWuKs8qby3794Zj6PhsyqDooJELZ91RQW1BQ3dLaBglWAIMAQYAt0QAUZAd8NGZVViCDAEuhkCVJ3DTPvqum4W8VAVlf//7N0JmBTluTf86umru2c4gCwz0z29d8/KAO5BjDFHeVnkGNAYJTlAzKsmOeaoMaKvon4oGtkOoJ6YhKMxvq9bNGpizBhkCQwoiMq+KLIvAgPMPj3dtdf9XVXPzEMxLA6L0N3zr2suqK6urnqeX3U0/rm5n1Rqz54977///sSJE0eNGsVbdvBW0U6nMy8vTxCEHj168FSaFUrbs2mHw+F2uwcOHPizn/1s9uzZH3/8MRGlUma/PUmSjg2js4wa04EABCAAAQhAoOsIKJrZykGT6PM1VBrcGC3Uo4V6cfDz2c82SDrJbY2Gu47HeZ2p9UcCrK2iJGqGRHvX0mXRTyK+wz27bR1UsfHgVtKSpKmabOgS6TKpKgLo8/rEcHMIQAACpySAAPqUuHAyBCAAgfMgcGwArVsbHwrrm2EPiCVJOnTo0MKFC2fPnv2jH/2ooqLC4XB4PJ4OVdIdXjqdTrfbzVp55OTk8A4e3/72t8eOHfv000+zPJrfFzsQgAAEIAABCEAg0wSOtHiQZCuAlqmuhkpDq+NFerRQLQlvmzBhb1uFdKbNLYPHq5sdt9liginFbPA84//QxYGvIgX1xcGd/999otxo1qprmiiTLJGMADqDnzWGDgEIdEkBBNBd8rFj0hCAQFcSYP00NFVbs2bN66+/PnHixEGDBrGu0DxiZi07OuTRgiC4XC6+vCHLr10u16WXXjp27Njp06evXLmSr6yoqZqiKB0aRivWZq/d7krwmCsEIAABCEAAAmko0BZAm3+fTBOJdE0lKUmX9V9bGlSiXrk8tv+mmzYcOGiOXFfScPzZOCTDTJ9ZAC0TSUQHDtFlJRsu8SvR7rXBHov2bDUjaUMl3RBlEiUSVbP5hsF+7EvTZ6MO5gQBCEAgGwQQQGfDU8QcIAABCHRGQFM1exZcU1Mzb968Bx98cMSIEV6v1+VyscTZZW0sm2aLFgqCYK+eZgse8rcuvvji8ePH/+EPf1ixYgUbhq7r/Ea8fJsd5C87M2CcAwEIQAACEIAABM62wJEA2jA0XVd1XZdSdP3QneXhRLRIKY0c+talHymymT6nWo6US5/tYeB6Rwmw9Fmx1iJMEv31PSrzb473SJT32nvPuKRklqqT+bCsAFom0er+jAD6KEO8gAAEIJDOAgig0/npYGwQgAAEzoKAoiiiKCrKUTU8rGsHj4mJqLa2tqqq6vHHH7/++usjkQhLmVkYzSujnU4n3+f9o51OJyuU9ng8LperpKTkpu/fNGHChCVLlhw8aJYP2Zc0PAvzwSUgAAEIQAACEIDAGQuwPxRnbc3kFN3zM7EsXBvzy6HC/SXxxQ11JCUolUAf6DOG7twFdDL7byhmmw1KKnTNd/9ZUri9PL+urPcnH/7DvIRmkGqoqiGrJKqGbNY+G+ZBzSBUQHfOGGdBAAIQOJ8CCKDPpz7uDQEIQOBcCsiyrCgKW73QHj2zMXRooFFTU7Ns2bInnnjizjvvHDBgAM+dBUHIy8tzOp28Apq/lWNtvK2H09r8fv/gwYOnTZs2b968w4cP19XVdWjTcS4FcC8IQAACEIAABCDABDoE0FMnUXl4d7QoVZRfU1m+fuWnlEygBcc5+7KYGbJGqkIk6rTon3RR+YpI7+2V/j3XXblST5jDUDRSdd0MoM0fFQH0OXs2uBEEIACBsyKAAPqsMOIiEIAABDJDgHfA4DudH/e8efPmzJlz1113XX/99Tk5OWzFQntrDlYK7bE2toYhO83pdPJUWhCEYcOG3X333a+99trq1avZ3VkaLlqbWeGiavZR8drtZDJpP459CEAAAhCAAAQgcCYC/P8OqRLNe4/Kw59Hfc3+/Ibi0NbXXqGWpjO5Nj57SgJmAbRkyJJOzQm6edS2i4t3F+fviuYvefl5ItVsAK2phlWurpp10LrOy59RAX1K0DgZAhCAwPkSQAB9vuRxXwhAAAKZKmAYRnNz87p161599dWnnnpq+PDhffv2FQSB1USzOmheFn2iHYfDweLpwYMH/+pXv5o5c+aiRYv4koaGYRy7gKEoiplKhnFDAAIQgAAEIJB+AkcCaJlWLqPS0MqYvynkTUUD+5+eQa3NZtth6yf9hp5tI9KJlKZkslWm9Wup2PfhwHBDqW/7ZZVL164mg0jTzQJp1i/FrINGAJ1tXwDMBwIQyH4BBNDZ/4wxQwhAAAJnLmCuFK9qrH0H+3//vIkHy4X3799fVVU1efLkoUOH9uzZ80S5syAI9mpodprD4ejbt2+3bt0EQbjsssvuuOOOSZMmzZ8/v6mpid1Fsjb07jjz54grQAACEIAABCDABY4E0Art20XxosVlkeawV414G+75D7KWz1AQQHOub3JHN0iRVDNr/tXdXw6Ibi0vqu8X2vzH/zEbQ+tm+w1zJW22mc03bA2gUQH9TT4XXBsCEIDAWRNAAH3WKHEhCEAAAlkswP4ff4cJ8jrlDsc1Vdu/f//ChQtnz559/fXXB4PBY/Not9vdvXt3QRDYAoasbpr3lWYhtdPp9Pv911133aRJkz788MOtW7d2uBFeQgACEIAABCAAgdMWaI80DU2hVBOFfX+tiDdGfUakQBozqtVMQ1n+edo3wAc7K6BbjTZoz04qi/09WrCn2Heof/HyL78wS9A1ajJIOfKwEEB3VhXnQQACEEgjAQTQafQwMBQIQAAC2SqQSCSWL1/+1FNP3XLLLX6/3+l08tpnQRDc1sbaRrPj3bp1c7lcx8bWvXv3vuaaa5588sn33ntv7969rGUHK81m/1mi6zovzc5WTMwLAhCAAAQgAIGzK6BrZsONm0ZvLI/WRL0ULaBg748VtP46u8onu5qeSDU1NdHUJ6hfdG+Z36gI1zw4oU5Wyez1TJJhaNYPT6EN1htFa/8jAvayw68nuyHegwAEIACBcyuAAPrceuNuEIAABCBAlEwmq6urn3zyyZ/+9KeDBg0SBKFHjx7du3d3u93Hhs72I05rY/XROTk5vXv3HjFixFNPPfW3v/1t//79RGRPnw3DXKzGfgT2EIAABCAAAQhA4FgBXaNkK/3izp0x//ZYIRXnUyx/41c70X7jWKpv5IhOJCrmlQeWrS71SzGvFg9sXL7MPKIbpJOOAPobccdFIQABCJxDAQTQ5xAbt4IABCAAgeMJ6Lq+ZMmSp59++uc///lFF13k8XiO7RNtj6F5I2mHtfG3vF7vqFGjpkyZ8vbbb+/Zs4ffCkk0p8AOBCAAAQhAAALHCug6iRLNnCH68zdGC6jUSxX+7R/+kzSNrEYcx34CR86mgK6bV3vlVQp614d9Ykmw6Qeja1MpfosOlc3mS3YIFdDcCDsQgAAE0lwAAXSaPyAMDwIQgEDGC7D8116MzJpm8Il1eElE1dXVc+bMufXWW6+44gqeLx+7wzpH24/z5Nrtdvfs2XPo0KETJkyoqqrau3cvv91p7Bz5C5+G2Q8SGwQgAAEIQAAC2SSg66Qa9MorVNDrs3Bfinupf2Tvn18lHWsQnpPHrGnmOoOXX/ZByL+vNKoEvevf+hNJCXbv46TPCKDPyWPBTSAAAQicTQEE0GdTE9eCAAQgAIFjBezpbYd9+8nsLfsRtq+p2urVq2fNmvXjH/940KBBbOnC3Nxc1kiarVvIc+fjhtHs4In6R9vv2GFZRRada+qRhddPMn77dbAPAQhAAAIQgEAGCejWny9/+CEVBz8P9dGj+eS/YNN/PVlPitVjOINmkmlDVa3i50QrzZ1L8fjq4miiOF7/nW+vb2lkMzHa2qAYVik6+9V6RzeLoI/zk2kAGC8EIACBriKAALqrPGnMEwIQgMB5FOiQ2/KXpzEkRVE2bNjw6quvPvzww0OGDHE4HHl5eT169PB4PCxodrlcLJXuEEZ36NfB6qMnT5783nvv1dTUsP7RhmGwcmxN1RRFsUfPevvGB4/u0qfx+PARCEAAAhCAQBoKWB0gaOMGqohsivShSF+KFOy87xe7SbF6PaThiDN/SPz/R7GdO/9DrOzXFCtO5ReufuElElOk1BGJZgdoc0MAnflPHDOAAAS6uAAC6C7+BcD0IQABCJwLAXtoa98/pXvzJh6GYciyLIpti9OvWrXqxRdffOCBB66++uqCgoKcnByXy+XxeHJzc+0Z9Mn3Wf/oSZMmzZ8/v7Gxkf9HERthe/hs/n7a4z+lyeJkCEAAAhCAAATOmQDr8lBzkAaWbi4uoGgBlQX333DdCl0iXTtno+giNzrSUkNWrZUHidavp+LoZ+Wl1Ltw32VXba1pIF2l5AGi5hNWoB+3/Flvi6u7iCSmCQEIQCCTBBBAZ9LTwlghAAEIZKiAPbS173/tdNjJPHrW2SI1RKIoplIpwzAkSdJUTRRFSZJkWVYUZe/evVVVVRMmTBg6dOjJQ+cO7zqdTpfLJQiCx+MJh8M33njj448/vmTJksbGRgTQX/ukcAIEIAABCEAg0wVkkS6pWBvzKVEvlUfqB120WEmaSSi2syqgE6lEqk5qs9iSsiLoX0/eHA9uC/nkcHzbL37VktJJVUhvJGpFAH1W7XExCEAAAudPAAH0+bPHnSEAAQhA4OsEWBdme2bN90/0UX6CYRiiKH7xxRd//vOfZ8yYcfXVVwcCARY68+Jot9stCILD4XC5XGyfp9I5OTnO9q1Hjx5XXXXVY4899s4772zcuFFTNUmS+AAUxfyPJ0VROtRN8xOwAwEIQAACEIBA+gvIKRo/pi5SdLBv99qSUEOkaNGOzaQhgD5bT66tgzMLoGUzgJZbiOhwLX3rsuq4rz5c0BwKfLB+PckaaewsxWy+wUum2UDYy/Z9sw201Sea/3q2hovrQAACEIDA2RRAAH02NXEtCEAAAhA46wL2QNm+38kb8YUEWfX03r17P/jgg0ceeWTYsGH5+flsJUMWOjscjhxr4y9Z/nxsR2lBEIYNG3bnnXfOmTNn4cKFJ8qdeXreyaHiNAhAAAIQgAAEzo+AtQihJtI9v0hEg7t8feqigYZI0WfLq0lr6xJxfsaVVXc9EkCb6bJGaqsmqkRPP0sV8fWR/ERx0f577tzf0EiK9TjagmVbusw0EEBn1bcCk4EABLqMAALoLvOoMVEIQAACmSlgD53t+2cyGxYZi6K4devW999/f+rUqUOHDi0oKHA6nW63O9faXC5XewG0k5dFOxwOt9udl5fHj7jdbpfL1a9fv7Fjx06dOnX58uUtLS3JZFKSJN4w5EyGis9CAAIQgAAEIPCNC7QH0NOfpLLormigKeyvD/vXvvp/EUCfPfujFxJkvbXrWui73/nE13NjqHdtcdG65cvM27W13W5PmnXrCK9wbj9snsk6QdsyarZk4dkbM64EAQhAAAJnSQAB9FmCxGUgAAEIQOCbEbCHzvb9r72bYRiaqmmqxiuU2eqFsix3iIbZmYqi7N+/f+7cuQ888MDw4cN5+szroB0OB8+dBUGwV08LguByufgJgUBgxIgRU6dOraqqqq2t5QP42jHjBAhAAAIQgAAEzoMAC6Alev63VFm6oyTaHPbXR4q+nDmNrD5b52FEWXhLFkC358caUVOK3vu7Xhb9uDxYd2H88PBrvtCsrPmoANpqwcGO2zNo5nNM/w0E0Fn4xcGUIACB7BBAAJ0dzxGzgAAEIACB4wjYA2u2f5yTbIfs5xPRV199NXfu3N///vejR48uKytjSxSyDJp1iHZZm9Pp5NEz6+PhsDZBELp3787qqQcNGvTQQw+9/vrrGzduZHm0ruuaqimKwiJy1q9DlmW2mmKHiNw2RuxCAAIQgAAEIHC2BdoD6Or5FPKtKI03RAMNsaK9P7zpK0Xu2GO4PUE922PI+uvZA2jD6vJM9JPx66MFX15SnCr2f/Ty/yPZ7Pms6cR6cFgith7QxwbQbbXPR9dWZz0kJggBCEAgEwUQQGfiU8OYIQABCECgUwL2QLkzAbT9ojwglmWZHa+trV28ePH9999/8803l5WVud1uj8fDo2fWsoO/ZBm0vak0P7l79+4XX3zxz372s9mzZy9fvryhocF+X0mSsJ6hHQT7EIAABCAAgW9eQCcyVInWraRYcFlptKY4nIgXHfruFRsQQJ81fFsArRMpGi2aR3H/ggp/S7j37sqyv9Y3UaNIIjXrZC0+yG6MAPqsPQBcCAIQgMD5FEAAfT71cW8IQAACEPhGBU47gDYMQ7E2Xp7MX/KaZSKqrq6eM2fOT37yk8GDB7PaZ5ZK9+jRw+Vy5eTkuN1u1p3DvpJhh/3c3FyfzzdixIgZM2bMmzevpaVFFMVvlAUXhwAEIAABCEDgaAFrWTyZDu2n8tjyiH93aTRV4m8uDVUrkr0CWreaDptHsJ2yAAugNatzM5Gs0L13JitDNcGeLZXxvbOfrm+RSDQroA3d7AKtmbvWZi985vvtd7cOoAK6nQO/QwACEEhbAQTQaftoMDAIQAACEDhTgTMPoHkrjK/t46woyqpVq2bMmDFu3LjS0lIePXs8Hta1gxVH22uieR8Pe2tpQRBKSkrGjBnzyCOPVFdX79mz50wV8HkIQAACEIAABL5GQNdVUVdJkah/+WIzgA4qpX6lNPypLJJ+pAhX1UllGejXXA9vHyvAY2Ld7LIhilQW+jR4QV2gV11JaHlNXVusb4X7PIA2M2geOtt32i+PALpdAr9DAAIQSG8BBNDp/XwwOghAAAIQOB8CXxs3n3xQuq4bhrFu3bpnnnlm3LhxV111VYeI2eFwuK2Nt+xgJzidTpZcs7rpvLw8QRB8Pt/3vve9KVOmLF++XJIkc3X4o1dW1FSNN49G+46TPxq8CwEIQAACEDiegK4pqWSr2RfiRz/cEgvui3up1Efl4c3rVpIkm+W4VhIq6yTbY1C2f7wL4thxBcx4WWyhVIr+a5pSEdtSEUtEir6c+CC1tP/tLyuA5ln1UUXQx70iDkIAAhCAQEYIIIDOiMeEQUIAAhCAQCYJ8PxaURSWFxPR6tWrZ8yYcfvtt1dWVtq7cHTIpgVB6JBKsxNYJXVOTg7Lox955JFFixbV1taylQx5AK2pbUvHZ5IXxgoBCEAAAhBIAwFdN2PQsePXlYS+insp7qXy4K45z7YmE+bgVLM1hGj9dKzJTYOxZ8oQ2pqXHNpPlWUL46H9Ie+eSOCf23eQZEXNtkCfZ9Dm1GzHM2WmGCcEIAABCBwlgAD6KA68gAAEIAABCJwVAU3VePsOnkHzK8uy/PHHHz///PNjx44dOHAgi5gdDofT6eT7rPzZflAQhJycHLbaIY+tI5HI6NGjn3nmmcWLFzc2NiaTSWTQ3Bk7EIAABCAAgU4KSOYqwCSq9OSvG0rCO9oD6D1/eI50hUTZbEiMALqTmF9zmk6vvESx4PryuBgL7R4zZmNLa9snThQ0n+j419wIb0MAAhCAQNoIIIBOm0eBgUAAAhCAQLYIyLLcYSosFNZ1nRUsm/+VK0msPpqIZFlevXr1008/fdttt1155ZUsevZ4PBdccIE9kmahc25uLk+f7Tusbrq4uPiWW255+OGHFy1atHPnzg7DwEsIQAACEIAABE4i0NhKU6YfKA5/GfNSrJBKAntvH7tRSpg9i5NKqxVAowXHSfy+7i1W5qzT1VeuL4/VVRRL8fDad/9GsvXXt6yI//hXQAB9fBcchQAEIJA5AgigM+dZYaQQgAAEIJD5AnxdRN228YOGYUiSZBjG5s2bX3zxxV/84hfDhw/v2bNnbm6u0+k8UeMOvrCh2+3Oy8tjDaa7d+8uCEIgEBg9evTkyZOXLFmSSCR4cbSu64qi2Gu0WQ7OgGVZ5uF45pNjBhCAAAQgAIFOCRhELQr9YwEVRzbEvIYZQPsPXHnRXDVllj+LekojSSedLZDHIlEEo52R5Uq6ToZB8+ZTqOizWLC5sNfW64ZuU2SyOpad/Ep2b369k38E70IAAhCAQBoJIIBOo4eBoUAAAhCAQNYL8KzZlj8f2bWvLmin2LBhQ1VV1ZQpU4YMGZKfn88Knx0OR05ODl+0MCcnh61hyIumeX10t27dBEFwu93BYPCaa665++6733777S1btjQ3N4ti26I/hmEcW7htHwP2IQABCEAAAlksoGtmo+EU0bovqTi8OlqoRguo2FdzReXi+gNmAC2TqJGik7kgodbelRhRaGe+ElxJ00mS6Mc/3hou2h4uaowF17/+snkBTev4V8eOuSwC6GNIcAACEIBARgkggM6ox4XBQgACEIBAhgucPIDmk+PLGCYSCcMwRFHkR4ho586df/vb3+69995rrrkmPz/f7XY7HA6Px5OXl5eTk+NwOFibjg79o3lszZJrp9N5wQUXXHHFFffee++cOXM+/fRTexE0Hwl2IAABCEAAAl1BQNHMWFkmakxScfjTqFeOFurFvprLSj/6ch2Zpbuk6ubvCKBP+etwJIBWaeVn5Pd+ECza26fH598ZvKb2ILua1ZvjZBdGAH0yHbwHAQhAIP0FEECn/zPCCCEAAQhAIHsETh5A23tiSJLEps2LlI+roOv6vn37qqqqpk2bNmrUqFAoxIJme6to3ruDB9Nut9vj8bhcLtY5WhAEl7UNHTr0jjvuePbZZ5ctW2aPvI97axyEAAQgAAEIZIeAoZvpsmyQRJRQqDj6YdybjBaq8aLagbGVny4h1QxI23oUswzaHohmB8I3NAvGpVrBvazQhF9KxcGdgfyDA8r3PDapsanJcv36e9u9eaD99R/DGRCAAAQgkCYCCKDT5EFgGBCAAAQg0LUEeBJt37EH0KfB0dzcTESNjY3V1dWPPvroj370o9LS0pycHI/H43a7ndbGw2hBEHittCAIrHqadero0aOHIAjdunUbPHjwTd+/afLkyR9++CG7OBEpisIzcRZS23t3JBIJ+8vTmAU+AgEIQAACEDj3ApphBtApK4Ae+8NEv0hrUa+WcGFjcWjr735D9U0ka21/MMwD6HM/yMy4o2Flym01zbpOekpRRSuAPtRAF1V+EclPhPs2DyjZsOlzc3XHzm0IoDvnhLMgAAEIpKsAAuh0fTIYFwQgAAEIZLWAPXe275/JpPkag+wiiqIkEonGxsZ58+bNmDHjuuuu8/v9vDE0C6CPbRjNa6IFQejwbiAQuO6666ZNm1ZVVbVjx45kMslu1OG+ZzIFfBYCEIAABCBwXgQ0g1SrB3RCpZ+Mb4z5DsR8Ur84xYL7HnuMmlpJ0TQ2MNTffs0DYgG02VJbJVKt3tqkELUa9N+/l0L5WyoDFOmz656fJWWl/Ur619ZBI4But8LvEIAABDJTAAF0Zj43jBoCEIAABDJcwB462/fPcFq6rsuybE+E2RKHvJ9GIpFYsWLF9OnTx48ff8UVV9hTZtYzmvXlsHfnEAQhx9o6dJH2er0jR46cOHHiSy+9tHr16lQqRUS6rvN7neFc8HEIQAACEIDAORPQyFDJEIlaFZr6FJWE9oQLkkV9ElH/odtvS6Zksz6abVYn6M4W7p6z8afRjUwonUgkShLJmhlDU0qnpgRdOGBB4b/sjvWp71+8/OOP2ofMsuV23vajHX5HAN0BBC8hAAEIZJgAAugMe2AYLgQgAAEIZIeAPXS275/J7CRJMgxD13WWBbNL6bquqRoPhTsExIZhLFq06I/hVE2CAAAgAElEQVR//OPtt99+ySWX2OujWTsOp9PJFjbs8BZLrllO3a1bN0EQevbsOXjw4Hvvvff3v//9mjVr7GM4k0nhsxCAAAQgAIFzIKCRppImktGq0oxpFPSuLwupJUGKeJtGX39YtZYoZMOwAmjVyljPwbgy8BZmlKxa6XOCSGQV0CrRH/6HLirfXBFIRfpuu/3WL2vr2qeGALpdAr9DAAIQyGIBBNBZ/HAxNQhAAAIQ6OoC9mib7Z9IhK15qCjK6tWrX3/99YceemjQoEEej8fhcHg8npycnLy8vGMz6A4dpR0OB6uVZr8OHjz45z//+Z///OfNmzfbQ3BzIScrKGeD0XVdkiQeWOu6rijKGbbDPtE0cRwCEIAABCBwPAFdN5tFqAqpok5vvUUV8fVRb7JflKJeuSy2UlXNJQjNul6D2IKFCKCPx2gdOxJAswpo86Cs0dWD1sQKdkXza0rDn/7pDetvTbFLIIA+ISXegAAEIJA9Agigs+dZYiYQgAAEIACBMxdgSTS/ztq1a1988cUHHnjg2muv7dGjR25uLo+hHdbGX7IdewBtbyedn58/ZMiQKVOmVFVVbdu2LZFI8FsoisLWLdRUTbE2TdU0VetQrM3Pxw4EIAABCEDgbAuwAFo2A2iDqqupvPiTqC9R4qdoAcWDa3ftRADdafK2qF4mkol0jUhUaUk1VcTWxL2Hi/27Bl++3GwOzSP8tp7RJ78+WnCc3AfvQgACEEh3AQTQ6f6EMD4IQAACEIDAORCQJCmZTIqieNx7tbS0sIx4z549f/7zn5944omRI0cGg0EWOnfv3t3tdncIoDsE0x1eFhQUDB8+/MEHH3z33Xe3bt1qGIYkSah6Pi4+DkIAAhCAwDcvcKQCWjZo23Yqj1fHilrC+RQroGDBug8+IMVqvWFVQMu62eAYbaBP8FgMy0bXmZBiUFMT/cfPPg8WrArm7+pXsu7V18wPNoniqQgigD6BNg5DAAIQyBABBNAZ8qAwTAhAAAIQgMA5ERBF8bjVx4ZhsON8FIZhbNu2raqq6rHHHhsxYkTPnj1dLpe9AtrePNpeDS0Igsvlcrvd/KDP5xsxYsSUKVPmz5/f0NDQ0tLC74IdCEAAAhCAwDkQ0M1aXfNHNqi5icqK/1Eabgz0MQPool7r/vC8KCvEMlX0gP6ax8ECaJVII90wm2/s20/lpVUx/87SyO5vD15aW0+iWSVtduSy/Zz8qgigT+6DdyEAAQikuwAC6HR/QhgfBCAAAQhAICMENFUTRfHvf//7U089NWTIkPz8fI/H43a7nU4nayQtCEJOTg5bsZCtXsjXOXQ4HE6nk53Qs2fPwsLC0aNHT5o0qbq6uqGhQVEUewtpTdUkSWKNO2RZZusrplIpTdUyAgqDhAAEIACBNBTQzbzU/FF0Sqbo2n/9pDx+MJAvxrxG/+KvZk8XUyJpVlEvi0LTcAppNCRW26yQKJNEdNeE+nBsg6/wYLho/SMPfp4y+z9TSrE6arep49/gafT0MBQIQAAC34QAAuhvQhXXhAAEIAABCHQ5Afu6gmzy+/fv/+CDDx588MERI0aUlZWxZQxZWXRubi7v2sEKort16+Z2u10ul9Pa7C07AoHAyJEjZ82atWDBgrq6OhZGJxIJ3dq6HDQmDAEIQAAC34CAPYCWJLrl5k2lsV2B/ESor3h5//o7frJdlUnTzK4SCKC/nl8nUswW0E3NdLCZYv2XxMtqQ4H6aHDp/j1tn27vv8Fif80qhf76C+MMCEAAAhDIUAEE0Bn64DBsCEAAAhCAQFoIsNyZlSHzAem6zlYU5N08dF2vq6tbuHDhtGnTRowYEY/HWXG0PWjOy8uz9+UQBIFVRruszel05uTkCILg9XpHjhz5yCOPsP7Roigmk0l+a+xAAAIQgAAETkOABdDmrxrJCt1376FIYIu/b2tZkCIF20ePXNvcZBZHawigO4Nr6KSIJhbRfz2jRks29em7Kxj48qYbt8uiWWAuKvwqvAsHP4IdCEAAAhDIQgEE0Fn4UDElCEAAAhCAwLkUkGWZrx+o6zoPow1rYyPhJ7DFDIno0KFDS5cunTx58siRI/Pz87t3784iZtYYmvWSdlgbj54FQci1Nt48WhAEn8931VVXTZgw4fnnn9+wYQO//rkUwL0gAAEIQCDTBXhps6aTqtKUKS1+70Z/n1TMSxWh2oro+8lmUjQE0J18ziqRRDq1tNBVV39WVnY4ULQvXrJ8+ceUSpGuYgHHTjLiNAhAAALZI4AAOnueJWYCAQhAAAIQOC8C9tC5MwNgwbQ9nmafWrx48TPPPDN69OhIJGKPmAVBcDqdLpeLlUt3eMteQ832hw0b9tOf/vS55577+9//bq5wZC2fqCiKZG1ExAasqZq9tTQ/3pkp4BwIQAACEMgyAd5YQ9fNoPkvf6HK0l2hAqO0iIq9jf2LV2xYa66nZ1VA83OzzKDjdM5gnroZQBO99QYFvJ8EvDXF8T1Dhy0xAa3WG2dw5Y6DxGsIQAACEMgIAQTQGfGYMEgIQAACEIBAlgsYhqFYGyugbm5u/vDDDydPnnzT928qLS3t0aMHC5fd1sZ6cfDo+eSRdEVFxW233TZ9+vSFCxdKkvnfwyxrFkVRUcy/A8y6iLA8mmXTx4bjWa6P6UEAAhDo8gI66WyJQd0wA+jqpVQW2xIupFgBxb3J/rH186rsAbRqteLIcrXTjonNFtCa0dRMN92wN+zbGy5qLImu/9MbJpduWP8S7gp8Wf7twPQgAAEInJoAAuhT88LZEIAABCAAAQicAwF7HMz6dcybN2/69OmjRo2Kx+Mul8vj8fAAusMOb9/Bj+fk5OTm5rJVEC+99NLbbrvtySefrK6uliSJNwzhk+IF2vwIdiAAAQhAIOsFWPpMpJJBBtGOHRQLbgzlU7APRfqK/WPbn51JssraGqvmaV2gjYQVQLcvFmj7Bpw8mGbdtBtb6P1/UKzo08qIWhFL9iv/kPV9tpy7hJ4NDLsQgAAEIEAIoPElgAAEIAABCEAg3QXYkoZ8lDU1NcuWLXvyySdHjRpVWFjYs2dPnjUfd8fhcLBUukPpdN++fYcOHTpr1qy33357y5YtLI9GAM2dsQMBCECg6wi0dYYwzACayGxeHPJ+GsxX/b2NcL7YL1Lzf34py0pXCKDb4mWWI2uka2TOWtNIU80GGpphvTQD+I5BPFvvQSNVIWpN0b13f1Xm31vmS5ZHtk55glSNkqkGIrmLxPdd5387mCkEIACBzggggO6MEs6BAAQgAAEIQCCtBZYuXfq73/1uzJgxlZWVLperQ9AsCILH2gRBcLvd9pA6Ly/P4/Gwjzgcju9973t33333Cy+8sGDBgoaGhlQqxaetWxtv2cHbdLC2HqybBz8ZOxCAAAQgkHkCBpFxZIG8//Wv+0LeFn/f1kB+ojTYcOO/7U3JZjqtKexfDccpDc68KdtHbDXHIBKtH7PAWyWjSUm2knYoRYfq6J+LaP0m87hsRtK6Ts3Wj2x1LzGPK7pMRE3S/iaRdm6j0uCKASFpQLCxf+y91nrzcppqtr0yDM38RSdTk/8cGQk/xHaOvIE9CEAAAhDIXAEE0Jn77DByCEAAAhCAAASOEtB1XZZlTdVWr149c+bM8ePHV1ZWsvJnFjrn5uY6HI7u3bvzttE8euZHcnJy+JqHkUhkzJgxjz766IoVK7766itJkjoEzbIsi6LImkofNRS8gAAEIACBzBJoiz2tFhHWyH90c0Oo6GDA2xzIT8QKW66+fEvKWkdAEhOkyVnYguPoAFojatXkmpZEgmh3HZWUvVES/cegb72xdRfJBilmZXS9TrU6iax9tgVnIspkBvT/898U6b29pHcy2mvj5If2E5HUarIaOsugrQDafG39HPmqtD2G9jescvQj72IPAhCAAAQyVQABdKY+OYwbAhCAAAQgAAEmYBZTqWY51YlAlixZMmfOnAceeGDYsGEej8ftdrMSaR46s5Da2b7l5OTYu3aw9h0ul8vv9w8aNGjq1KnvvPPO3r17WTW0+R/VkqSp2onujuMQgAAEIJABAkcH0LJED9xH0dC+oK+lqCAZ7tvcL/LpgX3mPDRF0qRkdgbQbRm0WdzN/q2WMiih0cuvUcy/JtR784Diz56fQ6JGitlRo1E3M+ikTqr1o+tmAbn5wfp6+u7lmweGWsr7tlQUrdy2qe35mz06dIN0K4Y+TgU5ewaaLX02LGfWFeQ4H8iA7xWGCAEIQAAClgACaHwRIAABCEAAAhDIBgHzr/PquqIosrVpqsaaZrBgmtUpK4oiSdKmTZteeumlu++++7vf/S7vDc1CZ3t3Dv4WO8he8hPy8vJ69+49ZMiQSZMm/eUvfzl48GA2IGIOEIAABLqyAE87DUqmaNoUCoe3hPzNgUI53DdRGvh01ackW0XQVkKadXmovfjYypFTmtaYpNXrqH/ZkrhvX6RXbbj3xhm/ZgG0rFFCN39EHkC3SqJKpKhU9S5dUryz+IK6UN6Xd45NSkmSrTxbklInDqB5+owAuiv/jxBzhwAEslYAAXTWPlpMDAIQgAAEINAFBVhrZhY9d/hVUzX+Y39r48aNr7322h133HH55Zc7nU5eFs2zZrfbzQ86rI236WCxNTvo9XqHDx8+ffr0Dz74oK6uLplMMv8OpdlshPzRsJcdzuHvYgcCEIAABM6RAMs/Wa2t9TdqXv8ThQIrw4GmYKEW6SuWFK158xUyS5/bthP+tZv2EzLtd7tAewV0QqUZ06nYv6oifKjUV1Pi2/TMDB5AyzrJrPaZrVVovlaopZa+c8nK8vzDF/rlMu+nf/0Tqe2Nta0K6A49N7gSAmhOgR0IQAACWSiAADoLHyqmBAEIQAACEOiyAicJoO2hs33fbqUoyqpVq2bMmDFu3LgrrriCZ9AsmHY4HKxLh32RQx5Ju63N6XSyd4PB4E3fv2nixInz589vbGzkd+EBNBsDP44dCEAAAhA4nwL2+NUgw6D5CygU+ijkbwx5KdJXLfFtmj21UUqw3husSvd8jvfs3/toAc3KoFtVev53VBbcWhGqPTqA1q11CHVW/swCaIVIlOnd16m//8tIXlOlt/HaKz4mItXsutG+sbu0v7L9jgDahoFdCEAAAlkngAA66x4pJgQBCEAAAhDowgK8oLgzO7qu89JjXdc7NJKWJPMvWq9cufKFF16YOnXq0KFDe/bs6XK5eCrNomf2Kz/IiqN5xbQgCLm5uYIgRCKRW2655fHHH1+0aFFLS0sXfkSYOgQgAIH0FNDNBfGsCmhDJ0mmzzdTOLI44Dsc9lKsr1Hi/fLOn6yXE2SY3STEE9XxpufcOjUqlgAzBMNs5SyT2qrRO29RZWRbub+lpKCpuHDz7GkkKqRY8bSVPou6WRItaqTWtrSkRPrl/5YHeGv79TXifTb/9R2z+YZqb5itH93h+UgdOQLoTj0lnAQBCEAgQwUQQGfog8OwIQABCEAAAhA4jkBncucO5xznKkcfUhSFZdOJRGLv3r0LFiyYNWvWyJEjA4EAz6BZh2h77swjafsOy69zc3PD4fBN379p8uTJS5cubWpqOvqGeAUBCEAAAude4EgArWvUmqK6WorH/hH0HQwVUriQYr7t1/2vJclWMtfa05PZHEBbUbBGlCI5adA/F9DA4h1lvmRx30Q8/8tZU80yZ1sAndQpqVFSIZIN2rub+gc/61/QNLAocc2l2xqtf78dFUCbC/i2/7Awuu1RI4A+99953BECEIDAuRNAAH3urHEnCEAAAhCAAATOjUCHiPlELzs/GPsV7J9au3btiy+++MADD1x77bU9evTweDwsbua9oe3NOgRB6NatG6+h5osc5uTkFBYWDhs2bNq0aXPnzm1sbEylUva7HHdfUzVZlnkF93HPwUEIQAACEOi0wJEAmogUkdQWGvHdFRHvAX8hFfkMf3BvvwsXJBWzSNogyV7U2+lbpPeJPBe2qpI10lMkmgH0QhpYsqWsKHHcAJrMRQiTGomKQZpCv/p5TXnBl5W+2suKv5w2mZoSlDLa0+ojbTh0Q1M1RTGrrNsOsiiatf3AIoTp/T3B6CAAAQiclgAC6NNiw4cgAAEIQAACEEhjAXtefJL9szIDFgGbCysRbd++/e23354+ffqNN94YCAQEQXA6nSySdjgcbrfbXg3tcDhYBs36StvXP2T9ox966KF58+Y1NDTwcR7bNtreRYSfhh0IQAACEDh1ASsKZQ0oiAyZ9Gb6yfc3xq0A2uszvKEDxQOXf76LFDOf7VjUe+q3S79PHBVA6xqpRwLo0s0nCKB1i0LVSVU0StbTpSUrK321g8sTl5TN37eHEqm29NmMmtttzQpojQzF+mhbCw7daumBADr9vhUYEQQgAIGzJIAA+ixB4jIQgAAEIAABCHQ9AdYnWpZl868UG0c6WTKJpqamBQsWTJw4ccyYMf369evWrRtbopB16uABtD2V7rDPSqrD4fDNN9/82GOPLVy4sLm5mV2cBetdjxwzhgAEIPANCdgCaMPMRrUWevTemrhvr7+QzAA6eDheufLdDyhp/iM/GzceQJtlyapGcicC6LZmGjqRotDTv6ZvFR8s652o9O+ZeP+B5oSZPlN7tKyTrpEmK6RIpImkpUiXzX4m7e48fUYFdDZ+uzAnCECgywsggO7yXwEAQAACEIAABCBwZgKJREKWZU3VWB30SS62YMGC5557bty4cZdddpm9BUeH3Pm4L1kBdV5eHlvPcPbs2QsWLFAU9l/3J7nnyd46NjQ/2dl4DwIQgEA2C7D1B82mEIrZToKUBD3968Z40c62ADrQEC37/LcvUCKZpQpHBdCyRrLMekAvpIrohopAqrQgWeLd+sx0ew9oc0lGXSdNJyVFF0U+Lu19aIBf/lbFtvnzzTYlrQo1p8xOG9aPbEbLBu3aRu/9WfzNjK1SK6lWHw4rxm4/yzyXD6V9XUgzpraS6iy1x7QgAAEIZL0AAuisf8SYIAQgAAEIQAAC50LgVEuSFUVZtWrVzJkzx48fP2DAAB465+bmCoLA6qNPtKqhw+Hg/aavuOKKW2+99fe///3ixYvtCTgPlyVJUhSF/WqHYO07eIsS+1vYhwAEINDFBNpaSbCcU1E0MswS3aq3qdS/JeQlfxH5A4lobPevf21WQGdnFGpPfUnVSVZIlgxasIBKg2v7BcWywlSpb/uzM44KoHXV+qZo9P471L9oazjvcP9gza1jDrYqlCKzObRsmF2i2VmiQa0t9O83fTQgsqC86P17frpBkcwTdPN2HXJnPpou9k3EdCEAAQhkqQAC6Cx9sJgWBCAAAQhAAAKZI5BMmgV11dXVb7755q9+9asRI0bwtQoFQcjJyXG5XG5rY008eFrNo2p2giAI/fr1u+uuu1544YWNGzdaizx1LJE2DEPXdU3VWMk2AujM+ZpgpBCAwDcnoBPJZt8Nq9BWU82WSppEa1ZQaeDzcKEVQPvFknjTuLENBpnRbBZuR0W+uk5qQmshohdfpIr4+hJfU6x3c6zv5plP2QPotiheF2nolR9VFB4aGFSKi5b/7V1q1UkkQzYopVJC0WSiFtnM7l/9I10YX+XP3XJZbN/gS/7W1ERNCqkkI4DOwm8UpgQBCEDAJoAA2oaBXQhAAAIQgAAEIHDOBdjSgrxg2Uw9rG4emzZteu655+6///7hw4eXlpay0JlVRns8HpfLlZOTY0+ij7t/7bXX3nXXXa+88soXX3xx3JkhgD4uCw5CAAJdTKA9gLZCWPa3STSZDn1FpcH1bQF0kVocFb91yQZZJYUV9GaZEQug2yZlloS3SE1ENG2G0r/s83hhXaRXfbjX5hlP2gNoVaekrNBHiyjuXVqa31Dq++qaf61WyCx/ZgG0SmYnaDN9NqixhQZfuHWAX+7vpXj+1ptv+lC23pXMvFo5uvPGUXF4lkljOhCAAAS6oAAC6C740DFlCEAAAhCAAATOswCLfVkTDJY4swHxI8eOr66ubvHixY8++uioUaP8fr+9RFoQhNzc3J49ex5bHy0IgtPpZIG11+u9/PLLZ82a9fbbb2/ZskWSJJ4+2+PvY2997BH7B0/1s8deDUcgAAEInG+B4wXQCh3aT6WhlVGfVlSo+ov0kE8uj62pO2R2Pc7CzVpJt63Xsrmvi3qqvoWmTaPS2BfF3vpo3/powdbZU+0BtMnQ0Ey/uONQoOfaiqLWi0t2vviCopnpM8mkqVZhOVu1USUa/+9bQ712ledTWT71C25Zt54OJ8xW0SlKWm2ieehs38lCaUwJAhCAQBcUQADdBR86pgwBCEAAAhCAwHkWYAHumQzi4MGDc+fOnTJlyne/+91AIMDKn51Op8vl8ng8vJG0y+VyOp324miXtQmCUFpa+oMf/OCJJ55YtmxZS4v596xZFC5Zm6Io9jRclmXeM/rY9h32PPpMJoXPQgACEDhPAqwHtJkrGzqxf6bpGklJGnLl7niR7CsQy4qpsGeyLPjFiqWks2rd8zTWb/S29gBaI0U26NdPUHFgX6SgPtL3YIlv+3OzSFTMcmW2aCAR7f6K+pcui3sPFLh3DO63SWkgkkgzSCVJJUkhPWXF0P95576od02lXyovoIqi1CVla2oOm2XRVlT9jc4JF4cABCAAgfMvgAD6/D8DjAACEIAABCAAAQickkBzczNLhBVr03V99+7d77///uTJk3/0ox/FYjGeODscDlYBzYqgeULNTmDxNFvqsKKi4pZbbvntb3+7ZMmSxsbGZDLJlzRkLar5CA3DYHdnzUN4MH3mqTq/BXYgAAEInHOB9ujVCqDZP9+kFI0Z3RD3J7z5rbEw+fsoZcGtf/0T6bLVLuKcD/GbvqFuxcpWDG9WQKuGLKo04T6KB+sjBY3R/JqywPY5z5KotgXQikGtIt37yy3xwMayYKLEt/PXD7YVP5PZ1FmxMmiSdHrnHRo04ItI7/2BnvWl3vrKyIZXX6SUZDbe1r7pWeH6EIAABCCQBgIIoNPgIWAIEIAABCAAAQhA4FQEWJGy/RP2amVRFJubmxctWvT0009/73vfC4VCLG5mYTTbZ3k0P84yaPaSde3o37//HXfcMXPmzGXLliWTSVEUFcVcdYutYagoCmtUzRtY8yJo+6iwDwEIQCDjBNrKn61/ukkpmnA3xQKHfYWJgE+PFFFJcPvsKQlSyVyuMOu2owJonWQt1SLS+PHJkmhzrKi12AyOd7zwOxINkimhmGsK0v79dEn/6oFRqTKk9YusPLiLWg5bLqpZS87C5Y+W0Hcv3xgr3BbpczhWcPiSii/v/eUWIpK1rFTMuq8FJgQBCEDgbAgggD4birgGBCAAAQhAAAIQOLcCuq7LMuurSZIkJRKJZDLJ0mEWDbPh6LquqVpjY+OSJUsee+yxG264oaSkRBAEl8vldrs75M4sena73awyOicnh53gcDgqKiquu+66p556asGCBfxGqIA+t88cd4MABM6FwFEBtEhTn6BoYE/A2+z3asUhihdt/z//uS/7A2irHDyltDYmaPTompJoojSolPkb+8e2v/S82bVZpkaZRFGn/36aykKbygv10vyGW2/ZIyfIxNHMXw0rg97yOV118WeXltSV+1srIy2XDth5zz2H6622T6h9PhdfaNwDAhCAQHoIIIBOj+eAUUAAAhCAAAQgAIEzFmABNM+Fj7sjSZIsy6tWrZo5c+YNN9zQr18/j8fDImlBEHJycngdtCAIPKFmx/nKh4WFhax/9Icffsj7RyuKIooimwRv33HsnNCp41gTHIEABNJKgP+VDlWi1/8fxYObQ/7mgI8KLkhGC3fcdN1KNZHtLTja+pGYj2XEiN3RQFOJX4v7GivDX360yKyATlGyxTBXKhxYXl3qPVR8gTgwsHv5QmpuJFkkw4qWFZEO76Fbb9xxYWRnuGddsFciHtx2+51bm1Wz9XNC4uXPCpktPbBBAAIQgEA2CyCAzuani7lBAAIQgAAEIACBDgKGFRkQEWupQUR1dXXV1dUTJky4+uqrWRG0PYN2uVwOhyMnJycvL4+37MjJyXFaG0uoI5HIqFGjZs2aNW/evKamJnYL1rWDdYtmY2Dl2Jqq8TF0GBteQgACEEgHgSMBtEzz/kHFobXRQJPfa0T8FPHtvqjsfbWFBdDZ1objSAsOra3HiE40ePDGkL856tPC+fWlRZ8vXUCtMrXqZvr83t+oPLauxNt6eVS57ls7mmtJEkk137E2iX52y1eXRXcMKGoozq+vLD408vrtX+ynfSlqtuTa+TQE0O1k+B0CEIBA1goggM7aR4uJQQACEIAABCAAgeMK8B4dhmFoqsYSYU1t+8vQ69ate+GFF+66667KykqWODudTl4BbS+RdjqdbmtjzTp4JO3z+a6//vpHH3107ty5e/bsYXc57khwEAIQgEAaCtgD6E0bKB5eHgs25veWyuMU8e4rKXpv/w4WQGdbK+hjAmhDVKmkpDoaag0VKsHe9cWFn1fPpaREKZXEBI296dOA74uIt6GiaPNbfyA5aS48aFhNOBpq6f6fHy7tvfmyAAU8+6KFG/597M7N+6iV6IDeRGT28TAD6PYQOg2/BhgSBCAAAQicRQEE0GcRE5eCAAQgAAEIQAAC6S7AO0eb/+FvNZJm0bMkSawsmpcns+D4XWt74oknrr32Wq/XyyJp1rXDXijNi6NzrY337hAEobCw8Morr5w1a9bbb7+9ZcsWdqN0Z8L4IACBLixwJIBW6OBBikcXFscae3VP9CumiO/wJeWffbKYJaeylbVaGaphRdK8+Dcz9VgAbf5ppLWnGZQUqW/B+yUxKeyVA70Oh/us+ef7Zo2zqtO6T6gyVh30Hy6PJwZVfirVk6aa0xaJDrbSpIcT8T7LSnu0RvPEC0M1Y248IOnUqJm9NhqoXjSDaGtDAN0Ggd8gAAEIZLkAAugsf8CYHneWUukAACAASURBVAQgAAEIQAACEDgTAR7EsGB6+/btr7322qRJkwYPHtwhgGarF7ImHk6ns8O7rKO0w9qGDBly3333VVVV7d27l41NUzVJkvjKiqK1sbcMw0ilUrxA+0zmgs9CAAIQ6LyATqTo1Jqkiy5aUFbaEI9Q739JxAPNxb5PZzzeai61Z2at7UXQhhXaZn4ArVgrCLIAWlXo0CGq6Le6NC6XhPVgn5pgr0+2baKDdVTXQhPu1X19dgV8VBytnT2VdKuNc1KjJoNmPEfRwEeVwfoBPiruU/vti1cdOkCNLWbzaJEMhWSDtAyn6vz3CGdCAAIQgIApgAAa3wMIQAACEIAABCAAgc4KsHUOedH0559//vLLL//kJz+5+OKLBUHoUBnNWkWzamgWPbN20qxxh9PpdDgcF1xwwVVXXfXII4+88ac31qxZw8Yhy7KiKLwWu7ODw3kQgAAEzp6AGUAbZruJ4detKCk5GA2Tt68S8TZVhrZOnaTrZp1wewDNyp/1jF+Z0JyyLYDWNdq2lUpLV8bjUnFEDRXsDRcs+WoHyRrVNlIkvLKoIFlQkCou2XzwsGkla9Sq0P2PHiguX35hReLCEuofTJYF1857n5JJklUz1mbl4gbpOmntRePIos/etxZXggAEIJCuAgig0/XJYFwQgAAEIAABCEAg7QUUa+PD/PDDD5955pkf/OAHoVCoZ8+erOqZ9YZmfaLtrTl41w6WSjudzry8PIfDMWTIkIcffvjll19eu3atvWEIvwt2IAABCJwDARZASxr9x127Q6Fd4RD5vUawMFEZ/urWH+zQzIJf1oLDGku2tOBQyIrWWTMOouUfUzT6aSTcGg60hLxfloTn1h80U+SZ03Vv7w1FhY2R6J6f35Pc32TGyc0p+ss7dOGAzwMFB/x9GkuDDaWh1X99g1SZWhPsuuy5mekzAuhz8B3GLSAAAQikjwAC6PR5FhgJBCAAAQhAAAIQyAABWZZbWlrYQNkahnxf19vaeRqGUVNT89577z355JPXXHNN7969eQX0sRk0T6JZ+w5BENxud48ePQRB6NWr17e//e0JEyY8//zzGzZsOMM8GiXVGfD1whAhkDYCrBxYJpr863pf0RfBAPny1WiRVFxwYFD/jzSzbX57RS8bc+YX8lpTtgJogxVC0z8+oGj8s3AoEfDVBws39iupSjZS7R7610Gb/L33xMMN+b73F35M9ToliV57g0qiH8S9B8J9ksFehyOFqx+cUCen2qPntpVuybq0Zv3KY/vMt0ub7y0GAgEIQCA9BRBAp+dzwaggAAEIQAACEIBA+grwRhwsgNZPsLH+0Wwa27Ztq6qqevTRR2+++eZIJJKbm8uCZtaIw+FwOJ1Ol8vFXgqCcMEFF7CCaEEQcmzblVdeeeedd7711ltbtmzRVM2eKbNRsdvpui5JUiqV4i9lWdZ13X5++vpiZBCAQBoIsCLgpELP/rZpwICaSID8RRTx6/GC1gHhFaST0XEBPZZHdzyaBlPp7BCsKbcH0Dq1tlL1EiopWxcJpwLexrD/y9t/fLjlML31IvUr2lnuT/kLN4/76ed1GtXp9O58quy3Iu7fU+5vifc+cFF095MPt3XeaAvqWcsNMshcwtD8aW9ZwmLozg4S50EAAhCAQCYKIIDOxKeGMUMAAhCAAAQgAIE0ErAvVGjftw+RpcOKosiybBhGY2Pj/PnzJ02aNHr0aK/Xe+yKhfYjtvw5x15AnZ+fP2TIkClTplRVVW3bti2RSPA7shuZhXaqJrdvLC4/0Qj5Z7EDAQhAgJU3a0QtIs2dT4GidfEwBQMU8VOJlypDG/dub49P27B0qyOH3LEsOqMoOwTQqRS9W2UG0OGgGCpKlsVqbhvX2HKQRl1lhLofHBih/uXb3/w7tRB99iVdMvijQNGOUH5jsOeOeMHKMf+2peEQ6byymcX55kszgLYyaJ7UI4DOqG8JBgsBCEDgtAQQQJ8WGz4EAQhAAAIQgAAEINBpAZ758k+wI/xlbW3t3LlzH3rooR/+8IeVlZV5eXmsZzTvzsEyaHsqfex+QUHB8OHDH3zwwXfffXfr1q2GYUiSxLuCmLGHYbAi6GPHw0eCHQhAAAJMgEemH62g8tKtRQVmAB32U0kBVQZ2zP2rQoZZ2qu25aiqtSYhW5YwUwl5AG3WcuvmooIv/LEuGlsTKJLDRVppuP7un9N7b1B5/sFor9ZYUet3rjrcJNKK9fSt73wcjW8tK1bKo6lQ709HD12ZPPIHgpYGb7ZhBtAdSsXtATRPrDPVEOOGAAQgAIHjCiCAPi4LDkIAAhCAAAQgAAEInH0BTdVYW4wOATRLh3mFMhEtWLDgueeeGzt27KWXXmqvgO4QTNtjaJfL5Xa7eYm0z+cbMWLElClT5s+f39DQ0NLSwjqF8PS58+04On/m2SfDFSEAgfMkwFJSmehwPRX2+ShSZAXQRRQvoH7+r34zu8aMaHVKqbIVQetktkFOWuW952nEZ3xb3WzXrLL2zJpOSYlmzN4fCq/3e5WQlwIF9ZMepFuup1jvRKB7sjTe9NY7tHUHff8H68KR9fFoo6/PwZLg1qHfWW4uVNi+GZpKumKytGXLXxtAI4Nut8PvEIAABLJIAAF0Fj1MTAUCEIAABCAAAQikt4A9/LXvn3zUsiyvXLlyxowZ48aN69+/v8PhyMnJEQQhLy+PdYjmMXROTo7T6ezWrZvL5WIH3W63x+PJzc31+/3XX3/9ww8/vHDhwsOHD8uyrCjKibpC2+umWR8PZNAnf0Z4FwJZKcCKmw2iksiqmI/C1k/MS2XB/bf97w1JlVI6tWosgCarBYdolfdmKoY9gFZ0akrQ9Bmt0dCWYKER8lIP96F7f0ah3oeivSjYKzlgwP71m2jEsMOx4PpA/sHyiBTzbR85dHP9YVKt2nDdjJwNw9A6Z8JrpDvsZComxg0BCEAAAnYBBNB2DexDAAIQgAAEIAABCKS1QFNTExHNmzfvhRdeuO222y6++GJ7Bm3v1MHrpp1OpyAIDmvjUXUwGLz++utnz569cOHCpqamVCrFI2ZWKM0VWOMOe+8O/hZ2IACBbBdo669x2zgK5utmAO2lmJdKgvtH/tvKhiRJRKKhaayzsdnamPWAzlwVXW+vgFY0Soh053/uHlh+2HeB5OujxYpoxNUUy9cKPWrMa0x8iG66icpih0r8jbHCpnjR7pFDdtTspUTSnL61RiOPkjsDwk/usNOZz+IcCEAAAhBIdwEE0On+hDA+CEAAAhCAAAQgAAEm0KEwmbMsX778zTfffPjhh6+44orc3FyeMguC4HQ6PR4PL4h2OBxOp5OVRbvdbpfLxeLpcDg8ZsyYxx9//IMPPti3bx+7siRJsixrqmZPn3lOze+OHQhAIIsFdF1taqAbRx4oD2vhIrMIOuajkmDNwIHzaurMEl+F1feafSPMjtCdq/ZNXzCrCJo0MruLiArdMmZNv/iB/O6tgXwqj1FJkMJ99WgBFQfouqFUGpX6x2lgVKoMf/Vv12yvraGWZkqlKCmJii4TGawIunOzZbkz6/9hz6B5w+i2Pwzo3NVwFgQgAAEIpJcAAuj0eh4YDQQgAAEIQAACEICAXYB16rD3ypBlWdd1TdVYW2dZlvn5uq4rirJ27do333zz3nvvHTFiBK+DZl077Nk03/d4PG632+l0snPcbndFRcUNN9wwZ86cTz75RDMbopp/jZxv/HbYgQAEuoJAsplmTaV4sDbs5wH0IV/Bu3v3m7Nvi5xZTMoS10xGYfMwA2jD7AF9yy0bvL02FfWUYj4KeSlUQL4LlJIg5f+LGPaZMXTcm4wVbjPT571kZs5EUpInxWaObGXQnRFBAN0ZJZwDAQhAIFMFEEBn6pPDuCEAAQhAAAIQgEAXEThR0TFPhDucYD8uiuK6deuef/75++677+qrr2ado51OJ+8fzSqgWRjtcDhyc3N5VN2tWzdBEHJzcwcNGnTrrbfOnj177dq1rCOHpmqKtbEdSZJEUTSTF0nqIg8F04RAFxLQafZ0iga3hQNquIhiRVQSqC2OfPzxx2b6rHAIXrbLj2Tmjk6kka4YpGg0bMgyb69NA4sp6qVggfnj66MFC6g4SP2i5O/dXNhj0y3fO9hwmFSxPYyXT28VQc7XYQcV0Jn5NcKoIQABCBwtgAD6aA+8ggAEIAABCEAAAhDILgEeGbPlBFevXv3qq6/ec889w4YN41kzr4bmOw6Hg+/n5ua6XC5+8mWXXTZu3Ljf/va3CxcutFPpuo4A2g6CfQhkg4BuFva+/grFouvCoWS4iCJ+PR6sjwfXvv4qtaq2AFona9W97Ji0qlgxcv/yd8tj+6OFarDQ4D/FQSrsJfUrpmDh58P+dePO7e1T5uXTjKL9cOd+75A785cIoDvnh7MgAAEIpLcAAuj0fj4YHQQgAAEIQAACEIDA6QoYhsHrlHVdZ806WOMORVFEUZQkae3atW/86Y2JEyce2z/avrwhD6N5MM3KqHNyci655JL777//lVdeWbVqFREpilkQyZqEKIpibyF9uvPA5yAAgfMmYOjU2kLLllO8eEU41BwMUDigxoKNsaIvHnlAaUqZRdBtG0tKT6/8t/0aafK7TrJikGFQqOj1/vEab4+mYKHm92p+n+T3auVR6hejeGTHJZf8c9kn1CqRbHYqstpfK9ZCjIqVxZ/aZHji3GEHAfSpOeJsCEAAAukpgAA6PZ8LRgUBCEAAAhCAAAQgcNYEDMOQJImvYchWF7RfnTWPlmV5zZo1b/zpjXvuuWf48OE8dM7NzWV9ovlihvwtvsOWN3S5XEOGDLn99tvfeuutDRs2yLLMWnPY74V9CEAgUwRYM+PmBG3bQSVlS8Lh+mCAgiE5EmqOFu4ae9OBuhaz6Lmt8jmrAmhV0SnZSvHA+6G+Owp71Pl9qaKilN8v+r2Kt5fuz99/4cXV676glGWUFGVzCUa2CqPc3ovj1B5zh9yZv0QAfWqOOBsCEIBAegoggE7P54JRQQACEIAABCAAAQicIwF7z2jdtimKsnHjxj/84Q/333+/vX90hxja4XC4rM1pbS6Xy+PxsH4dDofj6quvfuqpp958881t27YRUSqVkiRJURSehrMVDs/RVHEbCECg0wKsFTIRtSiUUigS/0c4cigYIH9IDgZaK8PS5f1WNbeSaJgr9pk/mtk7mQXSnb5JOp3II1/SddIVlb5YRxXhVdGC/SVh2R+s7+s7XORTSmNUHqULB2z+dL05V8WKnc1pGNYey6DbHVh4fCqTPPVPnMrVcS4EIAABCJwvAQTQ50se94UABCAAAQhAAAIQSAsBewDN9+0jY4scKoqyatWql19++b777rvuuuvcbjfvCs3qoB3WxvZZ22hBEHjLDo/H071792HDht1///1z587dt28fb9Mhy3KHSNp+d+xDAALnRaA9gDZEopRKg7/9cSSyPxhU/WExGEhdGKW4d2lTMyUUzar4zZYA2qpkNgNohVYsodKijXHv4XhQKvAd9IUaCwpae3TbFfavfun/UpKoUU1q9gCaPScWZFv7px4nn/onzsuXAzeFAAQgAIFTFEAAfYpgOB0CEIAABCAAAQhAILsEeOhs3+GV0GyurJNGc3OzpmqstbSmahs3bnzttdcefPDByy+/nOXRTqfT7Xbn5uay6LlHjx72cml7Qi0IQiwWu+GGG5599tnq6uqmpqZUKmUvi84uY8wGApknwAJoiZISUVKmseN2xSM7IsFkMJQMB1rihQ2Xla5ZsaJ9XrqeDRXQbU00VN1sZ09V71C8cF2JvzFUKAWKVF9hMuBtrCjf/N4H1ChTvUQtqpm+s0Yl7RBH/X7qcfKpf+KoG+IFBCAAAQikqQAC6DR9MBgWBCAAAQhAAAIQgMC5EbDnzvZ9fne2liDrlSGKYiKRYIsNslUN2ZKDiqKsXr36pZdeGj9+/MCBA51OpyAI7FdeH52Tk+N0Oo+tm2ZHSkpKxowZ88gjjyxevHj37t387tiBAATOl4BOelJt0YlElR544GBZeHM80BwJNUaDB8pD2+Letz5dQTpvPZEFLTiODqD/9CJF+q6pCDYH+rRWFlPvf9lTWrz5N7+lBokaVKvtiGHVS5/48Zx6nHzqnzjx3fEOBCAAAQikjwAC6PR5FhgJBCAAAQhAAAIQgECaCtiDaV4cffKdNWvWzJo169Zbb7344ou7d++el5dnr4bmqxceu+N2ux0OR0VFxR133PHSSy8tXrxYUzVd11knkJMAfe0JJ/ks3oIABE4ioGr0yktq/+jGaP4hb68vv3Xp3kjw3Qfu26aqpKltaxC2ZbHWooQnuVT6vmWOnLVw1s3qb5n+6zG6OL6j6F/2lAWUfnGpJPr5Pb+qISLJ7DmSufNM3yeAkUEAAhDIYgEE0Fn8cDE1CEAAAhCAAAQgAIHzIGAYhqZqmqrxexuGsXTp0t/85jd33HFHRUUFX7eQrV7otjaXy5XTvvGiaUEQPB6PIAiDBw8eP378zJkzV69ezS7OmoHwEJzfCzsQgMDZEbD3Mtbps4/p8gFVMe/8f71y9WcrqTlp9uU4shnWCoR65i9C2F7TrMk07oaNg8r2XFaiVoZb+8W/vPeXycYkiVbHayuFtjJoBNFHvgTYgwAEIACBEwoggD4hDd6AAAQgAAEIQAACEIDA6QkYhqHruqIokiSxTh0sj2a/NjU1VVdXP/7442PHji0pKREEgXXn8Hg8vH80b9/hcDg8Hk9OTg5fz1AQhKuuuurOO+98409vbNq0iY2Q12if3oDxKQhAoKMAy5RV67BOSbP1Dn3yGR2oM0PY2qT5UtRJ0bS21Jl1j7DF1h0vmOav20be1gRDk+kXY3deGttR5msoD+66aMA7GzfToWZSzTJpRmMVTGd05p7mTwTDgwAEIJBFAgigs+hhYioQgAAEIAABCEAAAmkpwNYwTKVSbHSGYfD+0bIsNzc3V1dXP/PMM6NHj45EIrx/dM+ePe2l0C6Xy+l0spUM2T57Ny8vb/DgwQ8//PCbb765cePGQ4cOpaUBBgWBTBOwmjtrorXGnkGKbC5HWG+VPRtmFbCqk9YiNVmzsv66Q3YF0LpCm1bSD4ZtHBBZOmrEhvf/QUnVrI62tvayZz7ltuP4DQIQgAAEIHB8AQTQx3fBUQhAAAIQgAAEIAABCJwbAVYuzRtrJBKJ5cuXP/XUU7fccovP5+uwaKHT6WTps9vtZpXRgiCw4miXy8WaewwePHjSpElVVVXbt29njaF1XZdlWVGUDjNiZdqytelm31dsEICATcAgXWlvNGEtuMcWGtSsJsg6GVYt8NE1z0e/sl0rU3bbKqB1w2xvrcmkSaQopOiktHcZOWombacfdcz2gr1t/9X2JnYhAAEIQKDLCCCA7jKPGhOFAAQgAAEIQAACEEh7AdZJgw9TUZTa2tpFixZNnDhx1KhRfr9fEAS32827dtj7cvC37AsbBoPBkSNHPvHEE++9997evXslSSIie+TNly7scGs+BuxAoEsLsED56JLfY/6spv1t839dmdwG2nzSRxLlI3vtR4+ZePsbJ/yK2KNn+/VO+AG8AQEIQAACWSmAADorHysmBQEIQAACEIAABCCQ8QKsJJn9ymPiurq6efPmPfnkk8OHD+/duzfrDc36cgiCwOqj7QG0fd/j8YTD4RtvvPHxxx9funRpUxPrHkB8JUNd1/mNMp4PE4AABE5H4EhMfGTv9K+jW2sWHhtDn9m1T2c8+AwEIAABCJxPAQTQ51Mf94YABCAAAQhAAAIQgIBdgNUm24Ng3hmD77ASZiLSVG3//v0LFy6cNm3alVdeWVhY6Ha7HQ6H0+ns0aOH0+n0eDwul4v16HC73WyfvXQ6nW63OxAIjBw5cubMmfPnz6+rq2N3RwZtfyLYh0AXEzgSDR/ZOx0C9mkVAfTp4OEzEIAABLJOAAF01j1STAgCEIAABCAAAQhAIEsFWJeMkwTEBw8enD9//sSJE0eOHJlrbbxHB99hNdG8aFoQBB5Mh8PhH//4xzNnzly1ahVbMlFRFNa1Q1GUDvcVRdGeiWcpOaYFAQicngALoP9/9u48vory3h/4nHNylsSwBrKf7GQj7LuUolZAVFxLtRa1rdK6UC3Fal1wuxRua1161Xv7E7GKtApixQVQMWyyE5IQ9p1AgIRsZ5195vvrM08yTdGiIGiAz7xicnIyZ87Me47/fPi+Ps/Jv5/ekfEqCEAAAhA49wQQQJ979wxnDAEIQAACEIAABCBwYQqcPIA2TVO1NjsXPnTo0IIFC2bMmDFmzJi4uDin08k7OuLj4+Pi4lwuV1xcnMPhiIuL83q9dlkHj6o9Hk+fPn1uvfXWZ599duXKlXzgWpblE2LoC/NG4KohAIGvEjh59Mz/+lXHwN8hAAEIQOB8EUAAfb7cSVwHBCAAAQhAAAIQgMD5LnDyANq+etM0dU0XRdEOi1VVJaKqqqo333xz8uTJQ4cOdblcTqeTh84+n8/pdPp8PnsU2g6jeUjNm6aHDBkyZcqUmTNnbtmyRVVVSZJkWVZV1c677RPAAwhA4IIXQAB9wX8EAAABCECgjQAC6DYYeAgBCEAAAhCAAAQgAIF2LPCVAbSdOBORJEn2r4Zh6JrOr4xXaiiKUlFR8eKLL95+++0lJSUul8sOnduWdfDo2f5T2wejRo2aNGnSnDlzysrK2rEZTg0CEPhOBBBAfyfseFMIQAAC7VQAAXQ7vTE4LQhAAAIQgAAEIAABCHybAosXL37++edvuummvn37er1ej8fTdkqaL11oB9A8sOaLHDqdzg4dOgwfPvzxxx+fP39+dXW1JElEpKqqruk8NMeU9Ld5K/FeEGg3AqjaaDe3AicCAQhA4DsVQAD9nfLjzSEAAQhAAAIQgAAEINCeBEzTNAxDFMW1a9dOnz79pptu6tGjh8/n4wG0nUq73W6XyxUfH+92ux0OB/+Vj067XK6EhIQrrrhi+vTp8+bNO3jwIB/HNlo3XdN1TUck3Z5uO84FAmdJAAH0WYLFYSEAAQicYwIIoM+xG4bThQAEIAABCEAAAhCAwNkQsPs6+MHtX03TbGpqKi0tnTFjxrhx4/Ly8tpWRbvdbrtLms9HOxwOl7XZ49KdOnUaNWrU73//+3nz5lVXV9snz8Nu+43s5/EAAhA4XwQQQJ8vdxLXAQEIQOCbCSCA/mZ+eDUEIAABCEAAAhCAAATOIwFFUcLhMK/O4JdljyorisKfqampWbBgwdNPPz1mzJi4uLi2ndE8dOYBtKPNZndMx8XFdenSZfTo0Q888MCiRYtqamrOIzxcCgQgcIIAAugTQPArBCAAgQtUAAH0BXrjcdkQgAAEIAABCEAAAhBoK2CvcHiSB60tGuwnEfGyjmAw+N577z355JMjR47s3LkzL+twuVz2oDSfibYHop3WxmNrn8/XsWPHESNGPPHEE+++++7+/ftFUSQivlJi2yJp+1TD4bAdhdtP4gEEIAABCEAAAhCAQLsVQADdbm8NTgwCEIAABCAAAQhAAALfnsBJcucv/sk+rS/WaFRVVc2dO3fy5Mljx461Q+e2U9Jer1cQBKfT6XA4YmNj+QN7T97X8dRTT73//vu7du0ioubmZkmS7EHstm9tP8YDCEAAAhCAAAQgAIF2K4AAut3eGpwYBCAAAQhAAAIQgAAEvj2BL6bMJ3lG13TF2nhZB4+hVVW1Z5MNw5AkiYiqqqqef/75n/3sZ4WFhXFxcTxo7tChwwnN0XYAbT+IjY3lsfXAgQMfeOCBV199ddu2bYZhKIqiqqphGCiP/vY+HHgnCEAAAhCAAAQg8A0EEEB/Azy8FAIQgAAEIAABCEAAAueLwEni5i/9kyzL9lTyCXGwYRi6pquqeoKNYRhr1qyZNm3aTTfdlJuby8s62g5HC4JgL2Do8XgEQYiLi4uNjbVTaUEQLrvssnvuuWf27Nnr168/4fin9Cvy61Piws4QgAAEIAABCEDgtAUQQJ82HV4IAQhAAAIQgAAEIAABCJwowNPqE5/999+j0SgRhUKhVatWPf3005dddlnnzp19Pp/b7Xa5XHzxQt4izX9tG0Dbyx7yLul+/fpNmTJl9uzZFRUViqLwI/N30zWdT2rbE9N2Mq6qKgLof78n+A0CEIAABCAAAQicLQEE0GdLFseFAAQgAAEIQAACEIDABSjwdQJovtIgx+GPVVWtqal55513pk6dOnz48A7W5vP5ePTs8XhcLlfbGJrPTbtcLrvKgz8zevToe+655/XXXy8vLyciSZKi0ag9i80LQy7Am4JLhgAEIAABCEAAAt+hAALo7xAfbw0BCEAAAhCAAAQgAIHzTeDrBNBEJMtyOBzmPdGc4IQej6qqqnnz5v3mN7+56qqr3K2bx+Px+Xw8a7a7O5xOp8vl8nq9J5R1uFyuSy655IEHHpg1axbvj7atv+ZJ2vvjAQQgAAEIQAACEIDAaQsggD5tOrwQAhCAAAQgAAEIQAACEDhR4Otku3Z5tL1uoa7poVBIkiRFUXh1hmptuqbznSsrK5999tkJEyYMHjyYT0bHx8e3nYkWBMHpdDocDl4ezeukeTZtT0mPGTPmgQceWLx48ZEjR048b/wOAQhAAAIQgAAEIHB2BBBAnx1XHBUCEIAABCAAAQhAAAIQOKkAj6q/+J2I+JPGl208kq6oqHjuuecmTJgwYsQIO4Z2OBx2U4fD4XC73R5r83q9vMSDJ9S8YzoxMXHUqFEzZsxYtGjRkSNH7ExcsTZ+DnZViGEYoija+5z0svBHCLQIRERR0f5tKU6dTP43g0jRVFGRvxJL0VTNML5yN+wAAQhAAAIQaM8CCKDb893BuUEAAhCAAAQgAAEIQOC8Ffhi9Myf+coAmovIMgvvFEUhoo0bNz7zzDPjx4/3+/12Bs3Hn+1fBUHg0bPD4XA6nTyb5i3SHTt2vnbr+wAAIABJREFU9Pv9N9544wsvvLBs2TJd0/lbtF2r0C6SbrvO4Xl7b3Bhpy9gELXkxTqZOpmaYah6yyfKDqD54fl+y5cvX7p06ZNPPnlJm23kyJETJ05ctmK5rLJPuKjI9kFO/9TwSghAAAIQgMB3JIAA+juCx9tCAAIQgAAEIAABCEDgwhb4ygD6P+2gKIodB/MM2jRbBktN06yvry8tLX3uueeuvvpqv99vz0e3DaDtJ53WZv8qCEJcXJwgCAMHDrzjjjvefPPNqqqqtu91Yd8xXP1XChhEmvXV8oE84QWiIq/fuPEf7y94etq0H4welZicxD97bpfLKQhul8v+4s937Nzpzb/NERVZaf1HkRMOiF8hAAEIQAAC54QAAuhz4jbhJCEAAQhAAAIQgAAEIHC+CfynfNmegP7SHex1C+1CDD4ETUS6predWTZN0zCMQCCwfPnyRx999Oqrr247Ac3rOOzo2U6ivdbGK6TdbrcgCD6fr3///pMnT37llVf2799/vt0GXM8ZE+Dps0KkWBm0sXzlivn/ePfPL7049cmpT0178p5J9wqCEOP12J86h8MR42S/uQQX+5PDE+OIiXEK/EmnM8bt8zpihBt/NP712XOO1jbIisE6PL483D5jl4EDQQACEIAABM64AALoM06KA0IAAhCAAAQgAAEIQAACZ0DgSwPob3JcVVV37949f/78Z599duTIkX6/n69PyNct/GJZBx+a5tl02/7oSy+9dOrUqe+++25tba2qqrqm81PlCbhhGHwiW5Ik+/E3OW28tn0KiKIoSZKu6YeP1KzbuPaz5R+Xrlj8x+eevvbG0V26XxTjtaJlwemIsQNnweP2uWO8guAQBIfH7Yv1ut3WX52C1yHEuYQ4j+CJcQlOB3uJw2E9cgoONh7tzOvR61f3PbR9214iCoej3ATj+e3zs4GzggAEIACBEwQQQJ8Agl8hAAEIQAACEIAABCAAgXYhcMYDaD5bbRgGX8mQiA4dOrR48eKHH3748ssvdzgcsbGxvCHaZW0nTEnbA9Qejyc2NpZPSfv9/quvvvq5554rLS0NBAKiKPL0WVVVURTtbNouCWkXsjiJMyGgKIphGNOnT09KSXb72LB8bAceOrcmzk6HM8bl8jgEFwuRfXEX+XxxVvosCIKTDzuzbLl1cwg+j+CLcQr8OYfD0RJFsx0cguByuuI6dug64nsjX3jhhcrKSrsD3TAM1drsD/aZuD4cAwIQgAAEIHDGBBBAnzFKHAgCEIAABCAAAQhAAAIQOBcF7FqPsrKyuXPnPvLII8OGDYuLi3M4HC6Xiy9X2HYCmgeGfHqaL2PIskJB8Hq9ffr0+cUvfvHcc8+tXr2aiNquWMjz9HPRB+f8nwQmTJjAPwatGXLLT6+vY1x8Z2+sx6rW4E9aU82C4HDFsNHmtptDcPsEr09gkbQQFyP4BB5Bs7nnlgzaGxcT18HHh6kdTtZUzj+WY8eOnTp16vbt2+0zRAZtU+ABBCAAAQi0HwEE0O3nXuBMIAABCEAAAhCAAAQgAIGzJcAroflIMn8P0zQVa+M9BnrrOm98nlRRlHXr1r3yyis333xzcXGxPf7MR6QFQeAN0W2DxLZhtNvaLr/88jvuuOODDz7YtWvX2bowHPe7ECgvL580aVJCQkLLB4CVatifBZcgxApCJ0HoLgipgpAhCMlJSbm/mfLQR4s+Xrj4k+UrP/9kyWfvvf/hW/PmPvzYg7+8Z+K1N1wzYsQ4QSh2CgMcQqYgxLMMujWAjuvAFsZkm0twtJmY5s/xBHzChAmzZ89uaGj4T7P2/+n57wIP7wkBCEAAAhecAALoC+6W44IhAAEIQAACEIAABCBwYQrwRuYvbfawnzT+wxYIBFasWPHkk0/ecP0NycnJXq/Xjv/s8ugTKjv4DnwyWhCEbt26DRs27PHHH3///fdramoURZEkSVEU3hzNo3B+X0zT5E+qqmqvtXhh3rL2c9X8psiyPPP/vZLcPTE2Ntbj8bhcLj78zu5yrC/2ojgWErN+DU9K0qCbr/lbn6yXe2e+dNnQ548eabkUk0gx//UVVeVgmEyFXvuzMjRvaWH3v//4+llvvbXq0cenDx4+LCbW7fLFWEUcrILD7b3I5Y4VnC7+Xm3XM+Qftuzs7JtvvrmmpkaW5RPoEECfAIJfIQABCEDg2xRAAP1tauO9IAABCEAAAhCAAAQgAIHvTMBOmU/y4EvzZ13T+Zd96seOHXv//fefeuqpyy+/3A6jeQjIE0m+dKHL5eKD0nZM2aFDBxZQOp0ZGRnjxo179NFHly5d2tDQwJsT+InZ78IfIDo8AeRb+7Xt7TBNc+nSpSNGjIhxOr1uj9vl4l8td5avG2h9Ap555v9t2lijBuknV24u7v5hUfKsQztbTlkyTf4VNU2RSCTSrL988Db1zy4t6rp2wpU1x2tIVlv2b4w2bahY//d579w/+fGC/MsFIdnh6MhmrZ0uX1ysLy7WGdPS5uGLY4G4IAhdunRxOBwTJ05cs2aNrul2vcy3hoY3ggAEIAABCHxRAAH0F03wDAQgAAEIQAACEIAABCBwHgqcJHe2//SlAXRbC17cwZ9RFCUUChHR+vXrZ86cOWHChKKiIjuGtkNnvlyhz+fjf+IBNF/n0G7tKCoqGj9+/EsvvbRixQp+cPuU2sagbc8Ej781gSNHjtxxxx181N3tclwU63W7HF6nw+NwxjhZKQZflDLG45vw0ztNk53Xw3cf65P0eVG3D9+Zo4oimUSSQWFd49FzlIh9mRRS6PPPqU/Wyr6Zm24cs/74YQpHKCqSopFmkmxGJTMkmyRKJAaooZamz3h9xMhLHS5nx86d4uLjPRfFCu5/NUo7nU6fz8c/eF6vd8yYMdt3bCUyEUN/ax8VvBEEIAABCHypAALoL2XBkxCAAAQgAAEIQAACEIDA+SZwQqT7pb9+aQB9kh4MRVF43YEdTIdCobVr106bNm3s2LEdOnTgc6l8INoOoNtm0/zJuLg4r9fL+3w9Hs/AgQMffPDBOXPm1NXVEdHpZdAYnf7mn2DTNBctWpSens4n2XkGHet1exyCx+H0CB6P4Nm6deu2Hdtf+J//+fNLr4VCZIj06L3HBmZ+2jft04V/ozD7FwoyrLg5wso2SLHS5zBRWKP1G2nEsIU9Uj7+0ZW7mupZ0CwppGqkWUPQJlFYJlUnSaTHHjhekPnfH3+ypzkS2ndw7/ibfpiene3t2NF90UXsLL6wOV1Cx47xgiD8+tf31dfXf3MKHAECEIAABCBw2gIIoE+bDi+EAAQgAAEIQAACEIAABM43gf+USp/qdaqqKopic3Pz8ePHFyxY8OCDD44aNSouLs7j8bjdbh4025mh0+n0WBtfupCP0wqC4HA4fNY2ePDghx56aP78+dXV1fxMeOptL5x4wunZV3HC8/j16wtw2+nTp39xwckOPi9fC3BI7+8pVr6sGUZUYZmxFqUnpzQN7/F5QcJbH7xNoWb2hhqRaFLUoCgZknUGEZ1CGjUEaNT3N/XusXT89UtqjpBqsJyab7LIfkoiy6/XrqA/z6ChxVUlOW99+umxoMTesjncKBn0yuy5g0f+oGUBRKsGJDbOzT9XDqfgi41xxbC1ETt16jRr1ix+ZEVRTvIPKi1vjx8QgAAEIACBMyqAAPqMcuJgEIAABCAAAQhAAAIQgMC5LGBHtyc8OO1r4mGfnRSXlZXNmjVrwoQJvXr1cjqdvCSaT0nzag77MY8R7ajanqTOzc296qqrZsyYUVpayjJKiUea7AQNw+Bd0qd9tnihzRgIBEaPHm2vIWkPrVvlGy6n4Lzr9nvDx7Vgo6rqOhErbg410X23H724YN33Cpf+43UKBRinRmpYi9gBdJQMmUgiqjlCY0cvyei2YGCvRXv2k0rEjsLGo1tzaIWkAP1w7LrC1NWFqZsLUpf+7/MUCJBiBdoKhcOqqhFFVXrltWWJyYMEZ6Ig8JoXHo8L7jaD0V6v98Ybb+T/bvHFJQpx3yEAAQhAAAJnVQAB9FnlxcEhAAEIQAACEIAABCAAgXNJ4ITc2f71lK7BNE3DME5owOCTp22fbGpqWrZs2eOPP37ttdd27NiRz0c7nc4TVjW0M2h7YtpORQVBGDBgwMSJE1966aVt27bZJ3l6p22//AJ/oKpqMBjs1asXH1dvy87+wcDl6hzXZc7MeWaEOekaq3w2iGoO0s/H7++btr2g68r/evCAYXVoGKSG9PqQEYjoVukzUdgaiD5wiK4dtb3Yv3TksPe2bydJJ8k0DZYsW+mzRkqY5Ea65Yqmwi7VfVKiRWlbn3j0sPVWrJFFo2aTHYm9b3MT3Xjd3F/89IOZL+/Iy7xaEBJdzo4tQ9Ct7dAOF4ukHQ5Hz549+ecEQ9AX+Icclw8BCEDgWxZAAP0tg+PtIAABCEAAAhCAAAQgAIH2K2BHtyc8ONUzliTJnnpWFMUeVT7JhPLu3btnzpx5//33Dxw4kGfQsbGxdhjtcDh4AXFLtuhg1Qpf3C677LLJkyd/8MEHdlnHqZ4537/t5Z/eEc7dV1VVVWVkZNgpP29/TkxMjI2NdblcHeM7vDf/A7aqoDWxHJW0qE61x+m39wVyu63M6rD29muPkkmKTgaZUb0ppDWGzXDEZEsOst5nnWpq6bZb1hWnrR+Qt35HFUudrWULiVgJBxkGm5EWG+mHo3YXdD6Y3ymc06H61uubZJUawmZziO1DFLYmoNmjKffvKcqc/etf7G06RBNveefSob8WhK4tHwyH4LQKOeLi42MviuMZtCAIn376qf3hPHdvE84cAhCAAATOIQEE0OfQzcKpQgACEIAABCAAAQhAAALnv4BqbZs2bfrTn/50xx13FBUV2UFz2xiaP3a73W1bOxxtti5duowbN+7xxx//+OOPA4FAOBw+of9XVdmYLl8+kT+2Rnp1RVF0TW+bQduPz1f9aDTKyzfWrl3rarPZBdDx8fFer3fYsGEVFRWsKUPRrL4MVvx85Bjd8bMDffK29cnZft0VFZpV3xyRSCNdI1Uy9ahJTRKbVpaJmoJ07eiKnG6fZXX58KO5pCnseetL1UiOqKSaJEVp/BXHe6cd69G5pjh5z+hhFdEmEq3DGuxt2V0yiEISvfZapDh73vWj9ysNdP9Pd/X2v/zUbzct+WRbUmo3wcGqoWPjrRqOlk4ONgTtcrmcTueKFSv4v4uEQlaJ9fl6X3FdEIAABCDQPgQQQLeP+4CzgAAEIAABCEAAAhCAAAQgYAnYubAkSbIs65peW1u7fv36p556aty4cd27d+dt0bw/2uVy8Xpih8PhtDY7gvZ4PHw9Qz463aNHj9tvv/0Pf/jD2rVrRSvOtPupVVU1rE3XWPrMA2j+DO8SOe8DaP7R27ZtW1JSkp0/27m/IAg+n+8nP/kJ303VWf5rtTVTY4iemKr5E5f2SN8yYtCWykpqDrFA2Wp/NjUyFWsFQoPYIoRNAbr1pk39cqr6+CunTo4aEauPg+1rGqRHNNax0RCgX93TmNf9YF7XcK/0w0NL1lSsZ3+WJVJVa+ianwRRVSWNHPrhyCFlFZ/T7Bepb/ZbN49dThGSWZZO9035hRAjCDGCw8OmoN1xPmcMi57tMus1a9aoqtq2Q7z1wPgJAQhAAAIQOMMCCKDPMCgOBwEIQAACEIAABCAAAQhA4BsKfLGpg88ps8XuZPnIkSMLFix46qmnLrnkki5dutiRIg9M7QCa/+rxeOzuDqfTyXuNXS5Xr1697r333pdffnnjxo1fTCHt9PkCCaANw9i2bRsP9+0A2uVyxTidnhi31+2Z9vTTfESa39moaYZUOlJLN1xbUZBdmZO2ecig8i1bKShSc5Q1roTFkG6QZpJCpmjNPjeG6LYfHc1N2FCYtHrq/QZbdpAlz/w/VqwhEzWE6NeTlVz/7qwuDRkdq3ukrPjgH2wvUTV0XREjrdPKJh0+SKOGL+2bv/alZ+m9t6jEv/Liok93VbbUeSgai8g//vSTbilJgjX+zGJo54m1LcuWLeOXg+8QgAAEIACBsyqAAPqs8uLgEIAABCAAAQhAAAIQgAAETk2AdyPw10iSxKeP+cxy2wzUNE0+sFxWVjZnzpxJkyaNGjXKTp8dDgfvj/b5fIIg8BUOT4iqPR4P72Tw+/0jR478/e9//8knn/CyjgstgF67dm1SUhKfdBYEgWXQMQ63iyW2neMvmjvnTSavk25SVJVNokaJjgdp6mPUu2hLYdaerLTPP/iIFTMHZIoqzYYpGYahG6wJWrImoBsj9JMfr89OKCtM3HX198sbakiX7U8FG5jWiKIqTbpvX3bmVn/3+uS4/YMLDzz2YDgSobC1p0mioUnsNQbb+5lptYX+hb+5m9atoAHFywYXLduwnK1OKMskWnvxYelDdUf6Dh4sCB7B2ZWNQ1ubwynExsa63e60tLT169fb54EHEIAABCAAgbMkgAD6LMHisBCAAAQgAAEIQAACEIAABL5tAdM0Kyoqnnvuudtvvz03N7dDhw5OpzMuji1A13bjQ772MzyGdjgcHo+nY8eOCQkJ48ePnzZt2po1a6LRqCzLvKPDNFtWy+PxtGmavMTj277IM/R+pmnytpNwODx06NC26bzb7eI4g/oX79tZSbokRSNihI0VR0kJGHS0ia6/YXtx/o6kruXZ/uV/fIYlyGGV2NCzEeWlzoZGUYkUkySVfnpLXWH61oLkbcP7bogGWZ+GLpOpssiY1zpHJXrrb5SXvSkno8Hfva5P7p4Zj1E0RCpbzJCVPlsZNfM3RFr7MfVI/nDk0HW7ttGwvjU5KUvnvEHH6tg58IFqsyWmppAeCqk0/odPC0LvmJiWxQm97hinILgE9k8UI0aM+OL8+xkCxmEgAAEIQAACLQIIoPFRgAAEIAABCEAAAhCAAAQgcH4KhEKh0tLSJ5988sYbb0xPT7eX1LOj5y99wOuk7UB24MCBd9xxx5w5c7Zs2dKWiQ35ai2txHzRwrZ/bf+P+Wi5LMsZGRn2xQoCmw4WBCE+znPzD68PN9bZF2KYLAtWiOoluu2OA6lJK7t1qMj2b7rr7pqowoJma1NYYbPG4mK+bGAgSA9MrknvVN4ro6EwY+mGVSSxNmfSra9IVFdUNltdsYHy0jdmJx3P8Yfysw7ccNXO2sPEljj8902MUF01DS1a2T9n2/JP6ae3BnrlV0y8o6mmjkIaK/HgZ2ENSbNTDeoUUeiRByqSOt0rCDlsFJpdmi/G6XQKbE1Cr9d7zTXX2Pfx398Nv0EAAhCAAATOjAAC6DPjiKNAAAIQgAAEIAABCEAAAhBoPwI8XdU1nWeLfNT30KFD8+fPf/TRR0eOHMljVh5A88T5hLFowQoo7YUN+Z7x8fEXX3zx1KlT33nnncOHD/PrjVqbqqr2iHT7cTjJmUiSJIrixRdfHB8f3zaI93q9Pp/vlpt/JIfZcn5yiA0WazpJOguWTaKHH2/omvBRTtau3KzyH/1wX1SlgESBiCLLItuDDytrpOsUCtKjD0SKs8rTO+zu22Pnkk9I0kiSSVZJ1XXZlP55NEWnHZV0ycCG7K6N/s7NfXo09C5eeay2ZZy57fkbOtXX0C3XlvfJWv6HR2jK3VSY/dkN138eEFnRR1Qn2WRv3jr+bChWXL7wfRpSuKwk7R8FmZPiPYVxns4uweG26q35Lfb5fK+++qooivxD0vYd8RgCEIAABCBwRgQQQJ8RRhwEAhCAAAQgAAEIQAACEIDAdyzAQ2e+bOBJTkWWWalwNBrdv3//q6+++qtf/apnz56CIHTo0MHn87WdBeaxLF/GsO3zTqeTL2yYkJAwevTohx9+eP369dFo9Cvf+iRn9a39qW1KPmnSpM6dO7dNn/kE9J/+9CdNVkyNVWSoIqkaSQobJW4M0cNTI0WFq9NSKrP9m8aN23nkKDtx3n1haApbWtAafzZUUhX67W/2lmSW5yXu75uz5++vsz1VYo0cokqSqURNllw3NVG//F35iWJ6nNgzPTys3+bdu9hihrJJJuvnkKwKDjJM0hSa+xpbb/CnNxhvvEz5qasu//6qnfvoeJiNZqtW3Kxb5Rv2BPQni6h33ifFyZsKun248B363/9Z5HZ14tfrcrncbjd/3K1bt7q6unO6UOVb+/zgjSAAAQhA4DQEEECfBhpeAgEIQAACEIAABCAAAQhAoD0KtE1XT/X8VqxY8eKLL95w/Q25ubkul4uvYeh0OttGzzyn5lUefAdW6RAf7/V6nU5nUVHRnXfeOWvWrNLSUlVVv06xwzc54VO9QL4/X7yRiD788EM7ena73bwIWxCEV199le+pa3o4EtTJjKgsfT54iO66O+hPKU/ptrtT3KqexUt37WFj0VZAbBKJRDJprLiZb8/OoKKstf1zAz0z9v1uckCRKSKRaLAh5ZDO6jKiREfq6HtDtmcn1BUmUnbH5qL0yg8WsFcr1iyzTqZmsMNLCqvjWL2Chvfd0C93/xsvUqF/1YhBS9d8bu1MhkS6ZgXQislGqgNB9vzWSrp88JG8zvtK0sqfflAJ1JMi06y/vu5wsuv2xvrcPq8zpqXt+o6f/dzUjW//dnArfIcABCAAgfNbAAH0+X1/cXUQgAAEIAABCEAAAhCAAAS+WoCvKGjnj83NzR999NG0adPGjh2bkJDQoUMHPi1rVQcLHg+rEuYbj6ftZ1wul9Pp7Nixo9vtHjly5K9+9avZs2fv3r07GmV1Fnzj5dHfybytfYH19fUJCQmCIHTu0NHr9rgEB7+ct99+m58kP2Er+GUzzc0R+uVdTandN2SnNmWn1RYXrOZzynz22XqJzNo3rPFnRaY/zgjmZ63xd99RlLP76tE7eR+0rLN+DI0oYLIAukmhib9Q07rtLvbrWV0aeiRWzHyJ1UObVo2HYhp6S680O7wYpqF955Zklr3yLA0pOdCnYMmnCykUYjvLVK+RqJDJOjcM1u9BRMEmum7MtuKUY/0zGh/7NUlhNkNNRBFZ+svMv7jcbnbFTgd7IAg+ny/O61uzarXtY10RvkEAAhCAAATOjAAC6DPjiKNAAAIQgAAEIAABCEAAAhA4PwQMw+B1wLyswzTN7du3v/baaw8++GC/fv14+UZr/izYs9K8SNp+nkfV/LvL5UpMTLzuuuueeOKJFStWBAIBDsWT6O8k9LzsssvsAopYj9ftYmPBs/7yCgt0rS0cjUZVMWxEFevX3z2i+FPXZKfXFGRFivN2vvMuadasMfsjL102WPlFJMTWIJz3Jvm7r+zTI1CQu/vqG9ZU11Eg0lLUEVKjujX7HCS6894af+qWjMRGf9cjhf7yRx+s1TUKsj2Jpc/sSCw1NkyKBOnWG/b3y6l68gEa1vdQUfayp5+IaNbwtWREZKNeNaKsL8RkATTbdJpyt57RaV1mp80/uvKYrlNDiMIyq+kwiUKSPP6Wmy/q3JHdrJbg3RnjdBbm5zc3N38nt8M6aXyDAAQgAIHzVgAB9Hl7a3FhEIAABCAAAQhAAAIQgAAEvqYAn4C2S5wVRRGtqV1d03mZRts/rVixYtasWVdddVVhYaHb7W67iJ+9tqGdU7tcLns+2o6ns7Ozr7322hdeeGHZsmVf8wzPyG587Pr555+3z8Tr9nhi3E5BeOfvf2eVz1ajRlSO8iA6YFK9SL97NNojtyyl2+7s9JrivO2zXqHmoJ1Um+wVRksMHQjQm7OpIHNTdtLB/KzqMVfs3XOcDTuLaoQoolm9z/uOq2GiV+dQVs66tO6H/N1q8tI3jhu7NhimCGvnbtn4qWgmaSo98XAwp/vGW66iKy9R8zJK7/j5nqjYmjWToppBRRd1MnWDNI2F4I8/WF+YsrF/9oHrRx88XksRjeqj9bXNxxXSo6zMg0IS5Rf9QBA6tDqwVo5Yr/udd95BAN16B/ATAhCAAATOmAAC6DNGiQNBAAIQgAAEIAABCEAAAhA4RwVOEjvytQ2/+F2SJCKqq6tbtGjRE088MXz48LZB8wnl0Y7WzWVt/K/8OafT2a9fvylTpsyePbuhoaGpqemsGh48eDAtLa01eBXi4+IEQZg2dSp7UzVAJCtqOKKEm5SAabUqT3k4kJKyMjP1UEFG2J+06aGHakIR0nUrcebLFBpsrUC+/XUmFWaXFefW9cjaPWTo0sodVKuQRKTqpqGxcoyASCGNZr9F/tQ1vfMj2d1r++btvv7qlZEI+6tisNlnzdSiiso7nYloRSmV5FUNLA7//BZKT1x33bitR+ooorJxZoPF4KzVwzR1XdNZAC3TisVUmFya23nDDwZuVaLsmCqr6VAkCmsUlai5WaHGBvr5Txc6nUMEIVkQLhIEweUWvD6H358my7Ki8LHvs3ofcHAIQAACELiABBBAX0A3G5cKAQhAAAIQgAAEIAABCEDgTAnwmg5WQWGa/HEgENiyZcsLL7xw99139+vXz+fzsY4Hh8PpdLrdbq+1ud1ul8vVGke3/LTj4CuuuGLv3r082j5T59n2OIqiXHPNNXzhxLi4ON7C8fNbb2OtF+EmKXSUKBKRAwZRhKhZot8+FCkp2pbUZU9mYm1h1oGf/ri2voEUrWXe2QqoNd1qbY5oNPvvRm7WyoKsYxnJu3oWrX5zLuvQCJnE09xQiC0/KOtUtonyc1dkJtQWJquFqXsv7rti+xYS5X+lz6ImiZpilTtTXSONGrFvYFF0SC/yJ20t7LFoy1bWIi2a7Dvv2+AXGA1rpNPh3TQwr7R3+qa8xA83rCRVJ52tSsjeOkphYvXTbAJ68j1H+hcuykp7zO38niB04f4ut+BwCjNnzjRN8+zdgra3A48hAAEIQOACEUAAfYHcaFwmBCAAAQhAAAIQgAAEIACBMyzAS5xZevuFmVlJkoLB4NKlS59//vlx48ZlZGTwMPqECWg7enY4HLyso1u3bmcv/XzjjTf+VRJirb83eODA+qPfot5iAAAgAElEQVS1JKtSkE9ea0EpJJnUHKaHf6emditP7libHB/IStx33dgqTSFdteadWbbM1vwjIokFvzR3HqWlLMhI3pGdundQ/8q35lFjmAXEkhUTRzStMUJBiRqaaHCf1ZkJ+/K6UJqvrtD/yacfspsiqaSZmmYqikmK2dLvIcl03bhKf0L50F5UkF6blV66aTPLnflmrXf4rwxaUyl4mG6+fPfArIohBZ8vWci6NnT27lGjJYBWZCLJoDfeoMK0TX0y9vfNXZzc9X5BSGm5C07BFeNITU0NhUKtb4KfEIAABCAAgTMggAD6DCDiEBCAAAQgAAEIQAACEIAABC40gWg0al+yHUDzkmX+vN3aoWu6oijbtm176+9v3XnnnYMHD7YnoPlwtNvt5qUc/Nf333/fPvKZfZCXl8fXRfxn7UaM19MlIaG6uvqLbxGK0iMPqTlpm7O7i5ldjeyE+oGFlbt3kNm6RKHVFs2iYN1gUfVHC6lfn3Vp3asyk/dnpK397e+OHm9kR9WtQ5tWDB02SFTphzdUpnfekNMpUNKdhvZo/OBtVvHcHCTVUFQzrOgRxWBT0k0Si43/ezrlpVUUpNZlJuzLTV/5xhvUECaRqFlWWV+I9cXnoNl5GXTPzTX90jYOzF4++39Z44bVTa2x/g+rMiSs0rFm2lROIwZuzO++tyh17w+v2h5qpP4DrmYBtENwxbCfbrd75syZusbPnY23t72nX7TCMxCAAAQgAIGvFEAA/ZVE2AECEIAABCAAAQhAAAIQgAAEvqmAnUebphkOh1evXj1t2rTx48fHx8d7vV4+hOt0Ov1+/7Fjx+wA9Ju+q/V60zRlWX7hhRc6d+gY52XFIHx75rlnW9JVK1luDkcCIqtJfv01SklY6e9Sl9mRsjqHijPXbqsgXbYS5dbaC1Z5YU03r1pFfXqvzMvYV5TX0LNg72OPUlOUoi35bcvpHw3pIZOmTJZTO2woTmrO8B3ul35k6n0kR1ihh2YYGkVVapSMSFCk2iaqD1JpKWUnb85NCBclRXtlbpk+vbYpSpLJRqoVK3qWTba8oUJsJrqxmZ7/w9GeKZ/ldPjouWl1hkqqRqom8rfXTC0oqapJTQG6/HuV/i7rcxLLr/rBtnorJV9XsUlwMA+n0+MSXIIgZGRk2OyGYdj/umA/iQcQgAAEIACBUxJAAH1KXNgZAhCAAAQgAAEIQAACEIAABL6RgJ1E20fZu3fvvHnzZsyYMXXq1MrKSt4rbf/1jDyQZTk5OTnO6/O6PXwIuqikZ0QUFU0NRyVWqGFS9VEKRunh3zX2zNuQk1xz+WDKSxD7Zh+Y+4Z1CnzhQavPIhrWgiGKyrRhI/Xvtzo/e09y132pSVvGjdt95Div3bASaNOKqDU2rfzUH+szUzbkdw/27B7I67T9x1dWS02kKHzVQcVgL4oQmSpRRKG166hn4cZiv5rVSRxSeHzyXUFJaan8YMUfJkk6ibpurxX4j3lUkD6nf96yST+tjjRzMHYCctTQ2bQ0m4Y+WkNXXPZxdvdVPVI3//Cag9WHKKyzEzNJvvm2Gx1s/tkR42BT0C6X67333uNH4RPQJ1mjku+G7xCAAAQgAIGTCCCAPgkO/gQBCEAAAhCAAAQgAAEIQAACZ1fAMIy2+eYZL3zgB582bRor+hCEGKfg8Xh8Pt9fZ/NcmURDDaiSTqSZ9Ojv6nJSP81L2TXhOipMayhI3Tj3dXb5UdaKrLHmDdZpYT2j0OpVNGhAWU76np49mrPSD4wbd6TeWmmwdUjacmOJMs1/l1JSl/TMbSpOCWRctOXa7+8NHmN10gpbJFA3DZJlWZQbZFMiouYIXX/N8Xx/c34SZXevHn99ZTBIoSgFRfbm7MtgGbSo6yKxIehtO+ji3htzEpbecsNaIgqxtQaJTJl0RY0qhsLi52AjPXJfc3H6yt7ZVQN7rly3oeU6TKKw3qRRKDbew6JnPgstCGPGjFFVte19+eI/G1hvg28QgAAEIACBrxZAAP3VRtgDAhCAAAQgAAEIQAACEIAABL4FAZ5ynvE3kmU5MzOT127EOIU4n6djx46yyjo0WD6sk2iyueO/v0k5yYsL07dPf4gG99CLUnfeN/Ew6awog7VvGEHWeKGRobKB4nWbWPrsT9ydldKYn32sb98Nh4+zOJivOqjJVgpt1T9vK6M+JRsKezQVZ0k9048NLdq4eS2JQTJMlgLrZLL/2LmYkkq19fTww/WpXSsyu4WLM0NXX360voGi7G1bNt1kxdOawc68KUr7q2n8jZ9nd18+7pIDYoSdmGKQwqJp1RqnZulzpJ7ee5PyE0pL0sqLsxZUVVGUqEExo1acHVCOE6nPPPcHl5sVofAhaIfDIYpi2yIUBNCtdwA/IQABCEDglAUQQJ8yGV4AAQhAAAIQgAAEIAABCEAAAueKgGmaM2fO9LrZhK8VsAruGOEPf5yhamRaHcpBjaXPc+ZQcfaGXv7qR+6hXmkHS7rtH3/pYZbUsiTZJD1o6FEi0yAKyVRbR8OGbO7WeXN+RjQ3JdCneHv5VgpbJRoSGaylQ2W76kS7D9GAi9emJG/JTGrKTQr2ytyycglJEZY4K4rG02S2n0GqQg0N9NeZlOuvSO9yKDNhX9/CNWXr2NKFkpUUs6iaTHZY60s1KRqle35+tF/hyiH9Plm5jN0QUWfna4XfOpuuJoo0Uul8GpRZld+5fEjRqrJN7GjWlxllWbqpUMRk9R6UkVEsCD6HECsITkEQpk+fxm+xLMuGzi7HzqDtB+fKZwDnCQEIQAAC360AAujv1h/vDgEIQAACEIAABCAAAQhAAAJnV+DWW29l/RLWUnuCIKQkdwkGg2Slz6womeiNN2lg78qeGfsenEi3Xkm9krbdMPxQ/U6+h04kWl9mY0CWiI400nXXHO6ZX5fc5UhmUk1Kwqr/+1+KWOUcUTIUK4BmITTR0XoaPqa8c0p5l857cvzHCjO3vvMmibwig/1dY0muVSrNJ5x3baHirPK0zgcK0qvzM1auLCVNI8ngKw3qOqmmyfo6DJOVR//z/B+ecrA44+N++UsWL2SLGKom1QfYLLWVQZs6UaCJdpbRiB5b+iftG5i1bvM6drQmMyKRKpOqshjcDEj1RBQMmm++sUgQOgtCvCCwJujcvEyTt40QIYA+ux9QHB0CEIDA+S6AAPp8v8O4PghAAAIQgAAEIAABCEAAAhewgKqqSUlJvOCYLbQnCL+8c6I11cxQmiV6/e9UkLe8MHvH5Ltp6q9pSE7txXlb91dYZC3NFyoRK+yQTDp0lMZdW9UjZ09GUq2/+8HC3I3z3yFZY8PGbHlAq9NDJ1J1ikbo4YcjWbk7c/PCKSnV+fllDz5Sw1Jvu02DTTTzWWT2yrq9dOmALXndD+UkH+pT+Pn71iqAgTDfQ1dI10jXydRNFkAHm+ivL1P//MUF/tdmv2bI1nKCokERlWSWWrOzVXWq2UM/6L32e9kH+yavf28OhcMUNSlkqjKriDat8WddNnRFZUcnIkHoJggdBcEjOARfbEzl5jIGZXz5+HPbhugL+POFS4cABCAAga8WQAD91UbYAwIQgAAEIAABCEAAAhCAAATOUYElS5a43e4YJ6uViBEEX4yjqrJcjOiSxALg2XP01NRXCvPWT76XHp5MOUkrSlJWvzeL5Cbrcq1B5pbmDZWONbD0uSB3e1LnA8md9xVkl789hx0kJLGhY9anYQXQikmSTM/9ibp3WtE1vsafGiwu2Tn5oUaJKKSxjLjlqOxnlGXPOhkRuuXKoxkXbSlMri3I3Pzf0yOSSpJOYYUH0KpEumI1ResmKRKtLqWLC5cPzl/+9KN7yErGJZNlyKykw0qf/7mgoibSHdfX9ey2vk9K6d/+Qg3H2fs1S6z6mafP1gQ01TWwimstTI/8+mNB6CsIWVYGzbj+9Kf/ZsPRAelL+zcQQJ+j/0fgtCEAAQh8+wIIoL99c7wjBCAAAQhAAAIQgAAEIAABCJxFAVmW2QKDqqooyp133hkbG+t2uQSr29if2pm9scm+bVhFhZnvFmWv+N1DtOhDKszYm9N97aL5pEdY3MuCXZbNkqibQYUkjX5599G0pHX5WY1FWYHM5LLHfhcIhljubOXIEh+AFq09N5ZRVsqmntmUdJGalXps9NUrj0vWgofWwoMGi4KtBQhJNlVSwzT7LzS86Hh25yN98/Y/+oARkdi6iK1lzapEskS6RBQ1KBShXVU0qMfC3mlL/2uyIoUpIvLDmQYb0Y6oFFWsWo9Jt9b0TdzbP23rB3PZVSg6KVbZszWprSgkqVafNRvDDtLLv6eSxPl9s170CKMdQqYgeHxxwtirLmWXH/63CWh2LGwQgAAEIACBUxFAAH0qWtgXAhCAAAQgAAEIQAACEIAABM4FAV1jS/CpqhoXFycIQoeL4p1W/8bDD95naJIcoeWLqU/u3/JTF986XinbQH17rx1csvOBezRFZFUX0SiFQi2TygbRoTr65b0HS4o3+5MOZ6U0+hMrJt5WF42w5NfKnRuJgqz/mUgVaddOGjRgQ35GNDuZSrKNoQN3NUTZEoVNBkVY8QXfrAicyAzRZ+9RsX95XvdDvTKPTryt/ngdW0tQZPUcusLWJpQlkkVSI0RhjfbsoRF9V/ZKW/6jH2xrriY1SqrG0nYr0o5orA6E7f3BHOqVsqKoy6aHJrZUfvCGkNbvmkKGZFAoSppMr/6ZhmRW9E5cc3HRa+OvfNYlZMTHdeWrNrKObBEB9Lnwicc5QgACEGjHAgig2/HNwalBAAIQgAAEIAABCEAAAhCAwGkJGIZhmuamTZu8Xq/L5XK7XJ07xsdf5Jw/d54h0baNNLxwcVFy6UOTIru30KiRoRz/+lGXLWxuZh3NEYmaQmHFNHhIrBDdNWlfWuon/pRdqV3rCzMPX3NllamTrvJJ6ihRM5lhNtMcpcBhGnf5/q4ddnS+KJCe1DywX0XVVrbOYRMriCZrPJqFxSy5NshsouqNNDx/c1bH6tyk3eNGH2isZz0e1qKHLb3PmhVDiySHiWpqaejApSUZay/tt0FqsKao/9UoTZqVbus6LXiLirsv75ey7vH7a6t3k6Swt7MrqlmhtfUVirIR77f/j6XPfbrtGN7j833bqLx8F5sUtxZsdLtdn376WShkzYFbp3xatwIvggAEIACBC10AAfSF/gnA9UMAAhCAAAQgAAEIQAACEDgvBSRJevbZZwVBcDgcLpfLZYWqTfVNpkK/vHXuwOwFN485VruPbv9RTVF6+bhL9zTx3meiZjEokxSxhpXrI3Tv/TU98tbk5xzJSj1WmFl96cXb6o5aETKbsWZDz2TIPOKVaun+2w5ndtuR3j2akRJMTVm/8BMKKBQyKUJRmSXbEcXKjVUiQ6Om/TRh1JqShEOFiYH8jOV7WJ8zS6tF0kWr9Jn1Slu9GRGioEJXXlGVmbKsOHvJqiUsUWatHHzj3c9Esk4fzKeC1Pn9/WvuublGCZNuUFgmyWCHbR1/ZlG5JFOomXZX0JX9DxZ2qCzqumTrGoqGWe9IZm6awCqg2TZ16lTD0KyrbW2ubn1P/IQABCAAAQh8TQEE0F8TCrtBAAIQgAAEIAABCEAAAhCAwDkjYJqmqqrDhw9nAbTL6XCxSHXE9weyoWWD1q5sfuXPNc2H6NF7qFfKsu8XL96zkV1aVGkJlSMUEomOR+ihx8LJSWsKskIZCeHM7vtHDF25ZxerrWAt0kZLl7RpvSgaoT//kfJSdqR3aU7pcrx3rz2vz2GzxjIr02jJfyUrfa4LmAGRwlG6flRVn7SdOZ2O9M3Zs2gRRWQWN2tEEeuLLSpopb5ilOqO09Vj12ambOhZULFwIRtqtjbrjU3SZcXUSFGpbAMNKFxenP7JlSMXNB8lTWG9z+wETF0h2foyW15KVL6SBmYvL+pY2S91zQdvkWGVg2imct/k+5wxrDJbEIShQ4fyMpNz5sbjRCEAAQhAoP0JIIBuf/cEZwQBCEAAAhCAAAQgAAEIQAAC30yAx6Yua+1Blj5b48+/nnwPb0xWJBYil62mouS3SxLnfTaXKMRGmTWDd2OwymaR6Kn/lgsKKnpkBAvSKatbXZ+8jbu2tzkta60/ItJMNtg8bx6VFBzISopmdA/nZeyZNOlYY4hl1DoZbJDZYLvx8JcNQZv0xFSpMHOnv/O+1I6rPnyXrSWosp1NjfVIm6K1j6mRIZEh0qMPhIqyV2Snrp72X1QX4OegsnM0WZ4uB0lsps9LaWifRfmpn/TLX1B7kKXPmsFKP2RSZFKsOmlVIZ1F0gpV76abRlX3S9nSL3XNgtdJDFFzqCV8L12+THAyL7fbnZCQYFgmbS4bDyEAAQhAAAKnJoAA+tS8sDcEIAABCEAAAhCAAAQgAAEItH8B0zSXLl3qdrvt8WfB6VhSWsrPXJTYBPO7c/f2zH7i/545TBrJUU1XWS4sWdPHQY3+8Hy0/4CtOf5j/fMpN7m+V87qqrI2180noA0WMTeFaNUqGjpwT4FfykyQspP23zVRVIkCdkWGRqbeEkCbxJb+e2c2Ffl3ZCUczEoq+8vLpOhsVFljAXREo5BEokQ6+1WlaAM9Oulw3+zVg4o3TZy4TbMOG9F4IYZVUm2tPxg+SlcM3dwjsfTSoR9XWtPcmkaKaSis+iNqBdC8gkNXDDp+mG4dt2uQf3/flMqZzxlikF0Xj9MlXY2qsjfWxyegBUHYw5tB2lw6HkIAAhCAAAROSQAB9ClxYWcIQAACEIAABCAAAQhAAAIQaO8CuqZLkjRnzhyPx8Nmn63xZ29s3PIVq1VrzFfVSbIaJ3SZolb8KmoNRBSIsMIKmegPz0k9e67JSqu+dAj1zpFyuq//x1sUskaPNa2RVWNY/Rs6mz+mmqPUq3hNTuqRtE6B5M4HJtzUfPAANbFVCVXdiJq6xqNljUgxWFHG9s3UM3VrRsfqvLSKp59iBc3W+oSkka5TRKeQTGHW12yQJtI//kr+uLn5CaU/umpHzRGSTBadi7outyyRyEo9Qkfpx1dsHJpbXpi8aPH7FAqSZGXfimnIbAI6KpOmmNa7G6SI9PMbdwzJ2TQsd9uMh9iENbHgm0KSHBSjx5ubRE3pkpDAA2ifzzd79mx+v03T5Es7tvfbj/ODAAQgAIF2JoAAup3dEJwOBCAAAQhAAAIQgAAEIAABCHxjgX9GpY8//jhPUe0KDsMkzQqgDTJ0K3VlS/wZJJtRky3gZ4ZNChv02hzKyFzuTzowvB+ldz7aK3PHM0+yZQFZ2MzKOUJsXlhjpxhSqaGJrrpqZ276weTO9ZmJtf17bt68hQJRVn9hmmFTC5AeZe0eLCg2ZYXC9TQ4f2Nuh6N9so89+HBtlChisj+zZQn5VZuk6LKss1B4/ls0JH97Scr2kb1Lj+0l2Rrc1q2dg7IcktgCg2TSz26s7p26fFj+p6+/wM6TzT4bbKTaWnXQZLUbrKqDbY119JuJBwf6t/dOrpg8cbupssy7haL1/WVDHzxsaHx8vCAIXq93+vTp/LwMw9A1HY0cXAPfIQABCEDg6wsggP76VtgTAhCAAAQgAAEIQAACEIAABM4BAcMwZFkeOXIkm4C2NmeMa9CQ4azNuDWA5g91ltaqBmnWPDTrfX73I/Jn/iOxa9XVl1NKfM2A/COP/doQm3jibBBFrTUFrWILkx3slgl7invsy0gJd+twOD9747491rwx6YYZJSPM0mcWQJuarEgyVe+nay/Z2idtZ37CnpvG1R2PUJ1KjRqrhm4JoK1mD12nUIjWraGCzPeLUneWpG3YU2nVQrdUbrDrCCgsSw9LNOX+I3ndPy/otuLpybVqA5vf1q30WbLqRCTrdCUegRP93x+pJOVTv3vFXeObxRAL3VvTZ01nc9oshP5nC8dvH/mdLy7W7XYLgnDppZfyW44J6HPgo49ThAAEINAuBRBAt8vbgpOCAAQgAAEIQAACEIAABCAAgW8mMGLECJ4+u9zuGK/n+5eMZmmr1jJpbBg8e9VUkqxpZmqM0Cuvm316L8/L2jZmJPXODeYlbb/zx0FWyaFbrzL51DQ7rWaJRcZ//ouSlbUmLyvYrUNTfs7B1/7KGjaslFgxzTCbPOazzdZwsRyke2+tLey2oV9m1ejvrThWy55tNGVW/aE3WisQkmGSYZAUpa1lNLikLMG77Hv9K2fPtN7dqohm7R8kGqRao8/0xFQqzt7WI7Hihh/sVhpIDxEbe2ZrD7Iya4XY+LNIJJp06DB9NI96p64c5N/0k6u2BmpZNwd/UyuDNngALZMhkzHtDzPY2Li1eb1eXdPNlhHqb3ZL8GoIQAACELggBRBAX5C3HRcNAQhAAAIQgAAEIAABCEDg/BXgNRG8QYKnqL5Yz9THnmCJrx0lmyztVUmTiMIm61aeOYuy/P/IStl0+3j6fj/KS9o+/soDTcfYSoAqm1FmDRmGxgJiXpr8t3cpKfXdgtyjPXOlnJT9Tz/Clg6UNFM3glZNR8TQJFMjU2VT1qTSjIdoSO6OksTNfTI/2VJBEZUveChqFBEpyJNq1SRVpeOHaEjJol4Ze3qkbv7ZbVvYuxtkKs3WoDZLwTWioER/m0v5uVsyU3b3yV9xdC+FG1gdB79A1QqiFXbipkgUVmnhh5SVMLdv2pprLt4cOEoKuyKSSbHWR2zNyYlCCqk6vfjiAkFg6xD6fHFeb6woigp/wfn7mcGVQQACEIDA2RNAAH32bHFkCEAAAhCAAAQgAAEIQAACEPjOBBwOtvig0+l0OAWPW5gx7TEyJatDI2otNKgbZKgsXqb6CH2wkHoXbkjvUnHvbTR2KBUnHrm0906piWSRJcJW+mwaJCskRk0zpNL6ChowoCwlcc+w/iyqfvxXEdYOzUapQ2TKpiGZJKpmOCRHQiITWPA29fdv7pW4b2jBuvJVLMgOy2yVQoW1aIQkEqOkSEQBmYJBGn9Fw+C8usL07ZPujIii1Vtt6KSHSQua1oi1JNPrs6h/n/K87J3FRevXrrGiaYNMNcRDdt4TrVsLHCpEZeU0sNeGXpnrfjBoYfNhFrpbSbWhkahZ12e1RVunT7RxFWUlPygIiQJbvtHrEmJXr1yjcwWevn9ntxRvDAEIQAAC56QAAuhz8rbhpCEAAQhAAAIQgAAEIAABCEDgJAKVlZV89pkXGbsE4f35s4mayQySYbVTkGyQGdSoup4WfkrpqR9mdq/4zZ102zjqmbxjUNbGbWtIjbBhY12XZD0Y1UJRknSrYGPPQbr0kpU5GQdSutX1yNz/k+sOS7VWpq2ZZETI0A1NV42o2TqR/PEiyk1+pyixvE/apoXzSBVZkh1RwgZFNYoo7DejIRrRiQIRmnR3Q07XHcWph68bs/fwIdYPorElBEWiiKaGpQgbqV4wj9I6L0pNWJ+Xu/rt+STyBmuKEEVYAG3NaBtEobASidLqNTRsyNLC3FWDepWWrWb9HnxOWmOzzpLOUviWyo5jDbSpjAblf5rX/VVByBYcgktwuQR36aelRCRJUjgcPok5/gQBCEAAAhD4UgEE0F/KgichAAEIQAACEIAABCAAAQhA4BwWWLJkCQ+gXS4Xf7Bq6Sdkhln6bLVwyFathkS0oZKys5aVFBz+yXh6fAqVpO4bmL1x72aKNlp1yJqkm82y3hjWxIjJZoQbonT1lTuL8w738Id75h2/ZMR6McyKls1oS+2FVTNtRkTZtJ5YX0ZD+q7PS91Qkr34f/9kaCqJbPZZV4yAbkR10nVrN9EgxaCHphh9cnflJFYO7Lnq4CFWDKKwN2WrEuoUYWsghmhnBQ0rKS9O25eXuuF/XqbmKNvNyrqt4LnlprFMWhapuY6uvGRvUdba4RcvXL2ONKugmldh62RYX6x/g3VG63TwIA0o/CjFs7x/zieCkO2IEVxO9vWHGb/XZAU10Ofw/w84dQhAAALfqQAC6O+UH28OAQhAAAIQgAAEIAABCEAAAmdaQNf0TZs2CYLgdrudTqfPx+qMP1rwnlXBoZrWOoQqUUSnjRXUf+DizPSyn/+EnnyIcpJX9c5Y/fYr1gkZxEaEtahhNKtmkFiNM4V1euEl6pm/P63L0dy0mgG9yjeVU1RqvQDZmoO2lvaLWEF3zTG67poNPfybUhM+m/70cdbQIVFEZlUdhhk1DdbEzOoyDNYf/fqrlJtUkdt9X2Hmp2s+Z88HFE2xij2sKWn2Lnt307Deq/OTKwvTKibeVt/YTPVhEnXTOrvW07BSZtLp8B667gcbBxVs7ZG+8GgdBa3eZ8k0ldbFFK3lB60AWidJpJuv3ZfVZUUff+WPxm4SBD8LoF0sgH7qiUfJZBPQrW+AnxCAAAQgAIFTEEAAfQpY2BUCEIAABCAAAQhAAAIQgAAE2r+AqqorV660O6DZaoRuz8rlS4lUk0RFUzUr1V1fTkMGr8nJXH/NuPo3ZlGh/1BJRtXMl0ixWptZTs2+DNNQNJOtwXc8QK+/TgV5Wwt7HM/O2FuYt7RqMzU1W60cHIUHukRyhP1+5DBdedn23OSNJfnrH5vKKjasxQjZgoJsYpnNK7Mk2mpXpvlvUI/EVf0yQ2kd1s2fS/XNrJ5DZMsksvFkIqqPUn0T/fDayt7ZlT2S144bveJ4HVtDkB2Cba0/rYeKSGITPfCLaEnqit5Z7330LkXZ2DVJZIjEAmgrJGcZNzsBgxqO0S3X7ClM3lKYvPkn12+tP0aC0M0ZI8S42NcTUx+zdiQMQXMHfIcABCAAgVMSQAB9SlzYGQIQgAAEIAABCEAAAhCAAATau0DbAJr3b3hi3Fu3VhGRqLQUJm8oo9zc13Oz11z+g/CK5VRcsLpXbtX9d0milT6rbG0+3VDJ1FhRhaKz6Hr1WspN3ZCT3pjXo6ZLwntv/o0C1pp/fIpZay1fZjoa1R6ie+/cWZy+LS9565VXrm9WWItzlKXKKg+gLURTlR7YdwwAACAASURBVCnYSMs+osJuawb460tS9/z2LrWxgSSVdVTz8WfJanWuj9BPbt3bq3DtgOItQ/qWbipjhdEGkVX1weum2X4im9UmsZkeund/74zPe2cue/s19ozVByJFSOVNIaqVQatW67Sp0QO/bMztunJoQXXv3FIxwkqlBWdHp5U+I4C27hS+QQACEIDA6QsggD59O7wSAhCAAAQgAAEIQAACEIAABNqhwAkBtMPhcLlcgUCANWBEWa/GmtV08aA1edmrxl1zoKyMhg045k/8bOzYT3hrs6S3dCWz3FYjQyNFpnWr6NIhW0r8kZQux/3ZG3/5m4NWUs2uXmfJsmJNGLNfg7VkhOix+0J5CStTLvp8+KCNRwMsfda/0NPM9taocjldWlxd0OFY37TqKXfVkEGyRJpGuhVABxRqUkkmeuQpNTervDhve5fOL23cxF5aH5StAeqWJQhZxmywJQqNKH3wJg3IWVqU9el9d1VLUVIUMkhTrMnsSOv4s2LNVocC9Nar1KPzmsG5ewYVL6iqJMlgfdCCM87pjIlxYgKaUWODAAQgAIFvIoAA+pvo4bUQgAAEIAABCEAAAhCAAAQg0O4EvhhAO51OIoqqsqhSNEpjRr1ZmL1g7OWHy8roqiv39incdsPV+5ojFDFJNEi02ixUhXRFN1XSZJJDNP7KA+kdq3qmKTmp1Xf/JqgSNSoUVFiorbEk15BIjcoSmaRF6M/TowMyKwu7bbms/6b92ymq03Gpqe0SgVYWTWKUIo10acmObN+ugk77rht5oP6otTKgQobKAmjNYCPTYY3+/H+UmV3aq2h/757r336HIhr7at1MFj3z3meD1DDNfY2Kkz7qkbjksd+xdQvVloUHRZW0KMvK2QnrrI6DHfydv1FR6me9UyoH56/cuJY1dfA82+H0OJ0eNgTtRAVHqzR+QgACEIDAaQkggD4tNrwIAhCAAAQgAAEIQAACEIAABNqrQNsA2u3zCg5BcAhr1q2NyAqrntDpqf9afu+kT+pq6Re3ir1yVg/tv2TVKnYxTRJrvZCtqJh/Y0FwhH4zsb5f7v6kuF0FGQevGVe94wiFW5NctpygledyDEWj9xdQbvrKguQdo/ruqdtKFLImjQ2dDN1g+/KomBqDdPwI/Wjs4cKEHYVdqy4uXhSqY7kz2wzW0yxFWFYuq/TOu1SYsy41YW1x/pInnqxrEtlAtGTlyNbeJpGuKVFJkprqafMq6pO1sH/m+luuORBV7N1Yn4fOUnL2jEkk62zM+fXXaXDJ9mL/5j45c8tXk6mzYDokqZKuCg63Q3A7HA6HU3jmmWf41eE7BCAAAQhA4DQEEECfBhpeAgEIQAACEIAABCAAAQhAAALtV+A/BdD8jEVWXMFC2G3bqW/+3KykN9esYqGzYUW6vBxZJzKsoLi5nl54mvr4K0tSj2d13z3i4oqDR1n6HLKKLPhQMy/uEK0+5dWrKDd3aY5/W0lu2ftvWtFzlFhgrOpkqCapoh6WrPNQTfrpTYGi1N0FiVv7ZH9WvpZUkcJBdkhDbo2pDdpSToN6leYmbe6VW3XbhA2S1hJgs3pok3SzZWHAaJgddPNaGjtsdVanD665bFvjMZY1y2yxQ3ZNBmm6dc58SUNVpfVrqVfh54NKqgeXbFhZSrqVfau6LqvKseN1DofL+mIR9Pz587H8IP/w4DsEIAABCJyGAALo00DDSyAAAQhAAAIQgAAEIAABCECg/Qr8hwB6tWSIPL+VdDbpTER/ebl6ZSl7oLcOFJutq/OpJskizZlJJWll/dID/TJDIwfvK9vMcuqQFSnbHRiqSc0iHaunDeuoV+HivMzybp0/fPZP0cbj1ryxZMXQmkqGrLMomuXCqkEPTdF65RwuyTjSJ7/0s0XWHDU7EaOpoVaOWCdn0tYyurikLL/7ltyEDT+8cmdjY8tEM69pVkwrg7aGqg2ZmqvpZ9fsK+r+/9u77+i4ymtt4O/MaGYkuTdZvfdiWbIxGBtCNQEMBDBOckO5ECD05tBDSEhCbm7KbSSEEiAQwPTQDC64N7lIli3LknsvaqNpp5+zv2+/Z6RwCXctbCDI5BlraUbyqb+jv5611/N+MKVm3vZ27tkw+KYitlz2kAew5W0aDikKHdlHp9bvKRzdVpg158035YnlOVVVdRxnw4YNHDz3vZqamhz5kpvgGwQgAAEIQODoBBBAH50XtoYABCAAAQhAAAIQgAAEIACBAS7wKQG017Ny9aq4odhEoSh/74p1G0Saxsv9heIc18o2Z13n0gtuwtAtalpLVTnzplbEqzO6Tihv39jE+XGPZfBAs/xyJ6B1iw4foW1baULNkpKctSW5y++5MxKJUUROJcts2yHHdsgwicImV0I//jiVFWwozz2UM3r1ww93a4acTybSjB7bURVZk9Gxj666ZGvxkKaS4e31xUv27uArdM/Iaw8S6Q7H6KZFSox6D9Jlp7eNy1x6Qsm7jSt5M9nRodgcQPOPbvpsOWQY1Lmfrry4vTqrvSZv0/PP8WF7NdK5lsOKxPiiFy1aJITweDzu98bGRtu2MQQt/0bwDQIQgAAEjloAAfRRk2EHCEAAAhCAAAQgAAEIQAACEBjIAoZhrFq1KhgMCvfl9fj8wZ8/+u+627Nh8+CwKSssdIt0k5fpM2TphUF6r95FcmS5s4vOO21z0ai28rQDlTlNb75KnT1ygJlIkRvo8nuvYpoObW2haae0jyveXVW08buXNcVjpCpuWOwQmbbN89bu9iGV3nqPMtMX5GVsLczZdPMtnDb38OKFRKTpTo9uaaZJeowuOXPrSYX7S4durc9e19LA1+dGya68SRQ1LIcoFKNID9190+HanFU1WR+89wbFwnIBQ+dvobMbQGsW72qodN8tdmXmipqcOa88R7qRuDCdKGbxdVrkPPbYYwk6+RYOh227P/oeyE8e1wYBCEAAAgNRAAH0QHwquCYIQAACEIAABCAAAQhAAAIQ+DwC8+fP/1uE6hH+YMpds+7lng2HTLkeH39w5BCx25GcGGrm5ueIxttcdfn68uzWmtyeKXV77p0VjhscUnP3hWOppGqka3IpPx4f7qKZ3zxUNLo1b+yGs89qPXCQYkqiQloOUmtxM6ISHQxZEYPWNNHEE5elj9lQkNv2zfM37zzEcbbb1GySqtoxXh5QoVuu3VU8YkPVmAM1YxtefZLTa0dG5P3fTZlom0SxOD10d8fkmoV1xfPe/Aunz7bDAbRj9WXWFv+oWRSKcA3How+HStOXVOeuev4Jjrktefvu4oSqw4m2Rc5DDz3UN/7sS05Oxezz5/lTxL4QgAAEIIAAGn8DEIAABCAAAQhAAAIQgAAEIPC1ErB4vT0SQni9Xm+STwgRTEme+Z3vukXPZl8fhZtB81J+8jduq0ZXlCJxuveuaFH6+pq8aEnWlmuvbe1VEy0WusNJrkbdOnUrpCsGHdxFV13UUT58Z05qy8STVm7ey1PSoajCoHxkx+Tl/Yw48dKFB7pp4gkNJYXbsnPa6yatPxDnU8s1Efn4qunELIqp9MuHqDZva+moXXV5Lb/9iRLhmWyKq25t9d+e1JEu6o3Qi89TZd6c8ty333yVOz4sd2VC91blWLVtc8rc3cNNHI//mqpyFhRkvvtvP3cMeY22DKDjRPG/HZguv/zyQCAghPAnpeRkF3zsf/ARAhCAAAQgcNQCCKCPmgw7QAACEIAABCAAAQhAAAIQgMAAF1BV1Z2ATgrKIDU5eMbZZ1ik6aSanMdy4OsWcfz/gV9b9ikbZOpEcZ2e+INTW7ylLLMzd9TG6ee1xS3OjkM6V1XIRJfTYJ3iik3ROH17+t66nJ2lg7ZNrWhbtJL2RXkzftl8XJO7mK0Y6QrRtv00/eI1eVkbS/MOTJ7UPmcBheSGKo9W88y1qlHUoBWrqSxzfV12T21e6723xEId5LZfRFWZQ7sH75uGnv0yVRS/XZL99v2zjrj/w/E6N07LTJ3zba4dsSwyDXr2CaU664PcEe/fftv+zh7eXNN4XNqQ6bMbQLtFG9OmnZWSksLBfWBIdVV93znxDgEIQAACEDgWAQTQx6KGfSAAAQhAAAIQgAAEIAABCEBggAuUlpa6Q9D83SeERxCpFvVYMvCVXROczjpkWKalW5rq9MYMev89yhzxemZqW1n2rvPPbzjQzav4xeWafqqMrblzo7fXTW8v/87misy2kpFbp5Q3LPwrGRrXScvQlze1bG7OcLugVYe+/b3txYUtxdkHijPXzH6a8dziC3f9Q/5RpSXLqKhgwYTCQ9VZm2ecvyoW7Rtq5i4PTXY+8466XKVwYxONHbMgL3vNrDt3cSgu824+eyImd8jW+jPzZfOoIufNqpwPr79qV8SkmKwcseTah7yeofxy9+vp6eprL/EMTh09ZlTOAH/QuDwIQAACEBjgAgigB/gDwuVBAAIQgAAEIAABCEAAAhCAwLEITJs2rS9Ile8eEYrvIYrplqZollu7wRExqfF4RJZ2UNsWmlA5pyZvS97I1vHlqxetSBRT9FqaG9Eacr7YvZr77uyqKVxVlr6lOmf9Wy9QrIt44NldKtDhoWPL4qPzioUOXXd9c0VJS37WnoKsNf/5K3KickuZVvNYtU2WTof305QTG9OHry3JbPruRXvjUVLlCoF80r8D2LONaqteLshdddFFh6NxOtzDJ+c1Bv+2sa3E4mRStIe2NdPUmiUVmfOumNGiqpw+x8k2iJdg7M+geUebFIVaN2//mFvSj3/06N+dHL+AAAQgAAEIHIUAAuijwMKmEIAABCAAAQhAAAIQgAAEIHBcCFimNWvWrI8Fqfxx/sK5RA4vQmhwpCtHlXWbB5H5pYRo5rnra3Jaxhfsqi6a17yB4+NOhXPdqB3XydbdhQod0sJ0742Hx2U31eXt/EZ9829/YalR2XXhps/yyKbN08WaxY3Sv36USrLWVuR15mesv2vWbm78kP3LfY0eJpl0aCddeGZT3pjmgoyWySd81Lie1wzsDvM1GInJa1tVTHeXI0fo9JOXleV+MO3MDztk94ZbKqLJi+y7tcT0c9c2qs/9oD5/xVUXb9+1kw+g8ryz7nZeywDadGNocijcQ988+5qU5CyeGOeXd/my1cfFE8dFQgACEIDAgBVAAD1gHw0uDAIQgAAEIAABCEAAAhCAAASOUcAwjMcee+x/B9CeX/zyV4qWGCZ2V+lzs1rdJlOjm6/cO6FwU/moLdXZq198njRuZiaVHIscnXT5xbPMhkJ3XXtwXEZD+YitVRlNd9y4TXXTZJk7uwfkgzs8XaxqtHQxTajYUjx2f8HYzRed167Kw/bdlcV5sEW2QjdefmByxc7SzPainIXLVlBMbhbVSHV4tNmUGTQ3bxD1hul7/7KsOHfOhKq5e3fwAThTtngtQ9VxEim5nNRWYxTaT6dWrJ5c3HzB1LWH9nBDCDd4yNFqN4A2+QZlHG/xf1w186nhg07yiLEewR3QY8aM6btUvEMAAhCAAASOUQAB9DHCYTcIQAACEIAABCAAAQhAAAIQGJgCtnwtWbIkEAh4Ei+fR/ivuPIa94INk2eTdYvX6+P1Am26987tRaMW1ufurc9t+u1POY/WLI59ZT+ybZJpykHpWC89cItan7XjzEq7PrNt5tlNllxD0A1z+2aKE40Zqkob19EpEzaNK+yoLth76UWt0WhiRcHEZaghUyFHo5/fH63Jbsse2lqcveD1V6kzIptBHFJkRYh7Gb0RikR4ncT7fhiuKv1gyqT3lyz6JL/u5tSy0JmIjuyji89sLB21tD5vwaolvA4hybTa4gCaf3Jnq02HLNnf8dCNyvicF8YMPccjRnrFUCGCkydP/uQ58DMEIAABCEDgKAUQQB8lGDaHAAQgAAEIQAACEIAABCAAgQEv4DiOoijuIoRefiV5vUnjxte7F65oVkwlu+8u3niFaorn1xfsqs9v+93DpHSTFifFMG05emyQY8jcNq7SHdeF6vJ2lw4LVacdvuSUtt2byLZ4grmvIdrsD3YNi7qP0PlTtxeO3JI1um18beNOXimQp5U//rJj9OozVDRmcWXWwZKMTa+8RHHZ+6ySpcqA2JSNGW6/c3cvPfKTrvK8D2vL5r78AhmJYerETLfbwkFEXWHbdCgSpisv3TEub0l13rzl8xPpM6ft/KVbZFtOYiBa07jA+qHbDtWkLRqf9ZZfnCBEskcMEiLw/e9f7fRXgHz8uvEZAhCAAAQg8JkFEEB/ZipsCAEIQAACEIAABCAAAQhAAALHg4Aho1lN0yorK71er8/nkxm0N5iatGvfNiJDN41wlAecI3GaM4cqC1aXZuwoz9x0y9XdtkpGohSab1Vm0BxAR8J0xw96i4a3FQ2NVGVGaws2bNuQGCeW3RWkc+dzyKKQQaZu0fY2uuSsXePSD5SkHSwqbVjdQppNqp7gs+Wu0Q7auoZqMlcWjdxdlrv5gXucnl6K6G5HM59UljXzNHSc6EiYXniZysqWluS89csfdUa7+5+EaZPTH6a7AXdPB82cvqM6e9PEsvV//pMVibkbyxvri8DdANomCnXTvz2oVY6dM7Vs8dTqPwV9pT6fTwjhS/I889wfFbVXMvSfDh8gAAEIQAACRyeAAProvLA1BCAAAQhAAAIQgAAEIAABCAx8AcMwVFW98cYbvV6v3+/nAJozVfHqmy+QHPwNxymuUUsrVZW+W5y+s2DkjstndIZ7eFLYNML9kSsH0A5pOt13u1abv7toiJKV3Fmas3HJR3ITOU5sJZJi1aZOm6IcHKs0/azWmpxdNRmHawtb33qfjiicZRtyWNmRFRkm0ebVdO6EBROzD9YVdFx3Ta8q/1ejuC6Hm92KjE6VU+POML3zPpVVrKiuWn//nYf7/BWiuEUxnQNqSw5MUzxGaoyu+vaRitzm2sLW264PuRs7pNu8mUy+bT6T7ZAlz/jaizShaEFV5rw7vt/+Lxc/EfClebxsFQh6Vzcs7Q139Gv0nRfvEIAABCAAgaMQQAB9FFjYFAIQgAAEIAABCEAAAhCAAASOFwHLtFpaWjhIDQSEEINTUz0ez113305EoVhEtamjiy46f1Ne2trK3AOTx7e3txP3cnAvskXEa/q5KwT2dtEVl20Zl7c9Z1BXyWizMm/XS6/QkYjbZUE272GqXM6sEoWJOMK+Z9bh/LEbaos6awpXPfXY3+ovXDrd4X13badz69trR+6tzzn4nQt7Wtv6+6Yjsp46kSibxKUcTWtpUvWaouy5l124vvOIexiTKGRSl0ldBnUS8UqIapT/6+6be4py2zJHN35v5hZetFDlGWqLU2RbRuURh0IOyaFoi+a8TrUFCycUr/rlQ1w44vNmeETQXbyxtKzYMBU3sXZPie8QgAAEIACBYxBAAH0MaNgFAhCAAAQgAAEIQAACEIAABI4DAcu00tPTg8Gg3+cbnJrq9/vr6+sNy9Is6u6iW25omVjTUlu664ypu9evSQS+tkm8NKEV57RWp1gHXXL22sJRS8vH9mQP7hhXuu+hH9HBCMe9MtU1LdINrtbgZf1sk4wovfkynTR+Y1XRgeKs9Q/e1ykTbZKJNs8bRzTbcKi3ly44Y13V8F2F/p3Tp+7Zu53TZ1m4oVgUt+VShe5Ic0ShvbuprnhFdc76S85p7jzA7Iqp2rxZyKJum3qJIkRmJERaL9174/7qguW5Gc3f+lZ3Vxd3jPRqpFiOm0HLMo9wf/r86INbJ5UurStYfdcNnWqc5i5o9Sb5PB4P92/4fFdccYXOdSR9nR3HwQPHJUIAAhCAwEAUQAA9EJ8KrgkCEIAABCAAAQhAAAIQgAAEvhCBK6+80ufzBf08BB0IJAkhtmw5FAnRI3ebtQUbsoevLi9a3LKZOy4Um+J6Yl0/MlUlRD276F/O2Vc2ek3RqO3Fow9X5m+5/sZNh+OcPsdlAC1bMkyD0+e4RaSEqXkFlYxeVpy2vbp44333xaNqYqE/GeMmmprjKv30PqrL316TtuPE0rXtLXyjusMBtCFHla3Ed5NXMjxEF5+5vTxzVW3xwlXLOe3mKg/um1ZlVB2XwTVfthKmH83qqivZWJbRVFH4VribIjE+YFQWf/QdWbW5+5oP8YefUX32knE5C394wyFHTkd/+4prvUncly2ECAaDr732mqqqjoMA+gv5S8RBIAABCPzzCiCA/ud99rhzCEAAAhCAAAQgAAEIQAACX3uBd955xx3pDfo5fRbC8+xTS2Y/a47PWTeh4GBl4fKXX+YoNyZT2X6NeIgO7aKLz2ipz9t5crlyWp1Tkd1+wbnNcYcHpeNkq2TrMoNWydFlb4dh0fJFdELph8UjthSO2nzBuU3aJw/LAbTp0Jy3qTKzeVzWofKx83bI9DmqO/3rDbrVz/zdIV2j266KVaavr8pZMOdNnpvmoNlyTLJs7nQ2EmkycWL9X7+yK/KWZg9fM75kbeMKeU1EimGHNU21OYl2vyyHPz16/+H6rFWVo1fecuXuaA8fdufBPaMzxnrkeo1CiJSUlL179yKA7v+TwAcIQAACEDhmAQTQx0yHHSEAAQhAAAIQgAAEIAABCEDgOBBIT0/3CiHX1RM+Mbqq6OqpNc9Xpa2rK9z4p6cpwov8cVWFbfMHXSclRpsa6MSqBSUZy845Wa8vVKpyd42vfK+3N9FGofI6gbobQCvcnMy/P3KEZlywI2PwR3UFbZdO2x6PcHezapPF/28S6ZalKgq1NlF13ryqsQer0jd/8FeKxUizSHO40EPnUNtW5fizStTZRT+9p6d6bNP49I1/eZwrnHWDU2ddrgnokGaQahLPJ9sGzXmDCtLmV+a2VeQtXbmwb9VAm1ca1CyOnokoJt90g157jiYULM8bPOfiM9ZGeykm1yZ84cWX3MFntwB65syZ3BuicRe287GXPBK+QQACEIAABI5CAAH0UWBhUwhAAAIQgAAEIAABCEAAAhA47gQefvjh4UOGur3GQgwToi5v1A8vOmPNE/9FnRGKOBRRZMuERbZCsRC99iKdUP1hRV7DrJvo2n+h8tztE6obGlZz6hySabVBYZ17nzkLVhyK6Uwy4+KNmaOX1ZVvP3n8sr3bSVNksmxbmqNatmyUJtrWQidVzRmf11Q0as1zj1E0xtGz5nBALNNnXSXd7dToVei1v1BF5rwT8zc9+AO7Yx+vZGhaPECt8wSzrVMsYsRtonicXn6eqoveLhzTUDhq8Vsv8SFsgyyDlyW0ZZzNRRy6c7iHVI3eeo2qcxZXZjRcdObGzgNkWaQYvCDhGWdMc6PnlJQUIcQzzzzDRR2G8bHwmT8ed08fFwwBCEAAAl+5AALor/wR4AIgAAEIQAACEIAABCAAAQhA4EsUOHz4cNAfCCT5/X6f3zdIiLHTz7+9o4PCGlc584gvWf2zzbN/TyeWNdaUz3/4IXrivyln9Mrykjnvv0+aHD12iLojPRZFZe8zZ8ERlUK9dOt1PVWFLQV5rXV1a3bu5rFkQyfD5AlozZahrUmRAzTjrPXVGStOrtrwy0eikZh7TC6PdgNomT7rMTkv/dxz8fKsZfX5bVdf0tq9nwxVRsmycUMnSydNJU0n2refnnyccrOX1ZTsLMtc+LN7wmTK9NlSNbPD4FUKeQ7bkDPaik4vPEM1hQvKMxvOmbKldSOPVPPQt6UsX7rGJ1JSAil+n08IkZaW1tXVxS6m9YkM+kt8Tjg0BCAAAQh8TQUQQH9NHyxuCwIQgAAEIAABCEAAAhCAAASIotEoEd128y2pweTBg1NlH7S/ftJU4sX7uPk5IiNoR+MY+JEfHqwYPb82Z8Obr9KCeVRTsrmiYMmfnqbOXupRSCNd0QxZ1KHpHOzyyoHdIXrpBarIWVOeu7W8csWGtgS6YSYCaNUiI056N9102d7SEQvr89b+eJYZjnDirZFtke4G0KoMmeNEMaL1zXRy/QcTCrdPrmg5sofj8VBPWDeiliO7PMhyC6N7NXriCaoqWZmXsTV/bOO9N3fbUZ55dnSefVaNI7rTJYs3eFhbNemN16i6YGnB6JVTJ65esYRbR+IWV1obtn79dbcGvEOE8KQEgkKIO++8023eMAxD13XbtvvnoPE3BQEIQAACEDhaAQTQRyuG7SEAAQhAAAIQgAAEIAABCEDguBFQFE5j29u3DBkyyOMVfr9PCE9g0KDt+3fIMeWoxqEuaVG67vv7SgveOX3SO5sbqGEZlRWsqClo+Ml9VqiXJ5QV29C5gZlniS1L162Yamm9MWpYTkXpi2vzd9aUNaxtpRBRl05hPaZbiQaMqEKOQr+6Nz65oKV02Mrrvr1XCbMel2PIJQ1lAG3rsnyDiLbtotMmbC4c3jg+v2HrBjITqyNaJEuq3QoOR05Jv/0e1ZRvLM5or85Z/73zWzp2c9LNd2Nb5BiWHdcsPpNBFFdp3Uo6obK5tmBfed7ypmY6wqPSpMjJ7/0HDyTKNwIpblP2jh07+Apt2zItN30+bp43LhQCEIAABAaeAALogfdMcEUQgAAEIAABCEAAAhCAAAQg8MUJOI5j2+YFF1zgTwoGgzzhK3zi908+oVhcjqHptGYVzbxkYVnJ2+ees6G9lXo76eQJjQXpH804t7nnMJc9K7ahOarNoTEH0PGYblr8sW0zTapsKE1rnVLbvmQxhR2KEimJOg/ewOAaZXr3JRqfueCU4i3fmbZXCfEihz0himtc6Gz1dTSbxPPY3SGaeeGGsrTWCXl7Xn+WA2Wbo2q3QkNOKxOFDdrfQQ1rqa56ZVnOwZr8/Rd9Y23Pvj4v2+IODttyHMcky42vN62nSRXNpWltVQXNzz9HhyPcPWIRxWUHx7XX/8DnC6SkDBo8eLAQ4uqrr1ZV7rq25avvuHiHAAQgAAEIHKMAAuhjhMNuEIAABCAAAQhAAAIQgAAEIDDwBWzb1nU9Ho9v27orOTBSCJ8vKAYPDxSWqdQpOgAAG25JREFUVqgqGWH660t00rgFlcVv3XRdQ1cn7d5HF1zQVjR2+bTJzRGuQeaXamkyeyZbjiG7v4x00HfO21yTs7EsY+XsFymqUafCATTPKhOF9YghP7Q20ilVzdVpq8+bsjJ0kP+rq5cPYJLjHs0dhVYsiit05WW7KrPW1uVv+NPvSI3wmoEygLZsOdkckVPVJtHadTS+fGV5zu7MoVvPmLSzvYUPaJGjaB1EMXddQ5mucxX1qvl0QlHLxMJDkyrb/ue/7ZDiHtO9Cdq+c1dSIFkIr/D6vElcAN2+fZv7f5bJKXZiO7xBAAIQgAAEjlUAAfSxymE/CEAAAhCAAAQgAAEIQAACEDgeBGzb5pFeh+649UdeT6pbNyE8waf/OL9jB00sfezkiXNefJGiPRQP070P2Fm5H06sWt68iu9NNw2LLHf2WWbBtkWk66RH6ObLuyYUr63M+ujVF6gnQr069WicPutEvbodMXhGuucwTamZV52xYtqkja3rSVO4+CKi2SZPSfMXZ9A2DyqHeuj+WbvH5a8vH7P+gtPWGtHE9LJNjinTZ64BIYrZtK6RJo6fV5K+pSbvcGVew6K5FOO2DyKKO9TjUK9DMYssU0bm8RCdPn5fdfqRolFr7rsjFo7zAHX/yya6+dbbEiDCI4T4wU03WuTEFAXjz/1K+AABCEAAAp9TAAH05wTE7hCAAAQgAAEIQAACEIAABCBwfAj0hmJjx2b05a0iN3ecGqbGdVr7Ps52bY3+8hTl5izKy1+0aBEpKk8KE1myJ5lnny2yIqqmGxQ6TFfP6KjKXF+VvfCtV3lLLtBwjJDZ5ZAZtcy4xYv+RUN011VWXWbzCWXvrVlGpkGKTjGDEtPUfWaWTIRnP0UVmfNKxzZccFqbEuFiEN0m3eFLUC1SecVCfu0/TFNOWF+etbU2p6ssffVLf+47Cr/HiSIO9cSNzpimRuMUi9AFZ60vG72zPG3nbdcecNw7kcUgqmVZRK1t7cGUVOH18ZcQeXl5XV1dbl6P2eePy+IzBCAAAQh8HgEE0J9HD/tCAAIQgAAEIAABCEAAAhCAwHEjEIlEnnzyj16fCAR5sT2PN/m//+M5t6k5RvTOX6mu8pXyknm//i11RihquAF0ooPC4iUDybRpz2666rKO2sKWmsJVr/2F5BqHFDc0xQ6ZPICsxB2KGxz+PnD79tq0hhPzmhbP4XFnm0jlTJknn22efdYNW+ch6zDNf5NqMj6qyVj/jbp1m9ZzTq3xJLWuWppqcrrdq1GvSp09dOZpzeOKDhaN2lc4cuV/PEoadzW7L1M2b8Rs4oUH43HSFXpgVrQ8Z2l55qabrjRsgzSDwjGK6zyardmO5dAJJ04WPPjsHTRkmBBiyZIl7rEM42Nj0n0nwDsEIAABCEDg2AQQQB+bG/aCAAQgAAEIQAACEIAABCAAgeNPQDfU006fKoQYOnTo8GFpo4YXNDVx5XGPTqd+48PSorcffGCLZnKbs1vlLO/QkcXOZDt0aB9969zW8uyW+srNd9y5JaZzOhzvS4HDWodK8YjOHR13ff/wCQWrJuYunDebj+FQYqLZkO3PFkVt7ou2yaLGhXTWuA2VIzaOy1j55ye57llxSCPTdHSLO5zViK5rRFGVLjn/QN6oHdU5sck1h275wVZdowg3i5g22Q6PN/Pag+76gUT0y4eoLKOpNLvpW+evPnCQLyAc5SuJJ/o66PobbuobBvcK4fn1b/+Dr1OWPiOAPv7+snHFEIAABAawAALoAfxwcGkQgAAEIAABCEAAAhCAAAQg8EULLF22WAjh9Xo9wh9IGl47fsrBjs5QnG69s+2aa5rds8m6Zw5t5YuLMHSDVq+kb52zvbJgc+boFffe5/QYdCRGiknRmElE0WhUc3S3fOP2mxonFzedmLvxNw/opJMRp95QjMNfLa7zkXSL4jyHTNS1lyaXLC4dtLouvfH+G3h1QovbNmwOoBM1zE7U4OLmO+86mJ/WUjiioyJr1/lnbeoJuTm1qlPUsCzbIsfWE6UhcZr/LuWPXjwmuHhK/dp9+927oLhuxBVbl8PNTz/zrBCewUOHJ6cOSk4ddNa0b+qmpes8ka1pGvdS4wUBCEAAAhD4ggQQQH9BkDgMBCAAAQhAAAIQgAAEIAABCAx4AUVRotHoaaedFggEUlMHC+ETIuX86ZcRUSxO3T1c+WzZZMrGDJvIsCgmey42rqEZ07qKxuzPGbPlvIvW7+rmW+2xtZjNc8WaGbW514LCcfrZg6HitPfrshoenUVKJ4U7yVRk7zKvXqjrlqaRGeeTUKyLLj5tZ33G9oqRDTd8p9WNjyPxsAyguXOam6eJNItu+mFPevbqsuzDNTk7zjtrXVzhAFshVaOo5sQ50uaK6DivV0j0wV8pJ2NN+pjGKRMXNa3j3WMGWWTrdm9M6yGyZ8+eHfAne71J/qSgENxGsmpVw4B/dLhACEAAAhA4XgUQQB+vTw7XDQEIQAACEIAABCAAAQhAAAJHJdA/2LthwwafzxcMpniEXwiRnDzqp4/8OxHZtuk4lmPLGFqOKPNSfURbN9I3alunVOj5Iw9WljR1KtTlUIRX/VNtmQKH1YhmccfFO2/RuMIltblrrrl4t95BvHogV0fLwWYeq3YssjSHuKbDoIvO3F2dvrVo+LrTxq0MHZRjz5qpGb2qpXFVtM2lGkT0+O8pr6ipvDJSkNE2sXJl8wbSiRSyFQppFJUtIBSNyOyZaNN6mjRucVlRW17u0g/eJ03h6mdeydCOyVUKzWdfeCo1NVVWP7sNHJ7p519omX3T3kcFio0hAAEIQAACn0EAAfRnQMImEIAABCAAAQhAAAIQgAAEIPC1EHAcp6enxzKte+65p68BOUnOQQcfeeQRWYLMAbRjkmVwdqxH6aUn6ZSq5oqRB2uyOqdM2NywjsubI1JDIyVihHtVLoHWNXrjRSoau7xw7JIp9QtCR0iLkRKVs8+WWyLNh9dsK6ZTVxf97CGqzmmryGqtLXpnRyvFeynSyymwQxqXSDtcOa0r9O5smlzZVpB2MHv0jok1q19/hSufYwYpFNcopJNqWJZhGIpKqkFdIZp+Vmtx5sqKgg//8ie+xFiM+z76Xy+98pLweoQQAX+qPykY8CcX5hVpim5qify6f0t8gAAEIAABCHxRAgigvyhJHAcCEIAABCAAAQhAAAIQgAAEBrSA4ziaplkmJ7KO49TV1fl8PhlDB4TwBIP+x//4P46TWM/PUknpoQ9fo4Ihi4qH7qxN76oraPnwPYrp1KORQdRp9nSbHQrpik2KRn99jSqyWiozd51ct3LlUo6P5XkkiMZlGm6ltLsa4U9/THljV1TmbD+5tuWN1xJl0zyGbFu6wT3RusOB8pYNVJa2tCrtcMnIQ+PyWx9+oNuWk8pyAjqsUFjnqmg+hWWRqtM3z1lYmruuOn/Nj2bt4TJpomjsb23O//bvvxZen5x95rsO+JOFEB+89yE5ZBuYgB7Qf7q4OAhAAALHtQAC6OP68eHiIQABCEAAAhCAAAQgAAEIQOCzCnC43PciIkVRUlNTPR6P20fB2awQN95wczwiw2KNHrxNqUhrnJAdnZQXPqm86cn/4unjUIxDYIP7LHRVhswRk5YupqxR71fl7KkuapzzAV9PIve1yVHI1GzL5EA4bvDXn1+ksoLGoswdRVkrZ87YEFYoZrnbG0SmZfFKgD1RalhFk8e3l6cdKR56qDqt+YfXh/UY6Sb3b+g8Gx1WKKrJeg9VZs2zbtfL8zcWpa/90SyyFL4FlUezuXVaN43rb7hp8NDhvPpiUiA5OdVN3i/51rc+qx22gwAEIAABCByrAALoY5XDfhCAAAQgAAEIQAACEIAABCBwXAn0hc/87l74ihUr0saO9vA6fCI9c7jPLzwe32Uzru3uogvPeap4zAelI/fUZkar0jffe+s+shKjyiZZquPIIJjiRBtbqaZyQX5GU+aoxX95nkIquRPPfAqbyzcs01EMLoImoqUrKSf77ZKCPSWFO6aesmR/B9dEy5fKjdGOSQ4ZNu3YTbXV68ak7ihPi5WP2f3ds9spRqbGCbhOjk6KQtE4ccDMUbhJv/h5Z1X+5urs3d+efrDnEFd/KEqMm58pfPDI/vET6t30WQjhSeKbHTJkSFlxiRKLJ06ONwhAAAIQgMCXJoAA+kujxYEhAAEIQAACEIAABCAAAQhAYCAJfCKAdtckbGnZGAiKYIqs4uBvHr9/bNBfU1pw94xpe86aGJpUuuP8bzRqcV7NzzItw4oYdtwg2yQ6FKJ1jTSh7sPstNWFeWtvu+tAj8aBcq+ZiJvdu7fINogiBq1cRxVlS0cMaczN3lNWsWLFBlKIeg2dOLKWgbZtkkHhXpp+fktx3v6yXKt47P4Lv7HH6CS1m2upZQBNOhkK6XFetpDiDj37IlVXbhqff+CUyi0H2rm3um8A23rj7ReHjeDB58TLJ7zJwucXI0aM2NS8cSA9HFwLBCAAAQh8bQUQQH9tHy1uDAIQgAAEIAABCEAAAhCAAAQ+LtAfQLu/1HXdHYV+6unfB4LCI+uRk5NTk5JGCpEhxMlnTn2tMv/F805f0HnA3YPnpm1Ttci2iY700MoVVFX6QXXxxrKCDeddsGVXJwfKUaKYwwG0Q2TJSeuYwbvv76BJJ83NSdtakRsqy2949VXeUucJaVs34rapu+PShkqXXthcmLM5fWTX2OH78zI+Wruc+z5I4/Fo0+FdVHLiZCtEmkOr11Fp2Zqygt11BWsa5pIVJTVChkbhsHHBpdOTh8mBZ6/Pm+Tz+Dl9FgHhD4hnnnmGbMfUuO4DLwhAAAIQgMCXKoAA+kvlxcEhAAEIQAACEIAABCAAAQhAYCAK9LdwuBc3Z847wWQugZblyAEhfEIEhSgSouyZZ1Zx1QWRbiTaMqIadYaoeR3VFjdUZG/LS1tfP35uyzbqJYrJL5UorClEpNmODJ+ps5smT1qenba5KC1aMqrlgRu2kOrOPMvzy8Zo06KoRTffsTt99NqsUT3pw7rLirbOfoW6e8ixiBcKtMmyOdpW5YizRnRgH500flVFVmvRmI/+8NseLUJmjJQIPf3k7LS0An9qsvAnRp8DgSS35Dp1sPfpp5+U9dC8EuNAfDa4JghAAAIQ+HoJIID+ej1P3A0EIAABCEAAAhCAAAQgAAEIHJPAq6/OHjJkkMxrPT6/P5iSLPxyXUIhTjvj9N379vL4s20bBkWjdGgfTSxtrsw4VFd05OT6lo0bORSOc/ocUWU7h3sJBlFMo+4OOnPqgoqCnaUZ4bqC6CWn747tJqfXnXiWWbLJCxraRH/4E41Im5855nDumHBx7o6fPkwdPaQ75PD8c4xsx+EA2nKD8GicLp/RWTRyXUX66ntv6HLPqETsb02fyXPO/S+PELLk2pfkEUJcc82/In0+pj8Q7AQBCEAAAscogAD6GOGwGwQgAAEIQAACEIAABCAAAQh8nQQURWloaMjNzfX7/cOGDZOj0IkQ1+PjBPfqa7+/c/du26Y97TS1dtn4jCNVaR2V2UuffZLCceqOc/+GSqpGMZV6Veo2SO9VSVXo5n/tKk1rLR7TVTxmb3Xekp3NculAtjNtkv9MbuL401NUkL2pOFfPGHm4pnz3lVdu643wMoL8j5ce5GJpGUArKlEsSjMvbKnM2pE/fNOpE+d27KdDh+jPL7w8dHB6IGl4cqpM0mX07EnihQe9PuHxiqv+9Qr3kTmOZRjucPbX6RniXiAAAQhAYCAKIIAeiE8F1wQBCEAAAhCAAAQgAAEIQAAC/zABRVGi0SgRV1IcPnx45syZPp/P65Vjw4lSDiF4ephfZ5xxxdmn/ueU6ncn5G2syVx5yzVbQt1c96zKVNkkw+DlBiMGxRWDVJXuvGl7ddaW8tGh0tH7p47b9uxjFOvmuFm+HFvupRrU3kbZGfMLM/SSTMrLaLv0km09vbyJxe0cOk9XOzq3b5j8G1WnO35woLZgQ/nYPWVZq5YvodmvrM/ILpUXGEhOHsVrKcrQmXNnGUAHAknXXf992zZt23S40YNfkUjE/YDvEIAABCAAgS9PAAH0l2eLI0MAAhCAAAQgAAEIQAACEIDAQBdwVya0+17u5f7+978fPHiwmzj/3Xe/EGOEqCnNuvvyS191bIqqFNX6b9OxSNdlwKzG6c4fdI3LaS8adagm68iEksZbrtlCmkyfZemzu0+3RjsP0fi6zRmjOnPTqDC7c0LdvF7Ow+XL5uIPcsL8ZZscScfod48otdkt5WN2V2avvPm6baeefnNg8DCecBZJQqQKkcydG3JNxf6Lnz37JUWJWZZuWbz0Yv+r7zR4hwAEIAABCHxZAgigvyxZHBcCEIAABCAAAQhAAAIQgAAEBr6AG8X25c8cDMfjcSJavXr1ySef7Aa4Q4YM6U9yhRDBYFDmu9kjhtZ957vXbtu92yIy+9bz0x2KK9RzhH71487q9IaSkYcuPJVqivZcfE5D9wF39jkxgOy+7QvRjKt25RSGho/QCwuViSe0rV5HqkGKLvFsnnomK052nCehVXrtWbUi85lxuStKM+emJN0txBSPHHmWV+jh9FkEEgG0EEOGDBo9euSiRR/phmpzfu0oSqw/fcYihAP/7xNXCAEIQOBrIIAA+mvwEHELEIAABCAAAQhAAAIQgAAEIHCMAv0BtPuh/yhuOPv6668PGzYsJSXlYwG0T04ZDw0G0kaMyJML/Hmysyv+/PwbZt9csxqhl/9Ak3LXlQ1f898/oRPrKDdr1UdzSedk2yGKEJc580u16Ppb4+kFe3PKKbPYGZXz0fuLSevLstVIiPufZfMGF0BHaNsGmlD2cHHWg0KcLnwnpgyvFt7Bwiv8qQGZifuF8HNdiDex8GBdfU1j47r+m4rGwv2f8QECEIAABCDwjxFAAP2PccZZIAABCEAAAhCAAAQgAAEIQGAgCvxfAXT/tdq2feutt/7vAHqQRwyRfRf8a58v2ecd6v546mnTHnnkiacfbz2x9JXajLm/vZ9mnrejIHfeH/9IXZ2kxkh2PsfcbmfLoGef0nMyV2dmRDJz9PyKPbPfpS6VIiqf3LJ0mVbLoWmZQW9r6qnMvyhjxKVCnCDEcD734EQ19cixY4THz7PPwst11XL5wfsfuJvI1DSl7176AvK+n/EOAQhAAAIQ+AcIIID+ByDjFBCAAAQgAAEIQAACEIAABCAwcAU+SyVFe3v7DTfcMHy4jH05+vUG/MnBYDBJrlXoEz6Pxye8MvcVKUKMTRKT0oZccsWMx/Mzv3fpRf8ZDn3K7W9aReNy3qtM21yetrMys+nRh7g92rC481lTLVXRbcPRIuq65Q2//cVv6isnBMTgJDHcI8YKMVpOOstUPNkXGJIsfJ6kQKq8Lo6kr7z6ip17djqOJdcb5BrpTzk9fgUBCEAAAhD4hwgggP6HMOMkEIAABCAAAQhAAAIQgAAEIDBQBT5LAB2PxxVF2bFjx+233y6ECAQCQggPp86JGWQOfxMfvTIdThFiWNCfKcQIIYacc/alV15x/X/87vFf/PQ3j/3XE7Nffv29tzeeUParsrSniob8uWjoU5ecPnfOazT3vR3z5zcsXrSyqXHTX99676477ykpLBmUPCglwB0gSZ4krzfJ4+Mv4feJoF8EfCJJFm5wAJ4khDj7m+esbVyr6Dz1jAB6oP7F4bogAAEI/HMJIID+53reuFsIQAACEIAABCAAAQhAAAIQ+ITAJ9qfP/G/n/jRcZyurq4bbrjB5/PJCWTR/8H9kXNpEfR4Bguu6fDKmowhMpJObC8E58iBpKFCDE/x1yT7xqf664UokFF1qhtje5MCqYOHB5MHB4McPft83K3Rnz57kwLC97HgW4iho0b86/evWbOe6541Q9cMXdE1BNCfeHb4EQIQgAAEvhIBBNBfCTtOCgEIQAACEIAABCAAAQhAAAIDReCzBNCapvGagaqsZybSNG3btm2PPvpobm4uB8RJ/ysO7p+FTk0Z4XZDez2pXk9ySvIwd6lArzfg9/s9PLIsgikB9wP/4E2E2N6kgM8f7K+ZHjRkGA9Yy9nnxAS03DAjN3vGd7/9xtt/7Y1HNUOPKYpNFI5GNEM3LO7fQAXHQPkjw3VAAAIQ+CcWQAD9T/zwcesQgAAEIAABCEAAAhCAAAQg8LkF3nnnnenTp/v9fncU2uPhMNorx52TU7ipQwhvcnCwRwR93lS/b5DXkyxEcn+4LIRIHZLq9cu9knw83cw5tMcvZ595Z/6N8PmDPn8wKZCcm19wxlnT7nvg/vfmzNEM/eOXbxOZtt3/hQD64zj4DAEIQAACX5UAAuivSh7nhQAEIAABCEAAAhCAAAQgAIHjXsAwDCLSdf3QoUNPP/30jBkzEjPMQgweKueZvdydkRwcLGNlv9eTLAPoAAfQHn/KoMFu9CwjZv7R3T1l0LChw0ec8o3Tzz7n3LvvvX/W3fe88OJL738wd//BQ3w60zIsyyKnn89dZ9AmsshBAN3Pgg8QgAAEIDAQBBBAD4SngGuAAAQgAAEIQAACEIAABCAAgeNSoL+UwzITcbBhau+8+/odd1176unVwivceg2P8AuRFPCnJgcHB/ypn6iN9if7hfAOH5k2/cJLfvyTn89b8FHjhmbDcnp6I0RkWI5mmO5nIrL+FjuzmEWO3SfnBtAWOe4XJqD7YPAOAQhAAAJfpQAC6K9SH+eGAAQgAAEIQAACEIAABCAAgeNawDCMcDjMMbFhKXHNcRxNUyw7Lm8qbDgHG5sXL16ycO6HHz315LO/+fV//vihRx588KH777/33vtm/fzffnzXPTc/8oufLFi0UDccTdZp6KblBsqmfDNk3hyOxtwkOhpXo3E1rvIag5qhf3wImogQQB/Xf0u4eAhAAAJfVwEE0F/XJ4v7ggAEIAABCEAAAhCAAAQgAIGvRMDtwzCJdPll8kU4H/tKXFR/bUb/BPMXc7XumoqO878npb+YY+MoEIAABCAAgaMWQAB91GTYAQIQgAAEIAABCEAAAhCAAAQg8H8LuMny3/1/fwb9d//zxf4CAfQX64mjQQACEIDA5xRAAP05AbE7BCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIfLoAAuhPd8FvIQABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhA4HMKIID+nIDYHQIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABD5dAAH0p7vgtxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIPA5BRBAf05A7A4BCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAKfLoAA+tNd8FsIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhD4nAL/D4zzOYFuvvENAAAAAElFTkSuQmCC" width="216.63181102362202" height="121.8553937007874" preserveAspectRatio="none"/>
</g>
<g transform="translate(48.97590551181102 134.85539370078743)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="15.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="25.119999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="35.739999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="43.019999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCAFB20A65E8FBEFE071D9C4C8EE95E49" x="56.959999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="66.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="75.97999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="89.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="99.66" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(9.937952755905533 172.01539370078743)">
<g class="typst-group">
<g>
<g transform="translate(30.124094488188963 0)">
<image xlink:href="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAB4AAAAPACAIAAABb1/PuAAAgAElEQVR4Aeydd5zcxNmAKb7bXa000qivVtv3iguGQEINxkBMDyWUEEpopsRgeicQCAFD6AbSgFASQgmEUD5Cx5jeCb0HMIRu+3x3e1skzcdodrXaa5wxARu/+9NvVyuNRjPPzN4fj957ZwUCLyAABIAAEAACQAAIAAEgAASAABAAAkAACAABIBAi4BIS2lyXDLO1FAkX9wgZdgvVGLrVoF1WqEZIbcT6B10BX4EAEFi6CaywdDcPWgcEgAAQAAJAAAgAASAABIAAEAACQAAIAAEg8E0TCLviYe2zGzbOg/aHtc9eq08esUMgoEdEAyeAwDJKAAT0Mjpw0GwgAASAABAAAkAACAABIAAEgAAQAAJAAAj8rwiAgP5fkYV6gcDyRwAE9PI35tBjIAAEgAAQAAJAAAgAASAABIAAEAACQAAIjEpgCQT0CPk3IAJ6VOBwEgh8hwmAgP4ODy50DQgAASAABIAAEAACQAAIAAEgAASAABAAAl+FwEgCujWPRqjUSGk3wsdDxUduU7hQeH/kK+AMEAACSzcBENBL9/hA64AAEAACQAAIAAEgAASAABAAAkAACAABIPCNEwir33AOaBDQ3/hQwA2BwDJPAAT0Mj+E0AEgAASAABAAAkAACAABIAAEgAAQWFoJhCXe0tpGaBcQGI5AeO4ukYAervJRj7Xeubm84agXwUkgAASWYgIgoJfiwYGmAQEgAASAABAAAkAACAABIAAEgMBSTiCcXiC8X292WKUt5T2B5i3FBNjU+mYbGJ67IKC/WfZwNyDwXSMAAvq7NqLQHyAABIAAEAACQAAIAAEgAASAABD4nxEIpFz9DqU+hxDi1uiqa9UyeeWldxd8PhC6e1B+2J1QQdgFAiMT8BxSGaCpL26/7b4zz7jg1lvuZGUrZdelE/B/8gpP2a+YdiPUrnBtbD90MtgNnwnvBwVgBwgAgWWSAAjoZXLYoNFAAAgAASAABIAAEAACQAAIAAEg8G0QCDSaf3OPVCv1Vvzlilsz9moCl1x/vWmPP/50o21B+WF3GqXgEwiMRMCjJ8r95OMP+zffdEcs2aqcVnDynLMupk8+HPK/c9DhKfv1CWg3CKZurZP1n91z6P5IdOA4EAACywYBENDLxjhBK4EAEAACQAAIAAEgAASAABAAAkBgKSAQSDm/Lb4crAyQq6/6P0Mdj+JpLGYlZM34xaGNprqE1BpbcG2w0ygFn0BgJAIe6e+lwfXrr7s54q2VVuAlZCk4mc9OWNRTrpTrDnqkq1uPBxNv0E5rqca3cKFWWRw6E047M3Tfr6pR2nVI0z77GrrmErY1itTTPbMWsION1sAnEAACyzIBENDL8uhB24EAEAACQAAIAAEgAASAABAAAkDgGyUQmDL/rh6plMmH7/d2F9cW+ZwiFlScj7ThQn58o1EgoBsk4POrEfAfclw8+y9YTCPekpBlaDnE64jXX3n5rUU95XqtfrEvu0MwewftDH9duNCSC2iHqvKRBHSttX7WHnf4ZsFRIAAElkECIKCXwUGDJgMBIAAEgAAQAAJAAAgAASAABIDAt0MgkHL+7X3rd9zRsyLjDEXsUMSCrhQNraDKdqN1IKAbJODzqxHw59hWm++MeEtTMrbVKSFLU1KWmb//3kdpdo4Bv8SYVikMZu+gneFbFi7UKohDZ4ZGPYeP+BU3Sg+yzy1fW+sfvj1wFAgAgWWXAAjoZXfsoOVAAAgAASAABIAAEAACQAAIAAEg8A0TaMg0dluPLg3X3bGmoXZhVJSELBazWExPnLBGo1kgoBsk4POrEfAXtzT1DtvqVOW0hCxdzSJeF+LaQ3OfCqr0XBJswcEhO8HsHbQzpKB/IFyoVRCHzoR189D9lnpajHOQCZrttNY/fHvgKBAAAssuARDQy+7YQcuBABAAAkAACAABIAAEgAAQAAJA4BsmEKg3/74eufmmuxUph1GeCWgUt7mo8eMtd2w0CwR0gwR8fjUCHnnsked1NR9tl5OJDi6mGVpOiGvju77H6qMR0F7TPnujJa4IZu+gneFbFi7UKohDZ4ZK5/ARv+JGaRDQw3OGo0BgeSAAAnp5GGXoIxAAAkAACAABIAAEgAAQAAJAAAh8LQSoTPM8x/PqeQ+OOeoUOzHB1Mab2kQaBy1mBS5x0IFHNm4GArpBAj6/GgGP/PnSa1VMF7fEko14U8EpLFk/332/cH1B+POoApqM4JHDNTX3G+KYrgw4woUuCevmoft+ZY16QEA32cIeEFjeCICAXt5GHPoLBIAAEAACQAAIAAEgAASAABAAAl+ZAJVprltzag6rYsvNd1SkHB+1hVgGxdMSSmtK7s+X/a1xAxDQDRLwuTgEXH9+DZRqCxeUjjziRFMv8JwuiaaCk1iyEK9fc/WNVP4S0nxnXxfnLl9D2bB0HrU6pqFbizTUNFPcrefgGxAAAt8lAiCgv0ujCX0BAkAACAABIAAEgAAQAAJAAAgAgf8pAarMPM9hAvq9d/+bSnZpcsHSJyAuy3JAR9vVJx9/odEIENANEvC5mASCWOb11t0YS7YkmrqWNvSMJJpIUD/7dFGLemYieDFv8TUUBwH9NUCEKoDAd58ACOjv/hhDD4EAEAACQAAIAAEgAASAABAAAkDgayJQj+N0XZqW4NZb/6XgVGScJnApXelWxIKhdWRSkyrl4G4goAMUsLN4BKpVGtI8/7M+xOtMQAtxjUVAbzBlGkv9TGscswJevNuPsfSY7w4R0GMkCsWAwHeSAAjo7+SwQqeAABAAAkAACAABIAAEgAAQAAJA4H9BoEWjXTj7j5qS0ZUiiqc13BVrT0goPXXKVqEbg4AOwYDdMROoVj2WhePeux/EkqWrWSGucTFFRAbi9VNOnkVrCstftj/m+r+2guE2jFppyy+nXpIdG+7MqFXBSSAABJY5AiCgl7khgwYDASAABIAAEAACQAAIAAEgAASAwLdFoCnLKpXaVlv+RJEyipRTxIIidhhqV8qa+OuTz6tWGpl5aXLbUbZvqxdw32WDQH9v7ezfXoQlG0u2KCSwZOtqVlNSD819gkbZB/J32egNtBIIAIHllwAI6OV37KHnQAAIAAEgAASAABAAAkAACAABILCYBOoC2nWIUyPdnZOpgPbtsyJ2iHxGkwt33fEIrbO5IhwI6MVkDMU9EiSA/umOezEBzd5NvWAaOc8lAyW3LqABFxAAAkBgqScAAnqpHyJoIBAAAkAACAABIAAEgAAQAAJAAAgsLQSoTXZdt1p13n77PZ6TwwJaVzoVKec5xK2BgF5aBmyZbIdHnKo/i1xSyK0iSWl/syXJFiVz5sHH1DvVfMixTPYSGg0EgMDyQwAE9PIz1tBTIAAEgAAQAAJAAAgAASAABIAAEFhCAlRAex7Nz3vLzbdHIxIW0xjlMSpilFek3Jab/bTU59+iKQchAnoJmS+Pl3suFdDz3v0c8VZDQKclyda09C233l2pkoq/ROHyiAb6DASAwDJIAAT0Mjho0GQgAASAABAAAkAACAABIAAEgAAQ+PYIuK77hR888ZenSKKJxWwgoJPm+ItmX1Et0/wJ9c2jr5HTQH97fYA7L3UE2IOKlmbdcMMdPBXQWUnKIpxGmAroUtkrV1xSn1WuS+jWchl8AQJAAAgsZQRAQC9lAwLNAQJAAAgAASAABIAAEAACQAAIAIGlmwDNweGQvfbcV0SGhNKSkJWEvCRkNSX3zFOvlks0dhUE9NI9hkth64JI+WbbTj31AiSkwgJ6rbU3dHzfXKqUmXoGAd3kBXtAAAgsrQRAQC+tIwPtAgJAAAgAASAABIAAEAACQAAIAIGllUC5XF13nSmI1xsCOiuh9CoT16Lt9YjrgIBeWkdu6W1XSED7+VvcGtlii51p7LOUR40I6JNOOZPFPveVB3z1XHNJzTfSweUQDb30jjG0DAgstwRAQC+3Qw8dBwJAAAgAASAABIAAEAACQAAIAIGvSKC/r5KyC4g3RT4l8hkaAY3SMw44sl6dN0hAN/Il0FQJwfYVbw2XfXcJsLlRX8Gy1Eey2clYKiApz6MMknOCbN875zFCSMUjZa/iq2cmoGuhefX1C2jv66/yuzuGy2DPYHyXwUFb9poMAnrZGzNoMRAAAkAACAABIAAEgAAQAAJAAAh8iwQ8l9x/38NYsgwth+K2JOTz6TVj7Ym/X3/r169yPF9Hsvdwn4ceCZ9t7g/vDqv05ZDmSonNC76dPb87dOU9h1SrXrXqOY00JjSmvJ5K+9tp2v/8rs1RaApozyUvv/gOxjksFXghx8VTopyT1VzF9e2z61Ro4HNzWxIB7bpuuVyuVCp+vnLaXdetT5tyuezU6JKb39ArPNtH3x9jg8b6MwlVN/p9g7OhK77CbsuU9p9XBZX4pxzP+9qgL0XjG3QSdpY/AiCgl78xhx4DASAABIAAEAACQAAIAAEgAASAwBIQ8Fxy2aVXKzilq3mRTylih6VPRlz2hX+/8TUL6MB2BTus2cHXprscqT/DC+iRSn87x4d0h2Fk3rNSqfT29n47DfsG7hr0nd6rKaAJIdf+7RZJyoooG+ezXDwj4sJGP9qOCega8WrEcUjVIVWmoRvXNmpYgpZ7LqlUavUhaJjoJahvzJcGKMayM5Zaw/WMpbyfP4c+lRnjNsY6hys2MDDg1IZXzF+7gB50/29tfAe1A74uZwRAQC9nAw7dBQJAAAgAASAABIAAEAACQAAIAIElJnDIzGM0JaPirIrzGu7io9mJ3etVK/Xsz0ta/Rj9V1BstPsNL6CdGg0xXuIIaKY7h76P1qBhzgUdafj0Spl88vF8VnJZts9DybQOx5CO0y6zg4Tst+9hIkpzMZuLZ3ghJ4jZ0864qOaRGiFLJKDDN/X3609NPPLWm+8+8/TzV1z+13POvuCqK/92//0PDDNYX/uhIe0Zk/8dSzPCNYfKs+hjtkxo6HCDfPiq0fdbLl68Ly+//PLcuXOvvvrq2RdcdN21N73z9kc0s0rZpa2iryWIgB7S5m95fBcPDJT+zhIAAf2dHVroGBAAAkAACAABIAAEgAAQAAJAAAj8jwhsvdVOhpZTpIyhdWCUN9Txe+x2aLVCqlWnrnuW5MZDFNKXKLkR7xWKhw3XScgH73/6wfufjnjdWE8MK1hbHetYqgq1zXPJ+ef9bpVJa4hI6e6acNdd91Sr1bHUsfSVGRVOqMvNwWV9YKcIWWetjZGQikYSUS4tiNm4YN9+x8OBgHYWPwK6mUyj9e6vvfLu7PP/NG3jH6fsDixZlpm3raJp5ESkbbnFNo89+lSYbZCdI3xwifZbG9OkMfrxkW/ZbGG4hlB5Knjdepb2sd4uXJW/P4y/Dt2CPkcY9Dvw82w8MOfxA2ccseoqayFeR4Iq8ArPqZqSWnklfu+9DlhCAb2Ujm8rFvi23BIAAb3cDj10HAgAASAABIAAEAACQAAIAAEgAAS+CoFKmUycsAYT0HzMYosQzj7vimqFODXqtr7Kyw/+rZTpxaV+qlwfmPPoscectOvP9tlw6ubdnat1dkxef72Nt91mpwtn//HNN97zXFLqa/wLP7Njw9y1KaBZq6plcss/75uy3lZJs4vn9IsvuoQQ0t83MMylIx5qqrjevh6/lOc4FRZN3Uhc2ywzYjVDTrg1emivPfaPtAu6ZnGcmEpl1ltv/W8uAfGQJi3mgZGMMw1Z9ki1Uh2oVCnqSsXvKiFD0/xWqvUg8L5+kkh0SVI2Fk3GuZSIsonkBEKI4xLHY6k6XBoJTbeR7ttofmM0KmWXwSwPOJUyPbtwfvnoI08WhaTIpySUllAai1lFyqk4r+K8JKUxTnFx9epr/t6oi1Scsktcfxt846DMl+w02hMe2fJAveOVMrnv3odmnX7ODtvvssP2u/xooy122XnP8879/cMPPk2tbmPKj3ILmtycEKdKFvWU3Rp5/rlX33zjHUJI8CQjLKADE+3WaHdosRrp63fKFTJ/YekfN91xxpkXHHvsKRfMvuTW2+4O37TWUNh+wHIjdN8vUe+XR3p7B/r7Kuyn98Ccxzfa4CeGsoqCxmt4ooLGK2KXv3UYWoepF3Qt3d016dNPP3ddd1HvQtpZPw56aP3hZtD9Bs+lZXwHtw++AwFKAAQ0zAMgAASAABAAAkAACAABIAAEgAAQAAKLQeCzTxeZekHgEklzvCRkJSEbWTnxwP3POlWaguOrvTyXDJSol/z4o8+PP+6kzo5JKbsgIsPQM7qW1pSUgpOWmY9FRS6G06ni7rvtM++9j6nbauin4e7bFNCEkHKJXDz7L5KQ1ZVuQ+0ShYSupW/+57+I52cO8Vok2nC1sWPB/erlBwaoVC2XfaNZv2xwmZFrq59xqtQtnnP2hSLSVMWyk3lJUgVeNIzEa6++4dTG2LYvvc//tMBIIriuiRt23m+DRyplOiIvv/T2O29/9NknpVIfcT3SXyLlCunr95544lVNLSIhw8VsJGR4Pj1l6jbeVxDQjaGggtWfnMEDkhtvuL2YnywhW+RT/kMUOpMxyitiQcVFFRd5Ps3zNi/omWzXq6+/7fiDUHUrSySgG+0hXv1Bi1MjAyXqfm+/7Z59px9YyI+XRN0PDZYVnNA1W8FJTcnYVufPdzvg5ZfeZnKZTvsRXjS3DCE9CweuvPy6zo7JsSiOtAvbbrvDokV9bH3FQDo3dxw6/coV0ttXqznkhZfemHnwURK2EDIMM2cm8ggZ0RjO5rpP/c1Z7LZNAe0nzRjUlgAyIdSDn3XmBQpO8dFsrC2v48mqOFlBq/jbRFWcoMkdmpJTcFJVrH323p+5ctetjUlAN3guLeM7CAR8BQINAiCgGyTgEwgAASAABIAAEAACQAAIAAEgAASAwBgIPPvMK4g3BS5h6l1M2CXNiZ99UmbmawwVDFfEF2qzL/hdLtuhKlbKLmhKCkuWKCSEuMHFNCFuiMjgOTUWxYjXhbima+k//fGKpoMeptamgHZq5MXn36QZq+UOkc+JfMbQCpJorvn9Hy5JswdKlS8U2+GHH5nJ5A4//MgF83sqFXrkK7xef/U9Vaa2UURGpF1QZEOSZEXWyuXvQgoOJuirVefFF1495+wLpm6wiYKTmXS3EDd0NVvIrTJpwpoXXnQ5g+d65I9/vEbXOhSlQxLzWCpwMfvIo09zWqKdxxYB3RCUbEQCMXrMUb/KZyekkl18zBxJQCMhI0lZjFMrrND227PP/9oFdHnA6e+rEI/ceMNtU6dsJokm4vVoROJiChdTYlEcjUiI1zUlpcppPmYqOKUpmauuuJ72ZWQBTQVuhcw+/w9YspKJDpZLJGXnTj/9jGq16tRokpzBmy+gGaJZs843E3kuripqSpJsTcvqei7OG7JiYznJI3WPPffvK9E5Ga4kmPBe8CDHo/+j8NKLb6y7zkZYshBvWvqEdHI1DXfp8gQN+xHQaDxGnZKQpUHoQgIJqiIbTz35jC/KF09ALy3jG4CAHSDQSgAEdCsP+AYEgAAQAAJAAAgAASAABIAAEAACQGBUAjfd+C9RSBpaQeCSApdUxMLU9bd1/BUIR72ucZI5wcY3+umRRx95cqstt420xzmOxjiLSIu0iVxMEYUElmy2tY9DkmhaZj5ldyg4GWkTRaSddeYFQRD0kPjrpoB2HbL3njMklLb0CRruSpoT+ZgZiyg8J3/430+rVadUomGowRZu3Uj7NDDZI4cfdnTSygg8xljfY4/pIxUe5Xipz6uWyfbb7a7KtiSaPKfayXzSyqmKOWPGQYQQprlHqWHpP1Upu9dde+M2W+9YyI/X1CQXw7EoxpItColga2tT1lp72k3/pKke9t//qGjEiEWT0UhCRNloxPjTpdcFo+PvMAHdeqw5gKFEMA0HzdJuEEL22etAERnJRCEWURQp4wvowSk4NLkgSVnLmiCKVpxXpm44rX+APlooVUpfVwR0pezeddd96627YSwqSqIpxDX2+CGT7rbMPJYsnlMRr1OJrHdE2hRRSK6wAqfK6TvveCAQ0E3h608Cln/j9dfe0ZRUKtkViyiqbGPJRIK80047l8vl+fPnh8Ux3ffts+eQefM+236H3WOcohsZhAxdzyGUiPOGpmWjUSVhdbS1i4aZS2c6DphxaKXaTCQdaH02D3t7+ymoPmfO/Y9Mmvh9LFlYsnQ1G4toSXM8H7NS1kRFLChiAaOiJORFPoN4S4gbPCeLSDn7rHPL5XJPz4LFioAmfkw9a8C3Ob5L/08RWvgtEQAB/S2Bh9sCASAABIAAEAACQAAIAAEgAASAwLJJ4MwzLpCQjeK2wCW5aEKTC/vufVTdAn9pjxo2MLDGhJCnn3oBS2awIUFtb+OFuCbENcSbqpxW5bQQNwwtZ1udNHWGmtWUjCrbSFAj7cJ5517M8kFXGxmEG61oUd3FwiRT79LkDoyKGOWxmMWSrWvpRuEWeRn2mkEBmjCaWchyteYbziv+fC3PqRKyDD3Dcgh8+glLDB2+6Mv359z3FJZsv6e2iAxJ1HlOLhYm9CykLm+ZflUr5I3X5u36s310Lc3FlEy6W1MyCk5JiEbFKlJGV/NYTLethMeNkzHOrLACd/Y5f8jlVjWMLl89J5CQiseTH3zQ28ohmEnhw8HB5tAzJ8sKzf+stM3WP1Vlm4spzIpG22VRSGhKZnzX92addt5VV1x/7tl/iLbLNEBeSktSWhQtCZuWnQ1u49BM1G54hrD9oMCgHeaIPZdmG2dTtFIm77z930NmHmXoKZ6jqTbY/PEtrWKZRVFI8JyOJVvBNPzZMjp1NS8hG4tpQ8ttvtl27Bae59GIZvby45ppiu2ye/55vxORoeBUY0sqsrHvvvu7rssyxtR/fS5hmcd7e9wXn397rbU3liTbMAqGUZCVNMYZhJKSlNb1gmF0yEoaoYSZyGtaWpT0x5/4t+s0g6CbXfZI7yJq6m+5+a5Im6ipSUNPRSNIiGttKwupZJeKsz/fbcZpv77g2qtvO+bI02LtCSzWI6CxZEXa44cddkSjttG51kuxpQvZl29lfButhU8gMBoBENCj0YFzQAAIAAEgAASAABAAAkAACAABIAAEWgh45Bf7H8GCRkU+xccsFWdPP/WiMQnoIXrQc8lNN/6fZWYD+6wqlq75MZu83j4O0RhV36NxMQ1LdiyiRNowXf/QF3N+dgLbMvNPP/mS17BpjdbSjMFBqoJSf1WVqTHno3ZYQE+csAZtuf9qRILSkNCwXmxU2Pys+ukYnnn6Zd8VJiVk62qej5mRNvzaK+82y41tz62RHbbbk4+ZiDd986hKohmLinf86z4W0z0ksnts9S4dpf5+3f8xxSwKCVVOr7QCb+odhpbTlIyuZtlSllhM0zI4g3EmzhuW1e3n3yhgqSCitKIU0ulJlQr1vo1XeCY1jtHP8HG6z1beq1RqTo3K1t133T8WUTQlgyWLxdGLyNC19KWXXBXUUimTE44/VdOyTEBLki1hc9Xv/YDd3KWppBdPQAc1BztX/PlvqmIZeiqdKlpmVuCVZKLQPg5F22WeoyHPllnUlAzT0FzUkJBtGd10XUSUVqSMoWfee/cjVttQAV2tkENmHiWJNGVHY0tirJ991rme59WTlXuNaH+f2dw5T3d2ri5JNhfX/Yhvg+NMjjOjUS0SUU2zU9cLGKcQSrD4aC4uHzTzyMECOmBPaLqbZKLAcyrrnaGnUnZBwYnNN9tu7gNPEo/095KBfuJUyOqrTlWknL8CpI0luvbmr3/9mwaoLxfQbEHL8oBTrSxF49toP3wCgSYBENBNFrAHBIAAEAACQAAIAAEgAASAABAAAkDgSwh4ZN21N0FxW0JpLGYRb2LJvu3We+u5mAdf3FSG9EygqPydmkMef+IFLCexnJSwSTdZl2QdS6aCE5JoHnrwsdf+7ZZnnnr1madevfZvt5wx6/x0qhPxOuKpq5WQxTR0tF2e8sNNnCpxWrIltwjoTz5eyHM6F00IXEoSi5KYlyRqGKdtsg3L7VuqlMcioEvlKrPPfiaHmSlroq4UdaWoyQUm5T+Yt2Awgy/7fu+9T8bjyUhERSgZjSqSZEci8l57H+g6hCWAdmm47TL5uvRP10rI1uSCJhfaVsKRNprygnl2LFmSSAdRldOaQg/6ljOjKLmVV8YiSmOc09SiYXQZRsdWP96ZLr7XxBAMbuPpQR1P6wzzny0wR/lFUoijjzxJV7NJsyvaLutaWsGJGIc3/tGWL7/yFk06TMPb/fX7CPnz5dfqei4koK0tf7xdY56UFkdAU4UaZMkYKNU8l+ZsEZGGBNX3s3ksmZaZjbSJbLHNGQccfuMNtz/1xIt33D7nhONON7TcyitK/mMemgsbY9Yq+9bbaKISyoTUA6BZYg3akRrZcOrmCk4qUqa+4ZQkqXPmzK06TqXW8iMhhLz11kdrrDFFFC3DKIiixQsmQglJsmUlrWlZwyiYZqei5CTJ5gUzxil+MujEpptt3SKgQ+A/eP/z9dfbVFNSQlyLRUXTtP0VNfH0fX/BBnHBwmae9J///KCQgKYlL/nTZSwHdMiR10d36IfnkvIAW1zyWxnfoS2CI0BgeAIgoIfnAkeBABAAAkAACAABIAAEgAAQAAJAAAgMIkBVmkcso1vkM4pYUHGeJvBFxssvvTkoD2zjwpYYxrqk9qMvXY/09DjrrjstnZ6gqCkkaoGAVhXrxBNOLZcaQrlRh+eSee99POMXh1KxFVHo8nFCUkLWSivwX0SMXnzhZfR//+tCkvkwJwiC/vSTHlFIKFLO1Cb6Apo56PQuu06v+f5qUV/vWAQ0y7zhEvLA3CdZQg87MQmjfLTNFLiUnZjkDvZ7DRKtn2Fcm222o2VNQChpmp2RiGzbHelM97PPvRyY09ZLl5lvB804NpUcr2Ka7cQyugUugXjL1AvJRMfUKZsdfeQvL/nTlQ8/+PR119y8y857KzgVi2k8b0Wjmml2xsQh3HUAACAASURBVGI084amFhOJLkXNnHjSrFI57JoD3zmUBjvVmDSE0KwXHjn/vN/Rpfw43dAKCk5FI5KItI2nbf7pZwtrLlXPDiH+0no0bP7o406RtUxYQO+5937Mfi/q71lcAd3fT/OoDJRqjz36zOrfW9s0ciyfjIKTQlwzjUx7G88SgLCEGP29NTaN3RrZZ6+ZhkafbUhClovZWCrIcl6S7Atm/zHo+aAUHMQlmdQEFWdpkhm6pbFkI0H+8L8fVx2n1niYwQB9Mr80ZcPN40hX9LSZyMd5jRf0VLpTVux11tlo5sHHXHjR5VM22ELTsiwfNJaT0RgWJX3jaZsPL6BdssvO00UhYeoFP/uzmU7lBV484qijCSHlist+bn399FdXLpOurh+EBbSqmDfc8A//VGksAtpPOUL/YeG8c3//bYxvMAiwAwS+hAAI6C8BBKeBABAAAkAACAABIAAEgAAQAAJAAAgwAq7rfvD+pyouYtSp4qKK8wJHBfSinvIQRExwBe80wtTxSLVGag7dCCG77XpgOj1ZlDNxZHKCppqpFcZFJ05a7Ymnnuvtq7WGMzerdx1y4IzD/OBZG/EWFzUMrYB4c+KENQZKbkPssgjZpoAulwgXNXg+nTBXEYWiiPKCmBXE9H4HHMHydPSVKzXXDbaGjHYG2cZyhTa+XCZb/3h3SchKQt5/zwpcytIndOR/UC41mzrKnlMjvb0DhJB773sU4xTGGVHOiHKKF3RNt085lWYhYG2g3BpafZQKv6VTQ0SwRxe1cyrkuKNnKVIu2CJtSj4zWYgb0zb+8R23zxkouVSzErKop1wp0wXr/vmPO0TJjPNGLKZxnIlQUhRtWc5qWj4aVW6++a5m9POXd7Vpn9l8ePjBZ/1nFTSHMou2LhYmrLvOlA8//tTnTKWzQ0iVkL4BUvPIOutPa48pPEpqZgcvJmQtdfe9D7DbNlYg/PIc0JVKxfOaSWBuufl2TUkZWsHUxsfaE3T1TpxiC2n+4oBDhumTj/auux/iOFOSqH22rVVFlDWMLk3Lvv8BbbkfuE1TgtCp4tHfl+eSDz/o4aIJP9WMn+jcF9BbbrENm1EuIQM1r+bR3+OAQ3bedR9ZSwpY1xIZrFoC1rFqmcncKb8+g9VfrhDXIyeffKampXlBlxV7XBsyE9kzzjyHxlz7LxZ2TV3wADn9N+ezsGs6q+VkJIpWGhc9/Mij2M/f8Sjemkdp95fJ40++LMvZlD3JMLoibQqW7Fy2o37fcmm4RQibf09YMabsH3rgOcRbLEf2Nza+rAHwDgTGSAAE9BhBQTEgAASAABAAAkAACAABIAAEgAAQWN4JuK77+GPPUvUsdatSJxPQEyeswdYAbKUTqKL6TiAFHZfUXHL6GX9Kp1bDUiEu2BxvxJHeFkPJTP7pf7/IVGN/b6080Ax6dV237L+o7XLI2mtOVaQMFW0xS5FyopDU1extt97dSJfMBHQ1iIB2qsQyOnk+begTqYAWigJ10OnDjzqZFS1Va4F9rrk0uNPfBgvomi+kL73k75raydQzeze18QKX0uSOCrXKX/5yHdKzkBbdb/9DwwJaN1K6kXzrP2/3l/sbbaAt+fIav50SgwV0tUJKfeTsM/+kK52BfVakjG1121bnuWf/rjzgVfynFUxAD5Rodmb2uuLK63lB5wXTMAosH7T/norG8H/e+bBSbTxc+PKeur679NgF/b3uJhvvgBFNoEzjgiVbiGuZdMf782gaZd/v1+1z1f/6h0uuVvRsMj1BkOxo3NQTxfGTvl+u1AV4b2lRw0HTa8NbuF2VCs0yUS6XWRLqyy67nIthntNNvUuIZTTcZekTsGRPnLDGbbfeXW1mpAjXQVPWvPPuJxhneN4WUdY0JsWiyWjEWH319Vk5v/F0itYFtJ8G/YV/vyXyGSGWqc9PlJaQdewxvyz1l1n2mL6Bel9OPfN8WUtygqJbaSud061sOyeuusaaL776Bqu/4q/qyUrPffCpddbZSFZsHqkHH3pkuVoL7DMrXC6R++5+ggaY+6k/mIBuiwg7/XRX+qRhoMwUORPQZYcMVMme+8wUJFuW85ramUlN1pTMkUcey2pzHKrv6+PoBfM/4O2X8g/39rjTNtqedvYbHF/WSHgHAmMnAAJ67KygJBAAAkAACAABIAAEgAAQAAJAAAgspwSqVRq07HneX666jqpncQIT0Ig3t99uV5rloP4KDBHbqRHCtnrEKCE0gvid93q4eEbEHXE+zfHJqGCsGEGCYs59/ElWTaXq9fdVygNOWDq6frhj2Y8xvvLy6wyt0L6yKvJUQ0vIbh8nzTyILozmv1g8azMCmhCyysR1kZCScScS/U0qCjh72hmzaeSmx1rp1Uh9a8hfJqCbnvGLVMKlEllzzU2wVGDOy18/LZ00xzMbPv/TMeXgYP36zzsfYzkpyikW/iwqSSTrx554okObxCJbfbe47Ajo3kW1a/56K83Nwmd8Ae2nIcYpXc3eesvdLF51UU+pUnYr5boGZekpiEdKZW/nn+0djWFm5Jl9xjhVKE6oOqRUrjYvqE+2kT6aAro84J14wiw6RgLNR6EpOcSbyUThyiuucR36IIRFQFf98OcqIU8//2Zx/BqcmGyPG6pRUI1CMt199HGnsDvVXLend+FYBDTNTVz2Z4JHzj7rfAUnFJwUhUQsYmhyh8ClYhFj8023f/c/HxOPBAq+0R/222EC+rNAQCOpGIkl22PaCSedzry5P10HC+h/3fagrnQijobnM+0uIeuhuU8smN9bdTw61T1SIeRf9zyi2wVe1rVkNorwyhyPNXPa5lv9Z95/S9VaqVyt+P+n0D9QqVS93r76U4KPPlnY21djOj7IbV2fni7ZcIMfYzHLxp0JaDORnff+R+x3WP9b4N+97JG/Xn8zj60IZ0hSVkTZyDi6yugLz7/SgOCNLKCDIqRcIiccd4bIZ0Q+M7bxfbs4/geDx/f4Xy3u+DZaAJ9AYKwEQECPlRSUAwJAAAgAASAABIAAEAACQAAIAIHllsBAiUZpep436/RzwgJaFBKHzDyK/TN+azzoiAKaELLnXkdw8Uycz3LxTFSgAjqKtD//9ToWCdo/UGFmcCht160wAU0IWX21KSuvQAV0tM2kiYYle4Mp0xoCum69/XUP69Wsv+7mvoAuIqmIxE7BF9CzL76cRqo6VDEH9rlWD3+myST8iOemgK7WyB/+8DeMc3EuxdSzhGz/f/+zKqYxtq+/8t+hzR7miEf6e92zzr4YoQRWsqKcQUoKqUlZT7z0+ht+eoQquztT4cPUsFQcGhwBfdedcxFv8TGLiyTrAhqnFJy69+6HWeg6SzwStJ1Z2uBJw2mnn8fFVVG0wvmXp226ZS+dE2My+/4sbUTOuuT++x6myxvSVSI7NLmAxazAJfbecwZ9EOLSwGe3oZ4rhGrZqdO2MezO9rixYruMlWxcsFb/wdSBan0C1OhykMHWnBUNYRx0i+5UKnTJwfPOvVCIa0LcEIWEpuQELmnqXbGIMX3vQ33zPlSqe65b8dtFJ+9ddz3CcRb1s+1mW7sV59N6ovPRJ19w6g92vJo/RYMIaKdKrrr8H0lzosjnEJfFKE/zRyOrZ+EA09yLBijG9z/uTWYnICWlJnJmurAyxyey+cmr/4DFPn+2sGdRX2/QmRIz6f53xyWlshP8POvLY3qkWqEiWJMLulJkke/0+YGcvOPO+5mtrj/j8e1zhZAHH39OkG1Jy63cpnIxO51aTeCSh8w8znNJqZ/l8xlRQIfF95z7HxO4hCZ3qJguBBoeX9f/UQfjy54xTJ22nWF3t3OJFdtVOr7IXH3NKQO1rzK+AR/YAQJjIQACeiyUoAwQAAJAAAgAASAABIAAEAACQAAIAAEqoA879BhFLChilyJ2KFIumSicMevcBhom4oZ/DyTdTTfdK+MiH8/KyvgVVzbaowmE03tNP4jlQ2hUNewnzZbB4qA9h2YZ1pVOkc8JMboiIhXBovnhf2luXI+m82WpNYLQbLLrz/bleVtROpiApu9S9oq/3MhiYPsrVRZPWqMBqU64D4SQqlOPrK5WSXf3miJKIyEVbdO5qJFJTVJxlosmFLGgyR0P3P/0sE0fdJBluJ686rqKksNKluUa1q387nvtz9pDDalXo5ufmbq+0Fwj5e6g2ob9Glwy7NnwQdd1q9Vq4PUqlYrDsnSHCw2/zwQ0nRgDpcqC+b1frAZJo4zjdqw9YepdiLdSya6773xk+Ktbj/aX3GuuvVkULYQSDQGdlrB11DEnVGpjD38m4czL226zs4ppcgZDpVkvRD61/rqb9y6qVf2I3opHFvjBvcxt77TrvobduVIEG3Y31vOinOFR8t45T7CxH6qKW5vf8o1FuF922eW6RjOVSyjNlgRsWwknza7DDjmhpXTLF69aK1Vr9aTqF8y+zLImxLmUiPIJa7KsdKw/dYuefhpK7m+DBXS1TE447rdcJCkJeT6axiiP4nZ35+pBRnWPkFKF7DX94FR+MiclOEFDsinriUQq+8Qz/6azjuaGpvOf/R5pqHWNruLINvqoqbGxJ1L011Eh77z9CRc1dKXoPw0q6krRNDtPPvms4Hfk+D9ERvKRJ57Hqo2VNFayWMnLuNjWZqyz5qbVMs2uQzeXxbA3HiQ0U3DQmRZMVELItlvvQsdXyNLxpYuj1seX2faaSxb0lli0OCFkp133TyS7x7UriWS3ovnjKybunfNY6/g2/2K0DAt8AQJLRgAE9JLxg6uBABAAAkAACAABIAAEgAAQAAJAYLkh4Dpkxx12DQtoQ89cecXVDQCBbhq6U48xrFTJKqusJ4n5SJtlmqvG+axmjNfMjpdee5cJ40ZVw37WdSdb7uzaq2+nYbZiR30lQD/X7WuvvuVfWfOzPzeXgCMeOeaoU0TR1tTOsID+02XXsDv5EZpU5w0V0AsW9VAp7OeI+M1p55tmp2l2a2pRkTJYTGMxbVvUfKF42tTG//Wqfw7b9EEHqxVy/72Px+MJXS8gnPbXuytg1Z778JPM/S0aKC2hgGZ3HEkle55XrVbDZ13XdWoOO1KtVuvBrYPaPfgrHZHAls74xcGaQjNvSEIWxW2WC/gvV1LFP8bX2ef8TtOyXFwXRbuxWVf+5ZpGFuyxykEWJn/7/92lymmBSxpql52YlE5OVnH+L1fexJJQ11w6J2kYsktKDtl+5z2QklopgtvjmmIUODHJo+SJJ/+2kfx5jD1oFrvllts0zTB0GimPUREjuiSgoRUOnHEEXZtwxJcfi984O22T7WQ5j4RMLJrSjIlYLh73y1lMEw8roCsDZL/pR9F8FKgoxDIY5fmYtem07Wge8YZBn33x5aKcWimiSFpGNTJINpGs3+mvsuj49rnW+r8M9bb4P77APge1MdV76MHHG1qHoXYpYoEtyGlZE95/f0H4D0HFH737H3wyme727XNdQCtKQdc6br917kB/U0C7bm24FBz1tlQq9AHC7bfd0zK+9qTw+Db+GYL+f8NAlWz/032QkhnXrkQ4mlyFR0leTJx48hlDxnesc6wxRPAJBMZEAAT0mDBBISAABIAAEAACQAAIAAEgAASAABBYngkwzeS5ZJVJa4QFtCrbc+fS+FbfV4Z106D9uoC+7LJrNbVIEzHzBVUbLytdgpg+4cQzXEIW9lVG83KUflNAV8vkpefn0cS+VO3V7R6W7IcefMwPkPQ8Ug5WIGQD9+dLr1WUnKIUwgL6wt9dEQgnP1NtIwQz5OBorga/UF+/UyhMFkXbMLpoPbwlCglRSLSvLNNEB0JWkzv2+vnMMc6Tww45IRJRx42TeZTk+ISeKG6w0RbMLRJCFvb3fmUB7dE8EW44UDRoUmCZmWuu+q9BhQMrXS7X43AblzP+zVFgx9mCe1dffY2CE4g3JZT2g8ELmpI76ZdnNK798s+aQ7be+qdDBfQzz77ALm4Y4y+vihDS09Oz0UabSMgyND/ncnsCo/wGP/zxwvl0lrEI7xohPaWBZ158ZZOttpP0VHtcMVJFxcy1xzVRTe8/48hShVQW666Npr34wqu5bIemJlTZpurZn6LF3OoH7Hd4pUyCeORG8UGftIWeS1568S0/EXZOEvNxLiMrXVguPvjIc6UqTR7S2FiucI8u8eeSygDZcrOfaXIH/QcFsUOTO7ho4sjDaY7jRT00zvul195VjRzHJxJpmoIjjnQzmTvznPOZ9h6o+UmiQ5O/Ya2Hj4Cm4c9V76knXrStTlPvMtQuFRfTyclcJHnSSef2l4jr1X/4LAz5+n/cLms0rtyPfabhz1jJG0bX1Vff6lRJJRQBPbqA9rtT2nDqpi3jK2aD8WXZxh2P9PRXnnvhtU232FHScu1xI5HsVo1ChDOwkh1hfIO/B4MGBb4CgSUiAAJ6ifDBxUAACAABIAAEgAAQAAJAAAgAASCwPBColP3UFx7BkuW7rXoKDkk0X3/tbT/jLUtcO8g7069+SoS6h1pjjSmG0dU2LmHoE6NcWjPGm9b4Rf2E5X1loZcj82xRnx/M6y1kfuDnGWgK6Nv/7y7mTx1nwHdmzcruunOuYRRoPClNvlFEUh5J2XMvuLTWME7sv//rOQBCDi6o4uRTZsV5Q1FyHGcilES8uevP9hWFhKl3xCKGnw8ks/qqU4Pyo+9YZjEa1SSJhj/7Pi4966wLg/wbVAhSCfcVU3A8+cSzd999/zV/+/vvf3/J3LmPvPnGe/29tUU95fA2772P33j93WeefvHhh56841/3/eWq62adfs4Rhx+31x7777jDrieecOqc+4emzmgZAtbBUn953rwPOjsn8JwciyhYTGtKzjI6p228jb9gJBWLY3m9+tp7omRKko1QguctUbQxzoii9e8X6gvTLZYKvv66f+iabWi5pDk+FjHsxCSM8tdfcwd1uw7p8W1sT3/lnjkPJnMdMVFdOSbpdgEbaV40sGrv9LPprM1NA/tlfQhCbgkhW26xjSSpfFyiAlqkuZiLudW33mqX/l631Oewxzmj1efPyV+ffDbGOUXp4ONZXeviebvQucaiEj3XsM/En67+SpW+gC6XyFrf39iPRO4w1PG60hmLGBfNvsJzyGefl6o1cugRJ3C80R7TJC23UgTHkX7gIUf0V6offfb5gN+uQeHPze77Iz80AvqL3/5xx54iIUtTcoqU46O2qY3HYvaDD2gW6bCAnn3xZaqRi8bNaNxi6hnLxS8E9O9/X/8Ximqlnn/DzzozWgQ0IeT66/6hqUl/fGlObTsxAYvZYHwX9dA519tfuef+h+1sdxzpK8dkPdmlaHn2cwuPb7OPdEgafw5GGx44BwQWmwAI6MVGBhcAASAABIAAEAACQAAIAAEgAASAwHedQOCR6x11aqRcIp99Um6Ec3b6KQXSWLLKAzRg0w+DZVeF2dAjTs0pl8ueS6668lp/yb60iLIiysa5FJYKv/7NBTQi1aPJZ9nSauHrR9n/9KOaInYgLo9RJ40wFbNYsh95+AmWO8JxaOhq0I1qjZQGiGkWFSUniUVJ9AU0Tp988pk1h65H50s9uuTg0IUHWRs++PBTCdP0xBhnYjEDocRmm/yEELLR1K1EISlwSRUXaeoDMfvB+58PbbbnUqHMjpfKzt9vuE2SbF0vmGZ3PJ6g6Sbk1Pwemg+AFXL9JR9ZxttB74Mqd2pOqVTyXHLpJVftveeMjuIqukpTPbBFEVHcFrgkiqclgabKDW/+UOZHfy9kfnDoQb9+4dkPBt00yMDQ3zdACDnl5NMMPdW2ctwy85qSUnBSle1nnqXimCnIQZcP/VqtkXPP/b2mpeO8oWnZWMyg+VK0vJXsLJWDyPgxyUGayaFKfrrjPoqUYdm6kZCKx5NrrbWpH7FLb+76NV30h0tMOyNgHatWG4clPRXlZVmxDpp55NAWfumRStmtlOnonXvORVgy2abgpKbkVJwt5ic/9+yroSB+Vt8wQp82r0r6e4mm5LCY9ecV3REl8+d7Ui1eayyv588Wtihi/QEPISSbnYxxjiVWVpSOaMS45Zb7q36W6zkPPM4LZjI9QVZzCKc1s7DelE16+unanzU/RUfwexmxs6y9rJxHw58/+3QRz6lYsv10NFnaTj51yknn0YTO/mqehJBPP+s76KBjEUqMGyfLaqE9msAy/QHq5oTrb7iH/gD9rVL16g9d/OznjRQcNBN0uD1s7u21576SaPKcLgpJRcqoON8yvv4Fv/v9JQkrJ0gmVu32mCJrmWhcx0p6xsxjwxXCPhD4BgiAgP4GIMMtgAAQAAJAAAgAASAABIAAEAACQGDZItBqonzrVC2T1176WBIawpfmtE2nU8Vq1XMdujhYI2g43FNajy+gqQDb4Se7UQEtUPssoiwXszHOzV/oUvvcENB1RxuuY9h9j7z+yicsFjssoF9/7W3mp2gQZUhA99OlyMgqk9cyjI6wgJ6+78yaS6oOzZEb2GendRHCUpk2fr/9DzYT+ThvcByN0jXN4q033+s55OILL19xBYFFufpSPnvN1fUsw8M2nHVw3/0OQShpGF2SRGWrpuX3O+CIMHQqoN36kmtfKqAJIbvtumc61akpGT8pQUFCaZHPiHzGT5Cdl/iiT6lzyDtLYBJ+H1wGcXlLn3zDdfcM2x1CyCsvv5WyOywzjyULS5ampGJR8bTfnDV2+9xfIpUqse2OGKfoei4SkWMxQ5LSul5Ya+2NQ/cdk4B2KuSjD8oClzLULhGlRZSmQlbOn3baxYGAfu31ebvstreA9UhcFJXEim1xpCY5QTMT2d+cfnbojouxS7O31Mjjjz1rJ/OBgMaSFYsohpa74/Y5AyW3Nb6W2dzBDrpSoj74sIN/ZeodjccD9PmKJOvnnk+f1lRHFtDlMrGsbiSkFKUQiyaxVIjHkw888Gx/iSxa5O6y636ynPXVcwfHJxC25zz0FE1XUqIPkYLpN9pvMCSgywPOwgWlK6+4hkZ5hwS0nZjw5mufUHAufWp18013do///srjRE3LI5RU9Q4k5WWlQzO67rznyQqzz/TxDP0ZjkVAE0I++Xi+wCsKTgpxw1/j0VZxduj4ipIe47CoJFdsE0Q5xfGGniieevr5izGoUBQIfE0EQEB/TSChGiAABIAAEAACQAAIAAEgAASAABD47hAIZJTfJeb9PHLvnU+LfK4ufH0B/b3V1vJcUq2yEEV2VZgCPcJyYsx770MRGRKiobgiyosoK4n5nXc+gF25uALaqZC597+AUdHUVlHEej4QBafmf76ICWjPc4I+uISUaZQn2WXX6ZqW9++eF0Rq4tafsmnNJZWaU65WRhLQX1z4+pvviJIuK3YspvE8jYPed9/DWDKH9975JJnoCAvorbfa+ZOPF4YpUBfnkHK1ueBZwurgecs0u9vaNMPo0LT8fQ882TfQjGOtC2jX19CtJnpQzYSQjz/6NGllNDWp4CTidS6mCXGDpcJQcV4RC41M2WHR7OctoemJh26NtNooL/KZaJtu6l0777Tv0PvSFfxKtX2nz1RwSsEpUUhwMUWIa+uuM3WgVA8/H/aqoQcvmH2JpqVZjLkk0RUIMc5oWv7nP5/RKDxY1DaOD/6sDJA/Xnwdy0ccjyclKWua3en05CeeeL1G164jf/zT1R2dk8e1ISSbvKS1c2IkjpVESjVTF8z+I6uOPbEYXPUYvu+37yHpVCdz8ew9mSgwHT9C5o1h+vXc0/NUnBe4pJ9v3U/oLOUULfHvF14idDKHFbGf8buhjz/7vCTL2Xg8qWsdkpjHUgHj3Kuv/pcQcu99j7OgcpYBIy5YBx58XNkhfeXa/EW9/uOjZjD1iB0NCWj6fw9lssmPth4koNdYbcMgjP+4Y06lE0O0dD0Xjyc0LS+IaUUrrrPelnMefI5lv2H/gjB2AV2tOueff5Ghp2JRzCKgWcqXoeMrYROJWnsMR+KKauRUI3f+7MtYD/zA/RF7CSeAwNdOAAT0144UKgQCQAAIAAEgAASAABAAAkAACACBZZ1AIG/9jjQCT6+9+g7EZcMCesr6PyIeKfsxwg0JFu47NWXVatWpeRdf9EfLzIcEdB4JmXvueYKtPLi4AppGVv7jgUBAq1KnyFMHGhLQVEQHGyFkQc/Amb+9UBQtP/66LqBz+YmOS8rVWqlSHkVA7/+LmUjURMnk4rphdKw8Tnz88ZeYZauUyVZb7BQIaEXKiULinbep8qPCMWQXS34u5L5S+Z775iKUYBHQdnKiouQmTVqLUQsaPEYB7dQ8x9d4HcXxSJBFpCk4oalJuikpTcmoclqRaGKQ4ba0nzZh6DsrTI/znM5zuoSsbbb+aXhc+/v7fftceWDOwwpOYomGoGpKjhYWzTvveMCt1SVk+Kqh+339juOS+QvK3eNXN8wcSwCNcUqWs5KUVpTc8cef3rgqhLJxaKTPbX+8p78QXyEWS0hSNp2e3NW1luuSTz+pTp9+mKbRSPa2dlHAuqwlOUGJ8vLUH20x9+EnP1/QG6w5OVLloxy/5eY7JNEUkYElSxJNJqC33+5n4UvYA5LwkUF5h90q2XnHA1E8vfIKKltLkL5LOU232VV9pWpjnjBl3Ew1M2/eZzxvxWIJw+jS1E4ZFzW1+NFH5f5+sv32e0WjWio1IS7YkVhilVV/2NNH+sseC3/245XrArq1ba3fgv9zcOlSiu++8yFNCu9PAEXKSCiNxeyZs/6waAG54/aH1vr+xog3c5mJfuKalK7nVliBiwvWzEN+OeCnBOkbIKWqn3/Dj4Cu+Wlq6mtvekEOaGfocppTN/gREtT2cchf9NLW1XzankDH99Py9OmHaFo2zmtt7aIo6Yqa4gQtyqtTN9567kPPfja/UnHp/1vACwh8wwRAQH/DwOF2QAAIAAEgAASAABAAAkAACAABILD0E2gILtbShq85+8xLRT5XjzgWC4qU2WbrHUNZBdhVw/SuUna3/vEOniGmiQAAIABJREFUsSgW+ZSfGiIn8rnVv7cxi0it+TkvHI+wbZjrwx63cfrIw07jo2kNj8eoU5U6+Zi16bTtSn3NdLFBH1x/OTLHJY8/8e9AQIsoi3HGMApvvjWvUvWqVIS6vgerp2p2/F739g88/+KrcQFjOaFpaYQSplncffcDaB6AjxZRvV4hf770WixmLX2CJGR1pWhouVmnnUcjVQe8oQ3v7a8ceNDhtBk0yDcnIppo4qijT2HdCi/a1ujoaJ+e5zk1x3Xdxx57Yu+9pq+z9vr5XOf47lVW/96aa625/pT1f/SjjbbYdpudd9l57/32PeSQmceccPypxxz1q0MPPnbGAYfv8fMDtt/uZ1M32GSN1dcZ373q6t9be4Mp0zbbdNt119koZXf44aWygpMiMhSc+M2pZwTtqPov9nWPPaZLoikhy/ePVAVusP7mLDY8KD/KTqlMKR98yLEIGZJk+1taktI0UwRKYpy7+OIr/MuZfW5MxFFqJGT+p1VN7oi1J5LmRBoI7EdAn3rqheeff4WmFk2zOxrVVCOnW3ma+jmGREk//Ijj+vqbM2fU6ltPshZ5pNTnVCtkvXU39BOhpAw9w6LRsWS99OIbFIhLnJqfrKYRzx6uqFQq0TI0jw2Z9ZuLuUhKkzskIdsQ0F2KWNhs823YJX2lMv2ltCSN8dhv5803P4jHE5F2nedtnk/TBQx5qq2fffYtw+iItOvjxqmKUpCk7I033u1L5/pDmsajkkZsddj2B+xD9pm4xKl4V/75byiuKKKlymk/vbstcImH5/77sENOlJAdbVclZPGcqsq2JJq6kdG09OVXXFcu15M++8aZJt8IbS7NwuFv4cwzTVYeeX/eR7pm8ZwcjUiN1B/pY4/+zcUXX4VQQlbSXFzXjYyZyMuKHYlIomgdfviJff1jmjzNG8EeEPhaCYCA/lpxQmVAAAgAASAABIAAEAACQAAIAAEg8F0gEJa3zQDNX/3yPIyKYQG980/3cJvibngBXa1S9YMlUxQSIQGd2W3XA/v7abpll9TV86gCejDW9dbeSle6/cZ0YVQUuOQJx51e9VNtsKLhPjCb/MmnPRinWAS0iLKynNX13A033lap0hzQvoBuZiGo0qQZNGXD9H1/oWhJLCcNMycraUmy773vUf9MfZm1BZ9XsJg1tfEpaxXL6Db1QiE3sVrxzwY5NHzLxvInWHaeCWiaoVi0RdG6+56HS3Qxv/qSfcNzHAyg/t3zPNeleU6qbKU5P91HterU46/r6pNUym49WzdNmeKx5fKaVXrMkNJitBkOeeH5Vy679Mrdd9vr0EOOPO/cCwdKdbJMC7ILFy5YFI0gJqCZf4xFtH/eeE9/b7PihtkMH2nuV6rkzrvmmIm8bmQGCWhJSiMh9de/3uSXDiRo89qR9h564DkVF7lIUpM7RJRWlIKI0lOmbC3LeYxzptmNcUY1cjQpsKCZydxNN/+LPkjws3OMVOdYjl/9179n0t2WmVdlOxqRkolCpE088YTTAvvMwtVZwnSK0Z8bg2p+4fnXuGgiaaySS63hB3H7+Tf8COjp+x7I9HCpXK1bWn+xPj9yvy6gn3/hTYSSPG8jgc3zbCazKiFkr70OkaQ0x1mG0SXL+V12OWDBwtrn8wdCv5Fg12/RGAS0WyW/PPZkLGgiMiJtNBuGpuSSZlcxvxoW06ZeMPUC4vVYFCs4aeipHXfa7cGHnqz4sc8h4xy2z3ShzmAbRkD7rbr/vgc1NSnENZ7TM6lJupoXuMSWm/1UVtK8YJpmMWF16EYGy8k4ryWswk3/vPNrGd9BIwVfgcBiEQABvVi4oDAQAAJAAAgAASAABIAAEAACQAAILA8EmI2q+Uks6v31auSgGceHpBiNgN53+oHML/uFhhenjkdDj7m4ysV1JKSQkEF8DgmZyy+/sebL668goF98/h2am1gbr0p++HPUxmL64QefDo9NYNSCZrmErD9l04aAphkeFDVzwIxDa77YawhoKsT7SvW81rfc+i8sJ3hBFyUzEpFkxd5m250dl4ZwsheNuXbJDtvtGW3TdaVo6l0Ssmyr+M+bbq9WGhmcfdVYdbxKzXnk0SexnKgLaGqf7VVWWcf1aJbqUnlw2pBwd0bYp52jCa/dmuPUHfEnn/hLwA25oFyuViq1atUZLgsELe259WwqVMY3OjiomkBzV8ruHy+5MhrDfl8s9r7uutNo7u2W11CX2Txdc8iWW+2YznTICgt/tiUpLUlZRSnQZfRiiTvvfMgvvRgC+re//YMk5uNcKs6lJCkry3mOs5CQwkpWkOz2mKYnOkU5pRq5vaYf1F/2+geoe2ZzoNmyMe41wmrLA95mm27LxbQgF7ampCZ0r967qObHPlOewcbUanh+Ol79acdmm2+jyYVcao22FQ02t+vvOH/WORey5yi+vfVF7RAB/ehjz0lSWlOLIkrHosk4l1p11Q2efeY/DCbGuWjEQCj54IP/pklpFtJk0o2t8ck6PtKgBaVojhgy7UdbYsmK85ppFhU1E48n2troiottK4uaklJwUtdsJKimkblw9u9df/lEmjm65lRqjh/BTR/8NIwzM9FfLqDPOvMCBSdEZCDeTCXHG1pBQnYmNSkSkXlBj8Yws8+6kdlnn4NKA6SfBpc3f7AjDOxiTLARaoDDQGA0AiCgR6MD54AAEAACQAAIAAEgAASAABAAAkBguSTAPFONkKaD9hyyx+4H6UqnnxaA5gRQpMwhM48pDzjUadLsAeyqwcB6+2q/+/3lomhpWp4JaBHRnWefpakJaK7kRvKNkSOgB9d55qwLI20KitsqLmpyITJO09UsDX9uCMFwegGXkP4BKmerDjnu+JNp3DGiGR4UlYZJrrPuVOb1wm6NumC/qm223ZkXzBVX5HlBT6U7Rcm86eZ/sRXqqlUaxOo6NAvHtVffJqG0356sKCRU2d5l572JH1bMAl1pSb8Txx534srj4rKSRigpy1lRtI4/4VSms0O5feuFB3d7mO/hVtN9160NDNAEzbS/1SpL1szSO7iuWy6X3XqKEVrA87yK/2J5PIIwaqfmVCqVcMmenp6gkgXzewZKNbdG1llnI1G0WEcQtgXJuuTP15Yd0rJIHmtK8z00QoT85rRzNS2raflIRPXVM7XPTEBrajHSrj/22Iv+pYvhB/fc82ARZeNcqq3N0DWag8LfLFHOcHzCssebVteqq//wqqtv7BtwS1WKo7d/4KsJ6FI/DegtD3iPP/Z8pA2beoeEbMRbttWpKanfXfxnlgrcqTXtM42AdutzPhi8vlL1i8Uwjzv+JB6pEqKzWhEL6eRkjPIqLupKUcXZa669iU1Ux2tECg8R0Pfe96gkpS1rgiRlV1gBISGz5pqb/PrXs1P2pHg8qSgF0+zcaad95i+oVqrhBx408L/l9zuSgA7GwR/GdKZDwhYv6HHe8BM9ZzDOIN6MRiSBVyRRl0R9j5/v98br/ykPNB9osPa3Cmhqn6uOF4qMdpsR0MEjDf/u0/eZgSWT5doW4oYiZUy9A0t2nNckbCWswrg2tNr31v3r1Tf2l+hzHTq+fbWRxzfcpZbJ2ZyzsAcElpgACOglRggVAAEgAASAABAAAkAACAABIAAEgMB3jYDrq+cWAU0I2eRHP+Fjlr8IYSdGRSxmjzziRNb13t7epjDyU9kGCpgQsv8BRwiSFRcsQUzzKCOI2UgswSITWwQ0TWs7mgNi0dbvz/tMwSlFyihSzt+o85p12nm9iyrM+bImBUYtvHP7HfdgOYlxihdM2+4SJVPC5ksvvx6+xPFoKozeXvLoI6+axoRYLIFxJs4bmpb+yfa7LOr1k2X4F9BQYt9f9feSpNkVaVNiEUVCFuJ1xOt33D6HWmA/DtqtUedICFlt9bVlxdL1HEIJGjTKa088+WKQgDjcVNaksb97njPC1hyZcG3hwqHMBzU39GpcWa/ZdWs0dYRDUx4v+LyiKLl4PMmjlKIVEU6Larqn3/Xjiel9PEKcxha+L4uBJYQ8+fQLsZjGxWwsdSG+YFmTdt/tIJ63Wa4MWc7H48m332bR3IElHFRTy1dGb621pyEhE41bPEphJc+jpKzmonFTMzvaY1oy3X3uBZc6Ls39Qjf28IPQNCYtdbV+YWf95TSpSGVfWZA4S1py+KG/ZBMSi1kJ2ViyDT3j1uopTQi7S3BTf4f+xlzS01/xCF2L79AjjxsXERAyZDkbjRim3tW2kiIhO21PsMwiz6n/fv411ihf4PoOeoiAvuHG2xFKiiiNcS6XWyPOpSZN/KGiFGQ5u8IKvGF02HbXk0+90l8ilWp9Qja8czD1/JsEvEM/x6AE23nl1f+oZooXDSRbeqK44jhRT9A4aNMsGmbO0FMbTt3079fftHBB3+B8L/4tAwEdPH/64vlQxU/XUyo7gS/u6ellyj54kLPeuhuyNR5FZHAxLRahMdeakkpYhbZ20TAzvz1r9uDxpcq+PqJBL0L9pP9A4KfpKDv+syA2svR9OA71iuADCCwOARDQi0MLygIBIAAEgAAQAAJAAAgAASAABIDAckFgeAG9zlobo7gdFtCHHnws41Eulxuykn6yg8z1EEJ2/tl0QbIRTgtiWsQFHmX0RCcz1HUP1fCAowhoFkT5hSn61UmnKTjZcNAZntNTdkew1BsVVf4rME0sxJUldH7/g49pSg2kStjyk8bS3Bq//8Pl4QYzU9yzkGy91T4y7pbEoqYWdb3AxdW77p5bqTmlSqkZa80UFSH77DUz2i6LyNCUlIiMZKKw4/a700QHnw84VTLQT/pL7oMPP47lhG6ksJzUtKwomak05VB1WP6BlsDYxZ1oYaHcut8cmXCd4TJjEdCuW/GLua5DnCp56IHn/EUUs0jKY7nIicl1N9h8oEoqHo05ZfHwwwroUrlaqTnlCvn+D6ZwnOmnZOngovmJE6bsuMP0dHpyPJ70I+VT0Yjx5psf+m1uUA53oHW/HlbskkJhtTiX4vgkkrKKlk8ku2UtE0dme0ybMfP4d+Z9XvMG22eHThkq2VttbGAf63d65JFHDjjggNdeoyK4Wq36qbfpVC8PeBO6v0+fhdB/C8gpUkaV07844BC/WMtvgYnRmkdq/uFKlUaLf9GeX/7qNMWwsWoJkmmanTQDiZRBvCUKCUPLWWZe1+yPPpnP2tEQ0HUHHc4BfcONt/O8xQS0ZU3iYnYu9z2Mc7KcxTilqJmpUzcP7PMQJRv8XocRr+FfExvWR554VtaSvGgIkrniOLE9pih6luONhFVIWIVzz7modXxavg3KuhM46A8//pyVu/b6f8yadSbb7+8bCOyz55LOjsks/FlEBpZsUy/4fw2SK63M77f/oW++Na9aax3f0D9YhHvhV94yxK3jSx+0NOPCG7BaugFfgMCYCYCAHjMqKAgEgAAQAAJAAAgAASAABIAAEAACywsBJqArjThoal/cGuksfk/6f/bOO86JOv//2V2yaZMpmUwmmfSyhY6gUuxYsJ0VRZE79YeiZz3reXL23vUsd+rpecdZvup5KirqiWLDQhUFVEClCdK3JJn++fmZTzI7uywIKgr6zmMeu59Mpnzm+ZnsH8957+tDp5wC+vennYdd4yZeRPdoJhq+3+EUHWeFrOUECx5frHe/oXrl6KZmFT7bFZH4YN0e00TlkrZk8Uo6GK4IaC7Jc8momD1u1InFNhy2W1kqAprMKFgpbTWs8NmSrO+9zwiGjdC0yHISw0b9gfA+ww8kV0A6TFKMn3t2ChXIpJO7UAGcI+zxhI8e+dtvcxKwPFU7iqBJjaQio1dfeYvn4gmpwNBiMCCIkTTLRF+Z9LYqY3S6itqL+qXjr+JCsZpa77fWW4xmA5RwxpnnkVMrml6Uy6qOT06WTUDd5OoOzbzplnNn51aOoudOzeo2WM46BTRC6Mbr76GD6RDfFOKbPIFEvT920fhrTWtMZYTKpm4Na6UI2nleWTGKZe2UU89kGAknNliZ4Bzb8NJL7x/2mxNZNkNRCZIBzdCpxUsqRtJ5hG7btoCm6LjHF6PoJMWmaD7tZ+LhWL7voN2nvD1TM/FwtRSNLuXPHQLaFpIb3YHP/vf5MB/J5xtOPPFkuwMkTfvjOZ9R/khFQFsOWooWXnn5jXKp68yGlRvMKgzHN6SlNS+57Do6HGeEhCcYiqcaqWD00ENH19eFBD4dDFTupUK+Fzmpwz53L6DtCmiOzVNUZQ5Glk2F+FRtHWVNuYmfczjuse7uuI04OHtOBPRzk14L8lE6HPfSgiAVODHj9gk0l/j9WRd++RV+bLC+BUfBlIqyjctu2KfsYqLJBtfdcBvDhhmG++8zzxHCHV9tA9nlzzwXF/i0z8PzXLx3r0GvTX6HzCTZXlJto92l4Tyv3RnSqI5v/sQTT+z4aDM7dGwELSDw3QRAQH83I9gCCAABIAAEgAAQAAJAAAgAASAABH5lBGwBTRw09mSqgqRogWezTgF9ytizupfFFi9ib2QdDdxlbz8T58U8x+cEscntCe+2x4GaiatlLQ2NratdCk2ULj7ARhKwZUP56COPD4cSPBcnP3ku7qkPzp41T9dQqah2K6B1pJOJzkhp8zXX3RQRk2SyMpoWA5QgRBKzZs+zM0OwndTRfvuNFCO9aSrrqY/6/VIgEJv4wmQSGGJtiTNqK50ktg6hQQOHhnnJ7+N9Xo446MG77GPfOS0tas9egyIijt2IiGleiLNc9L33p5PaStu/28rL3nELG1VZvLnfzkM5t+tknR1vqtt0I6B/N+Yshs7w4WYh1qfGHanzRv7x6DOEYdk0S4aqWCWkRFY6z4sQuunmu3HWhBWE7fdLHJe96KLrEEL7738MRSX8fikiNESEBpbNLFu2vsu+m3pLUrZ1A/mpWCCYCHIZbzDOhDM+Wso09v/0ixWtRbS+Fd8COBukc/6GdZlWBfRG4pWc7umnn/X5gvjJR0jcZ+/9yQyV5VJl1se/P/ivVKLZKaCz6d4k/dnehhyHDC5hYiK0rqV81vl/4qNpPyu66oN0OB5LFEafMG7u3CXfpsp43BzlD9f3oIVwvH/fXcgRtkRA4xkXuSxFpehg2ueL0cEkg6e7xPnIJHmj8z3W+R05zUYcnD0n/f/XE//x0jwbSbr9HCukvcFYMJQaOerkDW0aEesk9YLEWZAbgxzb/qJVjumoUEYInXX2hQwb8QdCdDB02613FdsVRTaIhsbPNAzEMjgAmqYi4VAiHEq565iEVFi6eHWxZLS2VUaki3fu8ta+YPLVQwhVxzfEh4R99tm3Y3w33tS+BmgAga0hAAJ6a2jBtkAACAABIAAEgAAQAAJAAAgAASDwqyDQRUBjaWcLaJ5pspYGns2e8v/OwTqpY4KxbujIOio0DQyL+bCYD4Xz4UgDzWYyuf6KgQW0Ys3218nzVH0uEdA6nuYNn71cRFdfdTNDi2IkzQRjPBeXorkwL9104x1kLjisrKv5GziquFpKTBrW3G+48POtd95nuWiIT0TEdExqCFAiF4pfedUNpOukiPLvDz4Vi/bm2IaAP+1ycdFo8957H1KS8SRplgE0NBNnJduFmWTfB+5/2O/D6jkYEFhaYmlJ4NNXXn6zruIK6HvvfYQPpyORrBjNUsGIGE0P2nmIXYvapbe2GusG6DZYVRXNm/qN5ayJVCunApMtthnD9z4sxBVCfEM01jsS7UWxqZf+9w7JfVZMJBuksN16wGAiTe8oub3vvn8GAjGKklg2heelpGODBu3Z1oal/4ABe3s9Ih1MkhQOjstWM6A7XTNh1WlV9c3ipd/wQo5mMzSb8QYkmksFgtIpp52/vlUnwRfkp1NAk2uuzhJo1UhbASLlNlOXUakVvfjcZIFP4wFlorlMr3PPvsg5pR5C6MILLsUjzmZYJmdNopgaPGRfWcGJxus2tK5atQYXAsuVxymygmngCOyZ83bfa0RdPR2gIz08TICOcOHE8P0O13T00qS3vPUhlpbisTzlx/X+Bx14JPG2mxfQ9z8wgWEStoBm6AxDp+hgUhQb6nowZ551YZfI9Sq2jX7b38HqJ9UvUUeu9533/LWHJ8iFE54ATzExj1+s94oTHptI/oGgi3GuHqab36QiHnfMwPY5mSrQjEAzghTNvPvONOcOiozWrWmPilmOlWgqyrEJJhgT+PTvxpy+YV2nOuuNv034L5qBFxJ3o5uovaQqqtlWVJ6f+IoQjpMpE3PZxksv/rMm49L1YmvR1A1TN3AkPF6sPygbkXH2ENpAYFMEQEBvigysBwJAAAgAASAABIAAEAACQAAIAIFfLQHiWhyTEG5CQI86xooj2KhU2QlOM9GQ3fbn+EwonOWFAi8UOD4XiTUSk1NUsGB2CqNKBbRD9Jg6UmT07wlPh0MJjsUlxiyN43EFPtm3z6BSUZXLuiyreLIyx8t5TGdb1VEm24xrkMPpUCgT4lMBSujXf1eEUFu7Jsto2bL1iXhvhs6EuMZkol8s1jMQiD3z31eJgLY0FhbQlVNVcz++Ld5cs2YDHxItkxW1BHQiEs7V14Ue//dEhFD//nuIYoM/EPH5hESiISZlzz3voi7X7uynk+G2bjuwddvsKqDLRTRop71CoRzD5UN8Qw+3SLGpT79YgfVuNbeF1MmSn9Yg44uYMOEZhk75fQlJ6iWKDe56juWkmbPmyjJSVbTnXocGAnGSwsHQKZbNTJ7cSUESDoQSaZPu2nxWr9kQFrMcn2NCWW9A8lMxjs+MOfEMhHDUsr1gAV0tvK0cwdAtB22pRjvBWkWPPPAMT+f83hhLp1g64fPwr77yllzGd/yG9e3kvKePO4ehRaeAPuKIMeQje+47QsCwvimqhu6864F4qjEkJAN0JEBH/EEhJCRHHHzMN2tKqor+8chTwQAOOBYjaZqK8Fz85BN/TxQtsajVn/g+dGZA3//ABJZNUVSCxHMTAc0wCY5LCkIKJ5ir+EkCXjY/4afj20cuhDB3juk/Jjzm9tF0SPJTYiicrXOHmFD2P/99zbk9aX/nT1K5fNbZF8cknLTOsFEhkhjQf1drFkecYENeqoLaWhUpmhP4JE3hr5jfJ0TCmROOP7XLKZzfI7uNH6HoSNXwAwBslS3l/dDDj7EcPg55wODzMpNeeFXHE0MitayCgO4CFt5+bwIgoL83OtgRCAABIAAEgAAQAAJAAAgAASAABH6pBIi06RDQpoEVcDSS55iMswL6gP2OIP8dvxkQOkIjR53sp0SOz/BCIRTGypLmUp8tWvJt9Wi7jGWPgUheM7ZCXQQ0nhkOoYnPTQ6HUqKQTUiNCamR55ICn67vQb/0AhZe5ZK2wapxddpTWzx1abSX1HGnnSNGs14vX1fHMYxkhUFHHnr4MVlGsozGjj1HFBtCXMHnjUtSH47LDhs2AiGkqJUiShLoUTmXJaBJ8bWiaBec/0csoHH5c4KlU+5a3ucR6UBi/+FH8nyW57MeT4gP4xSOEC9NfQ/b1S7ds99uBumP/pGTW3ftrgJaVVA62YehUxSdDjKZHm6RixSWfdNWMbyWg3bKSnyZJvr3o0/RdIxj8yxTYJlcKJShgpH7/voguRxZRkcc8TuGxrHFVh1x5tvsiDvu+PvGF0sQkfWkt6Rt4EJjXYjmQ+Esx2f8FC7L5YXcHnsfjMOpNyWgrar5apVrtdDVOscfz7vR30MKUTlffZxn8nQg9ZuDT8DXglNdKv3SNXTsMWN4Ls6y2JiTCuiGhp3Ix5r17ES1kiFkq0j3hRenDB26XzRaoENSWEwH2aiUbIjG84OHDV/41crWkqko6PIrbhb4NM8lSd4xz8WvvupmIkyr6pncit0IaI5LbyygaTqWSDSs21DqqID+wQL6hZf/5wlwATpCc4lQOOv2hAWx6drr73Xe0hVG3/Vr3vwvDz/iOFHM+wMRhpG8Xp4LxR+4/xHy3w/FtgprHPOtooRUiAgplpZ4Lkn5Ixyb2GuPg8iW9nnsL5GzoRtYPRP7TIrQL7zwSo8nxDAJn0cgsz7+5pBRasmaCdXa01H+XL0xNlLz9kmhAQQ2QwAE9GbgwEdAAAgAASAABIAAEAACQAAIAAEg8OskQCI4vltADx28L1E/m9HQBkKnn3mB2xvi+FQonMUCOpzn+MwDD0/QEM5qaJfLloCuqNiKgLYEkGo5uyefeImlE976MBOM05QUjzXUuAIcK912692KjJW1JQRxNIRTnjrdk7Otm+iZZ18IUDwVjKTTfQUhxzBSREz3HzB08ZLVj/zzSY5LUpREB5MhrsDQKVFseOHFKdiVF/Wq/jM0A2dA45cloEn5LEJo5ow5OKPWss8snaJ8UpjL+TyiJDZ7PaIVxZtw13MhPtG33y4KzqzeIQW0qSOGSeC85kAyyGQEsSmR7fvR/K86JK81z57toIsldOWVN/n8fIAS/b4Ey+S8HtFdz5151vnkC1aSVUVFv/3tGaFQLhTKcVyW47J0MHnOOX/e+BtIoJH19ijoGq7tRQhFYgVeyIXC2UBQ8gaiHJ8SovmlK9bbfXOWP+tmZeLKjmEgndbQyMNPTkX7iVxTmG7g6EKEb/bVx6e+/Qk+h4lITDB+LCEbBx14uMAnHQI6w/PZv/51QmvVnCKEH2w8/fSrQ4cegHWnTwyFMmEx66r1c+EExYgjDjn6s4XLiLpVVXTa6ReIQpZjcdY5y0R5Lv7g/RMq/tTKkei4DysV0DquaDaRFcEhMUyCZTNW+TOO4GCYRCLRdNLJuAy8raj8WBXQb7/3YYAO+4N44kE/FaPZTDjStPfwo+ywii2MkXnuudeae+7sD0T8gUgPN8swUjRaOPIoLPpbW+RyqfIFx18Va3yTiQYxkuZYHADNBGPe+lA0kv/8U/w0y351/VpZde2V3BUDaRoutz/yyBMlqZnn8Z3GMZkI3+irj019Zw4+CCmBxz9J+AZEcNhoofE9CYCA/p7gYDcgAASAABAAAkBoYnsZAAAgAElEQVQACAABIAAEgAAQ+OUS6CqgDR3JJSQKeTaY4eiCNQ9hgWMyCalArFC17JEUMhNXVKkVlBXjscef5SMpVx3NcckQnwrxKS4U32Ov/bGYU+2UggpOLMgMVCpjSYQQ+tvfHstkBoRCuaA/zrNZSWzmmFQ81nDG6ecT+7xlo+CUlkhVzXSqgefiPJvG0yoyGZ7NhkMpa8FiK53sY0UupCJ84bhjT1VlXHpZLhmVnAZrmr5KILJDQxMZffLvzo0KPYP+pN8TZ6g0Q6XZYAYv2AmmOC7NccmImL7kT1dUZmnbhIPesuv6abbC9CzzaVTUnokGDtyLohIRocEbkDy+WCAovfHWDMXAt4MdCU5qfhctWjlq1NhkslkQUqKYx0qUTkWjhVHHndil96eddhHHpWk6blFKs2yK45JLl65pL9qHxHvccec9+UKzGJNefW2yqmPxSnpFGkePPDEUymANHcmIYj7EJ/hw8sorb8IpHNXD2M9Liu1lVTXtae5w2oOJHnn4sebGARyT8taHJbGZpVNCKM/RuQf/9hS+PEuD4txzq6EZ6JxzL85k+3BcmlRAY3VOx30+4YwzLpow4Znrrr/76KNPTiZ7hUL4UUSYy4RCGazvg1GWk4RY9qSxZ9pyXLNU50EHHcOH0zQdE8U8FYxyofh/npmEBXTXBT8IsSI4KgL6vr8+hDPNuTSOgaZzeGEyHINF7YP3TyC07eByG0KXUejytjLiG92lLUVFiKUpRqSYGBNKM6Esw+WZUPqll1/HR7DgqKr1i4SzW/XLJE9DsR4srVi+/vI/35hO9pHERo5JUb5oPNbAsYl8tve8uV/IZZNUjpOjVQS0iU44fmwwIGTTvUUhK4mNLC1FwpnrrrmN/AnC0Rl6dZitPy+yjP+YkKGXy9g+P/T3pxsbd+WYjNcdweMbzFDeRIRv/us9T3a5dnwdZK7RjT+ANUBgawiAgN4aWrAtEAACQAAIAAEgAASAABAAAkAACPwqCGypgJaiOTsJtxqjgR205Z+qrg6hRV8s8weFIBvFAtqKXeZCcYaNPD9xkq2NSDgAVmxVfbRiRXHcuAsDgXiIK/A8nvOwvi7s98ZoShq+z8G4+FTRtlCiVe0ZHjxZVhXZOPOM8yoCmsnzTAPP5LGM5pJ4JZekKVy5HI/2pHzSlNenK2W8Y8U+68jyz4YloHW7Atf2eh+892mdKxIVelLeRFVA54iAZtkMEdBiNDv1vRkGQoqG52zrdtmebjTcQaeAVlS0224HMXTK6xGDTCoSbWZC6ZPGni3rSDFQ2Xpy0NKiKwq6/fb7+XA6mWz2+QSGkfyBSCzWFIlkjx89duMLvP32+xlGCgRiREATVgcfMvLDaXPWt5SnvPnerbf/JZNrDIWjYjTBhvi77r5X1U1Vx3eBvVx3/V0Mk8BPO/iUxxOKxnJeH8ew0YkvTJZl/GwDW0UDP4TodPNY659/7uXdhu2DEx6YqLc+5K0PMcFY0B8T+Oxf7nhYKePHMBUH3XF3o3vvfbi2lu4ioDkuLUnN2DVbwp1EWpOnHaLYwLJYi/Ph5LU33LFxPvXgIfuybAIX5keyAUpkOentd2bg+IiuAhp1EdAT/v0kEdD4UYctoNmEz8vNmP4xDkmvRpaTxsZDsPEaG2yXBkJo9732DwnJICs5BfTOu+y+8Isv7eOYVto0eWu3VQXdfdeD2XTPZLxJEhtFoSHMYVEejeSZYGzaBx+bOp53tLIXSbkhwE106833+Lyc3ycIfNrvFRNSM+WPRITESy+/1l6SVVIGb90PZHcDl6sjRcHq+b//fXPY0EPFSE9cg++Oet1RhkoH/VjW33jdA7iwvdNchvgAIKArwwC/fhgBENA/jB/sDQSAABAAAkAACAABIAAEgAAQAAK/QAJdBbSuoXIRRcI5hko7K6AjQmrhgq+IyNuUgF63oRUhdMzxJ/MRol+t/3nnkgwbpejQy6/+z4pXNhW1IgcRQp8vWHbvvY9ks/0jQoMQLlBUKiI0SWKz3xuTxMZjR55EKii3BjyxZ3iPUlE2DTRj+scbCeisLaC99WFRyDPB+NlnXorVczXwF2u7zb8sj3nBH64Jc3jmOoZKOiugbQF98CEjiXkvyWoXr2e/3Zqr29bb4k45BXSpjM444484gsMvcXwuFu/FCzmOT113450Lv1q5ZPnaSa++c9FF12Qy/Xw+MRptFIQcTccDlBigRD6cPPiQketbym3FqmKsdv+tt6dTwQjOieaS1oKrxUN8Agd2+xgpkfP5uWSqkErnY/G0GE28M/VDG5fd+GjOAlHM01yq3ifQdAwXGrMJmha/NdE33nRXSwvO+rBfioxK7fr8eYtuuenuPXc/gGOjUTEdpHifl5OiOYYWI0KK55KX//lGnF/RqnUR0KSGff6ni1k2YQloHAPNcdlQKMOyKbdbIPaZ5/OS1JxM9gpzmWikwecTaTq26+C9p7z5Ac6tVjrlU8sySqd7W4Y6TQWjAUqkaXHxktXO5BCHie5UAf3iS5NpOkbTcZ7HJduVCmg2ERWzLRvKclm3k0NsAt/ZsMF2aSCE7rrngbCYprmEQ0Bn/YFwoaH3y5Neb2vVFNmKmtYReYSjq2jy/9678PwrGvL9XS4fTUWlaIFjUmEuIwp5KVoIBsR3357h7BL+21JVz6Tx2fzFPBcXhazfJ1gPijI8lwyHEjEpe8ONt65d3+b8lwpVw+Enn3769a23/n3vvQ4PcYWo2IuiUjjeXWxmqGSEL/Bs9tI/3qjLSJeR4bg3nN2ANhD4gQRAQP9AgLA7EAACQAAIAAEgAASAABAAAkAACPzyCNgCmkgnXPxLBDQdSFkCumC5rRTHStOnzd68gCam9a13p4WENI5bZfN44bKRCHZVbChy8SV/njHzk4ULl0+ZMu0/z7xy6qnn0XQsFmtKJnsFAnGfLxbiCnheNSZDU9IxR1dyG0w8O6GpqMUto1+5EFL9Sjq8x27746rnagU0CSvg2ATHJoL+mCjkk/GeK5a1tazXcM61lSWwhQJaLqE9hh1EFDYTjJM0j2o+A5aqT/zf87ju1bLVXbye/XbLruun2Qp3yimgVQ1NmPCMxxOWpF5+Kh5ksYKkmFiQlbhwIshGA3SUYRKRSD4QiFGUJIoNfj92qYlEw29/d4pqCf2WVjwnnv36Nit85aoN/kCYsSrlSbE8MdGCkOLDyYiY7OGmeCHOclGOF48aeZxzX5ubLKNRo8bW+wQmlPZ4QkRAh/gUH8bkaTp28CHHnj7u/MvG33DG6RfuNmzfgQOGRcWs18MGAwLlD0XFdERIiJEky0SCFM9zsScee4acqDLTncOHknJbw0THjx7LcSQGGqesRKONHk+Y57PJZC9RbOD5LMumaDrG0hKHbXjsyitvWruuXCzhgnGy2Ckc7UWTpmMkCtkfwDo+QAmkdrsS32w6S6E7Cei33v6QZROBQCwiNFTsM5Pi2MTAAcPaWhU7acTmtiUNG2yXxob28ter1vJiwk+JWEBz+SCd49i834+NfzrZq2fToDGjx13+5xsvH3/zmNGnD9/7sOaGnePRpkJuQDAg8lzSWx+i/BEykaAULaRTze9NnYVMHP2MszuseO6Kfcbf2+pioKOPPIFMQuhx82EuI0ULUjTHclKIT4R46bDDjxl32h8uHX/N6b+/cNiw/QcO3EsUm7wekaISAX8yKvaKCE2i2MTSqaA/xrPpJx59gRQ+46cL8AIC24YACOhtwxWOCgSAABAAAkAACAABIAAEgAAQAAI7MAGna8KXgSMLZJSM96QDKTaYwwudwlPtMdGXXnyVXGg1i1bXcSlzJQzawJGspqLiudJOOvksipIYOuPzxnm+wZpoLk1iFlgWT5VG0/GOJZikg8lYrGcgECfxBQmp8bhRJ5MMDes/7BWEyggpjv+23wxx+4pQsYidtVzWH7x/gijkI3wjRxf8nrhTQHvrwyyduOmGu3HlpomrOMmrI8GgkgxLDtvpvLqGK6a/WLRst2H7+LxcOJTguaTAZykqQaY07Nd/GNnB8s+VA3c6xHb3Bl+mU0AjhJYuXSfFG1OpPiybCgRiLJsKhTKWhE0QFcswCb8/6vUKfn+UpuO1tazHEzr/gvH2SDguv+OCx449CycjCxlByBBrHIlkWTbh9XE0LTJslA8nKTp84EGHd4yFfSDiKBF67rnXfD7BH4hQFA70oCiJZVM8mw5zmTCXIcHfPJu1Gjh3JRxKkEUIx6NiWgjH6GCICrDpdN6+vTsEqG1Crexp0vX5ny7O5/uF+JQ1wySOrqbpWDRaIIXMRKPz4aTHzVx5xY1LF6/GgTNGdTFRxSxba2bN/jRA4biSmNTAMBLLJoYOHW5Ywei2gO5oOCvyDfT5Z1+xtCSJjSTrw76lzzzjAruKv4N155ZzXLa8fdkV11HBaERosOY8zHGsLb4z1tm7/iTY7bx1nosLfDIipA495Kgli1d2pNxY3zjyoKijm9XxfeXlNzlW8taHBD7L0gnrGY9UrZrHtfPWhJApMi0kmdCS/BTChWi02fqnCqm+LhSPNfzn6Zftx0sdJ4IWEPixCYCA/rGJwvGAABAAAkAACAABIAAEgAAQAAJAYIcn4BRQ+GKw7NPR0MH704FEZUo9LKClb7XdPXc/YOhIxTN/mbaDdghobAfJ4b5e0dq3724RoYFlCn5fiqaydDBtLdg1b2qJxXqm0/0ZJnH1VTeTMmRFJd65jFAbQsWtEtBW3XTliuQSGtB3d47BU5DhoAyi1GmJpSUmGNtv+GG2d7bHs0N6blpA2xu3tpTGjTuTY6M8FwsGxFisJ8fhSN+7/vKgvY3VqHq1zmu3p3d4AJ0CmuR033DDnT6fUM24iFkxFEmWTViTB6ZDfMrr5b1egaKkRKInz2fvf+BR/Giiej/Y3th5pRNfmCwIqQAl4sn3uCQfxjEU0WghGstFxHRETAco4fjRJ69vKXeMhX2gKsiWFv2aa+/wenlinysOmk5VZpvkCjzTkVBBsr+JgPbUB4MUz9A8HxJHHn3crFkfOfvW0a46aHItZP2iL77efY8DSWYIy0n+QDgipllOommRCkaGDh3+p0uvXLJ4JYk2LrYrHRK5s4B+5r8vU8EIw0jWDIq4bvqII0eThPSuu1j5Fh2RMAZqa1V4LimJjXjWRGv6QauiX7ru2lvkcvUpSsdldGo5x2UL2+SrPWzY/iybEcKNIa7R78tUZijFU5VaGSD2T9wfvIS5XJjL0FSUpiJiJE0F2GuvuZFkg3QIaMPouC57GsDq+JaL6Ibr7vDWh2hKoimJ8kWZYJxhEpWFxkEoLIPLsUNcofIvF9Z/XXjqI+Q5EMelRx93ypzZn3dCAG+AwDYjAAJ6m6GFAwMBIAAEgAAQAAJAAAgAASAABIDAjkrAKaDwNZBSxBN/exZDJasCOtFFQFv72IXPHQ3NwIJQ05FhoqlTPxbFpojQkwkWsIDucNAbmehqNTTHpXv3HvL885Ox7bIcmmGQ2uc2hFosB20LyM3g7npFZNMH73+UDiSkSC/Km+gQ0AxWYy9MnPydRaPdns+wrretrY18+vrkKWPHnppNN1FUIpnoM2rU2GLX//SverVuD7ddrMT0nAKaDKgsoz33OtAfCOMoFWxacXCEXX/q9fKCkCEG+ZBDR300Z1GJzOW4CQFNAklKsnn6788XhFQPN03ToiCkaFoMUILPz3OhmBBJ3H0v1vclGc88aC8dkEzU1q4ZJr7ZTjr5rHS6r2WfE4FAnA4kyN3L0VYJPy7kz7DYSuOUZyygeSlI8WE+mkxkb7n5NnLP65qua3iqyY5TOOIgKneV9aFuoFIZPT/xf2eedeFBBx+98y57Hnb4MWefc9Edd943c9ZcVUeKirfTtcr8h11tMqlxNtDV19xKBaOVIOxQ3ONhz/3Dn+ynOOSMlX03EtAIoSG77h0J53g2zTH40oiAfuetD4mA7nohjqtyfkO2pE2m+1NUc+as+U1Ng/lQExMsMMFGLthsOWj8jwWOJecsiPa4+VoXJQrZ3Ybt8957H8jV8AtrYk9invXqJJ+d4ZuoXMJTjxoaOnXsuQmp2ecR8FMxIp3ZjEM9YyEe4hpxUTZecPIPRaV4viGZ6HfTTX/Fl05SPhwQoAkEthEBENDbCCwcFggAASAABIAAEAACQAAIAAEgAAR2aALEQVUugZjfy8bfgGM3cKUwLn9mmShDC3ZGgbVDh3euFkHjIyiabkviqVM/7ttnr2rtM/HODvtc9c7WXGqxmNRwzbV3KCoqlioS3OqQhpBq1T5vdQU0lk6WTDQNVGzTkIFOOO40OpCI8AXr0vBFsUz02qtvxcpPw3G032MUdU0nQR9kX90qGF69ujRnzleqhoolG4Z97M5+0169vTTw2FYHFPt1EqtSks3FS1bvf8Dh/kCYCkZYTmLYKMsRB41nDgxQwvB9D334H08oKn4CQV5Ouem8PkU1VR21tuGZCceMOVUQUlQwEhGTIV7yeOnGpn7jTj9r7rzPZcVQddTSWrLtc5egBjuXuVRG5/5hfNVBS3QgYS0phkqTpZOA5qUwL3FcZNy4M+fN+7Rcwt1QVdXqodmNM7eeGjivpa1day/qiopKcsdothVxpTN56SZqayvqmokDbVRdM6rJG1YFND6dhkM5xo49h2UTxEGznFRT67/hxtu3UEDrGvr9aeextESClYl95tjohvXtqqoX260nAE7ojrbzWrakTXaVFWPN2vaP5izab7+RIa7AMoXO9rlaBF0pf7acOIP/egwdvM8Df/uXXCZ0cCi4qpUc0tkpoKu3TrW3GKAVvXPWGRcnpGaakoRQPhTK4YUrWEvFPlsCGifOW1E/OPBn3LgL581bVizhJwH2U6LqgeE3ENhWBEBAbyuycFwgAASAABAAAkAACAABIAAEgAAQ+MUQwOWTJpr04hsCn6SpSDAgMLTIc/E+vQe2tZUVRVNVrJhtR2lfODFZupWWq5vYI2MfraDx42/g+awoNlhxDdmI0BCJ5EN8imUTETHNh5ODh+xz5VU3qBq2cpqOZ10j/55fLeF0KjL7bFvU6CIuV369Ybdh+wYDAsdKDC0ytHDMyBM6Bf5u0VE33qj7umbS74233v7X2INrIIc5NVBLq3zNtbdkss1SIscL8YiYjMYy0VhmzG/H/vvRp9qL2B468443HjmyBg8xObKBR/z9D2bd99eHzjv/4ltv/8trr7+1vqWNlEjj6lcdL3gcq6/KeNkQrfvNsNzmf56ZNGLEUYKQ8daHI3whwhfctTwuha4mcljT2cWHDN7zkj/+eemSFeUSlqGKYs2TiA/o7K/jyQEZXudP++ybbpimaVRfTgFN9iBzMw4atCfPZ2tq6JoaqqbW7w+Ennr62S792OQZDPTpJwsFLkH78f3MsVI8lr9s/DVyWde1qgjfxM5drvM73+LInWp4CJlR8+57H8zmeiel3mwwk4r3Y+kUzlgP53guSeb29LhxJPqBI4646cY7yP9VWL0yEdLJ4hTQncl37jTBbo3GxOcmH3jAUZFwzuMJC+GCEC7U1Qp0MM3QGWzD2TxOiaHDAwYOOe/8S75a8nVJtm5IE1njoJEzVs/V+SzwDgj8eARAQP94LOFIQAAIAAEgAASAABAAAkAACAABIPDLJaCr+B/+h+9zYJiPRgRcLkoHwxP+9bidLWsZq0qdrI2BaCynqCIftRf1hQuXT5jwzIknnTl4yL6FQv+BA/cYMeKIY0f99o4773v/g1mqhmMWVB2pln12Cuiqg7ZPsnWNLgIaIbRk8dcjjz4uEc/xXOy3Y8ZuWF8CAb0xU4eAxvrXOaaKitqKyoyZcx59/KlX//fGp59/sXrNBmyTLZVMRtDe3mk2yVmca3QTP2wgtcC4oZsazv4wNMNQNFXXdOJvq+a58rurgO4sFGUFvff+7OuvvfPoI3/bu+fg5oadRSHfu+fgEfsfPWb0uAfvnzBr5lySjGFfNbHb1ltn7zYS0PYOW9ZwCmgbiG4iWdVUq8y3vWjGYk0cl6bpeCiU8QfCHi/90cfziZ23u7L5s91+y90iH6epCE1FLr7wz6T8efO7dBHc9ok207Ay3yu3gaKRUnH8bf3vfyZddulN+w8/smfTIFHIFvJ9dt15z+H7HHjK2DMeefix5ctW6xrOvnC8tl5AV1NQcEiOgcpF9O7bs6697s4jjzyxZ6/BjY27RoSGnj2H7r//qNGjT//b/Y9MmzFL0fSSXOkkObVp6oZREdBVDe3oFDSBwI9KAAT0j4oTDgYEgAAQAAJAAAgAASAABIAAEAACv0QCimwoVhbFjOkfH3TQb8J8dPg+B77y8hvYJVWjma3rtitCKxSIwLJdG1mrVEUQabS1G23tRrFkkApQ4sLsetiqgnTUvTo0YOU0W/Ori4AutmmloqpraMb0j6a88Q4yESn33thpbs1JqoZso30IkI1W7wArNiOgLUfccQmagWTFsKMnukyg53SaZB/nGnKrkBFubeuIjNCRXpSLXYyhXTC78WDZnEuy3l5S7VsO312kuNlAcgkV2/Cp5LJZLmm6hmRZVRSNlFd3XM+P2rLVuf2l0E3U2lYmCdHvvTcnEIjxfF4Um3g+S9NiNJZpK5ZlVbGuiDzg2XSHdGRYX66137TMmP7xqm82KDL+4mzJyzkKW9KuCGgrhxr/c0MZh5bg4nG5QtjQkK52cc0dHSG5NNZ7+4+GM+rku77kZCfre9Ylq93KYLd6olT+5ULVseLXTdReKpUUWdV1rVqHbg/HD3ys1XFh0AIC3REAAd0dFVgHBIAAEAACQAAIAAEgAASAABAAAkCgCwETp6YSe0sm71JkQ7XmVXNky9ouqbIzMVm2a2tpxRkcxZJBMhmcabnOs9mlr6quE1uEhZEdvPBdbsp5qI3bTgGtyJVjkeAFXcNTnGFhZ+utjv27WdXxYTet7rcnQLrZfLtf1VVAV4ug7dGoFC/rJk6I1nDGsf0RroZ2bG/7TXLR9ls73IM8hCCf6kjXTE01yope2ioB3YVol6ho+1NDQ9bzlcrNTNZvamN7r+/dsI2n/aWoBNRY1eJ/+9tjLJuJRpuj0Wa3m/cHwoN2HoLDOvA3ryOGe1NnNzUMWlesCBLrBlRkYwuvxTkKW9J2CmiEUEtbe5deGXjknNHtqFwuF4tFXdOr4drkPOSbQn46z9zleBu9taYQxFdn7doRM7/Rhp1vJ5P8VSHV9PZwgIDuDhus+9EIgID+0VDCgYAAEAACQAAIAAEgAASAABAAAkAACGxMwKmUukg3+6NKRnA1UhZvZlVW2vZZM7BHs5eNz/LD19gH34SwI4Jsy8+ztdtv+ZF/ni2dAtQeOGeDDC6phnYGHNujScbUuYvzSrqsr9wqyNRMzV7skmfTtB5HkIcSuGK5+sygmu1AjuY8fvdta0d76O1tNnEP2J9//4ZtPJ3Xi+cqNJBhomOPHcsyOSHcyDI5ls24XL7RY06yTkausPtnI5XeOCFsTTEx2d3Zn61tbwkO68K7TC1IztOl3/bbLTlqxzbOPnesdbTIBuQm7FIB7dgKmkBgmxAAAb1NsMJBgQAQAAJAAAgAASAABIAAEAACQAAIEAJOMVSxipZo7rTecMxrRzS0JaBJ+C/5aVvCbSQHv+v4xItt+ahu7fZbfuSfZ8ufUkDb9lnf1gLaYmkP/U9AtlsB3dqmKCpqb0f9+u2J1TNTIALa6+NuvOk20sfqTH2bva9sebs9CuhO9hk/QqhM8OjstLO9daPh/HvS7Z5OAa13TGCJB6Tb7WElEPgRCYCA/hFhwqGAABAAAkAACAABIAAEgAAQAAJAAAh0JeAUQ5sU0M7aZ4eAdv6bv20JQUB3RfyTvN9CAe0c4o42SQq2fjrvB2fHneudAlpHur1sfQW0U2g6z9DJOWIHadXXO/uzrdvO3sgKUlU0ZcoMls04BXRETE99b5qVIGGlmKDNVkDbwePkop0n2IKLcW6+te3q4Z20nW18POfYkTYI6Co3+P3LJwAC+pc/xnCFQAAIAAEgAASAABAAAkAACAABIPAzEnDKrA4jaaXU2h8513eWj6btoEFA/4yDSByow0FXilftEbTjm7sZymqgypZHcHS+B7aRgLY1rVUN+7MKaDKyV111B0WlGDrH0LkQV2DZTCrd3FbEk/tZedq2fe5kzzvdFV2tb9Xxdtqo+zfOodzadvWIztPrVsm2DfknENDfkZFNLqrj74ldiw4V0NXxg9/bjgAI6G3HFo4MBIAAEAACQAAIAAEgAASAABAAAkBgywgQT7XRtg5HtGnpttFesOJnJGAP2Y/Vh+oBcYDDJo+5ifun8/ab0qqdt+runSzLiqIgZKqabBiGFdpAJr/rbuvNrXMq2o7tdBWpMurVvCvlTfg9STaYC3MFmpJOOH4s2cgRWNGx1/ba2hRn5/pt0fdtffxt0Wc45q+FAAjoX8tIw3UCASAABIAAEAACQAAIAAEgAASAwPZLYBMCsSof8e/tt/PQMwcBe8gc635Qs3rAn1NA65pueWf9pZdeOvvss998883ve0nkRie1zJ2O8dILUxKxXr76mLtGFMM9GSrtcfOP/vspshEI6E6wun8DArp7LrB2eyAAAnp7GAXoAxAAAkAACAABIAAEgAAQAAJAAAgAASAABDZDgOjFTWywiQcYm9h6q1fLsowQamtr69u3ryCIHMePHXvq558tLJdwPsbWvLoX0KaORh55EuWTgv6k35OMCr3pQGrngXvL5cpzlx1KQG8ND9gWCPw6CICA/nWMM1wlEAACQAAIAAEgAASAABAAAkAACAABILADE/g5BTTBpmt6nz79RDHm8wX5kNi/36BXXp5cLmn40+8u0Cfq2RbQneJEXnrhdcoXZag0Q2XDbCPPNPBM/tJLrkcI6Ro+NAjoHfjOha4DAYRAQMNdAASAABAAAkAACAABIAAEgAAQAAJAALdFu/kAACAASURBVAgAASDwHQRkWR1zwkleD+3zMol4LhHPRcXsYYceO2P6x8hEhobUaj20oVlKupOV7l5At7a2l0va/vsezrNZypsI+tI808QGc0F/cuXydkOzBbRZddDf0Un4GAgAge2QAAjo7XBQoEtAAAgAASAABIAAEAACQAAIAAEgAASAABDYXgiYRkUEz5j+UURI+Ty83ycwwVitixL4NMcmLjh/fKkd+2ZdtfpsYB9tGnipvkgFd0cFtGFouobroG+79W6eS0pic1ToyQZzHN2YTgy85KIb21rwQQwdbVEKdvU08BsIAIHtkAAI6O1wUKBLQAAIAAEgAASAABAAAkAACAABIAAEgAAQ2L4IVHzxLffTgRTlkxgqyVBJmpJoSvL7hMbGgbfffn970ZRlZJh40XSkdxRBdxHQ+INySXvo7/9kaJHyRaORJjqQov0Znmno33ufYiuSSxWFbQloHaHNhpBsX6igN0AACHQiAAK6Ew54AwSAABAAAkAACAABIAAEgAAQAAJAAAgAASDgJEDUM5mKEBno0j/eKkV6cXROCOU5JsPSifq6UI8eIYaRMtk+l1xy1aefLbEdNI6H7tDQzqOie+5+ICKkwqGU3yuywQwdSIW5QoRvfOShZxDCgR6khhoEdCdq8ObXTcA08dep+m8Bm/hqbX+IQEBvf2MCPQICQAAIAAEgAASAABAAAkAACAABIAAEgMB2SMDyXXIRXXnZnZQ3EQjEGToVjTbTwaQg5Hg+G+JTDCOJYn7EiKNuve2+D6d9UiojWUaKglQrnUMp46ua8M//nnDcaT0bdxGFvM8jhLmc3xOXIr2EUP78P1yODFz+jNM8OvQaKX/uSPTYDtlAl35tBFTrRR7PmKa5cuXK999/f+LEia87Xu++++7kyZPfeeedefPmEXFsGIau6Y8/9vh+++03ZMiQQYMGDR06dPTo0TfeeOOTTz751Vdflcv4S6JaXxhFwcHqsiyrqqprulF92QLa2die+YOA3p5HB/oGBIAAEAACQAAIAAEgAASAABAAAkAACACB7YaANdmgXETldvTw359m6JQQLgjhQjTaKAg5hklQwSjDSByXxEsoLgiZTKbfzjvvd+QRY0895Y/jxv5pv72P7dmwmxBqYKi03xvjmAwdSEhiM0MleTa7x7CD5BK+2EqWdOW6bfsMAnq7uROgI1UCkydPvuCCC0RRZBimrq7O5XLVOl6u6svr9bpcrlQqddhhh5177rlky2Aw6HK5ampqamtr6+rq3G63y+ViWXbEiBHXX3/9559/Xi6XSckzOZutvKsi2gABXR0H+A0EgAAQAAJAAAgAASAABIAAEAACQAAIAAEg8AsgUC1JNnU8Q+C06fP33OtQQcj5fEKAjlJMLMhKQVbyBwVPgGf4OB/J8HyWoVM+b7xHXSToT0qRXjyTpwOpoD/JM3nKm+CYjN8bE/jsTv13mz/vy3KxgqnYbhVL43ebTvH4BSCFS9ihCBgGfgqyYMGCu+++e+TIkUQvE5tcVc1df9fW1nZd5XLV1dXV1tZ6PJ6NP3KukSTp5JNPnj17drlctpNwbPtsGCCgd6i7BzoLBIAAEAACQAAIAAEgAASAABAAAkAACAABIPAdBCwBrcjWVlY5cqmMrr7mVobB3tmxROmQVOMORmIFjkuzbIahM3QwHeYKbDCTiPURQnnKJ0lic31dWAjlw1wmn+07a+Z8hLDXxj91pGtV2w0C+jtGBT7+6Qg8/PDDw4cPdzrizbfdbncwGKyvr994s/r6+pqaGpfL5Xa7nQqb1E+T7e31yWTy4osv/vzzz51BHCCgf7qBhzMBASAABIAAEAACQAAIAAEgAASAABAAAkAACPx0BEhFsonsRIxFX3x9xJGjI2I6kWjwB8I0LQqRBE2LVDAqhAsRoUkIN3JsnqVTLJ0K+uM8mxaFvMBn47EGJhgbfdz/m/vJAtNAqoqls9WwEqN/ukuCMwGBTgQMwyiVrDgYhHRN/+KLLy677LJsNutI18B1zaSQ2eVydauYXS6Xz+cjwRoul8vr9xGt7PZ2LXxmWdZ2zSSUo4uwJrXStT3qdt9rz3/96192X0lAB8mVtjOmiZi2t9keGpABvT2MAvQBCAABIAAEgAAQAAJAAAgAASAABIAAEAACOxQBS0CTeGbS74kv/G/vfUaEeClA8WI0LQgpPpxm6BTL5Dguy/P5CF/gmFTQH2Npyefhk4mGVLLx+utuVfFEa8Q767qGlx0KBHT2F0jAvgnb2tpOPPFEWyJ3EdD19fW9evU64ogjDjvssCuuuOLYY49NpVId7rjGVVNXW1NX66pxVRbrM7yypsZXjzV0bW0tkdfdJnV0HApraXw0r98XDAbj8fjYsWNXrlxpmibRzbJM/jFhOx0LENDb6cBAt4AAEAACQAAIAAEgAASAABAAAkAACAABILA9EbAnA6x0yn5vILRuQ7uBkG6i115/a/SYk8RomgvFfH4+EIgHAnGKkmg6HgnnvPUhr4flWCkuZcdfetWSxV8X2xU7cGPdunWW+LNLq7enq4e+/JoIyLL8bXHxFVdckUgk7Npkq965R21tD6Khm5ub+/Tpk0qlPB4PG6SJTcaiucvLEsd11gSD9icNuYahOw/ZffBuTYUml8vVw8qJrutm5+oenQ9LbPW3+R633XKroenlYqVYe7sdIhDQ2+3QQMeAABAAAkAACAABIAAEgAAQAAJAAAgAASCw/RBwCmfcq67vEVIdtctvTJl6zbW3nXHGRYcddsLAgXsMHLjbiP0PP+Lw4664/LqXJ71GSp4RQuWSVf+MUDU3wLBmHdx+rhp68mskcMcdd2SzWWJ/PR4PEb6kge1znau2zkUSnHGIcw+SrVHnctW6XIzLxblcgrUw5Ah1brfX79v3gP3Pv/CCCRMmvDrpZRxsruPlL7fdVeNy+b31wQB19RVX59INLpfb5fJYP63jkeppy1J7/b4AHXS5XH6/nxzZ7/E25gvHjxrlcdenE8nLxo9f+fUKPGB2grpj9HRNJ5EdjnU/URME9E8EGk4DBIAAEAACQAAIAAEgAASAABAAAkAACACBHZ/AxtoZX5NzrbNdmUGwGhu92QkFyX47PiG4gh2KAAmvIGZWVdWlS5eOGDGixvGqxm7gwmeSxezz11Urk7F/rnX5Xa6gy0W7XFmXq7/LtbvLtUdN7W+ae/2/W++eMPmdN9a0rC3KRcsKW2IY/7MAQpq1qOipJx655uo/zZo1i2Bra0FT3/7ymmv/luvT21VnCW2Pq54NuHr0cNXW1faod9XW1bk7UqTralw9XHipr8H+Oxrmfzf6+E/nzpNLZYSQJmvkPwxkWVUUTddM08BxN+ZP+28GIKB3qO8EdBYIAAEgAASAABAAAkAACAABIAAEgAAQAAI/J4FOetnuiHOts21vsAUNENBbAAk2+VEJkKgNVcWTXra1tT3+2OMsy1IU5fDPNU4BTbyz11frrq8o6Hq3PxgQvW7p2CMvP/3k55qzN8SFmxrz9+y8y53vfoDWFpGMTTOpSTZNUzc0BSk6UhCSrQV/qCL8vvK65/YF55358tR3FAUba/XBp/52zvhzkg2ZOo8Xz2oYoHD1teNVV+Oqq3F5e9T46+u8PTqiOk4+8cTFXyypHhX/NnS8gIB2MoE2EAACQAAIAAEgAASAABAAAkAACAABIAAEgMCOQcApnZ3tHaP30MtfMQFVVU3TbGlpGT58OEnVqK+v705A4+QNV42rzl2xv3vvvee555757HNPL/piiaajb5ahk49a0Ss6q39mTv/mF1+ejNqqVcYa0hVdVnRZ1WRD05FiYuFctrQzVt/4pSNUltH4882m+Hs7Nbx52R+/QvjzdZaexhusWrP28f976pRxp6WzeZzCQVF4YsLayuKuc/k8dT5PnbuHy12HS6FramqoAH3brXesXr22VKxMUWjbZ6iAJtjhJxAAAkAACAABIAAEgAAQAAJAAAgAASAABIDAjkHAKZ2d7R2j99DLXysBkryxYcOGwYMHk1kESb3zpgT0PvsOvf6GK6e8MZWEmBuGoaioVELrV6HRR3zYP74wRy3tm5z31AQMtGxF06jIKGnlklKS1bKiWwJa1ZFqYAdNUjgQ0ky0/Bv0xz9+3ZT8rCG6Ii1OfuN/+Aiq2YJ/mUjVK6HOmoGKZeXLxUsvuOjCnQfvjDM6sBb3uHAMiNeK4sBK2vnq27f/U0/9h1RA2wL6Jx5wiOD4iYHD6YAAEAACQAAIAAEgAASAABAAAkAACAABIAAEgAAQ+HkIkLn4Vq9ejUuMFWXOnDkMg2cLJD99Pl9NTQ0pgna7cbVzPp8/++yzH3rooZaW9VZqhm5P8WdFd+B1fz4HJf2zh+S0fokv9xv6plqq5G6ouLQZR1/IpiKbimoohqGZhoKMItLLODrdeq1Zj+64FTWmZif5xQXp4wkTkGKgkoIUFbWsxxvp1pYmwsXTsmHiEmpcRa19s2HZsy9OPOCAU1yuBmtJ1tQ59bM9g2Htsccet2rVGnI6XetujsJKX7bJLxDQ2wQrHBQIAAEgAASAABAAAkAACAABIAAEgAAQAAJAAAgAge2QAHHQCKF77703Go36/f76ehzq7PP5SO2wz+fjeX7MmDFPPPEESYgul/GcflYghokFtIEMDanWuj//oa0p/FVzSOsrtfROvvPEo3prG5Kt5GfdytbQ8bY6DuJAmmZqhqEYZtEw8c4mQrKC/vkw6p2bF6XnF6SPrrsSbWhDsoHa2tDT/7f8qceWtqxHul6hqBkVAU0SpNsNXTHRY/9q6Z2/VQqNd7lGuGqTLo/H5a6vFkLX9KjH4dEulyuZTM+ePednGQ4Q0D8LdjgpEAACQAAIAAEgAASAABAAAkAACAABIAAEgAAQAAI/NYE1ayqFwBdccIHL5fJ4PC6XKxgMEktbX1+/3377/fvf/zZNU8ETAVZexWLRyuuwaoctAY3lsYoevgv1T87uJxVz7Lo0O+Pq8caGVpyuUZSRqiHdxFXOloauOGgdy2QsozUroKNUQhOfQvnojF7JFY3JORdftELWcfnzsuXonHHrG6VJjcn/e+NVpFWjog0dx3HgOmiESiZaW0LvvI96Zl5tDM/tG1+4e78Pcumz2fBADxXBDtpV66qtq3N7cMN6+XyByy+78icOgEYIgYCu3kfwGwgAASAABIAAEAACQAAIAAEgAASAABAAAkAACACBXzQB0zRXrVo1ePBgr9drlzy7XK66urpx48YtXrzY0FG5pBXby4paluWSDcPy0RUBbeiouAFNfBL1kt5O+j4dkG7vmVhw6QWmqaP1RbyHoqmqju1zFwGtWV5asUqpdRPNmoEGNc4vCMtizLQ/XYjWtVr2eRk6/qhPeqfnN0ifSZFnZnyIa6ex7zaRqSHTQJqBNytqWEP36j0xK36VDxWbwiv756e+/DKa8XHbPgcc5Q3StT2wg/b6A15/oN7ttTX0qFHHK4pVoW1f2zZugIDexoDh8EAACAABIAAEgAAQAAJAAAgAASAABIAAEAACQAAI/HwEWltbSeIzQmjKlCmkHNjlctXU1JC5B3/3u98tWLCgWMTyWC5b5hir5rK1WPIXIdM0NVRWDQXL3yJ69J8oK77dGF1VENb0yXx+5CEfb2jB0cyW2TUNvG8lOMOwdLOKjDIO7SiVkdqmYjE9ZzZqSEwcWFjVL//1kYcv+OwLtK4dLVmKDh2+vE9qea/kip4N0//vWfRNKzJJlkd10kICcl0rOuLIFYnYkiiztk++rV/zh39/CH9SQkg20S133Ekus6amzmrgImifL+D1+j0eXzKZfuONN0tFWZarxdXbcnRAQG9LunBsIAAEgAAQAAJAAAgAASAABIAAEAACQAAIAAEgAAR+bgKlUknX9IULF6ZSKb/fT+Qsb72mTJkiy3KnDlZm6Ss6BTTZoKxihTzhH6ghOS0vrs2GWwY2rt5/zxlr1lQmHiRVz9Z0hdjtGgivVxHO5SgjvYRKJWvNvHlo135v9Up+3Du94MDhy79cjEun53yChg1+rTG2qJe0qm/jR7Nmo6/bsMlGhok0HR9FtY6IkCKjO29XG3NLGrMoFWtJxj48+w9frGtH6xTUbphlKzRaN9G4089wubBktyqgiWzv4e7hqaurj0vJN954s9NVb7M3IKC3GVo4MBAAAkAACAABIAAEgAAQAAJAAAgAASAABIAAEAACPzcBRVF0TZ82bZogCH6/nyRvuN3uRCKxcOFCXAasquSnFfRsWN65iFBbRUBX+m+aCPvjuTPQTtlP8qFvUvS63qlvBg+YNnMm3qJkljTUSgS09ROHLRMBrVkC2nLQWhmhmdPRgXvMzfFze0qfDxn01icfo5YWNOV1NKjPtGzkg4bIR4cMXzR/ATbXVg12GZky0lWk4fpq08ApHpOeR73zb/dMt2fEYp+eyy68SMPzGSLUrqKSgorlSsKGLKtXXXVNXV29u4cHO+haUg2N9XttbY8wH3nwAatqehsPEAjobQwYDg8EgAAQAAJAAAgAASAABIAAEAACQAAIAAEgAASAwM9KYOHChYIgMAxjTznYt2/f1atX65ouy7KuVeIyrD4SAU3yN+ysZGyT17WiuXPQbn0/7ScV+0ooyy1tzkx5/z20ro2UP2sIyZ0FNN6LJGcolSJoVJbRIft80hSZ1yQuHNJ3/oIFaN0G9Oi/0JABs9PstL7puSMPWtjeim3yqmKpRdmAkGLoRaSVkaEiaxLDpUvQzn1ezwjz0pGVfRpXHHroZ8tX4bwPXPusIt2ogNaxlEaqqj/x+JM0zdbW9qip60EKokkBuN9PuVyuv9x1z7YeGRDQ25owHB8IAAEgAASAABAAAkAACAABIAAEgAAQAAJAAAgAgZ+UgK7ppmmWcOIFmjNnDk3TOImivp5EP48ZM4Z8tGV9Msrloiyj5cvR4Qd/3Tu+NuFb1xxe3zvx4XPP4hpnKxtD0VFRR+WqgJYNVDIsG0wEdNFErSVULqJRv/lkYHp5v/iKhvikNyfjguUJE1AmPGVAdmkvadZvj/riy4W4U4qJFKRrSNaRbBiGriu6USRy+YB93mlOf5qLLouxs3cfMnOuVSttm/Jur2jRl1/RLIe9sxsT8FN0TU1dTU1dnQsvzz//vKqq5TJO+9gWLxDQ24IqHBMIAAEgAASAABAAAkAACAABIAAEgAAQAAJAAAgAgZ+NgGFUKoHXrVuXTCbdbjeJQPb7/SeccMK6des21zOzMvGgc5tVy9ERBy/Zqaklz7cV+FUNkfdvvVYryqhdV3Sk6KhsLYqBQzJwTkZ1MUkGtGqidevQqN/MaY5Ny9GfNYpz/nE/KrWjW24286mnGqMzC+FpF5zeXl6PZBlpWD3jRceV0CrpjYZQsYzOOv2rnukZ0eCC3tnVQwbNmD8Pf1w0sQe3Xt113frgvQ8+7D1gJ1L73MPrq+1Rj6M5auvddTiX45///GflANvgFwjobQAVDgkEgAAQAAJAAAgAASAABIAAEAACQAAIAAEgAASAwM9KwDRNRVH23HNPXPhrCWiXyzVmzBiEUNdZBzfdTyJ0VyxCh+7+du/k4my4JRFclhennnfmPLJT2Wg3kGJgB63oSCMV0OQjqwJa1nB+MyqX0Jljlw/If9YYmZeLTrrvLzhR49KLUIp/vxCdnYtOump82/q1yESoXcYTDhoI6cjUcQV0O0KahtCGInr6P6iQfLVvflU+tq4x/fHEF3Hos9HJluuWsO50PYaVL6KbaMXqNQN23dXl8dTUe1yuWhwEbf0iodiPP/Z4p91+vDcgoH88lnAkIAAEgAAQAAJAAAgAASAABIAAEAACQAAIAAEgAAS2GwLEPpOyX5/PN2LECLtrdom0vcbZsOcP1BFqa0Hjz20dmJuboL7KCytz4oeXXtC28hsc7ryhtF5DRQN7Z0PHC9bB1WJkZM0XqKoIyRo665RvmqQZfVLLm5KfXXMlal2HzjoVDWiY1ze3PBt57693ozXrEJ7EUClrSFb0ds0wiIDW8OrS2jY071O086BXJO7DRmlJNvLBY4+gNS24y4qz3zgL2s6zxrXX5DJVDZVVXCv9xZJiWNjF5Uq4XB6Xy1VXQ9jgn6IoLliwoNPBfqQ3IKB/JJBwGCAABIAAEAACQAAIAAEgAASAABAAAkAACAABIAAEfj4CiqLYpc2maV599dUul8vr9WLTWlc3bNiwNWvWbGHvDIRkZMgIrWtBN9+EpPDMtPh179Tqxtj7xxz+nqlj+2xY4c9Gh3B2HttESG2R8elKZfTMk6hRmtsn1dqU+fQP56DP5qEjDiz1Tq5tTnzdO//uA/fjaQxbVVS2bLJqBXoouOoZZ0ArOIgDb3DwQTPi4Q8zkUX9s7MfuAVrZ13HPbB9s/P0VltBSC4WWxFC7e042UOW0fTpqG/DVTWug1wu3u2uqal11dS6autctdXXvHnzTBPPXrh5Qb/RuTa3AgT05ujAZ0AACAABIAAEgAAQAAJAAAgAASAABIAAEAACQAAI7BAEyDR6uoaV7JNPPtlR3OtyDRw48Dtynx1XaJcwlwz0+L9RMvZhmPs66F3UvzD3N/tOXb7YKnjGArqENTWOzejyMhGegVDFElpBk55DfbJTU+yyXin5iEPRJ3PQYQfqfXNLe6dW9y/Mf+45XMjcjlCLgQW05aAVFZUVpCvIVBAqamhDGzph9NtN2Zm5+JcNyRnnjl2Ot0P4zF1qrh39MCybXZmbUC7hXOovF6IjRkxqijyV4f/icvWqqfVjQe/r4RTQHMfNnz9fsV6Oo/2gJgjoH4QPdgYCQAAIAAEgAASAABAAAkAACAABIAAEgAAQAAJAYDshoKo4dKK1tZVl2Tprej2Xy5VKpaZPn76FPTQRkk0slTe0o2eeRZn4q03JZTmxpRD77PijZ69egZCGNljZF1baMpkksEsVsm6gdhzNbKBXnkUNwsydUnJzfM3IQ9C0qejAfY2e6W96ZxcOHfTeB++jdUVUrMZoEAFdRoqCymVk4rcm+mYNGn9xMRN9f0DjhsbknONHvYtLrmXcDWTNPegM/XBco2FtgUrtulLCq5USuuy8tl2yH2d8s3uG3+idvcxb16e+B+t211Wrn/Fvl8vl9/sXLVpkWC/HAb9/EwT092cHewIBIAAEgAAQAAJAAAgAASAABIAAEAACQAAIAAEgsJ0QUFWVlO4OGDCgrq6uvr6+pqbG7XY/+OCDq1atwmkYJcvFbra7hlWGXDLR7DmoV+P/8tFP+mXX9Yx/uVPzW+usAA88IWDlhUucLRksd6ywWtj+GmjmNDSo6Z1ekbadkqh/ruWJh9EeA4u49jn92U7Nb334AZ67sF1HraZZRoZinddy0FoZKVhAm6hYQi88hxpT07PiksbE57879uvVa5CmI41UQFcjp+2S7WrHyG+8Gk+AiJAmo4lPor7SO7tm1vaPLm4KT3r9BXTHzS+6XN66HjVOAV1TU+P1epubm5cvX05qyTsf8/u8AwH9fajBPkAACAABIAAEgAAQAAJAAAgAASAABIAAEAACQAAIbG8EZFm+7777SCUvieC4//77t7CTRbmidQ2EZn6Ehg6a1z+/tk+iJReav3OvNz6ehVR947gN0wph7gjiUFS0oRXXMH86F+3c57Veyc+z/Oohzejxv6J+yRXN4WW9ox8fvMfbH32IO1VWcN6zYpC8aUPtcNBmm46nI5z2Fuqf+7Aps6J3w5Kdd3r5y4VYJes6rq02rfBpUv68CQFdue72FvTRu2hI45Rmfn7P8Oe58H+ffQLJ7ai9DQ0ffoC7rsZdV9fDIaHr6+tdLtehhx6KEFLxHIo/9AUC+ocShP2BABAAAkAACAABIAAEgAAQAAJAAAgAASAABIAAEPjZCZimOX/+fJZliXp2u92HH374FvaK5EeXdVUx0NKVaPDgGZHAwuao2iwu7ZN+e95MZGjYPps4fdkKv+h0XN1Ogi7KyNBR2xo0Yvf3+zUszEureqZLV1+EBhXamyMLU963j9x77qrFSCki3UCyqiiqVdFsIMU0NBMpJiKl0Gtb0MLP0aD8jJ7iyjA7N5V5bdZstHYtrmg2dbyvNQsiTuPYRARHR/82rELH7j+vmZ85pLC8T2LqY/9AxXb8qaKitvaWMM+462psAV1TU+NyuTwej8vluu++++xJHTsOt/UtENBbzwz2AAJAAAgAASAABIAAEAACQAAIAAEgAASAABAAAkBg+yMwePBgYp9ra2s5jmttbd2S2A1yHYqGq31LZXTAAV+J4dWNMTQgLffNvvXJTGx5iyVS/qxYmRvd1AXbIrhlHRp9wOf9pS+ashvE8OoDh6Oc2LJTtjgo+9nJR81b8QU+m1lJjTYNHattQ0eagRW3ZuVBlzW0YgkavuvHg9JKn4SazE295T48G2F7EW9h6kjD8xPq9gyEm6iAxlkh7WvR+ad83TMyZ2jjugHZdx/4C1qxApVVJGtIt2ZPnPTycx6Pu66ukgTd0NBAHLTL5fL5fGRCwh84ziCgfyBA2B0IAAEgAASAABAAAkAACAABIAAEgAAQAAJAAAgAgZ+fwJVXXllbW0vmHqRp+tlnn1UU5Tu6ZVgT+VkbKQi1aeiMs6clxXlxTu2bUjL8Oy8+g6MqdAOtb7Pzo0nuc8eB9epkgJqJNrShyy9ZPCizIM+1pOLthQYjn1ai7KJe6Tmnjl7Wvg7rY1VG5XL5mxVfI8MS0DqyJvzTdKRiAa2jchEdvPfc5sjyPKNkhOXjzl61SkEbSECIhsM3LAGNJfbmK6BNDf3tdrRTdnrfxIr+2YWXnr9as3jIJlJUrJ91vVwsrRsyZFdLQPeore0xoP/OOw3YJUgxdXV1bnddPB774SkcIKA77hVoAQEgAASAABAAAkAACAABIAAEgAAQAAJAAAgAASCwAxEwTSxSVVX96quvGIbxer2kAnqvvfYyjE1UcyM2eAAAIABJREFUBlcvzzRNk4RZINRWRus0dNplK7L9p2eFxU3cF/3Sbz7+CJKLOKpCM3G9sGHgqmMDzy9YnQTQOpSi4XpmxUCGia6/2hzUZ16UWZxJ6Ay3ko+uSsTWpBPTLx3/dVsZlTWkaFaah4pMayHlz6ZRNswiyfHQVHTln9Y2xz7rJarNsdLIg0vri6hVR2XdCqG2yqUVE8km7oduIB3JOmo3cO9wL5C1IUKorQ098zjK8JP6pJf0b1h81KGLFizEW6gIx32olfppzdCLn302n6Zpl8vl9bAeN3fJxVf7vFy92+vGWdCuyy//s67p69ev1TXdNM1isVjlt6W/QUBvKSnYDggAASAABIAAEAACQAAIAAEgAASAABAAAkDg/7N33vFyVOX/n5vktm0zs7O991uTkITeBSSEgKgIoigIYqFJCSpFpDcRQUEpAoICgl++CiTSAyEkIb333svN7dumP7/vc87u3r03CUX8WeDsa157Z8uc8p7Z+8d7n/0cRoAR+I8iQAW0rukTJkyg6pnjOIvFsn379g8fp2li9bFOo5RNjNe4+zeqq2VB+5Fa0rXyIP+0yc9DXxfaZ8UEHXTdRPu8j4BWAVTUwRh3AX9/CQ5uXZ0K7o2FZI83G0vk4+mOcGTRFZOyvaT0WCE1y7iE4GABbZh5w8B3qDLc9rM97dH34sKukG33qMzqpUsgJ0PRQM2s6hjWYegkKprYcCKgCzr0EwFtGJA1oJjLm7oCs6fDYW1v+xvnj0nvbs68u3INlkvrYCgornHqhqGRTg1Dh+uvu3kYZ+O4uvpa6dBxJzz9hxcqMDmOmzZtGgAYhmaWo0M+nO2QV5mAHgKEPWQEGAFGgBFgBBgBRoARYAQYAUaAEWAEGAFGgBFgBBiB/w4ChUJBUZRp06YNGzasrq6utrZ22LBhd999t2EYNDviQCkcGGRhkMwLAK0Af30eWlpWCoGdvuiO9tjUV5/DYmJNISsEmhoxz9Q/qwba4Eqyh2qAqgAUZPjjYxCX5ob4NelQb1Oi6JF2R0LdwdCC235p9OuQA6ya7ujdlS12GoaCHlklm0byNyCr6Vht/cJTEOZfT0ubDk2ZEdfCyVMwFSSnDwhojQyb3qMTx0gPWQeZZHFoBvTpYOTyMP1tOCj5xuFN21qDOzOR+ZNfJ4XPZE4GGJqpaWRSmqkZJI26pxO8riaOs9YO5zlu2OQpL5955pm1w+0cV1dTMzwcDtKroVDoL8pZYtE/weXBBPQngMXeyggwAowAI8AIMAKMACPACDACjAAjwAgwAowAI8AIMAL/OQToGoPjx4+vrcWV9DiOczgc2Wy2UCh8ZHiximXAGIixaC4k/TOj3p1e7+5UeuXzT0OuE7QiRmKg6jWVsoCWdSgYmNKs0nQPg5RQF3SYPxeagwvifFezT45JXUHn5rB3pc/93h+eAR1AA8ibeJ8tditan25kMfSZCGhdpSsQgiLD21OgKfh2e2Bns7cz7l7wq3uxLrtIjq1UQA8S0FgSTQujdRoGjVrbgPWr4PCRb2TcS0ZHd7ZGl959B46hCFDAkeiqoShqUTVKk0ILL+P5fPR3z9Zw9bTw+YjDj8n2gUc8iON4juPq62vvvfdeWS4A6IZZZAL6P+f6ZyNhBBgBRoARYAQYAUaAEWAEGAFGgBFgBBgBRoARYAQYgf+/BJ544olKXoTdbn/44YeLxSJZ1s/AlGcSEn2gEezthHUr4bhDN4ScmxPejtbU6gvP31qguc86tc+aZipYMmwYWHFMNs0wVKNY0PM5TSvqsGQxjEx/kHTvjvNGwgZJId8e2dGSmPrHZ2BvDrVvj4IKGG8GmLiKoAKGbup0HzQNTffSBXBw85z2wM60qzfuWnLOWXOLKh5RAIx7VqgKryp/xvFAQcfyaFU3IZvDDGjDhJ3b4ITD57QEVreHu5LeRRectyxbwPCNIvHgmqmhfdZk1VA0tOeYQVK5ef2omzmuppYLux1HZULnNnCHcJzF6rDWNtTv3LMTczggS1qqHPTRO6wC+qMZsXcwAowAI8AIMAKMACPACDACjAAjwAgwAowAI8AIfFoCJl1i7dM2w45nBIYQCAQCHMfZbLa6urpoNFosFmVZrhbQB9LQcgGyffCFo5bEfeszwT2pwLJbboDuDpBJ7jPJqVCIfR4qoHUwC3q+t6AZAFu3Qnt62phMvtkPo0MQqsuO9He0R997/RXoypZKj3MavhM1sIYxzDTImQpozH0uwO7N8KUTlh2a6YoKe9pju489fOGO3ZA3oF81CwZmTB9AQOd0XJ5QxfpncuveCxO/OD3jXd7s7R4Z33XGhE179mK3uFAjgKrrslrUNZ2ob7TPCuiKiea6kEfbfe0Nk4bXDee4umFcUKw7+qDENY5hp9bWeq0OKzes5ubbbizoHQD9TEBT2uyeEWAEGAFGgBFgBBgBRoARYAQYAUaAEWAEGAFG4D+JABPQ/0ln4zMzlmeeeYbjuLq6OloE/cILLxiGoSjKvtK5LGnLU9ehsBceuFNpTy4cmdp+yOiNd94G+SzWI5OV/Wjis16tockqgLKGKw6qOV0xAHbtgQlfXBT3L28KFGKCFrZlR4W6xqU+eGsKFBW0zQqACooGsknts1Zx0KZpYEcAkOuD887Y0ubbPDqmtcY6WjNvTH0H9vbB3n7U1pjgMajwmcRS4zMGKX/ux/EQwdzZAWefsTDpmd/izcecu48Ys2TWLOjNl+xzriDLqqJrOvaLeSCmArqMMdembuJaiyZAQQWLLchxVo4bbuHihzXfctToOzhO4DhueG2tTbB09GwAjLOmiymWSX7UX1YB/VGE2OuMACPACDACjAAjwAgwAowAI8AIMAKMACPACDACn54AFdD73n/6llkLn2MCEydOtFgsNTU1HMeJolghURHQJBzZMDA7gt5MVK0qQB4mPw0Z14tp3wdhzztXXNmVL+AbVI2mKmNANFYKk/X6sA4aijqqZ1mDggJQNGHrdrTPozKbYq49o6IQsvaG7KuPGr1w8Wxsp78I/bKRV2UFS5mVUvmzWqoepvZZ0aG3D67/8YZxqU2tvkJU3DW6ecVLr0C/jIq3p5A1gchivSKdyU4lGwRXKCyg5tYxfOPWG/syoQWtoa6kc++hzdtefAGyJNzZAOjpyxcLiq4rpjlIQBdw/UUDk63J3B9/YoPDfswwLsRxXAMnjG26vHMbHHnEaSPqh2Ewxwju5tt/TCI4mIAuXUzsDyPACDACjAAjwAgwAowAI8AIMAKMACPACDACjMC/iwBdFK0s/cqjWLFsy2kTvumwBTKpMb954DGjlIxLX97/IeVD2V9GYIAA9cuvvfYaLXymyw9eddVVskyca/mNpILY0NHQKvQ5QytqOSjuhL8+AocG32vmpx+Smf3jKzqKKkpper3qYFL7THbovkoXHpTJJdtThO5+uOzizqh7SVTsDdqKKUnNeHedfvyWd94AVcN2ilCk5c50DcMBAU2SnWUZNBOzPm76Wd+41mVJ9872cO6g1NpJl/dhZTXWGOtFsx9Tns1SVDPugInV2QbZAdmAQm8+S+f14x9pbbGNcU9v0re3OTTvvttRn6s08IOmf2ASh2oCljqTFgwFy58NGUAxIJ+H5/4A8cCf46EbOW4kx9VbuLqgr60vC1Nef4NCRsXvtqpmlhRkk8jpMucP/8sqoD+cD3uVEWAEGAFGgBFgBBgBRoARYAQYAUaAEWAEGAFG4B8gMNgmm9DfJ4MJ4w76gsSnJT7pEhM+b/z3jz1dCgjAHgYf8g/0yQ753BDo7OzUNf3LX/4yx3GNjY2iKHIcR+1zPp+vYCCXlKFD0cBF+DCoQi7gun5TnoKD/TPahTljgzN/fuXe/m7UwdogAY0RzVWbrpHDsa5ZxXdedklHKrjIZ9nV7IOkqLUGOr42fve2DZhlQexzXsHaZFzijzaCQ6KBGuRLl0IR+nPw9FNwcNvysLQp4+9L+dec89W1u3di3LOMQSAFDRcYzOHhRIcPFtC6Bqja+/LQ1w9PPAxtkU1Be1/MYzSFt3/v3M1KrsTAwF7Lny1TBdxIrAc6brTPMkBRhj88DCn/wpg4//BRkznu5AYuYK2pra0dPvX9t2WzePzJx/1f+TPehnNT33uLlJMzAV25ytgOI8AIMAKMACPACDACjAAjwAgwAowAI8AIMAKMwL+BwGCbbIKuwm8eeDwRPchhjUh80mENWRrdmXQ7E9D/hpPzX96lqmIV8bZt22hlrsVi4Tjue9/7HopWw6CvVk3RJJY1h+IZoKcDXnoGRvlWtkvbM+Lb1168HXVs2dDSoyrXLjHGdLFAk+rp7iyoOjzyIETdaJ+TLmNkCDLeXV8bv7tIvDfaZ1JuTdSzoZGEZZ0uAoguGGOdTczEgDnvw7jWZc2hnSFhZ1DccPDI+bv2YP86quEiyZsumWdUz2iNSSpIKcFZ1fA5UBR49kkYHV8dEztjouK0bBt//O6u3aDJGNahGkXTJH3T6BtDBwMjODQTh6ISLtv3wkt/gZGRdUHLlox7c8bzctp7g72mvYYbznHcDy/7PoB5x723V4qgv/u9C8sCGoNNqjgfcJdVQB8QDXuBEWAEGAFGgBFgBBgBRoARYAQYAUaAEWAEGAFG4B8lUJF4pAHiv7502jm8LSzxSYlPup1Ju9UrCj4moP9Rwp/r40zTfOihh2pray0WS21tbU1Nzbvvvov2VtMVpZS2UQaEQcq0/NlQ4Zk/QFtkWpNr95jw7lOPeX/r+tK7DBNjlOmtcu1SAa0Z6JEV0opqwnN/hPbE0pjY2eqDkWGtPbr1Syds3rYBD1UBa60VkvNMBDRooFN9TFo2DKyQhv48LF0Cxx26qS3c1RzoD/HrWmIf/O//QHcWhW7RyJG8aRpCXXbQ1D4DrmUoq7hQomJCXoYXX4BR8aUtvr6MW23y9wRc78/+AMunDa0yFbJTEtCkHpsIaLpA4vZO+PurMDq5psWbb/X2NUlLTz1qxvRXoZ5LjeDq6+vrrY5GAFi6asmIeiyBHlE/wuNzUwFNrD0T0JQzu2cEGAFGgBFgBBgBRoARYAQYAUaAEWAEGAFGgBH4VxOoSDzSsQl7O7KCIyTYY4I94RJTDmvI5YxMOOUMJqD/1Wfmv78/0zRlWU6lUo2NjbQyNxgM0mmVCn4Hz9HQMXmjkIWnfw+jkrNTvvXjmvec/eWd+TymMGs6ZiKjgC7VQdMVC0sRE1i0DGZOV/pISPSy5TCqaWlc2pN2yk1S/8jIutNPXFbMo1dWMF8ZVbdO9C8V0Hq5tlpRSkpY0WDPLjjz1J6ke3t7SD84pcXdM+66fQ+aZRMUyKtGkcRG49KAOsilNGpaBE0UeX8RS7n7i7BhDYxrWdXk70lJcqu/vz26+Le/1voLmOmsQd4wNMMwcNVBUAFrn0te3NSxAjqrQk6FyVMgHZ3mtq4I2DaPjmw8d8ImtQvMAowbeVztiHqrw87V1fzxz38CgCOPOYKirm+s+9srL/dl+zGoWlNpGHdlycfB4EuPWAX0frGwJxkBRoARYAQYAUaAEWAEGAFGgBFgBBgBRoARYAQ+DYGyzaNtmPDWmzNEPuKwRkRHyu1MC46IKISuu/YmJqA/DeXP7bG7d++uqanhOM5ut3McN2nSpA9B0ZuHnl7461+gOfJ2zL3W71hyzBFL1qyBPMlR1uiifCTaojpcopK/UanyXboCRrZNywR3NfvUJldnq3/FFd/NbVqDSxyqpPyZCGhDB40YX5TR5GMwKKqiaw+cefo2v7A84c75Grcn3YtvuKbQ24c6WIG8AlnN1DTDIPa5gAHQZfVMdwzA7nSA5ctgTOtSqXFzQlKbfNn2yPJJl3X29kFfARM8iIA2UECj1i6YuJIiUenEtitEbC9ZAoeMXtYc2RF0bm5PbDztuGU9W0Htw5ncddc9lcyNb13wbQ30X97/y8ozV026WgdT0dRsPs8E9IdceOwlRoARYAQYAUaAEWAEGAFGgBFgBBgBRoARYAT+0whUpO1H7vynjXzf8VSmQF4y4dqf3OoSE3ZL2CVkXGJKEuKCIzT1rZn/fwR0pfePubPv+P81zxxoeP+a3v9be5Fl+f777+c4jjpojuPWbihHaZQrjitz0wB6dbj6+t62zLJMYOvI6O7W2Ptz5+LrsoFlyzpRz2SpQKyErujmyrlRwCyCuWknfPPcLUHXypaQlpI6mgMf/OzKvnwv9PVR+4zZGuUKaE1HS1zWz1iRTFJBFHzHLdf0pAKzEr7tLaFiW2TT+V9fv3sXFBTIa/1onyGPiR8ooEnt88Dyg6oGmPuMQR8GfDADxrRPjUd2hbxqewySnlXnfHWBaWBPBU3RDCzrxs0AHfrJZmJ4hwGmiWHWRRXmzoQJx3WlvXvjrh6vuPjU8at3bYNiHyARkNetW8eNoMsOcjbRnlPys2bPRAFdw9WM4NpGtiuaSqKzcYnFyq3CnOxQfrjLKqAHk2GPGAFGgBFgBBgBRoARYAQYAUaAEWAEGAFGgBH4txGoKK+P3Pm3DfFjd1yZAjnChFNO/qrbmbTUB6mAdokJhy3Q3Vn4/yCgK11//J2PPa1/8hsPNMJ/cjefseZ6e3sPOuig+vr62tpajuPGjh1bPUHClJQvEwUsq3DrPVqyeW7Etz3h3Zn0zlixEN+uEteKira0xB+mLVfsM5BEDupYe4uweRtMunpBS3p+MtCRdO9sDS+58ced2zeBqlLJq+m4bCDqYRrBQdwveYDr9Gk6QF8OikV46hEYnZ45MrHNZ13dFt529NjFixagNS5qpo4F2T0a9JEKaLrkoFlKgMaByRpqajTZHXvhnK+ujfsWRb39Cb8Wd28654ydXZ3ovAuqoYGqmyUBrZigQT/ZSHo0voAJ0YUcnHzUtqSrI+MpZALbv3jS6r3deDhKaigCGKqu+0JhFM71uBThtFnTASAQDnAcN7wOn+no7SQp0qYCOo7KxFlUQrTJ6SizNJmArr482T4jwAgwAowAI8AIMAKMACPACDACjAAjwAgwAv86AgeSjx/n+X/dKP/RnnAW+MN/QKu1fdtulzPidiZdYsolZNzOdP0I90lf+DImFJRXfiuXrpa91SfoeAgxrbwI3IF2hrz/H+jxEwzuAG/ddwzVzxzgIPY0IdDX12ez2WgFdG1t7UUXXUTBVBFUdMjjtafCXTfnxrQubontyIR7Yt75k/+GYdAGKXzGSuHyRiqgsUyYSFi8LA0Dr82ePBQVuO06NROY1RzZ2B7fPDox98ZrejWlFBtdPie0wrj8qDIgEpSsAezJwW+e1FvGLk7Ed43JFGP8qubQu8/9AXp7Ud1qePUbGnRpsFczsYS5NB5U0HJX/zYS2qx256Egw5dPX94cn5/2b2mV8nHL+qNHfbBwLigKJjtXgqc1wEpnBddOzJGNVEAXdOiFzs1w7lc3RKSVKV9vW3jHF45c0S9Djhh5zPcgSzjmZOXr553HcVyD3Ta8tvayH10OAIcdiTHQNSO4envd1Pff1sDc2d+ZJ9Y+B9BdpFXfGDddLObJx7n0mWYV0IMvC/aIEWAEGAFGgBFgBBgBRoARYAQYAUaAEWAEGIF/EYEqXYYi9jN2w9mZpm6QSIPJk19zOSMuEZcfpALaYQ3dcN3dOOd/soA+kHSuPF+N/d/IvDKMf+MY/lu7njp1akNDQyWS+OWXX9ZVtfRlBrmcdIC8AX15uOO2bEtsZsy9tjm0M+yd9/ij0J/DN5KsDcy5wMBm4qBpHXRJQJsluawZaJ8fekAfl1zb7NrZ7F8TFl65/foemShsIqgHLl8auTGYKUnMUGFvL7w3H1oOeTvassPl2ZsJ7kp7Zvz6Lt1UQdFAA12nHhz6sAgaM6BJXTboOhQATXpRAVUB6OqFqy4vxvyL2uJ74+K2jH1jyv7Wi09jnxi4ASUHrYGu4ft1IqB1sqPjl0E5gA742olzm/3z/LY1fseSLx69YuZ0yJtY9kzzQ3IFFcNJdHj62eeRcO1wroY75PDD/u/Ja6+/rrahHp+sq7n1zjuKJM2jW4O35sGR4/960oS/79gCKmp/yOb6mIAefCWwR4wAI8AIMAKMACPACDACjAAjwAgwAowAI8AIMAL/ZAJUsJqqij7ryit+Ui2gJT7pdafnzV6FfQ4YvE/pZCuHf/gO+sch2z956qy5/88EJk2aNGzYMCqgLTabrummomIMBC0ANtAvqyZcdsW6USOXtGX2xoMdkcCCH125zQB8HlcdxL8yLtI3WECjhsbQDEzSMAF6++Gl56EtNHdsZG/auT7hfOO+2xVD/gTTI78BwJzoo46cHQ4vSyV6I77tB6VXXnrh1lw/toMJ1OUN1TMpf64W0BpqY7ypOlxzRXdYmpv09rRFjJBt/ejorN/dgwHVxQKxz6BjEbQJxDgXFIzs0Is0HwN0dNJ74Dvjl7S55mWkdW2RDWNa31+4EAo6xnqQeGpEiMnTZO59eaXBYi1b/podO3a98cZbdbXU+9edPOHMrAz9RZj2HrS1zQgGl3mE6WeeNGv5B1DM0vEO3LMK6AEWbI8RYAQYAUaAEWAEGAFGgBFgBBgBRoARYAQYgX8bAZNYn49z/28b4iftGMu66S/6jz/u5GoBLToSkVB7qbmPJ6DpQmfoq6tun3RA9P1D7PO/ufh83zP+j83q83TUcccdh2K0Bu8mTJxYmjrVxiR4QinAZZfvSKRmhqLb44muaGLZRZd09imQM9Gx6iaYKKDVfSugMSTZxFpgjaz1N3sWjE3Ma5E2NzlXpqU3f3cPdGwDDb9Sqb4NXMHVz+LFj+HPUMzBlyfMCXnmJvx7op7dicCKCSfM69mLtdjdfZ1UeVMHXckDUXXUzQYOAxOWDVKS/NNJPRFpVtixqy0Aaam/yb/kZ5O65SxoZIFDskShXBbQpgJyRUAXSUCzUoArz99+eHzlKM/mNt+qU49fsWoF2ufOfClaGkOxqa0m+dcAMO6QQzmuJPqnTHl1xYpVJehcw6jRXywUYOkiOHLM6qS/O+BUo86OkYG3Hrp9Fw534IbngwnoAR5sjxFgBBgBRoARYAQYAUaAEWAEGAFGgBFgBD77BMxyxus/Y6q6Zvb350wDf8iPvkk2dA1kWaWOtLeHlDh+ko6KBZQ3xTysX7tzxvSFf3l+ym8eePzJJ56bM3spRsya0NdbxL4q1vLjNd7fV8B8ADJIeoSqqjqxYwdqwNBBUTT6qqFDPkcsF3lcyKumATIuuoYjUeRBwmlwRbOpa/qe3V0C75OEqCTEJT4p8emgr+3b37xUKWIDujZoYFQx65peLJKXAbLZbKGA4zdNM5/P05CEKgtd2qVDrb43DVBVHKSuYczC6rUbX339nd/+7vHf/u7xV19/Z+36rbm8rtIp7p9ntamubhj3e3t7VVWlg8znirI81EoOPoA2Nfi58qV4z933n/W1c7917oVT33pfp83sfzyDD/+cPTLNAc8bjUZralA/W2y2O++9RyMxL/gBLHSDBnI3fP9bXW2ZjW7PNsnXEW5a9Z2r1uxSoYeUNmPQBAl6Ll1IlUUIiZgm+hqyKuQVyHXDsQfNaxE3tPLrx8Xe/Z8nwaAyeBB5lWRXDHqKPtBNXDdwTwfceE3/6MTyiLg+6e2KOjcdMWbZ7NmQLWKaM70sdChlT6OGJsNQdVBUrESmwTHdOfjTMzC6eUXYsStu00YHYGRw41kT1q5djtc2if7QNMhpUKApHKSimS4PaKJWNiCfh+uv3jMmvjrNbxoX2nhs+/tyL8gyyAbI1DuX72mnVOZPuuba+gbM2uY47tJLrjAN4Diuvs46vLaR4+JL5sApRy8aHe1KeSEoQMzZ1+J+Y8ozQ1DoACoT0EOgsIeMACPACDACjAAjwAgwAowAI8AIMAKMACPw2SGgqqauQTZbUpmliQ2IrH/OTOmqZfSeilpF0UzTNPRPJrvlAqxbs+OOW399wvFf8kgprzsd8DZLQlRwhFzOyCknf/W9d+ehTlWrBPTHnouukhBZLEnWdM2s6N39IqD2uVpY01pR+mZdQ+lM51vR0ANsB4aEYjqbzT726JMOmwcFNLHPEp/+vyToh379jIxWeeBmmrquK4ZRst70BdM0s9nST/oRKclMwMGQW7WGHmho8N6smfOv/NG1sXir5Aq73TGeD/B8wO2OCULo29/+Yem9+xG+1fYZJ2IaUCwohby8ZfO2K6+8srW11eVynXTSSTt27KJIB3c75NE+Apr2CHDF5de5nBGHzeew+Tyu2EO/eRxDG/YzniENfn4fbtiwoZK/wXHcG9Pe0ciXHhTxls1w8Xf2jExu8UtdkXDeG13zhS8v367Bdg32kIJkFbPJwaRr/JVNNNW+1D4XTcyPXrcOTv/ChlH+DU38upGumf/7BGQ7KfOB65sEdcj7FdA066OowJ+egpHxeUHruhZfV9K9rj05d+a7kM1Djvhl0iLmP1MbjsMgQ8O5mFAoojvuL8DTz0AqPq013hN3aike2jwdJ4yds3UNVkeTWRs62ud+DY03jeAopWooAHkVcnm46rJNCd9bUWlda2jz0e0fzJkKegEDOxQDZJNsVQJaJxPTAf760hQin4dz3IhMptXQwWF31tfRXI740W0vHp7eErZ2tgTBJ3a3pTY89wgoXTgn1Rj0L5cJ6M/vx5XNnBFgBBgBRoARYAQYAUaAEWAEGAFGgBH4zBOg5YF9vcW33px+3y8fnDN7ka4Orbf9NBBKS5aRJn5+4+3tbWM97pDXE7z22us/UbPFPPT3wKU/vK6h1uMSUw5rhLdFva4ml5iShLilwc9xNkuDt6HO9fyzU7Dlagn2sXtatnTN+nWbiRQmK4VV4iwGVzDTUm500LJBS6cB4LVXpz78uyd+fuPt9/3ywVdefr1UqEu7rtjS6h18yejP9gLAmV/5hiiEBgloIbNhbZehokzXccU0jIo2y+bVNLFumrZN1zCsqHCze15YAAAgAElEQVRabD5UQBONWMJAxkCH987bsyac8hWHzed1x73etNudEISY25WS3CmHEBOlBO+MH3LYybt2Z/fHk/rMyj3aZyx87smddOLJ8Xjc4/HwPO92u3/4g0uohf/QImjaTmmMFb88ZfK7HGfl7UFJiIp8xONKNNS5Zs9aur/xlI/93P99/nmyOB6N4BgxrLeY10hIRX8BOrrh2OM+aG/eEPF2BKRcOLzlqPHT13VDB8BODb/YMIktxoJpupVVq0lKj6mALuiwtxN+/lNo8mxs8+weF17wP4+DNvBlSeWzpwJWD9Ovg4aeFYxUNuDVyTA6vaTJ35V2Z9Oe7W3JmX94Cj9sORmrm2nlMmAVMvl5QSkYpGBCgXwWStXNixfDqNZ5Lanupqga5PvbA8q4xLKZ08jhKKwxz1rH2ucCSeEoh0GT7I4iqX1+9mkYnZ4Z9y1JpdaPHvvBzPexstqQwVAxTkTRDiig93b2chw3bFjd8OENHDcCACaeesawYXUcV1PLjRkdfDlt2xC2dKeCe9vHzJ27CEwV5CwWVg+5MQE9BAh7yAgwAowAI8AIMAKMACPACDACjAAjwAgwAp8hAibs3tU94ZQzHHZXNJIWeM9VV/70nzY9s+SyO/f2jz/5dIH3CLwnGIjbLE6Lhb/zzrtp2ezH6e6Pf3iprfkoW0MoHBjN2+L2xqjoSAU87V5XE2+LOqwhl5iwW4J2iz8Sal2/ducnE5QmPPXkc4lYq1sKu13Br3/9XKpKZVnGCuJyEejAOMuGrb+vsGrVuuuuvVEUPbzDbWkURcFnt0m1w62pZOvNN92pyFCqV65Wz5V9Um29ZfMOlxMruCv5GxKfPvKw0+hKZfl+2LMru2L5utdfe/uZPz3/6CNP3PuL+6+79sbLLr3yq185+/TTvvLNb5x35RXXTJ78GnXQhbxMa7EHKqAr46/0a0Jfj3L1lT9zOSN2i98lxuyWoMUS4B0xp5iyWqIWa1R0ZiRXs+RqdgipCy64ghp4KrvLHCqSsuSODR3DVR544CG3K8g73B53yO0K2qxCa8uo8iEf8rfUSOkddKgGHHvUqYIj4hJjoUCz3eKXhKjPk37y8ec/2fn9kG4/iy/dcsstNqsDK3NHDAsmolkdk2IKOuzaC6d/ZWssvjns6w77etOxXRNO3bp5L+zV0BPL6JwNBXUrFheXBDRNuCBLF9L0Z0WDQgG+fOripGd2e2DnEZkt//ME9O2tcCx/Nkoqe4h9NknpMDppRYcFC+CQ0ctS/s6xKWgK5NriS67/SW9nHzZV+nYFq+oVgEJJQGM2SN7EJQcLNG+kmIcli+CE4xb5pHUht+ITculQ75jMupefx/iOgo7f2JCxUwEt41c5pdQOWQOsbi4W4X9fgIR/csS5MBFcNnrczLffRzOONwWhGApx0EZpBUe6iGNZy+O7AqHE8GEWjquzWZxvvP7uYYceheZ/+DCOa26S/jzWv749uOarE3ds2gUFgFwRv1JSdVPV9epvtZiAJsTZHSPACDACjAAjwAgwAowAI8AIMAKMACPACHxGCVz5o2vdrqDAeyTR7/NGA/7IX17466eZK01GpgEUqgKde/uPOepEUfAJfGXzeNyB5qbyInsf0hkRYTdcd6coxkUhKQppUUjXjggO43ySs8lqiTY2BP3+FkGI2GwBrzfd2OgWxfA9v3gQ9VdlO3D7VDT/9qHf49gcAdx4n80q3HPPfVSOV+xzJUWkEuisGXD7nb/0+WO84KlsguirbI0W6aLvXQ4A/dlBoRnVw1EUuOaaW2Px9vp6lyDEBD4h8CmBT5115iXHH3tmKnmYwKd4R4J3xPbZIjwfIhsmZvi88cmvvIE/7Vcx2KSyVY+/kNMNDeOz167e/oXjJgZ9TR5XorHeKzgiXleT25UR+JTozHi8o+yOlOhsFoUmwZHBTYjNnb8YG9d1VS+7wUGGckCmnTL+NN7uFx0J0ZHCez7CO7zdXRj2TRlWT79qf7CAJi889sgzIh/BTQiJQijgS/k8SVEI4EwrnrOqic/5rlwurP3amWeTXAiupq723AvPL5CPwqpVMGH8xnhkh08qJAOQinSceOLirTuhR0HbSzKRybqCA/KX4KRRxyRd3cDXoXM3XHz+1jHx5WnX0pGxWU/8Fv3sfk5e9cmgOhtPWQGgv6DnTYC9e+HUk9fHvGvCzu6kVz6oae+E8R9grDM5s2U7S1YZhCIZILaoq4VioRfAMEyQCzB/Dhw5dnnStyfkzrv5YtwPLYnt99wNnfi7AsjqvVQ3kwpoGe9NjLemjZsA2T6Y9hYcedD8w9p2RN1rM7Hpf3sReokBxynRoGiVHEKCpwfSP8p+3gA45xsXjhjh5DhLDWe9/dZf/uSan1H4w7hM0nXfwbFXrr1kPY2Txk+QhsXYqo4fhYHPDAAT0NXXC9tnBBgBRoARYAQYAUaAEWAEGAFGgBFgBBiBzxYBE8aNPUrgsW43GIgHfDFLo3jxD1GbfvqbrqF9PvKI4z3ukN0mVQloH62NLeQ/bGE6GhNxwfmXNta7ywI6yTsSDlucmuj6Op+lMeRxpwUhJIphyRW12X02u+eEE08dsM8HNpX5HMawrlyxnnd4S/aZCGhR8H33wh/IslosKNUCl4Zl04rm7t7cV8/8ps3hikTTFfvMC56KfRbEgFMK8YLv8h/99Fe/evicb1x4zje+Q7YLyf5F55zz/XPO+eGhh57SUO91OIJOZ6wioHlHwmaN2awxhy2O9tme2s9WstIR3oEmWhRC1193KwDIxQMKaLp+4/RpC0a2HRb0NbmluM/TVD/C7RJTlvpgQ31Q4FOSq1V0NkuuVsnV6hTRQeMmxh/87aMaqX+W1cpai9ShUcWHMg1TGjTIpNvdUly0N4v2VrzH8+Vbunj1R11OVUaOnLJVK7Z4XOiviYAOiAJKdrcrGAomhkaWf1TTn5PXK/Xpxx9/Qs2wBiyAbmj81YNPFDVYvY7Y3uC2MS0Q8UHM33X6hM6tO2HzHiiYkFWx5Je63qrTQLDRx0RAU4zX/ijb5Js7Krwh7Xr/5uu69u6hiRZDjeog5vSrIHyq38AOobMHJp6yJhXamA72p0K5kGvDyNbZy1dCUYOe3pLwJSEbdFAKqVomTZpgqKZCIiyyPfClLy4OC5viEjTHwC91pRK7rroa9vRC1oR+vVA0+xXAYBEd9NJWFtAK+cezdB4cPeqDkZE1EXFxJjb95b9BXw/pxcDwDRTQmIdNLuwDCGjdhBtvumNErcBxdo6zH3vUaW3NR3Bcvd0mcpw1JFx086SFoIGWw19CZLNZUvu8ny9imIAedMGwB4wAI8AIMAKMACPACDACjAAjwAgwAowAI/BZItDfp/J2v8sZ4h3ehnrBYfPYbdIp40/7NHOkfgVjf0245OIrHTYPDaYoVRmTOmifN37O18/HBQkPLIi3bNozccKZDpvPLUVFkW5xUYwLfCKZOPjmm3797LN/v/fe3zc2enk+0GiReMEniAGL1dXWPnaQgB7wX/uZ1q/ue8gthYmADgmOkOAIVAvoSikxTXymMRfz5y09+JCjnVLA441arC5e8FU2QQxUNqvNa7P7wuHmUKhJcoWrtqjkikpSXJKSDfV+zL7gQ4IQqQhorEQW0gKPhc8Oe5RUQCcG38fQOxP1TIug3VL4qSefp9OjSztWq3O6DwBT35rpsHm87rjHFfN50i4xZmnwS0I86GubOPHbd9/1+B//9NrFl/y8wRZ1e9tEZ6a0SYnrrv95pfyzDLEiLWnC8IcJ6L+88NKHnGjS4CDzqcow6aqbUGSXyp/xpAi8p6He9uBvHi4PgP3dP4FUKjNsRAPHDedGjHju+Tlrl8PhoxdE/WsTgWLCj/b52GMWbd4O/Qoq1sqtkrpRVZlrAlYfF7HiWIeuPXDtFXvHRDH3eUx8+YXnrOnshLxOBTTeV2R1pc2qHZ1EORc0gO5+uPqqjqBrbsTVFXTm0qHO445ZPX0GXiA6Sf/o2EO++DF1k2zEPpcvDxM6dhcUFfbugq9NWB9yLA/YuoOiGvOrPs/y07+yZPMe7LNX07tyBRKUQdRzlT7WwdQMUBRYugAOycweGdg6OtLRHJ3x9LNq3sAxYM23RgQ0OX7Q54is6VmepmGAoZna5L9PIbQtwznPMC7oEQ611DbV14o1nPXyS+6phIngNzSmSWufq7CUdpmA3pcJe4YRYAQYAUaAEWAEGAFGgBFgBBgBRoARYAQ+IwS2bdnrccUioWavJ+pyhiyNkiT6R7aP+5TTw6RVE35+4+0BX8LSKJXKn2nGBakyDofS27bsNTRcx2+QLK7qePzJpwd8CVEIeNwR0RkUxTDZok8++SL+mJ8setbTY1xzzc2SK+oPJG12j1MKNTTykWh6UJsfKqAvu/QaSQwT9VwS0DaLsxLBQY0z1dB0aPPmLEkmWuLJFtHpdzi8Vpu7Yp+pAacC2uFA+2yz+0Qx7JQibndli7ndMbc7IUlxpzMhCkmM3RAq5c8JksKRsFrCvCPicacDgdaSa6bGeZB3DvE85m/wgu/II07o75OLBQPdmY4umG7V+/PmLLE0ipLoD/qTlkapvla0NLpdYmzC+LNe+t93FLmUpZAvwEHjxkueFl5MO4SU6Ezxzugdd92LobhadcU6FXEDFdCUzynjv8Tbg1UV0Cm7xf+r+x6qLJNYdYardw2D1paTLyQe+s1TkhAXHFj+LIlhUUABbbeJ3/zGeXJRr6SgVB/P9isEBEHAlfGGWzjO/sCvlhw5ek7Gty0odGQixXS44/QJnbPnQ5EkqRSUgaUD0ZCSrdIOeVSyz3oBLv7O+kxgVou3o9m75eC217pI7nNOxxUOK1vZE1e1QXYNKJL6eJB1eOYZaErMj3h3pkO6T9iViS157Ano6oMCubjyeUxJxqt3QEBjq3h5kGvD1KHQB2dOnNEeWxuXsm1xCEq9LmFZS+vUtTswybpXMwuGXE6KIQLawFRrzN8wQTNBUWHLevjCoTMyrlUJcUNLeO5zf8JR5ol2VuknSBv4EFU+TcQ/01pvwwANI7M1dfXa9dywGq6mtqHOVcO5veLhHBeqwYJo7vqf3WiapqbkVTmHCypWatSH4mERHPsQYU8wAowAI8AIMAKMACPACDACjAAjwAgwAozAZ4bAxg07MehACDlsPo8b43p5hzsebcIJUh114ArlD4Ggq/DC838ThYAkBitb0J+uG+50OSOHHfKFpYvXopHRoFggZqksTAs5XS5il1de8RO6aCG993jDXl/8qKO/OG/+CsNEnUQ3AHjq6Rd5PmCz+3geUy/8gfipE7/68Qc//otn1NeKIh8rb5HGBnHq2+/RTIkhc9y1o6e97WCHzUMtc3294A8keT4wolYQxbDbHXM4/NFom9sds9l9DoffavM2NroDwYzN7qM5Ifik1c/zIavVb7OFHPZoRUA77FG3KyNJ6fo6D7ppMSoIlaDnkCAMbFRqO6WQ6AwedvgXrrjqp6qC6c/V9pmO3NCxnFNVzd27Og8++HCfL1RXaxEFn9cT9rgjbil89VXX6ypZGE0FVQVZRXJnfv0Hgisdjo4h9jnudEcfefQpzcAMaM0wqIarqk4tVUArimbocO43LxD5iGDLlCM4Ul538vvfu8I0SitSDkFaeahqGKxg6LBg3qqANxMOtLmdSVujTxRC5Mp0ez3B9es2YxDwASO1K419HndkWVZVVZblhsYRuA4epnC0jkw9MDK8ssWbj/AdmfCGtpZXVqzFBQn39smlimWEPiCeq8qfSwwNE3o64Pqru5r8S5Lu7XHPmpEt77w3A/ImlkaTjIqB2ucDC2idVlv/7SVIxWaHPbtSYYiH+lKxZbfdBr1Z6MqSaGZaBY2lx7iAaTmFwzRNXVaLuTxe4boCP75UD/Jzkv5tLYlC2NsfC28dddB7C1fiMHoUzPEozwKDnE1Tx9xy8n9M0dE+F7NwxkkbW4PrRoa3tMdnPfNHLMqm//BIlEyplpt6532uJCx8JptmANDYbRr6XFtbU8PV1nBiDSfVjmjkOO7Gm2/EwykUMgC6uy8lVgG9D2f2BCPACDACjAAjwAgwAowAI8AIMAKMACPACHxWCBRyZmO9W3AEXM6Iy4nVprzD6/VEP77AHUrCBEWGPbt70qmR4VC6Yp8lMWizeBy2wPnnXaKSCFdqeNGcKmii6UbWGYP77v1twBcTBBfdeMFltYunfelrO3Z2yQrxOWUBrWow6ZobU6nR1P9arC6rTbroe5eWxj90cIMe05rc1uaxdgtdNC9BF80L+BK7d3Wb+Dt9TSeFkPSwbL92xpe+7vPGR9Q6AsEUL/hEZ9BidUmu6Nixx/zgh5PuvvvBs876juSKimI4nhjpcPhtdl9jo1tyRUOhJqcUsdq8mMthC4hi1OtNWywBWu9MK6CtlrAoJJ1iymoN1tc7LVYPL/icUqh95CHHHz/h2+dddNXV1/7fsoePPPrU31+dOmfuklWrN2Vz6GJxWTPV3K+AxpET83XmV7/ukny8QxIEVygYE0WPwHuumXQ9mGifdZUsj6aCQgpHDzr4iw5nkheTHl9zg9U3vM7x3vQ5ZDk680MENE0p+dV9D9kt/ioBneDtwSOPOKGUHU0GUzkNpZJSQzMMTSeK0jRg4oSzvO6k25nk7UHBEbA0Sm5XMBiIvvnmO1iFLZftYqUVtjOYAFeD8RscV8dxx46MPdfm29zqyyVcaw8d/cHm7ZDT0RrjjQYsk6AJepEMbgZfx680ZLj6kh3NoVnNwc4xzYVDDln8+rvQT9YTpNnMZFU/XNhvX69a6cckicoLl8ChBy+IBzuifgh41Vh86/nf2dqbwwLq0vc9OJhyYnPpdwdox3XQC0qhL4/juftWNRNYk/LmIp6uVKLX610Tjr/7lymY+5w3Qa5cYJimoYKJKySaGh6Yz0MuC5174FtnLU+6locd64Li1L/+BbrpqoOIgAyk/MXbfqKaS+q5LKBNkLNo55syR3DDhtcM43Dj6mu4xtpaPAE33nIdoULuSLMVSkMuYiagh1x77CEjwAgwAowAI8AIMAKMACPACDACjAAjwAh8dggYJvh8KavVL0lxQYi43QmHI+hw+D+OwB1KoUrcfOubFzU2iB53pCyg/ZIY5O3+O267HxfKK6BuRqukon2mv7jXdNCI/Xz1tekYWOEJ8YILN9HJi87Djjhq05YdtMcBiUN+TT927DENDZLV5vX64rV1vOj0//Vvr+5XqA0ZsGnA3o4+txS1W4Konh0pIqBjp536NXq4rGq6iXpXN6CzK/etb33P441abW5BDFhtbq8v7nZHQqH0bx58UpahUCyVQ/7i3ocEMWCze9zuWEOD5PHEv3jyVwLBVEOjOHyEXRBCgWBmRK3g86Uw2FpIkgUVkzSLo7424PO2X3DBVY8//uzrb0zdtGUHllkSxZwrqD19eQD85X++qPX1l8ITNANkVSOuvLT84L7i7IYbbhIEl8Mh8LwoOd2iKFkstit+NIkCwarSsoCWNZg+Y5noSfFSosEa8AVa6i3uZGZUuWtUxQeqgKYOce2azbw9yNszvK1FcGQEPuHxJOvrnbv39OP5rfjB0smonEx8LMvyxT+8XBRCoUCz4Ag5bAGvJ+qwu+w28dFHfk+PKOTLX1+UWmB/BhEoFApYkIv+s4HjTh4ZfTEprE46N0Y9/7thA/QWYE+2LD/1cnZG+YnqhvDEGNCzGyZd3J3xzQ+LazLRXZHI9Kdehs0FyBKhTJI3VANyBkZfHPCmkTfv6YVjj14WdG8NONWIHzyBvnO+Azt7Ia+hNcbrnI5H1zELRldRH+N3RGUBbchdvfCnJyHifmdUsi/qKSSCaibd7Y29/ovHIAfQWYSsigkbeNNJbTauP2gCpj6jgO7HGAy49qrOUfHFEX5De2z9tT/ppYMm/7oUItXJJWqWZPqgq7Nsn8k/Kg0jODTYtRbOmTDFOvxEjrNg+fMwrqZmeE1NzfB6jhvG3XjrJAz2oLRIW5UGhyBnApqeCHbPCDACjAAjwAgwAowAI8AIMAKMACPACDACn0EC+YJx5JFfHFErOBxBUcRUYkGIORzBfUThR829bJ/BhN8/+ieXMxT0J8v2OSiJfkn0X3XFdYUcqp1iHgo5k6pnNNEkf4MK6HwBDj3shLpGyR9K2UWPXXTh5nSuXb8xmy9qBmTzCmav0nJLEx597FmPJ07zLtzuSH29kGkaNUTufMjQFy5YLonh+hFu0ZHgbXGXmBL52C0335PPYi1kpZ2erHzv/Q/VNYoWu7veKjmcuNQhL/gyTQctXbYeiz+rbroB702fc9DYw93uiFMKXXLJJFmGjo7sm2/NeOTRPz78yNN/fv7lN96YsWrVtscee75aQNPQ5wceeKqqsY+1m80Xdc3UNRTQ9L76sHemTrfbxHAoLgguUfS4XX6PO3DRd3+YzRbBhGIBczMqAjpfhK+d/T2rPeTxNdscYcmdsAu+7150CW1QVhXUgaUbTUioLD5X6tPQoL31cIctzttTAp8S+ITTGQuFmp599uUqTtUiju7j4TfddItLCkhiuHaYSNOfGxvExkb7ddfdUBqArFLVXuqM/RlMQJblmTNn0kQIjhM47pRR0edGBxcc0bJ44zroL0J3oWrhQVr7TMt5TSpuS98P4CkxQJXh+quVTHBJUNgWdm1PROfc/wjsMqCLWNVy+LdqQIHo3sFDKT8yyGs5Bc67YHUqsi4s5UMuCLg6I6lF81aVa7Hpm0tJ0lRA62ifMYUDh6QC5GR45x1Ihd9M+rfFPb0ee0fA3ZFILr35vkIPEdy9xD3nC8Q+K+Qpkg+CX3SRJgHgthu3NYXeGxnfeGj76qsuzemkYpr+6wJ06ESj72Of8bolbyKSHL04Nm+CmoezT1xzcPg1v/17NPe5ht6GcYMFdB8u5EjWN6y+7suE8C8T0NU02D4jwAgwAowAI8AIMAKMACPACDACjAAjwAh8RghUtN83z72Id4YbrD4SB5EShbQgxPqziv5xJHTZO2PCL/n9+sIFKwXeJ9D1BnmfzeISBZ/Aey6//CoqcUr3UPLOJZomyAr0Z7Wrf3yzx58ZXuuss7rrrWIwmrKLrseefFox0fjgRn7w359V8gXYvKVTkuJ0c0oRQQyMqLVdcdWPadXwAc5TZd74+tS33ndLUZGPuYSMrSHic7c01HreenNGZerUmb76xnuNvMfh9Ln90Xqr6HD67IJv/MQzl6/adIBe8Om+bK4gD6QdVNxTvmAo5Onf/e7pAQEtRh0Ov1MKzFuw5EPHP7RD2qxpmrjEmWHomkmzmOn75KJ+8MGHi4LP7QqKgs8l4Wp+qWTrqpUbKqfDNFBAo+ZT4fnnX/d6Wmy2iN/fYrH4AsGMxxt++53ptDWd1KgPFtADPCkrTYebb763ocHt9TZZLAGScx0WhMi3v31JvlDOLiDFpNUzMXS4/1cPiqLHbpOi4VbBEZKEqMcVq6u1XXPNtfSddIL0nnrJ6hbYfqFQUFX1tddes9t4UgIddAw7e2z8oVOPeHPLGsgXIK9jxkTV1wBUrOr4YwTTxHs0sKqqm4UCqEW48rKOiH9JOiYHxL6Aa9nFl2/tyAORqXi9UH1dXuuvgl/FRrApvBlgZlXIqfDbhyASWJQI9qQCasS1d0zLyqnv4nhohHTpYFoEXbpGSAfEBdOvgmbPgKD0cmt8Z8LbF/X2t6dz8eCKyy7pM0ntc6FUkS0regEnSQW0guI4349XGwDcexNkvHNGBra2heb+6LIFNIAkW1W6TZKdS19uleQ8xVVOpiYy3ejM9/cqsHE7TDxpbbu4eZx3adIzieMiHOfguBFY+VzDDaut4TjuZzf9jKjr/VT+l6Zc/sMEdJkE+8sIMAKMACPACDACjAAjwAgwAowAI8AIMAKfIQJUHOom3POLX4uukNVO8ogdGcHRLPCpFSvXD5jFA826bJ/BRPtMQ37P/Mq5JfvsCAi8r67WJoqeCRNO7+7qrxjPit4daNjECItp0+Z5/Bm7EHJIUckXd3mjNsH93R9c2tWXo+pZMVBAo5AyMa/jmGMmSlKyvMUj0eajjzmpP1uUVRoqO9B81d6gaT391J9FISQJcbfYZGuIeV0tPk9Tx25ckkwnphsA1m3cmW4bW1PvcHmjw+tsNsHt8oUPO/KELds7DYD8QOhsVSfEWymaqmhqxePTjnHhMsXQdPRcP/7JTaIYL0VwiFGbw+ULhAoYckxXhaviO8BuUC/UzVGlSB00RlfLhqqWSlnvuec+3iHZbZLHHfJ540F/0mHzPPvM/5Y0GzlSVyHbh3vvvrNQ4BM0itrjTnu9aUEM/OiKn6g6tka9c2WnvAjhAE9FNRXS77ZtnV5v0ufLOJ2J2lp3ONQuinGvt2nHzh7i+BRq+gAgnyvS+Tz26JOWRlEUfD5vXHAEajg7bw9KYvii75aKr4vFYkU9lw14aY5DiXxeH1MpP2fOnOHDG+pGCPaGpjruyAnH/GLtYujaBd1ZvIbo2aIXVqmsl5pkVMbEHQMu06cU4Y4bzKj3g3Q8l0xo6eTuk8ev3dWHardfx+yXysW8j4AuAOZhoKDOFrtNwHiNF1+CqH9WzN8TEnuaw10B5/RXXsTMjQLmM+NWutHx4XdZxD7TixMwVWPNGjhy3NLWWGfUlU0Hzai7y8PPnjhh2dr1eKhK3oN5G7i8olyaCq2n1kHJgybDC0+Z7cH5I/0d7YENE09YvHMP9Ba0YtX/icqMaOcVvV56nlyylFGfDDv3wPiTV7fFNmdsWw8Jzv3GGU9wnJPjbCR3mwjoEXUooH9+c3luH/GXCeiPAMReZgQYAUaAEWAEGAFGgBFgBBgBRoARYAQYgf9GAlSsFHX9g3mLnO4w7ww7hISDzzj4ZoeQ+uvfXqdvqKrGrSia8nQrgrTskB5/7Llq+yxgBbSzual9y+Zt5WMO+DdfgK+edf7wWjj6DQ8AACAASURBVKddjLl8TS5/2iJ4xxx2dF9RL+jonUubjrWcAHDmmRcEAq2SlCZbUpLivOB7+ZVXZVWrGvOQ7ipTKI34umtvslv8LjHlkZoFW0ri02NGHUcXQqSB1B3dha9/+6JGh6/O6rY7AzbR1+CQfJHkO9M/oPaqoJYnP6QrfEhirg1F0VTNwCrMClKdhN6OH/9lpzPhFDNOMeV0xuobHN/81nm5Ag13rsAdsjO0G9pm9bOmAcUCjmr2Bwu9nnAy0dJQ7xB4T30tHw6lb7j+tmK+PJSyicQ3z14ZiYyyNIYctrjDGpGEOG/3H37o8cVCydKRGVTyN8zBAnoohG+df4nFFhSlRH2j3ymlbY6o29v042tvJaOlNa4DQ37i8afDoaQoBCQx6HXHcSVMuz/oT3/ptLM7O3t1zSwWi4paNMhahbTfig0faIXtEQJTprxK6nBrOG6YW0j0duCz2SzeK+S0VzQ0Sb6hVwCtfZZR4RpgyvCTS7OjE5sC9t1xfy4WWT/mkL93F0slz32yXJDJRV8VVVHFXiZJyiqx29Cbh9mzIR1/PRPaERL63A07Qs55t/28H68AE3IFcplWHTzwPQv5CkYHQzWgtweOP2quX1yYDhQiEjQFoS3eddIXVq5ZB0UdN83AqGdyaWmYt1GamGqimsbE+UUzYFxi+ijflqh96VEHze7ajV325RU06dSgl+dS8c40gpqkUONbqHrG8A0Ttm+BL524uiWwtt2/JSVOve6Sbds2Aok9GYblz3SrRQF9w0037/vxrJ5uZZ8J6AoKtsMIMAKMACPACDACjAAjwAgwAowAI8AIMAKfHQLUjOQVtaAakjckeWLVAvo3Dz6OHhaX4KvUmdIjqowKlVfkiWIe9uzKppOjXc5IJX9D4D3BQPTNN9+m7vLD2Bnw/oxFvDNaZ/HzUsLla6q3+eqs0vN/faVAioUr9lnRoadXO+usC53OhM/bKjmbcEMNHb/5lrtyBVROQ23oQMf0Z/cDOQTf/tZ3bY2+koC2J3hb9ITjv6yr0NuNv8xXDHjymf+pt7saHT67M+Tyx92BhC+SfOFvU4paqX6zQmegE9yjJcxggKHocl+2t5odHZ6qQzozqroC2u0J3XHXPYqm5uV8uTp1iH3eT29V52NgCMWCYWhw1ZU/DfhiblcQT4Q/6ZbCiVgrnVppgKR5XYVp78yPREZ53E1uqdlmjfncLfUj3KFA5rVXp1JJVxG+lerjfQS0UVAQmgGY0z3l1fdsjrCdj7g86frGoOTOuDxpty9ZzYEWwj/x+J8E3mO3uu1Wr83i8XmSHldMEsOnT/w67bpYIKKQ2GfD0JiAHjjN++zJsnzH7XcNGzaiHAPNaUrR1DVFQYb07JDPgKnhyny4GSXpS0SsCUYRHvkVJN0Lo3xPyqe1xHcfctjc1Vug38DCZnor5EhZP7l49vmsUb9dKoxevBTGjnwnE97QFOhvDhbCwrKrfoBpyCYQ+2yW6t/LDZf/Eh2M/3wMKMpwykkLk6FViVBXKqDGPEbSt/eYw9fMeh/LsXEKpY8aHovFyyZuZBlC/B2EqsPapXDsqPlt3jXNriXj0jOXzC/1oqjmwHKdZBqV2ueKfaY7Cg19JrnPxSKcceLyMZG1o3zbopb3Jn1/G8jQ3wfDaol5ruE4zN4YxhEBfd3NNw+NSC9PcchfJqCHAGEPGQFGgBFgBBgBRoARYAQYAUaAEWAEGAFG4LNAgKrAgiLrJpx48mn1FndJhvItopA+deLX6CRVXAaM3uiic4OEpzIQ9wrX/fQ2kY/Q5ASXM2K3ugXe8/DDv6ft0PjgDwF36sSzG6w+n7+NF5ONjlCd1XvYkSdRvdWX1zTipHJFWLx0wymnnGmzYbiw25VpqA86xUwsOvbSS68dJDf339NQAX3SCafx9mBDrY9EcEQc1si1P75TLpTiRHbu6ROliChFeFdEcEetDg8vBX/90GM9WVnWsSiS6uH9dVWihMnYqMgGyp8rwm7t+s0NjXx1BnSjRZw7f6FGAmvJIbRSeEgcx/56q36OjMnUYeGClZZGyeUMVTabxXPjDXdhPWyfIcuY+IySXYGXX36b50MWS6C21mtriNQP9zfW+UU+9syfXuzrzdO2SbxDZezV/ZX2sSIabSD1xKgCz/nmDyR3ymoP8c54eYve8LM7sFMVE04A4InHn3U5QwFfglwwXpGP+DxpSQyf/bXvGBrks5glYmBAsVlqmAno/bAvPUU/Yn/7299qalCCklttz96CqZZMMwl7xqX9Kva5vAIo9GeLNJf8z3+AJv+igHV3wFZMh7rjsSmrN2L7Hx1jXDUw2UTfvWMnHHfU+y3xjS3hfMC2/dDmjrNPW9e9B4zSl0R9AH1kZFVHkl16nRmAYvfcs7d5HPODro6WpBYPZqOejrbU/FkzIT+Q3TxgoCsCGoNuNJBl2LQavnLi+jbvmrHR9aOTLy2cXerLGPLRJV3uV0Ar6ORhTzHXr8HOHXDWhLVt7sUHeda3umbd81PYtRn/CxSUwkGHZGj+MwroYTXDa+s5rubWe+4p6KW87A/78LBFCIdeAuwxI8AIMAKMACPACDACjAAjwAgwAowAI8AIfCYIUEWq6lir+JPrb7Tx3nI1bhOuQygGZMWgFdAHEtAYVkx+4a4q8OqUabzdHwo0i3zE44phHTTvO+fr54MJPd19H2mfJ788VRAivkCLnY+Jzkxto7/O6n3o4aeBpLvSckoDYNr7C0PRVpvdN2KE02YLOcWU1RKur/NdcvENlerOQYJ86JkaKqDHjT1KcIRsDSGJT9sbo4I99uAD2Kkig6rBjTf/oiKgeVfE6Q5/41sX6bTQsmyf91OTjJ1Sl4VxtuUNn6Ibda8v/vUVq02iCz/ivRDx+WM9fVlFo36ucuAnFtCkEBl++P0rRSFQsc8uZygZH7lx/e5iHtSyvJNluPHn9/B8wO9vctjDfl+bxCeDvjbRkfjN/U/29VYXqH4oV5IQXS2gAWDGrGVWe0hyp8r2Oc47o15vesnSDTTC+567HvS6MfGZt/vtVq8khi0N3oY619lf+07lvKF9RoIGE9AVJgfaob8zmDzlZY7jhhMFXTfcikEwZQFtmroOugY6RlsM0tB4ZRZleOMVaI3OyXh7fbZcxN/X3Lzszy+ieu6vykou9b7PdU8Fa0E2TYDeIuRVuOQHuzPRFelgLuMrJlxrR6em7dpCjsZjswA9eI+XOfkskVdKHxAsbYb+PEy6opgILkuFctGAEQ3lA971ban5j/4O8tUXJlXJpPCajoEks+Owc31wxklrR0fXtno3tIdn/Plps1wIXoWQdkmmUxHQlA8GbqB9NvIAvRrs2A2nHr/ikPjGUd71YwMLrvnOLiBhOQb+VKJ/4pdPLAloEsJR39gwoqFx8ptvZlX8oof+06jqdeguq4AeSoQ9ZgQYAUaAEWAEGAFGgBFgBBgBRoARYAQYgc8AASpeqLJ59/1ZLm+0WkBLruh70+dg7W559TmMPiDLfRGPigBMA+RiydycdMKX6kYIXneysd4d8KXcUjjoT27bugdrJzV8D/EwB8R21pnne71pbpjTaos4hFSdJXjU8afRseVlKJJa3V/e/3CD1eN0xUn5c4B3REQhKQixq6+6hbZbmRE9cH+dDRLQpgHRSLPgCPG2KG+Li46US0y9OnkGPXDOnBWSJyZKuPEuLII++rjxNJdDJqkgle4Gd0R9GI2N3b+AlhWketnlVwmir1pAn3TyaSjcP2UFNBlNx+6cz5OUxLDLGSEb1kHfefsDhXKMQl+fmcvBeedd5nYnLBafwxG02UK8IybxycZ677N/mlyaFDm9ZJ9Od/BcBz8iBbZYB62bWKDa2a398JKfluyzmOTFJO+MWyyBb3zjB4oC11xzK28PWhq8LjFWw9lFPtJY75aE6IXn/8igutOAbL+CBHUqoEsOmkVwDKY+6JGiKG++9ToV0LXDa+pGDJcLeVPXcDPxFwzUQVOolTpo8vGCPz8HbfFFMaE37YOIP5tuW/6rRyFr4Lp+/VT40k8PvRAGLgwcAFW39JWCAV1ZuOPO7nhoVtLfnQ6aYdf2w0YunDcT36fhyS2S2uciOvDBrdF2FEz+gYu+u7Y1vSgR3pWOG9GwGgn3tY1cdd/9/bv3YH40uSloqumoyooXTToW46OkvvKyjtbAolbfurHJJT++bJdcAJLmgv+6StQq8po8YZD1DIkvxouuWkBv3w6nnrAy41oxLrKn1TXr6gt2Yb/lYSh64dgTjuaGlyOgh3PDa2trGy2zFy0qkOhttfJPs9Tx0D9MQA8lwh4zAowAI8AIMAKMACPACDACjAAjwAgwAozAZ4BAtVDMyVognCYCOikKTU4x09jovuXWu7HAWTEwJhZvQwU0rRQ2dbj/vt973UmHLSAJUUkMN9QLjQ3iyy+99jHt86qVm5zOmNUadAgJ0ZmyWMMOZ/yuXz5CIRdV2LS148yzz5M8sXqLV3In3O6E05kQhSTviNxyy/3ZLKZJ/F8xL51R9bz2OU2DBLSugcD7yLBx2T2P1OyRMosXburvRbF09tkXON3RagH9xtSZOGUTcjIGz1a2wb1UBDTulMufB0Vw5AuGYcKxx5/slCICn+AdCVoBPema6yvLJ1Yd+AkroElN+mOPPCM4ArQUveygI+vW7AAT6AqEr7zybnPzofX1rkCgub7e5fe38I6YpTEU8DZPfvndkgKmUxmY3oHFPnlPtYBWNXTQK1ZvswshVM9i0iml7XwsFBxptQa///1reD4k8hGXGKMa2udJN9Q5L/zOZTR5A0tk+0n0s84E9MAJ+Mi9fD4/7b13aPqGzVI3vIabOWOaaSi4gUoENH6SgWTCYEQygIzGFj5YAM1Nf014dyckSPv1cGDZLb+EvSrkTCiSL5Cwa51UJmvlgt6KvcXrXFcAsyZ6FXzXn1+AWOS1VGB3k09PurpaQotf+CNoclnYQp7UPmv4ViqOy/5XJ5+vvApPPA4t6bnx0NaAuyMayvt9O9ItqyZdmzMBlFK+NP5zQrtb+UyT5zUgxrwAl/9op0eYPCa6uT2weNIlnfg2AFlFlZ7P9pTScypTKA9AJUzwK4//x955gMlNXX1/7PWWmZ1RGUnTe9vidadDGiWYZjoJHRKSEJoxEGJCCIFAIIHwvl/y0hIgQDAEQgmQmF4MNsa444K7jY3r9p2ukXS+nHtntLO7timhmjuPnhmNyi1/XWl3fjr6H+IUkgfoA+grwglHrRofXTshtLVFnn/TVJJnsUyfDd3IF0vqzb+/xUxAiCQajaDrpz+/hDZYJXfydkOhGYD+0LHNNmAKMAWYAkwBpgBTgCnAFGAKMAWYAkwBpgBT4KuoQBnVFktIbk448QyeDwT8owQ+IUlJRYp+99BJ2XT1s/cm6amASIJgNm/qFfkIEmExLIphSQ67PdEpU35BjSY+VJeiCn/8032KEmuod4tCvNEecvCRYHjMvIWrERUV4NHHp4ejbYIQSCTGuZQkz4UEIULDn++770mdeEObLNic2UW9A7rQ3ZV2u8Kc3aM445wjXFvrtlkDq1btAIAXXpjp9SWdUkhSYg4h4PKmLp78C4rL6Psuyu8HWoQgU0hNzTT6gXWuYGg60C4EfGM4e1SRU2538l//ftlM+aihT0J5+tgwWoczTvtxQ51sa3ArUlh2hppT4/fd6xCzzb+69lZJilLfZ7s9QGKfQ4qc2nffwxcuXJ3Lo/3IJ3uRGxWY240e/VwebrvtL24Xuop73G2NtjBB7RFBCDmlkKJEXK6ookScEtq2/OCcC/QSum+TIGqEmuWpXGg5gJeG8X6y5n0d9lqzZo3FYqmtGWa3NQy3WGa9OdPQdDKVkOWXbyqQMHsCRPOA9Hm/A94O+Zcn/IWoN9cS++CII97NAfQZUDAAb4rQQU+y/g2gxnhrSivo7X365jz05Aj8XbwERrbOSAS2jgxAzJEe71l28+V5LYdDohy5bJRI7LPeXxTm+yynSdzeBU88BU3JeS5pbcDb43J2xUO9o9rem/zztTkCwKsOokYYNHkegbSQdk41YPp0CHhnJfwbmtyLvjdxRfsW3KncZ5wtYVP6T9ZyLDOaaZBJx07rBQMbuEOFw49d0hJY0OZasld07nWXZ9ETunIJxDtSxeJ/tr7m2usw/pkmIRyO/LlmuDLtgb6nH4P/vSm9bBHWaqBnR9WeVT1hALpKDDbLFGAKMAWYAkwBpgBTgCnAFGAKMAWYAkwBpsCeo0AZQFPoec+9f7Na3S4FDaCdYkISwooU7u40zVZNdEspFGKUbLqkqXDB+Ve6lWQZCovh4cO5ltYJW7d3714nDYyCWqIBvxMnnohYmY+5lCZOiElKav8DjypqsGZ9xzk/vFh2R4ORkR5PiuP8ipwQhIgkxb/z7eNmv7V8kO+zSZ93zniwQWYvcJON729RpCDv8EpCVOBj1ga/KEa3bMkVi3Dyyef4/Kn6ermh0SO744mmvba1ZwcCaBNfmR01l+DMbgB0SYMFC1Zz9ihnjwtcyimmOEfYZvO8t2K9Rpi+iZ7pzMcF0GtWfSAJYb+niRpc2G0ujyt53bV/UFV49tkZ3/nOJI7z83yAJnKkQF+RE+efPzWbBUqfC2UYaHbto85QVkyMRCBXMAoFyGbh2986PhgY63aNtFnxKAsCAmi7w2N3eFyuKC946uuFCy+43KwDAfRu6TOxWDA3ZzNlBVRVNQxDVdVKBLTtP2G41197vUG8NsrItWwcoaOzcwF68zB7Hhxw0JxocF3A3R0LZMa2dR591NoPtuGpYoBa0nXclMY+mydAOSifDvgCYHBzexbjmmHtBhjbNj3qW+NxdIWFXKu84XcX68ZWjCvuPyuJXzN+L1+B0DZDAz1DrEDmL4RkYqZLXh0JqIkQRHx9kdCSs85ZtyODAc/lsOP+Y15CQw+joFVumWgAT/wDUtFXo96NYWXNAaNmrVuG4B2vcrS6AacpKZEuIc2hEdA64E05HWBzOxw0cbE3ODflWdQkvXTVRVtLaaJGfwOw8EJRv+nmW8sGHJiE0FJTaxlmCY+KPjg2MmdM+KVrr9hQKoJuZEmpVTtXZhmArijBPpkCTAGmAFOAKcAUYAowBZgCTAGmAFOAKcAU2KMUKOMfCj3bO/p8vmbOERaFpCjEHTa/W4k+eP9jlR5TdEsDBEsUoxg6vPbKHEWKClyI5yJ2e0CSMKD139NfU0uQK/Q/Kl8ppPypgaFqWkmHomp09+atVjfnCIpCvKG+7MJx5dSb/nT7Qx5fkyiFGjmPx5e02TyKEuM4v9MZueCCnxNTacjm+imWibPKvRpUZfnrAAC9aNFSSfSLQoC3BwU+xjnCAf/ITAbpMM9jX2w2jz/YJimJB6c9bYaBEgqnkxhJDJPc7USbNzgCGgDjgu2NEWt92GaNSM4muz2USu1lxh1jpjijZGLo6iqqgNkQFlfp8p/veqiuxlk/QhH5iEuOuZW4o9H9ykuzp0z5ZX290+NJCELIZvNQK20q7LRpTxeLSN3UEhSKeFwqhX3Cz5IO3b35Asl2+NKL823WkEse6RRTJoAWhIDVqvC8LxhK/ejHk/t6K4kRCbwfCKAHxD6zCOhdHZJiJcXesGHD6kbU1liG2eptN9948wAAjQdWxzOPRBNva4fDDl2RiryfCJUSoVLQs/b4Y7etXo85ADO60Z3dgX4dpvOGGQGNLFklPhQ5gHQR0nmM1oecAZOOXO8TVraGSwlPX1t4w6Xn5rKbSXsHXQzKzBfRM0BWI+0pGLBgMYwdNT/i3+R3dyfCkAzC6Jbe445dnCli4b10PA3of/mM7iv0IVLPw/TnIBl6ZUJze2tw+35jVix/19yaBFzTS9dOGTS5qFUYu64akM/DL36R9wYWp2Kbx8fmXn3hVp0O0qqTo6snk8khOH/plRkWzEI4gsZB19YOs43Yr8U9Y6y3c1x46Xf2+SdaSuu7vLHDALR5nNgMU4ApwBRgCjAFmAJMAaYAU4ApwBRgCjAFmAJ7kgKVYEhMfIcPyB951CkuBekzz0UC3laRD02ZfHWxDAb7ATTBKIigDB2+edBEzu4T+QjPRerrXIoSu2TyVKRThDcVS+jE0B/5WCUe8QIAzYC33lpIaG/S3hjhuZhTSnJC7NsHn2Cze+usEu8MOgTfsBE8z/sCgaZQqPWhh55CeAZlm4hB3Nn8Soxuq+orzw4A0DPffFsU0LfabsWUhgIfi8fG6zpceOFURYmhIUmgxcGHzjjrEs2AQsWxdiCA3j2D3iWAPvvsi23WUO0IPwZB8wlRiJ9xxk+pbYUGRjV91oh1gcmgPwqAvvjCqZIQlYRoXY1MTZbbWvcJBZobGiQ0FZHDPO+zOzw877M1uo4+5vvLlq0jLiwD5NIMPL6f+IVCV4w41CJccP41jbYoZ8dIcxoBLQgBp4RGHFOm/EIlzhsAkMvguOmnz6b5eCWBHqXPLAJ6p8dFI0ext7fX7/cTF46aupr6Q79zqEGpq27gTAWzFg3Y3gnf+MYrPnmRR2j3iD0+ZX1ry+wFC3Eb+uBDvtCLcdOUO5vvlNFinj906QDI0LjknjxMnrJ5dHJrXCl5GztC4rJTj9tQIA9CZHvoJkNbXdKRPmOS0bwGHT2w14RZErc06M65xL6QNz26OXvEoZu6+6Cb3Goi1HtoIRgW3VOEdAmWLIPW5DMxZWnK8/7o2LxH/wbbtuNaVc/rOjmBdwugTXFUA4oFuPH6Ytj/KokNn3/dz3JaX1m96hYUijq9kTbzrXcqAHqExVJXM9xuG/bdsYF3R3k6vjlm4cp30XRkF9dCLI8B6GpV2TxTgCnAFGAKMAWYAkwBpgBTgCnAFGAKMAWYAnuMAiatxafIwYC773wAeaU9bKv3y2KMs/tkZ6h9R28FRJaIP6qqaWVfjqt/8Ru/N1kzTLA1eBU5xXOhaHTM1m29JY3ARwydxF3NaafC/e73fxKEiFNMEDqZcIposkHspIN2h4fj3G5P1NYoi07/JZOnbti4bRdQtPIUfaUOQwdV1SotryzFtvRbiLz4wuuSGBT5kOKMu5SkJMWTib3XresShFBjo5fnQiQ1X2jmzKW5nFkCnTEqEdAlahdbBYjN7potxSXVS/v69H32+S4F0C55pMAnBD52003/R7cp6XrJKFVIK3paDKp7N1+1kqGXYP99D/O5m0UuJnAhTAtZmaxWxeWKNtoVq01ySj5J8d/2P7fnCv3l0wZoBt4YGAqgi8Xitq07ctn+UOXdtKS7N92XzmdzKML3v3cBz8Xqa30UtWOuS7QLD1qtyo9/fBliOQMKOZLDjnqXUItgkn6QeHqwCOjdKD14VaFQmDBhAnoQW4bV1dRzdp4yffTSKGG6zqIOfSpkSzDl0kxLYk3Q0xVwpf2uDcnEzLfexuWVgVtEh2V6xlQPXwqg8e4VZdC57kxfXoM/3w0t8XcTvu6UJx/kVk9oemvdeyTjJeGuOKJoKtOq8awDZFUcIgWArgwcdcS6kclOl7NHdhSkxrRPWX/QAW8vXQ4qMc+oGFFXWkf6jRcugHwJz+p582HCqFktgdXNrs3jYu/+/oYdPb0Y1I8j2TBwS9oL3EMfbABNAsMxRWdG1UtoKXLFpdvakvPDvqXxyLyJh8/Nk/GJpuzEyZqUhE82FEnb8iXjrXfmo+TlyTrc4rFZjhsbntkWmv38c9CToaqyCOjBw5V9ZwowBZgCTAGmAFOAKcAUYAowBZgCTAGmAFNgz1bApEqkmwZs/qDTJcfsDQGJj7ukhN3qEYXA7LcWVjBuOQaSPki+dMkKvzfO2X2SEHW7myQpLgiRe+/9ey6P0AejXwly0khKuX7yM0TRCy64HENiEcLiJArxfkBpk9yeqFPy7bPfN+9/8OFcQaNgdGAZgx6nL6+kbR5IS2kraAwkbvbiC6/LzpDABRRnnOdCdntg//0mTv35TUif0SI5MGKEfPTRZ9ASBz79/18B6C1b+xQZgTtnjytSK+31I4/8G10+MOfbJwfQugYd7X0+d0ri44IjIvFxWYyZANrjSQwbbvN4Y25P+MyzfrD8vdWDjgv9SkWmxizVUqsqiTyvXrTbecSLOf34E87kuYjF4my0hSUpaR5cUQx6PAmXK3rzzX/K0TsalSOJ/tmEPuu6XgHxgxn0bmv+Wq9Mp9MTJ05EAD3MUldTb62z9nRj7K6qoUtGZx+S0FwJJk/ZFAstjofSrSkI+jeOHfvOtL9X60bBM8Gr5QDqCsClZjRlDox3IwyAl1+AkYl3/M4PIr6+RGDr6Phbr/4b+rqhRHB2XsVHIsq5JCsAmhbTp+LtrO48XHp5eySwWhHSoiPjVbIRb/vYtsXLlwMlvCTaWq14UZdPYRrQDQC9vbB1G3zzwHkBYUnKvTXueuf8s9YXyaDSyIWIxtSXATS94VIZbP0kGnTcQAPIwjVXdI1Mvp2MrAn65x911NKOLigSkI2lka3ImVLSKgC6aMBAAO2wDWuNuH7QHLz7/nugM4O5Dcl+DEBXjzE2zxRgCjAFmAJMAaYAU4ApwBRgCjAFmAJMAabAnq8A5Y2ViEIDCnnjqCNO5u1BGZMQRiUhzNk9V1x+DYW5NMhXQ0ID2XzxtDN+MLzGLgghj6fZ42lubPQfccT3+vqwtI8CoEsYE4yvg77x3TKA5lKDALTbE5Xk4O9v+SPNH0a3J82gs/S94tqKDTOpEq6i0ZFVmw4If6YAWhKDAheQxRjPhWw23957H6bICZ4LNTb6eS7kUpJvvPFuiRgXDDSp+K8A9IwZC+vrPKKQlJwtmIHQHnU6Y8uXv4/tQ6NaBLAV8PoxIqBV4nuydMkqkQ8R+pxUnEnzUEpC2CmFBNG3/wHffvzJZ7L5Sta2KoFIaGgZ01WGRXk1tXfQSgathSw11e6Poa4ubMu2jknHnqwo6M3SaEOX7eq7C6IY5PlAY6PXZvM88OAT+i326QAAIABJREFUuQwpxED3a6TP5EWsNkwpBjDo6orYPFUgn8+rqqrr+k033WitH1ZXO6zGMsxiqVm0CI2Q8xreP8gQxDr1KkhGVvld7fFwKeDbFk2++egzaLtRNKA3W3XkzSvETmfwiKm6ASsWQ1vs9ZTvA5+zU5a3tI1e8eij6DhRUvGGSiWtHwl01w0MdycvnRhqUBPoyVN6mpKrIqG+kF8PhtRYYsf4cYuXLi0PRXJekwSECK+LxCBkwOjdvgUmTVzTFPwg5ekan9rwvRPeVosY6A3kjo7p6IKXh+prwAAsTXqoQWYb/O3/QUJ+JeJa6pTeGLv3jAVLcb/yHTWCs8klCOmzBlAgDiUFA2bNrY6AdtRZWsKe43925dM5AzXPk5qxoF28mAXHLoRhi5kCTAGmAFOAKcAUYAowBZgCTAGmAFOAKcAU+GorYFKl/m783x/vcdi8vD3I24NuJS7yoebUeATQxJOBBAgiRJn+4iuNnFxvUxRP0uVNNTrQLnnOnGVFFTJZTJ/3oRHQuYq3dDDYjL7AfELgUgKXoikQqUXD+T+9bOXq92njdNDVwSm8aPspgFZ1JFMmg0Y4NPPNt6644sr584mpLZZSDZ/w+4svvC4KAYELSAIiYM4RDPhHjhghe70tI0bIbnfTYYedjAyLPHffrxHOISOucuHoT0VIahkkLH41F+kAd9zxN0lKOsWUU2wW+ITdHpKkeC5fDn8uP+Vfdj3+GAC6WEQq98aMuQIXksWES2qW+KTgiEl8nN5OCIVa77jz3qJqZHIqDXCuYo3l/tHbDPS9qi/ltffd9+BNv72lIsXuAPT6DVuPOPJ4W6PsckUVOUH6m6gOf+Y4L8laGeccQZcr/tQTz1ED6EIBESpGgRuUXjIAXdH7I3wahlEsFu+75y6Oq6mvtwy34Ov5F18yANIaDo8cwF+ngUeZJ9nbE0GQ+Y3ByOwrrm7vUaErjzdZ+m/bUFxrvptHm8Y80+UalHJw+EGLm30bwkq3X9kSib3z21uhQAYWvZGQN4yCbqAFs06jiPECQkONiwA9JXjg7+D3v+W0fxAJaCF/xu9f4wu88Ox06M2YHdaBRjv3A2gMJS5q0JuGLVtg0pHTU6GVTb7cXs19o5Ov5rJ4IciUEHXjpUsvTzsB0BUbfGyPDnoOHrsLmsWnWuRVbeF14ya8NmcR2pXQC0clKSheanSsvJyHEbMxGjDrnaUWS60Fib/FYqmvtUQmHXlx0YDuAiH7pCVY0C5eDEDvQhi2mCnAFGAKMAWYAkwBpgBTgCnAFGAKMAWYAkyBPU6B9h29DrukSEHe4VUkDIIWhcATj083SOifGTY7fp+DLMOtnBgQpYjFYrXZvVf98ne5IpQMhDz0sXfq5FANXoeq1d7R45RCGBgrJEWhSRSaBD4xzOI88MAjZsyYT/cle1H6Zdq4VpdK5zETWFHLZQtZ8qg7PP74k4l4s+R0n3XWOZV6BwJoAx6Z9pTA+QQuIHAhnsM8ijzOhBQlJklRu933xBMv6UbZ9bVSSPlzF6B2p4RpcD/OP/9KUYg7xZS1IVhf63OKiX33O0wnSf+I43N176p6X2lBxREFKT990XByGpt87z3TZDGmiE2K2CLxTXxjXOQSDpv/x+ddTmhcpZSdf1Kdy0IRrxWkljoJV7/5t390NCqCID9w/9/IwpKmEWuBgVxNL8HqlVu/852jrTaJ47w+f8pq9UpSXJETLlf8llvvFJ1+0elvtLtp4kdRwFWhQPPCBe9VQkRxEBG+V6zy7K6WpdLznffia71UL2nz5s6ur7XU1FhGEAJ9w8239BRLvQb0Gkif44ll8VBvPGAk/IVkbOX5l6zrVdFnufKit5mIuTIdDpUVlU+85ZPPoblG52Y48fDlYxPrUqHOoNIeDy+6YipGW+sAfZhZEG03SuR2AugFMIq4ourQ5Qz462Pgjc0OhLaEfLmItxDybmhpevXBhyCbx7SfeD2hjJi+Y3tUYhmNpfcZmAPx0qtLgdDi1mg6wK8e1/TO6vegqJaNO+j1YoClDGXSWFoJJ1IsxmIbkE3D0w9Bwv7KXu4PWqR1+41csH4DtPfiQETYDaUi+mP3lqBXg4yGrcNbXlnDKBIA/a8XF1gsDcifyWRtELvaVbwVVzawroi3i08GoHchDFvMFGAKMAWYAkwBpgBTgCnAFGAKMAWYAkwBpsCeqMAJx5/idgVFwScKAZEPiXzovB9ckk3rmg5qCQoaXH/jHxySh1cCjZynodHjlKPNI/fuy2JYYIlgrI8JoAMYGFsFoAP+UQsWrDa9VskD+KbPxiAKOegrVl9Qi48/+U+PJyAIsiJ7Tzzhe+QomfS54gFNADTv8CN9tgerAbTX2yRJUY8nlcmiYUDFM2DAwf5vAPSJJ57rFBPUfIOzRxvqvSeccE4uT+I0McbT7FSlxoEcsOKIgmtJDsQy0sPYVQPuvedvihSVhZTEN0lci8vZ6pZbzj1zSj5DCu7njJXCB3yaAJrKRddpxWLpwp/+XBZjsjOgyP6//PmvdEWhkOsHirThANk+mHjYKVaru7ZOFMWg2x2XpKgghHg+cNfdD+Xy8Nf7H22wih4PWp0QX46kIqccNn8iNnrd2g8qzaHODQxAV/T46J+6sXnT+vpaDMS1NdRZhtUeNemkAnGBWLwK9j9ok9fVydva/Up3W2rzD8/p0gF6SJAviTImWBahK512OlwKOuAwLeXg0h8WI8KSpsC2cS2ZkH/paaevb++Bnnw2q1altsSWE6cNCqAJkE0XoKMLlq6E1Kgl8aZ8PAZOfkcitCUafP2uOw1VxetMkdJnejaYzzYggEYz6JwOaYArrk9HWtZ7/V0hZbNffO2xaUif8zrmJNQAL0dInwFj6fs9zXGMk5BqMmJ1HdLEtv7fT8A3Ri3dL9gxwbP9sPHrl8+DYhEdNjIlPaMVC0aeAOh0CdIaemirRTDyANsz+ChHoQQXXfSAxcJhzPlwZNDRaDSfK1b51XzI8WMA+kMEYquZAkwBpgBTgCnAFGAKMAWYAkwBpgBTgCnAFNiTFHjg/mk8p1QDaEkMqphsDONT5y5YwUlBm+C2i8igHc5AXaPy0GNPF3XIk4DCgoYe0CaDNmFqVeBjv1okAnowgD777MnU9YLuOxBA9++707liSb3/wYcisZQiez3usMMuXXThpWRLSlQp0CRtMWDaQ09wdp/IR3g7OhTjJEQEIeJyxV2u6Gmn/xj9N2hA9ZDKKgC6OqCz0t7BG1ctJ4B3//2/i+n40AO6SRTijY3+886bkskahCybglVK2RkDnD3nnTdnzc7miyaANgy0TqYAWhYx/SACaDLFQns989QbWBwNI60UvNtPbKhaIsa7AJMvmeKSYwFvqyKFRcHzxhtv0X3RV8EUgLRTLcApJ54nizGO84tiWJLDihJRlAjP+x75+7OajmMDAC6ZfKWiIJIuA2ipGVNfCuFkYtTCBUsKmPDRIJxRrYqAph0Yos9uu/H1XKmX8gEvN9xiqasdNqKuQXKF8jps74K99n0t4F+hiJ0eIeeX1h168IJt7chqqWMGSk3jgvsBNOW+qKKpu474FQn0X/4EKXlZwtkbdW1pSS7/9qEzFyzHLTuymPOwL5+jAcjkEBDgiy4c5QPSl4XOTmhtnuF0rkjGQGzMJkO9iejMfzyO6BnpNrFYxjPCnHCAGST8WdMN6OqBqT8vNafWRkJd8XBnKrL4hmuhpxf68tgjHDfUIof0iqZCLddddZOFOm8UNXj2nzAqNnuUb+M4/9YxgTlP/A09rGmv+/KFjp5uEgFdKhp6Ec8zowRaEQp5MHpK2KYnH4N46HqLxVM2PbEMP+KIo/DqQe/IlSve3QcD0LtTh61jCjAFmAJMAaYAU4ApwBRgCjAFmAJMAaYAU2CPUUArGcViqac7w3OSKHjKDFoIeNCi9wUA2N5RmHjMqZwUrmtU6h1yrU3kZP/BE48tGIiN/gMWu3rzBUqfiWUHTR5oEqShQg0F0G7XyDPPuCibhULBhL/UjYGGZA4tY8CS+x98WHEFRKdXFHw857ZZxen/fpFssRMA/dDfHnfYvCIfEUgorgmgnc6IJIeffOr5gdxtQEWkU2Vn58oK2tHKt/7PgcsNSCTGKXJC4GOK1Mw5wgH/yPPOm0IjoAlvq1BdSsqq3wGWL19x1JHHOGWXxxf427SHs3k0wzUzOuoaRkBLQpi3hyU+yTfGXc5WWUj984nX072k7J3h7P6WDpyjzhvnnXdePNbkcSXtVp+1XkrE2wZtVf5KSv7eyT8U+YjIR3y+Zrc7qSgRpxRyuaJ33f0Q3pPQoYDtxdekSd+rAOgmydnC2SL2hoDD5g2Hmv/1r+mEQSPBIwC6gi37YaS5pFwa+xiggK4dsM84WwO1gLbU1HHPv9x50gmLgu45LmHNqKTmc64+5Jtr2zvK6DmHZy85QXYCoPHENk9hehapOry3FCY0z4k720f6ICAvHdX28oJlaHZcAugqZPuK+YKu0TO2fKjoMCaZCDt6YO06mHTk+qbo5qg3F/FoXnFHLLDwttswsLo7DapeRN8O0ig0f6bVV0oAAwpZmPEiJPzzY66OVCCdCK4454z3u3ohR+C1SswxdgegSYE6GZBFFebMgYP2WxB3rwnxa8dEFzyJBjPoLo1Oz4ae1wq5EnanaGBQdpEEU+MMaDl0moaFi2B0/KWQfLfFEicAerjFMuLqq68ZcEQ+7AsD0B+mEFvPFGAKMAWYAkwBpgBTgCnAFGAKMAWYAkwBpsAeoUA6ncU0ZVn1Rz/6qSR6E/E2yqDdSvR7J5+r63DXnx/hnWHeGeakMCcFG+yyKAdmzVmADNTon0zT1f7H3ofoQ7GUDjCilsOUg0JcFJqcYrPH3XbkkafRzSv8Gv2dqzwBjGwhj+0sYCY90wdZB/jd7//klEJud5zjvCRWN3Di8aejWS2+KDor9QNNAx68vwygJT5eHQHd2OhVlEguD729qukEUs3gBs0P6Fw1Ly4jM3NzsqEBVqtit2Pwr1NM1Nd5amqk4447q1IIbadeKKiFPLWfrawB+OdT//L7wm6X32YX3J7AT356YUGlvStvo6rGM08/71biDltQ4pMOa1gWUrb64G233Jftg2KehJCaIK+/4P65vt6c+WXtmvdPOfm0+jqHJPo5u6+hTpbE4I2/+QPGfJZf/XNgwOSLr3IrcbeSFPkIx/ktlkZFiXi8sXvumZbJGrSlNDQeAN5bsb6t7QC3q4V3JASuWXQ0i1xC5GIiH3K7wg/cP01VNa2kGQaKkMvRVtGm94flVprBPqsUICLd+JvrSTY8+laz9z5T4q5/j/R3x5S+lsjm/fd544PNmEcPTzGa4Q89yOnZQe0rTBcOtHKmI5gOx3QW3nkH9p8wO+5eFZNzo6K5VPT16XizBjpLpRyGKGOYcCWa2qAOGLR9dLhs2QLHH7s66lkVc+W9XMEv7GiOL7xqandexcjlMrCunDRo1FwxqM7ncGVnOzx+H8TEeSODm4PC2oiy6jsHLEvn0Jg5T4w7SqCVQC1fkYZGQFekUg3IFGD+Qhg/alYytDHqT8cCK385dTsYkM2gOCUdUXgJrZ/zSJyRRyNhx1PUgEwRutLw/iaYdMTCpPLO6OhzNZa2YSOo4MNefeX1Sj0f6ZMB6I8kE9uIKcAUYAowBZgCTAGmAFOAKcAUYAowBZgCTIGvugL5HIanaiV4/PF/8pwS8Mck0S/wHp8n4Wh079iRHzXmoGoAzTl9Z//gAtrrjwugVYyPxNfItvHVALqh3m+3B959dwPaNejo30o+BwBouiPiZ/LSDVi3bsekSac2NnoFISKKUUSfUlQSg/Pmvlss+wvsBEA/8Nd/2K0+kYvJIsYjVyKgQ3aH59TTfgQA2ZxeDdMrTKzM48yvtBnld8pIq9/7NyebGOB2x3kuxDnCTjEhSUmeCx1yyPEVktwPoPFYqFDIY2JHowTX/fqmYCDudvl5TnLKHl6Q73/wIVMEWruqGosWLrdbPSIfiYXHC46YwxquscjHHHm6VoR8lhgL0LYNaHT/F3S0JR65j//jmUS8ze+NOxrdkhB2yTFZjJxw3BkIhCvY2TCMbDabzeQLee22P/yf3eaqGSa4pERDnWxrdEly2O2JXnf973t7MRub+TINed95Z4VTTChSm60hgQB6IIO+4frfm7uoqkrSM9KmV7XA3ILNmAoQkV564TmCQodZLDWWWpvHffLY8Pw43+G2Lh3b/PY7c3FQli0yzCjzXQLoshMGAKRzsGkDHH/kstHJdQlvh5vbmAovu+9eTNanY9xxtghF6lNhMmgKoOkTEt1Z6OyFC37S0RJdk/KrCS/4hY6Id/FVP0/3ZTETIBreUDNx2rgyjca+GRUznJf/DU3KqpRQbPX2jYpsjAdemDcXI5FzAHkMTAakzziRW2LYTYTgZPyUNdIB0gVEyQsXw7gx05PhdbFgj8e/8tyfZCnrxgyDxAYEw6jRW4gAaCy8VISieRcrnYXLL+kcFZ2TlBfJDXdbLCNtNhtn5231tg0bNtDKqustV7+zDwagd6YKW7YHKmD+3Rw0swd29XPp0iAZza+fS+WsEqYAU4ApwBRgCjAFmAJMAaYAU4Ap8IkUMB1LC3mtpXmMwy6R0FeX3eaqreGvvPIGSp/NCGg77353+Wp8XD1bhjIUzVRD2101pKAWKUA+59zzRTFI8hDSCOhWq9U7deqNNPS4hNRpcAR0rpgz+TUA3Hffk5HI2MZGv80aIDw3Iklx3uG9846/mqh0pxHQ99/3GAXQijNZDaA5znvHnX8tR+zSPGbk3fxpN2hmQB+r0XMZ9Zqbkw0NaG7Zy+mM2awBl9JEkh+GBCFUKaQMoCl9pgt3bO8584wf1tXaFdlvbxRkycPxkii5t25vR4xIsrrRdGeGDj3duWh4pOKMh/yjFWeyodZjrfO6pMQLz83KZQD5crlVlQqHfG7csOPaa26y1ku8w0u5s63Bzdl9AV/zwvkrcfMKgNZKmqri9Oyzz7mUkCgEeIffJSUkIeyUQoLou+jiK7M5PZMt4+diJZQVRwhhiw9Pe94lj+LtLaKj1WTQHqXF1uBWpPDJJ53+7uLl9L4I8QOhTWcAesgxq16AR0fvbN9aXztimKXWYqkd0dBYU3NQW3BmjH8v7pu+bDH09EGeJh4078ugP3iJelcQNG1UPXOAcLkE0JmB7e1w1ilboq7VTb6+VLB7TPOaX1ylp/NIfjO6oZMIZuqeQe8eUfhLfJLRH6OjD371q/ao/51UIBfzQEuo0BxbctWVeVVD+oyjxGxPJQ7bKGhqXqWJN0savPkaTEgta/PpSSe0utXW4OInn8TO53Q0ACmCUSzTZ41avmgkkyHiZ7T3wJdOHKL7irB0Few1dpZfXpHw5+Lxzd84bu6yHdBTgiKWBCT+HkolvPqUdB2vQYZehM4CdJZAy+vQm4VHH4EJqSWtnpVjovOE2mstloTDLtrqG1KJGK2L1mtWTRfu9J0B6J3KwhbueQqYfw4Hzex5Pf18ejRIRvPr51M7q6WswEe5yjOxmAJMAaYAU4ApwBRgCjAFmAJMgQEKVNji6aed63FHJdFvt8n/gblud1wUwyPqJFGKmAD6qmtuzOT1nKrnS1XBk1XEthKjPKAG+qVYLNLo3Rtv+kMFQMcxHlZOBAItw4bZH39iOsKochB0VSQkQa60kBdefP3QQ08KBcdbG5A+i0LSKaZ83tEN9d7rf30rfWC/QtWryRYpzYD773uMJiEcBKBFMTj77UU0BLIapps/7QbNDOjeRwDQ++x7sKLErFav1zPS52uz20OSFH/ssX+bYJcWWCC2E088Pr21ebwoeEhmSI/HExAEWZTcf77nfkrTaAsLBQLpDMhltKOOOFnkQ9Z6tywmMLkfH3dJiYO/PWn71nR/EPSARvd/+dP/uzfob/K44pzdF/S3+D1NijMucKFYePQLz72JUeFpihMxIlUraVrJ6Orsi4abOLuroc7pVuI+d8olx1yu6LHHfb+/XHIoq79qOmSyoKrwpz8+IjlbyvQZg6BTIpfg7eHhFs7vTQq853e/+0OVMQhNpEijZKvLY/MVBQiANvTiuDGjMfzZYrHU1tXVjfKLtzQH/vHMk+i5USyhxzqON/O06AfQ9GmDyoWAoGea1q9owNSpq6LK/LaA1uTra42v+d4pq/IaAcekMA1UPGNVRLxonaFjOtKSrhcBsgDdKvz1QUjFZ8S8W5NeTax/f2Ri7dSp2Z4MFEhD8LSk7SkSEk4zUGpQyGJAck8P/PsZCLmeT3k6mtzQ5DGSnjW/ux6zDhqV2OciqEXMkaiWwKA3OQakMSTFawB5HdZugMMPnzkyvjnpy3mcayfst3jpNoye7jXyReguQVoDRNgVAE0wNJo+78hBtw7QkYZ58yERmh4Xl8b5BeObnnaLF1gs4dp6h8ViuegCzF+Kd2oqr8qx2eUnA9C7lIat2FMUGPR3c9DXPaWXn18/Bgk46Ovn146vW034MA65p07fafcZgP66DQPWX6YAU4ApwBRgCjAFmAJMgf9WATM21oAnn3pedPoFIWBrdHGcl0x+zhF0ynGXN9Xo8Cme+Kq1m0sk/JaCLPP3zy6bUQVntZKhqpqhw6aN2zm7x2HzCpxPEoMiHxK4gMD5BN7zq2tu6O7KogcFIVOGhg4SeglWLt/8h1vuPnD/w0OBVpeUqqtx+d2jPMpIt9ziktBK+Korb8Kn7nXy2H45+raatJUB9NNPvUCqC7kkhJ7EgDgi8iFFCufRDZu8+kFcZcnH/hwojAGnn/pD3uEPeFsFR0QRmxB/c6F9Jhw6c+a7ZtnZHLz40syTTz6nvt7Z0jSO59xOyWfnZF6QGx3iNddeZ25Ju6mqmk66rJfgumtvcdi8bgWLlfg4TkJUEsLBYPMzz7ySyRrpTBnoqwREljR47bV3zv/pFW1tBzidkcoUk8WYw+aXxYjf0zRzxiKEg0BiqCt157IFrWSc98PzRcHj88TqRgh+T5Pf0yQKAZcSWrJ4NW1bZfNdfv76mtsc1rDDGhXsCcGeELmE2WzO7pGdgaOOPHbGjDdpUkQAPZ2hGRXLvdhluV/fFXqpmD337DOHDx8xfEQD8eJokFwH/Wv6pvZOKGkE0FaTfMKsCWqm6Ld8ztA7ItmCkSsh1r377lLY+2zctTGhdEXlxScc894H26GrgNyWMOf/AOoCqMSwHdmxbujZEmSLBvSV4IMcPPoCxFNzU+HeUTEYGc6Pa1p32eS+bAnpcyXtZuWAETuPsvE7Och9PZh1sDU8qyWyOeBsD0npUYkPTjlpUZrcpMmWnTeAuD9r5B0BNNJnajBC4ql7unHcZwqwfiNMOmp1IrDGL+yI+7eMbH15/hLowthnUBEtqOSpi/IFhAZf4+0o0LKQ7TOM9gy6Px+43/Im/6bRnvdHul+6784eiyVlsXgslkaLxfLPpx+njwlQ/lzp1e4+GYDenTps3R6hwMA/hHtEl77QTjA9vyD5yT+FfX2ZL6h6Vi1TgCnAFGAKMAWYAkwBpgBTYI9QoAoQpzO66PTzvE8QAiZ95hxBTog4+FCdVbnltjtM+kwh7Yf/HKoqn5q6qipmKzvx+DMFzudoVOpGcIieCX0WeI/Au1xK6OQTz77g/Ct/dfWtP/3xz4858vT99zncLTfJYkIWEz5XK28Pc42IWetqXFxjSHEm/3znY+leYvtKALTJjyrRlRVqacCsN+dLQljgQoieTQAtBPbd+1vUeflTOqgDhTHgjtvvc8kxgSuDb5NBu10tZ5x+8c+uuOmHP7jsoG9MdLmiw4dzihLhObejUXFKPqfkEyX3+RdcQqOeafMo5C3TdgLoO3bk7FaP3eqzW30mfZaEsN3hEcVgIjnq+6f+4Ne//t1ll1995lk/njTpVEWJSVKUThX6jBja72myWz3jxnzjjdfnU/o8VJBHHn7UpfgU2e/3xm1WxeNKKlLYJUeuufpGFR3FYWgqRbOQbFrXS5BN4xG56sqbFGfSLbf43aMkPmkCaJEPcXaM/pac7mef/TfeidDNrJKVQ2mWyGaqFHj0kYeHDcMIaF4UbHyj7PcQhxxD1bRytJZ5PvYHQpdNdEybFR2gN42FLlwIYe/To2Kbo8qOsLRyXOvLq1ch3e1W+9SyWwdx8EC8XUlIWgnp78zBm8sgPvZVkV8fkvTWoDoyvPKKS/raO5A+k2hpHL+kUvpeRtpIpjXQi7BuORw4+t2ovCkkdcd86ZGp9tFtM7Z2Qq8KOXL1MXMemjNlAG26ApHBki/A5q0w6ah5Ue+KqKsv5esc07r0gYewg3m8QAwImC6HL+ugqlqmkM9oaDRkYJZFOOWUJS2Rzc2+niZp1kO3w09/co/Fwg2zyBZLY11d3VuzXwfQPzp9BgAGoKtGLptlCjAFmAJfbgVmzHjz1ltue276C/RRly93Y1nrmAJMAaYAU4ApwBRgCjAFmAJfPgWqEJBagkMOPaZCn70ch+HPFEBbhjtHj/1GQUNqZe5BO0NR6y47Zm5NiTVJLKYW4YXnZ7jkiM9Dch5WAWhHo8LZXS4ZSai13s01BhRn3Odu5u1B3h7kGgO8PSjyEUkIc3af39MUi7Q98fjztPZqLFtpDw2CrlBLAzZu2CHyIZGP2Or9giMmOCICFxI434/Ou7hYKD9kWdn3v/kcDKCXLV0r8iHeHrRYeHtDSOQSijOJ+NXVYreHRCFutwcEAXMhNjZ67Q6PUwpIcjAQjNs5+YILJ+cKWjeFgqRR1T3FeRK9OmXyNdHQKFuDl8Q+Y/izJIR53lczgvd4Ek4pxAseXvDQ2Ha73We3+3g+wPMBQQiIYtAphZxSSHaGjj3m1O1b02XkW6muwhURLk865gSr1eF2BSXRLwoBRYraba7jJp1Gd9EoK96peBUXDdpgAPjtDX902PwuKVWB5lFycKNuJe5xR90u/90vlI5pAAAgAElEQVR3/YUB6J1qOXQhul8A2O12Ev5cfnt74fx++ty/Dx2flNTSd5VQ1gxgYj8jnYW5s2C/kQsSysaE3BeXd4xrXryyYgZeAHT4pkbkiHD1HOgZ0AqgGWoRejKQKcKmHfDtQ5aHQhtTAWgNwPjklp9dVMhkoGggYS71hxqbF4iKWYaODXl/ORyy96Kk570xcTXA52VufTz+6uy50JmFPg0HI+YGNPABAJM+owUHGIiTaYcgoyE3hs5O+P7xayKud5v9ubC0xet87R+PQS8Jo65EfffrUgbQhlEsaX3FUlrDQd1dhMkX7WgOr4hK25s9a6+8oCPfC4oywTKcqxnutlgckiR292xnALpfRzbHFBiggHmamzMDVrMvH1MBU0Zz5mMWwDb/GAoYsHrV+pNPOlWWPC6Xp3ZE/S2//wNj0B9DQLYpU4ApwBRgCjAFmAJMAaYAU4AqYP5+IYD4xt/+j93hsVqVQRYcohT5872PmJngKjAZi6jA3V0IOrB83Ig+Jo/w8bb6OofsJOYblQholxKy2+S6EQIx6EBSLAlRxYmOxrIY4xoD1noMuRU4nygEjj7ypDWrPjA9IqqxbKU1gwF0LmMIXEDkI/Uj3NUA+rc33KYWQSNgrLLvf/NpAmgiD9Hr9FN/JPIRkYvVDfcQBh1TnEmaQZFzhDlH0Odr5jiv1erm+QBl0HZOvvqXvykSq+dsnkQXk0ZV95TOU/Pob3/zaIELUPMNBNBikJQTcrmitkZXfb1gtUkc5xXFII19FsVwhT4HnBJO11x9o6FDPqfnMhoSeRJerZcgl1XxWGvwxhtv2Wy8KHhEweNoVEQhIDtDkhh86onn1CKUvVN2rZxOMGEuU0Z/hRzc/qcHFKmMyyk0l8VYwNfsUkK1I6wvvPASA9C7lnMna04++WTKnkfU11mGW86/+EICbHHLip8JPWtNUktz/5VIQHBGBw1tkXvh1GM6xoX7kk41yneOS6597GEo6oh2uwvbdShUAegSQB8YPaAXQMNUhwDQ3gXHHrugKbox6lFHhyHp3vCzi9SuHehzoaEf9eDxS+5qlQG0roKWhtOP2dbi3RBXtrWE1KCzp63p/T/fiz7O5XhkXcsWsqqmmQkPKX0uA2jiS4OmIzqGcp96ytxkYElLMNvk6ztwXPsvrurLmmY7VD96jSLzFEATrk0xN6YofPBhPe6d3RbonRDbevqx20GDZ55ebrHYLcPqhw93Wiy2QMAHUDCMSpg5LfbD3lkE9IcpxNbvAQoYoKnQvqP3hut/f+Lxp/7qmhs62vvwNtHQ/ww+x85i8lS1/Edo3txF11//28umXHnvPQ98jk34pFWRfyYMHab/6+XDv3vMpZOvnP3W/HJZpqSftGy23yAFcllVVY1surT/ft8Kh5IOu8g5nD5vIJVq1kpa1R/UQfuxr0wBpgBTgCnAFGAKMAWYAkwBpsDOFDB/sxhoFPvGm/Pq64VGuxKOtIhiECNkuZDV6p048WRVhVx+ZyXQZVUQZ8BPy6ry+5frkO7DQNnTTzvX7Qpzdo9LjtTX8qLgEwWfJPolMeiweW0NXq4xIIsxt5IU+VB9reSweR2NbrcSVaTgH//3z9TTYzDNog/Vl1tqgmDyneTrO2C/QyUhip4eQspWj37HAud7/bW3NeIFu+sefqw1ZoRpP59fMH+5IkUbaj1uucXnanPYgrw9LPAxuz0k8DGnM+Z2J12uuM/XbLN5JDk8sm2vF158Y3e1Em1p96mB9ZzZS9ta9wv4miUh3FDn9HuTihIRxSCFzm53XJLRlMNqVWyNLkkOK0rE7nA5pUCjXZqw1wFPP/O8riFlNietVJ4nxhoYXnrFFVMl0SuJXpIj0e12hSXR/91DJ+HB/SgvevuBtJzSar0ETzw+PZkYJfAeRQoLnI+z+9xKVBR8hx4yEXtnGLpeMjBqmqr6Uar5mm6TTqf/8pe/1NTUWIYPMyc8dph/EFQV7yJUXuYQpX7OiISKBlJmPDFP3jAu3p4UtYgtOya4+bqrs31ptNkgp0hRBw0BNB6PEsk12AOQMQwtR7IB9uXh7LM+CLuXBvl0k8cYn9h21WS9VDDvVNHbWAPO2jKAJi1T++BHp23ZK7kxyG2Pu9VUIJcIrLl6KnSnibczaZ6m5cFQDa1k4LAYPAFAL8lhqOlww68g7Jof9+2IedvjnhUnHbsmlyf4vKwC8b82qsYumdWJHUiHWsgDTJsGY1NLR/uySXHDCYe9l+7Cxp519vkWy7DhI+qGoQF0/VFHfZd0oXqUmlee/itARfnyJwPQgwRhX/dEBcgZdf2vb3UrUd7h/c+9yjGj9p/15ny0YTL/OfiC+r1p49Zzz/6JLPkE3sVzkscTGNk65vnnX/yCmvPRqiV6vvLSbL836Wh0K1LYrUR/fe3NuPMXredH68BXaatiAS/ff/zfu0LBlNsVVmS/xxNwu708L65ateqr1BPWVqYAU4ApwBRgCjAFmAJMAabAl0EB8zcL+V2zbUeP2xPmODfHuWvrRJ+vuaHebbP5Zs9e+iGNpeXQjarL3MW8WsToWjDgmqt/Y20QbVbJ740T9OwnGDogiUFZjMhizCUlXHLMYfNKQliRwqIQuGrqdevWfqCVoKsTQ6l2OlVaa2IgsoD08aILrlSccVlMNNT6RC7m9zQpUnDtmk2fXvhzdYRpGT/1dGdAh2l/e9olpRzWMG+P2ur9XGMoGBityClRiPNcxGr11tfLdrtPFMM/OX/KB5s7K73YxSfRlnbf3GLt6q3773uIxxX3eWI+T4zcRfBxnLfR7m60uznOSz2+6+udghBQlJDo9I8dv9/tdyDNx3ZX0efqebq2WNC/9c1DKICuYGhMHfnA/Y/QDT78vTIeyjFwZAddgzWrN5x99nked9jRqHhccUkMjh97wMIFy2jvdF1nAPrDtSVbvPfeexgBXQWgp02btltv4rxBbDdo+cU8TLmoL+FbMjpkxIXsKN+W807p7e6gwcug4V2qEhkjFEDrOhQ1dMXI5XVMWtiXh6t+0dUUWTomrjZ7CgnXminnp/u6QMdTjxpHV0bA4BMX68+l4bKf9o1LrR6XLMWUkk/IuvlVEw9d2d6OqBvJd/mEVjHgGgdo2TPDxNAlMPIa0vZiCa68fFtrfI2P3x7x9Prl5RMPXt7bgxy8hObPBnGuyQBkyhY2tP/kEkEBdI8Gby+E8a0rA40fBBvWjI3MyXTgRu+9t8kyzDKifoTFYhlmqR1mqb322muI8Uf1KDWvPAxAU2XZ+9dTAQPeeH2+39OiOOP0gaagb+R3DzlJUwkw/SI0obHPa9e8v8/eB7hdQZ5zYyYK3uV2+TlO8Hh8K1es/iLa9dHqNEBVYWTrAbW1iktJco5gfZ2LcwRnzJj/UW8Cf7R62FboJmaAWoSTTjyNs7sUKeh2BRXZqyhueyP39ttvM4mYAkwBpgBTgCnAFGAKMAWYAkyBj6dAPw4CVYOSDvsf8E1ecHm8EY5zO50RSYrf9Ns7SAAloT/9pdM9K9+rvw2dr15S2QMAshm0lXj+uVePmHisIiN6puHPkhgUhYAoBAQuwDv8vMNrt7naWve57tpbNr3fDgYUi6VCAcM5Tc/WQTOVSkwMRBYQujR3zhKRj8hiwu8eJXKxeHTUpZdM/VTDn3cCoLUSsafQ4cXn3vn2QSfYG0ISn7Q3hHguYrMG7HacEcVowD/yRz/62dy5xG0XoLt3NzHnlS7SyCdSZ7GAjzurRfjDLbcn4m2yM0DDnN3uuKJEFCUkyUGnFBCd/mAo5ZQChx426a677y8RRJYt5DEItuql6/ogBp3LqiNbx1QDaEX2jx2zz6fyy7dYLC1cuPiW3//Pj867+L57/r59a2+xUIGU2CoWAV11xHc7O2HChGFVr3HjxpUzEA7ai54ckNUhXSSnRq4TnngAoq45QXFrXEq3+DadccKGjq24m1HOOmiOCATQmBgTySuGPvdqkNPh4Wkgc3MSvu4x8cL41LopP+3sM/0u6EWAVETKw+/m/SM09+iA//0dhOSZzYHumLcUdWtesWPfvdYvfg860ugr3dGJls+IonUVjac1jbTAqMbQxBIaerJwxx8h6p8Xdu1Ihg2XvKWt7d033sSO5MpONgVEzzjlCBkvN8scyVoJVq2C5vjMuNyZFLd/Z8Li9xaV5bvl1tuJyckwi8XSYK0bXmN5++23SXQ5A9CDRhj7yhQw4PTv/0RwRGjSA1lMOGxBt9w0/dk3zJPt8xcpnyuecvJpktPN2V1uV1h2htyusMMuyZLPpfjmzV3w+Tfpo9ZowEMPPS1JSbs9ZLeHQsGxkpR0ionzz7/yC9Tzozb+q7Vd5Y+CtUHk7B6PKy47Q7U1DsnpDgbDCxcu/Gr1hrWWKcAUYAowBZgCTAGmAFOAKfClUKAKDBVVY9nyVSPbxlptoujEaNnTTv8xfXA/nanOLmfuU/kfnS6g/Rk6X72k0mf6dCOyLR3h7Fuz5l37qxsnHn7cqLa9aSh0LNL6zYMm/uiHk6+79pa3Zi5CAkn8JGkBWeLkWsVLB8xWKhkIoEmEr6bC9b++lThvhGQxcv6PL/tU3Z9pzWa9ZcgHgGi43PI+mPv2yl9fc9t5P7j08MNPmjTp9LPOuujCC6c+++xrxSLGivb2auVA0/5Ub5UOfdgnjStXi+jj/MzTz198yc8PP/y4aGxkPN4WjrTstfc3jzv+tPN+dPHjT0x/f2M7RqUSI8yCSmJChwJohND4otWqqnbwwd+VnG6TQTfUc3fcfk8fzen2YW0btN6kotlsls7TinIZDY9IJUIOISUD0IO02+3XBx54wOTPNTU1Vqt17ty5JIq8crbSWyQU6UNeg2IRoFCCJfMgJE1vCXU2+TIp38ZD9l+2cQP0ZcqeFcR2Q6+OgNZ0yqC1ggbpErw9H6KBhSGlNyhvGRlb/vPL0t1dCEUMjDgmzNm0fi1/708ZWCjBY49CIjwv5t0aUrJSY7dP2hqNLLrrLxg43achdsYXBdB4vygHJZUEZBvYCAMHiUYsRDZ3wt3355oTs5OhzqawGgt1JZqWP/gI7pqrnIMk42IOjAKZKRAGTconSF3VIZ+H7x2/PSyuCTduGxdZ88+/QyYDKrL2XDLRYrHUUqNtu6OuptZiGFoRJWQAmh4k9s4UqCiwefN2TPvLxejE28OURN/xfw9+gcB03twFsWhCEGTZiUkMyMNWEd7ht9YrihTs6shUmm/eTN7lgwxVW37ms9TO/8QTz3WKCV6M82Jc4GMCH2u0BQ8++Ljqfzo+86Z8bSpYMH+pJPoFLoDpqh0xgQtJojeVSn1tBGAdZQowBZgCTAGmAFOAKcAUYAp8JgqYP7HS2eJZ55zn9gTOOPPc6h9g5gaVAMaqZlDEvDPQXLXRl2CWtFDXYO2a91euWLt2zSZkYGYQ8afcQPMX4ccu19yzSvOPXcjH38GgEI2kU9Oq3g1qIlwsFq+77jf2Rk4Q5NoR1rpa27ix+1J76I9fF93DZHb0KyGkxCe6Pzi2DKCr4OknrWzP3s8E+tu2bUMbaPKqq6urr68/4fgTBvQdjzNCV60ARa1QMKAjB7MXwei9lnp9HyR86bC0elTyuTlvEzhN6CyGHWMQtK6h50aRekDjzQuDINw8rFwG++/3jtu5MhroDHjfvPyKjlyebIrQmHBfenEwRzY2yOjsRdSTL8BTT0M4vjAQSocCxbC/GPH1edxvnfPj+Vt7IQtQrOBrbAROOuhF0PKYMbGk45LyaYwR2Q89BcHmt92eZSH/1oi/I+ife/kvt3eptBEVGQxiwYHuzypARsc4aHypKvTkYEcOLr2y1Bxat1c4HXG8eectUCIIXQd4+umnqbBleestJ518tK4XNczdaPbtI521zAO6cjDY5x6nAL0YGYbxyssz+gE0H+HtQcUZ/09a4Tv+7/4vEEDPmjVLEJyS010B0DFZjNkbAj5384H7H1YskOtN+aCYZ/UXeZAKhQKVNJsvBYOttbVuTojxzqjdHuAcQacztv/+h5oN/UiXny+yN1+luh+4/xGXEkIA7YgI9pTgiMmS74wzzvgq9YG1lSnAFGAKMAWYAkwBpgBTgCnw5VPA/P1Cm1YsaTkSpWwur/pdM4Q00wVDFn/5elluEdpLlAhAo1GZn0lDhypXLdPQ+f5GDN2zf91nOLcrAI1CkRhPTGR38cWT/b6gLHkkp/uhvz1Gm4N+iR/7NbSXDEB/bBF3usOkSZNqazFKlwJoq9X6r3/9q39LCqABjEpm0a0dsO+33nR613oDhURga8z38msvo+cySdJXUgmmJfS5ROgznjl0QuiagewmOP6wd8e2ro2FNoWDCy/7WbdqQB5310pkIpCYHG5aNV5K8FiXAPJFWPou7DV+TiDc7fVDwA/hQFYW5x/0jTc3diIYzpdrx6rwhSXoaCGPADqPAFoD9J0ByPbBU/8EJTzT7nrfF2wPhzfHoksmnbB0xWboKlV2N1UoX6w0Yl6NttFo+EkaetvdEE8tTbi3jPGvOf/UtXrFRUTXYJ+996sG0BaL5c9/+SNh6GkGoE1p2czXXYE8sbrRStoNv7lZEoOSECVTmHf4FQmTOdxx+314JpdPws9NLrwG6Xpp+fLlsuRyKT5Z8pEI6JgsJnh7OOgbeeNv/gdb03+/0/wr9bk1cicVZbNZ+nzQwkVLGxpdohQLhsfI7rid89s5v+yOHjaRRUDvRLf/ftG5Z//E740PAtCPPPwIvSf/35fPSmAKMAWYAkwBpgBTgCnAFGAKfD0VMH9o6QAFtQwUqxdWAeghCpm/JSs/3AbtSPY1lw3Z/XNfQAA0trU6G96n3Qqzv6Zy1TINnR9cP91/8NLP9rsJCDE2uXqisKBQKOi6/uorr995590XXjCZtuWj5W8c2t+h+pT7NiD8ueIT/Nn2e88q/e677+Y4bvjw4Q0NDRSYHnjggf1dxIOs6aV8Ia8Vi5DLwvdP2RgJrgz7i83xXFN85pOP47Y9OSii3XKeAmgVPS+KKi4p02c8fgh/4cwjFjfJ7yTcK4LeGVMu78sWIUsy/ZkAWiPMGBFt+fqAgdM6YIj0vLlw6DfeC3s2hPylgA9CXogGt48c9eKy1dBVKDs0m/7f5RMJK9Yx/JlGQGtQKui5NLwzAw4cPzce3+p0dUvOzqbk5u8c9vam9rLTc3/3B85R2+hykQD33Q+j294LyOv3adp6/MHLt2/ErbNpfH/t1VmD6HN9w7COri0VAE39QWiw+MA6dvaNRUDvTBW2bI9QoKe7jzxQoJ526lkVAB2WhDDv8CpS8D9Wy3fcfk8/gK780/DZdx1Pc7VUKBQKI0eO8ngC1QDaJaUkIfrWTGL2Xm4Sbl+ZPvvW7boG8/GWaY/8Q5RCsitpFwI23t/IeTgx4A0kjjj6JLOh5r8buy6PrflwBfBvG8D4cfuFgqlBAHrNmjV9fTjC2YspwBRgCjAFmAJMAaYAU4ApwBT4ZAqYv1+o7UZJB1XTSiTupnrVzguvpotkC3MXc6byO44u2Hkxn9tSBqB3IfXOAbSO3tJ44PL5sl9zJcQN0um8qn4UglA9ROi8OTQG/2JmAHoXR+djLI7FYpSW1tbWUgz96KOPVu9PI+q2bYHLLtw2vnm9y77J4+hwCfOvu76QKULegLSmq5BVIV0FoM1oaOL+rIGWg8t+uGNCeFFSWjoqsvDKK7oLGtJnDJnHqRwBTaKnMW6ZBD0jwcY5A7ZshUlHLt1rdG/Mr8UCEPJD1FdMRJY88jj0lSCjQU5D2D14oJiDlK4rYezzmuUwJvpii399IpyNhAsRf9e4McvfXgjtGVrCLocoyaOIsdiqBovfhQljX034N4yOdezV8uaWtZBLQ7GgFwt4BrS2jLVaG6sZ9OETD6HBkrperBhUMwBdPcrY/NdIgQF/2g0dg4332/cgSQjT8GdJCAucr6FekCXfo39/qh9Af74S5XJouHPNL6+1NwqKFHTYvLw97FFGilzs2KPPNDR8uqLyGnzlqSz/Yj51gP/53//jxAAnhsgUoAC6kXOdfOq5X662fjEKfZq1qpqxbUdXMJQQxSDPhXguxjtSPBc77JBjaDX0obBPs0pWFlOAKcAUYAowBZgCTAGmAFPga6NA9e8XDQw67Q5ADyWKdAlRrLo0Oj+UI+3p0lZrsCuxqpd/GfSobk+5/dVx0Abmgux/UVJMQ4X6l+58rrrkofM734ct/cQK3H777RSVmn7QFotl+/bttEBNh+5eNK64/3ZIeRY1+3e0BrqT3vVHT9yQzkPGoN4XGRW6VeilUc8VDE2yAuYLmSzoeXjgTmjzrxwX6Wj2zT7v9JX5HDpv5Mv02RgCoA0dXS4yaJ9BEhge89332xLdPmd3QC7FAtAULcYCqydfks+qyK9pqHX1WVS5kpBriQb5HoKKNNi8Ds44YYPPvijlykRdfWHvlnj43YcfhqyG5ZAUhpWklkMFJbc/0nlYvAzGtL3WFF4TVd5vCy9482W0fi6htwe+pk2bZrFYhtdYLMNQ12HDcWbZsiXl1UjTqltaWbzrTxYBvWtt2JqvpAL9pycJf8Y/FcFAFAE0H69YcHgdjYpLCcx4fXYZQH/uPS0UCqqqvv76G6LocjQqshgRuZi9IWRvCMx4beHAP3Af75T+rLuiA1x+xdQKgA5wYsAh+ByCz+ZQpvzsmi9XWz9rLT778ks6vD5jttsTFYRANYCeeuWvsxmSFOCzbwOrgSnAFGAKMAWYAkwBpgBTgCmwpypQ/fvFBNAa8agwVw3o+1CKSJeQjcxdzJmPC2gG1PWV/GJ2nfpM70ovc/mXoZNmY/qB2ocCaIqhP6z11SUPnf+wvdn6j6lAb2+vKIrV4boWi+XSSy+lzzdoOqb+e/oJaAsuHxMsRsSO5uCGgw9aumEDxh3n0Xk5V4QuDTo16CXxy4iDzSlNfn//9lf5UdG5Xm5dUF456bBFm9+HUgk0EvVM3DHK4c8l0GgEtIb2HSVizgHpPFx84fbRTT0RN7jFUshrBF2FmG/TPuPf2boV7adpcHN1p83TCRdWAppLKrRvgzNOXDUu8f6osBF3a03+nmRgyWWXYJhj0QCCoGl4cmWf6kLJvJaDDzbDkUfNaGteGw9sbI7Om3YfFIj1cyGD9+Ly+Wwg6LJYLDUjED8Pr7HUjLBEo0GyNx3MZuvozJA6hixgAHqIJGzBV1uB/qGvlYxisdTT08M5nIMAtOwM+H3Rje9v+aIANF4B8Qko2H+/b/Ccwju8XGNIFlJ3/OlhtBca8Ko+qwes+KK+HHXM8dUAWnJFHIKvwS7ffc9DX7q2flEafUr16gA33Xwbx7l53sfzAZ6L0AjouXOWpNOVvACfUl2sGKYAU4ApwBRgCjAFmAJMAabA102B6t8vDEB/Gke/WtGhyHXokk+jzv+2jOpW9be/mkFX11DtlVG9fGfz1SUPnd/ZHmzZJ1Ugn0dCfOuttw4fPnwQg545cyYAZHIw+00Yl1owPqpGOLXJ07vXqOVzF2B9eQOILXJGgx4dunVI65jpr+z7jAyajIufT96S8r6W9L+neN9LjXpnxUrcF8cD2maoJZw0rX/SCX3Wi2jejKHCv/hldyy0MOjp8Tg1WVAVPhv35ALS7BmvYjmqgduUb1nRwVKVLJSWAMTIwyjBtVO3+bnXR4fV0TEIy9l9WvuOO3xdJot8SzP3rdodCzZfBkZrd66DE45aEQ8tjUU2yspLt/0x3ZuDYgEKGdzO0OHX10+lgc/loPIRlvqGmnvuvYsaowOgYfrHvcHGALR5ENjMnqGAeWLiTShDhzlz5kuiH2OfKxHQnN3jcUdDwQTaNtGT8wvquqHD7373B84hJ2KjfzH1tyuXb1YL0N2JDzxUPdFDe9Tfry+osVgtZqsAGDNu72oA7fImeGewwS5Pf+71L1Fbv0CZPtWqzzzrvAar2A+guRjPReiB+FTrYYUxBZgCTAGmAFOAKcAUYAowBb52ClT/fmEA+tM4/NWKDkWuQ5d8GnX+t2VUt6q//QxA/7e6fr77U3/nrq4uWZarAfTw4XX77ved7e1qRzucePTqZu/GkD0X4npGp1Y8/QwUiHVGCbFtwUAfjj6ALAZDo49FSacZBw0ks9dc0TchuajFu645slr2PvnSLIRJqkrYjVEw0E6ZZrA0aJJP6rNcJMV15eGBRyAWmamI73vkPq+r5PNCyN83Mrn6uqsMrQQdPaCXg5UJCafDsBIRTS5NSMMBIJ2G+++GVODllHdbwqWF5GLY/cGEltmb1uHaXJGUQ32nS4SgI4YeiL00ULvhtGNmhV3zk5GtTvnVyVcghGrvxRJ0FcOf58yZM6zG0mCzWK1WjhOstnrR6Tj00G8VihkCoPvTdVYxaNK+3b4xAL1bedjKr5IC/X8qqlv9zD9fFvkI0ucKgHY0uhUp+K1vHgZGmahWb/95zxswd87iYgGrzef6jZ+rCCPt1+fdLlrfIE1VDS+rvkBMdPrRldgZ5CU/x7kVJeTzJ9au+6AM9Kv/gn8xDf8K11qteWd3+v+zdx5wchNn/9eVvW1alVVZrbaXa+7GgOmh2fRqOgFCCPxNCyWE3gm9Q+iEzksJhBpCCWAc4wIYGxeMbWyKbYzrlb3tkub/PjO7ur2zzwXIG0xGH312tVppNPMbSbv6zjO/aRs0wukUQG0+rMjpQKD5lFPOLfVxIduCC0uzThWgClAFqAJUAaoAVYAqQBXYUhXoS3W21FLQfFMFfhEKWIBZUS6Xu+uuOyoAuo6pq6tjGCfDBPYZc95Rh744NDmlXVsT47sGxRY9+TRaniG+z2ss1ImsHmTlkFmo2BoDgM4XS3nTQvks+v3J3yTl6SNiPa3BNTHtg+efQx0ZGFUQBhY0rT6zUTVyxhi7jFDWRHffi1qSc1X/kohWDAXzAaVbUXqSiS+PORpCs3HoNiBwiCm2CsCA7VECIQSwVEaFTMnIlhbazDwAACAASURBVFB3D3r4ftQWntaqrxoUKaneFVF1TWvyownv4uhrC+eHGMnACIN4LiMgyqiILFQsQuEKRfTHs7si2ofJ6FetLXPGHTNl5kI4AwqYgGczQKW22WqUowEbPzOMyIGridPROG3Kh/hMqSUWtcsbP40ogN64RnSLLUSB9Z/69979lODrD6BlST/xNydvmm3Tv730fcfPJaWoPei6a2q//fcu99O0WLK+WbJcUcMVAC2FeCkkiLoaiEWi6VyhGlFOAfSPqJZazb/+9ju/pIv+kF+KqmoqEGgO6s1PPvU8dKvBEw5J/xEHo7tSBagCVAGqAFWAKkAVoApQBagCP0wBCqB/mG50L6rAv0EBy7Ly+XwOT4lEDJipqwFeG5U6JsYww0PKuVs1T0lKcxP+mVdegr7vhDjnHtSRQysh8NnE9BksNHDgsAWwtpRFnSvQYftOag1OSksr24K5VGjhReeXuzqB5AIyNnFQo/0Mb4ABMyqBDQdCqAuP5vfRDDRi8DeJYK41jmKhYiiQiUd6tOCyWOIdYuJRKKBiCQFAt0qYgBfAtINkw7QMAMkwlRF6fwJqTfwrwi/R3F0RPhORl7akPnvwAVQsQ35I5HUFoNsIG3hyCaFCCWemswudddZiwfdWS3KZKk8eNvKt5V2QchEHNhtlI5/P33zjjQ1MXWPVyaQBjz548QXnQ6h2JXW7wLULJJsbeqUAekPq0O+2KAXWc+qbZXT2mZfzbEzkkjDzcZGP8r6gwKu333a3SUaX+BkUslSy8rliCfffwJd0bZ5IuWrX/N8t12paNiH8ecIHH/KCWgugOS7gl8K777EvZKsWPdM/ZD+oomo1/9vLr7vcfEBLkAhoQYjyvJ7p6Y2UN+B3qkqjf9Dh6E5UAaoAVYAqQBWgClAFqAJUAarAD1GAPu/8ENXoPlSBf5cC2WyWOEG//fZ7DMPUNTTiUGgXw3ibnK0NzB5J9cHh8b8fefDkjrWAXLOomIOAYAPQLRBbC+YKgC6jIlq1CB0xZkFCeC8uzG1RutrCSw8/dPHaLhgwEPwtqgAadq/MEA1tmZAMAOg8mvYRGpSa0hxZGQt0B8RFxxyBmuMFTf5WC0667ibYplBARgllM2WcCHGNLkDWrDz6X7NnhLI4MtlA6KPP0FbDZ7VEOlrD5VSgFPJ1KNy0Cy/8vmCAf3Qf62eSGYPEPgN9JqimuxOdf053W3xme2JlS2LRyK3e/ugz1JlHK7qMfJUxfPDe+xXT5xoGfdihh5SLeYTMfLbHLuo6CxuvVgqgN64R3WILUaD3orczXCygcQefyHmjtQBa4HSeU15+6fVSCd9o7K3/QwvFQm0YKylFbVbWXVP77b93uVbTYskqm+jZ5//GcnItgHY6Bdan/uG8iyErFED/6Aqp1fyyK65RAxFB1DkuKIoxjgsdOu546OaDJ/wrSQH0j1acJkAVoApQBagCVAGqAFWAKkAV+AEKUAD9A0Sju1AF/p0KkPAso4TOOvMCps7Z0Oitb2AZGE2vkWFSvoZjD9//eUKdwWID0+cysoDeEsNl8opDgs1uNO5XXw/TloyMdY9uLbZoX+2166KlyyD3eNDCPgC6tnt9GVlFC6Dv2gzab+ySiLxQ47+JyN9dfj7aelBXWFw6vPXbI4+a35lDmSykVjYqA5hhBm2BBQfK4LloIpQpQtaWrEKHHfVFIrokETQ1sTMWWJsOfXvA2K+Wr0TZMubdxHmjliYANygQ+gzR3CV07u8XDIrNbNFXpfWl24yc88EkSLxKF1A2k8l0drW1tNgO2k2NDoZhRm+z7crvl9cMU9bvGPbHjdcrBdAb14husYUoQM570imgN8u77Lg/540KvqTgiwtcVODCoqDLkr5qZQfcI2j0aK9U61my7yUmgl4hMKrsbX/muIAghO2Z9WlBPXX/A48BGLUB9HoSo6s2SQHyA2CY4OK03/7jRH9QEHVNS6tqKhYbeu11dxZw3xkyPq4Biv+Iya6vDSz8iOTprlQBqgBVgCpAFaAKUAWoAlQBqgBVgCpAFfi/VMAykVlGIT3BMEyTg2XqnI0OFnPV4Hajj1nbgbp6IDtFy1zZudxEhUx+NUKoJ5cjgy3lutDCGWj34fMHKSuSXC7mLbQHV209eOJnM1BHN/hZVEcH7FMmm+Tm8OqVHejXxy0LB2akwysSgcXnjUeHj0UjYmua5UVDkhPmzEXdYMsM/LeI45fteGqMhPMI5Q2EcgRkF9ARR3+jhWay3Fd6KBuLduvBz7cZOW3mdLRiNSpCpPM64cgEziBEnDeyWXTPHSgsv5EKLpPdXwxKznj4IdRTrLh7GGXsGGKZ243a2qbPsl9iGCaoBubMmm2SDUhxa9FBHwE2/oEC6I1rRLfYQhRYB0BjNJeIDpf4FAbQhEGHVSU6YvjWlomKxTIF0Buu3FoAXcKdMs4552IbPZMF1qd5WWXu51/2AugNJ0q/3ZgCtsWzHk5ih5OoKEY4LqSqiXffm0LQs101G0tsg9/X/ngMtLzBBOiXVAGqAFWAKkAVoApQBagCVAGqAFWAKkAV+PkoYFmGUTamTvkEBz43MAyYQTc1NTY0wEJr++Bly1eZCJVN6FRcMDpIznvK4JzR1YXmz0ZbpWe0q51Dw2hwECXErmTgkyceh63yJQg3tlmzXWTi4UGMLDIGWptF55xXjISnBZU5LfFv9tvNfPLPaJCyol1anJbffe05iH1e0dENsdJg4AzmymRIQxiGEFIvAq9CqAcD6DP/8P2Qod9EYj3BWFZLdgYTi1NtHzzyBOyZJbR7AABdKKDVq1BPBj39JGqJT0zpiwanVse0T668vJQHW46agpTyxx91BPiWwHiDTfWYQ8t+afrHn1h2F+x+Xd7twm/yAgXQmywV3fDnrsB6APTqlTmPK9gPQCtS5NTxZyKEjLIxMIC2+V6/hZ+7CtX81Wa7um7z32tTMUzoG7LvfofxvC4IUTzjOGhRb24ZRiJ2f2Q87uZncAvdo1ZXe7lSFsNCZfyD9sWCxQ6nzy+FOS4oCGFJjilKnAyC+5MVeyDoXLv+JztYbUJ2qdf97a7d7Acv16ZfuzxQgpuyzUD7/vD1tUetXf7hKa53T7s21/stXUkVoApQBagCVAGqAFWAKkAVoApQBX45Chglcy04W5SNSy6+qoFx1zNNDMM01DNONwyo52P5X+2yRzYL/hcWDgLuKK3ttPIWQj0l9NEUtOPIz1r1Va2alZAyw5s7o+qkm29Aa7qAdhRNDG3JExZ5hMO6EQANUBubZlx8OQoGZ2jKgmhk6tjdl7/9EmpVFoxQOxPeaeedtghhC+m8YRRRuQwjbRkweKEJswWGIMiEsOZizkKZEnrscRSPzNfUlbEkUlMlIfVNZOiUsy9fsWQNHAvnPwd56jeDGTXkrCeDHrwHtcY+i6rfpMPLUvFPx5++3KgOkNjVXSj0ICuHrrn0UgKd3Y1NTkdTA1OnKer0jz/5aU8KCqB/Wj1pav9BBcgF18eCY8b0+S6HWrXgqERAc6z62KNPkYz+9wHo2tvSxiurdmsTG+QPHbo9y9oAOioIYUWJHnX0b4sl1JOrDM+6wXT7JbnBbX+xX5L+ML1SWJaBZzB07u7JkHI/+PBjWjCph1ocTWIgkBKE8H77H14s1bRS/mB9bCK5iQs/+EAD7thb9r6bDLS+dqvN3WZzt9/cY9VuP/Dy+qSuzVnt8sCpbP436zsu/HWqnTc/VboHVYAqQBWgClAFqAJUAaoAVYAqQBX4WSpAhhEsFgoQHnzG+LMbGPAydjYxTU6I7HW5gUePHNGW6V6Ry4EZRzdCOYS6yuivf0PRwBvDEmtbAigpWXFlWXN02qnjF2fyUNCiHTJMSHOvE4dlICDZOQscmR95FMUin8Uia1KJZUOHTfp6ETrmADQi9E07t2jMyLkrlqAcJsYw6iEAZ8PAJtS1EdAmKhcRyhlo2jTUnvo8GihGAsjv7/IFlvgiE7cZ8/rKItBnzF96EOoBRgBB1FUMjWO0SybqzqHHn0ItsdkxpSMeyOrS3D32+mh5J5TUnso96NlHn/M1NTnrQJx6CBev83nZObNm94l9rqb9Y55bKYC2ZacLW7oC5ELoA6DfeH1CQGnm2ZjIpfGcFPkozwXWrukuEXef9RS69oJad3k9O2ziqrVrOiF8dcDjbmIyG92M5BmZZrlYgtukBTdDMlmWZeTz2Wy2u1DIGWUjkwHWWYS+HeufastPtgjqzR6PJghxPIM1REBL3HnXQ3DXJnfljadUm2rt8vr33PLX1pbRXra9my3TLFcBNGBoUt5isXjeeReKYkIUUvAqRiKRtptu/nMOj4H7YzQp5A0T/96USnYe8IgCFpr3+aI335jwyktvPfzgU08/9eKypWvssRS6uroKBdxL58ccG/a1FagsdHauxYP/kr5DiPxLMEkWq8cqFEo1bUVlGBQYhmXI4p/Z6kaVd5IspIP/TJAymvk8bt8Gwl+Zqrv1z0+p3K+YcNWQy8SELlqINJVXdx/wnWTYsqxsT94sgwdZNgOvCKFcHk36cOarr757y63333Lr/e+8M8XEDdRrO0qlUqWlesB0N/ZFoVAy8UnUp35x4/i8z796842Jr7z07sMPPP/0k68tW5KBBnYcg97VlSkUNqUBaWOHp99TBagCVAGqAFWAKkAVoApQBagCVIH/pAKAYy0Ej5BgBm2gsWP2djgcdfWM2+N0uuocTqYBk+j2waFcrjuPB1ZalUXPPotS+kctwe+Gx1CbHw3VUbM275D9Zi/5DtAuAbyY+pbhQxGvgocpCNVDCGUKEOQz5SOU0D+VvN8F5WXp5JzJU9ETj6A2bcY20SWjItMnvoqKOehZDgMPVq2fSfgzMd8AMoDBsoXQgnloWMvbQ5NrB8eRxpdCSsfgtm/2P2D2l0tRZwk2wk9yRciSnT8T5brxaoS6C+jld1A0/ZkqfZ8Ko7jWtfVW8z9fjFblUR7HI5Eqevn5lwN+1dPkcNZjAs0wHqdr9mezKhFLeCP7mdlG3PYae2FTKpwC6E1RiW6zRShAzvxeAG2Z6MH7n1L8KZFL1gLokcO3z+dqWnz6F26zrqD+O2/0swG2QnATJNxno9tv/gaQf6DPxSLhZaVSiSzYSVU85u3PAKl7WWTNamQiE8/k1oaWLesKBJrd7mAtgOYF7ePps8vmhiOgbVVJBdkfaxdqj/xLWq4tY+XHANyj8nlSRwSImtUJtxlAdYzZcx+gz0IrBtAxjgu+9fYEY32GU5slVgXt1lT4O++8f8klV4RDSYFXXU5B9kc1NaVIMY9bOXzccatWdpFzdaCTZLOOXgOgN7QfgFgE1wg5NHhi4alYyuJf9x6EujCDrn7Rm5hJaH7vCrxkXwJV/myX366dyh7Am2vHWMBePeQ7Anb7pbxJH8lfgxx67ZUPjjj8ZLc7yLLhYLBdklI8FxXFhKa13XTTg+ALZMDwxD9mqmTSLh9C77w98ZKLrwrraYHTXQ5VFlo0ZagitnuckcMPPWnVykylfnvPzR9zfLovVYAqQBWgClAFqAJUAaoAVYAqQBX4DytQ+9yXyWRGjRpVVweAta4e6LPDzfASwziYbXfYalUX8OSr/5QZlJidFFe2KYWwq2eIhIaHCtsOnvLFPPg2h8pk7EGgzpYJ9LdkR0PhcCUcsPzFAjRy2D/jyrIWLTukbf6E99HMGWhE29vDQ18MC8484/ivUR5im8umWTbBeLPCoIn5hglYxkI9BgbQmQ50+L6zhsW/GJ4oRv3F1hAalurYbqupn81E2RIJnSaUBvdsrQHQOHYKlcrokxkonP5Ij3VpajYe6mxv/uKL+Wgt7Ns7XXnl1QxT56xramTqRB+M07jdqK2WL1sGW5Aus3hb8sxMAsvt5+d+C72JDrxEAfTA2tBvtjAFyPnfB0Cfe/alAheV+FQtgD7/vMs3sWT9rqgfyWdKJYtwNMKgSR7+TRgayKYBoyx2d+PhXRGaN2/+LTffdtVV14w79PDddtvj8MOPPP30M995532CqwbKRj8A/e570/z+uMejC3zSjoBONw+Fe1zJKtlj5w2o70+r6ICH2YK+MMpWqWQYZcs0oFmCVIdRtjrWdulavAKgIQg6JoqRji4Iaf+R5yGIU6WTH0z4cOeddmO9QkAN+VhJ4FVViepaWuDCPk9QEiOyP7zD9rsu/25V9aQlNfgTC5zLFqqgGXR495/vX3fdDaeffuY++xywzz4HnH7aOTfecPsnH8+sHrWEGXQOQcNt7/Ve/bbybsPruXPnzfpsDsH69r+QTYHppZLx/vsf3HHHXZdfduXdd93z6quv9zvEhj/a11Q+V7YM9NADzyRjwzyugMuliGJMEKI8H5aUtKa3K4FW3p/w8dHxp11UrZkNp72xb6upfDBhys477sF65IAa83kVgdNVKa2rQwQ27XMnJL5ZFpM7bL97Tf1uLGX6PVWAKkAVoApQBagCVAGqAFWAKkAV+NkrYD/6wRO0aa5d07nzzjvjofWY+kbG6QH67ORgRSC0/e9+O3F4y7vN8sKREatNKm4TRUNkNCy05NUXUUcGYp0tiBSC6Dx4Gq+dsQ55HBu1vBON3nZqa3Sx5lo0IrnwhefR0u/QkYeubQt9MSyyaHT7xFwXyhWAO5etImHQ4P6MwOgC3gBAGwbqNkzUvQZdcvbqobGpo5IrItzy9pAZ93dFlamPPwG+HNCn1urp/yRsWywiVCqieXPQ1iNmq/K3mpoJyCsS8ZlPPIM6ixXzjZ5CeeKkyclE2tGIQ8Fh4EEXwzAn/Pq4Zd8ugWdnsKOucANSXEKf+72uo8RGTgsKoDciEP16y1GAnPy9l6FZRkcc9hufJyTxKYlvFnxxkY+LfPSN199DViWyckOlw6GmtVfUTwD+sAXHW2+989STz07+8KOOtRW33w1l40d8192Vmzdv4dVXXzd62x3dbp+qhFmPXxKDqhKWxKCuxXUtvv12v3rqyWfhFrOe4pm4Wa5ymzVM9PgTL3JcyOuJCHyS58CFQxQjRx392x+Rx/++Xas/DIW8sWplx/wvFn3y8UybPtvtAdOmzvC4FVFohghoDKC3335PAvp/pGRGNcD2wgsu1wIxj4dXFT2ghgJqRJEiohDmfUHeF5KEmB5o8XkDoqAde8wJ1YOSC6L66ce8V3UgaVgmeuP1f55y8pnRSJqcpT5WksSQJIZ8XoVj1YAa+91Jp82dOw97dBCLrd5eT/0yYpko21N85JEnhg4dyXOSIgePPeaE7q4codI2m+7dy86MhfK58udzF1x04WWKHHI5OZ5TJDHIc0oknIqEU3fcfi9YW1QJb28K6yxle6C1IJ8rTp3yyf77HiGL8aYGf0BJud0BSUoIQlQUY7La7PWFXV7dx0fJ68OP/G2dlDZvRW/9nn8l1K9bVJVoQI0F1JgixUQ+zrMxnk1IfKuuDvF5oMaPPebETSnR5uWDbk0VoApQBagCVAGqAFWAKkAVoApQBf5DCtgA2igbpDtsZ2cvg/Z4m+oaMY52NjCMm2H2SmlPDNKnh13zIk3fDwsYad/Xd16DSEfxEsqbqARj+tl4qGplaCIYJzBjou860e77vJOMz03r37WHZ77yNOrpRI88hIam5w+JrRyRnvHuG6hQRN2F7jLYRGeBQVtlAxUAQBMOjbv/GhYqF9Bzj6Ih0SlJaW67tiYldoyM56P+T2+4GhVw9HLO6jZh9MLaaCxChsEGOt+DZnyMthk2rz3emYqU4qG18ejsP12HOgpgFJKz0Mq1Pccd/1tOEF0uT11dg9PpbsL0+Ywzfg9dckslg/TJpQD6P3Tq0sNuEQrYNwNMUvHdYYftxnLesMglFbEVnKD5uMetrPi+owpbzcpdqdrTn4SXkoRylaBMKHuhCHPvtAn4qXfjvkt7770vz4uORrcWiO01dr/p02eQzGSzWeLI3HfzTfuEbw2lkmGZyDZy/XT6nOOPO0VVopgnBnlfUOB0kY/2zkJYhFkXBf3MM84zypXw25pD9gHQZQPddPO9Xm+IZaNBbSjniylyWhRjTz39Yl/HgmoCNVAvly3lshVr3Vy2QMJpLRNitKtb/zLfiecU9v6G2N5C3vhy4bfXX3dre9vwsJ7WAglFAizYUM9tNWKne+5+tLsT99/JQ8CswEVrI/cvv/Q6olE/g4gfINzszxbustNYXPVaSE9ogRjr8Qu8KvCa7I9iTBkV+bgqpWV/VBQ0zuefOvUjfKCfAkDjE6MAgwyjYgEVcuj1197fc/cDWY8qCTF7rp6o0G4kcGE86wKvPvjAw+DlZYKrV/UvQF8N8OV56y13u128LOlhPe108KKg/enqm2wAXWnOrZ6isN5AuR5UKqBbbrpXkWJEh+px4egBJQE5FEO77boPzvl6Wmx681G9Rbzwwst1jNPtlHhfyOcNsB5VUeKSHPOyAUGIen3hxibF69MdTtknhIOhttE7jO1N5Icu1dSvHgqmtECC9cgCpwucLotJxd+Mz6sWVWqTxbQohDmfPHXKTzzA8Q/NO92PKkAVoApQBagCVAGqAFWAKkAVoAr8NAoQ4FN1uzRzudxvT/wdwwB7djh9TF0jU9+AP+oMs7PfdcWo+NQRWscofcUFp+XXLAfgjB8Zq/7PkCkD98cFjmEglDNhYKJv16BTzliWSE7VtS+ioWm33lzOZ9Dyr9Dg2NvpwLeDYl9ddnGXgR8fcUI9Buo0wGojh2eDREAXCzAiIUJo8Ww0KP5Ba2hZa3BNm9ozNGAN1hb/4YzVhlEhziYeNog8meOwySJCwIJgXK5O9NFE1B6fktJWtcdRW7w4pG3R789Z1V0E9FxG6La77vX6RKfTXV9f39DQxDB1dXUNDMP8+tfHb3S4snVZAFmz7vqBKo9GQA+kDF2/xSlgn/w45xaArZDWKvJxWUwTAM2zkR23H1OlzzBMn2liBm0D6GrUMyl82UDPPPvaOedcus8+h++z77hzzrkYhzTizgg/QB4L3XLzXW63T9PCxO7A5WS33WYHklIuVxmEbbMTrkI0ozqe2OxZ8884/TzZH/W4FRLNKnDhWpyHI8FJPDiEhBMMfcH5l61z6D4A2jDRaaf9kQBojk34xRbOF2ts9H86Y16pDLfm6lRdrGYMWXjsNQsV8taMT+defNGV++x90HajdznllNNnz5pX3euX/F7IG0YJvf3WhIMOPFJTUxyr8b6gIiUUKaHKSYJcPa6AJMTaW7Z58a9vF3PohF+fHQoMrQXQzz3zin3q/gCxKvtaaNrUWaoSFQUdv2qioMmSrmtxgVedDp71qHqgBTPfKMBKKQHfBqO33nI7Hqxy039cBsgjOSsQynSZyERv/ePDnXfYz+cJ6YE2cMsREvYMZym4t1dn3H1BFMKxaPNLf3sFp263QdccC6f/+dzFrEd1OkQAvlJCEmKuJv+hBx9TiX2uOTPJHwqjBOh51Yr8AfseLYtxjtU5Vnc2KgIXFXxxmHHeOG+YY3VFip115h9JyHC2p7ZhqpopCHwul0rWPX9+gPUKPAeXIesGuC+JEY4LqmqC9Wlut8L7Y5wQJ/TZLydEKR6KDvpiIbbcqinTpiwOUL/QvCT7w7qWFDgdBHFrujpI5NICm5aFFsXfLPujuha/9ZY7f/GtQZsiI92GKkAVoApQBagCVAGqAFWAKkAV+MUoUAOgK/Cns6PnnLMucTsD9fX++nqOwGhwhmYUhtnNwZyxdWLCuN3mrPkeDDfwg+O6j8CVMLM8Qt1llLHQ2Rd829b2WTy8UFUmnHzq2iJC+RI69cTciOSiUc1r999t+ZKlQKt7CigHA8YTAJ3D4c85iH7GHtAQ+NiDVi9Ch+85tz30VTqYb9GK7YFMjP1i+8GTV69ARaM3AtuGX9UcVmpszkw0KP6vhLq0WUO62DWk9atxhy348lv49vmXX2sd0uJodDY0uOrrGxsagDszDPhin3vueZtS4+sKYWejyoA2kgwF0BsRiH695Shgn/w4yxZaOH8J7wsRjCULLSKX9HlCV1x2IykRvhNBXwxg0ARAV69d04JxwO6664nBQ3cWpaSsNktKWlKSqprYc/d9TQMZZQhl/QHKHLD/OFFUZUkTeFWWdNYrcD7/p5/OtEdI2+w0a1AauDdY6I47/hyLNnOspkgJkY+S1yp9hrDWXqJXQXtpWCkAglwHB/cB0AihHXfci+eiHnfY5QxJ/laWjcbjwwoFVCxtEEDju9GkiZ8cevAxAq8R9KkqUUUG3+E3//FesRIbvdml3yJ2KBRK3y9fffppZ0EgqltLRIcLXDSktatSWhISgDg5qBfOGxa4aEBpVvypW2/6y8ihewhsWuRaMINOinx0+bIOfO5VY2s3s/ClkmWW0fPPvSyJIeIIzHpk1uPnfDLnkz1u8dCDj7r7zoeefvKlyy+5SZXSPBuBIGg56WMlVdFJf5z1RxxvNCfkLCWb4eVcBq36vnzKSRfo6iCPM4RNIWKa0o7dclLktXqipnspPAc6+LzKXmMPqHpSr+/YFrrtlvslIebzBGURrnrcCpU85Xd/AEpbc8n0LiM0//PlW2+1B8HfIh9n3TowcaDPScGX5NkEtq1olvhm6FQhaNOmfdzVtSELnZtvvFMSg5IY1AIxnzcg+6M+b4DnApIcGX/quffd//jdf3502+3GyGqzGmxpbJLUYIvXp3vY4HsffFzbFWN9JVzPuj71qyRItDXrkTlW5VjV45YOPfiYu+/8y9NPvnL5JbepUhvvBWd8VQKXFVUJn3H62etJlK6iClAFqAJUAaoAVYAqQBWgClAFqAJbrAKVLu/VN2wxAYW56I+31jGKszHAME3AYOsYpt7ZUB9vYIb5fXtNmpApVo0r+xcdP1ESR8ishdbm0bN/RZI0JR5aFg7MOP7EL5Z3ojUl9Mj/oKQ+d3BkTXNg4kcTII2eIsoVUXe+ZKASRs9g+4xNny2w3cBP+bkukkqXzwAAIABJREFU9Jt9vxoqLW7VsukAagmgdn35bqOnfjQZdWXxqEbrPM4SCkb6lS/5Ch194MpmbUlz0IjK+UGpZaO3f3v5GvTQk5PkcDPDME1NTQ2Mk2Eacewz5s8Mc8MNN+Vz64RV9S82fKYAen2q0HX/pQr0B9Cvv/ZuNDyIZ2Pgc8qlZTHNuvWXXnwLAnLxtQ5XexnmimCYTJkW9Gc46qjxitzCiylZbfWyUUlpkZS016c3OrizzvzjDwtEzXQXtUAiEk6xHr/sD8OYYLwqiuqqVWtIBiyrmpNNrMG+KG3a1Bl7jT3Ax0qyBH3t9UALjrGN4QBn7LYB/hvVwGegz4RvAuLkfSFVid5x+73EgxgfH/TEHtBlPBQhrAvqzQRAez0xnkuKQuqII07K5VGhCD7ReCJBqTWLuFqu+9MdrEdV5TjHao4GCLPlWM3jVmR/dNTInUtFsGIgIaWVZH4Zb7iCnnziGVnStEDM6eBVKS1yyYDcWomrxdG1PBshtBf780bcTUGeTShie1TfSuRaqvblUcL4O9Z2ZbPw47PRqfYshfYSC82c8Xk0khYFnecCATWmKlFZ0nlOGXfI0f94412jhIwSVES2G201fFeSGVmM1zFOUVQvv+zKfD6/vh+djWZkPT+Sjz38ckQfzrMJjzMi+JIBuV0RW8PBIb0AWkjUNJbUMGhg4hCs3dnRM2AXIQudc9YlqgTXOwHQnDfKs7Frr74TNOx71ZCP0z+eP2rEbjwbEbioprZy3rAqpavhzwCgBV/S7YgEpMEBabC7KRjSE2eeeVYvBK9JM5+DX//bbv2zLOnEbF0UNNYjS2KE5wJXXHb99yu6wT4MwX3m/fc/4cQo749JSlLRmlkuxInRf02G4Rb73s7WI/IA9dtCXLwDSkKV47I/zHOBcYcc+4+/v1+p3zzKdqGthu8pci08m5DFdB3jFQXt8suu3sS/HevJCl1FFaAKUAWoAlQBqgBVgCpAFaAKUAV+fgpUyXPl3Shb2YxpldADd7+W0Mc0MPH6Bg9TX0GxjQ7W0SQ2NHobm1x/e+WFkgmD+vSfMPAwESpaqLuIPvgQtbUsTEW7NHn2PnsvWLwU9VjomzWoecg7Mf3bqPT5DRcbKAeGzbkSIJOeQhkbPhsGHpaMZKuMrKKF8mV02SVfj0x8keK6W2Sgz61adlB0+nNPo54cyhkZhNbix8RKjgg8IvylM4u++RodtOfMpDxjeDIT8S8ZnP5qxIh3z734w+YRBzJNHA50JvHOdQzTQAKfGYZ5/vkX+hRwg9Fu5BG1dnv7obWKg2q/XM8yjYBejyh01ZasQPXMt9Ddd/5FFpOCL855oBO9KrWIfHTtatvpwjSMYrGUtwG0ZUA3/I8/nr/ttmN9fLw6RzkhjuckJ8RdLkUPtcya/SX0krBgrr3k1r0ga5Vc9OUSnzegSAmwOBAAQAfUSDrVVgVJG967NyWyPQyzlil3Z4qFIsoVrAceelz0h2pnTUs7nQIvaKI/NO6w4x546PHJk2d8PG3uiy+8KXBhCAslANrXJnIteqBNFuNHHn5iCY/wig9mIjxAqz0O4XfL10pyjPNFeC7ucoZ4LhlQ2x955IVCAZrwsO59LBFM3AxXKqCTTjyr1ku3Jhw7KnBhp0O68fp7KsNC9t7v1tV1U/XpVeo/t1StU3T9dbeKAgR9iwK0CkBMuj8l+OI+T0TiU+HgEJGPK/5UU4NfEmIeVwDCovGYmRLfKvGtgi8JAJqLHnv0ybZ/sQVDIWxcDWhlqV4NCKGlS1Zuu/VOHrdYcUYOJQVe5Xjlj+dfls1VtrObeQ855MRwaCjLhnk+zPrUaCz18COPlnsH/d00ZfGAfgTIQn8iDMELeev4X4/HZYQCygIQdp8nIvhAh+bkqPEnn//iX/85Y/rCiRNm/OGcK3yeEOeNEgRMrDACSoLzyc/8z18HBNAI7T32UI8r4HEF9UCb4k9JQsLnCb379jTSvASvCK4a8OYuoy+/XLb77gfyfFgQoqqa4rmoIMQ5XyQaHSbxKc4bVfzNJAMBuV1Xh/BsJBpJ77nH2N4mExtAw6AN6MknnhN4GDWRY1Vdi8uS7mjwKVLkrjsexAMKg980mZcu7dC0Fq83SIYlFISoyyWtXgP3qPVeALW6r69+d/G4JbdTkv3RsN4icNDScMH5l+Wr9VuqdjUYd9DJEX04uTFyrBaLNv/lL49W+2HUnDS1x6PLVAGqAFWAKkAVoApQBagCVAGqAFVgC1Sggp+rDzrFHPrkw9U7j7zg2ENuHXfIsUw943DUeTwwIl9DgwvbIoMxxXHHH9vd3U32NcpGiQzNh8cxMvJmTxeaNg0NHTq1LZVLJ9YceNDcbBFlTbS2B51wUiaVWhgQZ+689YyO7+DRziyjkmGVTZQrlMizoGUio2iU8gXLMsqo1FNCE/+FouEPIsmlsrQ2raAWMdMWmHftJfDEWoY0uhHM1QmPQmiaKFtAXRmU7URH7PPZyNisNnX+0Ni8VPitcPgmQTmSYXSmoQmAcwPD+1lMoB0Et7Msu+irxcXyQJHe1cgtfMD1PpxW5axmaRPeKYDeBJHoJluSAtWrwELnnn2pJCREjvSgj6lSevvRY3I9NuMEpw3DKGKcVynhe+98GouOFIWUj0tiAB318X0AtCSlGhv9V155M/Td2EwA/cGEadATX4Ru7wKnc6yqyKHDxh1VVXfjSLG6ZW+wcLGEsjnznHMvBPQsRiqzPxTQEmogwvHKH867cN78Rd2ZStvd6lXdloFee+VdWcQR0L420TdIBAYN8Z6HHnQ8cK+KQgRAF20APXnKdL8U5XwRv5hmvXHJ38pz8enTFxRLIAWerD4DsSK4zx571P9LRIeuD0BDLLYeaPN5Qi3pbYwSILnqoQfib9XK7RXi57tUKqKzf39hQI0R+kzi0ANKSuTB6Xi7bcZee/XdTz/52vv/nP7yi/889uiTFSnG+4LgBF0DoLHtA/DTyy65fnMBtO0JDpi1iMD+RdB4TnE0eANqhPPJsqRfedX1xRIqG/CrRqYCZpSx2HCWjfJc1O0O1NV7JCX44kvEdnmTz1LMZAl9NsoIGKiFJk/6dPfd9q1nuGoZwdGCdYU9rmAqPvL2W/7SucayzwFyPpx6yh89rmDVCgO8mDlW43zyQw8+OlDdFwtmMj7I7VQkIRbW2wJKithtf714ZS+AxmdsV3chmzPHjD3I41Xd7oAoxhQlKQhRj0cXxcSwYbtccN61t9700EH7HyeLSVmEtgGRw57dYnDcoUfCKJoFfE5WWwS6uwofTvpYCwB6JkP/8VxAC8QEXnv1lbdJhm36bBno00/nC0JYkhKSlGBZ3esN6qGWQmH99Lnf2W+ULbuBAep3v8Mhtt0XdDTwwOhZsJy+6sobS0W4DI3q/4oivhMkIiMxfU56nKF6hlXkUNVWe5PrdyD16XqqAFWAKkAVoApQBagCVAGqAFWAKvBzUqAKka1SEWMHE5WyCPUgAxPdW2+/xuGoc7lchMw6HIBoWRZwbXt7++TJk230XA3ZQaiEVn6LdttxRlCdFVIXD2qbPmMO6iyCUcZ7E1A8+tmwtkwiMuGDd2Gkwu5VnZYB44+VTbNQKtoAGp768NTRjb5disbu+VVI/zaQWqsnelrU3CBl8XEHfdnTSehzDtPnajwR3ssqo0w3KpdQOYeOP+Sj7domDQ6/1xp+Q2Zva2r8HcOMYhg/09AIAy424qDnRobEetfVNey8886rVq2qHH6gNxJlhb+lAHogkej6/3IFqhexhcbscZDARTE2asYR0Omzz7y0Rh0CjWAFtD6V0Afvz0hERrHeeFgfTgA0K0RZIcyJFQbt46NOd9DpDu6y6wFFA7Bd2UTVWEbAShuGNw898CTH6oRh8b6QwGuSGLzvvoeqWdrw3tWtcG5xpgHqrVyZ2Xb0rh6vrIfSohirzhGXm99pl91nfDarbKJsvliqEuJCoUQKGw3DQGSAnisAGoYju+LSW0nK+GD9AfT9DzwmCGGeiypyC8cmVKU9ldwawp+r7BIGlauMywoJlIro2KNPFvko69aJ0zHB0NUIaADQqtTCeQHIfjx13i8MQJ991vlOB9/UyPVaoEDYe+CA/Y586x8fFnIQbm9PlolefukNRYooUgxsiPlmEgHtc8dELimLyeeffX2zADTUchmsZqAiStYN19/W5ADOKPCqo8FLLMj/cO5FJOS5jAPYyTmSy6OJE2dyvgjLRlWlWRRjvKDFEs1dmR6c2009S4EjY8hrVE+P5555RRR0SYxEQu24jNjrWUhEw0MuuuDa5Uuxn7L9y4bbIHI91qSJn8LFQkYCxIMBikLY5eTmzP7CVo8sEEMM00DfL1/NemRRCMt+oNWSGJH90d133b+YB9cLe4YxgjPl408Yzwtao4PzeFVBCCtKXBQjLKvfc88TxaoRVsfq8kMPPCNwYVcTOGm4nZKPlW64/rZCvtLwAiWtCrPjDntIYohUJcN4OFZtqGdfe/WtfM7MZkCLSj3iG8dFF19NADS5cnk+fNJJvyfNL9C+heOkbUmqtzYoLriFla0+9dvIKVJM4HRHvShwYVmM/+Gcy6BDA24HqvQwQDA066QPZvFsjPPEAzKYbgucnoi1dndvZv32U59+pApQBagCVAGqAFWAKkAVoApQBagCP28FCoVSIW/YcTz4YdkwrfyMmdO33nprp9PJMEwDngiMdrlcDofjlFNOWbhwIWxsGD2FfNFA3y9D++w+I6rNb2/+fuSISdM+gWJ3ZlE2g7YZ8q+ktjQR/OLSi9YaBgYkFrLKyMQAumSA9XPFEdZ+wDPRWacvU8WP45GeQKQjHFszMr56723mLPkSGRiyAPC2A7WqCpfyBbOIUA5dec6CUc3PDI49ovJnsezBDNOOB1T0gb01meoxgGYYh7uh0dk4/vTxJI1iuVQoFWtcWKtJk/fqE/1PGB5II6D7Skw/bfEKABKCG4qFUomhBEDLQgvPQgT0ffc8WVO+KjxCgOqyGXP01mPAl9aXlvztGEADfa4AaDHq9YVZLiL60ywXE6XksuXdFQBd5UQbBdBXXHY9DIrIJcGR1heSxIgoaFMmw4BjeOpDb6sr1/Oe7QGqlM+ZU6d8OnjI1uFwc6OD80tRzLAS+DVy510P4PtjbxnthCwT0PDuux7Ya8Hha1P9gxKRUR9OnA2RkpWdagE04LXzL7yc53Wei6pKq9sVkaTmvfc6EiLBq/fNKoCuEMffnXRaLDLI4wrUM8L6ATS4IbdrymCejT3y8PPEARsGlO21eqiFb1XCZ5fkZ7hA7tEWuv66mwNqpMnBRsLNtQD66itvQVh/qMEsGC5D6DcWsFSyHnrwcVWO1wJo1hUl3hSffPR5BVzi1tte3jmwCIW8USpBQPGb/3jPx0ohPcFzio+VPG5RlvQDDzisWEAdXb22VplsESS20CmnnBcIwAiTPBcNh9t5QRt/GlBR3D1nk2uh+nNF/B+eeOx5SQwJnB7WWwDjCjF7njxpJonPtaN07TJZBpr92SKRh3EaKwyai7qd0uhtd153FFDiyFEqWQsXfKNryUi4mfcFVTnucSsCp1984Z8gENjsBdA9WevSy66T5AjHBRxNvNsjCaIuyZF089B335tWLKJcHkG8sAnQ1iyjV195e6sROzgdfDiU/N1Jp9lIF3JbBdDnn3e5KOgetyIKYV1LYwKu3ncvBGvneozKxUXcvvD/DkWJBrQE69N4PqxpLZrW8tZbk+zeFRsA0GBpUij11q9XCQVTvC/o8wY8roAsxg/c/5hiHnV1VCE6AsceQsnHn3y+prSTCOiIPljg9NNOhREIccP+JtevXUl0gSpAFaAKUAWoAlQBqgBVgCpAFaAKbCEKFAoF24W10p8V57xQKNxxxx2KojAMU19fT+KgPR4PQbg+n++yyy776ttvCCw5/oS5ieiUqDZvx22/nDwNre6uPBH+8cxcWJg6OLJk9NCZa1cj8M4kE6YcZRNsFOFxDzNowwT3DITQX+5D7bFpLZEuv3e1oqxQlbkj0x/OngyPmd3ZNQgVYI8+E7CaQi5rFdA1502I8ecJdac5mEMYJsww7krIc72TqXNDyDP232DqGa/giTfHZsz6pATcGhWLRRKO3Sfh2g/VJ3qyjjwo9nut3XxTlimA3hSV6DZbmAIQBfldpyTERD4ui2kCoF0OdeH8ZX1LAqC6WCx2dvSM2eOgaHiIIraKQquPS4v+Fr+ccnM6L0fjyeEsF3J5dY834mWjXjbK+xN/f3OiDaA3fhHi+85RR54kCQmMwltEPi6JkaFDtqnhaDaArgLdvnnt/WQBMf9w0sfp1CBHE+/xyn4pCuYYXEjX29LpkS+8+MZAGMk0KqYBe+52cCXMlmuXuHbWFR81Yo9MFxyk2h7YmwZh64cceqwkJThfrL5OFfg054tddeWdvbnCuxaKPaVyzigbfzj3AlHQseVIHANE8HoWuHA0PEiVkxBM6lAVf7PHGfG5Y4q/+YzTLiRJQQ4h9LSfqPbHvgf8P/jU97bb/4BV4gy/DV3YureMHvnLU7KkV2Z/2OOWBF5TpMiUyTOgWHgXQpNNHKRMzHzJjx85SUjViFwLceltSY+C49q/Xr3i9M9O7WeSoFFC++x9iOwPwyzpAq+yHrm9deSXC78F5lgGzEqaNIslVCyhRx97zi9Fvd5QINDKc1G/P64GYm+/8z5p761Nf6DlXBZCu/O5ooGdH4oFdPtt93GsGg23QXy3GGE9Ku8LikJ47J4HLvlmFbGkqCizTqILvliKA+d7ATTHapdcfNU6G0K4dz5XLBbMf7zxbq/tCR/VAy0+T/CdtyaTXbq6wI2iWEIv/u0fuOUm7JfCHq/saOI5LrD7Hvt3dBazOeDU/SazjAp5q6szv3p1Z7+vSKPOG6+/h48bJjH+bqeiyvETTzi1WIAmH5s+E3Kdz5m/PXE861NFf4jjghwX9EvRHXYYQyxQ7NO930LtcddTv/6wwOmsW2tv2ebLBd/BP5sS0HOYLMhDqYgef/SvsggW5JrSLvjishgPqLF3cP3a/8Nqj0KXqQJUAaoAVYAqQBWgClAFqAJUAarAL0UBeMAyYbiqMga7vfF3pICLFy8+7rjj6uvrnU6nTZ8bGhoIj1ZV9Zbbb7vplrea2//WPuSzQYP+/sxzaFUnEOLuEpo8FcW1qXF5cSr4zykfoELW1gyCyOzoIrIW3GANlC2iWbPR1oOmBtmFLUGUDiCN/2Zo26fv/xOe3aqPpEWIgCYxT2VUyhml4lrT7Jrw9r9OOPL3LibFMEmGSYPdMwMuInWNDCf4vGzA/uj0NLKC58KLLyDo2eiPs+18VmAFQRZ9Xms2+TGLFED/GPXovj9TBUwDffLRHAixrNjppmQxGQ0PyuL2pdpMFwq5YrF81JEnSGIkFhnmcATC0a3UwDBOSO/8qwOf+9ubf3nihVTLqGBokI+PuzxhHx9nuRgnxP983+MwfOnGBiHELLVywKGDR/MsDLYG6IeLikL4uF+fXNPmtqkAulgwp0z+OBZtZj1+Er/J87qXDTid8u67Hzx16pxSJdKxtqCV5WLBJL4BLemR9kBwEt8akNuvvuJuA4dL1gDocq7UQ/p8mAgNH7E9z4dFISX5WxWpzeuJvPrKB+U+TXFwh8zluh9//HFFDvq8is8bEHkI99bUZo7Vb7/1oY+nzjvu2FM1tdnjCuiBNp6N+TwRxZ8as/shJIskAhruz72YtZbCradQ/95VmwygQVgLvf7aO4oc6gXQkq4qYUUOvfmP9yCfVWBdAdAGYFO7z4tRQrff+gCxp8Dx6WkYQtMb3nvsYZV9K0W1Bdlg0S2U67GuveZWLZCwAbQs6YoUefWVtwGnFiEi2DCBxhIvjnff/5DjAi6XJIoxj0cPBFr9/vj5F1xJDrOhAQrWyQiJR85myjfecCcJzlWkGMM4FCnCcwrr8Z9w/CmVmG6z0mUBxOk7ZbrMSR/M9Hn6WHAElMSUydP7blj5VCyWLRM99uhTeODHCgjmWN3nCX779Wp7F9NCCxYubWkdIYh6UE+J/hAvaLygbTt618/nLcrmzEIRDHb6NARZUE2lklXIG4Sw26mRS7hYQLvtug9Eu/NRkQd7GdatDW4fvXplDmGHH0LYqxcXuvqqG3hOkeRIQEv4pajbrUhy7IUX3oQrqABbrXe2DwoL69YvNDNEFSnx6svvmWUI3yZ/cwh6Rgi9/+4U3hd0OyVJSLBuXVNbZTF+4fmV+rWtzfochX6gClAFqAJUAaoAVYAqQBWgClAFqAK/EAXsx6wy9rWoAGhiEk2KmM/n33zzzVGjRjU1VS0s+vpyOByDmtg/avH7X3kDHmFLCHWVUMZC2//qtZbktzFlwTmnrVj9PXnMtxAysHtrBUCTCGhbS8tCB+wzpT28KCHkEyJKSNmh6YX33ll5MiZ90u2NiwVkldA7b7511lknhUKCq95dx7jqGI+73u+oY+uJwXPFdINhGEcd43Y4HB5v08GH7J/Ndm6IO9vHqPIKG1xUFuwNftwCBdA/Tj+6989MAcJQLBM9/dSLtQBa8acOPvDX62Z29dq1N996e6OD5XmdZcFfQpLbHE3hCy68hWycK6MPp85StTZOgGEJRX8aL0RPGf8HYsdj38Dshdqj5HIk/hB1rM2C/wYPsYfupiDvC/G+4OOPPWM75GLihEc37Qu+SGp24iZCX3/7XdugYYoa9nj9AS3hZRW/FNW09A47jFmzFoh3d6ZMtq/NSSUdA8wE5s5ZVGP1AAPBaUr7gnnfk22qjAxud5kcBHuaCK1e2y3JEUGICnxSDw5TpDZdH7JsWcb238D7wu3qk+lTRVGS/AHZHxaFsCLFwnpLe+uoz+d8TYIxCzmw5w4oKUe9pCowkqEkpXS9rVS2BzMkpLa20PbyumX6N6/ZZABNAk5HjhjNevxVAK3Jksb5/G/+45+mAXHrlV8SIpYJTr61P3W5gvX4Ey+KYkzgkwKfFngY9Y516xecd80ABtkbKfuK5V2iGHG7Fb8Ecb5+SfdL+tXX3FIoVIxTSPtBqYwyPeWPp8/Ww8mGRp/Hq6pqKp0eqSjJ4SN27M4US32aGTZy0HyuCNYQuA4fvP8J1qPK/mhASUhiRJEiIT3BeoWLLrokly0QSE0w9HoT7cmiW259kGXDtv+GwIV32H739W4MB8TM+PLLrhb9QTwgJ7iiu1xSa9uovi0l6ITfnMpxAY9X9nj9iVS7X9LjibZPZ8wlZ3vZRIWiWSia1WsBDkgC1Qc69C033xUKpkQRXyNCXBDiipKcOvXzsoF6sridijhvmJDOffc91ORgRUEL6ilB1D1emfWpZ5x5/tqOAmkJsE/3fgv9jr5ieZckRjxuRfZH8QwA+k9X3UHQM0KA0Umce6bH/PiTuXooTeo3oKSaUyNVOTly+I6ZbohVr07kgNVP9J0qQBWgClAFqAJUAaoAVYAqQBWgCvzCFTCrz+XwbpQN8nrXXXf5fD4S+wyRxXV1VUtllmlIMowSSmx9/0NPvvfhpKyFrrqjIzFikhKas9NO3y5dgjrWEskKFioXkVW0gHWQIOgSOEPDtKYD3Xg1GhL+slnKjU6isKtzcPSrk05YbCFUNIFrg4M0fsKdP3/+ffc+eur/O6e9bbDD0WBD5gaGqQPHDZjqmfoGpq6hjoFXpo7w6IMPOXDWrE8RQqvXAO0plHodOEke/o9fKYD+PxacHu7fq0A+j68oC914w521AFrko2C/u840YeK/eEHmeAX6wosRSUrw/tjpv78E2I2FsgWrbKGePBp3+G+9Pgh/Fv1pXkyxXGTPvQ6x2ZDdmWIgeFPIG3NmL9ADLZrS3lSvhYNDfJ4gzwVmzfyihkja6fWJvCRZrv1u51+N8Ut6OJKSlBDHBdweSQsCKJy/YFmxhLKYeA+UE5LaXx5+OhJqrQ4E1yzxqZHDfoUs7BJQpXgEiJvQMwWGMfxs9jzWpwYCzSwbFYVmzhcbtdUe/aAeMRIaNWqbJoeH5xRR0HkuENbTW2+1y/ffdZeKwL4LOZjvufsvrEd1NcnBYDvPAa3TtJZsDtWAztoS1y6vU4X/phX9mv4GOAoZ64+0Cma6i6ecfKYoaE0OVhKDmEEDgH7u2RftGOfaZGp/5Mj6soFuuvleoPxCnDBoiU+5nYH77nlyswC0jU0vuuAaUYxoWhqbtIRFGeauLHhskx89YvhgmOjj6bNHbLWdw+mT5IjbI3FckOd1p9P//vtTsflG5ZevNv8DLROaaZnogwnTXE1+PdCCzXCirEeG2GevcOr408m+OM4duhKRgPd+5z0xwTjqqPGK3CL4wBobe3HoV1x+bVdXplgsDmQZcfLJp9r0WRRjXjZw4IFHGybK9JimBeT9scef10NpLZj0soqihnlB5XjlX5M+zhWMji7oKGVYKFcoZbJ9fp7XfziMlZGFBg8a5fGq0HgA1Qfz+PHnE3nhFUd5E9R+7z0PKjKcHpIYlOSIXwqnUkN22nnsmrV5sj0Jvq496e3lqm6VWPGLLrhGEiPEbLrKoKPQz4P0zwKfaNgD6veTuSNG7uBo4kn98r6gwOmuJv8EXL8wniGcFAS/96sHckz6ShWgClAFqAJUAaoAVYAqQBWgClAFfikK2M/7UKBeAF19LEL5fN7E04UXXqiqqssF7hYMw3g8LMDeBoZx1jW6mCZnfaPbOWz0EQ3CqUri4WT7q08/h3KVgXhKCOUMVC4gVAXQJQOVyhYwlo4M+tdENDj26rDwV23qsmGR5YP0zw4aO2vpElTCD2TTpn96/oWX7rjzbph9N9TXuRrqPQ0NDU4XAOgmGC6R8bFNPo/AYNxcjxm0HQc9Zo8933zj79h8Ep5q8/lsrgioyICI7M2JL/tJK5wC6J9UTprYz0OBYsE8+XdnQl94LomtDJKuJvmN19+DGFt8MXf3ZDPZ/NJlK0hMKAFzvBQjGZeYAAAgAElEQVTyK6FTTgM6RnwRiA2EYaLLr7jF49E5X0wUUn4xLQjxcLjVDpa0veTXLX0+nydhns88/SLgM19c8CUFX9znDYzedmcbFK67o72GsCdos1pdKBpo3BG/8QmaPeuhdFBPjRi5w+Kvvid2CvDa1xjETgoyjG15D9z/iICSEPl4QG4NyK2ymLzogmvtzaq5IpYgsLpQKj/9Py9iqJfgubgopDgu+LuTz/zfYdzsCOgy3ErR8b8eH9JaA0oiFEy5nEIs2jZ0yDbffLWC+A8QUFs20Ow5i7xsgGV1QYjzXJznANi9888PizhytieXI7fF6s3R5m8DojHs4oQwx4QMW5ZVKBQymUy1LHbhKgtG2bBnsgpsfEtGPlcu5A2jDLG04NuLI0OJ8UL/JPBny0T5XJmMnvfM0y8qcgioohjkOcnj4WOx1J+uuWG9O1YOCjm2jKr1RMFAhxx2fA2ATopCyuPRJ0yY/r8nYcWwAjfK4uaBfmpAKiTi3ihb3V2FxV9+31AnCEK0sdHvcPk5Mcz7I5defbOBUKEM7Su5IlRLZ6b8xNMvKsGExyu73KIaiBBjcadTeOWVt8ENudoW0e941XLZtVNdgUC6hfOXh4ODsM1LShISIh/1eRVJDJ588v8rABaFvkhkNgFuV2aSBEnRQGjOvKVNrqDLGeS5uCKnBS7MserncxfgIOtSlV9X5cNuXgih3XbfWxQTotDM+6E9SdFS551/lf0bu2p1dzjc7HQKeijd6ODcHpHl5Lv+fH8BhmCsXDuGhYplo9i3gcXqHUKiUlKST4TQnXc95HT68fifMUlK1DWKLq86acpnJpa6J2uRlP63Bi+/7E+cT3Y2+UJ6QuBVSQm53PyorXf65ttVBBbbaq6zYJrIzOV6IJNlo7srt3jRdw31nMhHmxr8riYZbndi5MorbzYtVCrBjY4k2N1tPvH0S4qWcrFyk1uUAzG7fl995W0yRCTcGSojf/ZWIl2iClAFqAJUAaoAVYAqQBWgClAFqAL/JQqQ+LB+hSUrv/zyy6uuuorneTsaGuhvfUN9PVDf+gaWqVexC/MQhhkUiY/Zd7/jrrzq2g//NfH775eWkZXvfZLMIpQxILgZHKJ33+724enHhqVeHJZ+ZljLg4nQhYeNu+f4E64ZveM+DNPEQLw1ocp1TH0dU99Q19BYV0+OzDidjvoGiHnGQyY24pwwHo+nqanp0EMOnT4dLCuJPQB+roRnSVI0y7Jjj/BDee/DdL+i9/lY+3Da54vN/EAB9GYKRjf/2StAmOOuu+xdC6B93sC3X68slqBPegl7NyOEfjf+98SaoAqgg9vv8qtVmdUFlDVQ3sBBn3ClWeiRR15g2bDXG+J8YI/g9ydFMbJmLQRLloyBICcohYdYhWv62j/dXAugOVY95ZTT1xsY209gcqlDtkvotjsfcXoCPkHHM2Bol1vUQ+nJU6ZDTCv284WeHQMD6FyP8clHcwROl8SIJMR8nhDnDfNs5B9//8A+Lr49Evpc6ZlfKJVvuPF2AqBFISWKCdan3nLbn8FsGt+wiG/A/zzzakgbDMxRgLHmBF5jPfKHkz4uEt5YbWMsFFFHVx4beoQJgIaAXyH6zLOvkAjoYhmqyJ6rsJUoYWezz4JRtoxy771z5Yq1U6d88srLf7/7rgdeevHvn8/9srurkOku47mY6S4u/26VPX86fdb77/3r+ef+9tCDj1504RVnnH7uMUf95oD9x918452fTp9DHH6JpwT4U9sgEx+/wqlLaMH8rwcPGuls8jmbfLKk85wkiurYMftmMn2iaPtkGgebk/oq4DbSb5au9XJaLYBWlVaWDS9aBKfupgBoHIReqbUzTjtfEmJ+f5zjQkw9J6lxRU+vWAvNGETKAt7wltvv4/x6ON7ml8KSHNGCcUUFv47HHn+e5JZsPLD69vdEkUoRD9r/BDyUIhi8kFNCFPSDDwYz6wJYsRD6XELQvls0UdGAueJRYh/rzLMuVwLtjiZo+1HktMhHR221IxB/6BVFmof6OKRAEzVCW2+zE5ylQisvpnh/QlKSt9z+gF1vp51+jl8Ki/6Qyy0GtITbI55x5nmFokkqgryWcSuOYVU8UvrVGvkI3bLwtVY2UFv71h42FAwNEsUYx4W8nHbYkSeS/OXh3wVMS5asPmzcMVogxnOKwKtaIMb5ZJaT2weP/GzWQrKN2ffKtZXFC+QfAwyaSjY+4/TzJCEmi3HeF6pnOFVOalp69eoCgd2EfSOEbrvtAU4Mh2ODRDnsVyKqnpTUKK7fZ0k61Vdb9eoK+k4VoApQBagCVAGqAFWAKkAVoApQBf47FFgvgCZFJ1+tXr36uuuuk/xKk8NVX99UxzgZpq6hnnU0+Oob2IZ6tqHewzCMl/PxouBw4RBlhmEFcbudfrXrbnvtuvtuu+65za5jRu2w8+itR40d0nIU69ifYfZmmLEMsxPDjGCYKMO4GcbBME11DY0YQANfxvQZM2hsAUKgM/6iz0skFr3+xhuWfresuweGPiuVSjnMMqoPlesLJ+vzML2haq4mUsXYG9p2Q99RAL0hdeh3W5wCcGvAlDAZH1QLoNtbR0GUHy5PoWiWDPTSa29yfk2UojDLYV7R3YL/i68XYetag+Aw2B5Tzekfz5fFJOvWvZ4IMGgh7peis+YsAN7XN0yyn2JG2SDI8sgjjusF0DACofb88y+UNkyvcVrkUi9baPqMr7w+nZNivQBaVFU9/sDDTxRNzPOIr9AGAbRRQkcdeSLvC3rcishHHfUi69aSsWGFXMU/l4QPk5hXhMqke0jJsE48idgaJAiA9njlyVN6B4LL9JS/W945bPgOAaVZEhIeV0DgdF1L3nzjnQYmpyT2uRIBjathm2135rggJ8Q5IQmvYvSmW++Bnin42DZ9xt1DNn67M0powRdLr73m9h2221MW44qUUOWkLMJYcJKQCCjNIa2dZ2M8G4PhH2ElkDtFisn+KLByThc4XRTCZLA+gdc4VlWVaDSSHr3tjrfcfEdvI0Mv5e6t6lIRnXnG+eFQMhpJ85zC+WTJH4hGkjNnzuoHrHv3qS6RshVNCEn+0/V3cmKYE6NYljgnxFWlOZXcKpOBQQI3AUBD5vK4w8+333wPpRPBX9vHRyUl6XArF11+QwZ7MhQt1J1HHT3mKaeeo4VSohxucouiP+j2QAQ0xysvvPh6sQSjFJZxU6ldAdVcD/yOzR9uvfkBno15nBGJb7UBtKpEZ332eZWfVsKfcbsJhD/jkRnKZDxC0vqx5PtuJdgmyM1eNu71RCQpJfujp44/yyjDVV49Rfv/ZpZNM5UeJPrTor8NDHOkJCdG//bKO2ULFJ72yRyI9fYpvBSS5IjoDw0fOTqTBaRLbDcMZJEODcRXZ+ByApsGAG2iBx580u0OeH1hVWuTlGRjk8T7Ix/NnJc3UK4MTL0zU574r09GjNxB9oe1AAQ+C7zqcnKKHNpp5z0/nwf3nA3YblTFr7RaE5chu34Vf0rgoqqcdDuVSy+7IYfbOwwTjIM6M+Yp4/+g6c2iFHV4JE4ONXklKRhhBVK/VrFgrnN+kqNtoNz0K6oAVYAqQBWgClAFqAJUAaoAVYAq8N+rwKuvvn7wwYcyYL7sYxiuoaEJZgDQXF19U10DjlIGON3Y4ABI3YcTg6EGw3J+hmlwNmkMwzOMiF8Fps7vdgcdTSKEP5PYZ7xnXXWCMOd6SK2uod7tBdhd1+TwCtzRx//6jXfeAuvUUiFXhmfbYhnoc3dPpvosuUFw3P+RuhKvVrvvT/WUSAH0f+9l8wsu+aIvv4EBwXhAjdiFI3nAfkdCxCSeyiZaszYbT7VLKqbPUpSXo7yi3/PQIyXAWmbByhoQlUmGBIR9Vq/MBZSUxxX0eiIsG+V8EUEIv/v+h0CO1teSVDlSzdu2W++EHWyj4MLBRSUxuHDBonXoT80OVS9m+1Ifs9cRbk5v8pIIaM0nqj5R/eOFl5PA33y5Eo9JojLtm0WfFBGaNPEj2R8O6y2hYLMsxpsawKJ37J4HA503oBt+Fe0RBmiWTDAmKBlozF4HVCOgm0Uh5XYrazsr4ysSY5PfnHiaIIRDWjvx6lWk2OHjjjMrwbjVzh3VW5thoeOO/53T6cf0GcZ15MTo+RddVaz2DMH4rxIEjVHjQAXC5bNQV0c5GRuhSmlJSCh+CLnlvFGfJ8J54jyb4DxxnzumiO14blXEVsXfjOeULCYlIaZICU1t1gMtZKw8gdM5VnM6eEWKcD7Z5WR32Xn3bE8xn7PL00fXz+culsRQKJgKqJGAGgHCKMg3XA+e48Xi+nep7F+NeCWGGNHUUFbUAUBXGbQgxHfd9YBsDkAnAGiY7ODffmdeRVzw8zXQU08+z3pUkQd7E5dX56VkKD7k84XLihb4TxVM9NRzrw0ZuWMwnOb8uhJMcH7dyyqCqGnB+NvvTDSwKYZdyA2qb29VqeVPPpqjqc0RfagiEvoMbRKSEHvhr6+TTXHw8noBNFwQduz9BZfe4PKFmHpVCQz2eiKimFCk2G23/rnaGEA27N8gUCyXwNZZTPFCK+dPcf4Ey4U+nDqLKHzEMb9VgglRDrtYGPcvFm/953sTe503cCsMQc8bB9AkStpE+x9wlKpCqDXLxSQlrWjNu+y2H0KoMwsV1NFTvv7mu/+3xwDrU8lJ4nJyuhb//+ydB9wTRd7HQ3meJJvN7M5utmSz6cnzPBRB7GejCFbsgg0LAnbFfnoeFix4iofl1NNTX7E3wH5ib4ddsYsVTz0bIjwldTfz3uwkm02eJw+I1HPCfvLMttmZ38xu2O/+9zeRcGqP3fezT6J8oeHPfEX8MoCua18eRFivFoCxaHjwok++Ja9BFA105z0PD8Ht2wKgHggm/YLuAZJf0KRQ7PGnXjBKjS5c5GiONqVJqgBVgCpAFaAKUAWoAlQBqgBVgCrw+1bANE0yOCGRIZvBb1f/Zcbf29Kb9evnIQDa3cS5vYwNoC1SXB4hsJZB92nyuPu7+/dt6uPCgwZa9hrNXrcHNDVzLhxYbVFqzKCtVAVA9+nTh+WAy+Xy+pjtR44Ys/NOx5x4/I+/LDURyhqF9mwmU8x35rJFVOrM4bik9mzG+XJ8wwasUBp7g8odaP0tqr3BKicogF5l6eiO668C8x9/GvLEZSJOXGgvumAWsmAf8To44MDDvYzIcZogYYtYIIYPnXxcBYmZeYs+OwE0Qmhg2xasF1sBWFOY47S77p63krRmyZJlgJWtMNsygN5s062Jt0MvImIibEHzfKF0w433MGwooCRZEBLlmKsvIyr6DjuOJTyRfBP03AuAzhfQPnsdpMjYH0OVMaCXxDjk9QunY1TaDUDjyhmVwGiOV7HFLXY2wAB68y1GLl2WKRRx5CZC6I475wCgiIFoACZkMaVIyY0GbfnB+zi0s9Hn2ONO9nolPxfzgwT+5iLjDpjUmS1DVeclr1EO1eUldP+9j0lCkmPDsphi3CHgi4hcUhLS3uYQ4w6znghgYjybgqDF8gRPQYCduIFPJ/COjJKHw6KtgGhJjKpyUhKxiwgHpICo6qHYnDkPWW+y1BDPooE6OtCRR54iiBEtlIJCyOXqAzhpi823JsXL5SoWDNXillMEpFqD4xWLJTRz1nWCFGVYxQmgWVY7/PATSYQsCU634m6tByX458D5wb8b7e3tZNG4fQ/BRih8nOcSLIg2ueXtho/F5UfY6uKkU6dxQliUY5wQdjMSFCN4NhDe8g/DX3v9XfKugLNv283hPF5dulAwujrx49axu44Pqa3N/WRVGiAJaY6N9nXxMy66shwFj3cjgyAatc8lcPnJQ6JiCb334WIoJqxA5hYotPBcAkJMsd9751PyUkKFVNc0B/ErZ3wCAdDEgiOgJD9a9I2B0KOPPycF42ooyQnhaGJgUEseeRTWtu5jFc7y5q4cqW4D5+w33/7McTo2MecSHIi5XJzXq0y/cBbZ5oNFX40/6AhZSwCg+FiJA4os4bcfOCAdc/RUckWytV1RAgPo7u0LQYJjw57mwIjtcfuaJXxKnnLKNAjDklTTvoIU3uIPI199o9q+zopU0s5SVJbRv1QBqgBVgCpAFaAKUAWoAlQBqgBVgCrQkwL77nXYuH0mjdv3ENaHxwPE//qVQ5VdLle/pia310PcmpvcXgsp92ty+60YZ48VQ+139fG5XJ4+fT1Nbl+/fuXRDvv27evxeGzXabfbPWbMmOnTp8+fP7+jA5ts2B9nBJXzZrZgGA0BNIHO3b+tTJ33hM60fcRVTlAAvcrS0R3XXwWuu/YmEYYsm2MLQPPxJ+cvsGnSnLmPEloqy3GXy+tmpJbBm/+wNGMDaMv9mXgPVOu49VajsV0yHjEPR5VynHbZ5Vfbw8dVt+sp9cbr73IAu1KUg6CBPn7cBGIr3NPm5WV2fHR7R1aPDvYwOuBjzV6JE8JA0ERFf/OdD1cIoLEVbB5PhSK64sobLPoc4vxBSYxy/lAAxgJC5N67HyK+JRVz/OpFxrBU+2LxN1AIOQH04ROPJxYNJkKZXGnwRpvLclwMRBUpSZDubbPn9FI1hND50y9m/bITQA/dZFuyC4k8twvRez5k7WOPPKNIccCqnmZB19pUOW05XAcZT9DPhDg2zIMIseDg2DDkYrjiMEYinTl/kPMHAasCVuU5VYQhDijuJo7xijwny5IWEFUpEPzHDf9HMD2WxJ4QeuWV92U5znEaFEIY0wtBHys++eSzpGBl34zKEIL1dang06++WdIyYFizV4SiFf5ciYAGIHTaadMxV7WMf8sR0BgjE3mc+VXyQuizT/8dEHQCoCGf5GCS8YUvmnFtRw7d98BTw0ftIUoJhg3q0YFyMOXnNY9P7u+GU46ciocxzBm5fHlAOrsJ7ITzeHVpwtPnzXkUq+rTRS4ZUge5+yscG95pzL54YyJaeTdbQWcCG7DkLAi9z7jDnABaFNOCkJADiWVLc1aXtCF5XSnQTz8vZUEAx9RzLYBPEXeXn5fhxwB77HMQCfdmuaCbkbbYcsTX3/zYlS3WvcTg/M2uz70yn8vlTANrdfXfbiIAmlwZZCnt8wXf/eBLE6HLr7gBQL1Pf06UIwAoPNQYr9jUzx+NpGdedhXJyRZ2JRK4UcjH2b7kAZufCV1y8d8yWTR33hMjR46VpITPF4xEatp30lG4fbvyRqbQy4CDzoJUjkf/UgWoAlQBqgBVgCpAFaAKUAWoAlQBqoCtQPXm2xreqHKr9tjjT1xx1VUTDj1k8622tMKcm/s1NfXt38/CzU0ul+xyhXlma5drQB/X0Ob+Q1wuweViXC4PNvTo00RCnhmGGTly5OjRoydMmDBt2rT58+d/+OGH+FY9U34HvVqKUilfLBAPSftGzubReHnlletKASu7Ou/CnWlrvZ1VXaKy86r/pQB61bWje663Chxz9FQM4PA4e2UA/f1/2vFQeHgANLTRkC2bmjme10kEdLNXvPP+h0uVYdGssGMcbFhxg0DER2LfvQ/B4305APSUI08gJ2SxioZ6luSmG2+DPHYZtgH0RRdeZhQr0cU971QOf8YDGM64LKAkoZDq3ywJgbgWbuXE0DnTZ+RL2CXEnnqMgCYXmqKBPvjgCy2UInTV6xZ5oPmZoBUEHf3i8/8QTlopSPU6Q6o278FH8bhtjgjoW2bfj/0lCljPaefM8Hghx2kej+hpDqhy+tijz8DjzJGP89JcWWaU0Ozb7uJ41QmgoRjJWn4VORPDTHuq7LSCv7NmXbnP3vu1tQ4M6/FUsm3woI2Hbbz5yBE77bH7foceMvnYY046+08XWNP5Z//p/NNOO/Poo44ft9+BO+809g9bbbfVlttuucU2W26xzU477j5m9G4bDd7Uz2L6zAGJAyLwC4oceuXlNwqFkkHGyatcow0TTZp0kijGvV6J9cs81HysuPc+B6ISIhHuZbLfE4AmxNZEqCtjnn7meTCg92vifUB1RkBznH7FFTcXCpjyr0QENJaoZKLrr/s/VYmT/k8AtB7Z+IWX3jvptAuCkcFNbpkF4YCcDoba5GBKlGOCFL35lvvsOGsitK2/M9F7G2Qzxe233REPccnHgS/S3E/GwblN8nPPvJHt6hFA95BfzkBXXH29n9egGLMjoCGfBP4wCfKttSKp5kCkXvTp5zxUnQAaijEToQWvvm9pq4tyzM3gpzg33Xwndo/p1j9Xsr444jtbHD1mDyeAlgKpwYO3fvrZN3bZ7QBOiLoZRZQSghSFQogFAUUOb7bp1m9YMea9iOwsgCNdvsqU21dOli9uXFLkktHwkH+98M6pp54bDre53QHgD8tSWtPs9g3fPPueEsJvdtgfR9JeZmN9cljncpqmClAFqAJUAaoAVYAqQBWgClAFqAJUgVoFzPJrvGaxCnDIFh1dXV9/+81rb74x/8mn7pnzwJ//fN1pJzyckM8Jev4iN82CrvPj8unnTLvpvOkXnDf9/POmnz/risufffbpH3/8PpfLtHcsI5l0deFXnAl6tgOfc7lcR0dHNps1zXJokeO2EdkAmrzObq+qKXcFaFRD68gSayN7l7pETQ6rNEMB9CrJRndaXxUgUcM777SHJIY5fxAPN8dhUkPKm8miGTOu4HhVkiIejxjU0j6gHjFl6pJ27NRbiYBG2AzZAaANy0Rh8hEnKlLSCaB32XVv4h6bK1jhqT1pQsoz7ewLRBjCw9xxER5EeKDfdccc4rBBKGRPuyLCOr9Y/I0g6pLSatkl48H6ANQ323I4YbU2fcblrx2E0B4+jmS+29hxrF9WlXhA0Hmgcf4g61U5f0iRsDiNADShVH+ddTUPNRH7dZQtOObPX0B45YsvvSmIugVeFVVNhdRWXWtbuiRHRKsEq9bXL1cozn/iGR5qHIj5Qcpy4Yj4gPrxp1/hbB30uQEmq8+wVDIKxZxh5AvFXN765HI5cpkumdiImQzN59ytEu7tXIYyXWXHjG++/vGBeY9dfNGlkycdfcbpf3rowcfKdXFcqc0SymQRz0dcLjfrVwFQJCnCgsCcuY+STEsmIuNM2nHQ1YOVEDGs6MqYL7/yFuOX5GAKu8EQA2grAprnYzwfuf32eV0ZDKktAG2UUKHUcwQ0znvJkqWmgY45eqrHzYswjJ8ZwDgHk8M2HZNMbylrg7xA93MRIZCUlFYhEGdYZc99DnlxwcLOLPpluTWAnVXEul8ae7Za/p5Sd985V5Yimpoi/VwWU5rSds7ZlxasZz/l37byjo7fN0dWBkLvfPBxON4qyjEMoCsuHF5PyOsNnvXHi/I5q69WvbCrO5dMZBRLb769EApBB4BOqNoAhNBRx5xB/HZEOcZywQMOmpLL4Sco3T92ZXvpe/l8vqOjCyEUjrRYADrGgQQHEsAfPfOPMzghzglxVRuAyy/iYGQfK0Wi6WlnX7B8Gd4LP7zJmbms4TyWM22TYDtB1i5ZsswsomOOOtnTLDgB9GbDxrSkNg8GW1lW4zhdFOOKkhZFq333PfjFBW91ZtHS5djghvB2klv3ultL7II0WE8XUwWoAlQBqgBVgCpAFaAKUAWoAlQBqkAJ0+fym+vdApuIPPiVdAMjjmweTT/zp8Gh+QPklwepLw2J3/fc4yjXhfKFbL6QNXHYo2maRcOowiVr8CRUKOC7Vhtf4FGhioZtSG3fvNkJCqBpx6QKrGEFKliQ+FoAf0CEIZaRgU8PwNRuOx+I3W/z6KMPv+zXl4W8BljZ5fKowUQivdHX3/2CeZAV8Fw5aSvZWaUmEdDTz5vpZ4K2jQPnD7YN3NgooVyh11Hm8KUCHXzQRMDKkhi1vIZjPNDfXfhx2V+5h+tUeRGJzZwx4ypNGyjAlABTFs+KARC8f85j+QIeG7BS4PoExrgWPyM2zeedd5nXK0lSDPI4MBzymEGzjMz5g9tts1MhXwegaxqraKKJk44CQFGUNM8lBNgiiukvvliC4RlCe+9zsBZKcbzK+lWe11U5fdvseWYRYQDdM2PEe3V1Zt9++52wnsZA35+y4F1MECOvvPp2zbHX+UxNRyiLTFq8s6uUyaJZs24MBjHJ9fNasxdKwejwHXa2wSWJyS3rYGXlbK+igYcWzBfQ6B3H9m8Cghhh2KAoJSzuHCPfqpx+4vGXHDLYQ/RVR8h0rMVJE6Htho/hoWYNGokBNOSTfi4W1Ib4WDwgIQ5/VpJuRmG54I033kXaMV/AhcGT9RjDWU5nuqsTQ2pibG1T9XIot4FGj9o1FExGwwMhF8GG2jDWlt4M02eiSOP+QB7kkIpsu/0oDyt42IADQKdEMe1xK3/5y3W5XOVBC/6tr4+UL5ro6Wefh0LQelLSysE0B5NDhmy/aNEPEMY1rS0YbAUgBGH4qadfIeP+1alnzdqtXndy2svxVu3LM58sWuz3KfiRkr8MoCGflgIt1tGTLhf0MWF3s8px+qiRO89//OmejtVwWWcm02m9Y+XUH29dQsO32wmfyOT1Di4tcmneH9ODAwGr2U+VvF4JAOXGG+8g7ZstoqLjhQlnns40eaiey+W6urosv5fyV8NS0hVUAaoAVYAqQBWgClAFqAJUAaoAVeD3qUDd/WIDEUrWUExfLUat6hNx34cDpc82Tjw7935jaTsewseJCxyReDgvcqfWINfVsth5L7jmj4YQjYBeLc1GM1mnCjhOWqOIPv/sazx2nBXhC1jsBnDsUWdmOlGms3TYoUdDXtPUBOQ1SYp4GfH2ux+wkA4uv33yVa4BlUpZl5XrrpkNWI1jw3jyYxtlWQl/+dW3GF4XewqktPbGUcwIbbXl9uWIbF4PwJgcSHz/HY5U7Sn8mVQG71WwzHCHDNke8kkngN5++K7Eq3d5Ow6L7XHKVV627+wq3X//44qSDGppQYxAXrcnlpFFGD5g/4m9AGhStW22GykGwrKctErSMmhg2az5uutuU9S4xwtZvwwhHpjxoP2PRLgtiwcAACAASURBVGbZtKQRgCbP7n74/idZ0jF69rdYDDr2X3799+tvqYi+3vytNkjND0DR6hWjRu3F8xFJTYtyLKBEpWD0qmuv78qTsfQqVXD0T2djEVeNyy6/WgulBDEiiJFU62Z+XncCaMhFXnrhrUpGpJPaUe826K6uJ+0uSiE8ImI5Ahoz6KCGPcQFMR2Q035eZ9jgPuMOe3Php4aJzcHtjx1E7yxnTdrAUcZk+xoAXUJvvfl+PNra3B9A6zkE45Wa+nF/u+rmrg7LUYWcZj3+QlsLc3kzXyidfMoZDMv7oSwF41CM2AxaEBI+X+iOOx7uHUAbpe4AOr31H8aefNJ5LKu7m2VRTHo80q67ja/zG7EVsBKOBqtZYS8vL73v3gdFiO3FeX8C92F/ShLbPO6QZRgSVeQBPl+IA5ELLyw7PuNrBX7X4td9nPoTHyFJDOtaixNA68HBrFeTxLgiJbG7jk/Zd79D3l74sbN9Sw67HmeezrRdMid9th+222tpgipAFaAKUAWoAlQBqgBVgCpAFaAKUAVWRoESQh059NfLP90k8eomkX8PCr1w4bRfflqOshbMqQHQ+NaY3J/hjKuplTnMqmzjvBdc80ejAHpV2ojus74pYHOhEka6d985V4QhwKqQi3D+EORi111zB0Loicdf4oEWECKWPW5IVqL77nfI8i6zWCpbo9onX139cBxrET384NOYOzsAtI8V7753bu8AOp8z25dn9FBCVeKeZgGwqiIlw6FWkxhA98DjSGXKRXjk0Wc4EJGlVieAvu++x8jqfLEGdNrlNxH6ZXlXvlAqFNFDDz/p8Yg8r+PwZyv22Qmg/+u/ce60GSRauScajjL53M+/LA+Goooa5zgdR2Hz6d12O8R6CwQNGbo1HnhQSWqhFq9X0vXWTxd9m8+ifBbHmzcC0PYrJJoa47mUDaA5Ths3fkKd+Ot+1tEg9iWZBKe3d6GmJpFldSGAA4oZvyQq+lfffl+PGB3909lGCKHXXn/Xx4qRaJuPVVi/GlCSEw473gmgGY/y9puLkGUhbUmx4gjot95+T1GjeDhEDKDxxHFl2w0WhKEYGzV67/vmzi+WkBXNXBa4M1Ow6bNzpAJngfFy6w2jXK5QKBjkCQrB0Lls6aSpZ0hiWJGjjFfSlBavW0wnh/7w3XL8AoF1YjbqDx0dWbOIOfg5510ciSZZIMCAJmuJKoAWE4KAA8PffPMTHKlNrGZ6ioAmAFoQNUcEdPoPW+0K+aQo4nB7K5/Is8++9l/vcvy0ueePo8FqNrCXlx8dTTv7AkmMQi4GQYoHLTxogXwa8klZao1Ehrib5UmTTnr7bUz5y440Nbn1NlM0zVwhnyvki7WuXgiht9/6SJWTPLAjoJO8P8b7Y5KQJMOKjtlhz3lz5hsm6rJ92BFqz+bsBxd1FjfOJiZlIi+RORl0b2Wl66gCVAGqAFWAKkAVoApQBagCVAGqAFWggQI4AtpEf7v6vcGx2YPCd37zJcoXUd66G62JKXOQB5KTzR8aZPzbFzvvBdf80SiA/u0tRnNY9wrYXMhKnH/eDBGG/D5JDsQIMv7nI/9CCA3fbhcrNjPJAQXymhgIf/DBF3bhcw47C3shSZgGymVLLy94mwe6E0ADTjrjzD/3bsFhFtGnn3wVEDVJDPfrCzh/UJGSidjgMoCuOxKerV51urLFU049m2E0ryfkBNC2IzBxebbzcF48SIDnK6++LYg661cFMcJxWlBLE/pMXDgwKFRTN95wey8AumAY777/IRSCYiDMMKoAUzyXmnTEacUiuvba22Q5zvhkt1vQQi2sX73kkqvtwtRWpWaxbaLf1jIE8mkHgNbTLUPqN13n89UGKT+BzORwwLuJ0AsvvS0FUoKQaPaQsebC24/aiTiJ15Ta0T+dbLezy9hm2x1EKRTUkpIUY/3qsM1GjD/wSCeA7teHX/TR1/hwBnZ9KpVsD+iGFhyPPPoUCwI+VuJxMHV58vhUUcJI94qrbspW4vUNaxhJhFBnppDJGSsE0CZCd9xx1+UzZyGEli/rckZAZzNmMjFA11KAlQGrBoQI5w9Omngcsa+pUaPbDDFsueLKv3sZyENVVsJAUFlOAVAvR0CLmD6LYvz7HzrJsIE2g67r8xaAfhEPmInNyokFRzqoDvJ6QgRAs6y+807756u2Wt1Kgxc4Gqxmvb0cL81ljWOOnopPJQKgOXxqcCAG/OFIZPAWW4x+5NHn7L2XL8tmM8WyO5i9tHEiV8jPnPXXmbP+mivksYcXYe7Wf08ee+Q5wKrWCKIxCBJ44mKsV5MDiQCMXX3lTbYjvYnbF/+/pj2b68rjSHd7curmTN977/2kfXHjOj6NS0rXUAWoAlQBqgBVgCpAFaAKUAWoAlSB9VqBdftOJwl8ynSi7C8IVW5F8xXry7Jw9r2mI0yK3KmtSWWd94Jr/mgUQK/JtqR5ry0Fas/VQw+ZzHMqYGXI69gRlQ1/tujHf1x/Fw80DG58ihiIcpx2+hnnl01vK9a3zpOve9EXf/G9yEedAJqH6q5j9yJb9rLv88+9ag39F/H7FMjrkhjdeqvRONzYcWVxHI5Uprxg8y2G83wsEt5YEtvIG/2nn35BVwbTT2Kb6zxuR2cxkyvZ5hsvLXhDC6Wamrk+fVhVTQEQ1EIt++51mMhH5UCiuZ8giVGWkV94/vXG4djYSPqOu+7zeDlBjPB8xMeERaH1ilm3Ll68DIAQAMF+/TnWr4qB6OgxZSkcdektaRSNUSN3FmBLBUAnBCHmY6WF73zc227rdB1RuyuLfzQyBXTSqdM4ELEcliN+XgdQv/RyjOBrHmPWFtgwEQlbz+RKU46cKoi6281zvKqqqaZmOHfuU7vtdiAHIvZYl5CL/PBdRwVAl+kzGYcQw+hSqSZu3foNu/2O+6AQYnwyx2nliVd9rDTxiOOW/NxpF8fuOaQjOelzd29lEmt/zvnTQ1qUA+K998wlYctkqF/TQG+/9QHwByCvhoJJWYrgBzww9M9Hn22kRT5X9uUgocEXXXiZFAh5PZwgamSM0L33OZjndUHAMcuCkGBZLRIZTApvG1U7ab5pWdYYJrrt9nsFEYfqC7ClMmH/dCudamqSbr/tYexvU6HwtiCOE7L2glLdwl5ejgTfd++DJTGOhzm1jJhFLulngiIMX3/dbIyxSdx6dadqRo1SXTlssf3Tz0u2GzFckAKyqph4cNQqgDaL6PZb50Iuwngs72k8oike1NTvUyZNPGHpEkfMs3V5KV8orGhxm9rX6Wa9w4HfpTjn/OmiIMmyesv/3WobrTQqKl1OFaAKUAWoAlQBqgBVgCpAFaAKUAXWfwUymYz1WmlNSdcNku4ZAVUioMgtugMIkQU15XbO2HeavSSc29ekbR5Ql6jZaLXPUA/o1S4pzXCtK+A83xAatvGWAUEngxC6m6DIR5ctNdLJYZw/6PcpHKcJYmTb7XZubzexn2yFPneHMnXVMIsI8nrZhcPygAacJMnawnffJ8zRPnHrdrzjtnmSGJXEKOfHcEoSozuN2bOGG9bsUL3efPvdT5IUEcUky0aa+gfxAIBC4vbbHyTxm5hMVR6a2YcmA44hhGbfdo+iRlm/LCtRH4uZezjc9trrHw7fbjcCoBmPIsLwf71i33vnUwLLegTiRgmdd/4MxhcgTg6imGZ9sf+7+cFJR5wiCDFZTipKkud1WY7PnfdETT16ncHg1DQnTzpWFFo5dgBm0CABYRQAZdYV1/a667pcSXTGXhUIZYtowmHHEljs5zCA5oTw7Dvu7R1AFw2UyWFrlNPPmEbos9vNS1LExyrnnHvpf005dt31ACeAFvnoZ598gxlxsWSaRdPMm6WsaeZt+lzXkYwSsgE0eUIAQBAA5aAJR/z40y9Fszpmpt1n7I6EuxMhlZbDhL2BZUdemnryqUJAhhBPN998K/biKFqTlbjh+lt4TuY5WYTBgKAHBF1TY+3Lc41aa9kvFgq3foBPOP4MnlMhr8lSBABFEPWJRxz34UdfQhi2AbTPF9x00xHENKMhgC7i09kC0JEKcSYM2gbQLaoy0BrYr3u5qudd5fffuYRsb19oqgBakZJVAM3HeU697rp/GEX8YKAMoLsfqsGSoolx8edffrHZFluIssSwbCQW/eY/3xZxw+NHQUVLahtAlx+GWZb0Ew6a/NOPv5hGvcc0aUS7We2E3biEUBeMcvuyPgCh+I8bbmpQRrqYKkAVoApQBagCVAGqAFWAKkAVoApsMAoQ8lCHm7vz6DVfHzISYSdC7ahi/lw9KLnRJDdpjttQsqC6WV3Kvj3tJVG3S3XWeUfoTFe3WBMpCqDXhKo0z7WrgON8+/GHZVIgJEuRgKBz/qCnWRCE2KxZN3q9CgAhltX06ECWC15/4+1dOdSeKRVL+LX07iS3vgIWKdty8+EW1AsRtMdDVZSC0y+8+Odlv/Ryyp477S880MkL8pw/pEjxA/af2CPttQ5avd68/MpbjE8WxTjj1fv1lTgQkwKpd99dXMZw5K18B4Mm6NMooaOPPVFRo24PCGpxHmqyEtVCqTff/PCXZcVkfGgAJiQxju1E/EHAqt//Zxk+bqNncQjtuts+rB+H00pSwusJKfKgO27/J8/j0FRRjEMY5nlMDHsKKa1X0Z43rDDgq6+6XhIHOgE065e32Gp74htgb7z+JOwfABOhnIFG7LAHtsvgEoCPARgRpOgL/3odv0rTa4nbO7I33jSbh6rbA9we4PFyWii10ZAtuzKYn24/fKwTQMuB2KuvvFsyUT6fLwNoM7/SADpo0WcMoG+59c66uGxnj7W5pJ1wri2aiNBnwEM/CyPhxEsvvmJH+BLMOmXyCfiMA0pzf+D3SYxXHLrR5nUy1BWgZKCPPvxyxPa7KlJchGFPswB5rX8TGL//IQihx/75nBNAAxDac8+DchbQdpbNmcZ8FqHbbrsfj+hYEwFth0K3nHjC9LpSVWar592vAdAHKlI8ABMBviXAtwVgivFCHFBcwIHMxMGikj85O+1LFVlcM2ta9Hnb4duzHPD6GCiK4WgEe+l0B9C8zngUC0BHOTbK+UO3zr7TEXlPssXamNZkIKN2wo8t7Mlq39OFgAo4kfXxsqQ9//yLjmLTJFWAKkAVoApQBagCVAGqAFWAKkAV2LAVwHaWRePqq68ePXr0nnvu+eOPP671+pQQylgTuTN23IHa94WOZXaYY8NyOvdquFGjFfbtYF2i0farZzkF0KtHR5rLulTAceIt+NcbeigREHTAypqaYhkZgJDHI/F8RBAwJfQBdfe9DsgWUVeulLfo8woBdDaTL1hWqlNP+KNF9LD1BABBHyupwdjgjYb1Hj19xGEn+hls/SwHEpw/pCktUyZNbSBXCb9wX4HBjz72dFBL83wkGBxgj5/2n//g0NGaqNVSmSUhhB559KlRO+yqh+OSrEMhqIeTPlYUpdD8J17I5VAmizg2jHkZnmKAVTmg5LKN2bNVylR6IwCCLKu5XJyPCUuBFuCPsmxEUVp5PsL6VdYvv/b6u7UDIjaoX2UxecH/4YfmSwE8dBsHEhyIiGLcx0qAk17816uVDdevv+TaTPQvFPEYjDwf4fkYAdCiHFv0+b87c8ViHWqtrcTs2+7iBTkYinK8LMm6pifUYOyppxeQrRwWHAkOxFQ5+fSTLxpFlM0QAG3RSLNIzDccMba4aKZpWhHQ90AhyPgClb4aAkC54657SLG7clkCJRugSYMwaOev0OFHTPb5OVFSvD6W5wMbD90MF9UaV9CO8z3i8GMVOcpzuEepchKw6gH7T8xgDNvzJ59Ff5lxjaa0NPWFPNADMAa5SDjUuvMue/68tAshdMvse50AmuO0SZOO7+jEyjrL5kwbJl41+9b7rME2k9Z4gGnIpytGHC0CTM2b9ywGxBXjLUfhnD/1jguKYwsHmCZao333xgBa5CsuHHycYTjDyCNULBQzVpS6UVte4hCOg9mduZGDvPPeR0OGbiGImqLqoqSomnbs8cdVAHQ5CBpbcNx2P+Q1xitVAHSc84fuuhO3L0LFbK7DYfVcNFDBMREMXTDwk46qjIdPPJpcJbw+jucD8Vi6PGhkTd3pDFWAKkAVoApQBagCVAGqAFWAKkAV2FAVMIpGNpvt169fc3MzwzBTpkxZFzUpIGR7QZbvDXExGtyAkru2huVssFfD7WtWOO8InemajVb7DAXQq11SmuFaV8Bx4t180+1SIGQBGlGEYR5oHKdDGGdBGIoxj0+V1OSzL77alcenfUem3Q75NCrYt1HpDRPdfsccH6v068+53YIkxSAM4/H3tLbZt84hyLFoonyxBu4ghMbvO1kWU34mJIspHkT8TOiQg49pcJQaAH3lVddbg8hFNG0g8Id5Pub1Kk8+ieFsoYjfx8/lUXtHmaUtfOfj444/LRJtY3xCOJICnOhy9RWlIC/IDz70WCaHKfOLL70p8vEATFnfGED/YcuRDUpSvgguXZZRgwmO032+EIRxa2y3JAdiLBsRhATG+mLkvPNn4CKZPVC9RpnjIfVM9NOPywEIYlwIw03NEAohAqDH7rEf0bOjK5srYJxrT40yXEvLrZ6Wz+HSGQXE8SppIAtDYym+/6G9o7NoWXSQEpULnrE+mKveejsviLISanL7ACdxvMxD9a6752VyJatLol122Z/nEjyX4kELz6XcTXDmZVeRweuW/dJuVzOfL5YPUA63NhEqGgYmvvfeP4cMQshxuhVMjcefvOzyK0kPL5j5RgDaztxOfP3N93vtM97nhz4/7N/MBENRUVAuvOCSXBYf1abPJRON3XU/VYmzflWSYpKE7bwHD94aD2/YiTtqtoCWdZh5q6hdWfTww89vvvkOemiQ161oSpumtIl8XJVbR4/c6+elXUUTu5T8edrFOJC54gHN8/qMS/5a8+gFu4Vg5uzsGwRA41OerwJoUWhlvBFRaJUCqZ+WtJOuZdfRSjiuICu6DpAdjaJhFEuTJx0riWGRj5YZNB/1s3Dx4i9K+H8VJeyXYubLht2oYC0kowCiQjFncWqcWcHAujz08Px4YiMfE5alASyrs0BgOfDuB+/ni4W6a9R9984D/oDfJ/FA5/0x3p/4rwf05TNnWfkjqw/YYw3WAOhKTasCfP31kr32PsjHSj5W6t/EBrU45NXp519C6ki/qQJUAaoAVYAqQBWgClAFqAJUAarAhq5AR0dHNovvlKdMmeJyufr16+dyuUaMGLGu60VuQnsuhX2TW715675htwwqe5VfhLUCtLrvRrYiy53p7luu/iUUQK9+TWmOa1sBBz4684/nBEQ8AJrfJ4kQsyGMTWFcCCQtAC0fc/xpXXnbKhkHA9p8p1GxOzM5ghQXffqVIOoABAUxoijpfv2gICR8TDiVGlYooo4ufFGrj4YuoZ1Gj5PFFMeGJSHJ+2OMOzThoKN7OhapRjUC+s675nK8iq2WpbTXGxTFuNsdGD9+IokDxeGOBsoX0IKX3zzq6KmSrEeibW43z4IACwIcH+AFORJNPvjQYwUL/BkldO+9D1ukLI1da/koD7Q9dt+vp5JYy6zivPrae7Ic5/kYyxKolyQMWoApny/Uty8/uOK0kCt2WaGXK4intg9XMrGR7qgdduWhapmZhNRgQhB1jpcBJz3y2BMmQl3ZfCZXqFxGMYZexx9LE8Niv2YRRcIpHmoVBq0DoHz/Q3e+WS319OnTeUGMJ9OAE60JR9ATfJ/LW1GpCB100NFOAA25yKQj8OMKPOifRe2zmTJ6JgJaZiaYPpOoW4TQCy+9pGrYTLkCoGMcp+82dl88cGI+Vwc07c5P8HRnJkPGwcPR9I89oWoRXpB9fuj2sKIUFKXgXnvtl+kqECDuBNCHTJgiSzgcXpbjohgH/jDDhi6+5O/FcmExg166DM2Z98zuex7KgjDDaMAfFrmkJKT7ugQl0LrLTvt/+/Xy9o58wcADaR597EllAA1T+FEH1G648VZyflUH0ysD6DKDxni6hG6ZfT8AobKGXIrnUrI0gPFGVGXw/vtPsRqDRCXbJ5rj8lF+9LziXkb+B3PmH/+sqQnIRSAXwxOvi4Jy1VVXFYrYK8SyTCmSOGg7GrpUMqzw5/IhSOeYfuElACgMo7G+hCQO9jFRNRi79PKZCKH2zo5KG+H4ZYTQSy8uUFXsdoIBNIhgBg303cfujRDK5TKFYs55RKfzBn4ekO3syuEAc+ttiedUNcXzuo+V3G5elEKiFBozeje8zgpvJ5vRb6oAVYAqQBWgClAFqAJUAaoAVYAqsIEqMHPmzJEjR44dO3bhwoUu6+PxeFwu18yZ+G5rvf2sFAMhN7KOOlT2ogDaIQpNUgVWswIOgjR61K6QV4kdrQ2gOQFHQIcTQyQt9dV3P5GjW8YVyHo/3bDxkCPWFmdqDSSGlnYsz1fGett1t/0YRvX5gpKU8PlCwB/lOTx6HsGImVyhLgLaLKBNho6ShHQApgIwZQHo8IQDj60o4Ch6GX7ZXAy98NIrAODxA3k+wjAqhGHGJ/tYafSYPc47f8ZlM685+eQ/DRm6FRRCLpeX8QUYX4D1y1AIehnYt79n622Gv/v+h4Rwke/Zt95XGTAtKfJxyOvHHnNSw4hPq2hX/+0mSUpAGOdAjKBn8h1UB3Eg4nYHbrr5zoKBcgUc/lwwuyoWIiuFoUsmuvKq6zlelaSIlxFlJSzJuiBqPlbcbIutycBr6yGAJsG/qIQ2HroFFEIkght7YUPtkUefKbdsrQAfffTRuHH7S5Iiq0HAw35NXo/XDzjxoAmHZ3JGAT9IKO9wyinTnACa8QQhr5NxCCt9Bg/9d/NNt7e0DOR5Yf78+VanxQDaMLIGKuQKWUlRg1rSAtAxDsQ4EFGU5PwnniPdoAxwHR7iZElnpjxmYEdXfvqFl0iyLishIaD2b2IFUROlkB5O/uslhzuKo/Oecdo5kNegEFKUZJ8+QNcHsCDECdHJR502c9Y/Lp15/cQpJ4eiQ6TgQD9MCGJaUVoVpTUAE5CL8SBy3NFnYVUtHfJFI18ojd1jPwtAJ7Cbs4CfTDz2+FOWH0XZsd3CsoY1OF8VQFveHfezrO4E0AJsgXya51J///udlobYwMbRUR3VWGkAnbdcPO668z5FDkNerzDoCPAHhg7ZNJ8vWp7d2BSFOEHX+UEbxVI+XywUjBdeeuWAAw+HQkjXW2UpLYltrC8hS62HHnYkGZMQM/fyyJAYQJdKRj6fl2U1pMV5oGEAjSddVeJPPFHue84jVvYtGahU074XzJSkiKxEBVHv3wQEURcDYV1Pf/7Z12YRGUVEgtztLkcTVAGqAFWAKkAVoApQBagCVAGqAFVgQ1HANM1CobB48WKv19vU1ORyuRRFIQDa5XJFo9G6YQnXbb0q4Lj65rdzScOykRtZa7W9vRVsVQXQzrefHbCLgAHb3rLhEVb7ChoBvdolpRmubQXKnNgK3IuEU5BX8XvxMCSJ0QCM4ehdEBallJtVr7nh9oyBludypoVdTRz+jD1SewXQpUwRhzabqNSVL8y8/FpVbeH5CIRRhtFEMQ35pMcjMT5h/pNPLe8oGzTb538hh5KxTQMwpQRaJSHNsVHGHT74ANuCozv8qgLoDz/6FHCSJEV8rGJZLatiIExMNnioehkxEm3DwwPyKserACjhSAvrl70MBJy0z34HfPvdT/miQQAuaZIzzzy/DkCfM+1CEs3aQ5tZRTtx6p+wDQJMOekz5JOKPEBV28aOPcjesWBilWrRnr2yYeKjj7/keFXX01AI9m9iZSUc1OKCqKlaZNq5FxSsyHNbTPsy2TC7Nb2iconHQdAltN02O2AAXWHQiho/6uiTC0Xste0kmdddd30ingJ+AfiFJrePBYLbwwZD0T33wk4j+UKJMGhS9gsunIXhKcDW2JBvhSARUltHj9pj4Vuffvft8pf/9c5fZ94waMDmkNcUOez1+q+66iongMYxs13Ltx8xioeaYzDDmKYN3HjYtt/+55fOrpJh4sjh7hMOoc2ja669MajFGZ8AOImHqsfLkRbRw8mnn/0XQqirM5/NFNuXZ8p1tDSZcdEswMqShEm3IGCvGI9PhWJMlBJ+Xvf5Nb8Q8QK9yRv0sGGfHzu6+HxB4v58xV9vRAhlrcBco4RNbAoG2vIPwy2yH8dWzjAuBsKvvbGQ+Bn3EgGNAfQtc7FfDbExsSKgSfizLA14+unXrROZPNooVn6Au5+DK9WNMpnMBx98xHMyJu+YQZeDoAOC/sczpi1d0mkW8aMCZ5w4UewXy+T67bc+mHrC6TzUGB8e4ZNhVJbVGUaTpfQBB07GHaNYIAzaAZFxBHRHR8eIEaMglC0AbQVBg4iutW2y8dbffftzptNwHtH5sKHcvtfcHNSSjE8GIMjzuscLg1pSEHVdTz/9zMtGAWUzph1lv1JC0I2oAlQBqgBVgCpAFaAKUAWoAlQBqsD6p8CECRPcbrdtu0FIdFNT0913371eFdZJPLqnGxa1QidskEzCrJzQ2Zmu3P+SI5Bc1zZioQC6YWvSFRuKAkaxRCjq5599JQVCIgwGBD0g6HIghsf9AxGfL8QJ8R3G7JMrYgRknXDkL/GQ7X6OmxWCiM9px0mLXS/aBmzG8zrLlgEf5JM4Qtkn7Ln3PkWzEp5Jwkut01lXh6jSINYTkWArBCnWE9lk6AjiI2yNh2ZbJztBWFn77UfsKEkRScKOCj5W4qEW1JJl6GmhT47HYwASMM1DTVairW1Db7xptrNK7R1ZC3Sio485zQGgoxxQZt9yVyW2u7618fISGjlyLI4/xQAao3Z7kqXWfv3EF198p+yKUEH5PV3U6nOumz/5lDM5XlbUKA9VFgSEgKqouiRrDAs+++LL/K8a3LAu6zUzm8sVDAssnnrKWaoSb+rn17UWHmiamlLl5KzLr//k428++vDLlxe8/aezputaSpZ0EQZ5nxTzKQAAIABJREFUTuY5POog4PDjij33Gl80cHciNNSOgH7++Tf79glI4sCmflERDgrwLZVBIxNW2+HQdWLhrSpxKRB85ZVX8OMTy2LYtGy4i6b5l8suV1RsnGKFPyc4gINqFXnA0KHD5859phM/JUHFIsqVI57x7JNPvjp58slbb70TDuXmdUmKsX45qCWJUbXbAx6f/6ztXNNd188+/TfLCF5GFET8bMbnw6NWQhi1ZsOcEOaEqMenNbllTohjJM0qPK+PHjX29Vffq8stV8C2HYoahzBq9Ter4wnBr77+lmzp7NuVc7NqzzJ37lMkYB/7aHMpa3xL7KktSwPyeay2gQpW3LQNoEl+PZx9dQVzzhILDoTQiOGjRRhSpLimtCmBVllMsV5VldOHHHzMewu/zFsPZQoVnc0Cynaiyy+7ft+9DlPltCTGVbXN6w2yrC6KcZbFdi7jxh363Q+/YHBcDnzGrWvP4v9bmOZll16uqjrkKxYc/pgipVW5ddjQ7R6Y81SmA5fULCBydFLsJ598efLkqVtvPcZq34gkJVhWCwZbAQhyvOp286R9c9kSfpmhNn7fWXGapgpQBagCVAGqAFWAKkAVoApQBagC678C3377rcvlIgDajn12u90DBw7EEGN94gy1d7j1cdANpe4GoCv5rHwEdMO819AKCqDXkLA027WngA2gX3hhATGAFmEoIETsCGjgDwM+9tyLC3GgZbF8PluU5VcD6EyudMvs+91uAcKoHWFqgTZNCMjffveDM+SQALt4eNMA3wKYGIaJfAvHxqPhIaaBL3nLly8vFAoVpeoRWL5QuvveB2Ql2tTMEdAMgCJJESeABkDxeKGPlRQ1Loj6IYce+dXXP2RyNQMhZnIGJpRFtPc+h9QB6Ecemd89Ajpng8kSGjBwywp9rgHQPiZ89tmXdVaiVi1YhsPJfy2ANkro5186Nt1sq/7NDBSCFoMWhIDKsIAXxGuu+3tFnPXob6FgFPDIcOiBeY+JMMQyAZeL8fsURcKuJprSArmInwlCLoID8LFRr2ZPTc2cxwsPn3gsGUbSCaCJz/jir5aoysCgMgxyg0S4kQWgsXlLgG8RuXRlSvZ1AU1NjNvvwELBsCwXcAsTAN2Vyy7v6PR4OauLxjh/ivOngupQryesKoMZbyQW3WzsboefPPXC0069ZMLBJ+yy88Gbb7aTLLVCSJh1BIAQx2mSFPN4oRZKtbYNffElEjvcWyscf9wpshKVlSiE4e4AGooRACMen8YJcSEQB0C58OJLC4VS92DbfNH47oefoRDCQzuWA5kTohSyH85WflbJiUx+XKsA+oUXFooiHieTAGjyDdj4FpvvmstZuL+U7+m9h/qzr7eqIpTP5zOZTMlEt916V3MTywNNlVs5NqoE8HdTX0mVBgBfZPtt9jh68pmnnXzRH0+bcfABx202bIwqDVClAZKAmxKClK4NZX0xPbQRfp0iEJ085QTSDar0GdUD6Gw2297e6fX6rUFWLQ9ofyKkbMS4Q5o8kPXoiegme+x26ClTp59xysUTDj5ul10O3HzzMbKEA8mtZxIR4A9zICIFUh6PpIVaWtuGvfjSm+SxeZU+Uwbdew+ga6kCVAGqAFWAKkAVoApQBagCVIH1WIGDDjqIhDzb9JkkbrnlFmv4nEqU0HpQhdo7XAqg14MmoUWgCjRSgIzGhhC66cbZIgyKMCRCbMzKA+zNKopJWUofdcwZeQNlrGhjcnqvGoDGFgQZdN3fZ3u9ksVxrCBTTpeV8IDBG5ESVhm0iUpF1Jbays+EIUhwbFwW2yBI+ZnQV4u/M4qlZcuWdatU9TFW0cTU+Kijpwa1OMfLZHRBHqpQCNqTJEVcLrcYCO+y676PPPpMLofaO3AlnZcw7M5sYMuFjYdt6wTQkNcWLnw/S0RxlKOry+LKJbR0SWfFfyPtiIDGJHro0OHt7eV9KuGZqwKgSRZvL3wfj5vHiVBUeEFmgcALos/PPfn0s0Vr6Fa7Oo5irrOkaaB8HkfpLl+WlcRwQNAlMQp5nfMHAwJGz5KQlMUU8OmsV+PYMHHptUg0jvydetLZpOjOCGhiLkGWTzriNJZJed1J4GsN8G3kuYUFoFtFjkxJyEV2GrPn0p/buzqzNoAu4QcA2O33vz+oZ551Lo515RIWgG4JKsMkcaCPiavKENaXEGCbKAyAfCvjjfmYqLtJk8Q2DsSAP8qyVnQ/pwEQ7N8E9thj/48XLc7kcEB83n5W0k37TKfx7sKP2wZuLIg6BtCWaQyEYRwBLYQ4McQJYTnY4vYGPT7tz+dc9uVX5XDm2pxwyQuGseDl13G8vwNAbzRkc2tVqa4/OCOgSQm/+OJHSUo4AbQAW3xMdMrkszIZEkpMxK4z3vl1ABqP6JjJ4AdameKokTsDVuVBxO+NilyaPGQCTIz3J0ja2xxi3GHAxDg2zvsTEKQgaOHZFM+mWCYlCgNkaQDPx045ZRpRo4Y+dwPQZJuzzpwmwhDkqgBaFtv83qgmDybPuiTYKnJpxhvxMWF3syoFWirtG2HZCAfwY4b+/YU99jjw40X/rrYv4c6UPtf2SzpHFaAKUAWoAlQBqgBVgCpAFaAKbEAKvPXWW7bzhhNADx48mNTif9UD2iInNAJ6A+qqtKgboAIkjPfC6Zda9BkDaM4fZL0qYLGnqh4a9N2PnZ1ZtLyr6ECZJYSpLD45a4Etma0CqQrkwmOd5QvYNsEsocf++dwWW46yYkV1jtM22XTLN9/GEdbLOzqdANosoI0GbevuLwVgCvgiZChCzh967BE8olpPnyqARgh1ZjDzO+PMczheJgya42Ung5akyKGHHf30My8XirhsBBHmCxgX2hPxfjVMpIVaHDYOUchr33z9fXt7p4lrVv/JZorvvbtIEGIQxqtOCBUXjieeeMW0KFVnBhs1r3IEdCaHbW3zhdJHiz7fYcwuNoNWNf2Kq/5G/DfsivRQyvpSr6X58hBtJXT5ZdcoclQSo6TLMV5JldMBmGA9uiSklQA2ca4waDxY3FVX31w08HMF0pHsCGj8sMF6SIAQuvvux2VpAGCTTf1D1QhomKqEP6dFLrnfPodiK+GSZTGMCXTZhWPp8qUmwnG+CKHWtmHlIGiQAGzS50326xPiQYuPifuYOORbg+pQT3M4om/GeGOQT7MsRpMEQPtYheO0c869BL+dVNGdZNujxNmMmc+hN996f+ttRkIh5GMlazzMEObRBECLoU02H3HGWRd8/Z8OEmGfNzKlkrFs2dJKVy2fcfliYe4Dj3i8sAygQQvPJfbca/wvyzvqR/jEe1YjoI0S6uwyOjpNWcZjZpLYZ8inRaHV6wnPuPiGri4CoPFofmRAv1LJGqQBnyvV873HCjZaaBrouWcXhPV0U18ockneHxO5tBIYoEobKeIgCFoAk4CgRRYGSnAA50v6vXHOlyT0mWdTPibKePVUctM773yks6vMfXOFfA2DdlhwkEdW5HI3oHWYyEfx4w1/jGOjfm+0qY+Cn295o35vXORaQ8pGHncoEt6E8UZw+/pi5YmN+HxBq30vrWlffC5S/41GTU2XUwWoAlQBqgBVgCpAFaAKUAWoAhuGAuPHj+/Tp08/6+ME0Hfdedd6WAEn8eieblhgBzqq3YsC6Iaa0RVUgdWgAHlz/MLpM70e6PVAPCYYr4dDA1ivKkvpefOebu8oZnKY0jk+5Hwlp6pjcbek82R2cqpMV+GJJ565+eZbH3zg0ZqdHCzLKKDDDjlekZLxyFBJSJJJU1NXXXltNpMnsdvlQcOsQNYKjKvmh7cpotdffeesM8/dZ+/xW26xzahRO44fd9DFF1368EPzq9v1msplS+8u/IQHehVAw7AeShADaMv/qKoDseAomejN1z/AseRczM+EJSFtDaKIZ884dTqOszUrk1Xy2oEcey1N7UqSD1n22aeL77rznptu+r8lS5aSKOMe4XhtBmt3zupCZd8SK73N1jtoagryutct8kDj/CGODTPuEPBFeBDh2LDXrfiZ4F57TPjog6+wbmSy1askzIqk/42r/ePp50pilIzRZ30nQuqAAEwoUjqkDrj2b7d2098g+ptm0TRN00CmgV55+a2Nh2zFcyrjlbzNQcAkAnybBFt5f0KTB4eUjSBI8f4E8YIAvoi3ORjRB0tCUuSjw7fb5cF55d5VbegKie5d8XvunnfcsSdvu93oP2w9Yvz+h43f/7ALL5758itv2Xth3FsyTLNIrKsRKlpTuQfmCsULLrzM65UsixsrghvEjj3uZPygAo9PWHMOV8CxnTdObD98Z56PedxBnktAPuljwpo2+KEHX8zlyry+ZutVnSHPzMnpefFFMxU56nWL7v4S4w4FIKbAJOSZY+OMO6yrQwJ8CwQpJTCA9ycAEwNMTJVbRRiadMRR33+3pFDARvZ4sj7lU6rSN+wmKG9j4GvCKy8v3HjI1jzQGY/idUuA1QIwIQkYglfaN2EB8SQECat9Q5HQxtj9g483bN86dVdVHLofVYAqQBWgClAFqAJUAaoAVYAqQBVYywpkMpmOjo7Fixf3sT59+/bt06ePy+XyWJ8dd9yRlGe9Cn9ejRJVmc5qzHS1ZkU9oFernDSzdaRAIY+53mOPPAN5LSDoihT3NAtet+hngn/5y3X4ffl6+kwi/SpDEvZa7EYA2ig2oDUOAF0y0E3/uMvrFgNCxNMsWK/qayIMXXvNDeSYHR1dZbrUI4B2HMHErg+oUMCLCDjutdSOlSWUz6EH5j6BDUm4JJ74uAjDf9hqOAGpFuStXqyILXXJRD/+sGzwwC14oBNPCU1pA6w2bt+JqI6L/TYATQpaQeF4LtNV9mMqFArE6MBRmXWddDQuKqFsxvz+P8vG7LA7BxSWkVlG9vsUOZAQ+bgkJBUprUjJ7bfZ9d67H8NRtsQgowKabapIEjaAzufMjo7spCOOkgIhwMqMVwSsqkjxcKh16glnffj+YqNQQf+kIbD+TgBdZtAIoU8/+XLHMbvynCwHEgGYssKxccwsGckQcjHiEwJ8uIlFPs4DfdCALWf/3322yoVCyVlOe/nKJ/AbA7Vbm8jsBUDni8bEScfgEGwQwUMI+vFAghddPIsA6LqsrIzLJwmJl/+vq/gJJ54eDLZ6vUGejwlCIhgcoKptxSJ+cQHXpeQ4qWoL9qvmqgDaChy++677gT8QECIEBHvdiqVnhPVqXrfCejXIxcjTCElIsl7Nz4TG73f488+/SA5aKBTKTw5sAF13llmzTgCN23fRtzuO3osHmhyIBYSI5QMTati+VoD2oLY/zL55jl3T396+dlY0QRWgClAFqAJUAaoAVYAqQBWgClAF1q0C+Xx+4sSJBECTbzsC+qWXXlq3ZVvTR68ynTV9pFXNnwLoVVWO7rf+KFDC8YBmES37JXPeuRdzQOE51e+TRBi67prZpJj1cZN46W+NgMZELJ+vDtnnFKSCKfM5VMijTTfZhmUCgJVZJpBKDt5tl73zOUzSjGIplysQqETQWCWOuJJXJR/CnTNdheXLO8rhtwiVjSAq2zb6WzKRUUDTz5sZgDEngJ542FGGBbWtHcmRHHmUcMmff+7VdHKop1ng/Hhcx4MPnJLLYJzthJJl/mwx0O4R3I4cV5AkahQKRj5fLBQM00AF62OaZuUQqwcdrqAcK1xdaRRUwiGrCGFSP+Piy1vSQ0QY8rh54siRiA45+MApN95wp1HA+pNPTeRyT4QRN5bVKNlM/s033pn116v/dNZ5l8+8+sknXjCLKNOJj1cjvkVUbX2sCOginjVx9yDFu/aaG1OJIQEhwngUXWtT5TQO0/aHNKUlog/0M0HGo6hyeucd97nh77eXDNTVYXa05/EDD0zYi87DrVAbq1f3sJVRsjE0DhouA+gKN69YYWCLjKKJNtt8WwCCTgA9Z+4/iQd0D1lbntf22nyhtODlNz1eKEmRpmaOh5qiJE8/4/yiYRnUrL4eRETGD04q3WDRx58ffeSJXg/kgSaJcUmMk+EoOX+IB7qfCQJWxSOjCvrEw46Z//jz1rMWbJdjBz6T8Gfc4Rv0jeq1wkS5DL7oIYSuvebmVHJwQNAZr6hrKVVONmjf/W647k6rfVFHe3GV27enJqDLqAJUAaoAVYAqQBWgClAFqAJUAarAOlYgl8stWbLE5XI5ATTx4hg+fPjqCkVax5VsfHgKoBtrQ9dQBVaTAkax/PY6NjvOGh99+PnNN91+yYy/vrvwYztSuEHg5K+PgLbBNQ5GLljmFY2rYdGuQqH0ystvbDx0M1nSEvG2c6ZdmM+ZJPCQwEQnVLJIIrFirWRbIcNGsRwabEded3VmKxv19tcs4vDwiYeeEICJcvgzjz2Lp519AbG5sHauHKY2p3wOw9M59z925hnn3XP3PHtlDSAr408chLvKANoCr+VgW5uwVw9XPsTqw4d21quW6K6WFWa+8O0PH3rw8fmPP/vJx/9ethSP3IdhvYFZYS6DSWWNbo0ho1HEUuDBJK2+YBq46e3O3N7eWc2nogz5Syw4cNrK3K7csl8yc+5/7LhjTx2zw+6bbrJNIjYwERu46Sbb7Dh6j0MPOfLWW+794bvlJP9CHj94ILtbzwDwyWUfzs6wl0R5r8oWuTzqyhYd1hm9AWgyxqAg6gRAYx9n0MKBxKuvvWcijKd7+tQsJUbVl11+JRSCshIWpdAJJ56es0YfxbvXbNtTZiu9zClypsuyXbfa65NFi2+68Y4jp0zdYrPtW9JDdC2VjA/aacyeO43Z84zT/vz4P58pmeX3GOzHP2QgUJs+rySAtvsDQvjZ25w5Dx137NQxo3dr2L5WX/rt7bvSCtENqQJUAaoAVYAqQBWgClAFqAJUAarAWlXgiCOOqAPQJAJ6wYIFa7Uc6+JgFECvC9XpMX9nChBeQzAZrjrBTNb3rwJna0O2CgKzC1aXWBNlMAqokEPp5LAATECQ8DMhyEVCweSDDzy6QgC9JsrTKE8iRaO1G9hyRyd0dshfC0Br8fJKz9XS57J0jiLV9brus+ShCHm041y7Uq1Q6eR1wdqVffHPorMmleXlv6++9g7rl/HwngAPjSjANp5L/bLMQsh1m/Y6+9nnX33w4SftHdmiiaOqi2Yjft1rLr99pUP2ck9okGdZZyJNg4cTK9UWK/Gc4ze1b4Py08VUAaoAVYAqQBWgClAFqAJUAaoAVWBdKZDL5V5//XVi+mzbbpDEyJEjc7kc8RpdV8Wjx0UIUQsO2g02eAWcMAunu7Ob1eT6uhqVKpe5W1FX3yGqoZ65DPrisx9FPq5IaQjwMGUiH2WZwHvvflQo2NHWDmq4+grxq3IiDferdlnXG5NHjM7vBiVaRXWxVcVKTPVnQI9K9nBedOt+9jYEUNbE5lsbN6hew8V2ho5w3RUA6OtvuA2HP3M68Echn5bEgZsM26HhAXpdQaKhbfpsYP9n/Ol1p3W2sqwVKWLjprElrSso2a+H756yWl3tW1cGOksVoApQBagCVAGqAFWAKkAVoApQBdaVAhMmTCDhz3UA+vnnn1++fPm6KhU9rq0ABdC2FDSxoSrQjdB1hzC2NURPVhyrv95OIlmXLh+sXMRubGj1laVK2Qp5dMdtD3rdiiSkAzBljVEWDQWTXZ357mYXjgLYoZuOZZXiV6w2SO26b7AqS4gmq7Ln2tunrjXt2SJCZLKX/MaeVs6n3LdRoVQ3lcF0t67eGBPX8M1u+9UtqLGDcKyzlLbr2EsPKTeJY1fSIe16VdfUtd74/Q/jeR3CqM8X4kBCkTY67NCT67bpdRaXqr1reb5YMFApXywULV8SA1uhlA/a6+6rttLWZIXt7tyyZuOaBiJXhh4fp9XsVC1tt8ug/eiiKrV9iGr7OvxVHA8JqtnSFFWAKkAVoApQBagCVAGqAFWAKkAVWP8VWLRokcfjcblcTU1NTgC93Xbbrf+F/52UkALo30lD/y9XszF5sRGME0A34DerUyEnY7LRZNEJbctMqEcAvYrRsnUVqAJohNDU48+GIMGxUSXQ2tfFS2J89Kix2UzRtpOu27kyaxPG7glnHSub/7a/RJPflsea3ttZ65VJr3J5ypmvTgDt4JCVZPUEqZxElY5ZJZR1dhnOWjt7Rc81rRwI/+2h/1urq3tafTbdMgTCsCjGvd4g8EdVZfD5511Z3WbFKVyqTD7Tme0slvAgfcVSsVgqGsgwkEHKs+I8ft0WTk1+bbp6JJsO40LaANpOO64V1X2qKStYvu4pBSpUmpU0NKm9lb2zfVeQc/UYNEUVoApQBagCVAGqAFWAKkAVoApQBdZPBQ499NB+/frZ6Llv374kPX/+/FwuZ5omteBY5w1HAfQ6bwJagNWrQCMARI5C1q7eI/aSm1kJjF1BeGxHR2U4QSfTI+lesm+4qoY+GwUU1gap0gDenxA57MKhKS2nnPynfM7sNQK6Ye50xa9UwNknf+WuyLlvXfrXZvUrtq+iSpyqcuqurnZHLs7yODuuY5Oa8juX16Yt22KE0IMPPc7xqscjAhAShIQiD+C51PPPv2Nt7TyEna7NpzqHy2ZaE0HP5Lu6fk2l7IL1kliNx7aPQtqi+3XG2UbV45YBtwM9kyXVLWiKKkAVoApQBagCVAGqAFWAKkAVoApsCAqYpvnNN9/0cXxcLhcB0CNGjNgQavB7KSMF0L+Xlv7d1NMJXJxpIgBZsjbFsBl098KUi5HpKiALwBnFmhEUq4PX9VZem0DZ0Jksqe7zxmsfKlIa+CISbJVgK/BFQmrrE/NfwIejn7WkgN36q3A8e19nYhXy+RW7NALQjiychTFrO65jqxUCaKvbmuT1AITOOe9iwEleRhQDUVGMK0prNDKsUCAZOru6nXYey5nGxVsvAbSzkL8xbYtgR5fXvGbhDDmvOxIF0HWC0FmqAFWAKkAVoApQBagCVAGqAFVgw1Vgl112cfDnPnYc9PPPP7/hVup/r+QUQP/vtSmt0XqlgJPTNSyYaTmx4tVOpuRMN9zVuZEzXd3h1JPP5diwtzkocmlNHiwJaR5oy37JUMvXqkZrL+XsD8702itB/ZGcvabyFKMCoKuxzyQOmuzb0zh+JJf6vHthoOVNrUcvhTyeKxlo08225ngZAMXtFli/qijpKVNO78qQbQ2EyFRXYnu2/uhEX+L+TL7rt1jf5509pHvarrgNoMk2K64VBdAr1ohuQRWgClAFqAJUAaoAVYAqQBWgCqzfCuRyuWw2u2DBAid9Jummpqbdd999/S7+7650FED/7pqcVnjtKuDERj0fuVAoff/dkjNO/9Ndd9736wF0I2hdPVY6OUwWW1hPxNscEjkcCj3hoCNxzGmFNjpT1d1oao0o4OwPzvQaOdiKM3UyTJK29mkAoEu5XO7+++dOnnzkggWvrDhzvMWK6lhC+RzKWYj5wXlPAqDwUON41e3mAQgyPnnu3KfMckelANopZl3UuXPViluGAugVa0S3oApQBagCVAGqAFWAKkAVoApQBdZvBbLZrGma+++/f1NTk5NBu1wut9v9wQcfrN/F/92VjgLo312T0wqvXQVWDIby+eL06ReqqiYFgttvN/rJJ14gJSQRyith09wdIpaMotHR0WUU0C033w25CAQJCFIQpHh/IqxtNP+fL+LMKYBeu13BOpqzPzjT66Aoq3BI00CDBg4NadGAqE48fMrX//7OzsQ08fCe3bqrs3Pa29Ynsl3IKKCDDpjMQw1PvM7zOuOTBwzcHOdZ7qjOrHpM12dL5jc8lav16LGaK1xY3Z+mqAJUAaoAVYAqQBWgClAFqAJUAarA/6oCuVzuueeec7lczc3Ntu2Gy+Xq06fPxIkT83nrTdv/1cpvgPWiAHoDbDRa5A1JgZXCXydNPcXjYTggNjexLCNMO/uCH79vLxnILKJctsqJG9S7O5BCefwpohIasf2uGEBzMcKglcCAoYO3a19eqDWAxuiQftaKAs7+4EyvlYP/5oOYBhJhEPJaQNBVJd7WsvEdt88hBhoIIaPYY1+1+2fPhzeLKNOJHnn4WcjrTgDN+tUZM64qGqi9g/y/wc6nUaJB/o4w7J63WH+XNqpp78vX3/rQklEFqAJUAaoAVYAqQBWgClAFqAJUgdWlQC6XGzduXJ8+fbxerxNAu1yuRYsWdXV15XK51XUsms9vV4AC6N+uIc2BKtCLAisFGW+dfbuiBIFfkCVdhKHm/qAlNezmG+82CqijfYVjBdbRqGph/nr530QYdgDoBMfGb7z+XuyLUPOpn69ZSWdWpwLO/uBMr85jrL68nCW0OomJxu93OA90yEUkMa5IScCq4/Y9ZOHC9wsFA9vB9NCV6vpnPaQu4f3Q8O12k8RoGUBbcdCyEv3o468cdemeT90Sx7aOpLMOjsUbRLKugis5u0FUjRaSKkAVoApQBagCVAGqAFWAKkAVoAr8JgWeeeaZvn379unTpy4C+tBDD/1N+dKd14wCFECvGV1prlSBsgIrxl+mgY0Ltt9uFIkt5YHGeKWAEIFcZJ89D33vnc/tCNOVF9U00Ouvva2HEpw/6ATQo0fugxB23c3nnKTQmV75g9AtV0EBZ39wplchq7Wwi7OE5U7y1hufKFIa+HTIxZr7BVQ5zXglnpPPPvvcXgvkhKf1G15+2XWhYLoOQJ/954uKFpuubO3Mocd0ZcPav8461K5Z/+d6rOYKF67/9aIlpApQBagCVAGqAFWAKkAVoApQBagCq6hAqVSOatpmm21cLlffvn3rwp+p+/MqKruGd6MAeg0LTLOnCvSugHXlNIto4dsfh/W0pqYAq/V1AZGPBmBC5OOJ6MZHHHbiW298bGNoo4QKRnmy8y6ayFpevhB/8tniSDRtDeYm+JlgACb6uQLN/YQnn3ih1nzDzoAmqAIrUqBkmVkgdPUVswMwAbmYnwkFYKxfX8ABRYTBTYZtcdmls5Z3dBYM3A8zuQJCqGhNsZBuAAAgAElEQVTiRCafMyqm49ZKVChgc+dMFt02+z7AyiwTaOrn5zk1IPw/e2cC50R5NvBJlt1ckzkymSSbc5PsLgie2E+rVq1WrVet1qqtVq1FEERFPFC0CloRrTfigYoXnm2tZ7WeqPWsitazoiIKci3skWyuuZ6v77zJ7LDsIqhcu8/8huzsZOY9/u8k++M/zzxvvGEIl02PWG1CTtI0S7z20076fj9v4m4kgASQABJAAkgACSABJIAEkAASGAAEdF3v6Oh46aWXqHd2OBx0QxAEhmFOOOGEUqk0ALo58LqAAnrgjSn2aIsiYBrjipmY6IXn3ggGSGaDZHw4x0YFjuRuNjV0Kig2jR1zxpNPvFAuGYoKmhmN2ituuUJ0HygqPPf8KyN33CUUTknBRDTW6nWHY5GtwsGhRx0xSlMNerdQUw06a9wWBQsbu0kJ0LsbBugKTJxwQSiY4f0xSUgxjNfrkf0+medkKRAOhWOTz7tw/ucLrbaqOkn6ohlQVtRyRadXbz5P3v/zFTeKQjyZaOW5cEiOh+Sk1yMFA/HZt93bI5yrd1VQQFtEcQMJIAEkgASQABJAAkgACSABJDB4CSiKsueee/YKfK6rq2toaJg/f/7g5bJ59xwF9OY9Pti6AU/AlGtWdPPLL72VadpaEhMCF+f9MYGL03y7YTkrCnFRiO44crczzjz/4Uee7upSVA1UjRhnTSfBpADwzjsfn3vuRYIYDYVTLpcQkOJSMCUJqZDU3JLZcflS0/kBlMtK2YxOHfB0sYM/GAGD5HfWFCgV9WK3US7CFZdfHwzEeS7s94V5f6PfJ3s9op+VvL6A1xcQxMi+P//F1IumvzPvQ5L1RelJPK4boGnwzDNv/Pa3J3FcTJZSspTiuTDHhsKhlNcjjRl9Kml2b+Hc+/feXcMI6N5E8HckgASQABJAAkgACSABJIAEkMCAIlCpVDRVmzt3bq+8z3V1dQzDHH300QOqtwOrMyigB9Z4Ym+2QAKF7gpxbbUJ3Oa98+G+P/tFMBA3NXSU9zcKXDQRG+puCEhiTOAjspzMZrdOpoa1to484IAjRo06beLEPx7+6+N32WU/lo16vRGOi7Fs1MeGA1IyFEqLfNJdH3rs4Rd1czpDRVFwKtgt8DLZDJpsgKKQK5VkcTGgVFTvvP0+Om1mJJw2ZbTsZ6VwJCXLSR8rJ5KtXl9QDMTi8Zb/22nP/fc//OSTzz755LP33/+Ibbf9iSSlBSEpSWlJTKQSw0UhynNhgY9st83OugrFbs3QzSkNzY+G2Xm95qT7QYECuh8wuBsJIAEkgASQABJAAkgACSABJDBgCJTL5X322cfKvGHFQTudzkWLFg2Ybg68jqCAHnhjij3awggYplijuk1TIddVBIDTJ5wVDiUkMeb3keQGxDtLCYGP8FyY56OCEBfFRCDQVFszopi2r4LQxLLRUCgbCDSFgplZN94LZviqroGimKk6tjBI2NzNggC9Sq1XAHjzzXd+uud+Ah8S+JCZQyMuBRMk7j6YEsWEIMR5PmqucUFI1tYm27WaioSyvL8xGslwbGjE8B0+m/+VdT/GXtFm0X9sBBJAAkgACSABJIAEkAASQAJIAAlsUgKPP/642+22vDPdcDgco0ePVhTFmqJwk7YRK++DAAroPqDgLiSwMQlYlo1u6BqpvFgoP/jAQ+nU0EQ8GwmnSHZdMSZLCVEg9jkgJckaaAqIzaKQNdcWUbDWLM81RSLD3K6w1xu56Ya7NMUMHqWxqxuzb1jXwCJAMojXFqtnpaJ65hmTOX9QEhtlidhneomKYkoUU1Q681xSEJqqK5+pXbRZUUzXOYRouDUsp5uzW3/80ee02EJ3RddA10gQNFnNxaoRN5AAEkACSAAJIAEkgASQABJAAkhgcBI45JBDPB5PLwHtdDo/++yzXC5XLJKQPlw2QwIooDfDQcEmDS4CNaFHftKe0+kBdQ3y+dIZEyc1Z4fVHHRjMBAPSGQVAzEi+Ih0HrrG2kIFXzw24uGHn7eS73Z12qeC7TWF4eBijr1dHwI6kGuIrIahWStJGmNo5XKxXC4Xu7V3533yy0OO4thIQCKJNUQxFQhkBKGJ55Lm2iTwmdraXLtZQu6duIbIfm/sqCNGf/VlG731QttmeWfrA7I+bcZjkQASQAJIAAkgASSABJAAEkACSGCgEXjssccYhqmvr+8loEeNGkUmH6pUBlqHB1B/UEAPoMHErmyZBCy/RgW0ppIQ6M7OzmKhTDv01r/fOejAX1oOmqhnuvYvoFk2ftRRo+d/tqRQJBPHAUBXZ4kkmybS0Kj5xC2TF7Z6YxOwCWhQjNoKYMbqm42huaE728sP3v/4/+20VyDQZDrodM0+J3nOLqBpxhgSH01WPnnl5Tcb1QTlmmEYuq53dnbaPxd0e2P3G+tDAkgACSABJIAEkAASQAJIAAkggc2JQDQa7TX9IDXRn3zyyebUTGxLHwRQQPcBBXchgY1PwK7bapq4pxWGDvM/XXDB+X/aceQuHBsKyclIKCuJCZ+vkaTTFbI+L4mG9nlTTakf/e6Y8a+/9m4+XyLZpelikGwGJKGBafdoEGtNQ1O9WDsSfyKBfgnoAKpttcR07xOefupfx/1ubDw6TBCS4XBLJNIqB5vpyrJxh4MLyfFYNJHNtlxzzXU0yUbvIsw7JdYzAWu+i3uQABJAAkgACSABJIAEkAASQAJIYDAQMAyjUqkYhnH/fff3Cnx2OBz19fXHH388Zt7Y/K8EFNCb/xhhCwcFAbuAXku8Zz5X+eD9T2+ffd+4kyYeftix++532M4//tnOP953332PmHj61EcfebG93cjnq8R0XTcMQ1MNTQVNNaiANgsniRRQQA+KC+sH7qTloC37XLvLYZh5xg3QVSh2G+Ui2Xj22devvnrW8b8ff9DBR+200z4jR+65x54HH3HEceeee94zz/6TNm312yE9zV3Lp6DnINxCAkgACSABJIAEkAASQAJIAAkggQFNgEYmVSqVrbfeupeAdjqdDofj88+rkwkNaAxbfOdQQG/xQ4gdGBgEqgKaTrlmvvbqV7mskPkJDaCZNABIbo18d1X/UelcLgNNeWToUKmQpAblcrmqnmszudly+NodYk0fQjUPddUm9moE/jrYCdivmb5Y1C4f3UypUahN/6BqoNVMdUUhwfjlMskwUyqV+hPQfZWO+5AAEkACSAAJIAEkgASQABJAAkhgcBFQFEXX9QcffHDN1M8Mw0yaNCmXyw0uIltmb1FAb5njhq0ecATWLqCpTa522oBySSsWFMVMr69qYGaNJm/WFB/ZpimkSbFUalcrsE8iZ5eJKKAH3CW1QTpkv2b6rYCmHS8VyfWo6T3XJ/nVNNRmVH41hTQK6H454htIAAkgASSABJAAEkACSAAJIAEkAJDL5VpaWjwejz0CmvroBQsWIKEtggAK6C1imLCRg4VAVRb3FQFtR2AdRuKVrdV+RL/bdoFo37ZKqYWwVsvttyB8Y1ASsF8z/QOwX010u49j7UVZ230ch7uQABJAAkgACSABJIAEkAASQAJIYDATmDlzptPpZBjGsfoyffp0M+8omc3eWgYzqM257yigN+fRwbYNOgKWWe6ZP7AvBtZhfb259n2W6eu1YVeGtIR+xeHaK8B3BzQB+2XzfTpqL8e+/X3KxHORABJAAkgACSABJIAEkAASQAJIYAASSKfTLMt6PB67f66vr//kk08085Fwyz7jVPab7fCjgN5shwYbNhgJWGb5WwR07cu1H0Z2m2xFNNNj7bLPvt3rFOvXfmrA3YOUgP2aWS8Eui1W31h9AszvXOZ6NQAPRgJIAAkgASSABJAAEkACSAAJIIEtj8Att9zCMExdXV19fb3TtpxzzjnFYrFSqRQKhZojIT+3vB4OjhajgB4c44y93EIIrL+Atss7yxr32rB33n68fbvXKdav9nNxGwnYr5l1oWE/3rqoUECvCzo8BgkgASSABJAAEkACSAAJIAEkgASgpaWFpn6mSZ8tBf3xxx9r6mrJN6iGRmSbJwEU0JvnuGCrkMA6ErALPvv2Op6OhyGBDUrAfk2uub1Bq8bCkQASQAJIAAkgASSABJAAEkACSGCLJFAul6lNvu222xoaGqiArqurs0z05MmTt8iODeJGo4AexIOPXR8IBNaUenTPQOgb9mHLJ9Df9YlX6ZY/ttgDJIAEkAASQAJIAAkgASSABJDAhiGg6zoAGIYRi8UYhnE6nXV1dXQeQpqOo7Ozc8PUjKVuKAIooDcUWSwXCSABJIAEkAASQAJIAAkgASSABJAAEkACSAAJIIH1JVAulx944AG7faYCuq6u7txzz+3q6lrfAvH4TUsABfSm5Y+1IwEkgASQABJAAkgACSABJIAEkAASQAJIAAkgASTQQ6CrqysYDDY0NNDYZ5r6mWEYURQ//PDDnuNwawshgAJ6CxkobCYSQAJIAAkgASSABJAAEkACSAAJIAEkgASQABIYBARuvPFGl8vFsqw16yCNgJ46dWqpVBoEAAZaF1FAD7QRxf4gASSABJAAEkACSAAJIAEkgASQABJAAkgACSCBLZRAe3u7y+WiUw7aBbQsy8uWLSuVSjRJ9Bbau8HZbBTQg3PcsddIAAkgASSABJAAEkACSAAJIAEkgASQABJAAkhgsyMwY8YMhmE8Hg/NAW056GnTpm12bcUGrRsBFNDrxgmPQgJIAAkgASSABJAAEkACSAAJIAEkgASQABJAAkhgAxOIx+NUPfcS0MuXLweASqWCEdAbeAR++OJRQP/wTLFEJIAEkAASQAJIAAkgASSABJAAEkACSAAJIAEkgATWl8Dll1/udrtp/g2HwyEIAtXQEydONMxFNxe6vb6F4/GbigAK6E1FHutFAkgACSABJIAEkAASQAJIAAkgASSABJAAEkACSKBKwDAMapwZhnE4HHTiQYZhRFFcvHgxlc6onrfEywUF9JY4athmJIAEkAASQAJIAAkgASSABJAAEkACSAAJIAEkMHAIKIpy6aWXSpJk2Wen09nQ0PC/aOipU6dWKhUU0FvuYKOA3nLHDluOBJAAEkACSAAJIAEkgASQABJAAkgACSABJIAEBgKBZcuWbbXVVk6nk8Y+07kHafjzihUrdF1HAb3lDjMK6C137LDlSAAJIAEkgASQABJAAkgACSABJIAEkAASQAJIYIsnoKna7NmzPR4PDX921BaGYaZMmbJixYotvoeDuwMooAf3+GPvkQASQAJIAAkgASSABJAAEkACSAAJIAEkgASQwCYlUCwWw+EwnX6wJp/JT47jOjs7DcPQVG2TNhAr/14EUEB/L3x4MhJAAkgACSABJIAEkAASQAJIAAkgASSABJAAEkAC34fAlVdeSWOfe0VAn3/++d+nWDx3MyGAAnozGQhsBhJAAkgACSABJIAEkAASQAJIAAkgASSABJAAEhiMBOLxuMPhcLvdHo/HHgG9ePFijH0eABcECugBMIjYBSSABJAAEkACSAAJIAEkgASQABJAAkgACSABJLAlEVAURTeXm266iU45aE08yDCM0+m89NJLS6XSltQlbGs/BFBA9wMGdyMBJIAEkAASQAJIAAkgASSABJAAEkACSAAJIAEksGEI0NDmUqkUj8d7CWin0xmNRnHuwQ0DfhOUigJ6E0DHKpEAEkACSAAJIAEkgASQABJAAkgACSABJIAEkMBgJlAulwHggQceoPHOloN2uVwMw0ybNg2TbwyYywMF9IAZSuwIEkACSAAJIAEkgASQABJAAkgACSABJIAEkAAS2GIIFIvFbDbrcDgs+0w3BEHA8OctZhTXoaEooNcBEh6CBJAAEkACSAAJIAEkgASQABJAAkgACSABJIAEkMAPSmDWrFmMudgnHvzfjqlTp/6g9WBhm5gACuhNPABYPRJAAkgACSABJIAEkAASQAJIAAkgASSABJAAEhhsBDRVy2QyLMu6XC67gPZ4PG1tbeVyWdf1wcZkoPYXBfRAHVnsFxJAAkgACSABJIAEkAASQAJIAAkgASSABJAAEthMCdDwZ7/fzzCMXUBPnjwZANA+b6bD9p2ahQL6O2HDk5AAEkACG5mAAWCtG7lqrA4JIAEkgASQABJAAkgACSABJIAEkMAPTSCVSjkcDrfb3UtAF4tFOj/hD10hlrfJCKCA3mTosWIkgASQQP8EdAC6kkMMnay6Wj1cUQy69H86voMEkAASQAJIAAkgASSABJAAEkACSGBzJFAul0ul0u23326Peq6rq2MYxul0XnTRRaVSyTCMzbHp2KbvSgAF9Hclh+chASSABDYggdUENIl9BigXATSoFImMBgBFUTRV24BNwKKRABJAAkgACSABJIAEkAASQAJIAAlsAAL5fL65udkuoBmGcbvdoiiuWLFCUZQNUCcWuSkJoIDelPSxbiSABJBAPwT6ENB3zv7bj3bYNxEdscuPd3/qqadKpVI/5+JuJIAEkAASQAJIAAkgASSABJAAEkACmyMBXdc1Vbvnnnt6pd1wuVwMw0ydOhXDnzfHYfvebUIB/b0RYgFIAAkggR+eABXQtWeODHjqH3PDclbwN0lC2uPmOY779NNPf/hqsUQkgASQABJAAkgACSABJIAEkAASQAIbkkAul0un0//LtmGPgHa73X6/P2cuG7JyLHvTENioApomcDEMo1Ao0O7qul6pVAzDKBaLdHZLwzDsz5XTPKdW7L21sWloYa1IAAkggY1EoCqgi8UirXC/fQ4Nyy0NzkgsMoLn5FAocs4kMi8wLkgACSABJIAEkAASQAJIAAkgASSABLYgArfccsv/gp1pxmdnbWEY5vLLL69UKltQR7Cp605gowroPptFrTS1zwBAlbT9SEs606sQr0U7HNxGAkhggBKoCmj6jbdwwRIa/sx5mwR/kxyMhcON48efOkD7jt1CAkgACSABJIAEkAASQAJIAAkggQFLoKWlxePx9BLQfr9/8eLFlUrFCsMasP0flB3bqALamsKyv9SliqLMmzdv1qxZF1xwweWXX/7pp58ahkFn2bKipwflMGGnkQASGGwEqjmgyVMgOtx5+30NdQG/NyH4M35vQhQikUj0mmuuo7MRDjY02F8kgASQABJAAkgACSABJIAEkAAS2EIJzJo1y+Fw1NXV9RLQU6ZMKZfLVnzqFto7bHZ/BDa4gCbyRNdp9TTzRqlUeuONN2677bapU6ceffTRe+yxxy677LLXXnvtuuuuw4YNo0H41uvee+990EEHjR07dsqUKXPnzn3ppZf66wnuRwJIAAkMIAJEQBuGBgCKok08/ZxYZKjgb/J7UiKXqXN6I5HoO++8O4D6i11BAkgACSABJIAEkAASQAJIAAkggYFPIJvNWtKvln6D/Mzn84q5DHwEg7KHG1xAl8tlGry8YsWKWbNmHXroobFYzG0u9fX1VsZx6+Jbl43dd9/99NNPnzNnjjVk1HHn83lrD24gASSABAYGAUXRth4xMig2BcXmoNAaFJsFPpRKpQdG77AXSAAJIAEkgASQABJAAkgACSABJDDgCXR0dADA7Nmz3W43VX80DtrhcPwvFPriiy+mBKwY1gEPZLB1cIMLaHqFKYoyc+ZMhmHcbjcNs2cYhk52uS7Gec1jvF6vy+VyOBzjx4+/8cYbC4UCzdQx2MYP+4sEkMDAJqCpxqf//YLzB+0CWhIbf/nLwwZ2x7F3SAAJIAEkgASQABJAAkgACSABJDBgCGiqVi6XrfBnh8PhdDoZhuF5nmXZzs7OAdNT7EifBDa4gC6VSoZhvPnmmx6PR5Ik60bHmk553ffQy5TeJGEYhmXZUCh08sknf/755312EnciASSABLZEAnQK1nvvfVAUInYBLQdj18+4YUvsEbYZCSABJIAEkAASQAJIAAkgASSABAYbARozOmfOHKr+qNajApphmAsvvHCwARmE/d3gAlo3l3fffXfd/fI6HllfX0+P9Hq9dKO+vv4Xv/jFnXfeiRH7g/BSxi4jgYFHQFGUYqE8buypfp9cE9DDgmJzOJR6+eXXDB22rEkIrXloB95IYY+QABJAAkgACSABJIAEkAASQAJIYC0ENFWLRqM0HYKV+plhGI7jcrncWk7EtwYGgQ0loHO5XKVSsRgtW7bsmGOOWdMsh0IhhmHq6uocDgfP806n84gjjqA76UXJMIzL5WIYpr62NDQ00CQeloC27LOV3COTyTz22GNUQxeLRcMwyuUyAGiqhgbEGhTcQAIDg4BhLgOjL332YljrthwbCYoZkgBaGBYUWrfbZpc+j/yhdtKnn+jXJi2zUqkoimJ9f2qqRieVXa8adY18CdOv4kKhUC4r63X6Wg5WFEVTDXoAvetpNXUtZ+FbSAAJIAEkgASQABJAAkgACSABJLARCOi6PmvWrPr6+rrVF7fbfckll2yEBmAVm5zAhhLQVseWL19+3nnnrame6R46CaHH42loaEgkEs888wwArFixYv/993e73aeccsqTTz75wgsvvPXWW3Nty5VXXnnZZZfttttuHo+HlmOpZ6fTWVdXR910Op2+/777LWmiKIqu69RVDXhjZfHHDSQwGAjQVBUAUCgUKpWK9QwEtZCGYRSLxS2Rg2EYn83/IihFZSllF9DHH3eyYt3gMwCs9QfqJMVVqVTohiVzTc9LDPJ3XnRd11SNroqi6Rp8z+/kNZtULpctB20V/p0bjCciASSABJAAEkACSAAJIAEkgASQwPckoKlaJpOh6Z7tCloUxa6urlKpZI9/+p514embJ4ENJaBp+PP5559Pkz6zLGs5YktGW9leXC7XjBkzAEBRlIpKYuJKpZJllHRdL5fL1CNTm6AoCr06X3/99ZkzZx5wwAFWNLSVHtrpdHq9XofDsfPOO3/8yYe6rgJApVKxfISlVDbPgcFWIYHBQEAH6HP9tr6veVLP8w1Lly794IMPnnrqqbvvvnvWbbc+/o8naGn2c76t/HV5n5bX95H2uuzbfR9N9tqP6tlWdf3PV17t8UqhUDYQyEhSS0BsDYjNDz/0tFIB81vNZp+rEcD9V7I+79gfYVm0aNFnn332yCOPzL7j9utmXv/0s89oYJSVim4WSF/Xp+zqN7yiaJWKSh9MMQzNMNZbbc+bN+/UU089+OCDL7jggo72LhpbDVCV2uvVJDwYCSABJIAEkAASQAJIAAkgASSABDYQgVtvvZVhGLfbbbfPdXV1kydPpjWio9tA5DefYjeUgH733XdbWlpo9gyPx2NNGGjZZ9bHMQwjh4MXXnThis6V7fkOKk8sl6GpWqVSyefz9NWOjAqLcrls6FAqqoYOXy36ZtZttyaTybp6kq+DqaWHptX5BHbipDM0MCoqeYTcWuxl4jYSQAJ9ELBCa+lGH0d8r109qnV1BftthfY6j6RCLuTVRx956pijTxD4EM/JnD/oZ6VwJOVyc6l0y5VXz7Cf823lm+/36rv1a/VkWl7fJdnrsm/3fTTZaz/K2iZv7PvzXwhCPBBoCojNktQiCi2BQGbRV6vIOeS22gYR0Lqpgssl7dFH/nH88Sdy/oAgBHlOCgQjXlbw+UU5FL36muvLpoLOF8hMs2ZT1vZSKeu6Bk//8/kjfv3b4Vttm4inzzzjHLrT/E7+LgK6OTs8Ec+G5GhQirS2Dn/xxZcBIJfL0S/5tbUG30MCSAAJIAEkgASQABJAAkgACSCBjUWgtbWVBozSNLyWhm5vb1+X/05urGZiPRuQwA8poK2soNOnT6fSuZd6bmho4HmeYRgn40wlW66dceOy9qV5g4Sttau5Ys3BrEt3qxJZB0MFTYMKgEqeQoeH//lM84G/YPgAVc/eBnOiwiHkNyEa/O8Xn2rmYYq54FW+LqjxmEFIoCf6VYN5by24+45HHn34+W8Wt2kqKIpW6C59HyaFUkWhfrMaQQsP/OWRgw4+nOWCjdHsz3/+q48/+bKiasVKuXY7ylK/q23oulpRSvThhptuuDcR3S4c3CoW3obnMtbKsWnOn+L8CY6LjTnptFyetLxQqmhgWGutL6tpX6p3i93kW6WYh68Xtr/97487VpU06nzJOdbx1WaWSiWa4LisqGbOefJdU6zAG2++f9fdf734T3+++pob7rv/718s+JqUWdZoUfSUWhuITtZBVw1VA8JoVXslEMgIQhPLxnmuSZaGCXzmJz852Ha82RQDFBUqCnmtQQOt5oSthq5+Ft1dOwhAU6CQ15Wy2TOAW2fd39q8A+9vFMWEtQpC3FpDofRJY8/UdFKpZvTgqNViDVZ1h6bA0/98KR4d5nGFeX8sERvq9UiPPvKPWhYOKqBpq2plkJ+9yymXqm0+dfwfRS5DVr5J5JORcGqP3femUdX283EbCSABJIAEkAASQAJIAAkgASSABDYJgY6ODgC4/fbbHbaF+jqHw3HZZZdZEaIo6DbJAG3MSn8wAU1Thc6dOzebzdKLyUqLQacQ5DjO4XC4XK4f77TzzOtuIP6GiONyESpFgBUAr3Z2zTdgHc2WXUAbKqgARYAOgFdWrbr1q29Oe/LpupEjGUFgHA0sF2CGOBkH0d4Mw8yePZvm+thCc8JuzIsD6xrMBGgCpinnXxeWtuF9Wc4X33P3n7/04qvfnwm1z5opSlUdLpx6aWM0LcmxIfUcxzXyfPxn+/yyUKqKXvOOkaUg6Ua1CTSr+zvvvHPQgb8Mis28r0VgW/3uLOtt5v2tZGW3IivZbua5JOsP3ffA38jHX+uxz/SOlFni6p7WgGI3UcCvvvzR/vseHZJas007tDRv8/yz/zLvYdE2rHZKdXq92tsdHXD9DXeP2HY3UUxQaRsKpzgu7PUFThw9funyDjDIdyBdiHU2F/sfXUWDG2+4V+Cbea6J55rCoa3kYCvPNZ199jTFnL2vu2B8uXD5c8+/9tDfn7551j2XX37DpHOmjh13xlG/OeHAg448/H1REPEAACAASURBVNfHH3LIb8+eNOXxJ56tVgNQ7kkd3VtAW8e8+dr8Xx92ohxokQNZnk2IYtpaBaHJWunOOXc/BgCqvk4C+qgjTuDZlN+TEvxNPJuQxNiUC6cRAa3TpBlaVX5bTalurDbumkL+bLz95udhaYToH0ZWrpU4aCHqZ8Wvv1qczxd6F4C/IwEkgASQABJAAkgACSABJIAEkMBGJ0BzG7S0tNj8s4NhGIfDEY1G29raUEBv9DHZZBX+YAJa1/XJkyeT6GZzGkCa39nr9VL7TPO8HHTQQffee2+xWCwVimZcm66C3gnwitZ5zcJPprWvmP7FgrZ1Q2EJaBImaPqLlQBvAFzevvSPbR3TivqUb5YfestdTHQE0yA7nSTdR5MghV1uhmFOPPFE6nrWrSo8CgkMLgJUpJZKpTffeFcWh4r+YZ6GWFDMhEOp0aPHKdQffz8kVnDuBRddygUiDR6RC0RZPiyFmjgxGZBT/3z6+UK5ZAuC7ru+B+7/C+vjSM4NNsH7sl5XKhralujm6trq5+ia8fPJYDj145/sSaKSFdUKf16LgDbt838S0W2ioa0lnqhYr0fe/+eH1AwzbdJqEbtGLfz4kcef3+FHPw2GWkSpKZoYGmpsDsgpvxAVxYTHKwWk+NBhO7z15gc0ztrQQVEMRdGqq0lH1eGbJat2+vHPebHFxybFQLMc3ooXs4Fg9vd/mLDTznunMyPC4Ww8PlQKpgKBJlEkr4Fglg+kWS7h9SUCIjHXAWloPLntqo48bW53z2SMq7W8yteAOXc+KnBJ1hMNihm/N+ZxyaKYslZOaLJWOTzUzydHbLtbSVknAf3VwqUcG5EDWcHfxPmSkpD2+8L77Xvw6gK674G276WZon9x4LG8L2sX0BwbikTi7as67QfjNhJAAkgACSABJIAEkAASQAJIAAlsEgLULdxzzz3UOFsOmoarTp8+Xddr/4XeJO3DSjcugR9MQB933HFWomd6MVmzDnq93jFjxnz00Ue6rmuqZj1yntdLi0GdD3Dj0q+nLFt68uJlV3R0L123/lMBDTqJITQMoxvgM4ALViw8tdRxcqF80sr8mR2l61ZV7n1n8dAdDiCJzpl6nnHQMGiv13vcccfRBwHWrTY8CgkMIgKFQoHeoZl87pSg0BqWthH8GUlIR8LpoBTtSYzx3ZAYUFGqKRTOnnRBQI75uKDLJ0mhZEBOeNmwj4v4uNBdc+4FgK58bi2VzLjuxpbmrUQxJInEj3saGkUuw7pJqgpzJYk4/FyzuRIB7WaDvBT+/CuSAWOtAtr8E2hAqQD77/fraGi4xLeEpFa/NyZwUb9PruaEqLas5++lpebPPud8vxANhrNSuCUYGcqJSZaLuX2RBo/s8YSpLHa75dbmHV6a+9Y5Z190wvHjjv3d6GN/N8pcTzj0V0ced/yYw3712+132JUTmqKx7XxsUpJbWS7FcolgOOvyyoIYleWkLDfxfJxlozyXlKSsHGzmxayfb/L6Ui5PQhSGej1NLnea5VLvfzi/WCmvDrO3gNZVmDnjToFLyoFsUMwExYzIJ1OJrS37LIopyz5zQlMw1FJXH5TkzOcLl61LBPQbr89jvaGQ1BwODg1JrcREc9Hhw0bSMHDzK518mdtjwFdvcM9vs268NyS1su4kiX2uRUBLYmzMmPEkvUmhV097TsQtJIAEkAASQAJIAAkgASSABJAAEthoBHRdj8fjdXV1ln2mG4IgrFy5cqM1AyvaHAist4C236CgWSyWLVu2//7719XVNTQ0WA6aZuHgOG7ChAmlUjWvBpULhkGef+9UKksB3gW4oW3l1CWrLljWPX2p/m8AMrVW38tqT2FXDzH3FQC+ALij2D1m8cJxunoKwOhcaeJX7Y8a8BVAvgwTJk51OhsahtRxfo8Vkb399ttbWTgKBXxku2/ouHdwEqCfiMMP+63ANwvcMPIqNIVC6VA48eVX31gGeb3h1D7EFQXuve9hMRATxKi18nzU4WClYMrtEZcub6uoitpjd2tVGSRdAxhw/nkXCXykunLRoNjUUBdgvaGwnB4/ftINN9x9zdW377zzAf6qg86wXEIKJUU5MveVVwpKuX8BrVazQBiwcMGyoNjEsynWHWfdcb835vc2huTk6gKaNMye8+GMs87mhSAfSPCBFB9Im2tKjrQEgtl6V8iey0LkMoK/SeCSApcU+aQkpCQxIVUTLleDjnkxS52yGGjmBKLRRanJL0RZf4jjwqKYkOWMHCSj43HH6pyywGd4rsnrSbpdMdaX4f3NYXk7zp/K5SuUYC+iipnLo6uzoKsw+Zw/8f6Y190YDQ8T+WSdQ+DYaFhOc1zjKaecO2fO32+55YGdfvxzMdDMB9J+PhkIpl3esF+IP/bkC1YO6No4Wbmbe3Y88/TL0Uizuz5Eek1XLi5wUXqE+dehXwFtf2albUU+ldg6EhrqqmsUOJJrhWOznD8hBmL/+eCTXh3sqR63kAASQAJIAAkgASSABJAAEkACSGDjErj11lutjM+Wg2YY5tJLL+3s7Mzl1hZztnFbirVtcALrLaB7haeVy+Xhw4fTWSzpVWW9Tp8+vVAoUPtMpLNalQuGYRQBvgZ4C+DSJcsu6lZPXtR1YQf86cviX5aoHUCTga4ZB1dzV2swyQHcl++e0pUbvarjhO7CCV2do7/+5sbOyrsAeYBuMxju1rvuafC5aNtoehC32+3xeN577z2zPLQWa2DFHYOewG677mUX0FIwJQUT7384vw8vvI6szA+xDvD6G/PMAN6kZZ8FMcowXpor+Z57H6qomtrnwzjmJ3XGtbfJUkrgogIxmERiikI8GIhPnXLZgi+WkABnHcpl+M9/vjQFdMbPN/n5JC/FRDky74MPy7q2LgJ67vNvSkJa8Df5vQnORzSxJKR22/VnVQHdM3sfmZiRAjh9whmcIHp8vCWgSciwmOTEpJ9PslyK55pEIWuuLRJvrVmJz0pCmq5EUlePIfbZWjkhQ0ujAtrrC7rdkssV9HjCPl+jzxfz+WKcPxEIZELy0Eh4uMcd47km1tc0dco1tHm9Y55ro1Yp65dfdg3HRsIyaYbX3RgUm8JyVhTik8/509Jl+byZwKNYhFde+8jliTEMF4luFQimab6Ut98l2neNwnt/Y3/x+TccG+HYKKVak+/RhQvIkJmKuWeGx1rTqj+tWTELeXX8yWfKUprzxf2elLshEZa34/3NXm/0mmtvpt/j3UWMgO7FD39FAkgACSABJIAEkAASQAJIAAlsbAKaqmUyGZZl6+vrLfvscDgymQyNB6URURu7WVjfJiKw3gKayB2V2BZd11955ZWRI0fSZC6Wd2YY5thjj/3iiy8sZVAsFjVV03XdioCm+ZovXL5yYpcypguOX1o5Kw/nL87NWdG9cn0EtAKQA/gPwLRv2k9tL4zNlce0d05atXLGqhXvAbQBmZywu0im6zIAXnnl5Wy6yVlHslQ7nc76IS6PxxMKB99/720Tvs0nbaLBwGqRwGZFwCagM4KQJJPpidGXXn7zu9+uMZ1kd0EbueMuYiDGcWG7gOa4cCicuu/+R1StmlO4DxoGPPbwy+76CM8maOyw+Urs86yb7qDHqxp0F8gch6vaK6a0NWOHhTjLhwOhxkXLltO88ZaDrtVCDWpPBPSMa28j0plkf06JHElJEQ23nn7auXYBncvlFEXJ5bo1Fc4661xBCMrhiCQ38lLMjIBO8YGUX4izXIwYcDEbEJtFocVch0q8tbYQAV1z0FRP08M4obm2ZmoCOu4XIjQCWhCjUjBBVX5Aigti1JzFMSoIcVFMxKOt++/3q5tn3a2YXrcvR1zt+kMPPSZLJMO1JKTcDcFIqMXvbQzL6dm33k8mGKzNlFguQ3cRfGzS54+7fVE+kJLkTDCcXtlRWMM+9xEBXezWUonhZlB5ohYBnRS46KOPPFWbjLF2ZfV216CpBs2vPfP6Wzg2JPJJMusgl3HVxxvDO0TC244dey4A0LkrK1aLa0OLP5EAEkACSAAJIAEkgASQABJAAkhgIxO44YYb/hfsTJMl2AX0lClTaHKFchmDhzbymGzK6r5dQFNrbLUxn8/TWSwnTpxIpxy0q+eDDz74ySeftNSzpq5mdTUDigArAT4GuKyz++wKjMqRdVw7TGorXrO07WOArrUJaFMckWkHyb+Kma/jXYAbvylOycOp3fr4ruI5bavuLuU/Mt8qadVZvVRTQCuKsnL5ir333ttR52QYJ8M4yMSbTkYK+D54/9/mIVYvcQMJDGoChULBMAySgkNoIkHQfFVA80LkiX88R9Cs9sleN1bUKhpwwqhxvBByuYReAnr7HXZ9/Y33qC0lt7jWLNWAN1+bH5KG8Wza0xCrCWgSAf3Q354w5/EjzaInagY89/xrAp8xBW6GE0kO6ECoMVcqG2vLAV0T0ACnn3auwMUlIW3a5+agmEkltr7h+jtIBbW+0DZqKkw+9wJBCHo8fkludHv8poBOmHHQibHjz555012nnX6B1xutyeWhokDtsy0Iuq8IaIG3C2gaTB3nAlGXm5PkWOvQbXf80a4HHHjYscf9YfJ5F15x1fVz7vnL08+8+Ml/v1zVXk0rRJ2sZZ/XpPrSi69GI02RcDoaafa6w5FQSyTUEpbTTz7xIpnuT4d8t14uk6By3YB//euDgNTi88c5ocnnjwbD6WA4RZmvWXKvAayUYZ+9Dw4Gkj1ZOEj6kei119xI/LJhu6TWENAAUCqq7733oRyMeT1SWE6nk9sExQzLJkPy0F1+vL/9ya1vbUmvhuGvSAAJIAEkgASQABJAAkgACSABJPCDE4jH41QbOp1Ou4Du7OykXvEHrxEL3JwJrIeAVhTFMAxFUT788MNhw4bZvTPDMDzP33PPPZVKpVwuW5HOJGZNNVeTQbcGywFeBDj/m5VnF+CkbhjdBeM74Py2/B1d+Y/1ShE0tScDR4+PMO2JAaCA0Q16QQc9D7DEnHjwyg6Y2AkndcDYleUzl6+4o5T7jKgS00KpACUDVJI0lsyRZYZVljRt8gUXuT0iwzQMcTQwDCMKrmDQ8+EH727O44RtQwIbjQD1dxVVO3H0ODEQs+agk+UmQYw+/cyLxEWan7C+4l77biYNXwWA62fMEvgQXXlO9voCXl9ACiYOPOjXJPBZI59ezSDfAjWTTApUaAZjDfba43Del/V70jxLE1akeH/jk0+8YK8111XUNSgV9YkTzq+msxDTgpBsjKZHnTi2bBpu1VDJquuqrtdCoTWN3NjqEdBHHXl8UCQ5mmOREZyPmOhYZOgXny3t6bz5FVUoqTfdfIfLzcmheECK1rt8oXBMlpNiIPa73499/6MvLKX+ySff7LTjPiFpmODP+D0p1p3cY7dDfvfbU4jj5ptCwUwomBGFuCjEG4YIvJ/MrEjUP70BwGdEMb39DnucddbU2+94YN67Hy3+pk3RQNHIN5uhf8tK+fQaL0UjHdj9J3tJYmMwEPe4JElMCBzJ+3zvnIe7OkjgtK5Csdvspzkgf/rT9Y2REW5Xo9cbZdloPD501KhT7PDXsm3oMOmsC70emWOj9gjo3x3zB3JHw66NawJaMeer1FQol7T5ny5obdma8wdlOekh0znKkUhzMjk8mRr21aLl3UXFfk3at9fSJHwLCSABJIAEkAASQAJIAAkgASSABH5wArquz5kzh8Y+U/vc0ED8G8Mwt956a7lctk8v94PXjgVungS+XUBb7aaZNx544AGGYViWZRjG7/e73W6GYbbffvuuri4re4tdQJMYOpUEHJbM6OZ3AC5Y2jVulXZSHkZ1wdhOOHdl6bZcYR5ACTTQyqD3pIq2qjZVlFYV0FCsgLEU4HOAWe0woROOz8EJHdoZ7d03dufeBL1ALJJGKq2QM2jthloV0CSSDmDchdMZl8AMIb1gGEYINGwzYuiyJUuruU5tFeMmEhhsBEwtCRXFmDb9CjHQaDrohCgmQuGUIEb/9tAT30FAU4affvJlQz1rCWiBD7nc3JB6do8992/vKPcnoA0dSgXId8G0i28g9tmd5X1ZwU9yYjQMEe6648Fidy1JBK3GAE2BFctyspSyJv0TxRQvhB7/x9Mkp4Sur4uA3vn/9gwFMzybkPgs54vLgeyOO+xJYp9tdrNQhH+98lZjNB2QogEp6vGKQiDE8RIvhK646vqSCp3dFUtAF4qglOHEE86QAy08m9p914PefnN+uQCffvzNE4+9dP11s6+/bvYTjz//9lvvL/hiyVFHnOBxkUkFaxHoTaKYeued/+oGdBcMRSXqWaWyntpn+rXbj4mmYGjDi2Xiamki70lnn0eUbjAWjWSikeZQsEkSE7fOuteyz+QL3FzyXfrCL1bKweaA2Mz5UyG5RRCSghD/5z9fKhTt8rh6/Jo/NAXeevODOidH0nZXJyEkEdByMKaZSULKZZIuyYoup/a5VFTz+VJnR/fIHXaSg7FgIM5xjWQ+zFBalpNeX+D5uf/SDCiUS7ZhsQ/Rmg3BPUgACSABJIAEkAASQAJIAAkgASSwQQgoikLT8O63334Oh8OKfabyjeO4xYsXo33eIOg3+0LXSUBrqkbt8xVXXOFykan8rHsXbrc7nU5/+OGH9p72CGhrS4cOM/PG1ctyk1bBsUuIfR7dBad3lmYUS28DeZdoL82AnkzRPRHQPQIaFB2MLoOEP9/WofyxyzixE47rNMZ3dV+nlv5laEtM7VxtDFVFNATblNG6Csu7lHaAOV9/c8hV1zKeAP0MkIcC6pgRI0aQiL8+pz6zdw+3kcCAJkDVpKrDE08+YxfQUjDB+kO33Ha3lXKBKr91h3HcsSeKQsQuoAUx8qP/+8nHn3ypGyT82R4BbdTcJ42Nffbpf4tcM4l99rUIbLPgz0hC6tTxJPPvmotSgd8cdYLXIwcCTXQVxcTePzuQdq2sVDQg8c612GfD3OgdAS2JMVlK82zC64qF5RaBSx73u5O1ymoCOpdXt97m/1wugfWH6ht4QYywXECUwlTTawAl1bAyEpuPZlRPX/RVR6VUy2Ri+lulUgv0BiLcDzrgCK87zHNNPJcxX5M7/3hf2tNCUSegjKpmtXffHgpN36Z76DG9BPTcl15OJjKsN8CxoUg4zXpDHpd0ztlTykVyuK5CdQRqzv3QQ34XCGTkYKvXE+f8Ca83MnLk7rl8vzMH2htG8iaZennXXfYWhdUEdFCKPvz3x6vttHKb1L7+6Vmj/jBOEhvjsYzAR0KhtCgm6ob4WX/obw89QWtRzS/uPh10r2bgr0gACSABJIAEkAASQAJIAAkgASSwQQn89a9/bWhosOyzw+FgGMblct1zzz3o3DYo+c258HUS0DQ75xVXXMEwjNfr9fv9TqeTqttoNPr223QSP/LUvG5bDCKQtAooRdDyAF8B3NyWv7gLxi6DcTkY0wkT2+Gakv4ikLwc5An72uPvlrW2gatqCR0gbx7/4IrcJe3dp+cro9q18Z3aVZr+DMnIobdrNJaOhD6TMmvqBFQS8UfPnVuBa3P56W1th11zM+MPMJ4GxuVgnI76+vopU6bY47htDcBNJDBYCCgaUb6aAR99PJ8KaEGIk3ntAjGPV7ryqhvXT0Cbn11NhRtm3ur1iLKUEPgeBy2H4i+9/CZVtFUBbZCqzS+BWvCtCX6vPX7Js9Q+t1IB/eOd9qGqtNfA/C9fx5QLpqdTIwQuagnogJR88p8vVFStUC51F4v9CWhNK5mGmBTJeoM0BUdz+kded2MkNPTWWfeDbmrZmumcOPGPghBn/SEpSCLEOS4sBhofevhxVQMa+FzWDWq9KTSiUw3I53qkba5LoQlGdJU4X2uJR1s5NspzTRybpgJ61KjTaSHlCkH0nQW0VcUeP93H6xE5f5Dnwh63yHpDmaatly3pXM0+m0crFbjk4iuDgWRAbPZ5UyF5aEhuEcXUo48+Y8V3W8X2u2EQw37N1TdxbMSMgM6YWbyjAh866qhjavMQ9kRA08B2pQLHHzfG7eK8HpHnZFlKRBozHNeYzoy46eY7SAYSM6M3rbQ2LBgB3e8g4BtIAAkgASSABJAAEkACSAAJIIENR4D6w5EjRzJk1jUSAU036uvrBUFoa2srlUobrnYseXMm0K+AtiYSLJfLiqI8+OCDbrfbCnym9tnhcMyePZt2z2aee2KYVdC6QV0G2kKABzsK03L6aV0wbhWc0g5/LMJVXfCcAkvN8Gcii1UzY4bekwR6TXBlgEUALwNc2p47rW3lmUVl3NKuK4skr/RXAN+Ypps+DV4yU23YQwRz5jEvAMwsaae1tZ/UtvISVdv71lsYSWIaSFg3wzBut/vZZ5+1erRmA3APEhjwBCyzqQMMHbZdQIrzfJTno4IQD0jJ438/jhKwZJ+VM4Fs9LUoFfhm8SqBj8hSgmMjrnoxEW/xeiQ/K91/70NdneZ0eQbRr2SlSY2JgTaz8Zif56uumOVpaOR9Wd7XUsdEJX5oPLLta6+8T42toQNN12BOVaffMPNWt0twNwQ8LkkUUxwXa2wcesYZF9iaRu6NWRHQtY7oOugVpUAjrz/66BOBj0hCikhSfxPPJgQu+erL/6FyVlNIkPKdt/8lICXNNR6Q4j5Wboxmb7yJfCWSTNZmfgxqimnVZPLC/lJk2CJ/uzpLCxcsM9MxJxsjI1hfkyS1BAKZv/+dTP/4LdkubOWsOS60p5pB0ndcc+3McCQeCafqnN5gIB4MxNOpES/NfWs1p28OqKbC1VfN8LNSNNLsdARZX4bnMuHw0NMmnEe+tjUolIhjt1Yb5z42O9oLfl+Ydcd5ls7u2FTnZEUh8sH7n1TTQBvQvrLb0KGQV/O5ypjRp4ZDiZAc5zk5JCfDIWL5A1L86qtv6qN03IUEkAASQAJIAAkgASSABJAAEkACm5TA888/zzBMXV2d1+utr6+nto1hGDpvXKFADMBqs9Bv0tZi5RuNQL8CmraAXhO6rm+//fb0unE6nW63u76+vqGh4cgjjyTGx7x90aeALoHRBfA1wH1dXZeuzJ3VTQKfx7fDpDa4thP+BcQ+r1KhaMrntUZAE+uimhMPzgW4pCN36sr2Uzu6Jq5cdW1BewrgU4BVAJ0A5Wq7q/mfaTpoGl39NRgvg/rn9o6JbV0ntRXG5LSx3aXzlq+64B/PMcEo4xxCPxWZTGbZsmX4YdholyBWtLkRsEyiDvCb3/5eDDQKYpTjGj0eWRDi/7fTnrTB1mFrik7yiVMNIoXNdMwAMO6kM1lvyO8L+31hj0vy+8Kp5LCLL7qsxz6b3pnaZ13XLfts6CR1QzI+PBnbNigMcw9JBvnhnDdz7NETdJox2DyANsnQ4aorr3c1+AU+Eo00R0JZp1MQhOS++x3e0UnnMawe2J+A1rSSblrtF55/WeCiIt9EsxXLgawkpL9Z1AW16hZ9tSqb3sYuoIfUc1OnXg4AxbJht892ob8uArrYbTzzz1dEPhkUM5w/JQotLJusr5c/+mghLXZtF8w6CGgyqaMGLa3DhUCozul1uwRZSrDe4DG/HQ06CVKuBmLXbidcdeX1Xo9oZuqI8FxG4FoFvvlnPzt85crq1y3V4j3XQ3/tMyOgyyXjgvOnhYNDg0Kr3xtzNwT9vnAwEB89unZjw5xAUldJnPiY0ady/qDXI0YjTW4XF482c2yoMZq95tqbaSLs/qrC/UgACSABJIAEkAASQAJIAAkgASSw8QkYhrHddtvRhBsNDQ11dXU0/8ZWW21VKpWoObTSHqB52/gDtAlr7FdAF4tF61KYMGEClbM8zzMMQ1/dbje9caEoil6b1KvXxdRtBiy/APDH5W3jVxVPzsO4dpjYrl/aVpxbgRUA3QDtFZIcg0Qkmi+kUt2ohkGSoDpqQXQApQOM1wEu68qNX9k5rrNw2squ6atyr5DMG/C1ASvNkGdzvkOinYmx1s00HKZ3KgG8C+rs4rJJy1ac1qacvhJOb4fzVLisQ/vLp223P/wsSQNtPhrg8XjGjRtnGIYVA74JhwerRgIbn4BlEnWA22bfxQshGt7r8cisPyIFE0uWmlkaakGvPQJ69baWiioV0A/e/6goxBvqAhwbIekX+AjPhQ864PDqhxuqH/eqfdZIHna7gL7pxjv83ka/N8G6k676eEAcFgqOeOP1+TTQmEzHV8tccfFFf5bEmNslRCPNrnoxLGcFIbnttj/5cmFbxbTVtQYaOpB4Z3tP6R4AQ1GJV519210CF6Xhz4K/KSQ1b73VrjTKl6SBBjj80ONJSgoSAU3CnwNS/NjjxuS7SZnlik4Dn+2JMmhd9j+0ZLsWEF1tmKmPDQ2mT7uOY6NhucXtajSzXiTS6e00HSoKybyxrguV0bajaRsqinHl1TOFQEiSY5FwWpZS7oaAwEVf/de7NOEyOaPm2c+bfDHrDbLeYCSUZT0RrycuS8N+tON+n3/WVixVZzKkOVssmLYKe29WyuSL+euFK1Lx7Vk3MezRSDPvbxSFqChEXnv13zQZCx3QE0+cwPpDydQwWU5GI5lsekRIjrPewHUzZvUuF39HAkgACSABJIAEkAASQAJIAAkggc2AwAMPPGCFPNPkG3V1dQ0NDXfddZfVOvv/i62duDHgCfQroMtlYmGKxeKrr75qT91SV1dHL6ZHHnkkn8+TYDpF6erqUg1VNchEUGbsH/EXKhAp/BrAFW0rzi6pY4rGmC44Y6V2ydL8X9tLbQCdCrQrROnQucBU0FRQyPPvVECTd6hPJmKqG0rzwZgD8IfFi04rG+NXFS9t7360Yiw1s0K3a5DTiA0hopqkBDW3VFNAayTCuh3gBYCpK786p1g5R4VJOThnFUxakptTItHTJYDDjzra7/d7vV6n0+lyuWbOnNnV1YUOesB/ALCDaxKwTKIO8M6891kuIMkxry8YkJIc18iy0YcfIWlqrMNWF9B0d0+pxW5j6+E7kfn0/LGgYSILEgAAIABJREFU2CQK8fo6f1CKfvThZ+USyfLc451pELR5F8suoHfYbpdQMCNyGVd91OtpYn2Z4487s1wi3xuKUl0XfL7syCOO49hQSE56XFIklA3LaUlIJRLD33vvcwCibm3LWgQ0VBSSkerSaX+2C2jWHf/FgcfQEgwVnnjspaDYxLERMRCzBPRXX7fR4OKKYvQvoDWza/S1589uT9tMv/yH35/CeiLR8DCfN8H5U4LQdNRRo8tlqCjrrp9ryZR7iq4OWb5bTWdGCGLU6wsGA0ne3yhw0SN//fue+wFmLpQVy7pPHnuWKMSjkWaOjbCeSCyyVTQ6PJnc9r33FtBSFQ3Kpi22LoZvyRACUC6Tkbjw/D/zbIL3N/p9Ya9HlkQSgn3AgYcXS9BdgFXtlSOPPCEUSrvdkiw3yXLSVc+LQjQkxy+5+M+qXlX8vS81W09xEwkgASSABJAAEkACSAAJIAEkgAQ2PoHdd9+dOkOXq5rqtqGhwev1UnlI/m9eqfT8T9hYn//hbvzOYI0/KIF+BTSdmLKrq2vYsGH06qFh8zSTy1577WVrBvEA9JF2Er9cmzmsS4MPAa5ctviczs5TupVx3cbYnPKnlcXn2tUlFcjpUDCMiumL1appJlKmJ/aZJASlq1YAbT4ocwrLJ65YdmpJG7WqMK1A1PYKgIKZhFRRyXP6oJIUqyqJpDaqp5oKugzwCmhXtq+asHLVqSXlpKJyUmfXpFUrH9DU13Rlsa6RVCH5nPXxqB/iYhjnvHnvkT4qZivMDwWd0dDWcdxEAgOfQEvrcB8r8ULE6wsJQlNIHjr+5D9qCtBoVjBseY3JHw/rY1slc8nFV3tcst/bKAnpoNhkJuKQ77/3IZrwl4QA97Fouq5rZjTsnHv+YmagjpsT8WV83hTHpv/91pfWn6mKBs899++tt95VFBNhOe1xSaw3RB30Dtvt9u+3PqbtqJj3uqzG9bdBPvFmBPSks8+zCeiMa0h49KgztQr5nikXYffdfh6NNIfkpCBGxUAsFE489Pd/kPBknWS3UG3Zn+35N0w521/NNXNr5qlobd4hEmrxe2OcP8WySVFMz7j+9nKFFL4+iz0fBzmP3NPT4d77HhbFhNcbiURaqzcGAsl33/m0UoJKCQwznPzVl/+z9fAfC1w8LGc9rrA5W2DS45J32vmn8979gHrwHslOLoE1Bn6tDVUUY+sRIz1eyeORzfTiSUFo4rmma6+9c8GClT/b91ecmOQDqWA4K0ey4Ui6voFnueD0S6/qFTNO611rVfgmEkACSAAJIAEkgASQABJAAkgACWxYArlcrlQqvfDCC3Z/aCWAnjlzJvkPqW2xNMCGbRaWvjkRWJuA1nX90UcfpVeP/dXhcCxcuJAaarMvRALUwvoMErVszmm5COC+le0Xrmo/pbt4crc2Iadd2FH8S0lfpIKiaGVdU0BXQK8AsTqqOSeYJaDNecCqRqYM2gJQ5xSWTutecWahe/zKzmlF/R9m/uhuVdc10xErNZOtVXUY0SEGyQTdDvAfgDlK+ZyO7rHdlTGl8piujkmrVtxayL0N+mLQi+ahXfnO22+/nWEYj8djpuMYssMOO5LeqabLNvu5xhPtm9NIYluQwIYhMGbsyR4fzwsRjmsUxbQsDd/9J4etVpXloKsCWjVtJDnk448WSGIiFMzwbEIS0rw/xnpDZ51J5gMsFSuaav3RsW9Uo4MV07YefsQxREBzST/f5OfJdHy77foLmqiBtuHaGXf4/FFRTMlyJhLKcmyEzD0oxH9z1AmVnhzF1ccj7J60z236NxEAxo45TeDiZgLojODPsO74lZffopRBKcMtN98Tj7aKQlSWElIw4fUFzzhzspUPpJd9XkNA22PHezXB7JABCxcsCctp1hORA9mA2CwITW63/PLL86hDX438t/yymoCuGW449LCjQ6GsqyEUkodyvjjvj+25+wFKmQyaUoZCDqZPuz6T2l4S0nIg63U3hoNDG+pCieg2v/zFMW0rSfYVlSQaIclAyGre8LP35FsaZb5dqVTuvuuegBSV5aQgJHkuyfrTfi4TCQ//6Z6/DASzbl/Uy8a8bCPDeEQp6XB6b7r5jmKBRE9TB01rofWuS414DBJAAkgACSABJIAEkAASQAJIAAlsIAL0v/R77LGHXR7S7VQqpSjkv3I0zsxMudljADZQe7DYzZBAvwKatnXHHXfsdfU0NDQcc8wxNEFHrT9mrgwikzVyEemgdkMe4BkDJn+96IxOhaR+7jbOW1V8NA9fGNABSgkKCqiWfa45aJLNVSMr8dE0A7UOsAD0R42uScsXn1nInV/qnt62/HXTPneZ0c1EQKs1B10Lpa4G45nx0YsAbqt0npFfeWyu+HsNju8m9vmB9u6PytABJDtHGQwFNEUvaVolFArRKRZpSuiLp12sglEhcY3W4+mk01b0ZY0A/kQCA5OAomn33Hd/KBzz+gKhUFYOtgbEVp5rmv/fxbTDJPZ1tTszNHNO1XYeecRxXo/sdYfN8OcM64n8dI8D87lKpWzeOjKLqN27suemqH78Fy1eFpDiPB+3BLSfb5o2/cbuInTk4YNPlvz6NycJMpGVoVA2HG6JNbYEA0lRiI4dczoA5HM9Ew/aDelatjUzwbOmGocf9luRT4pcRuSaRa7Z64pdNu3GSol0drdd9m0YInBsiOfCkcamEVuPpLHJNPaZFt4THVx7GKN/VWo1h+KAv/31Md7f6G4IiqZwDwQy8fhWq9pLqqWQ13at2aUz3dZMZ6uT50IAPv3sK0GIi2LK54tJUgvPJoJi01VX3NS+sgwGfD5/2QE/PyIoNsmBbHN6JM8mQlIz50vWO+VTxv2RVttdLAJAgeRPIc+afDcBDWYujoMP+bWPlTkuxnNJXmzhxRZOyLBciuVSXi4Vjg/3cFEPF+EDietm3Npd0BTFKJcVFNBrG398DwkgASSABJAAEkACSAAJIAEksHEJUEP4/PPPW3kFLJHocDimTZtmhT9rqqkNe/wz2rWNO1SbtLZ+BXQ+n//4449p9mfr0qEbX3/9ddF0ELWWWwKaPOVeMbXvvxW4qjN/4jdLT8vBhE44p125enHnZwZ0a1CAfMUU0NQ7216VCtCV5MSg6mg5wFNq1yUrvz6jUBy3qnN62/KnlOJKgG5VLdEwS2MNAU0TR5vhz8sBXgSY1Lbot21LD8sVTjTgtK6VtxZyH5Uhr5C5y3QNKqBWoKIalVKpcOqpp1rPCNTX14tBccGyr0skRtsM+TM7XLNtdtFTI4E/kcDAIpAvFLryOU4QJTkWjQ6Tg60C3+z1xG+75T46YR2RvNZHgdzSpOHPxJX+5cG/BwNx3t+YjA8n4c9sgvVEHvrbk7oKXV15cq+qOtlgL/VcjYDWNbj+hlnxeIspoJv8XIZEyEa3evmVDwDgqhm3c4G0GGr28gkv2+j1Rlh/JBhIRsLpO29/INdVLuRVRTEqikFTw1uWd+0bpRJ5fENTYZ+9Dxb5JktA82x69i0PAcD99zwuiQkyax8fcbsEXgg98JdHaJgzlc60/O8joC84f5ospQSOaF+Bz/Bccq+9DtHMtPa1i2stf6StwbA2iIDOF3P03Ntmz/F4ZBr+HBCbg2KzwCU/eO9LXYWrr7xFltJOhiPmnU+ScHVPJBJqYT2RGdfcWeom8r1cqX4TduS6LPtsPnayfik4aGNef2OeIEYFISkKWSqg612RgNTCS81CsIULpKVwts4TuGX2/XQCxlr3zZQf5i+UtrUfN5AAEkACSAAJIAEkgASQABJAAkhgIxOg+TN32203y6dReVhXV+d2u2lj+gx/poGnG7m1WN2mItCvgAaAiRMnMgxD5+WzEkCPGjWKTs2XzxOFVFs0g0YSqyT9xjyAa1Z1j1u2aqIKE3JwzhLtlhXKlwBdZHpATTMttEK0L0m+YVuJfS6BUgStCNBthjm/psG1nW2nr1xywpK2C9oLczWjk2T4UAwo04A+oj1o4LP1qpFqACAH8CzAJauWn1Moji1Xji0pozvbb9eLb4PeYfLWDCBTJqoqWYHkop07d67X66UfFYejzuFwHHnkkXRsyrrWUSHzZ5FVW79UrJtqdLFeJPA9CdAZ+Q499FchOS4JqaBIwoElPvubo0b1lGypzuqUpB2aqlUqajyWCclJjo24G4ICl/R7Y2NOPLPnLPKJI67Zlj24Rw7Tv0O/OvzoSITkoBD4jMA3C3zz9iP3+ter7+++58GcmAwE0yxHsjT4hWg4khYDsT123+edtz+wz2qo6iT5xtrTYvTUCkAFtKHDDtvtYhPQrfWO8KN/f6nUDT8a+VOaYNpVz0ti40ljJ9CcGvZXe4G9tu3dr23TQ8hvlQr5Itpz9wPi0WFB0w6LQpbzJ84/f7pVvhlwTpyyudbKWLefZUX95aFH0ohynmsShZag2LzTjvu8+MLbe+5+gN8XjkdbOTbi94XJrIPekNsl7LLzXu/O+6SznWQzITcXbEuvrlm/2g75ls1cvnLhlD8HAk0BsVkMtJprsxggqyS3etnYkAbprnv+XsGv228BiW8jASSABJAAEkACSAAJIAEkgAQ2JYGnn37a0oZWDKvD4bjsssuonqb5n2sKsefnpmw01r1xCfQroHVd33HHHevq6hoaGvx+v3UBvfXWW7SFPdcL2dIMKGpQ1gG+AfgrwOS88odVlQklOG1R5eolynwg+S4qZggdPVIlwc52+6zV7LPSDVoBoA3gNQPuLlf+mO+c2NUxZVX+rxp8ZdpmIruhaBgaMci6qZst+2yGP9Nowf8QD54b+82yUcvbR6/qmpDvvqSz/TXQl5K0GzWBoxmgamTVDfrUAMuyDrLUORx1dUy9k2lY8MUSMHNJLyT5QGCZmbijWvXGHS2sDQlsZALFYjcA3HTTLK9HlISUxGclvkXis5FQtlKuBaJaAtoMzKV/XaZMuSgkx4OBuMBFOTYaCQ1tzmzfvrJcyNsTSdgnLbQEJtmgd7niiazHI5sCulngSPD1WZOmuX0Rlm8MyCkfRzbMNcwLoT9Nu7xUVA29Oo8p0dC6rtrW/qKS7RXTxhs6jBi+oymgm0WuVeRaZXHo80+/89Bfn4tFhkZCWVlKkeBuTv7k0y96jYi9tDW3ex1s/kqOslLqawrEo61yIBsUmwlqqUUQknPm/J0KaLNAncy0up4Cmt4zUzTYepsdaUQ5zxGnz/mSo0edGRSbJDEhiQm/T46E0yE57mclUYhcOu1KM29HX63u874BfSql78NX21upkJHSdHjr7U8kKS1JWdM7t1L7TF6lTCCYfuwfL+cKgAJ6NXb4CxJAAkgACSABJIAEkAASQAJIYHMiYBjGIYcc4nQ6ezloQRBWrFihqVoul0MBvTmN2KZpS78C+vPPP2cYpqGhgWEYlmWdTifDMHvssQdtJtUlteStVQFdgnIbwEsAl+YLp+S10R1wRjtM/6r0DgAxuEQUKwYoRPkSGW2YK3XQVuYNpQjlblAKAJ8B3KmWJxc6JxQKF+VKz+mw0LTAJUPTSIZozczOTIrSjJqDrkVDFwHmA8xZAecsKoxZVvjdkvazurpnq5WXQFkMRjfoJRokTY43QCdpTGm/ioXyEUcc4TSXIY4hQxhvHSOePP7ithKp/XGAK5ctfBtgsRnojQ8LUGj4OoAJKCq5WdPWtkoOxuwCOhRsevaZV4rdfeeCmDfvPT8rcv6gwJO0GKFgJhJquf+ex9cAtTYB/fHH/x1Sz4XDLZaA5ti0X4hHoi0s39jgEb1+eYiLjzcN2+/AX771zn/KCnGaRNTalnUU0Jabpi1UFCObHiEJadO2D5X4oeHgVq+8+OEhB/2OY6M0AjoSTp95xmQdoLtIplPotaypnumeXoeZv5J3qHAHgI8+/CwYSAbFjMhlOG+TKGRlOfPJ/7P3HnBuVOf6/0haSSutVr1sr26YkEKSXyolBC65f0hILqEEMA644O51wWAbN6rB9DjkAgkdQkliWgyYGNNCCc1AMBCMwWtvX3Vp+sz7v+850mi2GQzG2ObMZz7aoylnzjyjHR195z3P++4OmoHwMwFofD6QF9Fa5MNt7f5AlQGgPRVN3oqGWGR0JNQcCTVGQvVVsWafNxIIRH/w/cOef+4l0IHPi+l0mud5A5Ebp7A752jsVCioJJh609Mv1NWNpQA6GBodDI2m6DkQagmEWv5461/yJJ/t4J2NBx6DV7D3TAGmAFOAKcAUYAowBZgCTAGmAFOAKbC3Fdi0aRMNWqUI0QhgXbJkCW2KKIoDY1hL7/Z2W9nxvjwFRgTQa9euNbu3UCvxO+64Q8jzoOFnRUNbZEUHGSOR0U5ZTAL8G2BtOjm9t39qRm1LwMod2osAH2oYcSxrkg6ijltiKLSEscyEXCNKRgxNX3nQ0wRYrxfkpZnE9FR8WYq/O48B0TJAXtcFXVUwgRmaRAskGFmgYdEEh+jEhLoL4L4kXNSpLOxSFyS0eT2pG0RlMwl8FjFrFuY/REtVTGA4AEADwMKlSy1lnNVqLbM4yjgPx5U7fWO7AB7OwNLujlV9Xbe993EvOTQD0F/e55Ydee8pQFwy4IRfnIhBsshkW0O+VpczdN65K2QJbRnQRWPgdMIJvwoEouVOr9cTjYab6mrGTJuyEEcdqCDwnyYCGqu78477vN6Y211l+G/4faPqmw7xBurCscYKb7TM6fP4I/MXXYAPkjTyaKtAn0vYuVTSNIMyU8tmMz81VtHzkEStvm508WRHh3xjy+01z256x1/ZRLIpNgX8ddFIQ/v2bklGBK9oQAuGDObKzWVjA1MB10uShBHBCtxx+73hYAOxzG70lDf4vE3RaKuqQTaHOQjpXXc3I6CR1/ISPkh46OH1FZ6IAaB93pZYeKyV85c7wjVVo3zeWDRSFwhEr712bSKekuUB11VVVDTtKj6rM0Vkl9yf6ZmaTm3EosAr6x/9R0PjuEikqQCgw63BcCtFz6TQFAw3r3voKVHB+gdMDEAPkIO9YQowBZgCTAGmAFOAKcAUYAowBZgCX6YChx12GIXONpvNoM8cx/X29hrNKiHngSVjA1Y44BUYEUBPnz7d+Nw4HA6bzeZyOOO9fYoooW8yAbgqyGQWJYKVdwCs7e2bH0+eLaqzZLi0B54D6CXYlxAExL2AbhcIfpFt0PyBJBQOh8vj0HmcUgAbAVb15qb0Jdq64/d0SwliCU2wtS7piLxI+LOeAz0JegKDmjFvId09AfBoVlraw0/v5s/tFy/uzd+ayr8CECcIG4kzaT9oOgHQ1NS5cKFFgD899BDn4AiDdpRxbldZgLMFJ9+67voe4cKu1M0J4T0J6TlacBSnA/5Twk7wK6lAASdSAP3A/et8ldXR0KhKd304MMrljPzw+0fTjIMFa2Ad8jlMHXrLLbe53R6fN1QVw6DaxvrxXk/VB+936CqoctG1oySoQRPNBeTaF668JhpuiQRbaSZA4gHdEgo1l7sC3mBNuSd8+sTJb7/7H1qTiVFi/HPxX3PAX+OYqqJTukojpvFWpBX+nek2qgI+bwxz8XlbAl504YgEDjrxhCkhX2uluzYWQQeS2bMWgV5gr0OJNtWO8GK8sxmz0YahBQqgp58zz++t83sbfJ5Gr7vJ52366U9/JZEYa1InPvYjAJraQA+tZsCSYjMKCy+8eLW7IuzzItf2eVt83hZPeZ3HVRPyN3rcUW9leOaMuVs/+Jj6YwzQTiMSaXjfM+qk2R3/76Fdjke6nRekvEBzxw5og/mNBpjGEAA2PPlsNFbv9cbsjoDPV1dfP97lipWVhSPhUdHI6GC4ORhp9AXrD/nGD9/f2imQ089kB1pQm+tlZaYAU4ApwBRgCjAFmAJMAaYAU4ApwBTYuwpkMhlBEJ566imPx0P5oWHBUV5efskll5ibwyI4zWp8NcsjAuhjjjnGSSbjOcaRRx5J8lChXTL1/yxYcICcI87ImwCW9yVnpLKTU/zCvvxTxA8ayUQBOBcANGUxSJ9VEggtI4lWCQfOkMyBG/JwcTe/MCkvSAqX92Z2kIMRk2fkzsYsgc6DmgU5DWKWGHcIxGn6ZYBrUvyshDA9Ja3sz/8pLrxK6DPabqDdMzkYQpQigKZgW0E6vg3gsr8/xLmtnJ2zWMutlnJnmZuzOL82bf6aD3tvjiv/JKkUoYirKKP5an502Fkf6ApQ0lgAnVve+U8oUB8JttZEx0dDY/zeOnTheOIFKoIRBL2jvau1dXRtTb2nwh8KVIeDdaFA/epLrx+BPhte7Gb6TGw9NFg0/9JwoIWaUQS8mIHQ72sJhhpqakcdfewJ/9j0T0HBw4qagZFpVG7pydAAhKpjtSKmEcXp97//wx2335XN5nEfdQCARhitATpRmAB0ffW3IoGxsfBYuzVEHEVaX39tyy6igIuUtoSeC/c9evjhXql79c+POwkBdGWTv7IFZ1/LxImzqak9qfNzAehzz1vqqYwSAN3iqxzlqxwVCYwN+VoDvqafHHHcE49vou3i8wOHRxXpM7aQ3vrJa5YYZKADEplWXXTxbXfcw4sD4qYL68gf4yHBuocei8bqGxpHe72xWFVzKNwYjbaGQs3V1WPLnTGPpyYQaghFm0LRpuq6MT86/L9oJTh2hk1MAaYAU4ApwBRgCjAFmAJMAaYAU4ApsG8oQH9xH3HEEYPoM8dxkUgkn8ef28bEALQhxVe2MCKAjkQidrudOm/QD9P111+vKmi+jPCBuifT1H8qJhjcDLA2r7QlkvMzmYsSqXsyYg8JeC7GPtOg52KuQF1DQw1iw0GiopEGpwE+AtgASJ9nbO9bnOCv7s28DdBBj0YsOwz6TAsqgmsBICdAKgt8HmALwI0qnNOVn5kSl6T5P/TzL2gYhZ0DyALkMRwb85KpgB4ieGiZRGjL+PcjgPuV3OJXNnF+B1du4+xuq82N527lyg7++iOdiVd02IGmHzroaDxi4K2v7KeHnfgBrQCFjSXs98tfnOawhUO+1khwtM3iD/ga2uYQRye6IaC9xnmLlmLsc1Udx5X5fVGvJ3rYj45RZRL7PDyZHISe6VvUdfJZC/3eBr+3EIZMAbTfX3fd9Tcms6IOQAE0QMF8w7gWlCAPfaWRzj3dfSeffGooGPF6/aIoZ7P5wpbk/7kQDa2B3xc1A+iQb2zIN9pujfi9DS5nZNrU+UIeObUZyA5X/rQAGg0uCAcfPeoQM4AOBkZddtlafIhXCD3eDQCN+VnxKRt63KugKxpMnjLdH6gxPLX93jFed1M4MOqaK/9kqEcLhZubCT1TlcznCAC8KEuKmsnlT/jV/3j9gUi0ZlA95rciCY++8ebbKzwhrzfm9cZc7pDT6S8vDwUC9WPHffvyy/9QXz/eYvF6fNXhWLPbE/P4qp0Vod+cMVlRIZEUZQUy2WFtoc3HYWWmAFOAKcAUYAowBZgCTAGmAFOAKcAU+GIVEEUMN924cSM177UUJ47j3G73ihUrvtjDs9r3QwUGA2jjoYQ5cp4C6P98uFXWJMJ8CXeRkd7qCggEyz4MMG9nfGE2uyqb/nMm105imYkgFPQOAtAKMW2lnhxYjwSwHeBlgBV9uUVJeVGSX76ze4Og7yRGHWk+Pwg907cYu6gKoGYUyCRA7AB4UIb5/erpHfz5GfGqRObhhJAh3FlQEUBnCIbmcXw/wiME0AIeXdHRpfpJRV3csW3Zjve4gJ1zWrgyJ2e147nbOc5T2QvQT8KfFTxtkQHo/fDTzpq8WwpQ2Ij/K3S3m/73Dr+3zl1e7a9sCgda/N66upoxSCFzuJ7P6c88/XIkXBsIRCPhaqejMhysq61uffSRjRJxXh/h2CMC6JNPnFrprvV5GokJRiEC+qab75IV4GVskw6Qp+YUA6seip4L8FSFnTs7f/Sjw8rL3Z4KbyQS6+joSibSpe1JlDQFwYMAtK+itSpySFXkYHri6x99igwH2ZMAWlV00MFVHjAB6KZAoPnOOx80hVp/RgAtKbIoK6f8ZkIwVGcG0C5H7e23PKTJIAl4SxSFwlOCkQC0qSUF0bt6+n58+JEVlb5AKOL1hT7c1j7waiAEN6Z1Dz1W4QlFonV2hy9W1ex0+svsXndF9Ovf+OGLL76l6TBr1pL6+vFOdyQcay5zBsorosFIvS9Ue8IvT2UR0IaMrMAUYAowBZgCTAGmAFOAKcAUYAowBb5cBdBgAIC6PxfhM/4tLy+32WyCIBh08cttJzv6vqPAAADN87ymYcjyyy+/TKGz8Wq1WkmjMd8gRkATywxFgYwOH5Pw50tS+rlp5SKBv7pr5zbCeQkdlouMuRj7jNCXRj5rCJBIDHKiF8OcNwCc19MzvSc1pz+7OpN/DKCHBCgbntFDC9gSXVTSfVk+1QXwN11elkyf06u0JeGadO4xSW6nDtQy6DLwJQBNmAghLQKvpSQE068DXPifbTO7dq5MdnH+cs5u5WwOzlrGcZyNUOg339lCbUB0CqBJ9kWKafady8lawhTYcwpQAF3yGm7/uLe+9iCfp765/ls1sXG+ytqaqlH33/uokCePdDQ4+qjjI+FaY/b7qs44bbLZIGO4to0IoP/rpydXumudZbGQbzSZ0SxCkvHRFcWgxaBgpMC7njQVJEnZuaP7qKP+q6G+pdIT8FYGR486CACSiWwBZherUBU9Ec8E/FXFpIuYhDDsGx/2jwv7x4QDLc0Nh1D6nE7lzRHBA8uDY593bcFBVdryzlaPO4px3wULjiaft+Hpp18pNo36FlG/otJ1wcBgEowMAL398cc3PLl9R0c2L5jbI8oKL8pHHf2zSKTBDKBrY4fwWaxe5BFAF+YCfsZhIoNmKrVchMrvvPveN771bbfHG62q9voDsaq6YlMLf7N5CaOwyW6b33zPH6hyuUNldm8wVFdV3RKJNAUC9d/5zpGbN29VVNxMFOHwI45HU45YI42P9vmrgqE6n7/q5FMmGpXTUzNfDbWrAAAgAElEQVTesgJTgCnAFGAKMAWYAkwBpgBTgCnAFGAK7GUFXnnlFbvd7vV6rVarwaA5jjv11FP3ckvY4fYLBQYAaOKwgeFqzz//vIGeaeH73/8+sf3UDACtE/q8FeBVgDW94rlpZbkAV3R3U8NlTVNAk3HWZSS2SJqNWdIwFSE+LtF0pNEdGrwAsLSrb04mO707vjyeWke4No611jDQEceSDzeT1QroclyFf0rqhfH4tP5kW0q5LKuvl9SP0S6DHIa4PCsavuUJ/ybgWhV4JasgfX4X4JqO3ivyMD+Ru16UOU8FZ7NwFjvHYQZPmwU1eOapTdhcTSWWsXhSRhD0fnGlWSOZArupAKV8JdApSzDh9HPqqsf7vQ3hQJOvsjYWaT77t7Mojb1h7W3hYEMkVG+et33Y+UkHHRFAn/jLSX5vQ7m9ygyg0X8eSgzaYKy7OApluzt3dH/v//0oFq2trWkMBKL1dc3Ll12I6NmwoaZFHfMT7hpAn3HaNNBAEkGWse4R5t0D0LT9L7/0htdTNQhAP/JIwZqZxHxT+iyT22EhtDgvSKKsqDr86dbbmltHuz3e+samrds+MjdMVnVJ1k/45cmhcL0ZQIf9Y1Ti04+3RGMeGUBT2A0Akqy//8FHXzvkW2UOd6y6xh8MuT3embPaBj0MoCkHRQlefOn1MWO/7q4I19WNjsYaPZXRpubxPn/V4Uf8f5s3b6Wnr6iQy8PLL7/jD9R4vbFAsNblDrkrwoFgbU3tKK83dtLJZ2RzSNuzeWkXZtO0NvbKFGAKMAWYAkwBpgBTgCnAFGAKMAWYAl+QAtls9thjj6XA0EomyqCj0WhXV9cXdFBW7X6twAAATc9E1/WNGzcOAtAXXnghz/OE1YiIkjV03viY0OdVSXFOWjhPhlV9qVcBDZezoEggEeqLDqS6rmqIjGjsc8H4WcNt0Pd5O/F9XtrVNy8tzuxNL+/seYAXPyasBVkGYc8aCbk2MWiKgakXtS6TZvyuV5zdk56TFi7LietUvZ2AZklHkxCE3MVMgwViJGFwdU5U8gDvAdwnZ5cl0/Pj4rntuYcAuHIfQc82jH4uc1o5K8dxt995N4by6QTT6DqB0QVOs19/AljjmQIjKEABZglA8zn1r395PBJqjoSa3eUxX2VtNNwSi7T2duf6e/lDDv5eXc2YSKixONevXLFaGJB1YNjjDA+gNQ0mnb0wGGxxu+oC/tFkHhvwt7773kfU9FkhgzUMxjps1YC21MgrH1z3aCgY8/uioUB1TVWTtzLsKvdtfgOzCKolj2usQy8C6FCg2hwBHQyMI/OYYLDl7+ufIW3A7Y0GDCnsHoCmw5ceW78x4K8xW3AEg0233X4/jfUeCUBTKLzo/CXBcNTpcgdCkVh1zRNP/sPcJHrvOmvS9ECwNhBoLuo5Nuwf8+83d5IzJ0bRlEGj079qmEeXCjrabed4TOT40MOPjx7ztUi0zueP+vzhaKy23FX53n+2Db0Qigq8AF875Lv+QI2nMup0BoOhhmCoLhiqa2gc9/w/XycjtyCPXy/4vFBW4I9/vNvrjYXC9WR7v89f5fNXVXgigWD1N771vXe2FID10GORJQUuP8JatpgpwBRgCjAFmAJMAaYAU4ApwBRgCjAFPq8Cr7zyCsWGDoeDAmj6Onv2bPJDW6X+Cp/3MGz/A0iBYQC0qqgbHnvcirn3StP6Jx5PpVJ44sh7NRUgQTL+XdMtzksqbXl1VV/qWYAuYnlB6LMiEINlCQmwSoafI4MmGBpfZdBo1sF/ASzu7puTFs7pyy9PyXen81tokDJVWYcCyCm+pVHPpB5dBi0L6gcAd0mwqINfEIeLc/CQAgXnDQ0nBNA02WCRiCM0knVC0ZGh3y+ll/V0tGWV2VlYA3Bde4ZzBtD42WLhLJzLVUlgtOXqa68rAegC2mEA+gD6V2CnMowCZABCIU4YV/M53e+tiYSaOa4i4GuIhJor3dW33XL//LYLfJXV0XBTkT4jhpZEyGc1WQJJHBQXaz7SCABah7lzl0UiLR5PXcDfWgSmrTfefDvdOZ3NmAGruUYsF2vVVFi18pJQoLrc6a30hEKBWq8n6vdFr7n69/msIolaPkdS45n2pxHQoUB1wF8X8DURB+oxwcA40obWYLAlV6Tqyq6SEO4egJZJNPX99/0tHKxDAF1w4WiKRFp+t/ZPkqwT0wt6VvRJHC1ju3v70pMmz6iqbvH6Ij5/OBKr8gWCyXTWrA+9AHPmLvL5q8wAuipy8A2/u0fIgSqZADQ+8CukLqQ3PeNV0UCSYcnSizyV0UCw1lMZDYXrA8HqYKjm2utvoETepCVurGpw6m/OrvBE3BVhu8MXCNRXeGKxqmavN7bhyWexa0JGxNC9qNEzL8Bll13rD9TQIGgaDe3zV3m84Wisvqau5ZFHn6Q7mo9VLNPzLr5jf5kCTAGmAFOAKcAUYAowBZgCTAGmAFNgTyvwi1/8wiCGZgC9fft2eihZxtAlNjEFDAWGAdC6rt9/95/dHOemDNrKcXZrIpsWebTEoFMWYBvAXwRY0SHM74EVO6V/pMV+YtmMv/41DE9UNMzslwM9BzqBGypxr0D6rIKW0LVegGcALktIsztzkz5OzusVbxLhTeLUTHGJAVAKOEkDkDScdZVCZR2gE+OXkwv7k/PTsDoHjyjQQ6CZThgKtkPTSkPLCbdGlIMIHe04ntPh0nxuRl6ckoTJKTg7oy3pSXIVQc7q4Bwc5+Ds7nL6T7VixQpjYHqpQrKoqAr7yxQ48BQogU7qFHz2b2eEgw10joQaw8GGXxx/alW01Wb11tWMqayIlTuCfm/NDWtvU2X0hqYOGJ9Bl/WPP1XuCZdXVPmCzb7AaJ9/rC/Q+oMfHmmuCjOJ0pSociF7HvUDods8vemlX594WiRc6yoPEO5c5fVUxSLNJ/7q9NK/8GDGDrKsdnX2OR2VFED7fS1+36iAf6zfN8rrbznhfyaKxUOJGpobU3Nn8koDoil6HlrGJcNNJWD6/HMvYRZHPwHQ3ga/t8Hlikw4c6ok66KsJNNZhXj0ExMSrEyS9Wefe7Wx8RBvZaPTXuPzNpW7Av5gdNLkaUOjsxUN1j30mBlABwPjQr7RRx/5a1nE08BnddSzqPCUD5O10lttPIXxyXkRNj714q/+Z4LXW11XNzYSaamoqI5Gm73e6l/9z2/Mp2ZcDVmB1ZdfQx2fff6qurrRsarmMrs3Gmu89bY/011UDRk09Ymmr3T5lKlzq6pbyl0BTJwYqAmG6iiJpqYcK1deblzrTJond3S6X+l7w9wkVmYKMAWYAkyBT1TA8OLTNK0Qd0LGBpkjmCQc4oiTUVAVlY7j+cT62QZMAaYAU4ApwBRgCuzvCggCgkEj/Nlg0D6fj+O4yZMn7+8nyNr/xSkwDICWZfmq1Ze7Oa5AXq1csK5KohhJ0UHEhxjbAdbl4NoULOmSzu/SbuhVtvIaulIg20XLDZwVZEM86DwB0IYThgqQJ04dTwJcnhDOT6tTO3MXZOCyrtw/AeJF8w3DcKNAbRA1EQAtqhgUjWREaQfpSRBX9rZP6elexsPfNMCx2RoJvVZpEJ+qaBpG8xH3DBXjnkEiLhp5gFdl8aZEcl6GP1uCiRk4KwNnZ6ULevo4d5CzEADt5DgHcYDmuLVr15YAtF5Mz8UA9Bf32WQ172MKiAJaM9x5+wNOu89g0NFwUzTc5PfWVFbE/N4alzPkdkW+c+jhfA4ogDbFT+/e+Wx57313ZaimfiwB0K3IoIPNXl9k7rwFsqobefDwVkCMcWjt+ORJhs1vvDf57DmRUGNz40FeTzQUqK+siHk9VbXVo6dNnY8R0obf8RAArSp6f3/K5434vTV+b4PP2+Tztvi9Y7yeZq+/ad7CVfSORG9QJvqMdyUTjx5a3hWAFkV0Yn7jjTdtVjcB0DQOus7rrQ6F63d29NEbmyhpvCjTNIz/B4uXXnBRKNwYi431VY7yuEchKA/Ue32hnR090kB/apo18OP2ToxcLlpwBAM0reKo+XNXYuN0yGdQxSJbAFGFnKD1JzHk+4NtnefMWFhTOyYWa/X56rzeWr+/qaHh67HY6ON/jikmREIkeFFNpHK0tbyo33LrPV5fJBiqw+SHgZporDFW1ewP1FxzLYZL02tnAOhBBVGEU049i/pBIzcP1voDNf5ATVV1S03tqEik6TvfOfLpTS+hHxSvSSJ50Ig3ZBU/plR+egz2yhRgCjAFmAK7VIB+B+m6zvO8GSVLkoQDdHS0NjJy2VPu3N/fj25UZK0kSaIo0uWapqkKG3K7S7nZSqYAU4ApwBRgCuy3CtC+AQBMmjTJQM+0YLVaHQ7H1q279kvcb8+cNXxPKDAAQNO+o67r1157rY1DA3FMwFdm+elxP1OBEFxZzctiF8DDAMv7+PO6lfO7pRWd6b8ToIzt0aFAnymDRqKAdskqSTaYw4BodGPuBXgW4JKkMKszvoCXFwj8eTt3vlh08BiachBrNjlxyAQ+dQM8mU9ek87M2dm9oLf7VknbSkKwacwe9oCNUeQDCrIEMg/wH9BuTHQvSSbmZPRJOTgjj+HP5/Vkr9/WxTn9HFeGFiSYg7AwPfjggwMAtOnNnrgQrA6mwL6uAA1nTqeEaKQhHKwjM4ZC220+Sp8rK2KxSLPfW/OX+9fns4X/us92ViqAoKrH/PfxLl/UF2z0BVpxDjZ7gzUOt2/CWVNe3fy2EWZLTYQFXstnlT/fve6XJ5xaXzs2FKiPRZq9nmhVrLkq2up2RXyV1Sf+agKfQz65CwCNob45qa62hdoxUwDtqWyu8DQEQk233PVXekaihlCXjuogr4M8N3YXQGOIcXdXb011AzkucYL21tkdgWiscdp0hOZScQCTosL/3njb//vekaPHfN3vr3O7a4KBMZHQuIC/1VNZ9Ze/Pkr5bxGIY0sogAaAn/33r8wA2utuqomOr4qOPf3U6e9v6dBkUBS0Y1Z0EBSkz8m8dNMtd/7q16d5gzXeYE041ux0R+zOsMdb63LFGhq+9rOfnUTtm6ksRkw6AOTyanPrQVXVTcFQXYUnQq2cI5GGY4/9ZTan0PyEeQHTJ5bmYjS0Srw+ZAVOOXViIFjt80f9gapgqMbri3i84WCortwVqKpuiYTqF8xfmkkjvsdrSgF0Ie2tIUDRkOUzPwz5bB9ithdTgCnAFNh/FBBF0TxOVtf19vb2F1544a677lq0aNFJJ530k5/8ZP78+ZdddtnChQsvvPDCZcuWrVy5cuPGjZs2beru7jYHRFOQvf+cOmspU4ApwBRgCjAFmAK7oYAoiu3t7RxHiCFNO0heOY6bMGHCblTENv3qKTAAQMuyTAMf1j/xOEXPXBkC6DmLFmQEPpNB09VugBcALhfVGUlpVlw7ryf/+3jyTZJOENUzwp8JgCaezxh1TAG0QOw1+gHeRfoszc+pc0V5VqJvRabvAV38qBi0ZsQ+GwXDalUliDkjonvGZoAbkv1LksKC3ux1ifRzqoZxeioOJNdUUIgPyBAGrSogZwF2AKyTMssT3W05YVYGzuqTJyaFuYnsldv77n7nY87msXJlg1ywn3/+eRNzHlD86n1s2Bl/RRWgpO+M0882A+i6mjG+ymqPOxrw17mcoWN+egL+EBWIU05h/MJuyyXp6P9w+5/vC1U1IoBGFw4E0NHqMTa7317uD4RrfvCDo844Y8qi81bObVt8+m+mHPffJ4UC9V5Pld9bUxVtDQcbYpFmjnMG/DWRUH1lRWTa1DaRR0wp00EQxSDogsOPqY2yrI8edXAoUOv31lEA7a5odFfUB8PNTz//KrnN4HOuIn1GTyEyLsPMoHcPQANokoTjTI4/7pcBP54CcYKuczrD9fXj/f660aO/dc60BQsXrjz1N5NbW78eiTT5/XWRSEs02mq1BkOh1pqa8cFg0+9/fwvaLuvAi9QepBAJrJL8gaKkPfCXR80Amjhct9RWHRQOtAR8Dd/7zk/POmvuuYtWzZh9/oknn/nN7/44Vj/KXRnxhWp9odpKf1Uw0hiKNgVCDYFQQ339uDlzl8gypg1Eai9gZHYyXXTIBpgzd5HLHfD6IiR/YK3PX+Vyh0Lh+vWPP0VdrSkWL9FnveDFQUOh0xnEypms9LP/PsEfqPL5o4FgtdcXcbkDznJvuSuAjhz+moC/5msHH4pBeAxAmz7DrMgUYAowBT69AjTGub29/bbbblu4cOF3vvMdq9WcCAZ/YRbjMThjVXl5ucViKSdTQ0PD4Ycf/utf//ree++l8dSf/uhsS6YAU4ApwBRgCjAF9hcFdF0XBOHkk0/2er0m+Iz9BKvV2tHRYTh07S9nxNq5NxUYAKCNz8rzL75A0TN9vfzaqwERs9wH8CrA2mSqrT8/T4dzRK2tp+c5gA5QeWIShy4cpZliGeQCErFqBRVSGvwL4HcizI5LZyXFuSC39W7/m5b7t24M+y4QEyN6jXiTqgIoAmgyxkWiPtsA1vR3zuzZcU5v6tKM8qJGY6tlXROoKSyOxB4Q+KyrJM8Wj/hbfwDkVbm+37a3z8qJs7Lq1J50W2/iNgK1H3j2DY5z2zirnQRAO+1lHMfZbLa33357AHU2vdmbF4wdiynwZSmgEs4IAPfduy4Sqg8FaiOhRpcz5PVUhQL10XBTONhQFW19fD1mlhPy5IHS52urqMKPjzgmHGuuqKyr9DV5/S2Vvgac/XWV/hq/v8GYA74mTNyH6fvqPK6qaLglEmosdwTdrlBlRSQaaViyeGUBNJvDYQcYXJfaKonaYT/6Kc0H6PM2eT3NFe5Gp6Oq0l9DiXrx7mQmzoYFx9A7WGlJ6RjDlZKJ9NVXXR+LUsOQmoCvwe9vMmaCwpvoayg0OhgY1dT0Tacj2th4SCDQGAjU33X3X4sNKx2RLiEx33hrlBVobTnUU9Hk945xORtDvtEhX2vI32zMiKcDFPrX+4I4R6tHlTl90ZqWYKTeYq90uAIeX8wbrDn//FWSDLyoy/jArzTTM3v7nfc93qDHG/Z4wxWekM8fdbkDFZ7QhRddYYRy0y3NbR50jVQZJBHnHx92NA1/DoZqfP6ouyJY7vK53Hhxw8G6qljjjvYuHPOCE7PgGO6zxZYxBZgCTIEhCnR3dy9evPitt95at27dKaec4rQ7cOxfcbJarWbuzHGc3W4vLy93OBwcxzmdTgNJ04LVanW73RzHRaPRyZMn33fffQaJNmw9jMKQtrAFTAGmAFOAKcAUYArsHwp88MEHNht6BQwC0NOmYSIiNjEFdqHAAACdz5MYYkVd9/BDGAFts3BWfH321ZdEjBrGIOU7Ben8nvSk3uxZWWU6z68RMlvQ01lVCO2lVLbIoBEESKAKxJNZ0CEjY+jxdXFhqQTTstrUjDyt6+N7QP0IMF0hTugyNwidYFibgpUoecAY5xRAO8AjIiyK98/IJs7P5u4l3h0YdImjxgUynBtJxFAAnQP4AGAjwHn9XXMV4RxenCFIczLZeR0dN/PS6wA7AdqWXMxxDvtAAG2xWBKJhIk5DyjStrNXpsABrgD59wSAt996Pxys83ljVdHWupoxkVAjpc8NdePOOG0qjw7AIKKlxGefBBX9JkQVnn7+X95AXSgyqtLXVFV9SKWvicyIoX1o0EznJn9laQ54WwK+pnCgpSo6OuCvGtU67v77/zJ8U0YA0LKsnzlhciRUTyOgvZ5mT0WTx9Pw/37wU8NdmGDTPQagRVEsBKBt74yEaz3usK+y2ldZS1Mg+n3o7+zztuBcOcpXOSoSGu+paAoGRnkr6z2VVU3N4x9//BmMxB58/xxmyfr1z9fXfTPgH+v1NCN9HgZAN5Oo80YKoMucAac7Eoo2eHyxULSh3BNsHfu1x558WpJ1XlTTGZ7abhgMmjL6xUuWR6I1FEDT13KX75uHfh/jxwfGxZvbPAhA07eqDNmcctLJZwSC1eUun88fNRh0LNoYjTRUxRrxi4MB6OE/5WwpU4ApwBQoKUC7+pqmCYLwox/9yPgBSSGy0+6w22yInk0B0DabjUJnGtxEt7Tb7WYATW0fjSU2m83tdtfU1MyYMeOVV14xAlzMyQxLbWIlpgBTgCnAFGAKMAX2HwWmTp3qIJMZQNtstg8//DCbzbLv+v3nSn4JLR0AoI0O4rPPPmvjLGVktlgsm157qRPkD0B7UE5f1pNv69NOi2cmJhNL0n1/B62bYGOa348OpkaSgnHQqgJqFmeQdEgDvANwY490uQQzU/K0jLwkJ/2hp+c9gqfx1CnaIQBFIRkHi0PkKSWSZFCShD4/BLCsu29aV+/iHH+HLr9BqLQOwAO61CJxwapILNzAIOh+gMc0WNEVX6zCmWn+bFmZLGTP4/tuyCU+AugjHHzR8kssnL2Ms1ACb7FytjJLQ0MD4vERpi/hurFDMgW+JAUkER8UjR93KI2Abm482OOO1tWMcdoDfm/NW5u35rN7oGWCig7POVERFPjfm+/0BRtrar/h9SOGNmZzRLC/sgVnzyg6B7xjfBWt7vLqiRPPSiYxg1/p/vIpWqcqcOWa66ORBr+3hkZA+7wt0cjYtgXLFMOwGO8tajEJ4TCc18xVjfKnODhcdeXvyp1+YiHSigDaO4bOFD37Ksf4PAe5nM3BwDiPB2PAzzhjyo6dvTQzoXGgXRRUFVZf9ke3qykYGGOiz400CJpEQA8A0NHqUaFok7Mi5AvVhmJ1M+bM29bewcuYDjGTKxhuUMsjyqCpHceYcV8rc7jNALqquunyK64bqoC5qcMCaPINgwovWbqipq7J5w/T2V0RjITqA/6apUtWybLOAPRQbdkSpgBTgCkwrAKpVOrb3/62y+WiHNlqtTqdTpfDWUb8NRA+lyw3MCWKCUcXIDP13zCIs1EwULXL4cR46jKLu6L8hF/+/K9/e6BwMyeJxIdtFVvIFGAKMAWYAkwBpsA+rsDWrVvpd315ebnVNM2aNcucEGIfPwvWvC9LgQEAGkMORYxFzqbSZZzFwVnKOYuNs+QJ9t0A4pr+znM75LlpmKTA9Hzy+mzfuwBJ4gBKATQFxzQQDXMPgpoDOQmQBNgOcFtGuzinz0mK89LiBfHMrXnxA4AdAjHV0IuReyYArWDsM84adlox/PljgKcBViTiU3d0zu9MX9GdfhnDlvU8AdZo9EFSUREahBBc11UVVBV0gbhUbwW4sl86Nw+TEupvU+IZifj03h1r+d5XAeIk3DKvw+FH/5fFgmdtsXI0AMRq444//nhVUUfgz8W40C/rGrLjMgX2lgKaCqKAH/hjjzmhtrqVGCA0uF2RUKA+HGxYfsHqPdgQ4rUDeREPd/udDwbDrU5XbTH8GTH0QABNI6ARQ1dFDg77x5zy6+kbN7wsy3I2lyRWwoniLYYCz+Fbiv/jGsbS/vWvD0cjdQigfXXeynq/v6mu7qAb/3iXRAF04cnWHgPQ+XxeFEVV0anPyfx559dWt4YDTYMjoEn4s69yTDAwzu1qGDfu+1esuYECX3o+Zpg7UlmS8J74179sCvip+UZjyG/MzYMtOEK1wUi9xxfzhaqP/+VJT2x8Jp7GEHdR02UVb60AIKvqIADd0dUXilS7KnzUf4Ni6ECwesfOXjrGxay+uZ1Y33AzdYtWNHh0/YYfH36UwaBj0fozJ0zVNdyrCKDJ6JfCEwHzcViZKcAUYAowBUDTtFQqNX78eI7j6A9I6rOBBhrOcpp+20Y86Ggebp+n7JCDxh112BEL2uadf/75y5YtW7JkyapVq1avXr1q1aqVK1e2tbUdddRRPp9vkF8Hx3HucofdXiDZFis3ftzYZUuXsmvAFGAKMAWYAkwBpsD+q8DUqVPpU2e73U7TQlAKvXPnzv33pFjL95oCXOnXvgaarGMGP1lXRMVqLXNYrG7OWmYp+yCXexNg+ccfndvPz+6AGXGYmJfm5fqfJEQ4TUZUK+iAUZgVQBsMSoE10JKgfwBwezZ/Xl/8nHh8ajJxQSLxcC7/H1XtBj1D8goOHNiOuyq4XCezKoOekdVegKcAVsazC/L6kjxcsV3cJEIXCVs28LXBvmkIto6D+EWV8OUPAG5Lw/lJmJyEiQltcn+qrbfjfzPdHwD0a0LR3haol43NQuizlbOXo8ndypUr2VCCvfahZAfaZxVA0kem2bMWhgLV3spwMRth3c+O/SWuISiwcFcpbPsZ/xhcEgErD2++9eGCBStCIeJQTJw3/P4mj6fO46mjTtCBQGMo3BiNNU44c+rGp178bEc1ThB0+NEPf1JXM8pbGfZ5I6FI9fd+cFiOl0VJw3EexaEVRiOLwgw6LF0/aOEu3xafZ1168dXjxhxaExtXFTkoFh4bDWG0cjQ0KhJs9XpqDj7oezesva0QbD6CkcjwhyEbI2RXoKcrPWfuklistcITC4Ya7I6A11vr9zd4Kqs8lVX+QE2lv8rh9sWq6k4747fPPv+SUaH5rGm5IEgxPPyFl172eIPRWG1NXZPHG6zwhIKhmoXnXkDzCg7yWTKqHVwYcl7GcR9+9O8XLL9w3vxFd9/1AN0LTaDokBnynHBwVew9U4ApwBRgCgBQ/42TTjrJCFgeWrBxnIPjvjW++YkH7/znk+tSPR+jcpJK7fVGCsWgy1955ZUzzjgD0XZZwaCDRnJYrJzVhjya47gjDz/ijVdfM8yg8/k8jfBg14cpwBRgCjAFmAJMgX1ZAZ7n33//faPnYLFYXC4XfXvWWWfJMlposokpsGsFTACa/NqnDLpzR6fVWlZmKXNjKsuyhza/ffP2joW98bkinNMHM/pgZkpcI+U2E9uKHHpoYIgxDUCmLhxogqEQGgXQD3B3Nrky1T8jnZyajs/PJtZm4u9rakaR87puYGu5OEieohzKoElINQY49wI8KcIlvdm2BH+uBAt3ZB4XoJPAa3KGGs09RV6xG0wBNGiiCrJITKLvTsKqPjgnDqcnYIOKZRgAACAASURBVGK/PL8/fV1/z5skuSKOz1clAHjrnX9bbOh8hz3mwmxxVbhvvPHGXevI1jIFvmoKTJk8s9zp9fuiVbHGcWO+/tbm91ABCg2HoMORxDGQ4rAAl9Js6hosSiBK8NbbW++8828TJ87+xjcOO/TQw2pqx9TUjjn00MOOO/6kpRdcsunp5xMpjM/FbHuqjo/BzPMwjRj2sGQ7HTY88XRdbUsgEK2qqjnmZ8dueub/Rl/gZNBnmtnPOAW6duArXTlw2ad7J0sIuW+75f5LLrxuwunTf3LEzyecPv2M06ZeecXa11/7N64dse0jrsAjFwE36IUaPty285Zb7zlz4rTvfPfw5paDa2pHtbZ+7aifHv+To342Z955Dz76GNWTxiAbJzuoYAbQAPBx+06vL1Rd2+j1hQKhWChS6w9UbfuoE4fX5BRZKcQnf4I6Qz5FxvaSMtBHmoY/MwD96T5abCumAFPgq6ZAf3+/KIqCIGiaRgGx8evRKNjtdg9JIeiwWBfMnpno/gggCxJ1pyPfHCodWbgrBI3jjTIZkRfWP/roxAmnez0VVhtnt9NYas7jLnc57dTNY9KkSe3t7QDA87wkSSzI46v2mWTnyxRgCjAFmAL7owITJkwweg5GwW63v/XWW/vj6bA2730FBgJoABVjHOBfL/6rzFLm4MqcnJUrK/vdY4/fsGPn7GTy1/3pSRmY3QcX9mb+DrCVwOU0QA4BNOYbRPKrEiosYWSyqmGE8nMAy3raZ6Z6pueT89Lxq9LxjaB0AOT1UtA0xdByiVqXpNBI/PIzAJf0pqdv71yQzC5LZ25M81uxa0xxipk+Y+ZD6ryBQ7JlVdWRUz8DsLIjPadPnhiHM+L6jKR0rag/p2DyQ0JrdEFAM9PVay5zuhxWG0ZqUA/scjJt3bqVdY5Ll4SVmALE6+b662742sHfPPKIo996c0s+h49w9uxkAEejWvMSXgBZwZknNh3GNgCQ40WRWAMNANAGey1tOjKr1UGWIJnIv/jCKzt2dBh2E8l0ltpNDMXQpVpLJXN7S0s/sTQILusqNgbZtwzUgxvLCojEvugTa9vFBrIK2bwkySiNEZ5Mt5dV4GWNPkaUFFlSZIXcBA3J6LnR10EAOpnOHnPscXZnBY2DtjsrFy9ZqRH63B/PmXc0ahumkSMAaOL4AbxYeMYuCqqmEv8NBqCHEZEtYgowBZgCIAhCPp9PJBKTJ08elDzQ/OuR47hjj/mvfzyxQRZzABKv9APkRTkFioAiamhRtSv8rOuCIBRDm3Ua13zfPfefM3l6c0Mrx3H00E5nITja7XavXr1aELDyVCrFrhNTgCnAFGAKMAWYAvumAvTL+uOPPy4vLzd6DkZq4l//+tfFb/99s/msVfuQAsMD6PWPrLdxtjKcLZzVNvOiy/+ek6/QYKYEUzJwbp98e1x8E82XMbq5CKBlxLmaCoqOWFfEiOg0wEsAV/V2L+azM/hUWz55cSZ+b6ZvB2HKNGjaiIA2GHQBSRD6oABQ6+fV3Rj73JbOLujuWv3RR+8DJAAygogxkoQ4m19VhDM4JhtUhNTYhp7EsowyK6ue1c/PSkhXSbABoIdEbQMA6ZlnAODEk090V7rNANpqtTY2NmazeyKx2j503VlTmAKfS4FMBgONJUmijsmfq66RdzYioInRMIgSJr4TZUVWickPQF5Q8iX7nEJFOHhCK2yAi8xB0IMZ9MiAWEeTikETvTV94QDa3EhTmRJnCe95e3j6v/x+MolwJgX6TI5oSI6jjJAwysyRzQCaDoJ5Y/O/f3z4UVU1DbGquobG0V096MRNJ/OOI56M+aoN3BFZeTaj6thmPo8YunC7ZwC6KBT7yxRgCjAFzArwPJ9IJA4++GCn0zksgHY4HOPHj7/vvvuEPI9f7rIga0JezkkYKIK3Y01RNU37RABNOwZa4dklZgvQSE+7J6vdfNf9To/H/KuV4ziXy+V0OhcsWDAUQGNEC5uYAkwBpgBTgCnAFNhnFDjllFMG9SIcDofFYnn99ddZsOY+c5X29YYMBtDUgmPTxqdtnI0waEsZZzvlpEk7dAxkXqPAwqS8OiW+A7BDQwScAC2DjFiTgNchB6pocIscwHsAN/RlF8fTs5LZ2enMRfnsn1X+feIKjcEV6N2Bs4lBazJmHSSTDhkROfaHAH/amV3QkZ2eEOdlU5cnerYCpAAEXZU1SdOK6a80xWDQKqg8KAldSRKX6qt39F0saItlmJUR5mX4a2XYRJanigCa9rYlWfD5K/FJDomALrxarRMmTNjXLyNrH1Ngryug64Zz+944tplamnHnyAiZtMrMMWl5QGNH3nvkX77m+K8BlZkNLgav+FLem89uEOktrKJ/hr7ubnOH1kCXbHrquTVXXPPnewpOzYVqi1bRBb8m88HM14tWYbpqdEEp9pw4b2j4vFFXFRKaRxn0oHM118/KTAGmAFPgq6EA8mLCcAVByGazP/jBD8zw1+Px2GzojFFZWenxeK666ipd1yVJ4nkE0KWJ8GM6nnC3flvS23AGYAdAB8BHJFplWyJ+0hmnmptBy3a73e12P/LII+SBoqoqqiRJLJaqdBVYiSnAFGAKMAWYAl+qAoIgbN++nT45tpgmq9X685//nP46/lIbyA6+3ygwGEDTJISbNj5t5azUA9nGWb8z7ocZHf4BcEVCXZXI3aVCO0ASIANaFpQ8AA+KAhnE0WoOZJXmmHoH4Jbu9PLe7Ny40JaQlyXFOzT9NdxIliAngErpswlAaxKUALRCoqTfAbgnDSt2pJfyMLMzfWFf7wZQ4wCaoqqqNBKAVkBN60Ia4G2AO9PS4q5kW0qalRBmdvT/TtI2EPrMY7PRp9qYXnjheY7jPJ5CBDQF0BzHrV27llmqGyqxwldegWKCUQTQxKS94OhrIoWfWqORwOXIyzUNzHPh2CMe0Aw0h2kgPc6Iew+7Yr8F0AaXLak7UEwMdf4sihT3MnYfsRJiPK2T+HRKn6m1dEln8/WitZiuGl1QAtCgU/ONARYchEGXKmQlpgBTgCnwlVQglUrRlINbtmw59NBDKeql2eopeqZLzpk8RVPUTAZHAWLKX1HQyVd7HqBfhF4eUio65gmqOtJomGHV1chPgwTAZoBHVLj2/Y51Pek0qfm5F/4ZiUTMGNpqtdKIqhkzZtA200hqozzsIdhCpgBTgCnAFGAKMAX2mgJnnnkmx3E2m83Eny12u339+vWqooqiuKvfyHutlexA+7wCuwDQmISPs2BAsIPzdvCwdnvmsoS0pjfxHKCrMgl8VkRQRLRyVnSMh+4FJQMa+on+B+AuPn/ezs65/VJbP2b/uzUHr5EdBQxfjgsg8qDTmURAI32WQJFxODVCkDzA+wC39igLe7Jzc8pyFS7tzjzWm0mQ2GdNUxSNBlvrOBxfVzVTBLSCIFz9APQ7VGlRIt2WhxkJZX5cvrxPfJ6EY2SIR4hCBhYarGTVhSscjjI8aZKt2wDQ27Zto643+/zVZA1kCnyhChh0EF0udKCe7ZRB03+mApv+9I2g/32f7tXMnel/v2Lw009/xIFbGv/9AxeP+A6334tfrrsQZsQmjrBiUFWFq0ZuooaYn13PQbXTt5iwSgVZ1tEOidip4PBtMhv0eTCANlqPEejmWnFFoVrMzliYGYA2BGMFpgBTgClgKKDrOo2A3rx5c0tLi8vlcjgcFPLSstVqPfzHh73/7rsYE6Io6WQiny8waI041L2oKA9lc+vSyTdJOEhKEIxnmMZRdlFQAdK6sBXgPoBVeenc7sSajp53QRFBz4kCz/NHH320zWaz2+2UiVMe7fF4WltbN2/eTGO3aRw08+LYhc5sFVOAKcAUYAowBfaCAtu2bTOeHJsB9JFHHkmPLsvyXvyNvBfOmB3ii1JgMIAGDfMQkgho8hmzIo61Wzy3P/TUuqR05bb2e3r725E0IyAWQSH+F6Bi5sEMGmOovETW3pfNn9/Xs1jVZqf4ZUn59hy8Qnq0OUBbZhWSPIg50HOEFAsEPRP6jN6tMsku2AGwLguLP47/tjc1W5AvTuTWZaQdJBMXoc+aooKCB0YArQKOv6YZCRWQs6B2AdyX7js/2TdDEqdm5Old2TW94hMSonOFZEkUsSU4Ud4NAAcdNJbjOJodxWLlbGUWq40bM2aMruuDxyR+UZeD1csU2JcV2PsA2gydzWUzM0VsSuDkZ5Bud3fE7ffilyttnvnVHHK+W+drrsQoD5JxDwNoSit0DZMlGuj50wJoPDmjnQXuQd8b9FllEdC79RFgGzMFmAJfMQXuuuuu/0v0Z+QLcjgcNHapqqrq4Ycfxm8zSQZJ0niePFGmd10c4PiaDn/i85f091zd1/5P0qtPipgpwPj6Gygk/XYecMvOkz7/45q8Ki/ME9QFWfWKnPIswL8Fnva9AeDSSy91u92Gm6S1zGYtQ1cQj8970003gYbPISVpz+c3Hth49o4pwBRgCjAFmAJMgU9QYOrUqRRAm+mzxWLZuHGj4dBldBLYk+NPUPOrvXoIgMaETuqWLVssFovL5cJwYKetzFE+dW5bH+lNxglp5olTM2JfjLKgEmI4pK5hWsL1Oizvz0zuy8wDmNr1/lqx5y3CElTCDyRQsiBmQSWznAM5jwm2sResEUsMhfg+r1NgeXfmrI+6JvYkF/XEH83ktktqnqQXw/DL4kzpM9asE6KsAw/iNpD/rKRXZBIz8vzZeXFKPL2qJ/2PlJoje9HRhdS/ljY9x/PPPve0xco5ymw2DPrG6G9Hmc1pL1u+fLnxCRlkxCGRCTNi4bBC1ks2dGKFA1sBiqHNcNAA0yMbJxckoXuV9DHXMlx50M9aM4MebnPj96/RotKhBpVG2n3QZsZbo0YjypvWYGywdwrDNvvTH9rYne4yQE8STv7ZWf4nNILen5EZk2hosrXRGqMwFDoXGjpwhbH9IK6Nb8lUbAzd0HztimvYX6YAU4ApcGApQFmtETDxhz/8obKykuJd+nOR4ziv13vJJZekUqlSh1ZDrqyhk54MIAk080oaZnUm5/XHr+lsf1rI9wPwJPcvvcEarzQERANBBUklffC8iJrqJE/4JoD52zundCfastpqAW4FuDoPv/uo+710zsjsvXHjxpIdh9POOW1k9CVXXl4+c+o0en1kWRZFrJdFVx1YH1h2NkwBpgBTgCmwTyugKipFyf39/UZHwmKxWK3W8vJyq9V67LHHGl2CQYV9+sRY475UBQYAaEVUED8AZLNZjuPKnOhHgZPDMv4bByugUnRAftOjWyh+zopDqrFrSIyhX9fh0u7U7BT/2zQ/Od59hdD+JCR66UkSbCxgKhI9jQBazqERhyhhKDONxcPDdwI8pMBF8czM/tSknkRbPHtNb+I/qi7pIOmahLafGLxcnAttwPcEQ7eD/A/gKX2elBOnpvjze5IPatBXiJAePlPY3LmzOY6zU/xMALTTanHayzZs2EDbbjzbAQDaFTZfOPNa83JWZgoccApQnGcwQPrwhy78xHOle5U2M9cyXHkQgAbDc6Pw2KtQ03C7GjC6VCgddwSeObBW8+b4g9qYzYcbsNHeemNuwC7aPLQ5dMfScrOe5kpLW+zBEjkAA9B7UFFWFVOAKcAUMCvA87yqqIlE4rzzznO73eFwmPbiqcnyMccc097ebt4ey7oO2IXVZNBEULcD3JuF5T0wqR+9754E2E5GJeZIN10rTvR3ZnEMYglAA0mvkgJ4FjASZYkKcxLyxSrcBrCsQ1oeh8s/in8gqoavna7r77777qhRo7CdaPxHrf9oq7nfnHKKubX0l7DxE9e8ipWZAkwBpgBTgCnAFPgiFJBl+fTTTx8EoOn39DPPPGN8KQ8qfBEtYXUeGAqUALSuoPkGBdAAQD9VDo/d4rRwDgtn4za/86YJQOOGJR9PDIiW+0HbAnBTrzi3MzUlmZmW678g1b4J+J2Akcs44T4gEecNSp8FEFUE12QMPSl1Ajwhqpf2p9qSmWnxzMIUf3Uyvz6v9AEQAI2vFD2XuIsptq4b4J8AqzO98zL81Iw6NSmuyikPKbCN8HEdGbpaBNGlaE1R5KMx7KYX+TNXxuFcV1NtpOE2okVEUXzwwQfXrFnzMJnWrFmzbt06+nSIYegD47+CncUXoIAZb5bKpdJgJDw0OHcwjB7YSFqTMTTCKIx8hBKYHmkbgzgPKgy7/cDmjPhu2H1LN7MR9xu8Ymg9g7cY7j3dq7RmaC2Dtyht+7lLQ6omC0a60KWMiCM1Eh99FJ+Algqk+2P6NBnu5PQimiv73GfEKmAKMAWYAvuYAo8++mhjYyPtw9vJ5Ha7/X7/+vXrdV2naf0kWVBVqfhUlZyABiJAB8AGkC/qTM3aKUzulq4jqbwzBEDHVRx6OOjnJR0DKaPbv6ajMz9W1a1hP/zKfLYtJ8xMyee2524HWJ6Qr1NhdUf+z535bh1jmWmHmed5TdMSicS3v/1tl8NJKXS5BY04nE58O/0cjIM2wj7MDdjHhGfNYQowBZgCTAGmwAGlQCaTEQRM24BPh02Tw+Gw2WxHH300z/Pm72Vz+YASgp3MHlWgBKBpx5FWLgjCDw/7gaWM4+wYkmArL+PKuGt/fx0Jgi5hGwNAKwBpTfoQ4BGAOVu7zlNhSn/vBan2hyDbRUKV0aaD0Gf0mAZdQutnmaf0WSO9WhK/nAT4B69f3Z1YkMjME9T5WeHyrHhfMvsR8f0QNRoEPRBA0wHxhJz3gPYGwO0AZ7e3T0vr0/v1izLwZwl2APSBxgNPzo4CaIQRPJ8j/Vr03yiEW5hiL8o4bt6smVQQXdcpgKb02WJBnw4nmeiOlZWVp59++muvvbZHrw6rjClwwChAbwGUC5cgYKlkQoZkIeWShYERwwbqDpTGXL9Bn6nB+8gHKd3Mht1mEHc23g678aeEyJ9nX/MZD63HvHakMt2rtHZoLYO3KG37uUtDqjZd1mEx9Cdcnk8BoOknwbhwX659yucWkFXAFGAKMAVGViCVSs2ejYP5aB+VJvez2WwTJkzo7S0MRAQAyqAz+bRMop7p16RKhjC+AnADn17UnZ7RI01PwCV5eKGYviWh7AJAk5TEuqSRUI9OgBtEaXYyPSuvtGW161W4uFtc3JFY9P72e/vVbQRna5qmKqqqqKIoSpKUSCSyqfQvj/u5x+50cJzLarfbkEFzHFdR7lq1ahUJ1MZ+OPtxO/L1Z2uYAkwBpgBTgCmwJxWgw5WWL19OHwnT72X6arPZXnzxRZru2PzVbJT3ZDtYXQeWAgMBNAleoMG8E8+eiBHBDmLHZkUMXd9YRwLOSlDAANB5HXIAL+iY6npqXjozHl+a6X8Mcj0EKoGE1st6iQVh2kABZAFI2AQJgAaALgXeBriuM3deV3Z2XGpLKZfm1D9L2rukW5zXdQqgjfDnUgAzuSQZgHcB7gF5TqLvtJ74QhUW98KdffrbSJ8hB6oCOR1yxGa6wCNEkQfQ8/nM6af/pszKlVk5Gwl8pqMAva7yV158ocDlNZ2mQ9E0bfXq1U6n02q1Op1Omr/barXaitM3v/nNq6++mud5SZJ24b++i1UH1geMnQ1TgCowPOocfineN4YlkgOiYgcqO3JNpTvW7m5jBpcjlc11DmzRrt6Z96LlXW093LrPVsPgYw2tZfAWwx17zy0bSVW6/PMcx3xm5qOYl3+e+tm+TAGmAFNgn1CAYtmtW7cecsghdrvd5XLZbDZjqOyUKVPMrcSYZQ2jlVWQZcy/ouVJhEc/wBsAN8q5Rcm+WZ3JhXk4h4eZHf13dnTuJD35PA3hMNdFyvSWKoHOa2KfIrYDPCwqS7Pi9Lx6Hg/LRFic0Rd0xi/ujj+QV7cSgw6Z/JagDNr4pYrpviVx3MHjObvNZreXWa0Oi7XMipPFYlm3bh09MrUAMe81pEVsAVOAKcAUYAowBZgCe0ABWZbz+Xxzc7MZPdPycccdRwczFa258C/7dt4Don8FqhgCoItY9+prr8IwijKcOSvndDmsdstLr7xo/vlOAbSiQQLgVRn+0M/PyuR/m84sSCTu0aUdVD6F5NYmAc44ShrN5lQdZAlETHii6iTvIPQCbAH43cfJpR1iWy8s6IcVCbhDglcA4qDLmiBqKjXfKAZSI1UyJpo1ZR3Askz/b+PxifHcgoR2cx42U+s6AAmjrXkVRA3NpgtsC73q+NyOHdvR8JoAaAexG3HZy8o47rvf+mait6fk+6oX0gxu2bKltbUVDaPtdiOleJE/Y8iGzWbzeDzTp0/HJOMkqSMdPyiKokwmVVGNf1HjFFiBKXBAK2C+c5TKpdLwEdBDMXQJJw+Ua+SaSnvs7jZmcDlS2VznwBbt6p15L1re1dbDrftsNQw+1tBaBm8x3LH33LKRVKXLP89xzGdmPop5+eepn+3LFGAKMAX2CQVkWX799dcPOuggGhLhdruNH4pnn322ke6PtpUAaIUCaAkTsahpEuP8BsBdWf78ZN/UZGKeCPMUmCLCrB2967PZHrInBmwMN5EetSqAmtCVraA/IgpXJNIz+3JTUtpiGRZlYXZPenFn772CuoXGPhP7PvNvVFpWQJcBekGMfvsgzuMos1pdXAFA22y2WCyWTqdFUWQAeriLwJYxBZgCTAGmAFPgC1Fg+fLlRqfCKFit1kceeUSSJEEQGID+QnQ/oCsdEUC/vvk1qx2NJqx2C81GaHPYTj3ttCKewL+YfkQHWdW3afD7PmFhXJoSTy7o67s/L2ylsc8k9JkEQBcNoxFBY+SFQv03sBsMaYAPAK7rzpzbkW7rhYW9cHEv3JpG+twBIEBe05KKjim2zfCg2BJdAjTZeELQL8kJMzK5SZnswox0QxpeBNgJkEeXOxl0WUEMTVMVFqrBYwMsPHf+IABd4XRUOB3XX30VXnoTu6C5xQVB6Ovru++++4466ij6f2jQZxvGbdjpQloYPXr0ZZdd9uGHHxqfIkEQzD1vYzkrMAUOaAWG/u/ikuGX4n/6UPRMl5RuAgPlGrmm0h67u43pn998IxhQNtc5sEW7emfei5Z3tfVw6z5bDYOPNbSWwVsMd+w9t2zXCn+e45jPzHwU8/LPUz/blynAFGAKfPkK6Lr+8ssvh8Nhm83mcrncbreNmFc4nc4TTzyxkMWkEFmia8SpWdMogFYVTAMuJwE+Arg9n1sa75uWSJzN8zMApsgwjYdLUgVqLAKIxUqK52x8VygAAg/iTpJ48OJkamZ/ak4Pf24eZoowpV9Y1Jm6LaO9h+nH0QhPxn64uRdcKAugx0ln/p6db3KtUavV6uWsZZYyi63MWoa97Llz59LwbaUYY1VsCf41WmNeyMpMAaYAU4ApwBRgCnxmBVKplNvtpr5eBn3mOO7www+ndYqiOMw3Oln0mQ/KdjzgFRgRQKug2suRpaILB8e5K90c4miu2MlTNZAUkPOg9YP6ZC67uD8/JSHO7U//Lp7+two5RLuIb2XS4ywxaLTiUFVMdpIjCbfRu6Md4I/9wpLezMK8Pi8BK+JIn59XkD5nAGQ9q0FaBdkIeTbyTimgCyB1gLyRl6/oTLTl5WkSnJfXrsvpL5GYjhRAUuKxFZqKfeQigNY0NAQRRT6VStTV1QwC0E6rpbLcmeojlnkmdmHOMUi79Vu2bJk7d64BoIf+fxpmfKeffvpdd92VTCYH/Zce8J8wdoJMAaKAGfyVyqVS8QdkcQkD0Lv+4BR1KuH1XW9P19K9SlsOrWXwFqVtv4iS6fY6AOvT5Z/niOYzMx/FvPzz1M/2ZQowBZgCX74CN910E3bR3W7qBWf8Ppw4cSK1esP0fYUbKgJojP/QpWIgCJ8DuQfgLYDl/T3TEokpOXGqDBP4/Jnx5NK8/iBAinSbJQKOydkWbqcyKLJpQGGCpCu8ISXNyYpnZZX5WbgU4Oxkcma8/+a88jr2+PG7SiAzJjMkAyIVTZNV7JzzxCvvA4B7sl2r298454GbOWeZk6M+HA5rmcNutwe8vnw2q2maQvriCmAIiTkw5cu/GKwFTAGmAFOAKcAUOIAUWLFixVD3Z47jNmzYQLOj0QwNg+gWfXsAycBOZQ8rwI1Un6ZpEyZM4Ij7M2e1FGfbrJltJCxYxkwmkN4J6ddAubjz/XmCOKk3fUVceJn0IxWExBLoIg2UJhbQOn0V0I5ZxF6olEYTDIAHAM6PZ+cmcF7Q03tpR+/6jNJDButJOogg8ZCXMGyC+GeoSKZIx1cWQc0AvAjK2lzu3Kx4Rk6cklVXd0n/Bugiu2d0VcCAa5VkPsQIaADALq+M7QeASy66mPbXbZzFPM+YNp1ugB33T5p0XX/ggQdOPPFEmpnQ4XAYuV+cTqfFYrFarS6Xi+O4cDjc1ta2detWWZYLkSmfVDlbzxQ4gBTYXbz52bZnkHGvfGR2lxLv7vZ74CR29/OzBw7JqmAKMAWYAntBAU3TXn75ZWKSXHjBMYtWq8fj+d73vme2qigCaOw8KzgAUVaJKx2AlgP9XyD9rqenLZWalBMn5eRpgnJaR+d5qdQ6EhktFs5EJn55NJcLZnXJYvdbUUhoSB7gTQWuj+vTOnKTRTgtD1MlmCVkF0jtVwnb3wLop6MJNeyE5wnLxqZgVLXEa2KehKH8G+AWFZb0xFf2fXxD74e+H32Xs9s4h8taVm4vc9KO+u+vvR5/eoiCSkB2nrwW88jsBcnZIZgCTAGmAFOAKXDgK0CNNTo6OlpaWowH29R+luO4o48+2iyBmT6bl7MyU2AkBUYE0ADwwgsv4GfOwhXps4Wz2so9/owgikpeAikH6ocAv8/umNO5dWE2e3FeXa+hG0YefZ5B0RUaZ4GmGxiqUJglLMggZYH0Sp/RYbUC0zLi9JQwP568qHvng3L+A4C4ij1lXQEelDyJti5gZwWZgkzCp/tI1/mWTPL8bGZqXpgqyOf3C/9E22iMthBUWcTA5wL4LhQ0jZdEhV+CigAAIABJREFUY1iiv9LrdpY7yuxm+sxxXFdHh5DnddWIuh5JwNJyVVG3b99+0003jR8/nv6vulwuSp9pHHR5ebkREH3kkUdeeeWVW7ZswZGDJBs4S0tYkpKVDlgFdhcIfrbt6V67u+8BK/oXdWK7C5R3d/s90G72GdgDIrIqmAJMgX1NAU3Tenp6fD7fIABts9mqqqqSyeSwAJpEhNCYDFlCDA0fgPzH3q5z23fOSItn5/QpWXV2SlzUE79bw7TeucJp09jlPPGxw14xAdB6BscgqkmALTrcE4dzO+QzOqWJGZgFcI6oTOn++Dplx8sgbkfmTGKVVdxRoG54OgJoFTAaZQeJnr4unp/Xyy+WYFFv1580vu2Rv3CVGLfhcrnsNpujzO6wWH/43e/RPjNpA+JsRp/3tU8maw9TgCnAFGAK7NcKGJ7Oa9asMdNno/zUU0+ZT5ABaLMarPxpFNgVgNZ1/WvfONjlKS8B6DK04VjzxxtyuryDz+wA2ACwsHPnjI6dV6fFjQDbicubomKvUNE0ERQJ450RPRc6m3S8HHlNA/xDgcvjypyUNjmtnZOSliWy92Uy71PXDpH0UhUQSB8XVBlTdqskakLDbmuK9Fn/mE4tT6WmZTPnpJIXpvN/E9FmLocJB3WDPhvsW1ZVScHQY0mSUqnUlVfg/1WZ1WqmzzbOMumss7GPi6fxqSbqDW1ENKuK+sYbb8yaNSsWixn/qzQmmqaIMZ4gOZ3OE0444d5772X0+VMJzTba7xXYXSD42bane+3uvvu9uHv7BHYXKO/u9nvgfNhnYA+IyKpgCjAF9jUFUqnUcccdZ6bPtJMZiUS2bt1qDIkt9Jix/10sqsiPQcXRh+0AD8QTS3Z2Te/JzEzCjCTMSOmL+vg7eczgHSc5UMiJayR2maBjTNyAEdUYvwyYgfxN0G+VtAsS0uwOcWaPPiMDs/KwMJ1bk+r/JwhpgBQyZwBdxxkjQtCIAwchalhRQoOtANcm8gvTuRmZ3LRE6mqAyxPZy7Z+MPqM0ziPM1jhKuM4X7nbVebgOG7H1m2kNtII+oPiU4xT3NcuH2sPU4ApwBRgCjAF9lkFJEnK5/OBQMAAWXSIFcdxRx555KDkxvvsWbCG7bMK7ApAA8Btd95WiICmcdBlJCA6UP7/s/cmYFJV1/r3qaqukaYbAg7xOlxF771G/dQb71/RT9F8GuPfSLgZ1CeiyExDMzXIPAgKiOAQURARo8YBMIQ4BEUig8GoARVFQBSQoaG7uuZz6szD+tx7VW8ODSgYwtCseopmV/WpM/yqumqdt979Lhdgm+0uA5hWnxqTkcfWZt/UIcnrSWZQ5rYEFKA18EzwPJeXvPyn57LqEwA+1uGRpDso5fbJQ++8OyitziqamwDSNlgYGm2zR5lsfR5L0bB4lgavOHVgNesrnjEuL1fLag85NySdfD6nNPBOKa7KVGa0PAv1GQf4TOTz+c8++ywcCkXDrKINSpJfg/5685aDSd5o8qSapolfGWHpj799/PHHf/3rX4um5BUVFeIvORQKRSJs65IktWvXbvLkyckkNhtvsmK6SQSaDYFDFQS/3/L4qEN9bLOBfKQO5FAF5UNd/jAcB70GDgNEWgURIALHGoElS5Zgs0G/Bl1ZWfnKK69gtxJ0JIl2viUBmqvPnsOK8CTA6znzwd3ZgSmtd97tl4cBGRiWMh7YmV/tQr0L5h5h17NZ3LPJe7g0zgv0mD/6c4CXzOJITelT1AflYKQCNQXov6Ph0Uz+b9yPojuY4cHTp3kUiAuuxrwpTEFWAbYBzEkqI7PaMID+hjYBYIxij9yW+l1tw3MbN0batgziPExJigSCLaKxl3//vFvUmYbe6KpGIftYe4Jof4gAESACRIAIHI8EWOsIgOnTpwvNSgwCgcCqVatEku3xeHS0z8cCgW8ToLGv5fnnn49BxuzFF5AkLpmOmzipHmB6pu5+rTgzpb+0NV/P7QisvOSCMVgsWcJghSa7gxWLPIBZ11yZT+v7wIG5DTCmHvpnoXvW6d9QfCxvrua+ZsYFdQOLPdD22ENLNS+fs2fbbMrefM8alktVqVbPojFUKUyu2/EFt06DZoJmgLsn9MM/NcDl7bMB4Prrr4+UhcuCQdZoUQoEJSkeYTFzv/nVr8H19lwP07P03HPPXXDBBfgHHIvFMBI6GAzGYjE8i8B0jltuueW5557DOYa6rvud0cJhLQ7nMO0arYYIEAEiQASIABEgAkTgGCVg8IvYuTPPPFOcEOIgGAzeeuutYoHGgeuC7fBugehbNrn6vAXgQ4BpKe2eBr1/mnmfq4tQkzHu37J7Nfc1O2iU5pU3D+BgaRulSrzxV2mAvwAMaajtbcjdDKu/BoOz7oi0/nhe/9BhBmp2YWZpVJ+54ZnNhnRMx9AcpkxvBZjjwIBUdmBGrVHMxwCGG9aQTPGBBu31vFcLMGDU0GAZO76gFAyxWl0aMqAGAEzbUi3D9FyT2VvoQgSIABEgAkSACBw2AoZhlJeXNykzJEnq0KED68Sg8mStw7Y1WtEJR+DbBGh08j7//PMiMoIFVrAQDunkk05/rzY5YcvG8du3vp6Ud4mwCi4Zs64ktus5rs3Nzjaq0jyqTeftAT8EeDLL1OcBGajOwOB6bcKOhtUAu3BeHtasOMfPZqkbtsfm61k8ME7lgXFvFJ37VGUAmF10q69ujmvY/SFPlLZNHQwebXcAAZq1PdS0VatWsYMKhbDJol+A/mL9hj3qs7vHAXJYXhrr1q0bOHDgWWedte+fNN4TDoej0ejpp59+2223bdmyRQjQKr+gek4C9GF5LmglRIAIEAEiQASIABE49gmgI8mxHcMw5syZk0gkhAM6EokEAoF27drV19djies7nL0FaF5If816d8Pk3UpNSq/KuX1z0C8HQ1VvbH1qJc/lKLlGHCYfO9w9orLmgR5P8eCFuAuyBR85cG99erBrdrW07o7TT3bvadAfy1qfYAtxk81d5NJ3o/TMbrOi2jGdIsAmgPk69E9n+4PbO5O5D2C0B4MyyrgG5em0vo1vR/ecUCTAvC9SMCxJYUm67rr/T/ac3WBuAyMJkGNXr8FQ0BLtO3AaEgEiQASIABEgAt+HwP333y8yN/ya1bJly3Qdgwy+z2rpMUQACXyHAM2MBqbZoUOHQIAVgCFJOq1FFL8Que5Xt38E3lpwU7aBJgfbM3njQdt1bc9hArTrgOOxopVlxZmskFVY4WvNyO8allX6FLxuMtyTd5/YoawH2G7oLiuOHX4tKc5MAeauCwdcHewcwBbufb5PVfoX8n0so4dl1uSy7wF845XIgmm5puOxjbJrY9tDodiinqsoSrt27TD9Ge3PISlQUd4yHArdUzNEV7V/nQDteZ5pmp7nLV68uFu3buXl5Xjm4P/bRtTRKLNjX3311bNnz8ZvAgDAsqwmx0KvYyJABIgAESACRIAIEIHmTUBMgzvjjDOanBkGg8HFixeLw8fGJI03vUb/BqvEdwN8BDA+b/ROK73zZk/F6VZ0+haMyYr6Z5tJulmvyBq3cNuHyXRnFrWhlARoG03QKsBqgGm1mdGadXeu0N1xemjmoLT5eBbet1kjFrZJp2iBaZXCMoSvpOTq2G7BHwrumKxenVO75zLjAQabct+CMTLjvKjAGosZqA1ubenao7sUDEqBYEQKMA06nigCrAVvrrz+hfTnH4G6i5lX3CxYJQ36MPtGGinS/0SACBABIkAETgACmqZVVFSgEuVXqK655poT4OjpEI8EgQMK0K7rapqm67plWevWrcNit0ySKiQpwXzQZZJU9sJbbyu4k1bBc1UbdBNME5gMzby6juvZjQI0z3TOAawHeNYuDExu61nUuhTtatV9UHHXeKWC1YOiBboFjgEe9iAsNSphvgu7CPZ2Pm1wRDY32IH+utOjLjMsk14K8DWzP9sqmDY4GAHCm6yUUjj8xuFvZNxRo0ZJkpRIJIT9OcT9FRf96IJMQ8pjfQ4PfwQHcvI8D784cmzHdV3TNOfPn9+5c+dYLCb+wrGTDN5EMfrkk0/u2rXrsmXLULwWGvSReIHQNogAESACRIAIEAEiQASOKgE0QS9cuBDrw2AwGAgEwuGwxHzB19kGz7nbzx563APC9NkMwBcAjxSgj2x1d6B70eklW31kY1g6/7Jm7mY2DssA1WFirifUZ5kL0DrrIWjaYBd4dMZDDQ3jLbsqq9zZkOmjKgNzmUcK9lILWCMWg7klNEdRQNXZjMg9F7SjpAGW5ODetN5PNvsX3bHfRG1Ycq9k7ZhM8fdF+BRABtDQvAKwK5mWQkyAjnMHdPwHlZvAnmVvu1f9/IH6Na9D7q/g/LnYsA6g3uP+atS692yTRkSACBABIkAEiMDBEsDwA8yGFfKUJElvvfWWZVmFQuFgV0TLEYEDEDigAC3CH9B+O3r0aHwJRgLMBx0IhKRAWetTT135wQdoiPCY4dnmJmifAO3YNitkLXDB8OBLGxbK9qis3K2o3mU5d6Tz4zPqO8ALVu59tkHjvbYtF1gLQczzcFlJ6RhOTgH4GGBSFnqloJ8Gg/Nwz6Zdq7ihI8fcGewhDm+xLdRncRRYuAPA31asxKznkBRIRJnsGw6F0Af92KOPMkp+9flwR3Ds91nwPG/t2rXTp08/77zzJElq2bKl+GsPh8PBYDASieDXUGeddVZNTc3WrbwJuG9deJimaeJhCoVaHL5vWRoSASJABIgAESACRIAIHDcEsM2153kdO3b0Nx6UJCkejz///POsU4ruguHXe/nReTZA3gJV4zMFp9aqQzLQvQh36dCjCAPy9oSC/Vht7kvegiUHngqsbndYL3BHZ1dXZRMQXRPsopexuYT9ZD7Vp762j2X0s5ze+cwoIznLzq7k62euEYdNXFTBUbkrhbVu4ZU9CuR5gL84MCVr964v3J1SBtvQO2/3yBujC8U/y+qXjsfr+VLmHm/7ArfedTc7TF6rSy0ic9Z9OCyzaYC25f70+jcBpoM9NqtM3ZL+mAvtmsK6p1D1e9y8smlHiQARIAJE4BggoOu667q6rv/Xf/0XKlFiUn40Gu3YseMxsI+0C82EwAEFaP/xWZa1a9eus88+OxAIBJgRQZKCAd4RRLryyitzuRwu7Hme67L8DeZ/5g5oNuY9ATXw6gH+ktOn7parcnYXzett2KM1648OfMm9FTYrHB2rFLyBac+ey9I7PJeHcmQ87WuARzPmPUWo0qFHBsan3Pmyx9wWrmO4JfVZxG7gQJShWLvncrm2P2hTFgwKDVqSpB9UtmpdUfnT629g0vMRF6CxXzl2HXRdd/Xq1TU1NZdddpnfB43vAolEIhKJMON2MPjjH/942rRpyWTSNFlJj65qz/OwTQ0etTh2/1NJYyJABIgAESACRIAIEIHjiABOgMtms/F43C9ARyKRiy++mB1IKTWDlX4mN3AwKZqlLjtqMWnz7imLLBiRgl4y3K2ya5UM4wvujJ3KF7wONz0WtaEwM4flsQAMywHHAdfhSXgmuAUwvgTjJacwqpDqZxjdNbMqqwzYtXu2nV0GWi0AC4a02RWToy3W/9DEFoQGj/LYDbDSg0k5vTqrVylmfw36yXbPuuKApPF4zt7klvbcZpYUF88EHIC/rvhbWSQWD5dFImVSItxl9u8GJL+6O7v5STAmZGoH5PPV9dnZBWadLgKouslPQVyqhI+jlzftKhEgAkSACBxFAvi5CQBPPfWU8EGKQSAQ+IBZTulCBA4PgYMSoFHi/PDDD1u3bo1ZHEyJ5qnQkiRdeumliqKg3YBr0PgaZgHQnmMDFE3QdvPojAd3Z2tSencF+upwX8F5HWAjQK3LVGc+L88z2GQ90W5wT5CbCvAVwBO1yXstZtnoocFQ2XzedjfwDiSW4zTRncVNIcI6lqUV1d49ega55TlSFo6GI5IktYjFy4LB1hWVu3fWssNUNVav+03Qh4fz/tfiuq5lWY7t+M0aju04trNo0aJBgwbhX35FRYUkSZWVlTjXUrwdtGzZsmvXrs8884zrurgSx3ZM08SxOPb9b5vuJQJEgAgQASJABIgAETgeCHiet2DBgkgk4hegA4HAI488giYG4KKrxdsGMicyCtAuGLqTBXgTYES93i8PXRW4S2Um6JFFmFanbAbQgCnNnsMUZJ0NLRaD51pcfy41YtF5C5YXCw3DlVQfQ682oDptjawtzkzpq7j3manPGIFnMQG6tANgW2Dr4LpcAf+LDQ/llar6TB/ZuMeCGtXqkyoM2Z2bnYMPWQAIe5TNVlNSolGDdgH+6z9/VCp9Y8FWN1wzJrtzpKdOtpzRDdkxijxh187VACmeWK07VskE41Ogj4enl/aRCBABIkAEiMBRI4CmxlNOOUUITTgIBoM33ngj9R48ak9Mc9zwwQrQeOxLly4Nh8OoPgsBWpKks846a+XKlU00aMf2mDAKRg6czwGeNe3hSaV/zumvwjgVFmiwlZebdfnShEFe8DLnBa92eZabx+cUAtQBvKJ641PFLvWFnoZ75+5dvwPzY55nVyyVzaW4Z5Se+aw9do9fhJ3+4DQ2iS8SDbJuiszGHSlj2XmRsvAfnnve0HSW/gzg2s4RE6DFK8rzPGxujn/8/gYyL7/0cqdOnQRt7Hsu3hGYJT0YlCSpqqrqnXfewRX6qu49Ir7YFg2IABEgAkSACBABIkAEjiMCju3cfvvtqD6HQiFR/m3YsMGySg1T0MEhfByspuWy8BoPpue9Hrv03gp0V5j6PCDvTkkqnwBrwcL8InZpyqHHamfuP7YcMD2mKfNIjTTAm6Zzb13d3al0V93unXUGbyvOrnc/4SV6SX3WuAvaYkU07yDI6FosNtpNASwDmFZQB6SVu5Ny36IzRHOGZIpjUoWZGe1DrjsXG9XnomPqnuM/iht+8tNQWUAqY7YR6fRTBqz9x4C6XePyzvhdygM7d63lpwM6V81Rffa3fvE7PI6jp5t2lQgQASJABIjAkSGAIa5z5sxpoj6j8XT16tWoUB2ZnaGtNHsChyZAA8D8+fNFTrFQogOBQCKRWLRoEas1eR3MjBcuyKaZAnet6z1XtEYni1W71cFZd6oJfwbYwWf8ofcZKfPQZ5bC4WLh6jEfhMy9z69p8KAKfdJG94LRM5uZUMws48nRKTtt+gRoIbziCsVsAgB4+qk5ZVyoLeN6bVkwWBYMhkOh8kSiqncf/9OM7QGbrMq/wL9u7PePow8af+IWn3jiiWuvvTYej/vfGhKJBN6M8kv79u0nT5784YcfYhxHk121+KXJnXSTCBABIkAEiAARIAJE4BgngMmMiURCzIe7+OKL8bzR9JjLmAdglH46/GYO4H0Pnsq6QxvsqixU56Aq5QwomGPqM3/nhbQOTGfWuE4Ntgemw13LFugeqCUnc63LWrA8kMoPaMj3zlq9s86AlPGoDB9akPbARpFb41ZqnT/El0RtgVsHsASsabrcP6t3zzo9M1bfgtUvq4xK5p6uVz5yG83L/KEmeLrncAM2M6SwNZkwbtjY0iG3TEgVLa557Hf3ZfOja+UZSWu1BWkWvmGbYDiOCawbTONETJeCOI7xVzTtHhEgAkSACBwrBC688MImvQfLy8t/+b+/xIZwx8pe0n4c/wQOWYA2TbO6uhrLX78ALUlSmzZt5s6di74DJCMDrHXhJdkaV2cMqnMG1TmTcvCqC19zZdnmlSWWqbxu9mweA40CtMuX+QLgTwZMSmsDVLirYPXKyiMyDS9a8jpwNLBUK8NT6kr2Z6Eao99BxCs/+cRMVGkjZWGUnvFnyxbll158STadtnQDd7iJaeII+yb8AvSe8pmdU7CLYRiFQmHz5s3PPPPM+eefj28Qwhkd4Rc8zHA4fOmll06bNu3jjz/WNM2xhRMF10Q/iQARIAJEgAgQASJABI4PApZlbdq0ifXNDocjkQg6oL+xgzz00EP7Vqour641YMrsanCfyhVH1KtVObeXwpwcYxR3aq6wHCDJRWceu8HSk5mLmQVJcwHadJgmze5ifcI/A5i+MzeoId87p1WnraH11kMKLOE9wG2PB04zGZvrxyiBl+pW1sQlA+7HAI9q6f65XNec1b0IPfPQL20NTyozM9pHLmRKujOTm/e9sjXpMP6eseGyKCtx43GpvMUPbu9878atMxq0FS7kPfBMywbdBpXl/pEAfXy8omkviQARIAJE4FghYBjGihUrUEdCfQ/HkiS9//77+5YZx8p+034cnwQOWYDGl2B1dXU0GvUL0NFoFO0Jt912Wzqd5lZopx7gBdkbXef0r4Mh9XB/HfxJYXkaLqsyPYNdwWgsWXnF7NmNDmide5//ZMDYfLFrQb69aHRRjCF1yefU4qesqnYs0F1PdV3brzuLcTqdRj33tddeO+ffz5Z47EZ5IuEXoNv+oE0+mwPXc3D24t5eCVzVkXxaxc43GeA+CB25UCgAwIYNG4YMGXLyySeLNwi/Bi3uPPfccx955JF0Oq0oijCnH8mDom0RASJABIgAESACRIAIfG8CpmmuWLFCVNqBQCAUCkUikZ07dzZdJ49es0vqs/KctmtMsq5/VumumV11s4+q3C/nMDfD5BZpNC5jerPGoji4AG04zP5ssh9fATyc1AbV56qySlVWGVqvzcjDcmAxegUW1mwaDnNOY69CphfzFDx221NlyK8D7/dmYWg60zOr9ShCTw26FrxBKXtWynvfZrnPvPNhSb52WPL0Xld2dDpMGDo2EuICdDAoxRPSqWdN/2TDKhdqASwTQDHAtj2Hx2844Ddw+MvppqDoNhEgAkSACBABIsAJnHPOOUwu4wFfQuK78847FUUhQkTg8BI4ZAHaMAxVVb+x4o8bN068OktfmISCgUCgRTza7qx/W77sbc2wVtQ2TNqV75+0ahpgfBL+kIf1POAZTAXAMsDhGrSHXUfQMOE2einqAf6iwuRUsWdOvsM0blflPtn0g7W7P+F9ri1wbdBs0BxgHfz2vaBlePr06axMlwLRcAQjOIKSJDTodZ9+hqHPhqbv633GdR5e3N++tn2Pwr8PGAztuq4Y4Nrefvvtnj17nnbaaeiGTiQSwWAwFosFAoF4PB4KhcLhcDwev/LKK//whz/U1dUJY/i37wz9lggQASJABIgAESACROCoE/jGUTF27FhMY8SSOxgMJhIJ7CBS2j10PvPuKUWAteA+qyXHpbYNTWeqZbWXplaphaGZujdZz0APwOM9Bh0dPK47sxRoDRyzJEB7YLBsjd0AcxvMEQ3GYM3rnc8MTicfU8ylXilGTwVdA9Uo9SlkyjOr5Fkrb3bVXW0HWG8CDK3d2S8t91GgjwbVebinQX08Y71vQx4g50JSNmSbZVg7LIy6dLV4DggTk4EJ0mOGjQ+XNQbQRWNSpMX0pSt2MQXcsTUDVAtMF2zXZj9AxEA3KeyP+pNIO0AEiAARIAJE4BgksGDBglAoFI/Hy8vLhb4XCAS2b9+O+RskHx2Dz9rxu0uHLED7D/W1115DB26wLMQSISLhUEBizf0k1inkpk4dH17y9oRdOwclk1MKxeeK1ke8TwhbA2v3x4rdxitLrEMB2uH68laATwDu360Ozpl9imYPXekt103R0qu4p4MvaRahWATVKT2utF+OWYqb8Fzoenf3YLBMkoKxGAtKjsUSoVCkRYyVsCe1afuP9z/AZoMo8mKdij0M/T/9x3sExvvVoP3b3e8CaEt/8cUXO3XqVPoyIBCIxWKRSARlaLwzEolIktSpU6ennnpqy5YtnudZlmWapqZpaBixLMuxmaDv3yKNiQARIAJEgAgQASJABI4igS5duqC3ACs6SZJqamqwbQnuleuyqpZnJsMmC/4oq2PzxX55o3+9MqroDtf1Cbn0m+BtZaZjh9mbDQtMC1wmOpvgMO+z6zBVmjk42IpMgHlFmJC2anLQP2f1y3z9iF33Pu9baHqskFfAk8E1gVupMcuj0UuiAWxhfQthcjo/qCFblS72zlq9MtbIusKrmeJmmxmfdb4d1unQZrHNnufwzeNP22FismvxZOlrb/nfUJRV8tE2raVwSKpMVE2ekPEMxdbYxlnPQjYb0l+9+1ZVWu1RfO5o00SACBABIkAEjk0ClmVdccUVorSQJAmzdn/zm9/g7HmSho7NJ+743at/SoAGgM8///zSSy+tbN1KKitLVFQynVeSTquUWpRJUllACkf/vbrf6M8/nVO74xMeJMe8040X9EqInzhvTwfY6TH1+aEGGJqGKhn6FM1BhcJUreEtcGt5ZAfTnD1bBb0IehMBms3V08zt23aeeuppkXBMkoJcg2Z/U6X8OEmKR6KfrPnIc3ipvleHkibFK7vZuLNH6P/96sv+be93Ac/zTNO0LMvzvLq6uilTplxwwQX4PiKCAnFWRTQaRRlakqQrrrjiscce27lzpwj3EBtCOV7cpAERIAJEgAgQASJABIjA0SLQqVMn0XsQC7xZs2b5Twt5uh3LtUsCvJZTpiXlvnnoXoThKoyozTxcn10BsJ1HXvBWfQaYBgrQNhegHeZ9dlgTQoNJymmAVS5rwTK4YA3KOCMyyu+s5BKQa7nFGRsdFvnaHI9H6TUK0NiSsI6rz1OTxuBkvlrWe+eUqnRxaL32ZIO+hdmdWSFvWDZ6lpntmQvQTENGD3SjucQE2GJbF9z0f6VYuSQFylqWM4dLPHDljdfYYFmujrvTKDf7y3i/nM3GR+uJo+0SASJABIgAETjWCKiqiiXEkiVLhPocjUbj8dJ8o6+++oraDx5rz1rz2J9/SoDGV60syzd3vIUJ0OUVrRKt48FwWJKiZeyVHCirlIIVUvnJt1XfszWjaLzidGyvZNLYB6EF0GDDRoAH027/tNsvzwTofrI9JpVbzuYMgswdGfxxrsV6XrPm2ziVsKQVuzB06LBEolz8IaH3GdXnQCB03jnt1n36mc3u8zqQAAAgAElEQVTLa78DGoXdvd0TR0GA3gdJ0zsOJECzat51ZVnWddY1xjTNbdu2zZw5E3uml5czICg9B4PBUIg71gMBDif2ox/9aP78+U23RLeJABEgAkSACBABIkAEjgECV111leg7jSXuRx991GS/LG5P/hBgcibdP6/1UKCHAsNV96Fk9v2sp/MphrxfoOOwVizsiuqzzeLsuABtOeB5CsAqA36XNGvyTt+CMSJTmFmUP/DV4Z4Lnsss0kyrbgx9Rl+HDlAP8BHA1Ib8oIZ8taxWacW75Wx1NvO7jLlSZ95noT47Hmt86HjAi9tG9dkXKa0DrNhdd2qHDlKiMhxtEYzH2UTLgBQqk7j6DIomG5beKEA3FZ399zdhRTeJABEgAkSACJywBDBT13Xdq6++GouKYJCl6aIDunPnzoZh+L/kPmFB0YEfdgLfX4B2XRfjGkzTNG1r0tQHpbKIFCznCRxSPBEOSIHKUKtYoCWbNBeubFne5mc3/nzxX96q2510D2BEUAE2A8zarQ9Km10KXo8i9CvAyJT+6I7ULu59Nn1Jcw4vYRkRnmUHHsx6fNZ/nvufrDLlgRtMAQ+EsFMLjq+5+lolzzr4sYvLdfBjzAFd2rcD/3cgARrfRABADFzXNQwDALZt2zZw4MBzzjkHvTOxWEyo89i3MJFgExtPOumkPn36vPHGG5s3bz7w9vf8ht6S9rCgEREgAkSACBABInACEDhaxc+FF14oijccyLIseLs8BqMA8CXA87o6JJvtUzSrCjA4C/dl5BU87wKlX5st6dhg4dVk7Vhs3TFszwbXsbmb42PbeTypjKjXB2SdYRn1SUVeaqkyL7ctANZ10GWqMV8VU6IdjynRXNpm1unPAF4GGNSQ7qOqvYxib0OuyicnF5WlNguPVrn3mfmmoaQ+N5o/uABte9DYGcbkwX3zN32VuPwKqUXrRIsfBCKNSdCStGz52y5rPmj7VeZvGQtWNCACRIAIEAEiQAQsy1q1ahVWFBjcyhWzQCKR2LRpE+pIRIkIHHYC/5QA/U1TFMwOtlmbEPjbus8vvOEXkhSXKiqC8XjrSJuYxDKISxVzkP3fomVlIFT2y1/fvm79JhdA1i2bH5PhQEE1t7nw6M66YVmlSrG7a+7dmjWs6DxeJ6/jGXCeyabtYWQHC33jKralOVu/2vr4754489/ODEnBkBQM8qvEPBJSWSQmSYFoNB6LJR6fMVMt6n4B93h0QB/oFbDXcfkW8t//+uuv33HHHRUVFeKNBidZYKNC8UyVl5f/6le/mjNnjji3wYwOjAECAEyO9m2EhkSACBABIkAEiAARaOYEsGcGHqRhGLqui9LIdV1/WqJlWZ988snUqVO7du3aoUOHW265RVVVrKb2zT07GGpYpAWDvJiWpEsuuUTTNFHjmTwNYyPAc64+TskOLcjDZGtU0pq0Q1nusuQNloCHgjGzOLPEZxH9rDtG0dEt8AyAHWB9CPCkoY7K6cNzMLHBfjbvrHEclrXcaPhA6RldIA7XnVVuhUYNeiPAbMMabmrdcrm71MLterqHkpyQqnvNsLfxrA4s+3F9JQc0eA7LlOYFvsP20zCgCPClA0vqC69s3y21/SHzskRbSQE+v5KX+NOmTbVcUzXUJqKzYNJkgFukn0SACBABIkAEiAAmuHbu3BmlZ9F7UJKkvn374nftR+sbd3p2mjeB7y9AY2GHArTpscYn2133+Y1bb3/0Sal1GymSKJPiLaQYa09YKhelFq0qApFoIBIPx8sr2p4SbdmqauDgWc88u2HL1zavSt/dsfPhnTtGp9LDUsV70sWROXlqfcPHwDpls4vNst6KmuEAvPXXd1es/HDcmMn/7xXXJqIsXyIkhfYWoFm38FA4KkmBSy7+788+/dzjrVH89eiJIEA3efni+8icOXPat28fjUZDoVA0GsUgDpH4g0bpeDwei8V+9rOfNUnnEOdaTdZMN4kAESACRIAIEAEi0FwJoOtiv+dj2CDesZ1kMvnII4907tz51FNPLdkvJCkUCsVisWHDhpkmi6z4fhcUoCORCGrQnTp10nUdi3DXdRWATQALDHWckhok54bniqO/Tj2dNDY05mZoXH9mSciOJ2I3HJ68YXu2xXzMrNheCzDDVgZlc/1SxTEpZ5EJa21mam4ycZGtpjF7A5M9VJ7+UQfwFsBoxbgzl++sKncqcnclM7ZY+JNpb+IxesJEghBYeocH3AHtuNiPnK/X4D0M/6Q4v9uyc9bnm6TKU1hjmWBCCsf4LEeG9vY7bjesJhnQLILDX+f7x98POz2KCBABIkAEiECzJFBbWxuNRjF5wy9Ab926VdM0Xd/buNksEdBBHQ0Ch02AVgHeK2Qe3r37gZ11T69e26VmlCTFQ1IwLElhSSpDx0aEh2NUVkplYVY88iRiNgiHTv+v/7j+Fx079uw1/LmX+7+wqPfLr/d++fUh816b8sqiN1atfOOd1996f+nQ+0eMnzzxmuuujcVbSlI4GGINSaIRFvGBsRtB7okobYp1IJRatzlp7u+fdWzWHzuXbQzfEKB5Coe/PG2cBrinjYlY9hgf+I/iQLuqKApmyePpE4ZEX3zxxSF+CfCwkkAgILoU4iwMDI/+7W9/+/TTTzc0NJimSTMyDkSY7icCRIAIEAEiQASaNwGPWYgdTWO2YNd1t2zZMnv27O7du59//vktW7KiVEwp4wVq6cfll1+Oc8i+HxwhQAcCgWAwOG7cOMMwhADdADDf1MfL+cGF3JCcMmpn5k861HGZWANXB0cHz2RGY6Y+K+AUwSqFPtss+MLk8vEXYC8EbUA+37VBHZf3XiyyNGebu5sVYBq3ztPw7MbJiI0ytIsP/xrgdYAHVeiXKt6Rlu9QtB55bWJBf8ViwSBZAN1xPIdNmdzf1eWZ0iwCxOSi+RsmjEvL9+yovX/Fe1KskptZwonWraVERGJ9TKT/ufIyJCmrBb8J2l8P+8ffDzs9iggQASJABIhAsyTQuXNnPrsoKtTnQCDQo0cPrG0wa1d8jDZLAnRQR4XAYROgDYCvAWburn3Ftr/mfU52peQ+vXqdeXKLKC8bQ0Ep1iIslQW47sxV4mhjGHEwIIV5OclKypAkJaRAhRQolwLlrU49PRQJMA91mSQ1Lo7xGsFQgovb7IEoOqMAjZV+2zYnjxgxqr4hreoH9pucYAK0/5QJbTgYpvHxxx/36dOnVatW8Xg8FApFIpF4PB6NRnFGhr/retu2be+4446XX3p5+/bt328O6VF5ldNGiQARIAJEgAgQASJwWAg4tqPr+hNPPNG5c+ezzz4bv7YPh8NoT8bpZfjVfpBfsKySJAnbBn6/b/GFAC0FpLJo5Olnfl+0XRkgxZv+rQOYUMhXK4WhOWVCMrcYYANannnUss3UZzC5Bq2DUwBLwSaEtgWW43iwE7xPAV6F4oNq/SA5N0wxnnWZpbrU6JtLzzK3MKt8wiJKzxYXuD2P6de7AD4BGJXM9UzJfQreHbW5XvnC2KL6igVrPaZcs+QN5nZ23MYgDrvRRo16tAO2xbRySAL81YVpWa1vQ2FUVh656A0pEMMGM21OOTXQMi5F+NlCLIg76FefyQF9WF7htBIiQASIABFofgT8U7i2bNkSiURQ+fEL0F999RUeuGVZQn32P7D5YaEjOsIEvr8ALby0TNbkc/eKvA5OcfWZlZUeuzfdUP/MU7O63HlbZasWKA2zn8GgFEDRmDtFQmXMwhwMSIGQFG0hxbCTIfdPx+JSJCgFpbLKSLw165XHL8FgMCIFwo3Kc+lelEovuuiiZ5999qA4NnYv5D1XDuoRzWahfd9Qdu7c+fTTT19yySXMkh7mFvVG1sg3xB3reApUWVl55513vvrqqyInGsmICaquy9o7NhtcdCBEgAgQASJABIjACUJA9HN2bAfjNQAgnU4vXLiwpqbm3HPPFVEYWCDF43F/4cTr3FKVi9PL8Lfr169nMqy9V0zEQSLFDZVFmfgarix/9+8fZgHWASz24Pe6N1k2+2rFakV5uGC8ZcNWXoqX2gTazPZscxVYB09jDmhLA4O7mdnGDYAPAWYa+j31DUMadj+g1s2D/KcAOdwzlzcf5D5o1j+QDxrbBLIlPLDSYH8OMKto9tjZUG3CYA8G5IwHiqkFTn6tiNETfmkuQOMa0EyN2zF4u5fdAPMzuWE7dw7OK0MUZ4bijXvuZYmdM7A4vxt+diPjwF0p8fKIbigWs18fuNo8get8pEo/iQARIAJEgAggAVHPAADan1H2icVioVAoEAjccccdopsFijlCMiKGROBwETg8ArR4ae41cLksDWCapuOYmlYcP37sNdddG4iEw/EEn6EYYoHQZbFQiNXTwRZcX45E9kRzBIOS/yZW36WfoXBZPBRmUwZQGL3uJx1Gjhy5Y8eOQ9A9T+DC1P9MiRcTTildv379xIkTL7vsMiQdDAaRsB8/3hOJRFq2bHnXXXetWLECVyLe14QSLTYktkIDIkAEiAARIAJEgAgcswSESblQKMybN2/06NEXXnghisii7BRFEYYyh8PhWIzN1BNWZfG1fTweb9Wq1YIFC/B4v99JXSLBiuRgWShazhqf/HXjV6sBntPsSYo9JG0MyFrVsnqfZrzuwhZuWOZdu1UHLI8L0CximadbcB+0YwJr663ZekpnavUjyeJo2RqiOKPyhfmQXQd6mgvNbIcb1V27UX3GXobiuTMBdgP8Xs6Nyua7Z5SesleVcgZt3vVHO78W1IwwYqMAzUVxg9/JO7Pw1fBNqMD25C2AifUNvfOZqqIyZHvDcoDBU6bx2ZFM0J8y9YGTTz1JkqR4IhxPhDd+sc4Fl2vQYnf2HpzAdf7eIOgWESACRIAIEAGwLEtRlFwu92//9m9YvWAGNFYv+TzrvLavjHMI8hoxJgLfReBfKUBz6VHXdXwdiz1RVHX5yhX3T5ncpUuX/+f8C2IhNmlRKgsGKhNSi7AUDrCYjkiZFIkEItFwNB4ui0ZC0TLe+DvKk50lKRAui1566Y+rq6uXLFniOKauqyZvRaKZmuWaTtN2KWLjew9O4MJU6MI4wO7t+GQJRmvXrh08ePBJJ7FaP5FI4DlVOByurKxs27Yt3sRJppFI5Jxzzhk+fPjSpUsd28F8jyabEKulAREgAkSACBABIkAEjlkCu3bt+sMf/tCzZ0+/lzkSiaDE7Jeew/wi7kEzUUVFRSgUuu6662pqaubMmbN+/Xo8nXNdF+3PWBhjmXSQENq1a8e3Egyy1iotXjPssQ3pAfliH9nql/PuSVkPF5j6/CVPc2br9FwHDBsc2wMWe4GyMRqPWaM/D1yWjLEGYEYK7i3APTIMzar3NdStBdZ1sMh8ylgls/8wCdrEzAu2ch6fYbOMjh0AfwV3RP2OntlMz6LRJ22MqzPm1BXX8mmRpeaH+BD+8D3W68aVAF/PToD3AQZs/bq/qveyrAF5+ZlcsRbgNv4sMNE5Gh47dvRl//Pf0RgL34tGw+/+Dd0Pe6TspjBP4Dq/KQq6TQSIABEgAic8AaxGhg8fHgqFUICORpmh85sC495778XipMnX5IdUq5zwgAnAdxP4lwvQwhKLrVewZ0smn7NL9mi2i++uWvXqu+/8ekT1/x3S8/ah/buPGDJo3Ohh48ePHjt+3OjxY0eMGTN05H3jJk6+9/5lS5e/u/xdMTXSMAyW/8FLZD5ga7M9FjR3UJcTuDD1q8OO7fgDnRVFQSUaf7quO2/evJtuuikej+MpFmYa4jgcDuObl/hVu3bt+vXrt2HDBvEWdlDPBS1EBIgAESACRIAIEIGjRCCXy7322mudO3c+88wzsQ1GKBSK8Qu2xMBePaL4QekZf0ajUUmSzjzzzE6dOj399NNLliwxTdNfAOMxieLKX4Md5OE2zksLRKQKSTppWkO+r6zdrTrdil7/nDOurviWzbzPpXbbLFbZcsAygQU020JC1rmx2WHSsw7wEcDjBRhY6/Svh/47tEcV+32uGptcfeaFOgtT4+qza4K7p7xuzNOQAd4FmJyqrdHknsViH9kYnlRfVJgOnmsUvZ1GDzUr0cEzwCtJ26hq8xgOGWAtwNjarwfIatec0U82R+xKfgWQAbjh5zeF2Kmx1LJFYtmyv/76178MlfHbkrRs2V+V4j4Nxv1AT+A634+BxkSACBABIkAEkEB9ff0pp5wiMlfD4XBFRUWbNm00Tduv95kEaHrlHF4C/5QA/T12BV/BNngqTu7DEhZgo5l9NvXZgxvf+cvWzzYkd2VsU/U8VrN63C/BzBq+ZiV7bXhPM20XXHHda5ED3fAXpgcaH+ixzeV+8Z7iPx3yf/GFB2oYxpo1a/r27XvaaacJrRkH+96Mx+ORSOTss8+eMWPGxo0bRYQiTt8QM1ubC0I6DiJABIgAESACROD4I/D5558/+uijN998c/v27UUTHvyWXUxK9Zc6whAdDodx+TPOOKNjx45Lly7dsWMHOi3+FRQ8z/vl//6S70kwFG4rJc6YXnAG6NBXh24p7Z50cVZO2cQzlEtbdyxwDY85oA2da9AscgNVZ4flONcCzFP1KQWtX73ZJwV9dzsPFeDvLjTwgGZg5TSbS8ht057LLNSWDabL7nDR/mxYTOzeDPBIOleTyfTMyd0zyrCM/qwJ6wEU3A9evfv8yczzbIPlMne1w1amg2sxt/WXALPBrs5neuft/mn3/npjKcBGVzXA/j/tLysLSuFQKChJa9asufnmm0Uu3Lt/W6HrqmUbB8XcX+cf1ANoISJABIgAESACzYqAYzsTJ07EwA0RwfHNHKOpU6eiUONXhPzjZkWBDuaoEjhqAjSaMFBWNj13FxiroPAu5LaBXmTtUlhd6iCaPQozl6F9lSz//Z5fC/WZD9i68XpAwv5i9EDjAz64uf3C/xbjNl7EO5E4rfI878033+zRowdzo7RsKUmScAbh9A08VYvFYvimFovFLrjggocffjiXy+3rBmpuEOl4iAARIAJEgAgQgWOSAGuabTtbtmyZP3/+XXfddf7554uzr3A4jB14/JUMnqGh0IyqNEqfHTp0GD58+KJFizZv3owHil/b/0sPuqamhtdXISnSWir/4UNZd4gCPRqMoRlz8s5dG0TPQHCYpusarN0gaA5oOvNB8+hlkxXWDjCj9LysPKS+rns+3zVnDMjDgwos4ao0W5Jpz6zURgG6pDeD4YEK7GqyvoUOG30O8FxOH95Q6JMp9k7pQ9LWTI3FaJQ8yRZf1l+0Mzu1xeM9iswJ7TBPtQ5MsH42q40znB6y2TsHI+rs103YzjbmKXpDOMy6lreIxSNlYQC46qqrsDdJy5Ytlrz9ppj++N3w/XX+dy9NSxABIkAEiAARaG4EstlsmzZtMHZDfO9eWVlZV1fn2I6iKH5FyD9ubiDoeI4egaMgQIPLXsylipQZnD3Xdf2JHKzqLbXuZjI0mzzI72GP2Y+iLO7dY38mAfp7vKL8bzH7jv0rVBRFVVXHdp5//vkbbrgBz9mERajJyRsq1K1atZIk6bbbbnvmmWfy+bw/8cO/5n3H/j3Z97d0DxEgAkSACBABIkAEvp2AYRhLly7t2bPn+eefj+VKMBiMx+PRaNQfIyZOxprYn//jP/6jS5cukydPXrt2LW4Iv563LAsHmqZh94tv341/5rfPPPNMyfkbTUgtfvBEUhuTsYdmzAm1qU89Jha7rEQ2HC46e6AxndcrekyANkwUnrn3eQvAIk2dmK7vns/fZZp9TWNcXl7Oo5xT4Cmgs4Q8bgDByYdsn20PmMu4wFVu1tmlwNXn5w1zREOmKq31Sdoj6uFJBZa7LBK6dMHyvfEW801bAJYFkAfIcn3cK3L1+UVdH92Q75+GqgwMTMGjMjNEY9zHpk8/jJUFWsTiQUlCAbpt27b4DEaj4ffff48EaAGYBkSACBABIkAEvp3AzJkzMf1ZFDyBQGD8+PH4PTqPt/WrL3vG375a+i0ROHgCR0eAZs1P0InA+2x6rDk3r5xFmxS3pEGbXIBuqkHvdXwkQO+F43vf2PMGs7+ROLPCPA3MMVRVVVGUDRs29OrVC93QQoYWJ3jYwBBFanGa16lTp7lz59bX13/n3vr35TsXpgWIABEgAkSACBABIoBdKFauXNmvX7+LL764SXFyoJvifEySpIsuumjw4MHPPfdcLpfzR4eh4oy9BI+A8Vk8lcuXL8ekaSkQkOLx2fWp+xvS42p3/xWgwfNcW3eZ0KzZjQK0B0UHijZoFug6sD7dWYCvmfe5OCXZMBmgl+X0spxhRfl39fW1PJ9DBkUDFVwHxezSNEQ2Aw7AtgBkrh2b2Hjw+ZwyPJUaUCz2zOTuSWtzFHjPg00m06YdANYYHBseCuuIByz7w3J4PkcGwDIAtgH8ISOPTjWMB6hOw6AkjN1lLuO7yg7cUt5c+GJIkqLhSDgUan/5Ffl8XpIkEcFRKOQEn4MaCBP0QS1NCxEBIkAEiAARaFYEzj333EgkIqZ8Ydmjqqrrutiqza+9+MfNigIdzFElcKQF6H0PFl/ZJT0axeRGbbqxx0nJ9+yfxrfveuiew0jA/3ZTeoL2Wbt/GUzsePmll7t06YJKdHl5uTjBw67x6DYSd2Ly/c033/z444/n83k8o8ONuK4r9G7/VvzjfXaH7iACRIAIEAEiQAROCAKe51nMS1u6OLaDTf9M09y0adP06dNvvPFGlGuj0agw+2AF4m+kHIlEgsFgJBKRJOnUU0+96aabHnrooXfeeadxxcfQ/67rlpeXB/EYyoIj/v7GQ6mNb3nyRmZL9kxwVTA1JvGWnBsuS7RjVwdUA7w6gH8ATKnPj8wYw3LG4ILVLasML1pPF+xNXH1mNmdXY6thRTf7t0eAdoE3DufheTZrDPhXgEk5vUqxuxWVwWrt/amvPkRxmrumeU6HxwRoFtdRquHZiHUNdwCMIsgFgCTAnxwYnyoOKurVmtk/Yw/4Ivknja1fFPwDq7pxxTkSDJZVVw9YsmQpqx7LopIUaN269aE+PVhqGoah67phGJZlHcmvEA51b2l5IkAEiAARIAL/PAFFUXRdN01z7ty5aAcUBdI3oakTJ0785zdBayACB0/gmBGgm+wyb5ntz9vwj5ssSzcPOwG/1OuXhr9zQ47tbNu2bdasWe3bt/dHc2CbeL/6LM4DsaVPdXX1mjVrxGxWkRbdZE/Eze/cE1qACBABIkAEiAARaJYEVFUFAFmW8ei2bNny8MMP33TTTSeddBKeXIXDYSwz0C0bCARQaI5EIiLuWZKkH/3oR1VVVXPmzKmtrT2WQbmuaxgGyzQr48cVlK4e02vuro82g54BR+XN/FSwdRZcYWMjFQdsGewC/7kb4G8AsxwYnPeqilAts8GwjP5gfeELbmxmYrHugWmAzQRo0fbbz8RzTdNzZYBPXZhjQo1i9lSsKjkzWd7yHphbQWehGTw4T8cADcyQ9gvQvJTXwKgHZzPAMoDpOgxS3L6aXZVXR6fUmbuKdQAya1XIrp5VvPHGa3iVWBYMls147ImJE++XpGAgEAoGy6677jrcvUMqU/1HZFkWfm/hv5PGRIAIEAEiQASaE4FCodSa4ZprrgmHw9FoNB6PYzeF8vLyg09GbU5M6FiOIoGjL0AfxYOnTR92Av5pqnV1dX379q2oqIjH4y1btixNHd1HhMa3P5xTefbZZ48cOfK9995jRhmbmW8auyGy/4X6/L1PNg778dIKiQARIAJEgAgQgX81AdY7hJcBYkPvvffeY489duutt5555pmJRCIQCOB0q3A4jBp0LBYTWQ3+7hQ/+9nPRowYsXTp0lQq5XmeaZpYXWDCmFj/sTZwbCcej5c1ZpkFzjv1g9wOmbcLtMA1wbF480GHJWigfstUZRngK25Ynmp4A2SvrwxVClQVYVjWebiu+AnATsxaNrkAbfPuhVyA3o/twzFVgC8A5srecNXtU9SrC6n7szvfdnIZgLxnG4YlYjcEPYzWKzmamZOapVN/DbDQg6k6DM5DdRH66G51ffaJHYVtooFhEZh1GwBrxkAgEC6LfvDBP/7P/1wRDJZJErs5adIk3IqwLIiNHmgglhR2hwMtSfcTASJABIgAEWgeBFBOeeedd7C1MptNFQxig67Ro0c3j2OkoziOCJAAfRw9Wcf0ruL5myjuAQANSgCwYMGCTp067aM8l+4Ih8PivFEsc8YZZ0ybNu3LL78kAfqYftZp54gAESACRIAIHBECmzZtmj9/fs+ePS+77LJIJCLSvUTlIAbhcBgjDvGea6655rbbbpsyZcrq1av9wR241/vec8x+yd2hQwdJkmKBEDuuWGhT/U5MyvA8xwbH5Ff0PzNDM1efdwG86cK0vFmVsbpp0EOBvtz+fH+y+K4N2x2es4HpzKbHRGzP8vfxRkQOn5VoelAPsARgeFKpVu2+Sn5sw9b5xd0sGVpVXQcMjTU73BOfwYfcks1Wgyux+V79HeABFbo2qH1VYNe8Oiktf+wBs7U7rHsiE7JdePe9FeI5jYRj2UwepWfmBA/HFi9ejM+Uv/L89lfiZZddhtb4ioqKn/zkJ9OnT1+xYsW3P4R+SwSIABEgAkTg+CWAyc4AcO2110YiEf/38eeff342m1UU5fg9Otrz45EACdDH47N2XO7zl19+OWPGjDPOOEOcTmD4BhqUGj09/l+y8WWXXTZt2rTt27cDgGmahmGgJE3ulePyRUA7TQSIABEgAicwAf80KUVRDMMQp0au66IWLGaDJpPJV1999YEHHrjiiitEpAYTH3lks/8kqknpcNJJJ910002TJ09etmyZf4v7BS8mV+33t8fUnR07dgxKUryMJVbHYrHePXoyoZapw54JpsIyoB3PZTHLsgkpgM0AL+XNB4ouS94oQK8i3Fnw+uWd8bWZt13YwVOa2cNtAMsD2wHX8oAJ0Cgjo23Z8XjjQB7ZvPn7KscAACAASURBVNKGKYpVLZvVsjqukF5kpbeCwSzUvFc4e3RjExfkhjZq9FirnlcARwH4hwNP5aFfATobcGde75XMPWiZr2haBtejc+3cgWI+N+upx1kj68oWkiT96je3jRwxNhqNR8KxSDgWLouKp8YTidHirsaByS94a/bs2TjZzt80G0vQCy+8cODAgXPnzt2wYQOaJzzP03XdL21j8dm44tL/4sVzzH5p0WSH6SYRIAJEgAicUASwsdabb74pSVJFRYW/mpozZw7OAzuhgNDBHnUCJEAf9aeg+e+ApmlYxGNc44YNG4YPH46ni/F4HLsRHkiADgaDiURCkqRbbrnlmWee0TTNX+X7x82fIx0hESACRIAIEIHjnIBIujBN07EdlJtRejZNs66ubtq0aXfdddc555yDQmEkEhGNBEU/CSwemDqZSKAefdZZZ916663Tpk177733xCYOBpXQEA9m4aO4jKIoEydOlCQpGmYCdFkwePYZZzK/sMn0V9PRVDBVsE0PNB5z8RXArF3y/VljcMHpw5M3+srQbbcyZEf9Eq5NM7sx0665Odll0R2e5zg80wOFY5YE7YFhurbLFOb3DJiZ0Qbn1WpZvzcnL7CMLeDIwERvpoOjaM290k0oYaRzDqAWnDUAz+TdkSm7qwadLfhtQ2pkPv1kZtdOAJMZsV12NV3e8xBuvOWnpa8WyoLTH370lFN+yPM3pEAgdMdv72yylf3exBNvbG09f/58zHyLx+N+g3yTby8CgcCFF17Yo0ePxx9/fN26dSL7xeIXEQcnNne8vH7EDtOACBABIkAEThwCKL9cd9114XA4Foth72VJks466yxVVcVX/icOEDrSo06ABOij/hScKDsgzE14PpDNZmfPnn3FFVeEQiGR2NjkNAA9PrFYDOMd8Yu722+//dlnn8WVCOfUiQKRjpMIEAEiQASIwHFLAIVmtJeKZg+ff/75jBkz7rzzznbt2jVpF+G/6f+iOhqNBgKBdu3a3XrrrfPmzdu2bRsAoNnZY4EULD4YL57nfbsJ+jgSEF944QW/cloWjz757Fw8TNvUPVfnPmjYzZOan8ra9ylu3waluuBWyyz3eXDeG1+beb4+vRtAA8tiV9MEy2QWZ8sBpj47XPotOZdddi9Tny1vswGzUtawDPM+jy7Ii3RrK0tptlytaDP/NU/Y4BHP3JHNd8rb03+wCMyRvQaKT+V3DsvleqlmN8Ppoek1amZKausGsIugux5ro+i5pu2ZHriKXWzZtpIFVkZY38WePXvitDksFDdu3Fh6gr/rP+Fi/sayMH78eP+rCFcV4Jd960/8YqOiouKaa64ZOHDgwoULa2trRbicEKaPo9fPd6Gi3xMBIkAEiEBzI6Dr+vbt28VnHzZkjsVic+bMadJao7kdOR3PsUqABOhj9Zlp1vul63o2m8XOP6tXr+7fv794W2xyDoBzbHGOZMuWLbF5PS7zm9/8Zvbs2aKva7MGRgdHBIgAESACRODYIvA9JiGhjXTNmjVTp079zW9+0759e2yJ4//oF50D8c4Qv4gFTj/99N/+9rdz587dsmULAMiyrOs6Ji0YhmFZlhAcMbZL1/Vv/676eBEQVVXduHEjcgiEgjj44Xlnp4oFRVV1VQPb1gB2AHwMMHVX5j7FvUeDIQYMLHiD895A2RmTKf4+md8MkNdlcAoO6DpoGhg616Btrj47HrMy7xXBAbDVtOfVJken9H6yO0zRZirFLwCKDnhaEfSiAa7GYzxYFIY/ggPHPB+jzrPXA7zsZGpqN1SphW6G1UvVa4qFyfm6DwDSoJpOxvMUz1Vt0A0wLbBXfrgq1oqFb5RFI6edcXp5eTmmr0QikWuvvfbg/xLQr7Bo0aIbb7zxOn7p0aNHVVVVp06dLrroIlSZUdpGZzQaxJjTnH/JIV54+EI99dRTO3bsOG7cuHfffVeWZfHiOaS/hUNa+OCPlJYkAkSACBABItCEgGVZXbp0kSRJTB2LxWIVFRWmaeL0IMd26FOpCTS6+S8lQAL0vxQvrfyABFzXdWwHz0Uty3Js549//OOtt94qav1wOFxZWekPeQwGg2hU8d8pSVLHjh1nzJiRy+XEG6h4GxWDA+4H/YIIEAEiQASIABE4dAJoAhWhBP6QXL+txvO8ZDL5xhtv3HvvvVdffTV+ygeDQXQ3l5eXx+Nx/HxvIj3jZ30wGDzvvPN69Ojx6quvCt+r/8P9RPCi4hRaANgzb6yMtyKUpHsnThBPXR3AIg/GZPLDDaem6NRktWkAw3PuGBlGppXJO3dt5h3+wLXBMsB1uNbM0jesxtxnFunBrw6YDvNHQy3Ay4o8RS32lpUBijYtV9wIkCtt0mA2aKZcN7YebBSgRfqzy7sObnLMP8uF0ZlUVaEw0IR+slnVkJ6QbljD16+DDpbqOTZ/Cdm2Zxtg9+hXJZVkdlEYSpFIWTAkrVi5TBzydw48z0ulUqeddppYC/a+jvDLlVdeecUVV1x88cXnnXdekyYlqDgH+aVJ2SlWdcYZZ9xyyy2PPvroypUr/V9+iL3CWldkwiiKouu6uCkWowERIAJEgAgQgcNIQHz1vm3bNvGZhd2bJUl6/fXXcVv4eeSvqQ7jPtCqiMB+CZAAvV8sdOeRJiAaxciyPG3aNNGpHG0p6I8W6nOTAaZIBwKBn//85wsWLGjSy3W/pwRH+vBoe0SACBABIkAEmikBIQGL4zMMY/Xq1VOnTu3cufM555yDPtNWrVrhWVAoFBLZGkJ0Fhof/qpt27Y//elP582bh05nseYTdoBO3pkzZ2I6GQZkBwKBs88+O9OQMgHqAf7mwFRF658rjLS8kTo8BjAq74wquvfszjzckF/uQhqVYsdlGrTHVGO8CtdzowDtWqCrYDYArADnPkWuyuUG6cXxBfnvfENW6WkwAAxc5Z5GgDwG2uWeaANAAdgO8Jqcm1xf17ugdzWgSrGHZIrTZe11l/m1ix6wyBTL9Gymgruua7tuMptu+8NTQtGIFAyIM2dWEIak66//iaYVcznWs/A7L2jv2rVrl3h14UsxEolgtpt/Xp0kSW19F7Teh0Ih/HbEvxtiLFaL91xyySVDhw594YUX1q1bh9IzC9nmITDCmI/3+L+h+c6joAWIABEgAkSACBwqAZREBg4ciN7nUCgUi8XC4fBVV12VzWbxw+j7zeM51D2h5YmAnwAJ0H4aND5qBDAXUuQ2Wpb12WefDRw4MBwOi9PUJrqzuIkidSAQwPPYUCh06623zpgxA99bj9oh0YaJABEgAkSACDRfAtjaAWdxep6Xy+WWL18+evTon//85/F4PBaLRaNRzCwWKrMkSWKMHeEkScJ0BUmS2rRpc8sttzz11FMbNmwQCdGO7aD22nxBHtSRYYGkKMo555yD3RfRohsKhX71q18VAV53YKpcGFNITVByT2qwAGBsEQarMEBWJuSyS1SvHlizwEbd2RXqc5MB9z6zOOkGgOVgT1NS1flCv2zhIUVf7EIDQBrFZs/j67OE+3nfwzAA6gD+DjAus7OnkrvLhLtM6JLN36eqyzzYCSB7rOOgwToQMt2Zt0JkMvS9E+9LlFew6q7R6I0KbyweWbfuU8PQ+Lb8O77vxtk94pUzceJEUSJilEcgEEgkEuiGFl4H9DsL6RkH3yJACyV630E4HP7Zz35WU1Mzf/78TZs24ak+WSL2/zzRvUSACBABInD4CGiahrVZfX39KaecEolExLetkUhk+fLlomcGCtCHb8u0JiLw3QRIgP5uRrTEESDg94agGG0Yhud5lmUtXry4U6dOGMYnRGf/AM8cMLBPjNHk0rdv38WLFx+B/adNEAEiQASIABE40QisX7/+hRde6Nq166WXXurX4DBOV/hDRZsHkbwRjUbj8XggEAgGg1dfffWkSZPeeecdPz3XdQ1+wZLA/6sTfDxixAhEjV/PB4PBcDhc8+jvpu2uG9aQfKCQfbwoLwWYVYTRKhOgB6Xq/whc7dW5Vrx3yrNfxG0cmxaYBYAvASbVbx2US9ZYzqiculC2Uzx8w7JxPR4Pi2Zu6n2fEVxVFuBTgLm2WiWn7rKNzhb0MGBwITeP26ItD2yHWbFNjwnQ7CFO6Xr2v5/nfzmJcc9e3U1Lb9xc4/7ubwcal2H/G4bh2I4sy8uWLfsmPfzOO+9s3749RnCIl2goFBKn6AcpQCN5fFQ4HMaBeKnjPouM6VNPPfXmm28eNWrUm2++KWRx/04ezNhvVaMZ0wdDjJYhAkSACJyYBDCC46GHHmrdujVOFsdPpZ/+9KeWZWFDXVKfT8zXxlE/ahKgj/pTQDtwsASeeOKJ8847D5u3Clt0OMzao+N8Xr8qjae1aGYJBoPV1dWLFi3CLe1bte97z8HuEy1HBIgAESACROB4JtAkt0ocCn4HrKoqdgwWfuc333xzypQp119/fdu2bePxuN/RjKZmFN3C4TCmDeJNXKyyshK/LW7fvv2kSZNWrFghNnegAX1ANyFTV1d37rnn4vmkKHKkRPmEzzZOqk29kC5+APAKwIiUPFiF4Qq8BPAJMOey4TEHtMNN0KxbIJeR/SIujllrRy4Qv1TMD67f0TtdPziZfcGGrQBMwbZ5uIbrgedwB7TDOw822UcmCec8JmHP0PIjLLVbUemimnfnraF54yXwPgPI46pQxMZ1ArA2hgBvvLEkXBYVorMYVLZq6XmOuO69+013YN/bfvUWf7t9+/a333573LhxN9xww1VXXSXszyglC20anebhcNgvLuNL3d+bRDwX/jub1KKJRAITVC6//PJBgwbNnj173bp16G33PA87o+C+YS4n/tGhRQMz1v1HQdrBvs8y3UMEiAARIALs8519qwtnnnkmfpYFAgGcbbZq1Sq/7Y9YEYEjT4AE6CPPnLb4PQnoOrO9rF27tqamBjOMxGRePNFtIkD7b+J81datW3ft2vXPf/7zvntAdfy+TOgeIkAEiAAROBEIWJbld2Vici4euGM727Zte/HFF4cOHXrppZf6VTmhDIp2bf57cByLxcrLy1GSa9++/cSJE1etWoVrVlUVJ4EKwiJLuonKJhbwD8Qy/jtPhLFhGPPmzQsEAti8EXVPKZqQ2l34J8X7FOAfAOOS2XttqGlwp6Qt3ujPU9CujIAaleZ91WeUk7MArxSKUzPZgQ11o+X83KL9PkABwGN2Zxc8VJ8xOHr/ArTODdTP59R7Xa+LovR3oVpx7klrj+W0zwAywJI3WLtDh8vZFv/JpHF2ueBHF/tfSIGgFAhK5eWJV/44X6jPHpO//btfeuzB/LdvvVcoFADAsqyVK1fOmTOnV69e1113He4DKsgo9/u/a/Gnc2C1eSABukktiqvFVeHKQ6HQ9ddfX11d/fJLL3/yySdo/MfvXUzTNAxDiAWoQYuf+x7IwRw+LUMEiAARIALNnoCmaS+/9LJw7OFHT4cOHUR/gmZPgA7wmCVAAvQx+9TQju1FAM9LHdtBkwgALF68+JZbbolGo+Xl5VjKN3GdNCn6hXUlHA63bNmyqqrqk08+QVEbs/n22h7dIAJEgAgQASJwQhJwbEfTtMWLF/fr1+/666/HmUZCZQ6FQn4ZWng8hTzn/+2VV145ZcqUZcuWiUDeJmoafqwLNXm/g/0+CWLJ/f62ed/p2M4vfvGLli1bCtFTKotJocqbBt77BcAjDebogje0wZy0VfsAoJZ1AjRNphy74Lhgu40x0HspuKjmWtz+/IkH9+2Sh6YLw5Opuaq+jidvGEww1htdz+ilRvWZu6n3Jp4DWGjAiHp9iAndClAlw5iC86IKa1zufXZdJj0bABq/8hxpTTF1zf7jH//UqD6X2g+WlyfC4dB1P+mgqvJhEaBxTw3D0HUddV70IKMB2f/63Lx588KFCx966KGOHTu2a9dOxEZjtYl/EaLUFM/Ft9ei4q9DDBqPVwoGg7FY7Iwzzrj66qvHjRu3aNGi2tpa3FtN03DHmqjPND9g79cd3SICRIAIEIESAZwshZ81+KX1u+++i9EcxIgIHEUCJEAfRfi06UMjgGIxTkgEAFVVPc9raGh44IEHrrrqKkx/FmcCTQb421AohI3jg8EgToQ8/fTThw0b9uWXXx7artDSRIAIEAEiQASaBQHUsPL5/JIlS0aPHn3bbbe1a9fOnxiISRrY6Veoz0J3FrobRm0EAoGzzjprwoQJb7zxBuIRih72FTT5RdwpdORvGewXs1h+v79txneapqlpWn19/UUXXSTgB4MRSYpJrc7s9fyfHqrLjc9rkzNMfW5g6jM4YFrAcy5sl/3v8dRklJwb1WOHO5JzAJ+6MGunNVr17inoU3Ym/84lZ9uzXaY+ay4YLkvyQAGaP9jbE8Lh8l/IAF8BTGgo3mNCtwanRoM+Xydny/YG7nhmT71lg+2B5ZUEaB4qbRtuIa+e9sPTJSnQeGXabDgcuvzy/8nnswDMgSCu39sBja8NoT7jTcd28LsQnLmMCRjiVYTzA/L5/N///venn3561KhRP//5zy+44AJ/qel7LoL++/1joTXjH0swGCwvL8eATvEr7JGI8/YCgcDJJ5988803jx8/fuPGjUKDFi9+EqDFc0QDIkAEiMCJTAA/DvCn67rLli3DjxWUPuLxeIcOHfxNNejj40R+tRzdYycB+ujyp60fAgF/wS08IOIk9qOPPqqqqmrTpg3mcuDXfbFYTJijxbnBfk8GJEkaNmxYXV2d2CGM58ebOF2F3qkFHBoQASJABIjAMUsAZ+7j7mHShZjuI/bZ87z169fPmzeve/fu//3f/+3Xv5qM8fMU2wb6f4Ufpvj97iWXXDJ48OCFCxdms1l/mofYnBiIj/J97xG/EgOxDA32JfDxxx+fdtppWOSURWLsqYlEpYrEwLcW3vf1Ry+p9Rn+GK4zu1x4tlnKMrYM9LhUzK3HuGaW2gywCeCRZHFIg9IznR6dyaz0IAWgMuezxXVnpj7zQaP32d0T7WEDFMGrA3gPYGZBHphRu+eMnil58O6Gabt3rfDsNNeM2eb84Rk4NpkoXtWnXzBYJkkB/pM5giVJKi8vX7t2LQuIdm3xwjhG6rE1a9YsWLBg7Nixd9xxx+WXXy7+OsSkATH3DktQ8bWN6JgdCoUSiYS/LsWxKFkxbDoUCuGqzjvvvG7dur3wwgvvvffevi+J0lPpuujpPtACdD8RIAJEgAg0MwKe56E5D79Gvfrqq9E9IAJLV65c6f8MPUY+RpvZs0CHczAESIA+GEq0zDFBoMmbprgpAjTQHL1w4cJOnTrF43H/9EZ/Kb9voY/3RKPRcDj84x//ePLkyTt37rQsCyt4wzD8XxgeEyxoJ4gAESACRIAI7I8AZgsIBQoHnuehBv3VV1/NmTPnt7/9Lc7NxJZokUhEKGX7imjiniaDiy66aNiwYa+88koymfR/ZSt2SnxDLO7Bz2v8+Pbf6b9ffLjT2VETRPvenDNnTjweZ2pm2f/P3pvAR1Gl68PV3fRKZzMQAtkkCRgQZAnDOqxDEG5QcQG5bPOxeUXlD0SEABdQhkUGdbw64gXRQZYRRC7rIMtFlss6rLIKAkJYshCSdHe6uqq6qs43p97ktewsRtYsp375dU5X13LOc6rOec9z3vO8JpPV4qhfh7NyXJTj3cObruHRRT7OQPQW7wUJZpFywQohhbwka4EHv+H9E3PyR9/Om1hwZxlRrmuiG16qlgG8M/3U5DOKfZ/BcdpPL+sj5CYhB4my0F0w+fadV++4R+UWjMvK+sjt2kn8GdoBPztLF3teE5X4Bb8r3/3V31dznMFitplMFoPBFOSk8So5jtu0aRP1nZfFgIekuCSP/j/4KAiCIPvlmzdvzp8/f9y4cR06dAgQ34RVBchNIweN3HRZ1inaqAAITDmAD3W7du1mzpy5atWqjIwMBEJRFPbuIBoswRBgCDAEagICEDgaGv/z589brVa9adelS5dK24fWhNphZdQjwAhoPRosXakR0A9K9Wl9ppEpzszM/OCDDzp37gwmfkUIaBDlwCFBmzZt3nvvvZJeY/rbsTRDgCHAEGAIMAQqJwKCIHg8HkLItm3bFi9ePHDgwMjISOCwsGeEr0aj0aJt+olboM8MBkNISAjEEuQ4rmvXriNGjFi8eHF+fr6+1Eh4KYri8/lKpZ7heOy+9aezdMURCMB20aJFaLfQ2rSbOTPHxYRvOr6/iONFqld/D5BgFjRpbuLP9fLZhGwnZFZ24RvZOZPy76xUyDFC3Z8LNeJYoOrRVHlDk5EuFt1QtOCBgibeQai48z5CPnEXTM7Jfz3XPSYnj7LPLs9uQq5A4EF9Bn6ZPnLoSFgYXcGmbVTuBVKLFy+GA3m+sBIOnvXCHZSC9/n02h2CIPz4449r1qwZN25c69atW7RoYTAYzGaznhTAiZ/y2Wd4MU0mk56/1qdtNltwcPAzzzwzffr0PXv2uFwufU5+CTb7xhBgCDAEGALVFgFRFF955RXsIMAnb9u2bTA3yWywalvxVadgjICuOnVV43OKLWZAAmQlgXqWJEkURT1rfOrUqbS0tF8loHEMAGMecC2BdEpKysKFCwsKCmp8DTAAGAIMAYYAQ6AKIJCZmbly5crXX389OTnZarXiMkzo1PBT3/EBgYU/YcJqtTZr1mzBggXbtm2DdZ3Q2yqKAlIboIhVcVCwB6/4KexIPQKiKOo5aK/Xu27durp163IcZ7VacQohODzs4sWLko9yzKVsisYriyohciFRbhGyTyb/5SETc3yT8u98QZTvCbmmEHcR+0wkSkDLhH4Ws8+gpOHX2Gc/VZa+TshCd8HE3DtjcgvH5vnSblHfZ2Cfb2tS1BLmA2RAtK++QuHCuQv1I+rb7bU16WcquwFbWloaTGzQhWh++ocPD0544CUrSQJeClx/APkEo1T2y263+1/SGTNnzkxNTQXJOJg8+FX2GasVtKEBHwz7WQwY/Y8cd7t27QYOHDhv3rxVq1bl5ORUEnxYNhgCDAGGAEPggSJQUFDgdDpBecNsNjudzg4dOsAdK38f+kCRYRevJAgwArqSVATLxr0ioG9SYTys30MI2bhxY//+/dFMNxqN+tWREF5Jb+KDHY+BmMLDwwcNGrR+/XrIKAz/BIEOh+416+x8hgBDgCHAEGAIlI0AsFrwCasscZ6VxmXzy6qqHj9+fMGCBYMHD27WrBnQkdjfQQJILpCUBY9m7ARB3xn5LLPZ3KJFiwkTJmzatAmptAD/U+hhy84y++VBIVBSYEFV1czMTKfDwXFckM3uNFsdnKm2wVy/TsThw4c1J+ci/QrMk+KXVUEmdDcNBHiSkHdz7kx3k2kF0oKC3F1EAf92P0QgpEIdlKouhYAuppIzCFnPy//pLnxdkMYWKpPz+Y/z7vyvKv1ASKbGPvuKL0WdBkRZKZaf3rF1R93wiNCgUKOxls3m4DijyWThOG7kyJE8z2OGq4etFWCX3rx587vvvlu2bNmrr77au3dvm81mtVpR7hmsULRL4fU0Go1FoiuaY4XZbDYaf455qHe20Kcd2tahQ4fp06dv2bIlKysL/bUhS+DKjcZzNYMdi8MSDAGGAEOgGiMA7ERaWhq4HWAorD179oAlgH1QNQaBFa3yI8AI6MpfRyyHFUIAm1RVVfUhCgOcs/Lz8997770mTZrAgNxisTgcDmimcXCO5j6O3nEZS2hoaFhY2PDhw48ePQqe19VjUFQhiNlBDAGGAEOAIfDQEYARBRDBsl+GhT6CIPA8f+DAgVmzZr3w/AvQWwHlhD0XJgL8K/Fgk8mE/Z3BYIiMjBwzZsySJUuAn9K72ZbKPrPu76E/C+Xd8Nz3p9u2aQOVG2KyGjjOajQ5nc4VK1boqw8uoSpE0vhnHyGXCVno9aV73JO8Qvqtm//jd/1IZLn4VsUMMzg+q4Ee0NoU/C1CNnrl+XneUTn5/1++Z2yed1Zm3k5FvkxIFqFu1KKm1SGqRFBUGl9D8Kt+SkP/9b8+oaohFjtEHaRT/rWsRmOtESNGFN+/2v4HqxWLB9NLhw8fXrZsWVpaWosWLcB/Tc9H4xsNiQD2GSMc6qlnmHAym83gZmG322GFX2Ji4ptvvrly5crLly+rqsrzPFrRsLhBFEWY2cIcsgRDgCHAEGAIVFoEoBMpKCjARW9AX/Ts2VMUxYB2vtKWgmWsJiDACOiaUMs1ooxoOpdDQIM9DYPq8+fPjxkzxmq1Op1OdPtCfxMck6O5H3AMx3EJCQkTJkw4deoUrEquESizQjIEGAIMAYbAw0VAURRYbSOK4uXLl9etWzdu3Lju3btD94QEUwCbDLyVvi8Dfgp4KOzR4uLihg8fvnTp0mvXaNQ60LDSez1DWfU9rD79cJFgdysPAT8v5OXlvTT6j5yVqlhYOSP1qLXbOI4bPnz47du3sSpBPINojsmXCdngJ2mZ+RMEfhKftVDIPE/8hUQmikqdnktsIMRRFEtQC2B4i5DNhfIsl++NQmlYjvu1Au+f3PyyAtdVSj3LHhrAkKpH+wlRi+Mg+gqpMEhqaqr++TSZTOAQMGLECL3vc4ksVLcdOJGDCSzh1atXN27cmJaW1rNnz+DgYHjlbTZbSeoZXSgC2GfwjwYuG9HGBFwwIiLi2Weffeedd1avXn316lW4OyytkCQpYCIK88YSDAGGAEOAIVCpEJAkac6cORBcGthng8Gwa9cuVE4D+61S5ZllpgYiwAjoGljp1bPI+iGx3gNa39TqB9WCUCSMuHPnTnQfQ7oZmWiU4KArW4OCUJcDErCKOTk5eeHChYcPH2ZmevV8tlipGAIMAYbAo0PA4/F8+umnY8eODQsLg04KYpGZtA2CB5q1DdPwE3JP2KMBS2WxWIYNG7Z06dLr169DsQRB8Pl8grZhRyYIgr7T1HeymH50qLA7/xIBlfjcNODkLZ9r7qcfOUMoWQkqkPDMtGvX7scffwTlmXeKhQAAIABJREFUFsotamdnE7KbkDk55E0PmezzvXvn8veEuOhPMlG0P+SgMVEsxAFkcgEh33rkP9/xvlHI/4cgjvPw73p938jyMUVxE6IofnCcVgiRVSrkQc8mJDc7N/l3Rc7aHMfVsloMJkqaWyyWmTNn/rJg1fwbaqmrqoq1g2XWv4Mej8flcu3du/edd94ZNGhQcnKy0+kE1W9c4lCSfcY9aN+azWaHwwF+0MhEY8Jut4eFhXXr1m38+PGbNm3CJgKzxBIMAYYAQ4AhUAkR8Hg8oigmJibCjCMYfl26dIGsStqmZ0UqYRFYlmoIAoyAriEVXVOKiaPigET55VcUxefzLV68OC4uDm10sM5Baw8+8adSE0ajMTU1dfny5eCqBpONoLJXo3x5yoea/coQYAgwBGogArA0kud5QRDAoxn7CJBHgE9FUUBhY9++fX/961/79evXsGFDZJcCEkgtGY3GoKAgm80GLBJ6N4PLM3RYTZo0GT58+MqVK10ul55WhroI6DEr/rUGVmVlLjI1ZmTJJ0unTp3q2LGjyWyG2g8PD4eAk/369Tt27BjMMdym7LP0Z94/tkAYm+dbUOA7qfHDRZobegK6SH4D/J4pkewnaqEm7nyOkLdv3Zng5scUekZlXvvY7/mWiD8RRSCEF4qCDqJjr8CLiqTOmvk25MrssJgsJqPZAF8NJuM7f5rFi2VETazMuD/0vIFVKQjC4cOHv/nmm5kzZ3bt2hUnqADPUj+NRqND0wq32+168eiy5DuMRmNkZGSfPn3ef//9nTt3ZmdnYwPi8/mgJVFV1eWi0xaSJGFdw2JEfUvy0EFiN2QIMAQYAjULgc8//xxje0DE2u+++w4WakP4YmyiaxYurLSVDAFGQFeyCmHZuTcE9MauPl3+VWGlIRxz9OjR4cOHgx1vNBotFovBYAAyulRrHneCNQ9Hjhw5cu3atYx3Lh929itDgCHAEKhRCIDprw8ih2txeJ5fs2bNtGnT2rdvb7PZQFgDPJpBWyOAfdYTRui9GLBGx+Fw9O3b9/333/9VN0Z9d/mb0jWq+qpKYTH0xRdLl9atF2GxWEACGIJemM3mp59++h97dp4W85Zk/DDhp0tjs3L/36XM9SKhHtSaPAfVygjYwH9Z2w+RCa8ScpyQ+VeyJuXzo3LuvJmb/anE7yPkquboXHS2ShRJFXjRL/gJIQf2HWzenEob061W0X+j2VA7uLattvXLFcslWS7kecZBB2BfzldcWC0Igtfr3bVr1xdffDF+/PjnnnuuTp06MBeFeqB6tzgq0mK16lsV/YSWPh0gQp2YmDhkyJBZs2Zt3749NzcXdHtgUg1oDqCeQa0e2jpoUsopBfuJIcAQYAgwBO4dgU6dOoEdCI1/jx49wMjEMLOMgL53kNkV7h0BRkDfO4bsCpUIgbJGzqVmER008FdFUdxuN7hyLFmyJCUlBVU19TOKRcOm0v6hr7TVag0KCpo4ceLBgwfBKMe7sARDgCHAEGAI1DQEwO7neR44I6/Xe/LkyaVLl44aNSoxMRHdljmOMxqNIKkBXqsBAhrIGSFJBAQ0UNImk6ljx46ffPIJdD0AMg45JEmChfwB4JfVdf7q/oDrsK+VBAGv1ws5uXr1atu2bTH0HJgtRfZMg5Cuaa/NOXZqcWbhiizfZThBlKlQRqlbsYKzQMhFhRwmZO4N9/iMvDfzPZOzs/9W4D1NyB1N8flnuY7iS127ciOlRy/6JJuMnNHAUb0NzhZsozS0iasd6jx1/rR2z59PLTULbCcgIEmSz+eDlkTvd6zHh+f5zMzMXbt2LVy4sHv37rGxsVarFcloq9UaMLOF7Yk+gW2LXvYHFH7gWYqPjx82bNiXX3556NAhuDu2NviVEdD6emFphgBDgCHwIBD47rvvoFkG9Wej0bhnzx6gIKCbCGicH0Qe2DUZAhVBgBHQFUGJHVNlEChrtFxqAcBBAxcj44BNf3BeXl56enrLli1h0SK07KV+om8RUgYgaGgymZo1a/bee+9lZGTor8zSDAGGAEOAIVBDEEBP5/3798+bN++5556rV68ediXIBAH1HDDfiYxzQELPE/Xs2XPq1KkHDhyAHg11nGW/DLIePm3D/i4A9rK6zl/dH3Ad9rVSIeB2uwkh2dnZ/fr1MxppTEKwZMxmsy0kiLMZOFstzvlYZPfnp3+xfvfZ65Jf814ukwSmP/gIySJkY574zvmbk28J0z1k4k/XvvTypwnJJ4RKPstU7lkm6p0cGvZwx9YdrZ5qU8tgAfdbqgoCvs9F6iBc/BMJV67/hPcUZaEowmGlgrKyZga0fWAZH/i4oWWLUQRR5Mfj8Rw8eHDx4sW9evXq1KlTvXr19E2Kvj3Rp7GZKqpBoJ9NpgBbFyzejh07zps3b/Xq1efPnwc9OmxDKiuELF8MAYYAQ6A6INC/f39oh2EJ3dNPPw1+dbAoirHP1aGOq0sZGAFdXWqSleOuENAvhS7rAkAc7Nq1a+jQoTB4w/XODocD3dbAjtdb6gFph8PRo0ePpUuXut1uIAX0nQHrHsrCn+1nCDAEGAJVBQGQeMbcyn756tWrO3funDp1ardu3bC/gPC2GCSwJA3kdDoDpJ+w38GepW/fvpMnTz5y5IiqqpIklexWUFe6rMC8mE+WqMYIqKoqiuLKlSshkDJVVKhl4moZOXMtzmzmzEGcMZTjgjjO3qZl23f+8+0tmzfzVK1c8nh9NByhxg0X8jwhpID4vyfyPwiZdSt7ao57podMz7jzrUIua3rQ19wCJaAJKci6k33t1oI/vVvbZLNwtewWu4kzmTgTfYbB/dnIBYeHcBw3ZNjg23k5XsFLiKoQBf+qcXU80KIh2xuQKOumOTk527dvnzx58tNPP123bl1oZGw2GzY+mMBmB7TpYKFGyUZJLw1kNBp79uw5ceLErVu3ZmVlyX4ZjV7Inj5XMGcGIRkFQQC5Uv0BLM0QYAgwBBgCZSFw6dKlgGYZ/d6wOyjrXLafIfCQEWAE9EMGnN2uSiKA6xw9Hs/KlSt79+4Ns4vAJoCryK8S0HqntpEjR27fvh2xKMsrDQ9gCYYAQ4AhwBCobAiUpFEEQZD98unTpxcuXNivX7/ExESr1QoCCNhfFHsQanycxuuUJKDhGOhcgoODsfv4l6Jfenr63r17wbtQFEUIBVYyJ4AVKE2VJKDLOr6yIczyc+8IgIEhCMK5c+eeeeYZneOqkaNaGBYjZ+E4M8dRethiosoMkZGRXbr1+M8Zb589/4MkU0VohRAv8V4S72wuyPw0O3NBbt6HXukvtz37CMkjVDwaPo+dOfPq6FfbNmtt5Qw2zkS9sSjVbTRyxp8JaANnqMU1iItauvJLKJ2kiKIsIPuslCkCcu9gsCv8jAD6TQMvLPvl/Pz87777bvbs2ampqQ0bNgTSGZov4JoD+GicQgOZIL3fNBjJVm0zm81GozE6Orpv374ffvjh7t273W43Lgr5OUNaCknqgP3sK0OAIcAQYAiURAD8D0aOHAmtLrTbo0ePhiORYWBNa0no2J5HhQAjoB8V8uy+VRIBSZJgJH/lypX09PTIyEho6JE+gK+/+glqevHx8RMmTLhw4QIsosRF01USGpZphgBDgCFQMxAA4gZbbNkv5+bmbtmyZfLkyX379m3QoAHHccHBweAMqO8ODAYDSq8G7MdORM/pwDHdu3efNGnSnj17MLCt7Jd5nne73b86okDPl1ITNaO6anQpA54QQRC++vtXztrBZqPFROWXKQNtpNwzDbZsMVmN2jcaI9BiM5mtHMdFx8b9vku39JnTZ//3n2cs/Sh99Yq3/mfdK0tXvrn6f744eOC/1q15808zJsyY3OP5f7PVCaVPrNFQizPVNtlsBou9lq34OTdQ7WfNA9oR5OjcrfPR74+JxC8pItDNXsHLCOhH+KRCFEGwRTEbGRkZW7dufe+991555ZWWLVva7Xa9+jPULLRXAdQzumUU1z5nMpkgpKrZbIapuOjo6P79+8+YMWPr1q2ZmZlwU6/XCw4fmAeWYAgwBBgCDIGyEABD9MKFCzALCEJJNpvt0qVLoMFV1olsP0PgESLACOhHCD67dVVCAEdxsl/2+Xz4dfPmzYMGDULuAK3tUhO4/hrUGJGkaNmy5YcffliqCHVJjPDWJX9iexgCDAGGAEPg4SDw448/fvrpp6+88kpiYmJQUJDBYLBrG7j7IS9Tal8QsBN7EFzA3rZt29dee23z5s05OTmKooC6a0lqRhTFkjv1xS+Vd8ad+iNZuhojAFMmYDz4fL6CO66hA4eYiwlos9lks1tMtQzUYdlMlaI5jrPXdlrtNGEw1aLuy2Yj5+C0Pxtnq83VfoyzOynb7KBuzkU0NjzW9DKcw2y3arrPHGeg16D6G0USHPPmzxVlwScLMlHcXhchqqb7TBgB/WifQJ7nkf9F92RY0oEZO3/+/JIlS9LT07t06YKRUUpln2FnQEOn/6qX7zAYDI0aNXrmmWfmzZv33Xff4d3xvizBEGAIMAQYAiURAEZi/vz52CDbbLbRo0f7fJqCll8ueQrbwxB45AgwAvqRVwHLQHVA4Pbt25988klycjIIMME8ZElXEb3xDccg3QAHp6SkrFq1ChABWgHGjaCIBxKf1QGvKlsGPfsPrBAhhOd5qBpc504Iyc3N3blz55QpUwYMGJCSktKxY8fevXt37NixZ8+e6enp77zzzjfffIOjLP1lqeam5t5YPq9UZSFkGWcIVDoESiVkA95KiCR+7Nix+fPnDxo0KCEhITg4GJp05F+ARw5o5+GrzWbDCUjYgweDb6DRaGzbtu2IESO+/fbb3NxcvZY0ZO+uUcPS3eN17joD7MRKh4BK4/xd/OHCKyNHlfq4cgbOYDJS8Qz9ZuJo/MBaRs5Ui6tl5kxmzmTQ6GX9QUVpI8fVMtQyGOjTrTlYmyxm29ixY7Ozs4vRANFnGq4Q/or3s/9VAwGIa3r48OG5c+eOGjWqbdu2yIDAQ2A2Fwea1L5TD3uTNl2hPRBwDO4pem446ivtcDhCQ0P79u07bdq03bt3FxQUBOhHY/gWaKVxjTmo3rOGrmo8QCyXDAGGwD0jAFGm9UGtOY7Lz8+/5wuzCzAEHiACjIB+gOCyS9ccBGCmkRBy7dq18ePHN2zYEPXydHqLaGCXlzCZTCEhIWlpaadPnwYuEiOY1xw8K2FJBW0LyJjH49m2bduRI0c+/PDDub/cYCSmF0wEv0icouA4LjY2dsOGDTCykv0yyLniGlg23xCANvvKEHhoCMh+GV55nue3bds2cuTIxo0bl9VwV4SAhhlHPBJIZ6vV2qdPn5dffnnJkiV5eXnllK4kG17OwQE/AR2DnwG/sq81EQGNgIY5zmPHjkFYC6fTSSMEcpzZZqVRCktu1JW56A999ksepd9jtdotZpvdXnvkyNFnz573eDy6lV6MgK7ajx42SqBASghxuVxHjx5NT0+fMmVKamqqTdv0ns64PBzawwCGGp8co9FoNpuBsIbTIyMje/fu/d577+3YsUOvH+3z+WAiH+WJVFXFdNXGl+WeIcAQYAj8GgKKonzyySfQeMJ83qhRo5gD06/Bxn5/xAgwAvoRVwC7ffVDAKzhDRs2jBo1qqRzB1rY5SfALu/QocP7779//fp1FButfnBVuRJt2LBh6NChXbp0QXLZ6XTqHX8ChlsBFY2/oj6s1Wrt27fvhAkTvvr7V8eOHYO19sAWVTlwWIYZAtUAgYyMjLfffvvFF1+Mj48HxVJ8bQNeZ/iKtDI6NZd6GOw0GAxt2rSZMGHCwYMHAStRFCGioNvt1rvy6ZFErke/k6UZAveIAJgroij+Sy8yLS0tLDzcYDKazGbq/kx9mI2UccatmH2m/tHFG/5YasJsNvf8Q6/jx09qs+nqL3PLCOhf4lEFv+mnySHeqaqqeu7j1KlTq1evHjduXK9evYBTBiVoaDNLtqsOh8Nms+l9peG50jetFoulRYsWY8aM+eijj/bt2wehWSAnuBaNWVBV8GliWWYIMAR+MwKKosTExMCA1GazGQyGq1ev/uarsBMYAg8XAUZAP1y82d2qLwKyX0azG/wvVFUFaY62bdvabBiKp9RhWtFOCATEcZzVSoP/cBwXHh7udDr79++/fPly9LOuvihW0pJJkvTGG2/Y7Xan02nQFhUXVZj2z2KxoN6rflgVEhKi9383mUw2my0sLEx/LpXatNv1YccaN26cmpr62WefXbp0qRw42JxEOeCwnxgCvxWBLVu2zJ07t0ePHuHh4fiGlmy3Yd4IZxbBU89kMuGLX5JSgau1bt361Vdf3bx58+3bt4GpQQ0ffVZBbUm/B9KMgC6JCdtz7wgggQjWRSHPL/58yRv/b2y7jh0oAR2w/UYCum/fvseOHXO7C2U/pZ59vPjLDDMC+pd4VLVvuFoLMi5qm76lgqcL90iSdObMmSVLlkyePLlJkybwcAU0mA6HA92iYfIPrCP9YVarFRhqaH45jmvatOnrr7++YsWKkyfpVMfdbcymujvc2FkMAYbAI0Tg22+/hfbQarXa7XZwf2at2SOsEXbriiDACOiKoMSOYQjcJQJooJ8+ffrNN9+MiIhAv1d06EAuA81x+Am96oxGI8xt1qtXr3///nv37gU1UswTOp7gHpa4CwQARkmSBEHQc/0+n++ll14CH2ccGsFKUuCOcZAOdDOMlPTVarfb8RhMFDFZZnMtqwXVOfBXSNStW/fjjz/+8ccfsTiCIMA8hyRJ+kziASzBEKixCKCouh4BVVVhPzoXQ2Lbtm2LFy8eMmRIVFSUw+GwWq366aKAN7Gsr0hA6/kRkNkxm80JCQkvv/zy8uXLL1y4gAoYmNBnkqUZApUBAYUQRcsHLwou3jt91ttxDRtyHFfLarHXdlBdDk2jI+B1MJvN+tenefPmixYtcrlcqNuLzzzzS60Mtfww86Cv+oD7ulyuw4cPr127du7cuSkpKWFhYWgpmc00FGbAYwbOfQaDAYhp+IToKQaDwWq12mw2sJZ79OgxadKkpUuXgu3k8/lEUcSnUZ8NQRC8Xi/0CCC7pP+VpRkCDAGGQOVEAKb3PB5PmzZt0P602+3li7lVzrKwXNVABBgBXQMrnRX5ESAATDTP8xs3bhwyZIjRaASnOavVCl7PkMDIhMXLW4v+6w1xu92ekJAwY8YMWGVTqlX9CEpY7W4J9K7L5Zo2bZpeYUNfF/q0wWDA4RO6OWPkMdTrgFP09DTsAcdqdPaBioezHA5HSkrKN998QwgRRRH9iSAEULUDnhWIIXD3CKBHJwjogxsITtUcPnx4yZIlo0ePhgkkfH/RfMc95SRKThDqD+7QocOYMWPWrl17+fLlgGLouRh8iwOOYV8ZAo8QASCg/Yri8Xp5v+j28ddv3vjq69UT3kxL6f10eERdeNQdTicQf/pIy926dfvLX/4S4IIKUZQhZBw+/4+wgOzWlQQB/VSEx+MB2yYjI2PDhg2zZ8/u0aNH3bp1cbkJPGYBRhQ8igHHBLTkNpstJCSkS5cuY8eO3bhxY0ZGBhQfvA1QKho7iFJDfVQSxFg2GAIMAYYAIuByuURRPHLkCCyVhvZwzJgx0JziYSzBEKicCDACunLWC8tVNUQAjV1JknieX758eYcOHfQh6dCVoyT7rPfv0JMdKSkpixYtun37NkiIVkPUHl2RNm3aNGL4qPj4+FKHPTBVgDyyqZbB4XB07tx5w4YNu3fv3r3nO6gmkDts3bpN165dO3Xq1K9fv86dO0fWjQA/HZPZHOBTpq96rGh0rA4LC/v666/1FBuoHz46kNidGQKVCAFYHKCqqs/nA6e2Q4cO7dmzZ+rUqT179uQ4Dr3qQOPIbDYHEBYBX/EdLD+RkpIyceLErVu3ZmdngxYTEBkQm0vRbcjBMQK6Ej03LCvFCAABLUhUK0NUFYUQmahZt3N4UZCJyovC2fPn/u/A/n8eO7pPtwF7iCsMIMxgwMPPnvxijNn/MhHQLxtXVdXtdv9rwd/MmTOfe+65Vq1agdFValOMKwtR00x/mMVCF5mBz0dUVFRqauoHH3zw3XffZWZm4qIZfHr19lWZGWU/MAQYAgyBR4cAzOwSQvr37w/uFCaTKSIiIjc3V1EUl8vFaOhHVznszhVCgBHQFYKJHcQQuBcERFH0er0oxwECGmBqnzt37qOPPoqLiwNzWc8/6tPBwcHIjJhMJnSXhrPq1av32muvnT9/npEa91JNhBCPx7N27drU1N5ms0kbydTWEDaaaxVJcutHNVqaRmgKCQl55plndvzvNkHgBYFXVbl165ZwpNlsGj9+PO8VPB6fxMtEUQlRJR8dmx87cfLvX68e/9aEf3su9fFGCSFhoSUuzhlpLugGLthBzhCbzREX13DNmjW6oRoum77H0rPTGQJVGwFJ244ePTp//nyQzTEajaCLB3N4JpPJYrFAGq32gGUHRa/cr/1LSkoaNWrU9u3by1rfja2xoig8z+tYaEXv/Ve1EWe5r14IYF9SyPOgxSETVSaqV/AphPCiIPolmajwExZdURQMgIFrDvQPPPOARqxYQo+AoiiiKKIxA1MX+gMwDT7LO3fu/Pzzz8ePH9+xY0c0ibGpBjPJbrcD3Yz7SyYwkkfDhg0HDx78l7/85ciRI/gM401ZgiHAEGAIVFoELl++DLNrMDk3c+ZMl8sFudUTDpU2/yxjNRkBRkDX5NpnZX94CADjgEMyvTcQuGAcOXLkjTfeiI2NxbXhFovFZrNhNELgndGPQx/zCqnq2NjYjz/++Pz587CiEG5HCJEkCYVQH16ZK9+d0MkFsub1enHks27dur59+5pMFuqHXstgNHGUluLMHBfEcU6OM3IGzmQxmG1mm8NOv9KfuNbJ7d6aPCUn905xWf2K6pUVz9Bh/26x0lOCgmpfuHBBklTi1w5RVepSpm0KIXcKC/1EUAh1N1MI2bhx47PPPtuqVStTLYPFarQ7KP1sKaa+DZzZwFm1P+3WrVtu276pwJVVdDXqrMY2hkC1RQAbT2C7gPaF0gqCsG/fvlmzZqWkpDidzlLpBmwk9dr6uNNgMDidTlR4t9lsENRFfymj0dixY8dXXnllx44dLpdLEARsT/R507ftJdNwpH5/ta0wVrAqiwDS0HdXAv3jXWr67i7LzqquCOBDAs2j7Jfhr6x2FUROc3Nzd+zYsW7dupkzZ3bq1Klky4+hNUCjXL+UDXsB7AKg8YdpxU8//XTr1q1lxYOFXGFd4EQj7mEJhgBDgCHwEBB49dVXgTEwGAxRUVF5eXnQHEGL+hAywG7BELhrBBgBfdfQsRMZAvcZAZix3Lp16+jRoxtqkX+gawEO2mQyORwOjP2NBjQmkKq2WCwvPP/C0qVLVVUF3Q82F4pVJYqiz+fDMYOiKPPnz4+PjweZC1BBKSKgTZzBYOI4u/Zn4jgDx5k4rrbF3NTEtYyKeP653u8c3EupZ8FHL6+oPlnxSHKhovpy72RNSBvbsVP7o0f/KfmFXzqMqYQQv0x8fkpFK4T4VMpAewXqF00IUVU1KytrwYL5tPZrFTFg1AWeEtBFfygmMGTogCs/XSwoKPjlLbC4LMEQqPII4NsKJVFVVZKkK1eurFixYty4cVFRUaCEExARFLljpBjKSeDBkIB5PvCw69GjR1pa2pYtW27evFkSyoC8lTyA7WEIVDkEgIAu+VnBgiCfWFaigtdhh9VwBMp6flDOLgCfmzdvbtmyJS0trXv37hiQIyQkBGOroHIauA3qo87i7CM0+06n02AwdO7ceezYsQsXLjx58iRa0YqiMJmOAOTZV4YAQ+AhI3Dp0iUY9UNbt2jRotzcXH2b+ZDzw27HEPhNCDAC+jfBxQ5mCNx/BFRV9Xg84EyHKxBzcnIWLVqUmpoKJrLVagVOBBhSJJ0DEnoaxWAwBAcHv/7666dOnbr/ma7KVwSR1v379w8fPlyPmEb4Gky1DKAVaKilEc7wSY8L4bjmHNfHxo2fM5E83+Vyy+iNbRr/952bxOsiXl4RFbefeIqJYJXn3V5tk2WREJUQSe/7LMkkP5eMGXGmfauVq1dKYpFXNAFy3Ov1qgq5nZP/+ZIvGz6eAJk0GDn4wzxbLbUd9rDIiITJb70j8FW5SljeGQKlIRBA7544cWLKlClURT0yEtzZzGYzxvmE90Lv5lYO4xzwE75TkOjdu3d6evqOHTtu376tzxcKhsJEkf4nlmYIVBsESlLPFfeJ1g+Ay0pXG6BYQR4VAjANiSvYQNcOeGHoNWS/nJWVtW3btvfeey81NTUuLs5isTgcDhBcCmjw4SvEBsefMMIHXYhmsQQFBUEwww0bNmRkZIAGq6ht+mw8KkDYfRkCDIGag4AkSUOGDMHGqlGjRvn5+awhqjkPQDUoKSOgq0ElsiJUbQR82gber6CIB9EDgOy4cePGBx980KxZM3RwDiCd8St0RcC/gOwpx3GQaNKkyRdffFGW20jVhq/CucegDYsXL27evDn23BC1BgYblH0uSUAbzRxXh+O61wmeEh/xVbOo4y3rZ8TbLzWPOPG7pK9c2TQHfpnIhJcJrypUMlNbpAmiG5A/v0ZAUx0OkRCfQnw+8szTx1ol/l+jqP+ZM/0W7yP+Yg0NRVE8Hi8N6yQolLgmZNPmDaNfGU7ZZ+qcQ1U4YBBlMTs0jtxuMUUkt/zDpYtZgq+Yya4wLOxAhkClRSA7O3vr1q0TJ05MSUmxFm+wsNpkMoGrGsYVhK/h4eEBms4BXHNZX3v06DF58uS9e/dCAMMAUx683iDYGpMKrbQPDMvYfUGAEdD3BUZ2kQeEADbO5TfF+vlLRVGuX7++d+/eKVOmDBw4sGnTpjabDY1nvSs0CEmD8ay3EvVpo9EYFhbWvXv3OXPmbN68OScn565Lqs/kXV+EncgQYAjUKATOnTuHwYE4jvv0008e0pDZAAAgAElEQVRBeLNGgcAKW6URYAR0la4+lvkahMClS5fS0tJiYmI4jsoTozUcFBSE3DSuNASSBczrIlkJ7d/w4cN37tyJqOGiwvz8fHAhwZ+qTYLnefArlyTp6tWrvXr1cjqdAV6TCCYuwwQkYX/nTiP+6wM+qeH2pKiLzRu4ksLFJ8OFFpE53Vqd3reb+BVKK8v0T5KJrCpE8WsezxRBOpDXqCuNSCakwEfWbSPXbpF+/S48EXesccyBJxv97cxp4pOIrJHNsl/2C6Lip99Umc5HKKpXIS6FeLKzMwe9/IrT0tTCxZuMDqOJM9TiDCaj2RpUq9Zj5lr1I+o+sfSLv0PF6V01q01VsoJUdQS8Xi/qJuvLAgGmJEmCFmnp0qXjx4/v3r27niAoizjW78cXGddfm7UtoM00Go0Wi8VqtQ4aNOi99967ePEiMBrAMqMbXVn+m7Bfn3+WZggwBBgCDIGHj8C9tMbbtm1btGjRa6+91qdPHzD50LQGyTvUOsPJTqPR6HA4zGazvt+BudG2bdump6evW7fuxo0bgAM4lOhZcj3djP3LwweN3ZEhwBCooggA0fzss89Co8RxXEJCAoR6KtW6rqLFZNmu9ggwArraVzErYHVAQPbLQCm63e59+/YNGDAgODgYFKLRYgbyRW8W6+kbSIN/dFJS0oQJE65cuQLWMNjHkiSBuVwd8CpRBp7nx40bBzPG+pWVyFhpEs8GZ+1Qo7FIdzkyssHwYeMyLhGpkPTufimuTsaTkSTWQZLCSas4d/umJ/95gAYQlDSnZpHIfiLLlDWmf5R51qSeCQQflOn/O7fJMwOORjXa3rz1+aioQw3CD7ZrdfDcOVIo0utADEEae0eSVFkhikoUWSWCSniVFAI9fecW6fLUe1ZuoJXrYOYaGo2PGU0Ok9luqlXbwD3GcWEcZx48eHCJ0rMdDIFHjwAsQdAHmJL9siiKgiBkZGRs2LBh7NixXbp0AY9meEn1LZi+ZSsrrXudaRJ8pe12O7SWsNZh8ODBCxYsOH78OC6JAGggtiE0g0gNlJN49ICyHDAEGAIMAYbAPSMAgh6XL19eu3btu+++265duwYNGoArtMFgCAoKgt4ETO4APw/ojKDrAQPbYDDEx8f37dt3zpw5W7ZsycoqihQNzBF2Mfeca3YBhgBDoAYhgBKdV65cCQkJQe+KefPmQduin9+qQbiwolZNBBgBXTXrjeW65iHA8zxYyaIogorxl19++cLzLwTQqXpqRk/flKp8N3jw4HXr1rndbnAADGBkqgHGMCG8cuXKiIgIm7bhpHEAV6V9NXGco7Y1rG69oOnvTBYFogrEd5vMessdHXr08TBf07ok0sw3jbrV9qm9J76n1LJAiI/+ySKR/ESlBHSxO7RGQIsK8clAUftJ+rjbwXUORDyeFxF167E6x5s/uffMGUoweyl5TbWji2QNi92ftStQYQ6FEFmT1nhlwKm2USc6NLjY0Pr3OobJZq67iWvIcRYaH5GzcpwtNLSO2Wzu1q1bTk4Os0WqwQNcbYqgZ3I1gRrF6/Vu3bp1xIgRjRo1KvkyWq1WkGLHRkzfspWVxusAEQB+0KGhof379//444/PnTsniiL4WQuC4PMVhf0khHi9XuAFAHB9bstKV5uqYQVhCDAEGAI1DQEwt6DZhy4pAAGXy3XkyJEPPvhg2LBhnTt3DgoKQrmnkhw0xGjRr5xD1xCHw5GQkPDss88uWLBg586d+tVp0LkE3Jd9ZQgwBBgCJRGAMZ3X623Xrh1Oj4WHh2dkZECrol9sUfJ0tochUKkQYAR0paoOlhmGQJkIKIoCatF4hNfrVRSloKDg3XffRVFjPTWD3A0k4CfgaPQ8bHR09NixY3Nycqrf+h1JksaNG+d0OsGHBR1YkKj6ZcL0u6e6fPJfS2iEMVIkybzuK9I07vDjj2U1rUcSg0lsUGbnNscOHwL2WeaJ7KN/kuYBTQlombLFmt8zdWmWZaLcuk3lnVd8ThKi98VE3QkKyq1fL7Nxo5MrV9KL5BYKud5Meiy9paIofs39mVAPaKJIChV1lmQi+siCWXLLuGMtI6RmwWrrOtlNQrfGhU55zNmjVq3HuCJFFoPmx03LVKdOnV27djEOGl8WlqgMCOTl5W3duvWNN95o3779L189+s1oNAZo4Og5aH3LVlYaGGer1dq2bdvJkydv3Ljx4MGDUHCUDcWvoiiC3DPs0b8sZZHO+v2VAU+WB4YAQ4AhwBC4CwSwMQ84F4Xp9PtFUVQU5dy5c1OnTh0zZkzPnj31fRAS0waDAXlnsDZtNpteIs9isRiNxiZNmgwcOHDJkiVHjx7V34WlGQIMAYZA+QgcPHhQr1D/2muvge2qRQ/ylH8u+5UhUHkQYAR05akLlhOGwG9AAK1nkE9VFOXq1asjR46MiorSe2GAJ2AA16M3nYGbhlN69uy5ZAmlX2GD9T56Xqb4lyrwXxCE27dvt2rVKqDs8NVgMFgsFmThLRZLjx49tn+7nco2S5QM9hNySyDfHiSJLU7UrZudWFdtVpckhfGtGp75bgfxitTxOV/kfUQV6Z8s0lMoAQ1UcpGgBiGFfuIhZOdRUi9+b1xcXmJkQXzYT0/FnVi9lPA+4lNpTELqMy3D+X7qdA0Utqa/4VMKC0WK9trVJCnuQGL9nIb11IQI8mR4fofHf2jfZMWls2TalI/NVjvHcc4QqspitlmhjFFRUXv27MHo8IQQt7bpnxx9ugpUKstiJUMApqxwxA5fA1qMixcvLl26dMiQIfXq1YO4TyVfSWyRAn4CQtlut5vNZpvNBofpdTmNRiMcY7FYkpOT33zzzfXr1xcUFIAnCLaNAVmqZCiy7DAEHg0CPM/n5OTAEoT09HTIhCiKuNS3+s1JPxqg2V2rHQKKopw5c+azzz5LS0vr0KEDBMUNWI8IUtHQqTmdzlKtcZPJlJycnJ6evmrVqoyMDOy5ygEMohSUcwD7iSHAEKiWCCiK0qlTJ47jgoODnU4nx3FXrlyBksLyvmpZalaoaokAI6CrZbWyQtVEBIBkkf3yuXPnRo0aFR4eDot0QHwDydaAxYNIQIOVbLVag4ODX3nllSNHjgSAWIVIHPB2HDx4MBQKwjDquS1cvhQUFNSzZ88dO3YQQkTRr7HPhBdJgUxO3SDNu+0IefxKdEOSVI8kOm91anx582rCe6k2hkiIT6VssV+jjin7rP2BlLOmnkFklbglci2PNO20uU7CjbqRnoTHrrSMPDDplVuql/gl4lfpn6wUXYKo0s8EtCqpRJAJ8flJxlXSIum7xAY3GtaTo+uTx+sLbRJyuzU7eWof8RdS/Y7DR461aN3CVttqMpuDQ0OgpFDGTz/9FB8M4KD1pLM+HVDd7CtDoIIIIEsFCdkvnz9//t13350wYUJ8fDzM9IBrs74V0r+PZRHQcAyM29HLDEb1FovFbDa3aNFi4sSJX3/9dXZ2dkAQcBAUkiSpCjVcFQScHcYQuF8IpKen2+12IM4OHjx4/vz52NhYo9HYsmVLWHR1v27ErsMQqMYIiKJ49uzZL7/8cvLkyV27dgX3Z1jBo+/1cDGivvvTp4ODg3v16jVnzpz169ejeDT1idA2CDVWjWFkRWMIMATKQeDAgQMWiwX6a4PBMGbMGLC6IYBTwDq/cq7DfmIIPHIEGAH9yKuAZYAhcD8RQIE5n8+3bt26/v37o9sF2sFI98CCQVgziL2a1WqFA9q1a7do0SJ0b7yfuXzw15o2bRoU3GQyWa1W/bpIjuPgpz59+mzfvj2AtxIEKqHh8ZPfd/9ncJ1jdWJyY+OkJ8Lzft/o8vqVRPASv5+yxhBlUKZ6G0XUMyS0YYIMIQh5kVy/RV586VJ07NnEJ8njj7sa1zs45y1vfjbxeolfpo7PsqIR0JQkkwjhiwhohWjsMxWG5nkysN/V2PBzCZF8w3qEekA3yGrz5L7d3xJPHpElUuglClF4kf+P1/6jltUSHBoSHBpipus+i0q9YMEC2S8XFBQgUQiKh4qiMAL6wT+JNeUOPp9vyZIlEyZMiIiIgBE1kM5WqxXZZ2CNSw7LsUXSD8UhZiC8qvD+2u12g8HQs2fPuXPnrl+/3uPxCIJQ0uaWJAk0nRn1XFMePlbOu0UgJiYGOkSn07lu3boBAwbgO7hx48a7vSo7jyFQnRFAw0lfSDCoUIb1+PHjq1evnjZtWqdOnVACDl+ukgmwxsFbAqU8oqOjX3zxxfnz5+/bt0/SNljTJkkSmnP6PLA0Q4AhUI0RSExMtFqt4Ptss9kOHToE7QA2DtW47Kxo1QwBRkBXswplxam5COiZYgxXSAjxeDyLFy9OTk7WM9HI+IBHBkqvgpshOM+iiTxkyJDt26k8RWXekIfy+Xxr167VRy0PWBfJcVznzp03bdoEfiVox8ua37JPIj6JTJyY1fKpmzENXPEJ/tiomy0aHt+yioia77PbSw9Qi7EIIKC1rzRioKySQh/5/DPSMOpoTP3c8DrXHwvdP3rYVW8u8fnoyZR9BgJaJSqh/s6UfVYlqv6sUD7ar9CLzJ7tahR9ommskBChJtSTE+vnNH78wPp1lL8ukqnWLqYQRZB8//3Z4lpWi8lsBgcccH43mUzz588HfGS/jLoEjIAursMa/f9eWNrDhw+///77gwcPjo2N1b9x0HSA3iXHcdie0FkRqxVoaH1YVGyOsM2BBLRLRqOxa9eus2fP3r17N6FTMjxOGsFTLWpbja5FVniGwG9HoKCgICQkxOFwwIsmiiK8dzB5CQpOv/2q7AyGQA1CAGwqatFpxhXYk2huIRCnT5/++uuvJ0yY8PTTT2M3ZzAYgHEO8JDAAyABHajFYmnduvXw4cNnzZp17NgxvDJLMAQYAjUBga/+/hWuYOY4rmvXrrAkAlb74RC4JkDBylgNEGAEdDWoRFYEhkApCAT4aEiSxPP8lClTwsLCgJ0EWVWgh5CixUSABcxxXEJCwrx580RRRMYKOzzcU0o+HtYunAG+cuVKnTp1IEqDyWQym82oEstxXL169fQ619SdpPhPJgqvFt52k799RpLizsTVuxHfwPOY43rTxHP/2ER4gZbEr9A/wU+pYTiRBh7UnKBRi8OvFVlQqHBzYsz2x+v92LD+jdioI3/occDnoxEFZUXjjmXtxnp8VPCcLpLxIIRs+ZbExO6IrnshNjy/eSxpHJn7ZML+ZUuJTySi5jKtXcOvEFHLFz1x5VdfRTZoULL6ZsyYIftliLrGPKD1qLM0zMR4PDSACcxPaIo0VH1c/457PJ7c3Nxvvvlm9uzZycnJJpMJZTFQ5wepZEzYbLbY2NjGjRvHxMS0bNlSr4dTck0GKGlyHBcZGfnC8y8sX7781KlTJSsIGzdMlDyG7WEIMATKR+Do0aPwnprN5sTExG3btsHqBJirVhSF53l8xSpDL19+cdivDIFHgoD+HdGny8qMJEmnTp1atGjR+PHj27dvDypVFosFwxWazWb9BC2ac0hYQzfaqVOn119/ff369VevXkWfaGCjkBbHrhw697KyxPYzBBgClRMBXFQRHR0NM1UwI7Vs2TJ4qdFor5z5Z7liCJSKACOgS4WF7WQIVHkEwA7GYiiKgt3YgQMHRowYAat4DAYDdGYwEEVLt5zE0KFD9+3bB1cGfqpSRT9o06aNPkQDFsRut8+cOdPlcmGEpaIiaDywTKgEhkDIsVOkacKRyNrXG9f3NI3Le+Lxc3P/RDxaJECRUFVmUdZoaJBvVikTrSegaUxCzTv66lXStvmhuMfOPBmX2Tj25B967LuRSaMOSppzNHVeBhWPn2tIY59V4nPnS4WUSs64QDp0PBn3+LXoyKwnG/KN6996Mv7I2tUkJ5cqUNPrEAXyorHPfoVekW4HDh0Mj6gL1Qq1DIusd+3aBRPmjIBG1FlCTzoDGsA04YqKo0ePzp07949//GNSUhJQxjB3ZdE2fL+QcQ5IJCYmwrQWDKpxZgimhWACDC7boEGDF55/4aOPPjp06BDOJwVUkH54r08HHMa+MgQYAr+KwJo1a2BAazKZunfv/sEHHwDtBRrQsI6KvWW/CiM7gCFwFwgAbQQe02fPnt28efP06dN79epVp04dEI7DCVrQx4OO1Wg0AvscoGRls9nat28/bdq0NWvWeDwe7L5L8s7Qt+LU8l3knJ3CEGAIPBwEcIXurFmz9OskkpKS3G435oFNDyMULFFVEGAEdFWpKZZPhsBvQwDGjYqiBITMhv1wrY0bN/bv3x/XziOXVDIBnhe432g0RkZGfvjhhxkZGeAmKQgCeFD+tlzep6Oxk/7rX/9qs9lQbASL1rt3b8wqz/P62yqUyaV/okrOXyC/73igcfT1uDB38zg1Ke6HyZOy7lDHUMr58pJfkIsiB2r+zpJef8NPVJGoPqLyCrl9m/TpcaJl/K0mkXcS6p3u2mn/gaPaLbQbaRob+iyAH7Zfu4lfc7EmBZdI/55ng53HGzUm0RGu1k3ynkzctfZrwkukQAACmopwgA6H5lGtKIT6XstEdhd6Dh4+FBYWhgMYIPvCw8P3798vSRIjoAPQr7FfA8xWeDVu37594MCBqVOn9uzZk+M4dHOG11//1WAwgJ4GPGkB1DM+fthuwLgaVmDYbDaj0ZiQkDBgwIAVK1b8+OOPiqJ4PB5w4NLXiJ4CKyutP56lGQIMgYogMHPmTFzz9Nprr/Xr1w/f2alTp8IV9G9cRa7JjmEIMATKQQDmdcBhGSwxEMqD1QagMXXhwgVYaZSamhofH48dqJ59xleV4zjYr3eajo+PHzJkyJw5cw4cOADXLCdL7CeGAEOg0iKgKEpeXl5UVJS+Hfj8889BRLHSZptljCFQPgKMgC4fH/YrQ6CqIoDjRp7nkZ8FJ2iwgGFpHiyrX7FiRbNmzbB7KysBE7DoMwX0EypEozDrw4cM1htevHgxIOc2m83hcMyfP1/QNvQBL1bdUBSNw5U09tkrkpf7X42NPN80TkmsxzdreGPcazywzz5CfKosKLKoOT77CfFTZ2ieyjhrHtAa+yz7COFVUiiQN8e6WiRcaBXLJzx2pcNT+78/Rgq8FBVQ3aCOykUa0prPMlXe0C5JuWdS4KJHpo2+/UT97xOj3dH1+Jg6N5o3PrFiKcnOJQU+ItLQg5R6lqkQND1F+4P/9FxKRUvk5PHLYaENHHaquIJbcHBwQUEBctD4kAQQkQ+/Btkd7wsCUKG/6VLQOFy8eHHJkiUjR45s06aNnmLGJ0ef0MtoBGkbKtOVykHD9BUMmOHcli1bLl269MqVK4QQr9eL3lj4QGIRcE/5CTyeJRgCDIEKIvDHP/4RCeh58+Y1atQIfazWrVsHF9G/dxW8LDuMIcAQ+FUEVFUVBIHneYgcDip5YIlhLHG4iNfr3bdv39tvv92vXz90f4YEil/p2Wez2RzgH92uXbuXX3556tSpGzdudLlczN771dphBzAEKgMC0CyMHTsWBrMw2xQdHe3xeOAn3ai2MuSX5YEhUFEEGAFdUaTYcQyBqosAmpv6wSS6wYKXNCHkypUrH374YUxMDCg24NAUvuoZKH0adOuSkpI++eQTnufdbjfeDjw79F/vO4aSJKHLZKtWrfQZMxgMHTt2PHv2rD7anhbiT6YEMnUjFhUi8qrbqxKPn8yaTRrUOd0gyBMbSpJi7gwacNnlpkSxTKU5/IJKhZdF4teoYlWmYs6SqsUJlFXiJ/Id4Y6fUE56+TKSnPRji5iCJ8JvtU08fuU0EWCllFpEFasKUUF/o0j0uQgVWSF5XuJWyCfLSULzU42fcCVG5sU6f2iRcOLPs4kg0Uz7i7lz7RxQDYHTi66VX0CDJfJ5RBbIuTN5oSGJHGcpgsXAOZzOFi1aeL1eURTB2xQfifteNeyCDx8BXNWLLx1yu4qiiKIIdDOMb3fs2DFz5syXXnopPDzcaDTCugH0aEbFDHh4goKC7Ha71WoNDw9v0qRJXFxcYmJi48aNga2GeIOo4Kx/DW02G1DPHTt2xECCDx8ZdkeGAEOAEOLz+bBxSE5ORj/KTZs2wYIhh8NhMBhu3LgB8R7ATsBuAs9lYDIEGAL3BQF8uSryrsl+WfbLx48fX7BgwdChQzt37qzvbfUTwGazWb8WELt4u92elJQ0atSo999//+DBgwUFBbiKEZZA+Xw+dM3WF1C/5F+/n6UZAgyBB4oALHEAP49/rfGdO3cu+lSxHvmBIs8u/uAQYAT0g8OWXZkhUOkQQEs3IAHhhoCiIoScPHlyzJgxdevW1Zu26Bul3wlpvZk7bNgwiNCN/WKA5MV9BMXn83k8HqDYxowZA90zfk6fPl1/ayiynoBWND3nf7kbu0WyZRtpnPB90zilaQyJdP409GXB5aJ6F3c8klso9Cm8SCP/UQ7aT2Q/kfUEdLH4BsktJMeOkeaNjjQM++mJureebHB4xzriydW4boU6UVOZDxq+kOaFctu/JKAFkeT7yIGzJDF5b1STO/VjChvVv9Yy9tDb6R63S5P+QPa5yIFaT0BLhKh5BQpRSfrr5xpH/vlvn94QPOT4YRJcuyPH1YaaqmW1mEymVq1agUSg/jG4j/XCLvXIEUAmGmMTEUJyc3M3btw4ffr0lJQUg8FgtVoh8BEsZQA5ZnhOAl721q1bDx48+IXnX+jVq1dcXBzHccBZwxWAqgbNcY7jnE4nNAhxcXEDBgz46u9fbdu2Dddb6LUpHzlKLAMMgZqGAEpySZIEL7vZbOY4btmyZehEGRsbC3NUOEvNeoqa9pyw8j40BPDlqggBjXY1eD66XC7ZL+/atWvVqlVTpkzp0KEDdsTwdoM9DOG4cU9AIiIiIiUlZc6cOZs2bTp37pwkSdhN69MASIB39kNDid2IIVADEVBV9ciRI8HBwfDOWiyWOnXq5ObmCoIA3lc1EBNW5OqBACOgq0c9slIwBCqEAFq6AQl9IDLU6xAEYc2aNampqdDzGQyGAFoKTVvwf4TDTCaTxWJp3br18uXLH4IqtCAIXq936NChaFIHBQVFRkZu2rQJbGgwl8Hti9ruxQLMIFtBpZ8l8tNPpHnjEzFh2XHhvidibqX84UR2LsXTVUg/RYn4Vb+/iID2+Ynkp+7PgkwEVfv0E0EkpKCQ3LpJ2j15MaleXpT9YnLiqa/+RhSRqILmtww601RwujgPSECrJC8vl/cRSSU3c0nPPqeCHzuekEDiY6VWST/MnSnJflLo+9n3uSjUICWjZYUGI1QJkRRSoBCpIJ9sWE2a1d+aHHt4UN/DfA5ZtYg0ippj4BIQH0i8/vrriAk8DBV6gNhBlRsB4J1xjEoIycrKWrFixdChQyMiImBNg/4tRlkMg8HgdDrhq9lsDgkJ6du3b//+/UeMGPH6668HrC0IeJbgK9BYcXFxL7744qpVq65evUoIYYPVyv28sNzVRASgi79y5QrGSOA4btKkSbjm6YXnXwBcoD3RLyHSty01ETtWZobA/UYArfGKENBUyc0v48ImCCsNqwDx3bx9+/b27dsnTZqUkpICS5pAkcOobbjoodR+HKI+9O3bd8KECV988cXJkydhdAAz2UhM328M2PUYAgyB0hHIzc0NDg42GAxms3nZsmVwEGOfSweL7a06CDACuurUFcspQ+CeEUBLNyARICOFHDTcMCcnZ/ny5UlJSaVy0BBSDHwerVZrUFAQyFQZDIbQ0NBBgwaB0us9551eQB91Abit7OzsJk2a6Dk1juNOnTpFCMnLy+N5HpSpQSQaCGhV0USTqXYzJZJvZZB/63Gk81NiTGh+i0Z5T/e4mHGT+Gg8P7paWRbgvnoCWtAEoIGA5mUi+IkkykQWSf++5xuH33oi3J0UdeKTD4pKrEog+CFTAQ9JoZ7MwEEjAa0dqBCS5yZvvpn5ZNPz0ZFZDeoUJMZlTHpLKvTS3AoqCD0XfWpRC1UtEKKs0OCHPoUU+gnJzSS9O+1p2eBiYsgPf51D/vEVaRZ1tFPz7eGhXXCwYTKZ7Ha7xWL54osv9I9BUXbZv6qPwKlTpz744INhw4Y5nU6od/0aBT1fjE/Fv1wg4+Pj+/fvP2jQoH79+nXr1i08PDwoKAg4Kfgs6VoFb3rjxo1feumlZcuWXbt2Dd4a0PqQ/bKobeD+HNDIVH2YWQkYAlUSAXgTjxw5gq9/cnLy008/jVpbkydP9vl8+fn5QHUxArpKVjPLdBVBAM2wihDQJSlgeJ3BIzKgxGDJX79+ffPmzR9//PFzzz2nD2kIpjtEqEZvEtgJLQPI65lMpqSkpKFDhy5YsGDv3r1Icwfci31lCDAEHhAC+fn5u3fv3rNnD848sdfwAUHNLvvQEGAE9EODmt2IIVDlEbh06dL48eMbNGjAcRzYpiEhIXqDVa9Ap09379596dKlJU3n34SI7Jf1egLg+tGxY0dw6ID5YYvFMnz4cOib9fobP99Io31FjVaGnW/9R2GzqAuJdbLqB59u02L3+R+o8oaghQtURYkooPn8s7OznzLOlH2WiQDBBN287Mon704jTzY41ygsu1Hds3+eI/q0W/BwCFWJ9tE/Wf4FkaxlhgYe9CpegSz6K0locDQq/FJ8TGZC7A8jR+a5RFKo/izdAV7UWuBBWdGUQDQ/bhod0SdTd+jhL/2UEPrPFjE3+7QlC+eSptEXGoX/kBS1YUr6qpGvvlJENxgNXPHfsWPHACWYTseB0M9wsVRlQgCI3ZKmp6qqBw8enDRpUvfu3Y1Go9VqDfBygikH5JtAUc5sNnft2nXcuHFDhw4dO3ZsZGQkHgAJnNeBd9lsNoOgs9FoTEhIGDly5Jo1a06fPh3gkAWA4bNUkUF1ZcKY5YUhUJ0R8Pl8wFjNnTsX3/eBAweGhdFwtRaLJSgoaN++fbJfBkoL3l/91G91RoeVjSHw6BDATrNkF38fM5WTk/Pll1+OHz++S5cu4C8C7LPVasU5ZltNxFIAACAASURBVIgbbLFYcI/e0SQyMrJ3797vv//+zp07cZETRBbBfMJ+r1eLvo17WYIhwBBgCDAEGAKEMAKaPQUMAYZARREAs9jtdu/fv3/gwIHh4eEQdgzZLj3prE/bbDaj0RgcHFzRO5V2XMAyQ7fbPX36dPDBtFqtJpPJ6XTWrVsXMhngxP2L62kCym4PZY9XLCYx1r2totyN6lzu0vbc6q+p0kWhTztcAe1mkaheovJEpYwzsM9IQHsFD1XBkMjhvaRFzMF45/m44KOjB+f6BJJdQArF4uvQkIOaUrQC3tfFWs5aKEKF6jaT/91JmsQdjrD/0DDiRpP4H/6t95nrmZR95gkVjqba0Vo4RJkoGgEtKVQJhKpRa37QxF1Itm4myQk/xDszW8bmfzybJNa90TDix6SY4+kTXYU+cut2dt16EfbaDmSfOaMhOjo6NzcXJtUfzuDnFxXBvvwWBALkNbKysjZt2jRmzJjk5GT94BBiDSF3jAkgm4KDg/v16zdgwIDevXu//PLLjRo1gv0QSxBFYJGZglcbHKjDwsJSUlJWrlx56dIlyDhQz6WOlvFxYgT0b6lkdixD4MEigJFIR40aha/5wIEDYZE+7MnIyIDQxJIk4fv7YLPFrs4QqPEIYKdZapd67/Do3SchLfvlixcv7tq166OPPurXr19CAtVqg5WOIKaHhgEujwBjA21+m80WFhbWrVu39PT09evXo20Aa6HuPc/sCgwBhgBDgCFQ/RBgBHT1q1NWIobAg0IAbVae50VR9Hq9X3zxRc+ePcEkBb9LPe+MaVzfB+HI7jF/wERv2rQJNSstFhpb718m8ty5c0Ejr0h/FmUuiqL20TsrhLh8kkrIxZPkyXqHngi62arBnaca7l/+N+IVNQKa5+lxVKGDEL9CxTUUnqg8KD6D7zN8ekUXjdl4kPRofaxZxNnWj/+Q2u2febmUUPYo1PXD4/XR+/m1uxZpf+jYZxCilsjli6RZo90JkT9Eh/yYEHlmQL8b126RfJGyzz6NBqe6HTRHSvGnXyOgBYnS0PR2tzJJas/vk+pntEskfTqQDk1J09jCxnFnx72Z5ZUJL9MCnTp7JvbxOD0BzXFc165doToe9OAH7sI+7wWBixcvrl69evTo0W3btgWqCEVv4BUzGAwhISF6wQ2z2dyoUaPu3bunpqb27t27Y8eOIPKIC28hkCCuaUBOCrQjQV5j4cKFp0+fliQJBW1ggqeccbL+cQpI3wsC7FyGAEPgXhBAX2ZsQziOGzhwIHTiHMfFxsaC6iv0s+VMMt1LNti5DAGGQAAC+o4y4Kf7+BWDo+BiCLw4ZOD48eMLFiwYPHgwNBE2m81isdhsNlj1iBYCWvUQhRj222y2Tp06paWlLVq0aP/+/RDYHOax8C73kkCI7uUi7FyGAEOAIcAQeLQIMAL60eLP7s4QqKoIAAOlKIrP5/N4PO+//36bNm2QcQ5IIFM8e/Zsl4uStveyyX7Z6/UGBQVZrVZw0IDBc2hoaHZ2NnBkNDihx6PTu1AJUfyqH1jlQpHk3SYvdL/ROOhKu1hPk7qHv15O5TG0rZir9gMBTWO+EFkgikBUSaWRAsEVWvKrxOUhF8+Q1N+ffiLsRJM6J37f7ODunVRX2iPTk11CriDpCGjN35myxeDMXBwGUfSRZ3peeTLmeuPI64mRp1L/cP7yZXIrT8c+F0UxVIoJaAJO0Cqh+tK38iWvTGb8p6954oXHw/MbR5AnIknj+q6m8Vef73cl309chAgKkWjxlL989GfOyGkcNGc0G4CFTE+fKvD0WqqmOKJilMN7qSR27n1C4MCBA//if1988cX4+Hggi0v6KevHhOCplJyc/Mc//nHIkCH9+vVr2rQpHAADRXhl9CQ1x3EOhwN8mho2bPjcc8+NHz9+165dGRkZ+pUEqqpK2oaOVOUUEQeKJRPlnMV+YggwBB4oAvA+EkLq1q2L7QYQ0NCNDhkyBDKABHQ580wPNKvs4gyBGoWAvq98cAUXRRHjMeB0FEYaLHnfw4cPL1u2LD09vVu3bgFmA9oVEIccZ7Vh3ZXJZHI4HK1atXr11VeXLFly8uTJ06dPl7x+xfc8HHwqnh92JEOAIcAQYAjcHQKMgL473NhZDAGGQCkIXLp06Y033sB1/ehU5XA4wI2C47i0tDQgsPTWZAWHuCBVLPvl9u3b4+AZ1J+DgoLGjh0LgQqpVa1JN1Oq168RvipRFNFPJJ+qenxElcmrQzPbxGQ0e+xWUp1D70wqEHSq0EUFU7QT4VP2UzFoyiArhEYS9PlUSlf/dJF0aXUwqc7pltGXWzfc9eV/k0IvKRCo57RE/DJRKJdLqW/wgC5GDPJGiCgRj0xm/klo0fBmw6Dcdo0L/v3ZHLeLand4VeIlXoH4QX9DVBWZ5lqVqSu0KlNNDhonUSYku5Bs2k5ionZH1cmNfYxEhZCYYNI0Lu+5Z87kFJAcgRRqPtQy9ZW+I5O8J59qDNDVshodDofVUpvjzCePZp47SnKuahy0TEuJtVOcafb//iDgdrsDxNADSF5FUfbs2bNw4cJevXqFhoYCoWy3281mMz7zZrMZh4Iw2LNarZ07d05JSRk+fPiwYcNatWqFB8OKWlwzi/vBg4njuLp16/bp02fGjBlXr14FTfAKvo8VQQQepIocyY5hCDAEHjQCoK2Rm5sLKyGg9ejUqRM2CwsXLoQ8AAFdkdmmB51ndn2GAEPgkSOgKArP8wUFBevWrZs5c2anTp2cTieYIjabDdlnbEn0qh2w02CgTg8dO3acMWPG2rVrMzIywBYqv5GBJgsDiaNpiolHjgzLAEOAIcAQYAj8JgQYAf2b4GIHMwQYAuUhANakKIr79u0bPnx4eHg4KNKiSepwOLp3745xS9CCrCDhBY4bn332GV4QEhAp5cqVK78koBUt6J9MadriTSCkoJD851u++ND9T9XLbh310zsTZcVHvLyikrzio7T/SByDhkax27LHe9vF+0SV5NwmL/XOaP349dZxmQ1Dv5szzSX6KCvsFkVJ5+VMr1WsBKIpQGu/+YkiUvHo5V+TqNg9iRFZLWIKevzuwpnjVIHaqxAf8fmIR6QEtAJ/OgJalokInLZESFYe6dp9b8PojHCHt0EoadaQRD+W+e8v+m5lUSrc5adsuFYUUSa5Msm7duNa6GMRlHysxRmNFg1Ao90c37rRW5+8+wNRqMwHI6B/8SQ8mC/oUCz7Zdkvf/vtt/PmzevZs2edOnX0j7d+3WsAiRwREdGyZcvk5OQ+ffr06tULBNlh1GexWAIOhiW0ZrMZtB3btm07derUr7/++vLly/BaFRQUPIiCMgL6QaDKrskQuDsEoLU5evQoNjItWrSAJUoGg8FqtW7ZsgWuHCA6f3e3Y2cxBBgC1QkBUNUQRRG8p69du7Z169YZM2b0798fFmlxHAexDeFTb4fAXLg+LkVwcHBKSsrs2bO/+eabGzduoAEP0vMQeDwgRLZ+1MCsi+r0aLGyMAQYAjUHAUZA15y6ZiVlCDxwBLxeryAIQEOrqsrz/LJly4YPH26321GFY9y4cbgAUG9KVjBzeXl59erVw8EzJoYPHw6WcVHQJFnTbiYFhLiJQmSFuEWfWyZumRz4J2mRcKx5/awnwi6mtDnPu0ihmwiU0S2xAQcNbtToSU39mYkrn/z7C5cTIs63fLwgKfLES/92Iu8OybpNr6B5K1PSGzhiugsIaLpDpC7Z1IuaZN0k3x8lTeOPJdS/2eLx7O5tfvjnQRpL0CtRxQxBJYJ2qUACWvOD9tMC0Wtl3CKT3pIS4y7E1CtsFE2i6yiNYrLa/+7/vtdWOgpaeEN6KM2OoElxKH4/WfP1/1qtj5ktIRznsJpDOI5z2qLr2F54tvtfAIK7qJcS2LEdpSAAnA4Oq27evPn555+PHDnSqG1ADUMwev2wDSJtwqOemJjYqVOn5OTk9u3bN2jQQH8Y6N7gi4avBiRiY2OfffbZjz/+eO/evRhhDIZ2mFEIUFa+OxIezBIMAYZAlUMAXvnPP/8c1icZDAboT1HPCtdAgMthlSsgyzBDgCFwfxFQFKV89S3ZL0O7sXfv3vnz50+cOLFdu3agy4ELrfQGCcqIgdGCP4WFhfXp02fmzJkrV668fPlyQCnAfMKwqGimBhzGvjIEGAIMAYZAJUeAEdCVvIJY9hgCVQmBUrUFBEHIy8tbsmTJlClTFi1alJmZCXakIAhoQVbQA/pfkbUnT56M1qo+cejQIVB/RgJaVXyEOjUXyET2a8LOd3zk+DnStu3WRpEXmkdlPxmzb8PXFF5/aeRzEe7AQRezz0QhHp7kF5Bpb/mbx//QNPpOdPCZjq33nT5JHY0JIbzsFVQR2eeiC/9MQPvBG1kRybVLpOvv9ifVz2gWl9v+qe+PHiKin/o8+2SNfVbpp6a/8UsPaE2Fw0+oELUokU8/8TVvdPbxSNdjtXMTY/2x9a82Tdrz/Wni9hKaCVo27ZPeVdRoaPrV6yU9erxgND7GcTabpY5GWdrtXMfP/3qcEuiSV1VlrBo4n33eLwQuX768atWqoUOHJiUlgec+nQBwOvFhBv8gcFWGnc2aNevSpUvTpk3btGmj948GfyI8UU9GAw0dFhb27LPPrlix4tq1a/pAQDBV4/P5YNCo1wChkxV+WS8Neb8Kzq7DEGAIPHIEoI+ePn06NhdxcXHQhphMpnbt2kE3Cn30I88tywBDgCFQGRAQRRGt9IpbCCdOnFi5cuUbb7yRmpoaHR3NcRwYNnonaGh8cA8m7HZ7aGhoamrq1KlTd+3alZ+fD7b9XRPQbGa9MjxILA8MAYYAQ4AQwgho9hgwBBgCDxwBZDPRhMXEr95bURSQ7FBVFdyf7Xa71WrVS861aNECrvMLC5UGDCyUqaKyoBCSJ1KOePiozJgGhyLsZ5JiTn6xmPKyPpn4Vao8gWRtYJZUoorEV0h4QfZJ1F06bVxBdPj+po/nRoX+9NQTJ//xLfg0E5n4FOLz00+q/vwLD2j0g9Y4aY+L/Mew3KToM40jf2re8PC3/6DCIKJKc+jXOT77iYp/RRIcGgENOfz/2fsS+Kiqs/07M5mZJCSBkH22ZGaSyULCaqnCpyIVxfoHF6rSUrFV8bOALSIqSF2wIFq0+rl+iloBbRW1tMinCBVB2XdZDWFNgJB19rvf+/4950wOlwQpFisEzv0NkzN3Ofec5w533vPc5zzvgd1Q5V1W6jxS7BRLfUJ25qaqyiWr1qIe8VJbJ7ANNdZgKwAaSbAoybB5c03XjCKLOYfj0jiuC8clpSeXXnrxTXwM7aJpCuWg2ypif0+FANEU068fmecuyzIpLFq06IknnujVqxcli0mByH+I/Dk1NZUMvQh3bLfb8/LyCgsL+/TpY8ULIYwsFgsdoZH/BUZvaI7jqqqqRo8ePXfu3G3bthlb3PH/IPpK4oXQzXQHMg329P+HGs/CygwBhsC5j8DVV19NlIk0XTC5I91+++2k8ey//7l/EVkLGQKdDoHly5c/99xzw4YNc7vd1DTMqJI2xjM0FkpJSUlPT3c6nddee+2zzz77+eef08lkxsfnJ71rkdiMPFmn7n+dDjfWYIYAQ4AhcD4hwAjo8+lqsr4wBM5DBCj7zPP8Sy+9ZLPZLHihvgQmk+nVV19F6mOeJ850hFDDbsa8hMhYpIUOyzBm3GG3Z4vLsbfIsWHqZKU1Di1xYopBCGjsWHEyNTRin4UEti88B8WuDSXuRk9unTNv7XP/g0huFZlqaBqyZpaw1vjEWqiVhwpqBMQY/P7BpjL35krv4VLXl88/AyHcDJy6EFWFrJ/xSyGJB098V3TMm8dhzMigr3t1aX7cndVY5N5dUrroy/WokUgfTZIqYjIZrzguxUY7yCBGYPjVv+c4B8d1xRy0heNSU+xZH374d1WVGAF9mv+R6CiIUM+RSISOcJYsWfLEE08MHDiQTES12+00bSCloY0EtNVqzc3N9Xg8ubm5KDmk3U7S+xC62W63E+qZ6hbJOM1mszkcjm9cbp566qmVK1c2NzfTlhNCud1HyjL/ywI9kBUYAgyB8wkBTdP69u3bjoAmN5ann36a9PSkVM75BALrC0OAIfADI0DiJXpv4Xl+9erVjz/++IgRIwKBANGU0AiHhkmUkiZBEbHvSEtLq6ysHDVq1NSpUz/88MO6ujo8ty9Oe0TORdhnOjVTxAvdhxUYAgwBhgBD4KwgwAjoswI7OylDgCHwHRCgAWu/fv2odNSOl5SUFL/fHwq16roaDLZIskCoQJxIT5EgIgAvA9RH4fEnwOv5Oj+30eXee/X/W9WCCeWYzksgKyAnCFoiWk44ZhxvYVxE5QgPc+dBUcEXlcXBwrxWv7/mpl9sVwF4gBYhSmw30H5tKQcTBVoN1lhLDfCX16DYsTY/Y3uvsp033fCZqBDSWlEQi40IaAVUBbdKhYQVBpU/I0G0Bq0heGs2BHK3BDLjVS7wOepKKj564z0lhjXU9IRIg000z22rdMw+t9bDrIcivQtfSbZcxnHdLfZUjjNxnJXjOG+JG4m4kYtIgqJsO5T9/dcILF++fNasWYMGDaKWGjabLT093ajWp8MqSgARBXS3bt3oJkI30490AEYo7PT09N69e48bN27OnDk1NTU8zwsC+tqT9hET9o7+rf+ScW63w7/uLduDIcAQ6GwIEC7GYrFYrVYqfzaZTERsuGrVqs7WIdZehgBDoJMhYHxyT8J7TdOam5uXLFkyffr06667LhAI2O12QkabzWbjxC8iQKHzwKiDmc1m69Onz/jx45955pmlS5fu3bv3pKAQ/5CTbmIrGQIMAYYAQ+CHQYAR0D8MzuwsDAGGwL+PAHGqnT9/PodMi5MpMUcKc+fOjcfjsiJi6W5CvashJleTICZigvhvi6DQubmqWAw46y/qs+XAMUD+0DKvgqgArxIDZ8I+EyKZGCi3NVnABs9z54HL8X/OzBp/Xouz++4bhx/dtReOhCCmA5Yq473xiRPuG7qGLDSwHQeqFeceXDgXAo7VvUpaA56agRevra2FkAASaJhxpgS0roJK2Gdkm6HLOsgKphglQB4fe3ZDv/Il/sxad2rI2WVfmW/tn99GPHhIhagSa2t1GxV+/DNulwoL3oVK94bi3M/yMn5nNfdMTsvGSFqSU9I5jnvp1T8punKhEdD0IYcBrdMq7t69e/bs2UOGDOn4zTR+UU0mU3JycjsRtFEBbdyZlC0Wi91uN5vNNrz069dv8uTJCxYsOHbsGGkZSQ1EiWNjc9tJjajbBt35XxaMtbEyQ4AhcN4gUFNTQ25WRgKa+Py0trb+23fC8wYf1hGGAEPgP4EAVSXT8IOehWYmJx70AHDkyJEFCxY8/PDDV155ZWpqqtVqJdPI2hl3GJnodkFUXl7exRdffNdddz355JMbN26kD+npSVmBIcAQYAgwBM4KAoyAPiuws5MyBBgCp4sAUWzxPD969GgyYKZRpslkSknp0tjYrOu6qiILZZy6j0cFXVeRdbMUkmD5aqgs31mcH/J1OzSo/IvdayEmQBwQBy0j5ldVAZlAI+sK+tIgHEwMxZFDtAorv4Cqsq3unNq8tMYqT/MlJcv3bgRVRpQxkS0fN7mgVekCQDQab0KmugBhEf7yNpQULfMV7C/x1JYHVq9cCYcbkEE1YqnbXh2U1BqgxsZlDfk6t0QhHIWfDt5VVXi0yiV6Mw/1Dqx7+88QDFMvEaJ5bmPQqQJaR1bXIR6WLoPK3vvz3U0eT63f9QHHDeO4bJPdxJmSOC6JM5m5JHNzayvKRqi0CcNP91p11v14nu84OKG2zh17tXz58hkzZtx4w425ubn023iKAiV6yOxRmgLeeAgdRxHG2W63BwKB0aNHT58+fcmSJXRU1rExbA1DgCHAEDhNBERRXLFiBcdxxBqITL8gN5++ffs2NTV1dIQ/zZrZbgwBhgBD4BQInP7DLSNDreu6IAjhcPjtt9+eNGlSnz59qE0HEUeTu5kxmiJl8uSeTu+w2Wx+v//KK6+cPn36O++8s2PHDiJtMTaYUOQkDQaxjSYP7437sDJDgCHAEGAInCECjIA+QwDZ4QwBhsAPgUAoFCLCB8rlkRBzxI03oQBRw4YRIOpIjhxDNLQGCqaED9TBxf2/8hYcLs5p7eXaseJ9RDwr2PWCZPxT8OHI+YK8CAfd1icZGy6vXw19yjc4Mg94soVSRyyQu+Ev/wN6Kyas24hjdATxeiYENGKAowBhAF1QIa7Cui0wYMDuUv/RkqL6QNGWl15GPHhEOE49GxXYbT4eGnaUjgKqAHl0RHiY9aRS5d3fx6t6M+u82atnv4BaHmwFYvuMu0FY8QQlTrqi4rSEGzfDxQMPZuU3ZhWq3XIbexfvcXebZbX2xGDaOI68zPc/OIWXRF4SETV/vi8dxcIn7fFnn302c+bMSy+9NDk5mYx/iCNhx2FPxzXtvrTEfINQP0R4SEhnjuM8Hs/NN9/89ttv19TUkGZQHvz0B28nbT9byRBgCDAEvkk+/thjj5F7FGWfySOxYcOGoeeOkkTZH3bPYV8YhgBD4FxAgMz3kmUkLgGA3bt3L1iw4IEHHhg2bJjT6SQ3tOTk5JSUFOImZAzDTCaT8QG/cdMll1xy1113TZ8+/R//+MeePXsikQjpLHkOZ8xwqCqqLMsdlQrnAjisDQwBhgBDoHMhwAjoznW9WGsZAhciAoIgzJs3j3rmUh202Wx+5ZVX9ONOxyjXoA4RHURVA0mCYBP8dPC2Ysf2MtfhnkVfv/AEpnNFbM8BoCLrDPRSE8SxirTGmoCYaA1EGZsyq1B7EAb2rfbmHi11aaWeeLFj+wPjokCMLk7geA0EtKYh+TVin6MAIKiwawdc1HOr33m4vCgS8OwecWN13VF86g7Xk9DQmPjV8OFBgDhOb6jFJPjnp9DDu6WysNWbWXdRYO/DD8hCFLVWbcuRSATZGrGSRqpoAfcZRAG2b4JeZSt8nrr09OY8D7jcUrnjSD//Eo9jFGfJ5jg7toFGHLTJZj9wuLZD087zFZSJVhVVEIRoNPree+9NmTKlf//+RhfmtLQ0u91ObJ07DnWMYxtapgQ0YXyofofYFw4ePHjatGkLFy5saGggEOu6LoqicfBznkPPuscQYAj8IAh8wy8/8sgjRBtoJKA5jps5cyYAEIqHctA/SKPYSRgCDAGGQHsEKOlMaF80r1FRJUkyZiYPhUIAsHbt2tmzZ0+cOPHyyy8n+clNJpPdbqcxGMdxJKszEUTTWWgkhKOBXEZGxqBBg+69997XX3/9s88+I7nNSXpz9jSu/eVhnykCHfIG0S2swBBgCJwUAUZAnxQWtpIhwBA4txC49tpr2xHQJGREo+XjBHQcIErYZ0UGIQb33qX0L633dt8XyN96y/+r5psRV6tIAuhINK3qCQ5axR+R0Qbii6OaooKWkP4ebYBrr97c0x+scEOlF1zdtg+9YmOkBeIJnUQHlFAgQmTLqDEaIJnz5k3Qv2pruael3CUVdP364r5rjx5BB7ajr0ldaGUimtEAggAtGmKwgdehvgkGXLSzwtVU2P2QN2v9w/erUgT4KOjEBETCB2JHEA1UDRmSSDrEdUBO2JEg3Di0ptx5wJ3T4swVsrIi+bnHqnx7Rl771eovwWTN5WxduCTswsFZObPl1Tdfj4vHWe3jbevQ43N2xXfVqhDe+dVXXx07dmxFRQXHccbUN5REpvJnMqQxjnC+rdzu2KqqqokTJ86dO3f//v1kEijN0k7BNE6EpytZgSHAEGAInCECl112GbmJtbsvEcKFTDlnBPQZgswOZwgwBM4cATIh49vqIbcpcstSFZVaamzYsGHBggU33XSTx+OhmWMoH22M62gUR/NzUH0AyXPet2/fa6655sEHH1y8ePGRIzhw/7bWsPUXLAKMgL5gLz3r+L+LACOg/13k2HEMAYbAD4KApmnhcLgjtWexWKqqqhJNSHDQSO2rq0jVLERg2pSYJ2NrWW7E3/3gjwJr1ShoMqFosRsF5n9pykBSTzjUCCCKSlzGW2uPwU9/ut3n2u3Nl305UOEK9itbJ8VBVolIGqUVPBmJjAhoDSREYwPEovDzEUd9eUd92WKVR6oo2rxmFbJjVhHHjV1AdC1hw0GCGPqO1sY0iMqg8DrEJLjrrrrCvB1FOUeK87dOmwwKj08vYYkzeUe+Hwo+tSQiB2qIiZIoQywMP79xmy9ngzer3l8Q6eHTXHktXtf2//fTVTyPkjBef8tNCGEr0o4QqB1uF6HIqa0Idan+QS77mZ5EFEWS1kaSJEEQqJpYFEVBEKjKj5xmw4YNDz74IJnISVWB7b5y7ciadlvJR5vNZrVa6WRPspKMZ8rLy8eOHfvKK69s27atsbGRnJcOn860t+x4hgBDgCFwGghompacnNy1a9d2D3StVmtTU5MgCDzPU/aZif5OA1G2C0OAIXA2EaD3Kw0vqqKSVzweVxVVFMWlS5c+//zzv/nNb3r37k0SO1OWmfDORM6SkpJCDdYIbU2V0cQkzWq1duvW7ZJLLpk4ceLrr7/+xRdfCIJA5quR+XNEoC0IgiiKkiSpikraRuw7iLV0NIqmRbLl3EcgGAy++uqrTz755MyZM1euXLl//37aZlmWR48effzZhtXW/6KLxowZ89Zbb9XU1JAHIVSnT83E6eGswBBgCDACmn0HGAIMgXMaAVmWly9f3sb3mSlDynHc7NmzEyrXxPNnJdETCT6cA71864sym0tyogN67PvyE9BExD5roOGcf2hH6rlM8v5hKlkFpCfWIjKSG1/909Xewh3FXjEzLeh1tBY7V67/EiUebPOLRgR0x0VDUmpRVIFXoLoGrr1mu8+x09k11MMDxfk7/vZXdEQkjnXSmooyIKJXW2so+5zwXhYlUMMy1LfCvLehR/lmR251wLtvruEgLQAAIABJREFU0j2oEZIEQkxENhtiGweNshnqWDEtRMRYS1RVdNB1uPc3TeWFmwKOw8V5sYIuzQFXtKDb1mLvP3btAV5D2uqvD9ZwHJeelYb4Z6sFcdHJ9g8XLJDVhD1Jwqvk5IR7RwzO/hoyW7NdO4jQWBTFw4cPU09nqouhdsxtX7YT/v5LArqdvUa3bt2uuOKKGTNmLFq0KBKJ8DxP7QuNrWIUjxENVmYIMAT+owjIsnzCfa3tQ3p6Oh0nU0KH3Z3+o9eCVc4QYAicOQLG+5WxbFQeEJU0yajx8ccfz5gx44orrsjMzGy7/yX+WiwWu91OeWeLxULCQvJOaWujqXTfvn1Hjhz55JNPvvfee7t37ya0I+GayTw2empkx4cJ6zPvMqvhB0CAUMwmk4la8I0dO5b8JlZXV9MvCfnq2CzHffl8Pt+wYcPojCKe58mTiR+gzewUDIHOggAjoDvLlWLtZAhcoAhIkvTwww9j+s/CccQjAv3ip6am7dy5+0RQMGurwkfvQr+i9RX5TcV5ojd/z8L5iH3WZcT5EiKVEMeUgCYOFqIu8VpQBSkoQFyGe8ZHyv0HPc6IwyHkOOor++x64cVoJIwIbA0bLROVdMIuI8GAo+ZooMWViArQ0go//3mNK3dtqTfkzg568qsffkgmOU6C4XjCpZnkCySUNtUY49qwOhvZgqgAazdCvz678rN3Fri2XP+z2qZmxD6rSD+N0ykS+bOMaWgkgo6rEI2JkqJDKAxvzYbCvHXFBY2+goZSt+DN1Hy5zX2r1q1ai4hrAXRRR4rsEbf8wpKcxJk4zsSZrSaO46659loUOmOb7BMJ6JMS7ydeinPgk67rkUhEEJASXNO0/fv3v/TSS7fddlsgEEhNTSVGgWlpaR0HIe3GJOTjvySgOY4LBAK33HLL7NmzN2zYQIY61K+QDEJkvBjtNRjFcw58U1gTGAIXCgJLliwxm83Ewt54o7viiisuFAhYPxkCDIHzCAEj6Wwsky7yPN/OjU2SJJJOUNf1urq6hQsXPvTQQ0OHDiWua4RYTE5OJrfH5ORkOq2N8M7UP5rw0dS7g95Ohw4dOnbs2FdfffXTTz81wkyaIcsynZBn3MrK5xoC12Djx26ZGd8kSLDbrVYrejhx6aWX9u/fPxAIkMuNn1ik2CwpHGcym5OIbQslrM0cN+rnv9iyZctJ43wy4DvXes3awxD4YRBgBPQPgzM7C0OAIfBvIiAIwrBhw3DMZ7GY08wmGhemIlKP6JbbpM+aAnt3wsU9VvRzN/UrlMq9+399W1M8CrIIupogoKU2GS8loKUEoazIEOcVEGR4YNLhvpUHHd1bityQlXMs27V84pRjClElJ1huxAujhdSCVxIvDRVAVKGpFe79XUtF8S53Tm3AHSx17Rsx7NCRo9CCMqYgm4wEAa3gcxv5XR00LbEdAFqjsGEr9Kj8osRTW+KpHXrNvn21iC9OLHobAU2IbJm0KKqCJKqIO178EfTwr/HkNHjz1K72A4HCaIUnVuzcsmABhOKIfZYgIumoy7VHWmgAbU+xpaalWZPte/bWIgJaQ64jigKqgtTdBPM2o2oCQVt7zrG/DQ0NL7/88i9/+Uuv10uUziQFDe3p6Re+jYAeMGDA2LFjP/zww3379hHfD+Noh0zMNAph6PxQMl2UjpfOMeRYcxgCDIHzEIHFixef9KY3ffp0cuMy3r7Ow/6zLjEEGALnFwI0iGpXIGJkURTpPU0UxUgkYmQDebwQPHRdr6mpmTt37qRJkwYOHEg56JPeMAlPTTjo1NRUs9lM5dIWi4VqpTmOc7lc11577fjx479Jai1JUjgcPr/g7zS9oXH46bRYA5j37l9NNqspKXH909MSY0+TxWyxokw5WMWSxHHmJM7aNaVbkinJKIu2WvAOHGfhTClJNq/bM/eNN9G4qW0xEtDG72TbdvaXIXA+I8AI6PP56rK+MQTOAwQkSWrLGZJkt2ZazGkkHBgz5jeUgI7zqKM8D4f2wbWDvq5wHOrpkHw5u2742RdhGf3ix3icchAxqLKC+GFZ15E7m4rFvxJAHOJRPdwUb1IAHpss56et8+c35HRtdOSLJSX7h1z1N0EEUUTy57alTfNMqGTCRusgarqoAC/A76c0u/PWlXjC7u6tVYVHr+yzPHoUwmEQdMQ8k/yHiMnFjtVImI3toBGdjbYGJZAUQDsfbYDLBlZ7Cw4XFzT/qKz6q1XYcMMQxKBDFFyPBrFgHAAkFcHBi/D+e9C3x1c9fLHyIsjvKpd4wOeu93qWzZ6diIIkiCkQQey3DpIMN938CxRRYfkzcjdLTfnjU2+CBp98AG8+B3fdfPR3d2xAmGOau42AVrDu+jgubfj8B/+2Y3XJmb5RyhNKd9u2bXPmzLntttscDkdGRoZRvXLSgYRxJREGGgcPRCht3IfjuMsvv/yhhx5at27d4cOHjXMqjeOfU/ffuCcLPU+NFdvKEGAIfF8IPPLII/QhHLndpaSkWK3WTz/9lNI039e5WD0MAYYAQ6DzIrB79+4XX3xx1KhRAwcOpEEgjQ9JgThHk600g4hRr0DLxHa/vLx8xIgRM2fOXLhw4aFDh4z8OPGII44NRCVNYloC4Ek93Dovtj9wy4kNd0ftuTH8Jr+AsiyLsvTSa68iQ0IzmhKKRgGIR0Yv9BFT0iaURyEpJbkrWZ2EU+jQL4ndaku1J+NDExvMHGc3Wx6e8lDjsQbad1GWjA2g61mBIXDeI8AI6PP+ErMOMgQ6NwK7d+8m4gKOS7JauppNyDyB47h3//oBtlZA4mcZK6Dr6+Dnw3eV5lX386lVntaLqtbvqYUWBWXxE2RivqEqIGICWtQxB40S9mnIRZlIkCWAl19q7eX92t8tGsiXstOPuJxHe/Zas2o1aEiYbEQSe2PoyFU6cXAbKRwX4a/vgNf1WbfknYW5MU9OQ2nB6t0rIXIEFBXxzPR0qo7VxISDJgS0oslaK0AsIsejItQ3wNVXrikvrM9JPerNrf7fP2Ke2tgKUiY5GHUQBZTeRFSRx/SmjdC7x2J37t689JjfAUVOyEqvL/HvfGqWHBVAQL3WMfscUVAB9WPhoo84juuS0YUw/habZeCAkdMm7+vt/mdl9v4few5VOd/ZsBy5ciDqPNFfAbH3CIIfYiG+FiclSpYsWTJ58mSv10tDQFogEyfpsIGu/5cFImewWq35+flXXnnl5MmTV65cSdLLCILQsRlGWvmHgIOdgyHAEGAIfBcEbrnlFjIXhM4cJ4Xq6uqON7TvUjHblyHAEGAInCcIUFqQ5LIm7xs2bHj00UeHDx/ucrnIbbOjl1G75K6UfTaZTPSWS3hqEn8SV4frr7/+0Ucf/fDDD3fu3El92yhbSgtIXyIlkqifJ0D/UN0gWWHoZSVDCfoRABoaGpYtW/byyy+PGDGid+/eHUcHJyQgQjlzunApqZzZynFWuyk52WQjO1gIY42Fz6SSNKvdynFdU9MIHz348kHz5sylDxt+KADYeRgC5xYCjIA+t64Haw1DgCHQDoH58+eT0M1iseFHzzaLxWKz2VqxmYWktyqAWFc+CuN/HQxkV5fnxQsz68r8Kxf8HbG9YUyNNoYETPvqCk75h+XPqq6jFHuCmmBPG0Iwfz4EXP/s649U5Or5KWFn5lGvZ9WijxHXGhWJOtnYOh3xwbqKNuggo3R9EAzDB/OhxPNZz+ImV/eGgKelV6Dm1T+BHIRQI5I7E7tm8o6EyzoWLxOnZ5QBERRdikiCDBCT4Oc3HvDm1vhz46WOhl/9/Bg6twCgIpnzyRbEoos6sjyOR+HifiuLXXuKXRGfU/c5we9SywO1Y8dFD7dAEO0CwYisImsNHr8TVbNQUelB/tpdkm22pOQuFo7LLXf+b1GX1WXpjSXpuweW/2MX0kBTAloDCOPXD0RAEzdnSZLi8Xg4HH7nnXceeOCBvn37ms1mo38fCfsseKGGfR0Dyo5r7HZ7WhqS2NtstuLi4rvvvvuNN97YvXs3SVyu6zrP86EQdlE58QIYqWdSPnE7+8QQYAgwBM4+AgMGDCA8iM1mS0lJIWWz2WwU4p39VrIWMAQYAgyBs4qAqqj0mZyu68aUhqIoHjx48IMPPpg6derIkSPLyspIMEm0MiTmNFLPpExiVGIQbCSjTSZTeno6SUyCEoBbrUOHDr3nnnvmzZu3bt06ksVEVVRRFI1M9FnFphOfnDDRhP+tq6t7+eWX77zzzl69etHhgJnjbJgqtnGcjWS9R6lxzBwy40hCjHNqKpeZhoTNNo5L47is1C4ZXZKxwsVqMdmtNgtnQrYbNrvZbLbZkJ8hqhzXSXw5uiSnlJeW3fHr2/fu3SuKYjz+bWO6TowzazpD4NQIMAL61PiwrQwBhsBZRuDJJ580mUx2nAMChwgmi8WWlpYWicQQ7yyHYqISE+DF58JFmav6uGVfZqMjY+WLL0JIgCAP8TbZMtEdU+8LxBJqiP+NYXF0fQgW/h8UOZYh8jpfrnRARYHeo+jgrKcgwiPWmFodt9VHViHeVlOQAYcESFa8aQuU+T7qFThW4oz5Hc35GWvv+e8gHwYpDpKAnS4MHDQhoBNqYmSujOpUAMISatXE+/ZXeg/28EBpQfCish31taCIEGwOyWITPvcJTWrLWIio5VgUhg1d587Z7sxqze7aGvBBqR+KXAdG/KyuNQKtAiKx+YSKQteRYFpUgQeQNQg/NetRqw3BbEni7F2Qf11B2qzS7M2lWbUV+ZvmvABSuM1C+2wooAHg7bfffuCBB/r370++Eu3s9ohjRkpKijGVOY0sv61AZCx2u71///533333nDlz9u7dS+J+okZpF/fTeLEj70zX0GvECgwBhgBD4CwiYNR5nWBSabWSG+bll1/O2I2zeIHYqRkCDIFzCgFCUJImEc83ms6azIFDahCc4Jrs09zc/Nlnn02ePHno0KEdqWdKQCM6si0DdmpqKrGZppPz6KNBEqnSGXh+v//222+fPn36xo0biRb7nMKqczVGVdR4PP76669feumlyGkwOZn+JtpsSN5EJMxmLsEw25CWOYnjkjlzKpeUwSVncIXezEGDcob8pN+YW4dMGvf7N19a+Okny5d+JvKCrmqg6WRIKPLCqlWr3vnrX3/569vsGWnmFDtn5pLsNmuynYw4yNUfM2bMzp07OxeGrLUMgTNHgBHQZ44hq4EhwBD4DyIwcuRIGh+Q2W0cx02a9AAJEAUZBBGWfgwljs8LM7+ucB69KLD3lz/7WgcIyUgBnXC2IMYXOqgaeiGqFyeA0DABLWqwehVU+NcUZh32Zunl+dCjAPw5R0f9LBgVoLXt4bQxZQQhi5F1BYCoRCOSxGuwcRv06f1FTsbWYles2BHtUXjkFzcei4dRC0U54fVBkwWSgoobokNMh4isCTEZscMREe67r7WieJfPGXZnHXNmLv1kAagCSgDYToaN/D8wI64DxEW9OarrAA9Oipf7vvY6QiVFUOSG7OzGXpXhq4fur2+GuA6Sjmh3xHqjAzUk3U4Q0HEAtbm51WZNM3Nm9LwfsRO5XcwTAo5P/AX/fPQBTeOxXvs/drUpe0sYE6I6iUQic+fOnTp1au/evb9NWkIjeBK4U0F0RgZKYE2EJ2jOXHo6zmdtp7vl5+cPGTLk8ccfX7p0KXGR7tg50qqO69kahgBDgCFw7iNAOYuGhgZy66Pv5M55++23M4PRc/86shYyBBgC5z4CqqLu2bPngw8+mDVr1uDBg8mwJS0tjbjttwtWya2YsNIn3UTv1bRQXl5+zTXXTJky5bXXXtu+fbuAl3YiiXYJ9wRBiMfj7Va2i7fPfWDPsIW6rm/ZsuXWW28lj11POjmS+FMhx2csWM7PzvrlT2+8Z9TYhQuW/+2LbV/G4dmauj8cOjajJfREQ/OzB4+siMiNgEZVbYNKHds1Jt6R2hr0iMBv2rFt+E0jKn/UF13ELnb0splt6chP0mKxpKWlvfjii6qikqmWABCJRM6ws+xwhsA5jgAjoM/xC8SaxxC40BHo16+fkYDGmYe51157jeKyeQ0M7Lc74KrrUVhf5t56zaD1rU2As/GBgrIOIpaYZMpTdGzAgZ0uSLigqtDcCjV7oKp0g6+gyd1d8uVBeQH0cIevHLi/BZtmkBORLIP0pMR2g3wk7hX1LfCTIStdzl3ugqjPIxc56y7uvXXbRhAFnJkQNLFN+2zkoLH/s6pCRIUodZP+7X0HnPkrC3Lq/EWCs2DbpAnHIq2gYZ9mZEWdkB4fbwvKW4j5ZFGGyQ/W9q6oLnFHnTmK3wddM0N5BXsHDNhZfwxEfEQb+6wiPhvJrmUdRB1t1PgY6uXwa+4yc8nI0gL9y+C4QaX+564Z+o9QCDPgxtO2JWI0rjvDsqZpsixLkrR379433nhjyJAhRBXSloiSO4W6hAboxqmOZMIj5aDT0tJycnIGDBgwe/bsZcuWET8NWZbbhe/GXjAC2ogGKzMEGAKdCwFCQOu6vmbNGuNNkpaffvrpU9wAO1dnWWsZAgwBhsBZR4Dopkkzli5d+v777//ud7/r06ePzWYjLCe9/dLCSR2l6daTFojYolevXjfffPOTTz758ccfHzlyhGgpVEWVJKmdc4gsy5SGPu8J6Hah+8SJE1NTU4mjo8lkslqtZBolwZDCi8YaFq6yV/mXG1YiXjkkgwS8DocApu+onVIfvqcxNjEszogqc6L6VwISOQlkfEiGYUjcQwloNMhCymhdD/NxBWD+Z590r/Bx6RYumbNmIkEMMehISUkpKyurra2NRqPEn/qsf4FZAxgC/1EEGAH9H4WXVc4QYAicKQJpaWkkPki840fTW7ZuQqyrAloYRg3bl5W+vsTXGvDU9C77564dKNefqCH2WUO2EjLhoGVsuKxpJJcgihGQ+leCPTugV2CdJ6c+L4135+gBF5S7o1cOrN24GXHUUQFRzdjm2UBBEwE16pmiohccPAI/GbwjN3OHqyBUVKTkuRorem2fOw8xtrICshYXQeJBIdbP7QhoFUDUBcIq17fAE09AwL8lP3dXgfNggWf/Vf9vfyiKSWesWdY0xDXTRVNBlLEDCH4IP/t/wetc78k/XORS/UXgKYQsV0tR1ZYv16MjWmIQEyWkfUZxkgqqjNquqqDJoOmKipoIIkwe/56Z654goM2czV46aMjvGsLIOfo/7fTc1NS0YMGCkSNHkhwvdryQeWokOiSGGyfloGn4SLlm4xqHw3HjDTc+8cQTtbW1AECFBhTJUxTaRbGn2JNtYggwBBgC5xoCZEKJpmmvvfaa8a5IHs6ZTKZVq1YZbTrOtfaz9jAEGAIMgU6KQDweFwRBlmVi2REKhT7//PPnn39+3Lhx/fr1I9PyyMw8qpYw3qU7lo1CacJlkyCZhspms3nw4MF33nnnCy+88NFHH4VCIeJnTVoiiiKloSkH3UmxPZ1mS5J08OBBklfQipf09HTivJFktyXZbSYLGu7QxZxkmT59elyMR9VIDGfcEQCOALzXqEw9HBrXFLu9IfK7o5E/t8IugFY0BRYkou5pkwKhH1PEQSN9D8oShNfrqhZSxRaADbH6Xz0/jUtPuELTq5aRkZGTk/PKK68AQHNzs6qoTAd9OteX7dNJEWAEdCe9cKzZDIELBQH682y3oizDJo6zWrgYj2THogR3j64rd20tLmj05B2o8P/zrTcBcb3YVAK7NssaoqkRc5qwvCCBATauUGWQojDimsbKwtaAA0oKwJcPpYXBHsUbn31ai8sQw8RzG9AG4hcrqVGuPzmmAYgijP3vYxX+ekd3scQHrsKWQNX2h6ZFjzagQ1VFVVUBE9DatxHQvKzoAE1N8NECKHFvcObU+opainx7SytXEO4YVYRZ744KaF5E3HUwCosWQbF7VX7mEXdepCAnmpHW7HQ15HrXLlkDTRHkspFYsOga2VEjylkDXsZlUGRERC+aD30CT3FcEUIaZd5AUdm4+x5sEVtkxOrTWtpqO+O/+/btmzNnzrXXXpuenk7SBpJ3Eg5arVaiCqEihZOyz8aInKQQ5DiurKxszJgxc+bMaW5uRvjpuizLPM8bmyzLcjQaJVoVEqN3JGIYAW1EjJUZAgyBzojAN2msJk+eTIfZSHuF3UgtFktra2tn7BFrM0OAIcAQOKcQoMEkjSSJu5EkSTzPUzckNDzRtEgk0tjY+NFHH02bNu22226rqqoy3p9PWjaZTCRCpkEvyZtNdjabzVarlW4iK5OTkz0ez7BhwyZPnvzJJ5/s2rVLEARRFCn7TJt6+kieybGnf5bvZc9PPvmEpnwkFL/FYknBiznJ0g7kQYMGrduAMq1LoEogRzVBxOzzxwo8eqjlt03iQwAPyNofo/waOqWV11UBi3N0PNRUkcMhSnQPaHYpGlapIATFoASNAFsAloL8p4Pb/rBqSZ8hP6GPH4zNuOOOO8jX43vpPquEIXBuIsAI6HPzurBWMQQuaARI7mlN0xYvXkz9N2xJ1iSUDoIbNGgQIn8leGyGUBjYnJN1qDKPL8vaPHH8uriUMKMgFsfY8DlhwUFoaLKeVwRRhoN74OZr68rctSUOsaRAL8mHPn7oUVj923E7IzzirIlZdMcrgZTVKgiq2hJVg0G4fywU5x11ZQZduarbrTvd20aPXk6P0rEAW8I+F4SAxpGNSj2gJR1iAoSD8Pe3wZOxqsJdH3AH3QWNhYWrFvwDSbATCyGgj38gFSCLD12FjWvhx702FbuOFBXwHmckL+eI11PnLVzx1w+QcpmnvDG1+VB0lDYxhl8iZrcBNm6C/v22FLn/ZuIGcFwKDYmKykrwaUUd+0a3Nei0/pJ8fcawG9HlweDChQt/+ctfFhYWmvFipJXJeeka2gxaIKnGyUcSUNrtdhJzDxo0aMKECa+++iqKICWJZNai4bUxaNY6LGTkQHc+re6xnRgCDAGGQCdBYOjQofQuSguZmZmdpPmsmQwBhgBD4JxGwOi80a6hxviTbiJ+C3LbcujQocWLFz/66KM333yz2+0mzClxK6YiDGPoS8qniJbpfd54lN1uv/jii2+//fZZs2atWrWKPoCkMm3SPGLWIUkSCeAJZ002GftiLNN+ncUCCe1JA6ZOnUo6Tu1NPB7PM888c/nll1Nk7CnJHMd1S894YvoMTdMkXYuCFsejIgWgXoFNAA83Nt8dEX8HMC6iPBI8/HeI7QMIkXOQRENkuIhdOMisWRmpegQFZF2DsAr7AN5pgQnVxya1ClNi/MzaukM6LF++3O/3W63Wrl270vZwHDdy5MjGxkZSvRH2s4gqOzVD4PtFgBHQ3y+erDaGAEPg+0GAWFJu2LCBEIsmkynJjEyJu6am3XH7RE2HuXOgtGJTpuNAbkFDr4KjNwzc1liPckFgjw2tjYBGhhOEeja+oybqcM+dEU/m1hJnpNihlhTopQ7+4orIbTcdU2T05JrUcNLOiGIi9Z+swKzpsbL8A2W5UF4IPo9YURm75L82hbCeLBKW41ENzcHCXhcScgUhz9VVCa1LJEiUMDv8+cdQlb+lOL2pOCvoyzvm9Xw9dnwwash/eGJLZGSWkXB1hq82wGUX7S52HHNnBz35gtcZ9bpqCz3L589HenBiUY0Ob4eFoCICus1WY8sGGPRfWxx5+7t3+7Jr6q84Lh+ZQJs4zmxK7mKPisc0iJLEhSe25FSfjJnEAaC6uvrxxx+/+OKLjZEWDZ1pgWxt95EoO6xWK2GfyWMJEp0PHjx4ypQpq1atIumtidK5Y7OMUTIZJLSjoI07dDycrWEIMAQYAp0RAV3XRRFNEr7qqquM915SHjBgQGfsFGszQ4AhwBA4zxAgfDQRTxCtxuLFi6dMmTJ48GCqxTFm0m4ndu54e2+3hmqB263Pz8+/6qqrZs6cuWjRoo0bNxJUSQBPAmOKc8fg+RyMnInHyN13352amkq6THTio0eP/vTTTz0eD8dxycnJVquVaJCzs7N37dqlyrKuagrKtq7FsfFhC8DXALP2H/5NS+hXojJOg0nR+HvA7wL9GECEKnKOJyGkwiVNQ8NEQQKUu/0owNxWeLQJxoVhTIs8NaL+RYJ6jGldXd3w4cNJY4wXpW/fvgcPHkRaqzgaBzJlDP0GssL5gQAjoM+P68h6wRA43xAgdmkff/wxSVhsxcFXRqqZ46xvvrlh9y5sdlwQzM5p8XvrBvddd+xr4GPAS3wb9ZxgkOlHBVl1yciLQ0MPpu+750iZ46vSgiAioJ1IAV3qOtardOm+PciaArlaHM/1R4KL4xn3FAUEGTlvvDsHAgWfX1QsBPIUd/eIx3WoZ//1y9eD0CZbVlSUPFBXkR21qoOK2iCi1Ig6/ohl0YII29fDwPIve+UfCnQNV+TJlUVHL7t05f7DSM2ttCUY1OgVRg1DxtHopYMYgZ/fsKdfcciVEcvu0uTKjXoLYj0rDj38+xDRPcdECR1KrJ+NNLyCzKfJpt3b4L967Szs3ljuhRJPbbFjloXrzXHJVoQ7mqS29J+f6AYqm7bl1AXyFOGjjz4aMWIEnSdI8n5YrVabzWbFJyD6jnaMM/1oNptteCEG0DabLTc3d9iwYU8//fTKlStJopVwONyuJUbum0bMxkC5HftMtB50h3a1sY8MAYYAQ6CzI3BS9mHSpElscNvZryxrP0OAIdDZEegYf1IxLwlot2zZ8tZbb40bN+7yyy+32+3EQ4mwliRgNjKY31a2Wq3JycnflgiRMtqXXHLJvffe++STT65Zs4YAa/yZoEH1uRk5y7I8ffp0ioDZbE5OTn722WffffddspLIyVEeQqvt7rvuisfjZLSiq5g3lhDwcYD9ALMOH733aOsdLcKYqHyfID6rxLYB4o6DeHRGhol0mImGjQmTQ+z+qEkSrmQxwAPH+LtaY+MleWo09n5crgZoVXWa+/eTTz7Jzs4mOujk5GSbzWY2m8v+4GqBAAAgAElEQVTKyqqrq+N4IY+QO/s3nLWfIUARYAQ0hYIVGAIMgXMFATIdDQBmzJhBCOgks9nCcV2SOasp75NFUOr/NCt9vztHdec0lHnXvz8H1Fii8TQUOLGgKsAj9llHxPHjj4h+x4qCtOpAvlDijJW4QqWu5grv+uqvUSVx4hJ8nHBWMRud+CxhRXFrE6xYCr6cxZXupr5+3ZsdLnY2FbpXPvliJKghjhmRxJgz1nTMPicIaF6FGPLkwAS0oiAb69oDcHnvVb2dB4q7NFZkxUtzjvYpXb92HXLIoDYdtC+oXhTykLAHNBEm/HddVeH2QC7vTFe72Y8UZB0sK9p3x+hgfQM6PCZoPB9DuxupZ71NfY0xO1oLv7plp697bbZV8eVDXrev+5XNTcIuHHY7Uhx/cwkef3w63ve7vYmiOG3aNMp6oOzSuDZCPVPemRaMMTQloElAXFZWNm7cuNmzZ+/fv5/4OEuSRMXOJDijwRwVbrRjmWl8b4ye6T7Grd+tn2xvhgBDgCFwDiMQiURURTVq6Mg43GazvfHGG8Tz6hxuPmsaQ4AhwBC4UBBQFZVEuSQo7dhtXdcFQdi6detbb701YcKEyspKSraeZoEaelitVkJkm0wmm81GrSrIyIv8ZNjtdo/Hc/3110+ePHnhwoU1NTU0bD4HCWhN01544QWidCFo5OXlffDBB2+++SbpDk326HK5Xn3lFTKcikajgiAoooSEy5Im6Yhlfv3YoQcam34bh98KML4l+vvGI59jS+gIoIw+ZKEZhhKTTclQSwJUj6aFAT4DpH3+naD/JhZ9oLH+L7KA2GcdRE035qRpbm6+6qqr6AMA0vLy8vLq6uq2U7G/DIHzBwFGQJ8/15L1hCFw3iBACERJkp544gmTyZRwQOO4FCtnNfW4+KJludnV7oKo1xXsUbj7mT/QWEDFT5+Pw4B5W11DomdRBknWQRHgrVeg1Lut2N1c4gqVOGOlBWKpo76qZMPbf4YYT6dUYY43oTqmCmhUs4q53z1boaf/8x7uIzn2huJ8xV/QWubd/YfpekSHSIJ5TjSDENAo5x9SIQsaCKSVMQHpsY8cgOt+sqMk6+vybLEyG/xdmysLVy14D2I4qzLhnY/3x1DSdJB5mHLvsUr3rrICHnlYF6g9vHyv8j233LRTFJFLNWm+Rv1EcHWtDUHUCylBYUeiMPK6mjLnnqLuYX8OVLih0ls7/OpPelbcxnGpViuhjM3XXjMCuVafxmK0exZFMTs7u11ATC5ou5Ucx5lMJiKLJptMJlOvXr0mTJjwxhtv1NbWhkIhWZZJFm9JkkjCQBIEn5o4bhcfG3c+afk0ush2YQgwBBgCnQyBL774gtxm6bO9ZLysWLHCeNPuZL1izWUIMAQYAucXAicNTY0C5JN2d8WKFc8///zw4cM9Hg8Js2lE3S5vCmVgU1NT09PT6ceOYfm3rUlJSenbt+/48eNfeuml5cuXExdpQRDI2I1oQWRZJoH6SVv7n1gZiUQAYNOmTUZ9d0ZGxooVK+677z7aF6IBr6ys3L9/f8LdgqR31xJeVQAQBviHFp3aUDeuOfKbCIwNy3/gxU9BPwhAnBHpnFJiAY1z/eChIp7rSnonAewFmNEkjwvDOFGcIQkfRWI1stYKIJxoaEim/Oq6PnPmTNpOUqisrOR5nohsyKPiYBAN4tjCEOjUCDACulNfPtZ4hsD5iQBhG7/p26OPPkqT1HGcOclks5uvqOqxLTunxekOeTy7b71xb5s1sQjAY2XvcUww46pqSPuMCN1oHFYshsqitcXu1iKn7nOJJc5IUfdjZY6vHprULCTY57Z0xiewv0SLnCBtG+tgxBVfVxYcKveouRnxojyhMnDkhut31TdBBBk9h4/bZQAyEkOTuhIEdFyDqAqaqqPGBBtg+OCvynKre7mgRy6UZUFJds0fpyHnDEEB5VssL0iuC0GEN16GgOOLMkekJB+KHXqJq7nYs3XolRsbGnAmRtJYEiURztvQLBX3srEV7rq7OqvL6nI3eDKVcjcU5Ry6YsDuY0dh4qQXLFaah9DqK+x5HNZTluLxOFFnhEKhd99912KxnDTRM6WbU1JSunXrlpyM0oBwHHfZZZfddttt8+bNa21tDYfDPM+TiJaEiUQaf1JO+dsa9W2h/Let/7Z62HqGAEOAIdB5EZg7d247AprjOJvNVldX13k7xVrOEGAIMAQYAmRWHyWpd+3atWjRoieeeGLMmDFer5cG2CTMpqpn8vHffic0d2pqakpKis/nGzJkyIwZMz777BvJL4iiGIlE2hlHtGvk93vViB6lrq6OGIwQsXO3bt1WrVp12223kSwyVPd99913A4CsqnFRwC6JCVdEDTk7q60An0N0lhAa1xq8MyL9d0iZxusLACUSRFNt2xLCk1mqbSNGVUEDLxVbLupqDCmkGwD+LogTGmJ3BdWHef5D0GtkTVCQjMkwGkvAQK4dz/Pz589PSUlJTU2laujLLrtMEAR6ccloiA5hvl8YWW0MgR8GAUZA/zA4s7MwBBgC3wEB+iD9jjvuIPJnHCElc1xehn2Uz78t29niLDny44Gba/fQ58gnEtCYfsUcsqwg1ws1LMOeavhR+fqCtH1FLrHQpfucaokzUpK/e9I4iY+3uVoADg1wLmNDjBACaEVKag0O7IYRV+woz9hWmRN3dOdL/JCXua+0ZNmxIApNJOT5LBLumrwT7reNAQ5q0KRCVNahqR6G/2RTIHtnea7UIx9KsrQqd+iOn8vo/DoIiq4hE44E5U2xI3kE4wK8/qruc/yzh6epxCEXO/RiJ19S9PUlAxYeOoL2DZN8gQkzMoOTtAKajF4AwMdh8u/DxSU7nLkN7hzdnQn5XQ9f1HvN19XIGvrNufPaolITx6XYrZnhIJ1zRptzkgLRPmzdutXr9aalpRElAg372upEfy0Wi9VqNZlM5eXlkyZN+vjjjztWRzXOZBP9SGMvWuh4LFlDdzjNwrfVw9YzBBgCDIHOi8B9993X0ezI6XTSJ3ydt2us5QwBhgBDgCFAqUkjFJqm1dfXf/TRR48//vh1113ncDg4jqOqZ5PJRBO0GOPzU5cpN0oeatKd6fpevXqNGjVq+vTpy5Ytq6+vJ2M6qokmIhJjI7+v8sCBA8mgIyUlxWazvf7666NGjSJ2IikpKRaLJSMj44UXXqCnU0CPgiaAjlVCaMB1APgVEJkR3juuNTg6LP9KVO5uDi7E7HMi1Qwe2qlouNemEkKMMkrMoyGpkwy63sLHGwCWg/Jk05HfHGt5oEX4m6TtBWglk2iJbYeGhpjkRcZ6uo7kR5qm7dmzp1u3bhRVjjNXVvYkwx+yg3E4Q/vCCgyBToQAI6A70cViTWUIXEAIkEflV1xxhYGATuM4f3bq7wqdm93uOnfxsuVr0PNmIRLFuJC8fG0+EXguFKZrVRl0EaD2KIy4fpUvZ5szPVjk1AtderFDLnPX/nTQ9mADCDzwkogjCgVFBNgvw0D/RrCMGmQRhv3kq75FdSVdG3vmQ8CteT31ZSWrNm+F5jiElKiMkw6SozsQ0JoGYcQ+A0gi/PaOhipPja9rqJcbPGmiJ+PQgF5b91VDLA4tQVVSZByZHCegyTNzlDhQhc8/hyLXoh6+hpyUxhKHjLxEivaWli5avRHiSlur6Qwx6v5MtNMYLCkOf52nlVd+VeBszcqK+D2Qm9nQp+ferTsggnnm7Xs2ciYuOcVst3UxcV2S7d2WfbbyNL9/uq5PnjyZpOo+aWibnp4+ZMiQF154Yd26ddS4WZZlYohGJqMZz0XCVmPI1bFs3N9Y7rjnqdcYj2VlhgBDgCHQ2REgyqkbb7ixHQGdnJx82WWX8TzPLDg6+yVm7WcIMAQuZARoXhOjTlbTNOqGQZKmqIqqKuqWLVuefvrpcePG9e3b96TqEAP1eaqi3W43OnhYLBaS8YWojykZzXFcSkpKRUXFyJEjH3rooaVLl+7du5fSqd/LVftm0CGK4mOPPUatq00m0+233/7000+jTIN2e3JystVqTUtLmzNnjqqosixTIwsedJQ2HquEYjhn4PP8vjsbdt4W5W+LwpiI8IdQZBc25Ug0FWca1IyZdNAUVxV0kciGNOwTvQLgRSE8tenYlKPH5sTFrwFN1uWJYooQ0CgvfeIlY09pUeRFPi6LvA7wxZZtXNdMzkbmhpo4jhs7diwl7o2jmO8FQFYJQ+AHRoAR0D8w4Ox0DAGGwL9GgIZQgwcPNidZTBYzZzZxXCbHlXqzZpR0W9vXt/OD96CxFQQRMb5tCzLKILQvtW1W8JPluAK33LKrR2B7eWF9wCOV+qAoXy8uaL6i/+54GEQBFMwcA8R0Ld6OgNZAk/TEfKkpE8MBx25fXtSTL5Q4xPLc1tLcL158rkXSgdeQcFjRQUIuHMcDCxphqKCIKAIBXYP7x9dXeWp6FUJ5AfiydH/3pp7edStXIOcNSUGRDBIp04fjmIVWNRBkVO3GrRDwryh21fsKJF+B5s+PeQt29Cj7cN0GaAqjU6MFzxFL1EAJaNQLtJ3n4cN3oMT9udfXkt494nbrHk+Tr/jLxcugPoxOoQOIStyEsg9yqfa0JC7ZZklZvTKRC7sN7ZP/Jddu1KhRNJkJsZ/z+Xw33nDjyy+/vHr1auORpx9I0W+F8XBWZggwBBgCDIFTIKAqqiRJQ4YM6cglTJs27RQHsk0MAYYAQ4AhcO4jcIbh8ZIlS2bMmDFgwACaM5xMUjT+ZBiNlS14IbG9kcKmCQaM7LOxEo7jiCmfy+W68YYbZ86c+f777x88eJAg3M6y4zvB3tjYSOTYNpstPT198ODBixcvJqcmhHhmZuaOHTt4nm+ncSHjIkVHc1j3A3wYDE5pPDQmfOxugDuC/FMRdQNAU4JuxiNLQh+3DdFQI1UdpZ5XBB2nno8DfMzDH4PiPa3C74Pxf4TCNYoUwr7PRDRNxUk0z7yoI+GPKotISa0gPnwfwKwly7jcAtyFJM6UZLWn3HfffVSyQ4dO3wkltjND4BxBgBHQ58iFYM1gCDAEjiNAY6kTCegsjutfkjvtR55/Pn6PhmTLEmJ7DV5aiOyltC1hgWMq4oUfny4UOTb4CprKfbzPEXdmST38Qoln9ZYNiMKWFdAl0NHEqaiO5mNh/hjRvigy0RAbi1jjSfc0Feas9Oe1FOVqzgKhyNHQ07l9+r3xlkZkMi2p6IUehGO7Z2T0fCINLWNiNxKB8WNqSvLXFGY0+zLBlwXubi29/dWvv4gOBACJzOWiB6NqJPLUPC7AoToYPHhTsbvOlw++PPAVKO7sGp9z0Zdf4rYaQyLCwdNIh0ztwhhv2wqV/n968w6Wl0KBU/f6xJz81X/+K9S2QLOACGi86IHiIhK9pVi7cBw36d6JiS2n8UcUxeuvv76iouIXv/jFG2+8sWnTJnIQ9dCgddAoil50uokVGAIMAYYAQ+AMEdA0TRAEI01AGYG5c+eeYeXscIYAQ4AhwBDo1AhQAbWmaZ/iZdasWUOHDiW/FMSvg5DLJIOfzWY7KcV8OgS00f2D1p+SkjJ06NBp06aRRILfFUxN0wYMGJCammqz2cxmc1pa2t69e4nZCGknYZ+JRckJlWOxDsrKA3AY4P1g9PHD9fc0N4+JRMfGxT/w6qdYzowoYTS8UhERrejEeoOMrvAGHRRNVxUJIAiwVYNnm+XfNsbubhZnhsRdqiYhjRM6CDsgahIgwTMho4ndIxr+aHj0qCE59iGAt442vnio/rdz3uOS0jlTCsfZiHHKokWLSPvp0Il8ZO8Mgc6FACOgO9f1Yq1lCFwQCFAu8kQCOpPjel/ad8YtQxeITcg0g7DPBgIaca4kJlBAllEyCAgJMP+vUFSwyZVVV1YIZR5wdIs7u7UGir5auAixvRKminXkiwGg8wC8ruFakFhYQly0BrIE8+dBv8D2wsw6X168KE8qyo/6ndU3XLUhWJ+4IgpWLmO1MWKzJVBlFHMgaTWJPBCzDPDn1yHgWBnIbah0gj8b/NlaVeHRqZNQAkRJgZgoKCrivJEXmC6jiAS1LKiCgPoShhuHH3bn7vU5BEJABwrCxa5lH85HbZAwc2xAAxPeVAoOmgaarMKuHfDjviuKCjYFioKFbtXnlT1FXz82A2V2lgHCMuLryTLihuvMHJeEeAtzis3+4P0PJDacxh/6lJ4EfB15Z1oHjaLoRaebWIEhwBBgCDAEzhABMhHbqF+jBPTWrVvPsHJ2OEOAIcAQYAicNwiQROIoR58sC4KwePHiRYsWTZo0ye/3U320xWL5twlo6pJBf4ZIhkCSFHfMmDHtFMqnA+zrr79OOfGUlJS33npr+PDhhLG1WCxOp3PDhg08z59slKGBhuwzGgHWADzYUD8mGLo9KoyPSDOa+U8B9gK0EAUQetcxB02miaIBXWIhLDLAUYAvZXitBe5vkO5pjP0hJv0d4BiSImn0JSP2OfGS8bgMq4d0NAIV0XhzH8CCsDJl74E/8sofj8R+MuN/uXQnxyVxHCLWMzIy9u/fTwZWZPTU1gj2lyHQmRBgBHRnulqsrQyBCwQBGiWcSECnV5b+bN0XypH9yElCwl7NbQHBcWCI/7ICqogJ2L8tROyzNydW6tKqvBBwQk7qUb9r94v/AzEJZSdEbK+KnbuQRJkHPQaaji03sJuFAqoAH86HCv+yUucRXzbvy5V8eWG/41CgaPGhAyBKEI+js6PkfigLsq4gvlrFiuoT2GdBgr/OgxLnJ76sgyXZUkm2UtitpcrTfNWl1bWHoKGJSI/1BAGNeOAYoEftIrGNbgnDxAnNZYWHcrtEEPtcoAUKouWe7S//D7LU4MXjCHQsaViOLWsgCDBk0JbCvG09y8P5WUcLXdH83F133yM2RyGiQQx0UYc4n6jgt+PG0wAxyWz+2Y0jOtZ80jXhcCJXh3ErCZUIFUKvrzGKMq40HsjKDAGGAEOAIfBvI6Aq6qeffkp1Z/SuznFcOBxmN95/G1h2IEOAIcAQOA8QCIVClPalvwiSJGkaYlnpGl3XN23a9MwzzwwaNKiwsND4U0LKp6OAbpcYhrDPdrudMNo9evQ4TTxJ28jOJSUlhNdOTU298sorp0+fbscLadWf/vQnAPgWfw8dVDkGsBvgZVG6IxT6hSDdwSsPheX5UTiArZ9jbfngNTS+I7NTE1In2lQN77kB4H+D0qRD4QeD8FhUfb8tdSFln0lBBkUCSQJJRqyzgrXPiQxEQYDPFXjsUGhSMHpvhJ9YJz5bK/90wjQuNYvw6SkpKbfeeqtx6ETbwAoMgU6EACOgO9HFYk1lCFwoCNBw50QCOuXHP7oBNFAUEEX0zBg/f0ZToki5TfucQEnQYeceKC1eXuqJB/KhsFus3KX4u8d7FB284479YlsCYkVDM6eQ3BlR0ZiA1pEPVzSEWVQedm2EgHe5133QXxDy58nubuFSR32xe8malcBjDxAF87uEgFZ0SYI4IaDxO8g62k0HWPoJlBetKXXUl+bHS3O1ku6iL/PAxZVrv94Oza0g6sg7WgUkHVaQi3RUhiYNe0bLABEeHp0K/ata3NnBwmy9qghc3Y758ldPntiITMNIdsHjYucTvifIRgQnuxAEuO/ecJFjQ4mnJT+n2VcYzu6+7afDDoYliKgoDiJP8RMJqTT991MeQpKEJCuJ4f7rkgEn1HsGH+j1PYM62KEMAYYAQ4Ah8K8R0DTttddeS04m6YyOkwaFhYU0S9W/roXtwRBgCDAEGAIXGALfFq6Hw+GdO3euWLHiwQcfHDFihMfjIT8txASDlE0mE81MSAyaqW7aaAllLM+bN+80ASYTK1VFffPNNwk5S3yrFy5cSMw3bDZbSkrK8OHDQ6HQqes8iNhn4b9bgr/mtdFR9QEFngkKuwCJgEQF+2UkJoaS+bHonVSooBT3Gg96EKAG4IWGhoeD4sRG5Q8h+IsGXwHUgx4/UQGtooGeJKOcPnEN4igDoqYi7ZKKUhQeAJh1TL4/DOMEuIeHyY3w7CG1BiDwo4EmWwpBz2QyLV26NB6PC4LAEgif+sqyrecsAoyAPmcvDWsYQ+DCRYBGPCcQ0Cbr1KlPoRx66HG1kYBucy3GK3VAdhWCAgcPwchbjnjd+0scUJwHrnTe373Jk7n9FzcerjmIBL/IriseV9AQHD3XxgR0DCCCog7kvAxCC+xdB0P6bvS79nucsaIC2Z/Pu7se6unb/OG7iPYVNVB0CRHQCnqhsAIZU1MCWpd0FKdIEqz9Eq4YsDvgbAjkQSAXSnOVwq61fYu3bF2DDhRV0CCqgqxoGmKfNU2BsARNMgR1gKYQvPEG9O/Z4M6Ku3NlX4HWswh6ePZNncTzMWx6jR6htyFCaOi27w6xs0aT6TS4Z1xDqW9jSWFDRurhAkfEV3LssiuqWyIo6BHa2Gf0NB5hASCrz8x6mgSRZo4zc9xl/3VpW63sL0OAIcAQYAh0DgQ0TXvkkUc6KqAHDRqk6zobwXaOq8hayRBgCDAEzg0E2pk/aJrG83w4HF65cuXYsWMvueQSSkATgbMNLx2NO8hj0W8Y1YEDB37++eeNjY1UiH06HZUkKR6PE/mz3W43m8233nrrlVdeSVOge71eURSj0agkoSx/HRcZoAFgUVyc2By9uZUf2Sz/Ng7TWmPrSeJBInc+4bDjSh9dR+xzGPR6UDeBMjsWeyQYezAO99Xz7yqwBZtvRNAsWSRPMoigFQ25OwoqhJFsWouDqugaskD8GmBuqzA1CON4uEuECVGYUh39VIIjANUNjTkuV2pqqsVisdvtJSUlABAn029PaB77wBDoHAgwArpzXCfWSobABYVARwLaZDGbLOb7J98va4gs1bDq97gDF5qPlEAoLsnhCIgRuG98s9Oxvjwg+5zg7ApleVDpbulV9n8bN6I96+NxCaTmcIOqY69okrIQPfAO6RBB06skiNbBZf5lPTKr/QWtLqdYlK/7C1r9BWvuG98YxfJoJFrWkH8YeSFHacQ2C9iFA2U1FlTgBVi3EvpUbA64jhTnK8W5EMiB0vz4RaW73puTUHEDmoIlkggFVYhk1FERggrwQQUWL4HeFdXunCZ3jup1SD5XS7Frz0P3IpNpDSeuQLWQRM5Ew0wE0RgPDVPPsRi88BwUOpc7c/fn5zQXOCLdHUfL+u5YthoFPTGMI55oh6ykMR2N6Pi/zHvbarEQEbTdavN7fRfUl5B1liHAEGAInAcIqIp68803E0bA+D5hwgR0x/+Wkfl50HHWBYYAQ4AhwBD4zyFAB2tGpw7CR2/dunXOnDm33nprVVWVkY82/gYRU+nU1NTk5OR/45eI5/l33nnHaCr90ksv0UetycnJixcvPnW1IYDFsjazmR/TpP2iBcaE4cFj0iqAZoAQqAqS7hC9c9sIkww226Q9QUVoAdgO4jy5ZXx9070C3B9Wng9qO3E2QhGlFVQkkAWUlCjBQbeN1gRsLt0EehhA4jH7/I4Qn9rUOCEujxVgXBweaUa21LVYiK0DvPPBfHvK8WlML7z8ElFinezinihEOtkebB1D4OwiwAjos4s/OztDgCFwEgRoCjuqgEYEdBK35LP/AyQXRobHbRYc+HDDr21cQPZab78KfUq2eT312d0jzmzITo36s4L9K3Zt3gQREVGu6KEz8HElospE/ow1wCDoEENKZBWaj8GQH3/cz1lTktHqzZc9BbI3Xww49468Ybsi4pTGgHln/Cxb0nA+Qx0lO5awlJrwuLwMR+vg4j6bewUaC7PjpQ5ABHSeVu6q+f3kmICNm9G8K13UVQUpj5GkWuHVqIidpcMAG3ZCsW9NsStWmK37CjSfq6m46Kubbqg5eADiAnqhBedxTjhooFyDCV4bxUg6muv1t7+Br/Bzn6euyBHzeWRfcWtZn12rtiHhM68j95HEgkhonEARQJfkT/7vY7sVZ17GNDTHmRO74UyL6LATngCgjcZgtK1S9pchwBBgCDAEzhoCsiwPGDDAOOwn5eeee444Y7L79lm7NuzEDAGGAEOgsyEgiiIdppG2q4r6bVQvMWvesmXLrFmzRo0aVVlZmZOT046STk1NJfV81xk5Pp+P/rSNHj3a7/cTrw+O46677jrSSJ7n2yRKx/XLCqDU6wcBng/yE0PynUEY0wwT6/hPACmOo8gaQ5bR+Aklk1cSNDQebSk6slbEWeUPqsoBgM8BZoaC44Px+wV4rD70JeavZQk0LCcSQOZRZiCkg24bnmGJE7QiBbSKMszXAbwdDE9tarxfku8R1AkxmNoCL9QBSXIf1yEOEq/JN9z0M47jklLsnNWSnJ4WEURRS7hRKziNfNuwzDAk7mxfLdbeCwQBRkBfIBeadZMh0JkQIHGMLMt33XWXOcliTrIQBfT6TesxTYv6QqZGJXS7lHKVIRaGnZuh0rPO3bXOnRdzOVRntlDsagh4l3/wHmJNZezqJSPiVVV0SSN0qgq6rsqaJOlIexyT4FejG8v9td7cUFGu1rMEPHlKwNE0sM8WPno8JKHCZxE0/CI0NGpeWED+Gwdq4coBe6qKgr7cZuSb4YKyfNWX/fXdv25GAmzUGElD87B4FJyouq4qohKNadEWKaQB7D0MgcCXntwWZzcI5ENxXszr2Dx0yNqYgLTVEuWOCQGNhM8SaEIiyAEQBTT766sd0KPPKoenzluk+D1Q5Ii4Xeve+zuKvcSTcchETC4L4hefLyfyBDNeTGYb6pgEezfBpNv333/XVi2GAjS6yHgxJgahm1iBIcAQYAgwBM4WAnSITtw2LRZLamrqunXriAUHI6DP1nVh52UIMAQYAhcUAsS+Y+vWrc8888ydd9552WWXDRw4cNOmTd8VhObm5nfffddsNlssluTkZJPJ9NRTT5FfOrPZnJWVdfDgweN1IgWzjgeOIoAq6dCkwx6AOa1wf33kzubQneHwAy2tK3DawDwG7dEAACAASURBVCBW4rRplhEBTcpojIVS1qNEPQq2a6wGmC/BlAPqhCMw4VjLU9HgZwBHE9NIQQA1BnIU5BgogpGA1rFvo4zz12OB8ztB8fdN0d+GtN9EYGIUHmtR32mFajwjFdDZNBUUXhMbQq0p3TKQJaINTU69/Td3Exqdx4LrJqTaRuNK0HUkPkpIk45jwEoMgXMHAUZAnzvXgrWEIcAQSCBACGhN0yZNmmQkoOOCJClqXJBkVT+BgCY/tSooItTugasHbqx0HHNnCAWZQmkRdEvZU1Gy5c9vQjCC6o8IsqQAeumaoiuoIvTUGLG/rWH0LFqQYOJ9B0uL97vyRGeB5ClQi/L13PQD/at2rF+NKF1k+iyjFzJ91kFEp1UIAS3qIOKpWqE4tAZh1E0byp0H/JmKNyteUaCWZEv9S0NXXrrx8GGkPsZJkEkaikSoIys8r0YVHJG08HD11Qe9zmOVXijMgtJ8qCo8+rNhNf+fvesAk6o623dmdrYBS9m+MzuzM9vYXarYSSxJLNhiFJP/t0YFpaMUQbBhwZaYGE2MBuzYEo2KPUpRmrRdeltWWLZPL7eX7893zszdAdSE/AKrOfOMd++Ue8657x253/ee97zf3r2EfUbdNj4TKmREQMVpe4jgzD0Zg6pBZzucddY/Kmuay8qhuEAtyvf367PittliXP0XsYmuap988gl1VUsQ0JacWAw6DsDJVSuGOupPqlz++ceIQBJ7Q1M1RVEYAc3+N2YIMAQYAj0HAZ/PZxLQtEwTfXngwAFN1di/2D3nSrGRMAQYAgyB/xIEqDxZ13VJIqtBj/C0dV2/6KKLqN45KyvryiuvpLUHKSX94IMPhkKhg5ukBLQCWG4eZc4v+mFepzbFL4wPhWaEfc8I0UaAsK7H0BNDknGZbOKZJKPJKk9VFQ2jg1QdfE2B+ztglg9m++EhX3gxKPtQT5RYHSqAEiFPSkCjJJouUEUCWkd7D8Jir9XgvnZ+SlgdF4OJYe2uoPZCGHYQsVRCM4X2HWpMFf4pn5p9952clcvI6c3ZrVxaWv2OPTzhu5sAPovEP49EGjWShUkyyQ4PW6Z6MCLsFUPgeCHACOjjhTzrlyHAEPhGBExB1vz58ykBTbc4s6uDJCmyqlHT5uTdFWsG6iq07YcrL2qs6L9rsEMbXAqOHKHKGRs6sGnWDD4UpawsKBo+VV0nfs2qRi2+DE0DQ1TwO3fNEYYO3OYp9LsK1bKSeJkjnJe935n7xRuv4oBVg6zF0nCrgaBClDh8YUCDTwMEHUQdHTSuvryxxrH9BI8y2AmDSqCuBEaUC0Mrv+hoR/aZENC6QiMVVHAboGsaaGExygMEYzBrtlGcv9WRG3bliafUgrvfvuEVqzdthLiIrDfl37tZeDI0ZJ8hQObCUf4sxODqX+11F613FIYGVkJRrlBR1jRjVrA9iFYjYhK7b7oM77+7uHd2dprVSp8cVxqNwQXn7R7sbc1N31Gau/7dN+GDj6B+C5ZzVhTFvGrf1CB7nyHAEGAIMASOMQJLliyhjLPFYuE4jtZ96tOnj67rR7re+RiPnHXHEGAIMAQYAj8wBFInPv/jxGHv3r30jmaxWNLT06+88kpKRmdnZxcWFoqieJglCFHLoDQYWohvxl3N4akdscmR6KyI/8ku32ZinRHDQkBixOBFLOdDCeiE4IkU2cFsLQTGNoC3AWY2R2eF4PYI3N3Kvyupu0gOhheLVOIRkV/W41hnEJemUhabfJZYtBsF+FyF3/u02/z6xKg6LhadGQi+RNhnpORVomfGZaaod0K2WhPawn5rr0wuzcJl2jmOGzNpCpB6iR9o8Aef8Juv2pdq6CqtKSYN/gP77bDT+YEgwAjoH8iFZKfBEPhBIvDEE0+kEtChIKn9R2hoWgQi6b2h4LooEZ77k1pduHFYKXhzjaFlUNov4MxvmDwhIkvk7p3EyDAMXVexOoSBC6k05HMNWQdJgUUvQoWjvrRfwJuvlxcYnuJ4uaOlwtVwy+Qg7Ry9OgwND0ACOq6iXQdlkwkBrQOvQjAKt0xs9ObVe/uGPTkxb9945QCpqrD9xIENq78AAUMJ6haNfiBIIhMSXMOCFTjEsAi3z1Y8zk1eZ6Ckf6TOpdY6W0YObWjcApKEbC8l3w/joFUDQoR9juk6xKNw64T22rIdtW7ZlasO9ECZ48CNN0j+GPaI1p/K11eFNq2c//7mmwcT0DXXX3+gpqrFXSBUOuD0ETCkrr2o+NOKyqfb2lklq+Rvi/1lCDAEGAI9CYEFCxbQzDw9Pd1OHhzHnXHGGaksQE8aLxsLQ4AhwBBgCPwwEUjlhemiyUPspL/ltClbTbczZszIIA+73e5yuU488UQ6z2q321944QUzkaGtkVSRLBhFP2VYCfBIW3BuWJkSjs+KBR4Ntn8SiekklRMBIoYYUqKCIRACGleamtkWMU5Ek433Ae4LahM75BkRmNMRefSr5i06dGmYzeGD9CcTm2kqNqIe0FpCBG2gFSRAI8BCEcZ/FZwUhokRYXq4bX77vm2m9pknBLSGVeZpeSEA8PPRa28ew6VZrL0yrb0y+7vdTRGlQYffdUgPBeHBvYEVxIhD0UUyiG/Bkn3EEDieCDAC+niiz/pmCDAEvh2BpUuXJqRbNuvpPxqZ+mVKQJthQVyAHQ1Q2v+t2pKuwS4o6S2X5ARqypr/d3Rzlx+Pw9ADb/qEfaWEr45MbihOjDkAYjy89jKU9F9b54bBLhhSipbNlfliYZ8vL7p4FQBKm9GrAyMLYmCBbaHthayjoJiSwu1BiPIwd1bkxLqt3gHNSD33FWvy41W5X9W5Pn/zDfAFkXQmE9uqjFEFeWlAXMBBagCBGLzxN3A51jlzW2vL+Dq3ONgpVBasWv4xiAnHMPymefpJCh400BQtzssR2dAFCf66CIZU7h7oEE4aCGUFapW79eKLmlo70SGEVB1UjO6FYqm4du/ffeddGfZ0u5U8sQ7hCdXepWVFsRMqIS9TLc2NDa6S3CXNFWWLOzu6CWjq70a33W2xPYYAQ4AhwBA4Hgjcc889HMdZrdbMzEy7HWVTHMeNHTtW1/X/WH12PM6D9ckQYAgwBBgC/70ImK4dAFBbW8txnN1uz8jIuPrqq+l9zWaz5Q7Ib2lpOxwjjaxSDQFaPz/eFr61JTDJL8yIxO/z7f9AjdDsihYHJGXmkfM1E0xzRwRoBvgElIej2pSgMTEEM/3CU+HQWjDaDb3beJnkihrJ7xIyI7TR0FXMQnWFeIBsAVgUl+d0CuMD2tiYMiUSfDLWuhrEGE0FJUJRq+jkrBABNVUOxQ3lvSWf4Mlm2jlc0cSNf3bB75r2z++I/94PS0QUdyP3jMnlv1rlejhG7B2GwLFCgBHQxwpp1g9DgCHwbyNgZsVLly61kYTZZrf/+KwzUxswGVhaBi/ghx+duMaTu2tYORTl8K48ucrdft5Pdrd3JA/Cu78EmoBbMqONomlSpkFQQZWhYS1Ulq6rdmll+VDaD8r6gScnNqg0cFLdl50BiBoQ0aAzHCQENDmMeHFogBUpRMJNRxVkkF9/HUYM2u7ObXH3D3v6iYMLYbgzONy74sUFEEiyzwpObOuUgKYcNB1lMA6v/RVqa76sqwx5S8Q6N1+ev3eIe8viV0GMJ08k+deknpNvGFpCQg3LlkJN2cpqR7i8wPDm6+685pOGbtm+Ez8m7LNGQhuJnEby6IP//tMY9O4777JyXAoBfeKgsrXuHL5yAHj6ieWFTUV9V5w6fNf99yihEJhxISU1GAF9MJzsFUOAIcAQOD4IjBkzhiqgMzIybDiViI8HH3yQuT8fn+vBemUIMAQYAgyBI0eAJhqGYWzevLlPnz70Xma1Wi+55BK6z3Hc5MlTBT5hKm0KYlQwgooQB6zs97oId3Txk/zS1Kh2b0z6mxQ5kDIS6rNBTJoxoUt96qTMzlJdejwSnBaQJobgloD226i6GqAL2W2ygjUpf0axkoFP820UCRHVEQ/6XoBFvDi3M3pzUBob0yaH47/hIytATrhWywntMxhU/owOHj4Zz0oFCEp8gduJBLTVwqXZ0n/6o8db9t/b1PaCX2shCSlRehMKPOW82C5DoEchwAjoHnU52GAYAgwBRCCVgMaogkzzchz994oIkLEQIEYGyOQaEBVg7txQcd8NVYWqK08sLYw7izpOGLajfguRKxsgShGcddYk0Ikll6EYBnp7yWRplaxA0yYYWff5kKq4twxKS0LnnwW1TqjI66h2Ln/jFQiQyXEBeBkXb5EHcfiigYWmA8qJSUHCF56DkvzlpXktjgFx1wDZm6tV5apDSnfNvGULdfSiQmlCQCP9Tc2goxrKq2UDln8BtZX1uX0aK5zhGq9QXhgoy1318jMgRknckei7O6Ax3yAxjyGi/wcIEfjZ6TtrPW3VpXJJ/4ir4MCIwQ2b60GUUJ1NHoS0N8gEOT2R1IbIviRJ48ePt9vtNls6edqs3ImV/T8ePCBS3ad9UMG2C360+i9/FDs70JNakBBnrKuh4dOgttps9v0wVNkbDAGGAEPgGCNwxhlnUALaarVS00yO49577z3zPnuMx8O6YwgwBBgCDAGGwJEiYEpbHnvsMZNxrqioqKqqoi9zcnK2bt1uZpGpBHSnGN0P8HeAWaH4hKA6JQpzBVggwR5zTathJkWJcZk6J0pDA6D5xp9C/unB8MSwMiWo/SYKS0nhHRWzUU0CTSQUM7LYZmM06yNUctyQcN0tyJ9HQ/e0R8eEtP9RlBuE+G/jsRW0eg/mchqmq5jkqgqKo1QRFdAQIAS0BBBSxZ9ePIqzp3HWNC49i8vOnL/005c727aSdBizSiSfKQHN0rAj/Ymx7x8jBBgBfYyAZt0wBBgC/z4CZmK8dOlSe2aGuXyYMKZIsRL7CLTlUgDrRLz3IZR7V7jzA9VOcOXzle7OYcN3rKsHH65lAg29tsjcs6oQBbQAhqJhcQkF3b4E2LgORg5aNti1p7iws7gkevHPwVGwb7CbH1iy5bGHFVkDJIiRfY7q2BThf6n8mN7cSVXDYBQ2boJhQzZ7XcGiXKE4Vy/NB28hX9hr068uafR14XH0IBrKUA46QUCrGDC0tsGpJ6xy53a488CVH/GW7B9asWXO9JgQAyHJeyPlbXadnFrXMdTAFtBxTIfRV7SV5O8tK4mX5Pnrqnxux5JPPsSiiFjCIiYnZvRpO2Sun0zTq8SjhDZjSAo2OOrCi/v06WNPy7DZs6y2bCs3bITrzZq+n19w4vaPXwc5isERBUClpZ0J+8wIaASaPRgCDAGGQM9AwOv1UgLazNgtFsv27ZilswdDgCHAEGAIMAS+LwjQhTvXXntteno6vaONGjXKvLXV1NTQE9GpYwUmPIaGlhdGG2hLQJqvSmOj/AQeZsXh8RisAwgi5csTiRK1rdCptIiyz6bUSSQE8XJNu7PLPzks3BKU5rbFPgXYR4REkMgoZRH5YsxMMTmiB6uUEcZXAVWmKuxnff6pXdKvebhOlKaFgktJIUGSyKm4SBdX1coKyHLimWhTIuUTN4RD/zt1OpeWyaVlc/Zsrm+/Kb/77cqIr9X07sCUzEwUvy8Xlo3zvwsBRkD/d11vdrYMge8FAqkEtI087Dab3WZrWL8ONNEwIjpEdJCxQgRAWyecdMq2ck+k3Kl5HZq7MHzayS1frEaWmgQB1PhLAEPGWzKhXLF+oIF0LQAcaILTh+8c6Gr1lPpKy5vGTobKcr4gp7nK0Xjtr5qDYQwaSPxg6KCQ45MENJnyToigJdhUD9VVHxQVbPWUyV4POIvBka+W5O8Zdf7auIAabV4yUBpsaBpIKlYilMnMthwjdSr2t8LF5+yudXS4c6C0Nzj6hAZ5N0+dWm/OXyPdTiMKOp2ejGnQ2VqLRvmITFaH3XKfP9fT4KjSc/KFktJOh+Od51/EuoUKDUjoEjGTfU7MzAuAZZOpU5kQE4OqBrwAlVXosGazZ3DWDI7LHNB35Mhhj/3x4ZAcw1CLjAV16FT7TFXPGPOZYY859O/Fb44NkiHAEGAI/OAQ0FSNCp8t5EET9aysrB/cibITYggwBBgCDIEfMgIieei6npuba5LO55xzjrk//ZbpqBFK1OrBrEbGDM4IANQD/EHunBT0TRRhckh7XEL2mWY+uOwWF7ImeGOKoEKSIpLvGZT5fV+HR0LClK7o5K74/UHpmdbYPoAoyeAkULTEilZZJyt0sREz1SL1giQDwmQYf+alGUF+DK+Pi6sPxrTnOqPUuFklwyBDxtJCSveTl3H1LnQCfAHw+N7W2W98zKUXcGn9OC6d4yxXjh0T0BXMxQxiDZlIw37IvwR2bt93BBgB/X2/gmz8DIEfIAKHENB2my3Dis+/vvIKqDzoEQPCkhYSFLzPX31tfVHBdkeRXjiAdxZ1jBi+/7NlePuNakgcE8EvCSSMBGkKOpaWwHu7DLt3wmXnBQek76rwxoudbZddDeU1zWWOYGlB469+0R7sQr5agLCOlY2RtSYBRRJwg+iNDQxSuvZDbfn73tJthfmtXi/07Sc4narT0TbipE1LV1H+miiMNQN0xYCoClEFRBHUOCgxgLAAo85f7s5tqOgvu3vBYAeU9t12xUVbNDIPHoyIvEBUzlQ7jSurNLIwi3iM0fiKDOrRPxslg1YOqPD196q9C/1VdXvufyQWiGJghWxwUjHdHRUlCGiJRFAaYdoTLmaKAByXxtltnMWKsZ2t3xVXTPe3Q5RYlAkar0OIPHGe3fTcYAR08sfB/jIEGAIMgeOMgKIoW7ZssR784Diutrb2OI+Mdc8QYAgwBBgCDIEjQUAURUmSIpEIXRdLeeezzz47SUBbFjyz0GRfFVJ1ME7SmyaABXz7PNk/TYiPbw89wsOHhM+lFDEZgpkgJQZEqwDqkGCfP1aNByLSlJA00Re/O6w80xrbRcv94dbgSTV68gb1b046YBARtKrhx5R9XhiTbg3JY6PG+Jh6H2881yE0k8NIhkkrE9EWRJ3ooHXSskiY7s0AD7bH72vnb1+6hetdytn7c5yNs9pOOHEE0VvrGuaqOn0eCa7suwyBY40AI6CPNeKsP4YAQ+BfIvBNBPTsW6cbInWtiJPQAhobobjg1aGDYoUD+CoPFOU3PPcy8AZEqbw5tSckSumaKJWXeAMg5INrLm929m509g2WuneMmQTnXADFxftrvYGThm5ZuxZVyuRhJGwrEgwufSkh8SzjlPn6pXD2iRuHVDR7SvwnjgCPB8q9UF7Bn/qjnavWgwBINuNqsMSCLpVw42EFZJFolqMK3HprV1355rIBHd4cwZXNu3N2/HTkslgYOw9GRADgBZ1S4NgQssYi6DHQeZR1E8ZYN2DVl1A3vMFdFcsc4HMNlMqqd0+bpUVkHCP2ToMrqko2p+WpjJrKlsm3cHBR2LEBLjj7CY7LSUZ1+PfJp56TE4DgV0lUJCcU0KbRmkGKbtDSG2iBxh4MAYYAQ4AhcKwR4HleUfDf6yVLlqTyz3ZS1Pd//ud/jvWAWH8MAYYAQ4AhwBD4fyBAi5wvW7bMzE1OOeWUnJwcqxWFMhkZGXu270BNDklVZIA48c0IAKyV9fsPtM+JxmdFQ/d0dnyso/VzmKR237RWUwVDIexzF8BiUB6IhSdEpJuiyu0x5Q+dsT1EgEQTKwX9O8yaPpQ+psJr4m0oo+YpBtAA8EcpfkskcmMMJoThkQg81yE0EWZZI5kdKaMj64mmSDtGwh0xCjjgpzqk+4LK7JbQA7vauHw3WnDY7JzNkpaRppEMzmSfiQT8/wE0O5QhcJQRYAT0UQaYNc8QYAgcOQKpBLTVak2zWtMt+Lzsgp/rvELIVORUQ2HoaoVK15cVrq7+vfdWlDUuWgStRKKLxKjJf1LulfLGhAeWFAj4YObE4FD39mFuodoVuWkCzHsQvN7WotxdxQP+8fpLEIzQcdNWqPYY13UZ6IUhU/pbV0EIwsVnba/M31WS01ZRop1+MuQOCLhd0YrKrS//DSOCKJFhY1ViyvaqBkBcQ1JaFgBiGixZBtXe9QW99w/1wImVMMTV/MtRX8XCIKsY2/CCzgu6oiY02Ngi6rBFMGKEvkaiXTegrRnOHPlFQX5Tbr7i9UJhyc5Rl2zjNQiK+PWE/JmyxeZp6SRKo2S0DpE4fhCKwD/eg1MGvlHa7+40a7UtI5PGeRl90j79/GMAk5RPiAySBLRmGIlnohAhLUdIej7y68+OYAgwBBgCDIH/HAFqlAkAf/zjH6n5Bt1S38w5c+aYN9n/vA92JEOAIcAQYAgwBI4tAg888IDdbqcFdYcNG9a7d2+bzcZxXJ8+fXAgNNUycIFshJQN3Anwql98wKdMbw490N7xphzfAaoPV6BiVZ+vJaBJxmbwAB0A2wAeifinhMM3xpUJIfGRYGwjcY42kpbRRAZEq/CI1ECje2uohoreHFsAXhZi0yOBG3nhhhhM8xvPdUjNlH2muRhyxri4lailCfuMUmYcnkisnxcG5IdiMLNLvDuk/c4X44rdnMXCZdhpjtbl7yQyp4T8mRHQx/YnyXo7YgQYAX3EkLEDGAIMgWOGwJo1aywWi42zpOHTlmXJwtiC6HkNYsH8u/ugpqSxzhOqqdz+/CKIqBhP0K90a37NlVUaVilWScTx8l+gIn91bXFredHWa66CxR9AeWVjqaOprnrTrVO/CodJCQckmmmIQZvQNFAUVdJJco8WzjJc9csd3oKGiqKot1gud4KzUCosOODxrP/9E+AXICgnTcVoSISVjYljBS6qUiSAF1+AKs/qgr77Kl3gKVJK+m/5yWlfNKyHeCzB8KpaYifBHlO+GPlsWnFQlXSQFLjx6q6CPpsL84SaKigr9p11+q64CKKBgQs9ge5W6MUzaJSWgEozkFmOROGheTDUu+aMIetzLLM4biDHWTmbheO4tF5cW2CPBoIGmkaiLboho6JDS/DryejPfEk/NbfH7LfDOmIIMAQYAv+lCMiyrKk4Tfvggw+mEtA0Wf3ggw/+S3Fhp80QYAgwBBgC32cE5s2bR9lnjuNOP/10u91us9lycnJOH3mqLCdXvxJeOQawQoA/+2JzD/im7ws/2iUtV5FTDoISB0nENaTduVEqE00lQz6A5QBPKPzsYGh6XLo5JMxsC6wkrLRItEC0qjumdYoKuql9Tt3RQ6LRAvARwLSO9hs7/VNEmKHAAz5lC2GW0cSQZkvYfQoBTXysZR14gEaAFQB3dsSnBLUpQW12l/BQsy/rp+dyxB+R3tOXr1hGF7qaIujv8xVmY//hI8AI6B/+NWZnyBD4niKgKMqSJUvQ6gttrtDpKo2zBVsjEtUmy/D2K3BKZf0J7tby4tW/+y3abojkVk6UvZh7JzhoukODCx2UMCx6Gry5i4c4WmsdHZdeyG/fAcNO6Cz37vW4vjz7jOUkbU+9lZMIBZXQWNBC13VcLUXmmufeLlZXbC7JbXfna8483ZEnFue1V1dtHT95X1CgX0EBMg6DWmdQApqQsV1dUL8RfnzijkpnsMINJUXCoNrQyNMaNqzHAzUFDJ3YaxD75m761iTTkSFPWGLce39XlXNnRTHk9hMry/mTh+7ctBZboFJtXIuWlDljqHXwQ9EMzQBegnAcxo5t9hRuqyhoOqFiaQZ3A8eVE+C59N42z8ACXusiBLTSzUEnQjczgDKjLpN9NgOr7jM4uH/2iiHAEGAIMAS+YwR4nsf7iKqdd955NEE1t3a7ff16cpv5jvtkzTEEGAIMAYYAQ+DoIpBKQNfU1NAZ1qysrEt/cYmsKqQuDxYB6gBYp8PzAWVWR+iWjtCDfultGfaRJFEEScYnEtCppdPNcatkhekmgD/K8rRodBovTWjz3x2IfQDQSmQ9Gk0IyeEkv9NBpyJoMw/CHQUgQFjsW5s7bgpGJ0XUaQHlwTi8B+A3c0OaHmGOqZMSRcSFw0BqWgHYC7Aa4L6O0JSgMjYK48Iwu0v6ze6W3LN+ymVyWb1QnMVx3PIVy1BrTeovMg9o8zqynR6LACOge+ylYQNjCDAEEIEUAprL4NI+evtjLNunQrQNBhY9Obigvjp/zcxpjbwCgViCaCUhASGJE77PcYC4TnhloQsWvwjVuSuHONor8/aeWNuyaSOcP6qjIH+Lt2zb2Wcv8wfQhgIfJq1qssaorhYoqb1/N7z9Gnjd61xOv6NI9zqgrBhcRWJ1RdP4KZ0RAzplWUOvDREpX8o+qyRA0dFZQ1egrQlOrvuiqqCzpJ/sqQB3TXtx5VvL1kEoBooMckzBosrUUdmcoje9RMg7CqiiAUuXgrNwRYVDKiuBvv1byqvWbVgHqkCCLOL+nGDAv4EBpoz0lu1w+WV7XCX1pfkBd/7u8tInOO40jivECssWJKB/ffP/4nkY6ASigUHsxpBcTgY6dN/knc3OUnfY75khwBBgCDAEjhEC1IXjnHPOMalnrCZrs1ksFkVRJEk6RuNg3TAEGAIMAYYAQ+A7QoAS0HZiu9GvXz+aJKZZrbfeeitd9xMH2K7pH6vaU4JyR1Qa5xdm+oX3AHYT6wySlGFyRb0Uv5aAFgF26fBaAG4PKOOiyk1hYU4w+qGCpLaA+ZdOStsn1NNkn2SMSAEfREBHAOoB7j4g3NIFYzu122LwYMh4T0IenLgemk6RJjS6hrUHsfaPSPxDNgDcHYneGIyMjcKN5Dm7S3ptf3DITy+wZXFZWZwV3UdMAhrHlszLzDbZDkOgxyHACOged0nYgBgCDAERKw2iektTNZo8UxF0r/TseXPvxY/iIAXg5Jo/1BS9dtvELtTwGuisnLyZJ5ySk0ii05emIS27aQ3Uli6pLeqsLQ6fXNe0ayvcMRsGltcPqfqqwv2P+o0YT0go8SXeyTTEoFUPMWZRcFAKRh/vLoIRAzf07b29tFTLG6CWOaHKA3VVvnNHbfyqAwMUQA9n5KDxghSb8QAAIABJREFUgQGOjuuzDJny2locrhjVWJ7bWJmnOvpLnnKft27la+9DF08cM4h0WRNQxYz1/FIJaPKCljOUiXL5xKFry0u6qt3gLA47XMtf+yvQEdLDaDnABDFP4ywDp8gpwW4AREXYuBlGnPBBbeUejzPkLdU87q2FRbdwnBOLENoyqQXHghefxvPQyRN57W5OPdmYqhM+mgyWnnb3wFPepB+xLUOAIcAQYAgcLQQo+6ypGq06mMpBV1ZWCgK5Rx2tzlm7DAGGAEOAIcAQOCoIzJs3j+O49LSE/TEloDmOe+ihh2QDDS2aAN4HeDTCTwvGp0aVWTw8Htf2EFGzRJQ0JJnDbEukyQlRH5NdpJB5gHaA1wP6/HZlWkCZFBSntvvfInQw1q8nWRwpPKjTnLM7R6QJHvHUoN7NzQCPh5TbYzApAHPicE8L/5aI5QRDCXdEWl0eKwuRTAob1yBK0lD8zh6A30fUcVHpegOu4+HGGEwOGg+0xDfy8LOLLrcQ6pkR0EflR8YaPcoIMAL6KAPMmmcI/NcgYJDH4aer67qiKJqq0apH9Gvf9GV6OP0mrXecn59vIw+O47LSMwZWDsTvEIY5GAC/v7tkg5pyCweMIhIPKvUS4rC5AQYNanA5Wp0D2k8Z6v9yDbz/Hnjy6wc7DwxyrX7zJYhGkDNGVwotwRRjINEdpJAGNdiyHoZ61jv67a+uUAuKY3l5sTK3VOnuvOTi/Xs7sNhxHMMaLWG+nDDNEAF4RUyIzsb+T2NNSWN1oVznhqGVwaGVK195NjFaDXXGCqigSzjJfggBTae2NeL7DAD/e/mOSucmd3HH8CFQXbX12YVSVyfluwkWVACO/hvEnkxXgbDw1GNEMEBU4eNP4PTTdpUW7+jbq7GqXCkq6PCUf85xI5F95rKRgCbRDY2NUAGN7DNVQFN+GYdtTrkzyjlxFdkfhgBDgCFwvBHQdZ3juFQPaJvNNnr06OM9LtY/Q4AhwBBgCDAEjhiBfy7fmT17NpLOVrRATrFB5u6/F/VJawx4XoS5YRgfgF+3qbe0ib9p8zcAdBHxsmzoqq5jBqpjboeJIpXToIOzKCt8nFQdXAIwranzThkm+8J3dvnf19GIOYLfJ7Iik7Am+R2VBFHdk0bqsCuaEdCQB3/JL82PwdSoNtYXntnS8UFU3c5rXQaKr5N6KUNPiIIoFJqOzDP20gXwh2Z5jh9u5uE6Ba4Sjcmidn9n/HOAVg0uumQ0nVfu1TeD47g161aTwoM4IKaAPuJfFTvgmCPACOhjDjnrkCHww0VAUdBwGACoASXlnVNPN5V9pixz6qfmfurXzjjjjMzMzFQBlxBLVJmQVUXUlORd39AAj8NGksEBvcHHZaRNmxphxNDPi4v3VlYKVeVNK5fDnl3wkx9vrC5oqsnffs3PN4GCfl2KliDKE6rhhIkHaLImCVjAcN1KOH3Y8vKCZm++3qeXr8TBlxSHy737a6qX1W/GaXURRMo+qwaoRL9MyOAIfmKAJsBTj8DAgnUD86XqfCjqvbfCseLPvyFz7oTlNUAwQECWVz2YfQbykmiQDQPiEXjyESjq9WmNu7PK0+nx1t81T+7sTPLOhzDBqLwWUYKtQzgk6ACdUZz5/9vfobpyY5mzzZEfKskLF+cfKCpaf+6FqziujktLJ/LnTJs945zzz9MIlIR6RvaZKKDNy0UJaCq5Pmjb/Q22xxBgCDAEGALHCgE64/vZZ5/Z7fZUAtpqtd52223fcvM9VgNk/TAEGAIMAYYAQ+AIEKA55kMPPWSz2TgLx1mQgDY56Hm/fXgjH3sqEJ4dkq8PwLVBmBSEO5vjn8nwFcmxVB3ZZ1XXSYJFDaANXLqpqmDwRA+NFs8rAe5qDUyLyeMD4Rktra/KaiPRLIu4BJRom0w7xJQdmopS42Ye4ADASz5tXrs4I6RMCcdvDwUXxuN7dLpA9tBTTsqfMX01IGqQOoefA9zbCVMjMFaAMSLcEORva/d/CmjfIQJcfMGlNjst08PZM+0rVq8gjTIC+lBs2eueiQAjoHvmdWGjYgh8XxEwlc4A8MYbbzz00EMff/yxeTL0U5NfNt8/ZMf8gmEYo0fjNG9GRkZ6ejq1sHz+uRcB7YcTt2wVjMSENjks0RQJCwRZiit4q97fBiNP2+gq3tYvc0tNRePLr8KuPXD1FfopAztqC/deeubecCdOWysqctjdg6GxBXKqWNAJAMId8MsLD5T221LSp8PRXyothOpyKM7fP3LkzjUbEpS1gh7OkgoaJaBJUCJrENEAIhF4702ozF8+1CEMK4HizFCdd/sds4SgH6ghZywWM0AxQMJTIdPZyCSnOEFjazqyz399EepKV7n7NVUXxcpLd4+Z3NQaxo8OIoC7XxIFNIZbGDwpAL4ovPkODBm0pczZ4XHE8vt2uQoCNRWNv7hs6xN/buMspYSATuds6b369P3bW2+rOsjqQc13o5Ts0wy/urtNfpQSXaUex/YZAgwBhgBD4Ggh8MknnxyigLZYLC+//DI1yjxavbJ2GQIMAYYAQ4AhcBQQMAxj2bJlqEki3LON4xJOHGncZXMnL2zbfk+odSofGyvBhDjMCcBzYazjF9QMiaSNJgFNOWgwFNB40CMAMYVUz9kH8HBbdFxbcKaqTutof6rNtxOgk8ifRVQmk/wmhXfGxC+RKmIyCpquAfLdHwPMOsCP75Bu9gVvDwQWCeoGgHCiOs+342KEAT4FeDQszojAOB7GSDCJh3s744sC4gGi4waAs390VlqGlUP1M2dLt+xq3EUaxaEwBfS348s+7QkIMAK6J1wFNgaGwA8EAcMweJ5/5513rrrqqpycHEoZcxz34Ycf0jNUFIWSy99+wqkE9J133mlacFgsFqvVOm7cOF3XeQl9olFtLYmp38dKEElumi6u+qoDLvj5ujLXFndRU1nxihcXQDQKc2+HGuee4Z6Oivx/1K8AgUdf44PY5+4h6mSpFnQegCsubKgq3lvrNLzFemmBktcn6HV2VlduXLIEggKu5/LHQwYaXggqKCkENHK+sg7r1sDI4Ssq8/YOLoETXFCRv++O2zRexG8baBpN7KWRcFboU8eD9ISPMyFzsfKyAru3wYk1X1QX7ajIb/EU7Pr5hftiBnSibDqF8U2lgZF6xiEAQAx12PDCK1A36HNH0f5qN5QVS67CjorS7SNPXrlpC/zs/GmcdYAlIxuDGmt6/9z8uCBpBsR4LKhoPrvhSb7JCOhUTNg+Q4AhwBA4XghQD+g5c+akp6enKqA5jlu5cqUsJ1YRHa/hsX4ZAgwBhgBDgCFwRAjQqdOGhgZrmo2zIQdtx1LpnMVm5XrbSi4780+d2x+NdNwbj84VlHti2kMHwusJfUxES5gbphLQWDbIUMCIAEQVECNEd/zigfjMlhg6R0dDD3e2rddRfxQjomP5WwhozI2IF7SOFs5LAeZ18FOjMDYMk9rbn+JjDd2+z/jVFKETAmAmVrSS+16AZzR1TGv7RBHGCTBBUO8IxRYF+H0APlJsBwAGD6xNXRmsoIUIXf/LCOgj+k2xLx8fBBgBfXxwZ70yBL5fCPxL1lgQhDfeeOOGG25IvSOa+6NHjx4/fvxFF1106qmnPv00lrP79x8rV66kGi6qg+Y4rl+/fijjJXYfuq5LEtELJ0loAJB0TTaQhA7FICbBeaPWupzr3cWNJblLXlkEfAz+tgjcuZsrC/dVF69Y/FdQiDOzaqjJNvCvOUIdQJDQVmPm5Hh54ZY6l5qbGa92gdcpDSz3OYr/8cILEJeA1L6QNJAA6eO4BpJpwaEAxARo/gpOHVI/qLRzkDPmymmtzNt7xQX7BRF49LPQNVyYhS7WhqHhExsRdIjpWBAZOWlCteM24IPLLzhQnr+rJGdnhaP+zJHL2zqwv5iCCmgsMHgIE4yxDS4uU4yYoCD5/uQT4PUs85Y1OwrE2nIY6AZP8c4fnfzpyuXQ0gKcNY/jsuwZvTKysv+J/Lx59yGPr3YDYiJzyA4NoVLfNIMqpoBOhYXtMwQYAgyBo4qAruuyLE+YMIHO2lpTHrRfylAf1TGwxhkCDAGGAEOAIfAdIkCL+iABnYYGHHaOy0QzDnz0PXfEM3s3LBXl9QCrAD6UYQegpQZSswYub026CKbuKCqpCEhZ5oX+2J3tkVs6hDuj+h+ioaUgB8nQzbwqUVjeVD2bO5ilCTIofgPlz4+2x8a1xn8dgrFB6Q+y8AWgqJk+vjaVwvaJF0icqKffjIkzQqEbhPg4WZkYiU9pbflLJEq1z7gQVcXTSbeY1iNcem+7pCQkWUwBnUSa/e3RCDACukdfHjY4hkDPQeAQf2dzYO+8886VV16JhlwpD1P7bL6XnZ1tsWCUkJ+f39DQQDjNxK3cbOprd5qbmzmOs9vtNpvNbse1Vlar9e2336Yc9CGeHoqmiZqiA0RlMaJAVIYp03YNrt46tKqj1rP27jlGJARf7YZT6/Z7+u+vKlo/5eZOmbDPsmIcoqSmgzGZ0wfvjVUUr3f3D+ZmxvNzdK8TSgr31dWuWfQqhGNI8WoGGCAhk2wgd4wENKAHNABEBWg7AFeNbh5Y3OLpz7v6tXny60dfsHv3DtqJoSHXjP4YCfa5m4CO6MBTApqOROLhsfkw2HvAUxgcWt184vClK1YDr0Cc+pKlRkkm+4ud4My9DiAp8MQfoLZqXXV5W6VXrS2HAX3C3pIDgyqX7dyMYc0D9/7Rbs2ka9vsGVnZvXM62rvwFKJxOtZv2TIC+lvAYR8xBBgCDIFjhoCu65qqnX/++SnMM+4WFBQcszGwjhgCDAGGAEOAIfBdISAIAq0w9OOzzqQEtA0V0BbOitllxcVnrpfC7cTpogOgGaCNWGeQVBMLDx5OQKugRCEcBy0O8IkMczoDN7T6JraEHwzEPwO1hSwd7db0EKkynovJOyd3iP5Z6wB9N8DTXbHZXcJNAWVMBOZElH8QEhyP+oaU12SfVR2CAO+HxPntgQnR+BhFnigLs8LBP0eCa4lOOykwMjRJ7pVF3DdIjn3iaSMC4UASZKaATiLB/vZgBBgB3YMvDhsaQ6CHIZDq7/zRRx9dfvnl2dnZGRkZWVlZhxDQGRndt0aTg6Y8cnp6+tKlS//9MxMEoaqqKoM8TA76yiuvpBUOUzXLxDYZZEOPyqIKKB6eOsdf5l1fWdQ6qKTh7pmNShw51isu+GpwWXNVyY4Lz12tqcgdi1pyVtugdstkS0INDUDX4fXnobxgbV1ZpKB3uNIFZU7IHeBzeb6c/5hPI6GIahDpMV09hTpmjRpKy2RlV5SHG65ucw/YOrRMrcgPu/pvu+icrW1tEFdQNx0X4zLx3sBayCi9Jv4bhIMm7LNIBc0GoE/0yo9guGetpzhaWynVDPx06ecIJB09ruoyB4BjIE9SBVEyUEYNAA/M0ytdq2q8baXO9uKiUGUZlDk7yr0ffUIsUrpa1ZJ8R5Y9zbxkDzz4ML1Sho4i6FRhOH0/dcsI6FQ02D5DgCHAEDheCNCbtcPhOKQI4TnnnHO8hsT6ZQgwBBgCDAGGwP8HAcMwZFmeNm0aks6kCCEpR8il98pKH9CPZkMC4Z1jZBsHVSF1Bom+x+SgsZS6BoYMRhy0VoAvAe5t998UDF/r898RCC/ixTZknw1s0CA8NLVI/Dr2GcvLA/gAdgM8Fo5MD/HjA8qkiD4rrL5sIA+eUDKZgqbDzl/RDEXDrK9RNR5t7ZwWjE/m5UmCOC0afsjftQrQwFrAAUsaKBooK1cttxLRV3avTM7K/fyyS1CSlXThYB7QhwHM3uhxCDACusddEjYghkDPRCDV3zk3N7d3795WK64Astls6enpmZmZGRkZlIbOysoyGcxDdiwWyzXXXKPrOBf97WymCQLP81dffTVVQGdkZGRmZqanpw8bNowm2MRUmhpWoLu0RvjWuASiAtNu21g+cG1VdUeNc/NtN0aVCOhxuPNWGOLZWuvaOXTgFxvWQ5hH54u4EgEAUSBsNDoua9TzAkXNBqxdBc4BSzz5gbJC2ZkHZcVQlBd2ubaNm9QlkrVQUZnIjzXyImHjjMNXAUSigH74odBA51ZXTrC8f8jdf/cZJ23yd5FqgOQkQ9GIQWpXYGSUIKAlSkOTaAOdoWUSwTTugZ//ZHdNcZO3sKvSs3Xx+9gIfUbjvBiXMAgy3yKN66ArgPpoSYH77zY8BaurnR3VbslZGCotCTmLW6or13/0IYTD6IT27J+fQ58TUlPabk13lJSGIjFF0RQlQdCbF+VrdxgB/bWwsDcZAgwBhsAxRoB6ZdIbdKoH9PTp0+nyI1E0V+we46Gx7hgCDAGGAEOAIXDECMiyrKmarutvvvkmXVNLc8w+ffrQnWhEAICQpPgVSUHzQVUEWcFqOmqizA8pqkOk0MhBC2DEALYBPBIMTfYHJyv6bbz0vKw2EEdnwKNIZqMSDpqaN1PVM11vmjwDnlhnPN0VmxHkx0bkSXFlTkh8MhTdkagZSBr5OvcNgyR3cUDtcwfA333h2b7wBEGdzMuzIvy8rs6/xmN+0gspbi+ouLhW+njpx/YsZKCpD8cdd9+BVo6JB1NAJ5Fgf3swAoyA7sEXhw2NIXAMEQiHExZViqIc7g65YMGCiy++uLCw8HBCmSa3h7xvvrRYLDabLTc399xzz33yySc3bNhAz+nfZJ/R0FmSPvjgA2oDnZ6ebrfbKfG9Z88eJHkl2cBZ36gBccMgLhNYhRje/xvUuL8szN1S4dlwx8xm4CHSBus+g+qitYPczSNqVn76EcRlJHYVkHRkocksN4YX1GELp6pFATauhlOGbKutDlaWo/C5tACqXeAp3Tf11qBBAhRzUjyhOD54itsAePUlqHJsceUES7PiI8r4s07YVb8OFJVGQ8nKhzqKl5GA1oG6PxsQp/GPREKWiAy8DJePbnSV7PQUt9QUrXpyPg5ZVEmZQrT9ICw1ZZ+VhChaBUWGqAT43/33+StK1tQ6IoPd4MnTygvAW+CvdK14bRG2Iwng7+yq9LjMC/fPnXvuuRdRMQzTfYVSzKlEc+o7h+/Ta822DAGGAEOAIXAsEdB1PRQK0RQ9lYB++OHEohZWh/BYXg7WF0OAIcAQYAh8hwiUlJRQS8aUtMXy+YpVkqIKippMhlBPpOFCVlKbnmqZVcxrVBQUawLAVpCfFdtn8uFJqj5XgoUqbDKwkCBNpBRy+KHDpmmiknhb1qQgwLNB7bY2bUKnOjEgzY3EF8r8JlAjyC8fkht1N2agZEiNgt4GsBHgRRHuCUrjg8LYqDgpFJvnC74rqV8BVhbSsbg9ap+Ju6N0/8P3UQIaEbBb3n3/ne5GMY/E8015h+0yBHocAoyA7nGXhA2IIXBcEBBFUVM1s7KfoiiSJC1cuHDMmDEpd/ev36UsM9VBU3aY47hBgwZdffXVzz//fENDg6ZqqfYdR3qCiqJQhbXZOMdxs2fPxnYMkMQYIF2LJLKqQTQCixZCVcG6OqevJPfL22YqAT+Ssy3b4Mc1n9UWflXj3POn3wPP05s6qBBPENCUg0YJMRpWCAJsXAfDqxqGVEqVFZqrDByFUNxfLC3cP3UytHeherqbfaZljJN2YIKkoAM0wIb1UFu2cXCp7u4jF6Y3n163d8cGMt+NZf3IAjBqu6GlENAo4xYMiJKyhGhjHdOQKJ84IVhcuNblCrgduyZd04xnTB66rqLzhkwJaANtp0mFChWMoITsswDwzAK9tvKzqpLmqkLV01939xNKc9pHVO55+VksyYgEtKg9cP8dGTbOymVwWFuaq6mqlSQl4QpC9eoGcvPmM9F7yjvmR+YO/Q7bMgQYAgwBhsAxRmDjxo10TVIqAf3RRx/RYRw+zXyMh8e6YwgwBBgCDAGGwH+GwPXXX394RrrwueclBYsO0pwsmYyQv1RsTGRHoGOepBDfjPeNyIPR1nGhjpt9/r+oWL0wQDQ8CvlC6hYtGWm7ycWmKmlHBfg0Gp3bKt3cCZN8xmxffKEsfolW1LoBdKEsZaxNb0TaCpLkCkg+0DYAPC+rsyMwPg5jovKEMH9HIPqSqDaSCvJYICjBPlMOWrluzLVWrIiECmhbum1/y34NlVeUdGYE9H/2g2JHHVMEGAF9TOFmnTEEeiYCqWIowzDefffd8847j4qOU2/wNJullQDN91OXQXk8niuuuOKFF17Ytm2beaaUvfyP011a8vimm24ye6Q7ffr0wS4wpCC+G8SMWRZh8Wvg6f+Rp+++Gsf+K0Zvj/IQCIMchyvPaanM3lU1YP+l53Q0fYWrleJkxZKKCmhSiBCb0wElxbymQ2cb/OqS1mFVQU+R5C3VHMVqUY5W5Y78/MKm/c2Jr+o0oOleV4WG0joGHJqsQcAHI09YUuvcV1UgePr6ap3bVn4GspBw+DAUlC0nVM96yg5xf9YAV1ppAH4Rh/rEH8HjXFPhaisrbRl5ys54F06sqyJoioCybxpJKTpoCuiSgQdKIggiQHsYXn4VPKWflzubvcXtPzkJqvIVV87+svxP3n4NAp2Jq7S5oaFXFglnOC4jLTuvf/7Sz5ZpqqEoWpJ8xr/JYC4R5hwc4eGbhzwTrbM/DAGGAEOAIXBsEXj++ecPrwbs99PlvMd2KKw3hgBDgCHAEGAIfHcILHzuWYvNak0jFtCkCCHHcTdPGE97oMnIQb0dvE5UJetMNwE8HgrdEQ5N72p5oLV5I6Gko0naN5V9pvsJP2gs6475jqCib0Y9wKMdvsnt8ng/TAvGnxT4DcRSQyIZ6mGJER2aSjrhNZBbARZJsbmR+PgYjBFhTIyfFQ4vEvTNpBEisDJkXDebYJ810OoG16JXogXZZ0+Fh+RipuSZEdAHXXb2omciwAjonnld2KgYAscagUgksmDBgokTJ6anp5sVBc30lRYV7N27N3oEH1xg8Iwzzpg8efI777yzf//+Qwat67qiKJTd1lRNEIRoNHrId/7Nl6+//vrhBPSzzz6rKYokyBgIKFhOYvdmOGvQxrqCve6+9Rf/rCkQAh/p8LfzAz+q7KrLDZ1et3fnFjTfMLBKoaiiEFnR8UlL/cm0HrEswqif1LvztnkKohWl4CoSi3N91WW+C37WFo5ib1gJQiGGyylhjoHtiBrqsEEzYOw1za6+awY5Q94BzUPL6/+2CHyE8MWSg6RgINpuoAJawy19ErpXI/JoOm8uA7y8CKo8X3qL93mLm7yeZe8uRscMXDmGreikugbdqrrGGyBoIMigiCS6eeFVOPnUHeVlPo9DrHLxpXltFYVtI6q2/f01UrEwif5JI4ZnZ6anWbmsDLuNs0yeMFFXDE1FZp0R0EmQ2F+GAEOAIfC9QeCuu+7KzMyk901znlgQ6J3je3MWbKAMAYYAQ4AhwBA4BIFgJJxfWIClCDnOYsOKRBzHnf3TnyTUxYeLnqhSJ+nNIQHsB3gxFLttX9ft7aE/BQKfxMJBQiyLoPNkTenXE9BywhRDBOgC2Azwh3D4zpg80a9N82uPC+pnhMUmi2DNIR8izqGCaB5ACIGxEWB+wD81Ko0V4GYBbo1Fn9HkzYA2IDx5CmCIoEmGTCw40DnEnmnnLJwljbNn2s+/8LxUA2iSFjILDhN5ttNDEWAEdA+9MGxYDIH/DwLUYZmWDTTVzbIsm87LdEfX9b1797700ktTp07Nzs4+zE6L3tAP2lqtVrvdfvLJJ0+cOPHDDz/0+XyUoPza0Zrdfe2n//6bkiTpum46UOfm5tIxDR06lFYLxKaIB8VZw/82uGDPCaUtF57zeVsHvica8MUyqHIsKx+wzzOg4YO38AgSgcRlEEhtCk3HtUsK0UEj5crHYMq48EBXU2WJ5HVoXoc2uAJqKw6MOq+htR2/hy4XtN4DDSqSCmgNDF4ReA1iEtw2o6WmdFtFbmhQUXRQ6Ya33sAxasSKDMlvqt3GP7RQs7lKK7HACwBtOCIq/H0xeEo2e/OjZQM6KkpW/WWBHIoju02sNQzcQ38zalOmyUpMx1Vl6M8hA3y2GsrKV+QV7Msr8PXrH66rAneRv7Zs4x3T/bHERADy7XffNSf1Gg+sqsAZe2onQkb6tZvUeOprv8DeZAgwBBgCDIHjgoCiKDfccENmZib1raIuHCNGjPiubsrH5aRYpwwBhgBDgCHAEEDHRV2/8pqrMXmxEAIaiWiOs1pIMR2QsXy7+UjmM8R0mSRJ0AbwfFSY3txyZ0j6bUd0uS8aw7xJ0LBquyKTwjqHE9CYoVETD0INbwd4Ih6c0RWYLcHMmPZASP5ANA4ARIh9R0LXhNkUVThRDw8zecIRrgXjoZZ9kxubbwmr46JwQ2voz6CsAggR9bSW7E0BELXEUt2ly5f07tubKqCtdsuzzz+vEoNrerZm6+bJsx2GQA9EgBHQPfCisCExBI4KAlqCNIU9e/YsWLBg2rRpp5xyCmUereTBcZwpeab+G7179zbfGTVq1O233/7ZZ58dvob3m3Lab3r/SE/PMIxIJDJv3jw6WnNrtVqfW7CQtIZRQcsuGFr2tCfnH5ectdfnR+pZ1CAQhDNO3l5etLO2bNe1/9sRJ9bJRG0s6Gi+gdpnSkDTeXFJhelTAoPKd1eWCN4ScDuNstJ4fk7DeT/d2emHzhAlr8VDToHql803X30FqspWVOQHh5aqlfkb33gBDANjEBoZJL+Gdh8kUAkRGlokL81VVOgxvbYBBg1amd+rpTRHHFjSNObqZlEG0TA09AwRkErHeEYCQwIdC0OTNWH4XliDDdugovZTp6utoEgurwOHR8ov9HtcO6dOCgZ9dAgqgLB+3Reoarenmaiu+HxZYqRJYj054IP+mlFO94gP+py9YAgwBBgCDIHjg4CiKOeee65Zs9disVit1tGjRx+f0bBeGQIMAYYAQ4Ah8N0hEOP5T5cu6ZXTJy0jHXXQyefGhnoNDNMJmhC5SECTaoSYNklEufxeBGbWTWdFAAAgAElEQVS1+ia0dzzgj/6DVB00RNFAa8Y4ERob2mEe0EgYUwpbhbgBuwH+FA1O93dOjUoTffH7w+JHAPsAOjT0YcQHzSq/joA2SL63E+Av0fCtre3jWgJTfNKMgPpwRF4J0Eo+TWSMSY/JpMzZmDh5ApbryUqnWduG+o00C0tNylhe9t390FhLRwUBRkAfFVhZowyB44uAyfyKohiLxSRJamlpWbFixeTJk4cOHWq1Wk2TDdPQuV+/fhzHZWdn03J/NHE9++yzZ82atXz5clEU0QJY1w8vJ3i0FdD0XCRJam9vz87ONgdMKfJyj1eI84ooYZFgAZZ9Yrz0F6GtBcIimaWOw/VX7Kgq3FxetP3Ukz9r74Qof8iVodpnRUX7ZGSrH/+d6iz+2F20z+tQ3E5wujS3t/lHI9dt34p66bgCqkHr/RGXDVwgFSfLsdAWgz7WroKT6taVDWhz5YRrHXunT2qSRYhgrT/0UMZQBB9m3UAaM/BJDro7bOjogh+NXFfm2F86IDjI3XXy0CXRMAhkChwbokUwUIgdNyBuUBIdIMgDr8O6LXDKaTsryyNOpz70JCgbBH1Km101m++4Hx2xEwpsnY+F+JICj0k9Z9jTnnjicTo+uj0koPmml6mHsH2GAEOAIcAQOL4IyLLscrk4jku91997773Hd1Ssd4YAQ4AhwBBgCHwnCAiyVDOoDv03kuwzZ7X85nePKZqm6HKSsaV5F3LQCvG12AHwNx3u8kfH+SJzQvxbcaGNjIYQ0OizjFktqeh3OAeNXzTQJHGLDi/HpLntgVsj0k0BYXpH8C1VawTwA3QpgIpkFD3raA1J9pLbRBYlAfLXLwXit7eHJgXFm8LCpI7g4wF+BbHvoBprDQj3rCfSRl4SBVmSFPHk007mOC6zVwbHcbkFuab8WUURUnepnu8EYdYIQ+AoIcAI6KMELGuWIXA8EeB55FlFUVyzZs2kSZOGDRtmKqFMtpESuHa7nWqcLRaLzWbLzc395S9/OX/+/C+//NL07kg9E8MwTCW1KIqRSORoE9Ci2C03fvvtt83xm3n173/7GC6KkkCMofOxogIvA2+gvHnlhzC8dHl1wXZP4fI1a6EzCOE4uZcn12MRVwyVOoOJGrz3Ibjdn5YUbist9nsdSllp3O1t9lYv2bgJK/qJCk5IkzCCWEbjjT6KhY7Jgi6JDNPnh7NOf7fWue/0GhjibrpvDvB8gjVWDdMTjPp/kcrGVBed4KOxed3AQ/ztcNlF71WUbHLnh4Z6I8OqN65agX3HJIjxPJYuVJN1C9GrQ9AMNAahg2tth5GnfT6w3FeUp9bWQu/+4fzSruKKhhsmdwoAQQHPIhYPgaH8+LSfclyvjLTsPr3Q3fvmsTdicGUkOPJvopsPfz/1F8L2GQIMAYYAQ+D4IiBJEjXfMNcwpaenv/TSS8d3VKx3hgBDgCHAEGAI/P8R0EgO9Njvf5eRlUmdoOn22l9fpyiKrquiyCcL9WBvlH3eCvCapt8Z56fEpJk8PB439gJENF2W1WSCh+wzpneJTAiPTRodIpcMgPYd7wFM39syV4DJXcLM9ujCuN4I0K6j/BkzPZrkYdInkp5NKhvzKxWgE+BdDe5sD93cHpvEwxRBuScU/YCXO8mhAKqKlo1kUSv17TBAEIQYz+87sI9mwbZ0G8dxvxj9C6pawg51XSXO1zRHIyNlG4ZAD0WAEdA99MKwYTEEvgUBKkamRKFOHuaXJUn68ssvH3jggVGjRmVnZ9MUlN6uqMvzIT4b9KNf/vKXDz/88J49e8x2KBFpcpGp75sfUeo5dXvI177zl4qinHnmmZR6pqaWdBsOh/m4yMdUQSQGzeSGryrwkyGfDx5QX5675MlHIc6juReW/TN4DA4S4YUq6TSigPrNUOZd6yz1uxzxsmKhrCjmKtoxYvhHG+ohGAYMTsxwJMEagw5xHVD5rBO3MX8ERl/VUlG5r9YRGVi05a5Z7fF4agyTigelwJMt0vEQh2hRQnJ54nVNQ0sbPP0PVOR1uPuvvmMmL8sYP5FFZCp+3SBPgBiPzHdckCRyHgda4Kenb6kqbqtyyV4nlJYaZWUxT8nmCWNCooQlGUnpRPzqjTdcm2ahzhuWrPSME08YBoAKdxJsIcWdZLm7p+/pMOk29WQO2jfPLHlyB33KXjAEGAIMAYbAUUZg+/bthxDQHMetXr36KHfLmmcIMAQYAgwBhsCxQAA1wgBVAwf2yuljipM8Hg/tW4pFQUUBsoF8LjLBOwCeFuQp/sjYoHDd/uA9B+TPiR2HbGA1d8obawayz0hA09e02jwptgOANsw7Af6qqvcF4tOD8qSIektz+GW/vosolwUdi9PTQ8nQcKkr0SspYAholkiq93QAbAC4szM6phNHMjks3Scof9WMZvNY3CGZFlVSp7Dh1/z6aqp9xvO1Wt59bzE9WTxJHU8VCwOltEM/ZVuGQE9DgBHQPe2KsPEwBI4AAVOkHIvFnnrqqeuvv76kpITWu7dYLKa6mYqdzdsz3cnMzLzwwgtfe+21zs5OVBDLsiAkXCQowa3rek8joAGgqamJjj+VgL7sF5chbZo0uU7wpCpM+3XjaZWfXnH+F/EgiBINBCQDCCuMMYKqgx6XgReheR+cMGS509VRXALOYigribuKdgwfvGzHDhQ+J6fGk5cmSa2qIKnoIo3+HYYKt9zylbe6yVEarihqvPrS/ZHgN7HPyXbMv4nlWqAqEArCA3eFh7i2VfXvdGW3DS3dd/n5m1URFAMUkDX0tU4S0ClBhkSsOf6ptr5tygFP/53V+eAeoJc7jeKiSMGAjRecXd+6FwcpaRAVBV7if/O73+DqbM6SlZ6VYc8cWFXFx2J0xl9TNUXTKPtMZNaMgDavE9thCDAEGALfAwQ++eQTOlNrLhXiOK6jo+N7MHQ2RIYAQ4AhwBBgCPwrBBRNkxT56QV/oWwsmkFzWJyvfs06XMwpkiWxyPtqPmJ58XdRmxWKX+MLXx+SpvnkV8LQSNaxqjqmVSaBeygBrWBuRDXN+wAWGeqcaHRKRJwcUsZ95XsqimYaPICgmcaI1PvZ3BL5syERCxD85nqAJzrg5vbYryPCuKgwNya8YsAWauaYwjVjAkmz2WTKGYlFKftss9s5jit2OhTslIyNsM+J5DclN/xXELLPGQLHBwFGQB8f3FmvDIH/DAHTiFkhj/r6+vnz5w8bNsz000i1SLZarZmZmam8s8Viyc7OvvTSSxcvTs6aqpqiKMg5ki2VM2sqVrSjBPTXctCpqufU/f/spI7oKF3X582b17dv31QC2mKxLF68+PDqiEidSsBHcTablvzTcHqYTlGrALwGIKoQjcLIkzZUe1pdjriz2CgrhHJH24jhn2zfiUNT9BTtc2JqOzFkBRQFFAlUWYZn/gDVJetc+a11FR2XnLdDjpGp94POLTWyOOgDGmRoBsTCMG82DCza48w6MMyp1uZ3njls814yDFJEWdSQg0bNNnmqGqhRURJkbE0W4MmH4KTKpoF5kcEl4OoHpQPkMkfrBefv95Gqg1Jy8C8v+qstrReJ0/DXkZmZ3dDQkEqWm+yzjDrobgLa3E+2dPBZ0FdMAf11qLD3GAIMAYbAMUPgySefTA0GOI7Ly8s7Zr2zjhgCDAGGAEOAIXD0EMA8RdcVTYvGYwPrai02a1pGmpXjcjju/hmz0IWSF2heEwDYBPAqwDxenugPjw2EJoYCj4nSBlLDRyBapFQC2tQR4+CTGmSVFBh8S43N5MPXS+KNcWlGWPp9e3QD8X3mSaJERDwm72zuJDInmjc1ArwQg1sPoPZ5bFyYIUafBmkzMXNELlk9mDzutovEscy9806a0dvsdovNetvts2UVl98eYr7BFNBH71fHWv6uEGAE9HeFJGuHIfCfI0Bcm/7dw7u6ut58881f/epXDoeDlhiy2WxU9UzvTLTevc1mowpoug63oqLihhtuePfdd6lMWNd1WZZNybDZN60x2JMJaACIRqNnn312KgHNcVxJSQl1vjbPJXUHVyd139l1wiojk6vo4PPDFb/YVdxvs7sgXlYslZVEyx0tVZ5lG+qBV1B33P04+K6OrYAmkiKAK1fCqYO3ObP3VBQ0XXpOR2dr90EYviQaIdPoKZ+Yuxjh6GhjvWIJ1Ln3lPaOefrJNUWh4Z6tryzAb6mgaEiX84SANhlhFERLWOMCj333DRhcunmYUx6Yr1Tm6hX5Rt+0bSMGr9/YADHiPi3gYjT4+zvv43SFNd1mz6I/mCeffBJ/CTjZbiiKIimypGsqcZk+RAHNCGjzkrEdhgBDgCHQYxGYNWuW6f5M/50/44wzeuxo2cAYAgwBhgBDgCFwRAgQchjzq2cWLrBnYlE+juMyOG6opxxJWWKNKAFsB3gf4B4FJgjqxEh8ejB4j6/9fYAAIXup/8bhBPQh+U4nwAdi5O7OfTeK/JWyMl6QHuXVZSI0G9hORKcrcKlO2qSe6Q6yyFh6h1DVbwWVO1pDsxSYEBVmCMIfQVpKbUAAk66EPio18Uwioup6UUkJPU1UQFu4vV81JeXPB5UfPDhVTR7P/jIEehICjIDuSVeDjeW/EgFa1k8iHgqUiU7lhXmeNwzD5/O99NJL1157bX5+flZWVqqyyWq12u32Q5TOHMdlZ2fbbLa8vLzrr79++/bth0CbKltO1ThT4bNJQH+7DvqQNo/ly3Xr1hUVFXEcZ0JhsVhOO+00OhUcIzUYJUUk1G9iBlkly59ISKFqEDPQkQJ8ARhzrVDn8eX1bh9UDoMrjSrP3pNGfLZ+IyqjVYMUMabT1ubSpuR56gCdfEQBaAvAJZfsrXUdqMz96qzh2zatAlkEZHTpgTSKwaM0k4pOttH9Nx6HtSvh1KHbPQUtFSWaIydeVrjjkQc1ajwdFwQdeB1iBxPQqoa2ZiApsHEljByy2d2/sc6hlueLuen7i/tsGzFo9boNICcn1FWAhs3bHQ5Hnz69srITsdqsWbNIvQ4dCWgs7pzw30iaglBx9tdsu4dOqkLTw79te9AB7AVDgCHAEGAIHC0ErrnmGpqNm5PTo0ePNjujAYD5ku0wBBgCDAGGAEPge4RAamYGAG6PJ1HUhqzu3LdzL5K5AM0AL4r8rV0d1/pjV/rjNwd89/jaPzWUVmLHrAB8LQFNE0aZOEfzRCi9FWChKk8N+cYo8nUx4T5Beh+gA0AysBCQRPIsw8AltmSVbSoHjcMIK0hAfwIwPyBM6QrfGhXmiMLToH9BRhgkHaFOiiZsBwufMcuTlGcWLuAsHLUZ4ayWn513Lr1YtGCPmaGaO9+jS8mG+l+IACOg/wsvOjvlnoVAaipIueBYLCaKSCyuW7duzpw5gwcPppmkWVGQapzNxJLqoOl3qBfHySef/Oijj1LDR9qUyTKb/s6p5LI5BrpDPzK35qc9CrjFixfTgoqUg6YlFq+66ioalKRQvUgA60g343Q4eepRww8A/jDMu1ut83aW5YMjVy0rilR59p44fPnW7RARCPsMCtpdmDUdDp5W1knEEFXg0tH7Kjw7i/tuH1xW/+HrIAVBx3LKMYxF9ISQGJnZb3jQAW/dDIMr17nzmgdVKB5npKRw32mnbW3pwICEVBkEHS2sZXNOnhhx4MuYCCIPw8uX1RS1lPXvqigUKopF54DGwVXLNxD2mZyyKqji6jUbLdZMW5rFhqUHrfa0rOuuu47OeeDPIxnxmOEL7ct8ecjOQWdDj/327UEHsBcMAYYAQ4AhcLQQOPvss1NDAo7jbrvtNnorN7dHq2/WLkOAIcAQYAgwBI4mAqkpiSBLz734gi3dhilwLxuXbnny8acAoAXgzah8dzAwTVWuDgk3Bvg5/q7nw/5WwvSicTPoWAuIlNYxPaDJkllDISlejMiTtwI82xWe5fPdKss3+gJzI/E3Ab4i1s+GinojWQdyY9UoBw2YQdLyhchEhxU5CrAK4P6gMLErMqErMrW9awGoywj7HCUENy5Q7RZMJ1JYKmPi40gIjLrwQrynUw7aann/ow9xuaoiMwL6aP7KWNtHCwFGQB8tZFm7DIF/HwFaS9BMC7ds2XLPPfcMGzYstXwQ3afUszX5QB6RKKBt5FFXV/foo4+2t7ebXStYkhcLDFLe2ezia3dQyfrND7PNnrNz9913Z2VlUTAyMhKS3oXPPUsrI8eEKBEdIwFLCWiZxBwioaGjGvzmUf2E/2PvTOCkKM7+Xz29czK7y3KznMtyHyHKG7yiqH+jyWuMb2IMRkQjRoMcCkJARBAIIopXNNGoYFAxihovjBeieCAgigoCIofAsvfs3H0fzz9VNdP0XgjKsbs8/enPTE0f1VXfnump+tVTzzNkZ4dwSbc2RvcO0K3jtycPW7l5G7X2TUpUtGZxj3WqXbu12Gz9DRuSabjkd5u69djSvfv+ol7r7lqQGVK3Lc2yqek6FaBZ68CRd7NnZ96pHw8bSkvg97+p+nHfaFHndOe21V267Cwesub9T+kxNem0ko0yQa2SbV4WzYSEDpJug6HAqN/sGtqzsl9HrbhDqnvb2ICu2skDdi1fDmmNXlYHKa5Gd+zZ2bZ9FyJ4xRzBm+MXSNsLL7hKZ86jFVmTJdWkzRh6RadV5660s9FJ1KrIwaXnrLRd6xT8gASQABJAAkeHAPfQxTVo3nhYtmyZaZjuf/ijc2XMFQkgASSABJDA0SXgdEZogB9D1wz9tDNOd4ZdB59+ehnAv8CeloiMjdRM1qzro/ItVcmlZVXbmbKsMZ8YEnMAbRsZDZp7f868gqWxEIXbAJ5WtFsqq/9UHZ2SVueU1bwoG3tZ91Kzqb2RoYNhsM+WzbqNdeyg7QhYawDuiskTq9LXRqTxlakFkfjHYJUyNyApZoVtWnTWrGPv5GanqvrKlas8OVRe58u5553H5/vKmspn27pp8LQ7B0wjgaZGAAXopnZHsDwnKIFkMrl48eLRo0fn5eWxuHABrqg6xs7hcJjLzVnxmb77fD6/33/22Wfff//9+/btc4ydeSeTo6RefbP+Pdydz/rpZidAA8Dll1/u9/vdtuGEkCX/fJxp6dzlBdVRLbAVW+PTqdIAVTK88gb0K15X1LFqSBH06qB077C3d9HqDZ9DXKHqs2UzBxq0GaKDaVLRl4eGyBoyWxYNPjhlQmRo/y2F7fb27rn717/+Qkpmv72mYlkaj6ScEaBrtQiyubBcVQ1GXrKrV+G2Tq0ru7RPtG+zq2evdXPuU2JMC47LMd7OoBlYzJabhmNWdZBodXSYNknu3fHrXu3UAZ2huL3Sre3eft23TJmUqo7Swsh20oTUo0sfzm+T16ZdJ1GkQSk9npyBfX+aZJbajmk8V59RgM7eQnxHAkgACTQ/AnxSS7ajSt/5JKE1a9bouu7+329+dcMSIwEkgASQABJw2cpQv8uWJWvqCy/+m/7heQjJpdM8r7z/vpmVeycoiQmydl1l7OaaxL2VVatYTHbWn7JUmzrQoJ6XDbAsy7CoJ2VX/BtLAigHeE1SZ1VUTpe1aUl9xr7ICzF5h01dZei6ST1Hm1SAphNsTRpHh610hirtA9Iw9ZYBsBNgYVX1dfurJ6Ts6yvk2yPyKoAyakBtpZnZkskMlVhBMoHfs3N5M3f6zJ+OEEQPrZ1AvAH/+g0bdGaZxHw7Ujvp+it+R5BAUyaAAnRTvjtYtpZAwLIs6leX/lNR4yNeJdu2VVVVFGXTpk1Tp04dMWJEIBDw+XzucIKtW7d2dFWnM8ndbgiC0LFjx8suu+zJJ5+MxWLcgNrxmGFZVmOdTPd2nm4QsXNYg3ub2sZTTjklFArxgEuOHfQrr7wiyzI17DVsVTeSiqqClbRNmf3Zf7QWunRcV9i6tLiDXdwO+nauGPaj9959Byoi1GqYzqXif+ZUd2bhC/lUKtrkyMQ6ltMwe6rUq+2Xxa0rftS1+qKz96pJsNTswDprzfBZXXxYm2boWBTT9k4mYkUsBpNuLOnd85PCdiV9eti9e0g9u2++6pqyuAVxZqnNaDM7Zu5q2cq0Mww2Q+ufj0PvLp8XtVeL2kBRG+iRl+rVYeOfp+5KK1Qwp8bvYPz9Hw94g3Tk3IEzdMggKanQUnzHUt+w+TtOwN1IAAkgASRwXAioqsqnOq1cudJpPPCEIAjcJZfz5+60Ro5LUfGiSAAJIAEkgASOCAFZlqlbxUjkpJOGUqeUAQ/xB0iPor/s3jU1FptmwHRZW5SoeM2KlbCJsLQ7pmZ8MjJXGVQ4NsE0QNdAZauhgl0C8Kak3VedmhqXJ0XlBWWp56vVMuYxg1o825mVasbcRIl1vmkf3LRs09AtLQr2FwAPq5EJ5dV/KJcm1MCdCVhtUvU5TUuia0wA51kZYGvU4smiUjZbOZybb5kpev1UeybE5w2MHn1VMpk+ItwwEyRwvAigAH28yON1TwgC7j4eF4h5tR966KErrriiffv23NjZ5/M53UVHa3bsnd1bCCGXX375ihUruGMNbvLM/WycsAK0qqqDBw/mAjS39goEAp07dFzx8ivUntc88E0rS+kJC1Z+ACcN2f2jPtA1z+rfCQZ2rRnSa82n6yCZBFkFw1GfuWTMfXLx2VV0Jx2WVjSYekP5TwZs6dumZmhh6szBX29ZC7bMWjNcg9ZpmyIjQLM2SkaA5m2KrPSbSsBf5kj9ij/qV1xW1CXVrWO6Te7mgYPfLq+hZXa1P7jz6oxTMIvaNVOhfPe3MHTQh0Udq3q0hR5toKitXdT+28sv2afqVCkHgKSiX3FlJhQV/xb5/d6hQwYwLfwAlsZTKEA3zgb3IAEkgASaGAE+2+njjz/2eDyOwy5BEERRdJxxORp0Eys7FgcJIAEkgASQwPckoOv6s8/+i1rb5Ppolye3TftfX/ZgTWry/srZNZGX7NQOgBgzE6J6MffJqDEzI+abygBbAVMGXQEjCbAb7Dfl1H2R2Jxo+ua48pea9Esx4xuTCseO9MwTmdmuzIEG7TKy2D+6aSeZ7fNjVuKmeMUfI/HrypJ3JOENZvtMQ9xTB416dqUzbQ22ugVoWdXXfbKhfcdOOb5AbjifEE/fvv113dWt/Z6o8DQkcJwJoAB9nG8AXr7FE+CdPcuytm3b9sQTT1xyySVdu3bl4nIdZbmxj6IoFhUVjR49esWKFfF43CHGLZ0ty3I8bDgatNPDdCvgzoktI6HreiKR4HVJJpNDhgzxsYUbiYf81NfEggULpKxfDAuoN4ptO+H007f075Uobg+d/dA9v+Kc4Ru3bARDBVWhc6VqzWXiNst8MJo6vqCtAykFU2+M9umyvk+Hfb3bVg0fsOu5p2kpaMQKgw2qs3H1BgRoy2ZNHoVNF4NUCp57Brp1eKdXYWlRYby4u9ylXUW/PhtffwtSOtO5D9ynAy47WMMGkjpU18Clvyrv26W8Rwe5Wzvo0RaKOkbOOePzHd9QXxomwMYvd//4pNPpZDRC/AFqAd26IO+P146RUhSanHbchRy4TL0UCtD1kOAGJIAEkEBTJWDb9n/9bMyePdstQBNCzjzzTN5OOBHaBk315mC5kAASQAJI4KgQUFWVetEAq0PPTrTbIxBPbnsS7vzH+xb/dV/5nC1fcfWZO1xm3TnuNCPjeVljs2PTzDBZoeozPGdq85Kxaen49Hj0b4nU64q5j3XytHoCdNZ+mWratINnUyVbsmAPULn55lRyrCRdG625LRpbZdO4iJpNLYxs28yqz7rJXD3yV257xF+Tael/hp/KbJ+p+TMhnkf+8RjtpTawuM9z2S81cCRuQgLHnwAK0Mf/HmAJWjaBLVu23HTTTYMHD+bCKPsLoS+OPwRnS52Ez+crLCz84x//uHLlSk3TVLYobHETSyQSkiQdxH2z++CWlObW306Nksnk4MGDuadsQRB8OV4mvZJfXfxzSU2ZTPpNyvCLCzZ1bv1Vu0BlURuje37F8P6bv/iExQk0wFC1jNVxQ//jlk3VZ02GW6fZJw/Y1avT/sL8XUWdPps9w6yOsgaHadGBbz6o3pAFtE0nZdGIFyb1HQaffgKD+77Tu7CsS5t0p/xYUWGkuOvm+XMhpYLCBOeMH2pWQ6p9Z9oc1HxaB5g7Ty/qtHNQd+jRXu/RIV3Usap3tzVfb6dG3BbAa2+sys/rLgjUbzhf/AHxj9eOiUYjlsHNo0GVaWDlgy4oQB8UD+5EAkgACTQlAtzT18KFC92xIgghl112WR0H0C14cLop3RAsCxJAAkgACRxdAqZhmoYZqakybOPhJx7L9nuI19uehDr+9cO1mwASTB1WTWq/XMdm2YkPVANQAfA1wOs2zE1Kk5T0jenojPJ9Ky0aMJCbAlHL5azzDSdhsMxlpl9TT486VAF8CnBHMnqjYl8vmbelUs/oyl7WFWVOP+j83O8UoK8bO65Vbn6OL8BdcBT1LG6cY0Md18aPxj1I4PgSQAH6+PLHqzdjAqqqcrdTvA6JRMI0TO7ZGQDefvvtyZMnn3LKKZ06scFY5/+QJfiUWJ/PFwgERLY4NtHBYLBbt2533nnntm3bksmMmapj2nxY/p25rVMzRnw4RaeNj0hk0KBBdORbEHI8Hp9XYGbQpO+A3q/9Z0M8Duef8+rgHl8M6BQrLtCKCvae9qMPt34BBjN8ptqxYbCJVRnnF04DxbYglabWy9VVcP8i6N7uix7ta3p0jPbosunCX32s29STGB0AoNOnNNqwoFO66rrg4M0UzdBtAMWE7TtgYPG7/bpW9S60e3eGH/eGos5bz/9/H5VX0hlZfKFKs2N8zU2z2Q5dh38+AcXF27u1TfXuBMUd1YFF+wf3X/nue3R3JCVNnzmbDf+39nvbUm9oPiEQzLlpyg2GxhRni03w4rEy3Apz5rLuN74b4vHo2rVrPvtsA413QfVz4MZ07kMxjQSQABJAAseRQCqV4hEITzvtNMG1+Hy+adOm8ec2b0ugHfRxvHyTLgwAACAASURBVE14aSSABJAAEjiCBHjXmGdYWVku+EXC5n0KJEhITrcf/Q+NEch7Z8yUh/fIqBmyRe2HZAM0kxov7wRYacGdUWlKLHVjWpsmqX+1jeV6qhQgRUMA6SrrotXXek1qQG2n2GFRgEqAdQD3JpPXV1aOTVkzkva/UnIpQKZLz0tC48rTnidbLZanZQF1I80rsmTJPwmhfVmBeAmh01iXLPln49DqF6rxY3EPEjjeBFCAPt53AK/fbAk4of94Dbh50apVqyZOnNiuXbvagvPBPjnenwcMGDBu3Lh9+/a5kfAYhqZhOhq0u+t4KGl3bi04zSM9RiKRk08+mRp/EZIbDvj9Dvl2A/qPG1B8f/c2rwzpvn1YcelJvddsWAOKxEIUmwroVmZQOhP9weYCtGnT1sl/nT6n0/DPR6FPt8/6dVO6dVCLe1b+eNj6TbsgaUEkRa2TbW4BzR1xNCRAc8tlC2B/GVx80fp+3ff07gy9O0HvztC1ddmg4rU7d0DcCSzBg1pkBejMyDvQiV17voGhQ78u7BwfUAy9Ohs/7hsfUPT+8uV0yP3Nd98vHtiViETwBEKBjrzJkuP3vfafl3VDBrCpBn2YAnQiEevRsxuNfeHL2bJlC/8K8WhXztevBX+vsGpIAAkggeZCgAeEOO+881z6s+D1eh966CHunQMF6OZyK7GcSAAJIAEkcLgEVF2ZNnM68Xu94aAo+kQxQETv1ddcS22D2MLD81BHFnom0p8EUAOwD+ClFNwZh2tqlFEpdWzamCNrj9ZUlXK30VR9VhsToHVq+2wngEaPLwVYD/CYZE2ujl1bEZkaVR6TadTBKPPgQQ2puXdHenG3+gwWlaQtri08sfQpUfR5PDmEeAL+sN8fPPfc85zyZ2pS6w0F6Fo48EMTJ4ACdBO/QVi8Jk1A0zTLsmRZfuGFF6ZPn56fn08ICYVCTkA8R/6sk3CiA4mieMEFFzz88MOxWIybl0YiEW5kKsuyoiiaprnV5zoW0I4CeJBEkyZ45AoXi8X4JKz9+/cPHTrUQ4hXpCPGfm/A7y0gpDUhbTz+YX36zPz5ea8OP/mpLz+jFs+SxIRj3aJmzAprjlDN1waLxqSg6jNQhxhxCZY8DsWFG4s7pbt31Hr3inft9f6KVSBlTtIroqWWE9SChQy0sxo0H2nnO7mt9CX/t6l34ZY+hTIVoAvtPl3jfbpsWfoovazGzZ8z4QtZ28ikzRULQDNMegkFxl1Vnpf3RXFf6NVL7d51b4/O700at2/Xt/C//zeGBkmmlSYeMUxI0EPCf7h63P7SSlWVo9FKAEilE7RadKXLd+GnFtBLly4JBH0ekYg5gs/nW7x4Mf+iur9y35UP7kcCSAAJIIGjS4CbP1uWxacBORq0KIpr1qzh/4/43D669wBzRwJIAAkggeNEwKR2yiCB2bNrl6Ao+v1ebgpNQjnvrHjNjlN/lZphUvXZYF6fFWpCFAXYBLAkbc1KWmOq9ZEx+IMGk01YUBPZzjVqWwdbZWGADnhqzFgrsQO4AJ1iNs67AR7TYVpKvi6anlyVergqvot59si6UcxEC2KnU8WZrTxbmlZV9auvvuLBogRBCARCgiCGQuF9e/dLaTqNlb/WA4wCdD0kuKEJE0ABugnfHCxa0yZgWdZjjz02bty4YDDo1pcFQWjdunUgQIPgHWQ544wzHn/88f379/NOI49Qz2vsCNDcmgkAHPNnFKAP5UsRi8WuumI01WF5DD5+G3JyCAkRof/wUyc988yeVIrmRFEbBh0GV9wCtGmDnrF9tiGtwwsvwYB+q7u2LS3qCB1a13Tu/PmU2YmYTce6NTDjZo1qSzSAIZ9XRY2gmUMPGg+Dt3NsGuDChrgKt82rKi7c2KMg3qcT9Ols9+mS7N/9m9//5lvQQZbpADjNxTAybRyDNm1MJkDLMkhR+Osc/cc9NvTuUj1ogNG2YF23riuGDlkybcqqcO4QXstgOEf0BgkJhIJtX37xTQA6YSyVSmk6bXgxX+FcgKYaNN/S+CsVoNes+TAQ9Ik5NAIG92M+f/78Oj7HG88B9yABJIAEkMAxIsDbDH6/31Gf+Wh3eXk5H8lGAfoY3Qm8DBJAAkgACRxbAnzuqAXw8jPP0k44D93HekdF3Qr3fr2ddl4sFviHHarY8C3ASzHt7urkPA3+pMAoBa4FmGTAX1LptcxsGWSF+u+gLjwOLDQwD10z8rHOXHBEgcYY/AhglqROkLWpMfOeau1LgD2ymgm5Q2fLHrB3qq8ZW2Bt2rQpPz/f6/XyDpfP5wuFQg899JCjO6tqrZJky1Q/s+wefEcCTY8ACtBN755giZoYAS4H81cA2LVr1xNPPHHOOec4QX54T8+tNfvY4t7C0x07drz66quf+dcz7k6gO91Y1d3HHG66sTxb+nbrmmuu5qboHo+ParI5ASKGiKcNEToS0u6nZ1305lurOAQzrdgyG5xmjQPbol6cE7JiAigWLFsOA/pt6NMr3qlNpE9PtW3e17/43z0xE3i4CRZ00DSAuuyg7ZGM42YZrDRYOvV3QbdSPRkA7rkf+hRt7d6uekBXKGorDeoqFbf7dmjv1XIKNJ1GJ7RBpwI0VbItaoXN3IKYYKdS1L/0mrfhJ90/PKnj3kHtyvu3+7Jv5392bjeOkP6E5BESDLbK59O1RDFw6k/OlFOGyS2u2aVN1lhyhbygYZdZuTKj8hyF+9U0tTvvukPwEGflYy2hUOjKK6/UdZ2PnfAYmO4TMY0EkAASQALHmIBt27Isv/fee6IougVoQojbReYxLhVeDgkgASSABJDAMSDg7s9c/L//SwgJtPLyDrjP72nXpmDnth1qGmQJamzYAbBChwX7kwtkmJaAcUm4xoQrdXu8ZU4t2/8x0ECCUiYUTgNlZ4pvxlmjwQykywE+BJhTER2fUibG1XtKta1ZzxsZix/Wx+SdRXdRee66ru/fvz83txU13HYtY/5wtSLJfHSZzs1lkXgaKBBuQgLNhwAK0M3nXmFJjyGBFLePBWo6ahqmoih79+5dsmTJSSed5PwpNCZAe72Zf45gMCgIQjgcJoRceumljz/+ODVH1enQZWMicmNVbOz4Q9neWJ4tdXsikaCmzSZ19zV/3r2E+JkLDp/gCRDRR3JySI6HeMRQOM/j8Zx//vkfvLeaouCx/5gHDFVJmWDXREHSYPkLUFT0Yod2O3p0MTq1jxYXlZx22le79kKcDmIbClDTZoPLziywMpN5bao+20mwVKYgQ1yzEhqs/xz69Ppi2EDo1w265MmDCq2eed8O6fHJa8+DpoJlaXzlArRtczGbbWQCdrwSLj7nzTP6rB3efeOwLu92b3VvgFxISKHzhWQJIRTKH3XZHyrLoqZKAyHyhTV33AGXda5EH1SAtiQpSQ0IXAK041smFApdeOGFHLVjp99Sv1FYLySABJBAcyGwfv36Oi44zjrrLKft0VxqgeVEAkgACSABJHC4BBRFiUajtm3HYrFu3brwLlIoN8D9E/5k6KmxiFUqw6cq3P1t6o40jCtN3iTDhBRck4TLZZgIMC0R+ZeWLKf9QmpZdCiLyoTmDQBz9u+fISs3pNRbq6S1TMKmfdFM6B1m9MMVbeeV5W5bYBr21q1bu3Xr5vd7vV5RzNpuDxk4iB5CYxPSSas4lnwotwOPafoEUIBu+vcIS3gcCPAHvSzL69evv/766zt16sT/w3jAwFAoRN07ZJf6FtD84Pz8/N/8+jf//ve/eQW4TsfDCzQmHDdW1caOP5TtjeV5ImyPV8LQfiNDOYMIaeshYUH0EB+hK1vC4bAgCKIoFnbqNH/evFSUBSjO+qVQ0vDic9Cry+sdC77o2bWqV49UhzalA/p9tnYjjQiYBjNpRQ0wufpM7Z65AE21XhtsGew02KoJugbUEHnLdvjRkPe6ddrRp4dZWJAY2B26h6T+HXbeN99MJajLDdvSMivoNlv5DVI16htaleGuWWU/6vlkx1ZzO4UnEnIqIT0Fku/N8QueTHWCvmDXzj2ee+bfusw9SdMMLJO6GTFsg76DblCh/cCa9T5GJ5HRiWHZVTdUVZW3b99WR4DOXCn7NmTIkPLy8hPhi4R1RAJIAAk0cQK8PTB37tw6FtDnnHOO4+mriVcBi4cEkAASQAJI4HsTcGIhaJq2a9euvLxwMOSnvjhyAtQvI/H++NRf/mPtN/d8G5sd1a8tq5mp2eMjybsBrqyUR8vKZFX+R6R6Owsn+B3qM+8zsc5THOBLgDsqK6ZL6QnRmvmJ1HOaXc4cUtOprXw6rEWTB1ZXDaM18RdeeDE/P19ksYsED/F5haDf27lj+y82fmoZGjuNytAWmyrrOhWTSKBZEkABulneNiz00SawY8eOqVOnFhYWcoGS2xMRQrgFqN/vP4gA3bZt22uuuWbNmjW8kI59qKJQH1A8En1jwnFj9Wrs+EPZ3lieLXt7MknVZD0NX31qPvrg290LT/YIIY9IBC9dxRzC/+aDwWDbtm1ZrEJfbijvqsv/8PGH69evXy9J8Nk6OH3Y00Ud1g/qlW6X922Hgq39em966GGIaaBSw2fVBI2rzTxWIQ82SIfLLRts3aYHqAaAZMKuvXDeeV/26727T694hzaRfj2tfoXysJ7SxWeXJmsgLVGZuI4AzWRiqoWnJWoL/e6qPd073JTvnUjICEKKCDngdpxZ2JOgXzzrp2d+toGp465baxqmTp1laIclQFs03CG1Il+6dInbAporz9wlGQ+22a5du48//th1QUwiASSABJDAcSNw9913u/1v/Dc9d+5ctIA+bvcDL4wEkAASQALHkIA7ws2yZcsyNjNeHxED+fmFRGydd9YFN73/8R3R+MyamgWq9gjATSnlhpQ8VZZn7d+7zjTLDTq91XGrzMte66Od3c18OpcAPJI0bge4QYrfWLH/8Xj8WwAWaYibPzN/jI0L0LNuva2ggHZFnSXoF/Nyg9u2bNZV2dAURUpT5dqyWQfzGKLESyGBo0MABeijwxVzbcIEuGjrLqBt24qi6Lr+8ccfX3/99W3btvX7/W4bIucvwZ3g1tBciSaEdOnSZcyYMStWrHDn7E6jWOymcSzSrtFpABgz5g8ic46S19rn9Qp+vzfEFh7qQSQCW0V2iz1t2/Tr1eP3RV0W9O76bt+ue4sLK4b0+/qPf9qsMPto6h3jgJExbaNw9dn9Gk2mEhoVwVMyjBq9p3OHL/oUpbsVxrp1TvXqYvbrGjn75O17vqZtCRMM3ZCZGw+Q5TQnY4Ela7Jm6Mv+9fT5F17QqUsxId0J6UVIB0JCOX5aBW6eTAj1KXLvPXdmWkPOADvLyLZty6Jm0G5j5wbTrnF5Bxxtbr377juFhXQGgIezYYC4l3Pn9f333+fF5gb+x+Lm4jWQABJAAkigNoFkMnnmmWdmZ2dl3h966CHLsuhIJPMAVvsM/IQEkAASQAJIoGUS0HX9wQf/Sv1vcKcWPkICgtChbesf/2jBu69vAtgI8HddmlhTNr6y5N7q6vVMOFZMndoFZUVmJ8GiDrJ+IBOgbYAYQCnAC3GYm4brI8k/RyMPpaM7ARIsRCFj6pxNLap1XecGUgCgacY323ee+dMRzDQ7M5u1XZsCQkhBbvi5p5exgIlWpiA2tWBrmTcJa3XiEUAB+sS75yd8jZ0+GBfLJElauXLllClTioqK8vLyuMTMA8dzI1m36MwdOhNCuPcGQsjgwYPHjx+/adMmHorNybw+ZhSg6zM5ulscKTbzl2299NLz7TvQv3Z3ZGR+f7kAnfVm4cnJaSMIAwn5GSHjCbmje+ErI85cuWMfxDKRjHlkwQPF5+0LR4DWbFBYjD8b4KabYicN2dO9S7xLZ6N7V6Vr53inNlXdOn72/kpQ0lS8NjLD5LSUmk4vYIH13vvv3jD5hvad2ojU2p41TkiAkACdQMY3eDx864gzf/r5pxsMTbIMhZ7qrnW2rdKg4lxnYz0BOiND27b5zTdfDxo0wJkHkCmB683j8SxfvhwAYrHYASiYQgJIAAkggWNIwLKsCy64wD1Dy+PxvP/++3zqFTriOIa3Ai+FBJAAEkACx5OAE6/vvQ/ead2pwN+uFZ0+6ick5CE5hHQIz1v++FrQHijbPbumZH609G3NyHoV1GzbNMHma1ZCpu4KWS+LKdMAGkAFwHNxuLPGGF8pTU/r91RVfMZUaYuHB6KheLJnUwfOB7x6RCLROXPmEeLJy2vtFqB51+qpx5dw54wHNOhsh+54AsVrI4EjRAAF6CMEErNpPgRUVeVK2UcffXTdddf16NHDsWLmz/1AIFBfeua7BIEOoQaDweHDhz/44IObN2/mXjUAQFGUg5t/ogB9rL8jzgwp/u8P9H989+49w4cP53fT5/MFAoGMBbRARIGaEvu9PmbbLgjeXBLoTIK9SegkknNyqO2Zw8/87WNLX9izu4xXpKY8rqR108g0Crj6zFxC00Fq6idagZdfhu4dV3cqKOnXBzp2NLp2tXr2TPUq2n3NNUlNox46VGpJnSnf8uXP3H77X664clTX7ixuBlOYPV6SExRFv494QtR9Ndvo84YDvjYFBR3mzrstlahhrSBWqDrqc7a9UkdrbvBjIwK0rRv095JMxc8666etW7fmPwEO0P0aDofnz59/rG8xXg8JIAEkgASyBHRd577C3EbQGC02iwffkQASQAJI4AQioKqqYVmKqX+6dcuAnwwjAR/xexwjJF+7gpNG/fb+L9c+UrV3SXnJHqYd26AApG0aL6eOAE3Ng5j9Ee1cqcz2eTXAzGppYly9KSoviiS3sWiE9DDboP1AqhE4vTwaSZCjX7p0abduPXzeACFCHQE6L9zqiX8uUVNJeqbNzJ8zryfQXcOqtngCKEC3+FuMFaxLYPfu3dOnT+/atasoioFAgE51KSjgzp1FtrhltTrpPn363H333aWlpfT/JDuSScc02VL3SrU/owBdm8fR/1RPgKaXtEGRtalTp/bo0SMT7YH5yxSZAO0VhbxwK6+XOpsQAx5uc0xHy8PcDpl27UUx0L2w569/dcmihfe889Y727ZtT8uqbtpuAZo3N7Z+DYP7P9C76zvFXbcNGxrr3m1Xz27bfjR48y/O/2r/fpBU6kP61TfefPqZZ6686oqCNvn8uvwr5/EKgVZ+fyjHw9yGsI0iEXK4AC2Q4KWXXBWPcX8d1Io6EYvy2h1pC+hMa0nTFU1XRo8efRAN2uv1jh49+ujfV7wCEkACSAAJNEyAB0nmw+p8Lhc/7uAD5A3nhVuRABJAAkgACTRnArppyrphAeyrrrnm+gkkJ4eIHuL1hbwsOKGPkJ6dr37g7q1MU6YR5NWIolQ1LkDrwOLP1wB8CHBnVJqmwU2Sfm9aWwtQxUFR9ZmG0skaPGeMoCORyAMPPNChQwevN9O183hymAydmdJKCHn2X8tsGt7eNhT5gADt5NScbwSWHQk4BFCAdlAclYQkSTz0nK7rzsAXt5nlciRPW1ZmWIwf4+zidrWyLLsdOzgjcibYhmXpZsaEUtaooSIuDgFu6cw/SpK0c+fOadOmnXzyyXXi8zgfufAnCEJubq7z3yCKot/v79Onzy233LJhwwYnc0w0DwJui+DaJd6+ffsZZ5zBb3owGOQevQUP9XTcsVP7k//nJDpCzrwee8M04p/Yio5V8CUUCvu8AUGgTsXYK+k/aODpPz3jxpsmz79jwYQbbnz2hX+vXvPlsP+5vG+fa7sXzujecVH39n/v2f6+4sJbO+VfdcOfnh977d/7DxiR14b6Vj6wCHV9g4g+l99lehxVpf/f+f9v05dfObWxTYOt9Zxv8Lo7x9GWEJ0+ljW4zpqFuw44lOQ999wjCIKXLU7JnR+RIAijRo2qrKykMQxZ/EPTMN2PvkO5BB6DBJAAEkAC34PA22+/7TyW+Qhr7969eT7OkPn3yBZPQQJIAAkgASTQHAlwo2XNpk4xNMPc+MXnffv3F71er8hecoPUsifcqvvgwUuXL9eo52eQpLhuaTShKqquqZYT9sdmU071OMBWgEV6fGys4vqKmjujyicA+zQ9bdm6aeqGatP48ZlFluXHH3/8+uuvd89MahUIBn3UtikcCgV9tJvZrk3b1155NWNFxDtrTh82mxV/d3fkau1xjs/YDtXaiR+QQNMhgAL0UbwXjothtxLqKM7uzoCu67Isc+f0tm3z+ZL8yDrl001TM3S+pmWZq88AkEglVV3jGrRm6HXOOmE/plKpjRs3zpw5k3tdCAQCbqXMnXb6bB6Px+/3c7cMQ4YMmTBhwsaNG1FBa2FfIdu2+c/z1Vdf7d27N3cr4XYuEWjl79Cl0Ncq2K1H98JuXenXI4d6X/bkiIJ4YPaWKPr8ftpu4IsnR/QG/PSAzOd2hBQS0o+QYYScScipLIpgPiGtqTONjMKdw1050zO4AM1f2XC4N8Asrz1Cjt/334Hx/oMGvvf+an4vMuZslm2bFl8zwZHd7Y/aTZAjIkD/18fo2rVr27dvHwxmKu4O18kZDhs2rLy83P2rcadb2HcJq4MEkAASaCIE1qxZw7u4hBA+jn722Wc32JhsIgXGYiABJIAEkAASOHoEHLmWxhVkBn+WZc2bN08UxWAw6BicEUICoWDvvn1umjpl89YtkqpU10SoMmOaFkBCliSdCjWaTOebagAfWsrs5P4JsfI7osrrBmQiyLPjTeZ3Y9OWr+69/74xY8bk5eWFw2FRFN0CdKabmO0Bdu7QecP69RRCxnjoYEZCTo2yFtZZeO4OYHYbviOBJkgABeijeFMc5/erV68ePnx47969c3NzM8qU6y0vL2/o0KHnn3/+rFmzJk2a9MEHH7z++uuyLHPJpo4V4eoP3nfWVavfe+e9d1OSxOuwYeNnqz94f9v27UexSk0+a67j27a9Z8+ee++9d+jQoQ5pv9/vdrngVp95mh8ZDAYHDBiwcOHCiooKSZL4TcS5q03+zh92AR1J9L/fmdtuu62goIArqqIo5vh9otcbyA0Tr+jJEc88e0T/QQPPPHtE3/79u/XozmVi0esNhcOZb5eHegb3BwN0F1Wp6Ys34BW93HFHmJA2hHQipJNI2vo9HQgJ55A8gft0poEw+Nwrpmsf0KA9RPAIoodLz+eed96K/7zGW0J82InPilBl5RgL0KZhmob5/vvv9+7d2wlLWOfXREfy27X76qsDZtrOw/Cw7xOegASQABJAAodGYPbs2fxfyev1csdiY8eORQH60ODhUUgACSABJNDCCfCQvACwefPmU045hf9jcn0g2CpEWIfOG/DnF7T+6YizfnfZyL8suH3tpxvKqssN6hVaBZPGiq+UUi9t3XLP7m2L9u9/U4JqAAng43VrFz++ZOq0ab/6v4vbdmjPO4bBYNDvp51Bj8dTS4MmNOYQv/qYq64xNdPU9QOGRJnpqg3fCxSgG+aCW5sPARSgj+K9KikpWbhwYVFRkSAIoVDI7/d7PB4+e92fXfijx3l1LDFFUbz44otvv/32+fPn33vvvdOnT//d73539tlnewN+ZyUeIa91/uNLl+qm+fY7K8P5eUQgoXB4yNChz73wPABEE/GjWL0mmXV1dfXf//73YcOG8We9A5a6UBBFQRAOYgR92mmn3X///SUlJU7NbNvm1uu2bSeTSa5uO3sx0awJ8DvLnXerqrpz587x48e3bt06Ly9P9HqJQHKCfsHnDYSonW+O35fj93lyxKLexT/7+QXnXXD+gMGDiECK+1AR9sDiEajTDIH6as7xZ+2gD+ymX0NCSMiX5xNbMSNol/pMGhCg+/bvf8WVoz/57FNZU9OybIKtGbrExpyopGvZlmEeMH+2bNp2sexabqBdN+mHW0Bz1d6yLF3Xy8vLf/aznzm/LEeD5tUNBoN5eXlr167l13c7EXKVCJNIAAkgASRwxAgsXLgwFAp5PJ5AIMA7vfPnz3dGW4/YZTAjJIAEkAASQALNloAkSZZlKYry9NNPd+vWLRMIyuslHsGTI1Ilmi8egXgEweflLhlp/45vFwUSCpGQn+QWEBIgQgEh1K2zJ4f69eAqdiaH7Fst9dlDe4heUexa2OU/r66gFN3GzHT2KlpAN9vvFhb8EAigAH0IkA75EJUtkiRt2bJl9OjRfDzN4/F4vd6Mh1mBPrjC4XAgEHA2Zh9Nh/3OTSPbtG+nGfpvLv0tH2oTRA81zBTIz35+wbbt21uS4aEkSaqq8q6Uu0OVSqU2bdq0bNmyU0891T29xVHE3K4VOGU+4yYQCOTm5p5yyimLFi3as2dPg/eZ++Pmc3acKIINHokbWwCB3Xv2zJpzW4dOHT05oq9VkLBohJ6cjCNmQfTQtEBnaTk/11NOOaW4uJj/2LMbmSdpj0j9SWeaKpk9osDNo+lHkYh+f5BFn8jszWtdwFKegrbtb5h00zPLnz+UUW7btDK6c+PS89G4Nbqua5o2evRorkHzOnDfNc5P77+/rzfeeMO5OpfOnY+YQAJIAAkggSNFwLbtCy64wHG+ITIHly+//PKRyh/zQQJIAAkgASTQrAk4/XpugQQAyWTy1VdfveKKK3hHhvpR5OZEbDKrkMMcJHqI6BNpxy47a5VuzfES0UdIkNBo9TQsUKY7V/uNC0F8SJjvCQaDBXn5N06caKjU03Qts6FG3GjU7w82IFE3cm6zvl9Y+BZJAAXoI3xbk8nklClTnJnphBDudkMQhLy8PK57/nDpufaTjfz1bw/eMHlSnY2i19uxc6fVqzMeY5PJpKOfutXbI1z/o5YdL7yTPRfWd+zYsXTp0osuusgB3qAAzR/9LN4AjzpA9cSzzjpr+vTp5eXlqVQKAOr46XYu5PxRNWt6TnUwcXAC3H96NBF/+JFHzjz3bCIKbq2Z/8Sod45QkGT9MvONfITpwG+QjZnTMfDarRHRQ2Mv1174EfS1W4+ef54+4823VzqFrN/gyOxyob3KGgAAIABJREFUNzIcw+djK0A7j5GlS5c6Dzo+ycMRoOmomN//t7/9jRe7JY2HOfcIE0gACSCBpkBA0zTudoxP9uImXatWrWoKZcMyIAEkgASQABI47gScfr0zBZYH5ZIkaU/JvpmzZgVbhbixUcZiyENntfI0jVTPlGYxu4G5XRSyM1hrd+8a+uTz+QoLC6dOnRqPxgBAkahfaRSgj/u3AgtwjAmgAH0EgCuKwudxLFu2rF27do6jH5/Px8e7AoHAyJEj33vvvX//+9+TJ08eNmxYp06dHM20oQdU3W11NSs2y4P6nPWQHF+AGlp6hFrRz7IZeL3exYsX84esI6G64x8egfof8yxs216+fPmll17KxX2v1+uMKzYoQDsW0OFweMiQIY8++mhlZaWu66lU6lA8AzjcHMXtmNcYL3isCUiqQoNOpJIffrzmn08+8fsrRvUbOID+ZrP6MW+dcI86dX27C4Q6duZrxnia/SAF2mzxeInXT1joY7qxqGfx7y69fOasuXtLymlcC+NA3GTTzkzBamCU283DLUC7tx/NtG3TUB7OFV566aW8vDz+1HHUZ/67E9kycuRI52BMIAEkgASQwBEnkEwmc3NznQYPfyDH4yecK7YjDhYzRAJIAAkggZZBwBGgbdvmUW0c4xju7RAAVvzntT/fMq1tp3ZuKyKPSESB2jl7XSs3iOb/tvS1ttWRu1vk8XgGDhz42GOPVVZWOle0mDfFWgJ0bcpuOyQnzQ9x9w0P9Mdqn46fkEDTJIAC9JG5L6lUatSoUVxTdqtRhYWFs2bNevDBB0eOHHnGGWdwe0BRFH0+XzgTwYzLVNlnl8AmdPi8xC8QHxtlY4NsOdn97iddjt/Hw6AFfUGBeQegSjSh3ov44Xl5YeqKKMfz7PPPmYbpCKnOg+/IVP5Y5WLb9sqVK6+88spu3brV6WJ5PB4eQa4xAXrAgAHz58/ftWuXU1gHQh0pzTnASTjcUIB2mLTUhAm2CbZhWbpp8sDHaVlOpqmNvGbon3/5xf0PPHDzLTMu/vX/nXbG6W3btuVzGrK/5eyvVCCC2JAAzfZ36hL+1f+dN2XqxH8te3Lzl5t0PaM4WwAGa0HEEikuQzdlAdr5AiQSCZ5eu3Yt16DdArTH4+FWeAUFBRdddFE8HjcN061cO/lgAgkgASSABH4IgWg06kS/cLxC4fP2hyDFc5EAEkACSKAlEXAL0HX+HxOpJJ8ISzt9oEdTNVu2bX34scVnX/jL9v0Gkhw/NSDyUEmGqzFeFszHm7GGZupzQwL06aefvmTJkpKSEh5Qiho+K4qp66aup+KsD+We1epi7SjOdRL8kDoCNGrQLnKYbOoEUID+nnfIkS95HNU+ffpwKSorQdH3vn37XnjhhaIoBoPB1q1bc4WUH5BxCpET9JA8gbQSBFHwECoWt2lT8LPzi8dec/79s6f8+9G1+7YDwOfrNjz6179d8LPz2+TltyP+Avb8y15ICAi+XLFVWMz1ia08YtgjhkRv0CuKjmZNAlSPXrp0qVNV5/HqbGk6CS7ycryKQkPNAsDLL788ZswYt7CVrX7mne+i4d1CNG4A97ItCEJxcfEjjzxSXl6uadoPkY8dDbrpgMKSHA0CXICu82pYFpek+VC52yH4li1bPv7449deefXpJ5+afessts6cfevM2bfdMvu2W25l68zZM+++7+6nn132+luvszCAhgUG0DXTWqjfaLAt4Ku7zXE06ntk8ywvLx82bJjbG4n7NyuK4siRI0tLS52LxuPxH/KrdPLBBBJAAkgACaxbt86ZWsdH/k499VRNoy4m8UmLXw8kgASQABJAAvwPkffrG6NhgWWAbgC1ENIBVIBPdZj9yZbfL3v2oulTz/rtxcPOGTHi/PM7FLTtEMgtIN4As3wWvd5WebkFbdteeuml06ZNe+qppz744IMDl7ABLPtA2B4uOh/Y/T1T7n6iO/09s8PTkMAxIYAC9A/F/My/ngkGg6FQyO/31zHLJYQ4ojOfh87tc93iaWGX3hdc8Jvb77jnxTdWbiqrXFVdfcf2rQ8kKu74dv1qqK4GW9JVqlPRiKhsicmfvv7utBsmn3bG6YFQq6Av2Ir4wsTnIwEi5hExn66ecI6Q4yMkhw/EBX2i1xsKhTasX6/KVNLlHZJsjk303bbtFStWjBkzJj8/v45jWTdn7gPB7/c7AwChUGjo0KGzZ8/+9NNPaRxZl6OA711VFKC/N7rmdWId6bnOR+drQDvzzPEFN583VI3GkbD4r7SBNoUJtqprsqYaFveqYbF3ysY9gu2wanYCNFc3+INl7NixgiD4fD63+sx/sz6f77TTTtu3b5/zFDoUHzgOFkwgASSABJBAYwReeOEFd+vI5/P9/Oc/d3e2UYZuDB1uRwJIAAkggROEgNOba6y+Flg6aDqbmCoBlAA8W6EsjKt3RRNLtm7+Rk1JADHdyJyuASiOTVFjWTIlBwXoxvHgnhOKAArQ3/92K4qyYMECt5rsyM18I58C6fP5AoGAny0Btvzyl7+cPHnyM/965pPPPjHB0OlED4gAfGTC3XtK5laX3rz7iw9A3Q267iqdDHYaTDp0ZmTU6C1btrz43PMzxk/61Tk/9/pzqUuinFxCcglpnUNC/iAJBkmrHE+uL8DLE/T5K8rKwQZdUV0ZH/+kZVnc5Nm2bU3TSkpKFixYwG2Z3XjdepZ7O7e4FAShV69e8+bN27Fjh1MlXdcVRWkWgrtTZkwcRwJ1FOc6H50mCxegbepMwmW+bINtWpmVHcq9eWiGbmQPs4GOp5tZ3dkZrK5TZUeArrO9wY9OJq6iNHjgUdzo6MjxeFyW5Ztvvpl7Znf/Zv1+P38khsPhb7755iiWBrNGAkgACZx4BBYsWOAI0NwCes6cOXz6l/PndeJRwRojASSABJAAEjhAgP8hHvhcN2VZYJh0tUyAJMBugEe+LZ2xf/8dkfIvAEpMIwIgA9utsRmtrhyo+0TLamC4l/YAbbryblsD1kquXA45yTNrsGvpdA8POTM8EAkcIwIoQH9P0PF4fOzYsdzKj4uhvLnvFkbdWwYOHHjdddetWrWKdwYsy9J1XdUVA7QIaFvTsDIBs7eW3by/el60/N+g76KStKkxy2fbtDRDT4GVBEuzqTcAoBqWraoqtbtkSxnAgv+8Pf6F16Y8+/qz//nkhutv7ljIwiES0krw+gRPjsfj9/raFhS8+MILzlnfs/KHf1otna6R00tLS++7776TTjqJM+RG5dyrBtet3GKWm/Pw4cNnzpy5bt06J9iOxhYAUFWVo27kmrgZCdQiUEdxrvPR6cNzAbrWmeBSn03a8qDRLZhHabcu3FhDoW5WWRccdbY3+NFpYbgv1OCRR2+jrus8modj2rx48eJwOMx/s27P7F6v1+PxtGvXbtWqVUevPJgzEkACSOBEIzBu3Dh30ygQCNx///1oAX2ifQ2wvkgACSABJHAQAryP1vgBtQRoCaAK4O1E6slkfCVAGkACSNiQMiAWTalJjbpUzC6aZqQkRVGUBnSPwxGgec8um+vB3hvrVzaFvuHByo37TmwCKEAfxv3ncfy4rHnFFVf4/X5CiM/nCwaD7lhkXq83GAwGAgGfzzdy5MhXXnll9+7d7svwB59t2wbYCrN9/o8Gc/ekb6xSJ1fGH5cSWwBizogaM3c2wGYW0LYC9CyTeoilQ2gG2DpAFOA/tr6wbN99VdWP7SyLmXSiR3l19OHHF7fvWsg7JB725hXFQCAwc+ZMXp5UKuV2Zu0u5JFNcwNJtyWy8/QvLy+///77+/fv7wRvdAvNgUCAf3QMojleQkhxcfGMGTOqqqqSyaSqNmDT7XBuYBzyyFYPc2spBNx/2PXTtWrpDhlRP80OrZ9DY1sazbnWjqb7wd3SMg1T0zRZlnfu3NmhQwfum8gZjXMM9ILB4OLFi23b5g8HSZLcz4emW1UsGRJAAkigSRIYMWKEW4AmhLz11ltNsqRYKCSABJAAEkACTZMA7dRZ1AQwM+PcYj42YkyxSTEBWgZQbeqhg9pIZ7t2NvOuaNo06IITLiiTjdNPZP4bqc9GZ4uTYDCymTm5ZhK1SB0oWt3DGjy91rn4AQk0AQIoQB/GTUilUjx06ZgxY7j67G7rOz6ICSGFhYWLFi1yVNFIJOK+jCOMygB7AdYC3LYnNjMO4/an79Pgc/aYO+B8gz396Fz+7MqtLy3LMsCWAKrB3ggwt7p8rizdHan+CKBCofNGoizzb8GYs/jB3M7teVH9HhqQ0BsKTJgwwSlSZr4/K1ZmY+aR6xzygxKapnGZmwOxbWq7LUnSU0899Ytf/MKJmcNLKAiC4/HZjZfL0IFAoEePHuPGjdu0aRMAyLJ8ENHK4YwC9A+6fyfSyQ3+czsba5FwWgwNJtihzonfmWg051o7msEHPuGA/94ty9q2bRuf0+Dozs6PmjsseuCBB1RVPcivuBnUGYuIBJAAEmgCBAYOHOg8YLl5xBdffNEEyoVFQAJIAAkgASTQXAjU79c5WjStgtOnc4nPmarxXbXqWSczFKBr0cEPJygBFKAP78brur5o0SKnic+9DxNCuI8IQsiIESNee+01Z0I69wWh69QJrJkdSXOE0SjABwBzy5VZaZi4T72nyvqImTPXKhN/cpk2df1MVxN0E3TqRShlagmAbaA/a8bHl1bNluCZtFTK9OsygK0Aj1aU/61083t25aptG0N5ubm+QDDHR3wi8Ys+X85JQ3/ML+Q4nM0ItTROK33UWnAgVFqtIn2vD1xjMg3z1Vdf5bqzIzTzGfpconKbP/MAg4QQj8fTpUuXGTNmbNmyhV/csqzvFK0czihAf687diKe5LQqGkzUIlKnSVHnIzu0wUwa3NhozrV2NI8Pzu+OegoyzGg0+otf/MI9Ysd/6aIocg160qRJpmHy4b06NXRnVWcXfkQCSAAJIAE3gfz8fN469fl8oVDI6/U6PpHch2EaCSABJIAEkAASOCgBd7+O+1hmE8yz59TpzWU3H5N3XjR2qTrFaPDjMSkTXgQJHAYBFKC/G5bjpEKSpA8++CAYDHo8HmdGuaNB9+jRY8WKFQCQSCRMw5QkiWdNJ2KYB5zOA9AYqAbYKYCdAPfGzalRmB6FOSXaahMqmecNVUnVGmuzgUrPug2aDZrJVipAVxtyBcCHAHemqqdJ+szK5FrmqKicqc//SJsz95cuKPvyDShXAZ569hkPIa38LCChSIhAcgj5w6irKsqjhk1d6fOpJTHm3oiWnE4ksUzQLBoiUWOadMOsDlHeffXVVydMmCAIgiiKfr8/GAyGQqH8/HyHpCPrc5tox+R5/Pjxn332maIo/PKapum6HovFAMAJfdZgyRz16hBL2GAmuPGEItDgP7ezsRYKd8ukfpod6pz4nYlGc661o/l9MA2TPz8nTJjg/oFz6zw+a8Tj8VxyySWyLNepnjN/DX+/dcjgRySABJCAmwB/SDrP2FAoJIriwIED3c6R3MdjGgkgASSABJAAEmicgLtrZwLoLIR83RniTv+u8XyOwh4UoI8CVMzyWBJAAfq7aWualkwmdV3//PPPW7du7Rg7Oz6LCSHXXHNNJBJxfG7UzdSm3n7Y8JllUf1YtQC+BniwrGSmalxbmpi7J/mOBuXMeFm1TJs+5lzPOP6g4Q85wwLdApPaKCsAGwDuTEg3RVK3ppLLwd7L/BN9CfC4kp66PzK7Jv5A5fY1UB1jT80rLh1J+ydhPwnnCH6B0PiE/l/+/BIJqPC9FeBFFR7etWeNrFOtl17E0EEyocai6nQm2mGdqsmyXL+HI8sy199Nw1y9evWMGTP8fr8oijxmo2PjzOUnQRAc/8485KDP5xNF8be//e3TTz9d53L4EQk0RQLuVoqrWVC/qE5L5TgGDKxfqqO9xWLL888/z53j8ykj/IHgeC469dRTE4kEH1XSdV2SJD6PxD2MxNNHu7SYPxJAAkig2RFYt26dI0DzxIgRI0zDdI/k4WBes7utWGAkgASQABI4XgT4XHDm25l34GoVxN2na2C3+9j6/UT3FveRLP0duf3g4+tlgBuQwDElgAL0d+PmTXZFUU455RTqQNnrFUUxNzeXzx8XBGHZsmWmYTomuvVztJj+ywVoDTQZ7B1gLZMiM/bvuaE6OrMy/XIa9gMoNlg62Daf6OESoGkUc5Yrd47BfA4pzID6JcucWa3cWJZcBvAJQCnAVgOe0uVbqksnf1t6d3XyE6A5y6wAe3buym0Vpj0TkYgBHpWQ+Dz5f5w2/+V9iQcj2t0Jfc6O3a8l5ASL6GqCoUHKhGoLapjcXVc0c7zs8ypzUPx148aN48aNa926tdfrdYzEHZ8b9R3C8sMEQTj//PP/9re/VVVVHdy6uT5k3IIEjhsBdzMCBejGb8Pnn3/u9/sd0ZnbQTuiSe/evSsqKpyz6+gmjhLtHIAJJIAEkMAJTsAxAnjzzTedZylPjBo1ymmk4fPzBP+eYPWRABJAAkjgcAkc3BmpWyZ2pxu4Sv1+ontLvRO+I7cffHy9DHADEjimBFCA/g7cXE7Vdf3hhx/m6rPH4wkEmCMLQsLh8KOPPsoNn1OpVGOaqUVnblg6dalspMHaAfCEEpkeKZ1SXX3LN6UvpWAf14g1NsODlqhhEYvlQy2pwYYkwBuGcX9SuqWkZt7uii8BvgX4FOCJuDQzHb+hvOTefRWfMn8asst6+e67qAPrYNgnBjwekYhEIMRLSO6Ff1n0l/KKOdHqR6prNuiQZubOTICWLEgAXRXmHaSuBs3x2dSrCC3Xzp07p02bNnToULfLV0KI3+93DJ95gvt95t0kr9d77rnnPvvss7FYjGfFraq5AvUddwh3I4HjTsDdjGj4t5spIm9SHG7D4rjX74gUgD8iSkpKBgwY4AglIlsIIfyh2rFjxx07dgCAqqrcbpq/OuoJfyAfkfJgJkgACSCBFkNgzpw5znOVR86YO3cud8SPz88Wc5exIkgACSABJND8CNTvJ7q31KvP4fYTD/f4ehfEDUjgmBJAAfq7cVuWtXXrVrffZ+62WBCERx55hKsqlmXJshyPxxvMzqLqs6aAJoFVCrACjJmR/ddWlk2LxP+xs2oXM0+2LLen5YZFLBNAAio9J5ncvKCi8ubK2Jw91U9Wp3cCfGnDkzFpTknFlPLKu6KJD1VIAagAcUnSDN0p2KnDf0KdLPsF0ScGcwK+nDwi5hJf3rWvvrIkFtnA3HEYzOCaueBQLHpNhRXOaMwTNDcAP+2007iTjQBbeF/I5/NxMdrj8Yii6JahA4FAcXHxjBkztm3bVicKmaqqqDQ5twwTTZ2AuxnR8G83U4MTWYDm4bBkWU6lUqeddhp/PnCPRk5AQkJIr1693njjDeoEyLWggNLUfwJYPiSABI4HgVQqxQfsJ02aVEeAXrJkCRegnXJhs8pBgQkkgASQABJAAseIQP1+ontLvUIcrqB8uMfXuyBuQALHlAAK0IeE+1e/+hWPjMeNeXkr/5577qG2yHZtXxkN5WeBpYEWA30PwBcA8+OVN8aqp6ZSC6vjmwxg7i6YeTHzrdFQBpltXKOuZP6j/6lKN0ZjU2LSw5Xpr1kowocqyhdE43PKapYn4GMJSlTmapp67bAtZp5sMkceb618O9NLySFEFIjopREJiRDo0mvD3vIKgDiAblBRnE08MZj0rB3E/FmWZdMwe/TowbOt417DsXDkjl+5YU779u1Hjhz50UcfaZrGg4+hneNB7jvuQgIthoBt23ymyNVXX+2WS/x+P/eqHwgEgsHgww8/zAXrFlNxrAgSQAJI4GgQ4E/Un/3sZ+4nKiHkgw8+aFCAdsbzjkZhME8kgASQABJAAkgACSABJNAYARSgGyOT2S7L8ttvU8U2Ly+PGz7zJv7555/Po7t8x/nZ3QqY+8H6AmBRTeVMTRpXVbEwnn6Dubegh3DbYivr6zl7Vp13ix1YBvBPxZ6VlibUpGZE5XcBVgPcWx19QNVvK698sCL+mQ4VBvPU4ZzPZGgTbAugxlZ/fM4ZtBYeQnIEkiOI4VZUWBcCI399WSQl8ZNUmUYiZCbPB7Pa5D2ZrVu3OgI9t3HmQrOzkUPz+XyjR49+8803D5SL+e7gJjx1XL46x2ACCSCBFkaAKybPP/+8KIrODAm/388dcYTD4WAwOGvWLADgA1QtrPpYHSSABJDAESHgDOkNHTrUPcOMEFJdXc3dGZmGydurzqwS3nI7IgXATJAAEkACSAAJIAEkgASQwCESQAH6O0ApitK/f38ukfCog4SQIUOGSBIVahtz+lw/05QBewDuiFaPram8KZ2aF4m9qdHwgMzZ8ncJz9nsdIBqgDUAN1cbE2Pm3Er1CR3+A3BfIj0zpd5cmbhvR8mXAOUAMeY1QwHqhUOmVto2WHZClhJg7wPz8bVvkYIgtXv2URfQ3vwQF4gFD3nqqSf41TICtDNDJFuG+u/ca/N5553H59GHw+GrrrqqjnnjRRdd9Oyzz5aWljqesjm6RCIBAJIk1VGfD8WuvH5JcAsSQALNiIAsy8uXL8/Ly+PPH/crt4O+9tpruY+jZlQpLCoSQAJI4JgRsCyL+0DLz8/noTX4a0FBAZ+ip6oqCtDH7HbghZAAEkACSAAJIAEkgAQOQgAF6IPAobuWLFniWO/yGeLhcPjdd9/lExsVhZsJuzLJOuTIRuujCq4CUAawuCQ6sary2nhkelnlizpVn1Pc0QXoLPigyXxBc8XXlaErJGGSefB4oFKapsIECRbG9BcA7oil/ry37JbK2H2VyS8BymyIAMRsSJqQtugl0gCmYXJJNwLwGcCje74a8LsLiUhIDls9tIreXC/xkQ4d20ipmKrKqirTQjQiQHPzGd7z0dli2/Ybb7zx1ltvcU1ZVdXHHnvs3nvvfeihh0pKSpz6NCbZ8wzdr84pmEACSKBFEkgmk5qmffbZZ/n5+XyQj88y4XbQHo/H6/WOGjUqlUq1yOpjpZAAEkACP5AAF5djsRifduZo0CeddBL3DV1nDA9bWT8QOJ6OBJAAEkACSAAJIAEk8L0JoADdKDpFUXRdz8vLCwaDjl9jURRvueWWeDzOG/G15FSbCcjMe7LODJBN6gZDAzCjAC8DTK1MTZSUW+KJDwH2MvWZqbvcsbNm0SN1loWZ1X1Z2SwWSVCjeVUCPFhaPitWM1GJjdfj9wPMMYwb4un5ceWlWHK7DlEWpVCiVs90VW3QbNAs0BVdMU0LYJ1pLopEZ5bvu+HdF0mYWUATpkFza2imtf/8F+exaZtMgG4UDzOrdndlDuoL+1Asmg/lmMaLg3uQABJorgRSqVSfPn0IIVx65q985M/j8RQWFkYikWQy2Vyrh+VGAkgACRwdArzhtHbt2kAg4HbBce6552oanWLHZeijc3HMFQkgASSABJAAEkACSAAJHAYBFKAPBuvpp58OBAI+n08URUEQRFFs165dgi1u6TWThUuANphonJSof4k4wNuqPL0iNt2ESVXRe8prdgMkbVCo3szP0bIOMxoyhbbAqqHm1NUAr2swL1p5k1Q9Ua2eqEdu0hMzTPk2zfp7TNpuWCoTsDWmeausADS8oQWWAYph1wBsAXhK0abElEnx+MzdnxRcfDqXeAghofxWYm6QENK6bT4h5JlnllFtPWvN3SAjNwGebvAwvvFQxOVDOeYgl8BdSAAJNFMCtm3H4/GRI0c60rMz5sefUcXFxbt3726mtcNiIwEkgASOKoHnn3/e7/e7Bejx48fzhhnOIDmq5DFzJIAEkAASQAJIAAkggUMngAL0wVide+65XHf2+/3cAfSTTz4py7IkSW759UAWB/xnmAC6pKtxgPcBbt9feXNcmlIRvWNn2QbI2CknAdK2bthcMeavXIB22UFb1CRalaiK/S7AvPJ9f05XTlRqJkmJSVJquqn+ubLiH9HEZoAapj7rTH3WmPqsApg09iBYJvXCsRXgH1piciL2h6h2Y1p7QN4/+dXFxEvlHY/HkxfO/fGPhuZ4qDMOr9fbrVs37uT6QNXqpdwEjogAXe8KuAEJIIETgoDCFtu2p06d6vf7w+GwMzbmJAoKCrZt26aq6glBBCuJBJAAEjg0ApZlzZ8/3+fzuQXouXPnYgTXQ+OHRyEBJIAEkAASQAJIAAkcIwIoQDcKet++fdzpMyEkGAzm5+d36dLFmczoll+dLJhcTH1lcM8bKsBGgL/VqJP2Vt0aS9xVWfMpM2Tm5slJ206ZWiMCNFeibZqXDSrABhppMDm2fM8NWmSiUnNTOjU9Id1aHXtCNzcCdSctZQVoFUCxbcWmwjb3Q60B7AN4wVInRcouq6oYVa1OT5n/iOzZAtJpF5wrimKO30cIGfX7ywVCRBqakPj9wdvn3+HUq8GEmwAK0A0iwo1IAAkcnIBt2zwAqcoWWZYfe+wxDxsJc6RnQogoivzj6tWrD54h7kUCSAAJnFAENE0bO3ZsHQH6ueee4y44TigUWFkkgASQABJAAkgACSCBpkwABeiG744sy7NmzXIrIISQJ5980vFDarkWLr9almVYlgKmDKYKVgJgE8DTaeO2iHFLTHsglX6X2T4DgME9bligmLphGzboNnXXrGbNlx1raJurz1sAHo6oEysTkwEmavHxqarrKstu+rbkecn+wubBDKnczEVrFSBtGLJpUv8b7Fp7AJbb5i2xyJiy8gmSMUWFOeXJz8BOgP7c08sCgkB8Asn1FfbtOfKqy6k7jlDYmxNs26bjzp07azm5bhgVbkUCSAAJfE8CzsOTP1ABQFGUlStXhsNhLkPz4ITuR/GTTz7JnNSjKfT3ZI6nIQEk0GIIcDPns88+OxAI8Il6wWDQ6/V+8MEHLaaOWBEkgASQABJAAkgACSCBlkEABehG7+OgQYM8Hg+XP0RRzM/PLy8v5xYlpmG69GfL0VA0MCRQ4mBUA2wHWCYZ8yqAA19NAAAgAElEQVTTUyqS8yKptwBK+KWYU2bNAoOulm2bjQjQ1IWGAVAK8CrAvKT9x5g93oLxqjo5Fb01Gl2clL6waVjCNJgaGI7zDm4BrWZl7r0Ar8swuyZ+TWXkxrQxKaLcHrdf1KE8W+8BvXoRD41G6MkP3HnvXczcuxXzy+GbPXs2AMgSCj1ZWPiOBJDAESXgPDwdAdq2bVVVd+3aNXToUEEQ6gvQoihed911iUTCmY9yREuEmSEBJIAEmg0B27Y1TRs+fLgzSufz0Tlt/PEos6XZVAYLigSQABJAAkgACSABJNCiCaAA3fDt3b9/P/eG7MgfCxcudBzq6bpum5ZNVWjDsgwqItPVNsGUQKoC+xuAlwCmR/WJ1ck5NYmnJamEOnNmiwqWDrbFHGRYNvXQbDsW0Aqzjc7EEdTBTAB8BLBQMm6QYGwCxklwfRpmyvqzNjWvLqPqs62A4RagDZaxztxAlwO8psD8CnXcfvlPFfoMGRZG7Zcl2M3MpQEgXR2ZcN11tN/CnEFPuO66MaOvZN0YkRCxTft2VZHqg4cibBgfbkUCSAAJHAIBLkA7MrRp0Mckf9JWVlaefPLJjqriJLg7jrFjx2LY0kMAjIcgASTQkgnwZ6bX6xVFMRgMcvXZ4/EANWEw+d6WXH+sGxJAAkgACSABJIAEkEDzIYACdMP3avHixTycC1c9wuFwebljNAyOAG2bVIA2QTdBt23TAD0O0h6ADwD+EodJSZgaV59QlC+ZrkyvZFimYli67QjQTHmhRtAmqCZoFmRiElpMfd4O8I94enwkeZ0EE5MwJQKzo+bTJnwNIDP1Wae2z5bJ1WymcXNlO83k6Q0ACyrS4/an/1ShT43C7HL5RQ12AsQAIqkUdS8N9peff0adPocDfkJyc7wb1673ECEs5rbN7fBfXfr2uxamTMtm9tScVEY5bxgbbkUCSAAJHAYBtwDtCMqWZem6zqWTq6++2pGeeSI3NzcQCBBCTj/99MO4Eh6KBJAAEmiJBKqqqviz0eulpgQej2fEiBGKovC64kyRlnjPsU5IAAkgASSABJAAEmiWBFCAbvi2XXTRRbwpzyLy+S+66KJahiSWDSZbLdMEUwFdY36cVdCizPXzwqQyNWFNrTIeScNXWe/MANREmkfc4rKLCdR3swaWRUVkg9kycwHaUAC2AiyWzWkxdUyNMVGDW9JwV5n2bsosY9bNXAjOlN5m2jMzsdbBrgHYA7ASYH51YkrKHJvUr48kZ5bXvCgb31DZmnqLNoCWnNtuDz/jFG+A9VsI+fv9D4y57A9thdYhEgj6gj0H99+aiCUAUgBJ3ZRV02RiOnrlaPh7g1uRABI4fAL8eVjnPEc3WbRokaNB+3w+j2s56aSTdu3aZdt2io6oZZYGc8vuxHckgASQQIsisHbtWkGg4aOd5bzzzmtRNcTKIAEkgASQABJAAkgACbQIAihAN3AbZVnu3r17IBDgUxoJIcuXL3es8+gJVPC1waAONEww02CmmAxdA9YmgIfj1bempRvLov+IWessaqoMGQtl26K+N6j1M5dIjIwADSYVoC2NrUCVaOpC+pmEemtEHp+0JupwfbV+e6X2jgnVdrbA1Hw5u1pZkdu20gD7AF4xzdtqUhOS2h+T2viUMjuZfkozN+hmJCNeWwaz2jaZDL1w0R1UgPbQzsv/DB22ad0X+SQvTEL0c9g368nFewBqmBE0N4WWsgp4tij4jgSQABL4/gQOIhmrKh3teu+99woKChz7PkeCZj7rg+vXr3df+yC5uQ/DNBJAAkiguROwbfv5558nhHANWhCEUCg0c+bM5l4vLD8SQAJIAAkgASSABJBAyyOAAnQD93Tz5s3c8Jl70/P7/bquu45jxscWF29tA+wEQASgCmAbwKO6dkNp2S2JmrsqKj6V7bTlnOeoz7bJTJ4t9sql6Yw5MxOUNRZ48KmUPrtanlqjTU7of1bNWbHE8yljv+NI2pGeecJkkrBmgUWV4ncA5kSrx5TWXJe2rk4kZ6TTz9mwmZlFpwEkViK3AL2nZE+gld+xnVGTWt8eQ3yefJKTQ/ICZ/5h1Odyugpo3MJKgCQrMfUmwtYD9XMqigkkgASQwA8mUGvSCcDmzZu7du2al5fnqM8eDx00485PX3vtNZxy/oORYwZIAAk0MwKWZd1+++3c84bTirv77rubWTWwuEgACSABJIAEkAASQAInAAEUoBu4yc899xwh/5+9O4GTqrrzhn/q3r610c0igr7GJ36yzRMXxiUMkfjgkjGZ+Jgxmcn4xlcRJygKioMgAoIiEBCMSzQaDUExErdEnZjRiahxQUVlgkJQMIoKAr131373e8//9ZxTfSkakEWa7q7+1ac+3be7q+4953u7i+JX//ofpuu6pmkDBw78wQ9+EIZhRRrSEUCLqmXuy6YWzbJjxtNEV7Zlppre3PqtT+Wz7X4oujrLDs2yyUaoKqBVvXNAaj8yiFaprmiKIbLsd4nmtliTM+HUrDezvTSvvf2PRJtk+CsKoDulz1ze2RMHKhF9QLSotXFyPn9pyb+ovTQx0/qr0H9H9tDIys7Rtmz60RFAewEF2UL2H07+h0RKrJzOGHvq6ecvuWIa63cI65dijH3hlJHtRBuJnmppWt7U0CJzZwpFHw+3I4zeBSK+BQEIQODzCahH3TAMVR30e++9941vfCMKoHV5UY/Vuq4/+uijhUIh8IPK1wujPh6fbyC4NwQgAIGeKBCG4fjx49XDoHoKl06nX3vttZ44VowJAhCAAAQgAAEIQKBvCyCA3sX5nzNnjso4GGPxeHzp0qWu61b0bg4C8nxxDUQj6JACV1QH/yfR1VbmJ2bxqkz20ZaWgqhWdim0yZNhbbn5xvY6aJlMB6IvNBepsiolLhK9GdIvW0rXtdOkVppV8G7NFdfI4uV2GR/7IYnMW5VMR0l0SEHJ50R/JbqjrXVuwbysNTOmPT/JNO8m73WijLyHLxt1uGI/fkUA7eVLmSnXTNJEF2im6/FxV05+bOVqlqxltUlmaGzo0D/ns78sNM9v/HBZseUNzypJM498V+TrqIHexa8QvgUBCBxAAc65ehXQNM1LLrlEvTcllUoZhqFpWiwW03WdMTZ79mzXddVxdw6jD+B4sCsIQAACPUTgzDPPTCQSURvoeDy+bdu2HjI2DAMCEIAABCAAAQhAAAKRAALoiGL7ximnnKLe2a3KSTZv3qwK8VRrUc53CKB9TvlA1B3PyWUuNTP/4VoLMi0fy14ZIdlixb5yAF0OjTvaQPNyAC0KpEUArQqKNxD9ut2euTU7vSFYVKJFDdnnibbJ2meLyBVNp3cRQAdEOVmCvcTxprRnr7a88Zncf+RyN7ulV2VDD9FFtSOt9kXlMpeLEHqB7ARNFP7+iUcGHFIbqxEzPuRLX/vDBxvZkUcwg7G4zur6X//H/5pXv+k2p7C4fvP/OCKADsizybLJQgC9/fcGWxCAQFcKqBiaiGbMmKFpWiKRUP03otcLGWNjxoxR/fo9zwt8sehrV44I+4YABCDQzQInnHBCTF5Ul/xYLBa9DtfNI8PhIQABCEAAAhCAAAQgUCGAALoCo2PzsMMOi97W3b9/f1Ge7AciwuWyXFnk0AFxh7hHPhWJ1hLd3pSZY/qTmltvzjS+JZYBDLjsdCHy2bDcuVlVLcvyZVUHHfgixvVskUGLrPoDoofzfGZT/qrG4k2tdOfH9mouVhQsyujZDciXPTpEvLJjBXRJ1j7/qt2f0mqPt8NxfnB5MXdTsfXpoNgsu0OXO1jL7JlCMXqfgiiDDkU/ZzJSooTQSKRYbe3cZ58edPY/ijQ6FWdG4qzJ19z2t01LtrZslYOR3Z89m0o2ldR9O+TwGQIQgEDXCnDOPc9bvHix6tQfFUFrmpaWl9GjRxNRRdOkrh0P9g4BCECgGwWSySRjrK6urra2ljF27LHHVrYh6saB4dAQgAAEIAABCEAAAhCoFEAAXakhImYiitYTZ4ydcsopjuMEnlfM5VXw7IuuGQFxi7jnctpK9MuWwrTGtsnbWn+WyS93ClvkLk2ZKYvkV/Volt8MO9bu82UE7JFnUmDKjLid6I+l8OZW65qW4vRt2Xsb3b841CiOJAqf/VCkzyqAFim0WMhQxNahbMRcT/SwTZO3Wf/ebF3q0mWuOT3f9Ei+YUNQkG9HF1mzCML9gDxOgQigXdE4JCjvSo7t1DNO71c3wKgRfZ8nPHzf3191MUsyUQSdTH5//KRVtphpKSCrEHKROqsA2kIAvcMvEL6AAAS6WMA01UKq9P7778fj8coi6EQikUwmY7HYiBEjWltbkUF38anA7iEAgW4WaG5uTqXE0zZ16d+//6hRo/DQ181nBYeHAAQgAAEIQAACENiVAALosooKNcIwfPvttzueyYvPk6ZMVrXPIu0NQ5eHRQpNsfyeaXN3G9GjmXBWq3nplqY5rc2Pe9Ym2UxDdVv2VCOOHQNoT8bNNnGbAk9EwGJf22QDjUWbmq5vzN9aCu/LlFThs1PeG3e5iKFFEi0qlx1OJU5WQLxEtInTG0SzmujiVhpfpCtNe2ah+T/JbivPLCDZp1qOpdw9OqTQpdBTddQd71CfeOW0eE1/xmpYqt/fTxjzL3f8lPWTAXTcOPGMfywQmaqSW0T0Ksx2A9kDGl04dvWXhe9BAAJdJRCtCrtx48Zhw4apZv2q+i969D766KPz+bwqhVZN/NVoOjopyQeyrhog9gsBCEDgYAi8/PLLqmYi6gE9Y8aM6FnrwRgBjgEBCEAAAhCAAAQgAIG9E0AAXXZSLfPCMHzuueeiCOPTt3gvvGlRR0JLPAj9MLREAC0ai2aJHs7ZP21zrmwtzLHcu5q3vivXCeQyqBW5b8c1LIe25c4ZHfF0oPo+14e0juie5tbrtjTMb8zeublhg2z6rNpsBKJomrtcZN+uXDxQBdCBaMFMWzitJrpxize+iS4p0kSTriuUHqNwA1GJ7NDOyQQ7kB+9UBZSkyiEVgF0uTrblT/++W9+z1g8lRzAGKv9x3+4/KG7WIoxI8b02IjTTisjqEbSwiwMK65798uGW0EAAhA4YAKqv3Mul/ve976naZpKYZLJpFqQ0DCMQYMGbdy4MTpexUKyIoWOvo8NCEAAAr1U4MEHH1QNoNUT11QqtWjRIgTQvfRsYtgQgAAEIAABCECgugUQQO9wfjnnS5curQygf/e736mownEcHsgI1w1dTs1EK4iuaW2/LJe91rIX1G9ZT5SXHTai3LlyQ6XJ4mAdiwGqhQe3yPbNN2Xs6S35ea0tt3z4t3VhUJSJcBRAqwxade3wxbKBDifHJd4ok+ufbc1MaiiML9B4i6aawd1e8BFRG1HJLfLQ7AigxVhUAK2aecgKaFHJHIZiAcONnOb98Sl22OFGPxFAsyMHznnyNzKAZkxjI08/NUrhd/DCFxCAAAS6TyB658oFF1yQSCQ0TVMtOJLJpCqIPvzwwx966CH1GO66blT+jAC6+04ajgwBCBwwgdmzZ6uX36Inri+//PIB2zt2BAEIQAACEIAABCAAgQMngAB6B0vO+U033RQ9j2eMvfLSy2oFwmKxKDYCTm5YJHqd6Ma23GTXnWgWFuVzy0OvgVyP3MrQWW17qvxY9msu94MO1BdUIFH7fEeLObXFFwsPbtn0P+RlxY3KtdJq/cJOAbRPnk88T/Qu0e2fNEytb7kyZ000/Wml4E6PniFqJyq6PAzF0oIdRdiVAbQbUmCLImiRPptEqz26d1PD4s2b2CEDGdMZi7Ha2ILf3ccSoiEHY+z/nNFRAb2DFr6AAAQg0M0Cqg7a87ypU6cOHjw4evROpVKxWEzX9XQ6/dBDD6keSgigu/ls4fAQgMCBEIheQhs7dqx6z4d66Kurq1u7du2BOAL2AQEIQAACEIAABCAAgQMsgAC6DGrbtnrT4oIFC6IIQwTQr7wSeGIpQQp54AeqELid6FchXZEpTi3Ys7Y2v0PUIMqfPZss1fe5Uwyt+j6LPFi15yAKfcqE9AnRPSV3Rot1TYNza4v/qus3E5eHCEluVBZBy27RgSsaaIhLE9EyP7y6tfWKTHZSsTSprf1203udqFUWYosRizurBNsLt7eBVkl06Mk1El1O9US/bLUX5Io/b2pkw44Tc9din36cc+etLKGzmIijTz3j9DITPkEAAhDoqQLPPvvs0KFDGWNRIhOPx1Vl9AMPPOB5HufccZwwDKOVDHvqVDAuCEAAArsWsCxLvfBGRN/97ndVBbRhGOq5a5RN7/rO+C4EIAABCEAAAhCAAAS6SQABdBnekykz53zy5MmVAfQzf35OVBE7rlM0vSAoEZfNN/jUfO5qn25oyP+hRI2i4TIVKbBEfwwR/O4cQNuyDlpVQIc+2UQfE/0poFnNpclN1q0t/vO+SLF37nSx497Ezx2izUT/ZQZzbeeSfH58sXRNoXiHaT1PtFU2obblAMS+RJodqPQ5LIffKoAOsr7pkBj5f+fpunZ/phXc1NSS/s53mC5rnhmbMn2a3vH/mTPOOKObfj9xWAhAAAL7ILBmzZqjjjrK6LioB/P+8jJt2rTK1Qj3Yae4KQQgAIGeIcA5V+3s1XC+9rWvVT5lPfLII4NylULPGC5GAQEIQAACEIAABCAAgQ4BBNAdEkSqbOTcc8/d/mxeY9fdfGMxcFUw7BOvp2AFFRYWP7q0tX6+R49n+FYRPYtAuShjaJEQ83IGrZpvqBUAbeKe7K1BJGqfRfpM/u3Z/LR656Y2etGnbR0LGIo775hDBxTKq+jYTKLa2n/QzF2Xy07IFC/JWRNLzoKC9TqJPbQRFTj525fXCjvSZ7XL7esj5sx8C9Fyojmt4RUt3iyLbq5vPfbicaxfrZr+eT86N2HENdECmp357W+LsW/f7XY0bEEAAhDoCQKWZalhtLW1HXeceDOHpmm6vKRSKfWwNmbMmJ4wVIwBAhCAwOcU4Fy8La9TA+izzz5bLan9OXeOu0MAAhCAAAQgAAEIQOCACyCA3k6q3tJ4xhlnVAbQ18y93ifitksyX15HtITaJtSvvTbb+Ktc4RNZjxwExAMR+4rkV8bHoax3djtWAPSJ26Jxs2ie4cl+Hc/6wR3Z9oXthZ83h8/4tEXupxw7q/LpHdJeHor8OrRle40/F3M3ZFvHFYoX550rcs512eJvi14rkUtUCMki0adadeAIRKsP7pfbeqiZippon4J24qtCfodF/5EJxjVY80t098fb/nnaNNavnwhuGDvzW6emjQRjrEbTEEBv/y3BFgQg0OMFGhsbx4wZM2DAABU9JxLioSwWiyUSiWHDhmWz2R4/AwwQAhCAwGcJBH5g2/b256ty64orrnAc57Puhp9BAAIQgAAEIAABCECgmwQQQG+H30UAzdhFF10U3WIb0WMlc3J949TW5sXNW1e5pXYZ+5IvP9mqrbLof1EZQIuS6CAMAzMMTJJlzq8Szdq0Zcamlp99kl1pUgMXBdTb657VlmigER1ZBNA+hW1EzxPdUjLHtxfObytd0FaYnjefDEXvDkveXAXg0d3kvbhfWVEt0m3XJ1pPdFv91tkZb2qWT2kwF21p/RvR9J9ezwxdBdA6iyWMOGMsHo9PmjQp2ic2IAABCPQKgZkzZzLGotaohmHE43HDME444YRMJhP4gWqlipapveJsYpAQgEClgOd5K1asqAygDcO49tpriUgtalJ5Y2xDAAIQgAAEIAABCECg2wUQQG8/BbsMoL/5zW+qguJtnF4n+kXevmJb7vrmwn9nW7eGZkl1dvZlAbNJZMokOhClzq68isUARfOKMAiLLrkZotU+3dzUuqBgzdnc/lg2aNh+/Iqtjkrq6Fsu8XYK1xLd7npXFf2x7e6/t9qT2s0lAW2UY9ixaUf5flGUXfnTEgV/I39Jru2Gtsz17fb0zdk7mkrriLJEi++7M6aJOkF1qdE0xlgikbjxxhujkWADAhCAQG8RePHFFwcPHmwYhqZpyWRS1UEbhnHEEUesWrVKzQItU3vL2cQ4IQCBSCDwg4ceeqgygE4mk08++WR0A2xAAAIQgAAEIAABCECgRwkggN5+OnYRQMcYSyYKRB+btI5oKdHMvDO5PveLvL3KtfIycPaJl/NmR8bQomGH6LNhl7PocvmxR+Fmcv/EnbuyhfmtxTmfNC/+uLFe7mH7CHaz5Zh+mx++Q3ypk5lp8QlFurQtmNbqLC2GbxG1yGNVRsy72Y34tkP0V6LfmqVpW5qvy9jzmwtL2wsbZAPrZj+3YvUKVhFAq//YxOPxRx5+5DP2iR9BAAIQ6GkCUaz81ltvHX744Sp9Vo9pAwcOZIylUqkVK1bkcjn1yN/Txo/xQAACENilgHrI+nQpwtmzZ1cG0Iyxl19+mYiKxeIu74hvQgACEIAABCAAAQhAoBsFEEBvx1dvxN6hB3SMMS323NvrthF9+qT+hoI7JW8tbMkv9+kjClW5czmAVgsOym4XqvxZBdCezJ9NGRO/SIWfmW3XNLXM25ZfXJ/7G1GORPcO1a95lwlyKG/QVgw2hvQUBVc3fzLZpolFmp6l21s9lT5nyTfJ2+Xdo7mpliBZz99M9DjRda3Z6Rlvbpt355bGD4habFv1+3j21ed3DqANw3jxxRejXWEDAhCAQA8XKBQK+XxevP+Ei05Gtm0fe+yxUVITi8XU9lFHHfXss8/28LlgeBCAAAQqBVzX5fIyduzY6GGNMabrum3b6ClUaYVtCEAAAhCAAAQgAIGeI4AAeodzwTn/0Y9+VPGEXqtLD7xr6cNbiZY052eVCnOt4rMetcrFAG25vl9AXPRvlisH8lB8Vlm009GFwyFqJlpLdJfVdGVr/bRM8eaPWv7CqUhUCEo+8UDuoLJdRij2yMvpM6dGosdaMte2fHJ1YI/P0aVb7JtavVVEogM1J4scixyxvuFuLr4cUrsMwV8iutHxJxWtSzc2/KLZXK9GG9q+J+plnn76T1rFJXLYsmXLbvaNb0MAAhDoBQJNTU3f+973osc0tWEYRiKRWLx4sejOb1m9YBoYIgQg0OcFVMTsOM63vvWtyse0Qw89VGXTfV4IABCAAAQgAAEIQAACPVEAAXT5rETvwp4/f370hF5jognyP//wvK1ET+XzN279YHFb/Tu2p2qcRXYsCuy4WCJQXgPZjUNm0aIHtKdaWxCtIu9us2WemZmWzd7QkF0pGy6LyMPLBRSIe8lrRQYdyv2JpQW3hrSS6LZcfkKmZbxjj29x57bRUwFtUQsPBr5PnkuBGMmuqqBVM5Ai0TaiV4juKjqTC9aVmeKtbcU1sgGI46jYJSSPFt95b02sJoqgdV0sSFhbWxvh9MRfYYwJAhCAwO4FonrAwA+mT59e2YuDMZZMJhOJhFq5q1Ao4LFu95D4CQQg0CMEov5Chx9+ePR8lTE2fPhwzxMrj+ACAQhAAAIQgAAEIACBHiiAALp8UlTuwDm/8cYb1RN6jTGNaUktdciAQwMKM2S2U9BOoUXkq8RZvQeSixLm6CqXHBQNLQLZcLlZpM/W/U7LlOb6qdnibVn7iXY3Vz4m98nyuS/qpjsH0EQUhMRLHm0I6B67NMUq/MQsTjC9GS3WY0QfyAjbpNAVyxvKm6rEesdfMV8k4EGWqI3oHaI78/7UnHVFuzWnPa/SZ05UFK1ExIVbdOOcRTWxuKaVM2gVQJ999tk77hVfQQACEOg1AoVCIfAD9Qify+V++9vf1tbWVqY2hmHouj527FhkN73mpGKgEOjzAoVCofJxjDF2ySWXBH6gnpn2eR4AQAACEIAABCAAAQj0OAEE0OVTouKJwA8WLFigntPrLKYqoA+pG/Rfjz8iy4WLoukFD0I/EF2XfU6hKIL2ZafmgMt+z6pxhlyHMEP0P0RL3bY5+YarCu3TW9sfztnv+FT0yLM9n8RV9doQAbSIrmUNtOhZSj7xAtEnIS23gmvaWi9z7Qken1pwf13w3yUqyNFYHQE0D8oRdjn+LhdkixLsAvFGoo+JnrLp2ow1MWvOaTMft/yCrL/O82KJ7GxerlfjdQ6glcMvfvGLHvdriwFBAAIQ2DsBW/S4LzeDtizLdd21a9cOHTo0lUp1im9+/OMfq87Re7dj3AoCEIBA9whwztesWdPpEWzBggXqxbaoRLp7BoejQgACEIAABCAAAQhAYFcCCKB3UHFd99FHHy0H0LqeTqfV9jnfV1XAgcwxuCiBdri4BiKAdmUzaAq5iKR92Qda9t/YQPQ7TjNL/mW59inZzYvD1jWyKYfo1xyWe3TscHgKKQwp8ImHBaK/cfqDxW9qdydn3UtaS9NNujljvSP34Mruz34ojhYG4qNa81Dl0J5YIDG0ybdlb+qtRH8shT9tyl7S2jojn3/BpSyJ2wfke+S7on5aXFwnPPt7/6xp2yugGWOGYaAB9I7nCF9BAAK9W8DzvGw2e9JJJ3WKbzq9h9113d49T4weAhCoXoGXXnpJ07RYxeXxxx9HE6HqPeGYGQQgAAEIQAACEOj1AgigdziFnuetXr1apRKaphmGoWk1cSNpGEahUFA3FR1F/VAs/+eKCmg/CqADTmK9P7GCYI7ofaJHinRDm3txS/EnjfV3UfvLZG6TKxOqQme3nAJXDKBcAx16Mn1+0vIWZO2pBXdsffbqjLugpfgWiT2L+DrYfuW+zKBJhM8iAQ+4J+ujCxRm5fqHr1p0c0tmcmPT1PbWBwK/Xu5BNqou78YX/ULE5Stf+Zrsv1FuwcEY+/rXv05EqApUPvgIAQhUjYBt28OHD1eP9nF5Udsnn3zy2rVrVefoqH901cwaE4EABHq7gGoWdPfddycSiYr8ObZmzRo8ZPX2k4vxQwACEIAABCAAgSoWQABdPrmq2I1zns/nZe4slh+MLoZhzJkzR91ULDoo1ggUX3kyUHblaoQi/PU4cbJDWkt0v0UzM/64psxlLf4jLQ0AACAASURBVI2z27euJNoqi5dF+uyXK6BVhbIqQA5ltbJaM7Ce6Pcun58zrymYV1nW+GzLtc31q2QrZ3vH9FlFyLIJiKy/DsptPFx5401Efya6K2de3dY8rb3lwVLpHdm+g2+Pr8UORMcP7hdKxZpEPKZr0ZUxNnHiRBTUVPHfP6YGgT4rEIZh4AeTJk3SNPFon0gk4vG4esz/whe+sGrVKvFSX7irpV37LBkmDgEI9AwBx3Hmzp3LGFMBtNowzfKSHnjg6hlnCaOAAAQgAAEIQAACENhBAAF0maNYlH2QiWzbTqfTav29KIBmjB111FGRnBcEwfb0mVQLjmjhl0aiPxJduaV9fMEbn8nMzTU8TVazqn3m8m6eiIlV1qwSY+IiBrbl0oKNROuI5ufsSSX3SseaYucmN370DFEjUdELVM+NygroMJCrInqyIlu1o/bFrjbJDtR32d71+cKMQvvPS+1vEW/lgSMScjskP6qiVgH0qtWrNCMWpc8xXYvH4++++66S6VhwUXyOHLABAQhAoJcKqN7Qrus+8MADQ4YMYYxFAXQymTzyyCPffvvt6FG9l84Rw4YABKpV4LzzztPkJRaLqQA66hrkOE61zhrzggAEIAABCEAAAhDovQIIoMW5UylDGIaquvnCCy/UdV2VxTHG1FN8TdOWL1+untbL/hUiQVbXdrvoyPi4mcJNRE8VnGsbsxOK/hWON7m98SG7eZP8qThSR0BMslO0J6ueRYmdWISQ2ok+Inqb6O6CN8Ohy5xwdLbxypaPV8pVBE0Kyfd5EIpLFB4HokaPB6oNBxeNpR0y26mNaAXR7EzLNcX89Fzm1taGvxI1iR+6skG0RSKADtRVBdBTpk5mGjOSCdH6OZmI6dpXvvIV9f8ZJVOZQUfbvfdXHyOHAAT6uIB8MBUPwE888cThhx/OGFOP/MlkUgU6d911l6olxKJeffxXBdOHQM8RCPyAc37WWWcZ8qJKJUaOHBnVB0QbPWfMGAkEIAABCEAAAhCAAAQQQIvfgSiAVnnEzTffbBiGKiqJ0mdN00aOHKla78lFBFUnZxEcOzJYzhKJVQfzpUWthStz1tVEU4vFe8ldT1z0zai8TygSZ9VzQ2XZxEWW3U70AdGSbDCr1ZxohpcU7CnFlvuptFH0zZAp884BtBpxKAPoQOwlCChDtIboxqbcdLM0rZSb19bwhmwGbZLLQ5s8l3yX83L6HMgG0CGFp5x6SlTxrdXojLGZM2eqv5DyQTo+Rekz/pODRxAIQKC3C4RhaNv2e++9d/TRRycS4hW4VCqlXoDUdf2Rhx+xLKu3zxHjhwAEqkkg8INEIqHLi3rmdv7556sJqoqBapos5gIBCEAAAhCAAAQgUB0CCKDFeewUQK9evTqVSqnn9JUBdCqVeuaZZ4LAleeeixRZXlTrjA3EnyT7+pI5rs28LG9e53p3FnNvqc4bstLZldvbq57lfWUps9iTS7SF6CVOs7ZkJzQXftKavzqXf5zCDUQZCn3ui+UOZc7ckQNv/8yDkAKPwsCWnTreIFrYlLu+4E9rK/w82/aUm8+IQzui9tlzo44hUQW05VoluyQLnw0jmVDpM2Pso48+UhP0PG/7wWSdeJRBqxvgIwQgAIHeLpDJZE488cRUKpVIJFLyov4VmDhxovpnordPEOOHAASqRqC2tlbXdVUq8WkX+4ULF6qHKTSArppTjIlAAAIQgAAEIACBKhNAAC1OaKcA2vO8uro69RZsVQenYuhYLHbqqafK3wAuKo1lBO3J1QXXEf2BzAVu6+Ulb2whnJApzm5ue7JUalS/L7LkWTV9tmUMHYijqrpo0dU5JMoTrfLpti3FmZnwyox99bbGZb7/vvy+Q34Y+mEgumb4ofhCNuLwfe67oiuH+CkFgU/UIDt4zG3NTC9501qdn2eD37e1N4sabS4ycN8mzyePxM1F049yEbTj2Y//4bF+/fvVJGpienn1xX/87nfU2DnngR8Evur9IYLoKH1GBbQiwkcIQKD3CoRh6LpuGIaqw9K5556bSqVisVjUhamurm7s2LGdJogyw04g+BICEDg4AmEYvvjii+qlsuhh6rHHHouezR6cYeAoEIAABCAAAQhAAAIQ2CcBBNBlrk6h6ujRo6N+FGojWublpZdeEPfxAtlWQyz39zeiBwL/mkzL5bn8pCJd59LETU1LS/5mIvHObdEomqs+HaFMn11ZEC12EnLyXQr9UHZ5XpKzrm7ITrVoRpP5x6L1MfGs3INDoctDV+5DbJMvYufQtcgtkm2R6ZIbuLzRo5eJbioEk2y6uLE0+xPraYs2y/YgqlSbB2FURh0QlwG0F5DHeXDhmAs0naXS4u3nInnX2Isv/lnly6LjtEyfK4mi7X36bcONIQABCPQ0ARUlR2/yCPzgiSeeUC9AptNp9ZDIGDvxxBPb2trU4G3b9jzvMx4Y8eJcTzvLGA8EqkYgDMOVK1d+WvWcSCRisZhaNPu1115TAXTVTBMTgQAEIAABCEAAAhCoMgEE0OUTGiWqKjhYs2aNyh0Mw4gKTNSz/JEjR4qKYJfbgVjW7x2i+wOaUbDGFewrXJpaosmfFBZtLawlsRJgEKoAOiQ3FEm0/KocQIck6pldh8JgG9GzPp/Z3Drd8qduLTzq0SYRVXOXuEPhjldR9RyGrs9dUwTQrkW2SWGDK0ZyY0Nxat6/3KKrM/6yDL0v825xVE6d1i3sKH8WAXRTU4NeE9NE22emPh5//LColEYtzFjpU7ldZX8PmA4EINDXBNQDWhRAq+k/8vAj6p8AtSCh6FBkGMccc8zq1aujd7gHfqBi6MqHxGi7rzFivhCAwEETWLBggVoiO5VKqceopqamg3Z0HAgCEIAABCAAAQhAAAL7IYAAuowWpQacc7Xk1Je+9CX1/N4wjGQyqUrhVBi97IGHPZ8afHqF6FdBeEWhcJHpXmzSZblwcta/bnPmOVusBFhUAXRAoscGD4lCTybCXnlNwpBCP7DyLaH7EtG81swVLdn5Jf5oi/OJvO9O6bOInnkgem7I6Nl3RO20uGaIVhLd1FC4oRRc0ZKdlskvDWkdUYs6UKf0OSBR1FzuvyEC6KX336uilgED62prRcXf40/8vqMxiYDp1Haj0mo/fudwFwhAAAI9R0A9oEUBNOe8UCg4jrN+/fra2tqoxSpjTNd1wzA2bNgQDd6Tl8r7Rg+P0W2wAQEIQODACsybNy8ej6tFU9W6qaZpHthDYG8QgAAEIAABCEAAAhA4sAIIoMueUWrAOfc8Uas8Z84cFcsyxoYOHfrVr35Vrfei6/Gvfv3vMyGt9WlJqXRVc/NleXu8R5fk6P/7oO3aNvP+fNBIlPfJ5bICOhA9pgORPocuhTZxmwe+7AAdULjNy/0Ptxa7zuVbGmcVgsWFsIHI9sSahDsWPoeO6NYhAmeX/KK4is4dfkAFoo+Ibm93p2a9y1uzs/KFX+byfyXx/ZwrukvvUPssFz0MQ7GqYZRBH330/5b1faIEWq+JffGoIxVKpcnutg/sryP2BgEIQOAgC6gHtyhEDvwgaqDR2to6cuRI9UqkpmkDBw6Mx+O6rq9cuVIN0nEc1Tw6apQfPVQe5FngcBCAQN8ROOOMMypfGxsxYoTrqvWx+44BZgoBCEAAAhCAAAQg0MsEEEDv+oR5ntfW1haPx6P+GyNHjjQMgzEWN5I1hxx67qzr/tMszG6vn5bNzsvSg0RXttK0dro9W3xNrhwoqp19ceUhBcRV+uxRaHO3xB2XRPPoT8hfQ3Rz46Y52cLsVucBm94iEkUsvu+HnTpviABaNn0WnTdk7bPYaZHTGqL7TW9qu3ulRROL+TnNDR/KAmpf1TCHIoDmsgJ7+0eumkKTZZWe//OzUecNwxAZ9CuvvKJSlShJ+YyNXfPhuxCAAAR6j0D0EBe111Bjd103l8udeOKJqv9S9JKkYRg///nPo46rxWLR8zz1sBkF2dE+ozi793hgpBCAQI8W+Pa3vx09HOm6/oMf/ACPMz36hGFwEIAABCAAAQhAAAJECKB3+1vguu6iRYuip/iGYXz/+99Pp9O6HhffTCcvfnjZzS1bf+E4TxLd2k7XtNDsJv8Plv2RDJdFDbMMoCmggFMgFh4MRdMNCtRPsiSy49utlun5tul5c9am9jdV04yAyLd9LjpsVFx9FUAXyC6S6/LQD0T6/J5PD5S8mZnClRaNazPnlQovEmVFhE3kc3HgTtFzKMqxo/+oeL4zcuQ3Vd/neLwm3S958sknKxFVBliZoexye7d8+AEEIACBXiJQ+eBWOWT1UBmG4aRJk+Jx8cgfVR3GYrEJEyaoG9u27bqu53lR+typbVHlPrENAQhA4HMKHHHEEerZqWEYiURi2rRpn3OHuDsEIAABCEAAAhCAAAS6WgAB9C6EoyK4bDZbV1cnqp7lZeTIkYMHD9Z1vSaZYuna2qOP/eOHm1YT/Ylo6uaG2Tl+V9Zf54cmkSUTYJECeyJ4JtEIQ13FJ1tmxBso+AOZVzTXT7TcqfnSL/Pux/KOsmWGE5DniqharUMo0mcVQJtkWmT7YViQ+fUDJe/abG58sTS+5N5QcF8IKF8+NBcJuFzucHvhswqjZdZCRK7rPvf8clX1HI/XiGxFY2vXrq18B3qkUxnQVG5HN8AGBCAAgV4qsLvHtOi1OiK67bbbEolEbW2tpmmxWMwwjFQqNXbsWPVYqibeKYDupRoYNgQg0JMFstlsTF4YY4lEwjCM3/72tz15wBgbBCAAAQhAAAIQgAAEPm10jAB6F78GgR9E373tttvUAi9qBaoRI0ZENdGM1fzbv1/2IdFdhdbpbfW3lOwnQ9oiUl9uyl7PInpWjTgCLrpghKHsCU3NFL5H9F9kLnSbJ5qFq0xvTkv7aqJ2kr0yyAvI8bcH0IEjem64lsigXZdsh/wC0Wai3xaD69oLVxQKE83S9Nb2P5FY+dASSxzK2mevHH9XBtCiHUfHhYhOPfX/qO7PqXQiprGFCxdEE++00XGnzp873QxfQgACEOh1ApWPa5WD55ybphnF0L/73e+ixWmjUuiRI0dmMhnVgLUygK7cD7YhAAEIHCiBNWvWJJPJqAKaMbZixQq1eMmBOgT2AwEIQAACEIAABCAAgQMugAB6F6RR3EBElmUdeeSR0VLjsZiuaTW1/fozpsWMfqwmPelXv7qp8Mm03Ie/aN+6hqieKEdhgUKLQrEfX17DQFYjuxQGTkCNRP9lBjObW68sZC5va1xo5lbK7FgMJSSbwpJYb1A061BXlzybPIsclzzfFgnzJ0S/baMpG83rHJrYnp+bbXuJU4Ns/SxWPpRXlTur7YC4aAQtL5xzyyoR0fLly5PJpKrmY4ydcMIJlRPfhQu+BQEIQKAvCewcTK9ateqII45Qb3uPMqCvfe1rtrxEt+9LSJgrBCBwUAWef/55xlgymYyemhaLxYM6AhwMAhCAAAQgAAEIQAAC+y6AAHrPZitWrGCMqV4csZieSKRkAM0S8X7pgUPYFw674JkHF7S8u9xtW09ukyxkzlFokh8QLxcjc88TrTOsEgXbOP05F9zZ4sywaIpNP81l/iRj61ANhJNNvESht0MAHch2HJ7syEHbiO7fym8v0fR2mtQSzGhsejx0mmTC7XT0nVbLH/rEOwXQROT5DhHZtn300UdH6XNdXd2aNWui3iN7RsEtIAABCFS7QBQoV74419raevzxx1f2g2aMDR06dN26dUQU+IFlWdUOg/lBAALdJrB06VLVfEPXdU3TamtrxVM7z+u2AeHAEIAABCAAAQhAAAIQ2AsBBNB7RuKc33zzzeoN1yqArkv3Txv9RACR6sc0xk746sKXn26WVcwZUQFNRVkBLfJf0fEiCMixqNBC+ffJ/zMPFm1t/mmez7BpZpv3p4A+JipUjIKrJs6yZ4cnY2VbfoeHorX0J0T3NZQW5Wh6lq43aVZ92/2tDZtItH52eceqh6oIWh5d1T7LjwHnorWIZZUKxdyUKVPk+zdjiUSKsdisWdd73vbGIxXDwSYEIACBPipQGUA7jnjpTrXaIKLzzjtPvQU+6go9YMCAt99+W0lVBtZ91A7ThgAEukZgxowZsVhMLYvKGPvOd75j23bXHAp7hQAEIAABCEAAAhCAwAETQAC9B8rAD4rFYuAHF110kSx5ExXQ6UQ6zsSqfaymhhmMaeyIE47d1Fwv4l1R+yz6b7iyA7PLRScNi7wmKr5L5tPk/NK1Z7QWrhX1y3zR1tLfiPK+CI47XUK5eGEgP7pENlGJRO3zb3LBLS5NzYdXtdlzM6W7mxrfFa05ysseysLncguOiuiZBxQE5cUQqVjK33nnHf3790+n04yx2n79z/6//4z0uZM/voQABCBQGUArjWiNVs/z5s2bF3WCVhuDBg169NFH4QYBCECg6wRGjx6t1kGVa3gY5557rnrvRdcdEXuGAAQgAAEIQAACEIDA5xdAAL1Xhp7nOY4zfPjwVCqlqt7iMU1sxMRVbQ47+ustTY2qylj2buYecYv8rG82kPMu+X8k86elzPjGlsuz7jW58KeN5kuyazOVu28QJ3El+dEmEuV2XCTQnidKpP9K9EDWndZuXp53JrQVZmYKS/KFN2W/adFXg7hKn1XZdUf6HFRsqAJn/uijDzPG+vfvryZyxP9z5F4R4EYQgAAEICAFVB10Pp9funSpip41TYtaQi9btsw0TUUV+AFaG+G3BgIQOIACp556aiwW0zT5LJSxa6+99gDuHLuCAAQgAAEIQAACEIBAFwkggN4H2Gw2e9xxx3UE0KL3hs5EIfTgdKpW1/olar454iTfNYv5rBs4NnctCmzZQ6OZ6Cmyb3ZLV+Stn2S9S1qca7YVnyXRfEOkzB2XKIAOiczoR6HYfp/oEZuubc9fZjnjSta0TP729sxKohaxbGFAoROUA2jR9KPjKqqeK7c5D9atW5tIGPL/LTHGmK7HV/+l/J7xjlHgMwQgAAEIfJZA4JcbFuXz+RUrVgwePLj870I8rmoSL7jgAiJSMXR048/aI34GAQhAYO8EjjnmmMoAesmSJej5s3dyuBUEIAABCEAAAhCAQHcKIIDeN/18PnvcsGP6pRLxmIie04wlGUsZshg6xeK1+ohvnlAqZDzf4URtoWnJ1hmryV6Uz03IuT8p0aVFmtpGi3N8syx/LhK3iXsiRy5fuNxWqwiG8jbrOP3eohtK3njHvjR0Jpba78hmlxetNtnlQ9Y+77DYYMfbxkXT58oAes3at+rq+sXjNbGYav2sLVr0s8BXVdcdh8dnCEAAAhD4TIFOcc/KlSvVsoS6vKi3mPzoRz/K5XKfuRv8EAIQgMA+C/Tv3z9aQZoxtmrVKrzKtc+IuAMEIAABCEAAAhCAwEEXQAC9T+Qiq81m24f/w0k1WjmATqjKN8ZYnIl+0Ix9c8RJa1a/lXecFgraiN7i7u0fvj9xa9OFWf/fHfoPk+4o0BqiBvJsskxyTAq2L17Otzfi8InniDYTLcu4s1uKl1v+FKIrgtzsUuPD7S0Naq1C2T/aJdn3uaP2eXcB9PHHD4sGyxj7/tnn7NPkcWMIQAACEFACYnlZP/A8L/ADx3Fc1x05cqR6gDUMI5FIpNPp0047LZPJoAUHfmcgAIEDIqAeTOR6JOJNbKr/T2trq+dtfxZ5QA6EnUAAAhCAAAQgAAEIQOCACyCA3g9SHob++Esv0SvTXLUtO/Kl0sahhwxetWZDG9GKIt3elJnRnB1Xn7204F3muBMbG1+VywkWyffJCkUTDk80e1YNOKI2HH6YC7x3iO4vONc05i7NeuMcGlcqzXKbfsNb1hLlqVwprZYrlAXUIVHIuSh8FrXPges4lppea2vrsGE7pM9f/vKX83mxDyw/uB+/AbgLBCAAgZ0Fxo8fL16LlI041Cph3/jGN0zTRAa9sxW+AwEI7L2A4zic8zAMn3vuucrnnrFYDOXPe8+IW0IAAhCAAAQgAAEIdKMAAuj9wC+HxLf87KaYVl6BsPL/A4YR65fsN+CQ/zX3nt/97uP8T+sLsz2aVHDGNbdMy7c9ELqbZGMNm3xPpM8dAbQaiGrAQZR1Re3zPU3t1xWcS3LOOIfGF7wp7e1LKLeS/EYiWwXQgUivXZFFi/SZKAxDPwhctbMgcD3P27Bhw6BBgxhjyWRSJSN1dXXqPZuWWdmDej8ocBcIQAACENgucNttt6nKRF0Xr1Emk8lBgwb95S9/UeHR9tthCwIQgMC+CDiOeMK2cuXKyiecZ5xxhngyGEZd3PZlj7gtBCAAAQhAAAIQgAAEDqIAAuj9xFYlJ6+99tpXv/rVZDJZ+f+BwUMHx/VEPDWIaQP/edZNt3zUcH1zZopVmJJpfqBofkCUk5FxkYIieR55vmjBUdEG2hdB8gaie5pLs236ScEZ69GlRWdmc/ZX+dxKok1EWbkH4uKWJaICiYUIVQAt58N91/ZdkVEvWLBAjU29VZMxlkql3n5bLDyo2pg6Dt65uZ+/A7gbBCAAgZ0F/vCHPxx++OGGYagMmjF22GGHPfTQQ8ViEe+U35kL34EABPZGgHPued71119f+YTzzDPPVOkz6qD3xhC3gQAEIAABCEAAAhDoRgEE0PuJr9JbznkulzvnnHOiDDpWE/3XoIbp/dmAw9kxJ1239q/XNHx8l1v4q6x9dmXTDZO42RFA+8RD0YajnCK3Ez3YFs5p9y7Oe5cTjTW9KW35JdnCq0H4CVGbDJ19eWNP9uIoiB1GAbQohGlvbf7ZohsPH3qopom2IKlUijGmadpRRx31xhtvRHN2XT/axgYEIAABCHxOgTAMPc9bu3btMcccwxgzDLkygMyg77333s+5c9wdAhDoswKqAnrhwoXRs8xPH2EWLFiACug++yuBiUMAAhCAAAQgAIHeJYAAev/PV8daf2JlwldeeeXQQw9VDS62/98glmBakqXr2OGHjZg9bcEbL24NKdgeH3M3sBxuc/LUGoK+JYqj1xE9VrIXtuRn5INLct74kj+95N2RK70ahDmZX0eZsRNQu2W3eU5RpM/iEgTuM//99EUXXnDYkMHRMDRNU4V4qVRq7ty5ROS65R4d+z953BMCEIAABHYvsHHjxoEDB6p2HOqfBk3T5s2bh4ff3ZvhJxCAwK4FojdPfOc734me3THGlixZou6ACuhdw+G7EIAABCAAAQhAAAI9RgAB9P6fiiiAzuVynPO2trYbbrjh8KGHxmv0QbX9O/6HILtE12gszlj/JKsxBh8y5N/GXHD/I8uaGuq5W14kUMTSshvzh6XgwS2bFm3aeEND/czm9v/Y1jK9vv1nDZmnneBDopbQby6UCrbny8DZ9kX27RM15zJLfrN09JgLBx0ygDFWI9dCVAOIxWKaphmGMW7cuJaWFjVbtAvc/7OOe0IAAhDYO4HW1tYRI0bE4/GoDlrTtIkTJ5qmKV4v9IO92w1uBQEIQKAscOKJJ3Y8vRSfX3/9ddBAAAIQgAAEIAABCECgVwgggN7/0xQF0KqizXdc0ZTZD+6/976j/tcXKv+HoLZTg9I1jA3qaBhdF48fesigYd88/t8u+H/vuOW2Z/74zIeftL7w3qZlGz+4t2HTndvev6v+w9s3bvz1xs1/ztrvE7WL1s/Bc6+/9vATTyy85dYpU6+ZOm3Gd/7prCOOOCKVSsVrym/01mNMj7GEUW4FolpwTJgwwbKsYrGoZosSvP0/67gnBCAAgb0QUK/zZTKZMWPGMMYSiUT0j8I555xTKBQQQO+FIm4CAQjsIDBkyBD1SKIW9rBtsdoHHkx2MMIXEIAABCAAAQhAAAI9UgAB9P6fliiALj/1D3koK9o82wk8Z+Wrr4y98PwThx0t3oLNWI3O0kmt1tBTeowxVptO1tX1E/+LSDIWF5Fx+ZJIs361TGcswdigBKurY6yG6bWMiarmWDrBamJqU95ei+uJhCburTOWiiei2ufBg0QptOr7fOutt1pWR6l1x9qD+z9t3BMCEIAABPYkoBq2hmHIOZ8+fbrqBx2Px1USfdJJJ23YsAFvRtmTIn4OAQiUBdTSI9GC0mpD/QwBNH5LIAABCEAAAhCAAAR6vgAC6M97jqIYutMGhQGJzhr08ooXz7vgvGT/NKth6bqkyoVFiJzUWK3OUiJhrompIFr+UI8xQ2e6Jq5iTcO4vG5f3LC8B5lJ6zJ6VvF1jVxvMPppPB4/7rjj1q5di4zj855j3B8CEIDA5xN46KGHBgwovy6oOnIMGzbs3Xff9TxP5Uqfb/e4NwQgUOUCgR+89dZb6m1tqrzgtNNOU3PGY0iVn3tMDwIQgAAEIAABCFSFAALoA3AaO0XP6svyfkUMTXbgvfrm69/5v99jjOlxXWTEtUk2uI7VMGaIiua4rIROiixaXXQZL2s7foyy5e03UgG0xpih64lEoiYRF+XW8jJv/vyAuEqf8Z+TA3CasQsIQAAC+ysQhuGbb745cODAWCwWtYQeMmTI888/j55I+4uK+0GgDwlwzpcvXx5VQOu6fsEFF/Sh+WOqEIAABCAAAQhAAAK9XAAB9AE4gbsMoCtj6EKhIFYLtJz/fPDRE/73MamauK7rImzWNY0lDRavkY2bRVm0iI8NJuqi4zKOrsygy8ly9ClKnxlj6XQ6+v65Pz7vgw8/JqJsvhiKMmzuh3LVwgMwV+wCAhCAAAT2WcDzPCLauHHjiBEj1GN1PB5PJpMDBgx45pln8BrhPoPiDhDoewL33Xefqn2OxWK6rs+bN6/vGWDGEIAABCAAAQhAAAK9VQAB9AE4c7sMoKP9Bn5g27Zj2RQSWQEFlNnWNGnqFDakliV1ZtQxPSUyZ3UVrZ5TjNXJkuiaPVZAi5t3XFL90ueNvvDVN95Uh3Y8PxpDSOLguEAAAhCAwMEXUO9EUZXOpmmOHj1alTGqj7quL1y48OCPCkeEAAR6l8CikuUufAAAIABJREFURYsYY/F4XJOXpUuX9q7xY7QQgAAEIAABCEAAAn1ZAAF01559lU2LGmTiFHKy5dUL8kQvhC2XPHnfSZMuZf/rcHZoP9ZPrxl6iAyTUwn9kPLqhHLBwY6EWXzWGEsnyo2k1ZKDX//6382fP++NVW/miyXL8QK+ixkFnPyQ1HJYlaXZu7gpvgUBCEAAAl0p4LruhAkTxLqyMfGeF9XUdcyYMc3NzTuXQle+wNmVg8K+IQCBniugXr66/PLLox7QjLFVq1b13BFjZBCAAAQgAAEIQAACENhRAAH0jh4H9KsoOAiIu8QD4uTKK1EDt56365c0rrvzo788UWq8r/7DH/z8lqP+5V+POvVMFh9gxGp1TV71pK7HDW37NV5jMMZGDD/ph+d8//ePPvL+e+v3Zsh+iAB6b5xwGwhAAAJdLmBZFhHdd9998Xg8KoVOJpPnnHOOaZqVGTTnoo9/5WuHlT/t8oHiABCAQM8QME2TiL797W/H46KHm2jjxlhbW1vPGB1GAQEIQAACEIAABCAAgT0LIIDes9F+36IygPZlEbRYFZDIJ25SkAmdreR8SHwd0awtG38WeAszuQea25qJ8vnia6/8j7i++uZrr76+8pXt13f+ui70A9+1iYgHPg+299lwfbHg4S4vAaeAUzQeRBi7VMI3IQABCHS1gGmaKoAuFourV68+9NBDo/e4JBKJ448/vqmpSY0hDEPLsjoF0F09POwfAhDogQKcc9M0jzvuuOjhoq6uTnWW74GjxZAgAAEIQAACEIAABCCwswAC6J1NDth3KgNf1YXDlaXQrkihy5dtZD+dr/9Ztvm6XPvCXP7PRFuJ7EAsV7W7SyAXsxKrGsoYmijMZrNEpJo+F02RTXe6IIDuBIIvIQABCHSjgEqOXNfdvHnzKaecEoVKiURi0KBBb7zxBhEFflAoFCoD6G4cMA4NAQh0o4DneZxzwzCiFhzf+ta3unE8ODQEIAABCEAAAhCAAAT2VQAB9L6K7f/t1UqAqgha7IWLhQHzFLxj5R9r++SeTRte496HRCUiV/xwLy688+12t9hgFIXvxU5xEwhAAAIQOHgCpmmefvrplS2hhwwZ8thjj0UjCHb/7pboNtiAAASqWIBz7jhOOp2OHij+9V/+Fe9mq+IzjqlBAAIQgAAEIACB6hNAAN2d51SsDUhkErUTtcno2SIqEtkksuk9XxBA79kIt4AABCDQowVUR44JEybE43EVMBmG6PU/a9Ysy7I8z3McJ/ADxNA9+ixicBDoYoEXXnhBvVVCFUFfffXVYbhXTxW7eFzYPQQgAAEIQAACEIAABPZKAAH0XjF19Y3yRBkiS7SHFte9/S/FXgfQXT1+7B8CEIAABPZDwJIXdcdZs2ZFvTgMw0gkEmPGjCEi13WJCGHTfvDiLhCoDgHXdV955RXVgkO9QLVs2TL0gK6Ok4tZQAACEIAABCAAgT4igAC6u090SBSQH5IrO3KI0ewUK+92iDvdcnctOHa7B/wAAhCAAAS6SWDnd9Dffffduq7HYrF4PM4YMwzjX//lX3O5HJKmbjpFOCwEeoQA53zhwoXqBSr14PDKK6+ol6Z6xPgwCAhAAAIQgAAEIAABCOxJAAH0noS6+OdiPcKwo/LZF2G0+HJvS6C7eHDYPQQgAAEIHBQBVeDsOM4jDz8ydOjQRCIRNXv94he/uHLlSjUKz/PQi+OgnBAcBAI9SMB13fnz5zPGVP+NRCLR1tbWg8aHoUAAAhCAAAQgAAEIQGBPAgig9yTUlT+X1c+y5NmVKw+q7hth56UFu3II2DcEIAABCHS/QFTj7DjOX/7yl9raWl3XVcFjXV3doEGDPvzww+4fJUYAAQh0k8CZZ56pHhBisZimaURk2/bO76LoptHhsBCAAAQgAAEIQAACENiDAALoPQB16Y8DuQKhR7IC2hWFz4GsgVZl0F16aOwcAhCAAAR6jkBli+fAD95+++0vf/nLUUtoxlj//v1//etfE1GhUOg5w8ZIIACBgyAQ+MEZZ5yRTCZj8nL66aerd0IggD4I+DgEBCAAAQhAAAIQgMABEUAAfUAY93MnKoAWy0upxQc5eSSuCKD3ExR3gwAEINA7BTjngR8EfqASJcuyCoXCUUcdVVtbq5pBJxKJT1cmXLhwYRiGSJ1650nGqCGw/wKxWCx6V8SPf/xjx3HwULD/mrgnBCAAAQhAAAIQgMBBF0AAfdDJKw6oWnCIhs+83PdZ9X9GC+gKJGxCAAIQ6BMCKk7i8qIm7LruJZdcommarutq5bFEInHaaacVi8U+IYJJQgACUoBzHovFGGOqO/ysWbMcxxFPHjmHEAQgAAEIQAACEIAABHqFAALoXnGaMEgIQAACEKhyARU9V35UDTcuvvhiFTzpuq7ipxEjRmzevFlxIIyu8l8LTA8CROvXr2eM6bo+cOBAxtg999yDFhz4vYAABCAAAQhAAAIQ6F0CCKB71/nCaCEAAQhAoDoFKqPnaFtN9dprr02lUpqmJRIJtQTZ4MGD33nnneqEwKwgAIEdBV5++WX1HgjGWCwWe/HFF9XPUQG9oxO+ggAEIAABCEAAAhDouQIIoHvuucHIIAABCECg7whEoXPlhpq+67qLFy/WNE0tS2gYBmNs4MCBDzzwABKovvMbgpn2WYF77rlHteDQdV3TtA8++EBR4M+/z/5KYOIQgAAEIAABCECg1wkggO51pwwDhgAEIACBviiwbNky1YKDMRaPxzV5WbJkieu6KrPGomR98dcCc+4DAjfccINqwZFKpRhjYYi1QvrAWccUIQABCEAAAhCAQHUJIICurvOJ2UAAAhCAQJUKBH6wbt26wYMHM8ZUDqVi6AsuuMDzPPSErdLTjmlBgFQjeE3T4vH4qFGjIAIBCEAAAhCAAAQgAIFeJ4AAutedMgwYAhCAAAT6rsB77713/PHHq14cqiFsLBY77bTTLMtSKHhXft/95cDMq1Rg1KhRjDFN02Kx2Omnn65m6XlelU4X04IABCAAAQhAAAIQqEIBBNBVeFIxJQhAAAIQqD4BzrnruoEf1NfXn3jiiaoOOpFIqLawJ5988rp162zbJiJk0NV39jGjvizwpS99Sb3a9OnHuXPn9mUKzB0CEIAABCAAAQhAoJcKIIDupScOw4YABCAAgb4oEIah6rYxevToRCKhaVoymWSMJZPJIUOGrFmzpi+iYM4QqGqB6B0Pn64+evvtt6tXmPA6U1Wfc0wOAhCAAAQgAAEIVJsAAuhqO6OYDwQgAAEI9AUB13VHjx6t0mfG2IABA5Lycu+999q2rULqvuCAOUKgugVyuVxlAP3CCy9wzrEOYXWfdMwOAhCAAAQgAAEIVJ8AAujqO6eYEQQgAAEIVLmAypdVBs0Y03VdRVS6rsdisenTp1f5/DE9CFS7QNTiedWqVZUBdC6XIyLXdasdAPODAAQgAAEIQAACEKgqAQTQVXU6MRkIQAACEOgLAlEjDiJasmSJyqdSqVT//v0ZY/F4/Ic//GFfcMAcIVCtAqqfOxE98cQTlQG0Cqajn1br9DEvCEAAAhCAAAQgAIEqE0AAXWUnFNOBAAQgAIE+J7Bs2bLBgwczxhKJBGPMMIxEIjF8+PCPP/6YiPBu/T73C4EJV5HAwoULo1eYhg0bxuWliuaHqUAAAhCAAAQgAAEI9AkBBNB94jRjkhCAAAQgUK0CqiJy9erVhx12WDqdjsViUb3kkCFD1q5dW60Tx7wgUMUC0RqDV1xxhWEYuryceuqpYRhGP6ri6WNqEIAABCAAAQhAAAJVJoAAuspOKKYDAQhAAAJ9TsCyLNu2N2zYcOyxxzLGogy6rq5uwIABzzzzjOob2+dcMGEI9FqBqMvzmWeeqV5SSqfT06ZNq3xDA5LoXnt6MXAIQAACEIAABCDQ5wQQQPe5U44JQwACEIBAVQpwzrPZ7IgRI1Qvjtra2qgdx9KlS5FBV+VJx6SqVSDq8vz1r389mUxqmqbr+o033ojQuVrPOOYFAQhAAAIQgAAEqlsAAXR1n1/MDgIQgAAE+pCAaZphGH7rW99SzaAZY+l0WsXQY8eOjSA8zzNNU/XuiL6JDQhAoOcIuPLieZ6maWplUU3Tnn766Z4zQowEAhCAAAQgAAEIQAACey+AAHrvrXBLCEAAAhCAQI8WUKGV67oXXXRR9LZ9VRAdj8eHDx/e2toa+EEYhupjj54MBgcBCBAxxjRNUy8prV+/HiQQgAAEIAABCEAAAhDojQIIoHvjWcOYIQABCEAAAp8l4Lru3Llzo2bQqoIykUj079//448/JqLKTrKftSP8DAIQ6A4B9QaFF154QdM0wzBUAB01hu6OEeGYEIAABCAAAQhAAAIQ2H8BBND7b4d7QgACEIAABHqaAOfcsiw1qsWLF6s6aFVEqUqhhwwZsnz5ciIK/KCnDR7jgQAEKgXeeOMNtayorutf/OIX0TanEgfbEIAABCAAAQhAAAK9SAABdC86WRgqBCAAAQhAYA8C0RplauOBBx6Ix+OqjaymaaomOp1O//KXv6wMoKPMeg97x48hAIGDIhCGoW3b0fsYdF0fNWrUQTkyDgIBCEAAAhCAAAQgAIEDL4AA+sCbYo8QgAAEIACBgykQhc6dDso5D/xg3bp1hx56KGMsmUzG43FVEx2Px88//3x1e8/zisVip/viSwhAoBsF1B/vxIkTNU2Lx+OJROL666+vfNGoG8eGQ0MAAhCAAAQgAAEIQGBfBRBA76sYbg8BCEAAAhDoWQK7DKA9z7NtW7V7fvfdd6P0uba2VhVEM8bOP/981RK6Z80Ho4EABKTAD3/4w6iT+w033AAVCEAAAhCAAAQgAAEI9FIBBNC99MRh2BCAAAQgAIGywC4DaM55GIbqo+M4uVzu+OOP13U96gqdTqcNwxg+fHhzc/Mu9wBfCECgewVGjRqlWrczxl566SX0gO7e04GjQwACEIAABCAAAQjstwAC6P2mwx0hAAEIQAACPVeAV1zUKHO53FlnncUYS6fTqheHpmmJRKKuru6FF16I2kC7rttzZ4WRQaAvCQwcOFC9YpRKpZ5//vnADyr+rHlfksBcIQABCEAAAhCAAAR6twAC6N59/jB6CEAAAhCAwC4FKoMq1YvDsqxcLnf55ZdHb+pnjKl2HP3797/33nt3uR98EwIQOPgCgR+YpskYU68V1dbWVv5Fq+2DPyocEQIQgAAEIAABCEAAAvsngAB6/9xwLwhAAAIQgECPFqiMqyoH+mk7jquuuipqxNG/f39VB80YmzVrVrFYRAV0JRe2IdAtAoEfvP3221H/jUQi4bpu5R812uZ0y3nBQSEAAQhAAAIQgAAE9k8AAfT+ueFeEIAABCAAgR4tsHNWpeqg1aCXLFmSSqWi1Qh1XR8wYABj7NJLL+00K+RcnUDwJQQOjsCDDz5oGIau67FY7Kyzzgr8AC04Do48jgIBCEAAAhCAAAQgcMAFEEAfcFLsEAIQgAAEINBzBVQMHfjBsmXLBg4cmEgkDMNgjKm+HLquH3fccY7jhGFIRCrw6rmTwcggUL0Cs2fPVn+YmqaNHj3asqzAD8KKS+WLTNXLgJlBAAIQgAAEIAABCFSDAALoajiLmAMEIAABCEBg7wVUUXPgB++///6RRx6p6qBTqZTqyxGLxY4++uiNGzeqHaICeu9hcUsIHECB0aNHqwBa1/UZM2a4rut5XkX+HCKAPoDa2BUEIAABCEAAAhCAQJcKIIDuUl7sHAIQgAAEINDjBBzHica0evXq/v37M8Z0XVel0GplwkGDBr300ksq7YpujA0IQOCgCQwbNky9L8EwjKVLl3LOPc+rDJ0rtw/aqHAgCEAAAhCAAAQgAAEI7IcAAuj9QMNdIAABCEAAAr1VwLIsVdRs27bneURUX19/4oknplKpgQMHqjromLwwxu65554wFIWW0Wwrt6NvYgMCEDjgAnV1dbquM8bi8fhzzz1HRAigDzgydggBCEAAAhCAAAQgcHAEEEAfHGccBQIQgAAEIND9AqpkMnoXv1rWTH0cPnw4YyydTqt3/asMOhaLXXzxxU1NTWropmkGftD908AIIFDtAi0tLdEaoYyxYrGoerJX+7wxPwhAAAIQgAAEIACB6hRAAF2d5xWzggAEIAABCOws0CmAjpLoMAybmpomTpyo3vIfpc+xWCyRSJx//vnZbBZrEu7sie9AoIsE3nzzTfXHqGlaXV2d67pEpJYG7aIjYrcQgAAEIAABCEAAAhDoOgEE0F1niz1DAAIQgAAEepbAZwTQjuN4njdx4sROFdCqMfSIESMaGxtV/w3Oeae+HD1rkhgNBHq/wJIlS9SioIZhHH300Sp9xvsPev+JxQwgAAEIQAACEIBAHxVAAN1HTzymDQEIQAACfVDgMwJopWHb9n333RdVQGuapstLPB5Pp9Mvv/yySp9N04z01D6jL7EBAQh8foGZM2eql4ISicSoUaNUA2gE0J8fFnuAAAQgAAEIQAACEOgWAQTQ3cKOg0IAAhCAAAS6R0Dlxbv8GA3oN7/5TTKZ1HW9trbWMAyt41JXV3fffffZtk1EqhrakxdVEI0kOgLEBgT2QyB6h4Ft2yeffLJafpAxNn/+fM65Sp+xCuh+wOIuEIAABCAAAQhAAALdLoAAuttPAQYAAQhAAAIQOHgCu4yeK79JRKZpPvPMM3V1dYlEQvUBYIypFPrTjXnz5hUKBdWU1nVdz/M63f3gTQZHgkCVCnzlK19hjKk/wJkzZzqOo4qgEUBX6QnHtCAAAQhAAAIQgECVCyCArvITjOlBAAIQgAAEKgUqw+LdbauGsy+++OJxxx1XGUAnk0m1MNq4ceMKhUK028r9RN/EBgQgsE8CUbjsOE4ymVQV0PF4fMWKFaoCGr3X98kTN4YABCAAAQhAAAIQ6DkCCKB7zrnASCAAAQhAAAJdLlAZFu9um4hUn422trYTTjghWgyNMabruvpy+PDhUR202k/Ul6PL54ADQKAaBdQfneM47777bvRHl06nly9f7nkeERUKhSikrkYAzAkCEIAABCAAAQhAoGoFEEBX7anFxCAAAQhAAAL7IaDS5LDjUiwWv/GNb0S5s2EYjDFVnnnCCSesWbNGlUtjebT9oMZdIFApEP0RPfHEE3V1dWoRwnQ6jZd2KpWwDQEIQAACEIAABCDQGwUQQPfGs4YxQwACEIAABLpKoFMArVpCX3rppYwxwzDi8XjUlGPAgAGDBg16+umnVVjteV5zc3NXDQv7hUC1C4RhqKZ4yy23aJoWvepT7fPG/CAAAQhAAAIQgAAEql8AAXT1n2PMEAIQgAAEILD3Ap0C6DAM1UqD48ePZ4wNGDAgHo8bhqFpmlqZcMiQIcuWLVNrEu79UXBLCEBgdwIXXniheqtBLBb7p3/6p93dDN+HAAQgAAEIQAACEIBAbxFAAN1bzhTGCQEIQAACEDgYAjsH0Jxzz/Msy1qwYIGqg46KoNWGrusXXHDBwRgcjgGBahfgnI8aNSr6Ezv11FOrfcaYHwQgAAEIQAACEIBA9QsggK7+c4wZQgACEIAABPZJQGXQOyfRRLRkyZJYxyWVSjHGhg4dqtoFjBo1Kp/PExGqofdJGzeGQCeBytU+b7zxxk4/xZcQgAAEIAABCEAAAhDodQIIoHvdKcOAIQABCEAAAl0r8BkBNBGtX79+yJAhlRmZqtaMxWJ/93d/t379+jAMOeddO0TsHQLVKOC6bi6Xi/6gGGOzZs2qxoliThCAAAQgAAEIQAACfUsAAXTfOt+YLQQgAAEIQGCPAp8RQKvq5jVr1owYMUJl0KoOmjFWW1urCqLXr1+/x0PgBhCAwM4CgR+sWLEi6r+h6/prr722883wHQhAAAIQgAAEIAABCPQuAQTQvet8YbQQgAAEIACBLhfYXQAd+AEReZ5HRPX19SqD1jQtkUh06g29ePHiLh8lDgCB6hJQf1l33nlnLBZjjKmPzz77bHXNErOBAAQgAAEIQAACEOiLAgig++JZx5whAAEIQAACeylQGUZXbhORaZonnHBCFJYNHjyYMaZpGmMsmUzOmDHDdV2VWVuWtZeHw80g0JcFLMu69tpr1cs5dXV16XTatu2+DIK5QwACEIAABCAAAQhUhwAC6Oo4j5gFBCAAAQhAoEsEKkPnym11sGw2e+GFF6rmGyqJjtrXJpPJCy+80JIXx3G6ZHDYKQSqSED1tzn77LMNw4i6cGBJzyo6w5gKBCAAAQhAAAIQ6LsCCKD77rnHzCEAAQhAAAJ7FKgMnTttE5FlWaZpjhs3jjE2cODAuro6FUZH8dnJJ59cKBSKxeIeD4QbQKCPC6jXaY488shEImEYhq7r3/3ud/HugT7+W4HpQwACEIAABCAAgeoQQABdHecRs4AABCAAAQh0iUCn0Dn6kohUe43ADwqFwu23367WIdQ0TWXQuq6rGHrgwIHvvPNOlwwOO4VAFQkEfhD4QTKZ1DRNFUGfccYZVTQ/TAUCEIAABCAAAQhAoO8KIIDuu+ceM4cABCAAAQgcKAHP837xi1/U1dVVNuKI6qA1TXvyySeJiHOuYusDdVzsBwJVIxCG4fr162OxmGqkruv6/Pnz1cqEVTNHTAQCEIAABCAAAQhAoG8KIIDum+cds4YABCAAAQgceIGXXnpp0KBBUSl0FECrjVtuueXAHxJ7hEAVCTz11FOapkWv4syaNauKJoepQAACEIAABCAAAQj0XQEE0H333GPmEIAABCAAgQMiEIZhsVgMw9DzvA0bNtTJS6f0+f9n786jpCrvff8/e293Telu4NCgizhcY/QHEi6CXhVZgnpNYtYxMTFRWSoQxqOgcQyixDFi9BiHZaI5DngQ4QSna9RcjXoSlRsUbhBc7cAxUa8CytBNd1dV17B37b2/P6se2JbNIEPT3VX13qtXs7uGvZ/n9VT/8+kv30cpFY1GL7vsMl0H3SX35SIIVJnA3LlzdfMNHUO//vrrVTZBpoMAAggggAACCCBQmwIE0LW57swaAQQQQACBLhPwfb+8sUYymfzWt74VVnGWJ9GxWOyoo47qshtzIQSqS2Dq1KnRaDT8lXnllVeqa37MBgEEEEAAAQQQQKBGBQiga3ThmTYCCCCAAAL7SMD3/ZaWlsGDB+sM2igdYaamlBo+fPibb74Z3j2fz4fnnCBQswK+7x999NGRSET/spimKSKO44Q7fwZBULM4TBwBBBBAAAEEEECgogUIoCt6+Rg8AggggAACvU7AK3hewWtpaTnzR2eG5ZydCqL79Onzpz/9SQ89lUr1ujkwIAS6XcB13T59+ti2Hf7NRkRc1yWA7val4IYIIIAAAggggAACXSxAAN3FoFwOAQQQQACBGhdoa2vzCp5uCX3OOecopWKxmG3b4e5qlmUppeLx+KJFi3TElkqlqIOu8Y8N0//kk0907bNuA/29731PmxBA89lAAAEEEEAAAQQQqHQBAuhKX0HGjwACCCCAQC8V0B0DHnjgAcuyIpGIXTpM01RK2bYdiUQMw7j00kt76egZFgLdK/DKK68kEgmllGmalmWdeOKJrut6BY8AunvXgbshgAACCCCAAAIIdL0AAXTXm3JFBBBAAAEEEBARXdTsuu7ixYvLSzuVUrrJgGEYpmlOnjy5paWlXMxxnPIfOUegFgRuvfVW/Wui/4vAjBkz9C8CAXQtrD5zRAABBBBAAAEEqluAALq615fZIYAAAggg0GMCYY7suu5LL70Ui8V0vhamz4ZhRKNR27aPOeaYDz/8UESCIPB9v8dGzI0R6DmBCy64IPw7jWEYt9xyi/5dIIDuuTXhzggggAACCCCAAAJdI0AA3TWOXAUBBBBAAAEEOgn4vq+7cIhIJpN56623dAZdHkDrxE0pNXDgwKampk5X4EcEakdg1KhR+tchFouZpvnkk0/qP8kQQNfOZ4CZIoAAAggggAAC1SpAAF2tK8u8EEAAAQQQ6GEBXc7suq4uhXZdd8WKFQceeKAOoHWjW9M0dTNonUE/8sgjuVyuh8fN7RHoRoGw5P+AAw7Q3Wni8bhlWcuWLSOA7sZ14FYIIIAAAggggAAC+1CAAHof4nJpBBBAAAEEalxAF0EHQeAVPH2eTCaHDh0aiUTq6+t13BYWQesf58yZEzbi0Duw1bgh069uAd/39W9H+S+CUipsjE4FdHV/AJgdAggggAACCCBQCwIE0LWwyswRAQQQQACBnhEoz87CoG39+vWjR49WSkUikU6hm2VZkUhk6tSpruuKiFfwembc3BWBbhHQn/BsNvvnP/+5/HchGo3qpxzHKf8l6pZBcRMEEEAAAQQQQAABBLpYgAC6i0G5HAIIIIAAAghsKxCGaLrhQGtr66RJk8oTt/DcsizDMI499thkMtnW1qaT6G0vyCMIVIeAV/C8gvfSSy+FvwJKqUMPPVTPLpvNhr87YUf16pg4s0AAAQQQQAABBBCoHQEC6NpZa2aKAAIIIIBAjwl0CtF0DH3uueeWh25KqYaGBsMw9IODBw/+6KOPemzE3BiB7hLIZDLXXHNN+e/CmDFjvIKXTCbLf3EIoLtrQbgPAggggAACCCCAQBcLEEB3MSiXQwABBBBAAIFdF7j33nt17mbbdiwWs23bNM0wiRs4cODSpUv11VzXJYDbdVheWSkCmUwmn89PmzYt/NgrpSZOnKjHn8vlyjPoSpkU40QAAQQQQAABBBBAoFyAALpcg3MEEEAAAQQQ6G6BhQsX6ugtjJ7DE8uy6uvrH330Udd10+l0d4+M+yGwjwXCv6mccMIJ5QH0nDlz9J31313CDHofD4fLI4AAAggggAACCCCwTwQIoPcJKxdFAAEEEEAAgV0R0LHySy+91NDQoAM4wzB0AG2aZtiOY+LEibprx65ck9cgUHECdXV15QH0o48+GmbTYfocPlJxs2PACCCAAAIIIIAWvAu2AAAgAElEQVQAAjUuQABd4x8Apo8AAggggEDPC7iuu3z58m9961tKKcuy4vF4eRhnWZZpmj/84Q+z2WzPj5URINClAvl8Pp1Ol3/glVKvvPJKGDcTQHepNxdDAAEEEEAAAQQQ6AEBAugeQOeWCCCAAAIIILCtwOrVq48//nhdAR2JRMojOcMwIpHI17/+9Y0bN+pgLpfLbXsFHkGg4gTy+fzy5cuVUvozn0gkYrFY+fabBNAVt6YMGAEEEEAAAQQQQKCTAAF0JxB+RAABBBBAAIEeE8jlct/+9reVUqZpdsqglVKGYey///4ffPCBHl9YItpjw+XGCOy1gOu6ixcvDrvN6P4zbW1t4YUJoEMKThBAAAEEEEAAAQQqVIAAukIXjmEjgAACCCBQhQKu6+ZyuTN/dGZjY2OYQYd7EiqldKvcBQsWiIhX8KqQgCnVkkAQBL7vX3311ZZlhd3PE4lEaFCePvMXl5CFEwQQQAABBBBAAIHKEiCArqz1YrQIIIAAAghUuUA2m02lUlOnTg0z6FgsZtu2jqFt21ZKxePxOXPmiAiRXJV/Gqp9er7vB0Ewbtw427ZjsZgu8x89enQ4bwLokIITBBBAAAEEEEAAgcoVIICu3LVj5AgggAACCFSPgA7a/K1HNpt98MEHlVKJREJHz6ZpxuPxWCwWFkRPnDjR9/18Pu+WDq/gkUdXzweiZmbS1tZ26qmnhh3PI5HIj3/843D2BNAhBScIIIAAAggggAAClStAAF25a8fIEUAAAQQQqB6BTgG0npjOoC3LMk3TKh1hTqdPjjzyyPJuudREV88HojZmov9kEo1Gww92IpHQ1f36w0wAXRsfBGaJAAIIIIAAAghUuQABdJUvMNNDAAEEEECgIgQ6BdC+74uI4zjLli0L226EIV35yWGHHbZy5cpwjjSGDik4qQiBdevW6aL+WCym20DffffdeuSd0mcK/CtiQRkkAggggAACCCCAwLYCBNDbmvAIAggggAACCHS3QKcAWkR0Bi0ir7/++nHHHVceOnc6b2xsfP311/WIXdcNhx5eIXyEEwR6lUAQBK+++mp5BXQkEnnxxRe3W/5MAN2r1o7BIIAAAggggAACCOy6AAH0rlvxSgQQQAABBBDYhwI6g972Brlczvf9I488UikVjUYNw9A10XrHNqN0KKXuvffeTu+lGroTCD/2QoG7775bbz9oWVY0GjVNc9WqVQTQvXClGBICCCCAAAIIIIDAHgsQQO8xHW9EAAEEEEAAga4U2FEA7ThOEASbNm0aOnSoDp2VUrZt6+hZf7csSyl13nnnlVeJlldDd+VAuRYCXSdw5ZVX6j+o6G02o9HojtLn8s92192fKyGAAAIIIIAAAgggsM8FCKD3OTE3QAABBBBAAIFdEdhRAK3fGwSB7/vnn3++UkpXjJYH0Eopy7JisdjZZ5+dTqf1Wwigd4Wd1/SswPe//33dUsYwDF3jn8lk9O/Ctt97dqjcHQEEEEAAAQQQQACBPRMggN4zN96FAAIIIIAAAl0ssPMA2nGcXC6XTCYvv/zyTgG0LovWNdG2bR911FHr16/3Cl4+n+/iIXI5BLpaYMSIEeU9zUePHk0FdFcbcz0EEEAAAQQQQACBHhYggO7hBeD2CCCAAAIIILDrAnpfwfnz5yul+vTpEyZ35dXQpmlGIpGmpqbwsslkMjznBIFeJRB+hvWJDqB71QgZDAIIIIAAAggggAACeylAAL2XgLwdAQQQQAABBLpPIJfLiUgul3viiSeUUn379lVKmaZZHkDrHh39+vWbN2+ebtwRNuXovoFyJwR2QWDdunU6d9b9N2zbnjNnDr2ed0GOlyCAAAIIIIAAAghUkgABdCWtFmNFAAEEEEAAgbCz84svvtjQ0BDmdzqD1j+apcO27WuuucZ1XV03DR0CvU3ghRde0J9YvYumUuq6667rbYNkPAgggAACCCCAAAII7KUAAfReAvJ2BBBAAAEEEOgmgSAIwvRZV4m+9957jY2Nugd0WASt0+e6ujrdFXr69OmUlHbTCnGb3RS49957OwXQr7zyym5eg5cjgAACCCCAAAIIINDbBQige/sKMT4EEEAAAQQQ2K6A7/uO4zQ3Nx999NE6xVNK2bYdniulIpGIUurggw9ua2vzCp6IZLPZ7V6NBxHofoGZM2fqj6tpmrZtW5a1dOnS7h8Gd0QAAQQQQAABBBBAYJ8KEEDvU14ujgACCCCAAAL7UMD3/SAImpubTz/9dB3kRaPR8gBaF0crpUaOHPn2228HQZDP5/fhgLg0Arsj8L3vfU93f7YsyzAM27Z35928FgEEEEAAAQQQQACByhAggK6MdWKUCCCAAAIIILCtQCqVCoLAcRwROe+88+rr67cNoE3T1JH0QQcd1NTUtO1FeASBnhI48MAD9YdTl+p/3gOadjE9tRbcFwEEEEAAAQQQQGDfCRBA7ztbrowAAggggAAC3SGg9xh0XTdsaBAWQcfj8fBcd+dYsGBBd4yJeyCwY4EwZQ4/nPoPJ6NHj/ZLx47fyjMIIIAAAggggAACCFSeAAF05a0ZI0YAAQQQQACBTgJ6c8LW1ta77rqroaHBtu1YLKaUisfjsVgsLIK2LKuhoeGKK64IgsD3fdd1dXjd6Wr8iMA+FdAf1/fffz8MoJVS0Wj0xBNPFJFwp819OgYujgACCCCAAAIIIIBAtwkQQHcbNTdCAAEEEEAAgX0lEObIra2tjz766IABA3TorBvsKqXCXgfRaNQ0zXHjxm3YsEFEwjfuq5FxXQS2EXBdNwiCP/3pT+UBtGEY11577Tav5QEEEEAAAQQQQAABBCpegAC64peQCSCAAAIIIIBAJ4GXX345bKqrlLIs66CDDgozaL0z4eDBgzdt2iQiYT+EThfhRwT2kYBX8Hzfv+2228oD6Gg0ev311zuO4xW8fXRfLosAAggggAACCCCAQI8IEED3CDs3RQABBBBAAIGuF/B93yt4QelYsWLFEUccYRiGbsdh23ZdXd3gwYMTiYQOoHU7jlWrVhFAd/1KcMWdCugP6oUXXlgeQBuG8corr/Bp3KkcTyKAAAIIIIAAAghUpAABdEUuG4NGAAEEEEAAgR0J6AA6CIJkMnnMMcfojK+urk4pVVdXN3DgwPKW0H379n3qqaf0W/L5/I6uyeMIdLnAmDFjygNopdRf/vIXekB3uTMXRAABBBBAAAEEEOhxAQLoHl8CBoAAAggggAACXS+gM+VcLnfssceGibNSqrGxceTIkbovh1LKtu1IJHLrrbfqvgfUn3b9SnDFLwukUqlcLiciAwYMML58tLe3f/m1/IQAAggggAACCCCAQDUIEEBXwyoyBwQQQAABBBDYicC5555rmmY0GjUMwzTNgQMHTpkyxTCMeDxu27auQj3vvPNEhPa7O2HkqS4UyOVydXV1ZtmhlEqn0114Cy6FAAIIIIAAAggggEAvESCA7iULwTAQQAABBBBAYF8JOI5zxx136G0Jbdu2LEsp9cMf/rBfv35KKf09FouddNJJum56X42D6yIg4vu+iCxdurQsfC6ejh49WvPQCoaPCQIIIIAAAggggECVCRBAV9mCMh0EEEAAAQQQ2L7Ab37zG13srAPoSCQybty4b37zm0qpeDyunxoyZMiyZcvCBDCbzW7/WjyKwJ4KBEHg+/5TTz2l6/HDGPq0007THWBc193Ta/M+BBBAAAEEEEAAAQR6owABdG9cFcaEAAIIIIAAAl0u4Lru7373u/r6ep0169D5jDPOGDZsmC6ONgzDtu39999/+fLl+u60hO7yVeCCvu8HQXDHHXeE0bM+ueyyyzROMplECQEEEEAAAQQQQACBahIggK6m1WQuCCCAAAIIILBDgSAI8vl8U1NTIpGoq6vT+xCapnnOOedceOGFOpXW323bXrBggYhks9kgCKiD3qEpT+y+gO4zPmHCBMuyyjPoX/3qV9Q+7z4n70AAAQQQQAABBBCoAAEC6ApYJIaIAAIIIIAAAnsvEKZ777333uGHH26aplJK1z4fe+yxV111lU6f9XaF0Wj0iiuu2Pam1ERva8IjuyWgA+gTTzyxUwD9hz/8gU/XbknyYgQQQAABBBBAAIFKESCArpSVYpwIIIAAAggg0JUCQ4cOVUrZtq1z5yOPPPKSSy5RShmGEVZDT5w4sa2tTd+V/Qm7Ur/mr6WUMk1Tf9gMw0gkEqtXr655FQAQQAABBBBAAAEEqlOAALo615VZIYAAAggggMBOBLLZbHt7++DBg3XWXFdXZxhGY2Pj/fff379//3BPQtM0R40atW7duiAIMplMLpfbyTV5CoFdFFizZk2nP3UopZqbm3fx7bwMAQQQQAABBBBAAIHKEiCArqz1YrQIIIAAAggg0AUCfunwCt6kSZNs2zYMQ/fi6NOnz2233TZixAgdTOvHhw8f/uabb3bBXbkEAiWB5557Lqyy1ye2bWODAAIIIIAAAggggEC1ChBAV+vKMi8EEEAAAQQQ2JmA7/tBEKTT6Ztvvlmnz5ZlKaXq6uruvvvu0047LezFYZpmv379nnjiCRGhS+/OTHlu1wTuuece/ekKP3gjR47ctbfyKgQQQAABBBBAAAEEKk+AALry1owRI4AAAggggMDeC+iezjpQvv/++5VSOoDWJ/fcc8+4ceNisZhulaCfeuSRR8IMOpPJ7P0YuEINCqTT6auvvlrvgRnWQZ988sk1SMGUEUAAAQQQQAABBGpEgAC6RhaaaSKAAAIIIIDAFwJh+hxWND/99NMNDQ1KKR06W5Y1efLkO+64I+zFobcrnDp1qoi4rus4Tj6f933/i4tyhsCuCZx00km69jkMoGfMmLFrb+VVCCCAAAIIIIAAAghUngABdOWtGSNGAAEEEEAAgb0UKA+gdT9oEVm+fHljY6NpmjqDjkQiU6ZMuffeewcNGhQG03379h0zZozrukEQeAUvHEYYZIePcILAjgT69eunP2N1dXW6uP7666/f0Yt5HAEEEEAAAQQQQACBShcggK70FWT8CCCAAAIIILDbAp0C6Gw26xW8IAg++OCDxsbGsC5VKTVs2LAXX3yxX79+OijUhauDBw/+4IMPyu9KKXS5Buc7Ecjn87FYTBfUh11fFi9evJO38BQCCCCAAAIIIIAAAhUtQABd0cvH4BFAAAEEEEBgrwSCINAV0OH3tWvXfvOb36yvr1dK6Wro4cOHf/LJJ0cccYRuD62jw759+7711lth4bPruns1Dt5cMwJLly6NRqM6etadoCORyBtvvFEzAEwUAQQQQAABBBBAoOYECKBrbsmZMAIIIIAAAgiEAtsG0CLS0tLyne98R28/mEgkYrFYJBJZsWLFOeecY5qmYRi6Drpv374PPfSQ7/ufbyvnOE54TU4Q2InALbfcEnZ0iZQOpdTGjRt38haeQgABBBBAAAEEEECgogUIoCt6+Rg8AggggAACCOyVgO7F4fu+TqLz+byI5HI5ERk3blx9fb1hGLpMNRaLLVu27PLLL9cNOqLRqFIqGo3efvvtIhKWQu/VaHhzDQjcfPPNkUjEsiz9EbIsy7bt8n7iNWDAFBFAAAEEEEAAAQRqS4AAurbWm9kigAACCCCAQLlAeQBd/rjuyDFu3DgdN4dVz/fcc89vf/tbXRxt27ZupDBjxozy93KOQCeB8hbhp556qlIqHo/rP2zYtj1kyJBOr+dHBBBAAAEEEEAAAQSqSYAAuppWk7kggAACCCCAwG4LhBsSbved9913X7hTXDwe/zw6vO2229544414PK6bQevG0Mcff3xbW1smkwmCgGrW7UrW8oOu64Y18olEQrdw0U3GlVInn3yyLr2vZSLmjgACCCCAAAIIIFDFAgTQVby4TA0BBBBAAAEEvlpgJwG03lrw5ZdfHjBggK5X1Rn0tGnTVqxYcdRRR+n6aKVUIpE4/PDD33vvva++H6+oPYHwbxKZTCYsnNctXJRSM2fOzGaztafCjBFAAAEEEEAAAQRqRYAAulZWmnkigAACCCCAwHYFdAC93ad839fJ4PLly/v27aszaNM0Lcv6/ve//+67744YMSJWOnQS3a9fv9dee227l+LBWhYIy59ff/11/VGxLCsSiRiG8XkvjptuuqmWcZg7AggggAACCCCAQNULEEBX/RIzQQQQQAABBBDYmcB2A+iwk4bjOLoOevny5QMGDAhLnk3THDlyZHNz8/Tp03UXDqWUbduGYcybN29n9+O5GhZYuHCh/gjZtp1IJCzLMgzjySefDEuka9iGqSOAAAIIIIAAAghUrQABdNUuLRNDAAEEEEAAgT0WCEtW9RXa2tpc1920adPxxx8fZtCRSGT//fdvamq67777dHF0LBbTDaOnTJmyadOmPb47b6wygXATwmuuuUZ/fkzTNEqHbdtLlizp9HmrsukzHQQQQAABBBBAAIEaFyCArvEPANNHAAEEEEAAga8Q8H1fF0HncjnHcY4++milVCQSiUajSqlBgwb97W9/W7x4cV1dnc4Wo9GoZVnnnntuMpn8ikvzdG0IhAH0ueeeq3Nn/V1/YFKpVG0wMEsEEEAAAQQQQACBGhUggK7RhWfaCCCAAAIIILDrAl7BS6fTuVxORFzXPfvss8M6Vqt0zJ8//4033mhsbNSP6zroY489duPGjTq83vV78coqFhg6dGinADqRSFTxfJkaAggggAACCCCAAAIiQgDNxwABBBBAAAEEENglAd0nQVez3nPPPTplVkolEok+ffrMnTvXcZzhw4cbhmFZllk6EonECy+8QAa9S7418KJEIlEeQBuGccIJJ+Tz+RqYOlNEAAEEEEAAAQQQqF0BAujaXXtmjgACCCCAAAJ7IKDjwmw2G24oF1Y9X3DBBW1tbWf+6EyllGmaOqFuaGhYtGhRPp8v7/O73Z0P92AwvKVSBIIgaGpqCv9ooT8zSqkxY8aICJsQVso6Mk4EEEAAAQQQQACBPRAggN4DNN6CAAIIIIAAArUr4DiOnnw2m125cmXY+llni2f+6My2trbLLrtMKWVZVmNjo2VZtm3fc889IqKrp4MgCJsC165jjc08CII//OEPtm2H0bM+mTlzZviJqjESposAAggggAACCCBQKwIE0LWy0swTAQQQQAABBLpEwPf9sJY5n8+vW7fuG9/4RiQSMU1TR4qjR49OpVL3339/PB4vTxuvvPLK8tw5vEiXjIqL9GYBvdY33XST3riy/FNx6623hn+Z6M1TYGwIIIAAAggggAACCOyxAAH0HtPxRgQQQAABBBCoRYEgCLyC57quLlx1Xffdd989+uijE4mEaZqRSER3hX733XeXLl2qe/5GIhHDMOrr64877rh8Pp9KpegKXVMfHf2Hh0mTJsVisfL0WSn1/PPP82GoqQ8Dk0UAAQQQQAABBGpQgAC6BhedKSOAAAIIIIDAXgnoImidROvi1nQ6fdZZZ+nWzzph7Nev37Jly1auXHnwwQeHjyilhgwZsnTp0iAIcrkcpa97tQwV9ebW1taxY8d2Sp8jkcirr76aSqV0T/Dwe0XNjMEigAACCCCAAAIIIPAVAgTQXwHE0wgggAACCCCAQCeBMCjU3Zy9gqdj6B/+8IdhwhiNRvv27fvss896BW/kyJENDQ36KdM06+vrly5dSt1rJ9Uq/lHvMWhZVtinJfycNDc3p9Np13XLP1RVTMHUEEAAAQQQQAABBGpQgAC6BhedKSOAAAIIIIDAXgmUZ4X6XPdY8Areb37zG6VUpHQYpeO+++4TkUmTJunMMRaL6X0LH3jggSAI0un0Xg2FN1eIwNq1a8PQOTyJRqMi4rqu/htG+LmqkDkxTAQQQAABBBBAAAEEdkmAAHqXmHgRAggggAACCCAQCoRBYfmJftb3/aefflopFS0dffr0UUrNmDEjCIIbbrihvr4+DB/79OlzxRVXhNfkpIoFfN9/5ZVXrNIRfgCUUgcddFA4620/S+FTnCCAAAIIIIAAAgggUNECBNAVvXwMHgEEEEAAAQR6o8AzzzzT2NiYSCSUUrre+dxzz/3000/nz58fj8ej0WhYJT1lypRNmzY5jqObeGQyGYLI3riiezemIAjuuOOO8uhZn3/729/WncRFhHXfO2PejQACCCCAAAIIINB7BQige+/aMDIEEEAAAQQQqFCBXC7X1NQUj8d1z1/TNG3bHjlyZCqV+uCDDw444IAwizQM47jjjmttbXUcR7fjIIis0EXf+bAvuuiicNHDk3Hjxuk24gTQO9fjWQQQQAABBBBAAIGKFiCArujlY/AIIIAAAggg0BsFMplMNpv96KOPRo8erZTSu8+ZpjlixIimpqZ169YdeeSRSqlYLGZZViQSicfjq1atEhHf9wmge+OK7vWYxowZE+bO4cmsWbN092d6QO81MBdAAAEEEEAAAQQQ6L0CBNC9d20YGQIIIIAAAghUukBbW9uJJ54YjUYty9KJc//+/d98881UKvW9733PMAyllO4Tfeihhz799NME0JW+4jsa/4EHHhjmzuHJbbfdpv/e4Louf3jYER2PI4AAAggggAACCFS6AAF0pa8g40cAAQQQQACB3i5w/vnnG4ahM2il1MCBA59++ukgCCZPnmzbdiwWCxPJxx9/XBfD9vYpMb7dEUgmk+ESl5+88cYb+jJUQO8OJ69FAAEEEEAAAQQQqDABAugKWzCGiwACCCCAAAKVJZDNZj/vrXHttdfqemcdQxuGMW/ePBF5+OGHdWW0bds6mpw2bZqIeAXPK3iVNVNGuyOBVatWKaX0B6A8gF6yZIleZSqgd0TH4wgggAACCCCAAAJVIEAAXQWLyBQQQAABBBBAoAIE5s2bp/tB6wzaNM0bb7yxra3tscceGzBggGVZOoOOx+Mnn3wy6XMFrOguD3HBggVhK/DyAPrjjz92XVf/vYEWHLvMyQsRQAABBBBAAAEEKkyAALrCFozhIoAAAggggEBlCZRHyc8++2z//v3DCNK27bPPPru5ufmdd94ZMGBAPB4Pnxo1atRHH31UWTNltDsSuPHGG5VStm2HbVh0NXSn14cZdKfH+REBBBBAAAEEEEAAgYoWIICu6OVj8AgggAACCCBQAQI6WPy8EYfv+++9915jY6Nt27ordDQaHTVqlFfwWltbjzvuOKVUNBrV7RoOPvjg119/vQKmxxC3JxAEgYgEQZDJZMaOHasDaNM09d8YTNM89NBDy98Xps/6jeVPcY4AAggggAACCCCAQEULEEBX9PIxeAQQQAABBBCoGAEdLKbT6VWrVg0dOtSyLJ01K6WGDBny6aeftre3T548ub6+XmeUtm0fdNBBDz30UMXMkIHuQOCQQw4xTdOyLKN0KKVM0zzxxBPLX04AXa7BOQIIIIAAAggggEA1CRBAV9NqMhcEEEAAAQQQqACBIAhaW1tPOumksOGGbduNjY1vvPGGiFx66aXh4/rkxhtvzOVyFTAxhlgmEBYy53K5sPzZMIxIJKIr3KdOnRq+vDx9Dt8YPssJAggggAACCCCAAAIVLUAAXdHLx+ARQAABBBBAoJIEfN/Xw9Uh44QJE3TPDV0KnUgkXn311SAIFixYYJqmbdu6K3QkEpk2bRq5ZCWttEgmkxGRXC63bNmy8vLnsNP3DTfcEM6IADqk4AQBBBBAAAEEEECg+gQIoKtvTZkRAggggAACCPRSgU4hchAEl112mS6JNU2zvr7eMIzHHnvMK3h/+ctfjjjiiLBg1rbtESNGbNy40St4nS7SS6da88PSmbKIPPnkk+bWQ+89qAvb77jjjhCJADqk4AQBBBBAAAEEEECg+gQIoKtvTZkRAggggAACCFSGgOu6IvLQQw8ppSzL0t8/z6N1beySJUuGDh2qtytUSjU0NBx11FGrVq2qjLkxyq0Ct99++9b82TQMQ+9DaFmW7riiNyokgN6qxb8IIIAAAggggAACVShAAF2Fi8qUEEAAAQQQQKD3C/i+n8/npdSr4eGHHx4wYIDeoU6Hleedd146nW5paRk6dKhpmrFYTDfrsG37nXfe0e0dev8cGaGIjB8/PgygdfqsK6CXLFmifTqlz1S487FBAAEEEEAAAQQQqDIBAugqW1CmgwACCCCAAAKVIaDLn3VX6Fwu949//KO+vj4SiRiGoVtCjxw5csOGDblc7vzzz9eRpa6SVkotXrx42wya4LJ3Lvzo0aP1nxb0d/23BKWUXq9t02fWsXeuI6NCAAEEEEAAAQQQ2GMBAug9puONCCCAAAIIIIBA1wjoGHrZsmVDhw41DMOyLF0q+61vfeuDDz7I5/O//e1vO2XQs2fPDpPKIAjS6XT4Y9eMiat0kUB5+lzeA3q70bN+sIvuzGUQQAABBBBAAAEEEOgVAgTQvWIZGAQCCCCAAAIIICAizc3Np556qo4pdQY9cODAFStWuK47f/78aDSqNypUStm2PWvWrGQyqcNr13UJoHvhR+iTTz4pb7uhlNKLO3jwYMdxdpRB98KJMCQEEEAAAQQQQAABBPZYgAB6j+l4IwIIIIAAAggg0AUCfukQEa/g6VrmKVOmNDQ01NXV6arnvn37Pvfcc/l8fuXKlbZtx2Ixy7J0Xe1RRx3V3Ny8bTuOLhgWl+gKgeeee862bb2O4fdoNDpmzJjtbj9IBXRXqHMNBBBAAAEEEEAAgd4lQADdu9aD0SCAAAIIIIBAbQq0tLToifu+n06nr776ap1Xhk0bFi5cmM1mP/zww2HDhuk+wvqpww8/fOXKlZ3QqIbuBNJTP95zzz1h5+4wgFZKTZ8+fUflz6xdTy0W90UAAQQQQAABBBDYRwIE0PsIlssigAACCCCAAAK7IRDGkeHmhPPmzQu7N9i2HYlErrjiCtd1m5ubv/vd74ZpZiQSaWxsXLJkSXgzEsyQomdPfN+fOnVquFLhXxRs277++utzuZwuftffww8Ay9ezq8bdEW409z8AACAASURBVEAAAQQQQAABBLpcgAC6y0m5IAIIIIAAAgggsHsC5eGjPheRXC737LPPRiIRpZROohsaGiZMmJDL5byCN3HiRF0BbVlWNBqNxWK//4/f67s6jrN7t+fV+0bA9/1TTjklzJ2j0aheStM07733XsdxCKD3DTxXRQABBBBAAAEEEOhdAgTQvWs9GA0CCCCAAAII1KBAeQCtp6+3FhSRpqamvn37hpvXKaWOOOKIDRs2iMjcuXPLq2vj8ficOXPy+byuoa5Bxl445cbGRqWUZVm2bR9wwAF690il1HPPPRcEAQF0L1wyhoQAAggggAACCCDQ5QIE0F1OygURQAABBBBAAIHdEygPoL2CJyKZTCaXy+XzeRH56KOPRo0aFWbNlmWNGDHigw8+EJH58+f3LR3hs2eddVYqldq92/PqfSag/3Kgq9QPP/xwpZQuaV++fLmIEEDvM3gujAACCCCAAAIIINCLBAige9FiMBQEEEAAAQQQQMAreDqP9n3fK3iO43gFL5/PH3PMMbZth0Fz//7933jjjfb29rfeeqtPnz4NDQ3hU8OHDw8zaNd1w2JqbLtZ4MUXXwy3i/z617+uz/Uy6ZEQQHfzinA7BBBAAAEEEEAAgR4RIIDuEXZuigACCCCAAAIIbF+gvBpad2lwXVe3dT7zR2fq+DISicTj8Wg0+sgjj4jIhg0bhg4dGgbQkUjENM33339/+zfg0W4RcF130aJF4aIMHz7csiz9Y58+fUSEFhzdsg7cBAEEEEAAAQQQQKDnBQige34NGAECCCCAAAIIIBAKdAqgw2roIAjy+fxFF10UZpq6ufBtt92Wy+U2bNjwgx/8QD+lNyccNGjQY489RkvoELabT3zfnz17drgi//zP/xwu3JFHHum6bljqvu2Kd/NQuR0CCCCAAAIIIIAAAvtUgAB6n/JycQQQQAABBBBAYPcEto0j9SO5XE435Xj++edjsVh5O47Jkyfre1xwwQU65dTPxuPxX//617t3e17ddQKnnXaabo1imuaECRPCAHrs2LHZbNb3/R2tddcNgSshgAACCCCAAAIIINDzAgTQPb8GjAABBBBAAAEEENgVAd/3deXsq6++2qdPH8uy6urqIpFIIpE49dRTs9msV/DmzZunt7nTjTiUUtOnT9cdPEQkPNmV2/GavRFwXffII48M/05wyimn6Mp0y7LOP/98vb1keQC9N/fivQgggAACCCCAAAII9GYBAujevDqMDQEEEEAAAQQQ6CygNxX85JNPBgwYEBbVWpZ15JFHfvzxxyLyzDPP6AzaNM1IJGIYxhlnnNHc3EwA3ZlyX/4cBIFenWg0atv2pZdeappmXV2dbduzZ8/2Cp5uAx1m0PtyLFwbAQQQQAABBBBAAIGeFCCA7kl97o0AAggggAACCOyBQCaTEZHW1tbjjjtO19jqxNkwjLfeektEVqxY0djYGMbTSqkhQ4a0tbXtwb14y54JvP322zpxVkr169fv9NNPj8ViSqlIJPLwww/v2TV5FwIIIIAAAggggAAClShAAF2Jq8aYEUAAAQQQQKCmBXQRtC6h/clPfqJ7O+i42TCMZ5991vf9bDZ7zDHHhBl0LBbr06fP8uXLaxquGyevW3Vr/2HDho0dO9a2bdM0o9HoSy+91I0D4VYIIIAAAggggAACCPSwAAF0Dy8At0cAAQQQQAABBPZGwHXdSy65RCkVjUaVUpZl9evX79577xWRtra2M844w7btaDRqmmY8Hu/fv/8zzzyjb6e7QOzNrXnvTgRuuukmpZSuT7/00kt1+bP+U8H777+/kzfyFAIIIIAAAggggAACVSZAAF1lC8p0EEAAAQQQQKDmBHzfnz9/vg6gw5LniRMnBkEgIpMnTw4fjMVi8Xj89ttv10/VnFQ3TnjixIkh+/XXXx/2SLFtuxtHwa0QQAABBBBAAAEEEOh5AQLonl8DRoAAAggggAACCOyxgOu6XsFzXfeRRx6JRqO6xtayLKXU2LFjddB8//33K6XKO3WMHz9+j+/IG3dF4KSTTtLgkUjk3nvv1eemaSqlHMeh/HxXDHkNAggggAACCCCAQHUIEEBXxzoyCwQQQAABBBCoUYGwH3Qmk1m2bNnBBx8cFt4qpY477ji99+CTTz6ZSCT0hniGYdTV1Z166qk1SrbPph2uhYjU1dUppUzTtCxr4cKFelEsyxozZoy+v95Jcp+NhQsjgAACCCCAAAIIINBbBAige8tKMA4EEEAAAQQQQGDvBXK53LBhw3RLaMuyDMP4+te/vmLFChF58803hwwZEovFdDWuYRiHHnroe++9F940n8+H55zsgYDrurrkfMOGDTp61gvxxz/+Udekx2Kx73znO/rKruvuwS14CwIIIIAAAggggAACFSdAAF1xS8aAEUAAAQQQQACB7QuEmeZZZ52lS251DJpIJBYvXhwEwfr168eOHav3JNTZ6P777//222/ry6XT6e1fl0d3TSBsrPHGG2+EOxAOGTLk6quv1vtDKqUmT56sL0Yb7l1D5VUIIIAAAggggAACFS9AAF3xS8gEEEAAAQQQQACBTgK5XO78888PM1ClVCQSuf/++0Vk48aN48ePt21bJ9S6GnrRokUi4hW8dDpNHXQnzN39MQgC3XRbd3w+55xzrr/++lgspjPoG2+80XXdfD7vOM7uXpnXI4AAAggggAACCCBQiQIE0JW4aowZAQQQQAABBBDYoYBX8HS4+eCDD+rOD/F4XMfNM2fO1PnynDlzzNKhQ+p4PH7FFVfs8Io8sWsCuqjZ9/3Zs2frXR8Nw5g9e/app56qF0IpNW/ePKd0lDeM3rXL8yoEEEAAAQQQQAABBCpSgAC6IpeNQSOAAAIIIIAAAjsX8EvHE088UV9fr7cftG07kUhMmDAhlUo5jnPffffpLhy6Gjoej0+YMGHt2rXlwSgb5e0cudOzugWHV/BGjRplGIZpmtFo9Nlnnw1Lzk3TXLFiheM4XsGjBUcnPX5EAAEEEEAAAQQQqFYBAuhqXVnmhQACCCCAAAIISCqVampqqq+v1xXQ+vuJJ564fv163/fffvvtsDhanxx//PG6kbRuE4HgbgnoTQi9gnfVVVfpnhtKqaamprvuuss0Tdu2jz322DVr1riuW57y79YteDECCCCAAAIIIIAAAhUnQABdcUvGgBFAAAEEEEAAga8QCILA9/0gCPL5vO/72Wz2iCOOCLtAKKUGDx68atUqEfnwww+HDRumO0HH43HDMOrq6t59910RIST9CuVtntbmQRCsWLHi7LPPHjdunN77MZPJNDU1/fWvf/V9n/Lnbdh4AAEEEEAAAQQQQKDKBQigq3yBmR4CCCCAAAII1KyA7giRzWYdx2lpaRk7dmx9fb1pmoZhRKPR+vr65cuXt7e3ewXvu9/9blixq5QaNGjQ448/rsPrmtXbg4kHWw/93ra2NsdxstmsiDiOowN9yp/3AJa3IIAAAggggAACCFS0AAF0RS8fg0cAAQQQQAABBHYo0KnLsOu6Z/7oTKWUaZqJRCIajfbt2/eRRx4REa/gjRs3TjeD1s2LE4nE3XffTRH0DnG/6gldhK47cW/NpTv/+1XX4HkEEEAAAQQQQAABBKpBgAC6GlaROSCAAAIIIIAAAjsS8ApePp8XkUwm47runXfeqYNmvTOhaZpTp07V7128eHGYQUejUaXUpEmTHMfRb3ccZ0e34PFtBQigtzXhEQQQQAABBBBAAIHaFCCArs11Z9YIIIAAAgggULsCjzzyiFLKKB1KKdu2J0yYoPceXLx4cWNjo35WKZVIJE4++eRsNqufrV2y3Z9552rn7f28+1flHQgggAACCCCAAAIIVJ4AAXTlrRkjRgABBBBAAAEE9kBAFzLrKPnll1+Ox+N1dXVq6zFq1Kjm5mbXdV977bUDDzwwzKCVUscff/zKlSv34I61/JbtBc6dH6tlH+aOAAIIIIAAAgggUDsCBNC1s9bMFAEEEEAAAQRqWkDvSRgStLW1jRw5Mh6PK6UikYhS6pBDDlm9erVX8Nra2oYMGbI1mi7+u//++69YsUI3lXZdl3YcIeNOTsK8eSev4SkEEEAAAQQQQAABBKpegAC66peYCSKAAAIIIIAAAtsX8Are4MGDddBsGIZSql+/fkuXLhWRtWvXXnjhhfqpWCym23EsXLhQp9gE0NsH/fKjBNBf9uAnBBBAAAEEEEAAgRoVIICu0YVn2ggggAACCCCAgG7Kcd555+n0OR6PR6NR27YXLVoUBIFX8G644QZdHK2UsixLKXXZZZfpOmj0EEAAAQQQQAABBBBAAIFdESCA3hUlXoMAAggggAACCFShQCqV8n0/nU7fc889ejdCpVTfvn2VUnfccUcul3Nd94EHHlBKmaYZi8UikYht2+PHj0+n01XIwZQQQAABBBBAAAEEEEBgHwgQQO8DVC6JAAIIIIAAAghUmsADDzxgmqbOmm3btizrsssuExHHcd56662BAwcahqFfoJQ65phj2tvbOzWVrrQZM14EEEAAAQQQQAABBBDoDgEC6O5Q5h4IIIAAAggggEDvF3j77bf3339/q3To7s9nnHFGLpcTkXfffXfUqFGJ0qFj6AMPPHDFihW9f1KMEAEEEEAAAQQQQAABBHpWgAC6Z/25OwIIIIAAAggg0CsE8vl8NptdsWKF3pYwGo1GIpFYLDZs2LCPP/5YRDKZzCmnnGLbtlk6lFKxWOyFF15wXbdXTIBBIIAAAggggAACCCCAQK8UIIDulcvCoBBAAAEEEEAAgW4XcF3XK3hr1qwZNmyYTp91HXQikXjnnXccxxGRKVOm6Acty4rH45ZlPfzww51G6vt+p0f4EQEEEEAAAQQQQAABBGpWgAC6ZpeeiSOAAAIIIIAAAtsR8H2/vb193LhxkUhEKWVZllJqwIABTz31lH71Qw89pDNopVQ0GjVN88ILLxQR3RI6m83SG3o7rDyEAAIIIIAAAggggECtChBA1+rKM28EEEAAAQQQQGAHAvl83nXdGTNmhEGzPrn22muDIBCR5557rq6uLnw2FoudcMIJukRav2AHF+ZhBBBAAAEEEEAAAQQQqDkBAuiaW3ImjAACCCCAAAII7FzAdd1MJpPP5x9//PEwZdYnZ599tohks9mlS5cOGjQojKHj8fgxxxzT1NQUlj/7vk8YvXNnnkUAAQQQQAABBBBAoBYECKBrYZWZIwIIIIAAAgggsBsCvu/rHNkreM8880z//v0Nw7AsKxqNKqWGDh2qi52bm5tHjhypg2nLsmKx2EEHHfTyyy+HvTjCW+owOth6hI9zggACCCCAAAIIIIAAAlUvQABd9UvMBBFAAAEEEEAAgb0SWLFihQ6aTdNUSiUSiaOOOuq9994TkWQyed555+lW0ZFIRDeMfuyxx/T99G6EjuPo7Q235s/FJh4cCCCAAAIIIIAAAgggUCMCBNA1stBMEwEEEEAAAQQQ2EMBr+Bt2LAhLHbWJc/9+vX761//qq84e/ZspZRhGHq7QsMwbr75ZhHJ5/Mi4pQOv3SEGTTdOfZwMXgbAggggAACCCCAAAKVJkAAXWkrxngRQAABBBBAAIHuFfB9P5VKOY4zderUvn37hgG0ZVkPP/ywHstvf/tb27aVUrpKWik1fvx4XQGtX0AA3b2Lxt0QQAABBBBAAAEEEOgtAgTQvWUlGAcCCCCAAAIIIND7BebMmaNT5kgkkkgklFITJ070Cp7jOCtWrOjTp08sFtONOJRSw4cP930/n8/r9Fnn0boIuvfPlBEigAACCCCAAAIIIIBAlwgQQHcJIxdBAAEEEEAAAQRqReDJJ59MJBJhpXMkEvnJT37S3NwsIqtWrTr66KMjkUgsFlNKxePxww47rKmpqTfT7HozEK/glb+4/Lw3T5CxIYAAAggggAACCCDQswIE0D3rz90RQAABBBBAAIEKE2hvb1+5cmW/fv10xKy/Dxky5NNPPxWRdevWfec739FtOpRStm03Nja+8MILepJBELS0tPS2Ces9Er9yVI7j5HI5Xcftum55g5GvfC8vQAABBBBAAAEEEECgZgUIoGt26Zk4AggggAACCCCwhwK+7yeTSb0toWVZiUTCtu2GhoZVq1bl83nXdc8777xoNKq7QiulYrHYwoULe09i6/u+V/BEJAgCx3EWLVo0d+7cs88++5hjjjlpB8esWbOuvPLKhQsXrl+/XsfQrusmk8k9FORtCCCAAAIIIIAAAgjUjAABdM0sNRNFAAEEEEAAAQS6TiCdTv/jH/84/vjjI6VDFzv369fvySefFBHf93/1q18ppQzDUEolEolIJDJ+/Piuu38XXOnTTz+96667RowYEdZr69GGP3Y6sW1bNx4xDCMej//gBz9YuHDh2rVru2AoXAIBBBBAAAEEEEAAgeoVIICu3rVlZggggAACCCCAwL4UyGazInL55ZfH4/FwZ8LPO3Lcdttturj4mWeeqa+v1zGuYRimaX73u9/V3aJd192XQ/vi2plMJvzBdd0gCFzX/eCDD2bPnj1o0CBdo21sPTolzrv4Y//+/U877bTrrrtuyZIl69ev17fT5d750hF2i9Z3L5+73pIxfEE4VE4QQAABBBBAAAEEEKgaAQLoqllKJoIAAggggAACCHSrgA6gRWTevHmRSEQpVVdXp0Pbiy++WA/lzTffjEQiOoaORqNKqdGjR69evbrb2nHoVhsiks1mdc574403RiIRPRjLsnSZto6gdzFxDl9mGIYui7Ztu66uLh6PG4Zx0EEHnX766YsWLXrnnXdEpLW1tTxx7rRCBNCdQPgRAQQQQAABBBBAoPoECKCrb02ZEQIIIIAAAggg0H0CQRCk0+kXX3yxf//+SimdRCulRo4c2dra6hW8ZDI5fPhwnfPq2Peggw5avXp1tw0xLIJeuXJlecONcLRbC6CL3UL24ChvzRGJRHSoHTocd9xx11577fPPP59Op/WUgyDwfV9vY0gA3W0fA26EAAIIIIAAAggg0FMCBNA9Jc99EUAAAQQQQACByhbQhb2u67a2tvq+v3z58iFDhuiOz3rjweHDh69cuTKbzX788ccTJkyIRCLxeNw0TcuyotHogw8+2J3z//1//F6PKoyYGxoadCDeVQF02PM6vEVYWK27S+uK6WnTpr3zzjvpdDpMn2nB0Z2fBO6FAAIIIIAAAggg0M0CBNDdDM7tEEAAAQQQQACBahPwfT+fz2cymZaWllGjRoXxq1KqX79+S5YsERHHca699lr9iG3bsVgsHo/PnTs37OORz+e70MVxnPKrzZw5c7sbDOpq5XDAlmXpbQb1I7qK+eSTT77mmmte3cGxZMmSv/71r3feeecpp5yiA+hwo0Lbtvv27RtevPwkkUhs2LBBRLyC123dSMpBOEcAAQQQQAABBBBAoNsECKC7jZobIYAAAggggAACVSug20roEHnSpEm2bevi4ng8XldX98gjj+iZz58/Pyw61kHthAkTRCSdTndhAK3TZ939edOmTWPHjtXbJJZHwPpcVyibpSN81rKsE0444fLLL3/uuefCdNjd3uE4ji4DD4Igm82mUqmmpqYHH3zw0ksvra+vD5Po8MphiXSffn3vvPsuAuiq/X1gYggggAACCCCAAAJlAgTQZRicIoAAAggggAACCOyFgM5hRWTu3Llh6mpZVn19/S233KK3AVy1atWgQYP0fn1KqWg0OnTo0JaWlr247XbeqtPnVCqlK7Jt2w7HU36iA+j9TFMpNXDgwHHjxi1evDiMlf3SsZ2rf/kh3c1ZRMo7abzyyisjRoywbVtXVYf117F4cbdGZVvKjvzrHb/WsXu4U+KXL8xPCCCAAAIIIIAAAghUgwABdDWsInNAAAEEEEAAAQR6iUAulxORZDL58MMPF4PWUvKrC5AnTZqUz+dzudz7779/xBFHmKYZ5sKDBw9evnx5104hmUwef/zxhmFstxJZx9A6gP7F1de8+bcVxXpkx+s0hnw+73qdHwxfEwRBmB1vPff9gpPJpEQkK/LTWdeo/WJqP1uZxn6m2k+pqKUMUxmxWLFZdl2dLgAPL8gJAggggAACCCCAAALVJ0AAXX1ryowQQAABBBBAAIGeFNDtOHzfX7p06aBBg/TWf7ZtJxKJUaNGNTc3i8imTZtOPvlkpVTYHCMSiTz33HO6iLhTB+ddnIzuhpHJZHTfjMMPP1y3vNApc1iDrKNn3RvkrLPOWrVqVeAVpCDilL4KEvjiiO8WH5J8Ppv2c76IV6xvDkT80td2RlR81vfEc8TPBL6TzDgbRVaJjF/wuGocpPbbr962TKXqlIoZhjJNZVpqv/1isdjtt9+ue2Sn0+ntXJeHEEAAAQQQQAABBBCocAEC6ApfQIaPAAIIIIAAAgj0SgEdJa9cuXLgwIG6BrlY85tIHHzwwa+99loQBMlkcsqUKWFDDP2a+fPnh22Xd2taejNDx3Gy2Ww+n//+97+vlOrbt2+YPusA2jAMXXY9ffr0ZDKZKR2+J0FBxC19FcTzJSfSIZISSYt8JrKmVM4s/s4C6OKzvicFRwq5QlBYXwj+S+Taj1vmtmRvXrrCPGywssyGmJ0oD6CNYuuPaDS6YMGCcLJ7Fr6Hb+cEAQQQQAABBBBAAIHeJkAA3dtWhPEggAACCCCAAAJVJeA4zpk/OjPstqGUGjBgwGuvvaYn+bvf/U5Hw5Zl6YR62rRpjuPsQQwdRreXXHKJUurzxtORSKQ8gNY3GjRo0OOPP64Da6/gOU7BL4hfKnwO/GLZc04kI7JJ5G2RRZnM3PY1/5ZcWyzb9qQYTvuF7RdBByKeJ25BCoWMyN9FHmhPzd6cuTonV69P/uvH67829hTVt6+yTdMuVUDb+9mxaLhV45///OeqWnUmgwACCCCAAAIIIIDAVgEC6K0S/IsAAggggAACCCDQ1QJBEOiu0JMnTy5vghGLxZ5++mm3dCxYsEDH05FIaYM+pe666y5dQL1bw9EtOHTvaV1YbZaOMINWSs2aNcv3/Ww2297e7vu+4zjF0LmUG3uBOBKkRZpF1om8I/KrTzb+omXznHzrPemN63UA7e80gA4CKfgFr1g0/SeRG1PpSzqcSwK5IO3Pau648a23Dz3jDBWLqIhVbMFhGGH1t2VZhxxySBig79aseTECCCCAAAIIIIAAAr1cgAC6ly8Qw0MAAQQQQAABBKpE4He/+10ikQhTV6XUzJkzddD85ptvDho0SBdBf94V+oYbbtjdOes0+e9///vAgQMbGhp0awulVCQSsSzr8zYX3/jGN5Yt+7+BX+zlXH7xwBfXKRYue0Gx9vljkfdFHnWCq9duuLR501Xtrb9q3vhHJ99SKoAu1T4Xe0Pv6Mh6wYZS6+drN7XMSHVM6cj/NOuOzxQu7cjdvm7dMs/9wfTJyi523rCiMaUjaEMpQ+0XjZw/YfyOLsvjCCCAAAIIIIAAAghUrgABdOWuHSNHAAEEEEAAAQQqRkC3vJg3b96AAQNisZht27o8+fTTT9eVyy0tLWeddZZhGGPGjFmzZs3uTsz3/ba2tm984xthGXV4YhjGlClTipsTesWr6pGE1y9WQPvF/s95kc0ir4rctan56s1tV7S2z9q47raN6/4m8v9K/aDdYgbtl7p0hO/+4qS0UWGxd8dKkXtb0pe2dUzOuD/NupMz+UmtrZdv/PR/l/pytIl3yP/3DTMeLwbxZQG0ZduxRPyZ55794oqcIYAAAggggAACCCBQFQIE0FWxjEwCAQQQQAABBBCoEIFly5Y1NjbqOuhoNGqa5tChQz/66COv4OVLxx7P4yc/+Ylu5RGNRnX6HI1G+/Xr9+ijj4pIS2urF0hHNp/L5bZtMN0u0iTyksgvO9ov3rTxFwX/ps2bF65f+7EELQV/S//nYv1zsQfHl0fo65bQfmkLw49EHsk5l3zafEHSm9wRTO7wZqZSc1rWPZz67EORdvEdcTe3b/7v/+N/lASKpdDFGFp/KTXooAO/fHF+QgABBBBAAAEEEECg4gUIoCt+CZkAAggggAACCCBQKQL5fN513ebm5mOOOUZn0Pr7gAEDli1bpnPhfD6/B9O544479KX0tn66BcePf/zjXC7nFTzX8zL5nL5swZfyTQ51Q42/iywKnGs7kj938ldms9e1t/+vwCv2fZZiv44gky39u/1x6Z4eOZFWkSfTm6/auHFGhzs1KdNSMj3lztrcOj+54X0JPpOOrOTyTkrEb8tkBh54iFJfBNCGVTyPfy3xs8su3f5teBQBBBBAAAEEEEAAgcoUIICuzHVj1AgggAACCCCAQCULtLS0nH322ZZlhTsTNjQ0FKPeLzdo3vkUi101SjsKNjU1HXrooaZpft4/Oky0n3jiiWw265eOYugcSEGKX14gXiHw3eKXBJIt7Te4yMlfk01flOmYlcne1tHxjOf+XYotoYu5c8Evvkf84rn+KhuWbipd8P1NIn8RmZvZfEE6NSnrT0vJzzLys/aOues3fCSSFnEC3/cL+hK+yJLXl/fp90/KtJRpJeoa9In+/vrrrwdBwJ6EZcycIoAAAggggAACCFSwAAF0BS8eQ0cAAQQQQAABBCpUIJlM5vP5GTNmFLfjsyy9W+Bupc9hWv3uu+8ecMAB4a6DSqlhw4Z9+OGHOnrebgBd3HjQK/Z9zor8Q2Rxzr0pmZmRyc5MZ/41nX224P1dgrQExV4bOn0unpUCaF+XRBfVt7Te8IrRdrLUwePfxPtZrmNK1pmU9WfmZMbG9luTqT+XKqO3ht9fevtfX1+WqGsw94uUQvOwE4dx0kkn6b7YFbq4DBsBBBBAAAEEEEAAgXIBAuhyDc4RQAABBBBAAAEEukkgl8u5rrto0aJvfvObpmneeuutu3vjIAgeffRRXfKsg+xYLDZ+/Hh9nVQqVYyJtx6FUvlxsZTZE88v7ha4WeRt6it77AAAIABJREFUkcdyHTemcpek3Jnp3PXJjhdzwRqRTDGgzkjgFmufddIcfi894JY6Phek2NQ5U9qlcGEueV22MD3lTe2QaWn3gnTqxo7Nf/Lz60sxd6n0unjr4tWKXT2KR8GXW//1dsPaLxpPlNpxmPq7bdtPP/30to2qt7yNfxBAAAEEEEAAAQQQqCgBAuiKWi4GiwACCCCAAAIIVL5AGK2GXSZyuS0NmndrcqtXr9bps1E6lFInnXRSLpdLp9NhBfHW/Ln475aCZr9Y+NwsskrkP5yOm1NtP0vnZ6YK1yXz89POR6U2HSJJ8dvEdzunz6UNCN1Sd46M/u7JRpG/ily3acPlaZnaLlOT/sxkx883f/qMBOtFOoJ88dbF3h+dA+i8W8i7hZNO+Z+WHS023ygehlJmNBo97LDDdouCFyOAAAIIIIAAAggg0GsFCKB77dIwMAQQQAABBBBAoJoFgrJj1+eZzWb1i5uamnTuHKbPSqn333/fK3hh6FxWAV0IA+i0SIfIRyKLPf+65uaZm1sudGXmxvSD61OtIsWqaclL0C6FpBS2CaBLbTnypZ7O6VJvjXUiSwK5M9NxeTL7LxtlyiaZ3JqZuX7d0+J8LOJIQbyM+N6W9FlXQJdSbBFJZ4qxe0t7sv6f/ims4w5PHln4aKEUmu86Dq9EAAEEEEAAAQQQQKAXChBA98JFYUgIIIAAAggggEANCQRBcXu+3WoAvX79+oaGhk4B9E033SQiemfCMIMunej2G0VSv1T7/I7Igmzu5rbUpZuTP0vnL0m5v04X1pSCabcYFXeInxIv2zmALm44WIyEc6WcOinymchrIvcmnSuTHRdmvH9plQub5eLm9ls3f/b3YosPJ9/RIoWs+H7nALrUhaO1vRR3izz93B/taLzUf2NL/tzQt8/wkSO8sFtHDX0cmCoCCCCAAAIIIIBAtQkQQFfbijIfBBBAAAEEEECgEgV2PYD2ff/www+3LKs8gB40aFBbW9uWi/iBFANtz/eL0fPWr1ILDpHVIo8F+SvWrrm8NfXzlPyiXW75LPluqSV0KRbOFps2B54EW7s/B6WuzaX0OQyg08UmHfKByD1p5/JkdkaHN71DZmTl50m5ddPm/xRvg8hmpz3I5Yqdnn0p9ZIujqq4tWHxq1gV7RQ8XyTrFnyR//nt7ybqGoodOJSyY7Y+eek/X67EpWTMCCCAAAIIIIAAAgiUCxBAl2twjgACCCCAAAIIINCrBT6vlb7uuusikUixX3LZsWTJEhHZ0vrZC0qBr1cICo44jjiBV4yh877XLPKSyNx06/QNG36el192yC0fpV715OMtk/aK/TeKX6VDR8/FU7/UGrq46aAvfl4CXf78F5Gr2jqm5rwpGZmWCn7uyC9T+cVt7etLJdJBUOq84Yi4vg7Ei48Uu0FvuY4Ue3QU+4F8KPLvr/0f6+CDVWQ/XQJtRYotob992ne3jIR/EEAAAQQQQAABBBCoWAEC6IpdOgaOAAIIIIAAAgjUjEC4XeEnn3zSv39/pZRZOqLRqGVZ48aN+5JEIZBCsca4IF5a3LQ44uUC32kVb5mfv6uj7eJk+5SO/OUdcucad5knLaUguHiFYovnL1LnrdcsPuKLV/pyfXEL4rWK/B+RX6z57KIOd1JefpqVi7Nyc679935qdSlTLobMTmnXwWLg7IvvBeJ6knfFcSXnScaTTC4odp1+VeTGtWt+3do26uZb1NcSdiIWtoFWSn344YfZbDaf35qJbx0T/yKAAAIIIIAAAgggUCkCBNCVslKMEwEEEEAAAQQQqFGBcONB13VPO+00yypWBydKh85qV69e/SWasAK6GEB7KSnkxWkXf7mXfaBt4xVtLTOc/E/b0ldsSL0qskHE1SXOfqnQ+UsX0j/oAFr3zvDyEmwU9z2R29avvWRj84yOYvnz9IxclfHnS8eb4m/Wl8mXekV7xVLs4m6L4gaS94pfjs6gc5LLi7wnckPzxpmp1CzX/+XGZnXIoSrxNaUbcJTmNmvWLK/gbWdQPIQAAggggAACCCCAQIUIEEBXyEIxTAQQQAABBBBAoIYFcrmc7/vPP/98sUWybRuGobtwWJY1adKkVGrLbn5b65e3ZMmeBF4g6dJugatE7k5vvrytZabTcXEhd2Wq9XcdmU9L7TCKRc/6HcU20eXHttXQ0i7ypsjtG/5xfap15vrNlyW9S9vk5ym5LZ1/Q+RTkYyOs4udN4o10NliJbTnlQJoCVx9J0/8ZKnzxm+bN85KZ3/anJ66MfmvHYUzb79T9R+ojGLCro+RI0fmcrlicXZQ6lBdPjrOEUAAAQQQQAABBBCoBAEC6EpYJcaIAAIIIIAAAgjUvIDv+6NGjdoazH7x77p16zKZYupbOnRkXIyTdaRc8KRV5G2Rx0QuTrVO8/L/IrmLU5vuyyabRDaWdgfcQQCtL1WKfUunfqmmeY3IgiB7VeqzyWvWXNqeu7S9cPVm99ctuaezwZpS6+diubJbTJ0Dv5g+pyXIilcQt5g++1ue7BD5ROTf2tpuzOX/pS37s4zMSQY3fPDZHz7eGD3oMKW+CKAty1q1apWI5HI5Muitq8y/CCCAAAIIIIAAApUkQABdSavFWBFAAAEEEEAAgRoU0CXAL7zwgm6+8UX2rNQPfvCDYsFxMW3Wx5bdAv1SAO2V6o3XiCwOvKvSm6e6zjSRyYXW2a1r3hNpK9UmB8W02N+mAjqQLU2ftwTQHY4kRVb78prInM3NF6WTF6Wci9LejGzhl1n3PzPyWVCMm72gVFPtFL8HvuSK/aCDrLiOuEHgBX6xJrqt1Hnjsax3ZTp5fnvrT1uSszbn7tqQ/b8im0RumHuXHf2aLvTWra4nT56sK6AJoLeuMv8igAACCCCAAAIIVJIAAXQlrRZjRQABBBBAAAEEalMgCIKTTz65PHrW5y+99JJX8Fy32Ma5lDYXt/wrffkSFNPeVpElBZnbnpyebJsuMj6dusZp/d+l2udiIiylquSw/0aYYxeLovWug8UA2i811vgvkSUi16/bfFlb7sJ0YWZSLkr6c5xgocga/SJv666DbmkInngSFMTLSd6RfBB4On1+V+SxTDA3mZ/Y1jo1n5/Vlr1zU8dbIs2lOfz9/Y+VUkbp0IH7IYccoidYlrPX5qeAWSOAAAIIIIAAAghUpAABdEUuG4NGAAEEEEAAAQRqRyCTybz77rvRaLRTAH3ofztMRAr5gk5mS2XMhWJZc/GrIH6xHfPfAnmwPT97c3p6e3p6Ln91NvO8+OuLhcmlvsx+KTLeYQDtFmPsUueNT0SWiVyzuWPKhvaftcvP2uTCpFyxWX4fFPt7bGlB7QfFrNrbmoG7Uuz87LmedDiSLRR3RCzuOvhY1rs+k72oI3tFJrhsTcu8zc47ImsL0pb3ktliL5ExY8aUzzSRSLz//vvZbJYAunY+88wUAQQQQAABBBCoJgEC6GpaTeaCAAIIIIAAAghUp8CUKVN0XXBZMmveecc9ZbP1fSl44nilANoXPyeyXuT37cGv2oIrWgszN6Znb9r8R5ENIpmgWJjsSbEnRjEvDgPoUr+N0jX1voSuK54rslnkXZE7WoJpLbnJuWL0/LM2uaxVfvmZ01R61inufqiLqYPiNbfE0EFxOAXXk2xW3KTIWpE/pLzb2zp+1pG6JJO57tPNv096/1XKr52tM/HEnffvD4fTjEaj8Xj8hhtuKHbh8IoV2sVYu2zIXxRtb70C/yKAAAIIIIAAAggg0KsECKB71XIwGAQQQAABBBBAAIHtCHwewuoAOhqNxmIxpUyl1Np1m8pe6ntSyEguIzlPnEDkQ5H5nzpXf9BxySf+9Vm56dP8EreYPutOzZ4ExZbK5QH0lvR5y96DgfgFyTnitYn8XWReUmZtkBmtMjUlE9q9iWs2/WpjZkWpb0ap30awJYD2AvGLVy4dnvheqfNGkC9dZMGG3FX/2PjzluxVycwNnzU/35r52JO0SL4UKIdzyeScMIDWJ/996LcKeUc8aW1PZbdG3t7WYm8y6JCOEwQQQAABBBBAAIFeKEAA3QsXhSEhgAACCCCAAAIIfCHw1FNP6RzWNM1IJKKUsqzIKad854tXlBo1+1JwigG0ky/VGj+VlevXOVesl1+0y5yPc48ni1v8Bf6XvrbUPpcupAuXi6XMpZcUxGvzN+dF/p/IU1mZs14ubpEL2+TCdpm8MXVdS+pFv3jBYuVyMcze2k66GEDr3HlLCO0U230U0/D/5cgN6zuu2Jy9aO2mmz9tftGXT7xiv+qw/DrMkbN59+j/caxpFkP20mSt+q/VpdK5jBTT6qW5jv9sWZ8s1UE7W6uhv6DgDAEEEEAAAQQQQACBXiZAAN3LFoThIIAAAggggAACCHxZ4Mc//rFSyjRNwzB0JhuPxP/9oUe2vGpL5bJf3PDPdzzxm0X+mHFvanZmbvIubpWbO+TR1vbVpSC4UwDtBcUI2C3lyO7/396dR9tV1XkC33d8U0YoC61xddvlWrVstLCrVtmWvayuVW11V5VTVUlXNzImxMwzhEyEBEKYMQqoiAqIOKCCyCSDgIYIgoyCyBBCkjfe+czD3vvbvfe59+ZlsMuqXkvvy/te7rrv5L13z93ncx7/fNdvfbdt45gUQOtK1BoG7gW21Pzldb2whYWOad7Yur/xfWU2HvRMLYZpfNbaNkprEz2bZ2rPm5ozesCbwHcSXFD3ljebq/3GlrHhe1qOY6ulswA66/voBtCJ1BdsuzC70m7xyPd3P1kB7pHYvGfvVyJ/2C7bpOXKLvlQMf6LAhSgAAUoQAEKUIACvSPAALp37gVXQgEKUIACFKAABSjQFpi84d4f//Ef53K5crmcz+dnzpyZy+XmzJmz59U95le7rc3Z4LJUPrAbuHSiuXifu6giNznYWW+9BO2blNkUNHefWfocwuxVaH9q6qA7489mX8FRYBf0VXG8rOktcdSSFpa20k0T/m21+IDtzYizCeROAG1KpbVNn22krSVCYAR4BLi4Fi2emFjt1zZP7L0HYdNeZWp3K8xaQLIm6uzipcZ99z/QDaCFEMW8WLXj8jsjXFbXW/14Z701Cqhubt1FyN7PVwpQgAIUoAAFKEABCvSSAAPoXrobXAsFKEABClCAAhSggBVIkiST2LNnT94+SqVSt5XipJNOUirNppUnhdBmlvkNYEe9fvZIbemwf/5IcpOrf2I2Hgx8NFO762A3gNYKUpsODcc+Ozv76RioAweAByE/GwTnut4SN1zbUqsm3AuC8JpG8xU7fWxmnyN7lGroRCKxAbSdfY7NFoch8JrG48COilzvynMDZ1tt38tA1YxOy9hub5h9aHcfxOySs1FoW3XdTqGLefGej37sspHmxmaycX/lQbtgM7xtW6z5J0MBClCAAhSgAAUoQIFeFmAA3ct3h2ujAAUoQAEKUIAC01RAKSVTM5F87733ZgF09polsgsWLZBIlBlZzp7aD00b8zhwR+SdPTr2iZq7YTy4oS6fsfsE+nBi1E1APGkCOjtObZOG19kGMIVuQr+G+EdQ10beBsdb6IULvXjhSP2CmrtzYvwlW8RsPja2A8ypNmGzijQiicRsbJiaXo4U2AOTPl98oLmppVeM1LdVR+6HrJrQuJ1WSxtfZxfQaaA+eLtPPPHEyUPQs0/8j1eOjW8aHf8u8ELWPZ31dxx8B48oQAEKUIACFKAABSjQiwIMoHvxrnBNFKAABShAAQpQgAJZAL1s2bIjA+h77rlLQ4WIEkTQCZRu+v448BDSbfXh02qtBU6y0492ATWTEkuNACoypRVZAN3eINB8kTAjz2bc2s4hS2AY6aNoXBfv3+DWF3nhmWF6Zhgvbra2j469an8rtRsNmvxaZ1sOJvbkJoM257Ozz6PA0zC9z4vH6+vdZMdY/T7Xa9rZZ4nErCg17c3dBP3IAHrevHm2fKO9FaEYLH/xtedvHd87ahNws2CdJeCTR8D5V0MBClCAAhSgAAUoQIGeE2AA3XO3hAuiAAUoQAEKUIACFDDZLiBT+YEPfODIALpam9Am9I1S04JhBqVHgUehd8aN1c2JlQ3v8lA/aHf/i0xLRYQ0QWoGoE0AfbSHCYNtIhwALwG3orZw37NLXfcsJz0tShf44Zqx0Uds8qsjs8ug1PZpTiY1EugICIBAI0ltycYvgKub0eKmvzKILpqo/sCWZigzuWzGn82SOwUaWQzd3YEwu/UKavtlF3d3IDSj0GVx29O79pm5b/OwddWdAPqwN/OvhwIUoAAFKEABClCAAr0kwAC6l+4G10IBClCAAhSgAAUo0BHI9iE84YQTJgfQ+Xz+xBNPtDvwJVmDhbLNG3bcuHb2WHVVpXGj4z0u5ZtAKxtt7m7Wp7rDwmbg2GTHWuvU/lIMlcIFXgW+FaTn1cYWOJUlMU6tBydPVFdOVJ8yk9GmLdoUb2hTsmEyYBtnSyQhotgMWXtQkQe8CFzTcNa13CVOvLnpPaJV1b4xgYohzUS2GZ0+uHWgMvm3njQPjTgJb/nebWLOoMgXhMiLQl4U899+8F4JBLEJ1c2je10Hz9Sx41cKUIACFKAABShAAQr0jAAD6J65FVwIBShAAQpQgAIUoEBHQGsdx6bWOdt7sJtBl0qlf/qnf1Iq1SprztAN4DlgZ6KW1xpLa+75+yeeSJMJaAdmG0AzKTw5qDVZbVZ3kQXQEqkyU9SR+eVh4E4H24ebS2vufD9dGGBezV/V9D8Xpm/a9NkBfBtAm/nl7GkyaBkjic0cdOLb9PmWwN8e+ssmxre4/u02H9cm5TbpcxZAS9Mb3d16MFuP7mTQWpnoXN/48D1m8LlQFLmiCaDz+c9//vNpZEzsw15V9qbOt/iVAhSgAAUoQAEKUIACPSjAALoHbwqXRAEKUIACFKAABShgBB599NG5c+d20+d8Pl8oFC655JIkSWyOnITAL4A7gDVjzRWj1UvHqrc7/j4bFvudALpdUDEpes7CY43EPGWKWMkEDeCnwIWj1RWVYHkDS1pY6ERrGu6XI/P98U4AHcKOP3cD6Owg0ZAmm34RuFbGq/3GWq9xfnX0rjTYa7s5uulzN4NOIe3gs4Kymyl2UujINoc8iXj1174kjpslSmWRL4p8XuTy27dvD/2g85fRjdVZwNEh4VcKUIACFKAABShAgZ4UYADdk7eFi6IABShAAQpQgALTWyCOY6XUww8/nPUg5yY9br/99qydI4EeBX4EXB1hfS3a0fC/OT5xwDZvhDZ9DrOSjnZbBtqBr6nQSJSKTXeznZCOE10HXgFu8qM1E40ljlpZx6oallfqO+r1HykzHN0y+weapwmgbWH0wSHoxPRrpNqc4RY/Xe25S0N3zdj+7yAZASqqGSPNcufJr6lpc7bptbRf7Tx0CkwA90J+avj1619/WQwOiNKgyJXNELQQF1+0XaUxoAPP6c5x24Pp/bfCq6cABShAAQpQgAIU6G0BBtC9fX+4OgpQgAIUoAAFKDAtBbJNCHft2lUoFEwTReeRy+Uee+wxrXVLmVqMx4Gt440VBxrbG/HX/XSPLebI+pllu9vZtDZnbR024zXhsVJxkgZSmjAZdrr5ZeAaz9vk+ata0UoHq+vYUNFXuM79QN3+UmjLN0J7KjNynG0dKKETxKH5Vwv4io81w+5aJ1w3XrldyZfNboROiEZsGqJN+cakZ5IiUrZQ2mTgKaIA9RQ14IEYO5qN8ydGrt2zVwwcJ/pmi/xATpSKIrd543pTXS1T8xehtFk7Kzim5f8dvGgKUIACFKAABSgwtQQYQE+t+8XVUoACFKAABShAgWkh8MsC6FKpVK1W4zj2bPp8ZbW1ruEtfmP05tA0QYem8TnOtvTLIuLYfjOr48hqO7INDKUM7QS0CoEXgOtbanOi5jWbi1vRslq6dlxd3lDfB/ZnM9K2sDmbl+7sPmh/kJr0WdoI+x4PG0flOS2s21v7VoqXzSyz9OCm8GxDtI7NyroZ9KQAOjWniu1J7nBwdTNaNlY9d7R60/6W6H+rKM0VuYGCKJRFbsuG9TCN0yYAN68MoKfF/wq8SApQgAIUoAAFKDDlBRhAT/lbyAugAAUoQAEKUIACx57ALwmgc4VCAYDv+28CX5D45FhjdcvbOl77KUyJs5lMVjaAtsXI0g4s+7a+2bMD0RYqi6Y1IDWSYeBmhSUTclmK053k1Erz7LH6lkrwHWnS5zBruOiUd9iBaYRQCWxxc2qy7nHg+zrdMVFbNKy2tvC1SvqamX3WHmRgz5CNYNu6jW4GnQXQdqJamSqQGvAYsGmssajqnDXcuKiqdwUQpT8UuTlC9BdEviQEA+hj7++cV0QBClCAAhSgAAWmgwAD6Olwl3mNFKAABShAAQpQYEoKmAqOnMgLURTmVYiCEMVxJ9qfqLvq7vp6sDrG+lrrdm1SYGkGg1MTQEubDmuTDic2AvZsgUZnAjrNUmUJjAG7gTUVvTDF/6qphRFOHR49d2L8a3H6kn2jSZzVpKYLexyZeWV7dm1aoe/z4x2V8c1Nb2sFX6rjDWDUD0MdpzAdH1lrh5ly1uaZmjnoJEQUIpKmhUNJG50/D1zdSFZ78uyqv+5A62suqoAo/K4Qs4Qo50W+IMTmjRuhOAE9Jf+SuWgKUIACFKAABSgwnQUYQE/nu89rpwAFKEABClCAAj0tcN999wmbPheFyJkAuizE0ARwh49L6+Hi4fr6WnRbgteByKTPsIFzBC2zUeXs2uwwdDuMtvXJJqlONSrAPcAmB0sCzPNwVgsLatH6WuPW1H8VcWKyYptqm9Me+khic4ZINYEHNC5rBMvGW2v3Ve7z1F6Jljb5tESahctZcYeyOXb2miD1EHuIzBg1UNf4GXDRgcbqplxSx7r94bfH3QpQVxBiUIh+e9X5vBCbN2+O4xgabrN1SAd0t4vjyKUeunD+iwIUoAAFKEABClCAAr9+AQbQv35zfiIFKEABClCAAhSgwK8k8NRTT2Wpc7kdQPeL/Akv2rh2bcVdP9r6cmAanN0sfTZxbmKzaAl9WBZr/pm2Wzh0YrcW/H6ILS0sSTHfx1ku5jfkipH6zWn6rBlbjoHAhLxZen34YqVMogh4yIkvb3hrGv6aevwZJ35dI06TTvgtFVQ3d548Rm1bQuIQqQSGU+wBvtKQ6+rJooZaXcfOCp6qeWYs2vXszovF7vz35k1bXNdvr2XyJoQMoA+/Qfw3BShAAQpQgAIUoEAPCTCA7qGbwaVQgAIUoAAFKEABCnQF4jgeGxvJ2QHgos1izWHf8V/6+Zvr9+3fWKneVE+f0qaqwqTLNutVkKnJoLOx48kZdPdXzOkbwIPA9qa7fDxY3hl/XlSrXzgx+rT9qY2d2/Fxdz2TD8Zl9GPgqgln2XhjZcP7TJw+bMugO+mzScSz9Nks7rCn6aA2P6xCvgpcW3W3tbDOxbLxZGtd3qHxpmnqwIuvvGovOmezd/P66Z3XhIGZgDYPBtCT7wePKUABClCAAhSgAAV6WIABdA/fHC6NAhSgAAUoQAEKTGMB3/eVSrMKDlsALUSuKHKFs796y6e8ys5G5YkEoynig2PGSCGT/2cAHQFN4BVge6txTpys8bG4hgVNLK0m6w8c+E7ojrenpE2gHdkG5/YMtI19lf1OBfEzKrx8ZHSLlywYrV8Uxg/Yc5pB7EmPg8PTkwPobLU2Jn8J6manfoGbLKok60Os3e99puI8A7TssPYjj+3uBNAiy6DvuP1OJZFGsUolA+hJ0jykAAUoQAEKUIACFOhpAQbQPX17uDgKUIACFKAABSgwnQVcr/X+9703mwE2aWxOiL7c4ltuuHbfS8/YGg0tbVibZpsCqgSp6W42+xFODn2zY5NMV4AngBvidL0fLwuwsKUX19XySrRtwrnTi1+348+m4NluNhjarQsn+7dM0By+Aly3f+/5jre05p5Tad0i9cs2mE4m/Wo3Fc8OzE/sfoZaZfXSJgf/RuxfEoVrXKxwsKKqdrrYLc1uis1UauC+hx4SuXbwPjRzthDi6aefTRKpEpuFH3l97auctAgeUoACFKAABShAAQpQoAcEGED3wE3gEihAAQpQgAIUoAAFfonAmrWr2vUb2Ze3zfngmgUPt/aP2uTZpM2p6aOwO/61A2h1lPTZFGI0gWeBL8bhJi9c7uNsBwsdrG7Ki8ad7/jqddsl7XcmoGEnoM3ehjY7zmaf34D+gWp9sVG9uN48149WVFs3KpNo103kbXYdPCx37q5KwfyHTvo8AtztB5vGxxfUnfkNubyBrePJ/TB1Ii0n8KI4SNL1528p9g8MDM0wwXuhKER+eHg0jlNznizOPmoGbX/IFwpQgAIUoAAFKEABCvSOAAPo3rkXXAkFKEABClCAAhSgwEGBKIpkKr/y1VsOCaCFOG3tYkd6XtSEjjSiFEmIJEYam/FnlZgU+CjRbAi8gPiWqLLVba305YIWFjhY7GDjeHCXG++1s8+eTZ9NRbN5mjTZPKQJjjVQA3bD/UI8vnZ4bJ0rz3WDnX7ynB3EVmmMyFMqllD2vdkZzEkSpD7i2LSDKKQmLR8B7tHRturYvAn3lJY+M8J6D9/xzOyzeThp9vXCHZeIYnFo5mybPosT3vZWs8dikmiptNngUB+9hSN7M18pQAEKUIACFKAABSjQMwIMoHvmVnAhFKAABShAAQpQgAJWoDvjC2DYa4h2EYUJoouz+t/3V39hJoCDJhBIBDGiAFGINOwE0KnZALCbA5szJsAo8NWwss0bX+0H8510voelDs6bCD69v7rHFmh4QNBOm2GDbNvrYXszYH/0OnA75Da3tqLa2hxgW6X+AOBktywKdOT+kgA69uAl5txaadPvfLdn0uelbusUJzktxLIYV7jxK0A8qUMjlPKvPvg35aGhdviez/35+/5z9lEyidI4NJF3NlOdpePdyD37Jb5SgAIUoAAFKEABClCQgql7AAAd7klEQVSgZwQYQPfMreBCKEABClCAAhSgwPQW6NYlS5sI1+xU8ivaG/i9t4pcTggxY8YMUczPPG6O1jpJI62lRCLNEHRk25/N+LN9yhSJQqCQJPYke4HHgAuCcGHknxmmZ4RqObDOad04PrrfjjD7tu45BOL2U8WmUiMr+DDh8TDMkPJ5B5KVE1gzVr+q2XjYNkqbwmiNVKexGXOW9tPb2yAmNviWiFNTreEkwGsJ7oyxoymXNaPT/fjkpn+2E15UcZ+3i7Q3X5opZykBnHjSew6OfudzGzdvtr+gkihIY1/L1AxbZ89uEt2u55jef0a8egpQgAIUoAAFKECBHhNgAN1jN4TLoQAFKEABClCAAtNVYHIAXZdJA9gP3PXG8x+ed5oQojQwWCz3F/sHZsyZ+/Jrr9uiDC0hNRJt4uZuHKsSEwQnNpWWTWAMeAS4ysEyPz0tSk9J1JlhusJ1draqtnkj8e2Ac2BfQ5t9B9ChOac5rQvsAb7rqSvG9IYm1ju4dKJ5t0xH7baCWfabQIVQcTv+PjyA1qhKeAeABxJc0pDL6vpMF2cGWOSFG6uNH9lSjnbZtPnEKDXj28h2IJw1Z6659v6+Bx/+AWBid5M+m4/qpM+m82Ny9fR0/evhdVOAAhSgAAUoQAEK9KoAA+hevTNcFwUoQAEKUIACFJhmAu3OZW0u20kTz2bH9732/Dfuv6c0NJTrG8yVB7LnZ79wgzZ1GVpCay21boewWQydmgBappChbd7YDXw2xMpquMSJzwzjU5J4oe/urLdeNsmviielz4FNn7MMOjSdzbEP/AK4C7hgX31LC5t9bJ3w7gySvXZQ2iw0NetI7Bs709PdMWpzkJh02PRV/xC4JopW14OzW+mZgVoVqx0N/87EVD+3ezzM6aQyJ8N9Dz0gisVs+8FCqW/WnNlm0lrLKPZkEkAn5oN10n4ygJ5m/6fwcilAAQpQgAIUoMDUEmAAPbXuF1dLAQpQgAIUoAAFjlmBdgCtzGixBDz7fEN6B5zmH/zRHwkhyoMzhTBdHJ8488zY/M7hATTsYHACGUFHttfiWeBzzXBtxV3ixIvceJEXLnXdrdXqy8CErd1oqdhTMht/nhxAB9AB0jcg7wI+5eu1E+EGT22p1j+1b9/LgKNt9BwDkcmYf1kAnX0/At4EbgXO9YNPtsKFXroiVhcGyTcaYbYGc0dt7G4DaOlE3o4rLjf9G/lCodQ3OGPG/E/Os+PPQZz4WoUHo+csg2YAfcz+P8ELowAFKEABClCAAseCAAPoY+Eu8hooQAEKUIACFKDAMSBwMIC2lRKxhguza9//jWfP37Zd5IrF/mxTvtwJb/ud1OwzeJQAGqY9QzVNfGyGiz8Xpmtdf5EXLvTihV58bs3/cjN+Vpt0O2ua7rY/dwafkR249u2PIrnCC5eMuwsr/urR2hVvvvo60AR0aqPnrDQ6QarNu+JJc9CJ/Wf2+qrGnSE2utEZLe/MZrA6xKaG+6n9o3tsiN2+cWYXQTPVbbdPxN9++EMzj5vT7YC+83t3ACpJAylt+oxJBdCs4DgG/vR5CRSgAAUoQAEKUOCYFmAAfUzfXl4cBShAAQpQgAIUmDoCBwNoaaNZdTDS9aI0Vx4Q+ZLIlYTID86YtfvxJ44aQCsoH3EI7AO+6ap1LX9+EC/w4yVOvKYef9bBc9Lk2tnQcDahfFj0nEXJNWC3Dr4Q1Ne1/MWtZGk12Lx/9BmY98babk+YNW7YMgwpEeuDzRshdNyZkD4A3Ofh8olkYTU63ZErIqwdd6+tuk/a6o+DN8emzzYVN7PQx53wFpM+m2lv8fu///sA4iRM0kCpuD3+zA7og3Y8ogAFKEABClCAAhToaQEG0D19e7g4ClCAAhSgAAUoMH0EDgmgbX1ylvRqGxf/8ydONwXQ+XJf/wwhxKmnn5HaCWizD6HpgE7bobWJls3s89e1XFttLHLT+b5a6KVra/H1DTyhUQEiM24MaGV3MmzH3J0YWmczxvuAL9fGt9RrK6JkdaI3VhvflaZ6GWkYI43M04TOZmJZQUozBC1NG0c7hvZ0ok3Fh/xJvXHVeLB8TH6yhqUtnNPAVTX1WGwmu81Wg1mHtDnMniZ93rVrV3v2OZ+bPXv21VdfbcefIylDbT7Btj8zgJ4+/2PwSilAAQpQgAIUoMAUF2AAPcVvIJdPAQpQgAIUoAAFjhWBIwNoKGhlEmUN7Hr8ySyWnXv8CULkCqW+bAK6U59sWpkV0qwH4+5m45xqZX6UzPewyMGaerpjJHhC295njdiEwyoLrJXtzei0P2vPln6MAw8n6ZZ9wytrrTWx3JKkX/TDAyayBuIw1bGP1IcKbNxsomcbQyttTppNVVelmcLeD3xtZOKcEW9+A8tbOK+JC0fDHwBV+6G29jlSSGzthrIxuvne4sWLhRCFQkHkRLlcdhyzSaGUsVKxCaCz3mcG0MfKnz2vgwIUoAAFKEABChzzAgygj/lbzAukAAUoQAEKUIACU0OgHUBn4XCWOtuFR0kaJanU+G9/8z8GZ8wRItc/OCREbvuOSxMpVWf/vghxjNQD7g7DHTVnkZueEWC+izVVXFPDIwlGAE8jkkjkIQF0ttthaGqjZRX6ZeCbYXrhWOOcqremEa6ttq6stl4ATAysNFITQNsJaBXZ2o0sgDZD2La6WkI5iGvAs8DNLW/zeHO5I//3WGtJLVj9xvADwF7b45HaX7fpeTb7jNQUS6PVasyZZUa8S6WCEOL0M07Nzpukgd1hUR7ldWrcXq6SAhSgAAUoQAEKUGCaCjCAnqY3npdNAQpQgAIUoAAFek3A5rd2UXY2uLu8IDLVF1GSPvDQw3YIumhf8+94+zuiIAxi+2M7ejwO+UPt76g3l7fieZ5Jn1fWcXXDpM8HbPqcSC3tnLKCsqPVJjQObR1zCNkCXoL6ThBeMN5aMu5ulFg+XLtkvPEYzOh0CGgz6hynOo21mUbOep9Tbfo3zHC0TZJTndahnkV6s9M8r9Jc1AxPq7rL/HjV8OhXU/0q0LCnSu07OldrdlMEkCTJ5Zdfasafc6J/oCyEGB0d7gxr66NEz9kcdFeKBxSgAAUoQAEKUIACFOg9AQbQvXdPuCIKUIACFKAABSgwLQUOBtCTLl8pZQeWEaemM/nP/vwvsiKOUqFw/ODMW2+4sdVqNX0fdkL5YbSubB1Y2XIXeFjgYlVdfaqBh1NTCR2lSFJ00udsWNm8mocyLdI+8Bpwa+puqo0vG3NXteT6RF9Qa9wVm7fXbUidKqVUOjmAzpqnzeiyqfRQSJVM5QRws1vdUB1b1Aznh/qfR8c3BsHNfvozYAxomm5o09TR/vTOxSaJfOWVV2bPnj1jxqAQYs7cWVu3bbHD35HJpjkB3YHiVwpQgAIUoAAFKECBqSXAAHpq3S+ulgIUoAAFKEABChyzAocF0No+TOKrTHAcp7LRcn+46/FCqU/khAmgiwNvf8vvpEESJGhKPK/kF9KJFa1984Nwvq/W1uJLR7wf2uaNJIEOVFYnnX1K99VoSiltM8ZDUJtqwwurlRWOPNfTmz33NuAVO7Ps2gDaDD6bmumDE9DdAFprjUQiVXXgSWDb+IHFrdr8UC5IsLg6vjPwfmHHqB2bPoedADobfO7e0ZNPPjmXyw0M9pXLZsq7WpvwfdP8EUauaaye3Ps8+bj7fh5QgAIUoAAFKEABClCg9wQYQPfePeGKKEABClCAAhSgAAUOFehWTSSJ/C/v/0A+ny8IURSiJMSlF17mxHgT+OrE+JrK3gVx/dQoWNIKrqv4e4BGZAsvYm3Gk7M25SNepcYw8D2k2/3aeVGwwg+Xt+I1E41bgMdtahwpxMoUbkRQEZTt32hXcHQDaFMrbaPqB9LkksroBrc5v1Y9pdFY7DjX6PAxoGJD59S+JnYDRABxbIanAz8K/Oj++x/M5XJZ/4YQYvnShTClHyZ3Vmls0mcom0FrU0U9+XmoFf9FAQpQgAIUoAAFKECBnhJgAN1Tt4OLoQAFKEABClCAAhT4FwTuvPOucrk8UCrOzBXmFPt/e87bRjz1kBt+ulZf1aotjN0lTvMS130JqCQagYQfm/zYFl50B5+7ByGwH/hBiu1+a5HTWBQES73gPNe7ymk+BuyxzR6pDX5ThQgmgz5qAB3YrQV/onBZvfHJidHlcTSvVV/QqF4UNh+FycdNS4i2z04C3g2gbfuzfOc73ymEyOfzxbwo5kWjNp5EnqkHkWkWQ3cmoA9Nn9Whhdn/Ah5/TAEKUIACFKAABShAgV+3AAPoX7c4P48CFKAABShAAQpQ4P9T4CMf+VjWBC2EmDv0W+/64Ieven3vhkp1nZdsaPjX1ho/A95A4kkfsY8oNo3LqQl/u7lz96AG3KNxsRMvboTzgvTUVmtF0LrcrTwIuc9MNEsXOoRpA4FtAklh9x7MdiDU5qzZM2veuK6ll1S8U1r+GTo506ludUa/q9yRTumzuepsr8LO9ZutCwHf99esWZNd0axZM8rFwpmnn3rI+LOdfdbadFV3nllDiV1Y52z8SgEKUIACFKAABShAgR4UYADdgzeFS6IABShAAQpQgAIU+KUCWuG11/Ycf/zxpq1C5AZKQ+K3f+8fPnf91j1vXjXhXbu/9iqwX8umDhPlm84MqUxIbBssuglwDHhAFfg5cInjm90CPSyIcUqtfm6j8jVvYsTMPqcxkgAyhDSVF1LrLIPOmjBMObVKoQOgZWelv+Tr8xrp/Jb6hJecEQQrG+Nfccd+jiA0l6JN10b34ydNLSulbrjhBiFE/0A5y6CLeTE2Mhz6XpZBd8efO9FzlkEzgM5A+UoBClCAAhSgAAUo0OsCDKB7/Q5xfRSgAAUoQAEKUIACXYEwiLPjyy+7MpfL9fX15fM2tx2aufO7d/14pOLaceMU8GTc3uIvK75Qtv7CVnHEwL5I7gV+CGyrHlgZOvP8YGGARc14caV2vYzf6H6e7V1uv9gA2swsZzPPKoKOUkgPeA24Q+H8VrS4lZzdShc1wzXjE7cm8RuQkY6zaetOAN5u4eh+wksv/Oy4ObOEEEMDfX0ls/fgRz/890kUZL+Qpc+d6NmEzhKHP7un4gEFKEABClCAAhSgAAV6UIABdA/eFC6JAhSgAAUoQAEKUOCXCnQz6D97758LIQYGhgYHZ5eKfXPmHPfiiz9vDxnbEWNTd9Gp3TCnsxm0tLXO+4BdwNb6vlVJ5azEOSMKF3rxiop7TSh3Z33Nkz9fd6ozsiw51UgTpIHZPhCqAtwPbBlpLWtG8514UdPf1HCvbzo/7UbNnTXYvo2D5w3DsF6v/8m7Tsx3+0TswTNPPdn9JQbQXQoeUIACFKAABShAAQpMUQEG0FP0xnHZFKAABShAAQpQYJoKZL3JAF588edCiFKxL583g8OmxaJ/8Hvfu9sLoix3TqQ2+wfa9NiEv3b3vhiYAJ4CLhs7sD6qzQsnTkmaZ8hwvuteUGv9RJufRkelzU5kwmgPyoHyJKQD7Fa4spYs3N86u5We7fhrvcZnE+8pBTc7SWI/t7uGQ8/8p3/2HpOh9xWy9eeEOOvUT6g09t2WiZ5NaC7NPoS2+rk7+5weOgTdvcDDAu5DP4r/ogAFKEABClCAAhSgwG9GgAH0b8adn0oBClCAAhSgAAUo8G8TSBKpJJJExnG6fv3GLIAeHJxRKvZlMe62iy7unrkbzposVyO06fPPgatGRs5360vc6nJEp4SNeZG7qlr5eqJHEqRZZ7MJrg99ZOeCUmho1DUCF9gHXDvcXPTyxNKaWtQMz3Hca6T3IJKJ7luD9iB0+93d7wOnnnZKNvt8/NyZQojBcmmwXGpWzFuzCg7zekQAnZo66UNaOLrXeMSKJ30YDylAAQpQgAIUoAAFKPAbEmAA/RuC58dSgAIUoAAFKEABCvzrBbSCtnsAmv0AU1O08cH/9t+FyILcXHbQNzC4bMUqJzRzzLGtv8g+RwI127xxbeRtDpyVobOo0dgAnNpqLK3Xrh2v7QPMKU3LtGnvOMrqbLNHgJaHRgD9isZle4fPHWutc7C6lpxbb12XRM8Cv5Cxa09h2qKjg2fyvTAb39Zan3zyyVlcnreLHuozTdaX77gYaWpnn02qrGWqpYJq7zfYnYA+7IAB9FHuFL9FAQpQgAIUoAAFKNAzAgyge+ZWcCEUoAAFKEABClCAAv+SQBZAZ68mX47TOE7/5N3vKRTKhUL5hBPelmXQhVLfiSe957v33ONFsW2yQGKrn58Dro2cc7zKeVGw2g/OB86qNZe0vAvrzWdgSzNSIEnMkDEUst0Lu0vq/DNE2IR6Dfh6pblurLa8Fa+sJ+eM1K51mj8G3oD5rCR715Fjz0AYxGeddVaWPgu73LwQ/YXCR/72bwHtt5pm6rmdPqdmbJsBdPcW8IACFKAABShAAQpQYAoKMICegjeNS6YABShAAQpQgALTVWByAB1FiRkRTvWrr7w+e/bcUrGvUCgLkRNCFEq2jiOXX3nOOU3fBzCe6ueAG93mOnd8ddjc7qbXAfNawel15yJf3p6a4ehUAqlCGtsvttDCjjy3sTsBNIADwM2xv75WO9dPljeCc2rNazxvtw4qQKV7a+wJJtdihEHsON6733VSf3//YQH0O/79v5OR7f4wsbfJrVUa2/4NBtBdUB5QgAIUoAAFKEABCkxJAQbQU/K2cdEUoAAFKEABClBgegp0A+js8uP2fDNeeP7FLIMWQuQKxVzBbkuYy4tisW/GjPWbt7aAOyrVK8eHN7oTG0PnJmBrLVjQbH2yUv2Sq/YCXnZGU3nRDaAnp8f2x9qMNjeA+/x4a9M5J07W1LzzDlQ+5zpP2gHqeuSYEDvr8OgE0K5vkuUwiB999Edvf/sf5XKFgYGBvr52Y3VWwfHcT5+KXMd8RmqHr5U0RRymAJoBdHZj+EoBClCAAhSgAAUoMFUFGEBP1TvHdVOAAhSgAAUoQAEKdAWiJH7muWf7BjqTxYWcKJhR6PajXH7LO9/91+sv2PLEs5/aP3oHcC3kufWRVe7oztR/CRgL4R/sfFYwRdPZwPPkEWiYTQGBRxSumIjOrQSbXHXhWOPWlv8iVKO91yCiWLWcyLwb8L1sqBkHDoycv/mCXK4wc3BWKV8u2DHtvpLpfS4Vcg98/96Dn5Z9rNLt73SvsHNwtFaPzs/4lQIUoAAFKEABClCAAr0nwAC69+4JV0QBClCAAhSgAAUo8K8UkNBxmjz30s9+620nZKFzrlwq9JUPxtCFsnjL74t3vPu/rlz36Wee2zm+d9P+F69s7bsfegIIIviR2YFQ2i0D7U6HOm3H0GYpCmjG5vXnwFXj0bYAW1pq877Krc3wBcDEzGbzwIMT047jBb7ZBXF0ZHzlitWDgzNKRTPyXMpnoXMha39+22+f8IMHHzBtG924+7CDIxwYQB9Bwm9QgAIUoAAFKEABCvS0AAPonr49XBwFKEABClCAAhSgwK8uIIE3Rw689fd+10S9g/2imC/09YtiUeRyZre/XJ95lmeKWXP/8O8/+LEd53/z9RcPAA2NuBMdtwuYTY2GjqCTbJLZTjePA68AX6nXz6s463y1vel+sVZ7Idu6MMxCaLNSrewmgsBNN37lwx/+6MwZs7Na6lyuIES+IAqlfHmof0AIcdK7/+QnP368fXWH5c7dfx5x8QygjyDhNyhAAQpQgAIUoAAFelqAAXRP3x4ujgIUoAAFKEABClDgVxQwQ9DaBMlBGn/oHz5q5qBLBVEq58p9uX4TRs8cmpEXol+IubNm535rjphRFjP63vX+91193XW7Hn8y1ghT8/7smUKHNoM2n277NBrAbcNvXPjqz7a1/PMOVG6o154D6oBKgRhIEDnp7t2PX3ThxR//+P8UQswYmmXGnPO2jVrk+vpM6Nx9fPjvP9SsN7IzR4HPCehf8S7z1yhAAQpQgAIUoAAFppwAA+gpd8u4YApQgAIUoAAFKECBowtk2bGEltBf//Zt5aGB8tCAKeLoPMo5MStf7MvnxGBBzCyKwXKuv9w/c4YQojw09Bcf+MuTT/nE9ksvu/Peex59Ytee2siIUzXpcKrcWP9434Evvfz8ztdfXvvI7i2P/OQzDz16033fv/CyK7ZtveTjHz/rXe96fz7Xn88Xs+esWXPsyHP7g/NCFPN5IcRgX/+cmbNuvvEmkzgrraUyxR3dxuds8PnoF8fvUoACFKAABShAAQpQYEoKMICekreNi6YABShAAQpQgAIUOFIgC6CD2JQv+0n08uuvfugfPprly6KUNWGYryaQLttnISfy9imEKOQKff3F/oH+wSFb35ETBfM7faXiUP9AecZsMThDzJwh5swSg3NE/2xRniHEQFH09RVmFfvmisIMkStl6XMuV8jni/39gwMDQ6VSqSByBZHrK5WPmz1n43nro8BURqtUtqNnpRlAH3kr+R0KUIACFKAABShAgWNGgAH0MXMreSEUoAAFKEABClBgugso292cKlPEoe3xEz99+slnnl24YqkZRTYzyLmifYp80TxFMS+KuVyhUCqJYq4zJ22/lgqinBNmarnzKPab6LnU3/n3QF4M5cWgaZc2j2z2OZ89Or9jvuaFGCj3XXrxjtpExXddUxLi+Wb8edJjut85Xj8FKEABClCAAhSgwLErwAD62L23vDIKUIACFKAABSgwLQVMDK2Un0ShTCTgx+b17l0P/93CM/7gvX9qc+eCMOPNBWHmoQvdsLgwVDbzyvYx6/i5ub6DPxIiNzA0u1gyZR12Wlr054f6xKyymDlYmDtQHigIk1+b9LlgthrMzvOWtxz/j//4sW9945tHuQ8ak/JnWzJ9lF/ityhAAQpQgAIUoAAFKDDlBRhAT/lbyAugAAUoQAEKUIACFOgKtLcQVCprgk6VSqRMpHx6fO/n9uy+/s0nb9314KLly//mL/96oNgvyu1x5nw+L/pzoizKfaJUFqLYHmsumJi5MxqdL+SLZZMuC5HL5fLml8xxX3GwVCqZ9Lkgcnkxe87Mj3z0777whc8//fRT7VUpie5zUsuz1iZ3zhY8+bV7LTygAAUoQAEKUIACFKDAMSDAAPoYuIm8BApQgAIUoAAFKECBgwJZmNsNoLMM+rWg/t1w7x3pvgnAiUOkOqy3vnX3XY/+9MltW7a99z+9x0wwF0zuXBgqi1kzRP+AGBoQc2aK/iykzvf19fUP9ZX6TdZsh53b+w0ODAx94AMf2HbhBc88+1OlUhspQ6lUa2mLQMxug0cNoLMVT46es+ODV8IjClCAAhSgAAUoQAEKTH0BBtBT/x7yCihAAQpQgAIUoAAFJgkcGUBHSjqQPrAf0QGnnpVEIzVV0eYhAdeXsWlnfvr5lzZdc8N7lq//D6s3/ekFl7xr7YaTlq74q8VL15y/dduWCy64cPP52zZs2LDh6qt33nbbtx968GFTNq0gUxknoe83zUSzis0pZWgPsjz66AF0N3qWR5uDZhjdvjv8QgEKUIACFKAABSgwxQUYQE/xG8jlU4ACFKAABShAAQocKjA5gJbQqVKpUpGSkZIwUbMPII3iJIzM+1Jl9ytUSJPsND+ZiD69z9lRUzuayY6x+ldr/nMKTrulWaaI4jTRnex68icnaQAgTtwodqLYswG0ag9BH62Co7NOE4B3w+jDDiafn8cUoAAFKEABClCAAhSYigIMoKfiXeOaKUABClCAAhSgAAV+JYFsoz8oDamR2qfU5p/ZQ9nvxBKxRBJrqapO+oKL6yeSNXvrKyfqVwXJU4APJDYjTpAk5vCQh1bZdoJSI7HPSCMCUvuUdr7atnBkIfOkDmgG0Ic48h8UoAAFKEABClCAAseoAAPoY/TG8rIoQAEKUIACFKAABWCi4Xb6LG0GnaXPyuTSB1PpRJvxZxXZ+BgTwMMJrtw38Rkv+J5p7TDJcVal0QmgO/m1Fc4ybq2PGkBnMfSksWYG0PyzpAAFKEABClCAAhSYZgIMoKfZDeflUoACFKAABShAgekk0J2AltAhdACd2nnldvrcHkLW0EkML4ZnG6HViJLPtZzXZDIGOEBox5htmUZ3ovkgIgPogxY8ogAFKEABClCAAhSgwBECDKCPIOE3KEABClCAAhSgAAWOFYFOOmxyZxe6BR1nAbQZiDb7B5o2ZwWJJIAXoAHdQNqKEXeHnEMkDoIYcadMI5th7v4869/IPicbgp5cwcEJ6GPlL4nXQQEKUIACFKAABSjwbxX4P/HZZ2lq2P/GAAAAAElFTkSuQmCC" width="216.63181102362202" height="108.31590551181101" preserveAspectRatio="none"/>
</g>
<g transform="translate(0 121.31590551181101)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="15.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="25.119999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="35.739999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="43.019999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g11C09650A1107877D1CACE85AD57EEFF" x="57.88949999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="67.1895" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="77.839" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="83.119" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="93.059" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="107.999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="114.759" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="124.879" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="133.81900000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="143.81900000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="151.09900000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="160.17900000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="175.04850000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="184.18850000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="195.02850000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="211.07800000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="221.83800000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="227.258" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="237.258" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="248.018" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="254.778" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="264.89799999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="273.83799999999997" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(94.32999999999997 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="10" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="17.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="26.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="40.3" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="51.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="61.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="71.48" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="80.42" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 433.56299212598424)">
<g class="typst-group">
<g>
<g transform="translate(8 18.5)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAA14E57E2DCC57A3F7809273EECD3C51" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="9.344000000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="12.812800000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="18.5344" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="23.296000000000003" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="29.1456" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="33.8048" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="39.2832" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="46.1696" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="49.638400000000004" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="55.116800000000005" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="60.96640000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g1CB3EC9D05726EBFDE8ADABEC8504FCD" x="67.54560000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="76.4928" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD62975B7DE3250BE5F195D0E8335F60D" x="82.3424" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="88.704" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="92.1728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="98.5728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD5EEFB9760BC9A91B84F628EDDA52971" x="104.4224" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="110.7328" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="114.112" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g83A6AA7A836EACB3652229F4716CDAF" x="123.03359999999999" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gDB4862E33098F259EEBBA99A57E5AFA" x="129.2416" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="139.3536" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="145.2032" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="148.5824" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g793DBE65A5AEC1A16A65955B6C0E046" x="155.1616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gA11612CECC8CBEF18835767DAB11B2F7" x="166.3104" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="172.7616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="177.52319999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gCEFEF3D67F35C6E83CC3757B1DD21B13" x="180.90239999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="190.57919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="196.97919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="201.74079999999995" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g645CA8FA3D9155E2CBD9F8EED3C1540D" x="207.59039999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="214.23359999999997" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(798.4017637795276 8)">
<g class="typst-group">
<g>
<g transform="translate(0 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1B31FFD796CA2E900A884ECD4210CED3" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" x="11.440000000000001" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.608 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="7.44" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="gF74D1E4498220F56E34936C81B24ED2C" overflow="visible">
<path d="M 2.292 1.464 L 2.292 6.276 C 2.292 7.272 2.496 7.3320003 3.336 7.368 C 3.408 7.44 3.408 7.692 3.336 7.764 C 2.808 7.752 2.244 7.7400002 1.776 7.7400002 C 1.38 7.7400002 0.792 7.752 0.228 7.764 C 0.156 7.692 0.156 7.44 0.228 7.368 C 1.068 7.3320003 1.272 7.272 1.272 6.276 L 1.272 1.464 C 1.272 0.468 1.068 0.408 0.228 0.372 C 0.156 0.3 0.156 0.048 0.228 -0.024 C 0.768 -0.012 1.3560001 0 1.788 0 C 2.22 0 2.796 -0.012 3.336 -0.024 C 3.408 0.048 3.408 0.3 3.336 0.372 C 2.496 0.408 2.292 0.468 2.292 1.464 Z "/>
</symbol>
<symbol id="g46E28FC12585DA626130081849FE40B4" overflow="visible">
<path d="M 1.86 1.464 L 1.86 3.744 C 1.86 4.3320003 2.016 4.224 2.292 3.876 L 5.112 0.120000005 C 5.292 -0.072 5.484 -0.144 5.664 -0.144 C 5.808 -0.144 5.928 -0.060000002 5.928 0.18 L 5.928 4.056 C 5.928 5.052 6.06 5.088 6.7920003 5.1480002 C 6.864 5.2200003 6.864 5.472 6.7920003 5.544 C 6.432 5.532 6 5.52 5.64 5.52 C 5.28 5.52 4.86 5.532 4.5 5.544 C 4.428 5.472 4.428 5.2200003 4.5 5.1480002 C 5.232 5.1 5.364 5.052 5.364 4.056 L 5.364 1.812 C 5.364 1.488 5.328 1.284 4.956 1.788 L 2.208 5.52 L 0.504 5.544 L 0.48000002 5.508 L 0.48000002 5.2200003 C 0.48000002 5.172 0.552 5.1480002 0.588 5.1480002 C 1.044 5.112 1.176 4.968 1.296 4.752 L 1.296 1.464 C 1.296 0.468 1.164 0.42000002 0.432 0.372 C 0.36 0.3 0.36 0.048 0.432 -0.024 C 0.792 -0.012 1.212 0 1.572 0 C 1.932 0 2.364 -0.012 2.724 -0.024 C 2.796 0.048 2.796 0.3 2.724 0.372 C 1.992 0.432 1.86 0.468 1.86 1.464 Z "/>
</symbol>
<symbol id="gA2769E14ED9B16297025579DD26D23A1" overflow="visible">
<path d="M 3.648 1.464 L 3.648 4.488 C 3.648 4.932 3.7680001 5.112 4.152 5.112 L 4.464 5.112 C 5.2200003 5.112 5.376 4.872 5.616 4.008 C 5.736 3.984 5.844 3.984 5.94 4.044 C 5.88 4.632 5.868 5.076 5.844 5.64 C 5.4240003 5.592 4.656 5.52 3.648 5.52 L 2.7 5.52 C 1.524 5.52 0.828 5.58 0.504 5.64 C 0.504 5.076 0.492 4.608 0.42000002 4.044 C 0.528 4.008 0.636 3.996 0.744 4.008 C 0.984 4.872 1.116 5.112 1.896 5.112 L 2.184 5.112 C 2.556 5.112 2.7 4.968 2.7 4.5 L 2.7 1.464 C 2.7 0.468 2.568 0.432 1.836 0.372 C 1.764 0.3 1.764 0.048 1.836 -0.024 C 2.28 -0.012 2.772 0 3.18 0 C 3.6000001 0 4.068 -0.012 4.512 -0.024 C 4.584 0.048 4.584 0.3 4.512 0.372 C 3.78 0.42000002 3.648 0.468 3.648 1.464 Z "/>
</symbol>
<symbol id="g48BCA4F06942DA5990D42018985FC781" overflow="visible">
<path d="M 2.292 1.464 L 2.292 2.5080001 L 2.9520001 2.5080001 C 3.408 2.5080001 3.576 2.112 3.732 1.668 L 3.996 0.948 C 4.272 0.204 4.68 -0.084 5.196 -0.084 C 5.376 -0.084 5.748 -0.048 5.952 0 C 5.988 0.120000005 5.964 0.24000001 5.88 0.336 C 5.448 0.336 5.2200003 0.408 4.98 1.0320001 L 4.632 1.932 C 4.488 2.304 4.344 2.5080001 4.188 2.664 L 4.188 2.688 C 4.596 2.832 5.208 3.3240001 5.208 4.152 C 5.208 5.1480002 4.584 5.568 3.1560001 5.568 C 2.856 5.568 2.172 5.52 1.812 5.52 C 1.464 5.52 0.96000004 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.212 0.432 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 0.936 -0.012 1.428 0 1.824 0 C 2.196 0 2.592 -0.012 2.976 -0.024 C 3.048 0.048 3.048 0.3 2.976 0.372 C 2.412 0.408 2.292 0.468 2.292 1.464 Z M 4.164 4.152 C 4.164 3.204 3.888 2.856 2.82 2.856 L 2.292 2.856 L 2.292 4.416 C 2.292 5.052 2.412 5.172 3.084 5.172 C 3.924 5.172 4.164 4.872 4.164 4.152 Z "/>
</symbol>
<symbol id="g4C6038BE04CA3E1481E54A97A0E34303" overflow="visible">
<path d="M 6.324 2.82 C 6.324 4.524 4.956 5.64 3.3960001 5.64 C 1.728 5.64 0.444 4.428 0.444 2.664 C 0.444 1.0320001 1.6800001 -0.120000005 3.3 -0.120000005 C 5.268 -0.120000005 6.324 1.26 6.324 2.82 Z M 3.288 5.244 C 4.356 5.244 5.28 4.26 5.28 2.652 C 5.28 1.176 4.548 0.276 3.48 0.276 C 2.316 0.276 1.488 1.332 1.488 2.808 C 1.488 4.428 2.388 5.244 3.288 5.244 Z "/>
</symbol>
<symbol id="gE1B486BBD379D5D210F28624A61384AE" overflow="visible">
<path d="M 1.776 5.52 C 1.452 5.52 0.912 5.532 0.444 5.544 C 0.372 5.472 0.372 5.2200003 0.444 5.1480002 C 1.176 5.1 1.308 5.052 1.308 4.056 L 1.308 1.464 C 1.308 0.468 1.176 0.432 0.444 0.372 C 0.372 0.3 0.372 0.048 0.444 -0.024 C 0.90000004 -0.012 1.44 0 1.788 0 C 2.1 0 2.58 -0.024 3.54 -0.024 C 4.872 -0.024 6.36 0.6 6.36 2.7 C 6.36 4.296 5.376 5.544 3.372 5.544 C 2.556 5.544 2.124 5.52 1.776 5.52 Z M 2.256 0.912 L 2.256 4.776 C 2.256 5.076 2.556 5.1480002 3.024 5.1480002 C 5.04 5.1480002 5.316 3.744 5.316 2.496 C 5.316 0.816 4.572 0.372 3.252 0.372 C 2.34 0.372 2.256 0.576 2.256 0.912 Z "/>
</symbol>
<symbol id="g9FB16590C6D64699AE0CE54876927A05" overflow="visible">
<path d="M 5.2200003 4.056 L 5.2200003 2.532 C 5.2200003 1.5 5.2200003 0.372 3.636 0.372 C 2.448 0.372 2.196 1.308 2.196 2.424 L 2.196 4.056 C 2.196 5.052 2.328 5.088 3.06 5.1480002 C 3.132 5.2200003 3.132 5.472 3.06 5.544 C 2.592 5.532 2.112 5.52 1.716 5.52 C 1.284 5.52 0.816 5.532 0.384 5.544 C 0.312 5.472 0.312 5.2200003 0.384 5.1480002 C 1.116 5.1 1.248 5.052 1.248 4.056 L 1.248 2.172 C 1.248 0.372 2.124 -0.120000005 3.432 -0.120000005 C 5.292 -0.120000005 5.784 0.936 5.784 2.688 L 5.784 4.056 C 5.784 5.052 5.916 5.088 6.6480002 5.1480002 C 6.7200003 5.2200003 6.7200003 5.472 6.6480002 5.544 C 6.288 5.532 5.856 5.52 5.496 5.52 C 5.136 5.52 4.716 5.532 4.356 5.544 C 4.284 5.472 4.284 5.2200003 4.356 5.1480002 C 5.088 5.1 5.2200003 5.052 5.2200003 4.056 Z "/>
</symbol>
<symbol id="g6799D348D26A0968EEDA80A0E5D50B73" overflow="visible">
<path d="M 3.312 -0.120000005 C 4.248 -0.120000005 4.824 0.228 5.388 0.984 C 5.364 1.068 5.244 1.2 5.1480002 1.224 C 4.596 0.576 4.176 0.336 3.372 0.336 C 2.184 0.336 1.488 1.62 1.488 2.808 C 1.488 4.824 2.424 5.244 3.3240001 5.244 C 4.284 5.244 4.848 4.716 4.992 3.876 C 5.112 3.8400002 5.232 3.8400002 5.352 3.912 C 5.352 4.404 5.328 4.908 5.208 5.448 C 4.752 5.448 4.212 5.64 3.252 5.64 C 1.668 5.64 0.444 4.44 0.444 2.688 C 0.444 1.932 0.684 1.104 1.272 0.564 C 1.752 0.120000005 2.424 -0.120000005 3.312 -0.120000005 Z "/>
</symbol>
<symbol id="g45E4C10E27056C5AE488FE2D8290DF06" overflow="visible">
<path d="M 2.34 4.056 C 2.34 5.052 2.4720001 5.088 3.204 5.1480002 C 3.276 5.2200003 3.276 5.472 3.204 5.544 C 2.748 5.532 2.232 5.52 1.86 5.52 C 1.5 5.52 0.996 5.532 0.528 5.544 C 0.456 5.472 0.456 5.2200003 0.528 5.1480002 C 1.26 5.1 1.392 5.052 1.392 4.056 L 1.392 1.464 C 1.392 0.468 1.26 0.432 0.528 0.372 C 0.456 0.3 0.456 0.048 0.528 -0.024 C 0.972 -0.012 1.464 0 1.872 0 C 2.256 0 2.784 -0.012 3.204 -0.024 C 3.276 0.048 3.276 0.3 3.204 0.372 C 2.4720001 0.42000002 2.34 0.468 2.34 1.464 Z "/>
</symbol>
<symbol id="gD77922058D8F1A3A631DDE5946887BDC" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z M 3.384 5.112 C 4.764 5.112 5.88 4.008 5.88 2.628 C 5.88 1.248 4.752 0.132 3.384 0.132 C 2.004 0.132 0.90000004 1.248 0.90000004 2.628 C 0.90000004 3.996 2.004 5.112 3.384 5.112 Z "/>
</symbol>
<symbol id="g5ABA589ED074A65FC8C929AB4EB2344C" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z "/>
</symbol>
<symbol id="g6F0940D406D545443F0C3F5AB20F1452" overflow="visible">
<path d="M 1.55 0.78999996 L 2.1 2.24 C 2.1499999 2.37 2.21 2.4099998 2.45 2.4099998 L 4.56 2.4099998 L 5.14 0.71999997 C 5.2599998 0.38 4.88 0.34 4.4 0.31 C 4.3399997 0.25 4.3399997 0.04 4.4 -0.02 C 4.77 -0.01 5.3199997 0 5.71 0 C 6.12 0 6.5 -0.01 6.85 -0.02 C 6.91 0.04 6.91 0.25 6.85 0.31 C 6.46 0.35 6.12 0.38 5.95 0.85999995 L 3.8899999 6.58 C 3.74 6.49 3.47 6.3799996 3.34 6.3799996 L 1.0699999 1.02 C 0.81 0.39999998 0.51 0.34 0.07 0.31 C 0.01 0.25 0.01 0.04 0.07 -0.02 C 0.32999998 -0.01 0.65999997 0 0.96 0 C 1.37 0 1.87 -0.01 2.24 -0.02 C 2.3 0.04 2.3 0.25 2.24 0.31 C 1.86 0.34 1.39 0.38 1.55 0.78999996 Z M 2.6299999 2.83 C 2.4099998 2.83 2.34 2.86 2.3799999 2.96 L 3.3999999 5.5499997 L 3.46 5.5499997 L 4.4 2.83 Z "/>
</symbol>
<symbol id="g6D72A0AB4EFB019D977FFECF4A1600A9" overflow="visible">
<path d="M 3.79 0 C 3.79 0 4.02 0.96 4.0899997 1.38 C 4 1.43 3.9199998 1.4499999 3.81 1.42 C 3.6499999 0.83 3.36 0.34 2.73 0.34 L 2.28 0.34 C 2.05 0.34 1.91 0.5 1.91 0.69 L 1.91 3.3799999 C 1.91 4.21 2.02 4.24 2.6299999 4.29 C 2.69 4.35 2.69 4.56 2.6299999 4.62 C 2.26 4.61 1.8499999 4.6 1.51 4.6 C 1.1999999 4.6 0.77 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.1 0.34 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.89 -0.01 1.55 0 1.55 0 Z "/>
</symbol>
<symbol id="g7035BD9A81EA6DB089327941BB80DFF8" overflow="visible">
<path d="M 4.72 0.90999997 C 4.72 1.74 4.7799997 1.77 5.0899997 1.8199999 C 5.15 1.88 5.15 2.09 5.0899997 2.1499999 C 4.91 2.1399999 4.63 2.1299999 4.3199997 2.1299999 C 4.02 2.1299999 3.56 2.1399999 3.27 2.1499999 C 3.21 2.09 3.21 1.88 3.27 1.8199999 C 3.8799999 1.78 3.9299998 1.74 3.9299998 0.90999997 L 3.9299998 0.37 C 3.61 0.28 3.28 0.22999999 2.9299998 0.22999999 C 1.68 0.22999999 1.27 1.51 1.27 2.33 C 1.27 3.54 1.8499999 4.37 2.81 4.37 C 3.8 4.37 4.22 3.87 4.37 3.23 C 4.47 3.1999998 4.5699997 3.1999998 4.67 3.26 C 4.66 3.6699998 4.63 4.0899997 4.54 4.54 C 4.24 4.54 3.5 4.7 2.9399998 4.7 C 1.51 4.7 0.37 3.78 0.37 2.2 C 0.37 0.93 1.3199999 -0.099999994 2.75 -0.099999994 C 3.4299998 -0.099999994 4.17 0 4.83 0.35999998 C 4.7599998 0.42999998 4.72 0.52 4.72 0.59 Z "/>
</symbol>
<symbol id="g7FD6A8241485CEBC032BD9E4CE659816" overflow="visible">
<path d="M 5.27 2.35 C 5.27 3.77 4.13 4.7 2.83 4.7 C 1.4399999 4.7 0.37 3.6899998 0.37 2.22 C 0.37 0.85999995 1.4 -0.099999994 2.75 -0.099999994 C 4.39 -0.099999994 5.27 1.05 5.27 2.35 Z M 2.74 4.37 C 3.6299999 4.37 4.4 3.55 4.4 2.21 C 4.4 0.97999996 3.79 0.22999999 2.8999999 0.22999999 C 1.93 0.22999999 1.24 1.11 1.24 2.34 C 1.24 3.6899998 1.99 4.37 2.74 4.37 Z "/>
</symbol>
<symbol id="gFAD9169AC3141E7FC4EA568E3BBD2E9B" overflow="visible">
<path d="M 1.91 1.22 L 1.91 2.09 L 2.46 2.09 C 2.84 2.09 2.98 1.76 3.11 1.39 L 3.33 0.78999996 C 3.56 0.17 3.8999999 -0.07 4.33 -0.07 C 4.48 -0.07 4.79 -0.04 4.96 0 C 4.99 0.099999994 4.97 0.19999999 4.9 0.28 C 4.54 0.28 4.35 0.34 4.15 0.85999995 L 3.86 1.61 C 3.74 1.92 3.62 2.09 3.49 2.22 L 3.49 2.24 C 3.83 2.36 4.3399997 2.77 4.3399997 3.46 C 4.3399997 4.29 3.82 4.64 2.6299999 4.64 C 2.3799999 4.64 1.81 4.6 1.51 4.6 C 1.22 4.6 0.79999995 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.78 -0.01 1.1899999 0 1.52 0 C 1.8299999 0 2.1599998 -0.01 2.48 -0.02 C 2.54 0.04 2.54 0.25 2.48 0.31 C 2.01 0.34 1.91 0.39 1.91 1.22 Z M 3.47 3.46 C 3.47 2.6699998 3.24 2.3799999 2.35 2.3799999 L 1.91 2.3799999 L 1.91 3.6799998 C 1.91 4.21 2.01 4.31 2.57 4.31 C 3.27 4.31 3.47 4.06 3.47 3.46 Z "/>
</symbol>
<symbol id="g5503E15E5E4E70E9E217A15BD1ECD752" overflow="visible">
<path d="M 1.9499999 3.3799999 C 1.9499999 4.21 2.06 4.24 2.6699998 4.29 C 2.73 4.35 2.73 4.56 2.6699998 4.62 C 2.29 4.61 1.86 4.6 1.55 4.6 C 1.25 4.6 0.83 4.61 0.44 4.62 C 0.38 4.56 0.38 4.35 0.44 4.29 C 1.05 4.25 1.16 4.21 1.16 3.3799999 L 1.16 1.22 C 1.16 0.39 1.05 0.35999998 0.44 0.31 C 0.38 0.25 0.38 0.04 0.44 -0.02 C 0.81 -0.01 1.22 0 1.56 0 C 1.88 0 2.32 -0.01 2.6699998 -0.02 C 2.73 0.04 2.73 0.25 2.6699998 0.31 C 2.06 0.35 1.9499999 0.39 1.9499999 1.22 Z "/>
</symbol>
<symbol id="gA419F36517085793EDBF3FE4736A2E59" overflow="visible">
<path d="M 3.04 1.22 L 3.04 3.74 C 3.04 4.11 3.1399999 4.2599998 3.46 4.2599998 L 3.72 4.2599998 C 4.35 4.2599998 4.48 4.06 4.68 3.34 C 4.7799997 3.32 4.87 3.32 4.95 3.37 C 4.9 3.86 4.89 4.23 4.87 4.7 C 4.52 4.66 3.8799999 4.6 3.04 4.6 L 2.25 4.6 C 1.27 4.6 0.69 4.65 0.42 4.7 C 0.42 4.23 0.41 3.84 0.35 3.37 C 0.44 3.34 0.53 3.33 0.62 3.34 C 0.82 4.06 0.93 4.2599998 1.5799999 4.2599998 L 1.8199999 4.2599998 C 2.1299999 4.2599998 2.25 4.14 2.25 3.75 L 2.25 1.22 C 2.25 0.39 2.1399999 0.35999998 1.53 0.31 C 1.4699999 0.25 1.4699999 0.04 1.53 -0.02 C 1.9 -0.01 2.31 0 2.6499999 0 C 3 0 3.3899999 -0.01 3.76 -0.02 C 3.82 0.04 3.82 0.25 3.76 0.31 C 3.1499999 0.35 3.04 0.39 3.04 1.22 Z "/>
</symbol>
<symbol id="gFF65128B49BB3276E17D04989ECB7ACE" overflow="visible">
<path d="M 5 3.3799999 C 5 4.21 5.1099997 4.24 5.72 4.29 C 5.7799997 4.35 5.7799997 4.56 5.72 4.62 C 5.37 4.6 4.93 4.6 4.6 4.6 C 4.3199997 4.6 3.8799999 4.61 3.49 4.62 C 3.4299998 4.56 3.4299998 4.35 3.49 4.29 C 4.1 4.25 4.21 4.21 4.21 3.3799999 L 4.21 2.52 L 1.9 2.52 L 1.9 3.3799999 C 1.9 4.21 2.01 4.24 2.62 4.29 C 2.6799998 4.35 2.6799998 4.56 2.62 4.62 C 2.24 4.61 1.8199999 4.6 1.5 4.6 C 1.1999999 4.6 0.78999996 4.61 0.39 4.62 C 0.32999998 4.56 0.32999998 4.35 0.39 4.29 C 1 4.25 1.11 4.21 1.11 3.3799999 L 1.11 1.22 C 1.11 0.39 1 0.35999998 0.39 0.31 C 0.32999998 0.25 0.32999998 0.04 0.39 -0.02 C 0.78999996 -0.01 1.1899999 0 1.51 0 C 1.8299999 0 2.23 -0.01 2.62 -0.02 C 2.6799998 0.04 2.6799998 0.25 2.62 0.31 C 2.01 0.35 1.9 0.39 1.9 1.22 L 1.9 2.19 L 4.21 2.19 L 4.21 1.22 C 4.21 0.39 4.1 0.35999998 3.49 0.31 C 3.4299998 0.25 3.4299998 0.04 3.49 -0.02 C 3.86 -0.01 4.2599998 0 4.61 0 C 4.91 0 5.33 -0.01 5.72 -0.02 C 5.7799997 0.04 5.7799997 0.25 5.72 0.31 C 5.1099997 0.35 5 0.39 5 1.22 Z "/>
</symbol>
<symbol id="gEDADDD9BA25BBB833C1F4B684DC50419" overflow="visible">
<path d="M 4.83 3.82 L 4.9 3.82 L 5.0299997 1.23 C 5.0699997 0.39999998 5.06 0.35999998 4.52 0.31 C 4.46 0.25 4.46 0.04 4.52 -0.02 C 4.87 -0.01 5.24 0 5.52 0 C 5.8199997 0 6.1099997 -0.01 6.3799996 -0.02 C 6.44 0.04 6.44 0.25 6.3799996 0.31 C 5.87 0.35999998 5.8599997 0.42 5.7999997 1.23 L 5.6 3.81 C 5.5699997 4.21 5.66 4.25 6.16 4.29 C 6.22 4.35 6.22 4.56 6.16 4.62 L 4.81 4.6 L 3.31 1.02 L 2.03 4.6 L 0.64 4.62 C 0.58 4.56 0.58 4.35 0.64 4.29 C 1.13 4.2599998 1.22 4.21 1.1999999 4.02 L 0.88 1.2099999 C 0.78999996 0.38 0.65999997 0.34 0.28 0.31 C 0.22 0.25 0.22 0.04 0.28 -0.02 C 0.48 -0.01 0.78 0 0.94 0 C 1.14 0 1.51 -0.01 1.7099999 -0.02 C 1.77 0.04 1.77 0.25 1.7099999 0.31 C 1.14 0.35 1.15 0.47 1.23 1.2099999 L 1.52 3.75 L 1.54 3.75 L 2.96 -0.04 C 2.98 -0.089999996 3.03 -0.12 3.08 -0.12 C 3.12 -0.12 3.1699998 -0.089999996 3.1899998 -0.04 Z "/>
</symbol>
<symbol id="g1E8994F5C297EC73FA26D93D22635023" overflow="visible">
<path d="M 2.82 -0.14999999 C 4.11 -0.14999999 5.16 0.9 5.16 2.19 C 5.16 3.48 4.11 4.52 2.82 4.52 C 1.53 4.52 0.48999998 3.48 0.48999998 2.19 C 0.48999998 0.9 1.53 -0.14999999 2.82 -0.14999999 Z M 2.82 4.2599998 C 3.97 4.2599998 4.9 3.34 4.9 2.19 C 4.9 1.04 3.9599998 0.11 2.82 0.11 C 1.67 0.11 0.75 1.04 0.75 2.19 C 0.75 3.33 1.67 4.2599998 2.82 4.2599998 Z "/>
</symbol>
<symbol id="g5396A27CA60B9808846A090320835A9F" overflow="visible">
<path d="M 1.91 1.22 L 1.91 5.23 C 1.91 6.06 2.08 6.1099997 2.78 6.14 C 2.84 6.2 2.84 6.41 2.78 6.47 C 2.34 6.46 1.87 6.45 1.48 6.45 C 1.15 6.45 0.65999997 6.46 0.19 6.47 C 0.13 6.41 0.13 6.2 0.19 6.14 C 0.89 6.1099997 1.06 6.06 1.06 5.23 L 1.06 1.22 C 1.06 0.39 0.89 0.34 0.19 0.31 C 0.13 0.25 0.13 0.04 0.19 -0.02 C 0.64 -0.01 1.13 0 1.49 0 C 1.8499999 0 2.33 -0.01 2.78 -0.02 C 2.84 0.04 2.84 0.25 2.78 0.31 C 2.08 0.34 1.91 0.39 1.91 1.22 Z "/>
</symbol>
<symbol id="g97A8E46F7A64F11D13C6F357868587EE" overflow="visible">
<path d="M 1.89 1.22 L 1.89 1.9599999 C 2.07 1.88 2.27 1.8399999 2.52 1.8399999 C 3.86 1.8399999 4.27 2.8 4.27 3.3999999 C 4.27 3.9199998 3.97 4.62 2.55 4.62 C 2.18 4.62 1.76 4.6 1.49 4.6 C 1.1999999 4.6 0.78 4.61 0.38 4.62 C 0.32 4.56 0.32 4.35 0.38 4.29 C 0.98999995 4.25 1.1 4.21 1.1 3.3799999 L 1.1 1.22 C 1.1 0.39 0.98999995 0.35999998 0.38 0.31 C 0.32 0.25 0.32 0.04 0.38 -0.02 C 0.71 -0.01 1.06 0 1.5 0 C 1.93 0 2.28 -0.01 2.61 -0.02 C 2.6699998 0.04 2.6699998 0.25 2.61 0.31 C 2 0.35 1.89 0.39 1.89 1.22 Z M 1.89 3.84 C 1.89 4.16 2.01 4.29 2.49 4.29 C 3.08 4.29 3.3999999 3.98 3.3999999 3.28 C 3.3999999 2.56 3.1399999 2.1699998 2.54 2.1699998 C 2.34 2.1699998 2.09 2.2 1.89 2.28 Z "/>
</symbol>
<symbol id="gB844DCFB76B4CC44608DB013C9764E9C" overflow="visible">
<path d="M 1.8299999 3.62 C 1.5899999 4.19 1.5999999 4.24 2.1399999 4.29 C 2.2 4.35 2.2 4.56 2.1399999 4.62 C 1.8299999 4.61 1.49 4.6 1.0799999 4.6 C 0.76 4.6 0.45999998 4.61 0.19999999 4.62 C 0.14 4.56 0.14 4.35 0.19999999 4.29 C 0.69 4.24 0.76 4.13 1 3.56 L 2.4199998 0.28 C 2.55 -0.01 2.6 -0.12 2.71 -0.12 C 2.78 -0.12 2.82 -0.04 2.96 0.28 L 4.42 3.55 C 4.63 4.0099998 4.74 4.25 5.2799997 4.29 C 5.3399997 4.35 5.3399997 4.56 5.2799997 4.62 C 5.06 4.61 4.8199997 4.6 4.56 4.6 C 4.19 4.6 3.9099998 4.61 3.6399999 4.62 C 3.58 4.56 3.58 4.35 3.6399999 4.29 C 4.18 4.25 4.23 4.13 4.0299997 3.62 L 2.9399998 1.13 C 2.9099998 1.1 2.8999999 1.1 2.87 1.13 Z "/>
</symbol>
<symbol id="gDAA1267270512376F631C9A10449D5F4" overflow="visible">
<path d="M 2.48 2.25 C 3.1399999 2.25 3.1499999 2.06 3.1699998 1.6899999 C 3.22 1.64 3.3999999 1.64 3.4499998 1.6899999 C 3.4399998 1.92 3.4299998 2.26 3.4299998 2.4199998 C 3.4299998 2.56 3.4399998 2.8799999 3.4499998 3.1299999 C 3.3999999 3.1799998 3.22 3.1799998 3.1699998 3.1299999 C 3.1499999 2.6799998 3.1299999 2.57 2.48 2.57 L 1.91 2.57 L 1.91 3.99 C 1.91 4.16 2.04 4.27 2.23 4.27 L 2.8 4.27 C 3.62 4.27 3.75 3.9399998 3.9299998 3.37 C 4.0299997 3.36 4.12 3.3799999 4.2 3.4199998 C 4.16 3.76 4.04 4.54 4.02 4.61 C 4.02 4.63 4.0099998 4.64 3.99 4.64 C 3.85 4.61 3.75 4.6 3.58 4.6 L 1.51 4.6 C 1.22 4.6 0.76 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.76 -0.01 1.1999999 0 1.52 0 L 3.06 0 C 3.46 0 4.12 -0.02 4.12 -0.02 C 4.24 0.39 4.35 0.94 4.42 1.36 C 4.33 1.41 4.25 1.43 4.14 1.4 C 3.98 0.81 3.6899998 0.31 2.86 0.31 L 2.4299998 0.31 C 2.01 0.31 1.91 0.42 1.91 0.75 L 1.91 2.25 Z "/>
</symbol>
<symbol id="gEEE4EC0F13100E99C1017169F912BE3E" overflow="visible">
<path d="M 1.55 1.22 L 1.55 3.12 C 1.55 3.61 1.68 3.52 1.91 3.23 L 4.2599998 0.099999994 C 4.41 -0.06 4.5699997 -0.12 4.72 -0.12 C 4.8399997 -0.12 4.94 -0.049999997 4.94 0.14999999 L 4.94 3.3799999 C 4.94 4.21 5.0499997 4.24 5.66 4.29 C 5.72 4.35 5.72 4.56 5.66 4.62 C 5.3599997 4.61 5 4.6 4.7 4.6 C 4.4 4.6 4.0499997 4.61 3.75 4.62 C 3.6899998 4.56 3.6899998 4.35 3.75 4.29 C 4.36 4.25 4.47 4.21 4.47 3.3799999 L 4.47 1.51 C 4.47 1.24 4.44 1.0699999 4.13 1.49 L 1.8399999 4.6 L 0.42 4.62 L 0.39999998 4.5899997 L 0.39999998 4.35 C 0.39999998 4.31 0.45999998 4.29 0.48999998 4.29 C 0.87 4.2599998 0.97999996 4.14 1.0799999 3.9599998 L 1.0799999 1.22 C 1.0799999 0.39 0.96999997 0.35 0.35999998 0.31 C 0.29999998 0.25 0.29999998 0.04 0.35999998 -0.02 C 0.65999997 -0.01 1.01 0 1.31 0 C 1.61 0 1.9699999 -0.01 2.27 -0.02 C 2.33 0.04 2.33 0.25 2.27 0.31 C 1.66 0.35999998 1.55 0.39 1.55 1.22 Z "/>
</symbol>
<symbol id="g14F95E5F274105B73EC9103738D4C7FD" overflow="visible">
<path d="M 15.144 0 C 15.144 0 15.024 1.704 15.024 2.448 L 15.024 12.288 C 15.024 14.424 15.432 14.544 17.112 14.712 C 17.256 14.856 17.256 15.384 17.112 15.528 C 15.936 15.504 15.528 15.4800005 14.52 15.4800005 C 13.440001 15.4800005 12.936 15.504 11.736 15.528 C 11.592 15.384 11.592 14.856 11.736 14.712 C 13.416 14.544 13.824 14.472 13.824 12.288 L 13.824 5.544 C 13.824 4.9440002 13.512 5.064 13.176 5.472 L 6.816 12.96 L 4.68 15.4800005 L 0.768 15.528 C 0.624 15.384 0.624 14.856 0.768 14.712 C 1.8000001 14.64 2.52 13.824 2.664 13.2 L 2.664 3.192 C 2.664 1.056 2.256 0.936 0.576 0.768 C 0.432 0.624 0.432 0.096 0.576 -0.048 C 1.752 -0.024 2.208 0 3.264 0 C 4.32 0 4.752 -0.024 5.952 -0.048 C 6.096 0.096 6.096 0.624 5.952 0.768 C 4.272 0.936 3.864 1.008 3.864 3.192 L 3.864 10.32 C 3.864 10.56 3.912 10.8 4.056 10.8 C 4.176 10.8 4.368 10.632 4.632 10.32 L 12.672 0.768 C 13.152 0.168 13.632 -0.288 13.632 -0.288 C 14.472 -0.288 14.712 -0.216 15.144 0 Z "/>
</symbol>
<symbol id="gFC5C8D23DE5E426807758A924FDBA2FC" overflow="visible">
<path d="M 10.104 15.144 C 8.784 15.336 8.28 15.792 6.048 15.792 C 4.968 15.792 3.552 15.456 2.544 14.64 C 1.656 13.92 0.984 12.816 0.984 11.64 C 0.984 10.728 1.224 9.576 1.776 8.856 C 2.88 7.368 4.872 6.552 5.9040003 5.8320003 C 7.008 5.064 8.088 4.104 8.088 2.76 C 8.088 1.584 7.056 0.768 5.592 0.768 C 3.984 0.768 2.328 2.088 1.848 4.272 C 1.464 4.416 1.08 4.32 0.72 4.224 C 0.696 4.224 0.672 4.2 0.648 4.2 C 0.648 2.4 0.84000003 1.128 1.104 0.24000001 C 2.4720001 0.24000001 2.544 -0.24000001 5.856 -0.24000001 C 7.32 -0.24000001 8.496 0.192 9.4800005 1.08 C 10.344 1.824 11.112 2.928 11.112 4.416 C 11.112 5.664 10.584 6.504 9.864 7.296 C 8.928 8.328 7.584 9.0720005 6.6480002 9.552 C 5.688 10.032001 3.984 11.28 3.984 12.648 C 3.984 13.992001 4.8 14.808001 6.024 14.808001 C 8.064 14.808001 8.736 12.96 9.168 11.376 C 9.504 11.28 10.104 11.28 10.368 11.496 C 10.368 12.768 10.272 13.752 10.104 15.144 Z "/>
</symbol>
<symbol id="g47EDFEA5ED41C2BE4D53DD4DC8C28ED" overflow="visible">
<path d="M 13.8 14.712 C 13.344 14.616 12.672 14.616 12.36 14.712 L 8.928 5.04 L 8.76 4.416 L 8.52 5.184 L 5.9040003 13.752 C 5.664 14.544 6.528 14.64 7.6800003 14.712 C 7.824 14.856 7.824 15.384 7.6800003 15.528 C 6.7920003 15.504 4.392 15.4800005 3.456 15.4800005 C 2.4720001 15.4800005 1.128 15.504 0.24000001 15.528 C 0.096 15.384 0.096 14.856 0.24000001 14.712 C 1.176 14.616 2.04 14.448 2.4 13.416 L 6.912 0.264 C 7.08 -0.24000001 7.44 -0.288 7.704 -0.288 C 7.9440002 -0.288 8.328 -0.24000001 8.52 0.264 L 12.12 9.84 L 15.792 0.264 C 15.96 -0.192 16.224 -0.288 16.584 -0.288 C 16.896 -0.288 17.232 -0.168 17.4 0.264 L 21.912 12.552 C 22.416 13.968 23.376 14.64 24.432001 14.712 C 24.576 14.856 24.576 15.384 24.432001 15.528 C 23.64 15.504 22.824 15.4800005 21.984 15.4800005 C 21 15.4800005 19.872 15.504 18.984 15.528 C 18.84 15.384 18.84 14.856 18.984 14.712 C 20.352 14.496 20.808 13.992001 20.52 13.104 L 17.808 5.04 L 17.52 4.176 L 17.16 5.184 Z "/>
</symbol>
<symbol id="gF7DAC8BB30649014016B28F6AD7EC048" overflow="visible">
<path d="M 12.62 0 C 12.62 0 12.5199995 1.42 12.5199995 2.04 L 12.5199995 10.24 C 12.5199995 12.0199995 12.86 12.12 14.259999 12.259999 C 14.38 12.38 14.38 12.82 14.259999 12.94 C 13.28 12.92 12.94 12.9 12.099999 12.9 C 11.2 12.9 10.78 12.92 9.78 12.94 C 9.66 12.82 9.66 12.38 9.78 12.259999 C 11.179999 12.12 11.5199995 12.059999 11.5199995 10.24 L 11.5199995 4.62 C 11.5199995 4.12 11.259999 4.22 10.98 4.56 L 5.68 10.8 L 3.8999999 12.9 L 0.64 12.94 C 0.52 12.82 0.52 12.38 0.64 12.259999 C 1.5 12.2 2.1 11.5199995 2.22 11 L 2.22 2.6599998 C 2.22 0.88 1.88 0.78 0.48 0.64 C 0.35999998 0.52 0.35999998 0.08 0.48 -0.04 C 1.4599999 -0.02 1.8399999 0 2.72 0 C 3.6 0 3.9599998 -0.02 4.96 -0.04 C 5.08 0.08 5.08 0.52 4.96 0.64 C 3.56 0.78 3.22 0.84 3.22 2.6599998 L 3.22 8.599999 C 3.22 8.8 3.26 9 3.3799999 9 C 3.48 9 3.6399999 8.86 3.86 8.599999 L 10.559999 0.64 C 10.96 0.14 11.36 -0.24 11.36 -0.24 C 12.059999 -0.24 12.259999 -0.17999999 12.62 0 Z "/>
</symbol>
<symbol id="g8F63AAB7FFA6B186E1B4BC124750174B" overflow="visible">
<path d="M 8.42 12.62 C 7.3199997 12.78 6.8999996 13.16 5.04 13.16 C 4.14 13.16 2.96 12.88 2.12 12.2 C 1.38 11.599999 0.82 10.679999 0.82 9.7 C 0.82 8.94 1.02 7.98 1.48 7.3799996 C 2.3999999 6.14 4.06 5.46 4.92 4.8599997 C 5.8399997 4.22 6.74 3.4199998 6.74 2.3 C 6.74 1.3199999 5.8799996 0.64 4.66 0.64 C 3.32 0.64 1.9399999 1.74 1.54 3.56 C 1.22 3.6799998 0.9 3.6 0.59999996 3.52 C 0.58 3.52 0.56 3.5 0.53999996 3.5 C 0.53999996 2 0.7 0.94 0.91999996 0.19999999 C 2.06 0.19999999 2.12 -0.19999999 4.88 -0.19999999 C 6.1 -0.19999999 7.08 0.16 7.8999996 0.9 C 8.62 1.52 9.26 2.44 9.26 3.6799998 C 9.26 4.72 8.82 5.42 8.22 6.08 C 7.44 6.94 6.3199997 7.56 5.54 7.96 C 4.74 8.36 3.32 9.4 3.32 10.54 C 3.32 11.66 4 12.34 5.02 12.34 C 6.72 12.34 7.2799997 10.8 7.64 9.48 C 7.9199996 9.4 8.42 9.4 8.639999 9.58 C 8.639999 10.639999 8.559999 11.46 8.42 12.62 Z "/>
</symbol>
<symbol id="g1E298373CF470F56F03EC97C7DE8EA04" overflow="visible">
<path d="M 11.5 12.259999 C 11.12 12.179999 10.559999 12.179999 10.3 12.259999 L 7.44 4.2 L 7.2999997 3.6799998 L 7.1 4.3199997 L 4.92 11.46 C 4.72 12.12 5.44 12.2 6.3999996 12.259999 C 6.52 12.38 6.52 12.82 6.3999996 12.94 C 5.66 12.92 3.6599998 12.9 2.8799999 12.9 C 2.06 12.9 0.94 12.92 0.19999999 12.94 C 0.08 12.82 0.08 12.38 0.19999999 12.259999 C 0.97999996 12.179999 1.6999999 12.04 2 11.179999 L 5.7599998 0.22 C 5.9 -0.19999999 6.2 -0.24 6.42 -0.24 C 6.62 -0.24 6.94 -0.19999999 7.1 0.22 L 10.099999 8.2 L 13.16 0.22 C 13.299999 -0.16 13.5199995 -0.24 13.82 -0.24 C 14.08 -0.24 14.36 -0.14 14.5 0.22 L 18.26 10.46 C 18.68 11.639999 19.48 12.2 20.359999 12.259999 C 20.48 12.38 20.48 12.82 20.359999 12.94 C 19.699999 12.92 19.02 12.9 18.32 12.9 C 17.5 12.9 16.56 12.92 15.82 12.94 C 15.7 12.82 15.7 12.38 15.82 12.259999 C 16.96 12.08 17.34 11.66 17.1 10.92 L 14.839999 4.2 L 14.599999 3.48 L 14.299999 4.3199997 Z "/>
</symbol>
<symbol id="g73F93EFBB215913414E078CF4300A07" overflow="visible">
<path d="M 2.1599998 10.46 L 2.1599998 2.44 C 2.1599998 0.78 1.5999999 0.7 0.5 0.64 C 0.29999998 0.52 0.29999998 0.08 0.5 -0.04 C 1.3 -0.02 2.78 0 3.58 0 C 4.38 0 5.8199997 -0.02 6.62 -0.04 C 6.8199997 0.08 6.8199997 0.52 6.62 0.64 C 5.52 0.7 4.96 0.78 4.96 2.44 L 4.96 6.3599997 C 5.56 6.22 5.8599997 5.94 6.2599998 5.42 L 9.28 1.48 C 9.679999 0.96 9.96 0.39999998 10 0.08 C 10 0.02 10.0199995 -0.04 10.099999 -0.04 C 10.5 -0.02 11.559999 0 12.16 0 C 12.94 0 13.74 -0.02 14.5199995 -0.04 C 14.639999 0.08 14.639999 0.52 14.5199995 0.64 C 13.92 0.71999997 13.48 0.88 12.96 1.48 L 8.58 6.66 C 8.24 7.06 7.98 7.3999996 7.98 7.56 C 7.98 7.7 8 7.94 8.22 8.139999 L 10.4 10.08 C 11.58 11.12 12.7 12.099999 13.88 12.259999 C 14 12.38 14 12.82 13.88 12.94 C 13.38 12.92 12.679999 12.9 11.98 12.9 C 11.179999 12.9 10.28 12.92 9.5199995 12.94 C 9.4 12.82 9.4 12.38 9.5199995 12.259999 C 10.7 12.139999 10.62 11.5199995 9.62 10.5 C 9 9.86 7.48 8.599999 7.48 8.599999 C 6.18 7.44 5.62 7.06 4.96 6.8399997 L 4.96 10.46 C 4.96 12.12 5.52 12.2 6.62 12.259999 C 6.8199997 12.38 6.8199997 12.82 6.62 12.94 C 5.8199997 12.92 4.38 12.9 3.58 12.9 C 2.78 12.9 1.3 12.92 0.5 12.94 C 0.29999998 12.82 0.29999998 12.38 0.5 12.259999 C 1.5999999 12.2 2.1599998 12.12 2.1599998 10.46 Z "/>
</symbol>
<symbol id="gD9D3B6C4D6AB50B3CADCA65007C1BC50" overflow="visible">
<path d="M 8.62 2.58 C 7.7999997 1.74 6.72 1.52 5.96 1.52 C 4.4 1.52 3.4399998 2.4199998 3.4399998 4.38 C 3.4399998 4.52 3.46 4.6 3.46 4.7 L 8.26 4.7 C 8.74 4.7 8.84 5.04 8.84 5.3199997 C 8.84 7.02 8.179999 8.88 5.24 8.88 C 3.1399999 8.88 0.74 7.02 0.74 3.9599998 C 0.74 2.8 1.16 1.5799999 2.02 0.79999995 C 2.78 0.12 3.76 -0.19999999 5.18 -0.19999999 C 6.56 -0.19999999 7.9199996 0.5 8.92 1.9599999 C 8.92 2.22 8.82 2.58 8.62 2.58 Z M 3.54 5.5 C 3.56 6.2 3.6599998 6.96 3.9399998 7.3599997 C 4.2599998 7.8399997 4.7999997 8.04 5.02 8.04 C 5.56 8.04 6.2999997 7.52 6.2999997 5.92 C 6.2999997 5.7999997 6.2999997 5.54 6.2599998 5.5 Z "/>
</symbol>
<symbol id="gAFD7B3D7EB6599FB514B70015F312425" overflow="visible">
<path d="M 4.8399997 -3.36 C 5.16 -2.8 5.46 -2.08 5.7 -1.48 C 7.2999997 2.3799999 8.28 4.54 9.34 6.7799997 C 9.62 7.3599997 10.219999 7.98 10.96 8.04 C 11.08 8.16 11.08 8.599999 10.96 8.72 C 10.46 8.7 10.099999 8.679999 9.54 8.679999 C 8.84 8.679999 8.16 8.7 7.4199996 8.72 C 7.2999997 8.599999 7.2999997 8.16 7.4199996 8.04 C 8.059999 7.98 8.7 7.8799996 8.38 7.16 L 6.3199997 2.54 C 6.3199997 2.52 6.3199997 2.52 6.2999997 2.5 C 6.2999997 2.52 6.2999997 2.54 6.2799997 2.58 L 4.42 6.7599998 C 4.4 6.7799997 4.4 6.7999997 4.4 6.8199997 C 4.04 7.6 3.8999999 7.94 5.08 8.04 C 5.2 8.16 5.2 8.599999 5.08 8.72 C 4.3399997 8.7 3.1399999 8.679999 2.4199998 8.679999 C 1.74 8.679999 0.59999996 8.7 0.19999999 8.72 C 0.08 8.599999 0.08 8.16 0.19999999 8.04 C 1.0799999 7.96 1.24 7.8199997 1.78 6.56 L 4.36 0.64 C 4.42 0.53999996 4.5 0.45999998 4.56 0.38 C 4.8199997 0.02 5.04 -0.28 4.92 -0.56 L 4.44 -1.66 C 4.18 -2.28 3.9399998 -2.6399999 3.3799999 -2.6399999 C 3.02 -2.6399999 2.96 -2.56 2.6799998 -2.56 C 1.92 -2.56 1.48 -3.08 1.48 -3.48 C 1.48 -3.74 1.54 -4.06 1.7199999 -4.2799997 C 1.9 -4.5 2.24 -4.64 2.5 -4.64 C 2.76 -4.64 3.36 -4.56 3.6399999 -4.44 C 4.06 -4.24 4.62 -3.76 4.8399997 -3.36 Z "/>
</symbol>
<symbol id="g1E934D63EFC0D2D779AEFC9122E70AE4" overflow="visible">
<path d="M 2.28 10.46 L 2.28 2.44 C 2.28 0.78 1.7199999 0.7 0.62 0.64 C 0.42 0.52 0.42 0.08 0.62 -0.04 C 1.42 -0.02 2.8999999 0 3.6999998 0 C 4.5 0 5.94 -0.02 6.74 -0.04 C 6.94 0.08 6.94 0.52 6.74 0.64 C 5.64 0.7 5.08 0.78 5.08 2.44 L 5.08 10.46 C 5.08 12.12 5.64 12.2 6.74 12.259999 C 6.94 12.38 6.94 12.82 6.74 12.94 C 5.94 12.92 4.5 12.9 3.6999998 12.9 C 2.8999999 12.9 1.42 12.92 0.62 12.94 C 0.42 12.82 0.42 12.38 0.62 12.259999 C 1.7199999 12.2 2.28 12.12 2.28 10.46 Z "/>
</symbol>
<symbol id="g5A467C6F5424E9C7BB01147ABA438205" overflow="visible">
<path d="M 7.1 0.96 C 7.14 0.48 7.18 0.14 7.18 0.14 C 7.2 -0.099999994 7.3599997 -0.19999999 7.64 -0.19999999 C 8.38 0 9.58 0.28 10.96 0.45999998 C 11 0.58 10.96 0.97999996 10.92 1.1 C 9.84 1.1999999 9.62 1.52 9.62 2.6599998 L 9.62 11.66 C 9.62 12.96 9.679999 13.7 9.679999 13.7 C 9.679999 13.88 9.54 13.96 9.36 13.96 C 8.62 13.719999 7.02 13.5 5.6 13.44 C 5.54 13.2 5.56 12.94 5.66 12.759999 C 6.92 12.66 7.02 12.639999 7.02 11.259999 L 7.02 8.66 C 6.64 8.78 6.16 8.88 5.58 8.88 C 3 8.88 0.74 6.62 0.74 3.9599998 C 0.74 2.78 1.16 1.4 2.1399999 0.64 C 2.86 0.08 3.36 -0.19999999 4.48 -0.19999999 C 5.02 -0.19999999 6.5 0.68 6.92 0.96 Z M 7.04 1.9 C 6.62 1.56 5.56 1.12 5.3199997 1.12 C 4.3199997 1.12 3.54 2.24 3.54 4.58 C 3.54 5.64 3.6599998 6.56 4.04 7.18 C 4.38 7.72 4.92 8.04 5.52 8.04 C 6.04 8.04 6.54 7.98 7.02 7.3199997 L 7.02 2.3999999 C 7.02 2.24 7.02 2.06 7.04 1.9 Z "/>
</symbol>
<symbol id="g50FEF586148C287DB923CFE895D558DC" overflow="visible">
<path d="M 5.9 0.97999996 C 6.04 0.16 6.58 -0.19999999 7.46 -0.19999999 C 8.559999 -0.19999999 9.34 0.22 10.08 0.91999996 C 10.04 1.16 9.96 1.3199999 9.719999 1.48 C 9.46 1.28 9.26 1.1999999 8.88 1.1999999 C 8.44 1.1999999 8.32 1.56 8.32 2.54 L 8.36 5.42 C 8.36 8.3 6.58 8.88 4.94 8.88 C 3.48 8.88 1.24 8.04 1.24 6.72 C 1.24 6.16 1.48 5.72 2.26 5.72 C 2.98 5.72 3.5 6.16 3.5 6.64 C 3.5 6.74 3.48 6.8599997 3.46 6.98 C 3.4199998 7.18 3.3799999 7.3799996 3.4199998 7.58 C 3.4399998 7.7999997 3.6 8.04 4.2599998 8.04 C 5.1 8.04 5.7999997 7.68 5.7999997 5.14 L 4.46 4.72 C 2.36 4.06 0.88 3.48 0.88 1.9 C 0.88 0.52 1.64 -0.19999999 3.3799999 -0.19999999 C 3.9599998 -0.19999999 5.12 0.44 5.7799997 0.96 Z M 5.7999997 4.36 L 5.7999997 1.7199999 C 5.2999997 1.3199999 4.7999997 1 4.44 1 C 3.58 1 3.28 1.5799999 3.28 2.2 C 3.28 2.9399998 3.34 3.56 4.7599998 4.02 Z "/>
</symbol>
<symbol id="gED653E9CCAB5F6C6237350979071A74F" overflow="visible">
<path d="M 1.1999999 1.1999999 C 1.1999999 0.44 1.8399999 -0.16 2.6399999 -0.16 C 3.4399998 -0.16 4.12 0.48 4.12 1.24 C 4.12 2.02 3.48 2.62 2.6799998 2.62 C 1.88 2.62 1.1999999 1.9799999 1.1999999 1.1999999 Z M 1.1999999 7.16 C 1.1999999 6.3999996 1.8399999 5.7999997 2.6399999 5.7999997 C 3.4399998 5.7999997 4.12 6.44 4.12 7.2 C 4.12 7.98 3.48 8.58 2.6799998 8.58 C 1.88 8.58 1.1999999 7.94 1.1999999 7.16 Z "/>
</symbol>
<symbol id="gC1513612DA0E34F2B247DB2830CD7DFD" overflow="visible">
<path d="M 1.24 4.6 C 1.24 3.34 2.26 2.32 3.52 2.32 C 4.7799997 2.32 5.7999997 3.34 5.7999997 4.6 C 5.7999997 5.8599997 4.7799997 6.8799996 3.52 6.8799996 C 2.26 6.8799996 1.24 5.8599997 1.24 4.6 Z "/>
</symbol>
<symbol id="g187DB76C80CD961C20BAB3AF6259527" overflow="visible">
<path d="M 3.4399998 10.46 C 3.4399998 12.12 3.74 12.219999 5.2799997 12.28 C 5.4 12.4 5.4 12.82 5.2799997 12.94 C 4.3399997 12.92 3.36 12.9 2.58 12.9 C 1.8 12.9 0.97999996 12.92 0.19999999 12.94 C 0.08 12.82 0.08 12.4 0.19999999 12.28 C 1.4 12.219999 1.74 12.12 1.74 10.46 L 1.74 4.66 C 1.74 0.58 4.38 -0.19999999 6.42 -0.19999999 C 10.5199995 -0.19999999 11.5 2.34 11.5 5.9 L 11.5 10.46 C 11.5 12.059999 11.84 12.139999 13.04 12.28 C 13.16 12.4 13.16 12.82 13.04 12.94 C 12.28 12.92 11.46 12.9 11 12.9 C 10.58 12.9 9.599999 12.92 8.679999 12.94 C 8.559999 12.82 8.559999 12.4 8.679999 12.28 C 10.179999 12.139999 10.5199995 12.08 10.5199995 10.46 L 10.5199995 5.54 C 10.5199995 3.3 10.219999 0.62 6.8399997 0.62 C 5.8799996 0.62 5.06 0.97999996 4.46 1.56 C 3.48 2.5 3.4399998 4.02 3.4399998 5.3199997 Z "/>
</symbol>
<symbol id="g67483374C2628B9150A7D3585AC4A61B" overflow="visible">
<path d="M 0.96 2.76 C 1.04 1.78 1.1 0.84 1.1 0 C 1.3 0.04 1.5 0.06 1.5999999 0.06 C 1.74 0.06 1.86 0.06 2 0.02 C 2.54 -0.12 3.08 -0.19999999 3.82 -0.19999999 C 4.94 -0.19999999 7 0.34 7 2.32 C 7 3.6799998 6.02 4.48 4.66 4.98 C 3.46 5.44 2.6599998 5.74 2.6599998 6.8399997 C 2.6599998 7.66 3.3799999 8.12 4.06 8.12 C 4.5 8.12 5.66 7.96 5.92 6.2599998 C 6.04 6.14 6.44 6.16 6.56 6.2799997 C 6.62 7 6.66 7.74 6.68 8.4 C 6.06 8.5 5.1 8.78 4.06 8.78 C 2.58 8.78 1.24 7.8199997 1.24 6.54 C 1.24 5.08 1.9 4.46 3.4399998 3.82 C 5.1 3.1399999 5.48 2.72 5.48 1.86 C 5.48 0.88 4.52 0.45999998 3.78 0.45999998 C 3 0.45999998 2.56 0.71999997 2.36 0.94 C 1.92 1.4 1.6999999 2.28 1.5799999 2.78 C 1.4599999 2.8999999 1.0799999 2.8799999 0.96 2.76 Z "/>
</symbol>
<symbol id="g7FBC39AA6D9FB89D8B638A3651405A80" overflow="visible">
<path d="M 7.72 1.86 C 6.98 1.1 6.3999996 0.78 5.24 0.78 C 4.52 0.78 3.6799998 1.1999999 3.06 2.22 C 2.6599998 2.8799999 2.4199998 3.8 2.4199998 4.96 L 7.74 4.92 C 7.98 4.92 8.12 5.04 8.12 5.2599998 C 8.12 6.94 7.52 8.74 4.74 8.74 C 3 8.74 0.74 7.08 0.74 4.04 C 0.74 2.9199998 1.02 1.8399999 1.68 1.0799999 C 2.36 0.28 3.3 -0.19999999 4.74 -0.19999999 C 6.2599998 -0.19999999 7.3399997 0.5 8.139999 1.54 C 8.08 1.74 7.96 1.8399999 7.72 1.86 Z M 2.48 5.64 C 2.86 7.8999996 4.2599998 8.08 4.74 8.08 C 5.5 8.08 6.3999996 7.66 6.3999996 5.98 C 6.3999996 5.7999997 6.3199997 5.7 6.1 5.7 Z "/>
</symbol>
<symbol id="gAC7FD886AB12F72ED3B61B0327264BE7" overflow="visible">
<path d="M 3.12 7.3599997 C 3.1 7.96 3.06 8.48 2.96 8.679999 C 2.9199998 8.78 2.8799999 8.84 2.72 8.84 C 2.1599998 8.62 1.64 8.44 0.26 8.26 C 0.22 8.139999 0.26 7.8199997 0.29999998 7.7 C 1.38 7.6 1.5999999 7.5 1.5999999 6.3399997 L 1.5999999 -2.2 C 1.5999999 -3.86 1.38 -3.9599998 0.16 -4.02 C 0.04 -4.14 0.04 -4.56 0.16 -4.68 C 0.85999995 -4.66 1.5999999 -4.64 2.3999999 -4.64 C 3.1999998 -4.64 4.16 -4.66 4.8199997 -4.68 C 4.94 -4.56 4.94 -4.14 4.8199997 -4.02 C 3.3999999 -3.9399998 3.1799998 -3.86 3.1799998 -2.2 L 3.1799998 -0.04 C 3.1799998 0.22 3.26 0.19999999 3.46 0.12 C 3.9599998 -0.08 4.56 -0.19999999 5.2 -0.19999999 C 6.3199997 -0.19999999 7.3199997 0.14 8.139999 0.91999996 C 9.08 1.8399999 9.62 3.08 9.62 4.7 C 9.62 6.8199997 8.12 8.78 6.08 8.78 C 5.16 8.78 4.14 8.179999 3.34 7.2799997 C 3.22 7.16 3.1399999 7.16 3.12 7.3599997 Z M 3.5 6.62 C 4.02 7.2599998 4.94 7.8599997 5.52 7.8599997 C 6.7999997 7.8599997 7.8999996 6.42 7.8999996 4.16 C 7.8999996 2.52 7.3199997 0.48 5.08 0.48 C 4.72 0.48 4.02 0.58 3.6599998 0.9 C 3.26 1.26 3.1799998 1.38 3.1799998 2.1 L 3.1799998 5.74 C 3.1799998 6.16 3.26 6.3399997 3.5 6.62 Z "/>
</symbol>
<symbol id="gB9C04FB79CAD4691AB5EC7F01BE2AD7F" overflow="visible">
<path d="M 3.52 7.16 C 3.48 7.96 3.46 8.48 3.36 8.679999 C 3.32 8.78 3.28 8.84 3.12 8.84 C 2.56 8.62 2.04 8.44 0.65999997 8.26 C 0.62 8.139999 0.65999997 7.8199997 0.7 7.7 C 1.78 7.6 2 7.5 2 6.3399997 L 2 2.44 C 2 0.78 1.76 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 2 0 2.8 0 C 3.6 0 4.52 -0.02 5.22 -0.04 C 5.3399997 0.08 5.3399997 0.5 5.22 0.62 C 3.82 0.71999997 3.58 0.78 3.58 2.44 L 3.58 5.22 C 3.58 5.74 3.82 6.2 4.06 6.56 C 4.2799997 6.8799996 4.74 7.54 4.98 7.54 C 5.16 7.54 5.3399997 7.5 5.5 7.2799997 C 5.64 7.08 5.8799996 6.8199997 6.22 6.8199997 C 6.7 6.8199997 7.16 7.3199997 7.16 7.8199997 C 7.16 8.2 6.7999997 8.78 5.96 8.78 C 5.02 8.78 4.2 7.8999996 3.74 7.12 C 3.62 6.8999996 3.52 7.06 3.52 7.16 Z "/>
</symbol>
<symbol id="gFB78EB03C35D4F852337F4EC6AC104AC" overflow="visible">
<path d="M 0.82 4.1 C 0.82 2.06 2.18 -0.19999999 5.02 -0.19999999 C 6.2999997 -0.19999999 7.2799997 0.26 7.96 0.91999996 C 8.86 1.8 9.26 3.06 9.26 4.2799997 C 9.26 6.3599997 8.12 8.78 5.06 8.78 C 3.74 8.78 2.6599998 8.24 1.92 7.3799996 C 1.1999999 6.52 0.82 5.3599997 0.82 4.1 Z M 4.7599998 8.08 C 6.48 8.08 7.54 6.52 7.54 3.6399999 C 7.54 1.12 6.24 0.5 5.2999997 0.5 C 3.22 0.5 2.54 3.02 2.54 4.56 C 2.54 6.2999997 2.96 8.08 4.7599998 8.08 Z "/>
</symbol>
<symbol id="g5925E4E4FE8F59A76637BD462660B390" overflow="visible">
<path d="M 3.6399999 7.16 C 3.1799998 7.8399997 3.32 7.8599997 4.22 7.96 C 4.3399997 8.08 4.3399997 8.5 4.22 8.62 C 3.6799998 8.599999 2.8 8.58 2.2 8.58 C 1.5999999 8.58 1 8.599999 0.48 8.62 C 0.35999998 8.5 0.35999998 8.08 0.48 7.96 C 1.16 7.8999996 1.7199999 7.56 2.28 6.74 L 4.02 4.2 C 4.12 4.06 4.12 4 4.04 3.8999999 L 2.36 1.74 C 1.56 0.71999997 1.12 0.65999997 0.42 0.62 C 0.29999998 0.5 0.29999998 0.08 0.42 -0.04 C 0.82 -0.02 1.26 0 1.86 0 C 2.46 0 3.02 -0.02 3.54 -0.04 C 3.6599998 0.08 3.6599998 0.5 3.54 0.62 C 2.82 0.7 2.6599998 0.78 3.1 1.42 L 4.36 3.24 C 4.52 3.48 4.6 3.46 4.72 3.28 L 5.8799996 1.68 C 6.58 0.71999997 6.2599998 0.68 5.62 0.62 C 5.5 0.5 5.5 0.08 5.62 -0.04 C 6.22 -0.02 6.8799996 0 7.6 0 C 8.36 0 8.9 -0.02 9.38 -0.04 C 9.5 0.08 9.5 0.5 9.38 0.62 C 8.48 0.68 8.179999 0.74 7.3799996 1.88 L 5.58 4.42 C 5.5 4.54 5.48 4.6 5.58 4.72 L 7.2599998 6.8599997 C 8 7.7999997 8.48 7.8999996 9.2 7.96 C 9.32 8.08 9.32 8.5 9.2 8.62 C 8.8 8.599999 8.34 8.58 7.74 8.58 C 7.14 8.58 6.58 8.599999 6.06 8.62 C 5.94 8.5 5.94 8.08 6.06 7.96 C 6.7999997 7.8799996 7.02 7.8199997 6.54 7.14 L 5.24 5.3199997 C 5.1 5.12 5.02 5.14 4.8599997 5.3599997 Z "/>
</symbol>
<symbol id="gE68C39294AA7FBA9B91EA2F8E9CC3997" overflow="visible">
<path d="M 3.62 2.44 L 3.62 6.42 C 3.62 7.4199996 3.6999998 8.7 3.6999998 8.7 C 3.6999998 8.78 3.6 8.84 3.4399998 8.84 C 2.8799999 8.62 2.08 8.44 0.7 8.26 C 0.65999997 8.139999 0.7 7.8199997 0.74 7.7 C 1.8399999 7.6 2.04 7.48 2.04 6.3399997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.71999997 0.59999996 0.62 C 0.48 0.5 0.48 0.08 0.59999996 -0.04 C 1.26 -0.02 2.04 0 2.84 0 C 3.6399999 0 4.4 -0.02 5.06 -0.04 C 5.18 0.08 5.18 0.5 5.06 0.62 C 3.84 0.7 3.62 0.78 3.62 2.44 Z M 1.8 11.98 C 1.8 11.46 2.28 10.94 2.76 10.94 C 3.32 10.94 3.8 11.48 3.8 11.9 C 3.8 12.38 3.3799999 12.94 2.84 12.94 C 2.36 12.94 1.8 12.46 1.8 11.98 Z "/>
</symbol>
<symbol id="gD3761FB0B01B207797C607CDFB6E3A0B" overflow="visible">
<path d="M 3.3999999 7.16 C 3.3799999 7.7599998 3.34 8.48 3.24 8.679999 C 3.1999998 8.78 3.1599998 8.84 3 8.84 C 2.44 8.62 1.92 8.44 0.53999996 8.26 C 0.5 8.139999 0.53999996 7.8199997 0.58 7.7 C 1.66 7.6 1.88 7.5 1.88 6.3399997 L 1.88 2.44 C 1.88 0.79999995 1.62 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.88 0 2.6799998 0 C 3.48 0 4.1 -0.02 4.7 -0.04 C 4.8199997 0.08 4.8199997 0.5 4.7 0.62 C 3.6799998 0.71999997 3.46 0.79999995 3.46 2.44 L 3.46 5.72 C 3.46 6.14 3.6399999 6.3799996 3.8 6.56 C 4.6 7.3399997 5.3399997 7.74 5.96 7.74 C 6.72 7.74 7.2799997 7.2599998 7.2799997 5.92 L 7.2799997 2.44 C 7.2799997 0.79999995 7.12 0.7 6.04 0.62 C 5.94 0.5 5.94 0.08 6.04 -0.04 C 6.54 -0.02 7.2799997 0 8.08 0 C 8.88 0 9.54 -0.02 10.04 -0.04 C 10.139999 0.08 10.139999 0.5 10.04 0.62 C 9.04 0.7 8.86 0.79999995 8.86 2.44 L 8.86 5.62 C 8.86 5.9 8.86 6.18 8.84 6.42 C 9.8 7.48 10.7 7.74 11.48 7.74 C 12.24 7.74 12.679999 7.2999997 12.679999 5.96 L 12.679999 2.44 C 12.679999 0.79999995 12.48 0.7 11.44 0.62 C 11.34 0.5 11.34 0.08 11.44 -0.04 C 11.94 -0.02 12.679999 0 13.48 0 C 14.28 0 14.98 -0.02 15.54 -0.04 C 15.639999 0.08 15.639999 0.5 15.54 0.62 C 14.44 0.7 14.259999 0.79999995 14.259999 2.44 L 14.259999 5.6 C 14.259999 7.3799996 13.96 8.78 12.2 8.78 C 11.179999 8.78 9.94 8.4 8.9 7.2999997 C 8.84 7.24 8.72 7.14 8.679999 7.3199997 C 8.5 8.139999 7.72 8.78 6.68 8.78 C 5.52 8.78 4.48 8.099999 3.6399999 7.16 C 3.54 7.06 3.4199998 6.92 3.3999999 7.16 Z "/>
</symbol>
<symbol id="g22D858CFD6AD86697C1391C74FD687D1" overflow="visible">
<path d="M 0.85999995 8.58 C 0.58 8.58 0.5 8.34 0.5 8.179999 L 0.5 7.9199996 C 0.5 7.8199997 0.52 7.7999997 0.59999996 7.7999997 L 1.78 7.7999997 L 1.78 1.78 C 1.78 0.35999998 2.3999999 -0.19999999 3.32 -0.19999999 C 4.24 -0.19999999 5.24 0.24 6.02 1.12 C 5.98 1.3199999 5.8599997 1.4399999 5.66 1.4599999 C 5.14 1.06 4.54 0.9 4.02 0.9 C 3.48 0.9 3.36 1.5 3.36 2.74 L 3.36 7.7999997 L 5.44 7.7999997 C 5.64 7.7999997 5.92 7.8799996 5.92 8.059999 L 5.92 8.46 C 5.92 8.54 5.8599997 8.58 5.7599998 8.58 L 3.36 8.58 L 3.36 9.36 C 3.36 10.66 3.4399998 11.46 3.4399998 11.46 C 3.4399998 11.58 3.3799999 11.639999 3.28 11.639999 C 3.1999998 11.639999 3.02 11.559999 2.84 11.46 C 2.62 11.34 2.4199998 11.24 2.1599998 11.179999 C 1.92 11.099999 1.7199999 11.04 1.7199999 10.9 C 1.7199999 10.66 1.78 10.8 1.78 8.58 Z "/>
</symbol>
<symbol id="g21D1E528F66DB45787699F71DA377CC5" overflow="visible">
<path d="M 4.08 -3.1999998 C 4.4 -2.6399999 4.66 -2.08 4.9 -1.48 C 6.5 2.3799999 7.3999996 4.44 8.44 6.68 C 8.84 7.52 9.12 7.8399997 10.059999 7.96 C 10.179999 8.08 10.179999 8.5 10.059999 8.62 C 9.66 8.599999 9.2 8.58 8.639999 8.58 C 8.04 8.58 7.4199996 8.599999 6.8199997 8.62 C 6.7 8.5 6.7 8.08 6.8199997 7.96 C 7.46 7.8999996 8.099999 7.7799997 7.7799997 7.06 L 5.7999997 2.48 C 5.66 2.1599998 5.48 2.1 5.3199997 2.5 L 3.54 6.66 C 3.1799998 7.5 3.08 7.8799996 4.2 7.96 C 4.3199997 8.08 4.3199997 8.5 4.2 8.62 C 3.46 8.599999 2.6599998 8.58 1.9399999 8.58 C 1.26 8.58 0.71999997 8.599999 0.32 8.62 C 0.19999999 8.5 0.19999999 8.08 0.32 7.96 C 1.12 7.8599997 1.38 7.68 1.9 6.46 L 4.16 1.1999999 C 4.3399997 0.79999995 4.64 -0.12 4.44 -0.68 C 4.2 -1.3399999 3.9599998 -1.9 3.6599998 -2.52 C 3.4399998 -2.9199998 3.1599998 -3.1 2.6599998 -3.1 C 2.3799999 -3.1 2.3 -3.04 2.08 -3.04 C 1.5 -3.04 1.1999999 -3.6399999 1.1999999 -3.8999999 C 1.1999999 -4.3199997 1.5999999 -4.64 2.1399999 -4.64 C 2.56 -4.64 3.36 -4.48 4.08 -3.1999998 Z "/>
</symbol>
<symbol id="gFB54B84572F46C3C9CB2B1A90182D6B2" overflow="visible">
<path d="M 8.88 7.74 C 9.26 7.74 9.62 8.099999 9.62 8.5 C 9.62 8.92 9.24 9.24 8.7 9.24 C 8.179999 9.24 7.22 8.9 6.7 8.22 C 6.46 8.38 5.7999997 8.78 4.62 8.78 C 2.84 8.78 1.1999999 7.58 1.1999999 5.74 C 1.1999999 4.66 1.68 4.04 2.24 3.5 C 1.68 3.02 1.36 2.1599998 1.36 1.48 C 1.36 0.76 1.76 0.19999999 2.28 -0.06 C 1.1999999 -0.7 0.64 -1.62 0.64 -2.48 C 0.64 -4.22 2.28 -4.7599998 3.82 -4.7599998 C 6.52 -4.7599998 9.44 -3.46 9.44 -1.3 C 9.44 -0.65999997 9.139999 -0.16 8.559999 0.32 C 7.7799997 0.96 6.3799996 0.97999996 5.64 0.97999996 C 5.2799997 0.97999996 4.7799997 0.94 4.2999997 0.88 C 4 0.85999995 3.8 0.84 3.6999998 0.84 C 3.12 0.84 2.4199998 1.12 2.4199998 1.9799999 C 2.4199998 2.3799999 2.54 2.8 2.78 3.1399999 C 3.26 2.86 3.82 2.72 4.6 2.72 C 6.3599997 2.72 7.98 3.82 7.98 5.7799997 C 7.98 6.72 7.7 7.2599998 7.12 7.8599997 C 7.2599998 8.059999 7.66 8.34 7.9199996 8.34 C 8.059999 8.34 8.2 8.28 8.32 8.099999 C 8.4 7.94 8.66 7.74 8.88 7.74 Z M 2.6399999 -0.19999999 C 2.86 -0.26 3.1799998 -0.29999998 3.4399998 -0.29999998 C 4.06 -0.29999998 4.62 -0.24 4.9 -0.24 C 5.9 -0.24 6.74 -0.26 7.3199997 -0.58 C 8.099999 -1.02 8.34 -1.3 8.34 -1.8199999 C 8.34 -3.26 6.22 -4.02 4.42 -4.02 C 3.6999998 -4.02 2.02 -3.4399998 2.02 -2.08 C 2.02 -1.4 2.06 -0.9 2.6399999 -0.19999999 Z M 6.3799996 5.58 C 6.3799996 3.72 5.44 3.34 4.7 3.34 C 3.02 3.34 2.84 4.7599998 2.84 6.04 C 2.84 7.44 3.34 8.16 4.44 8.16 C 5.7 8.16 6.3799996 7.24 6.3799996 5.58 Z "/>
</symbol>
<symbol id="gAA212A9DBB5FA7333A767E41B2F6A3B3" overflow="visible">
<path d="M 5.8599997 0.96 C 5.98 0.34 6.2 -0.19999999 7.2 -0.19999999 C 7.96 -0.19999999 8.679999 0.14 9.099999 0.53999996 C 9.059999 0.78 8.98 0.96 8.76 1.0799999 C 8.62 0.96 8.28 0.76 8.0199995 0.76 C 7.44 0.76 7.4199996 1.54 7.4199996 2.46 L 7.4199996 5.4 C 7.4199996 8.24 5.8599997 8.78 4.4 8.78 C 2.76 8.78 1.1 7.7 1.1 6.56 C 1.1 6.08 1.3399999 5.8399997 1.8 5.8399997 C 2.3799999 5.8399997 2.74 6.2599998 2.74 6.52 C 2.74 6.66 2.72 6.7999997 2.6799998 6.8799996 C 2.6599998 6.94 2.6399999 7.06 2.6399999 7.2799997 C 2.6399999 7.8999996 3.48 8.12 4.24 8.12 C 4.92 8.12 5.8599997 7.7799997 5.8599997 5.52 C 5.8599997 5.38 5.7999997 5.2999997 5.74 5.2799997 L 4.02 4.8599997 C 2.1 4.38 0.71999997 3.32 0.71999997 1.9599999 C 0.71999997 0.32 1.8399999 -0.19999999 3.24 -0.19999999 C 3.9399998 -0.19999999 4.54 -0.04 5.42 0.64 L 5.8199997 0.96 Z M 5.8599997 4.66 L 5.8599997 2.02 C 5.8599997 1.76 5.74 1.62 5.58 1.5 C 5.06 1.0799999 4.38 0.62 3.82 0.62 C 2.82 0.62 2.3799999 1.42 2.3799999 2.04 C 2.3799999 2.9399998 2.8 3.86 4.2799997 4.24 Z "/>
</symbol>
<symbol id="g3C2FFF86BC828E66F78F8A687CE12C70" overflow="visible">
<path d="M 3.34 5.72 C 3.34 6.14 3.52 6.3799996 3.6799998 6.56 C 4.44 7.2999997 5.46 7.74 6.24 7.74 C 6.64 7.74 7.06 7.48 7.2999997 7.02 C 7.5 6.62 7.54 6.08 7.54 5.48 L 7.54 2.44 C 7.54 0.79999995 7.3399997 0.71999997 6.2999997 0.62 C 6.2 0.5 6.2 0.08 6.2999997 -0.04 C 6.8599997 -0.02 7.54 0 8.34 0 C 9.139999 0 9.8 -0.02 10.46 -0.04 C 10.559999 0.08 10.559999 0.5 10.46 0.62 C 9.34 0.71999997 9.12 0.79999995 9.12 2.44 L 9.12 5.42 C 9.12 6.52 9.04 7.5 8.58 8.099999 C 8.24 8.54 7.62 8.78 6.92 8.78 C 5.94 8.78 4.74 8.5199995 3.52 7.16 C 3.52 7.14 3.5 7.14 3.48 7.12 C 3.4199998 7.04 3.32 6.92 3.32 7.16 L 3.34 11.66 C 3.34 12.96 3.4199998 13.759999 3.4199998 13.759999 C 3.4199998 13.9 3.34 13.96 3.1599998 13.96 C 2.6599998 13.759999 1.16 13.48 0.35999998 13.42 C 0.32 13.259999 0.35999998 12.94 0.48 12.82 C 0.53999996 12.82 0.59999996 12.82 0.65999997 12.82 C 1.54 12.759999 1.76 12.759999 1.76 11.179999 L 1.76 2.44 C 1.76 0.78 1.52 0.7 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.02 -0.02 1.76 0 2.56 0 C 3.32 0 3.98 -0.02 4.54 -0.04 C 4.66 0.08 4.66 0.5 4.54 0.62 C 3.52 0.7 3.34 0.78 3.34 2.44 Z "/>
</symbol>
<symbol id="gFE29E79896646B3825DA2D41961151C9" overflow="visible">
<path d="M 2.96 12.9 C 2.24 12.9 1.16 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.16 -0.02 2.24 0 2.98 0 C 3.6999998 0 4.22 -0.04 5.9 -0.04 C 9.88 -0.04 10.94 1.9599999 10.94 3.6799998 C 10.94 5.6 9.599999 6.7 7.8599997 7.2 L 7.8599997 7.24 C 8.86 7.74 9.76 8.78 9.76 9.86 C 9.76 11.2 9.179999 12.94 5.46 12.94 C 4.7599998 12.94 3.6799998 12.9 2.96 12.9 Z M 3.82 6.64 L 5.2 6.64 C 7.94 6.64 9.08 5.1 9.08 3.3 C 9.08 1.8399999 8.5199995 0.62 5.48 0.62 C 4.08 0.62 3.82 1.14 3.82 2.36 Z M 3.82 11 C 3.82 12.059999 3.82 12.259999 5.56 12.259999 C 6.68 12.259999 8.139999 11.66 8.139999 9.62 C 8.139999 7.9199996 6.96 7.3199997 5.2999997 7.3199997 L 3.82 7.3199997 Z "/>
</symbol>
<symbol id="gD8CB364949770E6EB9E57283C62D30EB" overflow="visible">
<path d="M 4.3399997 -0.19999999 C 5.12 -0.19999999 6.06 0.19999999 7.04 1 C 7.14 1.0799999 7.3199997 1.12 7.3399997 0.97999996 C 7.3999996 0.48 7.56 -0.19999999 7.56 -0.19999999 C 7.72 -0.26 7.8199997 -0.24 7.94 -0.19999999 C 8.38 0.16 9.08 0.45999998 10.3 0.59999996 C 10.42 0.71999997 10.42 1.02 10.3 1.14 C 9.0199995 1.24 8.84 1.62 8.84 2.6 L 8.84 6.44 C 8.84 7.04 8.92 8.5 8.92 8.5 C 8.92 8.559999 8.86 8.62 8.76 8.62 C 8.66 8.599999 8.36 8.58 8.059999 8.58 C 7.4199996 8.58 6.7 8.599999 6.02 8.62 C 5.9 8.5 5.9 8.08 6.02 7.96 C 7 7.8999996 7.2599998 7.66 7.2599998 6.3399997 L 7.2599998 2.48 C 7.2599998 2.1 7.22 1.9399999 6.94 1.6999999 C 6.2 1.06 5.44 0.74 4.94 0.74 C 4.3399997 0.74 3.34 1.02 3.34 2.8 L 3.34 6.44 C 3.34 7.04 3.4199998 8.5 3.4199998 8.5 C 3.4199998 8.559999 3.36 8.62 3.26 8.62 C 3.1599998 8.599999 2.86 8.58 2.56 8.58 C 1.92 8.58 1.1999999 8.599999 0.52 8.62 C 0.39999998 8.5 0.39999998 8.08 0.52 7.96 C 1.48 7.8799996 1.76 7.66 1.76 6.3599997 L 1.76 2.52 C 1.76 1.14 2.36 -0.19999999 4.3399997 -0.19999999 Z "/>
</symbol>
<symbol id="g1788914935A6D7BFA016214155630E72" overflow="visible">
<path d="M 1.9 2.44 C 1.9 0.78 1.68 0.68 0.45999998 0.62 C 0.34 0.5 0.34 0.08 0.45999998 -0.04 C 1.16 -0.02 1.9 0 2.7 0 C 3.5 0 4.2599998 -0.02 4.92 -0.04 C 5.04 0.08 5.04 0.5 4.92 0.62 C 3.6999998 0.68 3.48 0.78 3.48 2.44 L 3.48 11.66 C 3.48 12.96 3.56 13.759999 3.56 13.759999 C 3.56 13.9 3.48 13.96 3.3 13.96 C 2.8 13.759999 1.3 13.48 0.5 13.42 C 0.45999998 13.259999 0.5 12.94 0.62 12.82 C 1.78 12.74 1.9 12.679999 1.9 11.179999 Z "/>
</symbol>
<symbol id="g42587C4E387B2C5F870DA01C2914651F" overflow="visible">
<path d="M 6.68 1 C 6.7799997 1.0799999 6.96 1.12 6.98 0.97999996 C 7.04 0.5 7.2 -0.19999999 7.2 -0.19999999 C 7.3599997 -0.26 7.46 -0.24 7.58 -0.19999999 C 8.0199995 0.16 8.72 0.45999998 9.94 0.59999996 C 10.059999 0.71999997 10.059999 1.02 9.94 1.14 C 8.66 1.24 8.48 1.62 8.48 2.6 L 8.48 11.66 C 8.48 12.96 8.559999 13.759999 8.559999 13.759999 C 8.559999 13.9 8.48 13.96 8.3 13.96 C 7.7999997 13.759999 6.2999997 13.48 5.5 13.42 C 5.46 13.259999 5.5 12.94 5.62 12.82 C 5.68 12.82 5.74 12.82 5.7999997 12.82 C 6.68 12.759999 6.8999996 12.759999 6.8999996 11.179999 L 6.8999996 8.62 C 6.8999996 8.48 6.8599997 8.44 6.72 8.44 C 6.64 8.44 5.8199997 8.78 5.16 8.78 C 3.84 8.78 2.96 8.34 2.1599998 7.58 C 1.3 6.72 0.78 5.54 0.78 4.06 C 0.78 1.5999999 2.02 -0.19999999 4.18 -0.19999999 C 4.96 -0.19999999 5.7 0.19999999 6.68 1 Z M 6.8999996 2.48 C 6.8999996 2.1 6.8599997 1.9399999 6.58 1.6999999 C 5.8399997 1.06 5.2 0.74 4.7 0.74 C 3.62 0.74 2.5 1.92 2.5 4.42 C 2.5 5.8599997 2.78 6.66 3.08 7.08 C 3.6999998 8.0199995 4.54 8.08 4.94 8.08 C 5.66 8.08 6.16 7.8199997 6.56 7.3599997 C 6.8399997 7.04 6.8999996 6.8999996 6.8999996 6.2799997 Z "/>
</symbol>
<symbol id="g35631D62198EF939061DC90C9391724A" overflow="visible">
<path d="M 3.6799998 7.16 C 3.56 7.02 3.4399998 6.98 3.4399998 7.16 C 3.4199998 7.7 3.3799999 8.48 3.28 8.679999 C 3.24 8.78 3.1999998 8.84 3.04 8.84 C 2.48 8.62 1.9599999 8.44 0.58 8.26 C 0.53999996 8.139999 0.58 7.8199997 0.62 7.7 C 1.6999999 7.6 1.92 7.5 1.92 6.3399997 L 1.92 2.44 C 1.92 0.79999995 1.7199999 0.71999997 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.92 0 2.72 0 C 3.52 0 4.12 -0.02 4.72 -0.04 C 4.8399997 0.08 4.8399997 0.5 4.72 0.62 C 3.6999998 0.71999997 3.5 0.79999995 3.5 2.44 L 3.5 5.72 C 3.5 6.14 3.6799998 6.3799996 3.84 6.56 C 4.6 7.2999997 5.5 7.74 6.2799997 7.74 C 6.68 7.74 7.1 7.48 7.3399997 7.02 C 7.54 6.62 7.58 6.08 7.58 5.48 L 7.58 2.44 C 7.58 0.79999995 7.3799996 0.71999997 6.3399997 0.62 C 6.24 0.5 6.24 0.08 6.3399997 -0.04 C 6.94 -0.02 7.58 0 8.38 0 C 9.179999 0 9.9 -0.02 10.5 -0.04 C 10.599999 0.08 10.599999 0.5 10.5 0.62 C 9.38 0.71999997 9.16 0.79999995 9.16 2.44 L 9.16 5.42 C 9.16 6.52 9.08 7.48 8.62 8.099999 C 8.28 8.54 7.66 8.78 6.96 8.78 C 5.98 8.78 4.8599997 8.5199995 3.6799998 7.16 Z "/>
</symbol>
<symbol id="gE8171CD7697771DDE124968BDB3EF0D7" overflow="visible">
<path d="M 5.42 4.46 C 5.68 4.46 5.96 5.02 5.96 5.2599998 C 5.96 5.46 5.8799996 5.66 5.68 5.66 L 1.3 5.66 C 1.06 5.66 0.79999995 5.2 0.79999995 4.8399997 C 0.79999995 4.64 0.91999996 4.46 1.1 4.46 Z "/>
</symbol>
<symbol id="g713198A7DA4F5CD7D462D4529B1D64BD" overflow="visible">
<path d="M 7.96 1.8199999 C 7.8799996 2 7.72 2.08 7.54 2.1 C 6.8599997 1.22 6 0.78 5.14 0.78 C 3.6799998 0.78 2.46 2.26 2.46 4.6 C 2.46 6.7999997 3.4199998 8.12 4.74 8.12 C 5.92 8.12 6.08 7.4199996 6.16 6.72 C 6.22 6.18 6.5 6 6.92 6 C 7.3399997 6 7.8999996 6.2599998 7.8999996 6.8799996 C 7.8999996 7.98 6.7599998 8.78 4.8399997 8.78 C 2.86 8.78 0.74 7 0.74 4.16 C 0.74 1.5799999 2.18 -0.19999999 4.7 -0.19999999 C 5.9 -0.19999999 6.96 0.17999999 7.96 1.8199999 Z "/>
</symbol>
<symbol id="gF9DE6E66E5D3ACB0B17DC7988DD660B8" overflow="visible">
<path d="M 1.7199999 2.44 C 1.7199999 0.78 1.5 0.7 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.04 -0.02 1.7199999 0 2.52 0 C 3.22 0 3.8799999 -0.02 4.3399997 -0.04 C 4.46 0.08 4.46 0.5 4.3399997 0.62 C 3.52 0.7 3.3 0.78 3.3 2.44 L 3.3 4.18 C 3.6799998 4.16 3.9599998 4.14 4.16 4.08 C 4.38 3.9199998 4.56 3.74 4.7999997 3.4199998 L 6.2599998 1.4599999 C 6.8399997 0.68 7.08 0.29999998 7.1 0.06 C 7.1 0 7.12 -0.04 7.18 -0.04 C 7.58 -0.02 8.0199995 0 8.42 0 C 9.04 0 9.66 -0.02 10.059999 -0.04 C 10.179999 0.08 10.179999 0.5 10.059999 0.62 C 9.38 0.7 8.88 0.78 8.34 1.4599999 L 5.7 4.7799997 C 5.62 4.88 5.56 4.96 5.56 5.06 C 5.56 5.14 5.56 5.18 5.64 5.2599998 L 7.3999996 7.08 C 8 7.72 8.7 7.8799996 9.5 7.96 C 9.62 8.08 9.62 8.5 9.5 8.62 C 9.04 8.599999 8.48 8.58 7.7599998 8.58 C 7 8.58 6.2599998 8.599999 5.7999997 8.62 C 5.68 8.5 5.68 8.08 5.7999997 7.96 C 6.92 7.8799996 6.44 7.18 6.2599998 6.94 C 5.7999997 6.3599997 5.18 5.68 4.66 5.2999997 C 4.22 4.98 3.6799998 4.74 3.3 4.68 L 3.3 11.66 C 3.3 12.96 3.3799999 13.759999 3.3799999 13.759999 C 3.3799999 13.9 3.3 13.96 3.12 13.96 C 2.62 13.759999 1.12 13.48 0.32 13.42 C 0.28 13.259999 0.32 12.94 0.44 12.82 C 0.5 12.82 0.56 12.82 0.62 12.82 C 1.5 12.759999 1.7199999 12.759999 1.7199999 11.179999 Z "/>
</symbol>
<symbol id="g936880EEF467D45CE0F64A721CAEDAB8" overflow="visible">
<path d="M 4.56 5.3599997 C 4.56 6.08 4.7799997 6.3799996 5.04 6.68 C 5.2 6.8799996 5.38 7.02 5.68 7.02 C 5.8599997 7.02 6.08 6.8399997 6.24 6.64 C 6.3799996 6.48 6.72 6.3199997 7.18 6.3199997 C 7.7599998 6.3199997 8.32 6.92 8.32 7.7599998 C 8.32 8.28 7.72 8.88 7 8.88 C 6.2999997 8.88 5.54 8.28 4.62 6.96 L 4.54 6.96 C 4.5 7.56 4.4 8.54 4.4 8.54 C 4.38 8.72 4.22 8.88 3.9399998 8.88 C 3 8.639999 1.9399999 8.36 0.62 8.22 C 0.58 8.099999 0.62 7.72 0.65999997 7.6 C 1.76 7.5 1.9599999 7.3199997 1.9599999 6.18 L 1.9599999 2.44 C 1.9599999 0.78 1.74 0.74 0.52 0.64 C 0.39999998 0.52 0.39999998 0.08 0.52 -0.04 C 1.36 -0.02 2.2 0 3.26 0 C 4.3199997 0 5.14 -0.02 6 -0.04 C 6.12 0.08 6.12 0.52 6 0.64 C 4.7799997 0.71999997 4.56 0.78 4.56 2.44 Z "/>
</symbol>
<symbol id="g7B316FC97C7634445DBF19AF1976B5C8" overflow="visible">
<path d="M 8.44 1.74 C 8.44 1.9799999 8.4 2.36 8.179999 2.36 C 7.3799996 1.62 6.7 1.24 6.12 1.24 C 4.62 1.24 3.4399998 2.32 3.4399998 4.72 C 3.4399998 6.94 3.9399998 8.04 5 8.04 C 5.74 8.04 6.04 7.2599998 6.1 6.62 C 6.16 6.08 6.7 5.68 7.3399997 5.68 C 7.98 5.68 8.44 6.18 8.44 6.7999997 C 8.44 7.7 7.3599997 8.88 5.18 8.88 C 2.82 8.88 0.74 6.98 0.74 4.02 C 0.74 2.72 1.1999999 1.5799999 1.9799999 0.84 C 2.76 0.099999994 3.6799998 -0.19999999 5.1 -0.19999999 C 6.2999997 -0.19999999 7.68 0.64 8.44 1.74 Z "/>
</symbol>
<symbol id="g37DC97609493A252C8A67743647C955" overflow="visible">
<path d="M 10.559999 2.56 L 10.559999 5.68 C 10.559999 7.8799996 9.62 8.88 7.8999996 8.88 C 7.16 8.88 5.74 8.139999 4.6 7.44 L 4.6 11.66 C 4.6 12.96 4.66 13.7 4.66 13.7 C 4.66 13.88 4.52 13.96 4.3399997 13.96 C 3.6 13.719999 2 13.5 0.58 13.44 C 0.52 13.2 0.53999996 12.98 0.64 12.799999 C 1.9 12.7 2 12.679999 2 11.3 L 2 2.54 C 2 0.88 1.68 0.7 0.45999998 0.64 C 0.34 0.52 0.34 0.08 0.45999998 -0.04 C 1.3 -0.02 2.2 0 3.3 0 C 4.2599998 0 4.88 -0.02 5.74 -0.04 C 5.8599997 0.08 5.8599997 0.52 5.74 0.64 C 4.9 0.7 4.6 0.88 4.6 2.54 L 4.6 6.64 C 5.44 7.16 6.1 7.3999996 6.46 7.3999996 C 7.2599998 7.3999996 7.96 7.04 7.96 5.9 L 7.96 2.56 C 7.96 0.88 7.64 0.7 6.8199997 0.64 C 6.7 0.52 6.7 0.08 6.8199997 -0.04 C 7.66 -0.02 8.3 0 9.26 0 C 10.36 0 11.24 -0.02 12.099999 -0.04 C 12.219999 0.08 12.219999 0.52 12.099999 0.64 C 10.88 0.7 10.559999 0.88 10.559999 2.56 Z "/>
</symbol>
<symbol id="gF418DD62CA77762FBF8DB07ECAE6BC0" overflow="visible">
<path d="M 6.92 13.08 C 6.12 13.08 1.42 12.94 0.62 12.94 C 0.42 12.82 0.42 12.38 0.62 12.259999 C 1.7199999 12.2 2.28 12.12 2.28 10.46 L 2.28 2.44 C 2.28 0.78 1.7199999 0.7 0.62 0.64 C 0.42 0.52 0.42 0.08 0.62 -0.04 C 1.42 -0.02 2.8999999 0 3.6999998 0 C 4.5 0 5.94 -0.02 6.74 -0.04 C 6.94 0.08 6.94 0.52 6.74 0.64 C 5.64 0.7 5.08 0.78 5.08 2.44 L 5.08 10.48 C 5.08 11.84 5.22 12.259999 6.2799997 12.259999 C 7.44 12.259999 8.78 11.78 8.78 9.34 C 8.78 7.2599998 8.2 6.3799996 6.56 6.3799996 C 6.2599998 6.3799996 5.8399997 6.3999996 5.56 6.44 C 5.56 6.06 5.68 5.7799997 5.96 5.6 C 6.24 5.56 6.18 5.54 6.66 5.54 C 8.42 5.54 9.66 5.8399997 10.46 6.5 C 11.46 7.3199997 11.8 8.62 11.8 9.679999 C 11.8 10.48 11.5 11.679999 10.26 12.42 C 9.5199995 12.86 8.42 13.08 6.92 13.08 Z "/>
</symbol>
<symbol id="g814D257E196F777517493FCE505E18DF" overflow="visible">
<path d="M 0.74 4.14 C 0.74 1.52 2.82 -0.19999999 5.5 -0.19999999 C 6.92 -0.19999999 8.099999 0.19999999 8.92 0.94 C 9.94 1.8399999 10.28 3.1999998 10.28 4.3199997 C 10.28 6.94 8.5 8.88 5.52 8.88 C 3.86 8.88 2.62 8.3 1.8399999 7.3999996 C 1.0799999 6.52 0.74 5.3199997 0.74 4.14 Z M 5.2 8.04 C 6.56 8.04 7.48 6.42 7.48 3.6799998 C 7.48 1.28 6.54 0.64 5.8199997 0.64 C 4.18 0.64 3.54 3.1 3.54 4.58 C 3.54 6.42 3.86 8.04 5.2 8.04 Z "/>
</symbol>
<symbol id="gCD50B0C5537328D0484BBB5C5B7C30A" overflow="visible">
<path d="M 0.96 2.9199998 C 1.04 1.9399999 1.14 1 1.3 0.24 C 1.68 0.12 2.96 -0.19999999 4.08 -0.19999999 C 5.62 -0.19999999 7.54 0.64 7.54 2.3799999 C 7.54 3.06 7.3799996 3.6 6.92 4.1 C 6.3599997 4.74 5.52 5.24 4.6 5.64 C 3.8 5.98 3.52 6.62 3.52 7.2 C 3.52 7.66 3.8999999 8.04 4.48 8.04 C 5.18 8.04 5.8599997 7.3999996 6.3599997 6.18 C 6.72 6.12 6.94 6.14 7.14 6.2799997 C 7.14 7 7.06 7.7599998 6.8799996 8.4 C 6.24 8.679999 5.74 8.88 4.64 8.88 C 3.58 8.88 2.58 8.48 1.9399999 7.8399997 C 1.48 7.3799996 1.26 6.8199997 1.26 6.2799997 C 1.26 5.68 1.5 5.2 1.88 4.7799997 C 2.5 4.1 3.6 3.3999999 4.2 3.12 C 5 2.76 5.22 2.04 5.22 1.56 C 5.22 0.91999996 4.58 0.58 4.04 0.58 C 3.1399999 0.58 2.18 1.5 1.76 2.96 C 1.4399999 3.02 1.28 3 0.96 2.9199998 Z "/>
</symbol>
<symbol id="g3BBBD96D467CC564123619D79E97B4D6" overflow="visible">
<path d="M 7.8999996 12.62 C 6.74 12.78 6.7799997 13.16 4.8199997 13.16 C 2.8 13.16 1.02 11.82 1.02 9.7 C 1.02 7.6 2.76 6.64 4.52 5.96 C 5.72 5.5 7.2 4.94 7.2 2.98 C 7.2 1.36 6.2999997 0.52 4.7 0.52 C 2.84 0.52 1.64 1.38 1.1999999 3.36 C 0.94 3.4399998 0.74 3.3999999 0.53999996 3.3 C 0.62 1.76 0.7 1.24 0.94 0.26 C 2.2 0.26 2.76 -0.19999999 4.54 -0.19999999 C 5.44 -0.19999999 6.2999997 0.02 7 0.45999998 C 8.16 1.18 8.88 2.3999999 8.88 3.6799998 C 8.88 5.7999997 7.2799997 6.74 5.64 7.3599997 C 4.44 7.7999997 2.44 8.559999 2.44 10.24 C 2.44 11.36 3.46 12.48 4.64 12.48 C 6.58 12.48 7.2 11.24 7.6 9.92 C 7.8199997 9.88 8.08 9.9 8.26 10.04 C 8.179999 11 8.099999 11.559999 7.8999996 12.62 Z "/>
</symbol>
<symbol id="gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" overflow="visible">
<path d="M 13.259999 2.32 C 13.36 0.7 13.28 0.68 11.98 0.62 C 11.86 0.5 11.86 0.08 11.98 -0.04 C 12.719999 -0.02 13.5199995 0 14.12 0 C 14.719999 0 15.639999 -0.02 16.3 -0.04 C 16.42 0.08 16.42 0.5 16.3 0.62 C 14.94 0.68 14.88 0.76 14.759999 2.4199998 L 14.16 10.84 C 14.08 11.92 14.179999 12.2 15.54 12.28 C 15.66 12.4 15.66 12.82 15.54 12.94 L 12.92 12.9 L 8.679999 2.76 C 8.599999 2.56 8.54 2.48 8.5 2.48 C 8.46 2.48 8.4 2.58 8.34 2.74 L 4.24 12.9 L 1.3399999 12.94 C 1.22 12.82 1.22 12.4 1.3399999 12.28 C 2.72 12.2 2.84 12.16 2.7 10.66 L 1.9 2.4199998 C 1.78 1.22 1.54 0.71999997 0.39999998 0.62 C 0.28 0.5 0.28 0.08 0.39999998 -0.04 C 1 -0.02 1.64 0 2.12 0 C 2.6 0 3.3999999 -0.02 4 -0.04 C 4.12 0.08 4.12 0.5 4 0.62 C 2.6799998 0.71999997 2.58 1.3399999 2.6799998 2.46 L 3.4399998 10.48 L 3.48 10.48 L 7.62 0.099999994 C 7.68 -0.04 7.7999997 -0.19999999 7.9199996 -0.19999999 C 8.04 -0.19999999 8.12 -0.06 8.2 0.099999994 L 12.7 10.679999 L 12.74 10.679999 Z "/>
</symbol>
<symbol id="g17AD34DB90B05275C6F1422A9B4B5274" overflow="visible">
<path d="M 6.5 7.96 C 7.58 7.8799996 7.7 7.64 7.2799997 6.62 L 5.66 2.7 C 5.3399997 1.92 5.24 1.92 4.92 2.76 L 3.48 6.62 C 3.12 7.58 3.04 7.8199997 4.1 7.96 C 4.22 8.08 4.22 8.5 4.1 8.62 C 3.4399998 8.599999 2.74 8.58 2.08 8.58 C 1.42 8.58 0.82 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.28 7.8399997 1.42 7.52 1.8199999 6.5 L 4.38 0.17999999 C 4.5 -0.12 4.62 -0.24 4.88 -0.24 C 5.08 -0.24 5.22 -0.12 5.3599997 0.22 L 8.0199995 6.48 C 8.4 7.3599997 8.62 7.8599997 9.74 7.96 C 9.86 8.08 9.86 8.5 9.74 8.62 C 9.34 8.599999 8.86 8.58 8.34 8.58 C 7.68 8.58 7 8.599999 6.5 8.62 C 6.3799996 8.5 6.3799996 8.08 6.5 7.96 Z "/>
</symbol>
<symbol id="gE7450862BF743B056E90C8779357A05F" overflow="visible">
<path d="M 6.92 -2.22 C 6.92 -3.8799999 6.7 -3.9599998 5.48 -4.02 C 5.3599997 -4.14 5.3599997 -4.56 5.48 -4.68 C 6.18 -4.66 6.92 -4.64 7.72 -4.64 C 8.5199995 -4.64 9.28 -4.66 9.94 -4.68 C 10.059999 -4.56 10.059999 -4.14 9.94 -4.02 C 8.72 -3.9599998 8.5 -3.8799999 8.5 -2.22 L 8.5 8.34 C 8.5 8.62 8.42 8.84 8.2 8.84 C 8.059999 8.84 7.94 8.679999 7.7799997 8.46 C 7.52 8.099999 7.44 8.04 7.2 8.2 C 6.56 8.599999 5.7799997 8.78 4.94 8.78 C 2.5 8.78 0.7 6.7799997 0.7 4.14 C 0.7 2.28 1.9599999 -0.19999999 4.8399997 -0.19999999 C 5.38 -0.19999999 6.04 -0.08 6.3799996 0.12 C 6.8399997 0.38 6.92 0.42 6.92 0 Z M 6.44 7.3599997 C 6.8399997 6.92 6.92 6.62 6.92 6.14 L 6.92 1.54 C 6.92 1.18 6.8999996 1.0799999 6.64 0.94 C 6.18 0.7 5.64 0.68 5.3199997 0.68 C 4.16 0.68 2.4199998 1.52 2.4199998 4.54 C 2.4199998 6.62 3.26 8.099999 4.8599997 8.099999 C 5.46 8.099999 6 7.8599997 6.44 7.3599997 Z "/>
</symbol>
<symbol id="gCF24A1AE12C8178F68C1BA3421208D44" overflow="visible">
<path d="M 3.6999998 0 C 4.5 0 6.14 -0.04 6.94 -0.04 C 8.7 -0.04 10.679999 0.39999998 12.099999 1.64 C 13.059999 2.48 13.719999 4.14 13.719999 6.18 C 13.719999 9.88 11.32 12.92 6.3999996 12.92 C 5.3399997 12.92 4.5 12.9 3.6999998 12.9 C 2.8999999 12.9 0.62 12.94 0.62 12.94 C 0.42 12.82 0.42 12.38 0.62 12.259999 C 1.7199999 12.2 2.28 12.12 2.28 10.46 L 2.28 2.44 C 2.28 0.78 1.7199999 0.7 0.62 0.64 C 0.42 0.52 0.42 0.08 0.62 -0.04 C 0.62 -0.04 2.8999999 0 3.6999998 0 Z M 5.08 2.3799999 L 5.08 10.58 C 5.08 11.679999 5.6 12.08 6.3199997 12.08 C 10.26 12.08 10.7 8.7 10.7 5.68 C 10.7 2.04 8.5199995 0.79999995 7 0.79999995 C 5.6 0.79999995 5.08 1.04 5.08 2.3799999 Z "/>
</symbol>
<symbol id="gD5518A84533F4D2E67DB7AABF1806BFD" overflow="visible">
<path d="M 9.639999 6.62 C 9.26 7.58 9.0199995 8.46 9.0199995 8.46 C 8.66 8.44 8.28 8.44 7.8999996 8.48 L 6 3.1999998 C 5.94 3.06 5.8599997 3.02 5.7799997 3.22 L 4.64 6.62 C 4.62 6.68 4.6 6.72 4.58 6.7799997 C 4.2999997 7.62 4.18 7.94 5.3599997 8.04 C 5.48 8.16 5.48 8.599999 5.3599997 8.72 C 4.62 8.7 3.76 8.679999 2.74 8.679999 C 2.04 8.679999 1.02 8.7 0.28 8.72 C 0.16 8.599999 0.16 8.16 0.28 8.04 C 1.4399999 7.8999996 1.5 7.52 1.88 6.5 L 4.3199997 0.17999999 C 4.46 -0.19999999 4.72 -0.24 4.98 -0.24 C 5.18 -0.24 5.56 -0.19999999 5.72 0.22 L 7.6 5.16 L 9.5199995 0.17999999 C 9.66 -0.17999999 10.04 -0.24 10.3 -0.24 C 10.5 -0.24 10.84 -0.17999999 11 0.22 L 13.46 6.3199997 C 13.799999 7.18 14.139999 7.94 15.259999 8.04 C 15.38 8.16 15.38 8.599999 15.259999 8.72 C 14.82 8.7 14.46 8.679999 13.94 8.679999 C 13.2 8.679999 12.34 8.7 11.599999 8.72 C 11.48 8.599999 11.48 8.16 11.599999 8.04 C 12.679999 7.96 12.78 7.44 12.4 6.46 L 11.24 3.3 C 11.16 3.06 11.04 3.08 10.96 3.28 Z "/>
</symbol>
<symbol id="gB1351C61B7F6B471ABB1B8F64AC9D816" overflow="visible">
<path d="M 1.48 2.54 C 1.48 0.88 1.4399999 0.64 1.36 -0.12 C 1.5999999 -0.19999999 1.8199999 -0.26 2.04 -0.26 C 2.3 -0.04 2.5 0.24 2.6799998 0.59999996 C 3.46 0 4.68 -0.19999999 5.6 -0.19999999 C 7.8199997 -0.19999999 10.16 2 10.16 4.8599997 C 10.16 6 9.719999 7.12 9.08 7.8599997 C 8.36 8.679999 7.3999996 8.88 6.3399997 8.88 C 5.72 8.88 4.66 8.179999 4.08 7.7599998 L 4.08 11.66 C 4.08 12.96 4.14 13.7 4.14 13.7 C 4.14 13.88 4 13.96 3.82 13.96 C 3.08 13.719999 1.48 13.5 0.06 13.44 C 0 13.2 0.02 12.98 0.12 12.799999 C 1.38 12.7 1.48 12.679999 1.48 11.3 Z M 4.08 6.96 C 4.74 7.3999996 5.18 7.46 5.64 7.46 C 6.62 7.46 7.3599997 6.56 7.3599997 4.6 C 7.3599997 2.96 7.08 0.64 5.5 0.64 C 4.92 0.64 4.46 0.88 4.08 1.3399999 Z "/>
</symbol>
<symbol id="gB591690011940384999C1B007F794058" overflow="visible">
<path d="M 2 2.54 C 2 0.88 1.68 0.7 0.45999998 0.64 C 0.34 0.52 0.34 0.08 0.45999998 -0.04 C 1.3 -0.02 2.2 0 3.3 0 C 4.18 0 5.06 -0.02 5.54 -0.04 C 5.66 0.08 5.66 0.52 5.54 0.64 C 4.94 0.71999997 4.6 0.88 4.6 2.54 L 4.6 4.18 C 5.16 4.18 5.7799997 4.12 5.98 3.8 C 6.44 3.12 7 2.3 7.3399997 1.56 C 7.6 1 7.66 0.82 7.66 0.52 L 7.66 0 L 7.7 -0.04 C 7.7 -0.04 8.599999 0 9.3 0 C 10.12 0 11.24 -0.02 11.98 -0.04 C 12.099999 0.08 12.099999 0.52 11.98 0.64 C 11.2 0.71999997 10.76 0.65999997 10.16 1.56 L 7.8399997 4.98 C 7.74 5.12 7.7 5.2799997 7.7799997 5.38 L 8.78 6.48 C 9.42 7.18 9.96 7.8799996 11.48 8.04 C 11.599999 8.16 11.599999 8.599999 11.48 8.72 C 11.04 8.7 9.78 8.679999 9.26 8.679999 C 8.5199995 8.679999 7.58 8.7 6.8399997 8.72 C 6.72 8.599999 6.72 8.16 6.8399997 8.04 C 7.9199996 7.96 8.24 7.7799997 7.66 6.98 C 7.22 6.3799996 6.7799997 5.9 6.3799996 5.54 C 6.12 5.3199997 5.2 4.98 4.6 4.98 L 4.6 11.66 C 4.6 12.96 4.66 13.7 4.66 13.7 C 4.66 13.88 4.52 13.96 4.3399997 13.96 C 3.6 13.719999 2 13.5 0.58 13.44 C 0.52 13.2 0.53999996 12.98 0.64 12.799999 C 1.9 12.7 2 12.679999 2 11.3 Z "/>
</symbol>
<symbol id="gB8789F2F5F06048D4163694E4C0F3B6C" overflow="visible">
<path d="M 12.36 2.44 L 12.36 10.46 C 12.36 12.12 12.7 12.219999 14.099999 12.28 C 14.219999 12.4 14.219999 12.82 14.099999 12.94 C 13.28 12.92 12.259999 12.9 11.5 12.9 C 10.76 12.9 9.8 12.92 8.92 12.94 C 8.8 12.82 8.8 12.4 8.92 12.28 C 10.32 12.219999 10.66 12.12 10.66 10.46 L 10.66 7.2599998 L 3.82 7.2599998 L 3.82 10.46 C 3.82 12.12 4.16 12.219999 5.56 12.28 C 5.68 12.4 5.68 12.82 5.56 12.94 C 4.7999997 12.92 3.98 12.9 2.96 12.9 C 1.9599999 12.9 1.14 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.26 -0.02 2.22 0 2.98 0 C 3.6999998 0 4.68 -0.02 5.56 -0.04 C 5.68 0.08 5.68 0.5 5.56 0.62 C 4.16 0.68 3.82 0.78 3.82 2.44 L 3.82 6.42 L 10.66 6.42 L 10.66 2.44 C 10.66 0.78 10.32 0.68 8.92 0.62 C 8.8 0.5 8.8 0.08 8.92 -0.04 C 9.82 -0.02 10.78 0 11.5199995 0 C 12.259999 0 13.219999 -0.02 14.099999 -0.04 C 14.219999 0.08 14.219999 0.5 14.099999 0.62 C 12.7 0.68 12.36 0.78 12.36 2.44 Z "/>
</symbol>
<symbol id="g54DD1A53056317C9D72B591A0D7293A0" overflow="visible">
<path d="M 7.54 13.16 C 4.2 13.16 0.74 10.54 0.74 6.14 C 0.74 2.54 3.22 -0.19999999 7.04 -0.19999999 C 9.4 -0.19999999 11.259999 0.29999998 12.62 1.4599999 C 12.4 1.64 12.3 1.8 12.3 2.02 L 12.3 4.3399997 C 12.3 5.04 12.639999 5.24 13.219999 5.2999997 C 13.34 5.42 13.34 5.9 13.219999 6.02 C 12.74 6 12.24 5.98 11.44 5.98 C 10.78 5.98 9.84 6 8.96 6.02 C 8.84 5.9 8.84 5.42 8.96 5.2999997 C 10.059999 5.22 10.599999 5.14 10.599999 4.3399997 L 10.599999 1.28 C 9.92 0.64 8.58 0.52 7.5 0.52 C 4.3399997 0.52 2.6599998 3.8999999 2.6599998 6.54 C 2.6599998 10.04 4.94 12.44 7.2599998 12.44 C 10.16 12.44 10.98 10.78 11.5 9.059999 C 11.719999 9.04 11.94 9.08 12.16 9.179999 C 12.12 10.0199995 12.0199995 10.82 11.7 12.259999 C 10.5 12.46 9.76 13.16 7.54 13.16 Z "/>
</symbol>
<symbol id="gA1481BA28623480CC7E6165783E2A864" overflow="visible">
<path d="M 4.06 7.96 C 4.18 8.08 4.18 8.5 4.06 8.62 C 3.46 8.599999 2.76 8.58 2.04 8.58 C 1.28 8.58 0.74 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.16 7.8599997 1.38 7.66 1.8 6.62 L 4.42 0.16 C 4.54 -0.12 4.7 -0.24 4.9 -0.24 C 5.08 -0.24 5.24 -0.12 5.38 0.19999999 L 7.3999996 5.12 L 9.46 0.16 C 9.58 -0.12 9.74 -0.24 9.94 -0.24 C 10.12 -0.24 10.28 -0.12 10.4 0.17999999 L 13.0199995 6.52 C 13.34 7.3399997 13.679999 7.8999996 14.7 7.96 C 14.82 8.08 14.82 8.5 14.7 8.62 C 14.299999 8.599999 13.86 8.58 13.259999 8.58 C 12.66 8.58 11.82 8.599999 11.219999 8.62 C 11.099999 8.5 11.099999 8.08 11.219999 7.96 C 12.719999 7.8799996 12.5199995 7.2999997 12.24 6.6 L 10.559999 2.44 C 10.36 1.9399999 10.28 1.9399999 10.12 2.36 L 8.4 6.74 C 8.0199995 7.68 8.059999 7.8799996 9.12 7.96 C 9.24 8.08 9.24 8.5 9.12 8.62 C 8.5199995 8.599999 7.72 8.58 7.12 8.58 C 6.62 8.58 5.96 8.599999 5.3599997 8.62 C 5.24 8.5 5.24 8.08 5.3599997 7.96 C 6.2999997 7.8799996 6.54 7.2999997 6.8999996 6.3999996 L 7.02 6.08 L 5.62 2.54 C 5.3599997 1.88 5.3199997 1.86 5.06 2.5 L 3.46 6.62 C 3.08 7.58 3.1 7.8999996 4.06 7.96 Z "/>
</symbol>
<symbol id="g8D44D9C01F9AF6C3B1D634FDF54DE6FB" overflow="visible">
<path d="M 5.66 6.46 C 7.3599997 6.46 7.4199996 6 7.48 5.1 C 7.6 4.98 8.0199995 4.98 8.139999 5.1 C 8.12 5.6 8.099999 6.18 8.099999 6.8599997 C 8.099999 7.54 8.12 8.059999 8.139999 8.58 C 8.0199995 8.7 7.6 8.7 7.48 8.58 C 7.4199996 7.48 7.3599997 7.22 5.66 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.9 4.04 12.099999 4.92 12.099999 L 5.8199997 12.099999 C 7.94 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.92 9.34 9.96 9.5 10.0199995 C 9.4 10.84 9.099999 12.759999 9.059999 12.92 C 9.059999 12.96 9.04 12.98 8.98 12.98 C 8.639999 12.92 8.54 12.9 8.04 12.9 L 2.9399998 12.9 C 2.3 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.06 -0.02 2.06 0 2.96 0 C 3.86 0 4.8399997 -0.02 5.54 -0.04 C 5.66 0.08 5.66 0.5 5.54 0.62 C 4.14 0.68 3.8 0.78 3.8 2.44 L 3.8 6.46 Z "/>
</symbol>
<symbol id="gCAFB20A65E8FBEFE071D9C4C8EE95E49" overflow="visible">
<path d="M 1.22 9.36 C 1.22 8.94 1.5999999 8.58 2.02 8.58 C 2.36 8.58 2.96 8.94 2.96 9.38 C 2.96 9.54 2.9199998 9.66 2.8799999 9.8 C 2.84 9.94 2.72 10.12 2.72 10.28 C 2.72 10.78 3.24 11.5 4.7 11.5 C 5.42 11.5 6.44 11 6.44 9.08 C 6.44 7.7999997 5.98 6.7599998 4.7999997 5.56 L 3.32 4.1 C 1.36 2.1 1.04 1.14 1.04 -0.04 C 1.04 -0.04 2.06 0 2.7 0 L 6.2 0 C 6.8399997 0 7.7599998 -0.04 7.7599998 -0.04 C 8.0199995 1.02 8.22 2.52 8.24 3.12 C 8.12 3.22 7.8599997 3.26 7.66 3.22 C 7.3199997 1.8 6.98 1.3 6.2599998 1.3 L 2.7 1.3 C 2.7 2.26 4.08 3.62 4.18 3.72 L 6.2 5.66 C 7.3399997 6.7599998 8.2 7.64 8.2 9.16 C 8.2 11.32 6.44 12.2 4.8199997 12.2 C 2.6 12.2 1.22 10.559999 1.22 9.36 Z "/>
</symbol>
<symbol id="g8C7315D77A5D71E18736DE61553C419F" overflow="visible">
<path d="M 1.4 1.1999999 C 1.4 0.62 1.88 0.14 2.46 0.14 C 3.04 0.14 3.52 0.62 3.52 1.1999999 C 3.52 1.78 3.04 2.26 2.46 2.26 C 1.88 2.26 1.4 1.78 1.4 1.1999999 Z M 1.4 7.16 C 1.4 6.58 1.88 6.1 2.46 6.1 C 3.04 6.1 3.52 6.58 3.52 7.16 C 3.52 7.74 3.04 8.22 2.46 8.22 C 1.88 8.22 1.4 7.74 1.4 7.16 Z "/>
</symbol>
<symbol id="g560AC22EF992EFD90E66808483D7B3BA" overflow="visible">
<path d="M 11.12 10.24 L 11.12 3.6999998 C 11.12 3.32 11.12 3.1 10.98 3.1 C 10.9 3.1 10.599999 3.46 10.0199995 4.2 L 3.1599998 12.9 L 0.45999998 12.94 C 0.34 12.82 0.34 12.4 0.45999998 12.28 C 1.3199999 12.219999 1.92 11.5199995 2.04 11 L 2.04 2.6599998 C 2.04 0.88 1.6999999 0.76 0.29999998 0.62 C 0.17999999 0.5 0.17999999 0.08 0.29999998 -0.04 C 1.16 -0.02 2.06 0 2.54 0 C 3 0 3.9199998 -0.02 4.7599998 -0.04 C 4.88 0.08 4.88 0.5 4.7599998 0.62 C 3.36 0.76 3.02 0.84 3.02 2.6599998 L 3.02 8.78 C 3.02 9.46 3.02 9.76 3.1799998 9.76 C 3.3 9.76 3.52 9.54 3.86 9.099999 L 10.84 0.28 C 11.059999 -0.02 11.32 -0.19999999 11.639999 -0.19999999 C 11.92 -0.19999999 12.099999 0.04 12.099999 0.42 L 12.099999 10.24 C 12.099999 12.0199995 12.44 12.139999 13.84 12.28 C 13.96 12.4 13.96 12.82 13.84 12.94 C 13.0199995 12.92 12.08 12.9 11.599999 12.9 C 11.179999 12.9 10.26 12.92 9.38 12.94 C 9.26 12.82 9.26 12.4 9.38 12.28 C 10.78 12.139999 11.12 12.059999 11.12 10.24 Z "/>
</symbol>
<symbol id="g87DD77732F07A5C65A64D31E4C3C918D" overflow="visible">
<path d="M 16.199999 11.3 L 13.08 2.62 L 13.0199995 2.6399999 L 10.26 11.08 C 9.92 12.16 10.62 12.219999 11.3 12.28 C 11.42 12.4 11.42 12.82 11.3 12.94 C 10.48 12.92 9.599999 12.9 8.8 12.9 C 8.139999 12.9 7.44 12.92 6.7999997 12.94 C 6.68 12.82 6.68 12.4 6.7999997 12.28 C 7.8599997 12.219999 8.3 11.599999 8.48 11.08 L 8.94 9.76 C 9.0199995 9.5199995 9.08 9.32 9.08 9.139999 C 9.08 8.94 9.059999 8.78 8.9 8.44 L 6.3199997 2.58 L 6.22 2.6 L 3.3 11.44 C 3.06 12.139999 3.6 12.24 4.2999997 12.28 C 4.42 12.4 4.42 12.82 4.2999997 12.94 C 3.6399999 12.92 2.76 12.9 1.9799999 12.9 C 1.28 12.9 0.7 12.92 0.12 12.94 C 0 12.82 0 12.4 0.12 12.28 C 1.02 12.219999 1.16 12.2 1.54 11.12 L 5.2999997 0.29999998 C 5.4 -0.02 5.52 -0.24 5.74 -0.24 C 6 -0.24 6.12 -0.04 6.2599998 0.29999998 L 9.24 7 C 9.42 7.3999996 9.48 7.5 9.58 7.5 C 9.66 7.5 9.74 7.2799997 9.86 6.94 L 12.16 0.29999998 C 12.28 -0.04 12.38 -0.24 12.62 -0.24 C 12.84 -0.24 12.98 -0.02 13.08 0.28 L 17.1 11.059999 C 17.359999 11.759999 17.72 12.219999 18.82 12.28 C 18.939999 12.4 18.939999 12.82 18.82 12.94 C 18.24 12.92 17.6 12.9 17.08 12.9 C 16.56 12.9 15.679999 12.92 14.88 12.94 C 14.759999 12.82 14.759999 12.4 14.88 12.28 C 15.7 12.219999 16.5 12.16 16.199999 11.3 Z "/>
</symbol>
<symbol id="g11C09650A1107877D1CACE85AD57EEFF" overflow="visible">
<path d="M 4.2999997 11.5 C 5.16 11.5 5.96 10.98 5.96 9.7 C 5.96 8.7 4.7999997 7.16 2.82 6.8799996 L 2.9199998 6.24 C 3.26 6.2799997 3.62 6.2799997 3.8799999 6.2799997 C 5.02 6.2799997 6.5 5.96 6.5 3.6999998 C 6.5 1.04 4.72 0.5 4.02 0.5 C 3 0.5 2.82 0.96 2.58 1.3199999 C 2.3799999 1.5999999 2.12 1.8399999 1.7199999 1.8399999 C 1.3 1.8399999 0.88 1.4599999 0.88 1.14 C 0.88 0.34 2.56 -0.19999999 3.76 -0.19999999 C 6.14 -0.19999999 8.26 1.3399999 8.26 3.98 C 8.26 6.16 6.62 6.94 5.44 7.14 L 5.42 7.18 C 7.06 7.96 7.52 8.78 7.52 9.84 C 7.52 10.44 7.3799996 10.92 6.8999996 11.42 C 6.46 11.86 5.7599998 12.2 4.72 12.2 C 1.78 12.2 0.94 10.28 0.94 9.62 C 0.94 9.34 1.14 8.94 1.62 8.94 C 2.32 8.94 2.3999999 9.599999 2.3999999 9.98 C 2.3999999 11.259999 3.78 11.5 4.2999997 11.5 Z "/>
</symbol>
<symbol id="gAA14E57E2DCC57A3F7809273EECD3C51" overflow="visible">
<path d="M 7.9104 1.5616 L 7.9104 6.6944 C 7.9104 7.7567997 8.128 7.8208 9.024 7.8592 C 9.1008 7.936 9.1008 8.2048 9.024 8.2816 C 8.4992 8.2688 7.8464 8.256 7.3599997 8.256 C 6.8863997 8.256 6.272 8.2688 5.7088 8.2816 C 5.632 8.2048 5.632 7.936 5.7088 7.8592 C 6.6047997 7.8208 6.8223996 7.7567997 6.8223996 6.6944 L 6.8223996 4.6464 L 2.4448 4.6464 L 2.4448 6.6944 C 2.4448 7.7567997 2.6624 7.8208 3.5584 7.8592 C 3.6352 7.936 3.6352 8.2048 3.5584 8.2816 C 3.072 8.2688 2.5472 8.256 1.8944 8.256 C 1.2544 8.256 0.72959995 8.2688 0.24319999 8.2816 C 0.1664 8.2048 0.1664 7.936 0.24319999 7.8592 C 1.1392 7.8208 1.3568 7.7567997 1.3568 6.6944 L 1.3568 1.5616 C 1.3568 0.4992 1.1392 0.43519998 0.24319999 0.39679998 C 0.1664 0.32 0.1664 0.0512 0.24319999 -0.0256 C 0.8064 -0.0128 1.4208 0 1.9072 0 C 2.368 0 2.9952 -0.0128 3.5584 -0.0256 C 3.6352 0.0512 3.6352 0.32 3.5584 0.39679998 C 2.6624 0.43519998 2.4448 0.4992 2.4448 1.5616 L 2.4448 4.1088 L 6.8223996 4.1088 L 6.8223996 1.5616 C 6.8223996 0.4992 6.6047997 0.43519998 5.7088 0.39679998 C 5.632 0.32 5.632 0.0512 5.7088 -0.0256 C 6.2848 -0.0128 6.8992 0 7.3728 0 C 7.8464 0 8.4608 -0.0128 9.024 -0.0256 C 9.1008 0.0512 9.1008 0.32 9.024 0.39679998 C 8.128 0.43519998 7.9104 0.4992 7.9104 1.5616 Z "/>
</symbol>
<symbol id="gF5F8064101DBF0FCB4BCFDA7012527FE" overflow="visible">
<path d="M 2.3167999 1.5616 L 2.3167999 4.1088 C 2.3167999 4.7488 2.368 5.568 2.368 5.568 C 2.368 5.6191998 2.304 5.6576 2.2015998 5.6576 C 1.8432 5.5168 1.3312 5.4016 0.44799998 5.2864 C 0.4224 5.2096 0.44799998 5.0048 0.4736 4.928 C 1.1776 4.864 1.3055999 4.7872 1.3055999 4.0576 L 1.3055999 1.5616 C 1.3055999 0.4992 1.1647999 0.4608 0.384 0.39679998 C 0.30719998 0.32 0.30719998 0.0512 0.384 -0.0256 C 0.8064 -0.0128 1.3055999 0 1.8176 0 C 2.3295999 0 2.816 -0.0128 3.2384 -0.0256 C 3.3151999 0.0512 3.3151999 0.32 3.2384 0.39679998 C 2.4575999 0.44799998 2.3167999 0.4992 2.3167999 1.5616 Z M 1.152 7.6671996 C 1.152 7.3343997 1.4591999 7.0016 1.7664 7.0016 C 2.1248 7.0016 2.432 7.3472 2.432 7.6159997 C 2.432 7.9231997 2.1632 8.2816 1.8176 8.2816 C 1.5103999 8.2816 1.152 7.9743996 1.152 7.6671996 Z "/>
</symbol>
<symbol id="g3976D55F213F07C6469FD06EC16139AA" overflow="visible">
<path d="M 4.9407997 1.1904 C 4.4672 0.704 4.0959997 0.4992 3.3536 0.4992 C 2.8927999 0.4992 2.3552 0.768 1.9583999 1.4208 C 1.7024 1.8432 1.5488 2.432 1.5488 3.1743999 L 4.9536 3.1488 C 5.1071997 3.1488 5.1967998 3.2256 5.1967998 3.3664 C 5.1967998 4.4416 4.8128 5.5936 3.0335999 5.5936 C 1.92 5.5936 0.4736 4.5312 0.4736 2.5856 C 0.4736 1.8687999 0.65279996 1.1776 1.0752 0.69119996 C 1.5103999 0.1792 2.112 -0.12799999 3.0335999 -0.12799999 C 4.0064 -0.12799999 4.6976 0.32 5.2096 0.9856 C 5.1712 1.1136 5.0944 1.1776 4.9407997 1.1904 Z M 1.5871999 3.6095998 C 1.8304 5.0559998 2.7264 5.1712 3.0335999 5.1712 C 3.52 5.1712 4.0959997 4.9024 4.0959997 3.8272 C 4.0959997 3.712 4.0448 3.648 3.9039998 3.648 Z "/>
</symbol>
<symbol id="gB7BB853387AAC07ADB7DDEF96856059B" overflow="visible">
<path d="M 2.2528 4.5824 C 2.2272 5.0944 2.2144 5.4272 2.1504 5.5551996 C 2.1248 5.6191998 2.0992 5.6576 1.9968 5.6576 C 1.6384 5.5168 1.3055999 5.4016 0.4224 5.2864 C 0.39679998 5.2096 0.4224 5.0048 0.44799998 4.928 C 1.1392 4.864 1.28 4.7999997 1.28 4.0576 L 1.28 1.5616 C 1.28 0.4992 1.1264 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7808 -0.0128 1.28 0 1.7919999 0 C 2.304 0 2.8927999 -0.0128 3.3407998 -0.0256 C 3.4176 0.0512 3.4176 0.32 3.3407998 0.39679998 C 2.4448 0.4608 2.2912 0.4992 2.2912 1.5616 L 2.2912 3.3407998 C 2.2912 3.6736 2.4448 3.968 2.5983999 4.1984 C 2.7391999 4.4031997 3.0335999 4.8255997 3.1871998 4.8255997 C 3.3023999 4.8255997 3.4176 4.7999997 3.52 4.6591997 C 3.6095998 4.5312 3.7631998 4.3648 3.9808 4.3648 C 4.288 4.3648 4.5824 4.6847997 4.5824 5.0048 C 4.5824 5.2479997 4.3519998 5.6191998 3.8144 5.6191998 C 3.2128 5.6191998 2.688 5.0559998 2.3936 4.5568 C 2.3167999 4.416 2.2528 4.5183997 2.2528 4.5824 Z "/>
</symbol>
<symbol id="gF8EC31AC53CF59E01ED9143906F6DA7B" overflow="visible">
<path d="M 3.7503998 0.61439997 C 3.8272 0.21759999 3.968 -0.12799999 4.608 -0.12799999 C 5.0944 -0.12799999 5.5551996 0.0896 5.824 0.34559998 C 5.7984 0.4992 5.7472 0.61439997 5.6064 0.69119996 C 5.5168 0.61439997 5.2992 0.48639998 5.1328 0.48639998 C 4.7616 0.48639998 4.7488 0.9856 4.7488 1.5744 L 4.7488 3.4559999 C 4.7488 5.2736 3.7503998 5.6191998 2.816 5.6191998 C 1.7664 5.6191998 0.704 4.928 0.704 4.1984 C 0.704 3.8911998 0.8576 3.7375998 1.152 3.7375998 C 1.5231999 3.7375998 1.7536 4.0064 1.7536 4.1728 C 1.7536 4.2623997 1.7407999 4.3519998 1.7152 4.4031997 C 1.7024 4.4416 1.6896 4.5183997 1.6896 4.6591997 C 1.6896 5.0559998 2.2272 5.1967998 2.7136 5.1967998 C 3.1488 5.1967998 3.7503998 4.9792 3.7503998 3.5328 C 3.7503998 3.4431999 3.712 3.392 3.6736 3.3792 L 2.5728 3.1104 C 1.344 2.8032 0.4608 2.1248 0.4608 1.2544 C 0.4608 0.2048 1.1776 -0.12799999 2.0736 -0.12799999 C 2.5216 -0.12799999 2.9055998 -0.0256 3.4687998 0.4096 L 3.7247999 0.61439997 Z M 3.7503998 2.9824 L 3.7503998 1.2928 C 3.7503998 1.1264 3.6736 1.0368 3.5712 0.96 C 3.2384 0.69119996 2.8032 0.39679998 2.4448 0.39679998 C 1.8047999 0.39679998 1.5231999 0.9088 1.5231999 1.3055999 C 1.5231999 1.8815999 1.7919999 2.4703999 2.7391999 2.7136 Z "/>
</symbol>
<symbol id="g68DDE7C8FDC8A226B6C32EAD39AF7364" overflow="visible">
<path d="M 5.0944 1.1647999 C 5.0432 1.28 4.9407997 1.3312 4.8255997 1.344 C 4.3904 0.7808 3.84 0.4992 3.2896 0.4992 C 2.3552 0.4992 1.5744 1.4463999 1.5744 2.944 C 1.5744 4.3519998 2.1887999 5.1967998 3.0335999 5.1967998 C 3.7888 5.1967998 3.8911998 4.7488 3.9424 4.3008 C 3.9808 3.9552 4.16 3.84 4.4288 3.84 C 4.6976 3.84 5.0559998 4.0064 5.0559998 4.4031997 C 5.0559998 5.1071997 4.3264 5.6191998 3.0976 5.6191998 C 1.8304 5.6191998 0.4736 4.48 0.4736 2.6624 C 0.4736 1.0112 1.3952 -0.12799999 3.008 -0.12799999 C 3.776 -0.12799999 4.4544 0.1152 5.0944 1.1647999 Z "/>
</symbol>
<symbol id="g570B752173035444311A253BD2376AD" overflow="visible">
<path d="M 2.1376 3.6608 C 2.1376 3.9296 2.2528 4.0832 2.3552 4.1984 C 2.8416 4.672 3.4944 4.9536 3.9936 4.9536 C 4.2496 4.9536 4.5183997 4.7872 4.672 4.4927998 C 4.7999997 4.2367997 4.8255997 3.8911998 4.8255997 3.5072 L 4.8255997 1.5616 C 4.8255997 0.51199996 4.6976 0.4608 4.032 0.39679998 C 3.968 0.32 3.968 0.0512 4.032 -0.0256 C 4.3904 -0.0128 4.8255997 0 5.3375998 0 C 5.8496 0 6.272 -0.0128 6.6944 -0.0256 C 6.7584 0.0512 6.7584 0.32 6.6944 0.39679998 C 5.9775996 0.4608 5.8367996 0.51199996 5.8367996 1.5616 L 5.8367996 3.4687998 C 5.8367996 4.1728 5.7855997 4.7999997 5.4912 5.184 C 5.2736 5.4656 4.8768 5.6191998 4.4288 5.6191998 C 3.8016 5.6191998 3.0335999 5.4528 2.2528 4.5824 C 2.2528 4.5696 2.24 4.5696 2.2272 4.5568 C 2.1887999 4.5056 2.1248 4.4288 2.1248 4.5824 L 2.1376 7.4624 C 2.1376 8.2944 2.1887999 8.806399 2.1887999 8.806399 C 2.1887999 8.896 2.1376 8.9344 2.0224 8.9344 C 1.7024 8.806399 0.7424 8.6272 0.2304 8.588799 C 0.2048 8.4864 0.2304 8.2816 0.30719998 8.2048 C 0.34559998 8.2048 0.384 8.2048 0.4224 8.2048 C 0.9856 8.1664 1.1264 8.1664 1.1264 7.1552 L 1.1264 1.5616 C 1.1264 0.4992 0.97279996 0.44799998 0.2304 0.39679998 C 0.15359999 0.32 0.15359999 0.0512 0.2304 -0.0256 C 0.65279996 -0.0128 1.1264 0 1.6384 0 C 2.1248 0 2.5472 -0.0128 2.9055998 -0.0256 C 2.9824 0.0512 2.9824 0.32 2.9055998 0.39679998 C 2.2528 0.44799998 2.1376 0.4992 2.1376 1.5616 Z "/>
</symbol>
<symbol id="g9662C1D9A80FEB5040A57FD9DFCA7985" overflow="visible">
<path d="M 1.216 1.5616 C 1.216 0.4992 1.0752 0.43519998 0.2944 0.39679998 C 0.21759999 0.32 0.21759999 0.0512 0.2944 -0.0256 C 0.7424 -0.0128 1.216 0 1.7279999 0 C 2.24 0 2.7264 -0.0128 3.1488 -0.0256 C 3.2256 0.0512 3.2256 0.32 3.1488 0.39679998 C 2.368 0.43519998 2.2272 0.4992 2.2272 1.5616 L 2.2272 7.4624 C 2.2272 8.2944 2.2784 8.806399 2.2784 8.806399 C 2.2784 8.896 2.2272 8.9344 2.112 8.9344 C 1.7919999 8.806399 0.83199996 8.6272 0.32 8.588799 C 0.2944 8.4864 0.32 8.2816 0.39679998 8.2048 C 1.1392 8.1536 1.216 8.1152 1.216 7.1552 Z "/>
</symbol>
<symbol id="g1CB3EC9D05726EBFDE8ADABEC8504FCD" overflow="visible">
<path d="M 7.1168 6.5536 L 7.1168 2.368 C 7.1168 2.1248 7.1168 1.984 7.0271997 1.984 C 6.976 1.984 6.784 2.2144 6.4128 2.688 L 2.0224 8.256 L 0.2944 8.2816 C 0.21759999 8.2048 0.21759999 7.936 0.2944 7.8592 C 0.8448 7.8208 1.2287999 7.3728 1.3055999 7.04 L 1.3055999 1.7024 C 1.3055999 0.5632 1.0879999 0.48639998 0.192 0.39679998 C 0.1152 0.32 0.1152 0.0512 0.192 -0.0256 C 0.7424 -0.0128 1.3184 0 1.6256 0 C 1.92 0 2.5088 -0.0128 3.0463998 -0.0256 C 3.1232 0.0512 3.1232 0.32 3.0463998 0.39679998 C 2.1504 0.48639998 1.9327999 0.5376 1.9327999 1.7024 L 1.9327999 5.6191998 C 1.9327999 6.0544 1.9327999 6.2464 2.0351999 6.2464 C 2.112 6.2464 2.2528 6.1056 2.4703999 5.824 L 6.9375997 0.1792 C 7.0783997 -0.0128 7.2447996 -0.12799999 7.4495997 -0.12799999 C 7.6288 -0.12799999 7.744 0.0256 7.744 0.2688 L 7.744 6.5536 C 7.744 7.6927996 7.9616 7.7696 8.8576 7.8592 C 8.9344 7.936 8.9344 8.2048 8.8576 8.2816 C 8.3328 8.2688 7.7311997 8.256 7.424 8.256 C 7.1552 8.256 6.5664 8.2688 6.0032 8.2816 C 5.9263997 8.2048 5.9263997 7.936 6.0032 7.8592 C 6.8992 7.7696 7.1168 7.7184 7.1168 6.5536 Z "/>
</symbol>
<symbol id="gD62975B7DE3250BE5F195D0E8335F60D" overflow="visible">
<path d="M 4.16 5.0944 C 4.8512 5.0432 4.928 4.8896 4.6591997 4.2367997 L 3.6223998 1.7279999 C 3.4176 1.2287999 3.3536 1.2287999 3.1488 1.7664 L 2.2272 4.2367997 C 1.9968 4.8512 1.9455999 5.0048 2.6239998 5.0944 C 2.7008 5.1712 2.7008 5.44 2.6239998 5.5168 C 2.2015998 5.5039997 1.7536 5.4912 1.3312 5.4912 C 0.9088 5.4912 0.5248 5.5039997 0.1408 5.5168 C 0.063999996 5.44 0.063999996 5.1712 0.1408 5.0944 C 0.8192 5.0176 0.9088 4.8128 1.1647999 4.16 L 2.8032 0.1152 C 2.8799999 -0.076799996 2.9568 -0.15359999 3.1232 -0.15359999 C 3.2512 -0.15359999 3.3407998 -0.076799996 3.4304 0.1408 L 5.1328 4.1472 C 5.376 4.7104 5.5168 5.0304 6.2335997 5.0944 C 6.3104 5.1712 6.3104 5.44 6.2335997 5.5168 C 5.9775996 5.5039997 5.6703997 5.4912 5.3375998 5.4912 C 4.9151998 5.4912 4.48 5.5039997 4.16 5.5168 C 4.0832 5.44 4.0832 5.1712 4.16 5.0944 Z "/>
</symbol>
<symbol id="gEFCBD5CCFA072E8B49E2065B449FDBBF" overflow="visible">
<path d="M 5.6832 4.9536 C 5.9263997 4.9536 6.1568 5.184 6.1568 5.44 C 6.1568 5.7088 5.9136 5.9136 5.568 5.9136 C 5.2352 5.9136 4.6208 5.6959996 4.288 5.2608 C 4.1344 5.3631997 3.712 5.6191998 2.9568 5.6191998 C 1.8176 5.6191998 0.768 4.8512 0.768 3.6736 C 0.768 2.9824 1.0752 2.5856 1.4336 2.24 C 1.0752 1.9327999 0.87039995 1.3823999 0.87039995 0.9472 C 0.87039995 0.48639998 1.1264 0.12799999 1.4591999 -0.038399998 C 0.768 -0.44799998 0.4096 -1.0368 0.4096 -1.5871999 C 0.4096 -2.7008 1.4591999 -3.0463998 2.4448 -3.0463998 C 4.1728 -3.0463998 6.0415998 -2.2144 6.0415998 -0.83199996 C 6.0415998 -0.4224 5.8496 -0.1024 5.4783998 0.2048 C 4.9792 0.61439997 4.0832 0.6272 3.6095998 0.6272 C 3.3792 0.6272 3.0591998 0.6016 2.7519999 0.5632 C 2.56 0.55039996 2.432 0.5376 2.368 0.5376 C 1.9968 0.5376 1.5488 0.7168 1.5488 1.2672 C 1.5488 1.5231999 1.6256 1.7919999 1.7792 2.0096 C 2.0864 1.8304 2.4448 1.7407999 2.944 1.7407999 C 4.0703998 1.7407999 5.1071997 2.4448 5.1071997 3.6992 C 5.1071997 4.3008 4.928 4.6464 4.5568 5.0304 C 4.6464 5.1584 4.9024 5.3375998 5.0688 5.3375998 C 5.1584 5.3375998 5.2479997 5.2992 5.3248 5.184 C 5.376 5.0815997 5.5424 4.9536 5.6832 4.9536 Z M 1.6896 -0.12799999 C 1.8304 -0.1664 2.0351999 -0.192 2.2015998 -0.192 C 2.5983999 -0.192 2.9568 -0.15359999 3.136 -0.15359999 C 3.776 -0.15359999 4.3136 -0.1664 4.6847997 -0.3712 C 5.184 -0.65279996 5.3375998 -0.83199996 5.3375998 -1.1647999 C 5.3375998 -2.0864 3.9808 -2.5728 2.8288 -2.5728 C 2.368 -2.5728 1.2928 -2.2015998 1.2928 -1.3312 C 1.2928 -0.89599997 1.3184 -0.576 1.6896 -0.12799999 Z M 4.0832 3.5712 C 4.0832 2.3808 3.4815998 2.1376 3.008 2.1376 C 1.9327999 2.1376 1.8176 3.0463998 1.8176 3.8655999 C 1.8176 4.7616 2.1376 5.2223997 2.8416 5.2223997 C 3.648 5.2223997 4.0832 4.6335998 4.0832 3.5712 Z "/>
</symbol>
<symbol id="gD5EEFB9760BC9A91B84F628EDDA52971" overflow="visible">
<path d="M 2.1376 5.0432 C 2.0607998 4.9663997 2.0096 4.992 2.0096 5.1071997 L 2.0096 7.4624 C 2.0096 8.2944 2.0607998 8.806399 2.0607998 8.806399 C 2.0607998 8.896 2.0096 8.9344 1.8944 8.9344 C 1.5744 8.806399 0.61439997 8.6272 0.1024 8.588799 C 0.076799996 8.4864 0.1024 8.2816 0.1792 8.2048 C 0.21759999 8.2048 0.25599998 8.2048 0.2944 8.2048 C 0.8576 8.1664 0.9984 8.1664 0.9984 7.1552 L 0.9984 0.9088 C 0.9984 0.4096 0.9856 0.1792 0.9472 0 C 1.0112 -0.1024 1.0752 -0.15359999 1.2287999 -0.15359999 C 1.3055999 -0.076799996 1.4336 0.038399998 1.536 0.15359999 C 1.6639999 0.30719998 1.7407999 0.30719998 1.8815999 0.192 C 2.1759999 -0.0512 2.56 -0.12799999 3.008 -0.12799999 C 4.3136 -0.12799999 5.8367996 1.0624 5.8367996 3.0976 C 5.8367996 4.6591997 4.6847997 5.6191998 3.5712 5.6191998 C 3.0207999 5.6191998 2.5344 5.4016 2.1376 5.0432 Z M 2.2272 4.6464 C 2.56 4.9407997 2.944 5.0559998 3.3151999 5.0559998 C 4.0959997 5.0559998 4.736 4.1088 4.736 2.8672 C 4.736 1.408 4.1472 0.30719998 2.9312 0.30719998 C 2.5344 0.30719998 2.2656 0.5888 2.0096 0.9088 L 2.0096 4.1088 C 2.0096 4.3775997 2.0607998 4.5056 2.2272 4.6464 Z "/>
</symbol>
<symbol id="g83A6AA7A836EACB3652229F4716CDAF" overflow="visible">
<path d="M 5.0559998 8.076799 C 4.3136 8.1792 4.3392 8.4223995 3.0848 8.4223995 C 1.7919999 8.4223995 0.65279996 7.5648 0.65279996 6.2079997 C 0.65279996 4.864 1.7664 4.2496 2.8927999 3.8144 C 3.6608 3.52 4.608 3.1615999 4.608 1.9072 C 4.608 0.87039995 4.032 0.3328 3.008 0.3328 C 1.8176 0.3328 1.0496 0.8832 0.768 2.1504 C 0.6016 2.2015998 0.4736 2.1759999 0.34559998 2.112 C 0.39679998 1.1264 0.44799998 0.79359996 0.6016 0.1664 C 1.408 0.1664 1.7664 -0.12799999 2.9055998 -0.12799999 C 3.4815998 -0.12799999 4.032 0.0128 4.48 0.2944 C 5.2223997 0.75519997 5.6832 1.536 5.6832 2.3552 C 5.6832 3.712 4.6591997 4.3136 3.6095998 4.7104 C 2.8416 4.992 1.5616 5.4783998 1.5616 6.5536 C 1.5616 7.2704 2.2144 7.9872 2.9696 7.9872 C 4.2111998 7.9872 4.608 7.1935997 4.864 6.3487997 C 5.0048 6.3231997 5.1712 6.336 5.2864 6.4256 C 5.2352 7.04 5.184 7.3984 5.0559998 8.076799 Z "/>
</symbol>
<symbol id="gDB4862E33098F259EEBBA99A57E5AFA" overflow="visible">
<path d="M 2.1759999 4.5824 C 2.1632 4.9663997 2.1376 5.4272 2.0736 5.5551996 C 2.0479999 5.6191998 2.0224 5.6576 1.92 5.6576 C 1.5616 5.5168 1.2287999 5.4016 0.34559998 5.2864 C 0.32 5.2096 0.34559998 5.0048 0.3712 4.928 C 1.0624 4.864 1.2032 4.7999997 1.2032 4.0576 L 1.2032 1.5616 C 1.2032 0.51199996 1.0368 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7168 -0.0128 1.2032 0 1.7152 0 C 2.2272 0 2.6239998 -0.0128 3.008 -0.0256 C 3.0848 0.0512 3.0848 0.32 3.008 0.39679998 C 2.3552 0.4608 2.2144 0.51199996 2.2144 1.5616 L 2.2144 3.6608 C 2.2144 3.9296 2.3295999 4.0832 2.432 4.1984 C 2.944 4.6976 3.4176 4.9536 3.8144 4.9536 C 4.3008 4.9536 4.6591997 4.6464 4.6591997 3.7888 L 4.6591997 1.5616 C 4.6591997 0.51199996 4.5568 0.44799998 3.8655999 0.39679998 C 3.8016 0.32 3.8016 0.0512 3.8655999 -0.0256 C 4.1856 -0.0128 4.6591997 0 5.1712 0 C 5.6832 0 6.1056 -0.0128 6.4256 -0.0256 C 6.4895997 0.0512 6.4895997 0.32 6.4256 0.39679998 C 5.7855997 0.44799998 5.6703997 0.51199996 5.6703997 1.5616 L 5.6703997 3.5967999 C 5.6703997 3.776 5.6703997 3.9552 5.6576 4.1088 C 6.272 4.7872 6.848 4.9536 7.3472 4.9536 C 7.8335996 4.9536 8.1152 4.672 8.1152 3.8144 L 8.1152 1.5616 C 8.1152 0.51199996 7.9872 0.44799998 7.3216 0.39679998 C 7.2576 0.32 7.2576 0.0512 7.3216 -0.0256 C 7.6415997 -0.0128 8.1152 0 8.6272 0 C 9.1392 0 9.5872 -0.0128 9.9456 -0.0256 C 10.0096 0.0512 10.0096 0.32 9.9456 0.39679998 C 9.2416 0.44799998 9.1264 0.51199996 9.1264 1.5616 L 9.1264 3.5839999 C 9.1264 4.7232 8.9344 5.6191998 7.8079996 5.6191998 C 7.1552 5.6191998 6.3616 5.376 5.6959996 4.672 C 5.6576 4.6335998 5.5808 4.5696 5.5551996 4.6847997 C 5.44 5.2096 4.9407997 5.6191998 4.2752 5.6191998 C 3.5328 5.6191998 2.8672 5.184 2.3295999 4.5824 C 2.2656 4.5183997 2.1887999 4.4288 2.1759999 4.5824 Z "/>
</symbol>
<symbol id="g793DBE65A5AEC1A16A65955B6C0E046" overflow="visible">
<path d="M 10.368 7.232 L 8.3712 1.6768 L 8.3328 1.6896 L 6.5664 7.0912 C 6.3487997 7.7823997 6.7967997 7.8208 7.232 7.8592 C 7.3087997 7.936 7.3087997 8.2048 7.232 8.2816 C 6.7072 8.2688 6.144 8.256 5.632 8.256 C 5.2096 8.256 4.7616 8.2688 4.3519998 8.2816 C 4.2752 8.2048 4.2752 7.936 4.3519998 7.8592 C 5.0304 7.8208 5.312 7.424 5.4272 7.0912 L 5.7216 6.2464 C 5.7728 6.0927997 5.8111997 5.9648 5.8111997 5.8496 C 5.8111997 5.7216 5.7984 5.6191998 5.6959996 5.4016 L 4.0448 1.6511999 L 3.9808 1.6639999 L 2.112 7.3216 C 1.9583999 7.7696 2.304 7.8335996 2.7519999 7.8592 C 2.8288 7.936 2.8288 8.2048 2.7519999 8.2816 C 2.3295999 8.2688 1.7664 8.256 1.2672 8.256 C 0.8192 8.256 0.44799998 8.2688 0.076799996 8.2816 C 0 8.2048 0 7.936 0.076799996 7.8592 C 0.65279996 7.8208 0.7424 7.8079996 0.9856 7.1168 L 3.392 0.192 C 3.4559999 -0.0128 3.5328 -0.15359999 3.6736 -0.15359999 C 3.84 -0.15359999 3.9167998 -0.0256 4.0064 0.192 L 5.9136 4.48 C 6.0288 4.736 6.0671997 4.7999997 6.1312 4.7999997 C 6.1823997 4.7999997 6.2335997 4.6591997 6.3104 4.4416 L 7.7823997 0.192 C 7.8592 -0.0256 7.9231997 -0.15359999 8.076799 -0.15359999 C 8.2176 -0.15359999 8.3071995 -0.0128 8.3712 0.1792 L 10.943999 7.0783997 C 11.110399 7.5263996 11.340799 7.8208 12.0448 7.8592 C 12.1216 7.936 12.1216 8.2048 12.0448 8.2816 C 11.673599 8.2688 11.264 8.256 10.9312 8.256 C 10.5984 8.256 10.0352 8.2688 9.5232 8.2816 C 9.4464 8.2048 9.4464 7.936 9.5232 7.8592 C 10.047999 7.8208 10.559999 7.7823997 10.368 7.232 Z "/>
</symbol>
<symbol id="gA11612CECC8CBEF18835767DAB11B2F7" overflow="visible">
<path d="M 0.5248 2.6239998 C 0.5248 1.3184 1.3952 -0.12799999 3.2128 -0.12799999 C 4.032 -0.12799999 4.6591997 0.1664 5.0944 0.5888 C 5.6703997 1.152 5.9263997 1.9583999 5.9263997 2.7391999 C 5.9263997 4.0703998 5.1967998 5.6191998 3.2384 5.6191998 C 2.3936 5.6191998 1.7024 5.2736 1.2287999 4.7232 C 0.768 4.1728 0.5248 3.4304 0.5248 2.6239998 Z M 3.0463998 5.1712 C 4.1472 5.1712 4.8255997 4.1728 4.8255997 2.3295999 C 4.8255997 0.7168 3.9936 0.32 3.392 0.32 C 2.0607998 0.32 1.6256 1.9327999 1.6256 2.9183998 C 1.6256 4.032 1.8944 5.1712 3.0463998 5.1712 Z "/>
</symbol>
<symbol id="gCEFEF3D67F35C6E83CC3757B1DD21B13" overflow="visible">
<path d="M 4.2752 0.64 C 4.3392 0.69119996 4.4544 0.7168 4.4672 0.6272 C 4.5056 0.32 4.608 -0.12799999 4.608 -0.12799999 C 4.7104 -0.1664 4.7743998 -0.15359999 4.8512 -0.12799999 C 5.1328 0.1024 5.5808 0.2944 6.3616 0.384 C 6.4384 0.4608 6.4384 0.65279996 6.3616 0.72959995 C 5.5424 0.79359996 5.4272 1.0368 5.4272 1.6639999 L 5.4272 7.4624 C 5.4272 8.2944 5.4783998 8.806399 5.4783998 8.806399 C 5.4783998 8.896 5.4272 8.9344 5.312 8.9344 C 4.992 8.806399 4.032 8.6272 3.52 8.588799 C 3.4944 8.4864 3.52 8.2816 3.5967999 8.2048 C 3.6352 8.2048 3.6736 8.2048 3.712 8.2048 C 4.2752 8.1664 4.416 8.1664 4.416 7.1552 L 4.416 5.5168 C 4.416 5.4272 4.3904 5.4016 4.3008 5.4016 C 4.2496 5.4016 3.7247999 5.6191998 3.3023999 5.6191998 C 2.4575999 5.6191998 1.8944 5.3375998 1.3823999 4.8512 C 0.83199996 4.3008 0.4992 3.5456 0.4992 2.5983999 C 0.4992 1.0239999 1.2928 -0.12799999 2.6752 -0.12799999 C 3.1743999 -0.12799999 3.648 0.12799999 4.2752 0.64 Z M 4.416 1.5871999 C 4.416 1.344 4.3904 1.2415999 4.2111998 1.0879999 C 3.7375998 0.6784 3.3279998 0.4736 3.008 0.4736 C 2.3167999 0.4736 1.5999999 1.2287999 1.5999999 2.8288 C 1.5999999 3.7503998 1.7792 4.2623997 1.9712 4.5312 C 2.368 5.1328 2.9055998 5.1712 3.1615999 5.1712 C 3.6223998 5.1712 3.9424 5.0048 4.1984 4.7104 C 4.3775997 4.5056 4.416 4.416 4.416 4.0192 Z "/>
</symbol>
<symbol id="g645CA8FA3D9155E2CBD9F8EED3C1540D" overflow="visible">
<path d="M 1.9968 4.7104 C 1.984 5.0944 1.9583999 5.4272 1.8944 5.5551996 C 1.8687999 5.6191998 1.8432 5.6576 1.7407999 5.6576 C 1.3823999 5.5168 1.0496 5.4016 0.1664 5.2864 C 0.1408 5.2096 0.1664 5.0048 0.192 4.928 C 0.8832 4.864 1.0239999 4.7999997 1.0239999 4.0576 L 1.0239999 -1.408 C 1.0239999 -2.4703999 0.8832 -2.5344 0.1024 -2.5728 C 0.0256 -2.6496 0.0256 -2.9183998 0.1024 -2.9952 C 0.55039996 -2.9824 1.0239999 -2.9696 1.536 -2.9696 C 2.0479999 -2.9696 2.6624 -2.9824 3.0848 -2.9952 C 3.1615999 -2.9183998 3.1615999 -2.6496 3.0848 -2.5728 C 2.1759999 -2.5216 2.0351999 -2.4703999 2.0351999 -1.408 L 2.0351999 -0.0256 C 2.0351999 0.1408 2.0864 0.12799999 2.2144 0.076799996 C 2.5344 -0.0512 2.9183998 -0.12799999 3.3279998 -0.12799999 C 4.0448 -0.12799999 4.6847997 0.0896 5.2096 0.5888 C 5.8111997 1.1776 6.1568 1.9712 6.1568 3.008 C 6.1568 4.3648 5.1967998 5.6191998 3.8911998 5.6191998 C 3.3023999 5.6191998 2.6496 5.2352 2.1376 4.6591997 C 2.0607998 4.5824 2.0096 4.5824 1.9968 4.7104 Z M 2.24 4.2367997 C 2.5728 4.6464 3.1615999 5.0304 3.5328 5.0304 C 4.3519998 5.0304 5.0559998 4.1088 5.0559998 2.6624 C 5.0559998 1.6128 4.6847997 0.30719998 3.2512 0.30719998 C 3.0207999 0.30719998 2.5728 0.3712 2.3423998 0.576 C 2.0864 0.8064 2.0351999 0.8832 2.0351999 1.344 L 2.0351999 3.6736 C 2.0351999 3.9424 2.0864 4.0576 2.24 4.2367997 Z "/>
</symbol>
<symbol id="g1B31FFD796CA2E900A884ECD4210CED3" overflow="visible">
<path d="M 3.44 9.200001 C 4.1280003 9.200001 4.768 8.784 4.768 7.76 C 4.768 6.9600005 3.8400002 5.728 2.256 5.504 L 2.3360002 4.992 C 2.608 5.024 2.8960001 5.024 3.104 5.024 C 4.0160003 5.024 5.2000003 4.768 5.2000003 2.96 C 5.2000003 0.832 3.7760003 0.4 3.216 0.4 C 2.4 0.4 2.256 0.768 2.0640001 1.056 C 1.904 1.2800001 1.6960001 1.4720001 1.376 1.4720001 C 1.0400001 1.4720001 0.70400006 1.1680001 0.70400006 0.91200006 C 0.70400006 0.272 2.048 -0.16000001 3.0080001 -0.16000001 C 4.912 -0.16000001 6.6080003 1.072 6.6080003 3.1840003 C 6.6080003 4.9280005 5.2960005 5.552 4.352 5.7120004 L 4.3360004 5.7440004 C 5.6480002 6.3680005 6.0160003 7.024 6.0160003 7.872 C 6.0160003 8.352 5.9040003 8.736 5.5200005 9.136001 C 5.168 9.488001 4.6080003 9.76 3.7760003 9.76 C 1.424 9.76 0.75200003 8.224 0.75200003 7.6960006 C 0.75200003 7.472 0.91200006 7.1520004 1.296 7.1520004 C 1.8560001 7.1520004 1.9200001 7.6800003 1.9200001 7.984 C 1.9200001 9.008 3.0240002 9.200001 3.44 9.200001 Z "/>
</symbol>
<symbol id="g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" overflow="visible">
<path d="M 4.688 10.336 L 4.032 10.336 L 0.24000001 -0.94400007 L 0.896 -0.94400007 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
</defs>
</div>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(40 17.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gF74D1E4498220F56E34936C81B24ED2C" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g46E28FC12585DA626130081849FE40B4" x="3.564" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="10.788" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g48BCA4F06942DA5990D42018985FC781" x="17.136" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="23.268" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE1B486BBD379D5D210F28624A61384AE" x="30.024" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g9FB16590C6D64699AE0CE54876927A05" x="36.804" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g6799D348D26A0968EEDA80A0E5D50B73" x="43.716" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="49.620000000000005" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g45E4C10E27056C5AE488FE2D8290DF06" x="55.968" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="59.7" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g46E28FC12585DA626130081849FE40B4" x="66.456" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 28.192)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 30.592000000000002)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(6.768 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5ABA589ED074A65FC8C929AB4EB2344C" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 48.784)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(404.54488188976376 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6F0940D406D545443F0C3F5AB20F1452" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g6D72A0AB4EFB019D977FFECF4A1600A9" x="6.95" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7035BD9A81EA6DB089327941BB80DFF8" x="11.26" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="16.67" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="22.3" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g5503E15E5E4E70E9E217A15BD1ECD752" x="27.41" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="30.52" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFF65128B49BB3276E17D04989ECB7ACE" x="35.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="41.92" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 8.579999999999998)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.64 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 23.739999999999995)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 32.31999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(743.9997637795276 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g97A8E46F7A64F11D13C6F357868587EE" x="9.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.25" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.36" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gB844DCFB76B4CC44608DB013C9764E9C" x="24.89" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="30.37" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="35.14" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="41.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="46.58" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="52.599999999999994" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 15.16)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 60)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g14F95E5F274105B73EC9103738D4C7FD" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFC5C8D23DE5E426807758A924FDBA2FC" x="17.76" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g47EDFEA5ED41C2BE4D53DD4DC8C28ED" x="29.856" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 39.48)">
<g class="typst-group">
<g>
<g transform="translate(0 12.9)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gF7DAC8BB30649014016B28F6AD7EC048" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8F63AAB7FFA6B186E1B4BC124750174B" x="14.799999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1E298373CF470F56F03EC97C7DE8EA04" x="24.88" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g35249182E2B9A8D87270D5046FFBAC0C" x="50.44" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g814D257E196F777517493FCE505E18DF" x="64.56" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC3DD0650993487CD3F460FE3E213BEA0" x="75.58" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCD50B0C5537328D0484BBB5C5B7C30A" x="87.89999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1344FEF92B65FBC27D977C1EC5D9AECF" x="96.44" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g936880EEF467D45CE0F64A721CAEDAB8" x="103.6" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2EB1DC9A979CD3C8C9D80DB754EBF6AB" x="112.16" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7B316FC97C7634445DBF19AF1976B5C8" x="124.11999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1344FEF92B65FBC27D977C1EC5D9AECF" x="133.23999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE9BB2E81A58B731A2047F77D70267173" x="140.39999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g814D257E196F777517493FCE505E18DF" x="146.83999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC3DD0650993487CD3F460FE3E213BEA0" x="157.85999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gED653E9CCAB5F6C6237350979071A74F" x="170.17999999999998" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.06000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 39.06000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="19.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="32.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="46.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="57.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="85.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="96.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="106.53999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="111.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="122.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="129.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="138.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="147.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="157.48000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="168.32000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="179.16000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="188.24000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="196.80000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" x="208.12000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="229.90000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="240.74000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="249.68000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="258.82000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="266.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="275.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="282.84000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="294.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="304.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="314.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="320.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="331.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="337.34" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 52.06000000000001)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g612BB0D9B453ACEC45B2B13686D7BB71" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.5 6.160000000000001)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 74.5 0 "/>
</g>
<g transform="translate(17.5 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g98926218EB374AD77A2D864C6D10734B" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="11.140000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="20.28" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="27.720000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="33" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="48.3" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="56.099999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="62.419999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="71.56" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="81.56" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(107.99999999999999 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="9.719999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="25.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="35.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="43.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="49.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="55" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g17D0C844F22106CD9F208585DAE386D6" x="70.3" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="77.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="88.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="93.98" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="103.98" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="114.74000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="129.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="138.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g32FA8B29700389E7F9A58D039C5F66B2" x="149.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="161.62" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="166.9" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="172.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="183.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="193.4" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g612BB0D9B453ACEC45B2B13686D7BB71" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.5 32.32)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 73.6 0 "/>
</g>
<g transform="translate(17.5 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g607CD744DAB7515984E0B3F495F7DE81" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="10.56" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="19.700000000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="26.020000000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="34.96000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="47.400000000000006" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="55.2" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="61.52" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="70.66" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="80.66" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(107.1 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="9.719999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="25.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="35.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="43.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="49.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="55" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="70.3" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="81.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="90.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="99.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="106.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="115.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="123.24" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="134.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="145.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="154.34" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="159.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="169.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="180.51999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="190.57999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="200.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="213.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="218.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="223.79999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="234.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="244.88" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 117.54000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 117.54000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="13.979999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="23.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="47.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="58.540000000000006" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="67.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="84.62" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="92.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="101.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="106.48" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="111.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="127.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="137.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="146.95999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="159.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="165.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="175.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="185.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="195.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="202.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="212.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="218.26" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="226.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="232.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="241.51999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="252.35999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="260.91999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="274.85999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="283.93999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="294.05999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="304.05999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="312.99999999999994" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 154.44)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5AE3E73FF7353FF91276C30DF8EB5DCC" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gF7DAC8BB30649014016B28F6AD7EC048" x="14.799999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gF7DAC8BB30649014016B28F6AD7EC048" x="29.599999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8F63AAB7FFA6B186E1B4BC124750174B" x="44.4" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gBC3E99057185A77BABD844B7BE98A74B" x="59.48" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE9BB2E81A58B731A2047F77D70267173" x="72.52" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB88E546A1990E31D64B5C4B23478426F" x="78.96" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="97.06" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g35249182E2B9A8D87270D5046FFBAC0C" x="111.84" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g814D257E196F777517493FCE505E18DF" x="125.96000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB88E546A1990E31D64B5C4B23478426F" x="136.98000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB416F8956A8016097936DBEC1F135503" x="155.08" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC81C3C15134AD04FEC0FE7FCEBE8BB14" x="166.70000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="173.20000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4CEB3F42B775C8D3827D0A458A70771F" x="182.84000000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE9BB2E81A58B731A2047F77D70267173" x="194.06000000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1344FEF92B65FBC27D977C1EC5D9AECF" x="200.50000000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAFD7B3D7EB6599FB514B70015F312425" x="207.66000000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gED653E9CCAB5F6C6237350979071A74F" x="218.82000000000002" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 167.44)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="20.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="41.120000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="51.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="62.400000000000006" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="72.52000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="81.46000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="91.46000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="98.74000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="107.82000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="116.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="129.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="139.64000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g17AD34DB90B05275C6F1422A9B4B5274" x="150.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="160.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="166.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="174" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="179.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="185.73999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="194.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="209.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="220.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="231" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="241.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="250.06" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="13.979999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="29.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="39.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="46.879999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="57.49999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="68.33999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="73.75999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="84.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="99.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="105.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="120.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="134.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="144.54" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 65.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g612BB0D9B453ACEC45B2B13686D7BB71" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(34.52 65.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="10.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="16.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="26.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="41.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="52.059999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="61" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="71" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="78.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="87.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB91E67CF1B63A9F4CC30BB03AE35508D" x="96.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="105.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="116.26" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="121.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="131.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="147.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="156" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="166.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="181.88000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="192.26000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="197.54000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g5925E4E4FE8F59A76637BD462660B390" x="206.34000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="216.14000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="221.56000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="227.88000000000002" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 269.82000000000005)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g911507D70DD1D78477F3BEDE827F51DF" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gF7DAC8BB30649014016B28F6AD7EC048" x="16.34" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8F63AAB7FFA6B186E1B4BC124750174B" x="31.14" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1E298373CF470F56F03EC97C7DE8EA04" x="41.22" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCF24A1AE12C8178F68C1BA3421208D44" x="66.78" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="81.46000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCD50B0C5537328D0484BBB5C5B7C30A" x="91.24000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE9BB2E81A58B731A2047F77D70267173" x="99.78" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g80AF1C2942ED5136FA76CE028C280500" x="106.22" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC3DD0650993487CD3F460FE3E213BEA0" x="116.64" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gED653E9CCAB5F6C6237350979071A74F" x="128.96" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 295.9800000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 295.9800000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g187DB76C80CD961C20BAB3AF6259527" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="13.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="21.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="29.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="42.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="48.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="57.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="67.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="76.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="83.69999999999999" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 322.14000000000004)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 322.14000000000004)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gB2E338F181D915F0996F60E92302C895" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="11.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="18.98" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="28.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="38.24" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="47.18000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="59.980000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="67.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="78.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="87.3" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="95.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="109.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="116" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="126.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="138.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="146.32000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="156.84000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="165.92000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="175.00000000000006" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(494.80944881889764 0)">
<g class="typst-group">
<g>
<g transform="translate(0.000000000000014322751209022492 0)">
<image xlink:href="data:image/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgFBgcGBQgHBgcJCAgJDBMMDAsLDBgREg4THBgdHRsYGxofIywlHyEqIRobJjQnKi4vMTIxHiU2OjYwOiwwMTD/2wBDAQgJCQwKDBcMDBcwIBsgMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDD/wAARCAV0BDcDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwD3+iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCnqGoW2nQefeSGOLIGQhbk/QGrXp71meIRpz2sSartELTKE3Lkb8Ejsa0wAowOAKAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZutQ2c9vF/aJ/dxyB16/fAOOn41o9aytfgsrm0hj1Pd5bXEewLnmTPyjjtmtagAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKparqEGmafPeXLbYoVLMfX0A9yeKALbOFBJ4A6msy517SrWXZcX8CEYJzIOM9M+me3rXlGv/EK/u7IjUrOOG2kdiqQXO2QICANxBOcnv045FaWm6xb6Bp0UureEZ1tZUBnvov38WxsbCQMls8Z46jvwaAPULK/tb5PMtLiKdP70bhsfWrVcNdwafb3+k614cSKBLniRrZlVJkIAUOn8QHqOV6124BIBPFADqKKKACiiigAooooAKKKKACiiigAooooAyde/s9be3/tJ5I4zcJ5ZVmB8wcr07cfStasnxB/Zwto5NWLLDFKsikBjhxnHABrVz096AFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAornfF/iiDwzaxSPby3k88gSKCL7zepPXAHr615rqvixtd1MJejVk4G6ytcDjJXI5Gee4OT09qAPZVnidykcyM46gOCR+FT15r4em8E69dxQRRTW+oIP3X2ktDPIBwGVgQWPGRzkHsK6HwtLLZ3V1pBnuLyG2Y+XLPy0a54Uvn5hjoTznIPSgDqaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiijNABXI/Ey8nsvDDtbK2ZZEUuBkKOuSO4OMc5HPIrrq5D4iW/wBt0+2tGMISd2iJk9SpAx+vHfpQB4t4Q0iDxD4heNYiYYsMvmLvRZDgEYIB+b58KemK67Vr++8KC68Nx6iNQsCI0QSoGktGG3AHGGXOOMewA74Oi2HiHwZey3GhvamZysT2eogq6uVzuUnGQOcH0+tVdL8LeJNR1GS41iW3Sady8m6bc3zZYZC5IBGeOCcDrQB3fgaBdVt7O1gt5JbK1dXQztzCD8x2kdwRtwOg6+3q1YHhPRk0bT9iKUMoVipVQVO0A528ZJHOK6CgAooooAKKKKACiiigAooooAKKKKACiiigDK1xbJ7eOPUv9U86KgxnLk4Xse/P8+K0wAowOlZuuR2E0UEeptsiaZNh8wp+8ByvII9K06AFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooqGeaOFd0rqgPGWOKARJmjNYV74hgtd6Rhi6ZDF/wCH0yOpz29fWsDUfEH26XYkzldgkMKjJ6c8Acjjo2M5qHUSOunhKk1e1kdLqXiKxsVcvI0rKcFIhuI7844HHPPanaLr9lrETyWr/KnXdxx6+lcdZaXe6jIZ7ZYtgLENMxJY9Q2wYx2AOTWxbeGbmaBhcypEdxIwdwIJywI4GCe3Y1ClJvY6KmHoQjbm1OG+MmtRvfhLO5RjFEux0fmN8nPbBBVvfn0xWB8PfD13cwzaro+pCyvLMmVZpFBx8v3GBIHlscnp1rY8f+HIJHmS2klg+zTeUHOCuCnG4E4C7sAt2PPas251Lxnpvh3/AIROz8OKbmYLG11FL5hdcDbtPGDjpnNUlK+pzTdFU+WKbl3NDU/E765qmjXNwsNnfWPErx8qJAWzjIPyEA9O/fivR/CAe5lmvtzqs4DOo5RnPJKg8rjjI9eteXeDPB+p3uoKmpweWF3Z5XIkCkhW2noCck9Buxg17lY2y2lpFCABsUA7RgE9zj61ocpaooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKhldY0Z3baoBJPoKrajqMNiuXO9z92NT8zfhWdFZXGqSJcajlIgDtgGR34LD6VLNIwury0Rbhv5J7r93bk23K+bznPHb0PrTtb0xdUsGg3+TKPmilC5Mb4IDY/Gr4G0YUYAp9MiTTeiOPutG1u/gjgvotKndAVW52NvUevzZKk45wTz1zV3w94at9K/fMN9wWL8HhSc8DpnA9a6OuS8fajfaaNNm088m42Op6FSO9Ddi6VN1ZKCOtHQUtNQ5UGnUzMKKKKACiiigAooooAKKKKACiiigAooooAyPEMemvaxnV3VYYplkQE9XAOBjvxnitUHIHBrN120s722jj1AOYvOVl2Z5cHjOB0rSByM9qAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUmaTNADqDWbPrNhASJLlN2cYBzzWVqHiR4R/o8SMxBYbjkgdzgdccd+9TzJG0KE5uyR0p6Vm3WuadasVmvIww/hzzn0xXDSavqWo3SxGaUYIVlCfJIGOBgDvz3Pbmtq08N3U7ySTPHG5XYAq4XqDkjv04yTjJFRzuXwnU8JClrVl9xJqPi5Ah+woN5UkByAeBn7vX2+pHrWIuoa5ql44jhDxqhcMGIJXnIGehyOOgzxXV2fhmxt/LZ1aVo12pnjHr75Pfnmta2tobWFY7eNY0UYAUYAFLlm9yliaNJWpxu+7OAg8IanfTLJfSiLjqeX2/w5xySBgEZFdbo3h+z0sHyhv7jcBlec8Hritj61m32qxwSfZof3t0w+VOcDPTce386cacYmVTFVq65enZbFmaSGzty5AVEHAUc8dgBTbC6+1Ix2PE6nDI3Ueh/EVVs9Mkd1udSkeWdTkLn5V+gFaoGDwvNaI5ZWjpu+5zWqadeWmpyalplrFepcLsubZ32lwBgbc5X6gisG68M3d3dMtnpsWkDeQZkbJKle3JwOSOOOgxXo1NNMgzNG0e20uM+SC0jgb2bGeBjjAHFalcpoms3E/i3VNKnUlIDvjfPYgHHT3457V1QpKVzSrTdOST6pP7x1FFFMzCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAppalzVDUNSt7FMyv85+6g+8fw/rQNJt2Rd3fgB61kXOpPcfudOP7xv+WpTKjjP4+lRiG91YH7YWtYMj9yq5LD3b/62K14LaK3QJEoUelTr0NFyw1erM7TNIS3cTXGJrk4Jkbkg4xwTz/L6Vr0mKWmkZyk5PUWiiimIK5bxr/q7DrgT9m284457V1Nc74q83ztNWGUR5uOcnGflOOfrjjvUTV4m+GdqqfqdAnSnd6RegoNWYC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQBla5HYTQ28epttRriMx/MV/eA5Xke4rUA/KszXILCaCL+0X2RrKrKd5XLAEgcdeM8VqUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSVHLIka5kcIPUnFZOoa3FASsahtgJZmbaqADJJ4zwKTaRcKcpuyRsn6VVudRt7YYdsvgkIvLNjsB61yNxqup6iJBb/PGQceU23vxkDJBx1HftkU7TtGvrg7Jl8pCAwdfk+Yd/Uk557Go5ruyOr6qoq85JF/UPFUcLssCxnGD8z89MkbRyD16+lZM1/qWqXEawpKPkZgG4BYHI3Y7HPBHp71t6X4WtbeFhdIs0knLttxznPb6Ctu2sre0jC20EcfsoApcs3uy3Vo0lamrvuctp2gT3TxT3xEe5izIiY9uScHOfr75rYt9Ct4X375Ov3c8HjAz3yB6EVsgcUVagjlnXnLqVreyt4R+6iSPOScDnJ681YpaKoyu3uJio5pEiRnkYKigkk1Rv8AVYbUtGoM0+Cdi8464z6VXSznv3SbUX8sYG2FMgA9cnPf29qnm6FqF9ZaIbNdXWpEpp+EgG5WlLDJOO3cDnPr9KuaXpdvYJ+7XdKQA7nqx9fbJ5q6kaooVVAUelPos73YpT05Y6IFX1p1FFUQFNNOppoA5bR4z/wlmpOeOAB8o+bpyT19unSupBrmtI3/APCU6p+7Qr8v7wNk9BhfaulH0qY7HRiHeS9F+Q6igUVRzhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBoooAQUx2VVLMwAHJJ7VV1G+g0+Ay3LfLkAAdSemB+dZwju9XOZ08mzOPkP3m79QcEUFxhdXeiJZtVkupfJ0lFlI+9M2dg4zwR1osdGSCRbmeV7i4GTvY9CeDj+meladtbRW8QjhTYo9KmqbFOpZWhohR0ooopmQUUUUwCiiigArmfFsmy40xWz5ZnJcjHTHvgD6101cd41kb+2NGi3MqmVieu0njAOCOaiT0OnCq9RL1/I69fu0o6Ui/dpfSrOYWiiigAooooAKKKKACiiigAooooAKKKKAMvXLexuoIo9RBKGZRGBnmQ5C9Pr349a0h229Ky/EEGm3NtDHqr7Y/PRozuI/eDJXkfQ1rUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSVUur62tB/pE6R/U8/lQNJt2RbprMqruZgFHUmufuvEUe7baDPOGY4JHocA9DisJrjV9SVw6nehX5g4BDdDtXGMZHcn2rNz7HVDCTkrydl5nU3evWMAb99v2DLbBkKPUnpismbxILgFbVt+7Iwn3unUHjJGO3Xsaq6d4YnkMcl2dygbGR2zx16dBzjgV0kOl26uC8SPsGFyucck8enJNJOUjSSoUtE7s5WCLVtUBfcFYO2B8w+QnqCc+/8scZrS07wwDtnvZA0pADgL14x14z9cV0yRpGPlFSU+Qzni5bQVkU7WwtrY7o4kDnq20bj+NW8Cloq0rHK5OTuwxRSiimISlpprOv9Uhs/lB8yVgdsaZLH8s4HvRccYuTskXLiWOCMyTMI416knAFY7ahc6qXi01WihDbWuGPp1AHUfWmpp1xqTi41JnjB+7ArZUDsRwCDz16/St2GNIo1SNQqqMADtSd2a+5Bd2UdN0qGwQ7QHYnO5gM/hWgMU6koSSMpScndsMUtFFMQUUUUAFNNOppoA5zRmjfxFqm1gWRggAjwfU5b6nA9q6Mdelch4ZuTP4q1YMBiN2RfmGeMZ+Xt257114qIbHRiVaaXkvyHUUCirOcKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiio2cRoWYgAckk4AoAdWVqGo+Uzw24L3G3I+UkD/E/SmSXk2oSeVZIwhDFZJuOn+z+Perun2ENjAsca8jqx5JNK9zVJR1lv2KdnpQFwbu8czTnA9FA7DH4/StgDAwOBRS0WsRKbluFFFFMkKKKKACiiigAooooAQ1xHjOOabxNpPk7vkVmYr1AyBn3Fdua47W/Lm8X2cbb9wg4wCRyW9Ppn8sdOc57WOrCu1S67P8AI7CP7tOpqfdp1aHKFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZutWlrcwRC9LCOKUSrhiPmAOM46j2PFaVY3iaKwlsE/tWQxW6zI2QM5YcgHg8HpWx9O9AC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSdqry3UMX33x/T61l6tr9tYxkJIryHIAByAff8AwHNJtI0hTnN2SNK4vLe15uJRHxnn0zjP5ms668RWNqrEl2AXOQMA+gycDNc9bxXustIQoO4AfM3UZ5GSOfXt9K0LLwup+e5G11bjGCCuOmMADnPbvWXO5bI7FQo01+8lr2RTuvF73QddNik3cHOAMDgnJPr04+tQ2NrqmoXA82AphtwZgcL/ALQJ68nkDiuws9MtbZQIowCBgkfxfUVcxgYHFNQb3E8VCC5aUbeb3OctPDCQlfMkJwcnGRn6gHmtqCyt4j8sKrj0UD+X1q1ilxV8qRyzr1KnxMABjgUDjpS0UzIKKKKYBRRRmgBKbu4NR3NxHbRNLM21RWXE13qkscgJt7VHzjkNIO3pxSKUW9eg6XUJbz93piq3B/fNwo+nr9elS6bpMVnh2Zpbg/elfluevNXoYY4VAjVUX0AxUlJLUcp2VoigADilooqiAooooAKKKKACiiigApp/pTqaf6UAcP4Hd31zViQdjTMUzyR8xyN3Q9scmu4WuP8Ah7jy7wed5reczcMcDJPAz/ia7BetRT+E68b/ABWvT8hwooFFWcgUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlFZeoakIv3Nt+8uX+UAZIU9i2OgoKjFy0Ravr6Kyh8yZsA8ADkk+lZCQ3Grukt0VS1zlYjz0654GenXPHpViz0pmdLnUnM9x6Ngqv0GOlbHPajcu6grLV9xkUaouFUKB2UYqWiigyCiiigAooooAKKKKACiiigAoooNACdq4y8lb/hPAu6RNsCZwDhlzk85xgZ6/169mehrjoOfiBdOpYDykQ5yMnbnA55GOelZz6ep14b7T8mdguCgI6U7vSD7tL3rQ5AooooAKKKKACiiigAooooAKKKKACiiigDM1m3s7qCOK+kKRtMu35sEuOVA79efw9K0V6Db0rP1u3s7qGCO/maBTcRmMrJsJkByoz746Vo0ALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRXn3xA8ey+G4pBp9olzN8wAMoDjafnbbg4AAOC3U+3XyfTfHepapqqWyazeWV1NKEikuNQdUA2nCsSmPvHgkAHPPAFAH0zRXmEXizxN4d8hvEVsl/ZTNsS4iljfdxn5ZFCgnthkQHHDE9e80PXLHW7czafKzhcB0ZCrRt/dYHoR3FAEF1oUMsjEOwVjnbzwe2MEcVE/hqyaaKVstsO4g9CR0re60VPLHsaqtUSsmQpAiA7Vxnr+VTBcUtFOxm3fVhRRRTEAooooAKKKKACiiigBKzNT1RLNhDEpmuXHyRr6+57Cq9zrDy3H2fTF+0OH2yOOVj6f41Np2kQWoMj/AL64dt7SNz83tnp7UnrsbKCgrz+4gttOluJRcak29gOIt3yoc9gOMdu+a2UQIoAGAOBT6KaM3JsWiiigkKKKKACiiigAooooAKKKKACoZsrBIV6gcZ+lTVR1bK6bdMnDiJiPrg+nNA0rtHPfDs7tJLkIFLHZgfN15ycevbsMV1q1zXgFcaDE2wIDkgLznk8k45P1rpVqKfwm+Ld60vUdRRRVnOFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaKKAEpOneori4itYWlmbaijJNYoaXWmZG3Q2fcY+Zx6E9gfSk3YqMHJXehJPqE+oSy2umLgKPmnbgDP90Ec/X8s1a0vS4dPBKZaVhhnPfnPT6mrNnaRW0CxwLtXp1J/U81YC46UIuU/sx0Q6iiimZBRRRQAUUUUAFFFFABRRRQAUUUUAFBoooAQ9K5HTFV/Guouij5FUMNwyxwOceg/z1rrq5fSVb/hLtSZSWRtob5AACBwM9TUS3R00HaM/T9TqB92lpO1L3qzmCiiigAooooAKKKKACiiigAooooAKKKKAMvXbXT7qGEapIscUUqyIWcKN4zjrWpWbrVpa3losV8zCNZA42kg7hkjp6dfwrRx09qAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACq93J5VtLJjOxGbGcdB69qsVWv0LWswQEuY2AC4zkjtnigD5T8V6k+t6tcJJGX8tlit5FbI8oZLcEndnIAOQePqD6HF4etbn4fSySxo92wWWKKXBUK7JwCeQSCAOevT1rgLxZ7TxhdxXtlLNM0sjjKY3LzkYPXgc4+nIruZ7kTeH/AN5ayRWzuojL3AJkRM/fCfKACQDg9eOtAFuC0mi8B63Z2oubizRVjgWbLpE/m4JCgHIBzzjkDoeldX8Gbb7N4dIW6ubuJj8sssaqpA6AYJJIHBJ6/hXIXWt2x8Kz6fZzr5moNtjRI9qKu7duVRkbvXngEYOeK9K+H+nyad4ZtIpwgmaME+X0x/D7ZwRnHFAHT0VXa7hW5+zmVPOI3bN3OPXFT5oHZoWiiigQUUUUAFFFFABRSbqpX1/FZqvmNl34RVBJY+wFIaTehPcTxwRtLM4SNepNYkputbZRCxgsMfMSPmc+nB6cU62trnVJfPvzttyAY4lcjv8AxDv+NbkUaxoFQBVHQAYxSXvehreNPbVkNjaRWkSxRAAKMZwMn64qzRRVGLbbuxaKKKACiiigAooooAKKKKACiiigAoNFBoASs7Xv+QNe84Hkvz6cGtGszxB/yBb3c2AYWyeeBg+gzQ9iofGvUqeDkKaJAHVgWUNk/wAXv1reWsTwnzoFsdgXCYwq4HXqMjv19626mHwo0r61G/MWiiiqMQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBKKKKAEqjqGoR2SY2+ZKfuxKRub8PT3qlfa15kn2XSx59yeBJtJjU+hbpn8an0zTBCqT3TNLckfM7NnnOeO1K/RGygormn9xDBa3F9KJ79h5SMTHAoGB2ySRzxn+mK11QAbVCgDtTwMdBS00ZudxaKKKCQooooAKKKKACiiigAooooAKKKKACiiigAooooAO9cnoPzeK9Vw2ERsbPc4JI9P611RrmPDG0arqW2JxmXO8jGTgZGD29D3qJfEjppfBN+X6nUDpS0gpas5gooooAKKKKACiiigAooooAKKKKACiiigDI8R21nc2sEN/cGCNriPbjHzPnheR36Vr1m67BbT28KXdybZFmR0cOFO5fmAyfYGtKgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKDQAUnFFZuuSslmY4hmWX5EB/X9KCJy5YuRyfjrwt/aF3JesjlVQGG6tVJurKRTkOv94ZHIHNef3vhvU0jkNlqnhm8iRSN6yfY7jk4DOhG0sR64yeRXpY1I2s8NgHka4YBzjLgDt15HHOPSun+w21wUlubaGSZedzICc4x39jikncxoYiNZtLoeP+EPCOs6vrEU188UWm2e+MRRyhlYHILBcA7ieSSOnSvaVjVIwirgKMCmwRRQIIoIliReiqMAfgKlpnSYXiXS4L63W6aQxXFrl0kQkcjscds1H4b1sahGbe4Dx3kQO5Cu3eB/EPY5FbrxLIhSQblbOQe9cjrfhi5hf7XoUzxzRkERs33unG45OOOmazldao7KPJUj7Oo7PozshS1zvhnxAmptJZ3IEV9B/rIxxuH94Driuh6VUZcyujnqU5U5cshaDRRVGYlIaZI6xqWYhQOpJwKxnv5tTZV0vBh3hXn4O0c5wCfT1HegpQb9CxqWp+Q32e1Tz7ojIXoB9T/TrRZWMjubi+kE0pwQuCFTjsD0NT6dp0dlHxmSVjlnYck/0q6PpU2ZTmlpEEXHJ60poFLTMwooopgFFFFABRRRQAUUUUAFFFFABRRRQAGkFKaQUAHesvxLg6Fdhs4aMrx154rU71jeLWiXw/c+e+2MgA9twz0pS+E0or94vVEnhrP9i2245O3PXOOa1aztAWNdHtRCCI9gwG61o0o7BVd6j9RaKKKozCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKRqp39/DZRhpn27uFUdWPtQNJvRE9xPFbwtNPII415LHoK5ueW98QSGCyJg00na03KvIOM9eR7everR0+41S587Uf3cAA2Qhs4OOecfr+VbcSLGiovAUYA9qnV77GycaWq1f4Ig06whsYhHAoVRVykpaoxbcndhRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCNzgE+grnvDa41G/Pm78uBtJPGBngHr1HNb84zG49jWD4c2rqd8vcFN3TG7HPvnpn3qJbo6aX8OXodGKWgUVZzBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGXrlvZ3MMEeoTeUvnKY/m27pOdo9/p3rT9PasvX4bCS1Q6nL5UUUqyA7sZYZwPfr0rTWgB1FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaKKAGt0rmNT1CNb/AM2cvthyFQfMCAR8wx3zx/8AqrfupfKhZvvHoB0yfSuEuolv9S8mCTbIWAB25yoGDg8dTnGR+PNRJvoeXj6soxUYbtl7wXpz3eoy6tcEMXycE5IJ9/YcV2v8VVNNtvstnHHjBA+Y9Mk9at1UVZHThaHsqaXXdjqKBRTOsMUGig0Ac74m8PrqaLcWbC11KHmKdeCf9knrg1DofidLi7XTtTiez1DOBG/8fGdwIGOxx6109YXijQotb09kDeVcoC0Mq/eRu3I7etRJW1R005xmvZ1Nuj6r/gG31qrqF9b2EBluJAo7DIyx9AO5rg9B8Y6jplx/Y3iK33XaqRFMOA57A5/nXU2GkNJMl9fyCWcjO3+AA9AOTwO1Ln5loXVwrov949OluvoVDbX3iCQSXe+1ssZEXdvQkcYI75yPSukgiWGJY0HyqABUi9KdVJHPKo52S0SFoooqjMKKKKACiiigAooooAKKKKACiiigAooooAKKKKACg0UGgBO9ZHiUFtIlCybC3G/ggDvnPGK16xfFCpJpzJLkRtkPj0xmplsaUf4i9S3osZh0u2RuSIlyeOTjrxx71fqho426ZApz9z+JQp/IdKv047EzvzO4tFFFMkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEpM1Hc3EVvC0szhI16sawzc3OtM8VsHgtAcGbGfNHcdQQPp/9ahlRg5K/QsXmrhbhbWxj8+YttJ6Ip7gn1HXFLY6YFm+03bedcsCDySo5JwM9vbtV2ysobRAsar9doB/SrQHNJFOdlaAAetLRiimZi0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAQXL+XbSP1wCfWue8Mux1jVPlGNyEHeCRxwNuMj863b/K2UvlrkheBWL4ZO6/v23BsSLkjgk7RwQOOMcVEt0dNP+FI6WigUVZzBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGX4gsrK+tIodRfbF5ysozjLj7o6etaSngVl6/aWd5aQw305gTz0eNg+0715Az+BrVoAWiiigAooooAKKKKACiiigAooooAKKKKACiiigApKWo3ZUyzNgAZNAmc54s1FbWB8SbSgwOvLHjqPQc4rM8FWbz3X2y4T5AuU2gbeegPfI561l+K7ptR1OO1hZ9qv07biev1rvNFsxZWEcRO6QgFmxjJrFe9PyR4VH/AGrFOX2Y/maVFFFbHvBRRRQAUlLVO+vIrKFpZD9FH3mPoB3NA0rk8sixRs8hCovJJ4AFYz6jNeymDSwwQHElxgEL9ASM/XmmiC41kpLO7w2uOIdpUnjqTxnr9K17a2htUCRR4z1bufqaVzRKMNXqzC1Dwpaahp3lXOZLkDIuDncD7HqB7Vzuj6/feFr1NJ8QhpLckCK5AOFBzhT144716NwBjpWV4j0O21uwa2uUBzyG7g9j0rOUOsdzqoYiLvTrK8X+HoX7eeKeJZIXEkbDIZTkGpua8x07UtX8C3yWWqq93pbn5ZgMmJc+n1Nej2d1Be26XFpKk0LjKshyDVRknp1MsThXRd07xezRYpRUEVxFI7RxyI7p94KckfWpqs5bWFopKKAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKwfFkpj011T77BsDPPTsO9b1c94vV3sHSNYyWifPmdMcZ5+lRPY2w6Tqo0dEVV0y3CjGEA5GOe5/Or3eqGijbpNsFXA2DAwB/KtCqjsRU+N+ooooFFMgKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoNFFADW6VSvdQgslHnvtLZ2r3P8An1qK8v8AymEVsBNO7bcD+H3P09OKTTNNKYnvD51zkneTkD6DoKTNFFLWRn2+m3mpTCbWG2ojZjt0+6OnOc8/jzXQIgQYXgU/GOlLziiwpTcvQOlHSiimZi0UUUDCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCjqr7LKU43cDj8ayPCa+W99xIoaYttY9M+n+c/hitbV/+PMjgAkDnjv61k+EXaSS9ZvK4mKgrnJ5J5H9e9Zy+NHVD+DI6UdKKB0orQ5QooooAKKKKACiiigAooooAKKKKACiiigDL1u1s7yKBb+Xyo45hKh3hcuAcDnr3P4VqVm6xBZ3EUC30pSMTo6YcrvcfdU46g+netHHT2oAWiiigAooooAKKKKACiiigAooooAKKKKACg0UUAIRWJ4rvRZ6YxBwW/2c/p9cVtNXnvi6+OqaxHp8KlljYA4yQx9OOlRN2RwY+t7Ki7bvRE3gbSmnum1CccryOnU//WrvBVLSLKOwso4EHQZY+pq9RCPKrFYLDrD0lHr1ClpKKs7BaKSse51B7iU2+m8vld8nVQvfFBSjzDtT1X7Orx2ifaLgcbF5C/73eobDSHa4e81F1nmfkIwykZzxtzyOKuWGnRWhZ2zJM5y0hAzn29BV/nFTa+5o5qK5YfeCgDr1p1JilpmQUhpaDTAqX1hbX0DQ3cKyxkYIbuK4L7Jf+A7rz4BNeaPK582NRlos9GHryev516PUU8SSxNHIu5GGCKiUL6rc6aGIdNcj1i91/l5nKm0F/cx6/wCHroZdR5kS4xNj+HPRT61vaVqKX0Ks6mGYZDxHqpHX6j3rj7/RdT8J38mo+HF82wkO64sT36DKe/8Anmr9nfQa3EdW0B1N0uPNgfqD6EZ4P/6vWojNp2e501KSlFSi7x6PqvJnZUdazNF1WDVrXzYQyOp2ujfeRh1BrTzWqZ50k4uzFFFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVzXjBk+yyB5Cg8sn7oI69x1rpTXMeMZfKhkdh8u1VzuxyW4/WonsdGG/io2tLZfsEO37gXA6dO3TjpVyqumq6afAsv+sCDdk55xzzVqqWxhP4mLRRRTEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaKjZ1jUs7AAcknoKAHZrDutRkvpms9KJO1tk0wwVTjOBz1qOeS41e4MVq3l2yH94TkFwf6cdO49K1rGzjs7dYo+Ao5OACfyqbt7G1o01d6vt29Rmm2C2URGd7McsT3wMVeAopaZk3cKKKKYgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACg0UUAZniDP9ky7Rk5X8twzVHwgrfZJS0m8+Ycrj7v0PcfyrS1jP2CXa5Q4HK9etZ/g3cdJJk/ifI5JGMDpntUP4jri/3D9TfoooqzkCiiigAooooAKKKKACiiigAooooAKKKKAMrXra0ure3S9uTbKtxHIjhwuXU7gMn1wa1aytbs7a9jhW7k8qOOZZAd2MsAcA/wA/w54rVoAKKKKACiiigAooooAKKKKACiiigAooooAKD0oooAy9f1JdM02Sdj82MJxnmuX8DWD3V3NqM43c5Uk55I5/+v3qDxvenUNVj02E8Ljcdv4nn8uldnpFglhYJAAu7HzYGMn6Vl8cvJHjRbxWLv8AZj+ZeA59hS0AYFFansBUc0qRIXkYKqjJJ7Co7u5itITLO4RB3PrWOLefWGL3YVbPcCiZ+8AT175/Sg0jC+sthJ5bnW5DHZl4rMcNIQRu9Rjg1tW9vHbxiONFVR2AxT4o1ijVEUBF4AFSUhzndWQUUUUzIWiiigYUUUUAGKTFLRQA0j2rhde8L3FleHVvDb+Tc7gXgzhJOepHHP1z3ru8cUYqZRUlZm1GvKi7x+a6M8/0bUItSumvbBfsurRri5s8480eoB9/b8a67RtVi1O2EifLIPlkjPVWHUVjeJvCkWoH7XYs9vfod0ciPg7ugz9Kw9K1mZb1ba/xa6vERuBG1bof3uOScfUZrK7i7M7504YiHPS6dOq/zR6MKdWfpeoRahbiSLIIJBVuGB9xV4dK2TueW04uzHUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFcl4ukfz0h27UdUzJjgZfnPHTA711tcr4pyl1blUD9OMDIwTzyMkD071M9jpwv8RHSW67YEXjgDp0/CpabEAEAUYGOBTqa2OZ7i0UUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiimMwXLMcAUADsFUknAHWsF3l113ijylgrFWkUjMp9MEdP5/pSytLrTmOF2gtlYZYH74I6EY6EdP17VtwxpEipGoVR2FStTVWp69RLeCO3iWOJQqjsKkpaKoybvqxRRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUGgCjqylrCXbgHHUtjFUvCcbRaRGNu0FiR64/wBr3q7q3/IKuvmx+7OSMenvxUHh5dulwnZ5YIGAPyz/AFqX8Run+6a8zVoooqjAKKKKACiiigAooooAKKKKACiiigAooooAx/Elpa3lnDDeXP2eMzpg7gPMbOAnPr0rXrM1+yt721hiubl7YCdJEdCAdynIHPritSgAooooAKKKKACiiigAooooAKKKKACg0UUAJWdrN4llp8krNsOMA5xz9a0a4vxte+aFtoznccZVx+P5Z59KUnZHHjK3saLl1M7wbZf2hrD3kpJVWL/U9q9E6Vh+ErMWujwsQA7jceBn8/1rcqIKyM8uoexoru9WLVW8vIrSAyzMAg/U+g96L67isofMlY4zgAckn0ArPt4JdRm+0XiYh/5ZwuOR78HB+tWz04x6vYbDZzanN9p1AFYFz5MWSCAe7YODxWyoCqFQYUdBSgYGB0FOxQhSlzegtFFFMkKKKKACiiigAooooAKKKKACiig0ANxXN+K/DEGuW3yYhuYzujmUfOpHYH0rpaTFJpNWZpTqzpy5oOx5Za6zeaPqq2+tL/pkfCSxZIuBuxgjknvz15xXoGh6xb6tAXiGxwcFGPP1HqKi17Q7TWLUw3CDdnKuOCjeoP8ATvXBwx3fh7UBAu1JVyqNuADxgfe2569c9fzrn96m9dj1bUsbH3Vaa+49VozxWJ4f1yLVrcg4S4Th0znn2P8AnFba10KSaujyJwlTbjJWYtFFFMkKKKKACiiigAooooAKKKKACua8TpI93bCNMlmUA9Oeeh7V0tc94gRWu7JmMmQTs2ID83bOf5Dmplsb4d2mb6/dpe1IOgpaaMGLRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiig0AFJRWNqGu2ltcfZI2868PAhTkg+/p+PXtRexUYym7RL95eQ2cRluGCqPzJ9B61QgMmrhJZBssmGQmfmY56nHT86baafJeiO51YI8uMhADtT6Z71tBQqhVGBS3LfLBWW4yONUUKgCqOABUgFAFGaZj5sWiiigYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGfrMjR6dMysAQO67v071X8KbjosDP1cbif73vTvETBdIufcY64/LPGai8Iuz6JAWYsRkc1H2joS/c38zbFFAoqznCiiigAooooAKKKKACiiigAooooAKKKKAMjxHbafc21v/alysEUNwkyMzBQXGcDmtUHcBjkHvWZrlnbXtqkV5ceRG0qkHeF3N2Xn37DrWkvAGDkUAPooooAKKKKACiiigAooooAKKKKACg9KKD0oAqX8ogtJJD/AAqT361wF0Pt2sRRDDowxxye/wBSc+/aut8QS+Y6QKzKwIPB7+p9gOa57w/H5viORpdyFcnOecDpk+nPqaxm7tI8PHt1qsafS6O2t4xFDHGoxtAFRX2oRWRRZAWkkOEjXksapT6urzG108pNKDhju4jP9T7CpLDSVhuPtVxLJNcMBuLHj8B2rS/Y9+NNQXv6eQltZtdOLm/QbjnbGRkAds5zzWqq4opaaJlJsKKKKZIoopKWgYUUUUAFFFFABRRRQAUUUUAFFFFACUppKU0CG96ydd0W31e2Mco2uOY3HVT0yP6+orWoIoavuXCcovmi7NHlc8V7peqpC7mO5iBeJ3yI5Fzz68jAPPc/n2/h7Xk1C1QXv+jXQ4MUnysc9CATnBqzr2jW+sW/lz7kdeY5l4aJvUGuMutMksrhIb2cQXkYJtr9eNwHRZPU4H5Vz2lDXoes6lPGRSlpJHpApa5bw94iZpP7P1fEOoIdv+zJ7g11FbRkpK55dSm6bsxaKKKozCiiigAooooAKKKKACuX8SSMuoWgCZJbC4B3Z5+7yPxrqK5PxRIkOsad5jYy/wCR5wc44x79amWx0YZXqfJnVjpSikFKKpHOFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRWB4w1tdF00vu2yy5SMk4AOM5Pf8AKgDJ8W+O4tHlay0yD+0NTOAIwcRqcjgtnrz0HWqNv4g8Tw20t5rIh0yPdgGW0MkQ54+ZH3D0yRj36Vy/gXQB4t1G71LUBcxxmViUUnbzghSzfMcgg9+ewrp/EOmjRYDBotzcMlzHJHcRzyNLG5HUsW+4cE8gjnHBoA6TRtauJ7v7HqEMKTMoeKa2k3RTKRwRnlScHg56da0pdPspLtLp7eNrhPuy7RvH49a5rTIx5tnG67PKx8rLuwc5G0rgAc4546jGc12VAczWwUUUUALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBj+Kf+QJP8wAPBz6Z5p3h7aNJtlVnIVMDd1GO3PP0z2pvidPN0to1OHY/LxnnB6j0qbQYmh0y3RnBfbztxgH0GOKj7R0N/ubef6GkKKBRVnOFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZmr2cd5DBHPcSW+2ZHRo2CksDkDkHr0xWmOKytesrO7t4Tfz+QlvMs6vvC/MM4GTWpQAtFFFABRRRQAUUUUAFFFFABRRRQBG7iJWeRgEUZJPauG1X4hwx3gtdDsJtXbJWSSMEIG5+XPXPTtjkeoqj8V/E0EWny6bFMVkYhXw6gbuuDwTgDk4/WofBXg+6Gli9XVrnT2uCJP3a4ZeehySPxx6jpQBYj13UL+6lk+xxT4DN9nimPnqMdldQTj045rpPC9hZtpUjqEmW5BWQFe3QqeTXH6batb+I4o2dZfsMrgXSZ3AgYbKdz1Ockexziuy8ISDyZVIQMT0V+wAwSvRTzyBUqOtzgw9FtqrPSWpe0jR7LSldbFGRJGDFSxIGBjAz0HtWmB3NA6UtVY75Nyd5O4tFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAlLRRQAUUUGgBves/WdMttXsntbqPcjj6HPbntWjSYoaurDUnFqSZ5xqlq2khLbWvOnsIjiG9UBZLUgfKCe+Txnp071r6Jr9zbGK11RvPtyuIdQXgPyAAw67vX9RXTXtnFdwFJEQ8Y+YAiuPu9Ju9NaX7DEbu0kP7yzL4aP0ZG6DH+A6Vg04PQ9OFSGIjaa1O6UgjIpa4zSda+wom2Q3lg3Pns/zIfQ+v4V10MqToskbBge4rWMlI4KtGVJ67EwoooqjIKKKKACiiigArkte3/8ACS2LRrtAwC3Uc5OCuPb1Brra5XWYftPiO18tA7oV5OQY+vPv/SolsdWGdpP0Z1I6UopBQOlWcotFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXn3xgknh0a3nt/M3l2iOHx8pHI2989DjBxnnFeg1S1K0F1atGURzg4DrkH2/GgDgfAni/wAPWHhUh763hntwBLA03z7toydpw2PfniqtvezeJNSjjsU+0pGwDHOVRSwJZgeQST154A4rr4NB8O6nJvu9I02S7hO1yYF3qfxGeaZe21tZ2j6ZoNslsJeHa2jB5/ukdyR1JPAoAi0OFZtUdgyGOAkIsXyhMdQV4GCWJBx+ldbWZommLpkDKAnmSNudlH3jjHpWk3Q0C3FpMisF5NcWdtqRsnBQAcHjoecim/2rqsUQa403fyQRETuJ9hjp75pXNvZSezX3nQ0tc9L4iWDHm2F0AT7ZAx1wSOM8cVOPEmnrCZHd1CgFx5bZX6gCi6F7Gouhs0VQh1iwmA23MPJ24LgHPpirSSpJyjB19VOadyHCS3RNRSZozQIWikzRmgBaKKKACiiigAzRmkooELRSUtAwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMjxC22zU8jk8jg/dPfBxUmhIiaZEIw4TnG45PXrnvnrVfxL+8tgioXJV/u9R8pH86PCbbtEg+UKRwcdCfXqahP3jpa/cr1NuiiirOYKKKKACiiigAooooAKKKKACiiigAooooAx/EOn2uo2ccN5N5CLMrg7gMkZOMn1Gc45xWxWbrlrZ3ltFFfzGJDMhTEmzc2eFz3z6Vo46e1AC0UUUAFFFFABRRRQAUUUUAFFFFAHh3jB4IPiPIuo7o7LzCXOAC+Uzyw6gdMHn869F8SeI9N0jSI1S5idtilED43KOgwPXpgUviLw1ot7eedq2nQXEM52ys/BzxjPtx6iqz/AAx8JRskkOnNEIxgKJ32gfiTj8KAMjQ7r7UZr6SHYLfJ85gy+cxI2fNuI6gAiux8OwzLZF7kP5hwvzdQAPXvyTzWVPZm/eGx0xUtrC3VkEYUj1G8c8j0PXPPeuqjjWGNY4xhFGAKBEnal4qlqU88EO61iEzf3c1lf25e+Ssn9mtwwD4Ygr69RQ2aRg5bHQilrFOv26PtnhmgxnJZcgYx1IJ9afH4h0+SUxGby3DBf3ilQTjPBI5pXQ/ZT7GvSVQh1aymkWOK6hd2GQocZIzjNXg2ec07kOLW6HUUlFAhaKSigBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACqV7bGYBoziVPu+h9jV2kpNXGm4u6OH1DTfss01/YxDzet1a5LGVevA6Ke+AKh0fUn01ZLq03zWbMA8Tn5osDnA54yfXjpXX6hZfaVLxP5VwAQkg7H6d65JvDmpLri3VuFhD8S/NlSB2Iz0P04NYSg46o9WjWp1IuNR9Op2dleQ3kAlgYMCAas1wloX0qUy2ytG67jLbE8gD07YPGSOldZpeowajb+bA3fBB6gjqK1jK+j3OGtQcNY6o0BRQKKs5wooooAK5fVMnXYhvdMyKBtXk8Dgnrj6cV1FchrEnl6vD12C55OdpwQAcH+f8A9eonsdOGTcnbszrhR2oFL2qzmCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooApX2m2l8P9Lt4pT03EYYfRhyPzp9pZW1nH5dpCkS+iirVFACBaWiigBKMUtFADcD+7Veeztpf9bbpIfdQatUUWGm1sZcujafLjNuq4BAC8Adz+dRNoVptAhaWBlxtZGIIxnH1/H0FbFFFivaT7swJNIuvOgli1KfMWcgk/NkY6EkemMg461JHHrlvD80kN03oVwcY9Rgfp+NbdA5pNFe2fVJ/Iw01C/ju3Wez3RBc7wpB469c59gPWpItcg2n7VFJbsr7SHXdzj1XI9q12pjRI/3kU46ZGaVn3FzRe6M6PXdOdQxukTJC4bggk4AOe+a0I5o5Adjq2OuDmqN1othcxLFJbIFVt/yfLg5z2qvN4csXcuoKMc4ZcAqSeSpHQ9qPeKtTezaNqlrFOlXSQsiajN3256jPHJFNktdYgt9tpdpIwJIEo3duhY4J5/Si77C9nF/aX4m5RXPfa9fimCNYwSDj5ozwfXknjrxxQdduo/K36TcYZsHaSSB6jgDr2JHFPmH7CXSz+aOipKw4PEtjIzLIzwOBkiUY747Zq/a6hZ3Ehjt7qKSRfvIjgkZ55HWi6IlTnHdF6iiimQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFBoAwNeV3voEVGYeW5bb+FWPDEfl6TF8oXPPy9G96XUVT7SGZsYibB644PXvik8Nyb9JiZTkDhevQY9azt7x0yk3SSNeiiitDmCiiigAooooAKKKKACiiigAooooAKKKKAMnXbaC4t4FuLoWmy4SRHbbywOQOfUZ961qyPENpZ3dvANQuFt4op1lBZgoLAHAya1evuDQA6iiigAooooAKKKKACiiigAooooAimjWRGRx8pBBHqKzn0W0aLYHuUjxjyxO23H0JI/pWr3paAIYYEhjVEUAAYqbFFFACUEcUtFAEZQN97p6VA+nWTvua1iZvUqM1booGm1szIn0OxlwGiIAXbgMQMZzj8xmoZPDtuN/lySru65+b6e+Bx+VblFLlRaqzXUxP7N1GP8A1epuUwMqyjr3IYgkfrUWzX4Y3YTwzktlUMYJx6ZBAH5GugoosUq0uqT+Rh/2rfxRk3GmvuRcnYxxn2wDTv7cjSNDc200TN1wNwHGSc+gHfFbVRvGjrtdAw9CM0WFzQe8SpHq9i+MXUW4443jP4jtVmG4hlz5UqPjrtOarT6bZ3GzzoI224xhccZzj6e1UF8NWqXMk8Ek0UjoyHY2MAnPGAOmTigLU33RvUtczDompWbyNa6m7biWEcmSMnHqTxx2qxKutI37qSFvl3E4GA390d8f40rvqhukvsyRuUtYNxf6tasS9gs8eMnyyQRxz1z34wM+tNi8RNszc6bdRMMBsIWAJ425wM80+YXsZNXX5nQ0lYUXiaxeSWJllj8ogM5XK898jOBnjJxzWhb6lZzqrQ3ETA9MOPTP8qLol05rdF6ikByKWmQFFFFABRRRQAUUUUAJikxTqKAM3UrAXcWUIjmUgrJgHkHIB9QfSuWaO/0+58yKFY7jlpI/+WTjdxhsfe+n8q7qql/ZxXsBimHHUEcFT2IPY1Eo31OmjX5NJaor6LqkWoRMAQJ48CRPQ4zx7Vp1wOtWV/pF0LqEgZb/AF65C98bl559exre8O+JINWHlyYinyVCkjL4HJApRl0e5pVw14+1p6x/I6GiiitDiErjrhWmud06MVS9yByWPXhePQDuK7GuYuD5McbRuy/vy2DyeR/CCeB/nmokdNB2bOmHSnU1elOqzmCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACjFFFABgUYFFFABRRRQBXmtYJ1ZZokcN1DLnNZ83h+wkcukXlPksDGxXkjGeP5dK2KSla5SnJbM5y40vVIPKFhqDnYwJ80k59iOcjucYqN9a1nTiV1DTPPjH/LaFsDrySvJAxzXTHpSAUnHsaKtf4kn+Bz0Hi3T5OJkubf5N5MkR456EDJ9+mMd60rbVtPnCtDdRHe20AnBLdMYPOatTW8MqusqBg6lGyOqnqPpWc/hnS3xttFjwc/IxGc9c0lzIb9k+6/H/I1t3vSg1zk/hS1kvTcRzTwlsqQh24BOSBjHHAHfinf2PqsLp9k1mVo9m11lAP0KnBx+OaOaXVC9nTe0vvTOhyaWueEWvRTIRcRSozHdGyr8q9BhgBnscYFRT3fiSGR8WcE671VCoxx3b7x7flT5vIPYt7NfedOKK5RfEt6JSt1oN0qIm5jE2/nuBwAcZ9c57cZqwni3TSyb/PjWQEhjESAOTk45AIHHFHMh/V6na/pqdHRVOK/tZnCRXMbsRkKHGceuKshwe9O5jysfRTd1G6mIdRRmkzQBl3K+bfN5f8ABFhsEg8g4FHh6Ew6XErABgSWxxz3yPWoPEeu6f4dsnnv7iNXcERxkjfI3ZQOprnvBvjGfUrHJ0i+mRST50RRwR9AwPX0BqNpHRaTpNrZNHeiiqGmarZ6mr/YpSxiO11ZGRkPurAEVfqznCiiigAooooAKKKKACiiigAooooAKKKKAMjxDZwX2nlLu5+zwLIrliwAOOQDntnr6itUcBQKy/EFhaanaRQX0vkxiZWDbgMsOgBPr7c1qDkZFADqKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAryWlvJnzII23dcoOfrWdeeHtPuY9rQiP5dvyccemOmOa2KTFJoqM5R2ZgwaJdWRBsr51QYHlyKCu304/z19ahnu9csWlLQi8gGAo6P6cFQck9TkDHrXS4pNopcpp7Zt+8kznLbxda+YsV5b3FrK5AxInGSCeo9Mc+ladrrOn3TbYLyJm/ulsN+R5q5NbwSjEsSyA9QRmsubw7pcqhTbBAGLAKxXngnofYUWG3SfRr8TX3D+9SjPrXPHw0q+Y1teTxO64BDng5yp4OSAOMEniol0rW4PL8rVmk2kl943Zz14PYduafN5B7OD2l96OnzRXONN4lSBsQWjSDoF5B+uSMU4anq8URa409XdNudmQDlSTjqTg4HHvRcToy6NfedDS1yi+KZ0Be40e6jUIHYp82D37DgDqevbFWNP8AGGl3cKSSPJbFztCyoeT7EZBpc6G8PUWtvu1Ojo7Vn2erWV7I8dvcxu8bFHXOCD9Kv07mLi4uzRFPFHPE0UqhkYYINec+JtGl0CSS8tUZ7NyDmMfPAeOvqM//AK69JNMljSRCkihlYYKnoRUzgpHTh8TKhK+66owvC95qNzBH9sijaEplZ0fr6Ar2OK6GmRxpEgSNQiDoAMAVIOlNGFSSlK6VkNY7QT6c1zl+rPDbnyXfdccKGAwD6H/Gujddystcj4w8T6dohtrNpd0+8MYYhvdR64+tEjSjfmstWzsBS1h2vinS7iCKaWWWyEhwFu4miIPocjH61sIc8g5BGQfWqMCSigdKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEopaKAGYNQXFnb3K7Z4IpQezqDVqigabWxz134T0y5dmFuIyc5CfdJxgHb0yO1UJfBijZ9lvpoWVsljklhtwwbBAOTz2xXYUVLimbRxFSOzOOPhjU7RzLpuszhsY8t2JT0B+bPIyTznJxmkh8R6rpM9va+I7MMshKi8gPyDHd+gGfb8q7Ko3Xdw3Kngg96XJbYv6xzaVIp/g/vMiDxRokpwupW6sTjbI+1s+mDzWuzAKW7YzXM6j4G0K9ZHFoIGVg+6I4z7c5GM9hWzeW7DRp4LZjv8hkQ55ztOOeaI83UiqqVk6d/O58/+KbyfxH46a4itY7uJxhFcNgKThMjJ5OeBwe2BXYXXhmLRtPiElh/YOoYJi1KwnYqjgn76dNp4B+8MYzXO/DK3jj8VS6ysLyrYlhcRbNrxHBX5QeoAP3eo7dq6Lx54ttL15oYnkLN+4hjkSSMRN1LnGBnvg54T61VjK/Q6T4SavPrOiTXF7812krRzSgqRNzw3HAPXgYArva5H4aaTcaX4Xt0u08ueUeY4479OgHbHXJ9fQddTEwooooEFFFFABRRRQAUUUUAFFFFABRRRQBleILSK7tYxc3pslimSYShwvKnOCTjg1p5zyOQay9esbe/tY4rm48hPOVgcgZYZIHPr39RWp02gcigB1FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUYoooATH0pNv0p1FADcUY96dRQAmBVWWxtZv9bbRSdeqA1booGm1sYUvhfS2VjFbmCVuRJG7AqfUc8VQ/wCEWuLaNVstWu12kkqXOHHXtwDnPOOc11lGKnlRqq9Rdb+upyqaZr0fnP8A2nuZ23omQQh/u8jkD8M9yKpfafGGlpulgi1VA3GxQjbMcd/vZ5PBHpXbYHpSUuUpYj+aKfyOe0fxXp2oGSGVxaXUb+W0M5Ctu9ux/Ct1JkfmNg3GeDnj1rM1jw7purxut3bKWbOXXhu3Oe/Qdc9KxdA8DxaJqovrG8fZjyzC3I2c4Gc9Rx+VK8k9SmqEk5JtPtbT7zW8aawND8NXd6OXUBUGcZYnA57fXtXg3hK1PiDUXlutO1S7meZ2le1uRk7eAcn0JwD+p6D0j47EDQtPSV2ige5w8v8ACpxgbu3OT3FQ/C26sfDHhdRq0jWks+DBLL92VNo2hWGRjOTjrzmr3OeMnF6FHVr+88ORIFvZtT0hmSK507USrz2xz2bPI9zkenavU9HeFtMtGtuYDCnlfKV+THy8HnpXi2rTHxJ4mtLO2xdzmdvtDxFSoZjuwuOSoGcnt69q9vtIY4LSOONPLRFACj+Een4UySzRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHmWrfC9f7UmvdLnjZbhh5kc64ePrykgB45+6Rj8a0vC/gCLTrhrjU2W6lACrnJ+QHO1uxxgYOBXd0UANVQAABgDoBTqKKACiiigAooooAKKKKACiiigAooooAKKKKAMrXdNg1G3hW6m8uOCdZ9xIAJGcA57c1qAYrK8Q6dHq1nFBPN5CrMj5/vf7PUdc4rTVV2jHQdKAH0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFGKKKADFFFFAGD4x8OQeKdDk0y6fywzB1faG2n6H2JFecHwF4mgt4bJQuyAeWpW6Z4nU8HCtyuevQ4+nFey0UAcl4O8G2egyC7eINfsDmRzuZQeq7u/YZ74rraKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAzNZsRfxQxtcNbtHOkqsgBJKnOOfUZH+cVpDisrXrGC9tYTd3P2aO3nWfzNwXkZwMnp1rUGGX1BoAdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUVn6tpseqwfZ557mKPOSLedoi3sWUg4+hFAD9Q1Ww09N2oX1taL6zTKn8yKg0jxFo+sMy6VqdpelBlhBMr4H4E1hp4R8NWN/BDZ6PYfbZN0xmuYfPcIpUMQzHdnLKOvfPOK6qOKOFdkMSxqOygAfpQBNRQOlFAGVrenx6lbLDNP5KiVXz6kZwOfU/pxWkucDB3e9Z+tWn22CGJrl7UidHV0xklTnbz6gVpKMACgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKY7KilnIVRySeBXOah468N2U7QDUkvbpf+XaxVriX/vmMEj8cCgDpqK5K28R65qUqJp3hma0gcn99qk6wHA7iJdzn6ELXW0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUYoooA552z8QoE7Lpch/OZP8ACugIrm/+alfTSP8A2tXS0AFFFFAGZrmnRanBBHPK0axTLMCuOcZ4+hz25rTrK1mxi1C2SCed4gJQwcHadwzgA++ceuOnrWrQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBma3oWl63HHHq9jDexxtuRZl3KD64qpHaWNnqFppOn2tva25je5ZIEEY+RkA4XHds/hW8a59m/4r1U/u6YT+cw/woAmuJN/i+zh/55Wc0p9iXjUfyNbVc/afvfHWoN/z76fboPq0kpP/AKCK6AdKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKzdefVU01zocFpNeZXZHdOyRkZ+bLKCQcdOOtAGYv/ACUtv+wQP/Rxrpa82/sr4lXGsNqTT+GtPlaIW42pNMQgYt3wCcmrqeFfG14f+Jp48eGM9Y7DT44z+Dtkj8qAO8orO0mwGm6fFafabm48sYM1zKZHc9SWY9/09K0aAMvXLD7fDBH9rNqyXEcysMclTnbz1zWoKydd04ajDBG8uwRTrL9cZ4/X6+461rCgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArmj/wAlIK/3tI/lN/8AXrU1rW9O0WFJdUvIrVJG2q0hxk4ziuIv/GXhkeM7XVT4isltYrKS3kQl95cupXAAxjg5/CgDpdEJbxh4kb+79lj/ACjJ/wDZq6OvMND+InhiPxLr00eoSXQvJIGgW3tZpWkCwqDgKpPXiuw0fV9S1acSrpVxp9gOfMvcJLJ7LECSo92IPt6AG/RRRQBTj1CzZii3MJZeoDjjp/iPzpkesabLny7+2fGM4lXv071Cug6YoIWxgXOOi4PByPy7elPl0XTZZPMlsoZGxjLLntj+XegB02r6dBnzb2CPBKnMgHIGSPqBUn9o2e3f9sg24Bz5g6HpUCaDpaKVWxhUEY4XtSf2FphYH7HCSBjlc8Yx/LgelAD49Y02TdsvrdiuM4kBxnpmpTqFoI9xuoQm0NkuBwRkHrVaXw/pUshllsYXcjB3LkHnJyOhz39aH0LS5CTJYwNkBDkZGANo6+g4oAll1fTostLfQIA20kyADOM469cVJ/aNiP8Al8g4x/y0Hfp3qv8A2LpwjZBaxAMuDjjtjI9DgdaY3h7SH4bT4G4xkpyec8nqeaALP9p2Pl+Z9tg2EA58wYweh60kurafFxJeW6kccyAds/yqBfD+krt/4l8HyDYuVzxjAH4DgenanJoWlp92ygXjHC444/woAmbUrBclr23AXGf3o4z0701tV06NVdr23VZMFWMgwcgkc59AahXQdJTpp8HTb9zrznk9+fWnJommou2KziUbQmFXsBgD8B09KAJ/7Rsf+fy37H/WjvwO9Mj1XTpZ3hS9t2lUEsglGVx1JHaoV0DS127LCAFBgHHOMg8nqeR3pz6DpTy+Y1jCW2eWTjqvBwfXoOtAE1xqljbKGnvbeMHu0gH9abHqunvJsjvYGbG7HmjOMZz16YpsOjadHkpZxKWGCdvJGc8nqTnueaYdA0stk2EGQmz7n8OAMfTgUAWpL+zXIa7gBA3H5x06etRrq+nMzKL623JncPMXK4ODnn1qu+gaO/L6dbnAI3FPmwevPXtUh0TTCyE2MJKDAyuenTPr+NAEv9pWW7Z9st84zjeOmM5/Klk1KxTO+8txtG4/vBwPXrVUeHtITpp8C4BHC44PBH0PpSr4f0lW4sLfOSc7OeevP4UATrqmntI8YvbcyR53L5gyMdcjNH9p2CsEa9t8kZA8wdMZz16YGajk0TTpHDvaROQMYbkHnPIPB/Go18OaOjIy6bACg2rhOgPUfQ0AWf7VsGkeP7dbeYgyU80ZH1GaSXVNPiX95ewIOPmMgxznHOfY1HJoenM6u9nE+0AAFcg4xjI6HGOM9KSHQ9KgbfDYW8ZA2/Kgxj6dO9AEtvqlhPEJory3dGGQ4kGCMkZ6+oNN/tbT/MdPttvvUEkeYMjHXj8aiXw/paqojsLcBeANvGM5wR3GecetK2g6UyojWMGxAQAV6df8TQBYTULF13rdwEc8+YMcHB7+opjavp0a7mvbcAYOTIMc9OagTw/pUaqi6dAFToNnHXOMemecdM1JDoWmQNugsoYzgj5Fxwc5H60ASJqmntHvW+t2TZ5mRIPu+vXpUsd9aOgZLiFlOcEOMHBwf1qodA0s/esYT824nbyT060i+HtJTbssIAF6KF4xnOMemecetAEzappyLlr63AwGz5oxzwOc+1KNTsCu9Ly3YEbgRKDx69agi0HSof8AVWECjBGAnBBznI6HqaDoGkFRnT4Gwcglcnn3PNAE7app4j81r6ARnI3eaMcHB/Xilj1Owdcx3tu4xkYlB49etQRaFpkX3LCADkY28YPUY6YPcdKD4f0fbg6dbnnP3Oc/XrQBKur6b5qRfb7bzJCAq+aMkkZGBn05p0mpWEce9ry3CgA58wdOmetQtoumlUX7HFhDuTHGD7U6PRdNi+ZLKJTnPAx+H09ulADk1bT5NhS+t38zhcSD5jnHHNSf2jY8f6Zb8jcP3g5Hr1qqPD+ljawsogytuDDO7P16+30pf+Ee0nbj+zrfGc/c9OmPSgCZdV0+STylvbcyEA7fMGcYyD19OaP7UsFZF+2QZc4UeYOTnGBz61E+iadIqq9nCwQ5A28dMcjuPbpTR4f0oYxYQLtfeMJjDZJyPxNAFv8AtCz4/wBLg5GR+8HP61B/a+nNII/t1t5hAIUyAEgjI7+hpn9gaVt2nTrcgHIygO36en0FPOh6a0CQvZxNEpJCEZAoAl/tGxbYFu4CX+5hwc844/Him/2pp6zeS17AJT/AZQDzz0zUY0HSll8xNPtxJncCEA2n1Hp+FD6Np7wpC1pGYk+6pHCjjj6cDigCRtVsEj3teQBdpfO8Y2g4J+maWPU7GcZhu4HG7bkSDrjJH5VENC0vcXFjACTnhcc019A0uQFWs4zkk4OcZIwf0GPpQBKdY03zREL+28xui+aMnvxzUi6hZyLuS5hIzjO8YzjP8qgl0TTZVVGsoSgOQNvTnP5Z5x0zzTRoOl7di2MITJOAuBkgA9PUDn1oAnbU7BOWvIAME58wdB1pE1OwlUGK+t5ATgFZFOT6VGmiabG26OxhjJJPyrjrjPT6CmDQNKO7dYQvl93zruwR0xnoPYcUAWE1Oxk+5eW57f6wdcZ9fShtUsFXe95AFwTneMccn8qrr4d0gKyCwhVSckY7+tPOhaWGLrYQK3ByEx/KgCUalYyY2Xlu2TgYkXk+nWmjVdPKs4vICi/eIcEDgnn8ATUZ0LSyzO1jCXZg+WGcHORj059KE0DSkztsIFydxwvfGM/lxQBMmq2DqGS9t3BO0ESL19OtMk1nTYiiyahbKX+7mUDdk4GOfXio30LSnkZ3sYWcuGywzyDkYz0554pZND0ySNUksomRWDgY+6RjGPy/GgCy+oWcaM73UKqmdxLjjHWoU1jTGXcmoWxXOM+aMZ9OtMXRNNVw62MO8NuB28g5zkenPPHWlm0PTZt3nWULFm3HK9+P8KALDX1qOtxEOSOXHXp61E2r6arBWv7ZWPQGQDPJHr6gioX0HSnzusYGDHJ3JnnOe/TJ/OpBoWlrEUFjCFY5I296AJP7UsF/5e4MZIz5g69TT2vrNfla5gDFtuN4+96detVJPDukODu0+35AHCY6dOlDaBpTFmewhYt94lck5OSee+e/WgCV9Y09dga/tlLHC5kAyc4OPx4pz6nYR58y8t0AODmQcHGfX0qE6Jp23Z9mRU44BI6HPGDxTZPDmjSKytptswOM/IOcDAoAsS6tp8brHLfWyOTgAygZP50/+0LP/n7g6kffHXGf5c1XfR9OZPLNmgXO7jI57njuf1703+wNJ37hp1ur8HKpg8dORQBNBq2m3LN5N7bSFcbtsinGemee+KV9U0+N9sl9bKx6Aygenv7ioZNE02SVpGsYSzkFiFwc84PHcZP50v8AYWmGN4/sUQSQAMoXAP1oAr6qdM1a3W2l1GFNkiudrpnOSMc5xk5HrV8ahZLhRdwk52/6wE59PrWLrPhXSbpI1igtraQ3Ecu/YDvKEnb1HOM4x0rS/sDSPvDTrccAZCYP6UASxatp83+qv7Z+QOJVPPYde9Sx6lZuzql1CxT72HHy84/nVeXQ9LmcyS2MDsQQSVzwetR/2DpXOLGEMcZIXB46H6jPFAFxr+zT711COcffHXrUceradLny7+1cDAOJF79O9Qf8I/pQbeNPgVuOQmDxnHI+tK+haW7M8lhASwwcpkfl0z70AWF1KybO27hJXr844ycD9eKZHrGnS5MeoWzAY6Sr36d6hHh/SlywsYRkAHC4zzkZ+h6elPbRNLeRnawgZ2znKZznqfr79aAHy6xp0DN5t9bpjOd0gHQAn9CKf/aFk3/L3b9usg7jI7+hqEaFpQjKLYQhWG0gL1H+RTDoWmMdxsIC2MZK5Pp19cd+ooAlXWtNfdtvrY7ThsSDjPr6U/8AtKx27/tlvs6580fUd/SoJvD+lTMWmsYZCRj51z/nPehdB0wc/YYCcY+Zc8Yx39BwPSgCWbVtOi/1l9bpyRzKByBkj8qfJqNjHndeQDGM5kH4d6iGg6WqkLYwgEY4GOKjHh7SR/zD7fldp+Tk855Pfn1oAsrqNiY/M+2QbMZz5gxjqO/pUcmr6fE2Jb62j5xzIBzgHHX0NR/2BpWMfYIMYC4MeRgDA4PoOB6U6HRNMhVlhsoUDgBgq4GB04/CgCUalYsvy3tuw46SDv0796SbVdPijR572CNHGVLuACMZ7+1QHQNIGMadbfKCB+7HQnJz6/jUqaVp6bwlrEocAEDuBgD8sDFAEn9p2O0n7bb4G3J8wd+nfv2pq6rYPI6Le25dASw8wcYODn0waiXQNKXGLC3+XOPk980SaJpsnyyWcTfKUwQcEE5wfXpQBNPqunW/+vv7aP6yAf1pY9RsZOEu4Txu4cdOuarx6HpkalBYwBWHzfL15zk+pz0PWkTw9pKqQthAARsPydRkHH0yKALL6lZp967tx0z+8Hc49aYuq6czyIt9bFkyWHmDIx1zzUQ0LS928WEG/puC89QeT16inNoumu+97KFjjHzLkH6g8E+55oAkfVLBZNhvbcPgnHmDoBknr6U9tRsl3f6Zb/KMn5xwPzqrH4d0hMFNOgUgbeE4x6Y9Pal/sHSvlzYW/wAuSDs559+poAmXVLB2dFvLcsmdw8wcYODnn1pf7TsN2z7Zb5wWx5gzjGSevTHNQtoemPsL2MLbc4BGR69OhpB4f0kbdunW+FXYPk6LjGPpigCZdUsJJHiW9gMkedy+YMjHByKRtWsI4973kAUY5MgxyMjmmNoumOULWUTeX03DPvyD1/GiLRdLii8uOxgWPAXbs4wOgx7UASwalZTxJJDdwukg3KwkGGGSMjnpkGmf2xpjSOn2+23LncPMGRjg55qGLw9pMcaoLGEKgCgEEjA5Gc9eeeambRdNdUDWUJCJ5agr0X0oAki1Czdd8dzDtIyDuGOpHr6g02TU9OjXMl7bqnHJkGOc45z7GoU0HSkKgWMACjAG3jGc4x0xnnHrSxaDpMXzRWFuvGOE4/KgCZdTsCu9b23YY3ZEoPHr16U7+0bM8i7hxz/GOxwf1qsfD+kFf+QdbnknOznJ689aT+wNK+U/YIflOQNvA5z09M846UATSapYxrukvrcAAMSZR0PAP504anYtGHF7AUK7wRIOR61EuiaYigJZwgdMBeO/b8TTP+Ef0jaA9hCxGcFhubkYPJ56UATNqunrHva+twnIz5oxwcHnPrxSrqdgy70vbcrgsCJQeB1PWootB0uBdkNjCqcjaF4wTkj6Z5x60weHtIKhXsIXxkguu5vzPNAE39sab9pFv9vtvOJwI/MG4nGemfSnyanZRqHe7gCHHzGQY6gDv6moToemt5StYwsIeEyudvX/ABP50JoelpsZbGEGM8HbyPbPp7dKAJV1TT28vbe2583GzEg+bPTHr0p/2+z/AOfuDkbh+8HT161U/wCEd0gyB/7Ot96kkHbyCc5P60v/AAj2knG7T4Djkfu+n09PpQBKurae0gRdQttx5C+aM4xn19OakGpWPmRqLuBpJcbQHGWycDHrzULaHprxrG1nD5anIXbx69KYNA0nep/s+3DAlgQmME9cenWgC2L+0KhvtUOCMj5xyPzqP+1tOMgj+3W3mEZCeYM4xn19OarroGkkAGwtzt6ZTJHGOCegweB2px0HStqIbGABeg2/p7jnpQBP/aVjuRftcJMn3fnHOTjj8aT+19OaQR/brbzD/D5q56Z9fSoP+Ee0neHXT7dGDbwUXaQ3qMdKc2h6XLGsLWcJjToNvHrj6c9KAJH1TT0Xe95bgYznzBjGcZz9TTotTsJVLRXtu4BK5EgxkdR1qKPQ9LjbzEsIEfO7KLjnr2pp0DSm4azjIznBXv3/ADxz60ASPq+nLMIje23mMNwXzBkjnpz7U+PUrFyfLu4Dk4/1g64B9fQioX0TTHVQ1lEQDkDHHrjHpnnHTNN/sDSuV+wQ7SSdu3jJAB49wOfXvQBO2q6eke9ry3CBS+d4xtBwT9AaVNSsJEDJewMrNgESDk+nX2qIaDpYYuthAHJycDH8qadA0ktuewg3bwwJXJBHTGen0FAE8epWUv8AqryBwDjiQdcZx19DQ2p2CLlry3AAJz5oxgHB71XXw/pK/dsIV5z8oxzjB6eoGD609NC0uKYTR2EEcgbcCiBefwoAkj1fT5v9Vf2zZJAxIp5HXvTv7TsfLMv2yHy16tvGBxn+VQNoOlvu32NuxbGSUyeOnNLFounxMpjtIVKkuCq4OSACePXHPrQBJDq2nzY8q9t33EgbZAcnvTDrGnB0U31uGfBUeYORnHH4imvoOlyFmayhLNjJ288HIpTomm7Ngs4lXIOF457UATtqFlGNz3kChc53SDjHXv2qJdW0yZdwvLZ1yRkODz3pi6Hpsb+YlnCGznIXkHOevb39aQeH9KDb/wCz4N2Qc7OhHTHpjtigB1sdMsGl8mS2hM8pdyHGXkPBPXr2pzatpyMq/brYM/3QZQM8/wCNRf2BpZ+9YQHkMMpnBznjPTnmnPounSIqm1i2oQRjIx9CP19e9AFhb60Zgi3MLMSQAJATnqaKrjQtKEvmR6dah/URgdvb2ooA1KKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMrX9KTVbeBJZfKWCdJyfXbng/nWoOay/EOkvqtnHbrP5IWVXYjPzKM5XgjqDitJeFAHTpQA+jFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGXr+nDVLWOE3LW+yUPuUAk8EY5+taQGFAzn3rN1+wOo28EKXP2V0uI5VbaGyVOduD6itMDFAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZet6Z/akUKed5fkzLLnGc4BG3261qVmazpw1GCONpmhWORZCQoO4DIK89Mg4zWgPurzn3oAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBk+ItJk1ayjt0n8oCZXY88rzleD3BxWog2qB6cVn61YPqEEKRTiBopklDFAwO05IwfUVoD9KAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAY/iLTP7XsltvNEX7xXyVB3YzxyD1/lWsq7UC+gxWbrumPqcEEaTeV5U6yk+oAII/HNadAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRUUjrEjM7KqqMkngAetAEtFcprXi1LVIzpcaX+/B8xJF8sDIHJz7jnpzTYG8X3FuJlfTYGZsiNlLLtyMEMDnpnqPTpQB1tFc7o2tXk2oSaZrNn9ivYxvRoyWhmTsVY4OfVT+tdFQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGXrtlNqFnHDbXIgYSK5YjOVHUfXBrUrL1mze+ht0iljikiuI5gZFyDtOccHritSgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoNFRXEsUS7ppFRemScUASU3OPase/1+K3ido0ZwAcOeEyCBgnqOvpXK6trFzd4V522yDBUAqOmeFBLHIOPqBzUOaR1UsLOp5I9Drgvi/fGDQorRZBuuixaMjmVVGduc5GT6D2yM8x6HLe2dxJ/ZzTTIwDLHK4wwJ6hcZHJPUge+a5L4pjV7y2Wa8XM0aDEcfBKs3A2kfeH68j0pc/kXLCKD96St/XQ5CzabUNSilh0o/ZYGhWS3y26TZ8jJgfebgnPfv7dtcvZWNna694F1e9E7yeXJYzMZN+1fliKHJXGMDn2B5FZHwu1nQtE0m81fUtTWG7tlcvYyEBpHGdoAPORj8z7c5FrqsviTUhLbfu7m4cAGPoTu3LkAE547AsVHbmqi3LdWOarGEZWg7rvseyWE41LxVDe28IVGjKSFXOSyjoy9DgjAYHjODXZ1y3gfRhYadFcyjfcupVnJLEDcSQCccZ9q6mqMwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKimkSJGeR1VFBYk9ABXlvin4jCeKe2toruztRIYxdIwDygYBwOqKc9cE9OBmgD02a6trckzXEcR6ne4H8/pU0Uscqho3V1PcNkGvItI1nw9ZR/aNcsdZnSWMJLdXSGSEr/e+UkDJc5HbrjnNdJdWem6ZDYa14XmljhLBS1rJ5kEqYP31yc56bgMg49KAO9oqGJvMiV9pQkA4PUVNQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZWv6Z/a0EEQk8vyrhJifUAHj9a1ayPEGl/wBr2P2ZpPKHmK+7jt25Hfp/nFaqLtUD0GKAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJVa6vra1QvcTJGOnJ7+lc/e+MrWDP2eF5VBwWPygD155x+FS5JbmtOjUqfArnU1Wuby3tv9dIiE9AT1rj5tV1fUWC2srgkfMsSbAhBzks3PPAxjkHIqGHQdWvGWSdmG6XexbGfYnOTnnIx0xUud1odMcKo61JJfmaWpeMbFD5NvMNxwQe+D3Hbj+Vc1quu3V+YzawyM4faxbLKT/Dj0JHYCum07wfbRvFNdiKSeJywITIIznHOTXQw2FpD/qoEHvgeuf51PJKW7sbe3w9Br2ceb1OL0jQtT1BIpbuZ4ImJYKAdxBHQk9MkA9MDtz06fTdCsrQFlQO2R97nGOnXv79a1HZYxliFHUnpWSdRlvbg2+no2xWG+4OMAEZ4HfjvVcqic08RUrN20X3I0YI7dd3kqm7JB24zn3xXJ+NLG1N9FLqhWKwuEW3knGAyPuyp3HhRx1PHaum0+wjs8lCxZgA5P8AEfU+9UfEmr22n2jxuI5JpV2iJxkH6j0/nVbK5xV6kKS5pS0R5l4m8L6R9pg+2nTdRh8vassIIncdcttOPYEZ6fhXR+DPB9soW7XTLexiKKVES8kBuAGJ3A4Ayc8+1TeGvD73t+L65t0iiRtyxFABkdMAYAx9K6yTWbSPV10pnCXDIHQE/eHPT8qUZN7nNhKlbE3m1aPT08zUUBVAHAFOpKWrOsKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACikzQTQAtI1Z13q1rbxlzIJADg7CCAevNc7d+KGaNpVb7PGBuCjGTyAQT3POcDn61DmludFPDVKvwo6e+1G1sQDdTImSAAeue3FZP/CXaeL5bUrKrscBmXAx6+uPwrl5Zbi/KLB88suCm7K5GOGz1PPTsCe1alroeqq0KOI0VSrkx8AZOCOc7jjOQTzmo523ojrWFpQX7x6+pe8e6pbW3hm/j+0Q+bJF5YRiP4iF5GD6+leAeTDqniOOGWXZAzAAjcVzkg56EKTjI55z1r2rxD4egtLVTcNLeNcyrCOdu3IJGO3BHGe3HuPNtIsNT8Mazc6lYRw6oLcBLi1nm8uRG8w7BjBB5AYZ5x9Kd5swj7CF9HI6W6vNS8FWd1o95cx6jpUtttRJP9ZbFgQeMklMk53EYAxnJApvgV1vNFg0u3Yyxl/NU5KPGXyGI6DaGPTIyD0wa5Oez8X+IdXm1bVtMEaXcoVElICJxgBQTyOg7jvySK9e8AaAdIs/NYbjMu5iQcs+TkjJPGOh4yDnFanGdXAnlwKu7O0YycDP5VPRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZWvae+owQxRTrA8dxHMCy7gdrZxjIrVrL13TZdTht0guXtminWUujEEgZ4/HNalABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlRSypEpaR1VfVjise68SWcErxkk7PvMSFUenUik3Y0hTnP4UbpNVLq/tbYH7TMkeBuILc4+grk5/EN5cfJbBS+MkIcbTxwW56884/pUdno+o6hhw6wQYzkx5fJJJGSDxjA4689Kz577I6lhOVc1R2Rral4mitmVIEErOSqsXGMjnIXqwHtzxWZc61qGoM39mTSyozBVMahAD25PUHnt2q7pnhRUKSX0u5wQxVc43A55J69SPpXQ2tlBbR7IY1AzkD3otKW5TnQpaQXM/PY5VtO1O5lCyRIEBw0i4yx4BJJ5GOoxzxxVm38G2p+a5cyNyMjIO3OcE55+vUV1WKKrkXUx+tVLWjp6FGz0y0tCWgjAdlCsepYD19av4FFI3SqtY5ZNyd2LVLUL+Gxj3TNkt91B1b6VUvNTaV/s+nYll7v/Cv+NSWmmKj+bdsZ5XAyHwQCPSlc0UOX3pfcU/s93rTLJdE21p1CRudzf73bFbMEccUYSJAij0GM1MFAqpqN5FY27SzsFVafqRVq2jrokV9a1WLTrdiSPNKkovXOK5PRtLudcu0u73JgAIVn5J59/wCtPtFn8Q6r5k2QmOqjhceh/qO9dpZ2yW0KxxqBjqQAMn1rO3M/I8WMZYypzy+BbLuSRQrFGEUcCuS1OzSXx9Yz4bckHYZA+9154rscVzd75LeM7Xcx8xYCwXGR3x3479qqR9DhHyNpdmdKOlLSUtWc4UUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUZoAKKKDQAUlV7q8gttvnyom77oJ5b6Csy58Q26xM9ttkRQS0hbCpj170m0jSNOc/hRt1Wur62tFBup0iDHA3nGT6VxGr+Ir6dG2FoVC8rEcNzjBUkZOOvA9aZYaXe6pas0jszGQLLIUyzcjB7ZwOv6etZ+0vokdccHZc1R2R0V74tsoW2QhpWIJ3DhR+NYGo+ItVuYZGtYR8ih/LLjkdxngcfU57VtQ+FbYSl5XaTjaCR8xHGcnPU4x9DWzaadbWwHlRKGAwGPLAZzjJ5xntRaUvIuNXD0fhjzPzOEGia7qtvAJXRFMYLbyGXBBK4BHDA9cDpjHpWzovgyG0jVruTzZVfeDycHnPPfPGRgdK6zHYce1R3FxHbQtJM21EGSaFBdTKeNqyXJHReQiW8cZJVAMDH4en6VUOpp9oWIRuyZAaYfdBPT8D0zVQSXerSoYi0diSQ2DtZv8A6x9K17a2htoRHGoVR6f1qrHNJKPxasq61pyalYPbSAEHDLuzgMDlc46jPauE8S3Mz2UFnrWm2cuoxAKk6yhiOOWwMFc8YByK63xJrn9n2xjthunIwMdv6E+1Yvh7w/JeSC+1Es2W3beoY5zn8e/SlJtqyPIxOInKXsKG73fYf4R8NPHAl3f/ADM6rsjPOxQCMYORznJ/xrtQQAK5nxxqE+i6RBdWSndHMq7AcAqcgjFb1lIZrWGVhhpEDEdcZFVF9D04UZU6MZN3vp5lqigUVQBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBj+JNMn1WxSC2nMJEquxyRlRnI4+ta/p7Vna1Zy39tElvMkLpMkm54g4IByRg+o71oAdPQUAOooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKq3VzDbKrTSqgJwM9z6UDSbdkWM0dq5678SwR5WDBkyQN5xuIxkAdSefSsN9S1HUHG9ZsEkiMYA7EZA7g1LmkdUMHUkrvReZ2Ut9bxuyb9zjGVUZI+vp+NYN54nVWMcBCsmOfvcc+nA5HXOPwqG20G6mWM3FxIWkGWDDKg4HboeeueDW1aaLBb84BONp+UYIxjp2HtUe9LYtRo0t3c5qGbU9RfdFCX2Bkbex4b5e/TOMZ455+tXrDwu4cNeSK+3HHU5HoeMda6iKJIlCouFGAKlAxT5F1Jli5W5YKyM2z0ixtdphhTI+6xHI/GtEYA4p1FUopHLKUpO8mJRiiiqELTaWsW71N5nEOlbJn/ifqsfOOcdzSY4xvsX9RvoLKFnmIyBwg+83sB3rHjjvdakP2lTbWY52EYaTPY9CMfln1q7ZaUsUjT3bfap2/icA7T7cccVrdKW5fPGGkdX3K9paxWkIihGFWp+MUvWq91cxWkRkmYIo9aexjKe8pMS+u47O3aWY7VUfn7CuKl+1eJr8FhJHarjAHIx7g/rT7iW48R6n5KOVtlP3R2HqeO/TPauwsrWKzhRIVUAAAkDGccZNT8XoeU+bGS00gvx/4Amn2aWcCwx5+UYye9WwMUoGKKs9OMFFJIK524/5G+H5Af9G645UZ6jtjPHP4V0Vco8y/8J8I42O9bcBwTxjk8YOfzFRPodVBXb9GdWPrS00EelOqzAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACg0UUAJRmis+91SC0iaQkuBx8nPPYUmyoxctkaB6VHLPHCpaRgoAzzXJ6h4jmeVYbZ44+eVBySO2DwOfyxVRrXUrtw8cKM8qht27JBwOhIwPp0IPao5+x0xwvWbsb2o+I4LWBpI1HABVnOxW56Anv7VgXXiO5vlkSBt3BCmE4U84GTjIPp71pWfhVSyvdsWXcH8tm34bnjJ7Ak8Vt22lWVs++C1iRvUIAR0H9KTUpGqnQo7LmZx9hpuo6kY2cr5UkZk3SAOd5HTJHUED0rdj8K2+35pps5DZyM5z7V0GMUoFOMEtzGpipy+HRFODTreIJiIMyAAMwyeM/4mraoBTqKtI5nNvVsAKKhuLmK2jLzOqKOpY4rFe7utVDpZHyLcgHzGzuZT3Hp9OuPSh6FRg3q9EXL3U44pxbwDzbhsfKOgycZJ9sdBzUVlp0ryifUm818DCnoD9Bx/P1q7YWUdquQNznq55J/GrVLcbkkrR+8RV9KzNf1NdOt8/8tH4U9gan1fUrfTLfzJ3AzwF7k1ydraXXiG7+1TMFjPIUg4wOMjt/Ok5fZ6nmYrEtfuoayf4BomjtrF/LqN4T5ZIKgcc/nXboixRhEUBVGABTbeGOCJY0UKq8ACpqqKsjTDYaNCPm933Oc8cBTpKBhuAlXOBkj359K2rLH2WLHQIvp6flWP423f2XHtQP+/T5S2N3PStq2B8iMN1AGfrj24qftHpz/gx9X+hYHSiiirOcKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMrW9Pmv4YEhn8hop0mL88gZyOCPXvx7Vq1k63p82oW0cVtO1s6yBy4zkgAjHH1/D0rV9O9AC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRUbMF+8cVy+qeIAZ0jtHLDk/JzuHbn6jp1xUuSRpTpSqO0UdUOlZ1/q1tZA+YwZwM7QwyR+OBXHhdT1JQguC8iYk4kPKEYIx3OPUc1dsPB6yyRz3kkhAJwhOOOxAHAPtUOcnsdn1alT/AIkvkiW98T+czw2eN6lR8vPccZOAPwPH1qisGpXQlD7nRhsO7hscdTyeD0xz6+tdLY+G9Os/uQbuvLc/p0rVjjSNQERVA7AYoUZPdieIpQ/hx+85vTvDghAchNxUK2R22gd/Tmtu1sLeDf5caDdy2Bjcff8AKrtFXGNjmnXnU3YgHGAMClAAooqjEWiiigAooozQAmRVe7uYrRPMmkCL796r6hfrartjjMspAKovpkDn061XttMlln+0X8vmENuVB0Xrx9Ofx70Nlxit5FYm81iRch7S0Vsn1lAPqCCPXjP1rWs7KCyQJApHqerH6nqatYwMAYp1SkEptqy0QgFBpagnmEK5b6AetMybUVdjL27is4TJOwReg+tchc3Evie/NrH8tumPnA+9zz17elSXtzJreofZYWwqZyecNg9K6TTNPjsbcRoOTyx9T/gKnWXoeXKUsZPljpBb+fkP0/T4LGIRwRqvAyR3q6MEUnagDFUenGKilGK0HUUUGmWNrioZ1/4WTcx73x5SjHVc7Qfw/wAmu1PQ1xmnRq3jjUJfKferhd+eCNg4I9uo9ulZVOnqdWG2nfsztO1KKQdKUVqcoUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSUxnVVLMwAHJJ6CgB3X3ozWPceIbGE/LJ5uCMlegB6HJwCPpWFd65qN1Ifsx8rbwB91Sw5PzEHIPbjqMe9S5pHRTw1Se6svM6i81O0sw/nzIrIMlOrY7cDmsy78T2qMEibLnH8J79OmR+J4rEj0m9vbtmnYhJcjKkhVOfm4PJBxn0xW9Y6DFbLJuxI7jDMy8kYx169B9Ki8nsbulRpr3ndmPPeajqMymEbQSVYckAYbnjoc46jOe1SWmgXU0zi9kMkf3VfvgHIIH3VH611UNrFEAI41XHYDAqemoPqQ8VZWpqxl2ei2duoDRLIfVxnvWkqqoAUAAdqfS1aSRyynKe7ExS4oopkhScUE4qG5nitomlmYIijJJoGlfYmzWXfa1BBMtvEDPOxC7V6A+5qo91davIY7NJILPo05BRz/ALoI6e/Wr2maTBYqxj+Z3xucjk0m30NeSMNZb9inBpU9zPHdalL+9U7hGvRfbqRj6c+9bSKEHyjA9KfiimRKbYnbgVU1G/h0+2M9wwVQOB3J9BTr+8js7eSaR8BRmuQt47zxPeJPKAlqvr2+nJ5qZOx5+JxPJ+7pq8n0/Vj7K1ufEd/JeXGBAGKx8dh2HqPfHWuus7WK1jEUCBFHoMUWltHbIFjQLjrgdasURVtR4fDKl70tZPdgAAKWgUVR2HN+Nm/4l9suUAkuUU5Tdwc5IHc4rfjG2NRknGBk965f4gXHl2lkm8L5s+3B4z8p6Ng4P/6q6W1x5EW0YXaMD2xUL4jpmn7KL9SxRQKKs5gooooAKKKKACiiigAooooAKKKKACiiigAooooAytfsLnUbSFLSdLeWOdJdzruBCnJH4itQCsvXNPm1CC3jhl8oxTLKTzkgAggEdM568/Q1q0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUVS1HUbPTIDcX1xHbxA8u5wOAT/IUAXaK82uvitaLM32CyinhT53Z7xI28skDcBgrnJ6MVxwCcnA1tI+IuiXxCXrGwnGCUkdZFAIyCXjLKB/vEYPHWgDs6xdSe/W4CxqnlPwrZON2RgHHIz61rI6uoZWDK3II6HNOxStcqMuV7HJazaaxeQ7SR5TH7h9ueeM498/lWhpfh+G1CtKN7c5BAwSeOexrepOaXIr3NniZcvItF5EaQRIPlRR+FSAY6UtFUc7d9xaKKKACiiigAooooAKKSq93dw2sBlncRoOMn1oGld2ROxrFl1WS4n+y6cqZOcyP0H4dT9arzC51qQrte1s8ZGcqzn3HcDrjp61t2trDaxBIkC+pAxk1L8jW0YavVlbTdNjtPmYmScjDSknJrQAApaKoyk2wozQelRTypBEzyNtVRkmglu2rG3M6W8DSyttUck1yerag+pSmGBH3ZGGHpnp6/pVfV9Rn1CYsocW65CqD973P+elbvh/T1jgW4dCZCSVLZBwf88Vk5czsjyJVZYup7OGkepa0XSo9PiGAvmH7zDjNadGOOlLWmx6lOnGnHljsLRRRTNAoNFBoAQ1x/hiRZfEeqZkLMZWIXqNvTr/SuwNcX4JCyahqsil8G5fCsQcc8575PHWol8SOuh/Dm/L9TtBS0nelqzkCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKDQAUVDJKkY3McDOKrSanaxpvkmVB/tcZ+lDGoyeyLUkiRIXlZUQdST0rNn1uxhV280ybBuKqCT0zx9a57UtXk1RjFaQt5C4IPXPPfB288EdcDtUsPh+5mk3TRx/NJkshGdv5foOOO1ZubfwnbHDwir1XbyJb/xnbQqwt4XZ8jGQOR64ByOfWs1r/V9QkIjim2t867lyO3BA7fX+Yrp9P0C0slwUD8YGR07/AM8mtRIwq7VGAKXLKW4/b0qWlON/NnJWnhuaeOM3rbMDPl8cHjOD6cenFbtlotrbIwVN245O7k/ma1KKtQSMJ4mpPRsZHGsa4UBR7U+iiqOfcWiiigAooozQAUlFZF3qLPOLSzXdIeGkxlU/EZ5pNlRjzFrUNQS1VlUeZNtJWMdTis6Gwn1GRbjUiBEQNlupJX1G4HjNXLDThFGsl0BPPnJduSPYH0FaVG5fOoaQ37jI4wqgAAAdAKkxRQaDIKqX14tpAZH59qddXSwxlsFsDOB6etcjNJca3eRpCN8WfmJ4zzznoQBnik3Y48TiPZrkgryY0G98R3ikMI7dDu79R/npXY2drHawrHCoVQMYFR6fZxWkCxooB6n3PrVuko9WLDYf2fvz1k92FFFFUdgtFFFMZw/xHaZpNKihUkmZmOADwAOxBz/jg12MAzHHu67ea5fxhj+2tIy+MMxxyc8qD0OOh7j8a6tBgAZzx1rOHxM7Kz/cwXr+ZJRQOlFaHGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGbrlpPd2iRWs3kv5iktx93oRyD2NaVY/iLTpNVsBbxSCM+arknPQdRx69PbrWqvCj2FAD6KKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArwf4w+Mt2oXOixshiYM07xuC21chFHuW6jPfpXvFfLvj5Irrx7eRbZftElxGCpVS23gKq44ZTjGCO2ec0AP8ACXgifVLZ77Tr24gu7WLzFMEgAD7ckbWIIxn1wTnHrXdaZd3GuabLbeKbS2/tCKAyw6pboFlQiNjlwCCcgFSoOCQQRVXwvOmn+GGSMxBRbzSTRpMA6bmIBUADqT0z1HPIrT8KrBbwareOseyGDZIW/dxJ+6wwAON2cHDcA5OOBQBb+DWp391aTJJBciygd4EZ3HlO3XdGvUA8kjLBTwvGa9Qrzf4RQwGxublZJJJZJP40OIwAAArD5TjJyVJycknvXb63O8Fg0iBjt67TjjHU+1BE5ckXJmjzSYrkP7VuVZJZZSkPzbwGyf5flUv/AAk1n/yx1AgnA+ZMgcdScfnUc5xLH0vtaHV0Vy8fiXMu3zIXU4IIyOMf41Z/ttudpiduRwx65/l70c5osbQf2joKKwX17b8zQkf8Cx6eop0WvW7ru8t85xt75+lNSRSxdJ6XNyisUeILL5f9b8/TC5/zjv6U5fEGnnrKV5AyVOM+lPmXcr6xT/mX3mxSVmLrenN0uk79j269qq3utxM/2fT5UmmbglGGEHrk8Z9qTa7msKkZuya+8uanqCafHkgvM3CRr1Y/0FU7awnvpPtGp7iASEgwNo9GHcH360ulWVpAjTTTrcTu24yuQWGegz7VqpLG/wB2RSfYijc2dSEVaD17kqDHA6Cn00UyR/LQufuqCT3pmdzG8WeLdG8K2DXesXQiUYCoo3SOf9lRz+PSuFHxw0q6E7aXYPdRW4D5adIWZO5Ct1IHYZ5ry7xTqE3jXxddjU5njgtRlhF94jIG1c9Oh5PHfFbtx4E0y50C+1GO0ttKtVgdIYrht9w754fdj7wYYwvUgjvTGe6eH/EFhruiJq1lMjW7jLYYHYR1B9xWVq93PqdzHZ2sTmFj8zHjP/1uK8t/Zev3MmradK5KHa4jIGMjqxyc57dP5V7wkKx/cXGP8aTOetSlV0vZdSpaaZbQ26xeUrAYJJGcnrn86vooUDjFOop2NIQjBWiLRRRQaBRRRQAUGig0ANauQ8Cxsz3skmd3nPu3HJyTn+XFdc/auW8B7G0yRuGfzXyQhUnnvnqf/wBVQ/iR1U/4U/l+p1Y6UtIOlLVnKFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRWdql8thbNI/y8MQz5CDAJyx7fzrwPxp8VtRutVmtUWWGCAhMWt06rKpIJOVAIPGOTwDgAcmgD6NorxDwRf8Aia+0qK98Pa2uosnElpNfb2xxx5UqgjHqJAPTNd34X8cxai0VlqsElrfk+X8kThHYcFSpy0bA9Vbj0ZhzQB02o2Ed9EUZnjbs6NgiqI0C0aJo353DB64z64z69q26QCk0mXGrOCsmZ+m6XbWEeyFB1znbjmtGikxQkkKUnJ3kxaKKKZAUtJRSAWiiimMKDRSGgAqKaWOFPMkYIo7k4FV9Q1G2sFX7RJtL8Kvc1nWtnd6jKLjUpMQZJSBRxjjGT3/GlzGkYdZaL8yOSe51tJI7fdBaNlC5wC3r7j/Oa2LKygs4zHbxqi99q4yfWpooUhjCRoFUdABUgpbilPotAA4paKDVEDc8VWvbyOzt3mlbgdB6n0FS3E0dvE0krbVUZJrkpvtXiC8ZowRBFnYrdG9D07/Wpb7HJia7pxtBXk9kRzX11q12q25YDluOCF9OeDXS6Rp8en2oUAb25Y+pqpoOmyWyb51w/IUdxz1P+elbYWiK6sxwtCS/eVfif4DqKKKo9EKKKKACkpaSgDjfEMr/APCY6dGjAOImI3LkcnBxx14rsEHFcnqLf8V1bbWyVthwOq5Y+oxz+ddavSs4bs6q/wAEPT9R1FFFaHKFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGXrNndXkMK2syQSRTxyktkhlB+ZeCOo/z3rTHoKzNbsrm+itltLk27xXCSs3PzKM5X8a1KACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoNFFADWryL4oeBbXUNdtruwSOO/lJZY5VPlT4wSm7+FiRjJ45r1meVIIXmkYBEBYn2rAGppf2cyXtsrwnGVOTn0GD36d/ehuxjOrCm0pPc8U+32/h6Ga1uYn0t5ZMiG/sykiAEZxOoKuAR0I5xyATio4NT+1aQ9jY3VzeNNIruqlcRITjaxAPzMccEYPfHNe2pos9xbbLbWbkW0g5iuI45wOeg3LnHXg5/SnaD4WttLuHu5fJuLt2JMwt0RuVCnoOM47YFBomnqibwhpZ0jQLW2lQJOEBlChQAx5x8oA49f1qTxF/aS2rS6SyyugyYHAIkHcZ6g4rZoI+Wh7GkJcrva5g6L9h1fT2ljiKknbIhJGxvQe1EnhXS5Pm8orkYPOeOfX61g6jbanoN8dRijM0W4mRoz99Rk4ZTwOOOPzrqNC1m11qzW5tGBH8S91Pcf/XrKLXwtajxGBpSXtIpOPpsUZPCOmvamLa/I4JOSPz7e3Sq7eDbdIGWCVt+QQzj8xxjrXVA5oq3BHA8HQf2UchJ4L+QrFfSL0xwfy69Kk/4RWf5f9OfI6NubI/DPrXV0Z9qXJEj+z6Hb8TjT4XvldvJuwA4OeSec9vT/ACKgufCupeazLdKYDgksRkY7812F9fQWUPmXDhV9O5PoBWb5V1qkjG6DQW642xd26H5sHnHbtmk4RD+y6Mld3S9TkF0/V7lHW0YTRRAguoGH7YXPOcdPaprfSb+C1MctgJMBhzn0PIxnrXoMEKQwrHEoVVGABTtp9aSpIylldK/uNpebuefxAxXMaXFjNGwBOE+XcOPcVYjjsnLzNcXEAChtpDDHQ9RkY6fjXbmMEglQSO5qvNp9tPE0UkQ2P1A49v5U+Un+z3HaV/VHKpbnftttZjZlXoGAbHJ6+/Wrdxpms/ehu2YLzsLZVx3Xn1q3/wAIpp3y4RxtII56ce47962449igZzgYzTSNKWFkvj09Gz52j8N21l8VdZ0jVtTgs1vIGdZ7wCVZg2G5JYbWB9/bGDyye6u9LhOmeHRoWuTSxNCdRjtpC0Q5yTKSRuBGRjpXunifwvo3ii1WDXLCO8CZ8tiMPGTjJVhyucDoaxofhloMUIhEuptB08lr+UIRndggEcZ5xVnonnX7PPha50vWb2+mdJQYTGHiO5ASQcBscn3HH14r3rFUdL0+z0u0jtLC3WCCIBVRfT+Z/Gr1ABRRRQAtFFFAwooooAKKKDQBFO22Fm7gE1zvgdlfT5nXfvMp3bueeuPwzjr9a3b6Ty7SZ+u1GP6Vj+CInh0VfMGDIxk9cZPr3qH8SOmP8GXqjoR0paQdKWrOYKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPHv2h9Ulg0+1sYJvLe6O1lD7SY8/NnkDHA6+/4cH8MrVNR1hpLpWSPyxMPLC7gpO1FP94BcnBHJ9K7j9oe1vJItNuIYp5rSJi0yrgqMfjkEA5J6YrnfBF1cK66a9iqrOsTZ8xIA0WcM2cAkgtjjAwMEZFAF+/0e3tvGNzJpBdJfM2ReTgMcICysq/MAM5Py89M9Ku+Qy/GR53u7pGmcDyIirCUbY/vcj5cgc85zxjbVbR9Qg/4SESXOyGWSaSU4HmSlOSFVjyvDDjAJCg5BrZ+H8s+ueONT1mKzSOzZ9u6UF2GMYHIGMgZzg+maAPV93y7u3Wqb6rbp9/KjnkjipruaKC3Y3MiRpjBZjgVzbadcvNv4mSX+JCT8vHIOevPX8hSbsc2InUgr01c6QXduRlp05O3r3PapRIjfccH6GuJuZ9btGVIrZZo1IUAqT275HYgc1U+16nK7LJp+x0yXdVILDbg/nip5/I4XmXK7Si7+jPRM0teewaxN5202ThkBBBIyGGcZ6cY6CnLrhV9o+0orc+XtyBkex6UOp5FLM6fVHoFArhLfX3b5luJSvoVPHt3oi8QzxfKbosx6+YhIU45BPoD3/Ol7RD/ALSpHd0tcOPFE6eV5k8J3bgfk646GlTxXcND5mbVWC8gk9e5+n0o9oilmVB9TtaydQ1ZY7hrS0UzXeM7VwQn15H5VhyeIrzUlkgs402jhpUYg4PpxgH8alstWjsUJXTpPk+VpC2W7c5IJwfrRzpnVHG4de9KXyNjTdNMUpuLmQyzuMEnnA9M+1ao447VhSeIYotvmwuhY8c9Rxz+tOXxJZFdzl1IAyGAB/L9apNFSxlOb1ZucVyXj/xpaeD9KeeVRNckfu4iQoJ9ST/nitj+39O2eY0wReeWBH9K8F+Nd39q+IWmAssto7xkkfdZMr8pOSOx4OPUincqNWEnaLKR+IHxA1zbfhpVsvN25ixboM5+TcSBnjqcn8q6n4OfEq6uPEB8N6wZmWUnyGupt8sT90Zm5bJPFQ+D5DdanPb3emnVILWUCK1FzHHFbggkdWCnA6cHviuI1SSWy+NcMkbQvKbqPItDkBzgFd3G4g8E+tM0PpDWNOu9SMkTShIcjC8/MM9cj+VaemWCWFosCFmx1Y9Sau4wKMUrIwjRipufUUUUUUzcKKKKACiiigApKWkoA5UosvjWQqC3lwoZPT/Z79s56fjXUp0FcrCjL45uJVQHfAisShyPx6D9a6pOlZw2fqdWI+z6IdRRRWhyhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBl67Z3N/arFZ3H2dxKrFskcDORwQeelaXRRnk1m69bXd3apHYyrFJ5qli3TZ0bsecHitMCgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACkNLSGgDJ1iXeqWq5ZnYFtvVV9fpkYrlr5H1HxFbWdu+LaBsMVxgtk7vpjGBVnxJelLtpI2zgdUPbJCjI98n61o+CrIRWJuGGHlYtz19+3rWTd5WPCqSeKrezWyevounzN+CFYIljUYVRgd6mFFLWp7kUkrIQUtFBoGRsAwKtyDXJanoE2kXZ1jw6dsqjEtqfuSJ3A9COvFdhQaTima06sqb026rozH0HWoNYtVliIjlUfvYSfmjPQg/jWtwRwa5fxF4fnM/8AaehzGz1BcF1Bwlxj+Fv8fzpvhLxjba4z2t0v2TUYSVkgbuR1x61Cly6M1nQ54OpS1S3XVf8AAOsrD1XXVhlWz09Rc3jnG0chPdsfyqC81C61Cf7NpO5U3bXuNucDvtzx+P5VoaZo9tp8Y8tN0vVpD94k9Tntn2qr30RCgqavPfsQWmkNIVn1JjczE79rY2xnjhcduPetpVAFIKdTtYylNy3DFGKKKZIUUUUAFHaig0AJXNXfi2zt/EiaL5byTkje6kYjBHBPNb08giheR+ijca8Q8Vaj5t6b60/d3l8wdMNkxDIAUkZwSB7daxqz5bWPTy7BrFTaltbT1PX9ZuJoJbV4pNsZfbIPUGq2q3lzaahaSROptZ8K2/oP/wBeat2sD3OiwrcMsspiUl8YBfAOQO3NZ+oJ/aXhmdeZLiJWwSed4z/9erPnsTGUHKz818uh0aMHQMOhFOrC8F3327QoGY5kTKsffOa3RVrU6KVRVYKa6oWigUUGwUUUUAFFFBoApal8tlN1+6Rx159PesrwSqroimPzMMx5k6sehP4n6Vq6p8tm/fOB+tZ/hEsNIQSfeXKnjHI689/rUfaOmP8ABfqjdoooqzmCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDM12wbUdMuLSJ0SSVdo8xdy4PBDDuMcV5LrHgwWQNrY6nZ6STmT+ztTgEtqG6bopMZAJ5xk4PUd67y91Hyp5dTlcrbRcBUJDEdFH4nsa1PD90b2BpWDNGcMpdce/HbHvmknrY5KeKjOp7Nb/AKHjS+G9dWZrKGbSmmnPkmSzvCzRrtJYgsPl3Zyc884xzz6x4C8OP4b0cW90yyXZY+ZIjEggE7QM4JwD1PP4YroEtLWOZZI7aJJACAyoAQD1Gfwq1TOsgmiSaJopVDKwwwIyCK5OKRPC+oPBAssunv8AMyoCxhJ53E5+79P512dZWraNb6ih35jlxgOp/LI6H8aiSe6N6M4xfLPZl6KVJo1kjYMjAEEdDU2K4W1vrvwrdmHUwDpsjBI3HGztkkkADHbrmu0imSaNXjYOjDIKnII9QaUXf1FWo+zd1qnsxTDHuJ2Lk9TgVFLZWsv+sgjbvyoNWu1JirOdwi90URpWnn5RZwjr/BSNo9gybWtYx0z2q/j2rL1LVYrRxCjCS5f7kecfme386WnUlYenLTlX3Fa/0fRoITNcRKiDB4Y8ntgdzWWvh631ebcIDaWyEY4y0g6kE5IGOla9ppk9w8NxqzbpYyWWNcbBmtlRgccUrJ9AlhaCVuVP5HMr4LsElMiNKBjG3Ix/kVFJ4VmCymG/dXY5HUDvwQK6yjj0pckTl+o0H9k5gaXqisN7xvnn5wGAOBx68HPNULi6uoty3mkpIeoKnaCo59+a7bA9KTFVy2Ingk9Iu34mFpsFtqNoJTE8JycoXOcHjn2IH5Vx/wAU/h7PrVvZX/h2G3a/0+UyiGXgTIcZjB6dRkA8V6cFAoxRY6oUYwXmfPfid28RyjT5/BsXh6ZBGkkg0957pmHBCMq4K4PHJJHStDwB8MoJNViuv7PmtrK1cH7TcrJDPMQo4CHBAJPJ9uPSvdqguJo7eMySNtRepqjV6asnpKqyX9tHEkrzIqOcKxPBNWFYMMqQc9xQCknsPooooKCiiigAooooAKaadTTQBy1uhbxtcsv3fLGST324wPX3rqU6Vyml+UfF16d7NOPTlQAMY6cYGO+Px4rrFFZw2fqdWJ3j6L8hRRQKK0OUKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMnXLOe9t4FtXRHiuI5vnLAEKckce34VrVl65aXF5DElncm2dZQ7NkjcoBBXj1z+HWtL+EdzQA6iiigAooooAKKKKACiiigAooooAKKKKACiig0AFUdSn8i1Ztu7sR7d/pxVzNcn421H7JA+0tuIMYAOAFI5PT6Cpk7I5sVWVGk5voYls7arrKCA/wAfOeyg9D7Y9vWvRI0EcagdAMVyngCw2WZuXTDtwCRz15/DpXX44qYLS5x5ZTape0lvLUBS0UVoeqFFFFACUHpQTWTf6tHC4toMS3Lfw9gPU9fypNlRi5OyL11dRW0ReZwqgZ56n6VwviDwpLrUjanp0S2N1E++LcoPmnH8XYHNdNaaU8kxudSfz3K42OuVU+wPT/PNbIUDgcColHnVmdFKs8NLmpvX8PQ4jwV4njcHSdVQWd7EwQBgR5zfkMnpn1rtx1rmfGXhWDWoDPADHexcxuvXNY3hTxk9rL/Y/idjBeRkIkjjiTsORnPIPOaiMnF8k/kzpq0Y4mPtaC16x7ea8j0IdKKRSCAQcg0tbnmbC0UZooAKKKKACiikJoA8p1/XtQGreIrDzZvLmaKCJCQQoYYYrzkAgHkd+oFReEdKt9Q1LIlEkETqsalvmOB1OOOxPc9Oa5/Vrlp9Uv5YJirGV425yz/PhRjgHA/Tg16d4GsTbWjCSMbhj962N5Y5zkAkAjpXBG9Seux9XiXHCYf3NG0vyR1QHGTwBWOq/Z9aliYHyp4wwGBtz0P+fetms7WIm8uOeJN0sbccZyDXc0fHVo3V+xyOi3EujeK7izLN9mZydoBIGfun2POK7+NgygjkGuE8bWphvrXUYgAW+ViMg545z+WOK6rQrr7TYowO4gcn+VTHRtHmYCTp1J0HsndejNSigUVZ7IUUUUAFFFFAFTUDi1PTgjr65rN8H/8AIKDc/M7HJzzz7k1b1gqLVdzlAW7DOfbpWf4MVU0VNoQAkk7OB9OvX16c1H2jpiv3L9UdFRRRVnMFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFZevXXkWhTfs35UnOCFxyR9K1K5DxdeQsBHIdqqQDjkkdSQPToM5HWlJ2Ry4qr7Ok5GZqZ/tm6tdPtwyRcu7N/EcdweuBXbafbraWcUCDARcYHArn/CGmtDuuWdJFcHYR9ffkYHHSuqWpj3OTAUmk6093+Q7FFFFWeqFFFBoAhubeG6iaOeNZEbgqwyD+dcY/2rwVcFlWS50aV8nL5Nt+BHT05x7Z5PbmopolmiaKZA6MMFT0IqWjanW5PdkrxYzT723v7RLqzlEsUgyrA9amL/gB1zXm+v2mp+DtXXUtDy+lvkzWzMSoPUkAnj2x0rasdQTxhCogBgtdoZweWJOeODyBio59bM6Z4O0VVi7wfXt5NF++1S6vro2ej7HXH72fOQv0PTP1/CrujaSNP3M8jSzPy7n19v61as7WK1gSKEbdqgE4GTgdTirI61djmnU05Yqy/rcfiiiiqMQooooAKKKKACiig0AFVL+AXVnLCw++pH41aooE0mrHNpa/afDs1hJzNECoHcHqKl8J6hFdWRtxnfbYRgccdfT6VNK/2LV8scRXWBjI+8Opx19KwLSSPQfFtyk5WKC8+ZGwep56/XIqG7NP5HlSl7GpGXRaP9DuaKYrU+rPWCiiigAooooAKQ9KWkPSgDm9LXd4lun38LGAI9y8ZPLcc9RiulHSuZ0iNV16f5jv2biMZAOQBznjjjA/HtXSVEdjfEfEvRDqKBRVmAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZmtWlzeR24tJjA0c6yM2SMqM5HH4deK0wKyPEWnXGp2C29ncG3bzFZnyRlR1HHXNa1AC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUZoAr3EgghZyenSvOHWTxD4gMSZEYOCRyBg8n+ddV401MWtiYImHmy8AYzxVbwNpfkWou5MM0n3CPTuf6f/AFqyk+aXKeHi/wDasRGhHZas6ezt0tbdIoxgKMVPSUorVKx7UYqKsgoNFIelBQHpUTyrGjNIwVQMkk4AqK7u4bOEzTNgD8ST6fWszyLnVmzcr5dg4GIXAJcdcnB70mXGF9ZaIin1S51ScwaQCIRkPckcA46AHH49/StLTNLg02IpCXLHksxJJNWoYUt4UiiG1QMDv0qUdKSVyp1LrlirL+twxxRilopmImK5/wAU+F7PxBbhZ0KSocq6nBz9a6Km0SipKzNKdSdKSnB2Z5/omtaj4dvv7I8QsZbUEJDeY4x23HP4evetzXtQ1HTL6G6ihe404qUlSPBZWzwR0/r+Faes6TaazaPa30IkjYdx0PqPQiuLt73UPBMy2Wrb7vR5GYLc4LNFk8BvUf5FYtOGj279j0YuniHzxS5uq6PzXmd5ZXcV7AJoHDqeOPXvVnOelcx8lgov9JZJNPlO+RI/mX6jA4HrXQWtxHdQrNAysrDPFaRl0ZwVKdndbFkUGkB4FKasyErH8W3403w/eXZOCkRUfU/KP1NbFeb/ABs1TydFttNQK0lzKCSWxtA6H86zqy5YNnXgaPt8RCn0b19Opy/gO2S7uWvLh08qEtM8IGCxY8c9/mxjPH6169oluYbCLesauwy2zke3PU8VxPg3TVtNDtoWBD3kmZB5Q3AL09yAx+8eOPSvRlVVUKowB0FZUI2id2bYj2tVxjtfT5f8EXHFRzx+bEyHuPyqWjFdJ4r1OW1yD7ZoUiFdzW7YHHPHHvimeC7zfbhWO0ofLZR/e9cf1rTuIlTUJIwBtuY8Z9/X+Vcvo7rpmty2ygAyHaDj+MH9OQev51nLSSZ4tX9zXjU+T/Q9AXpTqrwSmWFXK7dwz6/yqxWh7Sd1cKKKKBhRRRQBk66GNqpjXMiEsuDjkA/pUXhD/kBwfwuwLNxjmjxLt+zrubAAcnnGBjr9KXwphtFhwQRyMg5z+PX8+az+2dX/AC4+f+ZsjpS0lLWhyhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBoozQBXvZvJt2fuBxxmvOtSeTUdZNrbt5qoQucYJweRk+57da6vxdqgsbJthPnEYQj+EnjNYXgDTDLI9/OeFPC46sc857/41lJ8z5TwsbJ4ivHDw9X6HZadbLa2cUCjhFA/xq5SAUorY9qEVFKKFFFIKWkWIaKTIozQMX61mapqsVku1QZpyQFiQ8knpn0HvVW71OS7n+yaYN4/juByi8ZGCM1Z0/S4rYiWXMs/eQ564x/k1N77GqhGPvT+4rRadLevHc6kSOpEBUYAIAweTkcZxXM+INBuvDt3/a/hsERBt09qvRh6AZwB7Y716CB2pCilCCMg9RSlFNeZpSxcqcr7rqujRheE/E9rr9mGjbZcoAJYT1Q9/wAK3lxjivO/E/hG8sL3+2fDLmOZSWaEHAfPXntkf5Fb/hHxVFrUP2a6Q2upRf623cEH1yueoxUQk17stzbEYeLj7ag7x6rqjqKKrXF1FaqGncRhjgE+tTK2e9bHBZ2uPooooEFFFFABRRRQAUUUUAZmtwl7cSqBuhbeM+g69jXL+OYPtdlZaivOwgOeOBnv+Pau3ZQ2VPcYrnbu1EuiX1iOseTlsc+/5DrWclpY8/G0ueEl3X4rVGhoF79tskJ4ZQP4cce35VrVwvge4MMzwSEYT5fmX5gCeOffiu4zxTi7q5eBr+2pJvcdRRRVnaFFFFABTGOA3tT6huP9TI3PCnp16UAc5oTbvEF62MxmJdrfKQT3weuB+VdP3rmtAy2tXEnyHzIkO5MdBxg9+tdKOtRHY6MT/E+S/IcKKKKs5wooooAKKKKACiiigAooooAKKKKACiiigAooooAy9dtLu8t4l0+ZYpo50ky+cFQeRx6itPtWZr1lc3kMC2k/ktHOsjHJBKgEEDHfmtPtQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUGgAqNztUluAOTT65zxvqX2DS2RWxJKCo47f060m7K5hiKsaNN1JdDm7yU+I/Egjj/wBUmVVgcHHAP6V6FBGsUSIvCqMAVyvw+0xreyN1Op3yHK59Dzke1ddgVEF9pnFl1OSg6095a/5DhRRRWh6g09aoajqEdlgH5pG+6mefqfQVW1PVPJZrezXzrkYyMEhc+uO/oBUmlaX5JE945numXDMScdSeAelS3rY1jFR96f3DLSye78u7v1y5UgREYABOea1wABgUtLTIlLmAUUUUyQooooAKKKKACql/Zw3ts8FxGHjkBVgRng1boo3Gm07o83ltNQ8E3jPZxy3uiy/KbXOfJ9SOCT/nNaum3ItTHqekkS6bcHM0I4MBPcD65zXWzQpPG0cihkPUVwuseHL7RrybVPD7gI5JltnxskX+LOeOnSsJRcPT8j1KdWGJ92dlLv0fr5+Z3FpdRXcCTQMHRhwRViuD8Na1bmGW805ZNhwk1kc5ibPLD2x6Cu1t5kuIlljOVcAg+3WtIy5kcNejKk7MmrxfxYx174pQ2kYeSK2ZEbB4HQk88DmvW9XvFsNLubuU4SBC5/AZryj4WQedc6v4iu4mOzc0TF+VyDleMZ4IrKtaTUPn9x6eWfuoVMQ+isvVno+nosurOQJNtogjRieD65Hc9ea3KxPCsZTS0lkIaST5iw5JGT1OATzk1uCto7HlVn77XYWg0UGqMjO1ZD5Ucqgb4nDc+nQ1yPikGPVIbpN+ZAJA2eARww6DjArupVDoyEZBBrltbtPN0l0c5azYuRjBwcg4Puf0qJrQ8vH03KDt6/NG3pEiPbhU6DBH5fjg1o1yfhS73KsbBgYztJOcdPWutpxd0dWEqe0pJi0UUVR1BRRQaAMDxVJ5dl/Byrr83+729/arPhpY00eAQD5Np527cnPcetU/FqoLWN5F3FC2B/CeO5yMVp6NuOmW7MWOUHUAH6fhUL4jqn/BXqXu1LSClqzlCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooNABTT0paxfFGpDTtKkfguw2qPek3ZXMqtSNKDnLZHIa48mta59mQkBTtwFyAf8A6wxXf6daJZ2kVvHjbGAB/jXLeBtMKtJfTL8zMSpII69fy5FdiorOC6s87LqLs68/il+Q6iiitT1RaKKo6hexWqfN8ztwqA8sc0FJN6IlubqK2i8yZgozgZ4yawXivfEBCkm1sweRzvcdvYj9Pr2vQWEt4fO1M7sMSkOBtUds+prVRAgAUYA7CpauaqSp7asjtreKBNkKKi+igD+VTYp1JVGLd9wooooEIcEc1yXifwkl9Omoaa32W/g3Msij75xwDn9PSuvpKmUVLc2pVZUpXizhrDVYPEdrLoWvo1pqMRAYMQu454ZDjBPsK09Inu9FeOw1WVp0Odt03A9geTj8e9P8WeF7fXog3+qu4uYplA3Kf8KwdO8QvHM+g+MVEVwDiK5wQkxzxgjjP5dOeayd4v3vv/zO9KNaDcNuq6rzXkd8rBxnPHtTugrmrLUJNJvE03UGaRJTmG44Ckeh5rpA2cY5rZO551SDg/J7MfRQKKZAUUUUAFFFBoAYw4rOuQIdQR2yVnXYU9+OcVp96parGXspGX5XQFgR9KDKrG8fQ4lImsPEvlhNyPlRjOMjp19BjNd3ayB4EPUjg/WuO8Wws9vbX6Jt3gMxGTgjgHp6dOlbnhu5F1bK5O7eA2R0z368isY6SaPJwUvY1pUn11XzN6iiitj2wooooAKr3p22czc8KenWrFVNQ/485ht35QjGcUDW6MHw15X9q3/UuwQ/MAGAAHHHauoFcv4ZzNq1+7KB5bbCNxyOAfmH8vauoFZw2OjE/wAT5L8haKKK0OYKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMzWbO6vIIUtLj7OUmDO3OSmCGAwRyc1o9h3NZ2uW91dQ24sZEjeO4jkbeSAyA5YceorToAKKKKACiiigAooooAKKKKACiiigAoPSikNADWYKuT2rzfXJ31vxBFHEQxRsKoPA57/lmuw8U3ptNKmKldxB74wK5/wFZmaaa/lDMcnaT0zzxn/Disp+8+U8XHSdetHDR23Z2VpCLe3SJRwi4qwOlH4UVrsexGKirIQ1kapfyvKLLTvmmb7zDog/IjNP1G/YzpYW6v8AaJh98DKoO5z6ipdJ06LT7cKqjzSP3j92bualm8Uormlv2DTNPWzj+bDyscs+OfpnrV/tSilprQzbcndgKKKKYgooooAKKKKACiiigAooooAPpTWVXUhhkHtTqDQBxPinwy7y/wBp6O7QXkOTsX7so/uke/8Akc1Q8OeKGaRwsbRXSvi5tJSd2ccsmeMcdK9CPSuP8ZeEl1T/AE2wb7PeoMCQfxDGCp9PrWEoOL5onqYbEQqJUq+3R9v+AZvxh1lIfCf2e1cM184j+U87QMnjr2AqXwnpLaN4VtbFgzy37hyiDawyASCcnpjGfevMtTa4vfEdtp91Ef8AR22yIBuI5BI+vHXvXsmkXUOraorwL+5tYwqnIwD2yB0PUY46VjTl7Sbl8j0sbh3hMLGnDVNtt/kdJDCsUKIowFGKlFJ0FFdp8yLQaKDQA01kX6rHqKs4wk8ZRvTPvzjpWxVLUoFntT97dH86kHBz9aT2MqseaNjibVW03UJIjIwCNt2kkZXPYdOcjpXf27b4kb1Ga4zxJEGntblP+WowShyCw5HHfOa6Dw5dedYnJG5Tg4zjP481nB2bieXgZezquk9uhsDpRSDpS1qeyFBoooA57xi3/Et+vGMZznA/kc1qaYirZQKvACLxnOOPXvVDxQu+xiG0M7SKgzkDk+vbp3rUtMG3i+Xb8o4HapW7N5O9GK82WKKKKowCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBBSmkpaAG8V534nu5db8QrYW3KwkYGeGOQSfwrrvE+oLpulSuTtZgVTjPNc/8P8ATWDSXs3LMOMdOf5EVlP3nynjY6Tr1I4WPXV+h11lbR2lukMSgIgwMDFWBQOlKK1tY9eMVFWQUGkJrEvtRe5l+yaawMhJDSZwEA649T+lJmkYORJqeqi3f7NaKZrxsAKASq57scYFLpeni3kae4bzLiTBZjzg98E+voOlT6XpsNjGWCAzv99+7Gr+M4zS1LlJJcsfvFHSlxRRTMgooopgFFFFABQaKDQAnesXxFoFprlsYrlBuAISReGj91PY1tUlDSasyoTlCSlF2aPMZLibQIm0bxQv2rTWGIrgDDrjG3v7fX+VdXpOpPZyxWk7LNaScW10HyHHYE9M1sajp1vqMDQ3UQkQ9mrg76wuvCM7tGrXOiSEboSdzQn/AJ6KSMLg+vGKws6b8j04zp4pWtaXbo33XmekUtcvoutRCKJZbpZ4pmJim9RxwT0BB4xXT1rGXNsedUpypu0haKKKozCiiigApGpRSGgDl9StA2mXlqz5aD94mM/Xp9OPSq3ha5xG0Sl8RyHHup/Dmt++CQXEc7jKyfuz7Z6/nXJL/wASzW3jnl2hm28Hd8hHy/kAM1lNWaZ4eIXsasai9H6dDvlOcGnVUsZhLbKwbJHBx61bzWiPai+ZXCiiimUFUdZ+XTbg4yQhIq9VTUOLKUtj7h6jI/Kk9iofEjC8JB2lvGljClX2gbTuxkn73QiunFc94RVtt1uUj5+M46c9CAPy7V0IqYfCbYn+KxaKKKs5wooooAKKKKACiiigAooooAKKKKACiiigAooooAytds7q8it1s5jCyTrI7AkHaAQQMeuf/wBdatZOv29/c2saaZJ5UvmruYvtwnIbscnB/OtQcAUAOooooAKKKKACiiigAooooAKKKKACmnoaWqOs3Bgszs++/wAowcEepoJnJRi2zkPF10ZpkAIcMw2jH8I4xn1JP/166XwvaC20mFc5LKDnGMjt+lchcRm51e3gb5s4OC+TjIxz2GPY13wZLS3zIyxoo5JOAB+NYw1k2eNgU6teVV+hYrNubmSeVray+ZgQJH/uD8eDVS4kvdVbyrQmK07yZ+Z//sfxya1rS2S2j2RKFHfHc1rc9/kUFd79iLT7FbOMIgBb+Jscmr1J2padiG77hRRRQIKKKKACiiigAooooAKKKKACiiigAoNFBoATvVXULhLWxluJGxHEhdj7AVari/i1qn2DwlPErYlvP3KjueecfhUzlyxbN8NSdarGmurR534X09/EGpavrUitmP50L/MmGOcHjk46ccelb3hu+udK/wBIiVg5ObhGXaAMEnjjPUH2z+d/wZZCz8DWttC7mTUGLnI6EYyvTjpx155rovEHhk3dvBPYMsd/aAeWzZIYd1Psa5IU7K63PocVjYOpKlP4b2XotDZ0jVbfVbbzrZgQDgg9jjNaAry7T3v7WaZ9OSS01BfnurOQgtMCeGUnjOOwruvDuu2+t2pkgJWRDteNvvKfcV0QqX0Z4uJwvs7zhrH8jYooFJWpwhRjiiigRzetWu6zuLRTztMsXA49QPc8/SqXhy8Ec8Yd93mJgnnC4PHf3/Ouj1EbQk4HMbfoeK5Fom0/VZ7WKMAviaKTjOc5wB7ZPbtWUlZqR42JXsqsai9DuweBS1V06cXFskg7irWc1qexGSkk0LQelFBoKMHxY0YsUWVgAXB7/MMgFR7nPetazObaJsbcoDj04rD8Ztt0+L73MoBwM8ZGc+3atuzKtaxbPulARn0xUrdm0l+6T82WaKKKoxCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACg0UGgBKM0Vn6veCzsmkz8xUhfy60ETmoRcnsji/GV8dQ1NLaMkKp2kc+vUjjHSu00SzWw02GAHOBknGMnrXF+FrZr3XzPKhKcuMtn6H6GvQenA7VjTV25M8nL4+0nPEy3k7L0H0UVi3t3NeM1pp+V5w8/GEHfAPX0471tc9uMbi6hcz3cklnp527ceZNjIXPUdQc49PzFXrGxhsYVihHQck9TS2VnHaQhI1HTBIGM1ZxiluOUrKyFooopmYtFFFAwooooAKKKKAAUhpRSGgBaKKKACq93bR3MTRyKCCMEEZH4jvViik1cadtUeW+ItHvvC87XmlRm402U/v7YkkLxyV/ujnqBxW54U8UW8lvHbM0ht+Qk7dPcZ9PeuwliEqFWGQe1eeeJPCo02d73TlAgm+WaMAbY06lh6ZIH09xWEoyhrHY9ilXpYqPsq2kuj/zPRUdXQFDkHoafXBeGvEslttt74g27YEcgIO3sAACSR69xXbwyLMgeN1ZDyCDkEVtGakrnm16EqEuV7dyeiiiqMAoNFFAFLUYvOs5Aq72UbkHuOR+dcr4gTcLbU+G3KYnODwRnB47np0xXascVg6rbGVL2yzgzp5iHPJbjA/Spmro8/G0vaQdv6a1Q/wAM3Hm2YT5flH8P8PXg981uCuF8MXAgvFV+C3yEdww46jgjHfNdyKIO6HgKvtKWu6HCigUVR3hVXURutJVVckrVqq9wP9Hf/dPv296T2KjujI8KArbT/LgGYnd03k9Tt7f161vVh+FG3acvzMQOPmGOec4rcFJbGlf+IxRRRRVGIUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZXiK2vLq1gFg6pLFcRync7KCoOSDt5P0rUArK121vLuO3Gnz+S0dwkjndjcgzkdD1z/wDr6VrUAFFFFABRRRQAUUUUAFFFFABRRWZreqppenSXDld2CEBYAE4J6kgdBnrQBYvb+1sYTLe3EVug6tI4X+dctqHiLTL65iWDUYfKbAByByfrgj/PevO7U33i/Uhfahp19qkQPmLFGxREyMfLyBnjPoQBzW1Az2OoC3FsYNjCM2V4BMGTHzAHBzgDPy8nPSpZxYttqMF1Z0+h6e95rclxKGRIzuGf4ueP1Gav2+mald6lL/bc8M1uBmJYeB6cgjrjPc59sUeGo10+/nsLZdlv1SEn5ofbaSTjHGRxmunA5pRikb4Sn9Vi4x3fUaihFCqMAcACnUUtUbBRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAG9c1418Wrv+1PFVtpkYZxAACq85J5PHbtXr91OlrbyTTMFSMFmJ7ADmvFfDONa8dm/mU7EZp38xiAWGeRgY46AH0rlxD0Ue7PcyeKhOeIl9lO3qz0zTrXzdZhEYVobGIICwydxHPXofpXS1k+HVY2jzSlmlldi+eApz0HtWtXRFaHk1pXl6GJ4i0VNThWSJvKuomDxOvUMOn4VxcP2w3QR1+w61GQhmJIhusngZGOf616disjX9Ft9VszHKh3AhlKcFWH8S+9TKn1R0YbE8vuT2/r8CvoPiCO+ZrS6RrXUYvvwP391PQjvxXQfWvNLmObS5Vg1QeakYC2mo9WRv9rB4H+R6V0+k6+wZbbU/Ljc8Rzb8pJ6EHAHPapjO2kh18N9qnsdKKDQKK2OAimRXQqw4YEGuQ8S2zxrFdkBpbZ/mPJITOeR3rs+tY2u2YmDFhuV1KkbsDOOKmSujhxlLnpu25D4bvAzNARgvmRCf4s9a3wa4PS7qSzdEdnJsWCMOTujPr9OK7iNw8St0yAaUHoRgKvPT5XuiWigUVZ6Jy/jT5oLaP7xMn3cckZGcdB+B61v2S7bOFd5fCKAxGM8dcVgeL22tZfMF/efeP1B6+vGeldDa820Jzn5Rz+FRHdnTU/hR+ZPRQKKs5gooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigANJS0lABXH+LbtGMsanJUbckHjJ5A9c9PrXUXc4ht3kPYfT+dcHr2RHGCWk8yT5snI49u4J5rObsjysyq2pcq6m34FtjHYGeQfO3yj1IHr610rsqDcxC47msSzv7TStJt/Ok/eFBtiAy7E9AFHOTT0t5tXG+8DQwK+VhzgnGMEkY9+KIbJHfg6Hs6MebsP+0yarn7ONtrkqzk4Lj27j+taNtbR28QSMdAFz3OPXFPghWFAicAVNV2OqUui2CiiimZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVHIoYYIyD61JSEUAefeJ/Dr6asl3p5kNqX3yxKTuBPBK9cep4+lN8N69Lps0MFxIj6e43Bxz5fQfO2ePoa790DrtcZFcdq/hn+zJJrvS41e0fJmsXX5COp2Y6E/zrCcHH3oHrUcVGrD2VbV9H/XU6+2uIriISW8iyIeQVqavO9G1WTR0E0Ej3GkqAHjODJb9eDgcgeo613Fhf21/bJPaOHjbowrSE1I4q+HlSd1qu5dFFIDxS1ZzCVR1CPMPmJ9+NgwIAzgHkZxxmr1MZQcr2PWgmSujhLyBrfWnjgUbboB0Ydm6/wAwR2612Wl3AurNH+XdjDAHO09xmuc8R2zx2aSJ5ryWbhl2nGVJHXg56dqveG7jnavMUy+am3nGTyCemeazjo7HkYb9zWcejOhoooFaHsC1V1FitnMy8kIe1WaqaicWM27n5CPSlLYuPxIzvCZd9NZmUBWclcDC49h6VuCub8ByrJovysDtkZTjI5+h6V0g60o7GmI0qMWigUVRiFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGR4is7q/slhsZjDJ5iuXDsnyjORkEHnp6VqKvyj2qhrkF5PBCLCREkSdHbc7KGQH5hkc9K0RwKAFooooAKKKKACiiigAooooAK8r+LM8094mnM0qLOsaxrgENlsMwJOFPIABGSenrXqlef/ELwh/b+o21wtzDbSKgjDSL7k9ScdcYGM9+1AGt4U0xPDfhdQ5kMioXfPHzAYGF6A4AHv3rAurmPWNbV0Ec2CPllYhMqOWAAJGcgZ9s4ps2k/EE2kdi15pLxQbQs0O9JJAM9QcgHHf8AnUFpZRaOi5uY5dX3NGVWNggHQEAjk4xye/tUt2MKtT2dmdV4dZXnd42dolG3zMghyOBzySc7uCfTFdPXNeEZkWzEczBbkgM6AEY/pk9eAOtdBLLHGu6RgqjuTgU07mkZxnrF3JqKzv7WsOf9MiAXOSWwPz6VajmjcZSQMD0waLo05ZdUT5ozTc0ZpiHUUZooAKKKM0AFFFFABRRRQAUUUUAFFFFABQaKDQByvxI1EWHhqdQMvcnyV5xjIJJ/IVxvwntX/si7nQDfdT+U4Z8bwPTvkAkfjU3xb1OOW7j09TuMCbmTPUsP0IAzz6jFb3gbTha6fp0BhyiReb5nA5b1xnORjv65rjfv1bdj6GK9hl+u8nf5I7C1j8m2iTuqgfpU9FFdmx883d3FooooAzdVso5oZB5SSBxh426MPpXH3dq1i7EL5+kAb0IzvticYCjHAHY+me4r0Aisu/smO57XZl+HR/usp68Dvj86znG51Ua7j7r2MXTNaayuEt7yQS2jAiK5DbgxzwPXP+R3rq1bdyDn6V5zIw02YhIs6dOG3xPlXiJ7DvkfqOO1aunancaZJEvNxYN8qupyVyTjj6+uDjrUwl0Z018Mpe9Df+vxO07VDdReZCy4XPbPrS206XMQliYOjDIIqWtTypR6M4m+QW2oI5TdFOrJLx7jnt2rotGlPlvA2MRn5cf3c8Vm69as/wBqhB5lAeL/AHhzj1puh3heOKcn7x2Oex+v9KzWjseNS/cV2ujOoWnGmocgEd6dWp7Zz3iLmWL9y07BeIwMgncOT6AeueK27dmeKNiu0soJHpxXPeKpGjIf5dvyLz05bnnqPrW/b8QoOclR1Oe3r3qI7s6J/wAOPzLAoooqznCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAA1z3izxbp/hq3Q3O6e5kyI7aLl2IGefQe5rR13U49K097iQjP3UBONzHoK8b0W1ufGniq6/wBKkiSOQhZc724znoBwW5B6YHUGgDqpvFmrX9vGb3To9NiY8NOXCnI4BO0jv6ir2mKdR1K2S/tTA3lh4yHEkU65zuVhyOnQgVU8TaLPpcEE39pTak6gxmO8YuGOM4GAcZUckjBxyasaQm21060AWNIM5zmPaM5BVuS2SDnjHsKhxucHsfaVJOotNLHUXmiWN3dxXc0A8+PGJFOCQOx9R7GtUYHA6Uo6UVSSR6Dk2kuwAUtFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAlFLRQBx+s+HJIb99T0lhFI6kTRBdyzDrgg8c+prG026e0u3m0UeXJHxc6W3TfjkR/ln9eleilA2d3Irmte8PxXYSVGaGSM5SZeq98Edx/LtWUodUehQxCkuSr6f8ADmvo2pxanbCWLKt0eNvvIfQitGvPbaW5t7wmXFrqa8KFY7LxRgbsYwP85xXVaLrUd6PKnUQ3KbQ6ZyMnoAe9VGV9GZ18M4e9HY2RRRRVnGZOsQ5G/ap81TE349P1rldLleyMsTdbJhgYxvQnOenXOK7m6hE0Dx+o/KuM1GP7LqUVwoJRjsmXqRnjP5ms5aO54+Ni4TjUR20biSNWB4IzT6xdAeRYWtZmzJGeOnzL0zj+fvW3V3uenSn7SKYlZ+t/8gq5GN2UIwelaFZ2tj/iWTqrcsMDIyDz0olsdFL416lLwfxokS7ycErgrgj25GTit4daxfC8TR6apZEi3HIRc/Ljjv1raHWlHYuu71H6iiigUVRiFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGXrlte3ENsNOnEEkVwsjk9GQZ3CtSsfxHa3t3YLHp8zQSeYpYh9vydx/nH1rXoAWiiigAooooAKKKKACiiigAqvd20dzE0b9DyD6H1qxRQBimTWLZBGLa3uyBhZBJ5fpyy4P6E/hVWXQWuZWu7h1S7I5A5XIHGRxkCukoNJq5E4Ka1OTkhk+0DzGSG9j5Urwsnb34/zita0vBdRmC7URT9GX+97r6irWoWUV7CY5R/usOqn1Fc/cRywzCLUCdqj9zd9CmfXp+IqbWOFqWHleO39bmu+h2LxsvlAq3O3sD7VXk8OWe9TE0kDqBzGcZIGMn1PNPsdT2Sra3jjzGGY5R92Uex9a1hVWTPRpYmUlozC/sCSOVWttSnTbgAEk8ZzyM4P1xSS2mvLtaG/RjkkhlAB68Ywen1roKAKXIjX28+tn8jB87XoutvBIAAMrkZPc9f/ANdSHVbqI4ubCUDPLryvXA46j1/rW3ikxTsx+0T3ijFj8R23nvHPFPD5YBJZMjnr0yRjvmrkGq2U6bormIgdeQCOccg9OasSQRS/6yNXB4O4A5qCXTbSV1YwhWUYVxwR9MUaivTfRosQzwygmKRZADglSD/Kpqxk0C1jV/LaQeYckg89c4yO2ajfTtSSERW1+2Ap+8Oc5yOcE9fc8UXYckXtI3d1Fc+0mvQXMKlIJ4cEuQu3nHA65HPsc0qaxext/pOmPgYBMTEndjJ+UgcD1z3pcw/Yy6NP5nQUVjDX4CiskNw27GAE57+uPSpE1vT/AJRJcrGzgEK+VP607kOnNdDVoqrFe2szbIriN2HZXBNThqLktND81FNIIondzhRkknsBTz1rnvHupSab4eneDb50uI0yCeT16e2aUpKKuXSg6k1BdWeWa9cXGta5HtkLpcS+cm0bTtGcYzg52genPHWvWvC0SizaZVwJCAqhsgADAH4CvJ/D0f2jXH2COfyAI0CkheTk45znn8/evarGIw20cbAblUZ2gAZ79K5sOrtyPeziShGFFdEWR0oopa6z5wKKKKBhRRRQBSeytJJfNkgjZwQ24gZyOhz7YqhqOjozyz2udzp80OQEc8kH2Oe9blJSauXGpKLumcLpd+2krK1qu63DgSR9Whx1zgn0P+FdlY3kF7AstvIJEI6iqWoaVHOzzRDyp9pAYdDkd17/AI1y0l9Pod4zRLtB+Rrd+Me64HI5PSsruG52uMcT8PxHV6paSzXdtJFjCMS30xXPPbfZNbktSN0c+ZVGMgj8x79K6XS9Ut9SgWW3fORnafvD6iqPimzaa0S4iBLwNv8AXjvx3q3Z6o8DGYW15W1Wpc0eZ3g8uU7nj4P07f5NaR6VgaRODcxkKpWVN2/jJ6fjW7mqWxvQqc0Fc5TxN5cstyv8S+X1baOoIz7c9ua6PT1ZbKBW4ZY1B79vWsHWII1kvZmU7naNevByQMY9SOldBZbTbxlPulRj6fmamO7PSq/w4r+uhYFFFFWcoUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBxXxX3Dw3HKCAqzqDvClRnOWO7uBnHvWT8JdQ0mHw9LOLoRug2y+dIoOQW45Pbr2HPSu91axhv7NoZ4o5QeQsgyM1y9v4C8Jampkn0W3S6j+SRlchwfcgj9RQBi6n4iXVNSWGzY3MbO2fKxICxOACAcnAGOBjnrnFb+nwS/2slqgIhibD7csNx5ZTnt8ox6fjUo0bR/DMTJotpHb3Ei7Q+Gfy1Hc8kjGau+HtKksg090ytcSqqALk7B1P5nn+tAG9S01s9qwbrVdShuvL+wo6nIVgScnn29qRcYOWx0FFYJ1q4gh33lhMGzgiL5scZA5wSfpT38SWUW3es4ywX/VHg+n4d/Si5Xsp9Ff0Nuispdc057fz/tkYjHJYnGB756VcguoJ03QzLIOuVYGi6IcJLdFmkNIDSimSLRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFNZQRggGnUHpQBzOs6TFd4t7qLda7gY2UkNE31689+cEVz96bmK/W1u2ZbncTa3cfCyL1UNjsOR+GTXoMiB1KMMq3UVzOv8Ah572M28aCWAgFCThoj3+oPespw6o9DDV1flnsWdD137UXg1AeTcR4ydpCt7j24+ldCDXCSabNFaWy6rG+7oZUIJXj7rEc9sZHH41raLrDQyR2V8OCB5cvG0+gz+QFEZNaSFWoRd5Ujpa57XrXzm8sMq+aOBnHI5H69q6BWDLkVma3H/onmhtpibfVyV0ePiYc1NoxdEug4hnXCtETFKDjO317V1ucjI6GuKj2WOqks2Le7UOuMY3k5wc/kK6XSroSR+Sxw8fHJ6gY5qYPocuBqWvTZo1Q1nb9j+bpuX+dX6zNaP+iqGUn5h/Dn8SPSqkevS+NEXhfb/Z3yuXG7klNvOB26flxWwK57wVMZtKJYMHVyrZbI46Y9BjFdCKI6xKrq1R+otFAoqjEKKKKACiiigAooooAKKKKACiiigAooooAKKKKAM3Wba7u7ZEsbgW8glUsxJ+5/EOCOa0B2z1rN1uC7mt4BYMyyR3EcjASGPcgPzAkA5GO3etSgAooooAKKKKACiiigAooooAKKKKACiiigAqCeCOaMrKoZT1B5qeigTipKzOU1SxNqpjkgkms25+T70R9V7inabq8lntjvJPPtH4hue556N6Y9a6WWMOpVhkVzmoaWImOEUxORkY4PHf8fSoaa2PNqUZUpc1M6KJw6hlOQaeMVyENw9tHJCS8iP8qxklTnvtPt2rS0K7aLfaXEu/afkY+nYU1LobQxUZNRasb1FA6UVR2C0mBS0UDExRilooAbge9GBTqKAIpIlf5XVWX0IyKguNPtZ8edbxyY6bhkCrlFJq4+ZrZmHJ4b01twWF1POMMePce9RHwxCtx51vc3ELCMxjaccZyMkYJAPOM10FFLlRftp9zn1sdbgG1NQSUbicSLyF9M85/H864fxpqmpS6lbWN9HGxtkMziIlQN3AyMnOAOucc9K9WLAHmvHtcuDdzalesSGnkMUcgydoBAweRxge/WsK692x6+Vvnrc0ktPzGfDy5tv7SMl9M6K7bizuAnBODkfgOvNev288c0YaF1dT0IOa5nwnotoNNV3gQsyAAkcgY5AJwcY46DHap7jwfZu7SWc89mzZz5bEgZ6kZ6H3qqMXCNjPMK1LE127tW07o6YUtcx/ZWt2ys1rqjSsX3bXUYI59QcduBgU+3utejnVbizhZAp3tGep9Qefyx171rc890V9mSZ0dLXLxeJbhWdbrR7ldhAJQ7hjHJwQDwePerlv4l06Z3j3SxyRttZGhYMMewHSjmQnQqLp92pt0VlQeIdMnDsl5GNgy+/K7ecc596nh1Syn2+RdwS7iQoVwSSOuOe1PmRm6cl0ZfzRmm5ozTJFrP1bS7XUYtlxHk9nHDD6EdK0KSk1cpScXeJ5tPb33h/ViBKV847llYDEuP4Tzj0rrdL1+x1BRbySLHcH5Xibg5PQY+laGpafb6natbXUYkjb8Cp9QeoNUdA8P2+kWyxbjcNGx8uRwNyj0z1rNRknZbHbVr069P8AeL3vLqQ6rbG2i/0JArwkOoyTkZ5wK3I2JhVm64GazNeDwiG8i3HyG+cAZyp4NacMizQpIvKsM1ot2eNSSjUa/AwtXaT7FfbPlbcvoRgke/Brbsg32OEN94IM857Vm3sUcWm3Lzn77Bicc8HjjnntWnaEG3jI6bRjtSW56M3eC9f8ieigdKKowCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACqNzpttcy+ayFZRx5kbsh6EclSM4z3q9QBigChY6Xb2f+raWRvWVyx/M1eAx9aWigAoxRRQAlQzQRSLtlhWReuGAIqeigadjPk0qxl377WL5xg4HUdqqyeGtOK7Y4jHzuyGJ59wcg1s0UuVFqrNbNmCugC33/Y7uSAnBJA7+4GAfypXtNYXZ5N+rbSCxcDBGMdMfj1FbmPajFHKg9tK+uvqjDS61i2Y/aLVLiPgBoyAx65JGT2x3oGtXC3flXFjIi8DcD359QBjHvW5ilwKVivaRe8UZkGt2kjMGcwFQCRMNnXp1qWPU7KT7t3FxzguAceuD2qd7eKRXDxoQ4w2R1+tZt34dsLiPY0O0F9x2nr2I57e1GvQlcj30NmkzWFN4cTeHtLmaBgdwG9ivTAHDDilFprFvGRHeLPsAC7wAzcdzjuaLvsPki/hl9+huZpawidch7wXABUkOMNyOcEccfTvUUetaiNv2jRplbHzbWzz2xgYPHvTv3D2Mns1950dFc7N4nht2InsrmMqVDZAHXqeTkgDk8VctvEGnz7h54iZc7lmBjIx1+8BRzIHRmldo1qKrwXME4/cSpIOuVYH+VTbqZm00OopN1G6gQtFGaKACiiigAooooAYwBXkZHoa5XXNJdZd8amS2Ys7qoG6Inqy9OOB34/GutoJpNJqxrTqypvmichpGry6c622psrRM+xJRnIbPKtxgfhXTTxpcwvG5yrgg4rC8RaNJcI8loFbdlmhPG5vUNng9MjHOKxNG8Q3GmXIsro+ZErlctnKAZyST27559PplzODs9jqlQWJjz09+qN3xJpf/EpVrYbWtvmX3H+eaZpNwGuIZoh/rVAYcdf1reR4bu23I4likGMg5BFc5DZz6ebiJgzQxN5iPjH689KrZ6Hztek6VVVIrTqdUCe4xWRr0hzaKisztJkbc8cdePTNX7GdLm2jkQ8MM1Xvow1xbPnaVJwR+Axn0q3serQkm1Iq+FIli091VSMSN16HHcDtW5WN4eZzaOjNna23PGM98YHT0zWzRHYus71GFFFFMyCiiigAooooAKKKKACiiigAooooAKKKKACiiigDJ8Q2t5eQ2y2EzQslwkjuG2nYAcj8c1rVk69a3V5Y+TYzvby71O5HKnaOoyCOo49M1pqvyj2oAfRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAYprorKQQCD2NOooAxtQsF+8wJQZIYdYz6isOW0ntHVnZVUZ8u43ZVh2DgnGfQ12bKGGDzmsu5tPKLlYvOif76HkAewqJRPPr4ZP3kR6PqwmHkTkLMvUE9fce1bA6VxF/anTWWZWeSxJBJBHmQnt+AxW1pWqEGOK7kVw+THOh+Rx7nPWiMujIw+Jkn7OrujfopuRilzVnpi0UUUAFFFFABRRRQAUUUUAYPja//ALO8P3UozvZCqkdj6n2rz3Ty97fWdstyiPEd5/iJY8rng84IGRznr0rofiXdb2t7ONyuxt0mMcjqR6/dGT+FUPh7At5qMlwYUaIMShblkAzjoevzHPH8q5Kj5qiR9DhYKjg3Vlu7/wCSPRLKExWsaOPmVQDyTz+NWcUDFFda0Pn27sMUmBTqKBDSoqvNZ283+ut45MjB3ICatUUDTaKX9nWYfzPIXdt2Z5zt9KzZvCukS4DW54zjLseuPU+wrepMe1LlRSqzjs2cvH4Qii3NZaje28jNuyJMj3yOM8cc8ipP7M1y1uhJa6gs0Z2gxSk7cDOeoJyfYge1dHj2/WlFLlRf1ib+J39Uct/bmt2zt9r0dWUFRmJznnpjAO736YqEeMpIn8u50uVJGBKlXG04OCASB0PrXXkU0oD1HtRZ9ylUp9YL72cxaeNtMd2W6E9kykA+bEcc9ORnsM56AdTXRwTR3EQkgkWZG5DKQQaiutOtbxDHdW0U6EYw6g1zcnha50y4nu/Dd4bd5VA+zycxg+o9PxB+tF5LzGlQqOyvF+e339DrHQOpDDIPBB6U1njghZiQkaAk9gAOtcZZ6v4vj1iC21PS4ntnPzyRLnaMcZYHGc9sVofEW+lsPCN9Lbl1kcCMFOvJwRnBxkZAPqeooUrmdSh7KWrTv2dzzDxh431XxVd3GnaWbOGwhcL/AMfIBlbJ2kv0IOMADv3rasr2fwpaQQ69Hqek+YGEF1Be/aYDIBwrKQQuT04wc81g/CHw7beItYvr7U7ZdsLDMZ53AghRnqMDBPJzxWx8QxaWVjfwacVhs5mFo8ZK+VuGQSE3Bhg9x2z1p9bkym+VQ8z0/wAOzXc2mRSX53zN/GABvU8g8Ejoe3Ga1q5/wRZyWHhewtpmy8cY9RgHkDBJOPTJroKZDCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKMUUUAJik206igCKSJHXDqrD3Gaqz6XYzIyyW0RDHJwuCSPcc1fopWQ1JrqYM/hy1kuBcxSTQSgj5oyM4HQZI6e1QNa69aR/6NeR3GOnmADj0/pnNdJRRyo0VaS319TlpfEd5p+f7S02QhTgywn5DyOmcevJz2q7D4m0qXAa48nOeZAVAxxyenPb1rbwPSqcunWcs3mPbIZefnAw3IwefoaVmtmVz05bxt6Mmt7m3uIxLbyxyof41II/Op6wJfDGmFVWKJoQuSdpzuPA5znJ44qC68PXoZTZapNEq5whkfB4xzz+P1pXYlCnJ6St6o6alrnILbxBbRwoLm3uEXIk8wEtjPBBzyceuPrTFufEiXH761t5YiyD5Bggcbjnd+XFPm8h+x7SR0tFc1da7qNuzoNM84quQVdgGPt8h4/Go4fGNs9ysEtldQyFS2GTJx26Z7ZP0FHOgWHqNXWp1VJWFB4n0eRUcXYQOQoLoyjd6ZIwDWvDPFMgaKQMCMgg9R60+ZGUqc4/EmiUjNYHiTw9FqkJlg2RXijKPjqR2PtW/wAUGiSUlZjp1Z0pKUXqec+G7/UEvZ7aziVLmHiW1n+UccAo3cH0rtb8lLATzr80Yy4U4GO/4Vc8pPM8zy13gY3becfWlljWWIo4yrDBHtURg4jxdZYjXlsUdCtVtrIeS4aOQ719s+/en3bFr6BF525Lew6U3R7aWzt2hmAIUnYQe39Kdf3VnpkMl9ezRQRKMGRzjA9M9/pVW0sYYe0YrS3kVfDK7baUlNmZWGB0PPXHatuuJ8NeNbG9Dx/Z78qXb94LdmjXnAGVzjNdNp+qWOpBhZ3McxTG5A3zJkZww6g89DTWxvWTVRp7mhRRRTMwooooAKKKKACiiigAooooAKKKKACiiigAooooAyPENpfXlisOm3HkSmRS7Zx8nccc8/UfWtYcCsvX4b+W2i/swr5qTxuwZioZAfmGQR2rVoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApMClooAzr2zBDGNQwYYaM/dauUa0+wP5MarPazEjym5II7j3z3ru6y9V0xLtS0eBJ156GolG+qODFYbnXNDdGdpWptaEQzP5tsoO2Q/fTnGG9veuiVgygqcg1xjwmOQwPBiTgZHBwO49j6flVzTL5rBxFIWcMxJ3HdxnGQe/07VMZW0Zz4fFSg+Sf/AAx1SmlqKORZEDocg8ipAa1PWTuLRRRQMKKKKACmnpTqqalcLbWUsrEqFU8jrntigaV2eaeNbtrm7uZPKCbFXDyHgfNgcDk5Arf+F9n5GkSSuDud85yMY9v/AK9cbqIa6vFjxFMJP3eVJyOcY7D/AOvXrGiWUdhpcEEQUBUBO3uepP51yUlzT5j6HHyVHCwpLqX16UtA4FArrPnRaKKKACiiigAooooAKKKKAExRUcsscSlpXCr6k4rMutetIQdpMmOMjpntz6H1paGUqsIfEzWqOWREXdI+0dK5yXWbqXb5KfJ1y52j0xmsu4uXllIa/kGQR5aDGDgnnnPpUuZxVMfCOyudTPqSrH+4G9j93PQ+3HNYnjKzvtY8PXdt5TMrRhgEHJI56Edfas6CC/m2vBvXGSeSS4yM/wCAxxWhpuk6t56TyXPyNjcjE/d+g79weKSbfQxhiqtV6xdvLQ8z0DVbrTbKTyreeG7RzFNIjlZgoOMOhXkAcg88DGc1f0XQL7xLcxXV+XuLNHBIfbh1yDxjADEcH6fSvV20OwlZGuLaKZ1XG5lGe3fr2q9DbRQgLDGqKOcKMCqszujTnu3+IsEaxRokSBFUcAcAe2KnpFHHNLVHUFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAYooooAKY6hhyAfrT6KAM6bSLC4bMtrHuA2gr8px6ZGOPasxvCViLgTW8s9uVG1RE5ULxjgjBHvzz3ro6MUnFGkas47M5OTQNWjg/0XV52mDKwaSQ4xzkEHPGPxPtTJLHxRasrWmopLGiklJcMWYjoDgHr0z24rrsUED0pciNViJdUvuRyMHiW/0xoo/FNl9mWSTykuIeY2PJ5UElRgep/wAOittTs7mHzIbmGSPnkOOMdamubaG4jMdxEkqN1VxuB/CuT1r4d6TqTRmLdZqpyVj5XH+6eBnjP0pNSW2pSdGq/f8Ad9NV91zsc5HFfP3xV1l9d8aRWnk/a7C3kaNY0lI3bFy7ZGAMc85x717rY2j2Wmx24k3tFHtDFfy4zXgXhaxN141e6uU89bWZxdQLxIFDbjui+8yknpgntyKo5GknodVpfh59L0kTpHqvh+5EZeK6W+EsJfJKgxsScEYByO/410Pwy1ebVrrUTqsSDVoXMcsscYCSqMcqRkcHjBJ9uKzviB4v0y5txFbXu+Ncjy1bYzyEEAEMM4xx2wavfBzS3s9Ee7mh2PcsTuULtdc43AjnnH0PX6Md23dnolFAooEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGT4hhvbmwEenSNFIZFLMrlDsHUAjnJ6fWtROAB6Vl+ILa+uILZdPnMLpcK8jA4ygB3D8a1u9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRQaAKGp6dHfRbWyjjlXTqDXNvH5VwbS8RY5jjYwbhwO6/3W/IE12VU9Qsor63Mcoz3BHUH1FRKNzixGHU/ejv+Zz1nqDWdwQCdmcNjp64I7H8O9dJaXSXUIljOc9j1FczcQy2lwEvJMEcQzdc+m4fj1qOGe6spt0QdCpy0OQQ/ckHofzzSTtozko15UXyz2/I7NaKpadfW95FuhkD44YDPB9KuA5rQ9ZSjJXi7ocKDQKKChKxvFc/kaS7ZA5zyM9AT06du9bNcl8QbgpZCCIFpXVgAAT1GM8dxUzdonRhY89aK8zkfByPqeuQs0bNEgb+LCkZ7eo+U8e/WvWUGAK85+F2jyWss8s6YaP5QfQnHA/X+tekYrKirRuduazjKvyxeiCloorc8oKKKM0AFFJmmuQOWbAFADqO1Zl3rdrbYzIGyccVkXWp3M+4K4jTouDj16kc9O3tUuSOSeLpwdk7s3rzULa0QtLJ90E7RyTisy41qSUFbXahzj5uW/KscSo5feyHf2H8PbgAc5NOtY0n3bYJHjGM4wqg4xnA6nkZ71Llc4Z4upUdoaCz3XnDdOTOWXABYj5u64B4yRT7eC6uGlEMCpIMfMy84zyOc+v6Vat4dQKJts7eMPkcDlDnGTnOa1bWylikWR3BcZBPcjqB26UJNip0ZVJe9f7rFG30WRtj3U5fIGVPP4c1ct9EsIAMW6uepLc8+uK0wD3pcVSiejDDU4dL+oxY1QDaoHHYU8UUVR0WFooooGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAleW678NruLXrnWNHlilNxuMke4wuuSTwQcOCTyG7d69TooA8w0P4dTz3qS+IZXkhiG1FLhvMHoynI65Of0Fej2sENpbx29tGsUUYwqKMAAdgKsUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBj+JI9Qks400p/LmeZQ7ZA2x87jz6deOa1UHy8nJ9az9ZS/MEP8AZ2N6zoXBfaDHn5hnB7f57HSXpQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRQaAK13bJdRlJFyD+lc3dWUltLslwVLfu2XPHPr2/P1rrKjdVcbWAI7ik0mctbDKrr1OIF68F6Hjcxzr8zxjP74c+2Poe59DXUaNqsWpQKyfu5RndGeo+vpWfeaGxk3JhohllGOYz2C98e1VdN067iufMtGgRScS4yucZ/h9f0rNXi7Hn0fbUJ2aun0/U64UVStLrflZQY5EGXU9vfPpXlfxC+NVlpEwsvDPlXd0sjLLJKjeWABn5cY3E54PT65rU9iMuZaHr7V5x8RZ1g8SaWPOKM2DwQMAHk+3WuBi+LHijUby3FxrWj6IlwWiUi3EkasMYZ2LFlyTg8YA59cdB4q1a/jezPjKztVkmDrpupabJ5kUjYBAZDk4I53AYx25rOpFyjZHfgakaVZSntr+R6N4Lhjj0kTRpj7Q7S57nnqfc9a6AdayfCwiXw/YCC4S6j8lcTRkFX9xjitbvTgrRSZzV5c9SUvMWkqKaeOIZlYL9ax77xLa28RaM+Yc4AFU2luctWvTpK83Y3qpXeoW1rnzZQCOqg5P5Vy/8Abep35KW8HAyCeR16fX6Utv4dv7k5vZuMk4JznIwTgf41PN2OJ42VTSjFvz6F7UvE8UMZFsCXzjJ7Htke9Y0uoahf4VI5mZhuAHp3PrjI4FdHYeG7G0AyhkIAHPTj2rWigSJcIuAAB+FLlb3ZDw1es71J2XZHG2eiX0oQt8qGPhm+VlYdOOvc1o23hhhKss1y7H+JRyOmDj0zXSqKWmopG0MBShq9TMh0i1hj2BFZc5wfTGMH1FXY4YohiOML2+UVNRVnZGnCOyGhfalxS0YoNPQWkpaMUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFQXFzDbQtNczRwxL1eRgqj8TQBPRUcbrIAyMGUjII6EU24lMULOkbyFRnYmNx9hkgfrQBNRWDbatqFzq8Ns+jT2lq8bu01xLHuyMYARWJxzyTit2gBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCrdXMdnBJPO+1EGWO0n9ByT7Cuefx1bbttlofiC+H96LTZFH5yba6usZ7uQ+K0ss/ulsWmI9zIAP0BoAzbfxB4g1Fylj4Ze1QnaZdQvI02n/AHE3nPscV0kPmLEnnlGlx8zIMLnvgE9Pxrl4riWB74wsU8zXY4iR/EpEQYfQ8iuvoAKKKKAMzW4tRkit/wCy5UjkW4RpN/Qx87h/KtMdKydfgv57BY9NlMcpkXcwbadnfHv/AFrUTov0oAdRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADWqncWm7LwuYZefmXpn3Her1FBMo3PLvijrU9naT6ekiCVIxLNInynyjwFbnOSewB4H5+QeE9J03U9Qls/tccNtcHdJNIxbyVJ58vBH7wnbjgjjnGK6L4oPDda7rMtzu3I5JeFyHCB/LSNeqknbv65GCMV6L8EPDdppng+G5aCB7u4bfLMqdSpIHUA5GSPrmgyjR5Zc1zHl8B+HpNMv9Tl0QpYQWEskctw26W4YKf3j8hg3cYK4NcL4VWOS38DzqHEn2iT7RGWfy3VHC+YADkNtOCQOSnOa9n+J+otH4bv9OsomnuZ7aQyFSAIIQPmZvTP3QO5+hryX4bfNLHrclq0VpotsLOJWABknYMT0xkF2LZOcBBzQXVlyxuel+Dr+LT7nXkhXbZyXplt04VVyDuAHbkZ7eg6VevPEV2cqgK7s7GC4HB6flUXhzS52soQVYZRZH3c7m4ODx65P456810Vho8FsNzqHxjjHAOMEj696yvJnmNYivazsu5gLZ6hqs2HEiRvjJ3HhT15/pWjYeFraNN1yN7HqvbGcge/410aqB90YFPpqK6m8MDTT5p+8/MrWlpb2yBYI0QD0qxS0Vod8YqKshKKKKAFooooGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFZOurAYoJJrdJJPPSKMuoJQu4UsuehA5zWtWJ4m4bS1/v6jCPy3N/SgC7qOnQX8CxTtOAvTyp3iP5qQazPB6S29rd2kt3cXS2t5JFHJcOXfbwQpY8tjOATzgc10FYvhpv3WpNnA/tCfJ+jY/pQBfi/eajLJ/DEojH1PJ/TZVyqenjMAc9Zj5hz155A/AYFXKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK55f+Sgz/7GlRfrLJ/hXQ1i29u//CZX1yyERmxt4lb1IkmJ/mKAMNfnt4m/57+IWP12yMP5JXbVx1qmyHw+jdZtUnm/NZ3/AK12NABRRRQBna4l89tH/ZuzzVlQsHcqCmfm6e1aArM1yG+lhg/s6Ty5FnVnOcfJghuxz16cfWtSgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA+efiVpDaR4x1mKSMnT9WjW680AOYCCx3ZbBUb89DgZ75ArtvD/hjxj4atJIPDeraJd6dchXjWeB4vIJ6uoUlTkckdM9AAMV3Gv6FZa9ZG3v0bAOVkTh0PfBweCOCDkEcEV5zqHwu16G2Ww07WfO00eYXiBaBmBbcE25MZ7YO0AEdOuQDmvFv9u3Grx+HJbiG5udUJ+2X6TiZoY1bLKsYIWPGeQxI46gV2PgDwtbm0t7OAO2k2B3rKduLyY/ecrjlduFAIGByDzT/CPw9uNOtpbW6S3ggmZvPx80ksbqMqHzlSGHPYkDqK9EsrSCzgENugRB+ZPqT3NAmk9yZUCDCgADoBT8e9KKWgLBRRRQMKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKxvEXzX2hr/0/5/8AIMtbNch4q1DUU1nS4dN0aa+MFwzGQzJEhYwv8oLHJwDnOMds5oA66uc0j5rPUIFbBm1KeP8ADflv/HQan0/UdeuLhUvdASzhJ+aQ3quR/wABC8/nVbwwyy3+pL1+zXsw/wCBM2fzAH5H3oA6ONcCn0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVUvb20s133t3DbJ/elkCD9TUsq+ZE67iMgjKnBH0PY1gJ4F8MCUzTaJZ3UpOTLdJ57k+pMmTmgDK1jxb4Vh1jRSPEWkrFaSyMwF3Gdo8plHQ+rVdl+JngtOB4ksZD6QuZD+Sg1tQ6BosP+p0mwjx/ctUH9KtxWltCcw28Mf+6gH8qAKWiapBrFo13ZwzxwMxVHuITGZRgfOFODtPQZAzj0xWoue9LRQBl6wl/Jbj+zmCTBxkt024Of8A63TnuBzWpWZryX7wQHTNpkW4RpAzbcxg/MM1p0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAmB6UuBRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABULwo0iSEfOhJU+mRg1NRQAlY+gaW+nXWryyFSL2/a5Tb/AHTHGvPvlTWzRQAUUUUAFFFFAGXf6fPPN5kGoT23BBVQCuPoeM55z1qBdKv1ji3axcNJF0bYMHj+Id/89+a26KAMWTS7tpg41e4A5BRQMY54Hp9eTxTV0i/jV0TXLk5JILopIz2z6dP6YrcooAwv7K1AKiHWZ96AhXCDqc8kHOccdeKX+ydRMgb+2ptmwoU8sAc8cYIPHYkk+9blFAGLHpl3Gskf9rXJQklSwBZevGTnIx+o7dKbHpF7tCtrNycDHCgH+Lv+I/IVuUUAYsek3scZQavcspbOWALD2BPbHrnnpio/7GvioU6zc5GcEAdDnIOevXg9R+WN6igDFXTbxN+3VrjDHOGQHBz2PpjjH5YNNbR7/cu3WrkbdwHyA8HOM+pGeprcooAw10q+3SMNZusNyAY1O05Gcfhxjp3FN/se9+zqn9s3HmociQDtnOCCTn2zW9RQBhf2ZqYmica1K/l5yDCuDkAdB+J5z7VKumXn7xDqlzhzuDYXcp46E5GOvGPy77FFAHP/ANi33lqP7cvAVbIIA6ZyQc5z+P0p/wDZepedG/8AbM2F6p5YweAD39cnnPtW7RQBgtot5tH/ABObwODkMMY98jv7dgO3XK/2XqCzRSNrMxCHLDylw3AHT8zznFbtFAGG2j3rsdus3SR54AAyOn8RyT04/XNH9k6iShfWrkuvdUVR1GflHBzz1zjtW5RQBgro19tCPrVyQCTlVwTnHU57dv8ADilbStU3RMdbkfyzlg0KgN+Ax/P6YrdooAxItKvIt4Gr3LBum5QxU8cgnPvweOfUZpq6Le+WY21q6IyeVUBuoPX8D+dbtFAGG2laiZI3GtT4UgkeUMEj1wf06e1H9lXqTExa1cop/gZFfHHYn3z1z+ma3KKAMSHS9Rjj2SazNId+8HYM/Q+o9uBSf2VqCyM0es3CIexRWxx2Jz3/AArcooAwV0jUNrCTWbgneXVgoBGSODzgjA6Y7/hT/wCztQVXZdYm3sOSYlODxyAeB9OnrW3RQBhf2Rehsx6zcgbw4VlDDHoc8kfjipP7OvVaUpqs+ZB3QEKcdVB4HPbp/TZooA57+xb145A2u3g3MSpAAK/48fh3qWTStRaUEaxMACDjyx82CTzgjtgdgcdK3KKAMH+yb9ZN8euXIyCCCikd8YB6YP8Agc8YX+ydRWORX1m4YszFW2AFM/TAPHbHXpit2igDFm0u/lVPL1i4iKtk4iX5uT1/DA9OM45psmj3bxlTq92Dg8jAwT0PHp6f/WrcooAxJtLvZFCrq1zGytwQi4PJxkd+MZ7HHTrSNpN1ufOsXeJF6ccHuR3H0HStyigDFbS7xo9kurXOQuA6ALyCcMcdT0BHQ+meaZ/ZF8WkD6zdOjHONoBGQRwR0HPb0rdooAwpNMvnjCDWJxtx8+wZOCcZwRzzjjGccinSaXfNP5sOr3Ee4fMhQMuc9QO3bgcdexrbooAw49Iv9sySazcMJTkHYAw+hHT3wBRcaTqEy4GtzREHjbEvrxnv044Iz3zW5RQBiLpF6k5kGsXJ3DDKwBX3IHGPbHT6cU1tJv8AdJnWZ9rYPyoARgH3xznsB0FbtFAGEujXkcwf+2rtxj51kVSDzk9MY9sdPelXSb3975ur3MgcDBChSpGeRg4+oxzW5RQBgro9/wCYkv8AblySCd48tdrAnOAO31/pxQ2j33luv9tXILjk4Gc+o9PoMVvUUAYTaTfNKJP7buQc8gIu33GD/kfTilj0q/8A3pOszOJMY+QAqQO2OBk9RityigDAl0nUJIPKXWrhCABuEa5PTqevr0x75xUh0u/3I/8Aa87MCd42gK4J6Y7fUcjt6Vt0UAYi6Te7n87V7lkKgcAKQR3BB49+OaY2jaj5Bj/ty5z/AHvLXPb8fXoR29K3qKAMYaZdv/rtVuDxtOwbenTHPB9T3+lQNpOp+UYhrlxk9T5a56+vX1xjHueK6CigDEbSr9vm/tidMjEmEBB9wCflP0pn9k3/AMytrM+zsAgBHH97k8HJ9exJFb1FAGGmkagrktrNyysgQgouRjqVI6H3wTRLpWoNbmNNYnj4wCI1J6dyeevOc5963KKAMNdIvhcJMdXnLKACNo2NjHJGe4z0xyc0iaReh+NYuOgHzKCeoPrjt6dDW7RQByWraNrv2WKOw1u53+cu5iqghOd3PU8ngfhnHI1Dpl8Hjf8AteXMahSNg2vjHJGfzqbWkv5II10uQRS+aMljgY7/AMJrRB5HvQBi/wBlX5uGkbXJ2UgDb5Sj+LPGPy6fXNO/su+VkZdWn+XjBQEEdu/69TW1RQBhSaRfPclzrV0IiMGMBRxnPBHTjvjNOh0q9RYz/bFyzRZ+8i4b/eHf8effvW3RQBiXGlXjZ8rVrqIkMucBuD04PAI9Rzj35pF0m+VY/wDidXBkTHOwYbAxyueff/HmtyigDFbS7xpt/wDa1yFIIK7R0Jzx6HsD1qL+yNQWN0XW7k5zglFyuQeM/l7+lb9FAGHHpWoL5e7VpiyDAOwYb3I7n6//AKmtpOotNubWpzGUKFREB37EHgjsTk+9b1FAGLHpN4sZi/te5POQ5Ubh14z6cj34681H/Yl8eJNbu8cD92qqcc9zk556/wBea3qKAMSLS72OHyxrN02STvdATznjPpyPy4IzSf2TeiNEOr3IkHBcAcrz2JPPv1/puUUAYf8AZWoIz7dYnYM24B1HHXIz1wePp2xTW0fUCo/4nVwDhl+4O+ffrz19q3qKAMIaPfoZNuuXLBskbkUkE++On8u2KF0m88mNf7YuBJHn94qj5uuMgkg4JH5YrdooAwW0nUWkRzrU5QKQU8oAHIx2IPHvk1LHpV5GjourXJRjkZUFl9gT2/yMVs0UAYP9jX+1P+J3dh0OQQowRycEHrz69uPo7+ydR85HXWJsKCNmwYPGM9fx5zzW5RQBhTaNeMo26xdI6nggAjGSTkHr1/Lij+ydQ86N/wC2ZiFBBQxjB4x259+Sa3aKAMFtHv2yP7ZuQP4cKMj0Oe5+vHrml/snUGaNm1m53r1KooB9tvT15Oa3aKAMOLR75Y1VtXnO3OG2gE5z15OcZ+ntTP7K1PzUb+2piEzkeSoB4x2IPqeSccYxW/RQBixaXdw71XWLgoW3DcASvTgE9uD1z19qj/si+8vZ/bV0PQgDPUHvnP8ALt0reooAwv7K1ITxu+szMEwSojADHAB6Hucn0HpS/wBlXokPlaxcohOdrIrlenQnPv1z+YzW5RQBhQaXqCxhZNYmchtwOwevQ88j0/yKeml3q+YqavcYJ4yisV6dCc+/XPX1Ga2qKAMFdIvhGgm1m5LK5dXCgdSOCMkEemelSrpt6u9U1W45yclFJBOORnj14xjn1FbNFAGH/ZV+rIya1cALJvCFAwxjlSSckfU/rzT1028Ekh/tSdg3UYHB4+76fTGPx5rZooAwG0e8ZXT+2r0c5UjAI6ZBPf8Ap/N8mkai0kbjW5vkIJHlDDY9cEdfTp7VuUUAYH9mairbk1m4Gck5iVs+mAeBj6Y9exo/se/aN1k1q6yXZldVwRkjjrggAccdT+Fb9FAGNNpd/IyP/bE6OpBIVFCtj29+/OPao20e7KYOs3gOPvLgc4Az+nA9+9btFAGLJpl++P8AibzoykHhRg4J6j34z2PpTW0i7/ef8Tm7ww4HHynuc9ce3atyigDFbTL5lw2rTbgBhggHIJ5IHB44I6d8Uz+x7w+YG1m72Ek8AAjPv7e1btFAGE2kaiVTGtzBkYHJiHzYJPOCOowPTjpSzaVfLMXg1i5jDdUKBxn1GenOOOnbpW5RQBhrpGoGOdJNauGWRy6kIAy+gyO3qBj2xSzaXqMipt1meMr6RrzgnBP4Yz2OOnNbdFAGD/ZF6szuus3e1gQUcAjJB5HpzgjH0o/sfUPn361cHc+/hMevHB6eoGPbFb1FAGF/ZF5HNvTWrogjDLIFYZ9R6c+n0pV0q+2zB9XuHMhyp2gFevpgfhgCtyigDAXSNRWYP/bdwT3BjXaeSenbtj6Y6USaLfNv261dKW56A85PPtwegwK36KAMFtKv/N3rrNwhzkjYCMEk4wfTjHft04oXSdQZZlm1md/MOVOwKynGOCpA/DGP51vUUAYc+k6hJbCNdZuEdeNwRctzxnvnHoRnvTv7LvvND/2vPnnIKDaRknGOxGeCPT04raooAw4tJvf3nnazcv5gGCFClDzgjBx9RjBpraRqXkbP7duM5GD5S5x79/1HvW9RQBkHTLp3Pm6nclWA3BPk+m0jp7+tFa9FABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRQaAMnXI71oIP7O371uYmcK4UmMH5hz2x2rWxWR4gj1GSO2XTJDE/2hC5GPuc7uvX/PTrWsaAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiud1zxRBpNxHbpDLeTuQCkeML/vHOAT2FVrXWfEF2gnh0CPym5VXudjYJIBzgjtk/hjPWgDq6Kw9H177fdzWN3Zz6dfQ/MYJyCXTs6sMhh9DxW4OlABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGR4k/tEWaDSF/fvKqseOEOcnkjp1rVXhRnk1na1/aH2RP7I2+bv+fcQBtwc9R9K0QOB60AOooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACikooAWisq71a2tt3PmNjOE5H59O1czqOv6hPLtilW3jyRwQCMc/eI9PaolNROmlhp1dtDuzXF/FHVZ9P0AQW7yRyXTlS8b7H2AZYKSDyemOpGcVX0rVr20mkaS4a8jXC7NmOMZ3bs9ice/J9K5L4q3+q31jHPLa+VDEjHaPm+VztDZ68jgjHSl7RFvCOMrSkrdzj4Name6ZLRb2PTbYhpgj/ADMrEITtOcEMoJxwecDtXdXWp6n4f06y1zQPEx1zT55Cv2WVPlCBfujHzBhjPQHrmsT4SCxt4L/VdQu7eO2tvneOVhlZAflPtnnPesSO9a6vVn0xDarPKZVRMKhkyMMuScE9CTx6cVSbe6OetGNOfLGV/M9etr2LU/E9heEXBhljUxhPmVH2dG7qRkg9jxnpXbVyfgXTpo9LgvLiXzJGRlC8fIS3zfjkYzzXWVRmLRRRQAUUUUAFFFFABRRRQAUUUUAFBoooAy9dOoC3iOlJ5konTeu4LmPPzcn2rT9Ky9bW/wDJhbTDiQTqX+Yf6vB3devsPWtUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFGaKACim1x/xM1Waz0IW1s7RS3rmPerhCqhSxwx6HjH50AXvEXiiLS1Vba2e/mY7QsTDaCegLe/sDVZNS8VXULTW2l2cRPIhuHOTzxhgSOmDnHf258MtdVupZvLsLS6jtrcYljSZz53OxvlORvPOcEAgfhXdzzf2FoyeJfB3iS5uYPMEUlnd/OpwuAhU4YMCpxyOOme4B6VpeuST6hLp2o2TWF6g8xVLh0lj6bkYAZ56ggEVt1w9pqKaprunX0O543jjEoRtwViCygqRkYyfmHbqcV3FABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUlFAC0nNMaRV+8wA9zisefxLpsO4xzGbadpMYLKD6Z6UXSLjTlN2irm1mmSyrEu5mA+tcXd+Jr66YJZGKNc44UyMOCeo45HbqCRVEQaxqyKFDvulZvMOSCvTqcYHQgYweazdT+VXOuOCdr1JJHU33iO0i+SGaJpPQnp6cZHf1Irkda8TS3RMEZeQs2CoXbsYEYI7cgZwT0/GtbTPBUfmxXN8AZEPKA5DrgYzgAevGPxretNB061VfLtlABBweRkHKnHqOx6gcVLjOS7G8amFoO6TkzldMstT1Mxkr5UDZkBkwxYYHBwMDBH1re0/w1HFMZb1jdPxtZiQQBnsMDPTtW+qqo+VcDtisy51PezQ6erTS52lwPlX8elCppb6mE8TUqfDovIs2ml2dkD9ngVCeCR1Ncx4s06K81cJds8UV5bLDHcBuEkD5A2gjJ5B/DtXSafZvasWa4klL8uHOfm45Hp9KqeKZbBNNZNShjnUnKxMM5Ycj6Y9a00SOGtVVP35PRdTyfxX4AsLedf7XsYYgSTJPaS7ftOSTuKYJUge2M8Z71t+B/D1umo2yRWzx20KK1u8z5bAYENkfKW4x7ZOKteHNAbUtRWYwKlrER8p3fdzkAEnn35rd8UX8Gn3kRs0U3ECgMmMAIehH0z+tRzNq55Ht6leLr8vup3XpszrookgjVIVCqowAPSpKxPCl617paTOxYk4we1bdaJ3R6dKoqsFOOzFooopmgUUUUAFFFFABRRRQAUUUUAFFFFAGZrP9oGGIaWVEplUSFiAAmCCeQenBrRHbd1rK8SPqSWiDRxmd5lVjgHCHO48kfWtUdATzQA6iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopKjmmSJd0jhR70Ba5JTGbavJ2gd65/U/Fdla/LFPEX27uT29h6/UiuZ1rxDLejyIZN25vLbOQA2flcYBwpxnr61m6iR2UsFVm1fRHZ3muWVum5WaTqAUGVyOvPtXMarr11K237UII24wPkweo+Y8kEe3Xoah0zT9W1EwglobZ8sWYbuMAbcEYH3f165ro9O8M2lu4mmT7RIFAVn5ZcEnr65NQ3KR02oYd+87swdKur2wvpJI55b2LaDsJySOuRk5zkjsARXNfE6bVNQsBLcW7r9nWQrGqAnY2FBwec9j+I64r1e3sbW2cyRRKkjZy2OTk5P4ZrlvGVnbPqcLaigFldQG2eVjwjbvlwOuTnr7VShdWZhLFRb5oxV+7POvhI+k2v2zUdT1SG1W1J8yCYgeytjIOfvZGKyX1R9VuDd2Z+yLdzl0jUYEzblww5OWyAASeAOOldL4q8E6bbmIanbWFzg5+0QMY5ZQWJy6L0wMgEEgn8q0vBmgWX9p2Yhia2to0D2/nSbnBBweRxu4OOmM5A6VSsrJHmYrGSnUV7N3Sfkuh1Hw/0loLGO7nctIwYAMuCuTkg8DOOmfqK7Ko4Y0jQKihVAwAO1SVZqFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRmigAopDWbdavaQyGMSebJ/cXnBxkZ9KTstxxjKWiRpVHLKkcZaRwqjqScCuXvPE823fa2+V6hQ25yQMkEfw8cj1rMiXU9VuCoRJIl3ESSncxAJBU4IHYD8cio5+x1wwkt6jsjp77Xra0ydruN2zco+Xd6E/1rGuPEl66ubXy3Kn7kSlz7gk4H45/Ciz8L3MvlG9lEaRlXC7tzE9wTxjIJB69a3NM0a009SsUZP7zzAT1Bx29uv50veZo3h6S095/gYE0F/e3CxXEMjIxw+4Fhwcdjgdjn6/Wm23g55Znku5cLgqo4II7Er93P+e1doqAGn0+RGf1uaVoaGbpuk21gWaJcyMFDMe+AAP5VoKAO2KWkxVqKRyuTk7yYVBc3cFqm6eRUHbJ6/SqeoaskGIrdftFweBGvOPr/h1qG20t5pVn1N/OkA+UBcBM9QKGyowtrMjma91bCwKba1ycs3Vx246/5/CtKzsYLOMiFAM4LH1PrVhEWNQqKFUdAOBUN5dpaW7SykBQOMnGT2FSTOrZdkiPU7+KwtzI74Yg7R6nFcRZWkvibUDcTq7Q5+8enBHH5VM8tz4j1AouUjB4B7AfjXZ6ZZR2NmkCfw9frU/G/I8PlePqf3I/iyW3gS3hEcahQoxxXEeJ9Kj1LxrAPMxKbVl2cjJ5KnocgH+Vd7XM3S/8VjbfN/yxLEHjpkAcDn15OKqcbqx71CMVGUOjTX4GT4IvHtdRkspDiJzhf9/vXeCvO/E8Mml6+skXCSfMp6YJOTyMdxXd6dMZrWJz1Kj1/rU03vHseHl03DmoS3T/AALYooFFansBRRRQAUUUUAFFFFABRRRQAUUUUAZmstfLDCdNUyOJ08xQyjKE4bqCOBz61pDheOayvEI1A2Kf2S2yfzF3HjhOc9Qf5VqLwoz1xzQA6iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopKimmihUvNIkajks5AFAEvWjmsO/8R2lohZQ8nzbPl4ycZ4z1H0rFn8SXdyzLYSb+B8sCFmBxyNxGD0PvxUOaOmGFqSV7WXmdhNNHF/rXVPqcVi3vi3T7WNnUSzhHCFkX5cn36VlS215fPCklu5V8eeXGc84wfT6/0p6eDI5Zd1zJ/q8hSBlipGMHtgdQMHnNS5SeyNoUaMdakvuILrxDqFxIiWxQbxnbEmWA6j5jxnGO3v2qqtjquqq4YSNvkJ8x8g7eM4zjAPGMDsa7Kx02G1WNVy7qmzcw6jAHQcdun1q/zjjrRyN7sf1qMP4cUjkrHwXbpOkt0sbSRPuXqeMgjOMc5z/+rituy0WwtQfJtkXJ3cjODkkY7DGeMdK0wMVXvLmK2j3zuFGcD1J9BVKEUc069Wq7Ntk4AAwOBWRPqrTvJb6ZG0rjgyAfKp+uRUQkvdXx5Sm1tQzBjn53x7Y4BrVsrWK0i2xqAcAE45OPWn6E2UdXqyvZWJtm8wSuzv8A6zec7j2P4fyqHxHf2ljp8gvFSZXG3yiM7j7j0qxql/Dp1s0krAE52g9zjNcXbW9z4l1ETTrmEHhz2HXHr9KTlZ2W55WNxTjanDWT/Ar+G9A/tO/E72ywW6kEx7cLwen862vFd/b2E8UVqii4txuVeApTvj3BxXUWttHbxCOIcD865PxXpa6h4t0/c33oGQAfXOTweKhpxV+peEwC9lKEn7zTd/O1zU8GXxv9J8xmO4NggnJFdEK888IXLabrclk5YRyYUKezd/69ef1r0AVcHdEZfV9pS97daP5D6KB0oqz0AooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKSmM6xrudgqjuaAH0lY994htYFYQg3EgBOE6HHXnpxWDe+IL2ZAYy0abmQlEIHbbz1BqHNI6YYapPpb1OxmuIof8AWSAZ4rEvPFNpAzRj/WAgbCfm6Z6dc+1ZNtY6lcrGzTo7uxLAgqOgxk8HPbHatiz8OwRyO8ihzKP3me/UHnr3OKV5PY19lSp/G7+hlTalcXuxog0yM2HHGAc9AvPUep4pbXwzc3Esc16UZvlLbs59wBkgj69O1dVbWkNshWBFUE5OBjJ9as0cre4ninHSnoYtn4esbUKQhYjJ5JwcjHIzg1qwwxxLtjVVHXCjAqWirUUjllUnN3k7gKWijNMgSjtRWXqGrC3dYoU86ZzgKOg+uM0rjjFy2Lt3cx2kDz3DhI0GSSaxvtV3q7NFbA28K/xkkM49iOn0zmprXTZLphdak7OxGVj5UJ68A1rogVQFAAHak9TS8YebKlhp8NpGuyNd+MGTHzH15+tXcUGo5ZViUtIwVQMkmnYylPrJhNKsSM8hwqAkn2riNSu7jxHfCC3J+zg8Dt9SetTapfTeILz7DZyYtwfm/wBr1yf5dq6nS9Oi0+3EcQBJxvb1PrWfxaLY8mbljJOEHaK3ffyRFpGlxafbhEGX6FuM/StKjFGOK0StselTgqcVGOyA9a5q4jVvGVvI0aswhIVs4Ixkk4xyOQM10veuYluGXxvGiydbcKVA6D5j+vHT060pdDrw6b5rdmO8aWH2vTTIqAvFlie+P680/wAI3Ky2SnI3kc47YJ4/Ktm6iE9tJEQCGUjnkVx3hOU22oTWkgYGNyMnoPbP58VD0mvM8KslSxMan82nzO7ooFFanrBRRRQAUUUUAFFFFABRRRQAUUUUAZOuf2h5MDaZ/rPPXzOnEeDnr17cetaveszXJb+G0U6dEZZTIqkDHCngnn061qd6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopM0lADqKqS3cEH+skCngYz+X0/GsO+8VwQvKi7cxnBAyT+Q/yO9JySNYUZzfuo6RmA5zgVmXOs2kMvl+Z5j5xhOcHtk9s9K5u51O61ExNCjTIrYkUc89R0yMkHH161PZ+HLqaWObUJI25yVZOR04wDjpx6DtUOTex0Rw0Iq9SVvIkuPElxMn7hNjMCVjQgsSM8FuQM4rNtotT1e5Hlfu4kO4SSrvYE84Bz0I7Hjn1rqrLQLC22sIA7Icgt/e5ycdOc1prGqjAGPalyt7h9YhT/hr7zkNO8KTFY3vJgrKwk+QZORj16dxxXSWOlWdmmyGMBd+/wDGru2jFWoJGFXEVKnxC4FFFFUYjWoNRXd1FawtJO+1VGTWKs97rDtHHutbYf8ALQZ3MM9M8Yz7UXLjByV3oi7fassf7q0U3M/dUP3frUVvpjzSGfUn+0OclUdcbM9hyQKvWNjDZRCOFcepq19aS1K51HSP3jEQIoCgADoBUd3cxWkJlncIi9SafPIkCGSQhVUZJNcVfT3HiS88mEsLZCO3B9z05pN22PPxWJ9krR1k9kRtNL4l1FUB2KvQ7c4AJ/Kuz02yjsLVYY+3U+pqDSNMi02AJGoD9z6e30rTpRVt9zPCYZ0/3lR3k9xBXL6in/FY6e24D9yWOc5PzAAcepPfgYrqK5vU1RvFmntuRnCNhCDkf7XHbnvTZ61Dd+j/ACMHxfCdO1aK5ibCM+4gAdyM9h3HrXa6TP8AaLCJ+5ArN8Zaeb3SXZQN0eW98e3vVfwhdLLbgMRvPHHGO+MdKzj7srdz5+knQxco9JanUCijtRWx7IUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaSuc1bXvJulgh9CWPcjoMdQASOpqXJJGlOnKo7ROjqtcXUUEbPLIQFG44BJx9BzXGy6rrNzEIlWdZhnJjwVI6A9P5Hr09KS38Mahe4e8vJ0XdjYvB29iSTk1HO3sdawkYq9SSX4mtqXiRVUraGMvkBd55I+nb8etY01zf37sZUaZDgDHTtgqDgKRnk/lW1Y+D7G1IMrvKcgkNgDI/X9a347aKIfu0AqeWT3K9tRpaU1fzZyVj4YZnE1woLFf4uSGPJOfXPf1roLHRra0hKKgOeSTyc+uf8MVpKvrTq0jBI5qmIqVN2RpGFGFUCn4paKs5wxRRRQAUUUGgAqNmVBuZgoHc1Wvr+CyjJmf5j0VeWP4VQewnv5lkvWxEjh44gOMD1B/X9KCoxurvREL319qspTTcwW6PteQj5iPVcgj+tatlp0NmD5Q+dvvOepPrU0UaRAJGoVFGAoGAKm7c1KRUql1aOiEwaOKWoppkgXfIdoH61Rk2luLLKkSb5Dha47WLuXXrwadaNhA2Sw7+vI9KfrV5Nqt59hs3XHU8jHXpz3rd0XSY9NhGFHnMPmYD9Kyu5Oy2PLqSli5+zjpFbvv5D9G0uHT4AqjMh+83rWkBQKWrSsejTpxpxUYoKKKDVGg01xB8v/hZDfvE3eSuAy/N93se46de9due9cPp6RzePrydZSTHhdoAIOFGefUHFZz6ep14Xab8mdsRXFa1ENP8AE6ziTy1u0GBtOCw7cdz7121c748tDPpP2hB89uwkB9B0NOaujxcfT5qTmt46m/aSeZbq2c8VNWP4Zu/temI4bIHHXP61r1a1Vzqoz9pTU11FooFFBqFFFFABRRRQAUUUUAFFFFAGZrj3iQQNp6SOwuI/MC4z5efm6+3pzWnWRrv9oeTbf2UxEn2hPM4B/d4O7Of85rXoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooqpdXsNojPI/wB0Z2ryT9BQNJvYtUyWZIkLSMFUdSTXM3/imJlaGzZFl+XDN6H27cetZLtql9LucNMrAKd2M8YPQgKCMkZ6+nNZuaOuGEm9Z6LzOkuvEdnHvWI+Yy5A+YKGI7ZPvxXP3HiC+ugrqZBCZMbVXYSPTg5H1q9p/hxkZZ5FBmwck84yOx9R+tbllpVvaK22NSX+8eufzqbSl5GvNQo/CuZ+Zz1vpuoXUILzfM5wUZSAB15PBPp1wc1q6foSW8ryPtd3+9nkHt0OeME/nW2BgcDAp1WoJHNPEzlotEV7e1jt1IiQIDzhRip6WirsjnbbeoUUUUCFooqGaWOJGaVlRfVjgUDJqydQ1Py2WGyTz584wuSF+uP5VUluLzVpfJtla3tlbDTZwzD/AGT2/nWrY6dbWW4wRgM3Vu5pGvKoay37GbbaU9wwudXYyyYyIzjbHz7cH/PWtsKFGF4FLS8U0iZTchBzUc0scKb5GCgdzSXE8cCeZK21a5DVr+XXLk6bYglM/Mw4B5zj2xjr3qW7HDiMQqUbLWT2XdjNSvbjxBfLZ2bbbZT8xGefcn0rqdL0+LT7ZYo1XdjBI7+596bo+mQabbhI0UMcbj71odM0orvuZ4fDyj+8qu8n+AKMClooqjuEPWuZvJ2XxraxKz8w4Kg8Y+Yk++ePyrpj1ribpo/+FjqsjAYgUgFOvUcH8RnP4VE+nqdWGjdyv2Z2U8SzQvFIMq4Kkeorh/DzPYazNayI21G3AnJA/QevpXeYrivFMf2TxFaXxciOZfLb5cgY56+9KfRnh4+PLy1V9l/gdr2p1VrCQS2sbrkgjuMVZrU9GLvFMKKKKCgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKgllSJS8jhQMkljgY6n9KAJ6K4e8+JmiQXssEUN7deXj5oI1YOpYKGUEhmGScYBzg47Z1tM8Y6JqU6QJd/Z7lsbYLqNoJDnkYDgZyORjqKAOhrE1G/vIZdiwNgghSCME9uT0PtW5TaTVy4yUXqrnKaxc61PbgQIERx1Xg5z0yCak03w6ol866y7YIYNzk9Mj0/DFdOVU9QKQip5e5t9ZajyxVirBp9tbuWijCse/oPQegq2oGMUtFVY5nJvcMCloopgFFFFABRRRQAUUmfSo5ZFiRnkYKo6knAFAElZN5q3+lLaWSfaLjvzhU+p6Z9qp3V5d6tui0pgsI4ef1OOg7j8q1bCwhtYwIl+Y9WOSSe559altvY25FBXlv2ILLTSgE123nTuPm3YIB9uK1KAKWmtDJy5hMUUuajZtuWbhRTJGySLEpdjhQOc1y2taqbsiK0Z9+cAqCQR65HQ4qHW9bkvJjBakrCrEbx/GR/TtWh4a00LGtxKwdieDjg9v59KzcrvlPJqVpYmfsqe3VlnQNHjsYRLLGDM3OTyVz2rbooq0rHpU6caUVGItFAopmoUGig0ANrkvD26TxNqryOAVkKqmME+5/l+FddXF+DkMus6ndM/DXD4BHO3J5zyPT0NZz3R1UPgm/L9Ts6rahbi6spoW6SqV/MVaoHSrOKUVJNM4z4fzPFJdWMqqjQtgjAB69+/wCddn0riAh0nxyzDIjuQCTu45z/AFrth0pQ2t2ODL5NU3Te8W0Ooooqj0gooooAKKKKACiiigAooooAyfEX9pf2eP7KbZc+YOcAjbznqD29q1EzgbuuOazNee/S1ibTEeSQXEXmBduTHu+brx0/GtXvQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLWJqt1eRSBIYuH4VgcDORjJ7HtSehUYuTsja7Vzmq66sMgit3AAzuPUnqOMdORyTVTVZNbntSsabFbA465z6jBqxpnhwRlZbp/Mfb84POWIwT/nms229jrhSp0/fqO/kjHnvdZvIUSFpN4/eZjfHHQfX6d+oqSDwtcXZie5u5zHG/EZYj5M5GSeSe5rroLK1t3LQRJG5HUDt6fTirdNQvuVLGW/hxSMGx8L2Fp/CZMdjwCc5Bx6+9baRRp91AKkoqlFI5J1Zz+J3AUuBRRVGYUUUUAFFFGaACkorJvdT/erb2irNMW2nnABwT19ePw70mxqNyzqeoRWMYaTLN2ReSf8AAe9UUsLi9l8/UGBjBDpGD9369vrU2n6YIsy3R8+4f75bp17D2rWoNOZQ0jv3GqAowowPaloozTMgPSoZ5kgjLyHCjj3J9KdLIqKWY4UdTXK6xqjX7eRabwTjay8jHr9aTdjmxFZUo369EM1e/n1O8+wW+0nJOQcDGcD6+9bujaZHYW4IRfOYYZgP0qHQNJSxiErqpnYZZuvWtnvmklrdmGHoO/tanxP8EAFLRRTO8Wg0UGmMaetcVDaRz/EG7lbeJI1jwQRtxt5B/Tiu0bvXJaU3meLdQ3TAMJMBNv3htHOR3GO57VnPp6nVh21GbXb9UdfXPeNrP7RozSAZe3IlXjPT/wCtXQVFdRCa3eNgCHBBB6VUlfQ8/EU/a05Q7oyfCN8L7SwynO3A65x7VtjpXF+CJZbbULzT5yu2I8LtAINdoKIPQ58DU9pRV91p9w4UUCiqO4KKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvFPi/wCK0F1c6OiLPIVkMmZlxDGq8kE/dYnPAwTyM8ce118u/EKD7X4/1BMxyY8vepjMYIBzhlyTzwCwPUg8CgCHQfC2qajDPf2V9+6gjMrRzW5njODuZScHcPlQncO4zXb6RFp3iDTngbR49D1qO2LpNYjdbTbVJ2lclWGB0OSOoORVrwqzaP4cvJ1Q7Xt52YqmEYc7erEsvIGccjFW/CSpGuozugkFvZ/Ksbl0VfLb5WJJ5zuOAT1OM9gC38HvE9zq0c1nJMWt4i0cCbHfYQSRmQgEqV6bgDgYJzXp4zXmPwWtf9Hubw3BkSV2EcAwohw3OVAGGOfQcdAAa9A1W5+y2pfJGO4GaTdhTkox5mXqWuXOsXKhWLlYyMkuq8D169KsLrqY+S6tXJAxufbz+fSjmOP65S9DoKKwDr+W2iNS3B+V8jGKli11Wzuhw3bDjBPpn1pcyKWKov7Rs5orK/tq23fdf9P85pf7atlQNltrYwQAf5H9OtPmRosRSf2ka1GazBrVgf8Al7jHTqcVJ/athu2/a4s9PvDrRdFe2pvaSL9JVZb+1c7VuIifQPzVW/1JLXbHEjzzN0SPnA9TS5jSLUvhZY1G/hsIvMnbk8Kvdj6CsaG3udaYyX4MdsG+SEAg+xznB59sfhVjT9LZ3+06jK1zPzhc/IAcfw9Aa2xgcDgUtzbmjD4dX3/yGRQpFGEjUKBxUlFMkkWNGduAoJP0qzFu+pR1vWtP0Oya91a8jtLZSFMkrYGT2HqfYVyEvxc8NLvNkbzUQh+Y2sO8KvOWPPAGO/NeQ+PNXv8Ax14gv4TN5Fppw3udxdY49wHGODzj3J71O/w6huNJvdQ0QXUFrDA5NxO21pGIJ4VT8qY4wQc8imB7/ZeIbC98t7eXfBOu+ObPyMOmc/Xis3xBq32p1sLLe284couePT8a8n/Z11C61HS9Z0qYpcxxhJUidmBGeDjsAR2HevVdLvvs5YyR7ow20Aj54sdAT+dZyZ5uJnO/s5OyfW3TsalroVrFaCCRdxJ3E9Oa1YlWNAiABRxgVkXeqzQSRvFAJrRhlpFOSP8ACtK0u4bqMPDKHFNHTS9lH3IaMtCij60ZqjqCiiigAoNFFACVyPgmMFr2YRhPMncseBk56DHYDqe5611prm/Bh36a0gPzGV9wHOTu6ntn6dveolrJHRTdqUvl+p0tFFFWcxyHj212wW9+i5eFwCfY+vFdLpsxuLGGYn7yAn61DrFot9plxAwB8xCBnpnsfzrD8C3u62ltJWLSRNnls9ew/wDrVG0vU87Sjin2kvxR1tFFFWekFFFFABRRRQAUUUUAFFFFAGVr0moJDbnS40dzcKJQ/Ty8HdWrWP4kl1CCxVtITfcNIqn5N2EOcn8Ota/pnrQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABVaa5hgj3zzJEnTMjBR0z1PtVmvGPjN4qiimbSFj3+ZIyTEncqxKuWYHHytngAAng0AdXqfxN0yyvZLeG3muwhGJY5oUVwcDI3uDjJPOMcZ6VpaP480bUhl3m08jBIvUEYOenzglfpzzXz74X8G3eq2xvrS7uYXtwzBfs4eIEZYqd2TgDqCD1wa7rQEt/EERsdZ0Gz0+9kt1NtqGnwqu7AyA55HzbTkEHvxQB7eCGUFTkHvS4PqDXlPwT1/UNQF1ZTlzZwYWMBWZFJyw2OedpHQHgY4I6V6vQAm3npS4opaADFFFFABRRmigAooooAKDRQaAENRyypDE0krBVHJJ4FQ6jfQ2EHmzE4zgAdSaybe2udW/eahmGENhYCOox13Zznn9KVzSMLrmewXFxcayGi0+Ro7flWmHBJ9B3x61pWVhBZIqxRqrBQCwHJ//XVqKNIo1jjUKo4AFPzRa4pT6RFpazNe1vTdBsWvdXvYrOBP4pG6n0A6k+wribn4z+G2DnS0u9S8sbj5CAcdSfmI6DnmixB6RTHdURmb7qjk1iaZ4js9TtoLq2bdbXCZSXqM9wccDB4qnr+pPcPHZWaSMshxK4B5HTHvn19KbOariI01fr2K+v6rJes0Vu0ggQkErnLkenqK0PD2moq+fJ8xz8p9f/1dqt2Wi2sFiIHQMCdx+vtWnGqooCjAHQCpSd9TlpYaTqe1qu48DApaKKo9IKWiigYUGig0AMzzXHeFf33iHV593H2hgBgZGMgnI6Z9Djp3rsjXK+E0Z9R1CdsAtOwY4wc5wB7jH61Et0dVHSnN+S/M6yjFA6UVRynC6hE2k+NI7nIWG6AB5A575/HFduhyBXL+P7YvpyXUQJkgcHj0/wA/zrb0W4NzpdvM42lkBIPY/jUx0bR5mGXsq86fR6r9TQoooqz0wooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK8T+JngF7rxFFqGlb7i8f52s/M8oyoPmIV+csMEbeMZGK9nkZUXcxwAMk+wrCuLu01W3lS8tT5cZyj56HPBUjlT70rmc6kYP3meJ6NeaVZWt8lvdwEswSNZ5niuUUsDjymAAAOCSCMgHBqS316eLSzYXdwHmvGDYiQEeXg8OSdp4GAuc8kjnFepX3habVoVS8i0bWICpVJNSs8zR9vvKeTjjI2nin+GPh7pOkXM1xJp9mZncMpjRgigDHCkkD26ketMtNPUvfD7Rk0Pwra2qw+XKy+ZJ8xbLHvzz0x6Vc8Q3N9bWwlsrVLqMHEsODuZe+3/wDVWzjuBQQMe1Jq6sXFpPVXRz+nWOn6hYebCzbZAAy7gShH8JxnkVVfwXYO+5ZHxjGD2yO2KzpZL/w7qRl2SC3lYeao+aN+eSgA+U465/Wut0zUbbUrRJ7RldWAJAOSp9D71C5XpLcjE5bSfv8AKnF9Tnh4KiS0aOO5bzf4W24xx04o/wCESuERtl4xbgjHGT64zgV1/Wjmq9nE4P7PodF+ZxU/hrVR9293N1yz5/DBB9+acfD+rbFja6VgDkFcYBAOM8ZODXZ0UezRH9m0el/vZww0DVk3Kjodwzkqo2nngGobnQ9V3twsiHa3b5Tn29B39DXdXM8dvE0krqir1J7VjM91q7YhJhtFI+bkGUf/AFj2z9aXIhrKKUteZr5nI3KakzywRW0Ujw7iZIwWHocEd8Hn1+tLbpLCryz2M6PyNysQQeR3GcYH4EV6FZWyWtskMY4UAZxjNWCgP3hmodPzJeXKN1CT+Z55azqr8TXESkEnqQ445HB/LtzV9f3spNpqoiUAbQ7YOB9T0/x5rrZrK2lZWlgRmX7pI6VVn0azlgaLygoPGep/WmoMyjgakNpJ/ejG8vWE/wBVd7+DkZBP65AxU08muDKqyuqZZgVB3rwNowPvDnHrQ3hOBGVred4tuOepxznPr2rpFBxk9auKfU2o0Kn2m187nzVp3hG4/wCFraroLTxrNcRs26Zym4Fdyuu0ZyDjg4q5e3F14c26Xeaba61qrQ+TbhNUaWKFy2QWjICgg5Iz3r2Lxh4B0TxU0c97C0F/F/q7y3OyVfYn+IexzWHp/wAKYrC1S0h166W2TPyJbQKxycnLbSe56YPPWrPSOB/Z20PUdL8VX0l5G0e+0+6HJwSwI3YOMkc4PPTpXtuo6Ylw/mR/I/cHo/1H9aXw7oOn+HtPWz0yHy0AGWPLMQMZJ9a0xSauROCmrM4oT31jcyBlVRnJhxw3GOD6ewqxbzhd1zpjFW3Ze23YAbPIH4dh1rpry0t7pNs8Yce/+Nc3qvh+aOU3di7tJuztz+WeeR7VnZrY8mrh61H3oar8fkb+n30V2nynbIOqngjHtV7tXCrqLbxHcM8FxGCFkbrIB6jvkj8K27HWWG2K9IUs2xGXkE8f4/41Slc6KGOjP3ZPU3xS1Gjh03KQynoRTweKo9EWiig0DIpvuN16Hp1rnvBXzadI7bt7SksCoXB+gx+PvW7fN5VpNJk/KhPHXpWH4HiaLTGMisjPMz4YEHHTnP0/SofxI6IL9zL1X6nSClpBS1ZzjcVwZd9E8WSLuAinIYdvlJyex78V3tcb4+s2Yw3MZG5Tyc4IA71E1pc83MU1TVSO8Xc7HtTqy/D9ybnTYyWBZRsODkZHHXvWnVLVXO6nNVIKa6i0UUUzQKKKKACiiigAooooAzdZkvYreJtPieaTzkDqjKDsJwx+YEcD8a0AcKO9ZutyX8UdsdMj8x/tCCQbQf3fO7qRjtzzj0rUoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvmL4pKL/AOJeoQctgKMbGU7SQcbQTuz0+hzj0+na8g+KvgKLUNWt9R0oRjU7ltqRSsUjkwMnBGTuzjHbnjmgCHwcJPDuivc2YiYmOWdpIiv3P4cDOWXcODyMDnpipfBqC3nu7sqHENqZRsyI0wrfe3ZALYySpxz+FcXBqOlaWt5YYt7SWVdvl6gJIbmPlSVyx2EZB546cYNTRa1Olj9njv8A7Q96NwERB8qP7p3kk8EA4XGTnqO4B3XwST7RFd3n2pmUyNst8EeVkKST2JOepyTz716Nqlw1raNKu75euP8A69Yvw+0X+xvDcEckYS5lzJLwQckkjIPQgHp2rR8QPqMVl5umoszJy0JXJkHoD2pPYHBz91Oxkpq90u2TzG29WQlemPvc8gf56VOniCH/AJ/4G4wA3GT2P+IqbTobDU7dmijKk/u5Fzkxnj5f0qIeDdM37iGPGCDisve6HlVKGMpO0Wn6saniNi+0CFuh/duW45yeP5Vdg1nzMt5Q2jK9e+enIHas5PBdkISgml5/i7j6e1Rr4NEcLL9rZ2OCCARz37/lTvPsZqWNjvFfejWbxBCvWFx9WApf+EgtgMhXb6EHnPTr1rEk8LX4/wBTqLvx1dyMHPoOKcPDupLsU3QdQRn5jx79OeaOaXYft8Wvs/kbKeI9PZdxm2ezKc1MmsWJz/pUYwcHJxz+Nc2fDeqr/q7pWyCTux94+nH45qC48P6s7ycqFYDuD0PHTHbv70c0uwnisUt4fgdb/a2n/wDP3B/30Kr32rxR7YbUC4nbnYrcAepPT8M1xcsOqNM1vapHcMiljIqZGBx19cdPX3otbK6gheSfTpOOCVJVhn0yOnY1PO+xSx9SD9+D+467TrBfNN5f3Amn7DOFUemM1tgjHFed2rwrLGsi3ERPpyJB06Z68ccVoI9vK4ZL/wCzJtGxWJB9uf7vr396qM0+hosxlU1cfxO0oYgDPYcmuQWLUf8Al21ESAgn5WGecY65H0q1LHrw+WGftu5VSDjqufftV8xrHF3+y/lqeE+OtXvPG/iu7sp7k21raIS7oRJ5aEgYVQRu6jOAee9XYvhrp2raPd6jpyvaWsMRZpbpsSu+SQQvRORjBznPFRS+FW/4XDdaPdXMUMlynmr9oYkTKVzxgAgjHqenU9an1CS48MNFplvp+h+INSO5I5kuZJRC24kb1bCAgnIBJ5BqjuTurjv2cruaabW9I3pcW5iEixPkBmBxkHtkZyOD+Veu6bemxZ/3WI1OCrcGI9hnoQe1eU/AHw9qWm+NrqbUI1VhbkyDAcqxPAJz8re3X1r3XUNMiupEkA8uVSDvUckelJo4q9CUnzw3RTvNUuQsU9jCk8HV/wC8tX7O/gu1/dMM/wB3vx1rmH+3adfPuIUcEKq8SHB7/wA8U6CYTM0+nfuLlSC8RPDZ6H8cVClZ6nLHEzUve+5/odlSis7T9QS4GyQFJRkFCMdO/wBK0a0PUhNTV0FFGaKCwoNFBoAY1c34K2+TdtuDSG4k3YOSPmOM9q6Vulc34MKtFdv8+WmYkMQe59B6Y571EviR0U/4UvkdMKDQKKs5ypqFst1aSwOARIpU5rmPAd00STafKzGaNs4J/DArsDXC6ix0TxaZg22OfDHHfJGRxyeR+tZvRpnmYt+yqQrdE7P0Z3fWlqNGDhWU5Dc0+tD0k7i0UUUDCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMzWZP3KxLkeawUnsB1OfwFcjqRlfXbfT7F2RUkAkcZUEntnPOFGPrVzxNfyw3zOOFA5I7KD69sk1c8JaaipJfSDLytuGRzkjJP15NZN3djw6sniavsodHq/JHQ20PkxBFH1Pqe5qeiitT20rKwUYpaKBkNzbxXULQzoskTcMrDINcfeafeeGboajpW6ewGBPaDqF/vL6nvXbU3FKSua0qrp3W6e6KWlanbaraLc2j742/MH0Iq7XGa1ol7pNzJqnholGb/X2vG11B/hGOD1/pWr4Y8UWWvQMIT5dxFxLAxG5DUqVtJGs6N4+0p6r8V6m9WZrGsQ6cir/AKy4fhIgeSff0HvVXUNXl+0LZaXGssudry9Vi+oH/wBbFP0fQo7GTz5HM1y2SZGOdufT/wCvRzN7GcYRiuafyXcjtLCfUGju9SfAZMC2CFQvOR39u4rdVQopQMUtVbuRKbYvUUUUUyAowKKKADFFFBoASsS78SWFrrMemOztdOVGxFztB6E+3rWvKwijLMeByT6V4p4i1GVdUl1m1UpPcyfuD3eMYUKemMgZAx09ayqVOQ9HAYNYqTi+2nqetaxfT2T2zRhfLeTa+R096g1XVbqx1K2jESyQTce4P/6qmgWTUNDhe8jQTvGHIU5UNjIwfSs/Uw9/4cadNv2iBN43L0IHpVNtHg4n2lNtJ+f3b/edIDkZ9acaxPCN61/ocE0j735DH3zW0OlUnc6KU1UgprqjM1jQ7PVUAuFw68rIo+Za5y/0m90qPlTf2477TuB7ZA6jHFdqelL60nFM562Dp1dbWfc4fRtY+whFDl4jnejZ3Kfb8+ldXYanbXy/uXyf7p61Q1rw7BfZlhZrebOTsOA/1rmbnTNQ0udfmO7k+aowOg/r+NZ3lH0OFTxGEdpLmj5HoWaXNcrpfitJNsV8nlsB8z/w+x/GulikSRN6EEHoRWyaex6dHE06y91kGqFjYT7eGKHHGayfBGToikyeaN7ANyO/v71q6tJ5VjK+MgDjH1rO8INnTQGUI285A7E84Pv+JqH8SPRT/cv1RvCiiirOYXFY3ia1+06c6fzGeP8A9eK2KrXieZaug7g4xxzSexjXhz05R7o5TwhcG1vpbNuFc/LvPIIGccjJJ5J9K7OvPlV4Lz7QrmB1PKkNkZHp+PqK7jT7pLu1SePO1h/F1qIPSxwZdU91030/ItiikFLWh6oUUUUAFFFFABRRRQBla1LqEdrG2lRiWYygMDjhMHJ59Dj3rT52jsazPEE19b2sL6bC0z+egdUIz5ZPzHkVq49aACiiigAooooAKKKKACiiigAooooAKKKKACiig0ARs2OewrC+3QajBPHe2qyRKepbI9vcHnqKva5MFtxCud0hwSP4V6kn24rj9YeaXWbbTbN/LEZAZl+VTnsCPQfrmpkzzcXiXSa5fS3ds15dCnv7by/tFre2ufli1KzExUZORvyCeOORnHfvUfh/wVYabdvdT2envNgIphtwg24IPy5IGc/l35NdPZ24t4FjXkDuep+tWKZ3wvZXEwBwBgCig9aKDQ4S/j1LQb575FleNmzKYzuV0z/d42kDqfyrqtH1W11eyW5s5A6t1H909wauyxLKhSQbgQcg9CD2rk7/AEK60O6bVdBOVQfvbMrw65ydpz970zWesHdbHZzQrx5Z6SWz6P1OxoxWZouq2+r2Kzw5QkYZG+8p9K0hitU01dHHKLi+WSFpDRWVq2sw6ePLT97O3AjXt7tjoKYRi5OyRoXVzFaQNLcOEQdSayGa41WUqheC0XHzY5l9iDSWthJfstzquG67ISuAnPXr7VtqoUYAwB2qDV8sNN2RWNpHZ20cEWdqDFTlF9KWlpmL13IJbeKTHmRh8HIyM4PrVeTS7R42Vol2sMGr9FFkQ4Re6OabwlZqd0MkkWMYI6jGe5+tb8MflRqmSdoHJqSmyMqJuY4AoSSIhSp0tYqxzfjHwr4d8QWBPiGyikMYys4OyWP/AHXHP4dPauJ8KeD9Le7Nrpepa1FbR52+W0URXJzncEDH8TnNbeu60utXQs7RSUVxg9ORkHn3HHpV6w1jTNCuIdLEUz3k7KXRUyQD/Fx2H585qHPW19Djo1amLxHJR1UdzoPD+h2Hh+xSz02EIigAseXc+rHvWpWRrt7NYpayxD920m1/oelRazqFzZ3lo0QRraZtjZHQnvn6VdzrnWjBtPoa9xbRXCFJkV19GGa5zWPDhZmuLNmDg5C5x+H0HYV00Z3KCO9OoaTFUoQrR95HBSX7QvHb3oljdPuStwzAdSfqe3atq01trchb4q0ZIxKvIHHf/Oa1NU0m01NNt1ECR0YcMPoa5i+0G70xGktP9Lh7h/vj8B1Hb6VFnE8yVOvhpc8NV/XQ7KORZUDoQwPII71IK4DStWlsJQiA7CcPE6nd+A68V11hq1ve/wCqcA5xgnB//X7VSkmduHxsK2j0fY0qD0ooqjuILltsEjdlUnisHwOrrp8rSQ+VvlZhn+IZPOe9bl1/x6y/Nt+U+/asfwUu3TX+YsPNbGV29+fl7c1EviOmH8GXqv1OhoNFFWcwlch47szJAk8ZUOh/j/nz39K6+s3X7f7TYuvpyflB/Q1MldHJjKXtaTiQeGLr7VpMXK5jGwhfb+f6VtVwvhOQ2OqPbMcJIeCxOcgcYHqcc13IpQd0TgqvtKSvutBaKKKs7QooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKDQAVTv5xb2xYnrhRg4P4Va7Vy3jLU/sNq+G+bGxV7Ekc5/DoaTdkc+JqqjSc30MBZnvtWEVuqzqSFKkcYBwNw/MnHvXoVvEtvbrGowqjp/OuQ+H9iGQ3sgGecEjByc8e+B/Ou2461nBaXOHLKbVN1Zby/IBS0CitT1gooooAQ0UVn6jqcVoUiH7yeT7qA4z7k9h70N2BJyehbuZY4YS8rhFHUmvOda8PS3GoSar4aR4JIWLOBlPO9Rxg54xg11tvY3N/J52pFhHj5I1JUD8ufxJ59K2wNoAHQVnKPMdlGu8M3y69+xyXgrXrK8U2TbYdQi4lSTAZmJ6g966/61xfjXwo15s1LSWNvfwHepXoTnPNHgvxib9303VwttqEJC4YgeZwOccHOc9qUZWfLI0rUVWj7ejt1XVf8AAO1ooorU88KWkoFAC0UUUAFBooNAHmGv+Lr+PVtd00OnkqqRW524ZXYDPbnjcfTiszw3oy6prSRp5LwWm0Z5B3DG5ugOcjhegOKydddrjXtSmX5tssg/hY5DELgDlcc856c9a9D8AaZb20BYWx81VGZdpCuTnkZ56HB9etcKvUqWex9ZWVPCYbmgrSaX5I69RsUKDwOKyIAINXuLVwghlQMBjr2x/OtvArK1uMqILlRzE43HvjP+NdzWh8ZXV7SOX8PXb6P4in0x2UW27K7jjHp+mK70VwfjKE2eq299FwJl2sQ3UjHP4cV1miXIurFGY/MODznjtWcdHY8/AydOcqEujuvRmlRRRVnriEVFPCk0ZSRQyHsamoxQS4qW5zGo+HwUcx7rhVy6xv8Ae3cfxHr361mW02o6MzJA/wBphiB3RnIK9zgdxk9RXcVUvbGK7AJBWRTlXXgg1PJrdHn1cEr89J2ZmRaxaarYERMN5Zcxngg7gPxp3hKZrjTTIz7t0r8/Q4wBgYx0rF8QaI8cvmqWQgKFmjBJY99wHvzkVH4U8QvY20dtqMbiJiSkxORg9s1nzNS1NqWMdODp11Z336Hd0tQW88c8ayROHVuQRU1b3udUZKSugxQRRRQUY15oscl1JcLgM68jHVvUn6cVT8P3hS8k091EeCSg5z/ng5rpCM1jaxpsa772GPbcIpIK8Zx61Nrao4atJwkqsOm/obNLWfouox6nZCWNskcNx0NaFUjrhJTipLqKKKBRQWFFFFABRRRQBk65JfpFbtpibn89Q4wCAmDknP8ATn0BrWrN1ua8t7RW0+LzZDIqkegPfoen0rSoAKKKKACiiigAooooAKKKKACiiigAooooAKSlqpf3P2aAv36AetBMpKKuzlvFN7Kl0WBCqqnLDqACOp6DJP49KseD9O/1t/NkySNnDdQcZyffmsJbmS81dI4SrAPsC442j5RnsepPvmvQbeJIIQiKqqvQVlFczbPFwsViK0qr1S29SxRQKK1PcEooooAWkPTmloNAHI+IfD00d4dW8PyC2vj/AKxMDZOvofQnHWpvCvjGy155LYq1tfQna8Eh5z7HvXRzzRwxmSZwir1Jrz3X/DZ1y5k1LQk+yTxESB8Eecccjtjt61lJOL5onoUHTrRcK2nZ/o/I6jVNWuGn+x6XGHm3bGkPIQ/Tv/SpdJ0SKxkM0n725YkmQgnk9cZJP61ieCvENtL5mm30a2eowHa6njd6YPc9v/112Q61SfPqjKspUf3dv+COoooqzjFooopDCiiigBp4FcV4w1rzlFnZt82eex7/AKVa8Ra6kQIhdXiHHDY3txjBHasjwxpsmqXf226UHYT16E5/zisZzu+VHiYzEurL6tR36vyLvhnRiCLm6Xbnk553DOeT1z9a4bxRft/aU2s2YCTTybbUpjJQYUfLkdQpI6g59a6DW/FF1Ya/remrKsdssCR242gFJGxyP73BJ+oAGKy9F0WLV9aigjmhkitlVcdOgALYx97PIHT+Vc82naKPtcmy+OWwdSps0n6q2x6ZpqNqXh22+2bJJJYRvI6Zx1FUr6M3/h2dWGbiFSRkYwwzj27YroEQRxhAOFAArJ2m21tlxtgnjz0/iz/n867LaHzeLipSbezuvv2IfBN817oUfmsWkQlWJOfcfpiugrz3S7mbRPFk1iW22kj9D2yPlrvw3GacHfTsY4Ctz0+V7x0fyHmkPSlHSimd5jaroFpqDeaQYp/76cbvr61y97pN5pkuEkfJHyzJwM+n+eTXoNRzRJKm2RQynqCMipcUzgr4KFX3o6S7nJ6Z4oMbrBqKspHDMR+X4+3411UFxHPGHhcSK3QisW+8PxvGxhAYD5lhfkbvr1rEii1DSryRLCUkAfNA3X1yp75z2qbuO5hGtWwz5aqvHujsb/atnNu6bDmszwuZVsXSbZuWVhxjPXODjIOAeuajtNetdTt3jb9zOODE7YOcj+vY1L4XleWyleTd80zgZz24/ADpVN3dz2qNWNWi3B6XRuiiiirIEqG6j8y3kT+8pFTUUCkrqx5/KskN75wJgeMgkYJ+owD/AFFdlpF0t5ZpKueeDnrmobjS4Jp5JwMO6YI9fQnvWXol79n1GSwmbaNx2qfXHPP+etZpcrPJoweFqe89JM6miiitD1wooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAIZ5VhgaRuAoNeb6nPLr+tLbwklA2O5A9T+Fdf4u1BbHTHCn94/yqM/lWX4F0plVr2cfOchT/M1nPVqJ4eNvia0cPHbdnTaZaLZ2cUCAYRQOO59auGiitD2oxUUooUUUCigoKSorqeO3iMkzhI16se1YlyLjWy0MG+Kz43SHKtJ649qL2LjC++iJJ9Yaa7Frpe2R2+9MeY1A9x3/AEqzp+lR2zmSSQ3Mxxl5MEjr09OtWrS2jtIFihQKq4XgAZ9zVqp3G5JaR2GgU7FFFVYzDFcn4q8H2mtqJY8290h3RzIBuBFdZQamUVLc1o1p0Zc0HZnCeHfFN3a339i+I08u8GFjnH3ZPrxgc9/0rY1nXJ9J1GHz4t+nzDaZUH+rb0PXOfwqz4k8P2eu2D21yhBxlZF+8p9RXL2et3egXQ0fxYBLat8sF8wJDeivxjPvWbvDR/f/AJnalDEPngteq/VHeQTJPGskbBlI6ipa5gf8SHEluRJp8vJ3PkR+mDzkYrooZUkiV0bKkAg+xq4yvozhnDl1WxMKKQdKWrMwrJ8TXy2GhXdy3/LOM46deg61rV578ZdR+zeGltI2PmXUip8hHTryOuOP0rOpLlg2dWDpe2rxp92cf4EtFvLoXMuxIrdmuZXJJZjk4GPw9K9b8P2xh09C6NG8nzNk5J9z7kdcVw3hHTUtfD0QwVmvpgHPLsABnB6D72M46epNelRR7IlX+6MVjQjZXPRzbEe0qNLa9vuJaiuYhNC8bdGGOKkHSlrqPDkrqxyeuQrfeH2807TA2N+OnY4/Gk8E3jPYKhK4BwcdM9sY/WtOeLZcz25B2Xakg56HHNcxoci2GpyxkMPMG9MnguDgjGfr3rJ6O54lX91iI1Pk/wBD0BemadUNu4kjVgpXI6Gpa0PbTvqLRRRTGFFFFAGTrsm20RtpZQ2TgZ4wf51h6ZocV5oyOp8ppiWZQSQQTx1HBxjmtzXv+PZedo+bkf7pxUPhQsdJi3Nu28A+2PqRx0rJpORrUpRq4e01dXOdEGraBIzWq5jwR5fVfwPrXSaP4gtdQTBbyZuhik4Ofb2rWZFdWVlBB4IrnNa8MRT5uLLKTLyOen0/+vTs1seM6FXC+9RfNHs/0OlzS1xOneIbzTbj7NqiF41GA+PmH19a6mw1G3v4t9u+8dx3B9DVKR0UMVTraLR9i9TT0qG4uYrWF5riQRRRqWZm6KB3rz3W/jDo1q72+jQSancqxT5mESZ+p5I+gpnYd/ZWdvZ7xbxrHvO5sdzVqvHdO+NsDf8AITjtY/LJWZYmcHOTjY2CGOAOCVzng16ppWp2uqWMd5ZXCzQuOCrA4PcHGcEdx2pkqKirIv0UUUFBRRRQAUUUUAZHiKS/j08f2Zk3BkVeEDfL3ODxwOf0rVX7o9aztYmvLaCB7GF5m+0IsiIoJ8snDHkjp1/zmtJelAC0UUUAFFFFABRRRQAUUUUAFFFFABQaKDQAmK5jxnqf2G1O12R8YXb6kHk/SuiuJVhhZ26KCa811aWXXtfSCJifm24wce/XjgVnUelkeVmdd06fJD4paI1fANiXdryRNyjO1j1yfT8K7gCq+n2aWVnFbp91BjPTNWu9XFWR04Oh9Xoxh16+ooooFFM7BKKM0GgYVRv9SjtSiMCZJDhFHU9OT6Dms+61aS6u1s9KVJT0ef7yJ69D1q5pmlraDfI7zTn7zO2e+ePSlc05VFXkUodPmv5RLqxDL1VFJGw56dv15NbgUIAF4FO/DilAFMiUnL0OS8Z+FItVgN1Z5hv4vmjdSRls55rL8IeNWW4Ok+ISttex/KryEKrjHr616CcYrm/FnhOx8QQASxhJ0OUlXhh9DWThZ80dzvoV4Th7Gvquj6r/AIB0lFcDoGuX2hXB0nxSSVUgQXmMqw/2j+XJ/lWz4h1e70e7guDF5umsMSbFyyHt35zxVRmmYTws4z5FrfZ9H6HTUVWtbqO5gSWM7lcAirFUczTTsxawtcuWdfISQqvPmMnOBg8dv51c1a/S1RUDL58mdgPt1Ncb4gu2mZbC1DfaJM+Ye/PO361MnY8zG4pU4uMdypHCmr6qLazi3QJ74yB1z19eK9B06zisrZIYUVVUdF6Z71Q8NaLHpVmAUxOyjec55xVjX7z+ztGu7s5xDEz/AIgVMY2V2GW4JwfPP4pfh5Hj3iGRp/EOpXEON4lkA3Y3NjhSoHP0PGR713/w/wBOigtlkMAEwXLSbcbieeB2xnBxXAeDbdNT1I3FygEMLNcO5Y7toPyr0x1A6dq9f8PwCHTlPleW0rF2+bcSSepPrXNRjzS5z7jNKnsqSoLpY1ay9aiBiE6j54WDZC5OM8/h3/CtSopkEkboejAqfxrttc+WqR5o2OI8YwMl9a38a/fTDjPUcZPpxxXUaBdG6sVyyuRwTnORWXqluLvQpY5SCbc/eGeg4bH+cVB4Ju2aAoT8sbeWfQk9MYGKyWkjxqV6WL8pK519FFFanthRRRTATHaqt9ZQ3sYWVcEHIYcEH1FW6THFFhOKkrNaHF+I9Ex+8+crgBJkGXz33dMg9c1S8Ma9NpsIiu0820LErKhzs9jk8dOldfrbbbJdy7sMD0zx3rH0jR4L/TfNcGFpnLOE3Dgn7pDf5BrCSaloclTBShB1aDs7/J+p0dpeQ3cSy20oljbuKnrhJdM1PRbky2BJXaTtXlD7eo6Vu6N4kgvSILsfZ7ofejbufb2q4z6SIo4y75Ky5Zfg/Q36O1AIIyKBWh6AlZOq6bDNuu0hV50U7eOta9Jihq5nUhGaszL0LVI9TtsxHLR4WTIxzitaq8FvHAWMUaoZDltq4yfU1PQFNSjG0ndi0UCig0CiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKDQAUlFYXi3Vf7N0w7WxJLlUOeRx1oeiuZVqsaNN1JbI5nWXbXvEq2se4xxNtyBxxyT7nmu7srdLa3SGMYVRgVyPw/wBLdUe/nGWbKoWHPXmu3rOK6s87Lqbadee8n+HQQUUtFaHrCVV1C+isot8p5JwqryzH0AqtquqRWH7tfnuGHyJ/LJ7DNV7DS5nnW71RxLOB8qbRtj+nrSuaxhpzS0QsUVxqQWa9XyoCCPs/Oc56np9a1goUBV4ApwGKdQRKV/QMUtAopkhRRRQAUGig0ANqjq+mWuqWj295EsiOMc9vf61fpMUNXHFuLvF2Z5tDPqPgqd7bUd95oUjFY+MvGD6nOAOela2m3v8AZd0stuxn0i6OUdTuEBOOD9Tn9K6y7tIruBoZkDowIIPvXBX+lar4YuZJdLi+2aZICJbRmJAB4wo5wMc9K53Fwd1serCrDE6SSUvuT/yZ6DFIsqhkIZTyCKlrjNA1e3isxc2Evn6c5AEZP7yCQnkN6A+9dejCRA6nKnkEVtF3R51Wm6crMd3rxnx439vfEWDSySYoNqkKMnHU9O/bk969c1G5S0sZriU7UiQuSfQCvI/hrH/amtar4ivt8nlAuqbBhu4yemQAMe/Oawru7jDuerlS9mqmJf2VZer0R6NpUEZ1ERQ8R2Mfl4C4Bc/eOc9f85rfBrG8MpK2nfaLkfvJjuY8ZPJPOOO+K2ulbwVjyqz9536C0UUVRiZurqF8m4PWJwT9DxXIeI0NvrUN7CGG/bINq/mD69K72VBJGykZBGK5bWbf7RpWSyiS2YlmxllHIx+dZzWh5ePpc0W16/cb2lOptwoY8AHnOPwz2q+K5Twtd7lVPmTZ+765z6fhXVelVF3R1YSp7WmmOoooqjrCiiigDB8UuFtdrYwUfnJyuFJzjvU3hmNItEtxHjG3JIbIJ/Hp9O1QeLYt9mhzwpbIBOTx2wDzV7Rl2aXbjIb92OQMZ98YH8qhfGdcv4Ct3NEUUDpRVnIZmo6Rb3zrJJlZF/iXgkeh9qTS9MWwMgjfKEjCgYA/xJ9a1MUYpWRl7GHNz21POPiJeXuo+ItO8OafcCGCVHuL6TI4iGMrgnBG3qOOHHrXjGoato934kkihtpLnToZkji0yAFpbpuQoHykADAGQcnOMnt6JrOoQW2q+Jby5bzW8i6ZQ785VGBTO3hSAB6gYz1xXHfCLwxssR40la2KWkrNJ9ql2oo67uhOfxJORjBoNSv8T7DXrLw/aXuvadpto14U8pYXfzrcAcKV4A7ZySR0zxXW/AgzSeIJ3s5HgtBbj7RDLCOXPZTuJ4I+93A5Gea848feKrzxj4leeXbJFGdsapkrGmR/9frjOe3SvePhD4VbQ7B9QvI2W8ukAYOOUXjjgAc4B4z7nNAHotFFFMAooooAKKKKAMvW576CO2bTofOc3CLIv/TPncfatSsrXJ76C0V9Mh86YyqCpGcLzk9f89K1PTtQAtFFFABRRRQAUUUUAFFFFABRRRQAGkpaSgDB8X6iljprgn5mGAKyfAdhJhrycAnkBg2ck8nP+etZ2uXB13xLFbWzFliO3cv8J7n6iu7srZLW0jgQYCDFZJc0r9jxKX+1Yl1fsx0XqWqWgdKK1PbCikqle3sNoitJnLnaqjqx/wA96TdhpN7E9xPHbxPLMwRF5JPasadrjWJvLiJisRjeTlWfrkAg9KdBbTaqUuLz5YhuxAM4HYZPGe/P5VtIAqADgDoKW78jTSntqyGztktbdYoVCqowB3qwuR1paWqsZXu7sKKKKACiiigDL13RbLW7Vra+gEiHpnqp7EVx9rqd94Quhp/iRzdaVK22K7IJZfQMMY/zn2r0LAx0qrqFnb39q9vdxLJG4IIYZGDUShfVHTSr8q5KmsX969DBkRtH23Wl/vNOlwzqrbgnuvt+NdDBdRXFoLlHBiZdwbtivPWi1TwLI3kh7/Qnb/VtgtED1JJ5x29PWptQnkjsv7Q0W4WXSbkhpVXnyjxkbc8fTtWalylY2Ko0va/EujXXyfZlrVL87zfzjcXYpDH1B/u5BxwOpq/4W0MpK2o3Q3yyHcobtnnP1rD0Wzk1/U1lnz5EQyT2J/8Ar16FFGsMaxxqAoHAHQCnDV3Z8vg6TxFR1ZrRPT17knUVwvxh1H7J4Y+zIMvduIh82CB16dx+nrXc5A714z8SJG1vx9Z6cu54oFXeqZPU5Pbg9vxorS5YWXU+xyqip4hSltHV/I1fBunfZvDqbet5KqtgbmVRyR0+bJx7AHk16dBGIYUjXooAFYen28Y1eOCJQkVjHtVUGBk9c/n2/Gug4opQ5VYyx1d1qjk+uv8Al+A6kNKKQ1scBkyIIdQcMBtulI254zjnI5rk9NlNhrUsUwXfITgs5X5/YHrzj04NddrMIaASjrE4Y8du+e+K5XxbE8eo295DuUMA4I29R1H8qynpqeJjoyg1NfZd/k9zuLWTzoUc8Ejn61NWbo0itarj+JQw9K0h0rSLuj1qUueCkLRRRTNQpD0paDQBl67/AKmLd039jjtVTwkv/EoTD7+fvcfNwO46j360/wATMqWYZs9HAwcH7pPB+gpfCSbNEgTauQuDt9fcdjWf2jrtah8zXKhhgjIPY1g614chuwZYBslXoO34HtXQ0VbSe55tWjCsrTRw1jrOq6PefZb5GmhXC5x8yj1z3rqtL1W31JXNuWJQ4YEYwaXUtLt9QC+cCGXoynBqPT9OjsGby2O04AXoB/iTUJST30OahRrUZ8t7w89y1eXcNlbS3Ny+yGJSztgnArzjxD8XrO3lNvolm11Nu2iedvKgAIyDuOAc4OOR069qt/Ee5n1TXdJ8N2l2lrHKGubyRpAn7tR0Gc54ySPTr1rxrXPEVtdeMWgt7a6l063kESWFqdrXBUnYowCABnqAScnnnNanoWO/tPjTKq7r63j2xyYmKW0mxkyANsgY8kHjK47Z716r4f1yw1/TlvNLuUmjb7wVgSjd1YDow9DXzt8S7DXrDw7Hd+IINIha9jRbe1jL+faRDkKAeBjoep5POa3fgYrXPipLizeWxSO2AuIZFBE55yByDjIznBORSGfQQ6CigdKKBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBoooASvOPE90dY16O1iy6IcKvYnjOee9dl4huxaadKwJDMCq4rl/BFlLdX8l/I2ArklSvOTmspvXlPEzGTrThho9Xd+iO0022W0sooVH3FA/HvVqkHSg1qezCKikkLWTrGomAC3tMS3snCxgjK5/iIJo1XUjBILS3Aa7kHyA9FBOM0/SNNFoDLIXe4kGXZmzz7UjojFRXNIZp2mmP8Ae3n7+4c5LHt6cdOP07VrYoFFBnKTluFFFFMkKKKKACiiigAooooAKKKKAEpsiK6kMM06igDz/wAReHLvSLo6n4e2opB+0W5YlZV9l6Ej3/OneH/E8bEywEtbsV82EY3QN0xgHpnr+td4yhuCMj3rhPFfg93uTqmiYhvB1U/dfjHT+9+lYSi46xPWw9enXXssRv0f+Y/4v6wbDwhLHCw33mIRx1B6498VR8FaY1h4KtbZwhk1KTc21d2VI6Hjt+Qrz7Xb6XVtYsrKUyKsRO9XYtsbIB4xxkDt2r2DT5Yr3WbdLUMILSDChRgc44OfwGOv61jTl7SpzfI9DFYeWDwsaXdtt+mx0NpAtvbpEgwqAACrFIKWu0+Zk7u7CiiigQVkXscYvGWXmK5QoVIyM/59a16z9VthcQB87XhPmKcA8j2PtSaMqsbxON0maexvJIJDwJCh+ccH1x1z7130LB41YdxmuH8SJs1CG8UEJcKPvDGHAGBnr+VdToc5nsl3DDDqM55z61nHR2PNwEnCcqT+RqUUUVqewFFFBoA5/wAZLu0kjYHyehOPyPrWjpCqul2qrvx5Sgb8bunfHFUPFgT+zB5mfvgDHXOa1bLb9ki2rgbRgenHSoXxM6JP9zH1LNFAoqznCiiigDzXxV8O7y8ubmXSLqNorlmmMFyzZjlY/OyNyNpB5Uqc4HPp5ynwK8aCy+wrrlotmQzm38+Ux788DbtxyAOa+j+1ZWsamtnHtU/vGHB7L7nP8qTdiKk1CPM9jzTwF8GrTRr2O71vUl1K5gLDyolxGVK7cMDkkdfQV67Gm1QoAAHQDsK5fw/qFtHdtDLcGS4OAQM4yf6+vua6uhO+pnQrKtDmQoooopm4UUUUAFFFFAGVrt1dWdokljA08jSKm1QTgHjPAPAPtWp9azNcuLq1hgks0kkJuI1kEaBjsJw3H9e1alABRRRQAUUUUAFFFFABRRRQAUGiigBvFYnivVP7N0t5FYK7/KpOfz4rbavOPFN42ra1Faru2RuAoB6k/jjNROTS0POzDEexotR+J6I0fh7ppKSX06/OeEJHryTnr/8ArrtsY5qrplsLOxhgAUbFAOOme9W6cVyo2wlBUKKgFFIOlZeq6j5OLa1+e7kHyr6D1Pam2dkYtsdquppZDy0XzJ3B2p2+pPYVW07TJHlN9qp824J+WPqkY7BQRmp9I0w26ia7PmXb8tIeo9q1O9Lc0lJRXLH7wA9fypaKKoyFooooAKKKKACiiigAo4ooNAEFzGksRSRQVOc/SvKddsza6lOuks727Hm3ySPTCjp3r0jXdRjsbX5zhpcqn1/yaztC0SPzjfyPvWUZClcf5FY1I8zVjhr1KlRqhD4Xv6GN4R1CCC0NxYTO8I+W4tXX54nycHHYe/eu3tpUuIUljYMjDKle4rivFHhqeC6/tbQf3F0v+tT+CdP7uP8AHg1F4f8AFMUjSyxoyMhAnsyQDFyRkew7/WpjLkfKe99UjOkpUNlp5o7m8uEtbWWeQ4jiUsx9hXkPw6X+1/E+p69drmCIFlLLgDpgMenQZ78iux+Kus/YfBlwYHw1yPJBxnhv/rVkeBtLfTvBSRnb5upsDjZyARgjpyc5x25qZ+9UUe2p14aPssHOo95NJfLVnYeGkMlh9skG6S4JY8gnqeMjjr+VbgqrYQJa2kUMY4RQO39OKtiulbHjzkpSbQUUUUyBjgMpU9+K5jWLRp9LaMPse0bdkdQMHPfBrqOM1lXipDqCu5/dzqUcHnoKmaujkxMFOGvXQx/CV0TEsRDAxttz6jsT+HH5V11eeWkkunajNExQRo5UqGwOpwcH9K721cSW6MD1A59aim9LHNl9RuHs5bonooorU9QKKKKAMDxfH5mnLt/hJ45+YFSCOKuaDt/sq3MbtICuAxG0nB9KreLF3aadyhlG7IboflPsT+VXNHXZpduNpUeWDgnJGffvWa+JnTJ/uUvM0KKKKs5gooopgeOeI9TtbHxRrl7GZmlijnCFif8AWJGMoCeMEr0XJwF45rz74TeHDcWV54tvHs4odPmEx+17lQgZJIwO2OAOucV7L4n+H76lqE13pd79mW6Pm3NvJuKvKOjqc/IxBIJwwPp1z5uP2ftelxDP4itYoBuYKgkYBiey8AZ74oGcJ498Vaj4z8QtO7m5ij4hjQYWNOpwP6k5Peve/g/4ObQbI6leIi3F4gZAGLlYzjAJIz0CnjHXms3wP8HNJ0C+t7jUr8apd2zCRAI9ij2YZO4ZOQD6CvVYxtAAVfYDoBQK6exJRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBoooASkbpTqp6nP8AZ7OSTnIGBj1PAoJm+VNnIeM7zz3SMEFSwXAPVO5/X9K3/CVmbXSkUrtLEkjpXI3sX2jU4YvnZQ4zgYPbIH0HPb6V6HCixRKFG1VGMegrGHvSbPFwUfbYiVV9NCXtWbeXzCRYLMCWXIDHkhB7471Tu9Qub6X7NpiMEbO65x8oxjIHf2zWrZWqWsYVRlz95jySfc1qz6Hk5NZb9ivpmmi1UySO0ty/35CSc89vT8K0gMUUtFrGbbk7sKKKKYgooooAKKKKACiiigAooooAKKKKACiig0AGKrXTpHbu8hCooyxPQD1NWDXIfFLVv7K8K3CxttmuR5Sc4PPUjHPAqZy5Ytm2HpSrVYwj1djzHQrKbxBr+o6wmHjiYsUJwShOODng4Gea6bwhrEumq0yyF45HHmoRnZnOCSeRx0x1/OrfgXTf7P8ABA24eXUuRhRu2/xKTnt82PT9K1/EXhiZ4I7zTVQ3kSbZEbhLhQBkNx144NckKUkuZb7n0uJxtOpOVCfw7L5f8E6yxvIL2ETWzrIp7g1YFeZaHql5p8L3NgpZS3+lWrod8ODjKj0rvtH1S11W3E9oxZfQ9RXTCpzLzPn8RhnSbktYmhRQKK0OMWkNLSE0DOb1mwJsLi3Rtskf76FgTkduv0qp4Vu9rRLIeJl3KgXAB7k44565roNSjAWObbuKnafoeP61ySI+nX9zb7XLxsJ4m6ALnnOPbjHtWUtGmeNiE6NaM1tsd51FFQWUwuLZJF6MM1YrU9eL5kmgooooKMXxO5SxUqwXEity2OhHT39PetGyffaQtk8oDzjPT24rG8Yf8eEa8fO4UFsYBJHrwPrWxYgLZQhSSoQYz1xjvUr4mby/hR+ZaooFFUYBRRRQBWvbqKzgeeZlVEGSTXAHVJr3VbmeZgFVD5YxlTjBwcjkc+nofetPxZeyXl9HZwDEcTjzH3Dbkjv6Y65pmh6aou0RFPkohOX5BBPJI468j6c9qyleTsjwcVUniaqpw2T+8t+DtKEJ+3SJ+8cHBI55xn2xxxj1rrBUcUYRAijAAwPapa0iuVWPXoUVRgoIKKKKZuFFFFABRRRQBl61c3tvBE2mw+dI0oV1xnCkHLdR0OK0/TtWdrM95BHbf2fD5zNOqyDbnCc5PXj61pUAFFFFABRRRQAUUUUAFFFFABRRRQBma/di00ydicEqVX8q5LwTZteak9/J/AcEEd+fyxU/jK9M+xA6BC+0AHkgdf59K2PB1mLXSg2Pml+YmsZe9JeR4Un9ZxkY/Zjr8zoMUUVm3t2+7yLVcy5G47c7B6+9bHvRjcbq+oPblLe2G65l+6MHCj1PBp2lWH2aPzZSXuJOXYnP/wBYfhS6Zp62al3w875LyD+I5rQAxU2uXKSS5Y/eKBS0UVRmFFFFABRRRQAUUUUAFFFFAFW+ulsbSa5lBKRIXwOpx2FeGeOPiNJpOo28VteTi43l7oQ3IPnYOduOQi44yOfyFeifGbUbzTfAt5NZI5clQzjH7tcgk89/TFfNPhBJr7XTcpiSRMfNJk7Fzy7ZBHHXmgD2Xwr4h8B+IEW0e/1bTbxsMEvr6RgS391yxU5PrjnoK9E8PifTtXutImv7i/jijWaJrhB5irnBBcABxn2BGMc9a+drbwmLrwPrniS7u5I0Eqi2AGfMk3jLMAOB1xg/WvVvgPf6hrljcavqjyPPsW239EZVChSF9cDk8f4JExgottHqzKpXDDKmuM8Y+EvtrNqGlMtvqCY2nHDdju98E4NdqOlQyyJHE7u3yqCSfapmk1qdFCtOjNShv+Z8+eJJ7q91W10qdWi8tzuR8naTgbs4749K9e0ow6hf2cdsXMVjCMN93nAxkde3IwK800eyfxP4o1bVos7YsyRh/ukdME54HHHpW74W1KXTGe7UsXc/vomx8gz949yMDjH/ANauGlL3m3sz6vMKcatKMIaSitvN7nq4HPNOzxVDStSttUt1mtpAw7gHoa0M16Caa0Pj5RcW01ZiZpaKDTEFUtRtvtNsVPDL86kdQw6VcPSigmS5lY4bxEpaa1uULkTLsdD0DAAj0PftXQ+Hbr7TaZzhsnjOcc9M1V1mzDWlxbIvzsDLEQDkN9fXsMVm+FbvZLE0mQs+Uxn+Idz9az2kePH9zifU7WigUVoe0FBooPSgDF8Vbf7MLbSSGAGM9Scdq0LEr9jh2rhdo4PGKz/EwD6dhnC8g8kgYHJ/StCwffYwNzyg68np3qF8TNn/AAl6stUUCiqMQoNFBpgNzxWXrGpLaARp/rnUkew9at6hdpZ2stxKcLGpJ964A6lPe6rPcySukRUqmxSRwM8+oHf9amUrHm43FKilBbs2dB1K1TUTbGWSaaQZDfwjJ6fX1NdgoCiuV8LaOsO2+nQeY+SuQCQSBnBHUccV1PaiOxpgY1FTvPrt6DqKBRVHcFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRVHVr9NNspLmQFtg+VB1c9gKALckixoWchEXksxwBXP6tfxz3cUMEscmBnAfk59Mden0ry6/1698W6y0d7NeR6ejZENmpwMAA5H8Wc8ZPfgel2GC0tpBCtp9qgjdUliuohFMAWwSWGCvJ5Jzj1pPsceKk0lBdXY63SrKTUNfN18yJERuzn5sZAx6Z9v61o2w1nUb57fUrcW1ogyPLIZZOcDnIPI5xgY4607wzut55rRGeW2U5jkYsz4PIDMeTwQR9evaukA/KoUbGuDorCwasm3rcjt4I7eNY4lCqoAAqajFLWhve+rCiiigAooooAKKKKACiiigAooooAKKKKACiiigAoNFFADD1rx/4x3327W7PSVdljjG9vqfpnoPavXJpFjhZ3YKoGSScACvFdCc+IPiS105Z41kaUEBRwv3RzxjGOnWubEPRR7s9vJ4WqTrvaCb+fQ9I0yzEV/Y2Z2yJZ2wySerHq2PXIHX+ddPWN4f3Sxy3Ug2PK5yu3BAHTnqeMVtVvHRHlV5OU9TnvEWhm6K3tkfJvojuDrgGT0Vj3H1rlbG4nS6ll0r/Q9TXInsigCzYx8y9sn2PNelCsDxJoMeoxiWNminiO+ORTgqw5B9xnqKiUNbo6cPiFb2dTb+tPQs6FrkOrQttDwXEXEkEvDKfcenvWsOteb4lTUY49QLQX0K/wCjXo+VJz2Deuc9+nfNdbo+sG5dra+he2uV4xJgB/8Ad9acZp6MivhuV80NjcoooFaHGMkQSI0bcgiuM8Rxm2NteqSTbP5bjn7ue+PUV2r1h67aLMjAgssqFSo9cfnUyV0cONp89NtC+HLtZA8IZmAJZSf7vGAK3BzXB6Ne/ZfJM5ANq3lPwCxU5x+GfxrukYMAQeDzSg9BYGr7Snbqh9FAoqzvOW8dFjawRx53GQdOT1HOO49cc10FoNltCny/dA+X7vTt7Vg+LxuNmEUb1k3rk46EZ47/AE6mt+1KvboykEFQQR06VK3Z1T/hRXqWKDQKKo5RKzdcvxYafJLt3OeIx3Lf55rSrhPFd59tvfJPNqi4yOQc5BI7Z4IGamTsjjxtf2NJvq9EV9It5rqU3DqRM+GAY8yDIz83cnBA9q7XTrVLaDldrH7w6/h9BWX4Y0/y0aedVJDny+uVHTH4dK6EClBdTLA4fkhzy3YoFLRRVnohRRRQAUUUUAFFFFAGPr8+oQWKHSIRLO0iqQRnC9z+Hv8AzrXrN1+6u7OzjlsoJJ28+NXSMZIQthj+ArSoAWiiigAooooAKKKKACg0UUAJVPUZ/s9m8i5LBcLjrk8CrEriNSzEBQMkk4AFc5rWq2lzNHb291bSgjPEo5zkcEHrSbsjCvPkg31OdvUae/tomWVlyCQSAevb+dd/bgQ26fwhQOuOK5HTbKS98ReZ0WDgnnkDjv6+1aItdYv9VaHVUVNPTJXyyCsn+9nn8CMehrJPqcWVUL89SWiv13ZZuby71FzBp2UjYHdcehBGQBx9M1p2lnDbRgIg3kDc3c/j1qWGFYYljhXaqgAAelSgVqkevKd9IqyFA4paKM0yAopKaXVfvMB9aAHUc1Sk1K0j/wCWoOfTJqjceIrWJiqqzNz0IGfzpOSRzzxNKG8kbRNGePWuPuvF7jAtoRg4Pqcd/T86zpde1e7cx27YYgrwoHociodRHJPMqUdrt+R3xdV6kD61XuNStoATLMqY65rhPs2t3uXd5QSeBuPH4DtUsfhW6mUmYuMnbkn5iD1Jznip9o3sjD6/Wn8FN/M6Ntfjdv3MkJT/AH8nPHFMudfMPzEoecYCsTn+lZcHgZTtaS4ZSDnAroLfQrWJVEgMpQAAsf8APNUuZ7l0njKnxJI574m3Es3gG6NrFJLJPsRYkXJOWGRyD2z/AE5rwXSfC1/Yywvbypd6XcMTcIJQN0YLAHCkvgAHnHB619Paxo1vqumNYTlkjJBDJwQR0PpXNHwmt5Ziy1XQNBumQH9+YsBupU4xkHIGTnmtD1U2lZnh/izXrzXnsvDmlWogjLKILVI84Y4VSWz8zY4JOOR05OPoXwD4di8L+GLPSYuXiTdKSc5kblufr+lU/B3gLSvDc8l7DbW63sq7N0Ue1I1z0Qds9/8A9eevFAw6VynxK1T+y/C10QcPcIYY8dcn0/CurryD4z3zXmrWWlRFsIcsoYZYt7deB+HNZVpcsbnpZZQ9viYp7LV/Iv8AgHT/AOzvBS7zJ5uov8vyDIGPmBB7cEDPr0FdFr3hl7u2huLHat/bL8pfo/qrY6ipNLtwlzp1oD5i2kAdgWP3yBkleoI4xn19a6mppwvGzKr4uftXUW7bf9fI8y0i7vbUyyaVH5V0pLXdtMMvtB4KAdsdhXdaFrFrq9sJbZ23DhkcYYH3qv4h0SLUofNtz5N3Hho5V4II6An09q42M3cd83lYsNaQgMpwIrseuQAMnt/9elrTfkVLkxcebZ/1+B6eOlFYOgeIYtRLWs6tbXsXDwS8N9R6it0VumnseZOEqbtIDRRRTIKGqJiNZR1jOTxk4PFci8JsNWuUSIgOv2iJuCMjkj+eR7d67plDqQe/UVxviSFoYkuVCmWzlHqfkzkZ/Comup5ePhZKa6HVabdJdWiSqwORzj171crnPDl4srSxKSyufMBJPQgdPauiB4qk7o7cPU9pTTFooopnQc940/5BB+YjLAe3pzWtpuwWEAiBCbBtB54xWH48Zv7KWNfvNIMYOG/DPB+lbmlrtsIAr+YBGBu9eKhfEzpmv3MfVlsUUCiqOYKQ0Vl65frp+nSTd/uoM4yT0/xp7GdSapxcn0Of8Xai092LGE7ViZTIwPAJBwCPTHNLoGnq17EI1Y26LkluN/Tk9M5I75z+FZeiQ3F3cl53WRmwx3YJI4PXrk9B/wDqrvrK38mELgK3fFZpczuzxsLCWJqutPa5LFGsUaJGoCqMAegqQD1opa0PdCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK8u+K+pXJu101Z/KjdV2jlXJJ5Kk4GMdTnj9K9Rrzn4l+GtQ1jUIbjTMGVYgEUueWBLY249QOcj0PFAGt4G0SHw54a3MNrkGRgADt64CkDJyMeoz0rH1K4t9R8QLPA6Hy3UfIo3htvIDHrk8cepznpVa+v8A4gvp0enyeG4gUGyW4jnWQSc9QMgjgdP5cUzRbO70a3F3cT2/9oMfL+yq+4Bu270I7AH2obMKs+SzauvxOu0AH+05T5glcKBLKwy5IPTd0IzxwB0rpa53waYlsD5YCbjnyx25PP410DMqD5mx7mi5rGSktB1LUCzwn7ssf4GpQc0F2HUUUUCCiiigAooooAKKKKACiiigAooooAKKKKACg0UUAc5481BdP8OXPzYkuB5MfqS3XH0XJ/CuA+GFr5lhd3qR/aDJIsIG3OFx8xB7cZHANaXxf1Hckdgj/JChkmUDn5uFPUe/5960Ph9ZfZ9K06B1MckY85iucMTnBJ7ZGO3OeK5Je/Wt2PoqUfYZc5dZP8EdtaQ+RbxJjooB+tWqaOgp1dR883dhSYFLRQIxda0yK4tZFkj3Qtyy8Aj/AGlPYjrXJXMX2KaGK/Ak09CXtrrOPKIAwrfQ/gevrXo2KxNR05gkgSNZLaUFZIj0wfQ54/LjtWU4X1R20K9vdlsU9K1zyGSyv5PnVfllduJB2we5rpx0rzWVBp0gt3WW50xzuilIJNvn8Oxx/OtvR9Wns5UtdQYyW44WfqOvHOMnOQM980Qn0ZrXwya56Z19QXcbSQOE4PUGpI3DKCDlT0NSVseZJXVmcPLELfVcycQ3UexucAMDwf8APrXS6LKWtzC/DxHbyckjsTWR4gti8dzGOqgSJt447j06VJo95uCXBP3/AJHXB5wccfSslpI8ag/YV+XodLRSKQVBHelrU9o53xOy74Vk3eWMHA67iwAwecEVvRkGNNo4wOPSsHxFLsY7VCvtUA52k5b1zjj3ratc/Z4t+7cVGdwAOcdwOKlbs3n8ESzQaBTXYKpYnAFUYGZ4gvfsenucMWk/drtbBye+a5bw/YpqVyZQzlIyAA5BGOpGOeo7k07XdTk1LUDa2rqUVggxj5uuR756eldLoenpZ2mcDfKdxwKy+KXkeK/9rxGmsYmjbxLDEsa5wowM1NSUtao9lK2iCiiigYUUUUAFFFFABRRRQBl63Pe20MB06HzXadVcYyAhByT6AcVp1nazNeW8UJ0+3E7vMqMuMgKc5Y8jgHGavr24x7UAPooooAKKKKACiiigAqlql8NOsZbl1L7AcIvVj2Aq7Xl/xe1G5jmgso5BHHIgC/K27eScsp6cKM5PT86AOev9TvPGGvb7z7dLp8SlkgssjBHBIAyWP58c8Vcijit7iS3trYBEZfMttRjXcUJw3IHHXsTgfSu28DaJb+HPDivtUOymRiEAIXnaOO+0jOOM9BWBrmqRXusxSQjeFK9MZDjOSDjr057ZPXpUyt1OTEqL5eZ2Sd/U6PwuFs7+e0t9xtiBJHG7HfECMgfNzg84ya6SaeOFN8jbVHeuP0bVM3mfKkeRQRJJJgsepxu69Tj8Ola7aldz/KlmDwDtPPHv0FGg/rEPsfka4u4Sm8Nwe+DTDfReremcYH61ztyuv7wtosaxNknCgdfrk1Ug0rWbsOLlyig8A55Pc8noaTk1sjmnjKi0jBt/gdDc65FCJGGG2jucc+lZdz4qCqfKMbtnhRnOM06LwsGT9/Mx6H1PArQt/DdhCvMe/PXd3+tSudmb+uVNrI5xvFUr9YZizZ74x6dOOtON5rNwy+Takb8csu7PHfOK66HTrSHJjt41PstWdoA4p8su4lgq0/4lR/I4ePQ9Uu/9YxQZ5LHH5DrwTn3q/b+Dol4lnbptO3uPxzXVKKdgU1BG0MupLWWvqZEHh+xiiCGPfjGC3WrcWn20ahVgUDr0q5RVcsex2RoU4bRRGsSrjCgY6Yp+KWima2DFJgelLRQBi+KNUn0u3gktlVi0oRg3TGCf6Vk+ELm6l1m+S4nZ4yMhSenTt261oeMoEktICwyqzAmqfhNozqmoBV+bcCCc7gOnf1x+dZN++jyKkp/XIpvTovkdZgUtFBrU9gZK2xCxOAOTXh1g48R/EZJpA7RmYvgEL8ij5eeeNoHAxz6dvUPHuo/2d4duWDYkmHkx84+ZuPQ9Bk/hXn/wutZpUv8AUIo96vIsS7lBIHQ44ODtJBx61y1tZxh8z38tXscPVr9WrL5npHhxjPHNeO2TK3TbgADpz34IGfatuq9jCttaxRKOEXFWK6YqyPDqO8grG1vRo9StSrEh1O5WUkFW7MPcHnHQ1sGjFNpNaihNwalE82u4Htby3g1iRtyKTbaiGwQ/OAQM9z0J49SK6jStbLSfYtTja3mQDa7MuyX3U1e1WwSeFg0YeNhh4iBhh61yF3bnTgBOBcaKh3RsMZtMDgYAyQWHB6fjWFnB6HpKUMRGz3PQ6K5LStcFlIltfzB4mG2K44KHAHfJ59q6tTkA561snc8+rSlS3HVja1Z+arH5irrtZfXjj/IrZqC6j8yEr69PrQ0ctaHPBxZwul3LWskSuTusX+YkcsjEjk+xrvIXEsSSKeGGRXF3saWuqRySgmKZWikwccjofeuj8Py4he3JGYj8uGzlT0Pr+dTF9DzcDJwk6bZriigUGrPYOY8aLut7ddoZg5IyQAAMZ68H6d+lb9nIHtomUhgyg59axfFO1hEsillA3eWO53L+X1rcgx5aBRgbQMDtULdnRUf7qK9SYUGig1ZziVw/i27a6uBCpBgCEEg55OQTjoOAcfn0rp9cuhaWEkm3cx+VRnHJ4rktBs/t96zRkosYChGbPufwI6/X3rObvoeTj6jm1QjuzW8KacsQeaRVOX+Trxjjg9x2+tdRUNvCkESpGNqqMACpqtKyO7D0VRgooKWkpaZ0BRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFU7+0S7i2khXU7kcjO0irlFAGMl/fQRBLvTZ5JVwpe3Kur+4yQR+IrLm0GS+nGpFPIuGwwhccZwOD6c/nXWbaTaKTVyKlOM1ZnK+XKLjz7eNYLuMfPCejDp7ce9bNpcRapbNHLHtYcPG3OD7GpL7T47pQQTHIv3ZE4I/+t7VzzGaK8EN3mC5XPk3A+6/Hftjt61OxwXnhp36Mvf8ACK2R81STtY7lGPunv9QalbRJY8G3v5o2A6biQWx6EkAewqfT9RLuLa72x3KjkdmHqK1PSnZHqQxUpq6ZgtZa0syNDqCsigBlZc55yTj1PTqKGl15NrGGB+TuVVycY45yK3sUuBTsae17pGJ/al+iLv007to3fvON2Pujg5oh8Q27MkdzDLbSt2ZeM5x97pW3imOiv95VOPVc0WFzwe8fxM0a/pxlZHuRGUIBMgKjJ7ZNaEVxHMoaKRXU91IIqs+k2Mm/NtGBIpVtq7cg49PpUA0CyQEQx+WMYAHIHvg5596NQtTe10alJmseHRZLZXW3vJlLbSTuPBzk4HI5olTWY9qxyRSKc5cqMj064z6UXFyJuyZt0Vzv9q6vDfJBcaajIesiOcAY9cY60q+KrVJNlzBcW3C4ZwCCT24JOR34ouV7GfRX9DoaKzG1uwVUZrgAP93gnP5CrEd9ay4Mc8bZ6YcUJozcJLoW6KbmjNMkdTM/kKWsPxlfvpmgXU0P+u2hI+cfMTj9OtKTSVy6cHUkoLqzyjxTetrWvOAI2E04dGUFiUXgc45GBuH1r1jwtEotmlBcqSEUN/CqjAA/qe5ryjRIwdXd4pJESAKqCNwzDeDnJPOB04/KvaNNg8m0ijPUKMn1PXNcuHV25Hv5tKNOEKMeiLdFFFdZ84LRRRQMKKKKAMy50bT7iUNLbqTu3kdAW9SO9Z9/oq28Mr2yF4vvvFjJ4Bxs9DXR0YqXFM1jWnHZnD6Rqy6X8jyGe1wPm3ZMXGcbe3cde1dlFMk8avGwZGGVYcg1jaloCOZZrNVjkclmj6JISMZYetYdlqMuk3xRcm0xtMLYUxsW5yOfWpu46M65U44lc0Pi6+Z0esQTG6tZIBxvxJxn5awIYv7O1eWxkXEUhLJknnPTHaurtrqG8hElu6up6EH3rI8UwECC+iBL27fNzjI/z/Ohq+qPncZh+W8+qd/8zT0edp7b958rocEemKv1g6NKnnh9rfvUDA9uf8iturTujqoT54XOX8V/vTcRrlmRY2KYBzzzwenB71v6aXawt/NUq4QbgeoNYusRxma/aVm2kIAAM9wDW/a4NrEY2Zk2jBbqRipW56dVr2cV/XQnrD8WakLKxMattkk/MAck1su6qm5vlUckmvPtTupNX1EiEy43hQpBHy54xyeo69Kc3oeHmFd06fLH4paIteD7M3l9JczZ+X5juUg5Oe/fnmu6FU9NtY7O38pAAe+M4z07/SrneiMbI1wdD2FJRe/UWiiiqOwKKKKACiiigAooooAKKKKAMzW7m6tbe3ezgeYtcIkiqMkRk4Y/hWkB69aytduLy2ghewiEsjTqjgrkbCDkn6f/AFq1qACiiigAooooAKKKKACvPfib4avNdubdtO8lJfL2bmYhjhs4xkAjO3rz+Ga9Cqvd28dxCY5FyD0O3OD60AectH8SV02LTpLDT3Efym6SfczDrnDEYI7dRkdMYqtp+lNpiNNfXFu+o+YUNsGJViSTz19eg4HTpXfLdanbp5cun/aCOFeGQANzxkNgjjr1rPuPD7X9yt/MDb3BAPl8EAjoDjpjGeD1qGjlxEHJe6r/ANdB3g7yvsrFQI5X5aMY9Tzxxz7eldEzIi72Kr7niuZkhkMyuFW3vYueM7X5x+XStaxu0vY3huYvLlX5XRuQfp60LsRh6qvyT3/r8S2Ly1PS4j78bvTrU24dqyD4csT5i7MJJ/CRnH49aT+wI4/La3upomjHVW+8eeo/GqPTcaXR/gbGaeKwH0nUUeNotTk+UYIbkHJBOR39B0wKbMniBNvlyQS5bJwo4AHTBx165zS5vIXs4vaSOhpAaw/7R1aMKJtOVjtBJRyQTjoMA/rx70R68AVF5aywtnHAyvBwTng4z6inzB7GXT8zdorGPiPT0laOaRoSF3Espxj6jIrRiuoZwTFIjBeuD0+tFyJQkt0WaKYsgPQg/SnZFMkWikzRQAtBoooA53xZu8i1RPmzLzkA4wM59ePaqPgdM3V5MW+Z5Cdv1AJ5rQ8YGRbKFov4Zcn249e1UvAy8XLNt3ZHIBA5yT/TNZ/aPGmr45f10OtpGoHSkatD2TzT4u6lxHYRuzeWhmkjAzuzwPxAyaufDzTFg0fT4pNxZ83LbecE8AHj+7iuQ8ZXDa1rjqpjdbqYeXIinhFyowcZPAz6Zr07wrAkVmzxh1XhETBC7QOoHYn+dccPfquR9Hiv9nwUKfV6nQAcUtFFdh82LRRRSGFZN7YtHultUU7s+ZH0DZ7961qKGrlRk4u6PMLjy9MuDsill0uc8h2y1uwbHCnpg9PatvR9Un08rFKTNZZ+SUZJwxyMjGSSTjNdFcaVYzS+ZLboxyGJ9SOhP0qlqWigF57JQNx3SQn7rkZOR6MT3rLlcdj0XiadVKE0bMEyTxrLEwaNhwR0p/U1xOnam+klmDGa2wN6Dlomxzx2Gcj9eldhZ3cV3AstuwkRhwRVxlfQ4qtB03fddzB8Q2fmrcw4BLr5kWOPmHb6kcVHot6xhhmc4P8Aq5FI644x/WtTWbeWWW3eH+CUbxjPy1hTxtYa81rjEVwdwAyOvPb05pPR3Pn66lRre0S8vv2OwRwyhh0PNPrN0aaRodk2dynAz6dK0K0R61OXNFMwPFE+xB0XaBz0PLAdc8fjWzZMzWsTMHBKDhuo+tc54tVbj7TG27cIk4z8p+bOPbp1re0eNo9Nt45T86oAcnJqF8TO6pFKlF9S6M4pjuFTc3yqvJJp/asPxXqC2dkY/MVZJAQoIzkd6puyOGtUVKDmzntd1L+09Q8i2djghQAcA9c/meOeldR4fsUtLTI6uc8jFc14UsGu783c4c7Rlg/OScjr+uK7kccdqiCvqzzMBCVRyr1N3t6DqKBRWh64UUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFBoATFVryzhvYTHMuQeh9Ks0tFiXFSVmjkdQtEt2WK7LmJCDDMoyYT9euParmm63JHN9n1IxhicRyqflk6fkfrW5cQJPGVdQQfWuYvdNNuXVkLRMRlM8fVcnjn8+lZtOJ5lSFShLmhsdWpBHFLXJ2eoyW1u8Ls0qLgF0PzoTxjB6471oaBfSOjQXUgd0OA3qO3Pc1XMjphi4yai9zcoooqjrFooooGJRilooAbgUwxq/UAke1S0UBcpNYWrKgMCARtuXb8uD3PFVpNA01lH+jqNvTBIxznt71q0YoaKVSS6mBH4dWFz9nvLmLqflb+L1JGM/Q8fnUf9iajHdebDrE23YVKNlsnseSRn6CujwPSjA9KVi1Wl/SOfWTXoEVWhhuTnJYNjjPpxzj0FcX448QSX7W2nXVtJb43SzRDJBHIXJIGOMnp1r1E8dPwryTWrkalc6jetIhLuYbfIwSoIBXoSOBnPHWuevflsmerlfLUrc8orT8yv8ADspcavmaURszliMAcA8EZ6fhXsi9K4jwb4ZsY9NzJGkuQVR9vO09iOQT789u9Xz4aubUD+ytVuIBniNjlRk8nHT07Yp0YuEdULMqtPEV24u1tNf+AdTml5rmd3iS2V3kW3ueQQgXqMHIBznr7HrThr97E8UdzpM6Z4Zk5GcZOD0xjvmtuY8x0H0afodHzS1gL4ssvNKPBdIMhd5jyvQk8j0wavRaxp0qbkvYSoxn5hxnGM+nUdafMiHSkt0aVFVIr60uP9RdRS4/uOG/lVhJFb7pB+lFybMdRRRTEFY+t6HbauMyIBKowHHpnoa2KKTVyoTlTkpRep5pZSX/AIc1V7Z+S2CN2cSIOuAT1+ldvpup2usWuUI+cEFCeaNf0eDWbFrecsrdUlX7yHsRWfoHhtdPCS3hinu4yds23Bx2zWcU46dDur1aOJp809J/mF5CdPhxbiRzAd2CedvtXQwsJIlcdCAaydcc2xt7nO1EfbIPUHp/n3rUicGIOB8pGR9K0R4lKPJOUEYmrlhFfn5VyUGSD6gZB9R29DWvp422EQ9EHbHb0rN1O0U6bciVtqyMG9j82Rj68cetXXuI7fThKMKgQFQT146ZqVvc9CrJKF+3/AMjxbqGy08hXXa52y+wyOCOuD+HHek8KadHHB5xRsjhHfIP0/DpWRah9Y1cB0LR4JO/tzz+FdxbxLFEqIMKowKS953PDoL6zVdaWy0Q9F70+iitD1wooooAKKKKACiiigAooooAKKKKAMnXr+5sLaOSzt/tEryrHswT1yM8dgcfhWrWTr95d2VtDLZRNKftEaSKsRkOwnDcAj8+grXoAKKKKACiiigAooooAKKKKADApCBilooAqXtnFdxlXBVuzqcEfSudkSSG4W3vgylDmG5TjH1I+nOa63FV7m3iniMcqbl9KTRy1sOp6x0Zn6dqOXW1vmAnwCsnRZfdf8K1B1rl9Us/s37qZXez/wCWb/xQt/ez1P0/OptP1aS2lSG9cS27/wCquR0Ps3XGM96XNbcyp4hwl7OodJ9eaPpSIyuAykMD3FOqjuD60mM0tGaCipLY2sjFjAm8gqWAwcdxkc1WXQ7BfuW4Tgr8pIyD6+v41qZoosPnkupjQ+H4bVX+zzzo0hySrkfoMD9KQ2mqwRbYbtJcEk7h82O2Cc89ueK2qAMUWK9rK+pzy3mtQzwxyWccquRuZcjbx0JGeQepxil/t545WW70+5i4XBGG3EnpjrwOfTrW/TdvtU2H7SL3iZg12xCqxmYBhkfIx7kdAM9qlj1fT5cBLqInsCcH8jzVh7G1lGJLeNh9BVW50WwuMedbhgOgyRjnPb35o1GnTfcyvHBSbSYiMEeaBlSPTtTvA6t/Z0hdtxD4HoAOmKo+J9Cs7fTN8G5JPMBDM2ADk8k/T1OOlQeG9CmmsxeWuoXETFWUx8qAcfl1xzjpWXM+fY8b2cHj7qXQ7rmsfxVqL6ZodzcxECUALHnpuJwP55qEDX7fy8SxXQJ/eFkClBjtyM8+1cV4816eea10y/tyNrtM8cYYbl6JnPfBJxzyBVVJ2jqfR4TCOtWjFNNbv0Oe0ZI5dcLNIpEEeY1RsjcemSc9Dxx9RXtGmQ/Z7KJcYJUM3bnvXkXgGWFtd8yaXylZ2+8qquA2R8x7jvj+dezqVcbgQR2xzWOGWjZ353J+0jDsh9FFFdR8+LRRRQMKKM0UAGKKKKAMfUdFhnd54lCTEHOfuyHGBuHeubj1GXQrvCK/lp8ssHQBjz8vbrnkZ4/Ku8rN1nSbXVEC3CfvF+5IOGT6GoceqOuhXUfcqaxJLHULbUIFlt5A4PUDqPqKz/E9rvgju4lzJbNuzjJ29648JfeG9a2uxUOw2OeFdR1AycAn+ldjpGt22o2qrKyRTsPnjY459B3pKal7r0ZGMwN4Nw1i9mM0e4EkscyqWWdM59P8963a57UbX7JF/okbl4jvUk9u4H/1q3bVzJbRuRgsoNXE8vDc0bwlujC1mL/SbyZt+1Y0xjkHkcYrZsm/0OLr90Dnr/SsvWGbyr1U2fcX7/Izkc98YrT004sIN3B8sVK+JnqTd4InkcIhZjgDvXAatcS6zqMkcZZVRwo57Z7fUdeldD4rv9loLZTy5+fkjC+nvn8qh8K6dCifaCmRnK7hzn0+g4xRLV2PAxTliKioR26m1pdjHYwBIwoJA3EZ5xwOpNXqUdKQDFWepCCglGOwooooplhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRS0lAC0yWNZFKuART6DQJq5g6jpys6b1+UfdbG7B+nIrHkSe1uFyvlz9ckDy5enORyDz/SuxmjWSMowyD2rKvbQRxNHNGZrZ+NvdB61DiedXwy+KOhJpOpx3Uex/llXgg961K4m4tpNNuVcsxhbiO6HLJ1+U+3rXQaZqTs6W98nlT87cfdkA7g/wBKE+jDDYhv93U0aNgUUgpas9IKKKKACiiigAooooAKKKKAMTxhfrp2g3UzEhiuxMddx4FecWcV1eTWlrE0Ak2M7eYflZsjgc4PGDzXUfEm6Yww2SuMsR5gKbsAnr6dAe386yPA9lDd6u08cRaJG/dy9Dx3PGOQR3rlqO80j6HBxVHCSqPd6/oj0TToBb2UMWwIyqAQMdfwq5TVHFOrqWiPnpO7bCmsM9VBp1GaBFeS0gkyHhjO7rlBzVSbRtPd2l+zKsjdWXKnPTPFadGKVi1OS2Zjjw/pqLtSDapGNo6dd3T6iqK+EbNH3RXF1DySPKfack5PbPPfvXS4ox7UcqKjWnHZnLJoWrWsL/Y9bleQklfOGQck5znPtjH9aXzvFFlKd8cd/FhRgbVIP8RyD/7LXU4FGKXL5l+3f2kn8jmH8WGDLXulXkCjq5xhfTdnBGcdgam/4S+wTcs6TxuAGC7N2Qe+RkdOetbrIrffAOKryWFo3zPawtjPVfXr2796XK+4KVJ/Evuf+ZmWfizRrt3SO9RHUgESfJjJwOvr27mttGDKGUhlPQisi+8NaVeJtms1Qk5JjJQk9eSOuOoz07VjLoOsaHKx8PXXmWu0BbW5JYBs8kE9Bj0I79aNV5l+zpVPgdn5/wCZ188STRMkihlbgg0irFBCMBVRAT7AVxVj441AatDp+p6I8DueZA+cDt8uCe/rWz471NtM8K38yMqylNiZweT6AkZIGSB1OOAelOMlLYyq4edGSc+q01T/ACPP/HPjzU9QvrjRtCsphChAM0eDJI4IIC9gOnqc0g1jULTTVsr+71KGbcfk1CKPb64DDPPsScZ4rmPhX4Zg8Q3l7fTwyeRbY3ojsvA3bQu3gknk/wB3Bxya2/GqNFZ3UciPLET5X78sfLZgx4bHXPBBzj8KiS10ODFznOmsPHq9z0zwXZyw6Ykt2P378MMEYx04+ldEP0rm/h7Fc2/hOyiup/PkRMCQ4OV6gZHXGcZrphVxVlY1p0404qEegCiiiqNQooooAKKKKACiiigAooooAKKKKAMnW7q8s47Z7O389nuEjcc8Ic5PHp/n0rWrI8R3V9a2Ak0+IPKZVXBjL4Hc4BGMdc5rVX7o9aAHUUUUAFFFFABRRRQAUUUUAFFFFABRRQaAIp40mjKOMg9q5q/0kw5CKrQsR8vUevQ5Cn3FdTTJEDjDDg0mrnNWoRqrXc5Oyu20+OSHczxAHKltrqe4XPXHt+taOg3joWtbmXfjmNyRyPTjvUuoaepILrujHQjqvvWLdRXFs8YJaN15WcY2P0+8MZBz/Oo1R57dXDtX1R2faisfRtVW5QRTNiUfr/Otj2q07nrU6kakeaItFFFMsKKKKACjFFFABSEcUtBoA5f4gSeVoqn1lUdcVP4KVl0SNn3bnYk5PPp/Sq/xEwNCZj/DIuB681f8K4Gh2u37u38+foKz+38jyY/76/Q1+K8l8SXv2zUtQvd5JVmt4CQflxwV6cZwT+Nei+KdQTS9EuLljtO3ao9WPAFeaafBJdyWMEMkKNvLvkHrjK8Eeg6msKzvaJ9llcOXmrPbY6rwNoVommrJJFHIdu1XK/MAc9+mDnI68EelX38HxQgHTb64smXPKOT1x2zjt6Vv2EJgtY42GGVQDj1q1W8YJRSPOq4qpOpKae5zQtvENvu2XUVyA64DoMEc59MYGD3yaX+19WgdI7jTMjgM0b8dOeSABj8q6Siq5TP2qfxRTOZHi6DeqyWN3G3yjlVPLenOeO/FaMevac3/AC8opGMhsgjOOxHvWiYY26qD65HWqsmmWMj7pLWFpOhbYM9MdfpRZ9xc1J/Za+Y231jT7pN0F5C/0cZH19PxqzFPFIP3cquM4+VgefSs8aBp4+5bqiqNoGcgDIPQ5HUZqk/hCxdtyPLGwcyBkIU7j1OQAc++aV2PlpN7tfidJS1zC+HLizWX7DrFzHJI4fLgOB7YPPTA69qSODxJbOcTR3UfACsV+YZ5JOBg44xyKLsfsov4ZL8jqKbzXMf8JDf27s19pE6RDHzK447HOcZ5HGO3WgeM7VRiWyulk2llVQrbvoQcZp8wvq9Tor+htatplvqtm1reLlG6EcFT2IPYisrQfDMOnIv2p0u5omzHMUAcAcDJ70tr4u0aeR0a5MTIFY+apXg9DnGOvHXqK3I3jmQPGwdTyCp4NK0JO4SdWlFwd0mZmvl4Y4rmNiBC4LADOVrTgkE0CSL0YZpzKGUo43KeMeopIY44UxGAqjt2FUlY4lBqbkupl6hbZsL1pG/1vOfYHI4/mO9WoZ4oNNSXaViVMgHr9K8m8ceOtQ1y5udG8P2+YIm2PKkuHk54YHGAvTvnNOTVdQ0nTfsmqy6naTFv+XqWOWIewwCR09eM9qhvlZriq8aVBzvr2OngWXWtYbPzqckh+gIJHT0A9Pzru4YlijVEGAOwrA8EWrw6SslyweVyeQCBtPIxmujFOK6s4MFQdOLnL4pai0UCirPQCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKawBGCKdRQBkX9mArAR+dA4w8X9a5nyZNPP2aRnuLPOYnz8ykdcHtzxjvXeYrJ1XTPOjL264cfwjgGokr7HnYnDcy5oblfSdWIkEF46sMkLP0DexHrW7XEiAlpY2VlONjq3OByc49PfBI71q6ZqhgYQzF23tgA8kD17cURl0ZOHxLVoVPvOjFFIOlLVnphRRRQAUUUUAFJS1Xu5FhgZ5G2qo69/8A9dA0rux5t41vDNfTvGGCxKRuU4ABwvJ9wD/nNbHwutWTR3ndyN5wFwQMdd3PcknpiuR1iX7TK8ZSUfaAi7t/B/hGcduM16n4fsF0/SbeBRghct256muWmuao2fQY1qlhYUur/Q01HFLQOlFdR88FFFFABQaKSgAo7UtFABRRRQAlFJxVG61KCD+MMc7cKQeeuPrigic4wV2y/TPrxWD/AG88n+ogkI74HI7Yx65B7VkXF/ezuwe5jiTk7VyxPcEZH0Hao5kcdTHU4rTU6i71GCKNiVMhAJwB6c965f4hQz634TvbaKJ1dV87CjJO3J4/rxmotPu7+VkMZZ9oOAQAD07Y9e/v9a0LEeIHnDOf3RwCvC7QOD1Gc/SkncwjjJVdk/uPMfCviI6NprSWMstvMG8piFVoXGcDcm7IYZ6gA9yDzmRdM1LxhqkX20MbNJBJOEyM5OTIvJGcZIz3/GvUj4R02aY3U9sq3Mn+skRsGTkEE4xk++M1r6dpVnptuLayto4Yc52qOM07XOpQqPrYmsoIre2jhg/1aj5RnnFWaSirOwWiiigAooooAKKKKACiiigAooooAKKKKAM3WrueyghktoGmLzxxyBELlUY4LYBH51op90Vm65e3NjFbvaWxuDJcJG6r1CHOT+FaVAC0UUUAFFFFABRRRQAGig0UAFFFFABRRRQAUUUUAMZdwKnkGsm8shGjgx+dC/WP0z1IrZprUmrmVSmprU4i7tDprLKoZ7UtxKOZIfQHPRR+tb+mak4xBfFcn/Vyr91wOevrU1/Zbld0TzI3BDw9mzXLNaHT90S7p7KY8RluVbvz2P0qPheh5UufCzvHZndg06ua0vVJbcpDckSwEYWbkEYA4IIyfrXRRuGUMpyD0NaJp7HqUq0aquh9FFFBsFFFFABQelFB6UAct8RP+QCfQyLmtLwzt/sOyKqQDEvU5P596zviJ/yL0o/21/DkVq6CF/se124x5S4x06ds9qhfxH6HlwX+2y9F+ZzfxHvZBbwWkJJZzl8AH5fx6HisHwFZJeao7rErwhVCyZJIC4wQRjk4/wDrVN46u/Ovp3wp8oEKwJ/d9snHPPNX/hTa7bKe4xhnfaPkwCvXr65z/wDXrmvzVT7lfuMBfq/1O+A7mnUUV2HzQUUUUAGBSYHpS0UAGKKKKAEoxS0UAJiqxs7bzRI0Ee8EkPsGQT1OferVGaB3Zk3mg6XeI6z2cbbySWA2tk9TuGD+tYc3hvU9KuGl8MXqxxMObSblN3qOv9OnWuy4pjMq/eIA96hxRrGvOPW67M4SLxZr9vqcNrqeipHGSPNmjbOF9eMgc+proPHGovpvhS/uYiiy+UUQt03NwO49au3OoRxoxiG88+w/Oue8Zi71bw3e2tvbvvMRkAUZ3Y5A5BzzjIwc9KEuXqY1sVSk1yRs/LW55P8ADPw1a+Ita1BpLUtaW+MjdtOwAhVAH8TNySeMA9zmtvxWn9nafNDszbqfIaNgzKrMGyAxOQQfrjv2qh4b1mTRbec2olhuo3EUkkbqOBkAPE2WJGeCQOB14p/9l6n4wu4zckSwIwZ2KABgTy/HVgCcZOaNGcFSUKkk5XVuh6j8Nbaa18IWUVw7vgHy97biEPIGcDI/Cupqrp9tFaWcUNsCIUXCgnOB6c1aq0dyFooooGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFBoAytY0v7YnmQP5Nyv3XH8jWBh5J2gnVobhR/q+oAz95T3B6kV2dZ2q6ZDfxjflHTlHX7ymolHqjgxGGUlzQ3MbTb82chVn3I3ON3B46jPTp0JrpbedLiMPG2VNclLC8UoguAkcwO4MBhZe35+/vSwahc2DblQ+UhzLEU5DY5I6kj6UlKxzUcQ6T5Z7HZCiqtrdxXMe6GRXHfBzirIPFaHrRkpK6FoNFFBQlZHieUx6Y4BC7jjJOMYBb+la5rlfH115emeRwWcNwTjqMA/rUzdom+Gg51YpdzifDFuuqa7bhc4U7jkccHGQT1z81eugYGK80+FemSJfSzTF38pcDPRTjn3zyce1end6yw6tG/c9HN5p11BO6SFHSiiitzxwooozQAUGiigBKKp3eoW9sf30ig9MVkXOuTvujhhZODgkcn164x9aTkluc9TEU6bs3qblxcwW67ppVjHXLHFZk2thlb7LGW7Bm6fX6ViCY3A3sQV6hmOdp9ySPTHT/wCuz9z86mVuBvcqp447sTnkY9cVDn2PPnjZz+DQmuL17jd9pncoV4WPj5hwVAx1qOONpxIbW3dugII4PHHAAGeR9Mc1ZtwQQI9MbYWO2Q/MSwPXA6dK2bG3uFkSR/kyDuTgDrxwO4HehJsiFGdVpyf4GXbaRezQjzpSiMM9MHHpgVZtfDlpC26UvMfVuM+mcc/0reIz1pcVfKjvhg6S1tf1K0FrBAMRRKnXoKs0UUzqUVHRC0UUUFBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBkeIry8sbJX0+ETTPKseCCcA9+PT34rXFZusXN5aW0b2Fs1zI0qqygZwD1PUYArQXkA9PagB1FFFABRRRQAUUUUABooNFABRRQaACiiigAooooAKKKKAEb7tZmp6aLhSYjtfj2B+talJSauZ1IKasziGt2jleHy2VwNuWOTj6HtV/S9TNo3knc6M2FHJOPb/CtfVNOjvkyP3cq/ckXqD/AFrnZY3WZrS6VoZyMqQ/yOM8lT1B7kdKzs07o8idKeGnzL7/ANDsYnDoGXoeafXH2N61m+VJKNjO4k5HPbseO55rprO6juow8Zzn16j8KtSuejQxMaunUtUUgNLVHUFBoooA5f4hBf8AhHpt2fvrjHruFX9HmWPw3ayscbbdW/Sq3jxN3hu69F2sf++hUX2jy/B1ueD5kKqSx4AI71lJ2k35HBQhzY9x7pfmef65MJrxAELrIPLHJOcHqcHn1PHavT/CunppujQQAYcje5xgljyc15p4djXVdft49vyKxLZ6EeuTzycjrmvYEAC+/esqCu3I+tzWfLGFDtq/0Hiiiiuo8EKKKKACiiigAoNFIaAClNVrm6itlZppAgAzz1rNl1sPuW1UMVxyxx156delJuxjOtCG7NgkAcn86z7nWLWEcOr9jtbOD2FYF5czXQ/0mViDlCqHB3dwAB36DNNhilm3fZLZix7tyMfhgZBPTtU83Y4amMk3y00aB1u5l4ggKk8gED8RWbLf3ks7+beJGoHIjXJ7HOCDyOnatCHRrudV+0TMEYAsrD5h0+XjjpVu28O2Mf8ArkMxzn5z75H5UtWZeyxFXdnM2kt+xR7d5XkUknOcYyMjBz/k1pWVt4gmn81pisRIG1iFBGeeOSD9MV08NvDFnyogmeeKmxQoGtPAcvxSfyZgt4W066fzry2RpucyDhj9TgGtSx061sIvKs4EhTrtUYGfWrdLV2PQjTUQooopmgUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSGlooAo6hYw3sJjlHuCOoNc3dR3EMnlTEiTeDEzdz9a7HFQ3FtFOhSVAwPbFRKN9jkr4ZVNVucdaX7WdwxtUEXzgzQ8c8dgec11Omalb6hAkkDYzn5G4b8qw77Ril0WYfu1X5ZcAFQOik+lRaVb3VrcNJZwjbJjzGLA4Ht1PPpSi2tGcNCdWjPlktDsKKq29zHP91vm7qeCPwrz74g/FzR/CjJbWRh1S93EOsco2wcZ+YjJyfT8zWh7Caa0PSSa8/8AiDcNBr+mhZAgkOCepwM547DBzmuNT4z6/q10YtM0rSrJJiEt/t1y2WbbnlhheegyRyRV3xPrJvr23PijSrnw9q0autrI7h7a5IAJUSDAUjORnI9zWdVNx0O7ATjCspVHZanongu3SPTWuEJb7Q5k3EYzz1x2FdFWP4Vge38PWMcgG/ygTt6c8+/rWxVQVopGFefPVk/MKKY8ir97A5xzWdd6zaWsRkaQNj+6etVdI5KlWEFeTsadRzSpGu6Vgo6ZJxXKSeK5p1K2tsxwcE9RjOAc1Vi03V9Sk3TlkA+Uk8ZGMd+eOvTrUOfZXOGWPT0pRcmbupeIrW0iZo2DtnA7DP8A+rp61gz69eXYAXeoYD7i4GT2JPb3+lalh4TiiU/apmlYgA5GfTnJ+lbkFhbwAeXCikADIUdqVpS30MvZYmvrN8q7I4y1sL26WJ/KWRGwe5GcnqT1H45rRttAvGlV5ZQqFi20nkZ6jjg9ua6zHpSY9aFTRtDL6cfibZh2vh20ijVHyzBiQwyDz0z/AJ61qQWVvApEcYAb73fP1qzilAq1FI64UYQ+FDFjVPujH0FPxS0UzayCiiigYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBl67eT2EEEtsgbfcRxyZjZ8ITgkY6H3PFaYFZOv3t1Yw27WEKyu9wiMpBICYOTx6YrXoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApKWkFACHGKp6jp8GoQGO4XPdWH3lPqKu03GOlFiZJSXK1ochPBLaymG5bD/wTHhXx/fHfjjNJFcXWnTExRsm0hnjK8NnuDk5FdTe2kV5CYp03A/pXNXNrPaOEuCxTePKYc8/0rNqx5FbDypPmh9/Y6Kxv4b1N0LqxHUZ5H1FXK4eO8ezvN8R8mXgvGuP3o7cHvjuOtdNpeqQahHvh4OT8p+9/wDqqlK514bFRqe5J6mnSHpQDQao7jB8c/8AIs3nylsqOn+8KxL68it/Btgsaht8eSvQ9CMjPcE1veMoZJtBukjUk7cnHpXB+IFl06HQkmnVXkGFQnDxrnJ+nB9MflWFXRt+RngKbnmUXbS35Ml+FWkyRXck1wdxhBAzj5CeOnPXnmvUe9c94Nt1WwkuFJIuHLfMBn9OoyT1rohVUY8sT08wrOtXlJ+goopAaWtTgCg8UlRT3EUCbpXCj3oE3bckzRnjNYGpeJrWBWFu4eQdz0/Edaw5tZ1C7wiCQhsH5eMHv26en/1qhzSPPq5hSg7LV+R113qlragmaVR9DWPc63NJL5cQ2q3Rume/U9OP5VjWul6hOqYjHQ4JB4P1bqDn/PFaen+HLlX865mMeWDFQc4xxj0wRj/CpcpPZHL7fEV3aMWkVfPadgJipTA6MMj1yOpOeP8AIpsXllWVFkdOGbyxjHfJP4fh9a6KHw/ZJFteIOc53cg/zq7BaRQp5ccYCYx1Jz9aOWT3NY4OpJ3mznbVZmQLb2KCPcQrH5j16kcYyADWrp9jPHIs0jANzuA4GD0GBxxWoFCjgAU6rUbHZSw0YWb1ACjFLRVHUFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACVQms3VzJaybGJJKEZVj7+laFFBMoqW5558R/ENxpGnyLGoguxFvklDkBIidu7OMDLEKMkGvC9C0pNV1afTroQXL3ysYbmaYKLQ4IEh4ORnA259hXYfF2/W78RaiF1F41BEE8W0uoRCoAKcbm3FmA6EflXUfAnwRpcPhaHWLu3jmu7s7zu5EeGOMemRjIpGapyTunoY3/CqvD13YXt3ELu6htbKV/tcm5POkVMLtVcDaCuehJ79qwtH1CXVtM8Cw3F/PNbpc7J7adg5iKbV3Kxz8jI/wB1hgYIHTn2b4kX40/wpd2lsrfaLuGRESIfMECkyMPoufqSB3rxr4b29nc39lczB00/RLYpKCCRJM5YkAYBGTgAD0NDZVRuMeZHq3gm+j0u41iyjlzplvclbKLkmNeSygnjaOMAdFxWldeKMqRbgK3bvnnH4VieHNLkksCVj5uP3x3rhj3wOnc/lXVWOiRRKBNgleQvXBIwfz//AFVF30PLc8TXdoaLuYcr6jqc4SNnQnGCwzxxnpwMfmas2fhTzYt19NIWJPA647ck9a6uONYwAihQKfihRXU2jgIN3qPmZRsdLtrNAIowCMcnr0xV7HHHFLS1a0O+EIwVooQClooplhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFcprlx4wtZbqXTV0Wa1AJhE3mrKOwBxlSc/SgDq6Kit/N8lfP2+bgb9mdue+M9qloAyddvLy0sA9jEs0xkVdrDI2nqeCOnX6dq1E+7796yvEV9eafYrJYW3nzPIqbCCcA9Tx/UgVrdKAFooooAKKKKACiig0AFFFFABRRQaACiiigAooooAKKKKACkpaKACiig0AJTJYklQpIoZT1Bp9FAmjmL7RP9JGAWgUEqQfmi9h3xxVfT7G6t7lZLONcNjzCHwCOOxyR9K6+qVxaFm8yBzHJzyBwTjjNLlW5wSwcVLniOtbtZhtZWRx1VuD9a8/8AiF8XNL8Lu1np7x3+prJtkj3fLCMZO45GT6Af/rsfEnX7rSdIngRRHeeV5jzRkgRx7gpYnBxknaPc14boekRaprDWjSW8320nbJcTYEJIKhg3Jzk5CdSBjvkJM6IVfe5HudzN8X/E2qyiG3h0XS47hxFCblzJyy5Xc2doBHqBgkZ4ya1fEuvXM0tifGejnTpmR/seo2k6yW0r7AwBxkgdwen64bZ/C/w3cpPK1jcXFrFbyGS8uAwMr4I+QAggAjIyGOCQT0xxWjXjaj4c8K2UV7PI9tfvHJC0pkHybAHjJBC/K5wPujZjHqNJrU66dWVGanHSx9B+EYZINBtBLJHI7xhy0eNpzzxj61tD2FcF4UvItO1nW4LVlGmNMklrEi4VGK/NjnABPOAM/jmtC+8USjcsI2ddh253c46nii6ijjr4+mpOUnudVLIsQ3SEKOmTWbe65Z2iNuk37Qe/U+lc666lqsuIy8W8YySTgcZ9MD681bsPCKY3X0pfkjC+meKnmk9kcX1qtWdqMdO7GS+J7u5crZQZUDliOPbnmoYdK1TU5le6YovUnofTjPOMf5zXUWWm21moWCFQRjnHNXqORvdlLBzqO9eTfl0Ob03wtbWxPm5kyMEdj05Pcn9K2orOGIARxKpUYB284q1zRVqKR2U8PSp/BGwgHHSloopnQFFBooELRRRQMKKKKACiiigAooooAKKKKACiiigAooooAKKKKACikOO9ICG6HP0oAdRRXJ3+j69c6mAviqWGIsZBDFZRYVQeBk5J5I69cUAdZRXP2/iTRbSRNPvvEVhLfh/LcPNGju+cY2g8HtiugoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigD5x+IOi/YvHGuQXTGODUgktvcMWCxyM+4ZI4wDkfNgc8Gu38NweP/CdnLYWGg6dqlhLmW0aO9KeQSMneJDuYEnOAcjnk12nizwpY+JbUrcxLHP5ZRZtgY7T1RgeCp9Ox5BBANefHwz8Q9MtRpsGpXNzb9PPhuy3lxqcqoRgHVjxyHPHHAoAxfH2p63JLFZalZSDXNXVYEIH7uzj6sFVcs5I4z0PI5Nb3gPw1/xLLTRYJTNbQsLi5uSCyyy7jlc5wFCnGAc7ic8U7wn4C1ENdS6nEZLq5co9/cORcBCqlmTqM7geoB69M5r0zRtKg0mxjtbUHZH3PU8e3A+goE1fctwwJCgVFCgDHFSgc06ilYFFJWQlFLRTASloooGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBU1CW7jt2+wQxzTk4QSuUQe7EAnH0BrP0+71MX4ttWfT45XQukduXLEAgEgsB0z6Vt1k6wQupaOc9bpkz7GCU4/MCgDVqndjzZoLf8AhLeY/wBF5/8AQsVdqla/vJpp/vbjsX/dXI/9CzQBdHAooooAy9e1CbTrWGeGJ5czpG4RCxCscE4BHStOsrxBfXFhYCWzh86ZpFQKULgA9SQCOAOTz0rUX7oz1xQA6iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKMUUUAfPvxduvtfiLVFYzQxxbUkkRicRqoXG0jDMWcsMEdCOtdB8B/CGinw0mrT28V1eXDncJEyIirNjgjhiDzgnjHvXN/FDS/wCzPHupf2grtZavbBlmbcVhfcAGGDhQCoHzA8/ga6vw1ovjzwnp5j0KHR9WsJ0jaCMyvEYmIy0hVs5z3Ab6Y6UAdp471P8As7w9cQRRvJcXcbwxRxIWONpLHgjGFyevWvD/AIbWHnX9ncXcUkWn6AsjXCsgDSSvk4Kk9Sdq8f3Oorf+IN3r5uotPuLL7Trerxi3V423LaRkhmVVXk8HaSSD14wQa1/A3hJTpsWj2wdraBhJeXTKw+0zBs7cg4KqpxtB+9k+9BFSLlF2N3w3pdxNabmTHn/v3DBs85IAyT/n8a6mz0SCMfvlVumF7A+v17VqwQpEgSMBQoAwBipAKjlSOWng4RfNLVjIoo4kCRqEUcACngcUtLVnYkgooooGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBn3+lWOpN/xMIEuUAwI5RuQe+08Z96q+GINLTTo7rStPt7FLgAukSBfmGQQcAAkHIrarnfCLeS2r6e3Wz1CXaP9iTEy/8Aowj8KAOiqlbfvLqebHGfLU+y9f1J/KprqcW9vJK3IRS35dqZZQmC1jjY5cDLH1Y8k/mTQBBcCB9Qjt5IY2bY0xZlB4BAH05OfwrRrIVt3it19LFD+cjf4Vr0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAGKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKwfFT+U+jzdk1KIE/76ug/VhW9XPeP1kHhW7uIRl7Mx3g/7ZSLIf0U0Aa99K0VnIyffI2p/vE4H6kVJbRCCBIl5CALn1x3qtI4uLq1jjIKAGcn1A4X8yc/hV+gAooooAyfEF/dWENu9nAJ3kuFiZTnhSDk8fStUDFZXiLUZdKs45YIPPkklWFV9znB/OtRPu+/egB1FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAYniTw7p/iK28i/iyeQsqqN6g9QCQeCOCDwa86m8BeMNMiltdJ1ma6tMnygL2WEpGMYjCHIHTghh09DivYKKAPJfCXw8vrW6mm1G3Q3VxIPtF9cP5kpXHJjYfdfPBJHYEGvSdG0q00e2W2so9idWJ6scYyfyrRpMc0ALiiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK5tM2XxAmTpHqmniQD1khfa35rKv5V0lct41b7BLo+tAYXTr1ROR2hlBiYn2BZWP+7mgDav/wB7cWtsP45PMYf7Kc/+hbavdqzrSQT6zfN/z7LHAPqRvP5hk/Kpr+4ktrWSaO2lu3UcQxbdzc9skD8zQBTi/wCRvuf9mwh/WSX/AArYrif7T8Ry67dzWPhfazW8MQN7fxxqu1pDk+XvPO/p7V0GhjWTBIddax80t8i2avtVfdmOWPuAKANaiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACq97bR31pNbTDMc0bRsPUEYNWKKAOV+Hk09zoMUt2jrcQgWL7+CWh+Rz+Lhz9MV1VJS0AFFFFAGdrWoNp0MMqQtKHnSJgqliAxxnArRAxWbrmoS6bFbvDbNcmW4SJlXqqnOW/DFaVABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVT1TT4NU025sLxN8FzE0Ug9VIwauUUAc/4R0q+0fTjDqd4L26aT5pgpXeqqEQkH+Iqqk9s5xXQUUUAN2gEkAZPU+tLS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZmv30un6e88Kozr0DZx+hFaEJLQox6lQaKKAH0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB//2bhK9z8AAAAAxohUxJ9hU22RZEABJg8xfw==" width="237.4047244094488" height="307.15198820722014" preserveAspectRatio="none"/>
</g>
<g transform="translate(3.242362204724386 320.15198820722014)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="15.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="25.119999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="35.739999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="43.019999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g5DAB70659D3EBD6E0CC12EEF6796854" x="56.959999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="66.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="75.97999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="89.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="99.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA335A20E4C1D7F39210005AFF7F1A0EF" x="123.67999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="136.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="146.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="157.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="165.32000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="171.64000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="179.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="189.70000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="198.26000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="204.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="210" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="220.08" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 433.56299212598424)">
<g class="typst-group">
<g>
<g transform="translate(8 18.5)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAA14E57E2DCC57A3F7809273EECD3C51" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="9.344000000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="12.812800000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="18.5344" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="23.296000000000003" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="29.1456" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="33.8048" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="39.2832" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="46.1696" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="49.638400000000004" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="55.116800000000005" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="60.96640000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g1CB3EC9D05726EBFDE8ADABEC8504FCD" x="67.54560000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="76.4928" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD62975B7DE3250BE5F195D0E8335F60D" x="82.3424" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="88.704" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="92.1728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="98.5728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD5EEFB9760BC9A91B84F628EDDA52971" x="104.4224" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="110.7328" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="114.112" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g83A6AA7A836EACB3652229F4716CDAF" x="123.03359999999999" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gDB4862E33098F259EEBBA99A57E5AFA" x="129.2416" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="139.3536" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="145.2032" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="148.5824" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g793DBE65A5AEC1A16A65955B6C0E046" x="155.1616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gA11612CECC8CBEF18835767DAB11B2F7" x="166.3104" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="172.7616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="177.52319999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gCEFEF3D67F35C6E83CC3757B1DD21B13" x="180.90239999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="190.57919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="196.97919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="201.74079999999995" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g645CA8FA3D9155E2CBD9F8EED3C1540D" x="207.59039999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="214.23359999999997" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(798.4017637795276 8)">
<g class="typst-group">
<g>
<g transform="translate(0 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gEF535BAC325E1F03037EDB94EE368989" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" x="11.440000000000001" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.608 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="7.44" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="gF74D1E4498220F56E34936C81B24ED2C" overflow="visible">
<path d="M 2.292 1.464 L 2.292 6.276 C 2.292 7.272 2.496 7.3320003 3.336 7.368 C 3.408 7.44 3.408 7.692 3.336 7.764 C 2.808 7.752 2.244 7.7400002 1.776 7.7400002 C 1.38 7.7400002 0.792 7.752 0.228 7.764 C 0.156 7.692 0.156 7.44 0.228 7.368 C 1.068 7.3320003 1.272 7.272 1.272 6.276 L 1.272 1.464 C 1.272 0.468 1.068 0.408 0.228 0.372 C 0.156 0.3 0.156 0.048 0.228 -0.024 C 0.768 -0.012 1.3560001 0 1.788 0 C 2.22 0 2.796 -0.012 3.336 -0.024 C 3.408 0.048 3.408 0.3 3.336 0.372 C 2.496 0.408 2.292 0.468 2.292 1.464 Z "/>
</symbol>
<symbol id="g46E28FC12585DA626130081849FE40B4" overflow="visible">
<path d="M 1.86 1.464 L 1.86 3.744 C 1.86 4.3320003 2.016 4.224 2.292 3.876 L 5.112 0.120000005 C 5.292 -0.072 5.484 -0.144 5.664 -0.144 C 5.808 -0.144 5.928 -0.060000002 5.928 0.18 L 5.928 4.056 C 5.928 5.052 6.06 5.088 6.7920003 5.1480002 C 6.864 5.2200003 6.864 5.472 6.7920003 5.544 C 6.432 5.532 6 5.52 5.64 5.52 C 5.28 5.52 4.86 5.532 4.5 5.544 C 4.428 5.472 4.428 5.2200003 4.5 5.1480002 C 5.232 5.1 5.364 5.052 5.364 4.056 L 5.364 1.812 C 5.364 1.488 5.328 1.284 4.956 1.788 L 2.208 5.52 L 0.504 5.544 L 0.48000002 5.508 L 0.48000002 5.2200003 C 0.48000002 5.172 0.552 5.1480002 0.588 5.1480002 C 1.044 5.112 1.176 4.968 1.296 4.752 L 1.296 1.464 C 1.296 0.468 1.164 0.42000002 0.432 0.372 C 0.36 0.3 0.36 0.048 0.432 -0.024 C 0.792 -0.012 1.212 0 1.572 0 C 1.932 0 2.364 -0.012 2.724 -0.024 C 2.796 0.048 2.796 0.3 2.724 0.372 C 1.992 0.432 1.86 0.468 1.86 1.464 Z "/>
</symbol>
<symbol id="gA2769E14ED9B16297025579DD26D23A1" overflow="visible">
<path d="M 3.648 1.464 L 3.648 4.488 C 3.648 4.932 3.7680001 5.112 4.152 5.112 L 4.464 5.112 C 5.2200003 5.112 5.376 4.872 5.616 4.008 C 5.736 3.984 5.844 3.984 5.94 4.044 C 5.88 4.632 5.868 5.076 5.844 5.64 C 5.4240003 5.592 4.656 5.52 3.648 5.52 L 2.7 5.52 C 1.524 5.52 0.828 5.58 0.504 5.64 C 0.504 5.076 0.492 4.608 0.42000002 4.044 C 0.528 4.008 0.636 3.996 0.744 4.008 C 0.984 4.872 1.116 5.112 1.896 5.112 L 2.184 5.112 C 2.556 5.112 2.7 4.968 2.7 4.5 L 2.7 1.464 C 2.7 0.468 2.568 0.432 1.836 0.372 C 1.764 0.3 1.764 0.048 1.836 -0.024 C 2.28 -0.012 2.772 0 3.18 0 C 3.6000001 0 4.068 -0.012 4.512 -0.024 C 4.584 0.048 4.584 0.3 4.512 0.372 C 3.78 0.42000002 3.648 0.468 3.648 1.464 Z "/>
</symbol>
<symbol id="g48BCA4F06942DA5990D42018985FC781" overflow="visible">
<path d="M 2.292 1.464 L 2.292 2.5080001 L 2.9520001 2.5080001 C 3.408 2.5080001 3.576 2.112 3.732 1.668 L 3.996 0.948 C 4.272 0.204 4.68 -0.084 5.196 -0.084 C 5.376 -0.084 5.748 -0.048 5.952 0 C 5.988 0.120000005 5.964 0.24000001 5.88 0.336 C 5.448 0.336 5.2200003 0.408 4.98 1.0320001 L 4.632 1.932 C 4.488 2.304 4.344 2.5080001 4.188 2.664 L 4.188 2.688 C 4.596 2.832 5.208 3.3240001 5.208 4.152 C 5.208 5.1480002 4.584 5.568 3.1560001 5.568 C 2.856 5.568 2.172 5.52 1.812 5.52 C 1.464 5.52 0.96000004 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.212 0.432 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 0.936 -0.012 1.428 0 1.824 0 C 2.196 0 2.592 -0.012 2.976 -0.024 C 3.048 0.048 3.048 0.3 2.976 0.372 C 2.412 0.408 2.292 0.468 2.292 1.464 Z M 4.164 4.152 C 4.164 3.204 3.888 2.856 2.82 2.856 L 2.292 2.856 L 2.292 4.416 C 2.292 5.052 2.412 5.172 3.084 5.172 C 3.924 5.172 4.164 4.872 4.164 4.152 Z "/>
</symbol>
<symbol id="g4C6038BE04CA3E1481E54A97A0E34303" overflow="visible">
<path d="M 6.324 2.82 C 6.324 4.524 4.956 5.64 3.3960001 5.64 C 1.728 5.64 0.444 4.428 0.444 2.664 C 0.444 1.0320001 1.6800001 -0.120000005 3.3 -0.120000005 C 5.268 -0.120000005 6.324 1.26 6.324 2.82 Z M 3.288 5.244 C 4.356 5.244 5.28 4.26 5.28 2.652 C 5.28 1.176 4.548 0.276 3.48 0.276 C 2.316 0.276 1.488 1.332 1.488 2.808 C 1.488 4.428 2.388 5.244 3.288 5.244 Z "/>
</symbol>
<symbol id="gE1B486BBD379D5D210F28624A61384AE" overflow="visible">
<path d="M 1.776 5.52 C 1.452 5.52 0.912 5.532 0.444 5.544 C 0.372 5.472 0.372 5.2200003 0.444 5.1480002 C 1.176 5.1 1.308 5.052 1.308 4.056 L 1.308 1.464 C 1.308 0.468 1.176 0.432 0.444 0.372 C 0.372 0.3 0.372 0.048 0.444 -0.024 C 0.90000004 -0.012 1.44 0 1.788 0 C 2.1 0 2.58 -0.024 3.54 -0.024 C 4.872 -0.024 6.36 0.6 6.36 2.7 C 6.36 4.296 5.376 5.544 3.372 5.544 C 2.556 5.544 2.124 5.52 1.776 5.52 Z M 2.256 0.912 L 2.256 4.776 C 2.256 5.076 2.556 5.1480002 3.024 5.1480002 C 5.04 5.1480002 5.316 3.744 5.316 2.496 C 5.316 0.816 4.572 0.372 3.252 0.372 C 2.34 0.372 2.256 0.576 2.256 0.912 Z "/>
</symbol>
<symbol id="g9FB16590C6D64699AE0CE54876927A05" overflow="visible">
<path d="M 5.2200003 4.056 L 5.2200003 2.532 C 5.2200003 1.5 5.2200003 0.372 3.636 0.372 C 2.448 0.372 2.196 1.308 2.196 2.424 L 2.196 4.056 C 2.196 5.052 2.328 5.088 3.06 5.1480002 C 3.132 5.2200003 3.132 5.472 3.06 5.544 C 2.592 5.532 2.112 5.52 1.716 5.52 C 1.284 5.52 0.816 5.532 0.384 5.544 C 0.312 5.472 0.312 5.2200003 0.384 5.1480002 C 1.116 5.1 1.248 5.052 1.248 4.056 L 1.248 2.172 C 1.248 0.372 2.124 -0.120000005 3.432 -0.120000005 C 5.292 -0.120000005 5.784 0.936 5.784 2.688 L 5.784 4.056 C 5.784 5.052 5.916 5.088 6.6480002 5.1480002 C 6.7200003 5.2200003 6.7200003 5.472 6.6480002 5.544 C 6.288 5.532 5.856 5.52 5.496 5.52 C 5.136 5.52 4.716 5.532 4.356 5.544 C 4.284 5.472 4.284 5.2200003 4.356 5.1480002 C 5.088 5.1 5.2200003 5.052 5.2200003 4.056 Z "/>
</symbol>
<symbol id="g6799D348D26A0968EEDA80A0E5D50B73" overflow="visible">
<path d="M 3.312 -0.120000005 C 4.248 -0.120000005 4.824 0.228 5.388 0.984 C 5.364 1.068 5.244 1.2 5.1480002 1.224 C 4.596 0.576 4.176 0.336 3.372 0.336 C 2.184 0.336 1.488 1.62 1.488 2.808 C 1.488 4.824 2.424 5.244 3.3240001 5.244 C 4.284 5.244 4.848 4.716 4.992 3.876 C 5.112 3.8400002 5.232 3.8400002 5.352 3.912 C 5.352 4.404 5.328 4.908 5.208 5.448 C 4.752 5.448 4.212 5.64 3.252 5.64 C 1.668 5.64 0.444 4.44 0.444 2.688 C 0.444 1.932 0.684 1.104 1.272 0.564 C 1.752 0.120000005 2.424 -0.120000005 3.312 -0.120000005 Z "/>
</symbol>
<symbol id="g45E4C10E27056C5AE488FE2D8290DF06" overflow="visible">
<path d="M 2.34 4.056 C 2.34 5.052 2.4720001 5.088 3.204 5.1480002 C 3.276 5.2200003 3.276 5.472 3.204 5.544 C 2.748 5.532 2.232 5.52 1.86 5.52 C 1.5 5.52 0.996 5.532 0.528 5.544 C 0.456 5.472 0.456 5.2200003 0.528 5.1480002 C 1.26 5.1 1.392 5.052 1.392 4.056 L 1.392 1.464 C 1.392 0.468 1.26 0.432 0.528 0.372 C 0.456 0.3 0.456 0.048 0.528 -0.024 C 0.972 -0.012 1.464 0 1.872 0 C 2.256 0 2.784 -0.012 3.204 -0.024 C 3.276 0.048 3.276 0.3 3.204 0.372 C 2.4720001 0.42000002 2.34 0.468 2.34 1.464 Z "/>
</symbol>
<symbol id="gD77922058D8F1A3A631DDE5946887BDC" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z M 3.384 5.112 C 4.764 5.112 5.88 4.008 5.88 2.628 C 5.88 1.248 4.752 0.132 3.384 0.132 C 2.004 0.132 0.90000004 1.248 0.90000004 2.628 C 0.90000004 3.996 2.004 5.112 3.384 5.112 Z "/>
</symbol>
<symbol id="g5ABA589ED074A65FC8C929AB4EB2344C" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z "/>
</symbol>
<symbol id="g6F0940D406D545443F0C3F5AB20F1452" overflow="visible">
<path d="M 1.55 0.78999996 L 2.1 2.24 C 2.1499999 2.37 2.21 2.4099998 2.45 2.4099998 L 4.56 2.4099998 L 5.14 0.71999997 C 5.2599998 0.38 4.88 0.34 4.4 0.31 C 4.3399997 0.25 4.3399997 0.04 4.4 -0.02 C 4.77 -0.01 5.3199997 0 5.71 0 C 6.12 0 6.5 -0.01 6.85 -0.02 C 6.91 0.04 6.91 0.25 6.85 0.31 C 6.46 0.35 6.12 0.38 5.95 0.85999995 L 3.8899999 6.58 C 3.74 6.49 3.47 6.3799996 3.34 6.3799996 L 1.0699999 1.02 C 0.81 0.39999998 0.51 0.34 0.07 0.31 C 0.01 0.25 0.01 0.04 0.07 -0.02 C 0.32999998 -0.01 0.65999997 0 0.96 0 C 1.37 0 1.87 -0.01 2.24 -0.02 C 2.3 0.04 2.3 0.25 2.24 0.31 C 1.86 0.34 1.39 0.38 1.55 0.78999996 Z M 2.6299999 2.83 C 2.4099998 2.83 2.34 2.86 2.3799999 2.96 L 3.3999999 5.5499997 L 3.46 5.5499997 L 4.4 2.83 Z "/>
</symbol>
<symbol id="g6D72A0AB4EFB019D977FFECF4A1600A9" overflow="visible">
<path d="M 3.79 0 C 3.79 0 4.02 0.96 4.0899997 1.38 C 4 1.43 3.9199998 1.4499999 3.81 1.42 C 3.6499999 0.83 3.36 0.34 2.73 0.34 L 2.28 0.34 C 2.05 0.34 1.91 0.5 1.91 0.69 L 1.91 3.3799999 C 1.91 4.21 2.02 4.24 2.6299999 4.29 C 2.69 4.35 2.69 4.56 2.6299999 4.62 C 2.26 4.61 1.8499999 4.6 1.51 4.6 C 1.1999999 4.6 0.77 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.1 0.34 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.89 -0.01 1.55 0 1.55 0 Z "/>
</symbol>
<symbol id="g7035BD9A81EA6DB089327941BB80DFF8" overflow="visible">
<path d="M 4.72 0.90999997 C 4.72 1.74 4.7799997 1.77 5.0899997 1.8199999 C 5.15 1.88 5.15 2.09 5.0899997 2.1499999 C 4.91 2.1399999 4.63 2.1299999 4.3199997 2.1299999 C 4.02 2.1299999 3.56 2.1399999 3.27 2.1499999 C 3.21 2.09 3.21 1.88 3.27 1.8199999 C 3.8799999 1.78 3.9299998 1.74 3.9299998 0.90999997 L 3.9299998 0.37 C 3.61 0.28 3.28 0.22999999 2.9299998 0.22999999 C 1.68 0.22999999 1.27 1.51 1.27 2.33 C 1.27 3.54 1.8499999 4.37 2.81 4.37 C 3.8 4.37 4.22 3.87 4.37 3.23 C 4.47 3.1999998 4.5699997 3.1999998 4.67 3.26 C 4.66 3.6699998 4.63 4.0899997 4.54 4.54 C 4.24 4.54 3.5 4.7 2.9399998 4.7 C 1.51 4.7 0.37 3.78 0.37 2.2 C 0.37 0.93 1.3199999 -0.099999994 2.75 -0.099999994 C 3.4299998 -0.099999994 4.17 0 4.83 0.35999998 C 4.7599998 0.42999998 4.72 0.52 4.72 0.59 Z "/>
</symbol>
<symbol id="g7FD6A8241485CEBC032BD9E4CE659816" overflow="visible">
<path d="M 5.27 2.35 C 5.27 3.77 4.13 4.7 2.83 4.7 C 1.4399999 4.7 0.37 3.6899998 0.37 2.22 C 0.37 0.85999995 1.4 -0.099999994 2.75 -0.099999994 C 4.39 -0.099999994 5.27 1.05 5.27 2.35 Z M 2.74 4.37 C 3.6299999 4.37 4.4 3.55 4.4 2.21 C 4.4 0.97999996 3.79 0.22999999 2.8999999 0.22999999 C 1.93 0.22999999 1.24 1.11 1.24 2.34 C 1.24 3.6899998 1.99 4.37 2.74 4.37 Z "/>
</symbol>
<symbol id="gFAD9169AC3141E7FC4EA568E3BBD2E9B" overflow="visible">
<path d="M 1.91 1.22 L 1.91 2.09 L 2.46 2.09 C 2.84 2.09 2.98 1.76 3.11 1.39 L 3.33 0.78999996 C 3.56 0.17 3.8999999 -0.07 4.33 -0.07 C 4.48 -0.07 4.79 -0.04 4.96 0 C 4.99 0.099999994 4.97 0.19999999 4.9 0.28 C 4.54 0.28 4.35 0.34 4.15 0.85999995 L 3.86 1.61 C 3.74 1.92 3.62 2.09 3.49 2.22 L 3.49 2.24 C 3.83 2.36 4.3399997 2.77 4.3399997 3.46 C 4.3399997 4.29 3.82 4.64 2.6299999 4.64 C 2.3799999 4.64 1.81 4.6 1.51 4.6 C 1.22 4.6 0.79999995 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.78 -0.01 1.1899999 0 1.52 0 C 1.8299999 0 2.1599998 -0.01 2.48 -0.02 C 2.54 0.04 2.54 0.25 2.48 0.31 C 2.01 0.34 1.91 0.39 1.91 1.22 Z M 3.47 3.46 C 3.47 2.6699998 3.24 2.3799999 2.35 2.3799999 L 1.91 2.3799999 L 1.91 3.6799998 C 1.91 4.21 2.01 4.31 2.57 4.31 C 3.27 4.31 3.47 4.06 3.47 3.46 Z "/>
</symbol>
<symbol id="g5503E15E5E4E70E9E217A15BD1ECD752" overflow="visible">
<path d="M 1.9499999 3.3799999 C 1.9499999 4.21 2.06 4.24 2.6699998 4.29 C 2.73 4.35 2.73 4.56 2.6699998 4.62 C 2.29 4.61 1.86 4.6 1.55 4.6 C 1.25 4.6 0.83 4.61 0.44 4.62 C 0.38 4.56 0.38 4.35 0.44 4.29 C 1.05 4.25 1.16 4.21 1.16 3.3799999 L 1.16 1.22 C 1.16 0.39 1.05 0.35999998 0.44 0.31 C 0.38 0.25 0.38 0.04 0.44 -0.02 C 0.81 -0.01 1.22 0 1.56 0 C 1.88 0 2.32 -0.01 2.6699998 -0.02 C 2.73 0.04 2.73 0.25 2.6699998 0.31 C 2.06 0.35 1.9499999 0.39 1.9499999 1.22 Z "/>
</symbol>
<symbol id="gA419F36517085793EDBF3FE4736A2E59" overflow="visible">
<path d="M 3.04 1.22 L 3.04 3.74 C 3.04 4.11 3.1399999 4.2599998 3.46 4.2599998 L 3.72 4.2599998 C 4.35 4.2599998 4.48 4.06 4.68 3.34 C 4.7799997 3.32 4.87 3.32 4.95 3.37 C 4.9 3.86 4.89 4.23 4.87 4.7 C 4.52 4.66 3.8799999 4.6 3.04 4.6 L 2.25 4.6 C 1.27 4.6 0.69 4.65 0.42 4.7 C 0.42 4.23 0.41 3.84 0.35 3.37 C 0.44 3.34 0.53 3.33 0.62 3.34 C 0.82 4.06 0.93 4.2599998 1.5799999 4.2599998 L 1.8199999 4.2599998 C 2.1299999 4.2599998 2.25 4.14 2.25 3.75 L 2.25 1.22 C 2.25 0.39 2.1399999 0.35999998 1.53 0.31 C 1.4699999 0.25 1.4699999 0.04 1.53 -0.02 C 1.9 -0.01 2.31 0 2.6499999 0 C 3 0 3.3899999 -0.01 3.76 -0.02 C 3.82 0.04 3.82 0.25 3.76 0.31 C 3.1499999 0.35 3.04 0.39 3.04 1.22 Z "/>
</symbol>
<symbol id="gFF65128B49BB3276E17D04989ECB7ACE" overflow="visible">
<path d="M 5 3.3799999 C 5 4.21 5.1099997 4.24 5.72 4.29 C 5.7799997 4.35 5.7799997 4.56 5.72 4.62 C 5.37 4.6 4.93 4.6 4.6 4.6 C 4.3199997 4.6 3.8799999 4.61 3.49 4.62 C 3.4299998 4.56 3.4299998 4.35 3.49 4.29 C 4.1 4.25 4.21 4.21 4.21 3.3799999 L 4.21 2.52 L 1.9 2.52 L 1.9 3.3799999 C 1.9 4.21 2.01 4.24 2.62 4.29 C 2.6799998 4.35 2.6799998 4.56 2.62 4.62 C 2.24 4.61 1.8199999 4.6 1.5 4.6 C 1.1999999 4.6 0.78999996 4.61 0.39 4.62 C 0.32999998 4.56 0.32999998 4.35 0.39 4.29 C 1 4.25 1.11 4.21 1.11 3.3799999 L 1.11 1.22 C 1.11 0.39 1 0.35999998 0.39 0.31 C 0.32999998 0.25 0.32999998 0.04 0.39 -0.02 C 0.78999996 -0.01 1.1899999 0 1.51 0 C 1.8299999 0 2.23 -0.01 2.62 -0.02 C 2.6799998 0.04 2.6799998 0.25 2.62 0.31 C 2.01 0.35 1.9 0.39 1.9 1.22 L 1.9 2.19 L 4.21 2.19 L 4.21 1.22 C 4.21 0.39 4.1 0.35999998 3.49 0.31 C 3.4299998 0.25 3.4299998 0.04 3.49 -0.02 C 3.86 -0.01 4.2599998 0 4.61 0 C 4.91 0 5.33 -0.01 5.72 -0.02 C 5.7799997 0.04 5.7799997 0.25 5.72 0.31 C 5.1099997 0.35 5 0.39 5 1.22 Z "/>
</symbol>
<symbol id="gEDADDD9BA25BBB833C1F4B684DC50419" overflow="visible">
<path d="M 4.83 3.82 L 4.9 3.82 L 5.0299997 1.23 C 5.0699997 0.39999998 5.06 0.35999998 4.52 0.31 C 4.46 0.25 4.46 0.04 4.52 -0.02 C 4.87 -0.01 5.24 0 5.52 0 C 5.8199997 0 6.1099997 -0.01 6.3799996 -0.02 C 6.44 0.04 6.44 0.25 6.3799996 0.31 C 5.87 0.35999998 5.8599997 0.42 5.7999997 1.23 L 5.6 3.81 C 5.5699997 4.21 5.66 4.25 6.16 4.29 C 6.22 4.35 6.22 4.56 6.16 4.62 L 4.81 4.6 L 3.31 1.02 L 2.03 4.6 L 0.64 4.62 C 0.58 4.56 0.58 4.35 0.64 4.29 C 1.13 4.2599998 1.22 4.21 1.1999999 4.02 L 0.88 1.2099999 C 0.78999996 0.38 0.65999997 0.34 0.28 0.31 C 0.22 0.25 0.22 0.04 0.28 -0.02 C 0.48 -0.01 0.78 0 0.94 0 C 1.14 0 1.51 -0.01 1.7099999 -0.02 C 1.77 0.04 1.77 0.25 1.7099999 0.31 C 1.14 0.35 1.15 0.47 1.23 1.2099999 L 1.52 3.75 L 1.54 3.75 L 2.96 -0.04 C 2.98 -0.089999996 3.03 -0.12 3.08 -0.12 C 3.12 -0.12 3.1699998 -0.089999996 3.1899998 -0.04 Z "/>
</symbol>
<symbol id="g1E8994F5C297EC73FA26D93D22635023" overflow="visible">
<path d="M 2.82 -0.14999999 C 4.11 -0.14999999 5.16 0.9 5.16 2.19 C 5.16 3.48 4.11 4.52 2.82 4.52 C 1.53 4.52 0.48999998 3.48 0.48999998 2.19 C 0.48999998 0.9 1.53 -0.14999999 2.82 -0.14999999 Z M 2.82 4.2599998 C 3.97 4.2599998 4.9 3.34 4.9 2.19 C 4.9 1.04 3.9599998 0.11 2.82 0.11 C 1.67 0.11 0.75 1.04 0.75 2.19 C 0.75 3.33 1.67 4.2599998 2.82 4.2599998 Z "/>
</symbol>
<symbol id="g5396A27CA60B9808846A090320835A9F" overflow="visible">
<path d="M 1.91 1.22 L 1.91 5.23 C 1.91 6.06 2.08 6.1099997 2.78 6.14 C 2.84 6.2 2.84 6.41 2.78 6.47 C 2.34 6.46 1.87 6.45 1.48 6.45 C 1.15 6.45 0.65999997 6.46 0.19 6.47 C 0.13 6.41 0.13 6.2 0.19 6.14 C 0.89 6.1099997 1.06 6.06 1.06 5.23 L 1.06 1.22 C 1.06 0.39 0.89 0.34 0.19 0.31 C 0.13 0.25 0.13 0.04 0.19 -0.02 C 0.64 -0.01 1.13 0 1.49 0 C 1.8499999 0 2.33 -0.01 2.78 -0.02 C 2.84 0.04 2.84 0.25 2.78 0.31 C 2.08 0.34 1.91 0.39 1.91 1.22 Z "/>
</symbol>
<symbol id="g97A8E46F7A64F11D13C6F357868587EE" overflow="visible">
<path d="M 1.89 1.22 L 1.89 1.9599999 C 2.07 1.88 2.27 1.8399999 2.52 1.8399999 C 3.86 1.8399999 4.27 2.8 4.27 3.3999999 C 4.27 3.9199998 3.97 4.62 2.55 4.62 C 2.18 4.62 1.76 4.6 1.49 4.6 C 1.1999999 4.6 0.78 4.61 0.38 4.62 C 0.32 4.56 0.32 4.35 0.38 4.29 C 0.98999995 4.25 1.1 4.21 1.1 3.3799999 L 1.1 1.22 C 1.1 0.39 0.98999995 0.35999998 0.38 0.31 C 0.32 0.25 0.32 0.04 0.38 -0.02 C 0.71 -0.01 1.06 0 1.5 0 C 1.93 0 2.28 -0.01 2.61 -0.02 C 2.6699998 0.04 2.6699998 0.25 2.61 0.31 C 2 0.35 1.89 0.39 1.89 1.22 Z M 1.89 3.84 C 1.89 4.16 2.01 4.29 2.49 4.29 C 3.08 4.29 3.3999999 3.98 3.3999999 3.28 C 3.3999999 2.56 3.1399999 2.1699998 2.54 2.1699998 C 2.34 2.1699998 2.09 2.2 1.89 2.28 Z "/>
</symbol>
<symbol id="gB844DCFB76B4CC44608DB013C9764E9C" overflow="visible">
<path d="M 1.8299999 3.62 C 1.5899999 4.19 1.5999999 4.24 2.1399999 4.29 C 2.2 4.35 2.2 4.56 2.1399999 4.62 C 1.8299999 4.61 1.49 4.6 1.0799999 4.6 C 0.76 4.6 0.45999998 4.61 0.19999999 4.62 C 0.14 4.56 0.14 4.35 0.19999999 4.29 C 0.69 4.24 0.76 4.13 1 3.56 L 2.4199998 0.28 C 2.55 -0.01 2.6 -0.12 2.71 -0.12 C 2.78 -0.12 2.82 -0.04 2.96 0.28 L 4.42 3.55 C 4.63 4.0099998 4.74 4.25 5.2799997 4.29 C 5.3399997 4.35 5.3399997 4.56 5.2799997 4.62 C 5.06 4.61 4.8199997 4.6 4.56 4.6 C 4.19 4.6 3.9099998 4.61 3.6399999 4.62 C 3.58 4.56 3.58 4.35 3.6399999 4.29 C 4.18 4.25 4.23 4.13 4.0299997 3.62 L 2.9399998 1.13 C 2.9099998 1.1 2.8999999 1.1 2.87 1.13 Z "/>
</symbol>
<symbol id="gDAA1267270512376F631C9A10449D5F4" overflow="visible">
<path d="M 2.48 2.25 C 3.1399999 2.25 3.1499999 2.06 3.1699998 1.6899999 C 3.22 1.64 3.3999999 1.64 3.4499998 1.6899999 C 3.4399998 1.92 3.4299998 2.26 3.4299998 2.4199998 C 3.4299998 2.56 3.4399998 2.8799999 3.4499998 3.1299999 C 3.3999999 3.1799998 3.22 3.1799998 3.1699998 3.1299999 C 3.1499999 2.6799998 3.1299999 2.57 2.48 2.57 L 1.91 2.57 L 1.91 3.99 C 1.91 4.16 2.04 4.27 2.23 4.27 L 2.8 4.27 C 3.62 4.27 3.75 3.9399998 3.9299998 3.37 C 4.0299997 3.36 4.12 3.3799999 4.2 3.4199998 C 4.16 3.76 4.04 4.54 4.02 4.61 C 4.02 4.63 4.0099998 4.64 3.99 4.64 C 3.85 4.61 3.75 4.6 3.58 4.6 L 1.51 4.6 C 1.22 4.6 0.76 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.76 -0.01 1.1999999 0 1.52 0 L 3.06 0 C 3.46 0 4.12 -0.02 4.12 -0.02 C 4.24 0.39 4.35 0.94 4.42 1.36 C 4.33 1.41 4.25 1.43 4.14 1.4 C 3.98 0.81 3.6899998 0.31 2.86 0.31 L 2.4299998 0.31 C 2.01 0.31 1.91 0.42 1.91 0.75 L 1.91 2.25 Z "/>
</symbol>
<symbol id="gEEE4EC0F13100E99C1017169F912BE3E" overflow="visible">
<path d="M 1.55 1.22 L 1.55 3.12 C 1.55 3.61 1.68 3.52 1.91 3.23 L 4.2599998 0.099999994 C 4.41 -0.06 4.5699997 -0.12 4.72 -0.12 C 4.8399997 -0.12 4.94 -0.049999997 4.94 0.14999999 L 4.94 3.3799999 C 4.94 4.21 5.0499997 4.24 5.66 4.29 C 5.72 4.35 5.72 4.56 5.66 4.62 C 5.3599997 4.61 5 4.6 4.7 4.6 C 4.4 4.6 4.0499997 4.61 3.75 4.62 C 3.6899998 4.56 3.6899998 4.35 3.75 4.29 C 4.36 4.25 4.47 4.21 4.47 3.3799999 L 4.47 1.51 C 4.47 1.24 4.44 1.0699999 4.13 1.49 L 1.8399999 4.6 L 0.42 4.62 L 0.39999998 4.5899997 L 0.39999998 4.35 C 0.39999998 4.31 0.45999998 4.29 0.48999998 4.29 C 0.87 4.2599998 0.97999996 4.14 1.0799999 3.9599998 L 1.0799999 1.22 C 1.0799999 0.39 0.96999997 0.35 0.35999998 0.31 C 0.29999998 0.25 0.29999998 0.04 0.35999998 -0.02 C 0.65999997 -0.01 1.01 0 1.31 0 C 1.61 0 1.9699999 -0.01 2.27 -0.02 C 2.33 0.04 2.33 0.25 2.27 0.31 C 1.66 0.35999998 1.55 0.39 1.55 1.22 Z "/>
</symbol>
<symbol id="g14F95E5F274105B73EC9103738D4C7FD" overflow="visible">
<path d="M 15.144 0 C 15.144 0 15.024 1.704 15.024 2.448 L 15.024 12.288 C 15.024 14.424 15.432 14.544 17.112 14.712 C 17.256 14.856 17.256 15.384 17.112 15.528 C 15.936 15.504 15.528 15.4800005 14.52 15.4800005 C 13.440001 15.4800005 12.936 15.504 11.736 15.528 C 11.592 15.384 11.592 14.856 11.736 14.712 C 13.416 14.544 13.824 14.472 13.824 12.288 L 13.824 5.544 C 13.824 4.9440002 13.512 5.064 13.176 5.472 L 6.816 12.96 L 4.68 15.4800005 L 0.768 15.528 C 0.624 15.384 0.624 14.856 0.768 14.712 C 1.8000001 14.64 2.52 13.824 2.664 13.2 L 2.664 3.192 C 2.664 1.056 2.256 0.936 0.576 0.768 C 0.432 0.624 0.432 0.096 0.576 -0.048 C 1.752 -0.024 2.208 0 3.264 0 C 4.32 0 4.752 -0.024 5.952 -0.048 C 6.096 0.096 6.096 0.624 5.952 0.768 C 4.272 0.936 3.864 1.008 3.864 3.192 L 3.864 10.32 C 3.864 10.56 3.912 10.8 4.056 10.8 C 4.176 10.8 4.368 10.632 4.632 10.32 L 12.672 0.768 C 13.152 0.168 13.632 -0.288 13.632 -0.288 C 14.472 -0.288 14.712 -0.216 15.144 0 Z "/>
</symbol>
<symbol id="gFC5C8D23DE5E426807758A924FDBA2FC" overflow="visible">
<path d="M 10.104 15.144 C 8.784 15.336 8.28 15.792 6.048 15.792 C 4.968 15.792 3.552 15.456 2.544 14.64 C 1.656 13.92 0.984 12.816 0.984 11.64 C 0.984 10.728 1.224 9.576 1.776 8.856 C 2.88 7.368 4.872 6.552 5.9040003 5.8320003 C 7.008 5.064 8.088 4.104 8.088 2.76 C 8.088 1.584 7.056 0.768 5.592 0.768 C 3.984 0.768 2.328 2.088 1.848 4.272 C 1.464 4.416 1.08 4.32 0.72 4.224 C 0.696 4.224 0.672 4.2 0.648 4.2 C 0.648 2.4 0.84000003 1.128 1.104 0.24000001 C 2.4720001 0.24000001 2.544 -0.24000001 5.856 -0.24000001 C 7.32 -0.24000001 8.496 0.192 9.4800005 1.08 C 10.344 1.824 11.112 2.928 11.112 4.416 C 11.112 5.664 10.584 6.504 9.864 7.296 C 8.928 8.328 7.584 9.0720005 6.6480002 9.552 C 5.688 10.032001 3.984 11.28 3.984 12.648 C 3.984 13.992001 4.8 14.808001 6.024 14.808001 C 8.064 14.808001 8.736 12.96 9.168 11.376 C 9.504 11.28 10.104 11.28 10.368 11.496 C 10.368 12.768 10.272 13.752 10.104 15.144 Z "/>
</symbol>
<symbol id="g47EDFEA5ED41C2BE4D53DD4DC8C28ED" overflow="visible">
<path d="M 13.8 14.712 C 13.344 14.616 12.672 14.616 12.36 14.712 L 8.928 5.04 L 8.76 4.416 L 8.52 5.184 L 5.9040003 13.752 C 5.664 14.544 6.528 14.64 7.6800003 14.712 C 7.824 14.856 7.824 15.384 7.6800003 15.528 C 6.7920003 15.504 4.392 15.4800005 3.456 15.4800005 C 2.4720001 15.4800005 1.128 15.504 0.24000001 15.528 C 0.096 15.384 0.096 14.856 0.24000001 14.712 C 1.176 14.616 2.04 14.448 2.4 13.416 L 6.912 0.264 C 7.08 -0.24000001 7.44 -0.288 7.704 -0.288 C 7.9440002 -0.288 8.328 -0.24000001 8.52 0.264 L 12.12 9.84 L 15.792 0.264 C 15.96 -0.192 16.224 -0.288 16.584 -0.288 C 16.896 -0.288 17.232 -0.168 17.4 0.264 L 21.912 12.552 C 22.416 13.968 23.376 14.64 24.432001 14.712 C 24.576 14.856 24.576 15.384 24.432001 15.528 C 23.64 15.504 22.824 15.4800005 21.984 15.4800005 C 21 15.4800005 19.872 15.504 18.984 15.528 C 18.84 15.384 18.84 14.856 18.984 14.712 C 20.352 14.496 20.808 13.992001 20.52 13.104 L 17.808 5.04 L 17.52 4.176 L 17.16 5.184 Z "/>
</symbol>
<symbol id="gF7DAC8BB30649014016B28F6AD7EC048" overflow="visible">
<path d="M 12.62 0 C 12.62 0 12.5199995 1.42 12.5199995 2.04 L 12.5199995 10.24 C 12.5199995 12.0199995 12.86 12.12 14.259999 12.259999 C 14.38 12.38 14.38 12.82 14.259999 12.94 C 13.28 12.92 12.94 12.9 12.099999 12.9 C 11.2 12.9 10.78 12.92 9.78 12.94 C 9.66 12.82 9.66 12.38 9.78 12.259999 C 11.179999 12.12 11.5199995 12.059999 11.5199995 10.24 L 11.5199995 4.62 C 11.5199995 4.12 11.259999 4.22 10.98 4.56 L 5.68 10.8 L 3.8999999 12.9 L 0.64 12.94 C 0.52 12.82 0.52 12.38 0.64 12.259999 C 1.5 12.2 2.1 11.5199995 2.22 11 L 2.22 2.6599998 C 2.22 0.88 1.88 0.78 0.48 0.64 C 0.35999998 0.52 0.35999998 0.08 0.48 -0.04 C 1.4599999 -0.02 1.8399999 0 2.72 0 C 3.6 0 3.9599998 -0.02 4.96 -0.04 C 5.08 0.08 5.08 0.52 4.96 0.64 C 3.56 0.78 3.22 0.84 3.22 2.6599998 L 3.22 8.599999 C 3.22 8.8 3.26 9 3.3799999 9 C 3.48 9 3.6399999 8.86 3.86 8.599999 L 10.559999 0.64 C 10.96 0.14 11.36 -0.24 11.36 -0.24 C 12.059999 -0.24 12.259999 -0.17999999 12.62 0 Z "/>
</symbol>
<symbol id="g8F63AAB7FFA6B186E1B4BC124750174B" overflow="visible">
<path d="M 8.42 12.62 C 7.3199997 12.78 6.8999996 13.16 5.04 13.16 C 4.14 13.16 2.96 12.88 2.12 12.2 C 1.38 11.599999 0.82 10.679999 0.82 9.7 C 0.82 8.94 1.02 7.98 1.48 7.3799996 C 2.3999999 6.14 4.06 5.46 4.92 4.8599997 C 5.8399997 4.22 6.74 3.4199998 6.74 2.3 C 6.74 1.3199999 5.8799996 0.64 4.66 0.64 C 3.32 0.64 1.9399999 1.74 1.54 3.56 C 1.22 3.6799998 0.9 3.6 0.59999996 3.52 C 0.58 3.52 0.56 3.5 0.53999996 3.5 C 0.53999996 2 0.7 0.94 0.91999996 0.19999999 C 2.06 0.19999999 2.12 -0.19999999 4.88 -0.19999999 C 6.1 -0.19999999 7.08 0.16 7.8999996 0.9 C 8.62 1.52 9.26 2.44 9.26 3.6799998 C 9.26 4.72 8.82 5.42 8.22 6.08 C 7.44 6.94 6.3199997 7.56 5.54 7.96 C 4.74 8.36 3.32 9.4 3.32 10.54 C 3.32 11.66 4 12.34 5.02 12.34 C 6.72 12.34 7.2799997 10.8 7.64 9.48 C 7.9199996 9.4 8.42 9.4 8.639999 9.58 C 8.639999 10.639999 8.559999 11.46 8.42 12.62 Z "/>
</symbol>
<symbol id="g1E298373CF470F56F03EC97C7DE8EA04" overflow="visible">
<path d="M 11.5 12.259999 C 11.12 12.179999 10.559999 12.179999 10.3 12.259999 L 7.44 4.2 L 7.2999997 3.6799998 L 7.1 4.3199997 L 4.92 11.46 C 4.72 12.12 5.44 12.2 6.3999996 12.259999 C 6.52 12.38 6.52 12.82 6.3999996 12.94 C 5.66 12.92 3.6599998 12.9 2.8799999 12.9 C 2.06 12.9 0.94 12.92 0.19999999 12.94 C 0.08 12.82 0.08 12.38 0.19999999 12.259999 C 0.97999996 12.179999 1.6999999 12.04 2 11.179999 L 5.7599998 0.22 C 5.9 -0.19999999 6.2 -0.24 6.42 -0.24 C 6.62 -0.24 6.94 -0.19999999 7.1 0.22 L 10.099999 8.2 L 13.16 0.22 C 13.299999 -0.16 13.5199995 -0.24 13.82 -0.24 C 14.08 -0.24 14.36 -0.14 14.5 0.22 L 18.26 10.46 C 18.68 11.639999 19.48 12.2 20.359999 12.259999 C 20.48 12.38 20.48 12.82 20.359999 12.94 C 19.699999 12.92 19.02 12.9 18.32 12.9 C 17.5 12.9 16.56 12.92 15.82 12.94 C 15.7 12.82 15.7 12.38 15.82 12.259999 C 16.96 12.08 17.34 11.66 17.1 10.92 L 14.839999 4.2 L 14.599999 3.48 L 14.299999 4.3199997 Z "/>
</symbol>
<symbol id="g35249182E2B9A8D87270D5046FFBAC0C" overflow="visible">
<path d="M 7.94 -0.19999999 C 9.88 -0.19999999 11.66 0.71999997 13.0199995 2.5 C 12.92 2.6799998 12.58 2.9199998 12.36 2.9199998 C 10.94 1.36 9.32 0.84 7.9199996 0.84 C 5.6 0.84 3.76 3.56 3.76 6.68 C 3.76 9.78 5.3599997 12.34 7.74 12.34 C 10.5 12.34 11.4 10.78 11.92 9.059999 C 12.16 8.98 12.559999 9.04 12.78 9.16 C 12.679999 10.2 12.5199995 11.16 12.34 12.259999 C 11.32 12.36 10.42 13.16 7.96 13.16 C 4.04 13.16 0.74 10.7 0.74 6.2999997 C 0.74 4.42 1.56 2.22 3.1599998 1.06 C 4.44 0.14 6 -0.19999999 7.94 -0.19999999 Z "/>
</symbol>
<symbol id="g814D257E196F777517493FCE505E18DF" overflow="visible">
<path d="M 0.74 4.14 C 0.74 1.52 2.82 -0.19999999 5.5 -0.19999999 C 6.92 -0.19999999 8.099999 0.19999999 8.92 0.94 C 9.94 1.8399999 10.28 3.1999998 10.28 4.3199997 C 10.28 6.94 8.5 8.88 5.52 8.88 C 3.86 8.88 2.62 8.3 1.8399999 7.3999996 C 1.0799999 6.52 0.74 5.3199997 0.74 4.14 Z M 5.2 8.04 C 6.56 8.04 7.48 6.42 7.48 3.6799998 C 7.48 1.28 6.54 0.64 5.8199997 0.64 C 4.18 0.64 3.54 3.1 3.54 4.58 C 3.54 6.42 3.86 8.04 5.2 8.04 Z "/>
</symbol>
<symbol id="gC3DD0650993487CD3F460FE3E213BEA0" overflow="visible">
<path d="M 4.56 2.44 L 4.56 6.46 C 5.3599997 7 6.16 7.3999996 6.52 7.3999996 C 7.3199997 7.3999996 7.9199996 7.04 7.9199996 5.9 L 7.9199996 2.56 C 7.9199996 0.88 7.6 0.7 6.7799997 0.64 C 6.66 0.52 6.66 0.08 6.7799997 -0.04 C 7.62 -0.02 8.26 0 9.22 0 C 10.32 0 11.2 -0.02 12.059999 -0.04 C 12.179999 0.08 12.179999 0.52 12.059999 0.64 C 10.84 0.7 10.5199995 0.88 10.5199995 2.56 L 10.5199995 5.68 C 10.5199995 7.8799996 9.58 8.88 7.8599997 8.88 C 7.06 8.88 5.64 8 4.54 7.24 C 4.48 7.94 4.4 8.54 4.4 8.54 C 4.38 8.78 4.22 8.88 3.9399998 8.88 C 3.1999998 8.679999 2 8.4 0.62 8.22 C 0.58 8.099999 0.62 7.7 0.65999997 7.58 C 1.76 7.48 1.9599999 7.3199997 1.9599999 6.18 L 1.9599999 2.44 C 1.9599999 0.78 1.74 0.74 0.52 0.64 C 0.39999998 0.52 0.39999998 0.08 0.52 -0.04 C 1.36 -0.02 2.2 0 3.26 0 C 4.18 0 4.74 -0.02 5.6 -0.04 C 5.72 0.08 5.72 0.52 5.6 0.64 C 4.7599998 0.71999997 4.56 0.78 4.56 2.44 Z "/>
</symbol>
<symbol id="gCD50B0C5537328D0484BBB5C5B7C30A" overflow="visible">
<path d="M 0.96 2.9199998 C 1.04 1.9399999 1.14 1 1.3 0.24 C 1.68 0.12 2.96 -0.19999999 4.08 -0.19999999 C 5.62 -0.19999999 7.54 0.64 7.54 2.3799999 C 7.54 3.06 7.3799996 3.6 6.92 4.1 C 6.3599997 4.74 5.52 5.24 4.6 5.64 C 3.8 5.98 3.52 6.62 3.52 7.2 C 3.52 7.66 3.8999999 8.04 4.48 8.04 C 5.18 8.04 5.8599997 7.3999996 6.3599997 6.18 C 6.72 6.12 6.94 6.14 7.14 6.2799997 C 7.14 7 7.06 7.7599998 6.8799996 8.4 C 6.24 8.679999 5.74 8.88 4.64 8.88 C 3.58 8.88 2.58 8.48 1.9399999 7.8399997 C 1.48 7.3799996 1.26 6.8199997 1.26 6.2799997 C 1.26 5.68 1.5 5.2 1.88 4.7799997 C 2.5 4.1 3.6 3.3999999 4.2 3.12 C 5 2.76 5.22 2.04 5.22 1.56 C 5.22 0.91999996 4.58 0.58 4.04 0.58 C 3.1399999 0.58 2.18 1.5 1.76 2.96 C 1.4399999 3.02 1.28 3 0.96 2.9199998 Z "/>
</symbol>
<symbol id="g1344FEF92B65FBC27D977C1EC5D9AECF" overflow="visible">
<path d="M 1.26 8.679999 C 0.97999996 8.679999 0.68 8.599999 0.42 8.38 L 0.42 7.7999997 C 0.42 7.7 0.44 7.68 0.52 7.68 L 1.8199999 7.68 C 1.78 5.66 1.76 3.1 1.76 2.1 C 1.76 1.4 1.9399999 0.71999997 2.36 0.35999998 C 2.82 -0.02 3.54 -0.19999999 4.02 -0.19999999 C 5.12 -0.19999999 6.3399997 0.35999998 6.74 0.91999996 C 6.74 1.16 6.62 1.28 6.3799996 1.48 C 6.12 1.28 5.62 1.1999999 5.24 1.1999999 C 4.7999997 1.1999999 4.36 1.54 4.36 2.54 C 4.36 3.54 4.3399997 5.68 4.3399997 7.68 L 6.3599997 7.68 C 6.56 7.68 6.8399997 7.7599998 6.8399997 7.94 L 6.8399997 8.559999 C 6.8399997 8.639999 6.7799997 8.679999 6.68 8.679999 L 4.3399997 8.679999 L 4.36 9.36 C 4.4 10.7 4.46 11.62 4.46 11.62 C 4.46 11.74 4.4 11.8 4.2999997 11.8 C 4.16 11.8 3.4199998 11.58 3.1 11.44 C 2.76 11.3 2.18 11.179999 2.04 11 C 1.9 10.82 1.8199999 10.28 1.8199999 8.679999 Z "/>
</symbol>
<symbol id="g936880EEF467D45CE0F64A721CAEDAB8" overflow="visible">
<path d="M 4.56 5.3599997 C 4.56 6.08 4.7799997 6.3799996 5.04 6.68 C 5.2 6.8799996 5.38 7.02 5.68 7.02 C 5.8599997 7.02 6.08 6.8399997 6.24 6.64 C 6.3799996 6.48 6.72 6.3199997 7.18 6.3199997 C 7.7599998 6.3199997 8.32 6.92 8.32 7.7599998 C 8.32 8.28 7.72 8.88 7 8.88 C 6.2999997 8.88 5.54 8.28 4.62 6.96 L 4.54 6.96 C 4.5 7.56 4.4 8.54 4.4 8.54 C 4.38 8.72 4.22 8.88 3.9399998 8.88 C 3 8.639999 1.9399999 8.36 0.62 8.22 C 0.58 8.099999 0.62 7.72 0.65999997 7.6 C 1.76 7.5 1.9599999 7.3199997 1.9599999 6.18 L 1.9599999 2.44 C 1.9599999 0.78 1.74 0.74 0.52 0.64 C 0.39999998 0.52 0.39999998 0.08 0.52 -0.04 C 1.36 -0.02 2.2 0 3.26 0 C 4.3199997 0 5.14 -0.02 6 -0.04 C 6.12 0.08 6.12 0.52 6 0.64 C 4.7799997 0.71999997 4.56 0.78 4.56 2.44 Z "/>
</symbol>
<symbol id="g2EB1DC9A979CD3C8C9D80DB754EBF6AB" overflow="visible">
<path d="M 10.2 2.6599998 L 10.2 6.12 C 10.2 7.7999997 10.24 7.56 10.24 8.04 C 10.24 8.38 10.16 8.599999 10.04 8.72 C 9.679999 8.7 9.28 8.679999 8.9 8.679999 C 8.34 8.679999 7.04 8.7 6.2599998 8.72 C 6.14 8.599999 6.14 8.16 6.2599998 8.04 C 7.2799997 7.94 7.6 7.7999997 7.6 6.12 L 7.6 2.4199998 C 7.6 2.22 7.6 2.02 7.62 1.8199999 C 6.7999997 1.3199999 6.14 1.28 5.7799997 1.28 C 4.98 1.28 4.38 1.38 4.38 2.78 L 4.38 6.12 C 4.38 7.7999997 4.42 7.56 4.42 8.04 C 4.42 8.38 4.3399997 8.599999 4.22 8.72 C 3.86 8.7 3.4399998 8.679999 3.08 8.679999 C 2.06 8.679999 1.3 8.7 0.44 8.72 C 0.32 8.599999 0.32 8.16 0.44 8.04 C 1.36 8 1.78 7.7999997 1.78 6.12 L 1.78 3 C 1.78 0.88 2.62 -0.19999999 4.3399997 -0.19999999 C 5.06 -0.19999999 6.52 0.38 7.68 1.02 C 7.72 0.52 7.7599998 0.14 7.7599998 0.14 C 7.7799997 -0.099999994 7.94 -0.19999999 8.22 -0.19999999 C 8.96 0 10.16 0.28 11.54 0.45999998 C 11.58 0.58 11.54 0.97999996 11.5 1.1 C 10.42 1.1999999 10.2 1.52 10.2 2.6599998 Z "/>
</symbol>
<symbol id="g7B316FC97C7634445DBF19AF1976B5C8" overflow="visible">
<path d="M 8.44 1.74 C 8.44 1.9799999 8.4 2.36 8.179999 2.36 C 7.3799996 1.62 6.7 1.24 6.12 1.24 C 4.62 1.24 3.4399998 2.32 3.4399998 4.72 C 3.4399998 6.94 3.9399998 8.04 5 8.04 C 5.74 8.04 6.04 7.2599998 6.1 6.62 C 6.16 6.08 6.7 5.68 7.3399997 5.68 C 7.98 5.68 8.44 6.18 8.44 6.7999997 C 8.44 7.7 7.3599997 8.88 5.18 8.88 C 2.82 8.88 0.74 6.98 0.74 4.02 C 0.74 2.72 1.1999999 1.5799999 1.9799999 0.84 C 2.76 0.099999994 3.6799998 -0.19999999 5.1 -0.19999999 C 6.2999997 -0.19999999 7.68 0.64 8.44 1.74 Z "/>
</symbol>
<symbol id="gE9BB2E81A58B731A2047F77D70267173" overflow="visible">
<path d="M 4.64 2.44 L 4.64 6.42 C 4.64 7.4199996 4.72 8.54 4.72 8.54 C 4.72 8.76 4.54 8.88 4.2599998 8.88 C 3.6999998 8.66 2.08 8.5 0.7 8.32 C 0.65999997 8.2 0.7 7.7999997 0.74 7.68 C 1.8399999 7.58 2.04 7.4199996 2.04 6.2799997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.74 0.59999996 0.64 C 0.48 0.52 0.48 0.08 0.59999996 -0.04 C 1.4399999 -0.02 2.28 0 3.34 0 C 4.4 0 5.22 -0.02 6.08 -0.04 C 6.2 0.08 6.2 0.52 6.08 0.64 C 4.8599997 0.71999997 4.64 0.78 4.64 2.44 Z M 1.9399999 11.92 C 1.9399999 11.259999 2.4199998 10.599999 3.22 10.599999 C 4.12 10.599999 4.64 11.32 4.64 11.84 C 4.64 12.44 4.18 13.16 3.34 13.16 C 2.3999999 13.16 1.9399999 12.5199995 1.9399999 11.92 Z "/>
</symbol>
<symbol id="gED653E9CCAB5F6C6237350979071A74F" overflow="visible">
<path d="M 1.1999999 1.1999999 C 1.1999999 0.44 1.8399999 -0.16 2.6399999 -0.16 C 3.4399998 -0.16 4.12 0.48 4.12 1.24 C 4.12 2.02 3.48 2.62 2.6799998 2.62 C 1.88 2.62 1.1999999 1.9799999 1.1999999 1.1999999 Z M 1.1999999 7.16 C 1.1999999 6.3999996 1.8399999 5.7999997 2.6399999 5.7999997 C 3.4399998 5.7999997 4.12 6.44 4.12 7.2 C 4.12 7.98 3.48 8.58 2.6799998 8.58 C 1.88 8.58 1.1999999 7.94 1.1999999 7.16 Z "/>
</symbol>
<symbol id="gC1513612DA0E34F2B247DB2830CD7DFD" overflow="visible">
<path d="M 1.24 4.6 C 1.24 3.34 2.26 2.32 3.52 2.32 C 4.7799997 2.32 5.7999997 3.34 5.7999997 4.6 C 5.7999997 5.8599997 4.7799997 6.8799996 3.52 6.8799996 C 2.26 6.8799996 1.24 5.8599997 1.24 4.6 Z "/>
</symbol>
<symbol id="g8D44D9C01F9AF6C3B1D634FDF54DE6FB" overflow="visible">
<path d="M 5.66 6.46 C 7.3599997 6.46 7.4199996 6 7.48 5.1 C 7.6 4.98 8.0199995 4.98 8.139999 5.1 C 8.12 5.6 8.099999 6.18 8.099999 6.8599997 C 8.099999 7.54 8.12 8.059999 8.139999 8.58 C 8.0199995 8.7 7.6 8.7 7.48 8.58 C 7.4199996 7.48 7.3599997 7.22 5.66 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.9 4.04 12.099999 4.92 12.099999 L 5.8199997 12.099999 C 7.94 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.92 9.34 9.96 9.5 10.0199995 C 9.4 10.84 9.099999 12.759999 9.059999 12.92 C 9.059999 12.96 9.04 12.98 8.98 12.98 C 8.639999 12.92 8.54 12.9 8.04 12.9 L 2.9399998 12.9 C 2.3 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.06 -0.02 2.06 0 2.96 0 C 3.86 0 4.8399997 -0.02 5.54 -0.04 C 5.66 0.08 5.66 0.5 5.54 0.62 C 4.14 0.68 3.8 0.78 3.8 2.44 L 3.8 6.46 Z "/>
</symbol>
<symbol id="gFB78EB03C35D4F852337F4EC6AC104AC" overflow="visible">
<path d="M 0.82 4.1 C 0.82 2.06 2.18 -0.19999999 5.02 -0.19999999 C 6.2999997 -0.19999999 7.2799997 0.26 7.96 0.91999996 C 8.86 1.8 9.26 3.06 9.26 4.2799997 C 9.26 6.3599997 8.12 8.78 5.06 8.78 C 3.74 8.78 2.6599998 8.24 1.92 7.3799996 C 1.1999999 6.52 0.82 5.3599997 0.82 4.1 Z M 4.7599998 8.08 C 6.48 8.08 7.54 6.52 7.54 3.6399999 C 7.54 1.12 6.24 0.5 5.2999997 0.5 C 3.22 0.5 2.54 3.02 2.54 4.56 C 2.54 6.2999997 2.96 8.08 4.7599998 8.08 Z "/>
</symbol>
<symbol id="gB9C04FB79CAD4691AB5EC7F01BE2AD7F" overflow="visible">
<path d="M 3.52 7.16 C 3.48 7.96 3.46 8.48 3.36 8.679999 C 3.32 8.78 3.28 8.84 3.12 8.84 C 2.56 8.62 2.04 8.44 0.65999997 8.26 C 0.62 8.139999 0.65999997 7.8199997 0.7 7.7 C 1.78 7.6 2 7.5 2 6.3399997 L 2 2.44 C 2 0.78 1.76 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 2 0 2.8 0 C 3.6 0 4.52 -0.02 5.22 -0.04 C 5.3399997 0.08 5.3399997 0.5 5.22 0.62 C 3.82 0.71999997 3.58 0.78 3.58 2.44 L 3.58 5.22 C 3.58 5.74 3.82 6.2 4.06 6.56 C 4.2799997 6.8799996 4.74 7.54 4.98 7.54 C 5.16 7.54 5.3399997 7.5 5.5 7.2799997 C 5.64 7.08 5.8799996 6.8199997 6.22 6.8199997 C 6.7 6.8199997 7.16 7.3199997 7.16 7.8199997 C 7.16 8.2 6.7999997 8.78 5.96 8.78 C 5.02 8.78 4.2 7.8999996 3.74 7.12 C 3.62 6.8999996 3.52 7.06 3.52 7.16 Z "/>
</symbol>
<symbol id="gAA212A9DBB5FA7333A767E41B2F6A3B3" overflow="visible">
<path d="M 5.8599997 0.96 C 5.98 0.34 6.2 -0.19999999 7.2 -0.19999999 C 7.96 -0.19999999 8.679999 0.14 9.099999 0.53999996 C 9.059999 0.78 8.98 0.96 8.76 1.0799999 C 8.62 0.96 8.28 0.76 8.0199995 0.76 C 7.44 0.76 7.4199996 1.54 7.4199996 2.46 L 7.4199996 5.4 C 7.4199996 8.24 5.8599997 8.78 4.4 8.78 C 2.76 8.78 1.1 7.7 1.1 6.56 C 1.1 6.08 1.3399999 5.8399997 1.8 5.8399997 C 2.3799999 5.8399997 2.74 6.2599998 2.74 6.52 C 2.74 6.66 2.72 6.7999997 2.6799998 6.8799996 C 2.6599998 6.94 2.6399999 7.06 2.6399999 7.2799997 C 2.6399999 7.8999996 3.48 8.12 4.24 8.12 C 4.92 8.12 5.8599997 7.7799997 5.8599997 5.52 C 5.8599997 5.38 5.7999997 5.2999997 5.74 5.2799997 L 4.02 4.8599997 C 2.1 4.38 0.71999997 3.32 0.71999997 1.9599999 C 0.71999997 0.32 1.8399999 -0.19999999 3.24 -0.19999999 C 3.9399998 -0.19999999 4.54 -0.04 5.42 0.64 L 5.8199997 0.96 Z M 5.8599997 4.66 L 5.8599997 2.02 C 5.8599997 1.76 5.74 1.62 5.58 1.5 C 5.06 1.0799999 4.38 0.62 3.82 0.62 C 2.82 0.62 2.3799999 1.42 2.3799999 2.04 C 2.3799999 2.9399998 2.8 3.86 4.2799997 4.24 Z "/>
</symbol>
<symbol id="g35631D62198EF939061DC90C9391724A" overflow="visible">
<path d="M 3.6799998 7.16 C 3.56 7.02 3.4399998 6.98 3.4399998 7.16 C 3.4199998 7.7 3.3799999 8.48 3.28 8.679999 C 3.24 8.78 3.1999998 8.84 3.04 8.84 C 2.48 8.62 1.9599999 8.44 0.58 8.26 C 0.53999996 8.139999 0.58 7.8199997 0.62 7.7 C 1.6999999 7.6 1.92 7.5 1.92 6.3399997 L 1.92 2.44 C 1.92 0.79999995 1.7199999 0.71999997 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.92 0 2.72 0 C 3.52 0 4.12 -0.02 4.72 -0.04 C 4.8399997 0.08 4.8399997 0.5 4.72 0.62 C 3.6999998 0.71999997 3.5 0.79999995 3.5 2.44 L 3.5 5.72 C 3.5 6.14 3.6799998 6.3799996 3.84 6.56 C 4.6 7.2999997 5.5 7.74 6.2799997 7.74 C 6.68 7.74 7.1 7.48 7.3399997 7.02 C 7.54 6.62 7.58 6.08 7.58 5.48 L 7.58 2.44 C 7.58 0.79999995 7.3799996 0.71999997 6.3399997 0.62 C 6.24 0.5 6.24 0.08 6.3399997 -0.04 C 6.94 -0.02 7.58 0 8.38 0 C 9.179999 0 9.9 -0.02 10.5 -0.04 C 10.599999 0.08 10.599999 0.5 10.5 0.62 C 9.38 0.71999997 9.16 0.79999995 9.16 2.44 L 9.16 5.42 C 9.16 6.52 9.08 7.48 8.62 8.099999 C 8.28 8.54 7.66 8.78 6.96 8.78 C 5.98 8.78 4.8599997 8.5199995 3.6799998 7.16 Z "/>
</symbol>
<symbol id="g7FBC39AA6D9FB89D8B638A3651405A80" overflow="visible">
<path d="M 7.72 1.86 C 6.98 1.1 6.3999996 0.78 5.24 0.78 C 4.52 0.78 3.6799998 1.1999999 3.06 2.22 C 2.6599998 2.8799999 2.4199998 3.8 2.4199998 4.96 L 7.74 4.92 C 7.98 4.92 8.12 5.04 8.12 5.2599998 C 8.12 6.94 7.52 8.74 4.74 8.74 C 3 8.74 0.74 7.08 0.74 4.04 C 0.74 2.9199998 1.02 1.8399999 1.68 1.0799999 C 2.36 0.28 3.3 -0.19999999 4.74 -0.19999999 C 6.2599998 -0.19999999 7.3399997 0.5 8.139999 1.54 C 8.08 1.74 7.96 1.8399999 7.72 1.86 Z M 2.48 5.64 C 2.86 7.8999996 4.2599998 8.08 4.74 8.08 C 5.5 8.08 6.3999996 7.66 6.3999996 5.98 C 6.3999996 5.7999997 6.3199997 5.7 6.1 5.7 Z "/>
</symbol>
<symbol id="gA1481BA28623480CC7E6165783E2A864" overflow="visible">
<path d="M 4.06 7.96 C 4.18 8.08 4.18 8.5 4.06 8.62 C 3.46 8.599999 2.76 8.58 2.04 8.58 C 1.28 8.58 0.74 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.16 7.8599997 1.38 7.66 1.8 6.62 L 4.42 0.16 C 4.54 -0.12 4.7 -0.24 4.9 -0.24 C 5.08 -0.24 5.24 -0.12 5.38 0.19999999 L 7.3999996 5.12 L 9.46 0.16 C 9.58 -0.12 9.74 -0.24 9.94 -0.24 C 10.12 -0.24 10.28 -0.12 10.4 0.17999999 L 13.0199995 6.52 C 13.34 7.3399997 13.679999 7.8999996 14.7 7.96 C 14.82 8.08 14.82 8.5 14.7 8.62 C 14.299999 8.599999 13.86 8.58 13.259999 8.58 C 12.66 8.58 11.82 8.599999 11.219999 8.62 C 11.099999 8.5 11.099999 8.08 11.219999 7.96 C 12.719999 7.8799996 12.5199995 7.2999997 12.24 6.6 L 10.559999 2.44 C 10.36 1.9399999 10.28 1.9399999 10.12 2.36 L 8.4 6.74 C 8.0199995 7.68 8.059999 7.8799996 9.12 7.96 C 9.24 8.08 9.24 8.5 9.12 8.62 C 8.5199995 8.599999 7.72 8.58 7.12 8.58 C 6.62 8.58 5.96 8.599999 5.3599997 8.62 C 5.24 8.5 5.24 8.08 5.3599997 7.96 C 6.2999997 7.8799996 6.54 7.2999997 6.8999996 6.3999996 L 7.02 6.08 L 5.62 2.54 C 5.3599997 1.88 5.3199997 1.86 5.06 2.5 L 3.46 6.62 C 3.08 7.58 3.1 7.8999996 4.06 7.96 Z "/>
</symbol>
<symbol id="gAC7FD886AB12F72ED3B61B0327264BE7" overflow="visible">
<path d="M 3.12 7.3599997 C 3.1 7.96 3.06 8.48 2.96 8.679999 C 2.9199998 8.78 2.8799999 8.84 2.72 8.84 C 2.1599998 8.62 1.64 8.44 0.26 8.26 C 0.22 8.139999 0.26 7.8199997 0.29999998 7.7 C 1.38 7.6 1.5999999 7.5 1.5999999 6.3399997 L 1.5999999 -2.2 C 1.5999999 -3.86 1.38 -3.9599998 0.16 -4.02 C 0.04 -4.14 0.04 -4.56 0.16 -4.68 C 0.85999995 -4.66 1.5999999 -4.64 2.3999999 -4.64 C 3.1999998 -4.64 4.16 -4.66 4.8199997 -4.68 C 4.94 -4.56 4.94 -4.14 4.8199997 -4.02 C 3.3999999 -3.9399998 3.1799998 -3.86 3.1799998 -2.2 L 3.1799998 -0.04 C 3.1799998 0.22 3.26 0.19999999 3.46 0.12 C 3.9599998 -0.08 4.56 -0.19999999 5.2 -0.19999999 C 6.3199997 -0.19999999 7.3199997 0.14 8.139999 0.91999996 C 9.08 1.8399999 9.62 3.08 9.62 4.7 C 9.62 6.8199997 8.12 8.78 6.08 8.78 C 5.16 8.78 4.14 8.179999 3.34 7.2799997 C 3.22 7.16 3.1399999 7.16 3.12 7.3599997 Z M 3.5 6.62 C 4.02 7.2599998 4.94 7.8599997 5.52 7.8599997 C 6.7999997 7.8599997 7.8999996 6.42 7.8999996 4.16 C 7.8999996 2.52 7.3199997 0.48 5.08 0.48 C 4.72 0.48 4.02 0.58 3.6599998 0.9 C 3.26 1.26 3.1799998 1.38 3.1799998 2.1 L 3.1799998 5.74 C 3.1799998 6.16 3.26 6.3399997 3.5 6.62 Z "/>
</symbol>
<symbol id="gE68C39294AA7FBA9B91EA2F8E9CC3997" overflow="visible">
<path d="M 3.62 2.44 L 3.62 6.42 C 3.62 7.4199996 3.6999998 8.7 3.6999998 8.7 C 3.6999998 8.78 3.6 8.84 3.4399998 8.84 C 2.8799999 8.62 2.08 8.44 0.7 8.26 C 0.65999997 8.139999 0.7 7.8199997 0.74 7.7 C 1.8399999 7.6 2.04 7.48 2.04 6.3399997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.71999997 0.59999996 0.62 C 0.48 0.5 0.48 0.08 0.59999996 -0.04 C 1.26 -0.02 2.04 0 2.84 0 C 3.6399999 0 4.4 -0.02 5.06 -0.04 C 5.18 0.08 5.18 0.5 5.06 0.62 C 3.84 0.7 3.62 0.78 3.62 2.44 Z M 1.8 11.98 C 1.8 11.46 2.28 10.94 2.76 10.94 C 3.32 10.94 3.8 11.48 3.8 11.9 C 3.8 12.38 3.3799999 12.94 2.84 12.94 C 2.36 12.94 1.8 12.46 1.8 11.98 Z "/>
</symbol>
<symbol id="g22D858CFD6AD86697C1391C74FD687D1" overflow="visible">
<path d="M 0.85999995 8.58 C 0.58 8.58 0.5 8.34 0.5 8.179999 L 0.5 7.9199996 C 0.5 7.8199997 0.52 7.7999997 0.59999996 7.7999997 L 1.78 7.7999997 L 1.78 1.78 C 1.78 0.35999998 2.3999999 -0.19999999 3.32 -0.19999999 C 4.24 -0.19999999 5.24 0.24 6.02 1.12 C 5.98 1.3199999 5.8599997 1.4399999 5.66 1.4599999 C 5.14 1.06 4.54 0.9 4.02 0.9 C 3.48 0.9 3.36 1.5 3.36 2.74 L 3.36 7.7999997 L 5.44 7.7999997 C 5.64 7.7999997 5.92 7.8799996 5.92 8.059999 L 5.92 8.46 C 5.92 8.54 5.8599997 8.58 5.7599998 8.58 L 3.36 8.58 L 3.36 9.36 C 3.36 10.66 3.4399998 11.46 3.4399998 11.46 C 3.4399998 11.58 3.3799999 11.639999 3.28 11.639999 C 3.1999998 11.639999 3.02 11.559999 2.84 11.46 C 2.62 11.34 2.4199998 11.24 2.1599998 11.179999 C 1.92 11.099999 1.7199999 11.04 1.7199999 10.9 C 1.7199999 10.66 1.78 10.8 1.78 8.58 Z "/>
</symbol>
<symbol id="g8C7315D77A5D71E18736DE61553C419F" overflow="visible">
<path d="M 1.4 1.1999999 C 1.4 0.62 1.88 0.14 2.46 0.14 C 3.04 0.14 3.52 0.62 3.52 1.1999999 C 3.52 1.78 3.04 2.26 2.46 2.26 C 1.88 2.26 1.4 1.78 1.4 1.1999999 Z M 1.4 7.16 C 1.4 6.58 1.88 6.1 2.46 6.1 C 3.04 6.1 3.52 6.58 3.52 7.16 C 3.52 7.74 3.04 8.22 2.46 8.22 C 1.88 8.22 1.4 7.74 1.4 7.16 Z "/>
</symbol>
<symbol id="g713198A7DA4F5CD7D462D4529B1D64BD" overflow="visible">
<path d="M 7.96 1.8199999 C 7.8799996 2 7.72 2.08 7.54 2.1 C 6.8599997 1.22 6 0.78 5.14 0.78 C 3.6799998 0.78 2.46 2.26 2.46 4.6 C 2.46 6.7999997 3.4199998 8.12 4.74 8.12 C 5.92 8.12 6.08 7.4199996 6.16 6.72 C 6.22 6.18 6.5 6 6.92 6 C 7.3399997 6 7.8999996 6.2599998 7.8999996 6.8799996 C 7.8999996 7.98 6.7599998 8.78 4.8399997 8.78 C 2.86 8.78 0.74 7 0.74 4.16 C 0.74 1.5799999 2.18 -0.19999999 4.7 -0.19999999 C 5.9 -0.19999999 6.96 0.17999999 7.96 1.8199999 Z "/>
</symbol>
<symbol id="gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" overflow="visible">
<path d="M 13.259999 2.32 C 13.36 0.7 13.28 0.68 11.98 0.62 C 11.86 0.5 11.86 0.08 11.98 -0.04 C 12.719999 -0.02 13.5199995 0 14.12 0 C 14.719999 0 15.639999 -0.02 16.3 -0.04 C 16.42 0.08 16.42 0.5 16.3 0.62 C 14.94 0.68 14.88 0.76 14.759999 2.4199998 L 14.16 10.84 C 14.08 11.92 14.179999 12.2 15.54 12.28 C 15.66 12.4 15.66 12.82 15.54 12.94 L 12.92 12.9 L 8.679999 2.76 C 8.599999 2.56 8.54 2.48 8.5 2.48 C 8.46 2.48 8.4 2.58 8.34 2.74 L 4.24 12.9 L 1.3399999 12.94 C 1.22 12.82 1.22 12.4 1.3399999 12.28 C 2.72 12.2 2.84 12.16 2.7 10.66 L 1.9 2.4199998 C 1.78 1.22 1.54 0.71999997 0.39999998 0.62 C 0.28 0.5 0.28 0.08 0.39999998 -0.04 C 1 -0.02 1.64 0 2.12 0 C 2.6 0 3.3999999 -0.02 4 -0.04 C 4.12 0.08 4.12 0.5 4 0.62 C 2.6799998 0.71999997 2.58 1.3399999 2.6799998 2.46 L 3.4399998 10.48 L 3.48 10.48 L 7.62 0.099999994 C 7.68 -0.04 7.7999997 -0.19999999 7.9199996 -0.19999999 C 8.04 -0.19999999 8.12 -0.06 8.2 0.099999994 L 12.7 10.679999 L 12.74 10.679999 Z "/>
</symbol>
<symbol id="g67483374C2628B9150A7D3585AC4A61B" overflow="visible">
<path d="M 0.96 2.76 C 1.04 1.78 1.1 0.84 1.1 0 C 1.3 0.04 1.5 0.06 1.5999999 0.06 C 1.74 0.06 1.86 0.06 2 0.02 C 2.54 -0.12 3.08 -0.19999999 3.82 -0.19999999 C 4.94 -0.19999999 7 0.34 7 2.32 C 7 3.6799998 6.02 4.48 4.66 4.98 C 3.46 5.44 2.6599998 5.74 2.6599998 6.8399997 C 2.6599998 7.66 3.3799999 8.12 4.06 8.12 C 4.5 8.12 5.66 7.96 5.92 6.2599998 C 6.04 6.14 6.44 6.16 6.56 6.2799997 C 6.62 7 6.66 7.74 6.68 8.4 C 6.06 8.5 5.1 8.78 4.06 8.78 C 2.58 8.78 1.24 7.8199997 1.24 6.54 C 1.24 5.08 1.9 4.46 3.4399998 3.82 C 5.1 3.1399999 5.48 2.72 5.48 1.86 C 5.48 0.88 4.52 0.45999998 3.78 0.45999998 C 3 0.45999998 2.56 0.71999997 2.36 0.94 C 1.92 1.4 1.6999999 2.28 1.5799999 2.78 C 1.4599999 2.8999999 1.0799999 2.8799999 0.96 2.76 Z "/>
</symbol>
<symbol id="g612BB0D9B453ACEC45B2B13686D7BB71" overflow="visible">
<path d="M 1.4599999 1.68 L 6.74 4.64 L 1.4599999 7.6 Z "/>
</symbol>
<symbol id="g98926218EB374AD77A2D864C6D10734B" overflow="visible">
<path d="M 5.62 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.7 4.04 12.099999 5.12 12.099999 L 6.62 12.099999 C 8.12 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.88 9.34 9.92 9.54 10.0199995 C 9.44 10.84 9.139999 12.759999 9.099999 12.92 C 9.099999 12.96 9.08 12.98 9.0199995 12.98 C 8.679999 12.92 8.5199995 12.9 8.04 12.9 L 2.9399998 12.9 C 2.34 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.1 -0.02 2.3 0 2.96 0 L 7.2599998 0 C 8.22 0 9.82 -0.04 9.82 -0.04 C 10.099999 0.96 10.4 2.28 10.559999 3.3 C 10.36 3.4199998 10.12 3.46 9.86 3.3999999 C 9.46 1.9599999 8.76 0.78 7.24 0.78 L 4.92 0.78 C 4.08 0.78 3.8 1.1 3.8 2.04 L 3.8 6.46 L 5.62 6.46 C 7.3199997 6.46 7.3799996 6 7.44 5.1 C 7.56 4.98 7.98 4.98 8.099999 5.1 C 8.08 5.62 8.059999 6.18 8.059999 6.8599997 C 8.059999 7.4199996 8.08 8.099999 8.099999 8.58 C 7.98 8.7 7.56 8.7 7.44 8.58 C 7.3799996 7.48 7.3199997 7.22 5.62 7.22 Z "/>
</symbol>
<symbol id="g1788914935A6D7BFA016214155630E72" overflow="visible">
<path d="M 1.9 2.44 C 1.9 0.78 1.68 0.68 0.45999998 0.62 C 0.34 0.5 0.34 0.08 0.45999998 -0.04 C 1.16 -0.02 1.9 0 2.7 0 C 3.5 0 4.2599998 -0.02 4.92 -0.04 C 5.04 0.08 5.04 0.5 4.92 0.62 C 3.6999998 0.68 3.48 0.78 3.48 2.44 L 3.48 11.66 C 3.48 12.96 3.56 13.759999 3.56 13.759999 C 3.56 13.9 3.48 13.96 3.3 13.96 C 2.8 13.759999 1.3 13.48 0.5 13.42 C 0.45999998 13.259999 0.5 12.94 0.62 12.82 C 1.78 12.74 1.9 12.679999 1.9 11.179999 Z "/>
</symbol>
<symbol id="g21D1E528F66DB45787699F71DA377CC5" overflow="visible">
<path d="M 4.08 -3.1999998 C 4.4 -2.6399999 4.66 -2.08 4.9 -1.48 C 6.5 2.3799999 7.3999996 4.44 8.44 6.68 C 8.84 7.52 9.12 7.8399997 10.059999 7.96 C 10.179999 8.08 10.179999 8.5 10.059999 8.62 C 9.66 8.599999 9.2 8.58 8.639999 8.58 C 8.04 8.58 7.4199996 8.599999 6.8199997 8.62 C 6.7 8.5 6.7 8.08 6.8199997 7.96 C 7.46 7.8999996 8.099999 7.7799997 7.7799997 7.06 L 5.7999997 2.48 C 5.66 2.1599998 5.48 2.1 5.3199997 2.5 L 3.54 6.66 C 3.1799998 7.5 3.08 7.8799996 4.2 7.96 C 4.3199997 8.08 4.3199997 8.5 4.2 8.62 C 3.46 8.599999 2.6599998 8.58 1.9399999 8.58 C 1.26 8.58 0.71999997 8.599999 0.32 8.62 C 0.19999999 8.5 0.19999999 8.08 0.32 7.96 C 1.12 7.8599997 1.38 7.68 1.9 6.46 L 4.16 1.1999999 C 4.3399997 0.79999995 4.64 -0.12 4.44 -0.68 C 4.2 -1.3399999 3.9599998 -1.9 3.6599998 -2.52 C 3.4399998 -2.9199998 3.1599998 -3.1 2.6599998 -3.1 C 2.3799999 -3.1 2.3 -3.04 2.08 -3.04 C 1.5 -3.04 1.1999999 -3.6399999 1.1999999 -3.8999999 C 1.1999999 -4.3199997 1.5999999 -4.64 2.1399999 -4.64 C 2.56 -4.64 3.36 -4.48 4.08 -3.1999998 Z "/>
</symbol>
<symbol id="gFB54B84572F46C3C9CB2B1A90182D6B2" overflow="visible">
<path d="M 8.88 7.74 C 9.26 7.74 9.62 8.099999 9.62 8.5 C 9.62 8.92 9.24 9.24 8.7 9.24 C 8.179999 9.24 7.22 8.9 6.7 8.22 C 6.46 8.38 5.7999997 8.78 4.62 8.78 C 2.84 8.78 1.1999999 7.58 1.1999999 5.74 C 1.1999999 4.66 1.68 4.04 2.24 3.5 C 1.68 3.02 1.36 2.1599998 1.36 1.48 C 1.36 0.76 1.76 0.19999999 2.28 -0.06 C 1.1999999 -0.7 0.64 -1.62 0.64 -2.48 C 0.64 -4.22 2.28 -4.7599998 3.82 -4.7599998 C 6.52 -4.7599998 9.44 -3.46 9.44 -1.3 C 9.44 -0.65999997 9.139999 -0.16 8.559999 0.32 C 7.7799997 0.96 6.3799996 0.97999996 5.64 0.97999996 C 5.2799997 0.97999996 4.7799997 0.94 4.2999997 0.88 C 4 0.85999995 3.8 0.84 3.6999998 0.84 C 3.12 0.84 2.4199998 1.12 2.4199998 1.9799999 C 2.4199998 2.3799999 2.54 2.8 2.78 3.1399999 C 3.26 2.86 3.82 2.72 4.6 2.72 C 6.3599997 2.72 7.98 3.82 7.98 5.7799997 C 7.98 6.72 7.7 7.2599998 7.12 7.8599997 C 7.2599998 8.059999 7.66 8.34 7.9199996 8.34 C 8.059999 8.34 8.2 8.28 8.32 8.099999 C 8.4 7.94 8.66 7.74 8.88 7.74 Z M 2.6399999 -0.19999999 C 2.86 -0.26 3.1799998 -0.29999998 3.4399998 -0.29999998 C 4.06 -0.29999998 4.62 -0.24 4.9 -0.24 C 5.9 -0.24 6.74 -0.26 7.3199997 -0.58 C 8.099999 -1.02 8.34 -1.3 8.34 -1.8199999 C 8.34 -3.26 6.22 -4.02 4.42 -4.02 C 3.6999998 -4.02 2.02 -3.4399998 2.02 -2.08 C 2.02 -1.4 2.06 -0.9 2.6399999 -0.19999999 Z M 6.3799996 5.58 C 6.3799996 3.72 5.44 3.34 4.7 3.34 C 3.02 3.34 2.84 4.7599998 2.84 6.04 C 2.84 7.44 3.34 8.16 4.44 8.16 C 5.7 8.16 6.3799996 7.24 6.3799996 5.58 Z "/>
</symbol>
<symbol id="gD3761FB0B01B207797C607CDFB6E3A0B" overflow="visible">
<path d="M 3.3999999 7.16 C 3.3799999 7.7599998 3.34 8.48 3.24 8.679999 C 3.1999998 8.78 3.1599998 8.84 3 8.84 C 2.44 8.62 1.92 8.44 0.53999996 8.26 C 0.5 8.139999 0.53999996 7.8199997 0.58 7.7 C 1.66 7.6 1.88 7.5 1.88 6.3399997 L 1.88 2.44 C 1.88 0.79999995 1.62 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.88 0 2.6799998 0 C 3.48 0 4.1 -0.02 4.7 -0.04 C 4.8199997 0.08 4.8199997 0.5 4.7 0.62 C 3.6799998 0.71999997 3.46 0.79999995 3.46 2.44 L 3.46 5.72 C 3.46 6.14 3.6399999 6.3799996 3.8 6.56 C 4.6 7.3399997 5.3399997 7.74 5.96 7.74 C 6.72 7.74 7.2799997 7.2599998 7.2799997 5.92 L 7.2799997 2.44 C 7.2799997 0.79999995 7.12 0.7 6.04 0.62 C 5.94 0.5 5.94 0.08 6.04 -0.04 C 6.54 -0.02 7.2799997 0 8.08 0 C 8.88 0 9.54 -0.02 10.04 -0.04 C 10.139999 0.08 10.139999 0.5 10.04 0.62 C 9.04 0.7 8.86 0.79999995 8.86 2.44 L 8.86 5.62 C 8.86 5.9 8.86 6.18 8.84 6.42 C 9.8 7.48 10.7 7.74 11.48 7.74 C 12.24 7.74 12.679999 7.2999997 12.679999 5.96 L 12.679999 2.44 C 12.679999 0.79999995 12.48 0.7 11.44 0.62 C 11.34 0.5 11.34 0.08 11.44 -0.04 C 11.94 -0.02 12.679999 0 13.48 0 C 14.28 0 14.98 -0.02 15.54 -0.04 C 15.639999 0.08 15.639999 0.5 15.54 0.62 C 14.44 0.7 14.259999 0.79999995 14.259999 2.44 L 14.259999 5.6 C 14.259999 7.3799996 13.96 8.78 12.2 8.78 C 11.179999 8.78 9.94 8.4 8.9 7.2999997 C 8.84 7.24 8.72 7.14 8.679999 7.3199997 C 8.5 8.139999 7.72 8.78 6.68 8.78 C 5.52 8.78 4.48 8.099999 3.6399999 7.16 C 3.54 7.06 3.4199998 6.92 3.3999999 7.16 Z "/>
</symbol>
<symbol id="g17D0C844F22106CD9F208585DAE386D6" overflow="visible">
<path d="M 2.28 10.16 C 2.8999999 10.16 3.34 10.58 3.34 11.139999 C 3.34 11.78 2.82 11.96 2.46 12.0199995 C 2.08 12.059999 1.74 12.179999 1.74 12.639999 C 1.74 13.059999 2.46 13.98 3.5 14.24 C 3.5 14.44 3.46 14.58 3.32 14.719999 C 2.12 14.5 0.96 13.54 0.96 12.139999 C 0.96 10.94 1.48 10.16 2.28 10.16 Z M 5.42 10.16 C 6.04 10.16 6.48 10.58 6.48 11.139999 C 6.48 11.78 5.96 11.96 5.6 12.0199995 C 5.22 12.059999 4.88 12.179999 4.88 12.639999 C 4.88 13.059999 5.6 13.98 6.64 14.24 C 6.64 14.44 6.6 14.58 6.46 14.719999 C 5.2599998 14.5 4.1 13.54 4.1 12.139999 C 4.1 10.94 4.62 10.16 5.42 10.16 Z "/>
</symbol>
<symbol id="g3C2FFF86BC828E66F78F8A687CE12C70" overflow="visible">
<path d="M 3.34 5.72 C 3.34 6.14 3.52 6.3799996 3.6799998 6.56 C 4.44 7.2999997 5.46 7.74 6.24 7.74 C 6.64 7.74 7.06 7.48 7.2999997 7.02 C 7.5 6.62 7.54 6.08 7.54 5.48 L 7.54 2.44 C 7.54 0.79999995 7.3399997 0.71999997 6.2999997 0.62 C 6.2 0.5 6.2 0.08 6.2999997 -0.04 C 6.8599997 -0.02 7.54 0 8.34 0 C 9.139999 0 9.8 -0.02 10.46 -0.04 C 10.559999 0.08 10.559999 0.5 10.46 0.62 C 9.34 0.71999997 9.12 0.79999995 9.12 2.44 L 9.12 5.42 C 9.12 6.52 9.04 7.5 8.58 8.099999 C 8.24 8.54 7.62 8.78 6.92 8.78 C 5.94 8.78 4.74 8.5199995 3.52 7.16 C 3.52 7.14 3.5 7.14 3.48 7.12 C 3.4199998 7.04 3.32 6.92 3.32 7.16 L 3.34 11.66 C 3.34 12.96 3.4199998 13.759999 3.4199998 13.759999 C 3.4199998 13.9 3.34 13.96 3.1599998 13.96 C 2.6599998 13.759999 1.16 13.48 0.35999998 13.42 C 0.32 13.259999 0.35999998 12.94 0.48 12.82 C 0.53999996 12.82 0.59999996 12.82 0.65999997 12.82 C 1.54 12.759999 1.76 12.759999 1.76 11.179999 L 1.76 2.44 C 1.76 0.78 1.52 0.7 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.02 -0.02 1.76 0 2.56 0 C 3.32 0 3.98 -0.02 4.54 -0.04 C 4.66 0.08 4.66 0.5 4.54 0.62 C 3.52 0.7 3.34 0.78 3.34 2.44 Z "/>
</symbol>
<symbol id="g32FA8B29700389E7F9A58D039C5F66B2" overflow="visible">
<path d="M 2.1 13.96 C 1.48 13.96 1.04 13.54 1.04 12.98 C 1.04 12.36 1.56 12.16 1.92 12.099999 C 2.3 12.059999 2.6399999 11.94 2.6399999 11.48 C 2.6399999 11.059999 1.92 10.139999 0.88 9.88 C 0.88 9.679999 0.91999996 9.54 1.06 9.4 C 2.26 9.62 3.4199998 10.58 3.4199998 11.98 C 3.4199998 13.179999 2.8999999 13.96 2.1 13.96 Z M 5.24 13.96 C 4.62 13.96 4.18 13.54 4.18 12.98 C 4.18 12.36 4.7 12.16 5.06 12.099999 C 5.44 12.059999 5.7799997 11.94 5.7799997 11.48 C 5.7799997 11.059999 5.06 10.139999 4.02 9.88 C 4.02 9.679999 4.06 9.54 4.2 9.4 C 5.4 9.62 6.56 10.58 6.56 11.98 C 6.56 13.179999 6.04 13.96 5.24 13.96 Z "/>
</symbol>
<symbol id="gF9DE6E66E5D3ACB0B17DC7988DD660B8" overflow="visible">
<path d="M 1.7199999 2.44 C 1.7199999 0.78 1.5 0.7 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.04 -0.02 1.7199999 0 2.52 0 C 3.22 0 3.8799999 -0.02 4.3399997 -0.04 C 4.46 0.08 4.46 0.5 4.3399997 0.62 C 3.52 0.7 3.3 0.78 3.3 2.44 L 3.3 4.18 C 3.6799998 4.16 3.9599998 4.14 4.16 4.08 C 4.38 3.9199998 4.56 3.74 4.7999997 3.4199998 L 6.2599998 1.4599999 C 6.8399997 0.68 7.08 0.29999998 7.1 0.06 C 7.1 0 7.12 -0.04 7.18 -0.04 C 7.58 -0.02 8.0199995 0 8.42 0 C 9.04 0 9.66 -0.02 10.059999 -0.04 C 10.179999 0.08 10.179999 0.5 10.059999 0.62 C 9.38 0.7 8.88 0.78 8.34 1.4599999 L 5.7 4.7799997 C 5.62 4.88 5.56 4.96 5.56 5.06 C 5.56 5.14 5.56 5.18 5.64 5.2599998 L 7.3999996 7.08 C 8 7.72 8.7 7.8799996 9.5 7.96 C 9.62 8.08 9.62 8.5 9.5 8.62 C 9.04 8.599999 8.48 8.58 7.7599998 8.58 C 7 8.58 6.2599998 8.599999 5.7999997 8.62 C 5.68 8.5 5.68 8.08 5.7999997 7.96 C 6.92 7.8799996 6.44 7.18 6.2599998 6.94 C 5.7999997 6.3599997 5.18 5.68 4.66 5.2999997 C 4.22 4.98 3.6799998 4.74 3.3 4.68 L 3.3 11.66 C 3.3 12.96 3.3799999 13.759999 3.3799999 13.759999 C 3.3799999 13.9 3.3 13.96 3.12 13.96 C 2.62 13.759999 1.12 13.48 0.32 13.42 C 0.28 13.259999 0.32 12.94 0.44 12.82 C 0.5 12.82 0.56 12.82 0.62 12.82 C 1.5 12.759999 1.7199999 12.759999 1.7199999 11.179999 Z "/>
</symbol>
<symbol id="g607CD744DAB7515984E0B3F495F7DE81" overflow="visible">
<path d="M 2.98 0 L 7.24 0 C 7.7799997 0 9.62 -0.04 9.62 -0.04 C 9.82 0.96 10.0199995 2.26 10.139999 3.3 C 9.94 3.3999999 9.719999 3.4399998 9.48 3.3999999 C 9.08 1.9599999 8.34 0.78 6.22 0.78 L 4.96 0.78 C 4.18 0.78 3.82 1.16 3.82 2.18 L 3.82 10.46 C 3.82 12.12 4.16 12.219999 5.56 12.28 C 5.68 12.4 5.68 12.82 5.56 12.94 C 4.66 12.92 3.72 12.9 2.96 12.9 C 2.24 12.9 1.3 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.16 -0.02 2.3 0 2.98 0 Z "/>
</symbol>
<symbol id="g733371913480EE84B3609C9E9CD62F8C" overflow="visible">
<path d="M 3.34 7.8799996 C 3.22 7.7599998 3.1399999 7.7999997 3.1399999 7.98 L 3.1399999 11.66 C 3.1399999 12.96 3.22 13.759999 3.22 13.759999 C 3.22 13.9 3.1399999 13.96 2.96 13.96 C 2.46 13.759999 0.96 13.48 0.16 13.42 C 0.12 13.259999 0.16 12.94 0.28 12.82 C 0.34 12.82 0.39999998 12.82 0.45999998 12.82 C 1.3399999 12.759999 1.56 12.759999 1.56 11.179999 L 1.56 1.42 C 1.56 0.64 1.54 0.28 1.48 0 C 1.5799999 -0.16 1.68 -0.24 1.92 -0.24 C 2.04 -0.12 2.24 0.06 2.3999999 0.24 C 2.6 0.48 2.72 0.48 2.9399998 0.29999998 C 3.3999999 -0.08 4 -0.19999999 4.7 -0.19999999 C 6.74 -0.19999999 9.12 1.66 9.12 4.8399997 C 9.12 7.2799997 7.3199997 8.78 5.58 8.78 C 4.72 8.78 3.9599998 8.44 3.34 7.8799996 Z M 3.48 7.2599998 C 4 7.72 4.6 7.8999996 5.18 7.8999996 C 6.3999996 7.8999996 7.3999996 6.42 7.3999996 4.48 C 7.3999996 2.2 6.48 0.48 4.58 0.48 C 3.9599998 0.48 3.54 0.91999996 3.1399999 1.42 L 3.1399999 6.42 C 3.1399999 6.8399997 3.22 7.04 3.48 7.2599998 Z "/>
</symbol>
<symbol id="g560AC22EF992EFD90E66808483D7B3BA" overflow="visible">
<path d="M 11.12 10.24 L 11.12 3.6999998 C 11.12 3.32 11.12 3.1 10.98 3.1 C 10.9 3.1 10.599999 3.46 10.0199995 4.2 L 3.1599998 12.9 L 0.45999998 12.94 C 0.34 12.82 0.34 12.4 0.45999998 12.28 C 1.3199999 12.219999 1.92 11.5199995 2.04 11 L 2.04 2.6599998 C 2.04 0.88 1.6999999 0.76 0.29999998 0.62 C 0.17999999 0.5 0.17999999 0.08 0.29999998 -0.04 C 1.16 -0.02 2.06 0 2.54 0 C 3 0 3.9199998 -0.02 4.7599998 -0.04 C 4.88 0.08 4.88 0.5 4.7599998 0.62 C 3.36 0.76 3.02 0.84 3.02 2.6599998 L 3.02 8.78 C 3.02 9.46 3.02 9.76 3.1799998 9.76 C 3.3 9.76 3.52 9.54 3.86 9.099999 L 10.84 0.28 C 11.059999 -0.02 11.32 -0.19999999 11.639999 -0.19999999 C 11.92 -0.19999999 12.099999 0.04 12.099999 0.42 L 12.099999 10.24 C 12.099999 12.0199995 12.44 12.139999 13.84 12.28 C 13.96 12.4 13.96 12.82 13.84 12.94 C 13.0199995 12.92 12.08 12.9 11.599999 12.9 C 11.179999 12.9 10.26 12.92 9.38 12.94 C 9.26 12.82 9.26 12.4 9.38 12.28 C 10.78 12.139999 11.12 12.059999 11.12 10.24 Z "/>
</symbol>
<symbol id="g3BBBD96D467CC564123619D79E97B4D6" overflow="visible">
<path d="M 7.8999996 12.62 C 6.74 12.78 6.7799997 13.16 4.8199997 13.16 C 2.8 13.16 1.02 11.82 1.02 9.7 C 1.02 7.6 2.76 6.64 4.52 5.96 C 5.72 5.5 7.2 4.94 7.2 2.98 C 7.2 1.36 6.2999997 0.52 4.7 0.52 C 2.84 0.52 1.64 1.38 1.1999999 3.36 C 0.94 3.4399998 0.74 3.3999999 0.53999996 3.3 C 0.62 1.76 0.7 1.24 0.94 0.26 C 2.2 0.26 2.76 -0.19999999 4.54 -0.19999999 C 5.44 -0.19999999 6.2999997 0.02 7 0.45999998 C 8.16 1.18 8.88 2.3999999 8.88 3.6799998 C 8.88 5.7999997 7.2799997 6.74 5.64 7.3599997 C 4.44 7.7999997 2.44 8.559999 2.44 10.24 C 2.44 11.36 3.46 12.48 4.64 12.48 C 6.58 12.48 7.2 11.24 7.6 9.92 C 7.8199997 9.88 8.08 9.9 8.26 10.04 C 8.179999 11 8.099999 11.559999 7.8999996 12.62 Z "/>
</symbol>
<symbol id="g87DD77732F07A5C65A64D31E4C3C918D" overflow="visible">
<path d="M 16.199999 11.3 L 13.08 2.62 L 13.0199995 2.6399999 L 10.26 11.08 C 9.92 12.16 10.62 12.219999 11.3 12.28 C 11.42 12.4 11.42 12.82 11.3 12.94 C 10.48 12.92 9.599999 12.9 8.8 12.9 C 8.139999 12.9 7.44 12.92 6.7999997 12.94 C 6.68 12.82 6.68 12.4 6.7999997 12.28 C 7.8599997 12.219999 8.3 11.599999 8.48 11.08 L 8.94 9.76 C 9.0199995 9.5199995 9.08 9.32 9.08 9.139999 C 9.08 8.94 9.059999 8.78 8.9 8.44 L 6.3199997 2.58 L 6.22 2.6 L 3.3 11.44 C 3.06 12.139999 3.6 12.24 4.2999997 12.28 C 4.42 12.4 4.42 12.82 4.2999997 12.94 C 3.6399999 12.92 2.76 12.9 1.9799999 12.9 C 1.28 12.9 0.7 12.92 0.12 12.94 C 0 12.82 0 12.4 0.12 12.28 C 1.02 12.219999 1.16 12.2 1.54 11.12 L 5.2999997 0.29999998 C 5.4 -0.02 5.52 -0.24 5.74 -0.24 C 6 -0.24 6.12 -0.04 6.2599998 0.29999998 L 9.24 7 C 9.42 7.3999996 9.48 7.5 9.58 7.5 C 9.66 7.5 9.74 7.2799997 9.86 6.94 L 12.16 0.29999998 C 12.28 -0.04 12.38 -0.24 12.62 -0.24 C 12.84 -0.24 12.98 -0.02 13.08 0.28 L 17.1 11.059999 C 17.359999 11.759999 17.72 12.219999 18.82 12.28 C 18.939999 12.4 18.939999 12.82 18.82 12.94 C 18.24 12.92 17.6 12.9 17.08 12.9 C 16.56 12.9 15.679999 12.92 14.88 12.94 C 14.759999 12.82 14.759999 12.4 14.88 12.28 C 15.7 12.219999 16.5 12.16 16.199999 11.3 Z "/>
</symbol>
<symbol id="gD8CB364949770E6EB9E57283C62D30EB" overflow="visible">
<path d="M 4.3399997 -0.19999999 C 5.12 -0.19999999 6.06 0.19999999 7.04 1 C 7.14 1.0799999 7.3199997 1.12 7.3399997 0.97999996 C 7.3999996 0.48 7.56 -0.19999999 7.56 -0.19999999 C 7.72 -0.26 7.8199997 -0.24 7.94 -0.19999999 C 8.38 0.16 9.08 0.45999998 10.3 0.59999996 C 10.42 0.71999997 10.42 1.02 10.3 1.14 C 9.0199995 1.24 8.84 1.62 8.84 2.6 L 8.84 6.44 C 8.84 7.04 8.92 8.5 8.92 8.5 C 8.92 8.559999 8.86 8.62 8.76 8.62 C 8.66 8.599999 8.36 8.58 8.059999 8.58 C 7.4199996 8.58 6.7 8.599999 6.02 8.62 C 5.9 8.5 5.9 8.08 6.02 7.96 C 7 7.8999996 7.2599998 7.66 7.2599998 6.3399997 L 7.2599998 2.48 C 7.2599998 2.1 7.22 1.9399999 6.94 1.6999999 C 6.2 1.06 5.44 0.74 4.94 0.74 C 4.3399997 0.74 3.34 1.02 3.34 2.8 L 3.34 6.44 C 3.34 7.04 3.4199998 8.5 3.4199998 8.5 C 3.4199998 8.559999 3.36 8.62 3.26 8.62 C 3.1599998 8.599999 2.86 8.58 2.56 8.58 C 1.92 8.58 1.1999999 8.599999 0.52 8.62 C 0.39999998 8.5 0.39999998 8.08 0.52 7.96 C 1.48 7.8799996 1.76 7.66 1.76 6.3599997 L 1.76 2.52 C 1.76 1.14 2.36 -0.19999999 4.3399997 -0.19999999 Z "/>
</symbol>
<symbol id="gE8171CD7697771DDE124968BDB3EF0D7" overflow="visible">
<path d="M 5.42 4.46 C 5.68 4.46 5.96 5.02 5.96 5.2599998 C 5.96 5.46 5.8799996 5.66 5.68 5.66 L 1.3 5.66 C 1.06 5.66 0.79999995 5.2 0.79999995 4.8399997 C 0.79999995 4.64 0.91999996 4.46 1.1 4.46 Z "/>
</symbol>
<symbol id="g42587C4E387B2C5F870DA01C2914651F" overflow="visible">
<path d="M 6.68 1 C 6.7799997 1.0799999 6.96 1.12 6.98 0.97999996 C 7.04 0.5 7.2 -0.19999999 7.2 -0.19999999 C 7.3599997 -0.26 7.46 -0.24 7.58 -0.19999999 C 8.0199995 0.16 8.72 0.45999998 9.94 0.59999996 C 10.059999 0.71999997 10.059999 1.02 9.94 1.14 C 8.66 1.24 8.48 1.62 8.48 2.6 L 8.48 11.66 C 8.48 12.96 8.559999 13.759999 8.559999 13.759999 C 8.559999 13.9 8.48 13.96 8.3 13.96 C 7.7999997 13.759999 6.2999997 13.48 5.5 13.42 C 5.46 13.259999 5.5 12.94 5.62 12.82 C 5.68 12.82 5.74 12.82 5.7999997 12.82 C 6.68 12.759999 6.8999996 12.759999 6.8999996 11.179999 L 6.8999996 8.62 C 6.8999996 8.48 6.8599997 8.44 6.72 8.44 C 6.64 8.44 5.8199997 8.78 5.16 8.78 C 3.84 8.78 2.96 8.34 2.1599998 7.58 C 1.3 6.72 0.78 5.54 0.78 4.06 C 0.78 1.5999999 2.02 -0.19999999 4.18 -0.19999999 C 4.96 -0.19999999 5.7 0.19999999 6.68 1 Z M 6.8999996 2.48 C 6.8999996 2.1 6.8599997 1.9399999 6.58 1.6999999 C 5.8399997 1.06 5.2 0.74 4.7 0.74 C 3.62 0.74 2.5 1.92 2.5 4.42 C 2.5 5.8599997 2.78 6.66 3.08 7.08 C 3.6999998 8.0199995 4.54 8.08 4.94 8.08 C 5.66 8.08 6.16 7.8199997 6.56 7.3599997 C 6.8399997 7.04 6.8999996 6.8999996 6.8999996 6.2799997 Z "/>
</symbol>
<symbol id="g5AE3E73FF7353FF91276C30DF8EB5DCC" overflow="visible">
<path d="M 3.3 1.5799999 L 4.36 4.36 C 4.46 4.62 4.58 4.7 5.06 4.7 L 8.86 4.7 L 9.98 1.4399999 C 10.219999 0.71999997 9.639999 0.7 8.88 0.65999997 C 8.76 0.65999997 8.62 0.64 8.5 0.64 C 8.38 0.52 8.38 0.08 8.5 -0.04 C 9.24 -0.02 11.139999 0 11.92 0 C 12.74 0 13.86 -0.02 14.599999 -0.04 C 14.719999 0.08 14.719999 0.52 14.599999 0.64 C 13.82 0.71999997 13.16 0.7 12.799999 1.7199999 L 8.679999 13.16 C 8.38 12.98 7.18 12.28 6.48 12.28 L 2.1399999 2.04 C 1.62 0.79999995 1.02 0.7 0.14 0.64 C 0.02 0.52 0.02 0.08 0.14 -0.04 C 0.88 -0.02 1.24 0 2.02 0 C 2.84 0 3.9399998 -0.02 4.68 -0.04 C 4.7999997 0.08 4.7999997 0.52 4.68 0.64 C 3.9199998 0.7 2.98 0.76 3.3 1.5799999 Z M 5.46 5.66 C 5.02 5.66 4.88 5.72 4.96 5.92 L 6.72 10.4 L 6.8599997 10.4 L 8.5 5.66 Z "/>
</symbol>
<symbol id="gBC3E99057185A77BABD844B7BE98A74B" overflow="visible">
<path d="M 8.099999 2.46 L 8.099999 10.059999 C 8.099999 11.34 8.3 12.08 9.0199995 12.08 L 9.46 12.08 C 10.96 12.08 11.8 11.58 12.139999 10.04 C 12.36 10.04 12.74 10.059999 12.92 10.139999 C 12.78 11.059999 12.679999 12.099999 12.66 13 C 12.66 13.0199995 12.62 13.059999 12.599999 13.059999 C 11.92 13 9.7 12.9 8.12 12.9 L 5.2999997 12.9 C 3.76 12.9 1.4 13 0.64 13.059999 C 0.59999996 13.059999 0.56 13.0199995 0.56 13 C 0.48 12.099999 0.28 11.04 0.06 10.08 C 0.26 10 0.59999996 9.98 0.84 9.98 C 1.24 11.58 2.06 12.08 3.3799999 12.08 L 4.36 12.08 C 5.1 12.08 5.2999997 11.34 5.2999997 10.12 L 5.2999997 2.46 C 5.2999997 0.79999995 4.96 0.7 3.36 0.64 C 3.24 0.52 3.24 0.08 3.36 -0.04 C 4.3399997 -0.02 5.38 0 6.66 0 C 7.98 0 9.04 -0.02 10.04 -0.04 C 10.16 0.08 10.16 0.52 10.04 0.64 C 8.44 0.7 8.099999 0.79999995 8.099999 2.46 Z "/>
</symbol>
<symbol id="gB88E546A1990E31D64B5C4B23478426F" overflow="visible">
<path d="M 4.56 2.44 L 4.56 6.42 C 4.56 6.52 4.56 6.62 4.56 6.72 C 5.3399997 7.2 6.04 7.3999996 6.3799996 7.3999996 C 7.18 7.3999996 7.7799997 7.04 7.7799997 5.9 L 7.7799997 2.56 C 7.7799997 0.88 7.46 0.7 6.64 0.64 C 6.52 0.52 6.52 0.08 6.64 -0.04 C 7.48 -0.02 8.12 0 9.08 0 C 10.04 0 10.66 -0.02 11.5199995 -0.04 C 11.639999 0.08 11.639999 0.52 11.5199995 0.64 C 10.719999 0.7 10.38 0.88 10.38 2.56 L 10.38 5.68 C 10.38 6.18 10.36 6.58 10.3 6.7799997 C 11.059999 7.16 11.92 7.3999996 12.24 7.3999996 C 13.04 7.3999996 13.599999 7.04 13.599999 5.9 L 13.599999 2.56 C 13.599999 0.88 13.28 0.7 12.46 0.64 C 12.34 0.52 12.34 0.08 12.46 -0.04 C 13.299999 -0.02 13.94 0 14.9 0 C 16 0 16.88 -0.02 17.74 -0.04 C 17.859999 0.08 17.859999 0.52 17.74 0.64 C 16.52 0.7 16.199999 0.88 16.199999 2.56 L 16.199999 5.68 C 16.199999 7.8799996 15.4 8.88 13.679999 8.88 C 12.94 8.88 11.259999 8.08 10.099999 7.44 C 9.8 8.3 9 8.88 7.8199997 8.88 C 7.1 8.88 5.66 8.12 4.52 7.48 C 4.46 8.08 4.4 8.54 4.4 8.54 C 4.38 8.78 4.22 8.88 3.9399998 8.88 C 3.1999998 8.679999 2 8.4 0.62 8.22 C 0.58 8.099999 0.62 7.7 0.65999997 7.58 C 1.76 7.48 1.9599999 7.3199997 1.9599999 6.18 L 1.9599999 2.44 C 1.9599999 0.78 1.74 0.74 0.52 0.64 C 0.39999998 0.52 0.39999998 0.08 0.52 -0.04 C 1.36 -0.02 2.2 0 3.26 0 C 4.18 0 4.74 -0.02 5.6 -0.04 C 5.72 0.08 5.72 0.52 5.6 0.64 C 4.7599998 0.71999997 4.56 0.78 4.56 2.44 Z "/>
</symbol>
<symbol id="gD9D3B6C4D6AB50B3CADCA65007C1BC50" overflow="visible">
<path d="M 8.62 2.58 C 7.7999997 1.74 6.72 1.52 5.96 1.52 C 4.4 1.52 3.4399998 2.4199998 3.4399998 4.38 C 3.4399998 4.52 3.46 4.6 3.46 4.7 L 8.26 4.7 C 8.74 4.7 8.84 5.04 8.84 5.3199997 C 8.84 7.02 8.179999 8.88 5.24 8.88 C 3.1399999 8.88 0.74 7.02 0.74 3.9599998 C 0.74 2.8 1.16 1.5799999 2.02 0.79999995 C 2.78 0.12 3.76 -0.19999999 5.18 -0.19999999 C 6.56 -0.19999999 7.9199996 0.5 8.92 1.9599999 C 8.92 2.22 8.82 2.58 8.62 2.58 Z M 3.54 5.5 C 3.56 6.2 3.6599998 6.96 3.9399998 7.3599997 C 4.2599998 7.8399997 4.7999997 8.04 5.02 8.04 C 5.56 8.04 6.2999997 7.52 6.2999997 5.92 C 6.2999997 5.7999997 6.2999997 5.54 6.2599998 5.5 Z "/>
</symbol>
<symbol id="gB416F8956A8016097936DBEC1F135503" overflow="visible">
<path d="M 1.9 6.18 L 1.9 -2.2 C 1.9 -3.86 1.68 -3.8999999 0.45999998 -4 C 0.34 -4.12 0.34 -4.56 0.45999998 -4.68 C 1.3 -4.66 2.1399999 -4.64 3.1999998 -4.64 C 4.2599998 -4.64 5.08 -4.66 5.94 -4.68 C 6.06 -4.56 6.06 -4.12 5.94 -4 C 4.72 -3.9199998 4.5 -3.86 4.5 -2.2 L 4.5 0.14 C 4.94 -0.08 5.3599997 -0.19999999 5.8399997 -0.19999999 C 8.88 -0.19999999 10.86 1.8 10.86 4.74 C 10.86 5.8599997 10.44 7.1 9.66 7.8799996 C 8.96 8.58 7.96 8.88 6.92 8.88 C 6.3399997 8.88 5.2599998 8.179999 4.56 7.54 L 4.44 7.54 C 4.4 8.099999 4.3399997 8.54 4.3399997 8.54 C 4.3199997 8.78 4.16 8.88 3.8799999 8.88 C 3.1399999 8.679999 1.9399999 8.4 0.56 8.22 C 0.52 8.099999 0.56 7.7 0.59999996 7.58 C 1.6999999 7.48 1.9 7.3199997 1.9 6.18 Z M 4.5 1.3 L 4.5 6.42 C 4.5 6.54 4.5 6.64 4.5 6.7599998 C 5.08 7.2799997 5.8199997 7.54 6.2799997 7.54 C 7.1 7.54 8.059999 6.54 8.059999 4.2 C 8.059999 2.52 7.46 0.64 5.72 0.64 C 5.5 0.64 5 0.76 4.5 1.3 Z "/>
</symbol>
<symbol id="gC81C3C15134AD04FEC0FE7FCEBE8BB14" overflow="visible">
<path d="M 2 2.54 C 2 0.88 1.68 0.7 0.45999998 0.64 C 0.34 0.52 0.34 0.08 0.45999998 -0.04 C 1.3 -0.02 2.2 0 3.3 0 C 4.4 0 5.2799997 -0.02 6.14 -0.04 C 6.2599998 0.08 6.2599998 0.52 6.14 0.64 C 4.92 0.7 4.6 0.88 4.6 2.54 L 4.6 11.66 C 4.6 12.96 4.66 13.7 4.66 13.7 C 4.66 13.88 4.52 13.96 4.3399997 13.96 C 3.6 13.719999 2 13.5 0.58 13.44 C 0.52 13.2 0.53999996 12.98 0.64 12.799999 C 1.9 12.7 2 12.679999 2 11.3 Z "/>
</symbol>
<symbol id="g4CEB3F42B775C8D3827D0A458A70771F" overflow="visible">
<path d="M 3.6599998 1.4599999 L 4.9 3.1999998 C 4.98 3.3 5.04 3.36 5.1 3.26 L 6.06 1.4399999 C 6.3999996 0.79999995 6.2 0.74 5.5 0.64 C 5.38 0.52 5.38 0.08 5.5 -0.04 C 5.9 -0.02 7.16 0 8.22 0 C 9.26 0 10.5 -0.02 10.9 -0.04 C 11.0199995 0.08 11.0199995 0.52 10.9 0.64 C 10.16 0.76 9.48 1.02 8.84 1.9799999 L 7.08 4.6 C 6.98 4.7599998 6.98 4.8199997 7.04 4.9 L 8.82 7.06 C 9.38 7.74 10.099999 7.98 10.719999 8.04 C 10.84 8.16 10.84 8.599999 10.719999 8.72 C 10.32 8.7 9.7 8.679999 9.04 8.679999 C 8.26 8.679999 7.44 8.7 7.04 8.72 C 6.92 8.599999 6.92 8.16 7.04 8.04 C 7.7599998 7.98 7.9199996 7.7599998 7.52 7.18 L 6.44 5.64 C 6.3799996 5.54 6.2799997 5.54 6.2 5.68 L 5.2999997 7.2 C 4.88 7.9199996 5.14 7.96 5.9 8.04 C 6.02 8.16 6.02 8.599999 5.9 8.72 C 5.5 8.7 4.2 8.679999 3.1 8.679999 C 2.12 8.679999 0.97999996 8.7 0.58 8.72 C 0.45999998 8.599999 0.45999998 8.16 0.58 8.04 C 1.48 8.04 1.88 7.5 2.44 6.7 L 4.22 4.16 C 4.2799997 4.08 4.2799997 4 4.16 3.86 L 2.32 1.5799999 C 1.8199999 0.94 0.94 0.71999997 0.34 0.64 C 0.22 0.52 0.22 0.08 0.34 -0.04 C 0.74 -0.02 1.36 0 2 0 C 2.86 0 3.8 -0.02 4.2 -0.04 C 4.3199997 0.08 4.3199997 0.52 4.2 0.64 C 3.84 0.71999997 3.22 0.84 3.6599998 1.4599999 Z "/>
</symbol>
<symbol id="gAFD7B3D7EB6599FB514B70015F312425" overflow="visible">
<path d="M 4.8399997 -3.36 C 5.16 -2.8 5.46 -2.08 5.7 -1.48 C 7.2999997 2.3799999 8.28 4.54 9.34 6.7799997 C 9.62 7.3599997 10.219999 7.98 10.96 8.04 C 11.08 8.16 11.08 8.599999 10.96 8.72 C 10.46 8.7 10.099999 8.679999 9.54 8.679999 C 8.84 8.679999 8.16 8.7 7.4199996 8.72 C 7.2999997 8.599999 7.2999997 8.16 7.4199996 8.04 C 8.059999 7.98 8.7 7.8799996 8.38 7.16 L 6.3199997 2.54 C 6.3199997 2.52 6.3199997 2.52 6.2999997 2.5 C 6.2999997 2.52 6.2999997 2.54 6.2799997 2.58 L 4.42 6.7599998 C 4.4 6.7799997 4.4 6.7999997 4.4 6.8199997 C 4.04 7.6 3.8999999 7.94 5.08 8.04 C 5.2 8.16 5.2 8.599999 5.08 8.72 C 4.3399997 8.7 3.1399999 8.679999 2.4199998 8.679999 C 1.74 8.679999 0.59999996 8.7 0.19999999 8.72 C 0.08 8.599999 0.08 8.16 0.19999999 8.04 C 1.0799999 7.96 1.24 7.8199997 1.78 6.56 L 4.36 0.64 C 4.42 0.53999996 4.5 0.45999998 4.56 0.38 C 4.8199997 0.02 5.04 -0.28 4.92 -0.56 L 4.44 -1.66 C 4.18 -2.28 3.9399998 -2.6399999 3.3799999 -2.6399999 C 3.02 -2.6399999 2.96 -2.56 2.6799998 -2.56 C 1.92 -2.56 1.48 -3.08 1.48 -3.48 C 1.48 -3.74 1.54 -4.06 1.7199999 -4.2799997 C 1.9 -4.5 2.24 -4.64 2.5 -4.64 C 2.76 -4.64 3.36 -4.56 3.6399999 -4.44 C 4.06 -4.24 4.62 -3.76 4.8399997 -3.36 Z "/>
</symbol>
<symbol id="gCDF8B867C9AAFA36255BC29C36465E90" overflow="visible">
<path d="M 3.5 2.44 L 3.5 7.7999997 L 5.3599997 7.7999997 C 5.54 7.7999997 5.8199997 7.8799996 5.8199997 8.059999 L 5.8199997 8.46 C 5.8199997 8.54 5.7599998 8.58 5.66 8.58 L 3.5 8.58 L 3.5 9.719999 C 3.5 12.799999 4.42 13.28 5.08 13.28 C 5.68 13.28 6 13.04 6.2799997 12.34 C 6.44 11.98 6.66 11.7 7.08 11.7 C 7.4199996 11.7 7.8999996 12.12 7.8999996 12.5199995 C 7.8999996 12.86 7.68 13.219999 7.2599998 13.54 C 6.74 13.9 6.22 13.96 5.46 13.96 C 3.78 13.96 1.92 12.5 1.92 9.38 L 1.92 8.58 L 0.9 8.58 C 0.53999996 8.58 0.44 8.34 0.44 8.179999 L 0.44 7.9199996 C 0.44 7.8199997 0.45999998 7.7999997 0.53999996 7.7999997 L 1.92 7.7999997 L 1.92 2.44 C 1.92 0.78 1.5999999 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 1.92 0 2.72 0 C 3.52 0 4.48 -0.02 5.18 -0.04 C 5.2999997 0.08 5.2999997 0.5 5.18 0.62 C 3.62 0.7 3.5 0.78 3.5 2.44 Z "/>
</symbol>
<symbol id="g17AD34DB90B05275C6F1422A9B4B5274" overflow="visible">
<path d="M 6.5 7.96 C 7.58 7.8799996 7.7 7.64 7.2799997 6.62 L 5.66 2.7 C 5.3399997 1.92 5.24 1.92 4.92 2.76 L 3.48 6.62 C 3.12 7.58 3.04 7.8199997 4.1 7.96 C 4.22 8.08 4.22 8.5 4.1 8.62 C 3.4399998 8.599999 2.74 8.58 2.08 8.58 C 1.42 8.58 0.82 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.28 7.8399997 1.42 7.52 1.8199999 6.5 L 4.38 0.17999999 C 4.5 -0.12 4.62 -0.24 4.88 -0.24 C 5.08 -0.24 5.22 -0.12 5.3599997 0.22 L 8.0199995 6.48 C 8.4 7.3599997 8.62 7.8599997 9.74 7.96 C 9.86 8.08 9.86 8.5 9.74 8.62 C 9.34 8.599999 8.86 8.58 8.34 8.58 C 7.68 8.58 7 8.599999 6.5 8.62 C 6.3799996 8.5 6.3799996 8.08 6.5 7.96 Z "/>
</symbol>
<symbol id="gB91E67CF1B63A9F4CC30BB03AE35508D" overflow="visible">
<path d="M 2.08 1.9 C 1.4599999 1.9 1.02 1.48 1.02 0.91999996 C 1.02 0.29999998 1.54 0.099999994 1.9 0.04 C 2.28 0 2.62 -0.12 2.62 -0.58 C 2.62 -1 1.9 -1.92 0.85999995 -2.18 C 0.85999995 -2.3799999 0.9 -2.52 1.04 -2.6599998 C 2.24 -2.44 3.3999999 -1.48 3.3999999 -0.08 C 3.3999999 1.12 2.8799999 1.9 2.08 1.9 Z "/>
</symbol>
<symbol id="g5925E4E4FE8F59A76637BD462660B390" overflow="visible">
<path d="M 3.6399999 7.16 C 3.1799998 7.8399997 3.32 7.8599997 4.22 7.96 C 4.3399997 8.08 4.3399997 8.5 4.22 8.62 C 3.6799998 8.599999 2.8 8.58 2.2 8.58 C 1.5999999 8.58 1 8.599999 0.48 8.62 C 0.35999998 8.5 0.35999998 8.08 0.48 7.96 C 1.16 7.8999996 1.7199999 7.56 2.28 6.74 L 4.02 4.2 C 4.12 4.06 4.12 4 4.04 3.8999999 L 2.36 1.74 C 1.56 0.71999997 1.12 0.65999997 0.42 0.62 C 0.29999998 0.5 0.29999998 0.08 0.42 -0.04 C 0.82 -0.02 1.26 0 1.86 0 C 2.46 0 3.02 -0.02 3.54 -0.04 C 3.6599998 0.08 3.6599998 0.5 3.54 0.62 C 2.82 0.7 2.6599998 0.78 3.1 1.42 L 4.36 3.24 C 4.52 3.48 4.6 3.46 4.72 3.28 L 5.8799996 1.68 C 6.58 0.71999997 6.2599998 0.68 5.62 0.62 C 5.5 0.5 5.5 0.08 5.62 -0.04 C 6.22 -0.02 6.8799996 0 7.6 0 C 8.36 0 8.9 -0.02 9.38 -0.04 C 9.5 0.08 9.5 0.5 9.38 0.62 C 8.48 0.68 8.179999 0.74 7.3799996 1.88 L 5.58 4.42 C 5.5 4.54 5.48 4.6 5.58 4.72 L 7.2599998 6.8599997 C 8 7.7999997 8.48 7.8999996 9.2 7.96 C 9.32 8.08 9.32 8.5 9.2 8.62 C 8.8 8.599999 8.34 8.58 7.74 8.58 C 7.14 8.58 6.58 8.599999 6.06 8.62 C 5.94 8.5 5.94 8.08 6.06 7.96 C 6.7999997 7.8799996 7.02 7.8199997 6.54 7.14 L 5.24 5.3199997 C 5.1 5.12 5.02 5.14 4.8599997 5.3599997 Z "/>
</symbol>
<symbol id="g911507D70DD1D78477F3BEDE827F51DF" overflow="visible">
<path d="M 11.28 10.46 L 11.28 7.3399997 L 5.08 7.3399997 L 5.08 10.46 C 5.08 12.12 5.64 12.2 6.74 12.259999 C 6.94 12.38 6.94 12.82 6.74 12.94 C 5.94 12.92 4.5 12.9 3.6999998 12.9 C 2.8999999 12.9 1.42 12.92 0.62 12.94 C 0.42 12.82 0.42 12.38 0.62 12.259999 C 1.7199999 12.2 2.28 12.12 2.28 10.46 L 2.28 2.44 C 2.28 0.78 1.7199999 0.7 0.62 0.64 C 0.42 0.52 0.42 0.08 0.62 -0.04 C 1.42 -0.02 2.8999999 0 3.6999998 0 C 4.5 0 5.94 -0.02 6.74 -0.04 C 6.94 0.08 6.94 0.52 6.74 0.64 C 5.64 0.7 5.08 0.78 5.08 2.44 L 5.08 6.3799996 L 11.28 6.3799996 L 11.28 2.44 C 11.28 0.78 10.719999 0.7 9.62 0.64 C 9.42 0.52 9.42 0.08 9.62 -0.04 C 10.42 -0.02 11.9 0 12.7 0 C 13.5 0 14.94 -0.02 15.74 -0.04 C 15.94 0.08 15.94 0.52 15.74 0.64 C 14.639999 0.7 14.08 0.78 14.08 2.44 L 14.08 10.46 C 14.08 12.12 14.639999 12.2 15.74 12.259999 C 15.94 12.38 15.94 12.82 15.74 12.94 C 14.94 12.92 13.5 12.9 12.7 12.9 C 11.9 12.9 10.42 12.92 9.62 12.94 C 9.42 12.82 9.42 12.38 9.62 12.259999 C 10.719999 12.2 11.28 12.12 11.28 10.46 Z "/>
</symbol>
<symbol id="gCF24A1AE12C8178F68C1BA3421208D44" overflow="visible">
<path d="M 3.6999998 0 C 4.5 0 6.14 -0.04 6.94 -0.04 C 8.7 -0.04 10.679999 0.39999998 12.099999 1.64 C 13.059999 2.48 13.719999 4.14 13.719999 6.18 C 13.719999 9.88 11.32 12.92 6.3999996 12.92 C 5.3399997 12.92 4.5 12.9 3.6999998 12.9 C 2.8999999 12.9 0.62 12.94 0.62 12.94 C 0.42 12.82 0.42 12.38 0.62 12.259999 C 1.7199999 12.2 2.28 12.12 2.28 10.46 L 2.28 2.44 C 2.28 0.78 1.7199999 0.7 0.62 0.64 C 0.42 0.52 0.42 0.08 0.62 -0.04 C 0.62 -0.04 2.8999999 0 3.6999998 0 Z M 5.08 2.3799999 L 5.08 10.58 C 5.08 11.679999 5.6 12.08 6.3199997 12.08 C 10.26 12.08 10.7 8.7 10.7 5.68 C 10.7 2.04 8.5199995 0.79999995 7 0.79999995 C 5.6 0.79999995 5.08 1.04 5.08 2.3799999 Z "/>
</symbol>
<symbol id="g80AF1C2942ED5136FA76CE028C280500" overflow="visible">
<path d="M 9.34 7.8799996 C 9.9 7.8799996 10.219999 8.12 10.219999 8.86 C 10.219999 9.24 9.7 9.82 8.94 9.82 C 8.059999 9.82 6.8999996 9.16 6.3199997 8.639999 C 5.96 8.84 5.54 8.88 4.64 8.88 C 3.78 8.88 2.9399998 8.679999 2.28 8.24 C 1.4599999 7.72 0.91999996 6.94 0.91999996 5.92 C 0.91999996 4.94 1.5 3.8799999 2.46 3.36 C 1.8399999 2.82 0.88 1.76 0.88 1.36 C 0.88 0.97999996 0.94 0.74 1.14 0.44 C 1.3199999 0.16 1.56 0 1.9599999 -0.12 C 1.1 -0.64 0.22 -1.78 0.22 -2.12 C 0.22 -2.86 0.45999998 -3.72 1 -4.1 C 1.78 -4.64 3.1 -4.7599998 4.06 -4.7599998 C 6.8399997 -4.7599998 10.0199995 -3.3 10.0199995 -1.1 C 10.0199995 -0.68 9.82 0.17999999 9.0199995 0.71999997 C 8.24 1.24 5.24 1.38 3.76 1.38 C 3.3999999 1.38 2.86 1.42 2.86 2.22 C 2.86 2.54 3.06 2.82 3.1599998 3.06 C 3.58 2.86 4 2.84 4.62 2.84 C 5.64 2.84 6.58 3.1 7.2599998 3.6999998 C 7.8399997 4.22 8.24 4.92 8.24 5.8199997 C 8.24 6.94 7.68 7.68 7 8.24 C 7.16 8.44 7.8199997 8.8 8.0199995 8.8 C 8.2 8.8 8.34 8.679999 8.4 8.559999 C 8.48 8.3 8.84 7.8799996 9.34 7.8799996 Z M 3.5 -0.5 C 5.04 -0.5 8 -0.56 8 -1.62 C 8 -2.34 7.68 -3.1599998 7.02 -3.52 C 6.3999996 -3.8799999 5.38 -3.9199998 4.62 -3.9199998 C 3.3 -3.9199998 2.3999999 -2.9399998 2.3999999 -1.92 C 2.3999999 -1.24 2.3999999 -0.78 2.62 -0.38 C 2.82 -0.45999998 3.08 -0.5 3.5 -0.5 Z M 5.7999997 5.7599998 C 5.7999997 3.84 5.24 3.6 4.72 3.6 C 3.48 3.6 3.32 5.08 3.32 6.1 C 3.32 7.58 3.6799998 8.12 4.46 8.12 C 5.4 8.12 5.7999997 7.3399997 5.7999997 5.7599998 Z "/>
</symbol>
<symbol id="g187DB76C80CD961C20BAB3AF6259527" overflow="visible">
<path d="M 3.4399998 10.46 C 3.4399998 12.12 3.74 12.219999 5.2799997 12.28 C 5.4 12.4 5.4 12.82 5.2799997 12.94 C 4.3399997 12.92 3.36 12.9 2.58 12.9 C 1.8 12.9 0.97999996 12.92 0.19999999 12.94 C 0.08 12.82 0.08 12.4 0.19999999 12.28 C 1.4 12.219999 1.74 12.12 1.74 10.46 L 1.74 4.66 C 1.74 0.58 4.38 -0.19999999 6.42 -0.19999999 C 10.5199995 -0.19999999 11.5 2.34 11.5 5.9 L 11.5 10.46 C 11.5 12.059999 11.84 12.139999 13.04 12.28 C 13.16 12.4 13.16 12.82 13.04 12.94 C 12.28 12.92 11.46 12.9 11 12.9 C 10.58 12.9 9.599999 12.92 8.679999 12.94 C 8.559999 12.82 8.559999 12.4 8.679999 12.28 C 10.179999 12.139999 10.5199995 12.08 10.5199995 10.46 L 10.5199995 5.54 C 10.5199995 3.3 10.219999 0.62 6.8399997 0.62 C 5.8799996 0.62 5.06 0.97999996 4.46 1.56 C 3.48 2.5 3.4399998 4.02 3.4399998 5.3199997 Z "/>
</symbol>
<symbol id="gB2E338F181D915F0996F60E92302C895" overflow="visible">
<path d="M 7 2.44 L 7 10.08 C 7 11.36 7.2 12.12 7.9199996 12.12 L 8.36 12.12 C 9.86 12.12 10.8 11.599999 11.139999 10.059999 C 11.36 10.059999 11.639999 10.08 11.82 10.16 C 11.679999 11.08 11.58 12.099999 11.559999 13 C 11.559999 13.0199995 11.5199995 13.059999 11.5 13.059999 C 10.82 13 8.599999 12.9 7.02 12.9 L 5.2999997 12.9 C 3.76 12.9 1.4 13 0.64 13.059999 C 0.59999996 13.059999 0.56 13.0199995 0.56 13 C 0.48 12.099999 0.28 11.059999 0.06 10.099999 C 0.26 10.0199995 0.5 10 0.74 10 C 1.14 11.599999 2.06 12.12 3.3799999 12.12 L 4.36 12.12 C 5.1 12.12 5.2999997 11.36 5.2999997 10.139999 L 5.2999997 2.44 C 5.2999997 0.78 4.96 0.68 3.36 0.62 C 3.24 0.5 3.24 0.08 3.36 -0.04 C 4.3399997 -0.02 5.3599997 0 6.16 0 C 6.92 0 7.94 -0.02 8.94 -0.04 C 9.059999 0.08 9.059999 0.5 8.94 0.62 C 7.3399997 0.68 7 0.78 7 2.44 Z "/>
</symbol>
<symbol id="g5DAB70659D3EBD6E0CC12EEF6796854" overflow="visible">
<path d="M 8.599999 4.38 L 6.94 4.38 L 6.94 10.219999 C 6.94 11.219999 6.94 12 6.98 12.16 L 6.94 12.2 L 6.2999997 12.2 C 6.16 12.2 6.06 12.08 5.98 11.98 C 4.72 10.44 2.3999999 7.14 0.56 4.2799997 C 0.62 3.98 0.74 3.4399998 1.3399999 3.4399998 L 5.42 3.4399998 L 5.42 1.5999999 C 5.42 0.68 4.66 0.68 3.8 0.62 C 3.6799998 0.5 3.6799998 0.08 3.8 -0.04 C 4.44 -0.02 5.24 0 6.16 0 C 6.94 0 7.7 -0.02 8.34 -0.04 C 8.46 0.08 8.46 0.5 8.34 0.62 C 7.3599997 0.7 6.94 0.65999997 6.94 1.5999999 L 6.94 3.4399998 L 8.32 3.4399998 C 8.599999 3.4399998 8.9 3.82 8.9 4.06 C 8.9 4.2599998 8.82 4.38 8.599999 4.38 Z M 5.42 10.139999 L 5.42 4.38 L 1.5999999 4.38 C 2.62 6.02 4.04 8.26 5.42 10.139999 Z "/>
</symbol>
<symbol id="gA335A20E4C1D7F39210005AFF7F1A0EF" overflow="visible">
<path d="M 7.14 -0.19999999 C 9.08 -0.19999999 10.86 0.71999997 12.219999 2.5 C 12.12 2.6799998 11.98 2.8 11.759999 2.8 C 10.34 1.24 8.98 0.62 7.12 0.62 C 4.42 0.62 2.56 3.6599998 2.56 6.58 C 2.56 8.3 3.02 9.74 3.74 10.639999 C 4.74 11.86 5.9 12.42 6.94 12.42 C 9.7 12.42 10.8 10.78 11.32 9.059999 C 11.559999 8.98 11.759999 9.04 11.98 9.16 C 11.88 10.2 11.74 11.16 11.54 12.259999 C 10.5199995 12.36 9.62 13.16 7.16 13.16 C 5.46 13.16 4.04 12.54 2.86 11.46 C 1.54 10.24 0.74 8.28 0.74 6.2 C 0.74 2.72 2.84 -0.19999999 7.14 -0.19999999 Z "/>
</symbol>
<symbol id="gAA14E57E2DCC57A3F7809273EECD3C51" overflow="visible">
<path d="M 7.9104 1.5616 L 7.9104 6.6944 C 7.9104 7.7567997 8.128 7.8208 9.024 7.8592 C 9.1008 7.936 9.1008 8.2048 9.024 8.2816 C 8.4992 8.2688 7.8464 8.256 7.3599997 8.256 C 6.8863997 8.256 6.272 8.2688 5.7088 8.2816 C 5.632 8.2048 5.632 7.936 5.7088 7.8592 C 6.6047997 7.8208 6.8223996 7.7567997 6.8223996 6.6944 L 6.8223996 4.6464 L 2.4448 4.6464 L 2.4448 6.6944 C 2.4448 7.7567997 2.6624 7.8208 3.5584 7.8592 C 3.6352 7.936 3.6352 8.2048 3.5584 8.2816 C 3.072 8.2688 2.5472 8.256 1.8944 8.256 C 1.2544 8.256 0.72959995 8.2688 0.24319999 8.2816 C 0.1664 8.2048 0.1664 7.936 0.24319999 7.8592 C 1.1392 7.8208 1.3568 7.7567997 1.3568 6.6944 L 1.3568 1.5616 C 1.3568 0.4992 1.1392 0.43519998 0.24319999 0.39679998 C 0.1664 0.32 0.1664 0.0512 0.24319999 -0.0256 C 0.8064 -0.0128 1.4208 0 1.9072 0 C 2.368 0 2.9952 -0.0128 3.5584 -0.0256 C 3.6352 0.0512 3.6352 0.32 3.5584 0.39679998 C 2.6624 0.43519998 2.4448 0.4992 2.4448 1.5616 L 2.4448 4.1088 L 6.8223996 4.1088 L 6.8223996 1.5616 C 6.8223996 0.4992 6.6047997 0.43519998 5.7088 0.39679998 C 5.632 0.32 5.632 0.0512 5.7088 -0.0256 C 6.2848 -0.0128 6.8992 0 7.3728 0 C 7.8464 0 8.4608 -0.0128 9.024 -0.0256 C 9.1008 0.0512 9.1008 0.32 9.024 0.39679998 C 8.128 0.43519998 7.9104 0.4992 7.9104 1.5616 Z "/>
</symbol>
<symbol id="gF5F8064101DBF0FCB4BCFDA7012527FE" overflow="visible">
<path d="M 2.3167999 1.5616 L 2.3167999 4.1088 C 2.3167999 4.7488 2.368 5.568 2.368 5.568 C 2.368 5.6191998 2.304 5.6576 2.2015998 5.6576 C 1.8432 5.5168 1.3312 5.4016 0.44799998 5.2864 C 0.4224 5.2096 0.44799998 5.0048 0.4736 4.928 C 1.1776 4.864 1.3055999 4.7872 1.3055999 4.0576 L 1.3055999 1.5616 C 1.3055999 0.4992 1.1647999 0.4608 0.384 0.39679998 C 0.30719998 0.32 0.30719998 0.0512 0.384 -0.0256 C 0.8064 -0.0128 1.3055999 0 1.8176 0 C 2.3295999 0 2.816 -0.0128 3.2384 -0.0256 C 3.3151999 0.0512 3.3151999 0.32 3.2384 0.39679998 C 2.4575999 0.44799998 2.3167999 0.4992 2.3167999 1.5616 Z M 1.152 7.6671996 C 1.152 7.3343997 1.4591999 7.0016 1.7664 7.0016 C 2.1248 7.0016 2.432 7.3472 2.432 7.6159997 C 2.432 7.9231997 2.1632 8.2816 1.8176 8.2816 C 1.5103999 8.2816 1.152 7.9743996 1.152 7.6671996 Z "/>
</symbol>
<symbol id="g3976D55F213F07C6469FD06EC16139AA" overflow="visible">
<path d="M 4.9407997 1.1904 C 4.4672 0.704 4.0959997 0.4992 3.3536 0.4992 C 2.8927999 0.4992 2.3552 0.768 1.9583999 1.4208 C 1.7024 1.8432 1.5488 2.432 1.5488 3.1743999 L 4.9536 3.1488 C 5.1071997 3.1488 5.1967998 3.2256 5.1967998 3.3664 C 5.1967998 4.4416 4.8128 5.5936 3.0335999 5.5936 C 1.92 5.5936 0.4736 4.5312 0.4736 2.5856 C 0.4736 1.8687999 0.65279996 1.1776 1.0752 0.69119996 C 1.5103999 0.1792 2.112 -0.12799999 3.0335999 -0.12799999 C 4.0064 -0.12799999 4.6976 0.32 5.2096 0.9856 C 5.1712 1.1136 5.0944 1.1776 4.9407997 1.1904 Z M 1.5871999 3.6095998 C 1.8304 5.0559998 2.7264 5.1712 3.0335999 5.1712 C 3.52 5.1712 4.0959997 4.9024 4.0959997 3.8272 C 4.0959997 3.712 4.0448 3.648 3.9039998 3.648 Z "/>
</symbol>
<symbol id="gB7BB853387AAC07ADB7DDEF96856059B" overflow="visible">
<path d="M 2.2528 4.5824 C 2.2272 5.0944 2.2144 5.4272 2.1504 5.5551996 C 2.1248 5.6191998 2.0992 5.6576 1.9968 5.6576 C 1.6384 5.5168 1.3055999 5.4016 0.4224 5.2864 C 0.39679998 5.2096 0.4224 5.0048 0.44799998 4.928 C 1.1392 4.864 1.28 4.7999997 1.28 4.0576 L 1.28 1.5616 C 1.28 0.4992 1.1264 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7808 -0.0128 1.28 0 1.7919999 0 C 2.304 0 2.8927999 -0.0128 3.3407998 -0.0256 C 3.4176 0.0512 3.4176 0.32 3.3407998 0.39679998 C 2.4448 0.4608 2.2912 0.4992 2.2912 1.5616 L 2.2912 3.3407998 C 2.2912 3.6736 2.4448 3.968 2.5983999 4.1984 C 2.7391999 4.4031997 3.0335999 4.8255997 3.1871998 4.8255997 C 3.3023999 4.8255997 3.4176 4.7999997 3.52 4.6591997 C 3.6095998 4.5312 3.7631998 4.3648 3.9808 4.3648 C 4.288 4.3648 4.5824 4.6847997 4.5824 5.0048 C 4.5824 5.2479997 4.3519998 5.6191998 3.8144 5.6191998 C 3.2128 5.6191998 2.688 5.0559998 2.3936 4.5568 C 2.3167999 4.416 2.2528 4.5183997 2.2528 4.5824 Z "/>
</symbol>
<symbol id="gF8EC31AC53CF59E01ED9143906F6DA7B" overflow="visible">
<path d="M 3.7503998 0.61439997 C 3.8272 0.21759999 3.968 -0.12799999 4.608 -0.12799999 C 5.0944 -0.12799999 5.5551996 0.0896 5.824 0.34559998 C 5.7984 0.4992 5.7472 0.61439997 5.6064 0.69119996 C 5.5168 0.61439997 5.2992 0.48639998 5.1328 0.48639998 C 4.7616 0.48639998 4.7488 0.9856 4.7488 1.5744 L 4.7488 3.4559999 C 4.7488 5.2736 3.7503998 5.6191998 2.816 5.6191998 C 1.7664 5.6191998 0.704 4.928 0.704 4.1984 C 0.704 3.8911998 0.8576 3.7375998 1.152 3.7375998 C 1.5231999 3.7375998 1.7536 4.0064 1.7536 4.1728 C 1.7536 4.2623997 1.7407999 4.3519998 1.7152 4.4031997 C 1.7024 4.4416 1.6896 4.5183997 1.6896 4.6591997 C 1.6896 5.0559998 2.2272 5.1967998 2.7136 5.1967998 C 3.1488 5.1967998 3.7503998 4.9792 3.7503998 3.5328 C 3.7503998 3.4431999 3.712 3.392 3.6736 3.3792 L 2.5728 3.1104 C 1.344 2.8032 0.4608 2.1248 0.4608 1.2544 C 0.4608 0.2048 1.1776 -0.12799999 2.0736 -0.12799999 C 2.5216 -0.12799999 2.9055998 -0.0256 3.4687998 0.4096 L 3.7247999 0.61439997 Z M 3.7503998 2.9824 L 3.7503998 1.2928 C 3.7503998 1.1264 3.6736 1.0368 3.5712 0.96 C 3.2384 0.69119996 2.8032 0.39679998 2.4448 0.39679998 C 1.8047999 0.39679998 1.5231999 0.9088 1.5231999 1.3055999 C 1.5231999 1.8815999 1.7919999 2.4703999 2.7391999 2.7136 Z "/>
</symbol>
<symbol id="g68DDE7C8FDC8A226B6C32EAD39AF7364" overflow="visible">
<path d="M 5.0944 1.1647999 C 5.0432 1.28 4.9407997 1.3312 4.8255997 1.344 C 4.3904 0.7808 3.84 0.4992 3.2896 0.4992 C 2.3552 0.4992 1.5744 1.4463999 1.5744 2.944 C 1.5744 4.3519998 2.1887999 5.1967998 3.0335999 5.1967998 C 3.7888 5.1967998 3.8911998 4.7488 3.9424 4.3008 C 3.9808 3.9552 4.16 3.84 4.4288 3.84 C 4.6976 3.84 5.0559998 4.0064 5.0559998 4.4031997 C 5.0559998 5.1071997 4.3264 5.6191998 3.0976 5.6191998 C 1.8304 5.6191998 0.4736 4.48 0.4736 2.6624 C 0.4736 1.0112 1.3952 -0.12799999 3.008 -0.12799999 C 3.776 -0.12799999 4.4544 0.1152 5.0944 1.1647999 Z "/>
</symbol>
<symbol id="g570B752173035444311A253BD2376AD" overflow="visible">
<path d="M 2.1376 3.6608 C 2.1376 3.9296 2.2528 4.0832 2.3552 4.1984 C 2.8416 4.672 3.4944 4.9536 3.9936 4.9536 C 4.2496 4.9536 4.5183997 4.7872 4.672 4.4927998 C 4.7999997 4.2367997 4.8255997 3.8911998 4.8255997 3.5072 L 4.8255997 1.5616 C 4.8255997 0.51199996 4.6976 0.4608 4.032 0.39679998 C 3.968 0.32 3.968 0.0512 4.032 -0.0256 C 4.3904 -0.0128 4.8255997 0 5.3375998 0 C 5.8496 0 6.272 -0.0128 6.6944 -0.0256 C 6.7584 0.0512 6.7584 0.32 6.6944 0.39679998 C 5.9775996 0.4608 5.8367996 0.51199996 5.8367996 1.5616 L 5.8367996 3.4687998 C 5.8367996 4.1728 5.7855997 4.7999997 5.4912 5.184 C 5.2736 5.4656 4.8768 5.6191998 4.4288 5.6191998 C 3.8016 5.6191998 3.0335999 5.4528 2.2528 4.5824 C 2.2528 4.5696 2.24 4.5696 2.2272 4.5568 C 2.1887999 4.5056 2.1248 4.4288 2.1248 4.5824 L 2.1376 7.4624 C 2.1376 8.2944 2.1887999 8.806399 2.1887999 8.806399 C 2.1887999 8.896 2.1376 8.9344 2.0224 8.9344 C 1.7024 8.806399 0.7424 8.6272 0.2304 8.588799 C 0.2048 8.4864 0.2304 8.2816 0.30719998 8.2048 C 0.34559998 8.2048 0.384 8.2048 0.4224 8.2048 C 0.9856 8.1664 1.1264 8.1664 1.1264 7.1552 L 1.1264 1.5616 C 1.1264 0.4992 0.97279996 0.44799998 0.2304 0.39679998 C 0.15359999 0.32 0.15359999 0.0512 0.2304 -0.0256 C 0.65279996 -0.0128 1.1264 0 1.6384 0 C 2.1248 0 2.5472 -0.0128 2.9055998 -0.0256 C 2.9824 0.0512 2.9824 0.32 2.9055998 0.39679998 C 2.2528 0.44799998 2.1376 0.4992 2.1376 1.5616 Z "/>
</symbol>
<symbol id="g9662C1D9A80FEB5040A57FD9DFCA7985" overflow="visible">
<path d="M 1.216 1.5616 C 1.216 0.4992 1.0752 0.43519998 0.2944 0.39679998 C 0.21759999 0.32 0.21759999 0.0512 0.2944 -0.0256 C 0.7424 -0.0128 1.216 0 1.7279999 0 C 2.24 0 2.7264 -0.0128 3.1488 -0.0256 C 3.2256 0.0512 3.2256 0.32 3.1488 0.39679998 C 2.368 0.43519998 2.2272 0.4992 2.2272 1.5616 L 2.2272 7.4624 C 2.2272 8.2944 2.2784 8.806399 2.2784 8.806399 C 2.2784 8.896 2.2272 8.9344 2.112 8.9344 C 1.7919999 8.806399 0.83199996 8.6272 0.32 8.588799 C 0.2944 8.4864 0.32 8.2816 0.39679998 8.2048 C 1.1392 8.1536 1.216 8.1152 1.216 7.1552 Z "/>
</symbol>
<symbol id="g1CB3EC9D05726EBFDE8ADABEC8504FCD" overflow="visible">
<path d="M 7.1168 6.5536 L 7.1168 2.368 C 7.1168 2.1248 7.1168 1.984 7.0271997 1.984 C 6.976 1.984 6.784 2.2144 6.4128 2.688 L 2.0224 8.256 L 0.2944 8.2816 C 0.21759999 8.2048 0.21759999 7.936 0.2944 7.8592 C 0.8448 7.8208 1.2287999 7.3728 1.3055999 7.04 L 1.3055999 1.7024 C 1.3055999 0.5632 1.0879999 0.48639998 0.192 0.39679998 C 0.1152 0.32 0.1152 0.0512 0.192 -0.0256 C 0.7424 -0.0128 1.3184 0 1.6256 0 C 1.92 0 2.5088 -0.0128 3.0463998 -0.0256 C 3.1232 0.0512 3.1232 0.32 3.0463998 0.39679998 C 2.1504 0.48639998 1.9327999 0.5376 1.9327999 1.7024 L 1.9327999 5.6191998 C 1.9327999 6.0544 1.9327999 6.2464 2.0351999 6.2464 C 2.112 6.2464 2.2528 6.1056 2.4703999 5.824 L 6.9375997 0.1792 C 7.0783997 -0.0128 7.2447996 -0.12799999 7.4495997 -0.12799999 C 7.6288 -0.12799999 7.744 0.0256 7.744 0.2688 L 7.744 6.5536 C 7.744 7.6927996 7.9616 7.7696 8.8576 7.8592 C 8.9344 7.936 8.9344 8.2048 8.8576 8.2816 C 8.3328 8.2688 7.7311997 8.256 7.424 8.256 C 7.1552 8.256 6.5664 8.2688 6.0032 8.2816 C 5.9263997 8.2048 5.9263997 7.936 6.0032 7.8592 C 6.8992 7.7696 7.1168 7.7184 7.1168 6.5536 Z "/>
</symbol>
<symbol id="gD62975B7DE3250BE5F195D0E8335F60D" overflow="visible">
<path d="M 4.16 5.0944 C 4.8512 5.0432 4.928 4.8896 4.6591997 4.2367997 L 3.6223998 1.7279999 C 3.4176 1.2287999 3.3536 1.2287999 3.1488 1.7664 L 2.2272 4.2367997 C 1.9968 4.8512 1.9455999 5.0048 2.6239998 5.0944 C 2.7008 5.1712 2.7008 5.44 2.6239998 5.5168 C 2.2015998 5.5039997 1.7536 5.4912 1.3312 5.4912 C 0.9088 5.4912 0.5248 5.5039997 0.1408 5.5168 C 0.063999996 5.44 0.063999996 5.1712 0.1408 5.0944 C 0.8192 5.0176 0.9088 4.8128 1.1647999 4.16 L 2.8032 0.1152 C 2.8799999 -0.076799996 2.9568 -0.15359999 3.1232 -0.15359999 C 3.2512 -0.15359999 3.3407998 -0.076799996 3.4304 0.1408 L 5.1328 4.1472 C 5.376 4.7104 5.5168 5.0304 6.2335997 5.0944 C 6.3104 5.1712 6.3104 5.44 6.2335997 5.5168 C 5.9775996 5.5039997 5.6703997 5.4912 5.3375998 5.4912 C 4.9151998 5.4912 4.48 5.5039997 4.16 5.5168 C 4.0832 5.44 4.0832 5.1712 4.16 5.0944 Z "/>
</symbol>
<symbol id="gEFCBD5CCFA072E8B49E2065B449FDBBF" overflow="visible">
<path d="M 5.6832 4.9536 C 5.9263997 4.9536 6.1568 5.184 6.1568 5.44 C 6.1568 5.7088 5.9136 5.9136 5.568 5.9136 C 5.2352 5.9136 4.6208 5.6959996 4.288 5.2608 C 4.1344 5.3631997 3.712 5.6191998 2.9568 5.6191998 C 1.8176 5.6191998 0.768 4.8512 0.768 3.6736 C 0.768 2.9824 1.0752 2.5856 1.4336 2.24 C 1.0752 1.9327999 0.87039995 1.3823999 0.87039995 0.9472 C 0.87039995 0.48639998 1.1264 0.12799999 1.4591999 -0.038399998 C 0.768 -0.44799998 0.4096 -1.0368 0.4096 -1.5871999 C 0.4096 -2.7008 1.4591999 -3.0463998 2.4448 -3.0463998 C 4.1728 -3.0463998 6.0415998 -2.2144 6.0415998 -0.83199996 C 6.0415998 -0.4224 5.8496 -0.1024 5.4783998 0.2048 C 4.9792 0.61439997 4.0832 0.6272 3.6095998 0.6272 C 3.3792 0.6272 3.0591998 0.6016 2.7519999 0.5632 C 2.56 0.55039996 2.432 0.5376 2.368 0.5376 C 1.9968 0.5376 1.5488 0.7168 1.5488 1.2672 C 1.5488 1.5231999 1.6256 1.7919999 1.7792 2.0096 C 2.0864 1.8304 2.4448 1.7407999 2.944 1.7407999 C 4.0703998 1.7407999 5.1071997 2.4448 5.1071997 3.6992 C 5.1071997 4.3008 4.928 4.6464 4.5568 5.0304 C 4.6464 5.1584 4.9024 5.3375998 5.0688 5.3375998 C 5.1584 5.3375998 5.2479997 5.2992 5.3248 5.184 C 5.376 5.0815997 5.5424 4.9536 5.6832 4.9536 Z M 1.6896 -0.12799999 C 1.8304 -0.1664 2.0351999 -0.192 2.2015998 -0.192 C 2.5983999 -0.192 2.9568 -0.15359999 3.136 -0.15359999 C 3.776 -0.15359999 4.3136 -0.1664 4.6847997 -0.3712 C 5.184 -0.65279996 5.3375998 -0.83199996 5.3375998 -1.1647999 C 5.3375998 -2.0864 3.9808 -2.5728 2.8288 -2.5728 C 2.368 -2.5728 1.2928 -2.2015998 1.2928 -1.3312 C 1.2928 -0.89599997 1.3184 -0.576 1.6896 -0.12799999 Z M 4.0832 3.5712 C 4.0832 2.3808 3.4815998 2.1376 3.008 2.1376 C 1.9327999 2.1376 1.8176 3.0463998 1.8176 3.8655999 C 1.8176 4.7616 2.1376 5.2223997 2.8416 5.2223997 C 3.648 5.2223997 4.0832 4.6335998 4.0832 3.5712 Z "/>
</symbol>
<symbol id="gD5EEFB9760BC9A91B84F628EDDA52971" overflow="visible">
<path d="M 2.1376 5.0432 C 2.0607998 4.9663997 2.0096 4.992 2.0096 5.1071997 L 2.0096 7.4624 C 2.0096 8.2944 2.0607998 8.806399 2.0607998 8.806399 C 2.0607998 8.896 2.0096 8.9344 1.8944 8.9344 C 1.5744 8.806399 0.61439997 8.6272 0.1024 8.588799 C 0.076799996 8.4864 0.1024 8.2816 0.1792 8.2048 C 0.21759999 8.2048 0.25599998 8.2048 0.2944 8.2048 C 0.8576 8.1664 0.9984 8.1664 0.9984 7.1552 L 0.9984 0.9088 C 0.9984 0.4096 0.9856 0.1792 0.9472 0 C 1.0112 -0.1024 1.0752 -0.15359999 1.2287999 -0.15359999 C 1.3055999 -0.076799996 1.4336 0.038399998 1.536 0.15359999 C 1.6639999 0.30719998 1.7407999 0.30719998 1.8815999 0.192 C 2.1759999 -0.0512 2.56 -0.12799999 3.008 -0.12799999 C 4.3136 -0.12799999 5.8367996 1.0624 5.8367996 3.0976 C 5.8367996 4.6591997 4.6847997 5.6191998 3.5712 5.6191998 C 3.0207999 5.6191998 2.5344 5.4016 2.1376 5.0432 Z M 2.2272 4.6464 C 2.56 4.9407997 2.944 5.0559998 3.3151999 5.0559998 C 4.0959997 5.0559998 4.736 4.1088 4.736 2.8672 C 4.736 1.408 4.1472 0.30719998 2.9312 0.30719998 C 2.5344 0.30719998 2.2656 0.5888 2.0096 0.9088 L 2.0096 4.1088 C 2.0096 4.3775997 2.0607998 4.5056 2.2272 4.6464 Z "/>
</symbol>
<symbol id="g83A6AA7A836EACB3652229F4716CDAF" overflow="visible">
<path d="M 5.0559998 8.076799 C 4.3136 8.1792 4.3392 8.4223995 3.0848 8.4223995 C 1.7919999 8.4223995 0.65279996 7.5648 0.65279996 6.2079997 C 0.65279996 4.864 1.7664 4.2496 2.8927999 3.8144 C 3.6608 3.52 4.608 3.1615999 4.608 1.9072 C 4.608 0.87039995 4.032 0.3328 3.008 0.3328 C 1.8176 0.3328 1.0496 0.8832 0.768 2.1504 C 0.6016 2.2015998 0.4736 2.1759999 0.34559998 2.112 C 0.39679998 1.1264 0.44799998 0.79359996 0.6016 0.1664 C 1.408 0.1664 1.7664 -0.12799999 2.9055998 -0.12799999 C 3.4815998 -0.12799999 4.032 0.0128 4.48 0.2944 C 5.2223997 0.75519997 5.6832 1.536 5.6832 2.3552 C 5.6832 3.712 4.6591997 4.3136 3.6095998 4.7104 C 2.8416 4.992 1.5616 5.4783998 1.5616 6.5536 C 1.5616 7.2704 2.2144 7.9872 2.9696 7.9872 C 4.2111998 7.9872 4.608 7.1935997 4.864 6.3487997 C 5.0048 6.3231997 5.1712 6.336 5.2864 6.4256 C 5.2352 7.04 5.184 7.3984 5.0559998 8.076799 Z "/>
</symbol>
<symbol id="gDB4862E33098F259EEBBA99A57E5AFA" overflow="visible">
<path d="M 2.1759999 4.5824 C 2.1632 4.9663997 2.1376 5.4272 2.0736 5.5551996 C 2.0479999 5.6191998 2.0224 5.6576 1.92 5.6576 C 1.5616 5.5168 1.2287999 5.4016 0.34559998 5.2864 C 0.32 5.2096 0.34559998 5.0048 0.3712 4.928 C 1.0624 4.864 1.2032 4.7999997 1.2032 4.0576 L 1.2032 1.5616 C 1.2032 0.51199996 1.0368 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7168 -0.0128 1.2032 0 1.7152 0 C 2.2272 0 2.6239998 -0.0128 3.008 -0.0256 C 3.0848 0.0512 3.0848 0.32 3.008 0.39679998 C 2.3552 0.4608 2.2144 0.51199996 2.2144 1.5616 L 2.2144 3.6608 C 2.2144 3.9296 2.3295999 4.0832 2.432 4.1984 C 2.944 4.6976 3.4176 4.9536 3.8144 4.9536 C 4.3008 4.9536 4.6591997 4.6464 4.6591997 3.7888 L 4.6591997 1.5616 C 4.6591997 0.51199996 4.5568 0.44799998 3.8655999 0.39679998 C 3.8016 0.32 3.8016 0.0512 3.8655999 -0.0256 C 4.1856 -0.0128 4.6591997 0 5.1712 0 C 5.6832 0 6.1056 -0.0128 6.4256 -0.0256 C 6.4895997 0.0512 6.4895997 0.32 6.4256 0.39679998 C 5.7855997 0.44799998 5.6703997 0.51199996 5.6703997 1.5616 L 5.6703997 3.5967999 C 5.6703997 3.776 5.6703997 3.9552 5.6576 4.1088 C 6.272 4.7872 6.848 4.9536 7.3472 4.9536 C 7.8335996 4.9536 8.1152 4.672 8.1152 3.8144 L 8.1152 1.5616 C 8.1152 0.51199996 7.9872 0.44799998 7.3216 0.39679998 C 7.2576 0.32 7.2576 0.0512 7.3216 -0.0256 C 7.6415997 -0.0128 8.1152 0 8.6272 0 C 9.1392 0 9.5872 -0.0128 9.9456 -0.0256 C 10.0096 0.0512 10.0096 0.32 9.9456 0.39679998 C 9.2416 0.44799998 9.1264 0.51199996 9.1264 1.5616 L 9.1264 3.5839999 C 9.1264 4.7232 8.9344 5.6191998 7.8079996 5.6191998 C 7.1552 5.6191998 6.3616 5.376 5.6959996 4.672 C 5.6576 4.6335998 5.5808 4.5696 5.5551996 4.6847997 C 5.44 5.2096 4.9407997 5.6191998 4.2752 5.6191998 C 3.5328 5.6191998 2.8672 5.184 2.3295999 4.5824 C 2.2656 4.5183997 2.1887999 4.4288 2.1759999 4.5824 Z "/>
</symbol>
<symbol id="g793DBE65A5AEC1A16A65955B6C0E046" overflow="visible">
<path d="M 10.368 7.232 L 8.3712 1.6768 L 8.3328 1.6896 L 6.5664 7.0912 C 6.3487997 7.7823997 6.7967997 7.8208 7.232 7.8592 C 7.3087997 7.936 7.3087997 8.2048 7.232 8.2816 C 6.7072 8.2688 6.144 8.256 5.632 8.256 C 5.2096 8.256 4.7616 8.2688 4.3519998 8.2816 C 4.2752 8.2048 4.2752 7.936 4.3519998 7.8592 C 5.0304 7.8208 5.312 7.424 5.4272 7.0912 L 5.7216 6.2464 C 5.7728 6.0927997 5.8111997 5.9648 5.8111997 5.8496 C 5.8111997 5.7216 5.7984 5.6191998 5.6959996 5.4016 L 4.0448 1.6511999 L 3.9808 1.6639999 L 2.112 7.3216 C 1.9583999 7.7696 2.304 7.8335996 2.7519999 7.8592 C 2.8288 7.936 2.8288 8.2048 2.7519999 8.2816 C 2.3295999 8.2688 1.7664 8.256 1.2672 8.256 C 0.8192 8.256 0.44799998 8.2688 0.076799996 8.2816 C 0 8.2048 0 7.936 0.076799996 7.8592 C 0.65279996 7.8208 0.7424 7.8079996 0.9856 7.1168 L 3.392 0.192 C 3.4559999 -0.0128 3.5328 -0.15359999 3.6736 -0.15359999 C 3.84 -0.15359999 3.9167998 -0.0256 4.0064 0.192 L 5.9136 4.48 C 6.0288 4.736 6.0671997 4.7999997 6.1312 4.7999997 C 6.1823997 4.7999997 6.2335997 4.6591997 6.3104 4.4416 L 7.7823997 0.192 C 7.8592 -0.0256 7.9231997 -0.15359999 8.076799 -0.15359999 C 8.2176 -0.15359999 8.3071995 -0.0128 8.3712 0.1792 L 10.943999 7.0783997 C 11.110399 7.5263996 11.340799 7.8208 12.0448 7.8592 C 12.1216 7.936 12.1216 8.2048 12.0448 8.2816 C 11.673599 8.2688 11.264 8.256 10.9312 8.256 C 10.5984 8.256 10.0352 8.2688 9.5232 8.2816 C 9.4464 8.2048 9.4464 7.936 9.5232 7.8592 C 10.047999 7.8208 10.559999 7.7823997 10.368 7.232 Z "/>
</symbol>
<symbol id="gA11612CECC8CBEF18835767DAB11B2F7" overflow="visible">
<path d="M 0.5248 2.6239998 C 0.5248 1.3184 1.3952 -0.12799999 3.2128 -0.12799999 C 4.032 -0.12799999 4.6591997 0.1664 5.0944 0.5888 C 5.6703997 1.152 5.9263997 1.9583999 5.9263997 2.7391999 C 5.9263997 4.0703998 5.1967998 5.6191998 3.2384 5.6191998 C 2.3936 5.6191998 1.7024 5.2736 1.2287999 4.7232 C 0.768 4.1728 0.5248 3.4304 0.5248 2.6239998 Z M 3.0463998 5.1712 C 4.1472 5.1712 4.8255997 4.1728 4.8255997 2.3295999 C 4.8255997 0.7168 3.9936 0.32 3.392 0.32 C 2.0607998 0.32 1.6256 1.9327999 1.6256 2.9183998 C 1.6256 4.032 1.8944 5.1712 3.0463998 5.1712 Z "/>
</symbol>
<symbol id="gCEFEF3D67F35C6E83CC3757B1DD21B13" overflow="visible">
<path d="M 4.2752 0.64 C 4.3392 0.69119996 4.4544 0.7168 4.4672 0.6272 C 4.5056 0.32 4.608 -0.12799999 4.608 -0.12799999 C 4.7104 -0.1664 4.7743998 -0.15359999 4.8512 -0.12799999 C 5.1328 0.1024 5.5808 0.2944 6.3616 0.384 C 6.4384 0.4608 6.4384 0.65279996 6.3616 0.72959995 C 5.5424 0.79359996 5.4272 1.0368 5.4272 1.6639999 L 5.4272 7.4624 C 5.4272 8.2944 5.4783998 8.806399 5.4783998 8.806399 C 5.4783998 8.896 5.4272 8.9344 5.312 8.9344 C 4.992 8.806399 4.032 8.6272 3.52 8.588799 C 3.4944 8.4864 3.52 8.2816 3.5967999 8.2048 C 3.6352 8.2048 3.6736 8.2048 3.712 8.2048 C 4.2752 8.1664 4.416 8.1664 4.416 7.1552 L 4.416 5.5168 C 4.416 5.4272 4.3904 5.4016 4.3008 5.4016 C 4.2496 5.4016 3.7247999 5.6191998 3.3023999 5.6191998 C 2.4575999 5.6191998 1.8944 5.3375998 1.3823999 4.8512 C 0.83199996 4.3008 0.4992 3.5456 0.4992 2.5983999 C 0.4992 1.0239999 1.2928 -0.12799999 2.6752 -0.12799999 C 3.1743999 -0.12799999 3.648 0.12799999 4.2752 0.64 Z M 4.416 1.5871999 C 4.416 1.344 4.3904 1.2415999 4.2111998 1.0879999 C 3.7375998 0.6784 3.3279998 0.4736 3.008 0.4736 C 2.3167999 0.4736 1.5999999 1.2287999 1.5999999 2.8288 C 1.5999999 3.7503998 1.7792 4.2623997 1.9712 4.5312 C 2.368 5.1328 2.9055998 5.1712 3.1615999 5.1712 C 3.6223998 5.1712 3.9424 5.0048 4.1984 4.7104 C 4.3775997 4.5056 4.416 4.416 4.416 4.0192 Z "/>
</symbol>
<symbol id="g645CA8FA3D9155E2CBD9F8EED3C1540D" overflow="visible">
<path d="M 1.9968 4.7104 C 1.984 5.0944 1.9583999 5.4272 1.8944 5.5551996 C 1.8687999 5.6191998 1.8432 5.6576 1.7407999 5.6576 C 1.3823999 5.5168 1.0496 5.4016 0.1664 5.2864 C 0.1408 5.2096 0.1664 5.0048 0.192 4.928 C 0.8832 4.864 1.0239999 4.7999997 1.0239999 4.0576 L 1.0239999 -1.408 C 1.0239999 -2.4703999 0.8832 -2.5344 0.1024 -2.5728 C 0.0256 -2.6496 0.0256 -2.9183998 0.1024 -2.9952 C 0.55039996 -2.9824 1.0239999 -2.9696 1.536 -2.9696 C 2.0479999 -2.9696 2.6624 -2.9824 3.0848 -2.9952 C 3.1615999 -2.9183998 3.1615999 -2.6496 3.0848 -2.5728 C 2.1759999 -2.5216 2.0351999 -2.4703999 2.0351999 -1.408 L 2.0351999 -0.0256 C 2.0351999 0.1408 2.0864 0.12799999 2.2144 0.076799996 C 2.5344 -0.0512 2.9183998 -0.12799999 3.3279998 -0.12799999 C 4.0448 -0.12799999 4.6847997 0.0896 5.2096 0.5888 C 5.8111997 1.1776 6.1568 1.9712 6.1568 3.008 C 6.1568 4.3648 5.1967998 5.6191998 3.8911998 5.6191998 C 3.3023999 5.6191998 2.6496 5.2352 2.1376 4.6591997 C 2.0607998 4.5824 2.0096 4.5824 1.9968 4.7104 Z M 2.24 4.2367997 C 2.5728 4.6464 3.1615999 5.0304 3.5328 5.0304 C 4.3519998 5.0304 5.0559998 4.1088 5.0559998 2.6624 C 5.0559998 1.6128 4.6847997 0.30719998 3.2512 0.30719998 C 3.0207999 0.30719998 2.5728 0.3712 2.3423998 0.576 C 2.0864 0.8064 2.0351999 0.8832 2.0351999 1.344 L 2.0351999 3.6736 C 2.0351999 3.9424 2.0864 4.0576 2.24 4.2367997 Z "/>
</symbol>
<symbol id="gEF535BAC325E1F03037EDB94EE368989" overflow="visible">
<path d="M 6.88 3.5040002 L 5.552 3.5040002 L 5.552 8.176001 C 5.552 8.976001 5.552 9.6 5.584 9.728001 L 5.552 9.76 L 5.0400004 9.76 C 4.9280005 9.76 4.848 9.6640005 4.7840004 9.584001 C 3.7760003 8.352 1.9200001 5.7120004 0.448 3.4240003 C 0.49600002 3.1840003 0.592 2.752 1.072 2.752 L 4.3360004 2.752 L 4.3360004 1.2800001 C 4.3360004 0.544 3.7280002 0.544 3.0400002 0.49600002 C 2.9440002 0.4 2.9440002 0.064 3.0400002 -0.032 C 3.5520003 -0.016 4.1920004 0 4.9280005 0 C 5.552 0 6.1600003 -0.016 6.6720004 -0.032 C 6.768 0.064 6.768 0.4 6.6720004 0.49600002 C 5.8880005 0.56 5.552 0.528 5.552 1.2800001 L 5.552 2.752 L 6.656 2.752 C 6.88 2.752 7.1200004 3.0560002 7.1200004 3.2480001 C 7.1200004 3.4080002 7.056 3.5040002 6.88 3.5040002 Z M 4.3360004 8.112 L 4.3360004 3.5040002 L 1.2800001 3.5040002 C 2.0960002 4.8160005 3.232 6.6080003 4.3360004 8.112 Z "/>
</symbol>
<symbol id="g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" overflow="visible">
<path d="M 4.688 10.336 L 4.032 10.336 L 0.24000001 -0.94400007 L 0.896 -0.94400007 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
</defs>
</div>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(40 17.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gF74D1E4498220F56E34936C81B24ED2C" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g46E28FC12585DA626130081849FE40B4" x="3.564" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="10.788" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g48BCA4F06942DA5990D42018985FC781" x="17.136" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="23.268" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE1B486BBD379D5D210F28624A61384AE" x="30.024" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g9FB16590C6D64699AE0CE54876927A05" x="36.804" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g6799D348D26A0968EEDA80A0E5D50B73" x="43.716" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="49.620000000000005" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g45E4C10E27056C5AE488FE2D8290DF06" x="55.968" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="59.7" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g46E28FC12585DA626130081849FE40B4" x="66.456" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 28.192)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 30.592000000000002)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(6.768 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 48.784)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5ABA589ED074A65FC8C929AB4EB2344C" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(404.54488188976376 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6F0940D406D545443F0C3F5AB20F1452" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g6D72A0AB4EFB019D977FFECF4A1600A9" x="6.95" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7035BD9A81EA6DB089327941BB80DFF8" x="11.26" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="16.67" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="22.3" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g5503E15E5E4E70E9E217A15BD1ECD752" x="27.41" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="30.52" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFF65128B49BB3276E17D04989ECB7ACE" x="35.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="41.92" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 8.579999999999998)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.64 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 23.739999999999995)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 32.31999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(743.9997637795276 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g97A8E46F7A64F11D13C6F357868587EE" x="9.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.25" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.36" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gB844DCFB76B4CC44608DB013C9764E9C" x="24.89" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="30.37" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="35.14" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="41.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="46.58" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="52.599999999999994" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 15.16)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 60)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g7B578904031CC07414BF9948E9002018" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g767CEF02C917BBE3F159A8F04079F311" x="14.736" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g841363B3896A8C79F18618DF16186242" x="24.816" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g79601DAFF2C13DD0AF25B87F7A83C884" x="38.04" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g9AEC0E315A165F115D211DDAB68AA0F8" x="51.048" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g79601DAFF2C13DD0AF25B87F7A83C884" x="63.192" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g24FA36D774E663C81AD78F0ED3820373" x="76.2" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8D84A54D9303B24762DC3071B60ECD14" x="83.928" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g24FA36D774E663C81AD78F0ED3820373" x="91.728" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g10AC66E6714D96E9762627FFB6E156C6" x="99.45599999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g69FC55421D5675D87F2C509D9B1DBC44" x="108.04799999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFC5C8D23DE5E426807758A924FDBA2FC" x="127.43999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g225F12A4A0DFD089304CD4B2A01795A4" x="139.53599999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g24FA36D774E663C81AD78F0ED3820373" x="154.24799999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g9E7CBAD4E034259458BC3DBF06AA0130" x="161.97599999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD732D1B4380472337CC02C39F4184A6C" x="181.91999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g24FA36D774E663C81AD78F0ED3820373" x="195.76799999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDD7DFDEC0D240E3DC5A3664E12D4BDDC" x="203.49599999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g10AC66E6714D96E9762627FFB6E156C6" x="213.74399999999997" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 52.38)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gB0978DD106A095AA3B799B940A52F3E4" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2EB1DC9A979CD3C8C9D80DB754EBF6AB" x="13.08" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE9BB2E81A58B731A2047F77D70267173" x="25.04" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC81C3C15134AD04FEC0FE7FCEBE8BB14" x="31.48" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g5A467C6F5424E9C7BB01147ABA438205" x="37.980000000000004" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCD50B0C5537328D0484BBB5C5B7C30A" x="49.2" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB88E546A1990E31D64B5C4B23478426F" x="62.74" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2EB1DC9A979CD3C8C9D80DB754EBF6AB" x="80.84" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC81C3C15134AD04FEC0FE7FCEBE8BB14" x="92.8" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1344FEF92B65FBC27D977C1EC5D9AECF" x="99.3" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE9BB2E81A58B731A2047F77D70267173" x="106.46" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gBD4F3A667A4E81DD5512C606D2565A9A" x="112.89999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC81C3C15134AD04FEC0FE7FCEBE8BB14" x="120.05999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="126.55999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC4CA1C48E288D770EBFD587FCB4E243B" x="136.2" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="146.62" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC81C3C15134AD04FEC0FE7FCEBE8BB14" x="156.4" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC81C3C15134AD04FEC0FE7FCEBE8BB14" x="167.9" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE9BB2E81A58B731A2047F77D70267173" x="174.4" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC3DD0650993487CD3F460FE3E213BEA0" x="180.84" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB591690011940384999C1B007F794058" x="193.16" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="205.42" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g5A467C6F5424E9C7BB01147ABA438205" x="215.33999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC81C3C15134AD04FEC0FE7FCEBE8BB14" x="231.55999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE9BB2E81A58B731A2047F77D70267173" x="238.05999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCD50B0C5537328D0484BBB5C5B7C30A" x="244.49999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1344FEF92B65FBC27D977C1EC5D9AECF" x="253.03999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCD50B0C5537328D0484BBB5C5B7C30A" x="260.2" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 89.54)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 89.54)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gB2E338F181D915F0996F60E92302C895" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="10.680000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="20.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="36.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="41.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="50.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="60.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="69.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="77.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="86.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="94.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="104.83999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="110.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="120.63999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="133.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="149.24" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="158.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="169.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="184.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="195.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="205.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="215.70000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="224.64000000000001" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(390.9448818897638 89.54)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(407.9648818897638 89.54)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g607CD744DAB7515984E0B3F495F7DE81" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="10.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="20.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="35.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="44.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="56.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="61.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="71.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="81.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="90.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="97.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="105.39999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="115.11999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="122.91999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="133.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="138.57999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="148.95999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="161.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="167.95999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="176.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="191.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="200.48" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="212.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="223.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="233.98" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="244.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="253.04" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(76.18897637795276 113.54)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<image xlink:href="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAB4AAAAH0CAIAAABTo6d8AAAgAElEQVR4Aey9B7gkVZn//3Z1V+fuG+bOnRyYnDOTGcIwgKJgYBQQMKxxRYLrrgFRZEFR0V0VMGBEV0WRNS3KqgTDYnYxICAZBoY7N3RXVz7h/f/fU911q/vOncAO/AY59zlPzVvV55w69a3TPU9/6u3vAdR/WgGtgFZAK6AV0ApoBbQCWgGtgFZAK6AVeBoUECj2W9pOKxHjIhBFa1dVirpqq5/ciRt2BMk6iXi8gSWqtM4edTjOeMbrZ7zjbf0ndzqGHe8m6yTiv9f+x7uu8Y4nJDmg+9VWP7kTC94RJOsk4gMaT6L+6MTW/SdlieMOWeLduEJ7oPVvzqh2WeI9rY/WJ54MFMRvqI6grdLoziGbP4nTwWj3OtIKaAW0AloBrYBWQCugFdAKaAW0AloBrcChU2C8L7HJ421nS3xZJfqsAbRskye5k9QwGSfrtMVJbZNxW6XRnWSfyXi0RkeU7DMZd1Rr7Sb7/L/Erf7Uv8nzHg7zJzm45NiScbJOIh5Pk0SV9jDZZzJurxXv6f41oIwnAwXJOZOM2yqN7uj5o+fP6GzYx/xJzCUNoNsU0ztaAa2AVkAroBXQCmgFtAJaAa2AVkArcKgUGA9SJI+3nSvxZVUD6Ocm4EjOjQOJD+v5kxxccm4n42SdRDzetSeqtIfJPpNxe614T/f/3Hx/xROgM0jOmWTcWa+5r+ePnj9tUyM5Z8aJNYBuU0zvaAW0AloBrYBWQCugFdAKaAW0AloBrcChUmA8SJE83nau5BfXwyGD9QDGk7yWA4nbrje5kzxXMk7WScTjnStRpT1M9pmM22vFe/+v+h/vvOMdjwdMQfK6Dof5kxxccmzJOFknER/Q9Sbqt1277j+pTBQnNUnGY2uqI1p/DVjbpkZyziTjtkqjO3r+jP1E0gB6dH7oSCugFdAKaAW0AloBrYBWQCugFdAKaAUOoQJjv4QrW402Y+i20yW/2I8BiG01o51k/fHivTSjQ2PHFh1pq57sc8x4xuth7PG2PpM7yf7Hi5P1E3HyLInD7eF4fSaPt7eI957J/pPnSsbxYDqCceskr2vM/erohHaT9ceL99KMDo07hmT98fpMHk/WT8S6/wMHoAnZ2sOkzuPF7S3iPa2/1l9/PkTvgvhN0RmM954a57gG0J0C6n2tgFZAK6AV0ApoBbQCWgGtgFZAK6AVOCQKJCFO66ssccHk8bYTJb+4PoMA8amNJ9lq33HbNSZ3ktc7Xpysn4iTZ0wcbg/H6zN5vL1FvPdM9p88VzKOB9MRjFsneV3P4PzpGN7obnI848Wjtduica8xWWu8PpPHk/UTse5fA1YNWKN3QeJt0R4m30fjxe0t4j39/ho7uzSAjqeHDrQCWgGtgFZAK6AV0ApoBbQCWgGtgFYgUkAcIiEiCpjcUsf7/3Le8W3/YEeTbD5O2+QYxOhyh+Os+re3Djt62MfuOEMY//DeTtdRO3m6jpf2v3uY9Z+8lmQ83oXsv07yAse5peN1TseTzcept/8xjNNQ978PYZovaf33rZHWR+uTeI67bzH28uozOX8S59IAei/3Qh/SCmgFtAJaAa2AVkAroBXQCmgFtALPbQVaAFp9e5StvU5NCO0l4bKK4y+cVLvj1WYH6mgzD7qzz3g/7udpA4gceYQRD4g4RuOJh9eO0ZM4cmycaHRg4QFce/IsB9ZpotZh1n/yWpJxYsRt4YHUORCI3NZpcucw0yc5tAOK9fj3LZPWR+vzbAG449ypA/oMHKftgXw2HrL+E+81DaDHuyH6uFZAK6AV0ApoBbQCWgGtgFZAK6AVeO4qwBkP/CZ45n5Lhw7iLAVKhhio4tFWMqSDrZTiJICOvoi2eurIg46+7iZebDHh6NCYtm01D3KHM46II9YIkyyga0t8Re6M99518st5MkZEP/QECjdw995SH00ooMSnfGM3cH/6i5+++rWvnr9oXn9/f7lcPu644z7zmc8EQSDEeE8/OhKVx0yR5IFknBiADrUCWgGtgFbgaVQg8b+rBtBPo866a62AVkAroBXQCmgFtAJaAa2AVkAr8GxUIAgCRPze935w263/Izl6DUSGnEUZzYx2miVAVNx59IjoRLjx988oGTohRxLdPgMAWqq/6PxSSo6cI5Ho1qnjgSaDxHAT4diRCxStDgnSc+RhGHLGfd+PeHeitQ5JAYHCDz1EfHTXIy87Y2e+lIPWn2EYpmmm0+mzzjprn2Il71QUJ6onDyTjRBUdHhoFtLyHRkfdi1bg706B6MNBbTWA/ru7u/qCtAJaAa2AVkAroBXQCmgFtAJaAa3A/00B5rNXnf0qAEil0h//908FPkoeJTMHAp2ocHQ4NlQJOCFXFHI04XkUQ3eYcIz6abQtRdiBdDuHPw7h6mgV73Y2b+1LKQcHBy+88MLXvva1u/fsRkTHd1ovxv+OfmOOOzzAIELPiPjQow9df/31rkt50PvI4R2v23go/8fg8O5fDteH7/zznVOmTwGAUrWUK2QNM2WaZiqVarFoeP3rXz++gKN3Kkpjj6+3U7dDNH86u93ffjyejmB/7Q709ajbyOgmeYoDbb+/esk+k3FbOxmdX92Bthf2v5PsMxnvv+WB1Uj2mYwPrPX+ayX7TMb7b3lgNZJ9JuMDa73/Wsk+k/H+Wx5YjWSfyfjAWu+/VrLPZLz/lgdWI9lnMj6w1vuvlewzGe+/5YHVSPaZjA+s9f5rJftMxm0tEx/SGkC3KaN3tAJaAa2AVkAroBXQCmgFtAJaAa2AVuDKD37EAMMAAwB2HP+8yASBE1/uANCOwtAJAD2WQQtFppIYuqnvvgC0svBI3IdDBBDDMFyyZIlh0HW95YK3IGIoKNd7PBeO5JfqA4mZZPc/dN/Jp5yslINCofDFL34xcRmd4Xh9dtZ7qvuHc/+WU3d8Z9XaVZlcJsbNoMhzKpUqFAqmaeZylBb9pz/9iZ5sxCBjVI34UDNIXu9orfj2th2inWT9ZDym4lM8kOwzGT/F7sY0U2+T5lvraeo/2W0cjw4kps/RKEYfL41W2UcUd9gR7KPJQb3U0W28e1Cd7KNy3GFHsI8mB/VSR7fx7kF1so/KcYcdwT6aHNRLHd3GuwfVyT4qxx12BPtoclAvdXQb7x5UJ/uoHHfYEeyjyUG91NFtvHtQneyjctxhR9DWJPEhrQF0mzJ6RyugFdAKaAW0AloBrYBWQCugFdAKPMcVCIKgWq4Uc8UMmACpzZu2KfMNUoVzr6MIEUgM96VY9P0z4lMsypRuVu/41tqx29Zn1El0KBmrIx0NR+G1qhnZiUT+GxdddFE2m41w57oN61RrWW/UEnQz6r25Hdvzvo88+MiD8xbMBQNyhWwqlUqn06lUanh4uAlPn9L4R8HrPuheUpNkHJ1xNDE9fg4QXbq67madff6T7DMZq0ZjNWn2NaZmlA8e3RFEPO/C81IKPhfKeQB45Wteecev/ueJJ5646KKLAIAAtJnPpnM3XH8DdRgjzpYO0XmT9y45krbrSY4kGR/8+Nu6jXeSfSbjZ6T/cTOgx4wkHm9nkKyZjA9k/EK9qekXEONPp2SfyfhA+u8c6972k30m46ej/zHnT8661pxUlcaMZEzT1oFkzWSsXtf9/58+P1sa7+vfpObJWOsfqZbUJBkfiD5RfbXVAHpfk1C/phXQCmgFtAJaAa2AVkAroBXQCmgFniMKSNkEe7fddlsxly9k8rlUPpsyzjn7JYgW4sMSf4v4P4g/V9v/aW1/gfgLxF8h/gbxfxH/jHgP4v2IDyA+hjhIbaWNwkcuyacjKkrTsWAleaRN9uSX3mQ8Tj/Ntq2asYfDrFmzDPVXqVTWbVgXo+r280bNaJs8fiDxlf92ZZT7DADpdDqbzU6ePJmEbY2EBpaMD2T8o8NpXtZe/kn2mYybVWPuHAfqhb3U3Evf+z00VplmkzH9CyHCMIxux00330S5z5SMDpCCiy+5mCP3Qy+ah8cccwzdKHo59eErPkwdRsbj0RWoE0TnbQlKJ0uOpG3YyZEk40Q/e2k7pmZbn8mdZM1k/Iz032Lzoz8paA5tzEiSQ26LkzX3Eo/23My5jupE94Inbk3r2UBb5x1zPtm/qpdUvnVP1QtjanZ2G+8naybjg+1/TNvmGcY7frD9xwPuCJL9J2PdfyRUUpNkrPU5/PWJ7pfaagAd3S691QpoBbQCWgGtgFZAK6AV0ApoBbQCz0EFRnleTGnPP+/CNKRyRrps5koFuPLjr5H4Xw281MJXD7EdNba1s4THStwp8WyJr5N4PuJHED+J+DnEGxWb/gvxaPkECgeZaGJEUrqNarXAE42nFSduRxI6JOJo9DHAipYBjJYWpMatmhHT/Nvf/ha7OgDA8Scer05AzIzTEoLNIohjxmUvg4xPNzZ493vfTS7GeTOdTRuGkU6nTz/9dHWtBAmbqyC2RhVf3th+mi9FNZPbuE1HkOwzGTertXQaTYVWL4ypObbevo9E3e9n/K2hCiE44xGDbjQap77klCj9OVfItrLRafFGzriU8n3ve18+nz9kALo1hr3+e4Dj72ybVG9snDjyFPtX54vcb9pOnei5dbx5l+ITNY/vpWarRce/yZpxHNtrtN6SUf80laMTxug5RPoVBH+WZ0DH1xsroNB+h1Rjd2PZ46BZJ9HP2FZtR5I1k7GqFHcbB7r/pHqxLHGg9TmM9Inms9pqAJ28LzrWCmgFtAJaAa2AVkAroBXQCmgFtALPKQUiktS0RpCS2N+GdRsNSGUgXUrne7vgO/991pP+a++pLR3BORZWHczGxaPYtDHbEBUr7LP86ZY3r+GutJ3NjrPdarys4b/Tl59A/BLiNxB/pHj0bxD/gHinKn9B/Cvi3xAfRHwU8UnEBmKQKK2s14gNRfmVYwCNumFCDZ5HW4V7RwE0sWjOvv71r5bLxZQB6UwKDDjn1WcjnSnwhMuRqUK4OUnR9oL/9jk7rrnmmsi2OHL5MAA+f+1nnUajBX4lLdQ4ZvwxN4kCRb3UfUl8dR/bqm0gyT6TcVul/ew0Kebo6WnUzeUl1cGOOCHOXpuK1piTr9IYLMu+954HsibZbqSVBcfXv/5VxxldDdJ3vRuu/wYA5Mx8Pp371tdvoK7i9PlIQ+op6jmWKdqPH2AkBrj3S08OLJpp8bY1+PFSepOe1B3gsmO3de9bo41OqgZ04HeKhiFUpnHy3eGp90sdcQRxCHGPegc9qt5ND+5te796r/1N/Ubhr4h/UeVPiFG5U70xo/fmHxDvUO/WO1rBLxB/2irxLx5+o376cIfa/g7xd+pnEL9Suwe1jc6S3B5U8+jnF9FgOuKon2TPcRyfIr7S6MhflJKRNXzz5u19+rSOdrx/499VtOZ/q94+/k3OhGSsmuj+25TU+oydSElNkvHhMH+i8aitBtBjb50+ohXQCmgFtAJaAa2AVkAroBXQCmgFnlMKRGzL4aK+65FH02CmIWNCJg+5/i54YNcpw96chujzsWJjxkYjLi4aLhqOBEembW46ouDwksu63HCCy/rdcHojnNcIllhseYOtcfh6l29x5DaHn4D4BsQLEd+N+AHEaxC/iPhNxFsQ70O2h0o4gGwA2SCKISkcgo/j4UTF+yQXzQxmGaIMKY4cP1iLJwv/4nf/k5EmtwfDJL7+rovfqaie74oRgf64OZyJ78/EQZLQsuMliXseH8gQU01HAHrqxCmIWBsYbsFTBaBFYqtmWQJJRmGMQeMgedYEGx0zgCap6Ti+17ms6rT327y4mPTGWeGJI61LabshyW6iMSc5aRx7iiLTaM570zsMKGcgXylnFy+aLbmQDKMSDfYPv/5tpGEOjJHdA2HDxVA0C2OtbPUE0O8kxckhtRSLuo7EoYx0hiIqAQoPpYMYFU89AmGJm91SMO41Tv6lmRY2+4mT7puniFpFGJ+hDKUIqHBG16suWYTUOupAjjfDqRup5qeFOOzZ96pxDiLaiPcz/L3EX7c8cH6K+G3ELyN+HvHaMeWTiJ9A/DfEDyNejvg2xAsQz0V8o8DXcHwlx1dwfIWUr5Z4hsTtDDf7uK3Bttb99cPOyuHGUoetcsSqPdayPdbmWrDDCrbZ4qiG3FLn2xrB8y3v5BH/2GF/27B71JC9dcjeOkJlc6tsHLFHS83dRMXZUnO21N2tncXbXD/w0tl8W92Ny9aaN6b4m2v+xrq3UZ1iY91fUwvW1PyNw/5mC7cPeK+uu99GHI7nauvex3c3OtB2jxN1dKgV0ArsXQENoPeuiz6qFdAKaAW0AloBrYBWQCugFdAKaAWeSwoIxIAL56e33pZJZTNgZiCVB9i6HoatLa7MC8yFmHIRGq2iuDM0twIcAa6k4gtVEPxWcRHi4iA4mPOw3xNzPLnSY1s8dpIXnOYFZ3vOWxG/jvjD9nKzyru8G/FhVR5S7tIPqO2jymO6rkicQofCVWbTITLZ9PqIlj2kG8lfddYZGQOMNJVUBr797RvV/ZWc6LOriq+oU4tlRohp7DaikB3H1UF7xNl56svSkAVIG2B+7pNfpGEojw8FdyMTjtFtnMTbYo9R1zF3TjDQjtPtdTcCyGNfUkMYy6ajk42/HbUl2SuA3ttDgbiz5CXEcYDoWY1BRNy4/ri0UY0Q8yXve5cge44mVY4Ge8uPbgUAA1Kbj9wQOh5dWQSgycVFUCJ5yyel7bqocTyGFnceK0j8IEEq9Cw85J5i0Ao9S9bKwU/on9SQYqnykR3EOk1COYBiN/JdyB9F9hDyB5D9DflfUfwJ5Z1U8I8q0fjP7XnHf0W8G/Fetb1LVfgDEk2OcnIjd/Uo/hniTxD/S/HlbyB+zQuvQ/xe3b0hwBsGnA/Y4n2O847QPo95r+DOqcJ+Pms8Lyph43mhfaIqO0JnW+huZsF6FqwJ2NKAL2Ryvi9mOmKazSfbos/m/W44k54eIdj0TjcamKH3rHp3M8wJ7BM4xcO+msgNMbAx5WCqgVkLeyzRY8mCJcyo2Nykh1IsTYWnVAGHQxS7Iq2K6QrTl1kqIk8limXGp2Lss0R1oq3qIdmP6s2V2b0UzMQfR3Fg05WWG3iEhaeF4j8RBxTxj+56vI1mUudUiF/WgVZAK7APBTSA3oc4+iWtgFZAK6AV0ApoBbQCWgGtgFZAK/D3rkALz0mOkuNHP/yxbDpnQDoNUDTgwnOn1P31ARYCNANMR7wmYtBPDUArqgUNaVo8Z7FSPeiu+/11b7rlzWl4iy13bcPdaHubnGBzVBrBZsvfgfhWxPcgvg/x/cpj+uPKZvrLiD9QRgG/I4QnH0E+hMzBkJEjbaAIEpPou3QLJR65cmMmlSEGrf4GB3bT8Sb6dWmxREopjVKhWwz6IG8+F/ilL1+fMoqbNh33rRtvdj1qb3sYCAwkqvRXwZDHpQVdI+uPmJwqvNm6L0mgOgpb47pxtaZLw96oa3QVyZpj46YWMXsNUIHe+DwdwXhIOnIDHm/ryUCgeODxh8GM4DNAFn5/152+xKjQy0hafeX6GwDSkDK//B9fjYYfE2omkAv1iEHSNk4oJ3Horjtqq3SI8pTJm1hdF6U8t6w8oicTdFzVp/ULW+ya4LYQ6qYp2h07l0fieAo670Z8CPGulm3FX9QKnLcg/ifidSr1+NOIV6t0448gfgjxgyrZ//2IlyFegvgOlYB8IeK5Et/A8JU+vtyVL7LFSXV2TI1tHQ42UvE3D1O6blTW14I1w/7KEW/ZkL/MwU1PNE68f9d53/7RsbvFjhouH5HzbX6EI6a5wSTP63fdvqjYXp/t9bZKt+2XXVbxRdnDgo9ZhlmfEHNa/bghY2PRFr1U1G8dCChjzkKwEGxWErh8+MljfvfbGUP2hKGADnoEqTM1NFW1XEPmGtJ0BBWbp20+lj5HDBpcAS0GnVasOUGQk/S59RArfprVDNrY9DgkOqLPhJs7yujzsBaANlzMNPhUG09heKXyEqk1AXTbJ0H0tkm+naJYb7UCWoH9K6AB9P410jW0AloBrYBWQCugFdAKaAW0AloBrcDfrQItFilUru65bzyvkMkbABmAUh6uumqey1d5aEapiBF0/r8AaJUBDR4aPqZ9NH3FhnyZjRIhA8qzzoeYZ1gQqjBi3xMCvtBna1y2rhGubwSb68GWun/UiPc8gecK+W7BL2Ps3xFvQLwJ8TbE/2k5EvyKkknFLQoU1qb2dJtG1jAy6RRk08C8uxGfULa5wyqf+j7ERxAfV1nVlkqI5nu96a3UW94KyDshKojoBNRKIFruKLviCmz7lJ6dBNAySiKO246eLkm6Ro+2g+nWjWtS6VGA2hrO6PmTXewjlq3M38g0Q+X/RmdpdTlKwInSjpYkjx6PPoeIrgg9GVz12asgBZAjO5QZ82fbjI0CaJW57jH5yWs/C0Z62YqViBhyHoYhZUmrP0bZ0vSQgWHIiUXHA2moHPl7aNHLpqv4LnV/dynv478q7+PYcHyXqhaZHf9KMcc7VQ7yX5Q7+a/Ug40oBzne/lTNrltUhv63veCTHvtYwD4cBB9g/oeYf4kILxDiNXX7+Q37OMs+yrK3WM6GhnNkXBz7SNdZ77prXG+JG8zzwrkeO8Jjs2w21RZ9DVFpyJwlUnUBNd4qDGqqDHOgwkyO0zkuHPGWfPGrsHAJdPfDxR+H3TjNxrKHECCEqgQSotKJblWdQLFjT+Hd6GcNRJklWCJlCbMmcjWZpiIKI6IywntGgtmOd+w1H4eta2DWJLj6ahhyeiSlDBOGtjBtodmQZgPTDUw7kootUrZIJD6rH0k40ZZHALq5VZ8tSYisEp/HQ8/J420YOkqXTvYTcWeyCWovYwF0xpX5erCsHrxdZZoPqMcSIb1V2jzho8z36B003lt0H+8v/ZJW4DmtgAbQz+nbry9eK6AV0ApoBbQCWgGtgFZAK6AV0AooBUTIXInhpg0bs2QAbRTS0FWFe+47pRbMdGQTFY0HoCPzjWg7Fnu10gyJ+zjqN/sepj0C0JkA0wGmAgkhplRJh5gWmBWYRZlFmUeZF6LKeH/Ip/pysicmOnKCLbobWG3I3oaY3GAzLT7fYkstvsZiG+vsGJVDunkk3EQJpN4xQ86OkJ/35GMfq5hkbg0pM52GI9dllN3H55Vh7teVA/X3EH+s3A/uUsmtexSEGmd2CK6cfJnkyo94DKZS2bjjtH1aDkcQNjK7iIFsx0p5+zxx5EpBxtlRXvE+K+/1RepBthAxE4JJAuxtf0JQwvmb3vjmKP85lUpfcMEFYRj6flR83/cF4yjk7sd3ffzfP/rnP/xetVegPvJrppzlhnpUcG9rSb37VHCfSka+CfF6xK8h/ofKRP6SWgDzC62U5E+rxPkrVB79pYjvQnwT4isRz0JyPX5REJ7keNsd52jHPcpztjjuUY57lO1Rsfwtqmyy/E1WsKEeHlkP146w1XUqyy2+0GbznXChYsozPDExkKUAc74o+qIc8NHCWJHxPOOZVskGvBjwos8KPjd93nKwkU0HG0+RYkuQIYYlTMRllrX5uzfOOGYjAfyePOQMmDQd7nl0e41PsSOvG0kYeh8AOkLSqueUhymP1hHN21hsYL6BmRBzwwg1BIkTXCzvCSY1gpO+dcOiDathVh90Aczogind8MiDmxHnWpwGpkzhszZmFXpu2vKoHOemLU/y8yEZt8HxiCYn+fJTixNUOvnJ0x6PunDUOASY9mRPzT4W8XuIj9GPIciPXD3aiB6ttM1ivaMV0Ao8FQU0gH4qquk2WgGtgFZAK6AV0ApoBbQCWgGtgFbg70KBaPnBALEe4gOIT2Qz6Szkc5At5WDTVnh499G1sN+WLfNWWm+waQOdtOBIQqX9AWhi0Ap7pUI0iD4rWBalbYaY4jItMNMC0MSghcwzLIZY9DHvoelhSjGviHyNblVedqaO2Tpm6giqZOpYrMs+Xx79h1++osskZ2tIEV8/66zyUO2VtnOiZ73Qrb1EijcwcX6A7wzlZUx8TIjPKY75XcRbVT71L1VK9R0tc95kwmzS3vduWkSRZHyAsmvlPSq4F8Xdyg74r8jvoSLuQ3m/YtyPIQ4h1hRRtRXvdlTcUAeH1Upog2obxeNtB1XW9oAyrk1uo+PRdry20fEhOosYokKLQD6O7BEU9yt74rsof1zei/I+ujr5ABW6zLjcS9XkParchfIu5Xf8e8TfqrTi3yH+XpU/IP5OUnL6/Sccva5s5EupHAB8+8bLuLhdyavS1fEOwX6M+DPE3zB2sxL/Z8oE/HbE21UC8k8Qv6+w8qcEXhPiJwL8uMc+4oZXOuwSF//RwVc6+ApbnlYLXzASPK8WnEjFp6Duba+5x4zYm2v2xpq9zvKW22ymIyb5si/AnhDLoSyE0uTSFDwXFS4KXBRCmQtlLkAqnioO5mzitlFJO4SJU8qmJqeeqbTSkFvpxjTJVWEIbSXOU46c06Nt5KWuaLKnntm42LXH6/dw/T33rj/nDJjaDZPytNJlXpVqBa77j9m1cO4ogG51G7RAdhvqVWBXPQTKeVjwsGTLsi2rygQ5bynr52Es7QkmjfCV9z685ZxXwKRuqKagCtAN0JeFiQW44WtThhpThn1Qv2lI2eqnDON9JiQ/H5Lx2FEd2iPt0DmR+CyzypeDjgQI9RBsZxHivyDeKTGkByfKZJyeK0XPdA76xwR/F/856IvQChxSBTSAPqRy6s60AloBrYBWQCugFdAKaAW0AloBrcCzRgEh0BOUT1pHfFji7T+54wq18luJAHQe3v5uGPY2WKxiS7AF0A/qpeJNCkOPB5sOAECTdWz08/8oDdMnDJSOSohphpm4hJjxqRgeGg4aNtHnVLwQYkSik5hJLSZmqMXTDOVjm3ew6gQbv/aZ9d2Rs7UB+SL8+ydme2yLENMwnIv+PI8tasjlqqxqiDUNsU7lU6+z2PpGuN72j2wr7tGIr0Z5LuJbEN+MGAXnI74d8XLED+awfsAAACAASURBVCPZyH5UWQB/TuXeXov4GcTPIn4e8Ysq5/rLKj/3BsQfcfxFiD8P8ecMfxEXjj9LlF9wjMsdHJuF4a9UuYPhHa2GP2P4s1Yc9Ra9Gm2j+rQNVIl64PgrSQvf/UYtf/cbxXxvVamgX1OD/xjix1Ti8LWta7kW8dOJ8kn16ieV0/EViFcgXqpY3luVc/eFiBciXqDKGxFfzvk/LZoCvQCTDegx4Mndr3p8aEPN21bzttb8zUPOxhF7oxNu8wQVJ9jccDc2vPWWS0YWlr2OXMK9NQ2+whHLbVzZkMstsaweLqqzBbXwiGExZYj3DfG+mpho4SQHp6gyrYHTHJzm4gwXZzhypidmOnyGIyY5WFD2x2TR4MUzUJoRhubS5CIXFcWgC6EoUWqzLKgHIc1prOZwOjJJD1ugOcLNSZyanKUdcdMYvbW8Zzy9o+coI9jzpLeyHp71nn/t7uki9+wi2WPTSpcFMMpZyJrwk9vWNMIF0YJ7vswGPB+X5uJ+tL5fJjkeRdJLnuzyZBdZP1PpsrFioVnHio2LPTztPRf3zphIuLkrRdsJptmTMroNyrz+yX/PRVxiCSLvimXTU6Vk/0nQPF6crP90xB06x7tk+tFKr/YQ7LArdM5B/C7iE6NLa0b0OTKUedZ8pOuBagUOXwU0gD58740emVZAK6AV0ApoBbQCWgGtgFZAK6AVePoUEMg4NgSOIJW/1tk1137pBACYWJ6eBbNUhC9fP8HHxZYwifNKKpGDcxI9R0eSgKkJoMf8oJ7qtJxnOwB0hP88WueQSkg+ABlfGoo+NzGfo/AcLYbW4nTNfM8WSIqIkqsqqJdoYTEXM7Qemrfm/RdPLxvNhe9KFfjBzWvq3lQvhMBNBZ6qg2YDM00nXEl+uI1WCqri480MVp8uwXTZVMeb63pHuN5c31sQBAvDcEEYLPG9jb67zfe2+o2tbv1o6Z4YWtv92nZv+Dhn5HirdoJVO6Fh7WhYO9zaiY2RF7virQ3xLlteZMuLXXyfJ/41wMtVeV+A72N4WatcyvA9DC9heFmAV8TFwyuiEuD7VbksoApRHG+j+u9XXb2f4RUMPxRQuTLAKxl+iFGHl4fiioBfHrD3+uwdHrvQDV/X8F5i+Sda4VYqwXbL39Ggsr1Vjm34xzoeFTc4zvePC4LtQXBsyI4L+VbO13GxivGVAVvqhfPdYJ7jzXX8IxjO+utdi3tNSqSdALBkJjjeJo5ltcplQaUYmxxNiXlHwmADYstgm4HLwA6pNBjYnAo5w6jU48j7OJoA0dQiwwrlI1FLbBsI5BFBS+TlXFl0ZT4geNqa1aqrEFMMDZWPnwoxzWVczCaDplRoWpCzmbyviLMvDTVvKfE5TnYO1Mxsdx+OzYib2bhxLn/TV51GqH5hIM06dg/j1CGcP8CO/tRXJi1aTbM3n4PestlbKhmUyk9/Zgpe9Rp4cNdGm01VADrvyqIvyNajae5BNiCqyGxMXdU0Lij63OPJLgWpizafXGfzdjsL9nhHffH67rXrYEIBJmToLF1A4DtH7Dvbk4W3vRW8YMewV1b6k51O/I6OT5H8TBgvjis/TUFMnJMBnav16eSiMeSCxA0oPkU/U0BnLwCazPG14/PT9x+R7vm5ooAG0M+VO62vUyugFdAKaAW0AloBrYBWQCugFdAKJBWIALRye7AR/+pY77j4XzJVgBLks4pu3f3QigaWHcVhI9Ac52YqlqfMXhXwdcjEGbiibx4Hj4HHUm4Ibqg8bSXRw6QbQBLSqTilcF7ax7xPixAqAM3TAyMwaBHRe2SETGnVcmfgKwuOhrIyeHwEENN2AAzzcf8xbAqkEUijzqDmL33zmws5UxE7gGwGBgZe4fFpaim2XEc2a0Dut8AwW7eNUJRcYTYUN3cxjVhVZgvkxmvxgs1Nh+Uk9je8CsOKj0UPe0OcxLDHkxU/mMCCfulRYX6PH/RYfMIwdg1KY1cDapaBONv1ZhHIDua5/gLPXx54q0NvXeCtDIKFvj/P9xb53hLXX+CGM23Ra4s+O5zTCBZFhdJ+WyU6YgeL9lpoyTt/gR9M94OZvreAhas4W+s7q3i4wXWW+/68gYG+keE5iBv9cInEVba7wPLmWeEsi01riMk273fZZJdN9sQkVSZ6YrwywRNUQtkXin7l3N0VSpNuhMgGrNtrTP/al/M9VSjk0qYJO1+WdfzVctS8QvmxtDNcep4hsuSPLICmliqBBIaGzwGxzNDcYxGtRsxJNEMOXKZQrW9ZU5MzemgRQerEZCO+jDiBS3MwiCyPSxxzTAAiCLWOH1dTGhGGR4DRudIMDcsDjjSp6oFJE0AhY3pEETkvt9YAjCxl2rhqwpu4CUClEc3VqFogQWAGae1N0wkqNXfFowPHf+3GZRu2QaELwFAFoNKtuHOa7MwNMCpl+MKXC46c7ZKjuno6QmCdPEOSziGRf0gLnZPBtCMKnuwJsEKVQ/CdEgvWuN7O7/9w27btUCpDIU0WHxHmLqugmAITShUTPntdqiYmcqxyssSJADSh/OT7uu3a258SPWMvxR8FcdCUmucVlM+7vNcVSxHPR/ErWh8UxSiAHl1xUBtwJP/f0LFW4CkqoAH0UxRON9MKaAW0AloBrYBWQCugFdAKaAW0As9qBQQygTbiE4j/i/jtoHb+q3ZCBaACmUIGps2EIf/IGqdlxPwWg24D0K3U0QbCUACWqDCch7hR4lGOu+XJJ1c//PAiJ9hoh8t9eQTDfibLjGc4N5gwQmKOY2ljKlQAOsACa5aSj+UGmzDizX7CWvBEY/GAu/KeXTMG/RUWX7XHmhnIaT7vHrGziBNiAhiNtskEpdEIoR6seNlZkMoCMTsDFiyA4eGXEkslqJ2zCKI12VmE0RkCYhVxnu/PQVzNcTU5PLAZw6wckgUwoXDKB5eUoiuw3PAKiDMs0TPMynuYYSkKKTDFuYGhgQwEA18S5RxWZRDBU6ATBb0kORXkpuAF5FXBS8jTkgPnGc6yTJBrcIz2EuwyTqc1KANXkrDtBZhURQAX9HiACgfO8vX6/78G4yK3Ma8xssi1Fvr2ct/a1Bhc7zRWIa7h8ogRp9IQpYbM2UhuuQrlxwtFdub5Rtmv8TbAVEguFjmysJCpUctjnpf+qve+C7IFQqipMrzm3F6HrVI3LrIFH73M6Hqbueci47Ocz02Pgc/AU081EKsBm0K51WyVKzbV/XWDtZXW8BpraDnzVyCucVn/gJ1C7B4MKIk+aEfDdKOJU3d7XhlxQQNnCVwvcUXdgiAkoaKZQM9UQkBMMZ6R2CdxkR0ubfAVu0cWWv4mjpsEznKQMovjG9RyM6ce2kjr3gB0fDfp9mERZT+KeVKu5vykr351ys6XUsozpTmrLflumGCUYNocMGkypwHI0PzXd86QOCEag4dpV2YpHVsZiRD9b/2woEWfm+87K8z62Ovy3qGRHhSrMXz+F6/tPuE4KBVprc7oYY0B0JOG7gwsnQ19JaiY6RRkKzm49VfdNZpO+WcpgCb6zKuuqNrBAiHPIWMc/jhySnQWKFR5Vn+068FrBQ5HBTSAPhzvih6TVkAroBXQCmgFtAJaAa2AVkAroBV4+hUQiFzinxGvlPwt3vD5a+fTOmNFgFwWzni16eNmWxA53SuAjmG0JUuPuj3DcvNPf7Pubf+SX74Y5s+EKb1QLcHkKXD6OXDzLStHGtt8fw4PqxhkMTS4TCU5XStOKc+NfLQqWkOUaqynHi6pB6d841trX//6ytx5YFDeJ3T3wFHb4Nzz4e57tw/V1nliJsdqDCsDkYkSHgnd8oyH5rC/dtvxUTKnUSjCzpdB3T6BcnUJJZs2LS5H44mhJyfK3D1kz35017bPXNNz9svgpS+Eb95QDuQ6jv12i7xH2a+I3Y6YNlRb98QAWRj7uCxQidIunT0rWQZDgzFwBQHoPZgbwh4PJ3PsZaEZhpRayyUVoQCxwAyZDkuT8QxlDYtsh3XvXi0dIgAdZXxHW0WiFX1WqeLxpbmYsWXVwxkj7qoHHjz501fPPftlsHYxTO+C+VPgmPXwr+8Bn59c8+c12ISGKLgyqzqnrlq3ad8Amh4thJim9STVFREEj8bAy0MDR27d3ATQ2Qnw9suPqIv1NZY0wYg8hSmd1lOPPSKG6/Kcy7q8oOSxtMdSiFOsoN8XO35864rz/jm/dguY3ZApQG8VZvXDq14O371hLuJ2iXMY9pChsxpJcvwqTiH2Ou7sunPqlf+ef+Ob4Lbbl4/UpirbjRRNUWmqLOm0Lw2Osx3v2Ftu3/qWt1bWboAtR8PLXgFf+Ma8x/xNNZxhKwbdzK5tTaTIgmOUQe8TQLto2KK7ESwbGDzxc59esG4lZA3Im6AMMKBaBSMH2V5495Xdv7z3jNe8tQsACkXC0n2TYI+1mWM1usXKkTnysUmru9C0VleeIaOUXO0WrKDq+os4O/2aq5euWwe9XZBXNjWVLJTplxDQnYX3XjT5vvvfeN5buif3QhHSWTDmzIBdI6sbZFSSi2ZjtKaoWoYxerBE29EL7wDxz+BunPgcB81RiTzRZ9HbcDcjvxrFneSDT4nOkdWGNtx4+v/z0Wd47imgAfRz757rK9YKaAW0AloBrYBWQCugFdAKaAW0AqRAoNyfbwrwDCc8pjH4lt4MAWjKrTTgE59fWQtXcMwRgFZmu5ELc8ydKZBmg00aDpb/6bEjX3MhlPuoYS5NXrE5MLLRr/cN6J0Ip5wKnn0qayxGrxtZWuwdQJOvQohZj3w/+hs418ZjvvG9KZuOBsMgK4CJvUTc0gDFHFSKUCxAfz98+COVIfcoD2fbyoKASzMBoA3GsxyrQ87GFcpCF8Co9MA/vR2s4EhPVmIAHS06F1AqdG6PZyAu2m0v+/6Ppy9fCd0lEmRiDhbOBqt+HMfJg5aC8hI8tTYjw0kD9eXbjobublizDr50vVnHWY+Sf3HOZzkWphkDLk2HV4b4rIFw7WUfg5tuLe8ZmsP4ZJ9TV3HudpSl62HJE5PcYLYbzLODBXY42+aT1Rpxhk3LMI6WCP9FWbRJ+tzKhm5mQEckVHlnF2t8znCw/q5H1v7ze2D6DJhQhQklQo1Z5fBbyUBvBTZshJ/9+ohaONfihYg+k+XFwQFoAvqjAFo9CfD9OXf+4ZhMBgplyJSg0A8fuHrbUHja4/bMOk6zcIol5tpsoc0WO+FChx3hyAmxzbcrTJdVnKDiBQXH7/PE6r8+sPasV0G+DLkKEKY1KDs4b0J3HnrzUDHhJS8At3EcFwsbTp6Y8pgM6FDm/HDy/fcv3LQJKiWat/198NjjC7ygwHieC7KwCGSBYdced/Lje45+7RugVAXDBCMDuSIUq1CcAC9/E9w7sqEu+2Le2smdY946PoAm+oxGXUz9yFVw5Aaa4b1q1uWV83IGoNoFZ74Sfnffxl3Bjvusk088HVIFeqCSL8O6TTBib2wE6QivK3BP0Dmiz2FrZcV2AJ0K0HQxs6fWdd3n4KiNMKGP0HKlkDKAbDeKABPysPOF8PvfHhOIM58YfOFLXwaVPKVFV9Jw3DYYaKzyiLmbam3S+JnBKH0+nAG0S/YjOZtPbgTLavWzkN2GYR2Fh1EK9CiD1v9JaAW0AodSAQ2gD6Waui+tgFZAK6AV0ApoBbQCWgGtgFZAK/DsUWAI8X8DvNziq1y+6v67TisqEJk2IFWC63+4NsDViMUos7K1uF/Wxky0clqAeSuYWqttuOGGIyZOp5a5qsLDBhG66K/Y25Utk1FANQ8v3A6sfibyecgJQEd0sm0rUx6DR5+EAPN1nDbCT37npZlUDib0U2eZNHSVsrk0TOgqV4t0grQBpRKkTLj4smxd7GA4NYaeUf4sWUDwksTJjeCkUpk6MTLpQhU+fV2hxma5Mu8i1NFooFF3ydgBsWc4KA3yqRbueM8Hu8CATI7yuPuKRg5gahfseni75/cIBMGphBwc1rOnsejyD1HnhQxUi9A1Ae59ctUTfpclehxRIMQsIMSMFc54bPjU5euguxemToXL/xX8cBkthYfgiqoryjb5fqRDzO3xq7uHV9bqL/7lL7d885uz73tge90/ysNZNczU0YgG3FDDtpFcOOL058h/I86AJgMQ7HE8cEXawdweblq4xMPXfuCjM80SeTgUlLFDTvktFIxcOVMwM5DJkO1DqQqPPLnKYhVXWRvHucPRZGgl24LyUYncM2L4OGp2Ed9cIapOfbrwdh6/HSpVyOYMSGVSRTj1jAXf+cnOm3++9cc/X3fLT9ffetsxt99ywk9v3XH7T4760Q8WPvjwioboiyabizDsAmKX7ZYazpHf+/62MiUBE6DNFCMAbUAmQwnyAMUUFAB6THjhDhh4cvOI1RuIbHwJcRCIntrIqje/kSzPK8oVJJuBH/x3meN0FlbrNWDkRd5nyUU33tw3ex7kFPNVZ1VnzNBsz06Af76sq84W+ApwM+UtE8PotiAJoGMqrQJXratZYws2bYWuCnQVoZSGrjTZbJQNAr433zxr1+CSPf6MAb70cf8lq46GvHKFzlXhgnf01P11ZFkjifgrG+jUOAA6Nr2hCq7MjtTmH7USek2oVgipV0vq6Y4Bx2yEm74/lclNAU4dcKY8OnDCyjVQLkDBoDfyeedVayEBaHoWIppLQUYpxtF8aG2TCdd7j9v0addk3JeSMsbxPtvG6c9x0MCiI5fWG2cifhPFI/QkjqnsZ4wtOMQBfYzrhOkDkklX0gqQAhpA63mgFdAKaAW0AloBrYBWQCugFdAKaAWemwo8jHidJ85s8OkeLr3l5qMKKtGY8kkr8OfHTnVwYZw4qQC0QcBUZiMmOBxUnGD9t785p5CC7jIUi4RrKVHZJH5NCDD6y0Amlc0DTK7CWaeBVd/gemVCw60M2SgQZEORCjlYXtZiU0bYsRe+E0p9CrSR2wD1FQHTcpkCssNNEUXNlWiJto9+slxjC2xBibpcuTd4ZPJrcl4ROO3R3UcVVQ+08l0ebvnN1KEgr9KHIwBNqyYimooCL9zDTnzDP4NRgWwXmCUi3dVsyQRYOg9qg8chTucMMAQZQshMJ5jRCJ6/aRspUDAzaYBKF/z4N9OG5MQR3mXxgsPJJ9pFGPEXvf3dpZ5uKGagkoNtGyEIjrVllcQU3bTGIOYGmdmQ837/59kXXwLTplOf+Rz09sEpL4e7n1j2kNVTw3KSQSsAnfFl5NHcNIBOAmjXBcELI3Z2yO1/zFr2rR/P3HKiukEpyhjOZeh2RU8LSnl1tzKEVtMGFPJw7ZfAkTMlFjwC6Hu33TgQAN1wQPJp9V3H7jwJehQ1ThlFM9uTyRcgS5m8uSoUK7TqXaUAXTnyGi5noZyHo4+BOpujHnhkXDQ8hFB2W8OLv/3NeZGLdLG7mSGcLRE/TedoBhopKBrQm8/0mNBfgZ07oe5udXlvzJ3jIOCTwuCl61ZB0YRqntL1jRT8/q7FNa+H8y7BKq7oRtz4te/0dE+l/PAUzQVVLUepx5lcBgwoVo1qH9T9NQzJLX3IoW1c2ihqTEul0XZcOY00EGpswfI15H5TLEC1ANO64eRj4BtfWCLcl6BYIrH3yTrssiYNh2dXJ0OhG9JFMCtw1eeXjrgrOBZjAK3y6CMXFMqDVm/hsVsTscrFqmPXwZQC0LKQeUp+P/PFcP3nF6J/GuLCELMOwoBfqnlnTuyHYhZKJv3y4Oqr51pimYMZS9mgx1TXJfwdP4eIYffe0XP0DKNDh/3vJjVMxgcDoG3MuNg/5G1B/CSKPyBz0EcZohQoNIB+bv5PqK/6GVFAA+hnRGZ9Eq2AVkAroBXQCmgFtAJaAa2AVkAr8P9CAYVUIrBC2+Zf0+P0LyGeVw+X1FhXiEd+/N/mF8ymlUHvfBiUp4+EMx3eNGsOMOVhzhdlXwHoBhpP1Cd976b+cgZ60/Sz/QwQOOudDK97G1z11fJ1N/V+4FO5zSdQhnIlp2w9AEp5+OxXuga9xYGsjAJoSX67tEuLwmWHaxMt+8WXf2CaWjOQnGiNLqJjR22Eyy4zv/qNvq99c+J7L4EjpsKEChSqTQQ5bS7c8ccZe5yqH5gS060M6DTnFV9M/d3/Li/mIZ0myFqdCI+MLKu1iFXkKIKY4zwT4tQRduwLT1cilJUTAYHulJmBbBquuTojxArPz3IfMKAScmgEs0bs03OKbpeL2VKJnIgfGF78OIMRaVo8Z3PT4SkPDR83zp2rMHo6nQMirb7zEpf3Kn6XsWW5gdVhd/Hvfn382iXE1rMZcjwo5SBrkv/v1pNhl3NKTUxXuc8ZhWUNFzM+eTRnA6EYtMhEQZQTzYQhwrRbNwI2peYcdfkHpxl5yHRBvkrDmFCiZwYnvxg+/ZXyD25fdd4FFUrzLqgceJUE/Q9vBI4b7CCPWCGDbGUFHq+2Fyl8IADaDQH5kreeTetb0l8zPT5HV6VSmHMlKFehUobufKo7T2m2AJDNwymnQT1cZMuyK7pd0S2x27bn3fKtI8ug1pNMg9lF/hvdE+D8C+DGG7u+/o30JZfDqrVAbsWqEzpbHj77Hwsb4bzY4ztO4vbYjFr9nFKejDtyKnd6ynTY1VhdC9NSdqGc6QTLv/ejGeUemtyGyqA3C5AvqActAN0KpmdSkM3Cb++s1n2gWYRGTJ+j1TtHoer4wDT6eUFd9n/xenjl6+EtF8BV18Cdf1hY37MG+Up3qEs20n4NGM8P1uY88NhZqRwYBbq0dBXu+ONLB52FAgvJhwQqToVkxp0kwukAyVSECuboaQ3O+K//zLzq5fCBS+ET/wZ337nYG96A3rLAmiCCnOuDLaAWHvHAo2fkC1AwidT3VOA3v32xi8stBIuceQwPUzGDPjwB9OgtaLL+fAPn27T24E8x2IOhSn9mKDk54nPk0TqErc/Kff6rM6D3KY9+USuQVEAD6KQaOtYKaAW0AloBrYBWQCugFdAKaAW0An9XCrQAtBilKrTWlof4MOKNjfD4Ya9sCdPHDW99a7eZaZoBbzwBnrC3W2xagGYLbKUDWZBYYpwyoGvY95cH1y5dDlWzCS17svCPb8zc8+DzOJ4ygssfZ1Me9xc+MnLyey6b0lMmT16iilmYvQSG+YsdMSkBoNORRS+X6UYjE3rrP//p5cpKgZpAHrI9cO1nVtu1cxruRo7LG+E8jx216+FTjj4KKAe2BDkFB89/Bzy6Z47rVSVZOdMSdnQKXvLF9B/fekQxD6ZBAHr+ChgKF0eGCSGmVDa3YftpLmc1gm2nn00EmWh6Wq3CZlJe7ZSpcPXV8y33SMRpnOVlqDKgGXlrWMHcP971glSGVkcs5FJ5kwyUbVwzjFCTKUuYNsvZPB2gOeCu7uqCUibTW5hQNKCvAvU9Z/jhVLIMloYtegNce8dvV82fTfYLAJQFXDRzlSLR4pQJRhXOf69ZI9eOrCPMQK3/RusTinzAVaEVCwlDc6RlA13VreAlx5ps2Vsu+BfIRlYVabq0rjKcuRP++JftLj4/xI17+JrHhl58/AsVgE7TteRzZDrsyZUMexDz5FJ9oACaiGeEPqPV/BoueI3Zs4sQeWak1N1Kp/PdPXRphQLl/ObzhNorJnSZ0FuGeXPgdW+C+3Ztq/OZNtJ6cS7vYzh/9+7j1syj9fFoLnVTov25byv9+e4dw9ZagdMD1vv4wHTLPvUt/0jsPvrLVaAwAer+eoa5yE6k5R+Sstn8u+49LZ+DnKLVKYBjj4cRXOahIbBkW7P+dv+xS5fDhImUZU/zsAqr18OXvnLUD3/8ojefVyrmob8XugrkXPG7/800GAhMD9qj6c8HC6AbZH0+f9fw7ABXeXzeSKNoOylBzjBpxFRok0WMx5bdcusJ3RNaV1eFEe91Q/ZsjvnW+5RmfnwL9gGgB2wIsKvRmCX4Gtua5TtT3UYVcYJkmYYFgQduAC5mPFz1g5u39PZCPg35DPT2QN19nSXmttKfaabF5bAF0HTTW3PY5v2D3gmIn0V5Nz2UC8n8WXLKgFb/agD9d/U/oL6Yw0cBDaAPn3uhR6IV0ApoBbQCWgGtgFZAK6AV0ApoBQ6xAtGPyjkyoQr1TonQNcTrhsOXOGKej8UGWSGvOuZ4RV0LBF7fcC7UrQ0um8ow1wJbZihziNlGHQIsD7irT3wBLd2WAejKwPQuuPBN8PjutbVgeoP3NETJkiVL9AS40MYXnXEm5U6aak1Csxtu+OEaT8xuAmhKfzabAFoUEBf87o5FPUVKqTbAMLOQL8K3blzYsDe5/jSfdweyFGKZ4QQmZtUaJ1b6FSzOglmCGfPg8cHnO95kbGU3k1mzzHOc9+lrM+UimU4AwCmng41LQ7KjpJRVgQbDkoPTLX/Hi19EFfIqMZcuDMgE46J/goHHT3C9FS4r+QJYmOMsGypXjQbCcLD05tu2Gyak05ToPSEDl7691/KXWmp9QpunHWbaPO1i+qHhhRmFRQ0gf4meMgztPjtwFzFW9EXew8V/vnv7uo0EOnMVyBg02mw04pQJ6RTkKN11yN7qhCWH5RCrau3BjKLPZRZ2s7DKeDaQhsTCgA1DIdQYMDltaGjTth1QnAgEbjPUf/cU+NrX+4eHVu0emR3gIg/n75HzhnDrmW8gu22DMpMzUyfCd39QeXwkEyDd9BjeEddOlHbgOOrzEEpTlVwoTcSsbU96z4Uwq1uZqBipFOSyqeayhzOnwKY1cOZpcOG58LEPwfXXFf9y54KBJ5dIXBbi1N0+4dShEALsr1nbTttJFtLVcqUrk5pUgfMuhEeH5lpsWkNUHJl2RRqx23dm1kc2nPMKKGcI95P5Swa+dkMmwCmOhAE3oqWZBhZr4Yrv//dRhSJEq2UWs3DRe/prOK+BYHEI2IYzXwa9VTBNyOUIlF/wVqj7R1tssRWstbxjP/kpmD+H0vDf+DoYaUzy0XDUWp0xjY2eAURLRI5uE+ollVStMq5oV2u8owAAIABJREFUpntTwHM+pxU1mTKWCRAchLqYe82nlmTVAw8A2LEdGvbxtjedjWZA5zwsKNuNZO5zFKfpicVoMdQDjLLPq74oB7wYCJo/0b2Onjc4mH5kz7SPXTWrVCCVshnYdiw8WT++xqc0kNyfOy65fT6MZ74xdmDN4Y0ZdkcPHQ2j+dZxMN6NX20ayDCeYTzDOfjeEpSfRrwPsa4+DQUKeiinPhrpQV3zYHRIb7UCWoFDpIAG0IdISN2NVkAroBXQCmgFtAJaAa2AVkAroBU4/BRo0RQhaJktVaRE/APDcxu40MfeyOl1RK5asValP+chU4Vrrq541oqAT5KY503/XwLQ0gWUpUZwxFe+1QPKRzifSlWz8Pqzwa0fHfCJQw7lBfscXGE6IudioS4W/uj2TdVqk/9CDs59e8URC1oAOh0D6JD3DD6x+pyd0J2FPKS6i/l0Cq774iw/2OyyLl9CXEIESTnOS9/9/h5TGUpABsrd8J3vr3a9IxDTEdprAmi55IorgAB0CowsvOH8TJ0tcBFCyi3tr1tko/Ho8JZTdkKvytHNZ8j1IluG7SfBbT9cJZ1tjVov4xlfQijJ99nnpoNgURq4ORSsvvYLqzMmdd6Vh4lpuP27W213QS0Acn/mKYelbZ6uIzw0tNjIKgQO1P+COVDf8wrmLGFhbygmD1obXvd68o8mRmyS1XA6Db0Tm4YYigmnUiW49WczbLffCSocyzGAZqzMwyoPy0wYJL4kpD5CKdiT6+4xJz4PKn3qvEXqeetJ8Ns/nWTZixFnOkT8J9WwOoTT67jljDeQD4byUoapE+HR3SuGAwgwzaIJoDKgDwBAm5Q1L3OhLKiSCyRQWrp39FUf6S0VIJczc2beADh5R/HuP77ZGnqlNXyiCI6XwQbpL0c+F3EyYlmSdwTB7gBTe0Jw5OxrP9PbF12IUuh1LydGXGOpyESloSyYEVMyzCLO/dnPpnUXSchsjh6rvO1foOEtDrBATs0INq3lWB4M1332K8uLCkBHqP/7Nx09yKcPIzCc98EPE1ymHO08JWi/970Z2z3WwR6VXF/wxCTXX7Bnz5L6yOYg2OjLvgjFeuRUM2pJMcqdY/+NcQB0E0bH1aThCkLqihdTlrGtptyInPveS2flyX2a7Kjf8FrwnTV+OJljsfmgSJY8WQnQbGfBTSx7UONxFfLeVZt90bt76AcEKSjm4ex/gAF3ZU30/L8A0B0e0zFijqFzMohfjQB0KpAGvVO8qcLbifIXKvOZtfKfWzYcqAH04fd/mB7R34sCGkD/vdxJfR1aAa2AVkAroBXQCmgFtAJaAa2AVmCMAi0ArV4gx1IP8XHOrrPlcS72hMSt8g5mR8T6/hnKfSIN6QrcdvtK35kfyj6JWUE8DkLMCplHTDWGSoMjJy1fRWyumKc84Xmz4L5714RsUiCNRgA+T/us4LKKw0sqd3W+hzsXL6f6ZjoNBixbBw5fRABaprnIRenPZNHLZtz4HwsnqgUGSwaUsvAPrzFDPBFxqktctbM4fNZtv96cqUKmBGYOJvbDBz4wSfBVXtjM0lUAuuj5K88/jwB0Nkt+Gld8dO6T9QWOAMQUYpXh4keePPaEU2hZuWoZpkwgq4H+XrjsCnjk8dWOu9SjlOo+xN5QABVOhD0C0MOY2xMced7bqqYCgqU0LJsBtUd2ut4RNiMKr0rakek6Gg8NLo8BdArgxO1gD5/CvDks6A/E6m/95+RitAygWsZw6w74r9tn3/3EjlefR8v0EZXOQLoAF78HrPocn/U1gmY2a8DzjOc5y3JOt4kR38zWRMHBGSNy+84zCb/mK1DsopTyY0+CQesFgVjecIqByNQZuJgaQNiD3Q83tqzdSibdlAGfghefDLZ/pEccM82QsmJ9QeYSTjs/baec5DQSuQyHokRFFhjNH8Wj2SSrfnJPD5TL5YxBBifnvAoGhk8atOa74fSQT2d8KsrJiL0SS1yaPqPFGwcYDBEGLe0aXLJqmVoBEMAswuK5sPuRF/hyboi5UQCNQIYVnJbXq9nrNq2nKZcrQCoNxx0D9dpRIfYxRXJpxT/MDobrLrq0r1SkXOxShhbZu++BnUPh7Lo84tafrimYUKDZCoUyvPlCeOiJ1UNun4M5BaDT5IdOk6eP4WSGfR45ooCvDJGfXgAtlr76NbmCWj2ykIWrPgaOvSjgExErrecEBQ9L8dqhym9kFMsmc66bMLr9hiYrRAB60Fv4irOhoBzJuyrwwY/DUDjbkqXDHEC3/K+jHGp6mEE55rzPrT8f5acQH1BP43jzmVz8cG40/XnUMH/MZ6o+oBXQCjwVBTSAfiqq6TZaAa2AVkAroBXQCmgFtAJaAa2AVuBZpoAkq1PEPYi3ecEFI8Fsn9hilmHJxtII25YtQbaSorzmCtz+8wW+N41hl6QKEdnMEIAWeQxXvv9fCymA7ioUc1AqwGevXWW5SwJpUOoxpT+nfZZzecERucdtCHH6k97Kt11ENLCUr6RzcMRCcNgyBaBNLgpcRuscph1/7ZYjoawckPtKMGsqPPjgaTVnBkGxvQFoi00Z4Wf2H0E9p1UO8utfm7at5RJNnxb9AwLQourYZMhQylMybLYAX/jqkY8NHmGxjB1kPT7vrge2rlgHRZXrWilCyYS1q+CHNy+UuNIKs5ZLl4NYCLmiz2KUwzoIQ7Kwx9/yopdCziRSmTfgBceBN3wCYzMZZok+N5PBwULzocGVZgsxA8A5Z4NjHc386SycMzj8/BNPAjNNGbtdedj5UthtHfeoM2UE59/95JZsmUyZUxla++7UF8LI0Fo/nFp3U5GXAlk0KGMBLuk2BQh1Bk/Uy09Yq19zLpjNhf9IovVHwmOPnTIw0Md4BmkxOqLJlCiNMISTf3vPNrNIxiBZgAlluPaaeRzXhJhhaJCPcAygW07QEalMAOgo4VQBaMypDGjy3whEBrHocxCYG7E29PVDMZ/NpSGThosugUF3qYuTXJlF7JZY9MO044Hrg8+oOAI4lhrYMxTMu/h9UMkrF4gCXcu1n+ndM7RY4pQ9HiQBNPdTkmUEmasc+S9v761WoFim5OalC6FhnRLg1GFBqcQKQGcGw3Wv+8dsKU+yV/MwdzY88PALasE6H09dv4HW3MvSuwFOegFY7LRhfzriRBdHLY85mo4Eiflhn+Cmh6mnD0B7KhnZQhhha09+PpFxWk6zDN/7Tq/jTQ9lN2K3AtCpgBB57hAC6JpYs2MHrQyZATKA/vp38kOix1Lc/5BacETzJ05bjqB5hwXHQWRAKwBNuc8RgvfQbGC2HizzrEsQf4U42ELPXH0stn4dogH0s+x/NT3cZ5MCGkA/m+6WHqtWQCugFdAKaAW0AloBrYBWQCugFThoBSjxWa1ByBDxXsRLXLbek5QyWbNBYk9Ddv/mL/NSyvVY0Vy4+4HVIe+RWBTKgUEx6AyTZdfte+Sh9TMmUwYr+RtkYOECsOyz3WC2L8mPOJS5yEbWVymHjztgY7WG8y/9CKRSUMp15UtmtgQOWxUiUPqzKAxZEPC878341g3FHrW6WpaydeH9l6YG9qxCXMywEEhgskmj4iRNi0/cE75w2SYacjaTzqbISti2VgrMRhYEZErAJjr1HTuOIwCdTpPH8Y9/tr3OF9vY4+Lyn/x8/ppNkMlCKZdNA3QV4fTTwXJPdPgMj1bSI4DVtApBGkA0Bl+tcOhhtobVJ5yjl68gKah5CT7x0VxjZImQkwTmmgBaJQ5bmPvln6fnijTUUsHMFeCi94HtrRBsqu+seec7CxN6obc7XcnD8gVw/93Pb/gr6rKvhtXBcP0/vIHGVjAoC7WvBxg7zWNH+CJPJsuYDjHFyeqaaHvYymZtsDkfvbJQrarUaSDsvmY53HfXCSg3IO+TITBO6eSuAtCUAS0XvevSUiEPuTSdqKsM99x7UiOYES3dlrwQh/LQjbgo0NlEhy3f52hUo74HPk+H0nR4qmav7+6lJQezKagU4Vv/NXHQm2GFfZ6sKKuNpsLE+lXxCUCnn3R6G/4ZU6YSAE0BGCYsWQ119xjKZpVZZZ3chMKBBBGYyGnZTJvP/dCVM43IWQOgpwiN4ZdznKfWnIwAtDEYrt95OqmaA6hk4Xknw+7Bl3vB2e96twL3BvR2w4plMFA7ddibU2N9Fs+R0zTpZrg4KoIvDQ/Tey2xUKNB6x7F07gtSGibbBItqmkRXN4xdTI5pKcAigV44IG1btgTkh9LpunTrSyeWw8Gmvi1tZvay7nGHw9NDwFD/oaZM+nBDAB0VeGOP00bFoaF6UOUAZ3kzmTe0ppRBwKgRzO7Wxc42lv0vojsgzxM29hVw3kOno14M+KQWoU1+nEIbzk+x78ViYOD/qDVDbQCWoF9KKAB9D7E0S9pBbQCWgGtgFZAK6AV0ApoBbQCWoFnuQKyBVh4gGII8SbEF/vYy9DgSNmmEic0RP9Nt042yaE4DemM2QuP7VkbmScITEUZ0LRYn+h1nOXXfro8uQcKKbLIKObh41eVhq2VLu/zRT5g1YCXCYQpquUiDDFoYH4IZ737A5TGm03nChWjbypY4Wpiu9LkIjcwQpjYfnLLS/8/9s4DTLKqTP/frZsqV+fu6Z7YPd0zPTkxkRlgCAM6QxAQDAgYUBQTuuL6NyAqq64BwbgqZlBUVFxg17BGZFVc1JVVQCQNzEynCjeHc7//fudUVVdPICNhTz+H4vSdqnvPfc+9t5/nd956v52Q7SD2XMpCexruuXMdixckODBlA+W3NnYr0LaLUE16puKTRtbylAlVVQHOO0f3nVVxIrIgVB7rMas2dfK6lRSwQPkfGbj93hdPeGserA7/+Jejw0s5R+e8GwDee/Gsmn2SzeYI3hccGkBP+WCjbmPPPZPb2ngINUHVNPzkR7NsuztkhTDR69w2oeQKC/M/uKlDAOiMqaZz8KkvQi0Y8t2he/+6oacLVI5KTRWu/fpCFm72wz4b0xZqlWjJhy7rNxTIK5DljPtvd+/y4hEqOpeYHEATIievNzd7eqiOW9k7717RUyA7M4F8nfzdP7pxA8ZHIM5DLGAEYUQA2uH253st887x9UPDxDRNhUj9ps1w/4MbnajT5cbnRw+g6+yehpfoXgQhUjHDex4YzWRoRCkgz/hvbxucivJWXPJ5QUUBu6OkTp9F1AlV3gsXXXHFvHyeLrbObopb+din+6rhEhe1Rrk/wsEuQpAARhmMzYCqCA5f/O4ena+pKAAD3VCbPC2ikphNBzRMhOuO20GLBxmArArnnQ97J875063nFvJ8E6+D+fVrlpSdpbUgW4tydmRSqDerF99rhbkHpc8eqtMQuUmWDw18aYfNt7V2+IKHTSs6bXvKW7M6AWhToSTxmr01wpyfaA7PewnEp3hwNnf+Pk4Are1zU1Pe9kIeShkjq5vtHbDHXlXmFvJnCoCOST21lsxx8NQEP4F4O/c+N+lz1Hg+Nrlzs/MMf/LL4UsFnmYKSAD9NJsQORypgFRAKiAVkApIBaQCUgGpgFRAKvCEKcBQAOgIMbYQb0mCd/nx8gB1KuIXQYI6wy6bzfnklUQeqeadkZ01AtXwsISYZp0+R5iiKIa4v1o+9uhtFJj7v7hWA1iyFPZVV1ss57M80eewi14TQoE+y/os7RELy0+EC9/8TtANqtSX64BFK5oAWokTteoAJsvvuPnEbpODP77zN75Gi7zDkQJ2253I9KJp97EoyGZTkb3+SnL23MWQyYKm0JAuelMx8Ef59+4VD9WAznHOxL5T+7shbUI6A5l2sNjbJpyTv/OvQ/Pncd+yTkC0XYPPf7i/Wt4c40IvKTg88cChwauc8xJRFedFp8bN3RYaDs76ye8GOzuAG1JpDGNja9wgFTAjYHVHaoPFd171vZTIgNZSkCnAT37TW/bmTjy44Q3nExwHoOGdeBLUKpuisBgww8WUjSkrXHjTzduyGuSAsGPOgB/8YGOEK0Mks3nIzzHk9JmDNrCxu1w7btfx5Opt44kfqQx8+Aqo1BZiPAeTbmTZMFIp44KwOFSSwoPuygsugkIBsikOoDPwD/8Pyu4al+XrjDXhtQ1FBvShHdDCu8qZOPmyyRDNCiHL2THYFA/S9rs/zFVVwty5lNJRgn3u0jLprLqJ4bM0tYR0a/Jun3K69Thev2kD6WOYYOZg0Uooh6db0Xxuf54OxHAxRXEfoQDQSjVa/oY3d2om6BkFVFiyCCqTx1nBHBuNRgQHTERr1q0h63qBh5/849tNy3n7+S9ZSPkWKt0K51wI++y1taDHiXQ7Vm2muFwEMkHPjCJpBEPv74NuhdSPp+8hVIjjD/z+zytUfuuVMkZ3F7jRRh8pq8Shsp/UCGHzpQixfCJc/M3XGWNo0OoZG1v4uJukp/z22+/ZkE5T2E4ho8xbAC5uFpknIn9DlF5srATMiMgQB23h4PVvMDTcyq3+ZeFcfiId0AH/BgNPgQcP9Wq0HPGjiL9m+ECEzswA6CZx3q/zhD2F5Y6kAlIBRIpGkj9SAamAVEAqIBWQCkgFpAJSAamAVEAq8CxSgDI3xOlwpMIQA0R2P+KVnvNcP+mLeLJEGANizscOh41cfCmlIhDaMvUl68CK1ghTLbc/E32m6nbx/Bv+bUhLUZk+XYGeLnjHu9qtZCGVX2PZIGoLoo5pBzQhxWyMGuLAPnvtBW+hIAgKru2C9VuhGqyoYzJK0c3Z9qqL39jTLqI30pDOwq9+sSmKhxhqDNti8msbwgHdoM9KFbUptrCWvLZ/PhTyZKr9X0Z56bs7o3hYRCF7qFBybjxvz+4zTZUst7k8rNwIeyqXfPf67dksZS9wJEyn/e63drsTxzIcdBK1/kHOoClON8kJo3E9j4ITOsROFwtlXPDZq/MaQdWUocK6NTA+tcgOiezPANCJ5uG8T3+JY03gFL4Et+9dOu4t+O9bjy5q5PimHwP+eMdz/GA2a/jHXdTscHBq8ox8GnIqMeW0Bld+YZThOj/RRASH4IyMT6iNqWo8+v0b1ncXYKAAHSa0tcHxJ0ElXFXzIQlUDIwo1L2AhywzsFCdiobuGTu91Eul9mj6U6lcFr7w9ZKHI8SFBY58DAA60cMkE8alIMmJgo0h9v3oZ72mAXkDunPqQB+MBYMVLrLNwIl0sWLhJ4bL1DrnZep4WfntrbPbSiSaqCj4jveBxdbbrIs7oPcD0AYB6CRnx2o53PDyV3XqGci1ZVUT1q+HSnVt1e+xMW2jxjOgYSJatXCIUHNRpdcPfXTJX//61r4crayk2kDthzvGN04EnXZMJm4nBpsTXkGf/84A2kmgEqoMh35y02BWo9GWsqkNG6EaLCP16gBadZlOyeBPGIDOurjgxz8f6uyi+0tVYO0GmAxWCoLfXKRp0mdaA+CZMKIA4MwygA9Bn5VG7EYrgFZbOHXzs82OgNfTgRsNzN3cFVUdDIl3AWOqx3rL3gmI/4a4x8cpD22GYSMDWjqgn0V/+OSpPL0VkAD66T0/cnRSAamAVEAqIBWQCkgFpAJSAamAVOARKSDse/ytMwB0hEmAvofxfyK+zGdzA6SQXN6UBNN20O5Eq173eqJaGiiGCcftBDdew1BpOKDrANphI+/7SL7QSXkRpko10H5+8/HlYJDAXJTzw4If5fxYb8AgsgwnmENcXXZOWbeZM1YguPyy86EaLqbMBN4izOwrr9m2FYw05UXk+2BoMbjhjhDTHCXnYuyJMCtqFXIAnbIwX8GO+ypLfvabnVqa4LIK0JaB71+7IYjmNAA0RUzY8YKf/XxTIU/QHACOODp39TXni2QGIOuzDtCRSsEPfnxELTgMcbAWkcE5rNddhJBK8Gn8tQm/yOaJmPawZzw47KKLKQlBBUq4ftX5+cnKIjcCP6bMkLpjmuh83o3XXPw+yPOwDkjB0BLY7R42Hq5+yxvy/UVIK5DS4HVvg33OcsQFIaPQAIeSr3NeOFyePGV4iPzpaZ2Odcl7e/ZV5jms7sjmtFGJGNi+Uos775taf/g2Yuui3mEuC7/9/dZJt29vhTI6MAYMgQUUwZFgzsXuCX/70ceDmgPC2ylIZ3MpDW69YzTALjFBxKDpXKgdGBDBYb0iXqcd0DxZJWaZMMkEVBASbHKLz/vslyg0vJQmubZthclw0OKBGBzsqn6icaYsXoks2wl559/1QRDOcRX0tAHf+X6HG/W7SXp/326SimIjqmmYtE0G6XvK6zYeASkTwFBUk+I1au7satBWi00LtSrPHpkKV5XyFGxSSNEUfOiDR77tH1ZkgMzm7QX45OfnR7jVxQLZihvGZ6FA0wsv7PBiCoLpGOi6ILwsIV1Oj785CVSjdCWa9+nP061nANnttx0FZX9hLSGDOTmRk7SbZInjJ1rjBlfF2knjV34N8y8oNEf+EGNzWT7E0Y9cARr/UkI2C8ecAFPhmiqP4BBhJs1XHopNiyJxovL6otwC30iJaTwTmoBY8OWmY1pk5ggA3YqhRSR0663X7IuPmAG/xhr7p68s8EZvEwDacYypyhrESxF/F2HNwcBGFiLjofj7vz6iB618k1RAKvCYFJAA+jHJJj8kFZAKSAWkAlIBqYBUQCogFZAKSAWetgpMA2ikhNOkivFfMfp8kmwOMS3QjGBSfpKygy7b33DOOcRi0wAZE57zXPDJAa2K9GeRvxEhONGyF50HZhv3omrQ3QN7J1887vZXAnDjDNHniCrvtcAgiKIsi9f94pdHZPJUM01LURDzV65eUgkXOHV3LdQ8bdLeVuqBfJeiFmgQLzwXyg4laYSU35r1sE3kYDTiLDJVbKvigI+7PnjZ4rRJQNMAaM9BZersqWrB42nRRJ8Rqmzo699cXMxR4TsAeOk5Rxk6pUBQBUWCroYJHQbAjufCXXs2+bgkwjYBoJsGcD6MFI/1mD61GDU77ht3jz3zbDB5eUPThLe+vaNiLfLq9LkBoBPwow7b2/qGCyGf5yxPhR0nQTnZefMfF3cXaSQpgIUj8Nc966rYQafMwEHdwVyQFIJgqFJ5zpYtROfNDAHo8y8wJ5zhVgDtE3vVoqStFg9/7TtF4WUuGdCVh//3TpiwN3jYJjzv9B3oGJCB6wHiwFhl9T/9cz6d5SMwSPl0oZjOwV57g4N1Iy0ByscOoAkgeqjYWKiyRRdfCoYKRV70b+dOmAqHLYQaN0GLo4jifg1rc6qadI35W57/cg7HAYqZ7EAv1KrbKzWOwg8Au1GsIctFfqkSDfzX3w5Ti2Q5NzNGJg9fvArcuMsOCxbLWGhUMVVFEAC6oEBOIYP55z/9ihWLIQ/Ujt4KlcrOfbXuEDPCUFwHtZzCCxzfCuUF92wkQT/xANpHrRYVquHiS95HMSxphVD+zpNhyhvk6BnI+My/c0DfRWBNAK1wAN2M5OYX8KMA0EWXLX/nu4F7/MEw4JQzoBxusFBrcmfREaUg/STFD6cSg04o/luY9EMkP3KjtTLopoW5FT3vB6BbP9vciQDNOtHnJBcgpX7z1tx5/VMJxdwP+O4rEa9HvCdC38bYxkQC6Kft3y45sGexAhJAP4snV56aVEAqIBWQCkgFpAJSAamAVEAq8H9YAYGhKYtjD+K1yF4VRoO8HNw007EjsFlXxV6/c+c0gD7+OeBH6ziAFt7n+qsTrlu0HLQMfRk/k4bNW8HF54+57VWKJtDd2PRjlZt/pzlRxQbfX/e2t3brPCOjkCX39ET5hVbcT8EdPFg5xq4bfpLvmMV5cFEDDT76KRh35vpIERAOph3M8q/2025tQpYFC3snceDe6uHbjoQsB8ppgFe8AvZObLK8nCjHJ5IfymzRP32ws5inszMVSlfIpKhaYFsaOvNqm5HJ0A4IAZ93vjIZbg2wV5BxAd/rmJ4PVVQm5KnWNHIrnDXhnLhsHRVXVFXC0J/6zNKqs8hveJObPlk/7CtXjj3zTMhlKa4aTHjT2+funjrn9W+mWosmwEAP/NMHuyPc7KAufMcORRVzuBbNseztLz6LhqinQdNhx3PAYcspn5oZQZwW0BaxzQnap7zDdp4O2TYaT1qB0WG4f+wYF+dVGYx5RPPr5QoTeHAcIlz54x8elRdOaciAblKuig6DI1DDwy0iejz5mncORK51L3DdcEok0SPOqPDgBVWUl4wTPUTVZmAlbbVo3QvOprTrXIraOedAmY1WOIBuZDhQLUG7pVXZ7An3tKHlVDqS29Xh5J2pSmVDhFk+nulUbiF1xDOjXS9fjta+52OaWqDMaFAoeuW+B9fG2FUL0x7mLdJWr2KqEqxry0JJIctzToH3v/vlCkAxBZ1p+NpVXRV/4bitIbbxLIj6Jd2K4/+eABoxT/btYO3LXkGBLVQ40YRzX2razuIohjgGWoGIDd4ofFxctw0sK5AunUIdoz+yjht3We7hr3olX+BRQUnBS1+Vs9hWm8oeTq+vCPHFnrkXXvUww6EwPWcaGJqG1BgPx8fEjskgf4jWtEi3fqq1L1izzg8kjNJNnD3dcRI1iDZg9BXE+xGnYrQDdD30Q2Qxomj7BT83f/0//JdDnrpU4ElRQALoJ0VWuVOpgFRAKiAVkApIBaQCUgGpgFRAKvDUKcDo0EwkQXuItyK+A9nmMOngNG0a7lRCcJLucm3TkVuJhGaA0huO20EAumF8rtNnhqoTbAYVVN1UQc9l4bzXwP3lw8b9oocpsmEyip5oxa9+ogVx577xLQsHKTdAAeKPLzgDJqrbrKRDAGg/ScXYd+XXIF3kCSAZLd0OV323rRINeJjzUK2hbhOlIrIZoOKgvsdRIlx0vz1yzQ1Dug55ng+QV+ELX2zzcClFENSLBEIVocyWvu6NZjYN6RTkdTpBU4GRhfCdb5956q622V2UwJDibuj/dUhf/H5jr7PWwi6PEzpB8cIGrZsBoBlUvb5J58xCFw07pUJKh5/fdHLNHWly52bHDWePjT/3+GPzc/qbAAAgAElEQVQhn4VsDrQ8fPgTm2/5/Xl9PaRJexqWr4RJ97RKNCdGHVGLCbtrNvk6zSDutbz1b7qIlznkB1qxBnzc7CQQxOkgzgq/cLkKiEvu2bMtXYJ0jnBtWw5e+5p8iEdbrO7hbRBANWClEJfc9KuR4XnQXaA3kwSKASlaJdh+Aoz5qzzktewapfYeIYBuMmjhgRUAuhZDLe6sRsds207oPwM0Za97fXYqXlLmYQ5NAN1KnynPOhqctF+RMkDjlFwBOOUk2P3gSIJZn8diiNemzlECEQNSu/a80TUE+lWTFga2HQGWu5FhWzXQI8zzGGizikbF39iehiLQNZABWDUya16v2mHC5vVwz97l1ciwGVHO1jWbpw5At1e8dis4fNcu6MgRgM5n4PVv6HWclTEH0DEB6DSVrwx7gqAviHuDaMALh7xgqeOvdsJFDpao3mPjYn4kJNqN+sqVo888na6ODK+T+fq3dNm42cVM3RRPSyB5Sn4P+vxgrh0O1uLhajxaC1fa0TDH0ECeaFqHaC5miNgNla5tAtDmfgA6qm+ZfkYFVAqVCooerDUtz02QrdLY6Ilhekn7lD0b8ZX0APQdZC6iG6Md0asE0E/dXyd55P+rCkgA/X915uV5SwWkAlIBqYBUQCogFZAKSAWkAs9OBRph0EShI8S7EL8a43OjpJfjHoFs6iboSkgO6Jp9xLLF0JGBrEKg9phjwA/XR6iJVnWAoR6hNj657n/r9SlKXoVMJg1veSeRyjIr+Kg07cyULcvADsCOwGPdeyeXXPp+RVQIBICOPNz0i9EElzhYcDhQDpKMFfV+/LNg1Emwoebht/+z2sLZXlLw0BQAmrJlGQFZB00PCxUc2mufsXELR2M8tHfDCqh5RzlYClB3E6oXV2UwiTAerj7mWDI+ZzUoGgR8t2yCP/11tc221NxTTz2ZI2mORDMGZNNUiW7MW1/F0rgPSOkfcGATGSYVu++/7zwh006UE1LkTf6fO15s+cMHoj03mM+iV8/poxxn3SDafeOPX3f689q78tBfglIO3v9xKOPiGvaSt5eDNp5soFOkQ9Ju+0ve90HC3OJH1WGsutllecR2hpkxiwKjqxaUy3O/9JW+TAFMXtLQ1OHfbjjW99dFSZGRI5X2FmC+HHR4yebf/OaI0WFytlLlSQXOfPE6+gUoDPpF56kurrPJnM5znzmypD7T6q2RyEEbZzqgmwBasHsC0Al5uithnxOdMTAHcjoB95wKV3xi6VSwvMYt7U0A3YjgICu0iykrHLnvgZfm8qBy+qmpcNFFfYhH2r4SxnBg4+sfWds/7IMfmSe04kQdvn/9aJCMRpixYzXCvJWYDmWIZ+7es6zUANBZgDZda0vTGsl7Lu180Oqt1adekNC6qVZETBz4KirmtSRi1y+bAy+Gx7YFMY84VLWP23EsFHQC0ADwujfOrrlr3WYRwqjkhcOBtz1wTv/zH4668XurP/SergteDi8+Db761e59zpw9HjwiAN0I+3aj/nvv23DkVsinIWsqmSy8/qLiVLzE5crEaMbY50cjrr3ZrZx4123H3XDdyg9+rP38N9PS1FXXtNlsXoBKnFCzA0As2aFW81JORIx40uFfgKDrp86Oqx44scLQtCMI6eGjM8wk3G0do+bEtDFApSlghFANIEKlRjtPO1RStUCZ44lGDwHUKu4sxJchfhWTOwhARxw7J2GCIWvYn2O+Ttd0Pbd2np1/HORZSQWeOgUkgH7qtJdHlgpIBaQCUgGpgFRAKiAVkApIBaQCT6QCjBPngL9ysoJlhv8W4UVOMspBTytNI0dhNQIr6rSdY5cugo5sHUAftR28YF0TQCNmEHNeBHfds9CgMISMCoWMDm94K1h4mI+zIjTrAJpHatQoX7htogYVa+71Nw5mTJjVLXggnHeOXqtuQIq5yDgCPCWFitv78X8B2nNKBU1TsvCjmwcdnOOyvJsYVdQs1MLEbADowmTcs9c6/A1vzna1QV5NZRXIpuBznx22o1EBQAMC4qkaU8YZPGCtXrWa4GomReG5y5fAPfc9d8Lv3edCJeh3vJOPO4IodvMnnYYvfWPhmL/uzjEYD8BB5aAAmqFie3N//Mst6WIdQOtp+J/bn28HC5uArNlxg8H77z1jVjeYGoVjtPXA5Z9+UTpFNDyvwoIFMIVH+DirhgTcA073OIAWUcIZJ5531TfzGo+hyBcMSMEt/73cxwHLAy+GBAs2GlUHavbo+z/Qm+ae30wWNAOmyq+NgiWY5KIk7yWlGPsR14xVDv/SV+cM9EHegKwJpRJc8ZkTTjq908yAroNRgNe/o1DFpTUEEagi6DC5jB8xgG6GjIsgYALQwey/3XtiTw9kVWqmCld+Yd2Uv/LhAPTCP912imHQ4oSeAV2Dt799ds1eE2Haj6DZmiTaj3I1d+SqazoyGYqISeuQNuDl54ETHuknPRyX6x6aVmJ6WKyxwt0PrikalL9Bxn/ugs+kIJuHux7cORbmLT4RPoeexNl53HAj1FgU95t+nQmgpxctmtfA4+xEmHLYAOJLFg9BgVJq6OJ50z+sGKs9rxaudJO1Htv2y1/P+/RnzBeeASsWQbsJHTp0atCpU6jImadBlW20yf39CFI4mgA6nF2zT1q+lG4OI0VJJq9/8+x79m6uxcNjzqAVb7z1toWXfxxe8HxYPgIdaegqcSt9GjJFOOJoqEXLPVSoICG1dM1Nh/HsKB52nEHXm4c4hDirNYWD0+dMgGqMxSCa5fuDjjNo2bPcmDYi5suuYNYUSu4nBmJX2coznB8n89yoD3GOHWohGgHqDjM91hkl2xE/h/h7jMoYIIa8xcL9TN8PkREcT+QfH7kvqcDDKSAB9MMpJP9dKiAVkApIBaQCUgGpgFRAKiAVkAo8MxSIEC3eGCYCQN8d4ocreGwNZzW+7d4MSKXg1BoDO+6x7OOWDEN7hqyp6RQceeQhAPS9840cd/tCIaPBWS+FcnQYw/k+L1gnarUFCUSoIZYYlu69b3DlUjBTVNswrZDV92c/Xf3gA4WIpXwyF2dDTPvYVnEHPv4ZAaB1SoEw4OrvdQY44iZpF4EDaIMAdKJ7ZJjtvG/vui99eVTlJRNzSkYD2L4dnPBkO+kVAc0RYS/ySu8J4K6x5T3d5BhN8QCQq77RV/OWW3F7hAUfC4ir7vjLttER6Ozl7wBClm2d8Okrh8fCxTVUbQr9mOaJAkYHCIhKlCz6wleHzDyFb5ADOg233X6SHQ4eiBrtcPBHPzyso0QgL6WDkYflK7M5jXKHS3m4/DMDMR4xQcHEBLsDelUc3vjhdA97/vuONVn+8VJbTlHhHZeAFY4g5hLKGIEQ2yt+yg83vvKVps6NzHoaVqyD+/aelkQLkGkhKzhsVozr7h875tWvShVNMoNnDVA0eOc/zdo9cfGi5WDqvLXBR+nc51YpU4USvacBdKvxudk/mAO6FUDHiWqFUPHn/8dPtrQXqfCjAqAp8K1rt00Gq6t01vVD7Gd/Jgd0NPinP+8wTQ6g0zQ1r3plcaqyKmBGkz770bQV2vUH9jx44vJlRNIpaxtAV+EXNw8mOMwDHyDixlgrMX0s1Vj7vbs3FrU6gE7zSoftBTjieHjAXldmBT7vukfLJDyzmLUHcWeYZA60P4ckAuXDNBzQ0xfMgRfDY9viIkza3ZXKGZ3F+lpJe7vyonNXf/Yrx7/tkr7jd8LCYejtotwVkyovQlsK2gHagAJGeg3YsAr+tndZBbNC7YcZQwNA29HcB/ft6u+vp5zrJrzm/M1XfXHHFZeNvOy87NAScuWLvBctReUlaWop44a2r1oH1fCwJoC2I2A4x7UOc6d2Te0+5e7btt/5P2uicBNFhTRSOBBzAaoMM2E8uza+feKe03f/5aS7/7IuxsEI03asxmjWC0KytBv1I27ya8eElRfcc/uR9969LsEtftJjR+CjUXYKnrcW8SLEX2JcJfrsI70Shk7ICt2gz9IB/cz4yyZH+axQQALoZ8U0ypOQCkgFpAJSAamAVEAqIBWQCkgFpAIUuOHwJhKgy4g/8vHcSZxnUzYFzxQmoCYYNKWv2gSg+6zazsWD5JrMpcjezAH0ehG7EaFWdYgph6juqyyjvGMNVEgXdDh2BzwwvtnHgUnuTKxTrUSbcowAh/aODR9/HGVuZDgpzhtw+eWdFXt9krQj5epmfSzy1zbhgM6kgcdEE1/7zBc7Y1xvY9Yl4pyykQB0yApePKvmb7nmm2tMnslQyBJWXjgXfnbT8gl/0MaMANAcELd5WNzjZf9871pVIe6pcbj8vRvMcStb8YxaBB4q1cCM2NLvXNfTOQvae+jQGZMIblsXfOHatr3RSBW7bTJrCx90PXCWE3YdcfkHPtSdztUDIlQT/nj7Tis6GIAORr7w5cGcQKLcz5vLQ2chnU7BusNgrLajgvNtqrVI4JJnZZgOqg3wrfjYbkUntHfS8FIAaRVGR2Hf+Ckert9T7vv8VfCX+7srfinAw08+kdgu/SiUqX3X7lf67lGht9xxt9TsXZddkRpaQEErGg+e1lPw4U+U9tpnTHpv6e3nXBgg1w5fv371mNc3FddDvd2EADHPWaZEjv3boQE0FTyk+AW1FkDFX3j1VasK6Xp2hJqCf/33YyeDlVWKuj4kgLajuQ/s3VkogfhYJgtH74Cqf8S+KniRIhi0R+NU3ajgBHMq9tHHnQBk5TYhVyQRPnpZf6W2nCy0iUgQJmu8w3QqRRiX7t29rqhPA+iiBp0l+OinYSKaX0tyDpVVNBsAWglYKWDtdB3S1bt/e3QAukF49wPBjTBrsvf6LOvGHXbUb4fzrXDEilc8MHHEzTef3lGEtAbcPU9FKUVAtmGCaaSyeiajGWmdck46TOgyCEPnADoMOO+l4OHafQHV8JxO4aBhaKKYpI2GneRt1mHF/VY0aAVLLH9F1T7+57/c1dEGvb08OkYhffIalNJgcsoMGtn/jQxki9SMLJhc9kIRzjoXqvFSD+vlEG3U3GT4lefBYD90ZaDNoEWp97wDvHCoEcGh8uSNYhgtvOhNsHguzO2gU8il4F2XQC2a5WG+EtIkRgguy9v+steeD6OD0FOEuT3Q1wHveBuUawM1AtDm3mp31Xoh4ncQ76GHogTQ8o+jVOBpoIAE0E+DSZBDkApIBaQCUgGpgFRAKiAVkApIBaQCj0+B1uBn+no5VhF/FuK7ari2gnkenbwfgKboVZuBE8+p1k5bNB/ayQ2aNlUoFiHCwyPUQyQ+5QgWmaTK7prRleRR7sjlSgZ05uGmn2/0k3kewpQHbkJhxJW4UGWL/vOPI8/ZCd0d0JUj+Js34Y1vVKreRpe1RbERx1qQFLykECQZD3O1sP071xlFQ6QQE2PdeiSU/WND7HHJa2zWPIhiw3cXRMFZP/j3Uwxeko72m4ZiBj5+WcFha2LssppwLUkhdjvYM+4t+NLVpbReB9CmCT+9qeSyoh3rdlQnkgFlzo5+6LJ0ocgdnJrRUWjXDTA74e0fzu+ubagk/WMh1ChGIBslebumIcsi6gmufNvb85kCKDrk28j4uXv8RQSgm3ix0bGCxe/7QKcYtmmkDE7POSWGn/x0ru33uyzvJKqwAPuJ5qLGHdDCSKv4WCjbG489ksBxlloqnyIL847tFHpQysErXgEWLvVx4/mvyaSaYdEq7Dyp8ytfO/aqr2298LVzhucQl1YBusxUUYGBTvinDxTK8eZJtv72+56vqcR4dYCMDjfdfHiV9VcZTagfq4R3mdrKnVuxaWMxg5Y0KLG6zqOp4lwDQCvkgHaXfORDIzmDTsFIgabBr245bSpeXMWUmDVBRRth0HUkbcd9E+XjFi+BfDvoee6uzcGNv5uzN2xjWAoDlVHNxu69ljnpL/vbvTs3HM4F4my01AVnnwe14Kgwms+SLK9gSTPOC1SmPNQtVCvuhlIa+I6NDF0jFBR+3/0bA+wlIEvrATqvaCcuFUorbp1coUmrGo+oX8e+BlHmhCo91gIalUcRxiZim+/nPK/L9UfGJ9fvGdt5y607r/7m4c9/MSxdAymTm5EVUKmUZkkhvMw99TotO6hUIBTUDIHgrAlDs+GMU+HDH4S77lozURv2MWdRcUuaVmoMpmwIMe9FasVPTSWdE2xhOd48FT7vpluOuvqaw846F0aGoacTSlkwNDKVk9Of/4g1jpRBBJwuGhOMEhR6oWcu7NwJl39Uv+P2zXvGFzsUKUMAOqBSk9qd+xaUeiGTB8Mk9327ASUDXHdVE4IHqLrevPF7Tu5OQ187lDK0GGYqMG823Hn3CivpcHguOcOcy/L37BtNZ2kxjOZNp2WVWW3w4NgiHzM1NMfjNR5+HvFeWo07MGsjoUftgZtbA6B5FdfH90SWn5YKSAVmKiAB9Ew95G9SAamAVEAqIBWQCkgFpAJSAamAVOAZqMA0MZkO3/hoDZ9bwb4a2WlFmAC5nhth0NRxEtWJhqqVF4/MhZIKWcinVSgUYbK6IiTXM9X+siNwYmoVd8UFbyxlOVPuy5OH8cLzs653/Fi5d8qe7cSLbVw77h1x5bfaO+YQBetsI6RrKnDkUTBhPceK+32EiKWi2BAA2iPPcsZiuYnyYZtWUFyAIFqZLHzpquF91dUeLrD9foaj5fLovgd2vOui/rxGkJRIqkHk65JLwPE2Odix12+4OwnwGQm22cmsKe+wSy5V0hpRMorsSMNPbyq4SdaJyG4pyv1R5nJSqHqb/987IWdSQrHBiyaW+iBVgpe8Cu54YLuFmyb8+ZPVIcRVdrXT93Mhqn68/MK35AkrpyCVJu77X7ftOASAXvbS88g0SkkFCsfcJpG840+Amr0qYBpPW+aol4i/Ri5dzgp5BIfiY6bsLH3P29O9OZIoTzHFRh6glCJYnwJ4w+tT903OtnHZP/yjkjGgkIYUh/kphezApTzBvjR/f0mjEnbDc+E716732cmTcc9YMP/Xt+7ImpBXoKjArHa44/ZjPZxDLJhjSoeZbmxSAHTD/tyKWR8OQEOcKA4Dy1/xtosGcjoBaF0hmnnTb0+ZikeqhCZTLl/n4Gi46Yamjs06xqtrXn8hXUt0QirkB+Dlb4PxaIftrQm9UTdYWPaWjdlbv33DyMACyHfQVWH00mW0dQeUw2MnnM6JMthOHYM2ADTt3EKouavbGwDaJMoKA90Quod7QaoePIJqPViGU9R6BbzGusLjA9A00QJA04kzqFpp1549uW9h5B5z/XWlS98LJ58I8+aDkgLN5JxX45OdAkVReIx2pwoZU6PKmYYBnd2w82Q4/435K64cue6Ha2778+G2syMIt963uyvG2QG5+KEWgRuDzwG0w8xJt8+NVyV49ISz7err8+/+COx6IYyuIZ1TOiVu6ylK607zg+ka5LJKmlcKTemQKcDAPDhuJ7zpbV1XXDny3R9s+NPdp9aiszz3WBaswWQwwc6IViPqyldRu33faLYLRJS5ptJ8FlLgumuaIgSo2vbg+F9f3qVByQRTT6dVutnzaZiqnBBgD9mfYwOxzU2y9+xdSfU8xZcCKLaHFg/2lVdNxdkyzqvgWT7+KqJigzyMKMF6JBFHz4I+SwD9DPwrJ4f8zFZAAuhn9vzJ0UsFpAJSAamAVEAqIBWQCkgFpAJSgWkFCLVEmFQRb6pFZ1VwpIYlu06fBXpufTXdJO1FiytTZy+cA0UVckomnYJCAe7421yXUWZukz4TgPYHr/vhmnSWUl7JLgrkwPzHN/bcf/cFtvePu/de8KkrV23ezr+Gr3HLKlAhuJNOgr/cs2oq6LdZm8/SUWxEcboBoAmLVyNtsjL6pldDmwpdJT2lEjYttMHHPj165+4X3D/+/Ft+f/yl7527bjnkUzw+QlVLOvR0wVveCla4fl8tZSNMxAJA8/iChAqR1eLuirv9jDOJoHEAraUN+Okv2302A0CLWOdxN83w+Ne+luitwUEfP0V6ae+Bc16pf+YLC3/5yx2//e2qmj9aC7J+onnhije9qb1uZ06BYsD1P9xghSOtJlnRt/xVxx5DHE3sWQPIZ6HYCT/+5RY7GPFjVdT340RSAGhyqjYiONRxFwJc+LtblxRNCvYtQarIs31VgKIGfZ3w81+u3+N2TLHuX9y8vLOd/OZpxRCVFRV+LgZAUVE0gL4eeOl5cO++LU50+D5rdhXzIa76xjWrcxoR6s40DM2FsfHnWqzHE8kYCThMd5nOYasI4phRxe5hATRLwGcQJRvOPUvJ6YTL1VQdQE+wkcpDA2jMIi7/4U8XtPH863QWVB7V/PZ3j/7ptpdUaq/5853P/9wXRo8+DtJ5CqOgaQZIFWDT8XDHvi0VXPxgBXiycD0IohVAE5BtAGhToWUSXYHjjoaErXV8YZSun2ljoYJSnmfAd07kW7c8oj53Pbe+02Hgx0XXXfPlzxsvPg16clSaMsMTlcnPzrOVUylucE6BqlDTQNXATKfg5F3w2U+3/faWJYjPm3JWVvylDlvjsuV2NLfqtVfcvBNm3Nh0GSVx2yFVbgxjurQqrHOKbf/YlV0nngn5LkowN9JkT84WwEzTGgktHamUu23qZFo3lJTBnc9bjoUPf2b2n+/dUHbXWNGafdWFFlvssEGbzbHZnIAtiJN5AWv3WdpPUiEqPCBbr6Jx+77RQgfZnymbG6AjB+e+CFx/cVMKAtDO7PF7ntdtQkaBtKLkDegswGmngxOu89BgfPkKkWqT3rdnOY8i4eoo0F6AF74AxvzRqWT2Pm9niJ9BvJvoM3L0LAC0eOXPSmF2lkUIp/9wyJ5U4MlXQALoJ19jeQSpgFRAKiAVkApIBaQCUgGpgFRAKvD3UEC4+iYR/4D4xUq0uYbtPMKY0gMO1kzyIMcjlfILhuZAUYeCpmdUKOThlt93WCEgZqte3f7sxFALevbZR73oXMjr0GlAZ4pIdHcG5nRDRzuYWYoI0LP8q/op8qLmOuGEE2Fv+bQHnX4Ls26SDmIC0AEzgiTnYY6HNigTPoS4eHLvqWuXEKAEAFPX+P/BKEChmwywlH3MuVUb5Q9ApwbvfxdMldcF2IU8R9imtGjhn025FBtNubFV56RNG6j+oU410tJpHX7+i/0BNDmgESZDsOLZU7Vdu3ZSbrX4UVKQSberqmoYkMsRyG4vwY9/ZUz6HGH7y97wxgLxQf6jafDVq9ZZwZJWAC1SNSx/1c7joadAyF7l1D5n8ICI5Bgr6qVaf2SGbWl8SBxAKw6qPKSiM0jWve+9FDXQoUK7CiUdekuwoB+u+fqiPePr9znaZKiN11Zd+GaY1QVFk5IThGU2r0GbTuz+uKPhS1d1T4WrHJwVYu+4l6okStlffNlHh7MKTWVXFpYsAjfYNRWU6mkYCZBHnvEkiuSRA2g1pDqQwBJqQQKIW3Y9hzyqBMQVukJ+/tuTHhZAu4lRY+1OsP0NF2SyKrTzeTF1KBXJpN/ZA6V2wtn5DEFS8qHzGJGdp0GZnTweD1nYU/YIImMjibgJoAXfJwCdIes3AWgeQP6mC9O2PRgl+wFoQs+iNWkpOaOfIABNRNUfeOdFlHpc0mgiOtKprKJQIgqZnCmxRDUIEFMzBQ4mK33OgG9e1c+i9W4wK8Kcm4AdQ80HK1CcGKyQwj2cmCooRmjGmGZoxnFKAOipeM6F7wKjW4SWqKaRy2hpUwODQ3xKyciRZ9/M0X1t8igMMwX5Alz5rdXjMXnk7YgO4TDi2jZPZw4S8ELTCzIRZqmWYKLzZgZJxsL0X/cOt3VScUjDoLtx/Vq4884NTthbjwShkG7VdnvGd2/pzpMIGYVCfmbPglv/ODrl9JU9msc4hgRNP0nt3jtc4KsmNOcaLBmFv9y1bSxa6OK2SvTuBP8TsVz/UkgrfZYO6L/HnyF5DKnAwRWQAPrgusitUgGpgFRAKiAVkApIBaQCUgGpgFTgmaHANGGJkNmI/434hbJzisUWe1j0MRUSgNMiNMIDmo/pGEcmJ4/Zuhk6spTPkDOIPd34Q3BiBbFYdqnjxIrNlFqcCXDh7XevWjFKLJXcwSq0paGzSFBJTYOeg0wR0lmqAqcV4FVvhr3ejvF4eCrprKHpYipIIGKC3GV4hTeCvwkaiHMs57CrrxrMa5BTySlMGFq4QLlnNqcaXWaxQ6EiZ0M9cOUVqjWxMI5LAh+3+IVFbjI8UIUIl1UrLxzoInINHEArAHf8dbEbm06kugw4UmwGcZhO1Fn2Z5drx5z5fDBTUMxDLg2FbDGj5wzynEJ/G/kxxyqHB9gfY9ZxR997aZ+mQYaSeOnnda/tsPxVAjqLV15BMWUFy846A/rzMMuENoAuHbZthD3ldVNR3sGMixT63GzcU0w1D/lJqbwaoeKg6SSdLlt+7bXpM54Ha5fASc+BCy+EqnNMxV0yXitVAqgEUA2KZXv1Je+F/n5oyxMx726D+bPhJWfBNd/MVP111Xi+lXRYaFg8g6KCUPFWv+XCnhzFmVAVyhOOh5q/peJTeq+ArfxEpsMiWgksj6eYhrMiA7olBloRANqNAHHblo2U/GvylQXNgGtvPPxAAL3fznkWdmnfZP/u+zavWQoDRYopL6bJiFvIgWnwZQkV8ql0X6nQliW6/bo3g4e7xr0F5bjdYhmC+4ws2PvtWcR9WP6qo4+gmTX5ukcxD1/58rKErUUs+QmlcIhPNekzOaAb+RvTncbbDjzE/luan535kYkauM7Ss0+GboNuQGFa13nGjKFSwkahCEccB5d+VLv23xd89JOzOkt0SRsA7Tn41lWAYb/vZOLIiGK6ucKEmh+BF+p+ZPqxTus9jMp4xonKEoh4VclKNHLmuaDkeGR4hjKjixoFi1PiM0/YOOUFcMlHlGtu6P/ny7tKWejM0EJOext8+dr2iWCxz/IxA2oxWaqbjQJ2KGNHC5hGBRup6QHVcsxYwZKjT4BSJ2hZOP2FcNc9g4UXvpAAACAASURBVDW/gxLGG7HUiLkEZznO8uO305JJdx5OOQXu37PO8Yb8sBDG9cPFieom4HiLTnsufQMjC2QD/9vuJRbO2xPNDfBsxB8wHE+SeDp2Y/oJWX+i7xf33Pz1mfHAl6OUCjwzFZAA+pk5b3LUUgGpgFRAKiAVkApIBaQCUgGpgFRAKNDEK+hheC/if/jsZR6u8ZJ+H7MhQkQtdVAA7aJWC9vdaOMFryFfM5mFU+R5/MNtHQFVeMvzCA4C0MSgY9XBjBUu/Ml/LFu5BNqz0MYLlBk6BVCABopJ4cSlTlixDr55w4r7qkeMJXMmMTOFZo3bkynFlSyxKc6kdIFZawxc1Lykr2Zv/ewnR3SgYQgLtJHmOFuHnE5MqicP55wO++7b6ZRHkBVqFuFjvhPVQYK2zRZhxg7n/+HW1Tle2zAFBPJyBXhwbKkT6U5MJFEAaE7nIUxMbso2a+GcifJJp55Kec0Zkxg0lf7ToK9EhO5Tlw/U3LW1IGt54PjzvnfjMhH7AACaDi85B6xgWRNAC/psY8qK5v/5T9s2r4BeE0oAR2+An/142ZTXKxCzh3qTPhOjp+RcxUOF1yFsAmjFQd1ihYo7MFVdMjW1uVLZXLGHK1532aVakQFSvK/DwI07fNxk+Sf/+pYt19+4/H/+clTNOSHGDVNul41ZPiRNuJsdYtDqlLvp9JMJ5FGKbgrOPgc8dhjiQDNugr/50QFozqCVEAWAVrwIJiujO46hPF9DJc+yZsBXv726BUBTLb6DtCQ16UDVK2AyescfRndsgoLCZ6Tuj6epyalkYc4ArFgM3/32MMOjJ6yOWpSbcoGXTwQ/PjSADhZfcAFoCsVk53MUQPHrW7b43hI/MHkS998JQDPMuO7wT25Y1mZQ0T9KfAaiwMOD8KIXwNVXrbrjrl0RnmLj+goOV9i2iy8xXn6u+taLstd/fzCOlyIWEyywJM0SJU7qYSMEoCPFj/U6gI7TYUKW5JjiUOiLAtVo4fdvXNPZx9PEeZlQHWB0EM57KVz5+fl7y6ftc7ZWcN1uZ/7uysb3va/7JS/UL3i1edU1Qx4e5eNcytJhxLsjRpbqZos44KZFpjqA1sX9hdiNuHjC3v75q9Jf+XZ6zNkQ4axaCA5Z7Hlj5KdG7J6slfbuG/3ylQPXXbvMjbdOuR1ubIYxRBGwkF5DPqFu0OuWT7juGwu+940hq3rCWMWwsK2CO3y8jOFfI0ZBRBjzUoPNx6Po8Gdmkzjv15F/UqQCUoEnTwEJoJ88beWepQJSAamAVEAqIBWQCkgFpAJSAanAE66AYCYtu20SFqwi+y/ET1a9jSHO8rEjxCynzwJAU1HBmS1lM6gxPcC5V36F/KQaQHcPLF0FFXdZhHqIBpE4pgoA7URqSLG8A3Y0evvda/7hbdDRR4nPZqmemtzRDyc8D778Tc3DDRU2u4YdU2hOIfCoX8JeBKAJThkBUjlEwYvLIZRDgn2IvRFb+v3vZV78fCgYNBgKwchDTx90FOH8V8CPfzTgeJsQRxEHEIuMZ/Jy463JX5sAWvUQxm3Ni7YevpngdUohwvrSC6Dmj7oUaqwKziuKpNUZNB+eh/q4k69Gqz9wGQzMhbYCRQP3dcHhG+H73y3E0UrEDjcAHhPcfW95w2kvo3AQsxMGV8LPfjdoxf1NAC06nPlmrXBgsrLo5z/Pf+tbMD61qOIOTLiGzRSPRBCDmfEqwkk4gyYY3TjHHOKssl3aM5GJcX7F6aj5bQy73BC8mJYZElQizCD22ljycLaDvRORaWMmxGKEeZ9SUAw3oTklU3CsWqww5Rw1spDiDhQiw3DZx5QgWYo4x8c6FK4DaA6IBbluJcV8bGKEYpAqHyoxdJHCESdKzYMYN77sHLXEbfMqTwa57DNzJpgoQkgXRus+W/uIRoJm4JjoD+/924r3XQzdsyDbTpTW4MXxigaccBRc962SXVuZsCHXbveDTELLLRCiEiQpkfDQus9m345m//tPh4wsldRTM3D2q2HS3Vp1ZjkOl6gxqhkO6MbG5k4ef4fXw2wPceS6G+HNb4WXvgre88/ws5uHLPdwx1nuWvMtpzfBeWORticEDzun/Pllb4nFRjyc52M7j7LJuUmablUOl12sU936uVO6C4Xe8FUWSkShd0Z9jn3Y9deVLnglvPJlcPmH4Xe/7axWVu/dN992FzrxvAjn2dhtY6eH8yv+8vHaKiveuMea72G3hYaNhpukxbUkQH9TZ4rMTgSArtPnEMFyCC7HuOBBq3cqGprwexFnVWzwGDVi0AymHCi74KFuJ8WyN5fhigRnMQrcgCgGFqos0AWADmPwfM11Sk6tx6n2O1aHFyl2NMrwkz67LUqiSNDniAB0Ml2edfqZuR93bv46/Q7ZkwpIBZ5oBSSAfqIVlfuTCkgFpAJSAamAVEAqIBWQCkgFpAJPogJNWtLoJIKyJIgPIH7Xss7ycMghfJyOqGmMeBy1cGYTQQQRZSinp9ylJ58IuQys3wT/9h+LEZdxXy2FR/uJ5sSKFykB0yLMBJhzMBfgwgemDrt/4uTrfrThw5+e+8Vvrv7pb3bcvfeUMXurjwvum4QKgxpON4uTOw6nUiIQgCNgQsYxQjWgxAlEIKYc9djVbb//zcZvf2vksis6r/zKwlv+sH2qvN31ViAO761AhGZEkdYUo+FiijPcVgCteqhP+VCNwQrm/fG20ZecDc/ZBZ+7emCPc0Qt6OOZy3X7cxNAxzNjggMsjllD9+3Z+NOfrv7Xf116662bEE/0w37EfBTzTGHKNW6bYoO371v1ya/0vP8T6T3e9gourrGCQxCQcqhbGiCF8Joe5vaWoRaBhzzSJEo5CTwEgG4YugXb1T00EbsrAe1/bxXGqhr5neMiQzMh6YC/KpMujVDEkozz9AlG3nCF02cBDY3AT4VhxsXecWeHqkGWon/Jefv1b5bcqL8Wpt0ZALoVRs+AxQ8BoAMeAx0nCkPdiYa/891lhgH5PHR1Q7YEl39Wq7C51UZy96Ewbi0hZzei7lQgCnoq1cW333PUDf+x4bKP91319ZW/uXnXg/c9z3O22HYvYjEIIfYV2yIdXGF8jqEJRg88hM3aKsGaz33NfM2F8IHLu3ZXt1TZUM0p+lGGLvsGa36yATRSDEtq3INKXCi7a+z4KAfXOMncCNuQ0mnoBvF4ZIrN10gmIvBRDbl0PKHFdDBDRBg1Irli6oWtmPd5WogRJBla9eGR3MSj43wYdSMbcctLETf5XlcQZwNmeBFYPtnGY0wLHFyjZRIjoSWN4mRIqwVlOjQ9NKYP2jhuUzRegZAGKVqCwNch0vs8mPDVSZ+WshjqfswBNCMAHaIxadNtW42hQtHVGl+UUkKe2xOFahTqdat1pFI1xZBCOZIo5flGhHMm7eci3hSEThQhAWh6OsbIEgmgn8S/RXLXUoFHo4AE0I9GLfleqYBUQCogFZAKSAWkAlIBqYBUQCrwlCrAkDGMGAaIHtJrQF81ZxHGMeJfML7Q9pe5LO9SUS9OfyiGNROR97kOg1o7jQgLxcES4ro7750V41o7muvEOUF4KQyXgctAhN4KKu2j5mHWx14X57nJsJOMOslSJ17ssEGHzXKTbP1r9Q0npoBivG4bz9+gr+frITl/aZCitQ44iLuDaI4XDjnRsB0N2/ECO+6zWRuZLunQeqPV/bYO9xF79V2RlVh4dYmRxT12sNj2l1jRfDvu8VnWj1VePq5+3FY1wgZzdBKoRbla0FP1ZlfduTW3v+Z3OBHxMp/Co8FPiGxaLFOJuqb8uRPenHLQUQ2zDtPr504+0xS1xj6pw7cIJNp8FcsA3B5OecoC6Tagp/B0T1uMCSJTYDRxQJcVPdbtxIUIM6wetEI+6LAhKc/xICIpPNRN6cJEdy2IoqyPc66+PpstQTpTANAKefjbveudMOPGpsD0fMCUv1E/Yr3MIz867x8KQHu8al/IfdBODAy7xysDn/gXOHEXPPcE+NS/wHh1oYX5ZunIGSq1KFbHxww8ypRQ7SBb9XvK3tyKP2j5w5Y/5ARz/KjDZ1kxpzRBMXmffX7RikvX5UUFDzyEi5rN2qx4thUstsKRWtztxDk7TPmxWp84Pl+NuaDZOXAnT8AWcYthyk0Mj3U6rNfhvma+gKSJpSOfFlpSYkGCp82oDeVpuUU0cXWJ8bRi6MYkTueohKjSDZiYIctFrCNK2kLC07SoIz5OijUSq/kaD91oJBcv78kvhvr6Sl2olimrC5Kk+OzXnzk8eIeWLoQ7m64usUJAD5b6IgH/mgV3QzeWT4Q1vhnrwQOmKfSDVsJiIwoycZhnfi4IhuzkeRFehvi7mFWjGKMYMfER3SSJE8ZZdOOhLVbtxG/8WdpYxpvxrsa75f+lAlKBJ04BCaCfOC3lnqQCUgGpgFRAKiAVkApIBaQCUgGpwJOsgIAmHEBz+sxCItIYINuH+L0w3uGyomBAAuzy7NcMT944OIAWDNpr4GkrAoZU5ouwo2BDAkBzxiRgnNh/C7pNNZI9DO6YrjNrwn8NukR8ud5SAcEplQNopQGg67XsWqGV2L8YHieVKZGq7KDebCLwwUECZNxSTeEPASqtwLQBvsUAUn7cGAkHtY2zoMgIHtrAMVkjmrZ1/HWyxnVo3d7ab9Jnp4nwDmBzre8X+xSjFSPfD0Dz028CaGWaPlPptrTL8h5m+LnT5Iq4lYZu5F73uFZCpeZrgKrnQBjmLBx983sAMqCaRjpTyBehYh1OwcEU09FsjxFACwYdoMLQdGKwGUxaRhCtsu1Vbjg3wHa/SdIPkKgpdatWh+o330x8U1yrHEPzaAhukz9YEcLWT9VngV+rM4oW/r0AdJP2Nq5hupgb9xTF5vgtrTmPLdc8vb+5Ez8hZ32zTW9v6Fy/1OuLBPTFiCZkb0rRqs9B76nWNxy037iz+JXJ18Mo/aNRcrCuMy8RSTPL6sVO68MW3m0+4Pojgj89RPA0j/gwwqAQ+p1R0ON4Gxh+kOFPGN6ZJFXGGKMChK4E0E/y3yK5e6nAo1NAAuhHp5d8t1RAKiAVkApIBaQCUgGpgFRAKiAVeAoVaBr2+Bi4u89HJNryn77zj3Ywsl+iLjc26jx842EAdC0AxELVh2im07MO9eowiPBuK1ri/f0B9DTzagKmaQBNJmgBoFtBmIBcYkvr/mcCaM1GrUmfeUeU6dsfQNc5GndczgTQDfosiFjDLHwggDsQd7ZStgP/VWxpUr/9AHQ9+kAQQGLTM6IhBIBuBG6Q67m+eMA7fLtg0KqwoArjsHjlBuf6R8RctELMVljJ4xpIrgCVKAY/6N49deSKTbz+YBpAh+N3Qc1dG7A6eqaobupPA+jW44p+w4dbH17L4aaheYxmjQNohu1u1Bckc+woZzPFacxOq7D79Q+lc+v21o/ULc91+7Najyd+NABa7Ll1nw09H4EDej/DewP4tu7tIP2G15gXxmyuo8wA0K0wujGe6XeKLdM3XeNbC/U7t7n/xniaVzu/lx8pgD7IyBs7bP5TY5GJ7rIZd3HL7X8gehbjrAfNc3R+4CxM38X8pqCTZXkn7HbiOT47EfH7DO9GnEJ0GQsYixIMyf5M/9W9zc0nJw+Fpt/Et0lEWsfBXp/Cx7w8tFTgWaiABNDPwkmVpyQVkApIBaQCUgGpgFRAKiAVkAo8WxVoYhQ6Qf4Lc33EBxE/N145xo57nAYV4phJUKoDkXEdDwnQKdBn1QfENEPVmQnsngQADTMBdH2QonIdZ9DT9EpYgIX32aIQgEcBoAUXa4ViM/oNzstFqFuwxUda+Waz36RsTRdn85+anScDQAsEz1HvfgBaszHrYLuDBW43Br7MoPmJJuIUyOnc0poA2qNahWB7s++49zQq9ahBpo0qSV76oR7bXzYTQPPchpYIjlYG7dbDPZqsufVwzY1KjQKFKQLbZkotNKZc4H7eGVnSrdq29pvCPkRnxvtbkzfYEwGgk1QL8H24CA6Behs3YOvAHqrfBMQzjvUkAOgGH38aAeiW+XpYAE0MWtBnvnRRS3KVeLDsH53gBxFvS1hAsRuJzxKPsSBJKP05Tqg1n5nNjnh08iyjely0BNDP1r+Y8ryePgpIAP30mQs5EqmAVEAqIBWQCkgFpAJSAamAVEAq8DAKtDCUBjPBEPEHFjt1zO/ysM3HdEiN0jAaX+RPtboRH7a/PyxrwWoNdEUkqGU/0w5oftzpNIAZwLfFBdkKoGf2RRTG9M4FgG7AUwrfaIbe8s409GxQ14N6tKd32Bx241zq6Ln56/6n/2h4YkvhQR4A3UR+/NzFnpsQrXmgQzmgxTvFa8MH3cz8zdW8nr/8pePDH4DJ8aNsv3/KBj9W7YDALj+XegRHk0ELDfmvio1QDgYvemc2WwT6MUDLwJ9uP97yhygBmbeAaQGrA2gx1NZgk9bYkIZ0+3tyW9DtwaNRWpFiU43H1WmBudy7PWP8j2LPLfsR3yGou4wf+mJouVMe67GmNWx1PT+SfqvarW7oGf2W8Tdm7aGu/0O951DbmzfXQ3RanwmtY5uOTDlEZneAIPKgfV6S0cIOG3fE+CUk7zN9F4SgM/q8hdOVWQ/+QG0+Rx+ic/BPyq1SAanAY1NAAujHppv8lFRAKiAVkApIBaQCUgGpgFRAKiAVeAoUaPISTKj6ILn7cBzxOz6eXMO5Va+v5nU5QcGNM35iPDYA3azFV4doLVitAZ7+3gDaQxG18bAAmpj7wUJCnjUA2uShz6aXlMYme159Hszvgs1L4MZr+1xrA+IyP2gP0OQi6AGaDVhPmL4JoB00q1jca28YWQpmDjIFSOdh81EwXt3mhL2PEkBPu9dbAejB+pT33YKw6+UZD8TxjwLdtuDUGddqHR+TGbyOOA9850NvkQCa69O43/eH1Ifa/hDcuflPjxdAs5TL8hU218ajA3wPw9vpKcwQE+R5GxJAPwV/leQhpQKPRAEJoB+JSvI9UgGpgFRAKiAVkApIBaQCUgGpgFTgaaHANIAWPfR8/w+ud7XlvaHm7bLtIz1vbRAuCFg790Frwg19KKjXpEL7dVoBUyvCa2x/GAA9zR9bXM+t4Gmm65kKEjbSnw/igA5QETZekf7cgKrCCi0c0BT40KCuAkAfMnWkeaaNc9kfrh1Kq0eyvQWwzoiYEOcu9nAgchWfOjAD+gAHtO4lJS9p5wrk/Hj+Wy+EOWmYo8AAwEUva//b74+zy6uDuJcYdJIJkkyrSbzhIldt7JwMVr/lXZBrh2weCiUw8/CFbwDiYjfKPRoAnWp1BzcmXeg57eRtbKct5BBPDDfJ8pZ+JJI+uve0gGPpgG71F7fexY3rcP8rX9wRrYIf6h451PbmzfUQndbnQOsIH94BnUAcQxS22d4KO3hxjF9heFuEFg/RCBA90ZrpzwkPez7EU7v5HH2IziE+KjdLBaQCj0kBCaAfk2zyQ1IBqYBUQCogFZAKSAWkAlIBqYBU4KlQoMlLyAFNPy7ibsT/QrwO8UqMLkX2VsSXIZ5uBdusYLMVbHOCzU60zGODXtLvYQ9vFNbhYdHHrI9pHw0ey0vlyAQ5akGfPPe2wfUaMJHQFX+z+Ai9RqjxlmoJcVaCBCJGrZU67VegjL9fMOgmhp5G0mIkzQAKpyXUWKRJ8HBkmAmgmx8/iPG5icYOBdFaAdyj7T9SAD0zZODRAOh2YtAUvqx6rPeHNxRm6TALYGE+UwKY3wlXfKhk2yc4/monGnbYLAcLnNorDiq8k3OSzlq4+vd/Pj5bAlWHbA5AgRNPhXK02kbTZfX8DT9WH0EER4q7rc1G+EmrG1qsB+yPoV3UCECzPLUkvV/BzBlqNy65A8npjLchNCFmI/9Eo6PMaKnWeXnIfspFyk4JWlqY6PWGKt8+fTHvP5JDuKoPBLv7fbB5d7Qsw6gRavvdYs3bs3kNNzqpiO5csXhD9+aM/bcq2TLCR3L9H+o9j2f79NjqAxNGdcONzWbzWZq3rM/yftzmR11+1OMG8113lW0d5zivDqLPI96dYBQg8zFm9Bi0EB3EYBpAJ/VH5MGe083n6EN0DvY5uU0qIBV4rApIAP1YlZOfkwpIBaQCUgGpgFRAKiAVkApIBaQCT70CEccuk4gP8CzUuxD/jPgHxN8i/grxF4g3If47Cy8LgzdZ3mkV95iqs73mb63666rBMiuab7G+WtxZYwUb0y6mhA9XQKIIIaqDZo2n0Ipcab3he6WO8DJHmGIIoiFCs7EEWKKwRIlFayRHtwBuUViMAot542g7McMkEyZmSHka4g302vAINwvcNbdQp+GANjkV1R8HI5s+4jQsayF3T9nGRPNZ1k8MgVDtyHTdVVe83yjwGGdNpYKC2TSsWQWXf2ykYp8d4NE+DtmYsUl21UIjwvnjlcX/+evDNmyAUglK+ZQCBKC/eHW/h6NkkY7Bi+rNj6HeZhalnD59orSZIMk1BK8HPTemrM6g+QpBc8qEY73pXp8xg81lBm7czniYa2lmY71BfETssJmITTsUBnkHTdFsNBtNb62dOLOv2CiaaqNqo25TyLgaJyoyBWMVY5UxncWmaHGixwn9q2gtay201NE48Wan6cqna1us0DDUW5rKULUCcHnzQvAjCGNqEYM4mXbxN/csxG+C++b2KIGQUYuS+tEbUeA0Bh9TPt3aJJq4eFqrZT6lfdVhOi1FsLyXtPtJT4CzgmQgSOYEbEEQj3r+Ssfe8P/ZOxM4qYpr/9/unp6eGYYBBBEBJWyKEoKIQdTMDKOs8blE89RoMM8li0bjlrhAYAbCgEaM7+8a9yUaN3yJiS9uD1kCiBGRxB3BuLAOMNPb3avq/Kk63dW3exaG1Znk9Kc+d+rWrfV7l57+1bmnHHOCcM/i/s8EPAGwDOB9gC8BkiClZxmUNyJPbTNuiVp4MAvppiP44cCl62j6EAEicEAIkAB9QDBTI0SACBABIkAEiAARIAJEgAgQgf1EoJmw0qydFEhPqQsBfgdwF8CdALcD3AJQa7qXmP730v5ZCW9y0q2KO2ManZFx98i42z/p9kk7fdJu76RzUNLpnnZ7pL1uJutq+V2k5ihKtezogbTW1Bq0Vp8BlPrMo1LCkyHCwMCQtdzUUl0kW5vUyzzexeNdZRAxLbEFBOjmqqW2gM64nsi3yS20w83acbeYHvRLkOdGIye87r0YHTRK3Y14kSOKnawnZVtOD/T13crfzA8bISMcU6sJSkXZKI0ZRxxlXHmt8dKifh99MSTOj0nD6DSv/PjTMfPmGkcNNbrEjLBhFIeMkpgx9RJjh1VjQ/8drtGCAM0NZ5cCtLwYMt63le6vT6uEmS9AF+xmTmXwLKsapAPrjLotLzbUuFHgxsrxNGXmLYJeWbIytNSjswJ0JF90NrK7LajPGQEaDOAyyOkTntGgGY9pAVr7kMkfrx44RiLZIXSVlrx+F9sttd0upldq+jHTj1qsVPk8qXD97q5/kOv1ctyejtvTdnrYdi/HPdjyelpeT9Pvafo9UqxHyu+Z8g9Osz5p1sfk/Wz/sJ1uWBw2yGVDXTbU8Y/AYHpHpZxvxO1RjQ6G0Y1OJuywjs2G43ZYX3kYs8Mas8McuyP9rR3pcQ4/02Hfdfl5Lj/fExf44r+YuIyx6wDmqafW4wCvAmwCueaqz8Hl4GcVZ6akZXwO5mvMwUdhs+ckCdBBPBQnAvubAAnQ+5sw1U8EiAARIAJEgAgQASJABIgAEdifBJoJK5nGtCAjfBAJgK1ZE+l/AnwB8BnApwBrAT4AeEeZSy8EeEnAHwAeSaevta2LXev7rnOW7U6xvRrXP8Hxj7H5IMvvY7GDLF6hVsOLKNNjw4PirMvpsLKbRmvoMOOljHXlflfOukgbUh5VBtEZW2mWMYgOSTkPHR2oiBQceTcZRFdcSU9Jxqhdtqw+29JWWquWWhzPM9ZWGXaZElSl810ZFOjOzYXjggwFu3n50e3AHm2zAnRaWpqX+1Cedo5+/PGDBn3N6BYzukot2ohFpAwdK1Om0RGjTz9j7InGQT2l3FwSMbqVSvU5FjaKQkbNKcbHn49udPs40CUtDJM3s4BuW4BGmVgue4gCdFAjzqixWbv1oOVyToZGQ3V0H4GTE8pqPmM4r8TfiNxKO3ojEKRZPR7V9shMaBcu2h4ZdWqtCwdnFzIG2gWzEepCam56LDOjI3LU05VLE+nYRMvrWkPPTq6E5CXNunn+wZ5/iOf189jhnj/I845w2CCH93V4X5t/zfSOTNvHpNLHJ5NVycTJiXh1Il4db6qKN45LxGuaEtVNierGpAzbk6c0JKY0NJ3tiyt99gvGZjD/V8yv9/x6n93ss5s9f57nz3PZPNe7HeBZgBcD4SWAlwBeUeFVpeS+pmakFn7V20UAS5RR80r10sY76ln0NsCbACvlVrwNsE49rL5Uq63aIHVnF5QAHdCgcw+7Vh+1zZ6TJEC3yooOEIH9QIAE6P0AlaokAkSACBABIkAEiAARIAJEgAgcMALNhJVMy1qT4eCkTObYymAQwPGko1RXmRJKa0IALtQfR73VHgf4HOANgL8A/A/A7wHuA/h/ymJ6poDLHP+8hHWqdOXhVCa8byb8kQl/RMo/xvS/YbJhJh9i88Nt0dcRvR3Rx/UGuN4Aqb75hzC/B2NdlBlphAtpCp2T6qR8jEGKyEra7mKLrjZ0MaHUlilS4lRin9QxrZw7Dmn7jMpgoAatMutqdzeSUSr3pdUz6tF5MrR0N7x7QVWCXhQApCWvA0baj3nsxNdf/fqppxgVRUaxYXQvN7qWSlvooojRpdToWiKNnaXJs2GUFhWXRyNFhlEcNo451nj771Up9vUkizU5RjrrfAO9cOT8b7RhAZ1xnBINrvjX3Ci4DQ26dQE6KDc3j2fUZ2lWn3WIERCgpTdkrFlto8pmv2tmVgPnNuS2h1yw0T80GGx2qM0PMaGHDOLgM0lOgQAAIABJREFUtDg0yQck+eAkOzLpD1dX+6iEnx+80Qnvm0n3eB3SzvEy2JVpc1I6dUY69Z1k6rsAPwT4McBlavsDgB8A/FjAVQBz1BsJvwV4AOBBtcXIQwAYHlCJjwA8CXJ+aKFSbFcpTzt/z27XZKXbtwE+5LCZ8yYVEpwnhEgBpJWvHkut1OcEbIfRf8VXss23VhYgfOA+4z4TzBfczQTBhA7gCWkB7SojaH83BGj9MAy0SQL0AfuOooaIAKh3o4gDESACRIAIEAEiQASIABEgAkSACHRaAq0J0HpAQknMPCM6CcYF8zl3OfcFByFdqAomXan6HGwuF/IypRIt4gDb1Tvvn2UNpT8A+EhZTK9R9olLAF4D+F+A51xxmw+zONzE4aodybN3pE9tTJ/SaFbHzcq4dULKPjblHm2yATb0dqDChph0ZMwjpjDkmm+ZELWhyIZi5TkBHfKGTAibEE5B2BSRNA9ZwpBBqa7a4DSrO4cCKa1ZvAZFyTbiuvh+c8GBYvTebQPjjTp+b9sdvmXbcX/8n4ED+hldi6Xtc/eysiLDiErdOVJsRMLS23PuM+k0491PRjRaR5ruoZbfzfFLHS+CDoilz438oFfJK4goy2W1NB8vcljE9iMOi8oFDIWcXeBqjkH6DFG21SY30iIXzMBEgh6L9Fwscq1nmoNMis0yEVwkEK3mg4btOFdhQ8zk0SSPJFg4yaMp1k1ee+wIhx9psyNsdoRcodEfarojbLvKtiZgMO0JGFL2pKQzKWmfGrfObrIucOAah093Wb3r3+Z49zvuw67/iM8eFVIOflZN0rwIsFi9Q7Aif/s3gPfUvfORivwDYI1aL3Q1wCoV+Ye6oT5VbyRsUvfaJrWm6BcqBbf4psI6ZQiMObcC7ACIq+miJECSQ4JDgkGcQaMKcR8sHxyWCR4DT93dUrFtRbQNCrQHLK6fUG1FUCZWW+y/dL6hRtFaPwO1BbPgcoOYEshCUSJABA4MAbKAPjCcqRUiQASIABEgAkSACBABIkAEiMD+IdAOSUWaEHIpMwsGnHMubB9MH0wGTKXJIwGhR+X0s/kZcAY+51L1YeAy+fa7K7gPjg9pV2peG5QZ5l8BXld2088DPAXwKMD9HOZwqAO4EeDqlP+9FP+OKaak+XiTn2z51ab/rZQ3JumOTrjHNDojG90RO5yjd7hHNPoDGvkhjaJno+iRgIOTcIgt+rpwKIPePnTzQPpBzgSh3CLLbViLmIFIGypzG4c6iwCtnUhEbelAoyLNe6W9EZs3/8e8+l6jhitfHCGjvMjo0cU4pIdRWqRU6R7Gcccbt99Tuj09jsERO5yI43Xz3G6+F/O9iK8WwStQnx0uReEWg7JhV+bGIuzyYsePSSHb72J7MduLqt2Yw8tc0cWDcg8qXDhYrjIH0srY8nub3sGmd3DK7ymXwWQ9k/4hSb+fXBjTG5L2j0z7R5nsaAxpb3jSHhG3vhE3j4mbxybN45PmCSnrWxgS1reyoSpuVyWcmoRTk3RPSfjjU2xCyj+VwcUMfsLhcgE/BbgC4GcA1wJMB/i1col+D8C9gXCfMj1+DOBp5cVikXoh4B019fKZWu1zg5KJNwBsBtii5mlyNsW4LJ7ayhXudFA3f9DQOGuLK+eHAiGomcoyuM9AisgeB4b7uoSfeZOBu8Aw+MB8eV8zBlJ6VhEWuLt54WJ8++extEe16sHnSmdHKhcMzJfRdeaCSK5sBl4QGcYDWShKBIjAgSFAAvSB4UytEAEiQASIABEgAkSACBABIkAEvgICSr7hDCwpRSktCgVoLkwuTAGeyH5056SptNLPfKH8rQopN2cDOAIckMGXb8wzJkVpU9ljbgNoUJ6mN2d9TK8D+BDgXSVPvwPwtnLz+jdlPb0CYCnAImVDvUApfb8HeDhl/Srl3JDyf5wS522xTt5iVW2zqxvN6nR6nJuu9OyxnnOM7x/l+V9z/UMdv5fLeipX0S0uUpdZoS5oIdu+eM5fR07p1pI3RlpznVGQTe/m5d8j189Yg64QMiq5DRETStPQLQk9ktAlBeVJr4eAYQAn/PWvPep/ZVz1U+P0bxtjjzN+8mPjpunGH14xtrvDAEba0D/JoxxKPa+UuzHhGcI3fGZ4WSvjoAzdgvqsOoBOVJTX7yIfSnxRzqEH54f63iDfPcJzhrr2ENMchMEyR5jJSis52U5NsVNTUolJyfjEZHxiPDG+wRwnT3f621tSZ7nwMxdu8KDO43M9/muP/cZnd/r+vQBPqOtkgRKFlyhReKW6lppv31ROhN8C+Ju65N5S195q5aQCr8O3Vco7AO9njfo/UEbK7ymV+SNltrwO4FMhXaVvULbJW5UP4iaAhHJnkVZbC8BSdwNT7xLIWZ6sZNy20imPZqVVfedhRGj/GEpx9nyQwZOBefKmk3cl+s5R96DwwPfAd8FzVU6GfiqEBxwDk6q1boxnmyvo6YHf1V3KoJIiu4LpqEhWoMdsmT2uRo8MWutxdoDBvwV5g4coTgSIwAEhQAL0AcFMjRABIkAEiAARIAJEgAgQASJABL4KAkq9yQrQXArGWQHa5sKWts0yCBkCGg1T0jPKPBnpWSpcvpahXZWBCXTfIXzhZ4I0lJa20gG3HtJgmoHjC9fjLmPS9UfW5bQJ0KRk603APwf4RPklWAzwgvI9/RDAbwHuV9u7Af4bYD7AXIBrPO9S0zw/ZZ6dsk5L2VNSzoSUU5N0Tko6J2T88DonyLgO0j/vN1UYnXRHJ71RSW+kDP6IpD8i7R9l+wNtf4AKh9l+Llh+330fvP7WHgfZnz4W62Wxg2x+sPRWzPul2cAkGyqDOCwNB1u83OHlAP19Pty0JyTNc5uS/7Uj/oPtie/uMCc0+t9o5IMa2REujGy0B0n7YnOEZQ53rIGOPcC0jkpZI1PWyKQdCNaolH1cyh6TH45L2celnW+mnW+a7hjL+5brn+yxSVycIcQ5wC8BfgVIB8dXAVwNcA3AdQAz1Em8T3k6fljZyD8G8BjAI8rH8UPKcP4Pak5iqVKQ1yg5+GN1YaD3iQ1qhqNJWfK3acir3M4Iafgr5BUu9VcUdn0QXiZIIddXaq8+yrLycfBe5RkjYymPYtCGzIF7JlgiEw8ezcqpGVtndH6T6QH2Q23lpA4qzsGtkp6l+owCdECF1ZNAvsov55iEfM0hG+QMEd6rzYystf7b/kjBgPZyV7eL9UCBAI3nQp0QzFmoQbfWfAtnQiYFs7eShZKJABHYfwRIgN5/bKlmIkAEiAARIAJEgAgQASJABIhAhyCQfQFf6nAoDaNQlbV+ln8LOqrVIe2jo3kkWLzFuBa9cBkx6fwj81EymdTfXBCOMiO1lElpQtmZbgb4EqTx6afZsF6pkB8rk+r3862q0bD6TWUSuxwAw18BliiXINJLtYA/MHiGwZM+POrDwx7c58KdLtxuw69tuNmHX6bS37PTZ6hwmp3OBTN1amFITzFzYZKZnhTYDR6akimYyzxFZc7P37x+TMkrpaptlm6bp9rmqaZ5mmmeocJp6fSUVHp8KlmTTIxznSmp9LlN1vWN7s1N3m1x/zcp9ps0v9WEOSbMTsOvLFGPwWa32OwWl9Wr7X0+/E4JwU8pXE/48ASD55QovFyJwsj5DUX7jSzt5dndN5XF8dvK5v19ZV8c3H4M8E+1xOXnzbb/VIe+VA4u0NZ4R8DWGA2NbbWAnq3WoEM73jxhsuACzt/FnFpx1mKkvsy1YXB+ucI9XRAjhYfbt5+pJGs0HbROznhlV28gYBytqtuouNkQgn0MHtz7uK5ZdQfry+uZzlAQaTG/9j2iMwdJ5OLBFrBNPI+6WOGzK1ggF8fsuN88HkzJlaEYESAC+4wACdD7DCVVRASIABEgAkSACBABIkAEiAAR6JgEgtJTUEfOysHyb2s9D+bZ3biuEwsGBOhci8E6M/n3SAwK1MOkaxHpLCQtIC5gu4AtAjYI+ILDpxzWcVjL4H0G73jwNwZvKp16gTLF/R1I+TUY0ES3YPuIMtp9SHkKDm4xHbfBInufv8WaC/r5sOrPg8qa+H41nCd9+F8bXndgsQOLffirD39lsEKFNxi8qcJbPvwtE8Qaj69jYoPya7xFQcNto7QUxpOSf5lkJzbQP29uq8+7jOiC+ySiqsZ2lfsXP9iHVtvNqJkoXAbuhuZdytQvC6CdcyB3XvW7Pa6copoBlbVS1ubKeZF91m6woubj3d2U3eWzh/mDHp9lXE9lqQgJ0PmXIu0Rgc5AgAToznCWqI9EgAgQASJABIgAESACRIAIEIF9RCAg1OZFW6s+L9Nu7ug6sVx7BWhdbHci2a5J2+qsAG1lNehGJUM3CrCUMI3pSQEyXemtX2RNrbXNNUbWARSEtcpB8EcB38EYxy0exS0W3Jv8bdesu7pOdWmt6tKHID4A/j52W8nuW5RR+Ta1Vl6j8nmSAEhmQxoglQ2mtEYXWffCQf8QQZkycFKC4m8wHshCAnSWQEBFzQroeYpzgR4d1Fz3imewouB53LO46gpW2S6Bfg/z7xsBWg89D6CeFMHUIIfCfLRPBIjAPiNAAvQ+Q0kVEQEiQASIABEgAkSACBABIkAEOj6BrFBb+Le1nhfm2519XScWOrACNBpBW0p0Tisl2so5NdDuD3QXdyOCuhaaYTYzqm2hnj3Lr9UzHWmh6mwSqmhotusL6aoYZTYsm83Vzr9YWTBzKyJdUHQOxoNFd9tSONhW87iqOivg+gzIAjorcDdnhSn68kFP161la2d6hn+7LcT3MP8uBeiCweRdcXonOHSdKCM4WEwKDjwvE+0QASKwLwmQAL0vaVJdRIAIEAEiQASIABEgAkSACBABItAigaBw3WKGfZSIolNQHfYD7+8HGlHCU1Ciam7RqReby4+g4apUP7MhaMqacd0QKLJn+YN1Yrx5zdpNRE5az6pr+c4yAuNuJRrU4ZrRCx4MlA+KzsF4IEugO8FK9jiuqg62FYy32m7A+jhwMfAWxPFM/S0XaLX+9gwnUGWwz63HcwX2qt329K39eXaXzx7mRwE6t807axkweVRa3Ane3XkZ2jPevAK0QwSIwN4SIAF6bwlSeSJABIgAESACRIAIEAEiQASIABHYJYGvSIBWi8tpvUn2ElWpnDCqVaqAZJwRdguEWLUrfBA+MBU8H7xsHFPwKG7Rh8Xe5Mc6W6s5z0eG7kZW0MzJlxKBXvANR4tA8rK0NNZcCwGtNnCms23lhEJMCWTJcW5B7dXnpf0RVfVut5s3Un3CA4PSHcjU33KBvRpXoMrW+p+fniuwV+3qoe2TyO7y2cP8za+owFnLgMmj0uJOsExehvagyCtAO0SACOwtARKg95YglScCRIAIEAEiQASIABEgAkSACBCBXRL4KgTorPqshSipqNpyST0tROMhFKRwDEFxShfMRQRwAWiRLDzpMTnPUhmP4ha17r3Iv4uas1q67Fu2S1y5wBYsQzvraUToNfWY7pXyOYxD0Nuc5pkbsCwQZBI40/mCaU40DGQhATpLIMC2NW756bkC+5Fn8My2J666kn9xtNnPPcyfu5aQSfBaz8bzqLS4E+xnXoZ2jzSvFO0QASKwFwRIgN4LeFSUCBABIkAEiAARIAJEgAgQASJABNpH4IAL0Kg+5Rv/5gRoJapqR7KYV8tSWrhqbhTNBLCc2puvPjN5KBdA2VHvo/y5akUzTxwtNiGF75xjjtYE6DyNOyNOtyDwaTL5jj3yBdOcaJh3RQTL7n1cVb3b7eY0Un1qVaR5fzL1t1xgr8YVqLK1/uen5wrsVbvNx7g3KbvLZw/z564lZJK9JoOnL49Kizut5m4PgRZrpEQiQAT2lAAJ0HtKjsoRASJABIgAESACRIAIEAEiQASIQIcj0JLohHqT7Ko+2ma/26NPdcw8bQ4rd7C1zudydIJYVppsf1fx7Lc3/+7lbm+tuXz6WmwxksvXUWO7y2d382fv1o46fuoXESACu0OABOjdoUV5iQARIAJEgAgQASJABIgAESACRKBDEwiqeR26o19l50iAbgf93RdM21FpIEvwSm0eD2TsoNHd5bO7+UmA7qAnnrpFBPaIAAnQe4SNChEBIkAEiAARIAJEgAgQASJABIhAxyWw+2JXxx3LfugZCdDtgLq/ryGsv7VtOzr4FWfZXT67m58E6K/4BFPzRGCfEiABep/ipMqIABEgAkSACBABIkAEiAARIAJE4KsnsPti11ff5wPYAxKg2wF7f19DWH9r23Z08CvOsrt8djc/CdBf8Qmm5onAPiVAAvQ+xUmVEQEiQASIABEgAkSACBABIkAEiAARIAJEgAgQASJABIhAlgAJ0FkS9JcIEAEiQASIABEgAkSACBABIkAEiAARIAJEgAgQASJABPYpARKg9ylOqowIEAEiQASIABEgAkSACBABIkAEiAARIAJEgAgQASJABLIESIDOkqC/RIAIEAEiQASIABEgAkSACBABIkAEiAARIAJEgAgQASKwTwmQAL1PcVJlRIAIEAEiQASIABEgAkSACBABIkAEiAARIAJEgAgQASKQJUACdJYE/SUCRIAIEAEiQASIABEgAkSACBABIkAEiAARIAJEgAgQgX1KgATofYqTKiMCRIAIEAEiQASIABEgAkSACBABIkAEiAARIAJEgAgQgSyBf2sBmvksy4H+EgEiQASIABEgAkSACBABIkAEiAARIAJEgAgQASJABIjAPibQCQTo/ScTu64LAPuv/rbPFfPZokWLPv/8c8dxAMC27bbz79ejnudpFAjEtm0R+OzX1jt75UKIzj4E6j8RIAJEgAgQASJABIgAESACRIAIEAEiQASIABHYHwQ6tADNOd8fY8Y6ufrsv/rbrtnzvNmzZ0ej0YcffhgF6LbzH4CjnuehIu95Huc8ID7L6AHoQKdrgvkMpw3264Xa6bBQh4kAESACRIAIEAEiQASIABEgAkSACBABIkAEiIAm0KEFaEt9rrjiigEDBugetxEJaqZtZAse0kprMPEAxDnnw4cPD4VCa9euBQBUfg9Au601gejOOeecXr16Pffcc9oaWiNtrSClo/E4cSACRIAI7CkBDrAfZ1v3tFdUjggQASJABIgAESACRIAIEAEiQASIwL4h0KEF6I0bN/bt27dPnz6rV6/G4bZttqzV0vZb7K5evXrKlCmvvvpqGzjbsG/V7jvayNNizU8++aRhGCNHjvQ8TwiBOnhzKRPrx+G0Mag2DunWEU5wV8cxwjn/+OOPe/ToMWjQoHg8jokaaUFm2gWAe+6559FHH9XXADEhAkSACOwpAdSg9XZPq6FyRIAIEAEiQASIABEgAkSACBABIkAEOh6BjihAJ5NJAHj//ff79+9/zDHHrFmzxjRNABBCoJsI7S4ZFVuUXxsbG7VaWhBpA/tll11WXFz86KOPYqM6ZyqV0nFPfQBAN4eqcTKZ1JKxzqNLtRFxHOfcc881DOOuu+4KSuqO46CayTl3XVcIgd45tL5s23ZzW+nWtG/btk3TZD5DgZv5TOfUFQIAtqWtsG+//XbDMKZNm4b91yTbGE7w0O7mD5btXPF4PB5SHz1J8O8z9s51pqi3RKAzEOAAPoALYKstgMiGVnuv1eo2Iq0WpgNEgAgQASJABIgAESACRIAIEAEiQAQOGIEOJ0CjwNrU1NSrV68hQ4Y0NDQwn6EayzlnPtOKqmbkOI42ItYiYDCiczaPDBkyxDAMbfAbzOA4jlZssQ+u62rFOZgT45hHF2meQadYljV06NCKiop4PI79RHk9qAszn6HArfVNXRybwIJB/TrYDZ1ZR5jPsPNawkZfz5jB87xEIoEie//+/Q877DBM1xh1PQWRRCKhxXedOTiQgvz/Aruc8y+//LKurk4L0HhN6uH/C4yRhkAEiMABJ4AatC/dcQjlkwM1aNkPPxuCnjra0J31oQM+CGqQCBABIkAEiAARIAJEgAgQASJABIhAMwIdToBGkXTSpEkDBgxIJBKpVAqVU626on66atWqlStXLly4cOPGjXpQqMbiVquBbYihL7zwQnFx8YUXXqhrQCHYdV00staVBDOYpuk4DmrimI7Zgnnajr/55puGYVx22WXYXEFm0zS1NBw0W0Z1GFOay9zBYXqeZ5rmBx988Oc//3nx4sXbt2/XTViWpf07c851Q5gBDa4ff/xxwzDQE3SLBHRtGPnss8+WLVuGVuHtyV9QvHPtIvnZs2dHIhESoDvXuaPeEoGOS0DbO2vpmCsLaNljH8AESACkVDyYY5fxjjti6hkRIAJEgAgQASJABIgAESACRIAI/PsQ6HACdENDw3333WcYxpo1a4KiKp4S13V3SqvnnHNOKBQqKysrLS2tq6vTh3ZXgB43bpxhGHfeeedbb711++23X3fddY899hjnfMuWLbW1tStWrAAA27aZz55//vmTTjrpxBNP3HkIm1u1alVDQwOKuZ7n6TytXTrBsdTV1UWj0fXr1xfYU7uuu2DBghEjRhiGEQqFVq1ahXIn6sKWZS1evLixsRETcfvnP//52GOPLWh069atP/jBD6LRaHl5effu3efNmxc08b7rrrvuvfdeLO553rp168arDyrOrusynxmGMWPGDG2XHex8QVue502ZMqW8vHzFihVafW4jf0HxzrjLfFZfX4/nKBQKaat8PfzOOCjqMxH4dybw1T+yUIAO6skCTwhXTjlSAE1Kg3aVaXQwX9vxf+ezSmMnAkSACBABIkAEiAARIAJEgAgQgY5CoEMI0PrHv2VZDQ0NvXv3rqurC3phRlrMZ++8887hhx9uGMbll19+1VVXGYZRX1+vWV577bUlJSVr165Fn9E33XTTpEmTzjjjjHvvvRd9dGDOI444wlCf7t27G4YRi8V21hONRg3DuPTSS5PJJNZ87733AsC2bdsmTJgQDocx55w5cwDg2WefjUQis2fPRrlWCGFZ1tSpU2OxmO5M8wjabgshxowZ079/f3TxjI6tMfPEiRMNwxg7duzEiRNDodDw4cP/9Kc/oXdmIcSzzz5bXl4+c+ZMXLEQ08/6zlkVFRVYnPnMNM033nhjyJAhsVjsyiuvvPzyy4uLi6dPn47aKAA8/fTTJSUlZ33nLPT+PHv2bMMwIpFINBqdPHmyFsRHjhx58sknawG6+ViCKWeeeaZhGH/84x91N/RI0X+IdmydTCZRrg1utcV6sE7LsrSnb/k2evaDWn/ukJohwINYp1bngx5UUMHHbJgBh5ZKpXAXz0LwULbBvL+e52HT06ZNi8ViYfXR/ScBOg8W7RCBzkMg+BwO9lp/NwUTdRzdLundXUaav3SSXyTncUOlo0cOByCtpGe0gLbbbwQthFwAAAD06gL5zWX2kslk8AnZYh5KJAJEgAgQASJABIgAESACRIAIEIE9IGDbdtBYdv/Fte63B53EIpzztn88tlGzqz568TwttQWLdAgBOtihGTNmVFRUFCwJiIbG27Zt69evX0lJCWrTtbW1hmF88sknegG9qqqqcDiMtT31+6e0uNyrVy8AwFKO49xyyy21tbXHHXdcJBK56KKL7r///mXLli1evHjt2rWoS44ePToWi23cuJFzPmXKlIqKiscff/z555+fOnXqAw88wHw2fvz4aDT65ptvasUWAAYNGjRgwIDgWAriqF0mk0nDMM477zw8ipfI5s2bjzvuOMMwnn/+eUyfNGmSYRi6zwAwduzYUCj05ptvoqCA2Q455JBBgwahmmyaZiKRGDRoUM+ePbdt2wYAt912W3Fx8Zo1a1DPTSaTl112WTQafer3TwEArjd44403rly58qqrrjr//PNx+JzzqVOnohvo9lzB48ePD4fDoVDovffe03oNktHCrtZ2C5hoCNrBd8Fl6lg287yCUroVnZ5IJHDWQacETw36LcElGTGDZVmouaAGbVnW559//tprry1fvnzhwoXPPPPM9ddfX1tbe8MNN1xyySUnnXTShAkTKisrhw0bFolEDMMIh8ORSCSmPlihVp+b9013iSJEgAh0TAI4q4c3Lzq1x612grR+/frFgc/ChQt3zt7V1dXNnTu3blef2traGeozc+bMnb7jZ82aNVt+5qgwV25/VTd7zi9nzfnFrPqrZtVfOWvuT2VkzjUqXDe7/uez66+fPefG2XOmzZ7zy9m/minzty/U1dXdeOONEydOrKqqGtfKZ+LEicccc8ywYcOWLFnSMc8O9YoIEAEiQASIABEgAkSACBABItDpCGhVKqgX7b/4PuGDznW1NWr7e6ud/Qa9KGsC2LeOJUA7jtOtW7cZM2bohfKCBK+88kptaXvfffeh+2YhhLaHNQxj2LBhiUTis88+69q1689//vNFixYNHz48FAq99tprwao8zzviiCN69+6N4rXnebpFz/MMw0Ab4alTpw4cOLCpqSlY9rPPPotGo1pBxkObN28OhUITJ04M5iyIoyHwiy++aBjGQw89hLs4P/CTn/zEMIwHHnhAFznhhBOOO+44rWauXbvWMIyLLroIM+CQU6lUJBIZP368bduYE223UV9+7rnntKdplFGEEJWVld26dfM879FHH+3du/fy5cvRNhwvC9M0UTLeKZQYhoGXmu5Sa5GTTz4ZLcpfeeUV9DGNy0KiebguhXbieneXEbQQ92xHLp6onJxoGvpkoY8U1N9d15XTNZaNSFevXv3yyy+vWrXqtddeu/3222fMmFFfXz9z5swrrriipqZm4sSJJ5544pAhQyKRSHFxMcrKqCzjWArioVBIp2OkrKyMfEDv8iRSBiLQWQg0NjbudME0Y8aMkwOfoUOHhsPhaDQai8UigU8oFCouLjYMA7cFD4fmu7FYrLi4OBqNyjqMUDZEQkZpyIgaIcMIqxAxjCIVwkYuUR0KR4xwuEhu2x1C8r0d+YJL8/4UpESj0eLi4t/85jed5WRRP4kAESACRIDhrYD6AAAgAElEQVQIEAEiQASIABEgAh2ZwNq1ay+99FL85RX4KbkPouGiSLio1Xoq9+IzZcqUMWPGTJo06brrrkMjqvZvn3322WXLlq1cubK6uvree+/VgmfwHHUIAVqrlqtWrTIM47333tNGzai7A8Dbb7+NnjeampquvvrqaDT6/e9/H0eCJuKY4ac//akQYvjw4ahE7zRunzFjRnFx8euvv47Squd5juOsXLlyp33xddddZ1mWVp/R9vatt95CD8jTpk0bPHhwY2NjgWaPbis+/vjjIMcFCxZUVFRceumlwcRgHOm7rnv55ZcbhhGsdv78+ej9A+2dd8rECxcuNAzjqquuQg5CiPnz50cikXXr1mGdzGeO4zz++OOlpaU///nPMfGll14Kh8PnnHPOli1bLrvsslgsdt5556EJPWqyjuOEQqHKysqlS5d269Zt6dKlWLBAYd/ZVbQub6cAPXLkyEgkUlpaOmvWrNra2nnz5s2aNWvatGk33XTTggULTNNEe3bTNJcuXbqk2Wep+ixbtmz58uUr1GfZsmVowZ0BKCAVT2zY+MXLr76y/G8rX1648K4HHrj2ppt+ffut1//ymgnfrqw55YT/OG3iCWOP69mjWzQSkXJNOByLxdCtSjgc3ukrXAsusVgsqCajfhSNRgcPHlxTUzN69Ojq6uoLL7ywvr7+hhtumD179uOPP75ixYqXX3552bJlX375Jc7qTJs2DSsMhUJaHEdcWiXPdJ7+EAEi0BkIPPjgg+Xl5eiOKZr9hEIh9L9UIDRXVVWNGTOmpqZmwoQJAcPiqqoaDOOqagLJ48aNHTv2zNNO/9lPfzZn9uza6TfU/vKa2hk/rZ15SV3t1Nl1Z8/+1Smz64+//pcDrp958PWzSn8xq/SaWT2vnjn06ptqrv7FOdNrfzp9xnXTp8+YPr12+vTp0395U/vDnDlz5s6du3z58jfeeKPZozeTcNlllxmGUVVV1RnOEvWRCBABIkAEiAARIAJEgAgQASLQCQjMnTs3Go2WlJTgC/StCsYtHCiOREpUiESKQoHjxeGikmwolofyjsqM6JxAy1+7G8EX/VFJ08ueoeXlLrfoohZNOceNG6e13OCp6hACdCKRQPF3+vTp+mewtmv2PI9zfuaZZ3bv3n3+/Pn9+/cvKSl59tlnUelDYde27SeeeCISiSxYsKC2trZnz55vv/026p6oF7/22mtBAR4thd955x2sBF1zIqBHH300HA4/9funotHoiy++WOCt2HGckpKSSZMmFfiUqK6uNgzjySefDMJtHjdN85hjjjn88MOxLc755s2bd3reGDFixMaNG7EzmzdvHjVqVCQSeemll7T/lF69ep144omu6wbV8LFjx8ZisTvuuAMbOv/88w3DmD9/fm/1+ctf/hLsgOd5GzZs2GnwO3fu3MMPP/y2225DvRt7EhRPhRC33HILWkAHa2gxjgbdwcsaDYrLysrQZtAwjIqKCpRvSkpKgjnbjpcWxyLKGjBkSEtDac1XFDIiIaMoYhRFjYpylWwYqC0rA+UusSJdJ957ejcYCQrQoZC8n3dyKy8vD9zYMhqLxSZMmDB58uSAQeTJ8+bNq6+vr6mpQYUqEokUACQBusXrhBKJQAcn8MYbb+BT4uqrr166dOmrr76Kou3ixYvxHt9V/wUAA/DUNuC3XhYGwTj46L2ZK4fOnwL8TcAznM9m/iUOO9UR1TavMtmYFB+2A4ZuhdHrne9utZ4A2AAQB3DU2oPyZQ8Arpw7s/Zt9aO91ciZZ55ZUlJywgkn7GqAdJwIEAEiQASIABEgAkSACBABIkAE2kXgzDPPRB1swoQJu/LamH+8dk7djN/UzZwvU2f9sq5OOnKcOatuZt2c+pvvqJ19+6U/vnbS5P+oGV9VM/5bSq0aH9SsgtpXO+Nod4USczQaRRusdpbV2YKlqqur0VFBgVzWIQRoPHuO44wfP75AgBZCMJ9t27ZNq+mXXHJJKpVyHAcVavTGsNOH70UXXWQYxiuvvGIYxoMPPrht2zbUanfasYbD4X/84x/Ba2TQoEFDhgzByjFdr+w3Z84cwzCqq6t/+MMfxuPxoAANAKtXr+7ates999wDAOh02HXda665BqGvX78+2Erz+JYtW0pKSnB9P5SwL7roovLy8tWrV1uWxXy5ZtS4cePKysoMw1i/fj2O7pNPPonFYr/73e90o4lE4qKLLqqoqNhpOr1hwwYASCaTWuSdOnXqxo0bsXWsAcX3F154wTCM008/fdiwYag+u65rWVZQmcDx3nrrrZFIpD1a6pdfftm/f399zZWUlAwbNmzUqFEnn3zyscce269fv7KyMpz2KS0t7d+/f3Urn6C5YFVVVUVFRVE4XFHSLWSUFBml6lVy45TJJ1d9e+JJ3z79xG9POW7i8d84pe+xk43jv22cMMkYN9GYcHJ5zbcOH1d5bHWl9HY6adKkiRMnVldXV2U/NTU149UHjRarqqpqamoqKyurq6vHjx/fu3dvvGHC4XDXrl1xtkePS0cKzCEjkcjTTz+tHcgiyebnnVKIABHoyARc1xVCoMOK+vr6gvnFdvQc1w9EAdqTknPug8K0r9YS3ATwPsASgIearBu3NJ3liUoOQzn09KGLJ7q7oqsjwgko3gqHbYSzkvBHgAZV0AuuPdg+6RkV6uDTveU4zp5ecMEFuz/q3CApRgSIABEgAkSACBABIkAEiAARIAKawEknnYTr0s2cORNXGGr3VngOyCBft097vqWC4/rM8zM/NZkAH2wGjuCQCWr9ed36bkUSicQHH3ywTH3eeOON5cuXL1Kf1l6ibTEdl9Y7/vjjI5EI6rqocAZ/hXYIARp/93LOjzrqqAIBGvXTd9991zCMgQMHbty4UVtGM58tWbIE3SLbtt29e/cJEyYMHDjwggsuQNaoL0+fPh1X88Ndx3E++eST8vLyq6++Wp8Szrle7u+oo46KRqPdunVDYZcHPjvtkdH3wooVK1DO//TTT08++eRhw4aVlZUdddRRQSNrXXkwsnjxYsMwJk+ejEN2XTcSiZx++ulYW1NT0w9/+MOePXv27dsXDZDRiLu+vr6kpATdWDuO8+mnn44fP37s2LH9+/fv16+fZVmc86VLlxqG0bdv3w8//BC7jHW+8MILU6dORSm5rq4ONetly5bhSoamaaKLcX1NWJbluu7cuXMrKiqCPW8jXllZiUbEtm2jNxU8a+hdmnPe1NSkvVTrhgoiwfrzhG8mpM2fD9xnXJgMXCYtDDnApwB/tuCKL+3jN1mjG1KnpJI/c9OPA2xCk3msEN2f430erBZt3oUQKDxpY3DdDc45+gx59dVXg3fXTTfdNGfOnMmTJ6MkHY1G0Rg/OBxdCUWIABHoFATw4YC+em644Qb9rMCvm10ps6g+o9Csnk/SFFoFwUAwAEsZMq8AuB/g2u1OVRM/KgEDHejrQQ8HYmkIW6LY4t0tdpDDyxK8/1YxOQG/FvBRwKQ6Y0G9zy2gDzvsMMMwpk2bpkfdKU4ZdZIIEAEiQASIABEgAkSACBABItBhCdTU1KD94uzZs/eik0K9DuuoH4YcQHCfMVcIxhlPeSzteuC64HkCfcPq5d/a32IqldJ6nS6lRUWd0s4ImjcFXXAEtbIOIUDj717OeVlZmRagUVdFQXPJkiWGYVxxxRWobKJn5HvuuScUCj344IOmaaID6FAodMghhzQ2NiIarPa2225Dn84LFy785JNPmM8WLVoUjUYfeOABLXyPGzfumWeewcpRWLz88st1r7QEbdv2TTfdFIvFLr744ltvvfWCCy4oLi6+6KKL1q9fHw6Hp06d2sYpwevgzjvvjEQiF154Ia6e9/rrr+9srq6uDgASicTXv/71nj17vvnmmyNHjiwpKUEF2XXdOXPmhEKh888/f8aMGeedd55hGBdccMGWLVt2WkmjuOx53pIlS0Kh0LXXXhv00YGeNB577DFMnDx5cjgc7t+/P+ra6P+6wCQehzBixIgzzjijjeHoQ0IIXIQwHA7rRHRRHeyJPtSeiC7o2U7GllDg7WYCbAfYBPAOwHMp7wcbU4dt5yUmdE15RwjvCoCXlcFgexrJ5YnH47jDfIYLJ2ohJqhl5woAoJk8uvIpMH/WZYP5KU4EiEBHJsB8Zts2vvdw8803B+/iXU4rqmdUVoMWyvxZGkALpTtvV1NlKwGeA5iVhtN3+EcmoSIBRhyMJjBSYKRVUAJ0hRSg/YMS7jFbras9eF3VoLFJ5xv70AUHfr8IIUKhUGlp6Zw5c3RLFCECRIAIEAEiQASIABEgAkSACBCBvSFQWVmJ3l9nzpy5+/WgeRP+rtSeHh2ARvA/V+ZNaYAvBDQwYAyNoPfUAhoFT5SJdT/RiFNroe2JoANhtE896aSTULYtMILuEAI0AKAJqnbBYVmWoz44BjQcHjx48OrVq1966aUFCxaccMIJO730zps3D39F33333fj29EMPPYSKKoqY8Xj8jjvu6NGjRywWQ6cWQohXX33VMIyrr756xYoV99xzj2EY48aN27Ztm23bW7duRSP5VatWIfqgWm+a5rJly9C78U6fGDuXrVuyZIlpmuj347HHHtNnq8XITg16xowZ4XB4+vTpKHbjuEaPHl1bWzt48ODu3bsvXLjQdd3JkyeXlJRs2LABdZA33nijW7duOHkyePBgtL9+/vnnY7EYisuu6+K6hQMHDly6dOnChQsXLFgwZcoUXMkQZ0IAYMCAAeFwuL6+Xuv4LfZzxYoVsVjs/vvvb/Fo88SJEyeiaq8PoR8PfY0WXMo6W2sRzZz7TDgs4zs18177OoAnAa5Kmd803UNNHjWFYUOZy6rAfwrEJgC3tWp3ma7b1ZHWitTX1+NiZdoHdGs5KZ0IEIFOQYD5DAXo2tpa7HDB2yG7HgVn4JvccqTFswMATQBvAzwKcJUHE20YnoL+KdE9JaIpJT3j1oIiS5RYoszhZQ7r7nh9Us4EIQXrrbJFOcmtWpbbfSZA6wGuXbsWn957Ny2/azaUgwgQASJABIgAESACRIAIEAEi8O9DYO8EaOUHAGwBDucu5776MRgHeA/g/wAWADznwp8ErAbYBuBx4Hxfk9WyWDsj2D7ap3ZoATqZTKKlc1VV1ZgxY7Q8qs3QLMsaMWIE/k5Gl9ijRo164YUXcIS2bc+bN2+nN+RLL73UceTvfs/zbPUBgHg8Xl9ff9ddd3322WdYof7JHQqFevTocd1116EptBCisbExFAp169YN5W9tiosNoSnc/fffX19fjyowZjjvvPPKysrQZUdrJx3Lzpw5s6KiQv/UX79+/bBhw4qLi48++uif/OQnGzdu5JxbllVXV1dSUnLiiScCAPrEuP/+++fMmfOnP/0J60+lUhdffHFxcTF6nUZiw4cPR0SRSKS0tHTs2LELFizAHqL99ciRIw3DWLduXWud1FMWvXr12rpVyR9tZM0eGj9+PK50iQno3QJbbHEuJVuu1b/6+g54UhXqvnoLxP0CzmVwtOOXesxwhGHyqCWGgvgJsNVyAbC9+Oh2daS1yrQAHY1GW8tD6USACHQiAkuXLkVXQnsiQKMBtBSITak7iwaQ3jNe5nCbxS9Mi2+m4KAUhFMQMUXEFIYMIIMliqXurIPf27VHuPZlAO9KdFm7ahnRSnQ7FiEEzjDoR1lBBM+L53k4CYozsp3oZFFXiQARIAJEgAgQASJABIgAESACHZnA3gnQoBYBsgFsLt3RJlz4mMOrIO4C97qUdf6Wpku3J+5z4G8dU4Du0D6g8aJxHKempkYregUvPluWdffdd0+bNq22tva5555Dybggj/aloP1Eo/yaSCTQUBp3Xdd98MEH6+vrb7jhhrfffhs1X9M0UbyeN2/eX/7yF92lggsaa47H41gVelLu0aNHdXU1OnAoyK930bfDkiVLKisrsSHdSZR9tdrOOV+/fv0dd9zx4osv6uI6gisfAkDfvn3Hjx+P6ZrDrbfeesstt9xwww1P/f4pPJRIJLAhx3Gefvrp+fPnIwpdYUHk9ddfj0QiN998c0F6a7s7vX/U1NTgS9yYBw2utfmz9lCBR9GEr3lteelcAIZMvs1qkmc+g/9kcIwjenui1GdFDjNMEUm6A9POhQBPSecbrHnFraQEFwnLZsloNNn3F/QZyR7P/SUBOseCYkSg8xPgnC9atAhfa2hbgM57UumBo0AsZ8C2A7wJcK8HV1gwKQWjG93hSXdgincxhWHxiAqGJQxLqs+Gw0tcVu6yEoeXOLzccoc4ybMBHgHYrOuWEaw/M6nNmy9CqBXnZhH5LG3+wcqZzx544AGctkRPUHmN0g4RIAJEgAgQASJABIgAESACRIAI7BGB3RGgW/yVydX7/S4Ad+HjBPx3Er7vixNcd+g28/Avto23vRcBlNQplyGUBkuZTaa3GSOpPeq7LNT8V2TbKdhQTU2NYRgdXYBGPXfatGllZWV/+MMfcMFAHACuFIeCJgCgaW3zVePQbTZ6GEEfxMGVo7SNc4uqIudcm10jaBRttdqLpTjntm1r6Rm799hjjxmG8fDDD+Nu21vHcVCQ1X3TTTQ1NemjuhLdK50fW3/ssce6d+/+wAMPaO8lqGIjH6wn2E9dHC3Ndf0Y0UcBYPjw4UcccURBhjZ2TdMcN25cJBLp1q2bVvnxutQaNO7i3ZC9MbBK6ddG6b2Zd8ulzsJAaiiQVH5t3gd4g/kPp5zLkt6JNhzkgeGDwcBwheGI4pQ4aId9ku3dqewNbVm81Q++woDt43JeelGvTJnc+qFZDbq1ykiAbo0MpROBzkjAdd3ly5dHo9GdzvdRgMbvoOBXLI4r/wmG3rgECEd5n/8A4H9BzE35Uxqs/o1QGodokvVM+T1NHrO4FKAdFpERgeqz4fJil5WhAG3xCtMZ7admALylHoDyca6Cahkbxv8iOAgfmKtWY5VzdWjv7ADEs4/Nv8tHIv8MhNWiAK2/0erq6nY6s4rFYgsWLGjxy7Eznk3qMxEgAkSACBABIkAEiAARIAJE4KslUFlZiT4e2+EDGn/sBbxoZN6F9ZVfx7UcnojDf8ZhYMKTOpgNR6b9S9TSaHKIvnLBodTnQA3ySIsCWfA127YIBX8LtyeOdXUOAVoIgZa/kUhk1KhRDQ0NKNSipomiM0rD2qJWy5ptMdvrYyjOep6XSCQaGxu1gGuaJvNZMpkcMmTI0KFDdW/3rMHmp1Pr4J9//jnWqTV3y7IOP/zwPn36tNgWVlVAKSgxNy+lDajPPffcXr16ffHFF+hxvHnOFlNQgK6srET5G+cAUH32Ofc5ZyB0wBuLCaUzg8MhzeXdonZRIvYA/JRybfMswK8S6YmW/Q3L/ZrjH+SJGArQPhiOXLkrloRBFlwM8HcAyxeu5btu81ssk5JSt64JYKvX5FMAKRXxM4PSNobtmCgiAbrFK4ESiUAnJcB8tmzZMrQFfuKJJ/B7p+ApikPL/9cgDdDopreD9znAQoA74ubEhDcsxfukoDwFRWkZSqSLZyhyRDgYXCFn0XwednmRy4stUWbDQQJOA/gTwBaAdHaxY0c9HbNPJXxMMTkXzizwzeA/FQ7ARxwWcJj9+Y7vfd7wEw5PSz26JQto/DZxHOf666/HBRIWLVqkvwg66UmkbhMBIkAEiAARIAJEgAgQASJABDoIgdNOOw1XqmvHeu/4KxMdPavuS7tM/K23DmC+gDNsOMrkpaaUwsoTyTMB/gdgvVq1PsmkHTSumdZcDkMY2Z+TUpL21C9NL2fqtO94CSHGjRtnGEZ1dTX+pi6ou6MsQqjF5RkzZhiGcfbZZ2/btg37yjn/CgXozOkS4tZbbz3qqKPQIzMuTrXTPLm2ttYwDFz5sIDsbu02F6BR6b7tttuGDx/e0NCghW8AmD17djgcfuaZZ1psokUBusWcwUTP82bNmhWLxdasWYNm1+gnJJintXhNTU0kEqmsrNRnCqcTuFKfWxSgOZc+NiAgQMtdvOmgEaQn9Ydc+KHJxjisu88NDEyEmAh5EHKVAG3CwSmYwuB2gE+VBeJmAWsB3gdYo2pYpbZvK3PC5QB/AVgCfAMIMytANykNWgnQuvWco9XWhivTSYBuiw4dIwKdjUBQgF62bJl+BSf4ZMYxZZ5SmW92Sxk+bwJYDjDXZJNTvE8awsFgQdiCPOkZZWhXhFXAlzmK0ryXgJ1zeLUA/1BPMyfwb0Hg3wj9n4mP/zBw9RDbAvAxwMsOn58UFzfBmC/M4Vut/4LWBWgcSzwenzJlihag256n7GynlPpLBIgAESACRIAIEAEiQASIABH4ygj86Ec/wkWGdnoSbr0Tmd+XKgPG1ZY7amGh9wAeAjjVhUMtv4vLixgYCbs/wJ1K9dqqfgwmlMDVtjva7Ju7GZ8DWoNuvV97dKQzCdCoQZum+fWvf724uHju3Lk4ZO3JQYvUzUWBPYLTrkLoi0MIsX79+p49ew4fPvyJJ55Yvnz54sWLZ82aFQqFRo0a1X6ttrUmgyPCOFoTr1+/vkePHocddtgTTzyxaNGilStX4vqEo0aNaruqFm33WivCOW9qaiopKZk5c2bQcUdr+QvStQCN8wRafdYnLjg6WVarvZnpF1Wf1FhcgH8C/BngOh8mJPwh280yRxQrO0GpQWsB2oaIBbGUGOE5swFWgbMN3I0g1wD9fwDTAa4AaRb9vaRdk3SPT3qjkt5IBtUAV4NYKcUduYSoy6DJg4R8RUHf5gUDa32XBOjW2dARItD5CAQF6CVLluBDDL9x9OMLR5X7ByEjCzcq9fm/HThtm9U3LcpRcW57mzGFVhNplnyZw0j4QwDmASwF2JSdvlaPSv20xPdE0CdHZmo8qSa9FwE85MMvLDg9DkfGoccmCDXACIffrR6nyRYtoPFZzXw2ceJEEqA73/VKPSYCRIAIEAEiQASIABEgAkSgYxO48cYbi4uLDcNo3QUHOgHI2kTK4XD1yv4O4X8A8EcOV5ow1oJ+KRGzIOxDuQt9PX4WwArwmpSAhn5lsyJb5ieqsnfWRs/S3YClXrFFK2mk5qlfnSqes8JkaHS9x1x3Lq1UXV3dOSyg9SC3bdv28ssvNzU1YYrWMb8SATpoN75mzZqqqip8TTsSiRQXF59zzjmYAb1I77EFmdY4dERXu2bNmurq6uLi4lAoFI1GQ6HQWd85CwC082jNDSNYw24J0Fjw1VdfRfXZcZzgAokF9Tffbb8ALc2eM16e1Z2Vq4uptTvfAXgS4Kbt7rAm3iUlohY3HG54rNAC2oYuFgx03HPB+SPAFwCfAPyvgF84MNnmo3wx2Bf9PNbDZSU2MyxmpH3D5Icy/j0Qi0HY8qYGn8EOBps5bFWO29ERh6vu9sCLD7ke5sVIgM7DQTtEoJMTKBCgcf6vRQE6N1D5GHEA3vP4XAe+Y8HQNJRZUNS29FxwNA3hFJQlRO9GayLAq8r5RjLzMhRKz1pxzjyWdgB8rp54bwG84Iu7LPfnKfc7SX60Cd1SYCTA+Mw1mmASwCL5kJXuofW3Si7ieR6+6XL88cdrAXoPZh9zNChGBIgAESACRIAIEAEiQASIABEgAlkCN954I1pA33bbbdm0gr8oN7tSJctoxymALwHeYuIhj1+e4Edu88NxiKYgbEORA/3iZiXAb0F8JBf7kVrWP9W7sOvVi7mWrF3Ww+UWxW2564FcYm2TWjhNewtYKV+9le4HdNPonSPTj4KOtnN3PwrQ+Fu2nf3Ys2y4JhIao+V+OufH9qzm9pcKmsIBQCKR+OCDD5YtW/b6668vXLgwKE+jWtH+mtvOGRyl67qffPLJsmXLli5dumzZMlSHHccJ5mkt3nYr+qhW+YORYJ06Z/OIFqC16q0rEYwLptxtyJWyhLwH8E5wPG45YAsp4NgA/iaAVwTMTsKk7f7hSdHFzC7Spf1v5FlAs36+858A96uFtlaBmGc7pybtr3E4yPFjnh/1vShzIsyJeHbYs8OO3U/AWQC/kebSIilngIRQWs8agNcBXk+6q9XLC41qXqjtlxckABKgm18GlEIEOi+B1gTolkeUmai2ga8EuCPhVKfFoSZ0tSHqiLALEbt9wZSvcXSP+0ekxVnqLaoP1dNQLnMs20Vba1/9w2ADpDhYm0D8hcFvLO9ncfesHd5JTWxkwhuW5v0cKHbAMMFIQvcEVAm4GWBdgYAefJ5zzrdu3SoYj0WLS0tLd85RL1q0aO9f5WkZF6USASJABIgAESACRIAIEAEiQAT+zQjU1dWF1Wfx4sWtDN1X3jNsqZJJ4dcG+CeD1xy4Oe5OMPkgEw5KQVkSonEoaoRIIzvaMmsh/Ro4nwBfq9zMPgBwiwqPSLNo2A4+l0G/Pit/WQplOPUhwL0eXNoAE9dbo//pnbBF/NiUalgiYEmtfoe20tf2JGsXHOPGjWtRIN1zH9D4a7Y9ndjjPPoHs1Y2dYqO7HHl7SyoG0IHx9rLRDuL73E23S5GgrZpqMs7jqN13r3k09xpBtYc7EMbAykQoPN6pQVoueygAMakAbK8xLeqiZ3P1CTMKuVA/eceTEzBYXGIovosDZ+ZwVTQPqCVA+iQ7Q8AuArgCWXl95hvT3K8PgAxAIODwZkMzDWkAG0VM7uL5xwL8GuAxcpb9FZ5W8K7zH024dy8jV/zpf1LDn9TiXH1bgIJ0G2cbTpEBP4FCeyGAK19YvifMX6XB99N834mRFzpmz7kyki7BGgTImnoFveHpcV3Ae4GWKmeij5XM3ISsZyuY1kXz+tAvAPwgu1em/C+vcM5upEfnICSJERMiNkQ8cHwwbAhnBTDAOrUs67BV6u/Bh/jwbhsQkA0EjEMo6ysbNGiRXv8Bs+/4AVBQyICRIAIEAEiQASIABEgAkSACOwFgfYJ0CmpQWfMjrcyWJKCX8fhOyno60GRDcVpiCYgFJcy9JCk+A7Ai3KRM/YSuHeDexn4p4M4SVAH6xoAACAASURBVIgJm1JTTXhELkHvc6m8SaezKnAT4DOAZQC/bYKJDdBvC5RugbJNMCAFF3tSgG5SAp0JsszefvaxAM0599QHNdC97d2uygd/LbcW31Ude3s82C7zGb65jOJvUBTe22aalQ+2qw9almXbNsJnnsc8D02M5baVjy7bRiRYNE8+Dhxoo7gWoDF7Xg0ZARrUPSCU+rwJ4B2APwDcy2Eug6sZfNeDE235AnvvFHSXr7HzqOdHfC/i+1KARvXZFYYHuAJhyGaHAlwJcD3AubY9yrb6AvQCKAduMJDBB7m0l+WGLafEcXtwOB3g/7h8vyCh3l5/GuB65k6Om8d+mj7uc/dHAG8HHLfn3n9obdRkAd0aGUonAp2RQKsCND4MCh4JwpdzyPx1i5/T5PcxoYsLkezTqVCAbk2SNiGSFP0s6cDrTvlmBmxRT6cUhx1KdMY58AZ16C8At5re1M3xE3Y4R8f9fknoloZoWpo8h0yIuRCTE2/So3T3pHuKcuXR4ELaVjN+gad4Liqn123bTKXQo1R5efnb76x2PLcznjvqMxEgAkSACBABIkAEiAARIAJEoKMRaJ8ALZcQVO++ugzeTcEDDXD2FhhkQwWHsCc9bxiN8j3Xvg5MFdKq8gWA+wB+YPljklZ/2+rOzDIrNWhTamoKngFokD9VOZMv/TtKgBYfAjzuwKVpGLvFPWgrj26H6A742hZ+JsBjShxz1c9Pe5/Q28cCNAA0NSbMtM18lOi1MZhex615RA8ka85d8GNeH28Wyf1cbj3WrNA+TtAto/jeXHkPpLQxdtkrDhwDSgvY0WCZbNdlmgBPBsGENILLfHLuLACEw4TD5CyFD+oiA8GbBSFU/VxZ4bc6oaHHWGAKHUzPdqGFv+PGjYtGo5WVlQXFM2bUTDmgkW5oPDkhA0sAbk9ZF23cUbndGrPDG7SdFzeCEZc3lZGGYkuUubw4I0B7EZ+HfS7VZBSgXQjZELJFj5Q1Mpk+xoVDGJQBVMjAS3xfSc/Zpb0SnpH2ujne1wF+DrCKw2aAdwEWpMzvu96xQvRw4dAN1iku3OPC+/kTPtrxTYv6E7ngaOEyoCQi0HkJtCxAy8eAeqpq30GYImeJPwa4O8W+sTVt2Mr82QPDA8NVwZbGyDIdDym/HFGLR1yIuhC1odSEHkk+OGFPALlu6kr5+oV8zpvKFT66eP4I5GsZLwDcubFxylZzRCPrl4CuSShV0nPIVA43VCuyTiZCvqiwvW/Ek5cBfCSEsMGxwWHZLxH8KhGQFlLpXgewGuDDP/7P/yuNoQRtmI6p3tTqvOeQek4EiAARIAJEgAgQASJABIhA2wRQf0JFSsWDgscBi2e8DWJnsjph2x3PO4oFd712V16hA76zSwGay5XJEgwSXJorf2nDk03wwy0wbCsUe1AGotiXfp/DcfnT8jCAHypXG79g4j8tGJjkIUupZIyFLWeYeuN/jfTeKHE60raJ7wApcz0C8KO0f+Q2u8iF0hSUNLKyDcmvx/kcaUkNKXUpWKpIOwG1pefuMwHa85jr8Jkz5oRDJT269/lk7T9V75jyT+mo7uIqirjFFEcdxWHg2nNK18te8+0cXwfJFhCam/VIDgsH6CkUOPCccKwKCA4eB5YNLcjFWYXaZ2AxSDMpFlj5wmigaVzuEmEqroFjBVFPeZZwClKDu0GtucV4MHMwjl7Go9HoiSeeGBSg0fOML1/qxgcK59L6eCnAFUx8I2n1Tdq90l63tFuiVgg0LMAQdkSRK8JKd5ZblJ5dYThS2ZEvuUsBGmK26GFLBTnmQYRDEUgJJoLZLClkG2kIJ7ixLdlzy6bTAX4P8ArwJ31xpS0mmGxY0u+a8o3t6X4u3O3BWiGdsjd/8KEXdn155yiTBXTwGqA4EejsBJoL0Nxn6pnggnAz/yD5anVAOd23HsRvHfOsuHVImhvKxjkjPaMAnZWhQ7ZUnNWrG27EtYvSppFIhy12kAfHA9woXwRhq4Bvz9JzgH+mpOE/ANxowRkJOCkujk7AoQkoS4CRUk82JT3H5DMwq3fLpyIztu7okUz8lzJ/3iwE88D2pKItv5s83zIttb4EbAT4P096w79qW+rC5/5wVkZ+Noy006i+r5s/BrO9o79EgAgQASJABIgAESACRIAIdCICQalQihmBJe+khY1y0yCUYKOl4AMQkUqY9hDhKr1L2SwGe9sccu4oLshjZ7wntyDjNC/81aTsUoBm4NuQsGEbg80MXkvD1JRa2d6FKBflwLpzXuGLCoDuAEMAxnB2nOUMs/y+Jo+hgJaGojgcZMHpNjzvsE3ZcabUj8qHfHa5kxrNzUM9t4fjlyb9sAndNzT19OEHAIuE9EyLhs9ykbRsWbxOcjpjsysCJU15FvNLyQoYiHHjxhmGsbc+oD3P+8ff3wuHiw2jKFpUuvD/Fqn+adXVUz/NmdqiCGup9dy06NnpBejA+WgxqlEExffgWWRZARqtkjOahrp7hC+FaY+BzcD0Ie7LS/BLBp8yWCdgLWTCRyA+AP6hXPIS1nHvQ3A/BP9jYCqItSDWCqmlysBU8GCtB5948IkD6334gkGDUqJb6H+LonMwsYUy2aTx48cbhlFTU5NzvsEyrs/9nJqRdOAtB+a78A3bM2zPcHy5xYjHpIGzoyyXUXHWVs+4mzmUE6ClDO0qjxwehDiEOYR9+YaCVLFRfU5DsQ3lNgyXQo/4NTi1vnOJzUen4eA465JkMRO6JZ0JACtan1ogATp7jukvEfiXJtC6AG1nBGim/jWSs4qNAK9bqQsTqcFpv1SpwKGg7qzjWfPkEIcIQDnnFSmzfOv2Q5iYJOAGgP8FsQ7cJnBNEE3KJ/5KJR/f15CcmoARCbmcYJckFKH0rNXnrG11TNlTy6ZtiDRZsZR1IvCHAD5X89icyTe5dqhq1wF8oBwfLbHhkUZxdRy+3cC+ZkPNa4vOCoWNWMQIh4s8kVJf362+KPMvff5pcESACBABIkAEiAARIAJE4F+OQKFCiAK0XvLOVfoj2hFn5UQssv+2OdMeNKjMmlUGu9pG6/IUFQjQHff3S/sE6JQNX/qwwof5CTgmDUUMDIAw8HJgB3EVAPpxrwd4PQB6ApSgOIbCVxy6x+EkD2Z5sJozU4nyGwAW+jA/Lb5rsmHcKQXX4G7U86NpbiTZwXFrHMB/A6zTOhhKzOrqRwFTa845PVMnKYNaj4PX4t2yzwRoALj++p/HYtFQWJpMLV++PK89vESwUzKOHkfS0hw4dyVle59Lyauj8+/gwFCF11udiBp9FkJgtAqbx6XJ8w4XNnlSQVgH8KHy/rlQLdD3GMD9ytXLvQD3qBWr7lOeQ+9Uu/eo7b0AzcMDyvj3RYA3AN4R8IaA93nGLC7Qg0A0KDoH44EshdEJEyYYhvH9738/l1+9S+Az4L4M6vNZGm5OwPiE2x1FZxSgHd+Qiw1yGbSxs47graVvMGX7jBbQuN6XdAntQchX6rMSoKWLHBVCtujqi6EAVQDneOxbLh/l8KG26GvCQTvc4qQ4jMGpXMxTqAtHFNjH01d4yZIFdAARRYlApyfQXIBmGQto5eFILyIsleJ3Ae5qTHwz7XVV02B5ts/qGYWPICPzrgbEHCj1oNyFPik4qsn8jnwms3fB2wGuD7YL7pfAX1G+OK5PwYQt6aObxOAUHJyUVs/RJES07XM683DDFiOuKHVFqS3dQHfdbg5FR0PA0tLVk5zlNAH+CbAc4FEQN5rO+SnnP5Let+L+0XF+eBx6NaRP+uvSXxiGUWyUhIwuLrPUP3O5OcNOf1JpAESACBABIkAEiAARIAJE4F+QQEAMRJesuW3LOnKgAHpnRRnY5+CqgK+vZxzGZt/L36+7OXNM7BuepUA/ZYaMltiCJIMZs+K1ytsBz3PbArQaA1emmx8zuCcNZ8d5fxOivhSgDeBlygK6O+fdAXo5ZqljloLoAmrBM0dZXqbAiPvDLHGDWmNwh7KUepPDbz34ngmjmrz+cavc96Lck5qbJaSlZoPdR8BsZZzUKP3+5n0KVa+8g7kdljM1LqgAYJ+54DBNc8yY40Jho7QsahhGU2OC5WYaPJAeDLYoD79bQJrZblehUfUs11N5AaEzzWYdDWT614gG7xI0pE2qCwLJNChcmwC+APhImcevBLkA5YsAzwE8CfCI6cyznVrbvyrNfpDyzkh4E+NeTaNTtcOqbHSq4l5NQ/qkhvRJO6xKDI1OVaNTtb0g2OO322c0mP+1NXHjpsTsBNxuwwIGG9rQGHIicn6stbPS1NRUU1MTCoWmT5+eKxEQoOXbFfKzzITzG6Fv0i9yfGn+jAHVZ+nAtJkGXaA+W1J8yajPaP6sLaBRgPYyPtojWQ2o1PYHAnwzafV1RC8PyjwodqDMhvIGN5oSxwiYAfB/6kJtbXCtpqMAHYlEotFoq5noABEgAp2EQCsCdPb9I/zmkt95XwI8a5rnJZ3+Vs4DRk6DRr/PuWkwiJpytcBum83eO/zjPfgRwINSF2Y2+EkQm0D8HcT/eHx6mv1HnA1JQvcUFGcd4kfSEFIB3+qQr3dgzcrIOuSKLq7oakNpmg1O2VPVVOVmsE0QpvoufgvgWTv9Mzd9pm2PNp0BSad70itJeiUJtyLJBzO4dO6sbxcboZJQ10i4IvC2Sic5Z9RNIkAEiAARIAJEgAgQASLw70hA67ToIjDflLiZbqtzZyMcpc8DIjS3qGIXqs9ansr2MJOhUIDubOd6lwK0WiVwB8DrAn4ch6FJ6OZAka+WlwdRArycCxkSSUN65OD/n703gZerqPLH73v9uvvtycvyspAFSAhZSAgJWchGSMJqkEXFEQUUFddxUBkFHSGIgDqKoiKIGyozwziMG+qMIyIgi6KICMqO7GR5S/fdaz2//zl1b3V1v/eSlwSZkX/yOZ9KvdvV1ffWreXUt875ns448nge9ixGhsbuRB0L8B0CFZ+gcGufUfCGAGZWoVRJm/2kOWEZ+hzpgg9jnh9YRqijDzoeGYB24NoM19QE7fYBvADwFPnX/pkyfQ7rMr6elwyA3rFjhyWLnDZ1NrJ7cEhiRsS+2whB/y5Z6f47wE/J3vYBpLMUO0BEUmglMRKjoT3+X+42o4T1X7q7RO7nuAqwDeB+7BPie4DhKb9CNOEXcHVWyE4cDNb3+csq6aGBmh/o2ZE6MJGzEzknEXMTOSfS+0cwOYLOCDpD6AlhopFATRhWQjWhJnqSr2YOykO3y7XP8RP64Z843CshUHhK1jDAzZ+79+S2h1144YU1ABojJ2oMvalTOpD4I2ef8/mqGHoYFDk0IeHGcCbP1vbZMnJY8+dhAWjDCm2gZ0pbOLTyzCuhOYG2FMamMJZDp4KSoelIoTQg20M4BuDfaMwYmtThnzqjRRrCbm8AaM/zVq1ahTTX+/7ta4F9LfC33AJDAWguJbmxoI0ATpXGCBrDOJwbiVkxtDCiDCJueheANhhxMYaWGJoj8Hzl9Sdj+9JXJfBJgF8APAnIjPEMwC8BvqTgHKaPidWyUB4Q6LEBtFiqDSfMYFMezzALY2iCGTIoM93F5KQ4OQ7DFapnQA2C7qNp7Yc+vKVPLE7FbMWnKdkLMA6gS0NbkpYGBqckySmgr/zspW9pKzSVm5uQgsM4UTnKxt/y+9x37/taYF8L7GuBfS2wrwX2tcC+FtjXAvta4JXdAga9sYaPFtsZ9qkNbYUYSto7bOmX56KNiuawJrw8v/wy/crOAWi6iUGKBPjPCSwNoDXB2IMWgG4BXVJQkroodVHIFpKS4JhnujlW3QwWAVI73gVwp4BPhvC6fjikHwHAMaHoiEVHzFoSsn0OwKvq3io/DuCzAH9EA2LNkYJDkdhOZBoGDWiJPxjNsDQGSmSDoB4H+A2BvTcAfBXgcwCXxOmXyfIpa08ppFLqpJNOampqWrFiBQBwTr/itLfn5HeWveWWW3IAunDSiW9AwzDE3foV/D6CGwLY0hefUI3XVYPN1cqbAC4D/WUQ14P6KcC9xErZT+zDXGtpJEc/d/ajf5XP6gFoO0xfIhCRkZnzVsIXniTu5j/RC/4V2jWLz+jwfJ28O6meEvlH+f7SKJybsmlc9aayO5YYT0+QRb1NOXbB1hRNdzOK5Ny2DmEOwztuP7IZF8aVGAKrEEHXoDq4CqeHcCWDPxI96EsGQB911FGe57kAtERWeSkx+GZMjfBtxs6K2YESzZALhjfDvclh8/ZxjH/BqAFoHLTOd5vpEKkFtAfaU9iMnQEs4PA+dE7X4YgxHrPOFwFUyEp6kED17OonPvEJMxyOOOIIctX/q3TVfZXua4Fdt4BdLfZBh7turBFLjARAm6C6tDoInAr0TVIfG+uMeCtVralqz4MQGjrmDICmIIHlWHWHybSIbQKM+3cznRU/jNCz/IZmH+DsuFTPSvSYWHXHqjPWrQRb1yydc3tnwp2RcKPDkTb8XTmRx6tk/DE6i5YYHRFx7W8JODeEQ6p42teCZ2+6XelWBZ7UTZx3hP6hKtkC4pZPf/x9rcQB3dLsSUaN87fai+xKPuIr3vfBvhbY1wL7WmBfC+xrgX0tsK8F9rXAvhZ4pbSA0hBrCI2QFarZuKQKMbodDaIzuoLnQG+ljcPz5Nn5PGCIcpN/lq68bOkzhJg9C/Ai3pLsB14BFmruS7Wd661DBTFTCAlfSul5Deft/+ndyygA6KdBXi3YKQn0pgjcNfOcXdbEOVPQLHWTJQwQskXydiE6mWyNRa+ANQDvB/gmwBf6xcYdeso2VahgULT2WHRw3sF5OdYYyr4KpT42F+BSIut4BsDXUA9AZ9spBdqE9AvIaorYGuQdIH4MyVd1vCUJ35KEpyThiWlyXBit6R98C+1ws1GVJEmapitXriyVSps2bVJKcfrnDrrRAtAXXnghIW5Nntdy7Ve+BiCFelrDbRF8/nk49Skxrwr7RXoi0/sJfZDUhyi9FGA1g1en8CEG12j4CcAfAJ7X9lHdu9j9vN1ujggc1wPNtV9wrltiT9N53TptvvbFUeUG6FjgR8S8fA0C8fD3cfKaINyQslVMLOZsPhezhZrJ5VTEDmTP1u0ek51Cd2voFtAuoFVBSaC0cBQMrGfEgKo2wlXN/k4je7IgkcpzRUsPUMpcTPTjjQDXAzwmIWIUnjI/A7DPajKjek5bSGttAWh7UYFiwAVwtHuHB4R8b8Lmcd4BUEAEBImbCxwKw+LO9qIDImdQ+1AKjiEW0FlbNTQa0ugoEvBSNSORZ2v0U3iUSPdH7EEEPf8K4Ebybb8boIpHc/TvbwyA3odR2q75CssYagg7gvP++Qp7yr/a49TGvhT6jl/dZU6VbrvtNnTxEWgBnZCQcXAV4B6Aj4d8IQLQuhnRZz415VMRFIYCzUUZRQYBx0UFk4RYAcn7QX2TuJhvA/g2wEWgTwVxuIz3l+kEIVuZamESgexUdWKdutlaVdcAaESfu1CgTIbPHUgADQXGDhJ954H4FaAC+mwC10bwdh+OCmFuBJNj6EqgPYXOFMbGujXUXgQe4t3pMSB+AOnWT265oMnzSk1eocnj/G+391iDDnuq+lfrMvsq3tcCr9AW2BP97xXaFC/JY9llubbMvCT17qtkXwvsa4F9LbCvBV7yFnDQoaxud+889NOX/Ab2sELG9QscnjRCVqjPEZT8F4pYcy+xvP7eSX9HAcbuoR3NbQD/SRuTb2O0GGQIvPblla8CfB3gW+SS/kOA/wb4Fd6Y/iPZbt6j4NdD5B4J90v4k4SHJDzG4UkJT0t4FtF2nRhH/D1syD3+mu0nVANBi0gD4NY3CgD6PpG+Hj1WVTdhgM3GWNNJM4DLoGTIWytbhWhnqhTLCQAnA7w+hE3b0gVb2YQKdEfQFUFbqtFcWvOS4oVIexUoDsC4AbmJyDeeBNhaQ2WNBbRVXBB97qcwaXdTJ7kG4MNVfsq2yoowWMLZIQALAObHUW+a7MfTg+LwdHpl2UNzzqWQmzdvbm5uPuOMMzj52NpQh6bQqABopdTJJ59sNudNza333vtbuulbQ3VxFU7ugwO2Q8sA9wLuxdxLRMauIKAUqgl96rA+eHUF3hXD5URw/EuyiX6Y4iO9SIGSamTSDTTjivDLerUY37PdblKsJdtaecZ2hezt59PGkOvKOSoirBTh0rwWINYQSBVGVJQY18m9TxNlMSJ75+foDT1IQ/qnif8hHp3Jk1M53zQwOGfQn+KnY0NRjlUh1h6mKF4syzEfH6Uz77+/o1o9VIilAEtSMQeFz0/5IbnMT8XcVMxNxPxEHJLwxVF6WMIWJGJ6ontSXaqDnqWnXRHNwFuANwPrkfGCsHI2wIOG0zR9OQDoWKDt8HaAn8fJcXHSqVIkUyeL7Caui1yXEXnRzSS7jkA4OgvoRgCaA6I5OY+7p3R7xJYreSXo+8iumd6p7Rg4JiThzs8RPP2jAfWhp/0zKnBRCjdq5LvJ/lkKjtWrVzeMqLzI7v5v+53zRXtjdfOYU2CELI6QBu4nU/2eVjjC77wklwUxH7H61OB+Q9MIjwFgcDjpp7lyGx6iIlHvXwAeI3mC8n95ZaVPE6WPeeS/RjpIM3PDS9n5nxb7sz25ITOkT5reCEMCZdi+upP+5fbkhnzjt2q34dCc4TyfT/aYGwpAa3R5QAA6ynitdmj4r5h9qJouT8TMNJ2dJnMwZdMIFy7WA9BNiRqv9UpQZ1OE2B/ROdYVSpwVR4czMU7mE7VUeHaIM6EqMdmKSLRGBw5z0FgPQGegM31aZmoME/vx8FgYuJoOd+9O4Os71Gue4zP7oLMKhRg6GHQx6EgRg25PoLSNeYOiNRIrWfIhUH8CAZd9DM+VW5q9pmavQVtqbMW9/Dt716aW2htxXwG+Evsqa+uwU3jEadBoBKZ/mn64l7f7ivu6bdjRZBoaf+hXsuZxXk3DV3bnz3xUDv+dV9ybeFkfaOdvqOFW9gInHfo7Tt1D+8/eXxm+s9Tfxt78yh7X7zw33Q2yXuazHGV2966cCvcoa+ZGew8j1DHSXdUVt5XsqqeMVJu9nrWJ1f2sphfRehs4at5fQ73Z4zqrdHv2bneZYXWv3vYE2w4mY68P1YXcknXvYrf+sC9ut761G4XtD+wksxvVjVB0J5XvqkeOUGP95eHqr7HWDv8q3Xc3Yr7+Z3b7r+Hua7creXm/4PbbkfJDm2tnJe1cYdS8oUPPTB3uBFKlacRNzc6xnzaJT5O/oN0k7tY+8QnaWj4CMJI8BEjW9yfCfx8g8tX7h0vvI8qF35DZ4t6ktyq4UcH1Cq6X8B0J3xHwbQ7f4vBVBp9lcHkCl7kikKLgMlCfAP1xgI9Uq6chdUF4QjU8rhptepnFj48OkuPj9KQkPY2xt7DkXTw5T8YXqfgynlwWiY/7akujyI9z+CKHqwVcK+BrAq4T8G0J/yIRSb+dGvO3lN5Jdj+/zRv57vp2/i1RBz+UAwWmJ5j0L9RD+qn/BLQLdNC/Ybch2qixGanJSAC053nNzc233HKLGY12YNOy8gTA9ZwtAt0CulXpVjJCzYw1cww6B6DNDlF7yL+hSqluQV9bNrfC5iWwH4OeFDpiKKZQTqBgtpNSNnNR8BF9nrw1XQ5wMW0bK2Q1z6VGvmaizB2go4snqPf+hkgjr4vTj2wbfH1ftG5AzvdhcgLdCspSF7goJMxLZUHDZIB1AP9EuFndVHPRRRd5nnfeeecNC5SNCoCO43jOnDnGAvqAmQuqle30M9+Joo2S7Qe8A3iLFCXOy5y3cVE01rhcFJkYG4vJoZgRiVkRW5Cw5WlyHAvPCv0PMvgCgx9qeFJBoJQg8hEJgkEaQxqCCJQMJKQGBZbZE5lofhgKihwMkOcBkOfBCicA0e0gxkSQrkiQiZKJIrJt3Ow6U5piIDiymyAGbYSDiIBVJQxInUKqDQCNoDUDZTid/wxwO4fvRGJLKN5a5cdEakki56RqBhNTUjEhFl2RKEeiECk0PYuQJtwLEBoo9CUdMV/1utd63WXv1BO8H9+0istzg+SMF/tf88iTJ/7h/hN+efO6H9248htXz//8J/f/0Hs73vpGb8Mqb+0yb8Nyb/NG7+oveSlbFcsJCEATwCqlJ2VzZv4sm6UoSd6pWbdO2yA+IB04EY+Y1OMgEwkhg0gb82RDzl23EtT1nl3+MYIFtBDgS2Q7/YWEjwfRUp50QIrm2MqMHERbOplsR8wFYegMgHatnk3e0IyYdBQW0OizYM2fKYOBBxF/kV4kipGczvUbQd1Mb5DmFGsGr5GNQ7N+Db8F+FcO79oOK5/is5+T60K4LIKfcHhGKeOmDgaAbmpqWrdu3S6baBQFlAO/Eh5nZiZJBCF0KkIXTLiAurdlpzDUwMz6bZ7IntIYXxyTmgMWU2zobbnLP40BLXCQKI4imTaiuEYRUglb3dC6RnnFkNkP0EHOAB0JuFE6t9JU+Bxx+DxN6eO0ot9HU6e7ot9LS8sdNF3eBHADHeR+CeALANdQ/qtEVPS3mH6N7r8h/ReA/6HF1SyxJr2L6J/uJgr+vdFmfkOq0lN0erR9FOkOgv5jmodpTtWpVolWrE6k0FKAMKLMDE6RAYiJzMzZpje7UTSyI0GHncpsNdw5vrGv1cYEKQU2uHMigZGYeT7bWphvuwD097//fXNRoIuXjHHGDzW84Fd/EcfXCPVOrU8nsq3zFZ8Xp+1kAV00kLFEyovuVIzr3zEH4FOEPl8I8NYwXhmyOaGYFstxqUZKJTvp1fjudbMxfyaNoZgze3gJFInQo5hAk5kJQ+356TgRnAzwGYCbQH0N4O0JLPfFfoHqSpEHH7mbBBLftyhaIDhOvC2VdAGPLqVBhFPZReefbwDo1rZSYyvuwd/uxOJOJtZOH9+aBYvdLQShNPYIA9ngaOoBd7PBKIgEzXIWqs5u0lnJs9gGe3D3f0NfqfXw0e6KLcGeyeykgobGxxdBM6t3RQAAIABJREFUB/1umi1B7kDdSX74gysFJti6kKh3ZUPSVcCMGraTO33FfbSL9b3+eWvISI7gG6yzrhvXf6VRc6DRaL41pGDD+LV/NtZhvjj07TsVuj3H5t3blwqk+xBD+pspbIplhQXgrkFgqBE8KHS1HLM5kBmhYWbUgxusmtROuujBzEe2pNJZtabyXdZvvl7X8OYPnW8m7K5C5lpavoDZhh02M0ydu75kmh7bSQPtoUIBkYBEKaaUGHYfOGKl2YxtXkA2YGnk2vfr3rdbjXvd5O2npllS2nVXSXnYQQfqL5K+9xTtLv9ESojR6/ZSmXkJv34/xVfYSjHkR5P2IXhh1rK6ND+VQNhCZhq24lSS9Ju8d9gm27uMfVl5NfRC7NVRZNzh6uaz6cDt38ONRtxTj+JXdlFm55Xkz1b3/279aMNT0GJklye387t5pmBYccsM02I7vTEsL5HE0ggXmqFAgmLyWgilSHAdlRqb7q//D/ulsTBVShnwIIvvJZV2hNZ2q+2LbKk3+1kTKs/t9maHianMNwj135UM9CDADtqM7KB94g76c1s+b7yQm/0+R2QOj5Ml5n2EMNr0D2QCfC/tm35MTupfAfgiyVUUlGuU28NrAa4C+GfAmC6X18ulRGtwCcCFtEH4ACDV57sA3gHw9uHkDAWbE7U+YGv8dLWfrq4mq/ZIVlbTw6vpkkZhi6vskCqf3yABmx+m8+N0LsmckO8fimkkUwM5vIRiqpVYTN0tsV8MxfCVB3Iq/foMvBN+YMIORiPLdGHEFoZ8gS/qJJCHkCwKxOJILYnk4RFfEvHDQ7Y0TJeFyRFhfGQYbwzjI6P0MJToqCjaGMVro+SImK1L+FFMbODyaA4ncHUa4bCfJSpkm36Odtz/TRalD5J16QtKDeLuNQcihxtoNKWaeVsh97EZm7gEE7artbZmiwhA04A1mjHV9gzA56JkI5dTKVxZCW00DU8AOtca/1rkeHQhMtpCkgUnFBIoRzAmhJ4EjY0KZqto+RJigh8jaB2AriocIbH3/lqL5yXnkuMsY9R8Gl/3AXxfw5Uczk/gzH6+uioO9cU8Xx3gwxQfQ9B1JFCU4CntKVWUqiygzU9my/SDALfieMwXL0NOe/HFF/9/0PGWLVuGDZY2KgB6x44d5XK5VCp5XsvZZ/w96IrW331x+8mczQTRhMBi6gFvQT5sXuaiYABoIdoF70b7cAQZS5m5q+xkyYFhfPgz/trt8hyOtve3Kvi5httB/ZomiIcoTNPzNLNUaXLPThXoPeFrdiyXtcrgYrt2uLqOJkwkzryoza416zsIN5p6qBMIDowjPGGWDTM7CtM/BM7t26gjPkG6kTF2/q6Az1fSD/nszFAelcC8FDoN9CmINMPE2UPcU3kR+T4H4PngVZCRuVCFiX3B2vY2b0zR6272xrR648d5vVO9CZO9tm6vVPY6St7YstdT9npKXk/Rm9jqdRe8ds/r9LxxLV5nq3fjjU2xmFqzgEYAOuffyADodsm7QY5NKgtBXg7JLzEmpGQCAgbBXxWABtxPVjTcp+CKEF4dsJmCl4F5wNECGkcF2vohcw11DNM3EJFxR9deANAWg24mGpPWFNp9VQzVdAknAVwJ+slMIbIbBKVAV+ko7E4NV70QnxTDgm3Q+hx098EGCV/TSCCznToS9gZDwfESAND5WCWk2SAy1N0MiGy3dbm+anv5sBmj0+STo6C7jYkpqUJa/nbS75/NCMr1E2AEzwmepLPch/MT3ceonz8KYA5yDdT7B4J9/0CLutkY3A3waxIDfVpF3z1yNB+ZYm5hc/12orH/EYCRHwD8gAhPvkcWozcCfJcidt6AFOrwHQ1fU3ClhE8JuJyry4wIdRnjl6RsS8IuiPm5MX97yE8LxPE+W+fzNT7b6KfHVpOjq8nRfowSRkdHIUriiLli0jDCMq64n7rfehnyaXRsoyTHJfHrePg+Fl6QJB+J00wS9tGEfTTl/5Tyf2LiY0ZS+bFYoYQaJQAUkzep+dSkqfxYVl5cSj5Z31Wwa9HwHxpPnv8L4Od0APALgFsoAu/tdBx9ez1QbvHxe/OOZA6i/0Co6MM0Bv9C2qTRKc129GHqkI+TzcLj2Ev1wyAfyeUxEE+AfAr0c6SVDpATQ2gPJhUkRiQkEgIJkcQrLN9I44hxAejLL788SRKDlSYgE4gZDCh4jn79LiIyuhKjLrB3xOE0gC5iw8gAaIAeJsdrOAjgtSA/DMmHONsc8YOR4jln7XczQ2c8c4WoNrI6CYAuJnhy6cWAsVUFTJViFam5nwN2CfCzlZ4Tq0IqC1wXjQZDKaLPFoBOYGoiXgfpz0Ez1BK42nz00W3FFs/zesaNIe+P2nyUTyO783/D2mu+ai7a/Rb+gsGLhwDQ2QJtT+PM9GcW4YSO6BzrZve3cEq2GLRTZnfu/W+qrG1Nd8pvuDjsn6ZJnY9MM+JLMRedJSe74hRuvJIXrsNW6OTAvZKdIpj3aNPsuw4M7e5nG7W6Yde7V9ZF3HwPxd93+ozDtNhO3pb7kdPb3cuUr2HEeaewRexHmBnyos2V7ATIfqc+U/9XY4fa+acjAdBD0WfgiCC7/qS2n480w5kAOxaDttDzsOhzQ/12Lmqs3MXicugZ0WoHhd75I+8RqmSqpFesCeQdpAP+PtJgt+YuYs+AegLk43WiHgWUh0E/QgvuE6QZGnM/Y81nVMEHaLF+kFAeA+sYlMfaBNxHfq5GD3TTe/Prd5Of9U0A3yff3v8g71ij5l2n4SsKviDgMwI+yeFSDpfsgUi4xIqCS6wAXGLFXlROYbmzn/tnDl/l6vpdioB/0Rjk/EaAn5E6dCtpRLdR+it69jvJUOBuMhq4K1ekjS70AFmf/Rng4Vwepe3n405qTC9NgUcAHtLwZw0PGkEiTv0wvsfshdJrlY+DflajS3WUq0bGaMCQqNb6bt4lXdh0+Lw7O7lHQHaWNxljF7Zz+Dj/0fopgQwP3F/JlxycZVxxv+5MbvW1DZnPzLfc+t2ncPM0M2fzbW7WYCHmoQC0/UhQYXsb6EjtANZuMZO3VSU5dmE8Po2NjrHOMfkKIA2uYcINAQKSARrdhlH3KToseYqG8JPUcx6lQW07lck8RLu84VL9ENTETAgPE8frg7l5r63KnRzsJHB/jv8aVd+YDf2eLv6WOr9rPTPscDAbxntojNxM5Aw/RnuLbJP4n87e8F80fJvkOg3XSfiKgM8z+JQrqf5kqj+ZyE8l+uIY3hPDG/v4xj6xtp8f2c+OGkw3WqkmG63Yi/1so5HBdGMlXh9Gq+JgGcmKOMgkCpdF4dIoOixOFsXJ/IQdnIrZTM1i6gCmZwpVEyVnoqgpQndyXSQPyJb/lRQdLnOhCDQtI6W2WKp341bdb41Us7luSzIokov87qeE2OJ3VQfXCJKiqLKUHRS7DzdHXJe5bsMC0M3lVJ4u4dE6lqy3kqbro2SzgHNT2MLg0xyuosn8hxRc59eESt9PC58BKv9C48vsSR8F+RdQz4PqVzJQOhFa4PF4DkBfcMEFhUKhXC4jx2MdAM0BfpHIk6rxeA6dRL4xKgDabh6NaWZE0CJBXhhojRkcEpAWknifeyowZxCOlHABDah+mkGNCW8fzQx3Yyh7uCqAc/rhmBf0vK26dwDaQihaiaAYATr7IgBtQgqpjhSmJOI4EN8iZCkaCYAeNljaqADoX//6157ntba2llvav37VDQDPC70lksu56sDYbgKBRRCekB5XXqoJYdRIbcxEN5FalihtyTbeupTAuBRmRjB3gC0M1PIUVnE4nquzhPogHSt9k+CM39IEWkXA2V0iaKHMjaBR93SM4+3SY8/YfYyUqLcp1Q+SYelstTWLl6lYECQRKYhUxvlJnlbZiszJ9PJngKzBX6XzrndxODGBpRHybB6U6gOEnqT1GNCtaDwPzcoBoFPlIfNGPQBdhaZ+6OlPl80+2BvT7o0peF0tXnuLVyqgN7T51+J5JRKEBzyvyfPKntfqed2e1+V5Xe3eLbdOivk0ppuRCCbngMa8EbpCn46T6QloL+lvA5bRMgulslCQZkm16yNmdvvfUA5oeic+wJ0M3tknZgSqjUtPc08LtNdG+z60fW7PzmeM7zlycewlAF3j37BRHM1hQIpE7F0SNoK+CsTvEVMyMIUypjcJHTDcCfDZCpz0QnxYHxzgw9gXoXUbzA7w6PJXBOAaSAvb6CUDoK3ehJ2NtDU0OTbWQKQumZ5Pr8WA0q5W1JC3o0RDDPoFVEARN7+LrGV/QHbBhubpGwCufJ0OgT8B8DHyofgnSj8K8FGAD9L57dsA3gbw1lzeAnBGJI+J1IZIrQ/lkaE8MhDrArHGlSo7opKuHEhWDJFlA0ku6dKB9NABtnAkqbJFVbbI54f6/NBILI7EokjOj+TcBElp5iZyDjociLlxOidKDg7jOVEyK2b7p2oagykpTCSZFMN+EUyNYJqRRE9L9LRUoXCJYvImNZ8OTd0y5lsvTyrUdFeYnp7oqZGc7rMDKunsgXR/K4PswEF2oM9m+WxWwGeHDCXgmVTF7KqYXZEoJm9SW4C+MidkcwI+p5LMGYgX9IULdkQk4cIdI0tfvLAvPrQ/XtIfH15Jl1fS5VW2whcr3c5A3WNdnq4PxHrM801BenIQ/53C3vVOgPeQvcC5ZDvwCYradwXApwG2ENL6caLUv5wWiE+TAcJnKfbulQBXU+CFf6NjjF+QLfyfaNLepqBfwiDFXEW4mY5kjLFVP+nrOK6yTYiQd9xxh5l7P/jBD0ZRhANSZ2NSIvHLDiJ+2UEKx80gPxBXDuOINbeSBXTZzGYhawWYB7AKYCVjy+N4cSWYNhh1+aLZxZ1t3uoQDRk69DZG0AULQCfQFrIe5GtSbwM4H+A8gDdIdgRjs2LRFStUsMjqGcMlWwDazIEJjAvFRjLKfgxVBAUyZcuXHNbVWi40eQfNmaUAohRh973/Z2c1k8EKDeZiP8gc1qzZIxahDxkdEhhb9Zo3krFFysHKRkNRumFTdTat7/0j/E3XYJvZrgh5xkKWGMqaJKEGj4wKRHl0bBkqps6sWTLELbdUHR6dyE9N7d3sPJOpW7au2j00LHOvuD8VR/c7xiGhVJDH0bCo6q4vDgvKDNOZs9Ymcw6LJhub4lpqh6fN5HbHtTJWXXGUFvOiLSybz7Hu+x/mlvJLbjGbxw9d3Dabts2Z1dDeatDevMY9+d/9sT2r3/hrmkDcFETAPMye4HDOszc+izkTsNg8hqs3Q1tAKiAUsF3AUwz+zOB3DG4V8FMB3yNV8Hpi/LwuVwWNi5Vh/7yGltQvoq0Gxs79LJn1XUABjt5fn/59xE+NxOaE14SxzYyfwMQGJtcNkfVMrseLag1TqwaCBQPhvIHwYEz9Qwf8wyrREj8+LGSHRmJRohcmMC/WB6HArD2QVM+yQjDQLJMKOUvILG+u2GKprv8h8+s2VfNitTCWS+pEHB4PJ5ldXrosTFcEyfI6iVcG8aogXhNE64JwA8DrAE4HOBPgLQDnkMr9LoD3OnIuwIdAfwTAygWkn19MitDnSYH/EoArX86d/66jI/MbCA3/McCvBPxewgMKHlHwhIKnFTyvYJuCqtn/0lG9gUEtPFqbk+14zPuyXVBqVqwcIwChr6iVPQegaepwh587v7l598bcIeJeHynv1j/M4oK2WrXFaM+Gb/7TCh2+YXAU0i+hT8ILRHR7r4DfOXKPgHucP7OPJNxLxxv/Toy67v7Oek/a0X0N9Q2TXk2DfZfpNWT2ewVNBUYhN/tEk54P8AGAc+vlfdSB301d+myAM5Po+CQ+OkmOSpI1SboyYctrkq7EK+nKKFkRJUfUJF4dGcHry8L48CBa6odLjATR0ihZho71fCUTK1DkMiaXIVUpW4Aeh5lku6GQzQ2TxWGyOBIHRXJ6pCZFemKiJ2cCvQlMcCWCCVYCmBBAbwS9MUxKYRKDSQj7wGStp1qRMJmkV8I4Dt1Md2Twly4hXSox7BnoA60zRTsS+MoWoZr/FyUnQUVDWvS/HFnckqO/YfdbO6k8zbhY8TY4hgrbM2mqd383iFDOYoHoM0LPFMi9CyPuyLERnxixKSHrtRLxiYGYFIgZvpoVqDlVOa/KFlWSpYhjxKsrybpKvGkg2jwQnEYz8KXkhPpFsqC/jg5Tb6FDmmc1bFVQRX8FRNvw3xVXXFEul4vF4l133UUTGyoxdBx4fywuJayjYPxWBRAArYvZS9mp6ZIlp43Q8LmAAHTOcGtg6AgtX3squCV/F9ffJDPfbSB9+uknQd4C4ks0SDcDbAJYVREzB/i4Hbx1QBR81RQgetZioOcInXERgDbtzDCkUFckD6c9+914HoZWCNkE3GABvecA9HXXXVcqlVpbW1sLhUfv/wPA3f3h8TFM5ISCg0bqYam8VCL0nG2tVWeczonjJWF8OHofh+vCZHGgx9LDIB7vUzTGFFoEtEj0EW5lMCsWKwN2QiDOiNUHGPovfzf3NL+PEPonCZJ+gc79uDXAcDhEDcBsdL6YQmT6ZA3nP//8n3720+995aov/9t1P/jDbx4CkZBOJwiG+Et+oPcIEcU+S4aizxOE8QDAz7S8hqUfCMLXDVaOrgRrwuQIVDj0wTHMTPVMoScBlEE2AS+DbAXVpDTZ+WrkwnYBaEPB4eNxREsFuiti7uevwgBQrZ7XRuBy0fMKntdS8FpKXkeXN2WKt2i+t2b55CNXzJoxsbVEn/aUvLaC97Z3eH66Nha9CDHLEs1ixCVquSyUl+Cvd/rRIlwz0gfBnHbnXNc0IvJj3Zo2vycA9Pr165uami688EJn4Y8AnlJwfQDr+6EtoF7BkTGdzJx1CxPdeD5hzipwXm6neWovAWhr+JzRklgYmkGbhCW4RqrbIalkmhEeTg+SVeNviI79iq1sSQUmVaCnD8qDUN4me3fwV3H4HJ0eG80EfTBeegDaKjU6IZzLUBg/Qt3SHCPfSzRGri2JITmyRsfGsNSkdwLczJOvQ3IlsMtBfAzUuYQgvwngtDA6NoyOjcKapOHxabQxTQ9P2SImFhtJ2aKULUJfGDE9Fr2x6MWZmiRRk1I9QUC3hE4FHRLaGJRTKBFMhjOgkUh7ofJ8SaI8f48kovMbc5SnwbMC0DREmpWND0tDL3M+UNltVKXnii88X3ghicmb1C3j5t0y5lsvTxrJpkahmZPIfLwQ1wYUDC5njnagSeD5ZLOuFwnNMo+oa/ImdYq1AKBonJObGTSlujkGK0MPxrOPjL9PimTrzSz3/UGfj0YpRDqTQBcD1ebLiQE7JGRLI3EITacHpPqARM5OxCFRckQSHUmyOkkOS9JDk2RpEq+IkhVhjHs5P15WQVkxEB8xEK8dCI/u90+RuGe7kFDpr5NF1U1kX//fZJd9Gxli3w5wMzkK3UsDH1FmszeQDgB90UUXmaks5ugEQy6DoYJB4APAXgTxEMB/+AMbw3AiwGQ/8VwAGmBCKib44YQwmaDwFGSsz9oraUuoMvYMCz2bTAPubP804VUJhjYDqiNRkxJ2sF9dIePX4nYUPuL3r1R6voZJkWyKVYEBos8CShrKBoAW9CpTaEmgM5CLquE/UFMERvEBpTefcFy52NLaVjriiBWoCr2UALTdtRrc3yD4NsS2YdRpSB9T8IBEeUjCsxKqZBNa2/vlMFj2ypzlZl+2rgXy7W6t6dw9NuVVjj4H1M5V4xZAFxsA6IiOcHDP7DDv7yDt6AkaRDtJLfP+E2RmZQwn7yfzyQZiROsna20n3RXtFZy/k9xEbqV5yUxNd5KV6APUYo9RC9tm/Eve4Iap0CWgtAyGj+cmb8axydrBWVM4c91aUz6Wuz25tT2SEyOal2srbyhsrpsy5ibNiH6WwjBQUHu0uEQWTkK4BofrS7V+5eIypuSQ8i577w6Fh4IZZ5eC7VboorUTrNAWoDFVULHiFLBsYC4hGNoO28oVesL15aRhbrXGILFCH20nJ54nyYL1QUqfId4G6yo+kpWieS+P5paGf84zD1IElz86waPuyc1m76JY9nfk/ka3ksntLZTe7PPv+OKrvrrSh8t9uMCH9/lwTgJnBv5mVjmB5DhWOY5VjkGpbjLC/Y3c3yjCjTzayJINKVuTisWpmkdycKpQ8OxfHpioiYnuidXYVNYEdXtVcqGH4fIe8VrmGIEuk9laWxYbJgsPQ3sojVZNeyZcoVGUESFxAzJUbAFjPrXbP0S7PLPXsynT+FyCNC4FBY2aVTGXMkAbQCcARZ7X3Vz2MD4hZRMZm8rSGZzN4myWYHNQ+GwUNleki9BYL5eULUG9KFmWRGuj6KgwXN8gcbAh9Tel1WPwFQ9uZgMns4FTw4E3cbhQ4KHC1eRm/g06hLieNto/pb32L0hD+CVBmcaDzZqpugyqxlLbnbSHzbvGsGbyN6lLj2sXBbewWSP+lBvnmvImNQPBDgcTqWwnaUO1O/nTteI3RugP0dxoJr37aVq2Jvx2L2a3YA0ZW8BkzBfvpnn+p6SXjib9Xqg+G8Kl9XIJ/qkvpxF9uQ+X+nBpVV8yKC+uyvMS/gbOTkiT45Lo2Ezio9MIhYeNkkZHJ+FGI0hTkEsSbmQBzgBWWIBXWLg2jQ6P48UNksaHZAFR0tksMXIgSw5k6f4snYG9mvembHzCuuK0PWalmDXH3ItFvVAIsZB5O5EsxhjCCAhTDmM7TDhmIrHmkNcklgYPQd9rrroEtHNdTGUBb8OI8EJZE3e7WtVeJsqrKg9DeSNw0cRRuy6SlAWUKVMQOVtCSjuyoUp+PhNaCj4TBMum9vrLmrH7jtQieE7G/dRlDhx93q2hYQcUD6GVyPmOm3Y3g9sl3cHkRMZnJuKARO5Hy1NXAm25EU+Z8m0mTaGdZdIqkLHQSIkhjItgZk5p0CTAvNkiQ/i1g8H4VM9M5UI8+WAbabgdH4Yn+v7pg9V3k6HqTYTYPKchNuiz1vrHP/5xczNamN55569q5obwF6a+GIqTA9XrK486FW7iCERG03jDyjhSo5nr1gI6A6ARwS8iB7JsT0VvIg4J4lfFyT+C+g6FnXyEprI70WVZfJ3754YDG4WYZjaPlGJnJkvqFoYU0gbbQejZCG1LEXCIwAvVftX4dDrSfgGZ0PBAPNuM7B0A7dgvnHfeeZ7nFQuFA6Z1g/4DwDUxzAudN8TBAxhHPCNNDHe/Y7eH04Pgjdd+cdZrjvMOPQiJI059lffAQ3P60omDssUnMooIX3CJQyHVnoKmiHVVk2nbgoNfDBZWYcXTg3MqcnlFrEQ/+vRYso/7R4ALNPK6PvKFqz7whas/TP4mRld7jLDj5wAjxW0je9VIygEA8dijf/7I+ed1dqAlcVdXc3up2N3W/s+XbqFGep7exA10dPxlCsT5E4BfPP34j/7rJ+dXk4v6wlMBXhcmi4Q+SMMBGg6shvNC/7UP/uHE666d9b1/m//ME5uCwaUgx2nuQVIG1gqyYABo7MEEhBkLaKcDNaMztW6NxeQ4WfSbu2Z9+hLv3Ld7W/7Ru+qKwne+Ubzll+Pu+eOU5yrLt8WnvjBw/n/c+OaZU9H8uc3z2gveuHHe56/urMj1O+LJsW5FAFp0ItWJLAmFRsT4oxJ5wRNerPoHE8cNkW8w6h5osIIENUi3pHM0OtvRm31r3VZ2NH8ceeSRzc3Nt956q1N4K8APUzh3EA7sR4CsKaLekgIRMbOulE9mchKeQan2VHZjRmO0wJ1LDso0MWhy+aCJ99mwPzeTzmcnDqMCliTMBfh7jLKqH0MDEU7DHzfajwJcI/U7Anacrxb50OtDO0lnFcYMiqVcfZoMKrfRF2rP9xJYQFsLG+s+zgF0QDDZf1BXvArgQgbvCtLXh+zEVB0rYaPWG6XawMX6lK2rnRLjiTFhc+mKMF3hsxVhuixihyKPEpuX8Fl02DsllhNiOS5WY1F4D8n4mI9PGQkfk/KuRhEdqWhLRXkYkbh+51JM8z8zNyLSA6gfZscwVjW3mXz1ys48jT5hpl27M8mcaMiVxpAJAE41Q0R76IqhKNV4GGZ8ArLhQIe6MTSHjhho1RzJOjBrXZmh5d1v7fw496X61ECQbpqQo00ITVaifDiYAWKWbambAJqtKPTMMKMDM1ZsAcxg9INMiDsYF8J8LSyT75Kb5h5SuFobXcEdd+YQyA3ja6isME2gY4ffM1CdXxnYxJITK8E8DQf0Mw+gPBB7laQ94hOZmIJThBhHXD3tXHVxOQYj7ync7sZqbKi7M1FjAzUhUJOrcgaadbNDqumSIF4VRmvicE0croqj5THqzUviaCVZG/0TRXm+CRcLhR5SSN8g+O23324soLdswdVBKJUqnQPQUqGTo09wwA8GgzNTMVdAOyG8LRzJl9rzM+EmszwzaIp1KdbtJK3Uc/LT2RF0O3f2s+xdDE952xI1KQpWxwOn09bxYoCNaAuvxidIyIWEX/SjGQCtoIT6B3r2lWLdGsgxFXmgL07DzY/agf4fShtCrvXr1pZaCp7nrV27uja77XHOzmmogyR4AKxTarTn6dT9+7m13XW58Z2b+TbAtRopra8g+pf/ocl5AGnERX5K0HhjhlPQOYDOVZ/Ggq/Ev43po0mNHVpGgTCs9ael4TaLPDaUInewkPAyn2y8TDOZVmXE3bSdsDNDu+RCDL8kTiTXkGpo/ipSqwzH4uXkTPNOsrM4h9K3A7xVw9kK3iLgLAFnSHiTEQWnK3htJVlTSVdWk1e6pMurKEtw1mKHBHx5xDbF6SlJciZL3sPi95Pbx6fJEcSknyQXkMvo+icArJgrl5GFmktM+SlyerCpreozdFD3udyJ5AsUL+ELuSZszCevoXnyWsdc7hoitf9ynpqXbgzrjJ2dsby7jvwFv0NsWrcSZvo7B74xWMyepS6sYxCfobxehtDgHtpr/S7/9VFmzLdMOhJv2C7rv4tLgPgNAAAgAElEQVTA3x+S5em1AJ+ntv0G/Xk9TW6u3bFpvavJwPBKMjf+DMAlGv4hkW+uxqcH6RsTdgYTb2bizan4u0QcF/H1frq2Gq9BE1o0pF2JktnYHh4kDbIkSBcHbH7A5wRif6T4VL2hwlNSwXpJJgtmxVyppYgciV5UHY3eiGm3FVLgWzGkgS7lZHqYyW1icss+2dJo6IdXSugcrdooLWepLpLtGzJLouhibmqXe3ZaF8/RZSg0DpET5lF/6+K000W3TM2F1HEkrTmYWk9TN0MhFjJjF/e6m8/ulhoEn73VMYGs2Q/hw+JubizJOMHH5fmxgo9joiapGJfLBGMg4qSTYzE55VMR+MM32yvYBFMV470xmx2m89EUlM0J+YFE/zoDveWSxWG83OwjjBVqkq4iyUxT8z/pYnIUwN+RyfaZQ1MFZ5K8WYGVswFy0W+DmpwN2sqbQVs5G8uoc1C0EfoWusqdkztiGo/Mt5DZ+MhprU5beX0G3gyZmDvM/tRwBhOvDeITB/1Ng8H6SrQ2iNeEyWojQzdfTtPV2/Aae97MjPeIKFkWpUtzIY5aw1Q7bMoWRvxgNNfNZBYG00I5COlx2aEofKERXywIxcGRnI6WCplMRACOhMmJXNQJ4nRyYipwKqC9YV2aigmMT8CewzCTiRiHu/Whokw8J3JrlmTbm5n3mqnApK0ZUoG8rJ0YMEwUucA4ZrkgZEZTR4lMg1ud1IwR8vauH/hcesOKO2axQL4lxCEmW5C4lsYgBi2jO6GdrEFOvFjVxDWjsUY/FswxQcLd1MT6GpI2WcMsMiDNXBtJaUc0wxHiDzA8pS9XOor7R7TRirs3GU3eftFAlkMaJzOfssVGU6cpY75iKyR64gXf+rZ36mbve/++oK//1Ync8NzgjAE1hcMEisRejqHlxdTbLrwKWoI2xxSSLUZotSWCQkgWV2luha2yHTQCDgZ/oLQZYQrVweV4zqdwPp3z6UxMSeR+kZwZyll9/MB+fvwLA5dSGIOKBaB/+ctfep5XKBTuuONWsnztB70D1M9ScUooeyk43IgAtNkb2o43bMZYQBN63oT9X7bguWawBvSXQf2KzBnvJR6bqyW8V8Br/PDIKFzB4vkinSp5uxYtShVRyH3W4tEE0pY4lFJHIuLl8KFYUUvI5eIxsjMwppTZduslA6A3bdpULpfH9/ScftpKUF/V8PoYusy7N/0gJiu8BIp9urlfTwxh+fdu6l2zzBvT5E0sez1EHNHT4p1ykrejuqHK51ZhLL1+L4VWBW0aEKViML6Szv7Jz9s/+QXvP2/2EjgogO4EWujMoSvVM2N9cAjzquKkcz8wHTfNnnfhxUf76ZcDcVnMP5OIK1PxZSa+KuQ3mPiuhrvD6IHvf/9b+8+Y5nlemZgsCiXMFD2vp9178pEfxeF3ONvC4UwOr97qbxiM3/D81vd/+9snj+tACuaLLvH64lmR7NBQToSXyrFBMu/7P+g8cq3XWUBIvd3zZoz1vnX12MG+GZK3g+7QvIRmmPnJyVAA2oGlWhB7ZT1hMCWsHsTCJTxaxqJFQTjdZ90JTN7ODqyqV3/i0z1d3Z6h5Rjb6Z14knfHfSu2siXb1dQUxseAXDyIPvOx5NDRIozZtSwwMVaJWSx9LVIm6ecN6QRuUHN6dASgrewdAL1u3bpCoVAPQD8V88/0p8e/mI5/IfX6RLmPdwzybj+dJsU6woDWpnwyQc/t2A4UlcvFX4bNO9P0sAB0S3581JKfXDUL3Q3yANAn0SC5D01XJLFryecguI1XPx9Hp0ZyfggTI2iNcA5qjqAlgO4A9k/034H+KZkkB39FABoEqKpWLyjxuNQ/j9hFiX5rAq9P4IQIlgdqTiCnRtDDoMyhSeomVROigde11MC15tnJ+QJpgKy4TYqnjg1GJcPZcViwuDGDJxxWLAyNGZfHyl3UnfLZAYlbMsOdkZ6JhE4guaFwylNnAciAZgSdDe6sCH2WlCrcb5iNhMW4rTGvwZQt4jxKANqW/78DQEc5AB3h6Q4OBzs6LADtdBXsOVJnR8omb1K3DMgCnp8pFOMDZcIg5G8nR5wJ3MSL+JqMDOv6lOHROTxt7pAAaN3zxLO9B872enu8N53mfelL3p8fmZ7AwVU2rpKMr6RjfNZe5U2RIisA6sN5r8b+POxinBuDN8caGZ8Y6cFStGpe0qLZbDulbAkqY0VyuGSnh5XL0Z+GiDlGAqANrzBaQCNgFxLF1a9i/b4IVqe6l1boFlqe2znG/cNpxw43c5+IQYMxHh8GfW44/HdHaK0e3ZaI6cT4fBaS5LALgZ0Zi96KMBphU74QG4IzfEeKjg3w5ABafdk2IA7w5avp4PZxEAo5fiQC7gBw5JE1AHrYGBG7h9zWAOiITCAfINTpFgXfFHBJDG+ripN2RMdv94/d7h/bV7Vy9Hb/2BeDY1+INj6XrnierdouTqyq9zJ0KL6JzPruJU3uAQJDHwf9FNkSDhLGzRA5tb/7/ycAml6NpoUpImcvS+gZ0QH8M7ll66NkNvsk2SwbA1U3lMUdxG13G9lrGOvj3xCZ+39R49+g4WoFVyi4QsBnFB4PGLlwMHnNID92kB9bYcf66TCCjorhxv5w/UB0VCVd6es5AUwPYWYIM2OU6REyI6HkFElTEz010ZNTdInF9c4Oh3waf1ltgl7WH3XnDVVCpIlN4+nBPFnIo6U8WibilY4sF/FykRxOskQkS/I8XuHRMkdWsCiTJF6RxOQ+Eq6ohMsH/RWD/oqB4Agjg+GawXBNf7iuP1yPEmzoDzaNIBvoUzfNS/rH9AXH9AXH9QUnbCfZ6r+WwQWJusRIrC8xkqhL2HBiSyYqKzlc+YuZyiTRF9kYBqH+qJVYfSyVF6Xi4gaJ5cVWQnWxlVg6JeVF+F0SWzkFURimfiYurpeLMPSCvIDp9zN4x/Zg8/Zow/Z41fZ4VV+4qd8/od8/rt8/ZhBlE8mGwWD9YLCuGq/3kyMjvj4WR6VqY6JXxbAggP0DMSMQMyI500gipyTQYbgy7Uk/QbS7wmcNGJpDpc7isusxZWziSHFqCcEIntO7SlFtX1MfXHfkQdTMVEvGxam6MJMdY5NZtPGV1m1ct+W49m6wjlrFElHvXKRssaJFixa1P2VexhS2X8dM5hg+pJXcAbvLfO6WmrcGPnv+XMZO3FEbtPl0uOet947P2x/1ilz5MZnmGDJeV3qEWuWIkmvqKvX9IbsuWwxTqtH9yAShxUlrVgt4NiDGm3MLxiZbwT1dLmhflQcrIzR8mkhzSWaIZEbtT7w+dYhMwzLJ/iQz0JCWhLCe6UwY2Y8JFM5rItl+rgypdugP4RUC67PUPELMJsa8J+IdsWxDs1ncmKDGm5MDZBo1atH5DqWWIWXbVbOH+dYwZajOobUNeyU7vEGPAXNvhJNgsDKyzUJQz0pS10VrOwUb1LqhCxm9NO+u2PntWrxrC9m637IDh3q18XXG4E8mMBh1cjPEcESg0F4j3wba/WDe+HYrYTPuTe4iTzdG+4gmdLPADUInAtCigAh1DQe3gHjdxjZWhVgVIl1T4ylUeA2WHQFdbTLMvIa7wHoJ5xZF5l3URmhtZm5oxr/anxb2HeH+63qRLbxb92m/tZOfcMuMvnJboZkAfeioitmnvcHrHeONbfPGjfWOOda79NPe/9y+/45k7Xa2aFsyazufOggTA+iO0DW/YLbPMWaayaIL329K7MZkwlWzdbP4g6E0xB6IFBltTHfQ+oVbYIYUyeUI2ralC4mU40G0v8kYOHQ9AG22SHeCuIwlB6YaO1KKyGGLY/VFFBz5hnfYoeci0S4AnUoPoB3gUDr5+z46S+nbQNwAcgtTp8WwIEbIqyeSXYx4YKRslrKZ9v4EQGtrD95Ke9s6ADqBUggFH7oqcGAIbyKjySqZs9RtwF4aAFoBzJ8/HzHccvniLZtTcXqVjTWNRcOpbLpOAN528KowbgBWXvmlmW1N3vgWb78Or4PQ506imGjxvI9vmXnDjROfGZjTr7oIg26PoUNDV6g7Q3nAf/9iXGeb1zvOmz3PS2BtAhM4We2hlbRqjVTZB2+ALZwzyxvfhoH73vSm9r7w1ApfFKSLwqQmleiYrcEFF35yDcZN9JDmotTi7T/Xmz7baysizUVX2bvhX0/pD06qsIN9sZ8vJg2KydvCpc9vfff4MVhgQpt3xApvMDxMQHekPAXjmTji4xe27deLFRaJkbno4dONafbuum0mF/sDcZK4GMSQWdtV2mgi0x5TLQB4mu2nCL4kyDE0vp/N2brjDe97X3fB88aU8Z5n7O9d8y89W+WqfpgVwdQXZWkArdvwyJEA6G7JO6UoCY2eJgkvCjkLMODeZQD3CggwJqeELDInxudUFKElx6D3GoAuFov1APSTTF46mB7dl87u41MH9UGD4jA/PTryzwH+LTKeel3Euox65LaSybuDysJqDZncAhrHrWMBXRK6G/1r6AwA6VD5DEg3gr4I4E6NjpMR8avcDPKKJHmTHyxP+Cyux5H7TLbKUn8eF4k1Sm0hZ2ETNauOaXyvLaCN2bMhPEkAHudwUwW2DMBp/eywCj+gIqYjQQHNkrR0ZYzyDZhsTeNxdZRcs6FFOgMBLWzX0NpuU+9p3u3VqPtmokuRKu5EyD60ZNIEyiQ1Lw+jRblLkYUgGxoBg7HqJiXblOzAaAOqTcgs5Kn7sA1Pt5OPGkqaP93yL2e+odvn+iWCzo7UmE+SLGauhYazjNF4zDl8rv0gFpwjyJjJQWfEqc3v5qPMKLU7Sev0sFyZcMu7d1gM9aS+dN2CpV5HEQmI2gvetF7vnLd6P75pYd/ACbFcrWE+g3EhWQrT5raF7gcVNVdpdgHc7DXRJi1jxierB0kHEsbKSfMSqF5gC0CcQoZpzyIVMkKYalgL6AyApkDG5Kb9AMB1O9j6FA6ktambQ3t+LIyRTlMouT0225bvVIEYqS/l9RSR37lyKjE+vwfgxJQtjsVkJLchT0BagrHx0SUQzcdQMg0GPadaB6DDh1Uawdz7QG/ViplgZwz9PxCALhYzC+g9A6BH8Jp5nnhOrtDqHZXg6EpyWKTmJDAz1JNCPYUI2Q3aiGkEk40E0Bvg8jedwdwUDq0khw2ES6vJyohtiJLNUXwa8at8mswJb6Tz/EEyr06JTSvHY3cPMv8bLo2GFRBqeFLD/Qr+4Ao1/rdzA2QKmJlxuX6KPKIuIHvkd8fpSTE/OpZrY7k6l7WxXLujuqTPXzoQLhuMDq+yxb5YGMhFkVocqcWxJFELIjggQhB5ejyChGq/QE71xSRfTvRVj687fCgHuiboBEaCx0VGj8fQMYg6ZW74uDW1O9i6jN1/7jIzUg3/t64P3V5mfmzFhLUlrCNOOuOkO5dOdGRGaR0i7WHSlkncEQ6VtDNiY8itZKLQSGTJYArJVAZTGQ69mQnKATsVU2akFL8bo8yK4aBIL4jUwrrOQxS6qVhihfEljNf+TEU9x25eHovlFGFMLEYHWLkwEYcgZRNGhqiTRBxCNGKLU5ZJwhdboXgSi9004aYYMo9l/GNU82jqp2oXZbeh5gR6dgD7+zDDh2k+TPVhsg+TA4pCQbEl7NQ3OUHW0Yx4FHeD0BOqsZnozhDaQ92J0WuN6HZiFK0NCtfKzzHdze2OkVrUQRt1RkznqoLDqjoNF8MshJFXhWZXAmgmQUJFFwBt+PpO/qTFqyPRxkXaVSGK5CLdkUBH5j+EE0WmK44+Y0yzRzDQrjPZdks21m8V2jrMvYZD7eQBR/eR1Z93WWedf17e/vgW8vfiVXEPjpZ9dFSALYZ9JheLR7s9BxUk1JGapSgpWc6M4FQRdKleML4RhjjSaOHBWRNLm+PUs+IyJwTcC5grTWHaFCdNadKUxoWamCtZ6qWJFVOsmMYocVKMk0ImrAUJHKzkFAoJ86yw1LPi1Gkrb8zYR4jTGv9DzJoTUWCqZBBeo1mZ1JhoZGnNHsi1DWqqK4MmHWRaSLYdQz7KbD6Gr3Ckr8iykpmXgEHGjTltQt7G6BpfL8TR59rhFgwwaixy3L5k8tYU1NrumAOPhmrtn25Xr9NpdYvtfjR9lej8bER351zvraHk+W7FsB+Y1DpTNtX9lqNpj3Sd6m9iui0lq22K2u1x7QnhCV5QuWhW0Kz2p+IFwQtCoLW1MGYxpJm4aA/tTdxJDLcqOURWdgyf8dFyvcXa6PyvZfIGN3urhvuv+9Mt6W7GR5N3v5tvD2uVu5+Opja3jGl2c9YSgjcoW377gPeB87wxnRhWbWqPN7HDG9PiTej0jtvkffHKA+++Z81gujGAhRFMrkLRp310TKPGrHRm12n5N9zfMp3Kot5kMV0MEXHGgIdKe1yXEzUe+STFWej0mfogMRiy+ecA0HeQA+Ij6PDEjlJph4kb1whAI6NI3UhxR9nQvN3dc2hKpKdhHMBadFWRr2HJq4LgyCBcEYeHpulsdH0gpSJQbSGiyVmAIrPrJ1MqRJyN5DvczAI6wX1ls48LzcTB5DVk2fnQMBsxDXsNQOeer6US2g8Xmr1vfuPV2wYWDMTZKUGCRqNt+WRX3A49O+Dw91zgjenwxpW8nmZvrOe996zeqz61aeOaHsRSW72WJm/yFO+GH7b3qd4BfIbmCFpj6Ihh+ov+Ye/4e6+n1etu8SZM8H7/x5mJymmmyeneWBYnsKiriAbIZc876wzPF8sjaE+giC72yqvK5gor74jmfelb05vaECweM8abMdO7/objH33hHQ8+/sGOEhEuF7xrr53ri4V0aIDzch/zIlh8+x3HHzDd6ypglz3jDV7ElgsYH0BnqI447x+91iYEvjsLXnfR6yliMMCJzd74ovfeczwmFgDMsICI6RzuJJifV9e0DfMpB6QrAkBS3e1BIYGZsT7s+a3HveoYbArDCv3ms7p//9DJz6ULnoO2KnQG2OYdIbTHsswkqhd4iCEyAJqBV42LUi4HuAgJrOEZBoxpRJ2FFkoxgqENAK0zI+iXHoB+DuBbUp/H4c0CzhDwTgnng74S+L/iaQn/uhTrQoZwuTl75/mcToc8LaEaF6jJ5Co4NoHyUAwuh+GyKSwHoFuQwV13o8ZAAHSqJwt2JET/SISwDxBJy/0AP64G747YplTPEtCjoEtDUeW2IZzWsAimMf5O0D8g8+dhQIq9B6ApFHJC9mtPA3xPwgUVWL8d9qvCmBDKFHUUeUus2FnbnaxHzjeerCaO13/DcbdxLHrpUrMtaQmgxcdTMiNFH+d6lAAKRnJrGrSpyRnuM63IsAo0oJ9uN3CxdXrXBYQtVBeFF2ij7YQZaCPq9PVjc8RidpZ3y7+cefepTd40C6HPpntkSLTTXFY/q8tYL7Bcpcs+dTFoY4jk/FDWA233282Mi0HbfCHUk6qw4ajNXnu711HwxpTQJaWnw+tu86bt573zXd7Nt+//XN9hAZsbimmh7I1VN2lyRoEu5occ+Irr3oUxERrOCIu24kiXDzAx9g9O/TeD+nfQ/UCR0iQoLuVQCg6McqNBUqw1Inf6+UB8tg9zA+QU605RDADdQos02kHbIYm6qTHucNRi250og0c1dffvlKR6CkxOYvFSDHYh3hGFKxIxk0GXoDi3Eppyci7UHck9Apm/CIBuZVBM0ZNjrA+LFPwDhVHt07qK8z8xK7/UALQie+RBOt57CODHfv9ZLFot5QIN+wUsI9eLiTvP7dLUaWuaKNLLqKLPSz5H8pD8UKot0T2JmI6EQsnSJFrtB6cx9UUJPyLCytspovpvydr6AbL2fZasfQ0F7Q5yDUuIyttyIzdk3Bm+4aP6P11T61HmTZg0tAywXEsJ+d8N0uKyjVrsaVqbXEZdk38kJ8E0tuQNLJO/Abg5lFeF+lMNksBHA//VcbguJ1I/MonWpvG6NFmVsiUpn5+K2YncL5bjItVGzOz5QkOnGji+crin4QQxVsWUPkqwg5UYrs7DC6lkLTUPVlrLMjoysqhiyFaPpEAKCgAlDKSRSUmD8cQvjAQT5/s3u5EbMTNSDf8Xr9fD0EaHMa79CpoUFEiaKO86hNblTfn8W3UfGSUHj291k0C2QdNouAoYvr/6/UZrCkOlzg0zxelrJMlKkl2eQQ2wn+T2euaYYfiUTiMylkbL2Miyk4nsK1iGOp6BDm13zZeGlowUIov7VMPgDBpCJx+GHCmjSDJatLVLdRFJ7PA1FJLO1zMnG/SzQQc+FEJI0UAYAVkjFUA/XyMU+qX2kS3jZiya42RcW+Ns2+UuGfXdmIhEc1tCQhtraLVZmKwVVf4TLqbZCFo50LN5iuYKNFcwgA1KFSWDPnMAK3vAvPJhKnQ/Iq2vLYIus4vMdd2m/HqH2eaE0Lr3Yo+7Yp11BvfKyPWXaH9uUmsA7mbcBmx2n27U+QwszvXhERstb2RUrYOs/c1bMG/EvB1M6b20BIgstJpjDDrJ6I51u+08Ts+pWWTnwxP9qKwLtpPBiE1m0nZxmQYYbjgkzqgoiLKh0YwxkXGNZvI8WpMQlENmJZlzp2tn485vbt7aJ6p6gj63npHybv0Nz0WTZM04I7MNt6DwSOjz0OvmK0Ovmyu2wlrGANYjpwaAJn3PANCcTE/y3UG+oGdbSKN723DWaOhj9lx5r3O7NOYNXjE6D1Hssa5ma/sYZnCqpJMzZbh6Mk7bujKNei/2Fkcyfrlc07BINK5cI9Uz0nWq1gDQaIWdSkSfDQDdgD4PA0AbGJpiBuLwIZBhaOevv/Oic9ton24DuA3paaPFoN3uuvP8KH/CuWG32UfMj7JaU6yh8pH2jw3FRvMT5iumQgtAMwwv16ZgZRCdcu89m9/3ro4ZExBRNIHWuoped7u3cJF3wYXe7/50yPZ4VVUfXoV5AcwKYHKINtFZZzbVur3I/lD9xF4IEY5rkxqHKlcdCZ9VqZyAHKriWeR6FTAUgL7zjltI+f8ZwJsE60U3bgNYQSeX04SYhoST5G+xZwA0bvC1h3hIOo8lh6Zy/0gjWyMpOZ2cdyS8mIhCpMoYjQlXE1y4w4xlpSlX6hqUvdqfEZSqUBiEQ8LkE2jYBM+QeVaMJL+4zcliJu8dAE1U0lLD088+Xy4X20peV6v3Pz85tr//4IAVDNJqTPBCJHRu8mHq09HSy77U29zmtbUgSrvyUO+Onx9SHVg/UDn+0SfePWGS19HmNXnepEnejT+Y1y8mV4yBGz52R1XO28He1NqD1sfj2ryJE72nn1+SqPFmxVLgDVQwYpiE4oMPT+0qYH+a1OG94+zmQBxO5AmoIW3DO+ndKg+860+HdU/0eid5pbK3er13958WVmHl0wOLbrl9ZWcRj0TGtnt3331CJZkTKi8i2R55oV72tW8s6mr3Sp7XXfY+cak3mM6twpit6azPXjOj2OoVm7yxJWTe+PA5nVs+3NvehBbQYz3vgvM8IRfGaqzPKPRWjhua7ZbZgxk7vnxax1mY6eZENKWsqBED7Yqikh91C7X63t8cc/gCBLjHFBHKv3DLuCo7e0Bt6IODtsKYF6AwAGWmxgjWoTh6VBk1ESnVyAI61c39QatQJ1Cgg20AvgAuQAo8i0H+YwlSa2mJadCOyt1Lu5vx0eXXrVs3xAI6pEg4vyNTrFuJjO/PFJXlQZBXp+yNIZsdiYKg8JWaeZoVeOrFzPM5MsACHK3h9QBnALyO+kC2vcxVH0P3jPN1PkE0p+j/ji7ntOHB5dCX5VCt5vrDoG8hOtF7iSj9Y0xtrvBZgexJ5ViD2mv0VkAxvhV0wLWISAy3OsyYdW2xlwC0wiDRgmFA5BcBftqXHu+rmUiZr3tCKNNo8gxP+tC0fvrDtz8aaajHGEr8NVL3h4at391xWdsZV32xpzj5y7VvefiM+S7NRehQQ4Tjddh9vrFxca4s37DsDas6D10yh35rV1fc83yjTtVBww2IsPtnZkVrvS/rVb2Gdmv4c9gGdDYemVGhYzxVO94337UVjrKqxnYYwYAxVp3b09k/+82Ev3uLd9RGb//9s6Wh3OK1tXpjuvDgcP5s76rPH/jcsydv37FIwuxIlSn0R4eEcQJ6MuJ4o9oiByX6nDohg5sN+TKp1zhAzIMEUHpRdO/QxygMb7sd18nMZwinw1tvvRV/2PMsB7QEbWZL4uB4JIb3V+HQAG2KvQSRl2xJtgdgtFVrpU0aTiYEBxfMualpmfq+hBZe9K6HUfVQr1VjlFgOOBOuZuqARI8hFL6YH88U6Cwa/2REzkP7OgrMotsinEa8fjE5gXfT8dvDABWtEnP6qJTiPKPg2GMLaAvN0szISaO6R8H1KXwo1ZsVnweiF2Q3GVUVLCtODnvVwK8cjzYjAvV1ByQyGHQ5go4IxkR6PAYuV1NCOavKlw7y1RW5vqqO8vUxPhwbwmZyB/scEUx/i2b7nwLcRUwU28j3xYLBhhHZ8iKb9c88EB46UChnSrN4tQxPCpHBis4r7JObjEvGbHSvurXC/iEICjfRyR4lve0uor/4CQYngK+RZffnHLPlf9ZwoYaPAJyv4T0SXpPqowK2xk9X14St8PlhvlhYL8gFmYjpeHohkeeRq16uJ5CM43psTlmOsVao8bH71Q3wbLbJ/LhpcCHNqwH10DwZsT/kMTTApWFCH5rmbvX4rodOO8w4g9dTOtq5yICk9k+hctgi9++pd3B2HKJ3WSAHO3a2eaurxLpdvwyZRoduF1hx8sYd3jjIm3yGNe/soYY+OCHR+ash+NKcmY1se54XrjNI38nF+vFuXxMdlanMeRygM+AeQHesvIB7VUGBi1GzNSfTpQhKEbQmNWmPIBMyXulw0rYYykZSZHHJhK60xeBK47ds4TSvwVZV/8U283MpdKRoOuMK1k9wKqYBtJKUAigF+Cw7l5Lzc+UYTWqKlqEy/9NctGntAZ2bb0vBilugmGZ1mq9nrVT/o40XyaG4XJ/WHrD+evTK2L4AACAASURBVK0Y1WlvcqRMOUHLofYEOikt0XKGXjvO9U5qXvet/V/LN7bYcO05Ygvkhd2HMhXar9Tqz1vbbX83X2t/KokfUb91+2eHfTVOhynbDpOH5LKxubJMXsDtTjbf0K/snZtM7f7pFy16aKK3FXLdKeNw2+X05dpujya/ywp3XaBuLbAz2O7QZQydeBuu1H7CLDE5B7phQh9NapFoy483fMYeAWYZe+RGGYcTY3jVPV8j3FMuk88WjiHrwtCSNWabYWqzYPoQs5icYq7ea5OMPIb86PA3j8WyEwVqnIyY3tDREKxsGXsoM4KTBCLpGcnnUJy0cQeEiLPd62XbwIY1Mf9ztAD00B99Ca/k929uFQObDxHrNWt0+Lrbtjtosq/HGSk3pyuSUZ2bFkLkXHbFfIpXct6SjCIjd/atO1ZpwD0Ccv4gzKG5orsqctKOZGYKh/enS3/6y943nuGNH++N7UAr0jFtaL2KMeE6vTUbvKu+Puep7W/YHm1I4SCAKYbdYZDjUdn2FHVjAyCY7V6+gzMnOggjMDWGi0mST5RiPFNjwmQJhXN4AESE3rVmz0GbALPBLBaL99z1Q2A/kfF5YTTfT1HnCTFmZosQBw9u3QDwjiiZPBAhOwJ2bzqMQf283ho636Fbk1aMLff/2HsPMDuOKm24bs5zJ0sa5VHWKIxG0uQkjaItJ2yDMbacbezFxjbKWbKNwZiwsMAu4f/YZWEXbMnSKEcHMLC7D0uGXS/hw7ak0YQbOufz/afqdt+eqJHTenl2nvepqdu3uzrc7uqq95zzHicAGm0zmJgBcyYpKGUctUVgMNaczZdFyyehyRxtqE4eKTuNIerZDnCFdnyiZSjIYrTcrdQBCFM0U2SoEqDu0IkmjbLdu3cvm1MzPtqZDrEKGfB5wEfdhFd++CNC8JcrjpA//9eHsplpoh6iP0buhxHwh09y0Pbc8UWeEInESSRC5s0hP/23RelUJS/GBa2ym//Qglqkg71e4veTn/786rQ+Fhl35OmJCpGUOv/Qi22+GAZlF0fJxx4hfVKtYBYqlBY0gAgSkQ2iQuynv5hUQCWYyyLk8Y+HMIyOOoT3ATkPpA/lBT9w9c0kFiYhL5k4mfzkF3UpDAac3Ce1/NXDeOcVR8jiGtLH3ZxRJzgEdJ+CBPSnnq0Mh1AA2uMhh0+WXOAmirDw7L/OjBUTf4gEA6S+mvz0bLvUda0qfODA98YsW0KaqsnBF4hiVCpGYVYmAk2TykEuWapEXYpE1Nv1KpZjV6R0iem3UKWlHKDYMCOmOY7jazsPzpxURuJeJMHDHvLkvuZv/n3dX3+t4Cvf9n7rgO/bR8kFraVPbzC0OlCmgx4yqCaRAEQ3UcNFtYhkxjPybICN6DylYqZBSkBj6RDQlFXJU9DOHWPTMQPugst8HIqAtjDDoSXQdOHdWDFpwkP4La88mNHmcWaRYnkZAQ0aATWcTgUFscKCxQDXAzxIj/+OtMSMEKMhoBn7jKEuCsQNmKKZbSiZikzTL2gimr8FuE+3lgpmMfNGUSzMdYB6cAZKCTP/IAWHv2MVzLDx8xFO++0T0BrIBrwBcMqC7Zw5GdN46hHQIyp2vqPilAf0v1f0cQAL/A5+dB/G4Gbd37L6yBRnP1pkAEtif3Q7dDP6270Xh32mMWgDOWj7dZtnAO0XzMA13csHb3W5JW4C2hmOuCuDX/O5JexV4SpzwTLOdRuh4r56bo7ATesMrrM17dfbQK+ry7TjTrwzfF2xgr1qEQfzMlbtG6mGXuGmrt47T5xp27o90baMFBdh5EeQoLWvJE727iKXelbxWn1ams7rUzSYqsMEGYppBsJ4LpEpda9gL2zq5OVFTSergM7/vc59mIL4mzAvw/rGflwh8tDf//736bCE7Nu3z3n2Lcug/dglgM6suZKHJE9HJPR+QLsXhZcOAb2Ug2OZG9G1E1VN6EzD8ZJw30WYP9BKDENAe9ISMWEswBpNqVahzOUpzML6cj4sLLKPyqfkqCsFew9UsRehgocODb5OdYS6LItH/Q1TNS3ZtGRNV94RCQ56oWRqA39FMT8nmXfyZo1olRlmCCwvWF4mMs4kUBiNaA+4KS9pj86pb5EtIYISOjmgzpprEGxT8AEZA98YIgIgeIjyMIFXm3npOl65lpdvMuERHXZo+hcU9VsAp6ic9CsAr1jwMq3/gNLT/24LTP8aYGT8lopQvwbwexuv0SX/QVNTsm1/CfBL+u74d/rS+Xe7/hOAV0zrgAXfNeHvdesrKnxatXaq5id0eDAt3pCVV9K0e41ZCQVhab6jBlGtlfQlqrFYtWbRQaS7xxih7vQ2uW5tuPmJu9dy9xX96v3JaFulMaf/zkzC1Is5rxDqJDh1c8SD+5krXeJu7W3VB0z+h/yYZwQ8tnzne8A++3Ln5TokF+nsuDN7WYZYliuGln77mlMHQ9fml6FXKAFt/xDDSzcM35PnOKBhrAi6NfzxYEICnMrqdJ6DczCTpGSSUQmnE870cKaPt1jIVNBmcsP0GY/yGAWYgwCJQYjRDoFNfd1lrqOg38YEDCJ0I0KnyqNZf/Aeh15iH2TURUMzMpqVjJ5mZZSH6FDHw+bkozkq97n8z6iLEL8s+l+T/xnn9T/3mIf7Od65M8oz5kx2j9E6lNrw25zjQCOcuxPrRzoP1+24lr+tN0W/t0B/6nmEr0bf/brXzDdoc9CUU3ZLf7wb9X6UKyNh2dUb3Ofnr6qTSxNTiVIMyjKaa8r9TnFvxcTZ3SkKc3WWetR1ppd57dpJSgftaJgDcL/NB2ybC1gcxJi7DfB2ZMzQBLR7QDVyfbgh2cjLR25zqG9xKOgeb49ct31B+rucozyajVy4m50NCN/gOdORs3dboSJgG2KdgTpKVbjgZpl9ruXudQIuJnoAGe2WoMS6e9bPZnwiKkvgXrrlhAorz3fd+KUvVlTPI1EvKQqRAg+6sbK/4nHkqhvJSz+ZKRhtWXWeZM0wcJpZ3oMJzJCNoTQCHj+bwdkXCgfYuWyEepmqj5eUmZryYYCXQefR93k4Avon3zO1r0viHZy2kIeKtFYoWTNMWAvwAMBOg/8QL47pStsENLWm4Jj8CgloZvmgrLSfpVh0LuYgPYYcec0obJt67kdAu+JggrJVocK1lGf/v6jlC5ydyVyi7js5D+h3gIDWDOurf/f1YNAfDZI5leTC69dnhYk0vDfoFhvKWpP/7efXFRXjr5lMkvFTye9fX6cYVVnBL4hEMSdx2i2NywjxkmCQlFeQrvQH0no5EtAGwoRA2qy6/xGfN4B6zSVJ8tqba1L6VB7iEqX/2VtHswKCFX/lJ+MKfOh3XBggT+wu4M2ZIg1z6wXSgzFHtZ/5UkEshBTGuAR5/oUKHhalYPIFZenf/3NtxJaE/sfnJmpQz5lJkTnHWTj85c2aRzdFPD5SECexAvLnvsVdUiWv3VU1H/loQkh9E/nZL+q5zFxDnWia4wVxgq7Ud1+cLogVqGhsJQTNyxkuK43NPtsEdM5Y4dBJgk54FQkFDXyiNecbX58VpyolYT8J+RCxKO63tJQUFJJgBMWnQ8XkqptI55F6WbjGUMdbOvLOuek9jWwV9ArNvAvgEMAlUE3LQsdnxkEb6ASdQ55+flc8oNktaFFhcgEsid6jXQAnUnJ7CkkcjFVE64JFDIuoRpTTFsn6vWD+fwD7URnHuDErTJb0BL3vkc1xQG3mObObgjH4fruMKhDnUUdyAVgfA/NrVBz9VZp2fJtgNolQIaAhCLsqnj7PqunHS2dS+R56PCKUCvq1VD/+vENCDa68RQLa8TRHx7o+6h7+cQ0WqWYS87/pFIYP81j+RcCe2VIhQjp8cdOXQ9RtTrkfA3K5hW+HgO5PCI5EOr8TazoaFExKwh0QxySwhyjzwcUsKD4XHNcv5G04Dtp9Gd1Xe/Dv4l7C1mTbspaHb2eYYV//rD7OGBcJYmrUVSy/AcUpI9qtRHq1JA8Ts9bkrF6ZVqaLxtzfvTbpy18mC2ajsXBsAYl6UJ3jvnsj+w8tzRo3cVCH2ZmgJA0FGUB9TNWd1YS+pOktgfGndOafizDigaSsCVl4QMEepm/wQ33u3Dk2HGEe0FQon4ZQQQrgZcX6BA9V1BHPuU+8MuRAuyBGQxPaQeXkONiA0h6cMedlJoeNFCqlj/tlCrXX9ElGxIIxvBwDGENZV2enQxDQLPExo7ll+jYUYIIGN5vwrAWvYso+S7BM2TJFpKGhz4K0pkvvBAFN7fvWm6Z2XNWeQLFmY6JkFqomJuNl4bRs9qjbPikOF8/OlEWMquAB08NyYGKpeZ28kWDSduxUq+65qD2YRhqLGvy9ihUU9SJRKxP1ElErE/QJoj5DUBfycm2Gb05nW3qzzb3ZZtVak4NxPcAjVF97i11uA3Q63gaww4VdVH56F8AeF9hCtto2gE0AjwN8DOBeTlnLqa2cXs/pSxh4s5Y3l/DmEtGskazFolnDGwsErUo05srGTMWYohkTDKgwYKwBEykqdGuMbhZrRpKaWMLMVfmt9ULu59ddd7c2XB8yYDlGbuVsBmxuw6KRWGj2wNImFOgPlHettf2ernCJu7XB3tbDLXFvRetDuO24Zn0DZmuOs8+7WhmcwZWSs8xLC2PeB4CZuJwsMewjW8fpgvr5JblOkC3Pn2Zu1s1+C7t/vlK3MvrKYD8rc0bL1+2HdIjjYT2AaOAYWLLCAlrfi2QrKRoJ0UgIeozTE1ktnoNakM2jMKvmwGlFA6EnOT3B4eYDkKDLWZnkcDU3Bm8yzPqD9zjMEvsgC+gpRLPaANinpsXZqQ1xPEaEMyL9T2SYo+p3Lu7zev/WeaPosuh/Td6/5/KXcZzD/Rzv3Nnh3SvoMRsRyYpibDim7Yk6YgV2Rz2403BH0ozqPTKo/39Xe3J34/k+1u4DR14y+GTfiyXueUGu3k/+wnbNscdvrvXp9b/iV4brVxtE9ebM2/18nEe+aO77YVR+0O7fwnUutlxe/zGJi6HOz2FxroSe1PaVcVXcA6qR6/Y4f4hGRvhq5DaH+9bVIHNNGNZ3gfGPdslmKCFHBYtWclNUJwaOjgZZswPOJef67b7gg8Yh7js8Z5Ae6oF13wPuTRwZMVxh8EgGvemtgAFRHZKKXi7IEzL8JFFe+vK5cY/cT2aMwdllJE48UeKNEU+QeH2ktIw8+ljiO/88t1e4KaM367DgkhqhOqKEpSi0/dhwLu++sKhpY0zmuXUAX0UZQJ1mt3e5PwPAKy9iiG3QH/jJv3zvYubz5/n7Lsg3dSnXcnCPBk8BsLzfT2f7FglKvIejBDQ64tihvfbNOTAq2g6Ptn84d74lVs8T0Gyd0RPQbt7ZSUgr6/Mo+/xLdHlG3y2Dim8oeQkOOrt+GxIcucBkUHVty7btXh+JBklbIxG4mwRlrIasn5uADmXVho5VJOAloQBO4Q8cr+pVqgEq0a8Tdf1mpaWPVNcS4iHROFm5jmT0NWm9VDCJrCNU8GfMmoVL8A5Ixsijj074Y+9iAXN3YNi1YqL0uwUhHZIZvfTMSxMLPKTYE4oS8vlnSzlzqmAT0H8Ww3/ONo8bSwq8KBL90PqCS6nalD6ZhxX/+MK0QAgFQIJ+sv7uQJfULmB6kAAS0BYC81eaNevvxYMMhcnUWSQLK9JG/QMP4iElo2TiePKTn9XKUC3okUspooNfMXyyFlKNOEAZJ3t1iAka6lDnnS4vR0ArljeDsYfJS4r3wHEkviOYESr3F09ixR/EQ/L6kLsPhgkKWwdJyRiy/g6iSMt0dSxoQdCJRU+EM0JZZQl9Bn4DFg8mOAS0Qz2zyrtOQOcIHotFsVNX6B8BfD6lzcrQWAlbfsErmYU83i1bkCnWXwGjE7SHAFosKBUk4vDOTmUoAppQAqhANidlxGpFuR2Mf6Cyp68AfEuDuzmj+rzg7TOQxFGoOYu35V/QtmES6mcXEtEJZbGkfpJ6sXGDKSpnyVshoNkzxThoSKNEPXxBgzoZIugtaPjAIBQuIgYX/g8GskgusESrzF4ymPFkowE3PzKaOmOf2b3kVv9wm0Pzz2NO5Mjh8t77ymAO2k1Du3Mw5uoD1SevhIDOi5nQV5T7De0aWvUjkdk67A3nfku533lDtzOQdB7o3WD7tLK4frS4AsRS1Lzcq5M0Dul8AGFeJ6Ie0M05lrnutd9dd/d6tEcWFZJwhPjDZNZCsuez5NfnazLQnIZFaagUjHJVL1T1AsysbdKc8vTRpoFFftv1DA1OnBVLqfUqfE2D3+aUqpznGUBV9UwmE41GA4HA1q1bTdOURclSFTA0qsP7WUHvEKwxTO+CadDTqKU8By33E6SOU5dVNkbxqVZC1cehxo5ZpkChayQXcDQQXKMZoqJjYIxXApgBhuZHdg0u+xHQLK6K+Qgz1wMBSC/qb7SY8Cy1wL0BlmIZumWqNvvc884Q0NihqdSy+K+q+gw6Hetj8E1KfWeY8IgzTHe0R9mJuB9JKj1GCWjdAwbt/TQvvtEMBJgIt3pjnoO2rXRsjMteEEwh17L1lOhV9aHFVw/JWkgyIpIRUcyoasUUiCtWuaLPVlQ7O5laI6s1olYjakvyUGtFN9hXuSX1otooKs1YqvW4oT5PMKYKmGU77mirMXcMHMWagawe5M2EYBbKZolilerWGM0sV/ViXUMYeomhl5hGqWWWWVaJaRQbRlIzkqqZxFRdVoLqpY6yTLK0ZlT9rVQGBpr0zBorIypEc5yN8Si2rk+iJatMoh/7l9oUQZsi6lNFfZqgzxD0GaI5E2HMHhKCPssBr818m3CaEvRZQ+5uyIXurez6DKxoVYI2/zJQFwrvNnLHUCXocxBaFe5RWSoodYLcIMgNuVtLrccbrB/YbWnfgUqrKC8TlVbcSqm7PGjjgtzAS/W81DgI9bhcrr08cPORMOh4lgrqYoR9jpzS1J1e2tW39NwriVMvRs69kjj3SuLsy/EzL8VOngufOBs6fjp4/HTYhejx09Hjp+IMJ04n+uFM7MSZyImzoaFxJoLf5hA7gSszDLNJfuWIvSZdf8BOh/mIR3g6So88SM9icNnvvFy7YMcTOHHWgeuMhjuq/Ok45/W+rpw8G78sXNfkfX0ufxnHOdzP8Q6dnfPo5R+3X//n1NcvLsxKrZzSIsgMTa5OY2muo7D7tP69zeCOa+ASQW56b4Gdtuv46+jxs7MYvlQX0TeR/RZg74L3pOTV2aPAXF6dy6vzsMT3+PRhXuXT8Su9cmjgVg5cgwH3AWgz7Xf0LDbAyJXGNGEYDL2v4Y5Br3S34zqe3IEJWqUDSa20MUVRHUxS1EmKOkE2xskoB2fDKhPzKEGxOAaaWjY3EnvP6rm9l+ExQJIOGpO0gnluEc7hjVDBNdm2Qw44UaCfgsU0uH2nWMxijjVGXzq3p/9w9dxgfrDDu8sbb8ht7VmATSngfFbTUePLhKBuoAtsKo0kmwlBC3ONFGnaeFNZkj6/fP93KlddhZRarITEEiQSIDE/usAm46S+gWzcSn77p5W9yvI+a04axqWhKIsxl0gaML9YZ8pGZ16RrFot8zsA/gWsdM73meohO7NMh4B+9V8OmXDOgu9Z8G0D8bwOL+rWHwB+YBh3qdpUxQwLhkNAIwfNJuDu6bl7Ss7q7xkBrWjzACNrf0KJst/SyFEW9/l7mt4md8Zvi4A2JfSQMgz1xg/e7PV6o0Fy64cIx62U9HKqGOiXMQkSUSDCKzM+/QyJFxBviPgD5LENiT6pLWWOyVBJb9XyZrMT/+Wnq4IR4vWTUJR8+F7Soy7OmEWi5VP0iKLHBCv+b78Z7/ESnw9lOl442txjLOjFlGUh0QxgolI9YFpRUS26lJ34/AuT4h5ShHws+fa3pvPGBCQXgKQx3Vn13k+RCHWtjxDyo5euzUhLe4WlX/nb2UWFKKDhCZCmVUSCW3vMuWnMLuhHjoaKG5oQk8ylHSvQTdvrJ9d/yPfHdMdzp5KhEAn7kBp+bv/itFQjQCJrsvsvRBOhMBXFgGBiSiikbCidzUrGoOW8CCkHxDgd5gGNdxU9cpygGvNWrSF+ghLY/gAJxkn7VWTVjeT628iH7iLX30LmLUI/6GQRQQnqCIkkkZjeup2IUouhRamEsY+zIhl9NnXF+jEYPOi6hQHkTP0ZHZ9t0vld14Bm2pj0NrRNGSh2/BlebZUxMNzfpZDXRdIHpNcsymjrNPMZejf/lLo/bxOVRahcaZQYRoJGmObdn/vT0F7KOyOnnFYJr5elsnWqtAPgCFWdPmSajyvmyqxeyUMB87mmYjc+Sk7ltAUYQyFjZzpWhGodJVNftQVDna5jYOWKCWiUG7WokiytYBD310zrRtEcb0IEIAEQZjrUgDRcgMIP8A7CR1tmaawxXzPzmn9XS8ws7IJmoCVJM1Ds28JTi5oQkHUiGnmggo3pGT0405OxPGnwZFAbPY8MauTjcvzK8qRNwpA1yLsIk2RtMJmXXBofi2RMkrWwm2JcuW1H7UdfOu607oqtfuUOOHKZuGyBKrvBHKWuYHYOn5LXLkDZVt0FE0JDgq3DXFHcKoG2c8qw7UhoSAsBxCwIKgZRDN8ASKaPIhdJRF8fKCfC6DkZKdcAijjrRNE8shoR1FId5vLmkld/UfbwVlI5BwloPzVwlo8l6+/z/ewP153nWjl5umVVZLmooiUANSvimm1hEsDLxDfpLuKCVmXBY1QSwRj4PCMBrWqahgbqYPDhhx9G92f8EwE7rv2ycU1aLafEpdegdnUV9bZY5JdHRAkthJKLR/OpqICR5IwQp8YFqVISa1VxHcBdAGtlqwLFNzCYCxNtDSPBYWvyora118U+O5m182lkaPBaSEQZikAWbbFxHtol2C7rJ3TtTVM3UAxJB+SgrSx1f+6zrOw74AGNXXuWyusfySg3ZYzpAqZkzPlBoPYUlRJiv69jIpLAq9IXZR+QbpP0WKQX0Pwg60TTsLvQdJ+iefA20NEthbl/qpaX9RKSSSSTJlpA4y5mLBTNgJSDD79yIfcuBlxf0mmCex3V1kTdh5tgSEEU0xuaOHmQAcnZrFrYpxRk9GQeRiKTRyxjRhB6MqOV6zBTg/kmLFGtmow0NyPPzijTM8oUTh/P6WM4o4Qzk5yZwNIo4Y0KXp2clSqz4ixOmi1IMwVppijMFvg5AlclZOZIXJXEVcn8PAaBm89nq7j0vExmXio7L8VXpYX5aXneCBDNmkvZmZeyM3l9SYqvS3FNFC1pvtVGe5pvT3PLKVa8fr6uq6eFl9dywnW9Pbf0dq/Poee23p7bUr23p3pvT/etT/etz6TuyKTuSPetN/WPZVJ3/PsvVh46tfjgqaUj48DJJQ72n6h5m3CaOnByycj7dX/r3ipfP9F48NjaZ74wd+P2sh37JgyPih373iN8YkvxE5+asXHr+BtvJm3LSFt7Du3LSPvyfmhrJ63tpLmdNLWSxmbS2IRShokoSUQQBXFSkLgC4LaxQYjTNt+JcoiDKaCHFyMFDHHUXAoFSZgGxMaiGPYXj+WBR+hG/6ONR8kQcG3ubmqINZ3Nh9zE+fYtVWJhzG2AoCc1RMm+tct+hzfk8bCFb+lg+jX+/mhhiBuv/4+biA31474/Dv59eD3f/iEN94u8/ZaHbCEWJuEgiYYw7UciiimpwyHsCkKhYREM4ER+9MDW3ivEYqSoCJ3GFiwgTc1XglbSsYbs+eT4RzfFtu0p27AtuWFbcuP2oo3bizbvLN68s3jLrpJ3Caz9IcodpZtt7Ng3YcPW0s9+cd6Jczd0nlrWebppCJxp6ETUjQi2Di37NdLSebqFtXnoVCPidL0LtYdODwv3u340dXdTh8/Wf3v/7EOnl/z6Tzd38Q9e4h68xD1wib/vEn9fD5dHb/ZuB6nsnYjMh7P8tZJ6jaxcIwhrOW51JrsiD255Jo/2DPffB76ZkxZJRg0nz2fglQUU1bwyBDh5YYqf35up6uNncuoM0ZoiQoUI5TbGUpKElc7CchFKRfRvKDegQoVyBcp4M8Hp1BeTTu3RzZRKHYxcKia6G5pU1qO/c7rLt53OLxSUtEWfSwC/SfOLKKZrHeqfjr4v1HuVfuU1jJiiRnQ9DlAMUKZrxaZewXET0sLCP7xR8zdfJg11pChIkl4yPkGKgyRGNQ+CPrK4lvzDc/P/0LPy95lpWZh4icepmQqEVzHNDxVa9CpQIJqVurUevZgxsz1NFWOh/rMDAHA0oH/w4xd16DLgdR3+qMPvdXhNh9/o8DMR/o5XGzUo0HCWhE6xlJzMsc8YfUiDBhwFBVrxIvtMHStZOKld5v2gbaFIlIu0v3V7wrnruJVbgsMdfud4QOv6BIAPg/UwwH0A94B1D5h3g3GPjjkJ/+BMrt8WAQ2qiiKZprq8o91L8CXx0QeIILdIRjEloL0ioFcyZ5RxqWunTyHInnpIfQt5s3ddRpvKQSgFvgyQPoEIwrzPPDPZHyA+P1LAj+0kKX0eyl+YAUWPKWoJr0787vNhnw/5hbGTyGvnr+7WKy9pnowZEAxM16hoPgsSWb5Eg7Yvfak86SNJKhLa+cJiTpucI6DNBG9dPWsOSfjxWG6+NvzG6x/j5dsf+CiJeHFJIk6WX0X+mK3rgokX9YI/ppH7oAS0XzWDFkR4fcmSxSTgI94AufP+4jd671p3U84ZeduOgt7satEck6XzagXJd7/DHVDLAzICEnWCczhoFwFN7xKrnwQHWjNo7jvBJIpevXYtGVdKPngTOdDZkZIePp9Zc0lsSGk1GaP2fGqpqH/4/Pl7Tp+94Y6HYr5CvNqRQhIqIMfPzhLkYhNNQ14OKgTzgwD/CNabQCWXddO00w++1wQ0S+RElTiYEM7LinZzSipVkCjx9VmxS1pZL8zKwA0qfMmCc1RM87RpbubVZgE1TzHRIuZahKDp0t9wEdCYdZDpb6RVIupFmXQzAXeF0AAAIABJREFUwDMABwHOgPUtSfl4VqnhrWLeClEWb6CwMjMMUBYpJECSM+fqcA/Ad5Bycmhz52HqX3krBLQFuoS6q0KWU5RfCNyOdKaDkxcC1OhmlWrM0s3JmjFJ0afL6ixZnaXIM98NSNKM9wyiON0NQZrOICkzu/sq0tmpANW6NUuFGao1y4EMs2SYM3pIMEeAOSLMFVygH3G5AHMk/HYWg2TNetcwQ7IoYJpgTk6r5RmtXIQKCcaJMFawxiDw3Vx6RUAaawDMIpvYSlB6i5VJRpOl9WhaD6e0SEqLZNRYDkoiK+fBy4kRwNbMKImMkkipCFZn5TDtoFKEgS/OuAEFBhTokBgOBq6Dq5mQ1CGuQFSyggBJA6KX+nIjFaQRkUf2qEjRFvAwrUe6/h+/X3PDDSTkx0TGxUlSXEpuuIkc6Swz1FWW0aSqsyyYqKOsZI7Utp2gqQa0UaFrt1A1nu6c5H3uic4Zy1hePkKI1+u9/fbb7ce9B+CMbmwU9FlZzaPpAV0LWFrY0MMqduYsLCtPQPM0Fidl+rPGJF6vVo1WCz5AFe03UbvghxW9RjDGUuo5QGno0RDQ/v4EdD+XeSadRvN7hDIQTaPvbbMGuw04ZsGbmDNPQ7gI6DQVg36nNKB7RPWoYH36knIVB9UyVKoo/THJgCkqTKMP8mwRcpDxMZyTMiuzMCNlVr7Oj+FgNgdzszAnC+jwIikzeWUGL8/ipJmcNDMjz0yJ03q5GWmxSrIWG9CQkqpSUlVvDvN7JYaFKZFhPn4rzkoJs1J8VYqfr0GdBos1WKjCAtnEgbhkLpXMOtlqZJCMJlFv5rTmrNqUURpf757H660arOS0xhxQRmMAajm9ltOaOXUZr6459WLZsdNlR06UHT1ZTlF69FTxsTPJY2cSx87Gjp2NHDsbwvJM4tjpkhdfmfrNb/qe2Ef+/7Qce/aQfRR7d6HK+e6dWO7dRfbtRjy5jzy5lzz5BFaeeJLsfoLs2kd27r0Mdj9BNm8n6+8mbR1k5eo8Vq0h/bCarKK46WasrFyFtu1IEHNH5xBAZ5BoEBELIeJhJAgKYlgWxklZKfFHiSeehy9GBsMbJQ48EfQ0eTtwmvJGh9jX4L2zJe6tnLovSgJREi0gkQTxhXBQ6g3998MTwIMJRjHdiMeXg9eP/hBu+AK4QiBCgjESjpEAdfvw+YjPi/AH0DXhMgjQ1Wjp8+OwPAcfuoDkP/qJLzAinA2Hr+DxDD6kAPH7bPjxsKNRUl2NZHrHctLRQVasQKzsQKxe0R8dZLULK5eTgaBbsW1HKt0bjmYT9/qjq69YRnJYTlYMCWcFWsmfyGiOh60zuiPJt/x+Wt/9Ow5Xf38e+V/qUb03v8KKjvzjsHQxKSnC0GS/n8RiGCE9MiIxkkOUREaBkVt7Z7/1eLE3ThbhKeSOzTnakStxEitEEYBgHBEvJrEiEi0kkQJEOIELA7F3Bf4ovsrziBB/f3iDxBsk4Ti+LoNxumaM+N2IE//bBGuNNuKLEsRQw4khFzrv9FFW3I0ECkikiASTxBcngQTWo4VDI54kORSSgiQKokZiZG4VWU579bWryUhYQ9a+l3AfzBpy+3ry5NNkzz7y6c+QJ566PD75NNmxCzf5u2+SE2dKT5wtPHEufuJclJbxfHm24MTZgvxHXCd+7GzszCtFvdwyTlnJqcs4tZXPoRnDBBkwWHAgZL1Jh2bVrOekRSl+flpYyEmLcpAXcnnkaPSMNC8jzRP1atlcLOrVgrowx7ArVZwyh1NmMad+TslNJXi5ShJruWydyDfocnO6b65p1PT0jJHVWVlulqK0q/KtfGrjge9++JZrJ2NyQj8pCodjvnCQYDK5SJxMmUMe2EzO/XRiVqgCmEM9qf02Ae2XrbE6rAP4a6RfqeyGSWUpGPPlcNCMgPYFAj/40au6pVPfUE0HRQdBh9+L8L0MPMDDJFu2ETVMHHIZucT3DQFtmgWGMs2Q5xjqZF2p0OVJhjwD1EWacDdNOJSbPb8FAjo3G7cJOAssZfacSkLQjL9jJ1HNRtksw+tCvcz6dALQ+Oy+irEJlK3wxsk3nwuIMFk0Ejz4+jAlIOFMX5qrmzKJeHFuj3zul78RzerzeSNJPaBjkjJelOsefZwE/PgSWncz4WBlypzeo8Y5IyTqPkZAY45sbdL57vYbbsAsglFCYoT85AfrOHUGI6AzxrjjZ+YXJHAXIUK+8Y2bjxy/s34pGZskcWrNWH8v6VbrzqtFMhT1oWskchyYxRJQVsYAb0asmTKRhOlsZNOOud//3lWJBLLqcxaR7sytvfxEjmo4yOjsltuQBlA70QcRml8yZ45g7DPLiIXENPVlc3tDo5EHSJonAF5FifX1Fb9xcdzF1MysNleGubI1QdCSnBwU5IiqlarKFJmfx4tLX09X7/4CPXk/ekPf+XHCwbzzMskgG1JtwOepV7xo6WCapm7p/10EtAKWApaJd1IvwI91bS8vLcooXiroHhCRGfygZHzegrM0wv1nqP6sP6IZ9bxZzlmYRoZDqjqkoQDiYA9oZJ81CCuIAlEry6aaAb6H4Q9wAmBf1uygeq9RGUlq5m+Ixga3MgPjp2ie1kQGyrOwHODbAP9Fg8ovw0BfMQFtE1r437AAen78408cP7Hs+efn7d9fdeRIzeHDiw4fXnSos+bQodqDL9QdfKHu0P7adxCdB+o6D9QdPlh/+GD9kUMNRw41HO1sfLfBdjS4/NErV7/xp4/K/A5F2MRl7uWy6wfhTi47KmS5O9MUGeGutAv40f4qy92Zya5nyGbWv2u4LZvJgec/IskfkuQbs/y6dHZNhlubFdZQrMrwKxFCB8WyjLAsI7SNANt10fFhbE0LzWmhMS3UI8RahozUkJEaskptVl3A6VWcXiXq8xzI2gIHirrgsmAri/qCAXAakbV+jYjyDE6qELUxilkh6WMlfSxGqA2Cqo9T9XGaMUEzJujmRMOarBkVil6qmkUGFBqYqzcg0KAQpqbCYzfrMdFKVyDBVAlqRav1v/5U97nPBiaUk0nFJEJIoY/Mnkj+z1enivyH+7h5SJdTAhp7WivInncUQ1AWgPZ52tVoOETI/5kAMoBqmrqhG4yAXr16NQD2nwB/MGGvZrZJZqGgElOJgZQEqQDUqGKhtLQAHg48PLpaM/i70W46SYLrdRQR/mcq7HWIaiLdoxhVKa5YtpJM/Zkl4RlGgsPxgMYXh8tq3S8tNeqOUQjU1ktjetbpaIT7Ieo+A9rhkXpmYBIcJr4aLB00Dd3A29paAgFUfWppabKdvvOXZhS1i2nzu7+9+PB/9Kx/k7/1onB9N39tb/amvvStvb139fbc19t3v4Oe9AM96Qe6eu4F2N6deeDY2SWdJxZ2nqg5dGpx5+klx87UnjzTcPJc08lzLSfONp0423QM0Xbk5MoDnSu/83zr//luw44nync8Ub79yfLtT4xl2LFvrOOjumtvxa59Y3fuLd21e+yundN27ZiD7M9yZLKWdZC25ZjwurkD0bLCxnLS3EaaWtCTtL6JTJyEgXj+4PAOpHHqYWqXfh+JRkhxMTpvRiIUdEqcn9YmSDThmlHH0OErFiZFSfT6RCNKIdaLkqSQ6swUFZGiEkRhGSksxXCxUAThDxFfME8a5kg9F43IluA4LU4SNDoqGiMIOp+PJfC8YgUDge1HSaIQG89Psey5VqKIJIpIQTEiWUKSpaSkDBssLSFz5pAVV5EVV5NVV+Wwei0ZDDfr7SbE31rd3drgfQ23xL2Vu75yDbnnAbJ9F9mxZyjsJTveW+x7mmzeSfZ8kvztN8nxc2Mpyo+fKz/x4hiKcSdezOHUSxWnXxl35oflZ39Ucu7Hxed+XJhW29JaU1prSGsNGb3+cmjM6A6a6YZNWKoteWBruQbTWt0wwN3ZYOsPLhtc+xpwYM0ZrTWjtaJautrK6+293NJefhE1Js1nM0xOnMeJ80RxvigudGGRKC4ShcUMAl/TD0K1ICwQhHnDYAH9lpXVAq7MMNwmw6w/YKfDfOS4RRy3kOPnc3zVMJhPv6Ult9A+GPsUxLmCg35nNMxR5U/HOa/3dQV/x8vBdU3e1+fyl3Gcw/0c79TZcUI1J9RkRERaXMIgGS2i3vxm77ys2mB3Rw25PkdfmtaXuvuflFqfh9KYuhzsBgd3Te/8EgmW9yl1WaP5334z7sTLyRMvlVAUnXjpsig78eK4Tz5LPvksvgV2PkF2PUl2P4Wvgz2fJPueJk98mjz5zLuCJz6NjefxKfIEw9PkCRv7niJ7niT3P0g6VlGr9io0WveDy9p9xS93d1OryYqVNlaRFaNAx0pyRXC32bGSXHMd7mX+AhpkEyPxeD7yxh06kx/RMQMJHVklklS3gQ78YjE0nwyN4cJf3qvlRYUojevzkkiYREIjIRrG08cyimYhdEoIoi/CKBHyEZ8Ht8XBMN1XOIxjYxwej4wIqZpHqheRunrS3IrD9aGxgiyz0dRKFi0hy1eS+z5auGHzlA2bp2zcMnXj1okbt5ds3JHcvLNw887CjTuSm7YlNm1LbN1asn3LhC0bJuzYNHHP9olP7Bz79L7SQ/trjxxqOHG444XvdTz/3TXPf/8Dhw7f+fyhBz/9+Q/PnB3146wI9QiCHmQtPV4cDIci5KldHjWzyoRJJnoK5wSpZXMKwF6a2DxNZ5foAm3YHLRDQ7/44ovYqM/36qs/sEBiE082TQP4jQCf6IMqHlOaoaIsE3t0WMS3Q0D3l+Zw+zsPrqMHtJ3lBSv9PaAx0ziT2xZ1n6AGs2ooq8RSQlxUJltWPZiPAvzGmTa+BQJaZ0mXkDlE6lAE6C4dgz9ANEyeeZZosFS2ilQqvkEdzaKKuXrGOBRcJoQsbSe/uzhOBI9iYKArh+5gobRU+fTT6DVTUV5G+WfywuFJaKAwE6Llk/SYJE8VpauvXoveN8EgefKzpFuZzsOEjBkRTI9ook+cogYsqwJg9dEjNQVRUhZDAjrhI//xq5t5eVaOgNambdjoS0ZJkJDiOHnoY0tLSlHPBQ/eTz7zzPhusa5bi/aaJE05Dio9iRSwQm8jFUhvZmFRghLQQfL0s6uuW5MoT6JJ80tfq1VgVVaJYNI8SlvTaGvcFn8qC3lniqEJaNTxHIqARk9+KpcJQDSdCHJOFIJm5/MDqtUEdIMoCgYmm0YIoBSg8pIU/VOqkQSJN0ECJWTdenLJmpeFgh7MX3Q7wFmwMkApBtPUdUt1Sz+/exIcPp/vpZdecu48E9lnTQGNEtB/VOEzvHYNp8xKSaVZc4IIjRp8zLC+SbVjumh5sKfreoGrUqFMRSFmZJ+zqMGCpg5qaArqENWtOJaYNt1DwwSiChQqRiVlnz8JcBrgKMBnBbgqBYVUpxXtBAqEWRavwQQ0D8EsRPpgXJ9ZL6MI9S/oPa/QrsM5myEqV0xAo/SzackyaFmA89/99obiIowjC3iR0YhGcx10OJSLQQsH0NMzjwC+QvrhCsPKwiF8hFlwa4JG6SYLSB5JzB06HIoKyGhByRRGqSCrkhiIogQpKyTlRaQoQQoimFyu0A4BTkZRaX04DBcbiEGacUQigWAkC6vnltOgTicAsCCC+30P4CPITM2ZQxoaSPsyNJWjY9dKHLetWk1WryFr15K1V10eQxMrV5HVQ+JqsscetuLI9amh8eSTZDi4N2HD38HtDLHtU+STnyKHjoR/8GrFC53BYycTQ+L4icTxE4mTJwtOniw8cars5Ony4yeLjx2P/+CHpYePkpd/HO9Kze9T5vaqc/uUxSm5jpfqZalBl2o1uT4lNXVLreezDbJ1Szr7UF/Xp77xhfVtC8sSlIOOe8jYYvK956af713WLVdxMEkyC3SIoKILhAVjqqavB+0M5ibOibA7DzUjoGULNMNQ2VCjrrYB5Y2NHoAfataHTZiEoU8qMaUIEtByHJScB7QIPgF8VOijgIMJaZjbZ7UKGEjxNUyFDH9EqXf170H6mKLXSGahZKLHN82gwByZmYITe5X0K3MjDxRu8tPuiwmrYbpaClyZRm/4BAhloSgNk3lYo6Pu88uUfTbYAEi3wKCjIdNUTUtEJWgdTCSg8W3Q1tbipVkH3gIBTY3VPdWthBQQjEgqJP5CEkiSUAI7tGiIxIPoOeuAdT4x2tfFY+golCigJGmMMq1RzLLLvG98YeqXGibeCDqERhI4+EsU4tMdiiMCCRKII9jHUIyEYiQcRYfQEOtLg5hNIewhAQ8NafKhshYCh5QUARpCRVW50OvTh5ZmFGDx4QAg6OsPLwl6cSyBYN6lHm/Qg43VL527cP6UjmU1TQ2zEY0zmxpnNjfNaG6e1tw81YVpzc3T6pdOvufOq3ZsuecTj33w8ceue/zxqx9/fO1jj6/4xGPLH3+07bFPtD62ofGxTQ2PbWp4fHPz45taH9uw7LENKx/fsObxjas2blq5aUvH1i3Lt25t37q1devW5q3bGrdtbdy2tXnbllaGrZsbd+9s/+pXPnTkyOMHDnzswIGHDrzw0QMv3H/w4AMHD903GPsP3HP8xEPf/edb3zj/Nxcu/c2FS1+80P25C93PXuh55kLPM129n+7qe/pS6lOXUp/qTj/d3ffJrp4n3+zac7Frb29qV4bbkOEfyfCPZLlhkck+7CCdfYjio+ns/QjuXoq709xokeHvcZAV7mXghXsp7uaFO3lxvQu38SKCEz4yGFnhphS/NiuvzMorU+Ky/mhLiW0pqaU/mlJSQ0quy0j9wIl1AyEt5d4iFmfEGl6uoX7680VjLpO0lswqivmSmQPqjGtVvDaTU6dm1AkZbWxO7MWKcVaEio8XUM2xEUurkKegwTRJuyzicuE1bIk7wmbIurNhgqN756zIAPAQpWD5YJ0ySBXSvQL4eQvFcBSICgZqtTMVnZyEnYkJYFgGclvh0UkGlUtd4Oh6DayYRBsAWwFs4JrO8itd39lwmArTERp9OfDA3MczzC4GbvI/aDXnl6WToNyvPKg+8Ed0X5PR192Xxb2Ve/n/1g3n4RpYyd1muk/LIaDpbwWKHlL0kGQ4iBhQ0CeQHp5k1QBTlRUgRhERqAeSACFaYR8jNKsH61JGVdqtsTbfxZKHKOv6JEgIKJ47Voapo8YMDPbKzpLNxSY0yOZi2VyMLwIGfQnNS8GyUwzKUeHOV6EtsfNVuHIDKK2i0ooxW4OhtmaVlv5oyyptWWUZQu7Iyh0ZaXlGWsEpqzlldVa6mpduEeU7B2G9KFMot4kjgK2DpbuFu0X5bkGhkO/lxQd48UFaPpArpft4N3CFPLLC/Vnho/3AP5TN4WNZfiB44WGGDPdXfakH+lIP9Pbd39X1YNeFjZcu7HLQdWFX14U9Di5c3OPgzYv73rzwyZ7UV1798YaDnXccP/HRziP35HD4vs4h8EDn4RHR+WDnsPirzk6Ghzs7B+HQo52HHj3Y+ejBzscPHtpw8NAmii0HD1Ec3Hbw4Lavf/2BBx9cunPHVVs3r9q0sYNi5aaNQwK/3bhh+RP7PrBpw9pbbp6/rGXCsuYpy5orlzVNz6G5st9HZzmtNNdNbmmYHvBgorWgl/hHhNeHic0YfAHk2QJh4vHTUTqlEy9bhBMYx4Y+QzR8DWcNEeo7TycILGggGMFpRTiCbh9hP4kFSWEMNwl5SYCQZIhEvaQ0SkriSI+wqD782s7EFvRFnA/BACmMkjERUr+AKMZ8DUJsjiZDRFQbAb4P8GewVOq8iykIBxPQZ18aQECLmETHksFMARxVYC1V62a+R14a3G/7IVGWcigP6Jyygn0kbkI5L8HhIqDdKwxZ78c+D0lAU9UR58D8OHLTYzrMp3Ic38aLYP+NjoDOT8hNmlNIx83RdVUAuPCHP+8P0VR4kTD54pdDGiySIcZIWxECKXncd/6poCyCBHQwTJ47vEiEGTp4AWKyRhRUBZ354pklySjL/ufDQBsv+c1vGgV5CqbBNXyiFhGk6VzmxmmTMHNgUZR894UwD+N4lIkkQMlHAA9AWV/33B+9XD97Min0k2K/N0rI2ELC9d0hqDMFCPJAsuqCVR0kGSQFPhImuWx+wTCpbSY/+Peq11MzNZjSp5M+HQlNAw8yqlIjBuWRMQ/hpb75BRG8Tf0h8tW/fag8Rkoj5ObriCpfp5tzeDVn8WCx4cx1molvsBxQdsl+QpYjHskCZk+wbwIm0oo3B2WlvbpFDHp7Medou0R1Dmpg8WlWQFK9qhHO8AT5ehjzy9/Px6fHS0iYbHyiqFubLcPUtHUtwFcAfgumhk+Bih58piVbliP9bPPP9D9KEjtg90D+TrDvoNH9b29vJ4S8+OKLzuomaBpkNMhQJveX3dp1vVZln7ygj1sjclsM4Z9A+h1ofYC5+H4O8OmUsSprTRUgIaLKe4AmA4xwOPLwoL67RWQtpOljTGOqaY7XMSoftT5Rl1Yfx6caUXUE/gmMjbp2DWcu4GAsDznnR4n6qttXFSl+N7LgvQDkIlRxxj4T3QZ76COg0WyeBrXBDH1RrpiAZr6IeIH+L8ChF898BDvEQB5BHyVGPKh95o4sC4UxLAAjcGngrT+ENyeK4TqgrE0whlwMC+DKlzGM0s3B/jZAo48HxnNRNidAQ73CCYz58gSx4/WFSLIYdc3cQN+94TBoZfeGg+slhWhoZSgtIgNRTEptlBST4cB8BotLUZOBobQE3fQYBmw1cBeDdlpWTN4RoNGYWpId6jwWpzGGUcqUuUpGn2HpEGpxJNRytFocw99Gj3wjdgu5pqi3I/N5ZOXAe4CG+LFgOvaVe2Ws2w0i02eDLQzE8FaJF5LCEhJLYsgSIpGH24MgEqMZBUMY3M3+kP6j2vdlZZS7jJKCECkKkGLs6lGZKx6md2MY70z25/FiBHfEn+sIox5SHCYlMXyICuKkpoa8/ma5CSHBJH1CmaHdiVlJjT+CYdDxgdNRsYpJza6qYYqs8fb25QC6Bb+y4O9EealpxEzTZ+leUw2Ysg8kH2h+AJ9peXiZpGUPqp3oM7PaDQLsVaFTgZ8CvA7wJ6pr/0WwrjasqQoUKBi04afw0kyqrMxZ0Wlvn19OPaPZu8Omnq2AYfmcnB46jd3BlIN6qEuczSmPKvq3Af7VhP+rQZ8Mogi6CGaPkOVU2XB7fVNtMk4QDbBuuOkGRry2tbUMuCiX/agZxh9ffw3tvWEMYwyXkmg5CZZgRmlvgIR8OLaL+RHRIImHSCKM5qWiOCkIIzedU4ClBqRYDG+YcBTp5mAU5QUC4RxY4uKiEpIspBwx45EHlx6bYqZDWI8PX4+UUs7dMDkC2uGg8YbDW9rxLPZ6iceDRsFwCMshvIxphJaXNur1oO+z8+f30fgtX27MHfDjx5Avj7CXMODY10Pmzhjf1Di9qWlKQ/Ok+qYJ9U0VdY3j6psq6pvHNrRUNLRUNLWOb2od39AyoaF5EqJlQkPL2IbW0qbWwqa2+Oat7Zu3N27atmTz1trNW5o3b162ZWPblo1tWze0bd3YQtG0ZVPTlk0NmzYPi81bmrdta9u2rW3jpsZt29o2b2neu2/5o4/P33/w/gMH7zzYefvBwx8+dOTWzsO3HTly+5Ejtx89esexI4ijR+84euy2o8duuSyOHP2Qg6PHP9h59Pru1JOX+nZ3p3d0Z7Z0Zzd1Zx9HcI/mKuzjMOWlzGMOutIfZ+hOfbw79fGu1EPd2bv6pDtS8p09/G29iFsZUtytFLekOBv8B1P8Tb3i9b3itT3SuhHQK62zsSajrszqyy+ml7zZvZBXcUovKs2y3A+K3KzIjZo0CHK9ZkOVlg4NsU4V61xfLVYlhCYvoajV5DzoaosVsRohLVDl+apSRTFHU+ddCeZq6mhwuTa12YI0NssXWTBZkEsVbawDVR8/BIwxOiYFimsQtiAhaF7FCvKqR8Z4R4+kkb8MCCrVnR91+dbPWkeNe4lKbWLOdvDoKI45dJoHEwIm+GiyVo+JLk6os29i3pEIQMSiqposlasJ5J0CdSLBNx1OHqmCp2yS9w4uBVKVTiolg3AKXjGFGjmGzFoxIInFW/vIVDvfJ6WJWToSFkQ1K6RDWLNCihEYDPoY5p5EXiaS6pVUvyAHJCWqaElFLVLUEkUtGxKqVn4FUMeqar6vcDoNrOjlw8LVvfTb5H21XJ1As9WxnHWjKJVKRZmeQ059cbYiz9b1qmxmmmUtEvhZulaNUGt0dYmu1iKU+kFo1OVWXVpuKmss5TpDuFHL3qwIN6Wla3rkq9wvu27x6m7xGoYuYV0O/LVdI+H6Lu6mLu6Dg3ATXX7Zkm6YvaULcauN27qyt13M3nYh85EL6bvOpx85n9rw5iCcT204n9pwsW/Dxd5NF3u3UGy72Lvtja7Nv//z48dOrXvh8GpE59oXOq9+ofOaFw5d98KhG9w42PmBg50fOHT4xkOHb+w8clN/fLDz8K2dnetzOHzboSM5HOz8yFC4/cDhOw503kVxz4FOG4fuOzAKvND50c4jf7Vt5+Idu5du2Dx/w6aFNhZt2ORg8YZNizdsXLphY92GDQ0bNjQxbNzY+sgjdatWFS9rjzc1hpsaww2N0YaGgvqG8vr6itqGdwj1E2oRk2rrpowGdQ1T6xunNTRNb2qe1dwyG9E8r7FlAaK52kZNY3PN7DmVgSAOnP0h5o9qD6I9A8br9vLB//3EF0YRmEACPVRwBhjEilu8JTeNjSIlHQjjID8UwujAZAKZ6BiVm0tGSNxPCvwkGcBJDP55kb/GDwwEt0LXEyrh6yeeuJ+UhMmcaQRgJSaoQ2/UQkWrB9gG8G80I47K5pIm6G4naKYscebFc8Tr8fi8ki4boOfYZziPGcvUXZo4TdaIBb6MTjIa0WmCOoetYh7QLNkgS0VIS4cIHqlC55JISDLX4ZxvEyO1hypZUvfBJc49LcwtqWL2I2QyMb2k5dOgAOAqGu/7BvVBrP2QAAAgAElEQVTgzM0dR0dAM19n3IReEWTKgDqH/xbMc7/+/eciVKEpHCJf/LJfhWrZSjACWoCkZDTdfisZFyUlfjK/igj6B7rSETrU8CDxKvvlTP3aNpRgjlFLhYegnuDvfluTlcoEPSIYAVGLCeLc8298aEIZSRBSHicv/3iyChUpHUcqPQpy0Eg+KtUvnpjftgQdn6NUYSNEyIxJJJO+XtCm0FDrYFapLUmgLkdx2Fvgx3tr6iTyN39b2MXVS1ApoF9tgIlpou+zlchKZZw4RVIm0ixwAQ28fZklxQkSC6A/1Lqr5gcw2x85fahCyk7V9LI0h74YKmUwaTso0cJoZdtlnTEFQxLQjrWBEdAeSkD7Fcuvm8hBU6UO+x6iXm/2TYO5qiQrrEM0i4R+pWa1bN+ee1qCReRXb954SZ3ercxSYDfAiwBvYu5BDRCGji5v7z4BPWHCBEJId3e3w1mYoOmQMYGjHO5rGeNBFa4H2AjwDTB/BNobYMj0cf05wJcyZmuvlchiDkmUyBDBR2lollw1IFikjyeaMgNgralVmcZkqi2LxgBe9QHMBUwb+BXQPgPWatUaL0CMpxopIv2lWOk8xgMqWQhfhPF9cKsOpzF1KahUNZ7ZrkZi5a+AgM41owOIpnSJ9lOP9aZvLCnBsGsGQjDou3IqyiBiAqLlOdx9X+yBvyp69BPjNm4dv3VX+dbdxVv3FFIUbN0TZ9i2L/bZL0/63qHG0z+86vkjTS60PH9kAPDb5w43Io7Uu1D73NGa545WP3dswf6j8/YfnffCiQWv99wtwcY/XVx/se8+hkt99w2Fey71Mdx1qQ/R1bfexm1dfW7Q5b13dvXHpZ47B6J3fU/PbT29t17qu/VS3y0Ut3b1ORjUJt3jpdQdDrr77nBwqXf9FcHZ8C1V7uruy0GQHrrQtf5nv7r65VfbDh6uPthZQ7Fk/6GlFHX7D9XtP9Sw/2DTc4eanjvU8FxnHcXS5zqX2nVcsv9wYx6dzftHQuv+ztbte+L9sLtgO6Jw+65iitKtu/PYvKfUwaa9pQ4278F1tu8qtbei2+4uxHZyYM1iuXVPfPOe4m17pq5cRxY1kDXXk1XXkjXX5LF2HVl7TT+sWUdWXY1R/O2rSOsKUttIrroWY6+KSzAUriBKisKkJETKgojCKObICkVxqBEqQCdZJBPtPz8dgST8IWa0RjrUg98fPY79A8pMW3UAX0JpKlPC3MT45zzaTo+FC5kHNCFkzep1AJwIB1PGwym+UhT9khyQ5ICsBGUlqKghVpHkQk6ckhYWCvpKFT4K8A0LfgSQtlDTo4vmQf2Cad1owFgnVutyFTcBnbNc0pdLQIWQRglokxosDTqTz+gka5VL0Gxi13qGst4CgKqBLIMqgi6BpKIVsBtwlPMnNE9ihNQf6eGBbppbt2/BpLs+sryj3X0tLls3TVPVNc2wdKpncrH7l9/Zv/vQme3Pn3zon47e9v3DNxw52nHqeAvD6ROtFO1nT3W8dGb1mZMdp44tO3uq48zpZWfOtJ0623LyTNPJ0y0nTrUeO9V+7NTyoyeXIU50HD3R8Z1/XvzMZ8du2xnduSexc09y557kjj1F2/aUbN1btnXPGBfGbd8zfvue8Syh3O59E3ftnbBzz/gdu8YxbN87dtu+sVv2jd+yb/y2vRO37Zl8/8Oxq24gy1bmgL1uO41RWI2RfctWIdocrCRtFCvWkpVXk0W1pHQc3oqeINoCE0Wok+i1VTICQRII9gtYYbbGWAjv7VgI3avR0EgNTsxAGIjmLIXMgBQuIGHb3RuXJPDODxWQaDKnURhLompkLIle5IkEhoA4Kd0wDV2cxBOIaEF/MEkQWsYKUMqQqRkWFFKxjgQakIIRlFNj0h8hmhgK/dkp4hESj+TqzAQ1nHGL2a6Y+wmWUTQdRZPEE8IpQbTIhWISHR0iRajSyBAuJIikjUIcF05fSNrWkvarybKr8uhYSxysXENWriEdVyGWXY1oXzcS2Dq5ci15fDvZsJ08+WkUSdyxi+wahN07Uct7aOwiuyl27SC7dg7CDoLLh8KQrbE1d24nDO4Nh1x/iIX28bCjGqkc7ozcy3eRr32NnDxZcORI5MiRyNmzZQ7OnRvrQsW5cwzlR497U9mlnNggyE2S2qqZy5DQ19tkvU1S2220Sup/L5wjeSsVaqVgtopRlfZZX+m+WiWtWdIaJb1eVGsFdTEnoTd9Wlg0PBamhYWY1BSxEKBNh3peqU6LVRlpLq/OZRqa71ipzaQO+zNQlJMiI6PEP03ZOh1L9vG9Ki1Ywquz09IsQZuPybjkGl5e8i5BUJa+n1CnW8s5oSmVreOl5uHuT0FucZDhG9Ncw3/+fsapM6Ez52KIswVnzhaeOVNso/TMmTycB/9/K2/7Cow5e3bM6dOlhzvjzzxD9u0lTz1F8SR5ajg8QZ7aR57am8OD95KbriZXd5AbryPL15K2q/uhdS1x0LyaDI01pPmdxVA76riWLGoi5dOIL0k8iXxiiX5JJuKo1JzXqrZ1qxMlOKhgpSeEdU+Qgga3eVwlG6H5Qugrk/ffchy5nIodh5ePxgsj43kZ0GZZ46MpvUEcmIXjODQaILqNH52DCVOHM+Z2RstkEdKprGRi6OicROP/mPfGSKXjjvYuVJhn2xDnwq4nPSNPEL2Vw3EcuLJcF7lhc5g6nUQwG0cuQpHFKfYvAxFSNo7Mq8YMzC0dpHUlaVxG6lpJfRtWUGHPRksHrtCyDNdsbieNrVguX4Hxx+3tpK2NtDaTjmWkpZm0N5OOdtLWmmhsqphfPXnanCk4e6STyUgEHUomjI2UFKBbKptaLpxLPv3MWA2a3xQJB3HOnKuqHwN4AeANSh+prKQENHLQTAyaEdCnXzzHXFQkXdVy0hsizdr3HGTu1/qm63xM08sEtUi2inQoVFwc9FAENM2yOBSDPIBitrlEav0dxfruWao7GySLQsPUjpSpk4BGpxlhgNkAj+AUu79y7agJaJxDutyf8WMPwPOS+uS//uqRSDF6EiEB/RWiQrViVqhWTAGvYI271L1mUjkZFyLlfsyfk+JmpiQkxbNAOCsiKq0PP4RuUPEQmTnXS7zYTixMfvMfc7NyUtAjkh4T9SJeXPwfv/pQcRiZ5bFJ8sLREhUqeQjK6AEdlMxCXW351peLxwRJmQ/FnRMBvEXDhLQ1EkleIxjlEvgFiGal9pIYKQ96YwT5i0f+ivz2d/WcPL9XiPcqJKWTrOHlrYCB7GRM0WpfOjOhZTF5/tshSZmYEYhuxVOp5uIoifmQLE/E8T5cOp+Yyg26MsHQixTNp1BanJHFVJdzAAHtpgzcHtAeGi7tUM/o1YvSEKgpHtT1qKEHdRr9ZLAANBOXM39qdO9Hh9+oAXEV/Od7x371i+PLYmRMgSeRINs+Q84bi3ug0sBUV9+lt3IvmCJaX/DmFy1TRC0as5/vM/uQd382rTwh0/8GuiwNwVbweNArzLUy8jsmaLaQhQbwe4CfgvFzUP4T9DcpFfIyktHwWAaW9KLgBr1ncgS0R0RTQUS2ErKVFNWEqs4C406Ah011vmmV6VCkQ6InSwAmAKwCuN5UVulKvapPVMw4TfDlZVdYQu9pn2QFRcvt+OyV8MH2S+DNmhUcfFCDr1rwW7xWjIBm9BSez5BEFX5xBQR0TlZdBeijctidPVyzaFb2cfP6MrUMaa6Olxrp7KsFpxB0zCrptZK+hFeqe7OzLvROlq35MlQNhmjM5tQZvfzki6kKyZyTD9c1qqUBoDG8OV1gjPB1MFs0Z4rmdNGs5C3E+Uxp1pgiwrSMPjlrTHEjY04ZBpMyJiKlTx4GU1O6g2kpfQRMzeiTM/rElDExZYynmNhn2jAm9+Uxtc/IIWVWMmSMSjdcO3X2PlLFve1brJtT+FwGtlm8VYlXT6/kjBkUs3g6GbOndjjZExQKdTYGcwzEbFGbk4NaJQ4PbESdjXpEdg63rDjdhVlZcVZWmJMW80hJcxz0ynMGICXhmllhDm6Yh6tNqTIrVaalypRcmZKnG9DEGTV98gLOqMlo1RmtOqtWZ9UFDJh5WZ3HIGjzOX0+Z1RzRk1Kq+5VFqSUhVl9UVZflFIWpcUlGamOE5o4oYkXGjixLiMv7hEWXuQWdYvtItzRnX5Q0b/y0rktX/+bBx+5d93cSaUFHnyzlAQ9ySC6l8bCZFwF+fVrBSqU8PqYrLgC4DCSsI5daZjn2tSB0dorOlYBnM/Al7qMD2a0eZJeIRvjGURzPKrzmxM5mC5Y7aL5sKR9zsTEp/9Kg496qO32NQv+wYRHNGhQoRy5Y3RJc3s6D1cfgYAOUALagzZn2pQMRDCmKsZNAF+mZq0LGPZCNbRMGsGhYv8r0s72Vfp2eBZgkwmbTfiMph8A4AHgc597lp1ye3urqwO/fFXTtEGa0emU9PIl+VtvyNsuqLdklFpRmyVq7IaczW4hXp4jqlWcNDsjTMN8g8o0hDqVk6dwcmVWmpKlN1VGmOYgxVcamNugui87jZereLmKU6oyyvyUOj+lLEwpeM9QLM4qS7LKEk5dyqlLGRHDyzWYyYTmMMmqCzLagpQ+L6XPU2HpRW76m+kpGW1erziLoZub0ZOdnhbnZJSqlEQfB6mqW67qlucjpIUUizRo7xIWvJGel9bqeqXaLr6mV6pPKY1UfreRZSzkjUbeaBT1PJAe0hozwhIdWjlp6Wt/qDxxJnbsTPLo2eSR0wVHThccPpVglaNnceGxc4XHzhWyOi1jR8+Fjr4YOHo2dvRM0Y59ZOeeHA26fTfZvpts3UW278xh6y78uGU3YtOeYbF5D9n2BGLjLiw/9ddk6z6ydS9Zcx3aitZchVhNZYKYCtCqNWTNagQqKa9GJhfJXBe9O7i+fDXJYQ1Zez3OgUvGkYISlLcuLCGFxaSw6AqQLEQveAZMBETBpKujhZi1KVFOYiXoF+OL2mmRYjjPcZCjxSnXz3xkvAmUMkPEh0Au1VIU3W1CcVJUjqR/IonMvkPx51l+F7mPwt/DIBcdwmJERlEO2Q5rxAlDcbc55PojLRxgonA+DnP8QzcVx3CW4hIMbUkWopKeg1AIbS15MOmwEOp9RaIYc5CIo0ZkLEZCwX5CZEyO7L+/DKJu+1tDP820ARJqQ318a3vpd4mo4Oay5baGpq2Y6UhnYmWAwuYKcvd9kQc+Fnt0Y3Lj9qKtu4u37SnZtrfoncGeEmyNYvu+0u17yxkc4X67MoEZDt+FsgLzBNDkAblyX8W23eNXX02W1KPZu2PVu4srlsR9O3K6o9i2tRXDGT0EE8k6lsUBFUewNUSf1mgUH9JIxH6Kw9RC6X6oXXVH9fV/K2/9ClDRgDAtfQF8UbKSGYyxLBoGhaSggGawKMD3Y6wAA9MxaW0UX47xMTkkykmijMRL84iV4KvzvUYpiZWSaAkiXkaSY0nh2H7pB910s/MSR2N2JKcsjG/AOCbMaGi1RxrOkINV1pDlNtj4BHNX/D/2vgM8jqva/0q70qoXS5blIvcm23IvcW9xTDohIaHXBy//R304QIrjVJIAofdAqIGEXhKcTieFEHiE0JLQ0mzL0u5Onzu3nP87587MzkpygwQe34e+33d1d3Z2dmZ2bvudc37nJPQhOCROYTsyOP5kzHUxNuhQ5oDHVG7dyXaewt62m+2+gu25mu25ZixcTW+l5VVsz1W4ZdfF7KKr2A3fLHz9ts5b7u7JYu9dvXvv7tl7dw8lDxx3290pOjCXYAxKHmhSCP5DytvvbiE03XkX4le/nrp/cLXtbj5wYAXn2znfKvhWGW1RYqsSW3m4icLINlSV/qbQ3xR46313nees9b3jAn9NGK7k0UrfX2o7A6672PeXBsGyIFhhEIYrw3C1F6xyfbQskrjZSl+uDzWmRrRC1FizxJZBf9Mfnlprw+ueLL3jjh/uPutFK3um1CH7XIuKHCuWTO2fOb6vG5Pk5BhGbU4Yz+784WKc+Uc9RWgvw9QSP1nzm9C/RzsZAtpIGQtMJJTB7d+7GwUB8zWuMH47AOAiOaa+AfYebZ0F0U4ldmi9Xei1oZrnqxYfYrbK5JCr9oA+WgJ6BB99xJdZ0jlbT2WyODF1rpETEL0AZ5Hm5L5snC0mO0MZErjsf1Ous/9Nun6peTlibcnwM0g7cgCUa6C3NaUyvLzIz/7hL15Q6Iz1y5GA1ssDMS0U4wKoc8T0X/x8S3Mt8sLjatmXbmgadscHUDccsQi6S3rpxZeg0mt3O3r9XP/517A8TjcbG9nDj8wvh62ebI4JaH/ZA/ef2liLBHRPK7voIlYO10lYfNDpdcLFf/7z6gvehG9116LU5MkntK9bU19LXm+nncJCvgGFNZENb7G84zvyrLOGddSyEzYx2znb4TM4dA67TNOi3Yd8STRomDboLrjzzsXzp7PZE9hnP9rCg9lOUBtGrQcPbG6vYwX8Hhyh25vZpbsnBN56gEkAHRoKkih/4wBunKCrPaCPhoBG4U76bC4U48Kol/NJgneLqCAEkySLxlV9qBoM9eyinlSXhNkezPH1sve+H0MGOvKsuYbN62dPBut9GHg6WA/wYcq/VwRlgXKQg0aYyrNOQJvMXVEUmWcrZlzTBw19fzk4HDyFCsjql6BvlOoiX5/mwJxhqHNiWW3M6EUe0IzuamOgugIxg/urADVV3xqVTxfRTKHbIt0RQRuHghM0O/Ysz53veF2WV3DCOl8WAko5aAIEfMh7stkTXZ7o9FRdxv05T/aPXsvfpOFD5Lc4hEy9joivJ3MMnv8zS0A/AXCv5e4KYaGAgq9yJqbPj5gTIAJRk43UC2UuECyUJqCy1kQvGrmYtIyAaajVUKuI4aLIyhyFWB4y+jIjKp9N7WiEtrHE/KKKCajRUJfqaKMQSgbVuRyrUjs6lAIuU6b52WpJ9jGflPWknDu6zFM+N5Y5AtatDMpQm0G+DHkL8jYqhiPcaiRfl37vESojPn7sL3NuHJ+CVhAjT++hvyoGTAjU/DG3PW9+CIURrwa11eGuqPev8MfNaajLoKAhRWW7glqpa4yJMpIsFCyIxkY2ztcVKNZvYEuWwhUYBH2oIwSCZeFLfGYiqHUVK3OGssuqclg8VDVQ059CSYwlzzR/0monSX2ok9BAaJHQEUFPBFM4zB7y5th804O/Xnrp5Wz9OpRxaMyh5kZnA1olG2tQWHxhP3vjf7Pv3Db3Fw+jHcXT08veRoD3os6PDmMC+tDtmghodK5esWJFqP5iwQ1luDDCAIuXA7xcwcskvDSCl0TwEh9e4cEbOab7+y65FRdj2xVqCv1SwvWWfulB0e9DCyk11VCYMzaurG15rPoRCGiKisKDkGVuIcAbAK5H5XpVBhUi+5xVD0KL1/+gNpm6Kope5Uc7PDRBrfH9F1rlq8laCZdfcakhoNetPy4iWei02z7aCnlAKwGONwzwlIafhvCZEC70xEmRWs3VkkDOdsUkW7RbosFTdZhnUjFLoOZVCnwkMk+sz5mBkU91A+aFLCIbLT7bkvmK+SrnaYKqw75dFkLVEKoGrhsj3SgoyhhH0jjEmORlcTJXa4yR5tkrBUnUEWCqCV/gvVXkXZ7ajDP9Xg02Z42NuizYfoeF2NXUhtg8mwUUkmS5TGLmzApIQ6wmKeuBMntw1R7qnlD3eHq8p8e7qttUAugJoCeECSFMMHUquwPoCGBcoHs92edF89xwkeMvc7wVjo8ZwE3StqRcUAoWlML5w4QhPj8BqqvHCBcNRwMluaQklwwGWHnCmrnfm+/COldudaMTnfA02z/Tdk+3vOPL7mZMhWptJGwuWZuLNmLI3jpkbx10DLYPOiNxwNoWw94y6G4sR9vL4YmBPnvYPnPYeuFw+aXDpVcePYaKr0iRhKdguIkJwSm7r//x/du/+q2BW24/7pbb1yFu27D31hSbbt1bwd5bN+29dcMtt2245fZ130FsGI1bbtt0y21bELdu27t32y3f3Xr++fXXvHPCJZe0776gdfcF7RcSLriw/YIL299+UefbL+rEBDiE8y4aX8HurvMq6Nx1UfuhMW7XRQku7N5FqBwnc0zz1lsuGGdgXh5m/6qDVE6m67zdnYdF5swz3151tHj7hNf8V8fGbWzjNiQCNm2vYPPxrILtbHOCTdswAqCzGxd7DU3ElTSy2KXL6DtlWBjDxfzLlfUNSAAdPZ6BCyQl/VjFqBElMsdAY5XGUUMz+qM1d2CMggnpwKDmZxrG9814EebpxCrqcM+CO17VwRP1OaNNZ25ISweKyzW3E7VgCIZqb7vDOOId01tZH8x/fj2PdGQTJaptaombm2l02RJ5vaT1NbfiRyZOYZu2seM2HhnrNqG/4b/x996BzWwdYcfJ7JTnsV0XTLnw0hm7Lpi064LeXRf2YFcfjyOtuy7K4MLuXedP3XX+zF0XTDnvgp73fGjut/du//49J3/r1uO+e9c6g713bth754bb7thw6+3rb719owENlJtoWMyW6ej5zFVuW7f3tuP23r567+2rb7lj5S13LL/ljuXf/M7CH/xk3R/+eOb+0n8UvXMR/muL/mvLnsF/lL045UMl8YPzWsd5reO+YnD4ZJef/vTBrZZ/coITLf9Ey9+JoDQPRszaDnfY4Q6Hn+DwE1yx87DY4YoYTrTtEDjeiRLQMc2Rj1ia7y3724re1oP2miF/SZEvTEB+FTz1rlhS7WOxDL0uxCwO/QfDyR7MteRUS0515BRHTnHFFFdM8gmjFGy6Q5FiHPJOzwL8qNOPOj3ePgIBbyU0B7w5CBpCXlC6BaBF6SapCkoWlKoDjQnPAOqkrBUCc55VEOUEAXczedEE5kULQxZFzA+Y4zDXw4rZaErOGadFhBcwJ2SWx2yOq4YAClbUVA66htzJZX/R0+WVP//Diqs+2rJqK6oImsja+f09G9fOXtrfjL6zOdZUw2b1sVe/InfztzYfHD6Lw2IX2i1oGRaTSnKDy89Hx0pFeXWQRDUSHCkBbZygYxoaCehcDcvX+hF6RtOfT67TD4L8OsjryJfonQAXAzyf64W+aot9JXU9EdD5/1MENK6DoFAUiwGuArgXXZqSqzLXdkwEdADgSUleU3AA4Btlua2sV9957/GFNpREbGlm734vO1Ca4/OZoej2dYMTzb35WyvH1bPuHMou/+Te/rLoK6lmF6Y9Za3f845ce2vMC+y5eNbnvvS85g6MS62tY1/b2/SkVXB1i6+bfNXmhov++MfnNhKp2pZnp53MStauwdLzH/rNjiv2TO1tRj64mbGuRvbWN3fsH7p08QpMyskY+8//ZB5fgn6yKNrQ6no7cox1MtZew/7jZePtYLOArieGmIIChxpLsKGIHYzaXdh5+4/Wd7az7hacZf3+oaWAGS3zYdh88Olt7bWsgXV1tPSg4ngn+/0fnheK+Uo3ADQBNBj9TUMFGh/bQ/lBJ6miTMKoXHY1a6gWK2y0nYHS8KriUH8YzLWcTi9qDlWDRmm8Lle3+dAKMMmFnqKaHcKpD/3uOa95dW1bA+qmtxXQFHPHDxZZMKsEAxLeTQaDIpGnIWgf9bsRPrISKYk6ZgUfGWOCSN+OW8bR/2OM1dXVHYKAViAj4BJCCaEG+XuAyxWc6Muljpxk62biB2tJdqOOSvQNR6ZYN2Fn6q4DeCfA1Yof73qTuGpH3WfdzHVjkqamKVQtIbbPeqQeUGi1w1dt5aD+gMVKfiGQE/1ggWXP8/hkco6Oj28HvTI8iWLzf6ZhWEuh0V5FSD0l0TBj9GHTm2NcxNWVV16OVoqamk2bjsZz0IQX/EHDu2zYFkIX6tBppkUtCstGTEVM8hgqyqXQIp8B7qwlSwGqJgEDzUAhtGTxRpkDmQOdz6AWdG3lI7S/+VRaKs2UrgFUSEdCM0XWDnZ4A5phWhNRmlwijG7UaQr48xnoRkMYmbKSlkTV+SpHBFOFn/I06oAbuICZizKod1Hvuz5JBIrpQCvfAgXzbBx9mf3s31Svo2s3iksx4WgEEA2/bO4t/hApVC3+fKMhGUgGAqGjBJzpFOlGqpg9scRnYCzE2+PHRumaFOkPnVbwMVB0KHMaYx5Q4WnjdWkmZF7IBoMoKkRRQUR1KdJHmio0vVCYRcqoWR20MRwEoElBo4I2Bc0Arb5sHLa6ADYr/aK77lz1ptfXLh9AQWHU0q1Bo2Y7Oc21t7Pnv5B99ssdd97TVVLLyzDXhuk2TPKgy5bLlbgG4Ofo/qyTOA/s19LmnO3klFLCsLHrj1tL8RBDxNI+REf4OXkZ30+yzvcB/ELAIyE8HsKTARwIwRIQSMxr/GsNlwaww1YLHMxC0xCR4mQ19VxhmUkJOstKZ98yatGmrI9QPxqBSbr4xCA4HcQ1oL4H6o8x+6wiVLiWEriCEEAcALgd4D2We5IbLHf5fD+aMuzUY8rWoZMAPgPwxP8yznv27DaXvHbtGs75KKfm7P3J1k1HidONSnANppx1FBxU8CTA7wHuAfU1CN4j+ZtK5e12uNCDXg4tB31WlgwzFSN1izMqXxG5LJjKPufVz7Z5/oF6P6liS211drJaKSswXSt2gASl6uj5zBsLn6mj+JVKP8Jk0rWa46ee5qPsBCiCRpmgUT8UqXNSETU5G7I2JKAkFocoa8jsVC/AoEHAUYIy8eo2oTsi2RnJTq4Q2RUF5brscHWbq6vT0CV55yj73DhHJ1DdjurGl6aiejw10VOTCRMDNR4twQQuu7gcT1uQNPfUBFenmOhqhKN6U9higi0mJC97HNWD+6jJuGQSUx0x/W+AHU2rgM+w+QyH4AWzvGCOF8zx/Xm+Py/05nF/AfcXCA8h/QHpDygPYepRsDAKFvKwn2AElEeWUTBAwD2lX4H5LH0cPxJwhMcXuhHCFgsxwqMCs8WU/VY0/9BYYEUJ+CKLkDlO5ZjmrTKGAiDMy8PsX32QqvOxRcmD2z8AACAASURBVP+hkd2z8u3VR0u2R0vsaFkMvsKuACMSEqyx+Qikb62iCIblVogoB8tihEvK/1ykZ/IvUFlR9leV/TW3fy9/+/caEHc3HQItt9/Vcftd426/s/v2O3uvu4598IPsqqtilZjD6bFklFsuvYSluOxSdgRc9r8+UBVccgn7xyFzznhpl7B3v5vd9OXGe+6b9dN7p9+8t/nmWxtvvrXwLOG7tzX8H8Lt+V/+pvcvT88r+2us4LgUI3KrJi/Xlv21VF9VDlZgewwHyrw/RjiADXNUozDt99/l33sHMHxwTCzGfj4eJmgoEXMtAxxZFuCnMBQMe1EnXOoGS91gsRsu8oMFfoii0mFQGRaFt6gCd7EYgey7z1h9gfDmC3+u8OfyYDZhZhjODPn0kE/3+XQ3mu7i3IBA1GqGYJ3iR1Nj0M5Un4JEQTTFj6YEoq8CjFmciFATsvBFz5Ehu/0E6eRnVCWeCNF0qOorsl93iHr62S6arbUh1TgSHWYiV122kYNdo1ntmvVppAuRLkjVKGUzpquRzSAaK5AFqKAO5D8IKXEhZT4DnG+biTfOvVE+OFetNZxdDZl6PN8esRsyEkAuwDT9DjIq/1gnHynLM94quWGX2RGCMod12W6/WzzpB7esP+NEtHznSCCuvoFNn9q+aF7fhPaG9jrWWsvGNbLTnsM+/+nJZev0srexHCzDbPaYOq7GUY1WtMBXb9YovvE48s5aIEwIakwk4Sop6wF9zwP3I8edz7t+aFZQtL8HughyP0RPg3wM+E8APh/yTRGuYRtTToycMg23EJOK5oYcno35297Nsj1mkTViC9fodFiGhoPQU4bnC/geuXIb9ebKOvHoCOhYdSEACIiAtgB+zGFPSc8p6Tl3/HRjXRMr5HHBf/GlbMjq93ifH3U6qtEO+6/7xIzWPGbqKzD2ket6niiuLcst+0rPee3rkLPuakac+1q2f/CVd/zwjNoC6RV2scvey552pzuqNSClBU/MGCwdP7UPTQ2YPJCxtavY0gHMXNSRZ+2MddYiAf2+97QMOS95qvza7j5UlP5fVZBr3sU8MYeSIuYCaHb9rRNaWFcNEtYrFjI7ONXWkzlM8dQEm/faUZ8FC104fddltZ2TMD4ln2cXnM+K5aWWUw/QHkXNw/u3duRZgY1raegqNLEV69hf928OdQ+tKmsV5KnB0HNPGhqHcYI+DAHtISVRsIJJ5+9ii+ews5/LrvtYbam0s1jeYPurAr3O0xuGwzWD3qonrZVP2Ztu/9Hc8y6oaWhgE8ehPnVjA5ruP39TdwTbHZjjo7by9zH4Wmp08UPBjQh5ZwT586Zky5iVuKlk36s8QEdZw6yhuZxxoNOoOY3nkpA81AC5BF6C6GFQ1wPs5NDlqYKNNARyzYZMpIch56HTaM7i40K+GOAcgIsAPgbBWzif4woW04iqAbOl02crDUzXcqiLoCmEjkCNt/mksjvL9Vdb1lqAnQAvDsQMslXgl7q6JeTrILoM4Ieg9puuQxvJEMM+pwkInwECWlFUfhHgrhBe6sEMH9A3FgloojxGEdAsZevSTjypEAdNtLUWKZVMRGEVAZ2SjzUVljPlN4k0HIPuVEgjGkbSkKQpO6kS19pRmehHJssWiqUMZnUlR/nTTFknUc02poQMGZQk16Ys26PSkceJYky6mFTDCKXSK8i2uMx35dLR7igr2c/+HfWEu6fYi4R6RkV7vLcp9YyVsahns9FwvsRBVwjosYi5mJ4jqnpsAjomkYl6jim5nFIxxrxMpXKJJaMGZA2S2imyZDQR0BgaIuurCGhKkp4Q0GjETp5qNLegfVvmUWgItYbQSFDmrBQwT7b6fLplzwvCJUGw4YGfLdx9Pps3HQ3R4wqss4ApIBpr0P15/Vr2hjfVfGfv4oPOGY7a6sH8IjQXgdmxA36TDVNddTao2wCKgNRwPM5Rn5Z2T2kPh41UgWPYWMaY7/vJezLxK+agQ60CrQKhha9R3oJMfIEAR+onBfxcwyc5bCeX1Y4QU2zVk8P7CN/nLMuMkQ0ZZN8ag4AOYVwgFojobJAfAXk/5nFFLTHT50dkeiyCfpJ481tBvj3gOxwx01UdZO6tdxULxAxhvwbgVoCDURRdeukec8kbN64/avbZmOViDlpDRAg1REoJPBdB2ksYUHIQ4CHQ3wH4AsBFDj/jqdIyD1Y7sNASM4u8tyw6HWjzoDHUeSnRulZlREmft0xFS2SfTahQGhFm+iUpkUQ2SK10honGWS8aSKoJaIkJGDK0ddwhH4mAxpCUDOKfz0SlmFMy5HUVGW1adIaSNu8a09RRlNmwiVqzf/LYUL4NlPOKr84YdczImAn6YRTNhz7gaVhf6l5hsmi4mPkZlamwX0262TTaxhhNTRoMEwRmvMirvyIrdZXW8RvNBNqM8nQC6bvHVkktkaYSO9ErChWSzIwjprfRUb2O6sFAFEAUICKYOq3Ekj6wTqkxkKzWjBkj0w0mnbYZMc1IZ3KzUMxQmvAjWzEKbMd2sZRCOXuQuG7ueXorsj8BuUSM8ZFR2+PzSRwpDvPyaI4Wy8qNdbTsx41mXXZL5XuzV5EJO6gKvfr39sPdATTS5zxVh2F/stUT7Rj5d0h0edF4L5oQiD6h54VivuXMKpVnWXa/6y4+GnjekhS+v3RsBIv9BJ43gPAXev5C15v/D8QC112UXNEiz1/oh/N9PtsLp7nhJJf34H3AKMlnBSmT9X+iojooEjQdBTAe6GiRiYA8zEOYbcX/rj/Td6D26A4YD/HolSUbeOwXUi8SKlCLPKbRTgfHqB54w9jI7vOM1c235yGK17PptA1nF0lwZDoDSSujpyI43VIG5ExA60paXZqVZrIKy7hSJfunHzxExaihJglXzIxu7DJz8Oo17xjfPnIHo6KbfFfmcg55VmOeA81DaPGuaK5ScU0jciBdryXzlsOtOp/pfZJzo4R1Jm2dKSmdXTKRzi6CDl83c+90n+xUHJnZOEEfTYYBOhRgnlWum4tBi4TZEhZb1tqPf5A9ZyOSip151tpaW1PINXfkmluQVGyqxzTpc6ezy3eP/+XPT3Tts4Tcii4OstPRBR+DknGJEYpxHj8e4HPkajNMDA9x0IcloEMla+rRedasoOIFpiLiLiLn6cgBcT/A+325PIRmIqDrTGdrXF2NY1+WtU9bxzNYGUE3x63StE16VomAzheh5yCst9Dj6k8iXl5XuUAfHQEd+40HAFzjcvZRDu8/CDuL0FMWc2//4cZ8PauvQQGU1/0Xs5wl6N6vmlBzmS/6+reWtjZhdvtCHabo+fK3TrvmvctmzkKCoKsZcw++4Vzmeju9aMtjT5xZ6MC8OoyxhcexwfDUYthpljEedPgw8Ja3so46RirzKLjR1YgqEwWGG0/cwe76/ixLLPNh468ffx6rpzz1teyWWycGair6w1IyQDdc8/yT0B27hWFey8vfMe7J4ec8Za0d4hvK0Ul/fOq0j3928UlnUnBZgTV0sXNezUI4teh3c9kU8Roe5Af3rW3Jsxx+f01dC3vlG9g+b1GAPkpGoCBPP3xMQFNviGH1mWciNU3ElcTCk0ulDJD9ROa0vugNNNSwcTlMvdhaw8a3sRefXfO2t3V/4lPLP/GplbvO73nBS2rXb8Ar7e5k7U2svZG1FjBb1HEnsM9/t/UJa2o5muGKHQquxsBn9N6VRDpLpKGNJQa51KzfX8KomP+GhHk2CGhADhoPnJK5yEk/BPpSgB1cT/ZVzuXkO0arXDOmkshDjQsFW/dF4kSI9oC6HeB7IN4Icg1X7Z5kFGfdhDQ0ukjjWi5udRrTOZrxKYC6ECZEsCqSLwL5PgpqOCeCmeixhQYl5kKdFc3H1IX6VhBPgQjw7pngCRPAbggUbFHG/TltVPEtA1DHoAGNBykB/M7n77dhXQCtxLnjmcd9pa6tIlhpLU1ZuSs7JHvS8Jx0BNR3xx1x6mJpHPESbsI8t1Vl+tYhKkhnGHWICDKscca7MEPZ1MZTB6KEDHETjzej86cju12FmOgxdJJkKIOeRTyxiEfiSDODlAEZMR1JB+bDfEv2Gw9VH/Hxv/slehnHhD5JahhhjaQ8XJZ5c0WG0ooUizGKnY+SLdnpS/VEJ2cYf2Mqj0ijgOvGFBQZ0DiiJCkDY1ovSFUwR0jKyoNhaJcAagyxZSSJUoIpbqckthA/5Br1N4g2qnehwSHY0BhCO4dOB2ZE8PzfPnzmFZf2bFiJESoor8Gwn2xirH8ae8UL2Cc+mvvDIwsDucaJ5rpqmqsm26K9GLGyQm0EsmAxG3pL4dZIX0n6GD4R0DKxOVd3g8ksANB7t5QS0IDm7MDyBg37rCCSwAWEHIKQ4AP3QYSglA4oy98PBOzm+oRQThe6DVPMYzuqqNwkzS1LMZt6OpdCGZMMRhLQIdQHYj7IC0n34xEAGwT19jpE+zOWZVLbvxPgHQAvCIJlJWeCo3osaLNQpoaFUCiHAxBdj7lqQURRdPkVl9ZSwo3NmzeOeV+OtFEl7LOvwVeKKyVwzMEuU9BtL9F3PUYxOvdpJL5v8MXVB73/N+idPhiuPKimFen0Ql1PNgykiRNbUWYWnpmjmyQYCfsZr6Wztqikt4z9681LdLWOuddKJTtpy866sHNObMyHWWyPeCvDvpkAiLhMJtk1yTOAv/ixH7/GQ/EuhOn6zEma0047gWzFtLiYos0InsTxJShjgkomBkbPhIShYp/uUCd9DvW92c7Z9EVhpS1XolVGf13y0+RxPYzhKXXxlnT4PpZK1fHjS6i6ELqEOlx1KHqWyPAgdcovo9UtoYzjHyI7lKT17I+VDi6mYowH8UadM/1qGi6TjcVJ6qg8YzD6IUy2mLwUVOp6P0FyBIzsySLdYUQlu8+h65XzMT32WGV2n6qvHuuwuczDX+GUj2ljllsZ0bL+mS+PnqH7Z+5JvLMqeKqRUPCwfiigZlHc3qlLNMahEOpDaODQzKGV43B8BAjoSCFh3BGR7iyg44gHf1Z3CKEt0CQCqZsCaA7RbaWJLrz5GS8FtPxfgLmuEBpCyNNsbaQl7Cho6OwzFtMioxtmthX/u/6s3YHKHCa2IpPlOJ14m++lcZaWxipPs6B4/ZiQsBVf1DgmjMbKqjpFiSXzscz+f9v20cfPbokDIpNFPc0K0uE4tX+bBdGYy7dRi7UkxDNxtcGh/5Ar2SpfhJQTH3XMdA2bHFzXJGbsik/P0W7RNekXJZXsaYyoI/VZdT4Jn5vMVXDxnmUnsxRBsk92ufFPqVco48TzKcPUJ1dUmXGN5PezpoV0HUo+bQoXqkLW43JVNUrVaNlMYIq8tlBOt4OTH/zVibt25cd3stY8KtmOa0ZuLY8Z33CdmWtjsxewV7yWff+eqQKOF3DcUwcmC+iXMB1NuQp7vJD8/HTYyIO5WpxLsrcOxX2a/GEVD+is43NaB4C6pobqfGm4VtKYsk0JzYnOvk6q53GM4s15yEE3J07QZuZvcstVlhLZJcwzVc8uhUxzM1vMisPw0S7kh9TcIXiTD7f5MMSJLIuLZNF4TAQ0akBTYqKf2fD/HoepRWi0+Yy7f7CxrRXzPzbVsJe9iNnuSgz21LUu1Fti5hODp47vRVntDsoo0kz8cmsLZoLqamFXXNY2OLRTwyJPzXbhlCXrMD9MXSsyCm+6kJX9BbgUwWVe3ofu3/1pwZQJbEITEg09Tayznk0Zx+ZPZx9+/8KnD24vhbMd6Nofzrrrvh2o5JVHLelfPzrgQSfSKKSq7Ir+j31w7vgCEtAtjLU2sTVr2Qtfxv77fHb2S9niZay5heXr8WFr7GQvPpftD87a508eCpjtM4Bm32MH9i1rInEPxlh9K7v6/cySU4OKh1rtKAI6yz5X2lVmwYkbR7DPNrB9EfvZbzrqSS3EZE0cV2Ct9ayJKObaHErsN6IYKd6N9jrWnEOWv7mJve2iuied44vQXxRtDl8gxAXowwsein2jfnGIjHPaCoymRMqaJo9F/P8fQ0AjmasA9gF8WcLJgepKpY3xyaZ1uAfMUuSYDK2WmlfyTwb4KMBeUPejgKk8EWBCqGs9lRLQ+ZTYMjQE6uOoBg51vmqx1QxPbZPweoBr8ePiSl+sDmCcB+0uNLvQaKsZRecsMl79FSKO1HMEIARIj5wlH0dNVbifRG0epBRew0k2RRO8j8T00RLQhoiHpwG+4USvdGEm6pXHRog0F2L+UJO/ZGmanW2YiSNuITIiXuxRO8I6+UxVVoCju6QRa8LsAJ+xpoxwzIzFhZOJiyGGjFMh+b2KJhG1iahDRONkND6G6JJjItmBpM/HiQgRheOjYGLk94XBtNCfgWXQ54d9fjg5gXnZVwnCiqb6FLdlord4NCNFxGek4OH0Y0L6waQyLeLTqD4r4rOwEvVF0cRIjI9klxSd1aBLpgvEHcQEAyF7I0WQkyID1RPp7gjayGe/HrUIELUZ5GlZWGOmkpWJ/qFXudnJbkIo1JgKBgdQoFaU4Z25riKdyTyDKU8NAiCGukrPxOioVEqTGAF1dUm93Qi4Gxtb8pBn/GuqPWhcqHd0h6WmlMXc4Wgggm1/ODDvM1/JrV7HentwTGmuZ0155KBXDrAL3zrnh3efNDR09v7B1ZY/k0O3rTFFbYnjFMpTqPBV4mjbw84EaktqocN3YR8C+6l5h6YbSk1JI/pCGjg9BRZNRlhNrhYAQmkBykpwiUQvQkAUAg+Reg488HwIOAiNCXt/CvBuAZv8qFNAg9HjNjaGlIPOMMtZlnlEQ4tnhIk9qZZMQU2RHheqqZ5YbLsvBriLUgRzvAQp0e6IiSwGiXq+F+DrAFfb/iovGh+KZl8W0FQMDRYGTNUrmD1kn4IqIiRBxjl/xzuuqKvL1dSyrds2j7onR7WBIl4ijfpKYUxAg5Y4pzIWSFHtex4QH/2ghL0cPl1WFxyMXrQv2HaQryqHS5yg3wlnebzPiybgnE82ewq18g+ryVNRgvZRvacu0UrDFRea8ShswjetJpGnr7Qm6jDThmN6y0yLqzFpCQ4jeZ99y0Px95wHdZREN+XsKu0l7WATP9mKd+eIbjl9mTnVHB0cS9Pzp/ZXZORRGjsTPiJyoWjEB6AKrb5o96Mun4/PAu82n+jwPnT0CI2QxTzP7ze+itnS9wZ848boDTg+wg5SLDHJHkeUjr8EFWD8la6/2vVXe8EaL1hDL1fi9iRA2A0XVQEVY6aG0SRCLzo9JMieuamTI6fxYWxHx0/ViIJOKhePfRQlk/ESiOl7M/CZ+1w9CMYeBodZsJnVUbJDLtLZnzitVylBJfR05flMH9SkgjJilRgvEjQnyj6Ou6RLiA8eQGEE75y+HKFAZb53LMrYPJ/IMlfLZOHLhC5Pn+GqSnItlQuk/SuzjvTpPdTtHbEDvYxHOvNUV5kZDj3kmYnTiJ3jxn7oTx3r/oeanmW3Vxt1jEXkGMuMiSh75KOoZ5nBRuKdY345+Wyyg2x2VGsGzRjJquocXedhplxMulAMG4phUzFoqUZbMWgbDsYN+73D3pRhd+qwO73oTyP0Ff2+UjC1GtMpO/HsYjC76M8zGPLmJJh30J0bw5l/8FlF/EUzD3pTD/pThoK+IX9aMZxeDmdTOujZGOwvMaswauuniAWIUIYozT8cV0QfVUibSHdSVGUzGe+bKTp+RNlInG89kfvZ0sz3jqY0n8I9I8SIycPhX2Zt2HnTB45eEcSjXubxG91AElNlnS8bcUyRBdynevQ0Lw91/CNuH/No/1obM4P12Ddn9OUc8bYccodK9CdSzIRK3FL6qSyXdHT1KrP9mLb8wx7HfLzKUyqzbEwo7CzvnKljFJe5LsM+Jw7RIwZoQ4qNLius5QgeM0NijjqZjJdDtc+T2bPalSdDlWaOmRCpKR96DJXM+bCxiP5krZ0w/uTUmHJNuF5IZjLxWi9Z+mGwEc0Y0XHhsKjMQrMPcLZOmWzitQl9XdbBIj6BEb9R5mV6toeqxEdOJlTZl4f6SEK1a8zNnpmAFXxZQFU6MZnzObY1G2DT8MEl371l/Gmns/Hj49Ru9TWsoxn5NPxrZtMWsee/hn3sS7P3O8/b5wzs95qGMRlMC4emYZeVw1oy1uJd8tHjvpbzKaH3XIBPUu5BULg2DBKvT2TfUsZ5RCWMeG0e/X2IUDI+j8poBgilOB7kIYD3lK3jFSwtRR0edBIBXZdxPTEEdOUWpS39GaxkG3hMQNNjln6FC7UWdJT0dgc+xeExH9yYgM6GGR9tEsL4MwLA0bDfg2/sg51PQiOHek/2PfTwyW0trLcVf7mtxzHPWctlC6eBx4I2F1ZeeDnr7mItDawxj79mXQ5zW/dOZh/5VM1wuMKBqcWgRcHUYT1v12WY6SJXzzAbYR17y3kMg7/Q8ly732elaMq3b247bgXrKCDfvXkde8+1tZZ3us3XuKrPhVYbTQFrP/OlbayW1dayCZOYJTfYtBgzzkSemuAHzz/zVNZdzzpqkMse34Jew/iFNXiGHY1I8ra3sg9+qNONTiyGUx1o8ckRVch8FDAtNk+fgSrV+Fi2sfvu63O8lgiJITTK0dhvZgD485NbdMXBLfGSrvI2NTxCSg4m3nlsGFgJ5u84Af3K2/Lo4tdRj1QL3UJWS2fbTDT6xCZ8a8tG9q5rax99fF0EG0M+hUfdKAPKnwfiThCOBClAJwn0NC78E5An2uF5BLOrYaMPxVUf/giQSnCozB9+tfHFRg7oFoA3+3K5x1tDEaeTwrB99B8vlIENC+ZCsyX7fTQrfQHgl8TpXAHRDoAZGKRPjT+x6GKMsK8bcNFFlJMtmMULVtA55A4M+q8JMTLiflDfVbDL0xsclNJuNukcLejz9XNldAOIR8niQvcqkqAHAX7F9Q1ldcG+6PQD0SY72lB0n+eID9LJuMktiFvL0RLQMeP1CMDbhsU8B1odZJ+RpPB1LFvs07LTsCdEoCSr0HQ5OnaFBOmT4SfT3R9h/SwwXSEiHbpCjd7oLmd2yBxeg1InqpImztx5MxoZ+XLTHIgEKXjQjoKhYo7Hl7jhGtff7Ho7Xfdkwomum8Db6bmj4J/o+Tu9YIfn7wyCM7j/MuG/IfLPj/zLIv+KMLw44BdlEUa7Q3GhEBcJcZGUFxsocbEByEvHhr4ExoS6DNRl8VvZutwDWajdoHbjkcVVCLkH9HmW9QLLOc3yjne8LY67zXG3udUo21uK9uah8haDorW1ZG+zvONtf6fvnxaEJ0dyB1frXNFvR32O6MIAH4KrxrlqnKe7TEYyDzpdaHAh70Auhsbl4kjQuyRlY+TUcwHaJ1DphX4yDNTQkKM8D/WUyaEBoKCgHj2ayWgcyrpA5Aw8WUNIMg1KZHi96ryCJm+hJ5lHGQh9TR79idNoOlBhBV35muLWig0WY/yRs1Z1btgLcPLjfz31Ex+ffsYZbOJE7HhzOUyA09TGFq9i7/po4Y6fzRiUawdhYAj6h1HyfnIROkrQbGHyUjwO1+gXIAR6a5oO1oI2R59M4lz7AeWQq0xtSUMe/V8pxfEMSNFea01TCoyBMNMI0lc2KsuSg3RAOCA49nEPDTmvdfkSLsdLXRMLL2iGGia6XkE+GRqQTaY15KGWkZVZhaAAggiY1HWge8NggRBnUabZn4B+HGQZ9DDoEmVe9oiAfgTgei3f4PNTsZvVXQF2rci1BfHsk9kwftjfSikZn8ABAkAJecklF+fyNYyxLVuORst+9E0zW+LxBslovG/pXza7gNkoyS26TIz5EwB/oN71foDbPX6tL88P1esjeEk52FCOFtlqmg1d1HUXAnTdKkholFjWS8gT6jWy6gX0Nye/frSvoK4LLmNwZp/4TafdY9WTmXG8HbEyJEuGYZNzY83dx5yyY69OTF8jMhG6lcdo5ro5Pb1RlQLOns3Z0vrHLHiEqo0kCzh2y37EPJHDAUI3GObRVjW2Rqutq9DAY9afCS1I7KFuD+XMQCzy+EKHL7DDfjvsLwfzkR321mKv5W1x/a0GdrDV9ncCvErp10t9npSXyOidin9Y8c9ofgNEN4H8MqivgP5qDPiqhi9rtCh/WcKNEdwoEV8WcJOAmxRB6BsNlLpR668Qvqb118hA8nWtsY6AmzR8WsN1IwBwree+zPefSzjND04hnOQHJ+GQYUaNYIfnbSVs9vz1XrgCtZijWV40wRWNtmSWxFtkiRi2jG9X9rc2D4ZpoRoz+hqVJFOSgFUiWGQWmRn3okprTWaD8dwvyT9psgHXKexpCwLqzQ9t7CJGozANNhKxFHh9IgXeJMCgPrsqS3qSOKUtOfWjx3SWQcZQsFSMJakkDEXsZJ2+NK7oo1kGs52EzvAjmf2xPtbxY+7D3NsRrSy7njH1dIfK/hU+ZQwGJDmf2BKfvjzS+f+N+5sRKlnJY4MyBKJR4a8u4y6dLIW4HFAU+GJ8UEZf+OhbnWxBysaEFJjAUI4ztLxp1MZrNbXspvmZTaptM9aTATtLcdYHmBijnuxhBQ9acUYhp7liDiqV8yUGnljqiaW+XBqoZQi5xufb/PCEuJX5O51gpxc+x+Enufx0l7/ID9/g+xcE/uWhf3UUXhmFl0d8T8R3pwij3VxczOU7hPqAUB+X8AkJn4jgkxF8UsD1CT6j4LMKPisQn3+WYb7lOgHXCrhKwVUCrpRwhYTLJVyu4cJy8BIrPKvsn2m5Z5St00vl00qlk0ulExPstIox7PJz7NJJTvlUxzrRd7a5zkrbnWd5k+2g2+Xdrpjkyb5QTwv1NA4z4hImBqgxhfab1ETEkeuvFziQNah4OKs35DIN2TVx68AWkTwAOo8ZtIw9NfOcpONatmJ6DCTjcDaCCa6zEXhkEY/7rtHPZ0w3GH3VdHGRxFwm++OkC5HukKmYZ/hvKMdgvQ/Pif+z3zU/U3oTjC9UZXCJp8RZqm6M+ghnNZNbIrnP8c9k8iaqngAAIABJREFUuv1kWKkkN67eMnYwpRnUDl3WaMw2j7NWCbgwN2mfKeFzLYYN4fxqNNLE6Wn6dJMyPW+UFc1xzBgXSkwWNxpp0qO0EvGaiNeEES5DKHd0nAooHSyOWEl/i8NUjngQ8xzikgdXN7gcdqPaKiRp280i6O8snYiNAcEcgpm9aGjQmCCnWUGrRGU/5EZTBNAQYOTKSIRQ8BGNPjoVNXhJvKmJOs2U9Q7U21BnQ85CYpGVCSVgQxphhA0FOv/WgMyhWJksKNlIKGD+QJNoCrUlsxmn6mn5U690QwXxs5Q3vVDiZ1OZSmV/nWQNmw8waCOfrmcT63Vtsh3f8hDMg3xR5TX0D7lrn3jqpEcfOetd10yYNoXlGCuQQyeKbDSylhbW3cNOOo297+Ps549O/VNxalkvKMuZNkx0oZ08PBI/v3jFal7mHWg4oOqG9UoN15EnTWSUHUn8OMuhZevpaggkaMZQxoAi7kvkSGQBBMYJmvQnHtfBjdLd7bsv8PhxmIUlloGOJc7Mg53tNLJ37Jmtm17ILKPMnMTE7lvAhqCpDMsCeLOGH2mUuEQCMmYdK5cLR+cBbRaJ+OlAQcmH7xfh9cOwJoQZtj//6QMvGN+D7HNrjp2wlQm+EoU+abzxdf0Q7yyLDa9+LSo+tzawhjybPIW95W3sqdL2A8GcMrQ94TAJHSXRJGDWsDp+8kwioGtYSzs7/yJW9icLaPOR260bDnMC5g0eXPrUX3cM7TvNdrYeLM8thuNdaKUpVM6BhlK09i3nzaqpYTU1mG67rJY7RHnEBDSO5ct+/fDyVUuRMR/fiO7DOYYnnyMOum8SMrn3/nTt0NBqy5uo0CUWNZVCQCsTQJ3r9J98OqttRJmOfCOTfP2BfSzCwLTYOTExQacDQ0pA59MJKM1B48HAjBxRstCldpJ3KIVaCLMffXzdm97Mli9B0ZnmBnTZjv9qWUsjmzuRvfjk+ovf0n7PDzaVSjsDtQpgnoZu0PUi6Ar9TZJfAeovIECgHy9KcJIKhwYVA9NDHdrlL3lOnjUCWpN3Hopx/EbCha5ab4dTfdkYGV5A4fQlxFvRWNatQ9Eki68l9vmr5ID8G9BfBLEdZFuk68yQUNW6dK0Rt6JRv3a/UyiFsyWcruBiD30A/wCYSPNWW59Qhg4b6lzIoQ1DzQrk6QDvo0gHlyLWhwD+CvBAGN5U9q4c9F90QK7eDxOGsE/PU4z/JZR8zKbbVSHoj0xAx/t6oB4H+OZwsNaFcTZ29LUO5D3Mm5f3oOAlE1MM8SCk89QjVGIib6TbUTr0ZheuFa7ZEILkxRCqFqHbNHRoDKXsiuQUHs0I5fRQTQ3VFMreMN4Vk8p83nC4aMhfOOQvpCS8i8tqqaVXOnqtq7e4cAoq7cJ/U+bWawA+APAp8i7/PBkSvkDl52jLZyj12fUAKT4F2I9/nMovAnwb4G7yPX+YlBMeAvifDH4J8ItMIrh7MctZFe6lz95fXd6bZI2776gr95Lx46dJ+WOAH1P9Qfr2H1Nut+8CfDW5KHN15krT8nMAnwX4dAJT/xRd+2epfD/AFRreIuDVCl6s4IVUvlTCSwS8OIQXBvoFnni+p0531Qmu3uaorSMhtzsG9JYltlhyU1msK4lVxWh5MVo6zJcMRwPD0UBRYN6SgGO+rIgvIiyO+GIRLRVioZCzhJom9YwUAqYJ6BPQK6AnBYfxoe4O0OWn3Vct6J0aNfqi1RfNoWrhqp4GxbhjTB9CHMNkUyjbMFOoagqVMRrlfd1UCnt/cn/7m1/P+sZjVtX2BtaYw9CWvmns/D31D/7uxEHv5CG1bAgmDkP9MLBhqCtCfRHqy1BvQcGGgguYGtjkjkMCmjTlqbFvkKhB8fuki4v/H7EvVEqZHriuro6IVPwEkapyREnhEsKHsoCHOVxXitZ40Cx1LmafKSsjJXduoBVgapU8WgI6AnbQZxyaJcy3SmsA3kD29t8ie6tCEC6oQYC/UHzGAxG/zfM/4PsvDKPVgZoeQAcRFpX1Iakb1dmi3w13oagRuEib0993bv6WueRj1ICOPz7in0lIOGLjkV/ibS5Tt3+XRnLzEwquFPDfIbwyhLN9OMWH413YYOmVxah/KJw+FE4s+t221+E5bb7X6nvNQdAUBA1R1IipL1GLHLM1SF0TE9CxtbhyQ8x0qmpAScbodAFJBjYjWXs44dpkNmz64RqiAgskbtPMdWukWiM1kn024YFSNkvZLERTyAtBmPeDuiCsD8NmwbtlNFHLyVr2qWhKFE0WYkokpodibiAWhHLAl8gZOWI55Xlb5QZr3WCt46+zghjlcF3ZPx7gdQBvBXgb4e0AF1IXfSXA+zGtAnyCet3rkvLTAF8G+A7AHdSpPoRPl95P4lEl+nXKAFaCEm0fBhimOfTBpBwku4IpD9AQbN4aAhii6KJi9QHLtP1xgD9V48/0MOylU/oKwE2ELwF8CeCG6gHlvRTndC2l4d5DV/p6gFd5/ARPrHPwLi11otV2tM7ia4vBmmF/9ZC7ashbUXSXFb0lRW+g5C203IVSrhRihYiWYt8Yzed8VsinR3yaktNAT48B0xXMVFhOV5i2eqqCKYRJCnoJPU7QnEFjpo7b3bAFwZtc3kQ9Z6spsXsciY5QIlAdDmpSx660ezGDe/oAE1kZ+wrxiixmxbfLrCXS/Un+q+KkVu2EhZ/69/7G7u6rnCcKXtTo8oZqNLlhmx122LzN5m1uOBIeb0VnC9mB3liYuhOzd3I5ASEmVmC2UOnzCV7Qawe9bjDV9Wc64RyXz/fEYkcu9tRSR2LFEgPlaFGRD+CULFxUFItLYllJLLOiFZjdMVxLWG+H6x2+wYs2uXKrp7YFameoTgv02ag7B7sALqDcKhdTh3Ax1S+icg9pN32AOodP0kTuU1ReTzO3G6l/+BGl5P01+Wo9SHMtM1+6l0IGTXkf7fMIjVB/pQn2XwGeoBX7k1Q+TTGR+6g0HcWzUZrjm/KvpAH1AE3hfpac9r2YPgezSN2YdDI3USfzRYAvJtNXM7sz07nP0KTuBrobHwG4BvRbAM4FeCngFO5lEl4h4OURvCxQLwmiF3r8BS4/w+EnOOFWJ9xqhxvtcKMbIGxvTdlbXnKXlP3FdrDE5ctcvswTS91owI0WGtdsSq86zeF9rpjiqYkcJgjokdBNMIInHRJStElo0wkUtCrdQkNMq5StSsSQqpEmJLhuxUVBYqA1A+VoWYPUgjtmZcz9sxpQI+pZESdTz+5gYpX+hUrTSZquOKXSzNQ3kMzneTdoPCY4QaPLm7yokUtcmilop9VZN0AvYQLAaIwHSNEFkKITYAS6aM/RR0i39GjoVnq80uMjMZ7z3jCcGCOYHAaTKy9x+4QK+PgQ0RXyLh71cDExklOFnCHVHKnmCTFPiH5caBBUtDCF5gsrCAcUHxDRUi6W8mh5EC31+BInXGwHA2V/cenokKSrHcDcvGm2zLQSYsLeUrCAsKgUZEEbw/llPs+K5jtykacGfFji62WeWuqp5dVYShsHPDXg6YV/Jxy1oBrzHWWwgCpzbTXLVjMsOb0o+4qyb1hMGRZThqJJGfQWeW8x6inxnhLvJvSUo15bTLTUJEtNsXWfA1MdmObAjFGYRtv7bJhiwxQLJlowvgzjytBRhPZh3Tysm4vQauvmUGBWeSkaEFGTjJoMAY3LHJmrpp4NDU0EdIZ9JuN6vSHKUnYiOyepnkubGXXMMnvIluRTN7iMJxwGDSdUda0HDQejzo98jm3dyXonstZm1lCHvqetjayuhvV0s+eezq69tvfen63bV9wRwjZLzBbQkSHo8EtNE04WAhnVdV1vwbgDMGsIXiEx5rU6tjN+naWeK3yRWQRpjQR0Ll+TENDDNKMOiLIzIroHaej8OsClAC/Cnh/5z4LhxNNz+0cR0OgKgF75iSy7i+HFbAjYIEwO4BU0Gv6Jsi9SvKuhEjPrvaMjoJO7hEGzEfDIC+BnAj5dHD7nwODmA9YZp52DXmlNDZglGWAmPnCKgWiUsh1gvC96h+xZDz/Sd+PXam++tWPI2ShgkwdzI5jCoa0ErChqHGhzoHdILvrmnZPmLGGdk9iFl7OnytMdaDvgMIBuK6oJ0Lmpx+U9CuaV7IlW0OmoVg9Muk8MFbeh8HRx2dKl+CTV5tlbd08qoSo0as8ZAjoAZqs6bH7BgkuuYAv7UVi5rYFN7GHTZ7Jz38Bu+8H0x4dWDNlzAjV12M17Cl0bMOUOHcFzmBBTrv9irmk8a5/Izn0j890pvs+i2PySjZYy7h4m+ilP1mx0V1HaoIGMQoldiIxCCsVAkZ0JUYEhb6s6srRMctT8kr/8oLX6qeHlP3towlduYTffXXPPr7oee3IuLimtJVwsBVjg+J2+aI7I84vrWt/r5+XdEP0EUNvBFegA70uItOF8swR04o8Wu6glVooMF/MsEdACCXEdgvIBflqOThmW3RZv81VdfB80+lSWgRWhuQzzrehM1/0gqPswqAF+B3C9FC9QsgcAvXGNf2W2q+JJBj+ODsVNZbXYhVdLdJ3+lYQ/02T3xwouLcFsi/QuyHmkPVTbQX+GmKn9FLG+l5bfl0Xw6rJ4zn5/yUE5awh6h6HLQlHaGofPd6MP0wTaZCQzmtbYwg5JQKf9T9wa/wzw8UH/RA/m7odcCZpKyKBhqjQbTwxDvFP5gmw099HVa120+2HEtzHSJB4x2I2a22VC9hIdgDw+pWqiErMEnxsF/b630HMWe85S1z7OsXaic4dzkmOfAvrloP8L9AWg3yXgCxy+IeFbGm4m8dm9AN/VsFfCrQJu16gAcx/RxL+h1Gd/ppywj9Pa4y+Z0lAMj9FtfwQgxe9pYfBr+tEfAf0XUE+BPABiGOQwyJJSCJAEZaHXpyLoMugyqAy0hQ6hI2GhVO4xQVsJS5LyLIZGMWzLPnq6/kRP0W+pfITYk+zF/oW2PAbwaAJz4X+iG2Juzp/ps7+i8eY+gJ9R5RfEvPya7snDAA/TjX2A1kv3VbPt94zi083a74ekO/FNgG9q+AbA1xLc5PMPhvy9IX8vDxGRf23gvsv3L/KCl7n8dDs41fJPNrC9k21/px1sNgtaw3C5wdogXBfw1aEcCNU8rvuF6pd6gSJoPU1DY8qPpIyJ1DmBWVCaCA1cxW77jur59t1thXZWV8ta8iiC38jYisXsk9flh9yBA25PWU50oNeH8S60O9DkoBt4Q5IkLfH4U3lMeol5L1EfPFBGgmOxhHfR/SxlhsKjqmYI6Bz2peQnPIJ61jp2ghYYd/JwCJfbsNmCiRTCnEOBtoR9lgp9zEmIAzeSMbI28YBOmWhTGSHEURui51rzoD+95L1UIVf4U3pybAwqiThELshB8h3+LMBbHXXGcLjGkYtCPYNDbwjtIdrPjDduHbHPzIbOUridHoYDAJGWwtyR++/9aZ5cA/5WDeiqG3vsBHTaXYbEZj5FlPqj9Pz/MrE2PUAWoO8CfNFWlx7k/+9J76wD9ol2aTMvroqsxZEzW/iTJR8XT4gT1wyl6lLrvZlTZkeQ0fWK1YRW5jRFzgYAxsaVdOp82ApFCI5MiTMiMBODD9BlW7Zw0RHyLi/s8fzpnr3SK29wrQ2utcmzNzvOZtfd4jjP0frVUr1JyQukuEJF79fiU6BuAvlt0HtB30l2he+THtcPAX5EZNCvyIz3e+psH6XO+TEq/0Q32fROf0y2/4W6tf30K6BTBj78WV/22L3BjGpG5MuEEGLy6moYyXVThhSCYPY0nzJjaDofEfRZDzCjp5c5jk3iOU/QWY0oH6chJrvxSWodj1GP+hvqQh+gO2Bsh8Yw+TPack9iVvw+jWXfBOwkv0pKXzeq8AuCX8f5tWG0x+fneeF/2t45ln+y7W8nJ/Ed2Cv6O11vRwx/u4swjuSbXX+zF2z1wk0Ivs6LVnrRcgQ5mRo/U18u9dWArxYGesBX/b7q9+R8T8311GzCzEAhQongaoZQ05SeoHQXoJ24GaARV3omE05FGg6fzLTLFTrO0pmlhwx/ZBgTU2YZpeyepv7v/eN7pepRSgtFt/q4iBGIviCaFYQDXrjCC1Z5wSo3rMAJVjrBSjdc4wSrnWC17a+yvTW2u952N9ruZtvZWgV3s3kLM+W4ZwbuKwP39Tw4n/t7wvDikF/K5dWBfHcg3heKD5MT8ec0sqVfI9r024BTsr2EO5JWn5rhjYU+ffgfoAmGmWj9jqZbvwEweJgqhlM29d9R10HTG/178ud4lKY0T6IZSbsxMLWJsUINV0+ZjMnKzTRnzDCU5PI1yb7THqBqBHlGX6RfYXK8OLTaN5M6Ywkr02kb7nuQrGh/pr7xj8m07Q907eZ2PUJz15RJf4L2/B2Nwg8m87cHyEnil4nbxK/opVHzuxfgJxncQbEgXySL2udBf05E10f8U5x/jIv3hOKKUF3kqzcH6jUBvDiA5/rwHE9tcdV6JzrO5qtsfwXx18tK7pIUljtg4PhL/GBRwOeFYrZU86Sap+U8EPN0NEfJPuSmoc7QQOgincAY8ivJeylBeqJLG6f2HfFyxM6YH5hi0TDF9Fgw6dazZXa3LBn9L1E3djuKWMppqNPQCNAG0AEwTqsJKpougznCn30o8GC2QRjONsDEmMEsN5hu+VMtf2rZ67O82ZazxHZW285qx1t1CKxwvAT+MqeCJY6fYhntc6gjrMoIZK31grWut8Gxt9vlE6zSjgy2W6UE5a1WBZut8kbLWmvZa2znONvd7NinuOWXOaU3OcW3g7oG1LtAj4K8FkZDv0sjrlXwHoAPkXPS9YnVx1igjTX6UOWXyWh9Y8aAlLoEfYE2mhZ3A9mZzAHT8gaAz2McIXxcwgcEvJfDOzm8M9TXjIWrQn1VCFcSLg/hb0egLxsD6h2BeF8g3ufLK1zxdlu+vixfXoqeX5KnF8VJZfGcUrQzRZnvtMMddrjDCbenwBlLsLXsbyt6W4fdLcPulkFn62FwwN5ywN6y3z5uv7N0n9O/z+l/2p7vwCoHVrl6lacXhtAXwrhIdwjdYqjkdGkDcdxYrYm0SOMtyMqFLFkiLBmTEuncm1yY6wNoIiduwzhXlbRnPsRc7ga4UDLhoWaxGX81emE3gGqJVG85HFiyhnV3o0NnUwPbvJH991vY1e9m9z84f9Bap+B4Xy4N9YwQJri6xdM5jnFvGAFg5v+pr54hoDM8DEqnlnWvDed46MDxGAX4V02Rjzh4xQR0LkdLy4xUrg5JwECDcmly+xWAs4rBRFf2YjA0cdBGdi89yXT1kd7MZ7xCUyDSWY29RXF9XYb8ELSUYD1RZ7/CSTuSiUbA2Wj+Vm7D0RHQiQe0IaAlplVSOKFXN5I/4zu+d9/zz3lRxyWXzXDFTgV9qOot60A0Q9QqRYPjsoMlFEwpea0Spruq24qaPGh0IWcDGxJsMGIWylB2DoqefcHMg9Gyslg3jNb7tqGADTpMQ4evMfeFBLTiKtRFJT3fOKA7h1qlut2OOv/81HE1DG0aNfXsk19aXNaLPGSHYwLa/AD0ss4WExQ877HHTv3tb04dHH6pFZx9wFlzwJtcFC2WqLckCzBQDnNuYIAhPdNRxEJeKPr99z085fv3T7T5GrI6Yrh06upPrtDIRAeQS+oY9RZhyqk4atLQ0KCaRkBptGpG0BbqboCFRa83gqkHnVYOM/ZbXaVwkh31hTCnLPqKwQRbTNYwy+U9EvoUTPHCbpRujLp80WvzGZ7/vMj9OsinAAY1FAVy0GGGgJbGCTpLB6RzsbSSPCZmQ0oEHFuLMgcZS4KDCGh0zv8jwBcH+aIi5ByNdL/xPkOpVskOhK37g/5i9EI7fA+I34LykF6En3LxqkDOFhhnjT/u6KYVE9BRPY+6rXA5wNsVfDGE3/pyvx/9EeCnAq4pRTssdHI34dJ1EcwBeBVN++5BZ1v9oUD9pyV3ogsJzLBgvIVx/QUL6ixotlH6tsYJF7v+DeT/ZSbNJkchXvQRCOjKXf7jPmv30/yUJ8IlB6D/ICwdhkXDMLMEU0owgb50vA3jLd39N6EHzZui3xYDCRa6oh+FHcRCW6y0xXF2tM7hGyoIdwC8mpzj3gzwFoC3kzvMHsBUlh8hz9xPk2Ov8Yb7HsAvFDwRwbCAkoCShLJCPzgbwFXgKYyZ4Kn2K/YbipJeJs/WIf6nd0dTJ25IihCXKzogB08OQmkBKgMtyNJGJWp2pzDkRnZ1k75lKpVMmPRt6cssHzK6nhkdUOYXWUfSWI+7Wp8WV+apOESTMReX8i3H2MJQwAaz42qhhdAiUgHBi5SBeckjVQHuCYGEooRBBQdTABzUmHTuMQ2/TRaWaeU+ahHGOT1bfpI6//cATgTfTXgnPSSXkwvVGwE11l+n4FwF54I+F+BlQbApDFcaBIFZma/Buay7yfE2Of4GXJCHS61ogSXmDoWbvv/g6TP6WUOOtdSyJXPZx96/2Cm+JvC3e2qygHaB6lftnuiMc8erDnSg1iaVSq0JhxeKcmBSREVIip8BTNHwEoA7qRuJOdZDPIRjbD56Alqj7PJfBNxgw9Zh7C7qAtK0kcg+1yiF3KIhoMktGuMTyQg0gnc2L034reE3a2mm1RaqqVa4OkKHtZs0PKRhGIQHYRHCJ0H+npjZOwGud8NzXFjhI1PfFsA4Dt2Uy7E1xCkdCkF46CfObGguiWVD9n+R2xpeuFI8CLwwDG/+9jebGuobC3U7d+4Y444c46bsiHN0HzWtIk33apoxCnZTCzcvFaY3hP0arVY/V3BbADf58FGIroXoCpAXgXwjqJeDOlPKE4TcGoltPNochMd54TKHL3CiuZaY6Yiprpjki14DV/a6stcXPSlC0Z2CR9086k4F3DMV9AyKIbuiGJ2RbE/QSXTVZFSKD+dEwUIeLPHCFVl+Cut8BaoVBetRsMjfavvbAc4COIc86f4rCSW5lsRSPkS6Kx8mn0TjgXgnEam/xeAnPQjSBhWA4qAJYDJxJ/7tyW9gwuNMl8Y1ddmSZgwSc2ti9mJjbTE9mflNTMdlPmM6UvPJSCohleBScilNLxRIWYFWPAVIjsLp5guUxB7N9P3UteGPjNAZ0BbaxzxLRiAvu4vAhC0EEhpHuXGq0JHNxUTxUKEidKnAb6eYsKp+WpNwTZH8soeQe9KDoIfIov9boupMpMvXaFH6CfIZ/2Qmdud6ikj4JJWfoF/nozSAfoi6TeOXfSXA5eTJcimVFwPsptH2AvJMPw/gzUK/LlL/FalzI/3aSP9HBK+K4FVCv8JAqpdK9WKlzlH6TClOEeJEzneE4bYg2BCE61BKO1wz4tFCMhTlthG+V4HZYrjRbJnu/O/9XR+JYydYaYUZ+BsAXgjwylE4F/R5oC5U+kKld8dQe+iHvhLgMtSxkZfQ6PkeCrn7APEpH6GHJFt+KHn3k8SP3ExBYMaD+AEiNx9KrNG/U/Cogj9reFpjZzikMapgmGanFhlvMl4lScMf/Z8MqBG1+ygVlRqtMWVmHUphbqS4BZkuwqwWkzVjbKbKzm1MXYGWmI82wj9pIIU2LbKKix4xW3v2XsYzOuo7xugQRtyqdPaWPSFzCLLMmX4sUfeiD6d3Ad/DnFJSYD8ZhYIHMgxE4BvoIABug9pHXMNT5HPzdFL+NZGlupeCUb5JjtifoqQ45lF5P4WwvIN81a8ASHEZQIo9AOdTVCJO0qrxapS8CzfE8NejeBHBd9eNCddbNybG3Nl31znu2jHhOWvHRHZn21v7LwTHX+f463AcD9b7fEsQbY/kTiFPUfoMpc7R8lUg/xPnxkcNnEvjlM/gdTTH3pXELV1JUT5XjSqvBEhxOY04pjSDTlpenuw2+ghmy9Xo0Y+uG++miccHiGD6TBLBaUI5TTyEKdPYKRPD+lGAD9KT+SH64I1k3/0RzVSz9phfkXnYlMbPJlum241h7LeJ7dy4lD11FAETJvpqP43jT2dCLp5MtpiGlo2N2EehWvuoAT5BTfJPxFr8IfExyp6hqZvz/GVifHoQ4O/Bz2m+MaL8n8RJ6yFyPLqNLOVfoBnIx6k3+BjNST6WDCgfovHlAzT9MGU6dfxw9f5mujK6/DjR/R8CeGfSq1wOsEfCbgUXCXizgBcLeK6EUyWcqGCnhO1Cb4n0xkhu4GJ9yHFOksFxZIBf6YgUyzEcTS5Gt24921Fzyb97AW4RS9EHHCY50O1At1dBT6B7AzXVhGVjFiU9LsKcrihsqID4bp0HVQ+yCWQLyDYlJpXcgV/8uv8bX++/bHfdrbcsKJVP88JNRW+WFXaH0BlAS5mjJhugImUDlXVAa7dAYhCtIXY5xBkpDAHtYQB9g6May9FShanF7sXQPWHIiKppZTwsjBhM0peKPKCRgM4KQwqtAlrvAKj9IO4CfQXAugi6SIqzCxfCuJpDFY5/BgGNEaWGhXPQYbRjSA9weCM5uwzHuX5SArrqZhybBAdy2MrM6fEuhrjCwWxsvwT4eQj3eOpzLrzEhwEJk0iPplbpGi1qQdbJMOd7tSEvoC+PJDc38lp1KeePjax5oQyNZfRiRqEZRxcCpGvxURC4VC4Me0xBaznMl4N6SszVQpprmK6Xci80hbrX8ua9732slrHGAmvqZk86LyrpWWXSuDRKlyGqbaJWBnnyN3hqoitnoeSZnOXIKY7qdlC0Ggnr5IfMUe7juth/ROPz56sWV/a4YqoveoVskPhEYvZJk//HMNEm0ZCtaizJbFVDqr7MQ8HNHEfbckGgM+D/Z+87wOQozrR7ZnZmgwKSwAITLYINJicRJYKFTbRxtu/w7+PwOf4+39n4fAYjCSzAAedz+h3ucDyfzzlg2SAQ0SATTDLJgA2SkDZN6lTp/f191d3TM7O7SquEarae3upUXf12dXXVW1+9H+n10GCRDWq2lAfH8ohIv4SUGf3TrEiuH5xD4obxeUF8XqzOV+YFomS5AAAgAElEQVS1oXhlIzgnjM7zg3P85lk2hM3zIv+VQfDKRvCGevjuIP68Vn8At0EVTQMXknphNE887exRjytPB9gXI79MXwq7LWs8tZeg9KCJ/49JQNOQDk0S/58QbxvFXmzwm1jmhmyVXMcuIc6RJMT2KxpQ0k0yaJV3Af8Vq2MjDORl0aw4WrYUtvpQc6DeyF++24BnFeqK9KZ/L/HpEbVgbTQrpDEGsmGP9O7Aq5l7fQfwFqoc9b4+ZoeYFSbLSm4CCA05xChXm3PJYMpEOb4z6duPS0BnNYtFFKONcLmvvu/jMz6uDPDRiMLlMT6wqnnWan/ean/eGn/ec42TNzLUztb4sDZXG3ONMZ82+rNQ/wH1ZZhrFX6pyTw5r0FxF1tk3J+ykNbA9g9svnEPW8E8zhZnq9j6bBU/vmc1RrXxFZnYB5KDIpYzzgJ7aaO9ih2Rpcq5OVkk5gZS3iDWyELSJ0j0+401VLGMMvWmkuLKrEXS1E+7N+m+7KB2cjmhNnhjvmjn4/mC3x1Prp2mTypNWfbsQJ89gt6MjmNbO/KXy71C2fFjnpsyP5Zyt27mdOYHLxdJiKP8vfL7L7NHk4uE/HbUDZKQWoWPcCvNmmZnRtxP8gDvI1xOHmTW8v50eR+3lu7iMpNf/h64ic0wl6XLm3jLrXzk73mu6881vi3wpRifCvHlweiHRx83rex577jwZSufvXrN2rePjvxdvXYeGRLGc0N1XKyODcVhvjjIlweEag+uEGg43epsapRs4GH2nhCVAHspnMvtp/t4eGCDq7KMgPY8z/et6o42inuS3BXPrKGBZ7X+fqT/qYE5dR7iitkgkQhoXdKq18rnGfRL1VdrFgdH6EtHUsWtwfxsVN9upKYP60LOiuI9h4fmGfkFyOX8IEa5HIcwT8L/pQk/IaOLwvgMXx7W1Ps0zIwG+zX16VtZiWnqxoDA1IjCgE+aP4U18R4N8V6WjvmrFcVWIJoQwHW/+mV/mVwPnHTCcXEc89hzrqRuoajt7ZPcNo+lRxq+QtOW2Bi1GDVJn7kRhUFFIytZN8OavlqL6T9wXXeLwU0Gv1X4icC3YnwhwsciLJb4wGDzVdXGK6qNM7JQr59Rb7zMhkb9ZY36aTb49dP82suC+oIxQuP0oBVODRoUouC0OFyg4jN1/CrEFyB8O5oXo74Q1Y+p+hci8X1BLhB+y94js7fjVraSsy9X/p26h1+6J1JJCmuh/GcuBk+TmpNeBTVI30oV8ahY+sU3AkYYngVlfULYarTDOLlj1R5ja2HmhG2TgV032OouGfdjR9222qJiY58UPSxbmfNTs4nF9LlsC5Qxbgzkqs18xThmnK5B45n29iyRnNDguYtRzg0HekMihaahEPAhCVvE6XRX0VlhS7NNbWh7Ssh0Xo3ZvdU8/8laRGbPIjOTzLZkM12yiO2+5o1M7YwWa2GabbeRB9KW9r25ruwKnuNyO5v/L+e69Bbecjd/xO9J6+Fuaam8GIKLbygCmfTWbalN8YrcQ8mIhnu5vfRoaiprZxhk5cGWkKfSt3iC6V+PcDp2msLTMKugB2Hq9IIbO3OL7HaZbl6rsFZhSKHKFaPPzTBqiWkaje8cc2rV3Px+2ZeWmwqxgC8Q5onVfDwdy6IRLTvob8+lK9g3OPmuam4V83Uz/cekiqCLc5Re4fwLmOQqe+Xt8Zt1mV2rI8JZya6cNrroFhkNI2iGk+K+lZDki1hoRByyGR5R2pS1I2L2ePLHI6lfnoSMt7fXSp/LePVPbBBwI22E5Yye5SKU1SqP84fATqd7IqWo7GzCR5gvy5YPpbOI/sgfmvtT4u9urkMyW+zf8+y6DvJrE1etzsmOtrR27rbSuInn2dzLj6CbvlyfLdl34SFuDzwC8ycK+pGu8DB0GsyDaIX7YfLhwfSwXArmUWQhmZOalZ8sYk1Vso9X1hHoEEi8J+1FPkYcrnmOnJSQ4cugoVqLgqQltd9sYPUtq82VX1bZR4gA2Rw0NGpsTzPClV7T9jHTwbNsFK0V4T5mzHZRIaeTvaqt+Vh2b/rm2gZMyBt9tqmyZlX2jdY6qQ8iTq3Jg9Z2aSvnKo//2WHsjVxqDHeFUY0a335D0yyTQSbHn2Ja/PH0rc8qAVsP2OeVb1dkT9B+XLI5x/kTO+K23zfmkQ9xkbZz7G7jSiP7LI75pt9GZkC4jmfn/Ipn6vyETZ2+z+MTnwc+rfFxjasN8T+LDS4e8l85FC4YCheMBK1Q9c+sNl9Za7ySZp6F82gamXlJjH1ivDDSu8dqVzL4UDNjOV3oaaRoZ2YIvZtUB8h4ro6OkeJFQu0c651iM6Ul/8gEYObrmJwbKS+QSbA6+wE5PSJHvtZ+kXm/Wb54SbX+BoPraAxY+zyLtMPFelq7j/efCehyYgFt25k0N0jLMP0c3Vurvt2PD2f3gyUWgJ7Cy948AZ3xYDF1+sYw0JyUjWQBrXukHJBygHQXmM5dHe46Gl3EcqmPAw1uafO3LGsD5L6z62cBnbQnQqChTUhdENvUEBFknV+wQaaibuYRkg8CF2icpsxLFfYyag+I2RDTIPuNYHUYWVGqKBW5hCKrNJYaqKJUJTdZpOSd2Ckbrym92PT7ahqwJ7BHLeqPSFt9iqD+cx/bF9uDe6g7rfZtNl7+mvO8XaaR3vS887wnG3OfEzMaRCi33HbzWdbgP7PkL7DORuL5Kkisqu1e0v2I0SKgVSJPXCSdazmgZIV8AZHKR+KAPiWgKz7NCt+lgd187NHAXiyss5+Pl5AqUDzXj+YH8emheFksFwh1hjKvEPp1bG16GY9Lf4hfQjsZxA5q2VFEK7v2ZTZ6+n889ngtD4B/lxXKfshzRX/ZDH+osMJgle2fMyeolAH3HdPuKI/wb2UCmvqBKww+XMNRo+RDkgz4m4T/QEjzxA8M8EpJo0k3cw2rgLrR9wHfC4JXCrOLlSthSsV602pz4BCaaVIfrPUbuUzeRXZM2pANOJl5fr2JNw/rvUZ4OIvna/RK88JYHhfKU2IcEWN3SfbvyVQO9v/Tx1IVyfAXD4IVJU1VO49JjbRRSm3w5G2ZiIDOc9DUrR1lVvehVHjudo7cwJPvvsLGU1/lu7AjkBu0/DJbzSzjvujd3MR8kJqh5jGYZwGf28GkD2+H6mz3Orc03KoONJlzNjXNpGZnlpZtIC6qQUHHZMqSsB1Wf8DyAlK1bNEi7v+TGb61MOEOSFYNU9t7TAKaP/BZLyDjNaijY31Y2q5RnmPNH51dgCK5iq8t3nbQxq3Ya2bI5cjxpKPVTXDQlvwvn+0sbg/IVm0k7QsZ7v+MR0An1EwemQnjZH/YFaiGsH5Dk75mWlZoVWXca8xlIJZmokDHmDAJVGYokCGVffDwYwzGeDrGwzHuiXGfwGN/vO/6h+69SwZPcDPla/wWfJHtLz6eirp+EDTWShbWpGwbH1WLKJANaXw0zYCOjmyGhzXiA0kiLZ7LRkC/ZM5IZK9q/ilMHM8I6ELR+/2dtwsZxSIch4B+SMQfjMRcHzulw5lJ7WGnZCb+f8yAkjPDcHYYzo7ldMmftrE4aGsEPVXqverVl4rGeWTIYO4mtpHkca1J5nXK/w/R/Jc4OiuSB4ZmJrtg7fFTZ/R2/IwHbomAFhiISDStMoppI3p+JP+TP+Ij3LKnTrJlLG743VLr+fbkE48XQrS7EJwYrUnca19da5YmNVnlSomIQxCjEaPBn7mIP2+tdy17IXMRRSpiaAisEXhK4gGJOxV9Yn7NQp/XskHrt9Llf/HszjGXeQn7/CzOTBL0WlYCzU8a+Ap/sr9HjTN9A+QdiO9F/Lg2axRVpE1NfSqqbDmI/FvPZdUafVsuKf3QJHWapndXClZfibmKZZrE3ja99oaoWkMaXGzhmFT4eW514jinxC89XUkY5Elka0TMdsT2QvZafJit9g0PPdplO/vMUws3lIDmkrVOAjp56ExAM3seMXcTUOYTKjnBOGXBMjosw76rDOc+ItlBHad3nZM7sLPW7zp23A25CydfL1udCx4xskPgbSSjvaoFoSMH2aq9ml3NkstKmN2SHZx9sHbs4xOz+XTMQwp68ZKQH/3NcGtrbLQ/xhYNqZP2OQ0RtUKUe3Ho5bUfdXtWUoSTBEVatql4cyurReyOW6bsjqTFSis8ohMqNBSN8NG0h+6QvFbcFrTNgYRCtSckF7MjhWk11Z4D23JTyewDmfZJkno7OTYDKsNx0iPZJbojuQx3l/aUjrclgVq5HMjkImWviKtKBUZo4Eonx2QHJ3fNgCftLq6cbZ/MOulpbzt2PwnCnSt2Rs7mM5fxjmj3TdotfFgumo4NtD6j2YvfkWK22v1ksl3dkfTptxWt7hTyW/K3noLfmuK4/WxhBVMa3WnwGI9eZ86zG8/QaOHZ/TzHRLZjfMO2oZJl+uZRtcJWPNn1bCS76tglwOYga5ZkE1UtG5txuxkhW2V+tnUHnLztxQiBzpAO6nSAlIxv5+6VGiQciOWYOHTdUB7EJGP5Y9rjrRqVttt3NFd5tm6sLZa/xMbEO1oXvNr2bqaZtGy4tG28Vv4oozw9Vwk2SoiSJZmQRjRtl2buZlPB8kXCxtP7tCXEXqyjnNgyZgLQ1OcgEYuwM8/YYlVpdAYYniTaTcpb7VNr+mZdCNzKFNBSFkX5z7Rl/q20Zf6t1P/H19nQ8MPA+4C384Skt7FBIenvs4fqM4Po5VG4gMPLY//sKDgtjA4N4v3ZN/URgTwm1EeH5nBfv7ip92nK3RvyBXZ+baxeIPRuTGfvSiLmFHYJ5DRf9zfJS5kX0sT9vZR4jWh+EuZho0OjY66+x/4CthWQ/EobAW1lKxqAT/wKPfOnJL5Zi0/waeqqdX7eklfdKgQ0TTJm1W+pyG+Tj70CnM/P6BFm7exHkMelxyr760dAE0DkgRDwuZUjqA4gzk1BBgbVGIMhVkuaxP0Uzw+6E/hfqa8Q6iIlz4c4kWhoNd3EUymIASP6tChZr1CB8Rqp4q3PXla19LRKNDED1R/KOWuGXtQIDwYOM9jZkI0Y9eRzFH6RCOj4sD/de86A503xvJ6y96X/HViNfVbLEmvHkJd5lrwsWOqQLWcTY3U2We/l6dtkDMtyz+QjKPVw3dsioLVnlAfpQRQR9yEeMGKABEzJhXHZWkCnUug9JKmpDx6KTxwKFwwG50d4V2Q+GKlFUfxZNjS7jedN3MaaX7fw8k4eDv1TajexCnqY5okbS+7bkainmCOwUoaPkW2FecKYJ42x+oyrmHReHRGPU48RxTTBNSGOFLVv85XLFreA7ikIIYjMUjT9jOcUrAV+FeLctZgymkgelxqY6mP3CKfyzI4fE1uqG1z8GgHuB/6nIRaEemcrmcrqpWQFH7MROr+BZI0eotBU+4XyX3layn1krku1reD68TaJf2ng8Lqe2dQkxGmlggQNfvQ09JSm3iVQs5Qpw3hpKJJfR/SlGvmk1s1WlnvzZKhb2R4q4B5/i9RaBwGdVDp2VMh+YgP+PFvVuRq/vU/zYKYdqLQycxu6ZDcvZogsx5lETpe2XtDMJNO7netUjBvPGgJxYvdBBBB/+A0Nb2QWHXb2JX2Y0y8juvbm9tmD0krYrnVkx3IjSVc6a3kIHlyzJnt59iT7nGa8SFru25q82Tc0l/H8TWQNnaS7xzmjeJpavi9huxNJ+txESGjVlEBP7y/3P0OnI0L91bafNf/M1998RothzsOVSyx/xpjx1gOiImD7vWljrmU1YFlpS3bn+Odxy0mWG9sWzGPamnXBzbekx8V9b76KkAgljYuQoSKMDxVya6bJ8+Oe5hH+P2tQYMGQRwwe1LhXY4UmEeQbeET9ulSI/Jc8DPsDmK+CTFzfEuEd7CXpcbatiFrvahvaE61kBHS5XPrNb34dhn4Y0kA3zaXttIBeEfmvUWJXZWj80gZrBJ2tUkRPIz9m6ljoIw1mC0OfG/7iZObPPXw8feOE3Lc5chriS+gu9L1k70xeN68FFgHvMGpBJF5K3kH1zpGaHsgpgeoPVG+gS5FJ3BjwPKkKW0DT9JGIhqyLw9gnwrvIiI9mchD7KcmSi8gsIcQdN99cYC+Ep8w7eSuxz8nYkU4szsjy1r771LM3VA6zgZOOh5d7GUixmJvB1k7N8rx2+HyEy8Nq/rZmxh020mEAYletueLT7fM3re8sqz5sl9l0gadTL1tWHtROH1nLFx3hT1I2gcbWSVlFaxuv9OqmdVRWaSXHtOyLyZuCDYLJ6HydbinYFKSk3uAGQJpudoHuiH2L+cVPzP1sZ69Fl3AiubrE9ljYLWfSM8xzaqm9syWdTa6StqLSY9ZUY27seNjpMflboFKc1Uf5SFIyNKk40RhwGpLmEt8uaQukANnj7SWyOGUgGTdl+j8jIjs4yvzqunkTzmY+H/l4293YjHA9ZnOWFQ+K2Kzbm05ud5zPrt2bL3z5hPLnWsjd8dkrmm9s5OLrfso2hazYsVmxipMRpIhb79kySFdFKqNDPEti228fVWLnz7UhV4i59zF9T6ixye9mokpDfQJqbLQabKDuAr0LtlXF/UabUPpy8fH2BU+W9qNARYL11bg0pkxE0pShk1Mahd5IC1RMwkDZq5G1neh6dJ4N+cK3+eLZ5caLpBAmucpWk0guZ7koI8I1TFslk6+GbD2TFhxLBtkl1SWW2bYzOMhjTuuzl5abZCOzE4qfXFYy08vkaw8ywc5xQfZuO2+mreE+xs5N3dSGUK5GGi/d/PH5emnHjGfPdwvcfh759YjnP7z5YtaaHJAaDQjuTVBdwyHhoLPJBCn1POYtdvaO2iq6rHM45ql2Y3Yn3QVufeqc5C6znlC+9sxStAnZ62VPbKMj2duei2Sd9o6bSuxMTethGCagqdVn65m0lZhVvVlHUqtk+Gud/9Jmkb0KNRF5hr3tPMq01Ze2OLMHnQwP2IfOB5NdWjbIyh0Q++2wluPsxsl6ciL1MzudMWtXW3Nsa99t53PYWV8r0tm39/DcjgeYUrOm3w+z26TMecwypkq/DvM9g//WuJa96XwauCIU747kW3zxmiA+i0xFw/lB8+TQn6fj0yEXQCyAOlGZOaGZ2dD9DeKCPYWXQn4M8e95dnjA95Kxz+PWtFmJSSIZAZ19l63vE22AQYn/HjZvqZk57NDLii70Wg+EPutvZKZOW8wCOvGxpDypi4HYO9Z/x0Y2D5joOXaoYImmmBsCkrfU6KW3eJj1lOBIGr3ULmkR0NSyN1BCoRlhtKFGQvIml/2G2Yrzf4z+DyM+JMUbZPQy1ThJ1Y9RzUNUsK8MXyDJB3Q50ERA2xBYAloQAU2Otkm5fI81aw859BDv4vd7jeYCH7uH7BIwxz57EQYiMzsM51/6wRm9HklwFHu8pxpzQ8wa1Z5CX2yIgOaOPRHQLLVZyZzSUvfe9JILLF2xfkWIjNZTA1Pxjce0NRnY0om6SIoiGQEdTVfRLnG8m6/2Ij+k8mDyNC1OrIsTq/L4UXEGazN9jkUAvweaY7uMJzc9BlOjhqD1/kdNwKTaI2NDMhnVUhNzTDNoI45Iw3KKdkTFaBlHUSBkpFQshIilioURstVcydqPtrri5igrJWbUGdU41Hy0P/vMsmo5i6TP0m5IiwwXpXTX+v7vluAg0VIyf/5kDYcMwhtl75kkdiwPHwpfXlcfMkQnPadlnLRSyffgrwfjC+pmD8GS9ppHC9irnvWm1Uta7HpXX87x48NrjTdp/Jw4BTNMfg6pFq4zxf/tAAtC7BaYgUiR0yegaNjYWbKAjsAMiVkalZR99ljGvsjsM/uQJHUhT5A80Ak8nf82ZnWtQWWrolk/ApqwTUYsLZatBDJseVPre9Je90+8PSUPknYqFQUrwdz2NLMnnkZsoq0vu20oZN/PmBRdrPmhog8PDzsn5yRjoWm7MuMU+DOZaHHyxdNrJVdJ7raNtraHJASBtZu2m7Ix9/wH2fZncl0a+sCmZPFEkQ0BlO6S0+xgn9eDgM5Dzo2oDgSy1eQNs8fTSna7KSFlsc7uya52L7MUOyIdRyZPQCYz9FuthxYHnbLPyRzSdBJuRtskfeHWbPfUEiF/KbqPFGt7zXw7JymqqaVQQv9TsTDcK85eh6SnSh1whobzJmKEERqxGeEwpMywwSh5pCQ1hid4dti3yJMYHmXKzw4XdbVlWxcZO5YR0IWit2LFnUJGQkaWfWZTbrLK5/QfA74tgiPJ+7OmwdTMc0VOoqsQyxkiPBjxycACYJ7Us4Qh9rmDgOYx0ZI0uyp5NNt6f5xnuiyD+l+tPqPkBVoeb+Q+QvQHPKMoMF6gPaKeVX+gy0xAk2tHe2m2gO5jnwTESjcwayg6xxCLPUqYk/VskE3ZlkF0zx13Fvireur8eWODsiW20svQSUCnHfOk/uHClLRsxshS/j3KE775MpB7RZPvci6hbGdu2yZEbX5s7yF9r5Pc2yvl3/qOA1odm2yiaM64mKs9AiU1X7SvZX56g606yFo5C2mN3VFX2BeWxq4zO6PU2qij5m870bYurLU1Xdh+45IvXVZxdUQyhDcikr96duM2knZzk2asSCsOOmUDCejsKlkOqSJLzButGWwMmX2JuiKtCjP35erc2MXQZ1Q9fcbzd5NlJy2HWaGy32rLQbd/Ydufsz0xSyePXLYxH3HH5yFK4/ly3Ppa22cwwYNOG+qGXVuokIZbxVghChGl22lINmSzEmrd0MQzHiu0FxuzcFjrRSqx/LIn7LMtZdZKLeuDWDuCjFvJIuln237O87dr6xAuFracMEtqbR4DZpGz4UNrP0gnZwR0yrxSwbZgZoUtqQuz9c0Xyd7l7sZnflcWtznJVhPGp/29yogwOjjloPNUcD5u8ehkn211klpX2zq8u0glLzpdvYOA5j1Z1ZFEsiea0wBJK4/W//y9TX48HYpIykO22oVg8sizA7bzSFIPb2hBTiuZ5AWxD3zLLPPVyYbH80U8mazJFLPtOVoOmj5nDIg1DrB1Wf6OJyh+XF7He/vWB+VWgU9j9moTn0t1YH6Uzroh6WihZR/irBW3KU9srG9IRkDbB2P73bmct3peSS+Lu635+iCtxvNts8xqeeMiXL1YM4XWjGduOvJXJ+0Vtifeapjmc8JN06SDlxT9fFM9fWL8ibGTwKymSsgtYcHFqnUQpZAZrdAT4ymUZK9tJb9HWE5tFVs4PcCT2q9jPZBvM333RZbPtt47PsNuG65ho5+3Cby6KV9Ri+ZV42OEfivU70gQgtSx7By7LMe2PGSruYx1RDsIaPp2k/IE2zjeF+KDq+Uhdcz0SfLXBmsBTdbQOelgb3MT0In7Qe3Fhmx2A1Npyj1rzZcb8UWm+2uqUad2CmWelevo1mXqiJj5aH7X1tMCuqPysS0a27qg9yCd8MVY2neYrjqamq09zIZaN1G3OfqUGH6PP/xKv35UFO8tSFKjHMHKX7D1saFbst11Q9IWey397Z6zBry9d/aWXDYtNCc2MNVgWsicNYM+1WCfRrTf40+cOH0nr6/f65/ivfUfvbo8SIINljWZrwoyQysJ0lUosjx5Dy+JGtAkDE0HxKZIaJLKc9mXJV8VfOU1tWenMBMLYIqx7rETqKs1z2/MiMP9lTm5iXNDvNvgs2xva0V1l/GsgQe4QFuB/NVs0zqcU0XJ1RadfQTGtjUG0lFI7Wr+9NYB+a1ZPN1tN6RrW/B/NwHNM8e/2sD5g5hdh7cW3hC84WDuSPP/Ar+UZNi4Bohowr6MySkS/hSq9zbUYaF+gSR1+YTWieD5ur8ud6rKnUbDvZvBaTp+L8R/IryJdS1qNOqiAir85hng27Xm2ZHZj7RcNEmna12GIcV6iQopsZhKEwOB6bM28tZWMR2rKFotDl56IXZhj4X/yboWUYqlnXxEb9v6E9CddWWaFv2f4Pu70bvy6XM8KyfrHaG2o/2uJF+3tEpopZ3UA60NGxvLZypJI79pK8U7W8/5bHAuuzZs7P23tcs3+qFPcOK6QLVz9tsbDakNVdakaI+0Wj/tXdc84zxmvA0kWwHm6sY8pu3x5HG08zP2sxVzlTvIVqjPcNxu7y6ybRcfcyUjoD3PW758Ob2g3KtXTAqEyZv8BPDlRmMe5CxonkXBo57ZrB1gSjOuBP5s4HRgIcy/ajm3EewU6QHLPueXrDXmRaaizYuhTwbOhT4Har6Ux4Xx3GZ0iB/v5cczyd5Zl/w8Aa1LAQWP+OicthU3TUpW5SNGyRfH8ODoEN0vN5BoojebdepGTGqTIXq8QtHzMgLaIj8mPptpo+15prVhZ0eOCpsdzV3H5duLTK5ctc6b4DXJdrWO3sRYPj/dSeX3dpTVjl2t1ZTh5VHGLMMTRLovO9GW5EL8OFpPYaIz1rlvgrytc9c6E7cHTJxO6z5aMLaq3PHObbs0ndhOjkyc6OTvzWWn7S7yK7ljxo2648eFhnfk8dk88Y6C1Llqv8L20hvZOOwufR2FfJ0HdB7fgZmlRiyL1LGLVjtwy9imbPsY53RccUuujpGbrk3rzE/nTWf3uq7IOlPOHbCutMbNRNf9uA3bEAIb/Vgn98RNRiRXUls1Vz7VdR6QP5jjY56xBTaO+SZ1XHfMYyZxYwfzvh7cJkOWLxRdeG7yhjR1+mzlavpNS7cD2Gw1SdVeKKMos+vmLmpPyfa0UpBW1yGdAGep3sy3x0ruM2bK2nmd/ceBPzHzczd70bTy7n8kis9YEzhrbJV1WbLvXoJLLnPt0TwBzYMaPEZb0/izwneaWFAjN3Vln70KsfFlMuM/558s82CX13jI4lao1q52x/NbslPaIpYTU6akdVmbAnvX6x3G3muC81kU5UHIJsKA7MGS6YNJv5Lvs7PrvREEdPYYOzpF7Th2r5kA8imIO6F/waMKi4B/0jg7wkmBPjZQR/jqwIZ80Wg8eyTeaUT0D6lSFV7V7Lbi/oN3mYKsEKkAACAASURBVOnNqnjTe7wPX+qtHDm2Zo6qYv8G9glxQFUe2JAnj9TP+4e3edNfQFOFp73AW/HgvNDsSYarZLDco3WJCGgOzB5W0mVfGukRJOPAsh6mGJlKYAYCPTU0O4WYFWHnCC8IzZ7N+MBGcHi9eVS1OTeMX8HOr9/DZs7fYFWNJ0j+hqZt2lELn6edpUXQFvoEljyG+Xg3ahNvsedmDzWfVBbPp2A35rdsobjnVUqlPiHI77WVggVWVPVFK6MXPSP6hjAwjF0bmBerS7X+eYSno8RrotFk/zzMnmd/5IcvIxUeM0uiz+pmMDU8MFjdoxocK8m92DtJH1b/AuGfEdRBwu0xjR3pOuIacJ+WF2ocLMwMiYoyZfIDpssaJK9BoitmGnmYxECTyOhkQClMxV7sRHjJfiwlir7eH7jS4EbOm0xxpDns9oXbEAI6PXu7+t9BIG5XeXeZ3QAEOh70Zl3dgGxtjUPHJaCJp0VIamrDwG2xeQ2wO2js086fYDenifPbYi2e7ocHAGeSgI/+EMRFUr6kKXoiU8lTzzaeqmf0KrOfMUcCRymzX4xea+bMo6QFWhoaKLWBSOcsmG4CmobHA+0N1jxfltnz6i+g/8KjxWtYF2KUK7EI/ghEhCgukwV04dT5p1nIt/xXJCWgx37ktkCOvW8H25q9m5v7vrPmxQa2ArvylXUGNiLSlZjb4BB4fiPw/Kvr8jXJuF+WjagcJuWU53dhcnfnEHAIOAQcApOLQKJzlaP+kvTp+zbuN84ekyegWdyFLefXaPwmxMU+DghS6tly0B28c7ZqZ7uOtcxTzN3x/JY23jlLKiOgle5Vpuxj5jAOXGNeDXzfmLugmiQZYsUa7K3aD/E4CG9JAlqw1+YhkGXrkzq2zrtvZWGKa0P1yVpw8Wh00Yg4f0SfOowjhrDPIAbWYtpfmnMuXuSVS97Mfm9qrzfvZG/J1Xvddf95TVz01OiZz9Zfv6r2njf+vVfp9/qnel6vd8F7vSF9ZIAXCFOGngY5hYU1e2NQ4KnHdgLyADszHGBbsB775BL/h5gemt0is0+gD2rIoxrxifX4tGrwetZbuBbqZ1DLoG6HuYslNVawn+vVMFXiHyRr+ds5GmSalaf/s4dgn0z3MjtgPSM2hfUnoNcz2Uk9jIfmPG9GqTidXFjp2JgGMBLiZ6vUiU+pyjN6ag0nkiUgfsECPWsVAiueQPmgovwM8GMh3+HHhws9W5hZ/OB6InIvOZXGLYI3iegKdtl3O023V8MQAU+ysJ6XQppeYR4BvlX3j9N4gcBAi4BGpUVAoz8wfU30MQFdyl7mTO/FGubzG9jXEMcDPzJ4OmOcGTU704Oi60dATyrULjGHgENgcyIwHgFtJxAa8qp6L/CF0eAwYDpMQkBLdmzrJ0pTA6PNw6H+D9d4/6bFiVLvFeuZLNZcjkyPDSkTXRIoKhQlyrGZFqkZkZrBxs5EK/va85WXcNAp+5zR0PlIuwU0NSwsAd1UZWA+cCkPCX+bJ50tBW7hUf0/Ir4f5mmINX2eV/L6Tp93dgrtprKOaTru/w6PwIbyRDs8YA4Ah8AOh8CG1hKbcvwOB667YYeAQ8Ah4BCYJAS6vz65hC1nl9vQHu0ioHla6lMGVzUwv6Fns7c5L2cBTfbO3SHji7sieYq5O57f0klAW+o5SzBEuYmdauLoNbX3sfulB4ERou7CvMZdysK332W2tqEEdAdnmqWzQRGrxZLJ6IyyTsUKgevq4lrg6wqfELgkxrtqOHetPm1VfPbK2nsv/uBx/SVvSoVsnHt6vKkzvN3284493Tv1HK844HkFr3+Ads3YzXtkzdlNnFDH/qHeW8h9YzHHV/uQU0sOvnlREvS+vt7f1y/21YG+OrApD2qoQ3x9RKCPC8QZvjg/FG+M4ouAK4BrgP9gV5t3sHDEKJk5W80dYhxEcvMaiBUT0Om0cyuAOwY2HTBmq2McOuEme+J2QUDvUirMIhcqOjYY1Vg92Pj+WrzuWRwxgnMNrmTKY5TmL7TmkrBujmgAfwD+3ZdHhOqFwswQZkaEGT52aWC/qjx51H8rW/4vh3oM8TCJdVihRIsNjQHEPJPiN9XmhSH2i1AULLihmXq2S4kKe5LsZQmOniZR26UsROStqydKxcdpxELt3Wi+nlXO42yEgVkZW/fQQ3ME9IRF1+10CGx/CGQEdKFQyEtwkLQ6zYJ4FvjhqP/qAHNiFKxMkKQpFD0NVOqYWsXsujpKq3cCVwEfgX5NI9ipSaJPpchUMvY5Mj0ZAa1Icb6kuPIhxtlKarBd86YQ0DEJUvWF6G+aXeviyJHw1KHgzKHm6yTeL/ERqa+S8hrgq+TOUT0ypeRVvKkLTnll+sAcAZ0i4f5vIgLdjfWJt2zi5dzpDgGHwHaHwMR1wuTu3e7AcRl2CDgEHAIOgW0Ege7vUS5jlpfKbWiP5glo8sljpYyXKVzQwF5NMz1EL6s/Jxx0N/Vst2Q0cVckTzF3x/NbxiCgbWohCk2Ua9h1WJy0tvF/gZtN/FdyfaQjxKn/oEyU3KLRfpfZ2noS0BlDupE9z/R8q2gmU708m40QWA2Q0orBIxoPKTxocL/BPWxffCcrrTwODP30R/+135wXlQpENHsFz+she+dSv1fqI6+DhR6vd5r3+a+/4rnmB2r4x2p8fk2c3YjProfnVKPzquGrbKhF59ei8xvxqxvxa5vxm/z4wiB6bxBcCnwR+C5wHVtk3wzcyvTiH4D7We3lUc7hGha2brBwTOY2wyKduEqjZ0Di+6yBMy70KR6s1pE9jA2P5NPJxzc8pc13RmIBnRLQEAZVjec0HlD4qcIPFZYbPAI1Sv4WYZ2H2mET1iwny+VvSJwcYwpLePdEmO5j91FzQBOvZ4eb9wKPkeNRcpYaEaJZ0acBAMkE9AMx/mVYHFQ3/QF5GiRJlkSCI7GAroiEdLauRUvsfLI3RG+EvjQQBx0Yb6Q+IIMFPCbxNLvtGhs7R0CPjYvb6hDYbhHICOhisbhkyZJUA1rx3JcA+INSF4Zq/9DMjFGwXlKHIu+Zmrcy7BvWBwu8Hfgc9PeBzwDzydUtOQlMpDNIbaPTArocM/ts/aNaQ2ZaWmEN0tmwQs+s/jyBETTP27IzOWwiAsRxR6j46G9ipyZ2rmPXutmjrverqYNq8tCaPLyuD1u59jyY31c8r+L1nj7/5eSLjn4b2QzYbh+7y7hDwCHgEHAIOAQcAg4Bh4BDwCHgENgMCOQJaOpmDbJx8cLYzGVB4H4mpsYweWbeOdODbot0cdAZs2zp5s6lQCELKeNMp0jtSe5jjsJrYjcf5wb4ijb3QK+B8qFrFMjdmiBjLOtddFwKNIFuCxHQqQR35lKDu7BJ5jS5iSPpzBq7emT5kIxNtcckVrFka7zkox874shDpk3v9TyvUunxPK+vr8/zvGOOefF99/8AuFnjh0wlf4cNY7/JHOW1wLfT8B3WavgOr36H/CIS6Xwbu25cSSy+CTgbPrPMERk4k55GliGpEWqyMrcEdL4IsvONxPVrSkCP3VXPUht7dz7RCeP5dPLxCU/awjs7JDiIgG4ajBg8Z/BXJo6FpYwN7aobNMkImu5Gkr25+UEcXxSaPSV7HZREE89qmEObeLOPzwk8BDqLaWty6trlfIme1HPAj+p42TD6GzxbIUYhT0CTC0r0CFZoTac2lEL0hugPMSXC1AgDHIiJbsrewD8IwcXQS6GHNY81jKm86QjoLVzQ3OUcApsbgYyALpVKS5YssR4IufpqAo8CX5PhMUJPEVRp9JB/VHijetqaaE6Alyu8D/gBsBzqhyZ+f6B2aaY8spXL6CKgSzEo2KlPVv/HOirYdAKaUy7zJA8Su7f1XpMaFqUmeuvor2PKoOofCU8Hbj1r/illr+f0k8/Q0hLQmxtml75DwCHgEHAIOAQcAg4Bh4BDwCHgEHh+I8BMWQcBbf4Ec5WKF6h4D6X7yVEZEVMt/2TtFtBtvDMfRlsmhYCO4EnVo3S/xFQf+0q8TuDTEo8o0B+ETjhoU4cOSAdCrkN8wz7LzU9Ad1Pgdou1VJXWXlWz7z4Jpelm7EZ2Acm5lAYR26LbJ0Tb7r/vnq995ZufuOrTF//rv331S1/95U9/xIywD72aVTLW8mzoVewg7ik2Xs6WT4N0e58ksWA8zsu/sAm2ZcCt2zq7tPlIyO9EzTlZY3lwC6FlS60v54wEtoR1571nu/MRm8rGLfPp5OMbl9pmPCtzQmiMMiTPHNlApDNvYVa6alAlSWVbNsgg+t4gfldDHRZilkQFpqL1dN/sPRqfA/y3wqMh/BBaITQIiAVuPRZm9ulh1YA76vi3tWbOMNErXocFNHuhJPbZskUpAV3waabDlBAk9xGB5MIjTI8wqx7uAvMaxD9G+CTMCF2XbiH5pQMVhKQjoDdjeXJJOwS2BgIZAV2pVJYsWaI1f7AEoIeIXI7ejHAfqAFppvJUKc+n5sJBAV4HfIWHsh8CbpXy/c3wqLrsSWsbawFdYvPnItPQRSaIk6FpQapBJBxk+WjrljCydtCpEXRe8XmMeM4C2tpB26TSZdJw8WlqVUZA7zwU7GfwHuDuc1+2oOxVTj/pLJPKTW0N7N01HQIOAYeAQ8Ah4BBwCDgEHAIOAYfA8wMB1psFOZDzvEK5VCIqSTZkuFRE5+t4V4gpkP2x3snHNDYbGtMIen0J6FTNudP2OSa2umX+LJi8TjU9CpEoQe8FLADeD1IveEwgiGkWsLV3VtA+TJOCFiRK2cl/jvGktiwBbTOU2Lcy9ZxxzZZ3tpbbCSudiesSAc3KviCLM0sB2+cVMy9NBsoiuWe+R638xBBZQkulZaxlqGUIGZLOg4r5eEtq22V24Sxi+Vy6WMbsUqwbU5sTS0BnNDQdKtsPzpLpiIzxVNZ7U0dS2ep6J7ClDvQ8r1QqCfJCSD8FYp2TAMPPt87sM1ugk6F8zJbLP6/HpzUwq4GBQE8VenYkXtqIzx6sf4gHD1TEZuoyobM7CGg2QsezBl8ZNC9fi2kj8Grw6sYLYPkda12YmD9HTE/XUaphWg170Qz0+FgWnt4/wgxBQhxTQ733aP04kgXXf4Lvw9TZZDsiDp1/aWEhWB0BvaUKl7uOQ2ALITAGAa0NyC74AeBDOjwEYjbkDKl2b6o5o/olNcwP8TaJL2j9eyUej8VdGt+oBafW4uk+VUSpNwlT8rX1QEgjYRHJBLUaB5Z9FqRTXybdDJMck9lBR6Y4BulsSn4SkqtkzlQ5/cy8usTtjEKMUoSeAOUGeqroGZZ7rq2dBfwn8PhZp84veZVTTz6L5gLZBscWwttdxiHgEHAIOAQcAg4Bh4BDwCHgEHAIPC8RIPbQSHhesVzsA+phuLzeWBjGBytThipr1R/rmT528jstoFu8c2TaTJe4F1kOzTTf7BzqnUkZ0kyLTb8wZYESH9zqZnaxzyVBE3CJ6WZLqXJd9Al9DHAJ8GtgpdUoIB9omq1/pWZmNSINCdLCVe3859iPbD0J6LFP3pCtlhtNz7A0rt2WsdLdET6czWHpHtuTYC44E/zNn5tdRBNhzT/FFKEiUFp8ckYn25PT0zbif5a57I4sAd12rY1Id4JT8mDk4xOcsjV3ZQS0zv0sAc3T2BWMHUIQpKaqNGvf3AIsGVWHVjFQRV8NO4+aw5rm/wTxN5T+g8EqEO9s1Ttyt5Y8TFZ/JhGPuyJcOIQXDsMbgVeFNwqvDq/BoUmvlnU22OOjx0elil2GccwoLmiaj7N4y9XAmyO9e0TSH5WGeLERHwZuISlwYaAF2+ZbhRabh9azcAR07qm4qENgu0dAaz06OnrSSSf19fWVSqXFixdrrVW4hsQ3zDdhzorEbo3m9DjeU8vjpfk/AT4R4qcadwJP6mgtT7v55praeVUxp2HKRBnbTzvpanUT0C0OOrWA9jIVDjupKpOEDklvutegT6NfkW9iz6C3YcoGOwdmIDAVe2SegBak7GGl8EvKFLip0cuOWHsaKAzDWxW9pBZ9LAzuAIbmHXdUySueMHc+DEgFOpkGtN0/UHcDDgGHgEPAIeAQcAg4BBwCDgGHgENgiyJg7XGpSyWAyCjteT3lwnTg6UBf7KtjfL1rSHPxKTD73N+aOMv8laWwIlKR7YlUqeZ7QzUPqBiUhfICOa0RH1iNjq9H8/zwuEgeKPVe2uwcq4GuGbfUJVSmwKEkiKfuj7mL2iTbzf5h7BbgDRo/h17J0gKhJp+DbOiZEKuGVHCJeiZhgxRGy4nll+keYCsR0K0MrDuWz3iL3kvPM5oJeLuaY5Itbd1BQDMo+fTSVDbxf57+zgjQNvZ5E7Weu/OXRyIf7z5ym9hCBHRPQQhB/LOCZaEVDxBwkU3NoUk7RkFJNnD+chOvG8Leo5hVx4ubOK2Jd8b4JvBnMmCHr+HzcEL7DVr8CW8f5q/Ad5uYP4LKCBPQdlljU+gaemqYXpe71sU+1fiAanToUP1ofsEuB37sq9uAPxAHbd4amt0iFJuY2RALoH9Igi1ElyMZ1Ujk1u0jbj0LR0C3Pxi35hDY7hEQQpx55pnFYrFQKCxcuDCKInIbEK5A8PUovLARnRGpc4ALgIuBryvcHWNYQRglIUeBmyXePRjOqetpDSSOB9lymdhn39CIdMYRp7pddkpUsUMG2o5LBzRpo9jksbS6LjfUzFDvG6lDY3XsSP3FMeaMRANEQKM4FgFNpDM7Ym0R0BH6fJSrqAxi+sroVOB3Rq2FGn3Da87zPO+gFx9C1s+T/inb7guFuwGHgEPAIeAQcAg4BBwCDgGHgEPAIbB+CLQT0ACKntdT9IBbAizwMdAkL/EU/CSU8wQ0Cz2XWOi5FKM30gNhPC0IdhHxHKhDII6S0cuAfwEWA0uAjwDvBs422D/SnQQ09weZgIZHNkl6SmymWPPnJkrDeGEd50a4RuNxQxaicaI+QAQ0KYfkAmkcpFxrXkIiO6iFzGYioLMrdURaF56sWBsB3Z5oyj4ncORAyXLVfsIkr2VXyfswtBs39EpZUh0Rm87Gpbmhedik48e0gLYPaAwCmiyX747x9kHs/xxm1nBghIsMvsgiqk9TPogEidlXJNMh3QMANKC0BvgN9MVNeVADfXWUqkkgIY4aWUPPqsqXCrxKqH+K4g9F/qeApcBdwINB/JjWo0yCfymIz/Ix3UelFh/BL/Af8yLlPPrT8VAShsYR0JtUYtzJDoFtEoFDDz20UCgUPe+iC/+Rv8QK5KLgOeBe4GbyMYgbuaa612BEa80ubGvAI8CXGjhu1PQ2UGpXzJiAgCbvwyn7TErQmdMJn9jnngYFr4HKSLirH51s5LshPg/8FsGXgNfFNGRNQh/jE9AlZTICutykKSC9Q9hlEIcNxRfxHQXQ/qUf/oDnebN2mrFNPhCXKYeAQ8Ah4BBwCDgEHAIOAYeAQ8AhsN0hQL78AJTLnlf2BL5awxFNFPxcyLsfTE2UqIeYuqbvi8xsYQ6T8ozq2jeY+oeBrzOp9QfgQQ5/AH4OLAxxWMOUA1JcbPkcSghoeBqegscENOlN+yjV0T+sjlX4isYfyeJKG5jIWmGSIWZ3IGovrzbRTYEmpJkjoDdrMbUoW13pPE25oRfNn5uP23S2A5u09SWgSZVDkUdK/GHUvPs5nLwyPrFqLtT4FnA3szysrE33HQIN5oJTYe4OGhqDwHWRf+mIf+5weIINg9Fxg/HRQ+qwIXHMUHDmUP0fgK8CPyNVDfMwwkGEIbTF07CDymvq8fwGZtSway24APgp+6skCpypZ+MI6A0tyu54h8B2ioAdMLNVmed580+eR9VQEIeBjkIlZJQ6y20AazWGiXqO2UGweRL4qdBvHYpn0vA1aW7kw/oT0D1ZE8QntfpZVb13Ve1fjeb68ZugruDmxcPwH4P8VaP58oaZYd2ujkNAF5h9Jg6aJThKDXjDKK1VLxoRb65Gn2PSnKaGfeSSf/M8r+h5qfrGdvDF2U7LmMu2Q8Ah4BBwCDgEHAIOAYeAQ8Ah8HxHwFJXCQHdO+B5vZ6PhVWa95/qNKaRzCWg1XeOzZRYz4zlC4N4/0ZwfBC9Sup3Qn8U+AlwG8xD0KtgqkBAvgHxNPArjQ83cVCdvM0XxyCgTUHD08ZTphyj1zelJnaqqwOG/TcBtxlTS6lnlRk+j0NAZ77+uvnPFoc5uQR0K928QXYuvrUK0ngZ29z5mazrTlY6m/t+x01/AgKaNaCtdkyqIEMKG88A10v8QONXYBFVYIR1Z/zU+H+YhJiJ4BmLgKatscZqkmfFHcAy4KY0XA9cz1tuB+5jM+eVwDBUA6IB4bNhtc8E9x+Byxry5CG1ew0nSfVNqEeBIYMg0552BPS4j9ztcAg8vxBQUmmtK5VKoVDwPO+UU06xkzGkZt0gAwUjEUk0NUIaAbYEdBwCdxnzT021X5NNmElnwySyGKyP0cMyzT1jSXDkLaDJFHok8HzlGUwB9m3imCbeEJvLgO/x+NyfoZ+hGk//ysSX1sRLG6g02LdqnoCOjRcbT7CzY6v2pUxZUGuj0GR9/EF5UDP8DPAUDciz14TLLv2Q53k9JS/wR6KwZn0eP7+erbsbh4BDwCHgEHAIOAQcAg4Bh4BDwCGwBRCwjuysax3STe6f6nn93pronWuivUa0l4VRQz7MaMKrKQemL8SUyMyu+/uG/inafyvE1ewbcAXPW32IhGqJQ1tDLJm21soR6wp8sIHj6tilQeKNYxLQJa1L2hTICJqNpZpqzkj91cB3gfsNhg1GjfaJfbYsmBrPAjojoMdjL2n7JBLQE10m5aC3wOMc8xLj5W3Mgydx42Rdd7LSmcRb27CkLAFtGZzMDWFOI4WiiRaHVTFHk+2dVzHv3ORRl4hJYUsQN5h9HmUj6Djxtpm3gE4LHAMXajRYMDpMyesAlH7Ac+clvUBUCWhin2WtnYBe1FRnj+KUGP9MA0p62GBEohnDxIn/wzEfDYHjJDg2rIi4ox0C2zYCGQHtkT1wYd6pp9iXX2pNHoBtoBkcEVUoiiubCDBPANf60dGBqVg9jQ0noEl8g0NFmFmxmBM0j6xWz4zxLxr/j1WDVkNKGoyTGvgTcHWoTq9hVuZqdd0ENPs7ZlmP6Q2cpcVSrkFpYZT+wuc+awlofj7CEdDbdjl1uXMIOAQcAg4Bh4BDwCHgEHAIOAS2ZQQMk0l2GfVO8byp3oj8QFXN9bFnPjT1Hk01pxYfUY1OHAnmjTTOAv4V+CzwS+B+YJB4KQphymKxJaUS0AHMKuAnDbyihp1r6Gvm9DciU4zZKb2dEcsENKtwkLjHzJHascCXYe4CnjWmQcER0BtYmsZkCbfAPOLJuu5kpbOBsE3e4aSaWiySIup6/UjCnAz7jTKoG4wYVA1RxlKz9oUm20IrwTHITDTrcrQT0MRKW9hIDzpVTLdbaJ9IA9E2FExI7LOs8dtry8bTMJ9rBu+UWGhIA+RBg5EYoxEajoCevKLhUnIIbB8ItBHQqQU01zIB6WHZGoWUrxTVPJLbAHGNFH7MWwO5e2w8qSpSVWJNxs6WFF4/C+gegQoFPbtRPVTV34LwqzA3Aw8DK3kszQ6hcTMGKxRe3cCAtX1elwQHuzzmsW72d1xu4miNy9iMmkb9yMOEMD/7yY+ZcvfITbOxwkdb4Ou5fZQKl0uHgEPAIeAQcAg4BBwCDgGHgEPAIbDhCBABLUWjp+L1TPUC88WR+gWNxpkdoVp/E8gd2o9I3NncyjKJzwCriH0mk0rBZFfMAgCxZqMkCAW1lmRm9Ueb8eFNMzUwA5GpRIYn3RqSgc4R0CzBwTLQsZkSqUOj4B1kVR3WIWiGLwUlqXOoeY4vG3B2qnAwy5cScOOxl7TdWUBveDnZgDPGg34DkuBDJyudDb3upB1vCegJyGcFkwuKtKATi8JIocqhyexzwipz4Q5JOoOEOMYnoK0SekIIpYIZdFuZ7I5VqGGGWjWgfH7DrNjpiBI/H619ASQDskLhLwp1Nn+OYqiYMkz8zFivGV3AWUBPWulxCTkEtgEExiGgJVHAmgloO5hFlVdKQOtHgCua4uAQ/RG8WFdiRd6HU/bZYwKaZkL5xiPL6DTEKJO8l9o5lPv44hg/OpmCfx77Mv4R9BM0ryr/o2G2kGddfS/ES7P0swQ7IjFLcAjQTCvS/LLzrfSujfAtrIlfg4Fo8kifxu9vvzUloEMpnARHHncXdwg4BBwCDgGHgEPAIeAQcAg4BBwCG4EAEdB+Y7RY9MoDnsDvgB8A38iFbwLfZHFnNnam7p4ln4xBZJh91i0bTfJSxvSUhAig7gc+J8V5UbxnrAY49MW6J2b2OSOgyQ+h9UDIjg1DuVe1ei6Jb4i/EJUdk50VE9A6UYK2pptjOyHMLEDHpMiSjZNCQHdfYCPQfx6fYvF5Ht/gum+tWCwWCoUJjhujDBGlkoisMp1D08vb7e50OtrTvjl/GcszJ+nkd9h4+2Xt+E7rIjFr6KRKOggVBMu9kjBqJgPdnajd4gjo8ZBx2x0C2yMCHQR0qVTiuzDGaiXbuiSbh6ElorXArwTOGdGVRL2LFJmLTdZl5iXpcNnVAF7TkMeJCJ7EQDWY3gz2j4L5Rr47jr4m5VLgRlIBIjfEfwGq1BZIRtGSSlLhkSr+41n/LF/vKo2XD3GO3bbcdMgtjJhbGzAetKd0bxSfCPwPqz83yPlgoEiNH7jxhutJQ6noASIKG53V8Pb4LF2eHQIOAYeAQ8Ah4BBwCDgEHAIOAYfA1kSAOpBKxdTVqnjAWjYneoq7Y9nyaTZ2rrJ4bJ71moCOEsAQ1E8gzhyu9UZySiT7hZgiRL8loGNTjE1RsAQHLwsxvJB8HvbW4iOAz5F7Ib0WWhrJk3sVWMkgVSnI52Js9Lp4u9xhjoDOgbG5ohM9gM11zW0pXWPMxhDQXbew1XBMqHByMmbzkF92ZTPZ4Ajo8ZBx2x0CdF2JcgAAIABJREFU2yMC4xDQsBM7uu5oFPJ2mKt8vGQE5D6ixiHTZc5oaLvFR1+A3et6v7WN/VYOHhbGr4N5P/AZ4GdG/Vkr63yVh6FpMFqkqmGGB+dC0OSMG57Fm58MXxiYAaW8fJCaHA9G8Cz7nPpWLoRkB03sM0S/jF+s4rdza8Nq5SshhJF0W/fdfQ9pQBMBbeeOdN2r2+AQcAg4BBwCDgGHgEPAIeAQcAg4BBwCG4AAsUpKKppsWiySU7TJ+Y1QP1RcodWcRuxFyotkrxD94xHQMQohGUj11vSevnw98DuY56Cr0L5Rckz/bevK5kS8nSOg14XeJOyf6AFMQvLbfBJa61Kp5HmWv9jmsztJGXQE9CQB6ZJxCGwTCIxHQI+Tub/Q5Cn1+tF41ii8ei400NNA0fLODWKle2qYPqz2WxufNRT/c1N9QeifAQ8ATwN/ZV+szVSwPlP4sgS0pYMlyxD9uYYv/hVHP8uujY3ybLA0dJ6AbrIn5SYKTZR8lEIe+o7lXpH/GuC/aNSdxrQlECsV061ps3rlSs/zKj3lce7UbXYIOAQcAg4Bh4BDwCHgEHAIOAQcAg6BDUZgMxDQT0J9BvJVQu5KRkiagypHsrfbAjqm/iBNw61j2kh4Ops/PwBThwlgIq0dAb3BD3RbOGFHJ6CVVI6A3hYKosuDQ8AhsNEIdBDQxWJxwqQeBRZG8Ymj8S6jsq+uZ9bVzlWzU9XsVDO71Mzsqtmtql9UFYdUo+NHgpcPNv4B+LbBcoVHYzXYnrI1c5Y5FxNMQCf6QgqoCvPgsPjGKrx+lTmqFh0T+HOz0AzmNoO5jfCYRnxITby0KinU1ME1eWhdHloXhzejYxv+a+PGJ4D7YGqkLsTS9nZ0WgkR+oHneeVSSQmW5GjPnFtzCDgEHAIOAYeAQ8Ah4BBwCDgEHAIOgY1AYDII6KRbaBABI8DNIvp7Ee8nzQyJYgwvMmwHrcrjENCFOrwRs3c9+mdWfXwOWhn2Y5iZP7MER8uh27pucyL+cxMtoG3S3ct1Zcnt38EQsBIctrTtILfuLKB3kAftbnOHQqC3t9dOkspP6TDGRFFUr9ctFFEURfGK0cY76uLEuj6sag4ZlUePiGOG4yPXxoc9Uz9gKD6xqd4SyEvY6Pi3wD3Aoxp/jTAoSUwjIKGtFqyaTZLtd9aqfQniiJPNBggM6obMpe8GbgJuBW4H7mgP1wPf0vhcpK+J9DVCXRPLT8XxNXH4eXJ2oa8H/ox4NXQAZShlngEmmHHWUpV5CouWSkvip93PIeAQcAg4BBwCDgGHwFZEIJur3mJEtuHYxgGl843BsZKI49jikL/1sQ502xwCDoFtF4HJIKAVIAwihdXAwz4+EepjpZmq0W8J6Bikx2iln7NlpgEdor+B2VWcYfBdFqGOlaH5sJI0H41K9Cbz1cwmSYU4AnrbLYvPm5xprYvFouVr8iX3eXODY96II6DHhMVtdAhsvwjY9oHneUcffXSxWLzvvvtIBWMsuS6DJ4CvAZdwuNTg0gAfjnCZwGXAQuBT7O7vNpa88OnzLiAVYvrYGwmlyJ1xRvXmh3hTB6hsFU2eCHNEdQ5Yo8ljBHuKMIqiqANP+cFtUXwncc14BHgY+KORD9NZssZtDHI9yOrStM0YE4ahUVqEkcc/aOOMoHMgu6hDwCHgEHAIOAQcAlsaAWNMMkDOtnn5ruU2G99QjOwNxjGJoSmpxgxRFNlklVT5G9/Qa7njHQIOga2LwCYT0IZ7cJFGQ+MRhe+P4C0B9pEoEvtsPGKfEwK6jYPOCGjf7FzHXB8XA3cCoebeoHU9ZDnofA1j45uCmCOgNwU9d+76IpDwF0xqZCV4fU/ePo9zBPT2+dxcrh0CYyNg7VA8zysUCqeffnqpVFq2bFkYhtnRxhgr08FbfOBR/oqvYMPkBwTuk/gT8CT7Nf4LuzMeBprEDkfk1tgI4p5Z/cJYA+QsZbuVly0CmjhmSUEJKAkljWY3qdaCOXduFg1ghpVcAz3Ik7NqQJDtA6IHHrrjhht/seyGX3G4bulvr/v4xz++ePHiT33qU9bu+9FHH80d76IOAYeAQ8Ah4BBwCDgEtjQCxhit9Zve9KY3vvGNWady4yM6s+5LaFxr8de93PhLGHPzBv5uWr7sjjtuW7hw4ZVXXrl4nN+SJUueeeYZS1Xn87aln4e7nkPAIbBpCGwCAW2YKxaWgFYYBFaM4J9X4TAfu7H5M1HPkfYEeZ63oSRQittDU+9TVW+J8W02f1ZkTZ0GR0Bv2rN1Z28lBO644w7P80499dT813FMs8GtlMHNcllHQG8WWF2iDoGth8CXv/xlO5a22267FQqFgw466KyzzjruuOPOPffc97znPYsXL7788suvuuqqaz7z6c9/8fM3LL/uhpt/Rcvl1w2OrFJQUsNoIou1MFrGaVBaEAGNmD/1/J0fx67ZDkizyJehpLRKOOgbl91y443Ll91w87IbbuVw8w3XL0/DjTfwb+lvr7vttlt+9vMfffwTV374kg++693/9NrXvurU00974e77lXqmeDRHxSuVKZR7KNjfTjvt5HnewMBAoVBYtGjRDiWjtPUKmruyQ8Ah4BBwCDgEHALjIqCkqlQqpVKpvOm/nt5yTy8nUyqXC+UyJVoq96bLXo7Tkg7LAp3Ah9ByHb8S/4pj/kpe0Yb83pI3bXp/qccrpY2xpE3W9e+SSy4JgmADtVnHRdXtcAg4BLYKAptGQFuumHwCsRP7/xnEqSvFtBAzJPrIAyEpb1gCOjWFRiGGF6IQojc000K9az06KdSf1lgB1GjWRco+i1SFo4PE20Qebz0toPNTgO1zsVu641vlqbmLbtMIOAJ6m348LnMOAYfA+iHwzne+s6vxP8aGgv0VPa9A/YpSD/VnKpVKb29/Gnor+V+5r7fc11/pT0NvfyULdmNvf2+5vzfp/dhTe+nX31MZKPb0FYs9HlHIRc/r8byeIl+25JVsoOwUKRulSsHzvL4ppSnT+72SR6HoFXsqPb2Vjtug7lCxWKlUvGKh2FOye3v7+wQNirufQ8Ah4BBwCDgEHAIOga2JwOzZs61Pjv7+fksAT8TzpvRuoUANofZfgZpr9sctN14tpctez+vlBlPJ88oc7+VIexqbtlZM2llpLpiSJrOACrfscomXy2XaXiq99a1v/drXvvbcc891aEBvzUfiru0QcAhsFAKbQEDnbZb+Cvw4Fn9XD/YEZsW6InVRwVPwJDzBISLemYKfhGm+3M8P5tWq72YfQlVmninNdMotT83dqJua4CRHQE8Ajts1OQg4AnpycHSpOAQcAlsPAau1t3TpUjJ6Yad8uR7BuNGEjM7984q00n1C7pC2aMojF0qFhGO259qDuGsyRmrJMV2XKU8pEulc5s5Uujff8+nv758zZ86RRx55/PHHz58//7gTTzjhpBOLPaViT+m973tfM8irdmy9h+Gu7BBwCDgEHAIOAYfADozAK17xCtuKsZxspVJJSeaJ/k+bNm2sNljKQSf/LddsVzIC2q7aXeWEs07PS9tTG/y/1FPYeeeZJO9WpIF/+yPb6opXKHmVfmqw5XfZC/T29i5btqxWI1vFPAG9AxcHd+sOge0YgU0koNkfkAEeAz4VhWcGjX1hdo/F7EjuEuuZsekX6LG8cwivyaEOr44pQ8E+jfhsmMuAnwDPEYKpc8G89fHY/oY2Ae/1JKCtF8REnzKnR2mvnLeG3oS8uFOfpwg4Avp5+mDdbTkEdiwEgiC48cYbrUtVz/MuvPBCK7txefqzq0uWLLniiisWL168MP0t4l+6xv8/ctnCNFzGv7a9uZVFly3msHDRZQvtKZd9ZNFlH1n0kYWLP7Jw8WWLLr9s0eULL79i8RUfXfLRq2y48oqrrlpy9cc+evVVS2y48sorP/qZz1+z/NZlNyxfev1Nv1l6/a9/t2zpTbfcsPxWEhn89a9/KWQURQG0ocD9GaGUBiIRR1qVyuWe3sqKe+5u+H6+RbJjPX53tw4Bh4BDwCHgEHAIbAMIBEFw/PHHl8vl/v7+Aw444Kabbrr55ptvXI/fTTfd9Itf/OKee8iJ9Ab+NBBykLkTY94yNj9ze/q7jX+30u/m9nDr9Ut/e+vyW2+++fZPfuJTSVvyikVLlixecuXCxVf8+5VXX3r5Rz+8+PKPXH7FIrt30aJF++yzj+d5P//5z21rzXoo2cQZ8bk7clGHgENgSyOwiQQ0Z1cBj43Wrhyp/n1t5KygcXoULgjlKaE+NsRLAuzqY4oPr0G8s1dHsYrpoziwod4ozSeB5cAamCixdmatx80KwYYS0B0ctM3b2NXuZs23S3w7QsAR0NvRw3JZdQg4BMZDIIqim266yU5+LBQK999/vxCCfbAni5wTQkojE8yyCWarFFE6C/bktr25laQ1wNSwPYWknxWUaYUNGgSWCGMVCB0qCGlipWJAN5pkR2N/SqooimIpAERaSZhCiSSinxtc60fkGTkL6Rnuv0PAIeAQcAg4BBwCDoEthEAURe9617usOfCJJ55or6qkmjgIISzxQS00dsvRvaSZ59bujhx0jLDv6AfYm/SdwB0ssTrErThOAZFBYEzivTBru3W0DAX/4jF+KZfNVod0lIyEDLQJtQlj0TCIhGrGwqft/ANw2WWX/c1i+vLLLwcQx7EloLcQ7u4yDgGHwGZAYFMI6DQ7ir3c/xr4LsiX4DeAa4AlwCXAP1fj86tywQiOH8HcYX38sDptUJw3GFwEXAvcAqyCiqB1q4O3mTno9SSgs/5mRyS9ZfffITA+Ao6AHh8bt8ch4BDYbhDICGjP88rlctLot9Rw1u0YK5K/Q7ufDI0Vmxvr7ATFfZiOpWm1BtLPr+0vrYOA7mw6WC/JmaJXNqupfVA5d5bk25Mwv7txWbGn1NNbaQaBI6Dzj9LFHQIOAYeAQ8Ah4BDYKgj8+7//uyWgjz/++DzhO3E8a3IlEaahtYJJqWC6F9tWggAeMfiKj/cO4o2rzeuH8Laa+UwcP07UNFHGmv1H0yh+Nm89D0XntUw6uT1/kI0baC21jg0x2hSIg9Yxb5R5ghvA3+bY/a0VeuWVVypJxHd3Ym6LQ8AhsH0hMBkEtAFGgaeBJ4hQpvBn4E88ZnYvyLvgbcBNvPwj8BBvf4gPfhamCh3ZITWqynKdwc0EoyOgNxOwLtkWAo6AbmHhYg4Bh8B2i0CegO7t7U3a/cwLd3cz8lvyd0xnWfbZUsiTREDnL0HxztaDXc8I6Hwka2uY/Fl5AtoreHNPOB6A1eVImfDOa7p1h4BDwCHgEHAIOAQcAlsAgU9+8pOWgD7hhBNsi2ti6tnuTdtmPNgPQdyuplllhlTHGqyC+gxzNw/JcGk9uGYUrx3Coc9h9zXY7xl5WgMfA56lu0sI6FR8dSweOL1W6387LIZtrSOgCgwCaw2qBk0OAbPPyQ21zjcmDENrAb1o0SLHPrfj6dYcAtsrApNEQAsgIC+CWccumc2Rszoy7GVQcN2jASNgAg5RMpDW2X/cLJA6AnqzwOoSzSPgCOg8Gi7uEHAIbKcIdBPQJvUTTFbJ4//a7jdjn2ViBJ2e22H7bFfXywI6ST/faGg1PrKL20156tnGs0M7CGiy7bEW0J7nnX3eudbaJ2OfnfZWhqyLOAQcAg4Bh4BDwCGwxRCI4/i73/1uhwRH0gprtccSZYyEembps8TXhTYwgqneyBD7DAOh8dcYNyh8E7jS4B01ceYa//BRvHQEe4xgYAhzVjbfYvALgCXLbNPJNolyzag8AmO2Csmo2fgKgworNR4H7mObxBs0btN4UmOYaeiA8sx6a0SOW7UQTk5rfemll3qe97a3vS1/LRd3CDgEtl8EJomAVtb+yFZLAlpAxhRozoYN1PHTFLK+J3PQNOsiVVjcEig6AnpLoLyDX8MR0Dt4AXC37xB4fiDQQUDTTaUENMiQWfEkTiOhJPKCgCr9qPMHXxrogK1s1lKTgHdm7YBuFY5WZ4m0PpKZoe3Hp8RxviNEw9rWQiePfYcQR9cRuQ2SpcASArrgHTN3LvHRrMuRcdD5pF3cIeAQcAg4BBwCDgGHwBZAwPf9pUuXep5XLBZPOukke8UWAZ1w0MqQMaBQIjI6NtqHGQb+yrLOdvkAz0N/kueqrwB+LLAkxAVVcURT7eZjShP9dcyoYaca+kZxeIzP0pR22VDNmPibrDGUEdCtTSzKQc02BTSBIb7uIyahm38L/MzghwbfbupPNrGojg/VcLXEDQKPKazWxif2WdLZWvNEuZRV/9udLlq0yPO8M844Ywvg7C7hEHAIbAEEJomATuZlsMGziaHTgJjVgiwHLcE+hHjcLel1QlBVmVRfW+B2sREE9JbIlrvG8wkBR0A/n56muxeHwA6LQJ6AnjdvHuEgk0+6UZI8xvAspgZEAKHAtiukDChSQUEruAzoVcDNLMhVswR0alxMDiByfRrbubHXiNkcmVPiZJr1qoiroCFrRZkQIURs/CB5OooHuzvnhGYEdI5pbnWc+NT0FMURBVy//Eav4J18yvxIxFlvy0Z22JLgbtwh4BBwCDgEHAIOga2FQBRFt956q3XIUalU0mzkpmaxjTORv6ZpRJMPGAbuAX4IsnH+LvAd4Cvsp+tq4JJ689XNcF5THhTqXYXpVfAkvAheAM9HbwO7RXgd8DvINYirkCFMCGJ4uAlmm0RkGiBbgUU6ePezBrcK/FcTi4fwj4P67Fp4fMM/ut48aSQ4wccJQzhoJXZ/IjgsxMcjLBV4UmlfS6vI2unk8G9mAJaAPv3009O7dv8dAg6B7RuBySCgEwQ6empjrnaBlT+qa+dm2OAI6M0AqkuyHQFHQLfj4dYcAg6B7RKBiQhoHWsTyoSAVgHIGpplBZss7fcU8DBPtLwLuBP46XOj74vM54A1RGFzj4k//gkBnXHQzEdLDalp9JoPzXo7JmR3E4PASqPvMbidSe1beC7nHcC9bNHjM9AZ3ZwnoNNHkBHQWYT3tBHQXkJAp0T5FhwlT7Pp/jsEHAIOAYeAQ8Ah4BCwCNTrdc/zCoWC53la6ziO25ChRpViz1p1YFSJe4EbQlw1JN88os8bFm+oRm/wg1dE4clheGQoDgjVC2MzTZiyggcOCl7MIcD0APMVriDPXXEA5QN+SkCn7TVSZAuAEVaIfoJ9f1k3X8s1vhNjSQ0XDGHec9h3CDN8VQhjL4j6GnraKCqD8J6D9yz2FrhSYJkhjWlJqiBkRT0GAb1w4ULP8xwB3fa43YpDYHtGYBIJ6E2AwdLQm5DAep/qCOj1hsoduLEIOAJ6Y5Fz5zkEHALbEAJxHN944422t2MtoLWdtETOHCRP8EzcPRB7SzpbgqU27gV+yRY31wD/Drx5Zf3YJs4YCt8L/CVHQLfYZ2sHneptcEqUXqYHaH20V5livg34b+CzBu8a1Wesjo581j/o2fDoleF5q+qXAI+lql/WZXuegG7nm7tg5r4PEc1kAc0EdCyFI6C7cHIbHAIOAYeAQ8Ah4BDYCghYDWjP84RQUURNlNbP8Oi+BNspPwR8b3Xw8gBHDJoXDptdR8zeVb1nHTObmBJiIESfj3KIkkBJwbNBoBTSRq+B/QJ9MXCj0auMsu680klpWUNNy7S99ws2rL4S+MBofM5a/7hV9Zeuac4Zlns2MLuB6T56Y1MUygt0uWpKQ/DWwBtE/xBOBn4EPMOSHXkVtZavamPM3xQ5HAHdesou5hB4XiCwbRDQWw5KR0BvOax32Cs5AnqHffTuxh0CzycEhBDLli3LE9AqVolbB6ERx6ynodih+bNkKYPbgJ8BX1vT+IfB8OwhMXdE7zukB0Ywu45TgC8QAW0FoqmjtE4COhaoCawReMqQgfN1UN8Io0X1+B+q6tRh7LdWD6w0ZEcziL4qTq5jEfAIE+FRqtQxJgGdim60ParUK087AZ2fo5Wb6dp2pltxCDgEHAIOAYeAQ8AhsJkQUFIJIXzfL5fLRf7R6Lhqv5oloGnjMPCb4eD/s/clcFYUd/713pt3zDDDIacgIJfKFVAJAnIIgqKgJkajG6MmrBhdNZpjVTRcA15JjO6qcZO4xFXjETdrvAVEgYBxA+pGzd94gPFEHJh57/Xddfz+Vv1e1/Q7ZpjhkqPf5/vpqVddXV3165p+Xd/+1fd3/lbW63MgnwuyTZBGQbIilgWSl/wysRQc5e/sA1GIeZC0oM6EXiacSukDwD8AnlNr0VAYzVLRCBsUZfwWwJ+Vq8E9WWNu3jkt5x2X54MM6GhClQlxG+KK3Y5TiPsQo4IoAprkONkm3Z+rm2BMVvwA4M1m9bSQk0AQ9kNqXEcEdPFljr5FFjgQLBAR0OVXkZRntT0nHAG27UdFJQ8kC0QE9IF0NaO+RBY4aC3AOV+1alUsFqurq5szZ470Q/aEZJDRIcZn4DDwPgNYB3APwOUunJql45rYyCYY0AQ9VRybdFZ50wBcB7BaSnBgtMACAY1qG3JbENwo1O4z8H05idrkwwsO3JOHH9twuiPGWXy0wY/Ii7556K7qTzYB+ZR1ybGrAP4shKEulq9WhhaCIwd+NSqkoY5VqKc6AR2N7tYAsHhJ/RerXBcvqfeZ0hU5aC9/1PHIApEFIgtEFogsEFlgH7CAbcuIF8OGDYvH47FYrHKL5PMMBXgd4F9tGJmHOgOIWUDSgrQlKeaEBTEHiIaS3ZC+z4qV7u7D6QA/A/gr0Cb1+OQz13LMrQCfArwC8JgDN5twYR5mZPkEQ4w2xEALejnQ2YGMAzGvQGcTDoRDHCDOBeGCUEFcJrnvHMQa2BDTX6zCIRariOgHs+LuXX/99YSQY489tjg7+hZZILLA/mqBiIAuv3I7SUD7vu+6ru/7moMurzrKORgsEBHQB8NVjvoYWeCAt4AQYuXKlTH1ufbaa+WvG9WdRrWN1wEeZXSe5Z5qwOF5qM5BKg/JPMTyytFGbdMUpindjI9AGFpNOST3jOyz3ApoEtKL+TU1g3qZwzITrt8mztoOYwzoqaY3GQdqLKhW4do75KEuBx2yfILH7wXYKhVC5MdVKzq1Ckf5nEYohjqrfLcNFKXmDBiVh4cJaMojv2d9xaNEZIHIApEFIgtEFogs8CVYABWfx40bh4vSVAtwjVfwFl1mGTJIBjwq4BRXMsJpu5lojjmQDiDFNzQBrRJIT6cMGApyMdlKEB8pf+f31eK2vwH8BeBRyn6ady822Iwc9DeggyF1PFIOxF0VvdAv8qeW7LMkoEUVFzFNQJuQsaGHIWZx+qTUlS75lD+sqQJLly6trq5OJBIlxaOvkQUiC+ynFogI6PIL1z4CGpeHIPvsui6jLCKgy216UOVEBPRBdbmjzkYWOIAtsGLFing8Tgipr6/3PE9KcEgnYqbCzjwHcCnAeNM/fJtZa8qpSMKCKksuwEwEqLPFEIDLZUBCn0v5juYghFwFG2x2glZ+0B8CPAKwAGAuhdkufNWCIQYcZkA3B2pdyCiklExhwpFn6Zrzj/XhauWY44HvKYedPEA+WNepJzRCBbjhIMMbNgD8VcA6Aes4vMZgi4zAzqnvS0VFTUBTziMC+gAe21HXIgtEFogsEFkgssB+YQHOOaNs9uzZIQKaqVfpWgmaAnwCsK7Rv97hx/q8g8szrpDsMIYW9KR7ctKDtNomPUh4gSu0BTH1Xr+nA7MBHgN4F2AbwGaA5wHuAvpDzzrbp9M8dqxDj3LEYQ7UOpJ6TjlQ5UKVX0A8dKKEDykfUhQyTCQ5T1AuW2LyQ2x2PMD1ABtUAENLPZLt4Ap861vfQvHrHZSLdkcWiCywn1ggIqDLL1T7CGgA2LJlS1NTE8pLa/ZZiPA7yfKzRDkHrAUiAvqAvbRRxyILHEQWkALIK1Y+F0/IJ/+Fi66XrsW2AzYFd4t0kIH6rHu4yYktFKSjjSSFFZKKI06avC+FbyqBjo8K4tGBBrSadTSp+dK7crEn/K+SkH44m/2G4xxNxSAG3TxIK2nCuAupgH2uciGO8oVybSnv35Sfo4Sns1K9QwaF95X7s6n8oDFE+6cA7ymX6o0AL1nu/1j+fS7c6sINHvzU5g+Yzpt5ozEioA+ioR11NbJAZIHIApEFIgvsVxZwXfe8884rI6Bd7AQHB+BvFO76zJrp8MN9kfZ4yhOSFA5UnokinZF6Tqg0PrDFHMlEZ2zoDfA1gN8AvKCo5we8/FxqnOxZX3GdPj7rRCGjkAoYZ6SeJdGsUIWkNtZcRECLGOXEFXGDDjTsueqZ7RPlYW0GHHqLnMkX0bCnTJmSSqVaFB7Zry5i1NjIApEFpKIjZV/4NsXj8YOEL21jEMI2jQ3f9z3PW7BgQSKR6Nat2+bNm9t0WFToQLdAREAf6Fc46l9kgYPBAjLszIrnn4hXSQJ66Y3zAEA4DkiX4r8D1DvORNPtbdG0zZM2TyACz5okJvJ0pAqP/hZGORcUuIL0QvYawH8d4EmA2zx6kUVPNfxxFh3h0L4e6+qJOsU+V1GIU+lck/KhRnHQUrgwG4DBJOmt420Fx5GTL/y4rp/brnytt0rPa/7fwG7w2VzTPyXvT9jOvpplYxzvGNcda1iTbfdan74tu8aBUxm+Z+nSpbK/S5fi6+Sg0uhvZIHIApEFIgtEFogsEFngS7AA8hf4fPKFT4BqAVdRl5kPzAefQY7DizZ8K8d7u1DrQ8wTxBPN7LOSyIgpP2i9TSCV7EKVI1/zd7DhUJuNtv0JFh1ns2N8Opiy3pQfQkUtle7MVSGkVI7ehnfJ2INByTiTYtCEAnFFleFNAPgfwT90RNYF7iuXAQaUgadk2YKYHcUGPuOMMyIP6GKTRN8iC+zfFogI6PLr11YPaN/3X3/9dVyenMlk1q1bV15XlHMQWiAioA/Cix51ObLAgWgBKgnopHzyv/vXP5NTHWpI/Qr6OHdmG1Z3y+tk+R1sVm2zAg3tiipXVGmZrqt1AAAgAElEQVQa2vRGKffnV5SP898A3gJ4G2CTCj6zGth/cOPSXONklx7hQmcqF4cStVw04YNEMIGRExtfzo6qHBW6vRFkSHdTeutcDOyvIH1oHHAagX4C8KFaN/oGwCpw/kvk65n9Pc+bYdEhBq/LQyKvdEJ8yFDWG8SJgt/A2AcgQFBgSoKjvl4GIayvr+fqcyBe1qhPkQUiC0QWiCwQWSCywP5hAcPAAMuwYMGCYipWegQoAjrL4G8u3GXBGEc+SsXko1Qx+4wazYFKBkEmWhPQLhSe3CikFZIUksEzGBLKelvFIcUlHx1GOQGN5UmBgOZxzx/g+3MA/uJT2+auBcxTngIUXAY2B0s5cVcIvHHNNdcQQpLJ5P5xtaJWRhaILLAjC0QEdLmF2kpAA8DVV1+dTqcTiUQsFtuwYUN5XVHOQWiBiIA+CC961OXIAgeaBaQCB6xY+Yz0gI6RJ556mAsH+AdSfMP5sWUPz3lpiyYtmiwnoFF/QwZVp4MAfgLwa4A7AW4HuA7gxwBXAVxs2ida7rGUDxVwOIXOtkjZnNhqkaYr4j7EfIgpJ5rCHMZX3LQioOOSgPZ7MDgH4LfgvQ+WBd5HIDYAPAtwjw/Xmd63Le8kyxtruiNMb7BBexq8zhBJA6pyMlJiWkaB5wMBFgGskpEPGTCP+Y5cylq/cJEkoBcuYr6PlPSBdmWj/kQWiCwQWSCyQGSByAJfrgVCISra0hDf9xcvXhwioMNBCD8DuN+Cb+XY4Y5UeZYEdEj9WctAhxPSD9qHuIIU01CMc7ItBHQx9Yw0dIsENAcigxC6vf3c2QD3Ansd6DYmtjOxXYgccEOtkMur4BwNHAwul8gV0dC33HJLIpHIZDJtsVJUJrJAZIF93wIRAV1+jdpKQFuWNXbs2FgsVlNTE4/Hm5qaMIRReY1RzkFlgYiAPqgud9TZyAIHpgUKBPRzSECvf+lF128EeBXYDdSdYfndc5RYjFgsJt2fW/CAdnh3z51InVnUneE6Eyz3aNM7yvQHWryPA4fIoDcikWfEEkRqSSMBHYRT99WaTRpsAwI6bkFVEyc2DAL4PsD9IF4E8ScVNufupvycnDc753+1kfZvZJkmTnIB8oIYQBQB3aEJOjXCIU10qhIi/BiEzyMC+sAcxFGvIgtEFogsEFkgssA+aYF2EtAAsHLlSiSglXCqkN7PhfAa/8fh+yaMMKG7LUpiD4ZJ53B6pwlolNcIuz+XqHNoX+k4lfobcSaSzB3ArXOVO8J/Azyn3AWeBVihxKZfBPizWiH3iSKgg1jV6qIxyhYsWFBdXR0Ij8jcg0Q3dp8ctVGjIgvsBgscbAQ05/KlGr5BXLhwYUXGuK0EdENDA/4MEEIGDx4cDj8YaUfuhrGpqtC/MbZtAwDn3Pd9nSmDYrmF8Au764y7Xk9EQO+6DaMaIgtEFviSLaBCwkgJjgRJJTNr/7RaRYxZ48J5Du+X54k8JxaXHLRDYw4taECjErRU4eBVPiQ8Ue2x7h491Oe9fN7Dp9093sXjnRzooLykEw4kbagyeczksUIwQxXSEFeJ6sg5KlGFoQgdqGLSZ+dQgHMBrrPNcy1ntuVNt+gEg40wxEADeptQZwLRUNQzySvl6Cao3g79GsQ0BxYL+AuHHGdSmVpQEJ6MJn/jYinBsbS+XjAuGFea15V1CXf+ArV/2rnz54qO3H8tgOOkne1Xb47aeUxUPLJAZIHIApEF9qYFhHLz5W19uuCcM8qee+45ZB6QzlAEtAP0LYCHPJjoQK0JNbbIqDCAYa65YlorQceKgwpiaEH0iUa/5jChjOmwv3N5urm8dH+GKsarKT9E8EHUH+l6Ew13at6fkHXH5c3jDW9y1p/8mfFPAM8AfMTBa45UrS7HF0TVokVyXVo8Hrdtu9DxiIPem2M1Oldkgd1tgYONgGaU+b5/3nnnffEibVcJ6BdeeEET0GeddRa+kQvT0Lv7YkX1FSyABDSjzHGciIDeR4YFRsaIxWKTJ0/eR5oUNSOyQGSBXbMAX7HyqXiCEJJYu+55m79iwW0mjDMgk+OSzzWF5KAdKqHjENo80UxAQyLQGYzLGY7A4IQJFXJdhhN0ICHFN0TG4skdEdApFYQwpSokHtS6/ljGp/twlAs9XejuQlcHOjpQ60CNJYWeWyKg6xpg9Hb4gQtPuvChDZRyLigAEzKKD8BN9UvjhNywZClwIbEnyOI9UeeuXeno6H3RAhEBvS9elahNkQUiC0QW2GULaAIaOegd1SeEYJRt2LABmQeMSSgPopsAlgN8n9J+niCufKDSj0kVeWedufcIaF9UU6gJYkrX+FDrQsaDtMdTPq9zoIclTgF4CmArA15CQHPONQGNRmru+46MFu2PLBBZYN+0wMFGQHueBwAzZswghCxevFi/SAtfnbZ6QOtQAMlk8q677hJCcM4jAjpsyt2YLiGaK1653Xi6Xakq8oDeFetFx0YWiCywT1hAkV8rVrwQj6fisczq9Q8DPPap980m6JcF0sRJnscs5a3scuIWBDQSlpCwAUMRNhPNlgoeaEFMUcOSHUYoAjpjixqLp5GALggXFqK3SyVohAeyNldy1hI2EMvvbnmHutBZzWSqPahWDHXGhRQS3LYqJkuCVPkwgOQhnYVen7MZOfitD5vzYBnAPXAEt+SsZ3cQ0Oh/Wr4tuqYRAV1kjuhLCxZoAwFdPtIiD+gWrBllRxaILBBZYJ+xQFsJaHlH55wKIR3oPvnkk1ICmr8GsBT8Y4TTQ/gZj2UwCGEo2KBmnEsSzQS08phOlG8xHLR+DAslCpGigwIlgaObPaCVilqcQsaXEQuJUuQgIKpApEBUcY8ArabuVwCuBngNwGFAGajF6sGFChPQGIyxhBAICkZ/IwtEFthvLHCwEdD42mz8+PGJRGKXPKA551/72tfwZyCTyaxfvx4AvhAq2n8J6LCuxb4zflF5w3XdjRs33nrrrXPmzJk9e/aZXz/ziiuuePnll9Hm2Np9p/0RAb3vjJ+oJZEFIgvspAXU7GjF8rXxWCZGktuMjVm4NQ/nbuODG2nnrN8j73dBt2VXOt2ggrMU4kAC2oa4YoFjKmxggW5WpHNM0dAyJ/CALiOgRdxT0HMbNS+SVRWoZyB5TnJ+zPTjHiR8iFNIUEj6kFKoQi9p5LJdINq32mBdsmxMFq504U8OZA0AC8ADT8VX3MMEdDOZGHCGzTk7eYmiww5wC+xohAQjSQZsUuBcTt0l9pRlsEkVt7oVOlGxWNszw31o+1FKOyhY3B4YJjCLto9K6IbukUTQ/OY2lLdqRzlBHXvwr7YstrOtZ9qVXoWPLTtfpZ3Yxh1eJd2VPZ0obQkFKIcnf1sKcAAqwlLCVrk9tm3CwG5l2y0AHwF8UIb3AVrB/l6+la6V7PoA4JMAHwC8q6C7Hy6sM9uYwGN1YV3VJwCGkGrO5bduyT4z5gjwfep6vhMioAWIBoAXAWYB9BBuZ+HV+qJ6XyOglb5HjS856AIBzYEAxEFqQxPD7Gzlvw7wiDS4/OmSomjh20KYgH7ppZcAwPf9fdkLLdz4KB1ZILJARQscbAQ06mRMnjw5mUxed911qCZUQl221QN65MiRsVgsHo+PGjUK5Yk9z+Ohz35BRjPKXNetKIZdccTstUztUf7oo49OmjQpk8mk0+lEQq0GD7aXX365rz6Msn3n1ygioPfaIIlOFFkgssCesgAS0M+ti8cyX/xe+vDOp+at72fP/zR3qklP9sRJeWuEzTs3h1mXPstxV8GGuPY+xoTmjkvyJUcsD5Ee05ovrphAKY/C4QLDu0uHHR9ial1nOCpOFZUi0QRRkJPmhDLi+32puIzD7wX8Pwo5yoFSKQCt1nwKTuUKqRuW1CsJjno1D5KiHDv8hCmTYoZLE4IAuKxUsmNUkRGlcd7lU0SEg9ICRQMs7Ban5UELpGrrI4RzkCM6QOBEVlJhySCrSNW1ch7BoRyynVzKqEu6TRNtXivVNO+iAkrAhNTDYUoAR7eWqf8gjE1Vkom7Cv9fqnmy9gIhGFjDY+D5Ch54CtSTqx+aOcLytA7v5auT6/OEE+EymNZ7g1tBCTUZPo+2lRM0pKSw7mo4UTRedvkLC4KYeQJ8zmloElNIUs4ZCCavsbQsftDEngAXJOwicBsKcIFqeEA9ecdlFJhaaM8DiX2sEseibg8rFscVLV8EbXKsQdUWNpjez/S4KE40F8CBh61rZesD94G7EsIGYUrwnIRokuDbgTcA3yohtoD4pABJ+yI+BvgY4B8q8NqbAG8C/G0P4DUV2+1PACVYAfAowH1luBegFezv5Vvp2jIAjXuUWf4H4AmA/wF4AOBOhfsAHlS7wvWU2+Q+dcgDZbbFkngsVvWgsvZvAO4BeIzDW0LkQLiFB4+CEIUcx4JRwT0ZLZk6gnuJmKSgpT6Y/M97GeiNnI32RbXPO/i8gwdJJ5A+w6em8Lbiw5V6iiv3hg7nlKfL3aVlmZCLdOHBzJcPYykfahXi4QZYQD6HWBOMFfCfAO+BUD8ZhRtM8N8v5A9L/UIZmaMqVrV27Vqc7O87U37d3igRWSCyQNstcBAS0AAwbdo0Qsj8+fMrLuNoEwGdy+VqamoSiUQ6nT733HNRjBhpUP30tl8Q0G0fK3utJHo9M8ree++9b33rW4SQTCaDr3xxi2avqakhhMyZMwdfIJS8RthrrS0/UURAl9skyoksEFlgP7OAmsuvWL46Hk+p4OOfU1jJ4X41T7sD4BqA2Sbr0QIBLSUyEDjfQBY4PPcI70XaOry3PB0moIM6CxOeHRPQgvg0wWiKemNUEPbXAT4W3JKBB31FQEtia3cR0M3cmiZrpJB0MwGNJF1AQLfAmYT5kyh9YFug6M5Qwhfj8CgmoDVdVmYW/cIDE4WhWFT/rnxpbkwlGrqZgLYUDU3lsC9rYmlOCftMw+yzQK67+RD8J9J1akMU8hUJLpuBkFQvD8BkbKsCB+0DVZAkYjmDHM4pPUNxh8J79VE6sxIB3RL73C4Cuvm+0p6Lqe9BeDhXvLMNYCj32yaAJoCsSucB8iqdDW2bABqVI+0nAP8QsFnAZuU/+yFAARw+1FDU6j+C7WaQhcN4L/AqRd9SvX1bkbBvAPy1DK8BvLIjvKZW8f9VFdsguTmJvwBsDGEDgMb/AiD+rIja9QDry7jaEur2TwBrFF4EWAWwUmG5EuF9RkVRe0pJ2T4J8LjCYwB/UGzvowAPl+E+1/u569+E8LybPK+QtulNNr3JZBKYxq0u7Pqy8A7KsyUun+eKf0V4/F8RVFxhZs+0c7MDnGrnAuRn2hWhC5QkKhbOz2yucJ8qj63FJhW1/CQ7rzFdNr7xXLvx23Kbm22bE2xrnDRL9nS5K3xgSe/kV23V2UVGKD7KzJ2ey3+twTn1M/fULfQb28V8Vw5USz2RBG8+9I1P+gQzpKEFd5IJkk7F1f/+R+D+mlvf9GgfVy4aq/ak+3PCARImncPp8ier8NNUUBLJ5XLSOZzTDgLaVQS0K3WfU+ElcVlIbYPBDlyh/g1DLyz1D41KVCSg23Pri8pGFogssM9Z4GAjoJGlRAJ6lyQ4Xn755S9kpGOxWDqdvvfee7UTsWaf93E96DBdi23e18bm/fff37Vr17q6ung8jrxzJpP5xje+MXr0aPSDxpC46XT67LPPRmmVfSQuQURA72tjKWpPZIHIAu23gHRxW7HyOXUHTih3lAa5RtLfBGI1wDzTGW/xPh6kC47GIQ/oliY5LeYHrtMtFgDp8izFNBQwjZMl9LjB4DZUigymuEScAWGBE7TNqm2vp+cdCeJCgBXS9YznBPckAa3cn6U3DWecOjvnAd2abfVUClkzOaVEdkzRQHqvqkITa1HioLJA0fjRQ6Ik0cIIKT8WTccktYo0aytbZGBLtnIdeDk0r1pMAmvKW3teS55X6XjKdy6I8NUsajBA2FFDp9HfVv134v9oYSu9ogMKOFQP5jWTzmXexJUOaq5J761E7OJOvBbhguF83Bs0KCilLRNOaCtRzYwHPtrhYiWNC+/amTQDl0Ejhc/C8OETHz7y4B8ebPbgHQ/+nw9vUPg/Bq8x2MDgfxX+zKAZinJ9FOC/Au/O+wF+p9xCHyzePhA4gYb9QNH3E/1M7wH4ucJPARA3A9wspWxhEcBPAK4F+DHAVQDfB/gXgEsULgZoHVjsEoA5Jj3ZZFMl6IlhGP60UtATjAImG3SyQSfuGGyCITHO4GM18nSMRs4/tgB6dE5ilMLIHB2Z1/BHmf5Ikw5FWP7QArzhpi+Rp6XAfNxa3nCNFsvLyoeYbJDJBlk0jAEO7evRPg7TONRhAXhPpwR6V8VESWHes7mqfbx8Ucu7O1yjp0P7O3SA3PKeDnSQ4N1lv4oOaamnaNXAnqVHdXd4T4v3yfP+26H/VjjyH+5XZFRk/lf1xk6Ue0CreMggGBfcEbwgwbFq5XKA/+eZl3jucJfXyMch0cETHTAAhnrlH+aLC+kdPmLJAvg8Fjx0VT5EP7PphCpf0QPahSoXUop9TlkQx/gfFpAsdGPwHZBuDZvUc5FaERHcQHX854iADn5bor+RBQ4cC0QEdPm1bJMH9D333IOsaCwWe/XVV7UT7v5CQAPAZ599tmrVqmXLlj388MOvvvrql67CoTnxbdu2zZkzJ5FIZDKZWCyWyWQ6d+68dOnSfD6PLusbN24cN25cJpOpra1FhvqhBx/Sh5df0b2cExHQe9ng0ekiC+ynFsCw5vvOvavYjHIegAR0jCSl7p7jMjunVlpvALjS8I6yRHdPVCul5hiqNrdp6lI+sdFzGFG0QrN85rMTBLQHxGCdDG+EZZ8F8EuA/wfMAuZJfyLGhVRvkhqLioDeSQmOZruVkIYlHqDSj1XPrpoP0im9L0ocVBYoGhXFbGZhbBR7QGvjNO8tG2lKSbMV6lnvKmGfW3MK1oRyMQctVTsDNJPO4cKh8rJkqL9cCFYCJvUZpEoDBeYpYFptfcXbOhwklIS7Ffjwbi8Tum0A2FqsdasFED4ItG43Ke6j4jas1vq+KqYddXXibQCNt5Scgt7+DeCNQFThDZXGbblv71+V3+6GwBv3fwMXXe2f+7/KPxe9dP+svHTRV7eN2z8BPA/wJMB/B664jwI8KuARAQ9xeIDDfUwGZf2NB3c58O8O/MKBnzpwowNLHagPg8K1tnOO55zhOWc41izLPMXMzzQMiZwpkbUkVPqknClhSExHmOY0hRNM8wTDmKIwyTAkLON4CfM4yzzWskZZ1kjLHmo5R1rOIMsdYLn9Jby+bUAf2z/Mpj0UaZhUtFeV4r8KW+Ufmmh5GwtCF7SeKMTCRWmpcoGpAsUmZPBbTbfphI5JYAsZv1fDZ8Rnha9YRh6uIv3qQ3Rhl8vCu1RehQ7GUxS2QXBg3dSiBHYnvN2/yrfe2pK9upsl+bvpqyHp10QDVH8mBjSIM0BqUHwgF2/wigQ0A3mn5PKtuSKgk0nyp5d+B/CwaU9xWUf1Mp54os4TdTvnAV30rLX7Cei4CxIOpCyoMpUbgQWZLB8NcJe63W1XPwpKYkn/PgRPUxEBrR8Ro0RkgQPGAgcbAY2qQegBvWjRooous20ioOfNm5dMJgkhffr0yefzOCBwIqu3AOC6rhYqQvL00UcfnTFjRs+ePQkhM2bM2Lx5cyuDCd2oUXG/lWIYi+/WW2+98847Wy+GTXrnnXeuuuqqZDKJzsWxWKy6uvrOO++sqEji+75t26+//vrGjRt10D9tOM45dv/NN998/PHHn3322Q8//HCHbahYAEWf161bN2LECEIImjeVSp133nlhK2mbzJ49O5FIpFJyeXj37t09T3IH+8InIqD3hasQtSGywL5vASGE53lhAhoj2eqWu64b3qvz90ZCPf2jBEcqlZI3fw9psL9yuNWEsXnoYEG19IAWSSYKMdCDKOrNrjdFE5ty6hlz2kxAl9cW8rhJaA9oGWMdCFce0A6ktriZnJiiHPc2AzelC3J4mifTAgQIRgHgxqVLEjFy49IlAU3WqrGDOZL01sFPCYGo84P9wV/tCt28Kj/kFNksHRBlHtAWkC6xgVM8it7i/Ds8sCS7LOkHqc9bBElJ0MBduVAN1idlQzmnVOwIBXlfhgxys+5m0WjWjQkGb0t/S0Z70Vc94Is9m8sJcOGD8AVIqMCghbSykhWoQHwKEMb7iuHV0gqYeEVxtY8DPKQiXD0SbB9Sfru/U55396vbwn+p7W8BNLQg7DLFDf0HwL8B/Cxw1w077aLr7o0AGksAFiqRoh8oH96rAk/e7yt/3u8DXF6Gfwb4mu9Pt+xJpjUxhAmmFcAeZzZjrGm3C2NMZ7TpfKUI7gjTHdYMuXe06Rxj2mPk1h1mekcEGGx6ErZ3uOf19rxeEn4P6kl4voRLJWwFl3bT8OghGtTvrHAI9QN43aiGzOxMaS2lNZTWeKzWo50VsIbOHu0owWpbRY3HajyeUq9FC2EAdDwAX0oTtAFyNU/LaKGG8FmoCrYWaEPFVUKGX0Nw9duEa3S4IFwQxiWEAhOECUIVsLWYxi3uxW2byquasX69pUHv8PcUX+tG27AFPtxOOCRyjDBI2lAlIx5zApAuYuR3gYw2gOQhuR06NbCpTN6g3gduCXkbDvQ3QhrQ8lFEioVJGho4k2rIGbLm1csb/G+ZchUaDmnlAc07eZDGoM2Bnkbzw5gHsfInqN2bE3oea9aAVuyzXMHmQJUFcVMmarbm+gBcBvCCek3oNBPQ4Zep6pcnIqBb+r2N8iMLtG4Bx3GQr0MfU02gYUA8XHPWeg17bu9BSEDbtj1lypQv3Jd3iYA+/fTTO3XqlEqlZs2ahRdS8846gXyubdso0PHHP/5x7NixiUQiFoslk0nUkTjz62fmcjlNUusrjWMFx82qVatuuOGGe++9txUm4kc/+hEqI9922226kpIEetu98MIL3bp1S6fT1dXVtbW12IxUKlVbW/vee++VHAIAtm0/9OBDmUwmkUhcfvnlhmFgqzzPY5Qxyp588snRo0fHYjIsAjos33XXXe2lg7FOx3E6d+6MtHjHjh1ramqWLVuG/yGor61XaLqua1lWXV0d+qEnk8mbb7653Izl3dkLOREBvReMHJ0issABYIESD+gRI0YMGDDgmWeeCa9HCT8x7P0uSwI6JiX45S1a0kkNPvxnjp3VBN3zcvaVVBIcCSZiasKvZQGb5zxtmt7sPgJa6W+kkIAGSUDHLejcwIaY8D0BawWY0kUTQ80XZnqi4LQpCWi5Bn8nCWgOMmyasBUv9g85nxQam5Tg6dtq+zGI7Upi1QQwlTs5BiIr0qs9oCnXiFsPWyBMQCOFbAcDw1bxzWylp2ypTEONHJTozascHEWo2KsUcmRYs80yoJPcoghvs0qvlustS/wjGKLanxcTbyliVzvthj15dcw07fP7d4C/h3x+UbRXa+y25K5brrFbMWetEt5dAfBHJaT7UFjzQcAyDv/G4GcMfsYDKL54Ydb5dtY7M+dKGI6C+zXL+ZrlnB5gtuVIGPasApxT8vbJCNOaYVozDHOaYU80zOOaYX3VsL6at5uRtb8q4Rybc8cY7mjPHc7dYcIbrjBUeAH8I0UzhghfgfVlrI6yqsrgcbrzIJQHCGjNMKHZnOZxylKUZQoUsDxjcCAnjFVCQG5iJWHStrlaRadq2hQ5U8GIYAXWFVnRcPlCmhOPV3k8FUIVrrNpedvMGofp4HA6YOsq0dABLRvuSIvpMho6fJaAeq6igCjioL9cAlpfLP3THCZeozRagMr4xokcJxS6WLwng34UDrGhyqzk0r4TrLQkoHldIzvKZP8i5c59RT3LxSQtENCFfADO4jFC0uTB5cd9LiaaUBcM6YSS4JBO0FIMuoU4hPqi76HEjghouSDAlI+OvSzndBVQ5F2lmISvXZUHtH7dGSQiAnrvP/lHZzwwLIDcGvYFKUTOuWVZmkxrhVfc0xY4CAlo3/eHDx++qwT0iBEj4upz9dVXo+uu5p3DCYynxzn/xS9+oZWLk8lkLBaLx+MYW+/aa6994IEHSq40cqlCiLVr16bT6WQy2bVr1zArUVJ+2LBh8Xg8mUzOnTu3ZJf+KoS46aabkLHFCH6DBg3q378/IQTb9vvf/14XDie6du0ai8VSqdSgQYOwYZpfvvHGG6urqzt27IjVajp748aNWDI8+sN1lqd93xdCjB8/Hqvq1KnTAw88gCQ+egWG/2F832eUnX766RiiMBaLnXHGGV/iP1K4OxEBHbZGlI4sEFlghxbAO+r8+fMxrsA111zT0NAg9Ro4x9+XvX5z42phu7VixfPxWGbqtCnSA9oFgM3b6EXbYFATJJUbSxo1oAO15S+ZgEb2mUMKIA5AQHmcWXCYwb/lwX+a8IbJLMEKYoOFmR6TMtDSjVSAFOIAuOGGJbE4ueGG9nhA60Wjcsn/8sCz8v5Q4r+UH+Xv1N4NAt5RPPVWFfgLoxHKKgIdgyhxcFkAHZzVEmuHiwYmPmbiY8o/YkxBfMzgHwze5vCmgL8J0Mwvijygn+9qFQDtUeXbuwzgHqXSi1K8Jfq8Fb/eqxR46wFKsCCQ4kU33ta3V4AMJ3UZwPcA5gBcYNBZBj3ZYCcW1HjZFJNNsWkRLH9yOZQU7+Qca0aWTmzyj8+647LemEb36O3O6EZrVKM1stEamXVH5byv5Olwg42wYZQjCrD5SJsPdcUAF/o64jAJ3k9CHObyw1zerwRhPVyb9kK4tIfHenqsuy+6UX4IF1256K5BobuGBz01HN7Vo51dv64ZtIPbjGqXaqRdmnZZUpGqzfxpwHvGK5OtkpltG2RoMo2S+nV+xURR4coMeMCYY2NcURUgXGEzi00DV99y0jnob0F/1oa4DVUKcVO5TJqKt2r7tiVOsFINeIq4KcUBqkxItQFYUh8oExYkFJIWJB0ZbC2MKgeqHJPpwi4AACAASURBVClB0KwxpSLFFXhwGcs3RH8jOVjOBYdJw/aWD58iqD+u7FyyLQRaKDt7STH9df8qj63FxrfUcsmQNtJYE0t50K3R7Z61R2zPDs3affK0zgCiUXmMae0ORVVr7RSdwKMkAe33zdrnqAeDv8uFWeDJR5OKBHSzU7D0gE7ECYmTxXccspVNMkVPT3HlvpDeAJKDZl093kX5QceKV6TJx7PwENoT6YCAJj6gB3SVD3FfDvsqJcEhtWtsSDS5RwD8AuBNgM+VR0Bo9Q/yzqGHZs5g0aJ6Ffapau3atfuIq1mogVEyssB+YAFGmXaIDvNpX1bTDzYCGmfxXbp0IYS0Owhh+K6H3r6xWOz+++8PM87htJbgWLp0aSKRQN6ZEHLm18+88cYbTz755Hg8Xl1djcH01q1bV3EQXHTRRalUCvUo3njjjZIympVAB2RCyFlnnRUuE27zs88+m0gk0L+4f//+K1euBICPP/5YH/voo4+Gj/XU5+2339bU+YwZM5BSR1r5pptuQrfrVCqla0ZG+KKLLsIymqoO11wxjTzLE0880a1bt5NOOumFF15A/gULh/9bcN06o2zWrFmaT7/mmmsqVrv3MyMCeu/bPDpjZIH92gK5XK5Hjx54N8MXk126dJk/f75t218SB82VvqojCeh4aty4sYznABoFPPM5m7Qd0jlFBzjSyybhq3B/cikxTyATrVxyYqiz2aZJzi55QCfUnEeutuZQpVBgnyUBLToa/jgOv3BhXYO7yQEmvZylJC0qLUr350KAMw6MSR2n+hvqSYwsufGLdfTSH2nH40o6hqO8gAPwxjb7R03060306zk/BHpGEzutkZ69zf3eNmueJ6WoH1S+nM8CrC0WeNVKr39WmrAbAF6RHlKSdnwrEJzVErThxPsAH7SAj2T0SEmONyjKO4cXN4jV1qwBEnDzO+70l10CDR5uOaYdgJzqY1PZFjWCP1EmCmv+otRv+Rb91sMWfjewP/r8Iv/7hro66CP8mhLzfUVdMlSBKFHvDV/ckvR6ANTqfRwK4rwPcijAg9868EsbbtNw4TYXbvPErR7cQGEhhWs4XNFgfH27ecp2e2qjNSVrzMgaJ+fzbYNxYtaYkDXHlMIanXWOyroDEXlnYBimc7gGCvWatJ/FkO3t5UA3CzqZUKPoPEnYBZRiUcISiXIYkEDkIZGXaUn6KCJSMn22JPJQxrdZqLeMLwvYpWIJXU0D2UoAN9gmbJ6wGJHgEiaVsBUcJcurbi9EQCwMDokwKCQUkj5U+TImWBGrWOFrmRdthTIVKgnTu21PlzdGHYtEdoGkLi9TnhNyx2bNJDhSz3iJC5EA1F29pEdhT2e5K2SBECtaoJ7tnaKekWIuIwdjFki0TEAjp9wuArpKj8kSAtoCSUMHQGK60ABshlaaDo/bwAKFoRtuariYTu9c+eKjNI+sE8E/jhLq1eeqRFW3TuPqCksSX279ePbWWy5vNQ50dqB/gz3k/kfIjOnkG18nd9xJ3n5vhFzl4A3N0v552lPGluDVFk/iHUzeTIrvNmHBbkxjAUskslDd6I8x7ZvVr/yH6mfLkotdClIbyg86LJePQmGcgfCr4vJR8eJ55FM2MS/6KH9n6QpQTEAn1T+X9gkoJPDq77ltaB1ATLn/x4OclCvfwRBLvpjp+3njSQCrFfVsB6FqpQyaWmaH7/ObHzEYFREB3WyOKBVZoM0W0H6rCxcunDp16mWXXfbQgw/lcrkwpdbmynZzwYONgEbz4TS/3QS0vpAfffQReg1/4Xj72muvhUnncBq519tvv50Qgpz3uHHjli9fjkxrY2Mj6hfj3hUrVoQHBDLL+Xw+k8kg+5xOpw3DKLn+yC9//vnn2ov5sssuC5dxXReJ4PXr16Ozc3V19bBhw7LZLJ5i48aNhJBOnToRQl5++eVwGwDA87yHHnwooT5f0OW33HKL1om+++67a2tr0+k06nj88Ic/vPbaa9GyhJDLL78cD9cUebhVLaXbXlgI4bpu165dCSGdO3dOJBKvv/56S9Xu5fyIgN7LBo9OF1ngALDAcccdh/dPfJ+H6SOOOGLZsmVIQ4ffJu6N/qpZgCSgE+Skk6cBbGXwYg7mbWeD8lK+kGSB5ATJMZLjxPYJswiYRLhypbYnNf5iavqdViR1JeXBMOkcTrekEx3KD5EacV+ktdwnLm3myvcZGOFWnZkfbuS/q6Y6W32wPOllHJrkBGs8QQDl3FM+3guXLiJxsmDxAvkK2Xe0c3MJFR3kc1Ud42BR+JjB41lvhgW9LejtiCLINadwmMUHWuwoi46w6GjLP8agYwx/rOGPC8OiE2x2vAuTPJjG4DQmzub8O5z+i6A/Ev41ALcobYFbATR+AfDvAL8GuLcYqGz7AMDvAR5XztdrVcCfvyq9hU9BNABsU9gOsB2gUSk8+KpHZW5I4TEXsls4uygdLhNOFxUKfQmXCadDRUIN81VTG1Wbw9tPlQrE/wGEoYO8/QngKaUI/BuAuxV+rVYBo6fw7wJp4N+pzLuVVf8N4HaA25S1f6rchJcqN+H5gcjvZQCXAFwMcJFy+/0OwHkCvuGyWYZ7Yt6dlHfH573j8t5X24Zj8/7RpjeqBHk6Mk+H5+lQDZMOVTjSpENMNshkA0x6mMl6GbS7QbsarItFu1p+97aCdrVoF4t2KgWrs1gHS5IsFWCzdBguz9giY4uULVKOdAJNKpoYOWLp+BZmG3W6IhUSor1K6aqW6tEVliQq1r9zmSU1e6E70s5VuJ8eFbr9Sl3XdiFsw7Yc2MpIaH1XODxgON36Ubtrb/iMFdPaDq0YIdyYVorpXe0qj4X1sVFCW8BWL9dz0MGGr/z0NjJ4IKmNk2pCOmdITYqccAL5+W1HvfPBuRTO22aP2m71zns9XNHNEx1clpCRIRUoIwgMFOnTRAhJi3XYDr3zcK6A1cDzin3Oqa0R0qMIHjGaX2+jWhdNxjPJavKvN8c/8I7O8V7qrivvvQ5US8g4hNXBAIt5UidNYy94QGvhdSSgC7rnvvSATjny9eGhhjubuj8H+nf52y6KAgWoX3v8+W/+4acc5l3/E+n2l4g8oJvNEqUiC+zQAo7jIBXZpUsXlNKNqU+/fv2uvPLK1157DWvgnDPKkOT0PM/3/bY7j+6wDS0VOJgJ6J/97Gfa2mHetcUghMjkCiHWrVuHOs6EkMbGxjDpHE4DwHPPPaflKQYPHvzuu+/ilUDn4lGjRqEWRzwe37x5c7gRmF6+fHkmk0Ev6Xnz5pUTEFhs06ZN6EZNCLn22mvDF9txHOzkaaedhr7Jffv23bJlC5ZxHOfSSy9FpmP48OHocay7gGVuv/127QG9fv16zNy4cSNmxmKxY4455qWXXkKVjLVr106aNGno0KHPPvus4zjhluzetG3bP//5z7HX8Xh89uzZu7f+XaktIqB3xXrRsZEFDmYLvPHGG7fffvvcuXMHDRqkFY0IIaeddtoHH3yg3//tDRNJN2FYsWJFPEG+dvqpAA0u/E+De9nnzvAmv2MT65TlXUzoakE3F7pT0RP8PuD1Adad016OP8Rwv5L1xuT8o2zeUU/tihJh0jmcbgOjEWJA4r5Iag9oqoI7IQ1tZ2u48VXgP1CKse8DeD5wJf6M8zqlNihj+6D/Mve55/rOF1OfBUsWJjPJn976UyY9pcM+SEVWD2aHnAN1qaUUS/6yzb/e4EcELj96JrbTiTiFDnKNP+9P6VBGj2XeeOpMpM5k357oWce7xgQ7P97KjbOyE62m6VbjSWaTRD4rkc2dlM3OBPgnAReCuITzH3I6n/k3UXo79f4D4FGAxxQx/TjAE8od+3GApwFWKbHdNcE2LMhbLuMb3lue3r3ldZPWqEY+HTT+8VDiEYfe6vAbEB67QcJf4nqLHO96x/uhTb/r0K9b7CTLP8HyTzDcqYZTUPvNmScpzMxbp+TtGYY71fJPsOlU2zvB9k6w3MmWO9FxJzjeWMcf7dGRHhvqsSEeH8DEACb6FwC9GfTwRWfJR4hUuU9ciYvcgfQ1/N8d0B+VSefw3vBRbUmHj21Lui11RmUOPAu0NDYOvJ7uXI8iAroluyEBbUHtNnr4P19KOnYknapJ785yopypItUpEo+Rnn3IpBPJj64ji24mzzzfy6KzDW+iRUc7bLArevm8g5SsURx0QEAnfZoMOOikfC8I06l8l/yhCoks/bXUsiQrWIQUPF8UHkCoKuAgPU0ISWfI2XNJA0zMQg8DUghTxkiUUC//MA5HIsQ+J/eKBId+2kEJDk1Ax13I2FCdp8OpvxicNUBz8omqlG0uesrCLxzglp/dKi9APBFJcFQwUJQVWaBlC6Bn57Jly0444YTOneWNTDu/Yvi3s88++9e//rVmnC3LKicbW65+5/cczAT0Oeecgxyp4zhh7rdFAhqvIuf8V7/6VSwWSyQSXbt2LSFtNXvLOd+yZUuXLl1isVhNTU3Hjh0/+ugjfaGQy54wYQIqV9TV1ZXLHHPOL730UmSfU6lUOfWA7fF9/5VXXkEv6S9+IG+++WZ9FoyOCAB33HEHKm8kk8knnnhi27ZtyEo/9OBDhBDUg77//vt93w+3H+v54Q9/iMfW1NRgswFg8uTJmrbWrDqjDCMT6gbo8jpndyU+++yzjh07orAJIeTjjz9uu/f07mpDS/VEBHRLlonyIwtEFmjJApxzfDEJAKhx/9Zbby1YsGDYsGGxWKy2tjaZTI4ePfqXv/wl6iBZlrXnbrCykcox5fmVT1UlyKknzQDIAryU9/7d5BfbcKYJX7P4GaZ3muHK4F2WPcuxTnHM0wzz7Hx+LsBdAOh4e5PpDa480wuTzuF0GwjocIUq1HuB5/KV6DOVsQdrfXsC0OtBPK/UlnMAlKH2huxbyexOKg773LNpgYBO12b+9bqrbSrfoYaLhq8d5qvpIuXUA/iIwl0f21Mt6LX7CGicy1X5UOPxTh7v4tJuttfdcnsgPNbT57183kOhV3NadPNFN8z06KEO6+Oyw116hOuPcL3RrneM5R5rWF8t6C1Yx+TtY/P20YZzjOkcY9pjTHusbY0Jw7THGM4Ywxmbc0swJue2gpLCY1stPKas8pbKY/4xObcM3ley3pFZb0jWH5T1B+U9CcMfbNIhFj/CFkMcGGDDoRYcYkBHQ3TO80553iVLJZr8zhLeIVnaLUu75Vl3g/ewoJcjeqEzuwuHKpHfrh508aDOhRoP0lJtAJRwLc+4vMblGVekXBE/kJjlNval+L9yx9QzUoTho9qSbolYbCm/LXVGZQ48C0Tj4cC7pnu6R9qF3ATSBGSrn8iJ/q++0/XpVZ1++gty1Y/JjJPI8KGkYy1JJEgXuf6WxJIkU0eqDyHTTidX/CT9h+XD3tsyqcEYlvd6SWUMQQoqHErnXaZVjuENAFisNJcsGRIZo8/iI4XgoKGfPvSSIFXmkJou1RkybTb5nJ/YAD22AdkGpBFIDmJ5BROS0g9adFLqHEobWjpBJzyotBatnU9crV+F0MNPMwHtq1M4kLGgiyVOAXgefEu+3y/3fg4/Y6k0rjz77X/dj5zDmj+tpWoZW8mKtLLjoozIApEFChZAQhm377777n333XfOOeeMGDEinU5rPjqRSJx//vl33XUXai3s2dmlatfBTEBPnjwZSV3U2NQcdIsEtL6E8+bNw1vh+PHjWyGgzznnnLq6Ory6jz/+uP5XQPIXAAYNGoTcLnof6xagRofv+6NGjaquro7FYldddVX5GwkcH67rrl69GodRLBa766679IkAwLZtwzDwpUcmk7n00ktRmdq2bZSERhHn888/n1GG7z00B431fPvb30bBa2yk7/tz585Ft+66urpNmza5rouEiO/72us5n8+Hm7Hb01OmTEmn0yn1qa+v99Vnt59l5yqMCOids1t0VGSByAJIK+uXnWiQP/zhDxg5F19cd+/e/bLLLlu/fr1lWXvSYoJz7/mVTyTiZPyYMeBnAd4HWAfwiAqbs0zJFPwW4LeB7MMyFffsD3J2AW+o8DKrAH5u+EdUnrGESedwuj3TIVtqfTTDhY4yvBg9yrFOBvg3gBfA3wKOlFMUXMo+K6/uElZZTuk4cFc0E9BV1cnTzjzdA5ozskxOBwsTwbC1VSYqEVsANsALefj2VtrbgZrQHEx7A+1KQsbwUaqyVT6ktENTQXS1XHdSqFmu2vqcuLQZ1E9QX64Fdv2YQxO2TxwacyhxmYT2Kw/rtOq0nEu359Ls1cI4flTzwi8kNAnlKj1TS0WFMgXJ8wJMQUyVaRULnpqc5BnJUbk1ObGhygMU9tWKlpJgxWoLtEWx+mcbSdsDqVj4imvL7zARPqot6R1WWFKgLXVGZQ48C5QMA/31wOtp1KPdZQFNQBtKYazBJ42CZKFDDvqYMHKbdXTOmu7kz2lquHD9mhNuv7XfMceSrt1JrIokagiJEdKB1PYihw4kP1lKnlreqyE3Nm8fZXl9pRoSq5NS0UDkbxBPZ+3jAP4AsEU+eiD7TIPX41LTK+CgwwR0IXaFfBaZOGZ8XTWZdgr5MHfGZzBsK3TbCt0aoNt26L4dujdB9zwcatFBDu3v8lr1wJBW29heUA0KghDGgiCE0gPaVw9pFnTN0aOVgFXgjbcjAhofvQDgscefVCYmEQEdfgqN0pEFWrdAeC7p+7721ET+cNOmTbfddtuMGTNQ7Bfj0qVSqbPOOmvZsmWt11y+N8xhlu8tzzmYCehZs2YJIfAqhO3WIgGNxDHn/IILLkC/5tNPPz18pL60APDII4+gsDIh5Oqrry43/ZYtW1B/gxAyZ86c8LEAwCjbvHkz0tzpdBoj8pV4SWsH58ceeyydTiOXfd9994XPxTm/8847kUFOJBKvvvoqo8wwjN/85jfxeLympiYej0+ZMkUfEu4OZk6YMAE59PPOO49z/tRTT2lFjieffLK8PB6F+bra3ZJobGxESv2yyy5Dy8Tj8QsvvBAZ8z1xxp1r9kFIQAshXnzxRRxmkydP3jm7RUdFFjiYLdDSvRQdogFgw4YN5557rv5ZSSQS/fr1++d//ueVK1fiCz98/4cLqfRrTr2uqp22lU/+PjPv+PdbEnEydeJEkE6+OYDPADYDvKewWVHS4ehtHwB8pCLd+UqK998/c8cZvFvl+WGYdA6nW2U59RQRE2YQnUwRiJ22mwMd+2ygdwGsB/EP4FlgLjBRYJ8FMCGndAGfrInlgge0luCIJ2MTp0xE/5zyV7/otsMLc0dP9fcVgNtNGGXKKPPNHOUuMNFxHzK+5LJrVCLjQypAVUBGV6FPk6JcC55NkkSWoRcLYLygREkZ4bQAwYhgUqpbQsQQoXljRd9VOZ/UhUsTKgolC2+DaktLYn64JKbbWx6aW65OkWAiDN3UhG5AQK/HPV4ldcMlkko9PFG2lZ3Vui4tXcS9MJmv/I/T6j/Il34Ijsa2b9vb4LbX3N6S4Za0/cVA+Kgove9YoKWrv++0MGrJPmsBS8lAy1gX8m1l0uB1ButisC62112YfcHoz62+vnmka0x447Wjf3A56dObVHUgHZRPNFERAjNJcvw4Mm9e9dvvzMw7UzwY6EBtEyQ+tVONdJCAf5GxB5kN3AWqXozju/Hml93NDyfycUUEgfpUsVNnnFKdIhNOIFvN6xrYOdtgxjaYsZ1Pb2Anfk6nbvOnNrlTTfME1xrtsa7qRXVKbvfCD4eIqx/Twg8ohTiV4VgzLqSy8lFtAIOfqIAcn6n++Grb2pOp1udY9eKaiIBuzVLRvsgCLVughGAsL7ht27Z77rln2rRpyWQS/VkJIb179546deof//hHJN+0u63WY8ApJ6MMwxSF57DhdPnpMOdgJqCnTZump/Zh+7RIQGuuetasWbFYLJVKffe730UWWNsap/2MMnQ6TiaThx12mOYC8DR48W69VUoaIWs8f/78cAswfN/jjz8ei8UIId26dcO9+iyY0BNjVNhA57innnoqXJXruuPGjUsmk5lM5oILLsDhcuWVVyKB+0XgwZkzZ37++eeu66L/cvgUWM+IESOwGaguffLJJ6Nkx3XXXdfU1FRevryp4fbsenrBggVIdBJCBg8erMNztdSSXT9je2uICOj2WiwqH1kgskD5HSycg6/ZAMAwjKeeeuqiiy7q3r07CjThj8gxxxxz/fXXr169Gn8XbNv2fd8wDCHETi0Qkf42nHu/uPWmqgSZ+93vAGdysoRgPkgwYFxC8reK1C0sFOXgNQK8lIOzDOhryulHJefZMOkcTlcsHMrUHLQpZ4lpG7rnef9Ge/jWpkkAV4H4rYqwp+Kr04IvkWwduj8XPG6KZ3eqA2EN6FgVUQS0HJX4u180PmUlnIPHpW6jp1j43wKc70H3lsjK9udXuVDjQq3UEimmoV0ZzCeOcAAjvMktGjmgWZs5aD/MQTPCGRFcEdCcUE5KuFfN2oRrdiDmQYGlLeZ5NeerCV+d0LsqJnQxnahYTGfqYiUJXSDBRLJlyGJU9jdOWYrSGs46cFbNeZLzhEIylE5wEeOCaISJ9ZLrKPU3EMUO1MEQjdtQZUOVogDitoy/1CZgnW0sbEOhDftIeRV0NOFBQkUg3PG2ve1vb/1tL68NKBVUuPJVFDvetrf9unzz4NGjSFQeHjs3HvZ0/dpcO0xUbEkrnWplV8VzVaxfvZyrMPy0/StWVTFz59pTsaqKmXun/opWOoDb097+hsvrtTImJyZLSOdlnrSEXCck3CQ4CeET7hPqdTCaerj54z549+SHHp4ycTLJ1JC6WonOnUg8QWo7kHQVueA75NW/D9tiH2XCUZ+z4Tacr+JSbJaqYExFpig8PpU+ljS/KS8moMce/dU4Iaee3lcFFn4A4D8U7gb4pVI/u0uFKb4W4EwOh5mUoCpU5cew0JPVrhZQalSe8nf2VchZ9aa8o897uexwA44UcAHAMwCfqBVjgoPPVZiNooer4i8VCWimXAAiCY5iU0XfIgvsjAVwmolHMso2bdp0ySWX9OvXDx1kk8lkIpHo0aPHBRdcsGbNGs04o3CEnh9htDktn1AiK9FSsyICunx22SIBrY149NFHI4F7/fXXlxDQWGb+/PmEEGQHHn74YX0gJpAgGDZsWF1dXTwej8ViJW7LAOA4zg9+8IO4+px33nm6hjAlAQCNjY2WZZ100kkyKIESc9FBLfGQNWvWEEJQafqhBx965plnRo8erTVf5s6d6ziOfpsRrly/MOnVqxcKTN9xxx1PPfUUktEDBw7knLuuGz5EN7KiTcJ7dzp91VVXadHq/v37v/feeyXnCv8v7fRZdvHAiIDeRQNGh0cWOAgtUH4vDefoIMV4Z+acZ7PZe++9V8vxo0403p+PP/74yZMnX3fddb/5zW9Wr179t7/9bSfsiSe68calqWTshqWLBPekuwrzZCQ/DUFBqBWkQs2VcDGpMJRSx08b7aEO1MoJf8VJToh2Cc/9ygtrUhVVILTvs3J/7vhZdlDeOgf4rwD+DPxNEJ+AaAJBOYAnJD2Ma1uV5xCud608zUMCGgAW1S8ME9D6RW+zDSUBTTlg4EEH4DWfzRUwjPE0VyLUJTTlTnx1Ie5AlaMCxwce0NIb2oWMI0PJy10OVFmQUIhZELOLjdy85FwQnwdgxC9IbUhHYFdUqWhFSS3rUUIahkkcLIPli7cVWB5VT7K4mP66u8oniutPOzL4UjM8SHtQ8HRmIqnY5yrm1zC/Fvw6YGkQRIITYAkJHlNQObhLbTGmJW41Ga2uaczjKY9lXF5ri4x6HUKCbZUJGRNqFDK2SNlQZbYZSFvvp+UtKFxoC5Jtgak4+rbbp731t728NrgNVZZIGNAmtLf9WB71c0q2LRlhJ8ZDSc34dTfW31JV2obhRPAOBt/ENG9bqmS39NdT47B8BO7c9WqpqeFu6vROtH9P1x+NB1fId4H6GoUTeL1C27ihVlYVPKAFUV/V3UCkLV5ts2qbJ22e4CKTzxLP6GQ1HWpmh5vmtLc3TbziR6RLL1LdhZAkISnSowvpVEMyafK9K8kH2VM2N52e8/8D4DW5mEy+zhcSWmqjpYQuohjZycdPQQoC4GOADwA2KbynXr2/A/COXAEG/wnwHQ6H7z0CWj2B6AcPR37NyJCM3gjmnwniRoDnZAu5jD1IlYeA34IKdMGTQe1FnwHtAb167ZqIem5+Fo1SkQV2hwU0oYy6EL7vr169+pvf/Gbnzp1TqRTOKwkhnTp1OueccxYsWLB+/Xp04OWcoxQkSgdrDjo8e22pgREBvTMEdN++ffHuf9ttt5UQoABgWZYuMGXKFM55WHgFRSRuueUWFLJAinnVqlUlV8i27enTpyeTyXg8fuONN+J7hhLCF9dWL1++PJPJIMtMCAmHOvzCk3revHnanf7yyy/Hk6Iy9c9//vOSkzLKwqMQu1ZTU4P6Hvfcc8/MmTNra2vj8fj9998PAPl8vqVB1lJ+yRnb9XXu3LmZTAYdvTt27Lhx40bUSg+fC9Ptqna3F44I6HaZVL/qaNdRUeHIAgeYBcL3sZKu4RqaDRs2rFmzZvXq1WvXrl2zZs2LL76IiUceeWTmzJn4mjCmPnqNSCqVwl+HsM5SSeUtfWVUPvkvXrw4nU5ec+2PbDNbWC8pXaGFcojGVaPI5wZzKAZqRvQbqZYoerfIPmPctoocdDGR6kKzNrEmoE2IG1Cb44dl3XHS61kGPPxAdsQWYDEwTeFaHgeMGa+Ic1R/lj7Lgbe2arac18knLiFYmIAmcXL85OPRMi0R0AJMJb7xPsB/573jXMj4jHC55rTOFT2kFDUb6NLBDhvs8IEOP1xhoEq3aWvxgYYYbPEjLHaUxYZZdATC4MM08nSoBDvSpEca/hEKgw0/BDrQ8AYU4A4y3CGGc6ThDTO8EYb7FcP9St4flfdHmV4I/kgzjNCuvH90GeThBdCR+TB0fkkifmvxMgAAIABJREFUXCacLinWvq/lDZM5pidhuUdb3ijbGWE7X3GtMa451re+6tujfPdI3x3iO0N9Z6TCcN9BDJWZcq+E5w3RcPwhEt6Rlj/U8kaazmgZntEeZzhjct6InH+U3HqjVazFsTlnXM4dq4I3HmM4xxjuaLlrRzDc0Ro7LJzzmgvvI/WjzXGrRkswPPxRRcOjcOmHq9E4DLc5f5jCUdKSlTFMDk5vlBqiw3Hw59mReTZEgg8qh8kGaZTvDefk6MAcHWgo5L0BeW9A1t8xsDxusYYdbsOHlKTLjw0XKN9bMSd8SEm6vHy4QPne8pz2ltcmDR+o03uufrzo4euLaX1qQ13u8gaU5Ozv5fe0/dtrnz3dnl2pX/cl7/fP+/2zXj+E/OoNkLFtvaGN3nAJ/8isP6gh1zOX7+nLiIIjXHdwQ+OQz7PHbjPP/LDhiptuHz9yfLq6k2Shu2RIbZpUVZHu/cm9v5/G4DUutqqozrZ86pN8KgaTQGa10gvyYkZ2+tTphJCqBFFELj6nIEXNVI4H8BbAT11jsse6yzf6e1h/I1jxQ2wgUucaYhZ0sugAyxtnWacxZy6IfwP4i9S8FtsF9+Tzo2poRSq5uK+FOIVhArqlR9YoP7JAZIGdsICe42hvVE2M5nK5O+64Y8CAAci8xWIx9KxFdYfp06f/+Mc/xsJajSAsits6IxcR0NrO+qrtwAPa9339NuDuu+8udzV/5JFHtMCFFsTQLJsQYuPGjdXV1fF4vK6uDvmCTZs26dNjglHWo0cPZH4feeQRRhk21Pd9TAghDMPYtGlTv379UGED/ZpL5D4mT56MrUV6Ahs2fvz49evXl6zLxgP1+NMOd9XV1TjysF+ZTObMr5+JVLjjOK2QJiU9atdXzrmWLkX6/pvf/CZ2MJ1O9+nTZ+3atVgh7tXmbddZ9lDhiIBur2FxFF1wwQU4Pmtra/H/onw7JfQ5/vjjZ8yYMXPmzBkzZkyaNGn69OkXXHDBFwoti1r4LFy4cPny5atWrXr22WdffPHF1eqzZs2atWvXrlOf9evXh8fznk7jP3L50hX9ChF/FXRsT7wJ7M1tuCVtsUZ7r7su7/u+vvPozJ1O4N3DdV39s7rTVZUf+Nlnn7344ovr1q1bqz7ICL+oPi+88MKvf/3rm2++efHixbfccsuC0Gf+/Pm33HLLlVdeOWnSpGktfI4//ngU0wjfq1GmKZ1O6x8dTS7jPwsegrdo/a6xpAZcjoOvrFHGq7xfFXO++LFbvHhxTYfMwkXXe75V0VulZLYE0i/4JRPOysGhhuhsiHRrHLTmmisy0UGmJ+KeEjXWYd8MqNpm97fp+Yp6fhngQ4A8cCr9alAVw5ffmJTdYEyu9EQ36Aq9FBwY8xhzGHNUH6UHNCFkwvHj1LSwQE8H/LruLhXcUoLXf9xmfCvHD8M5mCeqHXqU5UzN5c/KNc21sldZ5g9N+xLTuSjvXpx3LglD5tuXbGv8zj8+OvvTT//JdS9D2O4VClea3pWG9wPD+9Fnjf/y903fXvvnmU8+M+7pp8f9/vcjH/vD0WtemP788ikKU1eumPrc8mnPrJj29MoSnPDUiikFLJ/69HMnKsx4+rmTn3nu1OeWz/7dAxNuublf/eKeGosX9Qpj0aLeGgsWHxbGwvq+C+v7IBYtPWzR0t5h1C/pXRHhMuF0ceHD6pcUoGo+rLBd0m/Rkn6YDgo0n2Vx/aGL6w9duERiQX2vBfW9Fi1uRtCp3osX9V6ysPeShb2WLOqxZFG3xYt6BLt6qHRhq/aq9OJuiwMsqu8msbjHosU9FtT3mr+o1/xFfeYv7LtgQd9FC3rVL+i15Cd9ls7vd8OigUvmD1wwr+/8aw5bdG2fxfMOK8J1vRdL9NJYeH0vDZ1ZlsCj5HZhCGXFdLXNZymUV2fZQXnV1F2pv/76Q4vwk55L5vdYuqDXjYt63rS4x81Lut+8pPuzT08PMG3504gTlj99wvKnJ0s8M1FhwvJnJix/dtzyZ8c9q/HM5BVPn7LiqVkrnj55xTNTVzw76aknjt6+7eItW77tOJc6zvcQlvs9y/2e6VxsOhdbtoRpzW0Fhj1Xo5ViepcubNitVWtahWpz9lwNPDZnz21ySpELNUOfQp+0YkLXtofqx5PqxhyE/TXMi3aInHmRRsXLVJIZtucOKzdCled21BhsRta6SEPnNNoXlSBrNTdbt7/t7cFeYNfwv6x8i/+D8rcvgM7JuReXIO/Kf9gSlNcZztG16fr1f8Su/H8Z5hzDnJM3vps1JXLWHGWfS7Lm5VnjKgnz8qx1cdb+znbz203W+TlvToM7Z6t7yTb3h1vy125puvmd92/5ZMu9L7909z9948TqGKmpKrACyQT5/hXnABicGa5nqucK6evVBuDTi3QLmDJ5KlYXPNAIABfAVu/XHQY5Ac8z8Q2XdrN5UhHQLaxC0w9gO5vAxx5DSWbbUqor2eCSrHeY45+ugg0+BvAngFcA3gb4HOQ7eydEmoeaH0pqb28ZjjF46Fz30suqy7HVa9cEZXfbX3QTLCeDdtsJdmtFQohcLlc+I9uNJ0E32F2cQCEtE25n2F9zN7Z2j1YVjvQe7kt709jI3UhVocoi8ni49Tyv9TEshNiwYcNzzz336quvrgp91qxZ88wzzyxbtuxG9amvr1+6dOmiRYsWLFhQX1+/cOHCH//4x8g7x2Kx8OwSp6W33nqr7l1Fs7R0gQ42Ahr/rXAKP3XqVJTHLBkSrRHQnPPGxkac8xNCfvWrX5UT0BdeeGEsFkskEkOGDMH/NxwTemScdNJJ6IOsL+Q777xTcoVyuVynTp1SqVQikVi9ejWqQmMZ27Yx8eabbw4ePBhJB6yqR48eJZ3p0aNH4XdP6U3X1dVhaEukmzVbjTca5Juwckd9bNtGp+lEInHhhRcSQjKZzMqVK7F8yVAr6cLOfdU3PkwAQC6Xmzlzpu7FsGHDwjIjnudhM3budHviqIiAbq9Vfd9fv379kCFDCCEoOaQvd8UEihOFKTkk4Eq4uZJjMepmSWb5V6wclybs0a0+NdKL5Wx7uIP6nqOP2muJ8W3+TAh9jm/zZ9asWSeccMI49Zm0mz5Tp07t37+/Dpe6e22VVB9UT9JXDcde+JKFTxqLxdLpNAYaTiaTqUofLB+Px5PJpK42PNQxs2SQ64GRTCarq6tbasDvf/97/K9klOl3e235P/2CT//ivIuXLqJSakN+NAWrE0y5Rit3aAvgLQF3bxPDs1BlSBWCzO4ioDG8niunOqlt9gAqhRTvU0tZTd0RGWyQSeqZUxBMCUDLX0Rf0eIGQBPAdoCtHD7hctXq+wI+FZAVgnEGQjDGHACov6GeEHL8xPE490H/6LJ+U1Xn/wlY8Lk9yoBaU6kAm7zb394ZfNwEUltLenUntSlSk5a6kJkOJF2GTA2p7UjqOqkCadKhA+lQI1ETJDrggTUkXUOqa0mnzuSQQ0jnjqS6ilTHSF2KdKkhh3SQ6NxBnrGmllTXlSJTSzSqO5ACakhtDenUUa4OTsZIJtGMdIxoJOMkGSeJhEKcJOJS11IjUUUkkhJVKYlUshnpJKmIcJlwuqhwlZTORITLpKqIhDpLoUDoLKkESSWko1lVVdBmbLnaYl/Kt4XehUpiTrjv4TTujVeReBWJJUgsLhGPSU+3NCE1CtUxeYFqE6QuSTqnypAm/5+9N4GTq6j2x6u7p5eZzEwyWUhYQghhxwhZBEKYJSFsgoCCiAtBAqjweE/c/gKRkCDLz+dTfAIqgorggk99sikSX1ZDEGWT1YAgiDHLbL3etarO36rTXV19e0nPlkySms/53Dm37qlTdc+tvvfW9546Z5yiBBmXIK0ajZMl+a0SK2VK5EsPFTVr5RXk9VaQR3nZ2wrymrbyJnT5toTw+GtrLJI4wbgYrs1RSTHSnCAtjaS1SdC4cpLjeZy2bW0mitrGiGHfNkZWHEMmtZG2FjKxjYxvJa1j8oRhWJvHiBisLU2CmhtrUVMTUVRbEo8q4aa6NTc2EZ3iY0isuYTw/tCo9QRbqd0f1RNdeWOTuNsMi35zvmMSZIfUmCCKal+vcnvuUPkYTXnjjjqjupFoJDrFmkSWPJ1iTSTWJGRUFWTq748+PvFXVr7F32DzGPFs0inRTOItJYQPqaZm8ZvVqVynXqIklXL8IQxx/KMRmmIidEYiXjRRIkGK1Cge3A0JEhlDomMJaRUUHkcaWkl8HIkkxPN6XCtJiEROJCEB6DFR0hiJCOflELn4oo/KlwqMMFEPAF2U6erqEu+BYaK9ywkAWn5+7/fhhRzcZsO7y6OZDXuJioeW5KF+v7nb2s+i8wEuBrgN4BGg68B/DtgLAC8CvADwZ8m8KLcvSzftTTJgyF8B3pLhRLrla1UQjweAX/7qIXxDRgC6ouu0eg/UGWWiV155ZV2Vvw0bNqxcuXL9+vWvvvqqjuiNNh7hnUwm881vfrOj7E/zzursGsLfAvmn/GQWLFig+DqZ4447rr29vaurq6Ojo6urCxUuWLDgnHPOaW9vP/jgg1tbW/X50SjnEV6bOnWqbuEB8R0dHe3t7WhJ5MuuXl0FnZ2dHR0d8+fPR/OihbFme3v7ueee29nZOWHChMD8MSz/cOJZzdToxqqmkwGxWCwWAKAVekkIOe+88zAcRwASVLv671Hn9zYAmjG2detWxIcxCaGChZVZagHQruu+8cYbCu2655579E86nHPHcSZPnoxA7bJly5RSZKhPL7vsMvRHw9jKsVgsHA6//bZcPqxJv/POO3goGo3+8pe/xFa04/DNb36zsbERgexIJIK4w8yZM3UZAGhtbcXeJhKJiy++uKenBwcK3lhVr5B58sknZ86c+fOf/xzxbtd1HcfBbuBwDIfD06ZNCzSxw0EWkB/Q7h133DFjxgxCSHNzcyQS6ezsTKfTSgMi5gHMXR3dVYwBoOu3vAr5cu655+K9T483FLgJDssufsGLyD+8L+O2GnI3LI1WVIJQO35A0h8Yig/UUuU7mQl0o8au3jHdtjV4leig2pOvRnPVDmE3qh0dSnkoFJo6dWpXVxei6+3aH74WzJ8/v6ura+HChQsWLFi0aNGp8u+000479dRTFyxY0NXVtUj+VXyNO+WUU84666wFCxZ0dHRgRbVFv+m5c+d2dXV1dnaiKnz5WLhw4bx589RLXuDspk2bdvrpp3/zm99UuSPq/2068q+zszMcDi+9/vqsZflMRD5WuLNIU6gRE3OCFMDPU3BhH+yXgrCMtlmf603B2bkkGHShUHpACydokRyMxzLuEY79aYAHAV6SbjX55Zwerj7lopM+FbGpMTy1OAwZ6a38ggxO/X8ADwH8FODHHB7m8CwHD9F1xgTIfvPNXw6FSXt7PgSHDNKhBxtBAzjC5xoeS8OZW73WjMDZGxyWyLqHvP9C0jqBtE0ksVgegY0mSEMTaWgk4aYiNTTKkoTYNo8lY8eTMa15amklLa2ktSVPY8eS8W1kQhsZ20yaEqQlIUC3/SaSSWMFBtfaKKhF4laJMQJrjpdSbAxBiksgG7eNjWTsWFFrbAuZsk8epMOJfXNC4IOKmhpJUymWofSI5pAk8D2mmShqbhaAeDVSYoopkSwFIJrHFNSOkRi93CrcQTCFhhC+RwRfgP4a4VlU2+qSyNcjKTAOCeLEmkhc4jhNcql1c1x8Idh3Ijn2aNLVTs44nZxxRhm9l5wxCknv52C7994zSZ7OIu+VdMZ7yWlnkFNPJ6ecShadIuiUU3dEp5FTKtLp5NT3SjpdKDzjdHLqKWTSBDJhnACgx7eUUFszUaTD2TufV+h5cwtRpH7vY1qLhSg50B6OtP7R1p+deb74maT+7YBtJT/D1K+/HsmWMQRJ3WDHlOK/qhzF6tFZLqOfqfqhVWTGtogHzdgW0tpapOax4sGHpMpRrKKSGoW6/mH5feHJtjSK72TqU1lrIcGg+L5VsHBTo4DLW8eRprGSxpNIM2loIWMmyU+REfEO0BgRX9oaCGkKkzAhCYlBT2hrY74IWCb/iuByweu3VsnCk7vi8WikIdTX11eAYj3hBC3Q7Hc4fL+Xn5thU4Ydbi5RKFMOFj2geWvOPcHOXgrwAwE9w89kEOpvA9wBcDvAfwHcBLAM4EuldB3A5wC+KI/eLnMzPim9BIRVlAkAYN3vN+DL7Zp1wiGvcNZ589X+xxi74oorakwx8FA4HI7H4+j2hzPE0bbVT0GfbSGvz7OG3vPAVKL+XeVDg8s3dYcbVPKvuLLogSM9eYKbSs45u6wMo+DiiejGr98awy6J1tPxX2wiFArpYF2NdhHrCHjaKW+twGmqXR2A1oUbGxvXrFmDP0AFBgaYaj/PvRCAfuaZZxKJRCQSGQwAbdv2888/r1Y6ozexbuu33noLL3wsFnvwwQdVcG7XdRljV111FSYeJIQ88MADaohs2rQpcIU2bdqEnm6JRGLZsmX4EQ/z/nV3d1944YX4kwiFQh0dHcpBuL29PaAHm4jH4+973/sw/DRGqQ6IUZ+uW7du6tSp8Xj829/+NufcsizbtjOZjBqsGEt0+fLl+mJ5/dwDOoe4+7Of/WzmzJn4MMCTveWWWxzHwS8GnufhcoMhLhIZYicrVkcAGh3sR84+FZveVYWc8zVr1uCI7ejoGFA38Aq+/fbba9aswfgYq1atwpgG+hYjZqi4GevWrXv66adxKGLsIWy0v79ft7nO488HAAIDGKPNqNAW+FVjJ2wzmQw2umHDhiof5tdtlH+PPvroPffcUyWyyIgX31D3n96VFXX//exnP1u9evVTTz21cePGanYYaPnatWu3bds2oHFYjzAG93Bd1/O8ineevr4+1BP4KqaWrQQ+WOrjEyvqg1N1KZVKYZQS/CiIdz/XdW3bpj5Np9NvvvnmjTfe2NzcHI/H8eVg0aJFq1at0kM24ffRwPhXTZQzuD4GM9wuW3Gj41X2gEYMWiyWFJOpv3K4tgcOT0FrVuYexKjNJfOWios9C1izDkC7EPGgwYWIxYhIpMOaLH8/EWw3uRhgNcBfEX3GhDaY00aG33BdSPnC07lH5PkRnjUvAqwF+IXMFP9f/dYV/c7FffT93fRDafiSBb+gvB8nNAqADkfQAxqnOYyLc9OBdwbQB/AXB76yxTu8B0IZaLB4wuVjbH/6Q78Zc+tXQ5/9HLn2mpal105Zeu2U65aOu+b65muub/risiJdc30T0vKbx3//h+9++NGFSI88uvCRR7seebRD0K9PeuTXJz7ymxMe/vXcRx6Z88gjsx56+Nj/W3XC65su6Ov9ZG/PJ5L9n5R0eTK5pDd5cXfqou7URdvTJbQ19TGk7cmPbe9fjNTTv9j2rtyy9YJ/bD4vmVrc13+xot7ej2u0pKdP0Pb+Jdv7LkPa2n8Z0vbk5YJSl25PXdqdvrwndXlPaglSX2pJDVJiigkKJy/vK9Ine1IFSl7Rk7yiJ/XJvuQn8wJaQ739lyB1Jy/Z3v9xnXr6Pl6DdEnkqwnrkluTH9/Sf7Gki7b1f3R734d7ej/c0/ehnr4P9SU/nM5eZDuXuHRxd2phd/qkUjqxO31id/p4QZn31CKUyW+xVvlW6imRxBKtFdFcocWK7YpClMGu6q0MTH9Pdp6k43uyeerNndBnzU/aHSlnQdo5pUCnpZ0aJMXck9NB6sjQEwX5XRn31Ixzds69IJW5MJ25OJlc0td3uU69vZcp6um+dNfS9p5LFW3rvTRA6tD2nkH2U9cQUL6tt9j0oPUP1Hoj3Z+R1q/Ot3v7kgGRqlgnMyDl9Qtv616iaGvPkgCpQ9u6B3Z2egf0E1Q/tGpMT+9litSjRDHqUI/2m62mqmK50rC9J/jjGsT4x9Pcvu0SJLHb/fHu7sWSPia3Hxcl25ds27p4+/aLevsWb+v9yNbexVt7/+PtLV/6y9//86+b77356xd0LBL5okJEoM8TWkmCkLHRxBf+/fM/uOs+9cbl+Y6GtSrQtRaz8OSulpYx0Whk8+YtNI/FUuEBzVMAGyhc0ccOyoqUxWSkSLywxYRDgFz4laLEgykApwNcA3AP+PeCc4NnXZ7JvT9jn5Gxz8jZp9jOibY713GK5NlzPedYlx7u0iMd74Scdb7r3cz8XwN/R4XpQCtQDpmcHYnGo/FGBKCpxNqVDXfI3HHHHe3t7R1V/trb288888yOjg5cNzl09HaENKiV7uPGjbu27O867W/pkP9uuummq6+++oMf/ODChQu1pa11sbNnz1aOj8oUO9/HSyFsQ2RwAevChQuH4FYu3JKOO+64c88996ah/S1btuyhhx56+umnMRTkBvm3Xv498cQT69evXy3/FGCiz52fffbZ9evXY0W9fO3atVj38ccfRwFEY1auXPn888+vWrXqq1/9qg5AYzjcCy+8cOPGjRihAWeL+nxW56v9PPdCAHrlypWNjY2RSGTRokUV42HW8oAGgCeffFJ5QN9+++2oghX+Vq1ahWM9Fos99dRTytGY+vSaa67BbxeEkK997WuPP/64+lU8/PDDgSuUSqWUnoULF1qWSFbwL+frW265ZcKECcpL9NOf/nQmkznmmGNCoVAikbj00ksDeiKRCH6PuuCCC5QbdTqdRghDoSSPPfYY+u03NTXhIhTHcTzPw26ozx2EkL///e868lLPIAt0qcYuDuKf/uSnJ554Ig5xHPSnn376unXrXnvttTfffHPLli3ox40mVx7sjuOk0+lcLvfEE0/84Q9/UOU1mhuhQ6tXr25qalqwYEEAbBqh5kaD2kED0Dh+AobSB5Xid3iaSrIeBrVVk9xhW3uVQDUrlZfv8WYpP+VASeE5IP7rh+qxTDV5dZdG1Nt1XUy+iruPPfbYaaedph4l0Wj0yiuv3Lx5M8LTQ+kPrpVZsEBEG1x+45fdordOxbPhwHo5PJKBhT28IQsxl4cpJ5QTDNy8g4lQJQDagwYfoh405ChJOg0Zf7LPTgf4NsDTwF4Hto3zFGOuiPzsA/VF8A35l2GwiQqE+gGAb3jw+RxclIZTUvCeXn5kHzsk4x2WpdNTMLkHDt/ivj/Fb6fwN6zJad4DOtYQaYxHcbfoh6OmhGLK9ybAXSk4eyufspWRDIRtiPjQwHiTT6f43sHMOYrZxzJrro+zLOdoyzkiZx+uk2UdrsjJHV6gQ73cDMuekXan9/nTkoKmIqW9qYoy7tSMOzXrH4iU8Q9M0YNS9KAkk0QPThaoz5+uCJOqYZYtmaRrOiZFFPmCCpT1DlaE+QxT/iGSDkv5hyXLiR6SLJCev0sldAowuozOl4hpeRRTvmg3T5iYTu7mcy0Wssap6rpOnVcCAUaX0XkUwxKdxxI0b8Gw0/ro1KS/f9rfP+sfoChHpwpi++bY5ArEJ+UETahJKCO3FZWwyVKJJpZXOynfIu5iXXWoQrsFedHb0g6X1NIa0nVqvA37SJqI55Vl4yVNlP3ZN8f2LyVsTt9KW+UbrWYc7O2+Nj9AEDswkORTDeZRwmTpdEVpNr0iKYEsLf4Y6+y/Xrei8jQrdmAQ+uvshhIb6f6MtH51Ijl/etY7aECk162HH5DyOoUz/kGK8LlQvlUCGX9gJ1hnH3Qxva3ynmCJLqPXrYfX6w7L+MdGM+40pEIf5JPRPSTrHpL1DrbpIS4cmqUz0u4MC45O0SMtWPTP3iXfv+/kCz5ycGOzeClLtMhXs5CIW7Xo5LY7vr48//KUR43VK0U9TL4qAHR1dSGct+73GwqOASA+irNnuX+bxedkoQGzN+/gvWvQCHUegI65Iu5zRKS+4C2C2GTbPTrnzMk6R2XdQ2xvhiD3cNub4dH9PD7RZ4IYFUT9CR4d6/CYxRMZf0LOXQj8bqB/Btav4GUFQDMA4YjWEEPAS70VF41iOGkBfR6xO/LmMu58CyhMD/2fkskkAOCq2bvvvvuII47Q4TiMprBlyxYVwrcikFrPWextADTnfMOGDehWP3gAWnm/33DDDfoMnzGGmfowiCeGzsBp/OWXX46thsPhq6++mvr0ueeew0dINBpdunQpXnJ1zVzXxVAeiCzMmjVr2rRpyvMambvvvpv61PO8eDwejUbj8fitt96qNCCzzz77RCKRaDR65JFH4nhSAwtRP+rT66+/HiHmSCSydOlSNZgw1D0hRLV79NFHI/irWtFvcKpwEAx6p/b19V111VVNTU3YYiQSUVh/4OsZLpZpa2ubPHnywQcffNRRRx133HGdnZ0YTjccDr/11luD6MawVFm3bl1TU9P8+fNHLknjsPRzGJUMEYDWR1E1foe9rVaxYjlqq3jIvNkETF3NSuXlgYp73m75KQdK9MeBfqgeU1STV57OKhPAvxbT9PT03H333Ycddpi6P0+fPv22227Dj4vYnMivrv1V01+jb57n1Q1ApwGedOHLSTikj4ms65SGgRJgxOd1uOFUAqCVB3SOk5Qz0WfvBe8W8P8o5ie0m0Mvg16ed3PeArBNxhB8AeC3HtzlwLU2fDjHO1Ls8DRMSUFjH5BeIEkgLotRFrchkoKpGfiEAz+hIoehyHyjAOh4tCEebWC+K4xTPjeUAPQ/M9dsthf1wrEpmJaDfWzeIjTzCEAYeBhYA9AY0ASwBECcsYjPiUdLyKdEEfOJIu6J8hyQNJCMRjK/PGaZJxYXpE8vLREdO5zJU0NGxOAWlIaIogxEMhDJiugoYRtCNoQ8CHsgPhIoKtUZtqSwrNKQLehUyiWjGg1nZTIi3KJvVPlWl9H5UknRLlIWRLsFimUhhnxBgJRWJLpOnQ+IqV1dRudRAEt0HkvwuqTlNcLLhFdHt56cnMv5OUTELB2iGmFJqCBTg0HJcg2oTT9aP1+xuUAPB6nfgwY5qMJ4asogeagib4oaXVV9K45JNTgLSpQlIwUDVhQeLYU2EEX6r1jnlYCt/Ri1E691LnpdXafO6zJ1qh20mN6W3ged12WMGjtWAAAgAElEQVQG2pBeV9ep87rMQPXr8moA18nodevh61Q7IDF1c5MPhcq3RF1mQMoHIay3pd9jdV6XGWgTel19DAT4eoYEylgSmcWHbMlzVvj8NkgiWU7SPvFhvM9n9GYO25Z9z+3fJ+0LRfis8ePlxD1CEuPIgrPI1+48Ye3GpQDPgyuQHZEn2cm/o1V6vSh/4cCS4ptaZ2enAqBdT5X/nbt329YHXW8fX374r3f92SBgaASgWcKFuMsbXd4imPyNK2RDVGT+4A3y6BiXtblsrAcxH8JIDMIMwpSHPOlAnRGP0TYLzpKxO7Yq66iXLwFKGABaXeeajP6evzvyNU/OHBwpC6jFspglaOPGjYsXLx43bhwikM3N4ntaW1vbV77ylb6+vuHy79w7AWhMHzVUADoej1922WXUp/qPfOXKlRiIIBqNnnnmmevXr//Wt741derUsPyLRqOXX365CiKhHKLnzJmDQIEaXIyxz3zmMxj1AvFuFQWcEDJnzpw//elPuKw7nU7jAoFoNPr4448H4LNzzjkHV0DE4/GvfvWrOvoMAAHvuY985COqA4hWYwgO7EYoFLriiiv0jx76iQfaVXrqZ5555pljjz0WDaUGPXpAE0JaW1tVOB4MCa0+A2BIb4Xmo3/7008/XX/Twyv5m9/8JhwOn3jiiSpBIhpqeFsZVdoMAD2qLsfwdibwM6+xO7ztjkJtNc4dD2l477B5QCs74NfpX/ziF5/73OfGjRunPs6dd955+LHTtm28PzuOgzfkofQHAP4VmqluAPrvAHdk4aw+b2JK4Kcx8MLgEaCDB6AtRnKUWIzYEHH82cB+APYL4L0JbDPwLR783YJXHdgI8CuA7wLcDPDpfueUbdlZm9MztmSndLvN/TyehHgSIv1AkHJAmBcBp9n3WrP2PIB7AV5jkPaBMuZTT8wLb7pxeTQSikZCvityEgb/8pPBbh8es+HrKefKnvRZtt/p+kd7bB+PjWG8ifEEgxiDGIcohygTyGPIgTx2jLNiNbkV81uNPEY8Rhwm8OUc5IFmiwk7OLRIAsv2Iz5tUOSyBofj3Lhkm+MRRXk9MnqjB8QDwiRRIIp8Li4Zkkj8WAZz67P9AK8DB4XpaBA402V0vkRetlveej5Ci5ww49GSWnICrOvU+XJJLNFldF4/qvMogyeuAA5xEeVV8xnxWVgQbaA8WkIsThXlD0Uo3yFpSlR1xQSaqHe3YqPRYveGoF+O/AYGDXhqwiByOKkBVmR4iBapYpekAA5OIRkR9sz3rZGyRsGLU45oenSdlXlPfHfZ2VQAygW8jt9+9K1+dHB90zXompHXjw5O/0Br6S2ORH9q6MdDeocHNDwCwvIXTerfBqrvcLd+zfVL5u+NZXfvkvubdo+tX/PgJEe6P7p+fWBU4/WxEeCxCroPqw/G6qxdCUAXcXM2zmWzNv157r3fOeTQo8iE/Ug0KtInJKJk5kzyhWXkiZcP6ofOfzgXyGVbvQJ8znjgyewU+ReLanBzeXnxTUQHoG1fpTF8Pmt/1HEP4m4zeGGflXyf1i/9MPACgBbvGxJ3jns86omAacQTDtHi6yA2ge8YWOJVgrlzQPqAdENjLxybg88CPAPgcBD5RPCs1DkbAFqZojazw0nKKBeofXbm6LBbAMcDqqU+vf/++88//3w1u0Rm+vTpd955p4o9gN6rQ+/J3gZAA8CGDRuGB4Buamr6wPs/EACgt2zZghcMs3xGIhEFIofD4WuuuQbRZ7zks2fPRrQ6Eol8/vOfVx7KGKbz1VdfnTJlCgoguhoOh1taWm677TaEntEzbtOmTf/yfY7H4+Fw+I033gh8mvj617+OADT2qr29/bLLLrv22ms/+tGPYnI/hHqj0eiSJUtwVKmksYyxAACNIUfUsAvcyFT5IJiXX3550qRJGFokJP/Qp1sHnSdMmNDS0qJwZ0JIuQxae/HixQE7DKJLg67ywx/+kBCCoZB1Ew1a4eivaADo0X+NBt1DfQzX5gfdxO5SsfbpD9HjWFeuG4Rznkwm/+d//uf888+fNGkS3uIIIQceeOC1116LCWwZY7Ztu65rWRbi1IHODCIkCC6FQQB6xYove55KmKP3Tjmp/NmFf0vCYT1+Y8ojlDYIANol4A8egM5REfo5R4kDDZTOlWkD/ySjPz8G8LhMJPhjgNtT6Y/nsmfknFlZ/4AMG5PmJM1JipEUkCQXlAKS4oIy0t2GOQTscdQ+PJv6mHBKErMd5gJzqYOI85dX3NAQJg1h4jlW2TxInruYG2VlFI4npc/O9xm70XOvtO33W86plrvQcjss/ziLzbT4oZbwj94/DROyvDnDo9U8mnUoM49NFxHniEMFeX6Aoj6NKXJpk8OaHJaQwRkbVDRtBJ31LU4OXQlA+0B8yeBcMeANjRP7Ac1Xq+G81cqV8h0KKEnV/4pVAmJqd0DCqpbeVqDQUZ8H0BtdAtD5hJlMfBgoQZ8RGkbwtAATy0l7BLfVkegiAC3m+TuiCo0WmlOH9HYVL44q3DkP7KqmBTqsJGszvoic0+ALz3oB8uaxodIxpgabxiAiHGhFh4nlIXH6cUmNHm+UDGIfEQUk7RDy2/kCqm8SoFEu3iWMLjPQHup16wHdBqp/oPIj3Z+B6tflkS+BLDUods8rL79r5e9pQztrhclWZuQ3p4rGDPSnokxlneLbXmXSlZRf68KPTn0KDeXvYHnYVPjh6oRBw8SXV5ZfsUQZoYxwsWIpkWXjU2xKih2Q8o7661szP/MfZNoE0pYgLW2kcSw5eib5yIXkD092+v4HPH4shXf1wHu288sBnvXtbBBVFW8T5UBztZLie5cGQK93mIRqRRrlPyUz51ruQdw6gNtTXH+8w5otFikxuPz2XFJSCReuS0CuWiuAy4W7N49KSDoAQIsbndKp/NBzcnVXL5AemJ5iF/twn8wULWzCyiyVB6CjZO261YhUFM1hOM0C+jxid+S1UzHsTrKAZVmbNm267rrrJk6cqCaYiLB1dnY++OCDKnUcejhhEMihd84A0Cr4iTJm1RjQtm07jvPqq6/GYjH0SJ87d66qpphly5Yh2tvc3ByJRDAr1JQpU3784x9jOA6U/Be2u2LFikQiobJMXnbZZZxzHTn97W9/O2vWLMSIjz/++BUrVugebajnRz/6EQ6URCLhOI6Cj/Eo9emiRYsQDVeRNFCh8jJuaWm5/fbbMb+WfsNCn/yDDz4YJWOx2Pr169VpDgujMPdzzjlHQe3K6/m88867/fbb16xZ093d3dfXZ1mWMo5lWS+88MK99957/fXXd3R0HHHEEfvtt98BBxxw5pln3n333Zj7cVh6OAglS5cuJYRgDOhBVN8dqwwagB4NJ6uP+dHQH9OH3dcC+ljS+frPCD8ucs49z/vtb3+7YsWKrq6ulhYMJZi/c1944YX33Xcf6q+mWW+9nK9WSy9HH2ps8pZbbsFDPB+7UAlyAE+iset6+BkpmJiFJhsafBbOA9De4AFo5QEtwxfsC3AewOUAFwF82HIW5byOHD0ux2ba7GCH7efAeBvGyLWfIiZDjgvKSifiLLoeS97hIroFcyfnkmdKRHsr5jB0AFzfQwD6P//fLfgEr5mw0QfIyDyH/5BI9CsAzwE8BbAeYJUEx+8H+Mb23BXb3Q9tpWf2+POz3tGWd4DFmm0RhUBMhh2IOBBR8zFb9DOUhTA6LFss6tCo50cF7ixjd+ge0JKPuKwBHZ8F7kzHWXS8xVotnsA1wgH3ZLWLDlyyrfzq7ByEFGGADtxWC3OhVJUzap5ZJ6M0FN3KtDgeWfnNQMnozLDI698DyvlAE3rrFXklnxOXtQLJkVwsVzbPVfKKtYU3mYjgoVTlILJDUsI1GK3dokKUD/RQFqLHbon/vvpeUs6Ujud6a5Xr0UpwcKquRnMQoEjhjERzegcUr39+KIBNOrqt8yVoVEFYOPdVoYHJ6z3R+SrKg+jYDvuj69T54dKvdSBw4pXto/dB54erP6U6xX0VL7o2fvKDUP089wJGBFkqvYcXgxrhvas+I6CSCkE8Kt4A8Z6vDlVsQh1Fps7HRF6sUqgu9akVGbyDaVu8iyr0mcibalQGjhgjtpUi3tiFZxDG4gAgtkWANVB/Qr99VHfujAcfnn3O+8i4JtLcQOIhsv/+5DPXkv95ZNLmvvd0Z44Q4aHd/Xx7Qi49W2ateErkQ+aeCCSBWZvVC1Q+ufGOQediDYDOjgWhUORf08x1v1/vC41cxvV4Mdn/xVz2/XbuDDvXaeXm5uwZDm0V37PxMSrWUUWElQYNOpdXzMPQekilqDS+MDv+xvGTGN43sGn9F9rPxmT9U7jzQ7DfAM8FH2Q2DxVYxJNvmMA5FTGgY2TtupUGgNYHQ4Avf9vfvUoCp2N2h9ECCDDiHFOFQ3jggQeWLFmigtxiPN5JkyZ96lOf2rRpUyqVUpLD2BNUZQDoAQDQiH4mk8lwOIwXCaN4BK4K9emVV16JcCohZOrUqddff73jOFgd20MnNcbYu971LuUr/dnPflZ9Z1BQdSaT2bx5cy6X45zncrkAAM05v+aaa3DozJs3z3VdBdFirzjnTz/99MyZMzFORTweV/AuAt9z587duHGj6p5+q8KunnXWWSpCtCP/Auc76F00AgC8/PLLCI43NTURQqZNm3bTTTdt27Ytl8thoq1AE+jch/GvsZN6ABCdD1TcObsIQC9cuHDnNDcaWjEA9Gi4CqYPu9wC+v1T5+vsWCaTue+++/793//9yCOPxDs2fumMRCLNzc2nnXbaHXfc8c477ySTSaW8tmYlFmBq18KjOgD9hc9+jsts69QNrIykMmBfGmDjVveybjgpyU9I08MtOt7zo9wPcxqM4VB58lNzYinmM7zR4VMcdqDP9/f5ZB/afGjxoVFmKQyXx5xFJ+JcYeolGi3MuxiMyaSOBrgN+B8x2iBOcShw37UdK7di2fWYc0MF3a5sLhk1mnPKORVTJiSOcHwPwJscnmbwOIUHKNwD8FXLvcL3LnTZWS4sdOEEB2ZZMDPNZvT7U3rcth5vbJ/f2s9aUtCahZYsNLk0Ib2bBZovPL9KfMrCcrKNMTckssBjDm116DiHNbs0IYBpdHDD2bXm7Cb8duXsWgLQoayAvAUpZFMhF1kZhRln9eVXTXc6GwqPmnGGrAMWOk5R3vrQ5fW2avPVeqKftbIqqgoAyuVOqRiUoACbCoBVD1NQj7xeV+d1PdV4TV6hugLmVsBBAb7JQ886XlCO6wVKFOYrP6iMBACt4GYctAhPV25I74zkxRkVzKuDJjqvBAKMLqPzATG1q8vovBIIMLqMzgfE1K4uo/NKIMDoMjofEFO7uozOK4EAo8vofEBM7eoyOq8EAowuo/MBMXGJ1QjX7m8h/Wde/rWpWoleqx6+mp5q5fXoHIRM4duheDrk7+H4kJUYYvn9c6BNVLsrDvR+XsR/tYeUvLWG5WoS8f6gERbW2qr1GeomVmwijzWLIMU2yLx5UBWAxuslv4CGXYgDzAB3ppXqvPNb4XfNJIkImdhMWqLksOnkm3ce/PrbZ3anj09603MwLgORHIv6fBzQI7h9EcATAGkAqwSALi4nYzK+8eABaCogbA7MAfa2/Pj9U4AfAnwNYAnAfB8mZbyRBKDlcCqYWv9VCh7X6+BjRQegneJXoqYszOLwBfD+DBYTobFdAJ8BVT7QDr6kGQC68ltoWWngVX+32y07IVMwbBawC3+oUaURUhBfJBI57bTT7r777p6eHgXQqbRww9aPgiIDQA8AgC4YDc4991z0C7vjjjtUITIqRPKmTZt+9atfPfnkkyq2N0bMUO3hfeGpp5464YQT9tlnn2uvvdbzPPVpQvnwlgOsCoNGtHrevHk4epYvX65aD/SK+vTmm28++uijlZfxoYceeumll65cKb4lYhO2bQfCiXDOXdf93e9+h/53iI+r/geaGMQunuy/fLQ3bNgQi8UikUgoFDrssMPefvvtaki3gp51lBnReewA+oDrRwfRsSFW2ZsB6HA4jLFHhmjDnVldf0LvzHZNW3ueBfSxpPP1nKlt28cff3wsFlNLVXAx1P7773/zzTe//PLLASWoP1AY2NX7oPMBsYq7OgB985dvyq+JLPGA5tKfxwGwOPyTwx8BVgI8CvCNtD83ScdYPFYOHVYuqQlAOzxssYhF4zk/btG4w2MyP2HYh5AvvGxIAYAWcx6cbKPXj4ihLAkblRPRuEsP9a1LRLRBOymda4RXt3C7AeFlk00nv/OtOwghjY2NaBacIOpbZS5p0jIAmguDSP/ofoDtAFsANgO8AfBngD/JoB9PA/yasbuzzrK0e0XK+WjKe3+KntFPT+plx/SxQ3rZ/hk+3qcJRPDF+l8uyC+gyRh+0RLp42OYE0lEY2QiHAelDdxHCmN1TsXaYUVUYtkuF96L+sy84JCoz/bFemdKyylMqVTuD8OWUqEN4ybn41dwgS/kIynLeMooo28HLi/ORQMyBsCriNg+FwuxFSmTcioKRd6nAnlaTG0KhPEgYRxk3Zm0GBm5Pnm9rs7reqrxBfkSl1XKQ6yM9NgLhVoBv9fgLgZ1KQ/tUmf1wjgs6VtZYbBRVF5AlisgkhKLL/qSSwQqWn2rSyJfQzhaydncyOsW2Pn2zLeooDFPfMUMq18oRmyvZ6uq1MnUo1OXqVPtQMX0aBUl93B5B8t/zix9BBQfB4X7WLHRMsngXbH0MYGt56vLukH5wo1Uv4vm+fxjRXuKBR402uOsvDqwEFLhbpZPb1C4RQgPaPnDj9sQl0xI/0yljJB/UeENlgj0PDOZPP2nPzjymBmkmZApY8iEMWRRB/nFL8f1Zd9jwaEABwJMotDs8IYci2Z5qwvvArgE4G6A1+QLkiO+VTMZXUJuC28RQwWg80E8GAU3Dd428P8J3j8B1gD8B8AcH9p2IQCtJ90N3P+leRsy/GAXruDwS4B/CugZ3cN9yeRdHbx8TkIOhIjAaCYER2HkVP6vv+fvjnzlszKlw2cB27Zvu+22Qw45BGFMxA/b2truvPPOf/zjH7i8AEeO53mO43ieN0KQmgGgywHVqiE41ADYsGHDpZde+rWvfU2VKEaHgHUegVHlnoxQL0a9UIWY9EndMlBnLpdDYdzVI3sCQH9/vwqL/NBDD+ktqi6pijiwXnzxRSzBYB2BkB2qdTXgXNd94YUXXnrpJcaYgsUDyge3q3L0vfrqqxMmTIhGo3PmzHnzzTfRLNhb6tMAIf6ut6hOQf9iowvsZN4A0DvZ4ENsrnzMD1Ghqb7XWkAfSzpfzSD698XHHnts+vTpuJwlFApNmTJlyZIlL730kvoqiUrUTR71V9OM5XofdL52LVUXZOZxQshDvxJRwApx+ZS3Dk4XhAMxB8djOcr7GfwN4JcZWNQHLWmRDL2+TDg1AWjlQeMXcL3AZMaDsAIaqgHQlswLb7MJ6eTpAD8GZ7OY8Ij4IfmE9DR/enzd6jX4QfSll17C9Os6+owIPG6lSUsBaOUKzTgwLnx5XA4+cOpznuE8Ix2l0eX6HwBPufRBgIcBHgD4PsAdFK5Ns09ssz7Ql3tvNrvQyZxo5Y6zrGMt+6ise1jWOyjrH5gpUIoeKIgdkKEHZKmI+UjdcdRr5W4z95q4l+BeTILRwg9dEaX5MJoS1Mtj0Lo91QzcBQGqKrxVMAJlUOizQrqHylDaQAvZFDGoiMqsKCIpa4TY+gDlRYclxj0YDLoajqPsiYyyKmIuOm5bwEEEvKsjIyiD0OpA5csA2TxcW64HS7AP+tEyDRHK4ow2gi+I0SLJXH+Y8Q/DLu9g60OTIhmmeQfyQRk2xquTRAzoArExHh3r0TaXFcnmbYpy0JbjE5CyMCELk2rSBCmjb428bgHdMsjrR8v5nSQvri+0Idl8rM3HukyQx1o81uLSZklNIly+3ygp7vg7ILGgZCC0Q4UBgQEpryrMYjq8XvuuJW7jaklNAFkuh571koJwHk2WEZk1dDv/PbJwvxULd/B+WBl91p5K4ltpCenPlNJDeq1KvAKggeW/qKmvffhoUyshtAUiJXF78k9AHnZYk+VPydhzH3506pGHkQP2Ic0REifk7FPI6pXHA3xwW3qyDU19jKSBcEEJCuN9PqPfmm35l8hn+rPiIzT3cKVU/h2MQWF+rd4s1DtVgKn8ptZ+Umc43IAhOJj4dC7DVjgybAUqgGczyffl3H3FKRTWgck8EMMdgqOmB3QpAB0ufc2IetCa8U4A+A6DFzhYHF8n1TZ/6rgvXj4JIRESWbt2LYIDlU2z15fq7/m7I7/XX8DhN4COct57771Tp07FPHgIQJ9//vkPP/yw53l6ZOfCDUp0BkfR8HdLZrkXcXXCYb25kWho9OgcahLCQZ+JuooIIuMuwqnqEK75xWDTFQNQ6rmkAOCuu+7CMdTU1NTf388Y0+HsQFd18FpvMSBWcRflB1qroiq9EIcdBjzdsmULQuq6gBr9yvcZLRCQGVW7ezMAHYlEotHoqLocpjPGAqPWAogmU5++/vrrsVgskUhEIpFZs2Z997vfxT7v2o9q+IH6XylVV//fKhmCA0MYIn7qFfxV8jMe2WEP4DUOd6dhXh80ZiAm1v/Wg0HrAHSZvASXa0ClIk6u9H0WISkUiemWzA6nJmBpRpLZGQB3An8ZaErmWrcEAK0mfQDU8zZueEKkVQjHNm54Eq+CmiYiUzqcZJnSgAzK4dQJj3PKRXp3iwuwXhAIR+ksQBKgF2Cb9JL+G8AmgBdlOOnnAF6W/JMAvwP4BcAPAL4FcEu38+Fu75xu75xeF+l9/c770s5pjn2Cbx/r2Ue6zkGOM9lx22y30aFRh6LrX1hfm2yL8NMNNoRLSczDMaKCLbEG4b0LIQ4RSVEOcS4WIyM1FhixyyE2FKIQoxDzywjLcavrryhPIc4KxKGRQ4xB1IewTIgX9qDBkWSLE6+LUB63HjQoKuTZw2x7+a3S70CDmnj7ogN5YhBVhIVKTDFK2NeE5VkIJSjmQLQiKSVuoUVdW3mLuhIb4o4/3nEn5cmZbLlFynmTFWW8fWtT1t9PUW3JKkf3z3gFcqdm8jQt404PkjMjI0l8m3GPyLlH2967HX+2RfOU84/NFCjtHZPyj0n5s5D6/Vn9/pwqNEseLd8aebRAuWWwZBfbR15ZvMrHpP2j0/TQLJ2epdNzviQ6LesfWKADimNsIONZDewaTJVRXfVXU0NV/Ycy/qQMa0yzSJpFsrRIOT+iyPYjBQrlaEjk+GWCMG1vcctC6SIJhfldmd03zfO1REWZJTjri1zBGY9k3SJlXFGS8oOU8UQ5ki5fkbc8kidf5AN0xRqgsHwehRlE5F09kLNU7OrLaJAXK6jkmwDmhMjkI1DpoHNYfyLIG37MhqaMt6/ln/z9H+y33z6kqYHEo6RrEXl87eFvbD7KgzkuHOhBmyfigDVSiPuQcPjEnHek5bxfOj6vAXhFZIngXt7xWcyfxefq/AtAftkVvisEXiDUbum7RmHvhONPLADQG/Jr0rgDviu+p/uOaNe6LWsdJxJCjFwSQu09TX3+r8F4EJMr1fJJj10+Jp2d2J86HWAlg14BBQSiu4mT9fL+3eKYO799DgmR9WtFEkLxdd/8VbKAjtXsjnylczJlQ7IATjNffPHFd73rXbi4MxqNHnnkkddff/1rr72GURB0aLEcDi4vGVKHCpWNB7T+bQCtsmMP6IL1Bva/4r1AxdNw5Z8KOqm6FQAgdCXUp+eccw7GdD7xxBPRUS4gr3dxdALQeEYq+LXy71M9V6esbDVCPwbV4hAZA0CP8gs0xOtrqhsLDJcF8HbHGNu6deu555578cUXP/HEE+l0usZtfLia3qEe/BVjEOoCAK1chjEwH04PpCacRolYh4+58Jk0PywNkXrRZwzQrDBobWJTCJ0RUm656ESjdkV2dVGxiDsX+JhF4xaLikyGTCQklL7YE2znfQDrgGaAesBkvGbuYBBFNMhwAtAq4xCVC2/Fkyw/+RQMA04FiWWnaL28DWVEEBFgWiDksswF6OXwdwnubyyA0d8DEVpa0Z0AXwFYAbAU4HMAFwN8WKZtPMtyO3TKeR0ZXxLrzLDOFG9P8fYMa8/w+ZLmpdgJKXZcks7t92clvWOTzjH91rs1OrbfOjaZE9SfPUZRX2bmoKknO7MnO7Nb0rbczG25PI8leBS32EQ1+R7rmB7rmL6coKQ9K2nPytizs+6cjD834x2X9k5Meycl/YFR2jtJUcY9SVHOOUmnjJsXQ/15C0s7i2yZBcILgbsok6IdKVq4InXLY63ybXm7WKK3qLcrNZyUoiel/IUAHwH4eBktkbFE1fYygB3S5TJZKG53KBwQ+ASAok8BfArgSklXAVwlF5X/R2F7NYCizwF8AeD/A7hWjv+lhe21sgS31wBcA3CdRl8CqEi6jM5XFP6SplAXvq6KciOvrDQS9sSrfI0cDFfLMYMjB7f/BnBFgT6ljTQ15CoynwQYEFVUUqNwQMrLhfGHdkm/c3K/24mUcjoVpe1ORVmrM2u3p532tDM/5c5PufP6PUXz+70Cue39AcofQuHjU66gpHNc0jkuJSlpvSdpvSctKWnPSdpz+pxZfc6sXveYXveYPqdISecYRWlrlkZz0tYctYu37pw3O+eJ70k2m2OzWTabZdFjLXpszn9X1j8y4x4h6aiMW6S0c2QpHZ7yjsj6hzt8hgvTPTjIgf1t2CfvLM8n5NjkHNtX0v45lqc0m5aDozNwyvfu3zeeILEwOWFu9Be/urA7d3W3s7CXH9nLpqbhgBwcnIMjcjA3x0/qzZ3o8vPlDed+EWuLbQWaBUoBn/7S61m+ADjyU7Qj435h6C8ZxLn4GVyhz1Ux1nnz5iMA/b8PPkzzUhYwS2DafCvAvVbu/Kx/4ABewMpeuuryGyjUqoE7Fw5FPUjIL7j52FxXEIUAACAASURBVF8UxgO8W97hH5Tf2l+XyZz/BuwtoP8EvlmGLnkLwC6svJMANDEA9A7e3BVgspsyOzg9c3jgFsBp5gUXXIAxeBcvXrxq1apUKoXlruvqjrA4bAKNjBCkYwBohfQqg+8aABr7Yds2AKAvcMVlJvo95aWXXorFYoSQpqamu+66C0+gxkDR61YcZMoE5Yxet/zooEtUNzA75w5PWXVj0C3uhIp7IQANAGvXrhUrpOTf6PdS3wnDwDRhLFC/BfAlgPoUoWfHcfT1UPXrGUbJTCbDOcfnSykAbUnXXavgnyLbxDjK8BbA9Q7MyvljfZYP++AWZim1pjQKfS6kCtSFZWjXEg9oWRJ1Ie6CCAldAJ1LYWjh/Jt3gk4z4sIkgDOA3wzwqkwHxCX6a8nsQIXwG0P0gNaBZIkgiwmhcEoqkMCaqWidezIWRyn6LGaSaEdRIQ9H56+o8j3PSHfpf4DAo98ppb/JSNOvy+nc8zLe9FMAT8okSE8CPFVGfyrIKLEnANYLgF5EkFwtPa9/C/AYh0c4PMThV5J+CSJiI9IvJBouthx+PhSi8HMKP/fKCMtxq+uvKE/hF6xAAL+S9CDAQzLIyW8B1gJs3Fn0pLT8brF9Qo6QJ+TwwCGhb58R0dIFPafRn2VA82rbF6XnPm6ryVQr1+u+LEcybv8CUJHw6KviRy0EcPsX6Xv4ilb9ZYCXCoWvSKaiNlWIMvpWHarI6JJGf7mJdrJ9sAPlF+JVbUi8WHMM6+NTH5P18Hrdevh6dNaQwSae027m5bd6vQRvSvirXy9v+LhV94EnKt27lPxa+WhYDfB/8gHxO4DHJf0G4DcyA8Sj8n77IMCDAP8rqfiYUM8LyeBR3KK8XuuXUuYBgJ+IkFlwH4N7Xf5dh93lsG/b7JsWuzXLbpC0IsuKlKHLS2lZ2r8+617jOP/mWZe61mIre2Eue142e2Y2e0Y2d1o2d0o59VvvezvzoTfSV//3905edFboru+d9Y9tN/fkvrg1u2SbtTgFiy24MAsfsmBJDj6fg//K+ffKu+hzAC+Avwn8d8BPguOIVU8iAFch9LMMVsYhy0WWCJFur/DxWQeddb7yC11X10IJQIduv/PbMmAyFa8xzAKBRr9AYUm3PTELDfUGQKvnDa2mTAFlDiYh1MqjLm90Re5HEZPNBuLDPgDHASyW3xGXAdwK8HWA78i4JfcB3Atwlxw8f5OvUMIO8+fPJ4SsXyNCcBgP6MojoxAwQUElux1T7bxM+eAsgJ6pjLG1a9d+8Ytf1F08VVyB8kEyuLYGWssA0KMLgMYBcdRRR33+85/HyN/6cNHjUXDOV6xYodzpEbMOCAdGw1AGmV43oHYouwG1FeOH6DKKH0qjI13XANAGgB7pMWb076kWoD71PE/Ftd+Fp+l53oYNG/CrUiUAWiZ21/vHLJmE/TwH2hwaoYwAJVwgv3WEgd4BAJ1Hn12RbxA9aCICfeaNLm+sDkCLdbu49jblhTx+LMANsodb8z41nMu5jSMniHk/oiF5QOcBaMSbZRr3CgA01wBoLmrgfDNvySIALaemslRNSIvu0jK6tO9DnpjAq33g+fksgt9SlYxJzSljHqcuRfI8KojyAlGPUo+5SC61XGp5LMe4LefJOfm9IS2jhfQB6NQr44fgtkcsNx4Ccejh0EMlIY/bajrL5bXO9Mp+9nDoZnybINZLqUizLM50IKSnoGA+1Qk8qogVklWgcrVaSzwKaWVCGZ8xX5euTx5rlW91Tdgului83m5eAxf/KXWZX4EKFhBhzAsDhmunrmyQZ8RILFANsR0f8sHbIYkrwLE5CfKId2SNtJUFxeDsVH77oQKsqUjlklhSUZjyvLbyWkYeLVBumRG3p4i/j3EP9IughqXPcKzq47kqr9eqh9d+I1V16jL16KwtIxfSiFS6A/lTP43C00r/elpBEcqjsCv9Um35XMiCWPaUBkgB9BfuwN3yK+k2gG0MtjCRhrcaCZnqhLU2y++s/wDAz65/B3gb4K/ye5gOrCv+DwABegrg94UMyb+WnyT/F+DnMvXCjwDuq0Q/5vArButdeAHgNZv/msFPXbhdSj4g6/4I4EcA/yNR+D/LvllFs4mAGBa4HoLMRQC6GInL0tBn9RKg37tKXguKmiV3yqLTEIBe8eWbEICWT+rt0mv4nhSf3U1Jtp73rmGS0YDmahg0ugtECgB0yGKtfdkD07l3Z+1jM/bsjH1cJteRyp6ayr43mTu92z49Bxc5cAuFZ2VKZ4Hgz5/fTgj5/dp1wgZVvcMDptrrdhVIspsye90FG8kTxvC2OjCILqpYrtDP8qEykp0q6t5rAeh/fUhbuHAhpv0rmkNyI+UBHWgGd/ULn06nLct67LHHCCHxePyWW24RC55lGkpVV42e7du3x+NxDAB95ZVXKoHajGqutthOPlrDa1vvCXZeLxmdvAGgDQA9Okem6ZWxQP0WYIytXr06Go2GQqHVq1cXXE4QIbXlVDNVcNnlItMO2wjuVyg9weJNTiHxfV3oc32zID3shpzw5EPiykT2ERvyhHMhGQtSRI10gFg8lvEnU/5B8H8LXl/BcTsw2ZOG8SgAPPF7AbsTQv745B/qN5cmKefqSr2a6UsJuYdFWg3F5p2gSzUoVbWZon68LKrh6s2pdqsyWDeAO9gFAAIZVzpz4RYly7e6TKC62tVldF4JBBhdRm9RL1c8YvNVz3MwB/TLMZj6ps7OtYB+vQy/B1tg5w6r3bO1wNMhsFt+TgEB/X6reHWzVQh14I496N0cQIAyGt6tfwetxiMmvkXmWkBE+20JZP8NRNrkcnobYDODbgmsp0AwmwtiuPAIq7wj0fOUfCD6eauJhziX8bNkCC38oeWPBcw4wK8GhcsiE3c1EBK6dumXJADNucil/CqD/0zBol7WlgaMOZZPAompIHGrry0bcV5zLJAvZvlYajaELB6zWLOMUt2c5c1ZNi5L98n6B2T9AzJsnz5+wGY+cztc6cMzImGGODu7s7O9sbFx3ToJQBdMYf4bCxgLVLPAKMfW9kIAeuXKlSH5t2jRIjFPY8FHwC4DoNHr7ZVXXhk7dmwkEgmFQjfccAMOLOpT7Ci6SAPA2WefHS38vfzyy9XGX6B8dALQgU5W2zUAdDXLjIZyE4JjNFwF0wdjgeGyQACALn2VceX0LwVAmfC7tcTid++/We58xz3IYQkRlxkjO9cHLtczEZJhN0KFbdHRRkHPinEh4kEI0WcHSJaNt/mJAMvB+6vwSBJ/Cn0pWiuXSgsnMIA1q1aHJQD9m0cfLR6un1O6daaw1LboxFwoKVGsV6mflypwalvQL8JHl1OhTZQtabmOHayFcIM+ka6jaomIXlfnS4S0HV1G5zURwxoLGAsYCxgLGAuMBgvgs7tyTxTigM+yykK1SwsANLl26ZeEj7+AaHsBHu/nZ23nbX0QyYxGADr/8iZ8AiAsSaDkpSTKs0CSML4PFibhyx68IgFoCyCz4OR5icaGdevX1DaOOWosYCwwIAvsKmxtLwSgn3nmmWg0GolETj311IrXaJcB0NibTCZz3XXXoQdWJBKZN2/e7bff/vrrrwMARgVljF100UUY/bmtre2SSy4phQYqnpQp3HkW2Ds9oNetW0fka1E4HFbfS3ae0U1LxgLGAsNqgZoANJNOrzmANIO0D2kK63PORyT63CwjMscEDM2aRHyMYcKgC9AzTmN0ADpkQwmhpJzniIWoGf8gj10pQlKyHoSYKwLQaDzfcX+/dl2EhCIkdM937x6MRcuBY6kFp5sFgLi44LmkifK69ZRU0F8Bfc5nNKzSckk3Ku/gGRgAurJ1TKmxgLGAsYCxgLHASFuAkHAkIvI/IQDNRQiUPzP4xlbv3b0QT4F47cEA0Lrv8671gK72HlgKQEs8mseS3rs8+IoD63zY6jGbQ5ZBqnPBnFicrFmzqqLn4Ejb3Og3FjAWGF4L7IUA9KpVq0apBzQGBMFwLZ/5zGei0Wg4LDyxYrFYIpHYf//9Z8+effzxx2Nha2srIWTq1Kn9/f3DOyaMtiFawADQBoAe4hAy1Y0FdrkFagLQGOTBlQtUtzJ4OQd3ppzZ0vcZMwEiAJ3YJQA04tHSlSaRgvFJ+yTKvgP8JbGMN+9+pGDdCmamnhcmJBqJfOWWWysc3mGR0q0YWUUB0MiobYk+VWVAjKYfkxWW+z5jyTB5QKu+I1NyBnXsBKqr3WpVlUCAqSZvyo0FjAWMBYwFjAX2TAsQEg6FIoSErrvuSyLxg0hH/OOUf0Evm5qSHsTV0Ge1LKwaHDzM5VoIjmqay7yhGyzvgGT2bBmzeyuFpMczHBzG7c6u+bF4ePXq/zMud3vmsDZntZdZYC8EoL/xjW+ge3FnZyf1qeM4gdR3O9UDutp4cxznpz/56YwZMwghoVAoHA5HIhEMuUEIiUajhJCJEyc++OCD5mNgNRvuqnIDQBsAeleNPdOuscBwWYAxtnLlSkxCuHHjRi1YFYaBFmggZy7AWwA/35w7K8v2l2H+4iI9IEQLDst1ZCCsz0W6oHDHHtA2hHIQ6acN7/Q3ZeEEgC8BPCUSJXFPBN3SqJqtCAk1hBq+vHyFiHyNWHDecRhrIBJapXY5diwFdfS0Sk3NM7tcSY0STV2hleJpagcVW7P/SirIFHQXUPzg8Xr3y/XU7s9A5evth5EzFjAWMBYwFjAW2L0sgAgAIeSrX7kV/BzABhc+1kOnZKA5CyL6WbnjsyqpBgTvmnIetqBBxIMWQTlIjpP+XAt1TwX4b4AXfEgJABr6KQiUpr39zIbouHVrn9CTqu1eF8701ljAWEBZYG8DoD3PW7FiBQLQCxYswFSQgc9powKAVldo+fLlRxxxRGNjIwIB2PVEInHqqac+/fTTSswwo8cCBoA2APToGY2mJ8YCg7OA67rPPvtsKBSKxWKPPvooAtA0j5EymYTc53Q7wJ/SsKQfjsxCo8CIeaMgwGwzIlDGcE1s6gegcxDKQnSbHbNgdk/uYzJV/T+AUQoeBYeBr7kDV7aNiCZEwl9evoKLGNfynA0AnbdAbbC4sj1LSwcKKA9UvrQ1s2csYCxgLGAsYCywp1hAoQE3Lv8c8FcY3JWFuX2cZCHm8JjLwz4jSAp3VsxwvY8Njx4eFugzT8htLMcabfdocL8I8DvgW33u+5DxIcPApww6Os6ORietXLkaQ9Y6jrOnXE9zHsYCe6MF9loAOhQKjYokhNUGnWVZ+qEXXnjh/vvvv+OOO6677rrvfve7mAeWc57L5cxdWDfUaOANAG0A6NEwDk0fjAWGYgHG2KpVq3Cqs2HDBiYRaA6gYgDL+BvPA3xri39UFhqzQGwBQI8pANARl05w6QQREro+H+faYgMEoON9MH673wnwE9d7FiDJBfps+WAxcJk4iVpAqgSgSR6ArmDEWnUriMuichi1gqTu5lzhsCzSZfLgeFG00Er9HtAqJ1JRSRWuoHuQHtB6dcVjU7ir80ogwOgyikfGbI0FjAWMBYwFjAX2cAugI1qYkD88+VOAH3mwpNc9pM9rtFirSxM+J3lixIMQJmQetQC0eD8U+UKaLTYu500GOB/oQ+C8A77tM5AYtM3ApuB0dJ0ajY394b33m2Xfe/j4Nqe3d1jAANDawuL8JR9dHtDl49C2bYwWXX7IlIwGCygAunxsjYbujVAfTBLCETKsUWsssKssoOJVbdu2jfq0P50CCUC7cisjD/6y2zsnBRMzKu+NmEskJFgcdekkl06qBUBzsVy0AlUKHSh1FnMPynAfERsiLkSdwvpNGyI2xHPQkmbTNmdOoHAzwB+538fBke7PFpUAtOy+DnoGDawAaOH+XOGvVt0K4rJIR1KryeS9rctg5RL54Qeg68Sg6zqDkq4Wd/S6Oo8SWKLzuozO6zLlPJaYrbGAsYCxgLGAscCeaQEBQIfEZvXarwB8Nguz+7yJSbcAQDMBQFMgnqCQBxGXh0cpAA3EES97MYc1Wf5+mdwcgBsANkHOBV8sVUMMmkGOgtWxoCsaH7N8+Y2BqKl75jU2Z2UssKdbwADQ5SDhaAeg9/Qxuduf3/LlywkhXV1de9Vj0gDQu/3ANSdgLFBqgRUrVkQiEUJILpfzPI8Cxxx3PgcqsNLnLLhiO5/aBw3FxOtiOtEgJxUNDmsSvi0VIWYx8cB0hQKDLs2EHpZLMhOFbUyGCGywIVoggTtLCrkQcyHhQDQDJElJym9wYLLDDu1Nnw7wC4C/cOhnzOecU+ASg/Y0H25WGnS5ePIYY3Hp0qXFogpcERitHVe6HF4tUVYHoFwir+/odfXyuvhi/wv+4OUlqGgHZ1CzNb1uTcEBh/go7239bdXuiTlqLGAsYCxgLGAsMBotID6QNxDSQNZs/Ow/c8dvY/E+1pDkkSwkbGj0IOFBgwtEkvhC7/GoRKIFJF31fWynHyrBxHk46x3E3CsAHgG2DRwAXyy688Xbm0ChKXgdCzqiifiyZcvKUZvReJFMn4wFjAVqWsAA0OW3MgNA1xwy5uCOLHDVVVcRQjo7O3ckuEcdNwD0HnU5zckYCwAoANp13XyqBC5wXBEZGf4J8JM0tPdBLAkkDSQHxOJ5kgB0OL+tNrERAHRMyAQE8ksyhSc1RgYUaWoAAeg87mzL5nIi6AdxBBjdkIVY2h+b9Q/vSx3vOR8F+AHAm9wHRgVxBhg3UADRJUBnZQS3s7OTEHL22WeXvx9o4wLhThGSxADQmlkCbP2gsA4oB5RU3NXldb6isCk0FjAWMBYwFjAW2O0tEIs1xGKERMjDKy/p5QuTMDkJ+yRhYpJN6nfH97vj0/5YEQxarA8T5PG4xKBHJQAtX/8snrDpPGDfBv4S0Cy44iWTMV+E4BAANKNAJQAdXbZsWSBt125/Oc0JGAvslRYwAHT5BNMA0HvlT2H4Tvq8884zAHT572r4DGw0GQsYC+wMCygAuuSN3wVgvQC/zTmXp93pWWiwGLF9QUUAOoApV9xVcTbk0bzDDidiuShrkItGZS6dQkBDykOFVaXCtceWZAGR0T/COZhi+/OT/R8FuAvgSaBvAM0h+iwAaM6BFagEc9Z3ivx7TjieEPLe951V08oIegYBaB2MLodFsaREbbHZgkO2PKzX1fmqdUsO1LODWjGmd8Wt3qwK04GF9esPKFF6yjWo/gSqlEtiiZJXEb0DFWu0VU2nKTcWMBYwFjAWMBYYlRaQMcHi0YZElITD5OHHPr0td9l27+TtfmeP395D5/XS9/T7c9L+kQ470OfjfCA+EI+NESSDcgS/91d8N9u5hRY0ZPwDAT4BsApYP1AHKOdUeD8bAHpUjkLTKWOBYbCAAaDLgTIDQA/DwNqbVXR1dYVCIeMBvTePAXPuxgJ7gAUUAK2dCwfPBXgR4JaUfYJFJzqUOD5xvJDthxwasZiAoStPchTirJjCPEctxsyjz6wBMehiOh0Z05DyiHDk4XGXN9owRsR69tr6rKnJ3GzLeb/nfgHgIWBPg71dOCVTLtZwSg/oIvrMeGmc5XL0V5ScfOopJEROPGm+duLlbBEALQWdiwkAdUAU61fARMu7IEWxLgUI+GyX9EOvW3Kgnp1i/wthScph6LrOoEpjuv5yPeWVhku+nrbKWzclxgLGAsYCxgLGAqPYAhKAJoQ0hEg8Rtas+y+AnwHcCXA7wH87cIMD17uwlMO/O9kzfPcoH5pGMwBtSTeCLEyy3DMB7gH+GvgeMAe4w5hbDYD2PG8UXyHTNWMBY4G6LGAAaANA1zVQjFD9FliwYEEsFjMAdP0WM5LGAsYCo9AClQBoC6AH4Oc2fCDFDrB4k8MkAC08oCOOHy8HoEV850JojnIGoWoXIg5vcCEu86E3WbTRoo05P5KVXtVuPp1OgwetDp9iuYdkrFk5+2SXfgDY1QD3A6wGeBbgVeBvAdsONC2caJgHjIrIGwKQLLg/1wdAt3eJEBwdC7pqXpQi0Fk/AJ1XqAPH5bwUKmovDRpS0qXyuuUlJRX0nWotVCvX69bDD1TPcMnreurpp5ExFjAWMBYwFjAWGLUW4I6bBgDH8YACJkluiJL1v78f4GWA56RPwMsArwH8FeBNgD8JYJpd6nlTGUR9SPiQkFE4IjKZc6iyi0DBIWDnHC1k/ojYMBvg2wCvA8/IPCNpDmkqEkcLR2gZNo0DsAULOxONsZtuuslxHNu2R+2lMh0zFjAWqMcCBoA2AHQ948TIDMACCxYsiMfjBoAegMmMqLGAscDos0AVAPpvtndfv/fhXveYtHN02j44a03JOfu4/lSfTfP5vh4f50GikANHJhtkIqBzJWpyWLNDWzP2mKw9LudMzHmTM/SANJueYYdZcHSOH53yjtqePnRz72E267L999rOBTnrMoCvAHwP4EGAP8ho1DnwXfCoyFUjPGgs4BbwwQPQiz9+MQmH5re3u34NX5si0GkA6EqDt2ifGhC6VnG45HU9mnrDGgsYCxgLGAsYC+x+FpCezwCY2Z6QUCREIhGybt1DAEngWfHCwzygHHAVE9sukjBbS1z7YAaNPsR8aJCrx6IyKvRoAaBl1sSDKHwM4AkQgZ99AJdCklYHoG+99VbGmC3/dr/LaHpsLGAsULCAAaANAF0YC+b/MFkAAeiurtrec8PU2KhRY5IQjppLYTpiLDA8FqgEQFMG/Vn3j2n/e1l6q+Pf7HnXUHoJpeen+07O9nVa6XlO7ljPO8Jn0xgcwGA/ClMpn1aJZlB2KGWHU3q0Yx/lWO92crOz1twe74Rt7sJt1rnbMh+3+Qoq1pY+APCYiA9I14O/Efyngb4sPX3eAdgG0AssCz4HT0aSoCAmY5AF7qH78yA8oK9deh0JkZM6OzK5XHVTFoFOA0BXslLRPgaArmQfU2YssDMtgL/HndmiactYwFhgWCzAXT9FWQZ1ERIKR0goQtase0y896hkF4qBF8H7gpuda9v7cGj2oUEE4oCQB6FR5QGdYVNs+j4ZP+R1AAcgxaCfQoaCTYVDgfKAZpzTrq6OeDy6dOlSNILjOJhZeljsa5QYCxgL7GQLGADaANA7ecjt+c0ZAJr6IoHxnn+lzRkaC+zRFqgEQIsTZtAPsAngz5I2AvwvwL0A3wK4DeD/AawA+DzAvwFcBrAE4BKASyvRJwGuALgK4GqALwB8EeA6gGVSybcBfixB56fFwkzYApAWDjIifnMBzMxHR6bS98fJO/74MmQydwAsuXhTxN8YBAC9/MYVhJCFixb5te5jRYDVANCVfgdF+xSuWW0IbLjkdT2V+mXK9iILsEJ8873nnPXxX87vPXYwZ2ossMdYgDOeA/GNnW3cuFEA0OFwKEzWrP0dvuFIKJYy5koM9y8AP3fsU7PptlwuAdDMIMyAqBzOAoYW2Z53IYUd3mDxWMY9yqMrAH4P0A3gMkhRQbZcy0YrAtCf+MQnVE5sA0DvMePbnMheaAEEoEOhkPpF79lG8DxvxQoxtQyFQosWLRJz2bIJpklCuGePgRE/OwNAGwB6xAeZacBYYOQtsGzZMkLIvHnzypryAXIAKbH8U4SE/ifA2zLy4GsAfwF4RQLTzwE8I2MRPi0DND9bafu8lHxRxjF8VQRxFrj2JoA3AN6Sansk9JyPp1ESyrkY1lnmGZRAc2Eyho4zEn3GOYq2LTuXCgXLly8nhLS1tVU4FixCiCdYOlz7I6td9LIcotJLhn4eAz2DkZYf+hkZDbuRBXx5m0qJHqvw6Cz/JWtUn4bqbQ0meAL428FF+K78YmcD2JLxC7/0YB2zbyxgLDDqLcAluCxCIUsAmkQiEUIIpa7PRMZlnzGf+z53Ad7MwXf/6Z7t0IOAJ4A3AIQZJ4wTyojK6uxRsgvJckjWjjpuG+VnAfwaoA/dC5iMoYbvcyXvAcIBmnV1dMajMX1tsfZalw9RMuqvo+mgsYCxQN4CnPNoNErI3gK6Up/eeOONoZD4fLhw4UIohFTSB8TeYgv9nA0/jBYwALQBoIdxOBlVxgK7ygLXXHMNIaTOcPYi29/A/6r5sOhTi0HyCEmXVa7HmHfeeWcoFGpsbKxDuGSiVIf8wERGVrvoC7ZQbTuw3laSHugZjLR8pT6asj3WAghAZ8Q4RyRXjfRRDlnUwJ3VoeBVw3MzAHTQLmbfWGB3twBjPp5CCQDt0wIALTBoEGErnkvBF7bB7KQz1rIjttNgOw2OGw0Qlu/cbUw05xLbabByY73cDPBPBrgR4DW8EzO5eg0XttHCe0n+qhkAencfvqb/xgKVLJBIJAwArRvGANC6NQw/YAsYANoA0AMeNKaCscDos8BFF11ECNFdTmr0UUd66weisVa5Wl3b8PLlbZWXPPLII+FwuL4Xo4ECpuWt1SoZWe2iZQXIVWRq9a2+YwM9g5GWr6/XRmrPsQCOKAnfCA/CAo0sAK2aUUwlgyooeTg7o1oMMJU6YMqMBYwFdgcLqMXaCECj5yD15TIvCpzKUGNAHVjbA5/sh3kpNsP2pzn0IEWef5DnH+R7gjx3miLqTttZtD/126i3r5c5BqyPgXcHsN8D9CvoOXDDUmEcOWXMp53tHbGGqP46Wv5muDtcSdNHYwFjgbwFYrFYffOsPcFixgN6T7iKo/wcDABtAOhRPkRN94wF6rFAe3t7a2vr/Pnz6xHWJwO7OwD9hz/8wQDQEqir58rXlsFJZW0Z/ehIy+ttGX7vsQDGoBD5uvKu0CN46uVAiirZYatKcijMDlsxAsYCxgK7kwUCADS+n+QB6EL8MQDI0Ke2+l9Ow5U+fBLgckmXMlhC4RLGPl4k/2K2U+kS5l/C6EWMn8foR6l9NdB7wH8G3G7ptQ35jB6Fj4N471OXRweg9QV5+jsn8qqKYYwFjAVGuQVeeuklDIjsuu4o7+qwdM8A0MNiRqOklgUMAG0A6FrjwxwzFthNLNDR0RGJRObPn69e9Gt3XIkNlKmtducfyrp/2QAAIABJREFUfeKJJ3CCp2Z9O78PpkVjAWOB4bAA97nreR6qoiyT83rlam/lYDccjZTqYIxRn3r45ztekCxKbUptxlzGXA4eB6dAntwd2pZjEHyxkN3zncKXJB3RLu2u2TMWMBYY3RawbVvEsed87dq1LS0tRP65nl24e1gc8Jduy6TNr8nsGk8DjBJ6FuB5mQUEM4K8JFKGsH6gNgXqA0eqcIeSa0RKAOj2DvEFkYk1IwZ0Ht1j1vTOWKCWBVatWkWICGePv+VaonvEMQNA7xGXcXSfhAGgDQA9ukeo6Z2xwI4twBhbtGgRIeSYY45Bj+Yd1hko7qzkd6h5Jwts3boVk/zs5HZNc8YCxgLDaAHGfMfP+Ay4B04WFXuW3ycx6HxM1WFsbhCqmABgOPWBesNPnMoeMfBc0YrmXziInpoqxgLGArveAhs3bgyHw6FQaM6cOTK1qsPB4pDlYElkVn5ck+s9OBW5CUV6QnmLQV7mKvT1rQv+yBJnLmeiCcFAgBT67MsgIgqDzhu6DIDuOKkdZEhoA0Dv+rFoemAsMAQLIAAdDocNAK2saGJAK1MYZjAWMAC0AaAHM25MHWOB0WQB27ZPOeUUQsgZZ5xRJwCtuq+Q5SoMOugVD6qKklFzkBF0USxtscIexljctm1bhWOmyFjAWGA3sQAF7ljg9gJLAnfynfaE6/Ew314wCyu+/DAqnPoAw37o97NAuFPdhkzKY636typpV4CRjVr9kO4Gqx9Y4cT1Bg1vLGAssLtYwJF/ALBhw4ZIJBIKhTo6OmTnAzcOcVujXFAA6t2lu8wFWxAHl4FL5ZaJHlYDoPW7My4o6ejoiEaj7e3tewlctbuMTNNPY4HBWcAA0NRHH4Gi/QwAXbTF/8/emcBJUZz9v2ZmZ2Z3We5j73tZEEVRiQcqIJ7xCCZ4xETNq0neHG/y94xGDYK8GDyReCZRExPfJK/6+vpGjUaMwCIKqGgUUfFGkXt3Z6an7676/VNVO729swfLssAuW/15Pr3V3dXV1b+u6e3+9lNPqVQPFFAAWgHoHjQbtYtSoE8pYNv2tGnTCCGzZ8/2YQ1j3RotqxUtd5zq6wCaUioHx3j55Zf71EVRlVEKKAW6r4DoqI0/PPjZjMnP1BU+9PifYGote3OnY+l3bPOhuzozx0KrmbCtruzNNyDt9dfw2iq8+kpH9jJelfYK7l/0ZYvduf3+O/T7b7fvv8OU9pvbbW63uR3a/be7991O71no3nOnfs+d2n0LdWHmfQvNYPo3d1nzrttw30Lt1ZdF8OvuC6dyKgWUAn1JAf8Z7JZbbgmFQuFw+JRTThEVlB+45HjC/MsV5b91/v3LzoT16QI9u5TvsOeNujC50QCAFoi8CwDtM2gFoPtSS1R1UQr0jgIKQCsA3TstSZXiK3DMMccEvk77q/fzRENDAyEkLCYFoPfzi61ObwAoIAF0PB6vr6+fMWPG6WK6/PLLr7322jvvvPPJJ59csWLFkiVLnnrqqZUrVzY1NfVxSb744otVq1YtX7788ccfv+mmm2688carrrpqWmCaMmXKIYccEgqFIpGIDAAdCoWWLl3ax89LVU8poBToTAHqwk3j4Jonx5Wvry7+fPKhn577jc1bPwNsrHoZzz2Lhx/Eoltw16246xbMuQaXnK9dMKv5glnJC2YlLzo7dcGs5HlnNc48bdNpJ26qr36tvuqtOmE11W/t3KrW1VS9J62u8j1h6+sqPmy1yvX1leuEra2vXDeu4r1xFesOqFgrbULZugll6yeUfsyt5NOWhFws/Xhc2afVFV9WVH9aWftWZd1r1TVvVVevq6n8sKby4+qq9dVVH1ZXbqip2lhV8Vlx4brqqg8PPvh5Q+9MJLVeKaAU6AcKyBer66+/XgaAnjVrFgDHcdq6BfCeHT6Tzjor2/Wkc7Sct7BqMYZhVs5eX0xpCdsxKaW269kOczxuHg8awifH82zXCUbhyKoABaYePz0nHiOkxUcwy7chK79aVAooBfq4AkEA3cer2ivVUzGge0VGVUhXCsycOTMajR5zzDF+jCr5n7Krffr/NgWg+/81VGegFGijwMknn0wIGTJkiHQHlq89Mv6gTPvzWCwWF1MsFvMBrr+17yRCoZBfGUmZ/UVCSDwe9xfD4XA0GlUe0G0ahFpQCvQrBagDN4EJlStrSpMlhV5VhTO2cmt90Rv1xUvrKl+or3lpQt37E+s21ZVsGV/WXF+yvWz455Ujt1SO2CbtwGprQpVZX6HXlBnVxaguQmUxKkp6asWoCFoJKktQXUy5lbjVpWZNiV5TYtYV23VFbl0RrStEZ1ZTiLISFJejpEIvqUyWletlZW5ZKVqtGGXFKByN0mKMHp0eO3b1q69CjmPWry6gqqxSQCnQRoGf//zn8ilFPswUFBSUlpYedthhM2bMkN/Tj5s+7bjp04488sgzzzzzJz/5ybx58xYsWHDZZZfNnz//ueeeWxaYFmSmm266af78+fP25DRnzpzbbrvtmmuumTlz5tTjp/t2xNFH1Y8fP3T4MBIioVjUt0g0GjSJnuWJSzkopUEG3UYjtaAUUAr0eQUUgFYe0H2+kfa3Ck6bNi0cDsv4XAPnH6QC0P2tnar6KgV2osCpp57qA1lCSG5urnznCYfDkUgkFovJQMnBPP6rkcwTyZ5ikUi2hcM54XBOKBRpZ6HemiKRSG5ubjweD4VCsVhs8ODBQRIt6xw8l3A4XFBQQAhZtWrVTjRSm5UCSoG+qgB14GiYUP1iTfnmkiJr5PBkXalVP3Jb/ajP66u+qCrfWDpme9HwRE0pqyjkCHhCHaqKnaoiVlXEKgpp2Si3bJRbVcQ4fRYAWjLoymJOontmrfy6FBWltLLUFWZWlierSzUOo4tQM0ZYIWo6syJwZl1i83kxrSyhlSUCjmf4eGURKgtRVYzKElo45otZ39gkL5Hfkb+vXjFVL6WAUqADBSyLx3H/1re+VVFRkZ+f7/c3bf/0RQiRMTrabwo+5Phb2z8L+Zt6MZGbm9v6yT8cCkXC4ZyItFAkTMIhYYSE2xk/HxLOiRBCItGo7wHtIfh63a3QcB3IqlYpBZQC+0gBBaAVgN5HTW//PezIkSMJISeeeKLsG+X/k9x/z5ifmQLQ+/f1VWc30BRIJpNyEEJCyA033HDdddfddNNNP/rRj04//fSTTz552rRpU6ZMOfroo6dNm3aimKKZSXpAd8KO21PmSOaFI8TfM7Kt196A4vH44MGD5QvY8OHDZbkyZJA/Ly8vP+SQQ+QmmWf16tUD7bqr81UK7DcKSAB9QM0L1RVflhRZFaVu0fDExDJjYknjhNrNY2s31VU111XqB9Z7JaO3jB6xvrriy6qyLVVl26SNHv5pyehN1WWNYysa68p31JRtD1hjTVkPbHt1+dYWq9hcXbG5plxYxRc1Vet5mA4eo+PjuooP6yveq696k8f96MjGVa+cUNUwoXrphMqXx1Xx2CA1lR9WV2yuLmusLmusKU3WFNs1RTi0FhUjtZrST39zL2QIDtt1duzYsd9cX3UiSoEBooDnerZty4eTUCiUm5vLgWwkEo/HIxEOZ+UkH2b87/5Z/dVk5n3VRy0/Pz/YySxTZf7QF4lGc+KxUCxKcsIdWIjE83Ij0WjB0CEKQA+QBq9Oc79XQAFoBaD3+0a+t09Qfk9WAHpv666OpxRQCvSeArZtz5o1Swam2NVSGwLTzWJasGDBL3/5y2BPz+mZSfYbnZqZjuul6atf/eoRRxxxyimnXHnllXPmzLn66qvvuuuu5cuXL168+LXXXsuiMP5nQvkhTQYeIYQsWbJkV89d5VcKKAX6iALUgbYD9ZX/qK1sHD8WVRVeTUXTgRWfHlz9zwljl9bXPV9XvWx83coDx782fuxLtTXP1NU9XVf7t7rav9fV/r2m+m9VFU9Xlj9TU/VcTdVzY6v/Prb67/XV/8jYkvrqXba6yueryp6tq3z+oHENBx/wysT6lw6qWXZQ9fIJ1S8cUPPkhNqHJ9QvHH/A9eMO/NH4Ay8YP/Hs8RO/0aEdeNA3Dj3grMPHf23ShDMOPPDc+gN+Ul3/y8q6P1ZWPVNd8Y/a0lfGV3xwYHlj/Ui7ZmjioLKP7r0Dtg053pcfd7WPXCNVDaWAUqA7ClBKfSfigoIC2amrFeNmHJ8lgz7uuOOOOeaYKVOmHHfccdJd4KijjjrmmGM6e7zKPH919+/JJ5/8rW9966qrrlqwYMENO5vmzp07b9486ccwe/bsX8y5wbfZc+fMnjtHLs6eO+eGG+e2txv/c97kI46I5salx7QcnFDdx7rTZlQepUCfVUABaAWg+2zj7K8VkwB6xowZygO6v15CVW+lwIBXwLKszz//PC8vLzc3t9fFYMyjzPSo5lHN8VKey416GmUmY16vHI4Pd2Pb/j94iZjbl8wYk93SZQYfQD/88MOLFy9un1+tUQooBfqLAtSFZ2BC3eJDJ7qVZRg3FqNHrL/4POg7oCeRTkFLchOjYMH0uFkOLBu2mJsmuDncdB1pDVqPLJ3ix0qnYGpwdcDKDBPm8OEQ4QAutGZoKVczvtTttzZsfXzDjoc2NN6/ofHeDm3Ttvt3bHqgadNvtm6994utj27Y/NEX27Fdh2YjqcFMQ0/g4Oq3J4xMjhucmFT28a9vVwC6v7RZVU+lQMcKJJPJ8vJySZxXrFjhOA4AGQpZDjgkvaSDjz3BgtqOVRjc0vM0FVP3S/Zcjz9xZe5/EiXzsxDWWT1s11mx8hUedSQncvwJMyR6VgC6M7nUeqVAv1BAAWj//dS/Xi1DrPrLKqEU2CUFggB6l3bs15lVCI5+fflU5ZUC7RWwLEu+7bTf1K01DBDjxMi3lLbvKi6QApqBhJg3A43CEgyOzOm5njTH83ZqfmY/4dfQsqz2kU8ZY7Zty1c4mTMLQD/66KN+CSqhFFAK9EcFqAfbwNlff7uqfGNNJcbVo7rq4/O+8UVqG6gBZoFaYBQU2028msL/GPibg88ptVsMLuAxUAbYHgfThsNNd6E7PTHPA1psB7y34D1F2W8oFlBcm7S+k3TO0eyva+7pafeEND0uzY5Ms6+kcXh7M70jPfs4z5pmuNOaze9vSTyzLbU9AZiALqKhfrkJh4z/24GjNo8vSB1W/OVvb4FtcQ9oT1h/vJSqzkqBgayARBWVlZVyROiVK1d2iH39vlzyy7oEvgAkm84auC+Yee9o2/5JrDvH3d64Y82bb4RzIjnx2PQZx0v07MPr7pSg8igFlAJ9TQEFoBWA7mttst/XxwfQ7dtWvz+3zk9AAejOtVFblAL9TwH5riLjDO5K7RnQdkCYliXOcAR03gp8BrwDPA/8FXga+Duwgq/xNsHVqGv7qFq+IElo0uHc5b6DLZQoKwOl1LVs5rW+p3Cva2p63hfANmAH8CnwobCPgc2AwRjzPaAXLFjQmSfRrqih8ioFlAL7TAEqelOce86rBx/UVFLoFY3Rams+Pfusd1NN/l0qAfzT8O5Iet9vck9rcr7hYoHtPmC7D7j0QYaHgT8Cfwb+F1gKrARWAasYXmV4neF1ivdtJAXHdi24IgGLwaZwW4y6MF00UnxG8TbwCvA3eH9k5k2W8aNE8uSEPilhVzQ7Q5rcSJNDEm4o6eakvYjOIgZIe7NALBCbEc/LcZ0haaeqKX0W8BLQ7MCywHS4zRY0E5dc9EF90YaaoalJpV/8+lZeOf8Ouc+uhzqwUkAp0CMFGGOWZU2ZMiUajcZiMRkczLIsz/V8J+isgimlexRAe65nGIamaaZpOl1Okjs7jmOapm3btuv4Jn0L5KLjeS6l7Y0DdLBINBrPy50+43iXtj7UZZ2yWlQKKAX6iwIKQLeHhMoDur+03j5az8GDBxNCampq+mj99ky1FIDeM7qqUpUC+0YB6V9DCIlGo7tSA6elM6UHuJTZvJeomNyU+QGwxsOjJuYb+K5mH2vZh+n2ESnrqwntMkP/b9hNmcwtfzNdNSlFi3ngTKm9OaIjuy0gt5i7rm3CsVsKkjSIV20L8A/gD8BDwN3A7cAC4Gbb/D2wwXO9pUuXSqfvG2+80XO9VCqVVSW1qBRQCvQXBSiF6+L881fVVH9SPIaOHmGXFn16wfmfWJzGgkEHNgKPNVsn6LTYcUc7TqnlHGTah/mWtg/lZn0lbR6TNo/T7GN1Z7rpnmp5p9v0jLR1JfBPl7tEJ4XpLnNdmvks5jBYOrwNwDLgfhf/4eCMpHWEZh2ctsennSrDLTLoMIPlGyxmIJzOmIGwMA6gJXH25zbj9NlmBIik9CGNzccCdwJvUyQsJHSkdtBtSRe6jXPPfau0YkPhmKbxVR/edwcH0L7DY3+5fKqeSgGlgFTAtvmH+WnTpsnnk4aGhvbwoj9q5d+UGGNB9Ox/LfPEfYtSKsdanD59es/cqPujOKrOSoH9WAEFoNvfwxWA3o8b/N44tVAoFIvFBg8evDcO1meOoQB0n7kUqiJKgV5QoKcA2uIouMVDRQeagK3A+8AKir+YmJPAt7bhqCSqbORRhB3km+4El14K52k4JneeDvhPtwXQLT6FWQyaZni0ZNBy7sGB0wR7C9gm4HPgA3D3w9eBZzTrPxLmzET6NN0+2XCn6c7UlHFKY+OlnrvWNM3Fixfn5eVFo9HZs2f3goiqCKWAUmDfKZAFoEcMccaM/PikGSv4ev6hbBPwootfpL1qBwReCF7EY1GnM0PEQchBxGF5jjfU8YanjROA5YxpjCWFafBM7vzMTNGpYj2wGvhfz7ne9r6hY5yBoTqi6Yxrs4+VrcyaNIi/Vbo/B/P49NlmxEVO2qhx0peJL2obwUODpCwkmr1NaQe2iXPPXVtY/emwkm1ja9+7d6EC0PuuFaojKwV2W4H9FUAHhck877WEhPYXZYTraDRKCDnnnHMUgA6KptJKgX6qgALQCkD306bbd6tNCMnNzQ2FQn23inugZgpA7wFRVZFKgX2mwC4CaCZckC3AEF7IFCwBvCkibPweuCZlnt5oHZRgRUkMSiKeRsQCcRAzMUqzTgAeA/2s/Ug0mTcQyYta/JtpSwd37hOdGb3GT/hy2QJ8vwMsAf5kapeZ5rdM91QTR2xOjt6eHtFkFjY7Zc1uUZNb3egd3mj8O/AWFR7QeXl5hJDvf//7flkqoRRQCvRHBagH18H533y9purz4tEYPcItLfr0W+etc1s6ZrwNzDUwVaelDh0ENw436rGojXg7i9qI2CAZC9ksz6bD0/pJPKqGY8Nxhdn8K5qbBN4Vt74FLi5OWscnrAPTtDyNkToG6YjqCLWHy3JNdwE0zdGdPMuYCvsxsO08oDV36XYAw7C22BYfevG8c9YWVX06opgD6LvvVAC6P7ZfVWelQIsCCkBLAH3ZZZe1pzaqlSgFlAL9TgEFoNvfypQHdL9rxn2rwrKHVDQabd+2+lZFe7U2CkD3qpyqMKXAPlZgFwE0FSNgJcCdCqW78VO2Pq95+7d3bD82kaxP28N1RvSMf58uPP50DNfcw1KpHwj3ZDG0TMD92R8bXbhTU8bxip3p3O4Hf7YBTYxe+KWI6fwe8Bawhvd5p3+AczPMSz3zG+n0pLRVknbjKY/olHdsd5DnYHAa+RoqTZzh4GbgIwArVqyQPT1nzpy5jy+AOrxSQCmwewq0AOjz/llTtbF4NMqKMbZ20+23wkhDfCp7AjjLQJFJR3reULh58OIOB9DtLWIjJOmzCcKNDTXtA9KJfwP7Jx+d0DLhNIJ+ArwhXJIfbNa/nqCH6aizUZKg8RSNpry4RvPSyOkwvMYuAuhYSh8CzASeEN/53gBeFQGmlzMeVX8NKC741hOlVWtHFO0YW7P+buUBvXsNSe2tFNi3CvgAWg4ytHz58v3PEdj3I8hKBD2g58+fL8eODo4gvW8vjTq6UkAp0AMFJIAeOM6anuvNmzcvFAqFw+EZM2bIsWGzdFMAOksQtbhrCkgAHQ6HTdPctT37c24FoPvz1VN1VwpkK7DLAJpagj6/CvyhSTs7aR6lmQfoVqVhF1rOUMuOWi6xPG4m5RQ4jZiBAxPad4HngC+zD5+1TBm4BdbKNV4K9GMBX54TYZ1vo/jhDueEbcahln2wa9e7To3jFDveSNsrsGnMpWHKQh4L2YjoCGkg21CawtVieLHtAJYvXy7HXTzqqKMCB1NJpYBSoP8pwAG0jfPPfbemckvxaFSVYlztxttvo7oOsFXA1S4mWsh1GHd8pt4gj+Y5wtO5hTJL1tx2rvO4zJFGrTjddAHYE/zrl2uKO9irwIPAFWn3pEa7PoXiFIamMSiNvDRy08g3aIHuDRLhnnMsFg7G1mgfgiNrq1xsDcHh5VKUATOAfwd+kkif0WRO3+FMbnIOa9YnJ/WZmxpvuOnWX5bXLRk5JjW25mMFoPtf21U1VgoEFJD+TDNmzNjPYkAHTrHTpHwWjcVihJDZs2d7rmdZlgLQneqlNigF+oMCK1eulHczwzD6Q313t44KQO+ugmr/nSqgALQcl3mnQqkMSgGlQJ9VYBcBtANsE754d+0wzkh6VWnEdEYMRizKzXQJB9AuMQWATlNio6TRmAY8DLwjvJi7VIJH+KC8Oz0zgATsj0DfBdYKp7+ngVsbmy/+YtuMJD0iifIm5DWLQ7sgLnd2DjkICXYTdmkYbpRHegV3x9aQ24zjLPwF2MpgMMbkhzRCyNe+9rUuK6Q2KgWUAn1dAQ6gLZx/zgc1FduKR6OyGOPqPrv9DtPmkervgnO8641xEPFYiNKIR6X7c8gUNwe903nERTHD8cAi3tPCWQGsAP6bpa/TUmfo7sEmRpjICRQS4l7PLFcMNijHG+wKQLcfeNCH0T6AtlhMt4cy1FEcaNGxGh2lIVcT/UtMl5hueWP6qzcv+requmdGj06Prf5UAei+3lJV/ZQCO1PAtu1LLrlEvmAuXbrUtm35kLaz/fr9dsuyGGOEkHA4PG/ePOkQ3e/PSp2AUmBgK/DMM8/Iu9kA+ZikAPTAbu975ewVgFYAeq80NHUQpcAeVGAXAXSTGOLvriRmbNQKNOTzHuWMB7uQHCdNibQUSAqkmcV1HK7THwnn5R0isEbLAIRthyH0T5DBs+BshbsOdDHwKHCzQ3+sOWem3Mk6xumsSkdJGsM1mpf0SLIlzkbYQtgEJ0qyh7vNCJxBcOKUezVGk5jocPfntQBlzPMBdCQSmTJlin9slVAKKAX6vAJZ/bb5IgfQJs4/+5MWAF2C+tqPbr9Dd50kNb4NZxR1B3veIOrlURr1+McqHl6jc/QsNw213SOBy4AHgF8Dl7vmVw39COCwpDEy7Q7SadxE1OIMmt955M2HQ2QWs2iuIUJw+EzZT/ghOHYKoC0WNmjE8PJsOjRlD0laeWnKg0pbIC4l1CLUKk+lvnrHwn+rrX2qaFSqvkoB6D7feFUFlQI7U0DTtNmzZ8sXzGXLlg0QagPAFNOoUaMikcj8+fN3ppParhRQCvQDBR544AEZUKgf1LU3qqgAdG+oqMroUgEFoBWA7rKBqI1KgX6gQLcBNBPjX30E/L5JP22jVpAWtJd3KhduyMLRmKRYiyVAEiCNbtEO42zgceBjsTsPrtEWPcug0k3ARhGd+W3gZeBJ0Pupd73lftNwp6W8cQl3VIJF0oLy2AhZ4MTZRcxFzEKOXPQZkAHSAqDtQZSFTK9Ys84TdUjyo1NQSqUHdK6YBki/sH7QFlUVlQJdKdABepbDk7YC6MothWNoWTGrr137q0XrGd60zCmghHpxT0Te8FjEEWMMdg6gQy1AmQ01zcOBi4GfMfNCyxzvYYSHfDlKocGI5pDGNBGLLWGjWygzy7FYSwBonzv7CQmg5dxfmZVo8YBGxGI5DnId5Fs0V/dCBmsZHdGjxDOJa5SmkmcuXPjdA+qeLhmZGl/5xd13qEEIu2pAaptSoI8r4DiO53rz588Ph8OhUOiVV17p4xXuxep5rmfb9imnnPKvl+u5c+fK2Kn7XwjsXlRMFaUU6PsKLFiwQI640/er2is1VAC6V2RUhXSlgALQCkB31T7UNqVAf1CgYwDdZpBAvkDhUaSAZZo9K5Eek3bjPLwpC9vChLMe4cMPCktTkqKRlBdPWke49LfAJ0CSk2fmCCdoW8BoqY4l0PMbwP9Q3G7jp5p1kmlPNp2DTXe8SSssNsbCMAv5FmfNnDuLUcIifnBVh69p4TJ+wgGBF4cz1HELLWs68F/AejCTw2/uMNkKoAlRo0H0h2aq6jjQFJDfqVpvRLTdwKT+CKVuC4A+56Oqqo2FhW5ZMRtfu+yO2+5PG7fq9kQHkYyFJH2223pAt40EHcqMQxi16XDbLXbcKscrczDE4V+8xCiFIuJQ2uXf3lrDZQjf5BaUzMLtQXO3oHOgQH5rpTm2l9tiNIcfS9zrXBDbIZo+WsfFd9x96UHjnq0cpY8v3XbPLdwTnIlpoLUXdb5Kgf1AAc/lPbRuvPHGUCgUj8fffvtty7J0Hsx+oExTp07NAtDyhqZuawOlBajz3L8UmDdvngzsvn+dVldnc+ONNxJC8vLyjj/+eMaY4zhZYZTUa2dX8qltO1VAAWgFoHfaSFQGpUAfV6CbABpIAx95eLAxNd50Q5yMBI2FW/ygMwA67ebpVqXtXAg0AKYgzg6oBjSJKNJbgA+Af/Lgqnjc8+bozoWNxrQmZ5yJYQ5yujDhctgKoH3oHEw4IA6LOm6haR/hWP8PWA2W5M7Pmenvf/+7fD5QADojifqrFOgzCvj0uU13CekB3cqdfSTNATSPAf1+VfXnhYV2aREdV/fcojuvN52fpN2xJqJBP2VJn30P6CB9FvcQH0Bnf9aSdxhLdLCwaEvPDx9A24wHx/Ct1wA0jXEATWM2C7uMuBkGbVHSbNTpuHnhvfceVP+P2iKjvqhpwfVwDQWg+0wzVhVRCuyiAhKzSn5BCJGPZwPKC1gB6F2rg1t7AAAgAElEQVRsMiq7UqBPKzBv3rx4PD5wXrU815NO3wUFBdOmTZODqcrRZf3rpAC0L4VK9EQBBaAVgO5Ju1H7KAX6kgIdA+g2NZReiNuAfzSZP0qZNdLr2RYe0MIPOocH4pDGiCHDQNtjjNSJYvyuf4qxB4X7M9smAjE/C9xn6N+xzdMte6plH2ba4wy7SrdLdXekRXNt7rHYKYPuDoA2EdIRT3njkvolIvjGpwKC2xSuBw/Am2++GY1Gc3NzB85TUZtLqhaUAn1WgSz6HFzkdaaA7aNnmaAUro3zz3u7quaTwiKztIjW1z69aNHPTPeHaa/WRNRExI/UHCTOMp397UoEieYfsQLm55GIWX5v8z2g5UoJo30G3XpX9G+PGULdPmcQZGfSon+J/52P9zXJMHFGKIbo1mm28/pdi9aOq1o9tsSoHt142b+3AOg+e21VxZQCSoEuFMgC0F3k3F83KQC9v15ZdV4DU4GBBqAppfImRgg56aSTOhxMVQHogflb6LWzVgBaAehea0yqIKXAPlJgZwBahH5mTARoXrglOcVwx+wEQDM+DqFu1rL0pcDT3PsY7whbDTwH3J1wfrBNm+a4NZQOYYgzhIAwEAeGMgxxEeuCPjvI2SmAFr6NoSRyk2xyypoLvAFsBWwK04Nt2AYnWLYtb+CEENu295H26rBKAaVAJwoEubOf5nk7BtCeh/O/+XpVzUejR6crSzBh7DO/uuuytHtx2qvutwCa+Hdam4UdhFyEHRDufO0OAg7V9asdy7jnV0Z12Zt1FW7F6OQl5zNbhODoRFO1WimgFOjTCmQBaDkCYZb3XJ8+gd2unALQuy2hKkAp0IcUGGgAWtO0E088MSymGTNmyFj2WddDAegsQdTirimgALQC0LvWYlRupUDfU6BzAC2pjwc48BxgpU3PTbijuIdyIPRziwc0C7fx+2Mx4DiwB4EVwgH5DoYfWThTx1eSGNdMx6VppecNhhcCI9zA55RGqBdniLp8gEFuThtr9YmWDFqEam0Z/sv3T8xEd40k2OA0pjL8GljLsIky3YVpw7YcU36R9gF037smqkZKAaVAiwKSyNDMxCDjyLcJxEEpmIcLvr1q1KjXR41I1ZZiwtinbv/V9xLW2ZpbYaBlSMD2vs/CLVrG3GiZOwh1aME7TPBeF/RlDqZlnmAgjmAM6IyPc2sI6c7WyHJsRhyEKCIuckyXWFYNvP8Alpo2FtzSWFq6trKMlRfZ55/t2fz2pialgFKgXyog73MvvvhiSEz98hx2r9IKQO+efmpvpUDfUmCgAWgAxx9/PCEkFAqpGNB9qy3uN7VRAFoB6P2mMasTGeAKEEIikUhHIjAe/Zl9BOc3tnOYQds45clxCFvmmd7lFh/gK07Z4XDnAPcBl3s408A4DQUpkBRIErE0cj0BnX36zAE0C3EGnaHPuwOgTURSLM/EJBdXMfwOeBZYRvEKxTsea8wC0MlksqMTV+uUAkqBvayAjPLsx3q2AR1oFlHjNwKfAZsAjcHJwtCUwjSw6E6jqurdkiKrqojVVT12023nbdZO0byy/QFAi2AgLnIcFrW8qOseCfte0C8MF3f/1iksebekDKVlxnnnWqa1ly+ZOpxSQCnQawr4AFq+YHbYfbvXDtYnC1IAuk9eFlUppUAPFVAAWg1C2MOmo3brTAEFoBWA7qxtqPVKgf6lACEkHA53UGc+bt8W4C/MucBKV3luzGMR30Mw6Anop22ELOS4GMYw3sPBDmp0jNGQq4GkWyxsiL7kHgg3FvFYVMxDIuhqG4fEjJtzKBiXo2sPaN9X0UK+g3oTk5u9o7a50za7p2xKX0axLgtAv/322x2ceH9bFUR3Mt3fzkDVd8Ao4IfUkOHlOzhvKoK2NwMbRfSe5cBfgb+IGD5fihFNKWOeCMfBGztlSOt45L8wtva9ylK3fLRXU/HnG2/7+pepqZpX0o8BdOarHr+nMWI4xPKiDh0EnArvb56gzX/+P4wuX19cjuKKpnPPb7KdDtRUq5QCSoF+oYAC0ApA94uGqiqpFOimAgpAKwDdzaaisnVXAQWgFYDubltR+ZQCfVsB2V2otY4SDDFBePAJ8J+2NdW1yjwn32PRTgE0H5aQx2i2wCNymIGht9p3Rc9g4oiNuMPyHBYXxRKfOGcldglAOxJtgxiMaNztOq8ZRdsxaYv5AzEKIj9ReQOPRqMvvPBC64n32xQFzWLQmYHa+DeE1inI/rpO82C7u25dlxnc2lqnbqZ2sTLBY+3f6Tb6+Srt5OK12amTBRmfp5ONna9ur3ZL4GYNSAKNIib7l8AG4GNgPfCe+FW+BawRIeNXAsuBJaLjwv8Av9tuXr7d+e5298KtxvW686bnyaDt/plyAG1ZWHj7jqqKtWWFTlUhuAf0nd/YbE5PsjHy5mOKD2PthiIMmWjzxcu/uWUlMvcrPgyg/7HNElzYZi1rej8EhziWDeIybppO0tYQ25kMXAv2tmPDAp5ZiqLS9WXlKC7dce75OxSA7rxdqi1Kgb6uAGOMUvriiy/6HtCU/2MfQJMC0APoYqtTHQAKKADdcwAtw//btr1hw4aNGzcOgNaiTrFbCsjng0gkYlkDqNNjQ0ODdJYMh8MKQHeroahMSoG+rcCyZcuyATR3Es4Y3k82XZFIHOnSSqDECQDoIKPJhOPIkQxaYOg2pCZIbdqkBbbmu7fQFsmDOOgJWBtIlMWmxWJrZp8+u0y4DSJHQ76GQxrTPwBeBFLM42908gYei8WWLVvWZ65PK1PrDvwN5KYUblsGTSl0Cg2w2xTFKLprLljAeDkdWTAPT3e7/J0A0sDJteQUYX/9w3VYGdiBOmdq0r6kvbOm+1J0JycVl7fNPHNhM37EIocrWgJvDJ5wFe5sHtCAF5opq02CMY8xj1LXpVSW6zGetd1Emecyj/K8Dmu5MhY4H7V5DHlQV3DnzwRrXiPg8l+BPwH3A7cBNwA/A34MnE9xiu0ebdmTbPNQSz/M0ifr1uGad5DGJiXZtDR+xvA25aXJj2MttaUUtoGFt6Vqyt4rG8OqxqCu8v/m3nbOBu24JEZYIC6/t+RYKLBQIMYkbLmftLkRtSXLfWeTDcIoN4AYdh1wL9gaoNllPEDJP15CZfH71UUoGpU4e1ZCjajarnGqFUqBfqbA4sWLByyAnjt37r/Ofe7cuXLwLkqpHAZAzvvZhVTVVQoMeAUGIICeMWOGBGXBQQiD97FuDUJoi6c5x3HuuuuuSCRSUVGxefPmAd+clABcAQWgFYBWvwSlwH6ggATQhLT9n9gCoD3gA+BB4HwPExiGdwdAW4xj6PaxoTtlOpxBdw2gu8eyJcIW3oLSZ9BmYYPlOyhvNI4H/gx8BDjU9QDE43FCSB8D0N1sTRnu1koNOYLjLs+SywlKKAG0WN+GKrbu1Al2DGQIDvXWEX2WB4WfrccHagNWg6g1UBma8emWh+usPkIHXqVMZfxPKTKRWe1v74VE1iHkYnfL9dVrl/BpO3M5w20RKZNmghu3HIu3nAyAtilsCtfriEE7AghLKp1RojMAzQTBtkU0DF04Lyco206xGfgCvGPEB8Lez3gxvwce32YN8FpbWw00uPYjrnevy25zceP21CXb099stL6edE513KnwjgQOAeqAMS5i/JdLCXO4UTvuOHEPuSbKDZzhYiHwaeZHkqk+uI8gB9C3WDVlH5aPRtUo1FW8eNPtv9im/1RzjjDpaINy9GxhmADQEZN/3OIMutM7Ul+C0TYjHiPMI8BI5n0NrAGOLqG+TrF0OeoK368didJR+gkzNioAnWke6q9SoL8qsGbNGh9Ae67Xw54o/fDsGWMKQPfD66aqrBToVAEFoKUf8y4DaKnoBx98EAqFImJasmSJpNKdiq02DAwFFIBWAHpgtHR1lvu5Ah0DaDAwjxsf+GspcI1NDzXcQZwQCY9CV4yLJaI2EwehoAf07gDo3UdCsiM8955mxEBOmo4wcbhJfwC8DpoA466aAOrr6/sNgA5Axo7aok9maatjaAuD5t13O/OB7d56KjimnLsex5pBC27tyYEkD5Xz9kQ5uDVT2+ARgzUJpv08PalS5kA93tc/ukzstJys/C2LGZrMPY87Ie8SsvMWkWGx0hHeF1LumNkossmzc9q0CrlXi+t022OZYgDAz4EPRZSMV0VwjMXAk8AjwAPAr4F7gPnAXOAXwBW6+TXDOtE33Txes6emrKOT9qSEfUCTM7bJrU14NUlWnWTVKVae9oosd5TtDrO9ApvGLEocSlyPuC5xnYjjRiyPd25IY6zt3gi8CqR4I287cQCtY+EtXk3pp+WjUDkS4yrWLrx1uZF+HdZtzD7XsieZXrFg0GFTRAcSvSv6B4DmgT5AbHeI504Ffgn6pjh77geuUzQ0oK7w3cohrLrIOXjCGmcA9cdr2wjUklJgv1CAMbZlyxYfQA+oEByUUgWg94tWrE5CKdCigALQPQTQkjVfccUVoVAoHA5Ho9GXX35ZNSulgPKAViE41K9AKbB/KLBs2bJQKNTWA5oJR0mHky1sgfuIkb4gZdSn7ZjLBxjkXdr7OIC2eATqcBr5Sbem0ZgpeNnHAPUcC5QTLNlJqs96QPtRGXgba0fcRMPzwaIE0CLiRHCd2Euu6G2omsVMd8pYO84Q5Ms+NM1KBPMEziJYgQ7R804CUASK6rhuu54hWKUO010cyM8fzBP0CuewETygirSk8Ef2082ZwMpfCAfhjwUvXi8ckz8UaTn/WMRc/jDjsLw2E3P5ZYGVl3c0X2Lbf7Ldh1zvXse9xXZnW87lpvNjy/mO5Z1temea7qm6PSNtHp02JuvWoZZb72IkQz5QQIV5yHeRayNqgZNfXQxDmgBJgKRoKEVDOosYlFgesWiLOR6RZnl8k06jBkYZONV1HuOnyb3Cs++70gP6zlus2pINlSM5gB5f+f7dt38Gw4bzMujNwMk2RluIydj0wgOaO0Hv/ueuPVsCCxs0orNIGjmaU29bVwD/gL0eVJMe0IbHAXTtmHXlg2lNsVte8qIC0NmNQy0rBXZRgX3rcey5nud6AxNA/+vEFYDexdaqsisF+rQCCkD3EEADcBynrq4uGo0SQvLz87ds2dKnL/X+VTnDMPrsCSkPaOUB3Wcbp6pYX1agr0WNb2hoCIfD7QC0xd2fHcD9yHX/n2aPT1iDLRZzEfYBdABDh2xEeNznluAb3QjBIcNuBOe92O2dhQ0R+jmBEY3u0SKEyBoB6WDbtny97LMAOthRq23cQx5fQ8bkZdSWBsYj7GYjaubBc+B54CF7ufVo4vF/WwwO68L8bDyxC5NwsJdu9sFgE23SgTyZyjCvw8pk/ID7wk8/+B1ApttB0+5Xk+9qAzuAjcDnbe0TEfXiNeAl4AXgr8BfgN8L3+TfAFn2a+Bu7kKL64GrRMzl8zx2iuFM0Z3Jaftw3To8bR7WasZkzZR2mGYdrNkTNKdOc2s0tyrtVliscltyODAu7RXZKNzWFN6RCFtu3GZhDwQIAxExD1NEKCLiw1VOMPCFkfm9B0K9814L/lB+BqfV4SQtMnGWx0NFvykofAcxqDmAtnDnrYna4i8qR6B2DMZX/fOlpeCBObAB9LfAodLx2Z9zcBy8+ew0nantniXObY/C6TPN07yhjd6YZvur/BKzLXA3AQnw3zZMiuUvcQBdPRzVRU5NRYMC0N3/YamcSoEsBaS7sfwflrVpry3KOgxAAG2a5r9688yePTsajd5www2MMbkm+Eix166COpBSQCnQKwooAN1zAL1t27bc3Fz5z2Ds2LGO48iyeuXCqEL6rwIKQCsA3X9br6r5vlLAcRzOk2xbPlvvq2oEj9sRgPYAg/d2p1tg/6/pzdBoXpqGTIScjPuzj6FFFA45qFdfAdAGwhpiCYza4R2UYt8Tg55tFvTKdVyrlwC0BItBIXsnLV63PMpMyvSgiVC8GtAkSPoOQSR3ZBabRWKbCM77MfC+sA9EzOvPgN2xT0S0Xzn/SBQYnAe37s5Rur9v8Ih+TYIr2/v8So/g4HrpHbz78/fEqHpyvk6wYDlfKwJWrAXeysREXiMSbwBvCJC6BlgJvAy8ErBVQHt7RWRbCjwFPAb8d1v7o23fars3uu61Lr28KfHtptTXm7TTE9pJifQJifTxQUsbJ5jmVNs+wvUmMhxAUcUwykW+BL4yZnqbOSU2C9s0h0fGYDEZ1d3gHQuIwfKBOopxSaMwYQyxULC5iTCEdB70hliMh4xwQGirhT0WEeHjIw5C/IhthhgNLAoALbovEA3hJHKb3IM8/CfQAHwpfgIdAWgmAPRtO7gH9AjUFXIAvbwBcBJwVsCZw1Bnipr3LwBtsRwTg9K0MuFNNzCH//qoB5YQP/ZWAF0z+p3akagcY9SVv6QAdO/chVUpA1UBx3H2rQe0PPoABNCO41iWdf/994fDYTl4l2yDCkAP1N+iOu/9QQEFoHsOoP3haAkh3/72t3m4PR5WUU17XAHGWF9m/QpAKwC9x38D6gD7nQKMsb7WsaNzAP0B8MeUe26SliQlWsrEffbpswjEEeJQiVukA6fCtj59e9Z/ULgxCsdJkgRpYmU7jLOB3wky2EyhUZgucz3Rh196QEej0YaGhl1vZX7Y3MDTwE4iNXf3IPx1Cw5FM8V2D1sdtsVhW2y6mSfwiYc3KceUqwMmx3xbBSwTPrCPAL8VkXnvE4n/aossswhm14t/FiM3yvl/AR1aME/Xpe3+1uCxgpX5IyDtYeBmYF47myuCFM8FbgjYL0TY4t2ZXwf49nPAt6sBaVcAPwS+J83wvml439Td83RvVpqenGYzNHp8Z5b2jhc2TXOn6u6xmjtZcw9LOYek7UN0YaY10TAnWGa9YdZaVo1l1dhWlW1VOE6545Q6bqHtjW5nIw06xKAFBsu3aL5FcyVZFpQ5R85dL8f1cjxhrhdzvVxptpdr05aRRQ23qHHLtGf+b8yGTw8z3CM0r0RDzAHRRGwNDURn3Py7gc3CnD4L81jEpXyYQZeGfeOkmxt3f5b0mfs+I3cHRm21Z4iQ0xvEdxddhMbO/im1eEDftq22dH3lSNQUYnzFB8uXgNGNjnk99Y5xUeSjZ5noFx7QFgtTDLVwuEavAxoYNjGkhftzCuCR7KUHdHXh2tpRqBljjq1YoQB0duNQy0qB7inguZ7snbZv3/EHLICWV+lf4xDKwTmkr0ZfhgDda1Yql1JgQCugAHQPATRjbMGCBYSQeDxOCFm4cKG6G+7NX9KaNWtkGO6+4y3on74C0ApA+41BJZQCO1WAMUYp3bJly3PPPZdMJneaf69l6AhAO2LwscUUP2j0qhOIJkT8VhE7lbPmTgC0iKma1Zl9rwHoFvocbum5j1jCmWQYvxReqBsFtUkwpBgcl7kAm3HCdEJIOJzTsHypiN6wS3pz5CWMh7fge/LwGDIYhisC9W4V0XjXCw9Z6Wn7nuDgazMOsKuFD+xKMQ/SZLm+Afi7cHr9P+BJiv/x8LiLx2z83sRCAzcZuMkSZmK+Sf/ToHMM9xeme7lBL0l5ZyWcExLWlKQ5JWlM17RTtdTX0sk2pqXO6MLSqTMydlo61ZVp2mltrG2xmUL80jo9aFI7ozML1rOTypyaTmVMO1FLH6PpX2lrh2v64ZpxaFs7RDN23yZqRsbMA7X2Zo3V7HLNKU67JTottVBuo1JYkYXBFuImYp1YjgluFp9HTISk67HOvY+5WZR7DfsOyx6Ix0KeF/Y8n+q2bnUzHsfy80+LF3NrDAoeMKc9gxb0OeYzaOEHzQG0gbDhlF3+UzIsj4weRn78A/KXxwp26MducyrSKNEwRmPDNBbVOI+OaIgYyDEQdsSgoLKeLfSZk+6W8m0a4xUQDFoC6GaEmjBiK520Kf19GXyD8iH37A77HVAG28bCOzbWVLxVPppxAF35/kvLAKxK6V816Uibq90y/GD/AtDAMOBw8dXkr8BzwIsZewVYw/DBylXb6kpX1IymNYVafcUyBaB36T6uMisFfAUeffTRxx57zF/cV4kBDqD9AZak/i3PV/vqYqjjKgWUArungALQPQTQAM4888y4mPLz89euXSsvhOoSsnsNMntvSZmDa995552zzjorHo9ffPHFMhJ3cGtfSCsArQB0X2iHqg79RQFKqW3bw4cPJ4REIpGJEyfeddddn3/+uV9/6X0j/1dpmuav39MJDqAj/H4WCCVsiJHK7tHocdtoQQKRlBg9zETUZoNslid70GdiQIccHgA6ZHfImiWP7nBTr6xs5c487nOaDzxINOQmnDG2ezaspTCbeU98bwc32sS9BpkJ2Nf/4hpC4oTkNix/kfF4I93t2CQQGKXc+9CkcHlPHZPStCjDBlhaoOcXhef1bcB84BbgFpde6bKfeuz7Li6wcZbhHq85R6Xsr2j2FM0+Nmgp65iUdXTK/krKPjxpHdbG7ElJZ0LSGZ90xmt2W3Pq005N2q1Ie0Vpb0yajuLmjTHcEsMpy7K0W9LG+C6tZrhF3TR/L40WabS1BLm+fSFZ+dvv0tmO7YsKrBljuAHzRhh0WDdsiPAF3tPzAoPldmQxjnFlOIsu5133GLAZj3QRMN4XIWPB9YEYF21iX8iOC9nzTAl+UTy8u4mQLiyNUBqjV6wefswUMnIQySNkeIzUVZD/XFCy7sNTmhPHu97EtJuXYqSZ8jAaDvI8TtJ5fTiA9o1FPBb1aNyjcYdJizqIOPxY0UaEdqB2k36ecOrf4jG4gMvD0nfwQ6UMlofbF31QVfVaWaFVXYSK0f94+/UNwIO6c5iFXEtUQIopAbS4g3XUYyPr+5m/2Cs3q24W4h+UJ3IsjHBxEMM0D8cb3nFp82jdPNI2Dk+njtjcdMKj/3vp2OpHeQDoosb6ysUcQMuuGLsRdXxP/8dR5SsF+ogC0tnZc70HH3xQOt4OHjz45ptv1nUdgHwk8xmon9ijlR/IANo0Tcdx5Mv1HhVZFa4U2F8V+OlPfxoKhSZNmvTQQw99+eWXftgGz/Vkr4K9fOIKQPccQNfU1OSKqaamRtO0IHqW6b18LffLw8kfhvxnb5rmFVdcIf8DRaPRvLy8jRs37tsuUR1qrgC0AtAdNgy1UinQoQIyptBRRx0lbx2EkFAoFIlEDjnkkIceekjuIu+BAPZmn4+G5S+2A9BbgCc89/sJr2YH71YvAXQ4jRzReT83G0Cz6L4B0BLQsBzhZcnnAkCHNTrKwnROfp1PoXE14TTD3Q6vEbA8qgPm9bN/Rjg9y21oaGB8sMWeAOiWvfgogJYYHW6NCOn7B8e7rNk4PY1jdRyRpscY3jEm/YpNJ1p0rIVSC8M4ym9BhzkOcjMWcxCz+aZoZlDHsB/HIJOQAzy2n2fnFIhTAKzMyJC+Sr5QUq60+Log50Eq2jX9lDnlXsLdlXRdzq7m7/roaqtUQA7rt6fnJnj8d52jZ24pDAa+snHL8d88m0QJGZnLv+TEI6SkmJxxGvn1b6M2TtJwYBpjUyhKIlcTkF02+ACADnUAoEWYDh3xJAZvtCZ6uJfhbdFrgY/DaPOBNTv4oXIA7XIAXVG9uqTIqCpEbelTr658guFSndZZiPVvAC1+v+KeELcR5yPB0jC1ietENbv8mRfOH1v/u4pip6q4ub5yiQLQHf7zVSuVAh0qINHAI4884j+VEUIGDx4cjUa/+c1vPvnkkzt27HAcZ2++gQ5kAA3gscceI4RMnTq1w+ulVioFlAJdK/C1r30tEuEuRbFYrKCg4MILL3zhhRfkLpbVMgRO1yX07lYFoHsIoDdv3hyLxaLRaDgcvvDCC6UrrryEPonu3Us1kEtLJBKLFi0qKiqKiIkQogB0X2sPDQ0Not96OBwOKwDd166Oqk8fVEBG3gj6zmzbtm3RokUXXHDB+PHj5YOCfPmZNWvWU089BSCZTMq99vzp8MgRDS89F87hVcj4zlnAPymuNtlRCQxragXQnDBKjNgGQAtmtM8ANM0NRLMV8QGQk3TrgdnAC/C2wwJsD64OqnEDPM8G3Ot/cU04lE9I/vJla7hfZbenjAc0L4TDMA6umRh07k6K7zabpyTtIzUcYKGmkQ5tpoMTdHjKG5miwzU62GD5BouZiEiHUOG7GnOQH7BcGxwzCYuKkd+CrFkOB9fZPJhTptvkNFjMtzRiac7rfQtLGC2xdQZeZ0PtDATn62WeFuLPR31sKaGzcnY1f/BYKt2ZAvJDxZ6eizAgER3c0tyiTTQnSYsS5uGrXz/orl8Vj68hY4aSglwSipCCUaR6PLnp9pK31n91U/NROqoSLKLzJh3JfHSR3tkhERXad3/2m308jUEJFDbjTOAlz014vKMBbBg2Uh4CUdczv1kZA/r2hZvKq9cUFxvlhaiv/e+/L706zabrrMrCMAsFwg86bIH0Pw/ozAckEbCb/6J5uBKbuHSUjelLX5lTO+4vpSWsqtipr3zVMTN3cd8Dupdi02fEVn+VAvuPAvLBbMuWLeecc87o0aPl200sFpP+AYSQ0aNH33jjjUuWLLEsa+/4Dw5wAH3DDTcQQm644Yb9p5GpM1EK7EUFrr322oKCgnA47H9Ui8fjEyZMuPvuuz///PP28Qb2dNUUgO4hgH755Zdzc3PlhXzwwQelK3sfB9BB0rGnG1ZvlU8pfeaZZ4488sggjonFYioER28p3FvlKADdW0qqcgaIAtLx2feg8d9h5P+RL7/88vrrrx85cmQsFguHw7m5ubW1tVdcccXrr7++V/ThlKLhpecDHtBp4BPgCQtn2jyiaywJkhIW9JBtA6BFr3+5pgO/VNmdvJt9z3c1W4sHdMwfTo0zGndE0pgKPM6H7KO658Jz+Xi2lMngG3wRwPXXXx+J5BIS6wGAFtQ5A6CZBqwB+5VJT0m4pUk2qpkOanKjTR7XLc39RonOzyssrE1ghHYAmrtC+/TZRnsAneNDqHaJ9nUpdvMAACAASURBVPS5Swbdip5b3MbTPChEq3VGPIPrg0w540zNMXRn5exq/uCxVLpDBfY0evbLlwzaFAxaRyhBiRh6tKDRGNWsT04kZv396SmXfIcMHknCQ/iLT6yAjC4m3/0PsviV0m36V9L24bo71mTDRTmSAoekV29L/A3e8vMs5BosptFR2+yDgQU8hDrlw+253P053RWANrHwtqbyqrcKS4yyMWz82Ecef/acHU6NjqIMgM4XrtAtkaD5nUremro539Vb0+7kb1Ol4O+69XtS2grZ3gEeu2LFq89Ujv9bcTkqSlFf9ZYjgwkFo3AoAL1X/pWqg/RTBaQnjeM4W7ZsefLJJ88444xhw4ZFo1HpAiXHf8rNzZ0xY8YTTzzR9Tn6j3ldZ+t664AF0NLrYtGiRaFQSALo/kgzur64aqtSYE8rQCldt27dhRdeWF5e7jNoPzFz5sz7779/T9chWL4C0D0E0DIslKSiMgA0pVSWFdQ3Ky0zyBhS27dvl1s91+tiRxn5qIsM/iHkHbmL/3Oe68lDy12SyWRDQ8Mdd9zx4IMPrl69ujPHOtnj27Ztn4/4RwxGwgpGKfV7izPGgkcM7tg+TWlm1CZAnsXixYtnzpyZl5cXi8UikUgoFJJ9B+QP5ne/+137QvrCGlm9SCTi69AXarWn66AA9J5WWJW/nynQ3gPaP0G/Gw1j7C9//ktNTY28q/D+BeHw+PHjr7rqqjfffNNzvayv1u3X+GX2INGwbGU4zF1+dKMJ2Aos3sH+o4nWaCBJYSkeVZlbkpGkRxIuSTncDI/HlpUhaDsOAN1rFIa7Lu7EWA5QkNTzdL0euBR4i2U7NnuAx5hn2y51cc/dv5aOTiteXkKp3VHP/i60pByIQQdNAKuAa20cm2bFGh1k0AIRXLjAYPkmoiJ2QatKDogInB12IS3HRSxgOS5yZBhcGYfXZqSdhcVYbe3n7XPKNa05g8QtGGojmA6K3O7QbQ4hcwYDa3Rdzq7m7/roaqtUIBAAuv23jd5cI78w+XPpRyzn3K/fHWNY9Zo1aYd52G//QiYfSwYNJ0PHEBIl4UHkkCPIfz96GGPf3bh9bJKNSYuQPg73ic63kSe/uLg8kW8hT2PRlDfWxv8DngV2iP4Flsvdnw0bTschOChsAwtvTVdUrCsutkoKvbqxD/1txbebUWFimItcl4eBjpmIGnwoQh7POvhb6FZ6p/efXsywUwBNc7ckiO2eCPr86tVG+fhXCqudsgo2tuafK1eIOxkPCiRMds/wvaG7uKWpTUqBga1A8HnsmWeeueSSS2SQNPlOGo1Gc3Nzp02bdt999/kvfaZp+qE4dV3v8PV5V0UNAuiVK1cOKAj7LyYwZ86cUCh0/fXX81uXHOF5VxVU+ZUCSgGhwKOPPnrOOecQQvLy8qQ3bSgUCofDBx100OWXX75hwwZ/iDXP9TRNkyMVdQdFdl/gOXPmyO95qVSq+3v165wzZsyQnWlmzJjBO926vI9t8P8L6c7pXXvttfI/UHl5+bZt2/xg3p3tK//92Lb9hz/84ZRTTqmuro5EIieeeOL69et3ekVN0+wOxv3d735399137zRCqG3bn3zyydVXXz1s2LC8vDx5FtFo9O677+4QXssCN2/eLLsaZYklGyWAN9988+GHH3722Wc//PBDKYIjpg7LbK+SZDF+6IYnnnji5JNPLigoiEajkgVEIpGLLrpIcn/55Xnt2rXdLLz94fboGgWg/eu4R3VWhSsFBogCjLHPPvvsrLPOys/Pl/+9cnNz4/H45MmTv/vd77733nv+s4IUpFfedrgH9NLXwqFcQogIjrw+gTs/TJyQRK2BoTqGGhhu8pjFI0yMMjHGpCNNOtL2RlvuCMMdpHshne0MDfcAzbRBMCIQxE4LYTmaTZLpwdSZAswRsZi/BDaK0MyfCbfuj8XwgBsY+L/yhmUrY7EcEiIrXllMmd4pgA76ErY2RApmA5uAFcAtNo7SMUhnEYNGLC9qe7ncaEyg5BYIKAdsDMx9Bu2T6BxJpTNDwPEdexezBuFyEBYH08E8Pm3sMLELQFkMfLer+Ts8qFqZpcBeA9A7PZDN40RHdIQsFBuYseqtI+feMrj+IBKKE5JDCmLk8InkZz8jq14fa2OaiYkJt1Lj7slDLeSaiHPfZ+TpPGB0TMcRwEP8N0t5lBsGw0PK5XGevZaYN62/RJESIXYEgH6vuMgpK2aVVb997LkLPmuqbTJKk+bwlDUsZRek3TydxkUk9K5iy3TMo3d6/+nFDG3ufh14QBt0WEIvd72fMPvzl19C2bg3RtVaJZVeXW1bAC1V8kl0lmhqUSmgFOhcAc/1LMv605/+dMUVV8joHISQeDweiUTKysruuOOOrVu37glIGgTQr7zySucV3A+3SABNCJEAum+++++HuqtT2n8VsG07mUw+8MADp59++pAhQ+TnNNm9IxQKzZw5c8WKFRIAeq4nbz7S0ba3fn0XXXSRpN77r8bZZ9Y7APrUU0+V5H7mzJmSPnf9RU7X9eeee+7II4+U/ry+M+/ZZ5/tU/Dsmopl27ZXr149f/78rvv4XHvttRLLLly4sMNy/JVLliwpLy+XFQjGtSCEbNy40c/mJxzHeeCBB6QP8s9//vMsAA1gyZIlkydP9qlrXl7efffdJ9XoPgeR7s+O4zz//PPHHHNMKBSKx+O+SieddNLLL78M4Oabb5bEvLCwUP4Sdorv/RPZawlfCv9j+F479D48kPKA3ofiq0PvrwpQSh3H8f/9v/vuuz/96U9lRxB595Y3yZEjR1533XUyjFdvPRwIFPtyWASBBhwHb2/D7M/0k7dqU5pSh+7QDm3SJjal6ptS4xOJI5OJ49LJqXpqmpWabmlTDPNg3S7XaZ7BiLQgvtytdBsEs3MAzaESi1mIUZQCpwFXAr8E7gEeEPYr4E7gLuC3Fh408BzQtHz5iliUx9davuIflJkdA2geIlsYawVfYrBCCmoAr1PMtnBsGsN1Rkw3ZNrE8YjLhIG0jrcGQgMWwNDSIZpkHKLDbsaj3PcrbwMcO3CIDkBqwXm7yB+8IkHoHEwH87Qpql3hMqfcNxieRa5pX86u5u/66GqrVGCnXLgXMwTbc/u0w0M8RzSQHQ4xMGZrelTSrflyx4Rly8f96IekcAgZRMiwHFKQQ047mTzyX4e8vX5qk32UYNB5JnLTiDcjkkRM4w7LpwDL4XrgnRbAuOOzJQC0QzuKAQ0ProE7b01VVKwvLvJKi93qqj899cIvd6QvMvRzbf0025xu2ZNMt9rwRvAw6OgHALqlowPN4RGfGe/HICLC8ygchlPhud8E+yPsVMNyFI19Y3iVNabcqap+g3tASy9x3+tZAej99blBndeeUcAPmybfbSmlpmn+5je/OeOMM6qrq+WrHyFk2LBh11xzTVNTE4CsPmq7Uy8FoBWA3p32o/ZVCvgKGIYh05qmGYbBGHv66aevvPLKgoICeR+Li6mmpubiiy9etmyZ4zhdQ06/5O4nTjrppJCYur9Lf8/ZcwDtd6gBMHbsWAl8L7/88p26PwO4++67CSFZwFeGkL700ksfe+yxLFn9wBdr1qyJxWL/orpjxozJyhP8xFpbWysbzY9//OOsbH6joZTKIEqy5rFYrKysrKKiIi8vTw7v+9e//jXoCi7/1wIYOnSoHHhhwoQJsjQ/2/z58wkhBQUF+fn5eXl5smRCiIzpkVWTrhdlKJJLLrlkyJAhkUhE8v3q6upHH33UP9MLL7xQanjUUUf5K7sudu9vVQBaeUDv/VanjrgfKyDfdvyPbU1NTffcc8/hhx/uv/BIJJ2Xl3fggQded911zc3Nnut1//tfZ9I1NDTIf1IAc/CBgd9bmC8A7i/BE3OBq4GfA7cAi4T9SrDdecAsD5PSdJROo0Hg2AvpHgHohE0MOsTyJtrOcZZ9rG5NNcxTDfNU3Zmuu8emvWlJ98wPm8/90rjTpOuff/75aE48HM5Zvnw5pW7H4kgAzYEOBXP5qIMt/MuG+zl1HzPYWSlWqrF4moY0K542444Td70cl3IGzSEdC3ks6tE4RQ5FWGLodgDad4LmCeEB3eI33QFm7ZpBd29rNy9Q1tHb7xUk11npYGZZjlyTlS24GNwlmG7vBh7c2n/TWfL2bLEX+XJ3imrPnVvWsJCDiMF4uHObx5mJmmLAUoqhW5uKEqkZX3x+wc+vGnrUoWTUIDJyMCkeQ3ILyBU/J2+9PzHlHqWxSSnUbbIKdtAxGg4FruHuzzZgCgDNg+l4LhwXEkCLb0DBXyyVADpRUfFecZFXOMoYV/v8a6+tBJ4Dexi4FfgxMNOw6wxvlADQuxgAmnUjBFBve0D7AFrcT/htQcTjjht0iGZOBm4H3mQuljSgsO7NYZX26DK7omqNAtDBdqHSSoGeKZDVydjnOJTSRx999MILL5Tvy/K1/cwzz3z88cebm5t7dqysvYIAWrpkZWXYjxelB3Q4HFYe0PvxVVantjcVkL5KkizLe4thGJqmvfPOOzfccMPkyZMlhZNYr76+/oILLli8eLFPFHe/qlOnTpURDna/qP5SQg8BtI9cJfeUPW4IIX/84x87I6G+A+zVV1+dJyZ5IWfNmnXnnXd+4+vfkORXery/8MILQQXlt1MAF110UTweD4fDoVDonXfeCebxu11blhWPx+WHi+985ztZefxq/OlPf5IVCIVCBxxwwBNPPJFKpTZu3CjhxeDBgx955BH/NGUjkzHLZSskhJx11lmycFNM1113XTgclr3CJQoJh8MSEP/4xz9mjNliyqpPF4uO49x77735+flFRUXf+c53nn322WB9PNc7+uijI5FIXl7elVde2WcppwLQ3bw08uLK9hBMd9FC+tQm/wvNnq4VY8xxnF70bG1fYT8Gjh+SfvfxZfujdLjGcz0Z6b7DrWpllgIy6hEV0+uvv37JJZfI/yCyb00sFpO360MPPXTBggVbtmzxHzKyyunOYgBAA0gzfMbwLvA+sE7YWuCfwtaJle+Bb30P+F8H3zJwQJpyp8J9zAEFsBY0M4eHYPZGmGyojuEmKzJZibAiCyOTGPu5edoO3Llde2PVq6tDkXA4J9awfDXv2N/hRAVzdsG7/jObehrAdNNm3jZ4z+up6zzMSrr1aVaYpiPSVlHKLNKtMaY5yjRHWeZwoIK6RY412nVGOE7ctEl7A4YCBQxxzqm5RSSqZogwhIAwQNpaGMgRFgN8k2vaz/0MbRIMOe0szBBmIO0s7EEaj0/tImZzthjRGdEZSVOSZi2mU7JL5u/YkqCitOx5KE1DPMxLW+MrWcQ3jTve7sxYVGu1uMbiLYs73bEXMvD46SkhF/e9FWaAy+V3HTC6jGPDs1Hi8cud7/KhKcNGZt/e+t21xd8hm+NOjpKzLAOpQ+IzSUQ0iRyKCEXEQ9gGPyOb+/5HLB6LgxiIplheszd8mzXGwGFbtGP/8tfRM2eRgiEkbxDJyyND88hhB5Nbbi/+dMuZ271JW8wp25OzgbcBBxaYIb77iE4IwhkawgO63c9VAujbmngM6CJn9AhzQs2a15bbgAVzA/AScGkqPc5wyvjNATnGro5AuJcBtGDZ4rtL2PVyPG78axblkuYnzaKEMQtYBlieiyUvoqhm7cgyWlTiVlXuMoCW3zslXws+hwfTPn3r8B7ZfqWMXeB/SW2foTtreiVeZPAs+mlajvcgO0jJgIfy4a3rec+e62R/U3mU7sz9Lq22bffswVW+gcrnUvm0s9N58MRt2/bffLvTqGSenR7Of7WRH/hllaSkVmBatGhRbW2tZNDyjfjss89++umnfYdoTdPkEEq7RHNkZvmCuWLFiu6fV3/PqWmaaZq33357NBq99NJLASQSiW6elGx+PWgM3Sx/r2XbzdvmXqunOlA/VaD9vcgwjJtvvvmss87y+Z70VZ01a9aiRYveffdd+a9TRnHowU9s+vTp8nW1/aH7qYY7rXYPAbSkzFKmTz75RF4PQsgrr7zSmXaWZdm2fcstt0jsG41GJ02a9MILL0jgkkqlhg0bJsuJRqOrVq3Kqrr8FzV8+PBoNBoOhwsKCtpHgpb/+bZt2ybzEEJ++MMfZpVjmqamaevWrSsqKpJjWB166KEyUrP81iH5BSFk3bp1wf/xspzFixfLSoZCoZtuukmuTCaT9957r1wvo5F+73vfu/baa31Z5D+JrJrsdFH2NA9yveCjofTFlv/UZZSPvnlHliKoQQh3ernl05ht2x999NGyfTc17Ma0ePHihQsXzp49+199C27cA9Ntt902b968W/4/e18CZkVx7V/33rnbMAswwzYr+64IomwCA7JGXKIx8UVi4kN9auKLxvyjSEAgIpoIGBP1ueW5xBcx+kREVpVFEYgIJm7PNa4RGGbmrr13nb9VZ25Nzd3mDszAoN3f+fqerj5VdfpUdfXtX50+dfvtDzzwwIvttr3Et61bt27btg2NwX0/2cu8YRjS/+p2YQWimkuH+ZbLiBEvHA6Lx0Ftbe3KlSv79euH3spiEA4Gg16vd/To0ddee+3hw2zNrtZuzQFo27ZN2zYpGIJsqtpUtUCjoHGnxAjAFxSeicF5UaiI0aLjD0BzyEZ2p8Xl0Tg859YgT4M8Hh+g+pPI9yPwFxvY4sDEQ9xe1/Ydr2YFoG0wOdmmFquntkqpFY5++Oori9Y8M+25DaOefLb7xm3dNmzt+vwLJc9v6r5xU4+Nm3pt3thr86YeL20ue/+d0+sOza6rnR4OTQyHx6VSKHxqOHJqJDaa06hIDOmUSIxT/OQIo+ESndx4CgUy7kVRuTDJ1YWU4ZxODimMGpRTkOqUUXXKKAvONGBy3BwbUkc2qEMj2hBOgyLaoKg6KKoO4TQsqnJSTooKwhQuENGGCQppw0LaSZxGhLRkiqgjkiikjQjrpyCFjFPSkz4q1ESjQ3qCtNNDghoTuWSmctooPWyOCJsjGtThB0L9Pj9cFbdPUeyT4ubwmDkkqg+OqoMiysBMFI73Dyt94+YAzR4UNwfE9P4RtW9Y6R1WqiJq74hWxakiouVAellEkCQf1asl6hPV+yQOK6N6ZdQobyK9kp/qE9X6xfSBMX1g3GBaqdbAqNYvrPSOmQMUOihiDYhYA8L2gMNa7zqrOgyVDdC3jo5qsM76KnTZBx/Pv/zyPiNOyiOEFPlIXh7p1ZvMvZI8tf40gA+oEmKhbxQ+3rCvDth6enYitoTN2OZbMw9oo0epMrj6rdde5LNHWhjo82BdEIp15/E38k8gANq03Rx9ZgA0C+wDRKVdFH2Sbi+x4AP2RQYHoMt7v92tHMp62X2r9jd5QAsLpY9i33gap71VVd25c2emv0hfR+e79dZbb7rppkWLFi3NYbvpppvw/9L53z2/pjXbpEmTJkyYUFNTM2XKlEmTJk2cOHFS5m0y37D4KdImV4gyJ/r+rLPOuvrqq5csWbJ06dKFOWw33njj4sWL165du7n1m+g1rWXC4XBrswinriR349zLQSg507t57uUcmST+T/vrX/9aXV2NXw+j41TPnj3nzp27f/9+/Gvd2vkbvBz8g7djx44j0+1EzIVAx8aNG10u1+zZs3F6I/fGFVMgMp6Qibc72EYpfeONN1588cV9+/ZlGofl9PZ+k97qbMfVAm3Vvtu3b9+5c+eLL7740ksvvfLKKzt27Ni8ebNAALBH7dy5c/PmzRs3bvzDH/5w1VVXdevWLRBgawIhaux2u7t06TJz5sxly5Y98cQTRzCw1NTU4Etr7vfyEdTSobIcOQCNl0EpXbt2La4EVVRUdPjw4Uy2o5Q+9dRT+LQIBoMjRoz47LPPRCHozyuciz/55BNhJlHgxo0bsbH9fv8vfvELISAYHCrfeecdAT1cf/314izOSyiKYpnW7NmzEQevqqp677338AGvquovf/lLl8uF6uFkNZaJM94ieAgC3Pv27cMnwZ49e/C6/H7/qaee+sorr2Cgq1dfffX0008fMWLE+vXrUQ3h3i+mSmT1ZB6f2Qi7o+ZJng7hcBit8fVDaM+ePWIyWS6kI/BoGQeAzr0tKKVz5871HKfNexSb+IgBQ/Fi07ftHm/bti0zbWm4GgA2AgoUFhamlWzbRPQQcbvdJ5100nRnS7HAzJkzZ82aNXPmzOnTpw8fPhw/8BRN4PF4cFoRHwH4QVNBQQF+NyPEKioqcr8fhaQEQLNpwUwANMLQHNSpBXhFsX4ThTFRKIqx1cPy2soTs63KUdmSaM1WR9QhGLXGAqwG+AoAFBWIi3gCZNvLL7Iws6kbA25stgyaaWMsWgAwdRUgfvd9N3t8xOUhhSXM9oEi4i8keZ2IN0h8AeLzMwpwYu+lhHTtQgKBdBQkwQLSq4qcchqZMp3R5GmMJp3JaOJURmdMOSKqIWccGUnVTaohSEk6jB1P5swh//EfJfNv6jP/170W/Lobp5IFvy5ZuCCVui1ckIYWLOghaP6ve2QhISaY+b/usWBhT6T5i3pmprL5ixK0sGJ+E1XNX1jVeNgokKWQNjnV/cZFJTcuKlm4pPSW28p/u7L66Wen/u+zNc+snfLsczVrn69Z9/yU9RtqMtMZa547+fEnqzdsGfn+x987WDeP06UH6y491PATTpccamiJQnMPNdEPD4V+KB3OrQ3/uIlCl9aGLk0c/qg2/KPa8MXNiScysXm1Df+xYfOYDZsmbNg08bnnxz/73Jh1G89Yv2XSuo1nMNo0/pl1pz67/pRn1g/7y//2e2LNkDXrz1jz3Jw1z/5w06ZfPL9u8RX/fmZRJ3YT5XlIMEC8HtK/omT1f6+2oybEOdCMYXA4AI2B2FPgZ4ZM23H4/e2xqsqPevWkPbpFBvfZ99oLHLmGv0H8hrgyTLELFMpGKgXcHT0GdMID2rSJZbkty23abp2SiE0iRqVt/ALgRQsOIgC99QWorH63Zy8o72n3q9y/ewcGCpKGs6wANACsW7eODWKBQKa/SOL1RDxosjM+ny8/P//I/tIEg0F82OFXPtn/LeI3o9mV+WacFa9+LV6O+I+K/7halD96AZ/P16dPHxn3z5GfNm3auHHjFi1adP311y9o/bZy5crVq1cjtoLeFVn2+J2uwTd0cM4ETcqgNr4goyS+uopc4gbDCNGPPPJIRUUF3iniv26PHj3+8Ic/RCIR8bIvcmVhUBjbBQHoVmXPUnIHP4WXibDD+PHj0eC4b1Fz9JqJRqMnnXTS0XfpY1+CuMHxf/6xV8Cp8ZtqAfEgkB+XGP8Wn/h44UIMD91ut/wEx/4ZCATQq7XF+1EWcADopGcHpZTIBkrlLdP64x//iC1RXFyc5QHw1VdflZWVoWRpaSkG0KCUikndUaNGIehDCJEHU0qpwrdrrrkG+0FxcbGu6wKcRa2wasMwdu/ejf8t3G73woULk3S2bfu+++7D/5GEkMceewyDVtu2/dxzz2Fk6i5dutx///349E0CoL+eM0cZj8fDXs4VxTCM0aNH+3w+v98/evToTz/9VNSIT2g8xO+hxFxliwA0aoVu/Gmt+tZbb+EKhIQQsbxDWkmhz3FhxE17BJ8kHBeF26TSI1uE0DAMXdfff//9qqoqtNuJtZcH4nbV3O12Z3oJbJN0+QmEFyLmxtr1unAmz+/3H7Pq2vty2qN88eqIhSf9IfDxDaemUQDHSXxFR8NOnz79CG5zCYBudH9O6wFtU5XacQAF4C2Au+PWBVHoHYOARn1sdazmaO9xP1TBo7I4ACx4K/viHnw6rY4q3wfYbzGPf9ANYI+8ANm644X0RhMAtM0B6MYw0boFb7/70UPn/aCrn0/c5AWJP5/48klekLj9JM9H3JxIHnHnkUA+izYQyE9PviBxB0hePoOwC7qSgi6kU2cSLG5EtH0FxMuLzQuywpsoIPFyuuADJE+Qn+SlJR9TNZnSSmJi4rryvCTPS3xehrAHAySYT/IlKgiSJgqQgkzkJ/mBJmLlZCZZEvlgoKnSTLbNlh4kgWD6FsmWK0Mj5pSlEwlwCuazyQm0od9H/D5mSZ+P+PI4ccOylCTysVwl3UhxFzahUVjcREVdSCuoKynqSopK0lBxCUlPpaQ4MxV1JQXFpBPv4f4guy6Xh83BBPL5TEyA7T1e4g2Q/EI+PdOJ5BexXucPkE6Nq+CwTpIfID43G9U87Pq8pZ16ffT2P1kMaNwSHtDZAOgY/P42rXf5p716QM/u4UH9du/eCgB1APcqkWmheFcdPNIXEh17EcIEAK1TYtocfbbzFBqoVXxhbSLYfwb9QwviAoCuqnqvZy+o7JEVgE7YMul37969uByLQECyPNpyBEfwwZT0OMtSbNIpr9dbXV09efLkKTlsi1O2m6Vt0Tdiu+GGG87/7vkTJ06cNm1aDiaZMn369KlTp3o8Hlz6Kfd9UkPkeCjW8slRXhYTWK08xS7m2jMx4oqEgEhJZVBG/E1K/Q8s6yPzOM0vp6S+CLhcLuHAga6CQl5GcJ566qmk+y7LIb7tYjnbt28XfuJZsnwzTqEL8/r1610u11lnnYUfSef47o95d+/e7fP5RK/IwqT2k+Obgs2NboK5aCK6mcM4Fshiga9DGoiXbhxj0wr7fD486/F45FHO7/cLb2iXy1VdXX0EQ40DQLcCgMaBzDCM66+/3uVyBQKBiRMnYtQIND0OiOJj5x//+McIr3ztX/zMM88I3BkA8OtpBN3cbvfo0aPlwRQr0jRtyJAh+F8NIzvjUpWimbFA27Y3bdqEYoWFhXfffbcQQB/hSCRSVFSEE7DXXXcdBg4DgLVr12KugoKCCy64AL8JEugz6gAAc+bMwW+IBg4ciCX//Oc/xydrfn7+22+/jYmqqsp5xVyxmBbODkDLly/rL/MbNmzAqxgwYAA6a8vGlyWPL4+3seMB3apWWLZsWQ5fcC695ZZbXnrppe3bt2/ZsiWLU4M49eGHH9bW1nbMpog75AAAIABJREFUftIq+3yDhfE7RE3T3nzzTdFw3wDmscce+93vfjefb0taud16663XX3/9RRddNGPGjClTpkydOnXKlCnTpk2bOXNmTU3NpEmT0E8a/YmmTZs2ceJEHMyTYOiCggKXyzV48OBPPvkk+wictoO1CEBTDL5BNaAxsGuBrtfgu2HaXaWFuhUwzXzTCujHI0xqRpibulUWqtjPYWgXD/naXYnWANwP8KFFWUhnizIA2pVHXty6M61ZeCIPAk1lAPogwKba8E8Px6ZteTnwl6fJ1m1V27b32bq9bMuOos3bO23Z3nXz9u5IL77Sa8eeqq27Ktjhtp4vvFyWQj23vFyy5eUum3d03ritC9Lm7aWbt5du2dFty45uL7zc84WXe27c2uPZjZ1vXUFuXkZuvqU19Buy9Ddk8VJyzTXk/AvIzFmMZsxkNH06o2lnNqdpZBqnqdPJ1OlkzjmMxk8mvfuTws6kUzGj/CISLGSUX8RTOjeBoYVFpLiQUUEnUpBPuhSTki6kcyHjOwUS5Ced/KSTj+T7m4gBysFGCgaI39uMAnlEJr8nAdfmMbdZzxGQm3jcR5TxCOrCLHnEwynPw3T2eRn03CnAwfp8EvCRYB4Jejn5SDCF8v2N9izqRAJeRo0yzXH8VKQ+P8DaoriQ2TbgI506Mdi3U1GCCkmnBBUUsZmSRiokBYUJHhOLGdCcnjqTabMbacoM5rl/5iwy/Ttsj+lTZpAzppHxU8nkmaTmO4yfeCaZMo0MHUbOmBDsUUp8LvaVQB4hPuIPugpPHTbmlkW31x8IN32WIAHQiVtVYNGcsYBG4Q/Ljd7ln/fqAWW9YuW91uze+S+ATYr6g7hWrUIQJ6IEBq2lLnOaPeU4TbDplK2XqFBf1O4eo2MAbmJx+S3LwOj0JmzfAlVV75X1TAtAc+OgB3TCcKm/S5YsGTt27IQJE6Zm3hAOnjVr1qhRo/AFVaxGgDOj8t7v98trleP7Udr33tREl8slVjhIPfvtTMFFd7xeL6KoWWC17Ohqfn6+1+vNfXoA/SGyz0xge/n9/kwIskDTUG38AyO3IwLlckp78KhGkn0wMVN1ArhJ7cDoS4F7UWaqocQcwJw5c8S7duoNmJSCr8mo1bcKgEY8Ydu2bW63u6amJsksLR5aptXQ0DB8+HB5LMrEH7FDD/Zz0atzYXw+X1FRUWr3EB0vez8UYseG6VDKpL1knDFNe+roE+UByuPx4MMol97SJuNYcXHx0KFDJ/HwUxPbYps0adKUKVPGjRs3fvz4mpqayZMnjxkzZuLEieeee+6kSZPGjx8/Y8aMSZMmjRkz5txzzz311FNnzJgxZsyYUaNGsdhoRUU+n09A2OPGjfvggw9kJ9oWb0kUcADoVgDQOPobhnHppZeiU/B5550nwhYLpBUt++ijj2KPd7vdN910kwBZEDU2DOPLL78UEwiI/4o2Q6/hTz75pKioKBAIuFyuDRs24Nm0z6pNmzbhEBYMBh9//HGhCSp8++2345KJwWBQxI26//77g8FgUVGR3+8fOXIkujbrup6UFwAmTZqE/yTOPvtswzB27tyJ1+Xz+R544AGhs67ruE4awtByOTIv5I+AefDBBxGArqmpEWtBHEE57Z0F7eMA0K2yM4Z2yTELLmWDn85l3zvQc44m7SBi8iTWic4fjUlxzMQS0A7i8xT8ohBPRSKRf/zjH3Pnzq2ursYgg/hq5HK5cFnauXPn7ty5Ex9yqSNzixq2AoCGQ2D9zbZvV2BYFIhOg6ZZYBkFltkBAWi/CkGOQftNKIrEBgEsBtgCcJgB0Jy6lHYhbvLiVuZklGHDVQgTALRNAd4EuCVijrWgTKM+RS3S9TLDKNeN7nEjGNN9MbNTzCiOmIzitMSAnhp0Y4dGl5hdmkpRsyRqdYmYxWG9KKx3DuudI0ZpxCiNmt2iZreY1TNq9ojbvQzoHTPLdOhnwjCDntwywXADhhv0lHB0pG5MpPRM05oSVybElQmx+Bmx+BnR6MRodHIkMqmRwjWRcA3yoegZoegZkdiEiDZRtaZGzZr62Jl1kQvqYnPrYnMPR394KHLxocjFtdG5dbFLGEV/0hD5d06XNYSv4HRlKPJT0/p/Bw9d8equM9dvOHX9htMYrR/Dadz69RMYPT9x3XqkyVtemPWXJ0+7Y1XFTQvzl/ymBGnp0m6ptGRJKdLipaWLFndFWrikawYqXbgkQYu7L0yixlOZ8rZR+tLOC5d2XrSkiRYv7rxwYadVq6qefHLs1hfnrFtbs27tJEbPjV+37vR160Yn6HR+ePrzz4/dsOGMF7ZM2bhx4nNrxz23dhyTZDT2+XXjn39+bHbasWNaff11AEsPH776cP1PDjfMTdAlhxs41f+kruHSBM2raxDEE0M/rmP0oyYKX1zH6N/qIhfWRb5bFz27LnZWXWzmwfC0rxqmHI7OqFdmHQzPUOzzI9Z5DdrZtbGz/xU6/6uGiw9HLwsrv/zq4IIXX7j0sssqhw4jLjcDwYmbnDS834P3PPTu399nkdlUU49pTbckB6DZx3PNkiQMugmAZh7QFeVK335//dv+bTosiagjVOikNnN/xk8iGLDbCjpOADQPGJIXhfyQOVCjVwI8DfQQWGDwiNiWkQRA/715CI6cAGg0auo7jvyXXl4e2bZtPMQl2oyUDYuyTCsej4fD4Z07dz733HO7cts2bdq0cePGRx55ZPHixbk4K8xI2XDWFvfTTvwNJwXQ8Rmnoidn3nAae9q0adOnT5+Zsp177rkLFixYsWLF/Pnzc3ENv/XWWxctWrRs2bJ77rlne7pt27ZtO3bs2LVr1+7du3fu3PlK5u2dd97BINHyEoL4Dx8/ik1Kz34oepwQEympDMrI/4vEP6Xa2tq0sVZxoZRXX31169atInzqli1b1q9fv3z58sWLF998883Lli277bbbli1bdssttyxZsmThwoXLly+/6KKLZOcA5N1u95o1a5qGrpa4by0AjT3hiAFotCtaryUbgzy4tZbf0cpt69aty5YtW7JkyW233Zb2vsOvOBYuXLhgwYJFixYhsyDrlkMo+FaLyINl5rnI438GlyJDk7bS5ydZHC2P38xg0yxcuHDx4sUPP/zw5s2b0415LaS12PGyCOAETHugXvJNgaOfYRjxeFzTNPkUADz77LNXXXVVaWkpOqSi4+xtt9324YcfYgDeLPpnOuUA0K0AoNGIlmnNmDEDQcarr746NcQE9pXy8nL8hmjo0KHCo1luhlWrVmEhwWBw0aJF8iksYfXq1YSQ/Pz8Hj16iLNpAejly5fjt04+n2/Lli3yoAkAQ4YMwYp+9KMfIcx37bXXulwudIuuqalBcFz0NmRQB9u2hwwZgqAGris4adIknPWVdcZHu4BIkmySpI+4ltYyN9xwA0Ysufzyy9PaobUFtpO8A0DnOFBix8D/FtgW+F8wyx6Dg6Ow3K9S+XZqXKfY9rBAR76dj+x65ZVUxQK2qb00Uwq+wOOsXqoChmG8++6799xzT58+fXC0wb3P58NvU6ZOnfr444/X1rL19MSGQ7pcoziViUkLQFtgcTIsthohW36Qrwj2PsDdFr0walZFDJ9uFplGkWUGLCvPtAlz1jtOME1yvdStg1enQZ0WqrSLCZWWeQ7AZtA+B1sTAPQpp55C3GTrK2tNCHOHwlQLoQc0gj0Adghgo2rPVKFrRCM25AEUAe1k04ANeSbzVSS6nafZAc0OKDSgQycKnS0oYsFnaUCDfIkCGjDiELlXgbw49SDxMLV5CJ1rENAhaEK+QgMWFKkQjFudFLsoBypgQW/tAoBeOpTEzWK2fJnVVbG6xs2SuFkS00tjeveIKqhnRO2Jh2GtNKw1guBhvWvM6q5DlQ79FRigwIA49IvT3nHaW4E+KvTTGQ1AMukAkw5CUo0BkXjvULQqHKuOKX3jaj9F76/ofWWKGX2RImrfeqU6pPVX7CEqDFPsITFzEKchcSOZYvrgmD6YLdynD45obOXDkJ6FhoT0BLGlDptT46ks2dvyVGK1xiExY5hqDo9pQ+sj/evCA8KRQbH4UE6DY2rvmFrFqTfne6P1VH2QRYdrxtBIrH8kNigWH8xIGRhXB8XVAdmpIVytmYNZdnOwZg7UzP4JGshTBmvmYN0cJtFJunlS46E1RGc0KEEDdGuAbvfT7T46rdZppWZXqFa5YpYpZllE7R6Kl8b1XnGbLVoYsysjtLLBKKtV+oWMMzX78h3b5vzs8qKhlaQ0QAp5dI7uvckV13V9YccdFL4AiKhKyDQamkHNqTclS5HQZ2DzQ3YMfr/c6F3xUa+eVnWlNezkJ19//4911qQY7aGDl8UISg0TlBaA7iAjGFdDAXcM8qIQCENBvT4W6CMAn7JLBRaexAJoBKArPyjrAeU9oV9lEgDNF3DM6gGNr0b4jyvLNL+iKJqm4X/+9A2SLlW8srbq0S9USlfkty4NH+X4bxmx1FSMVaTgf3LxlpdkLLEaXiaBJHlxGA6H0/YNTdOETwmGSxaIsGBEXRiITxxi4a3qGEKfo2RwauQIuplhGEm5MGDmli1bVq9ePWTIkKSwaYSQyspKXLFJGKpF5dFE+GfvW+UBfZQANPbSpA7WorWPgQCqdGSrdB4D9U7EKjRNE6NZW+kvRloMKhCNRsUglgvT2odji2rLL3FHzGMt8sCFz3FRO4aQra+v/3qCJMA38bL54x//eMuWLRhNwTItEYxB5M2RcQBofGrIjZgtBjS+w2PsZkLI1xMjck48axjG7373O3TX93q9YnVIbKSDBw9i2wwdOhSbs6Cg4MEHH5QbDEel66+/Hv2sv/e976VOR4jwT7quT5482ePxBAIBt9u9d+9eWaXdu3cTQjp37hwMBp9++umtW7eOGTMGV07z+Xw/+MEPUuMUi2Eau1dZWRlGvFq2bNnatWtxbas+ffrgvwpVVRElwUoFdCjrIPPyZbaWnzt3Ljp6fz3P3Nq8x1Iem9XxgM7F5pTSpMjmLebCv2u5/2lrsUBHoINYAEcPebg4oXlhVRz5xWGLDA6tSWKIaH/yySfLly8fPnw4fi3r5xt+DhYMBi+55BLxuEF5wzDw2SFmB2WTJlWRerh9+3Z8kAGwGNAm5QTUBMsEwwTNAoVCBOAQwFYKl6swLMoQzAADoM0Ck6PPJu2YAHQn1ayMxiYA3AnGO6BTsBrdny2g02dNJx6ybeezcfMrDumk2oZDXZSDPbYO9tsAd9fGe9vgAfBrJlFUYprEpMSwiWqRmEkUkygGYxgPeSZDmX0Riy0gFgeJKIlTdhijjCI2CVuNxJYasxvTMUuDTg5ECIU8FUhryQZPg07qNWICscFjg8fiZDLdfAymZ+SXCFO8OrvGYMggdQrzGBUU5wrHuPI8uHbTrIPO+wDuVYsABAH8oTgB8AIrzQPg4kQAGNkJMrll0pZpAEkiHYiesIPQ6sRiVHCZ4DHBY4BbZ0weNgffs5ZKIpuZywMQAPAb4DJYdszixja1wZWFGmKsW+qUd07ePxWD9VKZVNOTgVyq6VJN0ows1ttVi2h82skEtw1eCnkG9SpWUIduBlRFzd6H4v2/DA/59PCwf3512h2/J6edStyElARIjwApcpN5F5PH/zLuo9r//Eq9HeAfFnyKUSWAjTaS+3PamzIdAL3qdg0XIayuoKee9j9vfParz7WuUXYDEh6n3sf8nWV8+UQAoCPgDUPXemtgbeyHAHvANICamh6zgMWkpwbs2AK9KzgA3QP6Vby5e7u8CGHLAHR666akJn1khrih/JSReZFbvHckwXZCIAuDTtbiXSOVSVtj0jRwaq4TOgVxEAE3pzLZnUJEK4i/DakliBTEU2SAONV0Sb0iU2viKzMqn+S3JP7hy63ZIi80EZIiJZVBGVk3fPm1bTsXDEvgSpZpKYqCBjl8+PDatWuvu+66OXPmFBQUuN3uQCCA6LPL5TrllFOuvPLKNWvWfPzxx3K9OfKongNA52guWQwXr5JTMvGi5xwBk6nMLOliKi6LzPE9Jd+kmT5tEYPDcWTEIIZDvXjlSb3xc0lJHRyObytg7WLMaStl5OeC3BUbGhrefPPNCy+8UMSHCQaD/fv3X7Ro0eeff46DM0YSPhpNBAAtP02OpsCOn3fq1Knowjt16lThTykPNdkAaDRTly5d8Iny0EMPJT018W1/wIAB+JCYNWsWWkRVVbw9sOWWLVtGCEEgOBAIiMgYKIx/AqZPn+73+79eymDFihVyL8FJGOwruq7j4m8IQBNCPv30U/liFi5cWFDQuKTLggULUCufz9elS5c777xTXD/Wi8CH+GuIFWGMG0LIfffdN3v27JKSEo/Hg98N4bWjbnKlWfgj6B+itKFDhyIacu+994py8JEsQHNkWov4iNLahHEA6KTumsWq2LhZBJxTjgW+JRYQ/5+SHsaWaX366acrV64cMWIEfoySn5+PgwwhpFu3bmefffbDDz8spjaTzCXGT/lRlSST6VBV1QQADRbDnanOCPheMyFmMfT5XwD7Ae5R6fgYLYhZnrjl0u08RhLs2AzfkbEe5GXEJ/VsG6VwfdwGRVDVG9OGgnELwGtghrnTIDOVBdQC69zzz3F7yYvbNwELNyt939/MUjY7YwHQgwDrFOXiulgPi4G2TcAoq5Gjohrbu3TwJIBdge26MllGoYSRhPDKvJwLq2jtHkvIlEsuP3c+k4ZyCXKNcnomHsuUz8olpPKy5InIy1eUhLCnPUwrj4nZLx8Ny2Y7BNkknkKN/RB7Yw77w2EC0LlxsoGj25Sh5PmHlS5fRvqF7en/Cl+4eees/7yp50mjSX4n0q2EFPhIeSn50ffJQ/eSSG2NGRlbf3hayFxiwSaADwCYY28OGzr0Nt9TsFT4/e/ivSs/K+sBVeX20JPu/Tj080Pgj0GeYhPF9iq2N42hjsmIlKbeHMY6BUgM3GHwRWFAXfz7AKsBvmRjEQWOMccZp8MrCEB3h/Lu0K/8g3YCoHNol7YXEQ+1LEzb19qBS0Q7ZAFWZENlug5ZJlNRsgyWI6fIfKZa5HRZ/njxmfSR0wUajq/MOK8vBCilDQ0N99133/e//31CCDps4V+1YDB4zjnn3HjjjXv27JHxHZG3VYwAoN1u90svvdSqvCe6sG3bRxOCA3vXiW6E46W/fG8eLx2Opl5Z/9z5o6mxg+dFjFHgZqgtBt8AgL/+9a9Tpkzp3LkzxmDwer1jx47905/+hLna8NKmTJni9Xrz8/OT3nnbsIqOVtRRAdAAoKpqQUEBrtiQCkDbtv3www8LCHLDhg3YxgJcAIA9e/YEg0EB7Hq93r1798pmwizdu3fHBShXr14tsie107vvvltZWYliXq83GAxGIhH5Bps1axZG58CYU/hoHD169GuvvYZxn3F2K8n3XrhX27aNTnaEkDVr1uTn57tcrmnTpgEAfjYi15ULL19mLjyqh3+GKioqEA15/PHHk/IqipI6GyPrkyTfroei9WUov11r7AiF40QILifiANAdoUUcHU5ECyBMjHtd19etW3fuuee63W7x2QoygwcPvvzyyzdv3gwAkUgky7uNPAwKPkfLqKqKoxl772oEoNkn3pw0EyLc/fl9gCcsuDpsVcVsBmah96uMPrccguOYwD2okgEunQZVu4dpngfWOrAamMsg8whk/68wwMjM2TOIm+zZuyemZgC/GNZjA7XBNtnaX3BzXD89pHTm/sIugQnKAFMCgPZwGFrsm9yEZWG+vBgHoDNAfrKwqK5VDJaQKYtcfu68DFZmyiXXmElGTscy5RS5hFReljwRefmK0iLOSYlp5TEx++WjYVMR56QUuU2z8I1e/JSo4AfopZjd43qlZg5UtIFhpXddZPiOvX1v+wM5/UzSqQcp7EHc+cRfwADoH1xA7v199acfnhmPTmCBRCIVACMALgR4nN9ZhzJ/gpA0jDWHnhkcyxFZDVbdEUUAuqIXDD3p7o+j8w4BiQBRbI9i+RkAneQBzTyjpTDQOYDC2U3dtmc5AO2LQfdabRzA3QCvA8SBou+3yXgZgO7BAOi+Fe/t2tEuHtBJbXBsDsWDLAtzbDTpILWgHTKhxvLccxLoIOsvGzNTUbIM5pVTZF4uORMvyx8vXtZN1kFOxxAQSe/yuq5/9tln99xzz1lnnVVcXCx8Arxeb0VFxdlnn/3kk0/i+7imaaqqyih2UuE5HqICiArdcsstAPDtecd0AOgcO0l7iGW5L9qjujYvU9Y/d77N1eg4BaIRkvSpra196KGHqqurcShzuVzl5eXz5s17991322momTx5svBwSlLmm3p4tAD0gQMH3G43LgGZCkBTSi+66CL0Wu/Xr59AcmVrjh07FgVw8eJgMPjJJ5/IAjjLip3g61Vft23bhgA0pVQ8w+Lx+O7duwcPHoy+2DjdWl5eriiKfIOVlJTgEoLoNFdaWnr33XfLdWGZOLMhL0KIT1xFUbB/BAKBuXPnIn69adMmAEBN5Lpy4eWqc+FlADoYDKLdNm7cmJRXIJ74t0l8/yVUSpJv10NsOCcERy5GxgbKRdKRcSzwzbaAbdvi041wOHzLLbcMGTIEF1IXrzfnf/f8lStXvvrqq8IU4g7KhEGLMVBmRPYsDKU0FYA2G9FnMEHh7s8xDn/cGIFTQlanqOSu2zrM5RjCPSxKAy2MKmcArGQIl2kyL+bmAPS0mdMIIes3rdcMNY2JGpEuG6gKtA7ghbg1i60iaHbS7HyOQTdGq2iEsTiAxQHoRodoGTRMbyjqZuhYZmqMXcsj2Epe1SJKRssMlpApr1x+7ryscKZcco2ZZOR0LFNOkUtI5WXJE5GXr8gAX4uUVh4TW7x8ub3ilistyTKpvAhQHgVPFDwRGozSrl+Fe4WVSfH4Rf/79KBltxR95zukT2/i9RNfkPgLia+Q9OxNfnodufcBT2391Lg20qYDTVoeUoqidmnYGNoQ/x7An/jAcgggZoOV8g1CWqw5bSLoBqxY0VDV+/2ynlDRE4YOv++fkUsRgI7bfk5BhebzAOvigwM3X+IvgUF3MABaY/F5isJwUhguA9hpGXV8ghAMsC02OchCcIAGr25huHNZTyjvpfetet0BoNOM5N+UJHy4Z0KNjwCAzlRg6r8IOUXmczGtLH+8eFlPWQeRjol4iAEn//GPf9x4440jR47EF1KMS+lyuUpKSubNm/fKK6+gMKUUoecsoL+oJRdGANBfrwO2ZMmS1kYvzKWKDivjANDHsWnS3hfHUZ/WVi3rnzvf2lpOOHmMNRSNRu+77745c+Yg1ud2u71eb1VV1S9+8Yt3331XjF2WaYVCIYFAtsnFogd0IBBI8qxtk8I7ZiFHC0B/9NFHhBCv1+t2ux966CHEOuU+jYv7EUKuu+46hIMxLA6a42c/+5mLbyIGtNvt/uKLL5KeJZ9//rmYUF23bh2CCxh/BwCi0ej9998vwkuhBzQhZODAgUmRzjDaCILU11xzDdaCjS2CIgl0e/fu3QMHDnz00UdFyxmG4eEbYu4+n2/IkCGyH7584bnwouQcGRmAxojYhJCdO3fK2Q3DoJR+/vnnmzZteuSRR+666y5KaSgUkvWR5dubdwBoMR/QoqmxjVoUcwQcC3xLLFBfX3/JJZeIDznxy5Xzv3v+qlWr5HlKjW+yTQ4fPiwfCl4eBgUvzmZhkgBoNuwzJ2gwKUM4LDAA6gE+AXiKwpwQFETAE5MAaBGNIT3AmoTpHCsAWuExgmN2ta5eA/ASi57BL4Y5eLMLlDygCVl118r09ml0fzYBann4kf86GOsToSRu+xUrqFERQJl7ViacK2XQWebT26cJgGYhAlIpEbvWx6uTIzXnymMJUojnZhnl8nPnZT0z5ZJrzCQjpzcGSaDsSpHkElJ5IXaCMvIVGRBokdLKY2KLFpDbK2560pIsk8rHbW/c9kYpowh4I3aXv7/vv/kWMmMGKeVOgXmEdPKTwiKS5yfF3ciMs8ltd3Y+FDn/X/WnhmJ9IlrnmE4aYiSkuQ2oCpsjPj4wA+C/TdjGI8vrNrsl7QQAnRZizp4Iug4rVkSrqj8s6wlVPWDI4Pv/Gb7qEHjqaZeI2SNi9ooY1TH15Jg6KqYNjZlVMchH9FmBDgxA213rzDEAvwX4BwtdzyLYgwEmB6Bt5vmtwK5N0K/iXQ5Aq32rX9v1suMBnX44/wak4pPdAaDFP5zcGbn15VwyJoJRqt9444277rqrb9++JSUl+JYXCASCwWBpaens2bOffPJJBPqxQFVVFUXBl2tsF7miI+NlAPrWW289skJO0FwOAH0cG06+L46jGkdctax/7vwRV3dCZNy7d+/KlStHjRqFQxk6OfXr12/evHnoY4px8DGqsHCNikQibXh1s2fPLioqGj16NCKlbVhyhy3qaAHoffv2Iarr9Xrvu+8+ERwDL/jjjz9GZ2SMWYFnEY+zbRvXFcT23rhxo0Aq33rrLfEpDd4e+/btQ+jha5nFixdTSnVdt21b07QDBw5cdtllbrcbYeWpU6dOnz7d5XK53e4xY8YkAdBYiNfrnTlzJvYh+RmJOmPwit27dyN0/oc//EE0Hrp7ezwenBv5+sKXLl0qzibVlcuNLedtFf/mm2+iYb1e7549e1RV1TRt3759d9555znnnNOzZ080JiHE7/e/8847eNsIlVpV11EKi2YVbXqUBZ4Q2TEEh8/n8/v9uq7nsojHCXFdjpKOBY6ZBa644oqvfVvEYHv+d8//y//85ZjVnlRRKgCNGDSDajH2MRwAeNaEn8WgT5SFJRX+g82Y9ABr0kfuMgAt80k49dEdMkyc+mLQRTHPBPsxgE/BVhlyw4M52/zXZmiXfcbkMwghCxYtSHrGSSbCkKsfADxYb5xXb/fg3t95Gs1DT2eMkyADzTIv2yRTiIlGGWYNVmxakr1fj4ZHN1u5hLTVtUmiXEsuvFxpa+W179jFAAAgAElEQVTlvCcKL19ji+7PWQTkctLyaJBUp+aklOx2447DeTFgFIW8qFX2/24g3buSznmkNI90C5JeXUmnfHLqBPJfT7r3f9H7C21YCIZF7Oq43UOlXXTaSQe/SrvEzEE6PZ/S3wKsA3gD4CAAxfjrHH1GlFncf9lBZ+ksBV2FFb+F3pWflfeA3j1g4IAHDxrLa6H/If3kw8rpdfGxdZHvxEO/BPhvgLUAv40a/WPNRzP5bu0IPAvBYZeGtPFsAVX4nC0/2Lix+UFTjZkhEw7D319kAHR5DyjvCX0r3/wmeUAnrtf5bbKAeNnJwjRJt8RlKUT4xLVUxol93jItfDWmlP71r38tLy/HNzt8Dy0uLvZ6vXPnzn3iiScEOiNH6sCLb1tbyQD0smXL8FPpE9vKOWt/lAB0zvU4go4FvskWeOCBBy655JK+ffvia6bL5fL7/YFAYNSoUatXr870HW07WWTy5Mlfx3ioqanB96x2qqVDFds2ADR6495xxx1JD5jnnnsOMVBCiPgSB69/0aJFAiS9/fbbn3rqKYwpUVBQsGvXLlVV5Uf+wYMHRTkTJ06sr68HgA8//PCmm24qLCzMz8/HT7MvvfRSABg+fDjq88Mf/lAuhFIqwNCLLrpIhHGJx+NidhefnZs3by4uLkZP6q9rwWWmAeDQoUMYQlpofuDAAdGcSXXlcijyZmfQyRo/d0IQf+3atcIrcN68eePHj+/Ro4fH4wkGg+hR7vV6cc1GQsiePXsyAwfZa26Ds8Lm30IAGpfW3L59exvY0SnCscC3wwKWaT399NM4bni93r59+65YsUIeaY+LGdIC0DjIg02ZYyK8bcKvY3RMGPIzoc8YDzo9aiMDzZn4o0Ock+rlwE3nuDXatK8DugtonAVxpvxq+GqC3NeSAdCzzprpD/qWLltqgSU/16SGsKkRofBaDOZ/ER0ZomUxWqTaJbpVYtDOBhSZUGxCsQFFCSowgEXn0KgvbnpihjuiIuVFNW9U88ZNb9z0KDYLCY1QdaPymSzD05uHkxZxpVvNGJBnQJ5cWrMYuFl1aK2kXEsuvFx+a+XlvCcKL18jtsuR7eVy0vJoEL4QH8myz2434SwcA3cM3FG75+v7K6+cRwoJKXGRnoXk6svI2++efyA09TCUhSF40PDUGoGoXRqzesbMiqg2IGqczqBnuBbgvwD+xqFnhd1o7DsDsTU74OcklLkx3HO6FASgf2ciAF3ZDQb0/UuDuiEKV9gwH+BmRvT3YGxgrsSwC2BlVB/cwQFojUWv7qwapwD8AmAN6C8DvMX13wfwNwpbbXs3qJ+8tVMbUPVqeU+bA9BvOwC06EzfSEZ+TmXic7/wTCVgeu7lnLiS4krvvPNOsYRSIBDweDwTJky47bbbPvzwQ/EBtKZp+CWuuF5hQJFy9IwDQAu46uiN6ZTgWODbZoGbb74ZF3JDJ9qCgoLi4uJf/epX+HGtPJGWBGy2k6FkAFpgku1UVwcpts0AaOYhtYB5SMnbU089hUsE+Hy+Rx99FCHIeDx+1VVXBYNBjKF83XXXaZq2f/9+dGH+GkJdsmSJeJKJx16/fv3wsef3+0fwjRBSUFCAqCsh5J577kGYNRAIIB69YsWKpGhfpaWl6FI3YcIEWU95wuGOO+7AteNcLtf111+PCwyi5l9++SXCIqh53759RQgY8XxtFZOkQ+ohQs+iLzY0NGzcuHHBggUiMjrGP8EY3AIW9/l8gUDA5XLNnDnzscceExPRQrfUitov5dsJQG/btk00x/bt24/N+NV+jeiU7FjgmFlAANCnn376n//856Svao7jraRpGk7vNc3noe+zbQE9BLAhas4O09Io839sXHtQRN4QTBIK3HSYC6x5RAC0vP5hU3Vcw6hZFVV/ZNPHAP4JoAKoFtgG+3qdeUJbLIgqo9PGnubxeZYvX6YbzSaGpS5hW3oUYH8EfvWVOqleGxlVTlKUUVp8lK6O0NWTDP1kQz9ZV09qJG2IYfY1rCrDqtLNSkUrV7RyTa/iVKEZZbrVQ7dKdLsYfUJ18GQH/vBsWmDxCBIdADoXax8bGbn5jgx6Tm1NuUyZl68oEwYty2ThG5Fomh9WSgAm/XEFeeyBgK7WAIysbeim0Z4x3VcfI6rdLaL2juunR7XpIfXcBuWnqvkghe0cP/0Y4DBQjUXFYTHZxd2WQJ/5Rwo8NR3WnB6GBt2EFasO9qn6v8oeUFECQ3rv5AuL7gF4h9M/2J5+DLAH4Pa4NSNmdcexSx46Ohqv2z4K3QFOAfpdMP8d6NUAP7Vhng4X/8us+Uw980D4os1bfjew3xOVvdTyXuo3LAa06BkOIywgXnayMEI4RyZTUTlm/waI/elPf0KwhhAycuTIn/70p3v27NF1PelPmrjSVIuJU0fPOAC0A0AffS9ySvjWWmD58uXoq+rz+aZPn/74448bhoELpaJNUgMktKutHAAanyPyU4NktziG4ECs7ec//3mS8N69e9FzuaSkZPLkyfv27bvrrruqqqpEXA5EeEOhUDgcFj7ww4YNwzd8AR8DwA033OB2u/1+vwA0BTN58mR08kWwGIHsrx+Qzz77rHwllNI5c+bg49Pj8axatUpc7dflq6q6evXq6dOnY7GBQAD9qXVdxy+PAOCLL77As4WFhYFA4OqrrxYlJFWU42GSudIefvHFF2vWrLniiitGjRoVCATQLxtXe0AwHXH54uLicePGXXrppYsWLXr66af3798vSlMURV5Q8RgjOKKZvlUe0AKAxhgpoi0cxrGAY4FcLCC+O8GJaDHVl0vedpKRAWicFGwMvmFZQP8F8HwoNids9o3aPWO0SIE85pqXQhmxm3YCoKlbp24DPKZNTEoQjGaK0UDM6hmOT9W0u/j6ZnUAus0AaF0CoBGGhqLOhYSQW25Zapia/GiT7IwhOD5W4QEDFgIs4vQbgN8ALOY8d65sTF8EcBPAFbrxo2jsB9HYDwD+nZE9D+il1PoJtS+xzIsM47uqdlZUmx5RJ0e0iWF1fIsU0Sa0ROMi+mkyxbTTGOmnxvSRMX0EUtw8JW6ewnjjpJgxLGYOieqD01JMHxgz+saM3jGzImaWKWbP1pJq9UpPdjdVIgbHc9LMrprVmVORTgs5dWIwPSM8lPedeODj1IgliXi+ufS6o5Q5olkTcZvwEC4u3BvgPmKSy8nAN5vkYAA0TSGbMHvaAc3O16wizeqsWKWK2T3R6GWKWRZrRhW14R7/Otg3Hj1Li59X1zAiFB1k2KPD0RGqMqaubgzAJbZ9GcDtAPcCPMbisMMXbMk8dudRYGHYOfqMkdkb77ejBaBXrfwKAejyrjC0+h80zhftMy0WvMKKgXUY6CcAGwF+Uq9VKDRftEXHZHRKDHBR8FpWJ1Pvrmu9Y0rfsNK7Qet52OxcB50OQad6KHvx1R8OHHh/ZU+9slf8GxYDWhqHHTZxk8gPqgx8a42VoZjE/dja4k40eUppQ0PDkiVLVqxY8dlnn2maZtt2KBQSDlLigjIZqm3fPR0A2gGgRZdzGMcCrbXA4cOHx40bd911173++usAgEHqceyKx+OZJtVaW0vu8g4AnQqotgBA79q1C0Fhn8937rnnJnkuHzp0CONjIAqJ7rperxejbWDYJsQlbdseOXIkYsder/faa6+VMeh4PP7BBx/k5+djRlxmlxBSUlJy7733qqoq4Ik333wzGAxidV9++WVS2z/44IMCDyWETJ069ZJLLrn++uvnzJkzYMAAgeoSQi677LImNzfeJfEpW1hYiO7PHo/nrrvuSiq/rQ6xroceemjw4MGywkJDEfM6Pz9/1KhRzzzzDF7ssb9nWrxkof+3E4D+upvt2LGjRSs5Ao4FHAt0cAvouo4fx4iPsyKRGDXQP7EWYK+p3sk/A/9eRO2v0kIVXKl0rEEcmqdbAYP6ATwUiGqQaJxEDaKYPW16AcAfwd7NHC2Z+7Npg26xlbts7v7MsC8WgIPC1+hznt99y21swQN0u5T3iVazAaIskDS8B/Aup/ckHlPE/m2ANwH+npn2c1j8dYDXuDPmnqPe7wJ4FWArwAYe3PZZG/7XgqdteIrTEzY8bMODSBQeovAQ5//LhDtMuM2A5YIsWG7B8kh8UUT5dVT5ZUy5Oqb9JKZdGNXOiWvfaSRldlyZrcabKM5ToursJIooMyPKTExEmbgyO6acGYuPj8ZPi8RGI8WioxjFTolET4pEh8Xig2NK/7jWRzGqVLMyQdWq2ZysXhp01iAfSYUgJ78K3gR5VPBgL5UnS+KUtEgxm8gUp0QFj8bmXdwquOKUnY1YJGJ3UIpRIigO6a4XCEuXiZKYGYzpXeJ6r7jaT1FPjilj4/HJsei0aGxGJDIzFJ1ZH5tZx6k2PrM2djaFaykstuidNr2PB1Z+AuA5gM3A1hXcxbv36wBvA3zAv0L4CiDe6PDM3JoT4dh5ZHYWHifJEzoZ+5LvyzS8zUNwrPxdqG/FBxXdoKyLNaRqvxnjtzVGmKYasFj2rwPcq9LpEaubQn3Heshq5YwFAtAGuAzqNWiQzQ3YBXGrU9wOxm1/FDwR8ITA86/Qzwf1e6iyFCp6aH2q9uzcAdRgCD+bREQPc/QjTwxnzq9jAccCwgJtix2LYo+G+TYD0ADwyiuvEELEx9yp0wBHY1snr2MBxwLH2AKTJk1yuVyTJ09G7PEY135cqjuqEByapr3//vvok0sIOf3005MA6K/jLN94442ICIu1pAghFRUVDz/8sFg0IB6Pq6q6dOlSdE9GRPuGG24QYZrRNM8999y4ceNQZsqUKatWrRIe8mKRt9WrVyNA3LlzZ+FDJyxrmdbo0aMFjIuBkgOBQEFBgVDP5XLhwoNJs7jYJ7p16yYkcdpEFN6GTDQa1TQNXZsRwPX5fCIwyLBhw6644gr0B8/Pz6+srBRVC2dtkXLcGQeAdgDo494JHQUcCxy9BQQAjUUZlmXaYJs8YoUZB/szHrP1MYArTBih0uJU9FkF1zFFc5jvap5u+wzqp+CjEDCsYs0oi+kDVWMO0BUcAjuU8LHET/1xz4EuxKFtBkATQs674GyOVNlJyFbCsDwZz0m4WJKwOEzk4r/ZQwhwEcyY0KgJB09TTjZ5EyAMUJegwxx8P8xBt08APkzQRwAfcf7/KOylsNuGXTaDC5F284bey/c7udfq8wBPAfwZ4OEE/QkgR3oI4CGABwEeALg/sf8jwB0Ay1NoGfco/zXADQDXAfwU4AqAeZwuB7gc4D8SdIUNl1nwIwsuMGGOAWdpMCtqTIvoUzhNiuicjDMiCQrrE8L6OKSQNjYdjQ9pCVLPqFcm1Cvj6tXT6rVTkUL66JA+OmycGtJH1Wsj69RTOJ1cpyZIG17XREPrtONCjTrUayMSNDKkj+LE9G8k7fSQTJjOVrr7LsC/AVwG8HPuyH8rwO8B7uEN9yBvSmxQbNM/89mOlwB2AuznPeorgAaOMuscATX4dI+4LZBJdGoZEuX3VPPTCbGm36Rykg9tG3QFVv5W6Vv+UWUplHe2BlW/rjMPaB5HmolbAJ8BrAa4Jm6eErWK8UuOYzpqtR6AZh92QKObPKoqvNc17skeAfKvyOUMgC6Biu5W34rXdm1zAOimfuNwjgVOOAt8mwHoaDT60ksvEULGjh1rGEYH9Dw74bqTo7BjgeNrAQeAbrUHtKqqhJDi4mJCyJQpU0TQDERvLdNSVfXKK6/08M3lchUXF994440YEcIyLeG5HI/Ha2try8rKCCEYv1gGoMXknmEYmqYpioIpQl1MoZRec801brfb6/VmWkryrbfeGjNmDL5RI1Qt/Kn9fv/YsWN37dqFA3oqAG3b9oUXXojlE0Lq6+uFYm3ecQ3DOOuss1BPXGhx1qxZ991331tvvUUptW37mWeeGTNmzAUXXPDoo49ilGdc+aHNNTnKAvESPB7Pt8cDmlK6detWvHDHA/oo+4+T3bFAB7GAYRj4IHvppZfw5Uc3LdtkQAboALrOwc11FM6zoEIFf8cAoN0akLhNQqovFOsejo4Mhc/VtIWW8WeOn/6LYWFs7cHmZHFUXefQtAVu4iXENX7C6eiT2eQfneqPiZBXxwWgbd5ULNp1CkW5BzfuYwAxfhjmCPUhCgco8wxFOswxxCiXiXAs+wB3/f4Q4P0Eofd3y3sK/0fh/7ir+PvcB/YzHoThC44DfgLwOacvAZA+B/iYV/EuDxP8Om9EdA9/jTuu7udO5fsB3uC0n/vYvibtk3zJ5VN/A9idIIG2y4yc9zVe9Ss8VsNagGcBnuH0vwnmWZ74HN8jL2RQ8mmA40LPJFRaB7AOYD2nTQCbALYAvMhpK7BAzC9z2snh45cBXuFO9Hu4nXmsZDZLge31OWc+5a3zcWL/EW/QzwG+AjgEEOI9SmXjBYuszpf7xL08AZN1sMPbK7NIMuKc9MVCZgDaBsr9q03gvWuBBqdFjXLFLtIoCyXU8SkjAE1ZHKQokAORSwf3u48B0N2gb/nfHQA6cy9yzjgWOAEs8K0FoBE22b59u9/vHz9+PEYQ1dn/T2dzLOBY4ES1gANAC0RXoK8thOCwTGvGjBmItd1xxx1JYSsAAMfKd9555+mnn967dy+mIACNsKmQAYCdO3eOGzeusrJy6VL2tS8iraI34fNGHMoMIt2WaU2bNg2VufbaazMhnrZtL1++fNiwYV6vF72MKysr582bt3XrVgS4MZY0LuMrDIERr5544omCggJCyPz589t7xLdM64477li8ePFf/ucvoVAoqTpKqWEYqqrKIHgWE8nmOpa8A0A7HtDHsr85dTkWaCcLCAB69+7dPGwqw1nZAoQmRzUNFYz3wbhfMcdG7KbIBkkw9DGFcmieAQEetbYAYADAGQA/APgVd859gQe1+DvHm/7JkTJ5/znQWqAHOa56sNAX8Lvyzz3vbN2K2dxJEkMCNIPDEETDWNBSA2SCxCQR7n0pY3BJPBfFcuR6m9WOxWFGST619vT1NnlUYw5xMTa6qVJbp7YOlg6myckGiwN2kmAjiI9FNS7fyMKZUMrIAkZmCulgImm2ZViWblqGRc0UMzZTu3F9Oe6rTjXUkAOazfBGarKeaRvUNi3LMCzDaF5IWx0pHFqt50D8YQq1FGo5at8AEElg+mE+N4P7Bg7f4164oh8zBusNc8ViAAonrWndTWbbnLeULpiSmeLnBRQMCog7N4eejwcAvep2pV/ZR9UljR7QmoIfNlhgaUDDPDbIBXEojVuFLNo1ZTNYHZ8yAtC42iqQAw3XDO73QHVXqCyFvmVvOwB0zr3cEXQs0BEtkApAy+/CHVHjNtXJMAx8uUYgxXGCblPrOoU5FjjWFnAA6FYD0ADwxhtvXHzxxStXrsQ4GAKxzcLk2LCthVMPHTokljdcs2ZNLrXU19cLMVlh27aTwokgGm4YxldfffXpp59+qx51wkRHwDgAtANAH0G3cbI4FuhoFhAA9ObNm1E302YbtWwGSrKVu1Yryr/Vqz0MFmOXBYAWsIhgjiWUo4Pfgu4AJwNM5KEDLuT7iwGuB7iVh3dYxYM//JmHjxD7xwAe4aEkHgL4L4C1XYLE7wpMmTKFI1VNYG1yAwngOPlEs+MU1K4VAHSavHLZEgCNyTnJN+ZCWTkOCfKYnrSXxcQpWZUmXi4XF3iU98x1PkFyunAzT8Lc+fJ0QhCl+ERIM/C5qY147SyUN585YCA48qhVk5bNOXFJWRieg3LoVktxJ0fneTm3bDFxxXpKxlTP9DZMEfWiMsJ6LA5wOmq0W8JiycFnMAuWIl+eKCpxv7ByOBKNCqCs3TiPIO6alN7bvE1yORI1s8DGqRt6QAsAupKH4OAANI8Ab9dxF+9bdTgtBn4ld9xZXqYy91xtJIkLq7IY0AnCMZbFNKdEpQw912l1JPzHwX0ery5xAOjUfuGkOBY48SwgA9Dz588/8S7g6DROBaBlBOPoynZyOxZwLHCsLeAA0EcCQGMr2bat6zquByiPg2n59mhY27YfeeSRLl264FKHtbW1YqmotNWhYrKMrCoHFmw5RfCGYei67gDQaa2amugA0A4AndornBTHAiecBTIC0Mw3Ng6wF+CGuD0qZPtVIJyOMwBtQMCCUoCBlI7U9dNVdWTcHBDSB9Rpp4WsmjrrjEPahAPK1EOxGYejjVQXmRGKzoxFZumRmWZ0tq7MioavzXcTN/GcNmZCTNNbgLhyANGwhGatn4TBJR1y0RbqxeJSak9Tl1xxckVyJRKfXozBiHYjNSGVqWi6CG7CPZLZymcy6WAjGWBzAoNjzAKAlvSweXWqDUg6P5SR0yY1JMw0baKcq5G3+JJsjZ7a1DSTyLZN225M5DxKWmBYYNigNyfmw50DpdXtGCVy/dkqdOwbhkRDJhi8Ut2kTcSv1LJoo++7fHU4ScDbF9eza7x2dC3GtuD2EDA1z53Ur1J6r9xVc+NlpdLkSADQMeYBXQqVnY1B1a8rKlfT0PlCiPdp8IMoVIe543Cus2UdFoAGErWIYRWDda4d2Tm08tlqHoKjT/nbO7fz+9BZhDBNN3GSHAucABaQAWj8/PoEULrtVHQA6LazpVOSY4HjbwEHgD5yABpbT6C02Zl2aurx48djjM45c+YgQCxiTKfWaJkWXq0IbSHrnAWAxtDVDgCdatK0KQ4A7QDQaTuGk+hY4MSyQDoAmofgsEywGwBeUuzz49AjDu4Yh2+Orwe0Di4TvAbk6dStmX7DKrFpDxuKdVoYp91UqIhBzzB0C0H3MBVUGqalMSjRaE/Q+oA2AOyBuvr9Lp2IP69g/JQzdY6NCpTryJoPs2Pe9I6a6coVlWbLkgLhyXWlKVVGANOc5kkZZGR9EggjwosCOs6JkZFP7iQrFSyqxrTGUC9xvoSdytymMR3rYV68CQ9fFn0jgXtL5WWDhCn3kG6MHJIAwxESZ3sWSyQdGSzMR6NiidpB5bE/MuLo2dTIUdujFEPjNLuipEvWwE5LBjOsXLtwUGf+zGlbPOHvDM1dnjP1t1any9rIfJqCGgHo30YGlH3Qp4RWdtYG9X6NA9Am2HGA1wy49gAMrIPCEJBY7h7KHQ+AZu7PnCIGodYgsH4LCgwt38oA6O60T8XfX9kBlsE+B+ChdNhqsrLtkE9jQSfJsYBjgY5hARmAvummmzqGUsdOCweAPna2dmpyLND+FnAA6KMCoJNWIJTx3CS+rZpSjtHx/vvvE0I8Ho/X67333ntbrEIsHRuNRlFYVtIBoFs0YI4CDgDtANA5dhVHzLFAR7aAYViePJcnzyVCcNgWhniN8gXf7g/po1TI14FEOoAHdCLoB4kaJKySuEpUnagGYyI6iVMSoSQEJA5eHQI6+HTI08Gtc9TJAAKmF7QCQ+sWipzlz2Oj+JDTTj2kxATglg0IztqKMrgj81kzNQP9MkpmBKBTwaXUlAylChS4eXzflPwYY8HMgEKmhSYxUXjFSkhls8vliCfDTDHWOIak0BtBXjsxJ8DOclQa+KlWAdAMVLV5kOqEW3NjzOq0oHPzRFQMYWgBRiNKKy46xVhN1ydk2olJW3UyAC3Q51TQWZxKMEcMQGNHQn2a+hIeZ+h7OSWnvcL0dycDoFVYxQDo9/qUWpVdlEG99yAATUGx4I0QLPg0PvWgcUa9NTQMnaM5+kF3CADaY4CHR+FgMTcUBqC7YxCoixebxtlA14MNQ3vtqi6Fql5WZflrL28H3QDdAp3FcncA6Jy6miPkWKDjWEAGoM855xxN0xC/6DgatqsmDgDdruZ1CncscIwt4ADQRwVAy3Bwm7QcLi3YvXv3K6+8Mm2BCBNbplVfX3/VVVcRQgoKCjwez8GDB9PKy4kyxCynyzB0i7yc0eHTWsABoB0AOm3HcBIdC5xIFuCQDo5mt956K1sjF9FnBUD/GOCekDI1Cr0V8GsJ50ED3EgmuE3GsyiliAvn+m177k6IKZI6uBgQQ4lmczKJZjbyCuXRUVmUaq9Ki1XaRYMiDfI1yEPFGAANeQAVEW2QCT/3BPC6Sb2tWJnaTAZqZT6DfCbYTE7HrDJEJ/ONBct1yXyGetME3pUk05QvnW3MK6dwPqEzix2RGoKjpZREbgRlm6BJVnTzc8mxKZor0lxWmKK5UNOREECmeW7mF9oYbILy5Q0b/wphwAr5fxGzSZKa6OrLa8JSmyplt01zSqq3zQ9FdVn0Adn7uxFel5eOlFF5WcFm18UORGWpTIpsYwJKZjqbmi7Xn8qnyjdLSQDQoSQA2mYrYdoGhHkUjtcBdvF1Sn9wmBbGEmNC8pAlg84ynzIQJWdsawEeA9pt2X7L9htADCA6m/9zxcEboeVhfY5mLAfYBzac0v/v1d2sflVQ1mvX9h2gmaDZDIC2wOStzjzYZZs2s51z4FjAsUBHsoAMQE+fPp2tC21m/HvSkRQ/Wl3i8TguUuX1el0uF3vwUIqAhtg3e0YfbYVOfscCjgXa3QIOAH1UAHSbt4+maU899ZTH4yGErFq1CsfZpFp0XTcM4+DBg4FAoLCw0OfzXXLJJUImOyYuxmghj1WI9FwYOa/Dp1rAAaAdADq1VzgpjgVOLAswuBkgvxPDYm+99RaGujEAmkLsMMBOy/yhCv3i0DUOeSpHWDgUcjwBaESfBQCtWkS1GO4siEPhft3uolvdDNrVgCIDAgbkIYijAYnaPUP6eQB/9hcSkkeIn0SZy2B658qM4FuGZpaBnkw8ZsWzqXxjwalYX3ZML1Ve0lCuS0pOsJlLFpcgw7GJbFl/M+iDBWZ3CxaVZmgSVq8sI/PNdErVwW7EnSGxEEZjrGTmd90YNxlT0pTDk2T9W1FvqiZHn5KDPvhPLxVqx7Dd8l5ukYzX1cwo2Q/w8rLLyGflOlN5WTIN3wRAl7/bp9So7BIb1GeXojEXYI1/y8HzmFQ7APBSA8xqgK4x8KVHkGXQWebbGl9OX7tUS3MA2h3m/KgAACAASURBVMXRZxIHVwz8YfMkzVpomJsofAYUJox6r7qb1ruK9irbs+PlRvdnHlbIAaDT9BYnybFAR7ZAKgCd/X2/I19Lq3TTNA3l3W43IcQyLUVREJV2AOhWWdIRdizQcSzgANAdC4C2TOvNN9/EwBqEkAULFqT2FRx2v//97zf6aBHy5ptvoljjS0VqnkSKwJcTCexXJObIyHkdPtUCDgDtANCpvcJJcSxwYlkAv9rv338gA6CXLwJQLDsM8C+wdwL8PqKcpkN3FfJVcHc0ABoR57hN4nYT+qxQooNHB79hdzKsYpN2NmmRCfkm+Azm8+iL0YI6ZbRl/xHo/kABIV5CAiTOXQXTN1wmoDC9dCMwinCeDKQJgE9OFAArJjYrspX1pgHKeXFJ1YnDo6qrWeYMB6n6S/oIa6RlhJLCPql1yDIy30wyVQc5JUWfFspprbxcV3vwrdUnRT6t8dvKWzap7TLatmkqIUvMFq565l0jAP27+gEIQHeNDOqzU9WBshgUYmYpCvAahZVfan0jkJcxErQMOsu8BA23iB23iQAHoIlFPRZlITh09mEHiYMnBoVhbSLAUwCfAcRtE86e/lXvHvHynlDW6x8vv8KWzjQAyeRhzptieGduhczGdc44FnAscAwtkApAH8PKj3NV8rWzaWbbtkxLoM9J0VCPs65O9Y4FHAvkYAEHgO5YADQuIXjjjTfilyaEkDFjxjz44IP79u0TrRkOhy+55BJCiNfr9fl8l19+OZ4S8LGQTGXSyojEHJnUYp0U2QIOAO0A0HJ/cHjHAieiBagNlgljx4xPANARC2oB3gZ4LBL9ngL9YuBXwXeiAdBeg/oNGjRpASMGQOcbENBo94gxQodrAHZ/9N5un58QN3OCVtmqXRm2TNBhBnEB8SQBeTLYJ2REpYJpKrWV9WYHoLH21Hobq2ttXU1aZuZSy+SyqINsjVQ+o55SbbKMzEsiWUNHJEKCyPq0UE6K/i3Ip1qgbVNaq0+KfKrlW+gnzYyb7QAtI0tktFUjAJ2EPpvNfdzlktLwEgD9dp9uWmUCgLbBSLQzAHwO8D8HYnPqoXtDlhjQMugs88cDgDZtBKBdFo+/wQNAd4rY/RqicwHeQkOYOvzw/EjvsljPUrui/P9efbUJ0TekEBxt1bJprO8kORZwLNB2FrDZuqFACHG5XNOmTWu7gjt6SQjT7Ny5E6/dCcHR0RvM0c+xQA4WcADojgVAi3m8+fPn41CLaCZG2xg+fPj48QwOwFNut7t///6RSCTJizmHdndE2sUCOB+LDeTxeMR3Q+1SWUcqlFK6detWvHBCiANAd6TGcXRxLHBEFqAs5saEM8YRQn76s8sBLMOuB9ijGP8ZNU+JQZcY87zL42GU3RoLRcrib2D0ZzkGdGMkaEp0yhbLOmYkIm+woByiXurW2SKEMgxdZNIi1Ryu0+sA1gB8tO9vm8RQposYi6kQYS5GxVySpAy3ZeelTC0Bpqm6ZU/hRWeqPad6mwm18iBVt6z65KSnpEJO8qk6yClZ9ZGqSrRLa+XlutqDb60+WeVzsmczo7TuQC6/eU75TCa+eY6UoyQAuqJLw5wZh1QdbNC5rA0QB3jVhEvrrcoI+CMIQMv4cou8GFuOFaNTYtpu2/LbttfiMaBVFgO6LKqcC/AEwCEM7WxrcNEFod5lkZ6lUFH+PgLQ2N34+psMzUpQs2DrieQUazoJjgUcCxw/C6CDms/n83g8U6dOPX6KHIeabdvetm2bm29YfRaHueOgn1OlYwHHAq20gANAdywAWgyptm0/8sgjw4cP93q9+fn5+D5cXFzs8/nEu3G3bt3WrVuHX6aIjN+SmFCt7OfHVBwbyAGgj6nRncocCzgWaGsLUEonTDyNuMjkyRMBYiz+BqxuMGZGoFcc8uMs+IYAoJtFf+64ADRzGHTp4DGol/tBF7FYHHZX3Zhs0QcA3gU4uGvn8748r9fTye32KfHG4IOZ/IhbMDniPZJQAvER0E9GRsqUADrbCqzkRWfSJKd6mwm18iD1KrLqk5Oekgo5yafqIKdk1UeqKtEurZWX62oPvrX6ZJXPyZ7NjNK6A7n85jnlM5n45jlSjprFgO6mVXRpOGfWQZXFgMZPC1R+y/9RhTER8MZ5vHitRcQ5SeBY4c44i8bRZw5A217b9iAAbYE/qg8FuAPs3WArDgCd0hGcBMcCJ7wFEIAuKyvzer1Tpkz5Vr3sOwD0Cd99nQtwLNDcAg4A3XEBaIxwdNttt40YMQJxZ1ycEN2fa2pq9u7dGw6H8ascB4Bu3rGP9RG2gm3bwhHYAaCPdRs49TkWcCzQlhagFLQJE0cSN6mpqQH4EuDRz7Vz6+iQKHSNMgA6oEJAY2t25WmATtAknQe0xwCPTt16EnDTzoeKTQQ1gkocKtL5R+sGw6D9LAy03dW0ugNcALAZIAIQffHFZ70eV+fCIl+e57NP/sn8AdOihLmYGjNKkgikSQkOAN1ojEwQY6Z02YYyn5N82gYViby4VpTTWnlRUTsxrdUnq3xOduAlHNlOLr95CfKZTHzzHClHKQB03XnfOazipBJbZLUB4PG4fW7ELI/bXsX26HbeiQFAU2JzYgA09RtQZdELAF4A9QugMbZqJgD3gI5Ulcd6dYPKivd2vgLMz7nRvdmy2JE4dDygU7qOk+BYoCNZwDItwzAopaNHj/Z6vTU1NfjW2ZF0bEddHAC6HY3rFP3/2XsX+KiKLH+87r10dzomAYaHjALKU0EdFBQCmaTTmYTHKsL4GF1FXZ8fh9EfA5kfz82DbEJwFIZFxP8ouAjDjIou6LhAks1zkgiLMu4gsj5/OOKioJCk6cftvvfWP30PORTd6dCddHc63XU/95NU161bderUuaeqvnXqFOdAb3CABaB7o/xeKDMnJ4cQIooibGGJUQAa0GdY8KSUfvLJJ9u2bdu0aVNpaemrr75aVVWFjxwOB3fB0QtyFKDI+vp6bgHNXXAEkA4ezTnQVzigUa8dnScjcwohxGKxOOT/sdHNX9nu+cHzsxZ1cpt2rU0ba9eutmsjndowJx3somkumiRTwUOJhxr1w/2I27tDXIg1ANpNiUKJogmUJruVK2RPBqX/rLu3ppTKVRX/QQi5zGwihBxobuQAdCf4e0+k2B911XNj4DDExboKBCIhUD4XpfengY3pkp5O8gk1PVtWJMKh0tNl+qD4eRFTQvvB5n/xm+yTQOGL3/D75Q9A//zWHxgA+jNKC1tc19nUVK+jHqW3AWi/NTkHFR26VxD8C3bQHo2olFDNq8Rkz4/bHD+j9EWqHqMemWouqrmppgPQdzhGXuH48VD1quFHmzkA7ScePIJzoK9wQJZlgAVmzZqVyAA0IQSajLW68wn3lTbldHIOJDIHsrOzBUGwWCyJw4SYBqATpxnitaYcgOY+oONVtnm9EooDmm5Gl5nh9QF97fjxlLqdrqMKbXA4X3F5ymRtkUwf/t72D9+fyz3jyGxzTDnnmujwDHNT0WtirF3mvXVb4wv+l6O7Vz1QubLuNZXq8A2lot05jtINlL5PaYu3fTVaW13nXaMmokSEv9TXdgJAM3LgD4wxD4MKsjkE9UJYE0HpYc2yR5mx3PAP9yjrbr0cKn9CTd8tokJ4KVR6/HnOxoRQcICkodJzwUj3wmJEgKw7i0YAeszwY1cNcV056Mydt591eP0/u7y+krUq6n7C6bnW6T1P1eucx31hP4eo7+royV9wT3Thr5NKTirpmLJ4TiXnVOJ1+nEBXxYdtJ9DM+p3kkNLcmjGc7TfOSqeo8TndoH6Ur0LaXb5OkpfpvRT3Z/1BYapLjpuZPOIYfIVlytXjfhvAKA7mKSoFyygVZXiSY9sa7Phjvf4f84BzoHe4ACYP7vdbqvVmuAA9LFjx1pbW3ujEXiZnAOcA2HjQHZ2tiiKmZmZYcsx5jPiAHTMN1FfJpAD0ByA7svyy2nnHDjPAdjgeefP7yCEpCQnU4/qvamb0i8p/S9K91H6BqWvUvoSpZspfYbShZTmaXSgXe1DAPQgj3IbpTWUymrHeYN/qfvLBQC6rv48osNaqjIywoI0oYNr3ozYHJiMoxTsHs2RI47lhn84cuUGyjlU/oSaPlC54YoPlR5/nrMxPacqVHou/j5CfrsTAHr+mQ4A+iuq/SfVnlHVf2p1zmiVb2x1TW1zTQ/bLd/SxtznXLecc91id99s99xoVyba1bHn1CvP0UE2mtxGJRsVbbSfjRptNOnc+dt4jgIA7Ys+n9NX8qhGqGJyu6/0yPd51890p9beP6q+d0X1WkCPG3FoxDAPB6B7Lrc8B86B3uWAqqqapnEAmhDS3NwM2757t0V46ZwDnAM94UBmZqbZbM7Ly+tJJn3rXQ5A96326mPUcgCaA9B9TGQ5uZwDnXFA1a/FixeDTyHF7dZTKbqj5DNe+0F6gtLPdM8VRyltoHQHpb/U6Di7QmRq0G9JpkIgS+Teiu/wAU3cyiCPYqV0DdX+x4vbXACgvW6UREIkgZy3gAaUGDFohl0sPBcCPMZkxebAZBylYAg0R4Uilhv+4aiQcFEhofIn1PQXFRaBH6HS489zNqbnBIZKT5gB6MHf331HS8fBomco/TvVjlF6mNJmSusprdX1WDOlB3p8N+g+5d+l1Od+i9JXNLXc5Vnk1O6103QbvaqVJrdSsZUm6YEkHYbuZ+swfAYTadCWoLtkSjxe5xuSWx5lb7mPajsp/fpC03QA0NRJx4z0AtBXDlOvHnmk6S9UVaiqAVLNLaAvMIyHOAdinwMsAC1JksViUTxK4pxDiD6g2+teW1tLKQX3qbHfcJxCzgHOgU45AGjsr3/9606fxmUkB6DjslljpVIcgOYAdKzIIqeDc6AHHFA8isvlWrNmjSAI6HevpaXFrShuRfGoVKGKSp2UnqPURuknlG5xnb3D7RmtQ8+CTAWZSjKVegtoDlSuTImTSnZqbvNc53Au9po/KyfcdmcHAK39pb6W6OizLwANMPTFf/Wd7D5HeAXBdASgNW9ixPiCeDPMSUIHBMNMgE92yIpOAz6Jo/AzVP6Emj7SVQiVnk7ZjpE9pzZUepiPoztUeL1LuOjvftsy+oqjVw1xjRx69t67bR0AtEc3FdbrpFLVrakeWVM8moeG4VY8mmbT6A9U+4FqZ6mq38pZSr/XT3P9b0r3U/p7D13upA+cU3NbPDPOuLLOuLJaXFNb3Ne3Kle3akNtNM3mNYL2uuk4D0BrRNa86LOsiXZ6WZs8zdG2jtKPdPdBuiphLKBZAHr0iCPvNVBFX0PUTaU5AN1zWeY5cA5EjwMcgK6rqzMYDISQ9957L3p85yVxDnAORIYDFouFELJ8+fLIZB+LuXIAOhZbJW5o4gA0B6DjRph5RTgHysvLwQL6k08+AaccHRCSpvtRdegG0T9QWud0LpDla1xKGuDOOgBN5A7oJBAcHP14JxXs1HSWDjqj5VG624sHaSepds4LdaleEOfdt98xGYzGfgaJCDX/WR3oCD7Ew7oIXCQ/LOjMhi9KxH9wDnAOhI0D3qUhN339D/TqYUeuGuIafWXr/fc67C7vN42frQLHrdILjpDRI3LPAopCvTcckKXbHmu6EbKLqm2Ufkvp55R+SOl7ugugKqrVUXW/vo9k3Q/nFpx15Z1x39iijmyhl7VRqY1K52g/OzW4qFGmJgdNbaVX2uldlP4Hpad1Jax4uYYVUygA0Ff+2DPicnX0iCM1ldTt8lZb8yLQih7S03s5gRVFrvgEwtYiPCPOAc6BbnAgwQFoWZYrKioAgG5sbNQ0DQzA8fjBbrCUv8I5wDnQixzIzs42Go2FhYW9SEOUi+YAdJQZnljFcQCaA9CJJfG8tnHKAVmWNU1bsmQJWED/13sH3E4duQHwlMr6mVeyDn8c8tDftrlv0g8eNHUA0F70OSYBaFMbvfwHOrWF/l+V/o16K9Km23FTcDNy6OBBk8FoNpr6iWJ9TS0HoONUwHm14p8DqkoVme57m4768cejhrnHDm+77x5bm90LuCLCqgPQqocqHSgsGEArekyof9F4+jymq2jefSKaSjVFR34B7fbCv4oXGlcd+n2OKg7qUah6zusVhB6k9E1KN1FaQumv2+itNvqzNprTqlpbPdkt7qyzcuYP8s/a6H0euo7SYx0LgZcAoI9+6LWAVj3Q6ByAjn/h5zWMJw4kOABNKW1ubgZjCPQBjehz4rgiiSeR5nVJcA7k5ORwABrc2aMqIwkuE7z6PeEAB6A5AN0T+eHvcg7ECAccDgel9NlnnjEZjP1E8T/3VSgu2UubF7nxUNXpvb0Ww19Quv4c/ek5OtDpdbsB3p8FdFcafRvnrkrU+jm1/q3uKd+58h20QqU/uKiqaTp2462atz77/mOvSEg/USSEVO2vCBsAzbYrt4BmucHDnAOR4YCqUpedHmqi40d+Nu5KbdQVLffe3dpi86LDHZemL0GBKyEHpT24NRfV3N7bCy53uFsGj8wXcGfdCFpz6QWd09e99BI113lImtop/YHS/6X0/3V42P8rpYco/cB70qA38F+60XSzmx5QvS74z+lmzG7VC3TrFyDrireEMSMPoQV0QzVVnLrdswbaRz2v2bgFdIco8P+cAzHLAQ5A79q1CwDopqYm72BNP5URgZuYbThOGOcA50CnHOAANDiyRyWmaRoHoDsVFR4ZFAc4AM0B6KAEpWeJYnzBP8bJ6xnvE+Vtl8tFKa2trjFI0oDUtP1/fteLVHgH/h6qyV70WZH1mP9H6W9/cM0567ml1XNDm3yL93bf1Oae1Oa5rs1zXav8k1b5xli5XVPbHHkt555qcf67kx6Xqaxj6tR5zuW179Yx6NKSEi/2rF/PrCnnAHSiSDyvZ9xxQNWow04//Yhed9VnE4fT0UO/v+/OMy2t1NWx5KQ7o4DNHG3enRDaOf12UO3iW3VRvH0e4c/zCdy6abOOQXvtnzWvu4vzFteAPrs16mBul0bdmqafJ+Y9IlDTFFVTVMWjwDGwqqp6wPnRxa3TYa993tQafqrgTkP2guqec3TMiP8eMcwz8nJ1zPCjG9b+r+0HbxY2m01fRdSB6/OOozEztAv3CVxcNv/FOcA5EF0OcAB6+fLlMCqrq6tzu90ul4sFbqLbGrw0zgHOgZ5ygAPQHIDuqQzx91kOcACaA9CsPEQojAgvoISgxRSPAlarUKjiUZxOJ6UU/kaIkk6z7Wy+fCEhuG+z2Wyyjv65XC6f9DCsvPCCX0iWZbdbP1DJ7xGPCC8HKisrJUkyGAxl/1Lqzfk8YHG+EE12y47vZc8RhdYpdI9CX1PpGx33axp9vePeRelbPreHvkZppUJfp/TfFfp6tO7dlDZSr+eNUyyjPGDcrUetWrUKvI4QQkpL9VqzSS8O++A0Xfy8+D3+y8sBVVVBg4G/F1X14m7g25FS6na7UdFFiF9R0I0AIwaaKtvtdh/tF6GaJki2Ph+gQmmbnR75gE664uhPBqk/GfrDg7d/B6xwOu1u1znqceq3nXrsXgthRT5/ezzU43HZ2s7zzXPevNj7U1O91soeT4els441e71sdNwdpsWBeY47IAInYZ6AFbVL8eLmoIA9lDo81OmmHvX8sqAse314tLbS705Sp5N+9y39Sz0df9U3Y6/QRg+j46744qX1uqm3Xo/zez7OO1Pyfoid3QwFPNglB1BNoT6BIVmXL51/CCOZKI9nNE0DZQuwZjB0+qSBCoJyk2WZKzEf/oT9JwtAE0IsFgsWAZ2L3W6HLpVSyk4EMFnfDbhcLsWjlJWVAQDd1NTkcDjwo+u79YplyjVNY6UINAa4C8CVUaBfVVW3fkWzOtD6LIVIDIwhWWLY0RcbVjwKfDVsYsyHUgpTVP+nPCYsHOAANAegwyJIPJPzHOAANAego/MxQNcLYC7biUIMDBRwOhQdkrAUmNvgz04Dbrebnbf4jCbZn6qqyrIc/Iyu0+J4ZDc44HK5qqqqCCFGo7G8vNx/YqOqqtPpdLlcstsmK9/J6tfs7aYn8FboNz637nm5xU1PUPq9Rr+Nzk3pWUq9vq19uKHquCeAnk8//bSgXxyA9uFS2H/CRw3TS1BZLpfLbrdDA7W2tra1dSCA4Svbv/XDkjerhGHZD0AZdoGNhdSBDK7WwsJ8zIRFUsHvhUbpX6qVKVe9d/MVJ0ck/cfPpr31n5Vf1TY2/HnvOwf/671T3548bw6MWbABTbeQZmJUN3U7FEXWNI/+SPelfB4DxmQ6YKy6qeLygtuyy3u7Lr4dMvXergu3N4Ge2O32nl2oKl6fGnjLCpV1q+0PPvx2339+fPi/z9XU2vfsPvvyy8fXrfto4+8+2bDuk8ceffvBf/qP9J++OnHSv4265uWRo14fc/Xha4Z/O3G4duPVJ58rlKnD6+hahw/AJJulmOUchPEpD4TAAfYbR6SmiwBkDetwIRQTA0l9RmVQxxigKz5JYAHo5OTkGTNmYD2howGIEFcCAIaLj79Q05KSEkKIyWR64YUXnE5nhPpx5CoPwHoGuzbW2trKssXtdsM8FP6CCRRKIJsyEmEYO4GEg/IBcJktq6WlBWrRqQaGlP6DTMSd+fCMZWbYwxyABgFjF0W4C46wi1kCZcgBaA5A95a4Kx6FHSsAGbBVjQVBIkqe/wjApzhN09xuN/brPumPHTv2/vvvV1ZW7t69e/XF16JFi+666y6r1Zqbmwt2qf6V9SmL/+w5B2pqaiRJSk5OXrZsGUBs2FkCYug1ffC4FMWpqHZFtSlqK94qteGt0XM+t1tpUalNt6l26nvUcRt4JAIIr2gdtn7neQPTGIfDgas1/fv3jwQAjRT4BHreRn03B03Ttm3bZjabCSFms3n48OHTpk2bM2fOggUL1q1bV1hYuHv37qoIXA0NDTCVstls4Zqiw7zr7Nmz1dXV9fX1VVVVr7766urVq9esWZOfn3/vvffOnDkzJyfnxhtvHDJkiCAIycnJhBBBED755JO+24KxRjn7cQEA7ZRpY63yk6v/cOPVuwiZR8gYw2X9vUBGSnI/YxIhEljVESLoYanjr4EQgzlp4E2Tpuf9bN70aT/LmJ43//b7fv1/Vq4p3VhU8Kz3/ud1Rf+8bsP6V87f617d4L13bFz/x+fXv/7Chrc2/+ueFze+u3nj3s0b9256vuPe9O4muL0x+733xspNGys3b6zc/K//uWljzaZ/rXvqif/vqSdeWvjEloVPbJk2+VfTJj99y5Snb5m86KfTl0/+yaIbrvs/kyctvW788mtGLx971f+9eviicaOWDBv86LXXLBl2xSOjJzyddvl9yYPv+fHVS4YMKRs+6K3xQ47fOPyLFU9947F7vdy73B7VexYhOB4B3cuyDcOx1rZ9gB5Zluvq6j766KPgredcLldfHMmA2mxra1M8Cq4g9oEW6rMksgA0IaR///4Wi+WRRx4pKipavnw59DgnT56E+kFiHKr19QDMF8rLywkhBoNh+fLlbrc7akBnnxWZHhHe0tKiadpDDz3U0T+SK6+8csaMGZnMNXv27JKSkrKysqKiol27dtXU1DQ1NVVXV3eK9oYxEhXmoUOHqpmrmLmWLVtmsViysrJg3JXT2ZWeng61wy2P8POhhx5CDLpHTOQvd8kBDkBzALpLAeEPQ+RAggPQon5yV0NDQ4hs48lD5kBjY+OOHTuuvfZag8FgsVhycnIyMjLmz59fUFCwbt26lStXrl27tr6+vqmpqba2tqGh4fPPP8duO+TCQnxB8ShfffVVfX19LXO9/PLL69evLywsXLx4MQxZHnvssdzc3IyMjAkTJqSlpeFAR9Qv/OkfGDhwYFtbGx+AhtgsoSV3uVwbNmwYPnx4SkoKTHgA/c/uuKxWa05OTnZ2tpW9cizWjjvnZ9l45+bm+Nx5eT+79dbZs2blpaZeJvUTIntLFy4UJ5PJJIqiIAiS5AWhRFGEQFJSEgegQ5OV7qZWVfWtt95CbguCgK1ACMF2AYUQxr8oA0ajEUrv4V9JkoxGI4iT0WgEyqEUiMQS2YDJZBIE4dVXX+0u//h7vhxA9BQP/3O56J23l6eICwaYHyRkNJG82owYCJEMREgixNxxJxOSwtxphKQRYYDQbxARfkTIZXqyywhJJaQ/IT8iZJD+90eEDNTvH3X8HEzIUEJ+TMgIQkYScrXfPVKPh7/wdLSXMDJWv68hZCIhkwi5kZDJ+n0zIVMJuYWQDJFYCMkkJIOQXEL+gZBbCZlJiJWQGYRkETKtn2mGnsnVhIzx5iD8zGx48sfJ/zZ28Ou/eqTJ4/AC0HanrAPQTn07iHdHSMeaHMs8xuWIL4/5b18OwOKlLMtHjx5NSUmZMmVKu7uA4uLiwiCulStXFhcXFxQU5Eb3gh6xC+3EaqpOwxaLJT093Wq13nDDDRaL5Ve/+hXwhZum+spHOH7DcNftdlutVmgOQRBgrILdjdFohEcTJ05kB2V9PZyTk5Oenj5mzBioHezGCwdTeR4BOQArTBs2bBg6dGinnz+O0EwmU3JyMsz9UTLDOFrzzwrpSUpKwrB/AEjyAZfZZEajMTU1laUcnt5///1o0x2QQfxBjznAAWgOQPdYiHgGDAcSHIA2GAyEkBdeeIGDg4xQhD84fvz45ORkBGjYPrWLMHa00EySJGFMF2914xFgMT4vsuMAnPYAuOmT0mfAwb6IKZcvXx5+tvIcGQ6cPHnSZDLhlAaGm34CA8f1Cbr9IPsXDQklQsQQb/bdcIW9xqY6yNxPFPuhFBkMBoAOwRYVaycIgtlsTk5OvqQPaIZh54M+KM4lf/rnkDgxqqqePHnSYrEMGDAAIOBJkybNnj07Ozs7NzfXYrHk5eVlZmbm5uZmZ2ebTKYLywiSxM49OlUR2MqRC0iSBFRBESGRAdpbkqSioqLEafFI19T3c1PpofdaDWQKISMN/cZfdtm1hAzQWu+/XAAAIABJREFU0eRkIvYnwgAdTe7v/Sv86MJNBhO4xctJvyuJ+GMdXEbceYj3qaD/9SYbpN8D9Jzh7yBChjAYNCLOw/XIYYQMJ8JIQq7wu4d7H3lh66v0G1+8Wv85SgeX4cUxhPxEB6knEDJej79STzNUJ+NHes6jiTCOkHGE3HjzDYu2b/0fVT9xVaGaosiUOin9Qb/hHNZIt0w854+Qa0NDAygBXFRjR1mCIBgMBp+1riT9ioSOgvU8n+KQMP8SO03ZaWRKSgqcDAGZGAwGURQNBkNNTQ36io3n9u6NusGUSlXVGTNmQD+IPaAkSbCOjgMYGM902nYxFYlCCDMCoB+mJxADYTB8hp1ShBDoMbmNatjFEKftf/rjn0CE4C8oMWgRdpCDrYPt2I0AmyErwF1kha+wdkudpseUnT6FSJzjwN7HdmOUkpISLl1hly7/DDkAzQFof6ngMd3nQIID0NBddQO16T7HE/LNX/7ylxkZGdOnTwcjiC46V3gE0x40lIAJQ6fg7yWzumQCg8GAI2N2sIulszkMHTqUtc4Ag6H28SVexfq1ffv2ysrK6urq3//+96IowkiUb12PqOy3tbVNnDgRR3g4SmObTxAkAHb9IOZ+hOAdKoiML4Yr4DVwFgTJZDKbzZcZDeeNJgRBMBqNBoPBZDJBpUBuIZIQUlBQcOTIkVCZ7AuBBTAvxGSh5h9/6TVNAyub5OTkhoYGTdPgTEL4C0M0/1qDiYrNZmtubq6pqdm/f//WrVsLCwtXXeoq0K/l+rVq1aqCgoJLvXHR833M1djYuGfPnvr6+jNnziCFgEaBQyREpthN0Ogi/5577iGELFmyBN/lgR5yAD+r8wGV7vrjEYlcZzANIyQlxTzDJFoIucZgmmq6bFq/y6ZKybfA3e+ydLily9Kly2bAbUjNNPW3GlItxJhO+t3i/WuaLiZPly6b0S/lp3rKdDF5mpg8jZineu/km0nyzXrMdNGcIZozpeSsfuasfsk/NZp/ajTPMJpnePMhEwi5PiUtIy01o3/q9IEp+p16y8CO+0dpU3+UNnVg6i39087faSk39x8wdeCP0lNSpiSZJ6WmTu2flp2WYk02z0i5bHpa2vTky6YMGDgtJeUm82UTk5InXGae3D91OiFXiV5Euz8hg179tyq3y8tdWfGe6KV7PToLPvF7yHP+On7mDQ0NbEeJq5uwhQi7zlzmslgsGRkZs2bNWrBgwcVex7r/Kz8/v7y8fPv27e+++y6zQ/2iYE9azaVfsOO+oaHh1ltvBeQIAOhAGrsnJfJ3EapYu3YtcPuqq64qKSkpLCxsn3AVFRWV6BcKDfyM/b933313bm5uZmZmXl5eTk7OzJkz8TNJTU3FMCDsycnJTz75pM9xC1w2ws6BrKws5HwXAXZOl9WDKyMj4+mnn167dm37AeAowF0EVq5cuXv37ubm5qampobAF+wArqqqagxw1dXVNTQ0HDx4sL6+vlK/HnjgAULIbbfdBg7uo7ZpOOwt2Ccy5AA0anWcIHAf0H1CdGOUSA5AJyUlFRYWxmjzxBdZKGx1dXVdnLSgqqrNZgPny+iasK6u7tChQ00RuKqrqxsbGxsaGiorK9mxQX19/VtvvVVXV3f69Gm2X8fJWxeNA2iO2+1uamoCMJ0Q4nMgRhev80fd4IDNZmsH/2FJyWw2f/rpp8G0VGcFabqj52D/NjX9Jex3bW3trl27NmzYgLO1goIC8M9bVlZWXl5eUFCwYMGCvLw8q9V6xRVXwJi7s7pcOs4XAuMAdGCeobkcTnJOnDgBvgJBoeGrcOgQHLYO55cCPK1pGux/dzqdYL+DI7lAAcgTsgKRDpSy03jWlaHiUZxOZyDApevvRZblzMxMo9GYl5eH1eSBHnLA9+vTqMNGf5r+oO4lY/SVAxbdMv7fJox47tpR5RPHl10zvmT8uPP3NeNLrxm3Zvz4NWOvgXvt2GvWjp/w2wnXPTd+wnNXjS4bcdW/XDW6bNSYNWPGrR07/rfjrnl27Pjfjh3/2zHj1o4Zt3b02HLvPeaZ0WOeGTPuWbzHjn9u/Ljfjh+/9ppxa68Zt+aacWuum1D+DzP/8NC9+x/6x70P3/vuI/e+89g97zx2778//o9/fPy+7d77H//wxH07n7hv52P3/RHvh/9x56P3v/7Eg7v+6d4/Lrh7m/fngj89ct8fH7pn+z/d+4dH7nvtoV+89tj9e/7pnjce+MW/PXj3Sw/94uXH7t923ejHdYcePxKIWTvvVMNNqfcoQuo9hxXsoLm3jR4KHcUvvaGhAaw177333rKysqVLl77++uuNjY379u07deoUKApwX8uqESheDt8FGaqqyp6I6F9JJNv/0SVjYP0PVG5eXh4ocA5AX5Jv3U6AY+avv/4aPIbNnj0bD66AbOEEcvZYNlbMYjN89uxZH56AUGGv+v7779fW1oLRiSAItbW1MJfpifT6lMh/IgfA8jcnJ0cUxTlz5lBK7XY7yp4/z7GZenKWBpYe5NICkAHLYF2UC9rPbrcHknw8RhX15Nq1a8Foev/+/XCUNNLGA2HngNVqNRgMBQUF/nIV9rJiJMOcnBzQ3jk5OfpIzHu0NDvR4AB0jLRUnyQDMUFJkvriwdbdY7qmabW1tQgitHv47V4+/K3gOeByubZs2QK2zFVVVZRSh8MBiuySmbhcLk3TIiqfbrc70GBClmUYE/jTCYAUq47ZNIpH+d3vfoeux3BUxKbh4TByYMeOHfBRp6Sk1NbWhjHnAFmxILUvlHQpILeL9F6sBS9NU1wuh8Nxzu3xGgTC0Aem05DGarXChmIY2uKLQQa6oKPTR0FmG5fJ4Ht3uVxg0tW/f3840oqdgsJnDn/ZiQT7+eMsKMpcUlUV5zBYNJ4WJcsyYuIs5Xha7KxZswwGA0zz8HUe6AkHOvnEFLpi2QZCTIQMG2R+tHTp/zq+p5pLVycK1TznbwpHFipUU6miUUX13qA4NEqdLmp3eP+6ZOpRvI/UjjQeD/V4qNt94YYY+Kt5HV5QzJwqVJOps42eO0vlNuq2UcVG1Taq2ig9x9x2Su1UPXfhVmzeGOqkso06zlLPOao6qeKgrjZvjHKOulqp5qCeViqfpa6z1N3iTb/1+b8ZyU8EMvDGSZPdHpdGXQA8dwDQqm4HzQHonkic912cPwMALUlSdXU1AM0ulwt3c8uy7HQ6WcUF77r0Dgk0SRd4SpCPkBioFTuawjCoI8WjsHoJn3YdgGwRRrfb7bm5uRyA7qkMXep9VmzAl8vMmTNlWYZhPCzHXiqP2H3uI7QAzUD3Sil1uVwgYIIgwBl3sVuTvkxZS0sLkJ+RkSGKImBkdrvd4XCArkCgFmvZK0MvkJZLFg3JupjnwvAMlDAs/61Zs8ZgMKSkpDQ3N7e1tWE1eSASHOAANMgw2+FyADoSkpYoeSYmAE0p3b17NyzstBuAcAA6CuLudruLi4thtRYsoKEf9R/JRYGYSBcBm9bdbnf72T6EEJPJlJ6ejvUF9R1pGhItf03TGhsbYdxvMBj2798f2NgTYJ9Y51BHN69omqKqHv2+MAHH4ezChQsBD8XtArFesT5Lnw8AbTKZoCodLeX932crd55wrAtWBJfZ4Dipxx9/HB/xQBg5AFrJo9Di4mcIES9Lufy+e5fKdnrORmWZyh79VqmsUrfivT2a762q9PytULUnd0c+VKGqhyrKhVv1eGNUcInh0QHhLv9ekgzNTc/fHlpf9d+EpEjElGPJZj4ltcMa2rvNIIwMT+SsAOZobm6GHrOxsRHRDRyoYGeDOoFplD7MvJycHNiM39jYGB81isHGwPFJQ0MDcDtxts5omgbD/vYjE2KwaeKGJPh42w3MV65cKYpiZmamz0a0uKmpf0XArL6kpATm1PX19f5peEx4OcABaA5Ah1eiEj23xASgNU0rKSkB36mSJK1duzbR5SDy9WcB6MrKSvBHARObyBce7RJ8AGij0fiLX/yCncXxaU/Ym4QFoAVBqKmpCVxEPADQaGGUn5+PADRGBq47f9J9DvgA0IIg2Gw2xGviQ5uhmkI2Qa1lWZ4+fTpfr0W2hD0AWkn2uJeuWE5Eod2b0Op/KaGUuhXFo6pg/YzWyVEGYoE29m/w1Wff8g+jvGmaVl/j3ZcmESHHko35874SWRGuAFgIUkrr6uoSGYCGrXiUUm48GC7RwnxwPaOhoQGObykqKkJUGpPFayA5ORkOJ4/XCsZCvTgAXVJSAl4Hjx49CgPRWGiXeKWBA9AcgI5X2e6deiUgAA2e5hYvXmw2m+Gc3DVr1vQO9xOpVASgzWYzgIPgJjUup5c+AHT7SLSkpAS2uuN8O5EaPxp1ZQFoQkhVVZWPw8FoEBHWMlBUAAFEezQIwBa89mleUVERHCuPLrrCSgXP7AIHWAAa1i/B5yDbUhdS980Q1gXJhxin0wnuYpctW4aPeCCMHEBwdv2G3wmSCAC0rcOjpddfqtffhtcGOMros08dw0sAyhs6RhMEITv7PAAdl8MDH3721k+32417hhLTArq6ujpxINEoixl+uQ0NDYIgJCcnr169Oso09GJxY8eOBWSwF2mI+6J9AOisrKwEtICGndzgmhw/urhv+l6pYHZ2tiRJ7SeB4+par5ARzUK5D+hocjvhykpAABrauKysDI//Xr16deIolN4ScVmWi4uLwSgAtn/izLO3SIpcueBwEFxwwHHY27dvB39kcVzryPEzyJxxOu3Fblav7utzSxSVTgFol8tls9kUj1JeXo62NlyPBSkq3UvGAtCEEIvFAqA/21Ldyzl23sK6IEkQQykFY8mCggJ8xANh5AACu/srK4hAiCjUNZzfV6t4FGyFMJbYvayQzu697vMWyps/AM2n0z68CuNP4G1bW1siW0DDsR9czMIoV/5ZgZ9xQkhCdRzp6ekcgPYXhvDG4JcLLjiysrJghBbeUmIzN3TBAQA0tz6JQjNxAJpbQEdBzBKoiAQEoOHk5dWrV8O+dcCqOHATUaHXNE2W5ZUrVxqNRlEUvduK3d7T7eP1AuNuVVXXrFkjiqLJZGpsbISjFHG+Ha9178V6ffDBBzCdjg8AGjiJAuMTgKft1tAFBQUIQOOIvBdbIY6LhrMfbTYb9B1gp4mW6WwDxRkTNE1zOBzwcZWUeP1C8CtyHEDPvE1NTSBUCEDDz8gV3bs5w9HQgiAUFhZyVRa5tmA1FQtAs/GBwpGjKmo5ow/oqJWYmAXBJ7x69WqQsdLS0sSZZ918881Go1EQhMRs+ijXevny5aIoZmVlwWCM1V1RpiRqxbEANCHeo+D6usFN1FjX7YI4AM0B6G4LD3+xEw4kIAAN7hFYALq0tLQT1vCosHJA8ShPPPEEjsnwpPWwFhIrmSHWnJ+fDyeAHzt2DCNheBQrtMYRHbIsg725KIpxc7IoO5j2CUPTbdmyhQPQ0ZFiBMVgRp2RkaGqqsvlivtpD1QczpIqLy+PDrcTthR/ALrTDz/++FNbWyvoV2FhYfzVLnZqxIoTB6Bjp13ijBIQswQEoG02W3p6Op7MEWfNGlPVgSWNZ599FgBoxaMkiKtDfwA6cVZ3eksCOQDNAejekr34LJcD0IQQDkBHR7jnzp1rMBgIIZqmgReO6JTbK6XAaODee++FQ4rb2tpkWWYnfr1CVRwXChiZwWAwmUztu9LA6XYc1JeVGTaMewhqamo4AB3Nhm5tbQXUBnwOgr+duJ/2wOoO7y6jIGmJDEDDsRwcgI6omLH9CAegI8rqRM4cxAwAaEEQSkpKcAU37tkCvlPBNDXuK9uLFYR51s6dOyVJslgsHIDuxbaI+6I5AM0B6LgX8qhWkAPQfEYdNYGbPn062NCpqtrXD4i7JNNgYDRz5kyY4MHhGOzE75I58AShcsDpdIIFNCFkxYoVTqczDnalsTLDhsGgnlIKh/zAZk9uBBGqzHQjPbgaFwQhNzcXXo97C2hKKfq3WblyZTeYxl8JngMIQDc0NCgeBW722w8+q76Vsr6+nltAR6HJWFlKTAAazAKiwOpELgLEDAHo1atXJw4AnZGRQQhJT09PZAGIdN1xuFtRUcEBaORGpNmesPlzAJoD0Akr/BGpOAegOQAdEcHqLFOLxQLj/ri3gIaRN6U0KyuLEAJAFZyPgXO/zjjE43rKATCxJ4QsXbq03e04mgn3NN/Yex+x9bq6OkBtEucE8N5qDZg/19TUwPlCxcXFsK0hEQDoqqoq+LieeeaZ3uJ/gpSLo7L6+np3x5UIdW9qaoIRAreAjlpzAwCN3sZxfBIoEDXCIlfQAw88wAHoyLEXcgYXAXa7HQHo4uLiBAGgVVXNzc0lhOTl5UWaz4mcP4pTdXU1B6A5AB3pb4ED0ByAjrSMJVb+ONWRJCnuvSJA03If0L0l4okDQMOZUQBAi6I4bdo0AEPZffq91QrxWi7wHKbTgiDEvZ0mDr7r6urQyh5R6Xht5d6tFwtAt/McAGhAn9lPG5umd6kNb+lNTU2EEEmS9u7dG96ceW4sBzRNs9vtsFXovffeYx/FfbixsRGQwY0bN8Z9ZWOkgokGQLfbARQUFJhMJn5AXKQlEE5HKC8vh/XaoqKiuOwZ/dnIAWh/nkQ0hgPQ3PokogIGmXMAmgPQURCzBCqCA9DcAjpq4p6YALQkSXf8/A7wAc2iVFFje4IUpHgUl8s1aNCgdgfQoiiuWrUqviuOczkWgOZGEBFt9EQGoA8ePEgIMRqNzc3NEWVygmcOmzbAkf2hQ4cSihvgzp4QsmvXroSqeC9WlgPQvcj8OC4ahiKqqmZlZbU7gBZFMXG2NXAAOsqCzQFoDkBHQeQ4AM0B6CiIWQIVwQFoDkBHTdwTE4AmhJSVlTkcDu6CI6KSBls+0en2smXLgOERLbQXM+8UgMbIXiQsjovuFIAGMWPXluKyFcAC2mg0/vnPf47jJo6FqrW2toqiSAhJNAvoyspKqHhtbW0sNEQi0JBoADSllLvgiKZg5+XlcQA6mgxPwLKqq6tFUeSHECZg00ezyhyA5gB0NOUt/sviADQHoKMm5Var1WQyDR8+HLVY1IqOfkEAQmVmZhoMhtWrVwMBrF/F6JMU3yUCw7Ozs2G/Z3Z2NkDS8V1rqB33aBmdVvYBoEtLSymlCQJAg6G90Wjk4GCkhU1VVdjGkWjG5hyAjrRo+eefgAC01WrlPaa/JIQ9BoygrVarJElGo3H58uVhLyI2M5Rlec6cOQaDYebMmbFJYZxRVV1dDceP+9gBxKUpALSdLMuKR1m2bFn7BJN7E4qOPHMAGqEbhDJIdFjPS4lLDnAAmgPQURPs2bNnE0KmT58OJTqdTtRi8TdQgMH3/PnzTSbTypUr3W63y+WK4/pGTYoCFQQMBwBakiQOQAdiFI/vNgdYAFoQhBdffDFxAOjKykpARfft29dtBvIXg+EAANDt+EUCAtCADPJFjmDkJCxpAIBubGxkByddhMNSaO9mYrVawdC+d8mI+9IRgDaZTElJSbt27YKYRKg4HEIIx4/HfX17vYLV1dVwQEXiANDwKRUUFAiCcOONN8JAtNcbIr4J4AA0B6DjW8KjXTsOQHMAOgoyB50lTHVycnIopS6Xy2azRaHo3i3CYrEQQhobG6HK7PCodwmLv9JBxjgAHX8tGzs1YgFoURTffvtt9otmUZvYoTlclGzbtg0A6Orq6nDlyfPplAMJC0BXVVUBAF1TUxPfX1On7d4rkRyA7hW2J0KhMCSDjY+iKDY3N8efoUmgdpw1a5YkSenp6YES8PgwcsAHgA5jzrGcleJRVqxYQQixWCxw4GcsUxsHtHEAmgPQcSDGMVQFDkBzADpq4mgwGAghibArDQ6SUlUVzsSrqalRPMrZs2dZuCpqbE+QgmBuk5gANIAICdLQvVhNHwC6qanJ7XazSBmGe5HICBVdXFwMhxAePnw4QkXwbIEDiQxAgyrjAHTUvgVgeENDA+qurgNRIyxyBXEL6Mjxls0ZAWhYVaqoqGCfxncYukuLxRLf1YyR2rEAdIyQFB0ywMIpPT0dppzRKTRhS+EAdPcBaHhTluWvvvrqxIkTCStDvOIsBzgA3e4xFl30spzh4TByAIAb2PYIFtCgjsJYRExlBSNvSinM7sBmUFVVxaPg7C6mCI4bYmDnY6K54AAxk2U5btoxNivCAtCCIFRVVUEMfNSxSXO4qCopKQEAuqmpKVx58nz8OQASBY7sE80FR1VVVacANHaawBx/pvGYbnMgJyeHEFJfX9/tHPrcixyAjk6TwdcKAtZup5lQfnXANwKfWkZH0iilkiSlpaVFrbgYKQgA6Ozs7BihJ77J4AC0P24TlA9omJq63e6NGzdKkjRy5MiTJ0/Gt6zw2gXDgQQHoEX9WrFiRTC84mm6zQEYiSYUAA0YNCHEYDAAZON0OjkA3W0RuuSLikdRVXX69OmSJBFCMjMz3W630+m85ItxkABOmaeU+o8P4qB2sVMF0GM1NTUAk1VVVQFtiQBAL168GFxwJBSO0FuyN3nyZEJIQ0OD4lHg7i1KolkuANCCIPhYQHMAOnKtAPhgXV1d5IqItZw5AB2dFuEANAegoyNplFKTyURIUGhY1EiKQkEcgI4Ck7EIDkD7TzBD+OQ+/fRTOCpUkqSamhpuMIWClbCBBAegrVYrIWTWrFkJKwDRqXgiA9CEkLNnz9psNrCAjg7DE7aUwsJCQojJZILjX0Dw4p4boigmJSWdPn2ab8SLaFsHAqAjWmiMZF5SUpKcnAyoaIyQFMdkzJ07Fw4PUDuuOK4sVg12UguCUF1d3VFv738OQCOLwh7gAHTYWcozBA5wAJoD0FH7FsDBYyIcLMSylAPQLDciHeYAdDcBaMCalyxZAqZSaJQX6Qbj+cc4BxIcgIYN+1lZWTHeTH2dvEQGoEVRdDqdYI2Lrjn6eoPGIP2KR3E4HL/5zW9EUTQYDFarNXEsgsE3wv79+xMEcO8t8UtkALqoqAj2FnAlFlHxU1XV6XRmZ2eLovjee+9FtKxYyxwAaFEUOQAdtaYBADqhtjVwC+joSBcHoOMVgI7BMQBsNv3000+jI9sxUgoHoKPZEByA7iYATSl1u91jx46FZaLk5ORvv/02mi3Hy4pNDnAAmhDCAehICycLQM+bNw+QQbRsinTp0c8frLfAB7QoiqB+KaUcH4xcW8BxcAUFBZJ+ZWdna5qWIBbBrOPUyHGY5+wDQCeU41QWgOYWqZH7FjRNk2U5KytLEATWB3Qi8JwD0JGTq0A5cwA6EGd4fA85wAHoOAOgYR9nbBp2iKIoSRIcptpDue1Dr3MAOpqNxQHo7gPQp06dSkpKgpnquHHj3G63f17RbEteVixwgAPQHICOghyyAHRhYSGlVFVVWZYBqI2/qTULQINjsgRBQqMgS4GKQAAaRqIJBUDDKfM1NTUxaJkSqL36YrwPAH306NG+WIvu0cwB6O7xrRtvAQDt44Ij/npJf85wANqfJ5GO4QB0pDmcsPlzADrOAGiUZGhZ/BkLAYPBwAHoWGiIOKaBA9D+oHGwPqArKysBfSaE3H///YABxbGs8KoFwwEOQHMAOhg56WEaFoAuLi6GJXQOQPeQq/x1lgMcgOYANCsPkQj7ANAtLS2Js7DEAehISFSneXIA2ucQwk65xCPDwgEOQIeFjTwTfw5wADrOAGhN0xwOh39Dx0IMB6BjoRXimwYOQHcTgNY0rby8HE5nIoSsX7/eP6P4Fh1eu045wAFoDkB3KhjhjWQBaBiTKR6FA9DhZXKC59YpAO1yuRKBLeiCIxEq24t19AGgKaUulwsie5Gq6BTNAejo8JlSygLQikdRPAq6qwI76KhREuWC0AKaA9BR43yiAdCaplksFtgzFDUmR6egWOuJgB4QMEJIQvkZLyoqIoTEGQB96tSpDz74IDrCHGopHIAOlWMxmz6YfZy4yTiateAAtD9uHKwF9Ny5c036lZycfOTIEWi2RNjWF00B9SlLluUPPvjgzTffXL9+fWlp6euvv/7tt9+yowRszt4ypOIAdJwB0CBdhw8f/vDDD2GXA8gYSpqPiEbtpyzLAJMtX77cxwd0XE6qVVVVPIrRaBQEITadpvW86TVNQ4RXlmVWs/U881BzYAFoQRDmz59vt9uRvFBz61vp4cuqq6vrW2R3TS2KE6BvcMiky+UKZnjadc7dfgok1dTUAMPBjxA7iEKau11EzL5YVlYGqA186VjrmCU4SMJYT/FwWDeltKWlhVLqdDqDzCS8yVgAGpdpw1tEbOZWVlZGCJEkqa9jVawecOkXpdThcGia1ovqq9NGT0AAOisrixCSk5PTKUP6YiSrjRWPAg42WSGEuYBbv6I2FwACEhCA1jStpKSEELJu3bq+KE6BaL7rrrsIIenp6b///e9lWbbb7T6y5CNygfKJRDwHoCPB1V7J0+1222w2TdMUj2K32/HwJOhAgSRYmI8yeRyA9vnevcdcBdkGo0ePTtKv0aNHQ+tipwWBIPPhyS7JAcWjnDx5ctOmTddeey3MVCVJSk5ONpvNhJDp06fv3bsXEWcYLlwyzwgl4AB0nAHQsiyfOHECpG7IkCHr168/c+YMzqsjJEVBZitJEiGkoKAA07MqCCPjIwAdJ/gjxh40PqoGtfjrX/+6du3aHTt2gMler8+rWQAaxCwGZ/sREgBABt9///0I5d/r2YJ0wbYJFjGMMmEwv2IB6MSxTr3j53cQQkRRdDqd8aS3XS7XmTNnqqur4VxuVo/BIC36k2oEoDds2AD9CA4XoyzwUS4OFjkkSYqDtTQQG9i0vm7dupKSksGDBycnJ69atervf/87OySDJo4yq7G4RAOgVVXNzMyMMwAaW1PTtPz8fKvVumjRot27d3/++efwSNavKG/ZgU8gAQFoSmlpaSkhZMWKFdg0cRAAVL3dslsQhMGDBy9duvSzzz6D8X+v144D0L3eBOEiAMbbTr5hAAAgAElEQVRgR44cOXbsGHajkLmqqtBdcgvocHG763xAe4uiCOu13QSgT548aTQaDQaDKIoPPPAApdTtdsPuUZxLdE0HfxoMB+DLKS0tTU1NhdkaKGuj0QiYIGDQMPo5duyY2+0GS8lgMo9EGg5AxxMAjVPlpUuXggQKgjBgwIAHHnjg+PHj7JwnErLURZ6qqjocDkm/Vq1ahSlR+SDl+KivBwCZMhgM8WoB/dBDD5lMJkJISkrK4sWLjx075t85RbMRofSCggJRFMHNVDRL792y4Mt655134u872rp166BBgwghRv2aPHny4sWLoabRN1AF9gIALQgCrHDEH887Feb09HQYzMSZOwhZlkePHm3Qr8zMzE2bNp06dQp3TvSKTkMAeunSpTHrc7NTIelhZFlZGSzZ1tfX9zCrXn8d5skul+v9998XBAF6JVEUYS6QnZ392muvsasdvUUwB6B7i/NhLxdG+LfddpsoirAmTQiZNGnS+vXrT58+DU9h4h8dwYOeMTEBaMBqH3roobC3cu9m+Le//W3evHlgSwSd5uTJk1955ZUzZ85ER6gCVZ8D0IE40+fiFY/y3XffAWJ23XXXzZgxIzc3t7i4+I033oCVeByeAYAQtQpyC2j/8XBQFtBNTU1JSUkwBtqyZQvsx4lxALovzutqampuuOEG8LUtimJSUhJ8RfgXFLcgCCkpKYSQnTt3whfl367R+ag4AB1PADR8162trZTSoUOHgrAlJSUZDAZCyCOPPHL06NHoyJV/KQcOHAD8YunSpaqq4iZBxKD9X+m7MTAUO336NCwDuN3u+MMRTp06ZbVaYapjMpkEQZg9e/a2bdt6q9UQgIap18qVKwEp6y16olkufFlFRUXRLDQKZWmatn//fkII9KSSJMEYBvrTmTNnbtu27fvvv48CJVBEIgPQubm50I/Afo640duKR1m/fj0gg2azGZYMJ0yYsGHDho8++qhXTI8RgC4pKYGFzKhJeO8WVFpaClhtHFhAs5x88803y8vLn3zySQTjQIMNGjTo/vvv//vf/84mDhSO0IQISKqpqQlUbpzFx6sFNBoGXnvttYg+g5iJomgyma699trnn38eusvozDdhGIwy39f96oT0IaxevZoQctttt4X0VownhjWMb7755vLLLyeEwHggNTUVFtXuvPPOvXv39lYVOADdW5wPb7lgkamq6uLFi8FeEwb/giDA+P/RRx/929/+BoV2YVQXie4y0QBoTdNAexsMhry8vE53cgcFQG/ZsgV8qxFCwAF0MIa30EtBx3b69Glo8q59rzidToCWLimUIB9dLJqh/xfIqrW1tb6+ft26dVu2bDl48GCg7dVgFSXLcqczB1g5QdelUEF2OQUqe0ni2QSQieJRfve737FWz5Ik3XbbbW+88UZTU9PRo0dXr15tMpnuuuuuiRMnIh6dnJxcXFwMuUXig2Hp7DTMAei4AaDxg9I0TZblOXPmgM93AKdw5ePmm29+7733WGGw2+1dfIZsyp6EGxoaYFhcX1+PJxAiitErwt+T6lzyXcWjNDQ0iKLYv39/Sqm/16NL5hDjCRwOx86dO0G64K8gCElJSUOHDs3Pzz98+DBOclggOHKSBjnv3bsXtGv8obFdyEO8AtCwu/Ptt9++4+d3pKWlmc1m0GPYgRJCBgwY8Itf/KKiogL502nXj097EgA1VVxcDB19pwOynuQfy+/CSNRoNMYZAE0pBT0GdgMgYLC3Y9CgQQ899NCePXtsNhuIIitaMBKOUM+Vk5PTvnWmqKgoQvnHpqSB2aAgCHGAVQUyzvr666/ffvvtp59+un///qJ+GQyGqVOnvvzyy62trdhpsu0Okxp8FN62g8VjDkCHl6vRzw1MHNxu90svvWSxWEwmE7teK0mS0WgURdFsNmdlZb322muI3bjdbgi7XK4wyhhMQyilU6dOhf46Dj7q4JsVVFlubm7wr/StlB988MGmTZtycnLMZjPY2QBcmJqa+sgjj7z77ruwzx5EC2GZMAqYD7s4AO3DkL77E/s+xaNUV1c//vjj6MwWYUxCyMKFC7/++ms4YIntbYPBNrvHnEQDoN1ut9VqNZvNRqNx5syZnTItKAB6xYoVsIAwYsSIU6dOgaVkp9lBJIyzZVl+9dVXZ82aNWrUKEmScnNzP/nkk0tqEKfTGQyM+8orrzz//POX3EUry/KXX365dOnSAQMGmM1mqIXBYHj++ec7xTIgw5MnT9bU1CDcjDgXnBpEKf3rX/+6bdu2vXv3gg8j0JXgEKMLtnTx6IknnpAkCSA2SZJmzZrFeuS02WyKR4GTbb7//vuMjAyY4cDntGfPHjzYp4siIvGIA9DxBECjnMMHfuDAgXnz5uF2PNjcSggxm80zZ87ct28ffss9kfwgxZIFoMECGqllO48gc4v9ZAhAt/sjhh4Rv/G4qS/UEY70gTkGbjSGvZ9btmw5e/YsNFan6jrs7bhv3z4OQIedq72SIQ5DsfTm5uYlS5ZMmzYNu1pA3sES58EHH4RlcoAL8a0wfm5AUnFxMYxDsIhECGRnZ8OXFWcANNhMvPDCC0899dSIESNgSCZJEnpLI4Rcf/31xcXFgXaxsAtsPZcEcG44depUk8mUaAA0mA22D8lqamrY4UHPuRr9HFj62TCsZGia1tbWtnXr1jlz5sBnBaps5syZlZWVPgfD+GvCMFYHAOjq6uow5hnLWcWrBTTwHGFfSumf/vinoqIicJ2EMobeIK+66qpVq1adOXMmQo0FXqc1TUMJ5wB0hFjdK9mCToPeqqqqKj8/f+DAgWAWnZaWBh2o1Wp97bXXwBE5nKYbOVI5AB053vZuznAa4TvvvPPwww+jHgMTkCFDhixcuPDLL79EKCOipCYaAK1p2s033wys7pEP6NmzZ8Mkbd68eQBOdT2msdvt+/btmzZtGoDfgKsajca77roLFhwCNXO76eXBgwdLS0vfeuutQGnaR2ArVqwABHb9+vVdJKOU1tTUjBgxAoFdVv5OnDjh/67b7X755ZeNRqMkScuXL/efLNXU1ABPYaZhNps3b94M3GDNW/xzDhTTfmRnfn6+yWQC+yxJkp588kngEjtjgS8EMHGbzTZt2rSkpKTk5GRBEKZNm4ZnGQUqJULxHICOSwAaVDYI4aeffrpq1aphw4bBtwPYjSRJJpPJYrHs3r0bRgaRxqATFoAeOHAgfPVwSh7ORSP0RUctW5fLZbPZAHw5fPjwgw8+CCY2gn4RQtq3d4DIPfTQQwcOHGAJ67r3YVOGGq6oqIBCuQV0qKyLzfSwbgFLOCg2n3322fbt2+fPnw9bQSVJApdWhJAHH3zwiy++gNOWutehd8EH+HiLi4vB6XYXKePvEe7F8x9T9fXKwtgMpEXxKO++++7atWszMjLQexXMq4cMGTJ37txXXnkFfCZEaEUNzkuYP39+UlISB6Dhi+uLAoYdvU8A6oLC43a7//73v7/yyis4K0lJSenfv/+jjz76wQcfYMVR9WFMuAKJBkBrmgZL5nFsnYqyAZrtzJkzZWVlOTk5/j4hCSELFixA+3c0i8Ycuh2w2Www4n300UdhSJZQADSspQFq020e9pUX24++hLnAkSNH/vCHP+CSA8wCjEajxWJZv379N998EzmgkAPQfUVagqTT/4SVdqjNZrNt2bLFarWCSgEQLykpad68ee+88w6qrwh1l4kGQFNKb7/9dlgat1qtcPy7D28DWkCzQ7dx48YB4Lt48eJLmj9TSp9//nloWmxmdC6xaNGiN954w0eGcIfFBx98YDQa21HdoUOH+qSBeQtEjhkzBnJeuHChTzKsnqqqGzZsEAQBKDcajcOHDx85ciRu9Hj77bd9xnag3fr37w8smzhxIuSGyeBo2pSUlOTkZLPZjGbI4NPDh5Igfy5evFgQBFhYbj8jftmyZejiw263w6wGNwXg2Z0ffvjhyJEjEaN57733FI/CNlmQpfcwGQeg+y4A7SMtKOQQgMNGUDza2tq2bds2efJkdlIN240zMzPff/99sErGeRG+yH62bGSoYRaARkXG0hxqhjGeHi2gs7OzEdyPdH1ReUaHOWj6B/r/+PHjS5cuHT16NNtrwBKmJEkjR44EVwkRJbKyshJK5wB0T2Qgom0UEmEgWna73eFwdAoov/3224sWLbruuuvAe68oigaDYcyYMfn5+fv27QuprEsmhu83MQHoW2+91WAw3HTTTTF+dgg2IjQW/rxkwOFwoJUW+HBTVfWjjz7auHFjTk4OGHDAGhshZOzYsYsWLdq7dy+Yd10y85ASyLJcWlra7u2EA9ChNmJIfI5oYravZ8MwF0AgBrZrgKnKxx9/vGDBAnB5D3OT0aNHr1+//sMPP0Q/gWGnmQPQYWdp72bodDp9um/EZY4dO7ZgwYLBgweznqyg37RarVu3bu10/N+96rS0tMCUdtmyZTAk4wB09zgZ0ls+TR/SuyElBnzQrV9QKOIelNLvvvvu1Vdfffzxx6+44gp2OjB79uxNmzZ99913IZUVTGIEoMMow8GU27tpLBYLISQ7O7t3yWBLD5cE4klRmDm0rCzLTqfzm2++WbNmzeDBg3FLhyAII0aMWLZsGXo1wBfDFUg0AFpVVVhIC9kHNI54AD8C93aEkO3btwdClHCIs3TpUlAZsF764IMPbty4cfbs2YBBw0C8oaGBbVTcyPPggw+aTCbY9f/RRx+xacDNBZgmmUwmMFnyPyUWydi5cycMwgRBmDBhwltvvdXW1nbixAlCiNFoTE1N3bFjB1YThF5V1aNHjwKFhJD58+cDAU79WrlypSiKiPlCdaAnXrhwIexdCnKbvOJRoJvfsmWLJElQosFgyM/PD/7z27Bhg8FggAlzUVERojk+TIvoTw5AhwRAgyff4FsE0BP84mDW4d/Q4BMZsmW7T/iscK7iUy7kw34CnYZ93qqvr3/ggQdgSwF8AmC5f/vttx86dAgowc85kC91nzyD+dnY2Aj+GQ4dOqRpGnImmHf7Ypp290n19fXt7iwtFossy4Ea8ZJVczqdNputa3aBzNjtdlYALplzhBLIsrx169YZM2aAf15CSGpqKsobIeTyyy9/5JFHqqurUYCREuQSPoIaYYJLBqqqqmD1EX3rX/KVOEgA/XVZWVnwvU/XtWaPWOjhMWiIGnctw53Sw8ozG/ZPrHgUh8Px8ssvjxo1ip3wpKamtrtW2Lp1K3jnQBrQTQfG+OcZKGb16tUw2wmUIC7jMzIyCCFgB9F1W8RI9VkZZkliW5xVL6qqtrS0uPQLNg+Bl2fwh3D69Ont27fDMNjHQcf8+fM3btz45ZdfItDDFte9cGFhodFoLCsrA92OirF7ufWVt8LlggOa2Ol0gsFHSH+x0XsYAGjG5y+OBMDxrizLcAIHK6vHjh177LHHYO4D1jZGo3H+/PngJBqbEtC9noscB6CRpcEEgOGnTp1ixQNexE+1t/azsvT7aAz4Cb4xT5w48cYbb0yYMAEssbC7NJlMQ4YM+c1vfgO+ImHCDh6K2JyDDOMQDqy+2mGyODtZtGs+wEERVqu162T+T/G8gU4/bRxN+b8IMez8MVCa8MaD7grkQNztdr/55ptoE402f7NmzdqxY0dLSwueGQbqutu0wWS2trY2+hzoNs09fxHg12gC0OzYL1CYrRfqgUCJu4jHjhvSgMqFzNFLVUVFxR0/vyMlJQXG5AaDAbrLF198Edw/gtKD7jIY61uWeJ9wAgLQq1atEgQhZAAaMC+Yjn755ZfYxzQ3Nweao7pcLlmWn3nmGdARkiSNHz++vr4eTCnb2tqSk5MlSQJUurKy0qdtQG8OHDgQQNWUlBR/T9CgPU+dOgVpCCHgrYLNCgCXo0ePDhs2DM7ouOmmm2BNw2azffTRR3j66tGjR1FAUemgBVw718rKyiDn1tbWF154AZiQlJRkMpkee+yxFStWIFsWLVqENLDfA0Z2Gjh9+vTgwYMBVhMEYcGCBcArxNA7fQsjv/zyS3AlKUnSggULoFx8Gp0AB6BDAqBhUQ6axmdq0elPSqnPAK61tRXMrFB0ITec98JPPKYPf4LyBW0OkfCXFdeuw2B6A3/dbvfGjRuHDx8OayfoNuH222/HE2YRo2GL63YYAejKykoYWvkMkbudc2y+GBYAmh1udtq4qPdQq2Oy3mILGHOpqvr5558vWbIEN7uA8/GkpCRRFGH1MS0tLSMj45lnngGPn+iwCBzIYEWwasHUqLq6OgEB6BkzZhiNxsLCwk4nLcHwLVCakJgfKBOIZ4G/rlPiU1YG2DAmwAA6HXK5XDt37pw4cSIcjAPTEhjSzJgxY9OmTZ9++ilwCXwdwDZhzCeYAAegu26LYHgYnTTY2QEkhNoSeluXywWmCdAjo/kzdkzQR/sswBw/fvxXv/pVWloaWELAhAcGgffcc8/mzZuPHDmCOYDM489gag1fXGFhoclkuuPnd4CsBjmkDCb/WE4TLgAa6sj2njFSa1adwkfUqcaG5bTNmzfDbk44vQPMbhYsWLB//348oR087fakdhyADol7qEPYt+x2O3zjnT5lUwYKsxq1e2E0c4GAj1zBT4wEnfbFF188+eSTANzAXBgto+fPn19VVRWI2mDiEXjiAHQw7PJJ43Q6/XuNYKQLujyf3CLxE3BnPMHS7XbDFiIfFYfzX4fDsXnz5pycnNTUVIALCSEDBw68/fbbfbbUd09vwx64xPFlD3yOQQAaha0bQ2t8t9MAYCCsgCEkbbPZtm7dOmHCBNBjqamp4CVv8uTJzz333Ndffw0jKFSAlFKcb3ZaVqeRiQZAa5oGADQcAdgpfB/QBQdwUNO0d955B6ZhaWlp33//Pdt+LJc1TXvzzTcRpb3++utPnjwJCVwul8PhmDhxIpg2G43Gr776Ct/FDPfv3w/osMlkWrJkCSbAAAzoP/74YxivE0Ly8/PxKfpNVjzKnDlzYNI4cuTITz75BPpUp9P5m9/8RhAEs9k8adIkHyAP9DU4DwGA+/Dhw6DLDh48CPUymUxTpkxpbGwEQWxubp46deqkSZP27t0LZITkp/W+++4zmUygAsDa2uVytbW1sTXqIuxyuYYNGwak5uXlIRu7eCXsj3wA6F6hIeyV6jpD6KFXr14timJubm5IADSIKKW0XYZLgrg2b968Z8+e+vr6urq6+vr6AwcOwHGUSCEg2rjG4/+Fg6Ai+oyjOuj+Qxqq+oPXikfZs2fP/Pnz2W0BkiTdf//9AEM7HI5wiQQC0IcPH8Y1SeRD/AXCAkCDPATfkbPy0CssRUcusB5DKT1z5swf/vCHWbNmiaKIJ7PDvBp0Mm5YufHGGzMyMh5//PEvvviie9v8NU2rra1NQAAanFquXbs2jI3OfvusXIUUBnpAKrqhSQKVhdVENYgxGHjzzTenT58OIx+QNNhsJIri8OHD8/PzGxsbMXFIcx4AoEVRZOf8mFW8BvqoBXSnvR7O5EHAoMnghGpVVQE1xhViTAzJELYuKysDGJr1dw+jwSlTppSVlX3++edgToF5BiMb8JkAAJ2enh6SZAaTfyynCRcA7XK5us23QDon1HhWfjDM2mHBoM5nWQ6gZ2gjcHm5c+fOyZMnQ48pSRIosXHjxv3qV78Ky0528CqDXoBjWTzCRZvFYhEEIS8vr9sZ+vdlYDLiHx9kEaFKl396tjNijyIEAljkBUmCcfipU6eeffbZzMxMdpsa9JiTJk165ZVXYDCGbwUZQMWbmAB0UVFRz30jgIoAY09QaF2oNRCJIFsnEslA+EHXgUEAYuggaZDg2LFjxcXFw4cPx3U1UEEIGcmy3A3jJ/io6+vrI1G1GMwTmttoNAqCEOMW0Nj9hRpA+YcX4Sc48HS5XDgwAwUFn8bbb7/9yCOPwHmYYCIAp16NHDnygQceePHFF7/44gtZlruBPlNKOQCNPMcv4hIAtOJRNm3aBN1J//79u+ggT548if560tLSPv74YygDu64ZM2YAKGw2m7F46PYc+vX0008b9Kt///7+SgSKdrvdBw4cgK5OFMWCggI2KwBcfv/734MfNELIjh07IFJV1T//+c/gmXrgwIEvvfQSWrWgdLb791i+fDmkkSQJVjncbvfNN99sNBpNJtPNN9/sA50jQ0G4WYCvC161Q+QAahuNxpSUlKSkpE8//RRwIthkhwNNn9rhKAHKzczMBA0ya9asLorzzyRcMRyADgmABh2nquqLL74IK2xd/GUtC+ADxL/sW6NGjZo6dWpOTk5WVlZOTs6kSZOys7Ofeuqp1atXr1q1qqioqKKiooa59u3bd/DgwRMnToATGP+RaBcxaOQFez9hnNrS0uJwOHbs2HHjjTcihYSQ9PT07du3f/XVV10MeoKXQwSgQ5qNB59/rKUMCwDd1tbW3Nz87rvvHjhwoC7AdeDAAZg9+shDLzIEVRmrBo8fP/7888/fdNNNgAnCWiZuZ8ElSdjmD3oSJTnIumiaVldXl4AANJx0/9xzz2FnHSTHukgGWTkcjgMHDjT04KqsrNy7d29DQ8OxY8e6KK7TRygAPgFMrHgUf7BJVVVYBtY0bceOHWPHjgW3YJIkoQ9fWA4ZMmTIN998g7kFGeAANNscXTMNVUHXySL3tLW19eOPP25sbKysrDx8+HB1dXX7ySKrO672jdLFxcUlJSVr1qwpKioqLS399a9/feutt1oslpyOy2KxQNecl5eXlZXVfmTCbbfdNn369Ozs7IyMDDjOF/pNVonBTrvRo0dnZGQ89dRT/kvLgaoMHAMAuicYWaD8Yzk+XAA0AB+apjWFfjWG6epUZdbX1zc2NoJGrdev6urqpqam5ubmioqKhoaGgwcPNjY21tXVVVRUVFVVNTQ0NDY2NjQ0wLwGdkyCNgMN9stf/rKHOh8sYDgAHcx3Ad9mdXW1j/HJ4sWL8/LypkyZMmvWLFAbVqs1OzsbVEemfgl+FzvYDmMYcWQIAP6CRzqBHb3ZbIaN1aiyYEoCZMAqWrsLIDAOGDx4cGFhYTD88UkD7OIAtA9buv65bt06q9WalZV19913d3RT3v/PPffcwYMHa2tr4YzlQJkoHuWrr76qr6+vjfBVU1NTXV1dWVlZUVFRX1//pz/+ae3atcuXL1+5cmVhx5WVlZWdnd3Rkebk5eXNnj372muvBTEDNAkkExGh48ePs9hioGr6x99www2EkJ6c5uWfZyzHAFQVmwA0dElOp/PAgQPQzXXvLzvlXbNmDWjdsrKyFStW3HbbbdOmTZszZ05OTs6sWbNg6wboK/BbBdKVnJwMfhRMJhM8nTdvHjja7UbjcgAa8VLkXkAAGpK2r6Ln5+cLgpCUlJSZmckiAtA9fP/995DXfffdB8kEQdizZw8Oa3CT1+jRo9G+A5/iwNrlck2YMAH0CHh2Zk2owBcBJK6oqIBkqampL7zwAtaEUirLcltbG9iVGAyGxYsXo3vcd955B95KSUm58847wUGVylyQz2233QYAxPjx4yFm0aJFsBs3OTn56NGjEOnjHg4NqdiZFfCHJY8NP/HEE0CPwWB47rnnYMgL5MDqn39Tsa9D5jNmzAAX0nfffTf7NGrhBAegZ86cKYpiVlZW143l0xyqqp44cWLr1q0LFy60Wq0zZszICnANHz48yJElyBIkFgQBFocNBgOY2MNYEFZ3cHQ4atQoK3O1T1aLiopKSkoKCgpWrVq1dOnS2traioqKd999t6amBmY1tbW1MKVpampqaGiAXgFmSjU1NXv37t2zZ8/s2bNhkwHq8fvvv7+6urqxsfFvf/sbfPi49hO8cS4C0GGBs31aJAZ/hgWA3rx5M1g8+U1eLooAGBc6WvybHeCaO3duRkbGvHnzCgsLS8N9tSMIxcXFa9asKS8vLy0tLS8vv/POO7Oysu74+R0wQATZvoh6QQCNjd4S2pf0wV0gauMg2zdhAejs7GxCSGFhYTc+riNHjpSWlt51111z587Ny8ubPHny5ZdfjmbpwagvVl8ZL75g9gt6DBaVQX3hvLfT/EHmfR6BzKB4oyChzsTDGJKSkkCdQmJWteLCNgxPJUnatWtXkNKFyTgAjR9mF2MkEEVN07799tuioqKBAweC9zaDwZCamgr8R2EBFMynxfGnT9NDs2K7g28fSOPzCvsihH2EAdOzAon70KEggGYA+4NFZZj1wbtGoxHTs7nB0V4QM3ToULvdzo6ZUZYCBYqKipKSkrKysgIliMt4FqtCGQuypnB8H2uNjg2EYhZMAEZZQf5FkA46L7BQ9pFPcNICRYMmTElJgZUwf5lE+YTRF0qUTwA8WUEkznSCZBQkc7vdYJYIQ82EOiCu2xbQmqYdPnxYFMUBAwbAyhPoDVAR0O7wF9vRp+EC/URJ6HYAVvSx64R+FnQjKFuz2QwojNFoBOnCPhSphRisCLwINDc3N4NZQPBzJfiEi4qKoFIJJWMrVqwwmUxTp04N6atsP77vl7/8JatAAgkMNg1Cb8BkVhS7kCUoAhKD1kIZgNE4SgLGo8mIP0kgddA5wjI/qju2Y4UdkGCXCpn4GGmZzeaPPvqoe/gggIPs0TIgfqHyv6+k7zkAXV9fP3fuXIt+wWTRarXm5OTk6lcg4fFv/ejHsLT5lI6DMVRirASKojhkyJBum8lzANpf+QcEoGFu4Ha7H374YVhlmj9/PgDQOLbD+cP27duhIcF7BjhMwYMyKKVff/11SkoKDFbu+Pkd7EQXvoTjx4+npaXB3A9Pn/cnl1JaUVEBMmE2m3fu3OlDzDPPPANHJprNZjzq8KWXXjKbzWlpaSaT6aabbgLT5k4PDMzKyhIEwWg0zp071+12NzU1Qb2MRuPLL7+MygVPOUfImCUDw5jeJ/Dll18CKyRJmjx5Mnro88/N50X255kzZ6CmRqMRt5+wCaIQTnAAevr06UajEczPodGD4Tmk3LFjB3gawmphVlUAACAASURBVA6bVYsQxlECBEDsobfGuQr7Fg4LuujsfRQuvo7YCtvBB4rE+RKgNjCPwqEGWwRMdYB+g8GQnZ1dWVkJeiN4jlFKEYAOhsNxkCYsAPQXX3zx8MMPX3LabDAYYHZhYi62Edlwp63MJohEGArFSREKbafELF++HATgknrYR044AM32yz7MCfRz0qRJ0OIs5NFpu7CCcckEbGIcFEIA1CBOfnwC+CL4BcLhI8gMO6wE3cVil6xrF0wZiFRRFPGYYhwIBeISG88BaPwwg+TbHT+/A5oVBAAmt9jQEEhKSkI5wS4VO0Rsa0QGIQ3gvPCi/6oJFOQ/wfYpGrLCSLPZjJoKIyEAsoQyCV0tAOs+KWFRUNAPoW2H4Fn5CSacmAB0fn4+8A0M2UIaYIwbNw7eRSmSJMlqtcIEO/i/WSFeM2fOzM7OHjduHCxFsNoMBAOsTUF9sYus/gITUgyeHzNmzJhgJIpNAxtHwDMS5JNQ4GC3AWhKaWtrKyweiKJoNpuTk5NBBeGQJqRGjERinDsA3ofdHwZQ3bExQAl0pqB14Sksn0D4tddea99kjLNdVqI6DYNd19atW4GkhJIx2Mzhs1m8Uy75RLpcrkOHDrWbPyMEDNxjGwvCYFeHc0zQLdh2bHp/MWNHU2gjj8nYp4SQG264Yfbs2RkZGdM7rhkdV7p+ZWRkZOpXhn6hBs3Jybn11lvnzJmTnZ09Z86c3NzcKVOmjBo1yoc2URSnT5+elZU1b948H24E/5MD0MHzClaSbr/9dmxxNoCjJnbpFCehOADrOgD9IOoiNv9whUHU4S8UByRB/vgUhQ0DM2bMAKQuJI5xFxxobczyLSAADYkUjzJz5kxokoULFwJYjPMHXNK88sorIc31118Plho4lYU5xnPPPQdayWw2FxQUoHMfzOH1118H64PLL78c6esUgC4vL0fYq6qqComBgtCP+AMPPAA0/PrXvxYEAcyis7OzwXsLznwgAF2dqqoTJkyAeQicKwjOMUVRZPcQgX9StOL04YkPPVgXNlBaWgrD3NTU1NLSUnDsiz6pu87BbrdDvZ5++mnIRBTFP//5z2z+UQsDAA1j0O65+ooaqeEqiPUBnZeXJ0mSxWLBhZkgS9E0rbq6OiMjIycnh92ui7uNIJCenp6RkQHritnZ2VarNTMz02q15ubm4kojrDfm6ReE4Sls4oN9fBZ9FzBMomCtEvLH9Lm5uVlZWdOmTcvJyZk5cyZkPn369IyMjJkzZ+bl5V1//fVw8hssnGB3goGkpKQU/fKfxsMyCczuYLhz+PDhIBmFyTgAjawIKfDXv/6V9dAdqPNmMZFAaTAedu+ykw3srXsYgCJg4AKDD9ZGDAUJASYYE8BfPDVu8uTJwCJUpEFyjAPQ2GsHybH2peVHH30UBSPUwFTmCmBw73VTcPfddy9ZsqRYv2CH5v79+6sDXA0NDdXV1du3by8pKVmxYsW6desKCgrmz5+fx1zJzIU0o+KCAEoyjjshJa6ltefMLhgHzzEOQOOHicMwf+6hEcNnn31WW1sriiJsh4RDz8AkAqfWuCiLCgFGm4IgwMzW/++8efNWrVq1bt26FStWtB83XVRUBPs92W2bsAsZDmDArT/g06BevyBxQ0NDc3NzbW1tU1NTdXX1Sy+9VFpaWtBxFerXqlWr2seQRUVFhYWFxcXFq1atWrFiRX5+flZWFqhTlEPEdwghQ4cOPX78uD9zLhmTmAA0+Bk3GAwbNmwAGbsko9gEON2Ak69UVQUjXzbNJcOsbAcThlLYHZCgVVRVhW1nzc3N6EGturq6tra2sbGxpqamsrJyLXPBNhSLxTJ79uxbb731+uuv76JPZ/eRCIJwyUr5JMCTyr766isY18GWI59k8fqzJwD08ePHYQxvtVoXLVpUWlq6ePHiMuZC/QPKB5ve3yMCpgQFpSuk7v+BHY0NDQ3g0aWuru6ZZ54pLy8vKysrKSlZtWoVBIqLi9v7L6AX9Njq1atXrFgxefJkURQRW0f7KlBroJbvuuuukLZxwKy8uroalgATR8ZUVcXNHN34iDRNu+eee8D0B4cxWcyVm5sL3dDKlSufffbZ4uLipqamyspKFDYYW1UFviABpAfJhPN44Xhe2PXu1i+k3+12qx0XKkZ0ywvJ/JU2mPpRSk+dOrVt2zb49GCEZjabJ0yYsHPnztbWVkwG+XRjHMsBaGypYAKKR/niiy927drFdEFrWe0TKBNs+iADrJYLNYw6E15kxRUe4dAORnf19fUVFRW7d+++9dZb8cNhu9H777//rbfe+vLLLwPVrut4bgGNQyxkVFcANHQAkydPhv6jfSDtIzTgyOLZZ5+FBGazGXekQk9z+vRpmEig457U/5+9N4GOqkr3xc+p0zWuVIA/0HJpkAZEBfWpwA0kuRlfBnwM3nZovWLLc8CHdnMFYSGQf8aXMDxB+TPoE4UrKN2K9hLQJQZexkeALEC4gHo7ghccrgheyEANp6rO2f9QX/v19lSlqCRVlUqd76ysyq5T++zht7+z97d/+9vftttff/11vhwwCQHjBUmSHnjggaBUJkSTZTkrK0uSJOhejx49yhfp8OHDgiAMHDjQarX++c9/rqurmzJlClhmmUymhx56KHD1FadA4Kxj+PDhoJxVVVXt2bMH3KWNHj0aVC6XywU9HWT6U3eq8GXgw4gy8Oz4NSMjA9YbBUEAp+bwEySoSQG+4rPgmeSDDz6wWCzQEYNNN0aIZQAJaIPBELTVYlmY2OTFE9BPPfWUIAgTJkzAwyfDLAO8Wbj6gkKoeRxfExzLezCygvygrEIWkCPehIxgFoRzISwMOGR3Op0o/4qi4GBQU1Ozd+9e8OR16NCh/fv3b9q0ad68eUAXDhgwICkpCa2KBEEoLCy8ePEiVg1zCR0gAjo0PkF/hROK3n///dKQV0lJSUVFBRB8+Fke7KqsrKyqquo8gbOiomLlypUrVqyojOilccEBMxwoXuepLFA28NQk/nQhcTNnzpyioqJ169a1tLQAGtiRBgUn8KZuCWhYZ4XxPRCW0HegR+K7jtDxNb9CTxhiERdP2VJV1e12Q0ageECvqPnUpI/xYfkdejw8nMTn9XV0dHzzzTeffvppbW1tU1NTc3Nz5xaNTpFDBRR0GxQzURTHjx+/bNkyTUbhf9UnAQ06T05ODr6VGsUmKIBwzIDL5SosLIQl1czMzLy8vMceewym0NhfffjhhzU1NYcPHz5x4kRgUppMYfgDlQ9HokBv4Bq1DZNFoeXnz3AUMJwzzO+ug6cwF/zq8Xg2b978y1/+EkULAxaLZdiwYUuWLMFj4rrLhOqTgIZDoTthLCsrC0e6sEG7CoTolwIlCu7wOlU44a50PywSXwaUIlQgMRoGQFS++uqrhQsX3n777ShU4E4BjO4nTpy4Y8cOcK3WA9/6mNeBAwcgQf2Qg4yx3hDQ0IJwLhwOZyFkFcUsUJbwp+uKELZX+AFFUdxuN1hrKYqCAY/HA0MqTPA//fTTkpKSIUOGoJjhuAlLhoIg3HDDDdOnT6+srLx8+TI/HIdTGEVR9u/fD7pej3e+h5NRvMXpHNcEQUhKSupZwUAkQDUCUzk+HVVVUa2CFsGOBaJdtysLIbF8RnxYkwX/E4Y1ycJZgqdOnVqxYsWIESOAmTGZTOPHj1+1atXXX38Ne9lRG3S5XCComGD4ASKgw8RKVVUYYoIuJmGnFNhfwR1e9w4RhlEvzCL1Jhov6j/88ENVVdXAgQPtdjvfj6Wmpm7YsAG8ToGtYQ94GLKA7rYFNHQZgwYNAv5oy5YtvDIEOpAsy2PGjIFJ2syZM0EU0GMdEL7r1q1D86LOo101ygq4PM7PzwfblrVr12p6TPQiLcsyMJ5AQAuCcP78eZT4zvIUFxeDnaYgCEVFRTAomkymQYMGrVu3DuYGKKzAJPKUtCzLaIT/2muv3XPPPYMHD5YkadeuXYAdemfmMw0RxrwgaxgVLl68CAUzGAx33303f2Ar/9JislBOPP+NMdbc3AxvCPTI27Zt4zOKZRiaAwyRgopXLAsTm7x4ArqqqgoWEtACGlotGiVBeYiGunndAgP7A1N0qCyqkqjKuFyub7/9dseOHVlZWfzGLtivMHjw4Pvvv3/v3r1OpxPkvFtYEQF93TZKvAjQ30K9Ll++vGLFiptvvhk6PZzwjB07duvWrbAdGCSzxzggAW0wGFatWqWTDo0xBpaDnQep9Ri6nj3I92ndDfNjZXf7E7DW4TtSUHVcLldLSwtsLeTXzIC7ycvL65llpQYcfRLQWVlZFotl7ty58Fph8/HtrgEKv4YTByOHGeDThHCYD2qi8elgpTRxOjo6YJQEZW///v0PPfQQmI5CP4a+XyZMmPDCCy98++23OLzy6WuSDfG1c0FREIRhw4ZBHF7LDfFUf/9JQ0D3SXX49godDl28oM/CIgeooCBLqqpqDtJ47733cnNzeYdIuPls5syZmzdvvnjxIhiLYBahSxL0V3i2vr5eFEWz2Xzw4EG+Ow36SMLc7DEBjRDhChY/cgGkXaGEjdXLQFfpa+5jLiByqOQzxjo6On788cfVq1ePHj0a1TAMwEzfbDZPmTJl3rx54PqZX5BDEDQ5Bv2qKEptbS1sCkGPmkFjJtJNVVV7YwHNQ9EttDUPogx0FeDjhxkOXR7ICNd9d+zYAccswSxbFMX777//gw8+4MuDY64mwMcJp2xEQIeDEjQNT3d09RSPPx/uKn5X9+HZrn7t1n3sxPi1EJ/X53K53nnnnSeeeAI6MXSJ9stf/nLhwoW8O6/eVIQI6KAT6lAW0HD0X1JSEripCiSgGWO7du0CDwwmk6m6uhoEAtZGoJmPHTuGB8hAAx87doyXG+iSfvnLX4ITtHfffReVb15QGGNffPHFyJEjIRr4LW1vb+dlYtq0acB2gQwBVTF58uQjR47AWhkM/IHHpEIZFEUBJ6iCIOzatctms4mimJeXB6674N3js7tumK8mVurIkSPA1xsMhtmzZ2OcEB0ozh8URdm7d++oUaNwvH/00UcxhdgHcD1AFEU4mDH2ZYhxjkEJaI0kRKNIfBbRSD9omoqi4JEOwAbi4pDD4XC73V999VWnx/bS0tLCwsKhQ4fCG4d7DgYNGlRQUPDyyy8fOHAAlqkhl/DVbiwVEdAIhd4CZ8+enTt3bnJyMnSbNpvNarUaDIZZs2bt27cP0YAXBL/2IIAEtCAIDQ0NPVvl7kG+ff5IVlYWHEIYenoQ8XLyfVp3w5rhEpfGu1tIqLLD4Xj//fdhcxX6QID9T4899tgnn3zy7bff4ipyL1HSJwEN5GBRURHvuwxbrfcvbw/aXSNy3U0B4vOJBMokVBBVoz/98U8ao1Q49WTKlClbt26FM67RsAiMEHFzVbek7pVXXhEEYdCgQVBInXRlCU9AgwxopkVglHr+/PkFCxYMHToUvNPgBGH48OFPPfXUjh07YKaN0xB+OtMDyQexr6+vh+xaWlq6JZ89yDF+HukxAY1V6EcENFJOQB8cPXp0/vz5KF18ANxuTJ8+fefOnVhTeMrhcPD9JP9rV2HcWQUEtCAIMInoKn4i3dchAc33aS0tLc888wy4dQU/6YIgLF26tKWlBR2oojgFHXN7oFcQAR3mGwQECOLf1VMYQRPoKn607yOHpqoqSJEsy2fOnNm4ceOoUaMkSbJarUAb2u32J554AqaW7e3t/EDZy7qQCw7+NYcWvw4BfeHCBXDtJIpiIAHtdDpnz54NtkK33norL0OYU15eHnhRgXSsVut3333Hx4R5HYxkBoOhvr4elCRY24eYDofj8OHDt956K+QFq6y/+tWvwB8FisXgwYPhCEFwezpkyJBNmzbxeaG9AOy+xAdhmHQ6ncBxWCyWRx99FNg0YNVhOMT4YQb4rCGsqurWrVshZYPBsHz5crgf2I3yWQCYLpdry5YtSJEbDIasrKzW1tbAXGJ2p6GhAZYfDAbDmTNn9KCD6oqA1giSqqqtra179uyZP39+Xl7eiBEjAv1XDho06Omnn96+ffvJkycDHwcnHiDtvIRrYgZ+1TkBjd1pIDIJcwfkAWQDNg9+/PHHwI3y1oJms3n27NlnzpyBzh+XtXuPAxLQZrO5qamJMYZkUO8Tj+cUUlNTk5KS7r///hgXku8BuhvuasQMpwqwhdDtdre0tGzbtu3hhx/GibTZbLZYLJMmTXruuedqa2sDU4NyBt4P/44+CeicnJxOp0wrV67UkBF8u4ePYe9j8vn2pk35dFAm+Zuqqh47duzVV18dO3YsillycvKAAQPmz5+/f//+1tbWoMQi1hFTwzuhA4qi7Nq1C1xgQUw9KGadJxXzBHRoiKL3KzbWdQOhy9DV4/iU0+lsb28/ffp0ZWXlxIkTUbTsdntycnJhYeGOHTsCD9uAGRD4Y8UsMM3wA/AsENCCIHTXRUz4GcVhTF0R0LBeKMvyxo0bZ86cCVNX3NAsiqLRaBw9evSTTz7J72zGyTsueKCwhdkXYZd44sQJkG1QyeJQHiJeJB0S0A6HQ1GU119/PS8vD01QJUmaMGFCWVnZN998o9HGUZxwzNUEMEKY8kYEdJhi3E8JaKwdUHnbt2/PyMiA8zPtdjvwfg899NDu3bsvXryIkWFc42WJD2O0MANEQAfyGNchoM+ePQuTf4PBsGXLFt72Hl5s2DxosVgWLVoEXAAYbkCTPPvsswMHDhRFEZVvSZIuXbqkscj45ptvUH/66KOPYNoPfrJgy8/mzZs7t0XDQedgAS0Iws0336xZnYCdGkBSz58/HzapQZ2dTieuqcJThw8fvvnmm7dv347S4/F48PBNOF1t/Pjx/DZwXvjCCWPKEADEwD0fmFkVFxcD963pPQNX8BRF2bJlCzgYsdlskiSNGTMGDqjRgKnJNKpfGxoa4B02GAywVSGq2cVD4jokoL/88svNmzc//fTTo0aNAuXAYrGgkw0IdG7DLCgo2LhxY2trK7DM8JbhDj6QUlBMQanl36Drtix4GxSE6/RX102nv0TweDywupOVlYVGcP2l8L0s58GDB5988smRI0ei20oYHW644YalS5fCERDg7s3tdvO+iXqZLxLQNputrq7O4/H02KNcL0sS48ezsrKMRuOMGTNinC/fA3Q33NWIGU4VWltbX3/99SlTpuBJDCBg6enpb7311l/+8hforEAPgR5MM5EOJ5eu4vAEdKBC1tVT/f0+qPsVFRUdHR1dtXUs6xhYhp7lzqfDy6TP66uurn700UeHDx+Oyq0gCPn5+du3bz948CCY5KCxBeQOKcDQCa7neFUwzBJ6PB4cLvtQOQyztBGMphMCGvZBzpkzZ/jw4WDcYzQaJUmaPHnyE0888ac//unKlSs8qth38Td5ueXvhxmGx5GADvOpxIimKwL6iy++WLly5Q033GCz2VDnBxp62LBhr7/+OuwNCmxZWZZdLhfMeXu24AFy6/P6oP/UjwU0HEIIpFggsN26Eyb9Gpgm3z90FQ586rp3gpbnzTfffPDBB0eMGAELG8gG1tfXO/wXjJXwyQ+Imp0E/PjLl/m6pUL3CDU1NZr0w3m2P8aBappMJlEUs7Ozw69C/yWgQZOvqKgYOnSoKIrAOxsMhszMzM2bN+MaKq8ygZt+Xpb4cPigQUwioAPnO9chdD799FOYpBmNxtdee02jypw5cwYUIFEUt23bBgQ07AjzeX2dJ9fDyCGK4kcffYRbw06cOKHphnCR02g0olEw7Nm/cOHC448/jkxEQUHBPffcI4qiwWCYMmWKhoAGdsxoNBYWFiIbrskL5Ozw4cPJycmCIGzYsAHFCMy9gVGFkldUVOCvmrx4QewqzD8LRDNj7MUXX4SBXBTFefPmAUsOc13kO6Cd4Kbb7b5w4cKjjz7KH8c5adIknCdrconl14aGBhQAnbiB6ysCOpbNCq/Mnj17Fi5ciI7eUDlA8weLxWK321NSUt58882ujn7idYKgYf7d6aqObrcbnL0MHDiwqzgJdh8J6NzcXGiOwL47MaqMJsyff/752rVrgXc2mUywi8VgMAwcOPCee+7h97IEChJKUW8wQQLaaDSCJpqomGtQys7O7tzi2nk2umas1ESLq6/Y4ppA0ELiYXEnT558+OGHwasYKhUDBgwoKio6e/Zs0GcjfhMIaLPZjN7wI55FHCaYkZFhMBiWLFkSh2XrZZHQLRWkc/z48cWLF/N+0gRBGDNmzNKlS0+dOhVmXijV/Hw4zGfBcSrsiAc3enwi/egdD7O+GC0eCGgsTAQDuB526NCh+fPnDx8+HDgaQRBsNtvMmTM3bdrEj4kgPEELgHLFB4LGDOcmaGX6MQsATHpPQIeYS4YDe8Tj8AIDc3xYxAJX9UA3g7OgpKSk1NTUtWvXfvfddzxT01WRUMz4LqiryJr7qH3BvF4/BHQnX19cXCxJkslk0mDS37+eOHFi79697777bmVl5fTp02GUBJNB4ATz8/M3bNgAp++i8AQSzfxP1w2HAxpZQIeDEppLIuZhPtUn0WDFwuPxuFyuhoaGRYsWwaQS/PSOGjXq2Wef/fLLL8HPRu/PRbhuHYmAxi4dsQqLgAbueM2aNRrldc+ePbg5GjfgQJzi4mK0+1i7du3OnTvBBYfRaDxw4ICGyL506RLS0wUFBTA8nzlz5oUXXrDZbDD8mEym+fPnt7W1jR8/HiI/8sgj+BpAAHKUJOnhhx9mjIH8weYOqDCQHfv27RswYABYUp85cwaWZxljFy9eBNHEkl+4cAGR0uQVzld8Fs8/hG0mmP6kSZN437hIUsNNaK3169cDVw5760RRzMrKunTpErw2fBaxD4ORJlSHCGgUidg3RGRz/MMf/oBrJNC4aWlpN998M3pHFUVx4MCBL7zwQktLS6BHdSxMoN7AT5MgjKBp+hZMBAL79+/vpAUzMjI09xP1KxLQd911F9YxTKwwfjwHwHeQy+X6y1/+8vbbb995553Qq6NTF5j2PP7444cOHYKlOL46GtGKCDJEQPMIx3mYb3E+zBcbBlCYJ3/88cdTpkwRRRE81MO66Z133rlz584O/xUoY3xSEQwDAa031iYzM1MUxZKSkggiGQ9JgbMgxtjOnTvv+819JpMJRAvELCkp6eabb37ttdfgCPVA/burKvAijeGuIgfer62thWPcXS6Xxvww9DgbmFQ/upOoBDRjbNu2bbz3cLvdPmTIkDlz5tTX18MeIF6zAoEJ2nAoS3wgaMwQNxVFAePW5uZmsE8KETnxfko8AhonobIsd3R0lJWV3XHHHdCPobnJTTfdVFFRcfjw4W41KC9mGO5WCowxmIM0NTWF3392N4u4iu/xeF5++WVwbxJXBetlYR599NHk5GSYWgIVCC0riuJNN91UXl7+9ddf88MTCgzfufErGRghdCCcYhMBHQ5K/YKAhk7M5XL5vL4TJ04sW7Zs0qRJ0JuZTCaz2fzUU0/t2bOHl7TY1IsI6MAOPFwCWhCEoqIijYzu3LlTEATYj//OO+/Arx0dHfPmzbNYLMAgLF261Of1HT16FNgrSZLA74QmqeHDh8NQZzAY7rjjDmC7rFYrzhhffvlleCQpKclgMHQul61du1bTGQ0ZMgRySU9P16SP0rZmzRpQzUVRXLRoERwwCFT1d999Bx0ilHzMmDG4xhu6g+vqV74MAL0sy8ePH7fb7WBnbTab33//fdgagCUE/p0xtmPHjrvvvhsKAwUzGAxwjjzG4bOIfVhDQMe+ALHPUQ8W0KAcjBkz5g9/+ENpaemTTz7JqwszZ87cvXs3IK8oCszA0TkP3yJdvRdd3eef1YSrq6vNZvOsWbM09xP1KxLQQ4cOxTryuOHN/hs4ceLEHXfcgd0+dHHQMQ4bNuyZZ55xu92gRoB0oa00j0NguMeAEAHdY+hi/2Bgu8OdwJL85S9/SU9PhyOFwXLQaDTe95v7jh8/rhnfA5+Nxh0koGHzUzSyiMM009PTO03OV69eHYdl62WRysvLJ0yYAKIF1hLQlQ0bNmzLli3o4rlbuQQV7/BTQAIa7Po1qYWfTv+KmagE9O233263241Go9lsNhqNt956a3l5ucYARdPE/GyCb8TAaF3F5J/ShD0ejyzLPq9v//79IOqaCIn9NSEJaGiyCxcuDBkyBPxPgl2qIAiZmZmo8KONVGtrKxzCEbqtIyJvMAVubGwMnVfC/KooClArRqMxYSoFm79zc3NzcnJE/yVJktlsHjFixAcffIDVBKcH+DWo/HT3JqYWIkAEdAhw+J804PM/xUMYVfo9e/akpKSggazBYBgxYsRLL73U1tYGnRhURJbloH42olEXIqB7RUA/99xzmlaBBXCj0ThkyJDMzMzq6urNmzffddddOHQBw9ve3n7lyhXQVNB3syYpOFoXeC5YrEA+Iisrq7m5WZblNv+Fv+7evVvzMsyYMQPdQL/88stgZw0Klsvlevfdd/Pz8yFZi8Xy+OOPg2N7dP7y7bffwq92u91isTz77LOYgiajML9q6gh20KqqTpgwAebDsIdu/vz5vAeD06dPr1mzJiUlRRRF0DihVCNHjty7d68sy1AjKENgFrG8QwQ0yJtGHmLZBNHI6+DBgy0tLZs2bbrrrruAHxRFccKECX/+859xbxRvMIgcNC4IQak0sFz3a4i6gAV0WlpaiDiJ9BMS0AaDAVebeAD7e2U7N0a98MILcOYbsDawrDh8+PCNGzcyxsBBAVRTlmVwTwRTXx6HwHCPkdEQ0Ah7jxPsLw+iC47+UmBomsCm15ApV65c+eKLL/BoYlEUk5OTlyxZcvbsWXBVD+nAwobm2ehBgQS0fky6GGOpqang8YwfOKIHcsxS3rZtG6q7cO6fIAijR49es2YNnHSNM2qPx6MhDUMU8rqyHeJZxlhtbS1M8pubm/npFiQb+tn++2sCE9CCIKSnp0+fpKiCrAAAIABJREFUPv3dd9+FCQvMTeCzvb09UGCCtmNgtB70ezDJV1X1zTffBEdGLpcLjHiCZppgNxOYgD5//rzdbof5piAIjzzyCLp4drvdDocDDALCb9CIyNvEiRNNJtP+/fvDz7dfx1QUpaamBnYE9uuKBC38okWLwPXwY489tmfPHkVRnE4nugvnHwkqPD24yafZVTg7OxtkDOewkFFX8fv7fahmD3xAa/CPNxxgOGtrazObzWDvbLPZhgwZ8uGHHyI3DXyFZuCLQbvrjYD2eDxFRUWiKEqSlJ+fH3RCfR0L6EOHDsGOCZPJdO+996KdI0jhDz/8wFt8gDW01Wq1WCwGg6GyshLsi4F4BdcZsCLx7LPP8oLrcrlaWlpAXOBxo/8aMmTIq6++CmdwQfzjx49DeQRBwKERk3rjjTdg7IQpQW5u7mOPPbZo0aIZM2aMGzcOmevOZ5966inNJBa4ebvdDsutkiStX78eU45UAIR+w4YNUE7gXCAsiuKoUaOwdrj1CfqIZ555pr29HVZvIlWY3qdDBHRCEtCMscmTJ4NJ16BBg5555pmjR4/iUXiagRm+gmE4duIoWprhKvArxgwRkGX5tddeEwRh2rRpIaIl0k9IQMNW/cCVw/5eWY/Hc+HChYULF0LvZ7VaU1JSNm/eHE69eiZF100ZCWhJkg4dOnTd+AkToT8S0OGAD+wMHJ06atSo119/HWbR4TwbvThIQNfV1YE+wMtz9PLt25SBtWlsbEwwu2+n0zlp0iQ4vBqsK7Zs2YJQayY5mq8YLeIB4C8EQaipqcHtpbiROVHlDe1LqqqqIg5pnCcYyzbFmXxZWRm64IiZbPd5Q0SEgO7zWgQtwPfff28wGIxG4+9+97uWlpagcWJ/Mycnx2w2v/nmmzqRMZ/X19TUFDi1jD3y0chx3759xcXFn332GdjShW5TvlvDcDRKNW7cOJPJVFtbm3hTraBw9ZKADppmPNwEcXK5XOvXr8/NzX3ooYfefffdMAsWWhTDTCRENL0R0J1utUtKSsApRV5eHu6e4SEKRUC73W7ghYHPTUlJ0RDQnXZqS5YsAc6UNwP51a9+BVo4aiqKolRUVADXAJ/Lli1Dz1NQoD179kyePBmKm52dvWnTJlmWIQVYXVcUZceOHZDRgAEDYBcYXxmf1zd58mQkmmHPmsViSUpKwlM7RFGEgwexO4MA8NFwPiaU8NixY3zikQ3Pnj0b0YAdT/AVjo6B0kqSZLfbi4uLwTUSHlEY2ZL0JjUioAO1hGj3Yr1przCflWW5rKxs1qxZb7zxBs8X8K8MJgU3kXrGtwki8I8EDWM6oQMrV640mUw5OTmhoyXMrzwBraoqUGkJUzvo+WEPryRJkyZNamho6FY1NbIUEWR4Ajp+Zl8RqVroRBKVgIYdTt98883Ro0cBAVVVA9WG0OBE/FeegMZSoTxHPLs4SXDGjBkWi6WmpiYBxkceUlmWwX/9XXfd9fbbb8P0taOjQ1PNGLfv8ePHQZ/ErXXIPnc1UvOV6qfhadOmgYHLypUr+2kVelxsFDCN4PU4wRAP4rSOCOgQKPXHnxRFqa6uPnfuXJ+Pkjx66enpZrO5srIywXbP8HXkw4lNQENNoZvCnoSvPh/muzUM8xEiFbbb7aIoNjU1RSrBOE8ngQlo8NzI79WIk0UFvRHQHo+nqqoKbJQzMzPhNEjNKx+KgIYTtAVBGDBggCAIOTk5GuXV5/U5nc65c+eKoghn+g0aNGj58uXQ9rBd2u2/GGMdHR3Dhw8HtVgUxUACGqaLFy9ehPMoGWPt7e0gOvApy/Kzzz4LlF9mZiae7Me/6qdPn54yZQrkArbMZrMZKGmz2Tx16tRDhw55PB4Nkw69oaIoDz74IKwAC4Jw+fLlKAkuZPf000/zZx4ajcakpCRBEEwm09ixY+fNm7djxw7Nnk1N4/EV75MwEdAJSUDjUhW8wl29LyByoBZoeoaIS2NZWZndboe3PuKJx2GCCU9Ag4zhvl2f16coSt9OMJCANplMDoejbwsTS5lMVAIaxln4RAfisQQ2aF76JKAnTpxotVoTchv1+fPnP//8czz1mg/gnBkDQUUigjeBaL548aIoigaDoaGhAUwr9EBAp6eng+lGampqBCGlpDQI4DREQ0CjkEOXq3kqYb4mpAU0ajto64CBPm+4wsJCo9FYVFQUP4N4VDFJbAIaJM3hcPC2TVHFM5zEgTLq7hmb4aQcn3F6TEDHZ3X4UjkcDpxXyv6L/7UPw3ojoBVF2bp1K7CvPSSgfV5fQUEBvJxr1qzRuK0Aypgxdvr06Q8++ODTTz9FWgGoWxzDQGWpq6tLS0sbPXr08uXLQQ40moqqqki5agYbVVVdLhdMlQVBeO6559B1I+o9kKaiKCtXrrztttuMRiOw7yNHjnzyySfr6urguD9wDKLhoN1ut6Io77zzDrDAy5YtwyE54iILtVYU5fz586+++uoL/uvVV1/dtGnT7t27v/rqK6wIAA4wIpgRL0+PEyQCOlEJaBAJfAd9Xh9QhJp3DTuEaBPQq1atMhqN2dnZPZbV/vUgEtCiKHbLNLi/VBNcv/GldTgcfdvF8QQ0zyLxhUzIcAIT0GDyjKcvxEPzAQFtMBjq6uqgPNipatSheChtpMoA/pHr6+sjlWD8pONwODweD2i8brfb4/HA8Vx8s2I42sUGx9OqqhoMBpvN9sorr4DHQz0Q0FlZWaCPBR5CHm3YdZU+EdCdxpLg1DKR2h03HAc17erDms6ZM0cURfCq34fFiFnWGgIa51YxK0C0MwJqJXoES5jlh4kVKF2w876pqcnhcOBgncD6WAIT0DwpAaxFmPIQ7Wh6I6DdbnddXR2wxzk5Oaqq8u6UAe3rWEAzxk6cODF79uyXXnoJXEDwL2dX7ycfJ0SjdvV4V4/AIYHggmPPnj0Qjc+LTxCc0l68eLGr1AKtmxVF8Xg833///fnz5wN/7SodPd8nAjqxCWjsylVVhRksvm682ONN/gXkI/QyrChKVVWVKIpZWVm9TKq/PI4EtCRJoCugxzRAu79UpKtyxmEHiwS00WgEge+q8Al2P1EJ6PhsJiSgDxw4AFb/mq41Sr1o36IBW7sOHjwYhy9+3yIT2dx5AloQhKVLl4K/Iz0Q0BkZGcAj6GenVGSFJ8zU8CgasoAOEzGK1hsESkpKOvclV1VVJeTIGIgMT0DDYgB4RNFJ9QMBidIdsE4AVCVJEkWxsbFRY5gYpaz7PFmegL733ns17nD7vHgJWQC9EdCMsfr6elDJcnNzg65rXp+ABlGAmZLL5dKcRaZhQ3gqSvNTL0XK5/Vt27YNfH3YbLbLly+Dgw5eseaXCoFBAFMUyDrM8oDbAZomhdNeREDrh4DWvNq8ePA/8fcjFUYCWj8TSySgRVGEw8f5xQDSRCMlWnw6SEBLkqQrhImA5sUg2mF0wbF//35Y1NcJAS1JUktLi67erGjLUmD6QQnooEpymPpwYBZxeycjIwP3e8ZtIROmYJ07OB9//HFQgDXKSWK/4wnpgiOexbKkpKTTWaV+ThblCegDBw7oyhgilnLIW0DDwFFfXw+bmZBKSrxREhDmCejMzEzgu3BrSyxbQT956ZaANhgMvSWgQUp4pinMcKTE68qVKzk5ORaLxWw23/eb+yDZjo4OjW6NcznMt7srWmA6TQQ0AhgiQAQ0EdCauUcIaenxT3omoM1mc3NzMzg74rvcHoNJD3aFABHQXSFD9yOIABDQJpNp3bp1+nmvYSOew+GIIJKUVCACQQlo3MCE6jEOJYEp9N87REDHsu1UVQX3jAaDQaMEEgEdy4ZI+Lz0TEBXV1cnfPv2eQVlWYbDA+rq6mRZTuxREtDmCej7fnMfOE3uWxeIfS4G0S4AEdCBAhauBTQ4d0a1NfxAiEbtlpoC/jfsdrvFYtm6dSski6tVgTQ05ksENEIR8QAR0ERAa+YeEZcx6HnABYcOLaD5g6T4XjcaOOs8TSKgdS4Asak+ENCiKK5atQpy1MN7DQR0bBDWcy5AQDPGwKQLXHAQAa1nkYhe3WHrjA4JaEEQEs8HdPTkpJcpFxcX69ACWhRFSZK+/vrrXqJHj18Xgba2NtBP6urq4DAwXVlAl5WVke3zdYWk9xGIgA4Us24Q0N3ii8NpLZ/X53Q6hw4dOm/evKDxUW/u6OhYsGABnGNjs9nAs3Mg6cyvXGGC/OwuzCrgI5gIBYIiQAR0whPQQds9xjf1bAEtCEJDQ0OMAddndkhAZ2Vl6WoHzOLFiy0WS25urq5q3VdCji44ysrKAHDUN8LUT/qq5N3NF86wdblciqKYTCZBuKZtJlgdu4tJDOKDlg+Aw3F8vIBpwjEoT8yyGDFiBBiyTZ06NWaZ6jAjOD1MVdVp06YNGjTopptuAhB40UpUWFRVzcjIEEWRDrqMWRMXFRUJglBSUqKTsQMU0U6310ajMdBmMGawJ3xGKE7gqVYQhNra2gQ7a6erRuQtoImA7gqlyN7XMwENc2qf19fe3s6j2g0Cmn8sImGXy/Xee++BpcbLL78cdHICLqevXLkyYMAAs9ksCMKTTz4JRpHwCgXS0KAGBZawq/tdxQw/fmAKOrlDBDQR0DEQdT0T0KIoEgEdAxmD0Qc0Ub0R0CUlJZ0HsOTm5gYuUMcGeV3lghbQCU9AQ7PyfGhQHU9XrR+DygJnMXz4cEEQdEVAwwTBaDQWFBTEAGfdZgHLZj6vb/LkyWazOS0tDZaa9EBAM8amTp0qSdJzzz2nWwGIccXhrMslS5bAykeMc++T7E6dOiUIgtFo7JPcdZIp2lsQAU2afwxkXs8E9I033hi09+5LAtrj8Zw8eVIQBEmSBEEoKioKFAI4pefRRx+FOIIgnD59mrd05pUe/n5gUuHf4dMM/ykdxtQ5AV1ZWUkEdAzEngjoGIBMWejWAnrFihWCIBQUFACPQJIQVQQCCeioZteHibvdbpzYkAV0zBoCLDMmT56MBDTw/rxai+GYlSoGGcE2arvdXlhYGIPsdJ6FoiiwyJGfnw++3VGo0LQw8SDyeX2pqakGgwEdKCVeHeOtRsuXL7darTNmzIi3gkWvPJcvXwZiJHpZUMoaAloUxbq6OjB5xK4sUVEiC+jYt6yeCWij0Qh7CzSw9zEBzRh74YUXjEYjbJ2bMmXKG2+88emnn2IpHQ7HU089ZTKZkpKSRFGcM2dOCG/UREAjbrEJ6JyALi8vJwI6BpKmZwKaXHDEQMAgC90S0FOmTOkcgsvLy2MGtZ4z4l1wJDBTwxgDU1xVVZuamoxGI7ngiIHYw/xZUZTCwkIkoGG2iZNqPhCDIsUsC7AZtNvt5B4hBpirqgom5zk5OYGTshgUoE+yaG1tzcrKEgShuLi4Twqgw0xLS0tFUczLy8PlTD2AIAiCKIp6qGlf1VFDQAuCQAR0X7WFHvLVMwHd6UNJVdVAI+i+JKDx/V+2bBn0tvg5dOjQ8ePHFxYWmvyX2WwWRXHUqFFXrlwJKqm8Sg3hoNHoZmQR0DkBXVZWZjKZQEvgJTCyIFNqOiegaaoTm1dAtwR0bm6uwWBYvnx5YvOhsZGi6+ZSUlICppr5+fmoAl33qX4aob293e12NzQ0GI1Gq9VKLjii3Y5gZgIEtCiKcECcz+vjXdUlqq4CNoMmkykjIyPaOOs5fZfLJcuyz+uzWCyiKMLR0DqxHGSMwdGLpaWlepaBWNa9vLwcCGi32x3LfPs2L/BN2rdlSOzcPR4P7Pl76623QCWrr6/3eX2JOj7yrUkW0DwasQnrnIBWFAWUBB7tviSgsRyqqm7fvv322283Go12u10QBIvFkpSUBNs2bTabIAgDBw7cvXt3VxM2vsuAMCZOgeghoHMCuqSkJDk5udMaQmNhFD3A9ZmyqqpVVVU41dEDCB6PB18uIqBj1uL19fWdG/H05gOaCOjYCBhYBIPDk86dDTk5OYlt0iXLckdHB2OsqakJjCXhWOnYoK3PXJAHLCwsRALa4/HogYA2m82wmXLkyJH6bP3Y1Bp7LUAbCGidEDdIQJeVlcUGbcqlrKwMCOhAA7oEBocI6Bg0LphcvPjii0RAxwBtnWehcwIatFCNkVO8ENBA4a1evXrixIloBw2dQufOiKysrMOHD7e2tnZFQINk8zS0zmU9NtVHjqzThejBgwdjk2nf5qIois/rKy8vNxgMFRUV2dnZRqOxtraWZC967QIEtMFgyMrKil4ucZWyhoDW9NpxVdREKgwR0InUmnFYF4fDsXv3bnDcNG3atDgsYQSL5PP6gHOvrq6WJMlsNkcwcUoqKAJg7KyqamFhYaeKAhbQOiGgk5OTJUnCWgfFh25GBAEwtIeZmq4I6M5tUmABXVFREREkKZHrIkAE9HUhogg9RqDTMwBswQdvhzoxJiML6B4LTI8fJAIapI4HMC4IaCgWzFUYYydPnnznnXfWr19fWlr62muvffTRR1hiOJMQv2oCRAJqAIn2V50T0OXl5dOmTev0tLh//36SvagKW1VVlQ4JaFiBKy4uDr3wFlXkdZV4fX09iJmuAM/LyyMXHDGQc1i8rK6uhvc6Pz9fDwtLqqrCFlcgqmKAs56zAAKaMcYT0DpxwQF+xvG4Sz2LQVTrDrpuU1OT6L/0SUBXVlZGFWRKHBGoqKggFxyIBgUihUB7ezsoYEhA19fXEwEdKXgpHQ0CuiWgJf8VdLITFwS0pp3oa39BgAjo3NxcQRAOHz6MBHR/abv+Vc7MzEyDwZCdnd2/it2b0h45cgSIqhUrVvQmHXo2fATKy8slSSotLQUCOuiQGX5q/SVmTk6OIAg0o452e4E41dTUwHs9fPjwy5cvRzvTPkwfxsROw4LS0lJBEHTVe/cV7Gh1DmaDBoOhuroalZPAQF+VMxr5wmslSRIcdxmNLChNQMDn9e3fvx8AB4/b6PsFZCxRgVJVFYbLqqqqRK1jvNULCOjx48cHuhCNt6JGsDzkgiOCYHaVFKhkCxcuhK6MJ6C7eiQx7vMW0FVVVehVKTFqF5+10CEBDZMdg8FgMpmCNgoR0EFhoZthIaBzAvrxxx/PyMgwGo0NDQ04tQsLOIrUTQR0RUCDv044uUsUxcWLF3cTLYreQwTKy8uNRiMS0Dqxg87IyLBareTUsodC083HQCeTJMlisTDGEljGYEwkArqbAtKr6DwBbTQazWbzsWPHNP55UVdJsAU2IBHgs1cg0sNhIHDgwAF9uuAAAprMAsKQkchEKSkpSUpKGjhwoK7OsCUCOjLS03UqwLqqqpqfnw+jRl1dHVpAd/1cIvzCE9DFxcW68q7eV+2nQwK6uro6KSkJXA4GnekQAd1X0pgI+RIBrSGgE6FR47IOmZmZkiTl5OTEZemiVSjQiu69917GGHooilZmlC5jGgJaJ5inpaWZzeY1a9aQCMQAASCgTSaTKIqMsYRX/YmAjoFQYRZw1DhjrKyszGAwSJJUU1MDv/K8M4bxwQQIEAEds0Z0u91AQAuCkJaWpiiK2+1GoUqwhQ0eVbSAXrVqFX+fwtFDoKioCM6wJQI6eiDrMGW32w0Tq8mTJyMBncB9F9/EUE3QQisrK3Uy0+ERiH1YbwS0oihNTU02mw1ervg9hDD2okA5RgSBhoYGg8EgiqI+DyEsLy8Ha4hDhw6B8h0RVCmRQAT0RkA7HA6f1wdGEOQ7NVAeIn4HFLLy8vLOvUJoAa2TjWmZmZmCIGzbts3hcEQcWEpQgwDuSrNaraqqBrUL0DzSr7/yBLROZnd92F68BTTo/evWrYPy8PwghvuwqBHPmgjoiEMaNEGf1yfL8po1a0wmk9VqLSgogGgoVAn8msMhhKIorl69Oig4dDPiCIAHJ/Crk8CipcGNLKA1gET8K7KuhYWFuiWgBUHYtGkTLO0ktke4iMtPdxOE02uLiop00om1tbW1tLTAmyVJUtBakwV0d6WI4v8NgYaGBkmS4OyX2bNnl5WVzZ8//77f3JeVlZWenp6Tk5OXl5ednZ2Tk5P707Vq1apO3rahoeHHH3/kFdbuhhljQA8dOHBg7969tbW1+/btKy8vLy0tLSgoyM3Nveeee7Kzs1P9V1ZW1vTp0+fPn7948eIXX3zx8OHDly5dwuEH9kFriAC32+1wOMCs428V9u+Y9nl95eXlncx7eXl5Xl6eIAjNzc1B3y7+QQr3BgG9EdCAlSAIkiSlp6d3dHT0Bj169roIuN1uWZaXLl3aeYZVWVkZvM58F3HdFPpvBCCgGxoa+m8V+lHJP/nkE4PBYDQaLRbLlStXQp+r3I/q1VVRFUVJT08XRTE7OxtG+a5i0v3eIwBmJsy/mQNU/4qKCujHgqpYvc8xflIgAjo2bQHLZiUlJXDeY05OjsfjgX4MZSw2JYl9LqqqZmVlSZLU2NgY+9z1mePy5cvh1daJQQC0MhDQtbW1+mz0WNZ61KhRYEWnNx04KytLEIT9+/fram9BLEWLzwusFfVDQEPdwU8XEdC8JFA4Mgg0NDSYTCYwgob9nnDeJVDSoDQMGDCAnxgIggD7PvLz87N7cWVmZg4YMAD8y0D6oA3DQALTe/CBCAM5lgHKlpycnJSUNH369DfffHPfvn1tbW1dWf9duXIFfPLiJ09A84cQRgZTSiUYAroloDuPuJw2bRpAgrM7Wu0IJiO9ugccTUlJSWd3oTcCOi0tTRCEpqamXiFID4eHwJEjR+CcNEEQDhw4EN5D/TgWENBwhCx4HuzHlYn7oiNH8+abb4LOs2DBArjJDx8YjvsKdaOAqOPRIYTdQK2nUSsqKmAhberUqejLPiHlikdIVdXMzEyj0UgENA9LVMPl5eVgihHVXOItcSKgo90iLpcLsrDb7cAb6O2l5gnoaKNN6QNZ9Mwzz+hq/k4ENEl+tBCAc9JAObjrrrsKCwsLCgry8vJyc3MLCwtzcnJuvvlms9ls5C70CAOOyQ09vfjJhsViAVoZRhEN49y5Xc5qtUqSZDAYLBYLPmg2myVJwvLMnDmzmruamppqamoOHDjw2Wef8fB5PJ5Or52wKay0tBR2VRw8eJCPQ+GII6BnAvqOO+4APHF2p6sBLOKy1FWCHo8HbG2KiopkWVZVFTXUrh5JjPspKSmwjUMnFt992GqyLH/33Xe4QPvhhx/2YWFikzUQ0JIkZWdnEwEdbcyRgK6trYXF/gcffBD8jPPDB4ajXZ5Ypo+qHRHQ0YZdUZSysjIAPC8vD/cjJqRcacAkAloDSLS/Llu2DOyc9u7dG+284id9IqCj3RbgA7pzt5DovwRBIAI62pjrOf28vDyj0Thr1ixdzd+JgNazzEe37nAIIdhzNTU1ORwOIG4gV+BqfV6foijgmhDCjLHW1taG3l0HDx5saGiora1tbm6urq4+cuRIdXV1bW1tY2PjwYMHP/roo0OHDu3bt2/NmjVLly5dvXp15/FiVVVVpaWlubm5eXl5WVlZvPU0GG7zExhg1TV3BEGw2WxWqxXul5SUwBIiGQ9GV84Yy8zMFEVRn4cQ4nQaZ3e6GsCiLVqYPp4v1K8PuO+BbEycOFGSpE8//RQ1csSEApFFwOVyybJsMplgQfTw4cORTT8OU9MQ0HjKPPRmcVjgfl0kJKDB1bjNZsvJySECul+3aXwWvqCgANTgBQsWYAlRRcE7iRcAYwjS+WPWsmVlZZIkJSUl6cofBRLQPdDoYtY0/T0jj8fT3t7OE9C6QpssoGMpwHl5eSaTKS0tTVcyBgS0wWDQOLkF5MkHdCwlMNHyamhoAENm9IOMCig6rIjzgNPpBNp6zZo1GRkZ+fn5UCM4dhk0bKCngTIATyMQp7Kycvr06ehEKdFaN27qoyhKRkYGtEXcFCoWBcGXy+12g3NPfJvwRdPVYBY90N1ud2dXkJmZabVaKysrXS6Xz+vrX4Rsa2tr+K7cwLjb5XIpigI+lOBA8OghTCmrqgr8IOwIslqtu3btcjqdCf8uG41Gg8GQnp4OMpbw9e1bUYdeq76+HkbMtLQ03MnBIw/hvi1qZHNHzzaCIADnHnTOE9lMdZiaz+vzeDyzZs2SJAmOTMBxBwUsUWFRVXXatGn6OXQ9Htpx2bJlsGcInNXGQ5GiXQaXywW9d3V1NXRi/UsXjTY+EUlfluWOjo6amhpRFE0mk9lsrq+v19UCORDQBw8ehL2PtAMyInLVVSK5ubmiKMKGoa7iJN59IDGIgE68lu37GgEBDadgazpuZMriPIDe6xhjDocDzldBZGtqapqbmw/+dDX5LzC+BguIzmleWVkZTvDwQQpEEAGPxzN+/HjwrxLBZOM/KUEQQPNmjAFXiG8TzvSIgI5IO4LuBWvUdXV1mCaPc+gwNg2/4QN3fkQ70DOqBfhQ2KoPxcaKUyDiCODggi44KisrNUIV8Uz7PEFVVYEZfO6554CogjeFr3ifFzJhCtDW1gZd2b59+4DCGDp0aCA/iOAnTMUZY+BOLTU1VRCEuro64KATqYJxUhcQsLS0NPABXVpailp0QsoVD7uiKOB2T2+79XkQYhx+8cUXQflPvDPigr4v8H5BlWGaCXdiDLseslNVtbm5GQZKm81WX1+Phj7YNAk8wwICesOGDcBg0IgZVZmHQwj1SUCLoujz+uBV4t8ssoCOqsgleOJAQE+fPh18a/CCxdMx8RyGFgL6RlEU3MEKvkRg2RnLDyySoihut5t0gpgJt8fjSU5ONpvNoijGLNN4yAgtoGVZRsWI6JsoNY3L5QIVoampSVGU/qiNuVyuMNVlsKkHJIGAbm1tJSubKIkWJBtIQC9atAjIQRw6o1qAGCcOQyRucV29ejUR0LFpAkVRamtrYZ3DYDDohIAWRTEpKSk9PV2SpJqaGsaYLMtOpzM2mOsnFxhiRo0aJYpi5+n2JSUluHsmIfsxvmU9Hs/kyZM793PoxxqXr36fhJctWyYIgtVq5S0D+qQkEc+0q/cFHCgJgvAVLejCAAAgAElEQVTee++hg/WI504JMsY++OADIKANBkNLS4ssy/qZYQEBvWzZMtL8Y/AuEAFNBHQMxEwXWYAkNTQ0mEymrKwsIGRxNIWZNvK28RzAuRnyTTyD0xXLjIQ1PqWLVu+jSsqyLAhCUlKSDgloQRCSk5MvXLgARkb4KvHvWh81S6Jl6/F4zGazwWBYv359fX19dXV1c3PzgbCvRu5qiPnV2NhYU1NTX18fZo8EPZuqqk1NTZ1OhNLT00kHjbZA8wQ0uB1csWKFZudQtMsQy/SB+/vhhx8EQTCbzcXFxW63G3dyUA8WjbZA7cXlcoHhudVqvXz5cqDqD/hHowx9lSbwCFOmTDGbzWCgSuxz9NrCbrfDQSnFxcXIkeFLHb18+zZlt9t92223SZL08ccf921J9JN7SUkJmGJ0nuKTYLUO+r4oinLw4EGLxSIIwtKlS3u2uS3BgIpGdWBMLCoqAje1cNaODgnoqqoqVVW74jqigbw+0yQCOlALJQtofb4Lva019FbgZzA1NVVjxoXDavwHQgCBc7kQceinGCDw1VdfwdzSaDSmcldaWlp6enpGRkbmz6+sn18QJzc3NysrKy8vLzs7e8qUKdnclZOT84//+I+VlZXLli3r3E8a9NqxY8d3330HleUFAxwXIC+MdBIEeHD4p/j7QPzxbwpjrKOjA93ACYJQX18f4hXjU6NwjxHweX1ocg7yFs+fsEMTSwh0AHwFn858BKA7c7jrwQcfXO6/HnzwQavVOmzYsN27d/cYOnowHASQ9J80aRJwN0888UQ4D4IHHk3MoBOGc+fONTU11dXV8SsgK/xXlf+q9F8V/qu8vPyll15atGgRJxehglyXmZ2VlZWWljZjxoy0tDS+uy0sLExJSSksLMz1XykpKWlpaZ2OYgVBeP7558EoFXpLTY+nqR197RkCQLmqqupyuUwmE5xkNWfOnMrKyqqqKmh9XgZQEsq7f/Ht3t1wWloadFBGoxFP1+C7LOzZuhsYM2aMIAi1tbWwrZg46J4JkuYp2PYHGwSBEYN2MRqN5eXl8F77vD75p8sT5UtVVVhqDXPBVVMd1KagL8IeCaOdPXu2sbFxy5Yt8LIsXLjwt7/9bV5eXm5uLrxTnYfElJWVYXzqzRCKSAVUVf3yyy/nzp07fPhw8DaemZlZUVFRVVVVUVFR5L/Ky8tXrly5Zs2aioqKJUuWrFu37sCBA83NzceOHauvrz9w4MDly5c7Ojo8Hk9X6jc0HJYZo2EAf+plwO12o5CguzOHw8EYO3fuXB13bd++ffbs2TBoLlmyhAjoXiIf4nGPx7Nhwwaj0Qho97gzCZEF/oStzwcYY21tbRCHd9MHd2AjZm9K1ZUYw+A4ZswYg8HwwgsvYCEpED0EUlJSBEHIy8sL3aCBlAIcR+R2u3vQFfD9Gzz+ySefQN944MCBffv2ffDBB3/645947W/FihWLFi16+OGHCwoKfs6s/O1bXl7eTTfdZLVaoWc2+i9Q5GCyqVHbTCZTUlLSmTNnNPASAa0BhL6GhQCI8pdffmkwGFJTU3Fqzfet/SIcorZd9d0hHqGfooHA+vXrgRkEJ4+arg2oHOgB4dPEXfCr1WrlJ7eBXSR0nYEp4x1QUDAvQRAGDx5cUFCQx108c/38888vXbq0rKxsxYoVS5cuXb169ZIlS6ZNmwa8DHxmZGQALY6JQ3aiKIJKhL5im5ubccoU+FpFA3O9pQkvO1idYKPHYQBEQpKkG264gSd9cnJyMjMzc3NzOxmBQFEHgec/bTabwX9BAGoKDgf11vSxr296ejoAPmbMmOLiYiAB4ZOnCPnwggULpvqv7Oxs6Deys7OBYYR2xB4Meg9JkrC5Q4ixJEnYyYSIBklhRpiX2Wy22WyYEQqepkODlCVJevrpp0GNxoU6Xj+OfUMkZI7QlcGgCQNWUlISNLTEXdCa8Mm3YPjhEAIT5k9GozGwy+WFjS9k6DA+BfKM7mI1w2VCtngMKgXkMmbkcrlgoBFFMTMzs7y8vLi4uLKyEuexfJ8WjXBxcfGSJUvKy8v5TDH38AMF3GXlLl6ARVGEs8eBeoaTOcxm85YtWwCQjo4OXswQJQr0EoGqqir+NHiDwWAymWw2G9xEvgNPhofuDpoJGwua0mAwWK3WESNGTJ06dfr06fxiam5ubkpKCtig8GNuUVFReXn5G2+8sX///tpeXPv27Vu6dGl5eXlJScmKFSuef/75hx56KD8/PzMz02KxQDm5Kcu1IIofLnKEJq16ibOeH7906RKel4A7OSIFiNvtPnv2bG1tbX0XF2xbPHLkyIEDB1ZxV2lpaVlZWXl5eUVFxYIFC/Ly8iZOnFhQUMDr/CHCIN45/is3NxcDOP0E4y1wvnfjjTfiCmKkKk7pBCIAs7PCwkI4byzoG/355583Njbu27fvwM+vxsbGbdu2dW4BKS0tXdHF1ZU8ZGZmZmRk3HzzzWazGVV3URSBPsauJvwADIiwbwAMCFDz7yoRo9FYUFDwxRdfoJNbwIcI6EA5oTvhIuDxeA4dOvTNN994PB5wMc7rYf0iHKKqRECHACeWP12+fHnIkCGCIGzevFkztXjuueceeOABGF/xE0fZ3Nzc/Pz8cePG2Ww2o9EIZ+ZoFFO+xxT9F3+HD5tMJovFAo4mr9vh8g9CTx30ETRc5WfXZrMZdFB8ZNOmTeCUPOg7Fcu2SOy87r77bphewgIAzgrMYVwY2WQyGaNzaUQXxQOEjZ+3oMiBSAd+glcEmMjB/O33v/892mIkdiv3be3mzp1rt9vBoZAgCHa7nW8dvh/gw0D1woRBEIQBAwYEWuvDYe5ADEFfB9ohTtQ1AqPpo7r1VRRFpA75cvLsgCbBcePGgbvYwE6sb1sk8XL3eX3z5s0DKlbTaWgapa++Ah8UmHtXk6hw7g8bNmzgwIEjR44UBGHfvn1obs/LW+K1dcxqdOrUqU8++aSpqamhoWH9+vXw+uPyVVfGAYFNHKk7mDXf/3Q3LAW7YAtRV+WEFwpXOHxeHxjYopjFrEUSOCOwuP/6668bGhpeeeWVqVOnmkymIUOGTJ06FbbdJCcnaxrIaDTCOTFAQ8MnKGPAmJhMJvBKpHnQbrd31UkiQax5pFtfcdjFAK5hgLhqtDWr1Yrpp6enR5wVTWCx6W7VgA7zeX2zZs0CzLFXwSbofSA5OTlYN3PtnsZeBPMCwQDNkFfsu0on6H1e3jDlwIDBYKirqwu6o667eFL8EAjA6bWDBw/OyMgoLCycNGnSsGHDeCMSmDVCq/GTAuAccMU3sAX5O5oH4SfoG6H3y8vLKywsTE9Pz83Nzc7OzvRfOTk5SJtkZ1/b4Ai0Nfwa9DMnJwesYTIzM7Ozs5F+waQ427y8lStXgvM9DT5EQGsAoa/dQwAdCGiUMNTG4jwQorZEQIcAJ8Y/vfXWW2vWrOGtgLEAgQLG/wSm+qqqut1uWHL0eX3Hjx8/xF1vvPHGsmXL1q5dW1lZWRLsKioqWrZsWaezsLKysoqKirKysuXLl4O/Dtja7N/d/rMNzr/97W9nzZqVm5ubmpqanp4OnX5+fj728rAunZ+ff++99/KW0Tk5OVlZWRkZGRBIT08XRXHjxo183TVVxvpSoMcIgJxs2LAhLy8vy3/xNjL84NpVmI8PKUTpc+bMmdnZ2WPGjOFVDdAzgNbk73cVBt0XCEogK0+ePEk6aI/lJ/wH16xZk52dnZ6enpqaCrpaBncFVfUyMzMLCwvB2UVmZuaUKVNSU1PBhCqNu+6+++7c3Nxp06ahWomSjEILUgr3U1JSsrOzNds4eK1REy7jrtLS0urq6pqamr179x7grkOHDjU0NDQ1NcHo2d7e7nK5GhsbOxXuDz/8EFDSdF80zoYvPKFjajw5vv3226+88kpra2vop0KMLIEtBXeum2CYEWAHepiRrxsN+vDGxsZl3KlKGr30uolQhEAE+DcUKJsTJ07AiAPLrrjrgp8JRzUsSVJmZmZOTg44WON60O4F+f6WL7DVajWZTBoGBwZNs9m8YMECcMiGIyb/pgQCSHe6iwC4I2CMod5eXl4OIwi85tBrXbx48fjx4zU1NWvWrAG1vLi4eMWKFatWrUpLS8vIyJg5c+a0adNycnIyMjKAjIa9QXxbI/sMK/GS/wKDFT5aj8NAf4uiaLfbM/wOA7OysrKzs/Pz86dPnw7jLz8vyM7OHjZsGJDU69evx/p2F0OKf10EfF6f0+nstFP+3e9+h9SzyF3dbXR8FB5EW9Gu0gFOUBRFTT+WlpY2c+bMefPmLV++fPXq1RUVFaWlpeXl5Z0W8fxG2+uGV61atXjx4kceeaSwsBC0PtT9ZsyYMXjw4EGDBjU2NrrdbvJVdV1p6WWEjz76CMUAjULwDgTGjBmTnZ09c+ZMvrGysrLS09Ofeuqp0tLSoqKiYBTFtXsHuriam5sbGhq++OKL0D0JDGG4nhq6srytUqC7UXwWPVzBnUCjbyKgESsKEAKEACFACOgRAX6Orcf6U50JgVghEFkSM1al7gf5QCdGXVk/aKp+WMSTJ0+CBfT+/fsPHz7c0tKCp2L0w9pQkeMagdBcSVwXPRKFe+ONNyRJWrduXSQSozS6RIBfNzp27BjuMNPQgvD11ltvvfvuuzMyMsA37n2/ue8Pf/gD+MrQ8MJAEe7cubO2tvbo0aOcf+9rwfPnz+OqMF+AeAh3iRT9EAkEDh482NjY2NzcXFNTc/r0aZ7G5e0AIpFV/0iDCOj+0U5USkKAECAECAFCgBAgBPo1AkRA9+vmo8LrEAE4DgvMycM0ktIhSlRlQqCXCCiKAg4te5kOPX5dBHjClzGmKMqRI0caGxs/+eSTI0eOfP/99xqDTVVVoXVkWQYLfY/Ho4mjyRRc58M2cc1P9FVvCHg8HtzyhVtn9AaCpr5EQGsAoa+EACFACBAChAAhQAgQAoQAIUAI6BoB3qYeTVORvtE1NFR5QiA6COCLFp3kKVWGPRi/c8jlcgE04M+K7/rgPnjtCISPT01RFGCo+UbECIHP0h39IABrEngKNy8h+gEBa0oENEJBAUKAECAECAFCgBAgBAgBQoAQIAQIgWsIwLQZsHC73WAKTdAQAoRAxBEAN+s6Z6YijmpggsgIA8uM1HNgTLgDtDJv9dwVSc3T1vAUf6er9Om+HhDo6OjQQzXDrCMR0GECRdEIAUKAECAECAFCgBAgBAgBQoAQ0CMCGuJGjxBQnQkBQiDREeBZY+j00HAVviY6AFS/aCFAYyggSwR0tCSM0iUECAFCgBAgBAgBQoAQIAQIAUIgARCgyXMCNCJVgRAgBEIjQAR0aHzo1x4jwI+hel7MIAK6xyJEDxIChAAhQAgQAoQAIUAIEAKEACGQ+Ajwk+fEry3VkBAgBAgB9jOf0XomDUkWeo8AP4by4d6n3L9SIAK6f7UXlZYQIAQIAUKAECAECAFCgBAgBAiBmCKg5wlzTIGmzAgBQiBuEOD7PQjHTdGoIP0MgUBZ0qdEEQHdzwSXiksIEAKEACFACBAChAAhQAgQAoQAIUAIEAKEACEQVQR4pxxRzYgSJwT0gAAR0HpoZaojIUAIEAKEACFACBAChAAhQAgQAoQAIUAIEAKEQLgIEAEdLlIUjxAIAwEioMMAiaIQAoQAIUAIEAKEACFACBAChAAhQAgQAoQAIUAIEAKEACFACHQfASKgu48ZPUEIEAKEACFACBAChAAhQAgQAoQAIUAIEAKEACFACBAChAAhEAYCRECHARJFIQQIAUKAECAECAFCgBAgBAgBQoAQIAQIAUKAECAECAFCgBDoPgJEQHcfM3qCECAECAFCgBAgBAgBQoAQIAQIAUKAECAECAFCgBAgBAgBQiAMBIiADgMkikIIEAKEACFACBAChAAhQAgQAoQAIUAIEAKEACFACBAChAAh0H0EiIDuPmb0BCFACBAChAAhQAgQAoQAIUAIEAKEACFACBAChAAhQAgQAoRAGAgQAR0GSBSFECAECAFCgBAgBAgBQoAQIAQIAUKAECAECAFCgBAgBAgBQqD7CBAB3X3M6AlCgBAgBAgBQoAQIAQIAUKAECAECAFCgBAgBAgBQoAQIAQIgTAQIAI6DJAoCiFACBAChAAhQAgQAoQAIUAIEAKEACFACBAChAAhQAgQAoRA9xEgArr7mNEThAAhQAgQAoQAIUAIEAKEACFACBAChAAhQAgQAoQAIUAIEAJhIEAEdBggURRCgBAgBAgBQoAQIAQIAUKAECAECAFCgBAgBAgBQoAQIAQIgZ8joChKW1vbK6+88t5777lcLp/X9/Pfr30jAjoQE7pDCBAChAAhQAgQAoQAIUAIEAKEACFACBAChAAhQAgQAoQAIXAdBE6fPn3jjTcmJycbDIb6+vrW1lbGmKIo/GNEQPNoUJgQIAQIAUKAECAECAFCgBDQBQIKYz+bFsRHpeOzVPGBDZWCECAECAFCgBAgBAiBeETgkUceEQTBZDJZLJbVq1d7PB7GmKqqfFmJgObRoDAh0FsENC9Yb5Oj5wkBQoAQIAQIAUKAEIg8AtdoXoV5/X+K4g8zdoWxvzB2hLFD/s/PGDvL2L8z9g1j3zN2ibH/9MdpY6yDMQdjcg8ZbJUxbj4CjLP/E0ryU20hWtDPa8z5T38/S+2vKfiJ9Z8ixCPN/lMd6X9fIKAoCq+x8+G+KA7lSQgQAoQAIUAI9HsEhJ8uSZLmz58fyD6TC45+38b9rgKo4Tmdzn5X+OsWWPVfPq8PVnuuG58iEAKEACFACBAChAAhEHMEgHqWFdahMIePyQrzqMzN2GetHQucrmkOb1qHJ4+x/5exDYy9wdgfGfuIsVrGmhk7zti/MvZvjJ1j7CJjLsYUVfUpitfnkz1et/zXyyu7FY9H9Xmv6UZ+svhnPDFfZYUxL2Oea59OL+P0Q3jO6//Z+zfCmakKU73cn3KNYb7GaCsKk33X/pjvWnSvco0ih+fj0NSbx4DCsUNAURSf14ebgh0OB+QNajx+xq5AlBMhQAgQAoQAIdA/EQB+T1XVEydOWK1WQRBsNpsgCJ988gn4gJZlGQdWVVXJArp/tnNClBokUlGURKJr4e1KiPahShAChAAhQAgQAoRAYiLwk7mxQ7lmy+zxsSsyO6myrQ5PppcN9rFfeFmSrNzh8eZ6fbNk5RGH+j8cyuKrSqlTWelUVjt9a6/6Nl31/Atje1VWx1g9Yw2MNTLW5CepjzB2zE9Vn2TsJGOn/H+nGfucsRY/c/29n7z+D8a+VZVvfeq3svKNrJ73sK8Udp6pV5jiZMzNVPkaswx0sp9RRqNnPwf9cxr62m9ehbn8HDRERAKa2OfEFOOe1UpVVY0FNJ8OzpP5mxQmBAgBQoAQIAQIgaAIAAf91ltvif5LkiSz2fzDDz/AfZ/XhwMrEdBBAaSbsUDA7Xa/++67c+fOXb9+vcvlikWWscrj0qVLRUVFZWVlbrc7VnlSPoQAIUAIEAKEACFACFwfgb+6pVCY4jcZ9rvRUFX2by625iq738HGedkALzN62S98PrvX8//43EPcnmFt7Ff/yUZdUcddUW5p8/+1e29rk/9Lm3viZdfft7pT2uTUdk9ahzfzqi/nqjf/queeq/LMq/JvrrofYuyfGXuescWMLfVbVVcwtpax/83YDsZ2+v/eYew9xnb7Weyjfrb63xg7w9h/MNV5zcDaf/2sbj8zp/b6DbEdfq8g1yyy/8pT/5WSvvaPLkIgEAFVVT0ejyzL+BM/ScabFCAECAFCgBAgBAiBrhAAu9Inn3xSEASDwSCKYmFhIdyER/ixlSygu4KR7kcFAfC84Xa7jx49arVaRVGUJOnVV1+NSmZ9lGhubq4gCKIo3nvvvX1UBMqWECAECAFCgBAgBAiBIAj8jYD+Ky/rYOwqY//HyWa3sdHua+bPST5mUtkvGDMzZmEsWVGHtrNf/ycb2cpsrUzoYIKDCTITvNf+RB8z+PyEtcyMbmZyMbOLWV3qAJcy2K0Ocysj3L5fu31jZN842XeL7L1N9kyW3Znuq/e42+93tz8oX71PdjzodMy5enWx48orV6/8C1Nf87v+eE1R32Ksxm9V3eT/POR3Tt3s908NnkD+1W9nfcRvdn3I//mvfjfW/87Yd36/1Vf8ZtFBcKBbhIDP63O5XEePHgWTEafTyU+SCR9CgBAgBCKCANiBRiQpSoQQiEMEwJ9BSkqKyWQSBMFoNG7cuFFTThxeiYDWIENfo44A2Du/8MIL4KPcbDbPmDEj6rlGOQMcV44ePQr1slgsZrM5ytlS8r1CAJwAtre3a1LxeX28OUyg+3xVVdHTNzY99qp4R5MsfSUENAioqirLMr8+zAtboBzyj+MGi0RyYcRXkMI9RkBVVRAPRVF4AYNd5x7/hd0UGAAGShFE0PSEPS4SPRhvCIBbCz//LF87WlA55pNfdqlT3cwuq1aFWT1MuOwWrrhEh3fw5as3Oj35312ae8n5ZCu75SqzuZjR7ZO8Hon5JEUVfUyAP4UZ/H+/UFSLotoUNemnP4vCTD/9alKUZMUzQvWMVT1jFc+NjI10yr/2sf92xTX3qzOVP/xH1Q9tBTKb9KNrvML+ocOT0iGnOeS0q65U+HPIaU452yXny57/5vHc6/M9oPj+SVUeZcocpjzN1EWMLWes2G9k/Qljn/lPTSQb6HiTwb+Wx+PxwLzA5/X5vL7m5mYIRK+46PrZ5/VVVlaC0p6fnw85ki4XPeT7KmVo0/b29o6ODhjUDh48iIXB0RDv9CCAiUAA9DoYXkGvg4kDeB4nGesBwvH5CHjywdZnjPm8PjC2A40Lj7zCbqc3FQFVDZNqaWmB1PBObxKnZwmBHiOg+C9Zls1ms8FgAA769OnTfIJ8v0cENI8MhaOOAPbRd955p9FolCTJZrOtWLEi6hlHOQPs+jds2IDE+uTJk6OcLSUfAQQuX77sdDpdLpeGB+T9A6LcQn5A68CUyel0OhwOt9vNd6wRKBYlkegI8EIFR3ZhNwJqKw8AiBzeuXz58rlz5/ArnxTepIBuEYADtXxeX1tbm9vt9ng8GgkBAQN9EadPfI/Hn81AHHRCCtJPfpXh8L9/97le8zgfUXyj2DWr5194rxHKImMj/lO++9vWB05/9fuXNt436x/zHn/qv37wf6ZecE9u997gVIxer8CUv1LPyEH7VNH/J/lU+PsbPf23OEzwKVafb4DXm8TY6I4fb269Mmvv/713cWnmvTNyn3kq7fyFmT424T9dxlZZcDODmxk8zCAzUWaimwlu1eBWf+FWLG4lSVYGyb6hsvfvZO9Ij/fXHvc4j+s22XHXVdfE1o5/9Dv3OMXYJf9RhMRBx6ksezyejo6O5ubmGTNmCIJw//33a7qsSJWbT/arr7564IEHYLYMmcJyHelykUI7ftLh2/3kyZMzZ84UBOGBBx6AEvK/9qzMkAI4OdWMmB6P59y5czAQY+IkYwhFfw9A0zudzurq6vXr18+fP3/OnDmPPPJIcXHxyZMn0VLE6XRq5pg9rjik+fbbb0+YMEEURTAyxWNUe5wsPUgI9AYBmMAePXoUqGeLxTJ+/HiUf1yEw66PCOjeoE3PdhsBENBvv/1WEASTyWQwGMxmM78Q3VWKvdcPuko5IvdxXMnJyQH/G0ajcfHixRFJnBKJOAJItTz99NOCINxzzz2nT5+GRgTmxePxgA2OLMsul+vYsWPV1dVbt25ds2ZNVVXVsmXL5s2b9+ijj1ZVVTU2NgITjb1qnMtqxMGkBKOHABCFra2t586dO3Xq1EsvvTR79uxx48YlJSWZTKY777zz/fffZ4whcx29klDK/QgBVVWPHj1aWVn58ssvr1+/fuvWrbt27dq/f39tbe2hQ4dOnTp15syZL7nr8OHD+/bt+9Mf//Taa68tXbr097///ezZs2fNmjVx4sSxY8cWFhbS3KYftX6YRVUY8/jP9vN7Rz7lcj2meMcyxc4UgbFrf04m/of7lvNt//OPH/1L9vTKG8e9Om70xxPG/e/c/JmfnSu/KE9pZ5KTCR4muK79iT//g5shPkXw0eFjw9uvZJ0/Vvlq1bpbbls0fOwrN4/aefuvl/x/L87+8dLDPuUWxuwOJl1l4lUmdjABPjuYoYP9ooNZOpjN/5f0U8DmUKwet9XjSHI6fnm5tZCxWsZ+UNglH2tTmDdMcChajBG4fPny/PnzYV5gMpkkSdq1a1c0yoBLa5988skNN9wApySB1ciGDRtwuQ7VuWiUgdKMPQKgln///fcgZtDigiDs2rUL+GJQ43tTMJwGMsa+/vrr7du3P/bYY+PGjUOpvuOOO9566y3GmMPhQAGj+UJvMO/zZz0ez5kzZ5577jm73S4IgsVikSQJpSspKem3v/0tz8H1psC4J/Lw4cOzZs0yGo2CIFit1rFjx0KyvAT2JiN6lhDoMQJr1qyR/JcgCPPnz0fh53s8CBMB3WOQ9ftgb8ZLMLnavXs3DMmg/IVIkBfZoIiHfjboI72/CaXi0wENRlVVi8UCjm8kSdq+fTsfh8LxgwCM02fPnoWVOlEULRZLXl7e3LlzH3744WnTpqWnp99+++2jRo0aMGCAwWAAa32DwQCKBfguhxUUQRCOHDnCC2oImYwfBKgkcYLAhx9+uGjRorlz595///0FBQUpKSnjx4+//fbbR48eDbKHwmYymYxGo8Vi6dw1AnIrSZLdbq+rq+Mdd8RJvagYfYjAZ599NnjwYJPJBJ6gjEYj9F12u91sNmMnBgdVY/+GsybYPYcxbTZbTU1NH1aHsu4dAmDj7L12Lh93wRc/J/s9Y7u87ql+d88iU8zOVhtjad9fmf7u3ofum/P0uLvX3jD64K9Gtg4fKI+94V//YWrZWzuev+TKar9GUv+VgHYw8ed/1zxEX+X+HH6f0T99SlfZoCu+O350T/+h7ffb/uWJ+9IXTnCzuOIAACAASURBVLlp59hxLUmDv711rPu2Ubty/n7Kj9887756W7tTCElAW/xMNPDRv7jKJNc1w22BqVbVd4vT8bj/MEOvh3XIrIMIaK794yi4YcOGoUOHQv8DQ1unFl1VVRWNIsJa2tq1azEj1OvOnTsHS7m8OheNMlCafYLA2rVrcQQEtcpqtVZUVIDPhN4XCTT/zZs35+TkJCcnW61WGEOBkQQxs1gsTz/9tMYYsPdZUwp9hUBFRQXYnCUlJWFPYjQak5KSBEGQJMlkMt12221XrlzpfQldLtd333337LPPiqKIWhyc9vbFF19o7O57nx2lQAj0AIHHHnsMJD8pKWnPnj3gMYYfUjFMBHQP4KVH/oaAy+WCQRcdHgW6kvxb7J9CCxcuNJvNwD7DHiiUyKBbg/lfIfxTSgycXfJrLGC4GrjpGB/RBMAhZgiFQFEUl8sF9epqgRF+PXjwYKdCYzAYbDab0WjUWI3hAjuAhpXSlIe+xgABsIJxuVygH4CaCHQMsjCapWxYMhEEARa67XY7LDYkJye/8cYbdHBNDFotkbIACdy4caPZbE5KSrLZbCh4fEAURaP/Ao3TaDTa/BcaWQwbNizQiXkiAUV16QECGzduBNIZZ0QoVKIoAjENd2AerokmSZIoinCGNaiSZ86c6UEx6JH4QMDLWJv/7yf7X5UxFYqmepXPGXvP1/FPzD2OqUa/7fOwth8LTh8rXjx/1Z3/ZdOoMXv/buTpG274jyl3srGD2ZSbzvz9Lf/9z2/9d4fjbo9P8PkEnyp6/J4xwD8GfPqtoa9x0P4/0cGEVh8YVouXnYKPJf94dfxV9j8/2Lf+n+a8PHLEpvEjPr1l+KWRo5zDf+0edWP77eN2/cPE27/+8glVvZMxm9vPdDu1n79wqjanavrrfdUEX91M8KlC6xWz2znD73/jIvPberuZ6ouP9tBnKdD0GKoPivfevXtvvfVWYHCGDBkC3RF0Tfv27YssUKC9O53OhQsXQreGvaLNZktJScHsUDknYwLEpL8EsMn4bWEff/xxamoq2AYBYQdNb7FYGhsbe1k1FOxjx44VFBTwg2lycrIkSXAH5rxQhvz8/HPnzkFR0QWWZm7by1LR45FFAM5r4dM8fvz4nXfeCYIExsiCIMBc0mg0ms1mXOISBGHq1KmBjvX41DRhnmoAesHlcq1cuTI5ORkMUGC6Cp/Z2dmyLKPka5Kir/0CgaDNJ8tyW1sbYwzpo/ivy0033QTDq9VqvXLlCt8PawpPBLQGEPoaLgLgtBR4248++qiiomLu3LkrV648deoU33UGTe722283Go3QO7/00kvgNivo66fhhVEv1CTr8/rACS/e15C/eD8wAEbZmLJGCYBz6uApKGFQhh3esdWrV4OSYbPZUlNTQ3QZfHaBRaI70UbA4/HAgJ2Tk2MymTTUMzIvOD8BnZXXJ6xWK/762WefwYIHNmu0y0/p92sEoIfcsmULPw0eOHAgShTIJKx5gCKLsxqDwQDss8ViGTRo0Mcffxy0R+rX+FDhe4nAzp07QUiwm0L5Aa4HLWhwemwwGKxW64ABA4YMGfKrX/2Kn1a9+uqrvSwPPd6nCHgZc/j//AS06reEvmb/7FXYt4w1uOQ5TsdkRb6LsYx2Z/7Zf3/8j/+yOPfv/8cdYz+5cdi3f/d3/5k84Icbb5BvuoENN3tvGfJ/59z7hx/PlXiu3sJ8AvMZFZ/Zp0oedo2Gxj8/DX3N/wYQ0PI1v9Kil5muuoe3tU+53Dq7semf/3nRc2PHLxk/4ejoEW033cBuGsZGjGTDR6kjRzkn3LJz3f/6g9zxuMpuUdkvrjl9DvwDN9B4XzW5FZtbNbnVX1x1i7LrDsb+F2MnGXMyxtz+PyKg+1QOf5Z5fX39fb+5D7Zf4K5B4HEkSZo1a1ZXM4KfpRLGF0VR3G63y+VyOBwul+uRRx6x2+3QPWI3KAjCs88+i4mhIhepMmDKFIg2Avy0S5blhoYG8CqO2rvZbMZ2T09PP3/+fI+LBJNHxlhHR8crr7xi8V+wf8hms1mtVrvdnpycnJqaOnHixEGDBsGoCrI3atSokydPgvE1yVuPmyCWD6LnRpfLtXr16qSkJDBCQtGaMWPGzp07P//88w8++ODuu+8WBAEtSywWy+zZs8MpLQgDH1OW5Y0bN951111gFAW6HE9Ag4bmdrvJCJrHrV+HsSmhQ+vo6Ij/6qiq2t7ebrPZDP4rJSUlNBFHBHT8t2k8lhDsnT/99NMFCxYMGDAA5rTofWLr1q0hCv3FF1+Augmj9bFjx4AKxDEYT0bSBDDC/8/edYBHcWTpnhlPXI0Qi0BCOQKSkIVAS9ISz6QTEjIyhiUuIiwgcwRzgGER4Ug+TFjiEQ9sWGNAB8IsYFiCWURYMGDimrREk4TCjCZ0T3fXMfNDuT0KCBAgrXs+GVd3V+pXr1+9+uvVeyUqhQUFBT/88MPGjRvPnj1bTkQGG9fUYlq6Ee3Wf97Bo84yarZarQkJCWq1Gv4cpk2bRiUIrU0a2pu+Dn0qJ94wBSwWy/Hjx6OiooAvQy+kIGCNGjWioqKSkpIGDBgwfvz4uXPnzps3LzEx0Wg0AtaBPwT4dHPbKXnDLyI3V+UocPHiRT8/PyiRGtcvICCgdevW/fr1Gzx48KBBgwYOHJient6vX7/k5OSkpKQOHTq0b9++VatWKSkpvXv37t+//4oVK7B2ouc/qhwR5A6/PgqsW7duuus3f/78BQsWLF68eOnSpStWrFi9evW6devWr1+/ZcuWPXv2nDp16urVq/fu3cvNzbVYLPB9//HHH2OJrlAoJk+eXIYJw+vrv1xzRVIAJs/491nwQULMHDlCyP/ctiRcyQ/5Z17K+evTV/zv6la/nR0TlhUTfCnU936gX35w6I9R9fJCaxeFVhcaBpGGod/Oyhye/6gXZw0knJLwWoHXPw+AdvriyOMZjsTeu9d7385p40etiI74U3SdvXXCLoX4361T21yvhiX81za/2oJfEAkM5KPrrd+546MHD6PNNiMhWqvI0L8SkGhg0OI7LvRZaRcMJmsQIR8R8nfCm4E8c0Tk3FyQVCR95brKSwHewe/YsaNbt2561w/qlk6nw8Yq3SfLzMzEKqO89ZYj35kzZxISEqhxFsMwy5cvh+5nMBh27NiBlQXVzJEoR8VylspIgcOHD6ekpEBX9/T0xN6GTqcDXAhOmzlz5qt03WazYZU3btw4Cmqr1Wq9Xv/hhx/u2bPHYrGAjeG9d9myZSqVSqfT4VjbkCFDZH/Qr0L/N1mWrv1v3LjRqlUruk4E1tamTZt9+/ZRlBAmJlOmTKEANCyjy7+Xj6jjLMuuWLEiNjYWzSkUimrVqoGTpQD0+fPnaffeJE3ktiqWApAVZ8+enTZtWmpqanx8/IcffvjVV19hiWcymaS7axXbdIXUJori3r17McMqFIqPP/64RLCOtiUD0JQUcqIsCrix0RPIODMzE7JVo9HUqFFDoVDQjeWOHTuW4VRr0aJFOKiiUqkCAwMfPnzopvDlSX5SDFqqHUr7umfPnu7du1NTL41GM3r0aGmGMtJWq/XLP3/55Z+/LMOFgt1u37Zt26RJkzIzM4E2sixbHPTJy8ujZ7u0Wu2uXbvcLMFtNttD1092wVHGiLyxR1JRvn///tWrVy9fvnzDhg379u27ceOG9CkhhGXZNWvWwC6VbrQkJSVdu3aNdljKxvSmnJAp4EYBiAVY5UCtDA0NvXDhAmRmaWAfDT+CkIMmkwlnPqjK69aKfClTgBBSWFjIO3jKVG7zON02A62wI/up6xwP5rLevXtD+rnNZTJtqxgFBPjcEJwYLABopwuOu4R88dAy/JY5/fgPgyfP6/Vel+HBYauCAy5F+HExYUJw0HH/kP+r33B7j1554f53GoaSKG/y23f3bts6It/UzMHWIg6tC4AuzQJawbqCExYRrUkIL2J7/u3QH/44cmCLuLG/if4usMb9wBq5gd5X6oTujw3f8bsOjxOjfwwPZmsHCoHBRdH1/3Tz7jhCQi0ONUd+Qp+tYkmm0D8ZQSudzjocvpw9lZD1hDwmVtFlAV0kEN7dB3YVG8J/he5u375dOvFh55VhmP79+x88ePC9996DAYdCoUBw3Yp6Z7PZvGvXLi8vLxocydvbe+/evePGjaNozv379yEnpZYoxQVmRXVJrqcCKSDdKuA4bs+ePW3atPHw8NDr9RhfwH/du3c/fPhwbGwsPJsxDPPNN9+8RDfcuKJ3796oELbPnTt3vnv3Lj17TidfQojJZJo3bx7FLjt16oTW5bXDS4zCWymycuVKWLID/QB3ZWZmQkHiOM5isUgtz+bMmUOxY4Zh/Pz8yhkz3Gw2r1y5MiYmBiLL09MT7ol8fHzGjx9/6tQpAN84rQvbZ+ASbsz5VqgkN/pyFPjqq6/at28PhoEfV6QnTJhQHHF6uSbcSlHJ43b/pS9nzZpF5dvatWvLrkcGoMumj/z0KQXg/wi+Mnbt2hUZGUlPscGcmSqOWq02NjaWmgwXX7i+9957lEHT09OHDRuWnJzcqlWrOnXqGI1GjUbj6ekJxbRz584UgBZFEVUJggDMhXfwVqs1PT2d7jGiWojpHTt22Gw26dwvHUtUdeLECR8fH5hvL1++XPopCoIAz6pLly4NCAiAdQZ2zmNjYzdv3uz2Xk+8O02aNAmkwCuMGTMmIyOjXbt20dHR1F+wRqPR6/VBQUFwqYn9LtquPHNIx+itpzHEGKP+/fuDu+Dj28fHZ9WqVW6W+/I4vvUhq7QdAG+ge0+E0uTJk8FIMLo/evSoyWQqjX+k96VpKhvlBXOlHfeq1TG73b5+/XqEaTIYDImJiVWr/3JvS6WAE24WCLER4vLC8dQVxXmODLv1Y9+5s6b9Jm5qZPgXder+PbLu/ZDQx3VDC0KC/hIZ32PUf03cmXM8tcf/1A3+rp4vF+5lblhv9YGcngWsH++oTji90wWHoIIbaOp/41lCJRBPi6N6ER/+/fddxqRPSIr/8jd+2xuHXg2tVVA3RIjwvR5Xb1PK+0NXrVm99+v79UOX16tzv3agNTD8es/+G3LNA1mitROGlZg//wyAhgsOl88NahZtJYydjyX8nwj5BxELCGchxERIUamUkR+8EQrs37+/efPmiJ/BMIxer4cn+tatW+/duxc7YUFBQVChFQpFxRr0SVE/tVqdkJBw5coVQRC6desGvS4+Pp7CRtJJVtbJ3wh3vGoj1FPikSNHEhMTYeEE0BkclZCQcPz4cViVent7I6i4SqWC4ZHbRmzZvSksLARzsixbUFCQmppKo8UYDIbZs2eXXbxFixYwvtZoNEuXLsUqQ8pyZReXn75FCnAcxzAMwoBDbkRHR588edLN/yftITAKbLkBR1apVAsWLCgNl6AFp0yZ4u3tDSMA+EZDWI4hQ4bk5uaKonj8+HGAEiqV6oMPPgD/oFpZZFEyVq3EzJkz4RUArIW1ISKlKRSKErfKAIVZLJbFixfv27cPQ+9mPCeFqliWpZfwSI5D+c9lSEhIGKOAqqdPnx47dmzv3r0bNGiQlpY2d+5cIGZJSUlwHWk0Gh8+dIbfKOMnA9BlEEd+VAIF5s6dC88D1MweAG7nzp3T09Nr1KjBMMzKlStRctWqVQ0aNIiS/OrVq6fVaqm1MhzAAW7Gv1qtliqpRqMRIAsVqdLv5Ntvv/X390eoWY1Gg61IeroqIiJi7dq1x48fL+EdXLdsNluzZs0MBgNOTk2YMAFCHPmhYfTr1w9wNj1dBevXWrVqNW/ePFbygxsHCA5p+CZ6B2oQVCKlUpmVlYV3sVgssvIBmlfCf0VRPHfuXPPmzcEA2G3u16/flStXsCMiHTtpuhK+i9ylt0gBzPocxxUUFJw4cQKHNKFhrFixAvKtNP6R3pemZQD6LQ7ov1jTmO8uXrzo7+9Pl9NHjhz5F3vNX+7rPAOgRcI5gWjn74FIsnLNLb7e/m6HZqOjfPeF1j4fEnw5JOxYcNimsLDp/dInHDw96aZp5vVHOzsmjYwMPhThUxQbXPhvictuPUq3EYPA/8oJQAsKQWSeIc4/+YB2hSVUFTkYk93LwidMzYxoFjYrodaVBrVvxAZd8au5Lzjo8/daLZk+bd73lybcvDtz28atcWFz6obf8g/KDar77Yg/rnhsT2Nd6HPpAPQ7TqfPT/0+u2yfCWMRawpCN0L2E9FMBAsRfw5AO+kg/940BWw224ABA6j2i5Nk4eHh69evx8qWd/Bms1mr1cKsLyoqSqrqv0p37XZ7RkYGVisAcVJSUuAYQRCEoKAg9GrkyJFoRTrDIv0qrctl3xgFsH/Qt29fGggOi6+goCCwGXpSWFiItRjDMNHR0W5GJOXpLYAb8GdqaqpWq8Xak2GYzz//HDWUxjnfffcdXFaib3fv3oU9rJTrytMHOc+bpwC09Hr16gET0Gg08fHxN2/eBOPZXL/iveId/JIlSyj6rFKpunTpgsOOdMereCkAKXTVqdFoUlNTDx8+TJGQLVu20G6MGzcOPEmfFq9QvlPJKdCrVy+AV9SRQFhYGKQEBNrixYvtdjuFj+nrsCwLm06VSlWixTE1nb5w4UJ2dvaGDRsKCgqkrpmBQVMRRGsuMWE2m7dv356SkoK+IZYbVrI1atTIzs4ODg6GPAwODqYWliVWRVwBr0t7JN+XKfATBWBkN2vWLCCw1E4hPDx83rx5169fF0XRZrPl5eVdunSJEALOQ9xh+hVRzYB6L5I+cksrFIr09HRq3IcEOmSz2Q4cOFCtWjUAgvDqFRMTk56eTp0lQeNUKpXXr1+XfmzOcDR2O+rx9PTEXvQTDH3q1KlS8S2KYmpqqqenJ91FRwI7VCCCdFLBPhW0Z/qanp6edDFP306hUISFhT169Ah9oJ99aSrLT2Mgp94sBaxW665du4KDgzUaDXabg4KCNm7ciF4AsnEbPnr5Znsqt1YFKIB96SdOshITE6FqIPARGIna4BSXA5Sp3BIyAF0FRr2KdBFzX9u2bTFPwU6nivRd7mY5KODyvYF8TlcUpEgg+3Md44qEFju+jouP+CCs1or4uKyg8P+Ka9y/Z3rSlh1JD02pBWzDHx91Pv33dTFhf2gQefHdSL5u4JX+vdfmc+k2ohR4PXGoicjwhHEixURR7I8pEhmTg7EIDadMDkmIHFE/cGud0LXh9cY3+7ekzP/uevLsgAf5qbnmuLzHf1g4eVVCcFaY313/kBsBscvnfbEkj0uxi0pWVNr5UlxwiEpW0Dj/RCf67HS+wXvb7W0Jme8yf7YTniOEc5k/FxHisvqGKxKpR+xyEE/O8ioUwAQ3YsQIjUYDCLhDhw6bNm0qKCgABIPYgGfOnKGac3p6OjW5epWmc3Nzk5OTNRqNh4eHQqHQaDQZGRlUz798+TLFIhG3xm2GLT4Xv0pn5LKvlQJAhEePHg1rJK1W27Zt29WrV2O4wWlWq/WHH36g2le/fv3K0LvK7i3Lshs3bqQepY1G45o1a8DJOChM2Uxaz4wZM2CApdfrU1NTn6v7ScvK6cpAgSVLljAMYzQae/fuDS8r9HB2ad3bsGGDFCsYMGAALEnL2GMLDg4GgqHVavv3779//35UbrVaAUFOnDiRRt7atGkTAOjSOiDfr8wUYFl2yJAhUoPOSZMmXb9+nRCC7bSyAei5c+dSKQSB5vayHMdt27YNWJxer1epVB4eHvPnz6dYdhl86FYVIWTatGmQnxQVoQajCoVCr9fDJJRhmLS0NBQvURLikWwBXZzC8p0SKGC323fu3Fm9enWVSgX7ZQ8PDyhtgHctFosbH4ui2LdvX2icUsSZYr40gUXvk/2T+Pj4Dh06DBw48JNPPsnOzqboMxRBHDewWq2HDx+G5TIOUgUEBGzYsAHxNwkhYWFhFAhmGCYnJ8ftfaAlXLt2DYEgcKZm8+bN0v5/+OGHDMNgsxrbO7GxsbTDdMebwsparRafJTBxvV6P/UmEwY2MjGzatGlaWlpGRsbSpUtv3bolxdOlWq9bV+XLt0iBNWvWeHh4qNVq+HhJSUmh6yV4c+M4Tjp20vRb7LbcdOWkAPa9Jk+eDDGiUCjCw8OpQklNGMBFbq8gZS2algFoNyrJly9EATe9cP78+XRl3r9//zKiOLxQK3Lmt08B0YW+8k/dQNu5AkKuEjLnjqVlniWcdfRYPC9j4n/OGT/xv77YsvDkpdmX73YvcASaBMZBmNzcpt9krwz3nVg3+HJY7QdBPttnTf881/a+SDQCr3X6gH4GQNuIotgfI7jcN5sdYd+f6/Tpf/3HJ/85f/b8P2V98+kDe2YBSTKRoMec8pGV4cU/ZI7433q1Dgb75gaFng9vMG7zXz99zLaxO+MKKu1CyQA0+xMAzdhFpVXUWdgYwfafhHxLyD0iOogId9dWlxtozkkF0eUCWwag3zhT5uXlbd26NScn5/bt21JNG5YrHMd99dVXFA7+9NNPXx2APn78ePPmzTHbQoefP38+4q8QQjiO++KLL6gCf+vWLTqxuiXeOKnkBl+MAnQiAy+tW7fu5MmTubm5giBg159CLTabDWyGcUcEQulwl6dhcC/LspGRkeAro9E4YsQIKZpcWj3x8fF0ks3KyoKpFgWs0ZPSysr33y4FeAdvs9l4B79///7r169zrh+6BN2eMgDtJ+6PHz9eCkAfPHgQ8odmK544e/bsl3/+8vLly1arFQALNZtD5p49ewKA1uv1p06dkjmnOA2ryp3PPvuM7rwyDJOdnU11748//piuFr/55pvio2w2m/v06YMDtQzDtGzZsriH8aVLl2JihY8BiCyGYbKysqhgLA+tCgsL09LS4F4D8lOlUkVGRnZ9v6unp6dKpaL4GJqAdJXO9cVbkQHo4jSR75RMgSZNmlDm6/p+1+e6dxEE4fr16126dMGZAp1OFxkZSW2HDQZD586d582bd/jw4Tt37iC+J/VHQ1UKt67wDv7mzZvh4eH0K4qKinJTIMaPH4/PA6cDLl686FYJx3G8g9+5c6dCoUB/NBoNx3FUsZgxYwYOv8DqeerUqXl5eYSQ7du316pVC8KiadOmBoNBqVQaDAa4rkMYRp1OV79+/ZkzZ27atOnixYv5+flu05K0t8XTbl2VL98wBSjjTZgwgZr5MwwzdOhQ6iyFdokigMCj6WjSDHJCpgClgMlkys7OhmDBztm2bdvwtMRJmmVZeoKJslZ5ErRFOSFToAwKSLnu1KlTmDQVCkVAQIDF9SujrPyoKlHgGQDtMoO2COQGIVty2d+ahGomTmdha5tsbQqL3s+3JudZ3ytgE0xcoFVQOW2KRSavqMO8hf8TGvpFRNCPoX5XIwNmb8ta86CwrcnOEIcePqB5UWUjCsuzP8DQVqK0InigwJh4fYE9pMDUOr+gc15RhzxbkzxHaB6pVkB0BeQdlng8MP/+932/CPK9FOxvCws+3qnzqOu35hdYf2MVVNafO4CmPqBZkXEISgevY3kdK2jsgsEi+LBsZ8JtJeSBC3F2PMPdYQfNuy5dNJAdcVQC9pXOZYSQ2bNnU9d8WGy/XB+xlbt582YvLy8Yw8Isa+XKlXhEoZzevXtD6EVGRmLdTjU6t769XE/kUm+MAtDbYdZDB9HNgAl5Fi1aBB1MoVB8++230oGmyn95ur1lyxY452UYJjIyEqyFplEP7+BNJhN1s2CxWFavXk3D1Ht7e9NWXqhdWkpOVH4KgCv8/f1h5fYEXoyPj6fsUZ5xB39KWRpIBQxalUqllJEqP0HkHoICWNkRQrKysiAT1Gq1p6fnV199hQyIHF6/fn1gbiqV6ubNm8XBZVEU4XO5WrVqTyL31q9fX8pUvIP/4osvlEolzvpTY1DgWi1atIBP/PIMCsdxSUlJdPOMYZiPPvro1q1bNMI5jLgxn8Ic8+DBg4DayqhfBqDLII786CcK7Nu3j6LPzZs35zgO9sg/5SgpRWdf7LTAhT9l4itXrtAdGEDP2Aouqaan9wRBaN68Od0vgg8mqQ4hCMKyZctwnEGn0xmNxoKCArcK0ejatWuRjWGYRo0a0e92586d+Irwvl988QXtJCHk9u3bS5YsWbNmDcdxNpvNbDZjj52GLoU3D0wYbu1K5xJpn6VptyLy5RumAECZjIwMb29vLy8vHLZq27ZtUlJSmzZt4uLimjRp0qxZsy5dusyYMWPPnj3gcHAIxvENd1hurqpQwGazNW/eXKvVIroxMOi4uLhevXotX748Jyfn4cOHYCSqnXAch6gRUhHx3HRVIYjcz8pDgfbt21P7iM8//5zOhpWnh3JPXp4CAKBdtr+EPBbJX81kdD7n5/Kb4XSdYSMKJ1jsdKDs/LOKDOeEdxlOYB6bu4zPXBMStj8sKC+u3tWGsf/5t0MLcs2JVkH9FIB26HlRbSOqkgBopVVQWURVkcAUCYxFYGy8E9S2i862zIQpIEweUZqIx52CYc1bLQ4Jzg0OEMOCD/TrO+z+vQlmW4z157bPAKPhbUMCQBvsgs7qqGV1NBWEcYQ/53RyLfKucIsAnaX/SnyRvDxB5ZIVQAHpREYIGTZsGHxDMwxz9+7d0uJ6ld2wIAh2u33RokVYY1NEe+XKlTAikUo26mQzOTlZBqDLJmwlfyrlpdLSeIUxY8bQ9d29e/dewgUHDj6OHj2aWlYtWbJECkDzDp7aM1F+mz59Om1XrVYPHjy4kpNU7t6rU4Bl2ZkzZzIMU716dWDQW7ZsAX9Kz0CXvyGK6Pn6+sICumnTpuUvLuesbBSIjIyEFSPDMAsXLpSianPmzIHE0Ov16enpeCQFo2Ao3bp1awT1VSqVbdq0occpCCEnT56kh/XhJBaGm9iBMxgMZ8+epQKqRMoA5iKEpKenU9jN09Nz586doihijoaFpc1ma9iwodFoRBM6ne7atWvSzpRYvwxAl0gW+aY7BaZNm4b9IklkIQAAIABJREFUE4ZhJk+ebDKZqB2Be9afX0vNrE6ePEmZ2N/fn35LONhS9pcARWHcuHF0FtfpdCdOnMjLy5MqHIQQHCVWKBRqtTo2Nvbn3XFeoUtTpkyhVY0ZMwbZCgsLw8PDcV+n0y1btkzaf+Qpfodl2YiICIZhAFkeOXIE8ZFp09INTLpJLu02TdMicuKtUIB38B9++CFs5yG7sTMJa3fqAB3eDBmGCQwMnD59ut1uh1b6VvosN1r5KQBZ16ZNG2y/wfkPVQ7g5sVgMPj7+7dv33706NEHDhxAgBp6EpmKiOcmKj815B5WEgqALXFGDz5SqVvMStJDuRsVQAGnxwkX/Ox0g3xbIDPv2eMfsR4i0bFE4XSdLEGfnwLQAuPgXQB0YffkLrMiwi6GBhTWCT3Rts2oy9cW5VsaE+IBAFoQ1BxxWkAXPbOABhLtsoBWWkQnAI06LS4MuhgArTORgJMXBoXXmR4WXBhQi48M+eu4T4bnFmQUsRHAmp09lNhBUwAaLjic6LOoMXMRFutAIm52mj87AWg43wD0LPW4AQBahqErgK1esQrpREYIadWqFcJ3w6bParUW17Sf2+KTML8jR47U6/VqtRoYdLVq1eAj1a3stWvXqP4/c+ZMu90u1dLd+uZWVr6sbBSQjldpafS5U6dOGPdatWrhjjR/ed4L+HJKSgp0Oa1Wu3fvXjf+gWmhzWaz2+3Z2dkJCQnUfgsr071795anLTlPlabA6dOn6RlrpVI5dOjQV3wdIHq5ubnUlD4jI+MV65SLvy0KjB8/Hu494THZZDIhRJkoijt27MD8Bblx8uTJEjvJsmyjRo0g0J5YSffv3x++cAEKJycnwyOzQqGIjY1dvHjxnDlzABADj54zZ06J1brdHD9+PIU+atWqBdlls9koloX848aNQ9gzhmGCg4PpJlwZey0yAO1GavmyZArA5RD23BYuXAjOKznrz+9SBxSCIKxfv57KzW7duv08Y8lXFKQmhOzatQuQDXzNrF69mpahh60IIYMGDaIOOrq+37U0LRahsfFG69atQ1UDBgxgGAYRSyZPngxM3G63U1ettEUKZIui+PDhQ9qiVqulzqGkGq1bWqr0SNPS+uX0G6MAZZIOHToYjUalUgmIEMqi0Wikk4HU1RFOmuj1+o4dO966deuN9VZuqMpRQBRFlmVv3LjRpEkTrFuo5gERBB0CsS7pwrhTp047duyADJRKibLTVY44coffIgUuXbqkUCigp9asWfPGjRuiKFqtVqktxlvsntx0RVBAIAJHeCsRzIQcMovJD1lPE9HaiMvPRkkAtN3BEKK0scrHeX9o8O7U0IA7IbWtdcL+lvL+Hx6Z5pq4eEKMxOUDWhBUnAt6LgOAhiHzzwBokVpAe9pJ46ztPUND5/n75Nf2ZiNDd8ya+4dCtnuRw68MANr5SFTaRY1V8DAL3oXWlpx9CREvEGJxAtDO/6jhswxAVwQTVXQd0lmMEBIaGorVQZMmTViWxcnCF22ze/fu0Nwwk8bExBw/fhy6OpR5q9WKdrOzszHPPlmcZ2VlmUwmqYru1rcX7Yac/w1TQDpepaVhMBgTEwONKzExEedupfnL023khztUsND06dPd+Ac629GjR+Gh1WAw0OBJer3ex8enPA3Jeao0BQRBaNiwIWSaTqfz8/N78OBBhbzRwYMHKZAyb96855ruVUijciUVS4E7d+4A1QV2hKiDkFEHDhzA+CoUCk9PTwBuJbb+JHZCVFQUpJBarR43blxBQQHcYsyePZuiFsnJydRl7qhRo+gyMyUlhVo4lVg/IWTPnj0AwfWuH1xUw3m9lPEEQRgxYgTdZmvZsiU1f5YB6NJoK98vLwUQThCMnpCQALtj6mGjPLVQBoWl1aJFi8pTCnbWaAgOccDigwcPtrl+tBKWZQF2R0REqNVqgNSTJ0+m2CLNiUSbNm1QlUKhOHz4MMuymzZtom5/i+Pj0o+NVgU9Y+/evTjUwDBMs2bNKOYu1WzKmaY1y4k3SQEM2cmTJxE6Ehi0TqeLiIho167dhx9+OGjQoLS0tA4dOjRr1szHxwdBNTFzgNO6dOmCtc2b7LbcVlWkwMaNGwcNGgSH+Hq9np47hmCkwDRYUalUpqam0uPDpS2SpeKlKtJE7vObpwCC2/Tp0wdxsRmGWbx4cYnT3Jvvm9xiRVJAJMThIMJ9Z3Q+cbLNEW0nGjt5hyNKWEBTnJcaF7sAaH2Rqdqpk31iIheE+JqDfNiI8D2DRwy6kZthJbEC0bsAaLUgMhxhLMUsoG1Os2iVlbxjJe/As4fFZcgMC2g7YYqeuuDwtoudFy/pGRn+v77eBf41HBEhGz/fPNhMWhWJnixh3PomvbQSZYFDkWevnmePt3L/QcSjRLQ4Iy06XTw/83vthKFlALoiuek11WUwGLANlp6e/twgXSX2ISkpCSqZVqtVq9Wpqalms1lqwoJYHbyDz8/Pnzx5MpYzKpVq9+7d2G8TRZHjOFiclNiEfLNKU8BqtWLQlUrlkCFD6M4EVZ/K83bgqFWrVoHNUOHu3bsRtANr1aysrP79++MRDa2p0+m0rl9aWpo8z5aH1FUrD9yw0D6npaXBRAmuPmEmT5++SuLLP38JUckwzJ49e6DIvUqFctk3TAHewQMIhokbZBFkwqpVq2AEqVarvby8cDofAqp4J0VRxOF7b2/vJ0fwFyxYAJn24MEDnU4HU6fg4OAHDx7QSe3YsWPUnLk0B+J00rTb7Y0bN2YYBsvSmTNnwsKarkOlcgzOA7BuHTx4MHDnMtBnQohsAV18TOU7JVCAOlbG0bbOnTtfvHiRRhl+rr4INm3RogWcGzAMc+TIkRKaKXaLgrkzZsyg+mJgYGBhYSEhBJO99Bs4deoUnKsCEV61alWxKp03RFFs1KgRRY1v375tMpkSEhKwZRQXF5efn499pLI9jeDrmj9/Pq0qIyND2h+q2ZQzUWJv5ZuvmwJYeHz77bcQ2e3atZs7d+7du3dh1wDFAkdO4BQpJydnyZIlELg6nU6v1yuVytGjR5e22/G6+y/XX7UoYLPZILtMJtPly5d37dq1Zs2a4cOHd32/a/Xq1cGEdPViMBg6duxICCk+95coVaoWKeTevkUKbNy40WAwYPIq0V3VW+yb3HSFUUB0qkpEvETIXMHRziH8WiCMgyg5ZwBARXEMmhUZm9MC2tNcGLJ3V3pM2NogHyHQh4SHbx8ztc8dU3cbqSsSPXFoCa96BkAzUgtoVxxCCkArnQC0E6R2/j2NTEiUZqLMc/qA9jNbe06f2iciZGOAjz2wphgZvm7b/r4mUqfI2b1SAWirE8JW5jkUeY5Qq/B7kXxOyL2nULOTcDIAXWHs8wYqki6YP/nkE6yiy9ku9O2ePXvqdDpvb2+ckpw/f/7t27cPHz68devWJ3Hnpk6dOnr06N69e7dt2zYiIgJn2hA2HF4B1Wq1v79/aGhoVFRUXFxcYmLik8Nwc+fOLWcf5GxVggI3btyAWqVUKidNmoQ+S5Wo8rwFlHyO41JTU6tXr07NDNu1a9enT5+OHTvWqFFDo9F4uH5obvjw4VOnTkVEGYZhNm/eTCGe8rQo56laFOAdfL9+/TD0AEzmzp0rCAJFM17xdebOnYs1gkKhOHXqVEVV+4q9kouXnwKiKNKpSqfTXbp0CTbFI0eOpPLkyRBPmTKFZVmLxVKGjEKIS6PRiN0I+AIdPHgwpI1ard66dSsWm+iexWIBAK1UKhUKhcVigStn2gQ8gQBemzhxItjYw8MDkRJgo00BaHC1xWKhsdOUrt+MGTNQoQxAl58r5JylUoB38A0aNNDpdFisqlQqo9E4c+ZMCraWDb092fApLCw0Go1qtVqn03l5eZVz1w7Vmkwmg8GAz8bLy2vz5s1U5sIhF/ptMplGjx6NI3j4bABz004iG47DBwcHU4cehJA1a9agCMMwmzZtwgHA576UKIq8g+/6fldYXqhUKnpCAY3Sr7qciVIHQH7wOilAtxmuXbt24MABQoj0BLrdbjebzVQuSzvStm1byjYajUb6SE7LFCiNApAb1EkWzQbRdOTIkR49eiCyBD3TtHjxYuycPVeS0NrkhEyBsinQtGlTTMp6vf7AgQO8g6eSsOyC8tMqRQGBcDZCcgj5ndXyKyK+Q0TGQTQc0bBE5fr7GQzNioyVY3jeaDU1W7eyb0z4VyE+JMiHhEdmf7ri9/fZjkVCoNMFhxOAVggEFtA/AdAu9FnhCksIC2jlUx/TPwOg3zGTd5wAtBCSlzdo+OAe4UFbQ/zFIF9Sp+7qg+d7PSZGi6tmV6TEp65Cfm7+7AKgibaIJIpkKSFnCbG6nG+4oc+yBXQVYNWcnBycJGMYZvny5Zjpyg/SDRo0CMeKVSoVtHpYhNHFPAxfgNpgrU7VNpVKReOv0psAEBmG2b9/fxUgn9zF8lHg4MGDdKW2atUqgCNShap81RAsD+/duxcXF+fh4QE2U6lUOp0O7AebQY1G07179wsXLhBCcOIWDFZQUFDOhuRsVY4CvIPv2bMn3HjCkcInn3yCI+NwSvAqbwRUYciQIWAkrVZLXSu8SrVy2TdMgcWLF2MaUigULVq0EATh4MGDLVu29HT9sOij1pMsy5YmowRBQD0Qa3AEeuHCBVp57969gWZQLIvjOMgioHnnz58HZk2boDltNhts7Dw9PRUKxZkzZ7BuxfYwxaCxaO3UqZNWq8UsrFAotm3bBrs9N/DNjc6yBbQbQeTLUilw8eJF+DtXq9WILq3RaKKjozds2EBZtrTCgiAcO3YMQlOj0TRr1qy0nG73eQdfUFCAgIGY5lu2bEn3c5AAGG0ymU6cOEE1SCRu377tViE+HrvdXr16dUDVNWrUIITEx8cjTG1SUhJ9HY7jrFZr8RpwB484jouMjIRqq9Pp3FqkX3U5E6W1Jd9/TRQQBAGm7viXjmzZchMKKO/gv/vuO3Aa/CfcvHkTETVfU2/lav8FKEDFC42cjmO/ZrNZaiWxdOlShL6EiVbDhg2pU62yhcm/AInkV3gDFFi5ciX1P96jRw+YYJQf9HkDPZSbeHEKlBhez0LEK4SsFEicnWWI6PwTRB1HPFiiphg0hXdZkeEcjN1W3W7pOnf276PCtob4kAAfEhGZtWpjn8eOJjbRl5BfEV5FBEYgDO9Cijmi4CRwts3pGPr5AHSuGHbv0ce/+6BnmP+OusEk0JeNjln8/e3f5RGGJQzv8u/hcuWhRFRDl9/nd1jhHTvPWAUPG4kSyB8I+SvhHzmNnp0/kRBO4gBaBqBfnIneeInNmzdT1X3btm1ov5ybYdOmTaN+q2iQc9QGtZzWLL309PSkzq+0Wq3RaMTZYa1Wq9frsZ5nGGbp0qVvnBhyg6+LAps3bwZArFart2/fzrKsm071Qg2zLHvr1q24uDisJXU6ndFoxNJYoVD07dt33759WKI+ePAAfhiUSuV7772H02wv1JacubJRoLQVYt++feEfQ6fTqVSqESNGoOccx0mt5V7uddBocnIyZJqHh0dp3Xi5+uVSr48CUtX6gw8+AFz7BGueOXMm3HFQY6OAgIBt27ZRmMvNQlnaQ47jVCoVrEIDAgLwaODAgSqVCnPi1atXcRMoGYCLgQMHgkVVKtWGDRtKq3/27NnY0NVqtTiWBCwbC1UKQ3Mct3XrVk9PTxp9gWGYU6dOyQC0dKTk9CtRAPO0yWTC0RKFQoGJFnIwMTFx586ddrsdeykUYaFNiqI4e/ZsZFYqlWPHjqWPnpswmUx+fn4oq9Vq9+3bRwOJAIiBWH+CcXfs2BHOeZHZYDCUqMICc6R+osPCwrKysmrVqqXX63U63enTp+mOU9nHB9Dzu3fvAnxkGCYiIsLtdcqGioo/dSsuX75uClAjCADQ5RkR+OVAvFrewSN0u1Kp1Ov1sJsukete94vI9VdFCkj5jW4pQ36KoghLB9hn6XQ6s9kszV8V31fu81ukAJgHHRAEoV69epgoFQrFuXPnEERBXs+8xQF65aYFQhyuv5/7PSa3ibBcZD+wc748cULGThccoodD9OKIgXOZQlN3HE7YlzCEf0cwh9utQz8e3TsqfFdwbRLkS+rWyfrLX/rZ2Loi+bVIVIQoCGE4nmFtDHFeehDBkPeQccHQChcA7cSgLU5n0Arbs1CHgLmt5KkF9AMScePB9MTED4J9d0WFigG+91u0WvLI3NfEMsTBEI6xO5hCnsnlFfnOejQOYiDk14T3FDmd1eJnI71sZAkhF5xRBwXXWxMbIWZCWFccQsDx0n9fmcZyBa+BApmZmZBFDMMcPXoUUojq4VKhBB9o1P/eo0eP9Ho9zrljAQxPu7Q2Ly+v+vXrd+jQIS0tbeDAgaNGjcrIyEhPT8dKQaPRjBw5cvXq1V/++cu1a9dOnjy56/td4+Pj6SHlJzdfw+vKVb4FCoiiOHHiRIA1arU6JycHK0epTiVd8SFE4XM7arVap02b1q5du27dug0YMGD27Nlbt26V6nIsy+J8LZjqs88+o9z73MrlDJWTAiaTiR7CFkURmrnJZGrXrh3UdU9PT4ZhBgwYgKPe4DEgD6/4RoIg1KlTByb2gYGBLMsWx1vgExVOI2FY8IqNysVfnQIAlGEv7OnpSd0JNGnShIaUZBjmo48+KhFAwAlsKYotiuIPP/yAmc5oNLZv355l2QsXLmg0GmygUi9DOFFEHVvNnz8fpZ44rVq8eDFO4kpXB+CfmjVrYkNXoVDcvHlTKtMwI4uimJeXx7IsIrsCrYaAzc3NlcrV0qgnW0CXRhn5/k8UAOfR6x07dsTGxioUCg8PD71er1AoDAaD0WjMyMjAzCrVFynTDxw4EKzJMMyKFSvc8tDKiyf27dtH7REaNmyICqXMDT115syZ6Aw0S4VC4eXlRScJabUoq1ar4QMuKirqvffeYximWrVqI0eOxLcqrV9atnj6wIEDSqUScHaHDh2kk4G0knKmi9cv33mtFMC4UNlafJiKty4IAmYIQRD27dsHkwqVSgXTBlm5LE4x+U5pFJDyG2VCuily6tQpql4olcrTp09L85dWp3xfpkBpFKBWFZ9++ilYS6VS9e/fn4bwLa2gfL8qUEAgTvjV5uwqAu85UwIh3ztsg1hbHU4wOpzen11/TwFoHeeMRuj8c/mDdtkdE4YIet4SZzL/sV96vzoRe4P8SIAfiaq7YffOVAfrS4jRITqhZzurtllqWQrCuPwoYmlMrIm8NcbOe7kiEMLps8pC1DbnnwqOOJ7aWYvO4ISFhHnEv3v6HzOaNPl9mO/e+oH2UJ9b/9ZqQb65t83GEDtDihhzEfNjofZGvvdtc/hjWwMr91uR+zfCNSNcIGdpJJBPHeQQIT9KXlkGoKsCq/68j0OGDKEuOK5cuYJlNrVO/XleZwQXeKLE/T179gQEBCC8G8I3tW3bduzYsRs2bIBvTahkMI5BkVmzZkH6PQkb/s0331itVrpS4B08y7Lnz59ftWrV2rVrEWzGrQPyZVWkgCAIQ4cOBZsplcqzZ8+Ci6hOBXyQWqKU8x2lODW1haKH27Ae7Nu3L/hNoVAcO3aMLorL2YScrVJRABGDqDzBYvD69evNmzcHUqFy/RBMVcpj0u2Nl3sjiL5q1arpdDoPD4+4uLiy6wEflp1HfvpmKIBJTRTF27dvI0IgNV6GG6jIyMgNGzZQNxe0V9JBlLKQKIp79uyBYNHr9QCvUlJStFqtQqHw8/O7d+8erQQJiKMNGzYAJVOr1WPHji0RgD506FC1atUAbgDZo+tTVEURvI8//piaYKpUKghYNyNRt27QSxmApqSQE6VSAJ+E3W6HRoh8y5cv9/X11Wq12NfFHk5CQsKTANPIQBkUH17Dhg3hnpxhmO+++066k1Nqw64HvXv3psriwoULpTuKUB2sVuuhQ4cAAVP0WaFQ+Pr6og/FjxiIoggA+klECOzeoIkzZ87gM6NKCX2LEjvJcdynn34KOaJWq8ePHy912SGtpJzpEluRb74+CmBcqGwtPkylNQ21IzExEb78GYbZvn07dg4pgIjaSqtBvi9TQMpvlAmpkmEymSCX4H3oxIkTMsVkCrwKBaCAms1mGkVdp9OdPHmS4i+vUrlc9m1TwEFIoevP4ezJU5cUhYT81VzUluOrO5wWxM8AaKJzEKDPSu4nb8tOANp56VCzjmb38+e0S+4XEXkoMFAMDBSjo1fs3t2edXgSp+MOhhN+xdnrCqau9rwxtqJld+4svHxhyg+XepgcMS7QmbERxmX7rLYRvY38yioarKLOLmpY4R0H73SjYRU1Bbbf7j8wrWnc4Jja++vXyq9b88dOLZaYzP2tNoYUqYmtOhGDeNKsgO9zzzT2zo+zb16dc+vi9If/HGZ63Dgvvy0hO13oc9HTt3W+ssNl/gxLcKntc4nOSd72iMntuyjQqVMnYDdarTY/Px/iyE2PotMi3eOXHmnfu3fvmTNnHj58CBEHvb007X3kyJFw16vVanNzc1GhdP6FGl9acXnQqiIFBEFISUmhy1X4S5UqYC/3UjjV7oYpS3nJbDb7+/vD+io4ONgt58s1Kpd66xQADG13/Q4fPuzj40NdKHh4eEybNk0aRujV2QzvK4qizWaDt3GlUpmYmAhOK7t+7JFI5edbp94vswOYUHJycqTuniAZhg8fLggCDERKtIAuTjFRFBcsWIDiarV6/fr1Bw8eBByhVquXLFlCJ0paFrtrhw8fplhcUlISjOjBQsjJO/jRo0drNBrYVn711VeQWlSsUZPq7OxsDw8PuPtISkpCfr1e72bHSTvglpABaDeCyJclU4CaJAD/ha/SgoKCkSNHKhQKuDxXq9UqlYrGyqQ8Cm0SPmKgZRYUFEBNLLkxyV3ewQcEBMA7s0ajuXnzJh5KBe6ZM2fq1aun0Wjgx41i0EFBQchsMpmk+dExANDYusGmjVvPaRFJd9yTFotlwIAB1Jh65cqV1GKCFn+hhHsD8vVrpgBGhwpWOlhotsQVCD30NGTIEEherVbbunVrij7TsqjtNb+BXH0VpgDlN6nJDJWNhw4dop6OlEplXl5eFX5VueuVgAKFhYVPjotmZmZSg8G0tLRK0C+5CxVCAYfL+4TZafXsQp9FUkTID4SsLWLjXFEHVS5PzQr4a+aIiiNK158TdHaF+3v6r8nBWEirG4+Xx7fsG1L3UGCQPTCIqxe1fttfhudZOlsc3fJMva9fG3hg9+DFM/uOHJTe+d8HN2uWnvibnsn/HvXY+r6FeFlcFboAaK2N/MomGq2Ch1XwsAsGltc9A6B1BZb22ZtnNY4aH1v7RKxPUbTvo44tNuU9XpWXnyQUfvTwWsaJo7/7emf/STP7D/6PjM5JAxMbdXs3rMWUT35/9/7HhCwm5JqLcE+x9md238VxZ3qnQugsV/KSFChRoSKEJCQkYGmg1+tzc3OxDncDoK9evbp///5FixaNGTMGDnxL7AR8reIRnUndcnbp0gU7u0ajETOv1HCEZsaj0vpMs8mJykOBMgaLd/DNmzfHWpVhGKmlFFXD7Hb75cuXs7Ky5s2bN2HChG3bttEFXYnvKIWKaJRyuppAAqGJ4Jmhe/fuJdYj36yKFLDb7SaT6ZNPPoGBiF6vB2aXlZWF16FGr1JR9opveuPGDb1eD8iiVatWVqu1uIFdfn5+Tk7Ohg0bJk+enJmZSdHAV2xaLv6KFAA/bN26FcFX9Hq9p6dncnIy4pRCCpV2GPHSpUtxcXHt27enoymK4ujRo8EJOMrTsWNHIBLY6CreW5zevnz5Moz0GYapX7++3W6n/IkiLMs2b96c2n1ij1Yq1iBmHzx4AG8wDMO0bdsW1nharbZatWoArKlcLd4T3JEB6NIoI9//GQUog7oBJQUFBefOnYMXG8DEDMPs27cPHwlYVhTFq1evwkRaoVDUqFEDHC9tgOp/NO4fYOv79+/jA9NqtT4+PtSJEmq22+35+fnUl6Vard60aRP2dtRqtY+Pj7QJaTovLw/6LsMwFOL58s9fYjdb+rLSUsXTgiAkJibi1XQ63fbt2+knhwQ1x7C6fqgBToTp9ywtUrwJ+U6FUwA8zHGcxWLBlCA1AMRwSBsFP9hsNpqNd/Bwhk6Z89ixYxhQFJTHVErAX3iaHtKUniApThPIQJrnzp07bdq0QUwkhmGaN29e2nK6eFXyHZkCJVLgic5qMpmqV69OlUtYN5SYWb5ZVSnwzNhXILes5Kv79n4mLtDOM6zgtDvmRLULenbC0A6nvbMzwYqM1cGYbIzNwfBEm0sUj0ib0/dWhyX0Dqq3zy+4MMjfERaR8/X+fyzfsGjExwvfT1kaE7YgJmh9/aDN9QL/EuF/qE7AiRifI7GB/7Fpc0uzGGYV1IRobURrIb+yEZ2FqO1EyxK9QDwd5FdWQW1yMPlE8cjSaemiT+uHLgzyPBtdW6wb/Pj9lGufb/z7kv/54qP+X3Zps6F+xKcB/gti3z0UGXU8JOyvgUE74qL+2rrV/1y9f5Yn5wixOF2MPP25Xhu+R0r791lW+f9vhQLSKcxut1MvpfXq1aMW0FC30L19+/ZNmzatcePGvr6+dAXBMEzX97vCFKb8b0FVMpvNFhsbi+YiIyOLm4mVv045Z2WjAHR79IoaftJOBgQEAKBRKBT379/HfVEUd+3aNWHChE6dOgFJhIPdJ6ER0tLSRFGUosy0qrITODQsiqLFYoF/c1gprVixwmw248x72TXITysbBdwWhk9W8ZMmTYIeBWGiUqnat2//3Xffoedw5iN9C3AFXUXCjA/chXWoNHOJad7BHzlyRKlUQoXr1KkTzZaXl5eVlTVs2LDY2Fgc76A63po1a6SYRhmbNLQ2OfE6KIChX7RoERhGo9H4+/tDZEmFDAaILhsJIefOnQsLC3uCrbVo0YIOpSAInTt3hjn8Eyh5y5YtsAFlGGbOnDngLqkZPn1cuOs9AAAgAElEQVQjlmXhWwMccv/+fd7Bw485FqEcx9WsWRMxFUJDQwVBeCLH0CuO4xCEUBTF1q1bAwDR6/UnT55s2bIlrD+NRiOWsbB3KSPmqgxA00GRE2VRgGpvbgA0NjpYlm3VqhW4WaPRLFq0iKKr0DhPnTqFT+6JA2g/Pz+pzicV62vWrPH19cUmD77VK1eugKc1Gk10dDTtIvj7wYMHcN+s0Wi0Wu24ceNYlkXwWWirUHCLC1wpAA2dIygoiJ6lojuKtLkyEpGRkWhRp9N9++23Jfq+OX78eKtWrWrVqnX9+nX4hJLSR0rbMhqSH1UsBaRrIZvNJmUSaRqN2u12q9WKIkePHo2OjqYOzREq3WKx0AqlA1q8qop9C7m2Sk4Bt3WyVNy59RysYrfbWZY9ceJEgwYNsDeGzeqcnBzqwNetoHwpU6D8FMjMzDQYDBqNhmGYuLi4cq58yl+/nPNtUgDA6zMAWiSXLWTBA/HfLWKIK+qgByfqOVHrRKJFp9WzgzCsyBTZVVabF8eG2i1Rpscxjx83sZAed9nPtn57KLzh/IDI7/yCzQF+fEjQjdCY5eH150ZE7AsPuB5R21bHj8SE2mMjC0J9L0f5n48LOJ4QOWLN2gb5bAhPPFlRaRONFlLNQrRF5B2zoLcIPgKJ5UlzK9v6sbnt7bz2P9ycMX3K142iv60bkBvkzUaGFoWEnI2L3x737l8ahN+ICTCH+jys7X3P1yffL+BxQOg/giNORNXLqRO17E4BcRDOCT4j9qDTBvqZmXNp6PMzO+m3OUBy2xIKUJXJz88PS1mVSrVw4cLhw4cnJibiVDuMxZRKJT208cTdGYLBwMxFUl9ZSalWhvBKOp1OBqDLIllVflai4o1xh/upefPmjR49OjEx0WAwKJVKrE+BuYAVGYapU6fOS8+PVFtr164dVqMMwxw7duyFVpdVeQT+BfvOuX6iKM6cORM7GWAehmF8fX0//fRTnIItKCjAy8NHEL2U7o4gdOHZs2cBdJSIG6ASWN2xLAuMcvfu3Yhw6OHh0ahRoylTpgwaNCg2NpY6VQMnwxwbjDdnzhyscKkM/Bccm6rwShAmX3zxBbajjEZjcHAwsAVCiBSDxtQGmOvMmTOBgYFqtdpoNH700UdS7Khx48YqlQoQVrVq1eB/IyIiAsSgZzLcaMNxHLXafLIK2Lp1KzKAPTApwy01wzDt2rUDV0Oigm8JIdQ1rlKpzMzMtNlsrVu3pl5o3MQmPhy3bhBCZAC6OE3kOyVQgEquEgFoQsiWLVukALQ0PyFECkB7enpaLBY6PdvtdpxyGjx4MHae69SpQz+/I0eO0Mk7ODgYObEpferUqbi4OJhda7XaDz74AN8J3ffTaDQ5OTklKqkUgFYoFLCY7t27N31tqSkrvVlaAgC0QqFQq9XZ2dnSyN3o58qVK/FUqVSeOnUK9UiFiButSmtIvl+xFLDb7YsWLerZs+eYMWOuXLkC4I82AT6nWiyE8oEDB/r06QMGMxgMOEGDI050W1s6mkjTOuXEL5ACgiAsW7asZ8+eqampu3fvBgUoX7kRhGXZmzdvjhkzBtGHtVqtUqk0GAwff/yxW075UqbAy1HAz89PoVBUq1bNw8Nj9erVL1eJXKqyUsBlD+xCYEVn8rKFTM8jHTkST0g4IX4i+bWDGDhRzYpKYNAieYeQUEL+rfBuipg77uH5P+7d+J9/+u//7tV7ZXz8wcDAf/oFm/0CSHBtEupvCQ25Ehp8McTvXph/YZ0gS52QR2EhF8JCdtUN/lN0+EdpnT/67NNuBfYkG/EucmhZ8VfOBKlhIdpChybXVOtxXqOi/IG2vLk/nFn09ZZFUyfN6tlteZBflrfXuUD/xyEBXGBtm793bnRw3ruhpnp+YnhNR6hPXnjAjciwUxF1/hIRtaxOTOaHPRZtyfq+yELsrOBy92xz+n0G6Ewx6Mo6PL/kfklnPaovnTlzZvHixdgPo6o7EnSPX6lUenh4AFgxGAzx8fELFy4svmIvm7ZUMeM4DjV7eHiEh4fDrWrZZeWnVYgCwPLQYWz/cxx37dq1+fPn0z0MpVIJZ9BSz5DSMELY5FiwYMELLQalVAJ4ZLfbq1WrBn5TKpVuGJM0v5yu5BTAGnDHjh2NGjUCqzAMg4RWq42Pjw8MDIyMjPT19Q0PD4+KimrRokXLli2Tk5NTUlL69+8/bNiw8ePHT506debMmZ999ll6enpQUJBGo0HsOMAUVEZRUrgtIQ8dOjR06FC960eBEUhL6tVXel+hUHTp0uXEiRPUbNatQtqQnHgzFJBGDgR4Bb6i9m1u3Vi7dq1erwdg7eXlBecBFD7y8fFRq9Vw7wP0jGEYeIApcaDRliAIvXr1oubSjRo1OnLkyMWLFydNmjR37lxCyKNHj7y8vMBXFIC2WCzA3ziO69GjB8JgMgwzdOhQcG9KSopGo4HV1KFDh6TbLWazWWrQTd9RBqApKeREWRSgkrE4AE0I+eabb6KioqQuOKT5pS44sLd85coV2lhhYeH9+/cbNGiAbRxPT89x48ZRVxj79+/Hd4WC58+fR8FFixZJvf6npaXh0yKEREdH41TCk1MqU6ZMQawA2hwSFICm/jpmzZrFcVxx3yBuBd0uqQsOfKuzZ892m0hGjBgB5UOj0bRo0QLF3WgopZVb/fLla6KA1Wo9duxY9erV6bTd9f2uq1evvnv3rrTFe/fu7d27d/Xq1X369AkODsYoMwxDzfk/++wz+PXHjp90KGlaWqGc/kVRwGQybdiwQafTQQjo9fpu3bpdvHgRUsKNFCdPnhwxYgRMvSinMQyTkZGBpbvbrrJbcflSpsBzKbB8+XKsmrRaba1atWSOei7FqlQGwRWCz+UAWiSiQARyw0xWWslYThgi8r8XxR4CSS20tiy0NS+0NS+wtWTFD+7d73H67333fT3ysz8OHJz6u05xKa2j/qNJ3S9iQk8H1TQH+5JAfxLkR0Jrkzp+YlSIqW7o3fDA70MC90ZF/1+zVhvf75k1ePi62TMX7tm57PatZQXmkT8WRBU4vB0k8JGpehEfWuiIz7d1eGweuPublBXLu4/I+LDrv/drFjvsN3Xn1A/7sl7QsVD/+/61bV6ej2r72EJ8SFhtNtznanCtg6G1N9cNXdUoZmHzhKmD05dMyly86vPVO/Zk3X1wwxlqkCeCM9SizeX2mn3q9vonO+gqNW6/mM5CKTp58uT06dOTk5Pr1Kmj1+up3wPMeiqVikKBMH/29/dv3rx57969ly1bduHCBVgU8g7eZrNR68LnkpDqY/n5+cBo1Gp1WFgY3GI+t7icoapQALZN0PDnzZvXvXv34OBgQM/UtBmchg1+CthVr169SZMm/fv3X7Vq1ZEjR17lfelJ9pMnT9L1QlBQkHQP5lXql8u+FQqMHTsW+xZarZauAaHb4xKizE2gwc8n5T3q/QB2aU8waMTEogLKjUk2b96cmZnZsmVL6jmNtggrbOliAV59u3fvPnLkyJUrV169epUim6XV/1Yo+YttlHfwJ06cMBqNQB6MRuP06dNLnINu3LjRq1cvhmGMRiN8i+/ZswcuB7CdIAgCYpip1WpwgqenZ9u2bYEvlajbAyV7wgnwCwQ7J8q6Op3Oz8/P4vqBqdRqNXXBgSHbuXNngwYNVCoVdoU7dOiAhngHn5aWBiZXKBQZGRnIf+DAgbS0NLVaDSel1M0AnsoA9C/2Q3j+i8NIgWKy0g0NfAYPHjzYuHFjUlKSVAImJSW5gbC8g3/06JFWq6VqZa9evcCId+7c+eSTT1QqVbVq1YBfd+zYUSoo7927h+iCOBHg5+fXoUOHmjVrItomBH2nTp2kkSJwNABS3s/PD14v3GT6o0ePqAqCz+/gwYM0GOjzSSPJAcc3qM3b23v//v1wsrFmzRp47cEJepVKdfr0aVCG7l8hIX1fScVy8jVSwGw2L1++HHY3sIIHSqhUKr28vCIjIxs1aqTRaDw8PJAH8p2qDgzDxMfH79y5Uzp2paVf42vIVVduCoiimJ6eDsgP8s1gMKhUqujo6P79+8+aNWv58uUTJkzo0qVLfHw8MtAo7RApONZXud9S7l2VoUC7du3o6qhfv34lKqlV5mXkjpZAgZ88IotOINpKyG1CLhHyPSGnCfmOkOOEHCXkqEiO8uTGrdvciCFbY8PmJ767M6zG13FBf3839Gi9gBN1fP8ZUuNxpB8J9SFhfiSkliPcW4gLtIXWOPlh8sU/zf/n//3l1M6cLd//uOkWu+1H2+rHhVMKTSPNRekWa1cL19rqaGznGlsdTYvIbx9bPvpy/X9/mDq9TsTMdxtkxzQ8EBr5t5Dap+sG3KwbcD+41sNAH6unrsDfmwTVJL6eJDLo1nvtNmeMnLFsbcaeb3tdvtH74aPf5ed252z9LFyfR4WfEHKJ43mby/hZJBwR7VLYXUqSZy45ZLtoKVXeTvrAgQMZGRkJCQk4G05R5mrVqsFsSqPRwAECwzBeXl49evRYsGDByZMn7927V7E9vnr1KjW4RrAmao5dsQ3Jtb0xCtAYQjt37pwyZQqCElE0hCKAOE8Gp44qlSoyMjI9PX3lypU5OTmFhYXUTcGrdxtVCYKwZ88eWC+qVKrGjRtTMym3NfKrtyjXUOEUEASBZVmKr7Vu3drT01Ov1wN9A26AwYVPDLrTIMVDkEYRMB61ecKjxMREyB/Kw2azeenSpUOHDg0PDwcP05BxMC+FSSx1d5CYmDh27Nh169bduHHDzeNfhdNErvClKQAMCthx48aNMfoGg0GtVmdmZj58+NC5nW6zWSyWHTt2UAcXYDO9Xr9mzRo0jVMUoiiePXsWa0bk0el0Xl5e27dvL7uHgCmuX79OJ0EsObGrkZaWZrVaWZYNDQ1FtU9A6lmzZp0+fTorK6t9+/YKhYJyY4cOHehxEzi7R53wBBITExMeHo5KVCqV1OqU9lAGoCkp5ETJFNi2bVunTp3Cw8O7dOkyceJERAfu1asXnMggpjB4V6lUtmzZ8urVqzh8RPE41NuyZUtITHAwwzD+/v4GgwHwH7ZiUlNTTSYTLSiKIsuyKEjPvIDFIfFVKtWoUaNQvyAI+BhWrlwJoBDOcSIjIy9evCgFoDmOe+LFiR5bwCbSo0ePpMpBybQo6e7cuXMx8aBRvV7v6+uLRT7uwL/YwYMHS0Sf5aMxJRH1Tdxbv3495gAMk3Qzmfo/Qgb8q9Fo4PArLi7u888/B0dJebW09Jt4GbmNykcBaK7fffcddteory6wEyZpymCQitilgzBs1KgRjaZd+V5O7lGVpACWQLArnDx5MmafKvkmcqdfhAKYm3giOojIEtFGRCsRi3jSI+1sQtTNaH9zoCfrqyehv3YaIEcGFNQNyA2peTvM907dgIf1AsyxQWxcoC2m9tWeKf/kigjLE5E84sl+Qr4m5EuBLCJkGiGZhEwiZCIhnxAyXiTjRDKuiBuzb/+UhpHjGoadCKt9LyiA9Q6wenmbanuzEX5cnZD8umEP64Y9DPF7UNurIKiGIzaMBNXeNXPu9ssPvrpjSs/lEgo4XwtrtJtrFOYGmouaEPJHQs5xvGhxxh8kzo4IvAxAvwgvvOm8Npvtvffe0+v1UPVVKhXsv6iWbjQa1Wo1sJUnkVTatGkD9xpShVyqwL/iC5w+fRq2hzB8gaM8eSvuFan61otzHNepUyeYCtJFJVaLVLcHj8F8tU2bNtJggDgpi6Xrq78LPDEKgnDx4kUsDz08PNq0aUPZ2M326NVblGt4HRSgXnS7vt8VWDA4CmMK2ziNRqNSqeLj4zt27DhgwIA+ffr07du3d+/eH374YbNmzYKDg1EQRSioh1PaLVq0OHv2LLjCarXa7fbt27fD0hmbJfCTQNEPrBdQCbDLpUuX4sUpa70OOsh1vjoFpPjA/Pnz6S4C5kGGYapXr+7r60stkKjUYhhmx44dsI+02+2IK8g7+L1799L1I4yge/bsWZ6JDD3p1asXYqdBKjIMEx0dDRycZdmBAwdimYDVKDWioi326tULh79hcInwmKiKMrynpyd4NT09vUQCygB0iWSRbz6lgNlsBsNRP1bUtz09yavVanU6nV6vHzJkiJuBPWphWdZmsy1btgxaJj0/AomMS4ZhUlNT3baFIVL3798PfzQqlUqhUNDz7A0aNNi4cSOaoDE6CSH5+fkeHh74BoCPN2nSRCqdsd8YHx8PmFihUNCQJi808Kjz5s2b+MZgwUEDKANtVyqVwcHBe/bsATjuZvvspoVIO/lCPZEzvygFwAPBwcHQHiBqFQqFh4cHOJw6SMIBPb1e7+3tnZqa+uWfv0QsY2mL0qmleFqaU07/cihgt9uhDVy4cKFbt2505pYmcJID9hG4bzAY/P394eMSW2W/HIrJb/q6KVCrVi0INKVS+eRoJ3UG9brblet/uxTArCQFoJ0YNEdS2p0Jr3E5Psge6mmu708ifIoi/O7EhF0M89+Zmnx29nQ+ezOp53chwuta5K+/jwncPaivcx/dITptijnyyEFu2Mg/eHKBOP/OE3JOYmp9kpAzRPzHib9dree1rp7X9foBhUG1Htf2eRQSVBDid8/n13+Pe/dQz17/nLeAjBpJYuvdCPH5ITLg+8jIJYv+d/mNgpX3rWPy7D0K7W1yHycQoQtvG0Qciwk5RMgjh+A07bb9BEC7bJ2fuoF2UpraPvOSNL2JxNsdkV9O65s3b6ZTHlW3qB1J+/btP/vssxEjRtA8CQkJ0IQBQFOduaLUYykArVAo+vbtK0W6fznj8q/0pizLZmVlUUtnykuenp7wadapU6fPPvtswIAB9FGrVq2KUwBysvj9l7uDwHFPIsVhfTFkyBBaj9sygd6XE5WNAizLbty4EUgCADvqbLdbt27Lly+HX9ASoQ8qWI4ePbp+/fpRo0alpKR07tw5KSlpzJgx27ZtI4SwLCvV88GigKd1Op1SqYSoVKvVERERXd/vum7dutjYWOo3JjMzE5balY1ucn/cKCD95AkhHTp0oNgujOKxGPRw/ei4JyUl/fDDD3A5AOdC1I/86dOnpdb0/v7+L+SQShCEGTNm+Pv763S6xo0bT58+Ha3AFe2RI0c0Gg2QPSozASgbDIbRo0cDB8c7Yr+NZdm2bduCM7GpDIRt5MiR9ENw2+GTAWg3JpEvf6KAzWbLy8ujzKdWq+EzS7qJp9Vq9Xp9ly5djh49ipIlTuG8g7darYMGDaI7h/QYCywB582bJy1Ov1Xsrnz99dc4l4fOxMXFTZw4EV+L9DOgXZ8xY4Z0HwluPehTmFf07dsXILVWqx08eLD06Yumly5dCtWH0oom+vfvT+UF1aTdEvRlK0rDftH+/wLzw/bh/v37s2fPbtasGd3WxsBB+iuVyurVq7do0WLo0KHZ2dlmsxnxiBHr0mazuVn6S8dRmv4Fkld+ZUoB+lHv3LmzS5cudL9Nq9V6eHgYjUadTgeJWr169Q4dOmzcuBHTOa1BTsgUqCgKjB07lto1nDhxAnMo1Q4rqhW5nspGAcxHPBEpBs0SYuPIV5+TRpE5MYHH6gWceDfsZIvfnBs2yLRiGfnuBDGZSF4ecdjJ138mc/5I5maSHZtIfq4TfSaEWF1h/1z21KzrZe2EOP8EYuOdDy2CaBEFPCITBj6u53Wwns/fAr331g0/3KrFxYkTSHY2uXOfWHln6fuPyMIFZMY08qd55NhxUiQ+IuQEIf9HyBpCFhIyn5DlhOwh5CoRcwUHywpO9NkJQIvEZQFdMgDNOxHqn8BoGYB+K2z5BMGpV68etfNSKpV+fn7Dhg07dOgQ9+xHCBk0aFBycvK4ceMuXLiAfkLFgplVBZ7VkLrggN7utip+K1SSG31FCnAcFx4eTvUrtVodHh7+0Ucf7dmzB8tP2DgPHz48OTl51KhRhw4dQotS+A8mUK/YE1ocThW+/fbbpk2bxsTEnDt3Do+kqwOkaRE5UdkokJeXB6wQXoMMBkPNmjWnTp16+/ZtqtuXqEHhADcgZoS45zhOGopNKnaAEnAct3XrVupXAYb82Du5cOECrKZsNtuVK1fatm3bp0+f+fPn5+fn2+126r5D6oy0slHyF94f6VcvCMK1a9fgKQhHY6ngwoaZXq83GAyrVq2iEx9sn2GSD04ghCQnJ8PouE6dOt988w3v4O12ezndsFDH0xaLhTrahTC02+2iKC5cuBBmpjgwhLmyadOmOTk51AjP7voJggDY+sSJE6GhoQzDwEVB27Ztd+7c6VQXrdYSR18GoEski3zTSQGI148//hionMH1o6b4QUFBXbp0WblypcViyc/PLw/JeAc/bdq0gIAArIGhIkyZMuXevXtSTFb6oUrThw8f3rZt29GjR4uLe5oN3WZZdvTo0QzDeHh4SLed0UnsI+3evRvmYAqF4uzZs6hTWk953ojmWb9+fbNmzQDQazQaX1/fYcOGHT9+nGYobtxN25ImpPnl9BujAMuyDx48uHr16sGDB7e7fgcPHrx7925polw6ZM9Nv7G3kBuqEhTIzs5eunTp6NGju3fvPmLEiOnTp69fv37v3r1VovNyJ6s6BUaNGtW5c+eNGzdCcGHmreovJfe/PBSgCCyQWU4krJ3cvEG+3U+++qrg1Gly8w6xcMTCE5tAOJeZsyASgSOCnfB2wnNOwBdl6b8OwjsI5/pzPuecLj6cJXgiON1R805LaWInty+R/13y8Out4tlz5N5jUsSRIocTfbYKxCa6/ngndM3yhBUI72z8ISG3nIgz+cH1d83lzDqXEAsvOHFuVnT+8SIRxWcgc0kW0PSViyfKQzE5T4VQ4O7du5MmTRo1alR2dvbFixeBKVPFSar8l5imOSni8yq9slgszZo1oyaE48ePp+v5V6lWLvsWKQA7pHv37k2YMOGjjz5av3793bt3wS045VMhnFNRL0j5uaIqlOt5fRQQRTEiIoIu7cPCwqixXTkbpYoWHfcSuVGKQWdkZEyYMGHHjh15eXkv1EqJNZezBjnbG6YAQN6oqCjszsLuTa/Xd+rUae3atWVwC0XAzGbzsWPHduzYUR7PG25vR48/urmBBZqMiXj37t29evWKiopq2bLliBEjsrOz3eZK2knM6RzH3b179+jRo9nZ2Tdv3izRPFTaDRmAllJDTv+MAhSTzcnJWbBgwQTXb8GCBevXrz99+jT2NMCOdJfmZ+VLuXiCDptMpvPnz2MHBnsvpX0MlL+pYHXbr0YjNBusm202GzzmlNIF5+3CwsLdu3d/+ecvf/jhB9RJK6FtlVHc7RH1AXLu3Dmr1YqtThrBAJml9ZeWdqtWvnzzFIBRDm2XjlQ5txBofpqgVckJmQLFKQBp8xIyp3hV8h2ZAmVQgB7ggCiT6p1llJIf/ctQwA2EfQbcEqcZsQsoZp04sxOCFpzmzFZCilx2zU4CPCsr8MTBu6yOqX2xw+mD2eld2pVwAs7cM9PjpyXxwOG8K4gEV6wriqDkXyeQzbv+XKEFAWLzLkNnRBx0EOdTwQloC4R1OX7mnWYSz95DBqArJafC8hSWgNRrJLSjEuHm4jepKlVRs+SdO3cmTpz4wQcfjB8//iWW7pWSzL/cTrnNa+AWjuOw/qoonqlY+qKTFVunXNvroIAgCJ06dYJHTT8/P2o4X/62qKwrW45RaI+CKlIT6ec2Ryt/bk45Q+WhADy3XL9+/Zjrd/PmTZPJxDt4nIJ9rWNaHsyNLk6pFKXwNGhIeRuzNs1WTgrLAHQ5CfULzVYGPyHoHwDfF6UOdD66jQMFgn5spSUKCwupaHZrkRbBfZwggPimrbgVcbukNSDh9vS5l3gjWtYNxERxtyZKvHxuQ3KGiqUA5Ck8ctDhowAN7+DpsakSx6s8Nyu2w3Jt/wIUoHN/GQL2X+A15VeohBSATHMTXJWwn3KX3gwFBBdY7ISPRYcL14UzDaDPBS4M2uV04xkELThNmx2uf523SvgBCEYhZ1p4ik4LgqSAQ3SiyaLTpNppVS2KxC4SuxPZFjlCTM4/wcmkgtMgO5/7//bObU1BEIrC7/8KXfeAzZTmAWE+WLoHDQ0r8rTmYj4k2Gx+SHG5Q/NT2i1DrO6M/7UpanNrrJrdaeMUoAODsZYsWYcPzjxzDz/Sn4HW8xGbNLIgAWx3ID8kxwJ+ln63oPNses0EVK0ul8v5fD6dTvit9lxvg6e4RyMo9pgfmSOtRJZnsQUJ4KGs3P3haRn88adBzJi+/ABVjAcTkXCCdePFaArQkZyPWAxfDywc/RWbpEV1fRppL/iwp4Gq1fV61VojVBk7UQansmTCwliotRTzXwUgXo1tpIC9ONDB+/0uRuS8IG5HJqRicOnj2x9LRzbEYikINE0jUyXLstL9QZvGgI6N2nR+CldpcwcE/KVD8Iyxgz6yC+skMDihrdNJepWUgKp1di+LqjQ2Blq7kGLELrtdM2wE9K8ToFX3aav2OgG61aADHnaCsDVpnPrc7thcGFPpvFG3Wpe50YXWyqrTjdtGQxdGFzZAulGu3V/dQJvOnPp89QVoF0N9U9a9kgJ0YAhWloW3scmO89PrpelPP9IzLNSx/v+IQRpZloC8aEdiR+JFkGU9Z+ubICCvd6uqau4+y8ETWrDX0CUxmf27g2DhQaa0Msjn4ZoJ+Jsjy0kMUXEyoCIrPXYE0STGGBG7HsuM5fj2x9Kip+FFl3hhpq/C+RXLsszzHEqa/wgQZYJuUIAOYmGmJTAx71MAkqmcwjhtksDLBPCI4stfh5e9ZcWNEuAE2+jAbdRtzreNDlwat0U2loRsnIFAZ+SjcS/txR2POIbCsNa0WncbtuzX6Gxa2RqF7aed2P0fc41yLvYZgrhvpJfuLPYyebA4AVnqRyYWd5gOkAAJkMA7BLjceofeAet+YcLI9fdNvLATNDLdBAXoIDRmLkBgeqYu4BCbJAFHAFeCL1wPyGw70ooAAACbSURBVJsESIAESIAEdkXguUjd7+5k+XhZOb5kv3kepSUgS/3IRFpvaJ0ESIAEEhPg/WNiwDQ/m4Bcf2fX7FeAnX5e1BEF6ChMLEQCJHBYAlw6HHbo2XESIAESIIEtEqAAvcVRo88kQAIkQAIkQAL7JkABet/jy96RAAmQAAmQAAmQAAmQwIEIUIA+0GCzqyRAAiRAAiRAAhsh8Ae3xm94aKMkSQAAAABJRU5ErkJggg==" width="609.511811023622" height="158.7270341207349" preserveAspectRatio="none"/>
</g>
<g transform="translate(183.95590551181098 171.7270341207349)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="15.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="25.119999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="35.739999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="43.019999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g356EE1FB649593768A2B4DFFAD44479A" x="56.959999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="66.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gDACA5EBB44D5F3DB530A1F5F650BFBAB" x="75.97999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="86.79999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="94.07999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="104.15999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="114.01999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="123.15999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="133.01999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="138.43999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="143.71999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="149.13999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="155.45999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="170.75999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="180.45999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="190.69999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="196.11999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g607CD744DAB7515984E0B3F495F7DE81" x="211.49999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="222.05999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="227.47999999999993" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="235.27999999999994" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 335.5870341207349)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gB8789F2F5F06048D4163694E4C0F3B6C" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="14.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="28.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="38.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="62.3" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="72.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="81.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="89.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="94.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="104.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="120.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="125.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="136.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="147.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="156.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="163.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="169.23999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="175.55999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="188.35999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="193.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="202.77999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="212.91999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="221.85999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="229.13999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="238.21999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="253.33999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="261.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="267.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="274.9" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="285.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="294.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="300.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="311.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="318.29999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="327.23999999999995" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 372.74703412073495)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 372.74703412073495)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gB8789F2F5F06048D4163694E4C0F3B6C" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="14.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="20.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="30.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="45.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="51.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="60.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="70.34" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="79.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="86.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="94.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="104.24" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="109.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="119.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="130.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="145.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="154.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="164.64000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="174.64000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="183.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g757CB60871AF468909C575234729D90A" x="196.38000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="202.34000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="208.54000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="217.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="225.48000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="236.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="244.60000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="253.54000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="262.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="269.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="278.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF5D967C73B153E080367AE40708278EE" x="289.28" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(390.9448818897638 372.74703412073495)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(407.9648818897638 372.74703412073495)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g607CD744DAB7515984E0B3F495F7DE81" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="10.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="20.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="40.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="45.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="54.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="65" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="73.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="81.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="89.17999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="98.89999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="106.69999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="117.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="127.53999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="134.98" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="146.29999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="155.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="165.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="175.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="184.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g757CB60871AF468909C575234729D90A" x="197.24" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="202.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="212.10000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="220.66000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="229.22000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="239.84000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="247.28000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="256.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="262.74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="276.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="284.48" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="293.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="302.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="309.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="318.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF5D967C73B153E080367AE40708278EE" x="329.15999999999997" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 433.56299212598424)">
<g class="typst-group">
<g>
<g transform="translate(8 18.5)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAA14E57E2DCC57A3F7809273EECD3C51" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="9.344000000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="12.812800000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="18.5344" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="23.296000000000003" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="29.1456" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="33.8048" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="39.2832" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="46.1696" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="49.638400000000004" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="55.116800000000005" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="60.96640000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g1CB3EC9D05726EBFDE8ADABEC8504FCD" x="67.54560000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="76.4928" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD62975B7DE3250BE5F195D0E8335F60D" x="82.3424" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="88.704" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="92.1728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="98.5728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD5EEFB9760BC9A91B84F628EDDA52971" x="104.4224" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="110.7328" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="114.112" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g83A6AA7A836EACB3652229F4716CDAF" x="123.03359999999999" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gDB4862E33098F259EEBBA99A57E5AFA" x="129.2416" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="139.3536" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="145.2032" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="148.5824" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g793DBE65A5AEC1A16A65955B6C0E046" x="155.1616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gA11612CECC8CBEF18835767DAB11B2F7" x="166.3104" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="172.7616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="177.52319999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gCEFEF3D67F35C6E83CC3757B1DD21B13" x="180.90239999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="190.57919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="196.97919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="201.74079999999995" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g645CA8FA3D9155E2CBD9F8EED3C1540D" x="207.59039999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="214.23359999999997" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(798.4017637795276 8)">
<g class="typst-group">
<g>
<g transform="translate(0 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g58626FCFBD19425464A4FA7F304374C4" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" x="11.440000000000001" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.608 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="7.44" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="gF74D1E4498220F56E34936C81B24ED2C" overflow="visible">
<path d="M 2.292 1.464 L 2.292 6.276 C 2.292 7.272 2.496 7.3320003 3.336 7.368 C 3.408 7.44 3.408 7.692 3.336 7.764 C 2.808 7.752 2.244 7.7400002 1.776 7.7400002 C 1.38 7.7400002 0.792 7.752 0.228 7.764 C 0.156 7.692 0.156 7.44 0.228 7.368 C 1.068 7.3320003 1.272 7.272 1.272 6.276 L 1.272 1.464 C 1.272 0.468 1.068 0.408 0.228 0.372 C 0.156 0.3 0.156 0.048 0.228 -0.024 C 0.768 -0.012 1.3560001 0 1.788 0 C 2.22 0 2.796 -0.012 3.336 -0.024 C 3.408 0.048 3.408 0.3 3.336 0.372 C 2.496 0.408 2.292 0.468 2.292 1.464 Z "/>
</symbol>
<symbol id="g46E28FC12585DA626130081849FE40B4" overflow="visible">
<path d="M 1.86 1.464 L 1.86 3.744 C 1.86 4.3320003 2.016 4.224 2.292 3.876 L 5.112 0.120000005 C 5.292 -0.072 5.484 -0.144 5.664 -0.144 C 5.808 -0.144 5.928 -0.060000002 5.928 0.18 L 5.928 4.056 C 5.928 5.052 6.06 5.088 6.7920003 5.1480002 C 6.864 5.2200003 6.864 5.472 6.7920003 5.544 C 6.432 5.532 6 5.52 5.64 5.52 C 5.28 5.52 4.86 5.532 4.5 5.544 C 4.428 5.472 4.428 5.2200003 4.5 5.1480002 C 5.232 5.1 5.364 5.052 5.364 4.056 L 5.364 1.812 C 5.364 1.488 5.328 1.284 4.956 1.788 L 2.208 5.52 L 0.504 5.544 L 0.48000002 5.508 L 0.48000002 5.2200003 C 0.48000002 5.172 0.552 5.1480002 0.588 5.1480002 C 1.044 5.112 1.176 4.968 1.296 4.752 L 1.296 1.464 C 1.296 0.468 1.164 0.42000002 0.432 0.372 C 0.36 0.3 0.36 0.048 0.432 -0.024 C 0.792 -0.012 1.212 0 1.572 0 C 1.932 0 2.364 -0.012 2.724 -0.024 C 2.796 0.048 2.796 0.3 2.724 0.372 C 1.992 0.432 1.86 0.468 1.86 1.464 Z "/>
</symbol>
<symbol id="gA2769E14ED9B16297025579DD26D23A1" overflow="visible">
<path d="M 3.648 1.464 L 3.648 4.488 C 3.648 4.932 3.7680001 5.112 4.152 5.112 L 4.464 5.112 C 5.2200003 5.112 5.376 4.872 5.616 4.008 C 5.736 3.984 5.844 3.984 5.94 4.044 C 5.88 4.632 5.868 5.076 5.844 5.64 C 5.4240003 5.592 4.656 5.52 3.648 5.52 L 2.7 5.52 C 1.524 5.52 0.828 5.58 0.504 5.64 C 0.504 5.076 0.492 4.608 0.42000002 4.044 C 0.528 4.008 0.636 3.996 0.744 4.008 C 0.984 4.872 1.116 5.112 1.896 5.112 L 2.184 5.112 C 2.556 5.112 2.7 4.968 2.7 4.5 L 2.7 1.464 C 2.7 0.468 2.568 0.432 1.836 0.372 C 1.764 0.3 1.764 0.048 1.836 -0.024 C 2.28 -0.012 2.772 0 3.18 0 C 3.6000001 0 4.068 -0.012 4.512 -0.024 C 4.584 0.048 4.584 0.3 4.512 0.372 C 3.78 0.42000002 3.648 0.468 3.648 1.464 Z "/>
</symbol>
<symbol id="g48BCA4F06942DA5990D42018985FC781" overflow="visible">
<path d="M 2.292 1.464 L 2.292 2.5080001 L 2.9520001 2.5080001 C 3.408 2.5080001 3.576 2.112 3.732 1.668 L 3.996 0.948 C 4.272 0.204 4.68 -0.084 5.196 -0.084 C 5.376 -0.084 5.748 -0.048 5.952 0 C 5.988 0.120000005 5.964 0.24000001 5.88 0.336 C 5.448 0.336 5.2200003 0.408 4.98 1.0320001 L 4.632 1.932 C 4.488 2.304 4.344 2.5080001 4.188 2.664 L 4.188 2.688 C 4.596 2.832 5.208 3.3240001 5.208 4.152 C 5.208 5.1480002 4.584 5.568 3.1560001 5.568 C 2.856 5.568 2.172 5.52 1.812 5.52 C 1.464 5.52 0.96000004 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.212 0.432 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 0.936 -0.012 1.428 0 1.824 0 C 2.196 0 2.592 -0.012 2.976 -0.024 C 3.048 0.048 3.048 0.3 2.976 0.372 C 2.412 0.408 2.292 0.468 2.292 1.464 Z M 4.164 4.152 C 4.164 3.204 3.888 2.856 2.82 2.856 L 2.292 2.856 L 2.292 4.416 C 2.292 5.052 2.412 5.172 3.084 5.172 C 3.924 5.172 4.164 4.872 4.164 4.152 Z "/>
</symbol>
<symbol id="g4C6038BE04CA3E1481E54A97A0E34303" overflow="visible">
<path d="M 6.324 2.82 C 6.324 4.524 4.956 5.64 3.3960001 5.64 C 1.728 5.64 0.444 4.428 0.444 2.664 C 0.444 1.0320001 1.6800001 -0.120000005 3.3 -0.120000005 C 5.268 -0.120000005 6.324 1.26 6.324 2.82 Z M 3.288 5.244 C 4.356 5.244 5.28 4.26 5.28 2.652 C 5.28 1.176 4.548 0.276 3.48 0.276 C 2.316 0.276 1.488 1.332 1.488 2.808 C 1.488 4.428 2.388 5.244 3.288 5.244 Z "/>
</symbol>
<symbol id="gE1B486BBD379D5D210F28624A61384AE" overflow="visible">
<path d="M 1.776 5.52 C 1.452 5.52 0.912 5.532 0.444 5.544 C 0.372 5.472 0.372 5.2200003 0.444 5.1480002 C 1.176 5.1 1.308 5.052 1.308 4.056 L 1.308 1.464 C 1.308 0.468 1.176 0.432 0.444 0.372 C 0.372 0.3 0.372 0.048 0.444 -0.024 C 0.90000004 -0.012 1.44 0 1.788 0 C 2.1 0 2.58 -0.024 3.54 -0.024 C 4.872 -0.024 6.36 0.6 6.36 2.7 C 6.36 4.296 5.376 5.544 3.372 5.544 C 2.556 5.544 2.124 5.52 1.776 5.52 Z M 2.256 0.912 L 2.256 4.776 C 2.256 5.076 2.556 5.1480002 3.024 5.1480002 C 5.04 5.1480002 5.316 3.744 5.316 2.496 C 5.316 0.816 4.572 0.372 3.252 0.372 C 2.34 0.372 2.256 0.576 2.256 0.912 Z "/>
</symbol>
<symbol id="g9FB16590C6D64699AE0CE54876927A05" overflow="visible">
<path d="M 5.2200003 4.056 L 5.2200003 2.532 C 5.2200003 1.5 5.2200003 0.372 3.636 0.372 C 2.448 0.372 2.196 1.308 2.196 2.424 L 2.196 4.056 C 2.196 5.052 2.328 5.088 3.06 5.1480002 C 3.132 5.2200003 3.132 5.472 3.06 5.544 C 2.592 5.532 2.112 5.52 1.716 5.52 C 1.284 5.52 0.816 5.532 0.384 5.544 C 0.312 5.472 0.312 5.2200003 0.384 5.1480002 C 1.116 5.1 1.248 5.052 1.248 4.056 L 1.248 2.172 C 1.248 0.372 2.124 -0.120000005 3.432 -0.120000005 C 5.292 -0.120000005 5.784 0.936 5.784 2.688 L 5.784 4.056 C 5.784 5.052 5.916 5.088 6.6480002 5.1480002 C 6.7200003 5.2200003 6.7200003 5.472 6.6480002 5.544 C 6.288 5.532 5.856 5.52 5.496 5.52 C 5.136 5.52 4.716 5.532 4.356 5.544 C 4.284 5.472 4.284 5.2200003 4.356 5.1480002 C 5.088 5.1 5.2200003 5.052 5.2200003 4.056 Z "/>
</symbol>
<symbol id="g6799D348D26A0968EEDA80A0E5D50B73" overflow="visible">
<path d="M 3.312 -0.120000005 C 4.248 -0.120000005 4.824 0.228 5.388 0.984 C 5.364 1.068 5.244 1.2 5.1480002 1.224 C 4.596 0.576 4.176 0.336 3.372 0.336 C 2.184 0.336 1.488 1.62 1.488 2.808 C 1.488 4.824 2.424 5.244 3.3240001 5.244 C 4.284 5.244 4.848 4.716 4.992 3.876 C 5.112 3.8400002 5.232 3.8400002 5.352 3.912 C 5.352 4.404 5.328 4.908 5.208 5.448 C 4.752 5.448 4.212 5.64 3.252 5.64 C 1.668 5.64 0.444 4.44 0.444 2.688 C 0.444 1.932 0.684 1.104 1.272 0.564 C 1.752 0.120000005 2.424 -0.120000005 3.312 -0.120000005 Z "/>
</symbol>
<symbol id="g45E4C10E27056C5AE488FE2D8290DF06" overflow="visible">
<path d="M 2.34 4.056 C 2.34 5.052 2.4720001 5.088 3.204 5.1480002 C 3.276 5.2200003 3.276 5.472 3.204 5.544 C 2.748 5.532 2.232 5.52 1.86 5.52 C 1.5 5.52 0.996 5.532 0.528 5.544 C 0.456 5.472 0.456 5.2200003 0.528 5.1480002 C 1.26 5.1 1.392 5.052 1.392 4.056 L 1.392 1.464 C 1.392 0.468 1.26 0.432 0.528 0.372 C 0.456 0.3 0.456 0.048 0.528 -0.024 C 0.972 -0.012 1.464 0 1.872 0 C 2.256 0 2.784 -0.012 3.204 -0.024 C 3.276 0.048 3.276 0.3 3.204 0.372 C 2.4720001 0.42000002 2.34 0.468 2.34 1.464 Z "/>
</symbol>
<symbol id="gD77922058D8F1A3A631DDE5946887BDC" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z M 3.384 5.112 C 4.764 5.112 5.88 4.008 5.88 2.628 C 5.88 1.248 4.752 0.132 3.384 0.132 C 2.004 0.132 0.90000004 1.248 0.90000004 2.628 C 0.90000004 3.996 2.004 5.112 3.384 5.112 Z "/>
</symbol>
<symbol id="g5ABA589ED074A65FC8C929AB4EB2344C" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z "/>
</symbol>
<symbol id="g6F0940D406D545443F0C3F5AB20F1452" overflow="visible">
<path d="M 1.55 0.78999996 L 2.1 2.24 C 2.1499999 2.37 2.21 2.4099998 2.45 2.4099998 L 4.56 2.4099998 L 5.14 0.71999997 C 5.2599998 0.38 4.88 0.34 4.4 0.31 C 4.3399997 0.25 4.3399997 0.04 4.4 -0.02 C 4.77 -0.01 5.3199997 0 5.71 0 C 6.12 0 6.5 -0.01 6.85 -0.02 C 6.91 0.04 6.91 0.25 6.85 0.31 C 6.46 0.35 6.12 0.38 5.95 0.85999995 L 3.8899999 6.58 C 3.74 6.49 3.47 6.3799996 3.34 6.3799996 L 1.0699999 1.02 C 0.81 0.39999998 0.51 0.34 0.07 0.31 C 0.01 0.25 0.01 0.04 0.07 -0.02 C 0.32999998 -0.01 0.65999997 0 0.96 0 C 1.37 0 1.87 -0.01 2.24 -0.02 C 2.3 0.04 2.3 0.25 2.24 0.31 C 1.86 0.34 1.39 0.38 1.55 0.78999996 Z M 2.6299999 2.83 C 2.4099998 2.83 2.34 2.86 2.3799999 2.96 L 3.3999999 5.5499997 L 3.46 5.5499997 L 4.4 2.83 Z "/>
</symbol>
<symbol id="g6D72A0AB4EFB019D977FFECF4A1600A9" overflow="visible">
<path d="M 3.79 0 C 3.79 0 4.02 0.96 4.0899997 1.38 C 4 1.43 3.9199998 1.4499999 3.81 1.42 C 3.6499999 0.83 3.36 0.34 2.73 0.34 L 2.28 0.34 C 2.05 0.34 1.91 0.5 1.91 0.69 L 1.91 3.3799999 C 1.91 4.21 2.02 4.24 2.6299999 4.29 C 2.69 4.35 2.69 4.56 2.6299999 4.62 C 2.26 4.61 1.8499999 4.6 1.51 4.6 C 1.1999999 4.6 0.77 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.1 0.34 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.89 -0.01 1.55 0 1.55 0 Z "/>
</symbol>
<symbol id="g7035BD9A81EA6DB089327941BB80DFF8" overflow="visible">
<path d="M 4.72 0.90999997 C 4.72 1.74 4.7799997 1.77 5.0899997 1.8199999 C 5.15 1.88 5.15 2.09 5.0899997 2.1499999 C 4.91 2.1399999 4.63 2.1299999 4.3199997 2.1299999 C 4.02 2.1299999 3.56 2.1399999 3.27 2.1499999 C 3.21 2.09 3.21 1.88 3.27 1.8199999 C 3.8799999 1.78 3.9299998 1.74 3.9299998 0.90999997 L 3.9299998 0.37 C 3.61 0.28 3.28 0.22999999 2.9299998 0.22999999 C 1.68 0.22999999 1.27 1.51 1.27 2.33 C 1.27 3.54 1.8499999 4.37 2.81 4.37 C 3.8 4.37 4.22 3.87 4.37 3.23 C 4.47 3.1999998 4.5699997 3.1999998 4.67 3.26 C 4.66 3.6699998 4.63 4.0899997 4.54 4.54 C 4.24 4.54 3.5 4.7 2.9399998 4.7 C 1.51 4.7 0.37 3.78 0.37 2.2 C 0.37 0.93 1.3199999 -0.099999994 2.75 -0.099999994 C 3.4299998 -0.099999994 4.17 0 4.83 0.35999998 C 4.7599998 0.42999998 4.72 0.52 4.72 0.59 Z "/>
</symbol>
<symbol id="g7FD6A8241485CEBC032BD9E4CE659816" overflow="visible">
<path d="M 5.27 2.35 C 5.27 3.77 4.13 4.7 2.83 4.7 C 1.4399999 4.7 0.37 3.6899998 0.37 2.22 C 0.37 0.85999995 1.4 -0.099999994 2.75 -0.099999994 C 4.39 -0.099999994 5.27 1.05 5.27 2.35 Z M 2.74 4.37 C 3.6299999 4.37 4.4 3.55 4.4 2.21 C 4.4 0.97999996 3.79 0.22999999 2.8999999 0.22999999 C 1.93 0.22999999 1.24 1.11 1.24 2.34 C 1.24 3.6899998 1.99 4.37 2.74 4.37 Z "/>
</symbol>
<symbol id="gFAD9169AC3141E7FC4EA568E3BBD2E9B" overflow="visible">
<path d="M 1.91 1.22 L 1.91 2.09 L 2.46 2.09 C 2.84 2.09 2.98 1.76 3.11 1.39 L 3.33 0.78999996 C 3.56 0.17 3.8999999 -0.07 4.33 -0.07 C 4.48 -0.07 4.79 -0.04 4.96 0 C 4.99 0.099999994 4.97 0.19999999 4.9 0.28 C 4.54 0.28 4.35 0.34 4.15 0.85999995 L 3.86 1.61 C 3.74 1.92 3.62 2.09 3.49 2.22 L 3.49 2.24 C 3.83 2.36 4.3399997 2.77 4.3399997 3.46 C 4.3399997 4.29 3.82 4.64 2.6299999 4.64 C 2.3799999 4.64 1.81 4.6 1.51 4.6 C 1.22 4.6 0.79999995 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.78 -0.01 1.1899999 0 1.52 0 C 1.8299999 0 2.1599998 -0.01 2.48 -0.02 C 2.54 0.04 2.54 0.25 2.48 0.31 C 2.01 0.34 1.91 0.39 1.91 1.22 Z M 3.47 3.46 C 3.47 2.6699998 3.24 2.3799999 2.35 2.3799999 L 1.91 2.3799999 L 1.91 3.6799998 C 1.91 4.21 2.01 4.31 2.57 4.31 C 3.27 4.31 3.47 4.06 3.47 3.46 Z "/>
</symbol>
<symbol id="g5503E15E5E4E70E9E217A15BD1ECD752" overflow="visible">
<path d="M 1.9499999 3.3799999 C 1.9499999 4.21 2.06 4.24 2.6699998 4.29 C 2.73 4.35 2.73 4.56 2.6699998 4.62 C 2.29 4.61 1.86 4.6 1.55 4.6 C 1.25 4.6 0.83 4.61 0.44 4.62 C 0.38 4.56 0.38 4.35 0.44 4.29 C 1.05 4.25 1.16 4.21 1.16 3.3799999 L 1.16 1.22 C 1.16 0.39 1.05 0.35999998 0.44 0.31 C 0.38 0.25 0.38 0.04 0.44 -0.02 C 0.81 -0.01 1.22 0 1.56 0 C 1.88 0 2.32 -0.01 2.6699998 -0.02 C 2.73 0.04 2.73 0.25 2.6699998 0.31 C 2.06 0.35 1.9499999 0.39 1.9499999 1.22 Z "/>
</symbol>
<symbol id="gA419F36517085793EDBF3FE4736A2E59" overflow="visible">
<path d="M 3.04 1.22 L 3.04 3.74 C 3.04 4.11 3.1399999 4.2599998 3.46 4.2599998 L 3.72 4.2599998 C 4.35 4.2599998 4.48 4.06 4.68 3.34 C 4.7799997 3.32 4.87 3.32 4.95 3.37 C 4.9 3.86 4.89 4.23 4.87 4.7 C 4.52 4.66 3.8799999 4.6 3.04 4.6 L 2.25 4.6 C 1.27 4.6 0.69 4.65 0.42 4.7 C 0.42 4.23 0.41 3.84 0.35 3.37 C 0.44 3.34 0.53 3.33 0.62 3.34 C 0.82 4.06 0.93 4.2599998 1.5799999 4.2599998 L 1.8199999 4.2599998 C 2.1299999 4.2599998 2.25 4.14 2.25 3.75 L 2.25 1.22 C 2.25 0.39 2.1399999 0.35999998 1.53 0.31 C 1.4699999 0.25 1.4699999 0.04 1.53 -0.02 C 1.9 -0.01 2.31 0 2.6499999 0 C 3 0 3.3899999 -0.01 3.76 -0.02 C 3.82 0.04 3.82 0.25 3.76 0.31 C 3.1499999 0.35 3.04 0.39 3.04 1.22 Z "/>
</symbol>
<symbol id="gFF65128B49BB3276E17D04989ECB7ACE" overflow="visible">
<path d="M 5 3.3799999 C 5 4.21 5.1099997 4.24 5.72 4.29 C 5.7799997 4.35 5.7799997 4.56 5.72 4.62 C 5.37 4.6 4.93 4.6 4.6 4.6 C 4.3199997 4.6 3.8799999 4.61 3.49 4.62 C 3.4299998 4.56 3.4299998 4.35 3.49 4.29 C 4.1 4.25 4.21 4.21 4.21 3.3799999 L 4.21 2.52 L 1.9 2.52 L 1.9 3.3799999 C 1.9 4.21 2.01 4.24 2.62 4.29 C 2.6799998 4.35 2.6799998 4.56 2.62 4.62 C 2.24 4.61 1.8199999 4.6 1.5 4.6 C 1.1999999 4.6 0.78999996 4.61 0.39 4.62 C 0.32999998 4.56 0.32999998 4.35 0.39 4.29 C 1 4.25 1.11 4.21 1.11 3.3799999 L 1.11 1.22 C 1.11 0.39 1 0.35999998 0.39 0.31 C 0.32999998 0.25 0.32999998 0.04 0.39 -0.02 C 0.78999996 -0.01 1.1899999 0 1.51 0 C 1.8299999 0 2.23 -0.01 2.62 -0.02 C 2.6799998 0.04 2.6799998 0.25 2.62 0.31 C 2.01 0.35 1.9 0.39 1.9 1.22 L 1.9 2.19 L 4.21 2.19 L 4.21 1.22 C 4.21 0.39 4.1 0.35999998 3.49 0.31 C 3.4299998 0.25 3.4299998 0.04 3.49 -0.02 C 3.86 -0.01 4.2599998 0 4.61 0 C 4.91 0 5.33 -0.01 5.72 -0.02 C 5.7799997 0.04 5.7799997 0.25 5.72 0.31 C 5.1099997 0.35 5 0.39 5 1.22 Z "/>
</symbol>
<symbol id="gEDADDD9BA25BBB833C1F4B684DC50419" overflow="visible">
<path d="M 4.83 3.82 L 4.9 3.82 L 5.0299997 1.23 C 5.0699997 0.39999998 5.06 0.35999998 4.52 0.31 C 4.46 0.25 4.46 0.04 4.52 -0.02 C 4.87 -0.01 5.24 0 5.52 0 C 5.8199997 0 6.1099997 -0.01 6.3799996 -0.02 C 6.44 0.04 6.44 0.25 6.3799996 0.31 C 5.87 0.35999998 5.8599997 0.42 5.7999997 1.23 L 5.6 3.81 C 5.5699997 4.21 5.66 4.25 6.16 4.29 C 6.22 4.35 6.22 4.56 6.16 4.62 L 4.81 4.6 L 3.31 1.02 L 2.03 4.6 L 0.64 4.62 C 0.58 4.56 0.58 4.35 0.64 4.29 C 1.13 4.2599998 1.22 4.21 1.1999999 4.02 L 0.88 1.2099999 C 0.78999996 0.38 0.65999997 0.34 0.28 0.31 C 0.22 0.25 0.22 0.04 0.28 -0.02 C 0.48 -0.01 0.78 0 0.94 0 C 1.14 0 1.51 -0.01 1.7099999 -0.02 C 1.77 0.04 1.77 0.25 1.7099999 0.31 C 1.14 0.35 1.15 0.47 1.23 1.2099999 L 1.52 3.75 L 1.54 3.75 L 2.96 -0.04 C 2.98 -0.089999996 3.03 -0.12 3.08 -0.12 C 3.12 -0.12 3.1699998 -0.089999996 3.1899998 -0.04 Z "/>
</symbol>
<symbol id="g1E8994F5C297EC73FA26D93D22635023" overflow="visible">
<path d="M 2.82 -0.14999999 C 4.11 -0.14999999 5.16 0.9 5.16 2.19 C 5.16 3.48 4.11 4.52 2.82 4.52 C 1.53 4.52 0.48999998 3.48 0.48999998 2.19 C 0.48999998 0.9 1.53 -0.14999999 2.82 -0.14999999 Z M 2.82 4.2599998 C 3.97 4.2599998 4.9 3.34 4.9 2.19 C 4.9 1.04 3.9599998 0.11 2.82 0.11 C 1.67 0.11 0.75 1.04 0.75 2.19 C 0.75 3.33 1.67 4.2599998 2.82 4.2599998 Z "/>
</symbol>
<symbol id="g5396A27CA60B9808846A090320835A9F" overflow="visible">
<path d="M 1.91 1.22 L 1.91 5.23 C 1.91 6.06 2.08 6.1099997 2.78 6.14 C 2.84 6.2 2.84 6.41 2.78 6.47 C 2.34 6.46 1.87 6.45 1.48 6.45 C 1.15 6.45 0.65999997 6.46 0.19 6.47 C 0.13 6.41 0.13 6.2 0.19 6.14 C 0.89 6.1099997 1.06 6.06 1.06 5.23 L 1.06 1.22 C 1.06 0.39 0.89 0.34 0.19 0.31 C 0.13 0.25 0.13 0.04 0.19 -0.02 C 0.64 -0.01 1.13 0 1.49 0 C 1.8499999 0 2.33 -0.01 2.78 -0.02 C 2.84 0.04 2.84 0.25 2.78 0.31 C 2.08 0.34 1.91 0.39 1.91 1.22 Z "/>
</symbol>
<symbol id="g97A8E46F7A64F11D13C6F357868587EE" overflow="visible">
<path d="M 1.89 1.22 L 1.89 1.9599999 C 2.07 1.88 2.27 1.8399999 2.52 1.8399999 C 3.86 1.8399999 4.27 2.8 4.27 3.3999999 C 4.27 3.9199998 3.97 4.62 2.55 4.62 C 2.18 4.62 1.76 4.6 1.49 4.6 C 1.1999999 4.6 0.78 4.61 0.38 4.62 C 0.32 4.56 0.32 4.35 0.38 4.29 C 0.98999995 4.25 1.1 4.21 1.1 3.3799999 L 1.1 1.22 C 1.1 0.39 0.98999995 0.35999998 0.38 0.31 C 0.32 0.25 0.32 0.04 0.38 -0.02 C 0.71 -0.01 1.06 0 1.5 0 C 1.93 0 2.28 -0.01 2.61 -0.02 C 2.6699998 0.04 2.6699998 0.25 2.61 0.31 C 2 0.35 1.89 0.39 1.89 1.22 Z M 1.89 3.84 C 1.89 4.16 2.01 4.29 2.49 4.29 C 3.08 4.29 3.3999999 3.98 3.3999999 3.28 C 3.3999999 2.56 3.1399999 2.1699998 2.54 2.1699998 C 2.34 2.1699998 2.09 2.2 1.89 2.28 Z "/>
</symbol>
<symbol id="gB844DCFB76B4CC44608DB013C9764E9C" overflow="visible">
<path d="M 1.8299999 3.62 C 1.5899999 4.19 1.5999999 4.24 2.1399999 4.29 C 2.2 4.35 2.2 4.56 2.1399999 4.62 C 1.8299999 4.61 1.49 4.6 1.0799999 4.6 C 0.76 4.6 0.45999998 4.61 0.19999999 4.62 C 0.14 4.56 0.14 4.35 0.19999999 4.29 C 0.69 4.24 0.76 4.13 1 3.56 L 2.4199998 0.28 C 2.55 -0.01 2.6 -0.12 2.71 -0.12 C 2.78 -0.12 2.82 -0.04 2.96 0.28 L 4.42 3.55 C 4.63 4.0099998 4.74 4.25 5.2799997 4.29 C 5.3399997 4.35 5.3399997 4.56 5.2799997 4.62 C 5.06 4.61 4.8199997 4.6 4.56 4.6 C 4.19 4.6 3.9099998 4.61 3.6399999 4.62 C 3.58 4.56 3.58 4.35 3.6399999 4.29 C 4.18 4.25 4.23 4.13 4.0299997 3.62 L 2.9399998 1.13 C 2.9099998 1.1 2.8999999 1.1 2.87 1.13 Z "/>
</symbol>
<symbol id="gDAA1267270512376F631C9A10449D5F4" overflow="visible">
<path d="M 2.48 2.25 C 3.1399999 2.25 3.1499999 2.06 3.1699998 1.6899999 C 3.22 1.64 3.3999999 1.64 3.4499998 1.6899999 C 3.4399998 1.92 3.4299998 2.26 3.4299998 2.4199998 C 3.4299998 2.56 3.4399998 2.8799999 3.4499998 3.1299999 C 3.3999999 3.1799998 3.22 3.1799998 3.1699998 3.1299999 C 3.1499999 2.6799998 3.1299999 2.57 2.48 2.57 L 1.91 2.57 L 1.91 3.99 C 1.91 4.16 2.04 4.27 2.23 4.27 L 2.8 4.27 C 3.62 4.27 3.75 3.9399998 3.9299998 3.37 C 4.0299997 3.36 4.12 3.3799999 4.2 3.4199998 C 4.16 3.76 4.04 4.54 4.02 4.61 C 4.02 4.63 4.0099998 4.64 3.99 4.64 C 3.85 4.61 3.75 4.6 3.58 4.6 L 1.51 4.6 C 1.22 4.6 0.76 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.76 -0.01 1.1999999 0 1.52 0 L 3.06 0 C 3.46 0 4.12 -0.02 4.12 -0.02 C 4.24 0.39 4.35 0.94 4.42 1.36 C 4.33 1.41 4.25 1.43 4.14 1.4 C 3.98 0.81 3.6899998 0.31 2.86 0.31 L 2.4299998 0.31 C 2.01 0.31 1.91 0.42 1.91 0.75 L 1.91 2.25 Z "/>
</symbol>
<symbol id="gEEE4EC0F13100E99C1017169F912BE3E" overflow="visible">
<path d="M 1.55 1.22 L 1.55 3.12 C 1.55 3.61 1.68 3.52 1.91 3.23 L 4.2599998 0.099999994 C 4.41 -0.06 4.5699997 -0.12 4.72 -0.12 C 4.8399997 -0.12 4.94 -0.049999997 4.94 0.14999999 L 4.94 3.3799999 C 4.94 4.21 5.0499997 4.24 5.66 4.29 C 5.72 4.35 5.72 4.56 5.66 4.62 C 5.3599997 4.61 5 4.6 4.7 4.6 C 4.4 4.6 4.0499997 4.61 3.75 4.62 C 3.6899998 4.56 3.6899998 4.35 3.75 4.29 C 4.36 4.25 4.47 4.21 4.47 3.3799999 L 4.47 1.51 C 4.47 1.24 4.44 1.0699999 4.13 1.49 L 1.8399999 4.6 L 0.42 4.62 L 0.39999998 4.5899997 L 0.39999998 4.35 C 0.39999998 4.31 0.45999998 4.29 0.48999998 4.29 C 0.87 4.2599998 0.97999996 4.14 1.0799999 3.9599998 L 1.0799999 1.22 C 1.0799999 0.39 0.96999997 0.35 0.35999998 0.31 C 0.29999998 0.25 0.29999998 0.04 0.35999998 -0.02 C 0.65999997 -0.01 1.01 0 1.31 0 C 1.61 0 1.9699999 -0.01 2.27 -0.02 C 2.33 0.04 2.33 0.25 2.27 0.31 C 1.66 0.35999998 1.55 0.39 1.55 1.22 Z "/>
</symbol>
<symbol id="g7B578904031CC07414BF9948E9002018" overflow="visible">
<path d="M 8.304 15.696 C 7.344 15.696 1.704 15.528 0.744 15.528 C 0.504 15.384 0.504 14.856 0.744 14.712 C 2.0640001 14.64 2.736 14.544 2.736 12.552 L 2.736 2.928 C 2.736 0.936 2.0640001 0.84000003 0.744 0.768 C 0.504 0.624 0.504 0.096 0.744 -0.048 C 1.704 -0.024 3.48 0 4.44 0 C 5.4 0 7.1280003 -0.024 8.088 -0.048 C 8.328 0.096 8.328 0.624 8.088 0.768 C 6.768 0.84000003 6.096 0.936 6.096 2.928 L 6.096 12.576 C 6.096 14.208 6.264 14.712 7.5360003 14.712 C 8.928 14.712 10.536 14.136 10.536 11.208 C 10.536 8.712 9.84 7.656 7.872 7.656 C 7.512 7.656 7.008 7.6800003 6.672 7.728 C 6.672 7.272 6.816 6.936 7.152 6.7200003 C 7.488 6.672 7.416 6.6480002 7.992 6.6480002 C 10.104 6.6480002 11.592 7.008 12.552 7.8 C 13.752 8.784 14.16 10.344 14.16 11.616 C 14.16 12.576 13.8 14.016 12.312 14.904 C 11.424 15.432 10.104 15.696 8.304 15.696 Z "/>
</symbol>
<symbol id="g767CEF02C917BBE3F159A8F04079F311" overflow="visible">
<path d="M 5.472 6.432 C 5.472 7.296 5.736 7.656 6.048 8.016 C 6.2400002 8.2560005 6.456 8.424 6.816 8.424 C 7.032 8.424 7.296 8.208 7.488 7.968 C 7.656 7.776 8.064 7.584 8.616 7.584 C 9.312 7.584 9.984 8.304 9.984 9.312 C 9.984 9.936 9.264 10.656 8.4 10.656 C 7.56 10.656 6.6480002 9.936 5.544 8.352 L 5.448 8.352 C 5.4 9.0720005 5.28 10.248 5.28 10.248 C 5.256 10.464 5.064 10.656 4.728 10.656 C 3.6000001 10.368 2.328 10.032001 0.744 9.864 C 0.696 9.72 0.744 9.264 0.792 9.12 C 2.112 9 2.352 8.784 2.352 7.416 L 2.352 2.928 C 2.352 0.936 2.088 0.888 0.624 0.768 C 0.48000002 0.624 0.48000002 0.096 0.624 -0.048 C 1.632 -0.024 2.64 0 3.912 0 C 5.184 0 6.168 -0.024 7.2000003 -0.048 C 7.344 0.096 7.344 0.624 7.2000003 0.768 C 5.736 0.864 5.472 0.936 5.472 2.928 Z "/>
</symbol>
<symbol id="g841363B3896A8C79F18618DF16186242" overflow="visible">
<path d="M 0.888 4.968 C 0.888 1.824 3.384 -0.24000001 6.6 -0.24000001 C 8.304 -0.24000001 9.72 0.24000001 10.704 1.128 C 11.928 2.208 12.336 3.8400002 12.336 5.184 C 12.336 8.328 10.2 10.656 6.624 10.656 C 4.632 10.656 3.144 9.96 2.208 8.88 C 1.296 7.824 0.888 6.384 0.888 4.968 Z M 6.2400002 9.648 C 7.872 9.648 8.976 7.704 8.976 4.416 C 8.976 1.536 7.848 0.768 6.984 0.768 C 5.0160003 0.768 4.248 3.72 4.248 5.496 C 4.248 7.704 4.632 9.648 6.2400002 9.648 Z "/>
</symbol>
<symbol id="g79601DAFF2C13DD0AF25B87F7A83C884" overflow="visible">
<path d="M 1.776 3.048 C 1.776 1.056 1.728 0.768 1.632 -0.144 C 1.9200001 -0.24000001 2.184 -0.312 2.448 -0.312 C 2.76 -0.048 3 0.288 3.216 0.72 C 4.152 0 5.616 -0.24000001 6.7200003 -0.24000001 C 9.384 -0.24000001 12.192 2.4 12.192 5.8320003 C 12.192 7.2000003 11.6640005 8.544 10.896 9.432 C 10.032001 10.416 8.88 10.656 7.6080003 10.656 C 6.864 10.656 5.592 9.816 4.896 9.312 L 4.896 13.992001 C 4.896 15.552 4.968 16.44 4.968 16.44 C 4.968 16.656 4.8 16.752 4.584 16.752 C 3.696 16.464 1.776 16.2 0.072 16.128 C 0 15.84 0.024 15.576 0.144 15.360001 C 1.656 15.24 1.776 15.216001 1.776 13.56 Z M 4.896 8.352 C 5.688 8.88 6.216 8.952 6.768 8.952 C 7.9440002 8.952 8.832 7.872 8.832 5.52 C 8.832 3.552 8.496 0.768 6.6 0.768 C 5.9040003 0.768 5.352 1.056 4.896 1.608 Z "/>
</symbol>
<symbol id="g9AEC0E315A165F115D211DDAB68AA0F8" overflow="visible">
<path d="M 7.08 1.176 C 7.248 0.192 7.896 -0.24000001 8.952 -0.24000001 C 10.272 -0.24000001 11.208 0.264 12.096 1.104 C 12.048 1.392 11.952 1.584 11.6640005 1.776 C 11.352 1.536 11.112 1.44 10.656 1.44 C 10.128 1.44 9.984 1.872 9.984 3.048 L 10.032001 6.504 C 10.032001 9.96 7.896 10.656 5.928 10.656 C 4.176 10.656 1.488 9.648 1.488 8.064 C 1.488 7.392 1.776 6.864 2.7120001 6.864 C 3.576 6.864 4.2 7.392 4.2 7.968 C 4.2 8.088 4.176 8.232 4.152 8.376 C 4.104 8.616 4.056 8.856 4.104 9.096 C 4.1280003 9.36 4.32 9.648 5.112 9.648 C 6.12 9.648 6.96 9.216 6.96 6.168 L 5.352 5.664 C 2.832 4.872 1.056 4.176 1.056 2.28 C 1.056 0.624 1.968 -0.24000001 4.056 -0.24000001 C 4.752 -0.24000001 6.144 0.528 6.936 1.152 Z M 6.96 5.232 L 6.96 2.0640001 C 6.36 1.584 5.76 1.2 5.328 1.2 C 4.296 1.2 3.936 1.896 3.936 2.64 C 3.936 3.528 4.008 4.272 5.712 4.824 Z "/>
</symbol>
<symbol id="g24FA36D774E663C81AD78F0ED3820373" overflow="visible">
<path d="M 5.568 2.928 L 5.568 7.704 C 5.568 8.904 5.664 10.248 5.664 10.248 C 5.664 10.512 5.448 10.656 5.112 10.656 C 4.44 10.392 2.496 10.2 0.84000003 9.984 C 0.792 9.84 0.84000003 9.36 0.888 9.216 C 2.208 9.096 2.448 8.904 2.448 7.5360003 L 2.448 2.928 C 2.448 0.936 2.184 0.888 0.72 0.768 C 0.576 0.624 0.576 0.096 0.72 -0.048 C 1.728 -0.024 2.736 0 4.008 0 C 5.28 0 6.264 -0.024 7.296 -0.048 C 7.44 0.096 7.44 0.624 7.296 0.768 C 5.8320003 0.864 5.568 0.936 5.568 2.928 Z M 2.328 14.304 C 2.328 13.512 2.904 12.72 3.864 12.72 C 4.9440002 12.72 5.568 13.584001 5.568 14.208 C 5.568 14.928 5.0160003 15.792 4.008 15.792 C 2.88 15.792 2.328 15.024 2.328 14.304 Z "/>
</symbol>
<symbol id="g8D84A54D9303B24762DC3071B60ECD14" overflow="visible">
<path d="M 2.4 3.048 C 2.4 1.056 2.016 0.84000003 0.552 0.768 C 0.408 0.624 0.408 0.096 0.552 -0.048 C 1.5600001 -0.024 2.64 0 3.96 0 C 5.28 0 6.336 -0.024 7.368 -0.048 C 7.512 0.096 7.512 0.624 7.368 0.768 C 5.9040003 0.84000003 5.52 1.056 5.52 3.048 L 5.52 13.992001 C 5.52 15.552 5.592 16.44 5.592 16.44 C 5.592 16.656 5.4240003 16.752 5.208 16.752 C 4.32 16.464 2.4 16.2 0.696 16.128 C 0.624 15.84 0.648 15.576 0.768 15.360001 C 2.28 15.24 2.4 15.216001 2.4 13.56 Z "/>
</symbol>
<symbol id="g10AC66E6714D96E9762627FFB6E156C6" overflow="visible">
<path d="M 1.512 10.416 C 1.176 10.416 0.816 10.32 0.504 10.056 L 0.504 9.36 C 0.504 9.24 0.528 9.216 0.624 9.216 L 2.184 9.216 C 2.136 6.7920003 2.112 3.72 2.112 2.52 C 2.112 1.6800001 2.328 0.864 2.832 0.432 C 3.384 -0.024 4.248 -0.24000001 4.824 -0.24000001 C 6.144 -0.24000001 7.6080003 0.432 8.088 1.104 C 8.088 1.392 7.9440002 1.536 7.656 1.776 C 7.344 1.536 6.744 1.44 6.288 1.44 C 5.76 1.44 5.232 1.848 5.232 3.048 C 5.232 4.248 5.208 6.816 5.208 9.216 L 7.632 9.216 C 7.872 9.216 8.208 9.312 8.208 9.528 L 8.208 10.272 C 8.208 10.368 8.136 10.416 8.016 10.416 L 5.208 10.416 L 5.232 11.232 C 5.28 12.84 5.352 13.944 5.352 13.944 C 5.352 14.088 5.28 14.16 5.16 14.16 C 4.992 14.16 4.104 13.896 3.72 13.728 C 3.312 13.56 2.616 13.416 2.448 13.2 C 2.28 12.984 2.184 12.336 2.184 10.416 Z "/>
</symbol>
<symbol id="g69FC55421D5675D87F2C509D9B1DBC44" overflow="visible">
<path d="M 5.808 -4.032 C 6.192 -3.3600001 6.552 -2.496 6.84 -1.776 C 8.76 2.856 9.936 5.448 11.208 8.136 C 11.544 8.832 12.264 9.576 13.152 9.648 C 13.2960005 9.792 13.2960005 10.32 13.152 10.464 C 12.552 10.440001 12.12 10.416 11.448 10.416 C 10.608 10.416 9.792 10.440001 8.904 10.464 C 8.76 10.32 8.76 9.792 8.904 9.648 C 9.672 9.576 10.440001 9.456 10.056 8.592 L 7.584 3.048 C 7.584 3.024 7.584 3.024 7.56 3 C 7.56 3.024 7.56 3.048 7.5360003 3.096 L 5.304 8.112 C 5.28 8.136 5.28 8.16 5.28 8.184 C 4.848 9.12 4.68 9.528 6.096 9.648 C 6.2400002 9.792 6.2400002 10.32 6.096 10.464 C 5.208 10.440001 3.7680001 10.416 2.904 10.416 C 2.088 10.416 0.72 10.440001 0.24000001 10.464 C 0.096 10.32 0.096 9.792 0.24000001 9.648 C 1.296 9.552 1.488 9.384 2.136 7.872 L 5.232 0.768 C 5.304 0.648 5.4 0.552 5.472 0.456 C 5.784 0.024 6.048 -0.336 5.9040003 -0.672 L 5.328 -1.992 C 5.0160003 -2.736 4.728 -3.168 4.056 -3.168 C 3.624 -3.168 3.552 -3.072 3.216 -3.072 C 2.304 -3.072 1.776 -3.696 1.776 -4.176 C 1.776 -4.488 1.848 -4.872 2.0640001 -5.136 C 2.28 -5.4 2.688 -5.568 3 -5.568 C 3.312 -5.568 4.032 -5.472 4.368 -5.328 C 4.872 -5.088 5.544 -4.512 5.808 -4.032 Z "/>
</symbol>
<symbol id="gFC5C8D23DE5E426807758A924FDBA2FC" overflow="visible">
<path d="M 10.104 15.144 C 8.784 15.336 8.28 15.792 6.048 15.792 C 4.968 15.792 3.552 15.456 2.544 14.64 C 1.656 13.92 0.984 12.816 0.984 11.64 C 0.984 10.728 1.224 9.576 1.776 8.856 C 2.88 7.368 4.872 6.552 5.9040003 5.8320003 C 7.008 5.064 8.088 4.104 8.088 2.76 C 8.088 1.584 7.056 0.768 5.592 0.768 C 3.984 0.768 2.328 2.088 1.848 4.272 C 1.464 4.416 1.08 4.32 0.72 4.224 C 0.696 4.224 0.672 4.2 0.648 4.2 C 0.648 2.4 0.84000003 1.128 1.104 0.24000001 C 2.4720001 0.24000001 2.544 -0.24000001 5.856 -0.24000001 C 7.32 -0.24000001 8.496 0.192 9.4800005 1.08 C 10.344 1.824 11.112 2.928 11.112 4.416 C 11.112 5.664 10.584 6.504 9.864 7.296 C 8.928 8.328 7.584 9.0720005 6.6480002 9.552 C 5.688 10.032001 3.984 11.28 3.984 12.648 C 3.984 13.992001 4.8 14.808001 6.024 14.808001 C 8.064 14.808001 8.736 12.96 9.168 11.376 C 9.504 11.28 10.104 11.28 10.368 11.496 C 10.368 12.768 10.272 13.752 10.104 15.144 Z "/>
</symbol>
<symbol id="g225F12A4A0DFD089304CD4B2A01795A4" overflow="visible">
<path d="M 2.4 3.048 C 2.4 1.056 2.016 0.84000003 0.552 0.768 C 0.408 0.624 0.408 0.096 0.552 -0.048 C 1.5600001 -0.024 2.64 0 3.96 0 C 5.0160003 0 6.072 -0.024 6.6480002 -0.048 C 6.7920003 0.096 6.7920003 0.624 6.6480002 0.768 C 5.928 0.864 5.52 1.056 5.52 3.048 L 5.52 5.0160003 C 6.192 5.0160003 6.936 4.9440002 7.176 4.56 C 7.728 3.744 8.4 2.76 8.808 1.872 C 9.12 1.2 9.192 0.984 9.192 0.624 L 9.192 0 L 9.24 -0.048 C 9.24 -0.048 10.32 0 11.16 0 C 12.144 0 13.488 -0.024 14.376 -0.048 C 14.52 0.096 14.52 0.624 14.376 0.768 C 13.440001 0.864 12.912 0.792 12.192 1.872 L 9.408 5.976 C 9.288 6.144 9.24 6.336 9.336 6.456 L 10.536 7.776 C 11.304 8.616 11.952 9.456 13.776 9.648 C 13.92 9.792 13.92 10.32 13.776 10.464 C 13.248 10.440001 11.736 10.416 11.112 10.416 C 10.224 10.416 9.096 10.440001 8.208 10.464 C 8.064 10.32 8.064 9.792 8.208 9.648 C 9.504 9.552 9.8880005 9.336 9.192 8.376 C 8.6640005 7.656 8.136 7.08 7.656 6.6480002 C 7.344 6.384 6.2400002 5.976 5.52 5.976 L 5.52 13.992001 C 5.52 15.552 5.592 16.44 5.592 16.44 C 5.592 16.656 5.4240003 16.752 5.208 16.752 C 4.32 16.464 2.4 16.2 0.696 16.128 C 0.624 15.84 0.648 15.576 0.768 15.360001 C 2.28 15.24 2.4 15.216001 2.4 13.56 Z "/>
</symbol>
<symbol id="g9E7CBAD4E034259458BC3DBF06AA0130" overflow="visible">
<path d="M 2.28 7.416 L 2.28 -2.64 C 2.28 -4.632 2.016 -4.68 0.552 -4.8 C 0.408 -4.9440002 0.408 -5.472 0.552 -5.616 C 1.5600001 -5.592 2.568 -5.568 3.8400002 -5.568 C 5.112 -5.568 6.096 -5.592 7.1280003 -5.616 C 7.272 -5.472 7.272 -4.9440002 7.1280003 -4.8 C 5.664 -4.704 5.4 -4.632 5.4 -2.64 L 5.4 0.168 C 5.928 -0.096 6.432 -0.24000001 7.008 -0.24000001 C 10.656 -0.24000001 13.032001 2.16 13.032001 5.688 C 13.032001 7.032 12.528 8.52 11.592 9.456 C 10.752 10.2960005 9.552 10.656 8.304 10.656 C 7.6080003 10.656 6.3120003 9.816 5.472 9.048 L 5.328 9.048 C 5.28 9.72 5.208 10.248 5.208 10.248 C 5.184 10.536 4.992 10.656 4.656 10.656 C 3.7680001 10.416 2.328 10.08 0.672 9.864 C 0.624 9.72 0.672 9.24 0.72 9.096 C 2.04 8.976 2.28 8.784 2.28 7.416 Z M 5.4 1.5600001 L 5.4 7.704 C 5.4 7.848 5.4 7.968 5.4 8.112 C 6.096 8.736 6.984 9.048 7.5360003 9.048 C 8.52 9.048 9.672 7.848 9.672 5.04 C 9.672 3.024 8.952 0.768 6.864 0.768 C 6.6 0.768 6 0.912 5.4 1.5600001 Z "/>
</symbol>
<symbol id="gD732D1B4380472337CC02C39F4184A6C" overflow="visible">
<path d="M 8.376 1.008 L 6.936 1.008 C 6.432 1.008 6.096 1.464 6.096 2.904 L 6.096 12.552 C 6.096 14.544 6.768 14.64 8.088 14.712 C 8.328 14.856 8.328 15.384 8.088 15.528 C 6.12 15.504 5.4 15.4800005 4.44 15.4800005 C 3.48 15.4800005 0.744 15.528 0.744 15.528 C 0.504 15.384 0.504 14.856 0.744 14.712 C 2.0640001 14.64 2.736 14.544 2.736 12.552 L 2.736 2.928 C 2.736 0.936 2.0640001 0.84000003 0.744 0.768 C 0.504 0.624 0.504 0.096 0.744 -0.048 C 0.744 -0.048 3.504 0 4.44 0 L 9.792 0 C 10.488 0 12.672 -0.048 12.672 -0.048 C 12.912 1.152 13.152 2.7120001 13.2960005 3.96 C 13.056 4.08 12.552 4.1280003 12.264 4.08 C 11.784 2.352 10.896 1.008 8.376 1.008 Z "/>
</symbol>
<symbol id="gDD7DFDEC0D240E3DC5A3664E12D4BDDC" overflow="visible">
<path d="M 1.152 3.504 C 1.248 2.328 1.368 1.2 1.5600001 0.288 C 2.016 0.144 3.552 -0.24000001 4.896 -0.24000001 C 6.744 -0.24000001 9.048 0.768 9.048 2.856 C 9.048 3.672 8.856 4.32 8.304 4.92 C 7.632 5.688 6.624 6.288 5.52 6.768 C 4.56 7.176 4.224 7.9440002 4.224 8.64 C 4.224 9.192 4.68 9.648 5.376 9.648 C 6.216 9.648 7.032 8.88 7.632 7.416 C 8.064 7.344 8.328 7.368 8.568 7.5360003 C 8.568 8.4 8.472 9.312 8.2560005 10.08 C 7.488 10.416 6.888 10.656 5.568 10.656 C 4.296 10.656 3.096 10.176 2.328 9.408 C 1.776 8.856 1.512 8.184 1.512 7.5360003 C 1.512 6.816 1.8000001 6.2400002 2.256 5.736 C 3 4.92 4.32 4.08 5.04 3.744 C 6 3.312 6.264 2.448 6.264 1.872 C 6.264 1.104 5.496 0.696 4.848 0.696 C 3.7680001 0.696 2.616 1.8000001 2.112 3.552 C 1.728 3.624 1.536 3.6000001 1.152 3.504 Z "/>
</symbol>
<symbol id="gB0978DD106A095AA3B799B940A52F3E4" overflow="visible">
<path d="M 3.46 12.9 C 2.6599998 12.9 0.38 12.94 0.38 12.94 C 0.17999999 12.82 0.17999999 12.38 0.38 12.259999 C 1.48 12.2 2.04 12.12 2.04 10.46 L 2.04 2.44 C 2.04 0.78 1.48 0.7 0.38 0.64 C 0.17999999 0.52 0.17999999 0.08 0.38 -0.04 C 0.38 -0.04 2.6599998 0 3.46 0 C 4.2599998 0 5.54 -0.04 6.74 -0.04 C 10.84 -0.04 12.16 1.68 12.16 3.72 C 12.16 5.48 11.28 6.62 9.16 7.18 L 9.16 7.22 C 10.24 7.7 11.08 8.8 11.08 9.82 C 11.08 11.2 10.34 12.94 6.2999997 12.94 C 5.2999997 12.94 4.1 12.9 3.46 12.9 Z M 4.8399997 6.68 L 6.2599998 6.68 C 8.32 6.68 9.22 5.46 9.22 3.74 C 9.22 2.54 8.8 0.79999995 6.16 0.79999995 C 4.96 0.79999995 4.8399997 1.1 4.8399997 1.68 Z M 4.8399997 11.24 C 4.8399997 11.82 4.94 12.099999 6.24 12.099999 C 7.16 12.099999 8.28 11.74 8.28 9.78 C 8.28 8.179999 7.3799996 7.52 5.96 7.52 L 4.8399997 7.52 Z "/>
</symbol>
<symbol id="g2EB1DC9A979CD3C8C9D80DB754EBF6AB" overflow="visible">
<path d="M 10.2 2.6599998 L 10.2 6.12 C 10.2 7.7999997 10.24 7.56 10.24 8.04 C 10.24 8.38 10.16 8.599999 10.04 8.72 C 9.679999 8.7 9.28 8.679999 8.9 8.679999 C 8.34 8.679999 7.04 8.7 6.2599998 8.72 C 6.14 8.599999 6.14 8.16 6.2599998 8.04 C 7.2799997 7.94 7.6 7.7999997 7.6 6.12 L 7.6 2.4199998 C 7.6 2.22 7.6 2.02 7.62 1.8199999 C 6.7999997 1.3199999 6.14 1.28 5.7799997 1.28 C 4.98 1.28 4.38 1.38 4.38 2.78 L 4.38 6.12 C 4.38 7.7999997 4.42 7.56 4.42 8.04 C 4.42 8.38 4.3399997 8.599999 4.22 8.72 C 3.86 8.7 3.4399998 8.679999 3.08 8.679999 C 2.06 8.679999 1.3 8.7 0.44 8.72 C 0.32 8.599999 0.32 8.16 0.44 8.04 C 1.36 8 1.78 7.7999997 1.78 6.12 L 1.78 3 C 1.78 0.88 2.62 -0.19999999 4.3399997 -0.19999999 C 5.06 -0.19999999 6.52 0.38 7.68 1.02 C 7.72 0.52 7.7599998 0.14 7.7599998 0.14 C 7.7799997 -0.099999994 7.94 -0.19999999 8.22 -0.19999999 C 8.96 0 10.16 0.28 11.54 0.45999998 C 11.58 0.58 11.54 0.97999996 11.5 1.1 C 10.42 1.1999999 10.2 1.52 10.2 2.6599998 Z "/>
</symbol>
<symbol id="gE9BB2E81A58B731A2047F77D70267173" overflow="visible">
<path d="M 4.64 2.44 L 4.64 6.42 C 4.64 7.4199996 4.72 8.54 4.72 8.54 C 4.72 8.76 4.54 8.88 4.2599998 8.88 C 3.6999998 8.66 2.08 8.5 0.7 8.32 C 0.65999997 8.2 0.7 7.7999997 0.74 7.68 C 1.8399999 7.58 2.04 7.4199996 2.04 6.2799997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.74 0.59999996 0.64 C 0.48 0.52 0.48 0.08 0.59999996 -0.04 C 1.4399999 -0.02 2.28 0 3.34 0 C 4.4 0 5.22 -0.02 6.08 -0.04 C 6.2 0.08 6.2 0.52 6.08 0.64 C 4.8599997 0.71999997 4.64 0.78 4.64 2.44 Z M 1.9399999 11.92 C 1.9399999 11.259999 2.4199998 10.599999 3.22 10.599999 C 4.12 10.599999 4.64 11.32 4.64 11.84 C 4.64 12.44 4.18 13.16 3.34 13.16 C 2.3999999 13.16 1.9399999 12.5199995 1.9399999 11.92 Z "/>
</symbol>
<symbol id="gC81C3C15134AD04FEC0FE7FCEBE8BB14" overflow="visible">
<path d="M 2 2.54 C 2 0.88 1.68 0.7 0.45999998 0.64 C 0.34 0.52 0.34 0.08 0.45999998 -0.04 C 1.3 -0.02 2.2 0 3.3 0 C 4.4 0 5.2799997 -0.02 6.14 -0.04 C 6.2599998 0.08 6.2599998 0.52 6.14 0.64 C 4.92 0.7 4.6 0.88 4.6 2.54 L 4.6 11.66 C 4.6 12.96 4.66 13.7 4.66 13.7 C 4.66 13.88 4.52 13.96 4.3399997 13.96 C 3.6 13.719999 2 13.5 0.58 13.44 C 0.52 13.2 0.53999996 12.98 0.64 12.799999 C 1.9 12.7 2 12.679999 2 11.3 Z "/>
</symbol>
<symbol id="g5A467C6F5424E9C7BB01147ABA438205" overflow="visible">
<path d="M 7.1 0.96 C 7.14 0.48 7.18 0.14 7.18 0.14 C 7.2 -0.099999994 7.3599997 -0.19999999 7.64 -0.19999999 C 8.38 0 9.58 0.28 10.96 0.45999998 C 11 0.58 10.96 0.97999996 10.92 1.1 C 9.84 1.1999999 9.62 1.52 9.62 2.6599998 L 9.62 11.66 C 9.62 12.96 9.679999 13.7 9.679999 13.7 C 9.679999 13.88 9.54 13.96 9.36 13.96 C 8.62 13.719999 7.02 13.5 5.6 13.44 C 5.54 13.2 5.56 12.94 5.66 12.759999 C 6.92 12.66 7.02 12.639999 7.02 11.259999 L 7.02 8.66 C 6.64 8.78 6.16 8.88 5.58 8.88 C 3 8.88 0.74 6.62 0.74 3.9599998 C 0.74 2.78 1.16 1.4 2.1399999 0.64 C 2.86 0.08 3.36 -0.19999999 4.48 -0.19999999 C 5.02 -0.19999999 6.5 0.68 6.92 0.96 Z M 7.04 1.9 C 6.62 1.56 5.56 1.12 5.3199997 1.12 C 4.3199997 1.12 3.54 2.24 3.54 4.58 C 3.54 5.64 3.6599998 6.56 4.04 7.18 C 4.38 7.72 4.92 8.04 5.52 8.04 C 6.04 8.04 6.54 7.98 7.02 7.3199997 L 7.02 2.3999999 C 7.02 2.24 7.02 2.06 7.04 1.9 Z "/>
</symbol>
<symbol id="gCD50B0C5537328D0484BBB5C5B7C30A" overflow="visible">
<path d="M 0.96 2.9199998 C 1.04 1.9399999 1.14 1 1.3 0.24 C 1.68 0.12 2.96 -0.19999999 4.08 -0.19999999 C 5.62 -0.19999999 7.54 0.64 7.54 2.3799999 C 7.54 3.06 7.3799996 3.6 6.92 4.1 C 6.3599997 4.74 5.52 5.24 4.6 5.64 C 3.8 5.98 3.52 6.62 3.52 7.2 C 3.52 7.66 3.8999999 8.04 4.48 8.04 C 5.18 8.04 5.8599997 7.3999996 6.3599997 6.18 C 6.72 6.12 6.94 6.14 7.14 6.2799997 C 7.14 7 7.06 7.7599998 6.8799996 8.4 C 6.24 8.679999 5.74 8.88 4.64 8.88 C 3.58 8.88 2.58 8.48 1.9399999 7.8399997 C 1.48 7.3799996 1.26 6.8199997 1.26 6.2799997 C 1.26 5.68 1.5 5.2 1.88 4.7799997 C 2.5 4.1 3.6 3.3999999 4.2 3.12 C 5 2.76 5.22 2.04 5.22 1.56 C 5.22 0.91999996 4.58 0.58 4.04 0.58 C 3.1399999 0.58 2.18 1.5 1.76 2.96 C 1.4399999 3.02 1.28 3 0.96 2.9199998 Z "/>
</symbol>
<symbol id="gB88E546A1990E31D64B5C4B23478426F" overflow="visible">
<path d="M 4.56 2.44 L 4.56 6.42 C 4.56 6.52 4.56 6.62 4.56 6.72 C 5.3399997 7.2 6.04 7.3999996 6.3799996 7.3999996 C 7.18 7.3999996 7.7799997 7.04 7.7799997 5.9 L 7.7799997 2.56 C 7.7799997 0.88 7.46 0.7 6.64 0.64 C 6.52 0.52 6.52 0.08 6.64 -0.04 C 7.48 -0.02 8.12 0 9.08 0 C 10.04 0 10.66 -0.02 11.5199995 -0.04 C 11.639999 0.08 11.639999 0.52 11.5199995 0.64 C 10.719999 0.7 10.38 0.88 10.38 2.56 L 10.38 5.68 C 10.38 6.18 10.36 6.58 10.3 6.7799997 C 11.059999 7.16 11.92 7.3999996 12.24 7.3999996 C 13.04 7.3999996 13.599999 7.04 13.599999 5.9 L 13.599999 2.56 C 13.599999 0.88 13.28 0.7 12.46 0.64 C 12.34 0.52 12.34 0.08 12.46 -0.04 C 13.299999 -0.02 13.94 0 14.9 0 C 16 0 16.88 -0.02 17.74 -0.04 C 17.859999 0.08 17.859999 0.52 17.74 0.64 C 16.52 0.7 16.199999 0.88 16.199999 2.56 L 16.199999 5.68 C 16.199999 7.8799996 15.4 8.88 13.679999 8.88 C 12.94 8.88 11.259999 8.08 10.099999 7.44 C 9.8 8.3 9 8.88 7.8199997 8.88 C 7.1 8.88 5.66 8.12 4.52 7.48 C 4.46 8.08 4.4 8.54 4.4 8.54 C 4.38 8.78 4.22 8.88 3.9399998 8.88 C 3.1999998 8.679999 2 8.4 0.62 8.22 C 0.58 8.099999 0.62 7.7 0.65999997 7.58 C 1.76 7.48 1.9599999 7.3199997 1.9599999 6.18 L 1.9599999 2.44 C 1.9599999 0.78 1.74 0.74 0.52 0.64 C 0.39999998 0.52 0.39999998 0.08 0.52 -0.04 C 1.36 -0.02 2.2 0 3.26 0 C 4.18 0 4.74 -0.02 5.6 -0.04 C 5.72 0.08 5.72 0.52 5.6 0.64 C 4.7599998 0.71999997 4.56 0.78 4.56 2.44 Z "/>
</symbol>
<symbol id="g1344FEF92B65FBC27D977C1EC5D9AECF" overflow="visible">
<path d="M 1.26 8.679999 C 0.97999996 8.679999 0.68 8.599999 0.42 8.38 L 0.42 7.7999997 C 0.42 7.7 0.44 7.68 0.52 7.68 L 1.8199999 7.68 C 1.78 5.66 1.76 3.1 1.76 2.1 C 1.76 1.4 1.9399999 0.71999997 2.36 0.35999998 C 2.82 -0.02 3.54 -0.19999999 4.02 -0.19999999 C 5.12 -0.19999999 6.3399997 0.35999998 6.74 0.91999996 C 6.74 1.16 6.62 1.28 6.3799996 1.48 C 6.12 1.28 5.62 1.1999999 5.24 1.1999999 C 4.7999997 1.1999999 4.36 1.54 4.36 2.54 C 4.36 3.54 4.3399997 5.68 4.3399997 7.68 L 6.3599997 7.68 C 6.56 7.68 6.8399997 7.7599998 6.8399997 7.94 L 6.8399997 8.559999 C 6.8399997 8.639999 6.7799997 8.679999 6.68 8.679999 L 4.3399997 8.679999 L 4.36 9.36 C 4.4 10.7 4.46 11.62 4.46 11.62 C 4.46 11.74 4.4 11.8 4.2999997 11.8 C 4.16 11.8 3.4199998 11.58 3.1 11.44 C 2.76 11.3 2.18 11.179999 2.04 11 C 1.9 10.82 1.8199999 10.28 1.8199999 8.679999 Z "/>
</symbol>
<symbol id="gBD4F3A667A4E81DD5512C606D2565A9A" overflow="visible">
<path d="M 5.46 4.2999997 C 5.92 4.2999997 6.3999996 5.2 6.3999996 5.46 C 6.3999996 5.68 6.24 5.8799996 5.68 5.8799996 L 1.68 5.8799996 C 1.26 5.8799996 0.76 5.06 0.76 4.72 C 0.76 4.5 1.02 4.2999997 1.5 4.2999997 Z "/>
</symbol>
<symbol id="gD9D3B6C4D6AB50B3CADCA65007C1BC50" overflow="visible">
<path d="M 8.62 2.58 C 7.7999997 1.74 6.72 1.52 5.96 1.52 C 4.4 1.52 3.4399998 2.4199998 3.4399998 4.38 C 3.4399998 4.52 3.46 4.6 3.46 4.7 L 8.26 4.7 C 8.74 4.7 8.84 5.04 8.84 5.3199997 C 8.84 7.02 8.179999 8.88 5.24 8.88 C 3.1399999 8.88 0.74 7.02 0.74 3.9599998 C 0.74 2.8 1.16 1.5799999 2.02 0.79999995 C 2.78 0.12 3.76 -0.19999999 5.18 -0.19999999 C 6.56 -0.19999999 7.9199996 0.5 8.92 1.9599999 C 8.92 2.22 8.82 2.58 8.62 2.58 Z M 3.54 5.5 C 3.56 6.2 3.6599998 6.96 3.9399998 7.3599997 C 4.2599998 7.8399997 4.7999997 8.04 5.02 8.04 C 5.56 8.04 6.2999997 7.52 6.2999997 5.92 C 6.2999997 5.7999997 6.2999997 5.54 6.2599998 5.5 Z "/>
</symbol>
<symbol id="gC4CA1C48E288D770EBFD587FCB4E243B" overflow="visible">
<path d="M 6.8399997 8.04 C 7.9199996 7.96 8.059999 7.64 7.62 6.62 L 6.04 2.96 C 5.96 2.78 5.8799996 2.9199998 5.8199997 3.06 L 4.56 6.62 C 4.52 6.72 4.48 6.8199997 4.46 6.8999996 C 4.18 7.66 4.06 7.94 5.18 8.04 C 5.2999997 8.16 5.2999997 8.599999 5.18 8.72 C 4.44 8.7 3.6399999 8.679999 2.6599998 8.679999 C 1.9599999 8.679999 0.94 8.7 0.19999999 8.72 C 0.08 8.599999 0.08 8.16 0.19999999 8.04 C 1.36 7.8999996 1.4 7.5 1.8 6.5 L 4.42 0.17999999 C 4.54 -0.12 4.88 -0.24 5.14 -0.24 C 5.3399997 -0.24 5.74 -0.19999999 5.92 0.22 L 8.66 6.48 C 9.059999 7.3799996 9.32 7.94 10.38 8.04 C 10.5 8.16 10.5 8.599999 10.38 8.72 C 9.94 8.7 9.3 8.679999 8.86 8.679999 C 8.12 8.679999 7.3799996 8.7 6.8399997 8.72 C 6.72 8.599999 6.72 8.16 6.8399997 8.04 Z "/>
</symbol>
<symbol id="gC3DD0650993487CD3F460FE3E213BEA0" overflow="visible">
<path d="M 4.56 2.44 L 4.56 6.46 C 5.3599997 7 6.16 7.3999996 6.52 7.3999996 C 7.3199997 7.3999996 7.9199996 7.04 7.9199996 5.9 L 7.9199996 2.56 C 7.9199996 0.88 7.6 0.7 6.7799997 0.64 C 6.66 0.52 6.66 0.08 6.7799997 -0.04 C 7.62 -0.02 8.26 0 9.22 0 C 10.32 0 11.2 -0.02 12.059999 -0.04 C 12.179999 0.08 12.179999 0.52 12.059999 0.64 C 10.84 0.7 10.5199995 0.88 10.5199995 2.56 L 10.5199995 5.68 C 10.5199995 7.8799996 9.58 8.88 7.8599997 8.88 C 7.06 8.88 5.64 8 4.54 7.24 C 4.48 7.94 4.4 8.54 4.4 8.54 C 4.38 8.78 4.22 8.88 3.9399998 8.88 C 3.1999998 8.679999 2 8.4 0.62 8.22 C 0.58 8.099999 0.62 7.7 0.65999997 7.58 C 1.76 7.48 1.9599999 7.3199997 1.9599999 6.18 L 1.9599999 2.44 C 1.9599999 0.78 1.74 0.74 0.52 0.64 C 0.39999998 0.52 0.39999998 0.08 0.52 -0.04 C 1.36 -0.02 2.2 0 3.26 0 C 4.18 0 4.74 -0.02 5.6 -0.04 C 5.72 0.08 5.72 0.52 5.6 0.64 C 4.7599998 0.71999997 4.56 0.78 4.56 2.44 Z "/>
</symbol>
<symbol id="gB591690011940384999C1B007F794058" overflow="visible">
<path d="M 2 2.54 C 2 0.88 1.68 0.7 0.45999998 0.64 C 0.34 0.52 0.34 0.08 0.45999998 -0.04 C 1.3 -0.02 2.2 0 3.3 0 C 4.18 0 5.06 -0.02 5.54 -0.04 C 5.66 0.08 5.66 0.52 5.54 0.64 C 4.94 0.71999997 4.6 0.88 4.6 2.54 L 4.6 4.18 C 5.16 4.18 5.7799997 4.12 5.98 3.8 C 6.44 3.12 7 2.3 7.3399997 1.56 C 7.6 1 7.66 0.82 7.66 0.52 L 7.66 0 L 7.7 -0.04 C 7.7 -0.04 8.599999 0 9.3 0 C 10.12 0 11.24 -0.02 11.98 -0.04 C 12.099999 0.08 12.099999 0.52 11.98 0.64 C 11.2 0.71999997 10.76 0.65999997 10.16 1.56 L 7.8399997 4.98 C 7.74 5.12 7.7 5.2799997 7.7799997 5.38 L 8.78 6.48 C 9.42 7.18 9.96 7.8799996 11.48 8.04 C 11.599999 8.16 11.599999 8.599999 11.48 8.72 C 11.04 8.7 9.78 8.679999 9.26 8.679999 C 8.5199995 8.679999 7.58 8.7 6.8399997 8.72 C 6.72 8.599999 6.72 8.16 6.8399997 8.04 C 7.9199996 7.96 8.24 7.7799997 7.66 6.98 C 7.22 6.3799996 6.7799997 5.9 6.3799996 5.54 C 6.12 5.3199997 5.2 4.98 4.6 4.98 L 4.6 11.66 C 4.6 12.96 4.66 13.7 4.66 13.7 C 4.66 13.88 4.52 13.96 4.3399997 13.96 C 3.6 13.719999 2 13.5 0.58 13.44 C 0.52 13.2 0.53999996 12.98 0.64 12.799999 C 1.9 12.7 2 12.679999 2 11.3 Z "/>
</symbol>
<symbol id="gC1513612DA0E34F2B247DB2830CD7DFD" overflow="visible">
<path d="M 1.24 4.6 C 1.24 3.34 2.26 2.32 3.52 2.32 C 4.7799997 2.32 5.7999997 3.34 5.7999997 4.6 C 5.7999997 5.8599997 4.7799997 6.8799996 3.52 6.8799996 C 2.26 6.8799996 1.24 5.8599997 1.24 4.6 Z "/>
</symbol>
<symbol id="gB2E338F181D915F0996F60E92302C895" overflow="visible">
<path d="M 7 2.44 L 7 10.08 C 7 11.36 7.2 12.12 7.9199996 12.12 L 8.36 12.12 C 9.86 12.12 10.8 11.599999 11.139999 10.059999 C 11.36 10.059999 11.639999 10.08 11.82 10.16 C 11.679999 11.08 11.58 12.099999 11.559999 13 C 11.559999 13.0199995 11.5199995 13.059999 11.5 13.059999 C 10.82 13 8.599999 12.9 7.02 12.9 L 5.2999997 12.9 C 3.76 12.9 1.4 13 0.64 13.059999 C 0.59999996 13.059999 0.56 13.0199995 0.56 13 C 0.48 12.099999 0.28 11.059999 0.06 10.099999 C 0.26 10.0199995 0.5 10 0.74 10 C 1.14 11.599999 2.06 12.12 3.3799999 12.12 L 4.36 12.12 C 5.1 12.12 5.2999997 11.36 5.2999997 10.139999 L 5.2999997 2.44 C 5.2999997 0.78 4.96 0.68 3.36 0.62 C 3.24 0.5 3.24 0.08 3.36 -0.04 C 4.3399997 -0.02 5.3599997 0 6.16 0 C 6.92 0 7.94 -0.02 8.94 -0.04 C 9.059999 0.08 9.059999 0.5 8.94 0.62 C 7.3399997 0.68 7 0.78 7 2.44 Z "/>
</symbol>
<symbol id="gFB78EB03C35D4F852337F4EC6AC104AC" overflow="visible">
<path d="M 0.82 4.1 C 0.82 2.06 2.18 -0.19999999 5.02 -0.19999999 C 6.2999997 -0.19999999 7.2799997 0.26 7.96 0.91999996 C 8.86 1.8 9.26 3.06 9.26 4.2799997 C 9.26 6.3599997 8.12 8.78 5.06 8.78 C 3.74 8.78 2.6599998 8.24 1.92 7.3799996 C 1.1999999 6.52 0.82 5.3599997 0.82 4.1 Z M 4.7599998 8.08 C 6.48 8.08 7.54 6.52 7.54 3.6399999 C 7.54 1.12 6.24 0.5 5.2999997 0.5 C 3.22 0.5 2.54 3.02 2.54 4.56 C 2.54 6.2999997 2.96 8.08 4.7599998 8.08 Z "/>
</symbol>
<symbol id="gAC7FD886AB12F72ED3B61B0327264BE7" overflow="visible">
<path d="M 3.12 7.3599997 C 3.1 7.96 3.06 8.48 2.96 8.679999 C 2.9199998 8.78 2.8799999 8.84 2.72 8.84 C 2.1599998 8.62 1.64 8.44 0.26 8.26 C 0.22 8.139999 0.26 7.8199997 0.29999998 7.7 C 1.38 7.6 1.5999999 7.5 1.5999999 6.3399997 L 1.5999999 -2.2 C 1.5999999 -3.86 1.38 -3.9599998 0.16 -4.02 C 0.04 -4.14 0.04 -4.56 0.16 -4.68 C 0.85999995 -4.66 1.5999999 -4.64 2.3999999 -4.64 C 3.1999998 -4.64 4.16 -4.66 4.8199997 -4.68 C 4.94 -4.56 4.94 -4.14 4.8199997 -4.02 C 3.3999999 -3.9399998 3.1799998 -3.86 3.1799998 -2.2 L 3.1799998 -0.04 C 3.1799998 0.22 3.26 0.19999999 3.46 0.12 C 3.9599998 -0.08 4.56 -0.19999999 5.2 -0.19999999 C 6.3199997 -0.19999999 7.3199997 0.14 8.139999 0.91999996 C 9.08 1.8399999 9.62 3.08 9.62 4.7 C 9.62 6.8199997 8.12 8.78 6.08 8.78 C 5.16 8.78 4.14 8.179999 3.34 7.2799997 C 3.22 7.16 3.1399999 7.16 3.12 7.3599997 Z M 3.5 6.62 C 4.02 7.2599998 4.94 7.8599997 5.52 7.8599997 C 6.7999997 7.8599997 7.8999996 6.42 7.8999996 4.16 C 7.8999996 2.52 7.3199997 0.48 5.08 0.48 C 4.72 0.48 4.02 0.58 3.6599998 0.9 C 3.26 1.26 3.1799998 1.38 3.1799998 2.1 L 3.1799998 5.74 C 3.1799998 6.16 3.26 6.3399997 3.5 6.62 Z "/>
</symbol>
<symbol id="g1788914935A6D7BFA016214155630E72" overflow="visible">
<path d="M 1.9 2.44 C 1.9 0.78 1.68 0.68 0.45999998 0.62 C 0.34 0.5 0.34 0.08 0.45999998 -0.04 C 1.16 -0.02 1.9 0 2.7 0 C 3.5 0 4.2599998 -0.02 4.92 -0.04 C 5.04 0.08 5.04 0.5 4.92 0.62 C 3.6999998 0.68 3.48 0.78 3.48 2.44 L 3.48 11.66 C 3.48 12.96 3.56 13.759999 3.56 13.759999 C 3.56 13.9 3.48 13.96 3.3 13.96 C 2.8 13.759999 1.3 13.48 0.5 13.42 C 0.45999998 13.259999 0.5 12.94 0.62 12.82 C 1.78 12.74 1.9 12.679999 1.9 11.179999 Z "/>
</symbol>
<symbol id="gAA212A9DBB5FA7333A767E41B2F6A3B3" overflow="visible">
<path d="M 5.8599997 0.96 C 5.98 0.34 6.2 -0.19999999 7.2 -0.19999999 C 7.96 -0.19999999 8.679999 0.14 9.099999 0.53999996 C 9.059999 0.78 8.98 0.96 8.76 1.0799999 C 8.62 0.96 8.28 0.76 8.0199995 0.76 C 7.44 0.76 7.4199996 1.54 7.4199996 2.46 L 7.4199996 5.4 C 7.4199996 8.24 5.8599997 8.78 4.4 8.78 C 2.76 8.78 1.1 7.7 1.1 6.56 C 1.1 6.08 1.3399999 5.8399997 1.8 5.8399997 C 2.3799999 5.8399997 2.74 6.2599998 2.74 6.52 C 2.74 6.66 2.72 6.7999997 2.6799998 6.8799996 C 2.6599998 6.94 2.6399999 7.06 2.6399999 7.2799997 C 2.6399999 7.8999996 3.48 8.12 4.24 8.12 C 4.92 8.12 5.8599997 7.7799997 5.8599997 5.52 C 5.8599997 5.38 5.7999997 5.2999997 5.74 5.2799997 L 4.02 4.8599997 C 2.1 4.38 0.71999997 3.32 0.71999997 1.9599999 C 0.71999997 0.32 1.8399999 -0.19999999 3.24 -0.19999999 C 3.9399998 -0.19999999 4.54 -0.04 5.42 0.64 L 5.8199997 0.96 Z M 5.8599997 4.66 L 5.8599997 2.02 C 5.8599997 1.76 5.74 1.62 5.58 1.5 C 5.06 1.0799999 4.38 0.62 3.82 0.62 C 2.82 0.62 2.3799999 1.42 2.3799999 2.04 C 2.3799999 2.9399998 2.8 3.86 4.2799997 4.24 Z "/>
</symbol>
<symbol id="g21D1E528F66DB45787699F71DA377CC5" overflow="visible">
<path d="M 4.08 -3.1999998 C 4.4 -2.6399999 4.66 -2.08 4.9 -1.48 C 6.5 2.3799999 7.3999996 4.44 8.44 6.68 C 8.84 7.52 9.12 7.8399997 10.059999 7.96 C 10.179999 8.08 10.179999 8.5 10.059999 8.62 C 9.66 8.599999 9.2 8.58 8.639999 8.58 C 8.04 8.58 7.4199996 8.599999 6.8199997 8.62 C 6.7 8.5 6.7 8.08 6.8199997 7.96 C 7.46 7.8999996 8.099999 7.7799997 7.7799997 7.06 L 5.7999997 2.48 C 5.66 2.1599998 5.48 2.1 5.3199997 2.5 L 3.54 6.66 C 3.1799998 7.5 3.08 7.8799996 4.2 7.96 C 4.3199997 8.08 4.3199997 8.5 4.2 8.62 C 3.46 8.599999 2.6599998 8.58 1.9399999 8.58 C 1.26 8.58 0.71999997 8.599999 0.32 8.62 C 0.19999999 8.5 0.19999999 8.08 0.32 7.96 C 1.12 7.8599997 1.38 7.68 1.9 6.46 L 4.16 1.1999999 C 4.3399997 0.79999995 4.64 -0.12 4.44 -0.68 C 4.2 -1.3399999 3.9599998 -1.9 3.6599998 -2.52 C 3.4399998 -2.9199998 3.1599998 -3.1 2.6599998 -3.1 C 2.3799999 -3.1 2.3 -3.04 2.08 -3.04 C 1.5 -3.04 1.1999999 -3.6399999 1.1999999 -3.8999999 C 1.1999999 -4.3199997 1.5999999 -4.64 2.1399999 -4.64 C 2.56 -4.64 3.36 -4.48 4.08 -3.1999998 Z "/>
</symbol>
<symbol id="g7FBC39AA6D9FB89D8B638A3651405A80" overflow="visible">
<path d="M 7.72 1.86 C 6.98 1.1 6.3999996 0.78 5.24 0.78 C 4.52 0.78 3.6799998 1.1999999 3.06 2.22 C 2.6599998 2.8799999 2.4199998 3.8 2.4199998 4.96 L 7.74 4.92 C 7.98 4.92 8.12 5.04 8.12 5.2599998 C 8.12 6.94 7.52 8.74 4.74 8.74 C 3 8.74 0.74 7.08 0.74 4.04 C 0.74 2.9199998 1.02 1.8399999 1.68 1.0799999 C 2.36 0.28 3.3 -0.19999999 4.74 -0.19999999 C 6.2599998 -0.19999999 7.3399997 0.5 8.139999 1.54 C 8.08 1.74 7.96 1.8399999 7.72 1.86 Z M 2.48 5.64 C 2.86 7.8999996 4.2599998 8.08 4.74 8.08 C 5.5 8.08 6.3999996 7.66 6.3999996 5.98 C 6.3999996 5.7999997 6.3199997 5.7 6.1 5.7 Z "/>
</symbol>
<symbol id="gB9C04FB79CAD4691AB5EC7F01BE2AD7F" overflow="visible">
<path d="M 3.52 7.16 C 3.48 7.96 3.46 8.48 3.36 8.679999 C 3.32 8.78 3.28 8.84 3.12 8.84 C 2.56 8.62 2.04 8.44 0.65999997 8.26 C 0.62 8.139999 0.65999997 7.8199997 0.7 7.7 C 1.78 7.6 2 7.5 2 6.3399997 L 2 2.44 C 2 0.78 1.76 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 2 0 2.8 0 C 3.6 0 4.52 -0.02 5.22 -0.04 C 5.3399997 0.08 5.3399997 0.5 5.22 0.62 C 3.82 0.71999997 3.58 0.78 3.58 2.44 L 3.58 5.22 C 3.58 5.74 3.82 6.2 4.06 6.56 C 4.2799997 6.8799996 4.74 7.54 4.98 7.54 C 5.16 7.54 5.3399997 7.5 5.5 7.2799997 C 5.64 7.08 5.8799996 6.8199997 6.22 6.8199997 C 6.7 6.8199997 7.16 7.3199997 7.16 7.8199997 C 7.16 8.2 6.7999997 8.78 5.96 8.78 C 5.02 8.78 4.2 7.8999996 3.74 7.12 C 3.62 6.8999996 3.52 7.06 3.52 7.16 Z "/>
</symbol>
<symbol id="g8C7315D77A5D71E18736DE61553C419F" overflow="visible">
<path d="M 1.4 1.1999999 C 1.4 0.62 1.88 0.14 2.46 0.14 C 3.04 0.14 3.52 0.62 3.52 1.1999999 C 3.52 1.78 3.04 2.26 2.46 2.26 C 1.88 2.26 1.4 1.78 1.4 1.1999999 Z M 1.4 7.16 C 1.4 6.58 1.88 6.1 2.46 6.1 C 3.04 6.1 3.52 6.58 3.52 7.16 C 3.52 7.74 3.04 8.22 2.46 8.22 C 1.88 8.22 1.4 7.74 1.4 7.16 Z "/>
</symbol>
<symbol id="g67483374C2628B9150A7D3585AC4A61B" overflow="visible">
<path d="M 0.96 2.76 C 1.04 1.78 1.1 0.84 1.1 0 C 1.3 0.04 1.5 0.06 1.5999999 0.06 C 1.74 0.06 1.86 0.06 2 0.02 C 2.54 -0.12 3.08 -0.19999999 3.82 -0.19999999 C 4.94 -0.19999999 7 0.34 7 2.32 C 7 3.6799998 6.02 4.48 4.66 4.98 C 3.46 5.44 2.6599998 5.74 2.6599998 6.8399997 C 2.6599998 7.66 3.3799999 8.12 4.06 8.12 C 4.5 8.12 5.66 7.96 5.92 6.2599998 C 6.04 6.14 6.44 6.16 6.56 6.2799997 C 6.62 7 6.66 7.74 6.68 8.4 C 6.06 8.5 5.1 8.78 4.06 8.78 C 2.58 8.78 1.24 7.8199997 1.24 6.54 C 1.24 5.08 1.9 4.46 3.4399998 3.82 C 5.1 3.1399999 5.48 2.72 5.48 1.86 C 5.48 0.88 4.52 0.45999998 3.78 0.45999998 C 3 0.45999998 2.56 0.71999997 2.36 0.94 C 1.92 1.4 1.6999999 2.28 1.5799999 2.78 C 1.4599999 2.8999999 1.0799999 2.8799999 0.96 2.76 Z "/>
</symbol>
<symbol id="gF9DE6E66E5D3ACB0B17DC7988DD660B8" overflow="visible">
<path d="M 1.7199999 2.44 C 1.7199999 0.78 1.5 0.7 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.04 -0.02 1.7199999 0 2.52 0 C 3.22 0 3.8799999 -0.02 4.3399997 -0.04 C 4.46 0.08 4.46 0.5 4.3399997 0.62 C 3.52 0.7 3.3 0.78 3.3 2.44 L 3.3 4.18 C 3.6799998 4.16 3.9599998 4.14 4.16 4.08 C 4.38 3.9199998 4.56 3.74 4.7999997 3.4199998 L 6.2599998 1.4599999 C 6.8399997 0.68 7.08 0.29999998 7.1 0.06 C 7.1 0 7.12 -0.04 7.18 -0.04 C 7.58 -0.02 8.0199995 0 8.42 0 C 9.04 0 9.66 -0.02 10.059999 -0.04 C 10.179999 0.08 10.179999 0.5 10.059999 0.62 C 9.38 0.7 8.88 0.78 8.34 1.4599999 L 5.7 4.7799997 C 5.62 4.88 5.56 4.96 5.56 5.06 C 5.56 5.14 5.56 5.18 5.64 5.2599998 L 7.3999996 7.08 C 8 7.72 8.7 7.8799996 9.5 7.96 C 9.62 8.08 9.62 8.5 9.5 8.62 C 9.04 8.599999 8.48 8.58 7.7599998 8.58 C 7 8.58 6.2599998 8.599999 5.7999997 8.62 C 5.68 8.5 5.68 8.08 5.7999997 7.96 C 6.92 7.8799996 6.44 7.18 6.2599998 6.94 C 5.7999997 6.3599997 5.18 5.68 4.66 5.2999997 C 4.22 4.98 3.6799998 4.74 3.3 4.68 L 3.3 11.66 C 3.3 12.96 3.3799999 13.759999 3.3799999 13.759999 C 3.3799999 13.9 3.3 13.96 3.12 13.96 C 2.62 13.759999 1.12 13.48 0.32 13.42 C 0.28 13.259999 0.32 12.94 0.44 12.82 C 0.5 12.82 0.56 12.82 0.62 12.82 C 1.5 12.759999 1.7199999 12.759999 1.7199999 11.179999 Z "/>
</symbol>
<symbol id="gE68C39294AA7FBA9B91EA2F8E9CC3997" overflow="visible">
<path d="M 3.62 2.44 L 3.62 6.42 C 3.62 7.4199996 3.6999998 8.7 3.6999998 8.7 C 3.6999998 8.78 3.6 8.84 3.4399998 8.84 C 2.8799999 8.62 2.08 8.44 0.7 8.26 C 0.65999997 8.139999 0.7 7.8199997 0.74 7.7 C 1.8399999 7.6 2.04 7.48 2.04 6.3399997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.71999997 0.59999996 0.62 C 0.48 0.5 0.48 0.08 0.59999996 -0.04 C 1.26 -0.02 2.04 0 2.84 0 C 3.6399999 0 4.4 -0.02 5.06 -0.04 C 5.18 0.08 5.18 0.5 5.06 0.62 C 3.84 0.7 3.62 0.78 3.62 2.44 Z M 1.8 11.98 C 1.8 11.46 2.28 10.94 2.76 10.94 C 3.32 10.94 3.8 11.48 3.8 11.9 C 3.8 12.38 3.3799999 12.94 2.84 12.94 C 2.36 12.94 1.8 12.46 1.8 11.98 Z "/>
</symbol>
<symbol id="gD3761FB0B01B207797C607CDFB6E3A0B" overflow="visible">
<path d="M 3.3999999 7.16 C 3.3799999 7.7599998 3.34 8.48 3.24 8.679999 C 3.1999998 8.78 3.1599998 8.84 3 8.84 C 2.44 8.62 1.92 8.44 0.53999996 8.26 C 0.5 8.139999 0.53999996 7.8199997 0.58 7.7 C 1.66 7.6 1.88 7.5 1.88 6.3399997 L 1.88 2.44 C 1.88 0.79999995 1.62 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.88 0 2.6799998 0 C 3.48 0 4.1 -0.02 4.7 -0.04 C 4.8199997 0.08 4.8199997 0.5 4.7 0.62 C 3.6799998 0.71999997 3.46 0.79999995 3.46 2.44 L 3.46 5.72 C 3.46 6.14 3.6399999 6.3799996 3.8 6.56 C 4.6 7.3399997 5.3399997 7.74 5.96 7.74 C 6.72 7.74 7.2799997 7.2599998 7.2799997 5.92 L 7.2799997 2.44 C 7.2799997 0.79999995 7.12 0.7 6.04 0.62 C 5.94 0.5 5.94 0.08 6.04 -0.04 C 6.54 -0.02 7.2799997 0 8.08 0 C 8.88 0 9.54 -0.02 10.04 -0.04 C 10.139999 0.08 10.139999 0.5 10.04 0.62 C 9.04 0.7 8.86 0.79999995 8.86 2.44 L 8.86 5.62 C 8.86 5.9 8.86 6.18 8.84 6.42 C 9.8 7.48 10.7 7.74 11.48 7.74 C 12.24 7.74 12.679999 7.2999997 12.679999 5.96 L 12.679999 2.44 C 12.679999 0.79999995 12.48 0.7 11.44 0.62 C 11.34 0.5 11.34 0.08 11.44 -0.04 C 11.94 -0.02 12.679999 0 13.48 0 C 14.28 0 14.98 -0.02 15.54 -0.04 C 15.639999 0.08 15.639999 0.5 15.54 0.62 C 14.44 0.7 14.259999 0.79999995 14.259999 2.44 L 14.259999 5.6 C 14.259999 7.3799996 13.96 8.78 12.2 8.78 C 11.179999 8.78 9.94 8.4 8.9 7.2999997 C 8.84 7.24 8.72 7.14 8.679999 7.3199997 C 8.5 8.139999 7.72 8.78 6.68 8.78 C 5.52 8.78 4.48 8.099999 3.6399999 7.16 C 3.54 7.06 3.4199998 6.92 3.3999999 7.16 Z "/>
</symbol>
<symbol id="g35631D62198EF939061DC90C9391724A" overflow="visible">
<path d="M 3.6799998 7.16 C 3.56 7.02 3.4399998 6.98 3.4399998 7.16 C 3.4199998 7.7 3.3799999 8.48 3.28 8.679999 C 3.24 8.78 3.1999998 8.84 3.04 8.84 C 2.48 8.62 1.9599999 8.44 0.58 8.26 C 0.53999996 8.139999 0.58 7.8199997 0.62 7.7 C 1.6999999 7.6 1.92 7.5 1.92 6.3399997 L 1.92 2.44 C 1.92 0.79999995 1.7199999 0.71999997 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.92 0 2.72 0 C 3.52 0 4.12 -0.02 4.72 -0.04 C 4.8399997 0.08 4.8399997 0.5 4.72 0.62 C 3.6999998 0.71999997 3.5 0.79999995 3.5 2.44 L 3.5 5.72 C 3.5 6.14 3.6799998 6.3799996 3.84 6.56 C 4.6 7.2999997 5.5 7.74 6.2799997 7.74 C 6.68 7.74 7.1 7.48 7.3399997 7.02 C 7.54 6.62 7.58 6.08 7.58 5.48 L 7.58 2.44 C 7.58 0.79999995 7.3799996 0.71999997 6.3399997 0.62 C 6.24 0.5 6.24 0.08 6.3399997 -0.04 C 6.94 -0.02 7.58 0 8.38 0 C 9.179999 0 9.9 -0.02 10.5 -0.04 C 10.599999 0.08 10.599999 0.5 10.5 0.62 C 9.38 0.71999997 9.16 0.79999995 9.16 2.44 L 9.16 5.42 C 9.16 6.52 9.08 7.48 8.62 8.099999 C 8.28 8.54 7.66 8.78 6.96 8.78 C 5.98 8.78 4.8599997 8.5199995 3.6799998 7.16 Z "/>
</symbol>
<symbol id="g42587C4E387B2C5F870DA01C2914651F" overflow="visible">
<path d="M 6.68 1 C 6.7799997 1.0799999 6.96 1.12 6.98 0.97999996 C 7.04 0.5 7.2 -0.19999999 7.2 -0.19999999 C 7.3599997 -0.26 7.46 -0.24 7.58 -0.19999999 C 8.0199995 0.16 8.72 0.45999998 9.94 0.59999996 C 10.059999 0.71999997 10.059999 1.02 9.94 1.14 C 8.66 1.24 8.48 1.62 8.48 2.6 L 8.48 11.66 C 8.48 12.96 8.559999 13.759999 8.559999 13.759999 C 8.559999 13.9 8.48 13.96 8.3 13.96 C 7.7999997 13.759999 6.2999997 13.48 5.5 13.42 C 5.46 13.259999 5.5 12.94 5.62 12.82 C 5.68 12.82 5.74 12.82 5.7999997 12.82 C 6.68 12.759999 6.8999996 12.759999 6.8999996 11.179999 L 6.8999996 8.62 C 6.8999996 8.48 6.8599997 8.44 6.72 8.44 C 6.64 8.44 5.8199997 8.78 5.16 8.78 C 3.84 8.78 2.96 8.34 2.1599998 7.58 C 1.3 6.72 0.78 5.54 0.78 4.06 C 0.78 1.5999999 2.02 -0.19999999 4.18 -0.19999999 C 4.96 -0.19999999 5.7 0.19999999 6.68 1 Z M 6.8999996 2.48 C 6.8999996 2.1 6.8599997 1.9399999 6.58 1.6999999 C 5.8399997 1.06 5.2 0.74 4.7 0.74 C 3.62 0.74 2.5 1.92 2.5 4.42 C 2.5 5.8599997 2.78 6.66 3.08 7.08 C 3.6999998 8.0199995 4.54 8.08 4.94 8.08 C 5.66 8.08 6.16 7.8199997 6.56 7.3599997 C 6.8399997 7.04 6.8999996 6.8999996 6.8999996 6.2799997 Z "/>
</symbol>
<symbol id="g607CD744DAB7515984E0B3F495F7DE81" overflow="visible">
<path d="M 2.98 0 L 7.24 0 C 7.7799997 0 9.62 -0.04 9.62 -0.04 C 9.82 0.96 10.0199995 2.26 10.139999 3.3 C 9.94 3.3999999 9.719999 3.4399998 9.48 3.3999999 C 9.08 1.9599999 8.34 0.78 6.22 0.78 L 4.96 0.78 C 4.18 0.78 3.82 1.16 3.82 2.18 L 3.82 10.46 C 3.82 12.12 4.16 12.219999 5.56 12.28 C 5.68 12.4 5.68 12.82 5.56 12.94 C 4.66 12.92 3.72 12.9 2.96 12.9 C 2.24 12.9 1.3 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.16 -0.02 2.3 0 2.98 0 Z "/>
</symbol>
<symbol id="gA1481BA28623480CC7E6165783E2A864" overflow="visible">
<path d="M 4.06 7.96 C 4.18 8.08 4.18 8.5 4.06 8.62 C 3.46 8.599999 2.76 8.58 2.04 8.58 C 1.28 8.58 0.74 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.16 7.8599997 1.38 7.66 1.8 6.62 L 4.42 0.16 C 4.54 -0.12 4.7 -0.24 4.9 -0.24 C 5.08 -0.24 5.24 -0.12 5.38 0.19999999 L 7.3999996 5.12 L 9.46 0.16 C 9.58 -0.12 9.74 -0.24 9.94 -0.24 C 10.12 -0.24 10.28 -0.12 10.4 0.17999999 L 13.0199995 6.52 C 13.34 7.3399997 13.679999 7.8999996 14.7 7.96 C 14.82 8.08 14.82 8.5 14.7 8.62 C 14.299999 8.599999 13.86 8.58 13.259999 8.58 C 12.66 8.58 11.82 8.599999 11.219999 8.62 C 11.099999 8.5 11.099999 8.08 11.219999 7.96 C 12.719999 7.8799996 12.5199995 7.2999997 12.24 6.6 L 10.559999 2.44 C 10.36 1.9399999 10.28 1.9399999 10.12 2.36 L 8.4 6.74 C 8.0199995 7.68 8.059999 7.8799996 9.12 7.96 C 9.24 8.08 9.24 8.5 9.12 8.62 C 8.5199995 8.599999 7.72 8.58 7.12 8.58 C 6.62 8.58 5.96 8.599999 5.3599997 8.62 C 5.24 8.5 5.24 8.08 5.3599997 7.96 C 6.2999997 7.8799996 6.54 7.2999997 6.8999996 6.3999996 L 7.02 6.08 L 5.62 2.54 C 5.3599997 1.88 5.3199997 1.86 5.06 2.5 L 3.46 6.62 C 3.08 7.58 3.1 7.8999996 4.06 7.96 Z "/>
</symbol>
<symbol id="gCDF8B867C9AAFA36255BC29C36465E90" overflow="visible">
<path d="M 3.5 2.44 L 3.5 7.7999997 L 5.3599997 7.7999997 C 5.54 7.7999997 5.8199997 7.8799996 5.8199997 8.059999 L 5.8199997 8.46 C 5.8199997 8.54 5.7599998 8.58 5.66 8.58 L 3.5 8.58 L 3.5 9.719999 C 3.5 12.799999 4.42 13.28 5.08 13.28 C 5.68 13.28 6 13.04 6.2799997 12.34 C 6.44 11.98 6.66 11.7 7.08 11.7 C 7.4199996 11.7 7.8999996 12.12 7.8999996 12.5199995 C 7.8999996 12.86 7.68 13.219999 7.2599998 13.54 C 6.74 13.9 6.22 13.96 5.46 13.96 C 3.78 13.96 1.92 12.5 1.92 9.38 L 1.92 8.58 L 0.9 8.58 C 0.53999996 8.58 0.44 8.34 0.44 8.179999 L 0.44 7.9199996 C 0.44 7.8199997 0.45999998 7.7999997 0.53999996 7.7999997 L 1.92 7.7999997 L 1.92 2.44 C 1.92 0.78 1.5999999 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 1.92 0 2.72 0 C 3.52 0 4.48 -0.02 5.18 -0.04 C 5.2999997 0.08 5.2999997 0.5 5.18 0.62 C 3.62 0.7 3.5 0.78 3.5 2.44 Z "/>
</symbol>
<symbol id="g8D44D9C01F9AF6C3B1D634FDF54DE6FB" overflow="visible">
<path d="M 5.66 6.46 C 7.3599997 6.46 7.4199996 6 7.48 5.1 C 7.6 4.98 8.0199995 4.98 8.139999 5.1 C 8.12 5.6 8.099999 6.18 8.099999 6.8599997 C 8.099999 7.54 8.12 8.059999 8.139999 8.58 C 8.0199995 8.7 7.6 8.7 7.48 8.58 C 7.4199996 7.48 7.3599997 7.22 5.66 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.9 4.04 12.099999 4.92 12.099999 L 5.8199997 12.099999 C 7.94 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.92 9.34 9.96 9.5 10.0199995 C 9.4 10.84 9.099999 12.759999 9.059999 12.92 C 9.059999 12.96 9.04 12.98 8.98 12.98 C 8.639999 12.92 8.54 12.9 8.04 12.9 L 2.9399998 12.9 C 2.3 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.06 -0.02 2.06 0 2.96 0 C 3.86 0 4.8399997 -0.02 5.54 -0.04 C 5.66 0.08 5.66 0.5 5.54 0.62 C 4.14 0.68 3.8 0.78 3.8 2.44 L 3.8 6.46 Z "/>
</symbol>
<symbol id="gFB54B84572F46C3C9CB2B1A90182D6B2" overflow="visible">
<path d="M 8.88 7.74 C 9.26 7.74 9.62 8.099999 9.62 8.5 C 9.62 8.92 9.24 9.24 8.7 9.24 C 8.179999 9.24 7.22 8.9 6.7 8.22 C 6.46 8.38 5.7999997 8.78 4.62 8.78 C 2.84 8.78 1.1999999 7.58 1.1999999 5.74 C 1.1999999 4.66 1.68 4.04 2.24 3.5 C 1.68 3.02 1.36 2.1599998 1.36 1.48 C 1.36 0.76 1.76 0.19999999 2.28 -0.06 C 1.1999999 -0.7 0.64 -1.62 0.64 -2.48 C 0.64 -4.22 2.28 -4.7599998 3.82 -4.7599998 C 6.52 -4.7599998 9.44 -3.46 9.44 -1.3 C 9.44 -0.65999997 9.139999 -0.16 8.559999 0.32 C 7.7799997 0.96 6.3799996 0.97999996 5.64 0.97999996 C 5.2799997 0.97999996 4.7799997 0.94 4.2999997 0.88 C 4 0.85999995 3.8 0.84 3.6999998 0.84 C 3.12 0.84 2.4199998 1.12 2.4199998 1.9799999 C 2.4199998 2.3799999 2.54 2.8 2.78 3.1399999 C 3.26 2.86 3.82 2.72 4.6 2.72 C 6.3599997 2.72 7.98 3.82 7.98 5.7799997 C 7.98 6.72 7.7 7.2599998 7.12 7.8599997 C 7.2599998 8.059999 7.66 8.34 7.9199996 8.34 C 8.059999 8.34 8.2 8.28 8.32 8.099999 C 8.4 7.94 8.66 7.74 8.88 7.74 Z M 2.6399999 -0.19999999 C 2.86 -0.26 3.1799998 -0.29999998 3.4399998 -0.29999998 C 4.06 -0.29999998 4.62 -0.24 4.9 -0.24 C 5.9 -0.24 6.74 -0.26 7.3199997 -0.58 C 8.099999 -1.02 8.34 -1.3 8.34 -1.8199999 C 8.34 -3.26 6.22 -4.02 4.42 -4.02 C 3.6999998 -4.02 2.02 -3.4399998 2.02 -2.08 C 2.02 -1.4 2.06 -0.9 2.6399999 -0.19999999 Z M 6.3799996 5.58 C 6.3799996 3.72 5.44 3.34 4.7 3.34 C 3.02 3.34 2.84 4.7599998 2.84 6.04 C 2.84 7.44 3.34 8.16 4.44 8.16 C 5.7 8.16 6.3799996 7.24 6.3799996 5.58 Z "/>
</symbol>
<symbol id="gD8CB364949770E6EB9E57283C62D30EB" overflow="visible">
<path d="M 4.3399997 -0.19999999 C 5.12 -0.19999999 6.06 0.19999999 7.04 1 C 7.14 1.0799999 7.3199997 1.12 7.3399997 0.97999996 C 7.3999996 0.48 7.56 -0.19999999 7.56 -0.19999999 C 7.72 -0.26 7.8199997 -0.24 7.94 -0.19999999 C 8.38 0.16 9.08 0.45999998 10.3 0.59999996 C 10.42 0.71999997 10.42 1.02 10.3 1.14 C 9.0199995 1.24 8.84 1.62 8.84 2.6 L 8.84 6.44 C 8.84 7.04 8.92 8.5 8.92 8.5 C 8.92 8.559999 8.86 8.62 8.76 8.62 C 8.66 8.599999 8.36 8.58 8.059999 8.58 C 7.4199996 8.58 6.7 8.599999 6.02 8.62 C 5.9 8.5 5.9 8.08 6.02 7.96 C 7 7.8999996 7.2599998 7.66 7.2599998 6.3399997 L 7.2599998 2.48 C 7.2599998 2.1 7.22 1.9399999 6.94 1.6999999 C 6.2 1.06 5.44 0.74 4.94 0.74 C 4.3399997 0.74 3.34 1.02 3.34 2.8 L 3.34 6.44 C 3.34 7.04 3.4199998 8.5 3.4199998 8.5 C 3.4199998 8.559999 3.36 8.62 3.26 8.62 C 3.1599998 8.599999 2.86 8.58 2.56 8.58 C 1.92 8.58 1.1999999 8.599999 0.52 8.62 C 0.39999998 8.5 0.39999998 8.08 0.52 7.96 C 1.48 7.8799996 1.76 7.66 1.76 6.3599997 L 1.76 2.52 C 1.76 1.14 2.36 -0.19999999 4.3399997 -0.19999999 Z "/>
</symbol>
<symbol id="g356EE1FB649593768A2B4DFFAD44479A" overflow="visible">
<path d="M 6.3799996 3.78 C 6.3799996 1.88 5.38 0.48 4.18 0.48 C 3.4199998 0.48 3.1599998 0.97999996 2.86 1.38 C 2.6 1.7199999 2.26 2.02 1.8399999 2.02 C 1.4599999 2.02 1.0799999 1.68 1.0799999 1.28 C 1.0799999 0.45999998 2.78 -0.22 3.9199998 -0.22 C 6.3999996 -0.22 8.16 1.62 8.16 4.14 C 8.16 6.08 6.8199997 7.8199997 4.58 7.8199997 C 3.72 7.8199997 2.98 7.64 2.62 7.5 L 3.02 10.84 C 3.76 10.76 4.4 10.66 5.3599997 10.66 C 5.96 10.66 6.64 10.7 7.46 10.78 L 7.7799997 12.139999 L 7.64 12.219999 C 6.5 12.099999 5.42 12 4.36 12 C 3.62 12 2.8999999 12.04 2.2 12.099999 L 1.52 6.3399997 C 2.58 6.74 3.34 6.8199997 4.06 6.8199997 C 5.3599997 6.8199997 6.3799996 5.96 6.3799996 3.78 Z "/>
</symbol>
<symbol id="gDACA5EBB44D5F3DB530A1F5F650BFBAB" overflow="visible">
<path d="M 2.08 10.46 L 2.08 2.44 C 2.08 0.78 1.74 0.68 0.34 0.62 C 0.22 0.5 0.22 0.08 0.34 -0.04 C 1.24 -0.02 2.22 0 2.9399998 0 C 3.6399999 0 4.8199997 -0.02 5.8199997 -0.04 C 5.94 0.08 5.94 0.5 5.8199997 0.62 C 4.2599998 0.7 3.78 0.78 3.78 2.44 L 3.78 5.8399997 C 4.22 5.7 4.7 5.64 5.4 5.64 C 9.04 5.64 10.139999 8.0199995 10.139999 9.719999 C 10.139999 10.9 9.36 13.04 5.66 13.04 C 4.9 13.04 3.72 12.9 2.9199998 12.9 C 2.18 12.9 1.14 12.92 0.34 12.94 C 0.22 12.82 0.22 12.4 0.34 12.28 C 1.74 12.219999 2.08 12.12 2.08 10.46 Z M 3.78 11.08 C 3.78 11.66 4.08 12.36 5.52 12.36 C 6.8999996 12.36 8.28 11.9 8.28 9.36 C 8.28 7.2 7.24 6.3199997 5.2999997 6.3199997 C 4.7999997 6.3199997 4 6.3599997 3.78 6.42 Z "/>
</symbol>
<symbol id="g733371913480EE84B3609C9E9CD62F8C" overflow="visible">
<path d="M 3.34 7.8799996 C 3.22 7.7599998 3.1399999 7.7999997 3.1399999 7.98 L 3.1399999 11.66 C 3.1399999 12.96 3.22 13.759999 3.22 13.759999 C 3.22 13.9 3.1399999 13.96 2.96 13.96 C 2.46 13.759999 0.96 13.48 0.16 13.42 C 0.12 13.259999 0.16 12.94 0.28 12.82 C 0.34 12.82 0.39999998 12.82 0.45999998 12.82 C 1.3399999 12.759999 1.56 12.759999 1.56 11.179999 L 1.56 1.42 C 1.56 0.64 1.54 0.28 1.48 0 C 1.5799999 -0.16 1.68 -0.24 1.92 -0.24 C 2.04 -0.12 2.24 0.06 2.3999999 0.24 C 2.6 0.48 2.72 0.48 2.9399998 0.29999998 C 3.3999999 -0.08 4 -0.19999999 4.7 -0.19999999 C 6.74 -0.19999999 9.12 1.66 9.12 4.8399997 C 9.12 7.2799997 7.3199997 8.78 5.58 8.78 C 4.72 8.78 3.9599998 8.44 3.34 7.8799996 Z M 3.48 7.2599998 C 4 7.72 4.6 7.8999996 5.18 7.8999996 C 6.3999996 7.8999996 7.3999996 6.42 7.3999996 4.48 C 7.3999996 2.2 6.48 0.48 4.58 0.48 C 3.9599998 0.48 3.54 0.91999996 3.1399999 1.42 L 3.1399999 6.42 C 3.1399999 6.8399997 3.22 7.04 3.48 7.2599998 Z "/>
</symbol>
<symbol id="g22D858CFD6AD86697C1391C74FD687D1" overflow="visible">
<path d="M 0.85999995 8.58 C 0.58 8.58 0.5 8.34 0.5 8.179999 L 0.5 7.9199996 C 0.5 7.8199997 0.52 7.7999997 0.59999996 7.7999997 L 1.78 7.7999997 L 1.78 1.78 C 1.78 0.35999998 2.3999999 -0.19999999 3.32 -0.19999999 C 4.24 -0.19999999 5.24 0.24 6.02 1.12 C 5.98 1.3199999 5.8599997 1.4399999 5.66 1.4599999 C 5.14 1.06 4.54 0.9 4.02 0.9 C 3.48 0.9 3.36 1.5 3.36 2.74 L 3.36 7.7999997 L 5.44 7.7999997 C 5.64 7.7999997 5.92 7.8799996 5.92 8.059999 L 5.92 8.46 C 5.92 8.54 5.8599997 8.58 5.7599998 8.58 L 3.36 8.58 L 3.36 9.36 C 3.36 10.66 3.4399998 11.46 3.4399998 11.46 C 3.4399998 11.58 3.3799999 11.639999 3.28 11.639999 C 3.1999998 11.639999 3.02 11.559999 2.84 11.46 C 2.62 11.34 2.4199998 11.24 2.1599998 11.179999 C 1.92 11.099999 1.7199999 11.04 1.7199999 10.9 C 1.7199999 10.66 1.78 10.8 1.78 8.58 Z "/>
</symbol>
<symbol id="g3BBBD96D467CC564123619D79E97B4D6" overflow="visible">
<path d="M 7.8999996 12.62 C 6.74 12.78 6.7799997 13.16 4.8199997 13.16 C 2.8 13.16 1.02 11.82 1.02 9.7 C 1.02 7.6 2.76 6.64 4.52 5.96 C 5.72 5.5 7.2 4.94 7.2 2.98 C 7.2 1.36 6.2999997 0.52 4.7 0.52 C 2.84 0.52 1.64 1.38 1.1999999 3.36 C 0.94 3.4399998 0.74 3.3999999 0.53999996 3.3 C 0.62 1.76 0.7 1.24 0.94 0.26 C 2.2 0.26 2.76 -0.19999999 4.54 -0.19999999 C 5.44 -0.19999999 6.2999997 0.02 7 0.45999998 C 8.16 1.18 8.88 2.3999999 8.88 3.6799998 C 8.88 5.7999997 7.2799997 6.74 5.64 7.3599997 C 4.44 7.7999997 2.44 8.559999 2.44 10.24 C 2.44 11.36 3.46 12.48 4.64 12.48 C 6.58 12.48 7.2 11.24 7.6 9.92 C 7.8199997 9.88 8.08 9.9 8.26 10.04 C 8.179999 11 8.099999 11.559999 7.8999996 12.62 Z "/>
</symbol>
<symbol id="gB8789F2F5F06048D4163694E4C0F3B6C" overflow="visible">
<path d="M 12.36 2.44 L 12.36 10.46 C 12.36 12.12 12.7 12.219999 14.099999 12.28 C 14.219999 12.4 14.219999 12.82 14.099999 12.94 C 13.28 12.92 12.259999 12.9 11.5 12.9 C 10.76 12.9 9.8 12.92 8.92 12.94 C 8.8 12.82 8.8 12.4 8.92 12.28 C 10.32 12.219999 10.66 12.12 10.66 10.46 L 10.66 7.2599998 L 3.82 7.2599998 L 3.82 10.46 C 3.82 12.12 4.16 12.219999 5.56 12.28 C 5.68 12.4 5.68 12.82 5.56 12.94 C 4.7999997 12.92 3.98 12.9 2.96 12.9 C 1.9599999 12.9 1.14 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.26 -0.02 2.22 0 2.98 0 C 3.6999998 0 4.68 -0.02 5.56 -0.04 C 5.68 0.08 5.68 0.5 5.56 0.62 C 4.16 0.68 3.82 0.78 3.82 2.44 L 3.82 6.42 L 10.66 6.42 L 10.66 2.44 C 10.66 0.78 10.32 0.68 8.92 0.62 C 8.8 0.5 8.8 0.08 8.92 -0.04 C 9.82 -0.02 10.78 0 11.5199995 0 C 12.259999 0 13.219999 -0.02 14.099999 -0.04 C 14.219999 0.08 14.219999 0.5 14.099999 0.62 C 12.7 0.68 12.36 0.78 12.36 2.44 Z "/>
</symbol>
<symbol id="g560AC22EF992EFD90E66808483D7B3BA" overflow="visible">
<path d="M 11.12 10.24 L 11.12 3.6999998 C 11.12 3.32 11.12 3.1 10.98 3.1 C 10.9 3.1 10.599999 3.46 10.0199995 4.2 L 3.1599998 12.9 L 0.45999998 12.94 C 0.34 12.82 0.34 12.4 0.45999998 12.28 C 1.3199999 12.219999 1.92 11.5199995 2.04 11 L 2.04 2.6599998 C 2.04 0.88 1.6999999 0.76 0.29999998 0.62 C 0.17999999 0.5 0.17999999 0.08 0.29999998 -0.04 C 1.16 -0.02 2.06 0 2.54 0 C 3 0 3.9199998 -0.02 4.7599998 -0.04 C 4.88 0.08 4.88 0.5 4.7599998 0.62 C 3.36 0.76 3.02 0.84 3.02 2.6599998 L 3.02 8.78 C 3.02 9.46 3.02 9.76 3.1799998 9.76 C 3.3 9.76 3.52 9.54 3.86 9.099999 L 10.84 0.28 C 11.059999 -0.02 11.32 -0.19999999 11.639999 -0.19999999 C 11.92 -0.19999999 12.099999 0.04 12.099999 0.42 L 12.099999 10.24 C 12.099999 12.0199995 12.44 12.139999 13.84 12.28 C 13.96 12.4 13.96 12.82 13.84 12.94 C 13.0199995 12.92 12.08 12.9 11.599999 12.9 C 11.179999 12.9 10.26 12.92 9.38 12.94 C 9.26 12.82 9.26 12.4 9.38 12.28 C 10.78 12.139999 11.12 12.059999 11.12 10.24 Z "/>
</symbol>
<symbol id="g87DD77732F07A5C65A64D31E4C3C918D" overflow="visible">
<path d="M 16.199999 11.3 L 13.08 2.62 L 13.0199995 2.6399999 L 10.26 11.08 C 9.92 12.16 10.62 12.219999 11.3 12.28 C 11.42 12.4 11.42 12.82 11.3 12.94 C 10.48 12.92 9.599999 12.9 8.8 12.9 C 8.139999 12.9 7.44 12.92 6.7999997 12.94 C 6.68 12.82 6.68 12.4 6.7999997 12.28 C 7.8599997 12.219999 8.3 11.599999 8.48 11.08 L 8.94 9.76 C 9.0199995 9.5199995 9.08 9.32 9.08 9.139999 C 9.08 8.94 9.059999 8.78 8.9 8.44 L 6.3199997 2.58 L 6.22 2.6 L 3.3 11.44 C 3.06 12.139999 3.6 12.24 4.2999997 12.28 C 4.42 12.4 4.42 12.82 4.2999997 12.94 C 3.6399999 12.92 2.76 12.9 1.9799999 12.9 C 1.28 12.9 0.7 12.92 0.12 12.94 C 0 12.82 0 12.4 0.12 12.28 C 1.02 12.219999 1.16 12.2 1.54 11.12 L 5.2999997 0.29999998 C 5.4 -0.02 5.52 -0.24 5.74 -0.24 C 6 -0.24 6.12 -0.04 6.2599998 0.29999998 L 9.24 7 C 9.42 7.3999996 9.48 7.5 9.58 7.5 C 9.66 7.5 9.74 7.2799997 9.86 6.94 L 12.16 0.29999998 C 12.28 -0.04 12.38 -0.24 12.62 -0.24 C 12.84 -0.24 12.98 -0.02 13.08 0.28 L 17.1 11.059999 C 17.359999 11.759999 17.72 12.219999 18.82 12.28 C 18.939999 12.4 18.939999 12.82 18.82 12.94 C 18.24 12.92 17.6 12.9 17.08 12.9 C 16.56 12.9 15.679999 12.92 14.88 12.94 C 14.759999 12.82 14.759999 12.4 14.88 12.28 C 15.7 12.219999 16.5 12.16 16.199999 11.3 Z "/>
</symbol>
<symbol id="g3C2FFF86BC828E66F78F8A687CE12C70" overflow="visible">
<path d="M 3.34 5.72 C 3.34 6.14 3.52 6.3799996 3.6799998 6.56 C 4.44 7.2999997 5.46 7.74 6.24 7.74 C 6.64 7.74 7.06 7.48 7.2999997 7.02 C 7.5 6.62 7.54 6.08 7.54 5.48 L 7.54 2.44 C 7.54 0.79999995 7.3399997 0.71999997 6.2999997 0.62 C 6.2 0.5 6.2 0.08 6.2999997 -0.04 C 6.8599997 -0.02 7.54 0 8.34 0 C 9.139999 0 9.8 -0.02 10.46 -0.04 C 10.559999 0.08 10.559999 0.5 10.46 0.62 C 9.34 0.71999997 9.12 0.79999995 9.12 2.44 L 9.12 5.42 C 9.12 6.52 9.04 7.5 8.58 8.099999 C 8.24 8.54 7.62 8.78 6.92 8.78 C 5.94 8.78 4.74 8.5199995 3.52 7.16 C 3.52 7.14 3.5 7.14 3.48 7.12 C 3.4199998 7.04 3.32 6.92 3.32 7.16 L 3.34 11.66 C 3.34 12.96 3.4199998 13.759999 3.4199998 13.759999 C 3.4199998 13.9 3.34 13.96 3.1599998 13.96 C 2.6599998 13.759999 1.16 13.48 0.35999998 13.42 C 0.32 13.259999 0.35999998 12.94 0.48 12.82 C 0.53999996 12.82 0.59999996 12.82 0.65999997 12.82 C 1.54 12.759999 1.76 12.759999 1.76 11.179999 L 1.76 2.44 C 1.76 0.78 1.52 0.7 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.02 -0.02 1.76 0 2.56 0 C 3.32 0 3.98 -0.02 4.54 -0.04 C 4.66 0.08 4.66 0.5 4.54 0.62 C 3.52 0.7 3.34 0.78 3.34 2.44 Z "/>
</symbol>
<symbol id="g713198A7DA4F5CD7D462D4529B1D64BD" overflow="visible">
<path d="M 7.96 1.8199999 C 7.8799996 2 7.72 2.08 7.54 2.1 C 6.8599997 1.22 6 0.78 5.14 0.78 C 3.6799998 0.78 2.46 2.26 2.46 4.6 C 2.46 6.7999997 3.4199998 8.12 4.74 8.12 C 5.92 8.12 6.08 7.4199996 6.16 6.72 C 6.22 6.18 6.5 6 6.92 6 C 7.3399997 6 7.8999996 6.2599998 7.8999996 6.8799996 C 7.8999996 7.98 6.7599998 8.78 4.8399997 8.78 C 2.86 8.78 0.74 7 0.74 4.16 C 0.74 1.5799999 2.18 -0.19999999 4.7 -0.19999999 C 5.9 -0.19999999 6.96 0.17999999 7.96 1.8199999 Z "/>
</symbol>
<symbol id="g757CB60871AF468909C575234729D90A" overflow="visible">
<path d="M 0.88 5.04 C 0.88 4.14 0.96 -0.48 5.12 -4.08 C 5.3199997 -4.04 5.48 -3.8999999 5.54 -3.74 C 4.88 -2.98 2.54 -0.22 2.54 5.04 C 2.54 10.3 4.9 13.059999 5.54 13.78 C 5.48 13.98 5.3399997 14.12 5.12 14.139999 C 2.74 12.099999 0.88 8.76 0.88 5.04 Z "/>
</symbol>
<symbol id="gF5D967C73B153E080367AE40708278EE" overflow="visible">
<path d="M 5.08 5.04 C 5.08 5.94 5 10.559999 0.84 14.16 C 0.64 14.12 0.48 13.98 0.42 13.82 C 1.0799999 13.059999 3.4199998 10.3 3.4199998 5.04 C 3.4199998 -0.22 1.06 -2.98 0.42 -3.6999998 C 0.48 -3.8999999 0.62 -4.04 0.84 -4.06 C 3.22 -2.02 5.08 1.3199999 5.08 5.04 Z "/>
</symbol>
<symbol id="gAA14E57E2DCC57A3F7809273EECD3C51" overflow="visible">
<path d="M 7.9104 1.5616 L 7.9104 6.6944 C 7.9104 7.7567997 8.128 7.8208 9.024 7.8592 C 9.1008 7.936 9.1008 8.2048 9.024 8.2816 C 8.4992 8.2688 7.8464 8.256 7.3599997 8.256 C 6.8863997 8.256 6.272 8.2688 5.7088 8.2816 C 5.632 8.2048 5.632 7.936 5.7088 7.8592 C 6.6047997 7.8208 6.8223996 7.7567997 6.8223996 6.6944 L 6.8223996 4.6464 L 2.4448 4.6464 L 2.4448 6.6944 C 2.4448 7.7567997 2.6624 7.8208 3.5584 7.8592 C 3.6352 7.936 3.6352 8.2048 3.5584 8.2816 C 3.072 8.2688 2.5472 8.256 1.8944 8.256 C 1.2544 8.256 0.72959995 8.2688 0.24319999 8.2816 C 0.1664 8.2048 0.1664 7.936 0.24319999 7.8592 C 1.1392 7.8208 1.3568 7.7567997 1.3568 6.6944 L 1.3568 1.5616 C 1.3568 0.4992 1.1392 0.43519998 0.24319999 0.39679998 C 0.1664 0.32 0.1664 0.0512 0.24319999 -0.0256 C 0.8064 -0.0128 1.4208 0 1.9072 0 C 2.368 0 2.9952 -0.0128 3.5584 -0.0256 C 3.6352 0.0512 3.6352 0.32 3.5584 0.39679998 C 2.6624 0.43519998 2.4448 0.4992 2.4448 1.5616 L 2.4448 4.1088 L 6.8223996 4.1088 L 6.8223996 1.5616 C 6.8223996 0.4992 6.6047997 0.43519998 5.7088 0.39679998 C 5.632 0.32 5.632 0.0512 5.7088 -0.0256 C 6.2848 -0.0128 6.8992 0 7.3728 0 C 7.8464 0 8.4608 -0.0128 9.024 -0.0256 C 9.1008 0.0512 9.1008 0.32 9.024 0.39679998 C 8.128 0.43519998 7.9104 0.4992 7.9104 1.5616 Z "/>
</symbol>
<symbol id="gF5F8064101DBF0FCB4BCFDA7012527FE" overflow="visible">
<path d="M 2.3167999 1.5616 L 2.3167999 4.1088 C 2.3167999 4.7488 2.368 5.568 2.368 5.568 C 2.368 5.6191998 2.304 5.6576 2.2015998 5.6576 C 1.8432 5.5168 1.3312 5.4016 0.44799998 5.2864 C 0.4224 5.2096 0.44799998 5.0048 0.4736 4.928 C 1.1776 4.864 1.3055999 4.7872 1.3055999 4.0576 L 1.3055999 1.5616 C 1.3055999 0.4992 1.1647999 0.4608 0.384 0.39679998 C 0.30719998 0.32 0.30719998 0.0512 0.384 -0.0256 C 0.8064 -0.0128 1.3055999 0 1.8176 0 C 2.3295999 0 2.816 -0.0128 3.2384 -0.0256 C 3.3151999 0.0512 3.3151999 0.32 3.2384 0.39679998 C 2.4575999 0.44799998 2.3167999 0.4992 2.3167999 1.5616 Z M 1.152 7.6671996 C 1.152 7.3343997 1.4591999 7.0016 1.7664 7.0016 C 2.1248 7.0016 2.432 7.3472 2.432 7.6159997 C 2.432 7.9231997 2.1632 8.2816 1.8176 8.2816 C 1.5103999 8.2816 1.152 7.9743996 1.152 7.6671996 Z "/>
</symbol>
<symbol id="g3976D55F213F07C6469FD06EC16139AA" overflow="visible">
<path d="M 4.9407997 1.1904 C 4.4672 0.704 4.0959997 0.4992 3.3536 0.4992 C 2.8927999 0.4992 2.3552 0.768 1.9583999 1.4208 C 1.7024 1.8432 1.5488 2.432 1.5488 3.1743999 L 4.9536 3.1488 C 5.1071997 3.1488 5.1967998 3.2256 5.1967998 3.3664 C 5.1967998 4.4416 4.8128 5.5936 3.0335999 5.5936 C 1.92 5.5936 0.4736 4.5312 0.4736 2.5856 C 0.4736 1.8687999 0.65279996 1.1776 1.0752 0.69119996 C 1.5103999 0.1792 2.112 -0.12799999 3.0335999 -0.12799999 C 4.0064 -0.12799999 4.6976 0.32 5.2096 0.9856 C 5.1712 1.1136 5.0944 1.1776 4.9407997 1.1904 Z M 1.5871999 3.6095998 C 1.8304 5.0559998 2.7264 5.1712 3.0335999 5.1712 C 3.52 5.1712 4.0959997 4.9024 4.0959997 3.8272 C 4.0959997 3.712 4.0448 3.648 3.9039998 3.648 Z "/>
</symbol>
<symbol id="gB7BB853387AAC07ADB7DDEF96856059B" overflow="visible">
<path d="M 2.2528 4.5824 C 2.2272 5.0944 2.2144 5.4272 2.1504 5.5551996 C 2.1248 5.6191998 2.0992 5.6576 1.9968 5.6576 C 1.6384 5.5168 1.3055999 5.4016 0.4224 5.2864 C 0.39679998 5.2096 0.4224 5.0048 0.44799998 4.928 C 1.1392 4.864 1.28 4.7999997 1.28 4.0576 L 1.28 1.5616 C 1.28 0.4992 1.1264 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7808 -0.0128 1.28 0 1.7919999 0 C 2.304 0 2.8927999 -0.0128 3.3407998 -0.0256 C 3.4176 0.0512 3.4176 0.32 3.3407998 0.39679998 C 2.4448 0.4608 2.2912 0.4992 2.2912 1.5616 L 2.2912 3.3407998 C 2.2912 3.6736 2.4448 3.968 2.5983999 4.1984 C 2.7391999 4.4031997 3.0335999 4.8255997 3.1871998 4.8255997 C 3.3023999 4.8255997 3.4176 4.7999997 3.52 4.6591997 C 3.6095998 4.5312 3.7631998 4.3648 3.9808 4.3648 C 4.288 4.3648 4.5824 4.6847997 4.5824 5.0048 C 4.5824 5.2479997 4.3519998 5.6191998 3.8144 5.6191998 C 3.2128 5.6191998 2.688 5.0559998 2.3936 4.5568 C 2.3167999 4.416 2.2528 4.5183997 2.2528 4.5824 Z "/>
</symbol>
<symbol id="gF8EC31AC53CF59E01ED9143906F6DA7B" overflow="visible">
<path d="M 3.7503998 0.61439997 C 3.8272 0.21759999 3.968 -0.12799999 4.608 -0.12799999 C 5.0944 -0.12799999 5.5551996 0.0896 5.824 0.34559998 C 5.7984 0.4992 5.7472 0.61439997 5.6064 0.69119996 C 5.5168 0.61439997 5.2992 0.48639998 5.1328 0.48639998 C 4.7616 0.48639998 4.7488 0.9856 4.7488 1.5744 L 4.7488 3.4559999 C 4.7488 5.2736 3.7503998 5.6191998 2.816 5.6191998 C 1.7664 5.6191998 0.704 4.928 0.704 4.1984 C 0.704 3.8911998 0.8576 3.7375998 1.152 3.7375998 C 1.5231999 3.7375998 1.7536 4.0064 1.7536 4.1728 C 1.7536 4.2623997 1.7407999 4.3519998 1.7152 4.4031997 C 1.7024 4.4416 1.6896 4.5183997 1.6896 4.6591997 C 1.6896 5.0559998 2.2272 5.1967998 2.7136 5.1967998 C 3.1488 5.1967998 3.7503998 4.9792 3.7503998 3.5328 C 3.7503998 3.4431999 3.712 3.392 3.6736 3.3792 L 2.5728 3.1104 C 1.344 2.8032 0.4608 2.1248 0.4608 1.2544 C 0.4608 0.2048 1.1776 -0.12799999 2.0736 -0.12799999 C 2.5216 -0.12799999 2.9055998 -0.0256 3.4687998 0.4096 L 3.7247999 0.61439997 Z M 3.7503998 2.9824 L 3.7503998 1.2928 C 3.7503998 1.1264 3.6736 1.0368 3.5712 0.96 C 3.2384 0.69119996 2.8032 0.39679998 2.4448 0.39679998 C 1.8047999 0.39679998 1.5231999 0.9088 1.5231999 1.3055999 C 1.5231999 1.8815999 1.7919999 2.4703999 2.7391999 2.7136 Z "/>
</symbol>
<symbol id="g68DDE7C8FDC8A226B6C32EAD39AF7364" overflow="visible">
<path d="M 5.0944 1.1647999 C 5.0432 1.28 4.9407997 1.3312 4.8255997 1.344 C 4.3904 0.7808 3.84 0.4992 3.2896 0.4992 C 2.3552 0.4992 1.5744 1.4463999 1.5744 2.944 C 1.5744 4.3519998 2.1887999 5.1967998 3.0335999 5.1967998 C 3.7888 5.1967998 3.8911998 4.7488 3.9424 4.3008 C 3.9808 3.9552 4.16 3.84 4.4288 3.84 C 4.6976 3.84 5.0559998 4.0064 5.0559998 4.4031997 C 5.0559998 5.1071997 4.3264 5.6191998 3.0976 5.6191998 C 1.8304 5.6191998 0.4736 4.48 0.4736 2.6624 C 0.4736 1.0112 1.3952 -0.12799999 3.008 -0.12799999 C 3.776 -0.12799999 4.4544 0.1152 5.0944 1.1647999 Z "/>
</symbol>
<symbol id="g570B752173035444311A253BD2376AD" overflow="visible">
<path d="M 2.1376 3.6608 C 2.1376 3.9296 2.2528 4.0832 2.3552 4.1984 C 2.8416 4.672 3.4944 4.9536 3.9936 4.9536 C 4.2496 4.9536 4.5183997 4.7872 4.672 4.4927998 C 4.7999997 4.2367997 4.8255997 3.8911998 4.8255997 3.5072 L 4.8255997 1.5616 C 4.8255997 0.51199996 4.6976 0.4608 4.032 0.39679998 C 3.968 0.32 3.968 0.0512 4.032 -0.0256 C 4.3904 -0.0128 4.8255997 0 5.3375998 0 C 5.8496 0 6.272 -0.0128 6.6944 -0.0256 C 6.7584 0.0512 6.7584 0.32 6.6944 0.39679998 C 5.9775996 0.4608 5.8367996 0.51199996 5.8367996 1.5616 L 5.8367996 3.4687998 C 5.8367996 4.1728 5.7855997 4.7999997 5.4912 5.184 C 5.2736 5.4656 4.8768 5.6191998 4.4288 5.6191998 C 3.8016 5.6191998 3.0335999 5.4528 2.2528 4.5824 C 2.2528 4.5696 2.24 4.5696 2.2272 4.5568 C 2.1887999 4.5056 2.1248 4.4288 2.1248 4.5824 L 2.1376 7.4624 C 2.1376 8.2944 2.1887999 8.806399 2.1887999 8.806399 C 2.1887999 8.896 2.1376 8.9344 2.0224 8.9344 C 1.7024 8.806399 0.7424 8.6272 0.2304 8.588799 C 0.2048 8.4864 0.2304 8.2816 0.30719998 8.2048 C 0.34559998 8.2048 0.384 8.2048 0.4224 8.2048 C 0.9856 8.1664 1.1264 8.1664 1.1264 7.1552 L 1.1264 1.5616 C 1.1264 0.4992 0.97279996 0.44799998 0.2304 0.39679998 C 0.15359999 0.32 0.15359999 0.0512 0.2304 -0.0256 C 0.65279996 -0.0128 1.1264 0 1.6384 0 C 2.1248 0 2.5472 -0.0128 2.9055998 -0.0256 C 2.9824 0.0512 2.9824 0.32 2.9055998 0.39679998 C 2.2528 0.44799998 2.1376 0.4992 2.1376 1.5616 Z "/>
</symbol>
<symbol id="g9662C1D9A80FEB5040A57FD9DFCA7985" overflow="visible">
<path d="M 1.216 1.5616 C 1.216 0.4992 1.0752 0.43519998 0.2944 0.39679998 C 0.21759999 0.32 0.21759999 0.0512 0.2944 -0.0256 C 0.7424 -0.0128 1.216 0 1.7279999 0 C 2.24 0 2.7264 -0.0128 3.1488 -0.0256 C 3.2256 0.0512 3.2256 0.32 3.1488 0.39679998 C 2.368 0.43519998 2.2272 0.4992 2.2272 1.5616 L 2.2272 7.4624 C 2.2272 8.2944 2.2784 8.806399 2.2784 8.806399 C 2.2784 8.896 2.2272 8.9344 2.112 8.9344 C 1.7919999 8.806399 0.83199996 8.6272 0.32 8.588799 C 0.2944 8.4864 0.32 8.2816 0.39679998 8.2048 C 1.1392 8.1536 1.216 8.1152 1.216 7.1552 Z "/>
</symbol>
<symbol id="g1CB3EC9D05726EBFDE8ADABEC8504FCD" overflow="visible">
<path d="M 7.1168 6.5536 L 7.1168 2.368 C 7.1168 2.1248 7.1168 1.984 7.0271997 1.984 C 6.976 1.984 6.784 2.2144 6.4128 2.688 L 2.0224 8.256 L 0.2944 8.2816 C 0.21759999 8.2048 0.21759999 7.936 0.2944 7.8592 C 0.8448 7.8208 1.2287999 7.3728 1.3055999 7.04 L 1.3055999 1.7024 C 1.3055999 0.5632 1.0879999 0.48639998 0.192 0.39679998 C 0.1152 0.32 0.1152 0.0512 0.192 -0.0256 C 0.7424 -0.0128 1.3184 0 1.6256 0 C 1.92 0 2.5088 -0.0128 3.0463998 -0.0256 C 3.1232 0.0512 3.1232 0.32 3.0463998 0.39679998 C 2.1504 0.48639998 1.9327999 0.5376 1.9327999 1.7024 L 1.9327999 5.6191998 C 1.9327999 6.0544 1.9327999 6.2464 2.0351999 6.2464 C 2.112 6.2464 2.2528 6.1056 2.4703999 5.824 L 6.9375997 0.1792 C 7.0783997 -0.0128 7.2447996 -0.12799999 7.4495997 -0.12799999 C 7.6288 -0.12799999 7.744 0.0256 7.744 0.2688 L 7.744 6.5536 C 7.744 7.6927996 7.9616 7.7696 8.8576 7.8592 C 8.9344 7.936 8.9344 8.2048 8.8576 8.2816 C 8.3328 8.2688 7.7311997 8.256 7.424 8.256 C 7.1552 8.256 6.5664 8.2688 6.0032 8.2816 C 5.9263997 8.2048 5.9263997 7.936 6.0032 7.8592 C 6.8992 7.7696 7.1168 7.7184 7.1168 6.5536 Z "/>
</symbol>
<symbol id="gD62975B7DE3250BE5F195D0E8335F60D" overflow="visible">
<path d="M 4.16 5.0944 C 4.8512 5.0432 4.928 4.8896 4.6591997 4.2367997 L 3.6223998 1.7279999 C 3.4176 1.2287999 3.3536 1.2287999 3.1488 1.7664 L 2.2272 4.2367997 C 1.9968 4.8512 1.9455999 5.0048 2.6239998 5.0944 C 2.7008 5.1712 2.7008 5.44 2.6239998 5.5168 C 2.2015998 5.5039997 1.7536 5.4912 1.3312 5.4912 C 0.9088 5.4912 0.5248 5.5039997 0.1408 5.5168 C 0.063999996 5.44 0.063999996 5.1712 0.1408 5.0944 C 0.8192 5.0176 0.9088 4.8128 1.1647999 4.16 L 2.8032 0.1152 C 2.8799999 -0.076799996 2.9568 -0.15359999 3.1232 -0.15359999 C 3.2512 -0.15359999 3.3407998 -0.076799996 3.4304 0.1408 L 5.1328 4.1472 C 5.376 4.7104 5.5168 5.0304 6.2335997 5.0944 C 6.3104 5.1712 6.3104 5.44 6.2335997 5.5168 C 5.9775996 5.5039997 5.6703997 5.4912 5.3375998 5.4912 C 4.9151998 5.4912 4.48 5.5039997 4.16 5.5168 C 4.0832 5.44 4.0832 5.1712 4.16 5.0944 Z "/>
</symbol>
<symbol id="gEFCBD5CCFA072E8B49E2065B449FDBBF" overflow="visible">
<path d="M 5.6832 4.9536 C 5.9263997 4.9536 6.1568 5.184 6.1568 5.44 C 6.1568 5.7088 5.9136 5.9136 5.568 5.9136 C 5.2352 5.9136 4.6208 5.6959996 4.288 5.2608 C 4.1344 5.3631997 3.712 5.6191998 2.9568 5.6191998 C 1.8176 5.6191998 0.768 4.8512 0.768 3.6736 C 0.768 2.9824 1.0752 2.5856 1.4336 2.24 C 1.0752 1.9327999 0.87039995 1.3823999 0.87039995 0.9472 C 0.87039995 0.48639998 1.1264 0.12799999 1.4591999 -0.038399998 C 0.768 -0.44799998 0.4096 -1.0368 0.4096 -1.5871999 C 0.4096 -2.7008 1.4591999 -3.0463998 2.4448 -3.0463998 C 4.1728 -3.0463998 6.0415998 -2.2144 6.0415998 -0.83199996 C 6.0415998 -0.4224 5.8496 -0.1024 5.4783998 0.2048 C 4.9792 0.61439997 4.0832 0.6272 3.6095998 0.6272 C 3.3792 0.6272 3.0591998 0.6016 2.7519999 0.5632 C 2.56 0.55039996 2.432 0.5376 2.368 0.5376 C 1.9968 0.5376 1.5488 0.7168 1.5488 1.2672 C 1.5488 1.5231999 1.6256 1.7919999 1.7792 2.0096 C 2.0864 1.8304 2.4448 1.7407999 2.944 1.7407999 C 4.0703998 1.7407999 5.1071997 2.4448 5.1071997 3.6992 C 5.1071997 4.3008 4.928 4.6464 4.5568 5.0304 C 4.6464 5.1584 4.9024 5.3375998 5.0688 5.3375998 C 5.1584 5.3375998 5.2479997 5.2992 5.3248 5.184 C 5.376 5.0815997 5.5424 4.9536 5.6832 4.9536 Z M 1.6896 -0.12799999 C 1.8304 -0.1664 2.0351999 -0.192 2.2015998 -0.192 C 2.5983999 -0.192 2.9568 -0.15359999 3.136 -0.15359999 C 3.776 -0.15359999 4.3136 -0.1664 4.6847997 -0.3712 C 5.184 -0.65279996 5.3375998 -0.83199996 5.3375998 -1.1647999 C 5.3375998 -2.0864 3.9808 -2.5728 2.8288 -2.5728 C 2.368 -2.5728 1.2928 -2.2015998 1.2928 -1.3312 C 1.2928 -0.89599997 1.3184 -0.576 1.6896 -0.12799999 Z M 4.0832 3.5712 C 4.0832 2.3808 3.4815998 2.1376 3.008 2.1376 C 1.9327999 2.1376 1.8176 3.0463998 1.8176 3.8655999 C 1.8176 4.7616 2.1376 5.2223997 2.8416 5.2223997 C 3.648 5.2223997 4.0832 4.6335998 4.0832 3.5712 Z "/>
</symbol>
<symbol id="gD5EEFB9760BC9A91B84F628EDDA52971" overflow="visible">
<path d="M 2.1376 5.0432 C 2.0607998 4.9663997 2.0096 4.992 2.0096 5.1071997 L 2.0096 7.4624 C 2.0096 8.2944 2.0607998 8.806399 2.0607998 8.806399 C 2.0607998 8.896 2.0096 8.9344 1.8944 8.9344 C 1.5744 8.806399 0.61439997 8.6272 0.1024 8.588799 C 0.076799996 8.4864 0.1024 8.2816 0.1792 8.2048 C 0.21759999 8.2048 0.25599998 8.2048 0.2944 8.2048 C 0.8576 8.1664 0.9984 8.1664 0.9984 7.1552 L 0.9984 0.9088 C 0.9984 0.4096 0.9856 0.1792 0.9472 0 C 1.0112 -0.1024 1.0752 -0.15359999 1.2287999 -0.15359999 C 1.3055999 -0.076799996 1.4336 0.038399998 1.536 0.15359999 C 1.6639999 0.30719998 1.7407999 0.30719998 1.8815999 0.192 C 2.1759999 -0.0512 2.56 -0.12799999 3.008 -0.12799999 C 4.3136 -0.12799999 5.8367996 1.0624 5.8367996 3.0976 C 5.8367996 4.6591997 4.6847997 5.6191998 3.5712 5.6191998 C 3.0207999 5.6191998 2.5344 5.4016 2.1376 5.0432 Z M 2.2272 4.6464 C 2.56 4.9407997 2.944 5.0559998 3.3151999 5.0559998 C 4.0959997 5.0559998 4.736 4.1088 4.736 2.8672 C 4.736 1.408 4.1472 0.30719998 2.9312 0.30719998 C 2.5344 0.30719998 2.2656 0.5888 2.0096 0.9088 L 2.0096 4.1088 C 2.0096 4.3775997 2.0607998 4.5056 2.2272 4.6464 Z "/>
</symbol>
<symbol id="g83A6AA7A836EACB3652229F4716CDAF" overflow="visible">
<path d="M 5.0559998 8.076799 C 4.3136 8.1792 4.3392 8.4223995 3.0848 8.4223995 C 1.7919999 8.4223995 0.65279996 7.5648 0.65279996 6.2079997 C 0.65279996 4.864 1.7664 4.2496 2.8927999 3.8144 C 3.6608 3.52 4.608 3.1615999 4.608 1.9072 C 4.608 0.87039995 4.032 0.3328 3.008 0.3328 C 1.8176 0.3328 1.0496 0.8832 0.768 2.1504 C 0.6016 2.2015998 0.4736 2.1759999 0.34559998 2.112 C 0.39679998 1.1264 0.44799998 0.79359996 0.6016 0.1664 C 1.408 0.1664 1.7664 -0.12799999 2.9055998 -0.12799999 C 3.4815998 -0.12799999 4.032 0.0128 4.48 0.2944 C 5.2223997 0.75519997 5.6832 1.536 5.6832 2.3552 C 5.6832 3.712 4.6591997 4.3136 3.6095998 4.7104 C 2.8416 4.992 1.5616 5.4783998 1.5616 6.5536 C 1.5616 7.2704 2.2144 7.9872 2.9696 7.9872 C 4.2111998 7.9872 4.608 7.1935997 4.864 6.3487997 C 5.0048 6.3231997 5.1712 6.336 5.2864 6.4256 C 5.2352 7.04 5.184 7.3984 5.0559998 8.076799 Z "/>
</symbol>
<symbol id="gDB4862E33098F259EEBBA99A57E5AFA" overflow="visible">
<path d="M 2.1759999 4.5824 C 2.1632 4.9663997 2.1376 5.4272 2.0736 5.5551996 C 2.0479999 5.6191998 2.0224 5.6576 1.92 5.6576 C 1.5616 5.5168 1.2287999 5.4016 0.34559998 5.2864 C 0.32 5.2096 0.34559998 5.0048 0.3712 4.928 C 1.0624 4.864 1.2032 4.7999997 1.2032 4.0576 L 1.2032 1.5616 C 1.2032 0.51199996 1.0368 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7168 -0.0128 1.2032 0 1.7152 0 C 2.2272 0 2.6239998 -0.0128 3.008 -0.0256 C 3.0848 0.0512 3.0848 0.32 3.008 0.39679998 C 2.3552 0.4608 2.2144 0.51199996 2.2144 1.5616 L 2.2144 3.6608 C 2.2144 3.9296 2.3295999 4.0832 2.432 4.1984 C 2.944 4.6976 3.4176 4.9536 3.8144 4.9536 C 4.3008 4.9536 4.6591997 4.6464 4.6591997 3.7888 L 4.6591997 1.5616 C 4.6591997 0.51199996 4.5568 0.44799998 3.8655999 0.39679998 C 3.8016 0.32 3.8016 0.0512 3.8655999 -0.0256 C 4.1856 -0.0128 4.6591997 0 5.1712 0 C 5.6832 0 6.1056 -0.0128 6.4256 -0.0256 C 6.4895997 0.0512 6.4895997 0.32 6.4256 0.39679998 C 5.7855997 0.44799998 5.6703997 0.51199996 5.6703997 1.5616 L 5.6703997 3.5967999 C 5.6703997 3.776 5.6703997 3.9552 5.6576 4.1088 C 6.272 4.7872 6.848 4.9536 7.3472 4.9536 C 7.8335996 4.9536 8.1152 4.672 8.1152 3.8144 L 8.1152 1.5616 C 8.1152 0.51199996 7.9872 0.44799998 7.3216 0.39679998 C 7.2576 0.32 7.2576 0.0512 7.3216 -0.0256 C 7.6415997 -0.0128 8.1152 0 8.6272 0 C 9.1392 0 9.5872 -0.0128 9.9456 -0.0256 C 10.0096 0.0512 10.0096 0.32 9.9456 0.39679998 C 9.2416 0.44799998 9.1264 0.51199996 9.1264 1.5616 L 9.1264 3.5839999 C 9.1264 4.7232 8.9344 5.6191998 7.8079996 5.6191998 C 7.1552 5.6191998 6.3616 5.376 5.6959996 4.672 C 5.6576 4.6335998 5.5808 4.5696 5.5551996 4.6847997 C 5.44 5.2096 4.9407997 5.6191998 4.2752 5.6191998 C 3.5328 5.6191998 2.8672 5.184 2.3295999 4.5824 C 2.2656 4.5183997 2.1887999 4.4288 2.1759999 4.5824 Z "/>
</symbol>
<symbol id="g793DBE65A5AEC1A16A65955B6C0E046" overflow="visible">
<path d="M 10.368 7.232 L 8.3712 1.6768 L 8.3328 1.6896 L 6.5664 7.0912 C 6.3487997 7.7823997 6.7967997 7.8208 7.232 7.8592 C 7.3087997 7.936 7.3087997 8.2048 7.232 8.2816 C 6.7072 8.2688 6.144 8.256 5.632 8.256 C 5.2096 8.256 4.7616 8.2688 4.3519998 8.2816 C 4.2752 8.2048 4.2752 7.936 4.3519998 7.8592 C 5.0304 7.8208 5.312 7.424 5.4272 7.0912 L 5.7216 6.2464 C 5.7728 6.0927997 5.8111997 5.9648 5.8111997 5.8496 C 5.8111997 5.7216 5.7984 5.6191998 5.6959996 5.4016 L 4.0448 1.6511999 L 3.9808 1.6639999 L 2.112 7.3216 C 1.9583999 7.7696 2.304 7.8335996 2.7519999 7.8592 C 2.8288 7.936 2.8288 8.2048 2.7519999 8.2816 C 2.3295999 8.2688 1.7664 8.256 1.2672 8.256 C 0.8192 8.256 0.44799998 8.2688 0.076799996 8.2816 C 0 8.2048 0 7.936 0.076799996 7.8592 C 0.65279996 7.8208 0.7424 7.8079996 0.9856 7.1168 L 3.392 0.192 C 3.4559999 -0.0128 3.5328 -0.15359999 3.6736 -0.15359999 C 3.84 -0.15359999 3.9167998 -0.0256 4.0064 0.192 L 5.9136 4.48 C 6.0288 4.736 6.0671997 4.7999997 6.1312 4.7999997 C 6.1823997 4.7999997 6.2335997 4.6591997 6.3104 4.4416 L 7.7823997 0.192 C 7.8592 -0.0256 7.9231997 -0.15359999 8.076799 -0.15359999 C 8.2176 -0.15359999 8.3071995 -0.0128 8.3712 0.1792 L 10.943999 7.0783997 C 11.110399 7.5263996 11.340799 7.8208 12.0448 7.8592 C 12.1216 7.936 12.1216 8.2048 12.0448 8.2816 C 11.673599 8.2688 11.264 8.256 10.9312 8.256 C 10.5984 8.256 10.0352 8.2688 9.5232 8.2816 C 9.4464 8.2048 9.4464 7.936 9.5232 7.8592 C 10.047999 7.8208 10.559999 7.7823997 10.368 7.232 Z "/>
</symbol>
<symbol id="gA11612CECC8CBEF18835767DAB11B2F7" overflow="visible">
<path d="M 0.5248 2.6239998 C 0.5248 1.3184 1.3952 -0.12799999 3.2128 -0.12799999 C 4.032 -0.12799999 4.6591997 0.1664 5.0944 0.5888 C 5.6703997 1.152 5.9263997 1.9583999 5.9263997 2.7391999 C 5.9263997 4.0703998 5.1967998 5.6191998 3.2384 5.6191998 C 2.3936 5.6191998 1.7024 5.2736 1.2287999 4.7232 C 0.768 4.1728 0.5248 3.4304 0.5248 2.6239998 Z M 3.0463998 5.1712 C 4.1472 5.1712 4.8255997 4.1728 4.8255997 2.3295999 C 4.8255997 0.7168 3.9936 0.32 3.392 0.32 C 2.0607998 0.32 1.6256 1.9327999 1.6256 2.9183998 C 1.6256 4.032 1.8944 5.1712 3.0463998 5.1712 Z "/>
</symbol>
<symbol id="gCEFEF3D67F35C6E83CC3757B1DD21B13" overflow="visible">
<path d="M 4.2752 0.64 C 4.3392 0.69119996 4.4544 0.7168 4.4672 0.6272 C 4.5056 0.32 4.608 -0.12799999 4.608 -0.12799999 C 4.7104 -0.1664 4.7743998 -0.15359999 4.8512 -0.12799999 C 5.1328 0.1024 5.5808 0.2944 6.3616 0.384 C 6.4384 0.4608 6.4384 0.65279996 6.3616 0.72959995 C 5.5424 0.79359996 5.4272 1.0368 5.4272 1.6639999 L 5.4272 7.4624 C 5.4272 8.2944 5.4783998 8.806399 5.4783998 8.806399 C 5.4783998 8.896 5.4272 8.9344 5.312 8.9344 C 4.992 8.806399 4.032 8.6272 3.52 8.588799 C 3.4944 8.4864 3.52 8.2816 3.5967999 8.2048 C 3.6352 8.2048 3.6736 8.2048 3.712 8.2048 C 4.2752 8.1664 4.416 8.1664 4.416 7.1552 L 4.416 5.5168 C 4.416 5.4272 4.3904 5.4016 4.3008 5.4016 C 4.2496 5.4016 3.7247999 5.6191998 3.3023999 5.6191998 C 2.4575999 5.6191998 1.8944 5.3375998 1.3823999 4.8512 C 0.83199996 4.3008 0.4992 3.5456 0.4992 2.5983999 C 0.4992 1.0239999 1.2928 -0.12799999 2.6752 -0.12799999 C 3.1743999 -0.12799999 3.648 0.12799999 4.2752 0.64 Z M 4.416 1.5871999 C 4.416 1.344 4.3904 1.2415999 4.2111998 1.0879999 C 3.7375998 0.6784 3.3279998 0.4736 3.008 0.4736 C 2.3167999 0.4736 1.5999999 1.2287999 1.5999999 2.8288 C 1.5999999 3.7503998 1.7792 4.2623997 1.9712 4.5312 C 2.368 5.1328 2.9055998 5.1712 3.1615999 5.1712 C 3.6223998 5.1712 3.9424 5.0048 4.1984 4.7104 C 4.3775997 4.5056 4.416 4.416 4.416 4.0192 Z "/>
</symbol>
<symbol id="g645CA8FA3D9155E2CBD9F8EED3C1540D" overflow="visible">
<path d="M 1.9968 4.7104 C 1.984 5.0944 1.9583999 5.4272 1.8944 5.5551996 C 1.8687999 5.6191998 1.8432 5.6576 1.7407999 5.6576 C 1.3823999 5.5168 1.0496 5.4016 0.1664 5.2864 C 0.1408 5.2096 0.1664 5.0048 0.192 4.928 C 0.8832 4.864 1.0239999 4.7999997 1.0239999 4.0576 L 1.0239999 -1.408 C 1.0239999 -2.4703999 0.8832 -2.5344 0.1024 -2.5728 C 0.0256 -2.6496 0.0256 -2.9183998 0.1024 -2.9952 C 0.55039996 -2.9824 1.0239999 -2.9696 1.536 -2.9696 C 2.0479999 -2.9696 2.6624 -2.9824 3.0848 -2.9952 C 3.1615999 -2.9183998 3.1615999 -2.6496 3.0848 -2.5728 C 2.1759999 -2.5216 2.0351999 -2.4703999 2.0351999 -1.408 L 2.0351999 -0.0256 C 2.0351999 0.1408 2.0864 0.12799999 2.2144 0.076799996 C 2.5344 -0.0512 2.9183998 -0.12799999 3.3279998 -0.12799999 C 4.0448 -0.12799999 4.6847997 0.0896 5.2096 0.5888 C 5.8111997 1.1776 6.1568 1.9712 6.1568 3.008 C 6.1568 4.3648 5.1967998 5.6191998 3.8911998 5.6191998 C 3.3023999 5.6191998 2.6496 5.2352 2.1376 4.6591997 C 2.0607998 4.5824 2.0096 4.5824 1.9968 4.7104 Z M 2.24 4.2367997 C 2.5728 4.6464 3.1615999 5.0304 3.5328 5.0304 C 4.3519998 5.0304 5.0559998 4.1088 5.0559998 2.6624 C 5.0559998 1.6128 4.6847997 0.30719998 3.2512 0.30719998 C 3.0207999 0.30719998 2.5728 0.3712 2.3423998 0.576 C 2.0864 0.8064 2.0351999 0.8832 2.0351999 1.344 L 2.0351999 3.6736 C 2.0351999 3.9424 2.0864 4.0576 2.24 4.2367997 Z "/>
</symbol>
<symbol id="g58626FCFBD19425464A4FA7F304374C4" overflow="visible">
<path d="M 5.104 3.0240002 C 5.104 1.5040001 4.3040004 0.384 3.344 0.384 C 2.736 0.384 2.528 0.78400004 2.288 1.1040001 C 2.0800002 1.376 1.8080001 1.616 1.4720001 1.616 C 1.1680001 1.616 0.864 1.3440001 0.864 1.024 C 0.864 0.36800003 2.2240002 -0.17600001 3.1360002 -0.17600001 C 5.1200004 -0.17600001 6.5280004 1.296 6.5280004 3.3120003 C 6.5280004 4.8640003 5.4560003 6.2560005 3.6640003 6.2560005 C 2.976 6.2560005 2.384 6.1120005 2.0960002 6.0000005 L 2.4160001 8.672001 C 3.0080001 8.608001 3.5200002 8.528001 4.288 8.528001 C 4.768 8.528001 5.3120003 8.56 5.9680004 8.624001 L 6.2240005 9.712001 L 6.1120005 9.776 C 5.2000003 9.68 4.3360004 9.6 3.4880002 9.6 C 2.8960001 9.6 2.3200002 9.632001 1.7600001 9.68 L 1.2160001 5.072 C 2.0640001 5.392 2.6720002 5.4560003 3.2480001 5.4560003 C 4.288 5.4560003 5.104 4.768 5.104 3.0240002 Z "/>
</symbol>
<symbol id="g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" overflow="visible">
<path d="M 4.688 10.336 L 4.032 10.336 L 0.24000001 -0.94400007 L 0.896 -0.94400007 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
</defs>
</div>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g/>
</g>
</g>
<g transform="translate(40 30)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(624.3697637795275 25.8)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6E7B5CC2B72AC8CDDEB63FB023F45240" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gAF2E61F9C5EC3B2D9B048D1511B1060D" x="29.2" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g385ED71BD3F10D2170A1311D8F1A15B" x="53.12" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g2192B3D4CEA94ECF87445F8EE62E404B" x="67.44" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g8F4F96B13A9D8B27A4F3C34609AEF61C" x="80.44" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9BEF8AB47349CEAA320776726D3DB3DB" x="93.32" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g5CEF84A95ABDCAB0EDEF87161576AC77" x="117.96" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 41.800000000000004)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g985B950D50769631420A9A59AEA7CEFC" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2F3EA0F52D7EBFDBD1E9205C07C62175" x="4.752" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAACD21C62EEBAEA5F571EAFD70656C36" x="14.384" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE307093CF7EFBC8D676E62CB78C07836" x="22.848" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA95D2B4A225624CA202B59CBD1BF487" x="31.024" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3B851FDBB4F3A7C5E304DE6F7DEA331C" x="40.032" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1BA4F60CE8E3A065D660EA7EA67004B1" x="49.071999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE3CB9A16B9DD884349EFEF95066B2206" x="58.288" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAACD21C62EEBAEA5F571EAFD70656C36" x="66.16" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDBEAA3BAB7923CD0435518D325CA6C53" x="74.624" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA95D2B4A225624CA202B59CBD1BF487" x="79.6" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2F3EA0F52D7EBFDBD1E9205C07C62175" x="88.60799999999999" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.24 10.528)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(102.24 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.9693496646252555 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.938699329250511 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.908048993875763 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.877398658501022 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.846748323126278 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.81609798775153 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.785447652376796 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.75479731700205 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.72414698162731 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.69349664625256 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.66284631087781 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.63219597550307 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.60154564012834 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.57089530475359 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(89.54024496937885 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(95.5095946340041 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(101.47894429862936 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(107.44829396325461 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(113.41764362787987 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.38699329250512 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(125.35634295713038 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(131.32569262175562 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(137.29504228638086 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(143.2643919510061 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(149.23374161563135 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.20309128025661 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.17244094488186 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(167.1417906095071 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(173.11114027413234 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(179.08048993875758 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(185.04983960338282 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(191.01918926800806 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(196.9885389326333 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.95788859725855 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(208.9272382618838 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(214.89658792650903 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(220.86593759113427 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(226.8352872557595 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(232.80463692038475 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(238.77398658501 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.74333624963523 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(250.71268591426048 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(256.68203557888575 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(262.65138524351096 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(268.6207349081362 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(274.59008457276144 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.5594342373867 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(286.5287839020119 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(292.4981335666372 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(298.4674832312624 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(304.4368328958877 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(310.4061825605129 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(316.37553222513816 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.3448818897634 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(328.31423155438864 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(334.2835812190139 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(340.2529308836391 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(346.2222805482644 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(352.1916302128896 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.1609798775149 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(364.1303295421401 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(370.09967920676536 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(376.06902887139057 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(382.03837853601584 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(388.00772820064105 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(393.9770778652663 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(399.94642752989154 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.9157771945168 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(411.885126859142 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(417.8544765237673 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(423.8238261883925 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(429.7931758530178 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(435.76252551764304 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.73187518226825 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(447.7012248468935 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(453.67057451151874 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(459.639924176144 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(465.6092738407692 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(471.5786235053945 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(477.5479731700197 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.517322834645 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(489.4866724992702 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(495.45602216389545 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(501.42537182852067 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(507.39472149314594 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(513.3640711577711 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(519.3334208223964 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(525.3027704870217 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(531.2721201516471 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(537.2414698162723 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(543.2108194808976 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(549.1801691455229 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(555.1495188101483 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.1188684747735 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(567.0882181393988 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(573.0575678040241 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(579.0269174686495 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(584.9962671332747 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(590.9656167979 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(596.9349664625253 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(602.9043161271507 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(608.8736657917759 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(614.8430154564012 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(620.8123651210266 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(626.7817147856518 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(632.7510644502771 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(638.7204141149024 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(644.6897637795278 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(750.4497637795275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="4" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 65.328)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g12DC86CA8D9D6E336118F1B6EDF218A6" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9C63C5DDFB4402181293B5DF9DB8FDF6" x="10.22" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gF73CF51A640CD9E8903A9C4D4B743CCF" x="20.006" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEC1365C4E13D8501FA131C6543C06A3E" x="26.796" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.60999999999999 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.196915517139304 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.393831034278609 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.590746551417912 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.787662068557218 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.98457758569652 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.181493102835823 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.378408619975126 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.575324137114436 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.77223965425374 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(51.96915517139304 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.16607068853234 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.362986205671646 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.55990172281095 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(72.75681723995025 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.95373275708955 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.15064827422887 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.34756379136817 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.54447930850748 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.74139482564678 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(103.93831034278608 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(109.13522585992538 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.33214137706469 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.52905689420399 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.72597241134329 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(129.9228879284826 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.1198034456219 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.3167189627612 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(145.5136344799005 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(150.7105499970398 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.9074655141791 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.1043810313184 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.30129654845774 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.49821206559704 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.69512758273635 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(181.89204309987565 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(187.08895861701495 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.28587413415426 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.48278965129356 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.67970516843286 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.87662068557216 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.07353620271147 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.27045171985077 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(223.46736723699007 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.66428275412937 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(233.86119827126868 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(239.05811378840798 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.25502930554728 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.45194482268658 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.6488603398259 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(259.8457758569652 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(265.0426913741045 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(270.2396068912438 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.4365224083831 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.6334379255224 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.8303534426617 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(291.027268959801 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.2241844769403 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(301.4210999940796 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.6180155112189 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(311.8149310283582 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(317.0118465454975 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.2087620626368 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(327.4056775797761 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.6025930969155 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.7995086140548 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(342.9964241311941 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(348.1933396483334 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(353.3902551654727 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.587170682612 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(363.7840861997513 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(368.9810017168906 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.1779172340299 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(379.3748327511692 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.5717482683085 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(389.7686637854478 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(394.9655793025871 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(400.1624948197264 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.3594103368657 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.556325854005 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(415.7532413711443 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(420.95015688828363 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.14707240542293 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(431.34398792256223 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(436.54090343970154 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.73781895684084 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(446.93473447398014 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(452.13164999111945 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.32856550825875 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(462.52548102539805 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(467.72239654253735 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(472.91931205967666 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(478.11622757681596 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.31314309395526 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(488.51005861109456 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(493.70697412823387 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(498.90388964537317 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(504.1008051625125 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.2977206796518 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(514.4946361967911 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(519.6915517139304 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(524.8884672310696 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(530.0853827482089 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.2822982653481 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.4792137824874 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(545.6761292996266 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(550.8730448167659 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(556.0699603339051 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.2668758510443 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(566.4637913681836 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(571.6607068853228 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(576.8576224024621 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(582.0545379196013 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(587.2514534367406 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(592.4483689538798 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(597.6452844710191 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(602.8421999881583 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(608.0391155052976 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(613.2360310224368 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(618.432946539576 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(623.6298620567153 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(628.8267775738545 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(634.0236930909938 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(639.220608608133 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(644.4175241252723 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(649.6144396424115 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(654.8113551595508 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(660.00827067669 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(665.2051861938293 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(670.4021017109685 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(675.5990172281078 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(680.795932745247 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(685.9928482623862 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(691.1897637795255 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(751.8797637795275 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g9696EE00168B299790D79B47B78C5F18" x="3.5" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 87.54000000000002)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g9C63C5DDFB4402181293B5DF9DB8FDF6" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gF73CF51A640CD9E8903A9C4D4B743CCF" x="9.786" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEC1365C4E13D8501FA131C6543C06A3E" x="16.576" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.39 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.1956278798483515 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.391255759696703 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.586883639545055 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.782511519393406 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.97813939924176 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.17376727909011 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.36939515893847 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.56502303878681 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.760650918635164 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(51.95627879848351 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.15190667833186 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.34753455818021 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.54316243802856 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(72.7387903178769 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.93441819772525 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.1300460775736 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.32567395742196 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.5213018372703 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.71692971711865 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(103.91255759696699 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(109.10818547681534 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.3038133566637 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.49944123651204 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.69506911636039 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(129.89069699620873 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.0863248760571 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.28195275590542 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(145.47758063575378 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(150.67320851560214 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.86883639545047 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.06446427529883 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.26009215514716 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.45572003499552 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.65134791484388 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(181.8469757946922 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(187.04260367454057 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.2382315543889 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.43385943423726 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.62948731408562 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.82511519393395 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.0207430737823 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.21637095363064 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(223.411998833479 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.60762671332736 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(233.8032545931757 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(238.99888247302405 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.1945103528724 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.39013823272074 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.5857661125691 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(259.78139399241746 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(264.9770218722658 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(270.17264975211424 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.3682776319626 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.56390551181096 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.7595333916594 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(290.95516127150773 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.1507891513561 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(301.3464170312045 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.54204491105287 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(311.73767279090123 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(316.93330067074965 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.128928550598 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(327.32455643044636 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.5201843102947 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.71581219014314 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(342.9114400699915 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(348.10706794983986 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(353.3026958296883 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.49832370953663 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(363.693951589385 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(368.8895794692334 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.08520734908177 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(379.28083522893013 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.47646310877855 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(389.6720909886269 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(394.86771886847527 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(400.0633467483236 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.25897462817204 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.4546025080204 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(415.65023038786876 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(420.8458582677172 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.04148614756554 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(431.2371140274139 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(436.4327419072623 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.62836978711067 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(446.82399766695903 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(452.01962554680745 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.2152534266558 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(462.41088130650417 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(467.6065091863525 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(472.80213706620094 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(477.9977649460493 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.19339282589766 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(488.3890207057461 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(493.58464858559444 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(498.7802764654428 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(503.9759043452912 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.1715322251396 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(514.367160104988 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(519.5627879848363 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(524.7584158646846 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(529.954043744533 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.1496716243813 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.3452995042296 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(545.5409273840779 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(550.7365552639262 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(555.9321831437745 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.1278110236228 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(566.3234389034712 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(571.5190667833195 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(576.7146946631678 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(581.9103225430162 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(587.1059504228645 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(592.3015783027128 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(597.4972061825612 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(602.6928340624095 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(607.8884619422578 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(613.0840898221061 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(618.2797177019544 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(623.4753455818027 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(628.670973461651 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(633.8666013414994 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(639.0622292213477 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(644.257857101196 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(649.4534849810443 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(654.6491128608926 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(659.8447407407409 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(665.0403686205892 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(670.2359965004376 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(675.4316243802859 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(680.6272522601342 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(685.8228801399825 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(691.0185080198308 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(696.2141358996791 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(701.4097637795275 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(751.8797637795275 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD0485EF23018DAF4BFC69AAD15075193" x="3.5" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 109.75200000000001)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g42427CF90B88C34047186DDCC0B8064E" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9AE4831982D6CA553E49B4F41E9A233F" x="7.574" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="12.67" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gC80234271A0A022352A099322F0FCD32" x="19.726" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g3649D621BC998C9216AD40BBEFAC3AB1" x="26.628" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gC80234271A0A022352A099322F0FCD32" x="33.026" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="39.928000000000004" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gBBFA548D7BC5ACA0036C5BF286E59830" x="43.722" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="47.418" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g88B62CE1F53AC1AE1D938018DA31319" x="51.211999999999996" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g5799677F1612AA2CF55B8D046D0457BF" x="55.635999999999996" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gF73CF51A640CD9E8903A9C4D4B743CCF" x="66.346" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gE2267284F842780DB4609789BADA809" x="73.136" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="80.304" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA0F6184C06096774B92DEFE1EDA388E4" x="84.098" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g1F652CD6CF98783FD5BC41E10F253E3" x="94.864" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="102.256" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g2027E4E303C701A0DF6BD0919BBDE7B4" x="106.05" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g88B62CE1F53AC1AE1D938018DA31319" x="111.50999999999999" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(133.434 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.214964099826504 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.429928199653007 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.644892299479512 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.859856399306015 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(26.074820499132517 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.289784598959024 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.50474869878553 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.71971279861203 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.93467689843853 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(52.14964099826503 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.36460509809153 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.57956919791803 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.79453329774454 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(73.00949739757102 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(78.22446149739753 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.43942559722403 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.65438969705053 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.86935379687704 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(99.08431789670354 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(104.29928199653003 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(109.51424609635653 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.72921019618303 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.94417429600954 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(125.15913839583604 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.37410249566253 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.58906659548904 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.80403069531553 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(146.01899479514202 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(151.23395889496854 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(156.44892299479503 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.66388709462154 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.87885119444803 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(172.09381529427455 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(177.30877939410104 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(182.52374349392753 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(187.73870759375404 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.95367169358053 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(198.16863579340705 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(203.38359989323354 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(208.59856399306003 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.81352809288654 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(219.02849219271303 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(224.24345629253955 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(229.45842039236604 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(234.67338449219253 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(239.88834859201904 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(245.10331269184553 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(250.31827679167205 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(255.53324089149854 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(260.74820499132505 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(265.96316909115154 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(271.1781331909781 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(276.3930972908046 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(281.60806139063106 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(286.82302549045755 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(292.03798959028404 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(297.2529536901106 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(302.4679177899371 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(307.68288188976356 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(312.89784598959005 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(318.11281008941654 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(323.3277741892431 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(328.5427382890696 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(333.75770238889606 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(338.97266648872255 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(344.1876305885491 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(349.4025946883756 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(354.6175587882021 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(359.83252288802856 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(365.04748698785505 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(370.2624510876816 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(375.4774151875081 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(380.6923792873346 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(385.90734338716106 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(391.12230748698755 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(396.3372715868141 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(401.5522356866406 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(406.7671997864671 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(411.98216388629356 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(417.19712798612005 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(422.4120920859466 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(427.6270561857731 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(432.8420202855996 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(438.05698438542606 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(443.27194848525255 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(448.4869125850791 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(453.7018766849056 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(458.9168407847321 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(464.13180488455856 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(469.34676898438505 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(474.5617330842116 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(479.7766971840381 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(484.9916612838646 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(490.20662538369106 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(495.42158948351755 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(500.6365535833441 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(505.8515176831706 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(511.0664817829971 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(516.2814458828236 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(521.4964099826501 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(526.7113740824766 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(531.9263381823031 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(537.1413022821297 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(542.3562663819562 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(547.5712304817827 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(552.7861945816092 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(558.0011586814356 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(563.2161227812621 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(568.4310868810886 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(573.6460509809151 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(578.8610150807416 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(584.0759791805681 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(589.2909432803947 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(594.5059073802212 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(599.7208714800477 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(604.9358355798742 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(610.1507996797006 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(615.3657637795271 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(751.8797637795275 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1A68EE8359C8016621D122AFF85D0AB2" x="3.5" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 140.964)">
<g class="typst-group">
<g>
<g transform="translate(0 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5D30492BABB8924F22FB3C21C3BB4FD6" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g10E21E0BDD9E8A3223AFCCC5FAB594B4" x="16.28" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA8310C128FB1A6882AC3541210480577" x="28.094" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFFAD8ECF2B9E19A17BA2A700D6B3A275" x="41.272000000000006" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g6724C1A826126332467C6264F812F404" x="54.230000000000004" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1707CF3A32B022CA2D70483E817BB0E1" x="67.166" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD56DD9CEC6529211EE0EE20264633A82" x="75.17399999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA105310788DE1650FF0BD6095C2860C4" x="87.88999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDC8BE94E2F4CFB356B16F8B3BD0C3FF6" x="103.59799999999998" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.15199999999999 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(124.65199999999999 0)">
<g class="typst-group">
<g>
<g transform="translate(0 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(8.786596625421824 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.573193250843648 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(26.35978987626547 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.146386501687296 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(43.93298312710912 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(52.71957975253095 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(61.50617637795278 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(70.2927730033746 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(79.07936962879643 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(87.86596625421825 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(96.65256287964009 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(105.43915950506191 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.22575613048373 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(123.01235275590557 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(131.79894938132736 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.5855460067492 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(149.37214263217103 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(158.15873925759286 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.94533588301468 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(175.7319325084365 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(184.51852913385832 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(193.30512575928017 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.091722384702 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(210.87831901012382 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(219.66491563554564 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.45151226096746 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(237.23810888638928 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(246.02470551181113 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.81130213723296 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(263.5978987626547 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(272.3844953880766 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(281.1710920134984 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(289.9576886389202 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(298.74428526434207 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(307.53088188976386 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(316.3174785151857 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(325.10407514060756 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(333.89067176602936 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(342.6772683914512 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(351.463865016873 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(360.25046164229485 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(369.03705826771665 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(377.8236548931385 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(386.61025151856035 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(395.39684814398214 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(404.183444769404 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(412.9700413948258 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(421.75663802024764 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(430.5432346456695 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(439.3298312710913 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(448.11642789651313 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(456.9030245219349 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(465.6896211473568 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(474.47621777277857 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.2628143982004 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(492.04941102362227 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(500.83600764904406 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.6226042744659 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(518.4092008998877 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(527.1957975253094 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.9823941507314 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(544.7689907761531 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(553.5555874015749 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(562.3421840269968 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(571.1287806524186 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(579.9153772778404 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(588.7019739032623 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(597.4885705286841 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(606.2751671541059 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(615.0617637795277 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(745.0817637795276 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(750.5817637795276 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE113D5FADA3BF383003A7B8BAFE64E49" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 168.154)">
<g class="typst-group">
<g>
<g transform="translate(16 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC9B6AFC3BF91192FF29E0E0E4938B0A3" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g41BD02C814E5F1F9CC57CE5A8E90AFBE" x="5.312" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g776E4106C35A60F8D71A42812632C381" x="16.432" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gED7EC3C91583B7E83C2EF7E7FEF37733" x="20.656" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="28.656" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="32.176" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g15DFEC786ABE57FB12A0CB4AD246101F" x="39.616" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFBB69929369BF0EC60A13F790CB240F" x="49.312" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9A2E3AAC6CC7A3D99F4D7199A710CE2" x="59.647999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g26508BD01E1C582AC0C2221BD9BE4224" x="67.71199999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7E49B8D69C443145BC38CA6BB9F62850" x="76.38399999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g94C24BD726F4D930F93182C299232222" x="82.62399999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7079AB3C3D467A375535C421787E42DB" x="87.67999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gC5015BCFB784037C5056D382F6B20C97" x="93.63199999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gC2B9BD65B0E3456A64080FDFF521F7E0" x="102.12799999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g94C24BD726F4D930F93182C299232222" x="108.97599999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8EC8620411AE7F46663E6890D2DD9166" x="114.03199999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9A2E3AAC6CC7A3D99F4D7199A710CE2" x="118.36799999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g26508BD01E1C582AC0C2221BD9BE4224" x="126.43199999999996" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.10399999999996 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.9780380179750265 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.956076035950053 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.93411405392508 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.912152071900106 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.890190089875134 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.86822810785016 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.84626612582519 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.82430414380021 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.80234216177524 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.78038017975027 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.75841819772529 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.73645621570031 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.71449423367534 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.69253225165038 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(89.6705702696254 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(95.64860828760042 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(101.62664630557546 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(107.60468432355049 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(113.58272234152551 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.56076035950053 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(125.53879837747557 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(131.51683639545058 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(137.4948744134256 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(143.4729124314006 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(149.45095044937563 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.42898846735062 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.40702648532564 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(167.38506450330067 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(173.36310252127566 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(179.3411405392507 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(185.3191785572257 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(191.2972165752007 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.27525459317573 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(203.25329261115073 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(209.23133062912575 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(215.20936864710077 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(221.18740666507577 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(227.1654446830508 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(233.14348270102582 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(239.1215207190008 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(245.09955873697584 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(251.07759675495086 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(257.0556347729259 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(263.0336727909009 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(269.0117108088759 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(274.9897488268509 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.9677868448259 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(286.9458248628009 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(292.9238628807759 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(298.90190089875097 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(304.87993891672596 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(310.85797693470096 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(316.836014952676 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.814052970651 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(328.792090988626 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(334.77012900660105 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(340.74816702457605 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(346.72620504255104 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(352.7042430605261 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.6822810785011 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(364.6603190964761 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(370.63835711445114 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(376.61639513242613 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(382.59443315040113 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(388.5724711683762 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(394.5505091863512 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(400.5285472043262 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(406.50658522230117 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(412.4846232402762 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(418.4626612582512 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(424.4406992762262 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(430.41873729420126 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(436.39677531217626 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(442.37481333015126 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(448.3528513481263 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(454.3308893661013 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(460.3089273840763 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(466.28696540205135 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(472.26500342002635 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(478.24304143800134 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(484.2210794559764 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(490.1991174739514 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(496.1771554919264 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(502.1551935099014 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(508.13323152787643 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(514.1112695458514 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(520.0893075638265 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(526.0673455818015 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(532.0453835997765 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(538.0234216177515 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(544.0014596357265 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(549.9794976537016 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(555.9575356716766 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.9355736896516 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(567.9136117076266 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(573.8916497256016 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(579.8696877435766 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(585.8477257615516 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(591.8257637795267 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(750.4497637795276 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gBC176529035DE42B8BD4625370C40E4D" x="4" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 191.68200000000002)">
<g class="typst-group">
<g>
<g transform="translate(16 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC9B6AFC3BF91192FF29E0E0E4938B0A3" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g41BD02C814E5F1F9CC57CE5A8E90AFBE" x="5.312" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g776E4106C35A60F8D71A42812632C381" x="16.432" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gED7EC3C91583B7E83C2EF7E7FEF37733" x="20.656" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="28.656" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="32.176" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g15DFEC786ABE57FB12A0CB4AD246101F" x="39.616" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1741EC601D45A91DF6927753AEFC05FD" x="49.312" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gACDA1EE5EEC178C67D037C3CDBE0EFC9" x="57.071999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8F0641061D7822251E2A1C9000154920" x="64.22399999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7079AB3C3D467A375535C421787E42DB" x="71.53599999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gC2B9BD65B0E3456A64080FDFF521F7E0" x="77.35999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g40BC2CA66BF08C308C98CB508D30B53" x="84.20799999999998" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(112.81599999999999 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.926296857752594 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.852593715505188 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.778890573257783 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.705187431010376 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.631484288762966 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.55778114651556 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.48407800426815 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.410374862020745 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.336671719773335 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.262968577525925 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.18926543527851 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.11556229303112 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.04185915078372 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(82.96815600853631 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.89445286628892 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(94.82074972404152 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(100.74704658179411 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(106.67334343954671 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(112.59964029729932 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(118.52593715505192 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.45223401280451 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.37853087055709 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(136.30482772830968 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(142.23112458606226 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(148.15742144381485 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(154.08371830156744 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(160.01001515932003 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(165.9363120170726 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.86260887482518 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(177.78890573257777 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(183.71520259033036 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(189.64149944808295 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(195.56779630583554 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(201.4940931635881 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.4203900213407 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.34668687909328 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(219.27298373684587 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(225.19928059459846 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(231.12557745235105 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(237.0518743101036 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(242.9781711678562 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(248.9044680256088 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.83076488336138 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(260.75706174111394 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(266.68335859886656 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(272.6096554566192 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(278.5359523143718 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(284.4622491721244 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(290.38854602987703 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.31484288762965 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(302.24113974538227 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(308.1674366031349 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(314.0937334608875 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(320.0200303186401 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(325.94632717639274 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(331.8726240341453 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.7989208918979 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(343.72521774965054 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(349.65151460740316 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(355.5778114651558 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(361.5041083229084 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(367.430405180661 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(373.35670203841363 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(379.28299889616625 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(385.20929575391887 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(391.1355926116715 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(397.0618894694241 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(402.9881863271767 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(408.9144831849293 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(414.8407800426819 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(420.7670769004345 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.69337375818714 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(432.61967061593975 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(438.5459674736924 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(444.472264331445 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(450.3985611891976 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(456.3248580469502 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(462.25115490470284 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(468.17745176245546 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(474.1037486202081 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(480.03004547796064 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(485.95634233571326 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(491.8826391934659 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(497.8089360512185 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(503.7352329089711 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.66152976672373 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(515.5878266244764 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(521.5141234822289 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(527.4404203399815 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(533.3667171977341 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(539.2930140554868 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(545.2193109132394 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(551.145607770992 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(557.0719046287446 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(562.9982014864972 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(568.9244983442499 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(574.8507952020025 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(580.7770920597551 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(586.7033889175077 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(592.6296857752603 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(598.555982633013 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(604.4822794907656 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(610.4085763485182 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(616.3348732062708 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(622.2611700640234 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(628.187466921776 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(634.1137637795287 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(750.4497637795275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g9519A9B09125702A7696E3BE317A1C17" x="4" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 215.21)">
<g class="typst-group">
<g>
<g transform="translate(16 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC9B6AFC3BF91192FF29E0E0E4938B0A3" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g41BD02C814E5F1F9CC57CE5A8E90AFBE" x="5.312" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g776E4106C35A60F8D71A42812632C381" x="16.432" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gED7EC3C91583B7E83C2EF7E7FEF37733" x="20.656" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="28.656" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1B31FFD796CA2E900A884ECD4210CED3" x="32.176" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g15DFEC786ABE57FB12A0CB4AD246101F" x="39.616" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFBB69929369BF0EC60A13F790CB240F" x="49.312" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g40BC2CA66BF08C308C98CB508D30B53" x="59.647999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9A2E3AAC6CC7A3D99F4D7199A710CE2" x="68.256" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9A2E3AAC6CC7A3D99F4D7199A710CE2" x="76.432" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7E49B8D69C443145BC38CA6BB9F62850" x="84.49600000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8EC8620411AE7F46663E6890D2DD9166" x="90.736" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g26508BD01E1C582AC0C2221BD9BE4224" x="95.072" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gED7EC3C91583B7E83C2EF7E7FEF37733" x="103.744" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g26508BD01E1C582AC0C2221BD9BE4224" x="115.744" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gACDA1EE5EEC178C67D037C3CDBE0EFC9" x="124.416" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8EC8620411AE7F46663E6890D2DD9166" x="131.56799999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gED7EC3C91583B7E83C2EF7E7FEF37733" x="135.904" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g40BC2CA66BF08C308C98CB508D30B53" x="143.904" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD032B844D751F1F27806C7004D4F5D2F" x="152.512" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9A2E3AAC6CC7A3D99F4D7199A710CE2" x="160.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7079AB3C3D467A375535C421787E42DB" x="168.624" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7E49B8D69C443145BC38CA6BB9F62850" x="174.576" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(200.816 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.985264041994752 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.970528083989503 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.955792125984257 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.941056167979006 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.92632020997376 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.91158425196851 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.89684829396327 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.88211233595801 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.867376377952766 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.85264041994752 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.83790446194227 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.82316850393703 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.80843254593177 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.79369658792652 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(89.77896062992126 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(95.764224671916 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(101.74948871391075 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(107.73475275590549 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(113.72001679790024 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.70528083989498 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(125.69054488188972 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(131.67580892388446 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(137.6610729658792 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(143.64633700787397 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(149.63160104986872 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.61686509186345 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.6021291338582 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(167.58739317585295 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(173.57265721784768 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(179.55792125984243 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(185.54318530183718 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(191.5284493438319 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.51371338582666 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(203.49897742782142 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(209.48424146981617 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(215.4695055118109 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(221.45476955380565 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(227.4400335958004 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(233.42529763779513 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(239.41056167978988 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(245.39582572178463 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(251.38108976377936 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(257.3663538057741 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(263.35161784776886 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(269.3368818897637 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.3221459317584 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(281.3074099737532 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(287.292674015748 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(293.27793805774274 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(299.26320209973755 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(305.2484661417323 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(311.23373018372706 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(317.2189942257219 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(323.2042582677166 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(329.1895223097114 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(335.1747863517062 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(341.16005039370094 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(347.1453144356957 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(353.1305784776905 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(359.11584251968526 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(365.10110656168 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(371.0863706036748 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(377.0716346456696 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(383.0568986876644 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(389.04216272965914 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(395.0274267716539 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(401.0126908136487 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(406.99795485564346 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(412.9832188976382 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(418.968482939633 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(424.9537469816278 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(430.9390110236225 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(436.92427506561734 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(442.9095391076121 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(448.89480314960684 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(454.88006719160165 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(460.8653312335964 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(466.85059527559116 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(472.83585931758597 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(478.8211233595807 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(484.80638740157553 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(490.7916514435703 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(496.77691548556504 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(502.76217952755985 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(508.7474435695546 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(514.7327076115494 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(520.7179716535442 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(526.703235695539 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(532.6884997375337 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(538.6737637795285 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(743.0097637795276 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g54C180954D544D3C78C9AD9E4F48A6CA" x="11.440000000000001" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 241.73800000000003)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g985B950D50769631420A9A59AEA7CEFC" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g20DDE86F15DD9C8B9599512790FC45E4" x="4.752" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3E944C953D169E97A30360D928248E70" x="15.424" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE307093CF7EFBC8D676E62CB78C07836" x="22.8" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA95D2B4A225624CA202B59CBD1BF487" x="30.976" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gBAC0ED7F2DB725071CE720AF8BC15D72" x="39.824" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDA675C10B642A458CD97A11D372FF5DA" x="48.592" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g20DDE86F15DD9C8B9599512790FC45E4" x="56.224" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDA675C10B642A458CD97A11D372FF5DA" x="66.896" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2F3EA0F52D7EBFDBD1E9205C07C62175" x="74.528" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAACD21C62EEBAEA5F571EAFD70656C36" x="84.16000000000001" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(92.62400000000001 10.528)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(96.62400000000001 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.952460775736366 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.904921551472732 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.8573823272091 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.809843102945464 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.762303878681834 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.7147646544182 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.667225430154566 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.61968620589093 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.5721469816273 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.52460775736367 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.47706853310004 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.4295293088364 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.38199008457275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.33445086030912 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(89.28691163604547 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(95.23937241178183 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(101.1918331875182 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(107.14429396325455 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(113.09675473899091 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.04921551472728 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(125.00167629046364 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.95413706620002 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(136.90659784193636 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(142.85905861767273 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(148.8115193934091 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(154.76398016914544 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(160.7164409448818 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.66890172061818 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(172.62136249635452 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(178.5738232720909 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(184.52628404782726 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(190.4787448235636 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(196.43120559929997 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.38366637503634 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(208.33612715077268 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(214.28858792650905 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(220.24104870224542 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(226.19350947798176 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(232.14597025371813 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(238.0984310294545 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.05089180519084 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(250.0033525809272 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(255.95581335666358 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(261.9082741324 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(267.86073490813635 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(273.8131956838727 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(279.76565645960915 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.7181172353455 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(291.6705780110819 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(297.6230387868183 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(303.5754995625547 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(309.52796033829105 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(315.4804211140275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(321.43288188976385 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(327.3853426655002 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(333.33780344123664 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(339.290264216973 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(345.2427249927094 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(351.1951857684458 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(357.1476465441822 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(363.10010731991855 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(369.052568095655 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(375.00502887139135 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(380.9574896471278 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(386.90995042286414 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(392.8624111986005 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(398.81487197433694 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(404.7673327500733 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.7197935258097 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(416.6722543015461 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(422.6247150772825 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(428.57717585301884 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(434.52963662875527 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(440.48209740449164 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(446.434558180228 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(452.38701895596444 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(458.3394797317008 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(464.2919405074372 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(470.2444012831736 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(476.19686205890997 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(482.14932283464634 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(488.10178361038277 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(494.05424438611914 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(500.0067051618555 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(505.95916593759193 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(511.9116267133283 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(517.8640874890647 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(523.816548264801 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(529.7690090405373 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.7214698162736 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(541.6739305920099 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(547.6263913677462 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(553.5788521434827 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(559.531312919219 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(565.4837736949553 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(571.4362344706916 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(577.3886952464279 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(583.3411560221642 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(589.2936167979007 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(595.246077573637 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(601.1985383493733 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(607.1509991251096 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(613.1034599008459 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(619.0559206765822 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(625.0083814523186 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(630.960842228055 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(636.9133030037913 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(642.8657637795276 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(743.0097637795276 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="4" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="11.440000000000001" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 265.2660000000001)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g176D627313BEF56D87624592E290FFD2" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="9.044" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g6D1F08816BC4457F813BBA2B6CEC4900" x="16.1" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gC80234271A0A022352A099322F0FCD32" x="27.160000000000004" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="34.062000000000005" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g77113E0CAAA23E0B77E89A338ACC30A4" x="37.856" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g634FF9E9D0A0144E2AFDD807D5ECB7D0" x="45.444" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEF9FD20106DF1BE872ABEE235642DEFC" x="51.800000000000004" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g3B79D8E86480C20827A395F926C73BE1" x="62.384" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="72.842" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g88B62CE1F53AC1AE1D938018DA31319" x="76.636" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gD0DD0C2B056F25673B3EED0135505F92" x="81.06" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gE0345006C183149AF583AF5DE80FA9FE" x="92.092" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g7E303FA8E2D87EE13FB94A41DEF3418E" x="96.586" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gBB75D665A04FFE2A82A14DE003A19CAC" x="105.714" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.00400000000002 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.188862404911251 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.377724809822501 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.566587214733753 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.755449619645002 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.944312024556258 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.13317442946751 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.322036834378764 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.51089923929001 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.69976164420127 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(51.88862404911252 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.07748645402377 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.266348858935025 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.45521126384628 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(72.64407366875753 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.83293607366876 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.02179847858001 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.21066088349126 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.3995232884025 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.58838569331375 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(103.777248098225 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(108.96611050313624 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.15497290804748 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.34383531295873 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.53269771786998 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(129.72156012278123 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(134.9104225276925 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.09928493260375 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(145.28814733751503 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(150.47700974242628 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.66587214733752 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(160.8547345522488 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.04359695716005 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.23245936207132 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.42132176698257 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(181.61018417189385 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(186.7990465768051 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(191.98790898171634 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.17677138662762 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.36563379153887 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.55449619645015 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(212.7433586013614 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(217.93222100627264 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(223.12108341118392 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.30994581609517 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(233.49880822100644 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(238.6876706259177 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(243.87653303082897 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.06539543574021 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.25425784065146 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(259.4431202455627 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(264.63198265047396 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(269.8208450553852 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.0097074602964 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.1985698652076 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.38743227011884 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(290.5762946750301 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(295.76515707994133 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(300.95401948485255 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.14288188976377 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(311.331744294675 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(316.52060669958627 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(321.7094691044975 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(326.8983315094087 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.0871939143199 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.27605631923115 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(342.4649187241424 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(347.65378112905364 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(352.84264353396486 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.0315059388761 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(363.2203683437873 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(368.4092307486986 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(373.5980931536098 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(378.786955558521 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(383.97581796343223 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(389.1646803683435 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(394.35354277325473 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(399.54240517816595 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(404.73126758307717 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(409.9201299879884 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(415.10899239289967 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(420.2978547978109 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(425.4867172027221 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(430.6755796076333 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(435.86444201254454 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.0533044174558 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(446.24216682236704 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(451.43102922727826 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(456.6198916321895 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(461.8087540371007 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(466.997616442012 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(472.1864788469232 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(477.3753412518344 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(482.56420365674563 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(487.75306606165685 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(492.94192846656813 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(498.13079087147935 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(503.31965327639057 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(508.5085156813018 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(513.697378086213 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(518.8862404911242 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(524.0751028960356 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(529.2639653009469 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(534.4528277058581 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(539.6416901107694 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(544.8305525156807 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(550.019414920592 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(555.2082773255033 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(560.3971397304146 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(565.5860021353259 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(570.7748645402371 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(575.9637269451484 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(581.1525893500598 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(586.341451754971 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(591.5303141598823 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(596.7191765647935 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(601.9080389697049 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(607.0969013746162 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(612.2857637795274 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(745.3697637795276 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD8D2A5E78EA4643EEAAC69DB934A336F" x="3.5" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9696EE00168B299790D79B47B78C5F18" x="10.010000000000002" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 443.56299212598424)">
<g class="typst-group">
<g/>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="g6E7B5CC2B72AC8CDDEB63FB023F45240" overflow="visible">
<path d="M 27.76 13.16 C 27.76 21.119999 21.84 26.32 14.5199995 26.32 C 10.5199995 26.32 7.04 24.6 4.72 21.84 C 2.6399999 19.359999 1.48 16.039999 1.48 12.36 C 1.48 4.44 7.7599998 -0.39999998 14.559999 -0.39999998 C 18.68 -0.39999998 22.039999 1.0799999 24.32 3.56 C 26.519999 5.96 27.76 9.24 27.76 13.16 Z M 14.04 24.64 C 18.32 24.64 21.72 20.439999 21.72 12.32 C 21.72 5.68 19.4 1.28 15.36 1.28 C 10.96 1.28 7.52 5.64 7.52 13.16 C 7.52 21.32 10.48 24.64 14.04 24.64 Z "/>
</symbol>
<symbol id="gAF2E61F9C5EC3B2D9B048D1511B1060D" overflow="visible">
<path d="M 20.4 5.3199997 L 20.4 12.24 C 20.4 15.599999 20.48 15.12 20.48 16.08 C 20.48 16.76 20.32 17.199999 20.08 17.44 C 19.359999 17.4 18.56 17.359999 17.8 17.359999 C 16.68 17.359999 14.08 17.4 12.5199995 17.44 C 12.28 17.199999 12.28 16.32 12.5199995 16.08 C 14.559999 15.88 15.2 15.599999 15.2 12.24 L 15.2 4.8399997 C 15.2 4.44 15.2 4.04 15.24 3.6399999 C 13.599999 2.6399999 12.28 2.56 11.559999 2.56 C 9.96 2.56 8.76 2.76 8.76 5.56 L 8.76 12.24 C 8.76 15.599999 8.84 15.12 8.84 16.08 C 8.84 16.76 8.679999 17.199999 8.44 17.44 C 7.72 17.4 6.8799996 17.359999 6.16 17.359999 C 4.12 17.359999 2.6 17.4 0.88 17.44 C 0.64 17.199999 0.64 16.32 0.88 16.08 C 2.72 16 3.56 15.599999 3.56 12.24 L 3.56 6 C 3.56 1.76 5.24 -0.39999998 8.679999 -0.39999998 C 10.12 -0.39999998 13.04 0.76 15.36 2.04 C 15.44 1.04 15.5199995 0.28 15.5199995 0.28 C 15.559999 -0.19999999 15.88 -0.39999998 16.44 -0.39999998 C 17.92 0 20.32 0.56 23.08 0.91999996 C 23.16 1.16 23.08 1.9599999 23 2.2 C 20.84 2.3999999 20.4 3.04 20.4 5.3199997 Z "/>
</symbol>
<symbol id="g385ED71BD3F10D2170A1311D8F1A15B" overflow="visible">
<path d="M 2.52 17.359999 C 1.9599999 17.359999 1.36 17.199999 0.84 16.76 L 0.84 15.599999 C 0.84 15.4 0.88 15.36 1.04 15.36 L 3.6399999 15.36 C 3.56 11.32 3.52 6.2 3.52 4.2 C 3.52 2.8 3.8799999 1.4399999 4.72 0.71999997 C 5.64 -0.04 7.08 -0.39999998 8.04 -0.39999998 C 10.24 -0.39999998 12.679999 0.71999997 13.48 1.8399999 C 13.48 2.32 13.24 2.56 12.759999 2.96 C 12.24 2.56 11.24 2.3999999 10.48 2.3999999 C 9.599999 2.3999999 8.72 3.08 8.72 5.08 C 8.72 7.08 8.679999 11.36 8.679999 15.36 L 12.719999 15.36 C 13.12 15.36 13.679999 15.5199995 13.679999 15.88 L 13.679999 17.119999 C 13.679999 17.279999 13.559999 17.359999 13.36 17.359999 L 8.679999 17.359999 L 8.72 18.72 C 8.8 21.4 8.92 23.24 8.92 23.24 C 8.92 23.48 8.8 23.6 8.599999 23.6 C 8.32 23.6 6.8399997 23.16 6.2 22.88 C 5.52 22.6 4.36 22.359999 4.08 22 C 3.8 21.64 3.6399999 20.56 3.6399999 17.359999 Z "/>
</symbol>
<symbol id="g2192B3D4CEA94ECF87445F8EE62E404B" overflow="visible">
<path d="M 4 5.08 C 4 1.76 3.36 1.4 0.91999996 1.28 C 0.68 1.04 0.68 0.16 0.91999996 -0.08 C 2.6 -0.04 4.4 0 6.6 0 C 8.8 0 10.559999 -0.04 12.28 -0.08 C 12.5199995 0.16 12.5199995 1.04 12.28 1.28 C 9.84 1.4 9.2 1.76 9.2 5.08 L 9.2 23.32 C 9.2 25.92 9.32 27.4 9.32 27.4 C 9.32 27.76 9.04 27.92 8.679999 27.92 C 7.2 27.439999 4 27 1.16 26.88 C 1.04 26.4 1.0799999 25.96 1.28 25.599998 C 3.8 25.4 4 25.359999 4 22.6 Z "/>
</symbol>
<symbol id="g8F4F96B13A9D8B27A4F3C34609AEF61C" overflow="visible">
<path d="M 9.28 4.88 L 9.28 12.84 C 9.28 14.839999 9.44 17.08 9.44 17.08 C 9.44 17.52 9.08 17.76 8.5199995 17.76 C 7.3999996 17.32 4.16 17 1.4 16.64 C 1.3199999 16.4 1.4 15.599999 1.48 15.36 C 3.6799998 15.16 4.08 14.839999 4.08 12.559999 L 4.08 4.88 C 4.08 1.56 3.6399999 1.48 1.1999999 1.28 C 0.96 1.04 0.96 0.16 1.1999999 -0.08 C 2.8799999 -0.04 4.56 0 6.68 0 C 8.8 0 10.44 -0.04 12.16 -0.08 C 12.4 0.16 12.4 1.04 12.16 1.28 C 9.719999 1.4399999 9.28 1.56 9.28 4.88 Z M 3.8799999 23.84 C 3.8799999 22.519999 4.8399997 21.199999 6.44 21.199999 C 8.24 21.199999 9.28 22.64 9.28 23.68 C 9.28 24.88 8.36 26.32 6.68 26.32 C 4.7999997 26.32 3.8799999 25.039999 3.8799999 23.84 Z "/>
</symbol>
<symbol id="g9BEF8AB47349CEAA320776726D3DB3DB" overflow="visible">
<path d="M 9.12 4.88 L 9.12 12.92 C 10.719999 14 12.32 14.799999 13.04 14.799999 C 14.639999 14.799999 15.839999 14.08 15.839999 11.8 L 15.839999 5.12 C 15.839999 1.76 15.2 1.4 13.559999 1.28 C 13.32 1.04 13.32 0.16 13.559999 -0.08 C 15.24 -0.04 16.52 0 18.44 0 C 20.64 0 22.4 -0.04 24.119999 -0.08 C 24.359999 0.16 24.359999 1.04 24.119999 1.28 C 21.68 1.4 21.039999 1.76 21.039999 5.12 L 21.039999 11.36 C 21.039999 15.759999 19.16 17.76 15.719999 17.76 C 14.12 17.76 11.28 16 9.08 14.48 C 8.96 15.88 8.8 17.08 8.8 17.08 C 8.76 17.56 8.44 17.76 7.8799996 17.76 C 6.3999996 17.359999 4 16.8 1.24 16.44 C 1.16 16.199999 1.24 15.4 1.3199999 15.16 C 3.52 14.96 3.9199998 14.639999 3.9199998 12.36 L 3.9199998 4.88 C 3.9199998 1.56 3.48 1.48 1.04 1.28 C 0.79999995 1.04 0.79999995 0.16 1.04 -0.08 C 2.72 -0.04 4.4 0 6.52 0 C 8.36 0 9.48 -0.04 11.2 -0.08 C 11.44 0.16 11.44 1.04 11.2 1.28 C 9.5199995 1.4399999 9.12 1.56 9.12 4.88 Z "/>
</symbol>
<symbol id="g5CEF84A95ABDCAB0EDEF87161576AC77" overflow="visible">
<path d="M 17.24 5.16 C 15.599999 3.48 13.44 3.04 11.92 3.04 C 8.8 3.04 6.8799996 4.8399997 6.8799996 8.76 C 6.8799996 9.04 6.92 9.2 6.92 9.4 L 16.52 9.4 C 17.48 9.4 17.68 10.08 17.68 10.639999 C 17.68 14.04 16.359999 17.76 10.48 17.76 C 6.2799997 17.76 1.48 14.04 1.48 7.9199996 C 1.48 5.6 2.32 3.1599998 4.04 1.5999999 C 5.56 0.24 7.52 -0.39999998 10.36 -0.39999998 C 13.12 -0.39999998 15.839999 1 17.84 3.9199998 C 17.84 4.44 17.64 5.16 17.24 5.16 Z M 7.08 11 C 7.12 12.4 7.3199997 13.92 7.8799996 14.719999 C 8.5199995 15.679999 9.599999 16.08 10.04 16.08 C 11.12 16.08 12.599999 15.04 12.599999 11.84 C 12.599999 11.599999 12.599999 11.08 12.5199995 11 Z "/>
</symbol>
<symbol id="g985B950D50769631420A9A59AEA7CEFC" overflow="visible">
<path d="M 3.0560002 1.9520001 L 3.0560002 8.368 C 3.0560002 9.696 3.328 9.776 4.4480004 9.824 C 4.544 9.92 4.544 10.2560005 4.4480004 10.352 C 3.7440002 10.336 2.992 10.320001 2.368 10.320001 C 1.84 10.320001 1.056 10.336 0.30400002 10.352 C 0.208 10.2560005 0.208 9.92 0.30400002 9.824 C 1.424 9.776 1.6960001 9.696 1.6960001 8.368 L 1.6960001 1.9520001 C 1.6960001 0.624 1.424 0.544 0.30400002 0.49600002 C 0.208 0.4 0.208 0.064 0.30400002 -0.032 C 1.024 -0.016 1.8080001 0 2.384 0 C 2.96 0 3.7280002 -0.016 4.4480004 -0.032 C 4.544 0.064 4.544 0.4 4.4480004 0.49600002 C 3.328 0.544 3.0560002 0.624 3.0560002 1.9520001 Z "/>
</symbol>
<symbol id="g2F3EA0F52D7EBFDBD1E9205C07C62175" overflow="visible">
<path d="M 2.48 1.9520001 L 2.48 4.992 C 2.48 5.7760005 2.6880002 5.6320004 3.0560002 5.168 L 6.8160005 0.16000001 C 7.056 -0.096 7.3120003 -0.192 7.5520005 -0.192 C 7.7440004 -0.192 7.9040003 -0.080000006 7.9040003 0.24000001 L 7.9040003 5.4080005 C 7.9040003 6.7360005 8.08 6.7840004 9.056001 6.8640003 C 9.152 6.9600005 9.152 7.2960005 9.056001 7.392 C 8.576 7.3760004 8 7.36 7.5200005 7.36 C 7.0400004 7.36 6.4800005 7.3760004 6.0000005 7.392 C 5.9040003 7.2960005 5.9040003 6.9600005 6.0000005 6.8640003 C 6.9760003 6.8 7.1520004 6.7360005 7.1520004 5.4080005 L 7.1520004 2.4160001 C 7.1520004 1.9840001 7.1040006 1.7120001 6.6080003 2.384 L 2.9440002 7.36 L 0.67200005 7.392 L 0.64000005 7.3440003 L 0.64000005 6.9600005 C 0.64000005 6.8960004 0.73600006 6.8640003 0.78400004 6.8640003 C 1.3920001 6.8160005 1.5680001 6.6240005 1.728 6.3360004 L 1.728 1.9520001 C 1.728 0.624 1.552 0.56 0.57600003 0.49600002 C 0.48000002 0.4 0.48000002 0.064 0.57600003 -0.032 C 1.056 -0.016 1.616 0 2.0960002 0 C 2.5760002 0 3.1520002 -0.016 3.6320002 -0.032 C 3.7280002 0.064 3.7280002 0.4 3.6320002 0.49600002 C 2.6560001 0.57600003 2.48 0.624 2.48 1.9520001 Z "/>
</symbol>
<symbol id="gAACD21C62EEBAEA5F571EAFD70656C36" overflow="visible">
<path d="M 4.8640003 1.9520001 L 4.8640003 5.984 C 4.8640003 6.576 5.024 6.8160005 5.5360003 6.8160005 L 5.952 6.8160005 C 6.9600005 6.8160005 7.168 6.4960003 7.4880004 5.3440003 C 7.6480002 5.3120003 7.7920003 5.3120003 7.9200006 5.392 C 7.84 6.176 7.8240004 6.768 7.7920003 7.5200005 C 7.2320004 7.4560003 6.208 7.36 4.8640003 7.36 L 3.6000001 7.36 C 2.032 7.36 1.1040001 7.4400005 0.67200005 7.5200005 C 0.67200005 6.768 0.656 6.144 0.56 5.392 C 0.70400006 5.3440003 0.84800005 5.328 0.99200004 5.3440003 C 1.312 6.4960003 1.488 6.8160005 2.528 6.8160005 L 2.9120002 6.8160005 C 3.4080002 6.8160005 3.6000001 6.6240005 3.6000001 6.0000005 L 3.6000001 1.9520001 C 3.6000001 0.624 3.4240003 0.57600003 2.4480002 0.49600002 C 2.352 0.4 2.352 0.064 2.4480002 -0.032 C 3.0400002 -0.016 3.696 0 4.2400002 0 C 4.8 0 5.4240003 -0.016 6.0160003 -0.032 C 6.1120005 0.064 6.1120005 0.4 6.0160003 0.49600002 C 5.0400004 0.56 4.8640003 0.624 4.8640003 1.9520001 Z "/>
</symbol>
<symbol id="gE307093CF7EFBC8D676E62CB78C07836" overflow="visible">
<path d="M 3.0560002 1.9520001 L 3.0560002 3.344 L 3.936 3.344 C 4.544 3.344 4.768 2.8160002 4.9760003 2.2240002 L 5.328 1.264 C 5.696 0.272 6.2400002 -0.112 6.9280005 -0.112 C 7.168 -0.112 7.6640005 -0.064 7.9360003 0 C 7.984 0.16000001 7.952 0.32000002 7.84 0.448 C 7.2640004 0.448 6.9600005 0.544 6.6400003 1.376 L 6.176 2.5760002 C 5.984 3.072 5.7920003 3.344 5.584 3.5520003 L 5.584 3.584 C 6.1280003 3.7760003 6.9440002 4.432 6.9440002 5.5360003 C 6.9440002 6.8640003 6.1120005 7.4240003 4.208 7.4240003 C 3.808 7.4240003 2.8960001 7.36 2.4160001 7.36 C 1.9520001 7.36 1.2800001 7.3760004 0.64000005 7.392 C 0.544 7.2960005 0.544 6.9600005 0.64000005 6.8640003 C 1.616 6.8 1.792 6.7360005 1.792 5.4080005 L 1.792 1.9520001 C 1.792 0.624 1.616 0.57600003 0.64000005 0.49600002 C 0.544 0.4 0.544 0.064 0.64000005 -0.032 C 1.248 -0.016 1.904 0 2.4320002 0 C 2.9280002 0 3.456 -0.016 3.9680002 -0.032 C 4.064 0.064 4.064 0.4 3.9680002 0.49600002 C 3.216 0.544 3.0560002 0.624 3.0560002 1.9520001 Z M 5.552 5.5360003 C 5.552 4.2720003 5.184 3.808 3.7600002 3.808 L 3.0560002 3.808 L 3.0560002 5.8880005 C 3.0560002 6.7360005 3.216 6.8960004 4.112 6.8960004 C 5.2320004 6.8960004 5.552 6.4960003 5.552 5.5360003 Z "/>
</symbol>
<symbol id="gAA95D2B4A225624CA202B59CBD1BF487" overflow="visible">
<path d="M 8.432 3.7600002 C 8.432 6.032 6.6080003 7.5200005 4.5280004 7.5200005 C 2.3040001 7.5200005 0.592 5.9040003 0.592 3.5520003 C 0.592 1.376 2.24 -0.16000001 4.4 -0.16000001 C 7.024 -0.16000001 8.432 1.6800001 8.432 3.7600002 Z M 4.3840003 6.992 C 5.808 6.992 7.0400004 5.6800003 7.0400004 3.5360003 C 7.0400004 1.5680001 6.064 0.36800003 4.6400003 0.36800003 C 3.088 0.36800003 1.9840001 1.7760001 1.9840001 3.7440002 C 1.9840001 5.9040003 3.1840003 6.992 4.3840003 6.992 Z "/>
</symbol>
<symbol id="g3B851FDBB4F3A7C5E304DE6F7DEA331C" overflow="visible">
<path d="M 2.368 7.36 C 1.9360001 7.36 1.2160001 7.3760004 0.592 7.392 C 0.49600002 7.2960005 0.49600002 6.9600005 0.592 6.8640003 C 1.5680001 6.8 1.7440001 6.7360005 1.7440001 5.4080005 L 1.7440001 1.9520001 C 1.7440001 0.624 1.5680001 0.57600003 0.592 0.49600002 C 0.49600002 0.4 0.49600002 0.064 0.592 -0.032 C 1.2 -0.016 1.9200001 0 2.384 0 C 2.8000002 0 3.44 -0.032 4.7200003 -0.032 C 6.4960003 -0.032 8.4800005 0.8 8.4800005 3.6000001 C 8.4800005 5.728 7.168 7.392 4.4960003 7.392 C 3.4080002 7.392 2.832 7.36 2.368 7.36 Z M 3.0080001 1.2160001 L 3.0080001 6.3680005 C 3.0080001 6.768 3.4080002 6.8640003 4.032 6.8640003 C 6.7200003 6.8640003 7.0880003 4.992 7.0880003 3.328 C 7.0880003 1.088 6.096 0.49600002 4.3360004 0.49600002 C 3.1200001 0.49600002 3.0080001 0.768 3.0080001 1.2160001 Z "/>
</symbol>
<symbol id="g1BA4F60CE8E3A065D660EA7EA67004B1" overflow="visible">
<path d="M 6.9600005 5.4080005 L 6.9600005 3.3760002 C 6.9600005 2 6.9600005 0.49600002 4.848 0.49600002 C 3.2640002 0.49600002 2.9280002 1.7440001 2.9280002 3.232 L 2.9280002 5.4080005 C 2.9280002 6.7360005 3.104 6.7840004 4.0800004 6.8640003 C 4.176 6.9600005 4.176 7.2960005 4.0800004 7.392 C 3.456 7.3760004 2.8160002 7.36 2.288 7.36 C 1.7120001 7.36 1.088 7.3760004 0.512 7.392 C 0.416 7.2960005 0.416 6.9600005 0.512 6.8640003 C 1.488 6.8 1.664 6.7360005 1.664 5.4080005 L 1.664 2.8960001 C 1.664 0.49600002 2.832 -0.16000001 4.576 -0.16000001 C 7.056 -0.16000001 7.7120004 1.248 7.7120004 3.584 L 7.7120004 5.4080005 C 7.7120004 6.7360005 7.8880005 6.7840004 8.864 6.8640003 C 8.96 6.9600005 8.96 7.2960005 8.864 7.392 C 8.384001 7.3760004 7.8080006 7.36 7.3280005 7.36 C 6.8480005 7.36 6.288 7.3760004 5.808 7.392 C 5.7120004 7.2960005 5.7120004 6.9600005 5.808 6.8640003 C 6.7840004 6.8 6.9600005 6.7360005 6.9600005 5.4080005 Z "/>
</symbol>
<symbol id="gE3CB9A16B9DD884349EFEF95066B2206" overflow="visible">
<path d="M 4.4160004 -0.16000001 C 5.664 -0.16000001 6.432 0.30400002 7.1840005 1.312 C 7.1520004 1.424 6.992 1.6 6.8640003 1.6320001 C 6.1280003 0.768 5.5680003 0.448 4.4960003 0.448 C 2.9120002 0.448 1.9840001 2.16 1.9840001 3.7440002 C 1.9840001 6.432 3.232 6.992 4.432 6.992 C 5.7120004 6.992 6.464 6.288 6.656 5.168 C 6.8160005 5.1200004 6.9760003 5.1200004 7.136 5.216 C 7.136 5.872 7.1040006 6.544 6.9440002 7.2640004 C 6.3360004 7.2640004 5.616 7.5200005 4.3360004 7.5200005 C 2.2240002 7.5200005 0.592 5.92 0.592 3.584 C 0.592 2.5760002 0.91200006 1.4720001 1.6960001 0.75200003 C 2.3360002 0.16000001 3.232 -0.16000001 4.4160004 -0.16000001 Z "/>
</symbol>
<symbol id="gDBEAA3BAB7923CD0435518D325CA6C53" overflow="visible">
<path d="M 3.1200001 5.4080005 C 3.1200001 6.7360005 3.2960002 6.7840004 4.2720003 6.8640003 C 4.368 6.9600005 4.368 7.2960005 4.2720003 7.392 C 3.6640003 7.3760004 2.976 7.36 2.48 7.36 C 2 7.36 1.3280001 7.3760004 0.70400006 7.392 C 0.60800004 7.2960005 0.60800004 6.9600005 0.70400006 6.8640003 C 1.6800001 6.8 1.8560001 6.7360005 1.8560001 5.4080005 L 1.8560001 1.9520001 C 1.8560001 0.624 1.6800001 0.57600003 0.70400006 0.49600002 C 0.60800004 0.4 0.60800004 0.064 0.70400006 -0.032 C 1.296 -0.016 1.9520001 0 2.496 0 C 3.0080001 0 3.7120001 -0.016 4.2720003 -0.032 C 4.368 0.064 4.368 0.4 4.2720003 0.49600002 C 3.2960002 0.56 3.1200001 0.624 3.1200001 1.9520001 Z "/>
</symbol>
<symbol id="gD91DF12E6685C776523A4EFE671EF7FE" overflow="visible">
<path d="M 0.91200006 0.688 C 0.91200006 0.224 1.296 -0.16000001 1.7600001 -0.16000001 C 2.2240002 -0.16000001 2.608 0.224 2.608 0.688 C 2.608 1.1520001 2.2240002 1.536 1.7600001 1.536 C 1.296 1.536 0.91200006 1.1520001 0.91200006 0.688 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
<symbol id="g12DC86CA8D9D6E336118F1B6EDF218A6" overflow="visible">
<path d="M 8.652 1.7080001 L 8.652 7.322 C 8.652 8.484 8.89 8.554 9.87 8.596001 C 9.954 8.68 9.954 8.974 9.87 9.058001 C 9.2960005 9.044001 8.582001 9.030001 8.05 9.030001 C 7.532 9.030001 6.86 9.044001 6.244 9.058001 C 6.1600003 8.974 6.1600003 8.68 6.244 8.596001 C 7.2240005 8.554 7.4620004 8.484 7.4620004 7.322 L 7.4620004 5.0820003 L 2.674 5.0820003 L 2.674 7.322 C 2.674 8.484 2.9120002 8.554 3.8920002 8.596001 C 3.976 8.68 3.976 8.974 3.8920002 9.058001 C 3.3600001 9.044001 2.786 9.030001 2.072 9.030001 C 1.3720001 9.030001 0.79800004 9.044001 0.266 9.058001 C 0.18200001 8.974 0.18200001 8.68 0.266 8.596001 C 1.246 8.554 1.4840001 8.484 1.4840001 7.322 L 1.4840001 1.7080001 C 1.4840001 0.546 1.246 0.476 0.266 0.43400002 C 0.18200001 0.35000002 0.18200001 0.056 0.266 -0.028 C 0.882 -0.014 1.554 0 2.086 0 C 2.5900002 0 3.276 -0.014 3.8920002 -0.028 C 3.976 0.056 3.976 0.35000002 3.8920002 0.43400002 C 2.9120002 0.476 2.674 0.546 2.674 1.7080001 L 2.674 4.494 L 7.4620004 4.494 L 7.4620004 1.7080001 C 7.4620004 0.546 7.2240005 0.476 6.244 0.43400002 C 6.1600003 0.35000002 6.1600003 0.056 6.244 -0.028 C 6.874 -0.014 7.546 0 8.064 0 C 8.582001 0 9.254001 -0.014 9.87 -0.028 C 9.954 0.056 9.954 0.35000002 9.87 0.43400002 C 8.89 0.476 8.652 0.546 8.652 1.7080001 Z "/>
</symbol>
<symbol id="g9C63C5DDFB4402181293B5DF9DB8FDF6" overflow="visible">
<path d="M 7.7840004 7.168 L 7.7840004 2.5900002 C 7.7840004 2.3240001 7.7840004 2.17 7.6860003 2.17 C 7.63 2.17 7.42 2.4220002 7.0140004 2.94 L 2.2120001 9.030001 L 0.322 9.058001 C 0.238 8.974 0.238 8.68 0.322 8.596001 C 0.924 8.554 1.3440001 8.064 1.4280001 7.7000003 L 1.4280001 1.8620001 C 1.4280001 0.616 1.19 0.532 0.21000001 0.43400002 C 0.126 0.35000002 0.126 0.056 0.21000001 -0.028 C 0.81200004 -0.014 1.442 0 1.778 0 C 2.1000001 0 2.7440002 -0.014 3.332 -0.028 C 3.4160001 0.056 3.4160001 0.35000002 3.332 0.43400002 C 2.352 0.532 2.114 0.588 2.114 1.8620001 L 2.114 6.1460004 C 2.114 6.622 2.114 6.8320003 2.226 6.8320003 C 2.3100002 6.8320003 2.464 6.678 2.7020001 6.3700004 L 7.5880003 0.19600001 C 7.742 -0.014 7.9240003 -0.14 8.148001 -0.14 C 8.344 -0.14 8.47 0.028 8.47 0.294 L 8.47 7.168 C 8.47 8.4140005 8.708 8.498 9.688001 8.596001 C 9.772 8.68 9.772 8.974 9.688001 9.058001 C 9.114 9.044001 8.456 9.030001 8.12 9.030001 C 7.826 9.030001 7.182 9.044001 6.566 9.058001 C 6.4820004 8.974 6.4820004 8.68 6.566 8.596001 C 7.546 8.498 7.7840004 8.442 7.7840004 7.168 Z "/>
</symbol>
<symbol id="gF73CF51A640CD9E8903A9C4D4B743CCF" overflow="visible">
<path d="M 5.53 8.834001 C 4.718 8.946 4.7460003 9.212 3.374 9.212 C 1.96 9.212 0.71400005 8.274 0.71400005 6.7900004 C 0.71400005 5.32 1.932 4.6480002 3.164 4.172 C 4.004 3.8500001 5.04 3.4580002 5.04 2.086 C 5.04 0.952 4.4100003 0.36400002 3.2900002 0.36400002 C 1.988 0.36400002 1.148 0.966 0.84000003 2.352 C 0.658 2.408 0.518 2.38 0.37800002 2.3100002 C 0.43400002 1.232 0.49 0.86800003 0.658 0.18200001 C 1.5400001 0.18200001 1.932 -0.14 3.1780002 -0.14 C 3.808 -0.14 4.4100003 0.014 4.9 0.322 C 5.7120004 0.82600003 6.216 1.6800001 6.216 2.576 C 6.216 4.06 5.096 4.718 3.9480002 5.152 C 3.108 5.46 1.7080001 5.992 1.7080001 7.168 C 1.7080001 7.952 2.4220002 8.736 3.2480001 8.736 C 4.606 8.736 5.04 7.868 5.32 6.9440002 C 5.474 6.9160004 5.656 6.9300003 5.782 7.0280004 C 5.7260003 7.7000003 5.67 8.092 5.53 8.834001 Z "/>
</symbol>
<symbol id="gEC1365C4E13D8501FA131C6543C06A3E" overflow="visible">
<path d="M 11.34 7.9100003 L 9.156 1.8340001 L 9.114 1.848 L 7.182 7.756 C 6.9440002 8.512 7.434 8.554 7.9100003 8.596001 C 7.9940004 8.68 7.9940004 8.974 7.9100003 9.058001 C 7.3360004 9.044001 6.7200003 9.030001 6.1600003 9.030001 C 5.698 9.030001 5.208 9.044001 4.76 9.058001 C 4.676 8.974 4.676 8.68 4.76 8.596001 C 5.5020003 8.554 5.81 8.12 5.9360003 7.756 L 6.2580004 6.8320003 C 6.314 6.664 6.3560004 6.524 6.3560004 6.3980002 C 6.3560004 6.2580004 6.342 6.1460004 6.23 5.908 L 4.4240003 1.8060001 L 4.354 1.82 L 2.3100002 8.008 C 2.142 8.498 2.52 8.568 3.01 8.596001 C 3.094 8.68 3.094 8.974 3.01 9.058001 C 2.548 9.044001 1.932 9.030001 1.386 9.030001 C 0.896 9.030001 0.49 9.044001 0.08400001 9.058001 C 0 8.974 0 8.68 0.08400001 8.596001 C 0.71400005 8.554 0.81200004 8.54 1.0780001 7.7840004 L 3.71 0.21000001 C 3.7800002 -0.014 3.864 -0.16800001 4.018 -0.16800001 C 4.2000003 -0.16800001 4.284 -0.028 4.382 0.21000001 L 6.4680004 4.9 C 6.5940003 5.1800003 6.636 5.25 6.7060003 5.25 C 6.762 5.25 6.8180003 5.096 6.9020004 4.8580003 L 8.512 0.21000001 C 8.596001 -0.028 8.666 -0.16800001 8.834001 -0.16800001 C 8.988 -0.16800001 9.086 -0.014 9.156 0.19600001 L 11.97 7.742 C 12.152 8.232 12.404 8.554 13.174001 8.596001 C 13.258 8.68 13.258 8.974 13.174001 9.058001 C 12.768001 9.044001 12.320001 9.030001 11.956 9.030001 C 11.592 9.030001 10.976001 9.044001 10.416 9.058001 C 10.332001 8.974 10.332001 8.68 10.416 8.596001 C 10.990001 8.554 11.55 8.512 11.34 7.9100003 Z "/>
</symbol>
<symbol id="g47288CF7D8F788F93B1406172900DCDE" overflow="visible">
<path d="M 0.79800004 0.602 C 0.79800004 0.19600001 1.1340001 -0.14 1.5400001 -0.14 C 1.9460001 -0.14 2.282 0.19600001 2.282 0.602 C 2.282 1.008 1.9460001 1.3440001 1.5400001 1.3440001 C 1.1340001 1.3440001 0.79800004 1.008 0.79800004 0.602 Z "/>
</symbol>
<symbol id="g9696EE00168B299790D79B47B78C5F18" overflow="visible">
<path d="M 0.85400003 6.552 C 0.85400003 6.2580004 1.12 6.006 1.414 6.006 C 1.6520001 6.006 2.072 6.2580004 2.072 6.566 C 2.072 6.678 2.0440001 6.762 2.016 6.86 C 1.988 6.958 1.904 7.084 1.904 7.196 C 1.904 7.546 2.2680001 8.05 3.2900002 8.05 C 3.7940001 8.05 4.5080004 7.7000003 4.5080004 6.3560004 C 4.5080004 5.46 4.1860003 4.7320004 3.3600001 3.8920002 L 2.3240001 2.8700001 C 0.952 1.47 0.72800004 0.79800004 0.72800004 -0.028 C 0.72800004 -0.028 1.442 0 1.8900001 0 L 4.34 0 C 4.788 0 5.432 -0.028 5.432 -0.028 C 5.6140003 0.71400005 5.754 1.764 5.768 2.184 C 5.684 2.2540002 5.5020003 2.282 5.362 2.2540002 C 5.124 1.26 4.886 0.91 4.382 0.91 L 1.8900001 0.91 C 1.8900001 1.582 2.8560002 2.5340002 2.926 2.604 L 4.34 3.9620001 C 5.138 4.7320004 5.7400002 5.348 5.7400002 6.412 C 5.7400002 7.9240003 4.5080004 8.54 3.374 8.54 C 1.82 8.54 0.85400003 7.392 0.85400003 6.552 Z "/>
</symbol>
<symbol id="gD0485EF23018DAF4BFC69AAD15075193" overflow="visible">
<path d="M 3.01 8.05 C 3.6120002 8.05 4.172 7.6860003 4.172 6.7900004 C 4.172 6.09 3.3600001 5.012 1.9740001 4.816 L 2.0440001 4.368 C 2.282 4.396 2.5340002 4.396 2.716 4.396 C 3.5140002 4.396 4.55 4.172 4.55 2.5900002 C 4.55 0.72800004 3.3040001 0.35000002 2.8140001 0.35000002 C 2.1000001 0.35000002 1.9740001 0.67200005 1.8060001 0.924 C 1.666 1.12 1.4840001 1.288 1.204 1.288 C 0.91 1.288 0.616 1.0220001 0.616 0.79800004 C 0.616 0.238 1.792 -0.14 2.632 -0.14 C 4.2980003 -0.14 5.782 0.938 5.782 2.786 C 5.782 4.3120003 4.6340003 4.8580003 3.808 4.998 L 3.7940001 5.026 C 4.9420004 5.572 5.264 6.1460004 5.264 6.888 C 5.264 7.308 5.1660004 7.644 4.83 7.9940004 C 4.5220003 8.302 4.032 8.54 3.3040001 8.54 C 1.246 8.54 0.658 7.196 0.658 6.734 C 0.658 6.538 0.79800004 6.2580004 1.1340001 6.2580004 C 1.6240001 6.2580004 1.6800001 6.7200003 1.6800001 6.986 C 1.6800001 7.8820004 2.6460001 8.05 3.01 8.05 Z "/>
</symbol>
<symbol id="g42427CF90B88C34047186DDCC0B8064E" overflow="visible">
<path d="M 1.4560001 7.322 L 1.4560001 1.7080001 C 1.4560001 0.546 1.218 0.476 0.238 0.43400002 C 0.154 0.35000002 0.154 0.056 0.238 -0.028 C 0.86800003 -0.014 1.554 0 2.058 0 C 2.548 0 3.374 -0.014 4.0740004 -0.028 C 4.158 0.056 4.158 0.35000002 4.0740004 0.43400002 C 2.982 0.49 2.6460001 0.546 2.6460001 1.7080001 L 2.6460001 4.0880003 C 2.954 3.99 3.2900002 3.9480002 3.7800002 3.9480002 C 6.328 3.9480002 7.098 5.6140003 7.098 6.8040004 C 7.098 7.63 6.552 9.128 3.9620001 9.128 C 3.43 9.128 2.604 9.030001 2.0440001 9.030001 C 1.526 9.030001 0.79800004 9.044001 0.238 9.058001 C 0.154 8.974 0.154 8.68 0.238 8.596001 C 1.218 8.554 1.4560001 8.484 1.4560001 7.322 Z M 2.6460001 7.756 C 2.6460001 8.162001 2.8560002 8.652 3.864 8.652 C 4.83 8.652 5.796 8.33 5.796 6.552 C 5.796 5.04 5.0680003 4.4240003 3.71 4.4240003 C 3.3600001 4.4240003 2.8000002 4.452 2.6460001 4.494 Z "/>
</symbol>
<symbol id="g9AE4831982D6CA553E49B4F41E9A233F" overflow="visible">
<path d="M 2.464 5.012 C 2.436 5.572 2.4220002 5.9360003 2.352 6.076 C 2.3240001 6.1460004 2.296 6.188 2.184 6.188 C 1.792 6.0340004 1.4280001 5.908 0.462 5.782 C 0.43400002 5.698 0.462 5.474 0.49 5.3900003 C 1.246 5.32 1.4000001 5.25 1.4000001 4.438 L 1.4000001 1.7080001 C 1.4000001 0.546 1.232 0.49 0.36400002 0.43400002 C 0.28 0.35000002 0.28 0.056 0.36400002 -0.028 C 0.85400003 -0.014 1.4000001 0 1.96 0 C 2.52 0 3.164 -0.014 3.654 -0.028 C 3.7380002 0.056 3.7380002 0.35000002 3.654 0.43400002 C 2.674 0.504 2.506 0.546 2.506 1.7080001 L 2.506 3.654 C 2.506 4.018 2.674 4.34 2.842 4.592 C 2.996 4.816 3.318 5.2780004 3.486 5.2780004 C 3.6120002 5.2780004 3.7380002 5.25 3.8500001 5.096 C 3.9480002 4.9560003 4.116 4.774 4.354 4.774 C 4.69 4.774 5.012 5.124 5.012 5.474 C 5.012 5.7400002 4.76 6.1460004 4.172 6.1460004 C 3.5140002 6.1460004 2.94 5.53 2.618 4.984 C 2.5340002 4.83 2.464 4.9420004 2.464 5.012 Z "/>
</symbol>
<symbol id="gA4DE3951E8A0322DEC5E3569D1D30666" overflow="visible">
<path d="M 0.574 2.8700001 C 0.574 1.442 1.526 -0.14 3.5140002 -0.14 C 4.4100003 -0.14 5.096 0.18200001 5.572 0.644 C 6.202 1.26 6.4820004 2.142 6.4820004 2.996 C 6.4820004 4.452 5.684 6.1460004 3.542 6.1460004 C 2.618 6.1460004 1.8620001 5.768 1.3440001 5.1660004 C 0.84000003 4.564 0.574 3.752 0.574 2.8700001 Z M 3.332 5.656 C 4.5360003 5.656 5.2780004 4.564 5.2780004 2.548 C 5.2780004 0.78400004 4.368 0.35000002 3.71 0.35000002 C 2.2540002 0.35000002 1.778 2.114 1.778 3.1920002 C 1.778 4.4100003 2.072 5.656 3.332 5.656 Z "/>
</symbol>
<symbol id="gC80234271A0A022352A099322F0FCD32" overflow="visible">
<path d="M 2.338 5.5160003 C 2.2540002 5.432 2.198 5.46 2.198 5.586 L 2.198 8.162001 C 2.198 9.0720005 2.2540002 9.632 2.2540002 9.632 C 2.2540002 9.7300005 2.198 9.772 2.072 9.772 C 1.722 9.632 0.67200005 9.436 0.112 9.394 C 0.08400001 9.282001 0.112 9.058001 0.19600001 8.974 C 0.238 8.974 0.28 8.974 0.322 8.974 C 0.938 8.932 1.092 8.932 1.092 7.826 L 1.092 0.994 C 1.092 0.448 1.0780001 0.19600001 1.036 0 C 1.1060001 -0.112 1.176 -0.16800001 1.3440001 -0.16800001 C 1.4280001 -0.08400001 1.5680001 0.042000003 1.6800001 0.16800001 C 1.82 0.33600003 1.904 0.33600003 2.058 0.21000001 C 2.38 -0.056 2.8000002 -0.14 3.2900002 -0.14 C 4.718 -0.14 6.3840003 1.1620001 6.3840003 3.388 C 6.3840003 5.096 5.124 6.1460004 3.9060001 6.1460004 C 3.3040001 6.1460004 2.772 5.908 2.338 5.5160003 Z M 2.436 5.0820003 C 2.8000002 5.4040003 3.22 5.53 3.6260002 5.53 C 4.48 5.53 5.1800003 4.494 5.1800003 3.1360002 C 5.1800003 1.5400001 4.5360003 0.33600003 3.206 0.33600003 C 2.772 0.33600003 2.4780002 0.644 2.198 0.994 L 2.198 4.494 C 2.198 4.788 2.2540002 4.928 2.436 5.0820003 Z "/>
</symbol>
<symbol id="g3649D621BC998C9216AD40BBEFAC3AB1" overflow="visible">
<path d="M 4.102 0.67200005 C 4.1860003 0.238 4.34 -0.14 5.04 -0.14 C 5.572 -0.14 6.076 0.098000005 6.3700004 0.37800002 C 6.342 0.546 6.2860003 0.67200005 6.132 0.75600004 C 6.0340004 0.67200005 5.796 0.532 5.6140003 0.532 C 5.208 0.532 5.1940002 1.0780001 5.1940002 1.722 L 5.1940002 3.7800002 C 5.1940002 5.768 4.102 6.1460004 3.0800002 6.1460004 C 1.932 6.1460004 0.77000004 5.3900003 0.77000004 4.592 C 0.77000004 4.256 0.938 4.0880003 1.26 4.0880003 C 1.666 4.0880003 1.9180001 4.382 1.9180001 4.564 C 1.9180001 4.662 1.904 4.76 1.876 4.816 C 1.8620001 4.8580003 1.848 4.9420004 1.848 5.096 C 1.848 5.53 2.436 5.684 2.9680002 5.684 C 3.444 5.684 4.102 5.446 4.102 3.864 C 4.102 3.766 4.06 3.71 4.018 3.696 L 2.8140001 3.4020002 C 1.47 3.066 0.504 2.3240001 0.504 1.3720001 C 0.504 0.224 1.288 -0.14 2.2680001 -0.14 C 2.7580001 -0.14 3.1780002 -0.028 3.7940001 0.448 L 4.0740004 0.67200005 Z M 4.102 3.262 L 4.102 1.414 C 4.102 1.232 4.018 1.1340001 3.9060001 1.0500001 C 3.542 0.75600004 3.066 0.43400002 2.674 0.43400002 C 1.9740001 0.43400002 1.666 0.994 1.666 1.4280001 C 1.666 2.058 1.96 2.7020001 2.996 2.9680002 Z "/>
</symbol>
<symbol id="gAAC2A4387B1619C03EEEB0968B96165F" overflow="visible">
<path d="M 2.5340002 1.7080001 L 2.5340002 4.494 C 2.5340002 5.1940002 2.5900002 6.09 2.5900002 6.09 C 2.5900002 6.1460004 2.52 6.188 2.408 6.188 C 2.016 6.0340004 1.4560001 5.908 0.49 5.782 C 0.462 5.698 0.49 5.474 0.518 5.3900003 C 1.288 5.32 1.4280001 5.236 1.4280001 4.438 L 1.4280001 1.7080001 C 1.4280001 0.546 1.274 0.504 0.42000002 0.43400002 C 0.33600003 0.35000002 0.33600003 0.056 0.42000002 -0.028 C 0.882 -0.014 1.4280001 0 1.988 0 C 2.548 0 3.0800002 -0.014 3.542 -0.028 C 3.6260002 0.056 3.6260002 0.35000002 3.542 0.43400002 C 2.6880002 0.49 2.5340002 0.546 2.5340002 1.7080001 Z M 1.26 8.386001 C 1.26 8.022 1.5960001 7.6580005 1.932 7.6580005 C 2.3240001 7.6580005 2.66 8.036 2.66 8.33 C 2.66 8.666 2.3660002 9.058001 1.988 9.058001 C 1.6520001 9.058001 1.26 8.722 1.26 8.386001 Z "/>
</symbol>
<symbol id="gBBFA548D7BC5ACA0036C5BF286E59830" overflow="visible">
<path d="M 1.33 1.7080001 C 1.33 0.546 1.176 0.476 0.322 0.43400002 C 0.238 0.35000002 0.238 0.056 0.322 -0.028 C 0.81200004 -0.014 1.33 0 1.8900001 0 C 2.45 0 2.982 -0.014 3.444 -0.028 C 3.528 0.056 3.528 0.35000002 3.444 0.43400002 C 2.5900002 0.476 2.436 0.546 2.436 1.7080001 L 2.436 8.162001 C 2.436 9.0720005 2.492 9.632 2.492 9.632 C 2.492 9.7300005 2.436 9.772 2.3100002 9.772 C 1.96 9.632 0.91 9.436 0.35000002 9.394 C 0.322 9.282001 0.35000002 9.058001 0.43400002 8.974 C 1.246 8.918 1.33 8.876 1.33 7.826 Z "/>
</symbol>
<symbol id="g88B62CE1F53AC1AE1D938018DA31319" overflow="visible">
<path d="M 0.602 6.006 C 0.40600002 6.006 0.35000002 5.8380003 0.35000002 5.7260003 L 0.35000002 5.544 C 0.35000002 5.474 0.36400002 5.46 0.42000002 5.46 L 1.246 5.46 L 1.246 1.246 C 1.246 0.252 1.6800001 -0.14 2.3240001 -0.14 C 2.9680002 -0.14 3.6680002 0.16800001 4.214 0.78400004 C 4.1860003 0.924 4.102 1.008 3.9620001 1.0220001 C 3.598 0.74200004 3.1780002 0.63 2.8140001 0.63 C 2.436 0.63 2.352 1.0500001 2.352 1.9180001 L 2.352 5.46 L 3.808 5.46 C 3.9480002 5.46 4.144 5.5160003 4.144 5.642 L 4.144 5.9220004 C 4.144 5.978 4.102 6.006 4.032 6.006 L 2.352 6.006 L 2.352 6.552 C 2.352 7.4620004 2.408 8.022 2.408 8.022 C 2.408 8.106 2.3660002 8.148001 2.296 8.148001 C 2.24 8.148001 2.114 8.092 1.988 8.022 C 1.8340001 7.938 1.694 7.868 1.5120001 7.826 C 1.3440001 7.7700005 1.204 7.728 1.204 7.63 C 1.204 7.4620004 1.246 7.5600004 1.246 6.006 Z "/>
</symbol>
<symbol id="g5799677F1612AA2CF55B8D046D0457BF" overflow="visible">
<path d="M 2.8560002 -2.24 C 3.0800002 -1.848 3.262 -1.4560001 3.43 -1.036 C 4.55 1.666 5.1800003 3.108 5.908 4.676 C 6.188 5.264 6.3840003 5.4880004 7.0420003 5.572 C 7.1260004 5.656 7.1260004 5.9500003 7.0420003 6.0340004 C 6.762 6.02 6.44 6.006 6.0480003 6.006 C 5.6280003 6.006 5.1940002 6.02 4.774 6.0340004 C 4.69 5.9500003 4.69 5.656 4.774 5.572 C 5.222 5.53 5.67 5.446 5.446 4.9420004 L 4.06 1.7360001 C 3.9620001 1.5120001 3.8360002 1.47 3.7240002 1.75 L 2.4780002 4.662 C 2.226 5.25 2.1560001 5.5160003 2.94 5.572 C 3.0240002 5.656 3.0240002 5.9500003 2.94 6.0340004 C 2.4220002 6.02 1.8620001 6.006 1.358 6.006 C 0.882 6.006 0.504 6.02 0.224 6.0340004 C 0.14 5.9500003 0.14 5.656 0.224 5.572 C 0.78400004 5.5020003 0.966 5.3760004 1.33 4.5220003 L 2.9120002 0.84000003 C 3.038 0.56 3.2480001 -0.08400001 3.108 -0.476 C 2.94 -0.938 2.772 -1.33 2.562 -1.764 C 2.408 -2.0440001 2.2120001 -2.17 1.8620001 -2.17 C 1.666 -2.17 1.61 -2.128 1.4560001 -2.128 C 1.0500001 -2.128 0.84000003 -2.548 0.84000003 -2.73 C 0.84000003 -3.0240002 1.12 -3.2480001 1.498 -3.2480001 C 1.792 -3.2480001 2.352 -3.1360002 2.8560002 -2.24 Z "/>
</symbol>
<symbol id="gE2267284F842780DB4609789BADA809" overflow="visible">
<path d="M 1.204 1.7080001 C 1.204 0.546 1.0500001 0.49 0.266 0.43400002 C 0.18200001 0.35000002 0.18200001 0.056 0.266 -0.028 C 0.72800004 -0.014 1.204 0 1.764 0 C 2.2540002 0 2.716 -0.014 3.038 -0.028 C 3.122 0.056 3.122 0.35000002 3.038 0.43400002 C 2.464 0.49 2.3100002 0.546 2.3100002 1.7080001 L 2.3100002 2.926 C 2.576 2.9120002 2.772 2.898 2.9120002 2.8560002 C 3.066 2.7440002 3.1920002 2.618 3.3600001 2.394 L 4.382 1.0220001 C 4.788 0.476 4.9560003 0.21000001 4.9700003 0.042000003 C 4.9700003 0 4.984 -0.028 5.026 -0.028 C 5.306 -0.014 5.6140003 0 5.894 0 C 6.328 0 6.762 -0.014 7.0420003 -0.028 C 7.1260004 0.056 7.1260004 0.35000002 7.0420003 0.43400002 C 6.566 0.49 6.216 0.546 5.8380003 1.0220001 L 3.99 3.3460002 C 3.934 3.4160001 3.8920002 3.4720001 3.8920002 3.542 C 3.8920002 3.598 3.8920002 3.6260002 3.9480002 3.6820002 L 5.1800003 4.9560003 C 5.6000004 5.4040003 6.09 5.5160003 6.65 5.572 C 6.734 5.656 6.734 5.9500003 6.65 6.0340004 C 6.328 6.02 5.9360003 6.006 5.432 6.006 C 4.9 6.006 4.382 6.02 4.06 6.0340004 C 3.976 5.9500003 3.976 5.656 4.06 5.572 C 4.8440003 5.5160003 4.5080004 5.026 4.382 4.8580003 C 4.06 4.452 3.6260002 3.976 3.262 3.71 C 2.954 3.486 2.576 3.318 2.3100002 3.276 L 2.3100002 8.162001 C 2.3100002 9.0720005 2.3660002 9.632 2.3660002 9.632 C 2.3660002 9.7300005 2.3100002 9.772 2.184 9.772 C 1.8340001 9.632 0.78400004 9.436 0.224 9.394 C 0.19600001 9.282001 0.224 9.058001 0.308 8.974 C 0.35000002 8.974 0.39200002 8.974 0.43400002 8.974 C 1.0500001 8.932 1.204 8.932 1.204 7.826 Z "/>
</symbol>
<symbol id="gA0F6184C06096774B92DEFE1EDA388E4" overflow="visible">
<path d="M 2.184 5.152 C 2.17 5.572 2.142 5.9360003 2.072 6.076 C 2.0440001 6.1460004 2.016 6.188 1.904 6.188 C 1.5120001 6.0340004 1.148 5.908 0.18200001 5.782 C 0.154 5.698 0.18200001 5.474 0.21000001 5.3900003 C 0.966 5.32 1.12 5.25 1.12 4.438 L 1.12 -1.5400001 C 1.12 -2.7020001 0.966 -2.772 0.112 -2.8140001 C 0.028 -2.898 0.028 -3.1920002 0.112 -3.276 C 0.602 -3.262 1.12 -3.2480001 1.6800001 -3.2480001 C 2.24 -3.2480001 2.9120002 -3.262 3.374 -3.276 C 3.4580002 -3.1920002 3.4580002 -2.898 3.374 -2.8140001 C 2.38 -2.7580001 2.226 -2.7020001 2.226 -1.5400001 L 2.226 -0.028 C 2.226 0.154 2.282 0.14 2.4220002 0.08400001 C 2.772 -0.056 3.1920002 -0.14 3.64 -0.14 C 4.4240003 -0.14 5.124 0.098000005 5.698 0.644 C 6.3560004 1.288 6.734 2.1560001 6.734 3.2900002 C 6.734 4.774 5.684 6.1460004 4.256 6.1460004 C 3.6120002 6.1460004 2.898 5.7260003 2.338 5.096 C 2.2540002 5.012 2.198 5.012 2.184 5.152 Z M 2.45 4.6340003 C 2.8140001 5.0820003 3.4580002 5.5020003 3.864 5.5020003 C 4.76 5.5020003 5.53 4.494 5.53 2.9120002 C 5.53 1.764 5.124 0.33600003 3.556 0.33600003 C 3.3040001 0.33600003 2.8140001 0.40600002 2.562 0.63 C 2.282 0.882 2.226 0.966 2.226 1.47 L 2.226 4.018 C 2.226 4.3120003 2.282 4.438 2.45 4.6340003 Z "/>
</symbol>
<symbol id="g1F652CD6CF98783FD5BC41E10F253E3" overflow="visible">
<path d="M 2.086 0 L 5.0680003 0 C 5.446 0 6.734 -0.028 6.734 -0.028 C 6.874 0.67200005 7.0140004 1.582 7.098 2.3100002 C 6.958 2.38 6.8040004 2.408 6.636 2.38 C 6.3560004 1.3720001 5.8380003 0.546 4.354 0.546 L 3.4720001 0.546 C 2.926 0.546 2.674 0.81200004 2.674 1.526 L 2.674 7.322 C 2.674 8.484 2.9120002 8.554 3.8920002 8.596001 C 3.976 8.68 3.976 8.974 3.8920002 9.058001 C 3.262 9.044001 2.604 9.030001 2.072 9.030001 C 1.5680001 9.030001 0.91 9.044001 0.266 9.058001 C 0.18200001 8.974 0.18200001 8.68 0.266 8.596001 C 1.246 8.554 1.4840001 8.484 1.4840001 7.322 L 1.4840001 1.7080001 C 1.4840001 0.546 1.246 0.476 0.266 0.43400002 C 0.18200001 0.35000002 0.18200001 0.056 0.266 -0.028 C 0.81200004 -0.014 1.61 0 2.086 0 Z "/>
</symbol>
<symbol id="g2027E4E303C701A0DF6BD0919BBDE7B4" overflow="visible">
<path d="M 0.67200005 1.932 C 0.72800004 1.246 0.77000004 0.588 0.77000004 0 C 0.91 0.028 1.0500001 0.042000003 1.12 0.042000003 C 1.218 0.042000003 1.302 0.042000003 1.4000001 0.014 C 1.778 -0.08400001 2.1560001 -0.14 2.674 -0.14 C 3.4580002 -0.14 4.9 0.238 4.9 1.6240001 C 4.9 2.576 4.214 3.1360002 3.262 3.486 C 2.4220002 3.808 1.8620001 4.018 1.8620001 4.788 C 1.8620001 5.362 2.3660002 5.684 2.842 5.684 C 3.15 5.684 3.9620001 5.572 4.144 4.382 C 4.228 4.2980003 4.5080004 4.3120003 4.592 4.396 C 4.6340003 4.9 4.662 5.418 4.676 5.88 C 4.242 5.9500003 3.5700002 6.1460004 2.842 6.1460004 C 1.8060001 6.1460004 0.86800003 5.474 0.86800003 4.578 C 0.86800003 3.556 1.33 3.122 2.408 2.674 C 3.5700002 2.198 3.8360002 1.904 3.8360002 1.302 C 3.8360002 0.616 3.164 0.322 2.6460001 0.322 C 2.1000001 0.322 1.792 0.504 1.6520001 0.658 C 1.3440001 0.98 1.19 1.5960001 1.1060001 1.9460001 C 1.0220001 2.03 0.75600004 2.016 0.67200005 1.932 Z "/>
</symbol>
<symbol id="g1A68EE8359C8016621D122AFF85D0AB2" overflow="visible">
<path d="M 4.466 2.6460001 C 4.466 1.316 3.766 0.33600003 2.926 0.33600003 C 2.394 0.33600003 2.2120001 0.68600005 2.002 0.966 C 1.82 1.204 1.582 1.414 1.288 1.414 C 1.0220001 1.414 0.75600004 1.176 0.75600004 0.896 C 0.75600004 0.322 1.9460001 -0.154 2.7440002 -0.154 C 4.48 -0.154 5.7120004 1.1340001 5.7120004 2.898 C 5.7120004 4.256 4.774 5.474 3.206 5.474 C 2.604 5.474 2.086 5.348 1.8340001 5.25 L 2.114 7.5880003 C 2.632 7.532 3.0800002 7.4620004 3.752 7.4620004 C 4.172 7.4620004 4.6480002 7.4900002 5.222 7.546 L 5.446 8.498 L 5.348 8.554 C 4.55 8.47 3.7940001 8.400001 3.052 8.400001 C 2.5340002 8.400001 2.03 8.428 1.5400001 8.47 L 1.064 4.438 C 1.8060001 4.718 2.338 4.774 2.842 4.774 C 3.752 4.774 4.466 4.172 4.466 2.6460001 Z "/>
</symbol>
<symbol id="g5D30492BABB8924F22FB3C21C3BB4FD6" overflow="visible">
<path d="M 3.6299999 1.738 L 4.796 4.796 C 4.906 5.082 5.038 5.17 5.566 5.17 L 9.746 5.17 L 10.978 1.584 C 11.242 0.792 10.604 0.77 9.768 0.726 C 9.636 0.726 9.482 0.704 9.35 0.704 C 9.218 0.572 9.218 0.088 9.35 -0.044 C 10.164 -0.022 12.254 0 13.1119995 0 C 14.014 0 15.246 -0.022 16.06 -0.044 C 16.192 0.088 16.192 0.572 16.06 0.704 C 15.202 0.792 14.476 0.77 14.08 1.892 L 9.548 14.476 C 9.218 14.278 7.898 13.508 7.128 13.508 L 2.354 2.244 C 1.782 0.88 1.122 0.77 0.154 0.704 C 0.022 0.572 0.022 0.088 0.154 -0.044 C 0.968 -0.022 1.364 0 2.222 0 C 3.124 0 4.334 -0.022 5.148 -0.044 C 5.2799997 0.088 5.2799997 0.572 5.148 0.704 C 4.312 0.77 3.2779999 0.83599997 3.6299999 1.738 Z M 6.006 6.226 C 5.522 6.226 5.368 6.292 5.456 6.512 L 7.392 11.44 L 7.546 11.44 L 9.35 6.226 Z "/>
</symbol>
<symbol id="g10E21E0BDD9E8A3223AFCCC5FAB594B4" overflow="visible">
<path d="M 6.578 0.924 L 6.138 0.924 C 5.676 0.924 5.368 1.342 5.368 2.662 L 5.368 7.436 C 5.368 9.262 5.984 9.35 7.194 9.416 C 7.414 9.548 7.414 10.032 7.194 10.164 C 6.05 10.142 4.84 10.12 3.96 10.12 C 3.08 10.12 0.682 10.164 0.682 10.164 C 0.462 10.032 0.462 9.548 0.682 9.416 C 1.892 9.35 2.508 9.262 2.508 7.436 L 2.508 2.684 C 2.508 0.858 1.892 0.77 0.682 0.704 C 0.462 0.572 0.462 0.088 0.682 -0.044 C 0.682 -0.044 3.102 0 3.96 0 L 7.876 0 C 8.514 0 10.516 -0.044 10.516 -0.044 C 10.736 1.056 10.956 2.486 11.088 3.6299999 C 10.868 3.74 10.406 3.784 10.142 3.74 C 9.702 2.156 8.888 0.924 6.578 0.924 Z "/>
</symbol>
<symbol id="gA8310C128FB1A6882AC3541210480577" overflow="visible">
<path d="M 8.822 3.014 L 8.822 0.858 C 8.338 0.704 7.854 0.65999997 7.216 0.65999997 C 4.62 0.65999997 3.916 3.322 3.916 5.126 C 3.916 7.898 4.994 9.548 7.062 9.548 C 8.712 9.548 10.054 8.47 10.3619995 7.04 C 10.67 6.952 11.088 6.952 11.352 7.106 C 11.33 8.052 11.22 9.0199995 11.088 10.01 C 10.252 10.054 8.514 10.4279995 7.304 10.4279995 C 3.674 10.4279995 0.83599997 8.448 0.83599997 4.84 C 0.83599997 1.584 2.794 -0.22 6.842 -0.22 C 8.338 -0.22 10.516 0.022 11.858 0.968 C 11.7039995 1.078 11.594 1.3199999 11.594 1.474 L 11.594 3.058 C 11.594 3.674 11.901999 3.916 12.606 3.96 C 12.716 4.158 12.716 4.488 12.584 4.708 C 11.924 4.686 10.89 4.664 10.274 4.664 C 9.614 4.664 8.382 4.686 7.282 4.708 C 7.194 4.466 7.172 4.202 7.282 3.96 C 8.536 3.894 8.822 3.718 8.822 3.014 Z "/>
</symbol>
<symbol id="gFFAD8ECF2B9E19A17BA2A700D6B3A275" overflow="visible">
<path d="M 12.122 5.17 C 12.122 8.712 9.702 10.4279995 6.402 10.4279995 C 3.322 10.4279995 0.83599997 8.382 0.83599997 4.884 C 0.83599997 1.3199999 3.454 -0.22 6.424 -0.22 C 9.68 -0.22 12.122 1.562 12.122 5.17 Z M 6.358 9.548 C 8.514 9.548 9.042 8.14 9.042 4.862 C 9.042 2.068 8.316 0.65999997 6.534 0.65999997 C 4.62 0.65999997 3.916 2.112 3.916 5.148 C 3.916 8.448 4.708 9.548 6.358 9.548 Z "/>
</symbol>
<symbol id="g6724C1A826126332467C6264F812F404" overflow="visible">
<path d="M 5.368 2.794 L 5.368 4.554 C 5.588 4.576 5.9179997 4.554 6.292 4.356 C 6.402 4.29 6.5559998 4.092 6.71 3.85 L 8.118 1.606 C 8.734 0.682 9.834 -0.198 11.066 -0.198 C 11.88 -0.198 12.518 -0.154 12.716 -0.044 C 12.782 0.088 12.782 0.506 12.694 0.65999997 C 12.1 0.792 11.44 1.3199999 11 2.002 L 9.35 4.532 C 9.284 4.642 9.196 4.752 9.174 4.84 C 10.846 5.368 11.572 6.468 11.572 7.59 C 11.572 8.734 10.714 10.274 7.59 10.274 C 6.776 10.274 4.62 10.12 4.004 10.12 C 2.794 10.12 1.826 10.142 0.88 10.164 C 0.748 10.032 0.748 9.548 0.88 9.416 C 2.222 9.35 2.574 9.152 2.574 7.3259997 L 2.574 2.794 C 2.574 0.968 2.222 0.77 0.88 0.704 C 0.748 0.572 0.748 0.088 0.88 -0.044 C 1.804 -0.022 2.794 0 4.004 0 C 5.148 0 5.962 -0.022 6.6879997 -0.044 C 6.82 0.088 6.82 0.572 6.6879997 0.704 C 5.786 0.792 5.368 0.968 5.368 2.794 Z M 5.368 9.306 C 5.72 9.394 6.424 9.416 6.732 9.416 C 7.942 9.416 8.492 8.602 8.492 7.216 C 8.492 5.39 7.172 5.2799997 5.368 5.2799997 Z "/>
</symbol>
<symbol id="g1707CF3A32B022CA2D70483E817BB0E1" overflow="visible">
<path d="M 2.574 7.3259997 L 2.574 2.794 C 2.574 0.968 2.222 0.77 0.88 0.704 C 0.748 0.572 0.748 0.088 0.88 -0.044 C 1.804 -0.022 2.794 0 4.004 0 C 5.2139997 0 6.182 -0.022 7.128 -0.044 C 7.2599998 0.088 7.2599998 0.572 7.128 0.704 C 5.786 0.77 5.434 0.968 5.434 2.794 L 5.434 7.3259997 C 5.434 9.152 5.786 9.35 7.128 9.416 C 7.2599998 9.548 7.2599998 10.032 7.128 10.164 C 6.204 10.142 5.2139997 10.12 4.004 10.12 C 2.794 10.12 1.826 10.142 0.88 10.164 C 0.748 10.032 0.748 9.548 0.88 9.416 C 2.222 9.35 2.574 9.152 2.574 7.3259997 Z "/>
</symbol>
<symbol id="gD56DD9CEC6529211EE0EE20264633A82" overflow="visible">
<path d="M 7.876 2.9259999 L 7.876 7.15 C 7.876 8.998 7.9639997 9.24 8.932 9.24 C 10.604 9.24 10.868 8.69 11.242 6.974 C 11.484 6.974 11.901999 6.996 12.1 7.084 C 11.946 8.096 11.8359995 9.24 11.814 10.23 C 11.814 10.252 11.7699995 10.296 11.748 10.296 C 11 10.23 9.24 10.12 7.502 10.12 L 5.2799997 10.12 C 3.586 10.12 2.09 10.23 1.254 10.296 C 1.21 10.296 1.166 10.252 1.166 10.23 C 1.078 9.24 0.858 8.074 0.616 7.018 C 0.83599997 6.93 1.21 6.908 1.474 6.908 C 1.914 8.668 2.156 9.24 3.608 9.24 C 4.906 9.24 5.104 8.888 5.104 7.216 L 5.104 2.9259999 C 5.104 1.1 4.906 0.77 3.146 0.704 C 3.014 0.572 3.014 0.088 3.146 -0.044 C 4.224 -0.022 5.302 0 6.446 0 C 7.612 0 8.734 -0.022 9.834 -0.044 C 9.966 0.088 9.966 0.572 9.834 0.704 C 8.074 0.77 7.876 1.1 7.876 2.9259999 Z "/>
</symbol>
<symbol id="gA105310788DE1650FF0BD6095C2860C4" overflow="visible">
<path d="M 10.274 7.3259997 L 10.274 5.9179997 C 8.58 5.8519998 7.128 5.874 5.434 5.9179997 L 5.434 7.3259997 C 5.434 9.152 5.566 9.35 6.908 9.416 C 7.04 9.548 7.04 10.032 6.908 10.164 C 6.028 10.142 5.148 10.12 4.004 10.12 C 2.794 10.12 1.826 10.142 0.88 10.164 C 0.748 10.032 0.748 9.548 0.88 9.416 C 2.222 9.35 2.574 9.152 2.574 7.3259997 L 2.574 2.794 C 2.574 0.968 2.222 0.77 0.88 0.704 C 0.748 0.572 0.748 0.088 0.88 -0.044 C 1.804 -0.022 2.794 0 4.004 0 C 5.148 0 6.05 -0.022 6.908 -0.044 C 7.04 0.088 7.04 0.572 6.908 0.704 C 5.566 0.77 5.434 0.968 5.434 2.794 L 5.434 4.95 C 7.128 5.016 8.58 4.994 10.274 4.95 L 10.274 2.794 C 10.274 0.968 10.142 0.77 8.8 0.704 C 8.668 0.572 8.668 0.088 8.8 -0.044 C 9.658 -0.022 10.582 0 11.7039995 0 C 12.914 0 13.882 -0.022 14.828 -0.044 C 14.96 0.088 14.96 0.572 14.828 0.704 C 13.486 0.77 13.134 0.968 13.134 2.794 L 13.134 7.3259997 C 13.134 9.152 13.486 9.35 14.828 9.416 C 14.96 9.548 14.96 10.032 14.828 10.164 C 13.904 10.142 12.914 10.12 11.7039995 10.12 C 10.582 10.12 9.68 10.142 8.8 10.164 C 8.668 10.032 8.668 9.548 8.8 9.416 C 10.142 9.35 10.274 9.152 10.274 7.3259997 Z "/>
</symbol>
<symbol id="gDC8BE94E2F4CFB356B16F8B3BD0C3FF6" overflow="visible">
<path d="M 10.516 8.404 L 10.559999 8.404 L 10.846 2.706 C 10.934 0.88 10.912 0.814 9.724 0.704 C 9.592 0.572 9.592 0.088 9.724 -0.044 C 10.582 -0.022 11.726 0 12.342 0 C 13.002 0 14.146 -0.022 14.894 -0.044 C 15.026 0.088 15.026 0.572 14.894 0.704 C 13.97 0.83599997 13.75 0.924 13.618 2.706 L 13.1779995 8.47 C 13.1119995 9.24 13.309999 9.328 14.41 9.416 C 14.542 9.548 14.542 10.032 14.41 10.164 L 10.142 10.12 L 7.7 4.07 L 7.546 4.07 L 5.346 10.12 L 1.188 10.164 C 1.056 10.032 1.056 9.548 1.188 9.416 C 2.046 9.35 2.442 9.064 2.376 8.58 L 1.716 2.662 C 1.518 0.83599997 1.232 0.77 0.396 0.704 C 0.264 0.572 0.264 0.088 0.396 -0.044 C 0.88 -0.022 1.518 0 2.068 0 C 2.728 0 3.322 -0.022 3.762 -0.044 C 3.894 0.088 3.894 0.572 3.762 0.704 C 2.508 0.792 2.53 1.034 2.706 2.662 L 3.3 7.832 L 3.322 7.832 L 6.292 -0.088 C 6.336 -0.198 6.5559998 -0.264 6.666 -0.264 C 6.754 -0.264 6.974 -0.198 7.018 -0.088 Z "/>
</symbol>
<symbol id="gDC78B3846EDAB84D21B8DADC57D4B72" overflow="visible">
<path d="M 1.078 1.276 C 1.078 0.44 1.782 -0.22 2.662 -0.22 C 3.542 -0.22 4.29 0.484 4.29 1.3199999 C 4.29 2.178 3.586 2.838 2.706 2.838 C 1.826 2.838 1.078 2.134 1.078 1.276 Z "/>
</symbol>
<symbol id="gE113D5FADA3BF383003A7B8BAFE64E49" overflow="visible">
<path d="M 9.9 12.518 C 9.966 12.782 9.944 13.2 9.768 13.42 C 6.666 13.332 5.016 12.738 3.3439999 11.286 C 1.6719999 9.834 0.968 7.524 0.968 5.412 C 0.968 0.704 3.564 -0.22 5.786 -0.22 C 9.218 -0.22 10.4939995 2.552 10.4939995 4.488 C 10.4939995 5.566 9.548 8.03 6.292 8.03 C 5.456 8.03 4.708 7.744 3.872 7.2599998 C 4.048 8.844 4.796 10.3619995 5.83 11.198 C 7.128 12.254 8.646 12.452 9.9 12.518 Z M 3.762 6.358 C 4.598 6.886 5.06 6.93 5.456 6.93 C 6.93 6.93 7.546 5.412 7.546 4.092 C 7.546 1.716 6.842 0.638 6.05 0.638 C 4.95 0.638 3.74 1.496 3.74 5.324 C 3.74 5.566 3.74 6.116 3.762 6.358 Z "/>
</symbol>
<symbol id="gC9B6AFC3BF91192FF29E0E0E4938B0A3" overflow="visible">
<path d="M 1.728 -3.088 L 5.1200004 -3.088 C 5.216 -2.992 5.216 -2.7040002 5.1200004 -2.608 C 2.9120002 -2.4320002 2.8000002 -2.1920002 2.8000002 -0.8 L 2.8000002 8.976001 C 2.8000002 10.368 2.9280002 10.608001 5.1200004 10.768001 C 5.216 10.864 5.216 11.152 5.1200004 11.248 L 1.728 11.248 Z "/>
</symbol>
<symbol id="g41BD02C814E5F1F9CC57CE5A8E90AFBE" overflow="visible">
<path d="M 2.48 1.264 L 3.3600001 3.584 C 3.44 3.7920003 3.5360003 3.8560002 3.92 3.8560002 L 7.2960005 3.8560002 L 8.224 1.1520001 C 8.416 0.60800004 7.8080006 0.544 7.0400004 0.49600002 C 6.9440002 0.4 6.9440002 0.064 7.0400004 -0.032 C 7.6320004 -0.016 8.512 0 9.136001 0 C 9.792001 0 10.400001 -0.016 10.960001 -0.032 C 11.056001 0.064 11.056001 0.4 10.960001 0.49600002 C 10.336 0.56 9.792001 0.60800004 9.52 1.376 L 6.2240005 10.528001 C 5.984 10.384001 5.552 10.208 5.3440003 10.208 L 1.7120001 1.6320001 C 1.296 0.64000005 0.81600004 0.544 0.112 0.49600002 C 0.016 0.4 0.016 0.064 0.112 -0.032 C 0.528 -0.016 1.056 0 1.536 0 C 2.1920002 0 2.992 -0.016 3.584 -0.032 C 3.68 0.064 3.68 0.4 3.584 0.49600002 C 2.976 0.544 2.2240002 0.60800004 2.48 1.264 Z M 4.208 4.5280004 C 3.8560002 4.5280004 3.7440002 4.576 3.808 4.736 L 5.44 8.88 L 5.5360003 8.88 L 7.0400004 4.5280004 Z "/>
</symbol>
<symbol id="g776E4106C35A60F8D71A42812632C381" overflow="visible">
<path d="M 1.5200001 1.9520001 C 1.5200001 0.624 1.3440001 0.544 0.36800003 0.49600002 C 0.272 0.4 0.272 0.064 0.36800003 -0.032 C 0.92800003 -0.016 1.5200001 0 2.16 0 C 2.8000002 0 3.4080002 -0.016 3.936 -0.032 C 4.032 0.064 4.032 0.4 3.936 0.49600002 C 2.96 0.544 2.7840002 0.624 2.7840002 1.9520001 L 2.7840002 9.328 C 2.7840002 10.368 2.848 11.008 2.848 11.008 C 2.848 11.120001 2.7840002 11.168 2.64 11.168 C 2.24 11.008 1.0400001 10.784 0.4 10.736 C 0.36800003 10.608001 0.4 10.352 0.49600002 10.2560005 C 1.424 10.192 1.5200001 10.144 1.5200001 8.944 Z "/>
</symbol>
<symbol id="gED7EC3C91583B7E83C2EF7E7FEF37733" overflow="visible">
<path d="M 7.1040006 6.1920004 C 7.4080005 6.1920004 7.6960006 6.4800005 7.6960006 6.8 C 7.6960006 7.136 7.392 7.392 6.9600005 7.392 C 6.544 7.392 5.7760005 7.1200004 5.36 6.576 C 5.168 6.7040005 4.6400003 7.024 3.696 7.024 C 2.272 7.024 0.96000004 6.064 0.96000004 4.592 C 0.96000004 3.7280002 1.3440001 3.232 1.792 2.8000002 C 1.3440001 2.4160001 1.088 1.728 1.088 1.184 C 1.088 0.60800004 1.4080001 0.16000001 1.8240001 -0.048 C 0.96000004 -0.56 0.512 -1.296 0.512 -1.9840001 C 0.512 -3.3760002 1.8240001 -3.808 3.0560002 -3.808 C 5.216 -3.808 7.5520005 -2.7680001 7.5520005 -1.0400001 C 7.5520005 -0.528 7.3120003 -0.128 6.8480005 0.256 C 6.2240005 0.768 5.104 0.78400004 4.512 0.78400004 C 4.224 0.78400004 3.8240001 0.75200003 3.44 0.70400006 C 3.2 0.688 3.0400002 0.67200005 2.96 0.67200005 C 2.496 0.67200005 1.9360001 0.896 1.9360001 1.5840001 C 1.9360001 1.904 2.032 2.24 2.2240002 2.512 C 2.608 2.288 3.0560002 2.176 3.68 2.176 C 5.0880003 2.176 6.3840003 3.0560002 6.3840003 4.624 C 6.3840003 5.3760004 6.1600003 5.808 5.696 6.288 C 5.808 6.4480004 6.1280003 6.6720004 6.3360004 6.6720004 C 6.4480004 6.6720004 6.5600004 6.6240005 6.656 6.4800005 C 6.7200003 6.352 6.9280005 6.1920004 7.1040006 6.1920004 Z M 2.112 -0.16000001 C 2.288 -0.208 2.5440001 -0.24000001 2.752 -0.24000001 C 3.2480001 -0.24000001 3.696 -0.192 3.92 -0.192 C 4.7200003 -0.192 5.392 -0.208 5.8560004 -0.46400002 C 6.4800005 -0.81600004 6.6720004 -1.0400001 6.6720004 -1.4560001 C 6.6720004 -2.608 4.9760003 -3.216 3.5360003 -3.216 C 2.96 -3.216 1.616 -2.752 1.616 -1.664 C 1.616 -1.12 1.6480001 -0.72 2.112 -0.16000001 Z M 5.104 4.464 C 5.104 2.976 4.352 2.6720002 3.7600002 2.6720002 C 2.4160001 2.6720002 2.272 3.808 2.272 4.8320003 C 2.272 5.952 2.6720002 6.5280004 3.5520003 6.5280004 C 4.5600004 6.5280004 5.104 5.7920003 5.104 4.464 Z "/>
</symbol>
<symbol id="g15DFEC786ABE57FB12A0CB4AD246101F" overflow="visible">
<path d="M 3.9680002 11.264001 L 0.57600003 11.264001 C 0.48000002 11.168 0.48000002 10.88 0.57600003 10.784 C 2.7840002 10.608001 2.8960001 10.368 2.8960001 8.976001 L 2.8960001 -0.8 C 2.8960001 -2.1920002 2.7680001 -2.4320002 0.57600003 -2.592 C 0.48000002 -2.6880002 0.48000002 -2.976 0.57600003 -3.072 L 3.9680002 -3.072 Z "/>
</symbol>
<symbol id="gFBB69929369BF0EC60A13F790CB240F" overflow="visible">
<path d="M 5.7120004 -0.16000001 C 7.2640004 -0.16000001 8.688001 0.57600003 9.776 2 C 9.696 2.144 9.584001 2.24 9.408 2.24 C 8.272 0.99200004 7.1840005 0.49600002 5.696 0.49600002 C 3.5360003 0.49600002 2.048 2.9280002 2.048 5.2640004 C 2.048 6.6400003 2.4160001 7.7920003 2.992 8.512 C 3.7920003 9.488001 4.7200003 9.936001 5.552 9.936001 C 7.76 9.936001 8.64 8.624001 9.056001 7.248 C 9.248 7.1840005 9.408 7.2320004 9.584001 7.3280005 C 9.504001 8.160001 9.392 8.928 9.232 9.808001 C 8.416 9.8880005 7.6960006 10.528001 5.728 10.528001 C 4.368 10.528001 3.232 10.032001 2.288 9.168 C 1.2320001 8.192 0.592 6.6240005 0.592 4.96 C 0.592 2.176 2.272 -0.16000001 5.7120004 -0.16000001 Z "/>
</symbol>
<symbol id="gB9A2E3AAC6CC7A3D99F4D7199A710CE2" overflow="visible">
<path d="M 0.656 3.2800002 C 0.656 1.6480001 1.7440001 -0.16000001 4.0160003 -0.16000001 C 5.0400004 -0.16000001 5.8240004 0.208 6.3680005 0.73600006 C 7.0880003 1.44 7.4080005 2.4480002 7.4080005 3.4240003 C 7.4080005 5.0880003 6.4960003 7.024 4.0480003 7.024 C 2.992 7.024 2.128 6.5920005 1.536 5.9040003 C 0.96000004 5.216 0.656 4.288 0.656 3.2800002 Z M 3.808 6.464 C 5.184 6.464 6.032 5.216 6.032 2.9120002 C 6.032 0.896 4.992 0.4 4.2400002 0.4 C 2.5760002 0.4 2.032 2.4160001 2.032 3.6480002 C 2.032 5.0400004 2.368 6.464 3.808 6.464 Z "/>
</symbol>
<symbol id="g26508BD01E1C582AC0C2221BD9BE4224" overflow="visible">
<path d="M 2.9440002 5.728 C 2.848 5.616 2.752 5.584 2.752 5.728 C 2.736 6.1600003 2.7040002 6.7840004 2.624 6.9440002 C 2.592 7.024 2.5600002 7.0720005 2.4320002 7.0720005 C 1.9840001 6.8960004 1.5680001 6.7520003 0.46400002 6.6080003 C 0.432 6.512 0.46400002 6.2560005 0.49600002 6.1600003 C 1.36 6.0800004 1.536 6.0000005 1.536 5.072 L 1.536 1.9520001 C 1.536 0.64000005 1.376 0.57600003 0.416 0.49600002 C 0.32000002 0.4 0.32000002 0.064 0.416 -0.032 C 0.896 -0.016 1.536 0 2.176 0 C 2.8160002 0 3.2960002 -0.016 3.7760003 -0.032 C 3.8720002 0.064 3.8720002 0.4 3.7760003 0.49600002 C 2.96 0.57600003 2.8000002 0.64000005 2.8000002 1.9520001 L 2.8000002 4.576 C 2.8000002 4.912 2.9440002 5.104 3.072 5.248 C 3.68 5.84 4.4 6.1920004 5.024 6.1920004 C 5.3440003 6.1920004 5.6800003 5.984 5.872 5.616 C 6.032 5.2960005 6.064 4.8640003 6.064 4.3840003 L 6.064 1.9520001 C 6.064 0.64000005 5.9040003 0.57600003 5.072 0.49600002 C 4.992 0.4 4.992 0.064 5.072 -0.032 C 5.552 -0.016 6.064 0 6.7040005 0 C 7.3440003 0 7.9200006 -0.016 8.400001 -0.032 C 8.4800005 0.064 8.4800005 0.4 8.400001 0.49600002 C 7.504 0.57600003 7.3280005 0.64000005 7.3280005 1.9520001 L 7.3280005 4.3360004 C 7.3280005 5.216 7.2640004 5.984 6.8960004 6.4800005 C 6.6240005 6.8320003 6.1280003 7.024 5.5680003 7.024 C 4.7840004 7.024 3.8880002 6.8160005 2.9440002 5.728 Z "/>
</symbol>
<symbol id="g7E49B8D69C443145BC38CA6BB9F62850" overflow="visible">
<path d="M 0.768 2.2080002 C 0.832 1.424 0.88000005 0.67200005 0.88000005 0 C 1.0400001 0.032 1.2 0.048 1.2800001 0.048 C 1.3920001 0.048 1.488 0.048 1.6 0.016 C 2.032 -0.096 2.4640002 -0.16000001 3.0560002 -0.16000001 C 3.9520001 -0.16000001 5.6000004 0.272 5.6000004 1.8560001 C 5.6000004 2.9440002 4.8160005 3.584 3.7280002 3.9840002 C 2.7680001 4.352 2.128 4.592 2.128 5.472 C 2.128 6.1280003 2.7040002 6.4960003 3.2480001 6.4960003 C 3.6000001 6.4960003 4.5280004 6.3680005 4.736 5.0080004 C 4.8320003 4.912 5.1520004 4.9280005 5.248 5.024 C 5.2960005 5.6000004 5.328 6.1920004 5.3440003 6.7200003 C 4.848 6.8 4.0800004 7.024 3.2480001 7.024 C 2.0640001 7.024 0.99200004 6.2560005 0.99200004 5.2320004 C 0.99200004 4.064 1.5200001 3.568 2.752 3.0560002 C 4.0800004 2.512 4.3840003 2.176 4.3840003 1.488 C 4.3840003 0.70400006 3.6160002 0.36800003 3.0240002 0.36800003 C 2.4 0.36800003 2.048 0.57600003 1.8880001 0.75200003 C 1.536 1.12 1.36 1.8240001 1.264 2.2240002 C 1.1680001 2.3200002 0.864 2.3040001 0.768 2.2080002 Z "/>
</symbol>
<symbol id="g94C24BD726F4D930F93182C299232222" overflow="visible">
<path d="M 0.688 6.8640003 C 0.46400002 6.8640003 0.4 6.6720004 0.4 6.544 L 0.4 6.3360004 C 0.4 6.2560005 0.416 6.2400002 0.48000002 6.2400002 L 1.424 6.2400002 L 1.424 1.424 C 1.424 0.28800002 1.9200001 -0.16000001 2.6560001 -0.16000001 C 3.3920002 -0.16000001 4.1920004 0.192 4.8160005 0.896 C 4.7840004 1.056 4.688 1.1520001 4.5280004 1.1680001 C 4.112 0.84800005 3.6320002 0.72 3.216 0.72 C 2.7840002 0.72 2.6880002 1.2 2.6880002 2.1920002 L 2.6880002 6.2400002 L 4.352 6.2400002 C 4.512 6.2400002 4.736 6.3040004 4.736 6.4480004 L 4.736 6.768 C 4.736 6.8320003 4.688 6.8640003 4.6080003 6.8640003 L 2.6880002 6.8640003 L 2.6880002 7.4880004 C 2.6880002 8.528001 2.752 9.168 2.752 9.168 C 2.752 9.264001 2.7040002 9.312 2.624 9.312 C 2.5600002 9.312 2.4160001 9.248 2.272 9.168 C 2.0960002 9.0720005 1.9360001 8.992001 1.728 8.944 C 1.536 8.88 1.376 8.832001 1.376 8.72 C 1.376 8.528001 1.424 8.64 1.424 6.8640003 Z "/>
</symbol>
<symbol id="g7079AB3C3D467A375535C421787E42DB" overflow="visible">
<path d="M 2.8160002 5.728 C 2.7840002 6.3680005 2.7680001 6.7840004 2.6880002 6.9440002 C 2.6560001 7.024 2.624 7.0720005 2.496 7.0720005 C 2.048 6.8960004 1.6320001 6.7520003 0.528 6.6080003 C 0.49600002 6.512 0.528 6.2560005 0.56 6.1600003 C 1.424 6.0800004 1.6 6.0000005 1.6 5.072 L 1.6 1.9520001 C 1.6 0.624 1.4080001 0.56 0.416 0.49600002 C 0.32000002 0.4 0.32000002 0.064 0.416 -0.032 C 0.9760001 -0.016 1.6 0 2.24 0 C 2.88 0 3.6160002 -0.016 4.176 -0.032 C 4.2720003 0.064 4.2720003 0.4 4.176 0.49600002 C 3.0560002 0.57600003 2.864 0.624 2.864 1.9520001 L 2.864 4.176 C 2.864 4.592 3.0560002 4.96 3.2480001 5.248 C 3.4240003 5.504 3.7920003 6.032 3.9840002 6.032 C 4.1280003 6.032 4.2720003 6.0000005 4.4 5.8240004 C 4.512 5.664 4.704 5.4560003 4.9760003 5.4560003 C 5.36 5.4560003 5.728 5.8560004 5.728 6.2560005 C 5.728 6.5600004 5.44 7.024 4.768 7.024 C 4.0160003 7.024 3.3600001 6.32 2.992 5.696 C 2.8960001 5.5200005 2.8160002 5.6480002 2.8160002 5.728 Z "/>
</symbol>
<symbol id="gC5015BCFB784037C5056D382F6B20C97" overflow="visible">
<path d="M 3.4720001 -0.16000001 C 4.096 -0.16000001 4.848 0.16000001 5.6320004 0.8 C 5.7120004 0.864 5.8560004 0.896 5.872 0.78400004 C 5.92 0.384 6.0480003 -0.16000001 6.0480003 -0.16000001 C 6.176 -0.208 6.2560005 -0.192 6.352 -0.16000001 C 6.7040005 0.128 7.2640004 0.36800003 8.240001 0.48000002 C 8.336 0.57600003 8.336 0.81600004 8.240001 0.91200006 C 7.2160006 0.99200004 7.0720005 1.296 7.0720005 2.0800002 L 7.0720005 5.1520004 C 7.0720005 5.6320004 7.136 6.8 7.136 6.8 C 7.136 6.8480005 7.0880003 6.8960004 7.0080004 6.8960004 C 6.9280005 6.88 6.688 6.8640003 6.4480004 6.8640003 C 5.9360003 6.8640003 5.36 6.88 4.8160005 6.8960004 C 4.7200003 6.8 4.7200003 6.464 4.8160005 6.3680005 C 5.6000004 6.32 5.808 6.1280003 5.808 5.072 L 5.808 1.9840001 C 5.808 1.6800001 5.7760005 1.552 5.552 1.36 C 4.96 0.84800005 4.352 0.592 3.9520001 0.592 C 3.4720001 0.592 2.6720002 0.81600004 2.6720002 2.24 L 2.6720002 5.1520004 C 2.6720002 5.6320004 2.736 6.8 2.736 6.8 C 2.736 6.8480005 2.6880002 6.8960004 2.608 6.8960004 C 2.528 6.88 2.288 6.8640003 2.048 6.8640003 C 1.536 6.8640003 0.96000004 6.88 0.416 6.8960004 C 0.32000002 6.8 0.32000002 6.464 0.416 6.3680005 C 1.184 6.3040004 1.4080001 6.1280003 1.4080001 5.0880003 L 1.4080001 2.016 C 1.4080001 0.91200006 1.8880001 -0.16000001 3.4720001 -0.16000001 Z "/>
</symbol>
<symbol id="gC2B9BD65B0E3456A64080FDFF521F7E0" overflow="visible">
<path d="M 6.3680005 1.4560001 C 6.3040004 1.6 6.176 1.664 6.032 1.6800001 C 5.4880004 0.9760001 4.8 0.624 4.112 0.624 C 2.9440002 0.624 1.968 1.8080001 1.968 3.68 C 1.968 5.44 2.736 6.4960003 3.7920003 6.4960003 C 4.736 6.4960003 4.8640003 5.9360003 4.9280005 5.3760004 C 4.9760003 4.9440002 5.2000003 4.8 5.5360003 4.8 C 5.872 4.8 6.32 5.0080004 6.32 5.504 C 6.32 6.3840003 5.4080005 7.024 3.8720002 7.024 C 2.288 7.024 0.592 5.6000004 0.592 3.328 C 0.592 1.264 1.7440001 -0.16000001 3.7600002 -0.16000001 C 4.7200003 -0.16000001 5.5680003 0.14400001 6.3680005 1.4560001 Z "/>
</symbol>
<symbol id="g8EC8620411AE7F46663E6890D2DD9166" overflow="visible">
<path d="M 2.8960001 1.9520001 L 2.8960001 5.136 C 2.8960001 5.9360003 2.96 6.9600005 2.96 6.9600005 C 2.96 7.024 2.88 7.0720005 2.752 7.0720005 C 2.3040001 6.8960004 1.664 6.7520003 0.56 6.6080003 C 0.528 6.512 0.56 6.2560005 0.592 6.1600003 C 1.4720001 6.0800004 1.6320001 5.984 1.6320001 5.072 L 1.6320001 1.9520001 C 1.6320001 0.624 1.4560001 0.57600003 0.48000002 0.49600002 C 0.384 0.4 0.384 0.064 0.48000002 -0.032 C 1.008 -0.016 1.6320001 0 2.272 0 C 2.9120002 0 3.5200002 -0.016 4.0480003 -0.032 C 4.144 0.064 4.144 0.4 4.0480003 0.49600002 C 3.072 0.56 2.8960001 0.624 2.8960001 1.9520001 Z M 1.44 9.584001 C 1.44 9.168 1.8240001 8.752001 2.2080002 8.752001 C 2.6560001 8.752001 3.0400002 9.184 3.0400002 9.52 C 3.0400002 9.904 2.7040002 10.352 2.272 10.352 C 1.8880001 10.352 1.44 9.968 1.44 9.584001 Z "/>
</symbol>
<symbol id="gBC176529035DE42B8BD4625370C40E4D" overflow="visible">
<path d="M 2.72 8.56 L 5.584 8.56 C 4.3360004 5.4560003 3.072 2.3360002 1.9840001 -0.096 L 2.112 -0.208 L 3.2 -0.16000001 C 4.112 2.5600002 4.992 5.216 6.7840004 9.584001 L 6.5280004 9.776 C 6.2560005 9.696 5.9040003 9.6 5.2960005 9.6 L 2 9.6 C 1.4560001 9.6 1.488 9.76 1.2 9.824 C 1.1520001 9.824 1.136 9.824 1.136 9.776 C 1.12 9.008 0.94400007 8.048 0.81600004 7.2160006 C 0.99200004 7.168 1.1520001 7.1520004 1.3280001 7.168 C 1.6800001 8.448 2.2080002 8.56 2.72 8.56 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
<symbol id="g1741EC601D45A91DF6927753AEFC05FD" overflow="visible">
<path d="M 6.32 10.096001 C 5.392 10.224001 5.4240003 10.528001 3.8560002 10.528001 C 2.24 10.528001 0.81600004 9.456 0.81600004 7.76 C 0.81600004 6.0800004 2.2080002 5.3120003 3.6160002 4.768 C 4.576 4.4 5.76 3.9520001 5.76 2.384 C 5.76 1.088 5.0400004 0.416 3.7600002 0.416 C 2.272 0.416 1.312 1.1040001 0.96000004 2.6880002 C 0.75200003 2.752 0.592 2.72 0.432 2.64 C 0.49600002 1.4080001 0.56 0.99200004 0.75200003 0.208 C 1.7600001 0.208 2.2080002 -0.16000001 3.6320002 -0.16000001 C 4.352 -0.16000001 5.0400004 0.016 5.6000004 0.36800003 C 6.5280004 0.94400007 7.1040006 1.9200001 7.1040006 2.9440002 C 7.1040006 4.6400003 5.8240004 5.392 4.512 5.8880005 C 3.5520003 6.2400002 1.9520001 6.8480005 1.9520001 8.192 C 1.9520001 9.088 2.7680001 9.984 3.7120001 9.984 C 5.2640004 9.984 5.76 8.992001 6.0800004 7.9360003 C 6.2560005 7.9040003 6.464 7.9200006 6.6080003 8.032001 C 6.544 8.8 6.4800005 9.248 6.32 10.096001 Z "/>
</symbol>
<symbol id="gACDA1EE5EEC178C67D037C3CDBE0EFC9" overflow="visible">
<path d="M 6.176 1.488 C 5.584 0.88000005 5.1200004 0.624 4.1920004 0.624 C 3.6160002 0.624 2.9440002 0.96000004 2.4480002 1.7760001 C 2.128 2.3040001 1.9360001 3.0400002 1.9360001 3.9680002 L 6.1920004 3.936 C 6.3840003 3.936 6.4960003 4.032 6.4960003 4.208 C 6.4960003 5.552 6.0160003 6.992 3.7920003 6.992 C 2.4 6.992 0.592 5.664 0.592 3.232 C 0.592 2.3360002 0.81600004 1.4720001 1.3440001 0.864 C 1.8880001 0.224 2.64 -0.16000001 3.7920003 -0.16000001 C 5.0080004 -0.16000001 5.872 0.4 6.512 1.2320001 C 6.464 1.3920001 6.3680005 1.4720001 6.176 1.488 Z M 1.9840001 4.512 C 2.288 6.32 3.4080002 6.464 3.7920003 6.464 C 4.4 6.464 5.1200004 6.1280003 5.1200004 4.7840004 C 5.1200004 4.6400003 5.056 4.5600004 4.88 4.5600004 Z "/>
</symbol>
<symbol id="g8F0641061D7822251E2A1C9000154920" overflow="visible">
<path d="M 4.688 0.768 C 4.7840004 0.272 4.96 -0.16000001 5.76 -0.16000001 C 6.3680005 -0.16000001 6.9440002 0.112 7.28 0.432 C 7.248 0.624 7.1840005 0.768 7.0080004 0.864 C 6.8960004 0.768 6.6240005 0.60800004 6.4160004 0.60800004 C 5.952 0.60800004 5.9360003 1.2320001 5.9360003 1.968 L 5.9360003 4.32 C 5.9360003 6.5920005 4.688 7.024 3.5200002 7.024 C 2.2080002 7.024 0.88000005 6.1600003 0.88000005 5.248 C 0.88000005 4.8640003 1.072 4.6720004 1.44 4.6720004 C 1.904 4.6720004 2.1920002 5.0080004 2.1920002 5.216 C 2.1920002 5.328 2.176 5.44 2.144 5.504 C 2.128 5.552 2.112 5.6480002 2.112 5.8240004 C 2.112 6.32 2.7840002 6.4960003 3.3920002 6.4960003 C 3.936 6.4960003 4.688 6.2240005 4.688 4.4160004 C 4.688 4.3040004 4.6400003 4.2400002 4.592 4.224 L 3.216 3.8880002 C 1.6800001 3.5040002 0.57600003 2.6560001 0.57600003 1.5680001 C 0.57600003 0.256 1.4720001 -0.16000001 2.592 -0.16000001 C 3.1520002 -0.16000001 3.6320002 -0.032 4.3360004 0.512 L 4.656 0.768 Z M 4.688 3.7280002 L 4.688 1.616 C 4.688 1.4080001 4.592 1.296 4.464 1.2 C 4.0480003 0.864 3.5040002 0.49600002 3.0560002 0.49600002 C 2.256 0.49600002 1.904 1.136 1.904 1.6320001 C 1.904 2.352 2.24 3.088 3.4240003 3.3920002 Z "/>
</symbol>
<symbol id="g40BC2CA66BF08C308C98CB508D30B53" overflow="visible">
<path d="M 2.6720002 4.576 C 2.6720002 4.912 2.8160002 5.104 2.9440002 5.248 C 3.5520003 5.84 4.368 6.1920004 4.992 6.1920004 C 5.3120003 6.1920004 5.6480002 5.984 5.84 5.616 C 6.0000005 5.2960005 6.032 4.8640003 6.032 4.3840003 L 6.032 1.9520001 C 6.032 0.64000005 5.872 0.57600003 5.0400004 0.49600002 C 4.96 0.4 4.96 0.064 5.0400004 -0.032 C 5.4880004 -0.016 6.032 0 6.6720004 0 C 7.3120003 0 7.84 -0.016 8.368 -0.032 C 8.448 0.064 8.448 0.4 8.368 0.49600002 C 7.472 0.57600003 7.2960005 0.64000005 7.2960005 1.9520001 L 7.2960005 4.3360004 C 7.2960005 5.216 7.2320004 6.0000005 6.8640003 6.4800005 C 6.5920005 6.8320003 6.096 7.024 5.5360003 7.024 C 4.7520003 7.024 3.7920003 6.8160005 2.8160002 5.728 C 2.8160002 5.7120004 2.8000002 5.7120004 2.7840002 5.696 C 2.736 5.6320004 2.6560001 5.5360003 2.6560001 5.728 L 2.6720002 9.328 C 2.6720002 10.368 2.736 11.008 2.736 11.008 C 2.736 11.120001 2.6720002 11.168 2.528 11.168 C 2.128 11.008 0.92800003 10.784 0.28800002 10.736 C 0.256 10.608001 0.28800002 10.352 0.384 10.2560005 C 0.432 10.2560005 0.48000002 10.2560005 0.528 10.2560005 C 1.2320001 10.208 1.4080001 10.208 1.4080001 8.944 L 1.4080001 1.9520001 C 1.4080001 0.624 1.2160001 0.56 0.28800002 0.49600002 C 0.192 0.4 0.192 0.064 0.28800002 -0.032 C 0.81600004 -0.016 1.4080001 0 2.048 0 C 2.6560001 0 3.1840003 -0.016 3.6320002 -0.032 C 3.7280002 0.064 3.7280002 0.4 3.6320002 0.49600002 C 2.8160002 0.56 2.6720002 0.624 2.6720002 1.9520001 Z "/>
</symbol>
<symbol id="g9519A9B09125702A7696E3BE317A1C17" overflow="visible">
<path d="M 5.2320004 4.096 C 4.8 2.64 3.7760003 1.024 1.6480001 0.224 C 1.6480001 0.032 1.7120001 -0.112 1.84 -0.192 C 3.456 0.28800002 4.4480004 0.96000004 5.3440003 2 C 6.3360004 3.1520002 6.8320003 4.6080003 6.8320003 5.872 C 6.8320003 9.120001 4.992 9.76 3.7600002 9.76 C 1.664 9.76 0.8 7.728 0.8 6.352 C 0.8 4.9760003 1.536 3.7440002 3.7120001 3.7440002 C 4.1280003 3.7440002 4.7520003 3.8720002 5.2320004 4.096 Z M 5.3760004 4.6720004 C 4.848 4.32 4.32 4.3040004 4.0480003 4.3040004 C 2.48 4.3040004 2.128 5.84 2.128 6.6400003 C 2.128 8.400001 2.8000002 9.200001 3.584 9.200001 C 4.592 9.200001 5.504 8.656 5.504 5.92 C 5.504 5.5680003 5.472 5.136 5.3760004 4.6720004 Z "/>
</symbol>
<symbol id="g1B31FFD796CA2E900A884ECD4210CED3" overflow="visible">
<path d="M 3.44 9.200001 C 4.1280003 9.200001 4.768 8.784 4.768 7.76 C 4.768 6.9600005 3.8400002 5.728 2.256 5.504 L 2.3360002 4.992 C 2.608 5.024 2.8960001 5.024 3.104 5.024 C 4.0160003 5.024 5.2000003 4.768 5.2000003 2.96 C 5.2000003 0.832 3.7760003 0.4 3.216 0.4 C 2.4 0.4 2.256 0.768 2.0640001 1.056 C 1.904 1.2800001 1.6960001 1.4720001 1.376 1.4720001 C 1.0400001 1.4720001 0.70400006 1.1680001 0.70400006 0.91200006 C 0.70400006 0.272 2.048 -0.16000001 3.0080001 -0.16000001 C 4.912 -0.16000001 6.6080003 1.072 6.6080003 3.1840003 C 6.6080003 4.9280005 5.2960005 5.552 4.352 5.7120004 L 4.3360004 5.7440004 C 5.6480002 6.3680005 6.0160003 7.024 6.0160003 7.872 C 6.0160003 8.352 5.9040003 8.736 5.5200005 9.136001 C 5.168 9.488001 4.6080003 9.76 3.7760003 9.76 C 1.424 9.76 0.75200003 8.224 0.75200003 7.6960006 C 0.75200003 7.472 0.91200006 7.1520004 1.296 7.1520004 C 1.8560001 7.1520004 1.9200001 7.6800003 1.9200001 7.984 C 1.9200001 9.008 3.0240002 9.200001 3.44 9.200001 Z "/>
</symbol>
<symbol id="gD032B844D751F1F27806C7004D4F5D2F" overflow="visible">
<path d="M 2.6720002 6.3040004 C 2.5760002 6.208 2.512 6.2400002 2.512 6.3840003 L 2.512 9.328 C 2.512 10.368 2.5760002 11.008 2.5760002 11.008 C 2.5760002 11.120001 2.512 11.168 2.368 11.168 C 1.968 11.008 0.768 10.784 0.128 10.736 C 0.096 10.608001 0.128 10.352 0.224 10.2560005 C 0.272 10.2560005 0.32000002 10.2560005 0.36800003 10.2560005 C 1.072 10.208 1.248 10.208 1.248 8.944 L 1.248 1.136 C 1.248 0.512 1.2320001 0.224 1.184 0 C 1.264 -0.128 1.3440001 -0.192 1.536 -0.192 C 1.6320001 -0.096 1.792 0.048 1.9200001 0.192 C 2.0800002 0.384 2.176 0.384 2.352 0.24000001 C 2.72 -0.064 3.2 -0.16000001 3.7600002 -0.16000001 C 5.392 -0.16000001 7.2960005 1.3280001 7.2960005 3.8720002 C 7.2960005 5.8240004 5.8560004 7.024 4.464 7.024 C 3.7760003 7.024 3.1680002 6.7520003 2.6720002 6.3040004 Z M 2.7840002 5.808 C 3.2 6.176 3.68 6.32 4.144 6.32 C 5.1200004 6.32 5.92 5.136 5.92 3.584 C 5.92 1.7600001 5.184 0.384 3.6640003 0.384 C 3.1680002 0.384 2.832 0.73600006 2.512 1.136 L 2.512 5.136 C 2.512 5.472 2.5760002 5.6320004 2.7840002 5.808 Z "/>
</symbol>
<symbol id="g54C180954D544D3C78C9AD9E4F48A6CA" overflow="visible">
<path d="M 3.6480002 -0.16000001 C 4.88 -0.16000001 6.7520003 1.088 6.7520003 4.848 C 6.7520003 6.432 6.3680005 7.7920003 5.664 8.72 C 5.248 9.280001 4.576 9.76 3.7120001 9.76 C 2.128 9.76 0.624 7.872 0.624 4.704 C 0.624 2.992 1.1520001 1.3920001 2.032 0.512 C 2.48 0.064 3.0240002 -0.16000001 3.6480002 -0.16000001 Z M 3.7120001 9.200001 C 3.9840002 9.200001 4.2400002 9.104 4.432 8.928 C 4.9280005 8.512 5.36 7.2960005 5.36 5.1520004 C 5.36 3.68 5.3120003 2.6720002 5.0880003 1.8560001 C 4.736 0.544 3.9520001 0.4 3.6640003 0.4 C 2.176 0.4 2.016 3.1360002 2.016 4.5280004 C 2.016 8.464001 2.992 9.200001 3.7120001 9.200001 Z "/>
</symbol>
<symbol id="g20DDE86F15DD9C8B9599512790FC45E4" overflow="visible">
<path d="M 7.728 6.1120005 L 7.84 6.1120005 L 8.048 1.968 C 8.112 0.64000005 8.096001 0.57600003 7.2320004 0.49600002 C 7.136 0.4 7.136 0.064 7.2320004 -0.032 C 7.7920003 -0.016 8.384001 0 8.832001 0 C 9.312 0 9.776 -0.016 10.208 -0.032 C 10.304001 0.064 10.304001 0.4 10.208 0.49600002 C 9.392 0.57600003 9.376 0.67200005 9.280001 1.968 L 8.96 6.096 C 8.912001 6.7360005 9.056001 6.8 9.856001 6.8640003 C 9.952001 6.9600005 9.952001 7.2960005 9.856001 7.392 L 7.6960006 7.36 L 5.2960005 1.6320001 L 3.2480001 7.36 L 1.024 7.392 C 0.92800003 7.2960005 0.92800003 6.9600005 1.024 6.8640003 C 1.8080001 6.8160005 1.9520001 6.7360005 1.9200001 6.432 L 1.4080001 1.9360001 C 1.264 0.60800004 1.056 0.544 0.448 0.49600002 C 0.35200003 0.4 0.35200003 0.064 0.448 -0.032 C 0.768 -0.016 1.248 0 1.5040001 0 C 1.8240001 0 2.4160001 -0.016 2.736 -0.032 C 2.832 0.064 2.832 0.4 2.736 0.49600002 C 1.8240001 0.56 1.84 0.75200003 1.968 1.9360001 L 2.4320002 6.0000005 L 2.4640002 6.0000005 L 4.736 -0.064 C 4.768 -0.14400001 4.848 -0.192 4.9280005 -0.192 C 4.992 -0.192 5.072 -0.14400001 5.104 -0.064 Z "/>
</symbol>
<symbol id="g3E944C953D169E97A30360D928248E70" overflow="visible">
<path d="M 3.0240002 1.9520001 L 3.0240002 3.1360002 C 3.3120003 3.0080001 3.6320002 2.9440002 4.032 2.9440002 C 6.176 2.9440002 6.8320003 4.48 6.8320003 5.44 C 6.8320003 6.2720003 6.352 7.392 4.0800004 7.392 C 3.4880002 7.392 2.8160002 7.36 2.384 7.36 C 1.9200001 7.36 1.248 7.3760004 0.60800004 7.392 C 0.512 7.2960005 0.512 6.9600005 0.60800004 6.8640003 C 1.5840001 6.8 1.7600001 6.7360005 1.7600001 5.4080005 L 1.7600001 1.9520001 C 1.7600001 0.624 1.5840001 0.57600003 0.60800004 0.49600002 C 0.512 0.4 0.512 0.064 0.60800004 -0.032 C 1.136 -0.016 1.6960001 0 2.4 0 C 3.088 0 3.6480002 -0.016 4.176 -0.032 C 4.2720003 0.064 4.2720003 0.4 4.176 0.49600002 C 3.2 0.56 3.0240002 0.624 3.0240002 1.9520001 Z M 3.0240002 6.144 C 3.0240002 6.656 3.216 6.8640003 3.9840002 6.8640003 C 4.9280005 6.8640003 5.44 6.3680005 5.44 5.248 C 5.44 4.096 5.024 3.4720001 4.064 3.4720001 C 3.7440002 3.4720001 3.344 3.5200002 3.0240002 3.6480002 Z "/>
</symbol>
<symbol id="gBAC0ED7F2DB725071CE720AF8BC15D72" overflow="visible">
<path d="M 2.9280002 5.7920003 C 2.5440001 6.7040005 2.5600002 6.7840004 3.4240003 6.8640003 C 3.5200002 6.9600005 3.5200002 7.2960005 3.4240003 7.392 C 2.9280002 7.3760004 2.384 7.36 1.728 7.36 C 1.2160001 7.36 0.73600006 7.3760004 0.32000002 7.392 C 0.224 7.2960005 0.224 6.9600005 0.32000002 6.8640003 C 1.1040001 6.7840004 1.2160001 6.6080003 1.6 5.696 L 3.8720002 0.448 C 4.0800004 -0.016 4.1600003 -0.192 4.3360004 -0.192 C 4.4480004 -0.192 4.512 -0.064 4.736 0.448 L 7.0720005 5.6800003 C 7.4080005 6.4160004 7.5840006 6.8 8.448 6.8640003 C 8.544001 6.9600005 8.544001 7.2960005 8.448 7.392 C 8.096001 7.3760004 7.7120004 7.36 7.2960005 7.36 C 6.7040005 7.36 6.2560005 7.3760004 5.8240004 7.392 C 5.728 7.2960005 5.728 6.9600005 5.8240004 6.8640003 C 6.688 6.8 6.768 6.6080003 6.4480004 5.7920003 L 4.704 1.8080001 C 4.656 1.7600001 4.6400003 1.7600001 4.592 1.8080001 Z "/>
</symbol>
<symbol id="gDA675C10B642A458CD97A11D372FF5DA" overflow="visible">
<path d="M 3.9680002 3.6000001 C 5.024 3.6000001 5.0400004 3.2960002 5.072 2.7040002 C 5.1520004 2.624 5.44 2.624 5.5200005 2.7040002 C 5.504 3.072 5.4880004 3.6160002 5.4880004 3.8720002 C 5.4880004 4.096 5.504 4.6080003 5.5200005 5.0080004 C 5.44 5.0880003 5.1520004 5.0880003 5.072 5.0080004 C 5.0400004 4.288 5.0080004 4.112 3.9680002 4.112 L 3.0560002 4.112 L 3.0560002 6.3840003 C 3.0560002 6.656 3.2640002 6.8320003 3.568 6.8320003 L 4.48 6.8320003 C 5.7920003 6.8320003 6.0000005 6.3040004 6.288 5.392 C 6.4480004 5.3760004 6.5920005 5.4080005 6.7200003 5.472 C 6.656 6.0160003 6.464 7.2640004 6.432 7.3760004 C 6.432 7.4080005 6.4160004 7.4240003 6.3840003 7.4240003 C 6.1600003 7.3760004 6.0000005 7.36 5.728 7.36 L 2.4160001 7.36 C 1.9520001 7.36 1.2160001 7.3760004 0.64000005 7.392 C 0.544 7.2960005 0.544 6.9600005 0.64000005 6.8640003 C 1.616 6.8 1.792 6.7360005 1.792 5.4080005 L 1.792 1.9520001 C 1.792 0.624 1.616 0.57600003 0.64000005 0.49600002 C 0.544 0.4 0.544 0.064 0.64000005 -0.032 C 1.2160001 -0.016 1.9200001 0 2.4320002 0 L 4.8960004 0 C 5.5360003 0 6.5920005 -0.032 6.5920005 -0.032 C 6.7840004 0.624 6.9600005 1.5040001 7.0720005 2.176 C 6.9280005 2.256 6.8 2.288 6.6240005 2.24 C 6.3680005 1.296 5.9040003 0.49600002 4.576 0.49600002 L 3.8880002 0.49600002 C 3.216 0.49600002 3.0560002 0.67200005 3.0560002 1.2 L 3.0560002 3.6000001 Z "/>
</symbol>
<symbol id="g176D627313BEF56D87624592E290FFD2" overflow="visible">
<path d="M 4.998 -0.14 C 6.3560004 -0.14 7.602 0.504 8.554 1.75 C 8.484 1.876 8.386001 1.96 8.232 1.96 C 7.2380004 0.86800003 6.2860003 0.43400002 4.984 0.43400002 C 3.094 0.43400002 1.792 2.562 1.792 4.606 C 1.792 5.81 2.114 6.8180003 2.618 7.4480004 C 3.318 8.302 4.13 8.694 4.8580003 8.694 C 6.7900004 8.694 7.5600004 7.546 7.9240003 6.342 C 8.092 6.2860003 8.232 6.328 8.386001 6.412 C 8.316 7.1400003 8.218 7.8120003 8.078 8.582001 C 7.3640003 8.652 6.734 9.212 5.012 9.212 C 3.822 9.212 2.828 8.778 2.002 8.022 C 1.0780001 7.168 0.518 5.796 0.518 4.34 C 0.518 1.904 1.988 -0.14 4.998 -0.14 Z "/>
</symbol>
<symbol id="g6D1F08816BC4457F813BBA2B6CEC4900" overflow="visible">
<path d="M 2.38 5.012 C 2.3660002 5.432 2.338 5.9360003 2.2680001 6.076 C 2.24 6.1460004 2.2120001 6.188 2.1000001 6.188 C 1.7080001 6.0340004 1.3440001 5.908 0.37800002 5.782 C 0.35000002 5.698 0.37800002 5.474 0.40600002 5.3900003 C 1.1620001 5.32 1.316 5.25 1.316 4.438 L 1.316 1.7080001 C 1.316 0.56 1.1340001 0.49 0.36400002 0.43400002 C 0.28 0.35000002 0.28 0.056 0.36400002 -0.028 C 0.78400004 -0.014 1.316 0 1.876 0 C 2.436 0 2.8700001 -0.014 3.2900002 -0.028 C 3.374 0.056 3.374 0.35000002 3.2900002 0.43400002 C 2.576 0.504 2.4220002 0.56 2.4220002 1.7080001 L 2.4220002 4.004 C 2.4220002 4.2980003 2.548 4.466 2.66 4.592 C 3.22 5.138 3.7380002 5.418 4.172 5.418 C 4.704 5.418 5.096 5.0820003 5.096 4.144 L 5.096 1.7080001 C 5.096 0.56 4.984 0.49 4.228 0.43400002 C 4.158 0.35000002 4.158 0.056 4.228 -0.028 C 4.578 -0.014 5.096 0 5.656 0 C 6.216 0 6.678 -0.014 7.0280004 -0.028 C 7.098 0.056 7.098 0.35000002 7.0280004 0.43400002 C 6.328 0.49 6.202 0.56 6.202 1.7080001 L 6.202 3.934 C 6.202 4.13 6.202 4.326 6.188 4.494 C 6.86 5.236 7.4900002 5.418 8.036 5.418 C 8.568 5.418 8.876 5.11 8.876 4.172 L 8.876 1.7080001 C 8.876 0.56 8.736 0.49 8.008 0.43400002 C 7.938 0.35000002 7.938 0.056 8.008 -0.028 C 8.358 -0.014 8.876 0 9.436 0 C 9.996 0 10.486 -0.014 10.878 -0.028 C 10.948 0.056 10.948 0.35000002 10.878 0.43400002 C 10.108001 0.49 9.982 0.56 9.982 1.7080001 L 9.982 3.92 C 9.982 5.1660004 9.772 6.1460004 8.54 6.1460004 C 7.826 6.1460004 6.958 5.88 6.23 5.11 C 6.188 5.0680003 6.104 4.998 6.076 5.124 C 5.9500003 5.698 5.4040003 6.1460004 4.676 6.1460004 C 3.864 6.1460004 3.1360002 5.67 2.548 5.012 C 2.4780002 4.9420004 2.394 4.8440003 2.38 5.012 Z "/>
</symbol>
<symbol id="g77113E0CAAA23E0B77E89A338ACC30A4" overflow="visible">
<path d="M 2.576 5.012 C 2.492 4.914 2.408 4.886 2.408 5.012 C 2.394 5.3900003 2.3660002 5.9360003 2.296 6.076 C 2.2680001 6.1460004 2.24 6.188 2.128 6.188 C 1.7360001 6.0340004 1.3720001 5.908 0.40600002 5.782 C 0.37800002 5.698 0.40600002 5.474 0.43400002 5.3900003 C 1.19 5.32 1.3440001 5.25 1.3440001 4.438 L 1.3440001 1.7080001 C 1.3440001 0.56 1.204 0.504 0.36400002 0.43400002 C 0.28 0.35000002 0.28 0.056 0.36400002 -0.028 C 0.78400004 -0.014 1.3440001 0 1.904 0 C 2.464 0 2.884 -0.014 3.3040001 -0.028 C 3.388 0.056 3.388 0.35000002 3.3040001 0.43400002 C 2.5900002 0.504 2.45 0.56 2.45 1.7080001 L 2.45 4.004 C 2.45 4.2980003 2.576 4.466 2.6880002 4.592 C 3.22 5.11 3.8500001 5.418 4.396 5.418 C 4.676 5.418 4.9700003 5.236 5.138 4.914 C 5.2780004 4.6340003 5.306 4.256 5.306 3.8360002 L 5.306 1.7080001 C 5.306 0.56 5.1660004 0.504 4.438 0.43400002 C 4.368 0.35000002 4.368 0.056 4.438 -0.028 C 4.8580003 -0.014 5.306 0 5.866 0 C 6.426 0 6.9300003 -0.014 7.3500004 -0.028 C 7.42 0.056 7.42 0.35000002 7.3500004 0.43400002 C 6.566 0.504 6.412 0.56 6.412 1.7080001 L 6.412 3.7940001 C 6.412 4.564 6.3560004 5.236 6.0340004 5.67 C 5.796 5.978 5.362 6.1460004 4.872 6.1460004 C 4.1860003 6.1460004 3.4020002 5.964 2.576 5.012 Z "/>
</symbol>
<symbol id="g634FF9E9D0A0144E2AFDD807D5ECB7D0" overflow="visible">
<path d="M 5.4040003 1.302 C 4.886 0.77000004 4.48 0.546 3.6680002 0.546 C 3.164 0.546 2.576 0.84000003 2.142 1.554 C 1.8620001 2.016 1.694 2.66 1.694 3.4720001 L 5.418 3.444 C 5.586 3.444 5.684 3.528 5.684 3.6820002 C 5.684 4.8580003 5.264 6.118 3.318 6.118 C 2.1000001 6.118 0.518 4.9560003 0.518 2.828 C 0.518 2.0440001 0.71400005 1.288 1.176 0.75600004 C 1.6520001 0.19600001 2.3100002 -0.14 3.318 -0.14 C 4.382 -0.14 5.138 0.35000002 5.698 1.0780001 C 5.656 1.218 5.572 1.288 5.4040003 1.302 Z M 1.7360001 3.9480002 C 2.002 5.53 2.982 5.656 3.318 5.656 C 3.8500001 5.656 4.48 5.362 4.48 4.1860003 C 4.48 4.06 4.4240003 3.99 4.27 3.99 Z "/>
</symbol>
<symbol id="gEF9FD20106DF1BE872ABEE235642DEFC" overflow="visible">
<path d="M 4.676 0.70000005 C 4.7460003 0.75600004 4.872 0.78400004 4.886 0.68600005 C 4.928 0.35000002 5.04 -0.14 5.04 -0.14 C 5.152 -0.18200001 5.222 -0.16800001 5.306 -0.14 C 5.6140003 0.112 6.104 0.322 6.958 0.42000002 C 7.0420003 0.504 7.0420003 0.71400005 6.958 0.79800004 C 6.0620003 0.86800003 5.9360003 1.1340001 5.9360003 1.82 L 5.9360003 8.162001 C 5.9360003 9.0720005 5.992 9.632 5.992 9.632 C 5.992 9.7300005 5.9360003 9.772 5.81 9.772 C 5.46 9.632 4.4100003 9.436 3.8500001 9.394 C 3.822 9.282001 3.8500001 9.058001 3.934 8.974 C 3.976 8.974 4.018 8.974 4.06 8.974 C 4.676 8.932 4.83 8.932 4.83 7.826 L 4.83 6.0340004 C 4.83 5.9360003 4.802 5.908 4.704 5.908 C 4.6480002 5.908 4.0740004 6.1460004 3.6120002 6.1460004 C 2.6880002 6.1460004 2.072 5.8380003 1.5120001 5.306 C 0.91 4.704 0.546 3.878 0.546 2.842 C 0.546 1.12 1.414 -0.14 2.926 -0.14 C 3.4720001 -0.14 3.99 0.14 4.676 0.70000005 Z M 4.83 1.7360001 C 4.83 1.47 4.802 1.358 4.606 1.19 C 4.0880003 0.74200004 3.64 0.518 3.2900002 0.518 C 2.5340002 0.518 1.75 1.3440001 1.75 3.094 C 1.75 4.102 1.9460001 4.662 2.1560001 4.9560003 C 2.5900002 5.6140003 3.1780002 5.656 3.4580002 5.656 C 3.9620001 5.656 4.3120003 5.474 4.592 5.152 C 4.788 4.928 4.83 4.83 4.83 4.396 Z "/>
</symbol>
<symbol id="g3B79D8E86480C20827A395F926C73BE1" overflow="visible">
<path d="M 2.842 5.572 C 2.926 5.656 2.926 5.9500003 2.842 6.0340004 C 2.4220002 6.02 1.932 6.006 1.4280001 6.006 C 0.896 6.006 0.518 6.02 0.154 6.0340004 C 0.07 5.9500003 0.07 5.656 0.154 5.572 C 0.81200004 5.5020003 0.966 5.362 1.26 4.6340003 L 3.094 0.112 C 3.1780002 -0.08400001 3.2900002 -0.16800001 3.43 -0.16800001 C 3.556 -0.16800001 3.6680002 -0.08400001 3.766 0.14 L 5.1800003 3.584 L 6.622 0.112 C 6.7060003 -0.08400001 6.8180003 -0.16800001 6.958 -0.16800001 C 7.084 -0.16800001 7.196 -0.08400001 7.28 0.126 L 9.114 4.564 C 9.338 5.138 9.576 5.53 10.29 5.572 C 10.374001 5.656 10.374001 5.9500003 10.29 6.0340004 C 10.01 6.02 9.702001 6.006 9.282001 6.006 C 8.862 6.006 8.274 6.02 7.854 6.0340004 C 7.7700005 5.9500003 7.7700005 5.656 7.854 5.572 C 8.904 5.5160003 8.764 5.11 8.568 4.6200004 L 7.392 1.7080001 C 7.2520003 1.358 7.196 1.358 7.084 1.6520001 L 5.88 4.718 C 5.6140003 5.3760004 5.642 5.5160003 6.3840003 5.572 C 6.4680004 5.656 6.4680004 5.9500003 6.3840003 6.0340004 C 5.964 6.02 5.4040003 6.006 4.984 6.006 C 4.6340003 6.006 4.172 6.02 3.752 6.0340004 C 3.6680002 5.9500003 3.6680002 5.656 3.752 5.572 C 4.4100003 5.5160003 4.578 5.11 4.83 4.48 L 4.914 4.256 L 3.934 1.778 C 3.752 1.316 3.7240002 1.302 3.542 1.75 L 2.4220002 4.6340003 C 2.1560001 5.306 2.17 5.53 2.842 5.572 Z "/>
</symbol>
<symbol id="gD0DD0C2B056F25673B3EED0135505F92" overflow="visible">
<path d="M 2.338 4.004 C 2.338 4.2980003 2.464 4.466 2.576 4.592 C 3.108 5.11 3.822 5.418 4.368 5.418 C 4.6480002 5.418 4.9420004 5.236 5.11 4.914 C 5.25 4.6340003 5.2780004 4.256 5.2780004 3.8360002 L 5.2780004 1.7080001 C 5.2780004 0.56 5.138 0.504 4.4100003 0.43400002 C 4.34 0.35000002 4.34 0.056 4.4100003 -0.028 C 4.802 -0.014 5.2780004 0 5.8380003 0 C 6.3980002 0 6.86 -0.014 7.322 -0.028 C 7.392 0.056 7.392 0.35000002 7.322 0.43400002 C 6.538 0.504 6.3840003 0.56 6.3840003 1.7080001 L 6.3840003 3.7940001 C 6.3840003 4.564 6.328 5.25 6.006 5.67 C 5.768 5.978 5.334 6.1460004 4.8440003 6.1460004 C 4.158 6.1460004 3.318 5.964 2.464 5.012 C 2.464 4.998 2.45 4.998 2.436 4.984 C 2.394 4.928 2.3240001 4.8440003 2.3240001 5.012 L 2.338 8.162001 C 2.338 9.0720005 2.394 9.632 2.394 9.632 C 2.394 9.7300005 2.338 9.772 2.2120001 9.772 C 1.8620001 9.632 0.81200004 9.436 0.252 9.394 C 0.224 9.282001 0.252 9.058001 0.33600003 8.974 C 0.37800002 8.974 0.42000002 8.974 0.462 8.974 C 1.0780001 8.932 1.232 8.932 1.232 7.826 L 1.232 1.7080001 C 1.232 0.546 1.064 0.49 0.252 0.43400002 C 0.16800001 0.35000002 0.16800001 0.056 0.252 -0.028 C 0.71400005 -0.014 1.232 0 1.792 0 C 2.3240001 0 2.786 -0.014 3.1780002 -0.028 C 3.262 0.056 3.262 0.35000002 3.1780002 0.43400002 C 2.464 0.49 2.338 0.546 2.338 1.7080001 Z "/>
</symbol>
<symbol id="gE0345006C183149AF583AF5DE80FA9FE" overflow="visible">
<path d="M 2.674 1.7080001 L 2.674 7.322 C 2.674 8.484 2.9120002 8.554 3.8920002 8.596001 C 3.976 8.68 3.976 8.974 3.8920002 9.058001 C 3.276 9.044001 2.618 9.030001 2.072 9.030001 C 1.61 9.030001 0.924 9.044001 0.266 9.058001 C 0.18200001 8.974 0.18200001 8.68 0.266 8.596001 C 1.246 8.554 1.4840001 8.484 1.4840001 7.322 L 1.4840001 1.7080001 C 1.4840001 0.546 1.246 0.476 0.266 0.43400002 C 0.18200001 0.35000002 0.18200001 0.056 0.266 -0.028 C 0.896 -0.014 1.582 0 2.086 0 C 2.5900002 0 3.262 -0.014 3.8920002 -0.028 C 3.976 0.056 3.976 0.35000002 3.8920002 0.43400002 C 2.9120002 0.476 2.674 0.546 2.674 1.7080001 Z "/>
</symbol>
<symbol id="g7E303FA8E2D87EE13FB94A41DEF3418E" overflow="visible">
<path d="M 6.2720003 8.596001 C 7.308 8.526 7.308 8.148001 7.0140004 7.392 L 4.802 1.778 L 4.7460003 1.778 L 2.506 7.4760003 C 2.184 8.316 2.2680001 8.498 3.22 8.596001 C 3.3040001 8.68 3.3040001 8.974 3.22 9.058001 C 2.66 9.044001 2.03 9.030001 1.526 9.030001 C 1.0220001 9.030001 0.532 9.044001 0.07 9.058001 C -0.014 8.974 0 8.68 0.08400001 8.596001 C 0.85400003 8.526 0.966 8.288 1.3440001 7.322 L 4.102 0.154 C 4.1860003 -0.07 4.284 -0.16800001 4.4240003 -0.16800001 C 4.578 -0.16800001 4.676 -0.042000003 4.76 0.154 L 7.6580005 7.294 C 7.9240003 7.952 8.148001 8.498 9.030001 8.596001 C 9.114 8.68 9.114 8.974 9.030001 9.058001 C 8.610001 9.044001 8.12 9.030001 7.7980003 9.030001 C 7.4760003 9.030001 6.846 9.044001 6.2720003 9.058001 C 6.188 8.974 6.188 8.68 6.2720003 8.596001 Z "/>
</symbol>
<symbol id="gBB75D665A04FFE2A82A14DE003A19CAC" overflow="visible">
<path d="M 3.9620001 4.5220003 C 5.152 4.5220003 5.1940002 4.2000003 5.236 3.5700002 C 5.32 3.486 5.6140003 3.486 5.698 3.5700002 C 5.684 3.92 5.67 4.326 5.67 4.802 C 5.67 5.2780004 5.684 5.642 5.698 6.006 C 5.6140003 6.09 5.32 6.09 5.236 6.006 C 5.1940002 5.236 5.152 5.0540004 3.9620001 5.0540004 L 2.66 5.0540004 L 2.66 7.5740004 C 2.66 8.33 2.828 8.47 3.444 8.47 L 4.0740004 8.47 C 5.558 8.47 5.908 7.9100003 6.216 6.9440002 C 6.3840003 6.9440002 6.538 6.972 6.65 7.0140004 C 6.5800004 7.5880003 6.3700004 8.932 6.342 9.044001 C 6.342 9.0720005 6.328 9.086 6.2860003 9.086 C 6.0480003 9.044001 5.978 9.030001 5.6280003 9.030001 L 2.058 9.030001 C 1.61 9.030001 0.81200004 9.044001 0.252 9.058001 C 0.16800001 8.974 0.16800001 8.68 0.252 8.596001 C 1.232 8.554 1.47 8.484 1.47 7.322 L 1.47 1.7080001 C 1.47 0.546 1.232 0.476 0.252 0.43400002 C 0.16800001 0.35000002 0.16800001 0.056 0.252 -0.028 C 0.74200004 -0.014 1.442 0 2.072 0 C 2.7020001 0 3.388 -0.014 3.878 -0.028 C 3.9620001 0.056 3.9620001 0.35000002 3.878 0.43400002 C 2.898 0.476 2.66 0.546 2.66 1.7080001 L 2.66 4.5220003 Z "/>
</symbol>
<symbol id="gD8D2A5E78EA4643EEAAC69DB934A336F" overflow="visible">
<path d="M 4.032 1.7080001 L 4.032 6.566 C 4.032 7.406 4.046 8.26 4.0740004 8.442 C 4.0740004 8.512 4.046 8.512 3.99 8.512 C 3.22 8.036 2.4780002 7.6860003 1.246 7.112 C 1.274 6.958 1.33 6.8180003 1.4560001 6.734 C 2.1000001 7 2.408 7.084 2.674 7.084 C 2.9120002 7.084 2.954 6.748 2.954 6.2720003 L 2.954 1.7080001 C 2.954 0.546 2.576 0.476 1.5960001 0.43400002 C 1.5120001 0.35000002 1.5120001 0.056 1.5960001 -0.028 C 2.282 -0.014 2.786 0 3.542 0 C 4.214 0 4.55 -0.014 5.25 -0.028 C 5.334 0.056 5.334 0.35000002 5.25 0.43400002 C 4.27 0.476 4.032 0.546 4.032 1.7080001 Z "/>
</symbol>
</defs>
</div>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(40 16.58)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="8.99" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.280000000000001" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.39" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gBFFDA84A1400D9E1136DF0DD93EA19F5" x="25.02" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEC3CC7DEE79E0AA801DFAAEF4B6C0B50" x="30.669999999999998" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g202CCBD46865F83C12D50E1B4FF9BBEA" x="36.43" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="41.35" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g5503E15E5E4E70E9E217A15BD1ECD752" x="46.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="49.75" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="55.379999999999995" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 25.159999999999997)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 27.159999999999997)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.64 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 42.31999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(393.5458818897638 10)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6D39B87B7095296261A07873F9B99896" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1B61845C1FB429ACDF5304290F5BF286" x="8.339999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC66F55FB8F08DA72FE76D3863D88042" x="13.511999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="20.003999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g48BCA4F06942DA5990D42018985FC781" x="26.759999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g45E4C10E27056C5AE488FE2D8290DF06" x="32.891999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="36.623999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FB89403B37B0F0F934DFEB7E5171B37" x="42.971999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFF269982F0E4C510F3A3BFF016D72390" x="50.303999999999995" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 10.296000000000001)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5ABA589ED074A65FC8C929AB4EB2344C" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(6.768 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 28.488)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 38.784)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(743.9997637795276 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g97A8E46F7A64F11D13C6F357868587EE" x="9.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.25" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.36" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gB844DCFB76B4CC44608DB013C9764E9C" x="24.89" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="30.37" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="35.14" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="41.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="46.58" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="52.599999999999994" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 15.16)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 60)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6C3A310EEC8A7EBBD176D179125951F0" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(9.528 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g2F0CE4BDC8DA4B92139017B781562218" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8D84A54D9303B24762DC3071B60ECD14" x="17.76" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3E9095A1FBD7854ED5F7B53469C97011" x="25.560000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g90B91206A818BADA9956CC42F47E57A0" x="38.064" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2B9D5A283BBC2ED0501C3A1039D04E5C" x="43.92" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.78399999999999 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g10BFE5E41011FF0F560FA08FAB260218" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(75.312 15.48)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(81.312 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1BED8054A02AECF3BF3EC56A671C1672" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g841363B3896A8C79F18618DF16186242" x="16.944" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g42F794F2554BA43C69EE8F3AA6FD9BAC" x="30.168" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDD7DFDEC0D240E3DC5A3664E12D4BDDC" x="44.952" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g10AC66E6714D96E9762627FFB6E156C6" x="55.199999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g767CEF02C917BBE3F159A8F04079F311" x="63.791999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA13EE5B65CBC719304B28920E2ACC2B9" x="74.064" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g9CBC2DB69173A0577335373434CDCDA4" x="88.416" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g10AC66E6714D96E9762627FFB6E156C6" x="99.36" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g24FA36D774E663C81AD78F0ED3820373" x="107.952" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g841363B3896A8C79F18618DF16186242" x="115.67999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g42F794F2554BA43C69EE8F3AA6FD9BAC" x="128.904" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 39.48)">
<g class="typst-group">
<g>
<g transform="translate(0 12.9)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g911507D70DD1D78477F3BEDE827F51DF" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gF7DAC8BB30649014016B28F6AD7EC048" x="16.34" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8F63AAB7FFA6B186E1B4BC124750174B" x="31.14" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1E298373CF470F56F03EC97C7DE8EA04" x="41.22" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1E934D63EFC0D2D779AEFC9122E70AE4" x="66.78" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC3DD0650993487CD3F460FE3E213BEA0" x="74.12" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCD50B0C5537328D0484BBB5C5B7C30A" x="86.44" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="94.97999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g936880EEF467D45CE0F64A721CAEDAB8" x="104.75999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1344FEF92B65FBC27D977C1EC5D9AECF" x="113.32" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE9BB2E81A58B731A2047F77D70267173" x="120.47999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g814D257E196F777517493FCE505E18DF" x="126.91999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC3DD0650993487CD3F460FE3E213BEA0" x="137.94" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gED653E9CCAB5F6C6237350979071A74F" x="150.26" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.06000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 39.06000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g98926218EB374AD77A2D864C6D10734B" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="11.140000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="20.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="28.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="44.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="55.120000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="65.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="70.62" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="81.46000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="92.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="103.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="108.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="117.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="127.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="140.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="154.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="159.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="168.74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="178.88" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="187.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="200.26" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="210.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="219.26" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="227.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="236.14000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="251.26000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="261.34000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="277.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="287.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="294.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="304.91999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="314.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="323.91999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="333.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="339.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="344.47999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="349.9" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="356.21999999999997" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 65.22)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 65.22)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g844C4CEA683BD523227FE7A466FBF8A3" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="13.660000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="23.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="33.9" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="42.98" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="58.099999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="64.41999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="79.49999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="85.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="96.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="105.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="117.03999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="122.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="131.45999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="141.59999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="150.53999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="162.97999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="172.11999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="182.95999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="198.07999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="207.21999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="212.49999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="222.77999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="232.83999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="241.77999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="247.05999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="257" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 102.12)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE264501C5759C04FD4041B484B9EC12C" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4CEB3F42B775C8D3827D0A458A70771F" x="12.18" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g50FEF586148C287DB923CFE895D558DC" x="23.4" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB88E546A1990E31D64B5C4B23478426F" x="33.519999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB416F8956A8016097936DBEC1F135503" x="51.62" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC81C3C15134AD04FEC0FE7FCEBE8BB14" x="63.239999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="69.74" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gED653E9CCAB5F6C6237350979071A74F" x="79.52" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 115.12)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDACA5EBB44D5F3DB530A1F5F650BFBAB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="10.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="18.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="28.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="38.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="47.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="57.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="62.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="67.74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="73.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="79.47999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB2E338F181D915F0996F60E92302C895" x="94.77999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="105.73999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="114.87999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="124.73999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="130.01999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="138.95999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g25F4C61DF17D6DB8640DCCCD57BBA830" x="148.67999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="155.79999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="165.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g6636102111388326E3C89C955A433A6D" x="169.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g70A876D91C5CC45BCC4BC8E88B98F10" x="178.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB91E67CF1B63A9F4CC30BB03AE35508D" x="188.10000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="197.50000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="206.80000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="211.20000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g11C09650A1107877D1CACE85AD57EEFF" x="220.50000000000006" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB91E67CF1B63A9F4CC30BB03AE35508D" x="229.80000000000007" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="239.20000000000007" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="248.50000000000009" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="252.9000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="262.2000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="271.5000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g6636102111388326E3C89C955A433A6D" x="280.8000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g4B7F995A2850EF666DF3EC5EDED0901C" x="290.10000000000014" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g2E0E67B6699615E51BCE03EAB1A37509" x="305.08000000000015" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g579F1BD1E42C90590E5C6584A163F6DD" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="11.74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="20.880000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="31.720000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="41.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="51.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="72.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="83.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="94.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="109.98" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="120.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="128.98000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="136.42000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="146.14000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="155.44000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g6636102111388326E3C89C955A433A6D" x="159.84000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g18D1F1E967E0B15C3E9466BFBC921865" x="169.14000000000004" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 65.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.02 58.480000000000004)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 74.32 0 "/>
</g>
<g transform="translate(17.02 65.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="9.3" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g6636102111388326E3C89C955A433A6D" x="13.7" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g18D1F1E967E0B15C3E9466BFBC921865" x="23" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gF4B93BD1FBF62234B86BB304CE1128E3" x="37.3" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="53.3" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="62.599999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g6636102111388326E3C89C955A433A6D" x="67" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g70A876D91C5CC45BCC4BC8E88B98F10" x="76.3" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="85.6" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(107.34 65.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="20.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g17AD34DB90B05275C6F1422A9B4B5274" x="30.740000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="40.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="54.46000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="65.08000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="80.46000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="90.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="101.38000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="115.32000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="120.60000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="129.74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="139.88" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="148.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB91E67CF1B63A9F4CC30BB03AE35508D" x="155.07999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="164.48" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="173.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g6636102111388326E3C89C955A433A6D" x="178.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g18D1F1E967E0B15C3E9466BFBC921865" x="187.48000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="201.78000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="213.54000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="222.84000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g6636102111388326E3C89C955A433A6D" x="227.24000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g70A876D91C5CC45BCC4BC8E88B98F10" x="236.54000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g4D85B33E992F6B39F8E7EBFD2F7ECE19" x="250.84000000000006" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="266.84000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="276.14000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="280.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCAFB20A65E8FBEFE071D9C4C8EE95E49" x="289.84000000000003" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 91.64)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.02 84.64)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 74.32 0 "/>
</g>
<g transform="translate(17.02 91.64)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="9.3" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="13.7" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCAFB20A65E8FBEFE071D9C4C8EE95E49" x="23" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDCA082B6FC1DB6288BEBFE25BA893B80" x="37.3" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="53.3" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="62.599999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="67" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g11C09650A1107877D1CACE85AD57EEFF" x="76.3" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="85.6" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(107.34 91.64)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="12.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="19.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="28.26" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="38.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="51.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="56.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="72.62" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="77.9" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="87.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="97.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="106.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g13CAD87D675A42FC6A129543D89F948C" x="118.56" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(465.13385826771656 0)">
<g class="typst-group">
<g>
<g transform="translate(-29.675590551181095 0)">
<image xlink:href="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAB4AAAAPUCAIAAADDkLNjAAAgAElEQVR4Aeydd2wU1/r3p2irdtdGVBGKQgCFAKLYggCiBFEFBG7AgGgR5IKoIhRhQkRVKBEEEFUQiADDDaaIFoUmquAGRBVVQLAggKjC2NZW78y8/PjqPjrvrHe9Xttg4Nk/rLOzZ075nDI+3/PMcySDP0yACTABJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwARKgYBUCmlykkyACTABJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwAQMFqC5EzABJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwASYQKkQYAG6VLByokyACTABJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwAI09wEmwASYABNgAkyACTABJsAEmAATYAJMgAkwASbABJgAEygVAixAlwpWTpQJMAEmwASYABNgAkyACTABJsAEmAATYAJMgAkwASbABFiA5j7ABJgAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmAATYAKlQoAF6FLByokyASbABJgAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmAAL0NwHmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwASYABNgAkygVAiwAF0qWDlRJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwASYABNgAZr7ABNgAkyACTABJsAEmAATYAJMgAkwASbABJgAE2ACTIAJlAoBFqBLBSsnygSYABNgAkyACTABJsAEmAATYAJMgAkwASbABJgAE2ACLEBzH2ACTIAJMAEmwASYABNgAkyACTABJsAEmAATYAJMgAkwgVIhwAJ0qWDlRJkAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmAATYAJMgAVo7gNMgAkwASbABJgAE2ACTIAJMAEmwASYABNgAkyACTABJlAqBFiALhWsnCgTYAJMgAkwASbABJgAE2ACTIAJMAEmwASYABNgAkyACbAAzX2ACTABJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwARKhQAL0KWClRNlAkyACTABJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEWoLkPMAEmwASYABNgAkyACTABJsAEmAATYAJMgAkwASbABJhAqRBgAbpUsHKiTIAJMAEmwASYABNgAkyACTABJsAEmAATYAJMgAkwASbAAjT3ASbABJgAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmAATKBUCLECXClZOlAkwASbABJgAE2ACTIAJMAEmwASYABNgAkyACTABJsAEWIDmPsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwASYABNgAqVCgAXoUsHKiTIBJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwASYAAvQ3AeYABNgAkyACTABJsAEmAATYAJMgAkwASbABJgAE2ACTKBUCLAAXSpYOVEmwASYABNgAkyACTABJsAEmAATYAJMgAkwASbABJgAE2ABmvsAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmAATYAJMgAmUCgEWoEsFKyfKBJhAiRDQdb1E0uFEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwATeCQEWoN8Jds6UCTCBuAiwAB0XJo7EBJgAE2ACTIAJMAEmwASYABNgAkyACTCBskqABeiy2jJcLibABAyDBWjuBUyACTABJsAEmAATYAJMgAkwASbABJgAE3ivCbAA/V43HxeeCXyYBPQ3n0Ag8GFWj2vFBJgAE2ACTIAJMAEmwASYABNgAkyACTCBj4YAC9AfTVNzRZnA+0NA07Rwfvjly5fRiqxpWrSf+DoTYAJMgAkwASbABJgAE2ACTIAJMAEmwASYQNkhwAJ0gm3h9XpDoZBhGJqmBYPBcH7YMAw22EyQZtFv8/l8uAnkEaaLRU+P73iXBKjhsrOzV65c2alTpypVqrhcLunNJyUlZeHChRTHMIxQKBTOD8NKGn/fZek575IjoOu6pmloa6/XGwwG/X5/ySXPKSVIAI829oeTID6+jQkwASbABJgAE2ACTIAJMAEm8NETYAE6wS4QaYApKqEJJsq3FYWACBxh7c2nKGlw3HdJIBQK+Xw+Gko//PCD2+2G6KwoivrmI0mS1Wp1Op0tWrS4evUqFVfTNBagicYHE6CBjBo9f/5c3Hj4YKr5HlXE5/OF88PPnz9/j8rMRWUCTIAJMAEmwASYABNgAkyACTCBskaABejEW2Ts2LHlypWrWrXqokWL/H4/DKITT47vLDoByFUTJkxwOp1ut3vu3LncCkWn+O7vuHr1akpKCqRnWZaTk5OdTqfVapXffHBdVdVy5cpduXKFzTDffYOVfgmysrJatGghSVLDhg2PHz9e+hlyDmYCmEuzsrLat29vsVgaNWp04sQJcdvPfAN/ZwJMgAkwASbABJgAE2ACTIAJMAEmEIUAC9BRwBR2efTo0bIs2+12SZJsNtudO3fYBUdhzEryd9JBfvjhBxIuXS7X3bt3YVFLEUoyV06rhAiQiKxp2t9//12lShUyfCa52frmo6oqrkiSpChKhw4dDMOg20uoOJxMWSEAhxs5OTmff/65LMuKokiS1LZt27JSvo+sHE+fPq1WrZrdbnc6naqqdu3a9SMDwNVlAkyACTABJsAEmAATYAJMgAkwgZIh8NEJ0DjcLJwfJoGSAiAaw4Q2GAwiztatW2Gbib+qqh44cACuaUumWTiVwgjAA8OuXbscDgcJlJIk7d27F7cGg0FyyU1OHsL5Yb/f7/P5gsFggSKmpml+vz83N/fy5cuFFYF/T5AA3DcbhpGXl/fkyZOaNWvKsoxGrFixIjRHSZLoIrxwuFwui8UiSdL+/fsTzJhve+sEEvOKM3z4cLQ+WjwpKemtF5wz/D9P6xMnTlRVlUZiUlISPQQZ0PtOQNf1UCgUCAToURjjn5/3vbJcfibABJgAE2ACTIAJMAEmwATeOYEPSoCm5RNpynSkFf1kIh4MBsWf6EZTNPFrIBBo1KiRKEBbrdbNmzdD3BRjcrj0CKClUlJSSK+Egrlly5a8vDzDMML54dhaidfrff78+YULF/bu3bto0aIJEyb06tWrRYsWVapUgeBSqVKlDRs2kIpdenX5OFOG6pGWlkb7B06nE2bO48aNO3z4cFZW1v79+yFBwhoabT1mzBhSTD5OdGW81jSjkvtmOqY1npJfunRJkiRsLOEVE0n6oJ5T8UAoC3EuXLhgsVhUVXU4HBh6qqqWhYJxGUqQQCgUOnjw4KZNm+7fv1+CyXJSTIAJMAEmwASYABNgAkyACTABE4EPbWEfCoVE2dHv9+fk5Lx8+fLp06f//PPP3bt3zwqf48ePnz59+vbt27m5uV6v1zAMMpU1YRK/nj9/HuaZpEGrqvrnn3+yBbRIqbTDuq5fuHDBbrdDoCQR89ChQ36/H+2Yl5cXzg/n5eXNnj27QYMGrVu3TktLGz58eK9evZo3b16hQgVJkiwWC9n3USJwq+JyuaxW66ZNm0q7Lh9n+rqub9++XZZlm80G8haLxW63Hz58WARy+PDh1969qZVVVe3ZsydGqxiNw2WNQCAQePbsWUZGRq9evdq2bUuvJsQu52urzGnTptFItFqtkiS53e7Yd/GvpUFg6tSptBNgs9lUVa1cuXJpZMRpvhMCoVDo0aNHHTt2pNdNFi9e/E5KwpkyASbABJgAE2ACTIAJMAEm8DEQ+NAE6EAgsHnz5vbt21eqVMnj8YjaoqIolv//A3VDVdXk5OQxY8ZkZWVpmubz+XThE9kJoI+Q+owsHjx4EBmTr5QegWAw+P3338NgVmxlNAQsZHVdDwQCEydOJD1LlmXY9NEVrL0VRVHffOi63W5XFEWW5TZt2pReLT7OlOHn1zCML774ApaVVqvVZrMpivLbb78FAgGY0MLLimEYnTt3RjRFUaxWa+vWrT9ObmW51qJNuq7rPp9v1apVFStWhHwsy3KzZs3iLH/9+vXRGWAErShKixYt4ryXo5UggVq1amE+dDqddrvdZrO1adOGrNpLMCNO6p0QCAaDUJ/tdjscrSQlJf38889iYYR/hXTxOoeZABNgAkyACTABJsAEmAATYAJFJVDyAjQcC4ZCIdGaGIbJoVAonB8OvflEc3YBpxkUH/WJFjmytuPGjcOaWRSIo4VJbUSgdu3az58/h4Nacd1FYXitbdmypckCukKFCvD5EFkevlJKBAKBQOPGjdEQdE5duXLlxMYKBAKbNm1yu93QqZX/fVRVhaBJHQDCNFJLSkqCZTT+1qhRo5Sq8JEnm5mZCf6wgJZleciQIQW+hbB06VKKKcsyLKDF6eUjJ1kWqo89g0AggLl65MiRNLgkSbLb7T179oynnGfPnqXRB9/fsiyPHTs2nns5TgkSuHTpktVqpUcnWnP8+PElmAUn9W4JBIPBpk2bYmtBHK2bNm3Ca2Sx/xd6t4Xn3JkAE2ACTIAJMAEmwASYABN47wiUvABNCAo8furZs2enT5/OzMz8+eefp0+f/trueMiQIWnCJz09ffXq1adPn3748CGS8vl8Xq9XtLCjLEwBr9dLr+rTyjlGQFx0wRp6zZo1Pp8PJcdfEjShjIfzw5AvxWTbt29vGEY8JTQVmL8mTMDv96P5rFYrCdDt2rUT28swjEaNGkHP+p/4/H+WznC7oaqq3W63Wq2wdIbaBW+n5HlWkqQvv/wy4ULyjTEIdOvWDS1osVg8Ho/T6bxy5UqBg2jr1q3U1oqiQAUjR8MxsuCf3hoB2nF89uzZV199paoq9hUwIdvt9uvXr8dTmM2bN2NzCBMsRuuaNWviuZfjlCCBjRs3is84DMBVq1aVYBac1Dsn8Pt/frdYLOQECa1st9tv3LihaVpOTk60/4Xeecm5AEyACTABJsAEmAATYAJMgAm8dwRKUYAGi/Pnz2/YsGHo0KEpKSlOpxOuJE0eD3DCmNVqtVgsomlq8+bN16xZc+fOHVhVFwr3zp07SB/vk4rr5wLDWG7hL97uX7ZsGQ6FF3VMChuGcfDgQUgqYoJz584ttGwcoWQJ7NmzB2/ow7oZjThnzhwxl/v375O4TAK0oiiwiZYkyel0wjGL3W53uVxIBHI29cNFixaJaXK4RAicPXsWgxTutlVV/fbbb+EAJzL9M2fOiEN1586dkXH4yjsnEAwGz58/X7duXWoseNJITk5et25dnMUbNGgQbSJiJDocjlu3bsV5O0crKQJDhgwRn3EYpxcvXiyp9Dmdd04gEAhomrZlyxbawaWRS46nWIB+583EBWACTIAJMAEmwASYABNgAh8MgVIRoDMyMiZNmtS0aVNoTBaLxeFwQOCTZZl8MZMChYskEaqqCp+wtBwaM2ZMMBgs0DpSbAmv14tbHA6HuHiOFqb0EUhNTb19+zZsmUl0FgPh/PBPP/3k8XhMGvS+ffvEYnD4LRCYN28euX6WZRlL6D179piy7tKlCxqLepeiKDi6sHbt2n369JkyZcqcOXNWrlyZkZGxc+fOmjVrYjvE6XTCJvrJkyemNPlr8QlMnjwZgw6msna7/dChQzBqjhzm9+7do7aWJOnJkyeBQKD4ZeAUSpBAOD989uzZqlWrYnPR6XSSo5u1a9fGPqAVcywKAwfQaG4Maj6BsASbKf6kGjdubHpuut1udgAdP8D3JWYwGNyyZYvpfyFJkiZMmACHSKRBi/8LvS+143IyASbABJgAE2ACTIAJMAEmUHYIFFeAhsdPr9d77ty5H3/8sU6dOtCOYcssy7LH4yFjUnGRg8WteCUybLPZoES433wyMjIK9XTRtGlTSZIiLXokSapQoUKNGjUqCx+n01mlSpWGDRu2bt36119/DYVCPp/P7/fHWGh169aNDPQgtUiS9PLly7LToh98SSBT9u7dG60M3yk4XdLr9YrVh5S5ffv2Nm3aVKpU6fPPP+/Tp8/s2bNPnDhx7949+FSh1bWmacFgEC47qMcOHTpUTJDDJUJA13X4HoX1uqqqTZs2NbWdmNHp06dtNlu5cuVsNhudR8catIjoXYWpFY4dO+Z0OsV9AkVRbDbb8uXLUbYYPrvpp+zsbGxPYrsIT4Svv/76XdXu48xX1/Xs7GzT41iW5a5du36cQD6GWm/dupX+JcMolmV5//79fr8f/qBNG/MfAxOuIxNgAkyACTABJsAEmAATYAIlS6BYAjQEvl27drVq1Qo6IFat5PcAApPdbnc4HJCkoSyQTkFrHrzhS24QcG4V6YBI9rWcvXjxYloOFQhi7NixdKAcLaEPHDgQQ97SNA3nIuq6jsSjCdCBQKB69ep0Zhq0ksaNGxdYEr5YGgRIq6pcubLNZqMOo6pqq1atSA4rMGtN0+g0S4TD+WFRgL5586bH40G3wTbD/v37C0yKLxaHwJ07d5KSkuBoG1PBlClTYiS4d+9ezBs2m23Tpk2GYXi9XpOrnBi380+lRwDOkY4ePYqXTmg3yPHm88svvxiGAa/6McpAo/LkyZPimwoYiUuWLIk9rmOkzD8lQEDTtJMnT9LTkwLz58+PfDshgfT5ljJIwO/3z5s3D+/9kCe0+vXra5pGx0rjcSm+r1AGK8JFYgJMgAkwASbABJgAE2ACTKDMEiiWAB0IBAYMGBDN4hgL10hjZHjYSE1Nbd++fb9+/UaMGDFjxowffvhh4sSJ48aN++Zf39SsWdOUJgnWkiQtXbqUVMhIrMePH6dT5ugN4idPntAiShQcxeW0pmkvXryIrXTcuHEDQjmKB6X7p59+iiwGXyklAtCqsrKySBbBGYOSJC1cuNDUMUKhkN/vR0mgglE3COeHsZAW+8OsWbMoWbfbXb16dcMwYm94lFI1P+xkV61aBfcmOP9KluXTp0/HqHJmZiaUzRo1aqCJfT4ftSALIjHQlepPubm5Xq933759kiTJsmy1WitWrIhdQ4fDMX36dOROTRatMHinIRQK/fTTT6IAjZdpbt26lZeXF+1evl7iBOBpSnzmYla8c+dOiefFCZYdArqujxgxAvvreH1BkqTJkyfDEQdbQJedluKSMAEmwASYABNgAkyACTCB95RAsQToBQsWuFwuq9WqKIrT6RSNoEnIgyVp+fLlO3fuPG/evN//8/v169f9fj/0o2jUrl+/vmjRoqpVq8KGGosi0rLv379foC8OXdfD+WF4YyD1WZblkydPQgQhUzvkKzphwBWTgmkq3q5du+jIO9TLarUeO3bMFI2/lhIBqMm6rmdkZEiSlJSUhG4GW9oTJ05E5gv52O/3v3r1Cr+S4iwK0OgJderUQYLobx06dAiFQixAR1JN4ApoY8snLS2NTGUlSapSpUrsBC9evChJUq1atS5duhQZkwXoSCZv54qu61u3bsXow8CBfOxwOGbMmIHXSkh9pq2gyLJhiAUCgb59+4oCtKqq2ARi18OR0ErpSjg/HAqF+vXrZxKgP/vsswKfoaVUDE727ROA87Evv/zSYrFQ68uyfOrUKcMwYrsme/ul5RyZABNgAkyACTABJsAEmAATeO8IFEuAnjFjBnQHUe2FRSokvCpVqkyePPnAgQMmLqRGxRaPAoHA5MmTcZgVDOvwF15BRftlpB/ODweDwc6dO2MFRaVav369qQCJfZ06dSp5BYEA7fF4EkuK7yoOgWnTplHj4gRLj8cTQ+EqMC9TJ7xx4wbELyRotVpnzJhR4I18MQECkPixA1SnTh3Rd8rw4cOL2nYJFIBvKUEC2Jg5efKkw+HAI0BVVbSpx+MZPXq0YRim3b5Cc9d1vX79+qrwcblcw4YNK/RGjlDiBGgrzmq14kk3ZMgQGKrH3qMt8ZJwgm+TgKZp586dE3dhJUlq2rSpYRh5eXlwxxH7f7a3WVrOiwkwASbABJgAE2ACTIAJMIH3i0CxBGgcnm6320U1EO9i9+/f/8KFC+H8cG5uLmxnwEU0OiYFMBoyHO43d+5cHPdHuUiSVODrwMFgUNO0YcOGlZIAPWDAAFgGwchakiQ+lyla25XSdcgfffv2pc4Avbhr166x3adElkdcSOu6/ueff4rWlxaLZf369ay2RHJL+AqOefznn39cLhdGKLStdevWsQCdMNW3f2NeXl7wzadNmzbQquivxWIZOXKkYRi5ubm6rsdvuRzODwcCAY/HI+jPqiRJOHiWh+HbbOXc3Fy32002sGjcjIwMuAB+myXhvN4+AU3T5s2bRyMaPsfgzJ0F6LffHJwjE2ACTIAJMAEmwASYABP4kAgUS4AOhUJt2rSBZwxREJQkaebMmWQwFc4P02lvFIAnBFEEjMRKNs61a9eGHTR5wNi2bVtkfEiQCxYsgFcQ0hNLygK6Tp06tCyHD4GSSjmyLnwlkoCmaYFAIBgM1q5dW+xvsiyvX78e/S3yrniuaJr2888/U4fBhse5c+eKk2Y8+X5scQKBwB9//AGXwfSi96NHjz42Du9vfckpzYYNG8ghviRJOISwT58+sH2mqTvOmgaDwUuXLsG3PmnQsizn5OQkYEwdZ6YcrUACJ06cwHMW+0No5RcvXhiGgScs7RwXtZULzI4vlkECFStWpJcb4CXp6dOnLECXwZbiIjEBJsAEmAATYAJMgAkwgfeIQLEEaNjBjR07VrSXQTgzMxN+A+GsWdM0yNBFEqCDwaCu64FAYPr06TabTVEUyI6vl0azZs2KpIzlcUZGhs1mEwXK4sjEokQOW294H7ZarbIs37p1K7IY8VzhpXs8lExxNE3z+XxerxcKptjEN2/eLOor/2Li4fzwqFGjRAFaUZRnz54V1apaTJPDkQT8fv+KFSvgpQd7ObVr12b71khQb/9KnDMS/DXn5eVVrVoVW4+qqtpsNqvVWqlSJejFhmHEb/uMmmqa9uuvv2JckwBdv379t8+Bc1y2bBke4hCgXS7XF198gZmQ5kPSoBnXh0cgEAisWbMGGw/YWFJVdfTo0RCg8ffDqzXXiAkwASbABJgAE2ACTIAJMIHSJlAsARo+l0+fPi2eQwUrtoMHD74WjunAt8gArWBjCx/4dc2aNRaLhQRoSZLwoneBdA4ePGgSoHft2lVgzHgu4mBDwzAOHTokKp6vXTTggKwEdM+8vDzTXWRpS2JcKBTSdZ2uRysqYaQIXq+XwsUPkO4QCASQsqnkcWaBDkCRvV4vOWMxDCP+g/50XT927JhJgK5VqxalXNQAAW/Tpo3YvikpKYnVtKgF+EjiE8zevXuTwqiqas+ePbFHRRE+EiBvp5p4aQB5YT/PMAzMKpqmkV6MwRhnkUKh0KJFi2RZtlgsqqpCprRarSdPnix0viowC4zBUaNGkcktHiIjRowoKbUr2vyDXhcIBGgiNT2PSnY6LbD6dLGoQyAYDFJTFngqb7SLlGNkIJwfHjduHGZCNIfD4Zg0aVJJNURkjm/nCtjm5OTouo6nD+BEa/e3U6qymYvP59N1vXr16uIDUZblK1euwJIgsWFeNivLpWICTIAJMAEmwASYABNgAkzgrREolgAdDAYDgcDTp08jLaD/+ecf2EdHSs+4EufCD9Lk7t27xbWQJEkxDog7efIkOcpAwfbv3w+gpDbGz5cE6F9//VUsg6qqvXr1ovfNqTqFpowEoS8bhvHq1SvxFr/ff/Pmzby8PCyPERAjiGHScBEgPUKMU5wwaTHELRgMxq+SwF0GFUDTtFAolJOT8/DhQ7oIbkXyLop3/8W2SEtLI9M8SjnOAFXHtN7u06cPak0ti0CcyXI0EwFqINNBc9OmTaMmMN3CX4tJAE63afAitby8PJ/P5/f7MQUV1VQZG1HVq1eHRgxfDQ6HY968eaaM4i98OD+s6/rXX38NryxutxvS59atW03Ccfxpwl+EuLMVY/4JhUIoQ4FjHF5HaDIsUhniiRxZxyI1CoYPhPJQKPTkyZOHDx+i4gmUWdO0Hj164F0QuJmSJGn79u0JN248BN5CHPIyHznb0Az/ForxHmWxYMEC8SEry/LUqVPRo8Rh9R7ViIvKBJgAE2ACTIAJMAEmwASYwLslUCwBmsxhTAK0xWLBMi8UChVTgMa6d926daa10Pr168mgjwgi8sWLF03lOXXqFPSFyMUn3RsjgGTJLgwlUVV17dq1fr9fVC7iX/DDuhkLuezs7LVr13bu3Pnzzz+HoKMoSqNGjeBmhFbOkSUUBejIX0vqCkmH8dcOWXvffAzD+Ouvv2bMmNG4cWOPxwP33Ha7vVOnTtu2bUtA15g4caKpM2zevBk2WYm1bzg/HAqFVFUVk509ezbqm1j7lhT8DyYdNNCjR48cDodoAb1v37733biyzLZRIBDASyqvXr3y+/1nzpzp1q1bvXr1MD02a9Zs4cKFCRR+1qxZOPlTURQk1bdvXww9r9ebgHWkruvBYPDzzz9XVdVqtTocDpvN5nK5srOzyV47gXIWaf4hFbKos1wCBYt2S+jNJ371mWLu27dv2LBhqampeBXJ4XC43e7hw4dnZWXFeHxEK0bNmjWxE4D2VVX10aNH4kT9DhFFK3M81+npQKcii43+nlYqnoonEAf/2FSqVEl8JjocDuxpJZAg38IEmAATYAJMgAkwASbABJgAEyiWAA18r169Mlkcf/LJJ1j3kkIaKUOLa79ozUD+H0aOHCkuhBRF2bdvX25urulGrDBv3rxpEqAvXLgQzg8HAoEExBFkoet6jx49xDKoqnrhwoWcnBzIZ1QdU5FifA0Gg3l5eb1798YRXm63m45YxBWPx9OtW7cYKYh4Dx8+DGPqkl1IBwKBFStWtG3btlq1agMHDoxtkR1Z1B07dqSmpsKSzuVyQVoSe8vcuXOBLvLeaFe++dc30L/IEcelS5cQObH35cP54Vu3bsHBC5pAluVNmzYBLwxFE2jfaOX/mK8fPHjQdNDcyZMnYaya8NgscZ4YQSU7jkq8kPEn+OrVq2vXrt7xMQcAACAASURBVHXt2hVmrXa7vVy5cqQd4zUOkjILTdbr9TqdTgidsFMmV/gJaJ3ITtd1v9/vdrsVRUGaFoulUaNG2J+jDbBCyxYZIf75hwa4qd3x9dWrVzTBRuZSnCs5OTlLlixp1apV3bp1+/Xrd+/evfhTw9Gp1apVAzq73W6z2ejZpyiK1WrdvXt3UdtFPFtSkqRPP/1ULFJRp2vx3ncY9vl8LVu2lCSpdu3aq1atAhP44qCmf4fFK1NZk4uwyZMni//zSJK0bt06Nn8uU43FhWECTIAJMAEmwASYABNgAu8RgWIJ0PCokJ2djRP5aK3SpEkTIDCJs7TSMwVi83r58qXVaoU+C3nC5XIFg0FyYEq3w0rr3LlzJE2iSPfu3UNJEha5vF5v1apVxUPqbDYbFrEmwYIKYwqYsg4Gg3PmzLFYLHa7He6tSTigk7ggBAwcONCUlOnr5MmTJUlyOp2vK0t2u6Y48X8Vl5e3bt1q0KAB9GKIyE2aNImnvjk5Of/888/gwYNVVRX9g5PhJOlfycnJBw8ejL94hmFUrFhRlmUcgCbLstVqpYaIp2yReYVCoT///JP4o75PnjyhkzPF7hp5e/GvwFkN0jE5/vZ6vX///fe5c+c2bdq0a9eu48ePX/j/P9evX798+fLZs2dPnz69bdu2JUuWjBo16uuvv65Tp06NGjWqV6/++eefDxkyJCMjgw4FLX6BE0gBPh8WLVpkt9tFC+jLly9j30g0sYwzfbT7ypUre7z5zJ8/H+bqcd5O0WBpSz0/nvKEQqFAIEB7YHAiTAnGDojbJOSKJ/Yt8f/q8/kw1ZC3nN9++00cd+IkhmFIb9bHk8uiRYswQWEjISkpaerUqWKN4knEFEfTtOPHj9O8pyiK3W7v168fxp0pcjxfE5h/Yozx9PR0y5vP692pOXPmmGbyeMpjioMUdF2/c+dOs2bNXp+pK0mSy+WyWq3NmzfHtGO6RfyKjbHMzMzGjRtXqFABkz/tnGEeoyFWvXr1+HcXDMM4deoUzYQIDBo0SMz9PQ3PmjWLthgtFsuSJUvAOUa749hkqq//zcfn84k72XQ7RYsMiE8lcrdCATF+MceRmFRxwnAcH84PZ2VlYUuD9oy7d++egGPx4hSG72UCTIAJMAEmwASYABNgAkzggyFQLAE6nB/2+Xx37twxCdA9evQAoBIRoMePH+90OrEQUlXVZrP9+9//NgwjcrUWTYB+9uwZFoH0Em787QeFyOv1wncEyTcpKSmJKRG6rufl5fXp00dVVZfLRTZriqJAiSDFFiKCzWa7ceMGvJRGFnvPnj0QIKAlud3uixcvRkYr6hUsPhs2bAgNgpyBKopy7NixQlPbv39/+fLlcUwZWbwCHbYQcHaZ3W5XFKVFixbxt4vX67VYLFarFQK0JEmpqankibvQghUYIZwfXrVqFeR+YMS7xvBMTRIDAgWmUMyLkD7ho1bTtD/++GPChAnNmjUrV66cx+OBYkuqEG3zQFVUVZXUfBiQWq1W6lS4S5Zlj8eTmpp69uzZBHTeYtYOt2McvXYsQ/0B3fvRo0eFCr6YZwoUPsaNG2ez2RwOB/pVenp6AgazuAWSkGj2jhwj2x2TSSgUWrBgwbRp037/z++apkVORwVyA3+0NQ77KjBawhdJ3MQMOXLkSPQBmrhMAUhLhw8fjpEjSfN+v79KlSo09CRJqlq1agLATXnpur5x40bqq5jk4VRaFO9Md8X4msD8Iw5zMeW9e/eix6KDWa3W69evixESCKOrZGVl1a5d2+FwoAloFB84cCBGmhAHly5dSpogjXoIrIqikPqMllq6dGn8E2xGRgZNNQgsWLAgRnnel5/Gjh0r9tvq1avTSKGmN9UFgxQXL126tGTJkjFjxkyaNCkzMxPdkm6M0UvxE22MhUKhnTt3zpw5s3///uPGjVu6dGmc84apbKX9lTTodu3aoRvQ/3jZ2dnv6iFS2rXm9JkAE2ACTIAJMAEmwASYABMoVQLFEqBhQ3T8+HHY8JK0MWnSJCq0uEiLFqbIpkAgENiyZYvb7YYmSwvI8+fPQ3M0ScDRBGjx1HtTFoV+hZXltWvXYGJmqmOMlWdkyvA1fPnyZfJKIWoutOyHfAA9FFVevnx5NF+oAwcOVBTF4/HgrtdKMTxHR+Ye/5VgMPj06dOaNWuiSNA1SO9YtWpVtKTQH7Zt20Z1oQqSDabp/W5Ipc+ePYuWpnj99UllcPBts9nInC09PZ2W92LkIoVHjRoly7LL5QLwxo0bF6g+F6m5i1QAWtIPHDgQJYHgBbNQq9WK9+tNAw2NAntwq9VqsVigRyuK4nK5oFwjDlKrUqXKy5cvi1SwkoocCoXGjBmDYogC2eLFi5GF3+8nRz0YKTAMJ/XTNNgNw7hw4QK6E+3ZKIpy9erVBMocCASOHz9++PDh7OxsZFSo65Wvv/6ajHbHjRsXf6bU1rjF9DX+dKLFpF46YsQIzFemuYsmMfo1NTU1hkZJEjPUSWimTqdTVdWNGzdGK0aRrk+aNIkmDfTkM2fOFJVMceYf8dkklrxv377oY06nU5Iki8Uyf/58MUIC4XB+OCcn58svv6SNIgxS7HGuX78+RpqhUIi0VPhCwWYe9EGUEPMAPUc6duwYI0HTT+np6WThjtH6119/FbUhTGmWha/f/OsbmlHhnAQ7tdHanczG79+/n5aWRg+y1x3AZrOtWLFCvJFGXIE1pZG1e/fuNm3auFwuSZLsdrv1zeebf31DD3caaAWm85YvQoPesmULzRKyLNvt9vXr1xOct1wkzo4JMAEmwASYABNgAkyACTCB95pAcQVowzB27Nhh0sVIVBJNCE0LNvFrNIInTpyw2Wxws0BL9LS0NDrbECqh6XZywQExUZZlMjKKvVA0pYOvWBNu2bLF4XBA9ITGB+Ul/pU5Yl64cKFatWpYzZJkIElSgwYNpk+fvnXr1qVLl37yySeyLJcvXx7RVFUdN24cyXBiIUOhUPPmzSE6wIBOUZShQ4eKcRIIh/PDXbt2hf0ySXtQhRwOx82bN6OlCZ+kULug10AbtVgs7dq1W758+cWLF+fMmYOkbDYbzhyTJOns2bPR0jRd//0/v6MhYJYoSdKWLVsSaFZKFveSh1x0s379+kUz3qcbSzaA9j169Cjcf0NxRgcgx7jUH0QBFxdxaBuQ4gr42Gw2+GahN/QzMzPj77QlWMfvv/8edvTYPBA1UKvVWrlyZbfbXf5/n3LlyiUnJyf976MoSpcuXSKHwF9//UW2+VTr3bt3F7XY165da9CgATg3adIEgpE4QUV2sKVLl0L4czqd6M9xZnrkyJGePXt++eWXLpdLUZT69esvX748Mv04U4uMRpRg+wyNMpI58adxdOHChcjUTFdSU1NxwB0OqWvTpg1lZ4pZ1K+9e/fG0IM2pygKnRQXf1LFmX/E5hZzbNGiBcnEmGnT09Mj90LEWwoNa5rWtWtXSZKSkpLQDWh4SpL04MGDnJycaOXBmQHU2xFQVXXw4MFbt279/T+/DxgwgBoXgSpVqpBjlhhlQyfs168fbVdg8k/sYMkYGb3lnzDdtW3bFu1ID52tW7fG2GQKBoOhUGjt2rXlypXDO0Z4X4cmnGvXrkVrI1MFARYv2UiSRNMg5g1VVadOnWoYBvnMMd3+Dr/iIQg3L5goFEVJS0srqVH/DqvGWTMBJsAEmAATYAJMgAkwASbw9gmUgAD9yy+/iCZXqqru2LGjODXRNM3v92/evJmENtgueTweh8Px4sULGEhGW/4dO3YMS2is9MqVK1d8vWDWrFnk8QC69pUrVwr0CRCj4rm5uTArBi6yVps7dy6t6Hw+H7ysQlmA+E42dyahyuv11qhRA+9cQ4BWVbVfv34xyhD7p0Ag4PP5JkyYILr1EMWOPXv2FJgCPIRs2rSJFtgQoCVJqlmz5pEjR8jIKxQKtW7dGk1Db4vfvn27wGQjL86YMYPKA8/gly9fjoxWpCvh/PCnn36qqiq5ll6wYIHYu8RwkVIuUmRN09asWYN2hJGp6KGF+gMZpMMVCfZ+4JeDyMCLLt0Cmzt8XblyJYz6qcsVqZBFiozu+tqdy5AhQ2gsQxQjRyIklkHPJUcEKK3FYnE6nUlJSZIkHT16lGwJUYzMzEyKj1GpKEo8QiqNXJ/Pl52d3bJlS3RXmCXCBBWUCqyvz+f75JNPoMggX7vdHpmv6M5b1/XHjx936dKF2ogCFoulSZMmjx49KjCvBC6+LvnMmTMpfVQqOTm5Tp06W7duvXfv3tq1a0n8wlQpSRJUsGjZaZqG3RHsCGJ+ICNlCFXR7o3nep06dagp7XZ7nTp14rmL4hR//qExTmki8Nlnn5HmiBl70KBBCT9QgsFgIBAYN24cdHZqIwr8/p/foUVSecQ5f/To0YhJ3o2sVuugQYOysrLIw/utW7docCFa27ZtkaapaqavEGobNmyIsYCOXbduXTilMUV+X77quo73Y2rWrAkPV7Sft379emxyEGrxVIlwfnjz5s3UJ6mBkIjpOWtKxwQnGAyuW7cOPGFdTg2E2c/lcj148MDn872TrUFTaU1f/X4/eh30d5SfdvRNkfkrE2ACTIAJMAEmwASYABNgAkwgBoESEKAnTpxoEqBPnTqVwFJKfK9zwYIFpO9AuoI11rp163A0UAyvCyavndWrV49R/3h+CueHv/32W3JrgDeynz59Gs+9YpyOHTtiHetwOLAcrVq16v79++FOxOv1Ql9bvHgxBHcyCdywYUNubi5UD1ot67ru9/sbNGgA5RSRXwtw5IBbzDp2GFoknFNv3LgR5yLC0BjwJUmqXr36n3/+ibPXCkzt8OHD8D4Mm1BQatu27aNHj9AZcG8oFOrQoQNKC/FUkqT4xdAhQ4aQBGOz2SwWSzF9SoTzw16vl5yMg/zWrVtFzmK4wLoX8yI0pkAgkJmZKZqc2998SCu0Wq2wP4UKANpwhw2epJSRdTne8ib1RJKkAwcOQJQpZpnjuR3tvnjxYnEsk+8UUmHIPQskddubD3o1lbx27dqRqt/PP/9MYwT+Rmw2W/wDE71u9+7dNHYgvS1cuJAU6gKrefbsWYxfeqlflmWTG2WozyTBHz9+vHr16lSdyEC7du2eP39eYHZFvYh9ICobJOZRo0bB5TR274YOHYpGAXxJkgp11NC/f38MauxnNG7cGO1LjlNomBS1wKFQyGazwQGFLMs2m61Tp06i8BpPgsWcf6IVvkmTJqIKqShKz549i1o22n4zDANuTGCNS20ky3KVKlWOHj2q63owGHzx4gVRhV8RTdN+/PFHEjHJz/vUqVPRjf1+Px4f2dnZYu+y2WzdunXDw4LqaCo/rH0NwwgEAhUqVEAuHo9HkqROnTqZdn3iaYsyEicQCBCcChUq0NSKBt25c2ekBTSR2blzpyzLycnJIkzsQOBvpUqVUE2MghhsT5w4QUbEBQrQkiStXLkycn4rCxg1TTt37hyIud1u7D/t3buXQJWFQnIZmAATYAJMgAkwASbABJgAE3gvCBRLgIZtVPfu3cm8EYFHjx7Rejh+CkjtypUrvXr1MinaeG12/vz5ML2JoT5rmobzrGhtX79+/fjLUGBMXddTUlJQBhhA1apVq8CY0S76fL6hQ4dCI0MKkHKOHj1qusXn83333XdwUgmDXKfTeevWrUAgAJNMcaEbzg9/9dVXVFMIB61atTKlGc9XqAxXrlwhERMaB7S51NTUhw8fFrjmxH7AgwcPPv30UyxT6W+7du1wC1QVKsYnn3wCB7J4kf+LL76gnwoNiHqQoiiffPJJobcUGuHmzZsQ48ga9Pr16yJnMVxoaolFILatWrUimUlRlKSkpFq1ajVq1KhPnz5Dhw6dOHHizJkzf/vtt+3btx85cuTsm8/Ro0d37dqVkZGxevXq9PT0qVOnrlmz5siRIydOnFi+fHn37t2rVq0Kwat///5QZCCaJFbUIt2laVqnTp3iEaBhAU0DH93Pbrc7HI5evXpduXKFEFEBBg0aRPKQ3W6XZblhw4bx+1HFgGrTpg21O1LbsmUL5D/KyBTYsWMHYqKrQ0k3vfYBbSsUCuXl5R06dIg86lCBxQDS+fHHH00ZJfD1r7/+gsgFs3FJkpKTk0eNGgV5i6TGS5cu4WUFOsSyfPnyMbK7efMmuhAZkGZkZBiGUaCnmhjpFPjT3bt36c0JPEEmTZoUZxctqfkHYzyyeOi9YmPBoDgyZjxXHjx4gG0kzP94UwEeiu7evSumgKch9cOdO3eiDHgnBuE5c+bQLXBLpev6oUOHxNK+Ptv2559/pmNaaSqjGxHAtHD37l1MPqqqYjNm0qRJ+MkU/335itng77//xiOVplZJkk6dOmWqha7r2AW/c+dOjRo18OoAydYmqna7/caNG7RTRWBN09SzZ89q164t3hu58eZyuTp37ozRZCpSWfiq63q1atXwjwF2iSZMmGCqZlkoJ5eBCTABJsAEmAATYAJMgAkwgTJOoFgCNF7shSYIYQLygaZpeXl58Vv0YPH27NmzqVOnQgzCakfUtSdOnEgvxUdb/ECMWLFiBflSkCSpefPmxW+D8uXLQySCZtq+ffsipblr1y4ouVgAwzPv7t27NU3Dy+MQCDRNe/XqVXJystPppPeFmzVrhryIJ611DcOAWI/1LZToJk2aFKlstO7VNK1Dhw60RIdGLElSnz59YrxyG84PB4PBwYMHowxkkdqyZUscLRh480EFDcP47bffJElyuVww3X0t68+bNy9G+qa6JCcnk+AuSdJXX31lipDA1/3795NAAPtc2IoSZzGQQPqxb6E33NGrdV3Pzc39+++/Hz9+TAchUgokSKHVgsGg3+8PBoMoIWl24fwwvRWOUXPixIm///7bMIxXr14hI4pMiZdSYMaMGSQrQ+6kTkJaDF5FlySpXLlyDRs2bNeu3ahRo5YuXXrmzJlXr15R5zGVsHXr1mRRiF7x7bffxtmXYB159uxZOENAkWw2m8PhuHfvHoRjU3b0ddeuXdRhVFXF2ZWZmZkUgQJ5eXm3b9+uWLEi4tPuDlVctP622WzFNOc3DKNp06bQ4mFK7HA4unTpgona5/NBgIYqV7lyZYfDgaaRJCm2AL1w4UKqsiRJtWrV8nq96I3i6ECYqh9n4ODBg06nkyZYRVGWL18ep+FtSc0/0UqOA+jEOSclJSXOeonRMOjatWuHCRbPEcjQ3bt3h4UySb2i+qxp2v3798mAF4fgSZKUnp6OdiRQCGBXhoaYJEnktV9sKbFsUFF1XT9y5AieudTWK1asiH9Hx5RmWfgKJocPH8YemNiO165diywhEMFDN0Yr9l0IiBig83gjLakpZXplhx6skWNfVdXk5GRsIdCNZSowYsQI7AXi7Yf69eujP9M/D2WqtFwYJsAEmAATYAJMgAkwASbABMomgWIJ0FiEwLAX76V6PJ5atWr533xiK1y0gAnnh3NycqZNm/bJJ59ADYESITquXbRoUTz4gsGgpmlz587F+X5YhH/99dfx3BsjzuPHj0k5glI2fvz4GPFNPz179gyLWJQHtfvll1+gMkBWJtcWEyZMkGUZ+iwynTdvnilB8Sv5RCZpr3bt2n6/HzIcadbiLdHCot9YWma3a9euQAGCjJrD+eE9e/agUkTJ7XaL5wqGQiHIoMFgsHbt2mLLqqr64MGDaEUyXX/69CksJck58vfff2+Kk8DXFStW4JQ29OGUlBSToBBDuEkgO9MtNBBM10kVEnOPDEMEFP+KcWKnGflryV6BOaHf7581axakH3haIKPCZs2afffdd0uXLj127NjVq1dfvnxZYGeLLFU4P5yXl4c+Tz7QLRbLyZMnY/A0pfP6rYL09HTq6gjEs1+1YsUKugubSZIkHTp0yJR+MBjMycn58ssvsalGIjtEc2zDkEtl6Dvbtm0r0phFjpqmgduECRPETTsccvj48WPoRNRJcFf//v1JXHvtuL9Bgwam8otfmzZtilrAbc6cOXPAWexs8ZMXUzYMg3jSBHLgwAFT/zfdgq8+n6848w+kwPv375Mda2QuCxcuFE8ETUpKatCgQZy9lFJD/NmzZ1O3wYRpt9tbtmyJMw9Mj0td17H1out6165dxSeILMu4y3SLYRgHDhygLPC46d69O4pRaOvour5s2TJRHpVlGW6X4mkLqmzZCWATzjCMxYsXo17ADkR+v7/AsTZnzhzawCZHQKJyDbCyLE+ePBlNQLt9GA5+vx8tDm9g2GaQZZlefkIKqqpSs742gv7rr79i9MN3S1XccgO9O3fuoEimZ+W7LSfnzgSYABNgAkyACTABJsAEmEBZJlAsAVrTtOfPn8NHLSyMHA5HixYtYJIZWW0sz+h6Xl5eVlbW7NmzyaoLooy4hHY4HNu3b6dbYgewFkpPT4d9GVabAwcOjH1Xob+eP3+eFq4IwEtsoTcahuHz+fr374/yYA1stVp79uxJ98JEC8SWLVtGdYcYGts9RTAY/OOPP6BnwcBKVVX4pixUbqACwPXnhQsX6C14Wn43adIkOztbjImw6N/20aNHZOBJUuDKlStNd0H86t+/PwyrcTqWLMuxjz4zJXLx4kVgoQORFixYYIpT1K+6rk+dOpXs/iwWS+/evcmm2KSvFYlqUUsSGT8y98grpCpSQIwTO83IX0v8CrRRv9+/ZcsWdDCIL+jnhw4dIhEN5t5iAcgOVLyIcDg/fPr0aVFshVlu/ApOIBDQNK1cuXJieSRJGjJkSGR2piskmOK1D8imFy9eFKNhjMybN8/lckFwh59xq9Xqcrnatm0rDjfyADNw4MAE+his5g8cOIDBRVisVuv+/fvRH6h7AHggEPj1119pNDkcjmHDhonlF8OYHGhqwplpJN7F7m9iOtHCP/zwAxJXFAWS3O3bt+FniRKPdm9x5h+73f7DDz8g5WjYDx48iBMXyVl2zZo1oxUm8jolC9cobrcbTxBUs3r16o8fP/b7/T6fLzc3N/J2v9+/adMmOLuHRwhJkpKSkuAkmhLHg+b+/fsVK1ZEypIkORwOu91++PBhGmKR6ZuupKeniwL06+GQlZWF13SoIcRMTbeXta+BQAClHTdunKleVatWDYVCZHKOkmuaduDAAWyS0UtIdru9YcOGZ86cSUtLczqdYjpDhgxB+qbnBVIL54c///xzekUDPbxjx46nT5/etWsXGUTjWWa32/EKRdnEG84P064hKgIPPIW6dilrXYLLwwSYABNgAkyACTABJsAEmMA7JFAsARoykOiVUlXVAQMGxLOI2rVrV5cuXcjkjdQN0mIkSWrbtu2ZM2eKREfTtGHDhpG4oyjK2LFji5SCKbKu69DOUDCsG3fv3m2KVuBXv9+/b98+h8ORnJwMnUtRlJSUFNgk+v1+URrYuXMnvQ4PCclisRw7dkyMY9LXwvnhFy9e4LQo2gCwWCxxeiEQy9ypUyc4/YRHAqgkcFFNShPFh6V5KBTKyckZPny42+0WVbzBgwebyowbx48fDxMwCNyyLDdt2jQ7OzsyfcrIFMjMzEQ1yR5t27ZtpjhF/arreu/evaHEQVyYNWsWlAtRc6FwUdMvTnzKNEZAFBYRFiNH5h7718j4xbmCeYA0mipVqtAwh9uKhw8f0mYVVQQlpLPX4GXYVAxd1+fMmUNKKwwVp02bFs/MQ0mtXr0aTj+oVJIkbdu2DYkU2IdxryhAo+dbrdbIIwRPnjxpt9shCOJIT1mWR48ejWMSHz9+XLduXcoaXdrhcIgNVKTqwNRaZDJhwgRN0+BPhvBqmgatMxAIVKtWDQPKarVG+qMnULNmzaJyyrLcrVs3n88Xgw/dGGegT58+lD5eboBjmUJvDwQCxZl/UlJSxJNvC8zu4cOHOBUTE6MkSR6PJ/6DLjG5vXz5skOHDna7HYfaoa1VVT1x4gTMnAvMGqp0zZo1KWt49N6+fXvknPngwYNmzZoRRtwye/bsaO5rCsyxV69eosCqqiokWvLyUeBdZfYiFbtdu3ZivSRJateuHXZexcIHg8EOHTqgucmFeuvWrTG0MzIy4KCJkortDRxea+APB0bQvXr1Ism7V69eSUlJ5LhMUZTp06ebnu9i2d55GG5JqIOlpaXRURzilPXOy8kFYAJMgAkwASbABJgAE2ACTKDMEiiWAK3r+rZt27C4opXJhAkTotUWRyQNGDCgUqVKMCujvzjchhKxWq2LFy9GOoVqBGJ2uq5DzoDBjqIoZOMmRos/rOs6+T+lQp4/fz52ClBngsEg3NSSGZTVal27di05sybPG1u2bIHmi7/gMHbsWF3X8/LyKC+s9OgrAvXq1UN8MiQnLSnOV8XxhjISgX8Mt9u9bt06qFe0jDflm5OTc/36dQheWEgrilKtWrUXL15ECmfjx48nFwTk/3T37t1er5fWsab0I78uXrwYSjFRKpLLhcgE4ZqAlDsku2HDBtMr1e9qgS3mGy0sCotlTYAmPQUd3u12o/nQ06xWq6mfhPPDcIkOZ+6wiY4UoDG4+vTpI4qtkiQVabMqnB9u1aoVCcQokiRJt2/fNpUqsttECtBOp1OMlpOTEwgEmjZtKssyJiLYOc6YMQOW0XDKDNe0mD/hgkOSpFu3boltLSYbLez1en/66Se8VSAyefLkCd0i9hNIb5qmrVmzBpqa6GGfbqFAkyZNoNTDZzTebyApjaIVKSBCbtGiBfG32+01atQgx+gFpoknQiAQOH/+fHHmn507d6IYkXou5ZuTk9OgQQMUD86mZFnev38/RYgdwAy8aNEiCP1IBwfirV69mo6WjUwE25MLFy6E3AnN2mKxDB06NFJTvn79eqtWrejYAGyKpKamwr1VPC0FDs2aNSN1VZblKlWqJLCXGVmXd37l008/FeulKAreizI9H6dNm4YNZlg6S5LUpEmTe/fuYbw8ffqUXHshtXr16kWr2pMnT6Av07E01AAAIABJREFU0wZVjRo1COZr2nB4Rc0qSdLgwYNpwoyW7Nu/Tv9+TJo0iXwHSZJUo0aNQCCAgVPU+ert14JzZAJMgAkwASbABJgAE2ACTKAsECiWAG0YxqpVq+idX6xP5s+fL4oLmqadPXt29uzZX3/9NakMWJXRV4vF4nK5sBiTZXnYsGF37txJ2MKucePGSBkFi+1DOZ42mDRpElQkvIWtqmqktaOYjq7rEG2XLl2KV6FhNydJUsOGDaE9iaf3LF68GNqB3W6HGbKiKMOHDxfTLDAczg/7fL7Ro0fDkFxVVWi7s2bNKlR0QBtpmnbv3j3T4lySpEmTJmExjLWlKXeSjAcOHAhZGZKKqqpwTgKFCOvtV69ewfMGIBDDDRs2FHXhOn78eCiYr48uhOOXJ0+eiJ3NVM54voZCoVq1aokd8vLly2XEAjqe8osMxXA8977lOKL67HQ6U1NTIwtAbjegQUN9NnVC+B+32+0W4dOwYUPISdj/IBSmLEhyun37NiYcuDaGO+kqVarEs92FHSlIt0ikRYsW6IcotmEY5E4Hh226XK4pU6aYChPOD8NqFZ0ZMZcvXx6t8Kbb8TUUCj169Ih8ScOBgCzLGzduJF2VqJIMjSzC+eFz584dP36cXqUXs8Ak9uTJE5qoYVd79+5dMVpiYWpZwzAwh5CPC1inFpqsruuDBw+muQuvjxQ6/8C1gs1my8jIIBpUGFNPMwwjFAqNHj2aOhokyJ9//pnExNjlDIVCf//9t/iiD3a5Zs6ciRuprU3zWCgU8nq9Ho+HHAejp505cwYxfW8+hmGcOXOmTp06mMEwD8uyXLdu3cePH2ODs9AnKRL0+/3iOwowE462+xi71mXq1xcvXtAGMHqL1WpdunQp6fio/rFjx6iV6UGMDU74EfL5fDVq1KD+Jsty5cqVo7H98ccf0SL4J0RV1ePHj4ttvWnTJkTAX7fb3bZtW9qZjg0QmVJkDHOa2WLfm/CvW7duFTdRLBbLy5cvaYZJOFm+kQkwASbABJgAE2ACTIAJMIGPh0BxBegff/wRC2NYzqqqun379j/++GPFihUjRozo3Lmzx+NxOp1Yt4tCBqk/oqTYt2/f06dPF4e+ruufffYZFnXIYvny5cVJ0DAMOHEWnT/ETpBWZS1btoTc4HA4PB6PLMvr1q0joQHOB8aNG+dwOOAfFuqzzWb77rvvoP96vd4YUjIMdbEyxBoboliPHj1il1C0tBoyZIi4qHY6nR06dIDuIC6YIxM8c+aMy+UiAVpRlMqVK798+RKqDRbJV69erV+/Pnx0wJMpvCUsXLgwNzc3dvqROcK2HcegoVMFg8FiSiQ4yw79EyreixcvTAcrFbWckSUvvSti2cRw6eWYWMovX74kARp2wWlpaTQWKE2qAomDdIXiGIZx7tw5dCfSjCZPnoyeEHkj5SJqNCNHjlQUBZ4xyPlM7969xVyihadPnw61lLwP9evXT9d1n8+HLO7du1e+fHl0VEx6HTt2LFCrmj17NpnzYwhPmTKlwCqbCgP5CWn++9//ttls2CTDNEVyPEY6MTEF8CvmK9ibi1mDJ5wX09T92WefvXjxwlSYxL5C9s3NzRXnEEmS+vTpEztB1B0FE+eueOYfVGTZsmWmgxmp4tRbqAw7d+6UZRmejjB9kRP/2JNPMBjMy8sbOHCgw+Gw2WzYNvN4PB07dgwGgziqLlq+mqbNmjVLlmV0TmxO9OvXj0oF/XTt2rXUNHQ0a926da9cuWIYRl5eXmR1xBQQpg5AjomRZp8+fehZFnnX+3IFHszFfmK1Wnfv3k1OxtGIbdu2pckE7xKtXbsWdURHDYVCLVu2FNNxu910zqFIg44dJldg3333nemtmsOHD+P/E3JI9dlnn4mJxA6jSBj+uq6TGB37ruL8eunSJYfDQT3EarVeuHChwDmtOLnwvUyACTABJsAEmAATYAJMgAl8wASKK0CnpaVhsUqar7isMll+IQ4tmK1WK4km/fr1u3bt2pMnT2Iv6WO3BI5LKleuHNkCy7K8efPm2HfF/lXXdbxKD3nIZrOVL18+xi0wf9Y07ejRo6S4ocq1a9eGP9ZAIBAMBm/cuPHVV1/REY6EZcyYMVANYGQXQ4DG8i8nJweOJmltXL16dQjBMcqJn3bs2GGyDnstAF27dg06WjRxBMtdnN0nikfiiYJ5eXmbNm3yeDxYsqLpZVl2OBzr169H7tHSj1bsRo0akRGWw+GoXLlyPPJKtNRw/caNGyQTOJ3OpKQk04lSYiGLn13swiTwq6l49DWBpEr1lqtXr9IWDpS4OXPmROoXVH5IpfTVRP7nn38W1SKLxXL58mUqf7R7IRDruv7y5UtMTbRthuNPyS6VkiowMGrUKNo/w/j96aef8GYDyglFGIljXMNw1VSLUChkOt/PYrG0b98etS4wa/FiOD8cCASuXr2KjOjlCVmW6YgwAmiSnvEVPk+wY4SUKT70WV3XRYmTHAWQ9ahYnqKGMdXfuHFDnEMkSfr+++9jTHr07sj3339vmvfimX88Hs9vv/2G8otMqOKmNjIMIycnh8yQMZtBeYynvvv378cES86mLBbLlStXMIWaREkxQZ/P98knn9B0B0n04MGDOG8Q6HB4IzYd3W43ykZnDMTfRvB7c//+fXoGIVBoQ4gFLrPhDRs20JMRAYvFcvfuXbGPkXMnmlW++dc35CSa/if59ttvxaQkSXr58iX9SgTgXoM2lipVqvTw4UNs9lA3e/DgAbYlyMG3w+EQi0SpRQbQbaBB06+Rcyn9lHAApUXJg8FgjRo1qEPa7faNGzcmnDLfyASYABNgAkyACTABJsAEmMBHSKC4AnTLli2xWIXmi/UJXgPHW+0m0ZmWuJCeU1NT586dm5ubGwwG8fK7ruuioWKRmkTTNL/fb7FYrG8+cIq6Z8+eIiViiqxpWuXKlUlEsFqtLVq0iLFQxKFSXq931KhR5B3b+eYzbdo0WKUZhjF37lyLxZKcnAzxxeFwwNht8eLFpIAE33ziWVi2adOGXmCXZdnlcp06dcpUEdNXVKFWrVomAXrJkiUQpGKIIzk5OeH88KefforCI2tFUeAaG2dnwTsH9Q10gzp16pw/f57MtWg1TlU2FdL0tXz58mI1mzRpQh4qTTHj/7p3717Y0sIVw6effooj2sSyieH4U347McWyieG3k3v8uRw7dgyE4TpDVdVNmzZFajdUBYiD9NXUQ9C74P8XmhEiQFGNfa9hGOnp6TQRYfsBatGvv/4aT40GDBhAO2cWi8XhcJDgaxjGhQsXyE4Qyc6bNy8YDBbotMHn86mqirPpVFV1OBwNGzZEreMpSTg/PGLECCBVFAWlatq0Ke4V6YliqxiGTAlf82J80sumTZsmssILJTSE4ylktDiY2U6ePGkSoOfMmROPI5RKlSqRN3nIgvHMPydPnkRDmNySmOpOZYYv5pSUlKSkJHHyOXXqFKbQ2CjIHxQYYm8AeVErUNbUaoZh7Nu3j9w3oRc1bNiQ7JH37dvXsGFDj8dDW7xut9vhcAwfPhxOYPLy8iIHF1UqMhAKhQ4cOECaKUr7008/oY7xPIMi0ywjV2bOnAmNnrRjVVXp34xAIHD//v0KFSpgt5gE6IcPH8JdO05DxXCYMmUKJYIn2uPHjyP/XYGmjKaxWCwLFy4MvflQQ6Pvud1u2qOCe/H4D7eE+ty9e3eLxZKUlJSZmVlKtKnLhfPDDRs2pM3a11sys2bNQqZivUqpGJwsE2ACTIAJMAEmwASYABNgAh8AgeIK0DVr1sRiFcfQYXlGi22T+owlmaIojRo1mjlz5uHDh2l5QyiLs5iBbSMEaLwrbbFY/vrrL0o8gUBeXh6M12hx3r1790LTCeeHcZARigEOV69eNQzj0qVL3bp1AyIAgf8Hl8v1+39+h5xhkttiZ6dp2q+//oriEX/RGFC8He99IxeYMONoOFVVXS5X3759Rf5iWEzEMIxNmzaRfTeW93BvHQqFdu7cWbt2bcKF9BVFad++/aNHj0zpxP81EAhgSwOyo9Pp7NatWzAYjOxC8adpGAbOB4PvVLfbXb9+/SIJN0XKK87IkHvgvzUUCsWp/kDPQhYmJj6fL85E4ixhAtF+/8/v6JxQSyVJunjxYox0YvQ9wzDq1q0LORvTzoABA5AUBg7UGaQQmcWTJ0/okDHTBHXhwoXI+JFXmjdvTjtS2HL7+++/yV6ye/fu6Pw4V5Dk4Mh0YM2KFyxIs/Z4PFC7YjcZaur1em02myjg2u32P/74g/ISMRYpTCmYrD4PHDhAXuwpTsIBTdPgDJd0PUmSNm7cGFuADoVCO3bsIGJoxDjnH5J9TQERTmR1fvnlF7J5x9Q9bdq0GA2E1klPT1dV1e12k0w8cODAON37DBs2jJ4O6GPkQzw9PR2ehW02m8fjgR8kSZKmTJmSk5MTWfg4r6xfv960Gfnrr79iJomx4Rpn4u8kGmbyQYMGmYZ58+bNxd2gQYMG4SGFKcVisYj7SRCLYXe/evVqtD79vXPnDgnQeKpOmTIFXQWacv369THMTQTg/93tdiuK4na74cH8xIkTpmgFfkVGy5Yts1qtcBv12Wef5eTkxO7DBSZV6EUwRMrdunWTZZnO/ICrHDHTIv3fUmjWHIEJMAEmwASYABNgAkyACTCBD4xAsQTo134qxSUrlEE6IA6LNFiNYQXYvXv3BQsWZGVl0UKFVi+Ela5QHPopnsD9+/fJqSJkIMi+8dxbYJxHjx7BkJm0XZMjzsi7vF4v/DKTqiLLcoMGDV4fKrV48WISI0hAkSSpY8eO9+7dw8Iyfn0HCoiu6+fPnwdtWhw2btyYfAIQUlg7QlO4cuUKraIByuFw3L17lyKbAqZqDh48GAabZOU9YsSIq1ev9uzZE6nZ3nysViu+pqenZ2dnmxKJ5yt1g6dPn1IHU1XVbrf37dsXjmvjSSdanOnTp4OD1Wp1Op1ffvkl5RjtlrdwHRJqOD+cnZ199+7dy5cvPxQ+fuHz/PnzmzdvHjlyJDMzc+XKlfPffFauXLlq1arNmzefO3eu+EbiJVLfhQsXYqNCVVX00sePH8eW8KgHigUIBAIvXrzweDxQedAlFixYgDhoO7rR1JSapuXm5k6aNAmqDQ1PdABFUe7cuSPmFS1cr149mg0sFovH4/F6vajL3r17obBjmNtstl27dkVLByO0R48eSI0mBJxxWuhGSDAY3LBhAwnxkKFr1qwZzg+LvtFFGvGHqcy9e/cmULIsw9VJoWWj22MEUJjly5eL6b8+qXXnzp2Yo8TSmtL57rvvyPwZqOOcf0y6M32NkZff7z979qxJgG7evPlrU3q8JmIqGwp/9uxZ9HOHw4ESJicnP336VMzIFKbUYBdPkzkcgBw9evTPP/+EGyLy24DWr1Chwu//+R1bIImJxZqmLV26VGwIWZa3bt2KXl0izW2i9Ba+othfffUVPekQGDhwIPlN3rFjB6yesVUsSVKPHj1EeZrKqev6li1bTEldv36dJrFAIHD79m0YNUNQliQJ7UKJUCCcH3797xBEavhWNgnfFDMyAMk7PT3dYrFgtqlatSq9soBOFXlXYlfELjp8+HBFUei8086dO4uO1MWYieXFdzEBJsAEmAATYAJMgAkwASbwYRMolgCdlZUlWgKSETQWaXBb2bVr15kzZ547dw4cNU3zvvngq67rolZS/EXUpUuXqEiQDIpjdWsYxpUrV7CYhEMPRVFGjRplErbELgIDt6FDh+LkPVrSjxkzBu5KIMgSIlVVly9fLi4aNU2LU0Sgpa+mafXq1YMqAR1KkqRbt24VyBPvaHfs2BFHqGENbLFY4NJRXEaKYbGOmqbVqFEDAjS5YV26dCmd6kZNoChKnTp1zp075/f7Q6FQbMNGMQsKE+rr16+LArTVah05ciRFSzgwatQotAi6a5cuXRJOqqRu3LVr13fffdeiRQscXIaugm0VkQApJngtGi6A7W8+1LsgXdWrV69v3747d+6Ms1+VVEXEdIYPH04CK4z+YIwvxhHD0fpeIBA4fPgwvQmOHQ5ML9RVxG4vpmkYxs2bN6GA08AkvwpWqxX+c0y3RH6tUKECyZEOh6NJkybQIg3DaNWqFeDj/QDskUSmQFc0TZs0aRJ6IJpYkqT//ve/ol9mimwKBIPBTp06iebPr9PBe/EiCtwl8ownjLs0Tfvqq69EVs+ePTMVI+GvEGpnzJghpi9J0rFjx1B+sZxiLq/f+YB/ZFGHjXP+IcXZFIiWFzlN+vzzzzGtYR9FkqSsrCyxVAjDZYfP5+vZs6d4CmVSUtJvv/2GLUYxLzGcm5sLzfTs2bNiD3e5XHXr1sWxmehdGNcWi8Xtdn/zr2+ysrLC+WGfzxcKhYLBID0XIotX4BX4o5g5cyY0fWoOuJwu8Jb34iK8Z1BXoYG5fPly+MR47eokJSUF1+n1mgcPHkSr3aFDhwgO5g16ZyI3NzcQCAwbNoye71arFRJtganpuj527Fgkgn5is9nS09MLjGy6iNdievXqBb9nVqsV5v+maCXyVeyfv/zyC86PheP71NRU7HWJcUokU06ECTABJsAEmAATYAJMgAkwgQ+SQLEE6EOHDpEQg9eEIZCNGTNm9erVN27cgIxC62Gv1wt9FusWnMVHb7CCbzEXMydPniT1E4JXcd5KNgzj5MmTZLNstVpVVZ08eTKkkxgdonXr1i6XS1ys2mw2qAYAZbfbbTZby5Yt//rrL8iCqHj8fp/JhynktnHjxiFlMg795ZdfTOfpUYFxsBjaDovJtLQ0NJPIXwzTvYZhPHjwwOPxgDN8j5I7DliTYUmvKMrIkSPBH4oSmXgjNdMxSmIWFIZOZBjGf//7X5PWNnnyZIqWcGDAgAFoX6gAaWlpCSdVIjd+//33aEds55BoSwK06XVyUlWoCRCggUmypsPhaNCgwZkzZ0qknPEngqbv1q0b1UWSpLp160Ivi5ZOtL6nadqiRYswssj6nkYQpUa30xUEvvnXNzBRpBRgQwopM1K3pdvFn+BiHuRtNlv//v0xoe3YsUNRFJfL5fF47HZ7hQoVLl26FMMCHWkuXryYRCs01vbt2/GyQgzLU03T4EvEZAF95coVKrMYICDxBzB7p6amivNY/G5qxdwLDGM2+P7778X0JUmCK2dxF0GEbxjG06dPqdu73W54vkaHL3T+EXVnHL6HiVTEYiotVN3JkydDeibj1mXLlkXu6ECgz8zMpAGIjaLevXvjSSdmFBlG1uvWrStfvjzqiBqhh1CauOjxeFavXi0+jGJ0GFOlxK+apr123D9x4kSTAI2NEDHm+xXG9jYwitMmrJJf/zcybdo0dB7yLLFs2TJ0vAJreubMGbGvkoMvnDx87NgxpGa32/GvArnUwIPYlObs2bPxDEWaVqtVfLnK1OfFe9EhmzVrRr3im399Y3q2ivGLExa76NatWyFAw+y6bt26gTcfMU5x8uJ7mQATYAJMgAkwASbABJgAE/iwCRRLgN68eTOWQJDwrFbrpEmTCnx9ldQE0T0rlm2JrZkLbBVN07Zt2wb9DgvOpKSkAmPGf3HLli1Y9rtcLrhbnTdvXuzbHz9+DCAkmIqrXxwtVa5cuVmzZpnqbpJCTLm8fPlSvEICNJZ/586dQzlhCasoSufOnWENhwh0bzAYrFixIol3DofD7XbD+QY1k7ikNN0OB9CiZEbCOkn/kiSlpKTs3LlT13U4ICbdR0zZZKwHGqaFN+SVYDCYmZlJPJH77NmzqVIJB3r16kUCtCRJI0aM8Pv94fywWM6EE0/gxrS0NMhAaE3I0BDHSfsg9S0ygB0g0lxwC7jhp5YtW9KWz9upIzY2yFk8ytapU6cE4OCWwYMHU/ez2WzNmjUrUN8R08dg2bhxI7ymklhP6UiSVLt2bdoqE+9FOJwfBrd//vmHNH2YqS5fvhw/ffHFF7gC5wnDhw83dWZTsvh1z549aCZSo+bPn4+RSC1luhFf161bB5iKokDc79GjR6QkWuC98V8kE1Hk9eDBA1HxjD+dAmMGAoG0tDTq2JgnYzsHNwwjIyMDhcHIheqHKzTTRpt/aCLCibViXRAucFdM07Rbt24hC0mS4DL466+/LrBSOTk51atXF2dFm812+fJlNLc46ExharsePXrgdvQ08vKMZwdmhv79+9+7dw8+EKgYkR2Y+i3FiQygYL179xYnWEVRRP8SkXe9F1cuX74s7tCgBa9du2YYxunTp/EQxNhxuVzwWxUKhXAObWQF79+/LyKCuxh6iPft25eOYpYkafTo0Ugh2iQgOvRAQ1etWpX2y03/KYmFQbfBIZz4b2f69OlihFIKHzlyBA7WcMp0+fLlsUclduNSypqTZQJMgAkwASbABJgAE2ACTOADIFAsAXrBggVQcEjhghuHArlglRJjWVXgXUW9iJOU8DqtLMvwjVjURMT4a9asgeEbufL86aefxAiR4evXr0MZERerOOYOa90hQ4Y8efLEpB2YBGXggg4F5xWiv2PIKKaFH941hkNJj8djs9mys7MJOGU3cuRImGjZbDZoN7/88guMAeMUoBctWkTtDk2EpBmLxVKhQoX58+eTFEI23aYy01cCSFozXSF32JqmrV271iRUlYgA3aFDBzQKajRq1KhAIEDQqBXEIpVq+NSpUwQTAciLNMTICwcsMfGVXvYnKVNMhG5RVbVChQpQTEyHoZVGpeiIyEAgAJN5jAtJkujYwATybd++PdVOVdWuXbuiLgUmRQojZEHcCJ1o8ODBDocDGC0WC44LKzAR6CzQB0+ePEn9ENrW4cOHDcPYvXs3EqfB9fjxY+RuGqeUBZSpU6dOUYJ4JZ98y0R7gwEp4KUH0tdeB+bMmUOJl1TAJECfOXOGFLfiZxHOD3fq1EmsvizLFy9ejKbZIUccHEpOKkQButD5hwTocH6YLKCRLNo3muivaVr16tWRKR1iGenXPpwfxgQLQ3t0iTlz5qBGYk+IDBPP5s2b0/6TuEcCwbR58+ZHjx4lRNTDMXtTIhRABFQc9vg0OSMOvqIhxGfW9evXxcQpwfcocOTIEfjOglCLzQNA6NChg9Vqdblc8KTscDi2b98OqqZxBz66rmdnZ4tzqcPhWL58OYbDb7/9RujwQLl8+bKJs4kbTm6g9sXYf/LkCXpmjPkZP+HxjbvWr19vSrw0vp44cQJeofDPTLly5fCihtiTSyNfTpMJMAEmwASYABNgAkyACTCBD4NAsQTo7777Dmst0oNOnToVbckqrlIoXOIQFy5cCENCaND16tWjhXpiec2fPx9rVzpPD15Wo6UWCoWOHDlC703TohQCXNeuXckdNinCJD2TJlsgnz///HPPnj24y6SQ6roeCoUmTJgA82en02m3210u15IlSygmCvzf//4X0gbeolUUpU2bNjBaj8ydimFiOHbsWCTicDjw8jKtosePHw+n2yaVinQfSpMAwhBe1/W1a9dGOhAgq8B58+aJQtXrVi4RAbpp06ZYw6MPjxo1yqQ+mOpOxS69wLBhw7CLQMMKdtBwlkKbK/SrGEB/oysWi4XugnTy1VdfoUsEAgFqi9KrI5rv7t276DD4K0nSlClTqGWLSrJatWpUQUmShg8fDov1aOmgdr1795YkyePxAGCfPn2GDh2alJQUpwCNIWYYxsqVK8V+aLFYYIjaqFEjKFko27Rp06DOmDZ1xELCR+29e/ewxYVkVVVt2bIlosWwxNd1vX79+qL67HA4CrUdFnOPM5ySkiLWNyMjg/S4OFOIHa1JkyZi+vEI0Jh/4LQdijAZPhc6/4gTEZoG7lM0TVuzZg2OWIxWYDqwFF41rFbrsmXLTG/8nDhxAtIz7bU0b94cz0RxuBUYpnwrV66MpxjGi6IoENkdDseSJUsomqZp8MYQo/+Tnn7jxo3NmzdTlSkRMmJNTU3FPhY9sz4AAXrTpk0w16WXHurVq/f6GYqmxJSIzoNdH5KMqYEwSIFL0zQ82fHXbrfDacatW7fwfKdzI8eNGxfD9w5Se/HiBTarqPfKsnzo0CHsi9CDGyUR20vX9efPn8MYGf+Aif9UiDFLNnzmzBmy67dYLMnJyeg8JZsLp8YEmAATYAJMgAkwASbABJjAh0qgWAJ0ly5dSFFyu92Koty7dy+aL0Ja0YmBEsc6c+ZMEqBVVU1JSaElZWJ5/fjjj9A4SGOdPn16DMEuFApt374dJkJQNvHX6XSuXr0asqzX68VxfDhNiDSRSAmYyjx+/HhZlj0ej7geNpE8d+6c1WqVZTk5ORmv9Hbp0oXWsbAmbtKkCUQr+gv7TXjDyMvLE9MUw1QSwzDwrjHkPLyN7nQ6U1NT4bwV50zCXhsHHooVjEwznB/2+/0dO3a02+09evQwsSXj1vT0dFGoKikBuk6dOmQcJ8vymDFjTKZnpvKIHEoj7PP5gsHgwIEDGzRo0LJly9atW7dt27Zdu3ZdhM+A/336/++DC8OHDx/95jN8+PAh/4+9d4Gx6er/uPc5O+eac2bIuDS0njxFo0W0NFUV4xKMRl2etuoJw0RdgrbRIsYlbg1KKI2i0WqjaFEatE1RwVQo0mqlbnENSnohzCXnOmef/fr7vs/vXe8+c44zY4y5fE9E1lln7XX5rLXXnvVdv/1bw4cPGDCgc+fObdq0Ua32Nm3aJHdEYl9UeotQxN69e3HWpQjHCxcuDAQCUpNylSt6DXKbNm1aCgHONM1gMDh37tzMzEzMDF6v1+PxXL16ddCgQThCE/k0b97csmtiqRVGwuTJk9Vx6Ha7DcN49913PR6PSF1PPfUUDiUrLCyUGxAo1Dxx3GhJSQkETWTrcDiaNm2KstQOslxuGAaaI2fi4Y14Nf9KCVsE6IULF6JFyTYa0yxUbqvmzZurPNMRoAcNGoT3UVwuF7bcPB5PmvOPOhehqpFIJBAI9OzZ0+VyvfQ4TelGAAAgAElEQVTSSynG5OHDhzHBiu7fs2dPC4euXbuq49Pr9e7fv9+yCZHYrZbORQ7qxpimaXl5eXhqQPKW/RsYzApPlKX2gmEY69evh4r96aefJp60CcWzVatW2GRVBejUd4RaSjUMx+PxpUuXwsZZBOguXbp8++23drsdkjHufY/Hc+XKlXg8Lh4wpI/wwMWoiMfj2NLDKxQOhwMzCQ6MBWEM5pMnT97zxN1AIPD444/LHwmoybx586QrpQ4SI5BPnDiB+kOArsSjQaWIxMCvv/4qE6bL5YJ/M8v4T7yKMSRAAiRAAiRAAiRAAiRAAiQAAvclQDdv3hzrHxy5o2naPa1+EpdSldgTkUhkzJgx0BMhut2Pq1lUTN5zF18TEydOTCFSmKYJNyBYiEIk0jTt+++/h7yrthdqiLrOlLCs/MPh8NixY/Hytd1uDwQC8pMkxmlLwWDQIn9omnbhwgVYYkYikRUrVoiMDg3ljTfeEHHEopSpmVt6rUePHna7HRqQ3++32WydO3eG4qzqOxJWfwre/QBCIBCIx+OnT59u1aoVToHr3LmzygdhWIiPGTNGFao0TXvjjTcs5oeJ194zBgK6GPLDcDV1/94zzypLIH2UusRgMPjnn3+eOHHi4MGDifpU6mvv/9d4PP7hhx9K30FnwTl7FRAvbt++jRzkzlqxYgWGLqoKJmgmNsPWrVvXoEED990PNsxgCpqbmyvHCTZo0OCJJ56QOytZq0tKSl566SVpi81ma9eu3enTp7H9hp2qO+/1L1myJFkOlnjcGk8++aQYQaOGcNEjiaGCSXfH4/Hr16+DAwSszMzMjh07Svr0A9FoVIxkxaEE+gX37+DBg9X2jhw5MhKJxEpjwWBQUKdfnKSUWwy7ZWoRhw8fxnNEba9ceMd7b69evTDJu91uCNDpzz+Bux81tytXrrRv3x4TrNieqwnUcKtWraAOw9bV6/VeunRJTN2XLl2KYYlOtNlsEyZMUC9PJ1xUVCQ9K1r2hAkTMAmrTBCWh4hkbpmu165dK9s/ixYtSrzpMLoaNmwIeV36oqCgAFmJ2C1FpBPAqy2oHtLfz4BJp0RLmng8PnnyZNktQBcPGTJE3ZDDuQ5z586F5yV5ZqmchXA8Hn/qqacgwqqbRnI0n6ZpXq936tSplpok+5qTkyNyP27kDh06ILHcX4nQQqHQ9u3bMTbsdvsjjzyS2KfJSryf+LNnz+J9Gvwt1LZtW7rguB+evJYESIAESIAESIAESIAE6hqB8gnQ6so2Eok0atRIVkFY5oVCITVNIs3UvyamL1dMrDQ2ZMgQEaAdDsfAgQPLlUNi4nHjxongBVlh/PjxqVsBARqKKha9LVu2xCXqahxlqQtdNSw1GTlyJIw3/X7/448/DqNp+VUugYgwZ84cqS0CK1euRNFXr169c/IhIvEibcOGDa9evVoBARrLZpfLhd53OBw4BElW7ykCYvodCoUikchvv/3WoEEDXddddz9Tp04tU1OORqMWAVrX9TFjxlRMGRF6pmlCQIdbBk3TZs+eXfUSrVqfcoWl91NfFQwGIa+kTvbgfp06daqoWhiB27dvr9jr24kC9IIFC8BBrb9IyTt27JA7Aqc79urVCynHjBkj7l91Xa9fv34KHUcEU0iQ0pzc3NzXX38dPlJwyzdr1uyexo9SVUjnffr0EQEarhu++OILpAmHw/ISgNyq8Xj8woUL0i6IoQMGDJBWS/7pB9B2/A9JGr4p3nrrLWnsHRcBkGhhNZyIPf3iUFXDMCwCtK7rBw4cQAVkeFvm2xdffFGsv2HZOmPGDPFNlGLywcsZeBcEfXTq1KkmTZp4vV5sReTn56fYQ73j8mL69OmapmVlZYnEvHjxYhjgX7p0CVOiOGRv2LChZSMhHT4iQKv9W1BQYBiGRZRMxkctZenSpVCffT5fVlbWoUOHyhwkhmEkCtB79uwBeQt/Nf9k4XA4HAqFpk+fPmDAgPfee+/YsWPQo5Olf0DxEyZMUDEirArQuq4/9thj2BtWR47KVg2LsTMmE7k1cNvabLZHHnkET9Vkr4KpLZ0yZQoePSJDa5qGF4nUm93CPxKJrF69Wv706tChgyWBWkQlhs+dOwcf0LhZOnbsCCcwKp9KLI5ZkQAJkAAJkAAJkAAJkAAJ1DIC5ROgxdQrVhr7888/sQiXBZ7H43koi0y1S3JycsQGzel05uXl3adG+frrr6tih91uz8vLEzVKLVrCZQrQ8qtqrWlZZKoLOTimGDx4MPDiJLrx48cjH3kvWL3ENM2zZ89aOqVNmzbYFRg7dqz8BPepCxcuRG5qJsnCUn/TNPv37y8271gGv/322+rqPUVYlR1PnTr1+OOPo4E2m83n8xUUFKgFSThWGrMI0C6XKy8vT/xoS8ryBiwC9IIFC8qbw0NML52VZh2QPs3ElZjs5f+8LEoNunvnzp0YJOUtRRWgkdU777xj2TMoLi7GTPXdd9/h2DHYJjscjmbNmsHON1Yamzx5Ml6lh4Ndh8ORQi6EbBcOh+H3XJrj9/uhPeHdfLfbvXLlyjQbJX6lp0yZIgI01GQc0mjRlaS74/H4r7/+Kq6BYL8/bNgwNDzN0tVkX3/99QsvvODz+VatWlVcXAwR1jCMO6dHLl26VNQxu93esGFDuOtJ9FRjqa2af2I4mQDtdDrhFCiF/+uBAwfKKwsYA+Waf+SJcPLkyebNmyMH2K7CXUZibRFzZ4Pz3LlzKFrm0nbt2uHX4cOHS484HA6/33/P42rLLChRgL7jqX/fvn1QzNUxoIbVrLCLEIlEli5dinri/2bNmmGEWF52wSyaKEB/9913ZarValkpwoFAQM4k0DTt+eefP3PmTIr0D+KnsWPHil9mbAbjyaVq0Js2bcIEoj62VLZquH///na7Hc521PtCSlm8eDFyw25BskbhZtm1a5fF7cmdl5Zyc3NTn0MQj8fz8/PlWOP7OdA1WfXKjN/45UZIz5gwc3JyKECXCYqRJEACJEACJEACJEACJEACZRIotwAN27RoNHr+/HlZuiNQHXwCdu7cGZXRdd3tdo8fP75Mi9oyWZQZOWzYMBh3Y4Vpt9sHDx6cjgAtvlkh0YpzSYthlLq4VcN79+6Fv2Ys9vDSK873g7hmOUROlIIXXnhB7RePx3PkyBHVDhReONq3b4+uhDytFl1mWIXz6quvut1u5IPWvfrqq+rqPUXYNE0QWL9+vdgdw4NBCnN1wzAsArTb7cbCO3VfqNVWwyKWWQToxYsXVyxDNfMqC0tPpVmitDrN9PefDCV27NhRFFsMmD179mAAl7eIwsJCdXhrmjZy5EiLAI0Btnnz5jvncOLtAdzCTqfz0KFDkUgkfPcze/ZscbPrdDrdbneKM+jQkLNnz6rSp81mw3FkaJ2mabBGTJMzfECbprlq1SqIWfLahN/vP3bsGG7qQCBw5cqV33//XbKNx+MHDx602+0+nw/18Xq9//3vfysgQF+4cAFTnDgowPjHLRwOhzds2ICpDP97vV6REWX4SSD93kwmQLtcrp07d2KKk2yl4cj/tddeE/23AvMPlNx169bJQIJThQEDBlgGkqU5UK47duwoBu/wvfDbb78VFBSoB4f6fL6WLVuCZGFhoUzOlgzL/JooQGuatmbNGiRWmahhNSv4dB4+fDiO63Q6nXjlZfXq1ZLMci0soC1Wvdu3b0/xToBklSywfv16DCo4a9I0bdq0aakJJ8uqwvEjR47EmZDoawjiqvrcqVMn2cVUH1sqHzWMmwUtUgVoHCfYunXrSCQSDAbR45Zxq7YC+yt//vknnqR4FGIwezyetWvXApRatIRN08zLy9N13ev1OhyOyZMnqzlXelgeiLm5uXC9hUf/a6+9BnRSsRTtrfRaMUMSIAESIAESIAESIAESIIEaR6CCAnSsNPb1119jvYT/XS7Xv/71L1nLPSwQsGgTl5fwqHA/lRk0aJC8WA1T6BdeeCG1oHDs2DEsvJEeS19Z/Iv9nWotLut8LOE+//zzhg0bij4CpyLvv/++rN4TfcJKG8X+GqtEj8czffr0Rx55xOv1wt8xst2/fz8E6BQL3WQLy/z8fJxACLNBaHxiPZoIR9Xci4qK4vH4G2+8AS1ADMcaN2588uRJgSPNkSa/9tprFhHz+eefV5OlHxbbtH/++cfn88kxUHa7/aOPPko/H6ZMk0BmZqbad3dOmzx27Fia11qSBYNBGcYwHmzatKlIJPA0csdNzcyZM+X2wRjz+XzLly+H9Ax98+OPPxY1GaNx7dq1Yj2qDlqpw/79+yVbBETCxjsKO3fuxIXJ7h3JClMlfEBfu3ZN5gqcNappWr169SZPnjxr1qyePXvCjnv58uW4vLCw8NSpU6i8rusZGRlOp7Njx45FRUUwTBYgUhwcOMD7BO6yaDT6/vvvu91u8EFDPvvsM1GR4Fn+119/Ved5TdPgPkXmDSmiXIF4PI7Osrgg0HX9gw8+gJvpZAzRudJ39evX13VdzmEr1/yDSVLTtKZNm545cyaRm9oozLqrVq2SnTOM6mnTpsmbHGIEDbtauDFRM0kRLikpQcOffvppyzB76aWX0HdyuWEYGGlFRUWYyWE2axjGsWPHnn32WZjqQ6nPysp6+T8vy7WJgXg8jt0UVVRduXIlbof0XcqoOR8/fhzn8mFs67r++OOPyxswMszUSyo9PHToUAtJ+QpT6N9++00KTUeAnjZtmuSgzmler9ftdm/evFke5ZJtikA0Gu3UqRO2x6D+w6WM3W5///33VRXbci8MGDAAMrqmaatXry5zskpRbrl+khsqMzMT706BwNKlSylAl4skE5MACZAACZAACZAACZBAHSdQbgEaS3TDMD755BN1AeZwOFq0aPHQaT7yyCMQfyFP4H3Y+6mVRYDWNK1NmzZl6qRSSqw0lpGRIdIGVmuNGjUSiRYpVbEjGAwiz6+++qpXr15i9Yy3fe12+7x58/DCvroQVcPBYBBLX1im+3w+VEDX9datWyOM3DRNe/HFF+846FSXympWZYaldaZpfvvtt7IIh/8BTdNGjRplmqaI2tJGERogjW3YsKFJkyaw3oKy73K5fD7fvn37TNOEubpagWQCtM1ma926tVqr9MPiVBcGaDKMVUvD9HNjymQE0PUlJSVer1cg22w2p9P5+++/J7vqnvEdOnQQDRr62ooVK6ApFxcX7969Oycnx2az4TV52eHIz89HfWTY//DDD6K9IpCbmytqS5nV2LBhg4x8BHCrwoFM//79A4FAKBRK4T7Cki12oWKlMWw4YdaC4Iv870hRaKzT6ZwyZYpcfuPGDakJbJP9fv+uXbvkfpGUCMhtiK9Hjhzp0aOH1+sVGdfhcGRnZ+N0QYEQK41du3YN+wcikVtc91gKSv9rmQK0zWabOXMmzh21zAOS8zfffCM6HTbnHA7H6NGjyzv/YFZ0OBxer/fHH39MvFxKlMA///xz+fJlTFwypKE+wz0uOmXgwIEy2NR5XvJJFoDzk/Hjx0vnyl6muAVHF8NBiroNECuN/f3337NmzcrIyIBPc/E80717d8sAsFQAArRlM2Du3LkYCXLLWK5K/TUej8Nbt7x/oOv6iRMnKpZb6rKS/Yrze1WYEna73SLKY7ylI0AvXrwYOUjvI6Bp2tChQ8u134A6L1q0SJ7UmBvR43a7vU+fPmfPno3c/ah1M03z+eeflzv322+/Tf0HSTI4acajv/bv3+/xeFwul7g4P3r0KNqb7D5NM38mIwESIAESIAESIAESIAESqCMEyi1Ag8ud1SxeYJdlmN1ux/unDxFcJBLxeDzwjeh0Om0225o1a1IvvO9ZW1WAhjDUuHHjFBZhkBsGDRokC10JZGdnnzt3zjTNYDCoqhI4I27btm15eXk+nw+amrzQ7ff7oZ3JMk/qnBgD555dunRBoYAgFYBq4/P5Dh48KCoGbDAlq2QBKdQ0zb///lt0ZyyeITHk5+ejXeIaUq66fv368uXLW7duDYZiou5yubxe79atW5ESZNQ6iKBmsYDWdb1JkyYQDqSU8gauXLkC8U5EhPXr14v6Vt7cmN5CAMrFiRMndF2XicJms+m6fvbsWfUWsFyY+uusWbPwWr3X6xXVb8yYMW+++WabNm1w+6jSqqZpb7/9NhRq9RWNP//8U4RsDMt69erh1k42BmbNmqXeTdBkUaLNZjt8+DAuVAfwPecfaNA47FTuJgjokMWR/x0D0nXr1qlk2rVrh/tOqvTKK69gB0i8S6vpET5w4EBOTo7T6YSKimsdDkfLli2xKxAIBMRfEG7kFi1aoA646wcMGGDZZ0osJZ0Y+JK2iJ42m23EiBFy15eZz82bN6XJUn9d1+HhAV0sm0zIIdn843A4PB7Pli1bkCxNIa9bt24ynlEB2clwOBw+nw8joQJyJAbDypUr1Qb6737q1au3bds2DKc7XoBDoZD0QjQavXNy3ezZs7EdgmeHyJpt2rS5fv26JC4TqWmauDFVC+gxY8ZU+CaFpfPq1atlTwUz7QcffGA5BSFZfe4//o4J/7Rp0+QdBUEqMUeOHJHnoKrwWnxkq7fzqVOncNfj2SrDoH79+hcuXKhAnf/44w8MnoYNGyIgQ1rTtCZNmuCARLUO0Wi0UaNGuCU1TTt79uw9J5kKVAyXyHtaeXl58Dzjdru9Xq/P58P9m2yqrHCJvJAESIAESIAESIAESIAESKC2EqigAG2a5htvvKEuVu+8mv3000/fp8Pl+6RcXFwsBnGQVzZ+ufE+F0iDBg2SQ8awlvZ4PMXFxcmWfKFQqLi4+KuvvpLlrhrIzMzMy8vb+OXGH3744aefftq+ffuqVavGjh2blZUlVs8Oh0PCbrc7Pz9fsFiW7pZFqYgF77//PpxjiNtWl8sleQ4ZMkQE9FhpDA5D1azKDEsdEBg2bBh8DogdFjzSNm/efNKkSVu3bj1+/HhBQcGmTZs++uij3r17IxnqowLx+XxQn++4TYAEUFhYqFZApCiLAI1jvnCVpW7pf71w4YIoCJAgN23a9EBfZ06/brUgJQToPXv2QLIR1JqmXbx4sWKc4/H4gQMHMIQwpHVdhx8VjHmJhMzk8/nUO8iiMNarV08djZqmLVmyxJJGOsIwjJEjR1rSozi32z1x4kSkhDhoGcOSSZmBeDx+6NAhEXlFWhI92uv1du3aFYbVoqRPnDhRjCVtNhu8iDz33HO7d++WG1yKO3/+/Icffti9e3fciai2yPfPPffcH3/8Ieq8qt7GSmPt27fHHIirWrVqVQFn01ITBOD/2jAMiwCtaVr//v0tiS1fw+HwqFGj4DIC3QF3Cn6/v2XLllOmTEl//vF6vVCfZT6HDbKlRMvX999/H4MZOyt46KAmdrt97Nix8Xg8EAhgb89ybbKvYvQdjUYjkYg6zPC+CG6i7t27r1279sCBA8ePH9+9e/fnn38+Z86cDh06iHYJp+S43O12v/jii7dv35bWJSsdArTlQLxXXnklRfp7/hQMBo8dO4bDOTG7apr2+uuvywC+Zw73mcAwjAULFuCgUQtPTdPgOjnR9hmPIfX+VcN3GtWvXz/cmDKh2Wy2Tz/9VDyipFNteVgbhjF58mQZPBkZGWLzDufdP//8cyAQsNQBe8m46oH+0QW3M6Zpwp84fKpkZma2adMmnWYyDQmQAAmQAAmQAAmQAAmQAAkIgXIL0LCJM00zNzdXXYBpmtatWzfJ96EErl69KroAlut4J/1+KjNixAjRg7A+13X9/PnzsoAsM3PDMJ5++mlIQurSF2FIY1BeZGUOY0acaqXrOky503RJbNEXzp8/jzORkKfsEyDy/PnzUmdZ1kpMmoGCggJZM4tMVmZL0Vipg5rm3//+96+//horjaUQfURiHjlypGSCgNPphEW5tMLCIVlbpO9OnTql5qlp2rZt22TJnexyxqdJAHs/2IyxzBUpjvtLJ/NXXnkFMg0UQIulP9RYbOSMGzcuVhpLNP+EjfCIESMsGrTX6923b1+sNGbZuMJZnYlvNthsNr/f37RpU8uhoOUdk9Fo9J133sGtJDeUBHr16nXjxg3kKVsyFy5cwN0kJ4Ji0nO5XM2bN+/Zs+frr7/+yiuvdO3a9emnn1b5g49IloMGDfrjjz+wWwCDR8uLBaNHj8ar97jE4XDcvHkT1ZBmptNrahrIrIZhNGjQwHIPPvvss2rKxLBhGAcPHlRnEmyGORwOOV8uca9LTY9w48aNf/75Z7UhwjaxUFHnTdO8du0ahpwMPJjkw/T44sWLGDyW/cIy85RIzF3Cc8aMGTJ7Q+BWnxToaOEmTYOLXpjP2+32vLw8VU6VssoMZGZmwm20DJVnnnmmzJTpR16+fBkbHrquY/D069evygToaDT69ddf4y0Ht9uN5zieR02bNk1z51V6BIFwOHz16tW2bduCOTTilStXps8EKdVHVXFxMV5awj4x6gm/N8888wxuTDX/S5cuwbmK0+mEW201NzVlpYSDweD27du9Xi9cu6BDp02bdvv27UrJn5mQAAmQAAmQAAmQAAmQAAnUEQLlFqDBJR6PDxgwQNa9CPTo0aPK1pZldo+8Hitr9QMHDpSZMv3IGTNmiAwkpkm7du2y6FOSIZaC0Wh037598oI8hAkRRxKlZwtJm83Wrl27/fv3m6ZZAUNRwzDatGkjYpaqU8yaNUuqWuEABNy33npLLSKxCRbpGdWALKjr+ujRo69du3bPOsj6f/bs2dIQ6ZHdu3er+lGa6/AUAvSePXtSi1D3rDATCIFwOBwrjcHJqahauDfhBEZSph+I3v2cOnUKkiiUODFEFVtUWOyuWrUqVhq7efOmvEhuKQjezGW6QG4ZGRlHjx6VQYJLIJhOnDhRxp464Hfs2GEZhzJu0xyTSIb83W43cLnd7kaNGs2ZMweVseRZWFg4duxY0UBRH7UtiIEJqsULCmyZHQ7H2rVr4RQImYuRtQpq0aJFLpcLL+BD+dq3b59amTTbqOYJ9xSx0li7du3U+9rhcDRo0CBRdFOvxVNm6tSp6C/pCMsYk3g1IBLtyJEj5dxCS99ZysJXDCEZFXCsLyI+3OvbbLapU6dacgOoMvNMjBSqpmm2atVKOhdzKRqSOK9Kp0N6hnnsRx99BBNsi0OJxEIR89RTT8nAA8l69erhMZfsYZcsK8TjnEnIqbqu45acOHFixXJLXVayX0+cOGHpfTyUP/vsM7wlIMDTDKCgcDg8adKkbt265eXlVXgqU+t87dq1Vq1aSVV1Xff7/a1atTp16hSO7VUTY/cFvpife+65B/rACgQC0Wh04MCB4n8Dldy1a1fiaxZqJRkmARIgARIgARIgARIgARIgAQuByhSghw8fLmfcW4qpmq+yMJOF3G+//Xafy91169ZhNQ7hCYrDrl27RImwNA3x4XA4EoksX75c0zT4O1bVZ9ELpJ6WQH5+figUSlaEpcTEr7HSWF5ensVKzm63P/LII5X4um40Gu3Zs2f9+vXFUk8VgFRRSQ3DkGr9+vWodprv8huGsWHDBjUfEKt0AfrYsWOJPBlTMQLJBGibzQbFtmLZ4o7esWMHtC0IWxgbNputYcOGfr+/S5cuO3fuvOexctFo9OmnnxYZETtMmZmZr776qqVuuHG2bt2q3qo2m83j8cyZMweSaDINy5JVsq+43//5559t27YtvfvZtm3bjRs3pBWW/LE71bZtWxCAD18IxPCtoc4z6r2JJrz8n5dPnTqFlw9EDi5TSsb5Y6KBulyuGTNmpH/QYrL2wv/PoEGD1Ps6TQHaNM3i4uK+fftmZWWpzVR7p8ywx+Px+Xyff/45agXT+HTaAlNi8aqRl5cHZV/TNL/fD+m2efPmgUBA5jS1v5JBsMSrlxw9elQ1z5ctBBWXhDF0cUxc9+7d4d0YLvXvKUADwsCBA6WIShGgI5HI77//LptD0OgPHz6MJt/nc9nCrcyv2MZ47LHHxGGFz+fTdX3AgAHybFWBpxMGq0gkIk/SYDBY5l1TZpWSRUaj0VAoNGzYsKysLE3TMjMzcRRnmTl/9tlnstMm5yg+OJ6XL1/GrYTTNTRN69ChgwBM1iLGkwAJkAAJkAAJkAAJkAAJkICFQLkFaNUFh6x+Ic6+++67KXwpWAp+EF937dolCzMsmc6dO1cBC2K1bnv37oXACjejWJmnc4QaPMmuWbMGMlmZaoglUtf1l//z8pEjR27cuCGOICqw0otGo6tXr5ZFo3TTqlWrkFsyL7dqw1OExfQpFAqNGDFC1aClrGSBhQsXXrt2DRWIRqNwXIDjjFKUaBjG/v371TxtNtuDcMFx9uzZFNXgT+UiAPUk0QWHrutffPFFmca26ecfDoe///77Z599FuoSXgx3uVz//ve/P/74Y/VVjBTSTCAQ2PjlRrztrt6M48aNS6xJNBq9Iy/C8zIS35kN5s6di5Tw0VGmhpWYVYoY1VhbvU8tOUsOp0+f7tatG7wDiWdnaLIWZVY06Oeffx7qPKRtzJCqvwiUJUX88ccfXq9XLne73f369YtEIuhfcV4s6dMM4FHy9ttvq/e1pmn3dMERiUTQp6FQaOTIkeXSoBcsWHD16lXIiMFgUAireMusvwjQ0KDnzZuHJwJGAix8ly1bhmuhTt4zz8SC5JJAIBAOhw8fPty6dWsZbCooSxhPmY4dO65YsaK4uBh9Kg6OJdsyBU08tcePH489S+noirngUIuYN2+eiL9Q6tFk8E9sfqXHGIYhJyI0bty4V69en376qQx1FUuaYalhKBSCox6MRrXVkib9AEqHYo5nkIzMRFagij+6Ro8ejaLv8++cZFUtLCxctGgRRqBMLzNnzkyWnvEkQAIkQAIkQAIkQAIkQAIkkIxAuQVoyWjLli0Oh0Pe+W3WrFlxcbGsmiRZVQbWr1+PKjmdTrygWiluChs2bCjONDRNg6eRNBecwWDwl19+GTNmDA/WpcgAACAASURBVN5ghZWi8+4HC0gs7R577LHXXnvt8OHDlbWMXLduHXK+Y6EJCSA3Nzd9f6Apeg1LZWQFOXvTpk2dOnVCQSgU/4tjVk3TWrVqtWjRohs3bgQCAUhXkk/ie+KJpYM2fGrjeMn78Tkumn6iD+iioqJIJJK45k+sEmPSIWAYxs6dOzEe3Hc/CM+bNy+FLpxOzqZpFhYWmqa5efPm8ePHT5gwYcWKFUeOHLl161aZ+xmJN6zETJw4Ud0lys3NTf1W+/Hjx7/66qvVq1efOXNGbgSLnamqZ6XZHDWZ1E2NVMNq/sXFxZBxcVqd3Ik4pg/SPPTKMWPGHDp0SL1W6o9IcR+hlhUKhZ555hnJBz0oU2vFBGjp/U2bNkHxlDl28eLFaullhqUJd1xVbNq0qUOHDrIPAe/PMvnAPBzzz82bN4PB4D39eyQrEZuCmK82frkROYOGpml5eXki+KozrYAtM9t0IufNm4dNPuwo4PGBcuHNSdO0vn37yjl4ap4CKvWIKikp+e6779DFeGvnTv7i+0UmTDXnxLCMpfDdTygUwsl1uq7j+AE5qDPNDBOLqFjMH3/8UeYfJ6mZpFOW4E0ncTppJMMUdXvrrbdws7hcrkWLFqVImU6JiWnQj4g3DKNJkyZ2ux2zCv5oOXnypIzqSi89sT6MIQESIAESIAESIAESIAESqB0Eyi1Aw2oVOsXbb7+NZXCTJk1++OGHh05k1apVUB+wLHe73ZVikT1r1izoU7quZ2Vl/fTTT+VqKYidP39+w4YN48aN69u3b+vWrTt16tS/f//c3Nw5c+bs3btXbIrVo67KVUpi4hUrVqB3fD5fdnb2zZs3K0UWwcpTtAaUaxjGTz/9NHPmzDFjxuTk5DzzzDOdO3d+5ZVXJk6cuHDhwpMnT6IjxPQMV6l6TToL7zlz5sgxTY0aNTp69GisNFYByV7kD4sAret6IBAQ2/NEpIwpLwHojPBxAStR2I2OHj36/lV+MfMss1Yy2sv8VY2MRqO7du364IMPVqxYcebMGVQsTWFFboSHKECXlJREo9FLly4tWLCgW7du//73v7FJ43K5mjRpkpOTM2nSpC1btmBzRSRmy41sqb/KJxwOjxkzRtRJvGWyZcsWpKnY/RKPx2VyfvbZZ+WMuH79+sF8WBRqtSYSlukCyaLR6NGjR2fMmDF69OjevXs//fTTlvlHTJIlh/IGMFmpu2Vr166V5wKqDb9JMiSkkmmOpWRVMgwjHA7v2bNn6tSpvXr1eu7up1evXoMHD87Pz9+5c2dJSYlMrShUskqnDrdu3YI7lyeffBKqusPhePHFF9FBqTtCCsKTKxqNorHwkux2u0W4rF+//qVLl2T4qRfW3LDgrawmSIYpxszL/3kZArSu6zDorqzSkY88H+PxOJwOYf8D+1sDBw60vO1RuaUzNxIgARIgARIgARIgARIggdpKoNwCdFFREVjAjuzq1av79u2DfooYWb1UPbL58+erL/xmZmamv3hOVttYaay4uHjChAndunWbMGHC9evXK6B4wiEAKFne2FXXmcFgUESZZPVJJ14y2bNnz7BhwyZNmgS3pOriFuF0crOkUTNBX0ciESgvwWDQAvyODIHKGIaRaB2vZqWGLSXK1ztOY6dPn96pU6dRo0Zdv349Ho8n5imJUwRkiFoEaLfbLdaRFeaTotw6+BMwLly48I6xnhzF+fTTTx8/fhzH+lWYSZkdVN4tDZSOuyMajWKsqrtByaon41wdt8nCyTJJEa9OC2UmU8uCB2dLssLCQskEvoCRAE5v1MvLDKu5xUpj33zzjerQQ9f1nJwcpJFbRr3knuGSkhKIueFw+Nq1a0OHDs3JyYE3bXRi6ltb6hyJREpKSjAn48A0tWiZf1THJmqC9MNSIgJo9eHDh8eMGTNlyhS46rYIc+ol6ReUmBIDEhq6YIlEIn///bcklgEpMQikU4d4PI7mXLt2bdSoUX379p02bVo0Gk2Wp6UI9Ss6IhwO43hPuMaGNfq8efOwtSPTr3phDQ0L3sqqv2QoN29izm3atJHjN3fv3o1uqkBnJeacGNOtWzd5O8Rms7nd7l9++UV2EVDbxKsYQwIkQAIkQAIkQAIkQAIkQAKJBMotQKtZYNWKJXE4HMbi8wEthNRyk4WnTp2KM7hg+ZuVlZUsZQXiRdUVCSDNTBK112g0KotwkbORbXkzL7MO6AL0CNwUoBR1cVvhpaOaiaV0KEpIALvI1CqGmpUatmQrX8PhcDQalTO+JL68AYFvEaD9fr8s+1Gf8ubM9BYCwWCwqKgoVhr77LPPxo8fP2rUqPnz59+4ceP+zZ9RELpSOhQ6ozoO79mPUN/UfkfOEmNpETaTMPUFAgF13CYLJ+Zwz5gUpUv1pDjJTSbkcDgMO9xQKASPN8G7H5ipyoUpApInxKa//voLk6r6/4kTJ2A5qyZOM6w2ULoPGityUBMk5omaSzw0a8slZUbKJeUNWFiJk3FhjgwtyeRreYuzpBe3RSg38SGLY2/hlViFIxWwwFHzj5XG5Olmmib2mEWVVlPeMwytfP369V6vV3VR0q1bNxhHq3W7Z27VP4HgrayqSoYp+gv2yLgTf/31VwyGSvnLQVqBW/LHH3+EDbvf78/IyLDb7XhzxTLvyVUMkAAJkAAJkAAJkAAJkAAJkEAKAvclQJeZr6gJZf76QCPz8vJUC+innnoqUXB5oBWo5plX4uK/srKS9XZVopMhahGgGzRogGoEg0GpWAohoCrrzLLKRUC6755XJevfZPGWDKWgNNNbLn/oX9Ov/+uvvw4n7KJBv/POO+lYiz/0NlZiBQRXsjwlwUMcD1VZNNRPlBiNRi9evDhq1Cj1eAO32927d2/I9MmgMf6eBGTL4ebNm3L6pcPhKCoqwkaLmgMGIbaOLPFiop6iR/B8jMfjvXv3ttvtGRkZHo8HDuVxQKK6UaTmzzAJkAAJkAAJkAAJkAAJkAAJpCBQ+QJ0isIe9E9vvvkmztrCC6r/+te/KECrzGVdqkZWLFxZWYleU7FqVOyqZAI0BoxpmhY3BRUrhVc9RAJVNq6koKpU/SoRbPr137FjB3x5iwCtadqePXui0Shes6jEWlXbrARXshpKgho6HpK1K0V8OBwOBAIbNmx47bXXID3b7Xav12uz2ex2+8v/efnWrVt3vCeJe+gUWfGnZAREgP7ll1/kuM569eolpoceLc84SSCOesSLWuohumXLFvjvltNHR48eLbkxQAIkQAIkQAIkQAIkQAIkQALlJVCrBOhZs2bhtV84K6xfvz4F6PIOiLqQXhbnFgvo9u3b4w13y4FsEJXqAhm2kQSSEYhEIl27dlXVZ03TOnbsWLnv/icrnfHVk0A4HO7Vq5emaW63G8Ko3W6H1+BWrVpt2rQpevcjHkuqZytqSq3i8fjatWvlHmzevHkgEIiVxsr0NhOJRP7555/Lly///PPP+/bt27p16+effz5lypT27ds3a9Zs1qxZ8hxMbH5JSUnHjh01TfN4PDC4btGiBZRrkcITr2IMCZAACZAACZAACZAACZAACaQgUKsE6MWLF2MZrOu63+93uVyW03LKNPlJsQxLAY4/1VwC0uMWAbpr166maUJQUy0ZKUDX3L5mzSuFAA4a3b17t4hfuq5Dahw6dGilFMFMaiKBAwcOYEjA3tnn8z377LOTJ08+evQolMpIJGIYRjgcpnB5//1758k1e/ZsAf7000/jhIlr164dPXp01apVM2bMGDRo0AsvvNCgQQO/3w/jZcs9q2ka4i9duqT+RaSGp0+f7vF46tWr57z70TRt79698Cx//61gDiRAAiRAAiRAAiRAAiRAAnWTQK0SoFeuXIm1Fmx27Ha7xUUpVmtYEmO5FQqFYO5aN7u/7rQ6cveD4+nQasMwLl68aFM+LVq0EHNOis51Z2ywpekTgJ99u93ucrlg6OpwOPLz8w3DSOFVNv38mbJmESguLs7KyvJ6vc8888ySJUsOHjyIByvOwFT/V+femtXG6lBbOay4e/fuNpsNTsYg+otHDhGaRaGGRzK73Y6nnCTAhbdv35amqV50Nm/eLClxp0+cOFFSMkACJEACJEACJEACJEACJEACFSNQqwTojz/+WEx+sEj7888/hQskkkgkEo1GuRgWLLUyEA6H8dK3atUFc/hoNPrXX3+dO3fu8OHDn3zyiaI/2/x+v9CgAC0oGCABIRAIBLp06SJGlA6Ho379+g6HY/To0eLkV317QC5koLYSwAslkUgkHA5jDGAAqOqzxalRbUXx4NolO6M+n099ZkEp9nq9uq47HA68l4BXE+RvIf3uBzK0aNO5ubkiaku1w+Hw+fPnH3nkEXjxxm3eoUMHScAACZAACZAACZAACZAACZAACVSYQK0SoJcuXep0OmGXh4XW4cOHQ6GQqkIGg8HDhw8vWLBg8ODBEydOvH37Nl8NrvDoqYYXBoPBK1eujBgxomXLlp07d+7Tp8+QIUPGjBmTm5vbvXv3pk2bwnbMbrdjfW5ZzEOkrobtYpVIoDoQiJXG9u7dq+u6vJuP+TYzM/P111+HETQF6OrQU1VTB3FnZJom3D0jRo7CExmao+L+e+T33393uVzqM8vpdOLgR7FZxgPO4/E0bNiwRYsW7dq169OnT3Z2drt27Vq0aOF2u9u1azd+/PgbN24k1idWGhs4cKBk1bBhQ03Ttm/fzpcbElkxhgRIgARIgARIgARIgARIoLwEapUAPXXqVLvdnpmZidPbvXc/gwYNGjNmzODBg3v27Pnss89aVmvNmzeHPM3lcXmHTvVMHw6H27VrB/t3WUhrmibWYfITRoK6mHe5XNevX6+e7WKtSKD6EFi+fDnuIxz66nA44PVoyJAhMpFyL6f69NcDrQkU55KSklAopO7mivSMgAwMdT/4gVasNmUOyP/8848438CTC9s/drs9Ozt7woQJy5Yt27t374ULF9S2B4NBi4IsPaImi0QiCxYsEIcebrfb6XTOmDEDfszUnlWvYpgESIAESIAESIAESIAESIAE0iRQqwTokSNHiuYo3g8tAVVwxIur33//Pc6RV1fIEk6TI5NVEwLffvstth8s/a5+xSvJ+B/eMPGr2+3+9ddf0zm4spo0ltUggYdFID8/HzeaKFaapnm93iFDhjysKrHcqicgD0oJoA7y1RKo+hrWmhKh748cOdLr9WJLtWnTpuPHj9+yZcvt27cjkQiszgG8Aq3euXOn/PmkaZrH4+ncubPafRXIk5eQAAmQAAlUmEA8Ho+VxoqLi3FeEVwLyknplhOMkNg0TTghVI0AsMgtsxqGYcRKY/LPkkZ9pUl9HFRx2FKrxK84IxfNDIfD2HaVN7HuuYEajUZDoRDABoNBS3q1sYlFM4YESIAESKC8BGqVAD1gwADVvlXVHCWsCtAOh8Pv9+/cuTMajarmWnzYlHcYVZ/0S5cuRV9DF5N+VwOqAK3GOxyObdu2wUU4x0D16VPWpFoRKCkpwfImLy/P6/VmZGTAKhPqldfrnTt3LlY+sgqqVvVnZSqRgDpPphOuxKLrVFZYD4dCoXA4/N13323btu348eMWArLYtsSn+RX+qXAX4++oXbt2qX2aZj5MRgIkQAIkcD8EcGSRnKshWUFijsfj0Fux7yi/mqYJvRgaNORUHDB769atffv2FSifffv2LV26dPr06UuWLJmrfLorn+zs7D59+tjtdr/fr66bHlZYqdr/L9i3b9958+bNnz9/5syZCxcuPHr0aOjuB2QMw5C/RePxuByoAL9hSIlj6oWk+s6QxUBN0jBAAiRAAiRQYQK1SoAWDxsOh0MVFtWwKkBrmuZyuU6ePInHtuWgJCy9KkyWFz4UAu+9956maU6n0+Vyqf2uhtU/ntR4TdOOHTuGanPh/VC6j4XWCAIlJSWmaZaUlLzwwgviD1q8G/l8PpifqH/E14h2sZLlJaDOk+mEy5s/0wsBKAuqnxO5vwzDwOnKkri8ga1bt+LPIdlMGjRokOVloPLmyfQkQAIkQAL3SQBidKw0JvbOhmEcOXKkoKBg9+7dG7/cuHjx4vy7n759+3bq1Klfv369e/fu27dvdnb2k08+abPZXHc/6gsuMs8jEusgsd+ypJRHQ2J8tYqBMYTaNI/H8+ijjz7//PMvvfRSv379RowYMXPmzGXLln333XdHjhy5du2aehKvOAfDaRZ4/Im7Kvnz5j57k5eTAAmQAAmYplmrBOjHH38cJ8t5PB5VWFTDFgF63rx5pmkWFxfL010eMwhwlNQsAuvXr0d3Z2Vlqf2uhpMJ0C+++KJpmpFIhDveNavTWdsqIyCGJNi0Kyws7Nq1q6ZpPp/P6XTKAubgwYOWdxirrIYsqCoJWB6X9/xalXWrTWXB5A0tehB/mXz00UdYt+PhqGna+fPnKUDXpiHEtpAACdQgAmfOnPn555937969devWuXPnvvXWWy//5+Xs7OycnJyePXs6HA4oy06nEyfc4KVPxEMXdrlc9evXh3zs9Xrdbre6DhLt2OVySTgxgD/qVF+FaiZVHFbX72pY0zQ5VR5hlQNSqk1DjJxFn5mZ2bp1665duw4cOHDBggUzZszYsWPH3r17T58+HQwGLX/V1KAhxKqSAAmQQLUlUKsEaLwr5HA44JzU7/fDlaHIIpqmNW3atHPnzuPGjVu4cOFff/0FPQVWRbSArrbDtFwV+/nnn+fOnfvyf14eM2bM9OnTV61atXnz5h9//PH06dM3b968ceOGaZrBYPDatWtnzpzZunXrkrufrVu3ihsWCtDlAs7EdZNAPB6PRqPFxcWjRo3CaYR4+WDAgAHxeBx/uNdNMmw1CdQsArHS2IABA/DakMvl+uCDD0zTDAQCNasVrC0JkAAJVDoBrBNxHCsyj8fjqvGsasCkLiTVmmBLPhwOw9vylStXfvjhh7Vr1945TmPRokWTJ0/u3bt3586doZP6/X51R18VT1OHVVkW6nBiTGK85Ol2uyUshs/qChq/Qo9WTXkeXBgHHuC4XbVu2DGVF+/E8FltrxpWr1XjLRq6/ARFGwf8du/efdCgQe+88878+fMLCgoOHDhw69YtbNDKe0jS17HSmBhqiEcUcaUtyRggARIggbpMoFYJ0N9884337keeVU2bNsWW5sYvN548ebKkpARvqsqrTLDjk1dvLFudEl+Xh0jNans0GoXyFQqF0JsiK+NFNgyAaDQaDocRDt/9YEhIYnUk1CwCrC0JVA0BrMFwQs7hw4c/ufs5fPgw/tSmBXTV9AJLIYFKIRAMBn/44Yf333+/oKAAfxepvjIrpQhmQgIkQAI1jkCylSDiLcK0tO7w4cO7du3asGHDwoULp0yZMnny5BdeeKFr166yWw8ZFzqvz+fzeDypjZFVCTVZWPRTsVlOjEkhQEPGlUtQiiryJiv3wcV7PJ5EBbzM4sRYW+qvBtRL1PhkYbfbjZ4SXJIDnHw+9thj/fv3f++999599929e/eePXsWXY/nJtaYcDONeHWcqBKEDBgGSIAESKDuEKhVAnQgENi2bdtrr7326quv4iACyzY1TumJlcbwbAiFQpZDHlTZEeG6MxRqR0vFKkFcd1nalaxbcRJ04gBI9qenJVt+JYG6SQCzqNp2OUNcrD/UXxkmARKoEQS4SK4R3cRKkgAJPCACqf/+x6+nT5/e+OXGJUuWjB49um/fvr169XI4HG63W9Rkp9Pp9XpFd4aPCLvdDsFUkkHfVNVem82m67qkFAE0RUCVU0U5lUjV2lciVXlXraSlFLkWF1p+fdBfdV1X61lmcZUrQKOIRCDi8ARvWiMZjN5QgW7dug0dOnThwoXff//9kSNHZE0K5eEBDVRmSwIkQAI1i0CtEqBx8q9pmjLj4yVxePVNoYaUKTsmUyprVgfXtdrK34vyYlQkEoFGZpGkcXCTnD8ptvCJg6GuMWR7SSAdAjLNqlMu3jzA3ZROJkxDAiTw0AngrXBUA/v0pmnCFdVDrxsrQAIkQAIPkUA0Gj127FhBQcGGDRsWLVo0cuRIOGKGzzFVUFbFWSi2uq47HA7RMeHYwaKfiqYpfiRUjxZVIEDD84bD4Wjfvn0P5dO9e/eBAwdOmjRp3rx57979zJ07d86cObNnz541a9bMKvlMmTJl4cKFkyZN6tmzJ6rWvXv3bt26de3aNTs7u8vdD3hWrgANfdnj8cCrp7xXrfady+Xyer12u93lcqmW2m63G5VBd9evX79r167jxo1bvHjxDz/8UFhY+BAHM4smARIggepAoLYJ0NWBKetQcwmI+lxzm8CakwAJkAAJkMB9EuAe/H0C5OUkQAJVSQBeDuRQn3A4DEsUOAQTt2AprJFM07x06dLRo0fXrVs3fvz4Hj164JhlaM1iBYwA5GZIjaouKWFJoKaBGG2320XTRG5yFX6Csik+MVwul81mw0GCjrsfl8vldDrFYhpSLP7v3bt3hw4d+vTpM3XqVJyq9+OPP+7cuXOf8rly5YooocmmelkQ1aDAXOUzZ86cvLy8Xr16ZWdnS1/g7EGYlkuHqh2kWlvbbDaxdMbBhs67H8Fus9mcTqfFd7aUJY5Q1C6Gov3yf16eOHHi2rVr9+/fH41G4bijpKREDKURYxhGOByG+VRV3kosiwRIgAQeKAEK0A8ULzOvYQTkz6waVm9WlwRIgARIgARIgARIgATqMAGIzpaD4PAVB6viRclIJHL16tUvvvhizpw5CxYs6NSpEzRfGLQ6nU4YJsthdPD8a5GeVakxdRj6MkRM0ZpFuNR1XcLwvCFG05CeNU3r0qVL+/btu3XrtmPHjj179uzdu/fGjRuFhYWhUAjukizrF9HZobzL66HpDw3JsAYFLK0TCGr8yZMnf/zxxy+++GL58uWzZs164403BgwY0LlzZ7vdLr5TZHsAerRqh66q1ehKS0yZI0E6Xd17wAaDw+Fo3Lhxdnb2hx9+eODAAdQ5Ho9j0OJNbnQfOkJtC8MkQAIkUBMJUICuib3GOpMACZAACZAACZAACZAACZAACfyf90Woz4liayAQ2Lt377Zt26ZNm9atW7devXrh3D+RBSE4er1eiZEADI3xf5naYjqRkpumaXASLRKnpmn16tXr0qXLuHHjpkyZ8t57761YseLo0aM7d+785ZdfIB9Ho1HDMIqLi8UwFvGGYYRCoaKiIrX7AQExombiq0jJavpkYUlcUwI4yyf6v4+0Sx0P0HNFmIa9PFLCrVwgEDh06NC+ffuWLl06ffr0JUuWdO7cuVGjRrBAV/sxWbjM8QDLazGdTrzW4/F4vd7MzExN05o0adKlS5dVq1YVFBQUFhai06U5DJAACZBATSdAAbqm9yDrTwIkQAIkQAIkQAIkQAIkQAJ1lICY+h44cOCHH36YNm3aSy+91K9fP6h+ov2JI2aJgVMLccHs8Xgkjdfr9fl8UI3LFBbTjHQ4HNnZ2Z06dZo4ceKMGTO2bNlSUFCwbdu2P/74IxgMirkrzs+IRqOIlI6EBBmJRGDEHY1GY6UxnG8EdRXaq3jzV4+QRQL4J5EM0wnUFN1ZrafaLlWXhxcL9X9cJYcDiUgNrV/ykXNNTNMsKio6ePDge++99+KLL/bp06d58+b16tVLlJKTDQl4lEZ6GXvq5djkwM4EbPA1TcvMzOzdu3d+fv4333xTUlIiFUszIO1KMz2TkQAJkEAVEKAAXQWQWQQJkAAJkAAJkAAJkAAJkAAJkEDZBESKTSacxUpjEA3hOffmzZvHjh1bu3btnDlzevTo0bx5c7j3hQioqnv3DEN0drvdqhdgeH9GJJxywBuD3W53Op24xOVyaZrmdrubNWvWqVOnV199dfr06atWrdq/f39BQcHPP/+c2FRV/RRVVBVS1bAqkiIeGaaTRi1avVaNZzgFAUBDF0Df/5+BddQ0zZs3bx4/fnzfvn1ff/31+++/n5eX161bt8SRBmfQOFtSvHmI0xWkh4m06s1DFbL9fr+maV6vNzs7Oy8vb+3atVevXpUDwCORCE4PDt39yL0Dc+8UreNPJEACJPBQCFCAfijYWSgJkAAJkAAJkAAJkAAJkAAJkMD/EYB2Fg6HIfaJlAbL31hp7Pfff//mm2/mzZvXo0ePBg0aeDwet9stLptF3UsUAVPHwDuzxUYVtqhirOr1esU18wt3P2PHjt28efOBAwdu3Lih9h/UQPFDLT+JZCyisxqQXy0BCtACsFoFZHCiVuh0mOFfv359165dH3300dy5c0eMGNGhQ4cGDRqI0AyVWcYV4kVuTj1Qcfgk0jz++OOTJk365ptv4vF4SUmJWM2LgxEMpGoFjZUhARIgAdM0KUBzGJAACZAACZAACZAACZAACZAACTxMApDwTNMsLi7+/fffv/jii/nz5/ft27dx48awR4avDIvWXAGTZ4vSpzpllp8effTRYcOGLV68eNGiRfv37//9999v3boFOtFoNBwOwwtzMi+9gUBAvDCLrKyKzmpYElgCFKAf5nBMXra4nIZVviSMRCLRaBSdiL7DT9euXTt48OCqVavy8/OfeuopTdPg7MUykmXsqQGbzaaeYOm8+9F13efz4fKuXbvOmzfvu+++KywsNE3T4khE6sYACZAACVQHAhSgq0MvsA4kQAIkQAIkQAIkQAIkQAIkUEcJHDt2bM6cOePGjXv00UdVAU4Nw1mB0+mE7wv1pwqH3W53jx49srOz8/Pzv/vuu6NHj/7111+iHUtA7RVV41N9LqtpcK5dmYKyKj0nSszqJYm/ooh00qiVQXo1huEKE1CVZbHcV3NL7B3118LCwnA4/NNPP23fvj0/P3/w4MFPPfWUx+O55wCGkb7T6YQZNfx44CtuB13X27Vrt2zZssOHD6slMkwCJEAC1YcABejq0xesCQmQAAmQAAmQAAmQAAmQAAnUKgLxeDxWGoPjAki6Z8+ePXDgwNy5282b5gAAIABJREFUc19//fUuXbr4/X6cw5Yow4mDAvv/PkgjPjGgvsGtgcPh8Hq9uq4nKtTQ+Nq1a/fWW2/Nnz9/06ZNly5dklo9ONyqHHk/4WQ1VPNMlobxlUvA4oKjzMzRL2X+VGbkmTNn5s2bN2zYsL59+9psNl3X4V5G9TmeeHf8756ww800tGmbzda+ffu33nrr22+/Fc/p4jY6GAyKixix1y6zSowkARIggUonQAG60pEyQxIgARIgARIgARIgARIgARKoiwTgEhdCM9pfUlJy5cqVb7/9dsGCBbm5ufXr1/f7/TjZD1qbKGvqUWyIFAFaviZaQDudTq/Xq2kazgaEGF2/fv0+ffqMHTt25cqV33///cGDByORSKw0Fo3+3yFypmmqNYQpK4TF8kqHyC31/6pMXLFwsvzV3JKlYXzVE6jAKAqHw7h3iouLDx06NH/+/MGDB4sLaU3T8AaA5ahMuS/wq9xKbrfb4XA4nc7u3bsvXbr0woULwWBQvNwACDzJwIpfBlLVs2KJJEACdYcABei609dsKQmQAAmQAAmQAAmQAAmQAAlUPgGYOYvC9csvv2zZsmXWrFnDhw+HLgzXt+oJbA6HQ74mSs+irKXw8gwxzu129+7du0+fPu+9997+/fuPHj2qumY2DANemxGpWoCCAlz6iq1oBaTDNGmKxleBQLIi1KySpWF81RMo7ygqKSkxTRNepFHbUChUVFRkmmZhYeH27dsnTZr0zDPPZGVlicRsCeA20XUdzjpgHI008NTxr3/9a/To0cePH7fQUIdQOsbdlsv5lQRIgATSJ0ABOn1WTEkCJEACJEACJEACJEACJEACJFAGgX379i1btqxfv37NmjUT+RhHpcHeWZXMPB6PzWbLzMxUIxPDYgENhVrX9ccff7xjx44jRoxYtmzZ/v37T548aZomhO9oNCoKuKV+8DYQCoXi8bjqgiBWGpN/qs9ly+WV8tWi9JXra7IKqJkkS8P4qieAfilvubdu3RILfbnWYqp/8uTJpUuX9u7du3nz5on3i8TgnQDVs43b7Xa5XA6Ho2nTpqNGjTp06FBxcbE65itWZ6knAyRAAiRwTwIUoO+JiAlIgARIgARIgARIgARIgARIoE4QUGXccDgcDAbhoSJR5N2xY8fcuXNzcnJwJBrEr2S2zPAhALcAqhsBOU4t8XK73e7z+Vq3bj1kyJBp06bt3bv34sWLZZ78lqxjRJ+F0JYot0F9ToxPliHjSaCaEIjH48eOHVu9enXPnj0hLuPWU/+Xm068RWNDSNM0m82WlZU1ZMiQvXv3wvC5qKgoHA4n28KpJq1mNUiABGo0AQrQNbr7WHkSIAESIAESIAESIAESIAESqHwCYowZDAbhDeDkyZNfffXV5MmTmzVrhvf6oWeJnbIYYJYZgMdnkcDUNDabDaeutW3b9tVXX3333XcPHTpUUlICzxjStvIaad5TgE4mTEuJDJBA9SQA1Th69xMIBAoKCmbPnt21a1f1tkLY5/OVKUC73W64x2nevPnIkSP3798Pa2uxuYZ3GvlaPTmwViRAAjWIAAXoGtRZrCoJkAAJkAAJkAAJkAAJkAAJPCgCqtgUK4399ddf+/fvX7169aBBgxo0aKBaLlt0rhSGz2pKm81mt9thB+1wODRNa9So0VtvvbVy5cr9+/errVK1ZhzOVgEHtSJAlzeg1oRhEqiGBEKhEN4GiEajctvGSmP//PPPF198MWHChNatW2NTx+12qwK0rusulwvSs/jogDOcJ598ctKkScePH8feT7neNqiGiFglEiCB6kaAAnR16xHWhwRIgARIgARIgARIgARIgAQeDoGLFy+uWbMmLy/viSeeEB/NUI01TYNqDE3Z7XarBwmqQnOycJMmTTp16jRmzJj33nvvyJEjpmlCOxM1TaQ0HB54nwjKqztL+vssl5eTwIMmAO8xGLEWvxny9dSpU7Nmzerdu7cqQDscDr/f73Q6cZO6XC5N01wuF04E9Xq9drv9mWeeWbBgwfXr1x90K5g/CZBAnSJAAbpOdTcbSwIkQAIkQAIkQAIkQAIkQAL/p/xGo9FIJGKa5m+//bZ48eKhQ4e2aNHC7/cnysfiZEOULDF5hm6FS/CrenmjRo169+49efLk5cuX//nnnw+LuyjLFjPqZPEPq54slwQeBIGioqIdO3YMHjy4cePGIj1rmgYP7NhGkjsarnI0Tatfv37//v137twZCARQK8MwIpGI3DUPoqrMkwRIoBYToABdizuXTSMBEiABEiABEiABEiABEiCB/48A/LqeP39+69atb7zxRpcuXRo0aOD3+1UdWVWQERYBWn4SZxoej0fXdVzudDqfeOKJvn37Tp8+fdOmTTdv3jRNU3xJ/3+VqPKQSGYUoKucPQusLgSw5/TVV18NGTIE5xPK7ex2u3GPI0bebIBa3bRp03Hjxp07dw4tgQZdXVrFepAACdQcAhSga05fsaYkQAIkQAIkQAIkQAIkQAIkUCECZ86cWbNmTZ8+fTIyMjRNkyMBRYRKERABGjbOYizp9Xo1TevSpct///vf7du3nzhxoqSkBG404LgZNa0OGnSFmPEiEqjxBJK5UN++ffvQoUMfeeQR9bUGubVFiYaDDk3TfD5fz549N2/efO3aNUCxbOfUeFJsAAmQwAMmQAH6AQNm9iRAAiRAAiRAAiRAAiRAAiTwMAgcOXLk448/Hjx48JNPPqnqy3a7Xdd1p9Ppdrs9Ho/6Vr5IzKoUJQI0Itu0aTNhwoRPP/309OnT8Xgcfjxg7GzRmuPxOPw7G4aBwMPAwDJJoO4SiMfj0WhUHENHIpFwOGyaZklJCaDs3r174MCBDRo0sNvtqh00pgjMGx6PB4GMjIxGjRotXboUHnWoQdfdgcWWk0D5CVCALj8zXkECJEACJEACJEACJEACJEACD4NArDQmJ/Wp5Uej0WAwWFJSsm3btjlz5nTt2rVevXoW4RiGzxKpas2QpG02m3rMIKyknU6n3+/v3LnzzJkzt27datz9wKmFWoHU4fKmT50bfyUBEkiTgGjEqiMa3MWW/7dt2zZ8+HCZAXw+n7o1Ba8dYi7tdruHDRt2/Phx0zShbmPzSf0/zRoyGQmQQB0hQAG6jnQ0m0kCJEACJEACJEACJEACJFCzCah+LaArhcPh69ev7927d/78+R07doSVot1ud9z9iEmjmDOL+gwnzhbXz7qua5oG1emJJ54YNGjQRx999NNPPwk1VMAwjPIKyuVNLyUyQAIkUCkEUgvQkUgkGAzGSmPFxcWrV6/u0qULJhNMFE6nE67eRYDWNE3X9czMzJycnBUrVvz111+RSCQajcr2mAjflVJ5ZkICJFALCFCArgWdyCaQAAmQAAmQAAmQAAmQAAnUfgKwNDQM4+LFi4cOHXr99dfbt28vOpHD4XA6nRZNWRRnSSYx0JIQj/979uw5a9asbdu2/fPPPyrNUCgUiURgfK3KWGqa1GEK0Kn58FcSeNAE1DvXYvtsGIZ45EA1DMP47bffFixYAD/vmqZ5PB5Rn7GzhZ0qTDhZWVnvvffehQsXcLm45XnQjWL+JEACNYgABega1FmsKgmQAAmQAAmQAAmQAAmQQM0mAPPhirVh375906ZNa9u2rcvlggUibJZdLpfoznCmkb4FdMeOHSdMmHDgwAE5PFDqZhhGNBpVtSRVwyqXhSMFaKHKAAk8FALqzZsoQOPlhnA4rN6q0bufjV9ufOmll9TjCmW2sdlsfr9f0zSHw6Hrer169XJzcy9fvgw30w+lmSyUBEig2hKgAF1tu4YVIwESIAESIAESIAESIAESqG0EIpGIvKWutk117hyJRCDvXrx48YsvvsjLy2vYsKHL5RLjZXGpActlsVLUNA1itChEYhYNc0W3252dnT1u3Lhdu3adOnWqpKRElaVU7UmtmxpOJ42anmESIIHqQyDxfkcMJGn1V9RZjVm2bFmLFi3ESbRMRzCIttvtsjGWm5t78eJFmejUTazqg4I1IQESqGICFKCrGDiLIwESIAESIAESIAESIAESqKMEYGYotsOGYYjWDCKhUKioqGjLli0TJkx47LHHbDaby+WCmbPFh4bqOgMWiE6n02azyblhcNuKnxo3bjxt2rTvv/8eTjxU+iI/qZEpwkifIgF/IgESqLYEVEFZDScToC0NMQyjoKBgxIgRPp9PVaIdDge8RWualpGR4Xa7HQ7HiBEjDh8+jGMJLfnwKwmQQB0kQAG6DnY6m0wCJEACJEACJEACJEACJPAwCcTj8VhpDHJwrDRWVFS0devW/Pz8p556yqIsw9WG8+5H13WxOkxMJjGwle7Ro8eUKVO2bNnyxx9/qKcXotkoOhAIiJXiw8TBskmABKqEgCo6q+F0BGjZOYvH47dv316yZMmTTz6Jacdms4keLROR1+vNyMjo0aPHjz/+KI2TTCSGARIggTpCgAJ0HeloNpMESIAESIAESIAESIAESKC6EIiVxkKh0Lp16/r375+ZmenxeFSvGm63W76KMw1N00R9ll9F/dE0LTMzs2fPnjNnzty1a5dpmrdv30ZrqfhUl15nPUjgYRNQRWc1nL4AHbr7KS4uNk0zEol8+umnLVu2xOwEDdoyO7ndbk3Thg4devDgwaKioocNgOWTAAk8NAIUoB8aehZMAiRAAiRAAiRAAiRAAiRQywhA04mVxqLRaKw0hq84yg8xn3/++X//+9+MjAwxGIQHVTEb1DRN9ekMNUfXdUmvaZrdbnc6nXa7PSsrq3v37nPnzr18+bJpmhafzrWMLZtDAiTwgAioYnSZRSABdGrDMPACh7zGsW/fvl69elnmLsxpcA1kv/vJyck5efJkKBQKBoPIBGUhHxRRZumMJAESqAUEKEDXgk5kE0iABEiABEiABEiABEiABB4yAegpqkcLMT3+6aefFi9e/Pzzz6sqM2wG7Xa76uJZEuDwQKjP8Obs8XggTDdq1CgnJ2fjlxuPHTsWDofhSBrWiOFw+J5C0kPGxOJJgASqH4F7zhsWAVqUaMx4mOvOnz8/YsSIJk2ayJwmrqL9fj9e4NA0bfTo0RcuXAiFQrhWVOx71qH6YWONSIAEykGAAnQ5YDEpCZAACZAACZAACZAACZAACSQjYBhGNBoNBoPFxcVbt26dNWtW586d/X6/ruuqJw1N05xOp8/nE5lGdOfEgBg+d+3adfXq1SdPnoyVxsLhMNw3x+NxnPEFKccwDIo4yXqH8SRAAskI3HPeUBNYwpLn7du34/H4jRs3ZsyY0bBhQ8xmmMEwAcrbHk6nc/jw4efPnzdNMx6PwyZazVbyZIAESKDWEKAAXWu6kg0hARIgARIgARIgARIgARJ4mAQ2frlx+vTpnTt3zsjISJSS04+B4TN8Oi9evPiff/6JRCLSMBGdo9EoDA/h8QMJKOIIKAZIgATSJHDPeUNNYAnHSmPqmx/YGwuHwzNmzMjMzHS73VCfsd/mcDhcLpfdbne73Xe8c8ydO/fvv/82TTMUCqnZplltJiMBEqhBBChA16DOYlVJgARIgARIgARIgARIgASqjoBhGOFwGDZ6aqniW8M0zdOnT3/yySc5OTnyjrnlDC74RRVDZtXq2eVy6Xc/DodDrurRo8fy5cuPHDmilsgwCZAACTx0AqpGLOEUtQqHwytXrmzatCk8DmETzuVyaZomM+ETTzyxbNkynGqYIiv+RAIkUNMJUICu6T3I+pMACZAACZAACZAACZAACTxAAmJoLGUcP3585cqVPXr0cLlcjv99dF2Hk1ORksXkGSqzfNU0DRd5PB4IMW3btp08efLGLzeK2B2Px+FlFSqPFM0ACZAACTwsAiI6q4EUlQkGg3BPv2TJkvr160OGxgGqmqa53W4cqer3+5977rmCggJkpb7wkSJz/kQCJFCzCFCArln9xdqSAAmQAAmQAAmQAAmQAAlUEYFoNBoKhUzTNAzjwoUL69at69+/f1ZWliolS1jU50QBGml0XXc4HPjfbre/8sorS5Ys+fXXX9GYkpISBODT2TTNWGksEAhUUVNZDAmQAAk8MAKYytatW5eRkYEZUiygbTYbNuQ0TXv11VdlJnxgdWHGJEACD4cABeiHw52lkgAJkAAJkAAJkAAJkAAJVCWBCpgSX7p0afny5dOnT2/btq0IzakDkKHLTONwOLxeb35+/g8//GCaZnFxserKAyhEfYYpdAXqXJVIWRYJkAAJpCAQiUTg3Bk7eaZp3rx5891334UXDqfTaZkq7Xa7z+dbs2ZN4tyYohT+RAIkUCMIUICuEd3ESpIACZAACZAACZAACZAACdwXAYi5hmFYpA3Lu+S3b9/+9ttvR4wY0bJly3saNVvUE3y1WED/61//ysvL27Bhw61bt+BR+r6awYtJgARIoIYTOHv27DvvvOP3+zVNgxjt9XrV6TQ7O/vMmTN4EaSGt5XVJwES+H8JUIDmUCABEiABEiABEiABEiABEqhbBFQN2jCMYDC4Z8+esWPHtmnTRjVhrpgA7fF4WrRoMWrUqE8++eTvv/+uW2TZWhIgARJISSAcDuNVjz///DM3N9dutyd6yYcYPWHChFhpLFYaU2fslHnzRxIggepLgAJ09e0b1owESIAESIAESIAESIAESKCyCOBYP1XI+Pnnn/Pz8zt37myxWYbubLfb0xegfT5fw4YNR4wYsWbNmsuXL0udY6UxCSdWQH5igARIgATqJoGDBw8+99xzqvmzpmninaNly5ZHjx6tm2TYahKoZQQoQNeyDmVzSIAESIAESIAESIAESIAEkhI4ceLE8uXLR44cicMAcfgV7O/EEM9ut4saIhq0xFgCOTk5M2fOPHLkCKRt+DxVdedoNAqLP1X7Tlo//kACJEACtZpAIBAIh8OGYageNj799FPL1Kppmtvt1jQtIyPj448/LioqqtVU2DgSqP0EKEDX/j5mC0mABEiABEiABEiABEigdhOIRCLiXtnyvnasNHbmzJkPPvhg4MCB9v99ICuL3pFMZdZ1Hf5JVUla07T27duPHj36wIEDkUhEwIqPaePuR3UtrcZIegZIgARIgASEQGFh4eTJkzEt67oOO2ho0JqmvfLKKzdu3IiVxkKhkGWSlxwYIAESqM4EKEBX595h3UiABEiABEiABEiABEiABJISUHVnSQTDunA4/P33348dOzYrKwsisqZp/9Of/1/fGokCtEWJttlsuNZmszVq1Gj48OGfffZZKBSSstRAmgI0kqkXMkwCJEACJAACP/74Y8eOHdXJGWK01+t98sknT5w4QVAkQAI1lAAF6Bracaw2CZAACZAACZAACZAACdR1AoFAAHIzvFvcvHlz27Zt77zzTocOHeBC1Ol0qv6dUwvQInlIoHHjxqNGjZoxY8aRI0cMw8DBWaZp4v3xeDweK42hAqZpUoCu68OR7ScBEqgMAsXFxXPnztU0zev1YuNQ5uSGDRv+9NNPwWBQZuPKKJB5kAAJVAUBCtBVQZllkAAJkAAJkAAJkAAJkAAJ3JOAYRjldZRsGMbPP/+8YMGC7t27N2jQQNM0j8fjcDigO+N/caCRWoCG+bPdbs/Ozv7ggw9++eUXwzBUJxvhcFiqF41GA4FAKBSSGArQ9+xfJiABEiCBMglgP0/96cCBA48++qhIzwjYbDav17tmzRo1JcMkQAI1ggAF6BrRTawkCZAACZAACZAACZAACdR+ApFIRAyK5Ry/cDgMrxdi7GwYRjgcXrt27YABAx599FGHw5EoUogzDZhCq2Z0OHhQ0zS4eMblbdu2nTx58vbt26Ejp/4fPp1Vz86p06u/1v5eZAtJgARIoJwEZCdPve7mzZtDhw7FxqFlkv/444+RMplPJDUfhkmABKoDAQrQ1aEXWAcSIAESIAESIAESIAESqOsE4vF4mRbQsEE2DOPmzZtbt27Nzc2tV6+eHA+oaZrqZEOs5ESAtsgWmqY5HA6n0+lwOJo3bz5ixIjVq1dD44YCoorFycIUoOv6YGX7SYAEHiSBSCSCPchoNLpkyRKfz4eZ3OPxYA7XNA0adCQSoQb9ILuCeZNApRGgAF1pKJkRCZAACZAACZAACZAACZDA/RPAu9jQnYuKik6ePDlz5syWLVtCgMCBVBa7Zrv9/84VFK1Z1GebzebxeOCCAxdmZWX169dv6dKlFy9eDAQCam1jpbFoNJpMdK6seLVEhkmABEiABJIRkPdgNn65EdKzTPKaprnd7rVr1ya7lvEkQALVjQAF6OrWI6wPCZAACZAACZAACZAACdRpArHSWCgU+uSTT1555ZWsrCwIx6I76Hc/UJbllCqLFw5VgIZX6L59+3788ce///77zZs34cFDRVxSUhIOh6N3P7DCriy5OTEftVyGSYAESIAEEgncuHHDNE05adAwjGPHjjVt2hSPA4jRLpfL7XaLL47ETBhDAiRQrQhQgK5W3cHKkAAJkAAJkAAJkAAJkECdI1BcXBwMBq9du7ZmzZpBgwaplm6QkkV9ljMGLTFw6Cz/w+Nzy5Ytc3NzV6xYARU4VhqLlcZUT6OIF38aqlicug/ST5k6H/5KAiRAAiSQSCBxji0pKTl37lyTJk3sdju2IcWz/65duyQHOUVAYhggARKoJgQoQFeTjmA1SIAESIAESIAESIAESKDWEoBXDUjAMDE2DCMajUYikX379r399ttNmjRJtGKG0KBqzVAc4FID8TabDRe63W5d15s0aTJixIgNGzacPXs2BU2L9Jx4nGCKa03TTBRHUqfnryRAAiRAAukTsMyx8Xg8FAqVlJQcO3asUaNGmPx9Ph/OJ6xXr97evXvFiX/6pTAlCZBAVRKgAF2VtFkWCZAACZAACZAACZAACdRRAqrm+8cff2zatGnQoEFNmjSxeNiw2+2uux+LHp0oQzscDr/fj2QDBgyYPXv25cuXATcej0ciETF2Vm3icNShWD2rAYvkUUf7ic0mARIggYdNQGZjVARbmJjJf/vtN5fL5ff75aHg8XhatGjx999/i8/oh119lk8CJFAGAQrQZUBhFAmQAAmQAAmQAAmQAAmQQOUSiEaj+/fvf/PNN5955hkRDiRgs9l0XXc6nRY9WhJYAg6Hw+Px5Ofn79ixQ+oZK43h6EKJMU1TVZ9VuTkxLJKHKNdqPgyTAAmQAAlUDYHUs/GZM2caNGggm5Q4gfaFF16IRCLiNrpq6slSSIAE0idAATp9VkxJAiRAAiRAAiRAAiRAAiRgJSBr/lhpTBb/4XDYNM1wOPzbb7/Nnz+/R48eFgU59Vc5RRBeOMQrdMuWLceMGbN58+bi4mKLsZtFsFBFZHk1O50DBq3N43cSIAESIIHqRCAYDO7YsSMjI0PTNJvNBkccuq6/+eabwWBQHg2BQKA61Zp1IYG6ToACdF0fAWw/CZAACZAACZAACZAACVSAANxchMNhi4mxaZq3b9/evHnz22+/3bBhQ5fLlVprTv0rxIWePXsuW7bs1KlTKeqZWoBWf00dTlEEfyIBEiABEqgOBILB4Oeff443ZmABjUfJ3r17UT3ZDa0OtWUdSIAETNOkAM1hQAIkQAIkQAIkQAIkQAIkUD4ChmGIlRkEaMMwLl++vGDBgpycHFilaZomr0jb7XZVI0gtOuPX5s2bDx8+/Jtvvrl586ZpmiUlJVLFWGksFApZrNtUWRnnBEp69ad7huUqBkiABEiABKozgcmTJ1ueJk2aNDlz5oxpmonumKpzQ1g3EqgLBChA14VeZhtJgARIgARIgARIgARI4IEQuHz58oYNG0aOHOnz+bx3P7qui+4MDdput1s0gmRfRXS+deuWVDcej8OWLRQKhcPhaDSq2lyryURcpgAtWBggARIggVpMoHv37llZWRkZGfDUZLPZBg0ahMNma3Gr2TQSqIkEKEDXxF5jnUmABEiABEiABEiABEjggROAmbNhGJFIRDRfwzCKiooOHTr0wQcf4DhBWDeL12Y1kCg967rucrngWAMytN/vz87OXr169ZUrV1I0SRWXUyTjTyRAAiRAAnWHwLlz57xer+x64qGzYMECuuCoO2OALa0pBChA15SeYj1JgARIgARIgARIgARIoCoIwHbMuPuRo/wMw/j7778//PDDvLy8Jk2a2O12j8eDpb7D4VBF5/+HvTOBraJc//8smbPltIWgQmQxKhBFiFIIa6BAWIMiVwEJIgZZAiJhTQEJFEjZclEbipd4WSIiV27FsBmWNsiSipDKlbBIwCspCrlsgS7pOWemZ2b+/vvc++T9zWlPT7HAWb4Tg++888477/uZOX2f9zvPPK+Y5lgckiR5PB5JkshJzePxpKWlTZw4cfv27bdu3aqoqLBtm2N61NpJCNC1YkEmCIAACKQsgUAgYNt2QUEBLzZAUaF9Pt/9+/dTFgs6DgLxSQACdHzeF7QKBEAABEAABEAABEAABOKCwMGDB+fNm9e+fXtSk10uF/uaybKsqqqoOEemyc3Z5XJRDOg+ffqsWbOmpKQksm8kMUfmUw4E6LrIIB8EQAAEUpNAWVkZxXp+6623fD4fDTckRo8aNSo1maDXIBC3BCBAx+2tQcNAAARAAARAAARAAARA4PEQuHLlytatW4cPH56RkSHLsqZp5OzMITUURSFHM5rwR+rOlKOqqqIor7zyyuzZs/fs2cOd0XU9FArZtk1fSXN8Dy4QmYAAHckEOSAAAiCQygQsy6KhpKKigt6S0pDk9XplWf7uu+9SGQ76DgLxRgACdLzdEbQHBEAABEAABEAABEAABB4WgaqqKl7Ej2TfcHWYQjybpnn8+PGZM2d26dJFEba6xGXyaKaQGuJigyRS+3y+vn37/vWvf71586Zt2+Xl5dwlkpJN04zu8szlkQABEAABEACBKARCodCRI0dUVfV4PMLwpSASdBRoOAQCj5gABOhHDByXAwEQAAEQAAEQAAFn3UOnAAAgAElEQVQQAIHHQCBcHWZHY13Xw9XhYDBo23ZpaWl+fv7rr7+u1WxqzSZO4GsVoNkVmmRo2nW5XC1atJg7d+4333xTWVlpWRY7OPOlbduGAP0Ybj8uCQIgAALJS4ACcYwaNcrtdovj19KlS5O30+gZCCQYAQjQCXbD0FwQAAEQAAEQAAEQAAEQaCgBWt+PvlamD5a/+eabWbNmNW/enCJpkI7M8TTECXytAjTHgybf5+HDh3/00UdXrlyJbFgoFHJ4OtMu/xt5CnJAAARAAARAoEEEgsHg1atX09LSxPHL5XLdvn2bXnw2qDYUBgEQaHQCEKAbHSkqBAEQAAEQAAEQAAEQAIF4JHDu3LlPP/10xIgRJDqnp6eT4qwoCi0nSLGeZVkWJ/C1CtCyLGdkZIwZM+bvf//7tWvXdF0PBAIkbZumGajZzJqNMgOBABNh6dkhTHMBJEAABEAABEAgdgL0Qc8f5XNycsTxy+VyLVu2LPZ6UBIEQODhEYAA/fDYomYQAAEQAAEQAAEQAAEQeOgELMsyTdMwDPoGmVb2syyLvJ5v3br1zTffvPXWWx06dCC5ud5/NU0THaJ9Ph8p1G63OyMj480331y6dOn3338vdozaICrL4tFa05Zl1ZqPTBAAARAAARBoKAEa9SzLcrvdNMy53W4ay37//XceHxtaLcqDAAg0FgEI0I1FEvWAAAiAAAiAAAiAAAiAwOMnEK4Oh6vD58+fz8vLGzZsmENNjqI+K4ri8Xhoxu7xeMTVBZ999tnJkyfv2LGD3JkjZ/IQoB//jUcLQAAEQCDlCViWtXnzZkmSPB6PJEmqqmqaNm7cOHEdgpSHBAAg8HgIQIB+PNxxVRAAARAAARAAARAAARBoRALkfbxr166ZM2dmZmaS0EzRMzhNHyaLmaIe7fV6yVmM/vV6vZ07d87Ly/v55585gAYJzfyxM7e/Qb7PfBYSIAACIAACINDoBNq1a6coSlpaGg1niqL8+uuvjX4VVAgCINAgAhCgG4QLhUEABEAABEAABEAABEDg4RJoqKNWSUnJJ5980rt3b0mSyG1Z0zSfzydJkqIoqrBFF6AVRZEkqU2bNuPGjduyZUswGKSWkNezbdvh6rBhGLU2DwL0w30mUDsIgAAIgEDMBLZu3Sq+Xk1LS1uyZEnMZ6MgCIDAQyEAAfqhYEWlIAACIAACIAACIAACIPBgBCh2M5/Li/uFq8OmaZL3cSgU+vrrr8eOHUu6szjT5jQvHijmkMrMOX6/nz5S7tq16/r160+dOsXXbWiCNeiGnojyIAACIAACINCIBHRdf/bZZ2m84zUJy8vLbduurKxsxAuhKhAAgdgJQICOnRVKggAIgAAIgAAIgAAIgMCjIGCaZrg6TJIuXc8wjHB1+ObNm/n5+YMGDfL7/aqqSpLEqy2xpswJFqDFhCRJ5BwtSVJGRsZbb721devWiooKWrpQ13XDMB6shxCgH4wbzgIBEAABEGhEAvTVzrZt22RZZvVZUZSlS5dalhUKhUzT5AELy+E2InlUBQLRCUCAjs4HR0EABEAABEAABEAABEDg0REQRWfbtin48q+//rp169bhw4dLkuRyuSIlZs4RE6w7i5mSJHXt2nXJkiVnz561LIu9rUngNk2TEpiTP7pbjiuBAAiAAAg0HgEa10zTbNWqlShAt2rVioa2O3fuQIBuPN6oCQRiJQABOlZSKAcCIAACIAACIAACIAACj4AABdm4ceNGQUHBhAkT2rVrxwqypmmKokRq0FxATLAALcty27Zt33333f3799+/f5+jOVNfSHTmfum6ji+UmQYSIAACIAACiUjAMIw5c+aIArQkSd999x31BQJ0It5TtDnRCUCATvQ7iPaDAAiAAAiAAAiAAAgkDAH2OKavgM2aLVwd1nW9vLw8XB2+ffv2kiVL+vTpQ1KyOHkW07TYoNfr1TRNFJ0pTTq1z+dr3br11KlTi4qKxMm2mBbB1ZUvlkEaBEAABEAABBKCwKVLl2iRA4pYJUnStGnTal1HNyG6g0aCQKITgACd6HcQ7QcBEAABEAABEAABEEgkAhR90tHikpKSBQsWPP300zRblmWZZWVRd+Y0HSVXaLVmY+m5WbNmb7755rp160pLSymCh2EYorgspsVm1JUvlkEaBEAABEAABOKZgBhCavLkybIs05taSty+fTueG4+2gUASE4AAncQ3F10DARAAARAAARAAARCIIwKk8FKDwtXhu3fv7tu3b8KECc8//zzLzZxwrJ7E0jMlvF4vqc+KokiSpGlaly5dZsyYceTIEdu2efpNHtZ0RVFf5rRIhzP5dPEo0iAAAiAAAiAQ/wTEofbrr7+WJEl8p5uXl4cxLv5vIlqYlAQgQCflbUWnQAAEQAAEQAAEQAAE4pTA3bt3P/vssz59+oiasjg9Jg1aVVWXy0XBNMSSlGZ/rkGDBm3atOnUqVNVVVW2bRuGoes69ZzDfZAkLerLnBYZcSYm5yIWpEEABEAABBKIAI9l1Oa2bdtyCA5FUV555ZUE6guaCgLJRAACdDLdTfQFBEAABEAABEAABEDgsREIV4dZ86WV/SzL4gX9jh49Om3atE6dOj355JMkMYuLBLLjMyU8Ho/b7ZYkSVEUUZtWFMXj8fj9/ilTpnz99ddUOU+2Lcsil2fKeWwgcGEQAAEQAAEQeHwExEFw1qxZbrdblmX6bMjj8Zw/f76qqopetYoDKF6+Pr47hiunBAEI0Clxm9FJEAABEAABEAABEACBR0DAsizDMMLVYdM0q6qq7ty589U/vho1ahStGcgqsyg9U5oPUcLlclGQDXfNpmmaqqrt27efOnXqsWPHbNsmsTtcHXZMniFAP4K7jEuAAAiAAAjEMwGWksPV4d9++41f5aqq6vF4FixYIDZeHEbFfKRBAAQalwAE6MblidpAAARAAARAAARAAARSlAC5P1dWVv7000+LFy9+6aWXSE1mF2aXyyXKzaIMzQK0oij8sbAkSc2aNRs6dOiGDRtOnz5NkTQMwwgGg4w4xgUGuTwSIAACIAACIJAiBEKhULg63Lt3b141QVGUNm3a8DAqqs8sW6cIHHQTBB4xAQjQjxg4LgcCIAACIAACIAACIJAYBEzTbFBDd+3aNWPGjHbt2pGC7PP5JEniSBqSJInKMi2LxBo0C9CUaNmy5dSpUwsKCnRdJzdn0zQpQU2iXV3XDcMwTdMxhabdBjUehUEABEAABEAgyQjoum6a5scff+zxeHgI1jStpKSENGiKxcFjaJJ1H90BgbgiAAE6rm4HGgMCIAACIAACIAACIBAvBDigs23bHG05FApZlkX/2rZ97969goKCt956i92cRSmZ9WVOkIOzy+Vyu92KopAMTacoitK1a9d58+adP3/+7t27tm1TPA2HvswrCopHGRmkZ0aBBAiAAAiAQIoTIKfm3377TRyaJUnKzs4mAdowjBRHhO6DwCMjAAH6kaHGhUAABEAABEAABEAABBKMADkac6NZkj516tTKlSsHDBhAHlWkL4vzW1acIxNcjAJDq6r6xl/eyM/Pv3jxIi+LRFGeQ6GQGNOZxWVKRArTrE1zg5EAARAAARAAgZQlEAqFbNuuqKjo0qULD76SJHXo0CFlmaDjIPC4CECAflzkcV0QAAEQAAEQAAEQAIH4JcBqLzexvLx87969b7/9dps2bdjfmZc24pxIxTkyR6nZxo8ff/Dgwdu3b9MMORAIkIJMyjJp37SeITWGmxRFgObWIgECIAACIAACKU6AhlfbttevXy8K0JIk/fLLLykOB90HgUdMAAL0IwaOy4EACIAACIAACIAACCQGAfo+98aNGwUFBRMmTKBozmrNxssZSZJEsZ41TYsUmiNzunfvPnfu3JMnT1KEjXpBNNQDut4KUQAEQAAEQAAEUocAReG4fv26KEC7XK6NGzdi1cHUeQzQ03ggAAE6Hu4C2gACIAACIAACIAACIPBICdACg1VVVSwEG4ZBETaCNdv3338/efLkrl27ajUbxWsWp6+UJsdnWZZ9Pl9kGU3TJEnyer1vvfVWXl7etWvXqqqqGhRx0uH7zIzqyucCSIAACIAACIBAyhIQR0l6ldu+fXuKmkWDdf/+/ek1c8oiQsdB4BETgAD9iIHjciAAAiAAAiAAAiAAAo+ZAM1LWXqm1oSrw5WVlQUFBXPmzCFxmaRnmq9GSs+ROaqqkh6taZrX6+3QocPkyZO//vrr8vJywzBoXUG6VuxeV+IUWqRWV75YBmkQAAEQAAEQSE0C4ihJAvTMmTNp6QVJkmhBYFpoITX5oNcg8OgJQIB+9MxxRRAAARAAARAAARAAgcdMwLIsCg2p6/qlS5cWLVo0ZMgQ1pQ9Ho/L5YpFeubQz56azefzdejQYdWqVWfOnKEe8rqFVVVVuq7HLj3T6eIUWkRWV75YBmkQAAEQAAEQSE0C4ihJAvTevXtpAQYKnCVJ0q5du1ITDnoNAo+FAATox4IdFwUBEAABEAABEAABEHicBO7fv79z584pU6a0bt2adWdORAbT4EOOBM1jPR5Pt27dli5deufOHeoVCc3h6rBlWTT1JYdrCNCP867j2iAAAiAAAqlBIFKADoVCHo+HBnEKkDVr1qwGBcVKDXLoJQg8LAIQoB8WWdQLAiAAAiAAAiAAAiDwyAjwHDIUCnE0Z7o6zUINw7As69q1a5s3bx49ejStJUjOULRUoENZpl2Xy0XTVJ6y0m5aWposy36/f/To0Z9//nlZWVmUnorT4CjFcAgEQAAEQAAEQKARCTjG3969eyuK4na76TXzyy+//ABfJjVi81AVCKQUAQjQKXW70VkQAAEQAAEQAAEQSGYCDv9iCrIRCoWKiormzp37/PPPk/eT2+2OUYBWVZUKa5rmcrloytq5c+dJkyYdPXqUVjK0bZvcnB1XZ9COCTDnIwECIAACIAACIPDwCDjG33nz5lH0Z3aFDgQCdY3dD69VqBkEUpMABOjUvO/oNQiAAAiAAAiAAAgkFQFxDkly8MWLF7ds2TJ48OAnn3xSkiS32y1JkqZpJCLXK0BHukW3a9cuJyfn8uXLtm2Hq8O6rhuGUVlZGQwGo09fHRPgpOKOzoAACIAACIBAvBJwjL/Hjx+n75lo/QaPx7Nnz57oI3i89gztAoHEIwABOvHuGVoMAiAAAiAAAiAAAiDgIEDOzoFA4OTJk3Pnzu3QoYMkSbxCIC15r9VsJECTD1S9IThatGgxefLknTt33rp1i+aogUCABGh2f3a0JHLXMQGOLIAcEAABEAABEACBRicgjr+0+DAJ0GwJrFq1iso0+qVRIQiAgIMABGgHEOyCAAiAAAiAAAiAAAjEEQHTNI2ajRb0q7Vlv//++6ZNm8aMGZOWliaGbKZ5Jv9LTs2iKk2HKMgGSdJpaWmSJLVt2/aDDz4oKiq6e/duuDpMQTZ4HltrG5AJAiAAAiAAAiAQtwToLXL//v3ZKpAkqUuXLrREcNw2Gw0DgaQhAAE6aW4lOgICIAACIAACIAACyU+AwmsYhqHr+tmzZ3Nzc9u2bcuTyUhxmQ+RQzRr0LIss0O0qqqSJDVr1uzVV1/94osvrly5Ytu2rusOmhCgHUCwCwIgAAIgAAKJRWD27NmSJLlcLjYPqP0IxJFY9xGtTUQCEKAT8a6hzSAAAiAAAiAAAiCQKgQsywpXh9n9uays7Ntvv504cWL79u0lSVJVVdM0VVVlWVZV1VWz0ae1PLfkhKg+U6bP53vllVemTZt25MgRAhoMBilBMT3I/Rke0KnytKGfIAACIAACSUqAAmft27ePonLxG+sLFy5AfU7Se45uxRcBCNDxdT/QGhAAARAAARAAARAAAQeBioqK4uLiFStWvPnmm6wmU0JVVa/Xy0sLOo46dkUBulOnTh9++OG5c+eif3tbVVVF3tDs/oxpquPuYBcEQAAEQAAE4p8ACdDXrl0j24DeW8uyvGHDBnrlHP9dQAtBIKEJQIBO6NuHxoMACIAACIAACIBAMhCgQM8U9YLmgZZl3b9//7PPPps0aZJDR6511+1285SS0vyBraZpXq83PT09IyNj4sSJn3/++f3795OBGvoAAiAAAiAAAiDQEAKGYTz11FMUlYu+lxo/fnxDKkBZEACBByQAAfoBweE0EAABEAABEAABEACBxiVgmma4Onzjxo0tW7a88Zc3ahWao2Ty57RUxuVyybLsdrs7deo0Z86cH3/8kZyXyam5cVuO2kAABEAABEAABOKcgGmaFRUVWVlZJECTtdCnTx+OvhXn7UfzQCChCUCATujbh8aDAAiAAAiAAAiAQGIT0HWddOFvvvlm0qRJLVu2pJjOUYTm6IdkWXa5XBkZGYMHD966devvv/9OgMRozomNDK0HARAAARAAARBoOAHTNHVdX7ZsmcOQoFhbbCc0vGKcAQIgUD8BCND1M0IJEAABEAABEAABEACBh0Tgyy+/JGdnt9sty7LX65UkyVOzqaoqSZLP53NMFKPstm/fftq0afv37zcMw7btiooK27YrKyvJt5q7gEkmo0ACBEAABEAABFKKwNatW9mQoG+nTp06BcMgpZ4BdPaxEIAA/Viw46IgAAIgAAIgAAIgkIQELMsKV4fD1WHDMCiUMwV3ppV/bNu2LMs0zeLi4nnz5rVq1cpbs2maJk4FFWFTVVXTNLfb7ShD2jTHfe7YsePf/vY3mkCGq8NYJzAJny10CQRAAARAAAQag8Dp06fJ6lAUhcyJL774gt5bN0b1qAMEQKB2AhCga+eCXBAAARAAARAAARAAgQcg4JjChavDoVCIVhfcv3//9OnTRSmZdWeKxijXvYklqXDz5s1Hjx7997///c6dO7Ztk/AND6YHuGU4BQRAAARAAASSnkB5eTkZCYZh0MdVqqqSB/Ty5csd1kvS00AHQeDRE4AA/eiZ44ogAAIgAAIgAAIgkOQEaCIXCASuXLmSn58/bNgwh4Is7sqyLDg9O5O8tKCqqm63+8UXX/zwww/37t1rWZZhGORSHQgEID0n+SOF7oEACIAACIBAIxFo3769JEn0RlxRlFGjRvGnWo10BVQDAiDgJAAB2kkE+yAAAiAAAiAAAiAAAn+SwPHjx2fPnt26dWuPx8NxnDliRuzqM6nRPp9v+PDhO3bsuH79eqSPEiaNf/Jm4XQQAAEQAAEQSCkCvXr1kiTJ5XJJkqSqateuXVOq++gsCDwWAhCgHwt2XBQEQAAEQAAEQAAEEpWAuKCfKAcbhrFr165Ro0Z16NBBlJhrTSuKQnq0y+Vyu90ul0tRFC7pdrs9Hk/z5s3HjRv3z3/+0xK2RKWGdoMACIAACIAACMQHgYULF7LJQeaHbdt4nx0fNwetSFoCEKCT9taiYyAAAiAAAiAAAiDwUAnQVO2XX3755JNPRo4cSXM5UUfm2Z0joSiKy+WilX/4kN/vJ1+k119/PS8vr7S0lKJq0KKCLEE/1B6hchAAARAAARAAgaQnkJ+fzwG+KHHt2jUI0El/39HBx0sAAvTj5Y+rgwAIgAAIgAAIgEBiEKBoy7TWn2EYZ8+ezc7OzszMpJV80tLSJEmiBeV5UkfiMq0syEKzoiiaplFA54yMDIrA2KpVqzf+8sa2bdvu3btHOHRdN02TLkoJ0qATAxZaCQIgAAIgAAIgEK8EDh8+zGYJJfbv3w8BOl5vF9qVJAQgQCfJjUQ3QAAEQAAEQAAEQKChBEjYjf2sO3fu7NmzZ/z48c8++yxN2MiLmaMoSpJEcnPkv46ZniRJGRkZHTt2nD59+rFjxxxtCIVCnFNVVcXuz5ZlcT4SIAACIAACIAACIPAABC5cuEBmCb8yX79+PQToByCJU0AgdgIQoGNnhZIgAAIgAAIgAAIgkFQEyMuYumRZFoW8CAaDlKPrOiXu3r378ccfv/GXN2hJQEVReMIWKSvXesiRmZmZmZube/XqVb5WUmFFZ0AABEAABEAABOKYgGmaiqJ4vV5ZlulLrNzc3DhuL5oGAslAAAJ0MtxF9AEEQAAEQAAEQAAEGkqAoluwT3EgELBtu6qqyrZtXdcrKytLSkoWL1788ssvS5LkdrtVVY1FgI6UpGmxwebNm7/xlzd27Nhx7dq1YDAoxnduaMtRHgRAAARAAARAAAQemIBlWU899RR9vyVJks/nGzt27APXhhNBAARiIQABOhZKKAMCIAACIAACIAACSUuAfJ9JiS4rK/vyyy8XLVrUunVrlpK9Xi+F2miQAE0uRc2aNZsyZUpxcbGIT9d1wzBY+xYPIQ0CIAACIAACIAACD5tA586dyc4hC6dXr14P+4qoHwRSnAAE6BR/ANB9EAABEAABEACBJCTQIG03XB0OBoOrVq3q1auXJEl+v59COXs8HgqdIQbQIA1azGGdmhIUoOPll1+eNWvWqVOnCC75OychaHQJBEAABEAABEAgAQkMGjSIDRiPx5Oenp6AnUCTQSCRCECATqS7hbaCAAiAAAiAAAiAQCwELMsyDEOUfXVdp4DL4eow5+/fv3/VqlWZmZmyLHOEDZ6PxZKQZVlRFCqZnp4+atSor/7x1YULF2JpJMqAAAiAAAiAAAiAwGMhsHjxYnqnLkmSVrM9lmbgoiCQOgQgQKfOvUZPQQAEQAAEQAAEUogALyHIqwvatl1ZWWnb9tdffz169OimTZtKkqQoisvl0jSNdeQYdWdVVd1ut9frpciJBQUFfMUUooyuggAIgAAIgAAIJCCB5cuX+3w+0ea5ceNGAvYDTQaBhCEAATphbhUaCgIgAAIgAAIgAAINJWCaJp3yyy+/bNiwYezYsRSa2ev1aprGy++IE7AY0506dZo2bVpRURE7Vje0bSgPAiAAAiAAAiAAAo+FwJYtW8giYrOH44Y9lvbgoiCQ9AQgQCf9LUYHQQAEQAAEQAAEUpfAhQsXcnNzn376aZ/PpyiK2+2m+M6SJKWlpdFnp7T8Dk/AoiQURenbt29eXt6PP/5o27ZVs7HGnbqU0XMQAAEQAAEQAIGEIvDdd9+RRUSmkaZphYWFCdUDNBYEEowABOgEu2FoLgiAAAiAAAiAQIoTsCzLNE3DMEKhUDAYJP2XIz6Hq8OlpaWbNm0aPHjwM888I6rJct0bzcFcNZssyzQZc7vddIamaePGjfv8889LS0srKipSnD+6DwIgAAIgAAIgkOgEjh075vf7eVFlTdMWL16c6J1C+0EgnglAgI7nu4O2gQAIgAAIgAAIgED9BAKBgGEYV69e/eKLL8RV3UlWpjV26haf/3tEVVWXy0Xe0DQfa9Wq1bx583bs2FFWVhYMBg3DqL8pKAECIAACIAACIAAC8U3ANM1r167RShgZGRlkKeXm5sZ3q9E6EEhsAhCgE/v+ofUgAAIgAAIgAAIpTuDo0aPz5s3r2rWruIqgLMuKoqj/22LRoCketMvlateu3dSpUy9cuEBgyeHatu1wdThcHU5x2ug+CIAACIAACIBAEhAwTZODkkmS5Ha7V6xYkQT9QhdAIG4JQICO21uDhoEACIAACIAACKQKAdM0LcuKvbeVlZV79ux5/fXX/X6/GGSD07TGoKZpJEHHIkAPGjRo7dq1Fy9eZJWZgztXVFSEQiHbtsnVOvZ2oiQIgAAIgAAIgAAIxCcBtpp8Pp8kScOGDYvPdqJVIJAcBCBAJ8d9RC9AAARAAARAAAQSmICu66z22rYdDAZJ8KUuVVRUkCh85cqVNWvWZGZmkqCsKArHLuRJVGSClh8k7x6fz/eHjw/5Sqenp/t8vqFDh+7cufM///lPFHy02CD/S8sPRimPQyAAAiAAAiAAAiAQzwTC1WH+dExVVVmWIUDH8/1C25KAAAToJLiJ6AIIgAAIgAAIgEACE6AYFw4P6HB1OBAIUK8uXry4ePHi559/XtM0SZJUVY1dgCaFmk6kIBuyLGdmZs6ePfvIkSO2bYdCoXqDO7P0LCYSmDiaDgIgAAIgAAIgkPIEMjMz6bU9GUudOnVKeSQAAAIPkQAE6IcIF1WDAAiAAAiAAAiAQOwELMsKV4fp39LS0qKioilTpqSnp5PoLEmSy+Xyer3kwsxRNSJdniNzNE2TZblfv37r1q0rKyuzLEvX9Xp1Z265qDtzmo8iAQIgAAIgAAIgAAIJR2DIkCHkBE0CtN/vT7guoMEgkEAEIEAn0M1CU0EABEAABEAABJKZQLg6HAwGP/roo27dukmS5PF4SEpWVZU0aIrpTJOlegVoKvbCCy988MEHBQUF5GdNojPF92AB2rIswzAcLtgiaBadxYRYAGkQAAEQAAEQAAEQSBQChmGYptm1a1eK/syxOBBkLFHuINqZiAQgQCfiXUObQQAEQAAEQAAEEoMAuTOHq8OGYfA6frZth6vD4eowrT1oWdbu3bsXLVrUoUOHemM611uANOsXX3xxwYIFt2/ftiyrvLw8FlhRBOhYTkcZEAABEAABEAABEEggAr1793Z8NEYWmm3b/JI+gbqDpoJAnBOAAB3nNwjNAwEQAAEQAAEQSGwCkXOY8vJyXddv3br1zTffjBs37plnniF/Z5/PR87OjumQuMvRnzkhSZIsy36/v1mzZu+///6WLVtoRUHy7qEoz4lNEK0HARAAARAAARAAgcYjQCs/Dxw40GF33bt3j5Z9xlv5xoONmkDgvwQgQONRAAEQAAEQAAEQAIGHToBkaNM0r1+/vmbNmgEDBjh8mVVVdbvdjomQKD1TWq7ZSHSWZVlRlE6dOn3wwQfFxcXUB7Nmo/S9e/fgxfPQby0uAAIgAAIgAAIgkGgEysrKZs+e7TC0zp8/T1+nJVpv0F4QSAACEKAT4CahiSAAAiAAAiAAAolO4Pjx47Nnz3755Zc9Hg9Jz1rNptZsPP9RFMUhTPMhUYDWNG3o0KE7d+68c+cOefFE8gmFQuS/EwwGI48iBwRAAARAAARAAARSk4BlWZ+dm4kAACAASURBVMFgcOHChRz9mayso0eP2rZdl2WVmqzQaxBoLAIQoBuLJOoBARAAARAAARBIaQK6rvPaNeTvXFZWtmfPntmzZ6uqqiiKy+US/Zc5hgaLzrIs+3w+x1zI7XaTv7MkSa1bt540adK+fftSGjQ6DwIgAAIgAAIgAAJ/ggBJzMuXL3d8eUYCNC3g8Seqx6kgAAK1EIAAXQsUZIEACIAACIAACIBAQwmYpkm6c2lp6bZt20aNGuX3+zVNY49mmuSQBi2qzw7FmV2eqbyiKCNGjFi6dOlPP/1EywnCMaehtwblQQAEQAAEQAAEQIAJsADtsMEgQDMiJECg0QlAgG50pKgQBEAABEAABEAgFQlcuHBh4cKFmZmZFGRD0zR2q/F4PBRqg6I2O9Rn9oCmpQhJgG7WrNmUKVMOHTpEjtW6rhuGoes6VsVJxWcLfQYBEAABEAABEGg8AqIATZ4B9C8E6MZjjJpAwEkAArSTCPZBAARAAARAAARSlgDJu7GLvGVlZd9+++3EiRPbtWvHMZpFF2aPx+P1eiVJctVskdIz5fh8PlKfu3Xrlpube/369UAgkLJ3AR0HARAAARAAARAAgYdHAAL0w2OLmkGgLgIQoOsig3wQAAEQAAEQAIGUI2BZVlVVFQnQ4eow9T8UCtFEJVwdJjfkc+fOFRYWTpw4kQVlDu7M6jMn2A9azKG4HIqi+P3+Zs2avfnmm5s3b7579y5flC5t1bGl3I1Bh0EABEAABEAABECgkQjUJUDTMhsUUa2RLoVqQAAE/ksAAjQeBRAAARAAARAAARD4LwHLsgzDcHhAcxCMq1evbty4sUuXLqqqyrLsdrtjEaAlSRKDbLAMnZ6ePnr06EOHDvHlTNMMV4d5l5Y0rFWCxg0DARAAARAAARAAARB4MAJ1CdArV66kQw9WLc4CARCIQgACdBQ4OAQCIAACIAACIJCiBPSazbbt8vLyCxcuTJs2rUWLFqQdK4qiqqrL5SJlmTToKB7QvL6N2+2WZfnFF1/Myck5f/48kzUMIxQKOXyf6Wit6rOoUHMlSIAACIAACIAACIAACMRCoC4Bet68eeR2AFsrFowoAwINIgABukG4UBgEQAAEQAAEQCAlCJSVlW3atOnNN99s1qwZx9CghQTZhZn1aHJwpqgajqOSJNFqhJ07d54zZ87ly5crKytjJwgBOnZWKAkCIAACIAACIAACsRCoS4Bes2YNPKBjAYgyIPAABCBAPwA0nAICIAACIAACIJCcBHbt2jVx4sQmTZqwpiyujU7iMudEas2cQ/7RTz755Lhx43bs2HH79u3k5IVegQAIgAAIgAAIgECiEahLgF65cqWu6/T6P9H6hPaCQLwTgAAd73cI7QMBEAABEAABEHioBK5cubJ169bhw4dnZGSICrIYWyMywgbL0Jzg0Bxut/vtt9/etWsXvt98qDcOlYMACIAACIAACIDAAxCAAP0A0HAKCPxJAhCg/yRAnA4CIAACIAACIJB4BO7cubN379533nnnueeec4TOkGWZQm2oqurwg2Z5OjIhy3KHDh2mTJly+PDhqqoq27bFxQyxnHriPSJoMQiAAAiAAAiAQJISgACdpDcW3YprAhCg4/r2oHEgAAIgAAIgAAKNSKC4uHj27Nldu3YVFWR2YeZM8mWORYBWFKVv377r168/c+ZMuDocrg4bhsHRA/kTzvv37zdiL1AVCIAACIAACIAACIDAAxOAAP3A6HAiCDwwAQjQD4wOJ4IACIAACIAACDxmAhzjIhAIsOxr1Gy8a9v2wYMH586dy0JzpMuzeIjSiqJIkqSqqt/vZ2FaVVWPxyNJUpMmTSZMmLB+/fqrV69WVFTYtl1VVSUuGPiYueDyIAACIAACIAACIAACdRCAAF0HGGSDwEMkAAH6IcJF1SAAAiAAAiAAAg+PAKnPpmlSwrIsckDWdT0UCt2+fTsvL2/EiBGapqmqKkmSqDKzpuzIjyxDywlS+TZt2owZM2bLli1lZWWR/YIAHckEOSAAAiAAAiAAAiAQbwQgQMfbHUF7UoEABOhUuMvoIwiAAAiAAAgkJwF2c9Z13bbtX3/99bPPPhs5ciTpyF6vl4Vml8sVKS7TUTFfTPO5o0aN+vjjj8+dO0cQLcvi63KQDdu2IUAn50OGXoEACIAACIAACCQXAQjQyXU/0ZvEIAABOjHuE1oJAiAAAiAAAiAQSYB8n//5z38uWLCgQ4cOkiSJDsukILtqtijLCYqis5ieMGHCF198wVE+bNs2TTMUCrHoHBnZmTXoyKYiBwRAAARAAARAAARAIB4IQICOh7uANqQaAQjQqXbH0V8QAAEQAAEQSHgClmVdvnw5Pz9/5MiRFJSZhWN2W45MsDbN8Z0pNIdYsn///itXrvz3v/9tGAaryaIGnfDs0AEQAAEQAAEQAAEQAAHbnjdvniMU28qVK3VdZ1cDQAIBEGhEAhCgGxEmqgIBEAABEAABEGhMAhTWmWoMBoP379/fvn370qVLu3Xr5vP5ROE4FgGa/KM9Ho+maXyu1+t9/vnnJ0yYsG/fvnv37jlazxq0Ix+7IAACIAACIAACIAACiUvANM3Bgwc7vpCDAJ24NxQtj38CEKDj/x6hhSAAAiAAAiCQWgQcjicXL17cuHFjVlaWLMt+v5+0Y4/HI8sy+a0oNRtp0KwsRybYA5rO6tGjx6efflpaWio6OFMsacLN6rNYILXuBHoLAiAAAiAAAiAAAslIQNf1rl27aprGTgyyLEOATsZbjT7FCwEI0PFyJ9AOEAABEAABEAABJnDjxo09e/ZMnjz55ZdfpogZLCiz0Ey6c2Q+50Qm0tPTX3/99a1bt167dq2yspJWDgxXh+k/0zQp07btQCAAAZpvBxIgAAIgAAIgAAIgkEwETNMcNmyYqD5DgE6m+4u+xCEBCNBxeFPQJBAAARAAARBINgLkRGxZVlVVFfXNNE1yN6ZD4eqwbdsXLlzYvn17t27dSFwWXZtZd46UlSVJ8nq9lM+e0eTmLEmSx+MZMWLEkiVLioqKysrKKioqHHBFodkUNjHfcQp2QQAEQAAEQAAEQAAEEpQALUKYlZWFGNAJegfR7EQkAAE6Ee8a2gwCIAACIAACCUyAw1yYphkKhXRd37Vr16xZs9q3b68oCi0M2CABmmJxOITp55577t13392/fz/NMcjZmVybHexEoVnQn00x33EKdkEABEAABEAABEAABBKUAAToBL1xaHZCE4AAndC3D40HARAAARAAgcQgwGGUg8GgruuBQOD06dOffPLJwIED3W43a8eyLHs8HlVVZVlmDVr8OpJLOhIkW3s8nueff37Dhg1nz56lqBpMJ1wdFl2tOZ+EadaaIUCLZJAGARAAARAAARAAgeQjQDYhPKCT786iR/FMAAJ0PN8dtA0EHh0BFl8o8egujCuBAAikBgGKvBEMBktKSiZOnPjss89ScAzWkUUvZo/Hw+qzY3VyLu9IvPbaa1u2bLl165YDp67rNMcwDMO2bXJ4YTWcCot/ACFAOwBiFwRAAARAAARAAASSjEAUAZpcFhy2YpJ1H90BgcdCAAL0Y8GOi4JAXBAIBALUDhJcRAkGMnRc3CE0AgQSkwBFc2bZ17KsUCi0ffv2t99+Oy0tjYRjcnAWRWcWlMVYz4qicHBnLkDR+lRVHThw4IYNG27fvt1QTlH+xEX+JYxSuKHXRXkQAAEQAAEQAAEQAIE4IaBpmviZnSzLCxYssCyLo7fFSTvRDBBIDgIQoJPjPqIXIPCABEgnIq/ASL+/B6wUp4EACKQwgVAoZNv2/fv3DcMoKCiYOnXqwIEDJUlSFIUVZPJupqAZnMkJ0qZVVSXfZ8qXZdnlcnk8nvbt248fP37nzp2//vrrw3BOgQCdwg8vug4CIAACIAACIJBCBCIF6LVr1/KqISkEAl0FgUdCAAL0I8GMi4BA/BEIV4d1Xb9//z43jQVozkECBEAABBpK4Oeff87Ly3vttddcLpeiKG63W9M0l8ulaRotMKhpWl3SM2vNLEZTwuv1Dhw48NNPP/3pp5+4PZZlGTVb48rQEKCZMBIgAAIgAAIgAAIgkMQEIgXor/7xVeMalklMD10DgYYSgADdUGIoDwKJTYAH1LNnz/bq1cvlcnXs2PHMmTPUK9M0uUBi9xOtBwEQeLQEiouLZ8+e3bVrV3JVliSJbHpJknw+nyRJ0UVnUXHmEBzt2rWbMmVKfn5+WVlZIBAQ/zqZphmuDj+MDyQhQD/aBwdXAwEQAAEQAAEQAIHGIdBQy1DTNArsxoE4Dh8+TAZnQ6tqnA6gFhBIagIQoJP69qJzIBBBgBZVuHXrVlpamtvtpgCsWVlZtm3ruh5RHBkgAAIpTYCi9JAJTov4EQ7LsoLB4JUrVzZu3PjGX95gq52iZ/D6gWK+Q2LmiByqqtIfIo4H3a5du5UrV168eJE/0eDvM+glGWvEKX1v0HkQAAEQAAEQAAEQSGEC4erwtm3bBg8enJ+fTxhEY7VeMMFgkKxT0V5lAZojVUbWQ24QN2/ePHXq1G+//WbbNi+tFFkYOSAAAkwAAjSjQAIEUoKAruuhUGjmzJlut5s+kJdluWnTpnjHmxK3H50EgdgI0Osoy7LYnjYMg2Rf27b37duXnZ3doUMHcm12fL3I6jNFcGabXhSgKU1Rnj0ejyRJTz311JAhQzZt2nT+/HnbtsvKylhlDleHydk5crnU2HqDUiAAAiAAAiAAAiAAAslGYPfu3T6fj0K9bdmyhZY1irGTpC/TJ3psrMqyzAJ0lNlxuDp88eJFWZbdbneTJk3u3r0bRa2OsT0oBgKpQAACdCrcZfQRBP4PgXPnztGnRoqi0KJekiTR62KMnf+HFHZAIIUJ6LrOfxbC1eFz584tX768X79+HEnD7Xb7/X632+34dDEWAZrcn30+38svvzxnzpzCwsJgMOj4DiMQCASDQV3X6bsN1qPFRArfH3QdBEAABEAABEAABFKawNKlSxVFoTAa2dnZFRUVpmmSSRkLl6KiokgP6MLCQjpXjPwWWduECRPIJPZ6vStWrLAsC/PoSErIAQEHAQjQDiDYBYFkJkBBVOfNm8cfvLtcrrS0tCeeeCL6EJvMUNA3EACBCAL0B+H333//4osvxo8fL0kSCc2SJJF2TLY+7To8nWMRoN/4yxv5+fmXL18mcTni+v8/IlAwGOTvKEXRWUxHnogcEAABEAABEAABEACBVCCwc+dOUoHT09N79Ohh23bsU9pwdfjkyZMej4diwbETdCwC9M8//8zKtSRJH3/8MdTnVHje0Mc/TwAC9J9niBpAIMEIdOzYkaOvUqJLly5RPjJKsO6huSAAAlEJsIns+NWTyV5WVnbs2LF33nmnY8eOYtAMtss5EXm0adOmYiaL1JT53HPPTZ48+YcffnB4NEdt7H8PQnSOhRLKgAAIgAAIgAAIgEDqEHjttddIgFZVVdM027bZyq0XgmEYhw4d4kkxW7BFRUXRzw1Xh9955x1eZLtt27aGYWAtpejQcBQEiAAEaDwJIJBCBMLV4d9++61Zs2bszEhj7XvvvceehimEA10FgdQjQF8IsnsIa9CnTp365JNPevfuzfY3eTdTmGYWncWEWJLSFM1ZkiSv10vzgVatWo0ZM6agoODGjRsi7IYKyg0tL14LaRAAARAAARAAARAAgeQjkJaWRiaoWrNduHAhdgE6GAz++OOPbrfboUHXJUCHQiFabPDy5ct0UZfLRYnkA4segcBDIgAB+iGBRbUgEI8ELMvaunWrJEnkmUiBOCRJ+vLLL2lMjcdGo00gAAKNSoB+7JWVlZcvX962bduECRN8Pp/b7fZ4PPw3gQLquVyuGAVoKkkLuUiSNHTo0Dlz5ly6dMnRcMuyQqGQrusQlB1ksAsCIAACIAACIAACINAgAi+++CJJwLQeyfr169m1ot56DMMoLCwkhwmuRJKkI0eO1Hou1zx+/Hiv10vqs8/na968OZWHE3St3JAJAiIBCNAiDaRBIPkJvPfeezzEsth0/vx5DJnJf+/RQxCoIXD48OFp06a1atWKxGV6I8VpSZJc/9s0TYtRgFYU5ZVXXpk4ceLOnTsZs1mzkdbMadM0DcMwTZM1aC6PBAiAAAiAAAiAAAiAAAjESCAvL48ntpIkTZo0iT/yi6WGjz76SDyd0nUJ0FThtWvXOMScz+fzer0ffPABadNw54qFOcqkOAEI0Cn+AKD7KUegXbt25KX4x4q99MFRy5Yted3eBo3ZKccOHQaBuCRAbsW07kq4OhyuDrPay7/oI0eOzJkzZ9iwYZF2dpQcWZb9fv8fi6ukp6c7PETI78Pr9U6aNGnLli3iFUlZJlSsMluWRWXqKhmXaNEoEAABEAABEAABEACBOCXw+++/cwANRVFatmzZoDDQOTk55DothpgrLy+vtbe6rpumOW7cOFmWFUXJyMigZbevXLlCVi5b3bWejkwQAAHbtiFA4zEAgRQicP/+fXpny46NkiSNGDFCFIlSCAe6CgJJQYDs3VAo5Ah798MPP6xbt65Hjx7k1KxpGsdojiI613XI5/PxoT59+qxbt+7cuXO2bVdWVoZCobpkZfFvCwTopHjc0AkQAAEQAAEQAAEQiAsCuq5nZmaSgappmsvl+vXXX2P/rrdWATpKx0pLS+laZFF7vd6nn34a6nMUYjgEAg4CEKAdQLALAslM4OjRo/Sal8ZOemO8ceNGUSRK5v6jbyCQpARYej537tzf/va3AQMGiAGdWTgmJVrcrTft8XhogZemTZvOnDlz27ZtpaWl7F0SDAbpq0MI0En6ZKFbIAACIAACIAACIBC/BD799FNaN5ts2vz8/Ng9kRskQBuGkZOTw75cdLn58+dTWLn4BYSWgUA8EYAAHU93A20BgYdM4OOPPxa/o6cY0CUlJRCgHzJ4VA8CD5HAmTNnli1bNn369FatWtUlKNOPXfz511WS8snf2ePx9O7de9OmTRcuXKCFv7kb4eqwZVnsYwIBmskgAQIgAAIgAAIgAAIg8AgI6LpeXl4u2rRvvvlm7NdtkACt63rz5s05ALTL5crIyDh79mzsenfsDUNJEEhWAhCgk/XOol8g8F8CNChallVVVTVhwgT2gCYpqmXLlhwxti4JCShBAAQeFwGHV0UgEKBYz6dPn16+fPnbb7/t9/s5oo6iKGIMOzEtmub0R0Ct2cR8l8ulqqrX6+3ateuaNWtOnDjhMKkduyKTWF5iiWXEtFgP0iAAAiAAAiAAAiAAAiAQO4GePXtyJGhJaoDA1b9/f/KepmjO9G/kdelrvx07dtDC3XQtt9vduXPnyMLIAQEQiEKgAb/PKLXgEAiAQEIQeOGFF2gFQv53zJgxEKAT4t6hkSBw7NixDRs2DBw4sGnTpiQck18zmcuqqoqKc11pRVFq9YNu1qzZ3Llzd+zYcf/+fdu2jZqN/jiQWMwvqGq9EbEIymIZMV1rhcgEARAAARAAARAAARAAgSgEgsFgKBTauHEjLY5N5vGJEyeinCIeqleADleH2fnjxRdfpBm0oiher1eSpL/+9a/8LaBYLdIgAAJ1EYAAXRcZ5INAkhBgp8VgMEijMslP9AFRQUGBYRgkLbHAxNpQkiBAN0AgoQiYphmuDtN/hYWF69atGzZsWMuWLcUId+y5TG7LpERHLuRdqwxN9fj9/ubNmw8bNmzdunWXL18mQvTbZ1qiDC3+feACnOA/GvwHhw9xQiwjprkAEiAAAiAAAiAAAiAAAiAQOwHLsu7evSsK0O+//36Mp9crQFM9FRUVhYWFPI/2+/1kS//6668xXgjFQAAEiAAEaDwJIJDkBKqqqmzbDgaDJSUlkiS53W5ygdQ0TZbl69evQ4BO8icA3Us0AsXFxWvWrOnatStZtywus+jMCYrUzLsxCtCvv/76ypUrf/zxR1KB6S+ACIlFZJLCxT8RdIpYmNKxCMpiGTEdWRtyQAAEQAAEEoWAI1RUojQb7QQBEEgmAmPHjnW73WQSv/TSSzF2jQRosp8pkJ2iKOK55P5smuZrr71GxTweD12lV69etm1TdA7xFKRBAASiEIAAHQUODoHA4yTA0o+u64ZhkF5jGEYwGKQgsKKCw4JRZItprTDDMNavX+9wh3zllVeovKMq3o2sjXJCoRAH7ogsQ40h38nKysrIAvXmUBCAcHWYQgFQebIA+FxqJO8iAQJxSIBir4sNC4VC4q5pmrquf/fdd/n5+WPHjm3evLnP5xPD2Inicl1pNoXrKiDL8vDhw7Ozs0+fPi1ePZY0fx6BX1wsuFAGBEAABFKNgK7rLMGI5qg4fJDhSl/2iGWqqqrI2AtXh8Uv2SmTq7VtW9d1NikNw2CbkPPLy8sjzeNUuxfoLwikJoHKysrdu3ezW4bH4yksLKQ/CNGBiH7T9Ilw3759HadUVFTcuXOH11khFy6fz/e3v/2N/jTxxFn84+aoBLsgAAJEAAI0ngQQSDwCoVCIRrhYBjwy33Vdnzt3rihAS5I0derUyHpiqZN04UAgQDME27YDgUBpaemZM2dOnz5dVlZGswjSzR+YL7WcBHTLshwuNmJAAEhjDwwZJz48AvTQUv26rodCIcMw+HLff//9J598MnLkyGeeeabWoMx1qcmR+RwJ2nFoyJAh2dnZhw4d+s9//kNze/7BcjPqTdCfCPr1wbCuFxcKgAAIgEBKEXCYZzTKbNy4MTs7e7GwFRQUHDx48NSpUxcvXhT5kFMF5VRUVNDpPFaKArTjQmIlZIXSWaIRizHLQQm7IJB8BHRdtywrXB2urKzkJVIkSVq4cCGpw9FN33oFaPorlJOT4/jKUFGUa9eu4aVX8j1R6NHDJgAB+mETRv0g0AgEDMO4U7OJH8uzJBSL/BoKhQYNGuQQoA8cOEAVOux13o3edMuyfv755+XLl3fs2FGSJIqHRRJYz5499+/fH/30KEfJvZo+a6IZha7rpaWld+7c4emEKEBHqQqHQODRE+CnlC+t6/rZs2c3b948ffr0Hj16SJLk8/nI6iWXCtaO6UfKuzEmKKS7pmmdO3eeMWPG0aNHxQk8r6DC7WloIsa/CQ2tFuVBAARAAASSgwBpQLZt7969m0YuVdjqGsuaNm2alZX1xl/e6NOnz6uvvrpo0aJ169YtWLBg6dKlR44cOXr0qPgq17btcHXYMAx+pysq1KZplpeXkxqFMSs5Hir0AgTqJUCfEpLhPWPGDFmWySRu1aoVfXQovuWKrK1eAdq27VAo1Lp1a4cAnZWVxR7W/Acn0v6PvCJyQCDFCUCATvEHAN2PXwKBQKCwsHDq1KkvvfRSs2bNyHZv1qzZzJkzb926Rf6MsQ94wWCwXbt2DgH67t275JUp1iOm66JjWdaJEyfGjBkjSRJ9iESjMjWSInCpqnrp0qW6aoglP1wdLioqGj9+fIcOHfx+P0FQVXXSpEnXr1+HAB0LQ5R5XATI4eKXX375/PPPu3Tp8tRTT6mqqmkafR4oBtlIT09XVdXtdj+wH3T37t2zs7O/+eabe/fu1dpfMohDoZD4gXOtJevK5D8LdRVAPgiAAAiAQCoTCFeHg8Hgp59+6vP5SACKFJ2V/21sjnLMVkmSxEGQRklxCQSXy+Xz+bp37z58+PCpU6cuWrQoNzd37dq1eXl5n3766cmTJ48ePXrixAkerSiRyncEfQeBFCFAGrRt2/v37xf/pJw6dUr8WrdWGuIfq1pDcFRUVOzcuVNRFDLg+W/Xpk2bAoGA4w8OBOhaISMTBEQCEKBFGkiDwGMgwGHsKDQetWDhwoXa/zZVVTnsFNnirVu3PnLkiMN5OUrTg8Hg7du3HW9uO3ToQBoZx7iodRAlXxKqnHwqi4uL+/Tp4/V6yev5f7OJ//9/GvV5wvDXv/41SqtqPUSXCAQCa9eubdq0qcvl4tpI7CZD4amnnjp8+DC9lK61HmSCwJ8nQHakGMeZolValsX+xXQVioAZqNlOnz69Zs2afv36tWnTJnL67fgZsiErPueemk3M4XpkWU5PT5ckqUePHitXrtyzZw95hIleYH++46gBBEAABEAABMR1OBwLGPDSW8Fg8Oeff16xYkXbtm3JIKx18JIkKT09nWRl0W7k0S1KggZK8SxyrebLiSMpX71ly5a9e/fu06fPyJEjP/jgg2X/dzsmbKL1K970YDBI3xrSiE8mQSAQoOVY2AygN7u6rgeDQV3X2aqnqliQIoHetm1aG1y8EJcMhUJVVVV1tSfyFOSAAAg4CFAUDpo4z5w5k+Lz1PWbOnv2LHuEsBI9cOBAsU7DMF5//XV2lJZl2ePxuN3ua9eu0QwaFriIC2kQqJcABOh6EaEACDx0AmJ0qv3793fp0oXFVk3TIgVoVVXbtm1bXl4uRuGI0kpd10+fPu0w0MeMGUOniKOyI01WNZnUVVVVpmlmZ2f7fD6v10smvizL4pSA5g80hMuyPGrUKLa8ozSPDoVCoUAgUFlZefjw4czMzLqmIvRplaZpbdq0uXPnTuSMqN4LoQAIPAABetLoF0E/WErfv3//22+/zc3NHTp0qKIoLpeLTdi6nuFaNWhJkrxeb1paGp1FPyuuweVy+f3+oUOH5uXlnThxgtuP559RIAECIAACIPCQCETacuHq8B9rfsyePbtt27Zut5tlXx62HAlyLay3mOMs2nWYr/XuipVQYTEnerpjx45DhgyZOXPmmjVrFi1alJOTs2nTpqKiomPHjh2q2SoqKhiyuGI2ycriUQp+RTkUn0RcrZEr4YQIma1xPooECIBALATeeecd+pxCVdUmTZrcvHmTf02UECspKSnhPwiqqnq9XkVR+vfvL5YJBoOSJLGXFVX+5ptviv5bYnmkQQAEohOAAB2dD46CwCMiQJJWbm6uz+cjEep/DtC1C9Capq1ZsyZGATpcHd6yZYvoRi3LMi3dsfM3+gAAIABJREFUS69tHWOzuEuRsyzLOnDgQNu2bXmc5pgbogDNMW1JQJ82bZpoT0dHSXJebm4uuX+ypwyN+iTE89SFEhs2bIheJ46CwJ8hwE8v/QroxxKuDpeUlOTl5b377rvt2rWjaM4kH/Ovo14N2jF/phPJpYseeEmSmjVr1rNnz9mzZ2/cuPGnn34KBoNk7FKP4HDxZ+4szgUBEAABEIiFAH1jziUty/ruu++mTZvm8XjY24DHvugJNuFEuzE9Pd3j8dR7omPQjLJL1qnL5XK73RzHQ1EUdprmZkS5KPk6qKqalpZG3/ZRZ71er9vt9vv9qqr6fL5WrVoNHDiwZ8+eOTk58+fPz83NXbx48ZIlSw4cOFBYWHjmzJlbt26ZpkluHOIITlRN06SQ1qIbimNNMyaPBAiAQL0EdF3ft28facT0q8/LyxNntWzYU1XFxcX0d0D8K5SbmyteaN26dfy3guqUJGnz5s1itWJ5pEEABKITgAAdnQ+OgsBDJ8B256JFi/g7oFo9oGn8IynW5XINGjQoRgH6j3DJS5Ys0TSN3SplWS4uLuaPK8VBVEzT8sGWZa1YscLv91P0q/T09LS0NLLgxVmEoiiZmZlko7tqNoqS4fgaMQrQt99+m+Q8DiCoqiq5lEbOHFwuV58+faLUhkMg8CcJkENTMBgsKSnZsmXL9OnT+/fvT69GxG/xJEniCM6apvGklw3WyETk5Jl+ns8888zw4cNXrVp16NAhmrhSF3iayqYz5VRWVvJk9U92FqeDAAiAAAiAgIMAfWcTCAROnjw5Y8aM5557TpIkUayJHODqynG73V6v98MPP+wnbD169GjTpk10UThyxIyeQ9FayRz1eDxiaOm62hb5ZRK/DOZTqJHkI+lyubhaSqiqSgU4n06kTE3T/H5/kyZN+vXr17Nnz759+y6s2datW7dz587CwsKioqJ//etft2/fFo1wHvEdNwW7IAACtRIIBoNlZWUtW7aUJIkM9e7du/NkmWLWiT+x7777jn6nFN2O/mgsX75crLxjx478R4AToVBIrEcsjzQIgEB0AhCgo/PBURB4WATI4Zcjwb333nsUUln8zEdRlClTpuzcuXPv3r0jRoxgtw76Dqh169Y8+NXbSjqdonnQ8FlRUcFri3M9jgQp1O+//76iKOztwss7kEt1+/btFy1adOHCBWrDhQsXli9fPmzYsEOHDpHpXO8gTRBGjx7NVjtZACTHT58+/at/fHXgwIGJEyeKAvof759btWoFP9B6b32KF6CHUIzjLM7oDMOgpfnYNUmv2QoLCzdv3jxr1qysrCyfz+f4ekCc+jrewdAurTfI8XPYYCWDmLRmnm/37Nlz7NixH3/8cahmc3g6s74sNpt+p+I6nPzLTfHbje6DAAiAAAjESIAGHS5M/hD0xQ9lmqZ58ODB999//6mnniITtK4lc0XzkqUfSZIyMjLcbveTTz753nvv7dy5k41eGtpoFCN5iIMjB4PB06dPFxYWHj9+/MiRIytWrMgVtkGDBvXp0+eVV1554YUXaGzlwVQcasmepEPs28Fvjkk+Js+GWk9nK5TGceo7uYZ4vV46Kl6OW0LmgeMQ2wyO/Lp2NU1r0aJF165dhw4dOnjw4HHjxmVnZ69du3b58uV79+49efLk/v37jx8/XlZWZtt2ZWWlYRiVlZVsJFRVVem6HgqFwtVhen9gmiZFl+awXVyYbgE5YvOTYJqmYRjkPkJruMHGYDhIxD+BqVOnUkw8+lv0ww8/cMx6x5x09erV9DPkvxJ/vF1btmwZ/bKqqqqKiooif6fvvfde/ENAC0EgbglAgI7bW4OGJTMBMZJsMBicMWMG2cqs7UqSNHz48EuXLjGFX375hSVgGgs7deoUi0VI1+rYsSMZ3DTEtmrVis4V5S2ujRN/HF26dCm1jQxustTp36ysrM8//5yXYSkrKyN7l3wz2boVg2RxJveLXkdPmTKF1WfqnSzLo0ePPnfuHJe8dOkS6YA8E+jRowcfRQIE6iVQ1+uKioqKc+fOffnllytXruzRowe7d/G3t/TI8RxSTNQqQLO1KsuyQ4yWZfnFF1+cOHHimjVrjh8/Hq4Ol5eXW5ZFv9PILvCPUfztUKY4dedikTUgBwRAAARAAAQiCZAcGa4O0wJ6pLlQtOKffvpp5syZLPKSjuN2ux3x0Hiwo1GS5VrKz8zMnDZt2smTJyMvzQ4Q4iEe5oLBoGEYvCuWiUyHq8OXLl0S1hQ8dvjw4T8kpJycnD9C1S1ZsmTAgAH9+/cfNmxYz549mzdvTsoUj92RkjEtsu3xeBRF4R6xDayqKh1iW1SEwK+rxUy2GcTMKGluEpkQJO5TY/hzK/Hqsiz36dOnX79+vXr1GjJkyLJly5YvX75o0aLly5cXFhYeOHDg/v37pmlyBGqyhSzLunPnDvGko/zugQwSNu/J2OB3BrRkOr+2j7wjyAGBx0jAsqy9e/fSFwk0XZ0/fz63h34FbD+vXr2a5sUOAZreigUCAfIP419rRkaGLMubNm3iCpEAARBoKAEI0A0lhvIg0DgEyDHBsqy1a9fSugfsM+JyuZYsWcKhOf5Y+i8QCFRVVSmK4vf7KbKVpmmjR48m1Sl6g2gV7yZNmng8HhqJFUUZNmwYWfasW9Wa+Pzzz8n8paGXTpckqUePHjt27AgGg3wWtYFmFOzMwplcLHI6oev6mjVreGjnOczq1au5X3ShW7duiQK0LMvvvPMOl0ECBGolwI8cPUW0eH1lZWVxcfHGjRvHjh3bsWNHTdNcLpfH4/H5fLIss5OU+FjSk8nTSE7wJFZMkF8Vf5D7zDPPjBgxIi8v7+jRoxUVFeyCRG9fuNkODVr81VCaS9IuG9BiSS6DBAiAAAiAAAhEJ8CmZigUMk1z9+7d7733nt/v5xGNxkFeYpftQMf4yLtut7tbt255eXnXrl1jyZL8EkjpJk+F6K3iozRw865t2+SQK+bQUGgYBn3AxCMphaiikuXl5dQY27bv3r1bUlJSKGw5wjZ06NBhw4ZlZWVRj9izW3QQYSOBwsRR0Dn6tom+YnRQYoOBKf3JBDeAJw6SJPEixpIkUTwBmi/QGhUcyTozM3PgwIG9e/ceMGDA6NGjly1blp+fv3v37hM1Gy2ZyI7q9DaC5Gld1/lpYf5sYnEOEiDweAnQp43PP/88R9Fp2bIlv2sRDWbLsuoSoKkLhmE4vKPo69v//Oc/j7ePuDoIJDQBCNAJffviq/GwQmK/H2TbWZb19ddf0wBJ9iuZpKS90rd19NFcIBA4c+YMu114a7Y5c+bQOBr9urqu37hxQ/xmUFGU6dOnky3uGIkdu08//TSFz6OPLql5n332WeQVSXomtwhypaE5hqNCx0Ny7969HTt2OPw4/hDKly9fTkKheKGjR4+KArSiKAsXLqQCsXAQq0I6/gnQo+J4YB6g2fRbozjOX3755cKFC3v27Ekvckhr9ng89HEAzxj561pyXqbfJrs18UySEjxLdyRee+21Dz/88MiRI3fu3BFfyTieVXbKZlejyJ8M53D3KQcCNANBAgRAAARA4AEI0AvRPXv2vP/++y1atGDJxrGybnTB1OVyybI8YMCAL7/8srS01LIsfs9qGAa5ypIGHb2FPO5TEAlehoTPcng58AAaudYIBbNiT14SUtmi4ATX7EhQzeSFTasIXr169cyZM6dPny4uLv7oo49Wr169cuXKVatWDRK2J554ggwJ9qYkbmw2RMfIR9PS0ijSNAX94HxeHoZz2G4RJWlaiELTNFpKkQrTKwRS0yifGknvy+k1PFfrdrtdLle/fv0GDRrUt2/fMWPGrF69muKgbNu27dixY8drtrKyModJ48AYb7uJ1dp4o5dY7ZkxYwb9NSOTfteuXezgz0Y1CdCO3yyF4CBH6a1bt9J8gX8akiRNmjSJ//IkFhO0FgTihAAE6Di5EXHdDHrjzX9tHWIK+zXUa8/FdScfbeN0Xa+qqrp582aLFi3IaqQVXdLS0rKzs2mMZODUtNdee43WOqOSHo+HrPxYGn7w4EFy7WQzdNOmTeIALKYpDF9VVdWMGTNYU6P1vl944YWSkpIoN5rqYV2MEmLljlADN2/ebNasGUU8SEtLI8s4Ozs7slOmaQ4dOpR8Pdiy58DT4iUiz0VOIhKgqM3iw0bOU5EOOJG9Mwzj/PnzmzZtmj9/fr9+/Z5//nmaTfE6nOKDTem65of81ke0Pl0uFzsT0TPZuXPnCRMmbNy48dChQzdu3IhsUoNyxF7XdaL4zIvpusojHwRAAARAIHUI8EtN9vxl1+BwdTgQCJSXl+/bt2/SpElNmjThT3z4Nb845Ilp0RFYkqQnn3xy7Nix//znP0tLS+mK4ngUma6Xf+QpjgFRLBClNi4WpUwsh7ge0bLlzCiJo8L22Wef5eXl5ebmLl68eO7cuYMGDerSpcuQIUP69etHMjEZ9syZJDMyiUXrnQuIcjO/MuejkT6bdMjtdvt8PrqDHIeE1DdZlp944gnymGYbmyt0vG5ne0lM9Be2VcJWLGwicBL3w9XhqqoqWorDqNlo7lOXpUcvErge8dmgx48fe3ptwC9C6BSawPJd43qQSDIClZWV3377Ldnn9HMYNGgQ/YQdPR08eDA95+KvJj8/n4q9+uqr/CughMfj2bp1K2vZjtqwCwIgEAsBCNCxUErRMjyKi/0nt1zKIU8EcfgXSyIdnYCu62PHjuVhj8y4cePG0Vk8T7BtOxQKHThwgMxT/hhw+PDhgUAgFviWZW3evJkcIuhtsCzLBw8eZAvMkeBLt2jRgnU6MlUpkF+tDwY1m6oSzXRRg44EMm7cOHa3oQ4OGDDAYS8Sgb179/p8Phbr3W73q6++ShUahiFehdoQeS3kJBYBy7I4BKToX+/oBZc5evToxo0b3333XQrizCajKD3Tr4wPcYLy6zrKP1KelWma1rdv3z/elOTk5Jw8eZK+7Ivx9+ho/wPvOn62vPvAFeJEEAABEACBZCLATsdkK7Kod+TIkfHjxzdv3pwHQbIt2Z2W88lC49e05AahadpTTz317rvv7t692+EqUe+ndfXi5bFMTIhn1ZUvlhGb4chv6K54uQdO80XJwKYQfHQ7+KYEg8Hff//91KlT33777aFDh4qLixcvXrxq1aoFCxasWbNm3rx5AwcOzMrKGjlyZFZWFq0JSbeJQ/Nx1C/P/za+jyRSsw1DHtB0uymeNa007vf7SYZzfPLFcwHRWKorzRetNSHLMtU2ZMgQCgYyZ86cefPmrV69evv27QcPHiwuLj58+DCvSEno6DGjx5gfObIMma04IbIsq7KyktiK+VSY7yOfi0TSEOCvFiorK9u1a0cPIX2icfPmTf65cX8dAjR9EFBUVGTb9m+//Sa+6aGq/H4/P4FcCRIgAAINIgABukG4Uqsw6Xrh6vCuXbuGDBmSlZU1ePDgsWPH5ubmbt++/ezZs7R2Fq2VTIVTC9Cf6K1hGAUFBRyUmT51bNq06b///W+SX8X3tD///HPbtm3JMYHsRU3TTpw4EeP1/wghnZ2dTWMqLSAjy/LVq1fZAnMkqNpDhw6JEw9FUaZMmUIjd70CNFUoytDiJah+Xdd37NiRnp7udrvZp7tJkya//fZbZL+uXLmSnp5Oxi4VlmX5+++/Z1MeAnQktKTJ4Tci/ORcvXr10KFDW7ZsmTt3bmZmplazpaWl0bMhznkUReF3NmK+I83zKDGfp2qSJHXp0mXEiBGzZs3avHnzkSNHeFF4Xmve0chHAF/8TYnpR3BpXAIEQAAEQCDOCThUkkAgUFRUNHHiRL/fL/rMknFYq/QsDoikGz733HMffPABf3xGUdeIA0uE4ngUma4XWuQpDgFRLBClNi4WpUyDDnGFDU3wVXi6xDmUEJcHpBzRv5K7z0sIhqvDXODEiRNnz54tLCz8Y1KQk5OzdOnSJUuWrF69emDN1rt37/79+3McD9EcEtPsCMKrsLDizAk2k+pNiI8Np6M8YPSFJSt9Pp+P2+NyuZ5++ulu3boNHTq0X79+S5YsWbZs2YcffvjVP77avXt3UVHR999/T97T9PhR7D5xkiL+Cthriu+g40ZgNwkIiM4r8+bN4yfQ7XZv2LAh0sOJBGhxuSO32/3TTz/dunXrs88+40eR63nvvfeSgBK6AAKPlwAE6MfLPwGuXlFR8cQTT9Diy6TIiGZE9+7dp0yZ8tU/vrp48WICdCZummiaZtOmTcnU4/DKBQUFtL5KKBQi4zIUCt2+fbtr166iFiZJ0vz580UDK3q3TNN8++23yd+BPr6TZZleEbMRJiZs2zZNMy8vzyFAb9261bZt0QU+8rpiPXUJ0GRDBwKBli1b0oguy3LTpk39fv/27dsj67x79+7AgQPpS0/6nEqW5VmzZtFKKeQlAQE6klvS5JSVlW3fvn316tUTJ05kVwW2BdlqpEkR5fv9fp7McMkoCXFCJUlS06ZNs7KyJkyYkJOTQ7M7Dtoerg5zREsmLEYloplkuDosTnu4ZCMmxN+amG7ES6AqEAABEACBBCVAUsutW7cOHDjw/vvvP/nkk+IgqGma1+sVc+pKq6qalZWVn59/5syZKCjIanWEOBDHJkpHqYEORZ7CCmxkgSi1cT1RyjToEFf4YAnxWqSRcWgUWiCRAlCQ8UD2A/l8iK+3yddH13WKeU23WHTq5LvAHsSi40gwGLx8+fKRI0d+/PHHoqKiLVu2rFixYuXKlUuXLp00adLAgQPJJfnll1/mkCyidRR7mmVrTtB7DvqXnAZ4LhnpOkBXdzyQVF7TNI/Hk5GR4fV6KUeWZbfbnZ6e3qxZs0GDBnXu3HnAgAGzZ89evXr1/Pnz165de+jQoW+//fbUqVPXr1+nNS35Doo3JYHSid7+h42af1/nzp3jp0jTtMzMzEjLfPDgwfRg06IvVL64uLiysrJbt26Rj+KXX35JCx097F6gfhBIYgIQoJP45v7ZrpHAV15eznGRHKHf+M86JchInT17dkFBwc2bN8m0IrEm8i/+gzWO7LMHOzeuzsrNzeXFqYneyJEjbdu+d+8eGZRkcV6/fv2ll16ibx5Zg+7bt29D+9K9e3dab42WGXnhhReiTBKo8rlz5zoMUFp70DAMspWjtIFto1oT5DKTk5Mj+uDIsjxlyhRyD6GayYy+du1a9+7dyWbldb179eolfl/puEqUhuHQQyLA6wXVWj/PHunNCk2HOJNeeNBTUVZWdvDgwaKiohUrVnTr1q179+7id6bRY1O63W4yIh2TalKoKWqzuPCOWFuTJk0mTJiQnZ194sSJ0tLS+/fvU/Oi/Ez4qaMu8y5HCxHPrRULMkEABEAABEDgAQjQCEUrJdi2TaMqC5GBQMA0zQMHDkyfPp3HUHH4c1jviqKwec8jo8vl+kOvWbJkSWlpKb2C1XVdHOlqbbY4stdaAJmRBESqUdwpqJjo28FmRmSdfz6HNe6SkpLjwnbixIk/IuTm5OTk5eXl5OSMHDmyd+/eI0aM6N27d1pamiRJ5MLMz5ioQZMlRoHRuIAjwU+gI593SXd2FCPzj8tQM7gkOa/wUb/f/8ILL/Tu3Xvw4MG9e/devnz5ggULsrOz165du2PHjsOHDxcWFv7rX/+6ffs2EWaYFNOGbgRn0nyE57kUe5q/k9N1PRQK8VHxLMq0LOvu3bu8QE5lZSWX4XQwGOQaxKdFTPNZSDCWYDDYvn17uu/0J+7333938OnYsSOrHLROjCRJhYWF//73v+kUcQaqaVrk3XdUiF0QAIF6CUCArhdR6hYgJcUwjFWrVolaIQ/hkQka7Ck/Kytr8eLFJSUljvE7dYHatmEYlZWV5eXlTz/9tMhKkqRI15IzZ85QNFu/30+joKZpXbp0uXfvnl6zsQtwvUibNm1KHgf0zV3v3r15eI5MkIfyu+++6xCghwwZ4pjk1HXdyDrFHNu2Kyoq2rRpQ/Xz0P7TTz/ZNYhIkbRt+4cffnj22WfJMvB4PPQQdurU6bfffqN4u2K1nK6rVch/xAR4Ikomu2maoVCIPPfpAf7xxx/XrVu3aNGiCRMm9OjRo3Xr1vSjcLlcNGNxuVx003kCE/k3J3oOfTXs+K21bt26b9++c+fOzc/PP3bs2LVr16ipoVAoXB3mZhMufq7qSkQWizKBfMS3AJcDARAAARBIbgKsO9MHOps2bZo8efIzzzzDgyPFXnMIdnyUE/QSV1XV3r17b9++/cqVKw5ujqHNcRS7D0xAtC4ckEWDhIpRAf6XMh/40rGcSPopX5HcP3k6QK8lqB4WScV41t99911BQcEnn3yyePHiJUuWTJ8+fcSIEb1qNlpanIx88pJh8Zo99BVFYWdnctzh6IUulysjI4MeYDL2aELB0wpylyYzkkVG0SCkNPv38G/BVbNpmkZn+Xy+9u3b9+rVq3PnzoMGDZo4ceL8+fMXLly4bt26nTt3FhUV7du37+TJkzQ3YaTkrEMLfrIbOy9bous628PMjY+ydzzVxt+8VlZW8o3g1w+P4BngTiVEgn9Q4erw7NmzyfWKZsEHDx6k12ncEXqE3DUbPQCKonz//fcrV66kXU3TMjIyaBqSnZ0N2owOCRB4YAIQoB8YXUqcSBaGYRizZs1KS0uTZZmNAx6nHQlaBIMD9dJr5/79+3/66adnz54larTqcUoQ/L+dJBti8eLFvJ4e2T1jx44lD1AS/W3bXr9+PS2NTZEEfD6f3+93BIlmi+T/XsS5p+u6GABOkqS33norigcxabvz58+nBvA3d2lpaStWrHDWXvc+WwCOxB/uAAsXLlRVlTRl6uAbf3nD0Z3NmzeTrUklqQstWrT49ddf6ZqOanm37hbhyOMhcPfu3RMnTuzbt2/OnDmDaja6m7Qwpt/v93g8PDfgBL/0onmF4+9MlF3+nJMcvrKyst59992PPvrom2++uXr1Kjn1OEBQ3AxHJu/yo1VrgorVeogzuSokQAAEQAAEQOBPEmBdkl0jt23bNnPmTPpgTvxsXFVVl8vFA2utQyeVeeeddz7//PPKykp6VRwMBskqC9VsFPyBBzVuwJ/sCE6PYo0TbUYkwnekucyjTNB3inRFNuAtywoGg/xSxLZtcVf0BXZE462srLx06VJxcfEnn3yydu3a3NzcpUuXrly5cvLkyUOHDh0wYMDQoUO7du3aokULWlCONGKaoWiaRl7V5LVAUiPFOic7sNbHnjJFLweyNlmPpu/nxN+OaKzy0u7kbS2GfVMUpU2bNn379h00aFCPHj1GjRq1evXqpUuXzpkz56OPPjp27Njp/8fem0BHcXR7nllZztpcJaEntmaxm7XZ3CB9PEDwhJAeQtCsn83iwWCPMR/HH9gDGB0soRZIGhbRgGEMhjE2DGD4DNgeL/BYDyA0EstBYB9A0GCgWQ8YeGh7taqqciz97etwVqmQAIGEbh6OiMyMjIz8ZVbmjX/cuHH8+J49ewoKCgiUOIs1bURURppKFKjRToQMLT4GT/PW1/FzERZVVc+cOUOtCZPJNHHiRE3l8RiYzWaxi27Pnj3t2rUTnxD0VZw/fx6FawrhVSbABGpEgAXoGuFqiJnxITxx4kTnzp3pJR70Ww7dR6NQ42sNx1tMCJacnLxz586LFy8+gv16pHKpp7cB1+twOJo0aUK97ghWe/jwYVwUJtOYNm2ayWSCNUMBBPr373/t2jW6dgzyotUQiStXrsBcIxl66tSp9HkOTMAo3Lx5Mz7GMO9kWTYYDL9OrJ2dnR3iXOKuwJLps01jQiExG43GnJwc8djU1FSSEUmG7tOnz6VLl8gyC1G+WBSnnw6Be/fu/fTTTwcOHFi/fn1WVtaECRPi4+PFG00O73h7iE4o2AU/F9xuyqPJFvTNg42YzTImJiY9PX3hwoVbt269cOECvE5gvsO1JMR0qeSEoiFW1ZNGz3P1G5CaknmVCTABJsAEmAARgLr0UPMYTnxOp/PEiRNTp05t3rw52eckn4l6SlWfTovF8upfX929ezdVoKrvIAtehOiJJ6pjY4Q2M554lcQCA7vt4WtPeQIfV9E6omwUbw2uu9CsyRFY3CsegjSsOJwXQS2w/ezZs4cPH87Nzc3Pzz9y5EiWsMyYMSMhIaFHjx6JiYnx8fFt2rSBZCwKx/Cswm+HfkE02Qx+NRC1Rd9qGpMntpJEYxWt3cAfHVxxkRMu3tQ6kyQpJiYmPj6+b9++/fv3T01NzcjISE1NTU9P37NnT15e3t69ewsKCoqKitgDOvDx0GyhHxS2t2/fHi1Kk8nUtGlTakViL91lSZLCw8Mx4HjdunXYjhmwkA4PD9eUrDkvrzIBJlBNAixAVxMUZ1Pv3buXl5e3ePHiDz74YMCAAVarlZRB0d6ltPjpRRc0Xuv0HtfpdG3atBk+fPi0adO++OKLn376ifrDxf7e06dPr1q1asqUKZGRkZBQFy1aVB/vByJ87dmzB9NlEKjevXuTMVdQUBAVFfWrzkvyK6yTMWPG0AAuXHugwVcVk5ycHLoXuAULFiyoqo0hFhIfH089/2SZWSyWqKioEydOoP2DMGc4KtBIpdJwOr/f/+usDrt27UJ9qPAOHTqQOHjkyJEePXqQTSbLclhYmMFgGD9+PJVWNxMwph0Oh8vlomhuuGtXrlyZOHEijOD4R13i4uIGDhw4bNiwUaNGZWVlpaSkLFmy5JtvvjksLEePHj1w4ICqqrDpRWcTtF5UVYU3U4i/NMsNRUQB8Fu3bkFi3rRp00cffZSZmTllypQBAwZ06NCB3OQ1CdFMh0BMDxI9k3jU6WEgf2faghnSMZRSp9Mhf3R09JAhQz766KNvv/22oKDg0KFDZBdqEk+/2YwK1M2nlGvFBJgAE2ACdZYAZsIgCw1RnkXjCrv27ds3bdo0TRcvfVWRIEUMsTXI5tTr9U2aNJk5c+YPP/xQIw54ZmwfAAAgAElEQVT8aasRrkfL/FDIGgvn0c7SkI+CWX7w4MHjx4/v27cvPz9/3rx5ixcvXrp0aUpKyoQJEwYPHjxo0KDo6OimTZsiMAicqGDf0q8MwjR+VtS8xY8OnkP0AxRFTDpcTGA8KI4Shy80atSIGtoUkg7OSXq9PioqCl7hSUlJs2bNmjt3blZW1pIlS5YvX56fn3/gwIG8vLzCwkLcazSrxZaj+CBV9Tw89GmkA9FzhrG8NJFm0NPRIU8n4XK5Vq1aZbPZzGYz3OQ///xzOO+jeuhFQGsFfQ+KorRr147aLxjYLUnSe++9R2/mp1N5PgsTeF4JsAD9vN7ZJ39dmsFWCPt16tSpb7/9Nisra/LkyQkJCW3btsUrnrqF6ROr1+vNZjMmmYWXNH2bKU/79u3HjRu3bdu27777bv78+XFxcXAEppzoVVYU5clf3tMq8b333pMkCSIajJL09HSogRkZGZD1AQRSncFgmDlzJqLTYjQWaip+10PX/euvvybCaId88sknIQ4nsfjEiRN0p+jewQ9akqSpU6deuXIFAaPFZ6OqytAZx40bBwMLVtSvgT4yMzOhdWZkZOCMYWFhqDNUyA8//JD006rKryPb6TIxL5DP5ztz5gweewptTGZN9RMwfPV6PWRcgkM/DXIiJj93g8HQs2fPIUOG9OnTZ/LkybNnz05PT589e3ZmNZbZs2dnZGT07dsXU4pjAC9Z2PQ4IaERncVV8QIlSYIfvTjfEfU0YGoa7BJF6sjIyJ49e86YMSM7O3vx4sWbNm06d+4cZHSghtUbODqYbGsWoOvIT4OrwQSYABNgAqEJ+P1+cSoCj8dDEQz8fn9OTs706dM7dOggfiU1X2Ra1XyyrVar2WyeOnUqZhwRbZXQVeK9T5PAQyU/sm0emvNpVru+nIvcmyBDwxmWWj1V/SjsdvuFCxfy8vIKCgr27Nnz2WefLVy4cMmSJR9++OH48eMTExMHDRrUv3//tm3b0q8PHtOIDYIg7LCBLRYLpmokZRmHoJlAJj1au+IqDqfGEQXbocORIBUbq2h3wO0pMjJyqLAsFJY8YdE8YBTxA+KyJ+QiPgaiJP1sw1UXFhZihCU6EkaPHu0t92IWJW+5V9NOIQ1a3I4bEThXk3i9nGYCTKD6BFiArj6rhp7T5/ORd2cgC3yZ3G73tWvXcnJytm/fnpKSkpiYGBcXFx4ebrFY0EuMv0FNZ+hW0NHEDNCkLBYLXCONRuOIESMCK1D3t0AjQzcsPmYGg8Fms506dWrfvn2xsbEiIgTGDQ8P37hx42P2uH788ccwRDCfhizL27dvD4ELp4Mb7/79+1u2bElmk8lkwuA1m80GaXjmzJnnz5+nSdirKpasOofDgcs0m82olclkOnHixK5du6KiooxGI2IRYpder4+MjNy8eTOKJQf5qs7yzLfjMh0Ox+bNm0eMGIH5tXv27IkuB01MbVGorWYaWOhugqQ4MFDMACsKKj/cKDR7Q6/iEaXbZLVaYY2RQRx4eOBVkAGHzOTdjK4XTVEtWrRITExcuHDhjh07fvjhh+PHj9+7dw8dDz6fj2YDD9EVEWg3k+ks7nrmzwlXgAkwASbABJhACAJQopHhwoUL8+bN69Gjh6Io+O7DHVLzDQ38KKNDuk2bNunp6QcPHqQZnu12u2ZQXYia8C4m8JwRgO4M+xA/BLGdBa8FCvdB7Rf6+QTSgKBJvjhut/vq1avHjh3btWtXXl7ed999t3Dhwrlz52ZnZ7///vtxcXGDBg0aMWJEVFQUfrM0TSimWxS7jpCG8Uy/d/LJxfBibKe9aEdTHrPZLLapNW8Jjd2u2Yu5IvE3Q1gOCgua/6Krh4YPKdHIg7+aPLW9ipcnRH+j0Xj37l3c97y8PGqnIAECGochs9ncqVOn6oe+rO3L4fKZQH0nwAJ0fb+DT7v+Pp+PJpDF5xljbVAPfIcQAaC4uBhfdLfbfevWrWPHju3cuXPs2LGasUgGg4FELvrykTskbUGiXbt2K1asuHHjxtO+7CdxPp/Pt3///sroGib6wkVEREyZMkWSJKvVir5Z2jV69OibN29CCBZ9n2tal7lz56JMaMeKouzdu7c6heDzfPXq1dGjR0uSRL7tiJNFVossyzNnziwuLg4hEEM9dDgcubm5kLNNJhO8ADp27Pj222+jhvhLPfzjxo27evUqDT4VDcTq1P8p56HLP3r0KGZMNhqNmNeCLhlTozzaXzFuHUDRqECiFxYWBi9pqM/ifClBNV86MDCBDgaaTFz8kcLkpZYwjqXnQUyIhp0kSc2aNevVq9fAgQPfeuut1atX7927d8+ePadPn8adwvPm8XgQOYR4IjA6mf7oCRObBNglSsxiWjSLsf0pPxh8OibABJgAE2AC9KmqDgpvudfhcCQnJ3fv3l3zgabObM12zWrHjh2zsrKuXLkiRtPCpIX0ea1OTTgPE3ieCIgPP9oXaFyITQyaU5Ei2sGHNygHim7h9/sDZxlxOp12ux2St7tyQSEUehGrpaWlR44c2bdvH8I9L168eM6cORkZGenp6fHx8TExMUOHDu3Xrx9iUeKXTnHqYPDD2QsbjUZjeHg4xXKkIZJkn9N4YoSlplYJBY5HzsDRzJqXDEqGPi7Lcj9hSROWA8Jy//79p2aK49a4XK41a9bAHQdM1qxZg9u9a9cusZ0iatB0Uejz++STT3w+H/ymgz4GvJEJMIHqE2ABuvqsGnTOsrIyyEOqqhYXF0P9oUD+CFqHsLP0Cb979+7u3bsXLVr0/vvvDxw4sEmTJuK3EN8wfOECv2f0SRN3KYrSvn37X375RaM91Zcb43a7lyxZgg5YXBcERPEDj2mdmzdvvmHDhupcF8iXlJSEyPzuu+9irBbCHRgMhnPnztV0PNTatWutVqvNZkMIDnzIcS2QJps1a5aenk6u0OQIgIrBl8fn8y1cuJDMGnzUYQbp9XqbzYYnxGQyWa3WtWvXojRYKlXZK3gYxL8hUNTqLvqBTJ48WXxuEXeC4q6Iux4nDXooQbQp4emAvYG/L6jGZG/BbKW/mvqglQv1XLMLDy3c1Y2VS8uWLXv37j106ND4+PgxY8bMnDlzwYIFP/zww6lTp3Jzc6tJXrzXYro6InJVrwWxnGpWg7MxASbABJgAE3jiBBC1jIr1lntdLhdUMETecDqdhYWF6enpGHyG7y85SNK3nrQn6hum2FaJiYnz58+/d++eKKKJ30ExTTXhBBNo4ATwuwgKoSrzUsxcVR7x50Zp8cCapmkC0uPHj+/YsePYsWO7d+9evHjxokWLMjMzU1NTZ82aNXz48KSkpJiYmK5du4rWO71AxISYgaRqUqID9wZuoXacZheVRgI3Wijkkd2oUaP+/fuPHDmy35+X+cIyZ86cjz76aPv27QcPHjwkLCI30v2hSyBqJSKFYtDkzZs3w8PDyUm8a9eu6A48dOgQNYg0LSYRkSzLly9fdjqdKPOJ3Eex/pxmAg2NAAvQDe2OP8r1olOX5GZ684rWrdvtzs3NXbdu3d///vfExEQKcRUoOtP3iV7utEVMaL4EpNvGxMTgc0LVeJRLehbHeDweODuL3aqyLCPuM1oROp1u4sSJd+7c0Qi4IeoL3ZN0/8Cc48ePxzBM2BMGg6GwsBBNnWoy9Pv9Dofj1q1bU6ZMgY8trArxfkHE7Nmz56lTp2CHaaoErfztt9/GncUnHyjIzdZqtRqNxnHjxl28eNFb7nU6nQ6HgyoZaN7Z7Xb4MpBvQmCeQCC1usXv92/duhUdCfgLywwu5BpiD101Go0QdocMGZJQuQyoXOLj4xMTExMSEgYMGJCQkDDw9yUxMTEpKSkhISExMTE2NhabcUj//v0HDBiQlJSU+Oelb9++GRkZs2fPFpwV0tLT0+fMmZOZmTl37ty0tLR58+b9Gqk8JSUlKysrNTU1Jydn165dOTk5hYWF1XEHIGm+VslXVXiI56eqQ3g7E2ACTIAJMIEnSwBD0clKocSDBw+85d5Lly5NmzbtlVdesVgs0JcRQBaGBAbUBxrGsCL0en1CQkJWVtatW7cwR4Jon2tsZv4mPtnbyqU9HwTwuwh6LfRTDboXG6vKI/7cKB2inIfuohOJ7UT83jH/OUYNIhsaYohid//+/VxhEW3+WGEhsRhNMxJtNQ2WoO8isXkbNIOmEHSwaeJdVHVGNDNRPRoAiswtWrQYNGhQfHx8dnb2/fv3wVB8B/r9/pEjR4olX7lypbS0tKCgoDoC9Lhx41BmjdrOD72VnIEJNFgCLEA32Ftf4wuHE6vb7Ybk53K5Ll269Pnnn0+fPr179+6Y90BRFJPJhHnk8Jmhfk7MgSB+e/BxEr8HgXvFLYiYbDAYNMpmja/kGR3g8/mio6NxRfTBI6cVSZL69Omzfft2GCjVrCPZFiHyJyYm0kkxoXONBGjqeEB3cU5OTmxsLHlAQz0Xg4c0btx4x44dFIyFKgbDqFu3brjvIgESoPv167dt2zbMukODRsliI6sLZfr9fpfLZbfbYYRhsnixtnTqp5OgznaPxyOMNjtw+PDhHTt2HDhwABGNH60yosIuchDTmpLJ9gJAcV4jMSccB8QIy9gbWLLIFpoy3QKxQDFGs7fcCyyB5WsOqb3Vqp6f2jsjl8wEmAATYAJMoCoCNCbM7/efPXt29erV0dHRsiybTCYaGYbRZpgYg6xlSsCoa9Wq1cCBAzds2ECRygI/3KiD+B0U01XVkLczgYZGAL+LoFdd1c9KzFxVHvHnRmnxwMdJwz8Mp6ZmgqqqZWVlZLFTAo04DCgM8Zcq6ff7c4UlQ1jihUVspwemA9v4NHRSp9NRZxuagfgb1Pla8+oLPBFNaS5J0ooVKwKFguXLl2M0MKq0evVqVVVzc3OpNaqpKp1Rp9N99tlndJtEPrSRE0yACdSIAAvQNcLV0DO73e6ysrINGzaMGjWKAvXiMwA3T/GzATFa/EhU9XIX81Aar35alSQJH6oOHTqIAbzq1y0hx3C0MUi3bd68+bJly3At1JCozqU5HI6TJ09u2rQpRObevXvDmwZIFUU5e/asx+Op0UcUIi/V7euvv46Pj4dXr16vDwsLIw9ufOA3b94M+0asmNPpNJlMqAZ98mno1urVq8X+fJhKOJyqKpaGtNPpPHv27Jf/+FLUPQOzPYUtMHcQYDHo6TD2NoTZp9mlMWcRy8zj8SDWDXUIIQg7jsUh0JodDgc2Iuocxo6JnlBIQ0oWI7mj8pqzUzgU/PqCOjW73W4KEO/z+eh3qrmtQeHU3kZ6eAKvqPZOyiUzASbABJgAEwhKAAO8Zs2a1alTJ7j1wUiDZUh2r6iAaNKDBw9es2bN1atXacoEt9tNoTwCTyp+B8V0YE7ewgQaJgH8LoJee3Wsx6ryiD83Sgc9SzU34kTwuaFDnJUL+Z3QdkpgehV4nFRVVcocOoHWB9yMxAaIz+c7KiyZwpIoLC1atMD8NGgRY94asUlIrUK9Xq8oCoUbohejJgG3a2yEzhARERHYJHzw4AHap5h1KSoqSlXVgwcP0qkDi6VwoHi1Qtanm/iYGENDfujeZ3v2h1aPMzCB0ARYgA7Np8Ht9Xg8eM9qPmN79ux59913IyMj8XK3WCwUeI5e2fhUiAY0tlAGzaxl2K6Zk5BiO+h0OpJrKUbtpEmTfv7558COzXpxn8rKysgfPDw8HCOPzGbzjBkzxM7q6lxLaWkpDtm0aRNUYCiwQY9t2rQpBm/iKytJ0qlTp8Qu8aBHVWfjt99+26FDh8BRWuiH2Lt3r8vlEkM0OBwOzKRH33s8IZMmTbLb7SGMP7EyqDkNZd2yZQsepO3bt5PiKeavs2nRiKkqTZVHBlKoxe2U1iQIERWuySCK0TUyZahASlDFahpbPLBKvIUJMAEmwASYwHNAQPywwj65du1adnZ2x44dEVgD8goEF9FFA2MKaagZYtk1adJk5MiR27Ztu3379nMAhy+BCTCBRyBAhneIhFismI1cVcRXk5j5KadzhUXQqzMRchB/abYktBw1q9QzJwb87NSpE5x10MzBVbtcrlf/+qper8cobaPReO3atfz8fBQrvn7RqDQajUiMGzfO5/MFdbsRcQEp/jocjrKyMmqTogJi5sA0vHbQTwBXHnLoEZ17aHBwVaNaA0vmLUygDhJgAboO3pRnXCUI0Bhcv3PnzjFjxjRq1MhoNGrezqLQjHd04F9Y1ZCPxbgcmpyi0IxddC4679ixY8+cOYP5iJ8xoEc9vShA0wWmpKTAgcXtdlfzcwL93eFwfP7558AVHh7+6aefVlUvCNDiJ/b48eOPaXx4y73FxcXQgrOyslANdDDQpY0YMQJVwkcUMcgCJ8GbNm0aacoPrRVykinw6aef0rP0ySefqKr6bJ1tq7oFQbeLRmFVaToQGUjnFbdTWpNgAVoDhFeZABNgAkyACTwFAk6nE/YMZIv8/PyUlJTo6GiyaRHJlOwlTNSBVfJUwOTM7dq1Gzt27Pbt22EAezweGEJP4Sr4FEyACdQ1AlW1F8TtYp3F7XVNgA6sp7glMH1QWDSC9dChQxMSEuLj40ePHl1cXIy3JTWafD6f0+n88h9fii7VK1euXLhwoTh0m1qUYuKnn35CTX4dBT5r1iwh+kj8kCFDJkyYkJKSsnTp0vnz52OOnJ07d+bm5paUlKiqarfbaZjp3bt3UQ5GwGjS4oudXADFsCoaGhgU+9BWs+YoXmUCdYQAC9B15EbUoWp4y70nTpyYMmWKwWCA5yxexLIsIyYdvZcpCgciOlH3Y/PmzWNjY/v37x8fHz9w4MAPP/xw9uzZS5Ys2bp1635huXjxYmFhYcuWLcnappLhB202m/V6/aRJk06cOEF+2fX3bSsK0DSn4q/NEswXoaoqrrE6j4LD4Vi7di3mA8RNOXz4cFUHigI0xh/l5uZWlbn628kP3Vvu3bVrV/PmzcXbhwvEFIIo0+PxlJSUkO8zdWUfO3YMActgJD20AnTeNWvWGAwGenjy8vIeemydyiAahVWlqcLIQLaUuJ3SmkRgmZoM7AEdCIS3MAEmwASYABN4fAJ+v//nn3+eNWtWx44daWyfxkwSV3U6naIoJEm3bdt24sSJu3fvJpsHccnqrw38+Ei5BCbABAJt+8AtIiVxb90XoMXawo0GTsEulyuEgxFektBkce3QcKnRBP/iCxcuSJJks9nCw8MVRYmLi8vOzg4hQOt0OkTqgN/x0qVLEaafGrDiwG5qjeKtrigKDWGRZbl169b9K5dX//rqe++9l5GRkZqaunTpUggjR48e3bVr1/Hjx8XJhNCLiYuCgxqAINoSgjpW03FNfB44zQTqAgEWoOvCXahDdVi7dm2PHj3w9qRxLpowTHjJhoWFdezYMSkp6b333vviiy+OHTt24cIFxFuw2+1Be+0Qi9bz+zJu3DgY3DTOBefFvHZmszk2NjYvLw9H4etCvYJ1CFm1q+JwOOhbZbVa4UJ+6NAh6M4PHd1D5/GWe1esWEGhS3Q6Xbt27WikD2WjhEaAtlqtBw8epL2PloCDPG4Kav7111+LTSm4vR89epS8kr3l3rKyMnqo8P3W6XS7du1CHWB2PLQ+uNLVq1dTBGpJktq0aeNyuepXw0xjZgVdJRrYS7aUuJ3SmkRggZoMLEAHAuEtTIAJMAEmwAQ0BILatJo84uqqVavatm1LbhnokhdXNfYSVmEST58+PT8/Hx9osUykfT4f5vAI3MVbmAATeO4JBNr2gVtECOLeuixAi3WuaRriAOQCOrasrIwaTWiuOhyObt26id2BM2bMoD4/zTtZlmWj0Yi5Cr3l3lOnTmkyBF1F0x5ueVQyDQcXD4G0YjAYSAOBz59Op+vXr19cXFxMTMygQYPGjx8/e/bs7Ozs5OTkRYsWffHFF7t37z5y5MgznNqdCHOCCTwyARagHxldvT8Qr2PMLXb9+vXU1NTGjRvTy5FeiNBM4ewsy3KXLl2WL1++bdu2y5cvh+iNJDqYohd9j1BaHQ7H5s2bW7VqhZIjIyNp7GFYWJhOpzMajZMnTz558iQV8nwk3G63zWYT+0htNtvatWurGk1J4Z8wyYPdbne5XB6PZ+LEidStivu1YcOGEPo1pF78Rf6tW7c+sviIA73lXnzvveVe0r7ff/99en4kSTKZTLm5uWT64BnAZBFUJUVRPv30U/qOUubAO47TuVwuu93+97//HdNWkCP59u3bi4qK6pcAHXiNobcQnOpfZvVzhj71Q/eKdRPTDz2QMzABJsAEmAATqOME4G5GlUQfPE2VDO+8GzdurFy5cvTo0Ro7p1GjRhSzzmw2Q4Y2GAwkT5hMptatWycnJ587d64qg1A8NT6ytIUTTIAJMIHqEGho9rl4vWhKz58/Hw1VvH579uxJ72GxAQtdApMZotmblpZGYgUCT0NlFoetUJuUitIUjjmTaG/QuWdpb/UTYWFhXbp06d+/f0JCwgcffLBo0aLk5OTFixfv3r37+PHjO3fuPHTo0JkzZ4qKivCQiG1Db7lX/Lph6iZICuTzh/zQcxBcG4eI5dDjBzdtzFFJp0OBNH0lZeZEgyXAAnSDvfW/XfiDBw/eeeediIgIvCVhJet0OrPZjFh14eHhnTp1Sk5OhkcGyY70YoIJTnJ2IFD0QEJ9vnv37qxZs9D9CBWV7HJMypeSknLt2jVI2w81xAPPVZe3uN3uqKgoCNAWiwUhTQYPHkx1DrxezeCagoKCnj17WioX4DIYDOPGjSMJmIoSE6T2UsfsqlWrxK9y0E+IWIImjU9I4B2fOHGi+L2UZfmXX35BDCx4D/l8vo4dO4r1URRl4MCBVBTVSnNGmnXh1KlTPXr0AEODwYArmjBhQlFRUWgIgQXWuy0Ep/r3q/o5H5OGWDcx/ZjF8uFMgAkwASbABJ4tAbSoxe8pTUThLfdevHhx+fLlUVFR8NvAfCeinQO7CGP7MPcgWUovvfTS7Nmzjx8/7nA4YAGi3S6eS3Pt+MJqNvIqE2ACTOChBBqafR54vadOnYLsi5dwYPRIejn/qjJnZmYS0uvXrzdv3lw8lnLCI4qa2NhuMpnQVsXAX71ebzKZIK0gDjVUFxoYTaXVKEGdnSgNmrioq6DCmHIANZEkKSoqavjw4XFxcSNGjEhLS1u2bFlqaurWrVu/++67AwcO5OfnHzlyZP/+/eIIZrTlNYNvQnynwA2fM1IAoO1gvDLdGiLMiQZFgAXoBnW7/3Sxv0YXmjt3ruZlqtfrzWYzpOHu3bunpqaeOnUKMTNggiMaEdw90J2Ivw8dn+hyuQ4cOPDyyy8jDLGoPut0usjIyJkzZ165cuU5DnLncrn+9re/oVlis9kQSUqSpE2bNoUOAO3z+a5fv/5r0ChJkijuNr5tSUlJcJQOIb+KDSF0LaSmpuJ+Pc4HQPzwXL58efTo0eKzpNPpkpKS8MCJ3tlvvfWWWB88Blu2bEHwFvLL/tOTWrnyyy+/zJo1y2w2K4oSHh5O39fevXuTfh141PO0hW6WSL6OXKBYNzFdR6rH1WACTIAJMAEm8JgEqPfd6XTevXt38eLF6BEX50chQ4hMHbPZDM84RVEgQ7/22msrVqy4cuUKRGey32BghzZp8IV9zAvhw5kAE2iABBqafR70etu1aweRV+OeHKj8nj17FhKHw+GA5+/GjRuzhGXkyJFDhgyJj4/v169fbGxsREQEhcekdz41V8XQH9WsQGCVArcgvocYchqe2hTxCZcJqRpaOWbYQlHYIs74BamBxhnj+5WYmNi3b9/evXu/+tdXU1JSVq5cmS8sIX5K5BBNA4aopc/fshDcnvtdLEA/97c4+AUuXbrUarVqXk94GYWFhU2ZMgWzvnrLvQ6Hw1W5oCCXy0WOuujaqo4AfefOnV69euGdKMsyzouXcsuWLbOzsy9dukS+1TgRgjzUQa0tONBqbHU6nYsXL6YROgj/JElSq1atNm/eTFMRako6ffr0okWLwIp6SgGwd+/eN27coCkLNAfSKlpB1E1qs9n+9re/Pb4AjfuVk5OTnJwshmPGU6TT6b799lvxe4P6LF68mFpl+E7r9Xqr1fr555/jXgd+kI4fP56SkoJPoDhLj06ni46ORqcFXexznAhqSNWR6xXrJqbrSPW4GkyACTABJsAEHpOAt9zrdDpXrlw5ZswYEi/gdCbqAlAEyNTBeDVJkoYMGbJ+/fri4mKYRjCi/H4/5k0RLeoQpm+gjfSYF8WHMwEm0EAINDT7XHO93nKv3W5/5513zGYzvcDFV7eYHjNmjMfjgRYBATpweArUVTw81HF4//59n8939uzZQ4cOnTx5ct++ffPnz8/KysrMzExNTX3jjTdiY2P7VS4DBgyAT5543hql0bQXDxGVaIy0lmUZzluUTbx2RVGMRqMmkAhyUjZKUAkhEgOEJTk5OTs7e/Pmzbt37967d29OTs7BgwfhRk23poH89PgyNQRYgNYAeZ5XfT6fw+EoKCgYOnQoQvRq3iCNGjVKS0vDEImSkhIxeH910hCmkRMuvS6X69ChQ++88w6kZ/prsVh0Ot1f/vKXr776iqIrEHp6KyFB25+DRFFRETpI0TKheNCKovTq1WvNmjX79+//8ccfDx48uGLFitTU1OjoaNwpfEXwhTBVLiNHjiwtLbXb7SEaKiCGGX51Oh3NfDhs2DANTIwnRe+Cx+O5cePGmTNnyDcH4adxouLi4vPnz69bt2769OmvvPIKpGc4MouPU3JysuYUtNq4cWPqEEY8LAwLGjRo0Jo1aw4ePFhYWPjNN99s2rRp4cKFMTEx1IqTZdlms9GHMCEh4f79+4EaN52IE0yACTABJsAEmAATqCYB+CBT9DOXywVZoaysbPXq1bB5EAAUf8mKI/sHwcHEPH369Fm8ePH169cxfyCcNjSGblWrqPbzZwxX83ZwNibABJjAEyGAwbgul0/itDQAACAASURBVGvr1q0kR1CLUnRPRou7sLAQDUzRze6hLe5Hqyo59uXl5e3fv3/r1q0Ii5Gamrps2bK0tLQRI0YMGjQoOjq6WbNm8E1GNCf4pVEznz5DojBN/mfIZjabqQ1OAaPg3YUmOZggD441GAxWq5VYUeEY0COelOojttwD05Ik2Wy2zp07x8bGDh48eMKECSkpKb96Ri5dunTv3r0FBQW7d+8mTQkdtERe9FbEmCQwJ4aBt4D6BlRVpUmncHOpWCpEzBxYFG95UgRYgH5SJOtoORTZoKyszO/3L1iwoGnTpoFy4a89ZgsXLiwuLsYPj/5WR3emPDSKEOrzl//4ErPN0puOuhxHjx59+vTpqpCJhnhVeerjdr/f73Q6k5OTbTYbXscQXumdTuGisAWDOmk2SKPRSH2YEydOxEtT8+oMiqVp06b4sppMJgwOjYmJCZrT7XZ/+Y8v0SULp56oqKg333xzxowZEyZMGDFiRFxcnDixO9x88DjRsFNFUd566y18IYKeJTMzE4cYjUaKSIUPGAohx3w8OeKnS6/XWywWRVEmTZpkt9vF4B5Bz8UbmQATYAJMgAkwASZQHQJkVGCSpdLS0qVLlyYlJcFtAt5qJC7DbhHHXGOXJEkRERHDhw/fuHHjpUuX6LyBsaRpFyeYABNgAkyg9gjQu/369es0ixKJp0g0atRIkiSr1fraa6+J6nNt6xKBg8s1nY7wEoNHNiSakpKSwsLC3NzcnMrlUOWSlZWVkZGRmZk5f/78hISE/v37x8bGxsXFIeq0psVtNBopeBQ14elzBrXaZDKRCkFDeejDp6GHVVHvFtvvYpo+lHQIFYUK6HQ6nFdRlOjo6B49egwcOPCtt9764IMP5s+fn5qampOTs3PnzpycHMysWFpaCu9Jen7E0B/Y+ODBA3iyIwYIPQ/wg6RuhodGlKVTcOJxCLAA/Tj06sGx6Djy+XxlZWU0/xsEPhL7hg4deu/ePSiGTqcTv0lNiAZSmUMk3JWLx+NZt25dmzZtYKnbbDa8s4xGoyzL3bp1O3DgQFFRkfhu1YiVtf2if1a3DXH3MRUhfGQoBgVe9PT+pTAdmDcA2ynP0qVLA9+eIS4KbtQ4HDe9VatWGuUa37MjR45QjGnykaeoFxaLBYdrdHOqLeq5fv16TeGaunnLvd27d0dIjcBLliQJs8NDhUekbPpuoQ/2448/xqelqrglmjPyKhNgAkyACTABJsAEqkPgwoUL69evHz58ODk4kyMFjBa0n8kqw0a9Xt+4cePRo0dv377d6XS6XC6PxwPjqjon5TxMgAkwASZQ2wR8Pl+HDh0gcWpe7GiB/uojlZGRQRH5RVEidPP2MWuu8eENei40fh0Oh6ifVnVejLmBboP4IR6Pp7Cw8MSJE3l5ebm5uXv37s2oXLKzs9PT0999990hQ4b07Nlz0KBBvXr1ioyMJD4IG00Oc9R4t1gsyAPdGfoAtdmrSlBm+sKiQFHsplMgSAjVBDoAHWgwGHCUxWLp06fP0KFDe/XqlZycPHfu3MWLF69cuTI3N3f//v25ublnz54FKHKXdLvdCDNLajXJ0EHhV8WZtz8CARagHwFaPTiEfjmwfdevX9+kSROSFPGrttlsbdu2/f7772meU000YfGdG0J3pl137tzJzMzEHK/0RhDfIB9//DHmM0S/otPp1LxtQVY8bz1gXfMq5ubmIgwFTR2AYS9YpZlzoT7jdY9X7aBBg06cOEGUqtmwSUxMJI0YZZpMJnpCqPoej2f58uXwTYavNNIkQNPrnqKIiKGmJEmaOnXqyZMnqcAQifz8fAz8oceDeinI/RldF6TU4zM2YMCA/Px8KrmaBCg/J5gAE2ACTIAJMAEmEJTAli1bXv3rqxERERaLBdYIDCEMI8OoZ8zXBA0aXektWrQYM2bM7t27MdZQUzKP1tIA4VUmwASYwDMkMHXqVLQuRacrsUE6ffp0ipX0FCbNgySKiE/kpSvyQY8maSbkpQvBhLRySojHIk3SCi4HGxGPgkJOBR6lqipO6vP5IFt/8803y5Yt+/DDDzMyMhYuXJiVlZWUlDRs2LA+ffq0atVK4zQWVIDWOGLT4GzwR/wTUek2GAyBfm/izUKanLg1s1KRiIHtKD8+Pn7YsGExMTHDhw9PT0+fOXPmggULNm7cuGPHjrt370LXCtRJgvLhjY9GgAXoR+NW148Sp+qeP38+eocwtIQ6kUaMGFFaWiq+kjRXRbs0CVH1QxDee/fuzZs3LywszGQy4a1B/q1QLRMTE2/evMk/ZiJ87Nixrl27Yh5CcQYb8Z2L7tmwsDCDwdC5c+eNGzfS6BsS/cVbQ4VrEqmpqZhhgBTk3r17a/Jg9fDhw5ohNlDGIVuLL3e87tEw69KlS3p6+vnz59GBQVUKegpVVTGn5enTp9u3bw8LgD4kiqKgl5V6QfHlkCQpOjp68+bNKLyqknk7E2ACTIAJMAEmwASqIiAOuXO73ZgQafny5YMHD9YYObDHZFkOKlIgEGdKSsqePXvQRCfjR2Pr0vaqqsTbmQATYAJM4KkR2Lt3L/oR0bOI3kRqgMuyHBcXR2rvU6vVc3Oi4uLiwsLCw4cP79mzJzc3Nz09fdGiRRkZGe+///6rf301Li4uNja2c+fO5GeGyNGQROizC+WBNCsSCsijDrvIa410g6A5cQrEnkYGGsZEKjk9ElRCnLAsEJZjx47l5OQcPXr04sWL0MQQZNXhcNDXX3RRFzszNHeZ8mM7fLHRkeDxeNxuN/lrw1bRHF5nV0WpEF6nmqqyAK0BUu9XNZbuO++8gyg/+EnT73P27NmQAtHxpfkBgAIVpUnQXlVVS0tL33//fcxuZzKZ0E+Fc+Gl0Lx58+3bt9d7rLVwAd5yb1ZWFkL4o3PPbDYj+gTefWgLJSYmbt68mc6PDtIaCdBfffWVWKAkSXPnzhXbYOQC7/P5hgwZIsuyyWSyWq1iL4LBYKDXN2Zv6NSp06xZs44dOybGXRIfFaqzJoEp4PE+ys7OjoiIoLAbqKfNZqMviqIoiYmJX3zxBQpB+ZoCeZUJMAEmwASYABNgAqEJ+Hw+slhKSko2b9785ptvwggh9YEan+iPp557DAQ2GAydOnV69913Dx8+TOeCc0BVo3erYxdRUZxgAkyACTCBWiVw6dIl6JiKopD6TJ8Ak8nUo0cPVECjo9VqrZ6DwuH+SHorRFgIDhAuAq/R7/ffvXv31KlTe/fuPXDgwJYtWxYtWjR79uxfZ+6dNGlSYmJifHx8nz592rdvTxIW7hr0E3ygdTodjVWSJCk8PBz+bZhriqQVUccQP/Q1TeNR0el0EL5gKvTo0SMhIaFHjx6JiYnJycnLly9PT0//+OOPDx8+vGvXruPHj9+6dYvUZG+5F6YIZGVxakTq+fB4PE6nU5xoUaRHqEM7sIuHPKt00IgxLEA/q9tRi+fFs+st906cOFHj0CFJUuPGjT/77DM6PcV6pi1BE6IBjdexy+WaP39+ZGQkTgHfZ7iEkJAaHx9/48aNkpIShHgPWnLD3Cj2jO3bt2/atGkjR46MjY1FoP0333zzgw8++Pbbb+EsLNLDy0i8HZQOQbJr1670eh0xYgT6HjT50QnhdDpnzJjx0ksv4VUuvqzNZnOfPn3mzJmzbdu2K1euiKN4xKKqUx/xdVlUVLR37960tLSxY8f27t27U6dOMTExEyZMmDp16tdff+0t9xKr6pQs1oTTTIAJMAEmwASYABMQCWzbtu3111+nRin8noxGIwkQiFBJq+h0b9eu3axZsxAEzO/3ezweakxqxmhrXDrIdNFsF6vEaSbABJgAE3g6BBwOR7NmzSg4AzRoDEemHkeHw0HOrU+nVs/TWeirhyZ8UB2fPqOiSxx9JSmeFbqNxTylpaU//vjjoUOHcnJyTp48OX/+/IULF77611eHDBmSlJQ0dOjQ+Ph4DPqHI534Kcf8ZPimk5O1JgMJJiES5JqNY3U6HU2UBac6OpZGctMWm83WuXPn2NjYhISEPn36zJ07d9asWRkZGatWrfruu+9yK5dz586VlpaKjwTsDbhIi9uRJm6Bu57VFrFKYhr1YQH6Wd2XWjwvfucTJ06k7iBKtGjR4sSJE2VlZZgQj7pZAp8MTf2QAS8UVVWXLl1qsVioWIourdPpzGZzWFhY8+bNV6xYQdY5nUhTbMNcRbcVboFmYILmRlAeAkUdBvRypwTl0STQuzhp0qR+/fqlpKSIcraY0263q6pKX9wLFy4cOXLk4MGDBQUF165dKy4uxmBV+orQwBBMFk9FPbQ+KIFkZRyIjXT5drsdIrX4yUFOykNn5AQTYAJMgAkwASbABEIQ2LZt2+TJkylSHFqDopcGBZqEHgETt2vXrjNmzLhz5w5sD0x9HNQOIeNHs7eq7SGqyruYABNgAkyglgg4HA5Mj4QQHJrYC0aj0WaznT59GmfXvM9rqUrPTbFipAgIC5CASktLnU4nGvtOp1Ns3VdF2FvuFbOJiNxut6gs4UQaxzhvuRcekHa7vbCwcN++fZiN8ODBg1lZWenCEi8sJBOHSEDsIg0aOY2VCx1Fg8ghdsO6QLgPBBuBgUH6Ne1C7FPKoyhKz549Bw8e3Lt378GDB8+dOzctLW3OnDmbNm3Kz8/Py8s7fPhwcXExzAwR0TNM43ZcvHhx0aJF8+bNy83NdTqdGj2dBehneINq8dSTJk3S6/UYGoDePIPBEBERgfcp3g7iw0r2cVV1In3w66+/tlqtNA4CvzREK6YTJSUlXbt2TfMiqKrkhrldhF9TAnSzqnpl17RA5EexGCOD2XJpEI14xsD0o50u9FHo4sO5QufkvUyACTABJsAEmAATUFW1rKwMBozD4YAVeuLEib///e+NGzemliH5QEF9IDuWxGiLxRIdHf3xxx8fPXr0oYYWMmhMI74XTIAJMAEmUGcJTJ48GW9+BBHV6XR4/5OqWFBQgMAI/G6vszcxRMUe+uEOcSztOnHiRG5u7q5du7755hvE08jIyHjttddiY2MTExMHDBggBpXG4wThmAJVQ1/G7Fbo/NZ4W+N5I09tGo+FsB50OFkvGJ4FtVqMHkNpQUuPXygsR48ezcnJyc/Pv3r1Kl2gxoMQej3NPEnZ4CtJU1yKShHkQTEnQsUuWbIkMjIS4nuzZs3g7Q4PSLvd7vf7WYAWoT0PaW+5d8WKFfQzkCTJYrEgdN2WLVvg4kpxnzVv1Yf+XHNycmC4U2QGdOBQP0/Tpk23bdtGT3BVPVfPA+jHuwaQf7QyxLv2aCUEPUostkbpoKU95kYWoB8TIB/OBJgAE2ACTKChESAHizNnzrz77rvt2rWDgapxmxClZ4PBYDKZ4EIB3fn+/fuiG1dogy2ovdTQsPP1MgEmwATqCwG/35+VlUUqIYX7f/vttyGZxcbG3rhxA1Ka5g1fX66xgdfzoYpW9fm4XK7S0lJyxHQ4HHa7HQIXjVMvKSk5Urns3r173bp1CxcuzMrKSktLGzZsWGxsbExMzMCBAxGag1ybMdmV0WikQNLQ7iBJozsEArQYbwDPp8ViobkTZVkm9VlMkGYdmKDCu3fvHh8f369fv7i4uDlz5mRlZc2ZM2f58uU7d+7csWPH0aNHb9y4gb58aMeUFul5PB6K8uz3+8+cORMXF0cmFgJ2k/szXBtVVWUBWmRY79P379//6quvAu1sSZI2btyIy8NDIP4yxXdrCAQej2fVqlX4wciyDFGbfgmSJI0fP/7evXsowe/3uyuXEAU25F2h2zPPhIz4GNQoXRu1FStQG+VzmUyACTABJsAEmMDzRMDlcl24cOGDDz5o1aoVNbowUxB5N9N2JNDAa9euXVpaGia3ED16aEr6EDabaK5Q+nmiytfCBJgAE3ieCHg8nvXr18uyjGgb+Ba0bt365s2bp06dOnToEM1VSz2a/G6vXw+AKHM9Ts0RNBWewhp/YZfLRX6WPp/P7XYjWilO5y33IhKFJlqIqqoPHjw4derUnj17du/e/fnnnyOkRmZm5rhx42JjY+Pj43v37o1nkvw7oUrD/VlRFEPlolQumtBhpEFrTB2syrIs2kIUNsRoNJLvP3JiFkcqpFGjRt26dRswYEB/YXnvvfdmzpyZmpo6d+7cefPmZWZmrlixonPnzvBVJV/vvn37qqoqRl71+XwsQD/OY1m3jvWWe0+fPh0WFoYbbzAYrFarXq+3WCyTJk1COGYxYg7Vnt6qD/253rlz5+WXX8bjaDQarVYrfEZatmy5fft2jHYMego6FydAAMzrFA3xMahRujauQqxAbZTPZTIBJsAEmAATYALPB4ETJ04kJye3b98eDSqIzhaLhZpPQRMdO3Z89913f/zxR0DAwFICglAe2BjCZhPNFUpTIZxgAkyACTCBukbA4/HMnDmTxLjRo0efOXMmMHZo4MRLde1CuD5BCTxU0Qp6lGYj2QCQoRGbgryhYRs4HA6n04nJIYIqYHiENHEtIFhTfnht4uwul4tiv6iqevv27fz8/JycnLy8vDVr1ixfvjwrKys1NXWQsJDorEmQlzTZP5oZEeFLSr8Cg8FgNBqxilDUGlUafs1QsQN34SyQxUk61+v1cXFxCxYsuHfvXm5u7vXr13FrWIDWPGz1eNXn83Xo0AHBMcRnLjo6+v79+0Hd5mt6tR6PZ//+/fQcw/15+vTp5Phc0wI5PxOoisAT+XhUVThvZwJMgAkwASbABOoLAY/H43Q6yYnG5XLZ7fZ79+59/PHHMH2p6QUbVZZlagJhC0YHms3m4cOHZ2ZmHj16tDrXHkJ6rs7hnIcJMAEmwATqIIHr169PnDhx6NChY8eORfWoB1FsgfInoA7eu6dWJfGRQFqMgIyAEppeiidSNzqvpjTaXlXi1KlT+fn5e/fu/e677zIyMlatWpWVlTVmzBj4VsfGxup0uvDwcFHKoxAfcKyG5zJk6ECVWdxL8Xgp4AYVC/9UWkXCbDY3adLk9u3bHo+HBWjNna3Hq8nJyVCESX2WZdlms+Xl5T3Bq/J4PH369MGT1KdPn5ycHEQlp2EIT/BcXFRDJiB+/hsyB752JsAEmAATYAINkwBNCIHLx7DW+/fvb9q0adSoUZiMHo0fEqCpNYWWEsZZG43GwYMHb9iwAWOry8rKMDDW4/GIMTcCIaOZF7idtzABJsAEmEA9JeDxeDA0HH8RLUEU9ei6uDVKKBpgQnwkHpp+gnweeq6gGWieQNQEHtY+n89ut2P6N2yHzVNcXJyfn3/s2LFDhw6tW7duyZIly5YtmzNnzhtvvBEfHx8XFzd06FAIiRD9FEVBGF6bzSbqy4qimM1m2mI0GpEOFK+xBSETWIB+gk/Lsyzq8OHDdO9FATolJQWBw59g5bzl3pzKxVvuJd2Zhhg8wRNxUUyACTABJsAEmAATYAINmQDGqzqdzu3btw8ZMgSzyVutVpopntRniM6YVxDpbt26ZWdnX716VTPoFauh1WeMyGYBoiE/e3ztTIAJPGcEMCi8tLSURof7fD5NuOfn7JL5ch6NQFCdt6qNj3aKoEdVdYqHbrfb7TRQzFvudblcFOgjaBgQhPtAHUjTC1QO79+/f/r06UOHDuXl5a1duzYrK+vDDz8UdWe4wJIUCQdq0TDT6XTQpo8dO+b3+1mADnrf69/G1q1b497DHCcNurS0FM/fk7ok8nf2VC4otrS0VHxqn9S5uBwmwASYABNgAkyACTCBhkxg7969o0ePxrwjNpsNs8kjpAamyhHbOfDW6dmzZ1ZW1uXLl+HyLLbBQFIzoVBVeNHeq2ovb2cCTIAJMIF6SgDahdvthh+0qO7V0yviaj9ZAuIj8dD0Ezz1Q89VVQZxKgv0nfv9frvdjr52euA9Hg/ih+DJR80xIMzj8cBjOlCGpgu8ffv2kCFDYGvJsgzd+aWXXlq2bBm67T/77DOEikYsafyVJOntt99GISxAE8z6mvjViSM1NdVkMpHojHlXZFn+7LPP6utVcb2ZABNgAkyACTABJsAEnmsCYmRnutCysjJvuTc/P/+9995DIwd/abYccSON9AwPDx82bNjGjRuLiorQ3BKnEESDjU7BCSbABJgAE2ACTIAJPB8Ego7WEqXqQItI3AsI4haMDBB9TJ1O55IlSyIjI0UbTJKkuLi4X375BU7W06ZNg78z5dHpdM2aNcvJySG9mwXo+v3I+f3+e/fuhYeHk/oMQ9xgMLRq1ap+XxvXngkwASbABJgAE2ACTOD5JeB2u51OJ1o4GLF3+fLlrKys9u3bU+tFTOj1eqPRSDPhmM3msLCwt99+e9OmTUVFRRpOgc0tTQZeZQJMgAkwASbABJgAEwhKgFTj4uLi3r17I+KC2Ww2VS7NmzdPTk5GKI+ffvrpL3/5i06nUyoXs9ncuHFjSZLef//9O3fuoBwMR2MBOijq+rERQV7mzJmj1+tFARoe0KtXr64fl8G1ZAJMgAkwASbABJgAE2hIBBDSja743r17GzZsQPNGkiSKIUjqsyzL0J2xxWQyjRw5cufOnWI58ADCjFKqqrIATXg5wQSYABNgAkyACTCBGhGAZLxv376IiAgacIa4Z3FxcTdv3oTFlZycjJk5EBtaURSdTtemTZucnByEAUFMDxagawS/LmbG7QwLC4NRLobAa926dYjQLXXxYrhOTIAJMAEmwASYABNgAg2JwK1bt9auXTtmzBgKrxEeHm4wGMxmMxozJEAjYbPZXn/99R07dvj9fnhM00RShM3hcMClmgVoYsIJJsAEmAATYAJMgAnUiMDFixcTExMxyRzCPVutVoPBsGrVKpRz/fr1zp07Y3QaZukwm806nW7atGk0uE08I09CKNKol+kdO3aQkwgJ0AaD4W9/+1s151epl5fNlWYCTIAJMAEmwASYABOonwTu3r27bt26jh07QmXW6XQmkwkSM1xsYNxihB9aPqNGjfrkk0/g10wXLcYrpI2UCL2XsnGCCTABJsAEmAATYAINmQCCK6iqioTb7V6yZAmNPDMYDDDSkpKSrl69+uDBA5fLlZaWBlUadppOpzMYDJGRkVu2bMEU0IE8WYAOZFLPtrRq1UrjG4LVK1euqKpKgxDr2VVxdZkAE2ACTIAJMAEmwATqLQFMA4jqY8p1pPfv3z927NigtqvBYEBLxmAwQI9WFGX06NFf/uNLRA8UJ8OpjrhcnTz1FjBXnAkwASbABJgAE2ACT57ApUuXkpKSYKqRBv2rypyVlYWTnT9/vmfPntCdyaLT6XRvv/32zZs3ScsOWjOOAR0US/3YeOzYMVmWEWOFbrwkSf369cMFIMxK/bgYriUTYAJMgAkwASbABJjA80LAW+4lyfjChQvp6ekvv/yy2WyGj7PJZGrcuLHVasUqphbU6/XwiR4yZMiGDRtu3brl9/tFLRtRnr3lXojLoVGxAB2aD+9lAkyACTABJsAEmICnclFV1e/3L126tFGjRlAXMbecoihdunQpKChAho8//hjOzhQV2mw2v/zyy1u3bgXJqtyfsZcF6Pr3vJEhPmXKFPRIaCZmmTt3Lq6Kcta/i+QaMwEmwASYABNgAkyACdRPApCeT548Cd2ZQjyTwwQUZ1o1mUxGo7Ffv34LFy68fv16WVkZSvD5fBCdaWoTu91OW0KzYQE6NB/eywSYABNgAkyACTABp9Pp9/tv3749aNAgo9EIm81gMMiy/OugtOzsbEjPN27ceO211wwGAzJQ8LSxY8eeP39eVVV4HsB1oCpTjQXoeva8YdIVVLpFixYw3BH9GWlZlg8ePFhaWuot9wZOzFLPrparywSYABNgAkyACTABJlAnCdBIOwy3LCsrc1cuBQUFkydPjoqKgmkqqs8U9BnxBG02W7t27d58883vvvvOW+4tLS0NfaHVcXwOXQLvZQJMgAkwASbABJhAAyeg8VNesmRJ06ZNSXpGeI2kpKTCwkIEht6yZYskSXq93mw2K4oCbdpkMn3zzTeqqqK06nT8swBdzx488gQ5d+6cJEmi9ExidElJST27Kq4uE2ACTIAJMAEmwASYQH0gALnZ7/c7HA5o0H6/3+12X7hwYcWKFT169IBFKpqpNJ0gWi9Qn/v167d582aXywXlGj7OVbnMAAy1beoDJ64jE2ACTIAJMAEmwATqIgGPx1NWVuYt916+fLl///5kuUmSZDKZXnrppVWrVqHet27dGjhwIDLIsmwymWRZ1uv1o0aNIrcAh8Ph8XjISAthy7EAXRefhhB1ImeTjz76KFB9liSpV69elCdEObyLCTABJsAEmAATYAJMgAk8AgG3203xne12+/r166Ojo/WVC/lDoH2iKAocanQ6HQJA9+3bd+XKldeuXaN2C6Tn0tJSt9tdVlYWoj7UtgmRh3cxASbABJgAE2ACTIAJhCAAn+Xly5dHRkZKkqQoCmJr6HS6uLi4ixcvesu9brd73bp1FovFarWKngQRERErVqxQVdXn8yEbTkRGGgvQIcjXs10I6+wt977xxhvilJQw93/1KMnIyKDIGxwDup7dXa4uE2ACTIAJMAEmwATqNgG0K27cuLFp06Zhw4bBnRkz1ZCDDMRo/DUYDIqixMTEzJ8/H2M5yVXC4/E4nU6Ss0PPnI4QhKJsXbc5ce2YABNgAkyACTABJvCMCQSVg69fvz506FBIz/B6NhgMRqNxxYoV0KZ/+eWX+Ph4SI6IvIGgz8OGDbtw4QIZbHBHKC4uxhQdpEFXdc3sAV0Vmbq7HTc7PDwcVr7412w2HzlypO5WnWvGBJgAE2ACTIAJMAEmULcJuFwuqL1QiqmZAQ/lFStWDB8+XFEUBNkQDVFskWUZe61W6/jx4z/99NO7d+9idhrNdVNDxVe5eMu9QZtJmqN4lQkwASbABJgAE2ACTKA6BGDLwb6CXrxixYrw8HC5coEV92s051deeeXHH39EgV988UWjRo0kNyeSUQAAIABJREFUSTIajWTmWSwWistRnfMGzcMCdFAsdXqj2+0+e/as+CjA3Nfr9Tqd7pdffqnTtefKMQEmwASYABNgAkyACdRJAnB7gWMyKgj1+cGDB1u3bk1MTKR2CBI0waDZbBZH5g0bNmzdunUPHjwoLS2lYB2BV6wRoGmVZehAVryFCTABJsAEmAATYAI1IoCufbLufvzxR4xdMxqNiqIYjUYYcmlpaXAUuH///vDhww2VC9l1RqMxNjb25MmTj2+esQBdo9tXJzK73e7Vq1drGgB4OFq3bl0nqsiVYAJMgAkwASbABJgAE6iHBBwOBzUw7Hb75s2bx40bR74OcG0W1Wc4QGBLjx49Vq5cWVpaqrnusrKyoHHhRMVZk9aUwKtMgAkwASbABJgAE2ACj0bA5/NlZmZKkoTIabIsI3ha165dEUTB5/Nt2rTJZrNhDg/YdSaTqXHjxh9++CE5E2DI2qPVQVVVFqAfGd0zO9Dtdk+bNk0jQGN16NChz6xafGImwASYABNgAkyACTCBukoAsjKJyyGqee/evfXr148cOdJkMlksFnKBIeOTJhjE1ILDhg3buHHjzZs34WITqDVDkqbQz2I0Z43uTKshqse7mAATYAJMgAkwASbABAIJBDXzzp8/36VLF4vFAn9nRHPW6/Vz584tLi5WVdVut8+cORNOBhCmYfv16dPnxx9/pFBsoWeKDqxM4BYWoAOZ1PUtTqezX79+iqLohEWSpIiIiIyMjLpee64fE2ACTIAJMAEmwASYwFMn4Pf7MUUMzizKwVSXrVu3Dh8+HEJzoO5MArQkSU2aNJkyZcpXX3117949HE7acYgEnShoHtrLCSbABJgAE2ACTIAJMIGaEvD7/d5yLxyWveVel8u1YMGCRo0aWa1W6MuyLBuNxqioqIKCAhT+5T++DAsLg40HmRHRn+fPn0+Tc8DxGcZbTask5mcBWqRRb9Imk0mWZUF/1mFo5I4dOwK9TurNVXFFmQATYAJMgAkwASbABGqHgN/v93g8omsM0j6fb+/eva+//nqTJk1kWYZJiaYIrE1Rd5YkafTo0Vu3boU7DErw+/0+n+9xmiWPc2zt0OJSmQATYAJMgAkwASZQ/whAEvT7/efOnUtKSiIrDgJ0s2bNPvnkE5fLZbfb7969m5qaKsuyzWbT6/UI/SxJ0qBBg06fPk2eCt5yryhAi5ZkTemwAF1TYs8+/6VLl6h5oNGg79y5Q0/Js68o14AJMAEmwASYABNgAkygjhFwu90ul0tV1SNHjkyZMgUT0cC2pFaKJtG8eXPoztevX8c0NdT8cLlcLB/XsTvM1WECTIAJMAEmwAQaKAGHw+F0OjMyMijUBow6q9UaFRV19uxZaIbnzp176aWXoDvr9Xqj0YhsM2bM8JZ73W43WXput1sjQNOumiJmAbqmxJ5xfr/fn5eXJ0kSHiYI0IjkYrFY2P35Gd8ePj0TYAJMgAkwASbABOo2geLi4unTp3fr1k2n04mTCqLhodPp0AiRZTkiImLixIl79uwJvCCahebBgweBe3kLE2ACTIAJMAEmwASYwNMncPHixS5dukiSpCgKphyEsZeZmQnp+fbt2wsXLqT5pWH+ybIcExOTn58viopQot1uN5yg4XDwOG4HLEA//efhsc7o9/tTU1PxrEiS1LhxYzxYkiR17dqV5qZ8rHPwwUyACTABJsAEmAATYAL1mYBoEyI+xrVr15YtW9ajRw9ycpEkyWw2IxogGif427Rp00mTJn3zzTfFxcXwla6KBDVFqsrA25kAE2ACTIAJMAEmwASeOAEKfuDz+UpKShwOh6qqU6ZMMZvNmmk8oqKiLly4UFxc7C33Hj16tG3btpIkYegbHFvDwsKSk5PFGsLAg7eBt9xLUTgo5NqjydAsQIuQ60Ha5/O98847eFzg+Exi9JAhQ+rBBXAVmQATYAJMgAkwASbABGqTgM/nczqdOMPdu3fXr18/btw4s9kMJxdycNbr9dREkWW5efPmM2bM2LNnj6dyQZRnu90eoqYkQD/yYMwQhfMuJsAEmAATYAJMgAkwgeoQKCws7Nixo9VqhbFnMplsNpvJZFqyZIndbodfQlpaGk3vYTKZrFar2Wxu06bNvn37PB4PDD+cSxSgIUPT38ex/ViArs6trEN5vOXehIQERVGgPqPvAl0cs2fPrkMV5aowASbABJgAE2ACTIAJPDsC27Zte/PNN61WK8VtQ5tEkiQMycQounbt2s2YMePo0aNOp9Pj8Whcnu12u9gg0VzN4zRCNEXxKhNgAkyACTABJsAEmEA1CYjeBmlpaTDtDAYDXJsNBkOXLl1Onz4NK27Hjh0xMTHYRSPhFEUZOXJkSUmJt9xLjgt0dtHGI/WZPaCJT4NIeDyebt26mUwmRVHIaUWv18uy/MknnzQIBHyRTIAJMAEmwASYABNgAlUQ2LZt2+TJk00mExmKGDlH7guQoSMjI6dNm3bq1Cmfz+dyuWggp8fjoXQVZ/hjs9g4+WMrp5gAE2ACTIAJ1IyAT1XLVdVX+a9mR3JuJtAwCfh8PofD8fPPP0dHR1NcBJvNZjabIyMj58yZAywej2f+/PkWi0WSJJKeDQbDyy+/vGfPHph88I/WmH+ijccCdMN8xiquGgH7JEkKCwtr27YtzVq+f/9+dEc0XDR85UyACTABJsAEmAATeN4JiPGdEfvC4XDs3Llz7NixERER5OasKApaGpjcHK4x3bt3X7NmzdmzZ+/fvx+UEwfTCIqFNzIBJsAEmECtEPCjVKeqlqmqs1KGrpXzcKFM4PkgQOPSfD7f0qVLw8LCKKAztMFevXpduXIFcwmeP38+KiqKLEMkzGbzqFGjysrKVFUNNClFSqIGHTQtZq5OmkNwVIdSHcpjt9vFjgvqwVAU5fjx46qqinNW1qF6c1WYABNgAkyACTABJsAEHpuAOOLS4/F8//33b731lsFgIJtQkiSMjUMzA62Rjh07btiw4dKlS6qqaoJsaGrEArQGCK8yASbABJhALRL4Q4C2s/pci5y56OeIgLfce/Hixb59+8LkQ6Q1WH1paWmqqhYXF/t8vuzsbETuhVmoKIrBYGjduvWX//iymsZeUNFZ3FhTqCxA15TYM85fWFiIyH3iOEqdTifLsqqqoSeKecZV59MzASbABJgAE2ACTIAJPAkC27ZtmzJliqIoaG/oKxekTSaTXq9XFMVisbz00kvvvvvu+fPnxWGVoZ0VqtkmeRIXwWUwASbABJhAgyfgV1X/b6E3fH614t9TDMOBc4l/G/z9YAD1gMDKlStbtWoFq4/+RkVFXb58GTbe9evXBwwYgKFvVquVYrKNGTOmtLTUW+5F7ATR/Tn0ZYuis5gOfVTgXhagA5nU6S2HDh2C3Gw2m9u3b4/ZY+ATraqqt9zLzYY6ff+4ckyACTABJsAEmAATeFQCYnxnWZZNJhMcnGlOcwzDbN269cyZM0+ePElas9/vh5UoNhuQ1tSFLUkNEF5lAkyACTCBWiTgr9CbfT7VV676XKrP/ZsGXYtnFIoWpeenKXwLVeAkE6gBgYKCgq5du0IGhBcCVOasrCwKzbF48WKj0QhfBBiKsiw3btz4m2++EW08MhGrc/pA6zGoDfnQoliAfiiiupXhhx9+QNMC7i14qmRZbtu2rSaAS92qN9eGCTABJsAEmAATYAJM4GEERG8UtBOqiu+MCWcgQGOIZatWraZPn15YWFhSUoLzVNVgELc/rEa8nwkwASbABJjAEyaAYFAOuwfluu1qYYH6zph/u3VRddhVn+r2+X6bk9DvLa8INFru9rgcXo9LnAyNBveQ9PZkawmFDvP0irP14izecq/H46mRivdkq8elPd8ENE+1y+X68h9fUrhncnzu2rVrbm4uZpAuLS0dNmwY7dLr9YgQnZSU9ODBAw0uUYzW7Kq9VRaga49trZQ8b948g8FgNpvlPy8DBgxAUD+n01krJ+ZCmQATYAJMgAkwASbABGqTQE3jOyMsW6tWrT788MMjR46oqio2V0SVOUS6Ni+Iy2YCTIAJMAEmEIQAxC+/T/V4VNWrqh71fx+76b++nP2PtaWqqpY5iv1+r9frVlV/bs7B3f+28/jR/H/b8f2C/zNrrrAsWLBg8uTJgwcPTkhISKz28q+DEkP8yxKW1NTUTz755MqVKxCaSbATu4qDXBtvYgJPlEBxcfH9+/dHjRqFiM9weUYUhHnz5sHnoKysbOXKlZCeKSS0Xq83m81btmx56PwfT7S+oQpjAToUnTq4LzMzE170iCNOKnRiYiJLz3XwfnGVmAATYAJMgAkwASZQIwLVjO/cokWLqVOnHjt2zO/32+12j8fzW3v+d7EZAf5+X6vy/xrVjTMzASbABJgAE6ghgT8FtyAZF4X4Ktyb1ev/S43q+n501w/+n7Wnx78xve+/xCYmJiqK/kWz0WysmO3A8IJe0esgwGHaAwz9URTFarViMBA5foZMyJJO+uOfLEniv4oz/GlByVartVWrVoMHD87Ozt65cyc7PtfwAeDsNSbgqVxUVfX7/d9//z0cmXU6ndlsxq+gc+fO+/btQ7k3b96Mi4sjYZq8pEeOHHn79m2MNigrK6txJWrhABagawFqbRaZlZWFN6LRaNQJyzvvvAOfF80LvTbrwmUzASbABJgAE2ACTIAJPBkCVcV3hskH80+WZYrvjMk/yA8Lo5IDq1Kl8Pz7jsBDeAsTYAJMgAkwgSdHgCIt/1Gk2+M/cerkocM54ydOaN++uyS9LEldDC/81xdf7CRJpheMBkXR62RJr6uQnisENUlS9Dr9b8qxXpIUSdLrX/hNMNZoI4JM8ntSlnSyVLmil2Txn1KxqtdV/pMkfaU2/bsEjanbDAaDLMvQu7EnIqLpx//XKuh6f1xSsFRVn+ZgeXkbE/iDgNPp9Pv9t2/fHjRo0O/Po2Q0GpFesGABYr/4fL7Nmzc3bdqU8siyHBYWFhER8dFHH4mj4v4o+pmmWIB+pvhrfvI333yTnq3f36YV/6elpVX0HfoqehB5YQJMgAkwASbABJgAE6g7BCATk50Gn2VVVW/evLlt27ahQ4daLJZGjRrRNOWSJFmtVji5mM1mnU7Xpk2bDz744OzZs0VFRbiu3wXkiv/rzpVyTZgAE2ACTKABEvCWe0ntwpy3BMHrrQjofPnKz3v27MqaP3/Cm2/1jonTGy2SotebXjC8aHzBZNYpNkkKlySzbIyA3GEwyrJeekGuEKCNygsvmo1G5YVKqdgsS2Gy1Fiva6QoOvkFSa9IlhdNJJIICbg6CxskKTw8wvLiP1Vs0pn1hrAKIVu2SIrhDwH6N4donSTTv0r9u0LrliXJIEmWiugHprDEpCE7d+0qKvp3ulJ0DGPVbrdjji6MT6JPtpiZ00xAQwBTRuOZWb16dYsWLRBszWAwwERs1arVtm3bEHLNbrcnJCTQ863T6aBQDx8+/Ny5c3XTOGQBWnPH6/rqgAEDoDvTc4bE8uXL8VKr6xfA9WMCTIAJMAEmwASYQMMjAFcptEjv3bu3evXqQYMGybJssVjIr4psPEVREGatTZs2aWlpx48fF5u1fr8fTlXcoG14zxFfMRNgAkygThOgWXAdDseVK1dSUlIGDxnUtFlj+TfnYp2kUyR9pV5s1EsGinlhlqQwSYqU9JXqcEUHbIXOIUsVGrSi15mNFS7Rlf7JRkmyStI/6SRbRZmypNNLiqLTyRqBJMjqnyN16CTpRZ3UTpJaS9KLkvy7K3SF7iwJ6jNW4RldUZ1K5+sK/2tJkhWT0WhU4hPiZs2alZubq6oqXT6i7nrLvZDj+Xtdp5/aulE5v9/vdrtdLpfH4xkxYoQYUgNOCaNGjaK5BHfv3t20aVPxkZZluWXLlp9//nlxcXHdCfqsQcsCtAZIXV8dOHCg+JDRa/Wrr74iJ/y6fg1cPybABJgAE2ACTIAJNCQCpaUVsyoVFRVt2LDhtddekyQJUfxkWTaZTBaLhXxb4PXcsmXLmTNnXrx4UVVVp9MJGw9+MWjN0oRI7H/QkJ4jvlYmwASYQF0ncO3atbVr1w4fPrxDhw5/DOvRSfILFUEw5BdMkmSWZMXworlCy61UmSWpiSS9YnyhvyT1luVXJMnc45+j+sbG9OnTK6Z3r3/p2ye2X8yA/rGx/WL69Ordu1dMn97/0qd3/5iYfn3/JbpP324x/aIGxPdNT09LD7KkVW7/bdes5JnzMtLefW/SgH/tlzAoMTb29cZhb+ik/1YZAMQm6V6UZKMQkYM8oCsTUL8pYPTvQgy6kDHtW+vWrWfPnv3DDz+IN4mkZ/5ei1g4XRWBbdu2NW/e/PfnS1IUxWazvfzyy/Rc3b9/f/DgwfhxwZhE5tjY2J9++snv91NwtqpO8Qy3swD9DOE/yqkTExP/eI/TUylJhw4d8pZ762xHx6NcKh/DBJgAE2ACTIAJMIHngsCGDRuGDh0qSVJYWJi5coE5Z7FYyK5TFKVly5bTp0//8ccfYdFRfElqtWJeQUJCzVrawgkmwASYABNgAk+QgOa7U1XJLpdrzZo1LVq0kGXZYDDQyB5K/C5dGCrcjSUpvHGTSlfixpL0F0V6LcI4s9U/pf5zVNaUyZ/fuac6vRXKRsXshBX/hMXn9fuxq2J6NlUtV1W3qtIWIWdAskKYK3dVHuJBoTcuq/+t/87/0mqJJP1XSYqQJFu1BGgo0XrpBeMLRnPFlcJBEBq0JEk2mw1fc0z7xh7QAbeCNwQnUFRUNHnyZAyAIzcFSZJmzZp1584dv9/vdDqXLl3avHlz0SdVp9NZLJalS5eWlJT4fD4yHYOf41lvZQH6Wd+BGp5fDPLy+0u84v/Dhw+jo6OOP3A1vFzOzgSYABNgAkyACTCBOk0AHgBiFZ1Op7fca7fbv//+e+jOOp1Or9cbDAZj5QITzmw2y7JsNptjYmKWLl169uxZGlkplsZpJsAEmAATYALPhIC33IsBNzi7y+WiQM/Ycvv27XXr1o0fPz4sLIy6VBVFoegBsixTP6skSS9am1TG1ZA6dvrL36cu3f6F/eWwL6L+05kezc92bf5v/z35tN+nen3qfzgxt1V5hV7sL6+UmL2Vf/2VujPU54oqOFyVsyA8ZCoEHOXzeDxlZRWhmcvd6o3/qf73qaU92x7s2Hztzv/3Xv6Ri8cLzu49eGjB/8ieMvXv/eL6t/zPL1V8rHWS7gVJVihUiKQYXyTPbVGQoTRF07JYLG+99dbRo0cRjbcu+6U+k6erwZ5UjM5Mv6+jR4+2bNmSniII0DqdbteuXegEcrlcr7/+uvhrQnjoAQMGnD9/vr7AZAG6vtyp3+oZFxdHc1/i1Ya/OTk5Doej4hVc+beeXRVXlwkwASbABJgAE2AC9ZkAWumqqj548GD9+vWvv/66JFUMnNQ0FdBasFgssiz369dv9erVp0+frmhJ/z6RIOJs0HSF9RkJ150JMAEmwATqNwF8kugLhYtxuVzecu+OHTsQUQo9qRRaCuqz/oU/FNsKFVdXsRr5T00GD/nr//3p5rP/8+eKosrV9yZe72j7qUfjO90a/7ToQ7X031W3S7U7VE85TlUpQFe4OUN99v6uPv9G9T/KfktU4z+vqpb7vKqn0gfaXaouSVF7/KfcHi9/v239H0f/h9terla4WPsqz3Tl6tXvd/wwc9aMfx30r02bNzNbIiSpkcX8nyXpnyoSmMyQJMM/J/R6Pek2vXr12r9/v0a7/+OsnGpgBDQ/KI/Hs2DBAoulYnLLivktjUYYkGPGjIG4V1JSsmnTJkjSMCx1Op3JZGrZsuWyZcvqV8cGC9D17GFv164d+c6IAjQuI9AHp55dHleXCTABJsAEmAATYAL1igCcnYuKitasWZOUlCRJkslkChh0/EfDtGfPnitXrrxy5YqqqqWlpSUlJWiUIrgzS8/16uZzZZkAE2ACDYIAlGi3233lypXs7OyIiAh85iCE4QsHr+fKAT96o0lvtZpkuSLM8yuvdJ8x/YM9uw+6XRWsfJXeyuXl6rZP1Zg2p3s2vxTd+tj+71W3U3W41KJSMZ5GoAAthOWoLMdVppY7Va+n6rvwm3O0S1UrT1+uqnY1a9bd7s3y//ml/2/vDxVit69CDPc6ff9R8c/rcvm8Tq/LUe5EoXaX80FJsdvv+1/XHsz+YO2/xs6UpM6S1EGSKoTCEAt1QuulCv39nbcnXTh/3lv+EG/tqq+E9zw/BCDc+Xy+nTt3du/eXZIkS+WiKIokSY0aNdq9ezcMwqKioqFDh+LHRdq0LMsDBgyAJSlOUl33AbEAXffv0Z9qiM5DcsgnDZpc9/+Um1eYABNgAkyACTABJsAEakIAnika/5QQBWzcuHH06NHktIK2KGJuiO3Snj17rlq16vz58y6XCy4tPp+PROfqny5ETXgXE2ACTIAJMIHaIOAt9zocjjfeeEOSJDH+LCbODex5tdoMnbu02/rl1z9fvOZ2+UqKKwJfqKrq9qiuSsH31jW1W+u83m1udP9P+/d8pf77v/9Wa7vL6faIEm2lOFzhAe1R1YrYzT6f6itXfR7V51ILC9T+vRZmZ+2qEKD/HCz6t+L+iNXhUlWvz63+xwN1y2fqX/7Lnn9ud+irzyv8nN0VZ/OrqsdfEU76t1P7K5yuK06lVjhEe8v95eWqv8yplpWo8+de7truf7Rr9X+8+b+lVX7l/+TrTd/9sLAwpI1GoyzJVrPVbDDbLGHff79D1KD/f/beBD6qIl3/P0t6NQvIDiExIYSwaQjIlgshTACZILIpXBXnDqOOd8Sro4wKDOsNEH94YQZU/uDghdG5oyAjIIMEBkgiEJBVwiIQULYJS8jSTXefvf7WeZPi0AkIJIRkeM+nP6H69DlVdb7dTVc9563nZRbbLKkDjgeuvXf/oiWv16upmizLEyZMsH5gQOtLTU09duwYqM9r1qxJSEjged5ms4nmBsmrly1bJssyVALZqusLKhSg68s7Vd5P+B+fBd7DQk5RFMHbvp5dDHYXCSABJIAEkAASQAJ1jIBhGD6fD2aAMLhnTwkhPp8vEAhcunRpxYoVgwcPrgj4Kp9/shWUNpstPDz8R/O+7t27L1q06PDhw8zf2TrJZNkF6xgD7A4SQAJIAAncvwQCgfLgX03VSkpKJEkaN24cOGmwADgQnZnLRGhoKKixthDX888/f+DgTjMwk8YmwwNoyqbQW3SFDHv8UEzzgrhW+1d/SkqK6IsqtX1mFs/WIo2J9hueAPH6CfHo5JPPtFdf++6HY2T0wHOPtlm5YbX5A2tVrSveOl0janlEtSpdJXqAbPw7ebjD7nZttyz4n7NXLpYfpxFNo+q2rBNdN8pjtCt6QLVvnV6ELhOyI4+0aPJFfLNdnVr9bcGsXUQhq1f9/eWXX27Tpg3P8yGCYBPFB5wut8Mpinam1IucTeQc5l+b2x36xhu/o1bXZii0bnbv8uXLlccGOEKoeBv/Ff41DAM0ZRhe5uTkxMbGBsUucBy3aNEiuNrS0tKnn36aydPMxyY1NXXfvn2Q+M36makvjFCAri/vVHk/4R4jePnDbRD4Tx8XbNazNxK7iwSQABJAAkgACdRJAoZhKIoSFIIEA63i4uIlS5aA6yXLsARWfSzQCfZ36NCB+WxUdkizzhmCGqqTSLBTSAAJIAEkcB8RYG7FhmHk5OS0bt0afuNAfbaKYuy3j+O42NjYjIyMc+f+CeqYol3V1HL1WdGMMq9HJ+SqQmSVPPf0oY4JeW3bHVzyISky1WdqzUEF3opMgwaz2qCxyQHdrxJyxfBfMsie70iHhz9vF5fdp+vJR6J3vP2bS/DGGDrNpgBb5beKCr4Syd9L2j20qmnjrKHD8q/6iUYMvyxB5LRGcx+qNML6mgBNJXQz8poeoxByppAMGng8psWRLm1+GJZySDF77iuTobnCwsJF773fNbGLTRRp7kK6CaBB8+UCtIPnbDxPX018JKn4Simoz3C6btkqroP+W/lacE99JMCcmj0ez4svvgjSM4Q8g5tNnz59cnJy4NJWrlwZGRkJyavZ161p06bz5s27dIl+4OEWUX38nKAAXc8+vYIgsPBnyKUuimJERAT+31TP3kjsLhJAAkgACSABJFC3CciyDOOroqKiefPmPfbYY2yVMThswMyBzQ0EQejRo8fixYtPnz5NCFEUBWYIgUBAURRN1WB2aZ0wQLluY8DeIQEkgASQwH1HAH6/WG40sKZl4c8gSjgcDtgfExOzaNEi+MU0f+zKvZt16l6hKYZXMcpkIvk0Uuoh//OOt33spsRHvs7+hhTJFZ4X5f/q12nQdKefEEkjxCPTUolOfvbYzujIb9q2PNG13bfPjMzRFeIxUxFWIUBT8VYP+IvBYuPk96Rbh51xLb95pMPKH2gWBuqvAVJ7xW8x1aKpBn3t3VZM52gqQF/1kTd/d7FT7Km45gWD+u66cJoESqhvNLsA+N33+/0nT34/b94fOnVMdLrCaOCqGMIJIs+LVH3mqMOv0+nmeT4pKQlOAQ9fNkgAUw42VLjWFyzVZwLgWHDkyJHu3buDpQa9OyEIHMeFhoYuX74cghUuX748ceLE0NBQ+GaFhdGPUIMGDRITE/Pz86mJjUxveLDsoPXuc4ICdD37FIuiCOHPVm/B7t2717PLwO4iASSABJAAEkACSKBuEygtLf3kk086duwIuTcglonneZgzwPwBPDcSExPnz59/+vRpZu7MIgNAepbNjTk+4/Sybr/z2DskgASQwH1NoKyszDCM0aNHwx1Wm7kxFQJkaBDI0tPTN27cCLAsy310RaX5DszlRFSAlgxZIUTWyCfLSGL79U0bfLJ8Gc0JWKqZzhsaM1+GCGjzLw3+1UCANgjxKMSjkgkTz3Vol9/uoYstwven9txbfKVcLPYF6A1j60a7RNMd6op0lRBysYiMHLEjullefMtaI+98AAAgAElEQVRt33xNNWZP2bW3GE6E55UEaOqRoapk2f+S6FZfxjU/2LNzft42ctVDDy++VOHica0yIsvqVT9NeHis4NyU6f+vVeuHOS7afERwvIPjBE4QRTPX3Pjx42k3qfcI/cu24AuxVI7FekpAU7X333/f7XaDoMcsNXr16nXy5Em4qK1btzZp0oTZ2sACO6fTOX/+fAig9vl8MJKE4+vj5wQF6Hr2AbYK0BB3Axkw69llYHeRABJAAkgACSABJFDrBEAXBpdnmCqzhcZs5lxQUJCRkREbGyuKosPhgKWRVp8+WILGcVyXLl0WLVp0/vx5n4+mV2I1WC/LOj1gArR1J5OqrWdhGQkgASSABJBAbRKw/j4SQp5//nlmYcwW+oAdqN1u53m+d+/eX375JdNPK3eVxj6rNHYYTJiPfEc2byQJUTvjo7ZNnlhY7KECtN8ABVmlRxnmX3DhMMwXaAhzuSu0bJA1q0mvbqebhp3s3LY0qcM323OpZzNNRmgEVEM2DM362+r1ekHYlSTiD5BfPvt9ZJOsNpF/f38+oSHRTPGu3G9LSLM3QKOnVT/57iDp0HZzi8b/6JG4ectGokrUsMPcLNHSlqogc6JKiF8iV73ksb7/5+Se5/lOHBfG21283caJPCfQx9p1lKEkSeARDBq09UIstWKxfhAIGtdpqnb27NkBAwZAHAP7NjVp0uTDDz+ET2lhYeGrr75qtXSDw3r27Llnzx52Z4KFLwCI+vg5QQG6fnyIWS9RgGYosIAEkAASQAJIAAkggWoSgEWRsiwfPXp03rx5rVu3ttlsEONsNzcmQMNkQBTFbt26ffzxxydOnKBpkfx+6ICiKKxs7ZJ1elB5YgmvWo/HMhJAAkgACSCBe0tg+fLldvu1HHpMMoPYzMaNGy9btkyWZdDObtLVopIiVSMeDzl/hvTutj7+oW1tI78d2O+I5ypRTVflEi+NFCZEpepzkACtlXthQEjyqVOkx8P50Y3PRDe9EN18z4oVpMxHZWSJlMkkYGYRNKwuHCyXg6qTzDlXEqJ2tmu567mn9hOZlFwgxs0EaHZBhmrIfh8pPkPGpOfHRm3v1Gn739fRVzWNeiDQjIVWuw52Hr0e+oJiZlyc8fsz7Vv/rXenrIxpxzg+kePCOAc14qAyNMe1bRevqZrf70cB2sKvHhdBfYaxJVzG7NmzHQ4HM22D9XOJiYm7d++GA7Zt29apUyf2LWOjzXnz5sE4s7IAbR1b1q+RJArQ9ezDjQJ0PXvDsLtIAAkgASSABJBAnSHAwlICgQDEIx88eHDGjBktW7YUzY0FfAmCYE0zyHHcwIED//znP586dcoa6QyVaKomyzI4ZgZda+VJQuU9QafgUySABJAAEkACtUzA+vsYHR0N/s5MNWPq2JgxY7xe03S5on/sxPIdFWnzIDbYIMRbTF4ed6b1gwe6JFzu1iXn0hUa+3xVI7JB/TcMQyOGUoUADfHQhKgauXCeDOi795GYwrbNLsdHH/70U3K5jJRIJGDIpvpsaAaBhwFpBCv65r1K/rSMtG+3O775nsSov2s0oJko/oqo7IrDqvoXzEBIWTGZ+OurHVrs6twxd8rMYk+ARmjTLusQqm1eZcUls3pUQjyEFGlk/nzSuW1eYnze3z4mibGbExOWNmjUk+M50WGn4a5OB8dxv/zlL1GAZuj+BQpslHjixIm0tDRBEFgoA7jZzJw5Ey7TMIyXXnrJZrO53W52mNPpTExMPHv2rGJuN7FnsY4n6ws3FKDryztV3k+rAA2fY1EU+/XrV88uA7uLBJAAEkACSAAJIIEaJRA8B66qcvDKCAQCu3fv/uUvf9moUSObzRYeHg7LisGSD+YAInVotImi2L9//6VLlzKHPsj9As7ObOhfVVPl+9gxNync5HR8CQkgASSABJBALRCw/j6C3bPV9BkE6GnTpnk8pvkxIV6vF3xpg/umU3GWOW/ohKz9K+kUlRfT5GRs5N5jJ4lXpekEFaL7FDP82UwVaJpiQFiy6blhGFTfNTVoRSKT31DiW33bvuX5hMgjE99UNUICZqsSCahEodKzTlSDPkwBurxHGiHn/kk6tj+QmFDYKXrjtq/MRnTiv8oMNK7ve7nbB41uJkShiQf9ZMtG0rbRxoejv/31yz94TbVZIxINtdYsArRuOoWUV0avB3IX/nmN0b7drgddu6f/jiTG7Y9vnjN0QE5pKVm34avQhhEcx4WYMrTT6fzyyy8xAvr6N6MeP4Ph6AcffNCgQQPm9QzfoNatW69btw4U6h07dsTHx7O4BzigVatWc+bMgbUFLN8gRkDX409Dfe+6VYCGJTB2u33QoEH1/bqw/0gACSABJIAEkAASqD4BwzBgeszWPxqGAXqxpmrr1q174YUXIiLoxI8FOPM8D2kGWYgKx3FxcXFvvvlmQUEBzMl/cqHxrfQcNOhbORKPQQJIAAkgASRQmwRANdNUbceOHSzXLouA5nl+xYoVP90f3dB1VdMCMpFlU+89f550i89PaP59h9jcFSuI18wlKFHTjIAk6wZLOkiuEnKV2i+DmKurRAvQfQpZ8znpGLsrIaqge8fjv3vV6w+QgE4F6ADRZKKoRAMBmjZnsNhkrUwm318inRPz4puf7hpzbNa0U1QWp87S6vVpBi3XRLMeGkSRaUQ2tfcgF06T9pGrH4n65rlR5w8W0EYV0y6kPOCaKtWmVzWT22llhk/xBwzy9X7SI2Vfixa7p75JkuKutorIe2704ZIieomyQf62eq0QQoOgHQ4Xx3Fjx/6Cdk+jD6puWx6W/mGxThOAJXGKohQWFqalpcEaArZ04EclesaMGSyo+a233mIvweAzLCwsJSXlyJEjlX3VbxLBwF6q02gsncMIaAuM+lC0CtCQedZutz/zzDP1oe/YRySABJAAEkACSAAJ3EUCEEAU1ICmal999dXo0aMbN27MhvtQsNvtLpcLBlSQ+6VHjx4vv/zy2bNnrWseFUWRJPCpDKr79p6iAH17vPBoJIAEkAASqC0CLCXvvHnzQIBmEdAul2vKlCm3diOW6qsqCfgNv0cixR7ym1+f6hB5uEPr/D/OIx6ar5dcvlomU+Nmr6pTe41y42biMYjHIkCbSrRE9uSQbh02JcYdb90o58Vf/lBSTGSNqFR6pg+qPhNqxqwZVDCWCQ1t1sykh8VXyej/KGkT90PX2MKX/70MKGq0wYAGdVQGaxCi6oZMUztoGtF85LknTvfp9F3PTptOFVDbEFP1pmHZNDKbhmhb1GfaKBWwaUZBjVzxkD6p3z4Ud3LoEJLUuTQu8tSQn53ylNKAbUklXl/AF5B7/1sfjuPNBVj2Tp0eBvUZBejKb0u92AOjREmS1q1b16BBA6fTaR1wRkVFQeIQQkhubu4jjzzCRp6g70VERMyaNetGXzGmMt+kUC8oEUJQgK4v71R5P60CNMTz22y2t956q55dBnYXCSABJIAEkAASQAI1RwBCt6z1Xbx48c9//vOTTz4JQSgwnYZxFMwKWGAXx3ERERETJkzYvn273+8PBAJVLyu21o5lJIAEkAASQAL/WgQgk8Hu3btZBDT8XDZo0OC2LlQlRqmsXigiK/9C/i1pX0L0hilveUrLSKmPXFWIaV8R0IhfM30sNGoHXaqRUoP4y507IKDYT66cJAO7HI8OPdQl7rsX/+OfFy8T2dSaNVN6VssFaM0wbaTNpwY14lCJpJC33rwQFXU0Jupsx+iNZ45Rbdj089CZBn3zK1JKye+eP9+peV7v9nnHjpKyABWg/abGDUo3aNDU8QMEaerOUZ7ZUNbIS78+GRvzbWIn5eH2SvNGe7slbTp8iHjLkxYTTaU2HTNnZjidbtCg7TZnleHPtH7c6jwBv9+vqVpRUdHAgQPtdjsTlzmOEwTht7/9LUtSPXnyZFEU3W43k6dFUezTp8/evXvhKqsMd7iJ7sxeqvOQyjuIAnR9eafK+xkkQMNvwzvvvFPPLgO7iwSQABJAAkgACSCBWybAMrrc5Aw45vDhw3/4wx969uzJ4p2DJtJs0A+68zPPPLN+/XqoVlM1SZKgHuscQNf1W+nATfqGLyEBJIAEkAASqBcETp06Zf3dtNlsKSkp1NdYUaz9r3zfl64cMo/QCA0B/uEHktJt9yNtdrz12/OSVG6tYZpMqBqNEpY0oph/PRrxaMRPZWSQnnVqdaGUkXEjDrR/8Gi7hgVPD/3+wnlatUHjlxXDoAHK8DAMDR6qoaqmu0VAJl+uITFR/2jVrKBju4L1X5T3OqBJpuGHbgZBB6y2zdbruuozND/507skMTI7KXrL3z4hAYX4DCNgUZ/liiDocstpatdBr77E55MJWbyYxMVse7Sz2rsriWya37nDPw4eIoVFVHE3z6OH+n3S++8vqhiQ8IMHp6MADRDr6d9Vq1a53W6nucHbKopiZGTkqlWr4Juyb9++5ORk5v/G83xYWNiPh2dmZsIlK4ri8/ng4MrfNSY036hQX7ihAF1f3qnyfgYJ0BC8M23atHp2GdhdJIAEkAASQAJIAAncMgG2NLjyGYFAQFO1M2fOzJ49u1evXhBvYo1udrvdLBrFbre73W673f7444+vXbtWU7WSkhLIK8jG9JWbwD1IAAkgASSABO4fAmlpaRXaKP03Pj6+rKzcxQIgKIqi67r1dxOkY9MimYY0HztKrTMSmue89Oxln5cUX6W+GTq5qtNIYsX03gD1WSlXrSsSAFILCz8JeMmH88lDYRsfabX/6cdOymVEVqh1skx8VgEapGfTO9nQZE1RiE8h+/NJcvfD7WPPxUR+mzmbFF8pt12WDBncn80gaDVIgNZk07mDum+QXdmkZ+yBzs23v/9usd9Lr/hK2VUIdLb+Be9peka5AE3NqfO/Iz277o9vVdghirSPvpjU5e/bdxG/QmO3Verh4Zf8PqITWVaTkrqFhdKMFKJoBwHaav3MyvfPp67uXylYZBiG4fXSjwVEKhQVFQ0dOpQlERFFEYagTz/9tMfj0VStrKxszpw5PM9DvkFIOsJxXKdOnQ4fPsy+RNYslNYvl/WAm5TrPj3oIQrQ9eWdKu8nCtD17A3D7iIBJIAEkAASQALVJgCJBIPc8WDB44IFCzp16sSbG0yYnU4nU5zB2ZkNnzp37rx8+fLS0tKgHlnH9EEv4VMkgASQABJAAvcVgSVLlkCeXofDYTe3p556iq0E0nX9RgK0TMgVPznxPRk++ERck6+ffaLwylmq/5rir0TTDF4ToDUzAtqMqobcg2b4tCqRgIdkrSExTbITWn777+knis8SPUB0XVephbLPMCOgIQjaIkAT1Uc0P7l0mQwbnteuzXctG+ePGX3eS4Vvqlyr1O5DrxCgdb08Vrv8XQX12S8pAT85/z3pEr+2R1z+z5P3X/onFb4VlR7NzDaYBq2ZFtA0qrmicOx7MvCxXZ3b/TO2WVl8yytRTf6xJZvaQlPfakM2dB+18dCp0r1r126O40XRLgghHMc/9tjPK7s/gwZ9X33w6v7FWgP/DcNYs2ZN69atOY5jsjLHcU2aNMnOzqZ3JlTtwIEDbdu2NW8ziBzHMW9oCHy2Dj5RgK777/792EM2g4L7KhgBfT9+CPCakQASQAJIAAncTwSYA4au6+Cjl5eX9+abbyYnJ1sjnUF9Znvsdjsb6A8YMOCv//fXoqIiiKSWJAnqBL9LjIC+nz5NeK1IAAkgASTwEwQMwxgwYEBoaCj8pDqdTlEUR48eDT/BEP5p1c7AfEMhJGCQ778nw9Pz27Xc1a3d3mPfEslHHZktG83Up1MtuPxR/pIp8co+IpeRU3tJcodvWrfYN/Txyye+o64VhkIMTVUNmt7QIBIxqAvHdUYcpngduEwmvR6IbrEzuvW3vZO/LfYTn06dPkz3ZyoEg44Mfy1dosHQkqQYhCgyGf6z420a7Xi0w9qrdH0U8V5VfWYQNI13NoVslRhMg5YN3UwraPgJueghE38vtU843rJRYasHf+gUt2PF/9EWJci1WH4O7WjRxaL4+ASn083zIscJPC9O+f00FvIcVLiun/jknhJg6rPf779w4cKoUaMcDgcIdJCejeO4IUOGeL1e3dzmzp3LVhJA+DPP8506dSooKGAmG9bvEZwFf637b6V8T8HcRuMYAX0bsOrCoShA14V3AfuABJAAEkACSAAJ1CYB2dy2b98+efLkhg0but1uGMqzkT0UIGKLxZh069Zt1qxZJSUlPp8Pxvoej4fmCZJlTdWKi4sVRYEVlNbBfW1eF7aFBJAAEkACSKAOErh06VJ8fDz8tjqdTgjw7NGjR05ODpgPVPxuUiGYCtAG1ZXlABk1+HDHyG86P7Rt6cJyx2MVzC2u6b4gQJMKDVotj0dWaRTzxrUkuWNuTJPshx/Zfvz7CjBUvVV1nWrQFQI0bV8jhmTIMtFkM8ngp38i3TsWtGr8XVybr7d8Tf0+iiVDpqYaN1OfddOMg7pkaOT3Ew/ENv5HuxbbvjtEm9YJkRVDM21C4AJN9ZkJ0IZGNEmj5iQelRw9ReLa7oiLuRLXurhN6/1/nK/7/eSqRGVrGt2sUmNrolD1+dGkR8042WYOh8scsbh37NgZpDuzpxUI8N97Q8C69g5uvfj9/tzc3ObNm9tstvDwcJu52e32tm3bfvTRR/Rjo+tbt26NjY1lI9WIiAiHw8Fx3Ny5c2EUClq21+ut+B7Rf++SAM1083tD8PpWUYC+nkedf8ZmVoIg8DwPK0xnzpxZ5zuOHUQCSAAJIAEkgASQQBUE2KpelgBQUzUY8cNLS5cuffLJJ6Ojo8FPw7rOka1qZAMkjuO6dOnywQcf7Nq1CyqxDuitcSVVdAV3IQEkgASQABJAAqaIduTIkYYNG4aFhfE8zyxufzTkmD179oULFzyeqzQzoUb/UknaR+QSMut33s7NjnZsnv/CM/tKi4iqmLkCDep/QeOQy42X1QrANObYjCDWNIOUXSH+YtKnZ1br6Kxefbd7fESSiaqalhWqTlTdoEMDlRhmBLRu6t3UFdrwEL9KyK69JLHz3ugmx7t1PvtfrxeWyaRMpg1CXsSKFoP/NfMdkkt+4iNk0RLS9qEvunbY+pdlNG7aE6DeHVQ+Nmi0tqYQTaVPafJDc79Gn5nW1Dq5fIkk99nUqvmhFk3OxkZ9O20q8QeIqtFOUg+xQEUQuE6GDx1uyvq8w+Y0s1aEJD6SVFbmZYpzUCG4x/i8dgnous5Wy9Ho9aKit99+m3luCIIAHjUDBw784Ycf6E0RVZswYYLD3OCLI5pbamrq2bNnb953qxh9i2WWIoWNpTVV8/v9cDosWdB1nR128w7UwqsoQNcC5JpswhrpgwJ0TZLFupAAEkACSAAJIIF7RADSrQQ1vmLFivT09AYNGkBeQesQSBRFp9Npt9sFQWA+G2FhYc8888zWrVv9fr8sy9aIjyANGsblQc3hUySABJAAEkACSMBKID8/PyoqCtYVgQZts9l4nm/VqlVOzteSpPj9fkUu97b4/W8Ku7Tc1rlxwaMxuy6dp9VooMDqxAAHZQiFJjq1hTaoebJuarylsi5r5OQxMuyxvQltN3bqkbXvOE3cx367DY2qz+YDBGjJMAVo6qBFyBWF/HCZpKYdbdX8UJuo7wakHivzU6sOT4C6d1gvJ6gMnZIIkQn530/1NrEb2kZnv/27S4WXaLdopKph2kYb5oWo5l+qpTMBWqHiNCGBy+SPmSQmcltUix9atzj60kvef16g8dQaFZ/Nzew8IWTcf/yS3jjnqB0wxD7/aN0wY8Z/UwMQk1Llv0F9xqf3kEB2dnZsbCzHcSzoweFwNGnSZO3atRD4fPDgwYSEBDCusSYjmTp1Kqy3I4SAKFzlVVR8XG71XwimhjWCGzduXGJuGzdu/FElZ81BQ3BMlY3W8k4UoGsZeHWbY7MvsJtxOByCIMyaNau69eL5SAAJIAEkgASQABKodQIwyoZmNVW7cOHC3Llzhw0bBgN3nueZvsyGQKwAEwBBEEYMH7Fq1Spr3zVVYwJ00KpGllvcejyWkQASQAJIAAkgASDA1g/5fL6jR4+CzwD8+IaGhrJf4b590rI3HyAq0X1k3SekU8PtSY1P9GrzzYEcoptRzuWRwma8cAVb04mj3I6DBkVrpkZcVEQG9M9v3Xx7fNymrGxSIpvWyUyB1i0CtC5R4w1DU4lRbMamSoS8MaGoQ/yxyGbf9u6Rl3+YlF0lHp/pv6ywaOuK9iv+ZepzgJCdu0nH9ms7xec9/tjhy0XEIxO/Qa5qAUm/Frptxj4bGo2NrhCLCdXBiUKO7ydJcbvbNDvVOe6fPx901uMlV2UqroMATUVqg/i83j7JyfYQG9BzOt0cRwNkO3bsHPDLAb9cWXqGPRX9xX/vDQGm5GZkZPA8b12EZ7fb+/bte+HCBZCVJ02aJIoiWG0w8/RevXrt27ePdd3r9QYCAautB3spKB/JrYjQYIazefPmpKQkpnfbbDa73d6rV6+lS5eWlpYys+kqQz2srddOGQXo2uFcY6306tULZmLsE8Zx3NSpU2usAawICSABJIAEkAASQAI1QYBJwD9ZWVFR0eLFi/v06eNyuZi/M4yh2UQX1jCyp5GRkc8+++wXX3xRWFgIMSAwEIehNrPasMxerxWtqvdP9g0PQAJIAAkgASRwvxGANfuKQmOci4uLO3fuDL+/zNa24uc4vEPcz1csP9cj4YNe0bsTm+b9cbpCJAhwJhpRaLwwMRQNrKIrfKAtCQFViRRfIqNHXngoen98/J533iVFpquHeu1Hu7xUEQFNZWtTgCaFxZonQBYuIA8nfBPX+kibyNwNG0lAJqppSE29m2+wgfOGREiAEJ9MRqafbN96Z9eOm/Z+Q0quUsNoiehXNVmmWQdpGLUZ/ayYl6PouqqpBlWHDU1TieIjo9P3JDTP79WxpMcje4uvEJ9G3Z6p3YgB/h3GwQMHOiS0B2KiaOc4LiKiIccJthDH3r37afCsRoPEq3zc4Apwd+0R2LlzZ1JSEqhwzIsmMjIyMzMTOnHs2LGEhISKbwQH3tBhYWELFy6kNjUK/SBKkgSxz9YIiaBruBXRGYIq2Dh2wYIFYE/H5EHmSc1xXHR09MqVK5kGHdTcPXmKAvQ9wX7njaakpLBPNvM9nDFjxp3XiGciASSABJAAEkACSOAuEKC+h4rCbOlolh6PJxAIMCu6goKCyZMnR0VFud1ulkAcLPNgJO1yudg6R5j0ut3uUaNGffjhhxBycqNew9Ac5qw3GtDf6FzcjwSQABJAAkjgfiZg/d0EDhcuXHjmmWc4jnO73TabLaLBA0IIRx/0tzmU4yI4rnN886nPPbFBLiN+H/HLfkJUWS/ViawaqgqZ/sAyA2rUzcyAhJT8kwxOORgbeSy2zaHXJl4qUYnPMAjx6AYNFKWuz+ajXHEzTLHWrCEgE4+X7NpJ4iP/kRh3KqZZzruZNOqZ+S1XWE4Hv5O0DkKKzdDr8xfJiPTj8Y2P9Wr/w7IPjasSlaRlIklmDDdIz+Zf0/3ZoBoxFYu1a4HVC9/V2jT9ql2zA6ndjhw+SO2ofabTCG2F9l5bvGhRiCCwB6TyAu/gzz77jBkyVKk+0whr3GqFAMRMGIbh8/kCgQA8lSRp9uzZEM4Mo1D427NnzwMHDui6XlRUNH78eDaCBaVOEIQePXrs3bsXPsBBf61frlsP1LAyAFtqwzAyMzOZNggdC/Ksg7F0Tk7OjWKurdXWThkF6NrhXGOtoABdYyixIiSABJAAEkACSOBuEmBhGqwRWZYVRcnOzh47dmybNm04joO1inBP3eFwwCifjeCtA+sBAwYsW7bs2LFjrLabFILG91U+vcnp+BISQAJIAAkggfuWgPVH0+PxEEJKSkoMw1i8eHHDhg3L9TgQoEWqQXM8laZdYo/4h0Z98P4Kr8+nET8hik+54pNLdKoEV2wVnszeYpUm8LtC1ecmEV/HRR8dnF5QHCCXJXLFf0klVwiRmfoMGjR9KsmKL2BU1Kf4yMA+2zpHH30k5vjLv7oo+S0pB0FmZsJ3RfuggauE9u/MFfKLZ690jTvZoenRGb+lR5T6iGzmRayIfaYhzmYQdLkArZkaNFSmqeTcWdI3eV98zO7Ixiv37SRXfTR62myZKscFBQUjh48IdbuZ+hwiCJDEguO4pUuXgvpcThsjoC3vUV0o7tu3r0uXLkGSriiKCxYs8Hq9hmFs3LgxISGBKb8wZOV5fuLEiWVlZZX935gSbf1+3cGVQnjH+vXr2ShaFMUnn3zyTXN78sknGzduzGJVOY4bPXo0BGJXs9076GrlU1CArsykTu/p168f+2SzTxVGQNfp9ww7hwSQABJAAkjgPiYA2bcDgcAXX3zx0ksvge4MPhs8z4PozPO8YM7K2NpGl8sF5T59+vzpT386duwYxE3fxDvPytg6yL5R2Xo8lpEAEkACSAAJIAEgYP3dZEzgV/j8+fMpKSnh4eGCyNGHEGKz2QTqKkE1aBoKTcVo7mcDUz9a/iEhmqxdNe0oWDUVCjQhgX+SZ35+rGHE9jZtv0vqmnX5CnXDuOKlfgXUoFmnEcQgPV8vQMuGQlXe0iLy/NPfd4zc07HF8RE/Oy/5yVWJWj8rikbPZ49rDdI+QPpDmZB/lpCX/6uoZYN9nVufHJqWR10zzE01qINH+cMUo03LDzDiUFTTVIT2UCGXfiD/9WJJbJtDD8Xv+OtKerKiEp1mNKQC+ax3/rthw4YCx9lDbFYBmuO42NjY1atXQ3PXUKMADUTu0V8WjGz6ipPJkydb7Z4hbj0xMTE/Px86+Pzzz4P3RWhoKIxXXS5XYmLirl27YKQKVhvX3t8blO7gciGcOTExEdoNDw/Py8uDqG3DMAKBwMWLF0cMHwG5Qx0OR2JiIiHE5/NZu3AH7dbIKShA1wjG2qsEBejaY40tIQEkgF8xq/gAACAASURBVASQABJAAtUj4PV6v/zyyzFjxjRv3pzdOGcqM0xYrX+Z80b79u2nTp0KQ+rS0lKI3bC6eVQOr7b21DrIvlHZejyWkQASQAJIAAkgASBg/d1kTLxeLyEE5LmFCxYLXGOBayZw4aLoDHEIIQ6B40JouGh5mj1qSxDxYPjQ4elr1v3NDIIG7Zf6UyheQsrI+BGnu7T8tmPbMzFtv84/RHwSbQpyA/oVKvRa1WeqR2v0QTeN+L3kw/dJ54d2tGt2oFf7A/m76O5rUvMNwp/ZblkjC/5Ikjrtb9PkWGrXgqJCoirUrJp2wPSPrhCgJZVIFQK0ZpYl2ezChTPkjV+VJLT6OvqhrUs+JleuEkkvF7dXrFnepXdHjucgYSPlYrHg6NSpU3FxMeSusHJGCw6T6z374/P54OO9e/ducHxmZingsDFnzhwYhebl5SUlJcFOtoyvVatWGRkZ8O2Aa/B4PNe9vzd4cmcXvHjxYo7jwsLCOI6bN2+e1VcalPSysrKwsDDwg3a5XPRLY2bnZr24s3arfxYK0NVnWKs1pKamwmcdQv1hCocR0LX6HmBjSAAJIAEkgASQQAWBQCCgqRoLT4ah7dmzZ99///309HTeslmF5splGEZHRES88sor4LPBRslBhYqWaXofFrHCdmIBCSABJIAEkAASqHEC8JtbbiMgk4unSOsHn3IIMRznon5atkYQcUldoelGRVeeF+koQOB4gWvTpu3rv31z167dvjKa+2/ii8d7Rx7pHP5dYtSOdzPkAFX/qH8FpCeUdSIbhJotU1mYpjHUTF3Y0Iki+QkhuRtIp+jtHVrnP5qwJ3s9kX0W9RmuHNTgShRkU6de+znpHJvXpsm+rvF7vskmgQAVvmGj3tQQAU0jmWnIs0wM2axeJlKJv8wTIFdLyau/KowL35XYes8f5hddLiWSRgKalpmZGRcXS0c4IZxou6bEcxznsjsaP9goc9bs8hjsG3Svohf4b20QMAyjpKREUzVd1yWJ3gB55513nE4nSG0srV90dPThw4chiHj8+PGCIEBwtMPhADmuf//+586dqzwiha9M5b/VvLZAINCrV6/Q0FBBENq2bQsZDpm/h67rhmF4vd4xY8ZA4sSwsDBZpoY21p5Usw93fDoK0HeM7t6ciAL0veGOrSIBJIAEkAASQAJVEVAUBUa0hJCzZ8/Onz8/MTGRWTlb9GdzUe71wjMb5UdFRb3wwgvbtm1jMc6sWutwmTVUVUdwHxJAAkgACSABJFArBBQy4debOke/+ep//k+XR/qEuVub/huCaZgbIgj2igfE/lJB2hbiMhdCOdu3Tf7tS8sTmk1NaZvbM2rrr5/a4ysiikQlYIhQBhkaEgAy6VnTiaYTQ6VisKeQJLXJ6xR5qm2LnL/8L/GUmIHTN7xulaYVpJHNRDJoE/l7yKMJWzq2OtjloX2L3qXitW7upwq4Vu71DL7PKgEPaE0mmkwUj6L5VXKliDz35NcJLf7Wvc3BJ1L2XjhPTp05O+rf/71Rs+bUlIRu5Rw4jhc5usceYvvFs2MvXbhI+wjSMwrQN3y/aukFXdetibL37dvXrVs3u7nBWBWs4aZNmwYdys3NjYmJsdvtIE9DiuxGjRotWbJEUzVFUViGbXYBlUew1R/H6rq+Y8cOtpRwyZIl4HRnFaBpIL+us/SJbrcbEoBb+8M6WcsFFKBrGXh1m+vfvz/4oGMEdHVR4vlIAAkgASSABJBA9QhAuMeBAwcWL17cuXNnJi+Hh4dD+UYCtM1mc7vdHMf96le/+uqrr5jubO2OdaBsLVuPwTISQAJIAAkgASRQ2wQU8njKwhFp/5+/jLb8/nuLGzZsJIiczUYzOlgMJ8rNJ0TR7nS63e5Qp9Mpik4b9yDHtea4dk0eGLT4/a35hy7JBin1l/gVVdbLZWgz+liigc/XoqCJIdHsgU/2P9Kx6emo0P2TJhSXlVH3DBWsOaqgoBPiI8RLiM8gNKr6uyOke8L2js0Pd439dvwvzmo0nLp8K2/IjLw2BWgDQrBNKZzae0gqOf89eW7Eji5tliXGLu3S7t03Xl338MODuJAQjhdCnFRhd4eG8yK1IjE33ibYX/zVi2dPn6FXBRsK0BUk6si/paWlCxYsiIyMhJBnprMlJCQcO3ZM1/XLly8/++yzoMJBmD+8u926ddu3b5+iUPtw+Fs7V/Tqq6+CqV14eDgzqas8Tl60aBH0Mzw8vHJUR+10tXIrKEBXZlKn9zABujz5rEBvr02fPr1Odxo7hwSQABJAAkgACfzLEcjOzp41a1ZMTAwM2VlidxiisL9Mg4ZxMPx96qmnduzYcfnyZUmSIJuKFQ+EpQStFmRja+uRWEYCSAAJIAEkgARqm4BK5BLqpMF0VVmWMzJmNmvexFSfWQR0ecEMCubNl6h8ASMEu80dGv4gyLXxHduOGD18+V/+b8+BfL9ClWIwXKaBzxqNQ9YU83GVTB3v7xqZ/3CzgicHXjhZQC07CCGqQfP+VbXpZi8DEAF9+nvy7Mj9HZrvb/vg/nFP/nD6OPH5iNcXoLHP0BBEQJuR1qb6DBo0/SspgeMnvL94ckWr8MmNnf/FcYM5LonjWnGc0wx85oUQmorxgbAIKg7aHG3btpsz5x1VUpWAopsCuSrJZSWlGAFd1dt0z/YVFBSkpKSIoggRzUxlzszMhD6tXLkSjJ5Z0HFYWFijRo0yMjJKSkpkWfZ6vX6/5T7GXb6UQCDARPCnnnoKXKclSWKDZAgN0XU9IyNDEAS73d60aVPoVNAxd7mnVVePAnTVXOrs3unTp/M8zz79cH8GBeg6+35hx5AAEkACSAAJ1HcCa9eu7du3b69evZKTk9PS0l5++eWnn366ZcuWTFmmBo8VG+xkWjMMVGw2myiKNptt5MiRa9asuXTpEgsVqaw+Ay5YS2gdK7NyfeeJ/UcCSAAJIAEkUL8JGBbDZhbSS8ipU6dmTJ8V2SrWJj7AcXa7LdRuC+U5hylA02x8PGczcxWG0D0Cz5v/cgJfcQD9N7JNs36Dkj9a/uHO3Xmq6c2sykTyEi1A/m8pebjFtkejvuvdfuMP1JWXGncESMBv+GUCx1q4VgQdGzrxXaVWG0+k7evW9mjbJvse7bDNV0YkmerOhJCSMqpB08SACq2QekDruqJpXq/XMIxt27at/PyzGTMnt2gZw3FNOS6B46I5LpLnWgl84/IBjyC6Hgh1u0N5Xhwx6qkv/74eKiwP59YNQ9Op0wd7XGfBod/cQ6S8KvznTgmAJmsYhiRJsrnBnszMTHj74I6I2+3meT4+Pn779u2QJfKVV16BA2w2Gxxjs9nS0tLOnj0Lg9I77dGdn/f555+DszPHccuWLbvRKPpHYXratGkw9m7fvn3l9phODfkJ4YDKLiKVT6zmHhSgqwmwtk8PEqDha8CMaWq7N9geEkACSAAJIAEk8K9OAEa6oaGhEOMsimZOIav8fGMBGlLAp6amLl68GEbzMFa2JgqHhYFVUmSis7VQ5ZG4EwkgASSABJAAEqgtAjpN0Qep+8C5uSKLX8CvHzl8atLEmW5XI5sY5nJG2G2hHLVCpgI0x9mpBi2IHCSGEDizIHC8QwhxcnbzKJ7jbBwfwvEiDZdOTOr5yvgZf/0k77O/nOjacVZCyxVJMWs3fUGNnQ2daMSjEJ9KXZ6r3miiCoUQhfz35BOPxm97OHp/r4e3H9wffDAVnc1o6iNHT2zYmDV33v+M/69XunbtynFceHi4w2FzOGmPBcHOc65Q94NOR7jAhXJUW+dtDtcDYRFNm7eY8vtpZ8+ev04IL4eDAnQw8Hv4XJKkgoKCDh06sGgJVnjttdcgQuLzzz9v2rQpy0MIQ9+IiIgFCxZA0r97JUCPHDkSgrVFUdyzZ8+NBGhZlp977jmbzSYIwtChQ6n3uFFxQ8ZEz0KnNVW7dOmS1+utHSMRFKDv4Sf/TpqePn06uKFb79WgAH0nKPEcJIAEkAASQAJI4BYIwJCDrb7ieR4imgVBYCp0RQB0+R42lIdCampqhw4dXn311YkTJy5atGj9ehoZZBgGZOWGLhiGAdlgrENkq+7MyrfQZTwECSABJIAEkAASuEsEIGIXEvUFlYnXG9BVIkvE51U/eP9Pjw0acl3Us5mgj8rR8OCpfsvxDo57gKrOAlV0ebuD5u1zUEcLh8vJcZzrgQgx5IEQKmQ34LguMTFPT564cPEHH+7ckXv42J4LV8/KxEe16Bts3hIyf9b+np0XdUv4a1zkwk8+8Z85T7I2H/vT/37+29ffHj7yydS0foPT0xOTeobYwt2hDRwuJw3NNq1CTNNq0WaD7IJ0p90G2nmITbC77C6OE4akD139xVq9yvZNAdowjCBXset7ao2ArhDyrz8Cn1WHABtYBgIBwzCWLl3avHlzFkcMI9U2bdps3rxZUZRz586NGTOG2nm73bCMz+FwOJ3OEcNHFBYWaqrm9/vv4Yg0PT0dOty+fXtw3qhSg9ZULSkpyW638zyfkZHBCDCMuq5LkkQIGTJkiMPhGDNmDHvprhZQgL6reGu+8unTp4uiCN8EZp+EAnTNg8YakQASQAJIAAkgAZPApEmTYO2hIAjW8TpTn29iwcFxHIsfgTJY6cHouWnTpt27dx8yZMjYsWMnTJgwa9asTZs2nThxQlM1NrivXLgbb0uVw/e70RDWiQSQABJAAkignhMAwRSCoEGGDphWy9eMmHWN+K7KukYUxTj47ZEJE96ObPWQGd5shjwLZpFGRfNUgOZcVIDmbZyNc4bbedsDpo2yzRVK1WfYQpxciIsTnQLHucQHGoU4qELscvDOB0Rno5AHmrqS+yb3+beUPpat77/16Zuckpyc8rPUZx50/zzc9jTHPc5xvTkulhMacUIDTgg15e+KsGsqinMc7+DFEMHGi3YqNNtCHKZYDrHZ9AC7jR6V0Kb9q6+8svx/l5WWeAJ+WVHK5We/TwpSog2d3nG/HQEaNega/n74fD5CSCAQ2L17d0pKCmTwY5Laj5bKmZmZ58+fl2X5s88+gwV/giA4HA6wsGjWrNmHH35o7RPL6WfdWTtlr9c7d+7c7t27FxQUSJIEA+agpmHk3LBhQ4fDwfP8Z599VmWub03Vxo0bFx4eHhoa6na7qzwmqObqP0UBuvoMa7WGzMxMmO+5XDTLKoQjzZgxo1Y7gY0hASSABJAAEkAC9w0BXdcvXLgwdOhQFgQNs8EqBWjrgB7ulFsPY2WooXI97ACe56Ojo1NSUl5++eW5c+fOnj37L3/5y6FDh7xer6ZqzKWuckwHdYTUdU3VqtSUNVWDgBH27smyHAgErJI3ewkLSAAJIAEkgASQwI0JMCX6WoGKXzo1x9A1+tBUAx6EkH37Dsz87+mPDx1sc4miXaRRxlTjpQbQQogzxE7lZpvTJtocNgfVOmAUAe4H5U9D6BFciF2gCQ05ked4MPYI4XkBEh6G0CVZImcuzAoRzJ08H8pzzTiutZkzsBknhHGCi+Pt1OaDmYFwnCC6HY4HTZ8QU4kG1xDavRYu4WE79zDHtRiY+uT/mz3v1IlTpcUlhkqUgGkaza7+OmfncmxgKq0Z1Fpau84FIYgrqyWoEHQYPr1VAtaxYiAQeOeddxo3bgxREWywmpSUtH8/NWTxer2jRo1yu93wSWOJ/tLT03/44QcIFr7VhmvrOHZjI6hBwzBycnLgSu12+8GDB60oNFXTVG3Tpk3du3eHr5jb7R45ciQK0EEY8SklMHXqVHrbzU4XpEBSSwiqRzpIAAkgASSABJAAErgbBHRd//TTT+lKWIeDjcuDxGVmwQFR0jzPN2/evGHDhlZB+bbK1oZYGUKtW7Zs2a1bt549e44cOXLOnDlTpkzZtm3bhg0b4Np1XYcMM5UFaHgJDqty1A4xI3eDIdaJBJAAEkACSOBfkQCopXBltFx53ZJhGObdX0WSFEWVdF31+nybs7e+8bsJffqlmPozL4TQVMWcQAvwoy+EiLxY7usFll/lgwGR5+mCcCHEfNCXxBBOtPOCW+CddJ9IVWWmQfNiCHtUvCBS3ZoXuJAQm8MFwrdZOc9xDl5w84IdPKtDbKEPtf63UL5fy7Ax7aN+sXbFyYCH+ErNi9U1JaBIflmTNWqFDY9KAjTsZuozCtC19hWAXNbQ3KFDhwYPHmwdx8LCvvHjx/v9fk3V1q9fDzlLQJgWBMHtdsfFxa1ZswaCncEjDsLYa+0SfrIh63fNerBhGAsXLgT/jU6dOkmSBENiwzB8Pp+mahMmTIAVjaArulyunJycyj7R1jprqowR0DVFspbq2b59O3wrIP0gJiGsJe7YDBJAAkgACSCB+5WAJEkffPCBaG5MC76JAG2z2WAcH3TMbQnQoDXD4ke7uUEqFZ7nYbgcGhrK8zz8ZS4fYWFh7du379OnzwsvvPD6669nZGT84Q9/2L59+8aNGwkhfr8fUqzIslxl6DQK0PfrZxyvGwkgASSABGqGgFUUY2VWNURfqtffIj5w8OCszDnDRoxI7tOH47gHwsOoNcf1m8jxtoocyNZ73lCm4c9cKH2AAB3CCWZwM41vFqlCDY9rAjRI1Nc3Ac+690569j+e/OP7/7Mha+v5M+TZkR88HJ351KC/HfuWXgQ1FZGILOmKosDdbkMlBHRn9te8WiZKa6Q89hlkaLa/ktEGvGJ11rYeC2UGEgs/TUBTNY/Hs3DhwkaNGomiCBYCdrvd4XC0b99+y5YtsPrtiSeegIElfAB4nhdFMT09/fTp0/BxhU9rHQyCZt+voDGtpmojho8A+/K3334bSIEPydq1azt06ACKIly10+lcuHAhJCH0eDw/jbV6R6AAXT1+tX72xo0bWQQ0WnDUOn5sEAkgASSABJDAfUogLS0taKZmFZSts0E4DNbMWo+5rTJrSxRFu90OsSqsZutUwXqkzWaDqYXdbrcahrDb9snJyT8a5z377LOLFi3atGnT/v37L1++bB3BBw3i79M3Gy8bCSABJIAEkMAdEQj6SWVPrRGpGjE0qtpe2zRiKJoGO498dzTn69xPV65466230tLSBgwYEPtQTMPwCKp+cLx1vGEp2wWugcCFlwvQNC7aLXAtBK4FjWiu0KCvE6A5zhEaGtOmbddHu0+eMm3Jnz7a+c3uwksXCU1mqJiiMlH8ZP3fij/6Y+mV00T20n16JdmYXgOTni0R0CAYU/UZBehr73PNl24UlWwYxsmTJx977DEQzWAwCSPGSZMmKYpSUlKSlZXVoEEDNraEQpMmTbZt2wYdLSsrqx1jijvjwr5cQWNXRVHatGnjcrlsNtv69etBXD579uywYcMgHQuL2+jevfumTZsgOOPO+nC7Z6EAfbvE7vHxu3btgo8L/AWTmkmTJt3jbmHzSAAJIAEkgASQwH1A4OOPPx49enTv3r0TExOZ8ltlwaoRW6Vn6s1oaspwFrP1CAsLA/m4cm3Xrb2t/HLFHmjFMh2lRdhZccgN/3U6nf379+/bt+/bb789derUBQsWrFq1Kjs7O+gtVRQFhulsrA+jf5hXW/9ajaqDKsGnSAAJIAEkgATuKwLsRxOuunJkb4VcS4Xp6+RpU9L1eb00iZzPvy03d9eOvC9Xr1n4xwVTJk+eybYZmTOnLZw5/Y8zZ86eOSNz5tQPH+s7uUnI+Cb25weljXt70uTJU6b9v3fn/W312r9/lbV5a87X2/Nulb8BErJpslH1OcY1AbrqA65ZdARd+PWHB71Y5dPrz8BnhMiyzOLpoaCpWiAQWLx4cbNmzWDYByNSQRCio6PBa6KgoCA1NRVehXEplNPT0y9evAjDuRvJu3WTuiRJPp8P7G527twJlxMZGQlMZs+ebQ3LcDqd3bt3//jjj5k7R61dFArQtYa6ZhrasGEDuD/DRwoWt86ePbtmasdakAASQAJIAAkgASRwUwLWYBCv13v06NFt27atWbPmo48+mjlz5quvvppubuCeAcMVu93O8rrA2kZY/SeKosPhgIkBU6JhbMPGObdeqI4ADSEh0BZI2BA0zXFcVFRU7969+/XrN3To0IkTJ37wwQe5ubmbNm2CfIawCJdNfoCcoiiBQEDXdViwGfTqTenii0gACSABJIAE/sUJVKmtBu0sRwAxxboZLm1QDVqVZE1RdFUjsJOhMio0YoP4S8nk19Z1jsx89/cFly+UH6ETIimqohlVBjGzam6zoNP4ZxYBfYOTgy6NPb3+cLb7JoXrz7jvn1XO56EoSmFh4eOPP85xnMvlEkXqFw4C2oQJEwzDkCRp7dq1zZs3hzSDcAzHcTExMatWrSKEQBZrCKxmGnR9IQ3dfuONNxwOh9PpnDRp0ubNm7t27cpyKoqiOGDAgC+//BKM6Vhywlq7QBSgaw11zTS0d+9eqwUHzJdef/31mqkda0ECSAAJIAEkgASQwI0JWIeqEA4Mx1rLMPyVZVkxt8LCwj179mzYsOG9996bPn36Cy+8MGL4iNTU1FatWjGtGeIymEMf23/r6jOcAs7R1iDoW4yAhobYmkTmQB0RQdf8wgYJW8BDEGR0juP69evXv3//sWPHZmRkLFu2LDc398iRI1YTPVSfb/xpwleQABJAAkjgfiRwE4WVvVTOhZlaMLmZCs2Goema6cIslW+KFDAkP4EHDTkmJFBaLkmrtyc5syaD3hqJEOn6XdfMOq7fH/yMXVRQ4frjgl6s8un1Z+CzCgIQ+QuBzy1btoSxH0Q5cBzXsmVLCHyWJGnE8BEwqLOurhszZkxJSUkgEID66mMENIw2JUk6ceJEWFgYXOPChQthZAsqfHx8/CeffMIMNyA1N+RHqQB51/9FAfquI67ZBjRVAxcbCBQSRdHpdKanp9dsK1gbEkACSAAJIAEkgARuRABkaAgMqXyM1+sNBAKQNxxeDVp7y06RJCkvL2/Lli3r16+fOXPmJHMbNGhQUlLS4MGDGzVqVC793to/1YyAhtG5w9ysCxVZ+Axbgmbdc6OuQWeSk5N79Ojx2muvTZ48+aOPPsrJyWHGggwCFpAAEkACSAAJ3FcEqtRWg3aWA7FGQOuGz+tVJTk49rkqdrpK93rKaPLhq34qHPsCMhyoaIakqNp1HtSsCua4EfSyQYjffFj3g8OzdQ+r57pC0KWxp9cddEOjDnb47eno11f+L/4MbDcGDBgA4QihoaEQNMBx3GuvvQajVjDlYOvbILlIo0aNVq5cqSgKCxcIBAJg68HCn280iK1rTKHbL7zwAkRRtGzZ0m63C4IQERHhdrsnTpwIAeP3ttsoQN9b/rfduizLHMeFh4c7HA6Y29jt9pSUlNuuCE9AAkgACSABJIAEkEDdJnD58uUDBw5s3rx569ats2bNmjFjxpw5c5555pl+/fpBADXTfyHrIMSzWCOgQUoGcZkdDPMTqxU1vMTzvDXThsvlgrEW/A06nb1k3X+L5e7du3fq1GncuHHTp09/7733Vq9evW3btgsXLkAgucfjgRWg1jkPczk0DMM6U7Iew24JyLIMyd/r9tuLvUMCSAAJIAEkUNMEfsoQA9qz/npaemBaapR7alh206JqPqw7K8VKV9oB4rH1nJ8q3/4ZP1Xjv97rYHZsjeTdtGkTuGpYAwgiIiJyc3NlWb5w4cKAAQNYbhKe50Gefv755wsLC5lbGsvkAaOsux0HzVw+CCGsreq8WYZh7Nu3D8JVWcyEzWaLiYn56quvaLJMc6tOE9U/FwXo6jOs7RqsHyZI19O/f//a7gS2hwSQABJAAkgACSCBWiTA3D+sk8aCgoL8/HwIo543b96kSZOee+65IUOG9OnTh/l42Gw2p9PJ7DWsK8mstmbgUg3iNTuXqcwsZIZJ1eylWxSd2WF2u50ZXkMwNVQOPWzQoEGPHj1GDB/x/PPPgzydl5e3adOmixcvwhTF7/fDKlEGhL0JoE2DSbfVqpsdgAUkgASQABJAAkjgBgSs4m8lLbnqc64Pf650krXGqisI3nv7ZwTXcB89NwyjtLR0/PjxzOOYDdJGjRpVWlpKCFm5cmWzZs1cLhcbetlstkaNGq1btw5IaapmVZyZDM1EYRYKXVNkoUVCyLZt27Zu3XrhwoXqj9lkcxs9ejREdjNru8GDBxcXF9985WJNXdet1IMC9K1QqlvHsDQ+ornZbLbU1NS61UXsDRJAAkgACSABJIAEapeA1+uFMBZrs7m5uVu3bs3Pz8/JyXnvvfcgTeKoUaP69evXoEEDyFEDhs4QQw0BMjBwZxIzFJiCDPI0e9W6/1bK0IRV0YaqBEGwWzZrFA9Um5CQ8PjjjycnJw8bNmzatGkzZ87cvHnzhg0bysrK4JIVRfH7/ZBjJyhQ2soEy0gACSABJIAEkEDNE0ABuuaZ3rBGWZY//vjjpk2b2u328PBwu90O1hNRUVFffPEFIeTixYtjx47led5ut8OQDxa6PfHEEyUlJZqqMdkXFpkFSc93T4AmhGRlZXXp0gU6/OOwcPr06Te8zlt+Yffu3TCSZGnAk5OT4WwwesYI6FtmiQdWEDAMIyUlhcXVQzQ0+2BVHIX/IgEkgASQABJAAkigfhPw+/0styFEPUMwC1yVruuKorDJg3VpoXWEDfMHsKRgOMAFj527ffv2v/zlLxMnTpw2bdqI4SOSk5MHDRoE0TRMZbbqxdUUoCGDNFRiVZlhHlJZwgb/EBa8A1MpdiLETTudzujo6H79+o0ePXrOnDlTpkzJzc3dsGEDu+RaLlij1Gu5aWwOCSABJIAEkMC9IYACdG1xLykpgXSCbH0bhGkOHTq0qKiIEJKdnd2sWTOQy2DIJAhCTEzMli1bCCEwAoT1ZFCuUn1mLhnWgWX1LzErKwsGey6XC8RiQRDAJeOOK9dU7bnnnoO4Co7j3G53amoq+FmzOmv2Kli1t1XACOjbwlUnDu7du7fNZnM4HOBcIwhCWlpanegZdgIJIAEkoqdsjQAAIABJREFUgASQABJAAjVEAAbKlf/ebvWVa7j1PYWFhdnZ2Zs2bfriiy9mzJgxYviIvn37Dhs2rHXr1jAMgxWdMP8JEqlBYhYEgYnFzH+QvQQzENCUK0vP7FXQpsHh2qqJ/2QZxO6YmJhu3boNHjw4IyNj2rRpWVlZO3bsOH78OETEwPyKUYWFqJWzogflrgkyALHmjocaGGRWMxaQABJAAkgACSABJHBnBCDTICFk69atcXFx4KJms9kEQQgNDW3cuPG8efMIIcXFxaNGjYIRFAzAwLf2iSeeAG2atc4GKrdYYCfeWQHuzWuq1qNHDxgxsu5xHPfBBx/cWbXsLBiXgreb0+k8c+YMjNyCQrnZ8fekgAL0PcFerUaHDh0KXzaY8wiCEB8fX60a8WQkgASQABJAAkgACdQxAjeaD9xuN29Uz63sJ4QwpRVirq2tl5WV5eXlbdy4cfr06bNmzRoyZEjPnj3j4uJcLhdTkwVBcDgc1j0Oh0MQBJgygabMhGZ2lrXADDpuV4C2VgJllozR2m7Pnj2HDBny0ksvTZ48ef78+du3b9+4cSMLNpdl2SpGM7sPJl6DM7UVCysDYfYUC0gACSABJIAEkAASuAMCcJ/b6/X+5je/AaMJNsgRBOGxxx47ffq0YRhZWVmNGzcWBKFBgwYsLCAsLGz58uWVG72VcaD1mMo13NYeuN+fnZ0dEREBne/QocPYsWOHDBmSkZFRzaVj2dnZMOCEBXzz58+HJI3WyO66MCpDAfq2PjN14uD//M//hHgWZqNut9vrRM+wE0gACSABJIAEkAASqCEC1kG/tXy71VvPvd0ya4v5dRBCWLSvJEmsDCs6rfOHnJycVatWLVy4cNq0aS+//HJKSkpaWhq4qDEbjcohzEwjZjOrOxagIW4aVney4GvITsMqh5gGNknjeZ7FNzgcjlatWvXo0SM9PX369Olz5sz585//nJube+DAAU3VwGOaCfRBdijMEcUKhMHEAhJAAkgACSABJIAEbotAfn5+z549OY5r2LAhrCTjOC48PBzE1nPnzj399NNsPMPGOSOGj7h8+bLH4wFB1triHY8JrZXcehkE6FdeeQU6+cgjj1y6dElRlMr5S269Tnbke++9x7zjIiMjYRgWlFwRrpedck8KKEDfE+zVanTKlCkwe4HoevhqVatGPBkJIAEkgASQABJAAnWMwI0mBrfbzRvVcyv7WfgzCKlWGwqWxJxJsfBqZcmV7QEVW1O1c+fO7dmzZ/369e+8886bb745ZsyYAQMGxMXFWedUbO5UHQHa6XQye0SWQQR2skkaK8DUxRqszfoAoQ+Q4YftbNmy5cCBA5OTk2fMmPHWW2998skne/bs8fv9IE8zvLf7fuHxSAAJIAEkgASQABKwEli4cGGrVq1gBAKeGzabrV+/fsePHyeErFy5MjY2FrRph8MBwxW32/3pp59adecgqZcNVG6xYO3PHZRBgE5KSoII7rlz5zI36juoLeiU9957z2ZuLpdr1KhRPp/P7/cHAgGMgA4ChU9vm8Ds2bOdTifMFtic4bZrwROQABJAAkgACSABJIAE6gwBMLWQJGn37t1btmxZsWLF/PnzJ0+ePGHChOTk5H79+rGlbyAHw0zDGo4gCAIk4QFXQfjLgqyZcMwKNpsN5OawsDDYeZODIdqIuVELN91CQ0OTkpIee+yx1157bfbs2UuXLt26deuRI0esftPMlBDeARZjrus6RO7AflmWJUnSdZ3dDKgz7xh2BAkgASSABJAAErgrBFga6l27dnXp0gVGKcw0uXnz5vPnz/d6vaWlpaNHj27QoAEb2zRu3JjjuJEjR168ePGu9OymlcJYRVM1r9dLCIHUgnAthmFoqtagQQO4ipMnT960ptt7cevWrTAC/HG0NmPGDAh9gEFXlfL67dVec0djBHTNsaytmpYsWQIfWfYd4zh8H2uLPraDBJAAEkACSAAJIIG7SUCSJE3VWByxNUBGluXz589nZWW9++67ED39zDPPDBo0KCUlxToshAAFEJfBExCmJRAWZD0SypC4hknMLL4h6EhrLPZN9WcB8s7D6aGhoVbpvHHjxomJif379586deqCBQtWrVqVk5Nz+vRpFpcE8zSfz2dVnMGTmsWSA35ZlmF56d18N7BuJIAEkAASQAJI4B4Q8Hq906dPB3HZqoC1bdt269athJAtW7ZERESI5gY3yDmO+3GYsXr1aqbA3oN+m02WlZW1b99eEIRBgwaxPpSVlbndbofDIYqiz+eDO+7s1WoW+vfvb7fb27Zte+TIEVmW2e18FKCrCfZ+P33dunUwoGdRKjzP3+9Q8PqRABJAAkgACSABJPAvRwCmDbCAFGZTTIQNBAIsPohptceOHdu4ceOOHTumTZs2d+7cYcOG9enTJzo6OjQ0FPRlp9MJszirQzSEVFuTHAZJz9aR582lZ3gVjgc/a+uk0eVyMUsQSMZobahZs2a9evXq16/ftGnTZsyYkZ2dvXnz5tzc3FOnTrE3FgKlZVm2TqjYq1hAAkgACSABJIAE6i+B8+fPwwKpc+fOdenSxXpH3GazhYWFvfLKK+fOnSsuLn711VetaTPgyFGjRl2+fJndxWeZKmoNCIxSAoHAkiVLbDab3W53u90bNmyADpw5c4bneZvNFhMTU+NdKi4uXrlypTWJtDUhh3XUxEaSNd6Hn6wQI2d/ElGdO2Dnzp3WaQDI0HWul9ghJIAEkAASQAJIAAkggdsn4Pf7PR4POPfB2Ww+wypj0jPsgaBpKBuGwVaAsgggiBQ+dOhQbm5uXl4eRE8//fTTAwcOTExMBB8PyE8IA0urLszKtxUBzXEchGBbK3SYm91uB/8Qm80GTYMfIswkIV8i06lZ62FhYQMHDkxNTZ08efKMGTPWrl27Y8eO/fv3Mya1ULiHc7ZauDpsAgkgASSABJBAXSDw0UcftWrVym63W+9hJyUlgZK7cuXKxo0bw+IqlmO5YcOGWVlZMHby+/3sxvw9uRxFURYtWsTyPI8bNw66ceTIERjVpKam1mDHwNxDUzXZ3FjNbC1dkPp8DwczKECzd6feFLZv3w6fWhjQw19Yg1BvrgE7igSQABJAAkgACSABJFCJgHWSwFyS2c5Kh1+3Aw6zJpy5lTJUIcuyz+fbtWvX+vXrP/zwwzlz5owfPz4tLW3gwIGtW7dmKjDHcRC5DAtIYd0rhE7DMUHCsdPpZAFKLpfLmhSR7bdWzsrWoCe2s8pCaGjogAED+vXrN2nSpHnz5i1fvnzz5s0HDhyQJAk8OjRVs3pPg6UJk+yrnIbBKVa4kHOyyoOth2EZCSABJIAEkAASuF0CMIAhhFy8ePHZZ59lP/dsUPH6668riuLxeIYOHcqWbYFCHRoaOmjQoPPnz8PqKGvTNetxYa0ZlqYxmwt4iWWzIIScO3cO7MhCQ0MjIiJ0Xfd4PPn5+XCzf/To0YFAIKjC6jxlebBvccRYnbaqcy4K0NWhd2/O9Xg8oihCZk+mQaMAfW/eDGwVCSABJIAEkAASQAI1R4DNHGAuEZRA5ubt3IEADYoqxM5U9lP2+XyEEJhfeTyeo0ePbtu27fPPP8/IyJg9e/bYsWMHDx7co0ePVq1aWQORnE4nM3222WysDDMxpixbT2FTTVZgh7E9NynABBVMRawnRkREdOzYMSUlZdy4cVOmTPn444+3bNmya9eus2fP+syNZTv0+/1wsTcnjK8iASSABJAAEkACNUsAhiKSJC1dujQsLAxMw+BHXxCEqKiovLw8TdWys7OjoqJgf1hYGKyyatiwYWZmpvX2MNOya7aTlWtjcccwfIJRhLUnb7zxBkRwi6K4aNEiQsiePXtANB8xfETNiuMoQFd+g3BPDRCAj6nD4XC5XEx95nkeBegagItVIAEkgASQABJAAkjgnhKwCtCVyzfvWuXjf3IPBPbCIk2onM1hWFu6rsuyzOJ6WLZAQogkSdYZ1N69e3NycrKysmbMmDFi+Ii+ffs+8cQTHTt2tOYkBCtqQRBCQ0OthtFB+rJVRw566VaeQqwGi5yCU8Dog63nDQsLS09P79ev3+zZsydPnrx06dJjx46BXyRws0agszLDggUkgASQABJAAkigRgiUlJQ88cQT7Aea/dAPGzasqKjI6/WOGjUKdkIEMZQHDRp04sQJuJcsSZJ1zFMjvbpRJUEjJRhKwfoqqwB9/Phxp9MJps9du3Y1DAPCou12e3p6+o0qv7P91muH8p3Vc7fPwgjou0245usvLS2tMgLa+lmv+VaxRiSABJAAEkACSAAJIIG7TKDyFMK65+aNW4+8xbKu6z6fjzlKW9VktpMlsWGts3WjzN3CMAy2kxUIIVAGnTorK2vTpk3Lly+fNGnSL37xi549eyYlJYGnB5tqssJtCdAwZYXIa+bsYa2BWYXAqzCQDprosuNFUeR5PjIysn///mPHjp0+ffp77723evXq3NxcRqA2CzjCr03a2BYSQAJIAAncJQI38mVeuXJl+/bt4Z602+2GkUBERMSyZcv8fn92dnaTJk3cbjdbUCWKYqNGjVatWgX9hKELSzwI45+7dAms2s2bNw8aNMhms/1oUzZ9+nTrkIkdI0nSpEmT2L3w1atXezweh8Nht9sHDhzIVpix46tTqDzqq05td+9cFKDvHtu7UjPEX3Ts2BHupbAg6C+//BK+eNawlLvSA6wUCSABJIAEkAASQAJI4O4TuLNJVOVJyE32wEVYdee7f1lVtHDkyJGtW7d+9NFHmZmZkyZNSk1NHThwYFhYGOjFTFNm8jSEUVufgposCIIoipDbEAbJDoeDLeaFCGibzWY1rbZWcitlZuuRnp6ekZExffr0rKysrVu3FhcXQ/QTwGSqMSvA3FhRFHCmDqKgqRoT7nVdh/G83++HCar1HQw6EZ8iASSABJAAEqgXBLxer7Wffr+/pKTkV7/6FZNowdyZ5/m0tLRDhw75fL4Rw0fATzPLlmyz2fr06VNYWGitqtbKcAmrVq3iOM7pdIJcLori+++/H7QmDLpUVFTUsGFDWAeWkJCgKEqDBg3sdntSUhK4SNdgz9l4owbrrPGqUICucaS1UWHPnj3RA7o2QGMbSAAJIAEkgASQABK4RwRqTYC+R9dXdbOGYbBIIk3VvF5vXl5ednb2559/vmTJkqlTp/7mN78ZNGhQ165dmzdvbjO3IOFYEASHuYHWXKV+HXTKrTwFj2kWTM1xHIuhZmFZTZo0GTRoUJ8+fWbOnPn2228vWbIkOzv7yJEjYGPChH6PxwOWJixDPbCwGn0wGfq2fMCrZop7kQASQAJIAAncUwK6riuKAgunoLBp06bY2Fi4WwzSMwi1c+fOJYRkZWXFx8fDLzhbohQeHv7RRx+VlpaycUJtXhOoz3v37rXb7WzYACOBZs2alZaWBnUGFOG5c+eygzMzMwcNGuRyuZo1aybLMrvxHHTinT1FAfrOuOFZP00gPT2dDXnh0zxx4kTmzffT5+MRSAAJIAEkgASQABJAAkigLhGQZZllAmTzKDbJtGa39/v9bH9ZWdmGDRs2b96ckZEBxtOxsbERERFsvhdUcDqdsKeawjTMh8GM0uFwsOkxpEViTzmOCw0NFUXR6XTGxcWlp6e/8MIL8+bN27Rp0969e7OysiAmWpKkKieiEFGFEdB16XOKfUECSAAJIIE7JwC/7y+++CJLIMxxXMOGDe12++DBg/fv3+/z+V577TX4pWbB0YIgjBw58tKlS7AwSFGUQCDAhgp33pvbP3PYsGHQq86dO48bNw5suziOW7t2beXKwHWkY8eOED/qdDonTZpkt9sdDsfRo0cVRbnfft8xArryh6Qe7Hnqqaes41qO4zIyMlgi73pwAdhFJIAEkAASQAJIAAkgASRwYwKKucEaVTZDg+EuvASBVFABzEIhLxCkA/L7/adPn962bdvq1aszMzMnTJgwevTotLS03r17gwYdFMwRpFNXfgp5hKyytd1uh2yKzC0E9liTLlqPhzp5nodc4nAYz/ONGzdOTExMS0v77W9/O2vWrGXLln355ZdHjhzx+XzgxcEu/55Mtm/8FuErSAAJIAEkgARulQDcY163bl1cXJwgCC6XC9YPwY3badOmybK8evXqbt26wc8l3Nzleb5Zs2bLli2z3qaFFUW1HILp9XrXrl0L4c9xcXHHjx8nhCQnJ0MQ96xZs4JAlJWVgZUWWHb8/+y9eUwV1xv/P3Nv5m7hsgS3uNS41LimblHAgEIEMa61tpqqNdXaVKupHzEFMQISQI1UzafVxqqNWz/VqtFaoygBgYBg0NZoq2ld0rrEjahAuBv3zvz88c73+Z7vsBQVhavP/HFzZubMmXNeZ+bcOe/znOdAqv7www8lSbLZbBCs37T/dxagdQ+Jf+wuX75c91mcmpqKD3Q84v5RDM4lE2ACTIAJMAEmwASYABNohMDL65jB53JOTk5xcXFKSsratWv/85//hIWFRUZGkjBtsVjQPUYPGbI13HrgO5x8SZOJlizLMHbWfajDLbV4kNZxaSyA29lstoiIiJiYmFWrViUlJR09erSoqOjGjRvoh5Mfj0b4afUFa1VVXS4XOeL01nqfrpJE5uSNpcPHmQATYAJMgAk8KwG4kCJDSZfL9cUXX2A0Fws24G/x7bffzs3NvXv37rJlyzA0Cz9aOBseHv7PP/80eGt8JDR46iUdnD9/PnKVmZmJpR1SUlIw0vzJJ580cdMZM2bg+8FoNNpstoCAgISEBBo7f/UFaSKrL/UUC9AvFe9LSVxV1bVr14qfsJIkJScnQ4DmL8iXAp0TZQJMgAkwASbABJgAE3hdCKiqqrOcomUAvbXe69evl5WV5ebmFhQU7N+/f9WqVatXr46IiBg7dmzPnj3J+aMsyxaLhdRnLEmEBRJJxRYtoLFGIiI0pjvTcZvNhmsx65HSQcBoNIaEhMTHx0dFRWVkZKxYsSInJ+fcuXP37t2Db02qKHI8LdqO0VkEYDmuO8i7TIAJMAEmwARekACNg5aXl/fs2RMqlqIotHbCwoULq6ur8/Ly6CytMxwcHPz1119j3PQFs9FSl/fu3RtFuHbtmqZpDocjLS0No9Fr165t4n/277//bteuHb4fFEWBG2h8h9BYe0tlsi2nwwJ0W66dhvPmcrn27t2rc8GRkJBA40sNX8ZHmQATYAJMgAkwASbABJjAG0wASiv1h8ksi45ArqU+JDqHcDmtqiotMeTz+c6fP19YWFhaWvrUCiQ1NXXevHkxMTEjRowIDQ2FEg0NGvK0wWAQBWVSmZsIoItLujMt0GSz2cgMJSAgwGAw4BZWq5WU8e7du0dERHz88ccrV65MT08vLi6urNtQ84CABQ9hwOXz+UR/Jm/wA8JFZwJMgAkwgRYmcPfu3QULFtCcIQhZJpOpd+/ehYWFd+/eTU1Nxf8XVGn8zQ0ZMuTpKfqbbuE8PVdy9+/fx/9vUFAQJTBv3jysUXzy5Ek6WD/gcrm+//57SZLEhSJ27dqFArIFdH1ifKStEKiurj5x4oT4PSpJ0hdffEEGDm0lo5wPJsAEmAATYAJMgAkwASbQlgi43W76ZoY/StpFAG6XyT6atGkYTTscDqfTSWdF33e4nE4VFxefOnXqwIEDa9euTUpKmjRpUnx8/MiRI+EFsgnpGafQG4eRNSnO0Jp1nqbRKYD3D10HgWRrpCD6m16xYkV2dva+fftyc3MrKipQOkLRlmqM88IEmAATYAL+SqC4uHjMmDGSJJHxL/TlOXPmeDyeU6dOde3aVfcf1759++3bt2uaVl1djb/UNvLfdOHCBWS+e/fuNFANj9WyLF+9epUqib4c6AiKMH78eEvdhiJPe3caIpARdP0LKYXXI8AW0P5Xjy6Xq6ioSDd9Ly4uDiWBHTQ9wf5XPM4xE2ACTIAJMAEmwASYABN4OQReZMogGVA3/aVNZxsLaJr24MGDvLy8HTt2LFu2LDMzc+nSpdF1W7t27dBRh9aMX+qcNxggzx5kWkWrIJInEDKO1qUgit0hISEjRowYM2bMrFmzVq9evX379uLi4itXrsBhNDx7oERkkubxeMCELKlhTO3xeKqqqjRNc7lcPp/P6XSyk8CX8zhzqkyACTCBNkEAY7f4d3C73Wjz161bFxISQv87AQEBkiS9/fbbx48ff/ToUWJiIp1CwGKxxMXF3blzx1vrFcd3X0EJafC4iXsdOnQIAnSfPn0Q7eHDh1arVVGUIUOGaJrm8/mQbW+tt6qqas+ePbm5uWKCN2/ebNeuHTkzMJvNV65coQjiNwMdfM0CLED7ZYVWVlayAO2XNceZZgJMgAkwASbABJgAE/BPAi0lQJNo66nb6sOoqqoqKio6derUhg0b1qxZs3Tp0pEjR44aNaq+gbMsy2azOSAgABIz5vaKcjPJ01artb7Zta7zT5436x8fMWLE+PHjFyxYsGLFio0bN5aUlOTm5lZWVlLmyW7L7XbX1NTQrqqqTqfT5XK53W5vrZeO04UcYAJMgAkwAX8n4Ha7NU2rqqqCqe+NGzeGDx9uMBiwoC48U1mt1vnz5zscjp9//vmtt94y1W2SJGGsNDAw8LvvvqupqYEW3BxFuGWhiX9PDSrgx48fh5OQ7t27Q2HfsGED/i6XL19OmQEKTdN69uzZpUsXCNOQ5p88eXLw4EGbzUYa9NKlS3FfoHvtzUlZgKbnxM8Cui9ItoD2s/rj7DIBJsAEmAATYAJMgAn4FQHROolsgeuXoH403ZH6VtgwJXY4HNTlVlW1vv0XOvb3798vLy8/fvz4unXrEhMTZ82aNW7cuPDwcOrTGgwGUYOmuc9i90EnMUPFhgANzZqsp+Hcw2Qy0RFKEDE7duw4bNiwcePGJSYmrl+//sf//Xjy5Mnz589jgXRRpCZnl/Wh8REmwASYABPwXwJQUfG7atUqTN+B+oy1Crp27VpUVPTUUDo1NZX+Tcgh8sSJE//++2/4tYD4K8rBrwALbrdkyZJ+/frt27dPVVU46RJvXVhYaKjb2rVrh+MxMTH4c7x48SLFhDH4zZs38T/722+/0SkEMjMz7XY7/ltZgNbB4d22RcDj8cCsQGfFwAJ026onzg0TYAJMgAkwASbABJjA60VApyM31j2uH008gtX/6oOhqbtkLUVxVFWFRRXd0VvrpfnO5BAD8SsqKk6fPl1aWvpUAsjMzJwxY8bIkSNHjx6tU5zr75JBFk4ZjUZRdFYUxWg0YhUpMltDTKy/hFMI41pJkkbXbbGxsXPnzs3Kytq1a9eFCxfu3r0LIFRADjABJsAEmIBfE6ipqXE6nZcuXYqPj6flBzAUajabp06deu/evQsXLvTr109RFDKLVhQlODh406ZNmqaJKzRomkbDsa8My+HDh2ma0a+//lr/vmVlZbDXDggIuH379qVLlwIDA41GY0REBCLjPxqTnH7834+yLCuKcvDgQUqK/sRTU1ODg4O7d+8uuuDA54H4wUAXvjYBtoD2v6qEtf+QIUMw/ILfkJAQlIS8oftfwTjHTIAJMAEmwASYABNgAkygDROg3mNr5bGxrql4vLHwhQsX8vPzd+/evWHDhpSUlNjY2PHjxwcHB5NnP8ySNpvNiqLQ2oZWqxVxYLNG/XPRztpkMsG5J5JSFIXkbLJ0I7WaDLHj4+OjoqIyMzOTk5P37dtXXFz84MEDnZ7exK5umjZ2yf9ma1UQ35cJMAEm8CYQgMwqlnTr1q1o581mM0QqSZKeri5w/Pjxqqqq7OxsSZLgQxkrFhiNxsjIyDt37oiJ0P/Xq194sLS0lP65xo0bV38e0oMHDyBAy7J86NChTz/9FAr71q1babEEmrq0ZMkSpW4rKSkRC9hEmMre6l8aTWTyBU+xAP2CAF/15aqqVlVVuVyu8PBwUYC22+3IyqsfKXrVCPh+TIAJMAEmwASYABNgAkygNQi0erewsQ6qeLzBMJYH9NZ6yQEIde9VVX306NGlS5fy8vK2bNmSnp6+YMGCqVOnjhs3TlEUSAmQFWh5Q9ol8Rq2z9R7x/EGo0GAJiFbvATxO3bsOHTo0JkzZy5fvnz16tW5ubknTpx48uQJxGiXy4WuPvJPvX1N0yorK8k2nErXGo8J35MJMAEm8PoTgPTkdDpv374dGxsLp0ywboYLjilTplRUVDxtw0eOHEmOoeBG2Ww2r1u3zufzkcdk8BL/v14xQY/HM2LECFrOd8+ePboRUFVVO3ToYDQaFUWZPXt2YGBgUFBQu3bt8JekaZrT6cRfj9vt7t69u9FotFqt4p9U0yVqxbI3nbEWPMsCdAvCfBVJ4SVXVXXkyJFkPiDLsslkotu/CQ8uFZYDTIAJMAEmwASYABNgAkzgDSHQ2He+eLzBsI4PlHT4nha1WofDQXJAdXU1whcvXszLyztz5kxqauratWsXLVoUFhYWHh5O06hJaCYXHHa7neygxT4LhXEJ7KPra9BkSU0pK4oSGBjYo0ePyMjIqVOnZmVlrVy5srCw8MSJE6KbabFcuiLzLhNgAkyACbQsAVVVt2/fHhoaSm01AoGBgd9///2DBw+SkpIsFgvUZ6jSkiSNGDGCfFyIDTgEX/oLa8GsNjPN48ePI/+yLHfv3t3hcMD9AOVk3rx5MAOF9+qnKyJkZWXRWVKf9+/fDz8k0dHROhWbItcPUCZbfai7ft5a6ggL0C1F8hWl4631Yl3ptLQ0+oBDgHLwJjy4VFgOMAEmwASYABNgAkyACTCBN4RAY9/54vHGwjU1NaLnaJfL5fP5qqurn2kCpaqq8PhHv3fu3CkvL8/JycnKykpISJgxY8bYsWNHjBhht9tF+2hdz0WWZbvdjsWpSLnAokxwJ00qAGkWFA2G2BaLxWAw0CJXXbp0GTFixPjx4zMyMlJTU3NycioqKt6Qp4KLyQSYABN49QSe+kF+7733yLEGDUnkBFVwAAAgAElEQVR+8MEH1dXVeXl5b7/9Nuyd0XpjGTMYPmua5nA4aEYOZV78/6KDLx6gZBtLikZep0yZYqzbLBbLqlWrMEyLqyorK48ePYqyWCwWo9HYqVMnjNqS7TPsoKOjowMCAiwWy1dfffX48WOdit1YHiiTLEA3hoiPtwIBvBtr164VP8JMJhPGW1wu15vw4LYCd74lE2ACTIAJMAEmwASYABNgAs0m4K31Op3OvLy84uLigoKCzMzM9PT0efPmjRs3bsyYMZivjR6NwWCATgFNWfRDLXZ5YFMGi2mYoZlMJijURqMRx0XB2mw29+rVKzw8/L333ktOTt64ceOJEydOnTqlqqqoxWMaODQCkiF0pXQ4HLTWjs/no8uxPrxoRa67kHeZABNgAv5O4PHjx7pW7ptvvunQoQN5W3oqttrt9sDAwHXr1mmaNn/+fLhLFgXoYcOG/fHHH7TeINbcgwYtSlgUbilo9ROsqanRjbyS5vvHH39gmUT4ifr999/pFPLTqVMn+lf65JNPRANnuI1es2YNFlQIDAysqqrSXd5ShfLTdNgC2s8qjt6TlJQUeu7xfP/666/eWq/D4aAXjJ91P6tdzi4TYAJMgAkwASbABJgAE3hdCKiqCg2aujDw0Uwir9PpvHz5cklJyS+//JKcnJyamhoXFxcWFtarVy9RtjCbzTabTfTUQYbPpF+Tf2rdsofUYxKPIzxgwICxY8fOmjVr1apV33zzTUlJyalTp2CXhxrweDyw0YNiomlafXs9iqlTZ16XOuRyMAEm8KYTwOAcxCWXy3Xr1q2YmBiTyQSLZovFgmG/+Pj4q1ev/vHHH0OHDjUajSaTyWg0oiVv3759eno6UkD7T+rzqxSgIZT9888/9X1riDoybD3xLzNz5kxd9ZMQZzQaJ0+eTC0/CvLf//6X/ms+//xzXNtMC2jdjV7LXRag/axaVVXFG1tcXEyfU7AFOHnypLfW63a78TKzDO1nVcvZZQJMgAkwASbABJgAE2AC/k9AVdX6Qi00aFKiYTjsrfXSEXTRHQ6Hy+Wig6Wlpb/88svWrVszMzNTU1PHjRs3ceLEdu3awfyZekMGg8FUt9ERBODTg2yiSReAlm2z2cT4AQEBiC9JUlRU1LR3py1evDgtLW3Lli3nzp0rLCxExry1Xo/H4631kq0PyuvxeEiJ8P865BIwASbABP4vAWrucnJygoKC4KTiqQdkOHc2GAzJyck1NTVZWVlYn4xGBCVJiomJuXnzJlpIpIM2kzRoUbkSw//39i8WEm8H+XjevHkNJknF7Ny5M/4dzGbzzz//jMg0dNqlSxfMubHb7Z9//vn169dVVb148eJ//vMfRVGsVqvBYOjSpcuDBw8avMubfJAFaD+r/erqarwVJ0+eFD+YJEkqLy9HYViA9rNK5ewyASbABJgAE2ACTIAJMIHXiABsYlAgeK6Ay+mqqqrGSkmiM1Rpb61X1HNJFxAvLywsLCkp2bNnz1NNIS0tLTY2Njo6ukePHmazWfTvQZ0mWLRBMcFBTLJGGDo1qdU4KMuyzWYjX9XBwcG9e/cePXr0e++9l5SUlJ2dvW/fvlOnTj1+/FhVVdagxdrhMBNgAq8NAafTWVNTs2zZMkmSAgMDoS/DAjomJuaff/45depUeHg47J3NZjPiyLK8a9cuattdLhc0XDTvrSJAG43GwMBAWZbXrl1LtSOOmOK/JjExEX8BAQEBYWFh1dXVFFlVVawx+DQRS90Ge1Aa4ERg9+7dTqcTZRf/yyidNzPAArSf1Tu9G//88w+ebAz4S5JUWFhIw0o0cORnxePsMgEmwASYABNgAkyACTABJuDnBKjP0orlOH78+O7du9esWZOQkBAfHz9ixIjOnTtDH0E3CssYQmWAggDlWrSMRnxZlqFo13czbTKZbDYb9cuioqJiY2Nnzpy5fPnyNWvW5OTklJeX3717V5yCDetpt9tNugwM9IiVGBndOjqFADT9BkV5XUzeZQJMgAk8BwGHw4Gr0Bzl5eW99dZbiqIYjUYatwsKCtq4ceOTJ08WLlyIhtRqtVKLOmzYsIsXL+puTTpVcwK6a19w1+12P3nyBAOQiqK8//77SBCuonQacWFhIQoCW+/9+/fDBRN+fT4fFGqDwRAQEIC/CZKhZVnet28fu8ZtsL5YgG4QS5s+iHejqqoKY/g0g2zz5s30CtH73KZLwpljAkyACTABJsAEmAATYAJMgAm0NAGfzwdfGQjAqppk8bKysjNnzuzYsWPVqlVZWVlRUVHx8fH9+vWD4kCG0oGBgSRAm83mgIAAmnKuM5TGqolYjwvrItKiiCTHBAYGjh07Njw8/Isvvli1atWOHTtOnjxZUFBARX/y5EllZSUcT9NB+CrBLhZLdNZtFIEDTIAJMIGXRMDlclVUVMycORMrCpIjfrRmV69ezc/Pf+utt3Ac6jP8IyUnJ1dUVNBirZQ90qmaE6CrXjBALb+maT169JAkyWazTZw4Ecli/E8cz/PWei9cuIBxR1h59+zZE5N4yGr76cIAK1asQFImk0mWZbPZHBoa2qdPn6NHj1LKVMwXLMJrczkL0P5XlfT+wPkOfSclJibyg+5/1ck5ZgJMgAkwASbABJgAE2ACTODlEBBlBbqD2+3G6oLQRxAHVj4ulys/P7+goGDXrl1r1qxZvXp1XFzc0KFDO3bsCDNnEpQRgEiBMDn3wEESa3DWYDBA2lYUJSgoiC5HoHPnzhEREePHj8/IyEhNTc3JyTl9+vTFixcfPXpE2caKjthldx+EhQNMgAm8DAI+n+/MmTNdu3YNCQmRJMlqtdK42pIlS+7evbt06VKz2YzFBjHwZjKZhg0b9ttvv2GeRxsRoMUlBz/66COUpW/fvjqrZ2LorfUeOXIE5SWb7q+++orUZ/qzKCkpmTVrVp8+fbp37z5x4sRNmzZRkaHasQBNVBFgAVoHxD928ZHUvn17cex9xYoVtDQzP+j+UZGcSybABJgAE2ACTIAJMAEmwARamoDOI7Pok9rn85ErUtwWaoLo5ZMWm9ItNnj79u0TJ06UlpZu2bJl1apVCxcunDRpUkREBJRli8ViNBrtdrvFYoH6HBAQQGFxmUSDwQDhhrRpqNu4SlEUnXg9YMCAmJiY+fPnJycnp6am5ubmFhUVXb9+vaWxNTc96mw2qO83NxWOxwSYQFslcP/+/ZUrV9I6rmjcZFnu3r376dOnz54927dvX1ppECptu3btaFI+ilW/fRCbjibC5O+iRfDgRkhq69attEKA0+ms7+8IeV62bBkGFLt164apLR07diQB2lvrJaFZ0zQKU2r4BxEL2CIFeQ0SYQHaLysRb8WIESPgf0dRFJPJtGLFCozk84Pul5XKmWYCTIAJMAEmwASYABNgAkygJQjUFz50qYqShO6UpmnP0Z9yuVzXr18/e/ZsQUHBmjVrsrOz33vvvdjY2KFDh7Zv316u2yA3Q7URvVHDwFAnOsuyrNRtJFJDB0E0srYOCQkZPHjw2LFjFy9evGrVqu++++7UqVMlJSVPZ4iTCIIS6YpJiOACFZFJedc0DZ6mNU0jy+unnk+dTmdVVZXIRwzrbsG7TIAJtH0CbrcbrYHL5YLr57KysqFDh2IsDe0PDB8TEhL++eefZcuWUSsEPcpms02dOvXevXuiGvusBachwOdeuA9DiVCB0XyRn33KjMvlat++PUy5v/76a7GdpKassrKyX79+iqL06NFj27Zt1G7v27cP6WBgkuJDmKZdalrpphwgAixAEwp/CuCZHj9+PL5C4O/8k08+QdvBj74/1SXnlQkwASbABJgAE2ACTIAJMIFXRaA5faXmxGkivzSzG702pHblypXi4uL9+/dv3rw5IyNjwoQJU6ZM6dChAzp0ZChNcrOlbhP9fpBCjYMwuyZxRBdA5O7du8PxdGpq6vLly48ePZqTk/P777/X1NRAeamqqoJGA0mFNCCHw4E4VEz40UZZyBKQp5kTHw4wAX8kgDEnp9Ppdrs9Ho+qqkuXLsWAGdoQ/A4ePPjcuXOnTp3q2bOn0Whs3749NTgdOnTYuHFjVVXVcxcfY2Dr169fsmSJzrj4X9NEY6uqakJCwqBBgyZMmJCTk5Obm7ts2bK///5bnMJCSc2ZMwcC2sSJE10ul8fjqaioENu0/Px8o9FotVrnzZv35MmTwYMHw/v/4MGD0UKKfxBwIc0tIeFtOsACdNN82vTZBQsW0KwHo9EYHx/fprPLmWMCTIAJMAEmwASYABNgAkyACbQqAVE7aCwjzYnT2LVkf0fTsWFELLoBIZNksjguKysrKir65ptv0tLSFixYMO3daVFRUSRPQw0hL9KSJEGeJg3IYDAoigJrRBxE2GAwkK00lhELCAjAEavV2r9//9jY2IkTJ2ZkZKxYseL06dPHjh27e/cuMgxFBms5ko7DAnRj9c7HmYA/ElBVFcbCqqqePXt2+PDh8H2MZgTqc1JS0t27d+fPny9JEpZjhUMhWZZHjx798OFDNGgQZ8kfRfNpqKp67Ngxi8ViMBgmT57c/AsR0+12z5s3T1EU8teMpnLYsGH1jZFdLtfRo0cNBoPdbpck6datWxiKEwXopUuXQqHeu3evpmkHDhxAwQ0Gw6FDh2DlLf5H4FrxyLMW4c2JzwK0H9c1lt0kf2HDhw/348Jw1pkAE2ACTIAJMAEmwASYABNgAi+ZQHNkgubEEbPpcDhISoZ6CxcWogYtSiHk1IKEXZfLRdbHZFIHWef+/funT58uKytLSUnJzMxcuHDhsGHDoqKiLBaLzWYjfRmLgEF3hraiU6Jp7ixsmEitNtRtSAe/mG4/duzYyZMnz5s3LyUlZdOmTSdPnjx//vz9+/e9tV5RrHlWViI3DjMBJtDqBDCNPj09nQa00IDABUdRUdHp06d79OiBESwSpjt37pyamgqjaRQBxsiwBX7WQn3//fcQu81m8+nTp5t/uaqqixYtkmUZjSHJ0PCkv3PnTt18FHfd1rNnT0mS7Hb7l19+SdmmZg1lDAoKcrvd0NNjYmLQNsbGxnprvTrHAyxAN7++WIBuPqs2FzM7O9tiseBNMBgMcXFx4mdNm8suZ4gJMAEmwASYABNgAkyACTABJvDaERBFWDHcYEERoekp2xSHNJEGA5WVldevXy8sLDx8+PDatWsTEhLef//9MWPG9OzZEw46SGU2m82wW4LzU1KaxADm3cNoGouP2Ww2WZbR30RMk8lks9k6deoUExMTFha2cuXKzMzMb7/99pdffiktLdX1RiFOkX0l0YDCTkq9y+UikUicgO92ux0OB7mipss5wASYwIsToLf1zz//nDJlislkMpvNVqsV40+SJM2ePfvatWtz586FObDYpIwZM+avv/4SGyU0WcgVpdz8TB48eJDaoo8//tjn84mjd7p0Hj9+TK1HaWkpLjSbzf3791+8eDHyL8uy1WodO3YsIrtcLvIH7XA4srOzZVnGaoSXL1/G8GFVVZXH44GbAUmSZs2aRff97rvvKHtXrlzBGoliU09huoQDDRJgAbpBLP5xsKioCK2AyWQyGo1BQUHin7d/lIFzyQSYABNgAkyACTABJsAEmAAT8GcCpD7oAg2WCXFaRIAWjQ3hKwMme7Daq6ysPHv2bGFh4d69e9etW7d48eLY2NgRI0Z06tRJkiSduAwvH4GBgaSzmEwmUp9hnEinRMtrrJRoNBohdttstrfffjs8PHzq1KlZWVmrVq06evRoXl7e9evXRSNxTdOePHkCcRnqsyhawUoRXqcbZMgHmQATeBECeBmfDhE9nd8QHByMV9tmsyFgt9v37dt36NChPn36QKU1GAxms1mWZbvdvmPHDpfLRRM1WsT+986dO7g7xskqKytpUKqxYiLCtHenwXdHVFSUo247d+4clnjFyFlhYSH0YhKgVVW9d+8evGqYzebIyEj4gNY0bc+ePdSOXbp0Cbf2+XwOh8NutxvrtuzsbJRd19pjt7Hc8nEQYAHaj5+EnJwcmkiFcR4/LgxnnQkwASbABJgAE2ACTIAJMAEm4IcEGlQiREVVLNMLCtB0LxgJioozXHZADyK1BeILMiAaFXo8nsLCwpKSkuzs7MTExE8++SQ+Pn748OHUwaTVhsxmM9x0wNO0oigwoyZLSYhWMJ2GfoREIAMZDIaQkBCKExYWFhUV9eGHHyYnJ2dkZOTl5eXk5FRVVUHTgYwu4hJNF8XjHGYCTOD5CEC6ffjw4YwZM4KCgvBuklv5ae9O++OPP5YtW4YpEQEBAbIsBwQESJIUFhb24MEDWohPN4pGTdPz5Wrau9OQE0mSdu7c2Vj7SR7q0bLB77PZbD527Bj51t+9ezeSUhRlwoQJ9Ye4XC7Xl19+SXHGjBlz7ty5ffv2YaQtKCho4sSJlBpysmjRImjWAwcOZAvo56tiTdNYgH5udK1/4aNHj/DO0Ih06+eJc8AEmAATYAJMgAkwASbABJgAE3iTCJDyogs0yABxdNqNLibFESe56ywN4YqU7AQpgKScdVt1dbXT6XQ4HDhIAjQFoFP7fD4yoIa5361bt3Jzc0+cOJGSkpKenj5+/PjRo0cPGDCA5Cpa70u0hhbFa4vFQnFIV6IAOrD4ham11Wrt1q1bWFjYxIkTv/zyy7Vr1+7duzcnJ6ekpAQG3c+xuJmOKu8ygTeHANoQUlHFgjscjp9++ikwMJAcbmBRQZvNtnXr1p9++mnYsGFwA0020SEhIZs2bUJ7gqScTidc2OsavSaEYzEPYhht1549ezB8pShKdHQ0IqCBajBNb603NzdXkqTAwMB33nmH4quq6na7w8PDJUlCE3T+/HmcFaeMuN3ubt26UYuEtgs2zmazuby8HJc4nU60locOHTKZTEjw8uXLugacIOAq/m2MAAvQjZHxg+Nut9tkMlksFlGAFse6/aAMnEUmwASYABNgAkyACTABJsAEmMCbRIDUigaFFZAQ4zQWfhnMxHs1lv758+dPnjz5/fffr1+/PiUlZezYsfHx8YGBgeRyWpIkLIoIc2lSeYKDgxVFwWR2+GAlLx8659Q0Ed5sNsPUunv37qNGjZoyZcrnn3+empp6+PDhoqKiGzduVFZWaprm8Xga9Bur6x3TLgI+nw+6dhMV0RgEPs4E2jIB8ZGGzTKE1MePH48dO5ZmKsC/s9FoHD169NWrV5csWYK3FebPCEdGRsKTsq68ogirO/Wsu/C307lz58DAQEVRTCZTRUWFpml4Pem1RbI02JaYmGg2mwMDAz/66CNdnMTERKhkRqNx2rvTcCF5DkErd+DAASjs1AqhvEuXLoW8XlNTo6oq6exwNGS1Wn/8349iOymGn7Xgb1p8FqD9uMY9Hk/nzp3FtuPy5ct+XB7OOhNgAkyACTABJsAEmAATYAJM4HUn0BzBQozTYLjtQCKp6+kSXnfu3CkrKzt27Nh///vf1NTU+fPnT5kyJTIy0mg0kssOWFCJ3Vi474BmDWNMg8EA167kCURRFIPBQKZX5JoWUnV0dHRYWNjHH3+cmZmZnJxcUFBw/Pjxx48fI28ul8vj8VRVVRE0aFgOh8Pn88EfLqla8GpCMTnABPyXAL2bKMLRo0e7dOkCmZUWFzUajXv37r18+fKAAQOwxhgiKIrSq1evH374AdquLikkSE3TiyOqrKxMT0/H8qeSJG3evBkDS6ITIbopLLtnz54Nq+Qvv/yS3l/E+fF/P1IBJUkqKirCJA/KMHz+fPvtt1RYSZLsdntkZCRNthAjq6oaFxcHVyQLFizQnaLdF+fweqfAArQf16+31jtixAi8MPg9efKkOAzVYBvhxwXmrDMBJsAEmAATYAJMgAkwASbABPycAKkVTfTXxDhiuC0Uvb6/ZhggQ+dFDnV6UE1NjaZp165dy8vLO3v2bGpq6urVq6dPnx4XFzdo0CDSpsW+LSbF45RoWw3bTAjQMJYUVWnMkUd8aNkdO3YcMmRIdHT0woULU1JSfvjhh/Ly8oKCAjiTRRU8XY1NVVXRq0Bb4Mx5YALPTUBsWxwOx4MHD9577z2M+lgsFoiziqIMGTKktLR06dKleInI3bMkSWPHjv3nn3+QAafTqXujnztjjV3o8Xju3r1LcnBcXFwTd4QDohEjRiiKIsvyli1bdMn+/vvvYqvSt29fmutAzSkuKS0tHTNmjMViCQ0NTUxMRFOAUzpt7YsvvjAajVi3kBLRBXTZ4F0dARagdUD8bDc+Pp7+pK1W65kzZxwOh/gO+Fl5OLtMgAkwASbABJgAE2ACTIAJMIHXmkBz+mtiHDHc6mBUVYXcTDlxu92qqmKaPx1EnmGo6K31QksSp8lDkkZ8uLe+efNmbm7uzp07k5KS0tPTIyMjx40b1717d3gJwCJpZDeNpRFJriJntZCe8asoisViEXUo6jtTNLvdPm7cuJiYmJUrV6alpR05cqS4uPi3335rQvyiMnKACbRlAnglHQ5HQUFBhw4dZFm22Ww0WhMcHLx69eq8vLwePXrgFcOqoTabLTAwcP/+/Siap24jY+SXUV6yONY07f3337fZbHg9S0pKRBldvLXL5XI6nV27dsXbfejQIV3M27dvI5Hg4GCDwWC32xMTE9EcUXNKCcJRPlKgF9/pdKJlo/hbtmwxGo0Wi6V9+/Z0UBegNDnQIAEWoBvE4jcHP/vsM5p8ZDQaT5482dhL5TdF4owyASbABJgAE2ACTIAJMAEmwASYQJskoBN6dHkkOUZ3nHYpAkRn+H6FQk0rLiIOLqHp/8XFxXl5edu3b1+9enVycnJ8fPzw4cM7duwIBQqGz+KkexhQkwtpSM8Gg0HUo6G44RTWHyOFGoub9e/fPyoqavr06WlpaStXriwqKiooKLh69WpNTQ08w1K5yJ7a6XSKB6HcwawSCzyKF3o8HiwRqdP0dSnwLhNoPgGSUHHJ4sWLJUmikRsszdenT58rV64sWrRIkiS43aAIkZGR165do/e06fe9+blqZsyioiJ6VRMSEnCVrkR41xwOR2BgIF7hnJwcXZzbt2+LbuXh0mfr1q2aplVXV7vdblqIFQKaaOzcWFYLCwupfRD5iOHGruXjIMACtH8/CU/nLtEQ1tO2Y+3atSxA+3eNcu6ZABNgAkyACTABJsAEmAATYAJvGIHGRByn0wmpCJbXTqcTK4mJeO7du5eXl5efn79mzZqMjIyFCxfGxMT07dtXkiSz2Wyz2cx1m6Fug4Sk1G04IrqWJhkOerR4SnQJoihKaGhoeHj4pEmTFi5cuGrVqk2bNp05cyY3NxeLIkJ3Fh0XPHr0CHmGow8IXmIpOMwEWoSA2+2GGlteXt69e3dZlsW1QJ+upJeenl5SUjJw4EAM21itVhgdt2vXjnxZNPY+tkgOm0jE5/NNe3caXtIuXbrU1NSIjn3oQjjMCQwMxJjT0aNHdUL5uXPnoK2/9957IICY0KBpXUExQSoyHdQFjhw5guVVJUmiyLqA7hLe1RFgAVoHxJ92fT7fzp07yVmPJEnLli0Th250L6E/lY3zygSYABNgAkyACTABJsAEmAATYAJMQNNEc8Xm8PB4PJjX73A4Ll++nJub+1SiSqnbJkyYAHnabDbrLKZJmxZtvCgM0+mgoCDqgJtMJjoryzKMMQ0Gg9ls7tKly8iRIydMmJCSkpKRkbFz586CgoJLly7BXIyKAPUKy6yJ/kkoAgeYwLMSgOeNtLQ0PLF4yLF6Xrdu3XJzc5ctW2a3281msyzLJpMJwzCTJ09++PAhPZ+irvqsGXjB+D///LOiKGazOSAgYMuWLVgjVJcmCdAYIvrpp590EUpKSiCvJyQkLF26lOY6mEymgQMHzpw5MyUlRWc0TUXWJUW7GzZsQBNhMpkosi5AkTnQIAEWoBvE4h8HPR7PiRMn8A7g7crIyKiurhbfAf8oCeeSCTABJsAEmAATYAJMgAkwASbABJjA/0sAHi1gNSy6jXY4HPDQqmkavFjgOnjz0FlikVuM+iJveXn5iRMntm/fvnbt2sTExKioqJiYGKvVGhQUZLPZyF+H1WrFcmeyLFutVoh6pD7D1hJdcnTPdb8U0263S5LUu3fv6Ojo6dOnL126NCMj48yZM8XFxbdu3fp/i857TKBRAo1Z0Pt8vuvXr/fr1w+PLpnwm83m9evXHz58uEuXLvRUY4pAu3btDh06hFEQ3M/pdLaWpoQ3NCoqSpIkg8HQpUuXBhGoqup2uwMDAzEvYe/eveSlGrLy9u3bobmnpaVpmrZgwQIYL2OKA36vX78uNhRU5AbvqGna6NGjkau4uDiKrAs0di0fBwEWoP37SSgvLye3VoqiLF++/MmTJ3CeJb4J/l1Izj0TYAJMgAkwASbABJgAE2ACTIAJvNkE0MN9bgai2PSviaiq+uDBg19//fXUqVOrV69OTEz8+OOP4+LiYmJiDAaD1WqVZRmrnEFrJhNLkp7JUJqEaRyBcw+o2JQC1G273W4ymcaMGTNq1Kgvv/wyPT19y5YtR48eLSkpqaioQJ4hpkNn93g8EOzIQlxVVbLr9Pl8cLFNZq1OpxP2amRVCh3/X2lwhLZGgPxsUOUih6mpqXC4QWMeBoOhc+fOP/3006JFi2RZJiczeFCjoqLu3r3bdkr3+PFjTdMOHjxIhtvff/+9btwIuz6fLzIyEqVYsmSJz+fDpAefz+fxeJYtW4aS7tmzB6WbNGkSjL5xSWhoqDhwRY0DDVbhKnjRuXXr1pw5c2CXLUlSdna2qLaJ4bZDsm3mhAXotlkvz5ArmjdkMBimTJmCkSt2xPEMBDkqE2ACTIAJMAEmwASYABNgAkyACTCBZhCAenv58uW8vLx9+/ZlZ2cnJiZOnTo1Li7unXfega00LCUhdekkP0SA3wO5bkM0+qX4ZL5KK8W1b98+IiIiNjZ21apVq1ev/vF/PxYWFp44ccLn81VVVZGI9nBc8CoAACAASURBVPjxY5fLRbIdAvRLEnYzyspR2iIBDDNQdSOLt2/fHjFihLjeoKIowcHBc+bMyc/PDw8PpwcMz163bt02bdr05MkTGo1oC0XFcp1PNeiBAwdidcSoqKgGc+it9ZK36JkzZyLzNPoSExMDk+eLFy+qquqo21JTU0NCQiRJstvtmzZtovLCv3xNTU1JSQmGdiDrV1VVXb16NS0tDfMeoF8/9asjKs66MKXJgQYJsADdIBa/OaiqKrUjkiRFRUWxAO03lccZZQJMgAkwASbABJgAE2ACTIAJMIG2SgBKn2jdJeYUS5nhiKqqlZWVEHk9Hk9RUVFZWdmmTZtSUlLWr18/ZsyYsWPHduzYER4DjEYjpGcKwCsC7KAhnJEFK/X3jUYjRaCDNpuNzFqHDx8+atSoDz74IDExce3atXv37i0vL79z546maaQ+U241TdMZe4pF47BfEFBV1Vvr9Xg8GzZsCAwMxDMDfVmSpH79+h08eHDFihVQcvHMWK1Wi8USFxdXUVHhcDhweYMKb+sS2Lt3LzIcEBAADxu6/KiqmpWVBX8ABoMB0jOe8wcPHtCMBLoKswE8Hs+5c+doRVAIzcCYkJBgMpnefvvtOXPmLF++/OOPPx40aBAGgfCeSpI0fvx48pStk56xS7fjQIMEWIBuEIt/HISrDXEsa8KECZiLIf5H6kbG/KNsnEsmwASYABNgAkyACTABJsAEmMCbSkBUN95UBq1Z7pqaGpfLJXalYSb55MmTBrNFMSGBiR51caqqqgoXOp3OvLy8nJycHTt2JCYmzp49Ozw8fOzYsWTmDL8cFotFlJvNZrPFYiHjaEmSFEWhVRDrq9WkUD/1GBAQECDLcnx8fGRk5NSpU9etW5eZmZmfn19SUiIqcQ2W69UfJJKv/tZ+d0dvrdfpdH744YcWiwXPgKIo7dq1kyRpypQpx48fHzJkiGhlbzab7Xb7vn376rteoee21SFgXMftdvfq1QtP78CBA8VcORwOyM0nT54kf9a0DqGqqgcPHpQkyWq1Tp48mbzT0GJpOs8baGl9Pt/hw4fx1tDbRM5zMCYEzxsYzhHbZzEs5pPD9QmwAF2fiZ8dGTduHN4Hg8EwePDgVnQY72fgOLtMgAkwASbABJgAE2ACTIAJvKYEaC42ucGlI566TSw3GfHAxEfTNOiPLWIiCs+k4u0gYVB+NE3DenoejwfiiMPhEEUNMaxLh3f9iADZUze2gpymaX///XdJScnOnTszMjKSkpJmzpw5atSoYcOGmes2ksZg4El6tN1ut1gsJpMJv6Q+U3z47UR8WZbNZjOWaEPMkJAQaNOLFy9OTU3Nzs4uKSkpKCjAmwKnBORRGpn31nppEUhVVV11G07hJRJN4nCtWFMkAuLZpvfO7Xa3HSVUzHDbCaM9gUy/f//+4OBgGDgbjUYE2rdv/+2336amporSs8lkUhRl0qRJ9+/fdzgcJMtSudqO7k9PzrZt22RZttlsTx9XEn+RYWo8g4OD4XVkxIgRKJSqqqNGjcID//3331MBERDbUl0YnqMhOhsMBrxNkiRFRkauX7/+77//1iXFu89BgAXo54DWti6ZNWsW/cEYjUaaRIDXqW3llXPDBJgAE2ACTIAJMAEmwASYABN4JQS8tV6Xy0WqBIxSIW891RrIZ66qqjU1NaIYgdxVVlaK2YR6CDm7mb+appHdK5Jyu92QtsWUIeRBV6K58KTikRzD/TsR2msZJoWa1ECx0mtqan7//fdTp07t27dv+fLly5YtGzNmTERERIcOHWhdKKPRaDKZDAYDFGqyDyUlmqQDMQAnHvA2IMuyoihYZRHJWq3W3r17h4WFRUdHT58+fenSpRkZGVlZWcePHy8vL8/Jybl7965O0KQV4TRNw7CKqDiL/qmhcWM1RSwfR9ria1nFL1IotEhgW1FR8f7775OJLhYetFqtsbGxx48f7927N9UvDOoDAwN37dpFz9WLZOMVXIvH3uFwhIWFwWtNSEhIVVUVNY+UhzVr1gQGBsJQesaMGRcvXpw/f74kSWazuVOnTo8ePdKN/4ntPIVpkBJi2sWLF0+fPl1UVPTXX39hUURyYkP35cDzEWAB+vm4tZWrfD5fYmIiNS6S9P9XKL1I/tK+tBWanA8mwASYABNgAkyACTABJsAEXgsCoowFdYwsK+lUTU0NPOGePXu2QNjy8/MzMzMzMjKys7Mz/8+WkZGRnp6++lm2zMzM1NTU9PT0/Pz8goKCkpKSc+fOXbhwQdM0l8tVXV3tdDqRK2QJv263G3PMSYPm/t1r8Ug+cyGoO49HgiyRkRBcglCid+/eLSkp+eWXX77++uukpKSEhIRRo0ZFR0eT4w5oypAOZFkWReqAgACDwQAf0+TWAwGz2QwFExof1mET9Qfog5D8unTpMnLkyAkTJnz66afJycmrV6/evHnzkSNHiouLz507B/WQZhXAzB/jK+LgEBzyUtmpgByAmq9pWm5ubvfu3TGoIPppyc7OXrFiBWoHIxBms9loNE6YMOHJkydEvu2zpRbv8OHDJpMJZVm5cuXjx49144IVFRWdO3fGSAkt7Amb6G+++ab+M0MpiwGY83s8Hpjq62Tumpoad91WPzU+8qwEWIB+VmJtK77b7V6/fj0tdWq1WlmAbls1xLlhAkyACTABJsAEmAATYAJM4JUTgMVldXV1cXHx2bNnc3JyJk6cOGrUqDFjxmDWNuzmINZAxMGMdcg6UN+MRiNEDRiH6nS3Zu6S3wOKj5nyNpstIiIiMjIyOTk5JSUlNze3sLAQGjSkEBagX/lT01Zu6PF4nE4nBkh0eYLJsKgh6mw8MbyBgQ0Y1z948ODatWuFhYX5+flr1qxJSEiYOXNmbGzsgAEDYEIL/wz0fEqSRH6ojXVb/eefVj7EVUrdhjcIWjYuhKNqUcWWJGncuHHR0dGxsbFpaWkpKSk7duzIz88/ffr0X3/9RWNCulLzLnSex48fL1u2zGKxmM1mtGAmk8lqtb7zzjtHjx4dMGAA2bwHBQWZzeYOHTps3rxZp6iKD0/bBAt1GDNIJk2aRE9mXl5e/Qxv3LiRFgmkNQnHjRunaRrZ3dNVou4shiHuk9DsdDrJqJ8ClAgHnpsAC9DPja6tXHjq1Cl6IY1GY2lpqahBt5Vccj6YABNgAkyACTABJsAEmAATYAICAafTSX4wyCrZ5XK53W4osGTj6fF4RA8VOgGloKDgzJkzsFSeP39+TEzMmDFjunbtKnq5pR7TswZIlW7aicG/Jqu7nHRtMYBEzGZz//79w8PDk5KSkpOTT548if4drWtXUVEBY1iPxwNpCVK1gJaDTODfCZDae/bs2cLCwsOHD3/99depqamTJk0KDw9/6623bDYbVjuEmbOiKKISTf4fyBU1vQU0ikNaNk7BU4T4zNMYD10LRZV8UqelpaWnp//8889nzpw5duyYKCmqqoq2okGpEa7VodcjGnzyUOvhrfWKqf07r1aKQW3juXPnunbtSqBgda4oyvr161NTU3EcIweyLAcEBERERNy4caOVct1ity0sLKSide/eXXRqhHUFNU1LS0uTJCk0NFSWZbvdPnDgwAsXLhC3FssKJ/TCBFiAfmGErZcAms7CwkLxa6a4uJgF6NarE74zE2ACTIAJMAEmwASYABNgAs0iAI+3iFpfLPDWemF6RuZ7BQUF+fn5aWlpq1atGj16dGRkJM0EJT8DojrTIuFXLEBDfcOMcuh6iqJYLJa4uLjx48evWbOmrKyMDGPhqQO9P2+tl5S1ZtHnSG88AXpgnE4nhfE40fvorfUWFRWVlpZu2LAhMTFx/vz5cXFxQ4YMkSTJYrEYDAZoyrCAJn2ZFEOLxYI1D+kIrK1hHw31WfeeQp4WD+IuED2gegcEBIyq22bPnp2UlJSSklJWVnbixIlz585h7Ap1S4Xy+XzUjJDfG4ziICa5N4FVbJt6NFRVraqqSk9PF9V8NA69evXav3//wIED0UwFBATIsmyxWAICAjZu3IhKpGGqNlWoZmYGzdqnn35Ko4nz5s2D3ySdYXJpaWlCQsKMGTO++uqrmpoaeoCbeSOO9moIsAD9aji/rLs8efLk0aNHGJaEF6fy8nIWoF8Wbk6XCTABJsAEmAATYAJMgAkwgRcmQMKQLiWIRzdv3szNzd21a9eXX345fvz4QYMGQV6B5kXmljTZHHItfAKIpjmihvXc4VcsQFutVhQHpatfWJg99uzZc8mSJaJxNNT8xsDqOPMuE2g+AXjzcDqdDocDPj3IGXF+fn5hYeF///vf5OTkmTNnRkdH9+3bF48ueY6G3bTFYqEXtrGXEZ6pdWfFNxoyNyKYzWb40hFlWQoPGjQoJiZm8ODBiYmJ69at++GHH06ePHn+/Hko0ZhRAYe/NJzTfCCvOOZff/0VExODZsFsNpMUu3DhwuTkZBin2+12slWfPn365cuXkUny+/yK89yCt1NV9Z9//uncuTNKarVaN27cCA0ad6E1LcnLPwVaMBucVIsQYAG6RTC2TiJPVyDE3wB9kLELjtapCb4rE2ACTIAJMAEmwASYABNgAs9IwOFwnD17dvv27ZmZmV988UVERAR8xYqSE2Qs0mGhPWEXp2ARqYug07BeZPcVC9BiVknCI1lNdIBgMplsNpvRaFy2bNn169ddLhdr0M/4AL7p0TFcoapqTd1GNsLV1dV4nCA0Q8TUGZzC6A1eehGGRx0wvXfvXllZWU5OTlpaWmZm5qRJkwYPHty5c2fx1RYfdYStViu9yFarVRSs4VdakiS73Q6P7bCeNpvNUGZtNhsljoDBYIALESQuy7LJZAoNDZUkqV+/fqNHj547d+7KlStXr169Y8eOgoKCoqKiwsLCtjaEk52dTTo7CmIwGPr27btt27axY8fSEQSCgoIOHjyIKoCDEXGWid897qIx+969e1FGDEOeOnWKioPnlkVnAtKWAyxAt+Xa+Ze8eTwetI/du3cnr0xJSUlkAf0v1/NpJsAEmAATYAJMgAkwASbABJjAsxPw+XzizG6IUxA7IAT4fD6Scnw+n8PhePLkSVlZ2f79+1NSUj766KMxY8ZAUCDJifSFZwqIhpCiYkU2OrrUzGazqOfCoBh5UBQlICAgJCQkSthWCduP//sxNzf33Llzp0+fLvi37XTdll+3nT59urCwEC5EcnNzN23alJGRsWzZsgULFsTHx48YMaJz585msxkaGbIHZQ0+DcjEm8oCNwWkuEmSNO3daTt27EBFOBwO1IJfuLh99qePr2hhAvA7gXcWYXp5//VO9NbTmpkNej8Q/U2fPn167969KSkp8+fPHz9+fO/evfHwi88zPeoI0Cpz2MVbjNfWYDDArQdd/iKDRiEhIe+8805M3bZo0aKkpKTs7Oxt27b9/vvvT548UVXV6XSKjZumaXAT0ZgACpIN8nS73RUVFZqm1dTUPH78GE6rAdxb6719+/b48eMlSTKZTFhbDx6Hpk6d+tVXX7Vr147Ed7QPcXFxon9kEoUarI5/rdY2GGHWrFn0VHTt2vWvv/6i/502mFvOUoMEWIBuEIt/HKQ2LiIiQhSgn/U/wz9Ky7lkAkyACTABJsAEmAATYAJMoLUJ1NTUkKUkGcRAhCKlw+Vy3b59OycnZ/369TNmzIiMjOzYsSM6LLBkxKx8EoJJVni+ACyFSXXCLYKDg2EgTGnCmTIU56SkpNWrV69fv764uLigoIBKBLqilEZhEpJ8Ph9WRGzxqrh//35hYeHBgwczMzPnzJkTExPTtWtXUtKhrwUEBMD3LpWLArIsd+jQISsr6/79+8ibX9s/tjheTrAVCZACC3/T4i7srK9du1ZUVPTj/35cvXr1ggULoqOjBw0aFBISIj7e8DJBTqVpigC9I2Lk+gfpbNMBWZbFoSw0UzCmlmW5Z8+eQ4YMiY+P/+yzz1JSUlauXJmfn3/s2LHr168TXpfLRY0h1g71+XxoOUWrXlVVSdLBtWhtXC7XgQMH2rdvb7FYxKw+NSFfvXp1dHQ0DpIKHxoaeujQIUjhlAcSoMUj/hv2eDxXrlwJCgqif42wsDBqk/23XG9azlmA9vsaf+oT5+OPP64vQPt9wbgATIAJMAEmwASYABNgAkyACbR5Ag8ePCgrK/v222+TkpImTJjQv39/WORJkhQQEADzPYvFYjabdWaMWDJLVFhePExWkHa7vVevXjExMR9++GFKSsqOHTvOnj177949cZEx+BYQNSC4hSV1rD77Jk7pIpNVqWgv+a/pa5pWXV1N6hUkqlu3bm3dujUjIyM8PBwuR3SgoLmj7NDdPv300zt37pCvXl3eeJcJtCIBvAWeus1b63W73TSUhVzpBk5+++2306dP79y5c/Xq1UuXLo2MjIRPZN3kCbwFcM2Bt4BaA9370tguVjuks7o1EmFqjQaNbk1tHZo4SZJiYmLCwsLmzp2bnJy8a9euvLy8goICh8NR34cJCutyuXDK6XS6XK4nT55MnDgRCjjdxWAwTJ48ef78+e3atYMfHvyaTKawsLBHjx4hKd1AmtjWtWJ1t+Ctt2/fTrXTrl278+fPQ2dvwVtwUi+VAAvQLxXvq0jcW+tduXIlC9CvgjXfgwkwASbABJgAE2ACTIAJvNkErl+/fvLkyTVr1syfPz8yMhImimSpB93HaDRizjhJQqQaiAGspkUii3iq+WFFUex2+5gxY8aPH5+VlbVjx468vLxLly41Jr5AoxF1ZFGAdrvdNTU1ZPUsOiWgasdZ2n2RgNvtdjqdJBt5PB6Hw6GqKtybeDweb60Xap14l9zc3OXLl8+bN09HibSwgIAARVHMZvOsWbNaMLdiHjjMBJ6JABmriov+4SA0aPE1bCzlmpoa8roAbxgXL17cs2dPVlbWhx9+GBUVRTMtnk+AJutaOJvG+wV3N1CfG2ysRHPp+pI3jsBaeejQoSNHjhw3btzcuXOXLl26d+/eoqKi0tJSjBVpmlZQUNCzZ0+YYBvrNkmSOnfuvHTp0qlTp9IIE8SfTp06ff3115qm0Sp8Om6NtYG6aP6yC79PSUlJqBeTyfTnn3+yAO0v1Yd8sgDtX/XVQG7dbveGDRskScJ8hFGjRomfUw1cwIeYABNgAkyACTABJsAEmAATeMMIiH0EWP5CuYDKCRiiWAmt5/r16yUlJampqXPnzh06dGhoaCgMmXXSp26X1B9dAP5MaeK8yWSCBq3UbTp7Q0TGpHtSgiRJGjVq1PTp0xMSEnbt2lVYWHjnzp3q6uqWrUwIN439PtO9KJGmr6ovFdGFFKifgrfWW1hYOHnyZDKLNtdtIq6QkJD169ej9mFzKj4J9dPkI0zgpRLA8yyO8ejC9MDrHlTxOC4Rj4h5vnfvXmFhYV5e3pEjR1JSUj7//PMpU6ZERkbqminaNZvNWMOQ9GWLxWIymailIic/proNFxqNRjEOpdZYAI1hY2c7deo0atQonIWwg3BsbOzs2bM7depEw0s4HhkZCf/RMB4HChHC6xpWVXXlypVdunRZsmSJ6GZE97S8rsX393KxAO3fNYjh8WPHjlFDFhsby++ef1cq554JMAEmwASYABNgAkyACbwcAnDpQB4e4DYUZraqqpaXlx84cCAlJWXOnDnh4eE6yYN6HLC/E3d1YZ3ujF1Mbxe9cNBkdtJ9KB3YUPfq1euDDz5ISUn5+eefi4qKqqqqsKqe6NTiZXASha364We6I13e9FUU7ZkC8NdRVVV14cKFFStWdOvWjUhSAFaTQ4cOPXnypOh/tun88Fkm4NcEaFaBWApYT58+ffrs2bOrVq1auHDhpEmTIiIievToYbPZ7HY7WrbAwEB4ihcbQDiepteKWqrmB5oWoGVZxmgcErTZbAaDYe7cuWPHjjWZTHRfo9EYFBS0ceNGl8slOiqhdkMs7+saRuW6XC63200FZxHML6qbBWi/qKZGM+l2u30+X15eHjV8gwcPbjQ2n2ACTIAJMAEmwASYABNgAkzgjSTgcDjg7YGcrt66daugoGDbtm2LFy/u378/xBeY9cGlBgQRTB7H5HQ4HqWuR2OBBgVo0l+MRqOiKCSpQNnp1q1bZGTk9OnTd+zYkZOTc+PGDbfb7XK5qqqqUF2Yoe+u22D45q31emu9L0N3EEWN+uFnenzo8qavomjPFIANO/16a73fffddfHw8qfxkwilJ0lPgaWlpd+/ebVCbazp7fJYJ+BEBDLDBvw3aClhMi0++uJiqt9ZbXV195syZ/Pz87du3p6SkrFixYvbs2b169UJLSC6GqMWTZVl8ueh4EwFqAJuIg0bYYDB06dIlMTERDo5kWUYGzGZzWFjY48ePURfkOFtsNPyoml48q7SgJQi8eIKcwssmwAL0yyb8EtPH55e31ltQUIAZapg88hJvyUkzASbABJgAE2ACTIAJMAEm4IcEnE5nWVnZmjVrZs6cGRERASs/0cSvQVlEdG/aYIQGDzYmQCOyoihvvfXWsmXL0tPTDx8+fO3atcZwQkgSf8VV9ZqzoF9jKTd9XBR06oebvlZ3li7XHdftUrRnDYjG7EhTVdUDBw5MmDABojM5pbXb7UajMTw8/K+//tLdnXeZgF8T0I1CPXnyRNM0h8NRU7eJurOmafVfmfoHMdyF+RbeWu9vv/22efPm9PT0jz/+ODY2NiIiomfPnnDT0WAD2ODBpgXowMBAjMmZzeaZM2eOGzcOCg+NBQYEBKxdu5ZWLER96UyAdRz8uk7/NfOoI7HB/NdLOEKrE2AButWr4IUygGF/t9sttnG6FvaFbsAXMwEmwASYABNgAkyACTABJtB6BDBtnKxcaRfzr721Xo/HAyfIlZWVZBp8586d/Pz8DRs2JCUljRgxAlbGot2x2H341zB0ajLEazA+LdWF5e/IPFBRlP79+3/00UcZGRlnzpz5448/NE1zOp1QUl6SCXPrVVcbuvPhw4d79uxJ66oFBwej4oKCgrZv305SfnMWf2tDpeKsMIF6BFRVxdRwVVVdLpemadiFskw+pltWrPTWeh0Ox4kTJ1JSUtLT08ePHz9x4sQuXbrQwI/JZKo/gIcBIZPJRCNDaCrJIX6PHj3gDARvKzzjjxo16ubNm2L+EUb7KR6vx4YPMIE2RIAF6DZUGc+dFVVVxa/AgoICfEY0OLj33HfhC5kAE2ACTIAJMAEmwASYABNoFQIwbcOvy+USRUNYn5w7dy4vL2/NmjUTJkwYNGiQzWYz1m1QQ2D9KnYZniNMmrLuWlmWITpbrVZFUeLi4hYvXrxp06bi4uJ79+6Jfod9Pp/T6fT5fLwa3kt9iqDBaZpWUVHx6aefor4MBgM5kzWZTBkZGTU1NS81G5w4E3iVBOh5huLscDjg3f4lCdDkTx8tMDmm9/l88G60c+fOzMxMuNSPiYnp2rUric6BgYHk8dlms1ksFpvNRu0qTKHJSVFWVhaKIArNjYVfJXC+FxN4VgIsQD8rsTYaH60VWrSnC1VjOZE2mlfOFhNgAkyACTABJsAEmAATYALNI+BwOMSJ1SQ9FxUVbdu2bf78+aNGjZIkCdbN4qxwqI1ms7kx4Zj0jn8NYEUs+CfFjdDv6N+/f2xs7Oeff56VlVVYWAj7a/REKM9YNd3lcsHqGabcbCjTvMp/oVjkIrasrKxHjx6SJFmtVrGup06d+uDBgxe6B1/MBNoMgY0bN8bExERFRZ09exYzRep7qCDd9rlzjakn1L7B1BoepalZU1UV7jt0d/H5fPfv3z9y5EhhYeHatWtXrlwZExMzffp02E2bTKYhQ4aguYbn/YEDB166dKmmpgbFocw3EdDdkXeZQJsiwAJ0m6qO58+MKEBnZ2cjIRr6fv50+UomwASYABNgAkyACTABJsAEWo8APukdDseZM2d27NgxZcqU8PBwUUaEjwXykgGTZ4vFoigK+WLWxX/WXQiXNpstIiJixowZWVlZpaWlDofD5XK53W6YM5OxITkJIT2aHIOgLLSuYOtBfVPuDIeNGLRISEiAtkVuAYxGY2RkJNmNvilQuJyvI4EbN26YTCbotlartbi4mEbCGpRrn5sBXM+T1kyWf+JIIWyi0SQ2eCPSr8VGEjGXLFmC9hmqDo04Iv0GyyIebPB2fJAJtBECLEC3kYp40WxERUWRe6+UlBSXy9XgmNuL3oavZwJMgAkwASbABJgAE2ACTOCFCZCKQXKt2+12uVyka1RWVpaWln733XfT3p02YMAAeAJtehkryBYkOsuyDOEYnjGos0DTwBGfJnrLsgynpbhX165dR40atXDhwnXr1pWWlt6+fRuFFsWO5oRfGBUn8EIExDo6cOBAaGgoHgBUtyRJHTt2PH/+vMvlEmMi/EI35ouZwCsksGfPHpqiIUnSmjVr4OVcfKpbJDs6C+gWSZMTYQJvCAEWoF+TihYF6E8//dTn8/FShK+gan0+H6YTYnbPK7gj34IJMAEmwASYABNgAkzgtSEA6zZo0D6fr7Ky8ujRowsWLBgyZAg8hBoMBpKem2m2LArQuATG0WT3Wl/FhhY5bNiwpUuXbty4MS8v7/r16/Uhw2pPFHSaE66fDh9pRQLnzp0LDg7WeWWx2+0XLlzA0yjWaSvmk2/NBJ6JwGeffYYmDuMru3fvfkkC9DPliiMzASYgEmABWqThx2EI0EajUZblcePGYb1XPy5Pm886JH6yWMESBLyKd5uvN84gE2ACTIAJMAEmwARajQCkPSwn5a31ejyeBw8eHDlyJDU1NTY2lvw4w1RZURSdSvgcArTVaoX6jAXo8Gs2mxVFGTZs2PLly/fs2VNWVnbjxg1N0zCBkj5rgam+uZ8oUDYn3Gq4+cb1CKiq6na7Hz582LdvXzxOZAcdEhJy+fJlLKRG1VovAT7ABNoogTFjxjw1fDabzcHBwYqilJaWttGMcraYwBtMgAXo16TyyQJaluXBgwe/eMT1PwAAIABJREFUJqVq28Xw1nofPHhw6dKlwsLCmzdvPn78GE7WKNe0Ei4d4QATYAJMgAkwASbABJjAG07g4cOHR44cmT17do8ePRRFsVgs5MRZXDCwvp3ycwjQMAk0GAxRUVFTp07NyMjIy8u7evWqWAXwywzd2ePx/KtFBamTzQyI9+Jw6xKAjXNlZaXT6YyOjsYTBSt7SZLefvvt6upqsVpbN7d8dybQfALJycmSJGG8zWaz3bx5s/nXckwmwAReDQEWoF8N55d+lxUrVtBsO5PJ5Ha7eXGPxqDXJ0OGzI1dIq4SgHUGvv/++2HDhtlsNnzWG41Gq9X62Wef3b17l5yf8CKQjfHk40yACTABJsAEmAATeL0JwHBY0zS32+3z+crLy7dv3z5r1qyBAwca/s+mk5jpY17no5lUwv9znUFRFOgsZMQqXmK32wcNGjRr1qzk5ORdu3adPXu2wY9SUWfUhV/vqnnDS4e69ng8brc7IiKCni6Mgrz11lu///47OSJ/w1lx8f2LwFdffRUWFjZlypSioiLknJ9k/6pBzu1rT4AF6NekilesWIE5evj6rL+a6mtSzhcuBtZ7oWT+VXomkjAG8fl8R44ceeedd7DAriRJVqvVZrPh081sNvfv3//XX3/1eDwOh4P/8IgzB5gAE2ACTIAJMAEm8FoSgJynKxrU54KCgg0bNkyfPh0filggi0Rkg8HQHAFalmX4gKZEKAAn0YqiDBo0aNGiRevXr8/Jyfnzzz9FywmHw9HY565OdBZ3dcXh3dePgKqqDofj0aNHQ4cOpSdKlmWDwTB48GCn08kdmdev0l/7EmGkzel0UknFxpAOcoAJMIHWIsACdGuRb+H7rlixAg6g4dktPz+/sW/NFr6x3yYHdxkXLlw4depUdXV10+XAbDVN07Zt22au20DbarUaDAaz2WwymTB5DQ71kBp/tzVNlc8yASbABJgAE2ACTOD1IADXuk6ns7y8/OkifpGRkbIs2+120TCZZD6YmjZTgMZVcNRrtVotFku/fv0++OCDL7/88ueff75z546maRBc4EOj+d+fouKsC78elcKlaJrA48ePNU2rrq4ePnw4/MDgYTObzUOGDMHZplPgs0yg7RDw+XxOp5PmIredjHFOmAATIAIsQBMK/w6IArQsy2VlZf5dnpeZe3yX79u3r2fPnjAb79Wr18aNG3HPBodJcXDLli1kgYLuhNVqFfsSMGwxmUxff/21x+NpMKmXWbL/m3ZjfY9WzNL/zZy/hRiav9UY55cJMAEmwASYwCslcODAgZSUlNGjR4eGhsLA2Vi34ctQkiR8QBqNRqVuw9nmC9CDBg368MMPt27dWlJSAttq0VMzpvfV/1yhtQQ9Ho/L5RKtAkFHJzqLu68UH9+slQhQf+HRo0d9+vQhX+To3Ux7dxoWpWyl3PFtmcAzE0Bj2FiT+MzJ8QVMgAm0NAEWoFuaaCuld+LECZrQJ0nShg0bvLVe+qpopUy10duqqvrVV19BeoZlCoyXz549C//O9b/gNU37+++/27dvj9XJ4X+jS5cumzdvPnPmzI//+7Fjx47wBw1/fGPHjm3dwteXv721XrggfL6MeWu9GFKG5bjb7Xa5XPXXqMEjV7+H83w3ffGryCCoQdeHSP/mzZulpaW7d+/OyspauHDh5MmT+/XrZ7fbo6Ojf/31V7fb3eDz8OJ54xSYABNgAkyACTCBtkzAV7eRLEuLS+Nr59ixY+np6QMHDsTHIZRl0pRFb84UJqsFnecNk8lksViMRiM+I9u1axcbG/vFF1/s27cvPz9fh4jyQwFdBHEXcZBzhMWzHH7DCdAjpKrqvXv3+vbtKz6iAQEBX375JTpHACXGf8PRcfHbDgH01JxOZ01NDXKFJpp7cG2njjgnTIAIsABNKPw7oBOgk5OTNU1jAbrBSr1586bZbG7fvj2+/smb859//tkgNGCcMWOGJEnoHkiSFBUV9fDhQ1Jay8vLMZsSa+++9dZb3lpva3lBaWwC5vN1PFBGt9vtcDju379/5cqV8vLys2fPlpSU5Ofnnzx58oiw/fLLL48ePWoQeysehPp89uzZae9OGzp06IQJE+bPnx8fH9+zZ0+q/fozZC0WS48ePf7+++9WzDnfmgkwASbABJgAE2hdAmRx7Ha7r1y5kpKS8v7775NOpygK7JohPcPkmRRnClB82IuIXx0mk6ldu3YRERHz58/Pzs7G52gTHnhFEfBfP+0QQRSgWZRp3cepTd1dfJZcLld5eXlISAgeToPBYLPZDAYDLeYGuxO6pE0VhDPzhhNAp/uPP/5Yu3ZtSkrK1atXAaS+sdQbDoqLzwRanQAL0K1eBS2TAQjQ5CBi7ty5tHpey9zgNUpl3759RqORJkViulloaOijR48alOy9td78/HzqOciyHBIScv36dU3TPHUb2ERGRpL1SqsL0D6fz+PxiEPBz12B3lrvhg0bBg4cqCgKzMaBwmAwWK3WwMBAmPzgV5blwMDAOXPm3Lhx47nv2IIXUi/r0qVL7dq1I5eLiqJQ30+0QsLSK3QqNDQ0MzOzBfPDSTEBJsAEmAATYAJtmQAptpjE7fF4Ll++vH379vj4eLvdTl+DsHqmXfpyEI+Q+ix+adBH1JAhQxISEnbv3l1RUYHvT4yX17dg0Lk0JQWQAk3zpGgUaDo+n31zCNAjgYCmaSdPniRn0OguWa3Wixcv6sYw6AP7zWHFJW2bBMjq+caNG1arFaZF/fr1o0aVVnJqm/nnXDGBN40AC9CvSY2TAI0v4IkTJ74mBXsJxcjPzxeFVHxdxcXFoafR4A1nzJiBSZGBgYFWqzUrK6u+dXNmZia5hG51Fxw+n8/lclVWVlZUVFy5cuXatWu3bt26d+9eg6Vr+uDhw4cNBgO0depfQailXhYFsEKOJEkRERFNJ/uKz057d5okSVgsXswtDJHoiN1ut1qtJE/Lsrx27VqM5dA3+ivOOd+OCTABJsAEmAATeMUEHj58eOTIkdmzZ/fo0QMfCRCRFUXBXDccJMsP+pCggE59lmU5IiJi4cKFP/30E2ycxRLBsxmZQeAjE7Z79X2I0QcJBcSk6ocpGgXqx+EjbyYBeiRUVaVpnbt375ZlGYuuS5JktVr79OmDYRIx/ptJjEvdNgn4fL7//Oc/kiTZbDb0+OC8yFW3tc08c66YwJtJgAXo16Teb968KYprAwYMoM+I16SELVcMVVWDg4N1pit79uxpbJLOhQsXoD5Dfu3UqZOmaTprFJ/P9+2335KB7fz58zVNq99nePFC0CguPgGRDYfD8dtvv+3atSszM3Pu3LmxsbHdunUTnwfqDplMpuHDhycmJv7www+YUkoFgS2D7rHx1nozMzNh3Yx/dJvNBhowIYf7bKylAymfWL1gYX0+H/IGU+7nSw11ev36deRQURS46ka3EHNmjUYjCevoWML0Aw4Zd+/e7XK5xA9uMfx8ueKrmAATYAJMgAkwgVdGQLcWH77i6CPN5XI5HA632+2t9RYUFCxZsmTo0KH04aQLiBYM9CEkyzK+H/AhhEuCgoJCQ0Pnzp27c+fO3NxcKixZktKRVzBnke1VRdocbowALd02b948WlsI3/+ffPJJVVUVLnQ6nfT6NJYUH2cCr5LA48ePR48ebTKZAgIC0K2DAI31V19lTvheTIAJNE2ABeim+fjNWbfbje9dWZbx+es3WW+NjH7wwQdYkRwqbe/eveuv2kf52rx5M/oVuGTFihX1zZ9FAdpkMh04cEDTNJ2YSwk+RwCLUFOC3lrv/fv3Dxw4sGzZstjY2ODgYOrzNGabDHGcVsiRJCk4ODghIaGiogJaOdnd6LKXkZFB7kokSSKnydTvIvXZaDTiI1WSpFmzZunSeaZdqM/IksfjQQDK7zOlA5OiGzduABGJ8rDsCAoKat++fXh4eFxc3MyZMz/99NM5c+aIBezSpQuWXsEyRLrFiLg790x1wZGZABNgAkyACbQWAfHLDW7KKCfXrl3buHHjxIkTdVpzY7s0aC165KCx+aFDhy5fvvzH//1YXl5OX1Zk0Qz3GvW/H+ofoey1SOBlp98imeRE2ggBn89XXV0N23+bzYbZjTab7ZtvvqmursbDzAJ0G6kszgY1bmFhYdRoy7IM3+Uwt2JKTIAJtB0CLEC3nbp40ZyQBIkh6xdN7rW+Pjc312QywYtxt27dysrKmihudHQ0+WSwWCyXL18mM2S6ShSgFUWprq6mUy0V8Hg81dXVJSUlSUlJb7/9NmxwRGUcy+DQ8uv0H0xKMayVFUWxWCxWqzU4OFhRlJCQkK+//lpVVbjAFs17Ef75558hXttsNoizMBxGIgEBAXZh69ixY2Rk5LZt216w1G63Gxo0rC3+/PPPx48fQ4V/1pRhRn358uVFixZ16NBBUZSwsLCEhIRt27b9/vvv3lqvy+WifmlpaSlM42HNtHLlSqxLyQL0s2Ln+EyACTABJsAE2hoB/N1DgD5+/PiMGTNCQ0Ppewmzoxr8jhLjIEyKc58+febMmbNu3brTp0/TDDlYDJAArWkalDvSSnRkGjuui8a7TODVEKipqbl06RIZk5J50507d7AEzqvJBt+FCTSHgNPprK6u/uijj6ihVhSl6d59c5LlOEyACbwMAixAvwyqrZNm9+7d0ezCBvbXX3/lz9kGawJ9gKioqMGDB6elpd28eRMioxhZRGc2m8lLQ1hYmKZpDodD7FTgcnLBMXfuXJ/P93xqqZgHMayq6rZt2wYMGEBzP2m8gXy0IZ/010tT53QBimA0GtF9Mpv/P/a+PCaqq/3/zkxmzYAaRYytGusSl5q6BQXCGgSMor7VauMatTZ1S10IIoY1IhgUG6s29qembm/rFhSJioY1gBCoGrUaF0xrbV63KEtmZZafL5+8T873zjAO+3buH3Dm3LN+7rn3PM/nPOc5yu3bt9tsNpgzsBy0wWCoq6uDAzgklslkQUFB2KnKooTWmhqvFsimjkXZ7fa6urpHjx4tXrwYlHdZWRmLifthKhz7Xi0NFgrgGEl6mtu3bwewOPj7wYMHdrtdp9NxAtp9tHlKjgBHgCPAEeAIdE0EioqKNm3a5Ofn5+npCdkGq86QoLCQTwbOJC+xATh9njhx4qZNm86fP4/TNeCqi7oMqYM1VvioTEiCChXCAxyBTkQAovKOHTsg/EulUgSmTZvWtls8O7GPvOoegwBWFs1mc2BgoCAIXl5eBw8ebMHG2R4DCO8IR6ArI8AJ6K78dJrXtvDwcIjIEJ1LSkqal5+nZhAgk9iTJ09KpVKlUunp6alQKFJTU5GK1SvgvC8mJgYm1ffv33fh0IOpxK0gKlq4cCEkP9KCYIxAFtDk+6Jfv35ffPHF5s2bExMTDxw4cPLkyYKCguzs7OPHjx84cGDjxo3Tpk3TarVgn1UqFXl2/uGHHyBTsgS0Tqez2WyRkZF0IvaHJeXIyEhyi+FWH9xIZLPZQGojbX19/cuXL+Pi4tBfpVIplUqDg4PbitkX9ZGepoeHh0qlwhs0ZcoUsmTnBLQbz5An4QhwBDgCHAGOQCcg4OjXwtJgwVYqs9n89OnTkydPLlq0aNiwYZCaRMcDkmTlGKDF/sGDBy9YsGDPnj2FhYV1dXW1tbXUT0gInOwgQHigZyCARZEv//UlqQBqtVomk8XGxpKlf8/oKe9FD0aAf5l78MPlXeumCHACups+OCfNFh2ZcvbsWSeJeJR7CBABHR0dDRsZKCE40AB+gUUlVVZWbtiwIS8vr63YZ7JHvnnzJlkxQztizXNUKtXAgQMXLlx47Nixe/fuEZdKviMw9UIZgw3O7du316xZI5FIPDw8FAqFp6enWq1WqVQ4lp0lZ9GG6OhohUKhVqthfz1x4sSmDmwUYdLin6dPnx4yZAhcTsNvNf7+8ccfdDhhiwvHggF1E4gZjcbc3FyVSqVQKGDwvmDBAmyhhRJLHDRl5PZKrXkEPC9HgCPAEeAIcATaBAGbzUb7mRB4+/bt2bNn16xZ82GvGw7wEJHL4KApEj7K4HwDkXK5PDg4ePPmzefOnfvrr7/QTjj1wuxPBxtyArpNHiIvpEshYDabIR4/efIE2wXg0M/Dw0Mmk92/f1+n03WpBvPGcAQ4AhwBjkC3QIAT0N3iMbnVyLCwMJKkBUHYs2cPJ8jcAs5ZIqJxQevD+njo0KFEvJIbB9CRzspogzg0o66ujghoaEcggkeOHBkbG0tHq8OnIZxL4K+LFlgaLD/99BNYdfyVSCQ7duzQ6/UswQrfFDk5OTi1j3AgnxUuqmjuLeh1V65cmTJlCjHsSqWSJaBLS0s/uo/VnXpFfcR6w549e+C+RqFQqFSqAwcO4A3Cs+YEtDvA8jQcAY4AR4AjwBHoYARIJvnnn3+OHj3q5+dH+8NInMBpFvjLWkCzkvO4ceO+/vrrn3/+Gc5DIW9gJR4yAPqFeGzbglhIQkUHd5xXxxFoJwR0Op2lwQI15JdffqHXBArI6NGj26leXixHgCPAEeAI9GwEOAHdQ56v2WzevHkz2Do46oqPj+8hfeuMbhCBS96fBUFYuHAhjGex2RNpRAQ0bGbbpMkQ+3BEHuuCQ6vVQhBcuXJlfX291Wo1Go3QvkgHEzUAxkGGxou4davVunHjRhSFMocMGcJ2ihYw/vrrLyQDVT1s2DC6JaqoNT+fPXu2ePFiqggyLlRHuFwMDg7Gpj9yV93i6khXZDvy3XffQTVVqVQeHh55eXl43GRLzlo5iZ57i1vCM3IEOAIcAY4AR4Aj0BoEDh06tGzZspEjR+K0ZDgZw8o969ZZrVbTOcPEQfv5+a1du/bs2bOPHj0ymUzwMGaz2SBQGQwGLFFbGiwGg8FkMsHwmRUMnEoUrekOz8sR6HQEYHtBZ7rMnDlTJpOpVCos7XxwTpiWltbpjeQN4AhwBDgCHIFuhwAnoLvdI2uywTt37gR5h79z5sxpMim/4QYCNpvt7t272LkJMnT//v1QOegIPpa+dKPI5iVhVRpLgyU2NpYcPQuC8MEYOSkpidjk5hX9v9ToIBkKeXl5/e/O//n/7t07uVyuVqthAT18+PD/c7uZP+CiRK/Xw6rIbre/ffs2JSUFmuEHR9vUHvDOGM8ajebKlStwfsISwc2svMnklgbLtGnT4H8DNb5//x6poYhyC+gmseM3OAIcAY4AR4Aj0KYImM1mEhLYgsk+4P79+wkJCcOGDdNqtQqFghatESB5WCKRsDM73AgsWLAgJibm2rVrdNIDqmDlLpr0Pxpgc7FN5WGOQM9AwGw2379/39PTk91PIAjCo0ePyGNhUz01mUyZmZmCIAwbNuzJkydNJePxHIHWIMDabLWmHJ6XI8AR6AAEOAHdASB3UBU7duwggVsQBF9f3w6quIdWY7PZTp8+LZFIPD09lUrlB0hzc3NBgJKBTIcR0Ha7/d69e+zzlUgkP/30U2uwh+m0QqHQarU4YESj0bDn6lDh9fX1Hh4ecIUhCMKoUaPoVosDkBXq6uqSk5MBr0wmk8vlUB3VajUr5sIBSHV1tdVqxZbAtkUepQ0aNEjWeEkkkqFDh6JrIvbZqYV4i0HgGTkCHAGOAEeAI8ARcESADDDZW1VVVZcuXVq+fDlcNmPKpp1qcKJFP0lkkkql3t7eX3311c6dO8vKylz4rmWp5I/yzpSAzcW2loc5Aj0DAbDMIjsnQRBmzJjx0Q7m5OTgTVQqlZ9//jnSw+feR/PyBBwBdxDABl+bzZabm/v5558LgjB8+HCn+qw7pfE0HAGOQHsjwAno9ka448qPj4+njVFKpfKzzz7ruLp7XE3YYvntt9/K5XKJRALXE/B3gXM5SN9ov65TFaBH//77b1jukOPmoqKi1tTuPgFttVoHDx6MjasymeyLL75oTb3I+/bt2y1btgwcOFAmk8H2mdUVPT09R4wYAbNrENNjx44lZa+Vdt9OG//mzRv414YGO3v2bPjfoEopIHouTkvjkRwBjgBHgCPAEeAItAwBvV4PX2c6nc5oNObl5a1du/aLL77ApjSsT5MPDYhGUqmUlsnlcrlGo+nfv39UVFRmZiYOWGZb0pQUwc7vNOl/NMDmYmvhYY5AT0JAr9ePHz+eZHW8jKdOnXJ6MDt1/PTp04IgqFQqvLYhISGhoaF1dXWUgAc4Aq1HAF/p8ePHY21SEIRVq1a1vlheAkeAI9AeCHACuj1Q7YQyTSbTlStX6LMLsaBNjmvrhM50YJVNGdKCZfbz84NpsCAIgwcPhucN1vy5qext0gORSlNfXw/pjeyFq6urW1kRXHDAsYYgCE254LDb7SNGjAABLZfLfXx8WlPvs2fPNm3ahCFK1DM6pVQqR4wY8eOPP9bW1m7fvh0emaFVLlmyhFwutgfsJSUltIFXJpOtX7/e0fYZ8o3oubQGCp6XI8AR4AhwBDgCPR6BFszaDx8+TE1NDQgIUPzvwh4p+HQmFkwulyuVSjjvAgG9aNGi3bt337p1C5XabDYIbwAZ+6jIb4BITmbn94/yzpSAzdXjHyXvYC9EgI6ZuX79Or16CEyYMOHVq1dNnUBjt9tfvnxJvjsg6ms0mmXLlvVCGHmX2wkBLCiWlpaSUimTyaZOndpO1fFiOQIcgVYiwAnoVgLYVbLr9fqKigqpVOrh4SGRSGC325SJR1dpdGe0o7q6GsfIwLiGVYpIV8H2zPr6elbMGjt2LJnEumg4aTUu0rTsVl1dHcx86CT3lpXDtjApKQm0Mv6uXbvWaZlms9nb2xtppFJpaGio02QuIiGblpeXf//991qtFjtkQXyzjp63bt1KpzjOnj1bIpGoVCrwwpmZmbBAJycYLqprwa2zZ88CWLw7x48fJ91SFOCqZgvg5Vk4AhwBjgBHoNciwMpaTkHAzP7mzZujR4+uXLnSw8MDZ13QX8hjOGSb9fKsVqsnTZq0devWnJycu3fvkgjhtJZmRbJzvTvhZhXOE3MEuikCX/7rS7yMtBFhy5YtLghos9m8YsUKqVSq0Wiwg1MqlQYFBXXT7vNmd0EEoLbn5+djTGJ8ck+kXfBJ8SZxBIAAJ6B7yEiw2WzXrl0jMhEf36dPn/aQ7rVFN168eDF48GBMTlu3bnVdpNlsPn78OKv5YCYzGAw4Pa+D/ZfZbLZnz54R9QyHhq674PQu2Gej0YjjfWBJBCtvuVyek5PjVHkjAhpk8dy5c50W7jrSZrNNmjQJXaCTBtVqtVarFQRh3rx5Dx48sNvtOHTIarVOmjQJSyk4erGoqIiIYKiCrqtr7t2MjAy8PkCjqqqKqhMFWEW0ubXw9BwBjgBHgCPAEejNCJCYAetjS4Pl6dOnO3bsiIiIgFcuGDLDwwakWZbwEgRBrVYPHz48ISHhwoULNTU1drsdIlnb7utn53p3wr35mfK+9x4E7t+/L3of+/bt+/jx46YWmUwmU3Z2NqyjOAHde8ZJR/YUU0lxcTFM7BUKhVKpDA4O7sg28Lo4AhwB9xHgBLT7WHX1lFVVVWQhi8C1a9e6eqM7sH3h4eGkyXywck1OThZVTsKTwWAoKiry8vIi3xQ4Qj0rK+v169evXr168+bN27dvnzPXw4cP7927JyqwDX/abLbi4mI6yV0mk/n5+VGDm1URHSv/9ddfAxAUO3DgQPi4cCyNCGgwwitXrnRM4zoGTR02bBjsi6leQRDCw8NPnTplNBrJgMJkMun1eo1GQ1ZOffr0gcrKKoGua2zu3WXLlkHdBRp1dXUi3pl+tl8bmttmnp4jwBHgCHAEOALdCAGz2WwwGEA6nz17duHChaNGjSJZC+Qy6+iZ7ADkcvmQIUO++eabo0ePPnnyBIwzHVSIxXUID22FBjvXuxNuq3p5ORyBLo7Al//60tPTk0xJYETi4mxPu90OsZ8T0F38yXbr5pnN5oCAAIw0lUrFOZBu/TR543s2ApyA7jnP19JgIdd4UqlUpVKdPHmy53SvdT2pqanBnESH1cyfP19UJIQng8FQWVnp5eUFtYfcLsNrBBCGQ0KEcQg7jGfbb0+Z1WrNyspSq9XgZGUy2fz584mxFXXE9U/oaXSYNXhehUJx/vz5pjISAS0IglKp3LhxY1MpXcSbzWaivAVBGD9+/IYNGwoLC52y3nhe1NmJEyei2awS6KKuFtwKDAxEdVKpdPTo0U05gCYHIGhJCyriWTgCHAGOAEeAI9CrEMCMeefOnR9++OHrr7/+5JNPIGLJ5XLsgmKXpRFWN14TJkzYuHFjdnb2mzdvaPkc68FOAWxDI2hW3nAn7LQ9PJIj0PMQ+Oeff/r164f3VC6XI1BYWOjULMbSYLHZbPPmzcPCEvZBtp+61PPQ5j1yBwE4HX39+vXu3bszMjKuXr3qTi6ehiPAEegUBDgB3Smwt1elJMfDUjUtLa29aupu5VZWVpKJjUQiUSqVqampJpOJVSowe92+fZucDIJ9xoo9BCwPDw+lUimVSiUSiUwmw0ZRmUyGwlt5Op8LUM1m8759+7C3SKVSyeXyzZs3s413KvaxBZrNZpvNZmmw6HS6pUuXQhDUarXwOBEZGWm1Wo1GY1PlkEIoCEJsbCxbspthS4Pl9evXly5dqqysfPHiBXKhC44lVFVVgQ4G575mzRqIsI4pWx8Db+AjR45EjTDloAMPyfCZAizsra+dl8AR4AhwBDgCHIFuhwCWaTGBiiZoYoHfvXuXk5MTHx8/Y8YMmmEhTtCh2VjdRyQkk8GDB69fv76kpMQRE3b+ZcOOKXlM10GABEur1VpXV0c/jUZjfX09+xwR7jot5y1xRMBms+l0OlixQBXC9sHIyEg8WacuCuHVEK+5UqkMCAhwLJnHcARagAA+GmQe1IISeBaOAEeggxHgBHQHA96O1ZnNZtYFh1wu/6in43ZsTRcr+ty5c7RKDwHo+vXrOFSQZF80ecWKFfB0zLLPYJyRUSKRkCsMGD6r1Wp556jIAAAgAElEQVSJRDJmzJj22+9jMpm2bt0K/U0ulysUit27d1PLXYvs5sbLYDDYbLbc3NygoCDS9NRqtVwuDwsLq62ttdvtrGLAPkC9Xk+W4B+6nJqayt51PwwO12w2f/R4zAsXLoD3VygUEokkIyMDFtDu1+V+SqhAHh4eCoUCCIPcJ8ZZFGBhd78WnpIjwBHgCHAEOAI9AAHaIURMInXKarW+f/8+Jydn5cqVw4YNI8mBZZ8hYkGswrK6Wq0eMmTItm3bLl++/OrVK6yFWxosHxUVqF4e6LII4Nxvu91Osh9LUFqtVsiouIuNfayUxYa7bB97VcMgM79582bMmDGgnslde0FBgd1ux3IUPTgc7nLv3j1BEOhc8QEDBvQq0Hhn2w8BjDROQLcfwrxkjkCbI8AJ6DaHtHMKhHGrp6cn+dhVKpWLFi3qnNZ0vVoTEhKg7ZAWZLVaHYUkm80WGxuLszJgiQNNCYytyE5Hq9WOHz9+4cKFMTExWVlZBoOhZT4x3EHLZDLNmTOHiGN4zIBRMyvkOS0KKtx//vOfDRs2qNVq9OKDDTgY+TFjxjx58sRFy61W64sXL5AYeQ8dOuS0IjcjwedSYkcN1m63Jycno0aor/n5+XRsEWVsq4ClwfLw4UPsCkSlx44dE5HO7E8C3GnL26pVvByOAEeAI8AR4Ah0CwT++OOPAwcOrFmzZtCgQXRaMgKYxCG9YIYlSUYQhNDQ0NTU1Lt377JettBlq9Wq0+n4PNstBkBTjbTZbCaTyWAwkPsUSKQik3mikIiG5s+9KUi7QjwUqEOHDrEEtEQiCQ8Px4mgrJxstVpxRtygQYNow6ggcP6hKzzJntAG+nog0BO6xPvAEejpCPAJoEc9YfixhYivVCpnzJjRo7rXis4sX75cIpFIpVKAM3nyZHh8ZoUkGESbTKaVK1ey7DM2ik6aNGnz5s3Hjh27fPnygwcP3r17B5HaZDJBcaqrq9PpdLTztBWNdZLVaDROnjyZ9DqFQlFaWipyIeIkW2PUixcvoqOj4RactZEXBCEoKOjOnTuWBgt0A9IQ2KLMZvPDhw9hpgQSv8W+xa1Wq6nxYvlup2rG6tWryWWKIAh///035Fe2YW0YvnLlCpRkDI/8/HwcbcTyzhQWjZk2bAYviiPAEeAIcAQ4At0CgYqKim3btvn7+6tUKmwLw5EY5MQMRDMR0FqtFoLE6NGjV65cmZOTU1NT47qnTsUD11n43S6IgNFofPr0aUFBQXJyMoYHtg9qtdp+/fr5M9eCBQt27tyZmpq6a9euYuZ6/vw5Nup1wd71wiaZzWaTyfT69WuWgIbeVFRUBGWKti9A4DeZTFFRUawO0gtx411uDwRsjRe3gG4PbHmZHIF2QoAT0O0EbCcUa7Va/f39iaMUBGHEiBHsTrdOaFOnVkknMttstokTJ5IWJJPJEhMTnTaNtJ2kpCSZTKZWq0GDarVaOKpzmqtjIvv06QPxTi6XS6XSf/75h60XZiZkaKDX681mc1lZ2ZIlSwYMGAB3FkAAVsxyuXzZsmVkc9TUzI2tkaWlpWq1mqyWLl++zFbdHuGpU6dis54gCIMGDWqPKqhMm8124MABKMbQn+vq6jgBTfjwAEeAI8AR4Aj0BgRg2Mi6RCChCN3/sI8+KSlp+vTpUuaiczJw+gjJWpAZaNuZv7//vn37KisrwRf0Bjx7dh9JxgbViGEDlxpGoxHGGeXl5du3bx8xYoSnpye5XwALyZrDkwM00eCB4Qgz1v4bDAoK8vf3j4iIWLZsWXp6enR0dFpa2uXLlwsKCnJycm7evPn69Wty2lZfX88+BXY8w6oAMXBSB+YUfx1tDvSNF5UMU18qH0K42Ww2GAwkWmOos5WyjekiYTwsWM+QpuOizeSBx2q1rl+/ns5mx7MbN26czWaDDoIOoihI2qRHCILQrmYlXQRb3oyOQcDSYNHr9Vartbi4ePHixbNmzcrMzOyYqnktHAGOQAsQ4AR0C0Drilkg/33YzMiKdH379sVZamazmbU57YodaJ82kaTo5eUF9hbnNBYWFjoFhESuvLw8lsofM2ZMu3rY+Gjva2trcfghUclkXEB5dTod5LlXr14dPnw4MjISXQDjjKNCYHuiVqsPHz5sMpmwv9VoNIKApqIoACeMV65cwVmFUBtg4EBp2jxgNpuxjVej0ajVaj8/vzavgi3wg1329u3b4btGLpcPGzbMYDBwApqFiIc5AhwBjgBHoKciwDJKxBbhdEG73V5eXh4dHe3r64sDnHEwA8sMwpoVIgrCtIFp9OjRW7duvXr1KglXwFD0s6cC2+P7JfKkgf6aTKYrV64sXLiwX79+LOHIhllVBWOGvQtRU8Q700+NRkOGFJQLBWKbI615qFSq8ePHBwQEhISEREZGzpkzJzk5+eDBg5cuXSotLb18+XJZWdnz58/1ej05e6GRCSqZfYJYnmFjyNQXEqPNZmOP+yb2mcoU5e06P2kfJJrk4kByETv/119/9e3bFwYc+CsIwtWrV9mBQd0vKyuj58VdcHSdp98DWoIx9urVK29vbyyEqFSqmzdv9oCu8S5wBHokApyA7iGPFXTksmXLIPeTEUFdXZ3JZILrgx7S1eZ0AwbgNTU1oF8FQdBoNF5eXpYGi2tC+erVq8AQf6Oiojr3PBwc30FnIcIomOh1QPLHH3/s2bMHZwzSAIC0RyeESCSS1atX//PPP+Df4TqcjD6cQms2m0+cOAFxH3rC/fv3naZsZSSaZLVaX758CV1CqVSq1eq1a9e2smTX2a1W6/z580HWK5XKiIgIR//gZAtDpuLchss1qvwuR4AjwBHgCHRHBB4/fnzs2LHZs2f37duXpn6SIkQOyuCjjOWVPDw8Fi1adPHixZcvX0I0BTuASZPm0O6IDG+zUwRw8mR1dfXx48eXLFkCk1hyzsCODTaMDWe0VkG32LUNIp3ZgLLxovRsQKPREA0ql8tVjReWTJBMpVKRwT7x1FANpk+fPmvWLB8fn4iIiCVLlsTExOzevTufuXJzc1+8eAEEiFSln2RPTRY/3YWARl/u3bsXHx+/f//+ly9furZNZter7Hb7N998o9Fo6CkoFIrAwEDYU8McnsxlzGYzJRMEwanTP6cDjEdyBD6KgKXBsmfPHgww7MVJSkr6aC6egCPAEegUBDgB3Smwt0ul7969S0hIYGd3QRBu374NXk9EVrZLC7peoZCrbty4IQgCbJ8FQfjyX1+CgBZJkGzzs7KySO8SBOG7776DyMWm6chwfn4+GFIwywEBATU1NW/evLl8+XJGRsaX//pyzJgx8JIhk8nIWlmpVHp6esI5oyAIwcHBhYWFMIoH6YyT/VxLgSaT6ccff5RIJNATVCrV8+fP26PvWC2wWq1Pnz4lL4EfKO/U1FQcq01SbNvWbmmwTJ8+HUq1SqVavXo1IGKVB05Aty3mvDSOAEeAI8AR6DoIgHSeNWsWnH2JJEn8JGqPZQPB4mm12jlz5hw9evThw4eQK2i+hqAlErdEP7sODrwlzUXg7t27aWlpw4cPh4jISs6QWslygh1UQ4cO9fX1DQkJCWy8hg4dSibMotHl+BPSmsjMguReqoV1CIOwovECPy6TyeSNF04ap7FN2Z0GZDLZsGHDQkJCgoKCZsyYMXv27Hnz5u3YsSMzM/Ps2bP5+fnl5eU5OTllZWXwZUFiZHNR7eD0t2/fJlQ/++yzkpISFw0QEdB///03rSJgOUoul+fk5EBur6+vZ48QB6r4aFRWVkL70Ov1/IPgAnB+66MIYCAlJiZigCkUCrlcnpCQ8NGMPAFHgCPQKQhwArpTYG+XSj/M3/TxJcnpxo0b4PVwYF27VNyFC4VPuoyMDIi2MpnM09Pzp59+cup/g+1HamoqSbcSieTgwYOdKx4dOnQI0iGebGhoqLe3d58+fXCqDwRo1kAJjYdbPblcvnz58uLiYraDIKDdFI5jYmLYfbWujSNEtTTrJ9pz7do1sp2RSCRnz5612+3tuoKCjaJSqfQDZZ+ZmQlxmcBxEWhW73hijgBHgCPAEeAItBMCkFJsNht7xjLqEnkPgAOuvLy8ffv2RUVFDR06lIRGODEgK1FM/ViBJotRqPdKpXLUqFFLly49ceLEP//8A1oK02U7dZAX25EI1NfXQ9jT6/VGoxGGvVhXMJlMT548Wbt27ZQpU2jkOAa0Wi1kUXY4IRwbG4vCwRxh2MCSuqio6OLFi6WlpWVlZdnZ2T/99NPOnTtjY2MzMjK2bdsWERHh7+/v6+s7ceLE0aNHY0zSyEQbUCnJ8GzD4GyNjUFY1EKlUgmtge6C4Aa9rtVqVSoVm8CxQEEQ1Gr1p59+On369NmzZ/v7+8+dO3f9+vWJiYmXLl26evVqfn5+cXFxWVkZiwPgxYsMoZfOOXfx6FmGF/saafnHYDBgF6yL7Ha7vaCgAKsF1Kl169aRqE8OsqkQkoph4/zNN9/AAgZfjw8E9NSpU9EGbMBFj6xWK4h+mUymUCjKysrgR5v110FV8ABHoFkImEymffv2YRhjNHIL6GYByBNzBDoSAU5AdyTa7V7Xrl27RHIYXCCxMk27N6KLVfDBpcN3331Ha/uCIFRWVpJw1lRjN2/ezIqwOTk5H+WsmyqqTeJ37NiBaRXaIJ6yUqlkqWfWzEQulysUiqFDh27duvX+/fvv3r2DMQLbGJIgXXDruLV27VrUCIMR1xbTbBXNDQPko0ePsgR0eXk5WW03t0B30tfU1EBYwcbPn3/+GWs2LD5Nhd0pn6fhCHAEOAIcAY5AxyNgtVpZcqqmpubs2bOxsbGTJk0CZQbvZCKrVZlMBumCaDXQRhCKBg0aNH/+/FOnTj169Ag9IgnThSzR8X3nNbYSAfJozJZTUVERExMzceJEuGmmEYIArJVFkYIgeHp6Ygj5+PhkZGQ8ePAAZWLAkEUtIsFpikRuRyNZS4NFp9Nh7BUUFNy8ebO0tLSgoODixYunTp1KT0/ftm3b4sWLg4ODAwMDAwIC/P39p0+fPmDAADQP7QEfzXqQgJSLs76RUkRki346dhbiK9kCw9MIK59DmFcoFCC1SWuTy+WBgYFBQUHTpk0LDg5OTExMTk4uLCy8ceNGUVFRdXU14EKXdY0XfE+z7zjZamCjJz07CLHAlpyE0N26ujpvb29IwtSjQYMG3bp1C9WJOGISic1ms6XB8urVKxoP4KAFQSgtLbXb7bW1tewOwlGjRlH5SUlJ1FrR46aG8QBHwH0EsI6CoSiTya5fv+5+Xp6SI8AR6EgEOAHdkWi3e13w1Uuz+4dAUlIS2LR2r7sLVzB16lRImTKZTKvVwpzWtVHAwoULieQVBOH58+edC+PChQtF4h08irBELZ67p6fnwIED161bV1RUhOO5HWVNPCuSIF0ojRA6Fy1aRJsrvb292wkKMtHatm0b2y+YVrloZCuHHvxr01tz5swZkompZBYrNkwJeIAjwBHgCHAEOAKdiADNkrSJx263l5WV7dmzZ9GiRcOGDZPJZGq1mpauwbWJqDFMhSwHLZfLNRpNQEDA3r17q6qqQEjZ7Xaj0UjCgOtTyzoRE151CxAATYmMNpvtyZMnp0+fXrJkCdhDDw8PmHTAvRsrrYFsJWmK3GJMmjRp7969f/31Fx1hR63S6/Us+ajT6fATw4zlpnFQnkg8a8oegkYmVQQ+vb6+/u7duwUFBWVlZXl5eR+McBMTE9PT03fu3Ll27dpZs2b5+fl9/vnnZO9MfYEErlQqsWZDFiroPpusqTBMHACRI4tN5G+/fv1QJvm1gOaCn2hYWFiYr69vcHDwpk2bUlNTt2zZkpKScujQoezs7LKysvfv39fX1wMoVv4nGZswQQCP22AwzJ49G46z0QWsS23evBnJWA6axODa2lpj4xUcHEzW0wgEBARQ+eT53c/Pj/oO93poJ327RG3jPzkC7iBgs9nwKTh//rx/43Xu3Dl3MvI0HAGOQKcgwAnoToG9XSp9//59UVGRSPTZs2ePo+lru1TfhQvt27evp6cnHTNCjslYqVfU/NDQUOzIg1CIbWKiNO39E82DWObv709CG4ygIQ2zov/MmTMTExMrKyvtdjtrEIF24kR7VsgjCZKNFHUKEufs2bPJAGrEiBEiBUCUpcU/aafh0qVLyd+IRCKhU19aXLLrjPCvTS9OTk4OKdiUkcWKDVMCHuAIcAQ4AhwBjkAbIuBianZaCzxvGAyGD85VY2NjZ86cKZfLidgiyowmOwqw0gVFgoOOiYk5e/YsNlGBPTSZTI4Cxvv37502iUd2NQTcHFRms/nevXtpaWlhYWFkoktjAwwjuFTHvzAoVqlU/v7+P/744/Pnz0UkI0xiMZyc4gPpV6fTEb9MYqfRaBRx1lQCSW4Q0hDP9pe8xFAWVITCTSYTnI3AdIM23tXW1v7xxx9FRUXXrl0rLi6Oj49PS0tLTk7+9ttvg4ODWZNewodsnMmzh4eHh0qlApLsQYiQdYm6hd88ygU5n+6ifPxkI4noB8fNvs4TJ04MCAiYM2fOkiVL4uPjs7Oz3759S6gSDtBxbDZbZmYmlU+HNy5fvvzZs2dQnUgAZuG12WxXr14FdY5GqtVqqVRaUFCA894pl6+vL8Dp27fv4sWLUe+HE4zYx8S2ioc5Au4gAM8z9JXAWMVJmO5k52k4AhyBDkaAE9AdDHj7VldZWckKQIIgrF69mtx4tW/dXbJ02G4AE8hSa9asIbHShcRDIrVCoRg+fDhl6cheYm8d5OP+/fuT9kjC5dChQ7/++uu0tLSKigrYIiGxi0a66LLTXCiQdfM3ffp0pylbHwmK3GAwBAcHC4JA1h9OZeXWV0clnDx5EnVh56Cjs2xKyQMcAY4AR4AjwBHoAARA2cByEFQdzrQAeYe7YNwMBsPvv//+yy+/LFiwYPz48SQhsOvTIsmQ3eDF3pJIJCNGjNi4cePZs2ffvHmj1+stDRYSRdiqWQSIXWIjebhrIgBDYOJqYcnOEjd37tyJjo4eMmQIttmBEqWTAGGLgDFDdCpZRYBbxHGUtbW1kJzJAwONk+YKohj/bPYWlODicaBkp+0UVer0J0o2m816vb6QuWJiYpKTk/38/MLDwwMCAmbMmBEaGgpmll5S0dunUqnYW2q1Gv70KBkO6AZDzfoJwVITPR3WqUjfvn2RHWcwqtVqF/sVrFbrvXv3oHHQwoNCoZg0aVJ1dTU0AjIWEUE6YsQIaid6ERISItJKZs2aJQgC2hkSEoJxSF85xwdNZxiyI5YWwPDI2GaQyTx8T7O3nIZNJhNr2c1+afHpg909m5fWJ9hIHu5cBNgXk4YcjZPObRuvnSPAEXBEgBPQjph01xir1Xrt2jWa/hGIjIyEUUx37VWr2339+nUyRviACQ4lcC281tbWEgEtk8mmTp3a6la0sAAofrW1tRDm6CDvxMTEe/fuUaHYWOe6U5S4WQGUOXr0aBpXYWFhzSrB/cQQBO12+7Bhw0hChcsU9wtpQcqffvoJOw2xsxIup1tQDs/CEeAIcAQ4AhyBNkcArAoIaJwxaLVaq6urf/vtt2nTpuEQXRF1BVtIuNcgSgt+aTGbkwWlXC4fMGDAnDlz4uPjb9++zXKRIBBBxEAYID2f7SNFtocQwlbEw61HgLwA08PCGv+JEydWrVo1aNAgCMwYJEqlEqftsc6d5XI5PFEgDdbv+/XrN2fOnF9++QVux+HjjihdBFozTti8CLceCioBBVJrHetyEUOFQA4nXxNEqhIdBsChkel0uocPHxYXF9+4ceP06dMZGRlxcXEpKSnhjVdISMinn35KRziSO2n4PMEDGjBgAEtAk4hO1tCCIMBZCm4RmywIQnx8PD19aj8CAKGioqJ///6enp4oDU57+vTpc/fuXVF69uehQ4ckEglIc7VajYHx559/smnWrl1L7gRDQ0PJF6LNZoPXlEOHDtFqB9h2GIkHBQVFRkYGBweHhITExcUlJibu3LkzIyPjhx9+yGcuE3OhXtaExWq14ic8NhCVjNqhcNFgIAKasIKzEXqgbL94uHMRYN/Qzm0Jr50jwBFwBwFOQLuDUjdIg4/v77//zm7d+nAKxIwZM7DFiZ2Du0F/2qKJEBr27t0LNhNL7r/++9emyia9q7KykiWg582b11SW9o43m802m+2PP/6gjXhSqdTb29tgMKC1JBhRSzAS6GcrA/Af5+XlRcLrggULWllmU9lJqoOwi5E8ZMiQptK3VfyuXbtAPUOsv3PnTluVzMvhCHAEOAIcAY5ACxBwdBeg0+kKCgpSUlKioqK8vb2JciJ+mZgmlsER+aiVSCRgFaVS6cSJEzMzMz+4wcXBGKCbiZTBIWZOfemKBA+u/Lfg+XaFLJYGy2+//bZixQqNRkOjCOIQ/IMrGy8QnaBBScWATKjRaGbOnHn69GnRkKDeEatLzGzLZFR2jLWsBGqS04Bj+W7GEO/stFjY7WJ7n+hUQKQHy8nmJQcjIGeNRuOdO3du3rx548aNy5cvg6fesWPH2rVrAwMDo6Ki/Pz8sARFHwQEwP/iseKpkUuNvXv3sjWyYaiKsIOGLQg5DJHL5d7e3ufPn6dttaQ0UQljx45F7VjfkslkK1euZL8hCQkJNITgJLq2thYF6vV6k8mESqkvUNyUSiWdbQgv9hqNhpbQoB+xHz1ocGPHjvX39w8NDfXz85sxY8bXX38dHR2dlpYWExOTnp5+6tSpa9eu5efnFxcXV1RU3Lp1C2OVeGcaumz70dP6+nrWIpu6zwOdhYDobe2sZvB6OQIcATcR4AS0m0B1j2RWq5WmbQTGjRvX1LkT3aNLrWglCM2NGzfC+zNW8ouKipoqknalXbx4kRVlvvnmG2TpeIEDW8OKioqgEqBVcIKBZX40jDRVmoOb6mNz47HVjgRQQRCWL1/erji8evUKmg9kynHjxjW3zc1Nv337dolEQsL6w4cP27WDzW0eT88R4AhwBDgCvROBe/fu7d+/f/Xq1cOGDYM3Z4VCoVQqMUuyLCGMnVnRBWERAT1s2LAdO3bcunXr1atXsAdsijp0H3ASPFpflPuV8pQtRuD58+cnTpyIiIgAu8cSeSINAj/Jml4qlcIvx6effrpo0aJf//3r+/fv6aHDtld03AjrEqE144TNi3CLu+80o2P57sfAU41jsazdD6RKYMWWzOayNFiw/ONoX0IubuERwlFGBUlqtVrv3LmTnZ1948aN/Pz8Xbt2xcbGftj3mZiYGB4eHhUVFRERsW/fPrL2YGtHGOVjteDhw4cDBgwAmUvnsmi12pMnT+JZOzKzCQkJGDPkel4QhKqqKvKtgQRYBlMqlY7uDUU+tWGPIhqWoLBhH40xzCag4UrG4GDhKZ4S06ILxSiVyhEjRvj4+Mxgrvj4+C1btuzcufO3334rLy8vKioqLS11hI7HdCIC7Dv1008/paamZmdnd2J7eNUcAY6AawQ4Ae0an25219JgAW1Hvv8EQWBloG7Wn7ZoLoRsrJbLZLKHDx+6KBXSYVpaGqvF7dq1C/GOq/0uimqTW5Ddf/33r5Cc8PfDVlmIjyT3oy5MwG1SLxViNpvfv38P+xcMqg973+huewQqKioAPuRdkf8Ttst6vb68vDwjI2PZsmU+Pj5eXl5qtXrUqFHNbdXmzZthywNB9u+//8amgeaWw9NzBDgCHAGOAEfAEQHMzrQrH3QMsUhkHIqMFRUVMTEx/v7+JIeIiBLMxTRRCoKgUqlYelomk1FezG7ffvvt6dOn//zzT1ZRZ8OObeYx3REBs9ks8nxKLOHjx4/T0tKmTZtGCoJoXGEZHmQcxCGkhDCmUqkmTZqUlpaGk67ddO7HjjE23AWxpea1oG2saNpUdiofAdfJ2LtsRjLLpY8G7iLedclsmU2F2brsdnt9ff348eMxJDQaDZhfiURy/vx5pyXo9XokZlc11q5dS1+8Y8eO0S0RAW0wGGw225kzZ1CCaHAi0s2/7Ah3DLsuhMa862SCIOCTq9VqYWcd+r/r+++/T0pKSktLS0xMzGMuePDAXxY91vWH40BCDFxak+pHxtpUDs0miCF1VZSFMoo8X1M53TRA/R06dCge3IABA548edJNu8ObzRHo8QhwArqHPGKaY8ibLU2iPaSHze8GMBk5ciQO/YCDhUePHlFJTmd6m822fv16VmT58ccfkQUFUvaOCVit1oyMDLY9S5Ys6ZiqYZvw/PlzaLBoQ2pqarvWnpeXRxv0pFLp2LFjwcKj0rdv3+bm5m7evDkgIIC1jIAhGE7LKSkpgbDrZjvXrFmDDkIsfv36taNRhptF8WQcAY4AR4AjwBFgETAYDEQCUjzED7AGf//992+//fbVV18NHjxYqVTirDDyewDTZpYNwVwMihlcM7lqxV51JJ46dWp6enpxcTGUc+zoZwkmd8LUYB7oFgi8efMGK+gYWpYGy++//7558+bx48fTwXSsPMmOKxDNEIcgMEMoGjduXExMzP37961WK7lfcBzSTvFpaow5Tdy5kdTUdmoGlY9AU7U43mUztjcBTabKpB9ZGizgoOFRmjjoX375he0CpV+6dCmGDTHIarX65cuXKDk/P59slmUyGXhVkKEYUfv376cEcrncxVgVDV32J5vLMcymdAwjvWO8Ywy9KY63cGAPEECB9LmWyWRyuXzcuHHh4eEbNmxIS0vbsWPHvn37zp07l5+ff/HixZKSkj///LOurg4vMr7eWFgimhW39Ho9xRAJQA+FnggF6FaPDOj1+uPHj+PDhSeSmZnZI3vKO8UR6AEIcAK6BzzE/3aBTB40Go3I8sVNMbGHAPF/u2Gz2aDLYTZSKpXPnz+nJKJZGavQdrs9PDycFVlOnTpFWToyQAYOa9asYduzYcOGjmzGnTt3gB7G1YEDB0Qr7W3bmHPnzkH6xHErn3zySVZW1t69e1esWBEUFISWyNTyzWsAACAASURBVGQyUqVkMhk0dpIFs7Ozm7VUsGDBAuwbQOG1tbUkyZHc37Z95KVxBDgCHAGOQG9AAMdbGQwGo9GIMxXQ6+zs7NjY2PDwcDpqDBMQbWJjBTmicpCGZTQoF0gfLy+vxYsXnzhxgrW2ZoVAmtRaGegNz6779tFgMOTn50dHRw8ePBiHoKhUKq1WS67GSKSk8YPxhuEH085PP/1069atT58+Fa3om0wm9zdWNjXMui+2LW65CIqmykEy9q4o40d/snlbEKby7XY71hvq6+unTJmi0Wg8PDzoeyWRSC5cuADdkzUT+fPPP/EtIplcKpXu3r0bo6i4uBi2wwqFgj1jnNQxlqEWBAEanEKhcHriIo1eUYCGt9OAKLHoJ7KIIpv6KZPJ2FM68RKxOwkQ01SZcrkcm1coC45wRHV4DT08PPz9/efOnevn5xcVFRUXF7dz586ffvopOzu7rKysoKDg/fv3dru9traWnjVOD4IljU6nMxgMpLWxcxCl7zGBjIwMjBnMmDt27OgxXeMd4Qj0MAQ4Ad1DHijNPX369GH1FqVS+fvvv5tMJpp+ekiH3evGq1evSG6QSqWenp4wD6FFfrYYIqDHjRvHSi2XLl1ik3VYmGSImTNnsu3Zvn27SB9o1yaVlJQAQzgAOXbsGK12tG29EGF/+eUXSF2w5Orbty89QdLM2RiEIb3J5fLhw4c/evQI+rab7YyIiGDXzI1GI7KTFE6Scdv2l5fGEeAIcAQ4Ar0BAaPR+PTp03379q1cuRJ7hLF06jiXiWKIv2DjIQ/gllKpHDx4cEhIyMGDB+/du1dTU+OIp77xYjfps7Nby8KOtfCYNkcAQlGzJJCsrKzly5cPGDCAZCfsFWMHEitPsuMKNJ+vr+/OnTvpNGbUjhUUdFDXeLnZ2aZGl5vZe1IyERRNdQ3J2LuijB/9yeZtQZjKZ/O+fPlyypQp4PWUSiXZ9p48eZL8VtNADQ4OpgQgBIcPH25psOh0uufPn2NFBH8dtxtaGiwFBQWrVq2aOnXqzJkzg5irf//+RGqz49YxzI5wx7BjejYG6dmYpsLUGBDulIxePYphA9QeimRdLMrlcryGZEUO5h3zBW0PRV6AjDCUoAkTJoSGhk6cODEwMHDjxo3JycmbNm2Kj4/PysrKzc0tKiq6efPmX3/91SwbHXYYdPFwfHy8IAhyuVyj0Xw4cjM5ObmLN5g3jyPQaxHgBHTPefSY+8PCwuAQkOangoKCntPJZvbk0aNHgiDg1BTse6J5l0QlKpJiPD09STIQBMHFuYWUtz0CIKDr6+tFhDhMCdqjRscyLQ2WCxcukLgplUpbc7CDiBEmI5oXL15cunTp66+/JmdztBUUpy/StmI4oftgT6FuvFQqFcyf+/XrN2vWrIsXL5rNZvZ4RsceOcYEBgaC2pbL5Wq1mozFSAoXBRxL4DEcAY4AR4Aj0BsQIDkBnRX9tNvtWOw3Go0PHjzIyspKTk6OiIggAzdaRgXpQLSgiJXo378/UkKdptO0WMlk4sSJcXFx9+/fhwVcbwC/t/XRarU6WixCRKF9Wna7/fXr11lZWQsXLhw4cCANJJacAgmIwUOsGZtArVb7+fkdOXKkqqoKlbJQsyIQuYBgE/BwhyHAPgu2UsSzMW0btjRY9Hr9qlWrIJyzTOjVq1dZry96vf7MmTMYXex37+jRo3q93mQykXIqCP+lIEjkblaDC5krJyensLAwLi4uNTV1z54927dvX7ZsGcjr8PDw0NBQ8ulBVdPnV6lUqtVqtp3sN5bCUqkUR7/ii42/yEVQ0AvF8tFSqRQeAnHuIsxrcJAsCkch0FLZjFQ1Ak2916JkNL84xjvGKJXKadOmzZ4929fXNzw8fPHixTExMbt3705KSjpw4ACcgZSVleXn55eWlj548AAPCN8HTHNWq1Wn05F9G+sXXvTtwnfD8RFDZWP9YlsaLOxyF3yPUBU4ONdutxuNRvZdgHegM2fOkIsYqVR65MgRxxp5DEeAI9AVEOAEdFd4Cm3QBixB2+32wMBAmgWx0amyspJY1zaoqVsVcefOHYlE8mEhFNKGTCYjT2SOeiNiXr16BRGBZuvOIqBNJhPce/Xv358VPuDWyrH97fFkLA2W48eP0943mUyWl5fXgop0Oh01GDLKzZs3Dx06tGjRotGjRxPUFCDpEMoShjR5VfPy8po2bdrKlSuTk5OzsrJu375NTTIajc09W4NeGaVS6enpCcxZyUYUprp4gCPAEeAIcAR6FQIwSjU3XpYGC/GDRqNRp9OVlJQkJyfPmzdvxIgRWPPGpCaTyeBUCj/ZCQ4unmmKRwLy+wxrOA8PD4glo0eP3rx589mzZ6urq9mNUOwk1aseR8/urM1mc5RniIt5//79kSNHFi5cyC7Y00BiFQEMKoVCAXcBMCnAivu8efP27t377NkzIIkaRZWyo8vRjr5nP4Ku1jv2WbBtQzwb0+Zh2MSsWrWK5XPlcrlWq7116xZx0GazWa/Xjx49mk5GlUqlMpnMx8cHbCN9A2UyWVFRkV6vpyHdsjZDuXDUc9liDcxVylzXrl1LT0+Pjo7e1Xht3bp10aJFYWFhgczFcu4y5mKNvdApQRA8PDxYkx3WIwRWE7HhEjMCrQYhFxXiGHDxXjsmdj+GGiCXy0VH1+IDAj6X3B7icfft2zcyMnLKlCkzZszYsmVLYmIiADxz5szNmzezs7NLS0vhw9pmsxkMBtqiDYdU9JRpv47NZsPYoPMYHU3jKYYeq9N3ISYmRiqVqlSqTZs2kZET1cgDHAGOQBdBgBPQXeRBtE0z9Hp9SEgIzT0KheLnn3+GKOk4N7dNlV24FJvNVlJSgumTdjOVl5ezahvbfMxq5eXlNCUDyc4ioM1ms9FotFqtINBJ/jh48CDMrGgaZnvR5uF9+/aRJiOXy6uqqlpQL7Lk5ORs3749MDCQ1qghnOEn0GbtC8jKQCaThYWFpaWllZSUvHjxwmQywTMdlKWWGVAQUCCgYZ7g5eUFmcZgMJClDznjxi3KyAMcAY4AR4Aj0HsQcKTnXr9+/dtvv61atWrixImwZaPzCUgSYwPY0+Oo6tP8zvqDQsZ+/fqtWrVq//798MbLzneYCnG6YO95Cr2wpxh46LjJZDp8+HBUVJTjUMGAYccSjT3WxlMul69YseLnn39mXdK5kOtYoocT0L1w+JHSBHI5NjZW5EFo4MCBb9++BTIYSGlpaTT2QLYKglBYWCiygO6AHbr19fWisY1FREuDBfFYR8RZSnSmH/uUoW7odLrS0tJ85jpy5MjOnTtTUlLWrVvn7+8fFhYWEBDA7uNkEYApNMUgIJFINBoNNCz2DRUlI7tmvNqOd1sTI5VKXcxZUqkUp7uDbSdlDW1G+53Wju4QYR0QEBASEhIZGTlnzpwPYyMpKSktLe3w4cMFBQX37t1zsYnHZDLhebFPxNJgEVlA0106JZVieIAjwBHogghwAroLPpSWN+mDaAgXSGq12tfXl47D7p3LgDab7caNG6CeacX+8uXLTdGIQOnSpUui2bSzCGisFf/555849IOUip9//tlut2NfUsvHits5U1JSCBC5XP7gwYMWDKeysrLx48djCxuVBoswx4V3EQe9dOnSuro6o9FoMBhIOoTKTVbVVquV3bTlduf+m5AI6A8LNoMHD0aZdXV1nIBuFow8MUeAI8AR6LIIsIfytaaR//zzz9WrV6Ojo8PDw7E5CVZvtFkHAdANMIKGFTNjOfffIDvN0eQukUhg6dy/f/8NGzbs37//3bt30LTZNsNeDFYF0M/Zuzzc8xCAA4R9+/Z9+a8vIUFhCJE0xUbScBLd9fT0nDt37rFjx2BLyErCNpvNhVzHCeieN6Ka2yMaLSBtd+zYgS22Wq0WDoK++OIL0Ihms9nSYKmuriZ3EzQOQ0NDWQL6A0eZlJTk6PKluW1j1+RYNYH4ZdcFEj2NljdlrSXaFkCkPBVO5SAGqoRer799+/aNGzdKSkpu3LiR3Hjt3r17+/btM2fOnDp1akRExPTp08HninbfEm7tSkCjFtbuCjZPVDvrGAT7UEmhZm26sVOWzJVEbqPUajX5MIFFOZWPADYrDxo0aOrUqZGRkTNmzNi6dWt6enpMTExcXNy5c+du3LhRVlZWUlICeFnDIFpCIBdYsMcnC2t6RjzAEeAIdBEEOAHdRR5EWzbjzJkzcXFxr1+/xnxJsmNb1tFNyiouLqbpED62kpKSiLV07IRer8/IyKAsmBezs7NFzosdM7ZfTGlpKR1iDink/Pnz0B+akpPasDEGg2HdunVkiSwIApk5NKuWoUOHYj2cFUpYiQeKulwu/+yzz8hoXaVSSaXSsLAwyJdN9RcjnMSRZjXMbrd/8cUXsCRSKBTDhw8Hxw3bc+Kg6SVyMXiaWy9PzxHgCHAEOAIdg4CjmTC2fmPxEgQfTTEUwMFZFy5cSExMDAwM7NOnj0htpp/E+okCjtMcBAyYlbF3g4ODly5deuDAATAyOMxARGp0DFa8lo5BAO7IWBcErK0fHOu9fPly7969Y8aMkclkNLRo1CFAxpUwVqC7WN338vKaO3futWvX4LYFxBkr0jRLqmEzdgxKvJauicCpU6cw0kCbyuXyL//1JXQTSNFLliyhzY40dNmT4QVBWLt2Lf/Esc9Xr9ffuXMnLy+vtLS0sLDwl19+SU1NTWi81q1bN3fuXH9//xkzZkyePHngwIH4JtD7TgH4ABFpstAfHbdNIBmcPjlaYbNcs1qtxnNEJBHTMpkM+jU1wDGAjNAlaTA4ttAxo4sYqVTq4+Mza9asKVOmzJ8/f9OmTampqTt37vzxxx9zc3PLy8tLSkru379PDkBAT8NPo9ForK2txUQPvx/sU/ho2MU3k3bo4ksLQ3ukx8xOdlQfrYUn4Aj0YAQ4Ad0DH67VaqX1wF4uLP7555+YvXAKhEwmW7p0aVMzB+IzMjJoWkXekydPsgvsHTxiysrKyNGYUqn08PC4dOkS2tAB05jJZFq2bBmEBsg6cOzVXBD69eunVCpxZiD2IANbtVotk8nGjBmzcuXKX//968uXL/V6fVJSEu5isf27776DxECkgKh2DHIioPFTlMbFTyKg5XL5hAkTgCo8e3IC2gVu/BZHgCPAEegWCIDXo6kfUwn9tNvtdJKSzWarrq7OyclJSkpasmTJqFGjaDKCCXNTOjOrVLNhUvhFcgXip06dunLlytOnT7948QL6agdM693ikfWeRorES9Alz54927t3LxzpQvSiozgwIB3/YmRCyhIEwdvbe+vWrRcuXIARvQhPVjVgXwRRMsefbEbHuzymNyAALweWBsupU6cGDhyIVTRYsC5evJgOkausrAShyX4P161bh4GqVqulUumsWbN6A2LN6iPMX5CFNu7QFEYvIJVpNBqrq6srKiquXbtWVVV1/fr1vXv3JiUlbdiwYd68eYGBgUFBQfPnzw8JCRkwYAB8p5AnDQ8PD5rg+vXrhzAdS4CfopkLB78LgoAz4SkLAk39xRhoWwJaVDXbNa1WS75N5HK5UqmUyWT9+/cPCgr68l9fBgQEhIWFJSYmpqSkxMfHx8TEpKennzp16tq1a1euXKmoqHjx4gV2hMCHNdYCoYfi+4xvJrn7MJlM7AGM9GjoIVoaLHSqk+gu/8kR6J0IcAK6Bz538uKv1+tprmqWiNljQDGZTFOnTsUshRnoo+LOkSNHRBrmvn37AGPHw2K1Wqurqz09PdlDzB8/ftxhT9Nqtc6aNYumebVa3TL1ODU1lQqB6KPVan19fdPT0x0Pyfzg9nrXrl0bNmxISEggtt21ETo7zpv7sEBAwwQ7KCiIsCX2ucXUdscPGF4jR4AjwBHgCDSFAOtLl9LcunXrt99+i46Onjlz5vDhwzFVsX/hQ4O1VmbvIsySLGwY2juWWtVqdb9+/QIDA7du3ZqdnW21WqHlYnYjDdapSaDjHOcYQz3igW6BgF6vB/tMUseDBw8OHz5MUisri9K5lI5jD7QOtsqNGDEiJSXl1q1b7II9Kz5BsBENHvfhYjO6n4un7GEI0DeqqKjIy8uLCE2JRBIbG0udHTFihMh9BNGCSqVSKpV+8sknlJgHgADmBReqFmYxnBLEuhwhAI1GY319vaPvJoPBQA/u7t27eXl5JSUlxcXFmZmZsbGxSUlJiYmJ4eHhYWFhoY1XSEiIn58fHi7xztBGWctozIxQsR2/Tuz82LYEtFarRdXkZBx1gXGmsKhJNFYFQYDhNvuZxbCkLB4eHmPHjvX394+MjAwMDNy5c+f27dvT09MTEhJKSkpyc3Pz8vLu3LnT1M5gfC3pudDeJvbjTHd5gCPQqxDgBHSPfdxYmuvNwiI+8fv376e5ZMCAAXfv3nXxyG0225UrVyg9Ah9mZezcISXBRQlteIt4T2gjcF6xcOFCVNFhE1hQUBBwkEqlffr0oZOIm9VTS4Pl5MmTCxcuDA8P37Bhw6///vXJkyeEJ2Zl/KR+mUwmnAToTkXsOBdN+R/NzhLQs2fPZltFHDRb/kcL5Ak4AhwBjgBHoAsiAOu8wsLCPXv2fPPNN5MmTXK9MZkVBohWZiMpTHdFAWjI8+fPT0pKKisr+89//uMIC7uviCYgUTJ2DmoqLMrCf3ZxBEAG2Wy269evb9iwYdiwYTScWDepNKLYu6Lw9OnTV65c+eTJE9jRg9emg6yBA4gtnU7nOH7cB4rN634unrInIQAjUDL/fPTo0YABA1g7WfLF8f/+3//D6MXyiWgRBcSf00XBngRXi/tCCNvtdr1eT5Q0607K2HiJrGubmkRgW20ymfDlgZcnLHwajUbyHYFd1NhIzbqGr6+vv3nz5tWrV6uqqvLy8nbt2pWSkpKamrpt27Z58+b5+fkNGDBA9F2inzQMyLwaMZSgxQEQyuTdsX///lSUsvHCz759+2KuJ19GlIUOInLdJIxwdpzT4opUKgUJTj6sYXX+/fffw+v3iRMnihqvvLy8Bw8esCuCLR4ePCNHoFsjwAnobv34eONdIYDZWqfTnThx4ptvvklISHj//j2r6TlmxsTs7e3NHgq8bds2pCRu1DFje8QQAV1VVRUZGdmnT5/ly5e3R0Wuy/T29sb8rVAovL294ZvCdZbW34WS06xymhK5PloIS0DPnz8f5RD4rLrVglZ9tHaegCPAEeAIcASaQgCH8eIuPstOU2KLK83RFCguLi4sLExJSVm7dm1AQADrqpK1eyKV1WlAo9HQuUzIBS3U0QWnRCKRSqUKhWLcuHGrV6/OzMzMzc3FCbpOm80jeyoCxBYRv0akj8FgsNlsz58/P3LkyNdff92vXz+MLtAf7LDEWIK7cIxM2jKPn6GhoSkpKdXV1dgk7tS/M+QWWk3nsk1PHXId0y/RcMJSR1ZWFgg+fBgVCsXo0aN1Ot3bt28HDRoEq1J8G9kPLBLfu3ePzHI7pgvdsRZWE2l9+9nS2DBKdoxpbo1Y6AXlir87mWsGc9EHjTVMplVhljLGKGJtqOEGhJ3TcSgiHL+Q+xeYbLO20mxdiMewZMPsQIW/LKpadIt+0gfcNZFN6UOYK465zpw5c+HChZycnOvXr1dVVeEVI86aVF2sSdBaI3t+gOh54eOPSPbUYkuDhV1goDBNXo4JQKFQY0QV8Z8cAfcR4AS0+1jxlN0MAZJpaGer6w7U1dXV1NTYbLacnBxayF29ejW7SdZ1CW1+l+QAlEwTT5tX5KJAb29vaEQKhWLkyJEuKAAXhTT3FjrerFwtBocloFesWIFKuZLWLPB5Yo4AR4Aj0B4IYP6FliUqX/TN1+v1z549Ky4uXr9+fVhY2IgRI3AWEzYLs7we1FoX2iapiJRSJpNB/4TuqlarsSUZnnlR+Oeff/79998fPXqUbSc1kjhx9i4P92AEYICMQ6iomw8ePNizZ8+ECRMU/7twQgkZBrJjTxAEDw8PlUolGr2TJ0/euHHjw4cPDY0XCsdOsqZEF05A0yPggdYgAOGchhOKMpvNWVlZNHTxaZ0yZcqTJ08WLVpENCIlQAAUIZwRtaZJvSEvKYM0obSm12xpbBhlOsY0ty7yWP3RjOA63717V15eXspc169f//Xfv+7Zsye28UpJSQkICIhovKZMmTJo0CC5XI7xQw4qYTdG5DLdBU9N9s4YnPiJcx1Ew9LxJ6Z+/BV9ih0Tt1UMHS2LgEQi8fT09Pf3j4qK8vX1jYiISEpKSk5O3r59e1paWmFhYVFRUW5ubn5+/rt37+x2e01NDUsoQ/wwmUy4i+ei0+nIyt5ms7E7ZjAGkIw4bvzEjnAK8wBHoGUIcAK6ZbjxXN0AAcd52qm3LLYn2HmEmMePH9PBRIihVUE2S3uHMQ3QROLYqfZuABHQMpnMx8envatD+ezk1941sgT05s2bqTpWCGPDlIAHOAIcAY4AR6C9EcCsB2aNzlj+448/cnJy0tLSvvvuu/Dw8FGjRol4Oiii0DZhqoxNsgqFgnRU93VFHLFFWisyfvbZZ/Pmzfvxxx+LioqgcpvNZkeu3M0l8PaGkZffkQiIxMWsrKzNmzcPHToUxnSiEUj29aIBKTIajYqK2rNnz59//gmyAN2B7T9202NvPiuuUJgYw6YY6o6XLTvycfC62goBjCjWppJKXrBgAcxRQdUJgjBkyJBr165hCZD1GoxxjtW7Xbt2UQk80BQC9CK3yXvKlsaGUbtjTFOtEsW74J1xi5wgw3OISLFl0xiNRvqE1tTUkCku634EU61Op7t37152dnZJScnGjRuJaBYEITw8/Ntvv/3iiy+CgoJo+IFBZu2m2aVosmKmTzHLPot8yFCa1gRQI5x4wBkIy3GzNDoWcuRyOSXAAVGovV+/foinWUMqlU6ePDkiImLq1Kl+fn7ff//97t274+Pjt23bdu7cubKystzc3PLycnDQtIcG/DIcsGBawcYa/IVte8tccYpGC//ZyxHgBHQvHwA9vPt0VgMt2dGUJuo5ZlxEIg2meXanSe+0YCIXHFKpNDQ0VIRbO/1kH0c7VUHFsgR0QkICzaysEMaGKSMPcAQ4AhwBjkB7IwA3GsnJyevXr581a9aQIUOgcUkkEhwei58g9cAUYysu4sHusX4MEN/cv0ql0tPTc/78+ZmZmQUFBXDYxUoFpF3T7isgA8+b7Y0SL7+rIVBXV3fp0qVVq1ZpNBqtVkukM860xPADWeDoy4UGp0wmCw0NPXLkyNOnT9kOWq1WWuqgg8dZQUUU5gQ0ix4PtxgBjCsaTlSO2Wyura0dN26cQqGAXwWtVqtWq728vHx8fCQSCTGA7NiWyWRr1qyhQnigKQTY17mpNO7Hs6WxYZTgGON+ySxB7E4uLNmy0yhyYYCBksZ86qi86/V6dqq1Wq0lJSW05CyXy/Pz86HIw+8E8d12u/3Zs2e3bt0qLy//cIrmwYMH9+3bl5aWlpycHM5c5HmD9j+1HwFNNLRUKlWr1SJP0zR3SCQSIqCRhvoLehpCEb1iCGArGMKUHTKSRqNhS5gwYUJoaOjEiRODg4Pnz5///fffp6Sk7N27NyUlpby8PL/xunXrljtPlqfhCLhGgBPQrvHhd8UI0H4NmgwgBDvOH+KcHf67NZMoNRaFiGxG6G5vCHz66aeYhgVBmDhxotMumxsvp7c6N9JoNOr1ehqctJwLlhnxEyZMIKOkPXv2sAJN5zae184R4AhwBLo4AmSahOVelgsjIYGNdGrABSni5cuXRUVFv/771127dq1Zs8bX1xf+Q8neBxoU2ShRgFW3KNIxQMZEZPGkVquRF/ZHbDkI9+3bd9GiRQkJCYWFha9evaJnQaZeJGaQwkwxlJgHeiQCtGEOPp2pj8+ePcvMzPzqq6+IiXMciqIhTbvIaTR6eHgsW7bs4MGD7owrdshRuAUB6gIPcARcIEBDi0RrSlxcXAyPBxjJCoVCo9Fg/BOJxn5mpVJpQEAAZeeB7o4AlOW27QXGm+syobjpdLpz586FhoaGhIRcvHjRdZZm3S1iru3MFcBcxFOLPu+SxguW1HD6gb9kW40E9F6IflI8y0pjOQeSjEql6tOnDyVz068IasFfakmzAvAQNXbs2ICAAD8/vzlz5qxbty4+Pj4uLi4pKenIkSN5eXnXr1///fffX716hSNwsWxPAiFZVeNwKXZVlZ4OTa+kmyMZfXwonrKQ5EkniJjNZkieaAblpSw80PEIcAK64zHv9jViP2ldXV1paSncCTlVKTu9nyQkdc3mdTo+bjZg7NixpB2NGjXKzVxdJFl9fT0mHkxIZrPZYDDQGdCwi0cHMXlnZGSQJ6wu0gXeDI4AR4Aj0GURgPTPCvQQ8anBpAzQ5pK///77ypUrBw8eTExMnDt3rp+fX1RUFKlPTQVYfUkUZrOIbtFPOOhgTYFgTMQaBAmC4O3tPXfu3J07d168ePHNmzcQHtAF9BHUM/QlVsZwhygkTHig5yFQUVERHx8/efJkQRDARNCwpEHIBnCX1kLws1+/fsuXLz937hxJre6MK3Yctibc8x4K71F7IMCOMbZ8ODlMSUmhzyz2o8DAH4OfXgoKeHh4kC0/WxoPcwSAAMabazTog9mJDq+sVuvr169v3bp1/fp1hq8uimOuYOZipwM2zNpZ0wTBkto4jxEcNDvXyOVy1gMJvWJOA6Iam0U9I3FTb7TT6hCpVCpHjBgxbdo0IqwTEhKio6PT09NPnTp17dq1qqqq3NzcW7du4YHW1tbSc2eFTJIqEWm1Wt+8eUMp2QANDLvdTrlEYTY9D3cYApyA7jCoe0hFRqNRp9O9ePGCPjHHjh0jBxddqpNNCUldqpFdvDE2m83Pz08mk6nVaplM5u3t7bTBomN2nKbprEhaLNXr9exURO0ZP348BvOH2TQ5ORnxjmuqlJ4HOAIcAY4AR4AQEH0tYQpts9lKS0srKip++OGHuLi4giuSRgAAIABJREFUFStW+Pr6kg9cnCBEm7LhH4NVsWg/KasmNRUmaaSpXEgAXY712uHl5RUWFrZ69eoffvjh0qVLr1+/JpYZLhHpYDe40cC586QIsTKGY5jw4YGehADtCoeXzEuXLq1fv37MmDEYeyRLsE5gmhq3sGiTy+Vjx47duHFjVlaWzWZj94nDQEw0tBzBFCVo8U/HknkMR8ARAXaAOd41Go0RERG03QQekOgVYL/VMG1Rq9WOhfAYjgAhgPFGPz8agELKso0fzdKaBPQ6GI1GkSyEDzj2yqBVtKBIp1nACUkhc6U0XklJSYmJiVFRUZGN18yZM729vbVaLcQYzB1w1oHTF+mNAw1NP0VvHP2kVxJuoFpGQGPrGLHk7CRIFZEnE7VaTa1i3YzgoF22EOQlHyOBgYGRkZFTpkwJDw/funXr7t27Y2Ji0tLScnJyysvLCwsLy8vLHz9+7FTBBz3FuhS3NFiaStmaYcDzNhcBTkA3F7Femh6eN4xGY1VV1fDhwyFSYPuqTCZbv36942e305GiWYF/a1r8LCwNFoiSGo1GqVRqtVrSvdky/2q8KKbrAP7w4cPs7Oxz587dvHnzzp07t2/fvn79+rFjxxISEpY1XgkJCew0uWbNGm6LQc+RBzgCHAGOgGsE6uvrCwsL8/PzMzIyFixYEBAQ8Mknn2C3Ne25FjHL7CcXYVXjxe4wJbdIsAZilSXHMFug413ECIIQGBgYHBycmJiYnJxcVFRUX1/vKLfAtJm6DDbQarWyR/TQXVbGcAxTMh7oYQi8efPm4sWLS5cuHT58OBHNpC2r1WrSpSEkNzUmR44cuWXLlvLyctF51wRXTU2NO+PKMU3LYqheHuAIuECAHV2iZFAV6+rqBgwYgM++aPCz32qcCisIQmFhoagc/pMjQAhgvNFP1wFLg6Wpz6nrjG7epQVIUMlEKDerkaiLKGlHlZk2WolaBecVdrtdr9fn5eUVFhampaWlpKQkJyfv3Llz5syZPj4+ERERkydPJumLfePYMPtitoB9Zi2vsZJEYp5MJtNqteCaVSoVyXXIwtbLtgdhMkqgW2q1mr4kFEkzrEKhYHltQRDAVAQFBYWFhc2aNWvevHl79uzZtm1benr6lStXbt68efny5dLS0rq6OhG2/GcHI8AJ6A4GvHtXZ7PZkpKS6BNAXwqpVBocHFxfX4/PqMFgcHQV3b173ltbbzAYJk2ahCeOU4O3bNly/PjxS5cuHTx4cNOmTV999RWOhFIoFCEhIdgv4zibdjB+EAXOnj0LZ1g07dHQbSoQEREBeUJkedTB7efVcQQ4Am2CAL5FrMKMMKs8QA3o7n/r6+tFtpNweQE7IEdrIDjEZ41BSLOiA9Ch59jt9gcPHhQVFR0/fnzXrl2JiYnTp0+Hg2b6kOIbCzWGIt0MQCFBXpgnK5XKps4MJCUHGgi0LKg60HNw/tX06dMnT568du3a1NRUHPjuOAYQ0ybDjOaLtiqNl9PpCNTX179//95sNtPeqXfv3u3fv3/u3LmuVWh22NNwhWIMtnrChAnJycmVlZXu9LFtR6k7NfI0HIHmIsB+XTG3Xrx4USaTwTaTpbecvju//fZbc2vk6TkCIgTgPhEnEplMJnL7K0rWe36Ch6mvry8tLb169WpFRcWVK1d27doVHR2dlpa2ZcuWsLAwHx8fGBfLGy+avOCaTC6XQ/FHPJ2ZQZbONMHhvWa3l1FRojQUTwHkZX9S+KP+rNnvCRsmedKF+g8ZUiKRBAQEzJw5c/r06VFRUfHx8du3b9+7d++ZM2dEPqzZkUOuPwAyBptT+zw2FyRqR2ncZrOhHPyF22t2ANfU1IjK6QE/OQHdAx5iR3SBXrbMzEyFQgHqGZ8VvMMeHh5Dhgw5f/48WkMsXkc0jtfRngj07duXDiHEVh1F48XuoVapVLD6uXTpEjn6bM9GuSqbCJclS5Y0l4CePHkyhm5tbS0rUruqj9/jCHAEuh4Cjsatjm1k3/HuG3bsF/oOrxFwiYgZHGfBIz0rK9fU1Dx9+rSwsPDChQvp6enR0dGLFy8ODw/38fEhd4RkcoKPKmYB4p1JYWhZAEe3i2x2ENmnTx+NRiPy1CyVSkE3KxSKwMDAoKCg+Pj4pKSk/Pz8Gzdu4BuOB0q7X0UnCdPjdkSvZTEosGV5ea4uiIDZbMZ79OLFi3379vn4+MC5s8jNS1MDHq8JRikE5kmTJh09erS6upqUTHd6zceVOyjxNJ2LAH1OsYqJr+6GDRuw4vJRAnr79u2d235ee09CICsrKz09/ciRIz2pUy3oCyvjsaQn7f0CZU8lw4JBp9OVlZXl5ub+/vvvN27cyMzMjI2NhT+Q8PBwf3//uXPnBgYG9u3bV6VSabVazG5E+LJb1jBXkpSIOZFESpo6FQqFXC5HMhIvSeCkZE4DLOksIrKdpmcjlUolJmi4qmdvUVhUZv/+/b/44ouQkJCZM2du3LgxMTExOjo6IyOjpKSktLQ0Ly8P6x/4C2BNJpNOp6Ot1TiJijA3GAyUjCJZGz7KaLfbHU1MKEt3DHACujs+tc5pM4a+0Whct24d+3KCnYTJkiAIkZGRNTU1+NjB/a47REDndInX+jEEDAYDni+tYeLR02zBThJarfaXX36BLdjHCm7H+7RYMmjQIExmLpZAaSQjMHz4cCiHZNHG1b92fFS8aI5AeyIA8RpufGHwK/rbnpV3dNmw4KbvFU27IKBzc3NLSkoKCwvPnz//ww8/JCQkfPXVVyEhIaNGjerfvz991cnCxelpNo6aA06XEn1FW/ZTtI8ShWDe8fDwwEnrK1asiIuLO378eF5eXmlpKT71JKyzKhbQB+lMT4JlSShMd3mAI0AIGI3GR48eHT58eMKECTQUcRKGmwQ0ObucO3fuwYMHq6ur6ZXs9EV66iYPcATaBAH6nBIBbbfb37179/nnn4s8zLKEEb1Zs2bNapNm8EJ6LQJYL7TZbCtXriT73BMnTvRaQNBxS4NF5P6YAGHpaYSJ6yRW1G63GwwGxOv1epYANRqNiDebzb///ntlZWVhYWFOTs7Zs2fj4uJ2NF6xsbE4czEoKCgwMJAVIEXErqPQCO/SjvGiGPZ78tEyRXnxExw0iA6FQgGZFrXTLaRUKpVkJAFuQalUYsudIAienp6i8idOnOjj4xMQEBASEjJjxozo6Ojdu3dv27Zt9+7dV69eLS8vz8nJKS0thYjOYk7PjgIg0+jZ9YwAJ6B7xnPsiF6w2t3jx4+XLVvmdNVIoVBoNJodO3ZgywDReU6bSNqy07s8stMR+Ouvvzw8PMAyy2QyfGphAk8fYvabW1ZWBjrA8WPakX3BNKnRaJpLQM+ZMwfH44rM5Tqy8bwujgBHoPUIWK1WSHhVVVU3/+9VVlZWWlpa0ngVFxcXFRUxB8B01yA6e/jw4dTU1MTExBkzZsycObNv376QoUWSNGw5WX2APuPgC/DlJENjkr89PDxQVMtkfarFMTBmzJigoKCVK1fGxsYmJycfOnTo8uXLFRUVINbpg8wODHznTSYTdiwajUacf0gEn06ngxk4crEsCYXZAnmYI1BZWRkdHT1y5Eja50dUMr1EGPyuX4GlS5ceOXKkvr4espDNZiP13tJgYf3Uccw5At0dAfqcEgGNYV9RUeHp6flRC+ioqKjujgBvf+ciAKrhyZMnEC0gunw48qFzW9W5tdPaPOtpzdJgoZkIghMaaWmw6PV6lpVGPCUGGU1l4gWnVVWdTsdyRC46jk8EpO6CgoL8/Pzdu3enp6enpaXt2rVr+fLlgf+7Ro8eDR8+KpXKUWJEDDsXu56RHUtAsSqVijWkkEqlGo2GJn3cdcyLvR3UMKVSiSFHnAOJ0KK8Ti0t4ERbEITx48dHRkaKDlq8efNmQUFBYWEh+yxcINxdbnECurs8qc5vJ0kYaIrJZCotLV21ahV5iMcrBIdBMFz66quv7ty5wzZdxEtioxabgIe7FAIVFRX4eqrVajpVgL6noCrwxLG9tNPNn0E94DDi2NhYrGcKgqBWqwcOHDhy5EhfX9/IyMg1jdeCBQv8/PzGjBmjbLzGjBlz7949dvu2aMx3qUfDG8MR6M0IvHv37vTp0+Hh4Z9++inrpY6+TghgJnIUUtkY2D5AXpTL5U5pWVGxXeQnpGSJRAI5mPajsEIw0oA7YwVrtptSqRTHAMpkMkjSMPZEGmDIevcjVMliGjFNweLPXDExMenp6adOnbp27VpRUdHVq1dtNpvTI/4wvOkjTJqPYzw+2o6f7qbimyqzN79QvaHvOKcE50yS5ozAiRMnNm7cOGrUKDh7Yb8PFIZhHasSk9GTh4cHbC/mzp179epVHBUlGrGEMA0/iuEBjkAPQIAGNo18vV5//vx5QRDw1rjYPSBSFXsAGrwLHYyAyWTKzc2FL2OwgWFhYR3chi5bHftusmFWRmLDTaUhgwCnNgHt132z2VxQUHDjxg2YjJw4cWLXrl1JSUkpKSlxcXHff//9mjVrgoKCfH19p0yZgn1LUqlUoVAQRyzSCETCKkRfHJnYlDTLHi9M2UGDkJBAq9RkoofSVCpVU+eaUFHUwqYaACpDEAQPD4+AgABYl+Pv5s2b4+Li0tLS9u3bV1RUdOHChYKCgrdv375//x4PxWQy0Y5AGGpAEDKbzUajEXbuRHDTB5zcGNBJGFhKZ/1T00OnFQi2InZJQ2SQyglogo4HPoIA+z2ipCaT6dGjR3FxcYMGDcLLA3cHgiBotVps4/Xz8zt8+PDbt29hoIS8GN90oisVyANdDYFx48apVCr2gyiVSn18fObNm7dt27b9+/fn5+e/fPnSZrNhI0lXaL/ZbIZZnKXBUlFR8fjxY3KEajKZ2I8gPqPGxgsfTZpWnQ74rtA73gaOAEfgg/QpkttEP0n+E8WzP+HATiKRkNLCfujYlF05zPLOFBY1WKvVEgWAWyqVCo6z5HI5e0uj0QAQ8niL9CgZdLb0/7P3JmAyXuva8FtVqfH0wOlubOPWhk23nLTwEe3QOKYc444pX0xHJPmS4A+Sg+hDtGPKjyR/CJdgfwQhoo9xo/lMvdt00GwhLlM+RG/j7tZVqbned/2qbp6svFVdqida96rL1da73jXe7xqeda9nPUurTU1N7dixY/v27Xv06DF06NBJkyZ9+umn06dPX7Zs2YEDBy5duhRhE4V4isE2ZJSixmHeP5KFEx+ed4fMVHhWPgRgigefnjGGhfTZs2cXL1784osvwqqYiiCjVWXIYQGeGo2madOm77333o4dOyhZftEVjCQ1v+BXwkcg8PwiQA2b+AtcujVo0CDoJxkMBlWfosfmzZvfvHnz+a27KHlFQCA7O5skH51O17lz54pQKlGG0iMgyzKt3HGEiLcHIssytLmh3+10OnF7cEFBwd27d7O5Xzr34wlcUkOhI4C8igY1KkjLIeUBChP+LQUrmYNf19DJEp1OBzvaqjLrdDrw7wkJCampqZ06dRo4cOAHH3wwc+ZM/qLF7du3Hz169Oeff6bTWjSAE0dH5DL/KUFqk/gNLhvCj9vtxtb+qVOnsrKyfvrpJz4i3IKADsZE+IRGgJct4MbeiCzLLpfLarXOmjWrevXqvEoU+iE6gMViGThw4J/+9KcHDx6gcRcUFNB+S+gshe+zRsBut+fm5qampsbHx/fv33/mzJk4E61aX2Et96wL+2v+pE+HloZRFVt8NLBSaBpYUYvgdh4cheIKh0BAIPD0EVAUpVu3biqGNFieA5EKXRhcmqf6i1P2SKdcpcbgspWJj8ViAS9MhUdl+cRpFoZyN70iO/4IUL9+/fbt23fp0qV79+4dOnSYNWvWxx9/DHN169aty8rKys7OPnjwYE5ODsZDSP+kRoqNPYfDQcNpUa0CBzBpmCVzGWHC84EpGHnSoW/IwZH482EoQeGo9AiQYs727dvHjh370ksv8Xr9uFeZGLFgB/oOBFqTyVS/fv2MjIwTJ04ANxKKhMBQ6RuSqGBIBDCuBr8qLCwkY1DB3Qo+BoPhrbfeggW84BSEj0AgEgRu375NEo7BYBg5cmQksUSYio8AyCKHw2G1WsF7wmYITl37vD7o81JF+Hv/yBOBcfIeUXBbIG+ihDHGm+Gbxf2GDBnSvXv3jh07duvWrXbt2lg+4Jg1HTqk5geD0bxkDr6YApTYAVpZtZkXHR1NyxmQ6ZQ+8sUwS56Ijkez2UyK2xBvoqKiUlNTe/Xq9corr/Tp02fatGmfffbZ3r17wSYXFBTYbDaI+iFlaSj2FRQU9O3bF8srk8mUn5/PfwjGmCCgVYCIxyIR4NsZ70YEXPdkt9vXrVvXokULNGvcYq/RaHhWWqvVtmvXbsSIEXv27KH9liJzFS8qPAL8PmRFKCw4EdXeBrSf6PQQY4xXhSa5mW/YvLsi1EuUQSAgECAEtm/fzl8JQnIVOXQ6Xdu2bXv16tW6det2Rfw6dOgQHx9PUZ47ByZWi8WSmpoKo89vvvkmjiXOfPxLT09fuHDh9u3bDx8+vGvXruPHj//888/QJQF1iwGTRHCM58E8ckj7gKCPIcoTGU3fKLwD4cHWkW5LcJSixmHen1QwVOdXivLn4wbnKHwqKwKrVq0aMGAAlDFpZajq9UURZGR5o02bNrNmzTp//jz0ndGAoe8jqOfK2nJEvSJBAONqcEiXy7VhwwacuSmqfz3shjNmzAiOK3wEApEj4HK5Vq5cGRMTo9PpunTpcv369cjjipAVHwGr1coYwwVjKC0/5zqdTtoGxltIgKp68VHoFakvkINekYNPHBJyfn5+VlbWfu63Z8+e+fPnT548ed68eenp6b179+7atWvHjh27dOnSpEkTXn9ZJXhE+EgpqGyFhYwOmyEURaUfHTIKDoGR8VKYMYB6NYXndVnac7+0tLRx48bNnDlz/PjxU6dOxZ1hsOb38Bh9RkaGys6SIKCpaQlHaRGwWq1k4jkvL2/ZsmWJiYmYCdBwVZKHwWCIi4sbPnz4vHnzbty4AcaQv+vT7XYXFhZiz+rChQtLly4dMmRI3759T548WdqyivhVEgGedwg5CVVJVESlBQLPHwJOp/Py5ctHjx796aefaA/M4XDk5eXl5ubu379/48aNn3322ccffzx16tShQ4f26NGjbdu2HTt25G1G8wYr+ONs/J0kJHXxDpXwp9PpoqKiiqK0JEmCYWU+BZUbk6NOp2vVqlXPnj3btGnTpUuXwYMHT5w4cfbs2QsWLPj4448/++yz/fv3nzp1au/evZDkiGClka30HxJJFSudMsy9WPlSYCpACRyUiHA8dwhgEi/K/BeWi/fu3duwYUOXLl1UPY5/JFPO4KZhhUar1cIuJNZvLVu2nDdv3p07d3iUSPueb3h8AOEWCAgE0BMfnqfBjikmSt7ukyRJAwcOpAMKAjGBgEBAIPCUEeAn8XLlB2ARNCsrKycnJzs7e8uWLYsXL87IyHhI2i5cuHDKlCmvvvpqWlpa9+7du3Tpwus1gx3Gsa2Qy41gT1Jt5gUeLEl4Yhpvq1WrBq6Z0uG1p8m+Lm+pjE9WRfHRI4Z96Fnv2bMH04HT6RQE9FNu4ZU/O/RhxpjNZvN5fXv37h09ejQdVaAWybdadIOoqKguXbp88sknS5cuxX7S0qVLZ82alZKSggMFSESr1darV6/y4yhqWA4IPLUJphzKLpIUCAgEHiGgkg5Xr15dr149XmaCdWN+lgG1BOJY5Q+miQho1duQjzCFTK8g5FWvXh0+0BpAXikpKd26dWvVqlVaWtrgwYOnTJny+eefH+B+RCLz6hV0gAMMF3ZhcfAQh5QdDofL5eKjlFXjoBk88gRpXI08StmGpAKUwFG2JRGpPSsEVOzVvXv3li1bhhOg1E/DO8CIqW40bdWq1bJly4JPjxL1TApT1PaeFQIiX4FAhUXA5XLdvn0bq7lgTqROnTq5ubkVtvCiYAIBgUClR4BmcDjKu76qVQyOZVOmLpeLP1Po8/rsdvuDBw/27t27f//+AwcO7Nu37xPuN3To0C5dujRs2NBkMsEQH4g1frAlOyFEPauMdfAWychuAe48JNkJ2/NE5UXiQFwsmj788EM6+ygIaPrcwlGWCPA9hzF27969/fv3d+rUiW+s1KDDOLRarSnw41XVJEm027L8WFUnrac8wVQdYEVNBQJPBwGyGkF3N+fm5mJDHjwy0dDwDMk404zDB+Z39VVH1Wja6t69e8uWLbt27Yorp6c+/s2cOXP//v2HDh3au3fvkSNHYIO+sLDQarV6PB7IjvzgUxRWuJwab3H7B4RU7OaChqZjRkUlUkr/pyN8l7KQqug8tsV1q5ISj88RArSEwwUPjLG8vLx169b16NGD+jj1a95H5YbdQ2xBYW02ZMiQuXPn3r17Fydt6YwFGZEkO5KCgH6OGowo6rNCABP3yZMno6Oj9Xp9rVq1du/enZOTs2vXrkOHDl29elVRFJvNVh5bqs+qyiJfgYBA4DlCQCU6lmvJQZGR9gms2KkUTcggvtvtJlEnklJhMx7Xs509e/bYsWOHDx8+evToNO7XuXPn1NTUVq1atWjRwmQymc1mEMQ8N60Sk+iRFkQROihxrVY7Z84cqoIg8ggK4SgtAoqi3L59++jRo1u3bp09e/bMmTOHDx/euXNn3BaFnRa+vULfBLdC4S1YZlIugwNRqOmbTKZRo0aVtqwifpVE4GlOMFUSYFFpgUC5I4AT9y6XCzLZggULMDsES04mkynYEzcTkC5AzZo1W7Vq1b1798dksv//jIyMr776asuWLTk5OS7uR3XDJRs0nsiyjFN1CMDzyPAhAktRFNJuptTIQRu3vLgJN6/gCVKbYpWtA5Uq2zTLOzX6ECVwlHfZRPolQIBv/2Gio9M5nc4TJ05kZGS0bNmSLibFHhI4ZVxGqjryTyIl7+jZs+fq1avz8/NpCYeeTrwzrpHg/woCOswHEq8EAowxTH92ux39GvcNWK1WfrhGGOwrC9AEAsVFAE0rwomjuImL8FUBAX44KteGZLVacSsVYwyma7HxRttvHo8HywQV9Ux3LdIBLJTZ5/W53e7gi1vIh1Km74iIeMS6w+Px3Lp169ChQ2fOnNm/f//ixYunTJkyf/78adOmDR48uF27dq+++mpqamp8fDzP40Xihha2Vqvt2LFjXl4eXTwuCGj6HFXXEdzTwqyQoffBGDt//vyOHTvS09NHjBjx8ssvN23aNDY2VmWthpfseTffZGmFwHuqFNMobo8ePVasWMFboK+6n03UXCAgEBAIVD0EIDmR7sBDc08ffvhhTEwMzs6bzeb27dt369atR48e77///ieffDJt2rQFCxZs2rTp1KlTp0+fPnPmDKQxYnsBoSpZSj8SgglxeZHuiZ+FojwxpAggEKhqCOBSa1o10f4NcIDIarfbN2/e/NZbb8XFxeHoqOrgAuRGuoxeo9FAp0Gv12NfCjJn48aNp0+fjjuxqVcGS8X8K9XgQI/FGgGq2jcV9a3KCFD3oc6CPR6VP537If+qDJqoe+QIkEopohw6dOj48eORRxchBQJPHwGMcjQk0qCncvAFU70K88jHKls3jAH6vL7s7OzNmzfXq1cPOs5g8yCGgcTT6/VGozE6OtpisXzxxRc2mw2cOEQ7QUCX7Xd5LlOjTZJgmZsx5nQ6CwsLHQ7HDz/8sGrVqvT09A4dOqCdQb7X6XQPL7gkyhgyPVHGIR0811wsAtpisYwdO/a5RFkUWiAgEBAICARKjQBELhLagk2nwcfhcFBWOKEPoQf2MfhYpE1AaQY7eDmPkiVH+LcUjHdQFN5TuAUCAgEgoJJL0SXxasOGDRMmTCB1B7LhHlLapBN1OGBH9wrWrVt3zJgxp0+f5uVePhfVh6AOG2a4QBhVRPEoEBAIUPfh51byVPUp3l9AJxCIBAHSKjhw4ECDBg0wFyxcuDCSuCKMQOCZIICBjoZEftzj3XzZeP/wbj5W2bohMoGArlatmsViiY6OJvaZ6EEoPlsslnbt2p07dw5bRLy4JQjosv0uz2tqpPDPGEMrOXny5ObNm+fOnduvX79mzZoZjUa9Xk+GmOn8Mh1wpsan0+mIjA65HiCTfKChi0VAI8ETJ048r0CLcgsEBAICAYFAKRCA1EVCW3BKvIjDB+ZDKoricDjCC3BFveXTgZsPGfw2pA9FCflWeAoEBAIwfIEj/Ddv3lyzZk3//v2rV6+OK0Y1Gg3k0qLkTPLXaDSQXbVabWJi4qRJk86fPw8Di/xYER5w6rBPdIRPR7wVCFRBBKjX0MQdUgMabylw5N2zCkIqqhyMgCzL/fv3h96lVquNj48PDiN8BAIVBAF+oAvj5ksbJpjqFR+rbN0Oh+P27dtjx46FiAXhymKxEA0IJWij0ZiQkDBv3jxsDgXfXiMI6LL9Ls9larAyc/HixVWrVo0aNapz5860gwGyGDcBEvus1+vNZjPu2cTlLZIkwdomiOnyI6Bxo1RmZuZzCbQotEBAICAQEAiUDgGIWbSOJUsapPKcn58PWcfpdEL0ocB4xMkemKRUCW2RPAYXn48V/DakD0UJ+VZ4CgQEAoyxS5cuLV68uH379iqp0mg0kkRKRHMYR9OmTceOHXvkyBFQWir1apvN5nK5aHAIiTx12Cc6QkYXngKBqowA9Rp+LiZPoQFdldtGGdZdlmVsN5KRpTJMXCQlEChbBPgBMIybzzRMMNUrPlbZujdu3Fi/fn2IW3TCjC5yI/6wc+fOt27dQta0TONLIghoHo1K7sYcT1vKLpfr5s2bmZmZQ4YMSU5ORmNSSfloUkWJ9WRKL/iCwaKiSJJE7RUO5Mgb5aC4JpMJGi4IiYOWb7/9dhgT1ZX8E4rqlQUCMNjPGHM4HE6nM+TIWBb5iDQEAgKBckGAl7RKozPFpxPeXS7VEIkKBKokAk6nE+KozWajfoeODDxOnjza7Wp6AAAgAElEQVT59ttv41LBYKGURESc8YSeBP6CdyDrHM2aNVu2bFlubm7ZwkxlVjnKNheRmkCg8iGg6jJPfKx8CIgalQcCmFMURaHZQZIki8VSHnmJNAUCZYgAjYFlmGaZJIXr1mi3njH20B7vpEmTiK8jg2Z8p4P687Rp03DZIFGOwUUSBHQwJpXWhxTgZVnesmVL7969SXCn1kPbhmazWZIkKDuDCMajJElGo7F79+5du3btFPilBn5paWmdOnVKe/zrWPSvZ8+er7zySp8+fT755JMZM2ZMmTJl1KhR1KCLWmzEx8dPmTKlsLCQrlSutN9JVKwcEMByFzec8CoYyCq86lM5FEckKRAQCJQcAZLYSHOK9ylWunzEMO5ipSkCCwQEAuERUC1LcLv1d999N2HChMaNG5N2M07a0SNJqsEOKChAgOzZs+e8efOuXbvGlwG9m/cpsbuogaLECYqIAoEqgkBRfaco/yoCi6hmKRGw2WzQJapbt64kSaAyYmJiSpmsiC4QKG8EaOgr74xKlj6KxxjbvXt38+bNQRuqLOhCHouOjtbr9bVq1Tpw4ADlFUZhVBDQhFKVcFy/fn3evHmk7xwsxGPghhBvMpkaNWo0ZsyY7du3Z2dnZ2VlkYVogIWNEU/gp4KPepTKAaYPKqhut/vatWtDhgwxGo0hCWiDwaDVatu3b79gwQJZlnHC2uVy8RsyqnzFo0CgKASIq/J5fbdu3crOzi4I/IiPLiqi8BcICAQqFAL8tFIaDegKVSlRGIFAVUMAamtZWVlvvPFGjRo1giVSHLODTk3wW7r+Ggx1SkrKokWLCgoKVKo3iqLQ3jOGjqqGs6ivQKCCIMDP3ZG4K0ixRTEqOAIejwcE9FdffYWZwmQyrVixooIXWxRPIFCREXC5XG63u7CwcMyYMSSAEV9HPlAUMBqNH374odVqjVDKEgR0Rf70ZVy20aNHY28Q2s0hzWtotVqz2dy7d+/Vq1ffuXOH+GKXy0UXwqBYPq8PRHCETY0qA82Xo0eP9u/fHyclqTXDAbvSer3+5Zdf3rZtm6IorsAPKdjtdkFAE5jCER4B3ryGx+PZsWPHa398LSoqyhL4aTSatm3bHj16VHDQ4WEUbwUCzxYBlb4kv3AVBPSz/TQid4FACRBQFGXnzp3Dhw+H5jKuD4FyjdlsjouLgyVBUM9FHYzD7SOvvvrqsmXLbt68CV0bt9sNutnj8TidTqgsCAK6BN9IRBEIlDkC/NwdibvMCyASrKwI0HLvp59+OnTo0MWLFytrTUW9BAJPDYFDhw41atRIkqSoqCiYQCDKjghoGEvYs2cP7tcBBw15LMz5ckFAP7WP+Mwyys/Pz8jIiIuLo0aj0+lgO88Y+KENabXa1q1br169+tatWzDWQayc6rbiEtQE9xwyxux2+/Lly9u1a2cwGLCogJozb/rDaDT27t376tWrRWUUpkEXFUX4VxoEHA4HyRmKolitVqfTifEuuI7YOPF5ffwOHkyKY/MDzW/lypWq/ZXgpITPExFQFMVut4vu+USgRICQCCiKQpuL5FYU5cGDByoCmo/OL2J5f+EWCAgEngkCfC9GAdxuN6TKW7durf92/bBhwxo1agRNCJJLw7DMtM7hrcZ179591apVBQUFGBxCjgPwJFEWj88EE5GpQEAgIBAQCJQfAmLpUX7YipSrJgLjx4+H9V2VnAY9UbKNNnHiRBjILRZKgoAuFlzPTWCf14dLvTdv3pyYmKjT6SwWi6oB4T5Ag8Gg0+nGjx9/+fJlVfVIai8NAU3EwY0bNz744INq1aoFLzPoJpmHFmRmz54Ny30ej0dMJ6ovUsUfZVlGq6Bl5JIlS0aMGDFz5swwZoZsNpssy6NHj6arMmkrD9clQ4vqxo0bVRzeUlYfFk5w9ln03FKCWdWik4l2n9dHdBLNO+HRCEk8hY8i3goEBALlhADsXVDi6M45OTkffPDByy+/TAYEeSqZRFOeaIZSAnxMJhM9jhgxYs2aNbgeB1vR/FE8kg1QADySKKt6S4UUDoGAQEAgIBB4rhEgiVHIhM/1dxSFf7YIQKDKycnhb+PghTSNRkPyWMOGDXft2gXF5+IWWxDQxUXsuQnvcrkGDhzIC/R0mBEUsF6vj42NnTRpUkFBgd1uR8WgUgo3Se2qYT1yCFwul9VqXbJkSWpqKg5aGgwGGPXjCyZJUuPGjZcuXcqnTMw17yncAgGsOS9fvpyammo0GmNjYyVJatWqVUhb5IBr9uzZ2OQwGAwmk6levXp9+/aFNX1qh3PnzhXYlgwBVVeF7qrgoEsGpoilIomeqFYvFhuizQgEKiACHo/nwoULkydPbtKkCeZZvV5P+gd06E0ll9KMDL0bHFTSarVdu3ZdvXr1zz//TDX1eDyYeiAShBwH4FliCZbyEg6BgEBAICAQqMgI8FMAuStygUXZBAIVEAGbzTZnzhyIXhDDSG8ANDSENJPJ9P7779tsNtg2KEFFBAFdAtAqYhSeA7LZbKdOnUpKSsIJR/4WF9rEqFu37syZMyHB03lJcEZQRnM4HKUhoH1e3+7du4cMGRIfH6/T6VASKO1rNBq9Xk+Nu2fPnlu3bnU4HC6XS1EUm812//59t9tNnHhFhFuU6Vkj0LJlS6jw63Q6rGlzc3NDFurkyZO0+tXpdGPHjqWmhR0arIR79uwpONOQAEbiSbsCq1atunPnjuCgIwGtlGFIwuYH/1Km+ayiP3jw4Pz585s3b160aNGUKVOGDx/etm3bunXrtm/f/sKFC+HN41QmHJ4V/iJfgUAZInDq1KkPP/wQvDOmV5L3iF8m6ZSEUuKmEQZRWrVqNWvWrJs3b+bn52OWQTlpsqZLQUKOA/AUBHQZflyRlECgrBCoBKJLWUEh0ik9AvwUQO7SJytSEAhUHQROnz6dmppKcpokSTqdDpYSSFQzm81RUVHr1q0jWEgeI59IHIKAjgSl5yCMLMuQzn1e3969e2vVqkXGWdCSLBaLJEkQ+ocMGVJUlWjUDu9AdN7uAe578Xl9hw8ffu+996KiomBpF7nD1gG0UFGGh7r9M2fOvHz5MhTciiqP8BcIBCNw48YNtCu9Xo9dDaPReO/ePcYYjD5TFJ/X9/rrrxuNxpiYmNjY2I4dO8JGhNPp9Hg8WVlZ2AvR6XSpqamqMVSWZVxnhNQURTlw4MCQIUNq1649duxYWLSkjIQjKysrOjoadk6WLFnicrl4vkDgQwjQ/gd8fF4fmpnP6+MNUNAIjMNNqvZms9koAJ15RwN2uVwnTpzIzMxcvnz5okWLFi5cOHfu3IyMjCncb82aNZcvX8YGJJ8OFbKcHB6PBxvmQ4cOjYuLax34xcXF6QM/g8FgNBqhJkmyzssvvxyegC6noopkBQICAUIAowSUEnABtcvlwlBGLNLmzZtHjx6N6wTpCkFScOaXNEW5zWYzbihp2bLl0qVLT506hQIg3+CRikqFIYICULHD+PNhhFsgIBAoPwQcDgfpOSEXj8dDNwOVX74i5SqFALWx1atXDxs2rH379ocOHSIEHA4HuYVDICAQIMYDtImiKDNmzID8FizFabVacHcWi+W1P74GG2ilVFQVBHQlaYTE9Wzbti0hIQHyPbg57GBgPZCcnHzy5MkwdSYJvigHmG5olBBdcu3atQ0bNrz++uu4K9NsNsPUhkqlRaPRVK9e/bU/vnbkyBHwU4qiqIiVMGUTrwQCoI8fPHgAI0SgqyRJ6tChA1oshFpqvT/++CP6QnR0tMFgOHHihM1mo85SWFiIjRlJkkaOHBkMr9PpVBQFGy0zZsxAUgaD4aWXXhLSDA+Xz+t77Y+v0e2OOp0uMzNTQMRDxLux+iIfNFd6hK1zmJTBXwSAeE2tlz+hwhjD2wcPHjRo0AAfAmyOahAm6sdoNG7atOmZEDQff/wxFSOkg9hng8EQFRV19OhREpUIJeEQCAgEniECPO88YsSI2NhYQ+AXvHRBd+Z7Oq8egT1gs9lssVjefPPNpUuXXr9+ne/vNNDRtE5Z8z68m4elKH8+jHALBAQCAgGBwPOLAI7CKIqye/du2FqUJCk2NhaaSSQhP78VFCUXCJQhAqSuhDTPnDmTmprKs886nY5XI4DMFhcXt23bNtrpcbvdJJ6V4JyZIKDL8IM+46QURdmxYwfIXxAQOPwIDRSLxTJ58uSrV6+GLyUvrId0q6K///77zZo1w9JCdcqSTG2AB2/evPmqVauuX7+OFEBO2e12fqWhSlw8CgRUCKBNejye1NRUk8mEtWtsbOzatWsRUtVo09PTjUYjFsD9+vVDGOzdwV23bl203pUrV6ryslqt2CCRZblv377Y/YMu/5YtW6xWq0qVVRW9Sj26XK5t27Zh9gKeMTExwfeaVilMIqksHSK5ffv24cOHN27cOGvWrPfee+8N7jdhwoQZM2bs2rULWs+QpDFy0tyPbTyPxzNx4kSe6IEbjZaXLTAptGrV6ukT0GfOnMFMQR0TRqKokKQyqdFo0Ony8vIiAVOEEQgIBMobAUVRHA5HQUHBihUrXn311ZiYGH6LC1d9qJYuwQQ0neuUJKl69eqDBg3auXMnDYZUBdqK83l9IZc3qumeHimFpz++8VkLt0BAIAAEcKBQdUJRgCMQKFsEnE7ngAEDIPdCzjxz5kzZZiFSEwhUJgQURVm2bFlsbKzRaITSEi0VeQJakqTX/vhafn4+jPS63W6r1epyuWgRGlJCCw+UIKDD4/M8vb148SJaT3x8PA7CS5KERb7FYtmwYQNjDKe8SXM5uHokwYdxINbevXvbtWuHgV6r1RqNRoPBQNwBTQBRUVHvvPPO2bNnKS9snoB3FurPBItwRIIAVJ88Hs+nn36KNhYbG9u8eXOr1UrRMQ7ib4MGDSRJMplMMTExa9aswUlAJALbLy+99BL2aYoyIW21Wvv06QMb/FCXnjFjBmmhUqbCoSjKunXr9Ho9abf179+fYCGdNfKpsg5A8eDBg717937yySe9e/euVasWbFAQcYNz6PCksTQuLm748OHUUPmJn4b0QYMGgdyBvSPE1ev1YHLxiL9arbZ3797Q8afRvrw/iqIo27dvp2JAZRKPBoOhZs2ajRs3rlevHuYRNKQ2bdowxoLJqfIuqkhfICAQUCFw79699d+u79GjByk3QMuMRE0MPjSOYQETTEBDQ+Lll1+eOXMmn4XH44GM6nr8wxEQQUDzKAm3QOD5QiA3N/fYsWOHDh3at2/f/v37z5w5c//+/eerCqK0FRwBRVGwvdGtWzeacbRa7b59+yp4yUXxBALPCoGLFy8mJyebzebq1atjIUbss0qKW7p0KaxB4hg61O8gmNFSlBaSEa73BQH9rL57Geebl5eXnJwMY+G0vIcjJSXl+PHjZZtfnz59sAKhJmuxWMAagPgwmUy9e/fetm2biqorbgMt22I/zdRwNuFp5lgV8qJx7fr167C/0bp1659//pmvO/Y2ZFnOycnRaDRRUVFmszk+Pl7V9mDIslq1apIkwc4sDa/YI3E6nQUFBW3atME9sHq93mAwTJ48mc8rQjcVmxxWq5WOsZAnRvYI0yynYGRjp6Cg4MqVK5HnAlslq1evBhmBkSEjIwMjQAl2RyPP+nkJqSjK8ePH09PTO3bsCHzIOD5sFqGN4cgIsc96vZ4MxVgsFo1GM3z4cDQVNCEaY91u9/Lly3kyCPsBCQkJpt/+mjZt+sEHH2D/T9UvigKT9njIKA0ZgS0qSrA/jhSsWbOmdevWkiQ1btx4+PDhc+fOPXz48I0bNyj8+++/T5cvr1mzhnoKBRAOgYBAoGwRoD0evrtBw+X+/fuLFi3q168frxFDblrtY0yjrS/yhwN7YNWqVRs+fPjatWvv3r0bpvw0KIGPxgoHnmFiiVcCAYFAmSCAvgZpMNhimMfjwekEaDXxgqvVaj1y5MiKFSsmTZo0ePDg5s2bm0wmuiqcdscNBsMPP/xAzAXkQ1xKwWtKud1up9MJw3rYnaKRgcRmaORRrSFjCFVrAqRKOXBc1Wg0ksxMRkdpgqtSgIjKCgQIAZXG5xdffBEXF2c0GkmWI+0xsmeg1Wo7dux46dIlfqwuyh08OFPWIR2CgA4Jy/Ph6XK5aA5+4403iHeAdolGozEYDE2aNLl06RLufSqrWtEVcDwHDcEiISFh+PDhX3/9dWFhISwYUKaQEngeil5VModKXKtktas41dm4ceOBAwfQovhSkc9XX32FowBms/mNN97gB0foVcmyjAF39erVlAItv/Py8jp06IBFNfrUuHHjePMdFCW8A8K6y+VCXFmWb968uXfv3pUrV2ZmZp47dw5CNhJ5hnIziEWXy+XxeGbOnInDE3v27AlfO7wlDtRqtc6fPx8K4ziaTSfgePwjSbOShdmyZUunTp0wStOdwmhdwX9JerZYLDSeo63ijr7u3btDLxjXaQIrj8dz4sQJgA8BYsSIETabLVjy9nl9aI2qewgjwRwd5Ny5c1u3bl3/7fpt27adPXvWarW63e7iWv2m+QttA7nLsty4cWOLxaLT6aKiosRtlpF8FBFGIFAaBFQkDpI6ffr0F1980bZtW0h3mEz5tQrcRDTz4xitZBBLp9P16tVr5cqV+fn5NpstzDTHTxMkNAoCujQfV8QVCBQLAXC+MPZFc3TIFG7evLlv377p06enp6d36NAhKioKg4DRaDSZTDgXy7PPeIsDXkuWLOE7O0QRn9enMm1Hp7vOnz//8CIW+mVlZUHkgMgabMuxbJe9IasvPCsaAi6XKz09nWaiGjVq3LlzB4WklV1FK7Moj0DgKSNw9+7dl156iSwl8EJdTEwM/A0GQ0JCwuLFi7HSLIp05v358TySGgkCOhKUKmgYt9sN3mfLli3QBqVdC1DDL730kjvwK9sKFBYWtmrVKioqChZ4JUlKSkqaMGHCpk2b3G43lhY+rw9iAbImRf3iNtCyLblIrTIhIMuyzWYLKVWgXwwcOJC0R5ctW0Z1x7IWWhVvv/32+++/zxhzuVwFBQUejweE17Vr11q0aAEuT5Iks9k8atQoqGBQOsVyWK3WCxcufPTRR61btyYmEQM9lMJwa59K+C5WFqUM7HA43G73unXrkpOTsZCIiYkB0fnElCH9OxwOnIMbOXIkiYCtWrVSFAWrCOr+T0ywkgX4+uuvSTGQGBkQ9KBvtFptnz59xo0bt3z58r17954+ffpK4Hf69GlY6ujZsyfUpYnZGTRoEK8HDZBlWW7YsCHMzkiS9O6771IHwaYLtkNgGhUgR7IpSFd3ZmZmvv7669WrV8fgjypERUXVq1dv3Lhx2CeP/NvhFIKqW61duxbzl16vJ7vtkacpQgoEBAIlRsDj8Vy7di09Pb1u3bp07QFsu2Hg4tcqIQlofqAzm819+vTJzMwsLCwEn0VblSplHJoanugocdVERIGAQCAIAZkx+hd4KStel9vlcHqcLgTGau7mzZs5OTlLliyZPHnyq6/2evllvxxLnZ3U6IiAhiPk7hQOd3fp0kVVGCKRZR/z/wv8EMblcrVr144/Ho7hSJI0aR07jxv3waZN/0XaIVDcRmUCtVPlIx4rJwK0WZKRkZGamtqvX7/Tp09To6qcdRa1EggUBwG3271p06aEhARaoeOYLMl1dPa0a9eueXl5siyD03uiYKYKEEmhBAEdCUoVOszdu3ebNm2KRoN1OxgKnU5HJ+jD6JuUoG5ut7uwsPDrr7+eMmXKsmXLcLEhaDsiOyhZn9cHohzCBN9GKUwlcwCECxcuiLuzyvXLkrRBa1rKDiqfTZo0wZaM2WwO1oZAg4RsHay5+corr0iSBMMykiQNGTLEZrNxci1lFZHj+PHjw4cPlyQJu4vQaYUADQoPc0BqauqmTZsiSrEcAp04cWLQoEGYh2hdodVqI8zK4XD4vL6CggLG2J07dxo2bBgVFaXT6YxG4/z58/mOTx8uwpQrQbCMjAxqijTxS5LUpk2bCRMmHD58OLiO/OoLQ8quXbuwax39+Efm7UArA9hhw4bh+IvRaExNTcVGS3D6vA99Hd5T5V6yZEmrVq2wdETXgAXnqKgo2AyBeZCRI0eeO3dOFZd/xB4PjtmGbAnvvPMO5ZKRkQGuvGynML48wi0QEAgwxnJyciZOnNi0aVNMUvwwxU8HtFAhh4pjio6OrlOnzrBhw77//nsClo7XEB1w584dGnaK5aA0hUMgIBAoNQK/ZZ/9ZLTXv1fkcvx05dKWLVtmzZrVrdu/1KpVKzAgaDUanVb7gslkMehNmPf5VScOeJnNZoi1/Ek4fjzB/E76UpKkkSSN2fwPgejm1q3bdOrUJfCvU6dOndLS0vz/BU6PwS4Zbi3mEtT5178vmCVJixy7deu2e/dONbFeaqREAhUfAYiUtN9J003FL7kooUCgvBG4detWp06dMGJj/AQXQbIc7OhWq1Zt4cKFzsAPa8/CwsJiCWkhV3bBtRMEdDAmz42Px+NxOp1Lly7lZmK/E9qLly5dqjg1UbXdilOw8iiJ2+3OysoCpbh48WJSCYcGEHi68shXpEkIuFyu69evU78gE88UQOWg9glV6MmTJ9OhY4PB0LdvX1X4SB5B/N2+fXvixIlRUVFarZbGfVrPExNNBn9NJtOwYcNwaiyYWI8k30jCEOGO2SU/P3/atGmoMkYPnU5nNpu1Wm3jxo0jSZDCeDweKHFv2bIF+Ot0upo1a6omMApfRRz79u3j9zOw93D58mVqeBFO2KdPn46OjqaGDWPQIHNJkXnevHlYB0qS1LFjR5xKiZDAhbyuKIrNZiMVxSNHjqSlpRkMBqPRiObBrwBNJhO1Z+T78ODtnDlziiv6EwKpqalYvhoMhvXfrqd7lqtIUxHVFAiUOQIw2Ip7dylxp9N5//79HTt2jBgxonbt2uCRVWwyDTVgdrBQocP1pCyDYNWrVx8+fPg333xz7949SDuUV0gHRr+Qr4SnQEAgUBoESHONDCsjNafT+egubp/MZIWycLv9vPO582f+/d/fTuv0T/9g0RgNWt0LGo2f1KWfTpIMgX8vSJKWHzHgVhEZFIDiw+EPppN+m7JWkl4IpGyi9FWxQj5qNDqNpH8c0R9XpzOYLUZJkpavWJr3t58Ze3Q3HWR7qq9wVGIEym/pVIlBE1WrTAgUFBRgCUa3kS1evLioAZkfWlNTU69cuRLcg/i1alHu4gIoCOjiIlaBwsuyXFhYmJiYyLceuL/44guynFVBSsw32QpSpHIqhs/ry8zMxIcwm80DBgy4efOm0+nEGXlYIymnrEWyQMDtdu/duxefQKPRvPHGG+GRocbp8Xhu3LhBFnglSWrYsOHt27fDRy/q7eLFi2vWrIliwBAeb0WBWDbog5BpBUmS4uPjjx07xttJKCqLkvkTOagoyqefflqjRg2ctuaZxOjoaI1Gs2bNmuJmYbfbnU6nz+vr0qUL+EpJkiZOnMibGy5umpUg/Lx58zQaDWn9xMbGYkygthdJHR0Ox/jx49FUDAZDUlISRSfHkiVLQARrtdpOnTqRmYtI0uebHMarsWPH4tyrRqOh5mE2m2NjYy0WS3R0NH1itPO4uDjsog8ePJg45SdmTcT3wy3VmjVrGgwG9I7c3Fw0G2qxT0xKBBAICARUCGA5QfadPB7PQ4tPkyZNwq2nNFE+cX2CEQCTBShpnU6XkpIyceLE7OxsZIq8ghcwqiKJR4GAQKCcEJBlmXgH2kh2u904oMYYczgcp0+e2vDt+o8mfNTnX/t26/qqyRhlNPyDpJHMUZLRLOn1Ab1kDA2//tVJkinwzyBJL/jJ39/+IiGgH8nAagLavyn/mIP2s9u/5vkEF2KBvAY57reYp9VJWr9itNT/j3137doFnCFFkBWycgJfJCsQEAgIBJ4hAlAsw/pLlmWn04kj3TRahxxTDQbD1KlTaS1Gl2mhIrTADOMobpUFAV1cxCpQeJfLtf7b9cRoUJPq2LEjpP/gu6cqUOkrdVHcbjf/XUwm09q1a1FjsTAr7y8PE8/QA4Xa6aJFi8Jnyg+po0aN0mq1BoPBEvht2bIlfNyi3k6fPp2/fQWL9po1a06bNm3JkiWZmZm7du0aOXIk+LuhQ4dCw9RgMGCRHxMTs2PHjqISL40/qcasXbs2JSXFbDbzCq00jICbuHnzZgnyQiPfuXMnTHBAUe78+fOEcwnSfK6jwNJL/fr1Cd7mzZuD7S0WJm63e/HixTjmYrFYEhIS3G43pA3C5/vvv4e6vdFo7NatG/lH4iDK2OFwXLly5bU/vkbmpMF6x8TEdO7cec6cOdu2bdu0adP3339PxmqSk5OJoUY1O3fuDF3IJ2aNqcrj8eTl5Wk0mqioKNj3IO0tdOpiYfXETEUAgUCVQsDtdm/evHnUqFFxcXE0EPGO8OsTConNoe7du69YsQJm32ncwFhEJ2yqFLyisgKBCoIALCK63W4yi2yz2bKzs+fOnTtgwID69etzyxOtRjJrpSiNJspoipG0Gr8icoC6DfR30Lu/dv2ArrGffS4NAR1inPEb4eD+UYbFd9CxQj5qrVq1pk+ffvPmTaEAVEGaaHkXw+VyORwO2n0p7+xE+gKBCoUAiWQbN26sUaMGBsMQA+/jUbJhw4bnzp3DQuypqfsIArpCtZliF6Zdu3ZoUo9bkf//ixcv4tpKFTFR7NRFhJIioCjKZ599hsvrqOePHj36xo0bkRxNLWm2RcajwajIEOX84mkWAKPn6NGjgXy1atX27NkTvn5EbF25cgWG7TQajcVimTRpUviIRb3t378/CDuLxQLquX79+hs2bIC1BMRCptu2bTt06BBj7NNPPzUYDNHR0WSpIy4uLj8/H8GKyqgE/h6PZ/ny5SkpKeC+Uc7o6GiTyZSSkjJ06NDHt7tIiYmJxd0vUX3oNm3agH02Go2TJ08mJegSFPu5jgJG5tVXX0WbNBqNAxAqIcwAACAASURBVAcOpFYX+Se2Wq3Lly/HEstgMLRo0UIFOGMsKysLOx8mk6lHjx6EWyS5wFS6w+HIzs6uX78+tkPQgA0GQ79+/WDZia4NhHr1pk2bcnNz3W73yJEjoQOl0WjMZjOqGYk0g3WCy+W6ePGiwWCoVq2a0WhMTEykwpOBkUhqQbGEQyAgEGCMfffdd/369SNRBLtKJDpqNBqcwgmzPkFcvV4/aNCg+fPnX758GcCSlgNpXDLGxLJftDqBwDNH4MGDB+fOnVu0aBEsaGEe1+l0er0ee0gBxlcrSUatNkZv+kfJb8sCP60kxUtSfUn6vSTVkiTLY3+JV1Km4YIcEWpAU3guWY591vzGuwQP2Ag3GAwQbiFR4ybVkSNHHjx4MPynwW53+DDibcVEAPLw9evXMzIy0tPTjx8/XjHLKUolEChXBJxOp91unzhxItlIhGl+jL2qQXXixIl0OAalIrmuXAspCOhyhbfcE69VqxbRVRqNxmQypaenU65irU5QPGUH+KZRo0ZBt5TMtiYnJ2/evBmF8Xl9OINf3mXDbWa0tZWVlbVv3z6n01lYWAhuKAxDRPRW+M0MJG61WumQr6pSsixbrVYa1HxeX1EhVRFxWhBrWsQCJUplvn//vioK7F3Wq1ePbFxgZw84BP9FdNR07NixRL+2bdsWeUW4nHYHfrdu3apfvz4Z8YC43717dySCLkmoUsnBzC5ZsoQuFtdqtUajcdCgQbCBW1wimFLma8cYW7BgQWJiIvRfUEhoy7744ou7d++22+0DBgyAyQWTyfTaH18r5RiyevVqSZJiY2ONRmOjRo3o6jnCIRgKVckr02PPnj1xbl2SpDFjxvAghMeBFIEZY++++y7Mc0uSBNsy1K2A1a5duzApmEymIUOGwDNCcx/o5pmZmVjCPV6m+sWVOXPmRPItRowYgdal0+nQwD7//HNEVJUzZGrr1q1DyzcYDCNHjqQwgoAmKIRDIIDhAjadaSqkuRL7Q9euXVu9enWXLl1APNGSg9gf3oG3MJ5DIckzNjb2nXfeWf/tesye/MAlvoVAQCBQERDgRcSLFy/OnTsXVxarunNRj1rzP0iGf5C05vad/7Vdu39LapiRYJhWO+ajlD9M2LDuyN7/85eDOVlXrp2XfYG6/mo7OqKqhxoxcPkhu3///qlTp3btzNr5593Hj5/Izs45dOgvc+d+OjfU75NPPsnIyOjUqVPnzp1xMyH+du3apcu/dOrb719jYn/lyvV6vyK30ehn1XUvaEBG4ybwatWqvfXWW999953b7cZSiL8kAwZMIqqYCFRhELDb7bAad+zYMSxh8PeHH36oMGUUBREIlBcCdOwMJob27dsXGxsLNoP2BTH4EzGi0WiaN29OV9mXV8mKTlcQ0EVjU+HffPPNNyRM4Mq76tWrR87rVfj6Pa8FxCyIJeLkyZNBBkHbFEz00KFD8/PzVURq+dWWBFO3292vXz+z2WwwGHr27Ilb8sgOQFEFIPo1PEe2c+fOP/3pT9euXUM6/KpYluVgi+ThUwsuDKixTZs2NW3aNC4uLj093ef1oWrBSR08eJAfaq9fvx6eQHc4HG63+9atWxBP8clIbzo4/eDiwUdRlLS0NFrwV69eXZIkUqMmwIuKXlhY+Nlnn5HqNKqQm5uLFlVUrAj9z58/X7t2beh3Y0KCbrJer58/fz7djdmmTRu8fUgjzpgxgzcKHGFGfDC3212nTh0apg4fPoyWEGpBwserhG5FUdq3b0+U7uzZs3kQwrQx8LYul8vj8dhstnr16ul0OsgW8+fPD0Zq165daEJGo3H06NFQ54F+YiQ0Lu5LBFEOKlmj0WzduvWJjRBf1ul0du3aFV8cavWtW7eGGTKr1RpcWpXP/PnzH5LdsL+B5kcDFA+XKpZ4FAhUWQT4qZYxdvny5YULFyYnJ6Mf0YBDSxGed+bd2CslhQZJkpKSkt59990DBw5QFoKArrLNTFS8giOATvqQPP3444/pYgbShCAZ7FcHTF4Entt3S/t45icbtu+0epjDzdavYc1rb06u9ef2L668cIYVFvqr7vIVyMzGgSBz7ic4VXN34NEny15Zdvt8bkVmspfJHuawMRY2VYhJIXey/ZctO32ylz34O8s+cOGblXsmjJvdpvU/46pD3Qu/UauGgKTX6x9eoTRjxgxa46AaZO/rCbUSrysYArCvsmTJEp6AzsjIgEUafo+hghVcFEcgUDYIuFyu+/fvv/7662AhcAqEJ6BNJhOkPkmS3nzzTaKtyyb7YqYiCOhiAlaRgo8ZM4bECywbPvroo4pUwCpaFkVRbDabz+sDrbl27dqWLVuSdVSIPnFxcStWrHC5XGGIpzKED/dVZmZmYjkKHcMtW7aAlg0pz1HuGzZsSE9P37FjR1FFxaWLaIpNmjQhvptSIIcn8MvNzV25ciXO8tOrMA6n04lyKooCShd3rH355ZeIRctjPDocjrS0NPQIKBSnp6efOnUqp4gfGUVJT0/HZ4LpABgRC1Mw1StFUQYOHAiFX5xoNhqN6JJoEqrwwY+KojwkGT/88EMYb4mOjjYajbweaHCUCH2cTueiRYvIGgYtQsaPH3/nzh2f14c24PF46NZEg8FA90pFmEvIYO+//z5lN2HCBNxFrlqQhIxYmTwVRXG73UlJScTvbNiwQcXFF1VfRfn1Gvfx48fTvWEWiyXkdTo8AY3NDwSLhDw6deqUyWSiHRR8OOzEWAO/8PIKipqfn5+SkoJj/gaDQafT4dhHmJGB6v7WW2/59ZV0OqPRmJmZGZJ9LmogokSEQyBQuRGgLuAM/BRFOX369Jw5c9q2bWsymdDp0HnphltahPCkM+/GDG6xWJKSkpYuXXr+/Hlg6HK5rFYrcoxkDKncyIvaCQQqLAI3b95MTk6OiYnhbx/BOICeTpKYVifF1Uh4bdDA77dsvmv9e777gZv52WWrzFYsZ0m/P5Rc52zbpINnTrJf7MztRo19jLkD/3yMeRjz+tnix6rQj/SZAwRyMIccUt5TFJ9Ptrs9dodLcTiYC+S2mzEf87kZ9EtUfxWfP22P0wUHC2TnDSi4+IsoM9nBCm4yXz77au6ds8eY08Zyc3MXLlyYlJT0uO4a/QtGnU6HO1f8woakif/HuGnp6Y5f7B6vK5Bkhf3ComDhEAhJQHfu3JkxRsbQw8UX7wQCzzMCsiwfOXKkbt26YJkw4pHgB0/sTT68QH7hwoUQ6gqxwfgsKi4I6GeBehnl2a5du8dzqv9/rVa7d+/eMkpbJFMqBCBvIQnsrs+ZMyc+Ph5DAP7qdLq2bdtu3bq1VDlFHFlRlDVr1vAG4BYvXvxEc42rVq0CZx0TEwN7xMEZ2my2hg0bktm1bdu2McZsNpvKkprT6fz888+joqL0er3RaDSbzb169Tp37lxwgiofUnN+eImK0Wgkla4pU6aoQuKR+gU/ClMsvsvAfevWLZiGiIuLg8pndHT0Dz/8EJ6XD876gw8+oA0hUOTjx49XWVYKjkU+BNft27fJZstD5dOWLVtSmNI4Nm3ahPpC7+Pjjz++cOECcYJut/v+/ft3794lw+V6vb5MZqbs7GwQ35IkNWjQAJsQIRckpaldBY+rKIrT6YTyMpSLDx06FCEBjQ0SRVEWLVqEZox75KdMmRLyA/EE9MyZM8H4gzl6ogZ0YmKiOfBD39FoNHQOgDEW/ngNbMXgQ6xevRosNoaFjIwMfkgM/lj0FmaytVqtyWQ6deoU3054d3AKwkcgUHUQQE90Op0nTpwYO3bsQz0+shyl0+mioqL4+Q7DBa1DeNKZd/ft23fRokVXr14NhhFbvFjeP3EMCY4ufAQCAoHyRiAzMxPUA60y9IEf7OoQAR0fHz9p0kc3btxwebxur88XIFydTMn3+Ano/72O/S7uz01q/LVFvZxt3zLlMZfs1wLxutwem8f9wOspYMzBFK//dYCAlv2kMfMpzOsL/POnqch+hjpAUrNAQJkpik9RAiY8EEuWPV6X7zGF/eAO+49/z+3U7vO8G0WSwE67w+twAUlZlr2K16t43Qpzy8zhYpcusjeH/2XVV+yP/3L4fzRZ8/brf3bZGCmvHD9+fNKkSbVq1Q5eAug0UpTFZDbqd/x5W4CDLu9vJdIvewTsdjusL6pMcKSlpeH4YNlnKVIUCFQYBO7cuZOeno77PHCSmw69kewHhehXXnnlypUrFaHggoCuCF+heGXAroXD4eDnUb1eHxsbi3FWLNSLB+hTCe3z+qxW60cffYSVIQzv4gu+++674EB5MxEw10CfskzKOH36dLq+TJIk3H0XJuXCwsJmzZqR1drDhw+HNMiwb98+Enm1Wu2XX37pPw3n8ouJqJHH47ly5Urbtm2hj0zLY61W26FDB9BwYYoBqYIxBoPC4HYlSdqyZQvxp7h1kzE2cOBAbPGB+YIIjsPIpAum0WhANMMfLPyCBQugeqnT6d59910+5TBlI3KcDBfgyxqNxokTJ0ILPkz0ol698cYbxJ7r9frS795DcXXPnj1Hjhy5c+dOUXqsx44dMxqNer3eZDIlJycXVbzi+jdv3pw4aGhV8yxGcVN7TsMXFhbi9BOg+PHHH4uqCKk3onWhg2RkZPCkUmpqKjjl4C65ceNGrDb1ev1nn32G1MgER0gdRlmWXS7XW2+9Rf0CQ9PKlSuD0y+q2HxIRVHQy0CH9erVi3pomOhut7tBgwYQm0wmU5iQ4pVAoNIjQNMo1RREsKIoWVlZY8eOrVmzJozVYGrjBULeTdwT74lRCNvAW7Zssdls/C2ClKPKQQIJjVGqAOJRICAQeGoIQI7yeDyZmZl876b79yDw+zv7C8Y6tetNmPBhgKfz8toVYIDvFbJvN7CXXzrTrP6lpNp/2fOtvxKKl/lIydnvITP/Y0AVWgm8CUR2evzv7A42dOCR//yPO3Y3czOPzOzM/8/rj/FIQTqgQE2PAXbb52PWX5i1kH3xKauTsP5f+x66+8AfmcY6jDlM9j365/P5aW0fKywsyC+8LzOP3ccK3Gz/UdY46XjT5nkNf3+1we8OdO+w7dqFQEl/+zFsDwrPnf3hnXfeqVu3drXqUZJG0usk/Qt+8MxGv5mOzl3Srl+/TvgIe9C/xa/iPsFGnMfjKSgogAwJgfnNN9+MZGqruBUTJRMIcAg4nU4sDIkvslqt58+fr1+/Pj8F8G6LxQI+JCEhYeHChbgjpCLIcoKA5j7sc+XMzc3lWxjMfZKuHLWt56pOVaKwP/74I46ZYwUIXdfatWtDH5nMVOHasTL5jrRWJFozKirKZDLhEsKimFYItVDpBRl64cKFkF9oy5YtvPrV4sWLfV4fDY6MsYKCghYtWmAEpEZLbBoqHjJleJLx2RkzZhD7LEnSuXPnKBfU0ePxqBg0yo7XTcZ+YM2aNceMGXPy5EkQZ6mpqfA3GAwnTpwIUx7+FQrg8/rS0tK0Wi2J+6/98TVoVfOBI3TLsjxnzhyy1aDT6a5fvx5h3FIG27RpEw4n6nS6fv36lTI1ij5t2jRw/RaLZe7cuVCVLZO2TVlUfMf58+fRBbBHHcmmAoC6cuVKt27d0ICNgZ8kSbm5uSGpZMbYihUrMLZotdrly5dT10D44Fi4h+f8+fPUix8y1zExMV988QXu1SwZth07dkRnNJlMqamp/sWr/FifKihFGJ+RZRn3K2q12ubNmweFEh4CgcqPAMz10HkC9BqXy2Wz2TZv3jxq1Ki4uDhoNWKzk7YqabKDA+b+eU+Y3pIkqXr16iNGjNi+fTvmPtUeMEbmkEDToE1CRchgwlMgIBB4aggcO3asWrVqfE+HdG0wGCByJCYmfrfhe39nDzUDQ0t5526W1PgvzRMvNax5aO4U2fO3gJkNn4qARp0U5meffUzx088uN7M5mdXJVv1vb1Ld7JcaHXmQz5wuP0sdIKDlR+yzP6ydMecjPlphcoC8ttqY18M2bWBN6hxPbnJz/ufs//no8oWLHiyFHA7Ho+HIT0B7mOxiPg/0qt2+R6rQNg/LOckaJh2p28ge/Y/WagkX69XbeeD/sML7AbY8UGT/+UKvT/HJPo/LVljg9jhl2fvNN6tq1koAbjqNFB1jhjs2NpZuTi5KVwNAiL8VCgGIkR6PZ+XKlbVr+1XdO3XqZLfbbTa/eRfaVKhQZRaFEQgUCwFSesPZ1vz8/HHjxtHgTxQE+WAx+FBjLyUlBcwGhLeKIMsJArpYn/7ZB8YYqijKkiVL+Bam0+nCWOl99uUWJWAMshT0bXNycgYPHmw0Gg0GAzR2DQZDWloaf+C9rAYI0ME+r69p06ZYrELvCYvPR+Ldbz+QoiiFhYV9+vRBG9Pr9Y0aNcIRp2Be9U9/+hONcUajccmSJWRNAqm++uqrBoMBR/JhfAPyMZi4Bg0ahCenqJwDBgwgAxGNGzfm9f2p+LNmzYLKNlBFRikpKT179hw3bty8efM2b958/Phxe+DndDrRoY4dO6bX68H5du3alXS3KdnwjoyMDGhPYzshKSnJ6XRCcg1pJCF8am63+/Dhw7DjCU785MmTYci78KnRW6QAdfKiUps7dy5R/LDeUNT+BCX7RIfdbj958qRerweF2rlz56pJQGOfBg0yISEhuB/xSOK+PrfbPWfOHN4ei9lsjo2N3bVrF7oMr0hOlNC8efNgf1mSJJhRRrCiCGi09u7du9OEEhMTM2rUKBLZaZuHL2F4t8PhmDBhAnqiTqdLTEwMH16WZbvd/vPPP9NIMnjw4PBRxFuBQOVDABf2ol4YpS9fvrx169Z33nknLi6OeijOqWAwIU+Vg/ZccWGpJEkPLUTPmzfv8uXLSD94bsLETaNKMLxlJZMEpyx8BAICgeIi4Ha7of1A+goYBAwGQ3R0NARs3HlOk7jnEW37KCuZsbt32Q+5LPXlnLpxh2tV2znlwxvW+8x5JxAgDAHtNwMdIJkD/928wdqmHEhMONu68e1/qv+Xif/rRxkvFbDA3gD7bPObkA74QCXa4VPcPpZ7nLVudvzFetY//M7TqPbtRvW2pk/dSFA8WqHISoCAdgQ4aL+fS3EWOBW3wn74kb3S5urvat75fT1Wvfq1Or//89rv/CWzOykNv8O/sefnnWHQ2l8IWP9Yt/67unXrS5I2OiqW9uAlSWrduvXZs2eLEpV/k7R4qDAIgIOG7MqbjHO73dQFKkxhRUEEAiVBgNZ6O3bswHU7NOwHE9BQA5o3b54qp4ogywkCWvVRKvojtvJkWf7ggw/49YZOp8vPz3+imc6KXr1KXT4y+YqjtT6vb8+ePcnJyaBKSV9p0KBBZ86cIdb1kfhVCmQ8Ho/b7XY4HLgaGDoRq1atQlsKmbAsy/fu3TObzSiVwWCAPiwGPtVO8pdffkmspclkWrZsGdKECsOyZcvAoGG1bDQaO3ToADIaFdfpdE80BgLurFWrVkaj//4QnU733nvvgT7GKxQJJi82bNhANBauAXQ6nVarFSYsVVWAUDJp0iRarm/atCkkJiE9HQ5HXl6e2WyGrB8dHW2xWJYsWYLANE+EjFuU50PyrrCwkDSRtVrt/v37VZgXFbcof4hiYJNxr0vw9KMoypgxY4i7XLduHVGQRSX7RH8yvhYTE0NTY0FBAXEcJYPoiflWwACLFy+mEfull14KX8K8vLxp06bFx8eTDRmY72jSpMmJEydgRztYlxlpTp06VZIktOesrCzaTQlDQK9bt466jCRJNWrUuHv3bik/zZdffmkymaCqWb169SemZrVa9+zZYzab0U5wfWJ4lMRbgUBlReDatWtr167t1KkT3zExgKjIJhpVVA5MuCaTKSkp6auvvrp27RqECsyDHo/H4XDgOCdYbzLxTINzMLbBs0ZwGOEjEBAIPDUEli5dGhcXR8IVPwjUqlUrOzubn3l9j64T9G9/o4T377DsvSz1xb80/d1/N6uX82//8+r9u8xlD7x3+zWmf2uCA5FghcMDahn/zf1P1qDGqT/UvtWy0b0/1Dj4n5PvBRHQzsAFhl4kAbPRXsauXmWpLx19qcHNxvF/axR//aVGF0f+zx//mvuIJsf1p/4q+AlovxK0z+Pw316o+NWg/+5g//c669ThRM3qlxvVVeol3KsZf3DVWuZWWIGDFTrsqq/gj+gDLe3XvvZb/7D6jVb/vUD5j08+lTRGP3p+OxwS8NTpdIsWLRLEpQrGyB/R9vgWGHnc0oSEng2vPSM2EkqDp4hbcRCg4Sg9PR2jfXiBsH79+idPniSVOLLgURFkOUFAV5x2FVFJYEqYMda+fXv+Aplu3brxujMRpSUCPUUEaCZGt+fJoLfeeguWHImDtlgs679dz3PQpSmpx+ORZXnLli04kQed6zt3oOFQZMKwZ48BzmQyzZ49m8qjOrE7e/ZsBIN69c6dO6Hl7XK5zpw5o9Vqo6OjwXq/9sfXkO/ixYvJHIFWqy3qOkEqHMZcjUYDLlur1a5YsQLkJpDkF8+MMWh/oFSbN2/GxgyPOe92Op2NGjUCh16jRg2wrhHKK263e9GiRTQN6HS6kSNHElBYyVMtInSgLrCXrdFooqKiijJ+EmGCqmD8xAM3Avi8vq5du1IjPH78OHGXqhQif6TJ8vXXXyeU1n+7nsoQeVJPDEldjFd84GOp5GC+7s7Ar/yOWz7Uy5g6dSoJCv3792eBIxEoHkoCQ8y7d+8eNWqUXq9XLSmjoqJ69+5NuKkcfDWxiwDtY1iYwVfg2zwfnTGWlpaGfXJkunnzZhVWfPqRuN1u98aNG3HlqVarTU1NJeNCIaMju6VLl2IMMRgM679dT0QYShsyovAUCDxHCPBLYio2KW0xxi5fvvzVV1/1798f4zDuD6RxA0OoJEl0jwL5oL/z5p67deu2aNGiW7duRdh9oP4cYWAqvHAIBAQCzxCBtm3b6nQ6i8VCVjgwXAwcOLAI020KYy7GXD6f0/ULO3WIvfKHk22a5DWtdbJfz6NOG/OrCONqQl9okx0B3tntVdxOr2J1+ong7zexpMTTDWv87Q918pMb/nX9an/EgLUPBfrOj/5yMPkYu3ufFRawLu1zmta+2KLenZZNzv6vf7vxw1nmcPvvMwz583mY3el1+lwyY/ftLO8+++d/Ph5rPtKw9v2Gdf/W6sUz/+9sr8fN5Ee5h0hDDlj+8DJmtbP7t9lf9rP/PvYo2KWrefUSG0kvaFWD6rBhw+7du0fHJUMkKryKQEBRFLvdDunObrdj+iMKDJFUoiYvmoZx89IsVGroL0zcksozJE8s6FQJhiw1FLaw9rHZbCgedD7oL2MMNvTAujid/l0N/A2ZpvAUCJQGAZ/XR61LluXs7OwXX3yRBnwar2JjY1Wn4jp27FiafMs7riCgyxvhMk6fuJUGDRrwBPTbb79NXE8ZZymSKzsEVPMfHhljffv2fWge12g0YvgwGAwjRowgHlM1Qxe3OJh6MzIy9Ho9bgbr0qVLmEQwYScmJpI9VkmSQCvTGpWPPm3aNNBGEHyvX7/uPx/ncnk8nv79+9OAOGrUKFDhuNajUaNGFGvIkCF8gio3drOvX78ObUqo6F68eFF1rxpJJD6vD2yaRqMxGAxHjx4lTpnC8I6bN2/C0oXRaOzTpw8sK6nKUNSjw+Fo3LixVquFsqokSVevXuU/XMm+3cGDBw0GA0GHww1FlaG4/nwjVMWtXbs2oNNqtRhqYItcFSzyR+Lxv/vuO0yTD+2Qzp07l8oQeVLFCqkiehwOx4MHD1Ra5P6L3T2B23MCxzPx1VRhipVpmMA+r2/EiBHoIDqd7u2330ZgcKwOhyMrK+udd96pV68eTyHBqrher69bt+7q1audTifhpnLwWQ8fPpxaDi47xo4R3+b56IcOHcLJU/THvn372mw22ADhky2uG4rYZrPZaDR27tzZ6XSG4aDRTWgkgZHr8riItbi1EOEFAuWEAD817N+/f/z48bislQ4qwSoU9WVaZsBhNBpNJhOuH8RuriRJCQkJ/fv3X7t27bVr11wuF7JAZ39iLfgx4YmBRQCBgEDgmSNw9epV0hjgxwcyYUwCWKCocoB6djDmCFgAY3/PY6lNT7ZteP8PtS4M6v23XwqYy+G/NdBPQBMF/MiGBl9Xxednib2/eNkvTnb1CmvRbF/dhAuJtfMa1z/zzSp/SLfCZH8SAT1runUwkKbit93h/3lcrO+rp5rWO96k7l/rxu1e+v8x+y/MHYgRylS1n9H2KswWsOFhldmdAjZ0+E91Es7Uqv5zvZr/t/Hvj83JsMquQPmRwa91ePTsl/ECFyIWOJnLx44cYO1S/uuV1ovcLlYQ0Jb++y+/vDZkkF8cekGHv1g0paSkQHWGH7R/TVS4ikAAe6s0DfG2FrGWxKHVspW6kR1p/6jWAqqSYq3Ke9rt9uvXr+/bt+/IkSPUfVSJqJZFtI7g0xFugUBZIUCn1e/fvz9x4kQY/OQH/GCfOnXqfPXVV2VVgHJKRxDQ5QRseSVLa3iQlcRBr/92PTYAyytjkW5ZIMCv8cjtdDpHjBiB0QQfVKvVrlmzhucxS585bsnDavaLL74Ik6CiKKtWrcIyGNKt2Wy+desWyqOaiR9uBY8fPx6GAnB3GU3GO3bsgFqWxWJp0KBBQUEBHxfmhnHYLSkpKUx5oBG8fft2Wma3aNECJnRxPyGQJH4tPz8fYGq12piYGBIcKYDKgXJC0Fy5ciWvjxamVHi1du1a2EZATUePHs1/NRTsiYmoAhQUFAwaNAgEtEajadGiRdlKvdTwVMn6vD7UAkYYICwSi6EqZISPJMAdO3ZMp9Oheb/xxhslQyZ8plQdOleel5eXnZ29adOmU6dO3blzp6CgII/7nTlzZt++fd98881nn302ffr0BQsW3LhxA3sk4TMqwVuf19euXTs0y4c31M+cOfPSpUvrv10/fvz4zp07m83mWrVq6XQ6UnukkEajcerUqWStlf92KKYBHAAAIABJREFUvJsvUs+ePRFdkqT79++TtWi+2fNx33vvPeovkiQdOHCAT61kblmWa9SoQbWAPfHwywxZlgcPHkx0m81mEwR0ycAXsSosAjQeYprYvXv3oEGDYKMZZqmo59JQzPuQm7oJ+bz11luZmZlQ+4JalsvlQg+KEA1+TIgwiggmEBAIPEMEli1bRiMAdpGjo6PXrFnjdPhtbRBt8biE3gD1/IvMXF7GCu+xtwZffzH+YlLCT/17/fRT4KJr2RMgcAP3EgZYYNmvzOy/uzDAJwcSkpkvL/9avsvuZez+31n3Tj8mJV5r1uhO5853DhxhDx5dP8j8FDSuC/QPdhyjHUjEa2XTx99rkXj2xT/82KPnwbMX/NcY2gPk8iP2+be0dYDUlm1eR4Gb3feyG39n3bpdblD7Wu3Ye4m/u9ckMXda+i8+H/NfTPiIOvcE2Hbi0f25IklvoFgnT7J2Lc78U/3z/6PF7rw85g7YB5EZ8/h8/zb6TUKVTp+kpKQUFBQ8RlL8XzwEIPth+sPV1tBTho/T6bxy5cqxY8cOR/zL4X7Zv/0dOnQoOzv74MGDhw4dOnLkyIEDB44ePZqTk3PkyBE++du3b+fn59vtdpVcev/+/eTkZDSA2NjYnj17QvsquMKIiHWHx+MhHdXgkMJHIFAaBNC0cnJymjRpgrPauCMqWA5Eu+3Tpw8U70qT6VOIKwjopwBy2Wdht9uxPoFOqEajOX78eLGIs7Ivk0gxAgT4NR65+/XrBzuPkHX0ev26desw4lCYCNJ+QhCc19BoNHq9Hlq6RUXweX3du3d/qKkKHStJkpKSkmiuJZqPor/77rsGgwEa3C1atCDdyTZt2pBt6MzMTNo7AUN94MABEMomk8lisVBqwQ5sZS9atEin02HfZejQoaRMzdNqcOMqM2wJxsfHU4LBIeEza9YswCJJ0o8//siz5BS3KMeAAQPISi+iIyR9uGC4ikqK/I8fP47eDQ24mTNn8rQFBSuxo6iy5eXlEcXfpk2bMiGgKa+ff/5Zr9dDx7Zdu3aApQTghKk1VLadTueJEyc6deoUHx+Ps+rIFFsdUHWnv6r5W6/X9+jR49SpU2ULOE7z1atXj0glg8FgCvxQAFjgwSAAw+h6vb5mzZrp6el0bpEqTpDyDnrLGEtNTcVaVJKke/fuYatG1fiBPHqW2Wy2WCz49B07dqR+yqdZXPeUKVNw2AJj2vnz55+Ygtvtbt++PeSnmJgYNL+i6vjE1EQAgUAFRMDhcNy+fXvdunWDBw+Oj4+PiYlBv8M4gKnk4QYVDVnEg6gc6FbVq1fv3r372rVr6bQKunnJek3JYlVAkEWRBAJVBIE+ffrQbdswTzdlyhQ/XcyYz6u4PfbHJo+BhzfAsnq8fgMcbOUSllT7VMrvfmpW8y8nTzG7zLwyc9odfq1l72MaF+wzDGoofiI68NKvpexi7IGVTZvkaFrrTFLdGykt/vrfJ5nVze784s/L6w8IAhoWPVAAPx3sV1L2sOWfsZTEfU3qHXjrzTsOmVllf542uiCR2GcvU3y4sNDnCVj1uOdh9zys3+C/1vnd1cTfyc3qOJrWOzdpkuP+A/aLnTl+eRDI6ZGZkcfVQO5+AhoQ/D2fde+ck1TnarNal/t0O37zb37e3Mn8ORXarLIsL1u2jIRhssLfrl07ko7KXER8VMRK+t+DBw/279/fp0+fXr16paWltW/fvlmzZmi6RqMRxiHphKtqsivNIyZWzKe8tA/bViHnWbPZjE9vNBq1Wi2m2jp16qRxvxkzZkydOnX69OlZWVlkZr1YK8dK+p1FtcoLgc8//xzLupBHXtBHjEaj2WxesGABGZMkR3kVq3TpCgK6dPg99djgJXfs2IFhkYZUFKRsCZ2nXrlKniFvSMHhcMiyfPHixRYtWmDexbCSnJx88ODBMgfi5MmTJpMpOjpaq9UmJydDeKIFpyq7HTt2gOellXDv3r3DyFujRo1CazQajcOHD0dq69atwzV6ZrP59ddfp7yoiRYWFpJgodFozp07pyoGPWJnhXIxm80qA9l84oqiHDx4ECnrdLpevXrhbbBiMsUaPnw4bB0kJCQE6YxQKdQOn9fndrtBZYJafeWVVxCIUqas1ZGLeHY6nYWFhS+//DIEIChBk02PIiKVmXdOTg4xpMOGDcNQAzsnJc6DoJBluWnTphivaL+BlOVLnD4fEXskPq/vjTfe4JsWGidWERB2cW4d346GUIikRqOxZs2aKp0IPpeSuWVZpk0FSL28wiOaH8ocHR3dr1+/FStWlCwjxljjxo1RWZPJhI+oYp+pL8uy/P3339NHlyRp+fLl9LYEBUBGOKyg0Whwo2CnTp34pGgE4D2Jo8dWUIMGDVSHHFWBxaNA4LlAANSww+E4e/bs4sWLk5KSiNegbTDeQXfP4rAIbLJjJxLjg9lsrlat2rhx47Zu3crvChd3rnku0BOFFAgIBMIg0LNnTwgwkNXT0tL88ya0lv0TrdWnFASIYD/xG2BfmeJiLg/76zn2h9+fSIy/9HKT499/y1yyXwXYH8gbuHSQ9IYVhfn/BWxp+PwErYt53Uz+u9f7i4d9+L7j97En2ibe/efk86eP+KN7vMwTMLHh86cHtecA3+x3M6/b6SxkPhvbtpHVqXEwPm7bpP84D0ZYCVDjIK39CSlevyFnr5+qlr3OAGFu9/h92c+FbMy/F9RtcLre7+xN6nqa1D499xO/6rRTgb2PQDUCSTxinx/Xxec34MEKPeznv7Ehfe41q5HXvNbf/kfz//7FxpwePyPv8fm8sgzTEC6X69NPPwVDyhOjuAsH4grlJBzQciAGFjKey+XKy8v7+uuve/XqlZKSghkNfzGX8T4kjZMnyfDQHSFBHWdz+UkTbtw4QotWPjrc2N/lA+PYKwRgSpCPiPmXp/yCOWu8rV279qBBg6ZOnbpr1y7SwcKq0+128/sWtCYqShIWzakqI0Ct4u7duzAsfunSpfbt29Mylm+fvPuh5mKTJk2uXLnicrn4FV9Fbm+CgH4um/rRo0ep5RmNxnbt2j2X1aiShQbFqSjKiRMnoLNgMBiw1zpmzBg6a09zeelBUhRlw4YNULqUJGnQoEFIkwYmur7S4XC43e42bdqAjEMb02g0Q4cODVOMbt26YVbW6/XTp0/H8NesWTNIEnq9/syZM5QXHLiBLS4ujrI4duzxVSBBOYGmbNWqFcwTwz4s+ClVsnhcu3YtcWojRoyAQBmGgO7fvz+W/Q0bNgzKvEgPn9d34sQJkloeIjBjxgyEVpWqyCR++8Ln9blcrgEDBhgMhtjYWMw3H3zwAUr+27Dl8pSZmUm6HmPGjAG7gZmsTPLjbVCQyl6ZpIxEcNuJoigDBw4kFWBJkiwWC84rmUwmdDQaPMnBm1uNiorCvjGJAqUv5PXr1+k+MZQBhTEGfiaTyWw2Dx06dOPGjbxl6pINAjVr1oTInpCQEGz9WfVBp02bBskeCsu4tLDE9ZVlGXtdYNmQ8tatW/G5iS8LTh9Qm0wmrB9atGhRGh48OH3hIxAobwRoasPshs67Y8eOsWPHNmvWDF2SBhw4+OmD3HT7KGZVnPvR6XRRUVEDBgzYuXNn8LBAM05511GkLxAQCFQcBHgC2mg0HjkSoIFZwGyG4lOYVWEBhWRYtfArAPuYz298ecTwHxPr/JDc8NLW/2J2u5/pfWT4gq8bqSEHuGvFx9yyX03YyZjNxzZvZk1qHPmnWtc7JF346yGm+M1K+0ljn5+s9vqY/1q2wM8FS9A+D/M4mLuQ7fiOtWiYk9zsx3feL/Ayf7h8t8cZYMcfEdD+fL1+tvtRsfwUstVTaGOswMPefPdS3d8fj69xrWHdgvioo1MmPPil0G9y2hOyCgHiG3+s/psLmdPL/tj3LykN81vVZy/Wzz2YxZwu5pJ9dIUdBCQIJN26dZMkidcVkCRp165dj6sm/v8VAZfLBXUH/8eyWufNm9eyZUuerqXj2kQlE9dM+sgqHwoJTWReSlfNpPRIUciHzhfiUCz4a9zyDWmTJHNeMYW/BtxisfAV4floyoV3NG3adNiwYYcPHwbvDDvXDocDEzdN1mW4vvj1MwjX84wAmgRWbajHrFmziA0I2fAsFgvaHuwcwvKSIKCf51ZQ4cu+bds2tDmM1+3bt6/wRa7qBcRNeiATZVnesmULuKf/n70vgY+iSNvvmclcMQlhuSKBIKchoHJkFWQ9YGGFBQUBwU8X/BZ0/6DyqYiCIOcCgiCyHLKo8AHqLriygvixAgIBkUPOhQXkJhe5JskcmaN7uvv9U/XOvDSTg4ABAvT85pdU91RXV71dXcdTTz0v9VsfffQRdlGlp5e/0HaSJI0aNQoVeAVBQAHoCAAXHQMCwKJFi7BFQ64o9tkIg5aXjUaNGtHq3Jo1awBgwYIFVqsV6QMjRoxwOp3aThe5wxeN0KZNGyy+0WhcsmRJeekjFGW1WhHVMplMqEugTVMbnjhxIll17Nix2JrjX200Cj/++OO4Nt62bdvy8lD6vKqqM2bMINTAaDTu2bMHo6GyAaVf+trSZ9BF24svvoiiJQaDwWazJSUlFRQU0OJ56auq9sycOXPwcV9EQCZNmkQIIAV+4e0GDBhACwNZWVm0JPALk424HF+fDRs2fPXVV2vWrNmyZcuePXsOHDhw6tQpNGZBQcHJkycPHDiwffv2bdu2paWlbd269auvvho9evTjjz/eqVOn8ePH4xOsQh70pk2biEeDvjHNZnNCQsLQoUM//PDDAwcOYLZRFw9L5HK5aEAfUcaKD3GdBtfD+ZxQOxoJhfE8AHTq1IlYlvXr1/+Fzzo9Pb1hw4a4sIQzgWHDhgGA1+uVJAldipc57EZv6aTYU819N1dsf/1X3QJHjhwZOnRo7dq1tRNXi8USwz/U62m7DwoTIQtX0Zo0afL222+jiA36PNBuHCG4BLsb3fK6BXQL3DkW0ALQgiCcOHGCcVFlkcO5TOuYyXGgpEYYY1YVmDsTmjfY1ereg2PHQEEhFJeUjz5zOJn9zEHlgMrwYmcQ/vdTqF/j29YNjnR+4PC/d4BaAj4nl+9gUUUZ/JwBjc8hwOU6wOsEyQuT3vElJ+5PaXT4/w3JZFkFcPmZT0KRcZ3ZYQgHx2yHHRJ6JIl5TlThxZcKGyceb9nc1TgpOzFhx38POiXLDEHGbF66PFQDUIiDcboVzoPOyYf+vQ+3bvyf5HqOB+45+/fP2LWiDIoSVIOcdR2UlSADo3EgVFBQgK4sqBk3Go2/+93vqnBkeHvUVTSX3+/PysoaPHgwUYVoIqZFlgkj1p7E7o/O0IVlBigF7a+EI5f5a1xcXESu8F7aFDBMOcHDmJgYTNBqtdI8N+Iq5JAhBRtZFBihSZMm06dPJ1YZjcavam54e9QQvRSVtADhP7t37ybOliAIWs3GiOqXmJi4bds23KyM0ytk3UUMDsuceVUyV9cpms6Avk6Gvb7JTp06laqg1Wp95513ru/99NSr1AK47R2fYExMTL169TZu3ChJEhKQ2WhMxP1wVXPXQCDQ9+m+1Ctv3LgRKVoR/tbQZ1Hbtm2xlyXfeiaTacKECRVkRSuCnJubK4pikyZNsHTx8fG5ubkRgKwclJER2bVrV0Q8jUZjxbcgv4KCIJCsc0QvTi0vwriYgTlz5mCDjs706BJtIDU1FRmyCHtVppnGNJ977jlCDYxG45kzZwgx1KZf2nSlb+Fyufr160cvNTKyFy1aFAgEtHBD6aSq8MyYMWPwcVitVvSijsPKXwhKUg7R2R0O5Y8fP45GoO6Wol1bAHtcNDumQLMIPMTq7ff7tf209l5kZxLTr8LXcPny5QRAm0ymhQsXpqen48IMvvjaXXuUq6syDlUqxK0MBkPbtm21AxEtDk17SGNjY3Fd3WKxtGjRgm59DYFNmzY1adJES2ZJTEzMz8/HPMhBmRa9ykz8/PnzyEARBKFnz55lxtFP6haothZQVXXjxo3PPfdc3bp1zWYzbm/SEp/xRaNpsLbv0IaxF2jRosWrr766c+dOfK+pdaLi474lbOWou6Ff9YBuAd0Ct70FIgBoVEIIq20EWfFRPYP73VM4nntwL/w6eV/ThP1vvu5xlzDt4xKuuhFpK9TPQPlljt76ZQYBl6iw/9/QIiktuf6RR9rt+/vSkNCF6JFVUeJIsl9hVGmUkVY5sMzSzj0HLw/JanL3lhZJB/7QP8/BnJqzD0pw+GTVr4QwaH4aZURY4kFg+tQ+Ff78nqNJ/aMtEqWEGllJdX7q++S+ggLw+CEQ9IZUosMQtobNzYygqBCUGCv7vwcfv6fevsSaZ5onHh/0X9kAUOxjyteqIrJ/QUUJA9DIkgGAUaNG4dQJedDYhp89exYzr/8lCxQUFIwfP544BNTN4XAUVQoj8GU61A4a6WTbtm379OkzYcKEJUuWrFu3bteuXZmZmUTSkkp9qCtEb+o0mRIEYd26ddu3b9+yZUta+LONOyrcvn371q1bt2zZsnXr1vAvaStXrpw6dWrv3r1TUlIwkfbt2yNVZerUqZ07d05NTdUmHkGQJ9loimMymUaNGoWKCkTC0E5VyIZ6QLcAjvfee+895PFomfhIXYpYBenZsyd6+sHGHweK2rkeDQ5phlh9jKwD0NXnWVQ2J4FAYNKkSdS6XWzx33vvvcperMe7URbQvvYI4SHGtGTJEpvNVrNmzZiYmNjY2Li4ONqqQ5zQKu+ccBkfYc3MTEY9CPBPBMI1ZAjz/kzMZaxjJpMJSdNlWi4jIwOTxTU6URTnzZtHmpWTJ0/W2iGiXCNHjsRbmM3mfv360X6liBupqrp+/XqMabFYOnXq5Pf7K0BFu3TpQsmuXLkSUys9gae7dOzYEVHRZs2aETO0YvAR7dajRw8aLRkMBnSpTMmWF0AWG/6Km7PS09Mff/xxwg2RkTpz5szwdKK8lCLPowZF5NlKH2udYS5cuBAtQHbG5QpVVbHmECxSsaG0Nx8/fjziLIIg4IoLWVsb7ZrDWgy6dK3DM9o14Wu+0TVcOHXqVASgLRZLt27d8AUkQFab22tIHM2INfzkyZOEeT3xxBMVA9C4rkPvb4RYc3k5ycvLw/xTBJ/Pt2HDhovuL4gtEhMTY7PZcK2LkLKI158ux8DBgwepevTu3dvv91fDAVNEnvXDO8cC5dXGjIyMuXPntm/fXtsXaAFlbZg2URKlzmazmc3m6OhonMc2bNjw7bff3rFjR5mGpYbiVplglFkK/aRuAd0CVWKBjz76CFsS9LjgdDrDA12EZPlNVPCUKH6R4bCH9kGnNrtTmx//w9MXAgHmSFDiEHBYJ7l0ptgvjNWMQDDAxu/hvpTdLRoebpTwf58vVxjDGi9GwPpSAoR8g1gCBeegd+d9yfWPJjf6T88eaRlZIDPec4jwLAMEVPbVkKD9HHYWUaOjOADzP4ImjfY2rJ3VpG5Ry7vPDvj9maCHJSIz6WfmPFBLgqbCKwAlIpT4wemCoS/kNaj7033N3UkJx3v8fn9xCbuEIfOKoipcWUQWVTmoMvYz++BY99ChQzibQBgarT1jxoyIqdOlct8xITkoI7dXVdX58+cnJCREbOrFDhGtR9t6IvBZQtNatmzZtWvXyZMnr169+iKWTfOO8sxJXWGZQ1ycWuKWWdyER5QLTJBdrlmm0KamDS9ZsmT27Nml5zgFBQXr169/+eWXU1NTCRbEiRs5tKeCY6Bu3boTJ07EwTPO9G/Y3tbybKifrw4WwKqOnDwAOHnyZM+ePbWDRhor0suCb5PVal26dCkuxEQURFuHteGIaDf9UAegb/ojuOoMKIoybtw4at2MRuP1cFt31dnSL7jcAvja01AGf1y3bh1KSeDfmjVrbt68mbo3URSvR2OhKArqSCK4TBuCEP/CjKE7Mtw9ZDKZ+vTpM2LECJwSVwxA79y5k3rcli1bOhwOBLstFkutWrVwUTqCAU0z+RkzZlA1fuCBBzAnpXtlSZKWLVuGba7JZOrevXt4kB2yOCWI5PHExERk8hoMhvJm8qEr+b9OnTqhyFdcXBx2BqqqOp3oTVsbMRSmsRHpXONIy+FwlN4iHXG9qqoRbv32799fv359HLuYTCbkzb322mv0mCJSiDjEO6IFEOnTWiMicsWHjz32GI4ODQbD8uXLKXKEtRVFyc3N3bdv38qVKysQTqHLKTB+/HgSWdu1a1eVj+C17055YXofr9lKVJyrCgwfPpzK3q9fPxwNlykLc1XJUmQahezfv5+EvPv374/lLf0X1zaOHTum5Wl27dqVErxigFotAFi6dKnRaMTmAv/GxcV9+eWXqEeG6opXNDj6wMTBVr9+/bTpXzEzegTdAtfVAqWb1mPHji1evPihhx6Kj4/HN64yADStMhJTDHvAtm3bjh8//tSpU9p5Mvab2nJRs6Z9o+nkFV8xbVJ6WLeAboFb3QK43mw0GpFwumbNmtLjZ9YLuyDghd07oP39P93b+ED/XukeB3PJp4DMudEhDLksa8gyKCKXv/AC7PgJ2rU53rzR2ZSmu/75D4be+jjNuqwL1eLiAq8nCEHIz4AnOx9qWndf07rHH009ksPWr8Hj4RexPDAgWAp/w5offoW5BmT+B3PdsPKf0KjhzuZJhY3q5ibEHniq8wlnFhf2kJm4BmKJpQHoIIBHYkVzuuH117KbJf0nqV5uctOCXz905MBxcDGHilDsFYOsnfUjBq0FoLFQRKfVAejST1kURafT+dprr+Goj3bZ0rQOqc0WiwUZ0HTebDanpqa++OKLK1asQP/z2Hlp2Tmlb6c9o+31tL0hhgOBwKeffjpp0qSIGUp5XaQ2NW0Y53q0sVWbAQo7HI7p06f36tULO3dkYmmxQkEQYmNj8Q2tVavWl19+iT5mKAU9cCdbACfC6PtnyZIlcXFxuPtci0FT1aLJXY8ePdxuN9ZM3F2qtaG2DmvD2jjVIawD0NXhKVx1HlDSlyrlpk2brjoJ/YLrbAF87bE7xAXPtLS0uLg4u92OLUtMTMzq1asjcnE9GguXy0UzZLvdHoEnYpd/5syZ2rVrI25rMplOnjw5atQoHC6YzebSDGgCYZcvX05o74ABA9555x0aZMyaNYtKp+34sdFUVXXVqlU0ZLHZbNgQR2QPMeWJEyfSHq7nnntOmxreAq+Vg3JOTg6miZrX6enplIfyAk8++aTdbscRQ0ZGBvJJKxgiUNkjAGiU6USRhzLvhSgGqoG7XC5RFOfPnx8XFycIQlxc3EWgPz4+3mAw/OEPf5AkqYJ0SieODxErm3ZdoXTMCs60aNGC9s0RAI2FdTqdW7ZsmThxYocOHRo0aEA+/Zo0aaJFTCpI/KJVEYBGHPbkyZOlH2LFl1/xV+27U14YTYS/XjHBKozQtWtX8rhNjIwqBKCJL7xp0ya8kcFgeOmll7C8pf+WBqDtdjstAlVccBQzQRK02+1+5ZVX6JXHVSJBEBYuXOhyubTrTxWnCQBr167FdIxGY//+/at8feKKGdAj6BYozwLYHfj9/mPHjg0fPrxVq1ZU1Y1GI7ncJAxaO3nQhulNwZNt27adOXMmdlKBQMDn81H3h51FRH6oWdO+0XSyylvUiLvrh7oFdAtUNws8+OCDhHaV9gakABQVMYh3+xp4MPnHBkk7722zOSsH3Nw3IQeQpWD5+LMMQZEpPENeCWz7EVq12tno7qw29+XNWwB+zom+3BoEJiO1GooLAdww8ImjTeufSap3pkvHA8cPcaRZCTOgL0efEYZmSiGcTy0BU/xY9U9o0fzHexqcqxt3qlmD0z27nHLmcuoy40tLwLU6kPKs/Rvk93EHocgL48a67m18oGGt/MQ6F5o137l2A8t1ZonqB8h3FzKtEHYlx7JlhRjQWDSPx0Mcc5px6wxoeu4vvvgirX9Q74aBCAa00STcd3+rV1555aOPPkKxckzE5/MR2wZhOFEUI+dfkfx60PZ62t4wFOaCby6PO8xyZv9pSImAXVBBwXH+7LXJacLM+6bCro3AoHHCJYqi3+/3elwim675M7OzJk35c/yvalntNmYBA/8KRsFoMhjYl+zz1FNP5ebkBwK4C4BsqQfuRAuoqur3+z0eD25BpkpC40ZSJkRP1NHR0TNmzKBNqGUydTRV+LJgdbOvDkBXtydSqfy8/vrrWuFdYu9X6mI90g20AGJMAJCTk1OvXj3kPeE+3G+++YbAO5x2RmzJr6psZmZm4hAK4UUENylxVGRu3769zWbDgez06dNVVX3zzTexKSwTgKa+fNq0aTgsMxgMb7/9Nk7La9eu3bBhQ2wiaYcU3RGrq6qqW7duxSYVITNixdIkHC8RRXH48OHR0dE4z//Tn/5ESVEAeR9yUD516pR2m/P58+cpTnkBFB7Bwm7btq0y03gsPkpwEBKxfv16eqDl3QvPX1R8PnLkSP/+/WnTFgHxY8eOxbKIokhGrjg1AJg5c2afPn3Gjx9/5syZ0suhV7wcI9StW5cA6M8++yw9PX3t2rXTp09/5JFHsAvEv7jPDmuUxWI5evQoIfIV30gLQGdnMwG+qv1c1tOWc4DDU/yxau9eXmponJYtW9IscfTo0Xiy9M6AytS9Mm9E6itff/01vk0mk2nkyJFlDM3DpyRJQgkOfJRGozEuLq7MxMs8GQgEvv7668aNG+OLg1QXXOj6+uuvabiPGHSZKUSc/OKLL6jBGThwYMSv+qFugZtogXXr1r322mtNmzal1h7rKv7FjSOosYOzbpo8RAQwfnJy8vDhww8dOoQl0rYGeKY8Ihi1auGXmP2nk9fcetxEw+q31i2gW+CXWGDRokXYquDgberUqTh+RjQ2qECJG1Ytg9YJu5rXPdKq9d5/fAsFod19AYAShZGYAxzQjcyFyhSdVR9AnheOnIbfPHykbty+hnWODnrW7eey0W7Jyy+UOWDMwDquAR0A8AEbphwvAAAgAElEQVSAq5CRlAf1Pp3S8Mi9DS90bJ999BC4HaCKEPAGZQlEiV3AQWdFAoVI0BwsZImJMpw4Be0eONSsUVaLRtkpTU/2efJc3oWwp0JZBsbP5vBxOO+hUvNkAwBFJfD6G6eSG//UuF5GUu2Ce5ucfv8vkOeDIgU8LHeSJ1gSUFRZRQwaVA0AjUOXr7/+mpp6QoJmzJhRyUFvOF+34X+v1zt8+PCaNWvSyBYNRXMZhsAKQqOmTUaMGPHZZ8sLnQXeAPLemTW8KhQDHCsq2XDwGNZHn5fJ+6GlSmEa+GD5jyF1cjnIl0aKAQoBinidY5hy2BOl38sqIRuIMgeWAJIo+VniRQH1P7m5O06cEEOyLYoCQVWVtd0ohcVgCCNm+plhl5h+tqqiulWJea5EYXUASeY/AxS63B/+ZW5C/foEQBtMUeYoq9EYdakiCYYaNWp+8cXfMYf63zvZAl6vd/ny5UhBw50ECHRoh45Yc2JiYlq2bLlnzx5sfHC8Jwfl4uLiCANSBY4IRES76Yc6AH3TH8FVZ0CSpM6dO2Mdxfp61UnoF9woC+DC6b59+x566CFC9+x2+8cff+xwOCgXCDViY0Enqyrg8/lIJUMQBDkoe/j+N+zsz58///DDDwuCgAjvM888g/edMGECCXcMGjSozMwoijJ48ODIYQc/Xrx4MV5SulAIrSqK4nQ6jUYjgrCCIIwaNQpxKzkoo+8yTEEUxe7du9vtdoz55ptvRgz+sCHGOfmGDRtwAISIGC2tl5l/PDlt2jR8my56OFywYEF5k//SKfTv3x/vFR0dLQjC2LFjaVnS4/GUuTKJxp86darFYkHiANYKTGHBggU0Ait9u/LOeDye1q1bo/KvwWBAje8IE9G16GFPy5JGRrYoishkR4QF17eQRU7PF3tEooHExcUlJCSQAwS6hTaAFRv/du3a1cQ/cXFxZRpHe+F1Cmv74+t0i4hkJUmSgzLWRqwtc+fOpSWWKgSS0MiLFy8mlb3x48dr09eGcXIliqLdbsdnjX/Xr1+P3BPtMgbm1ufzoYAMAJw5cwZdfeKLQ1SXevXqpaWlUenI2hE2KX2oKMrixYuxpplMpldffbXKfbGWvql+5o61AHYZqqriRBebo9Lj+FWrVj377LNxcXFEbY4IYI2lv9p+lpZkcM+T1Wpt3779ihUrDh8+/MvNTm9WROCXp6ynoFtAt8CtYgHsrJs2bUojWKvdtmHTxhJfQOb05kAAZk2DpncfSqqT07T+mR6ddys+8HupfH4u7yxy7JgBvwju8b+M+akCZBXCiXTo9sSRRnf/3Kbp+ace2ZF/FkSRqULLwJSaWVphgirKQSsgMnKpAm8Mg3sS0xs3yGrdeOeezaD42Ukmc6GIMvcKKKoggiyCJIJEGDS7rxegBM4ehfuabWrRILtpfUfj+od6/u7Qzp/Aj6IfTGJaZd8QAM3vp5GyDgLkFcGokcq9jU42Syhq00y6v/npcWMhpwicHH32Mn0PKQBBVhAOQGOnoB2BZ2RkNGvWDCdHKK1gNptr1669a9cuBqF6L9mRDHp7B2jXv6qqL7300iWsmXeBeGi1WuvUqfPqq6+uXrvGy+uHAorCHr7kB0mGgAzShcJCJ8BegGUF4l+P5x5iSi3lfEIi5CgVo4mj+vwAFwDWFovLcwq3BcHB2Mq8IgcZtBwMiAHJr6oyq6wuN3vUCqus6QCfZ2b/Lfu8m69S+NgKCITI0Jrk+SqHwpc4ZLbaouCqCovhAjgD7HZuuYSD2CKwAobEZBAAVwDStm/7zWOPRlktaBu7/S6jYKhhi7EKURYhKsoQZTRGzf5wjhiUAoEAjt4vu79+cHtZQDvmxHZbVdXi4uJhw4YR1kwjSZpl04Dz4sR88uTJHo9HO4/ThiOGgmUeVjeL6gB0dXsiV84PAtC46ojua658jR7jJlnA6/Xu378/ISEBB4iINn700Uda9Pl6Z01VVRqeCoLwr3/9C+8oB+UtW7YkJiZiG2c2m5OTk6kj/Pjjj6k1TE1NLTOTiqJ07dqVomHAYrEkJycTCFXmhehj+qIKR8uWLfEqtMzQoUOHDx+ekpJiNBq3bNkiB2V0effQQw8R+2D48OGUSUwcW3Y8uXTpUmqyDQZDZYDOZcuW0Rr+q6++ipRtTLPMzNPJRYsWIXCMAy+j0bh3715S46Vo2BPg4bJly1q3bk1LESi+IQhCixYtvvnmG3TxTBdWPnDffffhIzaZTNOmTSPzUidEO9pcLpe2aAcOHFi8ePGTTz6J9PyIR4mHiBprx5o2m61nz54LFizw+/1ut1ubYOk843Pxer2JiYmIjSYlJZWOdmPOkEEqznNVZQb30RcVFWnr5MKFC6kClzeAuNoM0KrJ7NmzaZ1g5syZ2vS1YUxfVdUnnnhCC0D36NEDJ2BoH6rMiqIEAgFVVTMyMl5//fUaNWogvoYvDtaNvk/3zc/Pl4Myelulal8ZU2sBaIPB8MYbbxCH+mpNocfXLXANFsC9SoFAoLi4+JNPPhkyZEitWrWo39S+v9owNZgXG16KjCfNZrPVarVYLO3bt589e3bFC3VXm2FtO6YNX206enzdAroFbl0LYN86b948anMEgxBTI27j90yVMTsbpkzMa9V4f7P6uXfXzklp9vPGNZw1egntY7gZR9cwcAmARijPq8C5HHi6//nmTY/cHX+oXfNdxedAcYIaRNd/HgAPYs3sSv7B/x4XvD8R7m2Q3qB+fuNGx9b8DfwFIPsY0VhVvKriVYIQlCHI+NAMfeYAdFCCoASKojIYUS6Agb870bL+yca18hrXO9v5N/tPnwIfYzyzL08n/FflF7DE2E9MMIF7NRz7jrtJ/RP3JqhtGrOc9O31H4cD/Ap4guADJQAi/waDwBnQLJHLPjk5OQ899BChz8TPqKRS2WVp3S4HSKhyuVzodBe9CuF0Bvs7FJXKy8tjFAfOh/cznJcx3H0g+5nmOCMkFwDsAphf6H0/x7uqGE7yJYyyjaQBoPHhBn0BXmmD+QDfA0xOL5qcV5gGkAeMEM+QbF69/V6fXw54vW41JDej+ABOqfC3TO+crJztHEFmIuDgc4eqVcT9+RvBmNGMHM3S9LMIeQA/ASzLyVp14Vy25PX4nArDvUMANK+cDG0HUKQgI1wfOLBvyJAhMTExgiBECeZYa6xFsFgES5SBYdA2m633031oT3BEDvTD29UCOMnavXt37dq1kYtGPDwaUuJ5RKJbt269Z88e3Lyuncdpw9pxYHnh6mZPHYCubk/kyvnRAtCCIDRv3vzK1+gxbp4FkpKSzGZzbGwsgpVIS7zB2enQoQNuEDabzY8++ujBgwe3bdv2yiuvoO9sJM/Wr19///79iGSpqpqWlkZNYXR09MmTJ7V5RnxZVdWGDRtSNEwnPj7+s88+00YuM4wgKSpNox9hgmXRZ8XatWtJ0aJ58+ZEKBsyZEhEgggZY5bGjBmjBQgiYpZ5uHPnTlQhMJlMqampCA4SYlvmJUjPzMnJQbDPZrMh1mCxWGbOnIn0bbSkyD+HDx8eNWpUQkICsVNxRIKmGzRoUE5OTmWw8jIzc5FgO3nyZHoKDz/8MNpN2wnhhX6/3+FwrFu3btq0aV27dq1Tpw5eRRajQy3oHBcX1759+2HDhs2ePXvVqlVHjhwBAHLSSCIzZeaNeKzffPMNdqUWi6Xv033Li3y9z5e2yXW9Iz7TEydOkIUNBsOnn36KovAI6WqzROGrzRWp94wdO5aGMp988ol2gKINY/qKosyZM0cLQBuNxm7duq1cuVIOyrgcggEA2LBhw5AhQxBxxtUgcmBoMBiQ1k3y7liQypdCC0ALgjBmzBj0yFr5FPSYugUqbwFaFCFtx4srZJ988smDDz6IbWBMTIzVaqVVN+37qw1Tg6ldj8F+sE2bNnPnzi0qKqJdOFXImKOGIiJQeQvoMXUL6Ba4PSxQUFDQtm1bGj9jozTr/S8H9PrmgSbr72t6uMP9Oa2anxrYN5MBxyL3Knh5ycPE5yChaaimUVAI3bruaZp0rMU95zo9+O9t34MUFo9mOgSMDOpl0DNCgyArYSbriFeLmtQ/3qTehZTG/54/h8G9kj+EMqoQUBkNlhFLgyDRV2JeB70yiIoMgTyY/Krz/npH2jcsbl7rXN/uudw/K7sPYozIfsa/vDFnLFTmVJHxshmpddif0pslHmwYX/jAPdCsVn6XDj8XFITKzIBRVRFDALQY5DlBrisfmDEthU8+WZyQkGC327ELQKfxOIJNS0vDhLRc6cvNeTsfHTt2DP3WEPpsNpstFsuwYcOys7Mjd14ySJg5sfRy/Fbkf/M4cDwzp2hmQdEKV8kZ7k4SH0qoHpVlP4U9VrZE4Stxqlx2Yweok3KLXskvfjk7a/LJE2xDMVsXUWUulrFje9qfXh7e7ffdP13INuOKAKcAvigJTjx/4WOPdxfAcVV2s/UTqVhyl8eAVhl4ztZJsF4XAmwBWFhYPCOv+NN897lwofiyCGaaONhYFEWWfKoiZpw526dnb3wxBWO0wWjjMDQT5TCahHbt2uXn55dVaP3c7WMB7ZjT4XCMHDkyVB8EAZUM6DAi8Prrr+PeU5rlaadyFI4YCpZ5WN2sqQPQ1e2JXDk/EQB0x44dr3yNHuPmWaBGjRoojWq32ydMmKAoCipgYI6wmbjeuRs3blwM/2DThsIX2gm2zWb78ccfMRsIPJ0+fRq99xqNRpvNFuGHkMZeCN1qW8xu3boRwbPicslBecOGDdprCdJKSUlBsQhMQcvPff755xG/o8SxdUawb9CgQVqAICImXaINpKen0ygzNjYWgWwCWLUxKayqqs/nUxQFhQhQtiIuLs5qtaICdatWrXr27PmHP/yhc+fOycnJWC6cIeBSBNLlUlJSFi5ciMm6XK5AIFAxc5wyoA1c5KHv2LGDkEGLxVJUVIT4HXVCeXl5c+bMeeCBBwwGA3HJtZaPCNeoUaNbt25z586lWqG9I4Urk1sckg4dOhStZLFYtN4pKakbEyCD0Gjgut4XlzH27NmjrZMrVqxAeq/H49HmRxu+2lwhli0H5REjRtBoZuXKlTQ6iQjg+ysHZZfLpQWgqRo0btw4NTX1Of5JTU3FtQqtJAs+TYPB0KtXr71799JaEeb8as2LADThfRMmTEDFj6u1gx5ft0BlLIBYsN/v37t37+zZs1NTU6nuIXxMLwJuUtG+v9qwNho27w888MD8+fOpiyf0mdSZKpO9K8bRthXa8BUv1CPoFtAtcNtYALdYBQKBQ4cO0eAZUS1BuCvW9HzvLju3roPGd29IrPW3Tf+CEi+jaxY5uNLuJeCYMzYZyCYFIXBJy1mC1151NKq/o3HCyeTG+/72BZnNx9FnNxfyDahMjJeNaNjPKrhdMGKEIzFxd+MGGc2S/vPuW14G/slcZJknIDMdhtA3jD4zYmwQfBL4ZQA5AKuXwP11dzaPPtHm7oyUxM2njkKQk1CJ4YqQINNa4AIaXEWB4d+SBAXFMPbdjCZJP9xTJ7NNE0hJdCX9auMBPrkRWeFYJlVVDapMR0SEYJDRclFPWnYU5m/durl9atvou7gfOd6+Iz8G0efu3bujfJmiKFckqZC9bpvAsmXLkN+Af61Wq8lkSklJOXr0KM0FLgUCPvZIFKbuzaReuIhFAcAxgEnZxaMyCv5aXLwfwAkgi4wuXdGH09M5AC2iVMu/ARYXFr1b4HrjgmN6kfOboOriADTW4fyCC/XrJwgGwWBl6oibfzxwDmAPwLsZWdMD4tcAy/Nzv8s452D5Y7z58gBoUEMAtKxACcB/AD4JKv+TnjmuwL9chLQiKV9hRQvJP7NM4sKNyIsrsrqm+P0+NyiyJMOilWvik9sI9njBEmcw2qIMUTjqiImJSUlJQXcOFRlB/+1WtoB2zNmoUaMI5CQmJiZiC50gCDVr1ty4cSM5+EGII2IqR4facWB54epmPx2Arm5P5Mr5IQAa6+vjjz9+5Wv0GDfPAkuXLkVoklwna/HZq0Vqrq0c2dnZuGpNg1SSVBYEoW7duriqTxmTJKZL1a5dOy2rYuPGjYjn0ip3cXExzsCJQWw0GtG3UiXL5Xa7hw0bRkoUeLv77rvP7XYTxg0AKSkpNNXHrlprB0VRiD7cp08fElQyGo0kTaCNXzpMS/pmsxnRNCpj6chssBt2/ZSRkVGrVi2j0UidhxbIIKgX1bQJvzObzYmJiejKlkyKadIjKPO+ZZ6Ug3Jubi4C3/ggcnJyImK2adMGgRWLxUJOGsmkiEqj87rY2Fj0DJmfn1+eknVE4hUcoldrh8NBNUQQhIMHD1Zwye30E74Fq1evRlNjNVuzZo3X68UKph0o/MKCY4LPPvssPdbvvvuORicUoDtiNQaATz/9FCdXEUMiSqfMANs82Lv31q1bCWKjlCv57mvLqyjKpEmTSNBj+vTpui6e1j56uPIWwPVI7D6oX8DLUVJGUZT9+/ePGTMmMTFRW7e1yLK2GddC0tp3hOLUrFnz+eef/+yzz3Jzc6lroNeh8jnXY+oW0C2gW6DyFkAAGuMfPXoUiRrGS42a/df3/7+nn/i+eeKy5wduDQbBFeIvc84ygrgq0+BgsC8DzwLcISHDoy/kwWfLoHmDg22TC5Lqpf15kkfi9GaF0Ys54MahO1UOKrIXgNE8MRtv/U9Ro8RDzZvmNmt6aOQbrqJCJD6rnOcqASOUItqLGHRQZmcYy1QGbxCgJAA/bIY2SbsfqJtzf+30Lq0OuzKZSkKIUIqS1SpToCYMmkv+gi/AvplZ0Lvn0aZJ+1OaZQ54Cu69uzC5wd7/WwtedxgbDIGFbNwtKWKJv0SS5WM/H3934oSGjZIMUQJ+o6xR6B6DnLUIgpCSkkLElGsY5FT+sVarmDQlmTZtmnZuZTabmzZt+sEHH/j9fursNAFZBVZlQtiuwpD+PBX2ASxwed7IK5ri8Gzzy0UMqZVBDYS46xxojiw+rpSwGsBEnj1cgvnD4vxJBXlTT2d+kevZ5WeaHp6QnLkogn/e/FnsJbBYBMEkCPbRcz4+AbAwr3CmxzdDkd8tzJmZfvInjyvsEjHsuDDyxgrLmCqpCvOqeRJgqVN8u8gzAWCcS30/w/1teqE3TN8OX4r8eykMQCMSHfTLUoDLT58CeOStCcI9LQRzaIUD+R+CILRu3RodxoST0v/fDhbAgaiqqn6/X1GUhQsXar1V4845fK1Qxg03Sdvt9ldeecXtdkeMYBEu0LxlVxesbgbVAejq9kSunB8CoJFX26lTpytfo8e4GRZAyR7qv9FdKR3esBGM1+sVRfHDDz/EBi46OtpqtRqNRlxz69evX0ZGBq7OuVwuXL5GXYVZs2Yh/RnlzxITEwk4Q7TL5/OhBAf6WbJYLK+//jr+VLrdLPMJ4A7oBQsWtGnTJikpqWfPnjNmzPD5fAhckonatWuHg2qc8xO/DNPEOyKg1rVrV+0gqaioCAkLZd6dTnbq1AnTN5lMpJBAd6doFKBWHwB+/PFH4pyaTCabzUYo/6WJQDhkt9u7dOkyb968CDeAmElKtoJbUx4oIAdlh8MRvoPQpEkT/Em74ioIArKzEQNFxBzx8Q4dOowcOfK7776bPn06RouPj7fb7Si6QnQGut01BObOnYvZs9vtjRs3voYUbsVL6E1fvnw5PR1BELZs2ULFubYnTpdrA3i7Xr160b127NhBuDMFSt9RkqTx48cTmkaXIypt5R9iSWO0Hj16fPvtt3R3rCSlU6YIVwwgAI2rOEajcf78+dqp9RUv1yPoFiALYD2kw4vVmxTMN2/e/MYbbyQnJ0fgyNppAE0PtC8CYtA2mw2VLs1mM0br+3TfRYsW5eXlRRDifsm7QDnXA7oFdAvoFqi8BY4ePWq3WI2CYBQEq0mwmQW75W5BeCzW/N+rVl7w+RlyrIJUwnFoVWISGIyioXLtDO5UkJFMVSZOsXoltGq6q178zw3q/fud0Z4LOciSdijgUxiFmEPYHINmxFZFlgNMIuGt/3HeU39P44QLDeoe6dlzv4fL5vL8B8IAdIhrzEnQTKAh/A36lGImtOuF53ofT6l/7r6789s1/OncAZCKQRZVHl9kmtEcfb4MgA6jlnk50PvJ/Q3q7Etu4hr639C44dnkpH2rloHTyUSm2QfxQBWYQLDfu2PXjncnvtsiOdkWbWdDX7uNAGhDlEB7CmlUvG3bNpprVP6h3AYxJUn605/+RDQFnGFZrVZSI9H2dzzM0GeZWT3I/FHyRQ43B44/yMgfn++Y5vb9zS+fkdQg+zHAJFqCTO6ClMQvMxoTiOGKzBxlPg7wcf6FCfm5U3PzNvuVkwFwKOCWmcqHj2PQQTX4zti3WG7tdwmCQRDuenHG4oWZhbOc/tkSTHa6pxXlfyX5TqoKF4tm7ixJROay+7KlGeYy0Q+QA7BahAn5rqG57tc8ylvZxYtzirM4s5stqlzKN6YWXtDhqyQyKF6Ac9zp4oKikvfSc6Yf+HfT33cXoq04xqD5Y9euXRFhvDwb+tEtbAFJkhAMOXLkSPv27XEmpeU6aPEKfMVq1ar18ccfk7glTuTJBKXetas4QYlUk4AOQFeTB3EV2dAC0EajsXv37ldxsR71xlpADsq0gYLcamnP3LDsSJI0Y8YM1PZFQDk5OXnRokVavJhwTww4HI74+HhUZDaZTBaL5fjx45hhRLtUVV20aBFqgUVHR6PrMGJWVqZomA6yxkiOE7OkKAoSsQFg5MiRSI5GiOrYsWPaxGlQiE4RtQ06oqhXRMPHjh2LyzkGg+G5557TJl5mmJp89IW9fv36jh07kvYu9i5oZIvFgkLbHTt2fPPNN48cOeJ0OlFeAN21oakpQQqUed8yT0qS9OWXX6IkgiAIr732GkajlL1eb+fOnc1mM3Gfa9So0atXr4ULF544cYL6OTkoT5s27ZlnnhkxYgRil+SDrsz7VvKk3+9PTU1FDjjK+1bywls9GtXnTZs24coEDjfRhXrVlo7e3IcffhgnTkaj8dixY4Q7U4AqGF2CQ94PP/ywcePGdrsdL7dardHR0UgCMhgMZrO5bt26/fv3X7x4Mcp9oOaG3++njahlplzJYiIATW/Q559/XskL9Wi6BUpbABt8rOEOh2PHjh1//OMf4+PjcXxPzSCSTbBPxL/Yd1ADThg01Uzs7Po+3ffbb7+NWEQEgCp5F0oXRz+jW0C3gG6Bii2AzZ3kDwzs1+cuC2u6zMzvWbwg1BGEZlZ7Yv9nn//n2q8YmCexlBj6LCsquFXwyQrDoGUQ+S9w+ii0b37o/iaOBg3O/u6pcwVOBNhKAIq4RgcHoBlqp6ogqYqo+CGQD++PlxvWP9IwsaBVk5xHH9x39jQjVCM9WZNzlXtsCzltC6PPIDNyq+R2wfxpkJKw/976Oe2TzxzewzFFLrQhySWBoCegyGUA0JwdXZANvbuebtPs7P0peUOGQJPmrmbNj731ZqbHCT4v+EsCSokKJXDyQNZni7/q+bteNX/FpBFtdzEQkDmQtVkFo4GJNnAStNHMxjw4FhIEISkpCScd2n2ZmkLd5kH04IJ7PWl6NXDgQCy23yeiT0gGxPKPzPjMTM6lBMQSJtzM9MLPASzOdk4q9EzIK/o2IJ3mlHTOp1cZ+ixy6e7wWgJPmbv0YyEFwK9C0AWwH+CvAc+fixzvped8H2SyGDIXmC6SZbfCxMWVIJPN+HDuB/wFsAmCVYhu0H30rKkZhW/mOscUeqY7nP8nw8/M/SB+0IMlq0Ph+4X/MwDa54dAETDi9vQi56uFnv+XHxyZH5x5IecQ06Fm2b3E8r6UIELmTNlD4ejzGRD3Akwtdr9W5HmtyDWpIG+DVDxpxUeC3YwTN9x+enF8MmXKFJrPhtLT/93KFsBmedKkSTExMTS3Kg+ANhgMAwcOxE2lNEEjJhOaQTvPutpwdTOkDkBXtydy5fxoAWhBEAYPHhyxQnLlJPQYN8oCbrebxB+xHfHyz426/2X3cblcp06dWrhw4YIFC7777jsEnqi3o/ZOe82mTZvq1q1rMBiSkpKWLVsW0RRizGPHjq1fvx51FURRvNohGt4X/yJMRvCBKIq4CeXHH3/EbJjN5nHjxkVkFfdcY2YiJDj27NmjxQW0RaOwoih//9vf2WDUxnZFtWrVin4qL0DtPvO4zTegSZK0cePGqVOn9unT56mnnnr++eeHDx8+YcKE2bNnHzp0iGQKtJnBuoG3oAQpUN6tS5/3+Xzdu3ePiYlBeY1//etfiN2Tlfz8M23atIEDB44bN27t2rUul4t+xQTxySIyjo4T/X4/8bJL37SSZ0RRRG+WCMTbbDai21cyhVs3Gi17OJ3OhIQEXJDo+3RffDqVIeZXvuz0Yt533304yjGZTJmZmYQ7U4AqmLYCYA1RFOWLL74YOXLk7373uyeffPKll156++23P/jgg6VLl54/fx5pzrhWRBlDMXQ8LDNlillxIAKAXrNmjc4Eqdhi+q8VW8Dtdn/66adPPvmkFnTGV8MS/qBrKVphxR0h5TGg4+LievfuvXTpUhTrx7srioLtJB6i+1msuvQ6VJxP/VfdAroFdAv8cgvQSB4U6esvl7Zt1cwgGCxCjNlUw2AMKxobBJvdMuSPfzp84BgHoIMcgC5RQwA0E03IToduHXe2bZCRknihXeqBPUcYiMylbkuA0Z+55DPzBsjQZxkRwyDMHC83rbez+T2+u2tnP5J6/MxRhr15A95S5VLkkDIDx/vC6h8yMPD7h03wUOMf2tQ/+UDzg3//HIJM/wATUAOiu8Tv9gXFMgBoGXKz4PePr0uu90OHlOy334CUlnuSGu95eYTbz8Wuz5/L2rr5+6HP/3dKo9YxQl1BsHFiLMOarXabLdoeZeWAPV9vJBI07ZJ5/fXXMRN35kT7+PHj6McI50cEQJ8/fx7NonCBb8ZR5kxiVZVljokbFugAACAASURBVD6LEPCCiK4qMziDeI5T+rPDt9ynniOuMy1BSByARk498uvDqLbCBcA9HH1e4fNPdrqnOFz7ADJCdYtVSB/7MgBa5GIu23d8H4VVPqa2UCPpv5Z/O+ps8eg87+SM3K/98kmAIk7I5wlckkJH4Dm8QMKwYxHkQoDjAJ9K3lEu5yg/TPLAB/nBnQCnGTlaBRnVrUP4dZAXgr8vrHojOJ4H8BPArKysEbmOEX55WJFzXG72lwXnc0HZe/RwrVq10NdldHQ02nbHjh2hkun/bnELqKpaXFzcvXt3pDLQglZ5APTnn3/udrtxaobT8NJ8PhpYXkOguplTB6Cr2xO5cn4IgEZi2uTJk7VQwpWv12PoFqi0BXBQm5mZWekrqiYitq1EzlUU5dSpUzNnzty9ezdhbXQnbf1PS0vDXdLY1qOgM3FR6ZKIQHp6Oi5Eo3vGPXv2EHoYETPi8Gr7gIjL6RDTocMKAsXFoZV7yuGsWbNQ0dtsNg8aNAiJ9mg6yh7hjxESpRXcCH/S2vaKkSMiIJw9ePBgxF5tNtuwYcNoPSYi8u13SM9UVdUDBw7ggkQEOPVLzKu1GL4UqqrWrFkTufxGoxFFx7SPnsJUMVRVpZMRdUMbp7ywNg/aONrzlQlHANDr1q3DzFfmWj3OnWYBOSijTBOR8dnualFEHYyFCxc+9dRT2P6TsEx0dLR20I/zAcSmSfglOpo5LEJaNEWoU6fOwIEDcUWkdNdT2vJV9UaXTlk/o1tAt4BugUpYQAVFAklc9sn/1oz5lcXMmjUt9iEIQu1aCfHxv+rfv//6b9dIAVKGBkcePN3tPw8k/tz4rmNtG+8+uB8cYaYo3jfIEGiugsEA6ICoQNYFePb5zGYtTje5pzCxRk5y4sG/LWfoG1fJUEWunoAaBwjtMSVfRZRlxm+4uLvRzXU6ZBG8BdD70d0PJR1u3+iHL1eBKwD+EPp8qcSyylKmj8wzkn4e/uuprzu0/GeHVutfHHimzb1//dVdrzVv8u4rw//RoWPfpKR7DEbBEmUyMUq40SxERQnmKKPRwJRKDMYoE2/zo8xRVkEwEOiM7X+XLl0OHz5Mt7ujAtTZjRw5MiYmBnVIqFucMGECqfOx1Quu4sJ1MkBlXiklH/h8EAiqwRKG1cJ6FSbleSfmB1Z64ShX0iBj4rgxhNcSHs0Uvjm3mC14gAPUQwBzC92Ti6X3XfCtCukqc1jJ6xWLxwn9zB9gCfvKAaVgzXdftP/to02f6t3t4/8dk+l61wETz7q/L/ZnykwtmjBino1QnUIAmqs4M11ykYPU/wH4UAr8qdjxsrtkrMu3ooSxsHNZEZQgW4RBv5iM0Y++Fr08wJLlmiLZANtU+EuRZ0yea2RhYKTD+8aZrM89vjPsFWUft9udnJyMhsURSMeOHQGASEu/ZFzN76D/uaEWIJdUqqquWLGiTp06OAqllZuIRgbJ748++mhGRnhJ5Ybm92beTAegb6b1r+3eOgB9bXbTr7pmCxDWec0pXO2F2k43NEDhSeCoiMZGmCzKxdLM/5NPPunfv/9LL720c+fOytwXmcgPPvggIhEWi+UPf/hDZS4sDSaWznbEmQqSpfyXFwdLjdFor/eKFSsIOk9ISDh58iQSbEVRjLh1mYfl3auqzh89ehSHVrGxsdHR0Xv37r1zWCRag+OqAIKqEeerxNSEHd9gAFpbFm34agsVAUCnpaWhdO/VpqPHv40tIAflS5NevnBCTgUPHz48ZcqUgQMH2mw25DXjBmrtWL9MABpbJ3IEhIc2my0pKemFF15YvXp1RN9HGbiN7awXTbeAboFb2gLBQMglYHFhUd+n+2IziDpCOMrFQaPBYIgyGqOMwm87P/Lss89++dX3w/+0IuWeL1o3+vH+RptnTwkEfBozIGiHJ5gshqxCwC9D32e2NWn+U+t2wYSEvOTEn996mfGO3WJIb1kEVWReB4NcZANZoUwnVwVJCvpE2ScyhQb2mT3BndpoY+va61bMB18o+9yHHSfYMuD7Mn0GyHcUbt+x8/u0bY888myMaUCD+DF1Y142Cb1MwmOC0EoQmghCPUEwM/TZbLBaWDFNTJNEMBkEg5F9o6wW+10MnRcEo8lk4dLZ7CA+Pv6ZZ57Zv38/OoW74sgc8387/ZWDMu5kzc7ORvjMYDDYbDYKnz59GsuLNGUtAM0EwZn6s88PkgpwAWC9KM9xusbmuhaUwCGOEaMnSF4bVBnYF8FrhihjNUNnfny9wQHwb4APTp8bc8ExqUD8VmGUZC+PySFjBa+RuaiMD2QfBALg8oF4FmDx+XNv5eS85nBNzZHWS5DJMOPQgwrznS97blhBkY1dAnAW4EsfjHC5B7mKX3d55pb4dzPlDaY3HVQY85uRoLnOBgLQXq4KjXi2BMw14jYV5hd6x+R53nQERhV4JuW5/h5gxfECyKKMBC85KLdv3x7HHvh35syZSH2NIBJdllf9oLpaIBAIOJ3O5557jsafWi8j2gdtMBji4uLmzJnj9XppyaG6Fqvq86UD0FVv0+udohyUO3fubDKZdAb09Ta1nj6CSqRefcMMUiaYhScRhogYFAb4B096PB6SC6h8hufMmYMDdKSKHDhwoDLXavNZmXBl0qwgDsLKWLqDBw/27NkT82wwGKxWK4oL+3w+ks64YpYquNcv/ykQCIwYMcJisVit1ri4uKFDh2ox9F+efjVPQWt8WjCIWLSoqiLcZgD04cOHI17wqjKUns6tbgGUHVcUxePxHDp06J133mncuLF2TI9ho9GIvn1oDkCYC9GiMSYhMlartWHDhiNGjNi3bx9aiVZBFEVxu91a0edb3Yx6/nUL6Ba4vS2gyiFqZ25ubo8ePVDmHhfbkI6HokOmKMFsFYwWQYgyCkJNQfj1XdH9OnQY//3mYjEIPq/k84iyX2EMzyD68VNBFEEWFSUYkGDwoB0vD4M+vaBp0rE+Tx7OywMvd+7GtDJYdFlkYgUIQAdlBkpKXJwAbR8ECEhBOLRX6tDq4183+2LMy/u8hUyO4/82bNy5e8+YsePGT5w8bvzEse+Of2fcu91/3/PBDg83aty0Rs1fRVlsURab1W4zmmIEIUEQGhmFJjZzC0G42yA0NAoNBCGOtflGwWw2GE0sgO4ZjSbBFGWgLsPOXNWxT+N7mg4ePPjzzz/XElywC7gzRyOKoixZsgT7TTQRuctDHgkzC8dxEYYOa2bIjN2rMIUKN8D2ILznKnnLUbDQVbgd1EIuvhHmGofQ5xCSq3BBFiVEhkZXl/lcv2JubtGE7MK5AXVRbvE5FfyMH82ZxlyEGZn1jIysyGxdRJVLQHYArAz4Jhbmv+51vVNctMbHzlyi+ocVnwmGZq8Kk27mP/CM5AP8U4LJLvFVp+uVQscsl2s91/1Af5oEQGPmCblm6fDXLpejz3OL/KPzvIg+v+soWOovOcEJ4BKAL8ByjyvcOTk55JoiOjq6Vq1aTqcTd4tq5xG3d3t1e5TO7/enpaUlJSXRgJNE3ogETWPOxMTEo0ePYoNzSUPp9jBEJUqhA9CVMFI1i6Ioig5AV7Nncttmh8QrbjDzS9vpykEZpaVJXRp1AyIGhYFAgPBNbVNOSVX8kHw+X2xsrMViQQC6R48eFcfHXynxSgYqk2bFcU6ePDlq1KhGjRrhmiqOCwcMGJCVlYVaCrRaUJksVXyva/sVwdZAILBv3z6DwYDb9+rVq+dwOLAWRZAKr+0u1f8qrf1J9xkrLf1UVaVAAFpRFGRAo+L2DZDgoIJEBK62XMSARrjwzJkzV5uCHv/OsUBaWtpLL73UsmVL3LKKbSCJ+NMhatHU5B/c50gkaG0cQRDq1KkzfPjwH3/8EW0Y0bNgi0qSfHeOnfWS6hbQLXArWsDr9eKQw+PxYAAA1q1bl5qaql2QCzWDTIUiRP+NrvUr7rzwV4KxtiDECIK5Tu27n+r59HuTZ8z88/tpG7dlnsoIuLwQDIIsqnJQlEAMwOpVkHT3lw+l/uvMeXBzQjNKcHAMWg5qAGgFgj6fOyv7/P4DezZtXrd7/6Z/fP352LHTWzTuVTd2iCD0addqSNxd9woCA4XNVjvPllEwmljAaDKYongYM8xPCkKUxRYmL0eZomL5tXZBiL0rhm1+R7IzE9y4/BMTE3NP0ybtUtu/+eZbX/9zbW5OPkMvuSoItv/oK/6meIy/6VXO7XbjHGry5Mno/h1VXBA4i4uLQyoMsnQVSVU5bZkB0AySVhkQHJR9AEcAVnhhYqFnYm7OZihJZwsX7KPlPiOAy0jQKnduyYFliUPBLo4+/00JTi6Wpnvg40LPKWDKGyF2PRPe4FngHGRVlZn4h8wkO1wAmxRlqrNorM/zRm7WSoAsflFoQSacB0SNUfYjBEBzQFpWGUP5DMD7bmmUV3qr0Dkh68I3Qfk/PGWVycsopQFoLBQ+OzcqbxR6x+R63y6W3sr3TsovXup37+a0aIzD61qoygHAokWLiGNuMpkWL16MAw/t0Bov1P/edAtgE1FmNsaPH49KnjgiRbqD1Wol9Blb4Ojo6Jdffjk7O1tRFEI2ykzwNj6pA9C35MOdPHkyrq5cnFbpGtC35CPUM105C5TX0GOvHJGGFnfGnwiqLi8dXGRGzHTcuHGCICCn2GazTZ06Fbd432DwPaJQdIiDY3RIjfns1KnT9OnTz5496/F4KBpybLWHNyv88MMPm0zMwbjFYvn8888DgQBC5BU8i5uV1et9X+0gUhuuwvsiBp2YmIga6IIgaL1c4o1wkYbo0tqclPlCVWH2UO2OEkTvhfRmXeTsjx8/Hmu11WrNysq6Y8dkZKI7LaDdJUDOWrHRw5nYl19++cwzz7Rq1YowFAoQ2SSC3YyNeY0aNVCRA+fSpPLcvn37pUuXHjt2zOFwlGntiBeEfBKUGVk/qVtAt4BugWpiARplad08qKq6Z8+el19+uV69eojHRnN5X8EgGGMsMXVrMZUK1phGCaY4QUB5CqGGPd5qsJmEqPDXGGe133P33b9ue3/XLr1+8/ALiQl9o21PJib27/B4/w6/7frwb7s83OV3Dz/25G8e7fmbzo/9pnOnLt0ea5N6/90N6tljLFabyRTFvQAaOG7MuMg1uFxGfUFIMhkSkblsjLIYoywINxtMUbbou8xWe5TFZjJb8ctUie3RPAmTIFi5SHE85l4Qokxmq9XO/NC1a39/v369p783ZeLE8RMmTNi6deuWLVtycnKIW4PPS1UYanoZkzf8IMmS4RN30P9JkyYh9EwOElAMmpT02IbUYECWRWY+9mWQsNcv+mXZDfAVwJ8vFP0lvfAHBTKZMoaPk98ZSZlw53CAgcf+sISFzNnKpwE+yM35f2fPvFns/yjAxKM5tx7YXZgITOjRhXnL4JcDLrGkAGCTDNOzHeM8JWPz89b5g0eCkBdOufTDU5h2B7KWEdFmLgrPACy74Hkjr+h/Cos/dLk3ARzj4huoZh5UGACN33D+VbbxNMi2CuQBUxqZVlA8zi1NKoExud7pDvfnXv8BVS3gELYfMyGHbodHp06dQowSX8xnnnnG4/HgZtaIEXvpIuhnbrAFtG0CTZ22bNlSr149q9VKo1BiPJBLkpiYGIPB0KhRo+3bt9/gPFfD2+kAdDV8KFfOkg5AX9lGegzdAsBX1cMoQsX2wCX9Rx55BLv/mJgYi8Xy9ttvE6G44stv2K/FxcXDhg376KOPjh49qs1buJRs/HfTP36/f+zYsQQPDRgwAF2E4UDqpmfvxmeAnk5EoKpyglsEACA5OdlutyPuf/r0aa/Xi6gZAXlIP4/IBh1WVX606VQy8ZkzZ+JUx2Aw7Nu3D5crtOno4dveAj6fT5Ik2iGBzcWiRYsGDx5MRBKEkhFxxrYa94LQWB9PEiStdcCFc4M2bdpMmjRp9+7dWnuW2TRR1dUGtFfpYd0CugV0C9wSFsBGDLMqSdLGjRvfeOONNu3bsQbTECcINsHCfM0JlkvyFBaTXRBMdlO0iclzmBCAjhJMUUzQIvSxmmuahLpmU0Orpa5gMzAomKl52AQhln2Z+EU4qlEQuBQGO4NfRmI2CUINo6GuyVSTX2lmfw1mzmsOXYhgtMHEYGWTmXkLpBRj4n7Vrn3HJ57oM37CezNm/mVr2s7NW7cdOHQwOzfbJ5UozJMceoNj5cZV7QieCkLPIfiUg6ghGFrT6N8Sz/d6ZHL27NnkftBut2MvbLFY1q5di7cLqkFJEUUQZZAYAC2rXr9YwhnH24PSX5wlH+Q5v3dJ+QzhZbITzLGfGigTgBZB9oLi51iwh4tdLM7MH52X90pu3iw/bAJwh0qIlGV2ILHIXDhDkQOqWAyBCyDvBZiV75ziDL6VfWGVKmdy6BkVO8o0UUhDmv+mADhUOA/wlRP+Uhx4M8/x56Ki9X7pPAeOGeKtMria+0eMBKCDAH6Fka93Ayx0ie8BvCPBu0X+d09n/b3Eux/UIg44+zkXmwHeWj42wIEDB3BpHLH+J554AgBoF6OmMlaLKV6ZlrwDT+Ly3sWqOHbs2HCjxP7jWgINSvHFwb+vvvpqXl6eypx1XnJqcgeaDgB0APqWfO46AH1LPjY90zfcApXstmlIun37dmTJ2fhHEITRo0eTEugNz/5lN0SIpPQYmhbJqw9Bb8OGDbjnCHfBZ2dn42Y97brxZWW73Q+09VAbrqpyawFomjDs3buXaD5Op3PdunXTp0+fNWsW7irVZoPCVZUfbTo40vL5fCtWrBg0aNBLL700cuTIcePGjRgxYsCAAQ8++GBSUlJsbCyO3ux2u9VqXb9+vTYFPXwnWEDLeRdFcenSpS+88AKJ5SE7HhdXIgb6SUlJEQP9iAgIRvfo0WPRokWnTp0KBAJ+vx/rvM/nKxN6RoPTe6EN3AnPQi+jbgHdArelBUo3d9t2Hm7U8qk2vxn6xrg59z/4G+aQz2xmctD8YxLMXJ8jyiSYjQyGDv/AHfpFMSzYaBQsJoHRjTUfA/89FNlqt5kspkuXht0ACkaDYDBz0YxYQYg2RdWwWuOjLNEms9UYZUL6c3RMnCAY6ybc3fm3XR/v8tuB//X8mLHjPvzLvK3btuc7CpmANIAoqfw/e2K+gOQTAwFJDKpBVZVFiUGasiyWhnvkoExf3JxHW/S0Df6dPGrdtWsXPlOkcGLYYrH06dMHOSWM5MMQ3qAIEnc2qQZkpnfxneyal3Nu/gXH9xIw9Fnhehky04YGVbocgJZlYGrlXDqauaT0AZyU4VOne3xx8SQZ3s1xbVYhM0x/Zqrh/OvnYsoBvuUTVNUlllwAeQsULZRzXsstnloCK4o9Z/EqDvVejveyqoJnOADNnCAywBfghAobVXi3wDPW5fvQVbLOL56TFT8rJUefJVAlBkCjCodWiKOEe1zcDfBxgLGe5wBMLlGmOIr/WpB7VA54OPrMOEMK811I6h+Uq9WrV5MMtCAIOgDNH0j1/YPjVVVVMzMzU1JSiOOsldrQjkutVmtsbOyaNWuwSB6P545tWOih6gA0meJWCugA9K30tPS83jwLaMeRFeQCewJczEQmJiKnNpvtogOBadOmEYG0gkRu8E9EEa1u3VhBQUGdOnWIgThv3jz0qV3d8nkjn5e2HmrDVZgHnDslJiZa+UcQhNjY2AceeKBjx44tWrQwmUxWqxUHuN27d9fmQRuuwvxok1JV1eFwREdHx8bGkqQgTmZILg1XLCwWi9FoXLZsmfZyPXwnWAAXS2bPnt2/f38czZNwHq2pkB8tQRAaNmxI82HtQB9P4l+bzda7d+958+adOHECAFCqiBoiEmgqz7zaV4PC5UXWz+sW0C2gW6CaW8Dv96N+Ai345TkCf12288gZcEngERk05nA4ftq986uVf586eeq40eN7dOv56CNdEHA2GEyssTUKJoNgNpnMJqbZEW22Rpvt2oaXRzYxwjN+jQaDyWgwcR1nwWoQahiERgYhRRBaC0JTQaglCHdFRf3q4Yef6N3n2Yc6PvbOuHdHvf32lKnTP136v8d+PuHyMO9xQYX5KxSDssxd38kcEvT6UVUY8BCNzxSog5I3wKQO/H4vMknxJ6/X63a7CXemgA5Al663uDo7ePBg7ZM1GAwWiyU2NpacvXPcVvYDoz+rCkOHf5QC83POzTh36hunmIXpyl4GT4shJ4FBRiMO9ajsFLuSiVsooHgBTgfhOxHG5ztGuzyT80u+BzijgifsUZMRjfnXywBo1c91oAGYbsZ+UBYq2f+Te3Si07fYzWQ0XIwmLbI8iRyKDslGszwR8suqFidTB7nIxi6A2YWet53uURcufAdwFsCrgioGmPBHkKHPCgLQEBRVhdU6rtwiAjgADgN8XBQcm+uZGoT3AzA917nQkf9vns9L5g0yABpZ3CjogT8NGDCAvUrR0Uaj0WAwDBo0CHlRpRdFLiWlh26qBTwez4IFCxISEmibHe7GQ+eu+BxpaNqtW7ezZ8+iuFwgECD5wZtagpt8cx2AvskP4NpujwA0VvrRo0dfWyL6VboFdAuUaYHRo0ebzWa73Y5OIYxG45IlSzCm3m2UaTFCZ1RV7dOnD3bAgiD069evzPj6ySq3gByU3W43dgpmsxl382EA5w8GgwFdsbVq1Ur7vLThKs8VMt8BYMWKFchmRShcy2zVTm8wPGHChOuREz3Nm2UBWsAj1ANRYDyfm5u7bt26Tp06kVNBBJrpL4n5tGrVqkGDBto1DNzViNUG1TlwlWXgwIGrV6++WeXV76tbQLeAboHqbAHs9xGJk1WmZoCyugowKWTuSi7kFK50KYrdxenp5/bs2bNhw4Y07Wf71jT2/SFt249b03bw7860bbvYme0/bEvbk7b5wKZ//Wfbv3xdHvjivjpf3ltz5T3xfz557NIdGAap0RhAoQL6K6sMaL7sy9A8pqJBXwQ0w7DmpdGNFmIO6/eSkG8ocCn25aFL+bvzQqdPn46Pj7darXFxccgPwN72xRdfRGOIckAC1QuyJDPA9yDAJwUFc85krHa40y+5/uPPkD9amcPHfN2AnUTpaFb7VMXnDWQq8C+A8Rc8b6QXfVAo7VAZgdqpsGjIIVZARvw6CGoApADIEkAxV21epcBop/OtvNx/+sTjHBH2YRbRbyESp0MLFmHcOlzZJAg5HpzjdY9y5U115n0pejI4yVpUIVR5eF4Z/Rn8AfZllY9hyQp4AE4BLC1Up+RKU5ziFLdnZnHxMo9zHwQdWrBbDemMYxEkmcHqfr9/yZIlpNKA2wGXL1+OedfWxDuv9lW7EuOQVRTFnJycxx57rPTkBblrqMKB07G6devOnz//hpUEmRwej4cG2zfs1ld7Ix2AvlqLVYv4CECbTCabzTZr1ixi9FSLzOmZ0C1wK1vA5/OJojhgwABCPUwmE/p9vpWLdX3zLgdl9CF2/Phxk8mEvr8EQTh2TDO3uL5ZuKNTR65ETk5ObGwswXa4DEAIHWK+dru9Z8+e2kGtNnw9jEjMVvQKjes6JhMjUqFWNeGJ2KMJgrB8+XKfz0eo5fXIlZ7mDbYAbf3GNTwkxa9aterRRx+lKkqjearDuI5itVpr1KgRHx8fHR2t3QuM2yzwKqvV2rBhwxEjRhB9Xh8X3eBHrN9Ot4BugVvFAtjvX0Nug4oSkPwByc+RX6auIMuiJMuSLIcBXcZWlmRVkkEKQlBGzVxQgiBzLurCaRe6pvx4X/wPrWpu/stExmdmpGaVqRPICotPiHNE4DLoGZFoTidVQndg2rwysNteBkArCFFrIehwTi85k2NntGMhbfgarHQ7XXLo0KFWrVphP2uxWOx2xnY3GAynT58WJX9QYWTiEg74ngT4xJn/F0feNx7lqMKoyrjCEfkcQx4EEYBGMrIi8xQOAozPKHjlXP4HDnl9kMkxc8eFJNQsc7KyxBOQAQISMG+HZwD+EYT3nIE3813T84qOceDYCyAiao1XSxwOly5/MlxBukRiCzDZAN8E/G/nnZ9QkvcPteRnACfj3V9eRVgtCYrgFYEVXAmCxFjW7Nq1npKZF3xTimGKU5yan/+/JUW7QbkMfdY4JcL6KQYlBeDIkSPoFJQGQm3atJGDsiiKpBV2zW/r5aXVj36RBWhKsm7duoSEBIIIaOCK6LPRaETBdKvV2qFDh/T0dHLa+YtuX+HFpCO6dOnSBg0aTJ8+nXJb4XU380cdgL6Z1r/meyMAjRP4d95555rT0S/ULaBbQGsBXDPEpnzo0KE4zELIQ5Kk6iOyrM1zdQhrAeiaNWui/sNrr72GG46qf0dYHWz4C/OgqurRo0exU4jA78xm80UlGbPZbLVa+/Xr53A4tJMrbfgX5qGCy3ft2tWpUydkp8bHx7dr165Lly69e/d+4YUXXnnllb5P93300UebNGlSo0aNp556SpKk6r96X0Fh9Z+0FtDOneSgXFRUtHjx4tTUVBy1Y5XAoTyukRiNRuQyYzWuU6dOjRo1MJp2oI+q0IIgtGnTZsSIEV9//bWiKCiyEZan1OZCD+sW0C2gW0C3QMgC2ma5MkYhDJEiq4zaGeKl0skrBBTI+hkeavbXNnd/0an5mqceWVOSz0iwqI0rcXEDpqvLwWW6IwWqGoAWFUXUAoyqyrQgwt9LI6MrFOq2/hk7U6fTed999+EwknjQBoOhdevWny5dcvz8OQ/Xr9ggud678PMKyYUQcJCTf7neMWfVIxdY5XIqMsOtuRdBxmxWOIt5L8DMLNeEQuekrKxtAKc5sOvm7Gh+qRRGn8MBlUlA5wH8ADA5v+TNgsL3nc61UiCH05kDKgOgL91YU1XDvGdOqlbB6QvmAvNzOLPQOTHz3BcB13FO0/aVAqBlzrgPaYYEg6qsFLn8+QBbAN7PyZ9Z5J1WLE4sKFng9O7mGeNVO1Q/LtWncEhRlKKioqZNm9JSusFgsNvt5OORC1yHY6MO9W1d2ap/4YqKip588nnq7AAAIABJREFU8klajIkYkeIhLiSYTKZ58+bdsBK53W5Jkrxeb7NmzVCHeuTIkdWchKED0DeselTljRCAxrreq1evqkxaT0u3gG4BANSGW7Zs2R//+MfXX389LS1NFMN7t3T7lLLApSGSqu7evXvkyJFTpkyRJAmNpuuWlDJY1Z9AxLZ9+/aEPptMpi5dugwdOnTu3Llr1qzZt28f3VX7vLRhilCFgUAg4PF4nE4nAJw9exaZ8vQ2oYvCiNspiqID0BE2udUPHQ7H4sWLH3nkEZxroTgMkt+NRiPiy0itql+/PtVh4gShVrjVakUZGUEQWrZsOWzYsBMnThC7BNcIAQDdDCIYfavbTc+/bgHdAroFqtwC2O9XPllCgcOkUpWDe5egvEom5c6BQU99NW9y1oE0OLqfKeqivrMkAQeglaAqMpiPg5LamzIcM0J/Q2UCvNyFHeM+4/dqGNA6AF2ph+Z2u3HY9uqrr+IiMSLRMTEx7NBsEaLMbbt1G7t8yd/O/7w45+fdAG4AvxRisiNoS4+SiV+ITA9aVVXmQVJhIhYuDjcvcMHYHO/03LwtwLwOFjFOtOpkIhvotC+MOzPgGr+MUn8KYJkb3sx1vlNc9JXiS+fMZVFh6HOQQcVh93/hsvKFk0sHKofOf1Lhrz5lSr5zaV7ePjVYzG8QgEj6cxiAZm8PKJKoKrkAP8jK/BJpdH7xVJdren7+omLvZhVyeArh24QVr7WjbVU9e/Zs+/btccNoTEyMIAh2u/2RRx6JoOzQRZSaHrjeFigTul2xYgXyq7TcZ9rBSWC0wWBISUk5fvy4JEmKotyY+S/S5hYsWIDCoWaz+YknnqCxMa5kXG+jXW36OgB9tRarFvFJgsNisTz++ONlvirVIqN6JnQL6Ba44y1Am4PueEtcRwPQIHXatGkzZszYtGlTBHtCuwGVIkcErmP+SiUdcWs6LBVRP1GtLYBrCaqq4mAXqxmiwIqinDlz5oMPPkhNTbVarYgva4fp5IISJVni4uJwDka4c2nic9u2bV944YWDBw9ShdGOf/AkVfUy41Rra+qZ0y2gW0C3QHW3AKJ62r+VyzGCf2HlXLyGCSQo3BUdwyIlGQIhcY8wf5awy3IClwSgSQkaA9o8hfByBaFAojlXELjUe2jTuaPCEf0pAGRmZqKXF+rHTVabYLYJlmjBGi1ER3d/8YWP133NmMnhD2p0yKBKshyQ/KLkV+UgA4a57z9vEThVOATwWQDGF4oz3fIWYMobOaAWglgCqsjkNtBNIOHOLKBwGedCgM/yxem5Ja+cy5zrde+FQAEwrpDCNKWZogtC11TjyPcg6kL7OU/5NMCneYUTz+Z8eC4vk8t3uLjnQPKUSFUBAWheMrYQg9LPqwDe8Uj/4/K/mZu9qCj/kMKI2Qxb13xQiU5zAjZt2oRyzwhA22y2WrVqpaSkFBQUaIc02mG89nI9fF0tgGsA+CDcbreiKC+++CJ5FCwdwNcBweipU6d6vV45KNNAFAXoqBZdv5w3b96cRKgtFktOTg7di0Tw6MxND+gA9E1/BNeSAQSgcfKmA9DXYkH9Gt0CugV0C9xGFtAOblRVxbV3OqmqanmDIW2c28geelFuggVw1O52u8+cOTNlyhTU2UC3k1rtZsKX69evLwhCcnIy8ppx+K71nIl8q5iYmOTk5IkTJ+7btw/Z8T6fr8x6iyepqpcZ5ybYRb+lbgHdAroFbh8LaKHnUhTTCooZIkwjkszcuXHaMqfKcsozB6B9nNQc4s+WAzprf71KALqyGPSl3qOCAt3eP0X0p1hYOSgPGTIEETdjlEUwmgWjVTDZjAab0Whh0lh3We9uUG/MuLcyMs4j8CoGL5NeFiHIUGmRizJzuPkLj/pueu5sl/R/ABlcjiMf/A7whbedkvTzJQzaz0BqWJ3nn53veycjf57H/z1AFogB1c8qB3epyTBozkT+/+y9CXgU1Z73X9VFdXW3nYWBAIMIjxfkAR1f1gkkmSQkExJ4BfRe9Oqfi6+vy3X0KiNLHpZkssDNOoAwLjDiyCMuVxjJKwITlvyzmhD4I8uAwquAI9wwQMIl6Y69VHdX1d/uX/LzWEkwhGwNv354wqlTp87yqe2cb/3O70BRqD5rqr9wu6Zd1dSvNO3d+sY3Gn5Y//2VwwFbbJ/qdzz9Q8D1x08XQSDUas2teDTFFaj5/1F9a2yO3193vPIX5+v2plLVfQMwMbeFz+uDKYCwp76+/pVXXkEFH01ohwwZ4nA4WHsdXel39sXWf1oHzjbh0lVV9dSpU7GxsWBZ3FZ6ht4smEqMGjVq7969brcbplBjR7QXBGiHw/Huu++CAQcugbh58+aWi7H1Suo/kDVNIwG6X52OzlYGBWhRFGfMmNHZwygdESACRIAI3IkEWjsYP02JdTgcGNnJwJ0IhtrUgwTgwwYUIMvyd999t2HDhkmTJnEcJ0kSO1ERh1s8z4eEhAwfPnzUqFGs62dIADo19OnDwsImTZqUnp5+8uRJLAgcPYNlCl7V2EKIwX4/JtCZFGF6ChABIkAEiMAtEuiqAO2XBh2Bf34r1RZxObACYavQDJ40Wnd1ygiaBOhbPHudTs6+QPEdCq/X1NRU/1vebDEMMHG8xPESz4kCx1utJm4Axxk5zuQXpadOm7puw+vfnD/nd/MNRtCq/IMmOzWv4tMcqt/R826nltfwQ/af67/waf8dMEC2+51v+Gw/ebFQW1cd/EmJbtK03Xbtn87VpzU15/3Q/EXAa4fTLyx7WlTngCE9Wjq3aNlgER2QmOs17azmK9bkrPON+Rcdx/36tdbsV8VVV0Ab96ntuM4IfB1RnJpWr2nVmpZz44d/qLf/vkFebfMeCkT6PUe3JaxqNputuLj4mWeeCQsL4zjOYrFIgR90lgYPHvzNN9/4KXlbHEfr4CP/tnlTTA8RUBQlJycHuqY3EaDBI83vf/979jODzkiCPZs9UVtZlh9++GGw2IAK8zw/bdo0mKGIF1VPFN3lPEmA7jK6vjwQBGie50mA7svTQGUTASJABPoHAbZ/A1/g2bl77N6bhPtHU6gWwUTA7XZfuHChsLDw4Ycf5jgO3DdDD9hgMICUDH9HjBgxcOBA8LYBCbCjjJswHfW+++7Lyso6f/48WANB75mdxAomKnglIy+IIQEagVCACBABItDdBLosQHt/SYBm1WTWzPkmYfaQn4XZVv/cBYd/7Ylf+oevl58+6rMZ3g3hnxC0hsChrcPhuHz58oYNGwZFDA28uwWOEziO5zhugMANsHCc6BegOYETjIJoknjBEBUT/Y9LFh/8f0tuNNscmrdZ8wYMkLXtf657478uvVFv+1zWrgZkX7dPc/pUe+BCaVVyQYD2nwhF09wB4+X/0rQ1/9XwTzY1zW7fEXAh7fDv97asaegJCN4BC2g5sKKg3wYbsgkYQtsD9svVmvau/ca6/2quCFhe/8WvjPudfngD/zoSoL2a0qhpX2vaNqd3+V/8ts9ZNuXfPX5P1lpANHeogcUPWy+RmqpDixctmTBhAvRz0OQZNx944IHDhw+z/oJbef/s/9b86P/eIHD27NkHH3zQYrFA9xUWL2nXAtpqte7atQvrBJ8KdH1U9kRiym4MfPTRR2D4bDKZ1qxZA5YcZrO5qqpK0zRcdKcbS7z9rEiAvn2GfZADK0CLotgHNaAiiQARIAJEIHgI9HQHKHhIUE07SwDcOjudTphR6B/+KYrL5VJV1Waz3bhxY9WqVdOnTzebzeHh4dD9hQW4scuOyjIbMAd+EGMymYxGoyAIoijGxMS8/fbbly5d6sy12pFBEHssG+5smykdESACRIAI/JxAq4WyXgj+eapf3ALnCN6AkNhRYiyqowRt4/EQDLRN0zYGEreNp5ifEcDXKC7B59NUp+y+fOXKmf/7zT9lZg8cFOH3xcHxgiAYjQNM90h+OVrwv+EHSAP8HYMBAi8Y8N/c38xb997bey/852dXv/nov89sOfvll87mHwLqM3jJ8LUaESua5v/w7HVpHllz+x1neAOLE36taWsv3XjtauNLV+q3eLVTAa8dgdPp9yGu+vzCs9//hn+ZSv96hS7I0O85w+MOrFLo0bTjqvavduf6qw3/cdVuC+jarR4//M33qZrH4wt8/G75AuF3Xd36u6JpxZqWXn/jlcv1OU2O3S7trEe7LrcYL9ddvvbxx5/krM6ZNjWa8xuEG5h/nCAYOc4QFjbQbDaLojh37ly73a6zUe2oe9NaPv3fUwTA6GHt2rWhoaG6OXwmkwlMjCVJslgsYG+RmJj41Vdfoek63iy6QE9VV9Pgm9CvfvUr6HUvW7bM4XDAmpaSJP3m17+Bfns/XNedBOieuyp6MGcQoMHXOAnQPQiasiYCRIAI3BEE2P7QHdEgakQvEUDrCY/Ho6rqiRMnsrOzx4wZw2rKBoNBEARQn9HwmU0AYbAfYeN5nh85cuSaNWs8Ho/L5dI5y+vCMIy9ztlwL8GiYogAESACdxwBVHZ1gZ5p6K1Kw7pK/eTs96bVu9VSbprZnbsTX6OsAO03NvY7StEcLrnuv6+sXb9hWGBFB0EU4f0+QPL7g+b9+nPgxwcspOEvxERIhqhxU1956uPjFc3+7xqa2yNDnsDSL/+2CNKegL+WFsTfadqWy64115yLr/5l5ZWrlQHzZ5uiOT3eZp/d6WuWvf6uiuxRXV7V7Rek/UbTXk3VVL9naIem/SXgr2Pz2YsbGpo3X20Er82+gBdyKEPxtajP/tlUXlnxym6nw/mDvaViAXPpdy5eesvW/HxF1T98tnfxv/zrssw//vqJp8aMGQuN80vxYotTbEZ9NkiSmef92rxRNIWGhm7bto11+tzSQvqv1wmg94xz5849+uijcBJ1f0F9BlXaZDJZLJadO3filwMI4M2iC/REg0B6VlV127Zt4P3ZYrFcvHjR4/GkpaVh5S9cuNATpd9+niRA3z7DPsgBBWiwG+qDGlCRRIAIEAEiQASIwJ1LwOl0gvqsquqFCxfeeuut0aNHg8oM1h9oIWIwGERRRA36JhbQMP80JCTkoYceeu+99y5cuKAoCnbikSV23zGmkwE8UBfo5OGUjAgQASJABHQE2kq8/Um+bVs7XfXb3exPLWi3gv0sUidAg0MMqGOzw+FVlOID+5evWvlXEYNR/ALzZ3bTr0oLBr9NsBDw1HGPgbP4BdkRI++Lj49/+umnC/658JN/31H5RdXFuj/LXo+itNodezRF1m5oWk2zVvjNn9dfby68eGW/31t0i++LgAMOn6x5ZFXxqa1uNFq9Ryua4vdBrXmaNfWipn1wo27dn7/b9P2VMwHraUfAeNmnaj843W6PVw0I34qiNDQ0nDn9VXVV1d7du9JWLF9fmPvrR+empMycHBPNmaycdRBn+SvOHM6JJm6AX2s3+v0BmziONxhapHdxgMQK0CA9cxwXFRVz4cIF7F/1s1N9l1bn888/HzRoEHrb0F23MMkPIqOiokDqBdtnMM7QuT3sBYhNTU1OpxNW8xYE4YUXXvB4PLIsO53OsLAw6J9nZmaCVN0L9bmlIkiAviVc/SUxCtA8zxuNxv5SLaoHESACRIAIEAEicEcQQJuOgwcPgpMN7JGDjznoqXMcFxERIYoiz/PoggO1aTwEAmPHjt2yZYvNZnO5XB6PB8x/0NJZVVWIRPn4VkHigbrAreZD6YkAESACRAAItJV4+5N827Z2nTlv/akFnalvX6dhBegfnE5N0xrtNtZmWfZ6YKXB/9i/Lz0jI/rvYsL/aiCYQuu6AbAp3GPyB0SB868W0foTDIYBAf8dgUTCAD7MbLx/2F9HT/zbpMT/+fKKPz7yj8sTs3KmrvynR3PXFZ3+9vPqYwcr/7/qLw5XV1WVfVFeVlNRfqi6ouZQRfXhiurDVYeOVB2qrTpU88WhL/bv3VW8d9f/2b93a/mBp/5tY1xB1u82vPH7nHX/mJ6dujztj7mF85/4f2Yk/v2kSVOG//UIk8liNpsl0ShwvMFfR95qMQ3gOLPYoiwbB7TYehsHiJIkhoTcA8sJgoGzwTBAksytMvRPLjjEAVJExNBdn+0Gz7yyLJMFdF9f1/7yz58/P3/+fFZi1rnqhpML121eXp7fi3zrcpFs/dluJxvfE2FwjpeRkYG98XPnzuFaKa+99ho0Z+jQoXZ7i/F+T1Sjy3mSAN1ldH15YHl5OQ78TCYTrJ3alxWisokAESACRIAIEIE7iwBIw+PHjweTZ/jbOlL0L4MMTpyhXw79XdCgYbqi2WyGVQfnz5///vvv19XVodYMnJyBcSzLDAyisR/P7qIwESACRIAIEAEi0PsEUOYHJdqrKKwkDXvZGKjhN+fPbfrXzS++9NK4hx70r1No8JvNWa3WAQaDRZT8FsEDRLPRH4CJUyaL2d+dAGcdBn9A4P1+lI0cb/Rr1WaOs3CClROt3AArJ1j8e7gBIPG2WFUbBd4oCZJlgNEiSvcMMJoEURQG8BLvXxnR4O+m+EvlTEbunhBu4GB/xv4S4J8hYLPc0qPxJ+Y4I2+QDH4Z2iwOkAy8KPAirLnIVLLlgFZ3z2FhA0GJhgIDe/lhw4Zv2vSvLqdsszX3/umjErWAS3EQjsEoGP4eOHBg1KhRBoPBbA5ce4FLkZ3GB2K0JEmjRo06fPgweFVGf3F9Bdbn9Z0/fx562hzHPffcc7jeoKIoN27cMJvNoaGhHMetXbsWPelBbcHOAy2jr169umjRooaGht5sCwnQvUm728oCARqed5Ikffnll92WNWVEBIgAESACRIAIEIEAAVVVhwwZElhfyO/VEQaKoEGj5w3orKMFNLiBtlgsycnJmzZtam72D7dglqLD4XC73Wj1A3o0yM3AG6VnNpJOBREgAkSACBABItBXBDojQGMar6KgcbRPUyHc7HB8ffbM3r178/PzF//ja8kJiVP+x0RrYD03URRh5TS/xTQ6jA4I0P7NVo8dRs4gcgMEv+KMi/u1ir6gLEMf5ae/gYMDm35D5kA+AqMK+/cYBI4Xec7/T5L8EqQkmsxGsygIoiDwfmVakAzCAH+80ThA9C+bbAyI4mjZ7C8EN0C1hhrw4IIjPPyvXn99oyy3uBNRfFo/XBSur66r3iwXZ/VhoatWrYI+rSAIIDRD5/anK6g1tHTpUjjc7xk88OvbPuqPAvTChQuhdiNGjGD71aBEr127luM4k8l033332Ww2bDIEwIBa07TKysoRI0YYjcbIyEhdmh7dJAG6R/H2VOYoQPO83wTp4MGDPVUS5UsEiAARIAJEgAjcfQSuX78OAvHRo0dnzpw5ceJEjuOGDx+OFtAtY6xAP8Q/KmPWIRRFMT09PTs7+/PPP9+7d6/D4VBVFWcCgqsN7M3r0LIatG4XbRIBIkAEiAARIAK9TADF5ZtYQGMaqJtXUTw+HywlqKvt9WabU/E0uRwu1VdVXf3qq69GRET4exSGgGSMGrQu0KoGBoypA3IyCr+Y0p8GNwK7Dbw/24CJs0H021FzHBdqEkNC/XKz+R6L+R6rxeL/5y/fYDAOEC2S35Uzx3HTpk6f+PCkWX8/838//b9i/i7q1088PvbhCX9930iTOWBLDeX4szYGllzE2vj3hoeHT5kypaioyGazQW/Hv9ai261DQZu9SQAn4Z05c+a+++6DC8pisbT1ucFx3JAhQ3ieHzFixMGDB9FfXGNjY3/oo7pcLjDZDg8PLysra3tpXb16FZZmEUUxLy9PZwQNzKurq8GGWhTFsWPH9uaJIAG6N2l3W1koQMN4r6ioqNuypoyIABEgAkSACBCBu56AoigoGRcWFoI/DbBu1hmJSJJkMplEUQT/G7hQODrugF5+aGhobGzs3LlzX3jhheXLl+fl5e3bt6+mpubrr79mYfeHzj1bHwoTASJABIgAEbibCaC43BkBmhWdmx0O+w8/czrh01T/6m2a9oPqAaSwJsSpU6f+9d0tKbNn/UxAFgJCM3jIAOtlkHmFgNsM2Iu20jw3LTpqWlQM/IuK+btpUTGRUdOnTp82afrUidMmT4ycMHnK/5j99/FLXnnxj2vSly9fuiZ3zZqcnJw/5uX8Ma+mpqa4uDgjPb26qiozPSt9ZXrKzFlJCUmh1jCO4/zrKwYWG4T+DJYcqMfPBOioqJg3/uWtS5cuoZcDl8uBF89PKytiFAV6hQCejvT0dHSdjF4s4LSyfw0Gw0svvVRfXw8ONxyOlpPYH/qoiqK8/fbb06ZNKysr04nLcDc5nc7MzEzotw8aNIj11gsNOXbs2ODB/iVDAcUHH3zQKyehpRASoHuTdjeUBZ9uiouL4Q6Brx9LlizphqwpCyJABIgAESACRIAIMAQ8gZ8gCCaTCRw6cxwXEhICa76znvIEQUANGiyJ4Bs5+uswGAxC4CcGfuzeQYMGTZw4MSnwW7RoUXp6+oYNG7Zu3Xr69OmmpiZYahwr5fP63IEf1A0WH4e/sAusjcDBNIQ9Hg+K6ZgPBYgAESACRIAIEIFfJIACtOLXjlX8x8azYb+r3NZ/v5C5qgUUaX8qyFbTtOMnT+QW5M998nHOKnLhJs7EByySOc4kcOYBfo8X/gUMDZzxpxULDQME0SRBLwUcgv1dfFxMbGxUTPS06Ki/jY6cGvW3UyInTp02eXrU1OiYyOiYyKiY6ROnTBw2fHir7MiHhoYHei8DwAI6sGngeb8TMkjDc5I4wGwcIIaYxHv83qc5o2gyDDDdP/qBpxYs3Lu32GZrlmWv4sNGK4HmqQHJHZHoApiYAt1PAPRZRVE8Hs/Ro0enTp2KFwnaUsAF03oZ+D1XhIeHv/fee4qi4Mp+WDMQoHGz/wRAJGz1EaI0NDQMHDgQGrVw4UJoCJhynzt3bvTo0f57SPR7ldm8ebPP6+tNYZ0E6P5z2XSqJvAR5siRI3DRgC1Sbm5upw6mRESACBABIkAEiAARuEUC4eH+UZkoilLgZwn4bcTOOgaMRiNq0DqX0Oi4o20AD2flbPAwBsYpgwYNiouLi42NXbhwYWFh4b//+78fOHDg2LFj165dw3mRsMKMTqrG6Za6+FtsPSUnAkSACBABInD3EmAVU1SffZrKxncU7pAaIz23m6ZZU2qbLuX/x8dz//DstFmJYUMG+xcl5DjDPRZ/t0EQONHoj/HrwAHfHYHOBPY9eMHgd77x056WvsYAyRD4N0AwCvwAv/OMVgdiA4wiON9oOSbgxBnCAdfTfuNrgZMk3ij6baLDQ1cuS/3Ttg//8/h/+he68KmM7qy1ypRAxUcCdLunuEcjYVFrNHxev349rput64hCxxWuD1EUH3/88cbGRqwbelCBmNYzi/v7SwAqhgK0zWYrKCgAA2dJkvbs2QM94cbGxilTpoCZCMdxmzdvdjqdsEwLatA93SQSoHuacDfnryiK2+2+fPkyGB/5neVLEllAdzNlyo4IEAEiQASIABFoJfDhhx9GRkYajUaTyQR9dBCLwagZHEBDPGjQaN3MuuzQ9fhxExx3tAwNOY7NDSPZQmFlFZw4OWvWrLi4uNzc3LS0tCNHjhQXFx8+fNjhcIA2DWuzgBINPezWNtH/RIAIEAEiQASIwC8TYMXlHhWgYdFCcNPh0rRtl4+/33Dq/2qOq3Kzqqq2602VX1T/y9ubkh955K/vG8kZBNEcEKP9XQS/PNyiPgscD1bS+j5EQKkOOPEA6Rn2G43GkJAQUQB76oDiLA4whlgH8AMMnEG6J4wzDuDGjnjgiZTxjyb949rVuw+X/ef33/g0TfH6NK8q2x2aovq8PlAqVUVTfCBA+5NomjegPvsCAW/rX5boL/OnFF0jAP3A48ePR0VF4bXA9kthMW2/72+jMTTwW79+vaZpsHo2WA2zpgxdq0bvHKUToMHh+NChQ8HPRnx8vCzLdrt99uzZoD6HhYV99NFHUDeUniHQ0xUmAbqnCXdz/j6vr7m5WZZlGPvBwvSJiYndXAxlRwSIABEgAkSACBCBAAHwGdfc3Pzj0tvnz58vKys7cODAu+++u379+hdffHHGjBkJCQk410+nQaPQfJMADgzAsRh0l41G/6RXHBXAYuXoxwOGEHAgrqMCowiw+DAajTNmzIiJiUlNTc3Ozv7kT5+Ulpb++c9/plNKBIgAESACRIAIdJ4AK5d2mwDdQfHg5cOrKH/RfLuun93nvnRD01oW73P5fC6v35BT9cu6l65cKfvii3/KXPP7f3hlZsrsCZOmtCxE8ZNnjtbOBSwYCP6j8W/LKoL+tQdFQRAFIeQe64y4hJTZ//Px//2/Xlu58p/z/7m6/IvSL2pqvvv2P2781weXTnxed/qC5mrUtDp3o0v1eVyBevm0Hxpt6Ir35wI0KM5gAY3qs7fVPQlw7QAERXcHgU8//XTQoEFwHfA8D51MtjsKu0JDQx966KFLly45HA48lTi1rjsq0uN56ARoKO/NN99Ee5Hly5dPmDAButYcx3344YeQBqRqVoPu6bqSAN3ThHskf4/HI0l+P0cwNps5c2aPFEOZEgEiQASIABEgAnc3AV2nFuf36QIAye12nzx5srKycv/+/Xl5eRkZGYsXL542bdqsWbPCwsLAgDo0NBQkZhgJgGcPmNEFCxiC1owDBpSe4SiQm6FLjRbZraNM//8wtGgbg/FDhgyJjY198sknCwsLs7KyDh06VFJS0tDQAHYuPy7eoqoqTtuE5rN+ACGGvShUVWVpsLsoTASIABEgAkQgqAmwAvSthrvccJ+mNWuqTVNdAXvin4yJA6sctlsNMFx1On+o+qKiusr/r+oL/7/KqvLKqvKKNv+OHTt6+c8X/YbMP/+5Nc2/QqLqF4oVTbNpWq3W9NHl/yz5y/nvNdmuade1gBDu18IDNs2BKrVIeIrfNUkgDBbQYAStE53Z6v+8bNq6dQLYYQMtFTL4/vvv582bB71ENG4A41/oaoKSBn3F7OxxaNnfAAAgAElEQVRsp9Ppdrs9Hg84vG05m4H/br1GfXNEu3WOi4sD3yPg/FqSpJCQkL179/ZNFQOlkgDdh/C7UjRM7nC5XOi6xWAwPPjgg13Ji44hAkSACBABIkAEiMBNCUCPlhVY24YhjSzL0IOHaY/wt63/5crKyurq6r1796anp69fv/7xxx9PSkqKjo6GcQIoy6GhoThgsFqtgiBIkgQiNassQwy640D1mTVv0YVZ02k2K8h/8ODBUVFRP37Xz8rKSktL27Nnz9GjR2tra2/cuIEDG4/Hg3o0NBlGLEAR3A7KssxG3hQw7SQCRIAIEAEi0H8JsHLprYa73ipwEh1Qgf0yMMi56k/5ta1Jq7cExen8QfV5VZ9XUfz/fD7Z55M9ys//ed1e2eXzuDWFyTQQ9KAArfpLdmnanzXtG817UfPYNU32x6gtojUYNweOapH/SID+6RT1agidrWmatmnTpqFDh8LC11arle3scRzHLmQybty42tpaRVFkWcZeK9Qb9dxebcZtFIYVBqsITdNkWf7000+x+aIoCoKwefNmTdNgpe7bKK3rh5IA3XV2fXikLMvscEuSpD6sDBVNBIgAESACRIAI3KkE2B7tTcLQnWWnLrJA4PN5U1OT3W6HQYLP68PEsizbbDZI39zcfPDgwSNHjmzYsCE7O3vlypUzZ86MiYkZMWIEfHoHpRh0auxVd0Z6bnsIfsuHNQ9NgR/OT8TVniHzuLi4WbNm/biY+IoVK9auXXvw4MHjx4/X19e3HbGA+Qzb/F4Otw7Ce7lYKo4IEAEiQATuQAJtpd7Ox3QZBxThPxz9J6t+LdgRUIfbrYDfalll1OROlq2ofg0a9e6A6BywaQ4UrmpOn++HgKGzf7FBf4CxmIZ6wLGBfPzmz2QB3Uny3ZQMJq5BZg0NDa+++iosFsJ259juIoR5nn/ttdfAjAC7o2yNsMfLRvbnMFaY1eLr6+vDw8OtViuIh5IkgQDdhw0hAboP4XexaBjFTZ48mb2RupgXHUYEiAARIAJEgAgQgY4JsD3am4TZDBRFAbfRoErDrFhIgDMlVVWFHr9OwIVkbre7ZT2fwGBSVVXM8Ouvvy4rK6utrc3Ozl67du1vf/vblJSUyZMnjxkzRmfs3O4m9p0MBgNYwcA0TEEQRFEEkVoQBDDHxhmaHQ1jYMkjjuNiY2NXrVqVlpb2+uuvl5aWNjY2tjueYSn1RBiM07syAu+J2lCeRIAIEAEiEPwE2lV7OxnZtdZD5i1CLzqxCKjPP3QsQMO7T1V9zT/Y/EsBKj5V9f8DO2iv6mX/KYrfnbT/5zey/rkG3bKj5T9Z9jodLW6ovW7ZK7t+2s/I1pBJq/qsqn4jaWgHeH/uCNhPmVGo8wTYfg5MUHM6nYcOHRo9ejTYFoD5M3b5dIHRo0fv2LEDLSGwh8lWAHu8bGR/DmOFMaBp2mOPPQZt53keVo+bNWuWqqpsz7yXG0UCdC8D74biYKiWnJzM3kg2mw1GHd1QAGVBBIgAESACRIAIEAGGAHZnOwowafsyaLfbz549W11dXVFR8cYbb2RkZGzYsGH+/Plz5syJiooaNmwYupmGThTOxNRJzDpzaXADggo19uYxGeaDfTNRFMPCwsB8e8mSJVlZWW+++eZnn31WVVV1/fp1YISuPGAT1HnU6HXeS3BOJSaGlC6XS1EUT+Dn8/o8Hg97jvryZFDZRIAIEAEiQATaJQDSbbu7WoXbFjNk8MIRsGwGjxeslNtBBrcSHRCgWUETDoZS2s+I1Z3bT8Hmwdb3ZrneLCfa14YAdIFAGWtsbFyxYgXMV4O1KLEzhgGe58G24Omnn4ZZd+AqrQ9nraG/aU3Tbt+AAGR0t9uNhh2LFi0KCQlBAoIgjBkz5tChQ35bfo/fz3mf/EiA7hPsXS8UDIJ8Xt+kSZPwYuI4bv/+/fDxpw8vpq63io4kAkSACBABIkAE+jEBVtNsN9zf6u52u3WrmUMNYZBZUVFx9OjR6urq1NTUrKysxYsXT506NSEhYcKECayLMwxDAOydRVEEtdpisYA/EFEUdbo29NAkSYLRDnjzEAQBPFBDZERERHR09IwZM1atWpWamvrZZ5/V1NQcPHiQdWbCDollWXa5XLBIjs/rgwEGyM2sLz+f18eeoP52Xqg+RIAIEAEiQARaXF50AOLmMi0r6HaQwa1EgwV0myNuXoeb1781M7ambLh1P/1/ewTkwK+kpGTUqFEcx1mtVl1nDGfCmUwmi8VitVqLiopQLsMVpKHXdHt1ubWjwVxA07Tq6ury8vKrV6+CyndrubSXGlYi0TTt+eefh7l9FoslOjr6woUL27dvv3LlCojd7R3aS3EkQPcS6G4sBj6VJCUlsQJ0WVmZpmm4Qk43FkdZEQEiQASIABEgAkQgGAmoqgrrImLPHrRaGH74vD5WusUGyrLc0NBQW1u7b9++zZs3FxYWpqenP//883Pnzo2MjBwyZAh2wMDQBiY2hoWFmUwmmPVpDPxAntYNh+BY9N0BBjscxxmNRtS7OY4LDw9/5JFHkpOTs7KycnJyNm3atHv37kOHDsF4CYcumqY5Aj/dOAo1aGwUBYgAESACRIAI9BcCN7WA7kwlf0Eg7kwWkOa2a9JxUazozIY7PoL23AoBt9udmpqqW1ewo0VBEhMTbTYbGAirqgqf89HumP3efytV6HraAwcOTJo0CXqDP5o1ZGdndz2vwJGwjiLogenp6WazGfzIjR8//vvvv4fMUS3EXvFtFtqFw0mA7gK0Pj4EBktLlizB8c+PljW5ublw/7Q7lOrjGlPxRIAIEAEiQASIABHoYQJOp5P1vOzxeGDT4/FgV1uWZVVVwW2FpmkulwtMhuFvuxUEW2O73Q57PR6Py+VSVfXs2bM1NTXHjx/PysrKzc1dvXp1cnJyXFzcgw8+GBoaCp00VJ8tFgt6+TAYDOhdmuM4DEMCTIbatBj4GY1GULRNJtOYMWOmTZv2+OOPFxYWZmVl7d27t7Ky8ttvvwWfHqg+99qAqtcKavcEUSQRIAJEgAgEGYHbln1JgA6yM96l6t7EP8bly5dHjBhhtVphkllHujMYQW/bto0tHzqHui/3bIKeDh84cAB6iSATw0S6ffv23U65aPucm5sLmVutVp7nwecG9NPYTvLtlHU7x5IAfTv0+uZYcO+Sk5PDCtBpaWlut1vnTLBv6kelEgEiQASIABEgAkSg1wmwwmtHYfhaz/5lU0KV2Rg2JYTZvTdv4okTJ0pLS7dt27Z+/fqMjIyFCxcmJCRER0ebzWb048HzPCjOBoPBaDSazWadcTRK2O0GULxm+4QPPvhgXFzcggULFi1a9NZbb23fvr26uvrMmTMdycS6eGgg+hAE79I4ZxMsyv3rNgXWh3QFfjeR72+OiPYSASJABIgAESACRKBdAmDVC7tY8fTNN98cPHiwFPjBXDSckcZ2hyRJSkpKOnfuHNuXw14c9GTYzXbr0I2R0HHyeX3Tp0+HqXIwbc5isfA8/9Zbb91+WZ/86RNU5CVJeuedd6CBt59zd+VAAnR3keylfMDrn6IoS5cuZe+u559/XlEU9rbspQpRMUSACBABIkAEiAAR6AcEcBRxkwA7COlIUGYP70z6dpvOWtbAIAcNscEBSElJSXl5+Z49e9LS0rKysmbOnBkXF/fwww+z6xkKggBuPbDLB246jEYj6NGwCiIYR2MMeJrGQ9iA1WodN25cTEzMo48+WlBQkJOTU1ZWVlNTc/bsWXZJdEVRcJ4mjJdAj0ZVuq1mfRMzpXb5UCQRIAJEgAgQASJABDoiAP0otr8hy/LFixfj4+OhYwPzyVCAxnWhITBs2LDCwkKY6Mb25dg+HhvuqBrdGA89pYqKCqzq6NGjn3322Tlz5mRmZoKZ6W0WN3ToUPTqtnr1alwX5Daz7cbDSYDuRpi9kRXcgbIs5+XlsSOKxMREtEbpjXpQGUSACBABIkAEiAAR6E8E2IFER2F2ENKjAnRHYFj3zZAG3IO4XK7m5mY0Nz5x4kRJScn777+/fv36rKys5OTkOXPmDB48WBRFs9nMcRyMuNACGgczrAcP7CjyPC+KoiRJ7F441mQyWa1WSZIgh8mTJ8+cOfPZZ59NTU3Nz88vKyvbs2fPtWvX2jYHZHRYBRFpt01GMUSACBABIkAEiAAR6DIBVVVBSP3R3Rn0VfAzPCzvjBo0x3EhISEGg+HHnszFixdBH3O73dhLuUmgy9Xr/IEgQC9atAg6XQ8++GBdXZ2mabIs49KInc+t3ZQ4qW7ZsmWw0gk0ud3EfRJJAnSfYL/dQn1eX3FxMY4rOI576KGHbjdTOp4IEAEiQASIABEgAkFL4CbjCtzVmwI065O6qakJuLK2PBCDZsVtN9sOG8DZWnV1dVVV1RtvvFFQULB06dL4wC8iIgJ6hpIkob8OcPcB8TBOA3+IIGGzPcm2YcwEE8fHx0+ZMmX+/Pnr1q3Lz8+vqKiora29evVqdw2cunbp4clty7ZrGdJRRIAIEAEiQASIQD8h4PP6XC7XpEmT0LYX+ieiKILXMhSgQX5duXJlY2MjW3m2n9BRmE3fQ2EQoCdPngw9ro0bN3ZjQdCZPHHiREFBwYcffogds7Y9yW4stAtZkQDdBWh9fAhcWyUlJexQwWg0ejyexsZG6nz38emh4okAESACRIAIEIH+SuBWBx63mp5td9tj2b1dC6Nnj7ZKOsYcOnRoz549mzdvzs3NTU1NjYmJmTFjhiRJsMoNLNQjCIIoiihJw6Bu0KBBkiSBhXVb22rw/sGq0uHh4XAgx3GDBg2KioqaM2fOSy+9lJ6eXlBQUFlZWVpa6nK5wPcIVk/XcFwfEvq3KMc7HA52+IRe5nxeHyxeD8tuO53OtpwhRlcQbRIBIkAEiAARIAJBR2Djxo3gWYKVv9qGRVGMjIw8fvw4TCnTNRO7Crr4bt+E7orP6wPPZrC0IPRnwJQ7NDQUXD+fPXu2G0vH7lM35tkTWZEA3RNUezBP7FIfP36cvet4ntc0DXvqPVgDypoIEAEiQASIABEgAsFJAEcgukBHrdElw82O0rPxmBgD7N6uhTsjQENxmD8qvJqm1dfXHz9+/ODBg1u3bs3JyXn66acTExPj4uIkSTKZTNCxBOlZFEVYXB7NnwVB4HkehWnshaL3D4xh84HDhwwZMnny5OTk5KVLl65cufKtt97au3fviRMnrl27hl5HwJtHc3Mzup9G5bpd6wqUpFHaBtuibqSNDClABIgAESACRIAI9AIB6BXAK76xsXHhwoWs9zBdTwM2JUniOG7Dhg3QW4DuhK6qvd83sNls48ePNxgMKSkpWBmbzWYymSRJslqtjY2NwaIaY/1vP0AC9O0z7NUcsFNeX1/P3n6SJJWXl4OT9V6tEBVGBIgAESACRIAIEIEgIYAjEF2go+rrkuFmR+nZeEyMAXZvl8OYGyu8Qpjd5fP64J+madA/BJcgrJgLxjiapkH38vz586WlpdXV1atWrVq9evULL7wQF/hxHAe6s9lsBrlZFEXwwAjxsBAQ2FZjGI8yGo2sSG0ymcCMGpZbFEVx8ODBs2bNiouLy8nJWbVq1ZYtW6qqqvbv3w8+HxVFgYZAzaGNMGaTZdnpdLIckADbzC6jpgOJABEgAkSACBCB3iQALps1Tdu9e/eQIUNw6QtW+2LDZrP54Ycf/uqrr0CzRrmsN+vMloULe2zZsgU6SxaLZf/+/ZDm0qVLHMeJojhu3Li7s6NCAjR7tQRBGBfHVFUVbzxw53fkyBFahzAITiFVkQgQASJABIgAEegjAqxAyYY7qg6bhg13lJ6NZ9NDmN3b5TBmywqvrADdrkEN2gtDuezi8mgijQovaNawCZ4uXC7XtWvXDh8+XFNTk5eXl5WV9fzzzycmJiYnJ6NpEi4KBB1UnWYNkawS3VGMxWKRJAnkaZ7nBw8ePHHixKSkpGXLluXn53/44YfFxcWVlZXQTI/Hw3JAOHfnuK7LFxUdSASIABEgAkSgPxDweDyXL19++eWX2864QvmLDbz44ovwuRpW84MmgPuLPmyOx+PZvHkzuCnjef65556Dypw5cwYqP2vWrLvTewEJ0H14WXalaBwbqKqKFiUGg4Hn+U2bNkEXvCv50jFEgAgQASJABIgAESAC/Z4Aq7G2G9a1oEelWMjc5XJ99dVXFRUVO3fufOONNzIzM+fPnx8TEzNmzJiQkBB2oMh6nQaLaXBFjcI0ytlwFMxURcfToHGHhoZCMkEQRo4cCdbTubm5aWlpu3btqq6u/v7773WDT7fbLcsymoQDonZFeTC41jRNURS73Y4DWlay1xGmTSJABIgAESACROB2CMBHZZ/XV11dPXLkSLbngGFYvgI3IyIidu3a1fYj9O1U45aOhU/grA0oftHXNK2urg68kFmt1rCwMOhUnD59GoT1BQsWwAf+WyrxDkhMAnSQnUR2pDF8+HC8/QRByMzMJAE6yE4nVZcIEAEiQASIABEgArdCgO0KthvWZdbTArTb7XY4HC6XCyqDpaMhtt1u/+677yorK4uKivLy8pYuXfrkk08mJSVNmzYNJqJCbxa8TqPWbDAYdGI0dnohgJo1bOKBmCwsLGz06NFxcXG/+fVvVq1atX79+h07dpSUlNTU1IDXEZfLBeNGdsEiWZZhuiHafOB4ErrZumZieylABIgAESACRIAIdJmAqqqvvvqq7uWO73Tduz45Obm+vl63MEYvv6DBj5nP6wMlmu08AIRly5aB3CwIwubNmzVN+/LLL0VR5Hn+ySefxG5Sl4kF44EkQAfZWWNHGpGRkXhDSpK0cOHCu/MiDrJTSNUlAkSACBABIkAEiMBtE2D7hDcZdPWoAK1pmsPhaNflIpSLAzNort1uB6/NbOuPHDlSXl6+devWNWvWZGRkzJs3Lzo6euTIkVarVbfsIQ7koAOMw1QMYLxOjzabzaIowl6wwuY4LjIyMikp6cknnwTnHjt37qyoqDh//nxjYyNUz+f1gYGSzlYaVjtkm0BhIkAEiAARIAJEoGsEFEWprKwcNmwYvKZhUUEI6/4KghASErJlyxYoyOl0drIv1LWKdXSUblIUdHU0TUNnIHDgt99+azKZeJ4XRXHKlCmqqoJZtCRJ8+fP7yjzOzueBOggO7/sDTZ79my8Ic1mc1JSEgnQQXY6qbpEgAgQASJABIgAEegSAbZP2IcCNE4+dbvd2BHtjOoNBsh4ODBQFMUT+MmyDLp2TU1NcXHxRx99tHLlyjVr1sTGxqakpIwcORLEaKPRiMoyOluE7jF4qMOuMgZgNIibEOB53hD44Qzf+Pj4yMjIp59+esWKFbm5ueXl5dXV1XV1deCXo0tnjA4iAkSACBABInCXErhJRyU7O1uSpNDQUFj+gZ0dhS9reOk//vjjDQ0NuHgyfA/WdYd6h29paWlKSoooivfdd192dna7Dp3dbndaWhr2Unbt2mW32yVJMhgMKSkp6OOrdyrcT0ohAbqfnIiuVGPZsmVwQ1osFp7nx44dCxcxewd2JV86hggQASJABIgAESACRIAI9FcC4BZDVdXq6urS0tKPP/44Nzd30aJFs2bNmjp16rBhw2C8B5bRoiiazWZJkoxGI4xgYROcUOPgluM4s9mMmzqrakEQTCYTZCsIQnx8fEJCwhNPPLFkyZLc3NyDBw9WVlZeuHCBVd5VVZVlGZdJ1EntOrRgTmW3231eH0rzujS0SQSIABEgAkQgSAnAaw4rD9+YDx8+PHbsWPgADH955gdvZEEQJEmKiIj46KOPYIUGzARerCh/sfE9FIYVJoqKijiOM5lMoJgLgvD222+zn+Gx9OvXrw8cOBCcQY8bN87j8YSHhxsMhokTJ6qqChbcmPhuCJAAHcRnOSMjw2QywW0pimJ4eDgsroJ3INsJDuJ2UtWJABEgAkSACBABIkAEiEArAZfLBdZG6OgDXFG37vf/39zcXFpaWlNT8/rrr2dmZv7hD3+YO3fu9OnTsfMMXWij0cjGoN20EPjp/FBLkoTSNqYEd9WwaTQaw8LCZs6cGRMTs2TJkjVr1rz99tuff/55TU0NeIdEGVpVVbfbzS6WCKo6upzGGb7YsWdbR2EiQASIABEgAkFNIDMzEz4M30SAhs/GkyZN+uabb8DnMs61grbjK7IXtC94ZR87doztG0ANhw4d2tTUpDsdUKW1a9fit+2CgoKUlBTQ02H9iV6otq5WfbtJAnTf8r+t0vPz8+HDC1hkCIJw6dIl9g68267m26JJBxMBIkAEiAARIAJEgAgEDwF2xiuYG2PdoQ8MBlYej4d1ywgOnZuamk6cOFFeXv7uu++mp6cvXbo0NjY2OjoaR4noRdpgMIBfDhxwtuueUhRFmFdrMBhA0RYDP7SkBkU7IiJiwoQJ8+bNe+655zIyMjZu3Lh///4vv/zy6tWr2BzUoLE5FCACRIAIEAEicGcQsNlshw8fjomJAekWFmZADZoxgObhjZyTk4PeKmBhhr7l8Nhjj8Gn6Icffvi5554TBAFe9Lt3725bMehyPPTQQ0ajked5k8mUlpYGnYqvv/4aFnBue9QdHEMCdBCf3LKyMuwlQ+DgwYO9Pw0hiAlS1YkAESACRIAIEAEiQASCjQA4qXC5XDqttrm52e12g/oM7qR1LQNDDV0kepOEub2Koty4caO2trakpCQ/Pz89Pf2ll16aM2dOVFQUKMsmkwk8csDgGTrhJpMJNGtj4KfrosMmpgeX0+hvGhOHhoampKQkJiamp6dnZ2d/8MEHVYFf2wr3TgzZsvQOZyqFCBABInD3EPi3f/u3iIgIjuPwnYjqM8wlQg16ypQpX375paZpsDhEn7+Smpubd+/eDV+jx4wZ8+2332qaFhMTAxXOzc3VnUSbzQaKObjsAKl6wYIFYEW6a9cunBSlO/AO3iQBOohPbnl5Ody0ISEh0HP9cY4hWUAH8RmlqhMBIkAEiAARIAJEgAjcCoGONOVbyeMW0jocjm+++ebQoUO1tbWrV6/Oy8tbsGBBdHR0SkoKGDfBIoew6j266YCOOlpDwyY49EBTa1h2CdNYrVaDwYDW1oIgjBo1Kj4+PjExcdWqVa+99trHH39cW1tbWlqKpmHQDBTlWSceSuCnS6BrNliRu91uWZZZt366ZLRJBIgAESACRKDzBECEdblcly9fnj59etsFGERRhHcfWBbDKzI/P7/zRfRayueffx6ql5ubCy/KzMxMeI+/8MILN6nGk08+KYoizKkyB35LlizBmU83OfAO20UCdBCf0NOnT8O1jq7r0tLSyAI6iM8oVZ0IEAEiQASIABEgAkSgXxIAPVdRFDTCwqEjzLEFRx9Hjx6trq7evn17QUFBamrqM888k5iYOGHCBBhygwEUjLFZ6RkGpTrBGhOYzWb0MW00GlGVhgTwd9iwYfPmzUtKSlq1atXq1avfeeedAwcOnDx5Esy6XS6X3W6HemL9wazM7XaDl5J+SZ0qRQSIABEgAkFMAJc6KCoqGjJkCKi37f4VRRHMKydNmlRaWopv2H7V+DFjxkDlz58/r2ma0+nMzs6GF3RBQcFN1hD+/vvvBw8eDNbTuKwivJT7VQN7ujIkQPc04R7Mv7GxEb4UQb9TFMWnn34ausVoB92DxVPWRIAIEAEiQASIABEgAkTg7iMASwiC6TF4mgZVFwaTOGx2Op0Y1jTN4XCcOXOmpKRk165dK1euzMzMTE5OnjVr1uTJkwcNGqQbkMM4HNx9wC7o8IMYzZqJ4YE4nRmG8eBYk+O48PDwv/mbv5kxY0ZKSkp2dnZ6enpxcXFVVdWZM2fsdjuePbQlbyu1YxoKEAEiQASIABHoPAG3293U1DRv3jxwgmyxWPCdhQFRFK1WK8dxBoPht7/9bWNjI8rWnS+oF1Jeu3YN6hwWFobFPffcc+BW68CBAxjZNuB2u7du3cpxnNlsxoZv3bq1bco7O4YE6OA+v3jtgh+Z2bNng/EFCdDBfV6p9kSACBABIkAEiAARIAL9jAD4c0QfF1A7m83GGj25XC4wB2GlZ7Yd4OACrI8x3uPxOJ3OS5cu1dbWbtu2LS8vb/Xq1bNmzZo7d+7gwYM5jpMkCb1zYAAnQXIcx/qeRofU7EgBRsiQFWjZuBfk6YULF7722mt5eXk7duw4duwYeN5kzaWxthQgAkSACBABItAZAj8u9nvvvfcKggDGv6wBJb6DIDB06NDKykpN0+Al2w+tg0+ePAkC+qhRo/C9P3XqVJjhdO7cOQTS9tWpKIqmabNnzzYFftDkRx99FA5pmx6zusMCJEAH9wmFWQw4EW/UqFHkgiO4zyjVnggQASJABIgAESACRCBICIDNB3hYhr9oR4x98o6awqbExJgVOxyFcXhZWdmRI0d27NiRmpqamZk5a9aspKSkBx54ALxnoioNw1q0hmZH+BCpU58xvdj6w0PAznrWrFnx8fGPPfbY2rVr8/LyKioqDh069O2334JbT7aeqqo6HA4YZkOLsO0+rw8VeVVVPR4Pm8zj8ciyzGaFB1KACBABIkAEgo6Az+traGhYsmRJRwsM8jyPKhbHcU8//XRTU1MfNlP3abndmhQVFYEAPXbsWEjQ0NBgNptFUZw0aRI4vII3o8/rs9vtH374YUlJCZvVpUuXBg8ejO9rURTPnTvHuvZiE9+RYRKgg/i0ejyeOXPmwIIn2MskFxxBfEap6kSACBABIkAEiAARIALBTACnIXaXnIr5QAAUaiCkKIrP6wM7rCNHjhQXF2/ZsiU/Pz8zM3PmzJmzZ88ODw8HNRl8TEMY5kGbzWbWvweKzuCbkuM4HFyAYM3zPNiv6dxVR0VFzZ079+WXX87IyEhLS6uoqCgpKbl69SpasTkcDjyfNpuNFaY9gR9q7oqigDdqbDIeSAEiQASIABHozwTguQ0fGh0Ox6FDh+6///7Q0DEy+isAACAASURBVNCOBGiz2SwEfhEREcXFxeDMqm8byL56fF4fSMlslYqLi0E0HzVqFLT09ddfh7dnamoqpkTb7V/96lf33nsvCNPw7mtqatq5c6fFYkENetmyZZBVfyCATei5AAnQPce2x3NWVTUhIQGueIvFAjfDtWvXur3j2+MtoQKIABEgAkSACBABIkAEiAAR+CUCrJUWGBEriiIHfrrBs6ZpoE3X19cfPXp079697777bnZ29ksvvTRnzpwZM2YMHTqUFZr5wA+snsGkC6YVg19OGHGgKo2CdbsqdmhoqNVq5Xk+JSUlNjZ25cqVWVlZW7ZsOXjwYHV1dX19vaqqTqcTnE2DcTRrE/1LDGg/ESACRIAI9C8CqqrC68nj8bz66qsosHYkQMNLZMaMGdeuXesPLYEX6KJFi8aPH799+3aY0KOrWGVlJTRn8ODBsCsxMdFoNAqCcOrUKUwMUvKlS5egjSdOnMBdEMjNzQ0JCeF5XhAEEqB1cGiz/xJwuVwrVqzA7qAgCCEhIVVVVSRA999zRjUjAkSACBABIkAEiAARIAK3QqC5uRnH9mhZrGkau4Qgm5+qqmCBhZK0z+uDIbHP61MUhV3fqaGhoaamZvfu3Zs3b87NzV21atWMGTOSkpIsFgvrYxoVZ1EUWdEZljpErcFsNmMYtGzUtY1Go8FgwDnXAwcOjImJmTdv3h/+8IfMzMzCwsLi4uLDhw+fOXOGbQuFiQARIAJEICgIyLJ88uTJ0aNHgz+nkJAQ+H6JGjS8DuBvREREQUEBTOKBiTKwmFkftvSzzz5DF1XHjx9vW5PDhw/DV1ur1VpXV3f69OnQ0FBBEKKjoyExvHPh2+onf/qE53lRFHfu3IlZ4Us5KysrPDx81KhR5IID4VCgvxOQZTkvLw+6gDB/geO4nTt3ogDd3xtA9SMCRIAIEAEiQASIABEgAkTglwjgqPWXEv7CfhgmgNcLEKPRA0bbI3FdxD179hQWFi5fvvx3v/tdSkpKUlKSKIqhoaGoJqM8Df4x28aDMTUI0CaTCSy/JEkCkRoP5zgOYkwm0+jRo6dNm5aQkLBkyZK8vLzU1NSampo9e/YcPnzY7XZD5XG037byGOMO/HCTJYkuR1Gg1zTNZrOBQ2oaUiE0ChABIkAEdATgCQn+JcAN7IYNG4YOHQqfIVFrZufZwHq5kiSlpKTo1u/VZd4nm7W1tfgBNSUlBWbqsDWpr6+H5vA8X1RU9OKLL4JnqnfeeQc+68J6wnDIokWLQIivqalhM2k3zL6Y2k1wx0SSC44gPpUej+edd94RRdFgMFgsFrj6c3JyqLcUxCeVqk4EiAARIAJEgAgQASJABPqUAOscw+f1sWov1AtGyxcuXCgpKampqcnMzMzPz3/hhRemT58eHR2NnjrQczTYwaEwzfqkZtVnDKMKYDAYYJVFjuNY82qe5yMiIiZNmjRz5swVK1YsX748Ozu7oqKiurr67NmzoAWAixK3241je1j/EMzDZVnWNQ1aDa5LcDyFx/bpCaHCiQARIAL9jgAuLdvY2Pi73/0OJ82g+gzfGkF3xvdCfn6+M/CTZRlXo+0PbfN4PJGRkfCu4Tjuww8/ZBctgPCQIUMEQRBFceHChaGhoWFhYYMHD8ZJRS6XC1oky/KoUaMEQTCbzW19SfeHxvZVHUiA7ivy3VCuz+vbu3cvemeDwKJFi/BjVDeUQVkQASJABIgAESACRIAIEAEiQAQYAiDLKooCnj1gyI1ihCzLbre7rq4OlkbMzc1dsmTJE088kZiYOHHiRFSZ0SwaJmiDVGEwGHiehxhBEECJBmsbOBCMb9BLNcdxsNaizns1xCcnJ8fGxi5dujQ7O/utt97atWtXdXX1+fPnNU3D2oKsgEIzxJMAzZxtChIBIkAE2ifgdDqLioqGDx8O7pjw8Y4aNKjPEB8TE3Pq1ClcycDn9bVdwKD9Ym47Fh/pN8+puLgYqsrz/KhRo5xOJ/um0DTtueeeg9eT2WyGlHl5eZgnqs87duyACT0JCQk6FRsT350BEqCD+LwrigJuaPA+5zguOTkZ+0/96oNSEIOmqhMBIkAEiAARIAJEgAgQgbuMAHi6gEY7HA7QmsFJBZJgpefm5mZUFjABjL0VRYHFBjVNa2xs1DTt3Llz1dXVO3bsWLNmzUsvvRQbGzt+/HjwGYomzygEgF9O9NeBltTsIKhtGCym0ewOc8NlFadPnz5z5synnnoqNTU1Pz9/27ZtlZWVJSUlKFWQWQ97HilMBIgAEWAJNDQ0JCQkwKMVns/wvEX1Gb4gQmR6errNZgNzYHhxwHIFNpuNzbOHwvhU7yh/mBmjadqjjz4K7m1NJlNGRobH40F5zWaz7d69G9oLjnCHDRvmdDplWUbbZ5hDk5CQYLVaTSbT+vXrGxsbdSp2R3W4G+JJgA7iswx3gq6zdf/990OTYIpZEDePqk4EiAARIAJEgAgQASJABIjAXUbgwIED4NajsLAwKipq5syZMCcaFzxEBx04DoI50cbAD12OomANyUDFxkzwWHY6KUaKojhs2LCpU6fOmjUrNTV12bJlmZmZ5eXlVVVVZ86cgeUfwe0pnByPx+N2u9ta/4Aij9IGnklQ81HXgHiXywXeTjAZBYgAESACfU4AHk0wcQQWxVUUZd++fTqhGZ+f4GQJZqsYjcYhQ4acPHkSfBzBYxPl4LbPzJ5oLBaHmTscDt3nUnwaf/3112C1bTQaRVE8deqU2+3GZ7iiKEOGDMGPoC+88AJr4Axuo/Pz8zmOM5lMoaGhdrsdc8bS7+YACdBBfPbhUtZ1rcLCwuD2gBVFgrh5VHUiQASIABEgAkSACBABIkAE7iYCOITxeDwYhtHNV199deDAgTfffHPlypVPPPHEjBkzRo8eHR4eLkkSa+YMfkhB+7BarRzHSZIE06VZ5Rp8fbAxqJ6AJI27YMI16NogSYCK/dBDD8XHx//ud7977bXXsrOzd+3aVVNTs3v3bjxd6PpTVVVY8FBRFKfTCZJERzZxYC3eO7oMVpUCRIAIEIGOCIBWi0LqtWvXli5dio9QkKHZ5yfHcbAgrcFgWLp0KYqw8EhHORgz7Kjc7opnS1RV9eLFi219a7A6cnZ2NsdxVqvVYDDMnz8f6on+ptLS0mD1NUEQ5s2bh89q0NbfeOMNfB+98sor0ISOnvbd1cAgyocE6CA6Wfqqwg08atQo3d3+/fffa5qm+6SjP5i2iQARIAJEgAgQASJABIgAESAC/YyAqqqwciA6/WArCLM8QZ6G+HPnzlVUVGzZsiUrK2vZsmXJycnjx4/H8RF4lDaZTCCIoDSACToZaHsgLgIPOUBBmNuIESNiY2NjYmLy8vJycnLWrl174MCBL7/88urVq22HaSBPoEk1yiVswylMBIgAEegrAigW19TUTJkyBZzsd2QBbbFYeJ63Wq2ff/45PNzASQU8t/H5hnn2dKPQ+PrHZ2xmZibHcc8991y7hUKVXC7XkCFDQGHnOG7v3r2YGOTmESNGwBIFISEhr7zyyoULF1RVPXXq1JIlS0RRNJvNBoPh3nvvra+vxwMpAARIgA7iKwHW/YD7H/s6HMd9+eWXmqbhp5ggbiFVnQgQASJABIgAESACRIAIEIG7iQBOdtY0zW63K4rCxtycBIgdqF9XB36vv/56VlZWbm5udHR0YmIi2E2zo6e24ZCQEBAROI4LDQ1FNx1GoxEto9mjRFGUJAm8fICtNMxSBa8goMVgep7nJUmaMWNGTEzM8uXLCwoKMjIyqqurDxw48O23316/fv3mbezpvb0vD/V0iyh/IkAEbocAGvCmp6ejjyOcKYJCLT7ifpSk5syZc/36dbvdzn5v6ysLaBDHoHRBEEJDQ3meLygoQCb48Q/toFNTUw0GAzzwExISfF7fjRs3IL3D4fj444+h+abAD9YbxI+UEPjggw/QdQlJc4iaBGhEEXwBj8cjy3JiYiL2deCe37ZtG3ufB1/DqMZEgAgQASJABIgAESACRIAIEIFbJ8Dqp+2GXS4XODM9duxYeXn5p59+unHjxoyMjMceeyw2NvZXv/oVKM4opoiiCD43QI+AeJ0XRIPBAE4/wOMHHovDNJSzYQlEcOvR9i/4D5EkacqUKQkJCdOmTcvIyFi6dOm2bduOHDlSW1vb1NQEhuE6UR7dfbDAUDZiI2GmLOvVFPYqiuJyuZxOp8/ra5ebLhPaJAJE4M4mwMqmZ86ciYuLa/fzGz7l4Lk3cODAffv2gR4lyzLIvm3/sg+ZHsWIdtaqqtbX14M6DL41oFxVVds636+qqoJnNTyTP/30U9CmsdqpqamQwGq1oktoeFnwPL99+3an04mJsQ492tKgyJwE6KA4Te1XEq7jjIwM7OJAIC8vjwTo9pFRLBEgAkSACBABIkAEiAARIAJ3LgF2zN9uGJvu8XggAcZgwOFwXLp0qaamZteuXQUFBampqQsWLEhOTv6bv/kbsIkGH6A8zxuNRnAwDetugSkcyNOSJIWEhIBIgX8h0FZ6Rk/TMKDDBRWNRiPqO6D+gCCSlJQUFRW1cOHC3Nzc9PT0srKyysrKr776CpxNa5rmcDg0TQO1HQR3t9sNTcZmYkBnmYhqEQsQE1OACBCBu4GAz+uDz1EbN26EB5fuwxv7WIMH12OPPXb9+nUQo1wuV3NzMz5MdIHeebaA8w04WaqqNjc3jxw5ElYInD17NsazFtDwie7UqVO4lKLRaHzwwQfbCsorVqwAb9c432XgwIFjx47FlQB6p43BdSmSAB1c5+tntYV7YOXKldABQhn62WefZb9W/ewY2iACRIAIEAEiQASIABEgAkSACNyhBNgxf7vhX2w3LAOIyZqbm10uF5qwgenxuXPnKisri4qK3njjjYyMjDlz5sTExNx77704IgOX0GgZxyo1HanPKDRjJmCsJwgCCBwgZ4eEhLC22KBHg/CNB0ZFRU2fPj0xMTEnJyc/P//dd9/dt2/f0aNHwYhPURSYSttWj2adpYIogwwRCAWIABG44wk0NTX5vL6LFy/OnTsX1nEVAz80gkav94IgwHKvW7duxcX98NOXTnfGTXyw4KO125Hq1GeQyBYuXAjzVB544IGORDOPx/P555+bzWZRFEFqE0Vxw4YNujq73e6qqqoFCxY88MADI0eOfOSRRzZs2IBLF9Dzs90TSgJ0u1iCIxImVX3++ee6zsrMmTPh3iA76OA4kVRLIkAEiAARIAJEgAgQASJABLqDAKsRtBvGQtxud3NzMziM1jTN7XZ3pEfgIZgAvVuAmAsJVFUFu+Pa2tpjx4698847OTk5q1evjouLS05OxiFbZwRos9nMitdsGFVpsOPDbI1GI3oLASWaPQrVopCQkPHjx8fExCQmJmZlZW3YsOG99947ePDgsWPHrl27hvIQBFiACKGHAr1ZVg81gbIlAncSgU8//XT48OHo9BkfNfihCwJWq3X8+PHHjx/Hp6Isy83NzZqm9a0FNDzE4IzIsgzi2KZNm9Cnv8vlwjrrTtyyZctAeh4zZgw08/7778dnlM/rY50gOZ1OkJtRfYa9mL7nRHZdtfv/JgnQ/f8c/UINy8vLdc+C0NBQ9J7+CwfTbiJABIgAESACRIAIEAEiQASIwN1HANQBlFxvXyxgc0ABF7mCNuF0Omtra/ft2/fRRx+Bc49p06YlJCRwHIezWkGhBqE5JCTEZDIJgmA0GgVBAE2Z53nYCz5AdHoQ5gOSNOwFu0X+5z/dgbApSVJCQkJsbOyKFSsyMjI2bty4c+fO8vJydO7h8XgURUEv0qCtsAoLhtGeGiEAInaTDbMAMYwJKEAEiEC3E0AFFj/Fweqvc+fOFQTBYrHgYoPw8JAkCR4mFosFLKNfffVVdulUuHPxudpRAG9wfFyAZn2rQhbkw2IBoRmet9g6NluYSiKK4qZNm2B9QvZwTdMaGxvHjRtnMBhGjhy5detW9I+0fft2KE7n27ptW3QZ0iYSIAEaUQRroK6urm3XATzXsJ9lgrV5VG8iQASIABEgAkSACBABIkAEiEB3EwDVAPWRnhYRwH0iNEKWZY/HAy5WQS4BoeS77747cuTIJ3/6ZN26denp6U8//XRycvLYsWNxuAe6M2zCtHdw7oGOODAliCyYHifOY4KbBNDTKygvcCxkFRYWFhkZOXv27Jdffjk3N3fdunVHjx6tqKiA4SeK1CgqeTwene9pWZZdLhe0GiUnPAsQ6Olz0d2XEuVHBIKbAN6wTqezuLh44MCB8HyA9Vd//t2Kx0fHpEmTvvrqK7hnsf2656ru1sZN9h6HZQDXrl27aNEinXExZttRACQvn9e3ePHiCRMmzJkzZ//+/SUlJcuWLbt48SLOWWEPf/7558GC87HHHoMHkc1mYxOUlJQYDAZJkp555hm73T558mSO46xW66RJk+x2O7jUx4ZggG0RmxuFWQIkQLM0giwMt5MsyziJAJ4FZrO5uroaOgFB1iSqLhEgAkSACBABIkAEiAARIAJEoOcJ6ISS3pEPUOhh24eRbEBVVTTiA4eqJSUl1dXVGzZsKCwsXLRo0dy5c6dPnw6rFMJCiGgWDaq00WhE3RkDKB7dPIAaNPjuwMMhEBoaioeD9g3xgwYNmjFjRkxMzOrVq3NycjZv3rxnz57a2lq2sRhmvcTCHHaSchAOBYhA7xBgP4w1NjYuXbrUYrHA7cze9ahBw41vtVpffPFF1qwYa6t7ruJNrQuwz1tVVffu3WsymQwGw7x58zCrzgQURXE6nc8884zBYAB7bfAZYjKZpk6d2jYHh8Nx8OBBdFh05cqVtq1YtGgRPEI/+OADTdOKioo4jjObzYIgFBUVwRKvuuaQx+e2qNuNIQG6XSzBEQkdFJvNFhISgk8HeCJUVlbi2sfB0RiqJREgAkSACBABIkAEiAARIAJEoLcI6IQSVhDpiSrgZHB34AeWdzDbHR1Ju1wuNNkD22GsCci1TqcT5BJMBvGXLl0qKyurra3Nzs4uLCx89tlno6KikpKS0JJRN1pE+bjdAJgHSoEf2lDDelzo+1GXIQrWuuUQ0fe0JEmjR4+eNm1afHz8okWL1qxZs3jx4tra2vLy8tOnT9OUdjzRFCACvUkAXQMdOnQoMjISTBvB/hfvZVSfITBo0KCioiJ4BLndbp/XB5lAtXXP1bZCLcTonrdbt26FR4okSeXl5Z0n4PP6XnzxRVhXUJIkURThaxx8fnv//ffxqx4KzS6Xa8SIEQaDISQkJC0trW1Z8FQMCQlBJ9EzZ86EL23Jyckej0f3wazdFrXNlmI0TSMBOrgvA5hxMHv2bOwKwCMjOzs7uBtGtScCRIAIEAEiQASIABEgAkSACPQkAVYEYcM9WaY+b7ZcNozpIPJ2LOwaGhpOnjxZWlq6fv36vLy8goKC+Pj4hISE+++/HxxGsx48dMoyak8gyoATakmShMAPDzQajay7WJ2ujZlAQLcXNq1W68iRI6Ojo+fNm1dYWLhixYp169aVlJRUVVWdOXMGZr6jzgXeS1wuV1ufkyiotSs8geLPSlEo5SNwChCBO54AOMbBZubn54NzZ92tik8D/BA1Z86cGzdugBuKdp9XcHOxuzoT/vTTT/Gx8OyzzyqKgp/osJIYaGxsxOn+x44dEwM/i8UyduzY1NRUk8mE38MeffRR9POD7p5dLldBQYHBYBAEQRTFb775Bh4CYAz+8ssvQ02eeuopWJxW07Rt27ZhnufOnYOs2tXW2cZihSmABEiARhTBF4B3qs/ri4+PZwVojuNeeOGF4GsP1ZgIEAEiQASIABEgAkSACBABItBbBFixgA33Vvn+cthy2TDWASJvR4DGrFBP8QR+LpcLVh777LPPKisrd+7cmZmZ+aPv1GeffXbmzJmTJk0C2yaj0Wg2m0F/wRUOQaMBPRqVI47jUIZmI28eBitpEINEUYQVF9s9JDk5OSoq6oknnigsLFy1alVRUdGRI0dKSkqggbA0IjYWNGtossPhQPkJIaD3WNKgERoF7gYCdrsdP8+cPn06ISEBHem0FaBBgxYEISQk5MMPP8SPQLpnF8uNfY51JqxpWl1dHVgug65ls9l+8a6EBPPmzQNxPDo6GqaDnDp1KiwsDB4gRqPx0KFDUDfwNC3Lss/ra2hoMJlMFovFZDLFxcWBoq1p2scffwwPOpPJdOrUKTgQZqgMHjwYnoevv/46CdDs6b6lMAnQt4Sr3yWGt2Zubq4gCOz35Pj4eHym9LtKU4WIABEgAkSACBABIkAEiAARIAJ9TaAjcaQ36/WLdWg3QZdriHaFqO94PB4cOSqK4nA4WLNiu93+9ddfV1RU7N69OzMzMycnJzk5ecaMGePGjUOPq6ggg+iDxpLtisidj2ybD5YIShDaJILw/cADD0RFRU2fPn3NmjXZ2dn5+fnFxcWHDx+uq6tD1QybDx5RcClIpNFlsHQgEQgiAvBJZt26dfBtief5dtcbBIlJFMXY2NjvvvsOfU2gQyF8OrFtx8jOBzRNe+yxx/DhoHOdwWYOts9wwyqKAqutWiyW8vJyaJSmae+//z5kJYri/Pnz4VuUqqr4rFMUJTU1FdIYjcaEhIRjx47t2LED5O+QkJDZs2fjPAkoHSyjjUbjxIkTSYDWnZHOb5IA3XlW/S4lfOH58UZKS0vTCdCjR4/Gl2u/qzdViAgQASJABIgAESACRIAIEAEi0NcEOtJHerNev1iHdhN0soZgFIxqETsbvampCTNhFWeMxICqqu3qsxB56NChPXv2bN68OScnZ8mSJQmBH7rmQEXp5gGDwWA0GlFxZif+m0wmjEf7a5S8dfOAOY4zBn48z1utViyU5/nhw4eDX+znn38+Nzd31apVFRUVxcXF9fX14NCj3TYiBAoQgTuJgMvleuSRR0BEglX7zGZzu+bPP96M2dnZHo8HPdSj0MQ+mlg4bHxnwpDhBx98ALezIAgJCQmQ4U3uSp/XV1JSYjQaJUmaMGECPNzgYSXL8pQpU2BShSRJJSUlUA18EmqaduXKleHDh8Nig/CgMBgM4M1DFMUjR45gi+D73Cd/+kQURfgGhlp8Wy8cbHsxBwogARKgEUXwBeBuVFV1165dBoOBtYAWBEGWZfYGC77mUY2JABEgAkSACBABIkAEiAARIAJEIOCpowsY0LS5C8fe5iGyLH/33XcHDhx477330tLScnNz4+PjH3nkEXZ2PKv+oAaE6jPKx20DIFTxPA/LjoHuDDq1gfl1JKix8aCVWyyW6Ojo5OTkBQsWLF++vKCgoKysrKam5uLFi8DB5/WpqupyuUAsg7+g76N5NdJWFEWWZVVVYRfEwwKS6LsWskW56jZp0+FE4BcJ4Hem/fv3g+Ew+/2Gve/QujE+Pr62tvYXc77NBODjwuPxDBs2LCIiQpIkg8FQV1enaRrUWSdD4+aKFSs4jjOZTM8884yuDkuXLoUW/ehM4ze//g043tHpxZ999llISAhAwI9bHMctX74ci2DtoNFJyPbt23VZ4Sbe0fg00FXsLt8kATqILwC8pk+ePIkCNNxmVqv19OnTQdw2qjoRIAJEgAgQASJABIgAESACRIAIBAjg0C8YebCVt9vtHo/n8uXLYICckZGxevXqlJSUmJiY++67z2g0ohAmSRL63BAEQQr8QIwGjwGoPoMJZ9cEaIvFgnI2rKwIq5OBRbbBYJAkyWw2x8fHR0ZGvvLKK+vWrfuxwrW1taWlpXV1dSCQQQPBvazNZoMZ+h6PhzU5Z08cGoopigLTmtm9FCYC3U4ALjmXy/Xss8/ix562n3bgzhIEwWKxvPrqq/hxpdvro8tQUZSmpqbVq1fjTb1+/Xr8WsM+QFARVlV14cKF8BFr+fLlugy3bduG8vqPTjYqKyvB8zUqxSAxv/nmm/D0AHf2YWFh8fHxqNTr8nzkkUcg2e9//3s2HzZMArQOmm6TBGgdkODbVFXVbrfjh154ZHAcV1ZWRi+z4DudVGMiQASIABEgAkSACBABIkAEiMCdRQCn7euaxUq3YKVYV1dXWlq6Y8eO119/PS0tbcGCBcnJyQ8++GBERARq0+CCQxRFVrAGKQpc2cLomLV07ih8EzEOlkOEQsFAElyFoGwHCpckSSNGjEhJSYmNjV2zZs3KlSs3b95cUVFRVlZ25coVXPwQbSphBUhWqIKwjgxtEoHuJVBZWTl27Fi4ekVRhDsCL2YwJYab6L777gNzxt4RoOH6l2X58uXLWJ+4uLibyFk+r0+W5cjISEi/adMmHavjx4/DnQs36eTJkzVNczgcrFgMh1RVVSUlJVmt1iFDhqSlpamqigI03rOQctmyZVBcbGwsmw8bZu9rXZVoU9M0EqCD/jJQVdVms6EAjXfspk2b8Mtq0DeSGkAEiAARIAJEgAgQASJABIgAESACQUUAXMeioANqbLtiNOg+uEtRFJ/XxwpAYCx84cKFysrK3bt35+fnr1ixYsGCBQkJCePGjYPZ8TB5H4fGHYnObDwoyzzPm0wmnZyNs/LBrzQOtNkAOI1lY9CvCJhvQyYJCQnTpk175JFHsrOzly9f/umnn1ZXV6N/j6A6pVTZoCRQWFiIvtThcgUNmr10eZ4PCQlZtGjRtWvXerORLpcLbZwXLlwI7kE4jistLcUHgq4+siy7XK4RI0ZA/YuKinQJvv/+e9gVERExbNgwnudTU1N1iwfic8nj8WBY0zTwluN0OllH+Zqmvfvuu7D8aUREBCs6s2ESoHUnQrdJArQOSPBtwiV+77334gdhWA44IyMj+BpDNSYCRIAIEAEiQASIABEgAkSACBCBO4gAWDKeOHHiwIED0CxWWYYYVrjpSNBh07BhEIzcbvfRo0crKys/++yzN998Mysr66mnnkpISLj//vtBngbxCGQpFONQZcZ4GFZjAph0z3GcKIroHwASo5ANm13+a7Vak5OTExISQ/RJ+gAAIABJREFU0tPTs7Oz33rrrV27dlVVVekkeI/HoyiK0+mEeNTswCkBIm1ubnY4HEBVlmWAozNNk2XZ4XCwDO+gy42a0kLAZrMpinLmzJkpU6a0vTjBNBimERgMhpCQkIiIiPLy8r7Fd+jQIdS1Fi9e3FFlwP16eHg4tGL37t06qfrChQvY5LCwMMjz448/Rjto8O+Bdw1bEKxkCE8h9h45cOAASG0cx7HPKDbMpmfzpDAQIAE6iK8E9uKOjIzEGxXutLi4uCBuG1WdCBABIkAEiAARIAJEgAgQASJABIKfgM1mGzduHIxSf/vb37IL9GHj2LFtR4IOm4YNg/akKIrD4WDFWafTicKrqqqlpaUbNmzYuHHj4sWLp02bFhMTw/M8CNAGg8FsNoOnaZSeRVEED9Gw3hLUv13nHih1dTmAwhb6oYbRvdVqHTduXExMTHJycnp6+tKlS7dv315eXn769OnGxkak53a7oe3gxgQUNFSoXS4XSNIIDQ9sG4O7KBCMBOx2O1S7ubnZ5XLl5OTc/JrEq33+/Pl1dXU6Gbf3Caiq+sQTT0Cdhw4dCi7j262GLMsoQO/cuRPvdEhcU1PDcZwkSU888YTVajUYDKIoCoLw9ttva5oG33JUVW23vR0J0Dt27MCPWOwzig3jDYV3X7uVv2sjSYAO4lPPXtzgfx2XXxAEIeb/Z+9NwKQqsrThmzfJ1ayFKbZGli62ZhUaaNkGiuIDlAGVVht4UHBQYBhbBrUYQPxYfwrxF5cPBUcBPzbbfVCgbZamWKbYumQZaGAAcViHtaklzf3eGx+Zr5yOzqwqEiiKrKxzH57iZNy4ESfeGzeWN06c6NGjCpeNVWcEGAFGgBFgBBgBRoARYAQYAUaAEaj6CMyZMwdH+YHtOnjwIDgguWTy3LYsQkeOI8u6ruMAQDlBeImVCaZYSigQCASDwZMnT27evPk6hzV16tS33357+vTpgwcPzs7ObtKkCehp+NmA+TN4YTihrigLaNBtxEEjcbPZnJqaClocEYgrp5iKorRp0yYrK+upp56aMGFCbm7uxo0bv/76a/ieltEg0i0qkGCMCuefVRQBcnPsdruHDBkC1rV8Dtpms23YsAG2wJXj9Ll8bNetW+dwOKxWq9PpfPfdd8tSCQQ0irZq1aqorzsvLw+fyaRJk1544QVEgw/3tm3bDh06dMqUKWUZQZdFQM+dOxctmMvlktsoWaYPKkqf8otcfe4yAV2F37VcuadMmYKPirYIKQq/3Cr8cll1RoARYAQYAUaAEWAEGAFGgBFgBJIAge7du2OnfFpams1m++qrr2JtD+W5bVmEjhxHlgkiv98vWz1TOAQ506it9/STCGsSAoHArl271q5d+/7778+ZM+eZZ57p27dvw4YNYRYNDrp8gi+eu8DHFrnIKFXe4uyIXMSjybcofYfDYTKZ8LjZbK5bt26nTp369+//3HPPTZ8+fdasWUuWLNm0adP+/fuvXLkiA8hkWVRVqbo/UZM/+uij2rVrK4oCf8pUo6iqkDB06NArV65Erd/cw/oAQ+bs7GzYVtatW7esdxEMBtPT01GQjz76iNa0gMDChQvBjM2ePTsQCIwYMQIxAQjWck6ePAmuOSqLsgjoLl26IJFBgwbJbZQsy59VVLL8kw8hTJ46MHfuXOqEsG1HUZSTJ08mTwm5JIwAI8AIMAKMACPACDACjMDdQQA+av1+P44+g2FUSUmJPJksS4ZGwWAQvlZlBWMfgVVm1GZh+RGWGYHkQyArKwtb12GPuX379vI/gdgPp/wQGTHElEPuXJZzl1Pz+Xx5eXnbt29//fXXZ8yYMXr06KysrKZNm8ouOywWC3hh2WyZ6D8SVFU1m81yHJhd0xxfURS73e5wOHB2XKnG1xQoPwXk5VskK4rSo0ePhx56qH///jNmzJg7d+6KFSu2b9+en5+PYvp8Pi2kaSGNGEkSZBzwNhFZDocMd72Qo7xax0bmkNtDAGfoweX3oEGD5IqEOgbKFTKY2Tp16syePbusun17atz5U3Bx/snvPklLS1MUxel0LlmyhFaDkD58+GghrXv37ijR+PHjDcNAP476NmnSJICwfPlyPD5o0CCXy2W32/FIenq61+ul5oIqttyP42RUwzDOnTv3zDPPWCwWPD5//nyZdJblRMPzzt9IxabARrIVi+c9S23r1q1oU8xmM/bsKIqyffv2e6YQZ8wIMAKMACPACDACjAAjwAhUKQTK2uobTyFk48p44nMcRqD6IDBmzBiQPpirHj16FEeBlYWATOLEI8vpEKMkB949magx2fe0EMLr9Z44cWLXrl3r1q3D0YIPPfRQnz59OnToUKtWLaABG0+bzWa3261WK1hjsGZlmazCUFrmlCkpOZAo5vIFOMlFCna7nRQwm83IKDU1tUuXLgMHDhw7duzUqVNnzZqVn5+/YcOGM2fOEKTBYJCIPwqEUxR42pUDhRC6rhPZR7dYuBMEUPd0Xd+7d2+bNm2oksh1Q5ZVVR0wYACsFeXv6050qKhntZAWDAYNw+jUqZPL5VIUpWfPnqV2zYFA4LHHHkO5hg0bBgVoK0P//v1xcOi+fftw5KbX6509eza+vuvbCV5//XW5HgYCAbfbnZ+fH4xcWIQuKir6/vvvZ8+eraqq0+m02+1ms3ngwIEy4xwlJxqeFfVeKiodJqArCsl7nM6mTZsURaG2Bp3HkiVL7rFanD0jwAgwAowAI8AIMAKMACOQ8Aj4/X4ikmhSClblVnXH/BOW1JjKyn8DkYvyutXEOT4jUBURuHDhwmOPPQanEEuWLIEBYzkFkUmceGQ5KcSXQ+62HPs5u91uv99PLQkMhKN8gxw4cCAvL2/FihVvvfUWrKd79erVtGlTRVHIsAycMoyjYUYNuk2mlWViUQ6PR4Y5JxhwsOFEf5vNZtxNSUmx2+3gGYhtQDSn09m8efNu3br169dv+vTpr7zyytq1a3fs2HH06FG32x0FO1ACFJX/jqKUSb6fuq5fXyEwmUz2yCXXCpLhsOK6H+S5c+d6PB6fzweqlz6xhIJl1apVILWcTueKFStiddNC2pw5c5xOp9VqVVUVnxuq2cWLFx0OBwoOE356PBAI7Ny588KFC1GfbTAYfPnlly0WS7NmzZ566qmXX3555MiRbdq0wWKM1WrFmtCAAQMuX76MdZQo6hk/CUz6/ClrFtgFR/LUAY/Hg++T9hRc73JmzZqFEpbq2iZ5Cs8lYQQYAUaAEWAEGAFGgBFgBO4Agby8vB07dmzdujU3NxcHkU2bNm3w4MH94rh69uyZnZ398MMPP/LII9Ola1MZ1+7du8+fP48d03egMj/KCFQZBMhFA1Z6brq0I5M48cgyEIgvh9xVGRaXZKEJ+80onxX42EslpMjbLB4kV7xbtmzZvXv3xx9//MYbb4wePXrAgAEdO3asVasWmF+ZXCZ68TYsoOGKAQSCyWRyOBxEMSuK4nK5TCYTvKbAqQjcicg5IlOExFptt2vXLjs7e8SIES+++OKMGTN27ty5a9euixcvEu95V19N9Ul83759v/zlL+ndWSwW2eEG3o7NZlNVtW3btgUFBUIIv99fXFzs8/nk7ysREKNPye12t2rVCvWwTZs2sm5utxtNyh/+8Ac6Au2LL75AHMMwPv/8c0VRatasOXjwYJ/Ph4+U+txSv0ctpH311VdRddtms4FkU1XVZrPB8wad58kEtPxS4pTZAjpOoKpANPRG9M2YTKbs7GzojS0wVaAMrCIjwAgwAowAI8AIMAKMACMQBwLYMEv7ba/bf4HUEEKQ7QUYH8Mw/H7/iRMnvv32288///yNN94YMWJEr8glj5xlTuemMj0oG3/gKbqFmbP8M0o2mUxdunTJysrq2bPn3LlzZ8+enZ+fXxy5CADDMFAu+KemcBYYgaqFALE/hmF4PJ4o88OqVZZb0vamBB8iwDFFqSS1nB2cCWzZsuXLL7985513pk2b9thjj/Xo0SMzMxOnq8kMNVhI8JLw0gmOGCEwrKZDC0ElW61Wu91OpB72WKs3LrlhjGrNbuknSL3s7OyuXbsOHjz4lVdemTx58rJly9avX19QUHDhwgXQi2j64JNXrjCoS0TW67ou++0VQsS6BJExrNIy8bNaSIMJ88yZM+N5Lw6HY8qUKYWFhcA2YUGQv5cVK1ZgQ0Bqaup7770n60xdP9x0KIrSoUMHinC9S0Xl//zzzynwpkIwGHzppZeoTzebzVar1Waz9e3b991337106ZKcgqxnWbIcn2UgwAR0ktQEXdd79eqFDQK09pWZmYniYRR+0/4sSbDgYjACjAAjwAgwAowAI8AIJCkCcLVMBoY0CwUBjZ8FBQWbNm2aPn36q6++2rNnz+bNm2Mu6nQ6ZWs+kCA4+EuewMcjy2wLsTlgaejxWHtAegpk0PWt0LF2aojTsWPH4cOHL1iwYMOGDSBTwDuQvST7UU3SCp6cxaLzwbyRC6tE1WRyKpNTpb5dRIiHgEbrF+VYWU6zpKRkw4YNeXl5ubm506ZNGzJkSO/evevXr08tD5HRiqLgPEOz2eyKXDCbhaUz2kZyAHKDf1apcaMIlPItCXic3F6DQ4xqnG02W8+ePTt27Dhu3LhFixZ9++2327ZtO336NCoPvGzDklc2qKfDYGNrV2yIDF0VktEX6Lr+ww8/9OzZs5xDKal/adCgwZYtWwCdDFcCllr+Xvx+f5cuXeDK2eVyFRcXxyo8e/Zsp9MJb+YjRow4cuTI888/73K5bDZbenq6z+cjyj722VJDdF3fv3//5s2bt27devTo0UuXLkElWkLDU7KeZcmlpl/NA5mATp4K0K1bN7T76BjQYdDoPHnKySVhBBgBRoARYAQYAUaAEWAEIghoIc3r9W7dunXq1KkTJ07MzMwkz4+YkRI7TCd1w6YJVk6wAcTpWzK3clOZ2Baa4VNIlOB0Os1/e8k8NSLD3pCsDsmaxGw2ozhDhgyZMWPGsWPHmHfmil8VEQgGg+vXr3/mmWf69+//wQcfoAhJQwiW/0ZkcqrUmHKEsjAh6lmOIC9HwYMHkbNElrndbhACV65c2b9/P1bm5s2b16dPn0ceeaR9+/ZowfA3tmlCA1XhBLSiKPArjfYNa3WxpDa1hGCooWRqaqrZbB4wYEBWVtaYMWNeffXVefPmzZkzZ926dbt37z537hwRjrLRdKnIV7lAf+TC+XgrV65MSUkh6KjPkjsguIQePny4x+Mhg/EEL7X8OQQCgTVr1qSmpuLVv/LKK7GbJy5evFi7dm15uddms6GSvP766/EXlvpWLaRRFcLj+JrkT4+W0GRtY+X4c68+MZmATp53/fLLL9N+AWq+fT5f8rW8yfPOuCSMACPACDACjAAjwAgwAreIwLlz5zZv3jxnzpynn366Tp06xDjTAJjckiIEe8yj7mK+ir+3QUBj1G2xWDp27Ni7d+/s7Ow+N67sG1f37t179+7ds2dPogZiBdo+DNZAVhKlAHcNEzBFUVq2bDl+/PitW7fyCP8Waw1Hv5cI+Hy+WrVqwZ+Doijbt2+/l9pUbt4yLVVqznKEKJJLjk9+b4UQHo+HDjnUQhptBIH9L/z2gKaUUyCZHFyAdPP7/WfOnNmzZ8/69esXL16cm5v7wgsv9O/fv1u3bm3btiX2mYyj0Y7JROetyrLvUHCLSAEHykFOiVyUstw2UuudkpIih1Nki8XSq1evbt265eTkTJs2bdmyZfn5+Tt27CAEqrRQUlLy+K8fR2GJowcmUWjUq1fv008/1XWdGNXCwkKSExME+XOAhfuQIUPQdJjN5s2bN8e6EHnjjTfo1UOwWCz9+vWLZavLLzJWdNC3yucSl5SUkF8XSkHWsyyZIrNACDABTVBUeWHatGmxBDR6d/hHr/Il5AIwAowAI8AIMAKMACPACFQbBDDPNAzjwoUL33777dtvv92zZ094zIDfOfAgZVntRc1IrVary+WCV0e6BUqFCGsKdzgcGRkZ3bt379Onz9ixY+fOnTtlypSvv/46Ly/vwIEDmKDquk4HjpHxVFkvx+/3nzx5cv369UuWLJk+fTr8PiM7HHNEw3jSAbw5aYhwkDVWq7VTp07Dhg07ceKEEAKaCCFK3aFclkoczghUGgILFy5EfQZNNm/ePHKhUGk6JHhG5VDPpHk8cShyRQkej0cIsWHDhh07dqxbty4nJ+ehyNW0aVNqrGRBVVV4kSYyFB6H8NNqtRJnStQzdqI4nU56BAneOdMtKya38z169OjWrdtDDz00fvz4RYsW7dy5My8v79ChQ0TOlurClFp+EKMyRwm0sRIAg1n5hLo7f3Ferxe5r1u3rkmTJlHlwgolAYvNNI8++ijVATCkpJJMmFKcBBRQ5D179sBkPj09vVWrVrK/b7fbjeWWGTNm4NRBRVGcTmebNm3279+PEtFugAQsYDVUiQno5Hnpn376Ka0qU5M0Z84ctHfUmCZPgbkkjAAjwAgwAowAI8AIMAJJhIAW0jDhNAwjEAjs3r07JyenSZMmmFdbrVaHwyHzFyAUbkpAy6QGZBhNu1wuHG1ft27dbt26DRs2bO7cuZ/87pNdu3ZFjZwxXQfS0BDUcyAQuCn1XOr7QSLBYDA/Pz83N3f27Nn9+vUDTQNPrDh5yWazyaaC8BmNEBDxiqJ07dr1008/BVkPW0iodOeUR6macyAjcBsI5ObmkhX/dSE3NzfWjPE2kk2mRxL2g/X5fLqu+3w+aIimj7TVQtrevXvXr1//8ccfv/7665MmTZo4ceKTTz7ZrVu3jh07EikBVlpRFKxAwPszZDRo1NCRPyLaL0KJ3LlgtVqRaRRtQjtR0EHUq1evf//+Y8eOnThx4rx581atWrV+/fqdO3fiJFj4UIb3J+opgsEgwuHpwu12g56WqV4C7TbqLQjx8ePHAwSCizbKgKIFerVr13777bfRyyCvKkpA67oO+viFF15IS0tDtzh69GjDMLxeL7UhhmGUlJQcOnTo5ZdfHjJkyPz587FqgrLfXh99G++IH4kHASag40GpasTZsWNHrOnErFmzhBD0cVaNkrCWjAAjwAgwAowAI8AIMALVBgFYMLnd7sLCwi+++OLpp5/u1auXzWaDWRzm27GjXCIjyLxOJprpLs3PQezabLY2bdr06tVr9OjRixcvzs/Pv3z5MkgEHGMITlkIUVJSghB6D9DTMAy3203R6G6cQhQHoYU00BYIP3r06KJFi8aNG1e/fn0Uh+gSuUSqqjocDpypaItcDRs2XL58Oezy4tSEozEClYbAzJkz5QoMC2hwmsTQVZoynNFtIxDFKsAWVfYBIoQoLCxE+mjT3G73sWPHduzYsXr16kmTJk2dOhUOi+C3l4x25eohN+lltepy/FuVS21UkYg1cuHAANjSyq75YbKdnp4+cODAXr16DR8+/K233srLyzt48OC1a9cIVXhqjmrqyWswRbsl4ejRoy1atIAyDocjCjf4ekZn179//3PnzkUlXkUJaOzv0XX90qVL9erVwyKWw+F45513qOukkmINACVN8IMWSedqKDABnTwvvbi4OGopT1GUvn37xrZ9yVNmLgkjwAgwAowAI8AIMAKMQBVH4NixYx988EFWVhbxCGaz2W63WywWm81GZIHFYiGZYpIRdDmbtR988MERI0YsXLhw8+bNhmHgiBRQJ8FgUDYTk4Gkfb7gnUFSu91uxLm9ATZmyLJHTiEELLzIkg7+NPx+/4EDB2bMmNGhQ4eowlosFrvd7nQ6ZVLeZDJlZGRMmjTpzJkzcilYZgQSAYEffvgB/JGiKA6H4/jx4/juiH2+vQ8qEYqW9DqgJcQLMgzD7/cTDY0lBI/HIxuZon0ry+8BOamASe/p06c3b96cn58/a9asefPmvfjiiz169MjKyoI7jnJadblVjF8m82oQuOhoynncarWi31FVNSUlBRbcMMUFS07P4md6enq/fv169Ojx0ksvzZo1a8WKFdu3b9+xY8f58+ep77jVChMIBN5999309HR0dmUx8nDlBOtDGCDKJGwVJaCDkQuIrVq1itB2Op3r169HeFFREZ29Sc0IKmpZnfutvgKOX4EIMAFdgWDey6Tg0CdqKUxRlAcffBBND42h76WWnDcjwAgwAowAI8AIMAKMQDVDwO/3yzNhWOkGg8GLFy++//77Tz/9NG21jppax4bLBLQ9ctGMFLZRKSkpYGb79u27aNGizZs3k4tkLaTJbBfJ5b8NikYz2/Ljl3VXTkeWySkn+c2Q70I+c+bMRx99FLWfHQU3mUzyXmyLxdKyZcudO3dCWxydVJZKHM4IVBoChmGcP3/+up/WmTNn7tu3j87HK6v+V5pinFFFIUANV0UlqOv65cuX9+3bt2nTpkWLFs2ZM2fcuHFPPvmk3E3AhxKM8GR3+WBFZH9NFosFXsgpMvw5UA9is9mcTif9lIX4eXC5z5L1JMvlbt269erV69VXX50xY0ZeXl5+fv7GjRvlDeuBQID4fSHEmTNnOnfu7HA45HY+Sjf87Ny584EDBzweD72IqD5LDpflinpfdzudYDCI0wgBRc2aNU+cOFFSUlIOy0yHc95t3Tj9+BFgAjp+rBI9ptvtbtWqldweQUYHH9UAJXphWD9GgBFgBBgBRoARYAQYgSqOAGa5UYXQQtqaNWvGjh2bkZEBmkCetMtD2ajwWEsLCnE6nU2aNHn22WdXr159/vx5sFowLiZHnKSGPPe+6QhZjkwp3IYgpyPLZRFwchxkFwgE9u3bN3/+fJz9lZqaqihKSuSSQUPgO++8g6fKmZzfRin4EUbg9hDAhyZbxaKGl1X/by8XfipZEUBtodIVFhYeOnRoy5Yt33zzzZQpU6ZNm9a3b99BgwZ17dq1QYMGDocDu0OwYCnLIKwRYrVaozaRYGdJVHNavt1xbORSQxwOh8xHg0KlMxhdLldaWlq/fv169+49derUK1euCCF8Pt/KlSszMjJwYgF5AolKH0lNmzbN7XbDZ1Rs3wHc5HBZJlQTXPB6vYcPH4YlOF5K+/bt6dyIBFee1SMEmIAmKKq2gF17WVlZctOGTSL79+/nxZ+q/XZZe0aAEWAEGAFGgBFgBKosAthqLYQ4cuTI+PHjGzZsCD+bmDmX4+6TCGgcM4iRLZ0WZbPZHnzwwdzc3HXr1p0/fx5MKxiuQCBAZxCVSjHHP/2OP2b570dOR5bLIuDkOEIIeS+jz+fbtm0bbMFARsAZtDwLsNlsI0eOlDfLl68e32UEKgcBeVoaCATkei7LlaMM55L4CKBWkJ5aSMMpfxQCe2Gv14tz/xDudrs3btyYl5eXm5s7ZcqUrKysPn36gMmF4TNRz3a7HX42wGnCUDqK5EVPFBV4Gz/RRGPdlFZPKR2y4J44ceLVq1effvppKAlXVMRWU3yklpmZefDgQZRaXuAhfEiQvy9ZpggJLqDpWLp0KRAwmUwOh6OgoEBuUhK8CKyeEIIJ6CSpBvjwxowZQ00SBJvNlpeXJ49Zk6TAXAxGgBFgBBgBRoARYAQYgYRBoKxJIE6rX7FiRadOneQtz+RMw2q1EtEsU6hkdyZP/l0uV6tWrZ555pkvv/wS1K1hGLRnGToQq1UONvFPv+OPWU52dPyUnBrkOAlo7Gj0er3g00tKSoLB4J49e0aNGoVt4ziwUWZPbDbbY489Bo/S5evGdxmBu40A6vnx48e3bdtGznCjDiGUv467rQ+nn/gIeDwe8ozv9XplxxS0rIj2nxrYqEIFg0FUKuyGwVMHDhzYunXrvn37li1blpubO2vWrLFjx3bp0gULolFcCnGdUX1TqdHKCaTE4ak5ik3Gibt4HGx448aNKWsS5K5QUZTU1NScnByYS6PXiyp+1E/5+5LlqGgJ+9MwDBx3OW3aNGDicDgOHjxY1tgjYQtSzRVjAjp5KsD1Bvq6Xy18jfJfuKKXm+zkKTOXhBFgBBgBRoARYAQYAUYgARCIcvXgdrt9Pt/JkyfnzZuXnp6uqirNwOVhKlhmsvyC+wh5rzEm6rDnXbVqVWFhIYy8YFVdqt/kBADjFlSQiYCyZKLaiXaRMzhy5Ejbtm1lcl8m9J999lnZNlx+kGVGoNIQMAzj8V8/DqvPunXrFhYWyrUaNb/SlOGMkgYBuc0sq1BynHjk7du3r1y58rXXXps5c+bo0aN79OjRq1evOnXqYNHUbDYTEYwQcMpmsxmnFModHJk8m81mq9VKy67YzYOk5Pixskx8w7WIOXKlpKTs27cPB+qW2i+UhUZVD0fXP3369EaNGo0bNw5nPFQrBKr6G2QCuqq/wb/qHwwGFy9eHNtsjRkzhs55+GtslhgBRoARYAQYAUaAEWAEGIEKRUDXdZ/PV1JS8sMPPwwbNsxut9P8mYTYwSpYZlVVoybwLVq0mDlz5vWzy2J1jGWviFmIjZzIIaR2OYJcWLkssAiDk+tJkybBUYnT6ZQJ6PT09JycHFii8CxdRo/lykQgLy8PayTg4N544w2yWqWaX5n6cF7JgQBVnnIaNznOTWXAQqkZhlFcXAwD6mvXru3cuXP37t3Lli2bNGnSzJkzu3fv3q9fPzjldzgcZrPZbrfLS60gneGvH8fkyp43yukTo3pJOabZbO7Vq9eVK1dwtC8ZiSfHC42zFGT1DM/X9FrjfJyj3UMEmIC+h+BXfNZbt26Vmye0XFlZWeR6r+Kz5BQZAUaAEWAEGAFGgBFgBBiBGwjs2bNn6NCh8vyZnGzIgVEyWYeZzeYBAwZ8+eWXtE9f13XyJgeZJp838vzpf8xCowIT/CfNnMsRyiKggYPP5wsGg1pIO3DgQMuWLQlt0NBgQ5YtWxYMBsvCLcEhYvWSAIGcnBz65FVVnTp1KtwjJEHRuAj3EAG52SxLDTlOnDKSwrodmk1d191uN7Wi6JKIp0acgoKCLVu2rFq1avr06c8991yXLl1e8FRNAAAgAElEQVT69OmjKAr29MgsjSzTd1GqQDHh8jg1NfW1116DelpIQ+NfVsGTOJx2XJGXFbzZJC5y0hSNCeikeZXhgnz//ffyqhpasWbNmlFbmVSl5cIwAowAI8AIMAKMACPACCQGArqub9iwoVu3boqiwKWGzWazWq2Ye2PXcKkTbGxGTklJGTZs2MaNG0tKSmDYdRvFqopT0HgIkbIIaEAEEgQT8mvXrrVu3Vq2gAa8aWlpe/furYr43EY14EcSEIHZs2djlgoL6GnTppFVPn0CCag2q5TgCMALE/6WpSpVsDiFwsJCJKXrepR9MZZFae0EbW9hYSHxobDrJ8/7fr/fMAy/3793794dO3asXbt21apVubm5o0eP7tKlS506dcrqE+VwbAxyOBxZWVnff/+91+sF3030d1kFT+5weT2V3mxyFzk5SscEdHK8R4HW0DCMqANbYPUQdVZskpSZi8EIMAKMACPACDACjAAjULkIyDNtIQRsb7ds2dK+fXvaegxfEPgLt87gnuiIPKvV6nK5YBo2cODAjz/++IcffiDnztV8Xh37Pml2fVNk4JSjQ4cOlshFW79NJlPXrl2FEETux59mrD4cwgjcKgIfffSRzKl98rtPUJnleijLt5o+x6+eCOBUOnCRZ86cGTduXN++fceOHQs0QB9jAU9expNrWqwcGxOpyTFltOVwWS4rHflZLMNs2bKloKBg+/btHo9nzpw5sUcmOByO6dOng93WQhobF8oYsly1EGACumq9rzK1pW0gderUka0esMh87NixqNlCmQnxDUaAEWAEGAFGgBFgBBgBRqBcBMgubO3atdnZ2aqqulwuVVXJmzNx0CkpKRRODJTFYunfv//SpUs9Hg/lI1tEUiALUa5y4wFEC2nt2rWDKTqtCphMptmzZwshvF6vz+eTiZJ40uQ4jMCdIKDr+oQJE2rWrKkoyiuvvIKk/H5/WeTgneTFz1YrBMBBFxcXP/TQQ/CA73K55s2bhxWOoqKisuqY3AbKclnEsRxHRlgOl+Wy0qFnEQHruHRkV25uLppu2jbUvn37w4cPIxpWfG+6EklZsMAIJBoCTEAn2hu5TX3AL+u63rNnTxrco/FSFOWLL77gduo2keXHGAFGgBFgBBgBRoARYARuIEC7knft2vXggw86nU6LxQJzZgxBrxOdxD5DACutKIrL5WrRosWyZctOnjwZDAZ9Pl8gEMAYlbbTYgJ/Izf+P4yATGrEicilS5eaNm0qu4FWFCU9Pf3IkSOBQEDm+nmOECekHO0OEcChRB6PB3sdYI9fFjl4h3nx49UHATjEOHz4MBbb4AQ/KysL1SzKR7DclsYvA0w5vgyvHF6+LD9FaZKbDoSsXr0aPqwcDofJZMrNzcWXAsNnbq5jMeSQqoUAE9BV632VqS0aIy2kRZ36Ao8c8+fPL/NJvsEIMAKMACPACDACjAAjwAjEjcCRI0eGDBkC586y3YPD4VAUxWq1ygQ0RRg5ciTMuIQQ4J1lx51wDUGz97h1qRYRCZZbYh8OHDhASwKgZpxO59ChQykRSrZagMiFvKcIwOheVsEfuZiAljFh+TYQCAQCuq5v27YNzZ3NZjObzdnZ2VjU1EIaNXS3LUAr+XFZTzm8fFl+CnLUJnU8npOTk52d3aNHj/z8fGxzJ9dJsSlwCCNQtRBgArpqva8ytfV6vVjlmzx5Mg30SXjqqafKfJJv3GsEyJKIzAHk/vJea8f5MwKMACPACDACjEB1RICcbOi6TrPfw4cPjxo1CufaRR18DbdvcOtMsqIorVu3/uijj7xeLw4sKR9K4kbLj8Z340HA6/V+9tlnFouFLNBBQ2/btg04E1cST2ochxG4EwTgnRx+BsAYxjoooArJ7cCdQF2tnsX0WQtpO3bsIOrDZDJlZWVhnwcWO6lqxQMOIscTs/w48aRDW3/KT4rvMgJJgwAT0EnzKsMF0ULaa6+9Ro0vCb17906qciZdYbxebzAYpI1CPp8vajk06UrMBWIEGAFGgBFgBBiBxEWAputwlCGEKC4uHj9+fN26daN4ZxptKooCC2iTyQTj6D59+qxbt44KSf4uKYSFu42A1+vt168fHKTQqsDAgQMx5qS3fLfV4PQZASHE8ePHJ06c2KdPn6eeegprWnA+QPVQFhgxRiAeBMh+6+zZsxkZGdQNzZ8/H0uecqWKc2EDj8STe/lxKiqd8nPhu4xA1UKACeiq9b7K1JZWlfPz8+WZAOT69euX+STfuNcIkIURfPzt2bPn22+/3bt377Vr16hPvdc6cv6MACPACDACjAAjUL0QkCfPixYtaty4scPhsFgsqqrWrFmTjraTh50Wi8Vms9WtW3fEiBHnz5/HoUk0zolz8l+9UL77pT179mxaWpr8mhRFycvLk11L330tOAdGQHTt2hUO4hVFmTZtWpQj8tsgChlTRoAQ0ELarl27fvOb3/Tp02f27Nl+v5/NuQgcFhiBxEGACejEeRd3pImu6+jFd+7cSUNMHDyCn3eUOj98NxHAu1u8ePGjjz6qKIrFYrHb7RaLJSMjY8KECceOHbubmXPaFYaA7MiywhLlhBgBRoARYAQYgXuEwJUrV4QQGzdu7Ny5MwaTdrs9JSXFZDLBBQcNOCE4HI66desuXLjw/PnzMtcMXgkHKPF248p/mV6vd+bMmSkpKfCOkpqa6nA4+vbtywR05b+L6pzj3r170XSguRg4cCDQiOKd6Wd1xorLfnsIFBcXe71e5p1vDz1+ihGoHASYgK4cnCsjF2xsLC4uRr+OFWaz2ex0OlVVzc/PrwwlqnEecGcmhPD7/Te1XMZqAc603bBhQ+fOnS0WCy0YqKqKTax2u7158+YFBQXeyFWN0a0CRacKQLoahoEXXVxcLITgWTchwwIjwAgwAoxAIiOApfGioiIcbY2RJJ0riHEm/DkQGW21WpcvX3716lVQz8QiGYYhHzKGxVrcTWQEkkm3QCBw+fLl9PT0qEMjCwoKUEx5tSCZCs5lSSgEtm3bRhMcRVH69esH9eT2QW43Ekp5VqaqIOD3+91u901n4lWlOKwnI5B8CDABnVTvFF14rVq1FEVRVVVeZ8ZWu6QqbeIVRgtpu3fv3rJlC4xKyl+A9Xg8WkhbuXKly+XCefGY0eGv1Wp1Op0ul8tkMnXu3Ln8pBIPiWqnESbYNIXDT1h7ERY83yYoWGAEGAFGgBFIZAQ8Hs+CBQusViuNJIl9lh1AwwtHq1at3nvvvWAwiE7Q6/XKLFIUAS3fSmQEkkm3kpISv9//4Ycfyu9OUZSxY8fi/JhkKiyXJWER2Lp1q8lkQqNhMpm6devm8Xi4fUjY91UVFeOpVlV8a6xzdUOACehke+O6rnfo0EHeGpmammq1Wl955ZVkK2oilScQCLz//vtNmzZVFMVut9eqVWvJkiU4WKNUNXVdDwQCH330kdlsNplMdrudeGe73W6z2WANbbfbzWaz1WpdsGAB28+WimSiBcIbuxbSojxysAfMRHtTrA8jwAgwAoxALAJer3fXrl2NGzfGsMRisVitVpg1EAetKEpqaqrJZOrYseNHH31Uqq2ZTDSzhWMszpUZ4vV6sQ0rMzMzytahpKSkMjXhvKo5As2bN6cdn6tXrw4EAli4kpsLkqs5Vlz8O0GAmeg7QY+fZQTuKgJMQN9VeO9N4n379sVUgUaZJpMpJyfn3miT7LmCF37jjTdA+jscDlVVU1JSXC5XQUEBscZRFrJCiHPnzmVkZMC8CLO7+vXrL168+MiRIytWrGjYsCG4bNzKzs4GkKVO85Id48QqH73TUtXSQprP58vPz//ss89mz549bty4Xr16tWrVqm7duv369Tt48CCs42XHi2Q3XWqCHMgIMAKMACPACFQaAiNGjMAWOrKWJd6ZBEVRmjdv/snvPsH2LLlbxLQ/GAzKrjaYgK6011d+RtOmTaOpAYQPPvgA9HT5D/JdRuDOEfD5fG63+9133501axZ2i8IVITHOUcKd58gpVAcE5GnUtm3bnn322UceeeSdd95B2eW71QENLiMjkPgIJBUBTX510dZgQEyGh1EvI4nHW0899RQc89Eo02w29+rVKwoB/nmHCMBsRAtpR44coVkZJmzYsnr48GGalcGdIv28du3aqFGjEA2b0Tp06EB1sqSk5PDhw4qiOBwOxGnWrJkQojLPVTAMw+PxEERy/02lAItKn5gchx6MFfCdBoPBixcvHpWu/Pz8vLy89evXr1mz5mvpggPlOBOPza7CQ4LBIKbcO3bseOSRR7KysrKzs0eOHNmvX7/mzZvTbmVFUWDGLofUqlXrxIkTQoiSkpKocTb9rHCFOUFGgBFgBBgBRiAWAbmjd7vdr732WlpaGvVc1HmRYDabVVWtXbv2ggULCgsL3W53OV2zfIs6uCghViUOuasInD17tnbt2rBsgNlEp06d7mqOnDgjICMgm9Houo4ZhNwsyJFZZgTiQQB7T4UQxcXF8nx8w4YNZPQTTzochxFgBCoHgaQioIUQwWDQ7/eDHnK73bquw70U9W1oiYjpqxyUKzmXyZMnk90KOGiTyZSZmVnJalST7K77PPn666/lDg+mQxkZGSAZgQN6R5qPwQ+aPXIpipKRkXH27FmcWQdb6eLi4uzsbNr32rx588rEEzqUlSOVAhFo4Qd+J8p6isK1kLZo0aKWLVsqimKRLqvVSvvyVFU137gcDscjjzxy6tQpSuHeCuDfv/vuu/r169MaD/YjO51OFAFbEDBXp6k7JnuzZ88Ghc0WYff2PXLujAAjwAgwAujR8vLyGjVqpChKSkoKEdDoiPETcmZm5sKFC4lC0kIarUCXjyQNwqOE8p/iu3cDgVGjRsm7JM1m8+7du+9GRpwmIxCLgOyckKYPcrMQ+wiHMALxIOD1epcuXSrPx+fOnRvPgxyHEWAEKhmBpCKgqScTQuzbt2/OnDkDBgxo2LCh3BhZrdYhQ4Z8/fXXUSRaJeN+V7NbunQpOC/ZDtpsNt/VTKtz4tu3b5frGCyahw0bViomYKKfeOIJRVHAL1ssloULF1JkbFwVQsydOxdG0IqiZGVlyXbHFLnChajvQv6p63pRUdEPP/xw8ODB77777sSJE4WFhYighbT4j0n88ssvLRaLzWZLT08n3GQml2a/EEDpdu/eXf7AK7zg8SeIIg8ZMkTWWVVVOMq0WCwoFPjzqLNAr/Ptubm5MGZnAjp+zDkmI8AIMAKMwN1AoLCw8Omnn4bLLzJZkHthLBObzeYFCxZcuHCBdACRFOfIRCaYZJlSY6HSENi3bx+9aDDRU6ZMKSoqqjQFOKPqjICu61pI27Rp06lTp9CGxLmIVZ1B47LfFAFMQufOnUvzSlVVX3rpJZql3jQFjsAIMAKVhkBSEdDY2P7NN988++yzdHwKneeG8TT2xSuKMmrUqEpDuZIzWr9+PYqJstNAs5LVSO7somyE5Q4PgC9btqxUBLSQ5vV6HQ6HzWZzOByKojRo0ECOSVvSVq1aZbfbTSaT2WweMWIE4siMsPxUBcroxU+cOLFs2bJXXnll5MiRXbt2hU9qzFWIYEURunXrNnbs2I0bN8apw6uvvirPdQEX/bXZbC6Xi35CAAcdZ/pytKiTAOVb5ciYHpcVIRAInDx5Ems8MAqz2Ww4RtJkMsm227EW0KqqfvbZZ9iBwQR0WQhzOCPACDACjEAlIPDWW2+5XC4YK6DDih0zq6r63HPPnTlzBobP8mJz/KvCMuksy5VQRs4iFoH777/fYrHQWKtx48bJvTE0FgEOuScIeDyet956C9sfHQ7HgQMHoAa3CffkdSRfptOnT5fn46+//nrylZFLxAgkAQIJTUD7I5eMsi6EfuO3ZtyQhPjzn//83nvv9e/fPyUlBUyQTGDJphyKaqJ/w0c8LYQoLCkOnw1dxr+/5lF1pLy8PBQfvvwIip07d1YCfVl1cKpITZ955hkYPoOi7d69ezmpT5s2LTU11Ww245G33noLkaPezrJly8BQK4qyevXqchKM/xaMlXw+Hz0C0wO/33/x4sWPP/54/PjxnTp1qlu3LlUbp9NJahABDVrcbrc7nU78VRTFZrO99NJLsJAqKioimpXygjBjxgwkTr4pCDokS7wtvlzYiQ8fPjwqnXh+BgKBUu2zdF0v9ZY8CJZlOS+/33/q1Cmz2Uz7DODxBi2Py+Vq167dww8//OSTTz733HMjR46kuX1KSkrDhg2FEFpIg+tMOQuS5bxYZgQYAUaAEWAE7gQBr9cL7tgXudAH5efnd+7c2W63o4fC3p2MjAzq+tHv9+3b99ixYziJ4U504GcTBwGv1ztv3jyM2fC6bTbboUOHEkdD1iRZETh9+jQaFpvNpijKs88+G3UiN42EISQrDlyuu4TA6dOn77//fszOUlNTz507h4yi5td3KXdOlhFgBOJEINEJaAyUMXTetWvXV6tX/39zc8eOG9e7z/9q0+4Bs8VmsVjsdjt6Mho3RwSToqgIKYuAVmuYc/51ohAipIdp7VI56DhxTKhohmFEbfwHDl988UVC6ZlMyqxevRog22y2Jk2abNmyJXbCpus6ArOzs1Fv8UhZ3veWL19OTlSOHj1aUXDBKFjXddDQBQUFOTk5HTt2JBYYWtFfa+TCXMVqtWJtGe4myNU4CRaLxel0Lly4UGafozr+r7/+GoljGArrZrPZnJKSkpaWlh650tLSUm9c/fv3X7Zs2W3s0YOVOuUuO56TKfgohpoMk+VxsAw+bL6OHz/+29/+tlGjRnXq1OnevfvEiRNXrFhBUzgtpJWUlOi6jr2uhM+rr74qhMDpjnL6siznxTIjwAgwAowAI1BRCOCglBdeeAGOsHAyATkEQ1eFXr5OnTqbN29GBypbPVeUJpzOvUJAC2mnTp1yOp0wKcB4bMaMGfdKH863+iCwdetWmJhgn27v3r3RItHAGzMUGhJXH2S4pBWFwNGjR6dMmfLqq69+//33SJOrU0Vhy+kwAhWFQOIR0IYQ9E8IPaShqNizYzKrdqfDZK7hdKVGxkxh7wTkbkJRFGwos9SwKUqNyL8wB10WAW1zOGtY7afOnkkyAtrtdhN7KAvsjL+iPpvYdILBYNeuXdu1a/fiiy9evXpVCBFLmGIid/78eQy/YNhbzvnjb7/9NiaHTz8dNtWvkMvn8xEtu3DhwiZNmkANnKGH2iKvXmA6ajKZaGMBjJTleoWPDk/hFD5FUaZOner3+0HCRml+7do1l8vldDopqYceeghHhsoxacSAo0RlyliOFo8Mv9uUwtWrV/dFrlOnTgUCAWSkhbSoswFJAaKwKS95Ni5bUiMRRIMv7ylTpqCNUlXV6XSeOHECDqDLMfqgXFhgBBgBRoARYATuHAHylbF06dJatWqBecRBBRaLhTopDJgbNWq0cuVKt9t95/lyCgmIAIY9HTp0gGEBrAWbNm2agKqySkmGABPQSfZCE7A4MPEhxeSpXOxsjqKxwAgwApWJQIIR0EQ9QxAi6A0T0N+s/vcbBJlqsTkUxRThv34ycDabzVarFWQWLDTNZqtJsSmKNcJBKyY18i/MQ5sV1RxxwfFX8+h/fO7Z7fn5Wpj2LsUIml7G7TmTpccrUwgGg5mZmeTfgLjC559/HmpwE1yxrwPdG9Ikc1oS5LxKSkqWLFlCHpBtNtu0adPkCLI8adIkOEqrQPPncCXXdcMwBg0ahKkmzheCF0iahZILLUVRnE5n165dx4wZM3v27Lfffvvjjz9eu3bt5s2bP/vss/nz50+ePLl79+6obERSI+W33noLLHysb8Hs7GwyvTGbzYMGDQpELpC2OKIkeOMi4lgG55ZkLaT5fL4lS5Y8+eSTtWrVslgsDocjJSXF4XCoqtqtW7fXXnvtxIkTV69ejbXCAFNcana0xhD7rr1eL0rRrFmzlJQUghHp0AcYNTCSK1KpOXIgI8AIMAKMACNwqwjoun7hwoUnnnhC7qYxODSbzU6nE4vN999//7x5806fPo1OyjAMbECM7eNuVQGOn1AI+P1+eOHAFjQMNRNKQ1YmKREo1QWHFtJix948Hk7KCnCXCkUdFtIvKSmBQBZXNNu6SwpwsowAI3BLCFQqAU0tAlQM9zehCPFL3pxJ0IUIhWNpnjD/8/TTT4RJZJNZMVkitLJVUcwRGtoU5qLxLzKUNlssN/hWi6LYFcWq1rAiJMxcmyKW0SbFVENRfwpW1BphG+qfNfjZ+BfHr17zjSYMj99HnqahKgwb5Z1Bt4RyJUcOBAJ9+vSxWq0YWZIBeN++fTGLkO03K1m36pxdSUmJYRjDhg1LT0+H4YnL5dq6dWtZmBw4cGDChAmbNm0qK8JthOPV79y5kzbeYjpKmzFhnZ2WljZq1KilS5ceOHDg0qVLN81oz549zz333I1PT8GENj09/fDhw6U++9prr2HCg0lvixYtoiyCMRilEQMxtqWmFhuI+MXFxcFgcP/+/cOGDYNuWKaC2Rf9BXuekZExcODAvLw8pIYU7oT7DgQCX375JeGsKMr48ePLobNjS8EhjAAjwAgwAozAHSJgGMaiRYtg6UwDQvSJ8oan559/Hkc43HbPe4d68uOVicD+/fttNhtZG6iqunz5cp4dVOYrqIZ5BYPBT373Se3atRVFefjhh69du+bz+ZiAroY1oWKLbBiGx+OhhVIS/H4/5CpkRFixyHBqjEBiIlCpBLQQIhAI+P1+8Lm0JRB+Nnwe739s3fZvi96bMjln4D/8r3atWiqK2aKEqTpcYZ5INd/wrXGDeL7x/41Yis1ht9jui/DU95lUZ4uWrQc+9lDHX7VTFLO5RopqdtkcTptTDVPZkeu+1PsURalhq4GfaTXTR48ds/tPe7wBf0jX/X6/2+32eDzYaE/j8sR8naRV165dURyabJhMpg4dOlCjTDFZqEwEtJDWrVs38rfYsGFDsqItS4074UBj08QHeOHCBfC/qCTkQr1BgwY5OTl/+MMf4Kkj9vFSQ6jXX7ZsGWyonU5nzZo1HQ7H5MmTr1y5EvvUxx9/TAo4HI569epVLAEdDAYDgcB33333+K8fx9lKDocDjLOqqkQ9QyALIBwL+eijj164cAHeum+V+JZLGgwG33zzTTL0VhTlzTfflCOwzAgwAowAI8AI3A0EMNgzDCMvL69p06Y06pDHhOSAq0+fPrt27aL1URro3kkPeDcKxWlWIALBYLBFixYyAU0nwlVgLpwUIyAjQG4AEUjNFFtAyyixfKsIGIYRDAbRYWkhLarnYurjVvHk+IzA3Uag8gjoqOYABTt06NCHH344YMAALIemprosVnKOET5D0Gy2qya7SbWG/WaYI3bP6l8jROizyG/45ACdpijh+Iq9du1Go8f8s9vjCxPfIU3TxcFDP8x/c9E/Pju20c8bqxYlPSO8Nd7hspvMN44rvCE47nM+8MsOr7/xhhbS6OyyqjIov94KT58+HQSfPNmoXbs2inC3axWnXw4CJpMJI36TyTR06NDYswrpWb/fD+cVFchBayHN6/UahjFu3DiQxTc+GsVisYwePRq5+3w+Wh8ifcoXEH/EiBFwg4NkmzRpUupTBw8eJL+Tdru9bt26FUhABwKBkpKSV155BduKYWQNGjqKesZPQkBV1bS0NLvd7nK55s+fL4QoKioSQtwG/vjQnnnmGeSOLDZu3FgqGhzICDACjAAjwAhUIAKeyDVr1izyuaGqampqqjwmdDqdTZo02bhxI/xs+P3+QCCA2TsNdytQJU4qQRDweDwY1Tz55JMyAd2wYUOMxG5qGJEgBWE1qhwCOGoFausRGy+YpjIBXeVeZWIqHAgE5s+f36hRI4vF0rt3b3Rt4f30N04US0y1WStGoLohUHkENNlWXLt27ZtvvvnNb37TunVr2F+AsVJV1WIxq5awcwyzQ1FtYaLZZK6hKC7VVMek1FWUmmEfGqa/JaDD1LMKLxz3paYMGDiwZ1b2/54+c/nKjz2+QMmPbv2GW49AmIgWHo/QQiIUEP919NoHi5d27/mrMK994zJbLGEnHmo4UZvD7rjP2fwXLZ566qm1a9dGEWSoKHDzmoCVJicnB2WSJxuqqsIFcAIqXE1UOnz4MA7fQ50Hy1l+2XVdvxtnARmG8eqrr2LuATcRVqu1HIfU5SuJzQ1CiP3799NZoKiB9OHLKRQVFdntdnJTjtNvaMYLp12yx5tSl68QGHvr66+/rl+/PnKH4TMcnpTKPoMgNplM8IUNI2gs3hAdL2t+S3JWVhax/CaTCScQ3lIKHJkRYAQYAUaAEbhVBL755ptmzZrRTiNYQMsDwuv978yZMy9fvowzEmirMhPQtwp1lYtPXMzSpUtlAlpRlHPnzpV6hnaVKyMrnJgIYG2DGpnCwkJYpzIBnZjvq8ppVVRUZIn4YsUEc8mSJbCOivIBW+XKxQozAkmGQCUR0FiDOnTo0OTJkxs3bkz7/nBYmcms4t9PPHANNWz8HL4XZsYU5e8U5eeK0tOkZDXNHDjxX1+bmTv32z+uLfjPP61Zv+bAwYMXLv/kozak6/gX0PwB7UdNeP0hj9BFyf+I5QtLCvL1QNijtAh4xcE94uz3IqCJYv/lgoP5o/7paZvLbr3PYXM5kXUNhy3sl8Nhg1PpevXqPfPMM4FAwOPxaCENRiIgc2EfTdxZgtSPQ4cO1axZU1EUMHHkYwHUXoIomTRqxHKgpRZN1/V33nlHdgq8e/fuUmNWTuCpU6fgIMLpdMJIasWKFVSTIdyqJiUlJUjT4XBgrnv69OlSE2nQoAE+f0VRMjMzoxZ4ZDVKfRzx3W43Bq+wFvd6vTk5ORh2mEymlJQU8L82m83lco0aNeq9997buXPnjh07jh8//snvPvnlL3+JNmf48OHUKFmtVjxlsVieeOIJ+KcrS4fyw/ENgv5u1qxZ+ZH5LiPACDACjAAjcBsIyCarp06dGujZtvYAACAASURBVDJkSBSxSKuwqqpardbf/va3Fy5cwKm/UdnxbuUoQJLvJw1ZDx48SKYAWIxfvHgxyktxSIgyJiAO8fbGismHKpcoTgSKi4vnzZuXnZ09fPjw8+fP+3w+uLgkDjqe8X+ceXG0aoIA7dmdM2eO3PfNmDEDPRqZQlcTQLiYjECCI1BJBHRJScnw4cNhZiibYKCZ+CsBXaOGYnGprp8pYdfPP1OUemZLx18/tqD7r97o3OadXg/+n/86Kvwh4Q2GDBEI879CC+qBkK4LEbZzDp9cCA7aCBX/eDXsxDkYxn9ov21/3/qzfxq5MvwjINZ8Kjpk/lu39m8a4ZMOfwyIYl34L1y9+C85L4XZKItkEW01K+afvHu4XK7GjRuvX79eCHH58mV5Q0eidZZwxu/z+fLz80+cOLFs2bLGjRtfp/mWL19ObXSC18uqoh7wjBNVwzBeeOEF8LOgOy9cuECmKJVf5HPnzoECtkYuRVE2b94sV2Z54hGneoFAAOxtSkpKZE+DxR+5Yh8HAY3I7dq1uz0Cmnx+BQKBwsLCx3/9ONZayLYadP+rr7565swZTLZ1XScHI4FA4P3331+3bp0QYvv27fXr16c9GSCmnU7n8OHDb8MFhxCiuLgYZx7CBq1fv36xIHAII8AIMAKMACNw2wjAixc2swshXnvttbS0NHkGTr0hetusrKy9e/fKxzxEdfRRP29bMX4wYREgyvjKlSutWrWifWCKoowdOxZqy9Vg69at/SLX1q1bZRMcebiYsIVlxRIKAb/fP3Xq1JSUFJPJZLPZsrOzoR6xzzfd+5hQxWFlEgcBzKbnzp0rd3+zZs3ind+J845YE0aAELjrBLTH47lw4UL79u1hYmk2m10uV8T/QA1VrUEEtFJDjfyzmtN+pliaO9J/43D8U4umb/7LuPMzXhYdm29q2fD9338troSJ3/DlF8WeUEkgQkMLYegiFDICISNERtBCiFBIFJ4Ts1+82qnB+ux2vz9xWIT8YuOXomuLra1/tmzKv/zJHxA+/Ue/cOsiTFQX/lhScGBf7359VYdNqWFSbD8x0WaLBUdFYwv/gH946NSpH2QjkUQbhNHgEsQZ+bCGgz95WPkTmvzf7SLg8/lu6WhdOhzSbDanpaUZhnEPV2WvXr0KmhUsrclkOn36tFyZb6Oq7Nu3D7uf8L23bNmyrL7//vvvh02Wqqq9e/eWP6goMvqmL8fv9x8/fvzBBx9UFAU+LkGsOxyOjIyMtWvXyiw/NgEEg0G4yETi8LV98uTJJk2aOCOXw+Egm+h33333pjrERvjuu+9APauqajKZXn755dvAMzZZDmEEGAFGgBFgBAgBLIFv2rSpefPmWOG22+3yJBwdfb169VatWkVPFRcXc5dEaFQ3gV79kCFDMGZDzWnfvj2goAhCiFatWsFMoVWrVrm5ufn5+XA/KA8XqxuAXN7bQ0ALaWidYJGmKIrb7Sa3e6ChuV7dHrbV/CnY3pFvSfSAU6ZMYecb1bxicPETE4G7TkB/9913LVu2tFqtjsiFcTD43AgBXSPs5bmGolgUxaoqltSBT039/Tbx7D8dbf2L3w/o898fviU6Nf2v5nV//9ly8WNxGMOgECX+EkNEPDrfAFUTfn/I4w+GNEOEdBHShK6H6ebXp4k29dd3aPjv/7FOaH6xe7vo1eZPHe7f/r/Hn9Mi7jhCEeoZBtSa0DUh3EHtD1v+1LHrPyhKHUWppSgWuyPNdV8qBmfQP72ma+bM6VpICwaDgUAgATtLmc7z+/1EwBmGcXvmnDeQ5v8FjcvBHZ89ezZ+UDIyMsgcicx+43+8YmMWFxfLBLTZbEY9uZP6/Prrr1OaiqI8/uvHy9IZzmHsdrvVah00aFCUFfkt6VBYWNixY0cAa7FYXC5X+HBRh6Nnz56g1KEDDj+h10f7SWkNQAtpR48erVu3rtPpBDlutVpdLledOnXKKkU54StXroQ5NuzOFixYIH+V5TzItxgBRoARYAQYgXgQMAyjsLDw5ZdfttvtNptNJhOJg1YUBQc8UGdHxzbEkwXHSXAE5FFNnKpiiCWEmDRpEq21K4pSq1atq1ev0ugIqcmDOovF4nQ6z5w5k5juB+MsPke7hwgoigIOGpYiMI1iC+h7+EaSIGtd1wOBgNvtPnfuHHV8qqqePn26qKiI/KYmQUm5CIxAciBQYQQ0BkBYgBJCwKnTwoULZYcbNIhxOZ0Wc9i+2GK+z2xxKFYlvdHfTXl9zvG/iNMlYu7/EU2ab+7S6dy/viA6tz7RuvG63BmXg0ERMsJONiL/DF0E9bDhsxHhjjVdBILhxkdoWph9LnGLkkKx8iOR2XD7A612f7JSBDzi8H7R9YG81nXXjX/qtL9YFBYKTQgtzFcHNOHXhF8IIyS0Qrco8og/btYaNRyvKH0VpZWq1DMpjp+UjzjksNpUcw1T9+7dt23bFlUPbok4i3qWf1YJBIgqPXHiRIcOHbAyMXHixNg5gK7rWKJAuZYvX26z2ex2u8VisVqtbdq0KWcxQE6NpgoVi8/FixdhogtLhMaNGyP9W63DXq8XizHXrl2rVasWDjuCVfU333wTXjQKRlzh/K32devWJS7+iSee+Nubt/Dr/PnzLVq0sNlsYI1p+v3YY48FAgFCmEa3Ny1dXl4eFJMHMeQYMX4SeebMmeR73WKx7N69W36nt1BCjsoIMAKMACNQvRGIGmPD/ZRhGGvWrKlduza6cnDQ8KgA3742m23QoEEej6fUXrh6I5o8pae9dHRgNRmd3LSQ+fn5IAQxcrNarZs3b4ZLcYx2dF2nuRuqmcViWb9+PY9nbootRygVAToIByNtxJFH5rJcagocyAiUg8Dhw4dnRa7Dhw9zXSoHKL7FCNxDBCqMgI4qw5UrV4YOHYrlTeKg5UFMhH02mc3WBzp2ev///ltQiFM/Bs55Rd6fRLNW+Zk/P/bem6J5/WMPNMufPiVsYRqK/LtBQIsI+xwmoyOXEWaSI5cWjJgxC7FxnWjdfN0DD+ydPTvsNvrsWdHzV7ua1d3wZL9dV88gLghooYeT0UT4OS3sSVqIyxdE5wc+adP0k41rRJ20MVb1QUVxyjYCJpyRGNnv/9lnnxEnxb6rfkI2qf/DRM7r9f7mN79xOp2qqjocDpvNlpOTIx8EBAxgIO/xeLZv3167dm0Yw+JDqFmz5pdffllYWHhFuk5L15EjR3AcOU010ZVWFLp79+6lgeD1GUXXrl3JXQb12fHnpev6yJEjUTSwwJmZmdfdvQWDQWKBKTXDMOrUqYN5sqIoI0eOpFu3JASDwYEDB8rss8ViMZlMI0eONAyDJmPYLhrP5j58y59//jnWFYiD7tWr1y0pJoQYM2YMXrfJZLLb7efPn5etz241NY7PCDACjAAjwAhQN33y5MnBgwebzWaTyUSdqS1ygUxs06bN1q1bYexMw1QGMCkRKC4unjx58oABA3JzcwsLC+MfK548eRLDNqyXu1yu119/HeQyWOwzZ87IczdVVTMyMk6ePJmUMHKhKgGBF198kbYUP//882jQaNIRJVSCPpxF8iGA6R7KRTUq+YrJJWIEqi4CFUZA02K4z+e7dOkSfN1iZBxLQDtslvucpj7ZD2784xq/EXamYQjxF12cLxbtf/ldZqOzo54SPX4ZbNvkwNh/PBkMCl8wTEBL7HPpMl6Dt0Ts2S7aNs9v27xg1jR3KCQuXRODHvtzh1989w89//N/TocNp32hcNwgiGcRJp7BZWuGKLwmnhv2l1b1/2v2RPFYn4sP/PyrLm3f/FXHX6tmBQWRh2LY7z916lRQXR6Ph1o6AqTqVg7WPBYBvF8hBE7wI0cNiqIMGzYsat8i7XLdtGkTPE7YbDY6mI78FFutVkvkgpNxkJ4wDcDJdXeJgP7kd5/QKNBkMg0fPhx7F2JLEYuDHAIHylOmTMGkF+yzzWb78MMPA4FAqYZXuq6Djse0+aWXXpITjFP2+/0TJkywWq3geS0WS1pams1mQ0GEEPgqZfb5pktEtISQnZ1N7LOqqg0aNJBtguLRMCsrC22FqqqNGjWCkXg8D3IcRoARYAQYAUZARoCGlDg/cNasWbVq1cI4gRa28VNRlLS0tKVLlxJVjXTIb6+cLMvJgcCiRYtUVYWhzOTJk+MfxQWDQavVmpKSQnvXnn32WYx2MHjbtGmTPOtxuVywjUgO3LgUlYyAYRjBYHDJkiWzZ8/+/PPPKXdq31B1aSpNEVhgBOJBoKyKJIfHkw7HYQQYgbuKQIUR0B5P2Keyz+crKCjo0KEDeCVYIxIB7XCEHVk4rLa/7941/z82/ui+KIQvEP4XPkzwcol4bsy55j///qnB4oHMULO6Rx7rf/Avl1B8I+Iug2yW/0pAh/uqGzwyol49LXr+ck3bFnse6vOD7hMXzosuf7+7QebGju025m8ROoycI1F/snyOUNsl7oAQYccdG9eIjpn/3ecB8Wgv0SRja6fma77bLvweMXnyZBrl02gM53I4nc6HH34Yfu6p1+TG7q5W3HuVONGpR48ehaNh8vmQm5sbq5Wu64cOHTKbzaj8IKyxjRH8JtUlCOCg8ddisfTr188fue5GvZo/fz4R0IqigAXGeSCxBSk/5LnnnpMLYrPZBg8eDIPfUg2vZALaZDLBPWX5WcTeXbx4MX2SYPBtNluXLl0wfiW+WCadZbmsLxT22nPmzCEC2mq12my2w4cPB4PBUosTq5thGM2aNSNMevToERuHQxgBRoARYAQYgXgQkMfYbdq0ka2e5X48NTV10qRJ7siFrpB23mARNM4uLB6VOE7iIIAtp+RMw2Kx7Nq1Kx71vF5vt27dMFbBxA3nEMKDnBBi+fLltLChKMr8+fPhV62sEVQ8mXKcaouAbJrq8Xi0kIa/MiB3Y74jp89yEiOAAy1RwKhtr0lcai4aI1DlEKgwAloI4fF4/vznP7tcLmKcTSaTw+EASQRPBYMGDcr74+aQP8z2RojfsCvnMPMbEO+9I9pkHu/ZUXRubjROP/VYn4u+QuH3i5AR0kWxJjTN+ImAJjI6kkjYjlnHMYJCFF0W//jI9x0ztwwctOvseSG8Iud5f5Ome1r/Mm/voXD0iCV1OP6Nf0hM/Pij8BaLkv8RXX7xHy3rnG/9s5IHW11s1/wPJ46FdQjrqokNG//QOPNn4bG+WTHVUFSLyeawYtxmsdse7Nb16rVrZOfIg7PI20m2P4FAAPO31atXy/XcbDZv3LixsLAwtsDDhg2DjTNmiUQuo+aAm7ZarRjik6AoSuvWrdetWxd1ymUF1qsJEybABQfI8bfffjtWeTlEnriSvHnz5s6dO9P8BD5JunTpUlRURHHkRCBrIQ2W4Kqqms3mt956KzZOOSFaSNNCGhHEqqra7XZFUbKysoqLI2eV3ngYYxF5OAv5xv0y/z979izAQSOmKMq6devKjB1zw+v1wsIdik2ZMqUcNGKe5gBGgBFgBBgBRuCnQ48DgUBJSYnH45kwYYLT6XQ4HLTyTcucqqo+/PDDJ06cwNafqF4P1tBaSKvAIQS/nsRB4NChQ/Xq1cP8C1WiTZs2UA9jyLJUNQxjzJgxqE5msxknlGC4Eohc2NyGNNu2bUvplFqRdF0Hn4hBmhbSkJQW0sglGtZFYI8fjFzkw5oWS8BxYwsdkoL1AKoxniJNWKhCCJART6xrvipUClY1AREIBAJYpnW73WfOnNm0adOlS5cMwyguLjYMg7a3JqDmrBIjUA0RqEgCuqioKC0tTWblTCYTTgZTFKV27dqbN28Or0eFfvLXHIE7FDJEwBCffy5aNfrP9pmBB37ubdvo/IOt/vNwQdjuWAsJw3Abhjv8nP6TJ2gioAOG7jNKtLD99E/XiF/veOBn3/btvK/gO/E/V8SEcb62mdubZm7ctltc9gstnJ4/coBhmIAOhX/iMEPh84qQW4z9zcUHm5xud/+lRjUP9+iy78B+4Q2FUw9q4e38uh7af6CgS9f2ZotSw6aaaoRpaFxmi8VssdSuW+fgwYPwSHBDI/4/qRAgG9i33npLruoWiwVdXeygPCcn57rZiMvlAtkKvzSoNjKFiqF/u3btBg8ePGfOnE8//RTAeTyeeOx2bwPlJ598EhwrfP9RjqUmhX1zKB1GkCUlJaNHj7ZYLLTIBMq1Xbt2p0+fLjURCrx27RroeJx/+P7779Ot8gVMpQKBwJQpU2T0FEVp0KDBsWPHonjeqEk4/Sw/F9zNyMjAywI+n/zuk6jEy0nk+PHjsFDDvO6DDz6I/1CgcpLlW4wAI8AIMALVDQEtpO3YsaNVq1bk61lVVafTiQ4Uq6RffPFFVC9D/Z0sVDfoqkN5MSTbv39/vXr16GAPh8MxdOhQbM2Uid0oQHRdnzt3LuyELBYLxjzHjx+nicwjjzyC8arL5crJyYl6nH6Wxe9QOOhscMrBYBDcNGqm3+8vLi7G+ArkMkwX5b/EaEdVclKAhSqEgGEY27ZtO3QobBdGNaQK6c+qJiACfr8fLcajjz5qMplSU1ObN29+7do1Zp8T8GWxSoxAhRHQRUVFbdu2hSGkTMy5ItcHH3wArMP8kaYbWuTkP10YhhYKinM/iM4tD7S+v/iBRqJ53VO/arNnf4EIBsL/9JBmaCFD03VNhLRoAloTotDrNiLmzFcuiH8d425bL69b628O7BQBr5j2v0seeGBvRvqXX30ZdvrsF+JK6GqEgP7JAjoktKAwwscbamHH0B8vEb9qeqRJysmfpx/q3G73/kPCK4QvnLghwk8H/b4wde4PXp0+M3yEgt0Z9igS5tFqmMMMY1oqeMZ9+/Z5vV5a5uVKlkwIYLis6/qzzz4r1/OePXuimKVylKNGjQLfCg4an8mgQYPGjRu3YMGCvLy8ffv2XbhwwefzlWOgRHPIisKzffv2pJWiKHv27Ck/ZbDPgUDgzJkzEyZMcLlcFosFJcJkWFGULl26gH0uf5Jw7Nixn76diNfCTz/9tFTcYvXBUHXfvn3ImjjoOnXqrF69Wt57hWcJtCghNuXYkE6dOpHDbrPZvGDBgnJmcVGPr1u3TlVV1BBFUXbu3Bn/s1FJ8U9GgBFgBBiB6omA2+32er2TJk3CsIF8eaEDxZhzwoQJfr9fHjxE9Xfyz+oJYzUp9cGDBzMyMlRVxcq33W4fMWIEOOiyENBC2tq1a1G7yKfZp59+CgNVwzAaNWoEr3Emk2np0qVl1SUtpF27dm358uVTp07Nla45c+asXbt2165d3377bZ50xeqjhbR4hklGeN6o4WSU2EQ4JPER2Lp1a2pqeL58/UDLd999N/EVZg2rEAIFBQWwGUIFe++996B8rHFYFSoUq8oIJB8CFUZAd+3aFbsC/9bvs/mJx4d+f+IMtlP99NcQYUI5aBhhtxoi4BGD+51oUe9s89q+hmlnH2iWv+WPYZz9EfvkcLRQmCTWQ0K2gA5GjhAMRlxqhCN7xcI3fuzYeFe7+js3/rv48S/iwwXiF5mftWz5+/+7XPh84kdfmEKOuN0I6BGXHXqYVA6EItSyLyS+Pya6d8zv2vIvjVKONKn3h1Ufh48ovHFKYdAQJbrhCUR8cRjixyL3mVWfLK+ZkaGoZrvzPkU1hW0/zard6XC5XCkpKYcOHZIJNW74kuzL0UJadna2TEDPmzcPuwjLete5ublgSzHQt9vt5VO0WMgFbn6/v6xB/50Am5GRgR4aU1kQx+UsnBiGUVBQAKtnnFeTkpKCQ28URXE6ncOHDy8qKhJClF80IURBQQEyBcO7Zs2aOI0gYIg9atSotLQ0Yp9VVR0/fjz2dUYBIuMmy1HR5J/05Q4YMICMiaxW65w5c3w+H92VH4mVP/zwQ6oeiqKcP38+zgLGJsUhjAAjwAgwAtUTgfz8/Lp164IZJH4QHa6iKI8++uif//xnIAM3Hbque71ejB9K/RtnP1g90a6ipQbFjMHbzJkzaXAFl9BDhw4tp1xaSDt06JD8yHW6GSeaoEYRm2OxWLZt21ZO/XnjjTeQTql/Y53GUDSz2dyrV68+ffr06NGjZ8+egwcPfuGFF2b87bVNujZv3nz06FEeU5XzWhP5VlZWltPphHu62rVrR7YX64msMOuW+Ahg7cowjLlz52Jair8zZ86E8txcJP5LZA2rFQJ3RECDFxNCtG3b1ul0YpjicDiwSdDpdK5a+amui/C/CPmrhd3ZaULXwkbQIeFzC+1HMW/atdb3F7TI+J/mtYpaNNj/1ZeixB+O79fC9slahHo2dBF2AG2IkDACwghGDi3E0YWFnkAwKD79SDzQ8I8dm2z44iPh+Yv4+hPRsfHWZn/3+aJ3Lgkjko4uQpHHRdjnRgBOPLx6MCTE+SJxpUQ8OvBox5b/Xfe+Qx1aHFy5SlwqCds+u7VQpFfUIlx0SOhGZEAfCBlhpx9Hj51o077TT244TIpaw6ooJrWG1e68L/3vav5p73fwVlat6lN1KCycTFmtVtRz/D116hR5uysVhA0bNpA9rKIojRs3vilLW2o6FRXodrvNZjPZL6empoLAjSLQ8fP8+fMrVqx4/NePY0MDaGvs1kTxa9Wq9c4778SvGzxo05xn79698T/7ww8/4PhHmBibzebMzMzvv/8+/hTKj0mWNbTzFH6EvvzyS7pVfgpCCPhdAbzNmjUTQlx3G8IDoJvixhEYAUaAEaiGCJCjXhpXX758uX///rBmRT+LHlNVVZfL1bJly7y8PLfbTa4MSqWbYwNBIFZDhKtPkTt37owlCnC+aWlpOGL6+shEdsRMgODICqKDr+/Z6t+/P+5u2rRJUZSUlBTc9Xq9MgEty0KIhx9+WK6oOO8EJhdy4ndPHjhw4IMPPvjwww9PmjRp7ty5L7/8cm5u7jfffLNFurZv375+/XqcWlSqPUHsyJyKiYEcTLCBj/w1wTwCyz+Y/UUNp7E4hMBgMIiPNyoOvZQkFsxms91uJyP9WMCTuOxctLuKwPUvesaMGXILM2XKFPY2flcx58QZgdtD4I4IaC2k+f3+OXPm2O12sM8w0FBV9aGHHrp8+aLXE/xbAlrThGYYmq5FDg0Miq9Xiua11jV0Hvjlz6/94mf7F7wpSrxhPxs+PUxAB8E+a2GL5cgJhEZIaOCdAxHnGGGO2Cu+yxdt6q/v2Lhg8m8LSy6KP20RXduuaVPv97MnFIdZZCEM7ca/MJ0cdv6si1AwfEJh+P5Vj8j9/72tf3HoF5mn2vziPz/7RFwsikQK09yBiKJG5K8eoc5DEW/UP63WXitxD3hkkGoxKapiczgtNgf+KYryq67hc9jIZfDtvR5+KtEQAId49epV9HCo8E6ns3z2WQjx1VdfyQR0VlZWqWPfSivvsWPHMD3A38zMTOgDej18LmhJyfHjx+fNm9e7d2+5O4esqqrNZsPU4oUXXrhw4cItLbfI56qrqnr8+PH4Cz527FibzaZGfHdYrVaz2bxixYr4Hy8/Jg7GwYC4Tp06iqJkZGSgmJs3b45/qoAj6UFAZ2VlYfMHj7PLB5/vMgKMACNQDRGA9ZbP56N1yiVLltx///2g89ABYYxtsVjq1q379ttv07ltcDx1b4cT1fCVJWyRDcM4fPgwXBzAdYbZbE5LS1u8eLEQwuv1xnLQgUAgMzOThnkmk6lZs2awp37zzTex3m8ymdLS0rBMQoSsLPh8vs8++0wmoCnBShPwpZhMJrvdTpsGcDI2NsxZIpfJZMLwFedXN2vWrF+/fn369GnXrl3v3r3Hjx8/S7rypWvnzp1472RMEAwGQcrjE/b7/R6PBwNFGi7quk7x5e8UEeDzGh6u6ZGErV13rpgW0lAf6IAomcS/8/Q5heqJANorLaS9+eabME5CNSMXHOXs7q2eiHGpGYF7i8AdEdBCiOXLl9MufmKf//mf/zlSKsMImxvrMH/WRfgMQC18nl8w7AI6KM78l+icub1FyvfN0y62qX8kZ/z5QOQ8QY/xEwENZxk32OcweR2SbJ99EZ56/y6R3XFnpybb/2n4tYBbHPyT+Pt2+9vdnzdz4v94rwkNTjMiTjwizp4j/HP4jy8oAgEhijxiwx9Eu5YHM+sfa9akYOVnoigQZqVDYcrZJ4TnhpOPiKNpPWK+bWihyEmKwchhimcunXzoH/ooYS/QiuM+p8VuU1RT+K+iNG3a1Ov10sjj3r5pzr1CEMBS6pYtW9C3YY/PI488Ig8r5YwofPHixXgEf8ePH39PxpqU6Zo1a2QCumPHjj6f74cffvj222/nzJnz5JNPNm3aFGYvGLjjgEGUF+Svoii9e/de///Yew/4qoq0D/gWb8umwIZmaBKK9CSAkLKpmwRYmooCn6CugryiuIiwCUmWtC+kvIDwySLv2hZBFlB4RWAhIaYaEpASpC71lSYQMO3mlnPvOWc+5jzJw3hvEkJv5/zyu5kzZ+pz5sw8859n/pOdDTJpCXkfSmbRokUoDTi/EQWFYRp1XLlyxc3NDacZCoWib9++jYa8PU84G4e38ytXrsQSqlSqDh063FKCgwYNAold59946623nMmpbyk1ObAsAVkCsgRkCTyuEhBFESl3z5w5ExwcDKMPMNopFApAnxUKxZQpU2pqamBF02KxAPXz4yoWuV63IQE4iau8vLx169bQcsDU1GAwfP75540mKIoiHNuFrU6lUgGd2qhRo5AAulevXg4G9SwADXbBZ8+e/fDDDxcsWPDuu++y7Ra1qfvmUKvVYKDgnCOg5PCr1+sdQHOghnCIxZqPILjv4eHRr1+/0NDQ4cOHp6ampqenJycnL1q0KCcnZ8+ePdu3b79y5UpVVRWcCcTOBFm3wxtBFd3B/3G6BVZx4N9r27ZtC5X/x0kCcl3uhQRgDLVYLMOGDYPvd/DgwVevXoXJqQxA3wuZy2nKErhtCdwRAA2bs5RKpUqlgqNRVCrVp59+Kq33mqUy8QLhEIO2i5xEf8HbQjj9OAAAIABJREFU6cF/5OXhu32ePt671aVBXc5NnVhRXU14Qkw8RZ9puIY/iTqD8JQImjJfcCI1S6YW0CIldx767Pd92v3w55fOXjpDjpaT4MFbn+2QPTJoV1UFzd9GqTKkmHaKfxOeCJJNswRAE5ON/PILCRx01KfXL528itIySIWJpmy0EyvNyiIxbwgNRtDUApoaQYs8L9JkrVZSx5kkJ4n563+7uvRSKH6HWotH61Zubm4vvfSS3OtJLeHx+bHZbMuXL4fVe0BCP/vss6aqByOfKIpLlizBtnF9S+PixYubinJP/VHVW7FiBcuhHBYW1rVrVywh0GsAhIraOcyBDQaDWq0eP358cXFxPau7VGIY+1tS+OvbAubPnw/0yhqNRqfTmc3mFloHr1q1ij2FSalULl++vOVZt6R4YOPj7e0NaDvI5M033wTb8BZ+zu3bt8cZS0pKCns8VEvKIIeRJSBLQJaALIEnRwIw7qSmprq7uyMEBoMvjLxhYWE5OTmCIKAFawsHoydHhnJNQSUDtfP8+fMRERGgwMChzQaDwVlZBcTzutkvaLOomF2+fJkQ0qlTJ1xKHzZsGJrbAxLNAtBgXo2v4NKlS3AsEGqV98GBpgloXYvoOehjYByNJUFaaqw7VF8nXVqtFonmUJ0zGAxarRYXhFA4GBE/XowC2fXo0WPo0KHBwcFDhw6dNm1abGxsYmJiTEzMypUri4qKCqWrqqrqSTAH3rdvn7e3t0ql6tOnT3l5OTuPwPYjO2QJ3KoE2HWdkpKSgoKClpxIdKu5yOFlCcgSuCsSuH0Aurq6ukePHnAGN3CE6XQ62OTVULJ6wgtqAQ0H/9GDAK0CITYbWZZF/Lr92L/9ub7tD00a9VPtr6TWSMFlC0/JNzigbBYl4mb4JdRN0WeRmEVSaSTnz5MXRhZ4t972YvjPl86R2ioyLupwv2f+PTpq++WLhLNRc2tRoKcXUgoOWpZau63KbqG3hJDqOmIykrg5V73b7hnU+z+z/3qiiiO/WigA7XQBBUe9ETQA0BaOnmBYY6LpmqrId/8ydW717lOKSJ2mk97FQK3Cn1KDDvTBBx+YzRSOfxJWtp1E97h52Gw2i8UyZcoUhGVVKtWePXtuWs/Y2Fg3Nze9Xg+aLm7lu2nEuxsAG2FcXBwLQLNKs1arRXUcbWdA7e7cufPcuXMPHz7MGsI4TEJuWmCr1Tp9+nSgp9DpdAaDoeX47JQpU3DyoFAo2rRpA1/WrZaBLaRVulif999/HxbVYFdH69at16xZg6JjQ7Ju1H4uX77MFvIf//hHC+F1NjXZLUtAloAsAVkCj7EEqqurYXu+IAh5eXkAysDYAUMwqBk9evT46quvnMfcx1gyctXuRAJgjCwIQm1t7ezZs6FFoTX9+++/z+IyZrOZ47iYmBjU+mADe05OztWrV2GfHOiHo0aNAq45bIqs3sW6q6qqCCFpaWmoJ6NGpFardTodaFag/sEjllQNVVMwb4LTSjAFLCf66HQ63JyHnsCzoZUuV1dXAIghXwzTlAOwYywGCAQh7KZigT8Gcy5n8xEdnvr7+wcHB0dGRo4YMWL06NFxcXGLFi2KjY3NyMgoLi4uKysrKirKzc09deoUaJ6CIKCOCi8ImhCuV1ksFlyyMhqNLPUHGxf1WIje6O49mAdBapAO/HLMhXNeMBABOsra2lq2ndxJI5fjyhJoRgK8nYf2Cd+C3OqakZX8SJbAA5HAbQLQoiiGhITAeAkQlU6n+/LLL3H8w8rU82+IlFUZLs5ONm0gPdrnDOh4qqtHSdiQH65eIpyFiITizo2jzw1INAWgBWq5bDKRd6Ye8/HeFj1s/08lxFpL/vTHTc923hwRWHT5MkWx7dKhhaJQjz7Tww9JNSG1RCA2iZeDELJuJfHptmNo7yNvvHKpykwu1QmXa2t4KKmENjcU+gYATdFniQnEaqMYd52FGGvI+s9IhO//Du35z1dfWK9QtFeqVawmoVarV69e7SyZBnnI/x8lCcBawpAhQ9ACwtPTsyXsE1OmTNHr9bAlUKlUnj9//oFUG5HQV199FRVlOOZIrVajPQhMBoAvz8XFpUuXLm+++WZBQQHopjBtbnQS0pJKcRz3yiuvQO5ardbT0xNL1Wh0pKU2m81ardZgMKDwR44cCfrxnagXUCneznMcZzKZPvvsM5irwKRLqVSGhYVBwVgN3rmoaF1++PBhtgdYs2YNq987R5R9ZAnIEpAlIEvgiZKAKIqgTlgsljlz5iCFHerVMAAlJyeD9ogDLowmskr5RLWW26gs8LqIojhjxgyFQgHNqVWrVkALZjKZBEEA3dVqtW7YsAFaIKqFycnJ69atUygUaPA7ZcqUZiygWR0MQcyqqqoi5tqyZUt6evrcuXMzMzPffffdESNGDBs2LDw83NPT093dHY8VYdUn4PHAHYc6nQ7QZCiYi4uLwWBgoV5UYsE2mX3kjIY7ZIS3IIQHC0BDYYCnAs2rAYtH+244iwX36rVp08bX1zciIiIoKGjs2LHvvPNOYmJiUlJSQkLCihUrioqKCgoKtm7dWlZWVlEh7RFurFXV1NTAaduIVsNpTxCWt/PsjkOgAMJlCWgDCD1j8qDho56PTQUDyA5ZAnddAtDMYNzEJiePm3ddznKCsgRuTwK3CUB/+eWXBoPB1dVVo9G4u7ur1WqwfTYajezgJDEuc9Khf/WwrkDI6ZPkD4N2Dux8aUDns88N3HTyBLHzRBCpWbQgSucNOps/i5SUuZ4Amie/VpA5M874eRf36Zh9aA+lypj9JunXsTQyuOCng5TBg9DAlCuDGj7bqfkz/SM2CYauJ6L+aR8JHrjft8tPE8ccvHaN/Goml4x00V6i6pAKDtg59bkBQBOJhsMmhauqpf+O7SWhffYP7PD9i+Hb7bUkL/uQu3srg+F3cFK5VvuUwWBo27Yt7DPiOLtkiy3Fl38eQQlYLBbezru7u6POFxgY2JJ6DB06FFRJrVar1+tbEuVehMGJgb+/P840lEoly2sBmn23bt3CwsIyMjLy8/Ph7G/cKFdTU+M8GUbV86bFFgRhxIgRqOt37969JToBx3F5eXkwG8GtkcuXLwfg+KaZNh8ANeOVK1fCjAUEAq8sNzcXkAJCCPBvNp9adnY21k6hUMCR65hF83Hlp7IEZAnIEpAl8NhLAEwCCwsL8fw3gAhx7JgwYcLFixdtNhuM2s5j7mMvIrmCdy4BWBePiorCdqVUKrVa7axZs2DnGXA979ixw8HOd450oaKrUChmzZrFNkJcCGHBHXADri0IAoKYbEUcdCGO42pra1E13cVcRUVF33777bJly5KSkhYvXhwXF/faa6+NGjVq5MiRQ4cO7dixI9giKJVK4BjBOoKdNQtGsxv7MFhTjgcOQIPpN4ueOxeVxdPVarWbm5vBYABPrVaLT9kD2dhEWP0/mLnA2nrhwoWxsbHp6emffPLJtm3bdu/enZubW15eXlFRAa8Yui/2tTq7WcUe3WyzcY4i+8gSuEMJONvsO3RQd5i+HF2WgCyBuyKBWwageTt//PhxZBKAEwjxmNHfos9EwnEtIjGTet4Lauk8cdzR7u1+7NbqRMTQn8vLqamyGQBdgfAcBaN5FoCWcGc8RJCmZSVr/0kG9cwb2LVgy1fEUk2W/bfQzaOk79O7N28iVcZ6q2WeAJ5dD0DTFVpCgLuZEHLtChkdscO3S+mY4JOVV8iv1ZR5w0YhbhshZom5owGDpmIGnmdaHYEW0G4jgpkQjifHyknYwFLfDrv/0LPo/w7Wl/XQwWNurvT0D49WbjDeu/xO6+MzgGp7EhTe8OYkUuoGK+sGT/n/Qy0BURSvXr3KqnFvvvkmopONFh0Ur44dO0IsnU7n5ubWaMj74IkndHfq1IlVQEHT7d69+8svv5yWluZAKgJH88G2TbBHZuch7OjewioEBQWhDPv374+2w01FhxlLRkYGxgKTkN27d8PWv6YittAfJj+bNm3SaDQw43J3dwcNHiZdLUwH3vWaNWvYcu7cuRMR/BamIweTJSBLQJaALIHHWAJHjhwJCwvDM1SQHEClUg0ZMmT79u047MLI6zzmPsbCkat2FyXAcVxFRQXYPsM+PFByVqxYgVYFVVVVwNGBamFgYKCvry8LXyYnJ0uzoBstkdX9WPctFR60JqANgTYPGSBk2XxqtbXUFKiqqqqwsDAvL2/JkiVxcXEZGRmJiYlTpkwJDg4ODQ0NCAgYNGhQUxbWrLYGbhDCg7WA1uv12CfARJvF0OGEcE9PT1DdwTIaAWuDwaDX65GZhK0ggvX4otmnYCkP6WBqDgHQml6r1Q4ePDiYueKZKyMjY/78+cXFxdnZ2SUlJTk5OZSv0mS67XbSfDOQn8oSQAlUV1d/+umn6enp+fn52Jlgw8NgskOWgCyBByiBlgLQSKZjs9lwLV2tViuVyhdfeLHJCgi8KJgIMYFZMW8jqfONvZ7e5e35U/end6xdRZk0jJYGCFakpwVSa+j68wLh1EDCU0YNIyE2C08qqsnXG0jX9jld2+T8f//NVV8mm1aR3u2zu7fdvGkdpe+wNpwbSEFjAHjttHQ20WilwDGpNVPy6JdHnujVJifMb9u1i8RoogHghEKBUkwDHI51khijpTvpNEWLjZ59SOHsq9fIxOHnOiizBz3zbfFWYrxGODPl9xB5sn/fwdatPTUaNWXHdtdo9XQEj0+Isdl43g6AtkhIHaUEoai3fD0yEuA4bsuWLXCwCahl1/Xd5ik4RFE0mUygQULEoKCgB1thjuNgBgJ2vnq9Pisrq7y8XBAEpzWkxkuKY7mDo/HQTr7du3cHO2u9Xj98+HCO426KQYuiOH78eFYVVqlUMPdwSv7mHtChIfe0KIrLly9HexlgIFEoFMHBwS0UCGQJtfjHP/7BlnPfvn0yAH3zVyKHkCUgS0CWwGMnAaPRiCaf4OA4Li0tTa/X44iDRAetWrX6+uuveTsPQ5vD8Nro7WMnMLlCdyoBdunCYrHA+vr27dtZtQRsh8HUAKBeV1dXFnJl3RBx+/btwK7gjOlgy7zTokuH5dzF1Botj9VqPXXq1O7du7Ozs/ft25ebm/vhhx8mJCRkZGSEhYWNHj167NixgYGBXbt2RboPkIBOp4NvFsFZWEBC43FWwnBCEsD6+KU7bDdE+jtMEOk1oE9gMWiNRmOQLta6GV8TAsqsw6E87G1TwcCfDXnX3SqVKjQ01NXV1WAwjBo1ap50LVy4MDk5ubS0NDc3d+fOnTt27CCEwJZTWIEDLRraNm/n4Q/sqVlDe47jkCdEFEWgE4GFE2gMzc81LBYLWBQhQY3D9ATSbLRdyZ4PVgLQbxBC2rdvD7sB3Nzcjh07BstszRuKPdiSy7nLEngCJdBSAJoQYrVaRVFcvXo1rn+qVKq+fftWVlY2KzhqPmwnpK6OFOaQAd2Ke3sdGtL74NpVRFq3BvNnm4QbU2QWeC8AOgZQmCdGnhg5wlvs5OtvyGCfnP49S+Jn00S//RcZ1KOob8fctL/VVFXVo892yXaZJmSnuLJoJ5xQayfWKjtXzZFfq8gLo4t7dyiIHnq4NJ8SaljsIkdMArFL+PIN3o0G5g0WgCY8sXPEbibEwpGkeZcHeu0P6nls/efEWCkVniecRDAtCmTfvnKwgFY9pXBvRVmhlSpFdjYdUxtYOOokDFoGoJttPg/ZQ5vNtmzZMjC/BY45YPhtvpgsKbBKpRo3blzz4e/109OnT4NCDCYhbdq0Aei5eSSdLRXOEBwcbJhm3B06dAAsXqPRjB8/3kHDc44IEyRc+gKFWKlU3jYADTUFOOD6b1JSEqYJL9dNug4dOtRymcDcjBCyePFiVmU/ceIEKEAttOhxrr7sI0tAloAsAVkCj4EEvv322x49eiDexI4Ur732Gm4fNhqNZrPZYXht9PYxkIlchbsoAcDXwKAYkgUO35qamtdffx3MhoCiQaVSubi4XLp0CaCZ8PBwRDMdHDDpAxsFpIG+R62RTfYuiqXRpEAlA7JsADHRNAGQTYgliuL58+eLi4sLCgp27txZVFSUnp7+0UcfLViwYM6cOdOnTw9mLvaLRtyZtVlBTBkAZQivVqtZHjxg6sOkGu0uEPuGl8UCyujGFJwdGMYhcfB3Dn93fZC5GxjG4axLnFjp9XqVSgW/gMhHR0cHBQUFBASMGTPm7bffTkhIiI2NzcrKWrNmTU5Ozr59+3bs2AFEl6IoIighiiI7ubBarcBwfcOG/7cueN24voKQJZxoB9A2fF9Aft1oo5I9H6AEeDu/cuVKbKtKpTIpKQkPJHyABZOzliUgS8BBAi0FoKFHrq6ubtu2LdCwqlQqtVpdWlrqkOJvb0WjudoiQaxnTpCwQT892+5gvy7Fse//ajLWB5TsnXmwCpY4O6gNNANAczypsRF7jZ3kF5GhvUr6ty/+f+ddsdWS1SuIX4+dfbtujZt7saaO1Nmo6bINLYrRjloknChUc3YLoTD21Nd+7eqZN7jvtqPltACcjWLUHG8WBACuAYBG0meKnoMXpGejjNOksobM+0uNb9d9g7qU/+09c9XV31ZauhMFUlJS7O7hgl2hTq/u9kz3y5cqaYr1rB5I7tFICrLXQygBQRDeeust1t4BCBaaLyqc5QItQalUvvvuu82Hv9dPs7OzQQmGgwdZEowW4q3sJIF1t6TkVqvVYDBoNBqYC02dOhUtkRuNjhYHvr6++DUB+n/bADRrEPHOO+8olUo0dQHJ6HS6wsJCtLxotGAOnogvJyQksOW8fPkyZNe85YVDavKtLAFZArIEZAk86hJAYOvMmTPR0dFKpZKlsAP0JyAg4MyZM4h3oEEfO7Y25X7U5SOX/+5KACw30egeErdYLMB+0KtXLxYVVavVEREREDgsLMwBd8ZbOO+HEFJbW/uoA9DATM1xHLJOo/xZuwT05O280WiER0BAZzab8QsFbKsp1a62tnbnzp1btmzZtWtXQUHBkiVLEhISFi9evGDBgtmzZ0+YMCFCuoKDg4cNG+bn5wdMGsi7rdFodDodeIKuDo9AWQV/fEcsoIxuVhF1cGOY+wxAs9khFg9lQ8tu3DCqUqnc3NzAThxMwjGMu7u7i4uLQwpKpRKPKA8ICIiOjh40aFBkZOTs2bNTUlJWrVqVl5dXUlJSxFz4onFSAAsS4M8u5GBIVPXRR3Y8JBIQBCE1NdXV1RX5dubOnYsD60NSSLkYsgRkCRBCWgRAwyEVHMdNnToV0GcYLTIyMq6f341jc1MCpWQYNvL+f53v73VgaPeTs976pfpXUmemts+I7UoHB1ILQolwg2MAaApGcyI5dY4E+H870Kvw3fGU5nl/MQkfdLxP513xMdeuGyNTKFn6uwFAA62GZFJtI6SaIzV2MvuvJwb0+qmHV+mmDdQi22ypL3KDSTIW5wYADaTN8IAC3AKxWEn2FtKnw65+bQ5PHHHCeA0SsdQZLyOuzHF2UFBKSoo9WrkBF4dOZ3B3+31a6n/ztgZK7KZEJvs/rBIQRTE6OppVek6ePNlMYUFTycjIQK1LqVReP5m6mSj3+pEgCJ9//jlYHGika9KkSZgpa/eBns6OO5kM19TUgEENiPG9995rXp9DddDb29tBh74TAJoQsnPnzmHDhmGaOp3Ow8NDoVC4uLjAyYHOFW/GB+cks2bNwjQVCsWVK1fAArqpWUozacqPZAnIEpAlIEvg0ZUAx3GXL19OSUkB5RlOGgQKV4VCERUVtW3bNkAAAdiC0RAO9G5qnGX9H13JyCW/FxJYv379pEmTYBP6xo0bUesALoL9+/drNJpWrVqBCSqA0f/4xz/MZvOUKVMQzXR2DBgwAMC4Rx2ANpvNzmYWQHqDrAvI/ACaG7wmQK5RWQU5cNLVlAkFErhhLOCRwPeOxrbggzrkrl27srOzd+/evXnz5tTU1KysrJiYmFdeeWX48OHh4eGotbKviQWU0c0qog5uDINzEwgA/g6B7/otwMpgRwKJI6oO1CVoDQ2IM+LOWBI0AFcqlS4uLhAAPIHnGkOCA6vJLsBAATCpTp06+fn5hYSEBAQEREREJCYmpqSkJCQkJCYmfvnll8UNV0FBAWwKx/coOx64BGDqytv5tLQ0rVaLk3Rgrn/gxZMLIEtAloCDBFoEQMMgen3bEezbgu570KBBDmk53wKs/Gs1+ewj4tN5f792e8eEHKmVEFvpkQ2ILxoiUqRaIGaBWAHwtRNispKKK+Tc/5EXxxzr+vR34UM2Xj1JfjlMxgTu7tep8KWxR2stxCidcmiRzJ8lI2i7hGLX8cRsFXijjULPVkLmxhi7dv2+h3f+2zMu1JioCbKT+fEN3Fl6COWxSuWhGLVRAqx/KiU+XXf18jg4xLvsl59JTQ0ttChKdtsULUcUu75a27fluf2urUKhUyrc1Cp3pcJw7Oj/Wc31ZB3OhWiQxuP//1GcRNlstj59+rAazMWLF5t5VaD9z5gxA9fwFQrF559/3kyUe/oI9OC0tDTQxmCcfvXVVyFTeCP3tACEkDNnzsAkHLTnrKwsVjtvKnfezg8aNMhBpzx27FhLEHOol9FoxMkYb+c/+eQTYPRDexNwdOrUafPmzU0Voxl/sI4hhEyePJlV7mH5nZ6DKjQstDWTivxIloAsAVkCsgQeQQnU1NSwnTzgXN9880337t1xlMEhrGvXrhs2bIBaIg7VkqHwERSMXOTblwA0CViGdzDatVqt0HJOnz796aef+vv7w/I5tDGwAQScFOh0AU5dvXq1A5zn6up6+vTp1NRUFtBk3QqFYtq0abAhDHIEvYvV4Vn37df2kYrJVhndbA3Q895911evXj1w4EBeXl5BQcHKlSvT0tISExMzMjKmT58+atSoqKio0NBQOH/S3d0dUV3shcAWBPVV1t/Bzc568BHOIxzMk1u3bg0oMMK+GMXBgSclYhkcHA7hHW4hMNtWwcchWDO3Dtnd0i0wq3Tr1i08PHzUqFH+/v5jxoyZP39+GnMVMVdlZWVtbS2MC7CeAa0FRg34BeYl8OftPMdx0HgwjNFoxOaEKxaiKKKdL7gxDGZhsVhYkx2bzfY4EYlA38hx3Np/rcVWp1QqV65cKa8WsJ2S7JYl8JBIoEUANHRko0aNwk7cxcUF9qc3Uw1BQoTNlA2ZeLfN9un4n3C/H6/9HzA0g32yTTr8D3FgBKBtAOJaeWK3E2s1mfH68QHdi/x6Fx/8kfxynLw++nTf9ltDh+T/coHyQ5uIYJGYMSQjaN5GOI6YOVJro0TN1DK6opb8fx+Tdm0LO3r9OObFfad/oUwdN2gwbtShEQBaMnq2CZRKmtRUkWPl5Dnvnwa2PzWk255je2hMaqwtEiKIDS7IkxJ68HYRbKv/sfwbF01PtaKLUuGpUXsE/yGct4s2m1RxrP2NYjz+LmhR90E5uxeixN09oJBdvdoYA0tDxlDTsWPHgoYEX9BXX33V8Px+/wcl5u2334aSaDQalUo1Y8YM4C92UFnuUeEOHjwIs3GwO1i2bFnz+YJeJQhCSEgIdkHg+OKLLxymZA5lhjYGUyY8kGTHjh2wFVorXTAZc5Gunj17wpkVICiH1Jq/BU1RFMUJEyawWqzNZnOYrTWfjvxUloAsAVkCsgQeLQmAFTOOZVar9cCBA6GhoThmAeWUWq3u2LFjQkJCZWUljDIII8Jo9WjVWi7tA5TAhQsXvvrqK7CHBU4zbGwACLq5uQFqzEIwNptt4sSJEBIpC6Kioj799FMWyGPdCoViyZIlMgDt8K7ZKQy62TDoid0C+/TuuoHvGBFJUDthyQF6GDC+PnjwYF5e3vLly1NTU9PT0+Pj46dNmxbFXGwTYt14OiKie6ypMstix8aCdsj6gNoP/CFKpRLZn9EYmVWe2bzYRNANgdm2Cj4Y4KYOh+xu6RbNbJ2r2Uy+IAGNRjNkyJCRI0cOGzZsxIgRISEhCxYsiIuLy8rKio2NXbRoERzGaDRSulLWJJ+dmzj4o2k/INfs07vb2B7O1HAyGBMTA/KPiYmBL8KBkujhLL9cKlkCT5QEbgJA46j5zTffwPcMRFRTpky5qZiALvnSFTIysui5vj8F+ew/sItGMpkJz0usGfVJ/AaCtRPeTk2KKUBssoqincz+80X/HqURQ3P2lxJiJf/PmFO+3X4IG/LD8aPEzhOzSDgiSqCvyBEbR6w2ItiIYBE5TjJjvlBJvvyKdPYq9X7m5wGDDxUdIPQIQSLWCcbfZPwbk2hEouuLaCfExpNzJ8hzPcr6/P5Yvza7N68ldbX15ss8kcyfeVEir7YQYpJw7xvWjnW1pEv7sRrFcwqFl0FHSbTfn/0OslXfVJKPUwCz2QzDJ6uZYTN7+GtqMpmAtkKlUgGKeu1aPQlLM4Xv3bs3KFKgeWzatKmZwPf0EYg9IiIC1SONRhMXFwf+9zRrTLywsJDV21atWoWPmnFYrdZXXnkFiw0K3+TJk/GQ90bjQr0AgLZK13vvvadWq3U6HRoB4VEwI0eOPHfuHGh7aE3QaLLNeNpstnHjxrFaLEzbHqFG3kzt5EeyBGQJyBKQJdCoBLCTP3LkyJtvvqlWqx12miuVyjfeeOP8+fPO82HUiBpNWfZ8YiWAjcpqtYJacuLEiY8//rhHjx5Idwtn1uG6PhgWKBSK+Ph4OISNtXwEDQdIYFALUiqVsbGxLJDHurVa7b59+2QA2qER4jfLOtgwTfmzYe66mwUoMXFBEHCLHiq3yBwC5cTA6Chlrq1bt2ZkZMTExGRlZWVmZr788stAshwYGBgdHY2m9xqNRqvVgvkzbDFklXYHN+LL0NhYtRndDlEcbiEY21bBxyFYM7eY0a06IE2ARDB9/KDQBxww9YNyOjxieU1ZE3WwcIKIEMXHxycyMtLPz8/f33/mzJkZGRnx8fHp6enbtm3bvXt3dnZ2cXExfOn4rtmVJ+eSG1U4AAAgAElEQVS37OyDr/6Rc0A/CSw6QDeEtQM4Hlo7eGKn+shVUy6wLIHHRgItBaD79esHmJFWq23fvv2ZM2ccRHADbZUeCJJJslEg8/5a4dMzu3/370oLKTx84wKyCnr/GxzYRvmiqd2wQEi1kcx5b9cf+vw4sF3xuv8htmoS9xfSq9OOoT47Dh+gQHadlXACsVPzZF5Cn80SAE0NnI12avt8oYps3EK8O+9+rn+1V9uif64kVQKpJaRarBToc7zAHvo3JblRMJHYBWK1kNEhJ3u3OeT79N5FCUTgSK2ZRjdZuHr+jRsAtIXQclGR1JpomMkTvujbba5eMUKh6OJq8HJz+52Lq+qrNXRjiHQJEhhtb/h1kGVDqMfl/9KlS5OSko4dO4YjwSM0GJw6dQrO4UTyMmD4bebliKLo5uaGALROp9u+fXsz4e/pI7AC7tWrF3vKx4IFC+7nK9iyZQuc4ghK1ddff918lXEP6dp/rXVQ3VxdXQsKCnDZ3zkdaGMAQMfExHh6emo0GlA0YfIGJhgKhSIhIQGNR5zTabkPx3EjR47EZJVKJdpftzwROaQsAVkCsgRkCTxaEgCIcMGCBQ7jFFBOTZw48eDBgywUWFtbW11dLU+MH623fHdL67wU4ZA+UCBardbDhw/Hx8f7+Pgg2OfM6wKg1eDBg2NiYlasWPHee+91795dqVTOmTOnpqYG0CiwEzxw4AAEVqlUcJhb69atWSCPdbu7u0MssKtFlYbV4Vm3QxUe11u2yuhmK4ue90LBFgTBarWi1gqmspA7nNuEJbHZbKgkIzyNETEYOrDY8KLxdWMA2O0nCAJi2fiIEHL+/Pni4mJERRcuXJjIXKHM1atXL4PB4EAD4gAEO/SlDrcQmG2r4OMQrJlbh+xu6RYoOCBxhJ5Z8xqHfD08PAwGA4RUq9VAaoqJwPeIq0p4ZgD4Y1LA3g63sKsGZnNoog4JqlQqPz+/6OjowYMHR0VFTZw4cc6cORkZGampqcuXL//uu+92SteZM2ewSbAv8ZFzwycGbRJ3o9qkCzb44jZfaN6PXAXlAssSeMwkcBMAGnaOA+6D3WJWVpbVasXxDCTCgKYUxgUE+ct1ZGDPfB/v7E3/S+o4YpNoKgSRUCpUu8ReQSMj7CvaibVGNFbaKLJrs5K1/yJdvL7r2zHv6xWEu0yS3+e9f5/rP6A4J4dUmyh+DGnwNFmOJybpl9Iw2wipMpNfjeSHMuI78PDAHleffbo84d3TRKBUGdJBhbz9Rr7NvFMa3G4jVdfIzLcu9fQ8/Fy3M3+dflo6Lbe+jvWRKQuH9FcPntfLw86TZVlkSI+8oIHrp036X5XiWYXid3SRU6No4+l16WKNxNFBya4JBcZrCDFK1WqmSI/2o9mzZ6P27OnpOXHixO3bt+M6PIwQoO7AyHEv9LY7keDu3btZ/UapVFZWVjaToCiKZ8+exWVtUE3gCItmYt27R4Ig8HbeYDCAHTfA4osXL753OTqn/OWXX8L+O4VCYTAYiouLncM4+EAzqKioAE0LVT0of1ZW1uXLl1HJwLgQa+vWrbNmzQK2DQAC4C3AmScajWbo0KFw5GB1dTVq3rfR8CAKb+d9fHwgO4VC0bZt25awVGOZZYcsAVkCsgRkCTzMEkBeTiikIAgAK8+bNw+IVgEyAGNAtVodFBS0c+dOB52ZraA8JWal8US5OY5j1yRYPBrcJSUlU6dO7dy5M0BOOp0OFBjWmlKr1RoMhoCAgPXr12/evHnmzJmdOnWC8AhS5+XloWAh5djYWIVCwbZYFn1jAa+RI0eCfoUAtNxiUZgPynEbOuqDKirmC8THvJ23WCyAmJvNZjyqsbq6+siRI0VFRTk5OSUlJYmJiZmZmfHx8dOnTx89erS/v39ERIS3tzdgEUjiAbMAmNRgo0UH6PwI8oI/YLWsHQzO0SA1jA4OB0xZpVKB4TOUAW4bjeiQDnxfLFzu7Ga/Qeen4OMchvWBTFmflpQNpBoZGRkQEBAcHPz888/PnDkzOTk5MTExLS1t5cqVhYWFJSUlGzZsKCoqYi2sYarO23nYY+oMZ0NfwS5mYHsghLCc1+APITGMKIqweIZsQvCIt/O4dsvbeecFFY7jrFYrHJ0KwLQDFyJO9zAv2SFLQJbAfZNAkwA0fMzQlURFRUHvrNFo2rZtW1FR4TzyMQA0JW6uNZIvVpGuXb/u1mHLh+mkxkThWaB8rgegAa6lFeUbassL9LBAUmknVbVk8/+SgEHl3bzK/udDYr5MVn1I/Dp9P7j795vW30CfIQ1eAADawlNODpqcTSBWnhw6TPwGHujY5ujQ/pdfiv6P+QIRquvh7huZN+Td3H+BxM76pX/XH/y6/efFyNPXLkhMGw2Ac31EBKAbkhYIqbOQzd+Sfp1L/J45EPvOOWIhXb1CtE+5q9QKnV6t1/4+OvJFKbpdoNCziZCqxx6ARvIHWPuFkVutVj///POHDh16+GdoAECj4qJUKg8dOtRM4xEEYd++fcAXgecQ3pQ/vZkE7/CRKIrV1dWwMw5R4L///e93mOwtRf/73/+O29bUavWePZRM3blLcUgTArz11luI7eI0TKFQtGnTZvLkyUuWLPn666/Lyso2bNiQnp7+7rvvtm/fHtnZ8AwWwAV0Op3BYJgzZw4CxOy+rZuWx6F4WAVRFH18fJRKJexD9PLywvSdo8g+sgRkCcgSkCXwCEkAtBSLxYLqysWLFxMTE11dXR1wCliA3Lx5M4swNlXT2xhxmkpK9n+EJMC+d0SfeTufnZ09Y8YMLy8vFjzy9PREQFmtVuv1epVKFRwc/NlnnxUVFb3xxhtt2rRBzIs1qNRoNAcOHECxQNO12WxDhgxhsTkWtMJ0rutXoCICeoj2sGzJMWXZIUvgphKA5rd3797CwkKO45zNqAF5cG5gLM81x3EXL17cs2fPdun66KOP5s+fn56enpWV9fLLLwcGBg4fPjwyMlKv12s0GhcXF3d3d9j+CGzpyFcDujqYG6OZHdhls59AC89UZKM4u+H7agpWbgpcdg7PfqfOsZzzvakPzMRhroSJN2ruA0mhoFq1ajVgwICAgICQkJDo6OjRo0cvYK4C5nJoFXBSYnV1dU1NDfR72PuxIQHXhgYD6xY2mw092RZiNpshBUTAcWEDNv5CRASdWQebo+yWJSBL4P5IoEkAGgcAIGyFLuk6pJKSkoJqd2NFrDdnLt9PfHvv6tl539/m1dUZyZUqGlYyVaYAcQNaLTaA0pCSjXI8S177ykn/XvmDe+z+YBqprSRbN5BBnY8M6br3q08IZ6OW1PSMPwlnrsegKSZMbZ/B/Jmzk8pr5MWRPz/T7vCA7qeHDfr3Lz9LtMwNJW5AiRvub/wH22yuvowCqbpEVn5EenkW9mxT9ge/7aeO3Qj6GxewRkvpUvtuQst57CcysPs3/Trl//W/6qz0IAHy6f+sVyhU6qeUWu1Tbq6tFQrFqi/rz6MzW69JGLRFsoBukNBv8ngcbjZu3Ojl5QUALjQqdmhUqVSurq4+Pj7Tpk3btGnTxYsXsc4PCYrHAtBgh4sH2WNRWYcgCN99951KpQK7FVB6ioqK2DD32X369GmEnoHJ+osvvrifZUhNTWVZz06cOCFtKbh5mxdF8fLly507d0YLaGg8MEMD2arVahcXF6R4ZhEBpVKJaqVSqXz99ddxSma1Wi0Wi8Py+K3KBJQhAKBxxa5bt26sknSracrhZQnIEpAlIEvg4ZGAKIows4WO/fPPP+/YsSNAgTAewUikUqk+/PBDysNWWws8vA9PFeSSPAwSYBUDRE8KCwunTJmC9s4ACaHeAsxvoP+MHj169erVa/+1dubMmR4eHnq9nt2DDxoI4kShoaHsaSXQgHk7X15e3qZNG9zjj9gTq2LpdLpLly6BxHg7z6pJD4MY5TI8WhKw2WwVFRXdunUzGAw6nQ4OlEITV6wLgInsN4KPwBK2qRP2OI4DZR7Dw/qfyWQqKysDYpDc3NzU1NSUlJSsrKz58+eHh4eHhIRERkYGBQXheg+cjgi/0KVD944cGjCLYacY7GS2UTd8X86AMuuD3yBLG80GYKfPGIaN1WjWLfFEmx7IDu2EEJ5G5klIzWAwuLu7w7QdRaTX63U6nVarhV22ONlkCzBgwIBBgwYFBgaGhYWNGDFi/vz5H330UXx8fFZW1ieffPLdd98BhcvevXuvXr2KrxvMImHpF5bBgFsGLJ3B2BksgYxG46ZNmzIzM9f+ay0O1hAFf2UAGj8Q2SFL4IFIoEkAGkvz+uuvwx4W6JcvXLiA60sYhrJZAIuyxL5x6SJ5YVRJz/Z7Joyps1pucC2LEkAswcRcA/TMsxQcFH3myd69pF//wqfb5E8YfpLUkj2lxLfPtt5tdiXMoBlK0DNkaJMwaJozQM/0V6QpcCbyfPTxAd4nvNseHtC9YMt3UiZI9SEVtjG4S5BQajhFkEYRrWTj56T/09kDOpQPe/aHsmJSJ3E680xStEx4ZqHELiII1Ab84H7i32/rwC7Zo0JKfjlDKaRrjVzlr9WtWrVCk0wwkDl16hRlkab1ABropuHxGxJ/VF2iKB49ejQuLg6ZlGFYghNR4CRlGPbAQLVPnz7Jycnnz59/SCrMAtAwWn/00UfNlI23859//rlOp4N1eJgPtIR0opk07/DRgQMHUMdSqVQGg+Grr+pXQe4w5RZGh42fOKe61Ze7bNkyWJmHNoM6ExwtiDM0VnlCi3XIdPLkyWC33uiSO+olLawOBgNdmQWgtVptr169mtKhMaLskCUgS0CWgCyBR0UCQMGRmpqKBqe4xgyIQFhY2KlTp2DCDPZ9zdptPCr1lst5TyRQUVGxd+/eKVOmdOvWDRnqWAgYkGW1Wu3h4TF16tQ1a9Z8++23s2bN8vLyAl0IfkGvY0GuHj16TJ06dePGjeysDdQe4HQmhGRmZoISjsdjQBsGZUmr1V5nlMbDw2UA+p60gCcp0etNMSkpibW737t3L7CTYys1Go1gtUoxAZsNVeiKigpovYAyAxcox3FGoxGCQQoYnmWpZntgYP+AxoyyBxoHSH/Hjh35zJWdnb1w4cK4uLjrdIVJSUnjx4+PiooKDQ0NDAz09vbG9RsWY23UzX6bDpgy3rJQMno6OJzDsD6NZn1TT1ysAkpuBNa1Wq27uzsymUA6OH1j0QwoJGYE3QhMxKBvgUdQVAzG5guesEUVOkBIBLa9enl5DRs2DGHrsWPHzmeunJycgoKC4uLigoKCV199FY7hUavV69ataxSDxokethZsCbJDloAsgfsggeYAaN7OV1RUIFalUChef/111Fp+UzheQm4lWLaujrww4mjX3//Qu8v3B/YQC08BaFu9RTGlYJaIMtgDAElV1a+SnUid3ULO/4cM7fdDl04/RP3x1OWfyZHdpO8zRX27lo2L+BFzBIDW+beqlhpaV1aQcVF7+3Y61rPDqT5di79dR62hG656hmYArBs8AUJG22eLnRJikGuXyIES8odeJ3u57/Xv8X32RlL5az3YXX/CIBMfnfT8wzqyt5j49y7t165g8p+OV18mHDXsrr+mTZuGSJn6KaVCoQgKCm6Mj/pxhqFBFmvWrAF2FzijDwc8wBC1Wi34qNVqV1fX1q1bJyUlwXIo8EaB2azDWneDmO/V/6tXr7q5uaGliVqtfuWVV5oZwARBWLJkCR7zAovn69atu1fla0G6e/fuhWEeBn6tVpubm9uCeHctyIQJEyBrFxcXjUbjvP+u+ZxMJlNGRgZUAfQS1FRAcUHNBnUyUJ5CQkLS09OPHj1qMpk4jmsUfW4+6+afQjNAABq00v79+zcfS34qS0CWgCwBWQIPoQTAtIotmNVqraioWLJkyfWlcRho4CwBHHT69OmzZcsWNLNChzzdZcX4hLjhmDik5wIH0CjbbLaqqqqtW7dOnz69TZs2CDejMqNQKFxdXWH+1aZNm2nTpuXn55eWls6cOZO13gBiN5ymgfmhq6vrtGnTVq9eDc0P216jYhdFEQw/AesBrYm1eVyxYgWSnrckwUZzkT1lCYAEeDsfFRXFIpj5+fnOwrlpo4UA8E3BQeUYBWdkzj63Ed65bE35nDlzpqSkJC8vr7i4eNWqVdfnKcCh/M4774wdOzYoKCgwMDA6OhoXmXDUYD9/Nzc3gGvZGTEYYmMwiIioNH7+rIWyRqMBsycI3Lo13XINaYIZHLjBVBlLwjpwAgU9g4PlNYbEp+ADXCUORYUVMqAlxIisA05TRDAa4WP2sCI2PPR7rIjYp85uV1fXPn36BAcHh4eHjxw5cuzYsfHMBecxwq+ZuRxeNFB/oCd7eBV6ggO5YqAF4soKBrPZbACLE0KMRqMgCHjLcRweIupMbI0pyA5ZAo+6BJoEoK1WK2/nFy5cqJMu+J7379/fVIXtNZbaCoEIZMniqk6tS3t5HVucQaprAH2up2am7M/UWpnjiYVNhye81UzNf6t+IROizg7s+tOIyJNnTpILp8nwkB3+A3+KDjpY9yuxW4nFTupsNL4z+lxv0Wwn8X/51c+7/Gn3Q92e3hM7GzkcKAxup+bRPFpMM2UQJetjTsLROaud8mUcKCFBvct6tz7Rr93+rz8jxgoaXCAmm4SngyE2kwJ1ggHz1avEv8+e3m1+nPyn07+epf4cZ7dYjYJIa71nzx7sNAGAVqmeyv++9LdJYf1+6/3Y3YmiuGDBAtBF0ExVp9O5urrCjh4Yh8AaWqFQdOjQYfbs2T///DO0T9i35bCOfa+FhDNPOEMPjmdpKlOO45YtW8YOq0io11SUe+1/+fJlYN6AdngdQwcSjHudL6Y/atQoZCc0GAyNr2lh6N86wIoBiE2AvhC/JjCpQGgbQOdWrVpFRETEx8eXlZXhWI7a6m/TvtO7RgHogICAO01Xji9LQJaALAFZAvdRAoIgsLwZsFp55coV2LwFgw5M3V1cXGCy7enpuWjRIigj4s7oaBQKuY8VkrO63xJwaEKgHoC2s3PnzlmzZqHhJLLQwqYumHNptdpOnTq9/fbbJSUl69atg3MIMYozvqPX69u1a/f++++XlJSAiQYoxixjBgJzDrI4cuQIZI0YE2rjCoXiypUr0P5RccLG7JCOfCtLoCUSCA0NZSHCRg9obb6NsU/B3Wg7x2Bsy28mfEsK31QYwBzRrgXWmSAw4o8wB8EwRqPx+PHjO3fuLCsrKyoqWrNmzYIFC+bOnZuenv7BBx9EREQEBQWNGzcuJCQEIGOAcXE6CSzw4AlsGAgxs+KFRSnoOhyYrLE/YcOju4UANISHqTr2S+7u7v369QNTLb1eHxQUBD2MQqHw8PBACB7JEhErZ8F0LAkA6w6PEKRmgzm4oQogIigMINdg3wYIPoZxiKtQKHx9fYcOHRoSEhIRETFixIiEhISlS5fGxcUtXLhw3bp1udKVn59/+PBhsKl3bhs2m81kMoFFPy5+sK0Ro7AW+uh5S7NjjCU7ZAk8EhJoEoCG0vft2xe+SaVSeRMy0zobqSab15CB3Qu82+0PHrq/qprUWuoPHgSLY0BVAYAWKBAsNvxKudWRCcP3P/t0SbDfwVNHyZXzZNQff+71TGmY//dXLxKrZERskxBiRGeRRgN86irJl8vJkG77/Lqe69HlcGhYaZ2F2BvoMuxE5Ahvp5nW49fMGxIbyDfqTbOrr5FJkSf6tj4Y2PdsRgLhqutNvAViB6ZqtOnGROyEWEVqbf3CiP/r1/Hg0N47q67UP7RYa2xmUbTRW6PR2KfPsyBVtVor9YzasJDR8LQhNeA0abh7TP/DMIzrfjabbfPmza+88oqHhweONBqNBoc0bIoeHh7Tp08/fPgw7M8SBOG+YdBWq3XFihVone3h4bF79+7m388333zDUh6rVKr58+c3H+WePuU4Ljw8HLdZvfrqq/c0O+fEAwICYOBXq9Wenp6gnKFO5hye9eHtPJy/DEN4Tk7OBx988Nprrw0ePDgsLGz8+PGvvfba9OnT4+Li1v5rLbQQiF5RIa0gNaQFOmjD3d35D0VCC2hQa0aNGnV3UpdTkSUgS0CWgCyB+ygBOPXIbDZXVFS89dZboJk4G6O5uLjMmjULtvIIglBbW8sCHw5Go41OPu9jneSs7pMEwEgCzdkEQTh16lRMTEz79u1xEyQcBw2aLYJBvXv3njJlSm5u7oYNG6ZOnQpUuRAGQ6IGBbu+pk6dWlp6w4oFsYwWtj2z2bx06VKAaUBvAYNEWGhBEMQB45Nb8n1qSY9dNm+//Ta2ZxcXlzNnzjhXEbtQ50cOQF4zgDImwrbVZsI3mldLPNn04aODWJAXFBh9YPMuO+URBMFkMoEPotVsAECu4fiB2tra3Nzc9evXL168OC4uLikpKT4+fs6cObNmzfL39x89enRgYCCivShnlisD8F+03XGYYmMU6Argl8VqwQeDsQ6YueOKGj4Ck7KePXuGhISEhoZ27NjRy8srODg4KCho7Nixbm5u4eHhYWFhoaGhPj4+/fv3DwwMHD169JAhQ9q2bQu7MXDYRQTZgRUE83J2IJ7APoIEgaK60QCA5rOPgGiL9UEoAFIOYa73338/JiYmMTExTbqys7P37t27devW62xLp06dgmks0FvjL+yYATSDXf9uSQuUw8gSeOQk0CQAzdv5kydPsp/rrFmz6qsHlMfSjWRQzFMnTw79QIL77+vtdcin584fy4jZTmqt1dTcWKAosF0yfxboUYEWnphEahvNC8RMmS/sRLCSv/2lekCnHYP7/vBjMan5hcT+5Wx3r6KhA/eX76a2z3BR8PdGUvWekmEyEWzkm3+SoT32P9f5knerA74+BfsOk0oTMfMVhIgCT82TbRJbdAMAjfC1VHpqlE3RZ5EQi4m8/cZOf++DPdz3/NeffzXWUl+eqye6thIatBEAWiQWKxkd+R+/Hkef7fj9D98TK0fMvNFsv0aIGcrK20VBsE+d+oZOp5HW9NS0j1O5KhQu3p0DdxU3INbAcX2jfo+5C3agoNLM2/lLly4tXrzY29sbWBrYdoibjDQaTbt27ebMmXPy5Mn7iUETQj7//PMpU6bMnTv3woULCKA3+pJsNlt1dbWnpyeO8S4uLnPmzGk08H3wBD1p3759ISEhnp6eb7zxBqs53YcCEEL69+8PUx2FQuHl5QWZwh7PmxYG9TkYs2FLFMyLwODIarUiGRySe0DTcjYIurv1hcIjAA11nDhx4t3NRU5NloAsAVkCsgTujwRKS0snTZoE25mBFQE6dp1OB7bPEyZMqK6uZkcuGIAQ+2ghCHh/qiPnclckACpHS5Kqrq4+fPjwO++8g6dyoTkC6oSg3/r6+k6fPj0nJ2ffvn0zZ84EenGwwDAYDAhPu7u7w0JI+/btJ0+ejPxpsOwB561BCwQIwwE1di4zNF1BEPr164cW0Gq1GgqsVCoBEXM2f2bbvHOyso8sgUYlwHFcTU1NREQEGMGs/dfaRoNh/3nTpxCy0XaOibBttZnwjebVQs+rV68CZMxxXFUVpQN1BpphSoJfHDoQdBZF0WQy4ReHWXMcx5pUoz8wZcP3jp7gAMxaEITy8vLCwsKysrLi4uKMjIyUlJSMjIy0tLQRI0YEBASMGjVq2LBhaFXNzrVvA4AGsBi22Lq7u2Nqer0ecFs8sZDNUa/Xs2g4IrwqlapVq1Z+fn5DmSsqKio6OnrEiBHR0dERERGRkZGjR49+8YUXI5gL80UHdLZsRvjIwQGMIgBMQ3VwBzYM+njcIoSBJUAWHwfTbOg/IV9XV1dwYDUxU61WGxAQAMdghoWFTZw4MTY2dt68ebGxsYsWLVq/fn0xczm84sfjtuWD6eNRX7kWKIEmAWhCCCyJ63Q6+JxOnThOLYcBhpUwZ0ouQSw2YjTz5PJ5EtB3b4/WJ59ptXvVF6SWklhQjEiwE9FOkWb6R0Se8mCY7aTOTuoI4aq5y7SPtpLEv17u0W7Ls522rl9PLBbywXRu0DM/PNdzy97i+qLaidVOEV0eaDLQpJqIxGoi5lqS/b+kZ+uSge2quv/uol+vA99lk0smCVEmvCjSg5vthBoZ8wIRKFMIESgiDZdIiK22jhpIclZirCYpMbX9uxZ1alXwp4jDdVZikmBrCApk1xZCrBLhRsP5g/S/pYo8P/xQ/y6Hgwcd/3odqTMD3k2PJCSEE4iR0IpbBGLftbuU9j5KhVKlUCp0SoWbQuHhru8/e/paSyWFvyWyjgbL7YZSPpn/jxw5kp6e7uvrq9FoYMRCRRzWJ7VarV6v9/Pz++yzz2DUR1UDHQ9WdBzHfffdd56enjBxfe+99x5seR547u3atcPRNygoCMqDADRohy0sJASGqVGjCiibDgZ2cLBh7sQN7Q0BaNB1XnvttTtJU44rS0CWgCwBWQL3VAI4/4dcYMGyqKho7NixLLMTDlswBX3xhRcPHDiAy5xsCR2GGLxlw8juR1cCrHkajPvI2ikIAkA/x44dS0xMhHMCQfdDxBkMn/XS5eXlFRcXt3379k2bNs2YMaN9+/a4j16pVML8C6wXAbyA/X87duyARtW8DLHhNaMM46Pdu3djCVHN1ul0ubm5bDqsu/nc5aeyBJwlgJ0ta1nvHOyWfG61Td5q+FsqDGugjRm1PAWMgh/mTeM2FbIp/0YThFHPYrHs2rVr69atpaWlmzdvTk1NjY2NzcrKiomJiY6ODggICAwM7NmzJ2t9zNL1sAAr9iGwcNu6dWtAlmH0ZEOyqbHm1eyUH1PDE5jQB8BfhK1xmAbHW2+9lZ6enpiYOH78+JSUlISEhA8++GDmzJkJzBXGXO3bt0ewGNhLIH1YCwQjaK1WC2GghIBQQ42wGABAY0iHUsEtiA73wWDVXFxcIB3M1NkCPZy5nn/++cTExCVLliQkJGRkZGzfvn3v3r05OTmFhYUwMOGuLOdXD6MV/Do8tdlsyJ2Bo/gAACAASURBVP4PJl8OAXg7z9p1OTzFW7DchxTAYg/t9nB5HgPLjidHAs0B0CEhIfCN6fX6Ll26iLzdZrLcAKB5YheIRRRNhBoaT3utttfTp32fufTmhNrqSipAq91ktxkFjuK+gp3Y+RsANEeMVlLDUUyZcDby7w2kb+fvenXcsvlrYuHIhm/Ic31+7NZqS/Z6NB028xSzNnOURoMCu5ItswA2zDUV5FAZ8e9Z3M3lzIB25q7uez9eQi7XkjrCN4C4FHOWkHDC8wBACwKg07SkPD1o1261UZtsakbdr2PpwGeODh5YcOgohcnR3hnIoznJx0rLINIIEn20WEv+9p7V75n9/TruT44ldRL3CBhcSxlSAFr6owD0dRPazp07UgZhF41SoVEqfqdQuOpU3Xp4TdxTzNEE6dVQdrh7Un9hBBVF8cSJE7Nnz+7QoQN0xDj2wCq6u7u7Wq1u167dxIkTi4uL8eyXh0dsJpPpxIkTjfbyD08h709J2rVrh4N0UFAQvGJY3r8piOxQQtTVcBhDH4eQjSqFENg55O35YFv18fHBGeO77757e6nJsWQJyBKQJSBL4P5IwCZdhJCKioqVK1d6e3vjjFGj0eBsGVRif39/lnoLzNDY2T4OQw6O+1MXOZd7KgG0BWZzwS3V5eXlsbGxffv2hROnWTQZcQ2FQtGlS5dJkyYdPXq0rKwMcGfEmqHhubi44EFter2+Z8+e8+bN27Vrl9VqhQ1/LdFe2ObHlrYpd//+/bVarZubGwumfPXVV2w6rLupdGR/WQLNSKAlTbeZ6M6PbrVN3mp45xzvnc9tlI0detiCNeXPhkE3YoLSsVX1ZKQObgyMqwjV1dWHDh3avn37/v37d+zYkZ6ePnfu3IULF8bGxkZGRgYGBo4dOzY4OLh169ZgFo2jKkzkgeoHEGqY1CuVSr1ej1bGcNISxkKHWq1ulGYEA7AO6HhhUoZuNkAQc73xxhvJycmLFy9OSkpKS0tLTU1NSkq6vpT4ySeffPjhh2lpacnJyQkJCaOlKyoqKiQkxM/PD4AIxCUAUwbjaOS51mq1AFgD0AzgMlsqeIoFgwMYcVcKa5Du4IYoUDXYrYUaC5tahw4dBg8ePHz48PDw8Jdeeun9999PS0vLyspKSkoqLS3dsWPHtm3bdu3adeHCBVwcAtpYQkhlJcX1bDYbbDsGY39oq9gqmnGgUT/bzJoJLz96EiTQJABttVrZ3QpxcXE2i0SEUU9EUS8co4QiZ2UJz3T4sUf7o/267jh7ij6yckIDStwAQEsW0HbpJECOmOtEukXFYiWf/J34ddvVv0vZ/ywjtVWkOI/49c0e0H3bsiyJqlmCYTnOzgnVEgBNYWMJgBakwwgpTmusIAE9yge0ueTbwfhsu8Nz3rtUbSRmkeLKDZcoUX/wPMWfKSOIQE2S0QIagGJirSNfLCXe7sUBPS8913vvz+dItZ2aPwMADTbXQEItlYEadlNLaIFUnyXx/1Xh+/Ren84Hxvyx9Mql+mwBKLdR7J1rMNnmBMJZLJbZs+coVQqNRq1SPSVh0BqF4ndD/cZKa0QQXQagqRxEUXQ4anbjxo1Tp05t1aoVrJpCnwvDFQ5anp6eMTExp0+fhg2JD0OXh2uAwDfS0DKfxP9PAgAN27h0Ot2D5ft+EpuXXGdZArIEZAm0WAIwS7darUeOHImJiWnbtq1CoYAdS3jMEZzdpFAoRo4cmZeXB5oJ5HDTSf5tAAotLrsc8EFKALRTmJYfPnx46dKlnTt3BhABAVyAA2DFXa/Xd+jQ4e233/7666+Liopef/11UGIRtgC1AZfnDQZD9+7d4+Pjjx49apEuOF0QG95db3sLFy4EJAX0aoA5pk+fzrZh1v0gpS/n/QhKgG2xvJ1H3sU7rMqttslbDX+Hxbul6LdRNlaqbF5N+bNhmnLbbDaz2YwvCAFElu7DYrGAaS0mwgKXwGoNtkGwZeT48ePFxcVgYf3NN998+OGH6dKVkpISGRkZHBz84gsvhoSEdO7cGWBTtJUG8BpBVeC+ANgaZ/2ItLIO6FFhFdDV1RUIPNGaGG4RzAV/FqEGHzZB2BHl5uYWIl2RkZFhYWGxsbFz58798MMPIyMjp06dGh8fP3/+/MmTJ7/11lvz5s0DzDo0NDQsLCw8PNzf379fv35QGIeUkZ1JqVS6SZdDCbGoDg40IcexA8qJ6cMZj/gUMXGAvzGYwWBg5alSqbp06RISEhIVFRUaGhoREZGYmJiZmTlnzpz09PQtW7aUMBe2AQdjL1yrwAAAYd9J48SkZMcjLYEmAeiLFy/CWaWgTm3cuNHZJBcw5u9zSb+epR3cf/TtdeCfnxGTiQrEylHT4YqKsxTstVEWDpuN5+w26SRAasVstFP75LztxK/n1p4ddsT9hfx6hezdRfx9dvfruiN+zqVaClDXX+Y6nqf8FWbg32gAdimKfPUXMulPxwZ7XRn0tK1/h1N/fuk8cF4wPNX0c/gt9ExRYMbEmKeMHDzZW0wGdvyxt+fxPk8Xf7OaossW6a8B8q63vIbcwZ6ammBbyUdJpHerfL+nDwX1Kz11jILNRisC5cRGzy1EABpKRwoLi0GwGo0GuhKFQuX6u1aVv9ZKvFEIjjeI4An+D+MxIaRWuoBXixBSXl4+Y8YM534cOlk4BuGNN97YtWvXAxSe1WoF0xiLxcKOzQ+wSA88awcKDhiHHjMLaFBcDAbD9eXlBy5wuQCyBGQJyBKQJdCUBL7++uuQkBCcnoFZFk5ENRqNq6vriBEjdu7caTKZWFtpOHLAYY3cIZfbABQcUpBvH04JwBmVmZmZYC/P4iM4pQeHm5vb22+/vX79+g0bNgAfNDY2dGAUtVrds2fPd955p7i4GPY4g4k9CsFisSDPOHo26rjVtldWVob6M5RHr9eHh4cjWMAmiJ6NZi17yhJoSgLXrl375JNPQkJCRowYceTIEWeIqqmITfmzzbKpMKz/rYZn495r922UrakvsSn/RquAZx5y0gVhYL8FuGH/LnR6sOoG/RKYebFh0A3dF/zCuAkMRZCsg2UYW1ro32w229mzZwsLC3Nycg4cOJCXl5eZmZmUlJScnDxr1qzx48dHRUUFBgb6+Pj06tUL+09nh1qtdnV1xQ0lgOoCsQbLHwIRsRtH8Bf8PTw8WHBWqVSCIbNDeGBbcnNzY8+v0mg0bm5uo0ePDg0NjYqKCgsLmz9//rx581JSUuCUwpSUlMzMzNTU1OXLl4PBdUZGRkxMzIsvvBjIXA64M95CUQFNgtLisALVhGVFnU4HpybiU8SpoRYoE0gELLhREXJxccHDadkUIDD7yxQ5cPr06fPmzUtKSpo3b96CBQsKCwtLSkry8/PLysrOnDljsVju/POH9ib/PnISaBKAXrlyJbRphULRqVMn2IghrYZRaBfIKERCSveQoYOOdO98wqfPf15+8UhFJbHyhBOJja8jxCiKRkrabBdEntKiWW12AFZthJgt5D+HyR8G7u7Rbkt87Bm7jfx8kgwb+GOfzrsmjj1VV0eqTDdMmG02UaAYrh3AX7opQGKqsFrIC8P/07fDsYFev/b2PDb2j/vsZkri4XRCoCCKlAmaYpcNf/VdpEDPFiSEnDhEnuud3/P35T3bFnz5CX+lgoa0N/EnSGA8L5DLF8iGL0m/tgeGdb44fPCRw7tJTQ2leZYIOijCTtk96PmIFunoRWoWDrQhlZWVCoVKoVCq1BITtIr+KhSKNWv/ydo43Of2xA4AgPPCdAvZf3g7j1xCMEyapAtGI4fSNtWtwPIXRIQxj+VPgLEKk8KNHgDgiqIIpzEUMpe/v7/BYMClTuwH0RQlLCwsIiIiKCho+PDhixYtoqb3FgtmcR8cIKv7kNEjkYWvry8Oh7169YIyO4gImgT7yCGAQ03hafNhHKLc0i37aTQFN2Cj6tevH2ghCoXi+k6uW8pIDixLQJaALAFZAncuAaBKwHTYW1gMvnbt2kcffYSzOJxSYu8N07MhQ4Zs27ZNFMWrV6+CXoRUUZi47HgsJYCgDNROEASTycRx3Llz52bNmhUcHIwWZGq1GvAIYHYGLdTNzW3q1KmrVq3auHHjiy+8iFAF7K0GlRXWqsGnffv26enphw8fflDCrKmp6dOnD6ISMAds27Ytcsc1pdU/qALL+T6KEkhMTMRpWlhYGHSq91qHfxQF9aDKzL4L1o3lAU8cB+EWnzo4MDCGdwhwV25ramognUuXLuXn55eUlBQXF+fm5qalpaWkpKSlpWVmZiLVc3h4uCtzsToAtkzY/wQ9s066cHEOyZqdYQeIDqbECN1CRLgFt6enJybiIl0QUavVurq66nS6Dh06+Pr6hoeHDx48eOTIkTNmzEhOTo6NjV24cOHaf63dsWPHsmXLMjMzv/322/z8/G+//TYlJeWjjz5asGBBRkZGREREcHAwEHa3atUKDMAhO+AtYeFj2H+DYxNWH8zMISRwUjuHwXTUajVkhKg9nN+IUTQaDXBSgbG2XjqUUq/Xw/AHyH5ERIS/v39QUNC4ceOuc1cmJSWlp6fPmTMnMzMzOzu7uLh448aNhYWFQAYC7xo2IbE81OxUHZArMG7DIYy388BtDf54gpQgCOzRDg5tkv0KEJ2A0RBatUN4gLkcPOVbBwk0CUBPmzYNtBCDwTBu3DgwqrcJlCYZjH85Qo6dJqNHH+v89PE2rX7yGZh/7hdKfEGhamIXBE4UjaJYQwQT4S2iwPHUDJoYObHKItZZSGUFCRuaN6z3jy9EHq2sJJcukeeHn+rUOnds9EljNcVwTZQuw0ITa0BtAfW2STUwchTqnT3jah+vU35drAM6nw3y3bW7hD6TmDeAVQPMoIE0hGLQLAAtEFJroh2W2Ux+OUteGXN2cI+jg3seiJn569UrFGBGqNrBYW8AkXmObNlAunjkPet5ztt1b/Y6UnVJwt9JjWT1TEsiAdCElw4hFGi1KAO1zUIPTlQoPBUKlVKppkcRSn86vXL4iD82CuY6vLZ7fYvfMJDNQXboyX6KiE2DKRAscuJKKajveCIwtRe3WjGdysrKAwcO5Obm5uXlMXhyYXJy8qJFi+bNmzdu3Dg4qBcPcmFXILGjBAf2dOiPnSP44GBw5coVKOF9U6abH57v9dt82NIPDg5G9qtu3brBW4AdplarFRYYsMxms5ldn2hKkg5tEqPfdQdYBzjMS202G6LPhJABAwYghJGcnHzXyyAnKEtAloAsAVkCN5WAww5iUFc4jvvmm2+ef/550BBw8omaAzi0Wu3EiROzs7Nx6xLON+7pRPqmlZID3GcJwJSVEHL27NmMjIyAgABUKVkeUjgoW6fTubm5vfzyy+vXr//000+nT5/esSM98QWamUMbg1tfX9958+bt3LkTkLj7XDuH7IxG47p162D/K5b2xIkTEAy1d4dY8q0sgZZLwMXFRaVS4QlvhBCTyXTfdPiWl/OJDcm+C9aNAgFPHAfhFp86ODAwhncIcNdvz58/n5SUNHz48ClTpgCiAuTF1A7SagU3ixvuZK7ly5dnZWVdn7glJSVNmTLl5ZdfHjVqVGRkZMeOHR32WwN06wBKIKs1dp5IDw0GyABEOOMVbHidTscGQCgDHQ7U2JCmr69vaGjoiBEjgoOD58+fn5CQkJqampKSsmLFih07duTl5X3xxRdA91xaWrpp06a4uLiFCxfGx8cnJiaGhIRESJePjw/yj7HZAeEJlAoqgk9hOg/HLarVarQ0Z4c8QPORYwQqi6cvgiSRigpFgdQi6AMpwAZ3Nzc3T0/PYOaKZ67Vq1dnZ2fv3LmzsLAwPz8fYGs8K5gFiNGov3lECJsx6gOoGQKK7dyu7nrDfswSbBSApjBp9+7dAUNxcXFZ9tFyqLZN4OzEaiOihZBfakhiEnmmy5FuXS61bV/0XQ6lS66jj4ycKNlIEzMh1USoIYJRFCx20Q6kzCIhldVk/PDDw3rvHRWRf/kcqbxKXvjTjz075IcO2bN3D83KJNkJ86SGkBoEgxGANomkykiS/mbs3enwoC6kx++Nvr3KdmRLEW1Wu8gJFChH9Pk3YLJEAE3PPpSMm2kUexUZ/8e9/Tse8etxYsLzP/L2eiNlqLLDL5pFiwL5IZc807roGfezz3Y4FveeSOtPiF2kDBxI+txA/UyfSDwfxGYjtRVkwphNnu7DDbpuSgU13ZUutUKhdnX5PTUvfzgu/BrR4XwiAWLNJSUlRcxVXFz897//PSkpaenSpS+//DKsyEVGRoaHhwcFBQ0ePBgOagNmIligw6NmnbshWCWDrs2ZmB+OoGV7KHQDdRRLeKRSqfLy8ng7j4fG3AdhNz8834cCPFRZsAC0SqVyMCiGNY/z58+fPHkSiv2QANDQ1C9cuLD2X2u3bNlSWlp68ODBkydPFhQUfPLJJ4mJibNmzZo0adLUqVNBI4G9XZMnT36ohC8XRpaALAFZAk+OBKxWq8ViAeCsoKDgukWqt7e3w+yuQQdTKhQKDw8PjUYTERFRVFSEegLH0aM7QGgwmstj+pPQhKABVFVVrVix4qWXXnI+jlKhUKAhm6en55gxY5YuXbp48eJXX30VJsm4xdtgMABaDfNzg8EwYMCAjIyM8vJylCQst+PtA3EgxOzl5QWbCHU6HeVglC9ZAndDArydxwkaTP1gLib3q3dDuncnDfZdsG5MnfVENz51cGAAdDgEuLu3oigOGjQI+i69Xr9kyRJch3bICPs6B39EPFgGEjbM1atXS0tLc3NzAdhdvHhxbGxsZmZmcnLypEmTwsLCIiMj/fz8unXrBn0+QBAA0cLSC5y1iDgy2AKr1Wq0zYJPQ6vVAuKhlS4ESWCOaTAYWPQDbezgKVptK5VK2COu1+thtFKr1RDGy8sLShsdHT169OiEhISkpKQFCxZkZmauX78+Jydn/fr1qampK1asyM7O3rZtW3JycmZmZlxcXFpa2tixYwMDA4cPHw6VRcoEBNxBrULEBr96tVoNb4eNAoXHXUEgCgiAtCEI7oO4IEFAh5x/cVyGmmKCKpWqXbt2gwYNio6O9vf3Hz169PTp0+Pj4xcvXhwXF7do0aLs7GwGyipi3zvrhkbCaobwlDWphgbPxpLdrAR+A0A3bFGkiK1SpWhozcqC/B8gjtlusRGrlQLNZNU3pLPXrm5PX+jT41RMrAB0yZIBtE0Akg4KQNcRu1HgTYJooUbRErR64QJ5ZcK/e7T7LqDfjz/9SI2EY2cZ+z3z78F9vj93muZjrz9mkPCkRiBGiiTzlMUZrJs5QmpMZOMG0qtLySDvukFdSW+vU6tWop00sQkWq9XcFAAt8UHbJG5nmqC5hsx551pAv6N+3f4zLvJMnbSHoxEEGHg6aFEov4dVIPtKydA+W/u2O9vf65c/T6ogdsJRuhGRpzbQJkcAGjBwnlqPcybyX69c8/He1tb9zwpFF4XCjRpBK9VKhUanaa19yn3bv7Ntdum8RxD6ff81mUzHjx8vLS3duXNnfn7+6tWrU1NTY2JisrKy5s2bN2rUqFDmgrUyPO8buxiVSuVASMTCyrAaxi6UYURwuLq64toXbOUAf61WC52aQ3hoqw0tlj7E1TlMEPcVpqSkgFDvGwYtd0PsqU2+vr4wN4NBKCYmZuXKlVu3bv34449jY2NHjhyJm0BDQkIqKysfBgAaNt5u374dFmBBk3BohHiL7VCtVg8fPvy+f8FyhrIEZAnIEnicJdDU1NGhzsAwWF5enpWV1alTpzZt2rAzH9BJEH1WKpUeHh7Tp08/d+4c2LYYjUY2QSQEuz8TaTZr2f1AJPDll1++9NJLaLcFu5JhNzGSbyiVynHjxn388ccbNmx46aWXWrdujZqAgwOUUn9///T09NOn6WwHj76AdXdodS1s23ddIA0TwPqEJ0+eDOVXqVSLFy9+UKW669WUE3ywErBYLPAhQPer1WqhPNipyi3twb4gh0PkGn0vrCe6myo2BkBHUyHv3N9qtR46dAg7XqVSGRAQAJZzjbYr6PSQlgGgat7Om81mXHLmOM5sNkPZLBYLEJMiqI0OQCQhrslkQqZ+2PltMplyc3NLS0vz8/O3bduWmpoaFxeXmpqanJwcFRUVGRk5ZsyYYcOGtW/fHgoPagkgxTij1Ov17Nq5u7s71hQfAd6K/gCGIHQLSSGuDXh3o6AKpgBQDPBog+fQoUODg4PDw8OjoqJmzJiRmJgYExOTkpKyatUqID9Zvnz5V199lZ2dXVZWtnTp0kWLFi1YsAAoRIKCgoYNGxYSEhIeHu7t7Q1QMmQB3YLBYGDBIsgRqU5UKhXaoYOnA9SDxWZRIECf2ZCo9QG+BGgVi1mx6UBS0JYCGq7IyMikpKTU1NT50vXFF18UFRUVFxdv2bKlrKzs/Pnz2GbuvFU/DCk0+vncYcF+A0ADPTwhJDt7m06nUT9F35FWoxfs9Iw++hWJXB2lMyZHz5L+PsXPeF1qqz84edRh0VxPl4yloWX9/9n7ErgojrT9nhmHa0E0Iho5FBHkEO+ASkR0RXFRc7mJu8bNbq4vh/lHjZ/ncuiiJp/GuDnM5k40JpuY3cRj1ehyqoABj6h4axQ1Xigwwxw9093vP9UvvFYGMGg8ALt//Iaanurqqrer63jqqedV7IosKk4mgcwgpNrf5k23hPh9OaDn6pKtIFth/hypR1D+gOgtBflw2cTUk+0qBi2CQ2I8ZRVJZpA2C5qsisMJ//kaIgJ2hLY71a19WbdORamzLGaVm6KKY0iSwhwfNnQoiG4zwJzpYCx+ReradUdE90O9o9ZUXuAvIk+H6o0lpruh2M0gM4XrXbtgUPTOiHYHunc4ev+IMks1o4XLDlAcwCRpwOFU/0i7g6HjCjCKtA3+8yX0Cjka2qGge9e/uRn7CEJrQa9TpThaMYTU3XPJ0tdUqJ0xoev+8Vm81jBOn1DiAEE9h8Pxzjvv4CrQoEGDfHx86LW81oDL69qYr/wt+PjXep6u5dsXOokBap2xKXntNdXINaT8azWkFv96LIAMYgDAvpBWNet93PgojUbjqlWrCIC+nrve0GtGjRrFs/VpWMBXNvR6j2dat27dt2/fG5oFLTHNApoFNAvc6RZA90eI37nYwm6343xy9+7dM2fOHDRoELbGLs21Xq/38vLCJW1BEDp27Pjss8+6JFXvV5xF1/uTdrJ5WcBisSDmi9pxCCVUVVV99dVXY8aM8fT0JBYVP+338vLCZYzRo0evWrVq/vz5Y8eOJdwZ5/ZY5Wjfsbe3d58+febNm7dr1y5CYW7GjO4G2v/1118nLGPp0qVE+Gou+b+BptCSurEWmD59ure3N2JJkydPRhBQq1c31si3ILVrasFuWb+5du1anKbhLLJ///5oChfhxFtgn19zi8uXL+/duzcnJ2fr1q3ffPPNW2+9NXfu3FdeeWX69OkTJkwYOXJkcnJyXFycn58fMo49PT0RrcZGGzFc1LhAO/j6+hILGGNip4arqrRThyazyClGkJdHhPEqTBOvwm4OE/fy8kL5JoyAeIufn1/v3r2HDx+elJQ0fvz4adOmLVy48KWXXlq4cOGKFSs2bNiARPLPP/s8Ly8PCciLFy9etGjRwoULZ86cOXny5Pj4+EGDBo0YMWLo0KE+Pj6YZ+pkKRsIJlARKAKuFvOlIESbj4wwERYHI7i5ufEb6PnILmF0AoFlx/y4DDgNBsOQIUOGDx8+ePDgIUOGvPjii5mZmVOmTJk3b96yZcvWrFlTUFCQl5eXk5OD1cbl5UKJaloUIfFbXC7iEFZ2NbaoiJxQJZScEi6l4DgHHarRXciVaF1eJgrXuNyCkv01gZ8B0ORq+Y03/s7qtGcrQWB7EhGAlhjBF0wyHDkD9w4t8vcvCWpfdk/EgWM7QVFpIiR1oZZfUuFYVQXZqTJ/nSDa4Jm/FPbqktut/YbirWAzwUdvQmTgup6ds9Z8CRUmOFelqO77FCdIMtNPriEeYwlFieHgpTvh3piTPTvZYgKtHX22pc4y20SotIMVZFJnvopFUAaE8axl+PRjiOiWHRi0Mzxia+E2xk22mOhSBKDV6CoFm0Hs6rF7Nwy9tzi8/dHQu473Dt92cD9YnSAqsuysAaCZC8YaANopM81nFUgWGR18y3+Yakdo+yMRgQWps0oFoasgeNcC0KoXQkFIm5umypXceACa9Jfff//9uLg4en9Qp4KaFR4QbHyYUmt8gE+cv+paz/PXNhR2aV5/kj2iF48euRa4qRZAANpqteI2IureqKPinx3iAp6enm+//Tav1XVTc3j1xB0OR7t27bCbxyJgzpHNja6HUBsLfQcjwb9jx45XT1b7VbOAZgHNApoFfr0FkEb6zTffTJ48GYV3cZkTe5a6fBmcxgQFBX3yySf8gP7qObllE+mrZ0P79VdagCco4ezryy+/7N27N41MePYZzV3d3NxGjx79/vvvz5s378EHHsRqhngH6UETWq3T6ZKSkl577bV9+/ahjyxUgyGs7VcW4aZe7nA4XnjhhYSEhKlTp5LYJU5um0X+b6pxtMSv2wKouffee+8tWLDg3XffRZTEbDZTpdKmZtdt21t84TU9qVvWbxYWFvJzyWa3CZV3rHd1o2FMbJytVmtpaem2bdsQwEUxjTfeeCMtLe2xxx5LSUmJi4tLSkrq378/bxwXrX/U3SVSMKpnGI1GXIil84Tv85N31KciLJgWL/nbuYT5ywkNp5Px8fEJCQmjR49OTEycNm1aunrMnj377bffRg+TOeqBvON89cA4+HnfffehePeQIUMGDhyIJUX1eRc4CHOFhdXpdLRJjhS3cOiIs376JHzZJTUqOEWgUtNPPDsblVL4dWsabPj4+MTExAwfPjw+Pn7UqFF/+tOfJk2atGjRInTMiO7T8vLyioqKduzYgYvo6I+xoReTx6+prcAGGfFlfs8fJYJ8jpsOhaVAagAAIABJREFUQNMQ/E+P/ZEZSC+4Gb1GJT8gS8yroBPsVhmqRZj1V2tI8OGI0EtRYbu++RIcFhWZVkuDGHRtwa7wkO02qfIyfPo29O6c36fbfz/7CGxm+G4r9OtW3K395owZZ6rNNQCvivsyP4cyQ5/Rh59dBaOZenJhFsSG7+oTUN3lNxW9u5y9P/mw2crQZ5PTgVAvUoZrM1DPf4cKKVda4KvVEB6yPaTTnp7R/924EZjohQoxV1WotGu6FFPEjDjg0mkYOrAwuP130Z3PdA8p3LKN5dKugFNxMgDaCYz3DVaJeVBUVL1pscaPIkDpNujfuaSLz4GYznv/NP646ICEoY8IghsPQBuMxuTfjbpJDGjUXy8vL6f3in8NcI2IB3+vKUzvWOMDfPr8Vdd6nr/26mEipCxfvpxqOz1qLXDzLED96OnTpxsDQKPXXXd39507d1I7ePOy94spYx5wKy71QBig/pLqHp7Bz1Gj2OusHZoFNAtoFtAscKMsQBQPTLCkpGTp0qWDBw+m1phG/4gnYuOMAwBEpfV6/UMPPbR27VoeXLtR2dPSafoWwOdeXl6+Zs2aBx94EKU5cWqNS8hYhWjQ2Ldv30WLFi1evPihhx6ivr6hwCOPPLJo0aKKigqi3WGNbUYALo55+Gkn4h1ICKARXdN/0FoOm6YFsGohMQWrE302zQxruWrKFqCKVFZW1qFDBwL7FixYgJN9XAJsykVwyVtDbSx1Jei01q4eNE3Gfg2/iqJIHRC15KgnibIk586dQ7VV9MKYmpqaph6pqalJSUk/ecIYOnTosGHDQkJCSDGV7/IIKqUADbSo36Qz/IUUJloAbR2m5VvUceWRWYSGESCiFPhAEndMmzZt1qxZc+fOXbBgQUFBwdatW7dt21ZQUCCK4unTp4uKitatW1dSUrJ+/fq33norPT39p3qSnp6ekZGBCiEpKSkjRoxwwev5e3l6eqIUJ8pz45iBdtThQIKPj8MJNzc33pJkN75QiGjTCBYT0ev1qPeN53/SxfLx8fH29ia4nMcl4rnj+eefnzdv3ooVKzZt2pSvHvv37zebzQ6HA1VicEyCgmD4abVakSVttVpxQyHVLpcq+iu//owBjWkpijIofgCDI92ZJsTg+JEqAM1gVosIq7+BPj32B/ufigkr+9PE/VINyOzKVmZJoRdANVF7Nfx3DcR1y+sV/N2CNMZ93rUdBvVee2+P7+dMUiyqzrOoimOoeK2zFoBWVDkNuxOg2gaOahh976m+QVVdvSrC7zp1T1TBj6dZ6lamflHDNSbNCixL3U9JYvzkXfsgrPu6iLCTkaH7VnzEYjH1ZwmcNo51TfnHREW4dApG3JsXEbgnovPJoLu3rPqqxl2hCKKs2BQnKMwc1QBWRcafGAbNUneAvRz+mLwnvM3uPkHHHxz5/Y+nmN7I/Q9PZDC/KsHBPhndXBgYP8gpyyp+fYMlOJitrNa9e/eii1WchuHLQNM2Hvy9pjD/pjUyzKfPX3Kt5/lrrx42GAweHh6pqan4mt2kl6purdPOUOd34MCBxgDQ7EUYOPCDDz6od8nu1ttTUZSfcpKens638gaDISwsrF+/fsnJyQ8//PAzzzwzbty4AQMGhIaG6vV6X1/f/v37FxerblVvfY61O2oW0CygWaDlWmDdunULFiwYPnx4+/btacyAJB3krpJ+Ak5ycGzg5ubm5eU1bdq006dP09ysrieZlms2rWQ1Fli3bt3jjz/evn17rBheXl4eHh78BBLpYP379/9JmyU9PX3w4MEIauAn1jQaOeP8+Sddy+XLl+/btw/nb/z8n+yucAedbIIB0kyjwRvOVDUAugk+rOaVJbPZjC8IImiUeXoz6IwW0CzQSAuQsIDVai0oKHjkkUd+Ut/KyMggqhl1941M8DZG43f9OhwOQip4p4jIeOVfGf4qySm5lNdqtWKTjsJldrudWvjGlJQiy7JcWFhYUFCQk5OzcePGN954A+nJs2fPfvrpp0ePHj1gwICEhITg4GCEkkmxijiO2OHWlbbAjhURVTc3NxSGxg365MHLw8PD3d2dut2GAB+EvwnLxmg6nY4AX09Pz3bt2qGmx+DBgwcOHDh+/PgFCxZkZGQgZr1q1arc3NyNGzcWFBQcOnQIhSnyuWP16tXz58/HyBkZGc8991xKSkr//v3j4+NjY2ODg4NdEGTMA6HPKO5BnDb8ld+x5+npiYWlpRR+HIvGRAopDnfrmgKNwPNNDQYD4uZkT51OFxsbm5ycPGTIkMTExLlz586YMWP69OmLFi365z//mZeXV1hYuGvXrtLS0sZUkmuN8zMAmrQ/vL291PwZBMHt8T9PYmIQAKIDfvgBekWUhgecjww5PnhAgdUGNoU55VMYzPozuYyf5cMJR3dAfMSGmOBvUl+ymiphzy4YELU7zG/LQyOLzxwHu8jc+qEbQyQMO8DJWNdqmiaRYbjnTsHYYcf7da7s1VHu1bF8QMSunUU1BGlU3kABaACHzBJTM8VlQnI4MINOCX48C4mJu7qF7g4LLXplITgdYLWoZGtZYYgvYumEZMsKKGCzg80G//NYVZ/wHyOCLvq32fr/pp6yAVQrLLqTgfNWVYDDDmCqAaBr7SFJYL4MDww7GB9+snfA/nujcyvPqfaUYfHfXxX0AvvTCaoMtF7QCUYPd9HpuEkANI4gn3/+eaqsxA/ClxMrK25N/cWXHBMZNGhQQkICNjoJtceQBo7BgwePGTPmqaeeQq+GKAO0efPmbO4oLi7etGnTxo0bt23btm7dum3btuXm5mZlZa1fv/6ZZ57x8/OjRoRKwWeVFohQGkkQhDZt2jz//PMrV67kaoQWvKUWwDkMdpbh4eHoOx7FKwwGg6+vb2xs7IQJE2bMmPHBBx9s3LjxlmauETejEQAAFBUVHThwoLy8nLrkRiSgRdEsoFmgsRag1+3YsWOvvvpqjx49XDbrxMTExMbGDhs2bPTo0cOGDZs6derChQunTZs29xoPdPm9ePHipUuX5nFHVlZWXl7e9u3bd+7ciQN9/CS2LA3u+emBS/FQtY2cLuCvklPiF9UsFgueEUWRSu2STgv4ijusyWiiKMqyTANOm82Gs0fc64dacPxsSlGU06dP5+fnL1my5MUXX4yKiqKu/yoB4obgoN/d3f2xxx7bunWr2WxG6gfeAveA00SuBT+FFlCRrqkIfAdNdW/t2rWTJk3CcS+NG3GtAuerWFvi4uKefvrpmTNnjhw5kvf1hJd4eHjgxmQcbT74wIPffPPN8ePH+ey1sBrFF4fCfHm1sGaBX7QAkuixjcXX02V5A6vWL6ajRdAswFsA6xWuZ1CN4medzateURH4MtYNUzvcUIC/hI/Dj3n4OFcJX2VcxKdcb/jChQu7du1CyYgvv/xyyZIlc+bMWbRo0YwZM1DPeuTIkbGxsQEBAQi2ugDH7u7u5KUQ6cbUcePwz+UrncRFYl4iAzFZl/hIX8CrkKRYd1SJBGRBEHx8fHr06JGYmDhs2LCkpKSJEyempqZOU4+XX3555cqVeXl53377bX5+/oEDB3hrSE5pw4YNubm52dnZmzZtwuK/8sorGRkZP41Lhw8fnpiYOGDAgIEDBxI6jLMePreEX2MO8SsfQRCE1q1bIzUb4+CyOqHhZA2E0XBsg1AMpkN4NxmBLkG43NvbO5E7MrhjM3fQvIkkPkT1wFE36kr/DIDGyZUoirUP2yAIHpOem66uIDFk9tFxBzt3PHH3Xaejw/OZaLITRCaMISIBuZ66yzwRgv0SjLqnMObunAkP7DNXwHdF0DPiq27tt4xN/KH8Rwbs2mXmeJADoEECUQLR4rADQKUFLl+C1P+FkLYHe/g7enUy9wgsyF5TczcEimvVnx0AVjWxnwHQDH0GsNvtNjtcugx/+MOBPj2OBHUsfGnKJafM7iRJokqktoOsIsqYKEOjnRbVDbrdAVNfOtuj+8ngDufCQ469+KJUITLoWazxE8hEn5n3QYVlQAEHC6rUZ9HG8Om/zTQFeH8X1elkfPTW4tyanNudllffWHwFgNYJOsOtAKBRJ5Gm09gSORwOGqDjO8NHo5pUN4CtkuSUaGZeTzX4+Smcb5vNZrvdTk5gsGrivJR2BOB1siz/tGXgpZdeQjcvqNRD7wa9h+gaFV8qHx8fvV7fu3fvzMzMsrIy7JZoyf3n2dG+3QoL8A1xcXFxv3792rZtO3To0Llz527fvp2cFGNtxBbqKh3ercjxVe+BEAlV16vG1X7ULKBZ4BosQJ3CJ598QmuN/BiLDyNL8Sreq116isZ/ReYFjoVcrvLx8Rk6dOiQIUMmTJiwYsWKnJyc9evXW61Wk8lEoCo2ZVhs3DKJnBRqCfk+l6zTlBs9yuT1BXBORTMrClBq5AUFxxInT55ct27dm2++OXny5EGDBuGoGh8EDaZdngv/lUjQXl5eAwYMWL58eWVlJd4UGUD0IPjJGJ6kLGmBZm0Bfsi3evXqMWPGtGnThmZ3RqOxbkWKiIjARamEhASqTvwEjJQ6jEZjcnLym2++WVZWhm+9S5WmCnaVQDMyb72laEb517LadCyQm5uLi4gBAQEVFRWUMapjdEYLaBZojAWo5tC4C2Evm81GP7W8wRVftHrDvOn4CPyYh49zlTB/+TWF+TTxQjyDEBOOil26ToxQUFCQnZ29devWzZs3v/3224sWLVqwYMGMGTOeeeaZeNUnYVxcXGxsLGp0XJ00idxhdJOILGOcRNCGORoJoO4H7mdCHBxJmbhiTdGI3UiDBAwgeouzBswSXZiQkJCYmJiQkJCSkpKenp6amopeJT/55JPs7OyCgoL169cj944kVqqqqvbt25erHkVFRR988MGSJUsWL148e/bsjIyMESNGDBgwIDY2dtCgQcHBwTqdzsvLywWhdskecTKwIGgQKpROp6PLeeUTSgRZqiRhR9vBXZbzMb4nd/Tt23fAgAGJiYkjRoyYPHny9OnT09LSMjMzfwZA4/t54lSZvpWbodVvBMFdp/ea89f5DI91wodLINg3J+Du06GRRz78mPGJ0VGgyDjETkaSruX8XqlwEkiXYMrEw2F3rR2dcMhmhkMHICakODJw5/3JOy6cZRFtKn/YDk6RMaEdTqanDBLYJLAxXrETTBZIm1PZrePuPl3Enp1svbrsW/Up80Zod4Kk3pHIysBwbIZZux4KOGzsvMMBv//DocCgkuD2JX9+5OzFC2CygwhWhj6DBWT7FQY0C1Wxk6pmdPpsKSbyaGDHH/3b771/XGnZBTgngk0tsFkud4IkKapqtQyKIrF3TAWgFSeTDVm3AqI75nbtdDK0y859uxlibTODpGLr6zdtZtzn2r9bA0CjcbB15kFnV6Op3xvT0JAvFz5yvakhI4ynpSDWbLfbca8iuulEdpIoiiaT6ZtvvomPj6cXANmy9JUC9Ar5+PiMGzdu2bJlx48fp/6Gn4fUmzHt5M22wC/WDZdVh5udn+tOX5blepGj605Qu1CzgGYB3gLUbo8fP56Gg9jU4zgSMSBq86kXILSazvxiANkBLoQL5B3w6ZPCg7e3twv8LQgCDtow/pAhQ2JjY0eNGvXUU0/NVI933nmnoKDg7Fl1uFPrn5rKiF0wWx232ag75q3RAsJUWCpL3flGSUnJhg0bXnnllYkTJ44aNarug0Oz0wC6bgT+DBJa+/btu3jx4hMnTqDiFlHR+c4Ix/q05Ik/UT61QPO1AD7ZTZs2TZkyxc/Pj685vKMhXMHq16/fyy+/PG/evPvuuw8rEhEaaP6J593d3RMSElasWIEjAapaNpuN3x+N4xmXmlb3azMyb93M132vm1FxtKzeLgsoihIUFEQ8u+eee44qEtWx25U37b7N1AJYcxBXlWUZ17CxXlGlomrWTMtYN9t80eoN85fwEW4ZAE0ZoLsT7kwcR8R/sD+lPhS3CSqKgorVDWE4lAiSIwu4Yx53DOMO3L3ED+NxeO/p6enu7u6yLE3DBoKwcTWaZgcGgwHpwyRtIQiCt7d33TmFIAjk8hHVnHHCQjnBNH19ffEWvr6+Xbt2HTx48NixY+Pi4lJSUlJTU2fPno2E69WrV2/evHnr1q05OTlnzpwhVE0UxfPnz+fl5eXm5ubk5GRnZ7/11ltpaWkTJ04cMWLE4MGDk5KS+vXr165dOyoa5haFeXGQg8gyguxUEIyAuSVqOT/qbiiMXBBKx8vL68pMjeoHBhRF2b1nj87Qyt3DWxCMgt59/sJlNivs3Q4J3Xf263wqOKho/mKGGkuqzLHM9I1FB6MCq2RgHoOWQbbBgunWvp1z+3TdWpIHxYXQL2Z1bMSBsUNPlf0AFjtYGTUZYWOnk6HNDqeELGSnA6DSCqZq+PhDiAzZEtnpbEjbU71DD/y/p046JQb9mi2WOpi36sLw51C4rEayiSA54a+zS4I7597tv2ds0knbJSyxFcAMUME+ZQcgiZkVxSlBFVPjcMKq5RAa9H1wwPngoGOxA3eWnYfz1VDJsm2xwWU7i6Ywn4kS+xOdzP0g+6rmZfUXEN1pfWzksd4996z4jFnKYlYFTdSPbzdlMwGO2wFAY+FvyCdOmxE7JiJzXa40wnZ8H4D9RN25qKIoRUVFzz77rL+/PwrlEA2NKrFLXW/btu24cePeeecdvkTUG8myjM1Z42nafDpa+NdbgLofqgD43Gk3OuIv9Ouvv6OWgmYBzQLN0QJEIs7MzHQhERCbwKX9pz10hBQ3MuDl5UUzYT5Nb29vOk83xQAfDdErF3kQPgJRDHDc5unpGRYWNnDgwMGDB0+ZMmXx4sXp6enoy/vEiRMtuPXDdn7Tpk0FBQXffvttRkbG/PnzU1JSYmJicM8gGg27exz+0rgcf6KvuAeTN7JLePjw4YsWLaqsrCQiCQ5O6F1wgZv5yRj2UxRTCzRTC6xatWrGjBkBAQH83gisQnRGr9f7+/v37dt35MiRQ4YMwVpUu/tT9cfCVSyj0ThmzJivv/6agGacEuPmP5r+8ebixzwNhfn4TTxcbxGaeJ617DVBC+Tl5dEuBEEQEhIS6nKYmmC2tSw1ZQtg60RTfhxDbtu2bd++fdRwNeX8X1/eqGgNBfhk+Tj8mIePc5Uwf/k1hcnnIQCYTCabzYZzf/J0hxug+VsT3EyIjdVqJX4GjZPpcVN++EToJJEMKD76/LBYLFlZWbm5uQUFBdu3b3/jjTeWLFmycOHCefPmpaen33fffYMGDRozZkx8fHxkZKSPjw8KUNBAFAf/BEnx2h04gsU1bBpEkHsJfgRrNBr5vX18mvyNKBEEqZGXQ34OydmJwWAIDg4epB5jxox59tlnU1NT58+fn5GRMWvWrGnTpm3cuHHz5s2o7Lx9+/Zjx47JspyXl7d+/fqSkpKNGzfOnz9/3rx5SLJ++OGHUeEwLi6uV69e/JyItEEok/yECwF0+gkjGwwGhN1/Vhb+geGifU5ersHNYPDQq9rE+jmpH54/DuOGHO7b/sygrmUjElddvMwukmuwZlW8gjGIVQFlFe6trDBVW+DSRVi1EnqEloQH7877L+wuhp5dd0YEbBmXUnzyKJjMIDJ1ZVXIQpFFRXYqTqcsKyrj2AlwvpKRkP/xthLSIS8q4FzvztWRgTufffI7xjhAxWb2u4rjXikD+Q1Uf1EhcqcqlOEE+Gwl9AzfGNZx++A+u4/uVa+pUa52MM+BSjUDm2XG9cZEFVUVZO1aiAzd59+6rFP7Y7365WVtYxdesjDEXQRRhGonWBFxBuaEEEyi6ADZZGG7io58D/f02BYcsO/uTlmvLb1wTqVASQ5gJVfvcamiSlWARh1ovcFo1Bn0vm3bVFtZmsTs5gNXytokQ/TOXyV31LjgsIOWvGRZLigoeOGFF0JCQlCY5so6iSDwuwPwLUX19LS0tM2bN5tVpRSXm1JmXAIu0bSvt8UCLg+Fvt6WzGg31SygWaAJWuD1119/9dVXFyxYMHfuXE5qLAO/ptcequPutLlz586aNSszMzMhISE5ORmHjwMGDKBtZQ3tm6MhUb0BQrfr/kq0CPKdgLA1jUqxq3J3d6cxIvokwKSI0E23MBqNISEhI0eOfPzxx9EjSmZmJiLUe/fu5Xcr8w+LH2HT6JyPcKPCtNiMCdKOJQDYvHlzYWHhxx9/PHPmzDlz5owYMQLHwfhZ13SNOUO6e/jgPDw8aFBL2wDxTGho6MyZM5cvX95IT/fU3bgEbpShtHRugQVQSkVySijeYrPZ8vPzn3zySfQrWK9WG9Y6XARCT0GIR+v1et5XEr2eISEhDz/88L/+9S+LxeKi9u5Sc/DrLSi1dgvNAs3aAjt37sRuERGZpKQkmr7RO9WsC6hl/rZYgCqPoijZ2dm+vr44vnr33Xdx89NtyVXTvClvq5udw19/Lz6Fq4cbKgt/FcbhzxAc39Dl/PnKyspDhw4VFRXl5+fn5eV9+eWXixYtmjdv3iuvvDJ79uxHH3102LBhcXFxAwYMiI6O5ke5uHETKTUEYfERcPHbaDTyExY+Qr3herUyMCbeEZUwEPXGT1qDp3nKUO5ISUmZMGHCSy+9lJmZOWPGjJdffnnFihXr16/PV4+tW7cSvRonJrWTMPY/ISEhPj4ehUForE4BPv9Go5Fh+rxlcRqTk5fbyr2Vu08rFtvoNS/jP/83A7p6bIv2PTwk6jvzRQa7Wm14nayCtNVMwkKp9eBXiwmXFEFYyMbIsP2fLocvPof4e4q7+OUmDdh59hTYHUxn42fosyw75ZorJdWHIACUbIde4Vmhfj9E+Ff26nJ8woOHzvzIaNJSDbzsZPrKqg4GX4qasMIgcqeav8s2+Go1hARt6B2+Lzmu9MT36lm8ukY9Wqw5pWLWJlFUJTng2y0QFrbD/66T3YIvRHX/PmcLWCREzNkn42uDHdWfGVqsYsZWSamwMWz+4H7oHrQmuH1J17Dvn59a8aPqeBDVtCVRkh01+D0PQNPjUbnULR+AptWtgoKCJ554Al9X2heAizxYd/ET90f4+vo++MCDr732Wnl5OU48aGXMpRrwTQwfdommfb0tFuCfCB++LZnRbqpZQLNAU7MAOpYhtkLjs4c9Ak9LpH02e/bsyeIOHtQezh0ozUG77wkgpj66oQB2VQiP4uX1Dr/o8qukTHv6eAlauhADA7ljyJAhDz7w4AsvvDB37tw5N+FYuHBhRkbGuHHjRo8enZCQgFwMXCTmP8k9t0tWG/+1XosR6QMh/m7duj3xxBOZmZmrV6/evXs39SCNryT1iiRc0+Va5NtiAbPZzHvslGV5586df/nLX4KDg1Hi2aUGYuXU6/UdO3YcO3bso48+GhERQbUR53vu7u5Yn5G7ZDAYJkyY8Pbbb6PCBrUeVF6qby4BiqAFNAtoFqjXAjt37qQtrYIgjB07Ft8y/lWq90LtpGaBq1iArz+jRo1CcM1oNAYGBuI+lZu6Nn+VjDXBn3hb3ezs8fdqTJjPT2Pi83H4a/lwY+Lw8esNk1NxrEiVlZU4DpGcktlsJlo3XetwOGzckZWVlZ+fn52dnZWVlZbG6DIZGRmpqamPPvrofffdl5iYOGjQoNjYWESfeb0LHKvgagoSsYnXQl4BCbNG0gY/hK47xcBfEZ6mmLi/02g08og23tTDw4Nnc2OC9MkTTaZMmTJjxoz09PTMzExKmfY4urm5DRo06I033pg3b15aWtpPEwpXAFpRFMaAdnczuLsxcWLD3Q8/8F73dt/2vftwYo8th3eB5ABRBYpVWq4KuzIJDQfItZIc6q9HD8KAPjnR3b6b9r/w7bfQJ/pYSMec8Q8WnzvDno5dTQIxW6cKPdd+MllnBcDigH37oGdoVte2R7p4n43oeOyeqHWXzrNrpRr6M8gsI7aGAGjmQFDlPldLsGMXRIZ+2yPkYFe//279L9irgAHMoMaoAaARqbaoLgkZEH62Cgq+g379dvq3Odgt+MegwE3L/lFzhd3J5DmY50IVfWYANPuzAlQrzJ8imK1w9hzcP+ZIZMjxQP/vHvvz/ksmDiZXmIC1wyFJToZB1wWg27ZrpxazxQLQklO6ePHim2++mZGRMWzYMOLne3p64lSBXg9S23Fzc/P29n7mmWfQYZ368NgHLWzyWAP9yjc6fJgiaIHbaAH+ifDh25gl7daaBTQLNB0LELGXskQNBaKHtKUOPZlQNAo4HA5+ox/zOWGzoTwUOT8hQQa6ig8oilLMHfO5I4E7EL0iYhfBW4hn0a+ohkZUCIpGAXTSjaNAPIl9IkWoN4BjQd7zdb3RbshJLy8vJHHgUjEPJSDwxxeWis8PRq87G0OHDp00adKGDRvqZYLTejb/+BoTpkqlTVAbY67bHgdnemaz+cCBA+np6REREegyCOsYbZUjwZzQ0NDk5OTRo0dHRkaiCCONM/m5GdbbcePGrVixoqKiwm6346xSG1ve9ieuZaAlWUBRlIkTJ2Iv4OnpuWfPHvQSrzW/Lekp3/qy8P04jTFQrPbWZ6aJ35G31c3OKn+vmx1uqCz8fRuK0/jzJOmmKIooighMEw+SnEPQ9ASFqnHcgmH0wYYR8L5864cTn3Pnzh05cqS4uDgrKysnJ+frr79++eWXZ86cuWTJkpkzZ06YMAEJM7GxsR06dKAKzw9pEFujgRDF4QMNjcxxAxn9iu8RfcWZjovUhkscPjKqhRCgJwjCyJEj16xZ8zMAmiQ4BKOBZVHvKQj+bX0eCvP7/N6ogq8/BacNRKfLY0LVC+Y3kMlKqJrQ5efg/t9tCe2U9+hD8OH7EBT4dXhw/tMTz7M4ACZzTRJYJxB6Zk77ZFlUoMLC5KTPX4A/PFTSv+upezpLPTqejYv47tA+qDKxy9l9atQ+RBks6gmXLLGvTlVa2qLAvoMw+J7CmC67wjpmf/I22C0sk6YqK8sqgtkMBxZVBJl5PhQBTDJ8fwgGDSqNCj27odcmAAAgAElEQVQb6PdDVNi+Zf9gPg8vmxj07HSC3QoOp10Bu8K8JoqSbFHAqoBJrTdw8gdIST7m3+67u/13jxxx+IeTLD8OBxOhBoV9yhL7k5yK5FRcAGiD0Tj0t8Nq6dQ1Fm1JEhyyLK9bty4wMBDFMbEe4zIOTVz51wNr6jfffEPTS3pRFUUh7bB6N97yjQ4frqe6aKduuQX4J8KHb3lGtBtqFtAs0EQtQAJNV88fNiAAUFVVxY8O8SrJKdHgj7oM/IkwbhwLUjr0K0VofBtltVqz1QO9eH/xxReLFi2aPn36ggUL0tPTn3zyyaSkpJiYGBfo1qXXI0U55Gb6+PjwAhQUmUQ8EBR2GfNRtBsVQOSOMHG9Xk9K2by8CW1juu77enp69urV6+mnn168eHFubu7OnTvJkQMOABRFQa8SuH6Ao38aG1y9trj82vgn63Kh9vW2WOD48eMZGRmhoaFUu3DZBoVlsULqdLpevXolJib26NGjc+fOOLbkR5jkY7BNmzYdOnSYPn16fn7+5ctMXhARZxpw1ltGvs7w4Xojayc1C2gWcLFASUnJ2rVrz5w5g402NuMucbSvmgUabwG+HUZIgRzKUave+NRadkzeVje7pPy9bna4obLw920oznWct1qt5LEG/Z8BgFk9GpkajmNtNpvVanVZ6sbxLZ8OzmLoDD/cxWtFUTxz5kxubm5+fv7XX3/95ptvzp07F30xZqgH54txWGJiYmBgIA6iiM5MY6q6AR8fH35gT3vFKMDPPuru2qSXESc+6A6nHgB63fr1Nfdu1UrQtxaE8Mce/mzzGrBZmHQG88vHINxaoQ00hsJ87tmqayzz12lidMiOhLiKj9+B0E7f9Y7KnfHSMXOVKt6MsG8NpFpTK9jcj2HA8iWzXQK4WAFP/PFkr86Ho/0uRrc/Exde/J9/QWUVuyWqdjAAmmHQzqswoFWwGk6ehnv7F0TdXRrWPu///nb2UrkKOqP6RY0GhgJgAqiQVG0PC4iVEpQegRHJ+3tGVsR0t0Z03ZueBiYLQ7QlWRVmdoLCON/MXyGjPCs2h9OqqNrVkgSSHeb8r9g18FC30BP3DNpysQpsDhDtKjSvsMsRfcaAIsPgIUNrMWidvhXD/Yf+dhg6dORxZwpT5Wu+geeee86lchuNRl9fX1TJNBgMbdu2RS7VQw89tH37dovFghWl+RZZy3lDFrhJHUNDt9POaxbQLNDiLVC3v6h7hjcC3wrVjcn/yl91o8IOhyM3Nxc36OXm5mZmZqanp8+fP//ll1+eNm3aH//4xxEjRgwdOhTlBWgLHvahOOYjRJgfApLYHE7GcMWXj8D3wghk01CybgDZDR4eHqQrh6QG8rJIG/dQfoSWlvEuPE6NieP51q1bDx8+fODAgZMnT87MzFyyZElBQYEsyxaLxW63E6nkRplaS6e5WIBkYVXZOkZd2bFjx5QpU3DK5OHh4eXlpdPpcNBI9V8QhPbt2yckJPTr1w+VoPmJkLt60NJOcHDwtGnTSktLUUuan841Fyvd2Hy6MLn4xGnPAd8YuoSRwMTPomlyzielhe9wCyCMQm07Be5ws2jFv4EW4BUD/P39ye/UDbyFlpRmAeoByRR4pt5dlTjAoEua1HgDGTP4uXbt2uXLly9atGj27Nnz58+fNm3axIkTR48enZiYOHbs2CFDhnTs2JGfO5CGATIAaEqCGjjIv/b29qatkwT0MSSaDIcBRVG2FhYIOkFopWcgoJdvePeB5RfYj6IE1XabxGBfUQV/OQxaYQxf9Ez44XsQFlgYE1r+28FKQPuC0OBN/3gLLKgZrULXDMpF4Qv2tQYGdnLY/pQXj/UIOtg30Bbqc6R3QMG6f4Kk8pUVMEssFyr6zABoWWYJ1aTAFwSlqX+sgrEph/p0OxgTvDttisNq4aOwwZKKRttVANrsBGuV7LQCVIgw5r4jQXcfCOxwoXPA8ZSUfZcqa9weshojqcLSNUVQVOKzVdWFrkl8/jwIuntLYPtDA+75YftOsChQYWJa0Qjbs09VgkNRsWwXAFpnYDZ/9E8TWzAALYrip59+6u3trdfr27Ztq9PpOnTokJiY6DJN9fT0zMrKcmGruTw/7WsLsEDTbI5bgGG1ImgWuGMtgK0KX/y6Z+r+2lBb1NB5PoVfGebplnyYknXBhioqKvbu3Zubm7tx48b8/PzU1NSFCxeSY8a0tLQ5c+ZMmDBhyJAhqBGN3auHhwcP1ZFbEmJPEw+ibgBHmYgju7m5IRUCoyGxlMe7cSTq7e09cODAlJSUuLi4+Pj4tLS0adOmffDBByiEV1xcfOLECSygRT3sdjvyzc1ms4ZK0KO/MwPE6CkrK1u4cGFQUBA6piaCM02BsPr5+voGBASEh4eHhIRgxfb29kauDVVXvKRdu3Yvvvhifn4+vWhNairYNB83mcjR8FHvO8vj0U2zaFqubq8FaMf67c2GdveWZIH333+fPAG8+eabuDbWkgqolaUpWICmBpQZPNPsAGg+/9jD4xkkghA6W5eUrSjKxo0bk5KSaDyGg39En4ODgxMSEgarx7BhwyIjI2kCEhAQwLzR0o3pFT32wwmD0V0wuLEX+De/CY+KYcqJDrCIkur/zyGDqKorcwC0moq5GsqOQVTI5h5dznX2vxDW+Xho6H+/+jdcqGA/WxkNWCUCk4ozqnfI7JExgBuUSyb46D2ICNwT5lfZo2PlvVG7X8u0KEyTg4lqyFAlMQ0MV2EK/Jn/dACYRPjLk0e7d94V4leQOu1ytVmFrpG4ze6G6LNDZWUrTpAsUGUFhnBPfsne0e+Af5uL7e86kpRcVnaBoc81hywx54l4kcjgawWqJTAhBF52HL7+CvzaF3Tpcjro7i1fr1IZ0+qdyisszFi1aiWEPtcDQOuEeZmZLRiARr9Se/bsmT179tKlSzdt2vSTJvjMmTPd3d1xauHh4fHgAw9aLBakwCiKgvMEGgHXPgztf0uwALXg2vNtCY9TK4NmgSZgAWxV+IzUPVP314baoobO8yn8mjAO7+x2Oy24ks8cFIzjQRzJKfGb9ZBjSANEzIaiKOiel88VqlRZLJaioqINGzYUFxfn1R45OTnoGoXzzuga3Lx5c1ZWVl5e3ubNm/Py8vLz8zds2ICRsrOzN2/ejIkcOnSIclsXkLLZGBOB6EhYXio+gux8nrXwnWkBu91+6NChqVOnxsTE4EzGhUGPsx29Xu/r66vX64ODgzt16uTC7ndzc/P09KST/v7+Dz/88KpVq+5Mkzay1PwwjNQq8UWuO/msN018nemSeuNoJ+9kCyA6c+HChU2bNpWXl7PZrizX7SzuZBNpZf/1Fjh8+PCGDRuOHDlCSfGNG53UApoFrtsCNDWgFOgMBug84at8BP7XphZGTULKFbbPJpMJh/c4vxBF8ciRI/3796fhmdFoxM0Her1+0qRJOOCnRPgXEMM/A6Bx6HCposrdw1sQDILBQ2jVSjAaCDsVJbuTyS7bmGCGIsmqpjOj9MogOhgwPOGBk1FBh6ODLnX2Pxjbf8fWIhbVdEU2WvUwiHISNZliX0zmSgC4ZIJ1/4HunbZ3b1cZ5W/r2mb3nMkXwMmc/VVbrTJYZLBI7FZXAGip1o9gTWLIL1aYVMikSSeiwnJiQvf8z2NVF1QGt022is4KlYGsJsGuYWi2KlsNlQAVMkyZdjmgw3fB/pc6d7wQd8+BbcVQ6YTLTDdaTVqRGQDtVBhYbmX3VoU77A4VgV6zCmJ7fBfQ6YBf+4IVH7G0zSaWVTvDqWuP2mQIg+YlOBjJyKD/4KMPWzAAXWsIoAGHw+HAbZXIzH/kkUdQsIn8SmFMik8paIEWYIHm0hy3AFNrRdAscIdYoN7BHz/6cbED3wo1dG3d8y6J/MqvhD6jkjUCtTyyXC9TDCMQ5svngZSvUZbObrfbbDZifaKyAcZBRIC/tjHhem+KF9bFzfG8w+FAxBzXoUldwWaz8SVtzN21OC3SAsXFxdOmTevWrZu7uzvy65HIptPpSEOQ0OcOHTogzZm0yF3Izjqdrk2bNi+88AI6r3apllVVVVarVat4fEUqLS3Ny8tbuXLl66+/ns4d8+fPf/LJJ5OTk3kRSZdwnz59cLUAt0d8/fXXlZWV2ridN68WRgv8/ve/R42mtm3blpeXa++gVjFukgX4UYqmCHSTjHzHJksTB7IAnak7X8AJCB+BrmpqgbqZxxzyqLSiKK+99pper6dlfmI3d+jQIS8vj+/6eUU1IqAAwM8AaFyKBIA2d/kLem/216qV0Er/fel+1MxgERQLQDUoDtkpSZJYg0EDVFyEGS9Uhvvv6hl4MSro6LixZUdU53s21RngFQgawewaexMN2Xb+Mny3C/r0PNy59bmIttYI/+MPjDzqsDGwV0WcMSYKUF95WAzeVTnM7FQtymuuhBUfQJ+wPeGBO1KSdvxwnBG2GWtZUpFguRa0VmU0JLmG0HzJAe8th7Cuu6NCKoL8Dg3st2dPKUtVxdUREOaQbzs4raDUlqqyGrbkwYCoPf1DT0YE/3fuXyuqLoOpirkZJKj7SonxHApaAyQkDhP0OvanY+Nqd0+PgqJCjMxD7RSuSadF/MPJsNVqXbZsGepCJicnN+T06SrwQYswhlYIzQKaBTQLaBbQLKBZQLNAC7QAuoxHRAA/TSaT2Ww2mUxFRUVTp07t1KkT+l43Go04IEQBQdQfd3d379Spk4eHR+vWrcl5DoLRxLvBrwaDISAgYMaMGUePHm2BdqwtUt0lK1phop+qqqo2btyYlZWVmZk5a9asjIyM1NTUoUOHDh8+PCIigvcphHA/EcbRkr/mMzIyMjMzc9q0aWm/4njllVemTp26cOHCrKys7OzsykrGVbJYLCjbXWsJ7X9zssDmzZtxocLDw8Pd3X3ZsmX8pu/mVBItr03SAoghEP6F0IG2yNEkn1XLzFTLQ6skp2Sz2ZCwYrfb9+3bN3DgQN63s06nQ+mzp556Cp05N+bRugLQaLiExOE8AL1+02ZF9boniqIC1QyAliU1pmwXmbbEpfPw1ccQFZDTo9OeHkE7XnjSZLfCReT/qhgu4deUp1r9jhrY+MIF6NVnZ0CHs+F+tlCfYw/89ujRg+BQNZ4Re60VsMAEUMxC5RerGDQ7K4PDzD5XrYCIwKxufsWxUcWle8AqMgDaBraaO2JyTnaZVCuuIQJ8/i/o3GVjcIcjEZ1P9e9VsnuXKnTtgh8TDKyAIoHVCiYbiE7Y8z0M6JMXF3EhouP3j4/fze4H4GCC0rUS1ayU6sU8+qwWPWFoIgHQOoPe8zdeP54/Z3ewJOhufIAM2AICxMayWq379u3Lzs6uqqrCNRbS0GloKaYFFF8rgmYBzQKaBTQLaBbQLKBZ4E6wAD8xM5vNRUVFU6ZMCQ4ORn1nVA9EDNoFgEZfguieWhAET09PFy+XCJWGhoa++eabJSUlZEyCYulMywsgtlJWVpaTk/POO+8sWLBgzJgxvBsuxPsInedVGvHkDcSdecz6BiZrNBrd3d39/PySkpLmzJmzbdu2lvcc75ASffjhh8iVMxqNOp1u8eLFPCfuDjGCVsybagFc4CTKs+ZV4qZaW0vcxQL8OMflp+b7FYcZklNasmQJ+UIn1jP6f/78s89RP7CRxXQFoBH3nPu3TEHvpUpw6IVWQtq8vzHesAQVVWZV8tjEdlAqYBWt1dVgr4bDuyEufHuvwOKYLv/85wqoqIJqFYRF6jGiz4ii1pMtCS6cgnGjdwf474zsUtmj04+/7Vt6/HCNq0JyWFgL3yL0XPOJ6hkqSZmxmxULbPgSegYUhLQuuLfXtv27mTBIpQUsiuJgeDIeKu6rfjHZHBKwCBu+hb499wV3ODKwT0VMxJa1a6Daompz1MDjtbmmm6uiI3i2ohxie5SEtDsQFXjogZFHL54Dux1Eh2K1VXKguVyjmk1Yci0knTA0UWfQM/eDep3OoA/pFsr23joZNE5x+UBtVpr9/3qRZZTdwM96IzT7YmsF0CygWUCzgGYBzQKaBTQL3EkWQDjAarXu3r17+vTpnTt3dnNz8/b2JgFB1NmoF4BGWBNxZ+Ta8AB07969U1NTS0pKrkJzQ2ZDyxtVXrhwYdGiRSkpKWgcHv9FghKhwJ6enmhqPM/HvBlhpFfXXUggVvsvBjDnPHqO+TQYDN7e3jExMTt37iSe4530JjXvso4dOxaXQPAVXr16dYvEa5r3Q2r+ucdeZvHixWfPnv3J0RTR3Zp/ybQSaBa4DRaQnNKuXbvi4uLQITltn0IMeuzYsaIoYndst9t56Zur5LV+APrr1Wt1ejdVf0MQWgm/G3ufVQWU7XaQwOEEB1NClsBmBWc1/GOJo3uHlX2Dtz6cdNh6md3LroAdbChQQZRfQlGv5EZVw5Ct8KdxR0L9i6K7no/sUhbTZevJQwx7NTsciD5z+DUBwFcAaFTUYIlLcLAEfjewpEeHHd39crb+FyQ1B2YHiCA7GZ0a4eQroHKlHcxO2FMKPaP/Gx1yMfCu46GB3674CCzMUw5Iospgpuwy1rMMcg1ybGd5hLNn4JGxB4Nb7+nuX9YnLOfSOXYPk81ey5zG0mM5RHZSRt1pFZpWLZKQOIwAaEEQhv52GN2QLMYH6NeWEUAfg4xZrzqiRFHIljpVaBmPTCuFZoEmaAFqQJpg3rQsaRbQLKBZ4A63QGFh4cyZM7t27Uqyzogwurm5eXh4YLghCQ5EHonVi5FDQ0Pnz5+/d+9eHDcixMAjkpJTEkUR5Rpa3qhy8eLFgYGBhDvr9XoPDw8XKBnPEIaLflYQ/rsFMDQtGJC+xzUFEKFGmNLb25tSa926NZbIz8+PdzJ2h79fzaX4U6dOpUfp7e2N/qw0fLC5PL5mkc+PP/4YF9sMBsO0adMAwGq18l1DsyiFlknNArfFAvXOpmfNmoVYs7u7O6qi6fV6Hx8fLy+vTz75RBRF2nDAexq/ev7rAaAB4OLFi0YPd10rhj4LrYTOoeE2B9hEkGSwO6G8iqWpOGBHLtw/+HjvgINhrbc98/Bx+2WQVZxa9VJoufqNLSYLiGCrgLRploiAXZGdzobf/WOnNv/d9B+wVjPHfSpeK8mgIPyqpuYKQOMtqqrBbIODByChT2H3doX3dN2yZiVUqVC4QyUeO5lcs0NWMejLldWgug+U1VyevQRJw/cH+u2LCqyI7lL61us2SfWpyFIm3BdvIyuSw0FNWLWDYc0P/e5MVKcfetx9Ki6iZO9OFk+Ft221ALSkCpBIKuqsemzk8XgRLp4Bvb41AtA6g95gNP41PU0ChclVc/enjNSSuDFDLeHzKoyVlsdVaQkPTCuDZoEmaQEUGKWlLOpBEXdoklnWMqVZQLOAZoGWYAEcGPONLSJKiqL885//TElJ6dixI894bQiI9PX19ff3R6AZd+jjVAfJ0Yiu9u/ff+HChSdPniShNrQgjhjrfqLvQf5887K4w+FAGB2znZ2dPWTIEH7rqwvozH81GAzu7u5ubm6oYYLAPR9BEASCp3U6ncFgMBqNbm5ueBLJ5p6ent7e3oGBgf3u6f/bEUnx6jE4Pn5wfPwg9Rg7duzzzz+fmpo6Y8aMF1988bnnnouPj09ISBg4cGBCQgJS3XHVwSUbBoNBp9MhHIlcacwPzW+xnpCPHD7n6Hly6dKl9DSx06cHTee1QJOyQGVl5cSJE0eMGJGYmIhbtptU9rTMtAALdO7cGVswNzc3o9FI04EWUDStCJoFbrYFEJezWCwmk0mW5d27d/fu3Zs6X+Q+u7m5+fj4JCcnV1VV2WwqaRfgWpf56wegAZT+cX0FvSC4CYJeMHp6V1UzTYxKFXp22OGHozDpib0R7fMj2hyNaXc+Mepo9Tm4dI4BrYz9DFUA5l+wkQiOi/B/qY7+EfuC2vwQFXixd9j+zz4Gpumhos8q8RlRY5VszJKrH4A2meD8eRj/YHH3TvmRHbeu+RQU1RoOFQ+vpVEz8FxBeWYVDzZJcKYcHhy3NzzkSJf2J8MDd82aWlVdA5ur6LSiMqcRUmZ4sKJIMjVkJjM88+T5rn4HI/zPRgcUlGwBkwlLrCpO1xTeDmBVMeha2rUKQCsS2M1MSfvx33+qFzoRAC0IwlP/8zTzWW9h+eBxZwr/glWb1c84Umwoy1f/taGrtPOaBTQL3LEWENWDik/rW9Ru009aQLOAZgHNApoFbogFiJmBPuJkWd61a9fTTz8dGBhIWzUbA0DjJIcgUfyKGGVMTMyKFSsOHDhgsVjwdnyrTrBj3QA/KWqOo0qa3W3atCkhIQExZZoNNjKAyDLhvwaDgWdAe3h4+Pj4DBo0qE+fPvfdd9+cOXPee++9oqKiw4cPV1Wpsz51bmd3iNVWK19h7Ha72WymHCIV3eFw4KPB/hcVfi0Wy65du7Kzs5cvX56amvqXv/ylY8eORqORyLC4sdclY3iyLgDtrh6CIIwfP54UhM1mM//0+Xxq4aZjAf4dpHYD3Vs1nUxqOWnWFuBbRb1eb7fbaS7QrMulZV6zwC22wE++i/Ft4gcMuIkqLS3NbrdbrVZRFIkNQAG+nW8ozw0C0NNnT2V9P+7oMnp9m1XCuM/l8OMxSJ0CfbvldfffOiD0fES7QyG+uUWboaoc7FdGJnaVXlw/YbdGw6ICNn4I3dttiw6qCPGr6BVxYtkyJtthrUWf6wOgazBoVUwDwWhWLrEa/jz+h5iuhb3Cs2a9dLHiHNgtIDH02VqLPqOidLUIl0UwyQCVTrApMGUKBHc8FNnVHtjh+8lTDl2qhGoHSAwyFkERGYytiDWcZs5+siw77ZCZCt0Dj4W2P3ZP5N7VX4Eq2gzVNkav5o5qAJMKQKvnalFodH6Y9uzF8Lv+rhci9K0M+CcIwtkL5y322sWE+jBoLvFmH2xMBW32hdQKoFlAs8AttIDZbD516lReXl5+fv7x48fxzlpTcwufgHYrzQKaBe44CyDm+PXXXz/++ONBQUE8AQ3JrYgtIgzdEAOa0GokzAqCMHDgwNdee23fvn2k42mz2ex2O0FX2LZf5bO5A9Amk+nIkSNDhw5Fk7rMA3mopW7Yx8eHdE4QzEVycURERHJy8vTp0996662ioiLsKK1Wq90qSqK6WRPAph5W0W4V7Ra7zeoUnUTHqVO7CXSmX5jfG6dDYv7aFad8ZTLolGUEsm022+XLl7OystauXTt48ODg4GCc1hIRm1HgVe84dQFoLKlOpxswYADe0WKxuNQByokWaIIWsNvttIBkV48mmEktS83UAnxL6OXlhVpMGgbdTJ+mlu1bbAEcXB0+fDgwMLBmExL3RhkMhsTExIKCAhqS4fuF0s83BICWV/5zuSAIrbzU2+paLfy/5YcPwJxp+3qH/juyU3Z3//xFs+CZh6BnwPf/lw5OK4h2sFjZIMPOcGhH7V/NUIbMV8NhdsLR7ZAQtqtn4KUQv4oAv/2TJ8vnKxD6BQfIDpWkLDPND+nKyIWlosigoEgGIwXLIFVD2tSTPYILozpvn/G/Z0UHczwoOh1OsDrAhvmohaHtTnYHqVpm6PPMWZe6BR4Oans+5K4jvx974qIq2WGVzHbHZQZAy06GPssoZE3ZZwHRAblZEN35QPdO5yO7FGamm212pk9y5agFmlX6c7ValCs/ygqIVlj9BUR3/E9n3w8EoYe+Fdv2pm9liIiOQu4zsgyI9cwHriTU/EMaKtT8n6FWAs0CTcUCn3/2+ejRoz09PYke5e/vP2zYsD179rCeQz2aSl7v1HzQnJMCd6oltHJrFmg5FiguLp4yZYqHh4ebmxuBy4IgeHp68nRmIkFTHJcARnZ3dw8ODn7//ffPnTsHACaTCX3aYKOBZEkXtPEqX5s7AJ2WltauXTtyvYgzQRSv4GaF9QcRfW7btm1sbGxGRsbHH3+8Y8eO8vJyrHmKoqBxaioizVzkGuINA5EdYGVu1dlsq/b0lXpbUVGBX0RRxK24/HzNCRImaXeIVtHqkMkVfE0KklNSFIXJs0qiyVy5a/eOd9/9x+wZM5OGjfD0/I1apN8Igo/65yHo2AmdXtAbmGwIipAYDIalS5dWVlZiinw1uJJLLdTELGDlePSiKGoC0E3s+TT77PASHP7+/tr4v9k/Ua0At9YCzz77rCAIvHMO1PISBGHKlCkXLlxAxWfcfiTLst1ur6qqutaxVkMMaFbWtu3a6Y06JsTRSu9316DooDd6Bq3p2fmzl545ffR7yFoN/UJ3TBj7o+kSVNtAlMDucKo+9hR1oOJUgVeJDWRIOQPAKUO1HU6fgeEJZV07XAi6y9S108n/96L5fAVUimBRGPFYYg4F2Z/M/dWmxiSaneBgQLL6PGZPEiP9C+NjDj418bTZBlYZRLA4ocIJDkSx1aREiTlNZLi4Auznf34B3UN2ht/9Y/TdR//4213O8+C0g6iAU5ZFh42NmvBPrlWgRgxYveOn/4KA4JyIwNP9wg88/0wxAIOzyVMiu8GVyIp6T6YBbXUwhQ7GrJZgRzF0D82KCNs2c2aVIPgJep3BaBQEYfqsmSJSqWvT4KHnK6ne2oqo3U2zgGYBzQI3zwK0hZZuQVSFX4QpkUdz+vTpxx9/nHetTtNxg8Hg6en55ptvUuJa4DZagJ7sNa2T38YMa7fWLHCHW8CqHrxnc/QbZjabN2/e/MgjjyDuTJAojykT4qzX65HdjB5sqH3W6XSkCyEIQkpKyrJly86fP49q/oQn8o+ATl5HgE+nCYapv0Nrnz59OjIykmxlMBhInRm1kt3d3T09Pb28vIg5jl4H0QHX/fffj4gzEpRQSBox3wbLzvtNB7hcaWWzKhukTb8UG/PFp8vLLpSDWdXkwH2clA4+Cya3DZLEHMAzZ/USOJ2qM3g2t6o5I0m1fn3o8ckym3hJskWWLLKTbQB1WiWHVfl2Y9HUl94KCR0rCKGC0L6VuxsrNZsqscOtVZwhhOUAACAASURBVE0IFy1SUlI2btyIyKaiKOh5kuxJ+dQCt90Csizv3bv35ZdfXrJkSV3i/G3PnpaBFmCB7du3h4aGenh4hIWFFRYWIgDdAsqlFUGzwE21gMPhyM3NjY6Oxp1SKPRc0+MKQmho6LZt23jFLer3eVfPjYehGwSgzRbxT39+0ujuqXb1OmOr8Gf++N1zfzi+rxgulMGPR+F3Q76NDvqstLgGcWX6ygqjDeOWK4nhw8g8VpfAa5fWbU42+hg1YvvdHQ51CbK2+c2e3yX/UHaeMZMvqwoe6nhFws86ADSjP8ug2BTRCWB2wGefQmTHonvDT6cMKTl3BixMPsMmwkURLjlr3A+ykRCizwyAlkFWYOVKCO6Q2y3gRGTQgYljy+AywGXmU7EG9pauoL+KzIrBTqiwNwBs3Qpdwr/r3LUsLHDvI2MPmiwMbRbVoqqIuXqtirrX1hJE3yWz7XK13WlxwNFjEBVa2D3kxJDfnvLy/asghOjc1I1mgrD2P+toq1pd6FkDoGtNqv3XLKBZoAVaANHJw4cPf/XVV/v377fZbNi91UWoqfCiKJ46dSoiIqJ169aCILi7u+MGXpyWI0mqbdu2BoMhOzsbaXR0rRa49RaQZdmhHhoAfeuNr91Rs8B1WIDELihQVFQ0fvx4Ly8vbGARQcZZCgLKPO5MYYyAcCGh1agLkZSUtHLlyvPnz1P2HKrHbwQQXWBEAi6vI0DpN8EAFpMA4j179vTt25fnjxNYj5b08sINqgI5JAwLCxs3btx777136tQpMhr6YET0mU42WHycZiB9SJ3NKAAL/3Y6KnhjVPCmNf8G2Q4fvn1szVcnalOoYTzTRJQHoGvc8LC5Iaiu4Bn6XBeAVhRJAYfqPagaFDs4wWlTt8ECnD8HvXrMjY564qPl2c9PnhI3oBeDnlXk2d3I8GgE4n18fDAcHByMwpSYPTJpbW61/7ffAh9++CE+LDc3t0mTJvFwxu3PnJaDlmUB7LN+ud1rWaXWSqNZ4JosIMsyrt3OmzcPV699fX09PDxo+GEwGEaPHl1ZWWm1WolFRBsLEHF2+eSHZw1lpkEAGgB27trr3fou1lXoBUHv9Y9lm62qZ0GbCd5eAH27frMg9RjIjPvMlDfYnyyCoo4z2KfKg1Yp0QyjrjkkJ7z4NAS1PRTU/nz3bidG37/7bAXYVAC3ygoWu8o8VpfQJSa+gbu+rmzqwtGRTYW3//0ldA/cGB1QkBRX+OMpNsSxsiGMU9XDYAi1+md3gkNGQjOwJfjvtkJcTEmfsAt9up0cN3rnhdNqxuyMqaw4azBoxLkldczkYPLOMgOvHXDoe+jXfWu3wOMRXY6kjCy5eJFdW2WTagFopwxOBlVfyS+Wuqb4ldVw6TyMf+B4dOey6K7noyMKW7eZLrTqJhj1Bnc3b9/WVeYaP4ZO9QnXi0HX2FH7p1lAs4BmgZZiAYfDIYrirl27Ro4cyTocvd7T03PSpEm/WL7Dhw937doVZTFxQo5oCLo2wnkOfv4keclv/PzFlLUIN9wCOCLBZF0WyW/4vbQENQtoFrghFsD1v6qqqoKCggULFvTo0YOJ8+p0NDnBBpaIz77cQegzMqDpElSFHj58+Mcff4zYKM5qUBRCckqIw9Ichi8InbyOAJ9OEwwTxP/JJ58EBASQufiODPtHAp27du06ceLEL7/88tChQ8wHPNtmKjskiXzJXFsxadahXlZtg399Ab0iNnTr/O9/fw4n9sP/+3NZZIcV8TFvKEyesEKl39TcAR+HSn9mFCKRsXoYO0dUwC6DU90nivMyvAmC0XgVm2MpdgWqVRiaJSgDmMzw1ITy8MB//f3vpbXC1HD5UtlHH/19SMIgFHjBeohKI2glfStDK3e3Pz/x+OHDh7HqagvP11YHbnLsiIgIpNchYwDvpkGEN9nqd1zypOuiVa077tlrBb5GC4iiuGfPnn79+tGqNu6pwk1XQUFBK1eulGXZZrMhc4iSx+7bBXp2mdxd5QVsAIBWIVPRAcFdQlin3kpo5en+xz89ZrIysPnUD9C/61f3hP7LUgHllTUUYAKg0X+fqqTBfiInfgyZBZibag5pfyyik9Qnqrx/vy3F+5hPwOpagNpazRTBcAkdAWhkI7NRqVpiGdg4xmSGTesgofeOqLsLB8b89+Aepuwhqgi4na3QO+1qNHXEY5dUAFqWGBFatEBs9LaY4CMh7Uri+2wt2Q52O1uRZ8M2FThHEjQPQIsg2lSRDZsFxiWXhfuVRgUcGRK758gR5jIRM85upIDKs2YaZ5RVekh4UnQy14Vhd5eG3nU+rMPxyNBVOv19gtBGEITftGkd2SPaKtrxErtDJJoADQgpZUpWC2gW0CygWaC5WwBn3SUlJQEBATiTxIm3l5fXyy+/XHeTJt+fPfTQQxgZJ+Tt2rVLS0vLUo+xY8ciPUoQBC8vL71eX15ezi/eNne7Ncf8y7K8XT1cGNA8ltQcy6XlWbNAS7XA/v37p06dGhAQgGgyNqpIk9HpdAhGE/rsApUiwZlo0fjrsGHDVq5cefky87tiNptrIEjOfEjabahN4M9fa5i7SVMMYte2bNkyQRB8fX2p/3KxqtFo9PT0fPHFF7dt24YsJL5fQyHE6yxe7VyMCQZKsH8/xERsDg3cOms6lJ+D3917oF+XnGE9t371Hiav+supvRM+CwSg1WkgYzUzlzw25qBedOIsSd1Rqs6Sfg5AKyBLCrD5GjreqbTA4kWmkI45j/8BKs7D6ZNw9AiYKsBhZ251JIfVXFn12muvJSUl/cw4tXqGBqPRw8Nj+PDhJ04QWbs2o9r/22oBXDnAp+bm5oZ5IbjwtmZNu3kLsQDNESjQQgqmFUOzwE2wQHp6uk6nQ0UvXOHGkZsgCGPGjDl58qTdbmeuGpwSP9K4aQxoRVVQBlj2zlu1vXsrnd7j4gUmSPHI6I/C/ZZ+9T5Um9nitgPAJtcwoFX8l/Gga6nQDBrGpW+7BB99ADHhO2K6OCK7mLqHr99ziF1VrS6Ms6V7tgbO2MZsQ5b6h+gzE8BQJKcsoztCazUc2AmDovK6+5XEdt++aR1UmkGUATVARIY+qwA0YyODOsRhoDlbjrfDhPsP9u/2Y++QUz3DV+0qhqrLqhqZCpIT/ZnlQlX6QAY0SnlUWOD34w5GBZ4I8jwY2WnT1iyoVsU3WMpsNKR6S2T/7Sprm2HQCENLDkCttEorrNsAYYG7gluf6epT1afL4cf/tFkQgvTubdHCs+bMRv6CBAo5j+Y3rFGaN6H6aUlqFtAsoFng9lhAFEVZlhMSEojVVdvpCK+//joqNvBAA9HEvvjiC/STQPGzs7NVR7g1Dtbj4uK8vb11Op2Pj4/RaCwpKaFr6y0qCo/iXGjFihXJycmDBg3auHEjAiX1XqKdbKQFZFkWRXHUqFEIXfXo0ePo0aN4rclk4p8vH25k4lo0zQKaBa7DAoqiiOpB8wr0LWO328+ePbt06dKoqChqXSlAcDMF8CfciYIvOKkSo1JHUFDQjBkzNm7c2EhEABuB6yhRc7/k/fffR+jZaDSiJdu0YSQVXJoNCwubNWtWaWkpzf1wu+TNKPX3O6B35NaOd2188s9QfgEeuf9ij4CSfl1ySgvAdAFvaCOCEX5HqhC627FLcOki7C6E+xK+j4/518HSK9AzzmVQ7JBdyDnOcQCYFKXSCd9mQc+e3/btU3hoH2ROh14ha//3+W1W1Ve8urv1SonLysrefffdkBCVLKXXuXt6MOBedavzm9Y+gl735yce/6HspFOWkV9/5co7O4RvoqIo+Mrz1DbkjDscjmvSx8CBE59OvQbW61vRn9HD3WK3iaLYmN1pyGcngW8cy1HDhQGr1drIFqbevGknW4wFcMBpVg8slFYxWszD1Qpy3RZAcTO6vKSkJCIiAtFn2nHl5eVlMBgCAwMXLFiArTrpYdYdmPHztYbCdDuXQAMMaDWWxebcf2gvG/oYWhndffQGr/ffXQ0OyJienza1WK5mK+ROxiGW7eq+KVGRRUVGIQ4CoE12udrBktuzD3pGbQ1sfyC4Y1lwcMFnq9hwpEIEESTmKZkNSRyMvsw+meNAxoSuAXIZlisDw3wddig7CP1D83oH7u4ZmP/NZ1BpqtnhZZdZAAFoUalV8VAYNMz8BJpg1vMXI+/Ojwo+2De6aOsWUBREn52IbjtlvK0KgxMArTBxapME4yeURobv6uJ3NLj1tuyvAWzIfa5WnWyo6HMN2O1Qce8rIhyKxPJss8H2HRAdXdDRe19w61OhbffMflF8970deg+mXMaGSjrh0NEj+Gwckoq2X1HTrnGEqAHQaB/tU7OAZoGWZAHc2kOdH8EcgiB8/tnn6GbQpWPD4kdFReEUHZHr119/HScnZJx3330XU3Nzc9Pr9aWlpfXuxmXbbpxs8w26fiosLOzfvz9dOH78eEpQC1y3BSSnNHv2bKPRiLu6BEEIDg7ev38/69x/fvDP+rpvp12oWUCzwHVYoLS09LnnnuvTpw/q6hKOzDfLhDtTAH/lPeBhm+zn5/fCCy/s3bv3p9cfdZZw/vOLKNV15LwFXPLBBx9Qv4N8c+oWe/Xq9eGHH9ICKnqcv+FFxlnGxUo4cxbGjjwReveeUSNMO4rht4nHuwVtDOu4essGsFfV8mu42yPhhgBo/GXTNxAfvSEutLBvt88qLwO6ycFboDgjXkUANDrUuWiFo+dg4L07AgKKXl0MycNOxnQuie2enbseFKuq68HdF4OIk27YsOGPEx9lW3ZVd4VoSS9vb0EQ2rZrt2bdWkVRGgN01km+5Z9AGRy+nBUVFRaLxW63FxcXf/vttzt27Mhp4Ni2bRvuObPZbBUVFV988cWcOXPmzp2bWvf4a3rqX9P1+lY6Q83fXe390uZmLFiwYP78+Zncwd+qpKQEM4YQMzISKKv1oor1nqRLtECLt4Asy++9995jjz2WlJSUlZWFIBp+tviyawXULHAVCyDnANvSOXPmIGmA4ZDqgUvdnp6ew4cPLyoqstvtvAcmmprx6dPJqwT4+Hy4IQC6ZmBgdVTfM+AeQa8zergLghAbN+zSBXBY2fhDllFkmW2YYjRhhUmPMWfGKgztVEnQoorTXq6GsjPw28S93YKPxURc7Bye98m/me6zA6DSZmN3QoeFjEjsqEGOUQuDA6Ax05Wn4L5Bp/p1+iHMN+frlVBViaCzwkjWMuNBMwxakZ1yDXzLMqaOdNZ8Bvd02RHmVxgW+eX2/VDJPC2royhJvRC9ZKgYNMpXIwnaKcH5SzBzzpnAu7d0DTwSEpD35ScstzbmBlqRwIwuniVZxaCZCoeEomfIg1a5eGx531IN9/TZHhlyLtS/LMSvYEF6lcUC9z34mCAIRg/mUCMwOAgLiPJtqL+B9GcXLQ6Mpn1qFtAsoFmgxVjA4XC0b9+exzhQH9BqtSJBj+/bJKdkMplWr17trh7YdyYkJJA1qMvcu5ctoOKh1+vPnj1bLwCNbDK26VgUX331VUyQPGu9/fbblLIWuG4LIACNCwaenp5o3pEjR2KCPAR93bfQLtQsoFngmixATeWpU6dee+213r17U2tZ23DW859wZwrQNAbVXf39/SdOnJibm0v8RGp4HQ6H2aw6k7mmjN4BkUtKStq1a0fbgEjXeNSoUbm5uQ0ZgCemYJjjEyO7mJPVaCgV9TxeXmljm0r/8PC+6O474uMu7CyB5JHnI0KLY/ts/q4ILGa4fFmyVNskUUEaDk6kKBssoE6D/vUR9A7I79d5y+9/t/7MKXYDldhzZVJ3hQHNzjHOEvsnQ0U1PPk/l7p0PRweVhnd/Ux0WMHvkr49cwKsTHsD2H35A728q303Gy04HcfLTs5bMJ9cu7Pqq2Mf7p4eycnJ5eXlVOf5ZO7AMKG0yG7DrWOlpaXLli174okn4uPjPTw8+PUnRCjqfmJFdXNzU5eWW7m5tfLwdPP2rvGQ+fPmg7mTEvQG9teqldCqlc6gd/escXVFevFU839+rdC7d++RI0fGxsampKTMmjUrIyMjJycnLy8Pnx2uzbD5snpg6ahaXv350vDy6tG0X5uLBdatW+fu7o6rd35+fvjKXxOdv7mUVMunZoFrtYAsy/v370dnHgyENBrxZXFzc2vdurUgCLNnz8bugFK+xQxoJ4BNlCudivj6W2/qjWoHrn588MGXsgx2VafLyeS6GH9ZYp73ag7VE58KQ4NiA7AAHD0Dvxt1oGtQaWhgWUyPA4v/AedFBK+ZOIbq4E9Fox2k3FyrysHYyzgmYXYwl8Njoy9Gttkb1/nI/GkqACwyr4MiSAwEV0HkWgBaBdBVcNlmZ44Ho4L+0zdgT0SnDR9/4agAxmt2KiJbkXfWyHcw4rYiM/0NJzBCnApnW0X45CMIDd4U3PFQTPjR1P/P3pcARlElf/fMZGaSmHAYjhAIIYSEBMIlyiELiosigngrfzz4UHEXRJFlFUERVFDRRREBVwRXZVFEEJEVOeSUU45wHwFiyEHIPXffXd/Wq5lHOxwioAs4zTB5M9P9+r3q7veqfu9XVaP8sg/pz5LbDxgCOsACR4cY0KResZ5Ru/0M5q4shz63LEqptzWlTn6rtL3z5yAh2itBlDNKiMKJOC4ubviIv9GVJhCfQ8+REBz8AYgUIhKISOAKlsDgwYPD7I2777qbE764hcCtpq5duxJSTDbSN998Q8IxE2Sqqqpi2Ga1WmNjY80/hUmSgm+MHz+enI94mMJ77rmHQydhh1z0j7xrF73mS6FC8ogcNGiQw+Gg0LFkHgwZMoRisIQ0iODi96XQ5kgbIhK4siXg8Xg+/vjjG264gaLkh43AZ/rIcWdeoD3r1Knz0EMPzZkzhyBmojxzDJokyUfyK1uw59G7bt26hUFvffv2Xbly5anzgq6rmiajayTLrMNGTAOChoiBJXxRCvcQQHvaBoWwXJWBvwqAWwO3AkOHlqc0XNO0cc7ir6Fzh/xmTVe1b7Pi0AEIKBBQZTSd0C7DjWXPIWuOIcsskqIegK8+hg5Nl7eos/Hemw66KnBPSceGkWVE72YA2lB8iBwaIMvwj4mQlb63acrxrOblyQ3XPDmkMCBiCp8AWnoG6AZ+kBT0wGVOuGCAFJCpPZoGVRWwc7t47Jjx5lvTY+PinDEOSxS7PZkB26lTpw0bNkQwaACgyBuiKG7dunXUqFE9evQgpwdSqwiY4AR8QRAcZ9j4KOGIsmH8UFsQ8UecmWJtWKIcAr6iLEh8JugZ3202wWaxRtkcDofT6SQI22az4SKWhVWCl8waG1vTZnPwszidzv9mB4mOjjY/LLfeemvXrl1fGT/+uVHPH8k7ismimDVPdxrdG2d5jwxKZxHO5fhT79696YahVY0VK1b8Ri4jl6NwIm3+g0tg6tSpRBSgUZSvedeoUSMzM3P58uXc7qY1G3rng2SYQmL+/kzlMwlc+LlKEKYeIBxaUJBft36dIAYtCIlJjRASVjGsBmULxNZghkEKnYEArqJpMqgqc5YKANz90PHkRoeS6x9LT909ZqxR6oFSH+YMxMgbFC1MDQHQmDKZvST2roKEiK/PjYAxPPlQYZf0Qy3rbhr3jBcUzG4hahhgmYX7UPC0+NI0jK6hYEpCtua+ewdkpaxqkZzTNm3ZZx8hbIynZt0O0pxZDTJIKmDkUBKuR4YyGf45G5okbW3eqCy1wd67bz+M0UaYzofgNyua5RX0I2MqnW6ggoSqnwHPPlmW3XhTZoMDGUnrF85FNrSmwkcfzcOlYLZZLJb169dTrq3TpmY608WLfB+RQEQCEQlcGRJYsGCBIOBqnNPppCCYq1atIhuJGMp8bpMkKTc31+l0kse33W7Pzs4OEwKfIwkicTqdAwYMIKDTvKfZNe+pp56y2Ww8C7DFYunbt6955wspmz1/NVWTJInP8QS88t5R4ULO9RsdS8Eiw+Ck8zjXY489Rvg+pSaLjY2dO3cuSSNCjTwPeUYOiUjgHCUQCAREUVQUxeVyzZw5c/DgwZx1SB4JYYAyB30sFktMTIwZjeKU55o1azZq1GjChAlbt27lqNY5tieyG5fAJ598Qnagw+Gw2+0NGzacNm3aqYOtQSlqMOWNRLH5KLu7jun7vCpLqRPKQ8O4QAyGPj0MR9+iwaL6VU+1KioAPoAvFkGDBmuSGxx6dSzceH1Fm+aHul63adNmwPCCQVdXFq7wpNGmk9HmQwYzqF74fgG0a7imXdLGP7ddfWw/82tFgwvtLfKX5XYT774aYIEaZVj9HWSnrk9v8FNWan5mxuq1m+G4C/fCUxiA04RuGLIEIr00tPNkcFUip15VwPDBgDu2tEmZ9flMzGVYXHri6RFPRcUgMMq3evXqrV27VlM186TMW3JFFjRV4/RPijbm9/u//PLLxx577FTPMxoEuLh4gb43jxh80LAKgo0ZtEGblhGd6cBomzPWflXtuKvpo5UB0YI9SnBECfYoa0wMrz9UAdbBkGxBsFoFS7RVwCAqUU6rgN7C57Q1SG3c+cZu4ye+vmzF8oCMUABpXEQmoJBrlFDrtNrXJauDXZE352/RKQKgnU4n5WvdvHkzABDGwjXt3+K8kTojErg0JUAW1r59+9q0aSMIQizbaMWR1vwEQRg+fHh1dfXv2f6zANAEteq6rr7w0gvOmJMrkB99MksDTVJEnaUHZOizBnoAIzhrCEQrmiEx9ywJYPBwsX7DnfUSjjZtcujBh/PLXAQMI/qM+hMF31CYLsPRZxlZxrSfx+cntWb0sPLMequa1Vz+YO/9J/JB9gelxCpA0JsB0EE6NmuSD1Rwl0G/Ow80S9p4bda2ef8GOcBIAiHQnbjbLM2gJiOdOYDJD3UQFQSw1+RAg7Ql6Snlja7Ov/mmA1XVmNM5uIVYBVyRQs2Lr++zCNSqAoEAfDIT0uqu6NKyqH3zjZvXYgP8fqioUNIzsu1RMYJgjY6OTktLo2r5yBhWCJ018jcigYgEIhK4AiVAeHFCQgJ3+Xzttdf8fr+ZqcRHRQCYNo1nx0VizmuvvRbGU+aAJnmMWq3WGTNmUA1cfOaQcIMHDyboOY6FjBQEoUuXLr/RZMyrPTXwormPvJ2XQoHLSlO1Q4cOud0Yhcp8dc6xkQSpDBgwgAAsIjE1bNiwvLycLIRzrCeyW0QCEQmcXQLm4U6SJI/HAwDvvffenXfeyTEmM5zE0WcztZBWiU6L+nTs2PHDDz/cvXu3pmrkQYKslFPypJ+9kX/wX2kILSgoiImJiYuLI0Svdu3aFFiAL6NyKSGIi9/6MD0NszjIBvGhYycSgpGSjKEAMftMKCk60maCjOWTFRnIjmHfKrrIcu/gbztzIavVmnp19zzzJNxwvadls2233rD/0B5En5F4xMjHmooANEvSDjIoIkgyIAYtMoz5q9nQLnlt6wZb/txu68Gt4KtGm4s1QDsVgD7ZKh0UN7iL4dqMuen117XP2HfHbYeOFYCf9dMPWkCVZVVBgo6mIrtJRTuT0OegOy3608LYp71tGy5vl7Jg90ZsJCNoSz9sWdW2fVuLzSpYkVIbHR0dGxu7f//+U8XLxXMlFbhqRJj73r17Bw4cmJycfOpDTQ87HxzCdjgXAJoOsToEi1MQiHgerAUxaYvFZnfGCE5nEIB2OpAEzbJMITCN3OkgdG2zIPiMn2zRgrWGIJw2oEdYA00fGRAeV7smMqit1vbt20+ZMoUH6+DXXZZlWpDjepe5cCXdA3+0vvTo0cNut0dHB6O7rFu3juamyPX9o90Jkf7S+O/xeD744AMaIrmRyykFKSkp//nPfwDgd16UPTsAHcSgj+YfIbauzYGzRUZWhqSIii4H9QqmmYDhAd0HmmGw4BUuP5RUwpcLICN9b9MmRZnND9305y1F5eBWwcuYyyfRZ1oTD8OgJYSkDQ2qqhFMnv0RdM7a3T5l9/23/ljKoomVlaMBzFjY6IWF+g3LN4j8Z6oQoKIYRv7F07LRj9lpS5d8i8oZ25/c04LQN+3LQjn7VPBpoGEsaRUOHILs1hsbJx9uWD83K2N9zj7wsLAhWAUHmkNANql3QQyaKXWSCooMW9ZAZtK3zRLWZzf+ftdWjFhN4dJmf/o5uRQR5DFjxoyweCthjD88LLJFJBCRQEQCV6gEXC6XoihjxoypU6fOo48+umHDhlM7ynVHXdd79OhB2RLoPS8vjxBnfhQZ9nl5eYRo16tX7yzsvAcffJAmZqJL2O327t27E8bKK7zAAtk8hmEUFBRsY9uxY8fMBDfeOypc4Ol+i8M1VcvLy3vkkUcoqsmOHTvOg7BM9CsA6Nu3r8PhiImJoUnwoYce4mbhb9H4SJ0RCfyRJbBo0aLHHnssLi6Omxw04v0iAE27UeJQoujWr19/+PDh+fn5RB4kw55Wj4hi9keW86/tO0nsmWeeITkT9H/gwAFd1/1+/ylDom5AgKHPHsz7zngwZnBZ9sPBXQyeRZdRTWW48Unz5GTjDEbwCTDij+GXNYkFS9y6D1pfsy49Pa/b9dC6eVWTeru7d8rZtxsPYzENQJJ1SdYJgCYoXAOfCh4FI2egD+n4l30ZSRtbJO3qds3afdvxQOMk+nx6ABrTtwPGd9a9cH+3vGbxG9s0+a7/PWuPl4MLGU3s55MtZ/aXoYMWCALQHDvX4KP3oG2jVZ0zflg8D3fzB1AIyIwGn6KLTw0bllAP80yQSlC/fn3uX2Wu/sorBwIBj8ej6/qCBQu6du1KrmPkgs0pzAQ9ExWOvqQb0vx+FgAad7MINrsQE2+NjbM6nIzDHCUIDrsQc5UQfZVgcwoYRoOFQbFYOANasFqjojkJmiBnBI/tnAQdZRUS6gqOeIu9noBU6J+R2c3No7IFcW88y1XOaHYyIQqRbKQpWCwWh8MxaNCgb775hoPyoijy2F9h/sdX3p3wx+nRvHnzaKazWq3t2rWjjoflM//j9x+bMgAAIABJREFUSCPS0z+yBPx+f0FBQbdu3Wju4wE3+OB57733EimK04x+N3H9IgBNGDQ8MvBhXEu0WwSrYHPYxowbw5SSoG5j6DL6PiGDGKMnawDFZbBmDaQ1WdUiraR967IuXdaXlONyNYtLwXpHmkUIAMZFbIwBTZoOK6gMU9Zg3hxok7GyVeMd3a/d9tPhoGQMDIJB6o2og4puaJQJUMPAHwY705TXizLrL81MXDtuVKnPj9oaaslMoTnl5MQXwAhjsgJHj8L99+xPb3IwNTnv2vZ7vlsJLnTnQicyds4Q8Mw+kQiY8xlqacjIVkFmgac7Za25tumWe2/OPbCNqU0AHjc6mtVJqBecLK2CxWI5ceIEd49ibWQnMQES/MtIISKBiAQiErjyJEDJds3DYBigbF6T83q9HEaJiYnJzMw8lYpLjLydO3cSWjp58mSCSMyYLx3F0WcKTCwIwg033EDQ6kWcj+fMmXP//ffXqVPH4XBYrVZ6FwShc+fOEydOPHbsmMfjMQ353NfmErrUL7/8MldZSErm63WODZVluby83DAMj8fTqlUr4kE7nc74+PhZs2aRNXiOVUV2i0ggIoGzSMAwjOXLl/fv379evXpOp5PATR7jnkAZApsIhj4tA5oohIIgtGnTZuLEiYWFhYZh0IMvSVIggDo/DaqBQOAiDphn6dcV9pMoit27dyez0Ol0UjipU2c01msCoAMYfwNNGdzQADHgRAlUFsNDfXdkN5nqqgYZVMoGz9Hnk1xjOgwPl9jL8MgIIecVQd+7cpKT9qQ2LEtNOtK43sY+PXLzc8HnZ6dAbg4oiqEoSEHGzD0YhhC52BpG/0AEevRzFdnp6xvX/bFbh/2HD4LLhcygskqFtUFh9ll4CI5g83TQ/fDsoMJrk3a3qr9l0ssehXWu1FdGHQxmtmdZ7vFmw9NLaFMh7I39kQLw1Ry4qf2GLi3XfzgJfG50Y/WJ2HK/6gloXpYfHt54cyKFNo6NjY2Pj7/33ntJrwiK5Ar94/V6P/7442bNmsX8LN5FcDKnDFR2u537ip03AC1YhD69ezzS/77n/jbsldcmjJo2edzns6d9v/yLzVu+3bjl+w1bvlj4zZvvvstiQNsEBwaFbt4y+9pOnWvUqh3iPgcZ0EhVtwqCUxCuctz/5htJvfp27v1/sXENfxGA5hh2tM3OAoNY8BuGQdtsNnrKrFZrhw4dJkyYcOTIEbzBTJtZBzOXr9Bb44rtViAQWLZs2fjx42fOnEmuPzRJRa7pFXvJ/9gdoxv7tDIYN24cjfxWqzU+Pp4CV1I2+Fq1an399denPer3+fIsAPTPGnDkyBHumBMdHW21WgsLC8lF2jAMltja7/H5A6pIqsHeg9Aq68e0pJ+ymhRc03bbnoNQicvRuNTN4oyFlrZJj+HvuAOLnMyW/lUNFi2CRlevyUo+cH37VUcO44K+qKCLma6iAoQ0alRydES9mYYVkFBz0WX4ZBp0ar45u9G3778Jqh8PYaE2ULExY9BBPSrU1/JKqHLDA/cebpG6K6X+7tTGq+bMhyJ38BCdIPRgG0PHsL+qzoKKAAQk8Ljg6znQMWPrNSlb7r9l74mf8BvcVJB8MGf2Yra+K1hYNuDHHhv4s4oiHyISiEjg4klA13WCMinuW4SidfFEe3FqoomTmwBmBfEU/lfwjOvXrzcjoX/7G2ZwDduZ1E1RFP/xj3/MmzeP7HlRFGW28ab36tWLbBLudd6uXTtzG/iev7ZAWu+2bdvuvutuc2t5mc+ngiDUrFmzV69eq1atImSH4zu/9qQXZX9N1cLQ/6lTp5J1Su+8C3v37v21ZzTXvG7dOqfTScahw+FISUkpK0PEIbJFJBCRwC9KgJP4ToV958+f/8gjj/DnlNxEOL5s/p7TYYgeSD9xMDQ+Pj4rK+uFF16orq7m7uo0tFLzwkbv/3qxRFiEv3jhwnaQJKlPnz40Adlstq5du566VnryEIr+F1ygDP6RJKgqgj5dtmTX3XFdsxWiH2TwI7cnlKKQcN6TlYRKOhgBgCoFPCo89ZSUmnQoOaEsrUFV88b7bu+Z4/eCJDFri6UzNBjuTHnaEX0O5RD0ejEi4tS3tLZph5rVz+3WZceWbXh6OWhq6TrabRJ7DwLQxDuSNfAFQFGg8gT0u/VY2+Qdzeos+GIWKFIwUiK3CxHgNnTK0B6MwoE2Ges+e3v3TbFF8prmDb+f9o5Schy755XQVJR1DBsis300AwKydM/999lNW3V1NWkOZ0D8Q5K6DP9Sv7744ov4+HgifZsf/Li4OHrM+Vq+1Wq12+2UCZCrQ7T+RNAtYRZ16tTp3r17t27dxowZM3bs2FWrVm3YsIG45KoYQDmJxDuHwwCLVdc7B3Ys81aWMMtfBPjXZ3OxGVa7EBUtCMKLL42TVSST+QLS2h/WB1/r16zb+P2iTStn5x6c7fV+oMqv5h5cX11VqWsywIqVK9euXTtu3Lhhw4Z16dKFPKgcUXan3RHrjI6JiYlyBuOF2pyO6Fj8SN0hljcttpEoUlJSBgwYsG/fPkqXalYjXS6XWQ80ly/De+EP12RuDnAvB/7NH04WkQ7/ASTAeQDUVyJg7d+/v1evXlzx46M6YdA333zzkSNHaOL7X41v5wRAU/z+v/71r+ZpbODAIHIqyzKmEwSc79n8A+Ue6NN3e+MGu9Ia5bfM3LT/AGbHYJvG0GcXvhNb2KxisPjRsiIqmiFr4PXDxvXQqf2a1Pr70pJ+XLkafb00gEpvGULOLMWhoQJGbSbatQZ+Ua6oUFQFvlkAWSnrWqVueetlyRDBkBGqZkv42s9PeFKPUn2oz3jd8NyzJakNf0xtcDA9Zd0HHyL6LLIMGArWEWDTKOstdYi5mCms/35ZCchQWQXffgVtU7ZnJmy788adKkHPtLMO7kpISW4dE3OVjYXHckbbVq5cQQh+qL7I34gEIhK4aBLwer0LFy7s27cvcWDPEofhop0yUtGvkUAYhGGeCM9UDqPirl+//tQTGoZBWDOBzrSDoigcrDEM4+9//zs3ugRBqFWrVosWLfbt22c+76k1/+I3mqopirJ9+/Z+/fqRnUPzPZXN2oDFYuHMRFIO7r7r7qNHj5LDrBno+cWTXsQdiNhIUaGWLVvWoUMHCqXHMWhaga5du/bq1asv5LyKoowbN44SYsTFxdWoUePxxx8/D1b1hbQhcmxEApejBGg9lVpOYx0A7N69e9CgQbVr1+aWBo05ZwGg+Q6UFxTTf7GorN27d3/77bcLCgokSeJIt3lEChu3+QpiBIA+j9vpgQce4BciOTn5jDXw6H8/M0GgvASGPlzUqenO1onbhz9aImO0QB/hw6EUhWhvhW06ptoxPAYaQa+8UZXd/KfmjdS0et4GNXJu7ra1qABDOyu639BF0GTcifxTWfIeyt9uqJjVRnTDrCmQlbS4eb297TP27dkNfoWMJl3BwIciQ58JgNbUUIhEFdDEA0B2Tv+7trdNybn52vz/fAk+D1J5gog5a3SQJc0YRyy2tYFMaEPUVE1VwF0Fzw8vzk5d0bZZzvAhStFx8IiIPmNEbBYNkgPQ5KU6/Z/vm/Bn+4oVK8ywY5iILqOPZgCCns1ly5Zde+21DoeDUrHRQi/dZrxM6C2xwvmXTqezbt26WVlZnTp1Gjx48Pjx4+fNm7dhwwa+PMyVKJIPQXu6TmmY8D7RNagE+Bakd6uO/fN4/j6Ao4pBaZse+H8DBUuUNSrawlIKrl699lQhywBugNVi9TvHj48uLBpXXj7L5zoKhh9U0dD8kkhhf2gx2+Vybd6w8fPZ/37+uZHXdepoj4sRrnIgddrOglCzMBxcdeERh8xQhiAIvXv3Pnr0qHnhh+TJh7UL1AlP7WPkm99aAubZ6rc+V6T+iAQuNQlMmjSJVEGzyUkKnt1unz17Nrmv0ej9vxrfzgmA1nVdkqT8/Pz4+Hiu2v53rX7lGrQ/VV0PqLJPk/3EQdZg4GNF9equyc4qSG70/Qo2v3hlEFVSmjQAF4AnqNDQUjhfTg/pVbIM2zZBp9Y5aYlbM1LXLFiIi91lIga3cEnFKoi6riL6jCoRRp3WGLqMjVHgi39Bi6bLWl+z7pmRxz1+jMWM59IxfTRpUFyhoQIuv7KWK+UwYzI0T8lpWD83I23Xk08eVVk2RJYQ0VBxVf40ADRjNoNXQUczWYPRz55oWndp+9RDd3XP9ZSD5MesjKqk+z04/44d87rFYnNECzGY11fo+qcbyM6PrM5dak9vpD1XhgQCgUBGRgZZ1127dv3jZJ65jC6fWdc3T4RnKt9zzz1kR5E7OQ9Cau6yrutut9tMa6LaOJiyZcsWYgDVrFmTqD1paWl79uwxV3IeZeYM5B09enRcXJzT6TQ7vVKIDwqzSDoBBx1ILXA4HGQQvvXWWwBQVVVlGEaYsXceTfpVh5BRJ4piYWHhgAEDeAu5Cccj6914442/quZTdyYLIT09ncfljImJIUTg1J0j30QkEJHAqRJQFGXLli1PPvlkUlISPa2Er/EnlwphRgj/NTo6mlR6gp/uuOOO999/nzzT6Vw0IJhHIfNwzQEac8E8bp/a4Mg3p0pg+vTpPO6BzWabMWMGn6fCYZQgNHuyDlWGEYPzWjVY2zrx+y8+QltGRUyZ5cUJBQs85SC0eBQAL6hlEixaBo0br2vWyNWsgZyVVNzzT7uOH0eDS9V1w/BicEVdCkLCLCLjyeTtKv7y4nC5WZ01LZO23NJ5/cFdyGjGFDiIQyqM9czfCYPGmsh0k1WMlXHP7ftapK5IbzR39iyoqMR+BbFyzvVmViEjLKERx+w4zS1WycwL9uVnAy0b7ujU8tjtPXN8fjyvR4aALmFgRsabxmgkzPlWB5AU+W9/H3FFAtB0Q5D3kmEYvXr14s84sZgJieb2O6ocdrtgQU/ctm1b9+zZc+jQoZ988smGDRsCgQCyypioFUUxOy3RWThpjuJXKIoiirgewG/KUoCNhjSpunBiZdFqFQoBihmm7AXocfsdFkeMRbA7bDG1467+ftn3AT8uF6jsgtF7OcBiDd70+p6vqny5umpGadkeAJ+hgOzTNFkH8Ekysb74Gangk8TigGvMzCl9Rg0ROjYTaghCkAwdFAY+ZTarNQpjcdhsNvPQJwhCt27dFixYQAsSkiRFxrQw8V4uH2kCotbypCOXS+Mj7YxI4EIk4Ha7N2/efNNNN9WsiSlYw8gHFoslIyPjwIEDNHSTdvE/jI1+TgC0pmrkyPDwww9HR0eTuS4IQnrzjGoPJgMsdVVRQDJPAEaNLmmRnpNUf1dq2pp3pmNwsZMbqRQE49KKOtMhUONgP+kG+GTwy7BnB9zSZUfjmj9mJu8Y86JHNKA0AB4DPblUqFLBq+uyoaksGhmGg8bEyBKiz98sgOwmqxvXWzpo6JEyXChlG8vZTIv2/Fzkv4W6FAaBQnVs43fQpM6aJvWOpqXsfnxQpRiM2gEiaAooTKei6B2haqluxgzwIMIOI5/bfm3mpk6ZR9tnrN2xHirKcY+AV6YDjuQestkcmOlXEJws78LS776XJOV3zjv5s9ZHPkQkcKVLoEOHDkR8iI2NjYuLmzp1auSJu6SueRiiYcYvzGXOrWvWrBnNrE6ns3PnzoFAwO12h02i5joVtlFV3LAn0hk5nBIDaOHChQBA2RjOWz6LFi1q2LAhNY+WPQiG5kbvqQA0hYTmCbsJCXr00UdJRTjvlpz3gWVlZaNGjSJQmNIlU8IikhIB0NHR0YsXLz7vU9CBFMJr1qxZXFxWq/Xmm2++wGojh0ck8EeQwPbt20eMGEHrN/yp5BRm/kxR4UwAND3mvXr1+uCDD8rLUWE1Q07knMfxJvOgakZnwsrmQfuPcCEusI+02peSkmK322nwj46OXrBgAU1VZlwPTxTEktFkkSQoK4HhQ3KbN5zbtvHiT98DH3O4JKMqyIAOHRFEdbEK4vtgYAqXBt9vhKzsjY0bFjdpUN20Qf4df84vziPbCHRDBE0EPXASgGbcZJnxcgI6BALw7kRokbKlTZPd6YkLd21FK0xWocqNkRh19BmllxZCojFQIgOgESkuL4P77trZvMmWpKu/GftCochoy4zoQ/Ygc3Rl0T+oQQgoI5qMcRiQuaTBW68YbVO2p199pHOL3AP7kGvtYpWgo5tWJWNgapW9y8hXAth/8ECDRg35XGy326+kEBx0q3zxxRd16tShuF7mQSA6OrpGXLyT2Z9ZWVlDn37qnzM/XLlmtSQFVPmkqQy6hnmcTrfROKCpGs/PrDPQmd+ixPHyAuwG+NzvffHY0RmaugtgdbXy3aHDe8pKK3Xty8XfUquujq3dvuV1hoLWNW3oycFw6sMArx6vGlp4YkRRyZTyyv3slhXdFRjqBSCg4BKLyxfiQePtgOmZDB2qAY4BbARtVuGBj4t3LyraM2vB3Mcff7xRo0Y1atQIRrq3WSkVolk4FuaSTLTozMzMOXPmcICGBrfImHa6O+KS/k5TtcLCwo0bN/JWRnh+XBSRwpUqgZkzZ9ati7l2+WbW/SZMmEBkAlmWqUCj9/9qfAsDoE9/UQwdFEWTZXXv3v2CIERHx9qjnPYopyAIo154kZQiWv2c/wVkNF7XoPaOllk735wmFblwETyI+VKBvxP3mTjJAIrmocDOogFFx+Hu2/KyG+9u0XDrK6MwlYRbCsbBYBG9vBpLwWGATwevpsmqivqJqwpefNbfosna9EY/dO+6we9HrBqjRWN2QgYzm6NvYAgPnGVRjdPw8Lw8aNdqXau0n5o1zLnnzh1VLvCK+H0oOaLEAkAz+YRo2qisA4gavvsC0LvntsyUjVkN97ZOWf3FHEVmmlDAj2kXMck0QOuW2WZySq9evU4v7si3EQlEJHDxJDB69Gg2amHIOdr69OlTVFTE1REOSvLCxTv5edbEY1WbPaDPs67L5DACO8xYhnlS1HWdro7H4zEnznrmmWeof6cC0PxwXid9o+v6ihUr4tjGEw9OnDiRT8znKDAeOonzrOlO466stFJLLJt+/fq9/fbbq1atWrlyZW5u7qxZs1q2bEn0w/79+9NtyVd2Cep94IEHzrElF7gbxQzxsG3atGlECSd6OHfRpU7xrgmCUFJScoHnJRsPAJo1a+ZwOChQidPp/Pyzz7mJe+GniNQQkcDlJQEO6FCzeXxSGgCLioqmTJmSmZlZo0YNGihC01r4X0KleWwNskP4IxwbG9u3b98vv/xS13WKe8MHTD4zmuXGB0/zbr9YNtcQKZ9JArquT5o0ia4fh6Fnz55Nzj3By6EbBvJsdEVUFM1nAFSWwOjh1ZnJ3zZt8PGiLxVvNeK2AUkj7irxlDkGzMwdsnhEAD+6g6pQUQqtW29Nb1pVv055coNDvW897HeDJAbtJpZQPhQOgxhCzCCSkDoNJ6rg9QnQtllOcs3lfW76IS8XQ2ogrYhBvdTTkPHHA4GA1y9WexRJg8IiuKvnwezUg60yjjzxmEcMxX0OYp8YbIQAaJUVGCSNwRQVH1qEaJfNng0ZiT9kJ/3UNnnfV58EResKINDskXyKLtIxOu6LLrKr165p2bKlIAgJCQk0uw0ZMoQULbqNz3R1LtnvdV2XZZmGBYltI0eOtFgs8fHxNpuNGHD8eY+Pj7+77x2LZs89vH23rmoYU5tsYDRzDSYlFUNbYopJum5n6zfek5j4SMOXrrGUmJhoSQY4CjBH014uKp/lg28A3tbUN8uKv87P23WipEJDP+gVK9e+9MLLU958t6LIpSrIGwvGC2d/dwG8V+wZU+J+udT9uVs5gO7SwG5FP2iybqDBLrHgKmyhxcB4H5iUEtwa5AFsAXizUpxU5fni+E/VzEIHgIqKipycnLfeeuvaa68NjpJRDsERjUh0lIDRqK2xAoPmOUM8Kytr/fr1NBTT+6VjHZztwkR+C0mAO0qmpKS43e4I6ygkmMjfK0QCPMEV+d0WFxd36tSJZ422WCzcv81ms2VmZq5atepS6/k5AdDokxLCoJ96apjFgiRehx0BHYstau+hQ5h1wID9e6BV6prWTQ5mpmx88UWl2AXVOiZoDi7ac+iZoj/z4Bs6aKoHQPaokluBsmoY+Eh+s6Qf2zTd//DdR/wu1GkI6mX5AzGsGE48CCkHNJCq3bgQamiweD6kJ27q0KqgVcslP+WDpOD8GJybeLxpflLMWsiAZ3TLQs3pwQfLmjXZ0zrz0N23Hz5ehOhzMGRIsPmUMJpUGjZdY1BpXIwtr4Zt26Brly1pifszEo81qb32n5NAFsEfYAB3MPg1jPz789wSILNhybdLL7W7IdKeiASuMAlIklReXk6UEBqaSSOvUaPGe++9xy1tIsleIn0nQJOg53AP3Eukib9BM2g21VQtDC/mwAeJYuPGjTyQn9Vq/eijj6gtlP/qLMfSTxgaUpa7devmcDjoTnA4HH369BFFkUKp8lvi7F0k9JnvfOTIkVtvvZXP/VSg+BvDhw/Py8uj5mmqxmMcG4Yxffr0JUuWiKK4ePHixMREri6QjRQbG8sTLZy9MefxK7WcFBfDMIqKisaOHRsbG2uOGULeW/QNt9wotEhSUtJ5nDTsEMotoev69OnTiRhOHe/Zsyc1L2IzhEks8vGPKQFZlouKiiZOnNi5c2fiOHOgJIinnOFPWNZQSiY2cuTIr7/+2uVyccd5Wt4zo8lnkrN5n3Mpn6meyPdmCSiKUlBQwGOF0cDrcDiGDRtWUVFxck8dlADyX+QAFOfBXT1+bJW6LqPxV5/PARd6ouIWkCVK1kfvlCMn6P2Jv2PsZQb0ITh3181FTZOKm6X4MzNO3HX38eITIEqgMEAvGOGQRy1kdpAKmIfdoyMf6JVX1ezmP2Snrr+vz77ifKRjY6pArDxEQg5ZfiHsGg2iag/ac5VlcG/vTS2S9zStu//6DtuPFWK8ZqJsUy8QFA0C0DKiooxKraLNhh0IACxcBG0y16bXPdC01o5RQ5RAFesbMmhxkzDwIm6qoWqg7di5vfufb7JHI2WKNovF0qJFC6I/k2cV7X/ZvfMpsry8/M477yTFI2xwyMjImDx5cllZmeIXkTAl66i9MEkG+2uwSwTswmNCI3qdgzCCBxJNHSH/PbrynQGTvfK4CnEhwMTSwFhP1RsVx/YBVLA7T2R05mDVKnKzVAUMBdc8ZIDjAO8XVE4odL9R7P63RzvEuPbI8JJV0P2It2sIQMsa7o9rKmjaa4yrj1GnNwBMqpRGebVxZdU7cZkFc1dSSA2ejC736JF/fTL77vseFKLjrFfXFBxWfNxiataoWVcQomw2B1dFLBbLwIEDCwoKXC70LPB6vecgkcgul4QEVq1aRc8Ccf4+/PDDS6JZkUZEJHBRJUCrYmRLkgOH1Wp1Op02m43SzBKr6eGHHy4tLb2oZ744lZ0rAM0x6KpKV2xsHOdWCILQJD3N6wdPOXTKWtWywa6sBuvGji7AWE6A8TfY8M9mNIqzEZwz2OxHyg0qVLpXUVCzUeHZ4ZCWuDc7df//e6D4RDG4veARMfwFYcgMgw6FizIQIyaY+Ot/Q5uU3EY19rZpsWXnQUZMZmcwswBQweHOaSZlJ+CFoY+XN6m3t0XKT52vW/3jjyhZDDSFm8LUKYnpPCFPIfZDdcBL0PqPm6FVs+3picXZjT3p9XKe+UsxqCAFQJbQLYg0p/kL5sXHx4eUH8Futz/66KNhPBc6X+Q9IoGIBC66BFauXBkTE0MDtNlbuUePHjt37sSAdyxx3EU/7/lV+PtH/j2/dl6so/x+vyiK5PrNEWQecINgDj5avvbaa2YAetu2bdQMM3Iddqy5TgBYsmSJIAh16tShnO8Oh+PYsWMETHN0+Be7RswpAnAPHDhAYV74CE+F+Pj4lStXUpR/c4WUQIyHVaWTrlu3jkKL1KxZMyYmhhOXPvjgA/OxF7ccCARyc3OHDx9OjwbxwjgR22azZWdnT5w4UZbl4cOHU6don3vvvfcCW8IxL0VRPB4P9Z2eTafTuX379gusP3J4RAKXqQTMi47FxcXTpk3r2LGjxWIxDwuxsbH8OQ0bduijxWLhY4jD4UhKSnrkkUfCKDD0DLrdbgqUaQaUzyQ68z7nUj5TPZHvuQSIu6qp2qFDhyjkkSAIvJCRkbFv3z6aLCSMbIHbwW1wX48D16YcvC79xxdfwHiORHRRNI2iAIemPNUAxTA05NvoRARSdfDqBlTkw1ujIL3uobTE8uQGO3retjevEGsWWSY5nYIpmKwkYIGd0eMToLgC3puqpDf64Zqs3Y8+vKOiFMjdU2anoBaiwRj+QltNUqCyFO7584lrUkpbNy5om7V+7Sa0sii4YdDqooPRVFTBYDngGQ87oEuYhV6E/yyHjCYb26VXdMw80b9PMc6wLIaEpskUv5gwR0mR1/6w7qYePQSrJRjv2MJy0glC586di4uLSUp8FZm3/PIqELTat29fSudLjkT0+Dds2PDjjz/m3UG0GhlheLf8DIA2k8N+dg1M3r68FioYBiD6jFvIjRmpyksUeOlw1cQi7xyANzQY61Iml5RsBMMdMqRPWtEaaKJuSMjFlwwoB8gB+GdB6dRqz9tFpV9VSYcAfBQeU0YAWjf8MrOqJQ3zKiFcLbNKZUSi3QA7Ad5V4S+llX+rrpjqqSwFJHMz5pxCl5hj0JpquKt85W7prbnzW/TpK0RFCUiqi4kS4ig1osVicTgctPSemJj49ttva6omSZLX643woOmiX+LvI0aM4Msw/72O48aN8/v9l/uTfonLPNK8/4kEdu7cef3115PWZ9YJyXs1JiZm3rx5/5OGnctJfwUATRi0LKtjx77sYJuFRVOyRtluu3XYHTetaJe8NqvO6of67Pe6UI8hdy/8E6aJ8NkutM5qMKjap8Gzo/Ib1tnWtEF+x3abNq5HGrJfCbBuoPrEMWhkN+M6Lp53o3fwAAAgAElEQVQlIMK4FyqaJeRk1CnIStk6Zw4ue1ZqInlpEQCtsfhQbLHUCPpzsXAcsoZM6g+nQWrdNWn1DmSnbfvma2RDi2z5XENInOKVSWy+Nqg23i9Rg7lzoVXz1a0aV6XWqE5LyO35pz1VZUGxo1cQm6D37dtTO+EqC66z4uZwOOrXr5+XlxdZUA1KKvInIoHfTAKkc+i6vn79+saNGxPQRk8irQnVrl177ty5RDq+dJRLwjffe++90aNHL1y48AIDE/9m0r04FVdUVFAQ55DZHPxrBjjo0miq1r9/fzMAzZHKcwSgFUXp0aMH3QDkifLOO+9oqibL8nmop16vNzc3t0WLFrGxsfzWItzn1ltvNa85m2lW5pHffMvl5OTUqFGD9GYyIGNjY+vVq3dxpHxKLdu3bx84cCARKnnjSYMhb/3nnnuOY2EPPvggQc8kunfeeefcwfpTzvyzL4h4PmLECApHS1bfqFGjvF4vj23yswMiHyISuKIlEAgETpw4MWfOnPvvv5/IsNyW5gMXFWiUONOvgiDUq1dv5MiR+fn5YQKjNU5yOuHRAM3jbdj+/KN5n3Mp8wMjhVMlQMveNDXQ/DV//nyeG42QRCKtP//88zRTSAHI2ws3ZG9pfvX2a1P2Pz2wPCCCVwK/rAVk6efos46p2lm4QhMAzcwgGaa/BU1qr23VqDit/p4nHq/MzUNascYCEiJsRy/iDLF2M64qos9+Db76Clo0W9Cu+Y9PPlpeWYHmkqQgVUgOwuPBjpJ5R9YeLxcXwD29dlyTXJ1xdXWr1K0Lv0K+tMgQxZPIJ1WAx6D9ZehIB9IYodVnQM5+aNduTZO6hakJpde12L43B3x+5CR5fUgCp6jEhmEsXbr0xpu616hVU7CwbHvsgaEFzltuuaWiooIw/fOY9E+9jv/Dbzwej9/v79WrF82bPCZP3bp1P/30U7ofkEilKJKE1HhiYQWJXCYyMi0t+BmiixeChB+K23KaDga5z0ELWWFXJx9gUim86oIPRJgegDFV/tfLqjeyDISlqubV9ABDq3n0TayWpcssB9gPMPl45fiiyslFxYtc7qNsqYOSM+EtoqoqiAGk/rPbjKBnkTVXQZz6GMBMyTe0qnqoxz/qRP4GwHjQKluW4CGG8PZgkdw0WVP9GClmqwKf/ZT/8eZ1tz0x0Fq/iRDfIGyApY9Op/OJJ57gHIjTSCPy1SUmgfHjx9PDTvlLXn/9dVqU+u2aSbPhb1d/pOY/rATOMklNmTKFu3fzsYszDzp37kyrbh6P51Qi1KUgT+GcGkHqA3sXA4jOpjZJY721CgK9mqTUHNMmec7/3ba2qji0HM+rNh2OE1tQrSFaMc5jEkCFB557vqpl5tbEq3e1bL5963ZMKBEwMOkEuZJp6BmmUPbkAFtF9UoQkOD5ZytSE1dnJRWmN9z61luVLoZX+3ScXTj6HNRsqBmYgZlNewrICqxaCSl1F7fLONQ0adFnn6IDmseHDkGo78jsPaRAMR1IC2h+A6DcBT4J5s+DpknLs1Pyu7eG65tXX99qw+6twJIyAiP0oTpWXeW/tkNrZwwFmAreIe+88w6R4LiEIoWIBCIS+K0lcPTo0e7du8fExFCUWxqmY2JibDZb9+7dN2zYQOm8f+tmnEv9bre7RYsWfEahEeMcVRweFpDPW+Rqyj+GNUCW5enTp3/wwQeHDh3isafN+3g8HgIiZVnmiCTtYMZPzYece7lfv35xcehS07Nnz71795oxaDPAQRWWlpaa0Wer1Uog7y82g3YwDGPNmjVcqoIgtGrV6tybat7TMAxRFPPy8tLS0mrXrk0ri1Szw+F48MEHydrh3TnHa7d06dLatWuT0kzu8zab7d///jfZkFVVzNPY3I4LKLdr147CyJrJkgR49e3bl0Arfs+0adOGABGi5u3YseMCznyaQ/fv3084ms1mczqdWVlZFODyNLtGvopI4LKVQBiKEbayWFhYOGPGjI4dO9aoUYPWe8zDHU8mQ+MDx5253wAtJtlstoyMjBEjRhw5cuRirRJdtvK+dBtOMwLnntPEahjGjBkzYmJiiOJjTil5bYcOK1bsz9kMnVouadPgUOvE/b26rC48GqS5YLxBXQ9bhdURjsVAhQRAkyxUEXb9CJkpG7NTi7JStg4ZeMLrA6+KxJ0A6DKLqYvmDwtxYDBSswLgZowiTwDeekNtn7WpRePlw588qMjEXFbJSApRbhh6GeIdod3E4h16fVBeAt07bm7R6EBmvdL26YfHjC4iNg9jF4Xjz1gL2yj/O0Z21qGwCtq2W5fRtDgtMdCk7sFvF0O1C1x+wJjABsKnrqrK96dOu+aaa8yzPD0gJMzJkyfzSTnMUyp4vsvkD6k0brc7OzubUg5GR0eTTjtu3Diz7kT9ZaR2XFmQmYHLEGfDD7oPjCqAbQDrAFYb+paAiOa1GkT/mbl+WomgOU1QsrtarVRhL8D0CvfYchjjhper4ZUi9xyPexOoRQAugGokr+M2dcYsBA0c0d1v6+0RFb8roAHkAvxLdL1U6Xq1tHK53+9jxjfehEGsWgNDkdGvWJHBQFSc8mAiMI3owWGAD2XPSG/l0x7/iKLSZYDBoKvZakpY04Ni0XHRogLgoxOVr+cf3cbY06//uLn32HFCfA2n08nX2vkYKwjC5MmTf2sQM6y1f7SPnHBgtjJcLteaNWt27NixcOHCl19++dFHH+3WrVvPnj3btm1bs2ZNfqXMz7u5bL6CfDWXz6SnLRAJw263t2vXbsCAAceOHSP8jsZqrpdyQj3l5j1HDf+Pdk0j/b1wCXArjMYfj8fzXyZWbm7uzTffbL6Bzbd9QkLCjBkz6NSX8nz3qwFo6tKiRYtZbzkAXS9WuP2m66ac+AmMQFAlwj3DoGf6GNQ0AgCYMEIECOgw62NISvy+eVpuerONCxbioSzUl2oCoDH3AEuRAAEZQ0JJCrz6cmXbjN2ZyfkZyXsHDyp3+XE28qFbDx5uBqBN2g1qS5iVWcKg1a0z5zdruL1p4vrPPoGqStZkndGdycGHrxSHnMs8oqTo4PXAGxOkxg2+bZa056//B3feAO3TcpZ/AwEfiQffA37MQ5iV2Qq5z1bB4URTQhCEu++62zy8mhWFkwdHShEJRCRwsSVAz93nn32enp4eFxdHgBqN2k4nPp/Dhg3zeDyXgtE+c+ZM7k1DBR7j+FxGjN27d8+cOXPu3LmUxUiSJJqETnvsI488UqtWLUEQ6tate+TIkVOlTgRhQlTpV0VRSktL9+/fT0GNw1CVU2s47TeSJE2bNs1isXDOV3p6+pkmS5qDb7rpJkJLOS7zxhtv5ObmulyusrIyl2krNm10dkmS/H4/Eah5AOj58+eftm3n8qWmarfccguf9UkV/m9Aj4EDB3JqG+/OOaqnuq7PnTs3DIDu3r07tef85HymvjRt2pQTpjikdeutt3733Xd0rUnmBLWnpKQQS5qemkAgcHGj1ui6fsMNN/DY2bVq1crJybkUnsQzSS/yfUQCFygBMlwRWfN43n///T59+lB6VRpSYmJiYmNj+UBHP5G9YbPZHA4Hz1bHcedWrVq98847OTk5YQ0zGzBhP0U+/q8kYJ6L+TSBQTBEcdGiRYSb0GAbBFksQkLdNhmpI1s0md28/qrUq7/YF1oElGWV1/DzAgHQCppCCLohCFhxDAY9lJeWsjul8fZRI/1FhRi+WdIhAGoAZMxNxwIuU9hojcW+kBm/tbgKXhjtbp6yuEXyqmGDyhQJWTgsGK9XDyWbJ3JRyOzDcA+YyJ0RhnL3w319t7doeLhtE09G0r5HH0L02adAhdfvk/1nuQpErBYBCkrhzz23Nax/MLluefPU4iF/ESUGi4uG4ZerlyydP2Too1fXquGIsguCwNdWOQLVvXv3/Px8rkeRoMxX4SxtuKR+4mqAKIodOnSgm4Ssy4SEhA0bNhBOwbuGTHjkPhv8xRx7DR9o1WAUg7YD9Kll5S8eOjLp8JGVFdWywUxgXdNwfeG0G+NwMYI6Rs4E2AfwbnXlmEDg6XLpBTe86TbmycZ2QzwBGuZ3MoJBWjQDBEuUYI2iIe7uRx+TAfIBPve6xhX+9Gpp6VcAwUilHH1G52dFwyAr+FIxULWBdr6MRr4f4AjAAkl6QfQM9Xue9wTeq/TmMvTZxzoR1nqUCYtgXgGw9IR7yrGieQArAeYEqt8r/Ok7v6dIksaMGcN1OVput9vttIaxe/duLvywmiMfL1wCZKARDH306NHJkyeTTkg2gnly5Fr3b1Gw2+14Rrs9Ni6OmCWPPfbYtGnTduzYQW4TXq+Xq6aU/PzC+x6pISKBX5QA1xgnT54cGxtLhjPHoOkBqVmzZps2bTZs2MDJDWaVgE8Kl4hOeJ4ANADccccdHH62CtF2ITkp4fqqEyAFQdjQ+jVRnnnYjZNeXbh8KgOuvX/1NTRP25zVPD+16cZ5i6FSgSoVqjV3AL27RJW9DLaSjwxoHcNu+Nww/K/VWY33NLjqWJu08jvv3L8/Dy9fQNPcMmbN5SE72Fo+sq5DL/RCklUoyof7eh+9pvmRtKQdz49A9x4Ea/AwlQWZpry+jASNq8F4uGzoPhEkN7w5Vm3WaFOTxH0vjoBbulS0bLTt2SEerxv3oYFJkcHv1QcNGszHx5hYnMXi4uJKSkponDUMw+PxXGo3xC8+A5EdIhK4fCXAMbXx48dTlnCy5An5iouLS0hImDlz5i8yan9TCSiKMn36dDP7yWKx0Ljxi5wdWZb37NlTt25dGnmeeOIJGm3OZG7NmTOHdGuCM55//nki257aQdILly1bdscdd3BKkd1uHzt2LNfGTj3qLN9oqtarVy+zpR0dHX2myVJRlF69epFMzKAMz+zKARr6lejDlIEkLy+PrntOTg7RWyg8Vo8ePc7SvLP/JEnSkCFDKFgnv4WI+0wmCgf9zZI/e538127dunH6s81mS0xM5GwLvs8FFkRRvPuuu+kmqVGjRnZ29nPPPbd27Voz9ExXnBJkEUvdYrHY7fY2bdpwr94LbAY/XNf1Dz74gORJt+ILL7xAty7fJ1KISOByl4D5ljYMY8mSJf3796fHkLLHkLFNfjk0WPHhjlsaXKskJDo1NfXll1/euXMnCYf73dOzTMTYS8TeuNwv30Vsv1nzpzmC8ysNw/jPf/5Tr149AsJ4fCRBsAvW5oJwXWrK8GXfnuS7aKrP0GVDYzC0hlRotqHvKPMc1YhIGpChrAReHS63Sd3WoMnKOx85VO6CympgNB/E9CRQCYDm3J0gAG1ApQQD/nK4SdL3HbK3IfdZQouJYkSbyD1h4tEpR4/XB7n7oecNG1o12ZUYfbRFo6K7bz9QVITmUoUHIWTMexfaQmYa/qqBIRmyqIFfhZIy6NurOLluQf1417VtxCeeLHGrUBGAzbt2P/3ciLhasXYHPhZOe5TdZqMHhOxzq9UaExOzdu1a8u6iWFtm4fNyqAmXx99AIPDQQw/xJWTq8ksvvWRGnwHTDRocgMZBgC4tu2aVmlgOsBukuUrZ+GrXywVl3xZ7XcwKBg3/Ue4lMn5NV5nQ5yDf3Ys1wL8BBpcW/0XyPBXwj6mu/srvycesg7IfVH5xNZ96aP/h4Nhlswo2S8f/+7+DAJ95lDcLK6aVVi/3e4Pos8QyTzKCtQ6qCpIMgQASzwKIPWssX6GC3DVEn2XfuKrSv3i8w0TtHx7fDwBlDPIm8liIBBe8prSsUgXwvWFMOVbwVaU7B2ABwDtl5fPLq3fL2FhN1Y4dO/bXv/41jKEiCEL37t151sfL4y659FppfsCpdQi5ABiGVny8cNKkt268sRsRYhxR9ihG2gveM4LAeRInv+Gli1cg9FmwBePFU8W0wCMIQrt27UaMGDFt2rQ9e/b4/f7IgsSld4tdgS3iAaMKCwtvvPFG4vJzm5drhhaLZdKkSUTY5/MaTQGkE5i/vBTEdG4AtKmlkqRoLPEfekOHAnBYMRCHYLPGtmnVkfJRsHGfHcYB6JPBN/B74hn7NNi1H1plbG9Sb29WypahQ46XejGfgIb+Vi4pCED7NZx4AjgjGhg340QxPP2XknZpec0SyrISK1s1yykpwwSGPpyY2Jo4O7MOiDWf+lLYeuz0ydA8cXNW8oEBD1VWu6DajfkMmbeaW9f8eKjOQkQzOgAqQwbi0q5yGPLwwezkNemN9kx7G8aOhKaJ3/W/44AuBtMhKqok+gN+rzr4r8NwwLQJdrvFGR1UiRYuXEAeHARP0Go8vydMYo4UIxKISOAiS4B0BYIAZFkuKip6/vnnuZZpMvMwR82yZcsu8ul/TXWDBw/mzB2aXTiawIeL02IKhmHcfvvtBLwKgpCcnEww4pmmny5dupg1t379+hEJixvDlJ2PRDdy5EgOPRNkT76ft99++6/pHO5Lja9fv36Q3sUa0aZNG2onby1dLMMwzFxjjsiQUkg11K5dmwRl7g6V8/LyaEVh2LBh1GwivG/atAnXLAOUZuDX9WDatGkkCi4Qh8Nxyy23cGQ2zBuarto5nuNvf/sbhf60Wq3Ef8/JyTFDV+dYz1l203W9qqrqiy++WLduXV5eHuk3tD8Jn98GtKRh1ngGDhxIM9dFXKeh4IxkeFAw6Hbt2p2l/ZGfIhK4HCVgju9MoXuIXud0OrlbhiAINCuFeXuYzQxBELp27fr+++8fOIA56Ahl5uMqSea0E8TlKLQrss3meZwH46ZxlfyWiouL+/XrRxQ8nLCibMzecgj2BoJQr0naDStWbuaSMXS/oYuh2VNG1o4hq4aKpFfK1q6B6IeP3qvu0GR9uyY7/t9f88uVoLGkK5jtT0ZsTyeX05MANDOiZAlGPHs8temilukrx4z0IfdZpGx2eP4QNEl0Z94iLKDNZ2Dkjftuz2mVsic7ubRjpvtP7fbv2Ipoog7gCWCCRL4R6MwhKoraICrg98Odvdem1t2anljSKOFgn9uObdkN49+dUy+1GTM9BcFqEayCLUqw2yw2IYgcWSyWlJSUV155pbq62jzLmyVvLvNmXBaF2bNnk3rjcDiio6MdDkfDhg056y2ob+gG6EEAWiUGtIYLFcA8ektksQTgB4ApVcdfOVb470o5nzGeMWSKgaEqWQ4/Wgngiw2GHjSpcdFABSgB+AJgTMA3wlCeqK6YqMpzJO8+xIv1AIZrDkbeQLTYgPemTMOLY8OLJdSscfvYcbN9gVd/Kpla4lljIJMaN0VEznwIfdZwfUQScbXFJ4MPdD/+qmHc58PIfdbGVZU+7Sl73FM9RhLna0oJgMgQcgZAc0Y+3qeaJspgVDPY+vX8o5Orq3MAtgC8fcL1z3LvTwy55smoJUlau3ZtQkIC18FIBTrVv+SyuFt+z0aefd7hT3fouddnz/7k/gfurpUQH1TdbULMVbGOKPtVzugwZZ4Hi8P84czRIWyHi/vR4kBfCtLAaWGYGuBwOLi12KVLl88/+3zfvn2/p4Qj5/oDSsDr9U6dOjUxMVEQBMpfFRZSpkOHDps2bVIUhefbpEi/ZlP0UpvvfjUAbRgGKUmaqs2bN4/DEA57tMVii3bG3d7nLtSfZA0z1bLt55kMMOqGzryyFIA1a6FV5u4OLTxNam/4+2MHpSqEmf04yche3Y8L8rj+KepIlUbisyShNtP3xqNNah5q10TOqFPQInnNtwvwNBgEDRnMLIEgqT7Ig8aTsxdOnDShBgLw7xnwp5Y72qbk3HbjruIyDHBGmXw1qFahAmHoYFWoHWkhX57CXHiw994mVy3pmLF31VL4Zj60SNl065+2n0BnMmRVswzDWB4wYAClJLbaMPqzw4kA/XPP/U1WRE2TmUeUahiaYWjm5FRMWpG3iAQiEvidJCCK4o4dOx599NG4uDhaXa9VqxbHMQcPHpyXlyeKIsFzFxFu+8XutWvXLjo6mlpFq+4ELvD5w1yDLMuiKHq9XsMw1q9fb1bCatWqRQA0PzBMOzSDuQkJCZwUTPtTUGxFUQKBwH333RcXF8cVLxr5+eGDBg2iFp4jI4ACO3CgnNo8YMCAkAmN1B1yEAGARYsW0Q7EXKZ5l/RCm81GbaCrRt5zhOCQ9MaNG0eXT1M1StTjdDrj4+N79+5NfTRL8lzKsiwHAgHecavVSt6+119/vdvt5u0PK5xJ/qc949GjR4nZROwtQRCWL19+2j1/hy81VZszZw6Jl5bc33nnHULDf5GP/6uaFwgEBg0axOnkgiCcmjztV1UY2Tkigd9TAqIoEtmEhmJ65HVdJ/CrpKRk6tSp/fr1czqd5NltBpTN44nVaiUnAPqS1qKcTicVHnjggU8++eRXjSe/pxAi5/pVEuA3Cc0XZFvpus7nrNmzZ9evX9/hcFhsVntMrMUZK1gcghDNXkJ2dvbHH810uyqYN2mQSCwbFTJUqhAorapQDfAHwDDAXQELZ0NG3bnXNf6hX6/dAT+aWjLDlynloIq2kyqDzF5oeWkMoK4uhalvyNnJa5olLh4+bCsihMjU4bgz7y6BfZzwg/iSLEHBUbj1+gMpNQ4kRRe0TSnt0nbzvhzwe5HUqjGGDzcPyVJTdV1mMTtY/kGs3OuCpx/N7Zi5unPLjc0bz0usO6ZWwv2C0EiwRWMwB4fDFgKq7HYk+tCCdEJCwujRo0n54U2kwuX+7LhcLgCoX7++eQD5L1+BqzpEeaawLMzE1GVD94PuBslt+P0MoTWQoQy7AKaVi++cCCwpdR+TggsSBEAHqdLsWiuhqMt+MPygSWAoCt5shQasVOGFwvJhFdUvytprFa6l3sARRfWw0JpkU5PMNRdW8c70qYJDEKIE4eqrhMRGN7084c3C/PdKS1bJRgE7xDAw7gdLTMgMerzLVA1kEfw+8AbADYobdFUFKAD4EmB0tfwXl3sEqEPdP30AVXtZJXh3qggEMAQCIXiGB2h+pbIKlD0Ak4uOvV5c8CnA1wDTK6V/FnpWy3CcHRvCy4O3zH/j4ZAqbh6fKQEG0QzDbq3IxzD7gpstwdtARQHLhl54omTewgX33HNXbLQDwRHa7IIQIwixeIfQlxZBiGKzIQ/TxzFoiyA4bUKsg6032diBLLKLRbBHWRw2wWZH8gYGqqK6aV3KaXfUTajT5U+dO17fMS2rqTMe/SZsUUJsHJ4yKsYmONnqiE3AlRKkWOJDhni3w0EFqs386NE3iYmJw4cPX7duHfmD8hWvi0scidxgfxAJ0CTFO5uXl9erVy9y2uZkfK4oRkdHk69zmNVJC9sEQF+as96vAqBJQ0DyGulJXq+X8nQTFkDPYXR07ICHBpDgxAB6V3ANg32p6phIGSeWXbvgT9flp9bPT62/564e+935iPWqOjDvLtlnSEEA2lAxbDOApkBRHjz5SEHLxPwmV1Wn1DzePuPAv94H1L5wfRPTPLIX+4inoNwbGsU0owSGBsCBXXBd+qrMOhvvuml/dTm4cV3Vw5qpKQhAuxQkAoCCqZlRFcKpugpyfoR+t+1LT1h+bdNNP66ATSuhc9sVrZsu3LUF98CwWQA+EdP2PvGXx4OiiGFeYYJgsQo3/bkbG4s1t7vaDECH3WdYS2SLSCAigd9RArqub9++/b777qPHlt5J0XE6naNGjfo9oWfqd+3atQmDIBVq6NChXJM77YihKIosy5qqPfTQQ0Smo17ccsstZMqeafoxK9ZxcXGcy2xeGNNU7c477yQmiNVqpVw31DB+uM1mIx/wUxXQ015JXdePHDlisViI90c5l2bOnMlnUHM9q1evJsPSDH8TiENBOQisJ7ZC06ZNe/ToMXjw4JkzZ5aUlNDZdV3/+OOPuXXqdDq//vrr00rytK2lL0VR1FTN7/cPHz6cd5y0gUaNGh06dIioiLwL5sKZ5H+m01F+Fc6+mTdv3pn2/K2/NwzjrbfeMivcq1ev5s4Ev7ZfZ2otaRSffvopfwbtdjtlXzzTIZHvIxK41CRgHrVoNNBUbfHixY888gjlFeR+LWHslbDxhD8FtJsgCA8++ODs2bPdbvelbE5capfj0m+Pefw0zxfUcl3X3W53WVkZhXuKcgYNClxhjY2hXIWCIDRPT331lVF5+QfpKBkqNWAJbQD8Evi8+PXKryE76ZtOzTbec9OGykJEmul0hqbTC1FLQ5WZ16kEumSg4SMHYPY0aNv42/Ypm54f7FJUjNocQp9ZJOEgdYdsw58FZwAVKorh3lv2ZyT8lFbD066x1Dxpy9xP0crzedA8Q35QaKPjQ6RIbLAOGPFXkmDsqBUdMmek1Z0Wbx1qF/oIQnPBkiBYYwSrVcBIDozjI1gFi8BI4pjK4tNPP5UkiceiCVsUD50T/5LELrv3r7/+mqupfGpeuXIl9UhRFAy/wi4wXVxV1yXMNyj7QfSAWAV6Kcu892F++QfVMLvcOCYFZYBELQrUoZNPMMK4BEBLDKL1gyayQgnADoDX8ytHnnCPqvKNKzy+BuAnSZWRPR28SYKQAbpTISh8orosq2tbBKAT4oQ/3TgmZ8/U0uKlulKACTDZMZohgxbAtQl+R+g6uj2LIng18LKTw08A3wK8WCU+LcIgWR3irXrXKF0HgWAEDxZxRg3xxnD5xcB1ET/4SwE+lctfqSj6DOAbgAku/yv5patkjEPtY7ec+Q4kLqEoii1btjSPzx07diwvL7/s7pnfs8GKoni9XvLzphQyiqJQuOT5Xy0Y/PRQvHujGNTLpzoLRhgSYiy4uGbFdYoYwRor2KJtdqcdGcecXEJHOCxCjVgHRROv0zC+U4/r7n+837MvjZn92aL163asXvXDxo2b161bt3Tp0m3bthFvFPV/m23Prt2Yd8HrqnThICkp4v5D+5av/O7TuZ/8/cWRra5ri/UHUWss0vPFqZZ0dnP0A2KkclgwLS3t8OHDNPsrisKdEn5P+UfOdWVIgNhOs2fPTkpKoiGIY610BwqCkJqa+vlnn5vjbNvmJywAACAASURBVJgVCV6+NGe98wGgCUhVVEnTZJerqlGjpLi4WHosEWu1RsXEXPXYY4NkWXVVe9hEGJzSgnMbyIoBhT9Bu8x1STX3XptV1rHdd9VlYIi4RqproBqyhO5ifglX43E+kzVcS/dWwsN3HLkmJbd5wvH0hMLWqbvHPCe5qjEbYYh6TMvvwbmLZSzEFMqsgC49igHeCuh3244Wddfc1HbblnV4l/o0MHAf1HZYakODEhDSu0fRZIB9O+H+2w63StrYNmXNhlVwPA9u71rUMXPz559oOsuNyBQmo8xV2vXGriSKKGeULSroC5bdqoUkBSQJJ1lU8xj3md6vjOck0ouIBC5rCVBgnC1btvTu3ZswAqLW0rOcnJw8adIkt9ttGAbhub9pZw8dOsT5xRSWeu3atWdhmxKbGABKS0vtdntsbCwBtRaLZcqUKaKInrlnmn7MirXVan3wwQdpJuOYu9vtHj16NEVF4P5oRAcgjJ5qEARh1KhRpyUcnVZWuq4vWbKEV0uBLKqqqsztDAQCRB8QRfHDDz8MTTFCrVq1KIZGq1athgwZMmHChC+//HLjxo2HDx/2epm1zXzSzeeVZfmGG27gk3fHjh15B827nb1MpIbNmzeHCa127doLF7LMuey8fMo3F8z9OvtZ6Ne2bdvS+jZpwFOnTqUazuXYi7UPt88ff/xxbuVaLBaPx2OOcH1RTkcZxk+cOMHXGCwWS+/evS9K5ZFKIhL4PSVAVOhly5b179+/Xr16NHBx6JlzsszPlHlIocE/Ojq6Zs2aAwYMmDdvXhiLigYWPqT8nl2LnOviSoBfRG5A8nGe/GcpJgAAFBQU3HnnnXwSNBeiY4Lcv/oNEp98asi333/FwFtFYuwZQp+7ZG1olbTirj9vKMqHahfSSlErMKPPJwFoVdLRqlIkWDIfrmm8vnWDLaOHVoGKKKDEksAxnI5SyBPPlQPQTDwGsoWqSuDhvvnNau5vn6w0rVncovH2f32ARFZdB081axlqJRr+ZyQlzp3mEj50pGj4iAmxMVl2y3WCkC0ISYJQizEkHYLAOIpWK8LQbHPGxLZq027BAvSHJeiZgj5f9PQJvHn/q4Isy+PHjyfAyzyGBKkGmq5K8s90D0xtBJgnUsbr5gMtFwFc5Q2v9+2ANqu4OjfE2yKXYY5BqywRkhJCk6m/mOiIpQrcBfDaCc/fS93j/cqEY0VrQTkO4GVxOXhwcA5AGxLI3iBH7N0tK/9v4b9fLC15uax8maodY+CvKjLAmDGXRSKtBVcHaJ1DRoBAFwHABfCtAq955KerSoeK7r/K3hc8VatBKwDtZP4pdiyFPmfNxk6UAWwytEkVBZM173KAKT7PP6TAW4UnclkDTGsRwSLnOI8ZM8Y8Plut1vHjx/8+tsD/6h678PMahuH1eknNrq6uXr9+/TPPPFOnTp3gwIVYc5Q1xslCLSPRWbDYBYsdU5Kji4clmr2ILs+DMZPzYo8ePR555JF/vPnWovkLNq5dV1l6gt06PgVEHxjVElSx+6C8suLrr79+/vnnP/roo8WLF7dp0+bGG29ctAgVdcWPNxJtfOTyKtrGrVsddoz7YWXjC+YyjYvv1KEjMaC5YyVB4eZHjzplsVjIvclut99yyy2LFi3C25X5K4TOFvkbkcCvkMDRo0cp4jN5v5ExyP1iBUEYPnw43WBhOqF5/A/7iZt1v6Idv9mu5wlAY2gvQ1NUCUDfvn1rcEzBxSIbPcD2KOc999wTCARU5C/ruKaq4zIkOtgY6FFz2417WiTnNq69s1Ob7Zs3INJMG63DSyAi+kzQs4IhoFwVcG+vjS2TtmQ3OHZTa/Wapgf63bXHH0Qb6NBQ7mW2ss74zphFgaHPuCSLC7kyvPp39ZqUNe2bfrt9HUb3oE3BJVY/Q58xXwdBz7TMK2pw9Ah0vW5Vu2Yb2qWtqi4GXYLXx7ma1v7PC09pIsvejBGrRaXMVZrVppkzNsoShe4bVjsOmzGxzmuuaev1uVHLYpumyREAOij3yJ+IBC4BCRCwSEa+oiizZ8+uW7cuxwsowIIgCB06dPjmm29+h/Z+9NFHFA8kNja2Zs2ajRo1OscphFDauLg4h8NRs2ZNm822adMmURTJEuO2LpGpqSNhWtSgQYOIi0p+ZG63+7vvvqPhnQwewnC7d+/eoUMHUso5Ut+5c2dSyrkJfRZZaapGrY2Ojo6JibFYLB07diQU8rSH67q+dOlSzjIgQsTMmTMlSZJlWVEUIgYSDZwCMfOzS5J05MgRriPabLbXX3+d/3ruBU3VAoFA//79KTIgt0meeuopqsQcbCtMA+DCP/v0z3/t2bMnRZ0jiveECRM4HnHuDb7APTlGT7ki6YmwWCxEaSGKGW/wBZ6LcJZAINC1a3AFVxCEhIQEqva0t8SFnzFSQ0QCF1cClFfw4YcfpgGcOw4TpkzLbBaLhUIJmcdePphYrda6dev2799/yZIlmqoRa4yjkF6v9+whlS5udyK1/dYSMM8LYbP8qaeWZXnnzp3333+/xWLhDkAszYyNyC4xV8VabAjIXlUr9vGhf5k5e7bbr3+/tLRL68+bJXx2feuFRXngFUEDDA/NAWg6L1KFiAHNEu1IfijKhS4tv8uqv7r/rUdFF3KAiJiMgYWxKDMokjijIayPONAycnTu7bWxWe0drRO92fUrmydue/cNQHsxtKmyqCkS6BiHEANVE/+VvR84nDth4pvdbrqZoUDxghBttV5ti6ppszttdrvNbsc+Wi3oI2+xMsqT48mnnt69d7+CaDaih2ELNqFzXjl/X3rpJa7P8GGE+o66kKLoqkbBN+gqY89lnUJslAMsAeV1T8kLnqp3/dK+0FXk6DMVWBjooC2M1ziEJesMAi4AeK/Q/cyx48NLjk8qO7EOMIQFYdOEPlPKJ7otVICAgsa2BLBVVV47euANX+VTR3NnBfxHGPirSYwCzShoZIBjg4M4MDuxoWKccjS+YasCk6v8T5dXjAb5ac+JMZ6Kubp8VNd9kvpzZ2usQ2GAOGDYENgK8E7esekB92cAs0D/R0Xp5JLiLSwUSQgJoDuEbmkqY46Qhx56iAuZQMaGDRtWVFRwBSm4a+QPkwDNUHl5eR999NGwYcM6d+7MWQXILY52sjjgDOWNsgiOaMERKziuEqLjBedVQpRdsNqiGPrc8P+zdyVwN1Xre5+zz+ybZMzYh2QqokuRDFe5XZJ73dS/G91U96a4QhEyZiolUUmiJEXDRcqYSCJkiCTz8M3zmfdw9t7vv3e95yzb+T5fKiqc/Tu/c9bZ01rr3Wuv4VnPet7USm2va9nvn33GjRq9dtXqPTt3FRbiandiC2EhjzrCxH0SBFSALICdEmzOCx7Izu/9z/sES9SbwocffggAxb5ilkDmzosVMEXBKZMgwEkdFWmmvjrP7k6p4EI16gpOx59aXR9RJCqHu3fvXr169dSpU/v27Vu7dm1zeaBmPTU11el0cpFAej1r1KgxbNiwffv2JYpGwgI/1wJz5sypUaMGFST+zQtYlSpVNmzYYB7Lm3lmccNP86HzOGT7uTkqff4vAKCpIcJvDcnBWFmPGDGcG8hiiTrcq1ix0oMPPkgtV1jGxiQsq4oKp07Av3ofvK7OifQrDl9T59OF88EXXS6GPgBZHygis95OMIRE6LAfvvkKbm7+VasG311fb+8zT0Cjqlvv+euB3GxkLLNNiU27RsWeSO45hkFTbwkCfpjzktbu6v3XXrlh2RLmSDFmDwXn+5UIqCrqROPqoYDGJlsBdm2Fm6/b2qTO6p5/2ZmdAUX5sGQ+NK71yR2dv8w6jteznMH2HXsbNW3iquAkO9icCENbRaFFi+tCIbbeDKux6CcBQMcMn/hNWOCPaIETJ040bNiQ3mXqXiQlJREAt23btguRYqLu0jq1AQMGUFyiKHo8nmHDhlGM5kbFPHAljo9hGC1asOVjvC4WsHonfNZ8PmcWHzhwwNyR+lEQY/LkycSjIQDa6/Wmp6eTzw0i7t11110nT56kNa09e/YkAQ1aXZ6UlJSbmxvnZf5stlJVtX///iTKTKD28OHDeTNZ5lW6rnM6IU0Fb9rE1rDEzjbn0RwGgJkzZ3L6s8fj2bVrV9yy3Ng9yvvVdf3gwYPk/4EWQImimJ6ebpYqNj8jczguPWVGwz2JKYpy4403Uh7pYRKZ4rcfV1MWatWqxRd8derUiWtwlZmLX7aT89SmT59OWaaS+fnnnxOj7Q/VbfpleUxcdZFagOZ+tIhG9bM5FzTYVlV16dKl9957b3p6OvkPNAPK5jqW10KiKHJJeirwlSpVGjRo0PLly811hTn8c+sTczoT4T++BczP+myppSbgxIkTM2fObNSokSAISRVS7Dan0+m2Wmk9uuDwJItOj2CzCRYkwdjtdapXvrfhVUO+/RZyCxFSjCAud8ZGUJqK0oMIEusKnPgOOly7tU2DL3vd9lmgGGnLZ8ByeDV3jhMNq5KKQ5ww5B+Fv/35yA0NctNTMuslH21Vb/+4oZKuQDCEC97DUjEbr6H+NDrEwxsb6zd9vuDdd+69v881zZog/xCRZRvTubY63JXsjlSXO9VT4Qr0686YPS63Q3SIja9r9s6S90sl7IysXZJ/OABNnQSqYbjYGoF0uC6YfbgcrQ9gL0Q+VIPPFBeOzM9bIAe+Yejb2UykAYQYPI2PlU0RRAwE7L4H+ECBKbmRMTlZs4pPfY/os+5jZ9JQnDwnIZTM1CnDbLIiB2ClAdOK5ckGPF1QsrikOJMxpnFtMs1lMBK0xnBy9kw51AA4W8KS8CXAtPzCYQVZ40AbLstDT2W+V1xQAqgWEgWbqTTEUOtIzA1iPsBLPu+oooIlTPp5dObxGXnZu1QEH+UoSF2GGQzDUBTFbGROTFm1atW5L/gr49YX565QKMRhd3OXjLrTiqIsX768b9++LVq04EMYPhyJ7mHrwm1OK77f6CArSah4pVCpmvDX21P63N1uWP9Rb85au3UT1gqyAbKuRzRV02hNAx8gYFXJaiRiFuIMB6Awy3aAaf7MF3OOvfvlFqvoEUWH2+22Wq2dOnXC2QhdYi40mboQuzxXgqOxC1cF1IefnyW40gTRYxFtjz85uCRUHDHIZZe57cUwAOzatWvChAl33HFH9erVie5DOaUmnnNlKJCcnNy3b19CDM2goTl8LvX/xVlqEqkuzwJ8KMpfoszMzFtuuYW/OERC4r6pnU5nly5dcnJyzC8gRWAuQmWGy0vH73Hs1wDQ0SyzV0h74IEHYjWOg+m3o/UqVqzY+//QJyEu/AlGpzSH989uUOXL+lVPNU3/4eP/sblvdoKqS0yADN1fyICrwHBTYe92uPHaNdddteNvf1benQPX1fuyafri/TuZPDOeQc0XrRMyA9DocjACBnW1QgFY8QE0rrWofuqnr0/DBWjkApqdoDOWtEZKHST6HFCx7dy5Ddo22351lS9u77QlOxMXoH29BZrX++TPrbefOopOESUV55V37vouJbWSzRlVzne6Ha4KTrvLfu+993i9xRLRpGPoM6DuGU7704dlMvGVsEDCAn8IC1AbIEnSkSNH0tPTCXV1uVxpaWnUk5gwYcIFSiiHF5s2bcqbHIfDsX79eu6biPeDzK0LjTe++uorwsp5u9WxY0c6ZGYWE3pITde+ffv4ycTRW7RoEWfY/agrPWLECKvVmpycLIqiw+Ho3r17cTGSCEjWY9u2bXw+lk7YuHEjT2pcCksbrXPnzhQppeGTTz6h3ljpZpX30migRSLUFoslNzfXfFtzjOYwANx1110EDAmC0L59+182cgiFQgMGDCBuI4lWi6K4cOFCngZCkPkzMgfi0sMv4QFd17npFEWpVq0aGYeYbuvXr+dn/mYBGn1pEc3lcvFx1wMPPED5Or/J4Mo2GzduNAN28+bNIwD6/EaXuFvCAj/LAnzUTVeRmzhFUXbt2jV48OBKlSrxipS0+83yRObyTLUHnUzvVI0aNQYPHrxjB7p3oybAXFeYwz+rPvlZuUuc/EewgPlZ/2R6VLbt2bNn8OChNWvUtVpcDnuSy+P2JKUw4rATdUxRoUIQLBUEy9VWsbHorlm5dnqH27r0/++js159ZcWKFSePn8BxCdtK/D5ZlUJKiaLAt9/A7Te/3aL2sr+223TqKB5ma0n96CCOLWbF9ay0kZ93QwYjSm9Wi6H37e9ef832a2odb1Tz0LV1v+57136VKW/ooMhqsawW5+XlbNm8dcH8t0eMGPHn2zrVvorxvPhKewT8OABtFwRH2hXs/bLY8YDd0vWvXZa8v6iwKD+a9MvsR5Zl6rlxYinVMLybRBMCKC3J5JzRryNAPsJz4fe08KTiwpF5RS95g9shphSuEpEs3o4ag6fZKl88wWAQ82GAD4r84w+XjD8VeCfo3w16PkqFSwoOt3E0ThQuQp9lDTVbSgAyAVYZ+nMl8rAC+alCab6KKDbqQus6+n0ikenY9RpKf+ga0a/ZEmqViX5sBn1KftHjuQUjpfAUgIHHMt4MyYwGFpsNoTtw4FrHUikbkAuwEWCKFJoMxicAM3KypufnfhpBIWxCEFQS/Yg3ABbyYcOG8bqdB5KSklatWlVmT7XUPS61HYZhcLoALQr0+/3r169/5JFHKleu7PF4eF+Rr+GjQQR2aEUhKQk1Llxu202dbh42dfKrq1dPWL9+7J694/LyRx4/NOfo7hOo1o0lA92kyljscIaq9BYDoAOMfb8bYF5u9kv+3Kd9x172n1r01RYBdaSjW6fOHTRNCqvB0wA0m/U4BbAyAi9lexcBvJJV/M73p2a9v3LMM8/PmPEyAITU4NkAaD5Yo1Z77969L7/88o+OZ2rVqsWJI0RVMQ/KkpOTGzVqNGzYMLPYIC8f5izynYnA5WMBAh/mz59vdp4ZK8ICyU6mpaW98MILyHz90T1Cqc1chMoMl7rid95xjgC0qUbH2oB/sPPCdKL0wqL8tm3bmgEFMpzVIbS6sVFI8Sky+HNh3MDCm9L3Nr3ySJ1ae54YAf6YFI8Wwalwtl5GkyESBqx8VAXR5z81+OpPDfbc3ePQD99Ct1uKGtb89H/v6/7AaQGNmAljs7RRCQ4EoFU2vSlr8NY8uKnplhsabBj75BEjAn5UYwZCn8kZBvWjSG6qhDW5G9fATdd92ajmF7d3/CYjCyeAi7Lg1rabWzV9d82nUFSMiVcMmPTs9CsqV3WSv0HWhUpJwxUc3Xp0KyjMQyeMuJ2mP7MwNyCh7LEcJH4TFkhY4He1AGcTHz582AxAUzciOTn5wrmDo+YnLy+Pak7SWW7QoAEBcIT5cgzC3LoQW7lfv368raLA5MmTuS3N59NOwzB27DitnsSoUva9e9FBB22c7Ut3a968eW5uLiWA4BgSVqajhM5PmTKFy1CUjjF2Y/yVJImWF3k8HoJszEdLh0ncg/p2BCVXr17d3Auk0Zc5UnO4Tp06xDf0eDyjRo0qff9z2ZORkUFuiGm8JwhCkyZN+IXE0eDZ50+KAubE8EtKB+jkhQsX8pbU4/EkJSXxMlD6kgu3hzCOw4cPczbHj6J406dPpzye33j5WC4cDnPzWiyWwYMHc2Du/MaYuFvCAj/XAlTv6bq+b9++4cOH16lTh2ok/oIQJCSyjZOgzQA0f68bNGjw0EMPmevbcDhMTYC5rjCHzVWKef/PzUXi/D+mBeiZlp82mqeUZTkQCFBfRVXVcEg9fDDnjdff7fTnLhbRZrNXs4jVBDFJsBInRhSEZEFI9lSshSvcBUF0RbnSVkFw2Ow33nhjx44dhzwxdNSYUVOnPTPq6Uk3NL+vcfq/77nzzQyGPjN4MKCAjwkqIn0HJaSZKAJ9G7oEeogUHh7q/eJ19Yc1uHpG9TqvVKv6Yt1aE2bN+mbUmNd6/aNPy5Yt0yomsQ6DxyFeEdVZtTKXX6TkbLOIFVwWhz1KghZcFuuVgpAqWIVbutw0YeLEdetx0bEvSEvp0VSlVRfKN+ClcdQwjI4dO8YB0OQZzzCMvOLCMGgKGEgMZgwsL8Bm8L+mZI/x+kfmBmYX+TeokXwGFiPSpzCffybT0LhUw4eKH2IfGwCnAJZKvhdzsyYezX4zP7SfjdnDEIkYCuqoMPeDpQHoHIAVBkwtNkblBSfkeBd65d0APoZuh5FtpqDTS8ZiRimWCD5TCRHtANN9jugMfV4LoRd82U/m5o8IwqgwTPLrs7ILdzHqawRdE6LrJiwMZk1yVL4Gnw6bAaZlFs1R4SOAcQV5M73ejQY6HvTi5ZEAyCFcAB2bionZQVXVLVu2cOIhdXTpOy0t7ZtvvomblYxddxn9rlq16o477qBZVQLIuJUIhrYKgtPuoNFTxStSx08Y/eFHi0+cOAKoMA+7QXrDe3JExuFJijTep7yYXfQ9I937An5clE4lKWZOc5MXC6OuaTHABoDZQWnI8YzRWdnv66EdIG/c922F5FSm0oMp6vm37hr6ziSefFSLPA/gQ68xIqv4iWJpkh/mBeA7gDyCpKKCqTh3w5iCGCHz60lc/FiayvrNyckZNWpU+/btiQpdISWZnKNS08+XQPXq1YuoRVSKYjmK/pZ148S+S9YCWkTz+/0lJSWdO3fmtTp/lXiga9eu5Ov+Jw0RV5z435+88Dc+4VcC0ED0XkkOABgnTx6vV+8qGudzk1nZTHz9hlft2Vn85H92tL5qzZ9qHGxZ98h//hMMxISX9IhioDM/kHSQdU02IKRBSIIP34Ora7zTos6W/7vdW5QFd3Xfd1WV5cMGFhQU4rSqn7w74/CUG41wXgJ8sQpR2T2/3w/Nrl52Xb0vhzzE3J5qbJlZFO+Ooun8FuhzV8aor623tmmdTT3/sjs7E9Fnvx/+fuuBJrVWvTIjGAxiTRZQtZs7d43Sva2oX4TdJtaRevKpJ5nIWoQcD7KbmzHoBADN7Z0IJCzwh7PAnj17uJwFdZ5IDePjjz++oJ1OkhClypOkQgcPHkzYXCAQOBsAoSjKiRMniKxN3T76fv311zlEy1sgjvRpEe2rr77iFTUB0NxjhmEYnTp1SkpKIrVlQRDIzx5R//hSuNGjR3N4RRCE+++/nyeydIzmx5ybm0vTvISzd+jQwXy0zHBGRoY5te3atYubBDbHaA7n5uampqaSfex2+6pVq8q8fzk7yWiLFy82J8Bisbz66qtcQJzrUHMLmAPm9JSOiD8UUutu0qQJrq1OorG60K9fP6Jsx+W39H3O7x6Cwz766COichDWtnTpUl6ozm90NIWgRTQzAN2zZ88EAH3e7Zy44S+zwBdffPH444/XrVuXBgkcd+awMr2zNBQvE4Bu3br1G2+8sW3bNnqXaZEBJYa3LOa6whw+9/rkl+UucdXvawF61uWkgaRgqI2g0/ikBVaeGsiKHghA4wZ/q1Gtq8NRD117CaIgOqzOinZ3FUFwWN0VBAcSA602EWEjRGjiN6crRRCqCEItt71pvfrtbul8a6ubW97Y4fobO7Rqe3O7tu06tG3XoV3bTqc/7dq3v7lVh3atOt3c8bqG7VzCNaLQShBaC0Ib9t2QKWlgLKLIorY6bLYrBMFutaZYrA4cMYmCxSk63BUF4UpBqCoIlQShFvM62KxWzY6vzfkAGZAgBcJ+pA0h0Ta6+XyBcKgMIljs+CX7q6rqrl27kpKSqFdDj3DixIk8w2HEZDWE8Ji1sgHeh+AI7/EnCkue86vrdP14VGwFEH1WkS2NW2wATYizCrrKpht00IOMZ7pSll8uyJmen/1BWN4DSG2mJxIxIhqgKgIpdRC7S2YIbw7qfsDUYngy3xiXE5ybFzgJ4Gc4I6LPhqQggTpCWh+kpGHoEML1xgE2y4GJ2grwYknukyW5owEmADzjh0lHS/YwYDoIiqQHw8xBoUbK0zS8ZmmRAA4DzPNrw08VvwcwM6yMy8lZyvISBAgZRgikYsMroYvGeAB6//79VapU4Yv8+HvicCCimpeX5/P5mAEu/S/eQUVecAgJeosXL65RowZfGErG4WMBCuBrbRXTKiTfd+8/129cr+OkSNTZlxeUbICPQRuafXhIqGSMbkwqDK+PCcJIIcYQNNsVFTdQ4p2KGEHT5LfyO4DZocCT2XnPBuS5Jf6jbG5j9+EDV1SrItispDfd+77eshGFliOs7OUAvHGs8Nm88IiQPiKkz/BFtrD5FTxJx5KBK9wxrFG8CEPrCmiKoSEGrRgo3lLC1hAUs/IsGYYSwdkeogppEW337t33339/tSur25yMi22NVraOCm6Lw06o9G233bZmzRpAfMlvbuvNWU+EL20LkDeduXPnpqWl8UqG8+hpT0pKygsvvPDjgoxwOMyhgHLMYi5L5nA5l/wuh34SgI7V5T+RuigGvG/ftzVqVBcEwenEmfboxrxiuMVW19QYdcNVHzSvuunv7X8ozsOZ1/wCkGUkKhsR0ECTdKx3QhFsE5csguvqr69fddXIwb68YzBuMDS6cs29f9vhL2aCzQZoEDTAz537mRKI01xSSQFEsA45dBSaXb2pUZ3t7W74WAmht0HmY1DWmYYHKnewNWWqgo6bcdPhqzXQ+pptzep+MXJooMiLLXgoCBNHFTSusWLow15Dg5AKqz7bXCENAQKn22G1W0SHRRAFT4qjfoO6W7d+Fb3RGVRxMwBtDpsSnggmLJCwwG9uAWJ66rpObq8XLlzIl1SLouhyuTweT5s2bQ4fPmwYBtGNL1AatYg2fPhwq9XKmXSrV6/mcZVuSAgiBICBAwcKgkDL34hQ/OMijB07dnCssPS1uq4vXbo0Vkfjb82aNSkuLaKtWrWKr6QTBGHQoEF0iEAQRgfAOn/9+vU0pU8DodatWyvKaQ/s5m4rzwUFPvjgA/LQRfg+CUATBMmTGnfJzp07aXaTcJ+BAwdyD11xZ8b9/fzzz8lTIlmVg+xxp5Xzlzi/d955p3l24OQ0XAAAIABJREFUunLlyoSNls995hY7W75wolSltgeT8Oijj/4oxu1wOMj7pcfj+V30N+hZAMDs2bPJ8Q51iTZv3lzOYy3HhudyiO7ctWtXDu2Rkc32OZf7JM5JWODnWoDEhWhtI5foIcLp4cOHn3322cqVKzudTpfLRVWWueYsHab6kOPUt95664gRI7Kysn5uqszn8wokLmA+JxG+tC3Ap37jyoDBKDyKBKEiaHjlU60bvfDshHVFRfDpqs3jJj73pxs7CtYkxjS2C1Y7ykOzzWl3OBgn2mlHiKRiSirrRdDEp1sQ3ILgRDUMaxTKtohWi2izWvFjs9hsDMO2ioKNfRyCzSG4HILDJngES5pgqcSg5BQWLxJ17C6n1SYykRCkYUcZ0AJbK+8UrfbaFuEvHmu/JvWGPDP88I0NPm9ee8nTT30UViEoE3h0xrNFLIo+l99wyjAMn8+3ZMkS0mqj5tJqtXbp0uXYsWOKJkdA9YYQHlUZRfSzEDxTXPxYzokXpMJlEN4HRjHDZ6N4MadwxQBoUn9WUHdDYtCumgnGFwAvFpY8fzJnaUg5ydA3Ju6MY3f64BMhFXHsdyoqU9ddHNSHHskdWqyM9UfeKlIPMN1nttg5Ajggl0BFl5hhwME/wpMMXFTwcsTOdYAdBszMVZ7MKhmuwsAIDA1or/phG6CwRojJTKsR2dCYIgOKNcRKBZME2Q+wOCSNzSyaA/CUVxp8NHN+SfAHlngE542Iqkv+UJEeA0YjMiZB1/UNGzbwGcTS1Xu/fv3QqVW4FE56Rgm9dP7Q1BeNJnbt2tW0adOzNYI0eCH2TFpyypDHBmYcOQYAhb6iEggH0M6GBMYRgA9AHV5Q9FB2ycOFoREF0v9k9GOJQq0G02g+w3gGFkJDovIlsecuMaB5B8BrIfXx/Kwnso6/nZd/gKm50KULP3jXXTHJkVahbbdO2VJRGNSALkUYWLwH4C2vMcarPZLtHRvU3gf4lk1mSPRScMI/lkYdtJhcqqYiaKShLrWXodXrAeYVSMuKfFksMey6aMXMk69EVF841PfhhwUX8xCW5CGSophUweJwuit4BEG45ZZbdu3axYeWie4ut94lH5BlOTMz85577uEvFB9300pfl8tVv3597n2aDMIHlRe7fc4nAM287Rkf/W9JUhK+VFaRkYOjsz5uQUi3C12qOPu3bfxW/hFsJDS2zMHvjy7mQveDrOZRVVi6BK5vuOyaKz9+6jEoyYEFr0GzGus7t9qamwGBAK6Wiei6Bn4DihGDRgF61vBEnwZrRQ1szQqyoHvXLQ1qbG/b8rsDB/CwwpoaBcLM8SC2g+i014BwUMP2WoVVH8A1VVddV3vriEHIc0aZKoDPV8K1tZf0+vP2jIOQnw99Hxwo2KO+Fq12we6Ohv/2jzu93mJNU2K6z7yLRA2juaPEwxd7EUqkP2GBS8QCuq5PnTrV5XLZ7XbCVT0eT0pKyuDBgy802YFDybfddpuZ/UrLKklqjY85ydwcXM7MzExKSqLuMmdAu1yuzMxM/mD4tWb0cP78+ea+dZcuXajzDQDdu3enQ3a7vWbNmqS2TN4LOREPADgrmRpLjsn+ZAM5bdo0SjDZecWKFaWdJfLEU2D58uV0Mg23pk6dSg4P404r/Xf58uUkySqKYmpqaiAQMBuh9PnmPTTgxw50YSGH2om1ffvtt5MyBsHTZxPf4Kbgj8B8fwoToC9J0syZMyl3FJcoim3btuXn/8YMaLLS6NGjOcFTEITvv/+ep+cCBfr168c7YcnJyYqi8LfjAsWYuO3lbAEa71F1ysNer/fEiROzZs1q1aoVbw7MteXZwnzqyOFwtGjRYtq0aRkZGUSM+pVG5hVIXOBX3jZx+UVngbgCgI669JABqh4BJQDbP4eM/RgAHcIyrhaNMB3Vj1d+/sJLr97b94HWN95MpZd0L1yi3WHBIOLMVis15Xw8jBRCJClbBNFiEW0cgMbmW8RRHup82BgGzSBpmyjY7YLDaRXxR8RPbKx0+pURLYTCCIJQpUbVDrfe8vys6XPnrW7b6rkOLRd/+wV0u3HbTVf98M+ux8mHj0RjxTOf0+UMQNP0sM/ne/vtt7mXDqqmKleuPGvWS2zYGpGCssF8Bs4rDIzMKxpVVPARhHeBSkgfws4cwWdBNDAbmBLShwN0lI9Ws0FbrwReKiyYlluwNBQ5wgBcpIOe+YkC0AoiuAromQCfhOTxRfIQr/Z0IPJiUfAgqU6jy0EdFAVUCWQJFAKgI2Emo0EANGNe4/D8hxDMydSfzoqMCcMYHQZ65Wd82udM0jpkIHQQ0Zl0PvORGC0SjPQtARwBWCyHx2TnvAgwWYWn8gKvBbUdLA2M6KqBoeoRSVPDekQymJNZQ9O3bdl6ww03mEX8rVYrZ5onJydXrVq1sLBQi2h8nvLMgnlJ/eNVDeVqwoQJVquVlOhOv85nhsg196RJkwJenxqK8ohliHhBCeITM3KR+6yP8XsfKfD1L5CfypffM+BgtFDFAOgzABIDUWvkJSLWQwB0PmPWzw5pI4p8I4oL5oRKvtN1P9Om1yPI6icavgpGELRcxRcC3WcYfoD9BjLiR5fI/ykJj4zAjOLQdyzqMgYFqOqKzGuaX0HEStUgoioAWQCfBozpeeEXiuS3fcFDTOW8wNAQX2cbLwSo4sGY0afyciZOn5ZSqxpqU4uC4BDtDJK2sy01NfW9d9+7fKY0uH0u88Ann3xCPo1I6ocGPsTNIvrCgAEDCgoKiCVNtqLRIn8xyyi3F49NywGgzeAphcvPlh4K+Q1QNU1asGCenbkqdjitVntUlUIQXHYbLrBy2Rtu+OwHavvojijcpKOvgHAEvF547hl//YrvNam2eMLw/VIx7NoEzetvbt30033fgJdpf0WQ/mxoKBNdrEOBDiXMkYEpeSy9Uh7c9eeDdVLXt2ry5bzXIaAAuhZEXNpQUF8aGc8MgI4wv7tYO+7+HK654oMW6WufeCQnMxO8TAw68wS0abS+6ZXLv9sO772zNyntKqxvcWWbxeW2WayC22OvWavapi8/x+ZalTSshXjbzs3IK9S4gCnZiWDCAgkL/OYWkGWZ0IdHH32UulJJSUk0AKtYseJ7775HHc0L2jmgm6uqWrVqVer7Op3O1q1bm3sz5iaHIDld1wOBwODBg2nQSJxZykK1atW4Ic0XUnNFl0+ePJlOpmZv0qRJdMlbb73FVwAlJyfPnTuX9nMveQSq0k7SZ6BliaIomrWqy2ka+/btS6IfxCjMy8sjAJqnuXTg+eef50v8RFFcunSpeTFy6fP5HsoOQbpNmjT5WSMHXjY2btxICSaL2e32V155hQRJfj0ATWyaN954gyje9G23210uFy3Qw6lTReEUCZ61Cx3QIlrv3r0py/RNqwQuaLzPPvssL5a01vWCRpe4ecIC9JpTPb9r164hQ4Y0bNiQyFxUbxDT0PwilA5TLZqUlNS0adOFCxfSnCX31xS30OEX2DyuGud/f8GtEpdc1Bbgj54CDIAOqBquB0VRZhXkYLyPHE5ypYyHQ/KaNes2b9o0eeKkLh07WQTBJdpT3MgcEhgMfbp4WxiRiAHQgs3KSNCxb5tgiX0Qibba8NsuWKKEHDb0I5CbbmcXRaej5U1tOtzW5YmnR6xYu/po5iny/WMwxHTjBt8Pe2BIn0jz6l/0uHlb3jFEKc+2RdFGLSYcETeuihdUONttLuL95FB6ypQpZF1an0Hh9No1NqxZCTrkybAC1Ekl2WMKMt821G8YUlbCqKbkepAPUE8P8olEjMwspECfAmMpRGYESp7POPZxKHCEUZgZWBwPQGtA0uAop1kIsNQvTS3wDyoKjQjpr/nU7wFOktSHzABoHIJLhq5EDJLgiEjIpI46TkRRAoCdOrxToE44XjIxCKNVfUSJ/7ncwKoISlGHgZVwBaEDhQABdimWCoZ5ngD4WAlMziscG1QnA4zIKVngj3zHmKphpJ0ZpK4QA94RZwQwpk+fzqdeOAOaOAGEQdesWXPfvn0XcaH5+UmnwYIW0fr06WO1Wqmr73A4yCzETrDb7dQ5/5G+M2nSpPz8fBIKwBVF4RASqBkhXQHIQWeY8ExQGhCUB/hDTxd5P5KMQ0RmZ+vRyxw1aAyrIb6gqrCZCYDFmj40N+upovy3w9K37ARDB0NB5RhVl8JayACQES7GLRjR83U4oMPCEm1YIDhAk/4bKJrmLznAJjPYSXF1JF2HGhwMNcK18rRioARgE8BLOcUvZGQuVtUvAMWj97KJjXAMgOYOyekuit8PaAG1QC5pfXtHIdnhtFpsgpDkcSFTk/iagvDggw/S+YnvS94CgUDg9ttvJ5RZFEU+xcXrn3r16m3ZsoXbgQtw0XjT3Afg51x0gfMIQGPedV0JBFEYasGCeeTtVGDejK12i1ltzGITHvx336zcDGyx2EIYBfXLIBSCUcMKr6n5fsu6yxfPhnARFGVAt5sPNav75bzZUcY0ks50ppuBs1F+HYp0dDOAU7nRjQnNB3Lh/h67G1bc3uCKrwf950hYgmLGk44B0OiygFYL0VxrcSHs3QY3Nlh7bY11jz94tCAHudIlIQiG4B93LGhWZ/6Dd2+vWqmL3XWFxYm9NItNcHqiC9nGjhsVDvs1TdI0iYTqES9QJZYo3r6X7h/RnliyE78JCyQs8DtZQJblO+64gxAE+hYEoUePHocOHSKyCdX+BCJw6vF5TCxhi4cOHaLmhxqk/v37UxTmxobCtD8QCBw4cICGHHHf6enpPHlxlxOa+SMpj+Q+qOMoCMLChQtpBfq1117rdrtdbGvfvj0Rb1H4zCSvQYvTAaBx48Yco/F4PEeOHOEU6TK7kpSqW265BZfeOhwul6tGjRrmCV6ebHPAMIzHH3+cU3GdTue2bdvOEYCeNWsWxSUIQvv27X8BG9EwDPNNqlSpYrfbt23bRhKu5wWAXrduHe95cHsOGzaMKJmkEmM2yG8TlmW5Xbt25qL1G8T7zjvvUIz0Jh49yjxh/QYRJ6K4jC1w8ODBoUOH1qtXLzU1lY8HOPeZD7bN70JcuEePHm+//XZ+fj7NC5prp/OyqDauGud/L+OHdplmnT96CiAArUmqFmSOtqIjIVlVQrIUlCMhGTEZLTZAQsdsGmiotsvWfgIQS3Hb5i1bvtg0Yey4f/y91803tU1LTjkNHSMJGhnQqKnKPlEY2uqxCFdahHSLUN8iXG0RrrEIdS1Wl8UmuDzuJs2vvf/Bfs9Mnfzu+0uWfbpi05av9v2Aq2eYZziQDC2gygqKO4PMRm/hCLp2f2nKkZsbfd6x2dY9m0Fj8s46gKyXBSdzxeHLeGglSZKiKJ07d6Yqi3oOpHxrE4Q7OnZ9b9Xq6Qd3Tys4uljyHWTwnz/q/Y/IWIjloegF48hHy0gMgNZQK9lYp4ZeCAYmF3uXhwMnGPLrk/xx3Gf6G0ElZUUBvZDRrp86lDmsRB4Z1MdmFu1gihkRQL1NdMGkoCBwBCQZBaCVEGpAIwCtMMapwuDIvRFYUBSekuudHNSmRODp4sKxx4+vDsExBiJjeWZjeAKgGasMd0QMCIYRnt4B8JKveHhuybMAw/N9M4r823VaKw1IEWPavvQdDqK2+MpPPm7YoJ65SjcD0C6Xy+12V61albuN9Xq956VW/+NXYTTe6dOnjxl0NhuKwnXq1BkzZgytlaRBkyyHdT1Cy8EDIUU30OvjPoAFoA0NGYNUGB0MzQv6TwIURgDVMdhW5qiBA9AqgF/W/QBfAbwYCAw7deS1YPFeViwRH0ZyIiPuR3AWIiZtjkXcq+GkyOJCY1KBPFiVBkd84wozvmIzJTH9u9KVDL4JHIBWWCzFgCVwXnFwRpH/Q0XdArAWYL7XP//QvhNMRobqZManV08v3cN6Ti+BcCGEC7Tgyo3rWrZsgQqudtQxIgOSL8frr7/+N17p+McvgZdeChcsWFCpUiU+0KMCYMYfRowY4fP5DMPw+/2c+qaqKvG04pS4Ll77nDcAmr11Ua0cqnHmzZ9rN629oi4LwtD0EYT0q2tPnfZMSA4Ew2FFhtzj0Lvbgebp3zSptWr1/yBUiHOgYwdntGy45rEHc2QZW0pqIBGA1okEreL6G9aP0g1ciaNFIOjHBm3of3JvSN/RvMb+P7fcJjOXqpIOkmFg22dEPxHWhAVVCIRg/w5oWW/NdbU/H9DnVH42PtBQGCWk/9VnWnrtv7vsNzC3GKJgFUSny+724OyVIDz87wfz8nJiWDMVA444xwUu417Sxft+JFJ+iVqA43pEYu3YsSO1AU6nk5zjDRkyxDzMI1CVyyzwQ+fXPB9++CE5/aM1OO+9+x7dn0fHAzzeTp06WSwWzoAm9rQgCO3atePn8KsoQCgzAPTs2ZPEkakP9N133wHAq6++Sqaw2+3Jycnke7DMW7EZR71z5850Pn0vX76ci07wq+IChmHY7XY+ZGrdujVpWcSdZv4bDod79uzJPZJbrdbc3NxzlOCYMWOGxWIheNesaGG+f/lhXdf//re/m7NpsVhIS5oXCQ67lxkwPwI+gcEL4csvv0yy4+bOaJs2bXiqiE/B//5mgXA4XLNmTZ7xSpUqlRM1lyuhAvaLBdM//PBD5kYCJfOcTufmzZtpPFNO1IlDCQuUtgBNksW9bvR6UoWjRbSMjIypU6e2adNGEIQ4B9q82PNDVC3TflqgkJaW9sgjj8ydO7ewsJCPDXidUOZYunQ6E3sSFvg1FiAwjS0Ux3aGLRRHkFkzkB8a0c78sOWidAmKD/IPH6DE9qiSfOiHg1988cWGDRuemTzpmcmTJrDPE08NHzFm9ITJkyZPfvuvHWenWp680jO+sn1c7eTnm9addPgH8PrPcOhGAyG2aNWIIA3QYHoJQGH2rSoQQCQ6BO1aTriu7rQ9mxCmDPpZ6hAxR1DpjI1SGzfGilM6POOCS/ZPOBw+efJktWrVqLn0eDypnqRU0V6BmOhW0dPy2vunTc0yIAAQjoFtRBT2G1pAi8i6QQA02SgUZBRigAKAL0B9IfPE1Pyi9xXjOAJwuqTJqq5EzhTfIABaAs0HcibAWgOm5Pv+WyL/JyfwfEFkJwO+JQCkJ6uEPmsGqBHU4KAPukxkHz2EmgnIJ11cJE8+WTQ8q2isrD7tLXrZl7sJ4JiO/uGwOOB98KNroBi6xMBBiWHrIYY+T83JmShLLwKMyQs9l1O4kbFXVZWBjIauqad9V5YUFXbpjP1/u4iCocTwpUre6XQSKlS5cuX+/fsXFxd7vV5zX+6SLVVnZmzWrFmcl2NuFon47HK57r777lJEAVzZzuoiYhniHU8AvKfJo/zF//arAwrDc4q8RxlxmPQymBzqmRHzf2y5ekTDMpwLqAD+nNc/JjtncUnxAfboNUaZR9VUYO69cH27rmo494a8fAOKAVaEYHyh+nih9FTAO82Xvxn0HDbVgbz7M2osipURnpG6jWUGFcN1yNZhTcSYkZM1Kyd7GcBugA0A40vkUZlZbx3/9gSyHNFFIXXXtYiBrPoYbCUD7AznZiLkrUQADhfnDhzzFDcmZ594PJ5evXrxfCcCF7sFzI6mFUXx+Xz/+Mc/zJNbvAwQ9aF69epbtmyhNXlUlug7jgHNd/Lq6GI01AUBoNUIVu6yHJ43f66rgjPGfSZPFjbmcoLBt6hiIdZNr//ijJfDQbjrr6tbNVjdpvGWFe/jUpxwAN6YAY1rL+zRdZ23mGnv4JuMNUUUgGbrbrAHgtAzfpPUjhKEoY8ealz761op21rU3XRwB2hh0PSQbIQkQ0H0WWcf03TXrm3QosGKxjXW9uzyVfZJfI77D/zwzDMv1biyhSjUF4TqNmcyOpS2MO0ehj33/df9x08dP/ORn61PRL0kOlr6+8x7JP4lLJCwwIW3AJdvKywsJPSZ+lK0EKZfv37EX+OVe1xLwPefx5Tquj5z5kyaFKXuCJdf4NHxAE2Sz5gxgxQwqHdYvXp13rBxAJpfwgOcAX3jjTeSrITVaq1YsSIhNenp6Rzn7d69O/fNRTnlN+HYSp8+fXgLKgjCrFmzeNN4NuNkZGSQ8Bl9/+Uvf/lJABoA6tVDforH4yHoh9pjnoyzxQUAM2bM4MhRgwYNyjnzbId0Xe/SpUtcF5wAaBLkMhePMsNmu9GEdiAQIOWNp556ymq10s3p8QmCkJaWZvYhSVj/2ZJ3gfaTc0USvKaE1atXr5y4KON0An8uv4AltGbNGq524nA4vvjiiwQAXY7ZE4fKsQAvflQgaRmHYRj5+fkzZ86kpR5U2Gjq0VyV8TBRk7gqkSAIKSkpd9111+uvv15Sggv+qDWhYSfpFPHyX07aEocSFjgvFsA2SGNUPayCIxrKPssIQAMCi9HhErF2YgoHuFY9OnYyYdAx6JmNqXC/FvOOG2FLOxHp01SfHPYrUlhXf2QFjRyYe13Nz6+pvKpV+ro21yzbtgFFXmljK1EZykzLQqOLQ8sEoFHuwRdSgn44fhB2bmZwUAy74SDzGbY622DLPMA644JL9k8ohBIH+/fvr127NikFOSxWF7qPZJtVECqlCKnJ6Vc3GvnEqP07vyMaV2EoSIbFtpVpUKK9yXrMVMUAu0B/OS9jtrdkfl7BIaa8YSiqrhrsfCNGgjYY+xj/+pjXwc90mJJfMii3ZGCRMr7Y+MwAUvxAJM+gwoZMNY0B0JHoN3KfJaSIapmgfAew0BuemhsaXaSMKA6PLfa95CvcCEoGpUFjcCAB0CpOaER0dFFH6sDFAPsBFsnGU4XFo6XIZH9kVkFwnYq6w6TFEPIzbiwWbP3QDwf+/VA/spPtNOGfV/wYsFqtt91224kTJxRFoT6buS93yZYqU8a0iFa3bt243i/ZyOVyValShXvJ5lRNBroyL4+gGoZm6CiLUgSwQYGpPu/j3uIhAWl8gX8Pk7+ITneQFk9soYYpfhZE3XAIGzgpshXg2RMnJhf7ZxZ6D7CyQGU4ROIruo5lKhTMPHbs348ObNvh9nt7DyiMwI9aBmNPFvy3MDxKgUlZWZsZ95nFiTVSfHTRN4HVqii9gaz9bB22qfBasW9ybs4iJfw1Q5+fPV40Ntv3UkHRQdALdC9KwsQ2qmN53neogWW5xzbJJXtD/hyATYGCz7KPv/D66w67KzkplSvV0hhn2LBhv2ClZqlcJHb8/hagYTUNV1esWNG4cWOqVfhQnXy8c+QhEAjQguBYOSrv92Kviy4IAK1pCiMF47Of+cqMqtWroKyYw8OgZ48gJGEgWt3bmKtlQRBqNr5q6A2Npn23CwryUPti9WfQuvlXf7puXVYGBCVsNHnVFO0msT00lx6bUccYp44KNq21vUHtjHp1vp3zEoRLQJdB10IqlMjgiwLQjASN438ZSgqhw03v1qkyq/utK/YfgGenL7r2+paseq3gcda12Sq7XJVQwNrtEey4u8ff7z1wEL17BaUgk3uOm3bn/aW4gLlnZA7//m9IIgUJC1yGFiD/szfddBMBENTBstvt5OHaXLOXEz6PdpNl+bHHHqN2iABoEpsrM3Zd17du3cpxVUEQxowZk5aWxlu18gFoVVUDgUCVKlgzE8J4/fXXY+U5dSo1h6R/unPnTs4fpJzGJQYAJk6caBZI/fe//21mwprtw0GZ9evXi6bt4Ycf/kmEUVVVekDET6lZsyZPjzmKMsNmANrpdJIqa1y+yryQp0pRlBYtWnB6MnW+fzEATXHR6rwhQ4aQz0nisNO3IAibNm1S2MYRtLOl8MLt13Xd5/OZcbdrr7329KLCn4qYPGf+1FllHN+xYwcVbCojGzdupN5bGacmdiUscA4WoJrHMIxjx45NmzatadOmnNpGNa3D4fB4ogK49HbHfXOdou7du7///vtxkjhaRAuFQgQ9n0NyEqckLHA+LWCAakDQAC+5ZI9CzwRDxxBnRKJNn3MBoJHpY4CqqqU9MEcQ6zFCEmz6FG5peqTN1bs7tFz3w350E2YwGIjBg4asa7KuqRp+CMIuiwGN7ELFQPEErx9lGIk2qMaAbD6OOsNkNITix3jgch1aqap68ODBRo0aRWeyBWRM4SDbEoWibSkumxNR1hpVrnzs8cHb9+31KwpOQjDcmRQpSeIWAOmiGyEwJ3Ry8slTb+WUFCJRNBLWNHwo7FTNgBgATTvQtVIewCcA4wqlx/J9jxeGJmeFPjNQ90BjpYU5HES+s8JAZw0LrYqSHLoGGhJNwwCnQN4F/oWhrDHZecOKtSESDC+W5xSEvzYgG5U3UDca1YRjLH5i1OO0IvNSJ6FmCHwIMNLr65/nHVYkTT1VsF5CSRBJ01RV1QxY9cWOiS+8ds+993Vof9oVZ0pSBaI/U7VPhAC32927d+/vv/+e3CBz0TnqFlJP+IwyeYn+WbZsWZxWAG8cb731Vm+JX5ZVWY5R65kRUDw8+lrL+IgZc3l7BOZ7ladLfMO9xVPz875Gf4D40LHKYBdgYaT3N2rJ03+MCMg6Qtg7AF4o9k8s8U87lv0NI7zjuZqBFxLZWAYI6xAIdGjVCt+ACpUFofpfB02ZmBMYWBwaGlTH5BXvAMjWGLGZKVPHahoevakSwfKJN/cCrIkg+jw7x7c4bGwFeFs3nsrJf9YnvZNXcgqw/sX4NVyIHzdKKmag+eTDB+YfPbkL4FuAhcXFr5cUzD12qBCAxnHcpBQQRXHnzp2/vdMXZsTE1/m0AI3gSkpKRowYQWM9u93Ox+k0qHQ4HG63+4033uARly5FcYWq9F9+7UUUuCAAtD/g1TRFjciSFArJoc1bN1eqWkW0uxkA7RIEjyDYiU1ss13hdFRnr1yKIFzjsrSdPm1JRIcTWXBz+9evrrNk2fvIbiZqMzerjtzn0x/yJagaUFgIi9/Um9f+stmVJ+tW/eGf/4fSTtGlOpGQpgdkI2QGoKmaef21461aPJ9S4eFatfsItqqCTbC5RcFqsQqU6SIOAAAgAElEQVQpDBy3uiskYQpFR/Mbrlv6yTKcDWM1FhOwNlVV0bqTd4XiAqXPpD08W4lAwgIJC1xYC3AMlKLp0qULNQDUaxdFcciQIRxHKF3Fl95zHpNLKhPU1SMYOicnx9zZNcceCASaN2/Oey2tWrWSZZmW8ND8KgHQ5kt4mJSsCwoK6HICoLt27Xro0CGXy5WcnEw6Hv369aO15OY88psQ8xcA5s+fTyg2WbJr165nA6A56/ztt9824c/iU089RVGUA25mZWXRM6I0X3/99YQjxz1Qc1J5mABorh9dWFhIVuUnlBOg3oMkSfXq1eOr5CgNvxKA3rZtW6tWrURRTElJIbyVyOxut3vZMmxlyN2fiVRSTjLP26E4ex45coSXMUEQWrZsWRqM4HF/+OGHzz//fN++fTt06NCgQQO3292yZUt+9NwDBw4coLfA6XSKopgAoM/ddJfVmec4hwQAhw4devnll9u1a0cvGjl+4QWb1mHwv2UG+vbt+8EHH3Cyc9xrQmYvc+dl9UQSmf1dLMAAaL8BxQyDDkeJz1EeNCNBm6BngqHPBYBGLjXbkJCFwB+yVok5LRvgk4yCPOjQYlXTaut7dd6TlwHeYHSw5VciqHZoQp9/EoDmC9VDUiQQUkKSooOuaBhvVGUxzrI0eIobY8VxgeIuuUT/UjWI6GpEMwxj4MCB2NWJfbA2syIMbU2yOZLsyS6nk7yeCULNq64a/sRTWd8dwWkGIggzA/oQI9NfC58ccvDrF44c/y5KMpVkQ0HlcDbeNlADU2XTCQhAB5lex/cAEwqkR/KlR0ukJ7OLPiqBPGZzRQMFpTbCDIOWpRgAzaBJFYtVBCHEIMABgI8hOPTYtwNyC//rjTzhi0zI9n+tI4odZuuiNZAjRkSBiGLoyDVlvu2Y602NZKDzAObkZD2Tl/dMbsm4A8ee3bLj7S82Pz99xr/uvqf1DS1tLrcgJgmCzeZwkWGotk/y4F+PC2EgQRAaNWr07LPPlpSUcMcnVHaoS2buA1+iZeqMbI0fP55YKXEd4F69elGTJ8tqKKiEgorOCOnoChXFN9hjx4BGEwPvBSLP+eWxvuBzxSWfBH2HAQVREbdmYu6kqsJZhiwFUcxEB+Q+lwDsBHgvBGMy8l8sCm5n7Gk8DQtBjMKssXIsww9f76jkSRasTsGaIlirp3bo/WSOf4isT/IGPgPIYF7EONptipRiJHgp5nOQ0Z9PAbyQmzOuIG+hYnwOsEjTJmaeHJ9fsAywkEfRdyqNEZYjRKGxTAaYZvS0/IwJeZkbmAPGJQY8l5M/5fjxDWymBwB27txZpUoV8wDH5XJ17NjxjMeQ+HNxWkDX9bVr16akpPCOpdPpNAPQVqu1c+fOBQUFJClJyyziVmCb65yzhc3muVj6ouUA0ObsnHs4vkegaYosy/v372/SpBniFHaX1ergT0IUXXaxgig6LILTIqRahEqCkJbkaXhV7W7XNfrPwrl5kSDWEnoEFDlaS7DZMmoEo689razxBuDt16Fpzc3Nqh9rXuNYo+orj+0DFVc5o/dRQw1qDDVW2G0MgCMnT73y+ty//eM+hztdEKoJQh1BqC5YPILVlpxWHSFywYp8NCvKQt3Wrdu7738QMSIRXacOHMtnXH8nASifezlJnJmwwO9gAYI4FUUJh8P33nsvByUtFovH43n00UfPliZzpX+2c37NfhLMveGGG6gHTAA0oZ88ar/fz9d633nnnUlJODEmiqLT6dy1axcAVK9enROoSVj5bElSVXXr1q0kGkjaI+PHj+/Xrx+pW1D9TPxrjhqXvhUZc+vWrcnJyaQlTcg1qXZwTxrkDtusCDxixAhzA/zKK6/QzcuJa82aNXRzym+HDh1Kp+dse1avXs0nGARBWL16dTlI99lucsMNN5BteeN17NgxOrm8JVJnHuPA95QpU/iDNt+2evXqn3zyydnSUM5+snY4HN65c2coFDp3bM58z7hei6qqW7ZsISyY3EVy3J9Unr1e73vvvjdmzJhrr72WiNJEFCXFbQ/bvvnmG3MU5xI+fPgwF4FxOBwHDx4825TGudwtcc6lagHzW6woCqlh0OpFmjkzDGP27NlNmzYlTRv+5hIPpTSri5Z9OBwOEuJPTk6+8847V6xYwauyS9WSiXxd5BZAvqEBMiLRKLBMG43FYjBLFMyJHTT/8kNxgdPnGER8ZeKFOIKSGBP1yUHL/nT1ggf+tlsqAUlCiqIMuhx1saOjUrAR4Z8YhI1ANsOUUTfxzOEi7aF9uH6fNGT5aZicuBSW+fd0si/HkCzLe/fuvavXP5I8ngouhFP55vY4HTZ0vsF40YJgFZ12V7Ldk+Ko8MTgYR/971NFRxR4fwTmHz0+NTfjucxjPwDkaJpfC2sogYsj7pCiBQIhOeiNSEFZlsMyYn9eJkcwJS8woDD8rxzfyJLQmyEtkwnshljRiRjoJ1PTQ7ohsSdrAv0YBCnrcFiDj0PGS5rRv7hwkBp5vCgw8VTBOgmRRzk2FUJPVAc9YuB4HlXCYioxQSW0YcuWKS+//I/H//unu++qcmMboVIVweUSHOjn7bTChsXqSj4NBjkcNgtbjW23i23a/Gn48OE7duyg7o2578Y74XGBy6GEde/enbeVHo+Hwvfcc0/ZeccHq+voQFSWsEZCve4cgNVqZGyBf7Q/8kKedzPDjhVGIsSb0BtPDOIoHM3uTUvdGX4dYm4tX/EGxmfmLSgKb4mgErQcvUMMfaaLWPH6bP1mq8UjWpPs7iqC4LK1vWO8Vx9TEt6g6tm6hrRr3Kj6iP6J/cW5FZxeiYJM+EbslCNzT2ZNyM6ZIgUWAcwBebI36yVvznpdy4hOz0AEdIlVaJgd5tmzJFAkM0GYuRm5U3NPvgPwOcDrxcrU3MBL+YG1kpYF4GfQuSRJy5Yto/fU7XYT3C8IQkZGBk9cInBxWUDXdQkZuKFJkyalpaWZFysTYYsed6VKlSZNmkRZM692PUcG9NlsYh7KlaaRne2q337/BQeg+fTsj0yusWPHWiyW5ORkzkChkSoteGEYAbpbZhodNQThql7dh74wZYmuYJ2koG57dIsAVmySYYRwUhRKwqik8e4CuKnxnqbVTzSvndWoyqY3Z4Dm5TWcBmD4feqB/ZkL3v7gv0OebNC4ic3lZqoajmhjLFgFi42tWXLYxKo2sSqVj8bNGq9bv15CSXtU90EAGn1oGNSF4nWWKRBLZeI3YYGEBf5gFuDA3EMPPZSammpuCfr06UOk2jKTbO53lnnCr9xpGIaqqp06dXK73VyNmvBKHjVNiuq63q9fP05GEEVx4MCBhMXUr1+faMiiKNapU4cnydyw0U4toi1evJiqOGoaJ0yYQCuDCJTv378/60jiPD6/T5mBvLw8uoSqcavVumvXrtKIocw2usPDDz/8cwHo+fPnWywWwmotFgvJRpeZntI7v/nmG8opwaNz5swxQ1elzzfv4QWmVatWvBdOuP/s2bNpCGQeqJwtTBjWj1rSmzdv7tmzJz0mShWt/Xc6nTfccAP5WP9Jm5tTyMOGYcybN8/j8VSuXLlPnz5Lly4992zym8QFVq5cSUmlRNavX3/58uVz5swZOHBgixYt+OMgwI6jz7wDLQjCW2+9FXfPn/y7c+dOKkskSELrAH7yqsQJl6EFuHNOWqxKqi95eXnvvPPOrbfeyr2zUm1DrxvNlBDr2cw54kfJ39TSpUvJP+1laNVEli9GC/B+Qnzi41Da+MOmsctZzzwDgFYYaVWVYOtGZdrYHwpO4DgLXR0yYYTYN0KEJPtMGPRZAGjCoHV2adQ7D4HdBECT1kIUrYxLXpl/S+fuMttDpF0A2LhxI3cQTY24xWKxWa0Omx0pXxbRarU57S6P01MB5TEFu9UlulN6PPDIk3MXzNyxa35ewXaGLJPUhgq6yvA1ZnXC2KKocIj5DHylRBmc5e1fGJwYgfkBOMrwQewgsfIVfQiaAhEJ/RfizTRDi2iqjL7amB+5byV47Ujx2KzA8GJ5mDc4JjtvKyNW47UYlaFEfLISzMnJ2rV7++cb1o6fOK516xtuueWW9PS62AW1W4TTMHO0OrdYBauIH77xsGiziDZLSkrSvffeM+Ol6ceOHwHQaRaTnHOY+3L85YoLXA6F65FHHjGTJBwOx913311u3xK5wxH4USJeDRpqCMXE4YWigicK8p7OK/iCyaQgaxD1U9iCimgg+pxJDQZfeVbUNFQGh8MAi3J9LweDL+UVfB1Dn6PGpwFKbJhCUtJf7/meSc+4EE2yV6rc457ncn3LATIMQ0eV+jLrjridmsr4y98Z8GZ24YTjmdMj+gKAif6CZwpOzvDlrAI1gyNMWNpViRXTKACNrH/IBFgegclZ+XMNeRXAyyFlWo7vpVz/pxE4AlAYwaTwRZbDhw/nwzoaYrz++uvlrDi8HMrexZhHRVH8fr8W0TZt2kSOizjgSTwtXhfVq1ePCDplIg9xVU2Zf8uxT5xuIV+yrEU0SZLKfX/Luet5PnTBAWhVVTl/RJbllStXpqenE3ePHgONDXDsakU2n8PucthSrEKaIKRZhSvczmqC4OrZ8+8zZszYv38fAIRi7mtJZIjs8fESuKbaikZVtzWvvbdZrS29uu7w5UNEhpPHij76aNnEieN63PnXqlWrMx+CGK3odIlOXHRzxkbLlhCEvsJpq/fXbr2PHj+hRNQI9pHQmYaqMbceCQD6PBfCxO0SFviNLEBqbo8++iiBieR4yuFwdOvW7XevkQ3D6NWrl8PhIPTN6XQeO3bM3OqQV4oePXqYa6377ruPQFJFUdq0acMBaIfDQRoRZ/NlMXLkSIvFQig8NZAcFXW73ZmZmRx7/clnU7VqVTOg/MADD9AlcXfguOpf/vIXM1hpZkDH5ZdHTaRp3j+76667+KGfDOTm5nKLiaL42GOP/eQl/ASO3T/wwAO8G0H83D59+pBtzQOVs4Wx5QqFSPGZE8+5+Lgoirfffju3eTlMcJ6wMgN33HEHz6kgCKX8kpd5UfxO6qlQxhctWsRhd2yd2Ua9KHri/GgcA9rtdrtcrqpVq3733XfxEfzU/+eff54GPEQSTwjh/ZTBLsfjVFHwnKuq6vf733jjjd69e/OJNHoXzK+t+e2gCS2Hw0GFrWHDhgMGDPj4449p4o3uHFeD8egSgYQFLh0LxAEv/O8ZOTxNViYykBKOcf9URBSjgBLj5jB6zumW0EzcidF3oqxHdlMiPhNwjRg0Qc8xADpKlGYRnANwdEaaL68/vH9F2aYW/OjRo0OGDKlWrRo10IJgsVlsDtFptzpEQRQF0YbEK1zma7eLgp12iELlatX/1PqBESN3HjwQjuDT9Ur+sC5LhhI2wiFU6pYkPYw60ADbZPn1/NxxmZkjcgtG5Xtfzg1lAvgi4GfKuSVg+A0VnUKpSgyLNhjyGJUqUAzwapClw5I9R+bty5hztGjMtoP3vrv82a17n57/weOjpowaPrZ9qza3tEdnLebN5ca11E4nc83ED4iYH75xAJrjznTIbhe7d//rkiXvhcPB0qUEgXEmacILsblfag6XvvbS2zN9+nTqeNvt9uTkZIfDcYYuHFUXZ2SbxCuQtBfScCpiAcDg3MzJxZnvBgryGccZTycBb/rG+gDLkmRizdMtJYAsgHfySuaXBN/MzPgWkPtMLPponNHpKVa4mJoH6OANSq60qlZ3ZcGWKlxRrcPIUcuLCnIAmCorzYnwao4CXHYjVskwj5ffAiwokSZmFk0KRF4GGB0MPCf7Z+RlfqEh+hxjUmNCSI4GQywNOjldDGkzg/6pangpwHSvb6ov8mxWyfqwfJKlJIRUa3TNSa9qVlZWrVq1Yu+p4HQ627dvn+iBRJ/yxfYzevRoPlwlt9XE07Lb7eSAhIbJfKxnGAYP/8q8xjUEsiz7fL7c3NyTJ0/6/X46GnfOr4zxF19+wQFoen/omyCevLy8xx57jA9czUgEbzZE0eF0VHC7k2P0ZPRF63K56l/doFfvu5574flVn61dvX7dyrXrQrKx6cuCzje+1bDa/D+3Wdu66ZJUcXjP2+e3bPl3mz3J7a6AT10UXG5cVimKDtHuFGw2poklYsDcLmEr7BKEK2pUa/vlxpOR05RrNG9cLyrBgP7FZS5xYcICv5cFdF0nkI6DrU6n85ZbbuHEh98rYRTv/fffT2iIy+VyOByLFi0yd3b37NnTtm1bqiSp/qxfv35WVha1W1pE69q1q8vlooXkgiB8//33HD8tna97773XarXSfcwEhx+XgI0fP563haW5zPxWXCy7U6dOfB6RAqNHj164cOHgwYMrVaqUmpqamYleWzmy07JlS3O1zwFoEjHkWeYRAUDfvn1puQxlv2/fvuaj5Ye1iMZbFrvd3q1bN+z9/hSzm9+Tmq23336bewgk4rzL5dqwYYOiKHyUUk5g2LBh/HIS3eYKKj/2OMePH0/RkcjgL5gL8Xq9siz36tXL4/EQg14URb62i1ueZ+psAcMwDh06tGjRonHjxjVs2JCgdj5vT6XFZdqIqUE9LfMzveOOO+bOnVvmxP7Zoub727dvz+VW0tPTiY7EjyYCCQuQBWhmIisr6/333+/ZsycBzaV9CVLlxjucvCqgtzgpKWnQoEFbt26le5LnT7OFaSmleU8inLDAJWWBOCiG/y03k1qErT+NncNXhiKpEWmGuFaUPgQtm10gngazGVxDgynOnzYB0PxEFg1PWDmBWHouw19aIUcZ57gV9SUkSfr4449HjhxZq0ZtjkGba0IEoF12wS46U5IsLuRmoVyynallWoQ6DdNv/1v3pq2uu7V714cH/nvkpJFvfPDm+q83fvX5xg1fbhu5+N0HFi3817L/PfjJyn8vW/Xq1/tXrN/3+do9KzduX/7l5hVfblz1xeebvtz4ybKl81577YWpUyaPH4efCWMmjx/36CP9e//zvpu6da/fsYtQp6HgqSpUvlqoeo2QVkdwVhZTa6ckVU+1JVXyJNtxFM/EMli6rSJDzAXB7XEidB7bMBdsE20WBxMcIQa0FaF1HOE3bnzNwP8+Rko1Zr0aSQqVlBSR9XgXlPfo+J64wOVQzJYsWULDJRqVPPTQQ7x0RbMfYx+brGGg7z4Gs35cDE9lF48qKng3kHMCOfV0tn4mAI2zERyAlki2hWmLZwJsAXjuRNbs7ILvGeYrcwjbFB8GYzcGQNmWN7/aXuvWnpbm7To8MerTnLxiBiirBA+XwYCOAdBU5TD+fhbAgoAx1iuPj8A0gIFZuSMzMucUFe9lEiJc6ohSEYXBmSyrxhKwJQIv53gnBL3zAeYDTMosGHsoc6WGguZBWZIQRY9uhEGHQqEHHniAAEq32+10Ot1u9y/rQsdunPi9sBYocxS5ZcuWJk2aUC1EQyWCnmmP0+lMSkr6+uuvuSNrqqIVRTm/VJtQKLRkyZIePXrUrVu3SpUq1D12OBxJSUndunWbN2/ehTXNud39vAPQ8dGW+YQAYPfu3R07drRarWY2ND0hHNPaBIcTP2Z8mB89M2BjXg2rCkINFHHG7zqCUNXlqWAVBacLWyaPx8MH/3gtNkOW2K2tFZJTrTZH42bXDnhs3KD+b7Zs8sjyDw4pYQiF0TtvXH7Olp240xJ/ExZIWOAPaAHSfaYKhGRtW7ZsiUJyEY36mtS//L1SPnr0aAJKCIDr1q0b7+pNnjy5cuXKvCNosViqV6++cuVKYmrIsqyq6tChQ3nWPB7PxIkTaYl6KBQy95spdy1atOAVqXkpev369c14Zfk1HvWc5syZQ2ReMxxJe8j3wurVqykllIz09HQzWDl79mzKpvkRxMXbCl1aCxwof/zxx+NOKP+RtW7dmgwrimJSUhJJZ5R/CT9KacvPzxcEgQRSyG70LKZOnVpQUMBPJu6MoqDnA8Mwtm7d2rdvX7vdXrlyZVKe5Tanv+3atduwYQNhrPwZ8YfOb/uTAZo/X758Oc1AECLcrFkzDrWbR6c+n4+ioGmGcDj89ddfT5s2rU+fPo0bN65UqRIlsmLFigRAu91uYspbrdaUlBSHw8Elvx0OR8WKFdu0afPAAw9MnTp18eLF+/fvD4fD5uh+MvF0Ak0/nDhxIikpicOFjz322M960OcYV+K0i8ICtHiOryVUVZWWsFBF8corr3Tr1o2/jHwRBnX3eYebv3FEeSZ9mFq1ag0ZMmT//v3l2IG/j4kSWI6VEocudQtwuNecUZ05rqPF7IT9aAa6CpMNA13hRdfW0wp703c88mO+pZkVfTocIyTyVJQfOOOGl9efc6ymDn5/cM6rcwb0H+AQnTZkC+N4GDeLFelZiNeiPofgsFicouAULW6bWMFh9dgFp4iukRynP7hWT7QJdpfgTBLcKYI7TXBdITivEGxpgi1FcHgEh0uw2wQbSjA7LGV+rMgDc7mECh6hAruDo7JgvwI/tjSHNbmCxV1BED0WllCrYCn14QobKG5tP82G5n1aqxi9atTTI9avX6frERPujCUkOl/CGhVznX8u4cuhhBmGQR1v6vEOGjRIkqQz+6hmb1hoElmNKAauZVglw+QTgee9xkcGZCNzWZUY8IwYspkBjYreUQyaOblE5MVgkPFKgDE5GS8WF3/GfFEy6W/OeY6Zn+qE2O6TGqwBmJhZ9GxeeFZW8ONsKZ8Rq1WUcyUnYgQz02UIPTPRZwZg63iGj+lWf+iFJ3P8j8raY6D3D/kmh4IfytphDaQIY2uzJMbiZCmJgdf5OnwLMC638D+ZOW8BzAQYnVPyYnbJFgPIKxlWbyhhHTZpeICiKDt27CDdMHLG43A4qBDG8pn4/WNZgLBjqnhp/DJkyBA+tiV/RaIoulwuqo5EUezfv39hYSHPBj1f6tDSHfihnxsIBAKUEsMwZs2aVadOHaJa02tLCbDb7bSuNDU19e677y4sLJRl+cx3+edG+6vOv+AAdDmpMwxj06ZNPXv2jI1mT09jYmsoCqI9hhJHW8gyfxyCEFtyE2tJWWOK86VuDzZIHH3mAdHu9CShI4J77+s765XZBw8fDYQkXYPck7BprYxpNiAcc3xgzsI5tvHmSxLhhAUSFvgjWECSpPr161MlQvNebdq0ycrK+iMA0ASy7N69OykpiUuXCoJQt27dW265pXLlynw5D6W8evXq69at40gxzabOnj2bckdqCddffz2ZPa4nTTsbNGgQV5+SOv97775H3nipa15+jUew8jfffMOTR/e0Wq20RxTF1NRUkvGVJIkgpFq1avFG2mKxjBo1ippA7jqsdK+LUstj+bkA9F133cX70A6H4/Dhw+Wwrc9WVh966CE32/iENqXH4/Hcd99948aNW7x48e7du5ctWzZp0qSHH364YsWKSUlJVqvV4/HwlPOA0+kcOnQoN2+c04mzpeFs+8PhMHEliAFKsaSlpXFqP+9kUF9HUZQ1a9aMGjWqc+fObG3QmY2vBZtSLk5NJ5ABLRZLxYoVO3ToMG7cuI8++ogsSUWFGPE8R5TUuL9nSz9RvwFg+vTppIpAHaZp06ZRJ68cLv/Z7pnYf/FagMggqqpyVghNlvj9/qVLl/bo0cPj8ZyGGFhtwwFoWtjBXzRzLdesWbMBAwasXbv2XIqludq8eC2ZSHnCAr/OAgTTqGashKFFElsKT/vRZ5eBogtBfGtMiHNcOB6AJtLiGenjrGcWKB9uLn30jFsl/pRngYA3sHXrtuenz7zvP482/svtjqsbCjYPk6m02kXRmeRypngQd7Yzx0xWNs62C/iXZDtsuC7ZZrG5BZtbcDgEh83isFhdguhB6NlJ6LNDsKHWMmpPlwFAWx0CHsWrXS52icdidTkEl4PdkN3Z6mZqvjZBEC34icOgOcEZ94unKdJU7VerXuWf//y/dZ+tQc94Ueg5BhPGbJMAoGOWKPtXi2g9evSgBYjUCfzqq6/4qbHlC8QgRlBWViMSA3C/NGBsZsnUAMz36scYnRl0VDGNRFFgplphhqFRRh550DpjQBcCbDXgWV9oVEHhJ4Ciyejwkqn9EFrNcBqWEALA2YW5ABt09ekc3xgFhueEX8oOEm9aAYPNmZmrl1IANKuOFIA8gA9L4NlC/b8heMSAR0KBEd78D0H/gcjXMo+fIclki1hVVgxwCOClzPxhIfkZgCm6MaGgeFqOb6WGzhhxIwV1zKhK96PdJOhHAoy808KHePycROAPYgEaQlIHVdf1/fv3N2/eHLHH2MYfIvVUK1eu/NZbb0mSxEWJ+RD7V47+yCB8DDVlyhSLxZKUlBTXB+acDNpvt9tvuummkydP8rHhb2/Y3w2ApsEqjSrD4fC6deseeeSRZk1bOGwpdhHJy7hkJgpA29iUa3zTwp4ueSxMYX4L2XKh6DO3OqxR+Y64Z/CnNjf1uf9fc+bO+3o7+rpFKpwBMlOn0sBQFAgzXZ+gVIYy1G//eBIxJiyQsMD5soCu6xMmTOBE2nbt2uXk5PDe5+8ON9AanCZNmvB5Ms4DJcSTaNEUXrlypdksVJ3u2rXLjjyQ02DiwoUL+SQtzyA1e8Rv5W0kNZx33HGHucdTDkxDduMOdn9EYOkO5PCXbktY+YIFC3RdD4fDsiwTQbh27dqxNhp/e/fuTRHRZKw5nTyPaWlp1PelOw8aNOhntZoTJkwwzwMvXLjwFzT5fr+f2MF0K0oJaUOJokj+wc2HiC5Nc84kt00C3y6Xa+DAgYcOHaIHEQ6HA4EAgf5l5p0boZwATWBoEe2mm1Aqkfdi9+1Dxwm0+f1+anDXrl1bv3795OTkSpUq8TJmtVrjxHPJYzC5a6O+i9Vq/fvf/l5SUnKGCOBZ9Ex4XigQS0V5v4FAoHXr1lSQ7Ha7w+Hg6f9Zj7u8OBLHLhILhMNhXv+EQqF33nnn7rvv5gWbV1x2u52meQiAprk34p6kpqYS3ePqq69+9NFHDx48yEuRJEkknsOjKHqdOW8AACAASURBVG0VcwEufTSxJ2GBy8YCGoOPgiYMWo/ptQZj3uYQP0F8iHDjs2DQ5wBAn2nU0hAz7TnzrMS/c7VADCbj5+sawm1z87JnF+S/8fX/s/cm8FFU6dp4dXd6JQuMCHMR5FPBv4MyIjgCySTEXAJygdF7HRk+F/iPOFw3BhgiJDKBwISQXBbnCuKgwnUERmFkkGUIJJctQwDFAKOCI4tDAiFkIUs33V1VXVXn89SbvCm7kxCWLIS3f/3rnK46dZanKl3nPPWc5z227I9/mZOS9fILUx79t9E/+glfdsZfNjOXP9tMQD1zNlkIswth8BnO1c7mcEGwm3R62mEWHGGC3cYdPMLCDAQ010GjFNoumO0CLyfMpHPQFptg4d84qa1nw09grsN0AjyUgwauAMbMJpMpMjIyPDy8V69ezzzzzB//+Edd7IwqVaP6FQHgCuhrftWX0qFTaWlpsP4PLgeXy1VaWlrXY1Xh8bbkAJf0ykzlGuUSxnI1T1ZV8ZRKz28r/X/Xfxr8oDRWOeWiE6+geg7opDKEHpQUJunxJrmHxm7G/utCZfo5z59FVsj48oqAviJd/4FRdU2zXwIGF9hvxioZ2898K5TK31xWfl2mZZ4uP6Y3pkL1XGZesVZxDLbyRtU2cMG8dFHPn8fYb8s9r1TLvw6wX1cHMioqt8q+8/jzpzI/U/w8kqa+Rr7uN0rWJc3nGHvroieluDpDY//NWFJF1YLyqj2MndN9OWQu9BY5zS7qlX1/jb3f7zeOcHr06AFzhDqo6W97RACIBZyfGue2MG8SBOGJJ5749ttvIRSQsQ/wy3MNs1FjIZD2+/3frUiG2E442wVCYNu2bZ988klGRgaE5oa9EK9+6NCh16m8Dm1J87e0GQFtbKJY95JENWfH/hVvrX7++edjY4fa7HxOobPPDv0hLPz6GT/DBOEHuufGjwXhXt3BGfaG9bv3J3FDR40cMXrOnDmffPIXkODJcu2/uxRQpIASqLsxXeasM/weKWLAqz+Y4g763CKeXoQAIdBREJAkafXq1U899dScOXOgT7Ca7IbcAG4ISFu2bDH+wMECDpPJhN6m/fv3z87ORv9lj8ejqioQi36/HyyAoQSn02k2m3fs2AF3JuMgW1VVIEONdVmtVuOadMjfRKdgOTwyOLGxsXBjA2rbZrMNGDBg48aNoigG8ZX33Xef8SYdExMDhXi9XuOJALYIdsHCeWztlClTgFhvonm4S9O0NWvWAK0JJcyePduIBnYBD2kwoQSUd955B0qAPkJ/wUwW9ZjfmS8DeQo5UTgM2Z566qmCggIsH4ljY8eb2R4sBJ8Z1NTUoCkBMMt79+41ZgPvkd69e1v0l8PhQH4ZjDWwF9D47t27owE0dCQxMRFtELCd4AMDFeETnWvo0aeffoqEOLiVQZnIGwb1hb52bATKy8tXr179+OOPOxwOkDzD7wZcnPAJj+WM8mfYHhUV9cADDyxYsODYsWNoI45XLOAGa1+CNiKkxp8I3EgJQuDWQwAJaFlfww4ASDqt5DMQ0HwRPRHQ7f/ykKSA280lVrKilfu9fw/4Mkv/uaS6LM8bqILWq5wn8+uz4vzPPntt7uyfPjac09BW3TEjzCZYHCYzf4eZbHYunK4joG36LNxuFmy11HMdB81/oU0W/mkz8Te8wkycgIY3Z5750jndBUT/5OER9ThNYWaufQbhtQX8M8Msgo07hOhkN18DHRnZOTExMTU19eTJk7AaDAOZ1J0RIqDrkLjKv+fOncO7LcTQ7tOnT92iNE1hAS+TRa7n5dSyzNh+TVlUWTyz/FzaZd82xuljLmrWWEDT3S40+JEIIqD54yuZqZd1ovY0Y8sui8nny9+rZMcY82q1cmGtXnzsZcwrMRVJGi9jpxjbwFiqv3LGZTmtUjyoa5kZY5e1qhp2yc8u69c1J6AVfmAdc8xpZM6eq3rVnzG2pCwwU2RTfCy5QvqvC+6dPvni9xG7zOTLLMBJInjp5boZK2fsT2UVc0q9KZe588acCvfcopKPRaW0joKXOcN+mak6WsZfU1ZvwfFdGB4Yhz/55JNEQNdB3E7/fv311/369bPZbDBABdcLnN7a7fbOnTsvXry4pqYGBFhBP0owyLyGuVKDcOzevRvChEZERAiCEBsbO2HChHfffZfpVxdMo1RVnTdvnnEIPX369LaaYbULAvp7UOpPaPWzorg91YWFhZ9+enjnjl379v1tX+hr76d5u0+tWvZV/x6/j//xKs3HV3eo+IYgGHzJMUQQ5GExmgyFgQ0JeUyMeyhBCBACHQsBMCVoP3TDnDlzIiIiQNMBNzZIWyyW5557DhbaQJvxE9hYVVVTUlKQFYV7TK9evYIYFrAnjo6OBq8PGOuYzeaPPvoIxpR1I8srnOYgxwxN0z744IOpU6f+x7//x7Rp09asWVNdXW0sAu6yjDFU6SJVxIet+svojAHNUALKqVOncNEQHPL4449flY/zkSNHQFkA056EhIRrUxzLspyRkQFW1+Hh4ThShFaFsmOQ02azxcbGLl68uLCwMOhcAD7Gaw/SRtyak8YBxIgRI5xOJzyuuO2224zHwtBHluUuXboAAQ2nPoh0vvPOO19++eWPPvro7Nmz352OOXPmQL/gkOeff95YZmNp44iqsTzG7dD+mTNnGq/eWbNmYZ4GccO9lLi5EPjulyoo3B9cnJqm+Xy+4uLizZs3g94Z5PzwUAefhYAXOTzRgScWIHyGKzk6OnrhwoWnTp3yeDxgjt8EONf279ZEgbSLEOhwCGi61A98WXFyBPQNbIQe4y4DTX2dWCBHhAlDgcbl9JA27KRkAwjIutwUlJuyoomMFTG2xV24pOSLzcx9DhwOQJOq2+Kq+on363JTL2PZ+/cv27D+lYyMLv0fEqwu7h8d0YXHAYyMtAgml5VLxvgSQ0dtwiKYwuw2WycnDJAMn2buDW21mMP403qL/rY67M5OLp7HJITZbdzQGcTP/B7Apc31h5tspt7/5wcJw/7P0z8f/tukl5Yt9egx7GrjXurD4qv6YUejmAYgu+U3wTgfwvzC+XU4HOHh4T/60Y/Onj2L8EiMq6ArJJbjUZdUeKaXV/22vGqvrvz16ldRQCegQeqs+2wAAV2rfYbnHX7Gzqhc+5x5oSqpuGyJR/pMj2TIqV7Dr4teKfwoBXSvaeUyY98w9qGkplwQZ5SKGVXlm5kMxDcXXKsKk6U6ew9Of+uaZ01m/M2/KRKT/SJj5xn7/Tkp3cNmXWZJReL735Z+eTlQDRbSOo0O4m2Zs8869Q0PNfRdFxnbLoqLyiqTKv3Ta5TfegKLyqp3e5SL+uGSTp1LTPYpXjmgL7RnDCZuwE/5/f7+/fvjRW42m48ePUoENF5g7SGBjnDQmCVLloSuJMYVzFardfDgwUeOHIGlvUaZjrEvxtmfcXtz0kExKu+77z64fkwmU3p6euhEHrZUVVW98847oCiCz6+//hpkTDiRbE7t15+n/RHQdX0KvX8Yz1NtWmGyj2X8dkd8/z/u/php3joCGqln/pwLXgH40zwCuq4R9JcQIAQ6OgLwy2D8eWnzHuMjSjRGGDVqVHZ2NtBwcD+r/WHT/8AYUVVVj8fTrVs34B/h1tK1a9cGu7N///777rsPctpstuXLl8MNMvSm1eDhMDBC0IDoCbodNnigqqqLFi2y6S8gjFwu15kzZ5SAAo+IsUwkoEtKSowLAAVBSExMRNlvg7UEbRRFEYgqwMRkMgW1Pyh/Y18B/48//jg2NhaoMRBWQ0eQPIVIxxEREQkJCUuXLt2/fz+Iu0OLxc4GJUJzXnGLLMslJSXQQWjVK6+80uBRS5cuhfC/uHAVhkopKSn79++HQ8CgANIZGRkvvPDCq6++unbt2qARWIPlXxu21dXV4EJutVoBTxgVGUtrrDrafnMhYLy6sOWiKL7//vujR4/GaxgoZlhFiEtT8b8M3G9gjYjVah04cGBGRsaxY8fQwh5/2LEKShAChMB1IAA08HUUcLWHIu+MCUMJREAbwLhyEm1TOFeo02HVjB1g7vfKv1h3+fQh5r4EFBuEgdNJOoX7DKhAQFdL6kWF+9vm1NSs+eofuWUVb+/P/89F//Wb9AWDY4fFJfwrcmcum9WhSwbqfTMtAnffMIcJYQ7BFsHJa4dLcLm4cbSl1nGDxzwUBFdkhGAWrE4Xd/DQX4/EDB0aNyw+4V9fT5mzaMHS3X8rWP/Z3//X61tZWry08Js1Jd9+Lro5AR3Qda11c38YUF0ZFD0HEdBNA6VpWmVl5UMPPQQ3X5g1mEymBx988PDhT/kITQ/cd05lnwXYm6We1y5cmnqhcnG5GyhgTvhqte/aaIO8vloCWuHWGjwt6Wz1EcbmFpdPO1e22BPYzthZ3deiXmv8vYZqjPk1Jl5m2hnG/srYUp+SVKKlXBA/ZuJxvUk8TKpaV5XhYZn+01HrP82bL/sZY98ytt4jzSkRpxYFUs+zDypYkaabbNT+L/A0WFTzVgD1HNDbp9eVG6haVF6W6g6kSOw35f6M8svbRO2S3mDU3itM9SuiXxED4ESi75UC8r6/5Q0aNAikHuDbMHv2bFTJfK/T9KXtEJBl2ePxKAHlzJkzI0eOhAEqWE3irx8kTCYTxvhRAorf729sza5x6ne1PcNg716vF6Z1MHVKT0+H2XRQgcgvV1VVrVmzJioqCv6XJ06ciLuCDmnRr+2XgIZuf+dpgqHPjeepNq3bZpQUqZ/nV6s+pkr8JqTv0gMxN3CAhr+DSu0yEFgMUvvZolhT4YQAIdAOETD+TrSH5kGMgqKioiVLlqSmpm7cuHHfvn3gnozNM7LPxjRjLCcnp0uXLkDiDBw4MNSEAQqB+82BAwfeeeed4uJi2Ag/tlhL0wkjbrCY3ahKbozIVlW1tLQ0PDwcWvhduOfMzEysqEHlrCRJyEnB/fXBBx9UVbU5fDeWPHjwYDgWyNmNGzca24/Zrpjw+XzQtV27dk2fPv2ZZ5555JFHhg0bNnbs2Oeee+7ZZ5+dPXv2+vXrP/2Uj8uBPAWPFHRNMVZhbIMxbczT/PTrr78OPs4gGD906FDQseCeIcvy6tWrJ0yYMHbs2BkzZqxfv76oqAhyappmDJEBynRQpzaTesZysDtBbWjwq6ZpK1euRPfqiIiIQYMGhRZFOugG0bvpNoICWlVVuNjWr1//0ksv3X777TabDfUjDocDTISAegarDfgXhsCeMNDv16/fBx98cPr0afg1CB1G0zVz010e1GBCoBYB5J0xoe9A6hn4IPxqTBCGQQiAb+5lnX0GM8pLjG1Szr9R/NkB5j7DJDfjASSBY5O4bDPgZ34/8+sJvtnDWA5jq91Vfy6r3BfQVp47vf7sKT4L96kBxqp8npqamtzs7QWHDi5/Y2nyjN/856TnfzZmdHTs0NhR/xr9byNjR46NfuzJgU882yn234SfDhcSR/145GOxCXHwnvTi5N9lZmQsylq7/qPN27cf/LygpLwCmuP2cwZSkjVVZqUyy5HUrJLi14r+saTi7N+kymo9PN33CGiF0468L/S6bgRguOvxeKqrq++9994goi0iImLpfy+6JJWeYTU7mbywtGxm6aXXLpS/ccmdLSlV+iMNZF1qry7+T6tysoZHHQz49Sccim5/cYixBWU1STXu1y6U/k1nn0s5t6tJwCMH90XTeNAuuYix/9W0pZKU7PbNLvf8/pL7KGNlddJpzhprtWx3LX0MPxOaxgMT6spqUQ9y+D5jydXeGaUV84svbbqkfFt3/QBxDZci/8fBBSF6OdplWWbsEGOLai7OqPK+JrGkGjW9zL/zMm+D/uLeROg5zZimMEVWJZ/k80mi+7LnteRZJgsP2242myFqRb9+/dxud2OUZTAM9L21EIBJ0BtvvHHbbbfhgryg/whBEKKionbu3Alj0SDPjdCW4kTp2kaqHo8Hyrzrrrtgxe2UKVManGyGVj1x4kRo/O233x7EMIRmbokt7ZeABuq5zh1alCQJBHrAdNR9akqgHhYw3+A3nsZf+FNIBHQ9cJQiBG5hBIy/Fm0OA/zuybIMYbIkSfL5fEZWpaamBu4uRt4Z00ABi6KYl5d36NAhMORtsFNA/YA9NKiJkTLGRIMH4sZQ3KBMY2sxMyZg7/79+1999dUXX3xx165dsAu6iQQ05ofEq6++ipx1eHh4//79gzI08VXTNLfbnZycDFJKYLgmTpwY2v4mCgndBXYBSMuG3vKVgAKBJf1+Pz6pDirH2AZjOijbFb/6/f5PP/0Uwh6CJnTSpElB41dg/fAc4V6g1OESgtGSElCQ3IeLATLjIVdszzX0ZeDAgRaLBWxhrFbr2rVrkb6/htKu2ELK0FYIwBXldruPHj06ZcqU7t27c+dPQ+hUEGVYLBawuEFDPYiKyVVyLldcXNzvf/97iN4J4eMxbewXXDnGLZQmBAiBmwYB5J0xoTcdGCQUJBp5Z0zfNH1srYaCAlqPFMkV0IyxS0zbUnFqQ/nXZYxVM+aTAzyEnM67ebkbr+TnNrteP5MgMtJpxt4sLHqrtPwzlR1nbO35wn9AqCQvn4f7maJyVpEpol+3O4COcfWnxF1veaXVjB1m7O0Sz5xvy98t9RRqzC1ern37fdVejy5X5a0I1KlNYYrvk9VqSS1n7EhAm3fy6znl55PPnMhmgUpu36tJ2vcV0ERA37iLCkZ9sOyyoqLiwQcfBA0HUFfc+jZM6HZ351G/fu613TkLLpTNKavJquDsc4luPWGkXDgBzU+wbgXNLxVOy8p6tirGxfXL/crM6suvXap8T5Iu6q4c1SzgZn6poYcJKl/xLpYw/x5Vfvuy9NLF8mnV1Ysryv9XCRQzVq2qPv0qAtsZv16apF9Ueht0Wlrlvh5+PfDg+sue5Gpvkj+Qcv7sJ4qvXAeQX7GX/f4Azwa/NrUENFyg3PGerw/4ginvyZ6Zl6tfcquvVCjzKuQ/X2YXak8BeOXXEtB1p0XzSb4aT/WM15LsTgcXXoRx+T+u7tq9ezdEJ7o2UrKuFvp7gxEoKiqCKDtWqxWE6iiNQhp68uTJOHtqTvU3ZHbz0UcfwWppu92O4qfGagdFlKqqmzZtgkmxIAhGO53GDrzh29s1AY29hTOEJEt9ApbbBGqfdnLqWeG/SfyzERoaRydNJLBeShAChAAh0JoI4G9dg9SJ8V7VdDrIoLk1uwC8YYPth11NNAZ9ooPyVFZWJiYmgo1GbGzsV1991RilG3Qgfs3Ly4Pnw7Xhb8xmIMLwATLmvKpE6w8QQcUM2mSo3e/3l5eXDxo0CNQT0M2TJ0+GdgRiHgZdOfX307qUMUNoITdqCz6o8Hq927dvhwEcmPnGxMTAXmhR64N8o/pI5QAC8L8GT2sOHz6cnJx85513on0NUMzwZMjh4Ku38UpGh43vlko4HI7ExMRly5ZdvMhjAjX2C0OYEwKEQAdBAHlnTOgda2L6hrs6CAI3uhtAQ4t6sVqA03+ibv3MZZ5A+uqLg3VdqqQwr8q8CpNq9AhvH10seedM0eegLdWYmzEeypCfGlV3xZU0JnPTjtoVxXAqas8cyEnLGVvt9712tmhJoXufxCo5GxlQmKLw6HRAffOW4UmEo0SZs9ABxnJE8Y2LxbMunM4oL9ol+Ut0/wOJyQGIKweEgP4JCmj4vNEQ3lrlBY0GKysr33nnne7duyPjJlgFoZMghJuEyB8KP47797fXrjpbUqWfGkXXrQfqpMSiHJBlEN/z64Zv1rh1qqg/lphfWDjd4/71pUv/VVT8pR7Qz8efW0ii5ld0bX7Q2VT4dSh9zeQ/Mza1tHxiSekct3svk/kzCY0/AZF0f2ggoMHYHMxn6iTM/MqU9ECFW5maVl4642LlYr+8RfKc1WlxJJ0l3X4aCWje7DpbD1nnzdcx7+s1l16u9k684Hm9XNsuMWDPZZ9XqygBkbUv4BdVBZj0Ldu2PvZvo7jLueEFTg4ulys1NTUI81vrgmsHvQU3S9BvoYT5wz99aDhdPAkcNOrWe/bsuXv37tZsvt/v9/m4n/jIkSNhdeAdd9zR/OlSbm4uPvP48ssvW7PlUFf7JaCbiwXc3SC3nubsMxHQzYWP8hEChEA7QgBGHo0JgY3jkqtKt3IPsW1XW29jBDSUU1ZWVlJSAvLwqyrZ4/G43e4+ffog+/zd4+IFCxaAYByZ0Ksqs80zo4Z99erVd9xxhyAIEBDDYrGsW7cOwjkGNRLPizFRRzvX/zXuDSqhhb7Gx8cDb+5wOMxm84YNG3w+HzgFN3841UJto2JvCALffPPNokWL4DEJjHrB7BsFzjC4R0UJ5AH/jcTExHXr1p0+fbr5Gvwb0mYqhBAgBNoSgVr2ElhOYHJ4c4wEZWPptmx2+67bq6s+63FEkAHKWrpNVTnly2PEqSxQxdhfq0veOfOPv5ZcugjKVYmfBp1aVBmTFOaXdUNeHtfte+cHS+cVXmJsZeXF/66pzJW4va/nSgQ0ACnzQHKc1HvzQmnK+fMZ5ee3aJx91sWlisgCREC33BUXNBpUAorP56uoqPj5z38OoVnCnFYhTBDCHULYbYLpduFf+gquH8SP/tnv0uZ9++1Zj1fi3i9+CVuoqwT584a6AH7sHGNLiy68VlH+cs2l31aVHWWsgsuiVYmfWf5q8HGCXxfU5zM289y5qZU1c2p8HzNWyJln/bmKxA0+4OEKf3yhW7LUEtDgpsHFy+pFpn3G2GJvTXJFZUZZ2RY1cFZ/JKPBcxWD8Pl7BDQ0XeMmGxtUb6q77FelF/+zzP16ubZOZKfrxPu8y6I3UH2JsYCoSe/8z6r/++wzzk6ueurZFERpCgMGDKipqQnCHKGjRGsigFOP7xaYjho1Clbm4QkDt0MMRP/YY4+Vl5cjW9067QSZfFFREVDhgiBMmzat+VVv27aNx4zVH4QcPHiQ2xxJ9f+nzS/nmnN2CAKa916/c+o3ztq7EtwZQ4BpbLBi3B5yEG0gBAgBQqA1EDCOPPD+hxUH7W3+VyyhdRLYsKutDg4MPQq2o/cI6B9DszW4BfhlJaAsXLjQSEDbbLYzZ840eEj73AgP5FH6XVVVtXr16oSEBJgGOJ1Oi8XSrVu3jRs3gilBaC/wvDQ/EVrIDd/y8ccfw/LDyMhIs9n82GOPQRUejyf0X+CG104FthwCoiiWl5e/8cYbQ4cOBYGG3W6HBIzjkX1G6xVc3ut0Ovv165eRkVFcXOx2u0H432D0wpZrP5VMCBACbYkAspeY0FtjnK81lm7LZrfjuo0KaKaLnetcN+pYfjS7rfMZkHXieFfFuW3n//mtFPAAv6bLS3UWmvPAKtdK84hw9QQ0nLI6KEAz6mHsc9F9nHGDAm4GwoO8oWasftJuPKfglqlo7Eu3P/10RUaJb5cY0O0dApeZz8M0cFowcpRB6bom0N9rQQDHiqHqkLy8vP4PPgS3cpvVFWHrIggOS+fugtlmdnaC7bfd3n3c+P+77K23z18o8Xh5rD/OyupvSBQy9m5x+fyKml8XX0irLN3MZG6UIfo1VVJVlQcoVGoDGNY+19DpHqbH/TvO2H/XVKZe9qaWVO1VOZHtUSRNvswfmiABDWSxTkUrIG3Wye9qxXeW+Q4z/0q5eOalyky3PyfgOcefo3BZNlyBSDobE/pDl4DC1CrGPmVsQfmlyRcvvlB2aXa1uFlh/9DXB+hOHZp62SvKgdXr1v3/v5oUeVsUj7epG4gZh0BIaFoslgEDBpSXl4MvIsJ+LeeMjrk+BAB8KOPtt9+OiorC02RMwHm0WCxLly7lF7MIC0uur+6rORrmtqtWrYJWWa3WP/7xj81sBsbdgYXFR458F/6TLyu8mvqvN+/NT0DXIqDfQ2uh88KD1QaxMd7YGks3eCBtJAQIAUKgpRHAYYfxFoiVBu1t/lcsoXUS2LCrra7BXjPGwFRL0l+wkP+q7pRwny4sLDQS0IIgPPHEE1fbwrbND73Ozs4eOXIkRmzD4ez48eNLS0ubaCGel+YnmijtOnfhOOn+++83juoOHToEjg3XWT4d3rYIrFq16sknn4QZl/H8Gu2ejQQ0bDeZTLGxsW+99VZNTQ1EgQdRRujst217R7UTAoRAiyOAvDMm9Cobm7sZt7d4227aCmTdzgKaL+uUnM6p6RuArVPq3HP1ibWsc2rnmHJJz1Lp9gKRx9XR3MYXCGg/ENDchQMFYQY2o860gMuqgXoG4dgVCWiQPwdU9mlhyTvfVm6VWalegZ9d9jHfZd3qIaAbOgTxzvj1pj1R7aLhQWPFoDaVVVxauDDLbLaFCVaLYOpkcQlCrazXHGYzh9ksVrs5zCYIQqeozv/S685RY8ekLpy/s2D/P0rPqfp19XHx+T9UlKedP59ZVvo/5ReKGJMCMhMlFqgloCVFd43GK7PONrqIseXlpUtkJdPt3yByOxcuc5ZETazhivwAv9I47QwxA40EtP4EpUjxHmOBjUx8veSbtAvlf9WfssjMp++sJaDxWYyRgNbTqhvMN3zq66VVU0oqU6svfyCzQqiRMb/f//7bK1547jmTs5MQHi6EcUzA6BnHQqhahS0TJkwoKyuDSC1GzIMAp6+tgABMGCsqKsaMGYPnC+dZxi39+vX7+uuvYYoKR7VC87AKGBv/6le/slgsYOHy1Vdf4d4rJpKTk7t06QL9Ki4uBjePKx51AzN0GAJav4HW3u3gTld/S72BeFFRhAAhQAi0NAJXxa62dGM6UvmzZ89Ge1kIfZaWlqZpGoptMahg++w1DHGWL1+OftY2m+3pp59ev359YWHhtRkUGAe7kG7Nvr/66qswngP+cfny5a1ZO9V1PQgYnxPAT1ZJScn69esfe+wxHKNDAsa4GEUQFv2B8gLCudjt9uHDhy9btqysrCzogryeFtKxhAAh0FERALq5o/au5fplxM2Yrq0RuH7k8nWVNBjpwsQYjAAAIABJREFUQgw33FN3LPwFvXSdahofGECilpPmNQCXB/NzneCrJ/uCSoavuv0G18BKOkV4SV/jrO8KBJgSAOdqXbOKjLPuLtxy+FHJwQjs3JkbGx3rsrsEQYDbOj5O5rd+s0V/mwWLWbAI3DM60ipYhNvv6/PEy5Ofmp+S/Mmflh3/7H+++fs/JH+5JCkBrY5y5hVJMquqk07rdDIPZXmKBfYzllFaMedc5f8UXy6qb5GmBLgzOZiGi6oGJh4soKoKv/a8dUY+J9TA+ktVC6vFtOKqPRJ/qqHL+bn1BjwawacnAZXJiqZo3NMDrtsSMVDI2Loaf9q5stkXqmafLXnvfPnms8XL1m98etKvbu/Zw+qo83c2CwLXPde/IsJBTmuChNlsttvtb7zxhl4tfbQlAhg8UJblDRs2dO3aNSIiIki0hJ4VZrM5PT29LZurO2b4fL6xY8fC5WU2m6+qPYmJiTAyt9ls/JrnkTJb9dVhCOhWRY0qIwQIAUKg5RAgArrlsH344YetVmt4eDi6zaalpUF1EOm75aq+ISWLonjy5MmEhIRZs2Z98MEH17/yK4jva81r7/3333c6nTyQuokrRMaOHXtDIKJCWgEBVVXxaY0sy5s3b544cWKU/oKzWT/l0lPGjZg2m80jR45csWIFxBWEZoMZOV6WrdAXqoIQIARuOgSAoLzpmt1BG2xgj4PYZ2TyQnreHALaUG7I8XWhaI3UM6QbyEqbWhIBt9udnp4OMRtwaF23wgkIaP0zzCSEmaxdOgkOXSptEYQICx8gRAid+9/zk7jY8U+NT3099Q9v/eFQ/qHKci5r5gG39ecWkOaRDBl3utjgL0v58pu1NdzOhQdigxCakEn/9CuKX1ECqgpvSVM9sizqjzG+ZOpfqqv/UOpO+2fNXzTOPusBEWttqVH4XCvS15/BYMGaHnvzQKX33dMXXtn5t/ilf+jx9AtC73uFzreZIpwCV3vXvUx6H0OMnnX5iA2k4k888URJScm1aUewSZS4fgSUgAID2pqamhEjRtjtdpibGAlo8H0WBOHBBx88fPiwqqqtrxo29hQGyXfffbfL5bJYLD169DDubTpdU1Pjcrluu+02QRBiYmKaztxCe4mAvhpg657lXs0xlJcQIAQIAUKgvSBw4sSJuuFh7V+LxTJ37lwwwAKH5fZMfgFBDC00YgpDWKMo1bi3HaZPnTrVpUsXmKs4nc7w8PDS0tLWpL/bISY3XZPWr18/efJknHAG/WfBV6SbTSYTrj949NFHV61adfLkSZx6Ae+MCLTn/0FsJCUIAUKgrRAgArqtkL9CvVdDQBv55Sumr1Av7W4jBEC6oWlacXFxWloaDgOAgLYIFotgCat9m8IEkyXMxDXC1jptcB1Fa3W6HA6X0+Z02pxWs80smHt07zEs7tF/+9njSTOT38hc8rvZaR99uGHn54f+evarVceP/Lno0gndx4P7Rvv5WwrIXtnnk3yiLIFmGQnogCb5ApVlzPs3xpZ7q39bUvr7Sv+mKh510G/wP0f2mYfgDChSQJEVLVCnDf3m29Nr/7w+Zf68ewY8bPpBT8F5u+DoKth/INhc3IPELNRKvG268LkhAtpudUS4IgVB+PH9P87JyYHxT+uLT9voSmm/1cLUY/PmzVFRUThMheA0yEHb7fbIyMiMjAwISdJOOgNcudVqHTRoUPMngJs3b7ZYLCaTyeVyLVy4EMfhrdkpIqCvBm0ioK8GLcpLCBAChEC7QgDGeStWrIiKijKb+fDXarXCasGZM2fCXmS+2jkZigGLwUzZ4/Fcvxq6NU/W8OHDQS8DcedWrFhBo/DWxP966lq/fv0LL7zgcDhMJpPZbHY4HPDfFBERAf9NOAWFBPjTOZ3O2NjYlStXfvPNN1zWJMuoOkFDcGzVzfJviA2mBCFACLQmAkRAtybaV1EXEdBXAVZHyArsFQyYJUk6e/ZsamrqbbfdZjKZLILJwD5bbAInoF22WoeK2tGC6Xv+yGbBDOxz3SjCbA6z2awOh8lWy1TbwoQuTqFrl/8v/mePjn0+9qf//ruUxbOnpS7NfOOjjX/Ozd/z2dHDZ8+d5V7SjHtvSBp/BzRJZZ6vPec+KD87/+zpRRXV6y4HihmrVrixBlhMI/sMRjGMscJzxX/N3rniDyvHP/3s/f0fCLPXKpxNFnMnRyebYLMIYWbBzI2v6+j02mYj+1xHr9d1R/jJwJ/kZOeocuNLAzrCRXGT9aGiouLxxx/HcwQJm82G7LPZbO7atev69etBq+T1esGwuw37CTMml4tb3wiCkJCQAKFTmtOk1NRUQRBgKfCuXbuIgG4OaJSHECAECAFCgBC4LgSmTZsGlBloNOx2u81mmzFjBhBhofri66qsVQ6G0X87J801TYNlbnPmzLHb7aCctVgszz77bKuARJVcCwKapikB5fDhw2lpabNmzerRoweMd42fdYtt6/8KguBwOCBP//79s7KyTpw4Adcnqn5kWW7wqYOqqkpAgcCDN+M/47WgTMcQAoQAIUAIEAI3IQL4wNjY9uVvLut79z2WurCE3HrCbrM67DhyMAtCmGCymcxhOjENWmnO5/JDgLit53FtgsWmi6n5h8MhOFyCpbNd6NxJiOokRDgEh8ViE2xmwa4XGiZwZjislhV2REX1faDfA48M6Dt0YM9h0f+SEN8zIfGe+BED40YOiUmM+WlizE//NSb20ZjYR6N/GotvLtXW37qHtQlaZLFY7Ha7xaY7h/BRTgj1DN0zCRabxWzlvQBf7Ntv7z5p0q/+cfwfXreXk5gBI1SUbiUEjFMk9NDYsmWLkWg2m81wymw2G6qhR4wYAav0jJ/G0lqpA9+vpqqqCls4ZMiQxnhkTdOg2SiR7tmzJ0h/unTp8v0iW+8bKaBbD2uqiRAgBAgBQqANEfB6vUpAqampYYw9/fTTdrs9XH/BGNFsNq9atQqeb7f5wKINUWq5qmF4tHXrVtTJwik4ffp0y1VKJV8zAn6/H0e0gwYNstlsQaHbcSZZTzzXpQRBiIyMnDdv3pkzZ2RZrqys9XOExrjdbqSY0XxD0zRZlkVRBCccbDb9MyIUlCAECAFCgBAgBNoVAkhAGxMBUdIU9fjx43MWzL/3JwPqNcI8FKHFYrWGmc12gb8dgkkXR3OzjsYIaDDxsAgWrqsOCzOZbXbufGFzCjZOPJvDON0cREBbLdwZI8wk2O3WTp0Ep0OwhvF3GGeWw0w2u8llF8Jtlk5WSyeL1Wmx2s1hNnw3RECbTSYLZ7p5sQJ3fHYIglMIc9qtdqepTgQd/oNOyFB3vi1q6tSpO3fuVBX2vfCYdbYe7eo8dvjGBA0mfT7frFmzYA0fctAwrEVnua5du3788cfI4QYR0HjBtz50kiRpmta9e3egy+Pj4zEuS4ONwcAtH/7pQ0EQgLlOTU1tMHMrbCQCuhVApioIAUKAECAE2gsCyKlBrAkkQwVBePjhh4mAbrnzBMj/8pe/ROLSbre//vrrYMgAI7yWq51KvjYEwCgD5MxWqxU9nfEkgpKijnmu/wuHREVF9e3bd/DgwfHx8UlJSd+J3xcuXJiTk5OXl5ebm1tVVWVslRJQjHYccEkEzRmM+SlNCBAChAAhQAgQAu0BgXo+TtVED5f6Msa8jFUy9s7BHY/NfTUq4SGhq0uwmzgRbDKHmc02Eydybdw/WTftaEQBDfpo+LQJYcBc27gHmK50tunsM3zq2meTxWyycHMMc5ge/1AQLBaH1Wyzmcw2QbAKXCrt5J/g3Iya67pxDdcum7n22WStV0DzjWGCqZMQFm7qZBU66e3mvDMv0hxm6fYvtw2OfeTnTz+ZuWjh9p3bC88Xur01qhrASYemqIosK7KsKSo3/sB3ezh5t0Yb4Fyoqpqfn//DH/4Qzjeyz7g0FrbHx8efOnUKhqBG6hnSeLW3yRgVbBjj4uJgCW/Xrl1BwNHYaUSTyYEDB8Kg3Ww2Hz9+vLH8Lb2dCOiWRpjKJwQIAUKAEGhHCHi9tcNiURSfeOIJHHBYLJauXbsSAd1ypwq4xZSUFCAxzWbzvffeyxhr21jSLdffm7rkIPJ32LBhFv3VIAENw/d67tlkQn8VFJLAgN5kMoF5tN1uN5lMdrv9rrvuio+Pj4mJGTdu3Jw5c1auXLlr166CgoLz5897vV4Y4t/USFLjCQFCgBAgBAiBDo8AUnJMrfU4Vhjz6QT0Z96SNf848L+ec+cYm7fmj2NfmDRo2DBud2ASLPpbHz9YDPH7OEuGbySgwwRLHfvMmeFaJbJdZ5RtZsHKeWf+5uEOQZNstljB94P7NVt1ttiua5c78U+zRbAIZlPtGyqs/cqZa85Xm+2CzS7YHdz6w+bqc/8j/R+MHhQ9ZOij0b+aMnn279Le+2D9tuw9Bw4drPJc4gNaxcuYJimirEq1Z5zrnw0nX9U4Aa1qREAbQGmNpMfjUQKKJElJSUkwXq174MCffuA4ltvFWCxvv/02xtpphwpoMKH+1a9+BYFYBEE4ceJEEyDCPCsvLy8yMrJz586CIIwdO7ZNqHNoJBHQTZws2kUIEAKEACHQMRGAxUqiKL777rsjRoy4//77x40bt3fvXiCgO2af27pXQP2rqrpkyZLBgwePGDHiyy+/bOtGUf3NQmD06NEwUoflfsgmA79spJ4hbbVacTQPnHVonqAJAM4EjIm+ffsOGjToscceGzduXFpa2rvvvpuXl3fmzBljo1E0De466OPRxP+ypmmiKOKzKPCbNpZJaUKAECAECAFCgBC4FgQMfCvYHVdr0kXJU8TY5uqa/zl7bl9x6WUei1g5fHD/uvWrf5Py6wcHPnjn/+ltd0JQNa4+hvCDxvGAngZ76HpLD76xXsHMnTDCzAL/w2MDWjjnDBYcdru1rnALt2i2h4GvsyB0iuxktghxcT+Nj4+bN39uaursPXv27N2bt3fP/l37Dmzd/3lOSdlfLtWsKDy39VI1j/dd++LBC1X+5pEM9QR8VVUWwHftTk3VPTgwr05JkwK6DsqW+6sEFPA+hknf3r17+/TpA4v5cFAK1xgqY+Li4j7//HOINBgqfA7agg9dWp/MlSRp+fLlMCa3Wq3vvvtug1FVAFsYJw8dOhQdrnNzc5vI33JnBEomArqlEabyCQFCgBAgBNodAjhWkCTJ46kfUpLiskVPlRJQfD4fgs8YQ/awReulwq8TgVWrVgVpn5E+BjFFkBEHLmnEbDjWD0qETC8b2GA2m611L4vFAqsWunXrFhsbO378+IyMjNmzZy9ZsmTz5s0HDx4sLCx06y/GZ4fcatHr9Xo8HrzqZFkGB2rABJdkYobrxIoOJwQIAUKAECAECAFAAJf/n73sX3OmeJs78E/GauXBiqQx2cs8XtknKwp4I5/559kdObnpGZkTfzkpOvqn0dE/vffe+5zOTjA4iIzsbLM6bLWvMJstLMweFma3hdltFntt6GPBaubhCbkNtFVw8PeP42Ljhg9PSp6dOi99Tlp66tzfvbl8xaYtm3ft3RXgMQHrKXNNU3RfOEWSNb/MShjbKvpnf/HFqoqab3RHEcNprSOUa5noYAKasUDDBDQjCw4Dii2cBALa4/G88sorEPIHVuDhWNQ46Fy+fDkMGmEAGUQ3h369BgL6Bg41jxw5go0fO3Zs0zbQq1atgo4LgjB16lTQYbQw9o0WTwR0o9DQDkKAECAECIFbAQEYnWiapgSUGzgyuBWgu6o+wnI2tMMj542rQq9tM2uatmzZsrS0tLi4OCPX7HJxvZKFhxTi9tD4uiEENLeEtFiMxDcskzT6tuPgG2pEx4/IyMjRo0fHx8cDPb1q1apvvvmGMQaRW1RVBV2MKIqqqsJTEHr41LbXGNVOCBAChAAh0PEQQAK6xO3927mqf+rmE1wz7AkwRfEG3AFO1PKXypikMb/CaWlOA+uvgMokqTaDKMoHDhza9b97dhleubt2wfuve/dsO1awcMdfJ23a8J9b/7J41/ZNZ098WHNx+dd//7y4+LIYqPFy3vtSVa3oRJQlTVM0TfF6q+WALyB5vZ4qpnKXBkVjAY2z5BcY+++S08vKzh3XWA22qbZp9QQ0EM11OuhaBbROQAf4p6a/QSrdwGdtcfSnhRAoKCiIjIzE4SIkcLwKX/v167d7924UBYdyzQ1uuQYC+sb28ZFHHoH2W63WzZs3N1b44cOHw8PDBUFwOBzdunUrLi5uLGfrbCcCunVwploIAUKAECAE2hECQDRrmobL8JGGbket7HBNAQ7a6/UiDU2M/81ykuFMHT16FEftQA3b7WCwyE308HVDCGicLUBp8BXIbtBBIzcNEmlQRlutVofDgd4gQJfDLkEQrFbr4MGDR48ePXny5O/syOfNm5efn79///7z58+Lokgc9M1yNVI7CQFCgBAgBG4WBGCtoT/AYxJyDjjAmJ8xDyd0L0s8LovEFJGpYr1mmBPQksbJWngpAU0JaMBEyzKPVyzVvURZgne1qp5mbMPF4mXnCtd4q//O2Baxcll54aqSwhLGLoucxVYYkxXmE2VZqaWTVTWgb1aBfQ5Ifmygj3EF9Ic1Fw4wVi7pueql0kCYf4+DJgK67nS1l7/FxcWTJ0+GcaDT6eS24zYbKBtwvCoIwqxZsyorKyEiOizNhHVyDZLOxo1tRUBrmgbzqWXLloWHh0OMlri4uMZwHzJkCAyk7Xb7W2+91eYzLyKgGztTtJ0QIAQIAUKgwyLQVoOGDgtoMzpGmDcDpHaaxXju0tPT77rrLovFAtSzzWaDBDC/QBMD4Ws2m0HFDBuBL3a5XMhZ80jz+nwAMtjt9oiICEhHRESgnBlWTSKp3VgCphNweBOfOOsIyg/C6j59+kycOHHBggWvv/76vn37srOzDx06xGeteuwamPAqAQUE1OjmAaoZkFeD9zSIrOF0KgE+Ww46tbIsq6pq9P8JykBfCQFCgBAgBAiBDoAAJ7x0G2TubxFgTNQJaJlTuipjMiegNUnnputMK76nEwYEwEi59tMwKFGYBm8PY19q7KPTZ3ZduPBPxvYztrq68sOq0uOM1QDHrAuVFY3xt35UrUUG1KYqjL95aT7GPPq7UhdBlzN+CG8oZ8TrDDS+10bORNcR0LWJ7xUektmwtwOc4TbugpFRxeFWfn7+nXfeCaNBGH/abDZYrgdjVIfDcc899xw+fBj0B8203bhRBDSuCt2zZ8/WrVsvXrwIW5oDJcRFVALKuXPnYOzqcHD/malTp9b+s2j8UYkoil9//XX//v0h6Pd3nwsXLmxO+S2dhwjolkaYyicECAFCgBBodwgYxq7f0zO0u4Z2oAYR5jfvyQw6dzD2Bae83Nzcffv27d27d/Xq1fPmzUtNTZ0wYUJiYmJMTIzT6RQEISoqCsbHVqvVGMMwiCM2mUxWq9XITWMG8H8GiUdj7DOQ3aiJxmObmQg6EL7iFEUQhIceeighIWH48OG/+MUvZsyYsXDhwtzc3KNHj5aXl4OzR+jJRc4aeGrMgF9hHUAQtpiNEoQAIUAIEAKEQAdAgN/mVJ0D1h0pOJMr60y0wu2Xudi5jn2+HgL6MmNVjJ1nzKczzh/885+rzp89qPgrde9mpY7xvTIBrXF99uU6DtrPqWqFKTILyLWxBCF+YAinTAR0W12rRgJaluXS0tIXXngBRQwwsIRPm81mMpnAj2LGjBlutxsIawwHYuSXr5i+nvGbKIq5ublDhw6FxkRGRiYnJ6MHSHOQBKHD66+/DgNd4KDHjBlz4sSJ8vLyTz75JCkpCYbfZrPZYrFMnz79qspvThuuLQ8R0NeGGx1FCBAChAAhcBMjcD2Dhpu4223adMK8TeG/rsqN507UX8bhvt/vx6+g4JAkqaamBqqUZfngwYNbtmz59NNP09LSFi9enJyc/PjjjycmJg4aNKhnz56wftBIAWOcbqfTCX4a4LnRBPt8nQQ0DN/BYxrSMHXBCYwgCHa7HbQzONbHvZ07dx41alRiYuLcuXMzMjJWrly5bdu2Q4cOoUrFOI0BWBAxVVUR3us6SXQwIUAIEAKEACHQzhDQmWddpAzSY5Up+puLiXUml2fQuDAa3t9ztdBZY+jQlRTQisQ0r85yexT1XHX1nrPffO4uLWQBn663bj4BDWJtReNEtp9pTJOZ4uPFBHzczZkU0O3sAoPmIIOcm5t77733wjgNRm5AOuMWQRBuv/32nJwcVVVh4Zqsv2CchuMxY8I4hDOmjXmuFpXc3FwIo4INM5vN27Ztu6pyVFX1+Xx9+/YFJzqHw4GOc8ZiLRbLz372MzQ/vKoqWiIzEdAtgSqVSQgQAoQAIdCuEbieQUO77lg7bhxh3o5PzhWaFnruYOAOS/wYY36/X5ZljMENw1z49Pl8QLaCIhiJV7CqkCTJ5/MdO3bs8OHDeXl5u3btSktLS05OBg314MGD77rrLojc3TT7fEMIaDAKDA8PB+02cOLh4eE4oLfpL6vVCnJstKKGnEZ6Gof+4eHh9957b3R09GOPPTZ37twlS5a8/fbb+fn5O3fuZIwBOAjvFU4D7SYECAFCgBAgBG4qBOoJaJ2+DdTpnYERBg5aU3VbDJ2GvmYCOqAFJEWUFUWUVN3egwuZq7m7NNdbXxUBzblwheuyA0zj3tTAPitEQLfTK8/j8cAIMykpCUzbIOAeKhtQLiAIwuTJk8vLy5WAgkNWMN8QRRFi0eOQDBNG0tmYxgzGkW3TGGHOQYMG2e12UCjDEkCHw7Fq1aqmDw/dqwSUXbt22Ww2UFLDeBXUG6CJNpvNK1asgAOx9tByWnMLEdCtiTbVRQgQAoQAIUAIEAKEACFw1Qjk5+dv3rx5xYoV8+fPT0lJiY+PT0xMhAE3sr3GhMlkgrjnsO4S5CGQAZTOEIgGtsDkBHLCjAUoZizQYrHYbDZkooGqDrKTDjKVxmObTtxzzz3Dhw+fPn36m2++mZmZ+d577+3YsQNMCRsz94DJEvhHNzad0DRNFEX0mEYfaliAWV1dfdUngA4gBAgBQoAQIASuCYFQWhkV0JyD1l+hea6qKuPdEAw/FJ13BuoZCeiGyjTUDPYaepNgqy55BgdrzNZQGfXbMFtQoj4Hpa4fAZRBqKrq9Xp37tx59913hw630PwtUn9t2rSpiaqNhPLVppsotqamBlsLywQ3btwIQVDsdnv37t2ffvrpMWPGpKenX4NFBsi3c3Jy7r//fiCycWDscrksFsuaNWuaaFub7CICuk1gp0oJAUKAECAECAFCgBAgBJqFAHhZgFsFHCDLMiQ0TSsrKzty5Ehubm5eXt6mTZuWL1+elpY2efLkuLi4+Pj47t27w0DfODPBkIk2my0iIgLoZrSoxoQgCKCGNspnoJwG2WeU2xjrumIaCPGgY2Ft5siRI2NiYiZMmJCSkvL+++/n6C9Q+sBEBT69Xi+IdwATSZLAaRqCJUqSBIETQXON6WZBT5kIAUKAECAECIHrQ6COzA0ppdZPmW8P4ms5Q32DXsaSGyrSsN/QnsZzNrSnfpuhtO/1qT4Hpa4fAZ/PxxgDt7dZs2aBlDh0uAXDOafTOW7cuJqaGrfb3XSsv6vlnTF/0z1SAorX62WMQQDq119/3WQyOZ3Ovn37lpWVgRZb0zSjKLvpAnEvGmv4/f6srKzevXsDCN27d58yZcrp06cBKMzfHhJEQLeHs0BtIAQIAUKAECAECAFCgBBoFAEItyLLMk4eQO6Eg29gV5GY9nq9sJoSRvyMsVOnTq1evXrBggXTp08fN25cQkJCfHx87969jeSy0+nESDUul8vhcATxwji9uSEENMhVwNMDKkJ1NqydxOogAfkh3bdv35EjR8bGxs6fPz85Ofmdd97Ztm3bqVOngiYbmqYBDS3LMsx/lIByDSqbRk8M7SAECAFCgBAgBK4bgVDi9rqLrC8AC6/fVJ/CnSpYgtTvCUpdgZ6G3IbSiIAOAvDGffV4PKIo7tmzZ9CgQTAogsGbcdRkMplcLtcdd9yxdevW2nOjqrgyrPltQZa5iUQTpXm9XuPYVRTFgQMHAmOemZmJB0I4RPza/ASKM2AAXFFR8e2330JpOCRufmmtkJMI6FYAmaogBAgBQoAQIAQIAUKAELhGBIB9Dj0YxLzAqKqqCksRYaMsy5qmQYQZ4KAxjbEBccWuLMunT5/et2/frl271qxZM2PGDOCpH9Vf8fHxJpPJKIu+gRYcxsmSw+FAFQ/Q4vCJZtMQyhwPMZlMYJAdNO9yuVx33nlndHT02LFjZ8+evXTp0g0bNuzevXvv3r2AYRBJHQosbSEECAFCgBAgBFoTgVDi9sbWDuU3VKah5qYp5qb31hZtKI0I6IbgviHbampqpkyZYrFY7HZ7eHh40AgNh0mjRo1CxlkJKNc2+GmCd8Zdxk7h2BJCpOzcudNILnu9XlhdZ7Vav/rqK4/HY9QEGI81ltlY2ngs6DAwJ6it8Wv7SRAB3X7OBbWEECAECAFCgBAgBAgBQqANEMBZRBOj/7179xYUFGzZsmXOnDnz5s375S9/OWLEiGHDhvXo0aNLly4w/zHOgsAzGjllpIlB8owTJLPZHBkZiXudTieooSHuIniACIJgsVgalEVDOUZFNpYcRJQLgtC1a9cBAwYMHz48ISFh3Lhxv/nNbxYsWLBz586CgoLS0lLjTAbZfNyIYnNN00DO0xhWONdCuXobnFGqkhAgBAgBQoAQIARucgRQPQD+Y4yxAwcOuFwu4/I1GPaAdxm4W3Tp0iUrKwu6DlQsKIVxsNdyqKDuWBTF/v37m0ym0aNHQ+0ej+fcuXMwLIyIiGCM4cjq2trT2DDs2kprnaOIgG4dnKkWQoAQIAQIAUKAECAECIGOiYAsy263u6KiYseOHZ9++un27dszMjJmzZo1b968mJiYESNGxMXFAR9ts9msVqsxniFGjBEEAQIngml16OQKplhmsznUGMRFg2c9AAAgAElEQVRIQDeRRm4axNRQFOSHXd26dRszZkxCQkJycnJaWtq77767b9++06dPQ0REVVXdbjdOeKqqqoyGHsA7E+ncMS9x6hUhQAgQAoQAIdC6CMCIwu/3Aw1dXl7+6quvCoIQNI7CsQ0k4uLiYNwCQZvhs9UIaHxsv3LlShjIuVyu7OxsCAd95swZUCr07dsXm9e6oLZxbURAt/EJoOoJAUKAECAECAFCgBAgBG4KBED5i6wrOCzDrAatlqEjoih6PB7IwBgD0hYC5hw9enT//v1btmxZt25dampqenp6WlpaYmJidHR0fHx8TExM0FQKv4KhIWqlcXuQ0rkxAtpisUBEeJy5GblssJ+GeZ2xZGDDQXw9fPjwoUOHJiUlzZ49e8WKFdnZ2bt377548SJOomCuiBw0TsNuipNLjSQECAFCgBAgBAiB9oMAhubTNK2goODuu+82PpuHUQ2OWOx2e+fOnRcvXoyDLhiE1NTUqPoL5c/4HL0leoojn5UrV0LbXC7XpEmTYGh0/PhxWOj22GOPXaf8uSUa3wplEgHdCiBTFYQAIUAIEAKEACFACBACNzcCEMQP+gBUcmh/jEHMYYaD8xykZTE6Ih7u9/sxGyzeFEXx4sWL+fn527Zte/PNN1NTUydOnDh27Ni4uDiMco6TrmYS0Ha7HZXXNpsNZdROpxNndHb9BSWDVQgeAnmA3QYi22w2w0abzdazZ8+RI0fGxMTMnz9/1qxZH3zwwb59+4KsD7G/lCAECAFCgBAgBAgBQuCKCID2ef78+fA43GazoTWZzWZzuVzw1W63R0dHnzp1ShRFWZZF/QWLt1pZAW204HA6nREREeHh4VFRUTA+PHr0qMvlMpvNEydORL+yK4LQkTIQAd2Rzib1hRAgBAgBQoAQIAQIAUKgIyOAEp6jR4/u2bPnyJEjs2fPnjt37iuvvPLEE0/ExsbeeeedsMATRM1INAOtbDTcgC1gx+FyuWAXHAsehUA0G01CjKw3zAbBq7qJT6vV2rdv3yeffHLGjBkZGRkrV67ctm3boUOHjJYdoCLH0+bz+URRNLL5uAtyosIIppeiKBq3YGZKEAKEACFACBAChMBNhAAQuBAwUJblL7/8cvDgwUEjGUEQjCE3BEFIT08H4TOOkRpLXA8UyGvD2AOlA4wxURRBXoC6Zk3TXnjhBXiKb7FY1qxZo2nasWPHQDTw7LPPXk9Lbt5jiYC+ec8dtZwQIAQIAUKAECAECAFC4NZCAOdUIPOBWZAsy2AMAhECAZGSkpL9+/d/8sknb7311rx582bPnv3ss88++OCDRqdpmMKhgAiiHUIMH9Q+w0wv1PoDJNVNUM9Giw+UaSOFDZWC90hKSsqSJUvWr1+fm5tbWFho9PTAuRz0EU82ioxwi3EqiBspQQgQAoQAIUAIEAI3EQJ+v18JKJWVldOmTYMxQxDdLAgChmUeNGjQsWPHGGNerxcHSE0krgcHeHCO4RAhvCEQ3zAmCfL6KCoqslgsUVFRgiDcc889qqqePHkSejRmzJjracnNeywR0DfvuaOWEwKEACFACBAChAAhQAjc0giE8rAwFwI+2qgLRutqxpgsyyUlJYcPH96+ffvChQszMzNTU1NjY2NjYmLuv/9+4JqBgIY5Hi56NZvNERERMH1yOp1Ns8+wFxnnoATOHoHgNvLdgiD0798/MTHxmWeemTlz5nvvvZednf3111+jjQmccuCmgzbe0lcDdZ4QIAQIAUKAELj5EcjOzu7bty+ME5xOZ9BKLOCjXS5XUlKSz+fD9VJN8M646zqxwYfiu3btGjlypNVq7dWrV3JyMhaLFUHiu7VfNpsNhlWffPJJVVVVRESEzWaLjo7GQ26pBBHQt9Tpps4SAoQAIUAIEAKEACFACHQEBHAWBMIf5GEh0joS00ZdMEZNDO0/Hs4Yg2WkxcXFubm5u3btWrZsWVZWVnJy8n/8+38MGzZsyJAhSBY3h4A2rpw1ek8H8dHGrzabzWKxoOIJAySaTKYePXpER0cPHz48NTU1OTl58+bNeXl5JSUlRjRCe3fDtxhRveGFU4GEACFACBAChMCtiUB1dfX06dNB44zDAOMIAdIPPPDAgQMHcOgClh1B5G+DX68TVRBBf/LJJ0FNWrx4MRh0GCtljJWUlNx2221AQA8aNIgx1qNHD6fTOWDAgOtsyU16OBHQN+mJo2YTAoQAIUAIEAKEACFACBAC9QjAtAdWgAatA8UZUX3uG5HauXPn559/np2dnZmZOWfOnFdeeeXxxx+PiYnp06cPzBvtdjsEfIepmsViMfpyALMcGRlpMpkgP3hPgyYa00hAg0OIcdaHVLjVau3Ro0d8fPzPf/7zadOmpaen79mz54svvqisrATFN5ozyrIsSZJRD45sMkxlcULLGHO73cDI+3w+jDypBBQ0PAFgbwSWVAYhQAgQAoQAIXALIVBTUwPrtOAuLEnSwYMHXS4XBkY23u4hKAVsQcWxcZlXKwAHNPdXX30Fy8KAVoZlYT169FBVFRefwRgMmrRkyRLIKQjCggULhg0b5nA4evbsCevVWqHZ7aoKIqDb1emgxhAChAAhQAgQAoQAIUAIEALXgkDrE9C47hVJXmM4QU3TPB7P1q1b8/PzN2/ePG/evKysrKSkpPHjxycmJg4fPhwE0SCRtlqtJpPJ5XKBWzSwz3a7HWlonIgaKWzcaLVaIyIijLuM4Rb79euXmJj4yiuvLFy4cOfOnQUFBaWlpSiahpiHKP32eDygHzc6a8P5MNLNmqZBZ1uI3L+WK4COIQQIAUKAECAEbgYE4BYM1LPH4/F6vS+++KLJZLJarfhoGW/xMDAIDw8fMmTI4cOH26p/QEAPGzYMGjZw4MAXX3xREAQIrZGdnR1EQCsBRZZlv98/ZMgQeLLeuXPnWbNmOZ1Ou91eXFwMeuq26k6b1EsEdJvATpUSAoQAIUAIEAKEACFACBACNxIBZEKbSNzI+kLKAk4WBMKwE2ZrmFGSJNQrQbwgxthXX32VnZ29d+/elJSU+fPnv/rqq/Hx8QkJCeHh4aCYNk5B0TkaZNFAXgeZTRtNP4zHgq2Hw+FAdZXL5YqNje3fv//EiROzsrLmzp2bn5+fk5Nz8uTJoBj30DXQN8n6K0gEjTJq7CwlCAFCgBAgBAgBQqAxBPC+eejQoXvuuec7gTDenS36K+huPmvWrOLiYqNw2Ov1NlZ4S2yXZTkvLy88PNxsNt91110lJSWyLAO5LAjC73//ewihjAvRsA0ff/yxw+GAlV4TJkyAkcy6deuMK64wc8dOEAHdsc8v9Y4QIAQIAUKAECAECAFC4JZAoAneGXfdWCBQRCxJkt/vR+NpZJmBxsVKkbqVZRlnnrAXvoJWCKZwMMm8ePHioUOHtmzZ8t1ULSUlZebMmUOGDImLi+vXrx9ojox+HS6XCy0j7XY7qqjQ+sNkMsG01qiVxmzIVpvNZpgfxsXFJSQkPPXUU9OnT1+wYMGWLVvy8/MLCwu9Xm+oyQl2kxKEACFACBAChAAh0DQCoij6fL4FCxaYzWZj4Ae4rcOKKLwvFxQUwEIlxhgIh9uEvZ06darJZLLb7fPmzYMxz9y5cwVBMJvN06ZNC1JAw+IwAGH8+PHgSIadffnll2EXjH+CBkVNQ3fz7iUC+uY9d9RyQoAQIAQIAUKAECAECAFC4HsIINd8i0xmvF5vbm7u3r17Fy5cOHfuXPChjo2N7d2793eKpM6dO6P3IrDPVv0FpDOoq4JCI0J+FF7BV1ReWywWp9MZGRlps9keeeSR0aNHDxkyJDU1df78+atXr96zZ8/evXshLCS4TuO5UVUVZstGdh73wskChTUs2oVdqqqKoihJ0i1yNhEQShAChAAhQAh0PAQkScJn1QUFBffffz9SzKEJeKI8Y8YMjMEAgLThOKdLly7gDPbNN98AIZ6enu5yub7bmJaWBg/OoXlw0weNtqZpJSUld911F/QRhN733HMPMNRwf79F7vJEQHe8f2rqESFACBAChAAhQAgQAoTALYpAG07M2gpxFGIbw/6A+FoUxf379x8+fHjDhg1z5sx57rnnYmNj77vvvvDwcJgHWiwWk8nUuXNnkFzZbDaYW4IaC3ylQdwUOjfGLbhqGIynYc7cp0+f2NjYJ5544tVXX01LS5s/f35ubu6OHTtwIq1pmiRJYEViVHJJkhRkXQIGIOBJfYvMUdvqWqJ6CQFCgBAgBFoUASWglJWVPf/881artcFID/jEt2vXrjk5OXiLx1a11TjH6/XC4CEyMtLv90PDnn/+edi4detWY2QIaC2w7aqqyrK8du1aIwEdFRW1bt06yNbgk2nsb0dKEAHdkc4m9YUQIAQIAUKAECAECAFCgBC45RAwTlCBroVVuqg7RkSMwuQjR47k5eXt3bt3wYIFKSkpEydOjIuLi42NhXhHMFF0Op2CIFgsFiPLbHTtgAxIRttstu8W58ISXYfDYQyiCCU4nU6r1dq9e/dBgwaNHDny8ccfz8zMTE9P371798GDB0+dOgXsM+igJf0ly/KtMzvFM0UJQoAQIAQIgY6HwEcffTRgwAB46CsIQpcuXfAGCndbCNUwceLEmpoaIHDdbrcRh7YioL/88ku4p6N4mTHWr18/q9XqcDguXrwoiiK2DRoMz4xhiCJJ0ujRo2ExFowi4uPjIRuqwo3d7JBpIqA75GmlThEChAAhQAgQAoQAIUAIEAK3BAJAzgZZVYAaOoiYDpUPu/UXGjWihlqSpJKSkpycnLy8vDfffHPmzJlTp04dMWLEwIEDu3XrhrQyOHWYTCan0wnzyaioKJxLo/c0aKjBzQPdP8AIEjIbC4TtAwcOHDFixPPPP5+UlLRw4cIdO3YcOnToxIkTt8QZpU4SAoQAIUAIdDgEqqurp0yZ4nK5IHQwrBmCdUh434Tb5Z///GfovaqqVVVVQUggyRt6Tw/KeWO/5uTkQDsHDRoEwSrOnj0LW3r37o2jDmiVpmnr1q3Lzc2FZU9+v58xVlRU1KVLF6vVCjd9l8t16NChoGgZN7bN7a00IqDb2xmh9hAChAAhQAgQAoQAIUAIEAKEwFUjcLWTUtBKw6TReGxz0qWlpTt27Dh48OBbb701e/bsuXPnJiYmDh8+vE+fPmAHabVajaEOISgixkiEOTY6gZhMJlRVo6QaMiM3jfPzLl269O/f/9FHH33qqaeSkpLS0tLef//9/Pz8nJwcxhgIqEVRVAKKx+MB4w5cFxwa/tHI0SPiQRslSYISMAMlCAFCgBAgBAiBphGorq5mjNXU1EiSlJeXBybIEHcBOGhkogVBsNvtUVFRTz75ZGlpqRJQwOOilSnmppXI+fn5cCN++OGHIdhDZmYmPFqeMWMGQAG3S0jfeeedUVFRRojcbvemTZu6du1qtVrhuXVycjJjzOPxGLN14DQR0B345FLXCAFCgBAgBAgBQoAQIAQIAUKgYQSuh4DWNA1mqpqmYdhAWX8xxvx+/5EjR3Jycj7804dZWVlJSUnjxo0bNmzYfffdFxUVhTQ0Ol2aTCabzeZyuUBMjVwzss8YLxGUUzhph6LgcFzR3L1797Fjxw4fPjwlJWX+/PkrVqzYsmVLfn4+2k/Lsuzz+YBTFkUR0EG7EhBqQTAlI3AAVyvTAcYGUJoQIAQIAUKg/SMAN0dYnOTxeNxu99SpU10uF9za4MZnJKDhiWzXrl3XrFnj8/kkScIbE4b1a51eT5ky5b777vv444+hOrwbwtfc3FwwCUFaediwYeC4tXv3bvDfwKDBp06dgjv4vn37jI3XNC0rKwvKEQThpZdegie+8Hi4w99hiYA2XgyUJgQIAUKAECAECAFCgBAgBAiBWwKB5iidm8hjjF8Ps+WgyapRbhw0o/7iiy9279597NixrKysmTNnPvPMMyNHjhw2bFhkZCRKoWHuil8d+gu5aZixA+kMeSA/fCIxDcprOAoU2V27dgUB9fTp0zMyMmbMmLFly5YDBw4UFRV5vV4IhyjLMiTgUwkoaELd4afHt8SlT50kBAgBQqAlERBFER5qfvinD3v27An3IJvN5nA4bDabkX02m802my0mJsbj8eAKntA7b0s2lpctSRI4bJhMJofDUVBQYCTBofZjx47hg97CwsKCggLoy7Bhw+DBszFgw7p166DXn3zyCd5SoRwloKSnp3fp0qVXr17Hjx9HEzDodUv3tG3LJwK6bfGn2gkBQoAQIAQIAUKAECAECAFCoA0QCJ3iNn+LKIpIN4NiCzsAdC18GgsEURhGQdQ0DUuAY5HnPXfu3NatW/Py8ubMmZOZmTl9+vSYmJjExMSoqChjYEOjqXR4eDiENoLpMYqsbTabUTQNs2Ujiw0ZrFYrhE8UBCE+Pj4mJubFF19ctGhRWlragQMHcnNzT506VVFRgX1s/YQRSSLBWx9/qpEQIAQIgWYiAMtrqqurJ02aZDKZIDQCej0D4wwuVcBEL1myBJ9xQhUoB8Zf/mZWfT3Z9u/fj0T5mDFjgpoEDldgFWK1Wj/66KNp06YJguBwON59912whDY6eKSlpQmCEBkZeeLECWNReP8qLS0Fwp0xBiJo6Oz1dKH9H0sEdPs/R9RCQoAQIAQIAUKAECAECAFCgBC48QjckMktFmL09EDbZeNeYzq0M0GHgzl10CdjrKysrKCgICcnJysra/78+QsWLIiJiXnkkUd69+5ts9mMkQ9BJQ32HTCvRj01JGBNtNlstlqtkMFut4MTCJLUFosFrUIsFss999yTmJj4i1/8YsaMGQsXLty+ffuePXt27doVZNkBPcU+glEJfjVmxtk4JHBCbswM1HxjkBpzUpoQIAQIAUKg9RFAKyrwbs7Nze3duzfeR0ITsFjnwQcfLCgoMN7m4N4BT2qbvmPe8D5qmvbII48AxWw2m1euXBlUhSRJvXr1AtJ5woQJnTt3tlgsvXr1UgIKPnjGZUPdunUDeh22BBWFXQva3uG/EgHd4U8xdZAQIAQIAUKAECAECAFCgBAgBBpA4IZMArGQIAbZuD00HdqaoMONc3LkXo1HwQJhKFlVVVzk+/nnn+/YsWPVqlVZWVnJycmTJk0aOXLkwIEDBUGwWq12ux3pZrPZjDEPkSBAktrIXONe8PTAXZgZCv/hD384aNCgkSNHzpw5MzMzc+3atTt27Dh27FhZWRlM0aH9YEKNsi+fzwfCMZSPaZomiqJx3g5LmxETI55GTChNCBAChAAh0CYIwA+4x+OZPn26IAgulwsD7eIdBBMWi2XBggWSJDXx296av/MQsHft2rV4T+zdu7fX6zUiqQSU5557DpYZweNbi8WyaNEiuLvBJyxs+uCDDwRBMJlMI0eODArqCwVi14zl3wppIqBvhbNMfSQECAFCgBAgBAgBQoAQIAQIgRZBAGeSQQyycXtoOrQpxjzItBoTKBaGjVAChhYEF0tYCIyFI6ULW0RRPHny5J49ezZu3LhgwYKFCxdOmDAhISFh1KhRKPtC+w67/nLqL2ANzGYz+H4giQAENKywNvp7OJ1OpLkxERkZGR0dPXbs2Jdeeik1NfW9997Lzc09cOBAcXExmmAajbOBETDO7RENI1bYWUoQAoQAIUAItCECBQUFkZGRQNGCxhlvFvCQEnb96Ec/OnToELSzmffNlu4URgIcN24chliYMmVKUL3Z2dngatWlSxdBEPr06ePz+Yw3Kcj/8MMPAwG9YcMGvHEbi8JbmHHjrZAmAvpWOMvUR0KAECAECAFCgBAgBAgBQoAQaBEEcCbZzIk05A9tSmPlIOuqBBTQBcOE1kg9g8dFg/4VWBEcpQQUUHWBK6XRm1KW5a+//nr37t07d+7MysqaPXv2iy++OGbMmKFDh3br1g15ZKMPdUREBPILDofDbreDDQhuxIRRK40bMQGsd0JCwuDBg19++WUwv965c2dubu7x48dramrQhQPQMGKFHaQEIUAIEAKEQJsgUFxcPHnyZGBd8WaBv/CQAN/n8ePHQ+Q9n88Hi3vwHodrfYy/8I3dMVuim36/v6ioCLhyCI1w8uRJY0V+vx8iLsCz2FdeeQWW8iAHXV1dDe7PVqvVZDJVV1cbD8c0dhC33CIJIqBvkRNN3SQECAFCgBAgBAgBQoAQIAQIgZZFAGeVV0w02I6mjzLO0htMGw8PLb/pvaH5jVuA2vZ6vfn5+dnZ2WvXrs3MzExKSho9evSQIUN69uwJy5bRmgMIZaMCzmR4ARlht9shP3zCfB6YC5PJZLfbYfk2FvLAAw/Ex8c/++yz06ZNS09PX7FixZYtWw4cOFBeXg7cus/nE0UR7DuQbTf2wpgGNDD0k3EXpsHVBDl6KBP3UoIQIAQIgVsNAePPIP427t271/ADbwrincG4CUw5Nm7cGIqY8d7UWDr0qGvb4vF4CgsLQ481Pj9OSkqy6S+r1Tp+/HhcXQR5MjMzoYPh4eE/+9nPgICGXZIkvfHGG3AvczqdkyZNAkcOj8djrNHYR+P2WyFNBPStcJapj4QAIUAIEAKEACFACBAChAAh0OIIGCeWTacbbErThxhnyK1MQBtJB3DGMDYA2d68vLyDBw8uXbo0LS1t0aJFCQkJY8eOHTx4MC6+NplMEPMQ/TosdS8QxyHdjBSGQ3/ZbDaQV8PyZ7PZjGQ3cNadO3cePHhwYmJidHT0vHnzZs6c+fbbb2dnZ+/btw/pBlVVwTgbCAXQ3yE1AExBY+dFFEW3293gXtpICBAChMAtgoDxXgCLcp566in4QUYOGn+9BUHo2rWrIAgWi2X48OFFRUWqquJPLiJ2xRufsVI8qpkJKBwyy7KclZUlCMLkyZODDjfeXmVZvv3226EXDodj+/btGDhXkqSqqioIRQgZXnrppaNHjzLGTpw4MWnSJLihmUym7t27V1RUMMbgztJYH4Oa0eG/EgHd4U8xdZAQIAQIAUKAECAECAFCgBAgBFoDgcYmmaHbm25NaP6r3RJavrGE0L1X3KKqqiRJDcZTCjpWlmXgeUEfh9zBwYMH8/PzN23a9MYbb6SkpIwfPz4+Pj4xMRENNx0OB0zpgadGfbQxcKKR2sA0zvmNS79BhY08tclk6tWr10MPPRQfH//zn/8cZNTvv//+jh07du7c+cUXX4APtd/vh+CHwEdg12BtOH6lBCFACBACtyYCcBdQVfXgwYO9evXCZSsNEtAmk6lr166ZmZl47zBGlwUAjfemxtLXAzU2uLy8HO8aWVlZxjKN9TLGkpOTMeeAAQMwJxT1zjvv4F54pBoeHg53HKfTCTey7du3Y08h0KKxCkxjybdIggjoW+REUzcJAUKAECAECAFCgBAgBAgBQqBlEcBZ5RUTTbfjiodfMUNo+cZDQvc2vQVJZFVVg+IE4i5YiWwsBwhoFB0bdyEZARqxmpqac+fOHTp0KD8/f/HixcnJyc8999yoUaOio6PvuOMOmOobvadtNhsyy+DUCR7TYOuB5h6hempkDSBhdKYG1sDlckVHR8fGxj7++OPf+XvOnTt32bJlECzxyJEjxi5QmhAgBAiBWw0Bj8ejBBRJkpKSkkwmE/7GIvuMv8zwGztw4MCzZ88GLR8x3jVAXGy8PTWYvh6cIRivElAKCwvBLcrlcj377LPGmL3GSmVZ3rFjh9lstlgs0MfVq1fL+gvl26mpqdB3CHsAD00xSO/q1avBFRqaTQQ0nj4ioBEKShAChAAhQAgQAoQAIUAIEAKEACHQfhEwTpJD0+233TeiZXl5eZs2bVq+fHlaWtrTTz89bNiwH/7wh6CexgXgZv0VxIAYuWZQqwEHYdyOcmmXywXbG/xEc8//1965x0ZVre9/z0zmmuktXCSIJSAYAQkiBGiJvYXeAgWOYkIQMIAa1EPwQii0oRdCsQ2tnCh6ghzJUVDgeIgUDdA2LS1poQZQc7wQD2CU4zeiEijTzLUzs3/8+iRvVmbaUqBAC8/+o3n32muvvdZn71mEZ7/7WUlJSSkpKU/95alVq1aVlpaK3ceFCxdkZS0kjGPdSHEsiVBeoIyEw2EoFJIxB2BwO+kLeGyDBEiABG6eAL5rgefGwYMHR48eDdMkTLl4k4dZFDMnxNlXXnlFpr6IBQZvvis3fqb6Lc7QoUM1TbNarbm5uX6/X2ysVR1c1/UTJ07I60mj0ThmzBh1csZbVZhBWzs3m82GTPCHH354zyd70Jo69ojhyz/fNz6agX0GBeiBff/YexIgARIgARIgARIgARIggfuEgPyvtcvgHoYgBp0YeLAjCMU2FAqdOXOmvr7+vffeKywsXLhwYUpKygMPPAARxGAw2Gw2VW4Wlw+ICyaTSVw7RLaWnL5oDdput0s19ajRaIQ2jXNNJlNiYmJqaurMmTNfffXVysrKoqIiLJkIhRq6s+SMQ6S+9t23mi2u6h2qOBIhYd/DN51DIwES6D8E8J5s/vz5MvWJ+ixarUynw4cPb25ulnkbUqz6z9bdGhdsmjVNGzduHPogM6p0L9gR/Pjjj9V/ODRNKy4ulvpQrgOBQH19/Ysvvjhx4sSRI0dmZ2dXVlZirpbRqQSkfTWQmvdJQAH6PrnRHCYJkAAJkAAJkAAJkAAJkAAJDFQCoVAIurN4gETYNMvAwuFwsCN45cqVpqam1tbWHTt2rF+/ftOmTSkpKTk5OVOmTMHn0lgaEZK0iM4ioIjIEh10qUFrmiblNpsNsclkko+yrVarepWpU6fm5ORMnz69qqqqoKBg69atR48ebWlpwbfqbW1tGI6IIzI6BiRAAiRw5wkcOHBg0KBBmA8tFktEBrS5c8MnKYsWLfr999+x/p6aBdwfhNedO3dCLnc4HN9++63qwiFIgx3BF198EW7Ow4YNg8nGyJEj//jjD13XPR6PWEi5XC5M0RgaWoBFSbAj2N3Y+wMHGewdDihA32HgvBwJkAAJkAAJkAAJkAAJkBhh+bkAACAASURBVAAJkMANEICmHHGC5EFHlGMXGgEcSyUrDWIBfDy///77Y8eOVVdXV1ZWFhYWLlq0aObMmdnZ2ZIlHS09izxttVodDod8cq6q2OJAbTabTSaTzWaDBi3ytNosGoRObTabnU4nXEfNZnNeXl5ycvK8efOKiopKS0t37drV3Nzc0tLS5WBZSAIkQAK3iYDX633++eetViukWxgZYX6TJGhMa06n89///jcWdEVnuhNhr9vVvnr3FuF98eeff8q8XVVVhat4PJ4IJXrSpEmapo0YMWL79u2SCv3+++8HAoH29vZwOOxyuXAWBhIOh30+Xzgcli9X2tvbuxs7Bejr3n1WIAESIAESIAESIAESIAESIAESIIG7QKCvxIhedt3tdv/yyy/Hjx8/ePBgRUXF2rVrFy1alJ2dnZeXZzabHQ6HaDEiKzudTk3TYmJiRF/GITiEItta0zRoGThkNptjYmKkhQj7aXVRL6mDxk0m08iRI9PS0vLy8pYtW7Zhw4atW7fW1ta2traeP38e6zoKMbfbLT6noVBI7D4iBBeVjGgoKPT7/R6PBw1GHFLPYkwCJDDQCVy5ckWmC4ylqakpJiZGvuSQ+U0Cm81msVji4uJSU1Mx+agQVLFVjdU6mIsqKyvz8/ORPuz1eiMqdLeLeemaIvz666/PmDEjJyfn4MGDn3/+eX5+/vnz5yGFR1x33rx5eM+XmZmJPGWxbEbWdl1dHVK5n332WV3Xk5OTobxPmjRJ1/WrV68GO4IRbUr31PLexHLifRIwA/o+udEcJgmQAAmQAAmQAAmQAAmQAAmQQE8EYOuB3GrRJtQTYN989uzZurq648ePFxcXl5eXv/jii9OnT58xY4bINAaDQfLmNE0TU47Y2FhT5ybyjZwiJT0HYrcaUU21+DCZTFOmTMnOzp42bVpFRUV+fn5lZWVd53bu3Dlk6kFqcXduGCA8XnVd9/v9Ip2oY5dq0YUsIQESGOgEZE1U+NG3t7cvXboUS/bBcCNizsEuHCq2bt2Kt1MR76hkJokIVFZer7eurs7WuUHzhRORWqfneMGCBSaTyW63ozNOp9NsNmdkZMBnX81E1nX9wIED+NzEbrf//PPPastw4V+xYgUE6A8++EDX9T2f7JGR7tq1CwNUh6O2oJb3JlbPvR9iCtD3w13mGEmABEiABEiABEiABEiABEiABG6SgPhNY/HDQCAAqQL5dxA4pM7FixdPnTpVX19fUlJSXFy8fPny5OTkqVOn2mw2s9msKsX4gN1qtcpX4V1KPBGFRqNR7KThPa2q0nJI8qxxutVqjY+PR2w0GqdOnfrkk08mJydv2rSptLT03XffPXDgQHNz89WrV6HaiM+piiwiO1I9xJgESGCgE5AvJ1paWh566CGxtjcajZbOTZ1qoE0nJSUdP37c4/FgSlSNKSJWT1UF2QhQ//jHP2BeZDabv/zyy4ijPe+uW7fO6XTikxFMsNLtffv2RXgxo6lx48ZhJrw2Reu67na74csUCoXOnj1rNBodDsfQoUMxFp/Pl5aWhhVrs7Oz0UJ3Y1HLexP3PLR77ygF6HvvnnJEJEACJEACJEACJEACJEACJEACN0nA5/OJ/Or1eiWGwoJGRXpGKrHUwdFooRY21uFw+Pz5883Nzfv27bvmQFpUVJSbm5uenj5mzJgIn40I0VndFYlZPKnlKFQYk8lksVjQYHcZ1jgaGxuLc7Ewo9FohJeIpmkpKSlpaWlPP/306tWrN27c+Omnn7a2ttbX1yNN8ibJ8jQSIIH+REAUZ3TK6/W63e7XX38dQrM6KdlsNtViCB92FBUVBTo3zHjR1hndibARDPbt2wfV2GAwLF++HGdF1Olyt7W1VbKzp06dunz5crxmwzKJWVlZPp8vIgNa1/WSkhKZ6P7v//5PRPNgR/Cll17C68CFCxfibZyu6x9++KHRaMSHLOfPn6cFR5f3ojeFFKB7Q4l1SIAESIAESIAESIAESIAESIAESODmCXSnxUh5W1vbuXPnGhsb9+/fv27duk2bNj355JM5OTkPPvggtOYIxRnykJo9DW0aajJS9qAvI47IXsRn5lhMLMJy+rq7Q4YMmTx58qxZs1atWlVcXLxhw4b6+vqWlpYzZ84glxCJh5C3/H6/quNHEGzv3GThMgjcbrcbidioHAgERNuCVUiEcBbRJndJgAR6QyDYEfT5fKLAnjx58pFHHoE3vUwC0GqdTifeZkHwTUxMPH36dMSLt95cscs6v/76q8Vigbd+fHx8KBSS33uX9aVwzpw5cM9PTk72+/2hUKilpWXo0KGapqG8oaEB5XKK3+///fff5aXdhAkTxG1p//794phUU1Mjp1y+fDk+Ph7zbVlZmWpSxIlIKPUmoADdG0qsQwIkQAIkQAIkQAIkQAIkQAIkQAI3T0CE5h4CaT1a12hraztx4kRdXd22bdvy8/PXr1+fnp6elpYGHw+bzaZpmiRHQ1yGNm00GiGdGI1Gs9lsMBgk+0+yDkVs6k0g2g2ugs/zJca1Jk6cmJ6evmTJktdee23jxo0HDx48ceLEF198ga/yfT4fdGrsyqhhPouFyFAYwSEUCgU7gqq6rZ7LmARIoPcE8EPDxxnXZOi1a9fKcqnqPIDfO2YY+AgtXLhQXilFf+3R+w6gptvt9vl8ubm5sIHWNG379u29aTbYEYTKbLPZDh8+LNfdvXs3tHKDwbB48WK83BKRXdf1a6uqFhUVyTyWkZHR1NS0e/duka0XLFiAlQDEF3vlypV4gTdlypRQKKTO4XJdBtclQAH6uohYgQRIgARIgARIgARIgARIgARIgARuiYCqWXQZQ/Lwd266rkOCESEmEAj4/X5VRlF743a76+rqGhsb33zzzcLCwpUrV+bl5SUlJUmaM3RhTdMsFovNZoMqLYWq3tRzLKoN8qyxO2jQIClHgHxJaV/1rXY4HGPHjk1KSsrJySkqKlqzZs2//vWvEydO1NfXYwlEjMvr9YrRNnVn9V4zJoG+IhAKhQKBwA8//DBhwgR4OsOSXp0EnE4n1Gez2exwOPbt2xcKhbAWH6TYW+9MIBDYtWsX1GSTyZSamtqD1Y8cOnbsGGabUaNGRbzKevTRR/F2zeFwNDc3y2qE0tXffvvtwQcfFFMRzId2ux0qc0NDA64if6urq2WK++2339QJXNpkcF0CFKCvi4gVSIAESIAESIAESIAESIAESIAESOCWCKiaRXQMJUgSfkVkkUvKIVGocSgUColXKb6Ih1Tt8/nwGbvX6z137lxLS8u1j8qLi4vffPPNZ555JiMj49FHH7Xb7TeRBC0f42uaZrfbxYPV4XCofiCi12BlsGgDEKha0eVjx45NS0ubNWvW0qVLr60wVllZuXfv3tra2m+//fb3338XIAxIgARunUB+fj4+nsDvET9bVYBGNrHJZMrOzr5w4YK8G7v1S6MFvGMLh8MPPPAAHDA0Tbt48SKOyrwnl7t8+TIE5YKCAvQWttGYBlH/1VdflbdfT/3lKcjl+HgC7fh8vurqavlkRN6QXTMA2bBhg+r/gwY9Hg9mqsGDB+/atUudwKVjDK5LgAL0dRGxAgmQAAmQAAmQAAmQAAmQAAmQAAncRgLROsstXkyVSLAMV3eXOH/+/LFjxz744IPS0tJNmzbNnj173rx5Q4cOVbOkIUhBrVY9PZBSjTxrxDByhZgl+o6I0WogIpda2Mt48uTJGRkZU6ZM2bx5c1lZWUFBQVNT0+HDh3/88UcMM8JDFgoUkKqZ5hD6VWVKxR6Rco5GAoFAKBRyuVwgrNZnTAL9mcClS5fUTOFTp07FxsZibT387uDnA6VV/fE6HI6qqqrbOrRwOFxYWCjfZ/ztb3/Db1PkaZnQxCA+Ly8P3d62bVtE3w4ePIjJChX27t2LClg/EBp6KBTasWMHXEfw5sxqtWZkZEQ0JdNmZmYmksRXrVolnYmozN2eCVCA7pkPj5IACZAACZAACZAACZAACZAACZDAvUkgHA5HyNOysFiwI3jx4sXTp0/X1NR88MEHGzduXLx4cXp6empqqiruYGlENX0yJibGbDbb7XaDwYCjCPCJvUjMtyJA22w2JGbCTkQUcLncsGHDkpKS5syZs3LlysLCwi+//PLw4cOnTp3C6MLhsOpD7evc4BUrepPcb5RAupIYR+kGK5QY9H8C4udz+fLlv//973FxcTabzWKxmEwm/BhFgLbZbCJAZ2VlnT59OhAIyMzQtyMNh8N4tXPhwgX5hGLatGlIQxajatF8UTkUCiUnJ2My+eijjyK61NjYKO/PTCZTSkoKZGtJ34bzta7rp0+fTklJcXRua9eujf70RFpes2YNLpeSkiKdkaMMekOAAnRvKLEOCZAACZAACZAACZAACZAACZAACdzjBCCw+v3+cDgcrcWI9ysoNDc319TU7N+/v7y8fN26dZmZmampqQ8//LB8z261WkXGUjVr6Di3IkCjBWjQiNW/0Lu7vLTJZLJYLMOHD582bVpubu7q1asrKioKCgqam5uPHz9+8ODBlpYWsTSBzITBwpBaEkhV4Z5q1D3+q7gnhifqc2tr6+jRo5HMazAYTCaTtXODlw406ISEBKPRmJCQUFpaCiE4+sVMX1ERadjlcq1YsQIuHEajsbW1Fb8sn88nPzHpRjgcTkxMRP8PHz6sVgiHw99//z20bLwJ0zRt/fr16DDeJOEzCCmBvC6v4uQq6hixSqGmabGxsbicepRxbwhQgO4NJdYhARIgARIgARIgARIgARIgARIggXuWQCAQgG2FaNDqUGE8LTIN8gclKdLn88n38kiTdLlcR44cqa+v37Rp0/r165955pnJkydjoTNRim9FgJZMSfhQi7qtis5yIVjcqruIxSVW0relRNO0+Pj4xx57LC0tbcmSJWVlZZs2bfr000+hueu67na7VbmKgpT6tDDubwTw07506dI777wT8XMwGo1WqzU2NlbSn2HBkZOTc+HCBcl6hvPM7RsXpp36+nqn04m3RC+88ILf74+24JA+OBwO1GxpaQkEAqoG/b///U++zDAajWazOT4+fufOnTgXbcqUJQ32HBw6dEgch/h775lVd0cpQHdHhuUkQAIkQAIkQAIkQAIkQAIkQAIkQAJ9RgDZjjU1NS0tLddsXgsKChYtWpSRkfHEE08gJRNmGlarFRKzCMqqNBwtJaMkLi5ODsnp0YscSp1bDEaMGDFz5sysrKwXXnihuLj47bff3r9/f1NT088//+zxeHRd93q9Ip+BYJfiPg55PB6ohJD8xKw2Og+9z24GG7oPCAQ7gngIW1tbR44cqT7z+E1Bn0W5GNqsW7euvb09FAqJAH1nUAUCgblz5+JXP3ToUHFyx8seeeWDzkBJt1qt1dXVEVnSp06dQiOLFy/GxAL/n507d4odvKQ5g0+XA5Thh0Kh+vp6NGKz2eTcLs9iYXcEKEB3R4blJEACJEACJEACJEACJEACJEACJEACfUYAmqzX6w2Hw263W8QgeLP6/f7m5uZDhw69++67BQUFb7zxRnp6enJycmJiomQ6I7FRdDQYCJhMJrPZbLFYnE4nDolyLTX7PEDqaEQ+KQwENE1zOp0TJ07MysqaOXPmxo0b8/Pzt2zZ0tjYeOjQoT///FO8aD0eD/QvFYWu6+puoHODkih6Yp/dEjZ0TxOAnU5paak8mfhcAL7PiNWXNKNHj25ubhbh9Q6zCQQChw4dMhgMkHq3b9+u67rP5+tSgHY6nbDg2LVrF4YpSdCNjY34rOGVV14pLCzESoOYAbKzs5ctW1ZSUgJrkR7UZxk7rN43b94MyZ4CtJC50YAC9I0SY30SIAESIAESIAESIAESIAESIAESIIE+IxAKhSTbUSyY0TrUaii2zc3Nra2tW7duLSoqKi8vz8zMzM3NhaEt1CUx07BarXCCjhCs+1CGhmwX4XMNVVrWcItwqZbOoHzWrFlJSUnz5s0rKysrKCiorq5ubW1taGhQBWhP5+b3+1VNkAmYffbk3dMN+Xy+1tbWiRMnymMPxRYvbORpNJlMMTExmqYtXLjQ5XKpmqz8Ku8MJzzYTz75JKTeUaNGYWlQyX1Wn3xJ6N66dauqUIdCoW3btmEqKCgoCIVCixcvxmwgHKxW6/fff+9yuXoelzovyZqHKSkpPZ/Fo90RoADdHRmWkwAJkAAJkAAJkAAJkAAJkAAJkAAJ9BkBeFOoKpLatJQj5VA9JKv/iS0svCmQHYm/TU1Nzc3Nez7ZU1FRsWHDhpSUlLS0NFWeFvmpT4LY2FjJKrVYLKpJCAQ+0byg9NlsNrvdLpdGfSR7qjYIyN02mUxDhgyZPXt2Wlra2rVr161b9/7779fW1tbX11+5coUWtBHPBnejCVxzbd6wYYMsNogsYJGezZ0bnkaz2Txs2LDDhw/LSw4k4N95+xe/3+/z+Wpra2EGYrPZtm/fjl+3ZDfLVCDCuqyUKDJ0fn6+qXP7+OOPL1++7HK55syZI7Y8BoMhLi4umlh3JZcuXVq4cKHVasUPuaKioruaLO+ZAAXonvnwKAmQAAmQAAmQAAmQAAmQAAmQAAmQQD8lIMqU6NfRHfV6vYcOHSovL6+oqFi9evW0adOSk5NVyVh0YRHsujyKrGeLxaK6FsAexGKxiO+HrK/YXYDLqUexBFx0iSwNJ4fgThATE/Pkk0/m5uYuWbJk/fr1VVVVDQ0N33zzzaVLl6DQQT0Ek2BH0OfzifqPQkl0FZ1RSqQFWFHfeS/g6DvIkh4IYAk+uFVARP7uu+9mzJghXury8Mhz63A4JM7NzW1ra4vIsu/hcrfvkMfjwcM5ZcoUmIRMmjQp+nI+n0/X9eeeew6/o9zcXCyLCt082BFMTU01GAxOp/PMmTM4PRQKvfnmm2IT/84776jNhkKhX3755auvvoIvh8/nA8Y///yzoqJCXiBpmjZ79mz1RMY3RIAC9A3hYmUSIAESIAESIAESIAESIAESIAESIIEBRiDYEYRO5/f7oXMFAoG2trZz5841NTXt378fMm5hYeHcuXPT09MnTpyYkJAgwrTJZLLZbLDOEOUOFroGg8Fut4uhgRSK6hcd9EaAjj4LJSJzQyu3WCxms9loNKqKeXx8/OzZs7Oysoo7t/fee+/IkSNff/019DWPxwOpzufzuVwuCNAogTF3IBBQzaaDHUGPxwPVT9yrB9jtv3e7K7cS99Hn85WUlKgPScQDiURgPIGxsbEfffRRD29u7jA2jEXX9U8//RTrkWqa9tFHH6ndgDR87bVTUVERRhEfHy9p0X6/3+Vy4VMDs9ns8/mABe7zfr//yy+/PHv2rFwILQcCgVWrVsXGxg4bNmzZsmVr1qxZsWLFtGnTxELHZDLZ7fa5c+devnxZ7QzjGyJAAfqGcLEyCZAACZAACZAACZAACZAACZAACZDAQCIQLbGJjBU9DK/X63K5oFjput7Y2Lh///633367qKgI2dNJSUkiTFutVjGelsIIyS9aSkZNtTw6A1o9qsbwUrDb7fD9gKuvqj5L45qmIVkb8rTUiYmJweqOzz77bH5+flFR0a5du5qbm7/66ivR15BXHuwI+js3qM/RGKPpseQOEwiHw/Ju4Ntvv83OzobPRndPo8lkggadkpLy66+/4oegJr/f4f7L5cLhMDw0UDJ16lRY3IwZMwbrdqIcXfX5fCdPnhSdfe/evXg1EuwI7vlkDxYjfeaZZ7xeL7L45Sp4B6PuIv7ss8/kHZI0qzLcsmULrIH6A6vo/g+IEgrQA+I2sZMkQAIkQAIkQAIkQAIkQAIkQAIkQAI3QwAinXhNQHSDOAVRSZVWJf9XLVSvitN9Pt/58+ePHj368ccfb968efny5WlpaRkZGapY3F0sGrFU6L0ALeqYxWJRM69tNpsoaAaDASJjdHY21Ek1Y1rOksxum802ZsyYGTNmZGZmFhUVVVRUbNu2rbW1tbGx8ccffxSMKhPGd5EAUvvfeeedhIQENcFZ0zSn0zls2DB5zPASwmKxlJeXw2iiX8mpwY5gW1ubruvt7e379+9HArLdbt+5c2cEXjyEcHiPi4sbN26crutYVDArKwu/r8rKSnlxgt8sljRUs/ulWbfbvXLlyri4OBiyy28hPT198+bNV65cQU2v18vnX6DdaEAB+kaJsT4JkAAJkAAJkAAJkAAJkAAJkAAJkMCAIaD6RHcXq4NBHbXkhmKfz3fu3Lkvv/zy+PHjJSUlZWVlCxcunDFjRkZGBpI6ZQk4yIVGo9FqtcLcGdnTsixhhKwsyjWcN6ydG9xyr5t2raqQEbGa6dmb2GKxTJs2bfbs2TNmzMjPz9+yZcueT/bU1ta2tLS43W6YEYvLAdJa29vbJRcVoqdInxJEQ4ZvNbJWvZ2b+B1HV76vSkKhEOAEO4I//fRTTk6O1WqVJHdN0xITEwcPHqzq0bGxsQkJCU888cSFCxe6e7lydxlG9GrGjBl4gzJy5EhIwBEViouLZcjz588/ffr0mjVrMOT4+Pgenqsehnny5MmGzu3kyZN//PGHPIEyb4iW3UMjPNQlAQrQXWJhIQmQAAmQAAmQAAmQAAmQAAmQAAmQwL1AQMSjHgJ1nLcoQKtNiVwFQRZ/f/vtt9ra2qNHj65bt27Dhg0vvPBCZmbmxIkTIf525zeNo0gLhcpmMpnEXiNCU76h3d6IzhF1JBHbbDZLN66l1opinpKSkpmZuWzZstLS0oKCgsbGxrq6uosXL4oHAqRq5JMiRoIqJD/Rr1WYEkcIkVJ+nwRqEu727dudTqfD4bDb7aLGapo2ePDg2NhYpLeLDF1cXIzFBj2dWz/HVV1dbbPZkM6/Zs2a6EciEAgMHjxY0zSHw2Hp3GBQo2naNfNzXdf9fv9NPCqqEwgQRcwb/Zxbv+0eBeh+e2vYMRIgARIgARIgARIgARIgARIgARIggVslEKEfdbmrXuNWBOhQKBQIBPx+v8/nE/FLArmKSGNQu6SCy+U6c+ZMc3PzF198UVhYWFxcnJWVNWvWrMTERLvdnpCQAHMAVWo0GAy3KENHiMvX3cXVTSYTzHaj62NdRKfTKf4eqBMTE4NE76ysrJkzZz777LMFBQVlZWW7d+8+cuTIyZMnf/vtN9CDGB2hOba3twOgqsAK0vsnwFuNixcvZmVlqU+C2WyGKbnNZkOOvBwdNmzYDz/84PV6xaqin+Nyu91er3f+/PkYgtFoPHXqVESfr72rKC4uli8ANE3D8oPJycl+vx8PyQ39ltXKMkvIL1RKIrrB3V4SoADdS1CsRgIkQAIkQAIkQAIkQAIkQAIkQAIkMPAIiHLUQ6COCtXUkt7HHo9HZFORla9cudLe3h4OhyGKwXgay6bBirq79mEjIA1euXKloaGhsbGxtLR0w4YNK1asyM7OHjVqlCxIeEOJz1I5WkG+bgnOhaOIZEMj/xT5tpJ1C8Vczc+FKi3atAS4KATH1NTU3NzcnJyctWvXVlRUQKFubGyEBi1AuuN2z5dv27ZtxIgRuO/gZjabncomd9BgMLz88svgFggE3G53OBweEABdLldDQ4OM7oknnoDLc8TNXbt2LZ5DPH6TJ0/+z3/+o9a5oZ+zkPH7/ZCeKUCrMG8lpgB9K/R4LgmQAAmQAAmQAAmQAAmQAAmQAAmQAAl0QUDVu7sTs9Q6aizNoVA9vcvY7/c3Nja2tLRUVlaWlpa++OKL6enpY8eOhZ4rmbDqaoeQ9mw2m4iVCIxGI9YqxK7FYnE4HMiztlgsMJ6WQ2jw5v6KAi7di+hJD7vJycl5eXkvvfTShg0bqqqqjh07VlNTI4vFCb2IAK8Egh1BLMGn67rX64XUKDUDgQBsQETuhG2FVLhjweXLl5EJrut6OBxG4jPygmH5DecNTdMsFsuoUaMSEhI0TYNJC9KBhw8fXl1drXa4y2dMrdBPYmRA67r+8ssva5oWExOjadrixYthrBHRyZ9++unll19esWLFW2+9dd1nIOLcHnZVVmrcwyk81AMBCtA9wOEhEiABEiABEiABEiABEiABEiABEiABErgZAqpoparGanl3sVwPFdTTu4yRT42zJPNa1LqGhobW1tYdO3aUlJQsWrQoNTU1PT1d0zTVRgPe09B8sShiD7qwHLo56VnVwSWZuge5OeIQ1HAYjyD7VWR0g8EwZMiQxx9/fNasWevWrausrNy7d29dXd3Jkyd9Pp+u6x6PJ9gR9Hq9ko0uqNVAFGq18K7E0J1xT3fv3j18+HDJLgeWUaNGjR07VhLJ8fLAYDAsWLCgra0tos/q8xZxqF/thsNhpP+7XK64uDiM1Ol0lpeXo5+BQEC+JLhNPVdZqfFtutw93ywF6Hv+FnOAJEACJEACJEACJEACJEACJEACJEACd5qAKlrdaCx97eWJqA/NTs6V/NmIEkixly5d0nW9ra3t9OnTtbW1O3fu3LJly2uvvbZkyZKMjIxJkyaJ7GswGMydm2i+yMC12+13RYDWNE3StGF2LF2F4wd2LRaLums0GuFZMXfu3OTk5Dlz5qxfv3737t3V1dXHjh37+uuvhZIo+O3t7cGO4N3KgA4EAlCfgx3Bn376acWKFTDXFq15xIgRjzzyCJy48UrAbrfbbLb4+PjPPvtM3CRkXMiklidKLe9vMZLQkZ++c+dOaO7Ivj969Ciec7yJwXDU/svtUwtvIhZQEcFNNMVTdF2nAM3HgARIgARIgARIgARIgARIgARIgARIgAT6mECEbnVDu9KVXp4l9UV2DIVCwY6gKsaJYKfruuTVut1uORdpp8GOoKwE6PF4/vvf/544ceLAgQNbt25dvnx5enp6UlISVnuzWq13RYBGBrSIztCjsWsymWRJRlUuRx2RpCWDG/WlKbPZPGrUqKlTp7755pslJSVlZWVHjx6tqan5/vvvodoLqzsWBAKB2tra2NhY6STGMnbs2AkTJqiF3qaugQAACrNJREFUiNPS0n766Sd0L2IxzAEkQOu67na7hXlGRobRaLRarXa7PTY29ttvv0UmO5KgoUcHAgH1ab/1G9TdT+/WW74/W6AAfX/ed46aBEiABEiABEiABEiABEiABEiABEjgDhFQxaybuKR6epfxTbR53VPUC0VXhpFFTU1NS0tLcXFxRUXFunXrnn/++ZycnGnTpsXHx0MPhSWxulBhtGbaZQksQaSdCDUZKdiS4HxdHw+bzWa32x0OB64F3VyuK6YWts4N5RaLBTo7/JSRdzx69Oi0tLTMzMznn3/+ww8/rKura25u9nq9qvQJ5VToidwPhiiP5omSYEcQ61XCJOTixYurV682m80wQTabzZbOLSUlBa4jkg0No+StW7eqV1H70N0V+2E5ui1WM4FA4Ny5c4MGDZLbnZKSoorp/XAI7FI0AQrQ0UxYQgIkQAIkQAIkQAIkQAIkQAIkQAIkQAJ9RkCkQFWp7H3r6uldxr1vqq9qyrJ40qA6NCSlXr169dSpU01NTeXl5VVVVU8//XRqauqECRNEVsYCeqILI7dXdEaozJCDZcVCUY3V8ojC6F0IuFBvo68CoVlUcpPJZLVaoUqrfdM0zWw2yyp/suIfdOEHHnhg0qRJqamphYWFlZWVu3fv/uKLL+rr61taWiSTV9d1n8/n8XjgQA10EKxBDAy9Xq+u60eOHHn44YfloujJ6NGjn3jiCThf4xD08XHjxp0/f17EbvUhkRs0UAJ0XgRov98fCAT27t1rt9tNJhNMVxoaGjAc9akbKAO8P/tJAfr+vO8cNQmQAAmQAAmQAAmQAAmQAAmQAAmQAAncGAHYdKiqnxqrbakeID6fLxQKtbe3ezweMQn56quv6urq/vnPf1ZWVr7++utLly6dNWvW448/Dq3Z1LnB69npdKrrFkbry70sSU5OHjp0qNFoHNO5Qem22Wzp6enipCzuHHC9MBgMNpsNV5dEaavVajabRbCWq0cnYhuNRpGwJ02alJWV9cILLxQWFu7evfvzzz8/ceLEDz/8AGihUAiqdLAj2NbWVlpaivbRH3R18eLFkpQti0ZeM7YuLS11uVzISUdr95IAHewI+ny+a2nmRUVFuE0mk+mrr75SHzbG/Z8ABej+f4/YQxIgARIgARIgARIgARIgARIgARIgARLoFwT8fj/SdWHUq+s6dr1eL6yldV2H+7DsSv1eDsDlcp05c6a5uXnv3r2FhYUlJSXJycnx8fHi7ywysYi/1w1wClJooRRbrdaYmBhIukajcciQIcmd25AhQzRNS0lJGTFiRGxs7PTp04cPH440ZzQC+wv8xelms7nLLmGdRrvdHnFU9QCxWCxDhw6dOHFiamrq5s2bjx8/PmzYMKRpy6ASExNXrFiBs3BdHEpKSvruu++EqrwMuJcEaIwOIyorKxs2bNiSJUtkyAwGCgEK0APlTrGfJEACJEACJEACJEACJEACJEACJEACJHCXCWDlt547cRMCqJwS0bKUt7e367rucrmOHTtWU1ODRQLnzJmTnJyckZExceJEm81mMBhgiwzBV2LkLItnBdRbSWFW05ktFgtylsW1w2q1zpgxIysrKzc3Nysra9asWbm5udnZ2XFxcenp6UOHDoUpR0JCgqZpsbGxyN2OWN5QpGQ1cHRuRqPRbrejqyIuI9vaaDRaLJbc3NzMzEyRsC0WC664Zs2aCFb3zK7cdJHU75mh3bcDoQB93956DpwESIAESIAESIAESIAESIAESIAESIAE+p7ATQiI6ildxpJPjQXoxEY52BFU42PHjp04caKqqqqgoGDBggUpKSkPPPAAjJLFQwNqr8lkElVX1YURixW1vXNTV0HEIZPJ5HA4DAbD448/Pm3atMTExPT09PHjx6cq2/Tp0wcNGiSWzepVRGKWQqRRo28ofPjhh+fPn2+z2aA4S/8nTJiw55M9qrV039/Cu9qi+gDc1Y7w4n1GgAJ0n6FkQyRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAjchIKqndBnruh4IBLxer9/vhxgtph8+n8/tdgO7HMJue3s7DEB++eWX2traQ4cO7d+/v6qqqqKiYs2aNSkpKfHx8QaDQbyV1ZUPzWazyNBwo8YuMqZNJpNkWCM2Go04RZZMzMzMnDlz5rx58954443s7OzCwsKn/vJUWVlZWlrarFmzUlNTJQsbEnlMTIxo4s8999xjjz1mNBpFgIYqvWDBAo/Hc28/Y+oDcG+P9P4ZHQXo++dec6QkQAIkQAIkQAIkQAIkQAIkQAIkQAIkcNsJ3ISAqJ7SZSwZ0Mh3hqzccxZwhIFDIBAQ6dbj8ajO1O3t7SdOnDhw4MDf/va3goKCpUuXpqWlzZw586GHHhJFWFKVEcjqgqJKRxg3S32xnBaZ22w2jx49Oi0tbeXKlY888ghqSpL1Qw89tGTJkiFDhkjKMyo8+OCDlZWVsNgOBAIRo7vtN/UOXkB9AO7gZXmp20iAAvRthMumSYAESIAESIAESIAESIAESIAESIAESIAE+jMBVe4MdW6qtnv27NmGhoaampodO3Zs3Ljxr3/9a15e3vTp0+HsIb7S0KNh4mw2m202m5rdHKFiGwwGi8UC5RoqMyrbbLanOze0gMaxcGJmZub58+fVjvVnpOwbCUQQoAAdAYS7JEACJEACJEACJEACJEACJEACJEACJEACJPD/CbS3t1+9ejUcDgc7gqr+iwTqS5cu1dXVtbS0lJeXV1RU5OXlZWZmJiYmImcZCxLCvkM19LDb7VCcIUzDyiMuLu6tt95KTEwU5RqLEJpMprfffps3gwQGNAEK0AP69rHzJEACJEACJEACJEACJEACJEACJEACJEACt5eA1+sNBAJY8NDfuXV5PVkO0e12nz17tqmpqbq6evv27eXl5c8991xaWtrgwYM1TROJWZYcnDNnzpkzZx577DFN07DkIILx48d//fXXsB9pa2vr8qIsJIH+T4ACdP+/R+whCZAACZAACZAACZAACZAACZAACZAACZDAXSMAs2nVNjoQCKi7anK03+/3eDwiRnfZ6SNHjjQ0NHzzzTc4Gg6HT58+bbfbkS4dExNjtVrLysp0XQ92BK/bWpeXYCEJ9B8CFKD7z71gT0iABEiABEiABEiABEiABEiABEiABEiABAY2AVWMvqGRjB8/Ht4d48ePr62thYStWlTfdMs31A1WJoE+J0ABus+RskESIAESIAESIAESIAESIAESIAESIAESIIH7lMBNy8RXr1492rldvXr1ypUruq5Ha9D3KVMOe4AToAA9wG8gu08CJEACJEACJEACJEACJEACJEACJEACJNBvCNy0AC0jCIVCcJ2WEsmDlhIGJDCACFCAHkA3i10lARIgARIgARIgARIgARIgARIgARIgARLo1wRuXYDWdV0aEekZQb8eOTtHAt0QoADdDRgWkwAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkMBdJSBK9F3tBS9OArdEgAL0LeHjySRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAiRAAt0RoADdHRmWkwAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJ3BIBCtC3hI8nkwAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJkAAJdEfg/wEX6dbI1XvumQAAAABJRU5ErkJggg==" width="356.1070866141732" height="181.76299212598425" preserveAspectRatio="none"/>
</g>
<g transform="translate(86.74795275590553 194.76299212598425)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="15.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="25.119999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="35.739999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="43.019999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g70A876D91C5CC45BCC4BC8E88B98F10" x="56.959999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="66.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8934F85724FE2A1B73A1C811C5B32995" x="75.97999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="81.91999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="92.75999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="100.55999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="109.49999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="116.93999999999998" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 433.56299212598424)">
<g class="typst-group">
<g>
<g transform="translate(8 18.5)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAA14E57E2DCC57A3F7809273EECD3C51" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="9.344000000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="12.812800000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="18.5344" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="23.296000000000003" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="29.1456" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="33.8048" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="39.2832" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="46.1696" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="49.638400000000004" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="55.116800000000005" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="60.96640000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g1CB3EC9D05726EBFDE8ADABEC8504FCD" x="67.54560000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="76.4928" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD62975B7DE3250BE5F195D0E8335F60D" x="82.3424" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="88.704" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="92.1728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="98.5728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD5EEFB9760BC9A91B84F628EDDA52971" x="104.4224" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="110.7328" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="114.112" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g83A6AA7A836EACB3652229F4716CDAF" x="123.03359999999999" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gDB4862E33098F259EEBBA99A57E5AFA" x="129.2416" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="139.3536" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="145.2032" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="148.5824" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g793DBE65A5AEC1A16A65955B6C0E046" x="155.1616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gA11612CECC8CBEF18835767DAB11B2F7" x="166.3104" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="172.7616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="177.52319999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gCEFEF3D67F35C6E83CC3757B1DD21B13" x="180.90239999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="190.57919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="196.97919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="201.74079999999995" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g645CA8FA3D9155E2CBD9F8EED3C1540D" x="207.59039999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="214.23359999999997" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(798.4017637795276 8)">
<g class="typst-group">
<g>
<g transform="translate(0 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gBC176529035DE42B8BD4625370C40E4D" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" x="11.440000000000001" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.608 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="7.44" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="g5396A27CA60B9808846A090320835A9F" overflow="visible">
<path d="M 1.91 1.22 L 1.91 5.23 C 1.91 6.06 2.08 6.1099997 2.78 6.14 C 2.84 6.2 2.84 6.41 2.78 6.47 C 2.34 6.46 1.87 6.45 1.48 6.45 C 1.15 6.45 0.65999997 6.46 0.19 6.47 C 0.13 6.41 0.13 6.2 0.19 6.14 C 0.89 6.1099997 1.06 6.06 1.06 5.23 L 1.06 1.22 C 1.06 0.39 0.89 0.34 0.19 0.31 C 0.13 0.25 0.13 0.04 0.19 -0.02 C 0.64 -0.01 1.13 0 1.49 0 C 1.8499999 0 2.33 -0.01 2.78 -0.02 C 2.84 0.04 2.84 0.25 2.78 0.31 C 2.08 0.34 1.91 0.39 1.91 1.22 Z "/>
</symbol>
<symbol id="gEEE4EC0F13100E99C1017169F912BE3E" overflow="visible">
<path d="M 1.55 1.22 L 1.55 3.12 C 1.55 3.61 1.68 3.52 1.91 3.23 L 4.2599998 0.099999994 C 4.41 -0.06 4.5699997 -0.12 4.72 -0.12 C 4.8399997 -0.12 4.94 -0.049999997 4.94 0.14999999 L 4.94 3.3799999 C 4.94 4.21 5.0499997 4.24 5.66 4.29 C 5.72 4.35 5.72 4.56 5.66 4.62 C 5.3599997 4.61 5 4.6 4.7 4.6 C 4.4 4.6 4.0499997 4.61 3.75 4.62 C 3.6899998 4.56 3.6899998 4.35 3.75 4.29 C 4.36 4.25 4.47 4.21 4.47 3.3799999 L 4.47 1.51 C 4.47 1.24 4.44 1.0699999 4.13 1.49 L 1.8399999 4.6 L 0.42 4.62 L 0.39999998 4.5899997 L 0.39999998 4.35 C 0.39999998 4.31 0.45999998 4.29 0.48999998 4.29 C 0.87 4.2599998 0.97999996 4.14 1.0799999 3.9599998 L 1.0799999 1.22 C 1.0799999 0.39 0.96999997 0.35 0.35999998 0.31 C 0.29999998 0.25 0.29999998 0.04 0.35999998 -0.02 C 0.65999997 -0.01 1.01 0 1.31 0 C 1.61 0 1.9699999 -0.01 2.27 -0.02 C 2.33 0.04 2.33 0.25 2.27 0.31 C 1.66 0.35999998 1.55 0.39 1.55 1.22 Z "/>
</symbol>
<symbol id="gA419F36517085793EDBF3FE4736A2E59" overflow="visible">
<path d="M 3.04 1.22 L 3.04 3.74 C 3.04 4.11 3.1399999 4.2599998 3.46 4.2599998 L 3.72 4.2599998 C 4.35 4.2599998 4.48 4.06 4.68 3.34 C 4.7799997 3.32 4.87 3.32 4.95 3.37 C 4.9 3.86 4.89 4.23 4.87 4.7 C 4.52 4.66 3.8799999 4.6 3.04 4.6 L 2.25 4.6 C 1.27 4.6 0.69 4.65 0.42 4.7 C 0.42 4.23 0.41 3.84 0.35 3.37 C 0.44 3.34 0.53 3.33 0.62 3.34 C 0.82 4.06 0.93 4.2599998 1.5799999 4.2599998 L 1.8199999 4.2599998 C 2.1299999 4.2599998 2.25 4.14 2.25 3.75 L 2.25 1.22 C 2.25 0.39 2.1399999 0.35999998 1.53 0.31 C 1.4699999 0.25 1.4699999 0.04 1.53 -0.02 C 1.9 -0.01 2.31 0 2.6499999 0 C 3 0 3.3899999 -0.01 3.76 -0.02 C 3.82 0.04 3.82 0.25 3.76 0.31 C 3.1499999 0.35 3.04 0.39 3.04 1.22 Z "/>
</symbol>
<symbol id="gFAD9169AC3141E7FC4EA568E3BBD2E9B" overflow="visible">
<path d="M 1.91 1.22 L 1.91 2.09 L 2.46 2.09 C 2.84 2.09 2.98 1.76 3.11 1.39 L 3.33 0.78999996 C 3.56 0.17 3.8999999 -0.07 4.33 -0.07 C 4.48 -0.07 4.79 -0.04 4.96 0 C 4.99 0.099999994 4.97 0.19999999 4.9 0.28 C 4.54 0.28 4.35 0.34 4.15 0.85999995 L 3.86 1.61 C 3.74 1.92 3.62 2.09 3.49 2.22 L 3.49 2.24 C 3.83 2.36 4.3399997 2.77 4.3399997 3.46 C 4.3399997 4.29 3.82 4.64 2.6299999 4.64 C 2.3799999 4.64 1.81 4.6 1.51 4.6 C 1.22 4.6 0.79999995 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.78 -0.01 1.1899999 0 1.52 0 C 1.8299999 0 2.1599998 -0.01 2.48 -0.02 C 2.54 0.04 2.54 0.25 2.48 0.31 C 2.01 0.34 1.91 0.39 1.91 1.22 Z M 3.47 3.46 C 3.47 2.6699998 3.24 2.3799999 2.35 2.3799999 L 1.91 2.3799999 L 1.91 3.6799998 C 1.91 4.21 2.01 4.31 2.57 4.31 C 3.27 4.31 3.47 4.06 3.47 3.46 Z "/>
</symbol>
<symbol id="g7FD6A8241485CEBC032BD9E4CE659816" overflow="visible">
<path d="M 5.27 2.35 C 5.27 3.77 4.13 4.7 2.83 4.7 C 1.4399999 4.7 0.37 3.6899998 0.37 2.22 C 0.37 0.85999995 1.4 -0.099999994 2.75 -0.099999994 C 4.39 -0.099999994 5.27 1.05 5.27 2.35 Z M 2.74 4.37 C 3.6299999 4.37 4.4 3.55 4.4 2.21 C 4.4 0.97999996 3.79 0.22999999 2.8999999 0.22999999 C 1.93 0.22999999 1.24 1.11 1.24 2.34 C 1.24 3.6899998 1.99 4.37 2.74 4.37 Z "/>
</symbol>
<symbol id="gBFFDA84A1400D9E1136DF0DD93EA19F5" overflow="visible">
<path d="M 1.48 4.6 C 1.2099999 4.6 0.76 4.61 0.37 4.62 C 0.31 4.56 0.31 4.35 0.37 4.29 C 0.97999996 4.25 1.09 4.21 1.09 3.3799999 L 1.09 1.22 C 1.09 0.39 0.97999996 0.35999998 0.37 0.31 C 0.31 0.25 0.31 0.04 0.37 -0.02 C 0.75 -0.01 1.1999999 0 1.49 0 C 1.75 0 2.1499999 -0.02 2.95 -0.02 C 4.06 -0.02 5.2999997 0.5 5.2999997 2.25 C 5.2999997 3.58 4.48 4.62 2.81 4.62 C 2.1299999 4.62 1.77 4.6 1.48 4.6 Z M 1.88 0.76 L 1.88 3.98 C 1.88 4.23 2.1299999 4.29 2.52 4.29 C 4.2 4.29 4.43 3.12 4.43 2.08 C 4.43 0.68 3.81 0.31 2.71 0.31 C 1.9499999 0.31 1.88 0.48 1.88 0.76 Z "/>
</symbol>
<symbol id="gEC3CC7DEE79E0AA801DFAAEF4B6C0B50" overflow="visible">
<path d="M 4.35 3.3799999 L 4.35 2.11 C 4.35 1.25 4.35 0.31 3.03 0.31 C 2.04 0.31 1.8299999 1.09 1.8299999 2.02 L 1.8299999 3.3799999 C 1.8299999 4.21 1.9399999 4.24 2.55 4.29 C 2.61 4.35 2.61 4.56 2.55 4.62 C 2.1599998 4.61 1.76 4.6 1.43 4.6 C 1.0699999 4.6 0.68 4.61 0.32 4.62 C 0.26 4.56 0.26 4.35 0.32 4.29 C 0.93 4.25 1.04 4.21 1.04 3.3799999 L 1.04 1.81 C 1.04 0.31 1.77 -0.099999994 2.86 -0.099999994 C 4.41 -0.099999994 4.8199997 0.78 4.8199997 2.24 L 4.8199997 3.3799999 C 4.8199997 4.21 4.93 4.24 5.54 4.29 C 5.6 4.35 5.6 4.56 5.54 4.62 C 5.24 4.61 4.88 4.6 4.58 4.6 C 4.2799997 4.6 3.9299998 4.61 3.6299999 4.62 C 3.57 4.56 3.57 4.35 3.6299999 4.29 C 4.24 4.25 4.35 4.21 4.35 3.3799999 Z "/>
</symbol>
<symbol id="g202CCBD46865F83C12D50E1B4FF9BBEA" overflow="visible">
<path d="M 2.76 -0.099999994 C 3.54 -0.099999994 4.02 0.19 4.49 0.82 C 4.47 0.89 4.37 1 4.29 1.02 C 3.83 0.48 3.48 0.28 2.81 0.28 C 1.8199999 0.28 1.24 1.35 1.24 2.34 C 1.24 4.02 2.02 4.37 2.77 4.37 C 3.57 4.37 4.04 3.9299998 4.16 3.23 C 4.2599998 3.1999998 4.36 3.1999998 4.46 3.26 C 4.46 3.6699998 4.44 4.0899997 4.3399997 4.54 C 3.9599998 4.54 3.51 4.7 2.71 4.7 C 1.39 4.7 0.37 3.6999998 0.37 2.24 C 0.37 1.61 0.57 0.91999996 1.06 0.47 C 1.4599999 0.099999994 2.02 -0.099999994 2.76 -0.099999994 Z "/>
</symbol>
<symbol id="g5503E15E5E4E70E9E217A15BD1ECD752" overflow="visible">
<path d="M 1.9499999 3.3799999 C 1.9499999 4.21 2.06 4.24 2.6699998 4.29 C 2.73 4.35 2.73 4.56 2.6699998 4.62 C 2.29 4.61 1.86 4.6 1.55 4.6 C 1.25 4.6 0.83 4.61 0.44 4.62 C 0.38 4.56 0.38 4.35 0.44 4.29 C 1.05 4.25 1.16 4.21 1.16 3.3799999 L 1.16 1.22 C 1.16 0.39 1.05 0.35999998 0.44 0.31 C 0.38 0.25 0.38 0.04 0.44 -0.02 C 0.81 -0.01 1.22 0 1.56 0 C 1.88 0 2.32 -0.01 2.6699998 -0.02 C 2.73 0.04 2.73 0.25 2.6699998 0.31 C 2.06 0.35 1.9499999 0.39 1.9499999 1.22 Z "/>
</symbol>
<symbol id="g1E8994F5C297EC73FA26D93D22635023" overflow="visible">
<path d="M 2.82 -0.14999999 C 4.11 -0.14999999 5.16 0.9 5.16 2.19 C 5.16 3.48 4.11 4.52 2.82 4.52 C 1.53 4.52 0.48999998 3.48 0.48999998 2.19 C 0.48999998 0.9 1.53 -0.14999999 2.82 -0.14999999 Z M 2.82 4.2599998 C 3.97 4.2599998 4.9 3.34 4.9 2.19 C 4.9 1.04 3.9599998 0.11 2.82 0.11 C 1.67 0.11 0.75 1.04 0.75 2.19 C 0.75 3.33 1.67 4.2599998 2.82 4.2599998 Z "/>
</symbol>
<symbol id="g6D39B87B7095296261A07873F9B99896" overflow="visible">
<path d="M 1.86 0.948 L 2.52 2.688 C 2.58 2.844 2.652 2.892 2.94 2.892 L 5.472 2.892 L 6.168 0.864 C 6.3120003 0.456 5.856 0.408 5.28 0.372 C 5.208 0.3 5.208 0.048 5.28 -0.024 C 5.724 -0.012 6.384 0 6.852 0 C 7.344 0 7.8 -0.012 8.22 -0.024 C 8.292 0.048 8.292 0.3 8.22 0.372 C 7.752 0.42000002 7.344 0.456 7.14 1.0320001 L 4.668 7.896 C 4.488 7.788 4.164 7.656 4.008 7.656 L 1.284 1.224 C 0.972 0.48000002 0.612 0.408 0.084 0.372 C 0.012 0.3 0.012 0.048 0.084 -0.024 C 0.396 -0.012 0.792 0 1.152 0 C 1.644 0 2.244 -0.012 2.688 -0.024 C 2.76 0.048 2.76 0.3 2.688 0.372 C 2.232 0.408 1.668 0.456 1.86 0.948 Z M 3.1560001 3.3960001 C 2.892 3.3960001 2.808 3.432 2.856 3.552 L 4.08 6.66 L 4.152 6.66 L 5.28 3.3960001 Z "/>
</symbol>
<symbol id="g1B61845C1FB429ACDF5304290F5BF286" overflow="visible">
<path d="M 4.548 0 C 4.548 0 4.824 1.152 4.908 1.656 C 4.8 1.716 4.704 1.74 4.572 1.704 C 4.38 0.996 4.032 0.408 3.276 0.408 L 2.736 0.408 C 2.46 0.408 2.292 0.6 2.292 0.828 L 2.292 4.056 C 2.292 5.052 2.424 5.088 3.1560001 5.1480002 C 3.228 5.2200003 3.228 5.472 3.1560001 5.544 C 2.7120001 5.532 2.22 5.52 1.812 5.52 C 1.44 5.52 0.924 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.32 0.408 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 1.068 -0.012 1.86 0 1.86 0 Z "/>
</symbol>
<symbol id="gC66F55FB8F08DA72FE76D3863D88042" overflow="visible">
<path d="M 5.664 1.092 C 5.664 2.088 5.736 2.124 6.1080003 2.184 C 6.18 2.256 6.18 2.5080001 6.1080003 2.58 C 5.892 2.568 5.556 2.556 5.184 2.556 C 4.824 2.556 4.272 2.568 3.924 2.58 C 3.852 2.5080001 3.852 2.256 3.924 2.184 C 4.656 2.136 4.716 2.088 4.716 1.092 L 4.716 0.444 C 4.3320003 0.336 3.936 0.276 3.516 0.276 C 2.016 0.276 1.524 1.812 1.524 2.796 C 1.524 4.248 2.22 5.244 3.372 5.244 C 4.56 5.244 5.064 4.644 5.244 3.876 C 5.364 3.8400002 5.484 3.8400002 5.604 3.912 C 5.592 4.404 5.556 4.908 5.448 5.448 C 5.088 5.448 4.2 5.64 3.528 5.64 C 1.812 5.64 0.444 4.5360003 0.444 2.64 C 0.444 1.116 1.584 -0.120000005 3.3 -0.120000005 C 4.116 -0.120000005 5.004 0 5.796 0.432 C 5.712 0.51600003 5.664 0.624 5.664 0.708 Z "/>
</symbol>
<symbol id="g4C6038BE04CA3E1481E54A97A0E34303" overflow="visible">
<path d="M 6.324 2.82 C 6.324 4.524 4.956 5.64 3.3960001 5.64 C 1.728 5.64 0.444 4.428 0.444 2.664 C 0.444 1.0320001 1.6800001 -0.120000005 3.3 -0.120000005 C 5.268 -0.120000005 6.324 1.26 6.324 2.82 Z M 3.288 5.244 C 4.356 5.244 5.28 4.26 5.28 2.652 C 5.28 1.176 4.548 0.276 3.48 0.276 C 2.316 0.276 1.488 1.332 1.488 2.808 C 1.488 4.428 2.388 5.244 3.288 5.244 Z "/>
</symbol>
<symbol id="g48BCA4F06942DA5990D42018985FC781" overflow="visible">
<path d="M 2.292 1.464 L 2.292 2.5080001 L 2.9520001 2.5080001 C 3.408 2.5080001 3.576 2.112 3.732 1.668 L 3.996 0.948 C 4.272 0.204 4.68 -0.084 5.196 -0.084 C 5.376 -0.084 5.748 -0.048 5.952 0 C 5.988 0.120000005 5.964 0.24000001 5.88 0.336 C 5.448 0.336 5.2200003 0.408 4.98 1.0320001 L 4.632 1.932 C 4.488 2.304 4.344 2.5080001 4.188 2.664 L 4.188 2.688 C 4.596 2.832 5.208 3.3240001 5.208 4.152 C 5.208 5.1480002 4.584 5.568 3.1560001 5.568 C 2.856 5.568 2.172 5.52 1.812 5.52 C 1.464 5.52 0.96000004 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.212 0.432 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 0.936 -0.012 1.428 0 1.824 0 C 2.196 0 2.592 -0.012 2.976 -0.024 C 3.048 0.048 3.048 0.3 2.976 0.372 C 2.412 0.408 2.292 0.468 2.292 1.464 Z M 4.164 4.152 C 4.164 3.204 3.888 2.856 2.82 2.856 L 2.292 2.856 L 2.292 4.416 C 2.292 5.052 2.412 5.172 3.084 5.172 C 3.924 5.172 4.164 4.872 4.164 4.152 Z "/>
</symbol>
<symbol id="g45E4C10E27056C5AE488FE2D8290DF06" overflow="visible">
<path d="M 2.34 4.056 C 2.34 5.052 2.4720001 5.088 3.204 5.1480002 C 3.276 5.2200003 3.276 5.472 3.204 5.544 C 2.748 5.532 2.232 5.52 1.86 5.52 C 1.5 5.52 0.996 5.532 0.528 5.544 C 0.456 5.472 0.456 5.2200003 0.528 5.1480002 C 1.26 5.1 1.392 5.052 1.392 4.056 L 1.392 1.464 C 1.392 0.468 1.26 0.432 0.528 0.372 C 0.456 0.3 0.456 0.048 0.528 -0.024 C 0.972 -0.012 1.464 0 1.872 0 C 2.256 0 2.784 -0.012 3.204 -0.024 C 3.276 0.048 3.276 0.3 3.204 0.372 C 2.4720001 0.42000002 2.34 0.468 2.34 1.464 Z "/>
</symbol>
<symbol id="gA2769E14ED9B16297025579DD26D23A1" overflow="visible">
<path d="M 3.648 1.464 L 3.648 4.488 C 3.648 4.932 3.7680001 5.112 4.152 5.112 L 4.464 5.112 C 5.2200003 5.112 5.376 4.872 5.616 4.008 C 5.736 3.984 5.844 3.984 5.94 4.044 C 5.88 4.632 5.868 5.076 5.844 5.64 C 5.4240003 5.592 4.656 5.52 3.648 5.52 L 2.7 5.52 C 1.524 5.52 0.828 5.58 0.504 5.64 C 0.504 5.076 0.492 4.608 0.42000002 4.044 C 0.528 4.008 0.636 3.996 0.744 4.008 C 0.984 4.872 1.116 5.112 1.896 5.112 L 2.184 5.112 C 2.556 5.112 2.7 4.968 2.7 4.5 L 2.7 1.464 C 2.7 0.468 2.568 0.432 1.836 0.372 C 1.764 0.3 1.764 0.048 1.836 -0.024 C 2.28 -0.012 2.772 0 3.18 0 C 3.6000001 0 4.068 -0.012 4.512 -0.024 C 4.584 0.048 4.584 0.3 4.512 0.372 C 3.78 0.42000002 3.648 0.468 3.648 1.464 Z "/>
</symbol>
<symbol id="g7FB89403B37B0F0F934DFEB7E5171B37" overflow="visible">
<path d="M 6 4.056 C 6 5.052 6.132 5.088 6.864 5.1480002 C 6.936 5.2200003 6.936 5.472 6.864 5.544 C 6.4440002 5.52 5.916 5.52 5.52 5.52 C 5.184 5.52 4.656 5.532 4.188 5.544 C 4.116 5.472 4.116 5.2200003 4.188 5.1480002 C 4.92 5.1 5.052 5.052 5.052 4.056 L 5.052 3.024 L 2.28 3.024 L 2.28 4.056 C 2.28 5.052 2.412 5.088 3.144 5.1480002 C 3.216 5.2200003 3.216 5.472 3.144 5.544 C 2.688 5.532 2.184 5.52 1.8000001 5.52 C 1.44 5.52 0.948 5.532 0.468 5.544 C 0.396 5.472 0.396 5.2200003 0.468 5.1480002 C 1.2 5.1 1.332 5.052 1.332 4.056 L 1.332 1.464 C 1.332 0.468 1.2 0.432 0.468 0.372 C 0.396 0.3 0.396 0.048 0.468 -0.024 C 0.948 -0.012 1.428 0 1.812 0 C 2.196 0 2.676 -0.012 3.144 -0.024 C 3.216 0.048 3.216 0.3 3.144 0.372 C 2.412 0.42000002 2.28 0.468 2.28 1.464 L 2.28 2.628 L 5.052 2.628 L 5.052 1.464 C 5.052 0.468 4.92 0.432 4.188 0.372 C 4.116 0.3 4.116 0.048 4.188 -0.024 C 4.632 -0.012 5.112 0 5.532 0 C 5.892 0 6.396 -0.012 6.864 -0.024 C 6.936 0.048 6.936 0.3 6.864 0.372 C 6.132 0.42000002 6 0.468 6 1.464 Z "/>
</symbol>
<symbol id="gFF269982F0E4C510F3A3BFF016D72390" overflow="visible">
<path d="M 5.796 4.584 L 5.88 4.584 L 6.0360003 1.4760001 C 6.084 0.48000002 6.072 0.432 5.4240003 0.372 C 5.352 0.3 5.352 0.048 5.4240003 -0.024 C 5.844 -0.012 6.288 0 6.624 0 C 6.984 0 7.3320003 -0.012 7.656 -0.024 C 7.728 0.048 7.728 0.3 7.656 0.372 C 7.044 0.432 7.032 0.504 6.96 1.4760001 L 6.7200003 4.572 C 6.684 5.052 6.7920003 5.1 7.392 5.1480002 C 7.464 5.2200003 7.464 5.472 7.392 5.544 L 5.772 5.52 L 3.9720001 1.224 L 2.436 5.52 L 0.768 5.544 C 0.696 5.472 0.696 5.2200003 0.768 5.1480002 C 1.3560001 5.112 1.464 5.052 1.44 4.824 L 1.056 1.452 C 0.948 0.456 0.792 0.408 0.336 0.372 C 0.264 0.3 0.264 0.048 0.336 -0.024 C 0.576 -0.012 0.936 0 1.128 0 C 1.368 0 1.812 -0.012 2.052 -0.024 C 2.124 0.048 2.124 0.3 2.052 0.372 C 1.368 0.42000002 1.38 0.564 1.4760001 1.452 L 1.824 4.5 L 1.848 4.5 L 3.552 -0.048 C 3.576 -0.108 3.636 -0.144 3.696 -0.144 C 3.744 -0.144 3.8040001 -0.108 3.828 -0.048 Z "/>
</symbol>
<symbol id="g5ABA589ED074A65FC8C929AB4EB2344C" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z "/>
</symbol>
<symbol id="gD77922058D8F1A3A631DDE5946887BDC" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z M 3.384 5.112 C 4.764 5.112 5.88 4.008 5.88 2.628 C 5.88 1.248 4.752 0.132 3.384 0.132 C 2.004 0.132 0.90000004 1.248 0.90000004 2.628 C 0.90000004 3.996 2.004 5.112 3.384 5.112 Z "/>
</symbol>
<symbol id="gEDADDD9BA25BBB833C1F4B684DC50419" overflow="visible">
<path d="M 4.83 3.82 L 4.9 3.82 L 5.0299997 1.23 C 5.0699997 0.39999998 5.06 0.35999998 4.52 0.31 C 4.46 0.25 4.46 0.04 4.52 -0.02 C 4.87 -0.01 5.24 0 5.52 0 C 5.8199997 0 6.1099997 -0.01 6.3799996 -0.02 C 6.44 0.04 6.44 0.25 6.3799996 0.31 C 5.87 0.35999998 5.8599997 0.42 5.7999997 1.23 L 5.6 3.81 C 5.5699997 4.21 5.66 4.25 6.16 4.29 C 6.22 4.35 6.22 4.56 6.16 4.62 L 4.81 4.6 L 3.31 1.02 L 2.03 4.6 L 0.64 4.62 C 0.58 4.56 0.58 4.35 0.64 4.29 C 1.13 4.2599998 1.22 4.21 1.1999999 4.02 L 0.88 1.2099999 C 0.78999996 0.38 0.65999997 0.34 0.28 0.31 C 0.22 0.25 0.22 0.04 0.28 -0.02 C 0.48 -0.01 0.78 0 0.94 0 C 1.14 0 1.51 -0.01 1.7099999 -0.02 C 1.77 0.04 1.77 0.25 1.7099999 0.31 C 1.14 0.35 1.15 0.47 1.23 1.2099999 L 1.52 3.75 L 1.54 3.75 L 2.96 -0.04 C 2.98 -0.089999996 3.03 -0.12 3.08 -0.12 C 3.12 -0.12 3.1699998 -0.089999996 3.1899998 -0.04 Z "/>
</symbol>
<symbol id="g97A8E46F7A64F11D13C6F357868587EE" overflow="visible">
<path d="M 1.89 1.22 L 1.89 1.9599999 C 2.07 1.88 2.27 1.8399999 2.52 1.8399999 C 3.86 1.8399999 4.27 2.8 4.27 3.3999999 C 4.27 3.9199998 3.97 4.62 2.55 4.62 C 2.18 4.62 1.76 4.6 1.49 4.6 C 1.1999999 4.6 0.78 4.61 0.38 4.62 C 0.32 4.56 0.32 4.35 0.38 4.29 C 0.98999995 4.25 1.1 4.21 1.1 3.3799999 L 1.1 1.22 C 1.1 0.39 0.98999995 0.35999998 0.38 0.31 C 0.32 0.25 0.32 0.04 0.38 -0.02 C 0.71 -0.01 1.06 0 1.5 0 C 1.93 0 2.28 -0.01 2.61 -0.02 C 2.6699998 0.04 2.6699998 0.25 2.61 0.31 C 2 0.35 1.89 0.39 1.89 1.22 Z M 1.89 3.84 C 1.89 4.16 2.01 4.29 2.49 4.29 C 3.08 4.29 3.3999999 3.98 3.3999999 3.28 C 3.3999999 2.56 3.1399999 2.1699998 2.54 2.1699998 C 2.34 2.1699998 2.09 2.2 1.89 2.28 Z "/>
</symbol>
<symbol id="gB844DCFB76B4CC44608DB013C9764E9C" overflow="visible">
<path d="M 1.8299999 3.62 C 1.5899999 4.19 1.5999999 4.24 2.1399999 4.29 C 2.2 4.35 2.2 4.56 2.1399999 4.62 C 1.8299999 4.61 1.49 4.6 1.0799999 4.6 C 0.76 4.6 0.45999998 4.61 0.19999999 4.62 C 0.14 4.56 0.14 4.35 0.19999999 4.29 C 0.69 4.24 0.76 4.13 1 3.56 L 2.4199998 0.28 C 2.55 -0.01 2.6 -0.12 2.71 -0.12 C 2.78 -0.12 2.82 -0.04 2.96 0.28 L 4.42 3.55 C 4.63 4.0099998 4.74 4.25 5.2799997 4.29 C 5.3399997 4.35 5.3399997 4.56 5.2799997 4.62 C 5.06 4.61 4.8199997 4.6 4.56 4.6 C 4.19 4.6 3.9099998 4.61 3.6399999 4.62 C 3.58 4.56 3.58 4.35 3.6399999 4.29 C 4.18 4.25 4.23 4.13 4.0299997 3.62 L 2.9399998 1.13 C 2.9099998 1.1 2.8999999 1.1 2.87 1.13 Z "/>
</symbol>
<symbol id="gDAA1267270512376F631C9A10449D5F4" overflow="visible">
<path d="M 2.48 2.25 C 3.1399999 2.25 3.1499999 2.06 3.1699998 1.6899999 C 3.22 1.64 3.3999999 1.64 3.4499998 1.6899999 C 3.4399998 1.92 3.4299998 2.26 3.4299998 2.4199998 C 3.4299998 2.56 3.4399998 2.8799999 3.4499998 3.1299999 C 3.3999999 3.1799998 3.22 3.1799998 3.1699998 3.1299999 C 3.1499999 2.6799998 3.1299999 2.57 2.48 2.57 L 1.91 2.57 L 1.91 3.99 C 1.91 4.16 2.04 4.27 2.23 4.27 L 2.8 4.27 C 3.62 4.27 3.75 3.9399998 3.9299998 3.37 C 4.0299997 3.36 4.12 3.3799999 4.2 3.4199998 C 4.16 3.76 4.04 4.54 4.02 4.61 C 4.02 4.63 4.0099998 4.64 3.99 4.64 C 3.85 4.61 3.75 4.6 3.58 4.6 L 1.51 4.6 C 1.22 4.6 0.76 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.76 -0.01 1.1999999 0 1.52 0 L 3.06 0 C 3.46 0 4.12 -0.02 4.12 -0.02 C 4.24 0.39 4.35 0.94 4.42 1.36 C 4.33 1.41 4.25 1.43 4.14 1.4 C 3.98 0.81 3.6899998 0.31 2.86 0.31 L 2.4299998 0.31 C 2.01 0.31 1.91 0.42 1.91 0.75 L 1.91 2.25 Z "/>
</symbol>
<symbol id="g6C3A310EEC8A7EBBD176D179125951F0" overflow="visible">
<path d="M 2.328 -4.632 L 8.208 -4.632 C 8.352 -4.488 8.352 -4.056 8.208 -3.912 C 4.896 -3.648 4.728 -3.288 4.728 -1.2 L 4.728 13.464 C 4.728 15.552 4.92 15.912 8.208 16.152 C 8.352 16.296 8.352 16.728 8.208 16.872 L 2.328 16.872 Z "/>
</symbol>
<symbol id="g2F0CE4BDC8DA4B92139017B781562218" overflow="visible">
<path d="M 3.96 1.896 L 5.232 5.232 C 5.352 5.544 5.496 5.64 6.072 5.64 L 10.632 5.64 L 11.976 1.728 C 12.264 0.864 11.568 0.84000003 10.656 0.792 C 10.512 0.792 10.344 0.768 10.2 0.768 C 10.056 0.624 10.056 0.096 10.2 -0.048 C 11.088 -0.024 13.368 0 14.304 0 C 15.288 0 16.632 -0.024 17.52 -0.048 C 17.664 0.096 17.664 0.624 17.52 0.768 C 16.584 0.864 15.792 0.84000003 15.360001 2.0640001 L 10.416 15.792 C 10.056 15.576 8.616 14.736 7.776 14.736 L 2.568 2.448 C 1.944 0.96000004 1.224 0.84000003 0.168 0.768 C 0.024 0.624 0.024 0.096 0.168 -0.048 C 1.056 -0.024 1.488 0 2.424 0 C 3.408 0 4.728 -0.024 5.616 -0.048 C 5.76 0.096 5.76 0.624 5.616 0.768 C 4.704 0.84000003 3.576 0.912 3.96 1.896 Z M 6.552 6.7920003 C 6.024 6.7920003 5.856 6.864 5.952 7.104 L 8.064 12.4800005 L 8.232 12.4800005 L 10.2 6.7920003 Z "/>
</symbol>
<symbol id="g8D84A54D9303B24762DC3071B60ECD14" overflow="visible">
<path d="M 2.4 3.048 C 2.4 1.056 2.016 0.84000003 0.552 0.768 C 0.408 0.624 0.408 0.096 0.552 -0.048 C 1.5600001 -0.024 2.64 0 3.96 0 C 5.28 0 6.336 -0.024 7.368 -0.048 C 7.512 0.096 7.512 0.624 7.368 0.768 C 5.9040003 0.84000003 5.52 1.056 5.52 3.048 L 5.52 13.992001 C 5.52 15.552 5.592 16.44 5.592 16.44 C 5.592 16.656 5.4240003 16.752 5.208 16.752 C 4.32 16.464 2.4 16.2 0.696 16.128 C 0.624 15.84 0.648 15.576 0.768 15.360001 C 2.28 15.24 2.4 15.216001 2.4 13.56 Z "/>
</symbol>
<symbol id="g3E9095A1FBD7854ED5F7B53469C97011" overflow="visible">
<path d="M 11.208 9.456 C 11.88 9.456 12.264 9.744 12.264 10.632 C 12.264 11.088 11.64 11.784 10.728 11.784 C 9.672 11.784 8.28 10.992 7.584 10.368 C 7.152 10.608 6.6480002 10.656 5.568 10.656 C 4.5360003 10.656 3.528 10.416 2.736 9.8880005 C 1.752 9.264 1.104 8.328 1.104 7.104 C 1.104 5.928 1.8000001 4.656 2.9520001 4.032 C 2.208 3.384 1.056 2.112 1.056 1.632 C 1.056 1.176 1.128 0.888 1.368 0.528 C 1.584 0.192 1.872 0 2.352 -0.144 C 1.32 -0.768 0.264 -2.136 0.264 -2.544 C 0.264 -3.432 0.552 -4.464 1.2 -4.92 C 2.136 -5.568 3.72 -5.712 4.872 -5.712 C 8.208 -5.712 12.024 -3.96 12.024 -1.32 C 12.024 -0.816 11.784 0.216 10.824 0.864 C 9.8880005 1.488 6.288 1.656 4.512 1.656 C 4.08 1.656 3.432 1.704 3.432 2.664 C 3.432 3.048 3.672 3.384 3.792 3.672 C 4.296 3.432 4.8 3.408 5.544 3.408 C 6.768 3.408 7.896 3.72 8.712 4.44 C 9.408 5.064 9.8880005 5.9040003 9.8880005 6.984 C 9.8880005 8.328 9.216 9.216 8.4 9.8880005 C 8.592 10.128 9.384 10.56 9.624001 10.56 C 9.84 10.56 10.008 10.416 10.08 10.272 C 10.176 9.96 10.608 9.456 11.208 9.456 Z M 4.2 -0.6 C 6.048 -0.6 9.6 -0.672 9.6 -1.944 C 9.6 -2.808 9.216 -3.792 8.424 -4.224 C 7.6800003 -4.656 6.456 -4.704 5.544 -4.704 C 3.96 -4.704 2.88 -3.528 2.88 -2.304 C 2.88 -1.488 2.88 -0.936 3.144 -0.456 C 3.384 -0.552 3.696 -0.6 4.2 -0.6 Z M 6.96 6.912 C 6.96 4.608 6.288 4.32 5.664 4.32 C 4.176 4.32 3.984 6.096 3.984 7.32 C 3.984 9.096 4.416 9.744 5.352 9.744 C 6.48 9.744 6.96 8.808 6.96 6.912 Z "/>
</symbol>
<symbol id="g90B91206A818BADA9956CC42F47E57A0" overflow="visible">
<path d="M 1.176 1.392 C 1.176 0.48000002 1.944 -0.24000001 2.904 -0.24000001 C 3.864 -0.24000001 4.68 0.528 4.68 1.44 C 4.68 2.376 3.912 3.096 2.9520001 3.096 C 1.992 3.096 1.176 2.328 1.176 1.392 Z "/>
</symbol>
<symbol id="g2B9D5A283BBC2ED0501C3A1039D04E5C" overflow="visible">
<path d="M 8.808 2.928 L 8.808 11.592 C 8.808 12.864 9 14.232 9 14.232 C 9 14.544 8.808 14.64 8.592 14.64 C 8.352 14.64 7.9440002 14.544 7.392 14.28 C 5.928 13.608 4.296 13.032001 2.208 12.168 C 2.232 11.76 2.4 11.376 2.736 11.136 C 4.032 11.688 4.896 11.736 5.232 11.736 C 5.544 11.736 5.688 11.64 5.688 10.440001 L 5.688 2.928 C 5.688 0.936 4.5360003 0.84000003 3.216 0.768 C 2.976 0.624 2.976 0.096 3.216 -0.048 C 5.184 -0.024 6.3120003 0 7.272 0 C 8.232 0 9.312 -0.024 11.28 -0.048 C 11.52 0.096 11.52 0.624 11.28 0.768 C 9.96 0.84000003 8.808 0.936 8.808 2.928 Z "/>
</symbol>
<symbol id="g10BFE5E41011FF0F560FA08FAB260218" overflow="visible">
<path d="M 7.248 16.824 L 1.368 16.824 C 1.224 16.68 1.224 16.248 1.368 16.104 C 4.68 15.84 4.848 15.4800005 4.848 13.392 L 4.848 -1.272 C 4.848 -3.3600001 4.656 -3.72 1.368 -3.96 C 1.224 -4.104 1.224 -4.5360003 1.368 -4.68 L 7.248 -4.68 Z "/>
</symbol>
<symbol id="g1BED8054A02AECF3BF3EC56A671C1672" overflow="visible">
<path d="M 9.528 -0.24000001 C 11.856 -0.24000001 13.992001 0.864 15.624001 3 C 15.504 3.216 15.096 3.504 14.832 3.504 C 13.128 1.632 11.184 1.008 9.504 1.008 C 6.7200003 1.008 4.512 4.272 4.512 8.016 C 4.512 11.736 6.432 14.808001 9.288 14.808001 C 12.6 14.808001 13.68 12.936 14.304 10.872 C 14.592 10.776 15.0720005 10.848001 15.336 10.992 C 15.216001 12.24 15.024 13.392 14.808001 14.712 C 13.584001 14.832 12.504 15.792 9.552 15.792 C 4.848 15.792 0.888 12.84 0.888 7.56 C 0.888 5.304 1.872 2.664 3.792 1.272 C 5.328 0.168 7.2000003 -0.24000001 9.528 -0.24000001 Z "/>
</symbol>
<symbol id="g841363B3896A8C79F18618DF16186242" overflow="visible">
<path d="M 0.888 4.968 C 0.888 1.824 3.384 -0.24000001 6.6 -0.24000001 C 8.304 -0.24000001 9.72 0.24000001 10.704 1.128 C 11.928 2.208 12.336 3.8400002 12.336 5.184 C 12.336 8.328 10.2 10.656 6.624 10.656 C 4.632 10.656 3.144 9.96 2.208 8.88 C 1.296 7.824 0.888 6.384 0.888 4.968 Z M 6.2400002 9.648 C 7.872 9.648 8.976 7.704 8.976 4.416 C 8.976 1.536 7.848 0.768 6.984 0.768 C 5.0160003 0.768 4.248 3.72 4.248 5.496 C 4.248 7.704 4.632 9.648 6.2400002 9.648 Z "/>
</symbol>
<symbol id="g42F794F2554BA43C69EE8F3AA6FD9BAC" overflow="visible">
<path d="M 5.472 2.928 L 5.472 7.752 C 6.432 8.4 7.392 8.88 7.824 8.88 C 8.784 8.88 9.504 8.448 9.504 7.08 L 9.504 3.072 C 9.504 1.056 9.12 0.84000003 8.136 0.768 C 7.992 0.624 7.992 0.096 8.136 -0.048 C 9.144 -0.024 9.912 0 11.064 0 C 12.384 0 13.440001 -0.024 14.472 -0.048 C 14.616 0.096 14.616 0.624 14.472 0.768 C 13.008 0.84000003 12.624001 1.056 12.624001 3.072 L 12.624001 6.816 C 12.624001 9.456 11.496 10.656 9.432 10.656 C 8.472 10.656 6.768 9.6 5.448 8.688 C 5.376 9.528 5.28 10.248 5.28 10.248 C 5.256 10.536 5.064 10.656 4.728 10.656 C 3.8400002 10.416 2.4 10.08 0.744 9.864 C 0.696 9.72 0.744 9.24 0.792 9.096 C 2.112 8.976 2.352 8.784 2.352 7.416 L 2.352 2.928 C 2.352 0.936 2.088 0.888 0.624 0.768 C 0.48000002 0.624 0.48000002 0.096 0.624 -0.048 C 1.632 -0.024 2.64 0 3.912 0 C 5.0160003 0 5.688 -0.024 6.7200003 -0.048 C 6.864 0.096 6.864 0.624 6.7200003 0.768 C 5.712 0.864 5.472 0.936 5.472 2.928 Z "/>
</symbol>
<symbol id="gDD7DFDEC0D240E3DC5A3664E12D4BDDC" overflow="visible">
<path d="M 1.152 3.504 C 1.248 2.328 1.368 1.2 1.5600001 0.288 C 2.016 0.144 3.552 -0.24000001 4.896 -0.24000001 C 6.744 -0.24000001 9.048 0.768 9.048 2.856 C 9.048 3.672 8.856 4.32 8.304 4.92 C 7.632 5.688 6.624 6.288 5.52 6.768 C 4.56 7.176 4.224 7.9440002 4.224 8.64 C 4.224 9.192 4.68 9.648 5.376 9.648 C 6.216 9.648 7.032 8.88 7.632 7.416 C 8.064 7.344 8.328 7.368 8.568 7.5360003 C 8.568 8.4 8.472 9.312 8.2560005 10.08 C 7.488 10.416 6.888 10.656 5.568 10.656 C 4.296 10.656 3.096 10.176 2.328 9.408 C 1.776 8.856 1.512 8.184 1.512 7.5360003 C 1.512 6.816 1.8000001 6.2400002 2.256 5.736 C 3 4.92 4.32 4.08 5.04 3.744 C 6 3.312 6.264 2.448 6.264 1.872 C 6.264 1.104 5.496 0.696 4.848 0.696 C 3.7680001 0.696 2.616 1.8000001 2.112 3.552 C 1.728 3.624 1.536 3.6000001 1.152 3.504 Z "/>
</symbol>
<symbol id="g10AC66E6714D96E9762627FFB6E156C6" overflow="visible">
<path d="M 1.512 10.416 C 1.176 10.416 0.816 10.32 0.504 10.056 L 0.504 9.36 C 0.504 9.24 0.528 9.216 0.624 9.216 L 2.184 9.216 C 2.136 6.7920003 2.112 3.72 2.112 2.52 C 2.112 1.6800001 2.328 0.864 2.832 0.432 C 3.384 -0.024 4.248 -0.24000001 4.824 -0.24000001 C 6.144 -0.24000001 7.6080003 0.432 8.088 1.104 C 8.088 1.392 7.9440002 1.536 7.656 1.776 C 7.344 1.536 6.744 1.44 6.288 1.44 C 5.76 1.44 5.232 1.848 5.232 3.048 C 5.232 4.248 5.208 6.816 5.208 9.216 L 7.632 9.216 C 7.872 9.216 8.208 9.312 8.208 9.528 L 8.208 10.272 C 8.208 10.368 8.136 10.416 8.016 10.416 L 5.208 10.416 L 5.232 11.232 C 5.28 12.84 5.352 13.944 5.352 13.944 C 5.352 14.088 5.28 14.16 5.16 14.16 C 4.992 14.16 4.104 13.896 3.72 13.728 C 3.312 13.56 2.616 13.416 2.448 13.2 C 2.28 12.984 2.184 12.336 2.184 10.416 Z "/>
</symbol>
<symbol id="g767CEF02C917BBE3F159A8F04079F311" overflow="visible">
<path d="M 5.472 6.432 C 5.472 7.296 5.736 7.656 6.048 8.016 C 6.2400002 8.2560005 6.456 8.424 6.816 8.424 C 7.032 8.424 7.296 8.208 7.488 7.968 C 7.656 7.776 8.064 7.584 8.616 7.584 C 9.312 7.584 9.984 8.304 9.984 9.312 C 9.984 9.936 9.264 10.656 8.4 10.656 C 7.56 10.656 6.6480002 9.936 5.544 8.352 L 5.448 8.352 C 5.4 9.0720005 5.28 10.248 5.28 10.248 C 5.256 10.464 5.064 10.656 4.728 10.656 C 3.6000001 10.368 2.328 10.032001 0.744 9.864 C 0.696 9.72 0.744 9.264 0.792 9.12 C 2.112 9 2.352 8.784 2.352 7.416 L 2.352 2.928 C 2.352 0.936 2.088 0.888 0.624 0.768 C 0.48000002 0.624 0.48000002 0.096 0.624 -0.048 C 1.632 -0.024 2.64 0 3.912 0 C 5.184 0 6.168 -0.024 7.2000003 -0.048 C 7.344 0.096 7.344 0.624 7.2000003 0.768 C 5.736 0.864 5.472 0.936 5.472 2.928 Z "/>
</symbol>
<symbol id="gA13EE5B65CBC719304B28920E2ACC2B9" overflow="visible">
<path d="M 12.24 3.192 L 12.24 7.344 C 12.24 9.36 12.288 9.0720005 12.288 9.648 C 12.288 10.056 12.192 10.32 12.048 10.464 C 11.616 10.440001 11.136 10.416 10.68 10.416 C 10.008 10.416 8.448 10.440001 7.512 10.464 C 7.368 10.32 7.368 9.792 7.512 9.648 C 8.736 9.528 9.12 9.36 9.12 7.344 L 9.12 2.904 C 9.12 2.664 9.12 2.424 9.144 2.184 C 8.16 1.584 7.368 1.536 6.936 1.536 C 5.976 1.536 5.256 1.656 5.256 3.336 L 5.256 7.344 C 5.256 9.36 5.304 9.0720005 5.304 9.648 C 5.304 10.056 5.208 10.32 5.064 10.464 C 4.632 10.440001 4.1280003 10.416 3.696 10.416 C 2.4720001 10.416 1.5600001 10.440001 0.528 10.464 C 0.384 10.32 0.384 9.792 0.528 9.648 C 1.632 9.6 2.136 9.36 2.136 7.344 L 2.136 3.6000001 C 2.136 1.056 3.144 -0.24000001 5.208 -0.24000001 C 6.072 -0.24000001 7.824 0.456 9.216 1.224 C 9.264 0.624 9.312 0.168 9.312 0.168 C 9.336 -0.120000005 9.528 -0.24000001 9.864 -0.24000001 C 10.752 0 12.192 0.336 13.848001 0.552 C 13.896 0.696 13.848001 1.176 13.8 1.32 C 12.504 1.44 12.24 1.824 12.24 3.192 Z "/>
</symbol>
<symbol id="g9CBC2DB69173A0577335373434CDCDA4" overflow="visible">
<path d="M 10.128 2.088 C 10.128 2.376 10.08 2.832 9.816 2.832 C 8.856 1.944 8.04 1.488 7.344 1.488 C 5.544 1.488 4.1280003 2.784 4.1280003 5.664 C 4.1280003 8.328 4.728 9.648 6 9.648 C 6.888 9.648 7.248 8.712 7.32 7.9440002 C 7.392 7.296 8.04 6.816 8.808 6.816 C 9.576 6.816 10.128 7.416 10.128 8.16 C 10.128 9.24 8.832 10.656 6.216 10.656 C 3.384 10.656 0.888 8.376 0.888 4.824 C 0.888 3.264 1.44 1.896 2.376 1.008 C 3.312 0.120000005 4.416 -0.24000001 6.12 -0.24000001 C 7.56 -0.24000001 9.216 0.768 10.128 2.088 Z "/>
</symbol>
<symbol id="g24FA36D774E663C81AD78F0ED3820373" overflow="visible">
<path d="M 5.568 2.928 L 5.568 7.704 C 5.568 8.904 5.664 10.248 5.664 10.248 C 5.664 10.512 5.448 10.656 5.112 10.656 C 4.44 10.392 2.496 10.2 0.84000003 9.984 C 0.792 9.84 0.84000003 9.36 0.888 9.216 C 2.208 9.096 2.448 8.904 2.448 7.5360003 L 2.448 2.928 C 2.448 0.936 2.184 0.888 0.72 0.768 C 0.576 0.624 0.576 0.096 0.72 -0.048 C 1.728 -0.024 2.736 0 4.008 0 C 5.28 0 6.264 -0.024 7.296 -0.048 C 7.44 0.096 7.44 0.624 7.296 0.768 C 5.8320003 0.864 5.568 0.936 5.568 2.928 Z M 2.328 14.304 C 2.328 13.512 2.904 12.72 3.864 12.72 C 4.9440002 12.72 5.568 13.584001 5.568 14.208 C 5.568 14.928 5.0160003 15.792 4.008 15.792 C 2.88 15.792 2.328 15.024 2.328 14.304 Z "/>
</symbol>
<symbol id="g911507D70DD1D78477F3BEDE827F51DF" overflow="visible">
<path d="M 11.28 10.46 L 11.28 7.3399997 L 5.08 7.3399997 L 5.08 10.46 C 5.08 12.12 5.64 12.2 6.74 12.259999 C 6.94 12.38 6.94 12.82 6.74 12.94 C 5.94 12.92 4.5 12.9 3.6999998 12.9 C 2.8999999 12.9 1.42 12.92 0.62 12.94 C 0.42 12.82 0.42 12.38 0.62 12.259999 C 1.7199999 12.2 2.28 12.12 2.28 10.46 L 2.28 2.44 C 2.28 0.78 1.7199999 0.7 0.62 0.64 C 0.42 0.52 0.42 0.08 0.62 -0.04 C 1.42 -0.02 2.8999999 0 3.6999998 0 C 4.5 0 5.94 -0.02 6.74 -0.04 C 6.94 0.08 6.94 0.52 6.74 0.64 C 5.64 0.7 5.08 0.78 5.08 2.44 L 5.08 6.3799996 L 11.28 6.3799996 L 11.28 2.44 C 11.28 0.78 10.719999 0.7 9.62 0.64 C 9.42 0.52 9.42 0.08 9.62 -0.04 C 10.42 -0.02 11.9 0 12.7 0 C 13.5 0 14.94 -0.02 15.74 -0.04 C 15.94 0.08 15.94 0.52 15.74 0.64 C 14.639999 0.7 14.08 0.78 14.08 2.44 L 14.08 10.46 C 14.08 12.12 14.639999 12.2 15.74 12.259999 C 15.94 12.38 15.94 12.82 15.74 12.94 C 14.94 12.92 13.5 12.9 12.7 12.9 C 11.9 12.9 10.42 12.92 9.62 12.94 C 9.42 12.82 9.42 12.38 9.62 12.259999 C 10.719999 12.2 11.28 12.12 11.28 10.46 Z "/>
</symbol>
<symbol id="gF7DAC8BB30649014016B28F6AD7EC048" overflow="visible">
<path d="M 12.62 0 C 12.62 0 12.5199995 1.42 12.5199995 2.04 L 12.5199995 10.24 C 12.5199995 12.0199995 12.86 12.12 14.259999 12.259999 C 14.38 12.38 14.38 12.82 14.259999 12.94 C 13.28 12.92 12.94 12.9 12.099999 12.9 C 11.2 12.9 10.78 12.92 9.78 12.94 C 9.66 12.82 9.66 12.38 9.78 12.259999 C 11.179999 12.12 11.5199995 12.059999 11.5199995 10.24 L 11.5199995 4.62 C 11.5199995 4.12 11.259999 4.22 10.98 4.56 L 5.68 10.8 L 3.8999999 12.9 L 0.64 12.94 C 0.52 12.82 0.52 12.38 0.64 12.259999 C 1.5 12.2 2.1 11.5199995 2.22 11 L 2.22 2.6599998 C 2.22 0.88 1.88 0.78 0.48 0.64 C 0.35999998 0.52 0.35999998 0.08 0.48 -0.04 C 1.4599999 -0.02 1.8399999 0 2.72 0 C 3.6 0 3.9599998 -0.02 4.96 -0.04 C 5.08 0.08 5.08 0.52 4.96 0.64 C 3.56 0.78 3.22 0.84 3.22 2.6599998 L 3.22 8.599999 C 3.22 8.8 3.26 9 3.3799999 9 C 3.48 9 3.6399999 8.86 3.86 8.599999 L 10.559999 0.64 C 10.96 0.14 11.36 -0.24 11.36 -0.24 C 12.059999 -0.24 12.259999 -0.17999999 12.62 0 Z "/>
</symbol>
<symbol id="g8F63AAB7FFA6B186E1B4BC124750174B" overflow="visible">
<path d="M 8.42 12.62 C 7.3199997 12.78 6.8999996 13.16 5.04 13.16 C 4.14 13.16 2.96 12.88 2.12 12.2 C 1.38 11.599999 0.82 10.679999 0.82 9.7 C 0.82 8.94 1.02 7.98 1.48 7.3799996 C 2.3999999 6.14 4.06 5.46 4.92 4.8599997 C 5.8399997 4.22 6.74 3.4199998 6.74 2.3 C 6.74 1.3199999 5.8799996 0.64 4.66 0.64 C 3.32 0.64 1.9399999 1.74 1.54 3.56 C 1.22 3.6799998 0.9 3.6 0.59999996 3.52 C 0.58 3.52 0.56 3.5 0.53999996 3.5 C 0.53999996 2 0.7 0.94 0.91999996 0.19999999 C 2.06 0.19999999 2.12 -0.19999999 4.88 -0.19999999 C 6.1 -0.19999999 7.08 0.16 7.8999996 0.9 C 8.62 1.52 9.26 2.44 9.26 3.6799998 C 9.26 4.72 8.82 5.42 8.22 6.08 C 7.44 6.94 6.3199997 7.56 5.54 7.96 C 4.74 8.36 3.32 9.4 3.32 10.54 C 3.32 11.66 4 12.34 5.02 12.34 C 6.72 12.34 7.2799997 10.8 7.64 9.48 C 7.9199996 9.4 8.42 9.4 8.639999 9.58 C 8.639999 10.639999 8.559999 11.46 8.42 12.62 Z "/>
</symbol>
<symbol id="g1E298373CF470F56F03EC97C7DE8EA04" overflow="visible">
<path d="M 11.5 12.259999 C 11.12 12.179999 10.559999 12.179999 10.3 12.259999 L 7.44 4.2 L 7.2999997 3.6799998 L 7.1 4.3199997 L 4.92 11.46 C 4.72 12.12 5.44 12.2 6.3999996 12.259999 C 6.52 12.38 6.52 12.82 6.3999996 12.94 C 5.66 12.92 3.6599998 12.9 2.8799999 12.9 C 2.06 12.9 0.94 12.92 0.19999999 12.94 C 0.08 12.82 0.08 12.38 0.19999999 12.259999 C 0.97999996 12.179999 1.6999999 12.04 2 11.179999 L 5.7599998 0.22 C 5.9 -0.19999999 6.2 -0.24 6.42 -0.24 C 6.62 -0.24 6.94 -0.19999999 7.1 0.22 L 10.099999 8.2 L 13.16 0.22 C 13.299999 -0.16 13.5199995 -0.24 13.82 -0.24 C 14.08 -0.24 14.36 -0.14 14.5 0.22 L 18.26 10.46 C 18.68 11.639999 19.48 12.2 20.359999 12.259999 C 20.48 12.38 20.48 12.82 20.359999 12.94 C 19.699999 12.92 19.02 12.9 18.32 12.9 C 17.5 12.9 16.56 12.92 15.82 12.94 C 15.7 12.82 15.7 12.38 15.82 12.259999 C 16.96 12.08 17.34 11.66 17.1 10.92 L 14.839999 4.2 L 14.599999 3.48 L 14.299999 4.3199997 Z "/>
</symbol>
<symbol id="g1E934D63EFC0D2D779AEFC9122E70AE4" overflow="visible">
<path d="M 2.28 10.46 L 2.28 2.44 C 2.28 0.78 1.7199999 0.7 0.62 0.64 C 0.42 0.52 0.42 0.08 0.62 -0.04 C 1.42 -0.02 2.8999999 0 3.6999998 0 C 4.5 0 5.94 -0.02 6.74 -0.04 C 6.94 0.08 6.94 0.52 6.74 0.64 C 5.64 0.7 5.08 0.78 5.08 2.44 L 5.08 10.46 C 5.08 12.12 5.64 12.2 6.74 12.259999 C 6.94 12.38 6.94 12.82 6.74 12.94 C 5.94 12.92 4.5 12.9 3.6999998 12.9 C 2.8999999 12.9 1.42 12.92 0.62 12.94 C 0.42 12.82 0.42 12.38 0.62 12.259999 C 1.7199999 12.2 2.28 12.12 2.28 10.46 Z "/>
</symbol>
<symbol id="gC3DD0650993487CD3F460FE3E213BEA0" overflow="visible">
<path d="M 4.56 2.44 L 4.56 6.46 C 5.3599997 7 6.16 7.3999996 6.52 7.3999996 C 7.3199997 7.3999996 7.9199996 7.04 7.9199996 5.9 L 7.9199996 2.56 C 7.9199996 0.88 7.6 0.7 6.7799997 0.64 C 6.66 0.52 6.66 0.08 6.7799997 -0.04 C 7.62 -0.02 8.26 0 9.22 0 C 10.32 0 11.2 -0.02 12.059999 -0.04 C 12.179999 0.08 12.179999 0.52 12.059999 0.64 C 10.84 0.7 10.5199995 0.88 10.5199995 2.56 L 10.5199995 5.68 C 10.5199995 7.8799996 9.58 8.88 7.8599997 8.88 C 7.06 8.88 5.64 8 4.54 7.24 C 4.48 7.94 4.4 8.54 4.4 8.54 C 4.38 8.78 4.22 8.88 3.9399998 8.88 C 3.1999998 8.679999 2 8.4 0.62 8.22 C 0.58 8.099999 0.62 7.7 0.65999997 7.58 C 1.76 7.48 1.9599999 7.3199997 1.9599999 6.18 L 1.9599999 2.44 C 1.9599999 0.78 1.74 0.74 0.52 0.64 C 0.39999998 0.52 0.39999998 0.08 0.52 -0.04 C 1.36 -0.02 2.2 0 3.26 0 C 4.18 0 4.74 -0.02 5.6 -0.04 C 5.72 0.08 5.72 0.52 5.6 0.64 C 4.7599998 0.71999997 4.56 0.78 4.56 2.44 Z "/>
</symbol>
<symbol id="gCD50B0C5537328D0484BBB5C5B7C30A" overflow="visible">
<path d="M 0.96 2.9199998 C 1.04 1.9399999 1.14 1 1.3 0.24 C 1.68 0.12 2.96 -0.19999999 4.08 -0.19999999 C 5.62 -0.19999999 7.54 0.64 7.54 2.3799999 C 7.54 3.06 7.3799996 3.6 6.92 4.1 C 6.3599997 4.74 5.52 5.24 4.6 5.64 C 3.8 5.98 3.52 6.62 3.52 7.2 C 3.52 7.66 3.8999999 8.04 4.48 8.04 C 5.18 8.04 5.8599997 7.3999996 6.3599997 6.18 C 6.72 6.12 6.94 6.14 7.14 6.2799997 C 7.14 7 7.06 7.7599998 6.8799996 8.4 C 6.24 8.679999 5.74 8.88 4.64 8.88 C 3.58 8.88 2.58 8.48 1.9399999 7.8399997 C 1.48 7.3799996 1.26 6.8199997 1.26 6.2799997 C 1.26 5.68 1.5 5.2 1.88 4.7799997 C 2.5 4.1 3.6 3.3999999 4.2 3.12 C 5 2.76 5.22 2.04 5.22 1.56 C 5.22 0.91999996 4.58 0.58 4.04 0.58 C 3.1399999 0.58 2.18 1.5 1.76 2.96 C 1.4399999 3.02 1.28 3 0.96 2.9199998 Z "/>
</symbol>
<symbol id="gD9D3B6C4D6AB50B3CADCA65007C1BC50" overflow="visible">
<path d="M 8.62 2.58 C 7.7999997 1.74 6.72 1.52 5.96 1.52 C 4.4 1.52 3.4399998 2.4199998 3.4399998 4.38 C 3.4399998 4.52 3.46 4.6 3.46 4.7 L 8.26 4.7 C 8.74 4.7 8.84 5.04 8.84 5.3199997 C 8.84 7.02 8.179999 8.88 5.24 8.88 C 3.1399999 8.88 0.74 7.02 0.74 3.9599998 C 0.74 2.8 1.16 1.5799999 2.02 0.79999995 C 2.78 0.12 3.76 -0.19999999 5.18 -0.19999999 C 6.56 -0.19999999 7.9199996 0.5 8.92 1.9599999 C 8.92 2.22 8.82 2.58 8.62 2.58 Z M 3.54 5.5 C 3.56 6.2 3.6599998 6.96 3.9399998 7.3599997 C 4.2599998 7.8399997 4.7999997 8.04 5.02 8.04 C 5.56 8.04 6.2999997 7.52 6.2999997 5.92 C 6.2999997 5.7999997 6.2999997 5.54 6.2599998 5.5 Z "/>
</symbol>
<symbol id="g936880EEF467D45CE0F64A721CAEDAB8" overflow="visible">
<path d="M 4.56 5.3599997 C 4.56 6.08 4.7799997 6.3799996 5.04 6.68 C 5.2 6.8799996 5.38 7.02 5.68 7.02 C 5.8599997 7.02 6.08 6.8399997 6.24 6.64 C 6.3799996 6.48 6.72 6.3199997 7.18 6.3199997 C 7.7599998 6.3199997 8.32 6.92 8.32 7.7599998 C 8.32 8.28 7.72 8.88 7 8.88 C 6.2999997 8.88 5.54 8.28 4.62 6.96 L 4.54 6.96 C 4.5 7.56 4.4 8.54 4.4 8.54 C 4.38 8.72 4.22 8.88 3.9399998 8.88 C 3 8.639999 1.9399999 8.36 0.62 8.22 C 0.58 8.099999 0.62 7.72 0.65999997 7.6 C 1.76 7.5 1.9599999 7.3199997 1.9599999 6.18 L 1.9599999 2.44 C 1.9599999 0.78 1.74 0.74 0.52 0.64 C 0.39999998 0.52 0.39999998 0.08 0.52 -0.04 C 1.36 -0.02 2.2 0 3.26 0 C 4.3199997 0 5.14 -0.02 6 -0.04 C 6.12 0.08 6.12 0.52 6 0.64 C 4.7799997 0.71999997 4.56 0.78 4.56 2.44 Z "/>
</symbol>
<symbol id="g1344FEF92B65FBC27D977C1EC5D9AECF" overflow="visible">
<path d="M 1.26 8.679999 C 0.97999996 8.679999 0.68 8.599999 0.42 8.38 L 0.42 7.7999997 C 0.42 7.7 0.44 7.68 0.52 7.68 L 1.8199999 7.68 C 1.78 5.66 1.76 3.1 1.76 2.1 C 1.76 1.4 1.9399999 0.71999997 2.36 0.35999998 C 2.82 -0.02 3.54 -0.19999999 4.02 -0.19999999 C 5.12 -0.19999999 6.3399997 0.35999998 6.74 0.91999996 C 6.74 1.16 6.62 1.28 6.3799996 1.48 C 6.12 1.28 5.62 1.1999999 5.24 1.1999999 C 4.7999997 1.1999999 4.36 1.54 4.36 2.54 C 4.36 3.54 4.3399997 5.68 4.3399997 7.68 L 6.3599997 7.68 C 6.56 7.68 6.8399997 7.7599998 6.8399997 7.94 L 6.8399997 8.559999 C 6.8399997 8.639999 6.7799997 8.679999 6.68 8.679999 L 4.3399997 8.679999 L 4.36 9.36 C 4.4 10.7 4.46 11.62 4.46 11.62 C 4.46 11.74 4.4 11.8 4.2999997 11.8 C 4.16 11.8 3.4199998 11.58 3.1 11.44 C 2.76 11.3 2.18 11.179999 2.04 11 C 1.9 10.82 1.8199999 10.28 1.8199999 8.679999 Z "/>
</symbol>
<symbol id="gE9BB2E81A58B731A2047F77D70267173" overflow="visible">
<path d="M 4.64 2.44 L 4.64 6.42 C 4.64 7.4199996 4.72 8.54 4.72 8.54 C 4.72 8.76 4.54 8.88 4.2599998 8.88 C 3.6999998 8.66 2.08 8.5 0.7 8.32 C 0.65999997 8.2 0.7 7.7999997 0.74 7.68 C 1.8399999 7.58 2.04 7.4199996 2.04 6.2799997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.74 0.59999996 0.64 C 0.48 0.52 0.48 0.08 0.59999996 -0.04 C 1.4399999 -0.02 2.28 0 3.34 0 C 4.4 0 5.22 -0.02 6.08 -0.04 C 6.2 0.08 6.2 0.52 6.08 0.64 C 4.8599997 0.71999997 4.64 0.78 4.64 2.44 Z M 1.9399999 11.92 C 1.9399999 11.259999 2.4199998 10.599999 3.22 10.599999 C 4.12 10.599999 4.64 11.32 4.64 11.84 C 4.64 12.44 4.18 13.16 3.34 13.16 C 2.3999999 13.16 1.9399999 12.5199995 1.9399999 11.92 Z "/>
</symbol>
<symbol id="g814D257E196F777517493FCE505E18DF" overflow="visible">
<path d="M 0.74 4.14 C 0.74 1.52 2.82 -0.19999999 5.5 -0.19999999 C 6.92 -0.19999999 8.099999 0.19999999 8.92 0.94 C 9.94 1.8399999 10.28 3.1999998 10.28 4.3199997 C 10.28 6.94 8.5 8.88 5.52 8.88 C 3.86 8.88 2.62 8.3 1.8399999 7.3999996 C 1.0799999 6.52 0.74 5.3199997 0.74 4.14 Z M 5.2 8.04 C 6.56 8.04 7.48 6.42 7.48 3.6799998 C 7.48 1.28 6.54 0.64 5.8199997 0.64 C 4.18 0.64 3.54 3.1 3.54 4.58 C 3.54 6.42 3.86 8.04 5.2 8.04 Z "/>
</symbol>
<symbol id="gED653E9CCAB5F6C6237350979071A74F" overflow="visible">
<path d="M 1.1999999 1.1999999 C 1.1999999 0.44 1.8399999 -0.16 2.6399999 -0.16 C 3.4399998 -0.16 4.12 0.48 4.12 1.24 C 4.12 2.02 3.48 2.62 2.6799998 2.62 C 1.88 2.62 1.1999999 1.9799999 1.1999999 1.1999999 Z M 1.1999999 7.16 C 1.1999999 6.3999996 1.8399999 5.7999997 2.6399999 5.7999997 C 3.4399998 5.7999997 4.12 6.44 4.12 7.2 C 4.12 7.98 3.48 8.58 2.6799998 8.58 C 1.88 8.58 1.1999999 7.94 1.1999999 7.16 Z "/>
</symbol>
<symbol id="gC1513612DA0E34F2B247DB2830CD7DFD" overflow="visible">
<path d="M 1.24 4.6 C 1.24 3.34 2.26 2.32 3.52 2.32 C 4.7799997 2.32 5.7999997 3.34 5.7999997 4.6 C 5.7999997 5.8599997 4.7799997 6.8799996 3.52 6.8799996 C 2.26 6.8799996 1.24 5.8599997 1.24 4.6 Z "/>
</symbol>
<symbol id="g98926218EB374AD77A2D864C6D10734B" overflow="visible">
<path d="M 5.62 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.7 4.04 12.099999 5.12 12.099999 L 6.62 12.099999 C 8.12 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.88 9.34 9.92 9.54 10.0199995 C 9.44 10.84 9.139999 12.759999 9.099999 12.92 C 9.099999 12.96 9.08 12.98 9.0199995 12.98 C 8.679999 12.92 8.5199995 12.9 8.04 12.9 L 2.9399998 12.9 C 2.34 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.1 -0.02 2.3 0 2.96 0 L 7.2599998 0 C 8.22 0 9.82 -0.04 9.82 -0.04 C 10.099999 0.96 10.4 2.28 10.559999 3.3 C 10.36 3.4199998 10.12 3.46 9.86 3.3999999 C 9.46 1.9599999 8.76 0.78 7.24 0.78 L 4.92 0.78 C 4.08 0.78 3.8 1.1 3.8 2.04 L 3.8 6.46 L 5.62 6.46 C 7.3199997 6.46 7.3799996 6 7.44 5.1 C 7.56 4.98 7.98 4.98 8.099999 5.1 C 8.08 5.62 8.059999 6.18 8.059999 6.8599997 C 8.059999 7.4199996 8.08 8.099999 8.099999 8.58 C 7.98 8.7 7.56 8.7 7.44 8.58 C 7.3799996 7.48 7.3199997 7.22 5.62 7.22 Z "/>
</symbol>
<symbol id="gAA212A9DBB5FA7333A767E41B2F6A3B3" overflow="visible">
<path d="M 5.8599997 0.96 C 5.98 0.34 6.2 -0.19999999 7.2 -0.19999999 C 7.96 -0.19999999 8.679999 0.14 9.099999 0.53999996 C 9.059999 0.78 8.98 0.96 8.76 1.0799999 C 8.62 0.96 8.28 0.76 8.0199995 0.76 C 7.44 0.76 7.4199996 1.54 7.4199996 2.46 L 7.4199996 5.4 C 7.4199996 8.24 5.8599997 8.78 4.4 8.78 C 2.76 8.78 1.1 7.7 1.1 6.56 C 1.1 6.08 1.3399999 5.8399997 1.8 5.8399997 C 2.3799999 5.8399997 2.74 6.2599998 2.74 6.52 C 2.74 6.66 2.72 6.7999997 2.6799998 6.8799996 C 2.6599998 6.94 2.6399999 7.06 2.6399999 7.2799997 C 2.6399999 7.8999996 3.48 8.12 4.24 8.12 C 4.92 8.12 5.8599997 7.7799997 5.8599997 5.52 C 5.8599997 5.38 5.7999997 5.2999997 5.74 5.2799997 L 4.02 4.8599997 C 2.1 4.38 0.71999997 3.32 0.71999997 1.9599999 C 0.71999997 0.32 1.8399999 -0.19999999 3.24 -0.19999999 C 3.9399998 -0.19999999 4.54 -0.04 5.42 0.64 L 5.8199997 0.96 Z M 5.8599997 4.66 L 5.8599997 2.02 C 5.8599997 1.76 5.74 1.62 5.58 1.5 C 5.06 1.0799999 4.38 0.62 3.82 0.62 C 2.82 0.62 2.3799999 1.42 2.3799999 2.04 C 2.3799999 2.9399998 2.8 3.86 4.2799997 4.24 Z "/>
</symbol>
<symbol id="g713198A7DA4F5CD7D462D4529B1D64BD" overflow="visible">
<path d="M 7.96 1.8199999 C 7.8799996 2 7.72 2.08 7.54 2.1 C 6.8599997 1.22 6 0.78 5.14 0.78 C 3.6799998 0.78 2.46 2.26 2.46 4.6 C 2.46 6.7999997 3.4199998 8.12 4.74 8.12 C 5.92 8.12 6.08 7.4199996 6.16 6.72 C 6.22 6.18 6.5 6 6.92 6 C 7.3399997 6 7.8999996 6.2599998 7.8999996 6.8799996 C 7.8999996 7.98 6.7599998 8.78 4.8399997 8.78 C 2.86 8.78 0.74 7 0.74 4.16 C 0.74 1.5799999 2.18 -0.19999999 4.7 -0.19999999 C 5.9 -0.19999999 6.96 0.17999999 7.96 1.8199999 Z "/>
</symbol>
<symbol id="g3C2FFF86BC828E66F78F8A687CE12C70" overflow="visible">
<path d="M 3.34 5.72 C 3.34 6.14 3.52 6.3799996 3.6799998 6.56 C 4.44 7.2999997 5.46 7.74 6.24 7.74 C 6.64 7.74 7.06 7.48 7.2999997 7.02 C 7.5 6.62 7.54 6.08 7.54 5.48 L 7.54 2.44 C 7.54 0.79999995 7.3399997 0.71999997 6.2999997 0.62 C 6.2 0.5 6.2 0.08 6.2999997 -0.04 C 6.8599997 -0.02 7.54 0 8.34 0 C 9.139999 0 9.8 -0.02 10.46 -0.04 C 10.559999 0.08 10.559999 0.5 10.46 0.62 C 9.34 0.71999997 9.12 0.79999995 9.12 2.44 L 9.12 5.42 C 9.12 6.52 9.04 7.5 8.58 8.099999 C 8.24 8.54 7.62 8.78 6.92 8.78 C 5.94 8.78 4.74 8.5199995 3.52 7.16 C 3.52 7.14 3.5 7.14 3.48 7.12 C 3.4199998 7.04 3.32 6.92 3.32 7.16 L 3.34 11.66 C 3.34 12.96 3.4199998 13.759999 3.4199998 13.759999 C 3.4199998 13.9 3.34 13.96 3.1599998 13.96 C 2.6599998 13.759999 1.16 13.48 0.35999998 13.42 C 0.32 13.259999 0.35999998 12.94 0.48 12.82 C 0.53999996 12.82 0.59999996 12.82 0.65999997 12.82 C 1.54 12.759999 1.76 12.759999 1.76 11.179999 L 1.76 2.44 C 1.76 0.78 1.52 0.7 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.02 -0.02 1.76 0 2.56 0 C 3.32 0 3.98 -0.02 4.54 -0.04 C 4.66 0.08 4.66 0.5 4.54 0.62 C 3.52 0.7 3.34 0.78 3.34 2.44 Z "/>
</symbol>
<symbol id="gAC7FD886AB12F72ED3B61B0327264BE7" overflow="visible">
<path d="M 3.12 7.3599997 C 3.1 7.96 3.06 8.48 2.96 8.679999 C 2.9199998 8.78 2.8799999 8.84 2.72 8.84 C 2.1599998 8.62 1.64 8.44 0.26 8.26 C 0.22 8.139999 0.26 7.8199997 0.29999998 7.7 C 1.38 7.6 1.5999999 7.5 1.5999999 6.3399997 L 1.5999999 -2.2 C 1.5999999 -3.86 1.38 -3.9599998 0.16 -4.02 C 0.04 -4.14 0.04 -4.56 0.16 -4.68 C 0.85999995 -4.66 1.5999999 -4.64 2.3999999 -4.64 C 3.1999998 -4.64 4.16 -4.66 4.8199997 -4.68 C 4.94 -4.56 4.94 -4.14 4.8199997 -4.02 C 3.3999999 -3.9399998 3.1799998 -3.86 3.1799998 -2.2 L 3.1799998 -0.04 C 3.1799998 0.22 3.26 0.19999999 3.46 0.12 C 3.9599998 -0.08 4.56 -0.19999999 5.2 -0.19999999 C 6.3199997 -0.19999999 7.3199997 0.14 8.139999 0.91999996 C 9.08 1.8399999 9.62 3.08 9.62 4.7 C 9.62 6.8199997 8.12 8.78 6.08 8.78 C 5.16 8.78 4.14 8.179999 3.34 7.2799997 C 3.22 7.16 3.1399999 7.16 3.12 7.3599997 Z M 3.5 6.62 C 4.02 7.2599998 4.94 7.8599997 5.52 7.8599997 C 6.7999997 7.8599997 7.8999996 6.42 7.8999996 4.16 C 7.8999996 2.52 7.3199997 0.48 5.08 0.48 C 4.72 0.48 4.02 0.58 3.6599998 0.9 C 3.26 1.26 3.1799998 1.38 3.1799998 2.1 L 3.1799998 5.74 C 3.1799998 6.16 3.26 6.3399997 3.5 6.62 Z "/>
</symbol>
<symbol id="gFB78EB03C35D4F852337F4EC6AC104AC" overflow="visible">
<path d="M 0.82 4.1 C 0.82 2.06 2.18 -0.19999999 5.02 -0.19999999 C 6.2999997 -0.19999999 7.2799997 0.26 7.96 0.91999996 C 8.86 1.8 9.26 3.06 9.26 4.2799997 C 9.26 6.3599997 8.12 8.78 5.06 8.78 C 3.74 8.78 2.6599998 8.24 1.92 7.3799996 C 1.1999999 6.52 0.82 5.3599997 0.82 4.1 Z M 4.7599998 8.08 C 6.48 8.08 7.54 6.52 7.54 3.6399999 C 7.54 1.12 6.24 0.5 5.2999997 0.5 C 3.22 0.5 2.54 3.02 2.54 4.56 C 2.54 6.2999997 2.96 8.08 4.7599998 8.08 Z "/>
</symbol>
<symbol id="gE68C39294AA7FBA9B91EA2F8E9CC3997" overflow="visible">
<path d="M 3.62 2.44 L 3.62 6.42 C 3.62 7.4199996 3.6999998 8.7 3.6999998 8.7 C 3.6999998 8.78 3.6 8.84 3.4399998 8.84 C 2.8799999 8.62 2.08 8.44 0.7 8.26 C 0.65999997 8.139999 0.7 7.8199997 0.74 7.7 C 1.8399999 7.6 2.04 7.48 2.04 6.3399997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.71999997 0.59999996 0.62 C 0.48 0.5 0.48 0.08 0.59999996 -0.04 C 1.26 -0.02 2.04 0 2.84 0 C 3.6399999 0 4.4 -0.02 5.06 -0.04 C 5.18 0.08 5.18 0.5 5.06 0.62 C 3.84 0.7 3.62 0.78 3.62 2.44 Z M 1.8 11.98 C 1.8 11.46 2.28 10.94 2.76 10.94 C 3.32 10.94 3.8 11.48 3.8 11.9 C 3.8 12.38 3.3799999 12.94 2.84 12.94 C 2.36 12.94 1.8 12.46 1.8 11.98 Z "/>
</symbol>
<symbol id="g35631D62198EF939061DC90C9391724A" overflow="visible">
<path d="M 3.6799998 7.16 C 3.56 7.02 3.4399998 6.98 3.4399998 7.16 C 3.4199998 7.7 3.3799999 8.48 3.28 8.679999 C 3.24 8.78 3.1999998 8.84 3.04 8.84 C 2.48 8.62 1.9599999 8.44 0.58 8.26 C 0.53999996 8.139999 0.58 7.8199997 0.62 7.7 C 1.6999999 7.6 1.92 7.5 1.92 6.3399997 L 1.92 2.44 C 1.92 0.79999995 1.7199999 0.71999997 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.92 0 2.72 0 C 3.52 0 4.12 -0.02 4.72 -0.04 C 4.8399997 0.08 4.8399997 0.5 4.72 0.62 C 3.6999998 0.71999997 3.5 0.79999995 3.5 2.44 L 3.5 5.72 C 3.5 6.14 3.6799998 6.3799996 3.84 6.56 C 4.6 7.2999997 5.5 7.74 6.2799997 7.74 C 6.68 7.74 7.1 7.48 7.3399997 7.02 C 7.54 6.62 7.58 6.08 7.58 5.48 L 7.58 2.44 C 7.58 0.79999995 7.3799996 0.71999997 6.3399997 0.62 C 6.24 0.5 6.24 0.08 6.3399997 -0.04 C 6.94 -0.02 7.58 0 8.38 0 C 9.179999 0 9.9 -0.02 10.5 -0.04 C 10.599999 0.08 10.599999 0.5 10.5 0.62 C 9.38 0.71999997 9.16 0.79999995 9.16 2.44 L 9.16 5.42 C 9.16 6.52 9.08 7.48 8.62 8.099999 C 8.28 8.54 7.66 8.78 6.96 8.78 C 5.98 8.78 4.8599997 8.5199995 3.6799998 7.16 Z "/>
</symbol>
<symbol id="g22D858CFD6AD86697C1391C74FD687D1" overflow="visible">
<path d="M 0.85999995 8.58 C 0.58 8.58 0.5 8.34 0.5 8.179999 L 0.5 7.9199996 C 0.5 7.8199997 0.52 7.7999997 0.59999996 7.7999997 L 1.78 7.7999997 L 1.78 1.78 C 1.78 0.35999998 2.3999999 -0.19999999 3.32 -0.19999999 C 4.24 -0.19999999 5.24 0.24 6.02 1.12 C 5.98 1.3199999 5.8599997 1.4399999 5.66 1.4599999 C 5.14 1.06 4.54 0.9 4.02 0.9 C 3.48 0.9 3.36 1.5 3.36 2.74 L 3.36 7.7999997 L 5.44 7.7999997 C 5.64 7.7999997 5.92 7.8799996 5.92 8.059999 L 5.92 8.46 C 5.92 8.54 5.8599997 8.58 5.7599998 8.58 L 3.36 8.58 L 3.36 9.36 C 3.36 10.66 3.4399998 11.46 3.4399998 11.46 C 3.4399998 11.58 3.3799999 11.639999 3.28 11.639999 C 3.1999998 11.639999 3.02 11.559999 2.84 11.46 C 2.62 11.34 2.4199998 11.24 2.1599998 11.179999 C 1.92 11.099999 1.7199999 11.04 1.7199999 10.9 C 1.7199999 10.66 1.78 10.8 1.78 8.58 Z "/>
</symbol>
<symbol id="gF9DE6E66E5D3ACB0B17DC7988DD660B8" overflow="visible">
<path d="M 1.7199999 2.44 C 1.7199999 0.78 1.5 0.7 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.04 -0.02 1.7199999 0 2.52 0 C 3.22 0 3.8799999 -0.02 4.3399997 -0.04 C 4.46 0.08 4.46 0.5 4.3399997 0.62 C 3.52 0.7 3.3 0.78 3.3 2.44 L 3.3 4.18 C 3.6799998 4.16 3.9599998 4.14 4.16 4.08 C 4.38 3.9199998 4.56 3.74 4.7999997 3.4199998 L 6.2599998 1.4599999 C 6.8399997 0.68 7.08 0.29999998 7.1 0.06 C 7.1 0 7.12 -0.04 7.18 -0.04 C 7.58 -0.02 8.0199995 0 8.42 0 C 9.04 0 9.66 -0.02 10.059999 -0.04 C 10.179999 0.08 10.179999 0.5 10.059999 0.62 C 9.38 0.7 8.88 0.78 8.34 1.4599999 L 5.7 4.7799997 C 5.62 4.88 5.56 4.96 5.56 5.06 C 5.56 5.14 5.56 5.18 5.64 5.2599998 L 7.3999996 7.08 C 8 7.72 8.7 7.8799996 9.5 7.96 C 9.62 8.08 9.62 8.5 9.5 8.62 C 9.04 8.599999 8.48 8.58 7.7599998 8.58 C 7 8.58 6.2599998 8.599999 5.7999997 8.62 C 5.68 8.5 5.68 8.08 5.7999997 7.96 C 6.92 7.8799996 6.44 7.18 6.2599998 6.94 C 5.7999997 6.3599997 5.18 5.68 4.66 5.2999997 C 4.22 4.98 3.6799998 4.74 3.3 4.68 L 3.3 11.66 C 3.3 12.96 3.3799999 13.759999 3.3799999 13.759999 C 3.3799999 13.9 3.3 13.96 3.12 13.96 C 2.62 13.759999 1.12 13.48 0.32 13.42 C 0.28 13.259999 0.32 12.94 0.44 12.82 C 0.5 12.82 0.56 12.82 0.62 12.82 C 1.5 12.759999 1.7199999 12.759999 1.7199999 11.179999 Z "/>
</symbol>
<symbol id="g67483374C2628B9150A7D3585AC4A61B" overflow="visible">
<path d="M 0.96 2.76 C 1.04 1.78 1.1 0.84 1.1 0 C 1.3 0.04 1.5 0.06 1.5999999 0.06 C 1.74 0.06 1.86 0.06 2 0.02 C 2.54 -0.12 3.08 -0.19999999 3.82 -0.19999999 C 4.94 -0.19999999 7 0.34 7 2.32 C 7 3.6799998 6.02 4.48 4.66 4.98 C 3.46 5.44 2.6599998 5.74 2.6599998 6.8399997 C 2.6599998 7.66 3.3799999 8.12 4.06 8.12 C 4.5 8.12 5.66 7.96 5.92 6.2599998 C 6.04 6.14 6.44 6.16 6.56 6.2799997 C 6.62 7 6.66 7.74 6.68 8.4 C 6.06 8.5 5.1 8.78 4.06 8.78 C 2.58 8.78 1.24 7.8199997 1.24 6.54 C 1.24 5.08 1.9 4.46 3.4399998 3.82 C 5.1 3.1399999 5.48 2.72 5.48 1.86 C 5.48 0.88 4.52 0.45999998 3.78 0.45999998 C 3 0.45999998 2.56 0.71999997 2.36 0.94 C 1.92 1.4 1.6999999 2.28 1.5799999 2.78 C 1.4599999 2.8999999 1.0799999 2.8799999 0.96 2.76 Z "/>
</symbol>
<symbol id="g1788914935A6D7BFA016214155630E72" overflow="visible">
<path d="M 1.9 2.44 C 1.9 0.78 1.68 0.68 0.45999998 0.62 C 0.34 0.5 0.34 0.08 0.45999998 -0.04 C 1.16 -0.02 1.9 0 2.7 0 C 3.5 0 4.2599998 -0.02 4.92 -0.04 C 5.04 0.08 5.04 0.5 4.92 0.62 C 3.6999998 0.68 3.48 0.78 3.48 2.44 L 3.48 11.66 C 3.48 12.96 3.56 13.759999 3.56 13.759999 C 3.56 13.9 3.48 13.96 3.3 13.96 C 2.8 13.759999 1.3 13.48 0.5 13.42 C 0.45999998 13.259999 0.5 12.94 0.62 12.82 C 1.78 12.74 1.9 12.679999 1.9 11.179999 Z "/>
</symbol>
<symbol id="g21D1E528F66DB45787699F71DA377CC5" overflow="visible">
<path d="M 4.08 -3.1999998 C 4.4 -2.6399999 4.66 -2.08 4.9 -1.48 C 6.5 2.3799999 7.3999996 4.44 8.44 6.68 C 8.84 7.52 9.12 7.8399997 10.059999 7.96 C 10.179999 8.08 10.179999 8.5 10.059999 8.62 C 9.66 8.599999 9.2 8.58 8.639999 8.58 C 8.04 8.58 7.4199996 8.599999 6.8199997 8.62 C 6.7 8.5 6.7 8.08 6.8199997 7.96 C 7.46 7.8999996 8.099999 7.7799997 7.7799997 7.06 L 5.7999997 2.48 C 5.66 2.1599998 5.48 2.1 5.3199997 2.5 L 3.54 6.66 C 3.1799998 7.5 3.08 7.8799996 4.2 7.96 C 4.3199997 8.08 4.3199997 8.5 4.2 8.62 C 3.46 8.599999 2.6599998 8.58 1.9399999 8.58 C 1.26 8.58 0.71999997 8.599999 0.32 8.62 C 0.19999999 8.5 0.19999999 8.08 0.32 7.96 C 1.12 7.8599997 1.38 7.68 1.9 6.46 L 4.16 1.1999999 C 4.3399997 0.79999995 4.64 -0.12 4.44 -0.68 C 4.2 -1.3399999 3.9599998 -1.9 3.6599998 -2.52 C 3.4399998 -2.9199998 3.1599998 -3.1 2.6599998 -3.1 C 2.3799999 -3.1 2.3 -3.04 2.08 -3.04 C 1.5 -3.04 1.1999999 -3.6399999 1.1999999 -3.8999999 C 1.1999999 -4.3199997 1.5999999 -4.64 2.1399999 -4.64 C 2.56 -4.64 3.36 -4.48 4.08 -3.1999998 Z "/>
</symbol>
<symbol id="g7FBC39AA6D9FB89D8B638A3651405A80" overflow="visible">
<path d="M 7.72 1.86 C 6.98 1.1 6.3999996 0.78 5.24 0.78 C 4.52 0.78 3.6799998 1.1999999 3.06 2.22 C 2.6599998 2.8799999 2.4199998 3.8 2.4199998 4.96 L 7.74 4.92 C 7.98 4.92 8.12 5.04 8.12 5.2599998 C 8.12 6.94 7.52 8.74 4.74 8.74 C 3 8.74 0.74 7.08 0.74 4.04 C 0.74 2.9199998 1.02 1.8399999 1.68 1.0799999 C 2.36 0.28 3.3 -0.19999999 4.74 -0.19999999 C 6.2599998 -0.19999999 7.3399997 0.5 8.139999 1.54 C 8.08 1.74 7.96 1.8399999 7.72 1.86 Z M 2.48 5.64 C 2.86 7.8999996 4.2599998 8.08 4.74 8.08 C 5.5 8.08 6.3999996 7.66 6.3999996 5.98 C 6.3999996 5.7999997 6.3199997 5.7 6.1 5.7 Z "/>
</symbol>
<symbol id="gB9C04FB79CAD4691AB5EC7F01BE2AD7F" overflow="visible">
<path d="M 3.52 7.16 C 3.48 7.96 3.46 8.48 3.36 8.679999 C 3.32 8.78 3.28 8.84 3.12 8.84 C 2.56 8.62 2.04 8.44 0.65999997 8.26 C 0.62 8.139999 0.65999997 7.8199997 0.7 7.7 C 1.78 7.6 2 7.5 2 6.3399997 L 2 2.44 C 2 0.78 1.76 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 2 0 2.8 0 C 3.6 0 4.52 -0.02 5.22 -0.04 C 5.3399997 0.08 5.3399997 0.5 5.22 0.62 C 3.82 0.71999997 3.58 0.78 3.58 2.44 L 3.58 5.22 C 3.58 5.74 3.82 6.2 4.06 6.56 C 4.2799997 6.8799996 4.74 7.54 4.98 7.54 C 5.16 7.54 5.3399997 7.5 5.5 7.2799997 C 5.64 7.08 5.8799996 6.8199997 6.22 6.8199997 C 6.7 6.8199997 7.16 7.3199997 7.16 7.8199997 C 7.16 8.2 6.7999997 8.78 5.96 8.78 C 5.02 8.78 4.2 7.8999996 3.74 7.12 C 3.62 6.8999996 3.52 7.06 3.52 7.16 Z "/>
</symbol>
<symbol id="g733371913480EE84B3609C9E9CD62F8C" overflow="visible">
<path d="M 3.34 7.8799996 C 3.22 7.7599998 3.1399999 7.7999997 3.1399999 7.98 L 3.1399999 11.66 C 3.1399999 12.96 3.22 13.759999 3.22 13.759999 C 3.22 13.9 3.1399999 13.96 2.96 13.96 C 2.46 13.759999 0.96 13.48 0.16 13.42 C 0.12 13.259999 0.16 12.94 0.28 12.82 C 0.34 12.82 0.39999998 12.82 0.45999998 12.82 C 1.3399999 12.759999 1.56 12.759999 1.56 11.179999 L 1.56 1.42 C 1.56 0.64 1.54 0.28 1.48 0 C 1.5799999 -0.16 1.68 -0.24 1.92 -0.24 C 2.04 -0.12 2.24 0.06 2.3999999 0.24 C 2.6 0.48 2.72 0.48 2.9399998 0.29999998 C 3.3999999 -0.08 4 -0.19999999 4.7 -0.19999999 C 6.74 -0.19999999 9.12 1.66 9.12 4.8399997 C 9.12 7.2799997 7.3199997 8.78 5.58 8.78 C 4.72 8.78 3.9599998 8.44 3.34 7.8799996 Z M 3.48 7.2599998 C 4 7.72 4.6 7.8999996 5.18 7.8999996 C 6.3999996 7.8999996 7.3999996 6.42 7.3999996 4.48 C 7.3999996 2.2 6.48 0.48 4.58 0.48 C 3.9599998 0.48 3.54 0.91999996 3.1399999 1.42 L 3.1399999 6.42 C 3.1399999 6.8399997 3.22 7.04 3.48 7.2599998 Z "/>
</symbol>
<symbol id="g42587C4E387B2C5F870DA01C2914651F" overflow="visible">
<path d="M 6.68 1 C 6.7799997 1.0799999 6.96 1.12 6.98 0.97999996 C 7.04 0.5 7.2 -0.19999999 7.2 -0.19999999 C 7.3599997 -0.26 7.46 -0.24 7.58 -0.19999999 C 8.0199995 0.16 8.72 0.45999998 9.94 0.59999996 C 10.059999 0.71999997 10.059999 1.02 9.94 1.14 C 8.66 1.24 8.48 1.62 8.48 2.6 L 8.48 11.66 C 8.48 12.96 8.559999 13.759999 8.559999 13.759999 C 8.559999 13.9 8.48 13.96 8.3 13.96 C 7.7999997 13.759999 6.2999997 13.48 5.5 13.42 C 5.46 13.259999 5.5 12.94 5.62 12.82 C 5.68 12.82 5.74 12.82 5.7999997 12.82 C 6.68 12.759999 6.8999996 12.759999 6.8999996 11.179999 L 6.8999996 8.62 C 6.8999996 8.48 6.8599997 8.44 6.72 8.44 C 6.64 8.44 5.8199997 8.78 5.16 8.78 C 3.84 8.78 2.96 8.34 2.1599998 7.58 C 1.3 6.72 0.78 5.54 0.78 4.06 C 0.78 1.5999999 2.02 -0.19999999 4.18 -0.19999999 C 4.96 -0.19999999 5.7 0.19999999 6.68 1 Z M 6.8999996 2.48 C 6.8999996 2.1 6.8599997 1.9399999 6.58 1.6999999 C 5.8399997 1.06 5.2 0.74 4.7 0.74 C 3.62 0.74 2.5 1.92 2.5 4.42 C 2.5 5.8599997 2.78 6.66 3.08 7.08 C 3.6999998 8.0199995 4.54 8.08 4.94 8.08 C 5.66 8.08 6.16 7.8199997 6.56 7.3599997 C 6.8399997 7.04 6.8999996 6.8999996 6.8999996 6.2799997 Z "/>
</symbol>
<symbol id="g844C4CEA683BD523227FE7A466FBF8A3" overflow="visible">
<path d="M 3.1 1.5799999 L 4.2 4.48 C 4.2999997 4.74 4.42 4.8199997 4.9 4.8199997 L 9.12 4.8199997 L 10.28 1.4399999 C 10.5199995 0.76 9.76 0.68 8.8 0.62 C 8.679999 0.5 8.679999 0.08 8.8 -0.04 C 9.54 -0.02 10.639999 0 11.42 0 C 12.24 0 13 -0.02 13.7 -0.04 C 13.82 0.08 13.82 0.5 13.7 0.62 C 12.92 0.7 12.24 0.76 11.9 1.7199999 L 7.7799997 13.16 C 7.48 12.98 6.94 12.759999 6.68 12.759999 L 2.1399999 2.04 C 1.62 0.79999995 1.02 0.68 0.14 0.62 C 0.02 0.5 0.02 0.08 0.14 -0.04 C 0.65999997 -0.02 1.3199999 0 1.92 0 C 2.74 0 3.74 -0.02 4.48 -0.04 C 4.6 0.08 4.6 0.5 4.48 0.62 C 3.72 0.68 2.78 0.76 3.1 1.5799999 Z M 5.2599998 5.66 C 4.8199997 5.66 4.68 5.72 4.7599998 5.92 L 6.7999997 11.099999 L 6.92 11.099999 L 8.8 5.66 Z "/>
</symbol>
<symbol id="gA1481BA28623480CC7E6165783E2A864" overflow="visible">
<path d="M 4.06 7.96 C 4.18 8.08 4.18 8.5 4.06 8.62 C 3.46 8.599999 2.76 8.58 2.04 8.58 C 1.28 8.58 0.74 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.16 7.8599997 1.38 7.66 1.8 6.62 L 4.42 0.16 C 4.54 -0.12 4.7 -0.24 4.9 -0.24 C 5.08 -0.24 5.24 -0.12 5.38 0.19999999 L 7.3999996 5.12 L 9.46 0.16 C 9.58 -0.12 9.74 -0.24 9.94 -0.24 C 10.12 -0.24 10.28 -0.12 10.4 0.17999999 L 13.0199995 6.52 C 13.34 7.3399997 13.679999 7.8999996 14.7 7.96 C 14.82 8.08 14.82 8.5 14.7 8.62 C 14.299999 8.599999 13.86 8.58 13.259999 8.58 C 12.66 8.58 11.82 8.599999 11.219999 8.62 C 11.099999 8.5 11.099999 8.08 11.219999 7.96 C 12.719999 7.8799996 12.5199995 7.2999997 12.24 6.6 L 10.559999 2.44 C 10.36 1.9399999 10.28 1.9399999 10.12 2.36 L 8.4 6.74 C 8.0199995 7.68 8.059999 7.8799996 9.12 7.96 C 9.24 8.08 9.24 8.5 9.12 8.62 C 8.5199995 8.599999 7.72 8.58 7.12 8.58 C 6.62 8.58 5.96 8.599999 5.3599997 8.62 C 5.24 8.5 5.24 8.08 5.3599997 7.96 C 6.2999997 7.8799996 6.54 7.2999997 6.8999996 6.3999996 L 7.02 6.08 L 5.62 2.54 C 5.3599997 1.88 5.3199997 1.86 5.06 2.5 L 3.46 6.62 C 3.08 7.58 3.1 7.8999996 4.06 7.96 Z "/>
</symbol>
<symbol id="gE264501C5759C04FD4041B484B9EC12C" overflow="visible">
<path d="M 6.46 7.2999997 L 4.8399997 7.2999997 L 4.8399997 11.08 C 4.8399997 11.559999 5.18 12.059999 5.66 12.059999 L 7.3599997 12.059999 C 8.86 12.059999 9.28 11.3 9.719999 9.92 C 9.96 9.88 10.38 9.92 10.58 10.0199995 C 10.48 10.84 10.38 12.759999 10.34 12.92 C 10.34 12.96 10.32 12.98 10.26 12.98 C 9.92 12.92 9.76 12.9 9.28 12.9 L 3.3799999 12.9 C 3.3799999 12.9 1.3 12.92 0.29999998 12.94 C 0.17999999 12.82 0.17999999 12.38 0.29999998 12.259999 C 1.6999999 12.2 2.04 12.099999 2.04 10.44 L 2.04 2.44 C 2.04 0.78 1.6999999 0.7 0.29999998 0.64 C 0.17999999 0.52 0.17999999 0.08 0.29999998 -0.04 C 1.28 -0.02 3.3999999 0 3.3999999 0 L 8.099999 0 C 9.059999 0 10.86 -0.04 10.86 -0.04 C 11.139999 0.96 11.24 2.28 11.4 3.3 C 11.2 3.4199998 10.76 3.46 10.5 3.3999999 C 10.099999 1.9599999 9.2 0.84 7.68 0.84 L 5.66 0.84 C 5.22 0.84 4.8399997 1.26 4.8399997 1.8 L 4.8399997 6.3799996 L 6.46 6.3799996 C 7.8399997 6.3799996 8.22 6 8.28 5.1 C 8.4 4.98 9.0199995 4.98 9.139999 5.1 C 9.12 5.7999997 9.099999 6.18 9.099999 6.8599997 C 9.099999 7.54 9.12 7.98 9.139999 8.58 C 9.0199995 8.7 8.4 8.7 8.28 8.58 C 8.22 7.48 7.7999997 7.2999997 6.46 7.2999997 Z "/>
</symbol>
<symbol id="g4CEB3F42B775C8D3827D0A458A70771F" overflow="visible">
<path d="M 3.6599998 1.4599999 L 4.9 3.1999998 C 4.98 3.3 5.04 3.36 5.1 3.26 L 6.06 1.4399999 C 6.3999996 0.79999995 6.2 0.74 5.5 0.64 C 5.38 0.52 5.38 0.08 5.5 -0.04 C 5.9 -0.02 7.16 0 8.22 0 C 9.26 0 10.5 -0.02 10.9 -0.04 C 11.0199995 0.08 11.0199995 0.52 10.9 0.64 C 10.16 0.76 9.48 1.02 8.84 1.9799999 L 7.08 4.6 C 6.98 4.7599998 6.98 4.8199997 7.04 4.9 L 8.82 7.06 C 9.38 7.74 10.099999 7.98 10.719999 8.04 C 10.84 8.16 10.84 8.599999 10.719999 8.72 C 10.32 8.7 9.7 8.679999 9.04 8.679999 C 8.26 8.679999 7.44 8.7 7.04 8.72 C 6.92 8.599999 6.92 8.16 7.04 8.04 C 7.7599998 7.98 7.9199996 7.7599998 7.52 7.18 L 6.44 5.64 C 6.3799996 5.54 6.2799997 5.54 6.2 5.68 L 5.2999997 7.2 C 4.88 7.9199996 5.14 7.96 5.9 8.04 C 6.02 8.16 6.02 8.599999 5.9 8.72 C 5.5 8.7 4.2 8.679999 3.1 8.679999 C 2.12 8.679999 0.97999996 8.7 0.58 8.72 C 0.45999998 8.599999 0.45999998 8.16 0.58 8.04 C 1.48 8.04 1.88 7.5 2.44 6.7 L 4.22 4.16 C 4.2799997 4.08 4.2799997 4 4.16 3.86 L 2.32 1.5799999 C 1.8199999 0.94 0.94 0.71999997 0.34 0.64 C 0.22 0.52 0.22 0.08 0.34 -0.04 C 0.74 -0.02 1.36 0 2 0 C 2.86 0 3.8 -0.02 4.2 -0.04 C 4.3199997 0.08 4.3199997 0.52 4.2 0.64 C 3.84 0.71999997 3.22 0.84 3.6599998 1.4599999 Z "/>
</symbol>
<symbol id="g50FEF586148C287DB923CFE895D558DC" overflow="visible">
<path d="M 5.9 0.97999996 C 6.04 0.16 6.58 -0.19999999 7.46 -0.19999999 C 8.559999 -0.19999999 9.34 0.22 10.08 0.91999996 C 10.04 1.16 9.96 1.3199999 9.719999 1.48 C 9.46 1.28 9.26 1.1999999 8.88 1.1999999 C 8.44 1.1999999 8.32 1.56 8.32 2.54 L 8.36 5.42 C 8.36 8.3 6.58 8.88 4.94 8.88 C 3.48 8.88 1.24 8.04 1.24 6.72 C 1.24 6.16 1.48 5.72 2.26 5.72 C 2.98 5.72 3.5 6.16 3.5 6.64 C 3.5 6.74 3.48 6.8599997 3.46 6.98 C 3.4199998 7.18 3.3799999 7.3799996 3.4199998 7.58 C 3.4399998 7.7999997 3.6 8.04 4.2599998 8.04 C 5.1 8.04 5.7999997 7.68 5.7999997 5.14 L 4.46 4.72 C 2.36 4.06 0.88 3.48 0.88 1.9 C 0.88 0.52 1.64 -0.19999999 3.3799999 -0.19999999 C 3.9599998 -0.19999999 5.12 0.44 5.7799997 0.96 Z M 5.7999997 4.36 L 5.7999997 1.7199999 C 5.2999997 1.3199999 4.7999997 1 4.44 1 C 3.58 1 3.28 1.5799999 3.28 2.2 C 3.28 2.9399998 3.34 3.56 4.7599998 4.02 Z "/>
</symbol>
<symbol id="gB88E546A1990E31D64B5C4B23478426F" overflow="visible">
<path d="M 4.56 2.44 L 4.56 6.42 C 4.56 6.52 4.56 6.62 4.56 6.72 C 5.3399997 7.2 6.04 7.3999996 6.3799996 7.3999996 C 7.18 7.3999996 7.7799997 7.04 7.7799997 5.9 L 7.7799997 2.56 C 7.7799997 0.88 7.46 0.7 6.64 0.64 C 6.52 0.52 6.52 0.08 6.64 -0.04 C 7.48 -0.02 8.12 0 9.08 0 C 10.04 0 10.66 -0.02 11.5199995 -0.04 C 11.639999 0.08 11.639999 0.52 11.5199995 0.64 C 10.719999 0.7 10.38 0.88 10.38 2.56 L 10.38 5.68 C 10.38 6.18 10.36 6.58 10.3 6.7799997 C 11.059999 7.16 11.92 7.3999996 12.24 7.3999996 C 13.04 7.3999996 13.599999 7.04 13.599999 5.9 L 13.599999 2.56 C 13.599999 0.88 13.28 0.7 12.46 0.64 C 12.34 0.52 12.34 0.08 12.46 -0.04 C 13.299999 -0.02 13.94 0 14.9 0 C 16 0 16.88 -0.02 17.74 -0.04 C 17.859999 0.08 17.859999 0.52 17.74 0.64 C 16.52 0.7 16.199999 0.88 16.199999 2.56 L 16.199999 5.68 C 16.199999 7.8799996 15.4 8.88 13.679999 8.88 C 12.94 8.88 11.259999 8.08 10.099999 7.44 C 9.8 8.3 9 8.88 7.8199997 8.88 C 7.1 8.88 5.66 8.12 4.52 7.48 C 4.46 8.08 4.4 8.54 4.4 8.54 C 4.38 8.78 4.22 8.88 3.9399998 8.88 C 3.1999998 8.679999 2 8.4 0.62 8.22 C 0.58 8.099999 0.62 7.7 0.65999997 7.58 C 1.76 7.48 1.9599999 7.3199997 1.9599999 6.18 L 1.9599999 2.44 C 1.9599999 0.78 1.74 0.74 0.52 0.64 C 0.39999998 0.52 0.39999998 0.08 0.52 -0.04 C 1.36 -0.02 2.2 0 3.26 0 C 4.18 0 4.74 -0.02 5.6 -0.04 C 5.72 0.08 5.72 0.52 5.6 0.64 C 4.7599998 0.71999997 4.56 0.78 4.56 2.44 Z "/>
</symbol>
<symbol id="gB416F8956A8016097936DBEC1F135503" overflow="visible">
<path d="M 1.9 6.18 L 1.9 -2.2 C 1.9 -3.86 1.68 -3.8999999 0.45999998 -4 C 0.34 -4.12 0.34 -4.56 0.45999998 -4.68 C 1.3 -4.66 2.1399999 -4.64 3.1999998 -4.64 C 4.2599998 -4.64 5.08 -4.66 5.94 -4.68 C 6.06 -4.56 6.06 -4.12 5.94 -4 C 4.72 -3.9199998 4.5 -3.86 4.5 -2.2 L 4.5 0.14 C 4.94 -0.08 5.3599997 -0.19999999 5.8399997 -0.19999999 C 8.88 -0.19999999 10.86 1.8 10.86 4.74 C 10.86 5.8599997 10.44 7.1 9.66 7.8799996 C 8.96 8.58 7.96 8.88 6.92 8.88 C 6.3399997 8.88 5.2599998 8.179999 4.56 7.54 L 4.44 7.54 C 4.4 8.099999 4.3399997 8.54 4.3399997 8.54 C 4.3199997 8.78 4.16 8.88 3.8799999 8.88 C 3.1399999 8.679999 1.9399999 8.4 0.56 8.22 C 0.52 8.099999 0.56 7.7 0.59999996 7.58 C 1.6999999 7.48 1.9 7.3199997 1.9 6.18 Z M 4.5 1.3 L 4.5 6.42 C 4.5 6.54 4.5 6.64 4.5 6.7599998 C 5.08 7.2799997 5.8199997 7.54 6.2799997 7.54 C 7.1 7.54 8.059999 6.54 8.059999 4.2 C 8.059999 2.52 7.46 0.64 5.72 0.64 C 5.5 0.64 5 0.76 4.5 1.3 Z "/>
</symbol>
<symbol id="gC81C3C15134AD04FEC0FE7FCEBE8BB14" overflow="visible">
<path d="M 2 2.54 C 2 0.88 1.68 0.7 0.45999998 0.64 C 0.34 0.52 0.34 0.08 0.45999998 -0.04 C 1.3 -0.02 2.2 0 3.3 0 C 4.4 0 5.2799997 -0.02 6.14 -0.04 C 6.2599998 0.08 6.2599998 0.52 6.14 0.64 C 4.92 0.7 4.6 0.88 4.6 2.54 L 4.6 11.66 C 4.6 12.96 4.66 13.7 4.66 13.7 C 4.66 13.88 4.52 13.96 4.3399997 13.96 C 3.6 13.719999 2 13.5 0.58 13.44 C 0.52 13.2 0.53999996 12.98 0.64 12.799999 C 1.9 12.7 2 12.679999 2 11.3 Z "/>
</symbol>
<symbol id="gDACA5EBB44D5F3DB530A1F5F650BFBAB" overflow="visible">
<path d="M 2.08 10.46 L 2.08 2.44 C 2.08 0.78 1.74 0.68 0.34 0.62 C 0.22 0.5 0.22 0.08 0.34 -0.04 C 1.24 -0.02 2.22 0 2.9399998 0 C 3.6399999 0 4.8199997 -0.02 5.8199997 -0.04 C 5.94 0.08 5.94 0.5 5.8199997 0.62 C 4.2599998 0.7 3.78 0.78 3.78 2.44 L 3.78 5.8399997 C 4.22 5.7 4.7 5.64 5.4 5.64 C 9.04 5.64 10.139999 8.0199995 10.139999 9.719999 C 10.139999 10.9 9.36 13.04 5.66 13.04 C 4.9 13.04 3.72 12.9 2.9199998 12.9 C 2.18 12.9 1.14 12.92 0.34 12.94 C 0.22 12.82 0.22 12.4 0.34 12.28 C 1.74 12.219999 2.08 12.12 2.08 10.46 Z M 3.78 11.08 C 3.78 11.66 4.08 12.36 5.52 12.36 C 6.8999996 12.36 8.28 11.9 8.28 9.36 C 8.28 7.2 7.24 6.3199997 5.2999997 6.3199997 C 4.7999997 6.3199997 4 6.3599997 3.78 6.42 Z "/>
</symbol>
<symbol id="gB2E338F181D915F0996F60E92302C895" overflow="visible">
<path d="M 7 2.44 L 7 10.08 C 7 11.36 7.2 12.12 7.9199996 12.12 L 8.36 12.12 C 9.86 12.12 10.8 11.599999 11.139999 10.059999 C 11.36 10.059999 11.639999 10.08 11.82 10.16 C 11.679999 11.08 11.58 12.099999 11.559999 13 C 11.559999 13.0199995 11.5199995 13.059999 11.5 13.059999 C 10.82 13 8.599999 12.9 7.02 12.9 L 5.2999997 12.9 C 3.76 12.9 1.4 13 0.64 13.059999 C 0.59999996 13.059999 0.56 13.0199995 0.56 13 C 0.48 12.099999 0.28 11.059999 0.06 10.099999 C 0.26 10.0199995 0.5 10 0.74 10 C 1.14 11.599999 2.06 12.12 3.3799999 12.12 L 4.36 12.12 C 5.1 12.12 5.2999997 11.36 5.2999997 10.139999 L 5.2999997 2.44 C 5.2999997 0.78 4.96 0.68 3.36 0.62 C 3.24 0.5 3.24 0.08 3.36 -0.04 C 4.3399997 -0.02 5.3599997 0 6.16 0 C 6.92 0 7.94 -0.02 8.94 -0.04 C 9.059999 0.08 9.059999 0.5 8.94 0.62 C 7.3399997 0.68 7 0.78 7 2.44 Z "/>
</symbol>
<symbol id="g8C7315D77A5D71E18736DE61553C419F" overflow="visible">
<path d="M 1.4 1.1999999 C 1.4 0.62 1.88 0.14 2.46 0.14 C 3.04 0.14 3.52 0.62 3.52 1.1999999 C 3.52 1.78 3.04 2.26 2.46 2.26 C 1.88 2.26 1.4 1.78 1.4 1.1999999 Z M 1.4 7.16 C 1.4 6.58 1.88 6.1 2.46 6.1 C 3.04 6.1 3.52 6.58 3.52 7.16 C 3.52 7.74 3.04 8.22 2.46 8.22 C 1.88 8.22 1.4 7.74 1.4 7.16 Z "/>
</symbol>
<symbol id="g25F4C61DF17D6DB8640DCCCD57BBA830" overflow="visible">
<path d="M 2.1599998 -3.86 L 6.3999996 -3.86 C 6.52 -3.74 6.52 -3.3799999 6.3999996 -3.26 C 3.6399999 -3.04 3.5 -2.74 3.5 -1 L 3.5 11.219999 C 3.5 12.96 3.6599998 13.259999 6.3999996 13.46 C 6.52 13.58 6.52 13.94 6.3999996 14.059999 L 2.1599998 14.059999 Z "/>
</symbol>
<symbol id="g616EA0B06482AD9EB82F211B94D5D49E" overflow="visible">
<path d="M 4.56 -0.19999999 C 6.1 -0.19999999 8.44 1.36 8.44 6.06 C 8.44 8.04 7.96 9.74 7.08 10.9 C 6.56 11.599999 5.72 12.2 4.64 12.2 C 2.6599998 12.2 0.78 9.84 0.78 5.8799996 C 0.78 3.74 1.4399999 1.74 2.54 0.64 C 3.1 0.08 3.78 -0.19999999 4.56 -0.19999999 Z M 4.64 11.5 C 4.98 11.5 5.2999997 11.38 5.54 11.16 C 6.16 10.639999 6.7 9.12 6.7 6.44 C 6.7 4.6 6.64 3.34 6.3599997 2.32 C 5.92 0.68 4.94 0.5 4.58 0.5 C 2.72 0.5 2.52 3.9199998 2.52 5.66 C 2.52 10.58 3.74 11.5 4.64 11.5 Z "/>
</symbol>
<symbol id="g316778D5069ED68A0C52C06F0AD18D23" overflow="visible">
<path d="M 1.14 0.85999995 C 1.14 0.28 1.62 -0.19999999 2.2 -0.19999999 C 2.78 -0.19999999 3.26 0.28 3.26 0.85999995 C 3.26 1.4399999 2.78 1.92 2.2 1.92 C 1.62 1.92 1.14 1.4399999 1.14 0.85999995 Z "/>
</symbol>
<symbol id="g6636102111388326E3C89C955A433A6D" overflow="visible">
<path d="M 6.54 5.12 C 6 3.3 4.72 1.28 2.06 0.28 C 2.06 0.04 2.1399999 -0.14 2.3 -0.24 C 4.3199997 0.35999998 5.56 1.1999999 6.68 2.5 C 7.9199996 3.9399998 8.54 5.7599998 8.54 7.3399997 C 8.54 11.4 6.24 12.2 4.7 12.2 C 2.08 12.2 1 9.66 1 7.94 C 1 6.22 1.92 4.68 4.64 4.68 C 5.16 4.68 5.94 4.8399997 6.54 5.12 Z M 6.72 5.8399997 C 6.06 5.4 5.4 5.38 5.06 5.38 C 3.1 5.38 2.6599998 7.2999997 2.6599998 8.3 C 2.6599998 10.5 3.5 11.5 4.48 11.5 C 5.74 11.5 6.8799996 10.82 6.8799996 7.3999996 C 6.8799996 6.96 6.8399997 6.42 6.72 5.8399997 Z "/>
</symbol>
<symbol id="g70A876D91C5CC45BCC4BC8E88B98F10" overflow="visible">
<path d="M 2.8799999 6.8599997 C 3.4199998 8.679999 4.7 10.7 7.3599997 11.7 C 7.3599997 11.94 7.2799997 12.12 7.12 12.219999 C 5.1 11.62 3.86 10.78 2.74 9.48 C 1.5 8.04 0.88 6.22 0.88 4.64 C 0.88 0.58 3.1799998 -0.22 4.72 -0.22 C 7.3399997 -0.22 8.42 2.32 8.42 4.04 C 8.42 5.7599998 7.5 7.2999997 4.7799997 7.2999997 C 4.2599998 7.2999997 3.48 7.14 2.8799999 6.8599997 Z M 2.7 6.14 C 3.36 6.58 4.02 6.6 4.36 6.6 C 6.3199997 6.6 6.7599998 4.68 6.7599998 3.6799998 C 6.7599998 1.48 5.92 0.48 4.94 0.48 C 3.6799998 0.48 2.54 1.16 2.54 4.58 C 2.54 5.04 2.58 5.56 2.7 6.14 Z "/>
</symbol>
<symbol id="gB91E67CF1B63A9F4CC30BB03AE35508D" overflow="visible">
<path d="M 2.08 1.9 C 1.4599999 1.9 1.02 1.48 1.02 0.91999996 C 1.02 0.29999998 1.54 0.099999994 1.9 0.04 C 2.28 0 2.62 -0.12 2.62 -0.58 C 2.62 -1 1.9 -1.92 0.85999995 -2.18 C 0.85999995 -2.3799999 0.9 -2.52 1.04 -2.6599998 C 2.24 -2.44 3.3999999 -1.48 3.3999999 -0.08 C 3.3999999 1.12 2.8799999 1.9 2.08 1.9 Z "/>
</symbol>
<symbol id="g11C09650A1107877D1CACE85AD57EEFF" overflow="visible">
<path d="M 4.2999997 11.5 C 5.16 11.5 5.96 10.98 5.96 9.7 C 5.96 8.7 4.7999997 7.16 2.82 6.8799996 L 2.9199998 6.24 C 3.26 6.2799997 3.62 6.2799997 3.8799999 6.2799997 C 5.02 6.2799997 6.5 5.96 6.5 3.6999998 C 6.5 1.04 4.72 0.5 4.02 0.5 C 3 0.5 2.82 0.96 2.58 1.3199999 C 2.3799999 1.5999999 2.12 1.8399999 1.7199999 1.8399999 C 1.3 1.8399999 0.88 1.4599999 0.88 1.14 C 0.88 0.34 2.56 -0.19999999 3.76 -0.19999999 C 6.14 -0.19999999 8.26 1.3399999 8.26 3.98 C 8.26 6.16 6.62 6.94 5.44 7.14 L 5.42 7.18 C 7.06 7.96 7.52 8.78 7.52 9.84 C 7.52 10.44 7.3799996 10.92 6.8999996 11.42 C 6.46 11.86 5.7599998 12.2 4.72 12.2 C 1.78 12.2 0.94 10.28 0.94 9.62 C 0.94 9.34 1.14 8.94 1.62 8.94 C 2.32 8.94 2.3999999 9.599999 2.3999999 9.98 C 2.3999999 11.259999 3.78 11.5 4.2999997 11.5 Z "/>
</symbol>
<symbol id="g4B7F995A2850EF666DF3EC5EDED0901C" overflow="visible">
<path d="M 1.14 0.85999995 C 1.14 0.28 1.62 -0.19999999 2.2 -0.19999999 C 2.78 -0.19999999 3.26 0.28 3.26 0.85999995 C 3.26 1.4399999 2.78 1.92 2.2 1.92 C 1.62 1.92 1.14 1.4399999 1.14 0.85999995 Z M 6.44 0.85999995 C 6.44 0.28 6.92 -0.19999999 7.5 -0.19999999 C 8.08 -0.19999999 8.559999 0.28 8.559999 0.85999995 C 8.559999 1.4399999 8.08 1.92 7.5 1.92 C 6.92 1.92 6.44 1.4399999 6.44 0.85999995 Z M 11.719999 0.85999995 C 11.719999 0.28 12.2 -0.19999999 12.78 -0.19999999 C 13.36 -0.19999999 13.84 0.28 13.84 0.85999995 C 13.84 1.4399999 13.36 1.92 12.78 1.92 C 12.2 1.92 11.719999 1.4399999 11.719999 0.85999995 Z "/>
</symbol>
<symbol id="g2E0E67B6699615E51BCE03EAB1A37509" overflow="visible">
<path d="M 4.96 14.08 L 0.71999997 14.08 C 0.59999996 13.96 0.59999996 13.599999 0.71999997 13.48 C 3.48 13.259999 3.62 12.96 3.62 11.219999 L 3.62 -1 C 3.62 -2.74 3.46 -3.04 0.71999997 -3.24 C 0.59999996 -3.36 0.59999996 -3.72 0.71999997 -3.84 L 4.96 -3.84 Z "/>
</symbol>
<symbol id="g579F1BD1E42C90590E5C6584A163F6DD" overflow="visible">
<path d="M 3.78 2.44 L 3.78 5.8199997 C 5.46 5.8199997 5.8399997 5.52 6.12 5.06 L 8.26 1.5799999 C 8.84 0.64 9.7 -0.19999999 10.9 -0.19999999 C 11.2 -0.19999999 11.54 -0.16 11.74 -0.06 C 11.82 0.08 11.8 0.26 11.719999 0.42 C 10.82 0.42 10.32 1.1 9.8 1.9599999 L 7.2799997 6.16 C 8.139999 6.44 9.94 7.48 9.94 9.58 C 9.94 10.58 9.599999 11.4 8.88 12.08 C 7.9199996 12.98 6.68 13.04 5.42 13.04 C 4.48 13.04 3.6399999 12.9 2.9199998 12.9 C 2.22 12.9 1.28 12.92 0.34 12.94 C 0.22 12.82 0.22 12.4 0.34 12.28 C 1.74 12.219999 2.08 12.12 2.08 10.46 L 2.08 2.44 C 2.08 0.78 1.74 0.68 0.34 0.62 C 0.22 0.5 0.22 0.08 0.34 -0.04 C 1.24 -0.02 2.18 0 2.9399998 0 C 3.6999998 0 4.64 -0.02 5.52 -0.04 C 5.64 0.08 5.64 0.5 5.52 0.62 C 4.12 0.68 3.78 0.78 3.78 2.44 Z M 5.44 12.36 C 6.66 12.36 8.099999 11.92 8.099999 9.559999 C 8.099999 7.06 6.68 6.5 4.74 6.5 L 3.78 6.5 L 3.78 11.08 C 3.78 11.66 4.02 12.36 5.44 12.36 Z "/>
</symbol>
<symbol id="gD3761FB0B01B207797C607CDFB6E3A0B" overflow="visible">
<path d="M 3.3999999 7.16 C 3.3799999 7.7599998 3.34 8.48 3.24 8.679999 C 3.1999998 8.78 3.1599998 8.84 3 8.84 C 2.44 8.62 1.92 8.44 0.53999996 8.26 C 0.5 8.139999 0.53999996 7.8199997 0.58 7.7 C 1.66 7.6 1.88 7.5 1.88 6.3399997 L 1.88 2.44 C 1.88 0.79999995 1.62 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.88 0 2.6799998 0 C 3.48 0 4.1 -0.02 4.7 -0.04 C 4.8199997 0.08 4.8199997 0.5 4.7 0.62 C 3.6799998 0.71999997 3.46 0.79999995 3.46 2.44 L 3.46 5.72 C 3.46 6.14 3.6399999 6.3799996 3.8 6.56 C 4.6 7.3399997 5.3399997 7.74 5.96 7.74 C 6.72 7.74 7.2799997 7.2599998 7.2799997 5.92 L 7.2799997 2.44 C 7.2799997 0.79999995 7.12 0.7 6.04 0.62 C 5.94 0.5 5.94 0.08 6.04 -0.04 C 6.54 -0.02 7.2799997 0 8.08 0 C 8.88 0 9.54 -0.02 10.04 -0.04 C 10.139999 0.08 10.139999 0.5 10.04 0.62 C 9.04 0.7 8.86 0.79999995 8.86 2.44 L 8.86 5.62 C 8.86 5.9 8.86 6.18 8.84 6.42 C 9.8 7.48 10.7 7.74 11.48 7.74 C 12.24 7.74 12.679999 7.2999997 12.679999 5.96 L 12.679999 2.44 C 12.679999 0.79999995 12.48 0.7 11.44 0.62 C 11.34 0.5 11.34 0.08 11.44 -0.04 C 11.94 -0.02 12.679999 0 13.48 0 C 14.28 0 14.98 -0.02 15.54 -0.04 C 15.639999 0.08 15.639999 0.5 15.54 0.62 C 14.44 0.7 14.259999 0.79999995 14.259999 2.44 L 14.259999 5.6 C 14.259999 7.3799996 13.96 8.78 12.2 8.78 C 11.179999 8.78 9.94 8.4 8.9 7.2999997 C 8.84 7.24 8.72 7.14 8.679999 7.3199997 C 8.5 8.139999 7.72 8.78 6.68 8.78 C 5.52 8.78 4.48 8.099999 3.6399999 7.16 C 3.54 7.06 3.4199998 6.92 3.3999999 7.16 Z "/>
</symbol>
<symbol id="gD8CB364949770E6EB9E57283C62D30EB" overflow="visible">
<path d="M 4.3399997 -0.19999999 C 5.12 -0.19999999 6.06 0.19999999 7.04 1 C 7.14 1.0799999 7.3199997 1.12 7.3399997 0.97999996 C 7.3999996 0.48 7.56 -0.19999999 7.56 -0.19999999 C 7.72 -0.26 7.8199997 -0.24 7.94 -0.19999999 C 8.38 0.16 9.08 0.45999998 10.3 0.59999996 C 10.42 0.71999997 10.42 1.02 10.3 1.14 C 9.0199995 1.24 8.84 1.62 8.84 2.6 L 8.84 6.44 C 8.84 7.04 8.92 8.5 8.92 8.5 C 8.92 8.559999 8.86 8.62 8.76 8.62 C 8.66 8.599999 8.36 8.58 8.059999 8.58 C 7.4199996 8.58 6.7 8.599999 6.02 8.62 C 5.9 8.5 5.9 8.08 6.02 7.96 C 7 7.8999996 7.2599998 7.66 7.2599998 6.3399997 L 7.2599998 2.48 C 7.2599998 2.1 7.22 1.9399999 6.94 1.6999999 C 6.2 1.06 5.44 0.74 4.94 0.74 C 4.3399997 0.74 3.34 1.02 3.34 2.8 L 3.34 6.44 C 3.34 7.04 3.4199998 8.5 3.4199998 8.5 C 3.4199998 8.559999 3.36 8.62 3.26 8.62 C 3.1599998 8.599999 2.86 8.58 2.56 8.58 C 1.92 8.58 1.1999999 8.599999 0.52 8.62 C 0.39999998 8.5 0.39999998 8.08 0.52 7.96 C 1.48 7.8799996 1.76 7.66 1.76 6.3599997 L 1.76 2.52 C 1.76 1.14 2.36 -0.19999999 4.3399997 -0.19999999 Z "/>
</symbol>
<symbol id="g18D1F1E967E0B15C3E9466BFBC921865" overflow="visible">
<path d="M 7.8599997 9.7 C 7.8599997 11.139999 6.74 12.2 4.7799997 12.2 C 2.74 12.2 1.42 10.98 1.42 9.44 C 1.42 8.32 1.9599999 7.5 3.1799998 6.74 L 3.6999998 6.42 C 3.12 6.12 2.58 5.7599998 2.08 5.3199997 C 1.26 4.6 0.91999996 3.6999998 0.91999996 2.9199998 C 0.91999996 0.88 2.36 -0.19999999 4.48 -0.19999999 C 7.1 -0.19999999 8.38 1.7199999 8.38 3.24 C 8.38 4.4 7.8799996 5.42 6.8199997 6.06 L 5.4 6.92 C 6.3399997 7.3799996 7.8599997 8.42 7.8599997 9.7 Z M 4.52 0.5 C 3.62 0.5 2.26 1.12 2.26 2.9199998 C 2.26 3.52 2.52 4.92 4.24 6.06 L 5.18 5.5 C 6.42 4.74 6.92 3.8 6.92 2.84 C 6.92 0.84 5.42 0.5 4.52 0.5 Z M 4.68 11.5 C 5.98 11.5 6.46 10.639999 6.46 9.719999 C 6.46 8.639999 5.4 7.74 4.8599997 7.3399997 L 4.24 7.72 C 2.98 8.54 2.84 9.2 2.84 9.82 C 2.84 10.74 3.48 11.5 4.68 11.5 Z "/>
</symbol>
<symbol id="gF4B93BD1FBF62234B86BB304CE1128E3" overflow="visible">
<path d="M 8.24 4.72 L 1.9 2.4199998 C 1.64 2.1399999 1.62 1.54 1.9 1.42 L 9.7 4.24 C 9.88 4.58 9.88 4.9 9.7 5.2 L 1.9 8.04 C 1.62 7.9199996 1.64 7.3199997 1.9 7.04 Z "/>
</symbol>
<symbol id="g17AD34DB90B05275C6F1422A9B4B5274" overflow="visible">
<path d="M 6.5 7.96 C 7.58 7.8799996 7.7 7.64 7.2799997 6.62 L 5.66 2.7 C 5.3399997 1.92 5.24 1.92 4.92 2.76 L 3.48 6.62 C 3.12 7.58 3.04 7.8199997 4.1 7.96 C 4.22 8.08 4.22 8.5 4.1 8.62 C 3.4399998 8.599999 2.74 8.58 2.08 8.58 C 1.42 8.58 0.82 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.28 7.8399997 1.42 7.52 1.8199999 6.5 L 4.38 0.17999999 C 4.5 -0.12 4.62 -0.24 4.88 -0.24 C 5.08 -0.24 5.22 -0.12 5.3599997 0.22 L 8.0199995 6.48 C 8.4 7.3599997 8.62 7.8599997 9.74 7.96 C 9.86 8.08 9.86 8.5 9.74 8.62 C 9.34 8.599999 8.86 8.58 8.34 8.58 C 7.68 8.58 7 8.599999 6.5 8.62 C 6.3799996 8.5 6.3799996 8.08 6.5 7.96 Z "/>
</symbol>
<symbol id="gE8171CD7697771DDE124968BDB3EF0D7" overflow="visible">
<path d="M 5.42 4.46 C 5.68 4.46 5.96 5.02 5.96 5.2599998 C 5.96 5.46 5.8799996 5.66 5.68 5.66 L 1.3 5.66 C 1.06 5.66 0.79999995 5.2 0.79999995 4.8399997 C 0.79999995 4.64 0.91999996 4.46 1.1 4.46 Z "/>
</symbol>
<symbol id="g4D85B33E992F6B39F8E7EBFD2F7ECE19" overflow="visible">
<path d="M 9.28 6.18 C 9.54 6.18 9.82 6.64 9.82 6.8399997 C 9.82 7 9.74 7.18 9.54 7.18 L 1.6999999 7.18 C 1.4599999 7.18 1.1999999 6.7999997 1.1999999 6.5 C 1.1999999 6.3399997 1.3199999 6.18 1.5 6.18 Z M 9.28 2.86 C 9.54 2.86 9.82 3.32 9.82 3.52 C 9.82 3.6799998 9.74 3.86 9.54 3.86 L 1.6999999 3.86 C 1.4599999 3.86 1.1999999 3.48 1.1999999 3.1799998 C 1.1999999 3.02 1.3199999 2.86 1.5 2.86 Z "/>
</symbol>
<symbol id="gCAFB20A65E8FBEFE071D9C4C8EE95E49" overflow="visible">
<path d="M 1.22 9.36 C 1.22 8.94 1.5999999 8.58 2.02 8.58 C 2.36 8.58 2.96 8.94 2.96 9.38 C 2.96 9.54 2.9199998 9.66 2.8799999 9.8 C 2.84 9.94 2.72 10.12 2.72 10.28 C 2.72 10.78 3.24 11.5 4.7 11.5 C 5.42 11.5 6.44 11 6.44 9.08 C 6.44 7.7999997 5.98 6.7599998 4.7999997 5.56 L 3.32 4.1 C 1.36 2.1 1.04 1.14 1.04 -0.04 C 1.04 -0.04 2.06 0 2.7 0 L 6.2 0 C 6.8399997 0 7.7599998 -0.04 7.7599998 -0.04 C 8.0199995 1.02 8.22 2.52 8.24 3.12 C 8.12 3.22 7.8599997 3.26 7.66 3.22 C 7.3199997 1.8 6.98 1.3 6.2599998 1.3 L 2.7 1.3 C 2.7 2.26 4.08 3.62 4.18 3.72 L 6.2 5.66 C 7.3399997 6.7599998 8.2 7.64 8.2 9.16 C 8.2 11.32 6.44 12.2 4.8199997 12.2 C 2.6 12.2 1.22 10.559999 1.22 9.36 Z "/>
</symbol>
<symbol id="gDCA082B6FC1DB6288BEBFE25BA893B80" overflow="visible">
<path d="M 2.76 4.7799997 L 9.099999 7.08 C 9.36 7.3599997 9.38 7.96 9.099999 8.08 L 1.3 5.2599998 C 1.12 4.92 1.12 4.6 1.3 4.2999997 L 9.099999 1.4599999 C 9.38 1.5799999 9.36 2.18 9.099999 2.46 Z "/>
</symbol>
<symbol id="g13CAD87D675A42FC6A129543D89F948C" overflow="visible">
<path d="M 5.7599998 2.44 L 5.7599998 9.38 C 5.7599998 10.58 5.7799997 11.8 5.8199997 12.059999 C 5.8199997 12.16 5.7799997 12.16 5.7 12.16 C 4.6 11.48 3.54 10.98 1.78 10.16 C 1.8199999 9.94 1.9 9.74 2.08 9.62 C 3 10 3.4399998 10.12 3.82 10.12 C 4.16 10.12 4.22 9.639999 4.22 8.96 L 4.22 2.44 C 4.22 0.78 3.6799998 0.68 2.28 0.62 C 2.1599998 0.5 2.1599998 0.08 2.28 -0.04 C 3.26 -0.02 3.98 0 5.06 0 C 6.02 0 6.5 -0.02 7.5 -0.04 C 7.62 0.08 7.62 0.5 7.5 0.62 C 6.1 0.68 5.7599998 0.78 5.7599998 2.44 Z "/>
</symbol>
<symbol id="g8D44D9C01F9AF6C3B1D634FDF54DE6FB" overflow="visible">
<path d="M 5.66 6.46 C 7.3599997 6.46 7.4199996 6 7.48 5.1 C 7.6 4.98 8.0199995 4.98 8.139999 5.1 C 8.12 5.6 8.099999 6.18 8.099999 6.8599997 C 8.099999 7.54 8.12 8.059999 8.139999 8.58 C 8.0199995 8.7 7.6 8.7 7.48 8.58 C 7.4199996 7.48 7.3599997 7.22 5.66 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.9 4.04 12.099999 4.92 12.099999 L 5.8199997 12.099999 C 7.94 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.92 9.34 9.96 9.5 10.0199995 C 9.4 10.84 9.099999 12.759999 9.059999 12.92 C 9.059999 12.96 9.04 12.98 8.98 12.98 C 8.639999 12.92 8.54 12.9 8.04 12.9 L 2.9399998 12.9 C 2.3 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.06 -0.02 2.06 0 2.96 0 C 3.86 0 4.8399997 -0.02 5.54 -0.04 C 5.66 0.08 5.66 0.5 5.54 0.62 C 4.14 0.68 3.8 0.78 3.8 2.44 L 3.8 6.46 Z "/>
</symbol>
<symbol id="gFB54B84572F46C3C9CB2B1A90182D6B2" overflow="visible">
<path d="M 8.88 7.74 C 9.26 7.74 9.62 8.099999 9.62 8.5 C 9.62 8.92 9.24 9.24 8.7 9.24 C 8.179999 9.24 7.22 8.9 6.7 8.22 C 6.46 8.38 5.7999997 8.78 4.62 8.78 C 2.84 8.78 1.1999999 7.58 1.1999999 5.74 C 1.1999999 4.66 1.68 4.04 2.24 3.5 C 1.68 3.02 1.36 2.1599998 1.36 1.48 C 1.36 0.76 1.76 0.19999999 2.28 -0.06 C 1.1999999 -0.7 0.64 -1.62 0.64 -2.48 C 0.64 -4.22 2.28 -4.7599998 3.82 -4.7599998 C 6.52 -4.7599998 9.44 -3.46 9.44 -1.3 C 9.44 -0.65999997 9.139999 -0.16 8.559999 0.32 C 7.7799997 0.96 6.3799996 0.97999996 5.64 0.97999996 C 5.2799997 0.97999996 4.7799997 0.94 4.2999997 0.88 C 4 0.85999995 3.8 0.84 3.6999998 0.84 C 3.12 0.84 2.4199998 1.12 2.4199998 1.9799999 C 2.4199998 2.3799999 2.54 2.8 2.78 3.1399999 C 3.26 2.86 3.82 2.72 4.6 2.72 C 6.3599997 2.72 7.98 3.82 7.98 5.7799997 C 7.98 6.72 7.7 7.2599998 7.12 7.8599997 C 7.2599998 8.059999 7.66 8.34 7.9199996 8.34 C 8.059999 8.34 8.2 8.28 8.32 8.099999 C 8.4 7.94 8.66 7.74 8.88 7.74 Z M 2.6399999 -0.19999999 C 2.86 -0.26 3.1799998 -0.29999998 3.4399998 -0.29999998 C 4.06 -0.29999998 4.62 -0.24 4.9 -0.24 C 5.9 -0.24 6.74 -0.26 7.3199997 -0.58 C 8.099999 -1.02 8.34 -1.3 8.34 -1.8199999 C 8.34 -3.26 6.22 -4.02 4.42 -4.02 C 3.6999998 -4.02 2.02 -3.4399998 2.02 -2.08 C 2.02 -1.4 2.06 -0.9 2.6399999 -0.19999999 Z M 6.3799996 5.58 C 6.3799996 3.72 5.44 3.34 4.7 3.34 C 3.02 3.34 2.84 4.7599998 2.84 6.04 C 2.84 7.44 3.34 8.16 4.44 8.16 C 5.7 8.16 6.3799996 7.24 6.3799996 5.58 Z "/>
</symbol>
<symbol id="g8934F85724FE2A1B73A1C811C5B32995" overflow="visible">
<path d="M 3.82 2.44 L 3.82 10.46 C 3.82 12.12 4.16 12.219999 5.56 12.28 C 5.68 12.4 5.68 12.82 5.56 12.94 C 4.68 12.92 3.74 12.9 2.96 12.9 C 2.3 12.9 1.3199999 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.28 -0.02 2.26 0 2.98 0 C 3.6999998 0 4.66 -0.02 5.56 -0.04 C 5.68 0.08 5.68 0.5 5.56 0.62 C 4.16 0.68 3.82 0.78 3.82 2.44 Z "/>
</symbol>
<symbol id="gAA14E57E2DCC57A3F7809273EECD3C51" overflow="visible">
<path d="M 7.9104 1.5616 L 7.9104 6.6944 C 7.9104 7.7567997 8.128 7.8208 9.024 7.8592 C 9.1008 7.936 9.1008 8.2048 9.024 8.2816 C 8.4992 8.2688 7.8464 8.256 7.3599997 8.256 C 6.8863997 8.256 6.272 8.2688 5.7088 8.2816 C 5.632 8.2048 5.632 7.936 5.7088 7.8592 C 6.6047997 7.8208 6.8223996 7.7567997 6.8223996 6.6944 L 6.8223996 4.6464 L 2.4448 4.6464 L 2.4448 6.6944 C 2.4448 7.7567997 2.6624 7.8208 3.5584 7.8592 C 3.6352 7.936 3.6352 8.2048 3.5584 8.2816 C 3.072 8.2688 2.5472 8.256 1.8944 8.256 C 1.2544 8.256 0.72959995 8.2688 0.24319999 8.2816 C 0.1664 8.2048 0.1664 7.936 0.24319999 7.8592 C 1.1392 7.8208 1.3568 7.7567997 1.3568 6.6944 L 1.3568 1.5616 C 1.3568 0.4992 1.1392 0.43519998 0.24319999 0.39679998 C 0.1664 0.32 0.1664 0.0512 0.24319999 -0.0256 C 0.8064 -0.0128 1.4208 0 1.9072 0 C 2.368 0 2.9952 -0.0128 3.5584 -0.0256 C 3.6352 0.0512 3.6352 0.32 3.5584 0.39679998 C 2.6624 0.43519998 2.4448 0.4992 2.4448 1.5616 L 2.4448 4.1088 L 6.8223996 4.1088 L 6.8223996 1.5616 C 6.8223996 0.4992 6.6047997 0.43519998 5.7088 0.39679998 C 5.632 0.32 5.632 0.0512 5.7088 -0.0256 C 6.2848 -0.0128 6.8992 0 7.3728 0 C 7.8464 0 8.4608 -0.0128 9.024 -0.0256 C 9.1008 0.0512 9.1008 0.32 9.024 0.39679998 C 8.128 0.43519998 7.9104 0.4992 7.9104 1.5616 Z "/>
</symbol>
<symbol id="gF5F8064101DBF0FCB4BCFDA7012527FE" overflow="visible">
<path d="M 2.3167999 1.5616 L 2.3167999 4.1088 C 2.3167999 4.7488 2.368 5.568 2.368 5.568 C 2.368 5.6191998 2.304 5.6576 2.2015998 5.6576 C 1.8432 5.5168 1.3312 5.4016 0.44799998 5.2864 C 0.4224 5.2096 0.44799998 5.0048 0.4736 4.928 C 1.1776 4.864 1.3055999 4.7872 1.3055999 4.0576 L 1.3055999 1.5616 C 1.3055999 0.4992 1.1647999 0.4608 0.384 0.39679998 C 0.30719998 0.32 0.30719998 0.0512 0.384 -0.0256 C 0.8064 -0.0128 1.3055999 0 1.8176 0 C 2.3295999 0 2.816 -0.0128 3.2384 -0.0256 C 3.3151999 0.0512 3.3151999 0.32 3.2384 0.39679998 C 2.4575999 0.44799998 2.3167999 0.4992 2.3167999 1.5616 Z M 1.152 7.6671996 C 1.152 7.3343997 1.4591999 7.0016 1.7664 7.0016 C 2.1248 7.0016 2.432 7.3472 2.432 7.6159997 C 2.432 7.9231997 2.1632 8.2816 1.8176 8.2816 C 1.5103999 8.2816 1.152 7.9743996 1.152 7.6671996 Z "/>
</symbol>
<symbol id="g3976D55F213F07C6469FD06EC16139AA" overflow="visible">
<path d="M 4.9407997 1.1904 C 4.4672 0.704 4.0959997 0.4992 3.3536 0.4992 C 2.8927999 0.4992 2.3552 0.768 1.9583999 1.4208 C 1.7024 1.8432 1.5488 2.432 1.5488 3.1743999 L 4.9536 3.1488 C 5.1071997 3.1488 5.1967998 3.2256 5.1967998 3.3664 C 5.1967998 4.4416 4.8128 5.5936 3.0335999 5.5936 C 1.92 5.5936 0.4736 4.5312 0.4736 2.5856 C 0.4736 1.8687999 0.65279996 1.1776 1.0752 0.69119996 C 1.5103999 0.1792 2.112 -0.12799999 3.0335999 -0.12799999 C 4.0064 -0.12799999 4.6976 0.32 5.2096 0.9856 C 5.1712 1.1136 5.0944 1.1776 4.9407997 1.1904 Z M 1.5871999 3.6095998 C 1.8304 5.0559998 2.7264 5.1712 3.0335999 5.1712 C 3.52 5.1712 4.0959997 4.9024 4.0959997 3.8272 C 4.0959997 3.712 4.0448 3.648 3.9039998 3.648 Z "/>
</symbol>
<symbol id="gB7BB853387AAC07ADB7DDEF96856059B" overflow="visible">
<path d="M 2.2528 4.5824 C 2.2272 5.0944 2.2144 5.4272 2.1504 5.5551996 C 2.1248 5.6191998 2.0992 5.6576 1.9968 5.6576 C 1.6384 5.5168 1.3055999 5.4016 0.4224 5.2864 C 0.39679998 5.2096 0.4224 5.0048 0.44799998 4.928 C 1.1392 4.864 1.28 4.7999997 1.28 4.0576 L 1.28 1.5616 C 1.28 0.4992 1.1264 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7808 -0.0128 1.28 0 1.7919999 0 C 2.304 0 2.8927999 -0.0128 3.3407998 -0.0256 C 3.4176 0.0512 3.4176 0.32 3.3407998 0.39679998 C 2.4448 0.4608 2.2912 0.4992 2.2912 1.5616 L 2.2912 3.3407998 C 2.2912 3.6736 2.4448 3.968 2.5983999 4.1984 C 2.7391999 4.4031997 3.0335999 4.8255997 3.1871998 4.8255997 C 3.3023999 4.8255997 3.4176 4.7999997 3.52 4.6591997 C 3.6095998 4.5312 3.7631998 4.3648 3.9808 4.3648 C 4.288 4.3648 4.5824 4.6847997 4.5824 5.0048 C 4.5824 5.2479997 4.3519998 5.6191998 3.8144 5.6191998 C 3.2128 5.6191998 2.688 5.0559998 2.3936 4.5568 C 2.3167999 4.416 2.2528 4.5183997 2.2528 4.5824 Z "/>
</symbol>
<symbol id="gF8EC31AC53CF59E01ED9143906F6DA7B" overflow="visible">
<path d="M 3.7503998 0.61439997 C 3.8272 0.21759999 3.968 -0.12799999 4.608 -0.12799999 C 5.0944 -0.12799999 5.5551996 0.0896 5.824 0.34559998 C 5.7984 0.4992 5.7472 0.61439997 5.6064 0.69119996 C 5.5168 0.61439997 5.2992 0.48639998 5.1328 0.48639998 C 4.7616 0.48639998 4.7488 0.9856 4.7488 1.5744 L 4.7488 3.4559999 C 4.7488 5.2736 3.7503998 5.6191998 2.816 5.6191998 C 1.7664 5.6191998 0.704 4.928 0.704 4.1984 C 0.704 3.8911998 0.8576 3.7375998 1.152 3.7375998 C 1.5231999 3.7375998 1.7536 4.0064 1.7536 4.1728 C 1.7536 4.2623997 1.7407999 4.3519998 1.7152 4.4031997 C 1.7024 4.4416 1.6896 4.5183997 1.6896 4.6591997 C 1.6896 5.0559998 2.2272 5.1967998 2.7136 5.1967998 C 3.1488 5.1967998 3.7503998 4.9792 3.7503998 3.5328 C 3.7503998 3.4431999 3.712 3.392 3.6736 3.3792 L 2.5728 3.1104 C 1.344 2.8032 0.4608 2.1248 0.4608 1.2544 C 0.4608 0.2048 1.1776 -0.12799999 2.0736 -0.12799999 C 2.5216 -0.12799999 2.9055998 -0.0256 3.4687998 0.4096 L 3.7247999 0.61439997 Z M 3.7503998 2.9824 L 3.7503998 1.2928 C 3.7503998 1.1264 3.6736 1.0368 3.5712 0.96 C 3.2384 0.69119996 2.8032 0.39679998 2.4448 0.39679998 C 1.8047999 0.39679998 1.5231999 0.9088 1.5231999 1.3055999 C 1.5231999 1.8815999 1.7919999 2.4703999 2.7391999 2.7136 Z "/>
</symbol>
<symbol id="g68DDE7C8FDC8A226B6C32EAD39AF7364" overflow="visible">
<path d="M 5.0944 1.1647999 C 5.0432 1.28 4.9407997 1.3312 4.8255997 1.344 C 4.3904 0.7808 3.84 0.4992 3.2896 0.4992 C 2.3552 0.4992 1.5744 1.4463999 1.5744 2.944 C 1.5744 4.3519998 2.1887999 5.1967998 3.0335999 5.1967998 C 3.7888 5.1967998 3.8911998 4.7488 3.9424 4.3008 C 3.9808 3.9552 4.16 3.84 4.4288 3.84 C 4.6976 3.84 5.0559998 4.0064 5.0559998 4.4031997 C 5.0559998 5.1071997 4.3264 5.6191998 3.0976 5.6191998 C 1.8304 5.6191998 0.4736 4.48 0.4736 2.6624 C 0.4736 1.0112 1.3952 -0.12799999 3.008 -0.12799999 C 3.776 -0.12799999 4.4544 0.1152 5.0944 1.1647999 Z "/>
</symbol>
<symbol id="g570B752173035444311A253BD2376AD" overflow="visible">
<path d="M 2.1376 3.6608 C 2.1376 3.9296 2.2528 4.0832 2.3552 4.1984 C 2.8416 4.672 3.4944 4.9536 3.9936 4.9536 C 4.2496 4.9536 4.5183997 4.7872 4.672 4.4927998 C 4.7999997 4.2367997 4.8255997 3.8911998 4.8255997 3.5072 L 4.8255997 1.5616 C 4.8255997 0.51199996 4.6976 0.4608 4.032 0.39679998 C 3.968 0.32 3.968 0.0512 4.032 -0.0256 C 4.3904 -0.0128 4.8255997 0 5.3375998 0 C 5.8496 0 6.272 -0.0128 6.6944 -0.0256 C 6.7584 0.0512 6.7584 0.32 6.6944 0.39679998 C 5.9775996 0.4608 5.8367996 0.51199996 5.8367996 1.5616 L 5.8367996 3.4687998 C 5.8367996 4.1728 5.7855997 4.7999997 5.4912 5.184 C 5.2736 5.4656 4.8768 5.6191998 4.4288 5.6191998 C 3.8016 5.6191998 3.0335999 5.4528 2.2528 4.5824 C 2.2528 4.5696 2.24 4.5696 2.2272 4.5568 C 2.1887999 4.5056 2.1248 4.4288 2.1248 4.5824 L 2.1376 7.4624 C 2.1376 8.2944 2.1887999 8.806399 2.1887999 8.806399 C 2.1887999 8.896 2.1376 8.9344 2.0224 8.9344 C 1.7024 8.806399 0.7424 8.6272 0.2304 8.588799 C 0.2048 8.4864 0.2304 8.2816 0.30719998 8.2048 C 0.34559998 8.2048 0.384 8.2048 0.4224 8.2048 C 0.9856 8.1664 1.1264 8.1664 1.1264 7.1552 L 1.1264 1.5616 C 1.1264 0.4992 0.97279996 0.44799998 0.2304 0.39679998 C 0.15359999 0.32 0.15359999 0.0512 0.2304 -0.0256 C 0.65279996 -0.0128 1.1264 0 1.6384 0 C 2.1248 0 2.5472 -0.0128 2.9055998 -0.0256 C 2.9824 0.0512 2.9824 0.32 2.9055998 0.39679998 C 2.2528 0.44799998 2.1376 0.4992 2.1376 1.5616 Z "/>
</symbol>
<symbol id="g9662C1D9A80FEB5040A57FD9DFCA7985" overflow="visible">
<path d="M 1.216 1.5616 C 1.216 0.4992 1.0752 0.43519998 0.2944 0.39679998 C 0.21759999 0.32 0.21759999 0.0512 0.2944 -0.0256 C 0.7424 -0.0128 1.216 0 1.7279999 0 C 2.24 0 2.7264 -0.0128 3.1488 -0.0256 C 3.2256 0.0512 3.2256 0.32 3.1488 0.39679998 C 2.368 0.43519998 2.2272 0.4992 2.2272 1.5616 L 2.2272 7.4624 C 2.2272 8.2944 2.2784 8.806399 2.2784 8.806399 C 2.2784 8.896 2.2272 8.9344 2.112 8.9344 C 1.7919999 8.806399 0.83199996 8.6272 0.32 8.588799 C 0.2944 8.4864 0.32 8.2816 0.39679998 8.2048 C 1.1392 8.1536 1.216 8.1152 1.216 7.1552 Z "/>
</symbol>
<symbol id="g1CB3EC9D05726EBFDE8ADABEC8504FCD" overflow="visible">
<path d="M 7.1168 6.5536 L 7.1168 2.368 C 7.1168 2.1248 7.1168 1.984 7.0271997 1.984 C 6.976 1.984 6.784 2.2144 6.4128 2.688 L 2.0224 8.256 L 0.2944 8.2816 C 0.21759999 8.2048 0.21759999 7.936 0.2944 7.8592 C 0.8448 7.8208 1.2287999 7.3728 1.3055999 7.04 L 1.3055999 1.7024 C 1.3055999 0.5632 1.0879999 0.48639998 0.192 0.39679998 C 0.1152 0.32 0.1152 0.0512 0.192 -0.0256 C 0.7424 -0.0128 1.3184 0 1.6256 0 C 1.92 0 2.5088 -0.0128 3.0463998 -0.0256 C 3.1232 0.0512 3.1232 0.32 3.0463998 0.39679998 C 2.1504 0.48639998 1.9327999 0.5376 1.9327999 1.7024 L 1.9327999 5.6191998 C 1.9327999 6.0544 1.9327999 6.2464 2.0351999 6.2464 C 2.112 6.2464 2.2528 6.1056 2.4703999 5.824 L 6.9375997 0.1792 C 7.0783997 -0.0128 7.2447996 -0.12799999 7.4495997 -0.12799999 C 7.6288 -0.12799999 7.744 0.0256 7.744 0.2688 L 7.744 6.5536 C 7.744 7.6927996 7.9616 7.7696 8.8576 7.8592 C 8.9344 7.936 8.9344 8.2048 8.8576 8.2816 C 8.3328 8.2688 7.7311997 8.256 7.424 8.256 C 7.1552 8.256 6.5664 8.2688 6.0032 8.2816 C 5.9263997 8.2048 5.9263997 7.936 6.0032 7.8592 C 6.8992 7.7696 7.1168 7.7184 7.1168 6.5536 Z "/>
</symbol>
<symbol id="gD62975B7DE3250BE5F195D0E8335F60D" overflow="visible">
<path d="M 4.16 5.0944 C 4.8512 5.0432 4.928 4.8896 4.6591997 4.2367997 L 3.6223998 1.7279999 C 3.4176 1.2287999 3.3536 1.2287999 3.1488 1.7664 L 2.2272 4.2367997 C 1.9968 4.8512 1.9455999 5.0048 2.6239998 5.0944 C 2.7008 5.1712 2.7008 5.44 2.6239998 5.5168 C 2.2015998 5.5039997 1.7536 5.4912 1.3312 5.4912 C 0.9088 5.4912 0.5248 5.5039997 0.1408 5.5168 C 0.063999996 5.44 0.063999996 5.1712 0.1408 5.0944 C 0.8192 5.0176 0.9088 4.8128 1.1647999 4.16 L 2.8032 0.1152 C 2.8799999 -0.076799996 2.9568 -0.15359999 3.1232 -0.15359999 C 3.2512 -0.15359999 3.3407998 -0.076799996 3.4304 0.1408 L 5.1328 4.1472 C 5.376 4.7104 5.5168 5.0304 6.2335997 5.0944 C 6.3104 5.1712 6.3104 5.44 6.2335997 5.5168 C 5.9775996 5.5039997 5.6703997 5.4912 5.3375998 5.4912 C 4.9151998 5.4912 4.48 5.5039997 4.16 5.5168 C 4.0832 5.44 4.0832 5.1712 4.16 5.0944 Z "/>
</symbol>
<symbol id="gEFCBD5CCFA072E8B49E2065B449FDBBF" overflow="visible">
<path d="M 5.6832 4.9536 C 5.9263997 4.9536 6.1568 5.184 6.1568 5.44 C 6.1568 5.7088 5.9136 5.9136 5.568 5.9136 C 5.2352 5.9136 4.6208 5.6959996 4.288 5.2608 C 4.1344 5.3631997 3.712 5.6191998 2.9568 5.6191998 C 1.8176 5.6191998 0.768 4.8512 0.768 3.6736 C 0.768 2.9824 1.0752 2.5856 1.4336 2.24 C 1.0752 1.9327999 0.87039995 1.3823999 0.87039995 0.9472 C 0.87039995 0.48639998 1.1264 0.12799999 1.4591999 -0.038399998 C 0.768 -0.44799998 0.4096 -1.0368 0.4096 -1.5871999 C 0.4096 -2.7008 1.4591999 -3.0463998 2.4448 -3.0463998 C 4.1728 -3.0463998 6.0415998 -2.2144 6.0415998 -0.83199996 C 6.0415998 -0.4224 5.8496 -0.1024 5.4783998 0.2048 C 4.9792 0.61439997 4.0832 0.6272 3.6095998 0.6272 C 3.3792 0.6272 3.0591998 0.6016 2.7519999 0.5632 C 2.56 0.55039996 2.432 0.5376 2.368 0.5376 C 1.9968 0.5376 1.5488 0.7168 1.5488 1.2672 C 1.5488 1.5231999 1.6256 1.7919999 1.7792 2.0096 C 2.0864 1.8304 2.4448 1.7407999 2.944 1.7407999 C 4.0703998 1.7407999 5.1071997 2.4448 5.1071997 3.6992 C 5.1071997 4.3008 4.928 4.6464 4.5568 5.0304 C 4.6464 5.1584 4.9024 5.3375998 5.0688 5.3375998 C 5.1584 5.3375998 5.2479997 5.2992 5.3248 5.184 C 5.376 5.0815997 5.5424 4.9536 5.6832 4.9536 Z M 1.6896 -0.12799999 C 1.8304 -0.1664 2.0351999 -0.192 2.2015998 -0.192 C 2.5983999 -0.192 2.9568 -0.15359999 3.136 -0.15359999 C 3.776 -0.15359999 4.3136 -0.1664 4.6847997 -0.3712 C 5.184 -0.65279996 5.3375998 -0.83199996 5.3375998 -1.1647999 C 5.3375998 -2.0864 3.9808 -2.5728 2.8288 -2.5728 C 2.368 -2.5728 1.2928 -2.2015998 1.2928 -1.3312 C 1.2928 -0.89599997 1.3184 -0.576 1.6896 -0.12799999 Z M 4.0832 3.5712 C 4.0832 2.3808 3.4815998 2.1376 3.008 2.1376 C 1.9327999 2.1376 1.8176 3.0463998 1.8176 3.8655999 C 1.8176 4.7616 2.1376 5.2223997 2.8416 5.2223997 C 3.648 5.2223997 4.0832 4.6335998 4.0832 3.5712 Z "/>
</symbol>
<symbol id="gD5EEFB9760BC9A91B84F628EDDA52971" overflow="visible">
<path d="M 2.1376 5.0432 C 2.0607998 4.9663997 2.0096 4.992 2.0096 5.1071997 L 2.0096 7.4624 C 2.0096 8.2944 2.0607998 8.806399 2.0607998 8.806399 C 2.0607998 8.896 2.0096 8.9344 1.8944 8.9344 C 1.5744 8.806399 0.61439997 8.6272 0.1024 8.588799 C 0.076799996 8.4864 0.1024 8.2816 0.1792 8.2048 C 0.21759999 8.2048 0.25599998 8.2048 0.2944 8.2048 C 0.8576 8.1664 0.9984 8.1664 0.9984 7.1552 L 0.9984 0.9088 C 0.9984 0.4096 0.9856 0.1792 0.9472 0 C 1.0112 -0.1024 1.0752 -0.15359999 1.2287999 -0.15359999 C 1.3055999 -0.076799996 1.4336 0.038399998 1.536 0.15359999 C 1.6639999 0.30719998 1.7407999 0.30719998 1.8815999 0.192 C 2.1759999 -0.0512 2.56 -0.12799999 3.008 -0.12799999 C 4.3136 -0.12799999 5.8367996 1.0624 5.8367996 3.0976 C 5.8367996 4.6591997 4.6847997 5.6191998 3.5712 5.6191998 C 3.0207999 5.6191998 2.5344 5.4016 2.1376 5.0432 Z M 2.2272 4.6464 C 2.56 4.9407997 2.944 5.0559998 3.3151999 5.0559998 C 4.0959997 5.0559998 4.736 4.1088 4.736 2.8672 C 4.736 1.408 4.1472 0.30719998 2.9312 0.30719998 C 2.5344 0.30719998 2.2656 0.5888 2.0096 0.9088 L 2.0096 4.1088 C 2.0096 4.3775997 2.0607998 4.5056 2.2272 4.6464 Z "/>
</symbol>
<symbol id="g83A6AA7A836EACB3652229F4716CDAF" overflow="visible">
<path d="M 5.0559998 8.076799 C 4.3136 8.1792 4.3392 8.4223995 3.0848 8.4223995 C 1.7919999 8.4223995 0.65279996 7.5648 0.65279996 6.2079997 C 0.65279996 4.864 1.7664 4.2496 2.8927999 3.8144 C 3.6608 3.52 4.608 3.1615999 4.608 1.9072 C 4.608 0.87039995 4.032 0.3328 3.008 0.3328 C 1.8176 0.3328 1.0496 0.8832 0.768 2.1504 C 0.6016 2.2015998 0.4736 2.1759999 0.34559998 2.112 C 0.39679998 1.1264 0.44799998 0.79359996 0.6016 0.1664 C 1.408 0.1664 1.7664 -0.12799999 2.9055998 -0.12799999 C 3.4815998 -0.12799999 4.032 0.0128 4.48 0.2944 C 5.2223997 0.75519997 5.6832 1.536 5.6832 2.3552 C 5.6832 3.712 4.6591997 4.3136 3.6095998 4.7104 C 2.8416 4.992 1.5616 5.4783998 1.5616 6.5536 C 1.5616 7.2704 2.2144 7.9872 2.9696 7.9872 C 4.2111998 7.9872 4.608 7.1935997 4.864 6.3487997 C 5.0048 6.3231997 5.1712 6.336 5.2864 6.4256 C 5.2352 7.04 5.184 7.3984 5.0559998 8.076799 Z "/>
</symbol>
<symbol id="gDB4862E33098F259EEBBA99A57E5AFA" overflow="visible">
<path d="M 2.1759999 4.5824 C 2.1632 4.9663997 2.1376 5.4272 2.0736 5.5551996 C 2.0479999 5.6191998 2.0224 5.6576 1.92 5.6576 C 1.5616 5.5168 1.2287999 5.4016 0.34559998 5.2864 C 0.32 5.2096 0.34559998 5.0048 0.3712 4.928 C 1.0624 4.864 1.2032 4.7999997 1.2032 4.0576 L 1.2032 1.5616 C 1.2032 0.51199996 1.0368 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7168 -0.0128 1.2032 0 1.7152 0 C 2.2272 0 2.6239998 -0.0128 3.008 -0.0256 C 3.0848 0.0512 3.0848 0.32 3.008 0.39679998 C 2.3552 0.4608 2.2144 0.51199996 2.2144 1.5616 L 2.2144 3.6608 C 2.2144 3.9296 2.3295999 4.0832 2.432 4.1984 C 2.944 4.6976 3.4176 4.9536 3.8144 4.9536 C 4.3008 4.9536 4.6591997 4.6464 4.6591997 3.7888 L 4.6591997 1.5616 C 4.6591997 0.51199996 4.5568 0.44799998 3.8655999 0.39679998 C 3.8016 0.32 3.8016 0.0512 3.8655999 -0.0256 C 4.1856 -0.0128 4.6591997 0 5.1712 0 C 5.6832 0 6.1056 -0.0128 6.4256 -0.0256 C 6.4895997 0.0512 6.4895997 0.32 6.4256 0.39679998 C 5.7855997 0.44799998 5.6703997 0.51199996 5.6703997 1.5616 L 5.6703997 3.5967999 C 5.6703997 3.776 5.6703997 3.9552 5.6576 4.1088 C 6.272 4.7872 6.848 4.9536 7.3472 4.9536 C 7.8335996 4.9536 8.1152 4.672 8.1152 3.8144 L 8.1152 1.5616 C 8.1152 0.51199996 7.9872 0.44799998 7.3216 0.39679998 C 7.2576 0.32 7.2576 0.0512 7.3216 -0.0256 C 7.6415997 -0.0128 8.1152 0 8.6272 0 C 9.1392 0 9.5872 -0.0128 9.9456 -0.0256 C 10.0096 0.0512 10.0096 0.32 9.9456 0.39679998 C 9.2416 0.44799998 9.1264 0.51199996 9.1264 1.5616 L 9.1264 3.5839999 C 9.1264 4.7232 8.9344 5.6191998 7.8079996 5.6191998 C 7.1552 5.6191998 6.3616 5.376 5.6959996 4.672 C 5.6576 4.6335998 5.5808 4.5696 5.5551996 4.6847997 C 5.44 5.2096 4.9407997 5.6191998 4.2752 5.6191998 C 3.5328 5.6191998 2.8672 5.184 2.3295999 4.5824 C 2.2656 4.5183997 2.1887999 4.4288 2.1759999 4.5824 Z "/>
</symbol>
<symbol id="g793DBE65A5AEC1A16A65955B6C0E046" overflow="visible">
<path d="M 10.368 7.232 L 8.3712 1.6768 L 8.3328 1.6896 L 6.5664 7.0912 C 6.3487997 7.7823997 6.7967997 7.8208 7.232 7.8592 C 7.3087997 7.936 7.3087997 8.2048 7.232 8.2816 C 6.7072 8.2688 6.144 8.256 5.632 8.256 C 5.2096 8.256 4.7616 8.2688 4.3519998 8.2816 C 4.2752 8.2048 4.2752 7.936 4.3519998 7.8592 C 5.0304 7.8208 5.312 7.424 5.4272 7.0912 L 5.7216 6.2464 C 5.7728 6.0927997 5.8111997 5.9648 5.8111997 5.8496 C 5.8111997 5.7216 5.7984 5.6191998 5.6959996 5.4016 L 4.0448 1.6511999 L 3.9808 1.6639999 L 2.112 7.3216 C 1.9583999 7.7696 2.304 7.8335996 2.7519999 7.8592 C 2.8288 7.936 2.8288 8.2048 2.7519999 8.2816 C 2.3295999 8.2688 1.7664 8.256 1.2672 8.256 C 0.8192 8.256 0.44799998 8.2688 0.076799996 8.2816 C 0 8.2048 0 7.936 0.076799996 7.8592 C 0.65279996 7.8208 0.7424 7.8079996 0.9856 7.1168 L 3.392 0.192 C 3.4559999 -0.0128 3.5328 -0.15359999 3.6736 -0.15359999 C 3.84 -0.15359999 3.9167998 -0.0256 4.0064 0.192 L 5.9136 4.48 C 6.0288 4.736 6.0671997 4.7999997 6.1312 4.7999997 C 6.1823997 4.7999997 6.2335997 4.6591997 6.3104 4.4416 L 7.7823997 0.192 C 7.8592 -0.0256 7.9231997 -0.15359999 8.076799 -0.15359999 C 8.2176 -0.15359999 8.3071995 -0.0128 8.3712 0.1792 L 10.943999 7.0783997 C 11.110399 7.5263996 11.340799 7.8208 12.0448 7.8592 C 12.1216 7.936 12.1216 8.2048 12.0448 8.2816 C 11.673599 8.2688 11.264 8.256 10.9312 8.256 C 10.5984 8.256 10.0352 8.2688 9.5232 8.2816 C 9.4464 8.2048 9.4464 7.936 9.5232 7.8592 C 10.047999 7.8208 10.559999 7.7823997 10.368 7.232 Z "/>
</symbol>
<symbol id="gA11612CECC8CBEF18835767DAB11B2F7" overflow="visible">
<path d="M 0.5248 2.6239998 C 0.5248 1.3184 1.3952 -0.12799999 3.2128 -0.12799999 C 4.032 -0.12799999 4.6591997 0.1664 5.0944 0.5888 C 5.6703997 1.152 5.9263997 1.9583999 5.9263997 2.7391999 C 5.9263997 4.0703998 5.1967998 5.6191998 3.2384 5.6191998 C 2.3936 5.6191998 1.7024 5.2736 1.2287999 4.7232 C 0.768 4.1728 0.5248 3.4304 0.5248 2.6239998 Z M 3.0463998 5.1712 C 4.1472 5.1712 4.8255997 4.1728 4.8255997 2.3295999 C 4.8255997 0.7168 3.9936 0.32 3.392 0.32 C 2.0607998 0.32 1.6256 1.9327999 1.6256 2.9183998 C 1.6256 4.032 1.8944 5.1712 3.0463998 5.1712 Z "/>
</symbol>
<symbol id="gCEFEF3D67F35C6E83CC3757B1DD21B13" overflow="visible">
<path d="M 4.2752 0.64 C 4.3392 0.69119996 4.4544 0.7168 4.4672 0.6272 C 4.5056 0.32 4.608 -0.12799999 4.608 -0.12799999 C 4.7104 -0.1664 4.7743998 -0.15359999 4.8512 -0.12799999 C 5.1328 0.1024 5.5808 0.2944 6.3616 0.384 C 6.4384 0.4608 6.4384 0.65279996 6.3616 0.72959995 C 5.5424 0.79359996 5.4272 1.0368 5.4272 1.6639999 L 5.4272 7.4624 C 5.4272 8.2944 5.4783998 8.806399 5.4783998 8.806399 C 5.4783998 8.896 5.4272 8.9344 5.312 8.9344 C 4.992 8.806399 4.032 8.6272 3.52 8.588799 C 3.4944 8.4864 3.52 8.2816 3.5967999 8.2048 C 3.6352 8.2048 3.6736 8.2048 3.712 8.2048 C 4.2752 8.1664 4.416 8.1664 4.416 7.1552 L 4.416 5.5168 C 4.416 5.4272 4.3904 5.4016 4.3008 5.4016 C 4.2496 5.4016 3.7247999 5.6191998 3.3023999 5.6191998 C 2.4575999 5.6191998 1.8944 5.3375998 1.3823999 4.8512 C 0.83199996 4.3008 0.4992 3.5456 0.4992 2.5983999 C 0.4992 1.0239999 1.2928 -0.12799999 2.6752 -0.12799999 C 3.1743999 -0.12799999 3.648 0.12799999 4.2752 0.64 Z M 4.416 1.5871999 C 4.416 1.344 4.3904 1.2415999 4.2111998 1.0879999 C 3.7375998 0.6784 3.3279998 0.4736 3.008 0.4736 C 2.3167999 0.4736 1.5999999 1.2287999 1.5999999 2.8288 C 1.5999999 3.7503998 1.7792 4.2623997 1.9712 4.5312 C 2.368 5.1328 2.9055998 5.1712 3.1615999 5.1712 C 3.6223998 5.1712 3.9424 5.0048 4.1984 4.7104 C 4.3775997 4.5056 4.416 4.416 4.416 4.0192 Z "/>
</symbol>
<symbol id="g645CA8FA3D9155E2CBD9F8EED3C1540D" overflow="visible">
<path d="M 1.9968 4.7104 C 1.984 5.0944 1.9583999 5.4272 1.8944 5.5551996 C 1.8687999 5.6191998 1.8432 5.6576 1.7407999 5.6576 C 1.3823999 5.5168 1.0496 5.4016 0.1664 5.2864 C 0.1408 5.2096 0.1664 5.0048 0.192 4.928 C 0.8832 4.864 1.0239999 4.7999997 1.0239999 4.0576 L 1.0239999 -1.408 C 1.0239999 -2.4703999 0.8832 -2.5344 0.1024 -2.5728 C 0.0256 -2.6496 0.0256 -2.9183998 0.1024 -2.9952 C 0.55039996 -2.9824 1.0239999 -2.9696 1.536 -2.9696 C 2.0479999 -2.9696 2.6624 -2.9824 3.0848 -2.9952 C 3.1615999 -2.9183998 3.1615999 -2.6496 3.0848 -2.5728 C 2.1759999 -2.5216 2.0351999 -2.4703999 2.0351999 -1.408 L 2.0351999 -0.0256 C 2.0351999 0.1408 2.0864 0.12799999 2.2144 0.076799996 C 2.5344 -0.0512 2.9183998 -0.12799999 3.3279998 -0.12799999 C 4.0448 -0.12799999 4.6847997 0.0896 5.2096 0.5888 C 5.8111997 1.1776 6.1568 1.9712 6.1568 3.008 C 6.1568 4.3648 5.1967998 5.6191998 3.8911998 5.6191998 C 3.3023999 5.6191998 2.6496 5.2352 2.1376 4.6591997 C 2.0607998 4.5824 2.0096 4.5824 1.9968 4.7104 Z M 2.24 4.2367997 C 2.5728 4.6464 3.1615999 5.0304 3.5328 5.0304 C 4.3519998 5.0304 5.0559998 4.1088 5.0559998 2.6624 C 5.0559998 1.6128 4.6847997 0.30719998 3.2512 0.30719998 C 3.0207999 0.30719998 2.5728 0.3712 2.3423998 0.576 C 2.0864 0.8064 2.0351999 0.8832 2.0351999 1.344 L 2.0351999 3.6736 C 2.0351999 3.9424 2.0864 4.0576 2.24 4.2367997 Z "/>
</symbol>
<symbol id="gBC176529035DE42B8BD4625370C40E4D" overflow="visible">
<path d="M 2.72 8.56 L 5.584 8.56 C 4.3360004 5.4560003 3.072 2.3360002 1.9840001 -0.096 L 2.112 -0.208 L 3.2 -0.16000001 C 4.112 2.5600002 4.992 5.216 6.7840004 9.584001 L 6.5280004 9.776 C 6.2560005 9.696 5.9040003 9.6 5.2960005 9.6 L 2 9.6 C 1.4560001 9.6 1.488 9.76 1.2 9.824 C 1.1520001 9.824 1.136 9.824 1.136 9.776 C 1.12 9.008 0.94400007 8.048 0.81600004 7.2160006 C 0.99200004 7.168 1.1520001 7.1520004 1.3280001 7.168 C 1.6800001 8.448 2.2080002 8.56 2.72 8.56 Z "/>
</symbol>
<symbol id="g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" overflow="visible">
<path d="M 4.688 10.336 L 4.032 10.336 L 0.24000001 -0.94400007 L 0.896 -0.94400007 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
</defs>
</div>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(40 16.58)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="8.99" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.280000000000001" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.39" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gBFFDA84A1400D9E1136DF0DD93EA19F5" x="25.02" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEC3CC7DEE79E0AA801DFAAEF4B6C0B50" x="30.669999999999998" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g202CCBD46865F83C12D50E1B4FF9BBEA" x="36.43" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="41.35" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g5503E15E5E4E70E9E217A15BD1ECD752" x="46.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="49.75" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="55.379999999999995" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 25.159999999999997)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 27.159999999999997)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.64 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 42.31999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(393.5458818897638 10)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6D39B87B7095296261A07873F9B99896" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1B61845C1FB429ACDF5304290F5BF286" x="8.339999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC66F55FB8F08DA72FE76D3863D88042" x="13.511999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="20.003999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g48BCA4F06942DA5990D42018985FC781" x="26.759999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g45E4C10E27056C5AE488FE2D8290DF06" x="32.891999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="36.623999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FB89403B37B0F0F934DFEB7E5171B37" x="42.971999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFF269982F0E4C510F3A3BFF016D72390" x="50.303999999999995" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 10.296000000000001)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(6.768 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5ABA589ED074A65FC8C929AB4EB2344C" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 28.488)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 38.784)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(743.9997637795276 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g97A8E46F7A64F11D13C6F357868587EE" x="9.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.25" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.36" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gB844DCFB76B4CC44608DB013C9764E9C" x="24.89" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="30.37" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="35.14" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="41.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="46.58" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="52.599999999999994" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 15.16)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 60)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6C3A310EEC8A7EBBD176D179125951F0" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(9.528 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g2F0CE4BDC8DA4B92139017B781562218" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8D84A54D9303B24762DC3071B60ECD14" x="17.76" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3E9095A1FBD7854ED5F7B53469C97011" x="25.560000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g90B91206A818BADA9956CC42F47E57A0" x="38.064" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2B9D5A283BBC2ED0501C3A1039D04E5C" x="43.92" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.78399999999999 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g10BFE5E41011FF0F560FA08FAB260218" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(75.312 15.48)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(81.312 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1BED8054A02AECF3BF3EC56A671C1672" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g841363B3896A8C79F18618DF16186242" x="16.944" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g42F794F2554BA43C69EE8F3AA6FD9BAC" x="30.168" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDD7DFDEC0D240E3DC5A3664E12D4BDDC" x="44.952" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g10AC66E6714D96E9762627FFB6E156C6" x="55.199999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g767CEF02C917BBE3F159A8F04079F311" x="63.791999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA13EE5B65CBC719304B28920E2ACC2B9" x="74.064" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g9CBC2DB69173A0577335373434CDCDA4" x="88.416" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g10AC66E6714D96E9762627FFB6E156C6" x="99.36" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g24FA36D774E663C81AD78F0ED3820373" x="107.952" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g841363B3896A8C79F18618DF16186242" x="115.67999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g42F794F2554BA43C69EE8F3AA6FD9BAC" x="128.904" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 39.48)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g629AE7F75F47B1FD947FFA2989B5B47D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(9.599999999999998 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gDACA5EBB44D5F3DB530A1F5F650BFBAB" x="9.719999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="20.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="30.619999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="36.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="46.879999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="58.199999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="64.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="79.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="85.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="95.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="103.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="112.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="120.03999999999999" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(190.05354330708664 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g278A59F111DD0614EC58EAA01A502EFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(210.05354330708664 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="9.719999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="23.699999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="32.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="41.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="49.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="65.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="77.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="91.10000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="100.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="105.46000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="115.46000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="126.22000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="136.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="146.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="158.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="168.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="177.44" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 50.81999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="16.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="25.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="32.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="38.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="51.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="57.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="65.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="75.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="96.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="102.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="112.48" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="127.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="133.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="142.27999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="152.41999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="161.35999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="168.79999999999995" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 87.71999999999998)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gF418DD62CA77762FBF8DB07ECAE6BC0" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g37DC97609493A252C8A67743647C955" x="12.52" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g50FEF586148C287DB923CFE895D558DC" x="24.9" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCD50B0C5537328D0484BBB5C5B7C30A" x="35.019999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="43.559999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g50EBB3D006215D0409E43740CDD42DD9" x="58.339999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gED653E9CCAB5F6C6237350979071A74F" x="68.61999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB0978DD106A095AA3B799B940A52F3E4" x="78.74" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="91.82" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g578059AE543193F568F4B7010D62E33B" x="101.6" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g814D257E196F777517493FCE505E18DF" x="109.41999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g936880EEF467D45CE0F64A721CAEDAB8" x="120.43999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="128.83999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gBC3E99057185A77BABD844B7BE98A74B" x="143.61999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g50FEF586148C287DB923CFE895D558DC" x="155.67999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g936880EEF467D45CE0F64A721CAEDAB8" x="165.79999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g80AF1C2942ED5136FA76CE028C280500" x="174.35999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="184.77999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1344FEF92B65FBC27D977C1EC5D9AECF" x="194.55999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gF410D7E2AAE9C85F7CA0EFFF491D43F" x="206.71999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g50FEF586148C287DB923CFE895D558DC" x="218.25999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAFD7B3D7EB6599FB514B70015F312425" x="228.37999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="239.37999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g936880EEF467D45CE0F64A721CAEDAB8" x="249.15999999999997" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 100.71999999999998)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="16.979999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="27.059999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="47.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="56.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="67.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="73.96000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="81.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="97" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="107.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="117.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="123.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="133.85999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="140.17999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g261101C75B6E2D92A65743C21553BE65" x="149.89999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="161.09999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="171.93999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="187.05999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="197.57999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="207.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="213.07999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="223.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="235.23999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="243.79999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="249.07999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="259.15999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="266.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="275.9" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="283.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="295.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="301.34" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(333.44 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g629AE7F75F47B1FD947FFA2989B5B47D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.82)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 39.82)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g187DB76C80CD961C20BAB3AF6259527" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="13.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="21.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="34.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="40.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="51.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="60.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="73.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="84.48" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g5925E4E4FE8F59A76637BD462660B390" x="93.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="103.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="114.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="119.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="128.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="138.95999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="147.89999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFDEE26E32361E56ABE6C1C3702B2C2B3" x="155.33999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="160.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="173.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="182.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="193.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="199.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="207.34" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 177.43999999999997)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gF418DD62CA77762FBF8DB07ECAE6BC0" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g37DC97609493A252C8A67743647C955" x="12.52" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g50FEF586148C287DB923CFE895D558DC" x="24.9" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCD50B0C5537328D0484BBB5C5B7C30A" x="35.019999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="43.559999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2C80519849984D6FD44691E994D5E329" x="58.339999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gED653E9CCAB5F6C6237350979071A74F" x="68.61999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g5AE3E73FF7353FF91276C30DF8EB5DCC" x="78.74" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1344FEF92B65FBC27D977C1EC5D9AECF" x="93.53999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gBC3E99057185A77BABD844B7BE98A74B" x="105.69999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g50FEF586148C287DB923CFE895D558DC" x="117.75999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g936880EEF467D45CE0F64A721CAEDAB8" x="127.88" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g80AF1C2942ED5136FA76CE028C280500" x="136.44" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="146.86" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1344FEF92B65FBC27D977C1EC5D9AECF" x="156.64000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gF410D7E2AAE9C85F7CA0EFFF491D43F" x="168.8" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g50FEF586148C287DB923CFE895D558DC" x="180.34" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAFD7B3D7EB6599FB514B70015F312425" x="190.46" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="201.46" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g936880EEF467D45CE0F64A721CAEDAB8" x="211.24" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gED653E9CCAB5F6C6237350979071A74F" x="219.8" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 190.43999999999997)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="16.979999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="27.059999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="49.112309711286095" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="58.0523097112861" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="68.8923097112861" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="75.21230971128611" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="82.9523097112861" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="99.50461942257219" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="110.02461942257219" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="120.10461942257218" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="125.52461942257219" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="136.3646194225722" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="142.68461942257218" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="153.65692913385828" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="161.4569291338583" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="170.3969291338583" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="179.53692913385828" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="186.81692913385828" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="195.37692913385828" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g25F4C61DF17D6DB8640DCCCD57BBA830" x="212.38923884514438" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g844C4CEA683BD523227FE7A466FBF8A3" x="219.0292388451444" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="232.9292388451444" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="238.2092388451444" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="248.2092388451444" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCAFB20A65E8FBEFE071D9C4C8EE95E49" x="252.6092388451444" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g2E0E67B6699615E51BCE03EAB1A37509" x="261.9092388451444" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="275.2815485564305" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="281.4815485564305" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="291.56154855643047" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(330.27385826771666 6.160000000000001)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 106.86 0 "/>
</g>
<g transform="translate(322.27385826771666 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="8.940000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA335A20E4C1D7F39210005AFF7F1A0EF" x="15.620000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="28.540000000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="38.620000000000005" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="49.46000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="57.260000000000005" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="63.580000000000005" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="71.02000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="81.64000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="90.20000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="96.52000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="101.94000000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="112.02000000000001" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 26.16)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="10.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="20.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="26.020000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="36.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="43.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="55.98" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="64.53999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="69.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="79.89999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="87.69999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="96.63999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="104.43999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="115.75999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="122.07999999999998" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(137.16 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g629AE7F75F47B1FD947FFA2989B5B47D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(146.76 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gB91E67CF1B63A9F4CC30BB03AE35508D" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="9.399999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="17.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g17AD34DB90B05275C6F1422A9B4B5274" x="26.34" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="36.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="50.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="56.38" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.22000000000003 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g278A59F111DD0614EC58EAA01A502EFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 65.98)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 52.82)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="16.979999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="27.059999999999995" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.85999999999999 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g278A59F111DD0614EC58EAA01A502EFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.86 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="9.719999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="20.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="25.520000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="34.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g25F4C61DF17D6DB8640DCCCD57BBA830" x="49.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g844C4CEA683BD523227FE7A466FBF8A3" x="55.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="69.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="75.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="85.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g11C09650A1107877D1CACE85AD57EEFF" x="89.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g2E0E67B6699615E51BCE03EAB1A37509" x="98.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" x="110.96000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="132.74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="143.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="152.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="157.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="167.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="178.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="188.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="198.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="206.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="219.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="225.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="235.36" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(315.66 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g629AE7F75F47B1FD947FFA2989B5B47D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 92.64)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 92.64)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gFE29E79896646B3825DA2D41961151C9" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="11.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="22.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="27.799999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="33.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="46.59912260967376" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="52.919122609673764" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="67.69912260967376" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="77.77912260967376" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="84.53912260967377" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="99.47912260967377" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="108.61912260967377" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="122.31824521934753" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="127.59824521934753" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="133.01824521934753" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="143.85824521934754" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="154.09824521934755" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB91E67CF1B63A9F4CC30BB03AE35508D" x="161.89824521934756" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="169.69736782902132" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="178.25736782902132" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="189.0173678290213" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="198.09736782902132" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="206.65736782902133" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="220.2964904386951" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="225.71649043869508" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="235.31561304836882" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="246.15561304836882" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="255.09561304836882" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="260.51561304836883" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="270.51561304836883" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="281.2756130483688" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="291.3356130483688" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="301.4156130483688" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="308.8556130483688" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="320.0547356580426" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="330.8947356580426" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="339.97473565804256" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="349.05473565804255" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="362.57385826771633" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="372.9538582677163" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="380.3938582677163" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="391.01385826771633" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="401.8538582677163" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="407.2738582677163" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="418.1138582677163" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 105.64)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="7.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="16.740000000000002" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(45.08 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g278A59F111DD0614EC58EAA01A502EFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.08 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="14.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="26.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="37.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g5925E4E4FE8F59A76637BD462660B390" x="46.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="56.379999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g607CD744DAB7515984E0B3F495F7DE81" x="67.69999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="78.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="87.39999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="97.53999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="106.47999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFDEE26E32361E56ABE6C1C3702B2C2B3" x="113.91999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="119.27999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="132.07999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="141.01999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="151.85999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="158.17999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="165.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="181.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="191.74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="201.82000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="207.24" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="218.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="224.4" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(490.751811023622 0)">
<g class="typst-group">
<g>
<g transform="translate(4.057637795275631 0)">
<image xlink:href="data:image/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgFBgcGBQgHBgcJCAgJDBMMDAsLDBgREg4THBgdHRsYGxofIywlHyEqIRobJjQnKi4vMTIxHiU2OjYwOiwwMTD/2wBDAQgJCQwKDBcMDBcwIBsgMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDD/wAARCAV0BDcDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwD3+iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKK8x+O/xAHhDw/8AYdPm26xqClYsdYY+jSex7D357UAR+Lfjj4b8O6zJpyQXWoyQMUke3C7EYdVBJGSOhxxWN/w0joH/AEA9T/76j/xr5yjSSeYJGGeSVgAByWJPA9yTW/8A8K/8X/8AQual/wCA7UAe3f8ADSOgf9APU/8AvqP/ABo/4aR0D/oB6n/31H/jXiQ+Hvi8/wDMt6l/4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6B/0A9T/AO+o/wDGj/hpHQP+gHqf/fUf+NeJf8K98X/9C3qP/gO1H/CvfF//AELeo/8AgO1AHtv/AA0joH/QD1P/AL6j/wAaP+GkdA/6Aep/99R/414l/wAK98X/APQt6j/4DtR/wr3xf/0Leo/+A7UAe2/8NI6B/wBAPU/++o/8aP8AhpHQP+gHqf8A31H/AI14l/wr3xf/ANC3qP8A4DtR/wAK98X/APQt6j/4DtQB7b/w0joH/QD1P/vqP/Gj/hpHQP8AoB6n/wB9R/414l/wr3xf/wBC3qP/AIDtR/wr3xf/ANC3qP8A4DtQB7b/AMNI6D/0A9T/AO+o/wDGj/hpHQP+gJqf/fUf+NeBa14c1nQ44m1jTLmxEpIj86MruI64zWTQB9ueDvFml+MtFXU9HlZoixjkjcYeJhyVYeuDn0Iroa8q/Zz8L3nh7wfLeagDFLqsizpCeqxhcKSOxOc/TFerUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFBphagDJ8W+ILLwvoN3q+ovtgt0zt7yN/Cg9yeK+NPFviG78V69davqLZmuG4QfdjQfdRfYDj9a7T48fEA+LdfGn6dLnR9OYpGV6TydGk9x2Htz3rnvhn4Qm8ZeI4rMZSyhxLdy/3Y89B/tHoPz7UAd/+z94DNzOvivVIcwQsRYxsPvOODJ9B0Hvz2r3iobK2hsrSG0s4VighQJGi8BFAwAKmoAM0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABVbU9RtdJ02e/v5RBa20ZkkZuwH8yegHc1Zr51+O/j/APtvUW0DSpc6bZv++kVuJpR/NV7ep59KAOM+IXi668ZeIZtRudyQL8ltCOkUeeB9T1J9a634DfDv/hKtZ/tbVYd2j2Dj5W6XEvUJ7gdT+A71xngXwte+MfEdtpGnrtDndNLjiKMfec/0Hc4FfZPh3RbHw/o9rpWlxCK1tYwiAdT6sT3JPJPrQBpgADGBS0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFeNftDfED+xdLPh3S5sX96v+kMh5ghPb2ZunsM+orvviD4utfBnhqfVrkqzgbLeEnBllI+Vfp3J7AV8ca3ql1rWo3GpahMZrq6kLyMe59vQDoB6UAQWVpPqN9DZ2URknuHEccY6licAV9afDbwfb+C/DcdguHvJMTXUo/5aSEdB/sjoPz71wX7PvgP7HaDxRqkX+kzqRZI4+4h4Mn1PQe31r2SgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopPu5ZjhRySfSvM/FvxTFvO9r4djSbYSGuZOVY/7I7/AFP5VnUqRpq7OzC4Kri5ctNX/JHptFfPV7438R3kpkk1SZPRImCKPwXFT2fxB8TW0YjGomQesiK5H4kZrm+u079T2/8AVrE8vxK/z/yPf6SvJPDfxWvFu1i1+OKS3YgedEuxo/cjoR9MGvWIZop4EngdZI3AZXU5BB6EGuinVjUV0ePjMvrYNqNVb7PoPooorU4AooooAKKKKACiiigAooooAKKKwvHPimz8I+HrjVL3DuPlgizgyyHoo9u5PYUAch8cfHo8N6T/AGRpk2NVvozuZW5t4zwW9mPQfifSvm23t5bu4jhgRpZpXCIijJdicAAepNW9b1W71rU7nUtSmaa6uZC7sf0A9ABwB6V7h+zn8OzEF8XavCCzgiwicdB3l/HoPbJ9KAPQPhD4Ei8EeHkS5RX1W8AkvJBztPaMH0GfxOTXeUUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABUFzcRWsElxcSLHFEpeR3OAqgZJPsBU9eCftH/EDYh8JaXNhmw1+6N0HVYv6n8B60AecfF/x3L438SySW5caZZkxWkZPUZ5kI9W/QYFP+D/AIHbxj4gWW6Q/wBl2RD3J/56H+GMfXv6D8K5LQdIvdc1a10vTYzNc3ThFHYepPoAOSfSvrnwd4as/Cnh+30ixXcsYzLIV5lkPVj9e3oMCgDXRVjjSOMKqqAAo4AA4AFOoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKRmWNXeRgiICWZjgAdySegrxf4k/GuO283TPB7rLKMpJqLDKr7Rg9T/ALR49M9aAPYZr60huEt5rq3jmf7sbyqGb6AnJqxXxHeXtzeXb3V1PLNO53NLI5ZifXJ5r62+GE+o3XgHR5tYLG7aDkv94rkhSc9yuKAOmooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKiluoIf9dPGn+84H8zQBLRWfNr+jwf67V9Pjx/euEH9aoy+NfC0H+t8RaWv/AG9p/jQBvUVys/xL8Fw/f8RWTY/uMW/9BBqjN8XvA0XTW/M/3IJT/QUAdxRXnkvxt8Ex/cvLqX/dtW/ris+f48+FEzstNSm+kaD+bCgD1OjNePzftB6Kv+o0S+f/AH3Rf5E1Sm/aIh/5YeG3/wCB3Q/otAHttFeCzftEXx/1Xh22H+/cMf5AVRn/AGgPELf8e+k6ZH/vB2/9mFAH0RRXzTN8dvF8n3F02L/ctyf5sapz/GjxtL93UYY/9y1jH8waAPqKivlCb4seOZeuvSr/ALsca/yWqU/xE8Yz/wCs8SaiP9yYr/LFAH15R+GBXxpP4r8QT587XtTkz/eupD/7NVGTVNQm/wBbfXL/AO/Mx/maAPtOW6to/wDWTxL9XA/rVWfXNJt/9dqthH/v3KD+tfF7u8n33Lf7zZqOgD7Gm8beFYf9Z4i0ofS6Q/yJqjN8S/BcXXxJZH/c3N/JTXyPRQB9Vz/F7wPFnOtb/wDrnbyH+lUpvjd4Kj+5dXkv+5bMP54r5jRGc4VSx9hmrUGk6jOcQ2F1J/uQsf6UAfQk/wAe/Cqf6qz1ST/tmgH6tVOT9oTR1/1Gh3z/AO/Ii/414nD4U8QTHEWh6m/0tX/wq/B8O/GEx+Tw5qIz3aEqP1xQB9QeCvFum+MdIGoaUzAK3lyxSDDxPjODjjp0I61u1578EfBd/wCEdDu21fEd1fyq7QBg3kqoIAJHG45OcdK9CoAKKKKAPO/jH4jksbCLR7R9st4C0zDqIxxj8T+grx/Hetzx1rP9ueJry6U5iVvKi/3F4H59fxrB714eIqc82z9SyjCRw2Gimveer9WFFFFc5644cGvWPgprktxbXOj3LFjARLBnshOGH0BwfxryWu9+CiFvFM7dltWz+JWunDNqorHjZ3ShUwcnLpqj2miiivbPy8KKKKACiiigAooooAKKKKAI7q4htLeW4uJVighQySSMcBVAySfpXyp8VfG83jTxAZULLp1tmO1iP93PLn/aP6DAruf2gPHonmbwrpE2Y4iDfSqfvt2iz6Dqffjsa8p8MaBfeJdctdJ0yPfcXLbfZF7sfQAcmgDqvgz4Afxt4g8y6RhpFiQ9y2PvnqIwfU9/QfhX1rBEkESRRIqRxqFVVGAoAwAPasfwX4asvCWgW2j6ev7uEZeQr80sh+8x9yfyGBW9QAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFUdU1C20rT7m/v5RFbWyGWRz2UDmgDl/iz46i8DeGJLlSj6jc5js4jzl8cuR/dXqffA718fXdzLd3UtxdSNNNKxeSRzksxOSSfrXSfEjxjdeNvEs+pXJKQA7LWEtxFGOg+p6n3rp/gV4D/4STVv7Y1OHOl2DDarrxPN1C+6jqfwFAHoXwJ8CHw9o/wDbOpRY1TUEBRGHMMJ5A9mPU+2B616hQBx7nrRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVk+KPEmleF9ON9rVyII/wCBOryn0VepP6DvXIfEX4taV4WEljpuzUtWHBjU5ihP+0w6kf3Rz64r518Q+INU8Sak9/rF09zO3TP3UHoq9APYUAdV8SPifqfjF3tYN1hpIb5bZW+aT0Lnv9Og9+tcfo2lX2tX8dhpltJdXMpwqRrk/U+g9SelWPD2l2mp6gsOoata6ZbDmSebLYHoqgEsf096928KeLPhf4KsPs2lakryMB51x9nkaSU+529PQDgUASfDr4Nadoix3/iRI9R1HgiE8wwn6H77e549B3r1QYVeMAY6V5zN8bfBUefLubuX/dt2H88VRn+PXhVP9Xa6pL9IkA/VqAPU6K8fm/aC0YH91ot/J/vyov8AjVKf9oaH/lh4cc/710P6LQB7bRXgs/7Q16f9R4dtk/3rlm/oKoz/ALQXiF/9VpemR/7wkb/2YUAfRFFfNU3x38YSf6sadF/uwZ/mxqjN8aPG8v3dRhj/ANy2jH8waAPqOivk+b4s+N5euvzL/uxRr/IVRn+InjGf7/iPUR/uTFf5YoA+vvwo6fe4+tfGs3i3xHP/AK7XtSf63T/41Sl1fU5/9dqN3J/vzMf5mgD7Tlnhj/1s0SD3cCqk2uaPB/r9V0+L/fuUH8zXxbJI8hzIzM3qWzTRQB9jTeM/C8H+t8R6WP8At5Q/yNU5viT4Mh6+I7I4/uuW/kK+RKKAPqyb4veB4s51rf8A9c4JW/8AZaozfG7wVH926vJv9y2P9SK+Y442kOEVmP8AsjNWItOv5f8AU2dzJ/uxMf5CgD6Im+PXhVP9TaanL/2zRf5tVGf9oPRB/qNG1Fj/ALboP5E14lB4V8QXH+o0PUpP9y1kP9KvQfD3xfP/AKvw5qP/AAOEr/PFAHqU/wC0PAP9R4ckb/fuwP5Kaoz/ALQ183+o8PWyf787N/ICuKi+FHjmX/mAXC/77oP5mrsPwX8cS9dMhT/fuYx/7NQBuTftA+IX/wBRpemQ/g7f+zVRm+PHi9/uJpkf+7bk/wA2pIfgV4xf77adF/vXJP8AIGrsP7P3iFv9fqmmJ/umRv8A2UUAY83xq8bP9zUbeL/ctY/6g1Qn+LHjeb7/AIgmX/rnGi/yUV2sP7PN91n8QWyf7tux/mRUknwIsLRgt/4q2H0S0yf/AEKplOMFeTsJtI84m+Ifi+f/AFniPUD9JiP5VRm8WeIp/wDXa9qb5/6e3/xr2Kx+Bvhq44HiO7mb0VEQ/kc1rQ/AXwpH/rLzVJfrIg/kopRnGXwu4Jp7Hz1NqeoT/wCuv7mX/fmY/wAzVYySH7zsfqa+nYPgj4KT79reSH/buWH8quQ/CDwND10bzP8ArpPKf5EVYz5V3eufzoyK+t4fhl4Kh+54ds2/39zfzNXofBHhWL5o/Delp9LVP8KLgfHNOVGb7qlvoK+0YvD+iw/6nSLBMeltH/hVuOzt4f8AU2sEf+5EB/IUgPiyHTL+f/U2VxJn+5Cx/kKuReFPEEv+r0PUm+lrJ/hX2aPal59f1oA+QIPh94umx5XhzUTn1tyP51dh+FXjaXp4fuE/33Rf5kV9ZYPrRj3oA+Wofgx44k+9pkMf+/dJ/RjV+D4E+MH5d9Oi/wB64J/kK+laKYHztD+z/wCIn/1+qabF9Gdv5LVyH9nrUT/rvENon+5A7fzIr32igDxGH9nmIf6/xG7f7loB/NqvQ/s+aLt/fa1fsf8AZRF/mDXsFFAHlcPwE8LR48271OX/ALaov8lq9D8EPBUfWC+k/wB+5P8AQCvRqKAOHh+D/gaPpoxdv9u5lP8A7Nir0Pw08GQ9PDtif99S38ya6qigDCh8EeFYP9T4d0xf+3ZT/MGrsWg6ND/qtI0+PH922jH8lrQooAjS2gT5UgiVfQRgf0qVcLwOPpSUUALu+tGfYUlFABQKKBQAVT12ZoNFvpUOHSB2X6hTVyq2q2xvNNubYHBmieMfUqaUtjSk0pq/c+YhuYZNFSTwyW80kMoKvGxRgexBwRTK+eZ+xwacU0JRRRUlC9K9d+CekGDTrvVZEw1ywjiz/cXqfxb+VcB4L8M3PibVlt4sx2seGuJscKvoPc9q+gbO3hs7SK2toxHDEoVEHYCvRwlJ352fIcQ5hFU/q0Xq9/Imooor0z4UKKKKACiiigAooooAK4T4v+PF8H6D5Vm4OrXoK246+WvRpCPbt6n6Guo8Ta9ZeG9DudV1GQLbwLnA6ux6KPcnivkjxX4gvvFOvXOrakcyzn5UH3Y0H3VHsB/jQBllpJ5i7EvIzZJPJYn+Zr6q+Bfw8/4RDQ/t+pxAazfKDICOYI+oj+vc+/HavO/2ePh3/al4ninV4M2Vs2LON1/1sg6vj+6p6ep+lfSVABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV82ftE/EEapft4X0mXNnavm7dTxLKP4Povf3+lek/HHx8ng7w81pYSY1jUVKQbesSdGkP06D3+hr5QG+aTHzNI5+pYn+pNAGx4O8OXnirxDa6VYDBmOXcjiKMfec/QfmeK+uPD+kWegaNaaVpsey3tk2qe7Hux9STya5P4OeCE8I+HxJeRj+1b5Q9we8Y6rGPp39/oK7ugAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiq+oXa2Vq8zdRwo9TUVJqnFylsioxc5KK3ZDqWpxaf8rfvJD0Uf19Kyv8AhIpt+fIQL6bjmseWRppmlc5dzkmm18dXzWrOd6bsj6Ojl9OEPf1Zsz+I5m/1MSqv+3yf6VD/AG9feqf98VmUVzPMMTL7TOhYSivsmvH4iu1/1iRsv+6RWxpupQXynZ8rjqp/pXIVPp0jR30LL13Afnwa68JmdaM1Gbumc2JwNNwbgrM7avF/j5491DS7lfDejym1aWAS3M68OVbOEU9hgZJHPOPWvZxyK4D4pfDCHxvLDfW14LLUYUMZZkLJKg5AbHIIyeRn6V9kfNny4SScnmkr1bUPgN4ot4y1pc6deEf8s0lZCfpuUD8zXBa94U13w/IV1fSrm0A/jdDsP0YcH86AManBT2U5oVipDKcEdCK7Twz8UvE/h9VjiuoryAceVdRh/wAm6j86AOUh0vUJ/wDU2NzJn+7Cx/pV2Dwr4gm4i0TUn+lq/wDhXtPh/wCP+myqia7pM1o/RpbVhIn12nBH5mu80r4k+E9Xlihs9et/Ol4SOXdGxPYfMBz7UAfNEHw+8XTfc8Oanz627AfrV2D4U+OJfueHrhf9+RF/mwr6xBzyT19KWgD5ch+C3jeX7+mwxf8AXS5T+hNXIvgR4vf77adH9bgn+Qr6WooA+doPgB4ib/W6npafQyMf/Qauw/s9ah/y38QWyf7tuzfzIr3yigDw+D9niMf6/wARlv8ActcfzarsH7PekD/Xa7fN/uQov8ya9jooA8rh+AnhZP8AXXuqS/8AbVF/9lNXofgf4LixvgvZf9+5P9AK9GooA4aD4P8AgaHpo5f/AH7mQ/8As1Xofhj4Ki+74ctT/v7m/mTXV0UAYMPgfwpb/wCr8N6WPrbI38wauw+H9Fg/1OkafHj+5bIP5CtGigCJLW3T7lvAv+6gH9KmB28L8o9qSigA3f7RozRRQAZooooAKKKhvLhbO2eduiDP1PYUpSUU5MTdlcz9c1cWMZihIM7D/vkep/pXIyO8jmSRi7McknqafcyvcTvNKcs5yair5DF4qdefl0PMqVHJ+QvfJ61pafrt3aYRn86P+655X6GsyisKdWdJ3g7MiM3F3R3Wm6jBqEe6I4cfeQ9RVyvP7O4ks7hZ4W2sh/Mdwa76GQSxJIvR1DCvpcFi3iItPdHo0anOtdx1FFFekbBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB5z8RvAD6lcPquiqv2thmaDp5p/vA/wB72715TeaffWMpiu7WeF1OCHjI/pX05R+tclTCxm73sfR4HPq2Ggqc1zJba2Z8z2Wi6pegmz0+6nA6lIWI/PFdV4d+GWs6jKsmpL/Z1tnndzIR7Dt+Ne2gfhS1McHBbu5riOJK80400o/izP0LRbHQrFbLTohHEvJPVnPcse5rRpKK7FFRVkfMTnKcnKbu2FFLiimJCUUUUAFFFFABSMyqrOzBEQZJPAAHc0teOfH7x6bK2bwxpc2LicA3siN/q4+0f1PU+3HegDg/jP49bxfrP2OwkY6RYsRDjpM/QyH+Q9vrWZ8LfBVz448TR2Kgx2MOJbub+5HnoP8AaPQfn2rnNI0y61jUrfT9OiaW5uHEcaDuT/QdSe1fYfw38HWngjw1DpluA9w3z3VwBzLIRyfoOgHp75oA6PTrK202xgsrGJYbe3QRxRr0VQMAVZoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKx/FPiCx8NaHd6tqUmyC1XcR3Y9Ao9yeBWwa+VPj18QD4q1z+ydMmzpGnMQCG4nlHDP7gdB+J70AcR4y8SX3irXrrVtSP72dvlQH5Yk/hQewH59a9K/Z+8B/bbseJ9Uhzb27FbJHXiSQdX+i/z+lcL8OPCE/jLxLDYJlbRMS3Uw/5Zxjr+J6D3+lfWVhaW+nWUFlZxCK3gQRxIOiqBwKAJulFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFc34mud90tup4iGT/vH/wCtXRnv6CuHuZTPcyy/32Jrws5ruFFQXV/gepltPmqOT6EdFAor5M+iEoooqRi1b0eEz6jCF/hO4/Qc1UrqtBsPscHmSr+/l+97D0/xr0cuw0sRWVtlqzixtdUqTXV6I06KKK+6PlQpskaSqY5EV1bhlcZB+oNOooA4nxJ8JvCOu75G00WNw3/LWyPl8+pXlT+Vea+IPgBqlvuk0DU7e9XtFOPKf8+VP6V9AUUAfHOueDPEegk/2po13Ag/5ahNyf8Afa5H61iKGZgqgsxOAB3r7hADAqwGDwazR4e0Rb4Xy6TYC7U5WYW6BwfXOM596AIvBwvh4T0gaoCL4WkYm3fe3bRnPv6+9a9FFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABWF4wm2WkMIPLsWP0H/wCut2ub8Y/ftfo39K4cdJxoSsZVnaDOe6iiiivkjzAoPSiigAVd2F6k8CvQoE8q3jT/AJ5oB+lcp4YsftN358gzHAd31bsPw6111fRZVRcYuo+p3YaNlzMKKKK9k6gooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooqrq+pWmj6Zc6jqEqw2tshkkc+g9PUnoB3NAHO/E7xrb+CvDrXeVkv7jKWcR/ifuxH90dT+A718oXt3PfXktzdyNLPMxkkdjksxOSTW14+8WXfjHxDNqd0Skf3LeHPEUY6D69ye5rtvgH8Ox4o1f+2dWgzpNg42q3S4m6hfdR1P4D1oA9B/Z8+Hv9hacPEerxAajepi3jYcwQnnPszfoOO5r2SkUcUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRXN+PfFNn4N8OXOsXuGKDbDDnBmkP3VH8z6DJoA4T9oL4hf8I/pR8P6ZLjUr+M+c6nmCE8H6M3QegyfSvmiytJr+8itbOJpZ5nCRxryXYnAAqzrmrXmuatc6nqUrS3V05eR/c9h6ADgDsK9r/Z88CfZoB4q1SHEsoK2Mbr91ehk+p6D2ye4oA774Z+DIPBfhyOzGHvZsS3co/ikx90H+6Og/PvXVUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAQajJ5VhcN6If5VxNdpqiGSwnVepQ/pzXF18rnl/aRT2se9lfwP1Eooor549kWilRWkYKilnPAA710Wk6N5OJroBpOoXsv19TXbhMHUxMrQWnVnNXxMKEby37EWhaQyMt1dLz1RD/M1vgUUV9phsNDDQUIHzFevKvLmkFFFFdRgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABWL4qtWmskmjGTC2SP9nvW1SOoZSCMgjBBrGvS9rTcO5M480WjzuitvVPD80Ts9kPNjPOz+Jf8AGsdreZDtaF1b0KkV8lWw9SjLlaPMlCUXZoZU9haS3twsMI5J5PZR61ZstEvLrH7oxIerycfkOprqtO06GwgCQjLH7zHqa6sLgZ1ZXmrI1p0W9WS2VrHZ26wwjKr37k9yamoor6eMYwXLHY70rKyCiiiqGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfOXx08f/2/qR0LSZc6bZSfvWQ8Tyjj8VHQepyfSu9+Ovj0+HtJ/sTSpgNTv0PmOrcwRHgn2Y9B6DJ9K+crWCa7nit7eMyzyuI40VclmJwAPcmgDc8BeFL/AMZ+IoNKsFKq3zTzYyIYx1Y/yA7nAr7I0DR7LQdItNL02ERWtqgjQdz6k+pJ5J9a5j4SeBIfA3hxYZlR9UucSXcq8/N2QH+6P1OTXdUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAEM8sdvE80rhI41LOzHAAAySfavkf4x+PJPG3iRjbuy6TZZjtY+m/wBZCPU9vQY969G/aO+IP2eFvCOkTfvZVD30iH7inkRfU9T7YHc14VomlXet6nbabp0ZkublwiL9epPoAOSfSgDqvhH4Ifxh4hH2hWGl2ZEly397+7GPc9/QZr6nSOOKNI4UVI0AVVUYCgcAAegrF8FeGbPwl4dttKs1U7BvmlI5lkP3mP8AT0GBW5QAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFc9quhuJWltFBU87OhH09q6GiuTE4SniY8s0dFCvKhLmicWunXuT/osmfcVbtNBu5SDNthX1PJrbutVhtpNmDIR1x2q1b3CXEIkhPB6+orzKeT4dS1bfkejVx2I5Oa1k+pBYafb2KYjXLHqx61bpKWvap0oUlywVkeTOcpu8ndhRRRWhAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVgeOvFVn4P8PzaneYeQDZbw5wZpD0X6dyewrau7mGztZbq5kWKCBTJJI5wEUDJJr5T+KHjafxp4ge5BZdPtyY7SI/wr3Yj+8ep/AdqAOc1rVL3WtTuNR1GUzXVy5eRz6+nsAOAOwr3T9nX4eCCFfF2sRYllB/s+Jx9xTwZcHueg9ue4rgPgt8P38ba9594jDSLEhrhv+erdViB9+/oPqK+sooo4YkihQRoihVUDAAHAGPSgCYD1paKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACuL+K3jeHwR4ZkvMhr64zFZxH+J8dSP7q9T+A711Oq39tpmnz317MsNtboZJZG6KoGSa+O/iZ41ufG3iabUJNyWqZitYSc+XGD/M9T7/QUAcxe3lxf3s13dytNPO5kkkY5LMTkmvor4E+BP7A0n+3dVgA1K/T90rjmCE8j6Fup9sD1rzn4G+BP+Em1r+09RiB0rT2DEN0nlHIT3A6n8B3r6YY56dBQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQByt7/wAfk3++f51raB/x6Sf7/wDQVk3v/H5N/vn+da+gf8esn+//AEFcsPjPfxf+7L5GnRRRXUeAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFcD8YfHa+EdD+z2Ug/tW9UrAP+eS9DIfp0HqfpQBwn7QHj77VcN4W0mQ+REd19Ip+8/aP6DqffjtXlnhbQL3xPrltpOmoWnnbGccIv8TN7Acms395PIerySHPqWJP5k5r6r+Bvw9XwhoP23UItusX6hps9YU6qg9+59+O1AHYeDvDdh4T0K10nTR+6hX5nYfNI/wDE59yfy6Vu0gFLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUV5z8bPH6+DPD3k2Uo/te+Bjt17xL3kP07ep+hoA81/aN+IP2+/bwppUubW2fN66HiSQdE+i9/f6V5Z4Q8PX3inX7XSdOX95OfmcjiNB95j7AfnWSxknn3MWkldsnPLMSf1Oa+oPgx4EHhHQBdX0eNWvlDz5HMSdox9Op9/pQB1vh3RLLw9otrpWnR+XBbLtHq57sfcnk1o0UUALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHK3v8Ax+Tf75/nWvoH/HrJ/v8A9BWRe/8AH5N/vn+da+gf8esn+/8A0FckPjPfxf8Auy+Rp0UUV1ngBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFI7KqMzMEUAkk8AAdSaAMvxVr9n4a0K51TUXxDCvCD70jn7qD3J/wAa+SPFXiC98T65c6rqT7pp24UdI1HRR7AV1fxi8dt4w1v7NYSH+yLJisA7St3kP16D0H1NZ/wq8DXHjjxIlqMpYW+Jbyb+6n90f7R6D8T2oA739nj4djULtfFesW4Npbt/oMbDiSQf8tMegPT3+lfRwqrp1nbafZw2dlCkNtboI4o1GAigYAFWqACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDL8Sa5Z+HNFu9V1KQR29rGZG9Seyj3J4HvXxp448TXni7xHcaxqDfPKcJHnIiQfdUewH5nJ713Px++IX/AAk2s/2Ppc5Ok6fIQWU8XEw4Le6joPxPcV5z4etbG91e2h1a9FjZNIDPOVLbUHJwBySegoA9R+AXgMalejxLqkRa0tWxaIw4lkH8f0Xt/tfSvoGuC074m/D/AE2wt7Ky1dIba3jEUUYt5BtUdP4fzqf/AIW54I/6DQ/78Sf/ABNAHa0VxX/C3PA//QaH/fiT/wCJo/4W54H/AOg0P+/En/xNAHbUVxP/AAtzwR/0Gh/34k/+Jo/4W54I/wCg0P8AvxJ/8TQB21FcT/wtzwR/0Gh/34k/+Jo/4W54I/6DQ/78Sf8AxNAHbUVxP/C3PBH/AEGh/wB+JP8A4mj/AIW54I/6DQ/78Sf/ABNAHbUVxP8AwtzwR/0Gh/34k/8AiaP+FueCP+g0P+/En/xNAHbUVxP/AAtzwR/0Gh/34k/+Jo/4W54I/wCg0P8AvxJ/8TQB21FcT/wtzwR/0Gh/34k/+Jo/4W54I/6DQ/78Sf8AxNAHbUVxP/C3PBH/AEGh/wB+JP8A4mj/AIW54I/6DQ/78Sf/ABNAHbUVxP8AwtzwR/0Gh/34k/8AiaP+FueCP+g0P+/En/xNAHbUVxP/AAtzwR/0Gh/34k/+Jo/4W54I/wCg0P8AvxJ/8TQB21FcT/wtzwR/0Gh/34k/+Jo/4W54I/6DQ/78Sf8AxNAHbUVxP/C3PBH/AEGh/wB+JP8A4mj/AIW54I/6DQ/78Sf/ABNAHbUVxP8AwtzwR/0Gh/34k/8AiaP+FueCP+g0P+/En/xNAHbUVxP/AAtzwP8A9Bof9+JP8KP+FueB/wDoOL/34k/+JoA7aiuJ/wCFueB/+g4v/fiT/wCJo/4W54H/AOg4v/fiT/4mgDtqK4n/AIW54H/6Di/9+JP/AImj/hbngf8A6Di/9+JP/iaALl7/AMfk3++f51r6B/x6yf7/APQVgreQaii31nJ5kE/7yN9pGVPIODzTJfG/h3ww32TXNRFrPJ+9VfKdsr0z8oPcGuWHxnv4v/dl8jtKK4n/AIW94G/6DY/78Sf/ABNJ/wALd8D/APQbH/fiT/4muo8A7eiuI/4W74H/AOg2P+/En/xNH/C3fA//AEGx/wB+JP8A4mgDt6K4j/hbvgf/AKDY/wC/En/xNH/C3fA//QbH/fiT/wCJoA7eiuI/4W74H/6DY/78Sf8AxNH/AAt3wP8A9Bsf9+JP/iaAO3oriP8Ahbvgf/oNj/vxJ/8AE0f8Ld8D/wDQbH/fiT/4mgDt6K4j/hbvgf8A6DY/78Sf/E0f8Ld8D/8AQbH/AH4k/wDiaAO3oriP+Fu+B/8AoNj/AL8Sf/E0f8Ld8D/9Bsf9+JP/AImgDt6K4j/hbvgf/oNj/vxJ/wDE0f8AC3fA/wD0Gx/34k/+JoA7eiuI/wCFu+B/+g2P+/En/wATR/wt3wP/ANBsf9+JP/iaAO3oriP+Fu+B/wDoNj/vxJ/8TR/wt3wP/wBBsf8AfiT/AOJoA7eiuI/4W74H/wCg2P8AvxJ/8TR/wt3wP/0Gx/34k/8AiaAO3oriP+Fu+B/+g2P+/En/AMTR/wALd8D/APQbH/fiT/4mgDt6K4j/AIW74H/6DY/78Sf/ABNH/C3fA/8A0Gx/34k/+JoA7eiuI/4W74H/AOg2P+/En/xNH/C3fA//AEGx/wB+JP8A4mgDt6K4j/hbvgf/AKDY/wC/En/xNH/C3fA//QbH/fiT/wCJoA7eiuI/4W74H/6DY/78Sf8AxNH/AAt3wP8A9Bsf9+JP/iaAO3oriP8Ahbvgf/oNj/vxJ/8AE0f8Ld8D/wDQbH/fiT/4mgDt6K4j/hbvgf8A6DY/78Sf/E0f8Ld8D/8AQbH/AH4k/wDiaAO3oriP+Fu+B/8AoNj/AL8Sf/E0f8Ld8D/9Bsf9+JP/AImgDt6K4j/hbvgf/oNj/vxJ/wDE0f8AC3fA/wD0Gx/34k/+JoA7eiuI/wCFu+B/+g2P+/En/wATR/wt3wP/ANBsf9+JP/iaAO3oriP+Fu+B/wDoNj/vxJ/8TR/wt3wP/wBBsf8AfiT/AOJoA7eiuI/4W74H/wCg2P8AvxJ/8TR/wt3wP/0Gx/34k/8AiaAO3oriP+Fu+B/+g2P+/En/AMTR/wALd8D/APQbH/fiT/4mgDt6K4j/AIW74H/6DY/78Sf/ABNH/C3fA/8A0Gx/34k/+JoA7eiuI/4W74H/AOg2P+/En/xNH/C3fA//AEGx/wB+JP8A4mgDt6K4j/hbvgf/AKDY/wC/En/xNH/C3fA//QbH/fiT/wCJoA7eiuI/4W74H/6DY/78Sf8AxNH/AAt3wP8A9Bsf9+JP/iaAO3oriP8Ahbvgf/oNj/vxJ/8AE0f8Ld8D/wDQbH/fiT/4mgDt6K4j/hbvgf8A6DY/78Sf/E0f8Ld8D/8AQbH/AH4k/wDiaAO3oriP+Fu+B/8AoNj/AL8Sf/E0f8Ld8D/9Bsf9+JP/AImgDt6K4j/hbvgf/oNj/vxJ/wDE0f8AC3fA/wD0Gx/34k/+JoA7eiuI/wCFu+B/+g2P+/En/wATR/wt3wP/ANBsf9+JP/iaAO3oriP+Fu+B/wDoNj/vxJ/8TR/wt3wP/wBBsf8AfiT/AOJoA7eiuI/4W74H/wCg2P8AvxJ/8TR/wt3wP/0Gx/34k/8AiaAO3oriP+Fu+B/+g2P+/En/AMTR/wALe8D/APQbH/fiT/4mgDt68Y+P/j02sD+F9LlInnUG+kVuVQ8iP6nqfbjvW54p+Mvh2z0K4k0C+W91IjbBGYnADH+JiRjA6479K+bbq5mvbqW6upGlmmYvI7HJdickmgCzoul3et6pb6bp0ZmublwkajuT6+g7k9hX2J8O/B1p4L8OQ6ZagPMcSXM+MGWQjk/QdAOwrif2fvh4fD2mDxDqsWNTv0/cow5ghP8AJm6n0GB616+KABRiloooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKyfFVpeX3hrVbTTpPLu57SWOFs4w5Uhee3Na1JQB8GX9hd6fdyWt9by208TFXjlUqykeoNVtrf3a++JIIpDl4kc/wC0oNN+x2//AD7Q/wDfA/woA+Cdp/u0bT/dNfev2O3/AOfaH/vgf4V4V8Q/jVPo3ie60rw/pOnyRWUpilmuUJMjjhgoBGADx3oA+f8Aaf7po2n+6a+yvhn4msfHHhpNVSxit5kcwzxhQQsgAJwccjBBFdX9ktv+faH/AL4H+FAHwVtP900bT/dNfev2S2/59of++B/hVe+jtLS0muWtonWGNpCqoMkAZ9KAPhLaf7po2n+6a7nXPit4r1LUJbm31FtPhZj5dvbqqpGvYdMn6moLb4qeNLdgy60z+olgikH/AI8poA43af7po2n+6a9q8G/HqeG4S38WaXa3Nuxwbm2hCSJ7lejfhivftGn0vV9Ogv8ATRbz21wokjdEGCD+HB9R60AfC+0/3TRtP90196/Y7f8A594f++B/hR9jt/8An3h/74H+FAHwVtP900bT/dNfev2O3/594f8Avgf4UfY7f/n3h/74H+FAHwVtP900bT/dNfev2O3/AOfeH/vgf4UfY7f/AJ94f++B/hQB8FbT/dNG0/3TX3r9jt/+feH/AL4H+FH2O3/594f++B/hQB8FbT/dNG0/3TX3r9jt/wDn3h/74H+FH2O3/wCfeH/vgf4UAfBW0/3TRtP90196/Y7f/n3h/wC+B/hR9jt/+feH/vgf4UAfBW0/3TRtP90196/Y7f8A594f++B/hR9jt/8An3h/74H+FAHwVtP900bT/dNfev2O3/594f8Avgf4UfY7f/n3h/74H+FAHwVtP900bT/dNfev2O3/AOfeH/vgf4UfY7f/AJ94f++B/hQB8FbT/dNG0/3TX3r9jt/+feH/AL4H+FH2O3/594f++B/hQB8FbT/dNG0/3TX3r9jt/wDn3h/74H+FH2O3/wCfeH/vgf4UAfBW0/3TRtb+6a+9fsdv/wA+8P8A3wP8KPsdv/z7xf8AfA/woA8n8Gf8ilpH/XrF/wCgivKfjz/yNFj8v/LkP/Rj17nqAxfTYHAc4UfWt/wnFHJZymSFHIkx8wB7D1rlh8Z72L/3VfI+JtrelG1vSvvX7Jb/APPtD/3wP8KPsdv/AM+0P/fA/wAK6jwT4K2t6UbW9K+9fsdv/wA+0P8A3wP8KPsdv/z7Q/8AfA/woA+CtrelG1vSvvX7Hb/8+0P/AHwP8KPsdv8A8+0P/fA/woA+CtrelG1vSvvX7Hb/APPtD/3wP8KPsdv/AM+0P/fA/wAKAPgra3pRtb0r71+x2/8Az7Q/98D/AAo+x2//AD7Q/wDfA/woA+CtrelG1vSvvX7Hb/8APtD/AN8D/Cj7Hb/8+0P/AHwP8KAPgra3pRtb0r71+x2//PtD/wB8D/Cj7Hb/APPtD/3wP8KAPgra3pRtb0r71+x2/wDz7Q/98D/Cj7Hb/wDPtD/3wP8ACgD4K2t6UbW9K+9fsdv/AM+0P/fA/wAKPsdv/wA+0P8A3wP8KAPgra3pRtb0r71+x2//AD7Q/wDfA/wo+x2//PtD/wB8D/CgD4K2t6UbW9K+9fsdv/z7Q/8AfA/wo+x2/wDz7Q/98D/CgD4K2t6UbW9K+9fsdv8A8+0P/fA/wo+x2/8Az7Q/98D/AAoA+CtrelG1vSvvX7Hb/wDPtD/3wP8ACj7Hb/8APtD/AN8D/CgD4K2t6UbW9K+9fsdv/wA+0P8A3wP8KPsdv/z7Q/8AfA/woA+CtrelG1vSvvX7Hb/8+0P/AHwP8KPsdv8A8+0P/fA/woA+CtrelG1vSvvX7Hb/APPtD/3wP8KPsdv/AM+0P/fA/wAKAPgra3pRtb0r71+x2/8Az7Q/98D/AAo+x2//AD7Q/wDfA/woA+CtrelG1vSvvX7Hb/8APtD/AN8D/Cj7Hb/8+0P/AHwP8KAPgra3pRtb0r71+x2//PtD/wB8D/Cj7Hb/APPtD/3wP8KAPgra3pRtb0r71+x2/wDz7Q/98D/Cj7Hb/wDPtD/3wP8ACgD4K2t6UbW9K+9fsdv/AM+0P/fA/wAKPsdv/wA+0P8A3wP8KAPgra3pRtb0r71+x2//AD7Q/wDfA/wo+x2//PtD/wB8D/CgD4K2t6UbW9K+9fsdv/z7Q/8AfA/wo+x2/wDz7Q/98D/CgD4K2t6UbW9K+9fsdv8A8+0P/fA/wo+x2/8Az7Q/98D/AAoA+CtrelG1vSvvX7Hb/wDPtD/3wP8ACj7Hb/8APtD/AN8D/CgD4K2t6UbW9K+9fsdv/wA+0P8A3wP8KPsdv/z7Q/8AfA/woA+CtrelG1vSvvX7Hb/8+0P/AHwP8KPsdv8A8+0P/fA/woA+CtrelG1vSvvX7Hb/APPtD/3wP8KPsdv/AM+0P/fA/wAKAPgra3pRtb0r71+x2/8Az7Q/98D/AAo+x2//AD7Q/wDfA/woA+CtrelG1vSvvX7Hb/8APtD/AN8D/Cj7Hb/8+0P/AHwP8KAPgra3pRtb0r71+x2//PtD/wB8D/Cj7Hb/APPtD/3wP8KAPgra3pRtb0r71+x2/wDz7Q/98D/Cj7Hb/wDPtD/3wP8ACgD4K2t6UbW9K+9fsdv/AM+0P/fA/wAKPsdv/wA+0P8A3wP8KAPgra3pRtb0r71+x2//AD7Q/wDfA/wo+x2//PtD/wB8D/CgD4K2t6UbW9K+9fsdv/z7Q/8AfA/wo+x2/wDz7Q/98D/CgD4K2t6UbW9K+9fsdv8A8+0P/fA/wo+x2/8Az7Q/98D/AAoA+Ctrehr134DfDeTX9UTXNbtnGk2bhoUkXAuZRyOD1UdT2J49a+mPsdv/AM+8P/fA/wAKlAx8oG0CgB2AAOOB0pRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV8P8AxB/5H3xD/wBhK5/9GtX3BXwv4wl+0eLNZm6+ZfTP+bsaAPof9lgf8UFfe+oP/wCi0r2HFeS/svxbPh1K/wDz0v5T+SoK9aoAQimMucgjINSUYoA8c1r9nrQb/Upbqw1K60+KVixgVFdVz2UnBA9jmsW//Zsj2Z0/xG2/0mtRj8w1e+V5J8X/AIu2/hhJNI8PslzrTDa8n3ktc+vq3ovbv6UAfPXi7w3feEtfudG1Extc25GWibKspAII78g9MZr2r9lXWZ5bbWNGlkLQwGOeFSfu7shsfkDXgN/eXF/dy3V5M89xMxeWWQ5Z2PUk19K/s4+C7vw/ot1rGpRmGfVAghjYYZYlyQWHYknOPQCgD2CiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKDRQaAPPtR/4/7j/rof510Pgz/jxm/66f0Fc9qP/H/cf9dD/Ouh8Gf8eM3/AF0/oK5YfxGe9i/92XyOgFFAorqPBCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBksgijZ26KCTXwZqEnn39zLnPmSs/5kmvuLxVdCy8M6rdZx5FnNL+SE18Kk5oA+tP2crfyfhZYPjHnzTyf+Plf/Za9Krjfg1a/ZPhd4fj6brYS/wDfTFv612WaACiiigDwT4yfGeSCa78P+FGKSxsYbm/HYjhlj9x0Lfl618/yyNK7O7FixySTkk+pr1nxt8FfFEXii7bRLP8AtCwuZmkimEyKVDHOGDEEEZxnocZ9q2fD37OlzNGJfEGspbsRnyrRN5H1Y4H5A0AeI2tzLa3MVxA+yWJg6tgHDA5B5r3v4U/G+4vL2DR/GJjZpSI4b9QF+Y9BIOnP94Yx3HepNd/Z2sI9Jnk0TVrt72NCyRzhSkhA+7wARnpmvn0qyMdwIYHBHQg0AffVFcd8INek8Q/D3Sb2dt86xGCZj1LISuT7kAH8a7GgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPPtR/4/5/+uh/nXQ+DP8Ajxn/AOun9BXPaj/x/wA//XQ/zrofBn/HjP8A9dP6CuWH8RnvYv8A3ZfI6AUUCiuo8EKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAOI+NN/wD2d8L9dlzhpYfIH/A2C/yNfHFfVf7Sxn/4VowhUmM3kXnEdk+bB/76218rxRSTyiOJGeRjgKoyT9BQB9KeHvjj4L0rQNN09l1LNpaxQnZbDGVUA4+b1FX/APhoTwV/c1X/AMBl/wDiq+ax4e1pvu6Tft/27P8A4Uv/AAjut/8AQG1D/wABZP8ACgD6T/4aE8Ff3NV/8B1/+KqnpP7Q3h+81MW99p15YWzttW5dlcD3ZRyB9M189Dw1rrfd0TUf/AWT/CtbRPh34s1m5SC20G+jVyB5s8LRRr7lmGMUAfZkUizRq8Th0cBlYHIIPQ1Pjisjw9DDo+kadoz3cck9pbRQYZgHfYgXdjOecVxPxI+Mui+FI5bTTGTU9WGV8pGzHEfV2H/oI59cUAdJ8QPGemeCdElv7+UGdlIt4FPzzN2AHoO57CvjCaYzyyTORukYuQOxJzWl4m8Q6n4m1STUNZunnnc8ZPyovZQvRR7Cu1+DnwvufGWoJqGoxtDoUD5kfGDckH7i+3qe3TrQB7f8AtLn0v4Y6Yt0CslwZLgKf4VZiV/MYP416FUMMccEaRxIqIihVVRgADgAD0qagAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPPtQ/wCP+f8A66N/Ouh8Gf8AHlP/ANdP6Cue1D/j/n/66N/Ouh8Gf8eU/wD10/oK5YfxGe9i/wDdl8joBRQKK6jwQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAq6hY2+o2k1nfQR3FtMpSSKQblcHsRXO+G/hx4V8M6g19o+kxw3JyBIzM5QHrt3E7fwrrAMUUAIB+VLRRQAVQ166ntND1G4s13XEFtLJEPVwpIH51fptAHwfd6hd3l897c3MktzKxdpXclix6nNRW8Us8yxQxvNI5wqqCST6ADqa+pNV+BPg/UdTe7T7daB2LPDBIBHnvgFSQPYHFdV4S+H/hrwim7RdNRLjbg3Ev7yU/8AAj0+gwKAPHPhn8DLi78rU/GqNb25wyaepxI47byPuj/ZHPrivoOztYLO2jt7SFIIIlCJGi7VUDsAOlWRSUAAFLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHn2of8f8/wD10b+ddD4M/wCPKf8A66f0Fc9qH/H/AD/9dG/nXQ+DP+PKf/rp/QVyw/iM97F/7svkdAKKBRXUeCFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAlLSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHn2of8f8AP/10b+ddD4M/48p/+un9BXPah/x/z/8AXRv510Pgz/jyn/66f0FcsP4jPexf+7L5HQCigUV1HghRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRWfrWq2mi6Xc6lqMyw2tshkkY9gPT1PYDuaAOV+LvjyPwNoBlgKSandZS0iPPPd2H90fqcCvmW4+IvjKeRpG8TamGc5O24Kj8AMAfQVH8QPFt34z8TXGrXeVjJ8u3hJyIox0X69z6kmuj+E/wybxqlze6jNNaabD+7SSIDdJJxkDIxgDqfXAoA5r/hYXjD/oZ9W/8C3/AMaP+FheMP8AoZ9W/wDAp/8AGvZP+GffD3/QW1P/AMh//E0v/DPvh7/oLan/AOQ//iaAPGv+FheMP+hn1b/wKf8Axo/4WF4w/wChn1b/AMCn/wAa9l/4Z98Pf9BbU/8AyH/8TR/wz74e/wCgtqf/AJD/APiaAPGv+FheMP8AoZ9W/wDAp/8AGj/hYXjD/oZ9W/8AAp/8a9l/4Z98Pf8AQW1P/wAh/wDxNH/DPvh7/oLan/5D/wDiaAPGv+FheMP+hn1b/wACn/xo/wCFheMP+hn1b/wKf/GvZf8Ahn3w9/0FtT/8h/8AxNH/AAz74e/6C2p/+Q//AImgDxr/AIWF4w/6GfVv/Ap/8aP+FheMP+hn1b/wKf8Axr2X/hn3w9/0FtT/APIf/wATR/wz74e/6C2p/wDkP/4mgDxr/hYXjD/oZ9W/8Cn/AMaP+FheMP8AoZ9W/wDAp/8AGvZf+GffD3/QW1P/AMh//E0f8M++Hv8AoLan/wCQ/wD4mgDxr/hYXjD/AKGfVv8AwKf/ABo/4WF4w/6GfVv/AAKf/GvZf+GffD3/AEFtT/8AIf8A8TR/wz74e/6C2p/+Q/8A4mgDxr/hYXjD/oZ9W/8AAp/8aP8AhYXjD/oZ9W/8Cn/xr2X/AIZ98Pf9BbU//If/AMTR/wAM++Hv+gtqf/kP/wCJoA8a/wCFheMP+hn1b/wKf/Gj/hYXjD/oZ9W/8Cn/AMa9l/4Z98Pf9BbU/wDyH/8AE0f8M++Hv+gtqf8A5D/+JoA8a/4WF4w/6GfVv/At/wDGj/hYHjD/AKGfVv8AwLf/ABr2X/hn3w9/0FdT/wDIf/xNH/DPvh7/AKC2p/8AkP8A+JoA2fC08914b0y5upmnmmto3eRjlmYqCST3Jrzv4xeJ9d0XXrO30fV7yxhktBI0cEzIC29hkgHrgCvUbPTotJtIdPgZ3S1QQq7dSFGATjvWTrvwy03xrcR3+oXt1A8CeSBDtwRknJyDzzXLD+Iz38X/ALsvkeFf8LC8Y/8AQz6r/wCBb/40f8LC8Y/9DPqv/gW/+Neyf8M/eHv+gtqf/kP/AOJo/wCGfvD3/QW1P/yH/wDE11HgHjf/AAsLxj/0M+q/+Bb/AONH/CwvGP8A0M+q/wDgW/8AjXsn/DP3h7/oLan/AOQ//iaP+GfvD3/QW1P/AMh//E0AeN/8LC8Y/wDQz6r/AOBb/wCNH/CwvGP/AEM+q/8AgW/+Neyf8M/eHv8AoLan/wCQ/wD4mj/hn7w9/wBBbU//ACH/APE0AeN/8LC8Y/8AQz6r/wCBb/40f8LC8Y/9DPqv/gW/+Neyf8M/eHv+gtqf/kP/AOJo/wCGfvD3/QW1P/yH/wDE0AeN/wDCwvGP/Qz6r/4Fv/jR/wALC8Y/9DPqv/gW/wDjXsn/AAz94e/6C2p/+Q//AImj/hn7w9/0FtT/APIf/wATQB43/wALC8Y/9DPqv/gW/wDjR/wsLxj/ANDPqv8A4Fv/AI17J/wz94e/6C2p/wDkP/4mj/hn7w9/0FtT/wDIf/xNAHjf/CwvGP8A0M+q/wDgW/8AjR/wsLxj/wBDPqv/AIFv/jXsn/DP3h7/AKC2p/8AkP8A+Jo/4Z+8Pf8AQW1P/wAh/wDxNAHjf/CwvGP/AEM+q/8AgW/+NH/CwvGP/Qz6r/4Fv/jXsn/DP3h7/oLan/5D/wDiaP8Ahn7w9/0FtT/8h/8AxNAHjf8AwsLxj/0M+q/+Bb/40f8ACwvGP/Qz6r/4Fv8A417J/wAM/eHv+gtqf/kP/wCJo/4Z+8Pf9BbU/wDyH/8AE0AeN/8ACwvGP/Qz6r/4Fv8A40f8LC8Y/wDQz6r/AOBb/wCNeyf8M/eHv+gtqf8A5D/+Jo/4Z+8Pf9BbU/8AyH/8TQB43/wsLxj/ANDPqv8A4Fv/AI0f8LC8Y/8AQz6r/wCBb/417J/wz94e/wCgtqf/AJD/APiaP+GfvD3/AEFtT/8AIf8A8TQB43/wsLxj/wBDPqv/AIFv/jR/wsLxj/0M+q/+Bb/417J/wz94e/6C2p/+Q/8A4mj/AIZ+8Pf9BbU//If/AMTQB43/AMLC8Y/9DPqv/gW/+NH/AAsLxj/0M+q/+Bb/AONeyf8ADP3h7/oLan/5D/8AiaP+GfvD3/QW1P8A8h//ABNAHjf/AAsLxj/0M+q/+Bb/AONH/CwvGP8A0M+q/wDgW/8AjXsn/DP3h7/oLan/AOQ//iaP+GfvD3/QW1P/AMh//E0AeN/8LC8Y/wDQz6r/AOBb/wCNH/CwvGP/AEM+q/8AgW/+Neyf8M/eHv8AoLan/wCQ/wD4mj/hn7w9/wBBbU//ACH/APE0AeN/8LC8Y/8AQz6r/wCBb/40f8LC8Y/9DPqv/gW/+Neyf8M/eHv+gtqf/kP/AOJo/wCGfvD3/QW1P/yH/wDE0AeN/wDCwvGP/Qz6r/4Fv/jR/wALC8Y/9DPqv/gW/wDjXsn/AAz94e/6C2p/+Q//AImj/hn7w9/0FtT/APIf/wATQB43/wALC8Y/9DPqv/gW/wDjR/wsLxj/ANDPqv8A4Fv/AI17J/wz94e/6C2p/wDkP/4mj/hn7w9/0FtT/wDIf/xNAHjf/CwvGP8A0M+q/wDgW/8AjR/wsLxj/wBDPqv/AIFv/jXsn/DP3h7/AKC2p/8AkP8A+Jo/4Z+8Pf8AQW1P/wAh/wDxNAHjf/CwvGP/AEM+q/8AgW/+NH/CwvGP/Qz6r/4Fv/jXsn/DP3h7/oLan/5D/wDiaP8Ahn7w9/0FtT/8h/8AxNAHjf8AwsLxj/0M+q/+Bb/40f8ACwvGP/Qz6r/4Fv8A417J/wAM/eHv+gtqf/kP/wCJo/4Z+8Pf9BbU/wDyH/8AE0AeN/8ACwvGP/Qz6r/4Fv8A40f8LC8Y/wDQz6r/AOBb/wCNeyf8M/eHv+gtqf8A5D/+Jo/4Z+8Pf9BbU/8AyH/8TQB43/wsLxj/ANDPqv8A4Fv/AI0f8LC8Y/8AQz6r/wCBb/417J/wz94e/wCgtqf/AJD/APiaP+GfvD3/AEFtT/8AIf8A8TQB43/wsLxj/wBDPqv/AIFv/jR/wsLxj/0M+q/+Bb/417J/wz94e/6C2p/+Q/8A4mj/AIZ+8Pf9BbU//If/AMTQB43/AMLC8Y/9DPqv/gW/+NH/AAsLxj/0M+q/+Bb/AONeyf8ADP3h7/oLan/5D/8AiaP+GfvD3/QW1P8A8h//ABNAHjf/AAsLxj/0M+q/+Bb/AONH/CwvGP8A0M+q/wDgW/8AjXsn/DP3h7/oLan/AOQ//iaP+GfvD3/QW1P/AMh//E0AeN/8LC8Y/wDQz6r/AOBb/wCNH/CwvGP/AEM+q/8AgW/+Neyf8M/eHv8AoLan/wCQ/wD4mj/hn7w9/wBBbU//ACH/APE0AeN/8LC8Y/8AQz6r/wCBb/40f8LC8Y/9DPqv/gW/+Neyf8M/eHv+gtqf/kP/AOJo/wCGfvD3/QW1P/yH/wDE0AeN/wDCwvGP/Qz6r/4Fv/jR/wALC8Y/9DPqv/gW/wDjXsn/AAz94e/6C2p/+Q//AImj/hn7w9/0FtT/APIf/wATQB43/wALC8Y/9DPqv/gW/wDjR/wsLxj/ANDPqv8A4Fv/AI17J/wz94e/6C2p/wDkP/4mj/hn7w9/0FtT/wDIf/xNAHjf/CwvGP8A0M+q/wDgW/8AjR/wsLxj/wBDPqv/AIFv/jXsn/DP3h7/AKC2p/8AkP8A+Jo/4Z+8Pf8AQW1P/wAh/wDxNAHjf/CwvGP/AEM+q/8AgW/+NH/CwvGP/Qz6r/4Fv/jXsn/DP3h7/oLan/5D/wDiaP8Ahn7w9/0FtT/8h/8AxNAHjf8AwsLxj/0M+q/+Bb/40f8ACwvGP/Qz6r/4Fv8A417J/wAM/eHv+gtqf/kP/wCJo/4Z+8Pf9BbU/wDyH/8AE0AeN/8ACwvGP/Qz6r/4Fv8A40f8LC8Y/wDQz6r/AOBb/wCNeyf8M/eHv+gtqf8A5D/+Jo/4Z+8Pf9BbU/8AyH/8TQB43/wsLxj/ANDPqv8A4Fv/AI0f8LC8Y/8AQz6r/wCBb/417J/wz94e/wCgtqf/AJD/APiaP+GfvD3/AEFtT/8AIf8A8TQB43/wsLxj/wBDPqv/AIFv/jR/wsLxj/0M+q/+Bb/417J/wz94e/6C2p/+Q/8A4mj/AIZ+8Pf9BbU//If/AMTQB43/AMLC8Y/9DPqv/gW/+NH/AAsLxj/0M+q/+Bb/AONeyf8ADP3h7/oLan/5D/8AiaP+GfvD3/QW1P8A8h//ABNAHjf/AAsLxj/0M+q/+Bb/AONH/CwvGP8A0M+q/wDgW/8AjXsn/DP3h7/oLan/AOQ//iaP+GfvD3/QW1P/AMh//E0AeN/8LC8Y/wDQz6r/AOBb/wCNH/CwvGP/AEM+q/8AgW/+Neyf8M/eHv8AoLan/wCQ/wD4mj/hn7w9/wBBbU//ACH/APE0AeN/8LC8Y/8AQz6r/wCBb/40f8LC8Y/9DPqv/gW/+Neyf8M/eHv+gtqf/kP/AOJo/wCGfvD3/QW1P/yH/wDE0AeN/wDCwvGP/Qz6r/4Fv/jR/wALC8Y/9DPqv/gW/wDjXsn/AAz94e/6C2p/+Q//AImj/hn7w9/0FtT/APIf/wATQB43/wALC8Y/9DPqv/gW/wDjR/wsLxj/ANDPqv8A4Fv/AI17J/wz94e/6C2p/wDkP/4mj/hn7w9/0FtT/wDIf/xNAHjf/CwvGP8A0M+q/wDgW/8AjR/wsLxj/wBDPqv/AIFv/jXsn/DP3h7/AKC2p/8AkP8A+Jo/4Z+8Pf8AQW1P/wAh/wDxNAHjf/CwvGP/AEM+q/8AgW/+NH/CwvGP/Qz6r/4Fv/jXsVx8A/DdvC88+tajHFGpd3cxgKoGST8vQCvCdbj09NUuE0ZpnsVkKwvPje6j+I4AxnrigDf0/wCJnjKyukuE8R38jIQdk0xkQ+zK2QQa+t/CWqPrfhrS9VePymvbaOdk/ullBIHt6e1fLHwd8BP438RL9qV00mzIe7k6bvSMH1Pf0GT6V9cQRRwQxwwoscUahUVRgKoGAAPQCgCeiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAr5l/aG+IK61qn/COaTNnTrF83DK3E0w7e6r0+ufQV6X8ePiCPCeg/2fp0mNX1BSiEdYIzw0n17D357V8rRJLPMqIGkmkYBQOSxJ4HuSaANrwR4YvPFviCDSrMEBzuml7RRj7zH+nqcCvrfQ9LtNF0m203ToxFbWyCNF9cdSfcnkn1rl/hJ4HTwZ4eH2pFOqXgD3T/3P7sYPoO/qc12tABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUALTZHWONnY8KCTS0yaPzYnjP8SkfnQ9rlRtza7GFJrFz5u4ABOybf61tWlx9pgWXG0EdK5Z0MbtHJ95Tg1taDc74vIbhkOR/tCuanUbdpM9nGYeHslOmtvyMu8/4+5/8Arof51reHuLaT/rp/QVkXn/H3P/10P860tIuY7axkkkbgPwO5OBUxdps2xMXLDqK8jRvLqO1iMjDJPQepqhaaw0k6pNGoBOAR2PvWZd3L3UpdxgjoOwFT6RZGaUSnhEOSfUjtTVSTlZGKwlOlS5qm50VFFFdR4gUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFcN8XfHSeDtB22rA6tegrbJ/wA8x0aQ+w7ep+hoA4X4/wDxADl/CelS/KrA38iHqRyIgfbqffj1ryLw3ol94j1m10nTIzJc3MgUeijux9gOSaozvJPMZJWaSWRixJ5LMTyfqTX1J8C/h4PCeiDVNThxrGoIC4YcwR9QnsT1PvgdqAOz8C+GLLwh4ctdIsVyIxmWUrgyyH7zn6np6DAroaKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACsPxd4isPCug3er6i22GBchc8yOeiD3J/xrZYhVy3AHJJr5S+Ovj8+LfEP2DTpQ2j6exWPHSaTo0nuOw9ue9AHE+LNfvfE+u3Wr6k+Z7ls7R0jUfdQewHFeq/s/+A/tMy+K9Uh/dRkiyjdfvMODJ9B0Hvz2rgPhj4Pn8ZeI0tMMljDiW7lH8EeegPqeg/PtX1jaW0NlbRW1pGsMEKiOONVwEUDAAoAlooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAyNes8j7VGORww/kayraZoZldDhl5/8ArV1bqHRkYZDDBrlryA21w0Z6DofUVx1YWfMj3cBW9pB0pdBs7CSeRxwCxI/Go8kAr2zmjpU9jatdzbF4A5Y+grJXbPRm4043lsiTT7FryXJyEX7zf0FdGiLHGqINqAYApsEaxRiOMAIvepO9dtOCivM+cxeJlWl5LYKKKK0OQKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAOY+I3jK28EaEL+aBriaaTyoIScB3xnk9gB1rzjw58ffMu1i8RaZFDbyHHn2pYmP3KnOR9Dn2rvvit4Kk8beHUtbV1jv7WTzrcv91zjBViOgI79jXzN4m8Nav4Xv/seuWL2srDKlsFXHqrDIP50AfYOm6hZ6lZxXun3MVzbTDKSRtlSP89qsV8eeFPGeu+FJy+jXrxRk5eBzujk+qnj8Rg+9et+HP2gLOUJF4k0yWBuhmtDvX6lGII/AmgD2ij9BWB4e8aeHfEK50jVYJ3A3GItskA/3Dz+lTXt61wcD5Yx29frXl5lmVPA07vWT2R0UKEqr02LV1qCxgrBtY927Cqv9oXH/PT/AMdFVaMCvz7EZxiq8+fma8lsezHC04K1jUtdREmFlwpPftV+ub6VsaZc+bGUY5df1FfS5LnM60/YV3d9H38jgxWF5Fzw2LlFFFfYHmhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFMnmSCB5ZTtSNS7H0AGTQVGLk7IwfGXiy08LWQeYeddSZ8qAHBfHc+ij1ryDU/HfiLULhpDqUkCnpHAAij8ufzNZ/ifW59f1u4v5ycOcRJn7kf8I/Lr71k8Y4rx6+IlKVk9D9FyzJ6WHpKVSKcnvfW3kjstB+I+u6ZcIby5/tC3z88c2M49m6g/mK9a0LxVo2uqgsL6IzuoIhY7XHtg+ntmvnSnRO0bh0dlZTkFWwQR3BpUsVKOj2HjsioYjWn7r8tj6joFea/D74ipcLHpviCTbP92O6b7r+gb0b36HvzXpXavVp1FUV0fB4vB1cJUcKi/yfoFFFFaHGFFFFABRRRQAUUUUAFFFFABRRR6/NtUckntQBneJNbsvDui3OqalJ5dvbrknu57KvqSeBXyT4w8SXvirXbnVdQb5pTiOMHiKMfdQewH5nmur+NXj0+LNa+wac+NJsmPlkdJ36GQ+3Ye3Pesb4Y+CLvxz4misY90dnDiS7mH/LOPPQf7R6D8+gNAHc/s+fDo6xfp4n1iL/AEC0k/0WNl4nlH8X+6p/M/Q19LVU0ywttMsYLGxiWG2t0EccajAVRwKt0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFcv8RPF1p4K8NXGq3OJJfuW8OeZZD0H07k+goA8//aH+IQ0fT28M6RNi/vEzdSK3MMJ/h9mb9F+or5z0+xudSvrexsYmmubhxHHGvVmJwAKl1rU7vWdTudR1CYzXN1IZJHPcn09AOgHYV7n+z74E+wWi+J9Uhxc3K4skYcxp3f6t29vrQB3vw68IW/gzw5Fp0RV7p8SXUy/8tJMc/gOg/wDr10tFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRSAKz9ZsjcwiSIfvE6j1FaFFKUVJWNKVV0pqaORWJ3fywpLnjHeul060W0tlXHzHlj71YwPSlrOFNRZ1YnGSrRUbWQUUUVscIUUUUAFFFFABRUUt1bw/wCunhj/AN5wP5mqUviHRIf9drGnJ9bqP/GgDSorn5vHHhODPmeJNMH0uVP8jVGf4peCbf7/AIgtj/uB3/8AQQaAOuorgp/jN4Hi/wCYpLL/ANc7aT+oFUJ/jp4OT/VnUZvpAB/M0AemUV5LN+0B4cX/AFOl6o/+8I1H/oRqnP8AtC2Az5Hh65f/AH7lV/kpoA9morwmb9oaY/6jw5Ev/XS7J/koqnP+0HrDf6jRbCP6u7f1FAH0FRXzbN8evFsn+rg0uIe0DE/q1UZvjb42l6XttH/uWqf1BoA+oKK+UZ/i345m/wCY9Kn/AFzijX+QqjP8RPGM/wB/xHqH/AJdv8sUAfXlB/IV8Zz+K/Ec/wDrte1N8/3rqQ/1qlJqN9Mf319cP/vysf5mgD7Sku7aP/WXMKY/vSKP61TuPEWh2/8Ar9Y0+LH9+5Qf1r4xeRm+87N9TmmdaAPsKfx74Rh/1niTS/8AgNwrfyJqjN8U/BEP3vEFu/8AuI7fyWvkuigD6mm+MvgaLpqkz/7ls5/oKoz/AB18HJ/qxqEv+5AB/NhXzZDbzzf6mKWT/dQn+VXYvD+szf6nSL+T/dtnP9KAPd5v2gfDy/6nSdSk/wB7y1/qapTftD2P/LDw9cf8DuFH8lryODwP4qnx5Ph3Umz/ANOz/wCFX4fhf41mxt8O3Y/39qf+hEUAd/P+0PcH/UeG4R7vdE/oFFZ9z+0Frrf8e+j6dH/vGRv5MK56D4NeN5fvaSsX+/cR/wBGq/D8CvGMgy40+L/fuf8AAGgCSb48+LnH7qHTYf8AdgJ/mxqjN8avG0v/AC/28f8AuW6D+YrXg+AHiVz++1HSov8AgcjfyWrsH7POpMQJ9ftEH/TOBm/mRQBxs3xY8cSf8zBMqnssca/yWqM/xD8Xz/f8R6kP9ycr/LFenw/s8IP9f4kZv+udpj/2Y1eh/Z80df8AXa5eyf7saL/jRddQPFJvFfiGf/Xa3qb/AFun/wAao3d/d3ePtd3PcY5HmyF8fma9/vPgl4N0jTbi/wBQvdUaC1iaaUmVB8oGTwF/rXg2rS2M97NJpVu9tabv3ccsm9wPc8ZPrgYoAzzRXQ+DPB2qeMdWWx0qH5RgzTsP3cK+rH+Q6mvo7w18LPCujaYlvNptvqVx1kubpAzO3sDwo9h+tAHzV4OjvpPEenLpm4XXnqUK9ueSfbHX2r6nP6VWh0jS9Nupf7N060tMEjMMKocfXFWa/NM8zGOMrKMVZRuvU97B0nTjd9RaKKK+eO0TvVrSm23ij+8CKq96t6VHm5L9lU16WVxlLF0+XujDENeylfsbFFFFfrR82FFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVyvxTvjY+C70q2159sC/8CPP6A11RrhPjV/yKcPvcp/I1lWdoP0O/LoqWKgn3R4pRRRXhH60FFFFIBa95+Feqy6r4TiNy5eW3doC56kDBGffBx+FeD9q9u+Dls0Pg9ZJFx50zuv0GF/mDXbg2+f5Hy/EsY/VlJ73R21FHWivWPz4KKKKACiiigAooooAKKKKACvIPj34+/sy0PhnSZ8XVymbuRW5ijPRM/3mHX0H1rtfiX4yt/BXh5719r3s2YrWFv439T/sjqfy718m397cahey3l7K0txO5kkkY5LMTkmgCTS9PutV1GCxsIjNc3DiONF/iJr7D+Gng218D+G49PhxJdy4ku5wP9ZIR2/2R0H+JNcN+z38PP7GsE8T6tBt1C7T/Ro2XmGE/wAWOzN+g+pr2igBAKWiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvc3MVpby3FzIsUMKGR3Y4CqBkk/hXyF8XPHMnjbxK88bMNMtSYrSI8fLnlyPVuvsMDtXo/wC0f8QRtPhDSZcE4bUHU9P7sX9T+A9a8R8P6Nea/rNrpenpvuLlwq+g9WPoAOaAOt+D3gV/GGv+ddxn+yrAh7g9nbtGD79/QfUV9SIixqFUBVAAAHAAHQCsjwd4cs/CugW2kWIJWEZkk24Msh+85+p/IcVsnkUAJRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUVl61qi2a+VCwM7/+OD1+tYV68aFNzm9jSlSdWajEsahqcFguXbdJ2jHX8fSufudavZz8r+Un91f8etZ7M0jFmbcx5JNJXyGLzKtXfuvlj2R9HhsBTpq8ldlj7fdr/wAvEmfqa1tJ11ndYbwjngP/AI1g0Vz4fG1aM+ZSb9TerhadSNrHe1578Z/Hl14L02zj0xEN9fF9kkg3KirjccdzlhjPFdtpExm02J35bGCf0rC+Ifgiz8b6ZFbXMz209uxeCdV3bCeCCD1U9xmvu6U1UgprqrnylSLhJxfQ+epvi344l+9rrp/1zhiX+S1Rn+IvjGfPmeJNQ/4DMV/lXpkH7O6/8tvEf/fFr/i1Xof2e9IX/X69fSf7kKL/AFNWQeLzeLfEc/M2u6k31un/AMaoz6rqE/8Ar7+5l/3pmP8AM19CQ/APwtH/AKy81SX6yIB+i1fh+CPguL79reS/79ww/ligD5iLM3VifqabX1bD8IfA0OP+JH5n+/PIf/ZhV2D4a+DYMbfDlif98F//AEImkI+RaK+yYPB3hiDHk+H9LT6Wif4VoRaRpkH+p02yj/3bdB/SgD4rW3nk+5DI/wBFJq1DoerT/wCo0u9k/wB2Bz/SvtONEiGIkVR/sqB/Kn5PvQB8bweCvFE/+r8PaofrauP5itCH4Z+NJsbPDl6P99Av8yK+uMmjmgD5Vh+D3jmfH/EmEf8Avzxr/wCzVeh+BvjOTG6Gyi/37kf0Br6c5ooA+cofgF4nb/XX2mx/SV2/9lq9B+z3qZ/12u2S/wC5C7fzxXv9FAHh0H7PCDH2nxKfoll/Ut/Sr0H7Pmj8edrWoN/uxov8817HRQB5VD8BPC0f+su9Tl+sqD+S1fh+CPgmP71teSf79yf6AV6NRQBw8Hwj8DQ9NCVz/wBNJ5W/9mxV+H4c+DYfu+HNPP8AvR7v5k11NFAGJD4P8MwY8nw/pif9uqH+Yq9BpOmQf6jTbKL/AHLdB/IVdooAYqIv3UVfoop24+tLRQAm4+tGT6mlooASiiimMKq6jfRWFuZpuewUdW+lTyypDG0khwqjJNcPqt89/dmR8hBxGvoK8/G4tUIWXxPYwqz5V5kl/qt3euS0jRx/wxocD8fWqe9/7xz9abzRXzE6s5vmk9Tz5Sk3e5PNdyXmmXOmXrvPaXcLQyKT8wVhgkE9x1Feb2fwG1i5v4yNTsf7MY5FwpYyFP8AcxjP44zXoFdf4TZn0oZP3ZGA/Q17GWYmcpOEnc6sPUbfKx/hnw/p3hnSo9P0iERQryxPLSN3Zz3J/wD1VqCiivfO4w9Qi8q4bPRzuH41DW7PClwpRxn0PcVnTadImTH8w9O9fnma5JWp1JVaS5ovXTdHsYbFxaUZblOijj6Ui/Nwq5J7CvmFCTfKlqehzIAc/jW3YW3kQ8j5m5NQ2Nj5YEsw+bqAe1Xq++yLKnh/39VWk9l2X+Z4+MxKn7kdgooor6w84KKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArlvifpr6l4OuliXdJblZ1Hrt6/oTXVUhAIIIyD1FROPNFx7m+HqujVjUXRp/cfLVGK7v4heArnR7mTUNJiM2nOSzRqMtAe4x3X0PbvXCfWvDnTlTdpH6thMZTxdJVIO/6CUUtEatJIqIGZmOAFGST7CszqlJRV2WtOspdRvoLO2G6Wdwi/XPX6Dqa+j9I0+PS9LtbGD7kESxg+uByfxPNcV8L/BL6Ov9rasmL2VcRxHrCp6k/wC0f0Feg16+Go8kbvdn55n2YRxNRU6b92P4sKKKK7D5sKKKKACiiigAooooAKrapqFrpOm3GoahKIba2jLyOewH9T0A7mrNfOvx48ejW9Sbw/pcudNs5Mzup4nlHb3Veg9Tk+lAHGfEDxfdeMvEM2o3JMcK/JbQjpFHngfXuT611nwH+Hn/AAles/2rqsOdIsHB2svE8o5Ce6jqfwHeuO8CeFb3xl4ittIsFxvOZpccRRj7zH6dvU4FfZHh7RLDw9o9rpOlw+Ta2qBFXufVie5J5J9aANJECKAoAA9KdRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVw/xb8dReB/DMlxEytqd1mO0ibn5u7kei5z7nA711OsalaaPptzqGoSiG2tkMkjt0AH9fbua+OPiP4wu/GviafUrndHCP3dtCf+WUY6D6nqfc0Ac/dTy3dzLcXMjSzTMZHdjksxOST9TX0j8DPAn/CN6R/a+pxY1S/QEKRzDCeQvsT1P4CvOvgV4E/4SLWP7b1GLOm6e42Kw4nlHIHuo6n8B619IdBQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFICrqd2lnatKTlgMKPU1xsjNK7SO25mOSfetTxPceZfCFT8safqeayhXxmaYp1qrgto6fM+ly6gqdNTe7CiiivJPTCiiimtxHW6B/yCYfx/ma0BVfT7fyLKGI/eVQD9e9WK/QsNFwpRi90kfG15c1Vtd2FFFFbmQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHP+K73Yi2SHiT55Pp2FczkZ4NXdal87VLh2PAYqPoOKo96+NxlZ1Krk/RHmVZ80mO60GiiuYyErsfCy7dIjP95mP61yCI0jqkY3OxwB6131hB9ltIoAPuIAfr3/WvXyqm3Uc+iOnDx1uTHrRRRX0h3hRRRQAySGOQjeit9RQsKR/6tFX6LWRrlxJ5wiUlEAB44yadoVzIzPEzMUAyM9q5eSl7S6ir97HoPDVFR9pzadjZ6jmigUV1HAJRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK5/VvBHhzVHaW501FlbrJGTGT9cEA/lXQUUnGMtJK5tSrVaLvTk0/J2OHb4UeHTyGuwPTzRj+Vbeh+ENE0JhJp9kol/56yEu/wCBPT8MVu4oqFSprVRN547E1I8s5tr1DrRRRVnEFFFFMAooooAKKKKACiisPxz4os/CHh641O8IYr8sEXeWT+FR/MnsKAOP+OHj/wD4RrS/7I0uUDVb5DllPMER4LezHoPxPpXzfbQTXlzHBAjyzSsFjRRlnYnAAHck1Z13VbzW9VudT1GUy3Ny5d27ewHoAOB7V7j+zl8PNir4v1iH5mythEw6DvL/AEH4n0oA774P+AovBPh9FnVX1a7AkvJRzg9owfQfqcn0rvqKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiivM/jp8QR4P8Pmy0+bbrN+pWEjrCnRpPr2Hvz2oA81/aH+II1jUT4X0qbNjZvuupFPEso/h9wv6t9BXmvgvw1eeLPENtpViMGU7pJMcRRj7zH6fqcCscCSaUKoZ3c4AHzFiT+uTX1N8H/A6eDvDwe7UDVb0CS5OOYx2jB9u/v+FAHVaHpNnoOkW2macnlW9sgRV7n1J9STyT61dJzS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRQKAOP1z/kLT/wC9/QVSrZ8TWLLcfalGY5AA/sRWNXwOOpyp15X7n12EqKdKNuwUUUVyHQFa/h7TzPOLiQfu0+77t/8AWqLStIa7cSygxxZ692+n+NdTGiQxrHGqqqjAAr3csy6U5KrUWi28zycdjFGLp03q9x+KKB0or6w8ASiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHB6pGYtSuFbtIxH0JzVWuz1rRo78eYh8uYDGexHvXL3mmXlmf30JK/315H518li8JVpzbtddzzKlKSbKlLSqrMcKCT7Vt6RoLyMs18DHEORGer/AF9BXPRw860uWKJjBydibwtph3fbZl9owf1b/Cuj700ALwvAHAxTq+tw1BUaagelCmoLQKKKK6DQKKKKBHP69/x/f8AFSaB/x9Sf7n9RUevf8f3/AAAVJoH/AB9Sf7n9RXL/AMvD6CX+5/I3KKKK6j58KKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKQBRRRTAKKKKACiiigCO5nitreSe5lWKGJDJI7nAVQMkn6CvlT4qeN5vGmvtNEzJpttmO1iP93u5H94/oMCu5/aA8fGaU+FdJlxGhBv5FP3mHSL6Dqffjsa8n8M6De+JNbtdJ0yPfcXLbR6KO7H0AHJoA6v4M+AZfG/iENdI39kWLCS5bGPMP8MYPqe/oPwr63hiSCGOKJFjSNQqqowFA4AFYvgvwzYeEtAtdH05f3cQy7lfmlc9XPuT+QwK38UALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUtFJQBk+KvENl4Y0K61bU22wWy5x3duiqPcnivjTxd4kvvFfiC61bUTmSdvlQdI0H3UHsB/jXbfHj4gf8JZrv9m6bNnSNOchSOlxL0Z/cDoPbJ71zPw08IXHjLxFHYpmO0ixLdTf3EB6D/aPQfn2oA734AeBBeXI8UarFm3gYizjYf6xx1k+g6fX6V73UNnZ29hZwWdnEIbe3jEcUa9FUDAFTUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAI6h0KuFZTwQayLrw/bSMWhZoc9hyK2MUVhWw1KurVFc1p1qlJ+47GB/wjX/Tzx/uf/Xq7aaHaQEM4MrD+90/KtKiuenl2Hpu6jr95tLGVpKzYmPTp6UtKKK7zlEooooEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUyWRYoy7HgVk3N9JKeG2r6CvJzDNKWBVp6t7JHTRw86u2xqtNEnDSov40LLG/3XU/Q1g9eaTkcjivm1xTNS1pq3rqdv1BW31OjorOsL0uwjlOT2P9K0a+twWLp4ul7Snt+TPOq0pUpcsgooortMgooooAKKKKACiiigAooooAaECngKD6gU6iilawBRRRTAKKKKACiiigDn9d/wCP8f7gqTw//wAfUn+5/UVHrv8Ax/j/AHBUnh//AI+pP9z+orlX8Q+gl/ufyNyiiiuo+fCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACuE+MHjpPBugeTZuG1a9UrAP8AnmvQyH6dvU/Q11PiXW7Pw5olzquovtggXOB1kb+FR7k8CvkjxZ4gvvFOv3Oq6gx3zn5U7RoOiD2A/wAaAMtmknmLEmSWRtxY8lmJ/XJr6n+Bfw8XwjoY1DUYh/bN+oaTcOYEPIjHv3Pvx2rzz9nj4d/2neL4o1iDNnav/oSOvEso/jx3Cnp6n6V9J4oAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvHf2hfiAdA0o+HdJlxqN/H+/dDzBCe3szdB7Z9q73x/wCLrTwZ4cudVvMMy/JBCWwZZT0Ue3cnsAa+N9a1a81vVbrUtSmM11dOXkc+p7D0GOAOwoAr2NpPfXkNrZwtNPMwSNF6sxOAK+sfht4Ot/BfhuGyXa97LiW6mH8UmOgP90dB+feuD/Z/8Bi0tk8U6nF/pEykWMbD7iHgyfU9B7c969moAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKgvm8uzdu+Mf0rCvVVKlKb2Sb+4qMeaSj3My/uTNNhD8i9Pf3qtQRmlr8ixOIniajqTd2z6WnBQikgooormLCNzHKrjqpzXQRsHRWX7pHFc7W5p3/AB5xfT+tfY8L12qsqXRq/wBx5mPSSUixRRRX3h5AUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHP67/x/f8AARUmgf8AH1J/1z/qKj13/j+/4CKk0D/j6k/65/1Fcq/iH0Ev9z+RuUUUV1Hz4UUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABR8q7mZgqqMknoBRXjvx+8ff2fat4Y0mbbdTL/psinmND/wAs8+p7+31oA4H4zePW8Xa2bTTnP9kWLFYSOkzdDIf5D2+tZnwt8FXHjjxNHYpuSygIlvJR/DHnoD/ePQfn2rndH0271fUrfT9PhM9zcyCKNBzkn+nqewr7C+G3g6z8EeG4tMg2tctiS7nxzNKf6DoB6e+aAOi06xt9OsoLKzhSG2t0EcSIMBVAwBVukAxS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFQTzJbW8kszhIo1Lu7HAVQMkk/Sp68E/aQ+IRhQ+EtKmIkdQ186H7qnpF+PU+2B3NAHnPxg8dy+NvEkj27sNKsiYrSM/xeshHq2PwGBSfCLwM/jHxArXCH+y7Mh7p/7/8AdjB9T39Bn2rlND0m71vVbbTdOi8y5uXCKPT1J9AByT6V9b+C/DFp4S8PW2lWILbBullxzLIfvMf6egwKANqNEjjSOJQkSAIqgYAA4AA9KdRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVV1X/jzf6j+dWqZPGJYmQ/xDFcmNpOrQlCO7TX4GlKXLNSfQwKKWRGikMb9RTRX5BODptxktUfSxaauhaKKRct8qrkmlGLk7IG7CxoZJFQdWOK6CNAkaqOABiqun2nkLukGXP6Vdr9HyLLXhKbqVPil+CPDxdb2krLZCUUUV9IcQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHP67/wAf3/ABUnh//j7l/wBz+oqPXf8Aj+/4AKk8P/8AH3L/ALn9RXKv4h9BL/c/kblFFFdR8+FFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRVXWNSs9I0251G/mWG2t0LyMewHp6k9AO5oA574neM7fwX4bkuztkvp8xWsJ/if+8R6DqfwHevk69vLi/vJbq8laaedi8kjnJZick1vePvF114x8Qy6lc5SEfJbw54ijHQfXuT612HwE+Hn/CU6udX1SEtpNi4wrDi4lHIX3A6n8B3oA9E/Z9+Hf9h6ePEerR/8TG9TFvG45ghPf2Zv0HHc17HSBQMcAAdAKdQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUVV1XULbS9OuL6+lENtbIZZHPRVHJoA5X4reOIfA/heW7DBtQnzFZxH+J+7Eei9T+A718eXl3Pe3U1zdyvNPO5eSRzksxOST+NdL8S/GV1418TT385MdspMdrCf+WUeeM+56n3ro/gZ4CPiTWP7X1OLOl2DghW6TS9Qvuo6n8B3oA9F+BPgQeH9IGuanDjUr9AUVhzDD1A9i3U+2B616jTev4UtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUARXFtHcLhxyOjDrVJtLBHyzY+q1pUV5mJyvC4p81SOvfY3hiKlNWizNXS2/ikH4CrkFqkC4Qc9yetTUUsNlWFwz5qcde71CeIqTVmwooor1DAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA5/XP+P7/AIAKk8P/APH1J/uf1FR65/x/f8AFSeH/APj6k/3P6iuVfxD6CX+5/I3KKKK6j58KKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvnP47ePf7e1E6Bpcp/s6yfMzKeJpRwfqF6D1OT6V3vxz8e/8I9pZ0XSpsanep87o3NvCep9mPQegyfSvnG2t57y4itraN5Z5nCRxoMlmJwAPcmgDc8A+Fb3xl4it9IsQUV/nnmxkRRD7zH+QHc4FfZGgaPZaDpVrpelwiK2tYwiDufUk9yTyT61y/wi8Bw+B/DypMqPqt2BJdSjnB7ID/dH6nJrux0oAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvm39oz4hf2lfN4W0icNaWz5vHTpLIOifRe/8AtfSvUvjf42l8G+EWex4v75jbwP8A88+Ms/4Dp7kV8iO5kcs7FmY5JPc0AbPg7w5e+KdfttKsFG+c5eRukSD7zn2A/Xivrjw/o1l4f0e10vTIxHbW8YUernux9yeTXyj4O8b6t4O+0HRRao9zgPJLCHbA6AE9B3ro/wDhefjP/nrY/wDgMP8AGgD6bor5k/4Xn40/57WP/gMP8aP+F5+NP+etj/4DD/GgD6bor5k/4Xn40/562P8A4DD/ABo/4Xn40/562P8A4DD/ABoA+m6K+ZP+F5+NP+etj/4DD/Gj/hefjT/nrY/+Aw/xoA+m6K+ZP+F5+NP+etj/AOAw/wAaP+F5+NP+etj/AOAw/wAaAPpuivmT/hefjT/nrY/+Aw/xo/4Xn40/562P/gMP8aAPpuivmT/hefjT/nrY/wDgMP8AGj/hefjT/nrY/wDgMP8AGgD6bor5k/4Xn40/562P/gMP8aP+F5+NP+etj/4DD/GgD6bor5k/4Xn40/562P8A4DD/ABo/4Xn40/562P8A4DD/ABoA+m6K+ZP+F5+NP+etj/4DD/Gj/hefjT/nrY/+Aw/xoA+m6K+ZP+F5+NP+etj/AOAw/wAaP+F5+NP+etj/AOAw/wAaAPpuivmT/hefjT/nrY/+Aw/xo/4Xn40/562P/gMP8aAPpuivmT/hefjT/nrY/wDgMP8AGj/hefjT/nrY/wDgMP8AGgD6bor5k/4Xn40/562P/gMP8aP+F5+NP+etj/4DD/GgD6bor5k/4Xn40/562P8A4DD/ABo/4Xn40/562P8A4DD/ABoA+m6K+ZP+F5+NP+etj/4DD/Gj/hefjT/nrY/+Aw/xoA+m6K+ZP+F5+NP+etj/AOAw/wAaP+F5+NP+etj/AOAw/wAaAPpuivmT/hefjT/nrY/+Aw/xo/4Xn40/562P/gMP8aAPpuivmT/hefjT/nrY/wDgMP8AGj/hefjT/nrY/wDgMP8AGgD6bor5k/4Xn40/562P/gMP8aP+F5+NP+etj/4DD/GgD6bor5k/4Xn40/562P8A4DD/ABo/4Xn40/562P8A4DD/ABoA+m6K+ZP+F5+NP+etj/4DD/Gj/hefjT/nrY/+Aw/xoA+m6K+ZP+F5+NP+etj/AOAw/wAaP+F5+NP+etj/AOAw/wAaAPpuivmT/hefjT/nrY/+Aw/xo/4Xn40/562P/gMP8aAPpuivmT/hefjT/nrY/wDgMP8AGj/hefjT/nrY/wDgMP8AGgD6bor5k/4Xn40/562P/gMP8aP+F5+NP+etj/4DD/GgD6bor5k/4Xn40/562P8A4DD/ABo/4Xn40/562P8A4DD/ABoA+m6K+ZP+F5+NP+etj/4DD/Gj/hefjT/nrY/+Aw/xoA+m6M18yf8AC8/Gn/PWx/8AAYf40f8AC8/Gn/PWx/8AAYf40AfTdFfMn/C8/Gn/AD1sf/AYf40f8Lz8af8APWx/8Bh/jQB9N0V8yf8AC8/Gn/PWx/8AAYf40f8AC8/Gn/PWx/8AAYf40AfTdFfMn/C8/Gn/AD1sf/AYf40f8Lz8af8APWx/8Bh/jQB9N0V8yf8AC8/Gn/PWx/8AAYf40f8AC8/Gn/PWx/8AAYf40AfTdFfMn/C8/Gn/AD1sf/AYf40f8Lz8af8APWx/8Bh/jQB9N0V8yf8AC8/Gn/PWx/8AAYf40f8AC8/Gn/PWx/8AAYf40AfTdFfMn/C8/Gn/AD1sf/AYf40f8Lz8af8APWx/8Bh/jQB9N0V8yf8AC8/Gn/PWx/8AAYf40f8AC8/Gn/PWx/8AAYf40AfTdFfMn/C8/Gn/AD1sf/AYf40f8Lz8af8APWx/8Bh/jQB9N0V8yf8AC8/Gn/PWx/8AAYf40f8AC8/Gn/PWx/8AAYf40AfTdFfMn/C8/Gn/AD1sf/AYf40f8Lz8Z/8APax/8Bh/jQB73rv/AB/f8AFSeHv+PqT/AHP6iuK+H/iXUPFfh4anq5ia5Mrx5jTaNoxjj8aq/Ejxbqvg/Sra80ZoVlmm8pvNjDjG0nofcVyr+IfQS/3Neh63RXzJ/wALy8Z/89bH/wABh/jR/wALy8Z/89bH/wABh/jXUfPn03RXzJ/wvLxn/wA9bH/wGH+NH/C8vGf/AD1sf/AYf40AfTdFfMn/AAvLxn/z1sf/AAGH+NH/AAvLxn/z1sf/AAGH+NAH03RXzJ/wvLxn/wA9bH/wGH+NH/C8vGf/AD1sf/AYf40AfTdFfMn/AAvLxn/z1sf/AAGH+NH/AAvLxn/z1sf/AAGH+NAH03RXzJ/wvLxn/wA9bH/wGH+NH/C8vGf/AD1sf/AYf40AfTdFfMn/AAvLxn/z1sf/AAGH+NH/AAvLxn/z1sf/AAGH+NAH03RXzJ/wvLxn/wA9bH/wGH+NH/C8vGf/AD1sf/AYf40AfTdFfMn/AAvLxn/z1sf/AAGH+NH/AAvLxn/z1sf/AAGH+NAH03RXzJ/wvLxn/wA9bH/wGH+NH/C8vGf/AD1sf/AYf40AfTdFfMn/AAvPxn/z1sf/AAGH+NH/AAvLxn/z2sf/AAGH+NAH03RXzJ/wvLxn/wA9rH/wGH+NH/C8vGf/AD2sf/AYf40AfTdFfMn/AAvLxn/z2sf/AAGH+NH/AAvLxn/z2sf/AAGH+NAH03WB448V2XhHw/Nqd4FZx8kEXeWUj5V+ncnsK8D/AOF5eM/+e1j/AOAw/wAa5jxh401rxhcQTa3cI/2ddsccS7EXPU4Hc+tAGbrWq3mtarcalqMxmubly8jn37D0AHAHYV7n+zl8O/JRPF2sQ/M4IsInHRT1l/HoPbJ7ivP/AIL/AA/fxtr6zXisNJsmDXLdPMPURj69/QfUV9awokUaRQoEjQBVVRgADgDHpQBNRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAcd8TPBFt480EafNObaaF/Nt51XdtfBGCO4IPPNeNn9m/xB21rTP++ZP8K+laKAPmr/AIZv8Qf9BvTPyk/+Jo/4Zv8AEH/Qb0z/AL5k/wDia+lKZLIkSF5GCqoJJPQCgD5u/wCGb/EH/Qb0z/vmT/4mj/hm/wAQf9BvTP8AvmT/AOJrq9T/AGiNHttYe3tNIuLuxjfabsSBS4/vKhHT0yRn2r1vR9UtdZ0221Gwfzba5jEkTjup/r7UAfPP/DN3iD/oN6Z/3zJ/8TR/wzd4g/6Demf98yf/ABNfStFAHzV/wzd4g/6Demf98yf/ABNH/DN/iD/oN6Z/3zJ/8TX0rXC+Pvil4f8ABM62t8091fMu4W1uoLIOxYkgLnt39qAPJP8Ahm/xB/0G9M/75k/+Jo/4Zv8AEH/Qb0z/AL5k/wDia7TSf2h/DV3crFfaff2KMceaQsir9cHP5A16ho+q2OtWEV7pV3Fd20n3ZYmyD7exHcHkUAfPf/DN3iD/AKDemf8AfMn/AMTR/wAM3eIP+g3pn/fMn/xNfSlLQB81f8M3eIP+g3pn/fMn/wATR/wzd4g/6Demf98yf/E19K0UAfNX/DN3iD/oN6Z/3zJ/8TR/wzd4g/6Demf98yf/ABNfStFAHzV/wzd4g/6Demf98yf/ABNH/DN3iD/oN6Z/3zJ/8TX0rRQB81f8M3eIP+g3pn/fMn/xNH/DN3iD/oN6Z/3zJ/8AE19K0UAfNX/DN3iD/oN6Z/3zJ/8AE0f8M3eIP+g3pn/fMn/xNfStFAHzV/wzd4g/6Demf98yf/E0f8M3eIP+g3pn/fMn/wATX0rRQB81f8M3eIP+g3pn/fMn/wATR/wzd4g/6Demf98yf/E19K0UAfNX/DN3iD/oN6Z/3zJ/8TR/wzd4g/6Demf98yf/ABNfStFAHzV/wzd4g/6Demf98yf/ABNH/DN3iD/oN6Z/3zJ/8TX0rRQB81f8M3eIP+g3pn/fMn/xNH/DN3iD/oN6Z/3zJ/8AE19K0UAfNX/DN3iD/oN6Z/3zJ/8AE0f8M3eIP+g3pn/fMn/xNfStFAHzV/wzd4g/6Demf98yf/E0f8M3eIP+g3pn/fMn/wATX0rRQB81f8M3eIP+g3pn/fMn/wATR/wzd4g/6Demf98yf/E19K0UAfNX/DN3iD/oN6Z/3zJ/8TR/wzd4g/6Demf98yf/ABNfStFAHzV/wzd4g/6Demf98yf/ABNH/DN3iD/oN6Z/3zJ/8TX0rxRQB81f8M3eIP8AoN6Z/wB8yf8AxNH/AAzd4g/6Demf98yf/E19K0UAfNX/AAzd4g/6Demf98yf/E0f8M3eIP8AoN6Z/wB8yf8AxNfStFAHzV/wzd4g/wCg3pn/AHzJ/wDE0f8ADN3iD/oN6Z/3zJ/8TX0rRQB81f8ADN3iD/oN6Z/3zJ/8TR/wzd4g/wCg3pn/AHzJ/wDE19K0UAfNX/DN3iD/AKDemf8AfMn/AMTR/wAM3eIP+g3pn/fMn/xNfSvFFAHzV/wzd4g/6Demf98yf/E0f8M3eIP+g3pn/fMn/wATX0rRQB81f8M3eIP+g3pn/fMn/wATR/wzd4g/6Demf98yf/E19K0UAfNX/DN3iD/oN6Z/3zJ/8TR/wzd4g/6Demf98yf/ABNfStFAHzV/wzd4g/6Demf98yf/ABNH/DN3iD/oN6Z/3zJ/8TX0rRQB81f8M3eIP+g3pn/fMn/xNH/DN3iD/oN6Z/3zJ/8AE19K0nFAHzX/AMM3eIP+g3pn/fMn/wATR/wzd4g/6Demf98yf/E19K8UcUAfNX/DN3iD/oN6Z/3zJ/8AE0f8M3eIP+g3pn/fMn/xNfStFAHzV/wzd4g/6Demf98yf/E0f8M3eIP+g3pn/fMn/wATX0rScUAfNf8Awzd4g/6Demf98yf/ABNH/DN3iD/oN6Z/3zJ/8TX0rRQB81f8M3eIP+g3pn/fMn/xNH/DN3iD/oN6Z/3zJ/8AE19K0UAfNX/DN3iD/oN6Z/3zJ/8AE0f8M3eIP+g3pn/fMn/xNfStFAHzV/wzd4g/6Demf98yf/E0f8M3eIP+g3pn/fMn/wATX0rRQB81f8M3eIP+g3pn/fMn/wATR/wzd4g/6Demf98yf/E19K0UAfNX/DN3iD/oN6Z/3zJ/8TR/wzd4g/6Demf98yf/ABNfStFAHjvhDwlc+CtI/sa+uIbmYSNL5kOduG6DkDnioPGnga88eWEFhYXdvavbyeczThsEYIwMA+tdt4q/5Cx/3FqXwj/x+yf9c/8ACuT/AJeHvv8A3L5HjH/DN+vn/mN6Z/3zJ/8AE0f8M3a//wBBvTP++ZP/AImvpJnVR8xC/WopLy0T/WXMK/WQD+tdZ4B85f8ADN2v/wDQb0z/AL5k/wDiaP8Ahm7X/wDoN6Z/3zJ/8TX0HLr+jRHEmq2S49bhP8arSeLvD0f3tXsz/uyg/wAqAPBf+Gbtf/6Demf98yf/ABNH/DN2v/8AQb0z/vmT/wCJr3b/AITPw5/0Fbb8z/hV/TNX0/VVL6deQ3AUciNwSPqO1AHz1/wzdr//AEG9M/75k/8AiaP+Gbtf/wCg3pn/AHzJ/wDE19KjpRQB81f8M3a//wBBvTP++ZP/AImj/hm7X/8AoN6Z/wB8yf8AxNfStFAHzV/wzdr/AP0G9M/75k/+Jo/4Zu1//oN6Z/3zJ/8AE19K0UAfNX/DN2v/APQb0z/vmT/4mj/hm7X/APoN6Z/3zJ/8TX0rUfmxr/y0QfiKAPm7/hm7X/8AoN6Z/wB8yf8AxNH/AAzdr/8A0G9M/wC+ZP8A4mvo/wC0Q/8APaP/AL7FPV1f7rBvoc0AfNv/AAzdr/8A0G9M/wC+ZP8A4mj/AIZu1/8A6Demf98yf/E19KUUAfNf/DN2v/8AQb0z/vmT/wCJo/4Zu1//AKDemf8AfMn/AMTX0pRQB81/8M3a/wD9BvTP++ZP/iaP+Gbtf/6Demf98yf/ABNfStFAHzV/wzdr/wD0G9M/75k/+Jo/4Zu1/wD6Demf98yf/E19K0UAfNX/AAzdr/8A0G9M/wC+ZP8A4mj/AIZu1/8A6Demf98yf/E19K0UAfNX/DN2v/8AQb0z/vmT/wCJqS2/Zv1rzk+065YJFn5jGjswHsCBz+NfSNFAGF4R8N2HhTQbfSdMTEMI5YgbpH7uxHUn/wCtW7RRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVy3xUuXs/h14gmjYq4sZQCO2Vx/WuprjfjH/yTPxB/16MPzIoA+Myc8nvX2x8NtNTSfAmiWcZLBLSNiT6sNx/VjXxPX3X4XGzw1pa+lpCP/HBQBpiiiigAr5E+MvhnW7L4g6rNc2088d/cNNbzKpZXQ9FBHdR8uO2PSvruigD4U1fw9rGjJC+rabd2SzjdGZ4WTePbIrV8A+N9W8E6st3psrNCxHn2zH93MvcEdj6HqK+xNd0ew17T5dP1W2juraUYZHXP4j0PuK+MfHWhf8I14u1PR1culpOURj1KHlSffBFAH2V4Z1y08R6HZ6vp7b7e6jEiZ6oehU+4OQa1a8U/ZW1KW48N6rp0hJS1uUkjz2Dqcgfimfxr2ugBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKzPEWvWXh+x+1ag7BS21VQZZj6AVp1xfxQ8PXuvaXbtp6+ZNayFjFnG9SMHHvQBR/wCFsaf/ANAy8/Nf8afH8V9Hb79pfR/VUP8AWvO/+ER8Qf8AQFvP+/VRSeG9ci+/pF8v/bFj/KgD1EfFHw+cbhep9Yf8DTx8T/Dv/PS5/wC/BryR9H1RPv6beqPUwP8A4Uz+zb7/AJ8rr/vy3+FAHsH/AAs7w5/z0uv+/Bpf+Fm+HP8Anpdf9+DXjn9n3n/Pnc/9+2/wo+wXn/Pnc/8Aftv8KAPZ4fiT4ZkbabuWP3eFgK6e0uoby2S4tpFlhkG5XU5BFfNWOxGd3y17h8NbG70/wnBFeqyOzNKqMeUUnIBHb1/GgDqCdv09axLzxn4ds5DHNqsBcdQmX/VQayviw90vhM/ZtwjMq+eV7Jg9fbOM14t160Ae6f8ACwPDP/QSH/fp/wDCrVt4z8O3BxHq1uD/ALbbP/QsV4Hsb0b8qZQB9JW+pWFwB5F7bS5/uSq38jVuvmLJ9anivbuH/U3U0f8AuyMP5GgD6Wqs+o2UdwLeS7gSc9I2lUMfwzXzx/a2p/8AQSvP+/7/AONVXkeSTfM7O+7lnbJJ9cmgD6arnvE/jHSvDxEd5JI9wwyIYly2PU5wAPqaTwDNe3HhSwk1AkyFDgnqVBIU/livKviTa3Nv4vvZbtH2zMGhcjgpgDj6dKAOuk+LVsP9VpUzf70oH8gai/4W4P8AoD/+TH/2NcVYeE9ev7dJ7XTLho5BlWICgj15Iq3/AMID4m/6BjfjKg/9moA6r/hbh/6A4/8AAj/7Gmn4uH/oDj/wI/8Asa5n/hX3ij/oGf8AkZP/AIqj/hX3ij/oGf8AkaP/AOKoA6X/AIW4/wD0Bx/4Ef8A2NH/AAtx/wDoDD/wI/8Asa5r/hX3ij/oGf8AkaP/AOKp3/CvvFH/AEDf/I0f/wAVQB0DfFy4z8ujx495z/hXS+DvHVt4kuHtHhNtdqu8Jncrjvg+vtXlWr+Fdb0hEe/sHjjb+NWDhfqVJx+NdX8K/Dd9Hqq6vcwyQQJGwj8xcFyRjIHoPWgD1kVU1K/ttMtJLu9mWKGMZZj2q1XH/FLS73U/DirYq0jQzCVol5LqARwO+M5xQBian8WYVmK6bprTIDxJLJtz+AB/nVL/AIW1qHbTLb/vtq5LR/DWr6vK0djYytt++XGxR9S2Bn261tj4aeI2HzR2w/3ph/hQBo/8La1H/oGWv/fbVJH8Wrr+PSYj9JSP6VlH4ZeIh/yztm/7bf8A1qik+HHiYf8ALlG30nQ/zNAHRR/FsH/W6OR/uz//AGNSf8Lag/6BMv8A3+H+FchJ4C8Sx9dLc/7rof5Gof8AhCfEf/QJuP0/xoA7X/hbVt/0CZv+/wAP8KrP8WpvO/d6Ohi75mO7+WK5P/hC/Ef/AECZ/wBP8atWfw+8R3MgVrEW6/35ZFAH5En9KAPZdD1SDWNMgv7Uny51yAeoI4IP0PFLrOq2mjWEl7fyeXBGOSOST2AHc1B4Z0lNC0S206Nt5iX5m/vMTlj+ZrL+I+i3eteHjDp43zwyCUR5xvABBH154oA4nWPinqk8jJpkMVpF6uN7/wCA/I1hy+N/Es/LavMnsiqv8hUmjeBNc1O7MT2cljGv3pLgFQD6Adz9K6y3+EkXBudWlJ9I4QP5k0AcM/inX266zef9/iKZ/wAJLrv/AEGb3/v+f8a9HX4S6V/FqF6fpsH9KX/hU2kf8/t9/wB9L/8AE0Aeb/8ACS67/wBBm9/7/t/jUy+LfEC/d1i8P1kJ/nXoX/CqNJ7Xt6P+BL/8TUb/AAm03tqV5+Kof6UAcGPGXiP/AKDFz+Y/wrsfhp4u1PVNUfTdTmN0jozxyEDchHUEjqCKs/8ACpbH/oKXP/fta6Dwj4N0/wANySTQPJcXDjb5r4GF9AB0oA6aiiigDiPEk8c2szLGcmIKjexxnH61yHi+6uLWwiNtPJCWlwxRyuRg8HFdd4kt44NZmeMY87a7fXGP6VStvDtl4jmNrfvKkcX7weWwBJ6dSD61yf8ALw+gemD+R5a9zcOcyTyMfdyahPzfe5+te3RfDbw5FjNrNL/vzN/iKuReB/DceNukwn/eLN/M11nz54MAKK+g4vCmgxfc0ezH/bIH+dWE0LSE+7pVmP8Atgv+FAHzpiul+GrXY8Y2Qs88k+bjp5ePmz7f1xXq2q+C9B1V0a509EdBgGH93keh29au6PoOm6MhTTbWOAN94gZZvqTyaANSigdKKAPMfix4j1GxvYNOsJ5LWIxeY7IdrMSSAMjkAY7V53JqF5J/rLydm95W/wAa908S+FtO8RRouoI4kizslQ4YZ7e49jWPF8MPDyKAy3b+5m/+tQB4/wDa7n/n6m/7+N/jR9ruf+fqb/v43+NeyD4ZeG/+eVx/3+NO/wCFZ+G/+eNx/wB/jQB4v9pn/wCfiX/vs00yO33nY/Vq9rT4b+G/+fWY/WZv8amT4eeF0/5hpb6zSf8AxVAHhhGe1dD4C1i90vxFZRwSsYbiVYpYc/KwJx09RnINelap8OdBurRo7O3NlMfuyxszEH3DHBFQ+E/h7aaJqH225uTeXCf6vKbVQ+uMnJ/lQB245FFFFAGP4u1c6HoFzqCoHeIDYp6FicDPtzn8K8t0j4ia3HqsT39wtxbO4EkRRRhSeSMAEEV6B8UkDeC73P8ACYyP++1rw6P76fUUAfTQIIBHQ0tR2/8AqI/90fyqSgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK4j43SeV8Ldeb1gC/m6iu3rzn9oefyfhTqig4Mrwp/5FU/yFAHyPX3josfl6PYpj7sEY/JRXwrZx+ddwxf33VfzNfedunlwxoOiKB+QoAkooooAKKKKAKmqX9tpWn3F/eyCK3to2lkc9lAyTXxL4w1yXxJ4l1LWZl2teTM4X+6vRV/BQBXsP7SXj9bh/+ER0mbKxsHvnRvvN1WL8Op98D1rx/wAI+H7vxT4is9HsAfMuHALYyI1/ic+wHNAHv/7LeizWXhXUdVmGF1GdViHqsYI3fiWYfhXsgrO0DSLbRNFs9MsF2W9pEsSDuQB1PuTyau/aYBP9nM8fnY3eXvG7HrjrQBLRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFeBeLPEd/q2tXEjXUyQJIyxRKxAUA4HA7nqTXvtfNF5/wAfk/8A11b+ZoA9j+E2p3uo+HphfyPKbeYxJI/JIwDjPfGa7QVx3wmH/FGwD/prJ/6FXY0AFFFFABRVee7gt/8AXTwx/wC+4X+dVode0me6FtDqNrJOekazKWP0ANAGhRRS0AZsWg6XFdm7TTrRbg8+asKhs+ucda0QABS0UARSorqyOgdGGCpGQRVO10TTLTc1pp9rCzdWSFQT+laNJQBEIYv+ea/98iql1oul3f8Ax86fayk92hUn+VaFFAHOz+BvDc/3tLhUnuhK/wAjVCT4ZeHH+7FcJ/uzH+ua7LFFAHEf8Kt8P/373/v6P8Kt6b8PPDlk4k+yPcsOn2h9w/Lp+ldZRQA1EVFCqAqgYAHao7i3imAE0aSAHIDKDg/jU1FADVUAAAYHpTqTNKDQAUUUUAFFFFABRRRQAUUVla34h0zRYt+o3aQkjKx5y7fRRzQBqZFFcDJ8VdHExVLO9ZOz7VH6E103h/xDp/iC1M2nTFivDxuMOp9x/WgDZooooAYfl+b8zXLn4g+HVv8A7L9rbrt83afLz/venv0q54/ujZ+D9SlRtr+SUU+7EL/WvAs80AfTKEEBlIIPIIp9c/4BS8i8JaemoBhKI8AN1CZO0H/gOK6CgAooooAMD0ooooAKKKKACivLfiv4k1K11aLTLS4ktYVhWV2iYqzkk9xzjirHwr8VXl9dSaTqU7znaZIZJDlhjqpPU+vNAHpVFFFABRRRQBxfiv8A5Cp/3FqXwh/x/wAn/XP+tReK/wDkKn/cWpfCH/H/ACf9c/61yf8AL0+gl/uXyOvooorrPnwooooAKgvbmGzt3uLmRIoowWZ2OABU9cR8YpjH4XjQNjzblFI9RycfpQBr6R4z0PVr37JZXgeY52KyMu/Hpkc1v18z208trPHNbMUkjYMjj+EjkV9DeHdS/tbRbK/27TcRBmHoeh/XNAGnRQKKACiiobm6htomlnljijXq0jhQPxNAE1FQWd5b3sfmWs0c0f8AejcMP0qegAooooAKKKKAOP8Ai3L5Xg2Zc8ySxp+uf6V4xYxmW8gjHV5VUfiQK9a+M8mPDtrH/wA9LkforGvM/DEXm+JNLj/vXUf6MKAPokAAYHAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV5R+07MY/hukYOPNvol/JWP9K9Xrxj9quQr4P0pM8Pfc/hG1AHz54Vt/tXifSrfr5t3En5uBX3VXwTY3U9jeQXlpI0U9vIssbr1Vgcgj8RXVf8LX8df9DLe/8Ajv8AhQB9mVHuXft3Dd1xnn8q+MLj4meNbgYk8S6iB/0zmKfyxWG+r6pLfjUJNRunvAQRcNMxk/76zmgD7vrzn40fEeLwVo32WycNrN4pWFRz5K95GHt2Hc+wNaPwb8QX3iXwDp+o6plrol4WlIwZQrFQx9zjn3zXzR8XItTj+Imtf2wJDM9yzRs+cGIn5Mf7O3AFAHKXE8l1cPPcM0ksjFndjksxOSSfWtvwh4x1fwbc3FzockMU9woRpJIldgAc4GemT19cV0vgX4N+IvFlguoKYNOsZf8AVS3Od0g9VUDOPc49q6z/AIZr1H/oZLT/AMBm/wDiqAOF1P4veOtSQpJr88KntbokX6qAf1rkhqd8uojUFvJxeK28T+YfMDeu7rXulj+zVhwb7xMSvpBaYP5lj/Ku68KfB3wj4ZnS5W2l1C7QgrNdsH2kdwgAUH8CaAOu8K3N5eeG9MudSTZeS2sTzjGCHKgnI7c5rWoAxRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfNF5/x+Tf9dW/ma+l6+aLz/j8n/wCur/zNAHtHwm/5EyD/AK6yf+hGuurkfhN/yJkH/XWT/wBCrr6AOG+KHiW80K0todOzHcXJbMu3OxRjp7815Zda7q93zPqd4/8AvStj8s17h4o8MWXiOxW3uy8bRtujlT7yHv8AUH0rzLx14PtfDGnWssV1NczzSlSWAUBQM8Ad84oA452Zz+9Z5C3rzT7VZWuYY7RXadnHlCP727PGMd81Y0WxfVdWttPRvLNw4j3Fc7c98V7l4Z8MWPh+1SK3hR5lHzXDIN7Hvz2HtQBrWXm/Y4ftH+u2Lv8A97HNTUUUALRXDfE3xVdaBBb22msFurnLF2UHYg44B7k1w+h+P9a0+6827uJL63Od0cxz9CD1H8qAPVvE3inTvDkKvfOWkfiOGPl2P07D3rzy++K+qSSkWllawoDwH3O2Pc5A/SuL1XUrnVNQlvL6QyTSnc3oPQD0A7VNJol/Foq6vNAY7RpBGrt1ckHkDrjjrQB6/wCBfGcXiSOSGaNbe9iG5kByHX1Heutr568FX7af4p0+YNgGZUf/AHW+U/zr6FoAKjd1jQs3yqo5J4AFSV5J8U/FMst6+hWZaOCMj7QR/wAtG67foO/qaANbxT8S7e0d7TQkF1N91rhv9WP90D736D61wl/4v8QXsrPLqk6qf4Im2KPwGKzNPsbq/u47WygeaaThVUdPr6D3r0TRvhWHhWTWrx0kI/1Vvj5fqxzn8qAOKtfFev2soeHV7rg9HcsD9Qc16x8P/FX/AAklhKLlBHe25AlC9GHZh9cdK8j8U6SdE126sdkgSNv3bSdWQ9D0AP4V3XwX06eM31+6lYZAsUe7+PHLEew4FAHp1RO6xIzOQqryT0AFS15x8Xtda2tY9Itmw1yPMnIPOwHhfxP6CgDP8afEmaeRrPw6/lRLw1yV+Z/930Hv1+lcBc3tzdSmSe4nmcnJLOSf1NP06xuNS1CKys4i8sxwo9Pc+w716ro/wy0m2sgup77u4YZZlYqoPoB/jQB5npOv6tpcoksb6ePHVS5ZG9ip4r2PwT4rg8S2R3gQ3kAHmxdv94ex/SvOviP4Xs/Dk1vLp8zeRc7l8ljkoRjkHqRz3qj8ObuW28Y2HlH/AFzmJx6qQf8A9dAHvGeK8U8Q/EDWrvUZDp1y1naqxEaooyQDjLEgkk/lXteNyY/CvnDV7GTTdWurOdSrxSsuT3GeD9COaAO0sviffRaJPDdRibURgQT7QFIPUsB6dsda4W8vJ766kuLuV5p5Dl3Y5yajrvPhj4Qj1InVtTiD2qHEMTdJG7sR3A9O5+lAHDyWlwlulxJbypDISEkZCFbHoe9dL8Lr57PxfbRI7CO6DROOzcEj9RXa/F7Tpbjw5bz20e77HOGdVHRCCM/QHFed+B4rifxdpn2WMuyTrIx9FH3ifwzQB9A0V5XrvxSuINQlg0i1gNvE5UPPuJfBxkAEYFVH+K+sbPls7Bfchz/WgDqPjFc+T4VEIPM9wi49hlj/ACFeSaRb/a9UtbYf8tpUQ/QsM1oeJPFGqeIljXUJYtkRLIka7QCePqaxlJUgg4I7igD6FvfEOkaewjvdStYX6bTKM/lWhbXEVzCs1u6yxOMq6HIIr5qr2X4Q295b+F2+1h1jeZmhV+u0gcj2JzQB21FFFABRRRQAUUUUAcl468Hx+JY45ophbXcQ2rIVyrKf4T+PQ1W8C+BT4dvHvby4Se5ZSiiNSFUHqeeSTXanpS0AFFFFABRWB4t8TWXhuz8y5YSTuMRQKfmc+vsPU15bqnxD8RXsxaG6FnH/AApCg+X6kgk0Ad74r/5Cp/3FqXwh/wAf8n/XP+tctomq3ms6cl1qMglmBKb9oGQPXHeup8If8f8AJ/1z/rXJ/wAvD6CX+5fI6+iiius+fCiiigArzP423WItMtQfvNJKR9AAP5mvTK8Y+MF35/ilIQeLeBVx7klv5EUAYHhPSF1vxBa6fIWWOUkuy9QoBJ/lXvtjaQ2FpDa2yBIYVCIvoBXk3wctPO8STXOMrb25/NiAP0zXsNAC0UUUAFeVfGu4m+16dbbmMJjaXZ2LZxk/QV6rXlfxuX/SNLb+8kg/IpQBk/CS7lh8Vi2SQrFcQuGTsSBkH617TXhnww/5Hay9xIP/ABw17pQAUUUUAFFFFAHm3xsk/wBB0uP1lkb8gB/WuI8BR+Z4y0oekwb8gTXY/G/rpK/9dT/6DXL/AAzXd4208HtuP5IaAPd6KKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArlviJ4Ms/HHh9tLvZXgZXEsMyDJRwCM47ggkYrqaKAPALD9mwfN/aHiLv8vkW3b33NVw/s2aX/ANDFd/8AgOv+Ne50ZoA8Rg/Zv0UH99ruoP8A7saL/MGtay/Z78GQMrXD6ldEdQ84UH/vlQf1r1iigCrp+n2umWENlYQJb20ChIo0GAqjsKh1HR9N1No21LTrW8aL7hnhWQr9MjitCigBqIFUAAADoB2p1FFABRRRmgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvmi8/4/Lj/AK6v/wChGvpavmm8+a8m95WP6mgD2f4T/wDImW//AF2k/wDQq7CuN+EjhvB0aj+CeQH65z/I12VABXlfxsuM3OmW+furI5H1IH9K9Urxv4yTeZ4nhi/542y/qzGgDO+GUHneNbDJyI98n5Ia91rxz4Nweb4nnlI4htjg+5ZR/jXsdABRRRQB5b8YdEvJrmDV4UaS3ih8uQDny8MSD9Oa81r3v4if8iXqv/XH/wBmFeCigDoPAfh//hINcSKVT9khHmTnsQOi/if0Br0v4m2cZ8DXKxIFS3MbqoGAoDAcfgar/CPTFtPDX2sj5719+T/cHCj+Z/Gt3xtCJ/Ceqx4z/ozH8hn+lAHgELGG4jmHVGDfkc19LwP5kKOP4lB/MV8znla+jPD032jQtPm/56W0bfmooAv18/8Aji2ltvFmprcKQzztKp9VY5Br6ArG8QeHNN162EWowbmX7kiHa6/Q/wBKAPEfD/iHUPD9y82mOgMgAkDoGDAdvUfhivQNE+KdtNIsWtWhtmPHnQ5dPxHUfhmqGr/Cm4QmTSL5JB2juBtb/voZB/IVxGsaNqOjXHk6natA56MeVb6MODQB74sel63bRXBjtb6EjMbsiyD8MirsaLEgSNVRF4CqMAV4J4T8TXXh2+EkbGS1cjzoCeGHqPRh617np97BqFnDdWj+ZDMoZW/z3oAdqF9aWFuZr64jt4h/HIwA/WvCfG+orqnie9uopBLCWCxupyCoAAxXUfGl7htTsIX3C1WIsvoz55/EDFed0AejfB2zgjGoavcusQixAjOwAUEbmOfyra8S/EjTtODQ6Ti/uOm7OI1Pue/4fnXkO9/L8re3l5zjPGfXHTNSWtpc3s6wWcEs8rdEjUkn8qAJ9X1W81m+e81CUyzNx6BR6AdhXZfCXw9Jcamus3ETJbW6kQlh/rHIwSPYDv61a8KfDKRnS58RMFQci1jPLf7xHQew/OvTIIIreFIYEWONAFVFGAAOwoAnrgvjFaQHw/HdiJPtC3CJ5m0bsEHjPWu8rjPi+ufCBI7XMZ/nQB4xX0D4QgFv4Y0tEGB9mRj9SMn+dfP1fQ/hdt/hvS29bWL/ANAFAGgyhwQwBB9e9QWun2dmzNa2cEDN94xRhc/XFW8UUAeTa/8ADC/l1CebSJ7d7eViypKxVlyc46EH2NUU+F3iBuHayX380n/2WvZ8UjsEUljgAZoA+cNa02TSdUnsZ5ElkgYKzR/dzgHjP1rpPhp4Ws/EU94+oCRoLcKFVG25Y56nr0Fc1rF02oard3bHPnTO4+hJIr1r4O2Qt/C73JGGup2bPsMKP1BoA29O8I6Dp2GtdLgDjozDefzOa2lG0YxxTqKACiiigAooooAKxfGWsnQtBnv0QSSJhY0PQsTgZ9h1rarj/iyv/FGT+00Z/wDHqAOF0z4la3b36SajKlza7v3kXlquF/2SAORXscEqzwJNGcpKoZT6gjIr5sjHmTIr/dZgp+hNfSdvAlvbwwRDEcShFHoAMCgDK8Y602g+Hrm+jUPKuFjDDjcTgZ/nXlWn/EHXrfUBcXdz9rgJ+eFlUKR7YHFehfFdQfBlwR1WSM/+PAV4lQBf1vVbrWtSlv71sySn5RnhF7KPYVHNp13DpkOoTQlLadykTH+MgZJA9PetDwdoUniHW4rTBFuvzzsOgQdvqegrvPjDaxweGNPjgQJFBOFVB0A2EAUAc/4M/wCQL/20au28If8AH/L/ANc/6iuJ8Gf8gT/to1dt4Q/4/wCX/rn/AFFci/iH0E/9z+R19FFFdZ8+FFFFABXzz4vvf7Q8UalcA7lM7Kp/2R8o/QV7xrt4NP0i8vCceRC7j6gcV847i5LscsfmPvQB6v8ABSyEemX94R/rZRGp9lGT+rV6JXOfDmx+w+ELFWGHlXzm+rH/AAxXR0ALRRRQAHpXl3xu+/pH0m/9kr1E9K8u+N3+s0j6Tf8AslAHN/DD/kdrD/tp/wCgGvda8J+GH/I7WH/bT/0A17tQAUUUUAFFFFAHl/xv+/pJ7fvB/wCg1zHwyYJ4108scZ3j8dhrt/jTaGTQrS6Az9nnwfYMP8QK818M3DWfiPTZ4wWMdwnyjvk4I/WgD6KormtV8c6BpkrRT3wklU4McKlyD6HHH61kyfFXRV+5a3r/APAFH9aAO7orzuT4t2A/1Wl3Lf7zqP8AGqzfFuP+DSH/ABmA/wDZaAPTaK8ub4uN/Doy/jdf/Y03/hbs/wD0Bo//AAIP/wATQB6nRXln/C3Lj/oDR/8AgQf/AImj/hblx/0Bo/8AwIP/AMTQB6nRXlE/xZvmXbBpUEb+rysw/LA/nWp4Z+JiajfQ2WqWgtZJWCrLG2UyegIPT8zQB6HRRRQAUVw+q/E3RbKeSGKK5u2jJBaMAISPQk8/lWBd/Fq6ORZ6XCno0shb9Bj+dAHq9FeMS/FLX3/1aWUf0jJ/marN8SfEzdLmFf8AdhX+uaAPcKK8M/4WL4n/AOf5f+/Kf4Uf8LD8T/8AP+v/AH5T/CgD3OivDP8AhYfif/n/AF/78p/hR/wsPxP/ANBBP+/Kf4UAe50V5Z4L+IGo32s2+n6x5cy3LbFdE2srds44IP0r0HXtUi0XSbi/uAWSBc7V6sTwB+dAGlRXid58S/ENxKWt3htkJ4VYg2B9TnNQ/wDCw/E//QQT/vyn+FAHuVFeIR/EjxKn3rqGT6wr/TFWoPilr0f+sispfrGw/k1AHstFeTxfFq+H+v0u3f8A3JGX+YNXrf4tWx/1+kyp/wBc5Af5gUAelUVwsHxT0N/9ZBexH/rmpH6GtCL4h+G5cZvmj/34XH9KAOqorAj8Z+HpB8mr23/Amx/OigDfrP1nV7HRbb7TqVysEWcDPVj6AdzWhXm3xk0y+u4rK8tonmgtw6yKqlihOMNgduMZoA0rn4paBFnykvJz/sxgfzIqhL8WrAf6vS7k/wC86j/GvNbfSdSuf+PfT7uX3SFiPzxV6Pwj4hk+5o93/wACTH86AOzk+Lq/8stHP/Ap/wDBagb4uXX8GkxfjMf8K5yPwF4nf7uluP8AekQfzNWV+G/iZ/vWUS/WdP6GgDX/AOFtX/8A0DLb/v41J/wtrUf+gZa/99tWb/wrLxJ/zyth/wBthS/8Kx8R/wBy1/7/AH/1qAND/hbWpf8AQNtP++m/xpP+FsakXX/iX2u3+IZbn6HNUf8AhWPiP+7a/wDf7/61Oi+F2vuwEj2ca9z5pOPwAoA9U8OazFrujwahACqyjlT1Ug4I/OtSsnwvoyaDo0Gnxt5nlglnxjcxOSa1qAOJ8Y+P4PD199hitPtdwgBfL7VXPIHQ5OK51vi1fn7ulWw+sjH+gq3498CajqmtPqek+XMLgL5kbuEKkADIJ4IIFc8vw28SMRugt1+s4P8AKgDS/wCFs6n/ANA60/76b/Gmn4s6t/0D7P8A8f8A8apj4ZeI/S1X/tt/9al/4Vd4i/vWf/f0/wCFAFr/AIWxq3/PhZ/+P/40v/C2NW/58LP/AMf/APiqqf8ACrvEX96z/wC/x/8AiaP+FW+If71n/wB/T/8AE0AW/wDhbGrf8+Fn/wCP/wCNH/C2NT/i0+zP/Am/xqp/wq3xF/es/wDv8f8A4mk/4Vj4jQ5AtD9Jv/rUAbOm/FdmuFXUdNWOAnDSQuSVHrgjn869MhmSeBJY2DJIoZWHcEZBrxm2+GniGS7WOeOCGIn5pPNDADvgDkn8K9isrWOzs4baIHy4Y1jXPoBgUAWa4nxh8QLbQLw2NtB9rvEAL5baiZ5APUk47V23avFfHnhXVo/Et1cQWk11b3cplR4kLYz/AAnHTB/SgC1J8VtZZv3dnYoPcOf/AGYVA3xQ8Qn7q2a/9sz/APFUyw+GmvXUCSSC3tt4ztlc7h9QAat/8Ko1j/n/ALEf99/4UAVP+Fn+Iz/Faj/tj/8AXqP/AIWT4l/huIB/2wWtL/hU2q/9BGz/ACf/AAp6/CXUMfNqlsD7I1AGR/wsjxP/AM/cP/fhf8KT/hZHif8A5/Iv+/Cf4Vtf8Klvf+grb/8Aftv8ad/wqO6/6C8P/fk/40AYTfEfxMykG8i/78J/hXK5y2TXo/8AwqO6/wCgvD/35P8AjVrw58MWtNTS51e7huYom3LDGpwxHTdnt7d6AOl+HFm1l4RsUkTZJKpmYf7xJH6YrpqaihQABgCnUAFeF/E6bzvGt9/djCR/+OD+te6V87+KroXviPU5wciS4fH0BwP0FAHbfBGHNzqk/ZVjT8yx/pXqVeT/AAu1/R9D0y8OqXqW808owuxidqrweB6k11c3xH8NQpkX0kx/upC+f1AoA62iuD0r4n6ZfaqlpNaz2ySMFSVmBGT03AdP1rvKAOb+I8gTwVqZP8SBR9SwFeDV7N8Yrkw+ExGDjzrhF+uAW/pXkFhCbi+t4R1klRfzYUAfQ+hWa2GjWNoowIYFXHvgZ/Wk8QJ5miagn962kH/jpq8AFUD0qrquf7Lu/wDri/8A6CaAPnBfu17/AOBZPM8IaW3pAq/lxXz+Ole7/DiaOXwZpwjcMUQq2OxDHg0AdLSHrS1l6xr2maMV/tO9jty/3VY5Y++B2oA1Ko6vplrrFm9nexCSFxznqD2IPY1NY3ttqFstxZTpPC/3XRsg1YoA+dPEGkS6JrNxp9wdxiPysR95eqn8a7/4Nau7pd6TKSRH++iyegJww/Mg/iay/jHNZTazatazRyTpGyTBTnbg5Gffk1nfCuZ4/GVqFPEiSK3v8pP9KAPYtY0ix1i0NvqNus8ecjPBU+oPUV4V4w0qPRfEd3YwBhApDR7jk7SMivoSvNfjDoTzxQ6zAufIHlTAD+En5T+BJH40Ac78M9E0jXL26g1ONpJI0EsSByoYZwenXtXrul6XZ6bF5VjaRW8foigZ+p6n8a+fNJ1K60nUYr2xl8ueE5HoR3BHcEda9KsfizamAfb9OnWXuYWDqfpk5oA9Iqvd3NvZQtNdTRwRDq8jBQPxNcHcfFnTgn+j6ddO3bcyqD+PNcL4u8W33iV4hcRpBDCSUjQkjPqSepoA90sb+11CLzbK4iuI/wC9E4YfpXNfFld3gyf/AGZY2/8AHq4v4O/aP+EinEJb7P8AZy0w7E5G38c9PxrvviNAbjwXqKDllRX/AO+WBP6A0AeEV758P5/tHg3S3zkiEJ/3ySv9K8Dr3H4WIyeCbLd/EZGH/fZoA6uiiigArH8Y3n2DwxqNxnBEDKv1b5R/OtiuI+MN0YPCiwqcG4nVfwGW/mBQB40vCivoTwhZHTvDOnWpGGSBS3+8Rk/qa8G0e2N5qtnbD/ltOifmwFfR6jAwKAHUUCigAooooAKKKKACuR+LH/ImXP8A10j/APQhXXVyHxZOPBk/vLGP/HqAPFof9dH/ALw/nX0uK+aIPmuIl/iLqP1r6YoA5L4rf8iVd/78f/oYrxCvW/jPePHotpaL8ouJize4UdPzIry/RrT7frFnZ9pp0jP0JGf0oA9e+FWijTPDq3UikT32JTnqE/gH5c/jUXxgTf4SDf3LlD+hFdpHGsSKiKFVQAAOwrmPifD5vgy+/wCmZjf8nGf0oA4Xwb/yBf8Ato1dt4Q/4/5f+uf9RXE+DP8AkC/9tGrtvCH/AB/y/wDXP+orkX8Q+gn/ALn8jr6KKK6z58KKKKAOO+LV79k8IyRqcNdSLCPpnJ/QV4zawNc3UNvGPnmdYx9ScV6J8bLzfcabZKeivMw/HA/ka4bw/fQ6Xrdpf3ELzJbvv2IQCTjjr70AfQ1rCtvbxwxjCxqEA9ABxUoryyf4tzF/3GkoB6PMSf0UVH/wtq9/6BUH/fxv8KAPWKK8ri+Lk4b9/pMbL/sTEH+RrqfCfjiw8Ry/Z40e2uwN3kuQQw77WHXH0FAHV15d8bv9dpH0m/8AZK9RFeWfG3/j50r/AHZf5rQBzvww/wCR2sf+2n/oBr3WvC/hd/yO1j/uSf8AoBr3SgAooooAKKKKAK9/ZwahaS2t3GssMo2srdCK4LxD4E07RdCv77R47h7uOPMe593ljI3FQAOQucZzXotBoA+ZApkICqzseigZJq9b6DrFz/qNLvXVvSFv8K9+ttI023uTcW9jbRzt1kSJQ354q9j3oA8Aj8HeIZOmj3Y+q4/nipk8C+Jn/wCYTKPq6D/2aveqKAPCR8PvEx/5hoH1mT/Gnj4e+J/+fBP+/wAn+Ne50UAeGf8ACu/E/wDz4J/3+T/Gj/hXfif/AJ8E/wC/yf417nRQB4X/AMK88T/8+Cn6TJ/jWh4Y+Hmstq0E2pQ/ZLaB1kYlwzPg5wACfzr2SigAqveQtPazQhtpkQrn0yMVYooA+fbjwlr1teNanS7mR1OA0aFlceoYcYrQtPh74luVGbJIAf8AnrIox+AJNe5UUAePR/CrWW/1l5Zx/RmJ/wDQatL8JLw/f1eEfSEn+or1eigDyz/hUc//AEGI/wDwHP8A8VR/wqOf/oMR/wDgOf8A4qvU6KAPLP8AhUc//QYT/wABz/8AFVVvPhTqkbr9ivracHqXBQj+ea9dooA4Dwf8Oxo+ox6hqF2txNDzHGiEKG9STycduBXS+L9Kk1vw9d2ELKksigoW6bgQRn8q2qKAPCdO8BeIbrUVtZrB7WMHEk0mNij1GD834V0f/Co5v+gxH/34P/xVep0UAeTt8Jr1f9Xq0B+sLD+pqpP8K9bX/VXVjL/wJgf1Fex0UAeHy/DfxLH0tYZf9yZf64qlL4J8Rw/e0ic/7mG/kTXvtFAHzjdaLqlscXOnXUZ/24W/wqm6PEcOhT6givpqo3hif78SN9VBoA+Z6K+jpNG0yX/WabaN/vQKf6UUAXqKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDg/i/ql5p+j20FpI8S3UjLI6HBwBnbntn+lePk19Fa7pFlr2ntZ38e+JjkEHDKR0IPY1zej/AA00jTrwXE7SX205SKYDYPqAPm/Hj2oA8ZByaeIZHPyRO30BNfR8VjaQriG0gjHokYX+QqZY1X7qgfhQB4b4Y8F6tqt7CZbSS1tA4LzSqV+UHJ2g8k/pXu1AGKKAOL+LOmXOp+HYzZxtK9tMJWVeTt2kEgd8ZrzjwJo93qHiSyMdvJ5VtMs0rMDhApzznuSOBXvdFACGobxd9nOv96Nh+lT0UAfMjjDsPRua9c+DVpNBoVzcSkiOef8Adr/ujBP4nj8Ku6r8OdF1LUnvC1xA0jb5EiYBWbueQcZ9q6iws4LC1jtLWMRwRLtVR2FAFqvBviTLNJ401AT5wjKq57LtGMfzr3kdK4/xt4Gt/EbC6inNrequzftyrjsGHt60AeZeGPF2o+G7aa309YXjlYMRKpO0gdsEdaTV/GOvasCtxfvHGeqQDy1/Tk/ia21+FWtk/wDH1ZY9d7f4Vo6d8JXLg6jqi7e6wR8n/gR/woA82C7nVVDMWPAHJJr1H4XeEbqwm/tfU4jDI0ZWCFvvAN1Zh244xXW6J4S0fQ9r2Novnj/ltJ87/men4YrcAoAUVFcQxzRtHKiujgqysMhgeoNS0UAeV+JvhfKsz3Ph+QMn3vs8pwR7K3Qj6/nXH3HhPxBbZEukXZI/uRlx+YzX0HRQB8+QeFdfnOI9HvB/vRFR+uK3dJ+GWtXUgN+8NhF/Fk73x7Acfma9mooAxvDXh6x8PWX2ewUkty8r8u59Sf5DtWpPGk0TRSoHRwVZT0I9KlxRigDzmb4T2T326PUZo7YnPk7AWA9A2f1xXf2FnDYWcNpaoEhhUIijsBU9FAC0UUUAFeffGqN20OxkUZSO5+f8VOK9BrO1vS7fWdNnsLxcxTDGR1U9QR9DQB4Bo18dM1a1v1iEptpBIELYDe2a71/i3Nt+TR03e9wcf+g1l6r8MNbt5m/s9oLyLsd+xse4PGfoapL8PvEzcHTgPczJ/jQBBrfjXW9XuRKLl7RFHyxWzsij3POSfrXofwt8TXetWdzbaiwlntduJT1dTn73uMde9ctp3wt1eZgb65trRe4BMjflwP1r0Pwp4YtPDVi1vas0kkh3SzMMFyOnHYe1AG9RRRQAUUUUAFcb8W4ZpfCTmJSyxzRu+OyjPP5kV2VRyosilHAZG4IIyDQB85aRZ3Goapb2lopaWWRVGO3PU+gHrX0cg2oFzuOOvrVWw0qx07f9gtILbect5UYXP5VcAFAHOeOfDP8Awk2lJDHMIbiFy8TsMjkYIPsa57wT8PbnSNXj1HVbiB2hyYooSSMkYySQOnYV6LRQAhFY/i+ze/8ADeo2sQ3SSwMFHqQMj9RWzQQD1FAHjXgwY0TH/TRq7bwh/wAf8v8A1z/qKq+JLeODVJBBGkauA7bVxlj1J9zVrwh/x/y/9c/6iuT/AJeH0Ev9z+R19FFFdZ8+FFFFAHjvxhtblPEcN3Ih+zzQKqP2DAnK/XnNcfYafeajJ5djbTXD9xEhbH1x0r6LuIIbmMx3ESSoeqSDcD+BotLWG1i8u3gigT+7GgUfkKAPEYPh/wCJplDDTxHns8yA/lmpf+Fc+J/+fSL/AMCF/wAa9wooA8Iu/AHiW2iMjaf5gHaKRWP5A1r/AA58KavF4it7++tZbSC23N+9XaXJBAAB5717BRQAleS/Gi536tYWwXAigL59dzYx/wCO163XMeM/CcHie1jPmeRdwk+VJtzweqken8qAPMvhe23xvY+6yD/xw17pXCeCfh//AGBqH9o3tylzcKpWJY1IVc8EnPJOK7ugAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAwPSiiigAooooAKKKKACiiigAooooAMUUUUAFFFFABRgUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRgUUUAFFFFABRiiigAooooAKKKKACiiigAxRRRQAUhpaaSKAGPNHH/AKx1XPTJxT88VwWrNI2oz+fuzkjnsPat7wvftNGbWVstGMqe5HpWXtFzcp3VMJKnTVRO5m+Kf+Qq3+4tS+EP+QhL/wBc/wCoqLxV/wAhVv8AcWpfCHGoS/8AXP8AqKx/5enoy/3L5HTXlylrA8shwqDNco3iO+87crIEz/q8DGPr1pviHU/ttyY4z+4Q/L/tH1/wqppljJqFysS8IOXPoKqdRuVomOHw0KdJ1KyO5tJhc20coGN6hqnqK2jWKJUQYVRgD2qWuk8d2voFFFFAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK5rx34w07wVozanqhdgW2QwpjfK391c/nnsK3bu4hs7eW5uZVihiUySO7YCqBkk/hXx/8AFvxzL428TPcRsy6dbZis4jxhM8uR/ebqfbA7UAemt+0rD28LSY970f8AxFN/4aWj/wChWf8A8Dv/ALCvHfD3g7X/ABPHLLoemy3aQEK7KQACegySMmtb/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZ/8AwO/+wrzP/hUvjn/oATf9/I//AIqj/hUvjn/oATf9/I//AIqgD0z/AIaWj/6FZ/8AwO/+wo/4aWj/AOhWf/wO/wDsK8z/AOFS+Of+gBN/38j/APiqP+FS+Of+gBN/38j/APiqAPTP+Glo/wDoVn/8Dv8A7Cj/AIaWj/6FZv8AwOH/AMRXmf8AwqXxz/0AJv8Av5H/APFUf8Kl8c/9C/N/38j/APiqAPV/DvxRs/HWstbf2W2mz+UWTM/mCXHUfdGCB+ldbbXctlILiFd7qCQhbAbj7pPb614Z4d+HXjzRNatNRh0GctBIGIEicr3H3u4yK9wxg4dWU9weo9q5KseWSaPewU/a0XTl0KGj+Km8Y2r6lJYHT5Fka3aEy+YVK9ecCtSC4eBJBGcGUbc/jWbpthFp7XQhGFuJ2uCPRmA3fmeauVm5XdztpUkqag+hDeXcFnaS3N04jihUyOx7Ack1xFh+0FaaZG0MHhl5FLEmQ3gUt6HGw447ZqX4o6N4s163i07QNKmmsWxJNKrqokPZRk5wOp9T9K83/wCFT+OP+gBN/wB/E/8Aiq6KcOrPIx+I5pezjsj0wftLRj/mV2/8Df8A7Cj/AIaXj/6FZ/8AwN/+wrzL/hU3jj/oATf9/E/+Ko/4VN44/wCgBN/39T/4qtzyz03/AIaXj/6FZ/8AwN/+wo/4aXj/AOhWf/wN/wDsK8y/4VN45/6AE3/fyP8A+Ko/4VN45/6AE3/fyP8A+KoA9N/4aXj/AOhWf/wN/wDsKP8AhpeP/oVn/wDA3/7CvMv+FTeOf+gBN/38j/8AiqP+FTeOf+gBN/38j/8AiqAPTf8AhpeP/oVn/wDA3/7Cj/hpeP8A6FZ//A3/AOwrzL/hU3jn/oATf9/I/wD4qj/hU3jn/oATf9/I/wD4qgD03/hpeP8A6FZ//A3/AOwo/wCGl4/+hWf/AMDf/sK8y/4VN45/6AE3/fyP/wCKo/4VN45/6AE3/fyP/wCKoA9N/wCGl4/+hWf/AMDf/sKP+Gl4/wDoVn/8Df8A7CvMv+FTeOf+gBN/38j/APiqP+FTeOf+gBN/38j/APiqAPTf+Gl4/wDoVn/8Df8A7Cj/AIaXj/6FZ/8AwN/+wrzL/hU3jn/oATf9/I//AIqj/hU3jn/oATf9/I//AIqgD03/AIaXj/6FZ/8AwN/+wo/4aXj/AOhWf/wN/wDsK8y/4VN45/6AE3/fyP8A+Ko/4VN45/6AE3/fyP8A+KoA9N/4aXj/AOhWf/wN/wDsKP8AhpeP/oVn/wDA3/7CvMv+FTeOf+gBN/38j/8AiqP+FTeOf+gBN/38j/8AiqAPTf8AhpeP/oVn/wDA3/7Cj/hpeP8A6FZ//A3/AOwrzL/hU3jn/oATf9/I/wD4qj/hU3jn/oATf9/I/wD4qgD03/hpeP8A6FZ//A3/AOwo/wCGl4/+hWf/AMDf/sK8y/4VN45/6AE3/fyP/wCKo/4VN45/6AE3/fyP/wCKoA9N/wCGl4/+hWf/AMDf/sKP+Gl4/wDoVn/8Df8A7CvMv+FTeOf+gBN/38j/APiqP+FTeOf+gBN/38j/APiqAPTf+Gl4/wDoVn/8Df8A7Cj/AIaXj/6FZ/8AwN/+wrzL/hU3jn/oATf9/I//AIqj/hU3jn/oATf9/I//AIqgD03/AIaXj/6FZ/8AwN/+wo/4aXj/AOhWf/wN/wDsK8y/4VN45/6AE3/fyP8A+Ko/4VN45/6AE3/fyP8A+KoA9N/4aXj/AOhWf/wN/wDsKP8AhpeP/oVn/wDA3/7CvMv+FTeOf+gBN/38j/8AiqP+FTeOf+gBN/38j/8AiqAPTf8AhpeP/oVn/wDA3/7Cj/hpeP8A6FZ//A3/AOwrzL/hU3jn/oATf9/I/wD4qj/hU3jn/oATf9/I/wD4qgD03/hpeP8A6FZ//A3/AOwo/wCGl4/+hWf/AMDf/sK8y/4VN45/6AE3/fyP/wCKo/4VN45/6AE3/fyP/wCKoA9N/wCGl4/+hWf/AMDf/sKP+Gl4/wDoVn/8Df8A7CvMv+FTeOf+gBN/38j/APiqP+FTeOf+gBN/38j/APiqAPTf+Gl4/wDoVn/8Df8A7Cj/AIaXj/6FZ/8AwN/+wrzL/hU3jn/oATf9/I//AIqj/hU3jn/oATf9/I//AIqgD03/AIaXj/6FZ/8AwN/+wo/4aXj/AOhWf/wN/wDsK8y/4VN45/6AE3/fyP8A+Ko/4VN45/6AE3/fyP8A+KoA9N/4aXj/AOhWf/wN/wDsKP8AhpeP/oVn/wDA3/7CvMv+FTeOf+gBN/38j/8AiqP+FTeOPvf2DKB/11T/AOKoA9N/4aXj/wChWf8A8Df/ALCtTwx+0Bpmq6xb2OpaRJpiXDBFnFwJFVicDI2ggZ7849K+cLiJoZnicrujYq2CCMj0I4NdP8MvB13408T2+nwqVtoyJbmbHEcQPP4noPf8aAPtGiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoorhPi747j8EeGpJoCj6pd5itIjz82OXI9F/U4FAHnP7R/xA3O3hLSpeBhr+RW/FYv6n8B614v4d0S+8Q61a6Vp0fmT3DbV9FHUsfYDk1RuZ5rm5knuHaWaZi7sxyWYnJJ+pr6U+B3gP8A4RjRf7U1GLGqX6A4PWGI8hPYnqfwHagDsvCXh6z8L+H7XStPGEhHzSY5kf8Aic+5P6cVsUlFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFVdS1CHT4RJKCxY4VR3qpp+vW93P5LqYHPTeeD+NYSxFOMuRvUhzinZ7mrRRRmrnVhTjzzdkaJN7BRTd3NMmnSGIyysFRepPavDfEWA5+SMm/kaeyla7FuLiK2iMk7hFHrUVpf2t5kW0wcjqOh/KuU13VDqEgWMFYEJ2jufc1HoQmOqQGDO4Nk4/u98/hW39p3qqMFeP4nC6/v8qO4xRRk+poyfU17R0hRRR+gHegAoqOG5hn3eRLHLjrtcHH5VIKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACuf1u38q68xR8sg/XvXQVW1K2+02rLj5hyv1rKouZHXg63sqqfR6HL96sWFubq5WP+Hqx9qr49a3NBt9sLykcucD6CuaEbyPexVVU6TaNRVCgKowq8ACnd6BzWXr2o/YLbav+vl4X2Hc/4V01asaMHOWyPlZzSvJlfWddNpOYbdI3dfvE9AfTirWjamNSgZiuySMgMo6c9DXGEl2OTljXX+H9Oaxtd0uPNmIYj0HYV4+DxVbEVm/snJTqSnPyNbHvRj3oozXunYJRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXkvx58ff2RYt4c0uXF/dx/wCkujcwxH+H/eYfkPqK7P4jeMbfwX4bkvpiJLp8x2sJ/wCWknv/ALI6n8u9fJupX1zql/Nf30rTXNw5eVz1LGgBNOsLjUr+CxsYmmubhxHGi8lmJwBX2F8LPBNr4H8NRWKhZL2bEt3MP4nI6D/ZHQfn3rhP2d/h3/ZdmninWIcXl0n+hxuuDFEf48f3mHT0H1r2ygBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAM7WtVtdF0y51HUZhFbWqGSVj2A9PUnoB3NfHHxD8W3fjTxHPqt1lIz+7t4N2RFEPur9e5Pcmu/8A2hviD/bWpnw1pU2dPsn/ANJkQ8TSjt7qv6tn0FedeCfDN54u1+30mxGBId00vURIPvMf6epwKAO2+BHgQ67qo13VIv8AiXWD/u1bpNMOR9VXqffA9a+jgMfSqWiaVZ6HpVtpmmxeVbWyBEHr6k+pJ5J9au0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAY3iPT5ryGJrb5mjJ+X1HtXJkMr4YYwcH2r0WsTxBowuVN1bKBMo+dR/GP8a8bH4JyvVp79Uctanf3o7jPD+s+fH9lujiUfcY/wAY/wAa2q8/VmVwQSpByD3FdXo2qpd25WchZYxlgeMgd/8AGvhc3+sVbO7aWlux0YKvF+5Pc0Z544ImllO1F6muR1fU5b+TA+WEfdX+p96XWdUa+l2odsCHKr/e9zVewsZb6dUjBweWfsBUYTCQw0Pa1d/6/EzxOIlWl7Ont+YWFnNfTCOIYx1J6Ae9dhpdhDp8GyIbpD9526miytI7OERxDAHU9yfU1ZHyj1q8LnPssUpte7t5+p00sGowu9yQUVj+KfFGleFtMN9rNwIY84jQcvKf7qr3P6DvXz549+MGt+JRJaaazaVpzceXE372Qf7bj+QwPrX6jCaqRU47Mg9e8cfFjQPCxa2if+0tRXjyIGG1T/tP0H0GT7V4F4w+IPiDxbMf7Su2itcYW0gYpEB7jPzH3Oa5bpV/RP7KF6ra59rNqOSloF3t7ZY4H1waoCbw3qWoaTrVpdaPNKl4sihNhPzEkfKR3B6Y719mJu2LuXaxAyPQ9xXz7oXxA+G+g3MV1pvg+7S6iHyTO6uwPqMsQD7gZrpz+0HoXfR9R/76j/8AiqAPXaK8h/4aD0L/AKA+o/nH/wDFUf8ADQWhf9AfUfzj/wDiqYHr1FeQ/wDDQWhf9AfUfzj/APiqP+GgtC/6A+o/nH/8VQB69RXkP/DQWhf9AfUfzj/+Ko/4aC0L/oD6j+cf/wAVQB69RXkP/DQWhf8AQH1H84//AIqj/hoLQv8AoD6j+cf/AMVQB69RXkP/AA0FoX/QH1H84/8A4qj/AIaC0L/oD6j+cf8A8VQB69RXkP8Aw0FoX/QH1H84/wD4qj/hoLQv+gPqP5x//FUAevUV5D/w0FoX/QH1H84//iqP+GgtC/6A+o/nH/8AFUAevUV5D/w0FoX/AEB9R/OP/wCKo/4aC0L/AKA+o/nH/wDFUAevUV5Na/H7w7NOiT6dqMEZOGkwjBfcgHP5V6nY3dvf2kN3ZyCa3njEkUi9GUjINICaq9xewwcFizegFQareiCNkQ4bGWPoK5sanuk+ePK/3s8181mOb1KcnSwyTa3f6ep1U40oWdZ2vsa08lrNN5n2YZPX5iM/gKtRakq4Uw7F6DZ2rMRhIoZTlT3p3TrXyizrGKfNzfKx68qNOcVfVG3PfQwWbXTN+7A/En0+tcRfXct3dNNL1Y4x/dHYCpr+8M8mxT+6U529ifWl0fTpNRvAgB8teZG9B/ia+heMq42MYNWfbzPlMS1KryU9jR8NaWJJBeTL+7H3Ae59fw/nXU47mmRRrGiqgCqBgAdhT6+mw2HjQpqK36mtOHIrCUUUV0moUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABWZ4h16w8PWLXeoy7E6Io5Zz6KP8gVa1W/h0zTp766bZDboXdvb0Huegr548Ua9deI9VkvbskA8RoOiJ2A/r6muXEV/ZKy3PbynLHjptt2itzuLj4v3Jlf7LpMfl/w75efx4xVFfi5rO75rGzI9MMP1zXADAHSk49K876zU7n2sckwcVbkX4nsej/FnTLgBdVtpLKQDl0/eJ+nP6V0uk+MfD+rSiGz1OJpm6I4KFvpuAzXzx9KD6ntWscZNb6nFX4cw07+zbi/vR9SiiuF+EXiC51fSp7O+cyTWJULIxyXQ5xn1IIxmu6r06c1OKkj4XFYeWGqulPdBRRRVnMFFFFABRRRQAUUUUAFFFFABUGoXtrptjPe30ywW9uheRz0AFT18+fHvx7/AGtfnw5pU2bK1fN1Ih4ll/u57hf1P0FAHFfErxhceM/EUl8+6O0hzFawk/6uPPf/AGj1P5dq6P4F/D1vFuuDUdSj/wCJNYuC+RxcSDkRj27n2471x/grwze+LvENro+nrh5TmSTHyxRj7zn6D8zgV9keGPD9l4b0W10nTYhHb2ybR6sf4mb1JPJoA1EQKAAAABgAdAKfRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV5h8d/H48I+HzYabJjV9RUpGQeYY+jP7HsPfntXa+LvENn4X0G71fUXxDbrkKOsjfwoPcnivjPxZr974o1251fUn3T3LZCjoij7qD2A4oAzY1knmVUDSSSsAB1LMTwPck19UfCTwOng3w6v2lQdUvAJLpv7vpGD6Dv75rz39n/wJ9omHivVov3UJK2Mbr95+hl+g6D357V7xQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFTLZgcx4k0razXdsvB5kUdvcf1rB5B616C3eud1XQWZ2mscYPWM8flX5fSxyVSVOs9m7P5kYjBv46a+Rh28LXNwkKffc4FdpYWcVnAI4gB3Y9yfWsfQtHuIbtbi5URhAdozkk9K6EdTXn5nivaSUKbujbBYfkXNJahijFLRivMw9GVerGnHds9BuyuzwL9pSDUP+Eg0y4lVjp5ttkJ/hEm4lx7Ejb9R9K8dr7cvrK21C0e2v7aC6t3HMcqB1P4HiuS1L4T+CdRyW0SO3c/xW0jR4/AHb+lft9Cn7KlGmuiSPNbuz5Por3bxB+z5GweTw/rJQ9RDeJkfTev/wATXmPib4f+JfDBL6ppknkA/wDHxD+8j/76HT8cVsIx9J0TUtalMWk2U15IoyUhXc2PpWp/wr/xd/0Lmp/+A7f4VhW1zNbTrNaSvDIhysiEqwPsR0r0/wAK/HLX9M8iDWlj1S1U4dz8s+3/AHhwT9Rz60Acb/wr/wAXf9C5qf8A4Dt/hR/wr/xd/wBC5qf/AIDt/hX13a3Md1aQ3NuwaOaNZEPqpGQfyNSUwPkD/hX/AIu/6FzU/wDwHb/Cj/hX/i7/AKFzU/8AwHb/AAr7AooA+P8A/hX/AIu/6FzU/wDwHb/Cj/hX/i7/AKFzU/8AwHb/AAr7AooA+P8A/hX/AIu/6FzU/wDwHb/Cj/hX/i7/AKFzU/8AwHb/AAr7AooA+P8A/hX/AIu/6FzU/wDwHb/Cj/hX/i7/AKFzU/8AwHb/AAr7AooA+P8A/hX/AIu/6FzU/wDwHb/Cj/hX/i7/AKFzU/8AwHb/AAr7AooA+P8A/hX/AIu/6FzU/wDwHb/Cj/hX/i7/AKFzU/8AwHb/AAr7AooA+P8A/hX/AIu/6FzU/wDwHb/Cj/hX/i7/AKFzU/8AwHb/AAr7AooA+RbT4deMLidIU8O36s5wDJEUX8WPAr6e8GaQ3hnwfp+mXEgmms4MOw6FuWIHtk4HtW7VTUWxaSfT+tc2KqOnRlNdE39yLpx5ppGJcj7Qsgc/fBzWFNE0MjK/XP51v4zUF5bCePp8w6GvyvDYpxqNy2e/+Z6WOwar07rdbFHTbrym8t+Ub9DUmpXX/LKI5/vH+lZ+0qxB4K9aQ/Xn19a9R4anKoqh4KxtaNH2HUWNWlkCIuT/ACrt9Et47bTo1jGGblz6mud0+28lQzL87/oK6u0j8u3jTuBXs5NV9tiJWXuxW/mdcMJ7Gkpz+J/gSUUUV9eQFFFFAwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPOvjbqLwaPZWEZI+1ylnx3VccfmR+VePmvTfjqG+16S2Pk2SjPvla8y7V42Jd6mp+l5BTUcFFrrdiUUUVyHvBRRRQB6l8B4xnV3/AIv3Q/D5q9UNeffBLT3ttBub2QYN3Nhf91RjP5k16DXuYdWpo/LM4mp42bXe33AaKKK6DyQooooAKKKKACiiigAoorF8Z+JLLwn4en1W+O4RDEcWcGWT+FR9f0GTQByPxu8ejwvov9mabKBq1+hUEdYIzwX9ieg/E9q+ao4pLqdYoUaSWRgqoPmLMTgAepJq5r+s3uv6zcanqMpluLlizeg9FA7ADgCvaP2c/h7vZfF2sQ/KpIsImHU9DLj9B+J9KAO/+DfgFPBPh4NdoDq96BJcv12DqsYPoO/qfwr0SiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAprfkOuadXjH7Q/xC/sfTW8M6TKRqF6mbllbmGE/w+zN/L6igDzX46/EA+LfEH9n6fLu0jT2Kx4PE8nRpPcdh7c965/4Z+D5/GfiOOzUFLKDEl3KP4I89B/tHoPz7VzljZXGoX8NnZxNLc3DhI406lieBX1n8N/B1t4L8NxWEZElzLiW6mH/AC0kI7f7I6D8+9AHQ2ltBZ2kNraRrFBBGEjjUcIoGABU1JS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRUFxeW9scTTIh9CefypkGo2c7bIp0J9M4P61j7alzcrkvvNFTna9nYtUUUVsZhRRRQAUUUUAFFFFABRRRQAUUUUgGMtNHFStTcV+f5zkFWVV18Pqnq12OulVVrMZS0HrRXxn1as5ez5Xf0Om63F605VpqrT+lff5DkUsPJYjEfF0XY46tVNWQUUUV9qcwUHkEHoeCPWiigDzvxz8INA8Sb7nTlXSNQPPmQJ+7kP8AtJx+YwfrXn+nfALWm1ILqGo2MdkrfNJCzM5X2UrwT7nj3r6EooAitLeK0tobeBdsUKLGg9FAwB+QqWiimMKKKKQBRRRQAUUUUAFFFFABRTZZUiQvKwRFGSx7VyeqeIbi5kK2rNBEOhB+Yn1JrlxGLp4de9v2M5VFDc66iuC/tK8/5+5v++zVy08Q3sHDuJk9GHP51wwzak3aSaMvrETsaKz9N1i3vsIn7uT+4/8AQ960K9SnUhUjzQd0bxkpK6CoLxN9u4X72P5VPTJHSFC8rKkajLO7YA+ppVaaq03TezTX3lwlyy5jB6UlZNz408JSaqLK212ze4dsbQTs3HsHxt/Wtr7PPnHkvn6V+V4rLK+GqODi32aWh9FTxEJxvcyb+0dnMsKgluopNPsiJPMmGNvRa1GgkVuUIPapYLOSVxuXaO5rSl9ZqWoRi+2zOGWEoKp7Zvzt5j9OtvOnVj91efqfStnpTIY1jQRoNop9foGV5fHBUeR6yerfmcWIrOrK/QKKKK9U5wooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDkvih4ek17w+WtUL3doxmjQdXGMFR7kcj3FeDkbT6HuK+pa4Xxp8OLPW5WvNNdbK9blvl+SU+pA6H3H4iuHEYdz96O59Vk2bxwq9jW+Ho+3/APFKSuk1PwL4j05ysmmyTIOjQYkB/Ln8xWcvh3W3baukXuf+uDf4V5zpTXQ+yhjaE1eM196M7vxWr4W0C78RapHZWgYKDmaTHEadyf6Dua6Hw58MdZ1KRX1Jf7Ot++7BkI9lHT8a9c0DQbDQLFbTTYfLXq7HlpD6se5roo4aU9ZaI8bM88pUYOFF3l5bItadZQadYQWVomyG3QRqParFFFeslZWR+eyk5tyluwooopiCiiigAooooAKKKKAGTzRW8LzTyLFFGpZ3c4CKBkkn0Ar5X+LHjiXxprzNblk0u0JjtYzxn1cj1P6DAruv2gPHpO/wppUvob+RG/KL+p/AeteQeHtGvfEGsWulaXEZbm6cIo7D1YnsAOSfSgDqPg94Dl8b+IVS5V10mzIku5BxuHaMH1P6DJr67tLeG1t4re3iWKKFQkaKMBVAwAKxPAnhax8HeHLbSLBcmMbppccyyH7zH69h2GBXQjrQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFQXM8NpbzXFxKscUKl5Hc4CqBkk+wFAHP/ETxbaeCvDNxql1tdwNlvCTgyynov07n0Ar441nVLvWdSudQ1CUy3V1IZJGPcn+QHQDsK6r4v8AjqTxx4jeWJyul2hMdnCePl7uR6tjPsMCpvg74Gfxl4g8y7jP9l2eHuG7SH+GMH37+g/CgD0H9n7wKbCzHirVIf8ASblSLJHHKJ3k+p6D2+tex5J601I1RVjjUKiAAKvAAHQAU6gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApsjrGjO5AVRkk9qdWF4nuyFW1Q/e+d/p2FcuLxCw9JzfQ3w9J1qigirfa7cPIfsreUg4BIyT+dRjXL4wGPeoY/x7eRWb1or4uWPryk3zPU+mjhKMYpOI5mLMWZizHqxptFFcjk27s6UklY6Hw/qjSEWty2W/gY9/Y1uVwaOyOHQkEHIPuK7TTbkXlnHMBgsOfrX1eUY2VaPspvVbeh8/mOGVN+0jsyxRRRXvHkhRRRQAUUUUAFFFFABRRRQAVUvtRhtCFbLMewq3XOaz/wAhF/oP5VnOTijswdGNapyy7G3aXMd3Huj7HBB6irFY3h77830FbNKCUlzNakYmmqNRwiFFBorU5gooooAKKKKACiiigAoqvPe21u6pPMkbE9CanBDKGUhlPQjvUKcW7JiTTFoooqxhRRRQAUUUUAFFFZ3iC7+yac7KcSP8i/j1/Ssqs1Tg5voTJ8quYXiPUzd3Bggb/R4z1/vEd/8ACsel5NJXx1es603KR5cpObuwpOKdWLr3irR9DU/bLtDKOsUfzP8AkOn44qYU51HaCuxKLbsjbjdo5AyEqykEH3rs7/XdM0rTUvtXv4LKBkDBpHA3ZHQDqT7CvnDXPipez7o9HhWzToJJPnkP4dB+tcPqWpXmpTedfXM1xIf45XLcegz0HtX0WW4WrQTdR79DtoQlDc928VfHqwtA8Hhmya8kHAubnKRn3CdW/HbXkPifxvr/AIpctrOpSyxZysCHZEv0QcficmqXh3w1rXiO48nRtNnvDnDMi/Iv1Y8D8a9b8JfATOybxRqAHf7LZn+bkfyH4161jpPF7GyudQu47WygeeeVgqRouWY/Svsnw1b3Vn4c0211F/MuobaKOY5zlwoB57896i8OeGNE8NQCLRNOhtBjBZRl3+rn5j+da1AwJ/OisvUNWaGcxQoG29Sat2F2LyASAYIOCPeoTi3odEqFSMFNrQs0UUVZzhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFcR8XfHKeDPD7fZ3B1W8BS3T+76yH2Hb1P410/iHWrLw9o1zqmpSeXb2y7j6ueyr6knivknxj4kvfFWvXOq37fPIcRxqfljT+FR9P1PNAGRLLJcTNLM5klkYsznksxOSSe5r6i+A/wAOz4U0f+1dVhA1i/QEhhzbxHkJ7Mep/Adq89/Z6+Hn9tX48S6tFmwtHxbRuOJpR/F7qv6n6GvpbH40ALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV4D+0f8QdoPhHSpuThtQdD26rFn9T+A9a9H+LXjqHwR4ZkuY2VtRucxWcR5y+OXI9F6n3wO9fH91cS3dzNcXMjyzTMZJJGOS7E5J+uaALmgaNeeIdYttL06PzLm4cIo7D1J9ABzX1x4N8N2fhXw/b6TYgMkIy8mOZZD95z9T+QwK4r4F+BD4d0X+2NRj/AOJnqCAorDmGI8hfZj1P4D1r06gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK4rUJzc3ssx6Mxx9BwK7C7YpbSsOqox/SuHzXzed1LqMPVnt5TBNyn8hKKDRXzB7gUUUUALXUeGDnTc9t5xXL/qTXZ6bbG2sYoiOQuT9epr3MlpydZz6JfmeVmc0qaj3Zaooor68+dCiiigAooooAKKKKACiiigQVzes/8AISk+g/lXSVzesf8AIRk+g/lWFb4T1Mt/iv0Lfh37030FbJrG8O/em+graNVS+ExzD+OxKKKK1OIKKKKACiiigAqvqN4ljaPPIfuj5R6n0qb7uWZtqryTXGa5qP2+5+Q/uo+FHr7/AI1w43EqhDzexjWnyR8yjPNJcTNLIclzkmuv8NRyx6VGJM4Yllz/AHT0rndD07+0LsKxxCnzOf6fjXbBQoGBgYwAO1cGW0pyk6sjHDqTbkwooor3TsCiiigAooooAK5vxjJzbx9vmb+QrU1rXNL0G2+06zqFvZRDo0r4J/3R1J+gNeMeP/jNYXsyR+G7N5zGCPPuV2qc+ijk/jj6VyYulKrScI7szqRcotI695EjQtI4VV5LFsAD3JrlNe+Iui6Zvjtna/nHGIuEH1Y8flmvJtb8R6prcu7UryWVR0QfKi/QDis+2gmu5litoXlkboqAsT+Argo5VTh71V3MI4dLWTOn1/x/rWrbkSb7HAf+WcHykj3bqa5Ikseetd3oPww1S+2yanIthCf4W+aQ/gOB+J/CvRfDfgfSdLlRbKyFxcscCWb52z/IfgK3liqFD3Kau+yK9pTi7RPLPCXw48ReKZwLS1+zwYy09z8iAeo7n8BXs3hT4I+H9K2Ta08mr3I52N8kI/4CDk/ice1ehaTYJp9qIl+aU8u3qf8AAVdGc81305SlFOSsbRbe5FaWtvZW6W9nbxW0KDCxxIFUfQDipsUtFWUNooopjOW1L/j+m/3jWn4d/wBRL/vD+VZmpf8AH9N/vmtTw7/qJf8AeH8q5IfGfQYn/dV8jVooorrPnwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKTj+LgDuaWvIvj349/suybwzpUpF5dJ/pUiNzFGf4P95u/oPrQBwPxt8e/wDCV6yNP02QnSbFiEIPEz9C/wBOw9ue9Yfwy8GXXjbxJFp8IKWkeJbuYf8ALOMHt/tHoPf2BrntPsbnU7+Cyso3lubmQRxRr1ZicAV9hfC/wVa+B/DUWnpiS9lxJdzD+OTHQew6D8+poA6LTNOtNK0+Cw0+FYbW3QRxIo4AH+fxq9SAYpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACqGsaja6Rp9zqF/MsNvbRmWRz2Uf54Hc1fr5q/aJ+IB1bUW8MaVNmxtH3Xcin/XSj+H/AHV/U/QUAef/ABG8Y3fjXxNPqVyWSAfJbQk8RRjoPqep966r4FeBB4g1b+2dShJ02wcbVYcTTDkD6DqfwHrXFeC/DN54r8QW2lWS4aU5lfGRFGPvOfp+p4r630HR7Pw/pFrpmmxhLa2QKo7t6sfUk80AaAAUYHX+VJ0o6UdaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiigUAV9QGbK4/65t/KuIFd86hlKnowwfoa4q/tHs7poX4x90/3h2NfM53Tek+mx7eVTSvD5kFBoor5s9wKKK0tI0l7xhJKGS3H5t9P8a1o0KleShBXMqtWNKPNJk/hvT/Mf7XOPkX7g9T6/hXSU1FVEVFACqMADtTq+5weFjhqagvn6nyuIrutNyCiiiuw5wooooAKKKKACiiigAooooAK5vWf+QjJ9B/Kukrm9Z/5CMn0H8qxq7Hp5Z/Ffp/kW/Dv3pvoK2qxfDv3pvoK2qdL4THMP47Eqjf6xZ2MgjmdmdudqjJA96vVxniSF4tXlMn3ZBuU+o/+tXLjq8qNPmiup5tWTjG6OttLiK8iEkD71Pf09jU1cd4e1MWNyUmP7qTqf7h9a6yWaOKHzScqenv9KKGNhUpe0k7W3Kot1ErEtFY1xfyy8I3lr6DqfxrNvb6S3i+Vm3t05/WvGlxFSdT2dOLl5nfPC8lN1Ju1ifxPqpybKA9P9aR/6DWBbW73M6wxDLucAU0ksxJOWNdZ4a00WtsLhtrTyjp/dHp/jUw5sdX1en5HiRTqyu9jQ02xjsLZYYuQOXb1Pc1l+NfFdh4Q0STUtSJbJ2wwKfmlbso/mT2FbchVVLMQABkk8AD1r5Y+MXjQ+LfE7fZXzptiDDbDs3PzP+J6ewFfTwgoRUY7HdFKKsjrNO+P2qHVlOpaXaf2czYZIdwkVfUMSQSPoM+1e9RTJNEksLB45FDow7gjINfK3wq8BzeNtZdJJDBp1oA1zKBknJ4Rfc889hzX1OWt7GzVpXS3t4FA3OwVUUDAyT6CrGS0V5p4s+NvhzRg8Olh9ZuRx+5bbEPq5HP/AAEH615B4r+LHifxHvia7+wWrceRZ5QEf7TZ3H88e1AH0B4s+InhnwtuTUNRSW5Uf8e1v+8kz6EDgfiRXkHiz466xqJeHw9bR6VbngSv+8mPvn7q/gD9a8nOXJJOSTz6k123hL4V+J/EgWZLP7DZtz592CgI9VXq35Y96AOQ1DULvU7o3Oo3U11O33pJXLMfxNaXh3wrrniScRaJp011zhnAwifVz8o/OvffCfwS8OaQEm1QPrFyOf3vywqfZB1/En6V6NbW8NpAtvawpDCgwscahVA9gOKAPENC+AU6wpPruoxySdTbW+QPoZCP5D8a7DT/AAcdFj8nT9LWFehMYBLfVup/GvRKK5MRhVX0cmvyMp01PdnFQaHqEz4MIiHrIcf/AF66bSdKg09Mj95KRy5/kPQVfoqMPgKVB8y1fmKFGMdgoooruNgooooAKKKKAOX1L/j+m/3jWn4d/wCPeb/eH8qzNS/4/p/941p+Hf8Aj3m/3h/KuSPxn0GJ/wB1XyNWiiius+fCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiq2paha6ZYXF9fyiG2tkMkkjdAB/X0Hc0AYHxJ8ZW/gvw3JeyAS3k2YrWE/xyY6n/ZXqfy718m397cajezXl7K01zO5kkkbqxPU10HxC8Y3XjPxDLqE4aO3T93bQZ4jjB4/E9SfWuo+BPw7bxXrY1LVIj/Y9jICwYcXEg5Ef0HU/l3oA9C/Z7+HY0ewXxPrEOL+7T/REccwxH+LHZmH5D6mvaqYF4AwABT6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiisjxR4gsvDOiXWrak+yC3XOO7t2UepJ4oA4r46ePx4P0D7FYSAaxqClYSvWGPo0h/kPf6V8pBWlkCqGeRzgAclif581r+MPEV74r1+61bUmzLM3ypn5Y0H3UX2A/xr0z4A+Azd3Y8U6rD/o9uxFnGy8SSDq+PQdvf6UAeifCDwQvg/wAOrJeIP7UvVD3J7xj+GMfTv6n8K7k4yKQCigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACqt/YQ30ZSUcjow6irVFROEakXCaumVGcoO8XZnNTeHrhP9TIjr78GmLoF6W58tR65z/Kuoorynk+GbvZ/ed6zGslbT7jIstBghw8585v7vRfy71rDpgdqWivRoYenQVqasclStOo/fdw6UUUVuYhRRRQAUUUUAFFFFABRRRQAUUUUCYVzes/8AIRk+g/lXSVzes/8AIRk+g/lWNXY9TLP4r9P8i34d+9N9BW1WL4d+9N9BW1TpfCY5h/HYlUtW09L+1MbfLIOY39D/AIVdopzgpxcZLRnDJJqzPPbmCS3maKVSrr1X1q5ZaiyKsMzM0Q4XP8P/ANaui1+wjurTzDhZk+63r7H2rkJEKMVcbSOor47H4dU5So33V/kc0faYaSqR2NyWRI4mkYggViTyNNIXc89qDNI6BHOUXoKfaW5uJwv8Pc+1ePQoLCxlOTN8Ri542cacNuxPp1rvPmsvyjp710ukS/O0f8PUVmhQqhUG0LxisnxZ4qh8H6NLqcyq82ClvEf45COB9B1PtSy7E1J4+Eo9Xa3kewsJChQ5Pmc38f8Ax5/Zmnnw3pc3+mXaZunQ8xRn+D6t39vrXz2o3MATj3NWdTv7nU9Qnvr6Vprm4cySO3VmPWqtfpx5J6xp/wAVLDwZ4Zh0Pwbp4nmUF5r+6G0SSnqwQckdhkjgDiuC8SeLte8SzGTWtSnuRnIjLYjX6IOB+VM8N+GNV8S3Qt9ItjM38TFgir9WYgV7J4S+AVtFtn8T35un6m2tDhPoXPJ/AD60DPDdN0+81W7W20+1mup36RwxlmP4CvUPCnwK1vUNk3iCaPSoTz5S4kmYfQHC/ifwr3rQ/D+l+H7byNG0+3soj18pcFvq3Un6mtCgDlfCnw68M+Fgklhp0c1yv/LzcnzJM+ozwv4AV1RJxjtRRQAlLRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHL6l/x/Tf7xrT8O/8e83+8P5Vmal/x/Tf7xrT8O/8e83+8P5VyR+M+gxP+6r5GrRRRXWfPhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXzx8evHw1m/Ph7SZc2Fm/+kSI3E8g7fRf1P0Fd78cPH3/CMaP/AGVpsuNWvkIJB5t4jwX9mPQfia+a4IZbq4jhhRpJZXCqqjJZicAD3JoA2/A/hi+8Y+IrbSNPXBkO6SUjKwxj7zn6dvU4FfY/hrQrLw7otrpOlxiO2tkCj1Y92J9Sea5T4OeAI/BPhwfaFD6regSXUgGdnpGD6Dv6nPtXoNACUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAAa+U/j18QD4p1z+y9NmzpGnuQpU8Ty9C/uB0H4nvXpf7QXxAGg6S3h7S5salfp+/dG5t4f6Fug9Bk+lfNVnaT393DaWcTTXE7iOONeSzE4AFAHSfDXwfceNPEcdiuY7OLEl3N/zzjz/ADPQfn2r6xsbO30+zhs7OJYbe3jEcca9FUDAFc58NPB1v4L8NpZDbJeTYlupQPvSY6A/3R0H5966oUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUCYVzes/wDIRk+g/lXSVzes/wDIRk+g/lWNXY9TLP4r9P8AIt+HfvTfQVtGsXw796b6Cto06XwmOYfx2JRRRWpxFbU/+POT8P51zl3bLcr6P611FwnmQunqKwGUo5RvlI4NfCcRxqU60a0drW/FnqYONOrTdOWpgTQyQNhgcevatLS4ikLEjhzx9KuYHfmjoPavnK2MlVhyMeHy6NCr7RO/YXHNeEfHm+upPFUNnKSLa3t1eFex3feb8xj8K9+tLZ7h8KPl7tUfirwXoXiq2ih1iz8xoARFLGxR4weoDDt7HIr6XhvBTVR4ma0tZFY6suXkW58d0V9X2Hwm8FWURX+xEuD/AHp5Hc/zA/Srf/Ct/BZ6+G7L8m/xr7k8c+Rau2+r6lbY+zahdw4/55zMv8jX1LdfCrwTcZB8PxR+8Uki/wAjWVc/BDwXJnZb3sH/AFzuSf5g0AfPieL/ABJGNq69qYX/AK+n/wAa9s/Z88Zaxrx1DTNZuZL1bSNZoriXlgM7SrN1PqM89asyfALws3KX2qKPTzYz/wCyV2vg7wfo/g+wktdIiYeaQ0s0jbpJCOmTwMDsAAKAOgooooGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAcvqX/AB/Tf7xrT8O/8e83+8P5Vmal/wAf03+8a0/Dv/HvN/vD+VckfjPoMT/uq+Rq0UUV1nz4UUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABWJ418T2XhHw9carfHdsG2KLPMsh6KP6+gzWxczw20Ek9xKsUMSl3kc4CqBkkn2FfKvxW8cTeM9eLwF00u0JjtYzxkd3I9T+gwKAOa17V7zXtVudT1GZpri5kLuew9APQAcAV7Z+zn8OwfL8X6xFxyLCJh+BlP8h+J9K4D4PeApPG3iIC5QppNmQ91IB970jB9T39Bk+lfW9vBFbwRwW8axxRKERVGAqgYAHsBQBYAwKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACub8feLLLwZ4cudXvSGZRtghzzLIfuqP5n0GTW9cTRW8Ek07qkUal2ZjgKoGSSfSvkP4x+OpfG3iN2t2K6VZMYrSPpu9ZCPU4/AYFAHJ65q95reqXOpajL5t1dOZJH9z2HoAOAOwr2z9n7wIbWFfFGqRfvpQRYxsv3EPBk+p6D2ye9ef8Awj8Dv4w8RA3KsNLsyHuXx9/+7GPc9/QZr6lREijWOOMJHGNqoBgADgACgBwpaKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKBMK5vWf8AkIyfQfyrpK5vWf8AkIyfQfyrGrsepln8V+n+Rb8O/em+graNYvh37030FbJp0vhMcw/jsKKKK1OIKhubSO4X5hhvUdamorCtQp1ouFSN0yoSlB80XZmY+lP/AAyL+INLFpfOZZM+wrQllWGJpJGwqjJrNi1qN5trxsgJxnOfzryY5Lgac+Zx+9nbCtiKkW1sjTjjEcYVBtUelLSk56dKSvbhGMFyxVkcMm27sKKKKoQUUUUAFGBRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAcvqX/H9N/vGtPw7/AMe83+8P5Vmal/x/Tf7xrT8O/wDHvN/vD+VckfjPoMT/ALqvkatFFFdZ8+FFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRXDfF3x3F4O0Mx2zhtXvFK26Z/1Y6FyPQdvU/jQBwnx+8e+Y0nhTSpcIpBv5EPUjkRfh1Pvx615J4d0S98R6zbaVpcZkurl9q+gHdj6ADkmqEjyTzM8jNJLIxYk8l2J6++TX1N8C/h4PCOiDU9UhxrN+gLhutvF1EfsT1PvgdqAOx8EeF7Lwh4dttH09eIhmSUjDSyfxOfr29BgV0AAAxS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFcV8VvHEPgXwxJd7lfUJ8xWkR/ifH3iP7o6n8B3oA87/AGj/AIg/Z4W8JaRP+8kAOoSIeVXtFn1PU+2B3NeF6HpN3reqWum6fGZbm5cIg+vc+gA5zVe/u5767muruVpp53MkkjnJdickn8a9N+Dfijwf4Qin1HV2uG1abKL5duWWGP0Bz1J6+2B60Ae5eCfDVp4S8OW2lWY3bBullA5lkP3m/wAPQYrcrzgfHHwYOk97/wCAx/xpP+F4+C/+e97/AOAx/wAaAPSKK84/4Xj4L/573v8A4DH/ABo/4Xj4L/573v8A4DH/ABoA9Horzj/hePgv/nve/wDgMf8AGj/hePgv/nve/wDgMf8AGgD0eivOP+F4+C/+e97/AOAx/wAaP+F4+C/+e97/AOAx/wAaAPR6K84/4Xj4L/573v8A4DH/ABo/4Xj4L/573v8A4DH/ABoA9Horzj/hePgv/nve/wDgMf8AGj/hePgv/nve/wDgMf8AGgD0eivOP+F4+C/+e97/AOAx/wAaP+F4+C/+e97/AOAx/wAaAPR6K84/4Xj4L/573v8A4DH/ABo/4Xj4L/573v8A4DH/ABoA9Horzj/hePgv/nve/wDgMf8AGj/hePgv/nve/wDgMf8AGgD0eivOP+F4+C/+e97/AOAx/wAaP+F4+C/+e97/AOAx/wAaAPR6K84/4Xj4L/573v8A4DH/ABo/4Xj4L/573v8A4DH/ABoA9Horzj/hePgv/nve/wDgMf8AGj/hePgv/nve/wDgMf8AGgD0eivOP+F4+C/+e97/AOAx/wAaP+F4+C/+e97/AOAx/wAaAPR6K84/4Xj4L/573v8A4DH/ABo/4Xj4L/573v8A4DH/ABoA9Horzj/hePgv/nve/wDgMf8AGj/hePgv/nve/wDgMf8AGgD0eivOP+F4+C/+e97/AOAx/wAaP+F4+C/+e97/AOAx/wAaAPR6K84/4Xj4L/573v8A4DH/ABo/4Xj4L/573v8A4DH/ABoA9Horzj/hePgv/nve/wDgMf8AGj/hePgv/nve/wDgMf8AGgD0eivOP+F4+C/+e97/AOAx/wAaP+F4+C/+e97/AOAx/wAaAPR6K84/4Xj4L/573v8A4DH/ABo/4Xj4L/573v8A4DH/ABoA9Horzj/hePgv/nve/wDgMf8AGj/hePgv/nve/wDgMf8AGgD0eivOP+F4+C/+e97/AOAx/wAaP+F4+C/+e97/AOAx/wAaAPR6K84/4Xj4L/573v8A4DH/ABo/4Xj4L/573v8A4DH/ABoA9Hrm9Z/5CMn0H8q5z/hePgz/AJ7Xv/gMf8a0LLXbLxLbrqumNI1tPkKXTaflODx9RWNX4T1Ms/iv0/yN7w79+b6CtntXC6h4z0bwaFfW3nVbrIjMUe/kdc+nWqX/AAvDwX/z3vf/AAHP+NOl8JhmH8d/I9Horzj/AIXh4L/573v/AIDH/Gj/AIXh4L/573v/AIDH/GtTiPR6K84/4Xh4L/573v8A4DH/ABpP+F4eC/8Anve/+Ax/xoA7zWP+QdN+H865sdaz7T4qeF/EVwml6bLdm6ueEDwFRwNx5z6CtDvXLW+JHvZb/CZ16/dH0pQDXnR+NngyI7HuL3K8H/Rj1H403/heHgv/AJ733/gMf8a6TxJ7npGDRg15v/wvDwX/AM9r7/wGP+NH/C8PBf8Az2vv/AY/40EHpGDRg15v/wALw8F/89r7/wABj/jR/wALw8F/89r7/wABj/jQB6Rg0YNeb/8AC8PBf/Pa+/8AAY/40f8AC8PBf/Pa+/8AAY/40AekYNGDXm//AAvDwX/z2vv/AAGP+NH/AAvDwX/z2vv/AAGP+NAHpGDRg15v/wALw8F/89r7/wABj/jR/wALw8F/89r7/wABj/jQB6Rg0YNeb/8AC8PBf/Pa+/8AAY/40f8AC8PBf/Pa+/8AAY/40AekYNGDXm//AAvDwX/z2vv/AAGP+NH/AAvDwX/z2vv/AAGP+NAHpGDRg15v/wALw8F/89r7/wABj/jR/wALw8F/89r7/wABj/jQB6Rg0YNeb/8AC8PBf/Pa+/8AAY/40f8AC8PBf/Pa+/8AAY/40AekYNGDXm//AAvDwX/z2vv/AAGP+NH/AAvDwX/z2vv/AAGP+NAG/qP/AB/zf7xrT8O/8e83+8P5Vg2+pW+sQJqVmWNtdL5ke4YO09MjtVXUPH2heDpFttakuFe4HmJ5Ue8YHHPNcsfjPoMT/uy+R3oorzg/HDwWD/rr7/wGP+NH/C8fBf8Az2vv/AY/411nz56PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB6PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB6PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB6PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB6PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB6PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB6PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB6PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB6PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB6PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB6PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB6PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB6PRXnH/C8fBf8Az2vv/AY/40f8Lx8F/wDPa+/8Bj/jQB2viPW7Lw5o1xqupS7IIFyc9XPZR6kngV8k+L/El54p1661XUW/eTHEcYPyxIPuqPYD8+tdP8YPiGfGWoRQaeZU0e15iRxtMrkcuw9ugHYfWsz4Y+CLrxx4kisU3R2cOJbuYfwJnoPc9B+fQUAd1+zv8Ojqt6PFGrwhrG0f/Q43HE0o/j91U9PU/SvpPFVNMsbbS7C3sbGJYba2QRxRr0VQMCrlABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV4J+034X1i/utM1iwtprqzggaCVIlLGJtxO4gc4IOM+3Ne90UAfB39kan/wBA67/78t/hR/ZGp/8AQOu/+/Lf4V940UAfB39j6n/0Drv/AL8t/hR/Y+p/9A67/wC/Lf4V940UAfB39j6n/wBA67/78t/hR/Y+p/8AQOu/+/Lf4V940UAfB39j6n/0Drv/AL8t/hR/Y+p/9A67/wC/Lf4V940UAfB39j6n/wBA67/78t/hR/Y+p/8AQOu/+/Lf4V940UAfB39j6n/0Drv/AL8t/hR/Y+p/9A67/wC/Lf4V940UAfB39j6n/wBA67/78t/hR/Y+p/8AQOu/+/Lf4V940UAfB39j6n/0Drv/AL8t/hR/Y+p/9A67/wC/Lf4V940UAfB39j6n/wBA67/78t/hR/Y+p/8AQOu/+/Lf4V940UAfB39j6n/0Drv/AL8t/hR/Y+p/9A67/wC/Lf4V940UAfB39j6n/wBA67/78t/hR/Y+p/8AQOu/+/Lf4V940UAfB39j6n/0Drv/AL8t/hR/Y+p/9A67/wC/Lf4V940UAfB39j6n/wBA67/78t/hR/Y+p/8AQOu/+/Lf4V940UAfB39j6n/0Drv/AL8t/hR/Y+p/9A67/wC/Lf4V940UAfB39j6n/wBA67/78t/hR/Y+p/8AQOu/+/Lf4V940UAfB39j6n/0Drv/AL8t/hR/Y+p/9A67/wC/Lf4V940UAfB39j6n/wBA67/78t/hR/Y+p/8AQOu/+/Lf4V940UAfB39j6n/0Drv/AL8t/hR/Y+p/9A67/wC/Lf4V940UAfB39j6n/wBA67/78t/hR/Y+p/8AQOu/+/Lf4V940UAfB39j6n/0Drv/AL8t/hR/Y+p/9A67/wC/Lf4V940UAfB39j6n/wBA67/78t/hR/Y+p/8AQOu/+/Lf4V940UAfB39j6n/0Drv/AL8t/hR/Y+p/9A67/wC/Lf4V940UAfB39j6n/wBA67/78t/hR/Y+p/8AQOu/+/Lf4V940UAfB39j6n/0Drv/AL8t/hR/Y+p/9A67/wC/Lf4V940UAfB39j6n/wBA67/78t/hXvfwnhlt/AljHPG8Thpco4II/eN2Ne7VxHiX/kMz/Rf/AEEVjV+E9PLP4r9P8jx747W091a6V9mgkmKvJny0LY4X0FeTf2TqX/QOu/8Avy3+FfZHgz/W3P0X+tdRVUvhMcd/HZ8H/wBk6l/0Drv/AL8t/hR/ZOpf9A67/wC/Lf4V94UVocR8H/2TqX/QOu/+/Lf4Uf2TqX/QOu/+/Lf4V940GgD42+F+nXsHjnTJJ7OeNA75Z42UD5G6nFe/E9cV2/iT/kEzfQfzFcSBXLW+NHu5b/CfqfLt3pOotdSkafdYMjf8sW9fpUX9kal/0D7v/vy3+FfdkP3R9KlrpPElufB39kal/wBA67/78t/hR/ZGpf8AQOu/+/Lf4V940UEnwd/ZGpf9A67/AO/Lf4Uf2RqX/QOu/wDvy3+FfeNFMD4O/sjUv+gdd/8Aflv8KP7I1L/oHXf/AH5b/CvvGigD4O/sjUv+gdd/9+W/wo/sjUv+gdd/9+W/wr7xooA+Dv7I1L/oHXf/AH5b/Cj+yNS/6B13/wB+W/wr7xooA+Dv7I1L/oHXf/flv8KP7I1L/oHXf/flv8K+8aKAPg7+yNS/6B13/wB+W/wo/sjUv+gdd/8Aflv8K+8aKAPg7+yNS/6B13/35b/Cj+yNS/6B13/35b/CvvGigD4O/sjUv+gdd/8Aflv8KP7I1L/oHXf/AH5b/CvvGigD4O/sjUv+gdd/9+W/wo/sjUv+gdd/9+W/wr7xoNIDxnwKjx+DdISRCjrbKCrDGD7ivPfjpZXV1q2mm2tppgsDA+WhbHzewr2nWP8AkJXP/XQ1u+Dv+Paf/roP5Vyx+M9/E/7ovkfGH9k6l/0Drv8A78t/hR/ZOpf9A67/AO/Lf4V940V1ngHwd/ZOpf8AQOu/+/Lf4Uf2TqX/AEDrv/vy3+FfeNFAHwd/ZOpf9A67/wC/Lf4Uf2TqX/QOu/8Avy3+FfeNFAHwd/ZOpf8AQOu/+/Lf4Uf2TqX/AEDrv/vy3+FfeNFAHwd/ZOpf9A67/wC/Lf4Uf2TqX/QOu/8Avy3+FfeNFAHwd/ZOpf8AQOu/+/Lf4Uf2TqX/AEDrv/vy3+FfeNFAHwd/ZOpf9A67/wC/Lf4Uf2TqX/QOu/8Avy3+FfeNFAHwd/ZOpf8AQOu/+/Lf4Uf2TqX/AEDrv/vy3+FfeNFAHwd/ZOpf9A67/wC/Lf4Uf2TqX/QOu/8Avy3+FfeNFAHwd/ZOpf8AQOu/+/Lf4Uf2TqX/AEDrv/vy3+FfeNFAHwd/ZOpf9A67/wC/Lf4Uf2TqX/QOu/8Avy3+FfeNFAHwd/ZOpf8AQOu/+/Lf4Uf2TqX/AEDrv/vy3+FfeNFAHwd/ZOpf9A67/wC/Lf4Uf2TqX/QOu/8Avy3+FfeNFAHwd/ZOpf8AQOu/+/Lf4Uf2TqX/AEDrv/vy3+FfeNFAHw3pHhjXdX1CGzsdKvJZ5DgDyWAHuSRgD1Jr61+Gfgy18D+GYdOixJdP+8upgv8ArJCOf+AjoPb3Jrr6KAEpaKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAOa+InimLwd4Wu9Zmi85osJFFnG+RjgAnsO59ga+ftP8Aj94ui1RZ777HcWZb57ZIQmF7hWByD7kmvSP2pJ/L+H1pEDjzdRjz7gRyH+eK+dvCWnR6t4p0rTpwTFd3cULgHB2lgDz9KAPt6wu49Q062vbcnyrmJJkz12sAR+hqzUNvDFbQRQQqI4olCIg6BQMAD6CpqACiiigDifjF4jvPC/gO91HTSFuyyQxORnyyxwWx6gZx7189eCfib4p07xXZTT6veX0M86Rzw3MpkV1ZgDgHoeeor3D9o5C3wtvSP4LiBv8Ax8D+tfK+lS+VqdrKT9yZG/JgaAPvOiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAriPE3/ACGZ/ov/AKCK7euI8Tf8hmf6L/6CKxq/Cenln8Z+n6oveDP9bc/Ra6iuX8Gf625+i11FVS+FGOO/jyFooorQ4goNFBoAy/Ev/IIn/D+Yriq7XxL/AMgif8P5iuKrlrfEj3ct/hSPRIfuj6VLUUP3R9KlrpPEluFFFFMkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoNFBoA4HV/wDkJ3P/AF0Nbvgz/j2uP98fyrC1f/kJ3P8A10Nbvgz/AI9rj/fH8q5I/wAQ97E/7mvkdDRQKK6zwQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDxD9q+bb4e0OH+/dSN+SY/9mrxz4Sxef8S/DiY6Xsb/AJHP9K9U/azn48PQf9fD/wDoArzr4EwG4+K+iDrsaST8onP86APsPA9KKKKACiiigDz/AOP8Jl+FGs/7Aif8pUr5EiOHU+hFfZXxni8/4X6+npbbvyYH+lfGVAH3tYS+fZW02c+ZEr/mAasVl+FpRP4b0qUdHs4m/wDHBWpQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVxHib/kMz/Rf/QRXb1xHib/AJDM/wBF/wDQRWNX4T08s/jP0/VF3wZ/rbn6L/KuprlvBn+tufov8q6mqpfCjHG/x5C0UUVocQUGig0AZfiX/kET/h/MVxVdr4l/5BE/4fzFcVXLW+JHu5b/AApHokP3R9KlqKH7o+lS10niS3CiiimSFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUGig9KAOB1f8A5Cdz/wBdDW74M/49rj/fH8qwtX/5Cdz/ANdDW54M/wCPa4/3x/KuSP8AEPexP+5r5HRCigUV1nghRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHzh+1hPu8QaHBn/V2sj/99Pj/ANlrnf2bYfM+KFq+P9VbTP8A+O7f61o/tSzeZ4+s4/8Anlp8Y/OSQ15p4f1zU/D96bzRbySzuShj8yPGdpwSOfpQB910V8X/APC0PHH/AEM1/wD990knxO8bt/zM2o/hLj+VAH11qPibQ9LvEtNT1eys7mTG2KedUY56cE1oxzRzxLJE6yRsMhkbII9iOtfCF9eXWoXcl3fXEtxcSnMksrFmY+5NfRX7Ll3qU3hnVYrppG0+C4QWpYkgMVJdV9h8p+poA9F+JsRn+HniGNep0+Yj8ENfE5GDivunxXF9p8MarB182zmX80Ir4WoA+3Ph1N9o8BeH5f7+nwH/AMcFdFXnnwC1d9W+GmniRArWTNZ5H8QTofyIr0MdKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACuI8Tf8hif6L/6CK7euI8Tf8hif6L/AOgisa3wnp5Z/Gfp+qL3gz/W3H0X+VdRXL+DP9bcfRf5V1FVS+FGOO/jyFFFAorQ4goNFBoAy/En/IIn/D+Yriq7XxJ/yCJ/w/mK4quWt8SPdyz+FL1PQ4f9Wv0FTd6hh/1a/QVN3rpPEluAooFFMkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoPSig9KAOA1f/kKXP8A10Nbngz/AI9rj/fH8qw9X/5Clz/10Nbngz/j2uP98fyrkh/EPfxP+6L5HRiigUV1ngBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHhvx++G+seI9Tttd8P27XrLAIJ7dGAcYJKsAeo5wR14rlfA/wE1nWI3uPEkr6LEMCOLYskkh7kjOFH159q+nKKAPDv+GbNK/6GG8/8B0/xpV/Zt0jd83iC+/CFBXuFFAHlWi/APwbp7q16L3U2HOJ5tq/kgH869K0vTrPS7KO00+2itbeIYSKJAqgfSrdFAEciLIhRwCrAhh6g18l+Kvg54r03xDNa6bpM19ZvIfIuIcEFCeN3PykDrnAr64ooA474T+GJ/CHgm00u8ZWugWln2HIDsc7Qe+BgZrsR0oooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK4jxN/yGJ/ov/oIrt64jxN/yGJ/ov8A6CKxrfCenln8Z+n6ou+Df9dcfRa6muW8G/664+i11NVS+FGOO/jsUUUCitDiCg0UGgDL8Sf8gif8P5iuKrtfEn/IIn/D+Yriq5a3xI93LP4UvU9Dh/1a/QVN3qGH/Vr9BU3euk8SW4CigUUyQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACg9KKD0oA4DV/+Qpc/wDXQ1ueDP8Aj2uP98fyrD1f/kKXP/XQ1ueDP+Pa4/3x/KuSH8Q9/E/7ovkdGKKBRXWeAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVxHib/kMT/Rf/QRXb1xHib/kMT/Rf/QRWNb4T08s/jP0/VF3wb/rrj6LXU1y3g3/AF1x9Frqaql8KMcd/HYoooFFaHEFBooNAGX4k/5BE/4fzFcVXa+JP+QRP+H8xXFVy1viR7uWfwpep6HD/q1+gqbvUMP+rX6Cpu9dJ4ktwFFAopkhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFB6UUHpQBwGr/8hS5/66GtzwZ/x7XH++P5Vh6v/wAhS5/66GtzwZ/x7XH++P5VyQ/iHv4n/dF8joxRQKK6zwAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACuI8Tf8hif6L/6CK7euI8Tf8hif6L/6CKxrfCenln8Z+n6ou+Df9dcfRa6muW8G/wCuuPov8q6mqpfAjHHfx2KKKQUtaHEFBooNAGX4k/5BE/4fzFcVXa+JP+QRP+H8xXFVy1viR7uWfwpep6HD/q1+gqbvUMP+rX6Cpu9dJ4ktwFFAopkhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFB6UUHpQBwGr/8hS5/66GtzwZ/x7XH++P5Vh6v/wAhS5/66GtzwZ/x7XH++P5VyQ/iHv4n/dF8joxRQKK6zwAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooNABSUViX3iGC2mMaRNKQcEhgADSclHcuFOdR2grm3XE+Jf+QxP9F/9BFdTp2oRX0PmRZ46g9q5bxN/yGJ/ov8A6CKwrO8T0cui413F72/VF7wb/rrj6L/KunBrl/Bv+uuPov8AKuldtq7jwo5JNaUvgRhjv4zH9qWuP1bXpppSlq5jjT+IdW9/pWn4X1Ga8SSK4IZo8EP/AHgaaqRbsTPCVIU/aSN6g0DpQas5DL8Sf8gif8P5iuKrtfEn/IIn/D+Yriq5a3xI93LP4UvU9Dh/1a/QVN3qGH/Vr9BU3euk8SW4CigUUyQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACg9KrtdwJL5bzxq56KWGanPSgdjgdX/AOQpc/8AXQ1ueDP+Pa4/3x/KsPV/+Qpc/wDXQ1ueDP8Aj2uP98fyrlj/ABD3sT/ui+R0dN7UtYPiHWPsym3tz+8I+Zv7o/xrolJRV2eJTpyqTUYm9xRXCaZf3Ud/Htld97AMpJORmu77URkpK6NMRh3QaTYtFAoqjnCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAae9ee3kZhu50k+8HOa9Erl/Ftj8y3cY4+6/9D/Ssasbo9DL6ihVs+o3wfKu+eP+Lg49qpeJf+QxN9F/9BFUrO4a0u0mQ/Mh5HqO4qxrcom1J5UOQ6qR/wB8isHK8LHqxouGJc+jX+RpeDRma4+i03xNqfmE2cJyq8SEdz6fQVm6fftYwXAj/wBbKAqn096pklycHJNNztBRRCw3NXlVnsth9vbyXU6wxDLtyf8AGu30uwj0+3CJyx5dv7x/wqtoOliytt8g/fSct7D0rXFbU6fKrs83GYp1ZckfhQ4dKDRQa2PPMvxJ/wAgif8AD+Yriq7XxJ/yCJ/w/mK4muWt8SPdyz+FL1PRIf8AVr9BU3eoYf8AVr9BU3euk8SW4CigUUyQooooAKKKKACiiigAooooAKKKKACiiigAooooAKhm3eU/l/e2nH1xxU1JQNHm772ZmkyXLHOeua6Hw7q7FltLlsk/6tz/ACP9Kn8Q6RHLC9xbKBKvzMB/EK5dTggrkEHINcb5qbPfi6eLpWS1/Is6v/yE7n/fNbvgv/j2uP8AfH8q5y4mM87yt1c5Nb/hSVbeyunkOFVgSfwog7zuPFwccMo+hp65qa6fbkqcytwo/rXFPI0shZiWZjyT3NWNTvXv7tpn4Xoo9BV/w1phuZ/tEg/cxngH+I/4U5N1JWFRpxwlJ1Jbmh4c0gRAXdwnzn7in+Eev1roaQDAwOlLXVGKirI8SrVlVm5SFooopmQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFcP8V/H9t4D0ZZ9qXGoXB221uzY3Y6u3+yP1OBXTa5q9lomlXWp6nKIbW1jMjv7DsPUk8AdzXxt4/wDFd54y8R3GrXuUVzthizxFGPuqP5k9yTQB23/DQ3jHJxBpYHp5Df8AxVN/4aF8Z/8APHS//Adv/iqwPA/ww1zxpp819YPb21rHJ5ayXLMBI3fbgHOO5rov+Gf/ABJ/0EtK/wC+5P8A4igBn/DQ3jP/AJ46X/4Dt/8AFUf8NDeM/wDnjpf/AIDt/wDFU7/hn/xJ/wBBLSv++5P/AImj/hn/AMSf9BLSv++5P/iaAG/8NDeM/wDnjpf/AIDt/wDFUf8ADQ3jP/njpf8A4Dt/8VTv+Gf/ABJ/0EtK/wC+5P8A4mj/AIZ/8Sf9BLSv++5P/iaAG/8ADQ3jP/njpf8A4Dt/8VR/w0N4z/546X/4Dt/8VTv+Gf8AxJ/0EtK/77k/+Io/4Z/8Sf8AQS0r/vuT/wCIoAb/AMNDeM/+eOl/+A7f/FUf8NDeM/8Anjpf/gO3/wAVTv8Ahn/xJ/0EtK/77k/+Io/4Z/8AEn/QS0r/AL7k/wDiKAG/8NDeM/8Anjpf/gO3/wAVR/w0N4z/AOeOl/8AgO3/AMVTv+Gf/En/AEEtK/77k/8AiKP+Gf8AxJ/0EtK/77k/+IoAb/w0N4z/AOeOl/8AgO3/AMVR/wANDeM/+eOl/wDgO3/xVO/4Z/8AEn/QS0r/AL7k/wDiKP8Ahn/xJ/0EtK/77k/+IoAb/wANDeM/+eOl/wDgO3/xVH/DQ3jP/njpf/gO3/xVO/4Z/wDEn/QS0r/vuT/4ij/hn/xJ/wBBLSv++5P/AIigBv8Aw0N4z/546X/4Dt/8VR/w0N4z/wCeOl/+A7f/ABVO/wCGf/En/QS0r/vuT/4ij/hn/wASf9BLSv8AvuT/AOIoAb/w0N4z/wCeOl/+A7f/ABVH/DQ3jP8A546X/wCA7f8AxVO/4Z/8Sf8AQS0r/vuT/wCIo/4Z/wDEn/QS0r/vuT/4igBv/DQ3jP8A546X/wCA7f8AxVH/AA0N4z/546X/AOA7f/FU7/hn/wASf9BLSv8AvuT/AOIo/wCGf/En/QS0r/vuT/4igBv/AA0N4z/546X/AOA7f/FUf8NDeM/+eOl/+A7f/FU7/hn/AMSf9BLSv++5P/iKP+Gf/En/AEEtK/77k/8AiKAG/wDDQ3jP/njpf/gO3/xVH/DQ3jP/AJ46X/4Dt/8AFU7/AIZ/8Sf9BLSv++5P/iKP+Gf/ABJ/0EtK/wC+5P8A4igBv/DQ3jP/AJ46X/4Dt/8AFUf8NDeM/wDnjpf/AIDt/wDFU7/hn/xJ/wBBLSv++5P/AIij/hn/AMSf9BLSv++5P/iKAG/8NDeM/wDnjpf/AIDt/wDFUf8ADQ3jP/njpf8A4Dt/8VTv+Gf/ABJ/0EtK/wC+5P8A4ij/AIZ/8Sf9BLSv++5P/iKAG/8ADQ3jP/njpf8A4Dt/8VTJvj/4vniaKW30pkYYI+zt/wDFVL/wz/4k/wCglpX/AH3J/wDEUf8ADP8A4k/6CWlf99yf/EUDTs7o9L0DV4dc0a21G3/1c6Alc/dboyn3B4rQ6nNc34A8D6/4OsrqDU7qyubNyJEELsWR+h6qOCMflXR1w1I2eh9RhqyrU1Lr1CuE8e/EibwpqUFpo0dtPep88xmUsseRwMAjnv7V3qRTzgxWioZmB2b87d2OMkA8eteV33wM8V393NdXOq6ZJNO5d2Mj8knJ/hq6MLu7ObH4j2cfZrdlX/hoXxp/zy0v/wAB2/8Ai6P+GhPGn/PHS/8AwHb/AOLp3/DP/iT/AKCWl/8Afb//ABNL/wAM/wDiT/oJaX/32/8A8TXYfPjP+GhfGn/PLS/+/Df/ABVH/DQvjT/nlpf/AH4b/wCKp/8AwoDxJ/0EtL/77k/+Jo/4UB4k/wCglpf/AH3J/wDE0BY1fCXxi8TeKPEFro+ppp62tyWDmKFlbhSwwSx7j0r0avOvCfwe1vwz4gtdYvb2wlt7YkukTOWIKkcZUDv616LXJW+JHv5d/Cl6nks3x+8YxSyRiHSwEYqP3DdM4/vVH/w0L4z/AOeWl/8AgO3/AMVUs3wE8SSytINS0sBySPnk+v8Acpn/AAz/AOJP+gnpX/fcn/xNdJ4Utxv/AA0N4z/55aX/AOA7f/FUf8NDeM/+eWl/+A7f/FU7/hn/AMSf9BLSv++5P/iaP+Gf/En/AEEtK/77k/8AiaZI3/hobxn/AM8tL/8AAdv/AIqj/hobxn/zy0v/AMB2/wDiqd/wz/4k/wCglpf/AH3J/wDE0f8ADP8A4k/6CWl/99yf/E0AN/4aG8Z/88tL/wDAdv8A4qj/AIaG8Z/88tL/APAdv/iqd/wz/wCJP+glpf8A33J/8TR/wz/4k/6CWl/99yf/ABNADf8Ahobxn/zy0v8A8B2/+Ko/4aG8Z/8APLS//Adv/iqd/wAM/wDiT/oJaX/33J/8TR/wz/4k/wCglpf/AH3J/wDE0AN/4aG8Z/8APLS//Adv/iqP+GhvGf8Azy0v/wAB2/8Aiqd/wz/4k/6CWl/99yf/ABNH/DP/AIk/6CWl/wDfcn/xNADf+GhvGf8Azy0v/wAB2/8AiqP+GhvGf/PLS/8AwHb/AOKp3/DP/iT/AKCWl/8Afcn/AMTR/wAM/wDiT/oJaX/33J/8TQA3/hobxn/zy0v/AMB2/wDiqP8Ahobxn/zy0v8A8B2/+Kp3/DP/AIk/6CWl/wDfcn/xNH/DP/iT/oJaX/33J/8AE0AN/wCGhvGf/PLS/wDwHb/4qj/hobxn/wA8tL/8B2/+Kp3/AAz/AOJP+glpf/fcn/xNH/DP/iT/AKCWl/8Afcn/AMTQA3/hobxn/wA8tL/8B2/+Ko/4aG8Z/wDPLS//AAHb/wCKp3/DP/iT/oJaX/33J/8AE0f8M/8AiT/oJaX/AN9yf/E0ANP7QfjI5Bh0r/wHb/4qu5+H3iw+LdHe5uFiivYnKzxxjCgnlSAScAj9Qa4j/hn/AMSf9BLS/wDvuT/4mum8A/CzxN4T1n7XJfadNbSIUmhjd9zDqCMqBkGsqkbo7MHW9lU12Z2lOjmuVVolkT7M6gldvzFs+vpjtTcZNL0rjWh9LJKSsyh4g1a30PSLjUbsgRQLkLnBdv4VHuTXl0Px88XW8Qjt7bSkjXov2dj/AOzV2/xA8AeIvGCWkVjd2NtYRjftmdwzOeMkBSMAdOe5rjv+FAeJM5/tPS/++3/+JrrpxUVdngY+vzz5VsvzGD9oTxn/AM8dL/8AAdv/AIql/wCGhfGf/PHS/wDvw3/xVRW3wfeN5E1LVYWkU4X7KhZfzbH8qLX4G63fRmaz1TTjFuKjzGdW49QFIH50oYilUm4Qd2jy1NN2uS/8NC+M/wDnjpf/AH4b/wCKo/4aF8Z/88dL/wC/Df8AxVL/AMM/+Jf+gnpX/fcn/wARR/wz/wCJf+gnpX/fcn/xFdBQn/DQvjP/AJ46X/34b/4qj/hoXxn/AM8dL/78N/8AFUv/AAz/AOJf+gnpX/fcn/xFH/DP/iX/AKCelf8Afcn/AMRQAn/DQvjP/njpf/fhv/iqP+GhfGf/ADx0v/vw3/xVL/wz/wCJf+gnpX/fcn/xFH/DP/iX/oJ6V/33J/8AEUAJ/wANC+M/+eOl/wDfhv8A4qj/AIaF8Z/88dL/AO/Df/FUv/DP/iX/AKCelf8Afcn/AMRR/wAM/wDiX/oJ6V/33J/8RQAn/DQvjP8A546X/wB+G/8AiqP+GhfGf/PHS/8Avw3/AMVS/wDDP/iX/oJ6V/33J/8AEUf8M/8AiX/oJ6V/33J/8RQAn/DQvjP/AJ46X/34b/4qj/hoXxn/AM8dL/78N/8AFUv/AAz/AOJf+gnpX/fcn/xFH/DP/iX/AKCelf8Afcn/AMRQAn/DQvjP/njpf/fhv/iqP+GhfGf/ADx0v/vw3/xVL/wz/wCJf+gnpX/fcn/xFH/DP/iX/oJ6V/33J/8AEUAJ/wANC+M/+eOl/wDfhv8A4qj/AIaF8Z/88dL/AO/Df/FUv/DP/iX/AKCelf8Afcn/AMRR/wAM/wDiX/oJ6V/33J/8RQAn/DQvjP8A546X/wB+G/8AiqP+GhfGf/PHS/8Avw3/AMVS/wDDP/iX/oJ6V/33J/8AEUf8M/8AiX/oJ6V/33J/8RQAn/DQvjP/AJ46X/34b/4qj/hoXxn/AM8dL/78N/8AFUv/AAz/AOJf+gnpX/fcn/xFH/DP/iX/AKCelf8Afcn/AMRQAn/DQvjP/njpf/fhv/iqP+GhfGf/ADx0v/vw3/xVL/wz/wCJf+gnpX/fcn/xFH/DP/iX/oJ6V/33J/8AEUAJ/wANC+M/+eOl/wDfhv8A4qj/AIaF8Z/88dL/AO/Df/FUv/DP/iX/AKCelf8Afcn/AMRR/wAM/wDiX/oJ6V/33J/8RQAn/DQvjP8A546X/wB+G/8AiqP+GhfGf/PHS/8Avw3/AMVS/wDDP/iX/oJ6V/33J/8AEUf8M/8AiX/oJ6V/33J/8RQAn/DQvjP/AJ46X/34b/4qj/hoXxn/AM8dL/78N/8AFUv/AAz/AOJf+gnpX/fcn/xFH/DP/iX/AKCelf8Afcn/AMRQAn/DQvjP/njpf/fhv/iqP+GhfGf/ADx0v/vw3/xVL/wz/wCJf+gnpX/fcn/xFH/DP/iX/oJ6V/33J/8AEUAJ/wANC+M/+eOl/wDfhv8A4qj/AIaF8Z/88dL/AO/Df/FUv/DP/iX/AKCelf8Afcn/AMRR/wAM/wDiX/oJ6V/33J/8RQAn/DQvjP8A546X/wB+G/8AiqP+GhfGf/PHS/8Avw3/AMVS/wDDP/iX/oJ6V/33J/8AEUf8M/8AiX/oJ6V/33J/8RQAn/DQvjP/AJ46X/34b/4qj/hoXxn/AM8dL/78N/8AFUv/AAz/AOJf+gnpX/fcn/xFH/DP/iX/AKCelf8Afcn/AMRQAn/DQvjP/njpf/fhv/iqP+GhfGf/ADx0v/vw3/xVL/wz/wCJf+gnpX/fcn/xFH/DP/iX/oJ6V/33J/8AEUAJ/wANC+M/+eOl/wDfhv8A4qj/AIaF8Z/88dL/AO/Df/FUv/DP/iX/AKCelf8Afcn/AMRTLn4DeILaCWe41bSo4YVLyO7yAKoGST8nSgB3/DQvjP8A546X/wB+G/8Aiq1/C37QOtHWII/ENpZNYzOEd4EZHjBONwyxBx6V4tMixTuiyLKgYgOuQGA7jPNd58GPAkvjTxJHJcoyaRYMslzJt4cg5EYPqe/oPwoA+u6WkpaQBRRRQAlFFFAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFeWfHn4g/8Irof9l6ZMF1fUFIVh1gi6M/sT0H4ntQB5p+0J8Qv7f1Y+HtMm/4l1g/79lbieYcH6qvQe+T6VwXgPwrdeMPEMGlWuUQ/PPLjiKMdW/oPUkVhQwPczpDCrSSysFVRyWYnGB7k19V/CfwRH4O8Ook8YOqXYEl1IBnB7Rg+g/U5NAHUaPplroulW2nadEIrW1QIij09T6knkn1q3RRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQA1wGUowyCMGufvdLlt3JiRnjPQjr+NdCaaa+azXO8Pg5clrvsunqzvws6lJtx2ZnaLYvCDPMNrEYUHqPetSmCnU8tz7DYmPK3yvs2vwehnieepPmY6ikzRX0UZKSujlCgUUCqEU9X/5Bsv4fzrnO1dHq/8AyDZfw/nXOdvwrlrfEj6DLv4TOtT7i/Snd6an3F+lO710nhS3A9aKD1opkBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAehgaxYtBKZYgTG3PHY1W0+3NxcKgGRnJ+ldQaREC/cULn0GKw9mm7npxzCUafI1qKOPlHaue8Qazs3Wlo3PSRx/D7D+tTeIdX+zo1tbN++YYZx/CP8AGuVA3YAPOfzNeTj8bb91Sep4Var9lDoUaZ1jiUs7HCgd67TRrE6fZ+S5zITvb0z6VX0LSRYxie4Aa4Yf98j0+vrWvW2X4N0V7Se7CjT5dWFFFFeudQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRigAopk8qQRNLK6pGgyzu2AB6k1yOq/Ezw5Zq4hmkvpF/hhQ4P4nAxUTnGPxOx0UcLVru1OLfodjRXmY+MVnvwdIuFX185c/liur8M+NdG8RMIrScxXOM+RKNr/h2P4GojWpzdkzorZZiaMeacWl950NFFFbHnhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXhf7QHj7zZH8K6PKSikG/kU9SORED6Dgn347Gu6+L/AI6TwdoJjtGB1a9BW2X/AJ5joZD9O3qfxr5bdpJ5i7s0ksjZJPJYk/qSaYGh4Z0G98R61baVpcfmXNy20eijuxPYAcmvsjwR4XsfCHh+10ewXKxjdJIfvSyH7zn6/oMCuO+BHw8HhPQ/7S1SHGsX6AsG6wRHkJ7E9T78dq9QoAWiiikAUUUUAJRRRQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFRu21dzMABySeABQBj+LvEdj4U8P3esai2IrdeFB5kc/dUe5P8AjXxr4p1698S67datqche4uX3EZ4QdlHsBwK7P44/EBvGPiA2Wnyn+yLBisWOkr9Gk/oPb61ifC/wZN4z8SR2pDLYwES3ko/hjz90H+8eg/E9qAO//Z98CCRx4r1SH5UJWwjcdWHWX8Og98nsK91qKzt4rW1jt7WNYoIVCRxqMBFAwABUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSGlprVwZjilg8PKt2X4lwV5JCGk6UtIetfi9ao6s3OTu3qz0UrKwUHpRRWAApp+aZ0pVr6rIMxrUcRGje8ZO1u3mYVIe7cfQKKBX6ocRT1f8A5Bsv4fzrnK6PV/8AkGy/h/Oucrkr/Ej6DLv4TOtT7i/Snd6an3F+lO711HhS3A9aKD1opkBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVV1K6+x2Mlxt3FBwPfoKtVDerE1pKJhlCMEetY15clKUtrJ6hyuWi3OTi1/UEl3mXzPVWUf0q/FqUl2m7zGU91Bxise+tDbksnKH/wAd+tQQStDKrxnp+tfBV69TFU/3c397M6FWeErctZaHSrdTp0lf8WzSahrzQWpQLm4bgHsB61Rlu40thKnU9B71kSSNI5ZzkmscvxGKhduTttZnbmNekoqFNe8+vkNdmZy5LMxPJPc11Hh7Rvs4F1cDMh+6rfwD1+tV/Deklyl3cL8ucxKe/uf6V0tfV5fg72rVF6HlUqP2pBRRRXunYFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKBRRQAtI/u21R3orjfixrZ0nw0YIWKz3xMKkdQuMsfy4/GpnJQjc6MNQeIqxpLds4D4keNJdevGsbBymmwtjg/65h3+noPxri6U02vBqVHUd2fq2FwsMLTVOC0CnxSvDKskTMjoQyspwQR3BplLUHTKKkrM99+G/iY+I9C33O37ZbN5U+P4+Plb8R+ua6jtXkvwLaT7dqiD/AFXlxk/XJx+ma9ar3aEnKCbPyzNMPDD4qVOG2/3oKKKK2PLCiiigAooooAKKKKACiiigArO8Sa3Z+HdEudV1Fwlvbrn3dj91R7k8CtD7u5mYKo5JPQCvmL40+Pf+Es1oWWnSEaTYsRHg8TP0Mn07D2570Acr4u8RX3inXbnVdRb55ThUB+WJB91F9sfmea9O/Z4+Hg1W+TxTq8IaytH/ANDjcf62Ufx47hT09/pXCfC3wTc+OPEsVjHmOzhxLdzf3E9B7noPz7V9i6bY2+m2MFlZRLDbW6COJFGAqgcCmBaooopAFFFFABRRSUAFFFFAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAV4p+0X8QDpNgfDGlTYvLtM3UiHmKI/w/Vv/AEH616D8RvGNt4K8Nz6lcgPOfktYScGWXsPoOp9q+OtY1G61fUbjUL+UzXVy5lkkPcn+noOwoAi02wudT1C3sLKJprm5cRRRjqzE4FfW/wAPfCFt4N8OQ6bDiS4b95czKP8AWSEc/gOg9q4P4A+Bf7NsB4m1WHF3dLi0jYcxxd3+rdvb616/QAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFNanU1q+b4lTeAlbv+ptR+K4lIaKD1r8lO4O9FBoNNBsLjNKopEp+K+84ayyTl9aqLRbHNWn9kKBRQK/QTkKer/8AINl/D+dc5XR6v/yDZfw/nXOVyV/iR9Bl38JnWp9xfpTu9NT7i/Snd66jwpbgetFFFMgKKKKACiiigAooooAKKKKACiiigAooooAKKKKACqGrybYo0HVjn8qv1maz96L8f6V42eTccFO3l+Z04VXqozXRXQhhkHisS6gMEpQ9Ccqfatyoru3W4i2n7w6GvznB4j2U7PZndj8H9YhdfEtjBz/9arthaiZt7j92P1NItjMz4K4HrW5ptuHdEQDanzGvWlVdWcaVHVydtDyMJgnzOdVWUe/U3IF2wRr/AHUAp9FFfo1OPJBQ7AwoooqwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvGvjXfi58QW1mjZFrDyPQsc/wAgK9lr508bzPN4v1SSTr55UfQcD9BXHjJWhY+l4cpKeK539lf8AxSaSg0uK8c/RA60Y7DkmkPpXoPwk8L/ANpagNXvY82lqf3QPR5B3+g/nWlODnKyOLG4qGFpOrPp+L7Hc/DTw42gaCPtKbby6IllHdB2X8B19zXWUADFFe9CKhFJH5ViK869V1J7sKKKKowCiiigAooooAKKKKACiiuW+JfjS38FeHJLx9r3s+Us4G/jf+8R/dHU/l3oA4b4++P/AOz7V/C+kzEXVwuL10bmKM/8s/qR19B9a8L0nTbvV9Qt7DT4jNc3MgjjjHUsf6ep7VDfXc+o3k13eTNLPO5kd25LMTya+kP2evh5/YmnDxLq8P8AxMbtP9GjYcwQn+L2LfoPqaAO4+Gvgy08EeGotNgAkuXxJdTheZZO/wCA6AenuTXXUUUAFFFFABRRRQAUUUUAJRRRQAtFFFABRRRQAUUUUAFFFFABRRRQAVXubmK0t5bi5kWKCJS8jscBFAySasV8/ftIfELcx8I6RLjGGv5Ebqf4Yv6n8B60Aec/Fvx1N438TSXKFl022zFZxHjCZ5cj1bqfbA7Vb+DXgVvF2vi4voidJsSHnz0lbqsf49T7fUVyPh7RL3xFrVrpmmx+ZPcNtHoo7sfQAcmvrnwj4dsvCvh+20jT/wDVwj55McyufvOfcn8hxQBqogRQFAAAwAOgp1FFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFZus6n9hUJHhpmHHoo9TWNetCjBzm7I0p0nVfLFGlR9a4qW/u3bL3EmfY4H5ConllflpWY+7Zrw5Z5BbRf3nqxyuT3Z3XXpS7a4RJZY+Y5HX6EinreXKdLiUf8DNCzyH2ov7weVSW0jt6K53TtdkVwl6dyH/lp3H19a6Lr7g16+GxdPEq8Dzq2HnRdpBRRRXWc4UUUUAFFFFABRRRQAUhpRQRWNejCvSdOaunoxptO4zFJT8UYr89xXCtZSboNOPmdUa62YzHNOxS4ortwHCzhNSxLTt0RM6/RAKWjFFfcU4qCUYqyRzXu7sKBRRVgU9X/AOQbL+H865yuj1f/AJB0v4fzrnK5K/xI9/Lv4TOtT7i/SnDrTU+4PoKbcTJbxmSQ4UV1HiNNz5USUVm2+swySqjRmMMcA5z+dadKMlLYdSlOk7TVhKKKKoyCiiigAooooAKKKq6lqEGnwiSZslvuqOpNTOUYRcpuyE5KO5ZdlVWZmAA6k8CqD61psfym4B+gJ/pXK6jqdxfyEyvtTtGOg/xqnXh1c11tTWnmck8Rrod3bajaXXyw3CM3p0P5GrdeddOh5rq/Dmqm6T7PcPmdB8pb+If4iujC5gqsuSasy6VfmdmbVFFFesdIVXv4POgOOo5FWKKwr0Y4ik6ctmXCTjJSj0Ob9qK2brT0mbcjeW5646Gqv9lv/wA9Fr85xGQ4ulNxhG67o9qGMpyV3oUVBJwOSegrbsbYW8IXHzHljSWlnHbjgbm/vGrVfTZNk7wj9rV+J/gcGKxPtPdjsJRRRX05whRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQKKKQBXjHxX8K3Nnq82s2sTSWdwd0hRcmJ++fY9c17PTHRXRkkUMjAhlIyCD1BrKtT9pGx6GX46WCqe0ir9Gu6Pl7ikzXruv8Awmtbm4afR7z7IHO4wum5R/ukHIHtzVbTfhAqyh9U1PcmfuQR4z7biePyrzHhal7H3kc+wbp8zlZ9ranF+C/Ct14n1JYo8x2keGnnxwo9B/tHt+de+6bZW+m2UVlZxiOGBQqqOw/x9aZpemWmlWSWdhCkECfwp/MnqT6k1br0KFBU15nxWZ5lPG1O0Vsv1fmH0ooorpPICiiigAooooAKKKKACiiigCrq2o2mj6bPqGoSiC2tkMju3YD+ZPQDua+SviB4tuvGXiKXUbnMcC/u7aDPEUY6D69ye5rtvjv49GuaidB0mX/iW2cn751bieUfzVeg9Tz6Vw3gTwte+MfEdvpGnpgOd00xGRDGPvMf6DucCgDs/gN8PD4p1j+19UhzpNg4wrDieX+57qOp/Ad6+p1UKAB+lZugaNY6Bo1rpWmxCK2tUCKB1PqT6knkn1rUAoAKKKKACiiigAooooAKKKSgAooooAWiiigAooooAKKKKACiiigAoorP1rVLTRdMuNR1CYQ2trGZZWPYD+Z7AdzQBynxf8cReCfDTyxODqd0DFaRnn5u8hHouc+5wK+Q7ieW7nkuLh2klmYu7scl2JyST6k10HxD8XXfjXxLPqt1uVPuW8WeIogflX69ye5Ndf8AAjwKNf1X+3dThzpti/7tGHE03UD3Vep98D1oA9E+B3gUeG9G/tXUotuqX6A4K/NBEeQvsT1P4elelUvBNJQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQKKKAGvtVSxbAHJrir24a6u5JX/iPHsOwrqddl8nSpiDywCfma5Cvl87rXapr1Pdyuno6glFFFfOHtBmiigUALXVeG5zLYKrHJicp+HUVytdN4Zj26eW/vyE/lgV7OTt+3strHmZnb2Wvc16KDRX2R82FFFFABRRRQAUUUUALSUUnekwWg6kzRmg099wClpKKOgrBRRRQhkV5N9ngeXbnaOnvWLDq9z5u6TayE8gDt7Vt3EYnheJujDBrlpEMUjIeqtWFWTiz1sDSp1U1LVnQaqwbTJGU5UgEH8a5ytOG48zRpYWPKY/LNZlY1Jc0kzuwlN0oyh5nXD7i/wC7WBrF7582yMkRIfzPrVzVr7y4xBEfnIG4+g9PxrGQMzhVG4ngCtKkr6I5sFh7N1Z/L/Mn061NxdIq9Byx9AK6eq+n2iWkAXqx5ZverArWnHlRwYyv7eppsgooNFaHGFFFFABRRRQAy4lS3ieWQ4WMEn8K4XUL2S/uXmk4zwo9B2FdP4pl8rSWXPLsF/Dr/SuQr57Nazc/ZrY4sRLWwUUUV4pyCVNYymC9hkU/dcH8M81FTok3zRp/EzAfmaum2pprca3PQ6KDRX3C2PXCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvMvjl4+/4RzSToulzY1S+T5nQ8wRdCfZj0Htk+ldh448U2fhDw/Pql6VZl+WCLdgyyHoo/mfQV8k61qt5rWp3Oo6hL5t1cyGR27ewHoAOAPSgCrbW897dRW1vG8s8zBI0QZZmJwAB6k19dfCDwDF4H8PKkyRtqt2A93KOcHsgP8AdH6nJrgP2dPh55QTxdrEXLgiwiYdB0Mv49B7ZPpXvlAAKKKKACiiigAooooAKKKKACiiigBKKKKAFooooAKKKKACiiigAooooAK+Zv2h/H/9s6m3hrS5c2Fk+bl0PE0w7e6r+p+gr0r47fEEeEdA/s/TpgNZ1FSqEdYY+jSex7D357V8rxpJcThEDSSSMFAHJZieB7kmgDZ8E+Grvxb4gt9JswQJDumlxkRRj7zH+nqcCvrfRdKtNE0m203T4hFbWyCOMd+OpPqSeSfWuV+EfgiPwd4dH2lA2q3gEl0/93+7GD6Dv6nPtXbZoAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACgUUUAZfib/kGf9tF/rXLV1Pib/kGfSRa5avjc4/j/ACPpMs/gP1ENFFFeMemLRRRTAI0Mkiqq5JOAPc129jbi1s44R/AMH696w/DdiXl+1yjIQ4T3PrXRV9blGF9lT9rJavb0Pnsyr88+RbL8wooor3TyQooooAKKKKACiiigAooooAKKKKACiiigAooooAKw9et8TrMBw4wfqP8A61blV9Qg+0WroOvUfWs6keZHVhKvsqqfQ5lZCisB0YYNMFOYY4NIa42fUJJ6iscsxZss3Nbej2PlKJ5B85Hyg9h/9eqmj2Hmt58w+QHgH+I/4Vvnmt6UL6s8XH4n/l1D5iU7pSUjssSs8jBVAySegFbykoq7PHQ6krlL7xHcPMfsRVIgeNwBLfXNb2kXv2+yEzDa4JVgOmR6VzUsZTqzcIvVGcasZSsXaKKK6zQKKKKAMfxYm7Ss/wB1wfzyK5Ku/vLZbu1kt3+7IMZ9D2NcJdW8lrcPBKMOpwf8a+czWk1P2nQ4cRF35iOg0UV45yiVteFrEz3n2iQfu4enu3b8qzbG0lvLhYYhyx5PYD1NdvZ2qWlukMQwij8z3Nenl2FdWfO/hX5nRRp8zu9ieiiivqD0AooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACo7q4htLaS5uZRDDChkkdjgIoGST9BUleEfH/AMfefK/hXSZT5UbA30in7zdRGD6DqffjsaAOF+KvjaXxn4gaaIumnW+UtYj/AHe7kep6+wwK0Pgx8P38beIVe7Rho9kQ9y//AD0PVYwfU9/QfhXJ+GNAvvEuuWuk6anmXNy+Aeyr/Ex9ABya+yPBHhmy8I+H7bSdPXMcIy8h+9LIfvOfcn8hgdqANmCJIY0ijRURFCqqjAAHQD2qaiigAooooAKKKKACiiigAooooAKDRQaAEooooAWiiigAooooAKKKKACsbxb4hs/DOhXOrai22C2XOB952P3UHuTxWsfrgCvlL47/ABAPi7xALDTZd2j6cxWJl6TSdGk9x2Htz3oA4nxb4gvvFGvXWrai+6adshe0a/woPYDivU/2f/An2mceK9VhPlRErYxsPvuODJj0HQe/PauB+Gfg648ZeIo7NNyWkOJLqUfwx56D/aPQfn2r6ys7SCytIbW0iWGCBRHFGvRVAwBQBLRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAQX1uLq1khP8AGMD69q4p42ikZHGGU4I9xXeVlazpC3bGWIKswHOejf8A168TNcBKvFVKa95fij08BivYycZbM5alqaezubY4liZf9rHH51Fj+6u4+1fJypzi7SVmfQxnCSumJVvTLBr2cIOI15dvQf41Np+j3N1hpAYY/U9T9BXTWtvHawrFCuAPzJ9TXrYDLZ1ZKdVWj+Z52Mx0acXGm7v8iSGNYY1RF2ogwBTqWkr7BKysfOuTk7sKKKKYgooooAKKKKACiiigAooooAKKKKACiiigAoopGZY1LN0AyamUlFXY0r6IjuZ1giLN+A7ms19UmJ+RQq+/NV7mdp5S79ew9BUWVH3jivzvMM8rV6jjQbUV26ntUMJGEbzWpBcAmVmPc5psEfmzIu7hjyassAwwenrSBVQjaK0w+funTSnG8l17+p6HN7tkdFGioioowqjin1m6besSIpBu/un+laVfZ4LHU8ZSVSHzXZnzVenKnN8wfdBZvlVeSa4/XdWN45ghytup/wC+j6/T0qfxDq5uGNrbHEQ++4/iPp9KxreCS6nSGFdztwK83HY11H7Kl8/M82tU5nyRH2VnLe3CwQLkk8t2Ueprt7CzjsbVYIucck+p7motJ0+LT4Aicu3+sf1P+FXq78Dg1Qjzy+JmtKly6vcSiiivSNwooooAKz9Y0uPUIgSRHKv3W/ofatCisqtONROMldClFSVmcdL4f1CNsJGkg9Q4/rSweHb52USKkS9yWB/QV2FFef8A2XRvfUx+rwKel6fDp8BWEZY/ec9T/wDWq5RS9q9KEI048kVZGyioqyEoooqxhRRRQAUVJFC0nTgetTC1T+Ik1z1MRCm7NlKNyrRVwwJ2Wq8sZQ+xop4mnUdluDjYjoorN1zU1sItq4M7j5R/d9zWlWrGlFylsZyko6kOu6wbEGC3IadhyDyFH+NVtA1q4uLkW91tbeDtYLgg9ea5yWR5JGd2ZnY5JPeul8OaX5AW6uFw7D92voPU+5rwaGJrYjEJx0j26WOOE5zndbG+aKKK+iO4KKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiszxPr1n4b0O71XUn2w265wOsjH7qr7k8UAct8YPHaeEND8izb/ibXqlbdf8AnkvQyH6dvU/Q18us0lxOWYs8rtkk8liT+pzWn4s8QX3inXbnVtQOZZz8qDpGg+6o9gP8a9T/AGd/h5/aV4nirV4M2Vs/+hRuP9bKP48f3VPT1b6UAeifAz4ef8IfoX27UosazfKDLnrBH1EY9+59+O1enCkpaACiiigAooooAKKKKACiiigAooooAKDRQaAEooooAWiiigAooooAKKK5j4h+L7TwV4cn1W62vIPkt4c4MspHyr9O5PYCgDgf2hvH/wDY+lnw3pcxGoXqZuWU8wQntnszdPpn1FfOGn2VxqF7DZ2cTS3FxII4415JYnAFTa1ql3rOpXOo6hM011cuZJHPcn09B2A7CvcP2fvAYsrRfFGqQg3M6kWaOPuIeDJ9T0Ht9aAO9+HHhC38G+HIdPjKvdSYlu5R/HIRzj/ZHQfn3rp6O9FABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUUtFS4Re6KuFFFFUSFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVT1WTbbY7ucfhVys3WT/qR9a8nOKrpYOc12t+h04WKlVSZnVjakzG6Kt0HQe1bPaoLm1juOW4I7ivzPC1Y0ql5I9LHUJ1qXLB63M6zvHhbDFmT0Pb6VrBg6B4zlT+lYc0TQSMr9Ox9asafdCJhG/wBx/wBDXpYrDQqR9pT3PJwOMnQn7Gt/wxt2f/HzF/vCovEGs/etLRvaRx/If1qje6gYi0cBw3QsO3096ywGdwqr82cADqTXflk6lGg6a0cmTmWJU58sGLDG0jrHFlnY4AFdno2lJYQBmCtO/wB5un4D2qLQdIWxiEsoDTsvP+yPQf1rWr6nAYL2a9pU+I46NK3vPcKKKK9g6QooooAKKKKACiiigAooooAKKKKACiigUAFSQxGRvYdajq0x8i3Z8Z2qWPvgVyYqt7KHmyo9ycAABRwKK82uNXv55jI1zIpzkBSQB9AK3dA8SMZEttRbrwkuMZPof8a+e+sKcrMyjiYOXKdYKjnXdEw/Gn1Xv7qGytnmuGwij8/Ye9dMJcjUux0Nqxl6pfx2Fs0r8seI19T/AIVxNxPJcyvLKxZmOSam1C8kv7ozS/RU7AelXNB0r7bL5sw/cRn/AL6Pp9PWsq9aeMqqFPb+tTy5ydSXKi14c0gSkXVyvyD7in+I+p9q6bpwOAKAAqgAAKOABRXvYbDxoQ5UddOmoKwUUUV1GgUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIzKqszMERRkk8AAd6+YPjJ47Pi7XTaWEmdIsWKw7eBM/RpD9eg9vqa7z4/ePjY27eF9ImHnzL/psiHlEPSP6nv7cd68P0XTLvWdUt9O0+Ey3V1IIolHcn+ncnsKAOi+Ffgmfxx4njshuSwgxLeSj+BM/dB/vHoPxPavsLT7G206yhs7KFYLa3QRxRoMBFAwAK534b+DrTwT4ch0y3CvcN+8up8YM0hHJ+g6AenvmusoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEooooAWiiigAooooAr3VzFawST3EixRRIXd2OAqgZJP0FfInxg8dS+N/EjSQyMNLsyYrSM8ZHeQj1bGfYYFejftH/EHYreEdJl5OGv5EPQdViz+p/AeteI6Do91r2sW2mabGZLi5cKo7D1Y+gA5NAHWfB/wPJ4v8QCS7jP8AZVmRJcN2kPaMH37+34V9SIioiqihVUAADgADoBWL4N8OWfhPw/baVYLkRDdLJjmWQ/ec/Xt6DArboAUmkoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACqOrRlolcfwHn6Gr1IVyMHkGuTGYZYqjKk+qNKU/ZzU+xztJjitK40wHLW7YH90/41ANOn7hR+NfmtXJ8XSnycjfmtj3Y4ulJXuZt5bC4j2/x/w/WsV1KMVcMjqcEHsa7qz09ISHk+du3oKpa5oovnM9uVSYdQejf/AF6+gwmUYilQcp79jwMw5KsuamtTk1XJAzljXWaDows1FzcAG4PQf3R/jVDSfD9wt7HJdYVYzkANkse34V09ezl2CcffqLXocNGlb3pLUKKKK9s7AooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAOjXc6D1NXmG7IPINUEO11Poav15WOXvJlxOIvfC16ly/2by3iJJUscED0NYcsbQyPFKpV1OCD2r1OsLxNoYv4TPbjbcoOP9seh9/SvGqUFa8TkrYa/vRKHhbXgqizvZMYH7t29PQn+VZniPWH1K52REi3jOEH98/3j/Ssj5lZlOVZTgg1Ja28lzcJDGMu5wBWHtJySpo5vazlFQLOk6dJf3IjUERjl3/uj/E120EMcESRxKFRRgAVBplhHp9usMfzEcs/qat5r6XA4RUIX+09zqo0+RXe4hooor0DcKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACuS+J3jW28FeHGuvke/uMx2kJ5y/diP7o6n8B3rotY1O00bS7nUdRlENrbRmSRj6DsPUnoB3NfJXj7xZd+MfEMupXWUi+5BDniKMdB9e5PcmgDEvLue+u5bq7laWeZjJJIxyWYnJJr6T/Z9+HX9hacviPVYgNSvo/3EbDm3hPf2ZuvsOO5rzv4CfDz/AISbV/7Z1WHOl2DjarDi4m6hfdR1P4D1r6lAwKAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEooooAWiiigAriPi145h8EeGZbhGV9QuMxWkR5y2OWI9F6n3wO9dTrGoWuk6bcahfzLBb2yGSSQ9Ao/r7dzXxz8SPGN1408Sz6jPmOBf3dtBn/AFUY6D6nqfegDnby5mvbuW5upXmnmcySOeSzE5JNfRvwM8Bnw3pJ1nVIcanfoNqMOYYjyB7E9T+A9a89+BngX/hItW/tjU4CdL09xtUji4mHIX3A6n8B619IgYoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBRRQKKQgooooASiiigYdsUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACrdvJuXaTyKqUoJByKwrUlVjyspOxoUlVUuGHVcin/aR2SvLlhaidki7oxPEXh8XbG5syEmP3k7N7+xqtoWjS2UpuLlgHxtUL82M9Tmt2Rix+amjpXTRwMIS53v+BzunHn5g6UUUV6JYUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiivL/jp49Hh/S20TTJManfJh2U8wRHgn2Zug9Bz6UAcF8dvH3/AAkGpnQtJl3abYyfvWQ8XEo4/FR0Hqcn0rjPAPhK98Z+I4NIsQVVzvnm25EMY6sf5AdzisO0tp7y6itrWJpp5nEccajJdicAAepNfXnwk8CReB/Diwyqj6ncgSXcw5+bsgP91f1OTQB0+g6PZaFpNrpemQiG1tUEaL3PqT6knknua06KKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoNFBoASiiigBaKK80+Ofj0eDfDv2XT3/AOJtqKskJH/LFBw0nsRnA9/pQB5x+0X8Ql1S/bwvpUubOzfN3Ih/1sv9z6L39/pXmPg3w3d+LNet9JsVAMh3SSY4ijH3nP0H5nArEJZySxbceST3Nej/AAx+I2l+BdPnjGiS3d9O2ZrnzwmVH3UA2nAHU88n8KAPozQNHs9C0e103TowlvaxhF9W9WPqSTk1fNeKf8ND2f8A0Lkv/gUP/iaP+GhrP/oXJ/8AwKH/AMTQB7VRXin/AA0NZ/8AQuT/APgUP/iaP+GhrP8A6Fyf/wACh/8AE0Ae10V4p/w0NZ/9C5P/AOBQ/wDiaP8Ahoaz/wChcn/8Ch/8TQB7XRXin/DQ1n/0Lk//AIFD/wCJo/4aGs/+hcn/APAof/E0Ae10V4p/w0NZ/wDQuT/+BQ/+Jo/4aGs/+hcn/wDAof8AxNAHtdFeKf8ADQ1n/wBC5P8A+BQ/+Jo/4aGs/wDoXJ//AAKH/wATQB7XRXin/DQ1n/0Lk/8A4Fj/AOJo/wCGhrP/AKFyf/wLH/xNAHtdFeKf8NDWf/QuT/8AgWP/AImj/hoaz/6Fyf8A8Cx/8TQB7XRXin/DQ1n/ANC5P/4Fj/4mj/hoaz/6Fyf/AMCx/wDE0Ae10V4p/wANDWf/AELk/wD4Fj/4mj/hoaz/AOhcn/8AAsf/ABNAHtdFeKf8NDWf/QuT/wDgWP8A4mj/AIaGs/8AoXJ//Asf/E0Ae10V4p/w0NZ/9C5P/wCBY/8AiaP+GhrP/oXJ/wDwLH/xNAHtdFeKf8NDWf8A0Lk//gWP/iaP+GhrP/oXJ/8AwLH/AMTQB7XRXin/AA0NZ/8AQuT/APgWP/iaP+GhrP8A6Fyf/wACx/8AE0Ae10V4p/w0NZ/9C5P/AOBY/wDiaP8Ahoaz/wChcn/8Cx/8TQB7XRXin/DQ1n/0Lk//AIFj/wCJo/4aGs/+hcn/APAsf/E0Ae10V4p/w0NZ/wDQuT/+BY/+Jo/4aGs/+hcn/wDAsf8AxNAHtdFeKf8ADQ1n/wBC5P8A+BY/+Jo/4aGs/wDoXJ//AALH/wATQB7XRXin/DQ1n/0Lk/8A4Fj/AOJo/wCGhrP/AKFyf/wLH/xNAHtdFeKf8NDWf/QuT/8AgWP/AImj/hoaz/6Fyf8A8Cx/8TQB7XRXin/DQ1n/ANC5P/4Fj/4mj/hoaz/6Fyf/AMCx/wDE0Ae10V4p/wANDWf/AELk/wD4Fj/4mj/hoaz/AOhcn/8AAsf/ABNAHtdFeKf8NDWf/QuT/wDgWP8A4mj/AIaGs/8AoXJ//Asf/E0Ae10V4p/w0NZ/9C5P/wCBY/8AiaP+GhrP/oXJ/wDwLH/xNAHtlFeJ/wDDQ1n/ANC5P/4Fj/4mj/hoaz/6Fyf/AMCx/wDE0Ae2UV4n/wANDWf/AELk/wD4Fj/4mj/hoaz/AOhcn/8AAsf/ABNIR7XRXin/AA0NZ/8AQuT/APgWP/iaP+GhrP8A6Fyf/wACx/8AE0xntdFeKf8ADQ1n/wBC5P8A+BY/+Jo/4aGs/wDoXJ//AALH/wATQB7XRXin/DQ1n/0Lk/8A4Fj/AOJo/wCGhrP/AKFyf/wLH/xNAHtdFeKf8NDWf/QuT/8AgWP/AImj/hoaz/6Fyf8A8Cx/8TQB7XRXin/DQ1n/ANC5P/4Fj/4mj/hoaz/6Fyf/AMCx/wDE0Ae10V4p/wANDWf/AELk/wD4Fj/4mj/hoaz/AOhcn/8AAsf/ABNAHtdFeKf8NDWf/QuT/wDgWP8A4mj/AIaGs/8AoXJ//Asf/E0Ae10V4p/w0NZ/9C5P/wCBY/8AiaP+GhrP/oXJ/wDwLH/xNAHtdFeKf8NDWf8A0Lk//gWP/iaP+GhrP/oXJ/8AwLH/AMTQB7XRXin/AA0NZ/8AQuT/APgWP/iaP+GhrP8A6Fyf/wACx/8AE0Ae10V4p/w0NZ/9C5P/AOBY/wDiaP8Ahoaz/wChcn/8Cx/8TQB7XRXin/DQ1n/0Lk//AIFj/wCJo/4aGs/+hcn/APAsf/E0Ae10ZrxT/hoaz/6Fyf8A8Cx/8TR/w0NZ/wDQuT/+BY/+Jp3A9rorxT/hoaz/AOhcn/8AAsf/ABNH/DQ1n/0Lk/8A4Fj/AOJpPUD2uivFP+GhrP8A6Fyf/wACx/8AE0f8NDWf/QuT/wDgWP8A4mkB7XRXin/DQ1n/ANC5P/4Fj/4mj/hoaz/6Fyf/AMCx/wDE0wPa6K8U/wCGhrP/AKFyf/wLH/xNH/DQ1n/0Lk//AIFj/wCJoA9rorxT/hoaz/6Fyf8A8Cx/8TR/w0NZ/wDQuT/+BY/+JoA9rorxT/hoaz/6Fyf/AMCx/wDE0f8ADQ1n/wBC5P8A+BY/+JoA9rorxT/hoaz/AOhcn/8AAsf/ABNH/DQ1n/0Lk/8A4Fj/AOJoA9rorxT/AIaGs/8AoXJ//Asf/E0f8NDWf/QuT/8AgWP/AImgD2uivFP+GhrP/oXJ/wDwLH/xNH/DQ1n/ANC5P/4Fj/4mgD2uivFP+GhrP/oXJ/8AwLH/AMTR/wANDWf/AELk/wD4Fj/4mgD2uivFP+GhrP8A6Fyf/wACx/8AE0f8NDWf/QuT/wDgWP8A4mgD2uivFP8Ahoaz/wChcn/8Cx/8TR/w0NZ/9C5P/wCBY/8AiaAPa6K8U/4aGs/+hcn/APAsf/E0f8NDWf8A0Lk//gWP/iaAPa6K8U/4aGs/+hcn/wDAsf8AxNH/AA0NZ/8AQuT/APgWP/iaAPa6K8U/4aGs/wDoXJ//AALH/wATR/w0NZ/9C5P/AOBY/wDiaAPSvHfiqz8H+HpdSvMNIPkt4d2DLJ2X6dyewr5N1nVbvWtVuNR1CUzXNy5eRz6nsPQDoB2FbvxH8cXnjjWFvJYzbWkCbLe237hGD94k8ZJPU49BWx8Fvh+/jTxAs97GRo9iwa5bHErdRED79/QfUUAegfs6fDv7PEvi7WIcSSKRYxuPuL3lx6noPbJ7iveKhhiSONI40CRoAqqBgADjGPQVNQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaKDQAlFFFAC1438e/hxq/iyey1fQFFxdW0Rhkti4VmTcWDKWIGQS2Rn0xXslFAHxt/wAKl8ef9C5c/wDfcf8A8VR/wqXx5/0Llz/33H/8VX2RRQB8b/8ACpfHn/Qt3P8A33H/APFUf8Kl8ef9C3c/99x//FV9kVVn1Kyt7pLaa8t47h/uxNKodvopOTQB8g/8Kl8ef9C3c/8Afcf/AMVR/wAKl8ef9C3c/wDfcf8A8VX2TRQB8bf8Kl8ef9C3c/8Afcf/AMVR/wAKl8ef9C3c/wDfcf8A8VX2TRQB8bf8Kl8ef9C3c/8Afcf/AMVR/wAKl8ef9C3c/wDfcf8A8VX2TWP4i8S6N4bthca7qMNlGxwvmEkt9FGSfwFAHyd/wqXx5/0Ldz/33H/8VR/wqXx5/wBC3c/99x//ABVfSEfxc8ByNtHiOAH/AGopFH6rXT6PrGm61bfaNJv7e9hP8cEgcD646GgD5I/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPjb/hUvjz/AKFu5/77j/8AiqP+FS+PP+hbuf8AvuP/AOKr7JooA+Nv+FS+PP8AoW7n/vuP/wCKo/4VL48/6Fu5/wC+4/8A4qvsmigD42/4VL48/wChbuf++4//AIqj/hUvjz/oW7n/AL7j/wDiq+yaKAPkLSvgz43vr2KCbR2sY2PzzzyIEQepwST9AK+n/Bvhix8J6Da6Vpqny4B88h+9K5+8x9yfyHFb1FABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaKDQAlFFFAC0UUUAFFFFAGD4+1xvDfg3VdXjAMtrbs0Wem88Ln23EV8U31/dX17Le3k7z3MzF3ldiWJPfNfVv7RN19n+FuoKDhp5IYgPX5wT+gNfJ1rA1zdQwIfmldYx9ScUAfYnwcutSvPhxo9xrBdrl4iAz/eaMMQhP8AwHHPfrXaDpUFvEsMSRRjCRqFUewqcUAFFFFAGdr2s2WhaRc6nqkwgtbVN8jHn8AO5J4HvXyF8UvGUnjfxXNqirJFaqixW0LtkxoBz04yTkn647V7F+1RqckHh3SdMifC3dw8sgB6hAMA+2Wz+FeCeFtBufE+v2uj6eU+03TFUaQkKMAkk4B4wDQBkVr+GfEWp+GdSTUdHumtrhDztPyuP7rL0I9q+oPhj8L7DwnoNxZ6rHb6pdXrA3DPCGjAAICKGGccnnuTXg3xp8GR+DfGDw2SEader9oth12gnDJ+B/QigD6a+Hfiy18ZeGYNVtgI5W+S4hBz5Mo6r9O49jXS18xfsy+Im07xlNo0sh+z6pCdqk8ecgyD+K7x+VfTtAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBooNACUUUUALRRRQAUUUUAeNftVXvleDtMsgcG4vt59wiN/VhXg/wAOrL+0PHehWpGVkvodw9g4J/QGvVP2sL7dquhWAb/VwSTEf7zAD/0A1x37Pdh9u+KWnORlbRJbg/ghUfqwoA+uQMUtFFABRRQelAHzx+1i5Go+H07eVOf/AB5K479naLzPivppIz5cc7f+QmH9a679rL/kL6B/17zf+hLXK/s4f8lVsf8ArhP/AOizQB9aV4l+1daxnw3o13/y2S8aIH/ZZCT+qivba8A/ar1mGRNG0SN8zKzXcq/3Bjamfr8/5UAeVfCyV4fiN4fePO77dGPwLYP6E19qV8afBuxk1D4m6FFGM+XcCdvZUBY/yr7LoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACg0UGgBKKKKAFooooAKKKKAPk39o2/wDtfxOu4Q2Vs4IYB7fLuP6tW/8AsqWHmeJ9YvyMrbWixA+7tn+SGvP/AIsSTy/EjxC1ypV/t0gAP90HC/8AjoFYmmazqmkiQaXqN1YiTG/7PMybsdM4IzjNAH3dUUkyQo0krqiDqzHAH418Sf8ACaeKf+hi1b/wMk/+KrOvtW1HUD/xML+7uv8ArtMz/wAyaAPsPWPib4N0kst54gs969UhfzW/JAat+FPGvh/xZHKdB1OK7aLBdMMjqD3KsAce+MV8SgDPFepfs36ZqVz8Qob+0RxZWkUn2qT+HDKQqH1JODj2z2oA7H9rGxdrbQNQH+rRpoGPoSFYfntP5V5X8Itcj0D4iaNfXLrHb+cYpHPAVXUpk+w3Zr6m+JfhRfGPhC80nKrcECS3ZuiyryufY9Pxr421TTrrTL6ay1GB7e6gcpJG4wQR/nrQB9peMPFWmeE9Gl1PVrhY40B8uMEFp27Kg7n+XU8V8d+MfEV14o8R3msXpxLcuSEDZEadFUfQcVmXF3cXAjFxcSzCMYUPIW2j0Geldp8LPhzqHjnVA5RrfSIWH2i6K9f9hPVj+Q6n0IB6T+zB4SeG2uvFN3EV88G2tMj+DOXcfUgKPoa95qppVjbaXp8FjZRLDbW6COKNeiqOBVugAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKDRQaAEooooAWiiigAooooA4zxp8M/DPi+5F3q1pIl0BtNxbvsdx2DdQ2O2RmuWb9nfwc33bvWB/23jP8A7JXrdLQB4/8A8M6+Et3/AB/6xj/rtH/8RWjYfATwRalTNBe3pHae5OP/ABwLXp9FAHK23w58G21m1pF4b07yn674Q7H/AIE2W/WtrRtH0/RbNLXS7OC0t15EcKBRn1OOp960KKAErmfFfgTw74uIbXNNjnmQYWZSUkA9NynJHsa6eigDzay+B/gW2lEjadNcYOQs1y5X8QCM/jXf2Vpb2VtHbWcEVvBENqRxKFVR6ADgVaooAao9adRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBooNACUUUUALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaKDQAlFFFAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUGig0AJRRRQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBooNACUUUUALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaKDQAlFFFAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUGig0AJRRRQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBooNACUUUUALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaKDQAlFFFAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRRRQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAAaKKKAP//ZuEr3PwAAAAAbdt+dTPZAhKzNAn39Fo5M" width="237.4047244094488" height="307.15198820722014" preserveAspectRatio="none"/>
</g>
<g transform="translate(0 320.15198820722014)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="15.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="25.119999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="35.739999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="43.019999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7490174898CD3BEE5501720224632ECB" x="56.959999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="66.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB8789F2F5F06048D4163694E4C0F3B6C" x="75.97999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="90.57999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="104.55999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="114.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA335A20E4C1D7F39210005AFF7F1A0EF" x="138.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="151.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="161.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="172.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="179.92000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="186.24" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="193.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="204.3" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="212.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="219.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="224.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="234.68" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 433.56299212598424)">
<g class="typst-group">
<g>
<g transform="translate(8 18.5)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAA14E57E2DCC57A3F7809273EECD3C51" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="9.344000000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="12.812800000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="18.5344" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="23.296000000000003" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="29.1456" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="33.8048" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="39.2832" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="46.1696" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="49.638400000000004" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="55.116800000000005" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="60.96640000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g1CB3EC9D05726EBFDE8ADABEC8504FCD" x="67.54560000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="76.4928" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD62975B7DE3250BE5F195D0E8335F60D" x="82.3424" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="88.704" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="92.1728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="98.5728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD5EEFB9760BC9A91B84F628EDDA52971" x="104.4224" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="110.7328" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="114.112" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g83A6AA7A836EACB3652229F4716CDAF" x="123.03359999999999" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gDB4862E33098F259EEBBA99A57E5AFA" x="129.2416" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="139.3536" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="145.2032" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="148.5824" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g793DBE65A5AEC1A16A65955B6C0E046" x="155.1616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gA11612CECC8CBEF18835767DAB11B2F7" x="166.3104" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="172.7616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="177.52319999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gCEFEF3D67F35C6E83CC3757B1DD21B13" x="180.90239999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="190.57919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="196.97919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="201.74079999999995" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g645CA8FA3D9155E2CBD9F8EED3C1540D" x="207.59039999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="214.23359999999997" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(798.4017637795276 8)">
<g class="typst-group">
<g>
<g transform="translate(0 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g61B7E1470B16535C69F53F42DA9B40BB" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" x="11.440000000000001" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.608 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="7.44" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="g5396A27CA60B9808846A090320835A9F" overflow="visible">
<path d="M 1.91 1.22 L 1.91 5.23 C 1.91 6.06 2.08 6.1099997 2.78 6.14 C 2.84 6.2 2.84 6.41 2.78 6.47 C 2.34 6.46 1.87 6.45 1.48 6.45 C 1.15 6.45 0.65999997 6.46 0.19 6.47 C 0.13 6.41 0.13 6.2 0.19 6.14 C 0.89 6.1099997 1.06 6.06 1.06 5.23 L 1.06 1.22 C 1.06 0.39 0.89 0.34 0.19 0.31 C 0.13 0.25 0.13 0.04 0.19 -0.02 C 0.64 -0.01 1.13 0 1.49 0 C 1.8499999 0 2.33 -0.01 2.78 -0.02 C 2.84 0.04 2.84 0.25 2.78 0.31 C 2.08 0.34 1.91 0.39 1.91 1.22 Z "/>
</symbol>
<symbol id="gEEE4EC0F13100E99C1017169F912BE3E" overflow="visible">
<path d="M 1.55 1.22 L 1.55 3.12 C 1.55 3.61 1.68 3.52 1.91 3.23 L 4.2599998 0.099999994 C 4.41 -0.06 4.5699997 -0.12 4.72 -0.12 C 4.8399997 -0.12 4.94 -0.049999997 4.94 0.14999999 L 4.94 3.3799999 C 4.94 4.21 5.0499997 4.24 5.66 4.29 C 5.72 4.35 5.72 4.56 5.66 4.62 C 5.3599997 4.61 5 4.6 4.7 4.6 C 4.4 4.6 4.0499997 4.61 3.75 4.62 C 3.6899998 4.56 3.6899998 4.35 3.75 4.29 C 4.36 4.25 4.47 4.21 4.47 3.3799999 L 4.47 1.51 C 4.47 1.24 4.44 1.0699999 4.13 1.49 L 1.8399999 4.6 L 0.42 4.62 L 0.39999998 4.5899997 L 0.39999998 4.35 C 0.39999998 4.31 0.45999998 4.29 0.48999998 4.29 C 0.87 4.2599998 0.97999996 4.14 1.0799999 3.9599998 L 1.0799999 1.22 C 1.0799999 0.39 0.96999997 0.35 0.35999998 0.31 C 0.29999998 0.25 0.29999998 0.04 0.35999998 -0.02 C 0.65999997 -0.01 1.01 0 1.31 0 C 1.61 0 1.9699999 -0.01 2.27 -0.02 C 2.33 0.04 2.33 0.25 2.27 0.31 C 1.66 0.35999998 1.55 0.39 1.55 1.22 Z "/>
</symbol>
<symbol id="gA419F36517085793EDBF3FE4736A2E59" overflow="visible">
<path d="M 3.04 1.22 L 3.04 3.74 C 3.04 4.11 3.1399999 4.2599998 3.46 4.2599998 L 3.72 4.2599998 C 4.35 4.2599998 4.48 4.06 4.68 3.34 C 4.7799997 3.32 4.87 3.32 4.95 3.37 C 4.9 3.86 4.89 4.23 4.87 4.7 C 4.52 4.66 3.8799999 4.6 3.04 4.6 L 2.25 4.6 C 1.27 4.6 0.69 4.65 0.42 4.7 C 0.42 4.23 0.41 3.84 0.35 3.37 C 0.44 3.34 0.53 3.33 0.62 3.34 C 0.82 4.06 0.93 4.2599998 1.5799999 4.2599998 L 1.8199999 4.2599998 C 2.1299999 4.2599998 2.25 4.14 2.25 3.75 L 2.25 1.22 C 2.25 0.39 2.1399999 0.35999998 1.53 0.31 C 1.4699999 0.25 1.4699999 0.04 1.53 -0.02 C 1.9 -0.01 2.31 0 2.6499999 0 C 3 0 3.3899999 -0.01 3.76 -0.02 C 3.82 0.04 3.82 0.25 3.76 0.31 C 3.1499999 0.35 3.04 0.39 3.04 1.22 Z "/>
</symbol>
<symbol id="gFAD9169AC3141E7FC4EA568E3BBD2E9B" overflow="visible">
<path d="M 1.91 1.22 L 1.91 2.09 L 2.46 2.09 C 2.84 2.09 2.98 1.76 3.11 1.39 L 3.33 0.78999996 C 3.56 0.17 3.8999999 -0.07 4.33 -0.07 C 4.48 -0.07 4.79 -0.04 4.96 0 C 4.99 0.099999994 4.97 0.19999999 4.9 0.28 C 4.54 0.28 4.35 0.34 4.15 0.85999995 L 3.86 1.61 C 3.74 1.92 3.62 2.09 3.49 2.22 L 3.49 2.24 C 3.83 2.36 4.3399997 2.77 4.3399997 3.46 C 4.3399997 4.29 3.82 4.64 2.6299999 4.64 C 2.3799999 4.64 1.81 4.6 1.51 4.6 C 1.22 4.6 0.79999995 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.78 -0.01 1.1899999 0 1.52 0 C 1.8299999 0 2.1599998 -0.01 2.48 -0.02 C 2.54 0.04 2.54 0.25 2.48 0.31 C 2.01 0.34 1.91 0.39 1.91 1.22 Z M 3.47 3.46 C 3.47 2.6699998 3.24 2.3799999 2.35 2.3799999 L 1.91 2.3799999 L 1.91 3.6799998 C 1.91 4.21 2.01 4.31 2.57 4.31 C 3.27 4.31 3.47 4.06 3.47 3.46 Z "/>
</symbol>
<symbol id="g7FD6A8241485CEBC032BD9E4CE659816" overflow="visible">
<path d="M 5.27 2.35 C 5.27 3.77 4.13 4.7 2.83 4.7 C 1.4399999 4.7 0.37 3.6899998 0.37 2.22 C 0.37 0.85999995 1.4 -0.099999994 2.75 -0.099999994 C 4.39 -0.099999994 5.27 1.05 5.27 2.35 Z M 2.74 4.37 C 3.6299999 4.37 4.4 3.55 4.4 2.21 C 4.4 0.97999996 3.79 0.22999999 2.8999999 0.22999999 C 1.93 0.22999999 1.24 1.11 1.24 2.34 C 1.24 3.6899998 1.99 4.37 2.74 4.37 Z "/>
</symbol>
<symbol id="gBFFDA84A1400D9E1136DF0DD93EA19F5" overflow="visible">
<path d="M 1.48 4.6 C 1.2099999 4.6 0.76 4.61 0.37 4.62 C 0.31 4.56 0.31 4.35 0.37 4.29 C 0.97999996 4.25 1.09 4.21 1.09 3.3799999 L 1.09 1.22 C 1.09 0.39 0.97999996 0.35999998 0.37 0.31 C 0.31 0.25 0.31 0.04 0.37 -0.02 C 0.75 -0.01 1.1999999 0 1.49 0 C 1.75 0 2.1499999 -0.02 2.95 -0.02 C 4.06 -0.02 5.2999997 0.5 5.2999997 2.25 C 5.2999997 3.58 4.48 4.62 2.81 4.62 C 2.1299999 4.62 1.77 4.6 1.48 4.6 Z M 1.88 0.76 L 1.88 3.98 C 1.88 4.23 2.1299999 4.29 2.52 4.29 C 4.2 4.29 4.43 3.12 4.43 2.08 C 4.43 0.68 3.81 0.31 2.71 0.31 C 1.9499999 0.31 1.88 0.48 1.88 0.76 Z "/>
</symbol>
<symbol id="gEC3CC7DEE79E0AA801DFAAEF4B6C0B50" overflow="visible">
<path d="M 4.35 3.3799999 L 4.35 2.11 C 4.35 1.25 4.35 0.31 3.03 0.31 C 2.04 0.31 1.8299999 1.09 1.8299999 2.02 L 1.8299999 3.3799999 C 1.8299999 4.21 1.9399999 4.24 2.55 4.29 C 2.61 4.35 2.61 4.56 2.55 4.62 C 2.1599998 4.61 1.76 4.6 1.43 4.6 C 1.0699999 4.6 0.68 4.61 0.32 4.62 C 0.26 4.56 0.26 4.35 0.32 4.29 C 0.93 4.25 1.04 4.21 1.04 3.3799999 L 1.04 1.81 C 1.04 0.31 1.77 -0.099999994 2.86 -0.099999994 C 4.41 -0.099999994 4.8199997 0.78 4.8199997 2.24 L 4.8199997 3.3799999 C 4.8199997 4.21 4.93 4.24 5.54 4.29 C 5.6 4.35 5.6 4.56 5.54 4.62 C 5.24 4.61 4.88 4.6 4.58 4.6 C 4.2799997 4.6 3.9299998 4.61 3.6299999 4.62 C 3.57 4.56 3.57 4.35 3.6299999 4.29 C 4.24 4.25 4.35 4.21 4.35 3.3799999 Z "/>
</symbol>
<symbol id="g202CCBD46865F83C12D50E1B4FF9BBEA" overflow="visible">
<path d="M 2.76 -0.099999994 C 3.54 -0.099999994 4.02 0.19 4.49 0.82 C 4.47 0.89 4.37 1 4.29 1.02 C 3.83 0.48 3.48 0.28 2.81 0.28 C 1.8199999 0.28 1.24 1.35 1.24 2.34 C 1.24 4.02 2.02 4.37 2.77 4.37 C 3.57 4.37 4.04 3.9299998 4.16 3.23 C 4.2599998 3.1999998 4.36 3.1999998 4.46 3.26 C 4.46 3.6699998 4.44 4.0899997 4.3399997 4.54 C 3.9599998 4.54 3.51 4.7 2.71 4.7 C 1.39 4.7 0.37 3.6999998 0.37 2.24 C 0.37 1.61 0.57 0.91999996 1.06 0.47 C 1.4599999 0.099999994 2.02 -0.099999994 2.76 -0.099999994 Z "/>
</symbol>
<symbol id="g5503E15E5E4E70E9E217A15BD1ECD752" overflow="visible">
<path d="M 1.9499999 3.3799999 C 1.9499999 4.21 2.06 4.24 2.6699998 4.29 C 2.73 4.35 2.73 4.56 2.6699998 4.62 C 2.29 4.61 1.86 4.6 1.55 4.6 C 1.25 4.6 0.83 4.61 0.44 4.62 C 0.38 4.56 0.38 4.35 0.44 4.29 C 1.05 4.25 1.16 4.21 1.16 3.3799999 L 1.16 1.22 C 1.16 0.39 1.05 0.35999998 0.44 0.31 C 0.38 0.25 0.38 0.04 0.44 -0.02 C 0.81 -0.01 1.22 0 1.56 0 C 1.88 0 2.32 -0.01 2.6699998 -0.02 C 2.73 0.04 2.73 0.25 2.6699998 0.31 C 2.06 0.35 1.9499999 0.39 1.9499999 1.22 Z "/>
</symbol>
<symbol id="g1E8994F5C297EC73FA26D93D22635023" overflow="visible">
<path d="M 2.82 -0.14999999 C 4.11 -0.14999999 5.16 0.9 5.16 2.19 C 5.16 3.48 4.11 4.52 2.82 4.52 C 1.53 4.52 0.48999998 3.48 0.48999998 2.19 C 0.48999998 0.9 1.53 -0.14999999 2.82 -0.14999999 Z M 2.82 4.2599998 C 3.97 4.2599998 4.9 3.34 4.9 2.19 C 4.9 1.04 3.9599998 0.11 2.82 0.11 C 1.67 0.11 0.75 1.04 0.75 2.19 C 0.75 3.33 1.67 4.2599998 2.82 4.2599998 Z "/>
</symbol>
<symbol id="g6D39B87B7095296261A07873F9B99896" overflow="visible">
<path d="M 1.86 0.948 L 2.52 2.688 C 2.58 2.844 2.652 2.892 2.94 2.892 L 5.472 2.892 L 6.168 0.864 C 6.3120003 0.456 5.856 0.408 5.28 0.372 C 5.208 0.3 5.208 0.048 5.28 -0.024 C 5.724 -0.012 6.384 0 6.852 0 C 7.344 0 7.8 -0.012 8.22 -0.024 C 8.292 0.048 8.292 0.3 8.22 0.372 C 7.752 0.42000002 7.344 0.456 7.14 1.0320001 L 4.668 7.896 C 4.488 7.788 4.164 7.656 4.008 7.656 L 1.284 1.224 C 0.972 0.48000002 0.612 0.408 0.084 0.372 C 0.012 0.3 0.012 0.048 0.084 -0.024 C 0.396 -0.012 0.792 0 1.152 0 C 1.644 0 2.244 -0.012 2.688 -0.024 C 2.76 0.048 2.76 0.3 2.688 0.372 C 2.232 0.408 1.668 0.456 1.86 0.948 Z M 3.1560001 3.3960001 C 2.892 3.3960001 2.808 3.432 2.856 3.552 L 4.08 6.66 L 4.152 6.66 L 5.28 3.3960001 Z "/>
</symbol>
<symbol id="g1B61845C1FB429ACDF5304290F5BF286" overflow="visible">
<path d="M 4.548 0 C 4.548 0 4.824 1.152 4.908 1.656 C 4.8 1.716 4.704 1.74 4.572 1.704 C 4.38 0.996 4.032 0.408 3.276 0.408 L 2.736 0.408 C 2.46 0.408 2.292 0.6 2.292 0.828 L 2.292 4.056 C 2.292 5.052 2.424 5.088 3.1560001 5.1480002 C 3.228 5.2200003 3.228 5.472 3.1560001 5.544 C 2.7120001 5.532 2.22 5.52 1.812 5.52 C 1.44 5.52 0.924 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.32 0.408 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 1.068 -0.012 1.86 0 1.86 0 Z "/>
</symbol>
<symbol id="gC66F55FB8F08DA72FE76D3863D88042" overflow="visible">
<path d="M 5.664 1.092 C 5.664 2.088 5.736 2.124 6.1080003 2.184 C 6.18 2.256 6.18 2.5080001 6.1080003 2.58 C 5.892 2.568 5.556 2.556 5.184 2.556 C 4.824 2.556 4.272 2.568 3.924 2.58 C 3.852 2.5080001 3.852 2.256 3.924 2.184 C 4.656 2.136 4.716 2.088 4.716 1.092 L 4.716 0.444 C 4.3320003 0.336 3.936 0.276 3.516 0.276 C 2.016 0.276 1.524 1.812 1.524 2.796 C 1.524 4.248 2.22 5.244 3.372 5.244 C 4.56 5.244 5.064 4.644 5.244 3.876 C 5.364 3.8400002 5.484 3.8400002 5.604 3.912 C 5.592 4.404 5.556 4.908 5.448 5.448 C 5.088 5.448 4.2 5.64 3.528 5.64 C 1.812 5.64 0.444 4.5360003 0.444 2.64 C 0.444 1.116 1.584 -0.120000005 3.3 -0.120000005 C 4.116 -0.120000005 5.004 0 5.796 0.432 C 5.712 0.51600003 5.664 0.624 5.664 0.708 Z "/>
</symbol>
<symbol id="g4C6038BE04CA3E1481E54A97A0E34303" overflow="visible">
<path d="M 6.324 2.82 C 6.324 4.524 4.956 5.64 3.3960001 5.64 C 1.728 5.64 0.444 4.428 0.444 2.664 C 0.444 1.0320001 1.6800001 -0.120000005 3.3 -0.120000005 C 5.268 -0.120000005 6.324 1.26 6.324 2.82 Z M 3.288 5.244 C 4.356 5.244 5.28 4.26 5.28 2.652 C 5.28 1.176 4.548 0.276 3.48 0.276 C 2.316 0.276 1.488 1.332 1.488 2.808 C 1.488 4.428 2.388 5.244 3.288 5.244 Z "/>
</symbol>
<symbol id="g48BCA4F06942DA5990D42018985FC781" overflow="visible">
<path d="M 2.292 1.464 L 2.292 2.5080001 L 2.9520001 2.5080001 C 3.408 2.5080001 3.576 2.112 3.732 1.668 L 3.996 0.948 C 4.272 0.204 4.68 -0.084 5.196 -0.084 C 5.376 -0.084 5.748 -0.048 5.952 0 C 5.988 0.120000005 5.964 0.24000001 5.88 0.336 C 5.448 0.336 5.2200003 0.408 4.98 1.0320001 L 4.632 1.932 C 4.488 2.304 4.344 2.5080001 4.188 2.664 L 4.188 2.688 C 4.596 2.832 5.208 3.3240001 5.208 4.152 C 5.208 5.1480002 4.584 5.568 3.1560001 5.568 C 2.856 5.568 2.172 5.52 1.812 5.52 C 1.464 5.52 0.96000004 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.212 0.432 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 0.936 -0.012 1.428 0 1.824 0 C 2.196 0 2.592 -0.012 2.976 -0.024 C 3.048 0.048 3.048 0.3 2.976 0.372 C 2.412 0.408 2.292 0.468 2.292 1.464 Z M 4.164 4.152 C 4.164 3.204 3.888 2.856 2.82 2.856 L 2.292 2.856 L 2.292 4.416 C 2.292 5.052 2.412 5.172 3.084 5.172 C 3.924 5.172 4.164 4.872 4.164 4.152 Z "/>
</symbol>
<symbol id="g45E4C10E27056C5AE488FE2D8290DF06" overflow="visible">
<path d="M 2.34 4.056 C 2.34 5.052 2.4720001 5.088 3.204 5.1480002 C 3.276 5.2200003 3.276 5.472 3.204 5.544 C 2.748 5.532 2.232 5.52 1.86 5.52 C 1.5 5.52 0.996 5.532 0.528 5.544 C 0.456 5.472 0.456 5.2200003 0.528 5.1480002 C 1.26 5.1 1.392 5.052 1.392 4.056 L 1.392 1.464 C 1.392 0.468 1.26 0.432 0.528 0.372 C 0.456 0.3 0.456 0.048 0.528 -0.024 C 0.972 -0.012 1.464 0 1.872 0 C 2.256 0 2.784 -0.012 3.204 -0.024 C 3.276 0.048 3.276 0.3 3.204 0.372 C 2.4720001 0.42000002 2.34 0.468 2.34 1.464 Z "/>
</symbol>
<symbol id="gA2769E14ED9B16297025579DD26D23A1" overflow="visible">
<path d="M 3.648 1.464 L 3.648 4.488 C 3.648 4.932 3.7680001 5.112 4.152 5.112 L 4.464 5.112 C 5.2200003 5.112 5.376 4.872 5.616 4.008 C 5.736 3.984 5.844 3.984 5.94 4.044 C 5.88 4.632 5.868 5.076 5.844 5.64 C 5.4240003 5.592 4.656 5.52 3.648 5.52 L 2.7 5.52 C 1.524 5.52 0.828 5.58 0.504 5.64 C 0.504 5.076 0.492 4.608 0.42000002 4.044 C 0.528 4.008 0.636 3.996 0.744 4.008 C 0.984 4.872 1.116 5.112 1.896 5.112 L 2.184 5.112 C 2.556 5.112 2.7 4.968 2.7 4.5 L 2.7 1.464 C 2.7 0.468 2.568 0.432 1.836 0.372 C 1.764 0.3 1.764 0.048 1.836 -0.024 C 2.28 -0.012 2.772 0 3.18 0 C 3.6000001 0 4.068 -0.012 4.512 -0.024 C 4.584 0.048 4.584 0.3 4.512 0.372 C 3.78 0.42000002 3.648 0.468 3.648 1.464 Z "/>
</symbol>
<symbol id="g7FB89403B37B0F0F934DFEB7E5171B37" overflow="visible">
<path d="M 6 4.056 C 6 5.052 6.132 5.088 6.864 5.1480002 C 6.936 5.2200003 6.936 5.472 6.864 5.544 C 6.4440002 5.52 5.916 5.52 5.52 5.52 C 5.184 5.52 4.656 5.532 4.188 5.544 C 4.116 5.472 4.116 5.2200003 4.188 5.1480002 C 4.92 5.1 5.052 5.052 5.052 4.056 L 5.052 3.024 L 2.28 3.024 L 2.28 4.056 C 2.28 5.052 2.412 5.088 3.144 5.1480002 C 3.216 5.2200003 3.216 5.472 3.144 5.544 C 2.688 5.532 2.184 5.52 1.8000001 5.52 C 1.44 5.52 0.948 5.532 0.468 5.544 C 0.396 5.472 0.396 5.2200003 0.468 5.1480002 C 1.2 5.1 1.332 5.052 1.332 4.056 L 1.332 1.464 C 1.332 0.468 1.2 0.432 0.468 0.372 C 0.396 0.3 0.396 0.048 0.468 -0.024 C 0.948 -0.012 1.428 0 1.812 0 C 2.196 0 2.676 -0.012 3.144 -0.024 C 3.216 0.048 3.216 0.3 3.144 0.372 C 2.412 0.42000002 2.28 0.468 2.28 1.464 L 2.28 2.628 L 5.052 2.628 L 5.052 1.464 C 5.052 0.468 4.92 0.432 4.188 0.372 C 4.116 0.3 4.116 0.048 4.188 -0.024 C 4.632 -0.012 5.112 0 5.532 0 C 5.892 0 6.396 -0.012 6.864 -0.024 C 6.936 0.048 6.936 0.3 6.864 0.372 C 6.132 0.42000002 6 0.468 6 1.464 Z "/>
</symbol>
<symbol id="gFF269982F0E4C510F3A3BFF016D72390" overflow="visible">
<path d="M 5.796 4.584 L 5.88 4.584 L 6.0360003 1.4760001 C 6.084 0.48000002 6.072 0.432 5.4240003 0.372 C 5.352 0.3 5.352 0.048 5.4240003 -0.024 C 5.844 -0.012 6.288 0 6.624 0 C 6.984 0 7.3320003 -0.012 7.656 -0.024 C 7.728 0.048 7.728 0.3 7.656 0.372 C 7.044 0.432 7.032 0.504 6.96 1.4760001 L 6.7200003 4.572 C 6.684 5.052 6.7920003 5.1 7.392 5.1480002 C 7.464 5.2200003 7.464 5.472 7.392 5.544 L 5.772 5.52 L 3.9720001 1.224 L 2.436 5.52 L 0.768 5.544 C 0.696 5.472 0.696 5.2200003 0.768 5.1480002 C 1.3560001 5.112 1.464 5.052 1.44 4.824 L 1.056 1.452 C 0.948 0.456 0.792 0.408 0.336 0.372 C 0.264 0.3 0.264 0.048 0.336 -0.024 C 0.576 -0.012 0.936 0 1.128 0 C 1.368 0 1.812 -0.012 2.052 -0.024 C 2.124 0.048 2.124 0.3 2.052 0.372 C 1.368 0.42000002 1.38 0.564 1.4760001 1.452 L 1.824 4.5 L 1.848 4.5 L 3.552 -0.048 C 3.576 -0.108 3.636 -0.144 3.696 -0.144 C 3.744 -0.144 3.8040001 -0.108 3.828 -0.048 Z "/>
</symbol>
<symbol id="gD77922058D8F1A3A631DDE5946887BDC" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z M 3.384 5.112 C 4.764 5.112 5.88 4.008 5.88 2.628 C 5.88 1.248 4.752 0.132 3.384 0.132 C 2.004 0.132 0.90000004 1.248 0.90000004 2.628 C 0.90000004 3.996 2.004 5.112 3.384 5.112 Z "/>
</symbol>
<symbol id="g5ABA589ED074A65FC8C929AB4EB2344C" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z "/>
</symbol>
<symbol id="gEDADDD9BA25BBB833C1F4B684DC50419" overflow="visible">
<path d="M 4.83 3.82 L 4.9 3.82 L 5.0299997 1.23 C 5.0699997 0.39999998 5.06 0.35999998 4.52 0.31 C 4.46 0.25 4.46 0.04 4.52 -0.02 C 4.87 -0.01 5.24 0 5.52 0 C 5.8199997 0 6.1099997 -0.01 6.3799996 -0.02 C 6.44 0.04 6.44 0.25 6.3799996 0.31 C 5.87 0.35999998 5.8599997 0.42 5.7999997 1.23 L 5.6 3.81 C 5.5699997 4.21 5.66 4.25 6.16 4.29 C 6.22 4.35 6.22 4.56 6.16 4.62 L 4.81 4.6 L 3.31 1.02 L 2.03 4.6 L 0.64 4.62 C 0.58 4.56 0.58 4.35 0.64 4.29 C 1.13 4.2599998 1.22 4.21 1.1999999 4.02 L 0.88 1.2099999 C 0.78999996 0.38 0.65999997 0.34 0.28 0.31 C 0.22 0.25 0.22 0.04 0.28 -0.02 C 0.48 -0.01 0.78 0 0.94 0 C 1.14 0 1.51 -0.01 1.7099999 -0.02 C 1.77 0.04 1.77 0.25 1.7099999 0.31 C 1.14 0.35 1.15 0.47 1.23 1.2099999 L 1.52 3.75 L 1.54 3.75 L 2.96 -0.04 C 2.98 -0.089999996 3.03 -0.12 3.08 -0.12 C 3.12 -0.12 3.1699998 -0.089999996 3.1899998 -0.04 Z "/>
</symbol>
<symbol id="g97A8E46F7A64F11D13C6F357868587EE" overflow="visible">
<path d="M 1.89 1.22 L 1.89 1.9599999 C 2.07 1.88 2.27 1.8399999 2.52 1.8399999 C 3.86 1.8399999 4.27 2.8 4.27 3.3999999 C 4.27 3.9199998 3.97 4.62 2.55 4.62 C 2.18 4.62 1.76 4.6 1.49 4.6 C 1.1999999 4.6 0.78 4.61 0.38 4.62 C 0.32 4.56 0.32 4.35 0.38 4.29 C 0.98999995 4.25 1.1 4.21 1.1 3.3799999 L 1.1 1.22 C 1.1 0.39 0.98999995 0.35999998 0.38 0.31 C 0.32 0.25 0.32 0.04 0.38 -0.02 C 0.71 -0.01 1.06 0 1.5 0 C 1.93 0 2.28 -0.01 2.61 -0.02 C 2.6699998 0.04 2.6699998 0.25 2.61 0.31 C 2 0.35 1.89 0.39 1.89 1.22 Z M 1.89 3.84 C 1.89 4.16 2.01 4.29 2.49 4.29 C 3.08 4.29 3.3999999 3.98 3.3999999 3.28 C 3.3999999 2.56 3.1399999 2.1699998 2.54 2.1699998 C 2.34 2.1699998 2.09 2.2 1.89 2.28 Z "/>
</symbol>
<symbol id="gB844DCFB76B4CC44608DB013C9764E9C" overflow="visible">
<path d="M 1.8299999 3.62 C 1.5899999 4.19 1.5999999 4.24 2.1399999 4.29 C 2.2 4.35 2.2 4.56 2.1399999 4.62 C 1.8299999 4.61 1.49 4.6 1.0799999 4.6 C 0.76 4.6 0.45999998 4.61 0.19999999 4.62 C 0.14 4.56 0.14 4.35 0.19999999 4.29 C 0.69 4.24 0.76 4.13 1 3.56 L 2.4199998 0.28 C 2.55 -0.01 2.6 -0.12 2.71 -0.12 C 2.78 -0.12 2.82 -0.04 2.96 0.28 L 4.42 3.55 C 4.63 4.0099998 4.74 4.25 5.2799997 4.29 C 5.3399997 4.35 5.3399997 4.56 5.2799997 4.62 C 5.06 4.61 4.8199997 4.6 4.56 4.6 C 4.19 4.6 3.9099998 4.61 3.6399999 4.62 C 3.58 4.56 3.58 4.35 3.6399999 4.29 C 4.18 4.25 4.23 4.13 4.0299997 3.62 L 2.9399998 1.13 C 2.9099998 1.1 2.8999999 1.1 2.87 1.13 Z "/>
</symbol>
<symbol id="gDAA1267270512376F631C9A10449D5F4" overflow="visible">
<path d="M 2.48 2.25 C 3.1399999 2.25 3.1499999 2.06 3.1699998 1.6899999 C 3.22 1.64 3.3999999 1.64 3.4499998 1.6899999 C 3.4399998 1.92 3.4299998 2.26 3.4299998 2.4199998 C 3.4299998 2.56 3.4399998 2.8799999 3.4499998 3.1299999 C 3.3999999 3.1799998 3.22 3.1799998 3.1699998 3.1299999 C 3.1499999 2.6799998 3.1299999 2.57 2.48 2.57 L 1.91 2.57 L 1.91 3.99 C 1.91 4.16 2.04 4.27 2.23 4.27 L 2.8 4.27 C 3.62 4.27 3.75 3.9399998 3.9299998 3.37 C 4.0299997 3.36 4.12 3.3799999 4.2 3.4199998 C 4.16 3.76 4.04 4.54 4.02 4.61 C 4.02 4.63 4.0099998 4.64 3.99 4.64 C 3.85 4.61 3.75 4.6 3.58 4.6 L 1.51 4.6 C 1.22 4.6 0.76 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.76 -0.01 1.1999999 0 1.52 0 L 3.06 0 C 3.46 0 4.12 -0.02 4.12 -0.02 C 4.24 0.39 4.35 0.94 4.42 1.36 C 4.33 1.41 4.25 1.43 4.14 1.4 C 3.98 0.81 3.6899998 0.31 2.86 0.31 L 2.4299998 0.31 C 2.01 0.31 1.91 0.42 1.91 0.75 L 1.91 2.25 Z "/>
</symbol>
<symbol id="g6C3A310EEC8A7EBBD176D179125951F0" overflow="visible">
<path d="M 2.328 -4.632 L 8.208 -4.632 C 8.352 -4.488 8.352 -4.056 8.208 -3.912 C 4.896 -3.648 4.728 -3.288 4.728 -1.2 L 4.728 13.464 C 4.728 15.552 4.92 15.912 8.208 16.152 C 8.352 16.296 8.352 16.728 8.208 16.872 L 2.328 16.872 Z "/>
</symbol>
<symbol id="g2F0CE4BDC8DA4B92139017B781562218" overflow="visible">
<path d="M 3.96 1.896 L 5.232 5.232 C 5.352 5.544 5.496 5.64 6.072 5.64 L 10.632 5.64 L 11.976 1.728 C 12.264 0.864 11.568 0.84000003 10.656 0.792 C 10.512 0.792 10.344 0.768 10.2 0.768 C 10.056 0.624 10.056 0.096 10.2 -0.048 C 11.088 -0.024 13.368 0 14.304 0 C 15.288 0 16.632 -0.024 17.52 -0.048 C 17.664 0.096 17.664 0.624 17.52 0.768 C 16.584 0.864 15.792 0.84000003 15.360001 2.0640001 L 10.416 15.792 C 10.056 15.576 8.616 14.736 7.776 14.736 L 2.568 2.448 C 1.944 0.96000004 1.224 0.84000003 0.168 0.768 C 0.024 0.624 0.024 0.096 0.168 -0.048 C 1.056 -0.024 1.488 0 2.424 0 C 3.408 0 4.728 -0.024 5.616 -0.048 C 5.76 0.096 5.76 0.624 5.616 0.768 C 4.704 0.84000003 3.576 0.912 3.96 1.896 Z M 6.552 6.7920003 C 6.024 6.7920003 5.856 6.864 5.952 7.104 L 8.064 12.4800005 L 8.232 12.4800005 L 10.2 6.7920003 Z "/>
</symbol>
<symbol id="g8D84A54D9303B24762DC3071B60ECD14" overflow="visible">
<path d="M 2.4 3.048 C 2.4 1.056 2.016 0.84000003 0.552 0.768 C 0.408 0.624 0.408 0.096 0.552 -0.048 C 1.5600001 -0.024 2.64 0 3.96 0 C 5.28 0 6.336 -0.024 7.368 -0.048 C 7.512 0.096 7.512 0.624 7.368 0.768 C 5.9040003 0.84000003 5.52 1.056 5.52 3.048 L 5.52 13.992001 C 5.52 15.552 5.592 16.44 5.592 16.44 C 5.592 16.656 5.4240003 16.752 5.208 16.752 C 4.32 16.464 2.4 16.2 0.696 16.128 C 0.624 15.84 0.648 15.576 0.768 15.360001 C 2.28 15.24 2.4 15.216001 2.4 13.56 Z "/>
</symbol>
<symbol id="g3E9095A1FBD7854ED5F7B53469C97011" overflow="visible">
<path d="M 11.208 9.456 C 11.88 9.456 12.264 9.744 12.264 10.632 C 12.264 11.088 11.64 11.784 10.728 11.784 C 9.672 11.784 8.28 10.992 7.584 10.368 C 7.152 10.608 6.6480002 10.656 5.568 10.656 C 4.5360003 10.656 3.528 10.416 2.736 9.8880005 C 1.752 9.264 1.104 8.328 1.104 7.104 C 1.104 5.928 1.8000001 4.656 2.9520001 4.032 C 2.208 3.384 1.056 2.112 1.056 1.632 C 1.056 1.176 1.128 0.888 1.368 0.528 C 1.584 0.192 1.872 0 2.352 -0.144 C 1.32 -0.768 0.264 -2.136 0.264 -2.544 C 0.264 -3.432 0.552 -4.464 1.2 -4.92 C 2.136 -5.568 3.72 -5.712 4.872 -5.712 C 8.208 -5.712 12.024 -3.96 12.024 -1.32 C 12.024 -0.816 11.784 0.216 10.824 0.864 C 9.8880005 1.488 6.288 1.656 4.512 1.656 C 4.08 1.656 3.432 1.704 3.432 2.664 C 3.432 3.048 3.672 3.384 3.792 3.672 C 4.296 3.432 4.8 3.408 5.544 3.408 C 6.768 3.408 7.896 3.72 8.712 4.44 C 9.408 5.064 9.8880005 5.9040003 9.8880005 6.984 C 9.8880005 8.328 9.216 9.216 8.4 9.8880005 C 8.592 10.128 9.384 10.56 9.624001 10.56 C 9.84 10.56 10.008 10.416 10.08 10.272 C 10.176 9.96 10.608 9.456 11.208 9.456 Z M 4.2 -0.6 C 6.048 -0.6 9.6 -0.672 9.6 -1.944 C 9.6 -2.808 9.216 -3.792 8.424 -4.224 C 7.6800003 -4.656 6.456 -4.704 5.544 -4.704 C 3.96 -4.704 2.88 -3.528 2.88 -2.304 C 2.88 -1.488 2.88 -0.936 3.144 -0.456 C 3.384 -0.552 3.696 -0.6 4.2 -0.6 Z M 6.96 6.912 C 6.96 4.608 6.288 4.32 5.664 4.32 C 4.176 4.32 3.984 6.096 3.984 7.32 C 3.984 9.096 4.416 9.744 5.352 9.744 C 6.48 9.744 6.96 8.808 6.96 6.912 Z "/>
</symbol>
<symbol id="g90B91206A818BADA9956CC42F47E57A0" overflow="visible">
<path d="M 1.176 1.392 C 1.176 0.48000002 1.944 -0.24000001 2.904 -0.24000001 C 3.864 -0.24000001 4.68 0.528 4.68 1.44 C 4.68 2.376 3.912 3.096 2.9520001 3.096 C 1.992 3.096 1.176 2.328 1.176 1.392 Z "/>
</symbol>
<symbol id="g2B9D5A283BBC2ED0501C3A1039D04E5C" overflow="visible">
<path d="M 8.808 2.928 L 8.808 11.592 C 8.808 12.864 9 14.232 9 14.232 C 9 14.544 8.808 14.64 8.592 14.64 C 8.352 14.64 7.9440002 14.544 7.392 14.28 C 5.928 13.608 4.296 13.032001 2.208 12.168 C 2.232 11.76 2.4 11.376 2.736 11.136 C 4.032 11.688 4.896 11.736 5.232 11.736 C 5.544 11.736 5.688 11.64 5.688 10.440001 L 5.688 2.928 C 5.688 0.936 4.5360003 0.84000003 3.216 0.768 C 2.976 0.624 2.976 0.096 3.216 -0.048 C 5.184 -0.024 6.3120003 0 7.272 0 C 8.232 0 9.312 -0.024 11.28 -0.048 C 11.52 0.096 11.52 0.624 11.28 0.768 C 9.96 0.84000003 8.808 0.936 8.808 2.928 Z "/>
</symbol>
<symbol id="g10BFE5E41011FF0F560FA08FAB260218" overflow="visible">
<path d="M 7.248 16.824 L 1.368 16.824 C 1.224 16.68 1.224 16.248 1.368 16.104 C 4.68 15.84 4.848 15.4800005 4.848 13.392 L 4.848 -1.272 C 4.848 -3.3600001 4.656 -3.72 1.368 -3.96 C 1.224 -4.104 1.224 -4.5360003 1.368 -4.68 L 7.248 -4.68 Z "/>
</symbol>
<symbol id="g1BED8054A02AECF3BF3EC56A671C1672" overflow="visible">
<path d="M 9.528 -0.24000001 C 11.856 -0.24000001 13.992001 0.864 15.624001 3 C 15.504 3.216 15.096 3.504 14.832 3.504 C 13.128 1.632 11.184 1.008 9.504 1.008 C 6.7200003 1.008 4.512 4.272 4.512 8.016 C 4.512 11.736 6.432 14.808001 9.288 14.808001 C 12.6 14.808001 13.68 12.936 14.304 10.872 C 14.592 10.776 15.0720005 10.848001 15.336 10.992 C 15.216001 12.24 15.024 13.392 14.808001 14.712 C 13.584001 14.832 12.504 15.792 9.552 15.792 C 4.848 15.792 0.888 12.84 0.888 7.56 C 0.888 5.304 1.872 2.664 3.792 1.272 C 5.328 0.168 7.2000003 -0.24000001 9.528 -0.24000001 Z "/>
</symbol>
<symbol id="g841363B3896A8C79F18618DF16186242" overflow="visible">
<path d="M 0.888 4.968 C 0.888 1.824 3.384 -0.24000001 6.6 -0.24000001 C 8.304 -0.24000001 9.72 0.24000001 10.704 1.128 C 11.928 2.208 12.336 3.8400002 12.336 5.184 C 12.336 8.328 10.2 10.656 6.624 10.656 C 4.632 10.656 3.144 9.96 2.208 8.88 C 1.296 7.824 0.888 6.384 0.888 4.968 Z M 6.2400002 9.648 C 7.872 9.648 8.976 7.704 8.976 4.416 C 8.976 1.536 7.848 0.768 6.984 0.768 C 5.0160003 0.768 4.248 3.72 4.248 5.496 C 4.248 7.704 4.632 9.648 6.2400002 9.648 Z "/>
</symbol>
<symbol id="g42F794F2554BA43C69EE8F3AA6FD9BAC" overflow="visible">
<path d="M 5.472 2.928 L 5.472 7.752 C 6.432 8.4 7.392 8.88 7.824 8.88 C 8.784 8.88 9.504 8.448 9.504 7.08 L 9.504 3.072 C 9.504 1.056 9.12 0.84000003 8.136 0.768 C 7.992 0.624 7.992 0.096 8.136 -0.048 C 9.144 -0.024 9.912 0 11.064 0 C 12.384 0 13.440001 -0.024 14.472 -0.048 C 14.616 0.096 14.616 0.624 14.472 0.768 C 13.008 0.84000003 12.624001 1.056 12.624001 3.072 L 12.624001 6.816 C 12.624001 9.456 11.496 10.656 9.432 10.656 C 8.472 10.656 6.768 9.6 5.448 8.688 C 5.376 9.528 5.28 10.248 5.28 10.248 C 5.256 10.536 5.064 10.656 4.728 10.656 C 3.8400002 10.416 2.4 10.08 0.744 9.864 C 0.696 9.72 0.744 9.24 0.792 9.096 C 2.112 8.976 2.352 8.784 2.352 7.416 L 2.352 2.928 C 2.352 0.936 2.088 0.888 0.624 0.768 C 0.48000002 0.624 0.48000002 0.096 0.624 -0.048 C 1.632 -0.024 2.64 0 3.912 0 C 5.0160003 0 5.688 -0.024 6.7200003 -0.048 C 6.864 0.096 6.864 0.624 6.7200003 0.768 C 5.712 0.864 5.472 0.936 5.472 2.928 Z "/>
</symbol>
<symbol id="gDD7DFDEC0D240E3DC5A3664E12D4BDDC" overflow="visible">
<path d="M 1.152 3.504 C 1.248 2.328 1.368 1.2 1.5600001 0.288 C 2.016 0.144 3.552 -0.24000001 4.896 -0.24000001 C 6.744 -0.24000001 9.048 0.768 9.048 2.856 C 9.048 3.672 8.856 4.32 8.304 4.92 C 7.632 5.688 6.624 6.288 5.52 6.768 C 4.56 7.176 4.224 7.9440002 4.224 8.64 C 4.224 9.192 4.68 9.648 5.376 9.648 C 6.216 9.648 7.032 8.88 7.632 7.416 C 8.064 7.344 8.328 7.368 8.568 7.5360003 C 8.568 8.4 8.472 9.312 8.2560005 10.08 C 7.488 10.416 6.888 10.656 5.568 10.656 C 4.296 10.656 3.096 10.176 2.328 9.408 C 1.776 8.856 1.512 8.184 1.512 7.5360003 C 1.512 6.816 1.8000001 6.2400002 2.256 5.736 C 3 4.92 4.32 4.08 5.04 3.744 C 6 3.312 6.264 2.448 6.264 1.872 C 6.264 1.104 5.496 0.696 4.848 0.696 C 3.7680001 0.696 2.616 1.8000001 2.112 3.552 C 1.728 3.624 1.536 3.6000001 1.152 3.504 Z "/>
</symbol>
<symbol id="g10AC66E6714D96E9762627FFB6E156C6" overflow="visible">
<path d="M 1.512 10.416 C 1.176 10.416 0.816 10.32 0.504 10.056 L 0.504 9.36 C 0.504 9.24 0.528 9.216 0.624 9.216 L 2.184 9.216 C 2.136 6.7920003 2.112 3.72 2.112 2.52 C 2.112 1.6800001 2.328 0.864 2.832 0.432 C 3.384 -0.024 4.248 -0.24000001 4.824 -0.24000001 C 6.144 -0.24000001 7.6080003 0.432 8.088 1.104 C 8.088 1.392 7.9440002 1.536 7.656 1.776 C 7.344 1.536 6.744 1.44 6.288 1.44 C 5.76 1.44 5.232 1.848 5.232 3.048 C 5.232 4.248 5.208 6.816 5.208 9.216 L 7.632 9.216 C 7.872 9.216 8.208 9.312 8.208 9.528 L 8.208 10.272 C 8.208 10.368 8.136 10.416 8.016 10.416 L 5.208 10.416 L 5.232 11.232 C 5.28 12.84 5.352 13.944 5.352 13.944 C 5.352 14.088 5.28 14.16 5.16 14.16 C 4.992 14.16 4.104 13.896 3.72 13.728 C 3.312 13.56 2.616 13.416 2.448 13.2 C 2.28 12.984 2.184 12.336 2.184 10.416 Z "/>
</symbol>
<symbol id="g767CEF02C917BBE3F159A8F04079F311" overflow="visible">
<path d="M 5.472 6.432 C 5.472 7.296 5.736 7.656 6.048 8.016 C 6.2400002 8.2560005 6.456 8.424 6.816 8.424 C 7.032 8.424 7.296 8.208 7.488 7.968 C 7.656 7.776 8.064 7.584 8.616 7.584 C 9.312 7.584 9.984 8.304 9.984 9.312 C 9.984 9.936 9.264 10.656 8.4 10.656 C 7.56 10.656 6.6480002 9.936 5.544 8.352 L 5.448 8.352 C 5.4 9.0720005 5.28 10.248 5.28 10.248 C 5.256 10.464 5.064 10.656 4.728 10.656 C 3.6000001 10.368 2.328 10.032001 0.744 9.864 C 0.696 9.72 0.744 9.264 0.792 9.12 C 2.112 9 2.352 8.784 2.352 7.416 L 2.352 2.928 C 2.352 0.936 2.088 0.888 0.624 0.768 C 0.48000002 0.624 0.48000002 0.096 0.624 -0.048 C 1.632 -0.024 2.64 0 3.912 0 C 5.184 0 6.168 -0.024 7.2000003 -0.048 C 7.344 0.096 7.344 0.624 7.2000003 0.768 C 5.736 0.864 5.472 0.936 5.472 2.928 Z "/>
</symbol>
<symbol id="gA13EE5B65CBC719304B28920E2ACC2B9" overflow="visible">
<path d="M 12.24 3.192 L 12.24 7.344 C 12.24 9.36 12.288 9.0720005 12.288 9.648 C 12.288 10.056 12.192 10.32 12.048 10.464 C 11.616 10.440001 11.136 10.416 10.68 10.416 C 10.008 10.416 8.448 10.440001 7.512 10.464 C 7.368 10.32 7.368 9.792 7.512 9.648 C 8.736 9.528 9.12 9.36 9.12 7.344 L 9.12 2.904 C 9.12 2.664 9.12 2.424 9.144 2.184 C 8.16 1.584 7.368 1.536 6.936 1.536 C 5.976 1.536 5.256 1.656 5.256 3.336 L 5.256 7.344 C 5.256 9.36 5.304 9.0720005 5.304 9.648 C 5.304 10.056 5.208 10.32 5.064 10.464 C 4.632 10.440001 4.1280003 10.416 3.696 10.416 C 2.4720001 10.416 1.5600001 10.440001 0.528 10.464 C 0.384 10.32 0.384 9.792 0.528 9.648 C 1.632 9.6 2.136 9.36 2.136 7.344 L 2.136 3.6000001 C 2.136 1.056 3.144 -0.24000001 5.208 -0.24000001 C 6.072 -0.24000001 7.824 0.456 9.216 1.224 C 9.264 0.624 9.312 0.168 9.312 0.168 C 9.336 -0.120000005 9.528 -0.24000001 9.864 -0.24000001 C 10.752 0 12.192 0.336 13.848001 0.552 C 13.896 0.696 13.848001 1.176 13.8 1.32 C 12.504 1.44 12.24 1.824 12.24 3.192 Z "/>
</symbol>
<symbol id="g9CBC2DB69173A0577335373434CDCDA4" overflow="visible">
<path d="M 10.128 2.088 C 10.128 2.376 10.08 2.832 9.816 2.832 C 8.856 1.944 8.04 1.488 7.344 1.488 C 5.544 1.488 4.1280003 2.784 4.1280003 5.664 C 4.1280003 8.328 4.728 9.648 6 9.648 C 6.888 9.648 7.248 8.712 7.32 7.9440002 C 7.392 7.296 8.04 6.816 8.808 6.816 C 9.576 6.816 10.128 7.416 10.128 8.16 C 10.128 9.24 8.832 10.656 6.216 10.656 C 3.384 10.656 0.888 8.376 0.888 4.824 C 0.888 3.264 1.44 1.896 2.376 1.008 C 3.312 0.120000005 4.416 -0.24000001 6.12 -0.24000001 C 7.56 -0.24000001 9.216 0.768 10.128 2.088 Z "/>
</symbol>
<symbol id="g24FA36D774E663C81AD78F0ED3820373" overflow="visible">
<path d="M 5.568 2.928 L 5.568 7.704 C 5.568 8.904 5.664 10.248 5.664 10.248 C 5.664 10.512 5.448 10.656 5.112 10.656 C 4.44 10.392 2.496 10.2 0.84000003 9.984 C 0.792 9.84 0.84000003 9.36 0.888 9.216 C 2.208 9.096 2.448 8.904 2.448 7.5360003 L 2.448 2.928 C 2.448 0.936 2.184 0.888 0.72 0.768 C 0.576 0.624 0.576 0.096 0.72 -0.048 C 1.728 -0.024 2.736 0 4.008 0 C 5.28 0 6.264 -0.024 7.296 -0.048 C 7.44 0.096 7.44 0.624 7.296 0.768 C 5.8320003 0.864 5.568 0.936 5.568 2.928 Z M 2.328 14.304 C 2.328 13.512 2.904 12.72 3.864 12.72 C 4.9440002 12.72 5.568 13.584001 5.568 14.208 C 5.568 14.928 5.0160003 15.792 4.008 15.792 C 2.88 15.792 2.328 15.024 2.328 14.304 Z "/>
</symbol>
<symbol id="g629AE7F75F47B1FD947FFA2989B5B47D" overflow="visible">
<path d="M 7.44 7.54 C 7.04 8.4 6.42 8.84 5.6 8.84 C 4.2999997 8.84 3.1599998 8.179999 2.18 6.8399997 C 1.26 5.6 0.79999995 4.3199997 0.79999995 2.98 C 0.79999995 1.24 1.8 -0.26 3.46 -0.26 C 4.18 -0.26 4.9 0.08 5.64 0.76 L 4.8199997 -2.52 C 4.7599998 -2.82 4.58 -3 4.2999997 -3.06 C 4.2 -3.08 3.9399998 -3.1 3.48 -3.1 C 3.36 -3.12 3.28 -3.12 3.24 -3.12 C 3.06 -3.1399999 2.96 -3.3 2.96 -3.58 L 2.96 -3.6599998 C 3.02 -3.8 3.1399999 -3.8799999 3.3 -3.8799999 C 3.6799998 -3.8799999 4.88 -3.82 5.2599998 -3.82 C 5.64 -3.82 6.8999996 -3.8799999 7.2799997 -3.8799999 C 7.56 -3.8799999 7.7 -3.72 7.7 -3.3999999 C 7.7 -3.1999998 7.5 -3.1 7.12 -3.1 C 6.7599998 -3.1 6.2599998 -3.12 6.2599998 -2.8799999 C 6.2599998 -2.8 6.2799997 -2.6599998 6.3399997 -2.46 L 9.04 8.54 C 9.04 8.72 8.94 8.82 8.76 8.82 C 8.4 8.82 7.64 7.8199997 7.44 7.54 Z M 6.7999997 7.46 C 6.98 7.04 7.08 6.7599998 7.08 6.58 C 7.08 6.56 7.06 6.44 7.02 6.2599998 L 6.54 4.3199997 C 6.16 2.8799999 5.98 2.1399999 5.96 2.1 C 5.58 1.4 4.48 0.32 3.52 0.32 C 2.74 0.32 2.34 0.91999996 2.34 2.1 C 2.34 3.02 2.96 5.2599998 3.24 6 C 3.62 6.94 4.5 8.24 5.6 8.24 C 6.14 8.24 6.54 7.98 6.7999997 7.46 Z "/>
</symbol>
<symbol id="g8C7315D77A5D71E18736DE61553C419F" overflow="visible">
<path d="M 1.4 1.1999999 C 1.4 0.62 1.88 0.14 2.46 0.14 C 3.04 0.14 3.52 0.62 3.52 1.1999999 C 3.52 1.78 3.04 2.26 2.46 2.26 C 1.88 2.26 1.4 1.78 1.4 1.1999999 Z M 1.4 7.16 C 1.4 6.58 1.88 6.1 2.46 6.1 C 3.04 6.1 3.52 6.58 3.52 7.16 C 3.52 7.74 3.04 8.22 2.46 8.22 C 1.88 8.22 1.4 7.74 1.4 7.16 Z "/>
</symbol>
<symbol id="gDACA5EBB44D5F3DB530A1F5F650BFBAB" overflow="visible">
<path d="M 2.08 10.46 L 2.08 2.44 C 2.08 0.78 1.74 0.68 0.34 0.62 C 0.22 0.5 0.22 0.08 0.34 -0.04 C 1.24 -0.02 2.22 0 2.9399998 0 C 3.6399999 0 4.8199997 -0.02 5.8199997 -0.04 C 5.94 0.08 5.94 0.5 5.8199997 0.62 C 4.2599998 0.7 3.78 0.78 3.78 2.44 L 3.78 5.8399997 C 4.22 5.7 4.7 5.64 5.4 5.64 C 9.04 5.64 10.139999 8.0199995 10.139999 9.719999 C 10.139999 10.9 9.36 13.04 5.66 13.04 C 4.9 13.04 3.72 12.9 2.9199998 12.9 C 2.18 12.9 1.14 12.92 0.34 12.94 C 0.22 12.82 0.22 12.4 0.34 12.28 C 1.74 12.219999 2.08 12.12 2.08 10.46 Z M 3.78 11.08 C 3.78 11.66 4.08 12.36 5.52 12.36 C 6.8999996 12.36 8.28 11.9 8.28 9.36 C 8.28 7.2 7.24 6.3199997 5.2999997 6.3199997 C 4.7999997 6.3199997 4 6.3599997 3.78 6.42 Z "/>
</symbol>
<symbol id="gFB78EB03C35D4F852337F4EC6AC104AC" overflow="visible">
<path d="M 0.82 4.1 C 0.82 2.06 2.18 -0.19999999 5.02 -0.19999999 C 6.2999997 -0.19999999 7.2799997 0.26 7.96 0.91999996 C 8.86 1.8 9.26 3.06 9.26 4.2799997 C 9.26 6.3599997 8.12 8.78 5.06 8.78 C 3.74 8.78 2.6599998 8.24 1.92 7.3799996 C 1.1999999 6.52 0.82 5.3599997 0.82 4.1 Z M 4.7599998 8.08 C 6.48 8.08 7.54 6.52 7.54 3.6399999 C 7.54 1.12 6.24 0.5 5.2999997 0.5 C 3.22 0.5 2.54 3.02 2.54 4.56 C 2.54 6.2999997 2.96 8.08 4.7599998 8.08 Z "/>
</symbol>
<symbol id="gE68C39294AA7FBA9B91EA2F8E9CC3997" overflow="visible">
<path d="M 3.62 2.44 L 3.62 6.42 C 3.62 7.4199996 3.6999998 8.7 3.6999998 8.7 C 3.6999998 8.78 3.6 8.84 3.4399998 8.84 C 2.8799999 8.62 2.08 8.44 0.7 8.26 C 0.65999997 8.139999 0.7 7.8199997 0.74 7.7 C 1.8399999 7.6 2.04 7.48 2.04 6.3399997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.71999997 0.59999996 0.62 C 0.48 0.5 0.48 0.08 0.59999996 -0.04 C 1.26 -0.02 2.04 0 2.84 0 C 3.6399999 0 4.4 -0.02 5.06 -0.04 C 5.18 0.08 5.18 0.5 5.06 0.62 C 3.84 0.7 3.62 0.78 3.62 2.44 Z M 1.8 11.98 C 1.8 11.46 2.28 10.94 2.76 10.94 C 3.32 10.94 3.8 11.48 3.8 11.9 C 3.8 12.38 3.3799999 12.94 2.84 12.94 C 2.36 12.94 1.8 12.46 1.8 11.98 Z "/>
</symbol>
<symbol id="g35631D62198EF939061DC90C9391724A" overflow="visible">
<path d="M 3.6799998 7.16 C 3.56 7.02 3.4399998 6.98 3.4399998 7.16 C 3.4199998 7.7 3.3799999 8.48 3.28 8.679999 C 3.24 8.78 3.1999998 8.84 3.04 8.84 C 2.48 8.62 1.9599999 8.44 0.58 8.26 C 0.53999996 8.139999 0.58 7.8199997 0.62 7.7 C 1.6999999 7.6 1.92 7.5 1.92 6.3399997 L 1.92 2.44 C 1.92 0.79999995 1.7199999 0.71999997 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.92 0 2.72 0 C 3.52 0 4.12 -0.02 4.72 -0.04 C 4.8399997 0.08 4.8399997 0.5 4.72 0.62 C 3.6999998 0.71999997 3.5 0.79999995 3.5 2.44 L 3.5 5.72 C 3.5 6.14 3.6799998 6.3799996 3.84 6.56 C 4.6 7.2999997 5.5 7.74 6.2799997 7.74 C 6.68 7.74 7.1 7.48 7.3399997 7.02 C 7.54 6.62 7.58 6.08 7.58 5.48 L 7.58 2.44 C 7.58 0.79999995 7.3799996 0.71999997 6.3399997 0.62 C 6.24 0.5 6.24 0.08 6.3399997 -0.04 C 6.94 -0.02 7.58 0 8.38 0 C 9.179999 0 9.9 -0.02 10.5 -0.04 C 10.599999 0.08 10.599999 0.5 10.5 0.62 C 9.38 0.71999997 9.16 0.79999995 9.16 2.44 L 9.16 5.42 C 9.16 6.52 9.08 7.48 8.62 8.099999 C 8.28 8.54 7.66 8.78 6.96 8.78 C 5.98 8.78 4.8599997 8.5199995 3.6799998 7.16 Z "/>
</symbol>
<symbol id="g22D858CFD6AD86697C1391C74FD687D1" overflow="visible">
<path d="M 0.85999995 8.58 C 0.58 8.58 0.5 8.34 0.5 8.179999 L 0.5 7.9199996 C 0.5 7.8199997 0.52 7.7999997 0.59999996 7.7999997 L 1.78 7.7999997 L 1.78 1.78 C 1.78 0.35999998 2.3999999 -0.19999999 3.32 -0.19999999 C 4.24 -0.19999999 5.24 0.24 6.02 1.12 C 5.98 1.3199999 5.8599997 1.4399999 5.66 1.4599999 C 5.14 1.06 4.54 0.9 4.02 0.9 C 3.48 0.9 3.36 1.5 3.36 2.74 L 3.36 7.7999997 L 5.44 7.7999997 C 5.64 7.7999997 5.92 7.8799996 5.92 8.059999 L 5.92 8.46 C 5.92 8.54 5.8599997 8.58 5.7599998 8.58 L 3.36 8.58 L 3.36 9.36 C 3.36 10.66 3.4399998 11.46 3.4399998 11.46 C 3.4399998 11.58 3.3799999 11.639999 3.28 11.639999 C 3.1999998 11.639999 3.02 11.559999 2.84 11.46 C 2.62 11.34 2.4199998 11.24 2.1599998 11.179999 C 1.92 11.099999 1.7199999 11.04 1.7199999 10.9 C 1.7199999 10.66 1.78 10.8 1.78 8.58 Z "/>
</symbol>
<symbol id="g67483374C2628B9150A7D3585AC4A61B" overflow="visible">
<path d="M 0.96 2.76 C 1.04 1.78 1.1 0.84 1.1 0 C 1.3 0.04 1.5 0.06 1.5999999 0.06 C 1.74 0.06 1.86 0.06 2 0.02 C 2.54 -0.12 3.08 -0.19999999 3.82 -0.19999999 C 4.94 -0.19999999 7 0.34 7 2.32 C 7 3.6799998 6.02 4.48 4.66 4.98 C 3.46 5.44 2.6599998 5.74 2.6599998 6.8399997 C 2.6599998 7.66 3.3799999 8.12 4.06 8.12 C 4.5 8.12 5.66 7.96 5.92 6.2599998 C 6.04 6.14 6.44 6.16 6.56 6.2799997 C 6.62 7 6.66 7.74 6.68 8.4 C 6.06 8.5 5.1 8.78 4.06 8.78 C 2.58 8.78 1.24 7.8199997 1.24 6.54 C 1.24 5.08 1.9 4.46 3.4399998 3.82 C 5.1 3.1399999 5.48 2.72 5.48 1.86 C 5.48 0.88 4.52 0.45999998 3.78 0.45999998 C 3 0.45999998 2.56 0.71999997 2.36 0.94 C 1.92 1.4 1.6999999 2.28 1.5799999 2.78 C 1.4599999 2.8999999 1.0799999 2.8799999 0.96 2.76 Z "/>
</symbol>
<symbol id="g7FBC39AA6D9FB89D8B638A3651405A80" overflow="visible">
<path d="M 7.72 1.86 C 6.98 1.1 6.3999996 0.78 5.24 0.78 C 4.52 0.78 3.6799998 1.1999999 3.06 2.22 C 2.6599998 2.8799999 2.4199998 3.8 2.4199998 4.96 L 7.74 4.92 C 7.98 4.92 8.12 5.04 8.12 5.2599998 C 8.12 6.94 7.52 8.74 4.74 8.74 C 3 8.74 0.74 7.08 0.74 4.04 C 0.74 2.9199998 1.02 1.8399999 1.68 1.0799999 C 2.36 0.28 3.3 -0.19999999 4.74 -0.19999999 C 6.2599998 -0.19999999 7.3399997 0.5 8.139999 1.54 C 8.08 1.74 7.96 1.8399999 7.72 1.86 Z M 2.48 5.64 C 2.86 7.8999996 4.2599998 8.08 4.74 8.08 C 5.5 8.08 6.3999996 7.66 6.3999996 5.98 C 6.3999996 5.7999997 6.3199997 5.7 6.1 5.7 Z "/>
</symbol>
<symbol id="gB9C04FB79CAD4691AB5EC7F01BE2AD7F" overflow="visible">
<path d="M 3.52 7.16 C 3.48 7.96 3.46 8.48 3.36 8.679999 C 3.32 8.78 3.28 8.84 3.12 8.84 C 2.56 8.62 2.04 8.44 0.65999997 8.26 C 0.62 8.139999 0.65999997 7.8199997 0.7 7.7 C 1.78 7.6 2 7.5 2 6.3399997 L 2 2.44 C 2 0.78 1.76 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 2 0 2.8 0 C 3.6 0 4.52 -0.02 5.22 -0.04 C 5.3399997 0.08 5.3399997 0.5 5.22 0.62 C 3.82 0.71999997 3.58 0.78 3.58 2.44 L 3.58 5.22 C 3.58 5.74 3.82 6.2 4.06 6.56 C 4.2799997 6.8799996 4.74 7.54 4.98 7.54 C 5.16 7.54 5.3399997 7.5 5.5 7.2799997 C 5.64 7.08 5.8799996 6.8199997 6.22 6.8199997 C 6.7 6.8199997 7.16 7.3199997 7.16 7.8199997 C 7.16 8.2 6.7999997 8.78 5.96 8.78 C 5.02 8.78 4.2 7.8999996 3.74 7.12 C 3.62 6.8999996 3.52 7.06 3.52 7.16 Z "/>
</symbol>
<symbol id="g278A59F111DD0614EC58EAA01A502EFD" overflow="visible">
<path d="M 19.1 13.7 L 16.279999 13.7 C 15.799999 13.7 15.559999 13.559999 15.559999 13.259999 C 15.559999 13.0199995 15.679999 12.88 15.92 12.86 C 16.64 12.78 16.8 12.54 16.8 11.5 C 16.8 10.5199995 16.5 9.099999 15.9 7.24 L 15 4.58 C 14.719999 5.2599998 14.259999 6.52 13.599999 8.36 C 12.9 10.36 12.54 11.719999 12.5 12.42 C 12.719999 12.679999 13 12.82 13.38 12.84 C 13.7 12.86 13.86 13 13.86 13.259999 C 13.86 13.639999 13.62 13.7 13.139999 13.7 L 8.36 13.7 C 7.8599997 13.7 7.6 13.559999 7.6 13.259999 C 7.6 13.04 7.74 12.88 8 12.84 C 8.26 12.799999 8.48 12.679999 8.639999 12.48 C 9.059999 11.98 9.46 10.8 9.8 9.8 L 7.3199997 4.1 L 5.96 7.96 C 5.14 10.3 4.74 11.78 4.74 12.42 C 4.74 12.639999 4.96 12.78 5.4 12.84 C 5.7 12.86 5.8599997 13 5.8599997 13.259999 C 5.8599997 13.62 5.56 13.7 5.1 13.7 L 0.9 13.7 C 0.39999998 13.7 0.16 13.559999 0.16 13.259999 C 0.16 13.04 0.29999998 12.88 0.59999996 12.84 C 0.9 12.799999 1.14 12.5199995 1.3199999 12.0199995 L 5.56 0.12 C 5.68 -0.22 5.8399997 -0.38 6.04 -0.38 C 6.22 -0.38 6.3599997 -0.24 6.5 0.06 L 10.26 8.62 L 13.48 0.14 C 13.62 -0.19999999 13.78 -0.38 13.96 -0.38 C 14.16 -0.38 14.32 -0.22 14.44 0.12 L 18.68 11.98 C 18.88 12.5199995 19.14 12.799999 19.439999 12.86 C 19.699999 12.9 19.84 13.04 19.84 13.259999 C 19.84 13.639999 19.58 13.7 19.1 13.7 Z M 17.42 12.84 L 18.14 12.84 C 18.039999 12.639999 17.88 12.24 17.64 11.639999 C 17.619999 12.16 17.539999 12.559999 17.42 12.84 Z M 12.38 9.4 C 13.12 7.14 13.86 5.08 14.639999 3.1799998 C 14.299999 2.28 14.08 1.66 13.96 1.28 L 9.9 11.98 C 9.78 12.3 9.639999 12.58 9.46 12.84 L 11.759999 12.84 C 11.679999 12.719999 11.639999 12.559999 11.639999 12.34 C 11.639999 11.88 11.88 10.9 12.38 9.4 Z M 3.8799999 12.44 C 3.8799999 11.44 4.8599997 8.26 6.8199997 2.9199998 L 6.08 1.22 L 2.2 12.04 C 2.06 12.4 1.9599999 12.66 1.86 12.84 L 3.9599998 12.84 C 3.8999999 12.719999 3.8799999 12.58 3.8799999 12.44 Z "/>
</symbol>
<symbol id="g560AC22EF992EFD90E66808483D7B3BA" overflow="visible">
<path d="M 11.12 10.24 L 11.12 3.6999998 C 11.12 3.32 11.12 3.1 10.98 3.1 C 10.9 3.1 10.599999 3.46 10.0199995 4.2 L 3.1599998 12.9 L 0.45999998 12.94 C 0.34 12.82 0.34 12.4 0.45999998 12.28 C 1.3199999 12.219999 1.92 11.5199995 2.04 11 L 2.04 2.6599998 C 2.04 0.88 1.6999999 0.76 0.29999998 0.62 C 0.17999999 0.5 0.17999999 0.08 0.29999998 -0.04 C 1.16 -0.02 2.06 0 2.54 0 C 3 0 3.9199998 -0.02 4.7599998 -0.04 C 4.88 0.08 4.88 0.5 4.7599998 0.62 C 3.36 0.76 3.02 0.84 3.02 2.6599998 L 3.02 8.78 C 3.02 9.46 3.02 9.76 3.1799998 9.76 C 3.3 9.76 3.52 9.54 3.86 9.099999 L 10.84 0.28 C 11.059999 -0.02 11.32 -0.19999999 11.639999 -0.19999999 C 11.92 -0.19999999 12.099999 0.04 12.099999 0.42 L 12.099999 10.24 C 12.099999 12.0199995 12.44 12.139999 13.84 12.28 C 13.96 12.4 13.96 12.82 13.84 12.94 C 13.0199995 12.92 12.08 12.9 11.599999 12.9 C 11.179999 12.9 10.26 12.92 9.38 12.94 C 9.26 12.82 9.26 12.4 9.38 12.28 C 10.78 12.139999 11.12 12.059999 11.12 10.24 Z "/>
</symbol>
<symbol id="gAA212A9DBB5FA7333A767E41B2F6A3B3" overflow="visible">
<path d="M 5.8599997 0.96 C 5.98 0.34 6.2 -0.19999999 7.2 -0.19999999 C 7.96 -0.19999999 8.679999 0.14 9.099999 0.53999996 C 9.059999 0.78 8.98 0.96 8.76 1.0799999 C 8.62 0.96 8.28 0.76 8.0199995 0.76 C 7.44 0.76 7.4199996 1.54 7.4199996 2.46 L 7.4199996 5.4 C 7.4199996 8.24 5.8599997 8.78 4.4 8.78 C 2.76 8.78 1.1 7.7 1.1 6.56 C 1.1 6.08 1.3399999 5.8399997 1.8 5.8399997 C 2.3799999 5.8399997 2.74 6.2599998 2.74 6.52 C 2.74 6.66 2.72 6.7999997 2.6799998 6.8799996 C 2.6599998 6.94 2.6399999 7.06 2.6399999 7.2799997 C 2.6399999 7.8999996 3.48 8.12 4.24 8.12 C 4.92 8.12 5.8599997 7.7799997 5.8599997 5.52 C 5.8599997 5.38 5.7999997 5.2999997 5.74 5.2799997 L 4.02 4.8599997 C 2.1 4.38 0.71999997 3.32 0.71999997 1.9599999 C 0.71999997 0.32 1.8399999 -0.19999999 3.24 -0.19999999 C 3.9399998 -0.19999999 4.54 -0.04 5.42 0.64 L 5.8199997 0.96 Z M 5.8599997 4.66 L 5.8599997 2.02 C 5.8599997 1.76 5.74 1.62 5.58 1.5 C 5.06 1.0799999 4.38 0.62 3.82 0.62 C 2.82 0.62 2.3799999 1.42 2.3799999 2.04 C 2.3799999 2.9399998 2.8 3.86 4.2799997 4.24 Z "/>
</symbol>
<symbol id="gFB54B84572F46C3C9CB2B1A90182D6B2" overflow="visible">
<path d="M 8.88 7.74 C 9.26 7.74 9.62 8.099999 9.62 8.5 C 9.62 8.92 9.24 9.24 8.7 9.24 C 8.179999 9.24 7.22 8.9 6.7 8.22 C 6.46 8.38 5.7999997 8.78 4.62 8.78 C 2.84 8.78 1.1999999 7.58 1.1999999 5.74 C 1.1999999 4.66 1.68 4.04 2.24 3.5 C 1.68 3.02 1.36 2.1599998 1.36 1.48 C 1.36 0.76 1.76 0.19999999 2.28 -0.06 C 1.1999999 -0.7 0.64 -1.62 0.64 -2.48 C 0.64 -4.22 2.28 -4.7599998 3.82 -4.7599998 C 6.52 -4.7599998 9.44 -3.46 9.44 -1.3 C 9.44 -0.65999997 9.139999 -0.16 8.559999 0.32 C 7.7799997 0.96 6.3799996 0.97999996 5.64 0.97999996 C 5.2799997 0.97999996 4.7799997 0.94 4.2999997 0.88 C 4 0.85999995 3.8 0.84 3.6999998 0.84 C 3.12 0.84 2.4199998 1.12 2.4199998 1.9799999 C 2.4199998 2.3799999 2.54 2.8 2.78 3.1399999 C 3.26 2.86 3.82 2.72 4.6 2.72 C 6.3599997 2.72 7.98 3.82 7.98 5.7799997 C 7.98 6.72 7.7 7.2599998 7.12 7.8599997 C 7.2599998 8.059999 7.66 8.34 7.9199996 8.34 C 8.059999 8.34 8.2 8.28 8.32 8.099999 C 8.4 7.94 8.66 7.74 8.88 7.74 Z M 2.6399999 -0.19999999 C 2.86 -0.26 3.1799998 -0.29999998 3.4399998 -0.29999998 C 4.06 -0.29999998 4.62 -0.24 4.9 -0.24 C 5.9 -0.24 6.74 -0.26 7.3199997 -0.58 C 8.099999 -1.02 8.34 -1.3 8.34 -1.8199999 C 8.34 -3.26 6.22 -4.02 4.42 -4.02 C 3.6999998 -4.02 2.02 -3.4399998 2.02 -2.08 C 2.02 -1.4 2.06 -0.9 2.6399999 -0.19999999 Z M 6.3799996 5.58 C 6.3799996 3.72 5.44 3.34 4.7 3.34 C 3.02 3.34 2.84 4.7599998 2.84 6.04 C 2.84 7.44 3.34 8.16 4.44 8.16 C 5.7 8.16 6.3799996 7.24 6.3799996 5.58 Z "/>
</symbol>
<symbol id="g3C2FFF86BC828E66F78F8A687CE12C70" overflow="visible">
<path d="M 3.34 5.72 C 3.34 6.14 3.52 6.3799996 3.6799998 6.56 C 4.44 7.2999997 5.46 7.74 6.24 7.74 C 6.64 7.74 7.06 7.48 7.2999997 7.02 C 7.5 6.62 7.54 6.08 7.54 5.48 L 7.54 2.44 C 7.54 0.79999995 7.3399997 0.71999997 6.2999997 0.62 C 6.2 0.5 6.2 0.08 6.2999997 -0.04 C 6.8599997 -0.02 7.54 0 8.34 0 C 9.139999 0 9.8 -0.02 10.46 -0.04 C 10.559999 0.08 10.559999 0.5 10.46 0.62 C 9.34 0.71999997 9.12 0.79999995 9.12 2.44 L 9.12 5.42 C 9.12 6.52 9.04 7.5 8.58 8.099999 C 8.24 8.54 7.62 8.78 6.92 8.78 C 5.94 8.78 4.74 8.5199995 3.52 7.16 C 3.52 7.14 3.5 7.14 3.48 7.12 C 3.4199998 7.04 3.32 6.92 3.32 7.16 L 3.34 11.66 C 3.34 12.96 3.4199998 13.759999 3.4199998 13.759999 C 3.4199998 13.9 3.34 13.96 3.1599998 13.96 C 2.6599998 13.759999 1.16 13.48 0.35999998 13.42 C 0.32 13.259999 0.35999998 12.94 0.48 12.82 C 0.53999996 12.82 0.59999996 12.82 0.65999997 12.82 C 1.54 12.759999 1.76 12.759999 1.76 11.179999 L 1.76 2.44 C 1.76 0.78 1.52 0.7 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.02 -0.02 1.76 0 2.56 0 C 3.32 0 3.98 -0.02 4.54 -0.04 C 4.66 0.08 4.66 0.5 4.54 0.62 C 3.52 0.7 3.34 0.78 3.34 2.44 Z "/>
</symbol>
<symbol id="g733371913480EE84B3609C9E9CD62F8C" overflow="visible">
<path d="M 3.34 7.8799996 C 3.22 7.7599998 3.1399999 7.7999997 3.1399999 7.98 L 3.1399999 11.66 C 3.1399999 12.96 3.22 13.759999 3.22 13.759999 C 3.22 13.9 3.1399999 13.96 2.96 13.96 C 2.46 13.759999 0.96 13.48 0.16 13.42 C 0.12 13.259999 0.16 12.94 0.28 12.82 C 0.34 12.82 0.39999998 12.82 0.45999998 12.82 C 1.3399999 12.759999 1.56 12.759999 1.56 11.179999 L 1.56 1.42 C 1.56 0.64 1.54 0.28 1.48 0 C 1.5799999 -0.16 1.68 -0.24 1.92 -0.24 C 2.04 -0.12 2.24 0.06 2.3999999 0.24 C 2.6 0.48 2.72 0.48 2.9399998 0.29999998 C 3.3999999 -0.08 4 -0.19999999 4.7 -0.19999999 C 6.74 -0.19999999 9.12 1.66 9.12 4.8399997 C 9.12 7.2799997 7.3199997 8.78 5.58 8.78 C 4.72 8.78 3.9599998 8.44 3.34 7.8799996 Z M 3.48 7.2599998 C 4 7.72 4.6 7.8999996 5.18 7.8999996 C 6.3999996 7.8999996 7.3999996 6.42 7.3999996 4.48 C 7.3999996 2.2 6.48 0.48 4.58 0.48 C 3.9599998 0.48 3.54 0.91999996 3.1399999 1.42 L 3.1399999 6.42 C 3.1399999 6.8399997 3.22 7.04 3.48 7.2599998 Z "/>
</symbol>
<symbol id="g3BBBD96D467CC564123619D79E97B4D6" overflow="visible">
<path d="M 7.8999996 12.62 C 6.74 12.78 6.7799997 13.16 4.8199997 13.16 C 2.8 13.16 1.02 11.82 1.02 9.7 C 1.02 7.6 2.76 6.64 4.52 5.96 C 5.72 5.5 7.2 4.94 7.2 2.98 C 7.2 1.36 6.2999997 0.52 4.7 0.52 C 2.84 0.52 1.64 1.38 1.1999999 3.36 C 0.94 3.4399998 0.74 3.3999999 0.53999996 3.3 C 0.62 1.76 0.7 1.24 0.94 0.26 C 2.2 0.26 2.76 -0.19999999 4.54 -0.19999999 C 5.44 -0.19999999 6.2999997 0.02 7 0.45999998 C 8.16 1.18 8.88 2.3999999 8.88 3.6799998 C 8.88 5.7999997 7.2799997 6.74 5.64 7.3599997 C 4.44 7.7999997 2.44 8.559999 2.44 10.24 C 2.44 11.36 3.46 12.48 4.64 12.48 C 6.58 12.48 7.2 11.24 7.6 9.92 C 7.8199997 9.88 8.08 9.9 8.26 10.04 C 8.179999 11 8.099999 11.559999 7.8999996 12.62 Z "/>
</symbol>
<symbol id="gCDF8B867C9AAFA36255BC29C36465E90" overflow="visible">
<path d="M 3.5 2.44 L 3.5 7.7999997 L 5.3599997 7.7999997 C 5.54 7.7999997 5.8199997 7.8799996 5.8199997 8.059999 L 5.8199997 8.46 C 5.8199997 8.54 5.7599998 8.58 5.66 8.58 L 3.5 8.58 L 3.5 9.719999 C 3.5 12.799999 4.42 13.28 5.08 13.28 C 5.68 13.28 6 13.04 6.2799997 12.34 C 6.44 11.98 6.66 11.7 7.08 11.7 C 7.4199996 11.7 7.8999996 12.12 7.8999996 12.5199995 C 7.8999996 12.86 7.68 13.219999 7.2599998 13.54 C 6.74 13.9 6.22 13.96 5.46 13.96 C 3.78 13.96 1.92 12.5 1.92 9.38 L 1.92 8.58 L 0.9 8.58 C 0.53999996 8.58 0.44 8.34 0.44 8.179999 L 0.44 7.9199996 C 0.44 7.8199997 0.45999998 7.7999997 0.53999996 7.7999997 L 1.92 7.7999997 L 1.92 2.44 C 1.92 0.78 1.5999999 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 1.92 0 2.72 0 C 3.52 0 4.48 -0.02 5.18 -0.04 C 5.2999997 0.08 5.2999997 0.5 5.18 0.62 C 3.62 0.7 3.5 0.78 3.5 2.44 Z "/>
</symbol>
<symbol id="gD3761FB0B01B207797C607CDFB6E3A0B" overflow="visible">
<path d="M 3.3999999 7.16 C 3.3799999 7.7599998 3.34 8.48 3.24 8.679999 C 3.1999998 8.78 3.1599998 8.84 3 8.84 C 2.44 8.62 1.92 8.44 0.53999996 8.26 C 0.5 8.139999 0.53999996 7.8199997 0.58 7.7 C 1.66 7.6 1.88 7.5 1.88 6.3399997 L 1.88 2.44 C 1.88 0.79999995 1.62 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.88 0 2.6799998 0 C 3.48 0 4.1 -0.02 4.7 -0.04 C 4.8199997 0.08 4.8199997 0.5 4.7 0.62 C 3.6799998 0.71999997 3.46 0.79999995 3.46 2.44 L 3.46 5.72 C 3.46 6.14 3.6399999 6.3799996 3.8 6.56 C 4.6 7.3399997 5.3399997 7.74 5.96 7.74 C 6.72 7.74 7.2799997 7.2599998 7.2799997 5.92 L 7.2799997 2.44 C 7.2799997 0.79999995 7.12 0.7 6.04 0.62 C 5.94 0.5 5.94 0.08 6.04 -0.04 C 6.54 -0.02 7.2799997 0 8.08 0 C 8.88 0 9.54 -0.02 10.04 -0.04 C 10.139999 0.08 10.139999 0.5 10.04 0.62 C 9.04 0.7 8.86 0.79999995 8.86 2.44 L 8.86 5.62 C 8.86 5.9 8.86 6.18 8.84 6.42 C 9.8 7.48 10.7 7.74 11.48 7.74 C 12.24 7.74 12.679999 7.2999997 12.679999 5.96 L 12.679999 2.44 C 12.679999 0.79999995 12.48 0.7 11.44 0.62 C 11.34 0.5 11.34 0.08 11.44 -0.04 C 11.94 -0.02 12.679999 0 13.48 0 C 14.28 0 14.98 -0.02 15.54 -0.04 C 15.639999 0.08 15.639999 0.5 15.54 0.62 C 14.44 0.7 14.259999 0.79999995 14.259999 2.44 L 14.259999 5.6 C 14.259999 7.3799996 13.96 8.78 12.2 8.78 C 11.179999 8.78 9.94 8.4 8.9 7.2999997 C 8.84 7.24 8.72 7.14 8.679999 7.3199997 C 8.5 8.139999 7.72 8.78 6.68 8.78 C 5.52 8.78 4.48 8.099999 3.6399999 7.16 C 3.54 7.06 3.4199998 6.92 3.3999999 7.16 Z "/>
</symbol>
<symbol id="gAC7FD886AB12F72ED3B61B0327264BE7" overflow="visible">
<path d="M 3.12 7.3599997 C 3.1 7.96 3.06 8.48 2.96 8.679999 C 2.9199998 8.78 2.8799999 8.84 2.72 8.84 C 2.1599998 8.62 1.64 8.44 0.26 8.26 C 0.22 8.139999 0.26 7.8199997 0.29999998 7.7 C 1.38 7.6 1.5999999 7.5 1.5999999 6.3399997 L 1.5999999 -2.2 C 1.5999999 -3.86 1.38 -3.9599998 0.16 -4.02 C 0.04 -4.14 0.04 -4.56 0.16 -4.68 C 0.85999995 -4.66 1.5999999 -4.64 2.3999999 -4.64 C 3.1999998 -4.64 4.16 -4.66 4.8199997 -4.68 C 4.94 -4.56 4.94 -4.14 4.8199997 -4.02 C 3.3999999 -3.9399998 3.1799998 -3.86 3.1799998 -2.2 L 3.1799998 -0.04 C 3.1799998 0.22 3.26 0.19999999 3.46 0.12 C 3.9599998 -0.08 4.56 -0.19999999 5.2 -0.19999999 C 6.3199997 -0.19999999 7.3199997 0.14 8.139999 0.91999996 C 9.08 1.8399999 9.62 3.08 9.62 4.7 C 9.62 6.8199997 8.12 8.78 6.08 8.78 C 5.16 8.78 4.14 8.179999 3.34 7.2799997 C 3.22 7.16 3.1399999 7.16 3.12 7.3599997 Z M 3.5 6.62 C 4.02 7.2599998 4.94 7.8599997 5.52 7.8599997 C 6.7999997 7.8599997 7.8999996 6.42 7.8999996 4.16 C 7.8999996 2.52 7.3199997 0.48 5.08 0.48 C 4.72 0.48 4.02 0.58 3.6599998 0.9 C 3.26 1.26 3.1799998 1.38 3.1799998 2.1 L 3.1799998 5.74 C 3.1799998 6.16 3.26 6.3399997 3.5 6.62 Z "/>
</symbol>
<symbol id="g1788914935A6D7BFA016214155630E72" overflow="visible">
<path d="M 1.9 2.44 C 1.9 0.78 1.68 0.68 0.45999998 0.62 C 0.34 0.5 0.34 0.08 0.45999998 -0.04 C 1.16 -0.02 1.9 0 2.7 0 C 3.5 0 4.2599998 -0.02 4.92 -0.04 C 5.04 0.08 5.04 0.5 4.92 0.62 C 3.6999998 0.68 3.48 0.78 3.48 2.44 L 3.48 11.66 C 3.48 12.96 3.56 13.759999 3.56 13.759999 C 3.56 13.9 3.48 13.96 3.3 13.96 C 2.8 13.759999 1.3 13.48 0.5 13.42 C 0.45999998 13.259999 0.5 12.94 0.62 12.82 C 1.78 12.74 1.9 12.679999 1.9 11.179999 Z "/>
</symbol>
<symbol id="g21D1E528F66DB45787699F71DA377CC5" overflow="visible">
<path d="M 4.08 -3.1999998 C 4.4 -2.6399999 4.66 -2.08 4.9 -1.48 C 6.5 2.3799999 7.3999996 4.44 8.44 6.68 C 8.84 7.52 9.12 7.8399997 10.059999 7.96 C 10.179999 8.08 10.179999 8.5 10.059999 8.62 C 9.66 8.599999 9.2 8.58 8.639999 8.58 C 8.04 8.58 7.4199996 8.599999 6.8199997 8.62 C 6.7 8.5 6.7 8.08 6.8199997 7.96 C 7.46 7.8999996 8.099999 7.7799997 7.7799997 7.06 L 5.7999997 2.48 C 5.66 2.1599998 5.48 2.1 5.3199997 2.5 L 3.54 6.66 C 3.1799998 7.5 3.08 7.8799996 4.2 7.96 C 4.3199997 8.08 4.3199997 8.5 4.2 8.62 C 3.46 8.599999 2.6599998 8.58 1.9399999 8.58 C 1.26 8.58 0.71999997 8.599999 0.32 8.62 C 0.19999999 8.5 0.19999999 8.08 0.32 7.96 C 1.12 7.8599997 1.38 7.68 1.9 6.46 L 4.16 1.1999999 C 4.3399997 0.79999995 4.64 -0.12 4.44 -0.68 C 4.2 -1.3399999 3.9599998 -1.9 3.6599998 -2.52 C 3.4399998 -2.9199998 3.1599998 -3.1 2.6599998 -3.1 C 2.3799999 -3.1 2.3 -3.04 2.08 -3.04 C 1.5 -3.04 1.1999999 -3.6399999 1.1999999 -3.8999999 C 1.1999999 -4.3199997 1.5999999 -4.64 2.1399999 -4.64 C 2.56 -4.64 3.36 -4.48 4.08 -3.1999998 Z "/>
</symbol>
<symbol id="gF418DD62CA77762FBF8DB07ECAE6BC0" overflow="visible">
<path d="M 6.92 13.08 C 6.12 13.08 1.42 12.94 0.62 12.94 C 0.42 12.82 0.42 12.38 0.62 12.259999 C 1.7199999 12.2 2.28 12.12 2.28 10.46 L 2.28 2.44 C 2.28 0.78 1.7199999 0.7 0.62 0.64 C 0.42 0.52 0.42 0.08 0.62 -0.04 C 1.42 -0.02 2.8999999 0 3.6999998 0 C 4.5 0 5.94 -0.02 6.74 -0.04 C 6.94 0.08 6.94 0.52 6.74 0.64 C 5.64 0.7 5.08 0.78 5.08 2.44 L 5.08 10.48 C 5.08 11.84 5.22 12.259999 6.2799997 12.259999 C 7.44 12.259999 8.78 11.78 8.78 9.34 C 8.78 7.2599998 8.2 6.3799996 6.56 6.3799996 C 6.2599998 6.3799996 5.8399997 6.3999996 5.56 6.44 C 5.56 6.06 5.68 5.7799997 5.96 5.6 C 6.24 5.56 6.18 5.54 6.66 5.54 C 8.42 5.54 9.66 5.8399997 10.46 6.5 C 11.46 7.3199997 11.8 8.62 11.8 9.679999 C 11.8 10.48 11.5 11.679999 10.26 12.42 C 9.5199995 12.86 8.42 13.08 6.92 13.08 Z "/>
</symbol>
<symbol id="g37DC97609493A252C8A67743647C955" overflow="visible">
<path d="M 10.559999 2.56 L 10.559999 5.68 C 10.559999 7.8799996 9.62 8.88 7.8999996 8.88 C 7.16 8.88 5.74 8.139999 4.6 7.44 L 4.6 11.66 C 4.6 12.96 4.66 13.7 4.66 13.7 C 4.66 13.88 4.52 13.96 4.3399997 13.96 C 3.6 13.719999 2 13.5 0.58 13.44 C 0.52 13.2 0.53999996 12.98 0.64 12.799999 C 1.9 12.7 2 12.679999 2 11.3 L 2 2.54 C 2 0.88 1.68 0.7 0.45999998 0.64 C 0.34 0.52 0.34 0.08 0.45999998 -0.04 C 1.3 -0.02 2.2 0 3.3 0 C 4.2599998 0 4.88 -0.02 5.74 -0.04 C 5.8599997 0.08 5.8599997 0.52 5.74 0.64 C 4.9 0.7 4.6 0.88 4.6 2.54 L 4.6 6.64 C 5.44 7.16 6.1 7.3999996 6.46 7.3999996 C 7.2599998 7.3999996 7.96 7.04 7.96 5.9 L 7.96 2.56 C 7.96 0.88 7.64 0.7 6.8199997 0.64 C 6.7 0.52 6.7 0.08 6.8199997 -0.04 C 7.66 -0.02 8.3 0 9.26 0 C 10.36 0 11.24 -0.02 12.099999 -0.04 C 12.219999 0.08 12.219999 0.52 12.099999 0.64 C 10.88 0.7 10.559999 0.88 10.559999 2.56 Z "/>
</symbol>
<symbol id="g50FEF586148C287DB923CFE895D558DC" overflow="visible">
<path d="M 5.9 0.97999996 C 6.04 0.16 6.58 -0.19999999 7.46 -0.19999999 C 8.559999 -0.19999999 9.34 0.22 10.08 0.91999996 C 10.04 1.16 9.96 1.3199999 9.719999 1.48 C 9.46 1.28 9.26 1.1999999 8.88 1.1999999 C 8.44 1.1999999 8.32 1.56 8.32 2.54 L 8.36 5.42 C 8.36 8.3 6.58 8.88 4.94 8.88 C 3.48 8.88 1.24 8.04 1.24 6.72 C 1.24 6.16 1.48 5.72 2.26 5.72 C 2.98 5.72 3.5 6.16 3.5 6.64 C 3.5 6.74 3.48 6.8599997 3.46 6.98 C 3.4199998 7.18 3.3799999 7.3799996 3.4199998 7.58 C 3.4399998 7.7999997 3.6 8.04 4.2599998 8.04 C 5.1 8.04 5.7999997 7.68 5.7999997 5.14 L 4.46 4.72 C 2.36 4.06 0.88 3.48 0.88 1.9 C 0.88 0.52 1.64 -0.19999999 3.3799999 -0.19999999 C 3.9599998 -0.19999999 5.12 0.44 5.7799997 0.96 Z M 5.7999997 4.36 L 5.7999997 1.7199999 C 5.2999997 1.3199999 4.7999997 1 4.44 1 C 3.58 1 3.28 1.5799999 3.28 2.2 C 3.28 2.9399998 3.34 3.56 4.7599998 4.02 Z "/>
</symbol>
<symbol id="gCD50B0C5537328D0484BBB5C5B7C30A" overflow="visible">
<path d="M 0.96 2.9199998 C 1.04 1.9399999 1.14 1 1.3 0.24 C 1.68 0.12 2.96 -0.19999999 4.08 -0.19999999 C 5.62 -0.19999999 7.54 0.64 7.54 2.3799999 C 7.54 3.06 7.3799996 3.6 6.92 4.1 C 6.3599997 4.74 5.52 5.24 4.6 5.64 C 3.8 5.98 3.52 6.62 3.52 7.2 C 3.52 7.66 3.8999999 8.04 4.48 8.04 C 5.18 8.04 5.8599997 7.3999996 6.3599997 6.18 C 6.72 6.12 6.94 6.14 7.14 6.2799997 C 7.14 7 7.06 7.7599998 6.8799996 8.4 C 6.24 8.679999 5.74 8.88 4.64 8.88 C 3.58 8.88 2.58 8.48 1.9399999 7.8399997 C 1.48 7.3799996 1.26 6.8199997 1.26 6.2799997 C 1.26 5.68 1.5 5.2 1.88 4.7799997 C 2.5 4.1 3.6 3.3999999 4.2 3.12 C 5 2.76 5.22 2.04 5.22 1.56 C 5.22 0.91999996 4.58 0.58 4.04 0.58 C 3.1399999 0.58 2.18 1.5 1.76 2.96 C 1.4399999 3.02 1.28 3 0.96 2.9199998 Z "/>
</symbol>
<symbol id="gD9D3B6C4D6AB50B3CADCA65007C1BC50" overflow="visible">
<path d="M 8.62 2.58 C 7.7999997 1.74 6.72 1.52 5.96 1.52 C 4.4 1.52 3.4399998 2.4199998 3.4399998 4.38 C 3.4399998 4.52 3.46 4.6 3.46 4.7 L 8.26 4.7 C 8.74 4.7 8.84 5.04 8.84 5.3199997 C 8.84 7.02 8.179999 8.88 5.24 8.88 C 3.1399999 8.88 0.74 7.02 0.74 3.9599998 C 0.74 2.8 1.16 1.5799999 2.02 0.79999995 C 2.78 0.12 3.76 -0.19999999 5.18 -0.19999999 C 6.56 -0.19999999 7.9199996 0.5 8.92 1.9599999 C 8.92 2.22 8.82 2.58 8.62 2.58 Z M 3.54 5.5 C 3.56 6.2 3.6599998 6.96 3.9399998 7.3599997 C 4.2599998 7.8399997 4.7999997 8.04 5.02 8.04 C 5.56 8.04 6.2999997 7.52 6.2999997 5.92 C 6.2999997 5.7999997 6.2999997 5.54 6.2599998 5.5 Z "/>
</symbol>
<symbol id="g50EBB3D006215D0409E43740CDD42DD9" overflow="visible">
<path d="M 7.3399997 2.44 L 7.3399997 9.66 C 7.3399997 10.719999 7.5 11.86 7.5 11.86 C 7.5 12.12 7.3399997 12.2 7.16 12.2 C 6.96 12.2 6.62 12.12 6.16 11.9 C 4.94 11.34 3.58 10.86 1.8399999 10.139999 C 1.86 9.8 2 9.48 2.28 9.28 C 3.36 9.74 4.08 9.78 4.36 9.78 C 4.62 9.78 4.74 9.7 4.74 8.7 L 4.74 2.44 C 4.74 0.78 3.78 0.7 2.6799998 0.64 C 2.48 0.52 2.48 0.08 2.6799998 -0.04 C 4.3199997 -0.02 5.2599998 0 6.06 0 C 6.8599997 0 7.7599998 -0.02 9.4 -0.04 C 9.599999 0.08 9.599999 0.52 9.4 0.64 C 8.3 0.7 7.3399997 0.78 7.3399997 2.44 Z "/>
</symbol>
<symbol id="gED653E9CCAB5F6C6237350979071A74F" overflow="visible">
<path d="M 1.1999999 1.1999999 C 1.1999999 0.44 1.8399999 -0.16 2.6399999 -0.16 C 3.4399998 -0.16 4.12 0.48 4.12 1.24 C 4.12 2.02 3.48 2.62 2.6799998 2.62 C 1.88 2.62 1.1999999 1.9799999 1.1999999 1.1999999 Z M 1.1999999 7.16 C 1.1999999 6.3999996 1.8399999 5.7999997 2.6399999 5.7999997 C 3.4399998 5.7999997 4.12 6.44 4.12 7.2 C 4.12 7.98 3.48 8.58 2.6799998 8.58 C 1.88 8.58 1.1999999 7.94 1.1999999 7.16 Z "/>
</symbol>
<symbol id="gB0978DD106A095AA3B799B940A52F3E4" overflow="visible">
<path d="M 3.46 12.9 C 2.6599998 12.9 0.38 12.94 0.38 12.94 C 0.17999999 12.82 0.17999999 12.38 0.38 12.259999 C 1.48 12.2 2.04 12.12 2.04 10.46 L 2.04 2.44 C 2.04 0.78 1.48 0.7 0.38 0.64 C 0.17999999 0.52 0.17999999 0.08 0.38 -0.04 C 0.38 -0.04 2.6599998 0 3.46 0 C 4.2599998 0 5.54 -0.04 6.74 -0.04 C 10.84 -0.04 12.16 1.68 12.16 3.72 C 12.16 5.48 11.28 6.62 9.16 7.18 L 9.16 7.22 C 10.24 7.7 11.08 8.8 11.08 9.82 C 11.08 11.2 10.34 12.94 6.2999997 12.94 C 5.2999997 12.94 4.1 12.9 3.46 12.9 Z M 4.8399997 6.68 L 6.2599998 6.68 C 8.32 6.68 9.22 5.46 9.22 3.74 C 9.22 2.54 8.8 0.79999995 6.16 0.79999995 C 4.96 0.79999995 4.8399997 1.1 4.8399997 1.68 Z M 4.8399997 11.24 C 4.8399997 11.82 4.94 12.099999 6.24 12.099999 C 7.16 12.099999 8.28 11.74 8.28 9.78 C 8.28 8.179999 7.3799996 7.52 5.96 7.52 L 4.8399997 7.52 Z "/>
</symbol>
<symbol id="g578059AE543193F568F4B7010D62E33B" overflow="visible">
<path d="M 4.6 2.56 L 4.6 7.68 L 6.3199997 7.68 C 6.68 7.68 7.02 7.7799997 7.02 8.0199995 L 7.02 8.48 C 7.02 8.599999 7 8.679999 6.62 8.679999 L 4.6 8.679999 L 4.6 9.7 C 4.6 12.679999 5.42 13.12 5.8599997 13.12 C 6.2 13.12 6.2799997 12.82 6.42 12.34 C 6.6 11.7 7.12 11.2 7.8399997 11.2 C 8.5 11.2 8.98 11.62 8.98 12.48 C 8.98 13.0199995 8.36 13.96 6.24 13.96 C 5.2999997 13.96 4.18 13.62 3.4199998 12.799999 C 2.6799998 12 2 11 2 9.08 L 2 8.679999 L 1.9599999 8.679999 C 1.28 8.679999 0.45999998 8.58 0.45999998 8.42 L 0.45999998 7.8799996 C 0.45999998 7.74 0.53999996 7.68 1 7.68 L 2 7.68 L 2 2.52 C 2 0.88 1.68 0.7 0.45999998 0.64 C 0.34 0.52 0.34 0.08 0.45999998 -0.04 C 1.3 -0.02 2.2 0 3.3 0 C 4.4 0 5.2799997 -0.02 6.14 -0.04 C 6.2599998 0.08 6.2599998 0.52 6.14 0.64 C 4.92 0.7 4.6 0.88 4.6 2.56 Z "/>
</symbol>
<symbol id="g814D257E196F777517493FCE505E18DF" overflow="visible">
<path d="M 0.74 4.14 C 0.74 1.52 2.82 -0.19999999 5.5 -0.19999999 C 6.92 -0.19999999 8.099999 0.19999999 8.92 0.94 C 9.94 1.8399999 10.28 3.1999998 10.28 4.3199997 C 10.28 6.94 8.5 8.88 5.52 8.88 C 3.86 8.88 2.62 8.3 1.8399999 7.3999996 C 1.0799999 6.52 0.74 5.3199997 0.74 4.14 Z M 5.2 8.04 C 6.56 8.04 7.48 6.42 7.48 3.6799998 C 7.48 1.28 6.54 0.64 5.8199997 0.64 C 4.18 0.64 3.54 3.1 3.54 4.58 C 3.54 6.42 3.86 8.04 5.2 8.04 Z "/>
</symbol>
<symbol id="g936880EEF467D45CE0F64A721CAEDAB8" overflow="visible">
<path d="M 4.56 5.3599997 C 4.56 6.08 4.7799997 6.3799996 5.04 6.68 C 5.2 6.8799996 5.38 7.02 5.68 7.02 C 5.8599997 7.02 6.08 6.8399997 6.24 6.64 C 6.3799996 6.48 6.72 6.3199997 7.18 6.3199997 C 7.7599998 6.3199997 8.32 6.92 8.32 7.7599998 C 8.32 8.28 7.72 8.88 7 8.88 C 6.2999997 8.88 5.54 8.28 4.62 6.96 L 4.54 6.96 C 4.5 7.56 4.4 8.54 4.4 8.54 C 4.38 8.72 4.22 8.88 3.9399998 8.88 C 3 8.639999 1.9399999 8.36 0.62 8.22 C 0.58 8.099999 0.62 7.72 0.65999997 7.6 C 1.76 7.5 1.9599999 7.3199997 1.9599999 6.18 L 1.9599999 2.44 C 1.9599999 0.78 1.74 0.74 0.52 0.64 C 0.39999998 0.52 0.39999998 0.08 0.52 -0.04 C 1.36 -0.02 2.2 0 3.26 0 C 4.3199997 0 5.14 -0.02 6 -0.04 C 6.12 0.08 6.12 0.52 6 0.64 C 4.7799997 0.71999997 4.56 0.78 4.56 2.44 Z "/>
</symbol>
<symbol id="gBC3E99057185A77BABD844B7BE98A74B" overflow="visible">
<path d="M 8.099999 2.46 L 8.099999 10.059999 C 8.099999 11.34 8.3 12.08 9.0199995 12.08 L 9.46 12.08 C 10.96 12.08 11.8 11.58 12.139999 10.04 C 12.36 10.04 12.74 10.059999 12.92 10.139999 C 12.78 11.059999 12.679999 12.099999 12.66 13 C 12.66 13.0199995 12.62 13.059999 12.599999 13.059999 C 11.92 13 9.7 12.9 8.12 12.9 L 5.2999997 12.9 C 3.76 12.9 1.4 13 0.64 13.059999 C 0.59999996 13.059999 0.56 13.0199995 0.56 13 C 0.48 12.099999 0.28 11.04 0.06 10.08 C 0.26 10 0.59999996 9.98 0.84 9.98 C 1.24 11.58 2.06 12.08 3.3799999 12.08 L 4.36 12.08 C 5.1 12.08 5.2999997 11.34 5.2999997 10.12 L 5.2999997 2.46 C 5.2999997 0.79999995 4.96 0.7 3.36 0.64 C 3.24 0.52 3.24 0.08 3.36 -0.04 C 4.3399997 -0.02 5.38 0 6.66 0 C 7.98 0 9.04 -0.02 10.04 -0.04 C 10.16 0.08 10.16 0.52 10.04 0.64 C 8.44 0.7 8.099999 0.79999995 8.099999 2.46 Z "/>
</symbol>
<symbol id="g80AF1C2942ED5136FA76CE028C280500" overflow="visible">
<path d="M 9.34 7.8799996 C 9.9 7.8799996 10.219999 8.12 10.219999 8.86 C 10.219999 9.24 9.7 9.82 8.94 9.82 C 8.059999 9.82 6.8999996 9.16 6.3199997 8.639999 C 5.96 8.84 5.54 8.88 4.64 8.88 C 3.78 8.88 2.9399998 8.679999 2.28 8.24 C 1.4599999 7.72 0.91999996 6.94 0.91999996 5.92 C 0.91999996 4.94 1.5 3.8799999 2.46 3.36 C 1.8399999 2.82 0.88 1.76 0.88 1.36 C 0.88 0.97999996 0.94 0.74 1.14 0.44 C 1.3199999 0.16 1.56 0 1.9599999 -0.12 C 1.1 -0.64 0.22 -1.78 0.22 -2.12 C 0.22 -2.86 0.45999998 -3.72 1 -4.1 C 1.78 -4.64 3.1 -4.7599998 4.06 -4.7599998 C 6.8399997 -4.7599998 10.0199995 -3.3 10.0199995 -1.1 C 10.0199995 -0.68 9.82 0.17999999 9.0199995 0.71999997 C 8.24 1.24 5.24 1.38 3.76 1.38 C 3.3999999 1.38 2.86 1.42 2.86 2.22 C 2.86 2.54 3.06 2.82 3.1599998 3.06 C 3.58 2.86 4 2.84 4.62 2.84 C 5.64 2.84 6.58 3.1 7.2599998 3.6999998 C 7.8399997 4.22 8.24 4.92 8.24 5.8199997 C 8.24 6.94 7.68 7.68 7 8.24 C 7.16 8.44 7.8199997 8.8 8.0199995 8.8 C 8.2 8.8 8.34 8.679999 8.4 8.559999 C 8.48 8.3 8.84 7.8799996 9.34 7.8799996 Z M 3.5 -0.5 C 5.04 -0.5 8 -0.56 8 -1.62 C 8 -2.34 7.68 -3.1599998 7.02 -3.52 C 6.3999996 -3.8799999 5.38 -3.9199998 4.62 -3.9199998 C 3.3 -3.9199998 2.3999999 -2.9399998 2.3999999 -1.92 C 2.3999999 -1.24 2.3999999 -0.78 2.62 -0.38 C 2.82 -0.45999998 3.08 -0.5 3.5 -0.5 Z M 5.7999997 5.7599998 C 5.7999997 3.84 5.24 3.6 4.72 3.6 C 3.48 3.6 3.32 5.08 3.32 6.1 C 3.32 7.58 3.6799998 8.12 4.46 8.12 C 5.4 8.12 5.7999997 7.3399997 5.7999997 5.7599998 Z "/>
</symbol>
<symbol id="g1344FEF92B65FBC27D977C1EC5D9AECF" overflow="visible">
<path d="M 1.26 8.679999 C 0.97999996 8.679999 0.68 8.599999 0.42 8.38 L 0.42 7.7999997 C 0.42 7.7 0.44 7.68 0.52 7.68 L 1.8199999 7.68 C 1.78 5.66 1.76 3.1 1.76 2.1 C 1.76 1.4 1.9399999 0.71999997 2.36 0.35999998 C 2.82 -0.02 3.54 -0.19999999 4.02 -0.19999999 C 5.12 -0.19999999 6.3399997 0.35999998 6.74 0.91999996 C 6.74 1.16 6.62 1.28 6.3799996 1.48 C 6.12 1.28 5.62 1.1999999 5.24 1.1999999 C 4.7999997 1.1999999 4.36 1.54 4.36 2.54 C 4.36 3.54 4.3399997 5.68 4.3399997 7.68 L 6.3599997 7.68 C 6.56 7.68 6.8399997 7.7599998 6.8399997 7.94 L 6.8399997 8.559999 C 6.8399997 8.639999 6.7799997 8.679999 6.68 8.679999 L 4.3399997 8.679999 L 4.36 9.36 C 4.4 10.7 4.46 11.62 4.46 11.62 C 4.46 11.74 4.4 11.8 4.2999997 11.8 C 4.16 11.8 3.4199998 11.58 3.1 11.44 C 2.76 11.3 2.18 11.179999 2.04 11 C 1.9 10.82 1.8199999 10.28 1.8199999 8.679999 Z "/>
</symbol>
<symbol id="gF410D7E2AAE9C85F7CA0EFFF491D43F" overflow="visible">
<path d="M 6.98 0.84 L 5.7799997 0.84 C 5.3599997 0.84 5.08 1.22 5.08 2.4199998 L 5.08 10.46 C 5.08 12.12 5.64 12.2 6.74 12.259999 C 6.94 12.38 6.94 12.82 6.74 12.94 C 5.1 12.92 4.5 12.9 3.6999998 12.9 C 2.8999999 12.9 0.62 12.94 0.62 12.94 C 0.42 12.82 0.42 12.38 0.62 12.259999 C 1.7199999 12.2 2.28 12.12 2.28 10.46 L 2.28 2.44 C 2.28 0.78 1.7199999 0.7 0.62 0.64 C 0.42 0.52 0.42 0.08 0.62 -0.04 C 0.62 -0.04 2.9199998 0 3.6999998 0 L 8.16 0 C 8.74 0 10.559999 -0.04 10.559999 -0.04 C 10.76 0.96 10.96 2.26 11.08 3.3 C 10.88 3.3999999 10.46 3.4399998 10.219999 3.3999999 C 9.82 1.9599999 9.08 0.84 6.98 0.84 Z "/>
</symbol>
<symbol id="gAFD7B3D7EB6599FB514B70015F312425" overflow="visible">
<path d="M 4.8399997 -3.36 C 5.16 -2.8 5.46 -2.08 5.7 -1.48 C 7.2999997 2.3799999 8.28 4.54 9.34 6.7799997 C 9.62 7.3599997 10.219999 7.98 10.96 8.04 C 11.08 8.16 11.08 8.599999 10.96 8.72 C 10.46 8.7 10.099999 8.679999 9.54 8.679999 C 8.84 8.679999 8.16 8.7 7.4199996 8.72 C 7.2999997 8.599999 7.2999997 8.16 7.4199996 8.04 C 8.059999 7.98 8.7 7.8799996 8.38 7.16 L 6.3199997 2.54 C 6.3199997 2.52 6.3199997 2.52 6.2999997 2.5 C 6.2999997 2.52 6.2999997 2.54 6.2799997 2.58 L 4.42 6.7599998 C 4.4 6.7799997 4.4 6.7999997 4.4 6.8199997 C 4.04 7.6 3.8999999 7.94 5.08 8.04 C 5.2 8.16 5.2 8.599999 5.08 8.72 C 4.3399997 8.7 3.1399999 8.679999 2.4199998 8.679999 C 1.74 8.679999 0.59999996 8.7 0.19999999 8.72 C 0.08 8.599999 0.08 8.16 0.19999999 8.04 C 1.0799999 7.96 1.24 7.8199997 1.78 6.56 L 4.36 0.64 C 4.42 0.53999996 4.5 0.45999998 4.56 0.38 C 4.8199997 0.02 5.04 -0.28 4.92 -0.56 L 4.44 -1.66 C 4.18 -2.28 3.9399998 -2.6399999 3.3799999 -2.6399999 C 3.02 -2.6399999 2.96 -2.56 2.6799998 -2.56 C 1.92 -2.56 1.48 -3.08 1.48 -3.48 C 1.48 -3.74 1.54 -4.06 1.7199999 -4.2799997 C 1.9 -4.5 2.24 -4.64 2.5 -4.64 C 2.76 -4.64 3.36 -4.56 3.6399999 -4.44 C 4.06 -4.24 4.62 -3.76 4.8399997 -3.36 Z "/>
</symbol>
<symbol id="gC1513612DA0E34F2B247DB2830CD7DFD" overflow="visible">
<path d="M 1.24 4.6 C 1.24 3.34 2.26 2.32 3.52 2.32 C 4.7799997 2.32 5.7999997 3.34 5.7999997 4.6 C 5.7999997 5.8599997 4.7799997 6.8799996 3.52 6.8799996 C 2.26 6.8799996 1.24 5.8599997 1.24 4.6 Z "/>
</symbol>
<symbol id="g8D44D9C01F9AF6C3B1D634FDF54DE6FB" overflow="visible">
<path d="M 5.66 6.46 C 7.3599997 6.46 7.4199996 6 7.48 5.1 C 7.6 4.98 8.0199995 4.98 8.139999 5.1 C 8.12 5.6 8.099999 6.18 8.099999 6.8599997 C 8.099999 7.54 8.12 8.059999 8.139999 8.58 C 8.0199995 8.7 7.6 8.7 7.48 8.58 C 7.4199996 7.48 7.3599997 7.22 5.66 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.9 4.04 12.099999 4.92 12.099999 L 5.8199997 12.099999 C 7.94 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.92 9.34 9.96 9.5 10.0199995 C 9.4 10.84 9.099999 12.759999 9.059999 12.92 C 9.059999 12.96 9.04 12.98 8.98 12.98 C 8.639999 12.92 8.54 12.9 8.04 12.9 L 2.9399998 12.9 C 2.3 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.06 -0.02 2.06 0 2.96 0 C 3.86 0 4.8399997 -0.02 5.54 -0.04 C 5.66 0.08 5.66 0.5 5.54 0.62 C 4.14 0.68 3.8 0.78 3.8 2.44 L 3.8 6.46 Z "/>
</symbol>
<symbol id="g261101C75B6E2D92A65743C21553BE65" overflow="visible">
<path d="M 9.4 2.44 L 9.4 6.66 C 9.4 7.44 9.48 8.72 9.48 8.72 C 9.48 8.8 9.36 8.84 9.28 8.84 C 8.679999 8.599999 8.099999 8.58 7.3999996 8.58 L 3.46 8.58 L 3.46 9.719999 C 3.46 11.62 4.14 13.28 5.5 13.28 C 6.3599997 13.28 7.04 13.059999 7.2 12.24 C 7.3999996 11.24 7.8199997 10.94 8.44 10.94 C 8.88 10.94 9.3 11.34 9.3 11.759999 C 9.3 13 7.6 13.96 5.74 13.96 C 4.8199997 13.96 3.72 13.599999 2.8999999 12.639999 C 2.06 11.66 1.88 10.44 1.88 8.88 L 1.88 8.58 L 0.9 8.58 C 0.53999996 8.58 0.44 8.34 0.44 8.179999 L 0.44 7.9199996 C 0.44 7.8199997 0.45999998 7.7999997 0.53999996 7.7999997 L 1.88 7.7999997 L 1.88 2.44 C 1.88 0.78 1.66 0.7 0.58 0.62 C 0.45999998 0.5 0.45999998 0.08 0.58 -0.04 C 1.26 -0.02 1.9799999 0 2.6799998 0 C 3.3799999 0 4.2799997 -0.02 4.94 -0.04 C 5.06 0.08 5.06 0.5 4.94 0.62 C 3.6599998 0.7 3.46 0.78 3.46 2.44 L 3.46 7.7999997 L 7.04 7.7999997 C 7.66 7.7999997 7.8199997 7.3999996 7.8199997 6.3799996 L 7.8199997 2.44 C 7.8199997 0.78 7.58 0.7 6.48 0.62 C 6.3599997 0.5 6.3599997 0.08 6.48 -0.04 C 7.18 -0.02 7.8999996 0 8.62 0 C 9.32 0 10.099999 -0.02 10.84 -0.04 C 10.96 0.08 10.96 0.5 10.84 0.62 C 9.62 0.7 9.4 0.78 9.4 2.44 Z "/>
</symbol>
<symbol id="g42587C4E387B2C5F870DA01C2914651F" overflow="visible">
<path d="M 6.68 1 C 6.7799997 1.0799999 6.96 1.12 6.98 0.97999996 C 7.04 0.5 7.2 -0.19999999 7.2 -0.19999999 C 7.3599997 -0.26 7.46 -0.24 7.58 -0.19999999 C 8.0199995 0.16 8.72 0.45999998 9.94 0.59999996 C 10.059999 0.71999997 10.059999 1.02 9.94 1.14 C 8.66 1.24 8.48 1.62 8.48 2.6 L 8.48 11.66 C 8.48 12.96 8.559999 13.759999 8.559999 13.759999 C 8.559999 13.9 8.48 13.96 8.3 13.96 C 7.7999997 13.759999 6.2999997 13.48 5.5 13.42 C 5.46 13.259999 5.5 12.94 5.62 12.82 C 5.68 12.82 5.74 12.82 5.7999997 12.82 C 6.68 12.759999 6.8999996 12.759999 6.8999996 11.179999 L 6.8999996 8.62 C 6.8999996 8.48 6.8599997 8.44 6.72 8.44 C 6.64 8.44 5.8199997 8.78 5.16 8.78 C 3.84 8.78 2.96 8.34 2.1599998 7.58 C 1.3 6.72 0.78 5.54 0.78 4.06 C 0.78 1.5999999 2.02 -0.19999999 4.18 -0.19999999 C 4.96 -0.19999999 5.7 0.19999999 6.68 1 Z M 6.8999996 2.48 C 6.8999996 2.1 6.8599997 1.9399999 6.58 1.6999999 C 5.8399997 1.06 5.2 0.74 4.7 0.74 C 3.62 0.74 2.5 1.92 2.5 4.42 C 2.5 5.8599997 2.78 6.66 3.08 7.08 C 3.6999998 8.0199995 4.54 8.08 4.94 8.08 C 5.66 8.08 6.16 7.8199997 6.56 7.3599997 C 6.8399997 7.04 6.8999996 6.8999996 6.8999996 6.2799997 Z "/>
</symbol>
<symbol id="g713198A7DA4F5CD7D462D4529B1D64BD" overflow="visible">
<path d="M 7.96 1.8199999 C 7.8799996 2 7.72 2.08 7.54 2.1 C 6.8599997 1.22 6 0.78 5.14 0.78 C 3.6799998 0.78 2.46 2.26 2.46 4.6 C 2.46 6.7999997 3.4199998 8.12 4.74 8.12 C 5.92 8.12 6.08 7.4199996 6.16 6.72 C 6.22 6.18 6.5 6 6.92 6 C 7.3399997 6 7.8999996 6.2599998 7.8999996 6.8799996 C 7.8999996 7.98 6.7599998 8.78 4.8399997 8.78 C 2.86 8.78 0.74 7 0.74 4.16 C 0.74 1.5799999 2.18 -0.19999999 4.7 -0.19999999 C 5.9 -0.19999999 6.96 0.17999999 7.96 1.8199999 Z "/>
</symbol>
<symbol id="g187DB76C80CD961C20BAB3AF6259527" overflow="visible">
<path d="M 3.4399998 10.46 C 3.4399998 12.12 3.74 12.219999 5.2799997 12.28 C 5.4 12.4 5.4 12.82 5.2799997 12.94 C 4.3399997 12.92 3.36 12.9 2.58 12.9 C 1.8 12.9 0.97999996 12.92 0.19999999 12.94 C 0.08 12.82 0.08 12.4 0.19999999 12.28 C 1.4 12.219999 1.74 12.12 1.74 10.46 L 1.74 4.66 C 1.74 0.58 4.38 -0.19999999 6.42 -0.19999999 C 10.5199995 -0.19999999 11.5 2.34 11.5 5.9 L 11.5 10.46 C 11.5 12.059999 11.84 12.139999 13.04 12.28 C 13.16 12.4 13.16 12.82 13.04 12.94 C 12.28 12.92 11.46 12.9 11 12.9 C 10.58 12.9 9.599999 12.92 8.679999 12.94 C 8.559999 12.82 8.559999 12.4 8.679999 12.28 C 10.179999 12.139999 10.5199995 12.08 10.5199995 10.46 L 10.5199995 5.54 C 10.5199995 3.3 10.219999 0.62 6.8399997 0.62 C 5.8799996 0.62 5.06 0.97999996 4.46 1.56 C 3.48 2.5 3.4399998 4.02 3.4399998 5.3199997 Z "/>
</symbol>
<symbol id="g5925E4E4FE8F59A76637BD462660B390" overflow="visible">
<path d="M 3.6399999 7.16 C 3.1799998 7.8399997 3.32 7.8599997 4.22 7.96 C 4.3399997 8.08 4.3399997 8.5 4.22 8.62 C 3.6799998 8.599999 2.8 8.58 2.2 8.58 C 1.5999999 8.58 1 8.599999 0.48 8.62 C 0.35999998 8.5 0.35999998 8.08 0.48 7.96 C 1.16 7.8999996 1.7199999 7.56 2.28 6.74 L 4.02 4.2 C 4.12 4.06 4.12 4 4.04 3.8999999 L 2.36 1.74 C 1.56 0.71999997 1.12 0.65999997 0.42 0.62 C 0.29999998 0.5 0.29999998 0.08 0.42 -0.04 C 0.82 -0.02 1.26 0 1.86 0 C 2.46 0 3.02 -0.02 3.54 -0.04 C 3.6599998 0.08 3.6599998 0.5 3.54 0.62 C 2.82 0.7 2.6599998 0.78 3.1 1.42 L 4.36 3.24 C 4.52 3.48 4.6 3.46 4.72 3.28 L 5.8799996 1.68 C 6.58 0.71999997 6.2599998 0.68 5.62 0.62 C 5.5 0.5 5.5 0.08 5.62 -0.04 C 6.22 -0.02 6.8799996 0 7.6 0 C 8.36 0 8.9 -0.02 9.38 -0.04 C 9.5 0.08 9.5 0.5 9.38 0.62 C 8.48 0.68 8.179999 0.74 7.3799996 1.88 L 5.58 4.42 C 5.5 4.54 5.48 4.6 5.58 4.72 L 7.2599998 6.8599997 C 8 7.7999997 8.48 7.8999996 9.2 7.96 C 9.32 8.08 9.32 8.5 9.2 8.62 C 8.8 8.599999 8.34 8.58 7.74 8.58 C 7.14 8.58 6.58 8.599999 6.06 8.62 C 5.94 8.5 5.94 8.08 6.06 7.96 C 6.7999997 7.8799996 7.02 7.8199997 6.54 7.14 L 5.24 5.3199997 C 5.1 5.12 5.02 5.14 4.8599997 5.3599997 Z "/>
</symbol>
<symbol id="gFDEE26E32361E56ABE6C1C3702B2C2B3" overflow="visible">
<path d="M 2.58 13.96 C 1.9599999 13.96 1.52 13.54 1.52 12.98 C 1.52 12.36 2.04 12.16 2.3999999 12.099999 C 2.78 12.059999 3.12 11.94 3.12 11.48 C 3.12 11.059999 2.3999999 10.139999 1.36 9.88 C 1.36 9.679999 1.4 9.54 1.54 9.4 C 2.74 9.62 3.8999999 10.58 3.8999999 11.98 C 3.8999999 13.179999 3.3799999 13.96 2.58 13.96 Z "/>
</symbol>
<symbol id="g2C80519849984D6FD44691E994D5E329" overflow="visible">
<path d="M 1 9.08 C 1 8.58 1.4599999 8 2.18 8 C 2.76 8 3.34 8.44 3.34 9.059999 C 3.34 9.16 3.3 9.3 3.24 9.48 C 3.1799998 9.62 3.12 9.78 3.12 10 C 3.12 10.46 3.82 11.38 4.7799997 11.38 C 5.7999997 11.38 6.5 10.12 6.5 8.92 C 6.5 7.58 6.42 6.72 5.3599997 5.72 L 3.6599998 4.1 C 1.18 1.74 0.84 1.18 0.78 0.64 L 0.85999995 0 L 8.58 0 C 8.82 0.76 9.059999 2.1399999 9.2 3.28 C 8.94 3.3999999 8.76 3.48 8.3 3.48 C 7.8599997 2.12 7.2799997 1.5799999 6.3799996 1.5799999 L 3.78 1.5799999 C 3.84 2.22 4.04 2.76 4.7 3.36 L 5.8799996 4.44 C 8.26 6.64 9.059999 7.12 9.059999 8.98 C 9.059999 11.059999 7.2999997 12.2 5.24 12.2 C 2.3799999 12.2 1 10.32 1 9.08 Z "/>
</symbol>
<symbol id="g5AE3E73FF7353FF91276C30DF8EB5DCC" overflow="visible">
<path d="M 3.3 1.5799999 L 4.36 4.36 C 4.46 4.62 4.58 4.7 5.06 4.7 L 8.86 4.7 L 9.98 1.4399999 C 10.219999 0.71999997 9.639999 0.7 8.88 0.65999997 C 8.76 0.65999997 8.62 0.64 8.5 0.64 C 8.38 0.52 8.38 0.08 8.5 -0.04 C 9.24 -0.02 11.139999 0 11.92 0 C 12.74 0 13.86 -0.02 14.599999 -0.04 C 14.719999 0.08 14.719999 0.52 14.599999 0.64 C 13.82 0.71999997 13.16 0.7 12.799999 1.7199999 L 8.679999 13.16 C 8.38 12.98 7.18 12.28 6.48 12.28 L 2.1399999 2.04 C 1.62 0.79999995 1.02 0.7 0.14 0.64 C 0.02 0.52 0.02 0.08 0.14 -0.04 C 0.88 -0.02 1.24 0 2.02 0 C 2.84 0 3.9399998 -0.02 4.68 -0.04 C 4.7999997 0.08 4.7999997 0.52 4.68 0.64 C 3.9199998 0.7 2.98 0.76 3.3 1.5799999 Z M 5.46 5.66 C 5.02 5.66 4.88 5.72 4.96 5.92 L 6.72 10.4 L 6.8599997 10.4 L 8.5 5.66 Z "/>
</symbol>
<symbol id="g25F4C61DF17D6DB8640DCCCD57BBA830" overflow="visible">
<path d="M 2.1599998 -3.86 L 6.3999996 -3.86 C 6.52 -3.74 6.52 -3.3799999 6.3999996 -3.26 C 3.6399999 -3.04 3.5 -2.74 3.5 -1 L 3.5 11.219999 C 3.5 12.96 3.6599998 13.259999 6.3999996 13.46 C 6.52 13.58 6.52 13.94 6.3999996 14.059999 L 2.1599998 14.059999 Z "/>
</symbol>
<symbol id="g844C4CEA683BD523227FE7A466FBF8A3" overflow="visible">
<path d="M 3.1 1.5799999 L 4.2 4.48 C 4.2999997 4.74 4.42 4.8199997 4.9 4.8199997 L 9.12 4.8199997 L 10.28 1.4399999 C 10.5199995 0.76 9.76 0.68 8.8 0.62 C 8.679999 0.5 8.679999 0.08 8.8 -0.04 C 9.54 -0.02 10.639999 0 11.42 0 C 12.24 0 13 -0.02 13.7 -0.04 C 13.82 0.08 13.82 0.5 13.7 0.62 C 12.92 0.7 12.24 0.76 11.9 1.7199999 L 7.7799997 13.16 C 7.48 12.98 6.94 12.759999 6.68 12.759999 L 2.1399999 2.04 C 1.62 0.79999995 1.02 0.68 0.14 0.62 C 0.02 0.5 0.02 0.08 0.14 -0.04 C 0.65999997 -0.02 1.3199999 0 1.92 0 C 2.74 0 3.74 -0.02 4.48 -0.04 C 4.6 0.08 4.6 0.5 4.48 0.62 C 3.72 0.68 2.78 0.76 3.1 1.5799999 Z M 5.2599998 5.66 C 4.8199997 5.66 4.68 5.72 4.7599998 5.92 L 6.7999997 11.099999 L 6.92 11.099999 L 8.8 5.66 Z "/>
</symbol>
<symbol id="g316778D5069ED68A0C52C06F0AD18D23" overflow="visible">
<path d="M 1.14 0.85999995 C 1.14 0.28 1.62 -0.19999999 2.2 -0.19999999 C 2.78 -0.19999999 3.26 0.28 3.26 0.85999995 C 3.26 1.4399999 2.78 1.92 2.2 1.92 C 1.62 1.92 1.14 1.4399999 1.14 0.85999995 Z "/>
</symbol>
<symbol id="gCAFB20A65E8FBEFE071D9C4C8EE95E49" overflow="visible">
<path d="M 1.22 9.36 C 1.22 8.94 1.5999999 8.58 2.02 8.58 C 2.36 8.58 2.96 8.94 2.96 9.38 C 2.96 9.54 2.9199998 9.66 2.8799999 9.8 C 2.84 9.94 2.72 10.12 2.72 10.28 C 2.72 10.78 3.24 11.5 4.7 11.5 C 5.42 11.5 6.44 11 6.44 9.08 C 6.44 7.7999997 5.98 6.7599998 4.7999997 5.56 L 3.32 4.1 C 1.36 2.1 1.04 1.14 1.04 -0.04 C 1.04 -0.04 2.06 0 2.7 0 L 6.2 0 C 6.8399997 0 7.7599998 -0.04 7.7599998 -0.04 C 8.0199995 1.02 8.22 2.52 8.24 3.12 C 8.12 3.22 7.8599997 3.26 7.66 3.22 C 7.3199997 1.8 6.98 1.3 6.2599998 1.3 L 2.7 1.3 C 2.7 2.26 4.08 3.62 4.18 3.72 L 6.2 5.66 C 7.3399997 6.7599998 8.2 7.64 8.2 9.16 C 8.2 11.32 6.44 12.2 4.8199997 12.2 C 2.6 12.2 1.22 10.559999 1.22 9.36 Z "/>
</symbol>
<symbol id="g2E0E67B6699615E51BCE03EAB1A37509" overflow="visible">
<path d="M 4.96 14.08 L 0.71999997 14.08 C 0.59999996 13.96 0.59999996 13.599999 0.71999997 13.48 C 3.48 13.259999 3.62 12.96 3.62 11.219999 L 3.62 -1 C 3.62 -2.74 3.46 -3.04 0.71999997 -3.24 C 0.59999996 -3.36 0.59999996 -3.72 0.71999997 -3.84 L 4.96 -3.84 Z "/>
</symbol>
<symbol id="gA335A20E4C1D7F39210005AFF7F1A0EF" overflow="visible">
<path d="M 7.14 -0.19999999 C 9.08 -0.19999999 10.86 0.71999997 12.219999 2.5 C 12.12 2.6799998 11.98 2.8 11.759999 2.8 C 10.34 1.24 8.98 0.62 7.12 0.62 C 4.42 0.62 2.56 3.6599998 2.56 6.58 C 2.56 8.3 3.02 9.74 3.74 10.639999 C 4.74 11.86 5.9 12.42 6.94 12.42 C 9.7 12.42 10.8 10.78 11.32 9.059999 C 11.559999 8.98 11.759999 9.04 11.98 9.16 C 11.88 10.2 11.74 11.16 11.54 12.259999 C 10.5199995 12.36 9.62 13.16 7.16 13.16 C 5.46 13.16 4.04 12.54 2.86 11.46 C 1.54 10.24 0.74 8.28 0.74 6.2 C 0.74 2.72 2.84 -0.19999999 7.14 -0.19999999 Z "/>
</symbol>
<symbol id="gD8CB364949770E6EB9E57283C62D30EB" overflow="visible">
<path d="M 4.3399997 -0.19999999 C 5.12 -0.19999999 6.06 0.19999999 7.04 1 C 7.14 1.0799999 7.3199997 1.12 7.3399997 0.97999996 C 7.3999996 0.48 7.56 -0.19999999 7.56 -0.19999999 C 7.72 -0.26 7.8199997 -0.24 7.94 -0.19999999 C 8.38 0.16 9.08 0.45999998 10.3 0.59999996 C 10.42 0.71999997 10.42 1.02 10.3 1.14 C 9.0199995 1.24 8.84 1.62 8.84 2.6 L 8.84 6.44 C 8.84 7.04 8.92 8.5 8.92 8.5 C 8.92 8.559999 8.86 8.62 8.76 8.62 C 8.66 8.599999 8.36 8.58 8.059999 8.58 C 7.4199996 8.58 6.7 8.599999 6.02 8.62 C 5.9 8.5 5.9 8.08 6.02 7.96 C 7 7.8999996 7.2599998 7.66 7.2599998 6.3399997 L 7.2599998 2.48 C 7.2599998 2.1 7.22 1.9399999 6.94 1.6999999 C 6.2 1.06 5.44 0.74 4.94 0.74 C 4.3399997 0.74 3.34 1.02 3.34 2.8 L 3.34 6.44 C 3.34 7.04 3.4199998 8.5 3.4199998 8.5 C 3.4199998 8.559999 3.36 8.62 3.26 8.62 C 3.1599998 8.599999 2.86 8.58 2.56 8.58 C 1.92 8.58 1.1999999 8.599999 0.52 8.62 C 0.39999998 8.5 0.39999998 8.08 0.52 7.96 C 1.48 7.8799996 1.76 7.66 1.76 6.3599997 L 1.76 2.52 C 1.76 1.14 2.36 -0.19999999 4.3399997 -0.19999999 Z "/>
</symbol>
<symbol id="gB91E67CF1B63A9F4CC30BB03AE35508D" overflow="visible">
<path d="M 2.08 1.9 C 1.4599999 1.9 1.02 1.48 1.02 0.91999996 C 1.02 0.29999998 1.54 0.099999994 1.9 0.04 C 2.28 0 2.62 -0.12 2.62 -0.58 C 2.62 -1 1.9 -1.92 0.85999995 -2.18 C 0.85999995 -2.3799999 0.9 -2.52 1.04 -2.6599998 C 2.24 -2.44 3.3999999 -1.48 3.3999999 -0.08 C 3.3999999 1.12 2.8799999 1.9 2.08 1.9 Z "/>
</symbol>
<symbol id="g17AD34DB90B05275C6F1422A9B4B5274" overflow="visible">
<path d="M 6.5 7.96 C 7.58 7.8799996 7.7 7.64 7.2799997 6.62 L 5.66 2.7 C 5.3399997 1.92 5.24 1.92 4.92 2.76 L 3.48 6.62 C 3.12 7.58 3.04 7.8199997 4.1 7.96 C 4.22 8.08 4.22 8.5 4.1 8.62 C 3.4399998 8.599999 2.74 8.58 2.08 8.58 C 1.42 8.58 0.82 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.28 7.8399997 1.42 7.52 1.8199999 6.5 L 4.38 0.17999999 C 4.5 -0.12 4.62 -0.24 4.88 -0.24 C 5.08 -0.24 5.22 -0.12 5.3599997 0.22 L 8.0199995 6.48 C 8.4 7.3599997 8.62 7.8599997 9.74 7.96 C 9.86 8.08 9.86 8.5 9.74 8.62 C 9.34 8.599999 8.86 8.58 8.34 8.58 C 7.68 8.58 7 8.599999 6.5 8.62 C 6.3799996 8.5 6.3799996 8.08 6.5 7.96 Z "/>
</symbol>
<symbol id="gF9DE6E66E5D3ACB0B17DC7988DD660B8" overflow="visible">
<path d="M 1.7199999 2.44 C 1.7199999 0.78 1.5 0.7 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.04 -0.02 1.7199999 0 2.52 0 C 3.22 0 3.8799999 -0.02 4.3399997 -0.04 C 4.46 0.08 4.46 0.5 4.3399997 0.62 C 3.52 0.7 3.3 0.78 3.3 2.44 L 3.3 4.18 C 3.6799998 4.16 3.9599998 4.14 4.16 4.08 C 4.38 3.9199998 4.56 3.74 4.7999997 3.4199998 L 6.2599998 1.4599999 C 6.8399997 0.68 7.08 0.29999998 7.1 0.06 C 7.1 0 7.12 -0.04 7.18 -0.04 C 7.58 -0.02 8.0199995 0 8.42 0 C 9.04 0 9.66 -0.02 10.059999 -0.04 C 10.179999 0.08 10.179999 0.5 10.059999 0.62 C 9.38 0.7 8.88 0.78 8.34 1.4599999 L 5.7 4.7799997 C 5.62 4.88 5.56 4.96 5.56 5.06 C 5.56 5.14 5.56 5.18 5.64 5.2599998 L 7.3999996 7.08 C 8 7.72 8.7 7.8799996 9.5 7.96 C 9.62 8.08 9.62 8.5 9.5 8.62 C 9.04 8.599999 8.48 8.58 7.7599998 8.58 C 7 8.58 6.2599998 8.599999 5.7999997 8.62 C 5.68 8.5 5.68 8.08 5.7999997 7.96 C 6.92 7.8799996 6.44 7.18 6.2599998 6.94 C 5.7999997 6.3599997 5.18 5.68 4.66 5.2999997 C 4.22 4.98 3.6799998 4.74 3.3 4.68 L 3.3 11.66 C 3.3 12.96 3.3799999 13.759999 3.3799999 13.759999 C 3.3799999 13.9 3.3 13.96 3.12 13.96 C 2.62 13.759999 1.12 13.48 0.32 13.42 C 0.28 13.259999 0.32 12.94 0.44 12.82 C 0.5 12.82 0.56 12.82 0.62 12.82 C 1.5 12.759999 1.7199999 12.759999 1.7199999 11.179999 Z "/>
</symbol>
<symbol id="g11C09650A1107877D1CACE85AD57EEFF" overflow="visible">
<path d="M 4.2999997 11.5 C 5.16 11.5 5.96 10.98 5.96 9.7 C 5.96 8.7 4.7999997 7.16 2.82 6.8799996 L 2.9199998 6.24 C 3.26 6.2799997 3.62 6.2799997 3.8799999 6.2799997 C 5.02 6.2799997 6.5 5.96 6.5 3.6999998 C 6.5 1.04 4.72 0.5 4.02 0.5 C 3 0.5 2.82 0.96 2.58 1.3199999 C 2.3799999 1.5999999 2.12 1.8399999 1.7199999 1.8399999 C 1.3 1.8399999 0.88 1.4599999 0.88 1.14 C 0.88 0.34 2.56 -0.19999999 3.76 -0.19999999 C 6.14 -0.19999999 8.26 1.3399999 8.26 3.98 C 8.26 6.16 6.62 6.94 5.44 7.14 L 5.42 7.18 C 7.06 7.96 7.52 8.78 7.52 9.84 C 7.52 10.44 7.3799996 10.92 6.8999996 11.42 C 6.46 11.86 5.7599998 12.2 4.72 12.2 C 1.78 12.2 0.94 10.28 0.94 9.62 C 0.94 9.34 1.14 8.94 1.62 8.94 C 2.32 8.94 2.3999999 9.599999 2.3999999 9.98 C 2.3999999 11.259999 3.78 11.5 4.2999997 11.5 Z "/>
</symbol>
<symbol id="gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" overflow="visible">
<path d="M 13.259999 2.32 C 13.36 0.7 13.28 0.68 11.98 0.62 C 11.86 0.5 11.86 0.08 11.98 -0.04 C 12.719999 -0.02 13.5199995 0 14.12 0 C 14.719999 0 15.639999 -0.02 16.3 -0.04 C 16.42 0.08 16.42 0.5 16.3 0.62 C 14.94 0.68 14.88 0.76 14.759999 2.4199998 L 14.16 10.84 C 14.08 11.92 14.179999 12.2 15.54 12.28 C 15.66 12.4 15.66 12.82 15.54 12.94 L 12.92 12.9 L 8.679999 2.76 C 8.599999 2.56 8.54 2.48 8.5 2.48 C 8.46 2.48 8.4 2.58 8.34 2.74 L 4.24 12.9 L 1.3399999 12.94 C 1.22 12.82 1.22 12.4 1.3399999 12.28 C 2.72 12.2 2.84 12.16 2.7 10.66 L 1.9 2.4199998 C 1.78 1.22 1.54 0.71999997 0.39999998 0.62 C 0.28 0.5 0.28 0.08 0.39999998 -0.04 C 1 -0.02 1.64 0 2.12 0 C 2.6 0 3.3999999 -0.02 4 -0.04 C 4.12 0.08 4.12 0.5 4 0.62 C 2.6799998 0.71999997 2.58 1.3399999 2.6799998 2.46 L 3.4399998 10.48 L 3.48 10.48 L 7.62 0.099999994 C 7.68 -0.04 7.7999997 -0.19999999 7.9199996 -0.19999999 C 8.04 -0.19999999 8.12 -0.06 8.2 0.099999994 L 12.7 10.679999 L 12.74 10.679999 Z "/>
</symbol>
<symbol id="gFE29E79896646B3825DA2D41961151C9" overflow="visible">
<path d="M 2.96 12.9 C 2.24 12.9 1.16 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.16 -0.02 2.24 0 2.98 0 C 3.6999998 0 4.22 -0.04 5.9 -0.04 C 9.88 -0.04 10.94 1.9599999 10.94 3.6799998 C 10.94 5.6 9.599999 6.7 7.8599997 7.2 L 7.8599997 7.24 C 8.86 7.74 9.76 8.78 9.76 9.86 C 9.76 11.2 9.179999 12.94 5.46 12.94 C 4.7599998 12.94 3.6799998 12.9 2.96 12.9 Z M 3.82 6.64 L 5.2 6.64 C 7.94 6.64 9.08 5.1 9.08 3.3 C 9.08 1.8399999 8.5199995 0.62 5.48 0.62 C 4.08 0.62 3.82 1.14 3.82 2.36 Z M 3.82 11 C 3.82 12.059999 3.82 12.259999 5.56 12.259999 C 6.68 12.259999 8.139999 11.66 8.139999 9.62 C 8.139999 7.9199996 6.96 7.3199997 5.2999997 7.3199997 L 3.82 7.3199997 Z "/>
</symbol>
<symbol id="gA1481BA28623480CC7E6165783E2A864" overflow="visible">
<path d="M 4.06 7.96 C 4.18 8.08 4.18 8.5 4.06 8.62 C 3.46 8.599999 2.76 8.58 2.04 8.58 C 1.28 8.58 0.74 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.16 7.8599997 1.38 7.66 1.8 6.62 L 4.42 0.16 C 4.54 -0.12 4.7 -0.24 4.9 -0.24 C 5.08 -0.24 5.24 -0.12 5.38 0.19999999 L 7.3999996 5.12 L 9.46 0.16 C 9.58 -0.12 9.74 -0.24 9.94 -0.24 C 10.12 -0.24 10.28 -0.12 10.4 0.17999999 L 13.0199995 6.52 C 13.34 7.3399997 13.679999 7.8999996 14.7 7.96 C 14.82 8.08 14.82 8.5 14.7 8.62 C 14.299999 8.599999 13.86 8.58 13.259999 8.58 C 12.66 8.58 11.82 8.599999 11.219999 8.62 C 11.099999 8.5 11.099999 8.08 11.219999 7.96 C 12.719999 7.8799996 12.5199995 7.2999997 12.24 6.6 L 10.559999 2.44 C 10.36 1.9399999 10.28 1.9399999 10.12 2.36 L 8.4 6.74 C 8.0199995 7.68 8.059999 7.8799996 9.12 7.96 C 9.24 8.08 9.24 8.5 9.12 8.62 C 8.5199995 8.599999 7.72 8.58 7.12 8.58 C 6.62 8.58 5.96 8.599999 5.3599997 8.62 C 5.24 8.5 5.24 8.08 5.3599997 7.96 C 6.2999997 7.8799996 6.54 7.2999997 6.8999996 6.3999996 L 7.02 6.08 L 5.62 2.54 C 5.3599997 1.88 5.3199997 1.86 5.06 2.5 L 3.46 6.62 C 3.08 7.58 3.1 7.8999996 4.06 7.96 Z "/>
</symbol>
<symbol id="gE8171CD7697771DDE124968BDB3EF0D7" overflow="visible">
<path d="M 5.42 4.46 C 5.68 4.46 5.96 5.02 5.96 5.2599998 C 5.96 5.46 5.8799996 5.66 5.68 5.66 L 1.3 5.66 C 1.06 5.66 0.79999995 5.2 0.79999995 4.8399997 C 0.79999995 4.64 0.91999996 4.46 1.1 4.46 Z "/>
</symbol>
<symbol id="g607CD744DAB7515984E0B3F495F7DE81" overflow="visible">
<path d="M 2.98 0 L 7.24 0 C 7.7799997 0 9.62 -0.04 9.62 -0.04 C 9.82 0.96 10.0199995 2.26 10.139999 3.3 C 9.94 3.3999999 9.719999 3.4399998 9.48 3.3999999 C 9.08 1.9599999 8.34 0.78 6.22 0.78 L 4.96 0.78 C 4.18 0.78 3.82 1.16 3.82 2.18 L 3.82 10.46 C 3.82 12.12 4.16 12.219999 5.56 12.28 C 5.68 12.4 5.68 12.82 5.56 12.94 C 4.66 12.92 3.72 12.9 2.96 12.9 C 2.24 12.9 1.3 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.16 -0.02 2.3 0 2.98 0 Z "/>
</symbol>
<symbol id="g7490174898CD3BEE5501720224632ECB" overflow="visible">
<path d="M 3.3999999 10.7 L 6.98 10.7 C 5.42 6.8199997 3.84 2.9199998 2.48 -0.12 L 2.6399999 -0.26 L 4 -0.19999999 C 5.14 3.1999998 6.24 6.52 8.48 11.98 L 8.16 12.219999 C 7.8199997 12.12 7.3799996 12 6.62 12 L 2.5 12 C 1.8199999 12 1.86 12.2 1.5 12.28 C 1.4399999 12.28 1.42 12.28 1.42 12.219999 C 1.4 11.259999 1.18 10.059999 1.02 9.0199995 C 1.24 8.96 1.4399999 8.94 1.66 8.96 C 2.1 10.559999 2.76 10.7 3.3999999 10.7 Z "/>
</symbol>
<symbol id="gB8789F2F5F06048D4163694E4C0F3B6C" overflow="visible">
<path d="M 12.36 2.44 L 12.36 10.46 C 12.36 12.12 12.7 12.219999 14.099999 12.28 C 14.219999 12.4 14.219999 12.82 14.099999 12.94 C 13.28 12.92 12.259999 12.9 11.5 12.9 C 10.76 12.9 9.8 12.92 8.92 12.94 C 8.8 12.82 8.8 12.4 8.92 12.28 C 10.32 12.219999 10.66 12.12 10.66 10.46 L 10.66 7.2599998 L 3.82 7.2599998 L 3.82 10.46 C 3.82 12.12 4.16 12.219999 5.56 12.28 C 5.68 12.4 5.68 12.82 5.56 12.94 C 4.7999997 12.92 3.98 12.9 2.96 12.9 C 1.9599999 12.9 1.14 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.26 -0.02 2.22 0 2.98 0 C 3.6999998 0 4.68 -0.02 5.56 -0.04 C 5.68 0.08 5.68 0.5 5.56 0.62 C 4.16 0.68 3.82 0.78 3.82 2.44 L 3.82 6.42 L 10.66 6.42 L 10.66 2.44 C 10.66 0.78 10.32 0.68 8.92 0.62 C 8.8 0.5 8.8 0.08 8.92 -0.04 C 9.82 -0.02 10.78 0 11.5199995 0 C 12.259999 0 13.219999 -0.02 14.099999 -0.04 C 14.219999 0.08 14.219999 0.5 14.099999 0.62 C 12.7 0.68 12.36 0.78 12.36 2.44 Z "/>
</symbol>
<symbol id="g87DD77732F07A5C65A64D31E4C3C918D" overflow="visible">
<path d="M 16.199999 11.3 L 13.08 2.62 L 13.0199995 2.6399999 L 10.26 11.08 C 9.92 12.16 10.62 12.219999 11.3 12.28 C 11.42 12.4 11.42 12.82 11.3 12.94 C 10.48 12.92 9.599999 12.9 8.8 12.9 C 8.139999 12.9 7.44 12.92 6.7999997 12.94 C 6.68 12.82 6.68 12.4 6.7999997 12.28 C 7.8599997 12.219999 8.3 11.599999 8.48 11.08 L 8.94 9.76 C 9.0199995 9.5199995 9.08 9.32 9.08 9.139999 C 9.08 8.94 9.059999 8.78 8.9 8.44 L 6.3199997 2.58 L 6.22 2.6 L 3.3 11.44 C 3.06 12.139999 3.6 12.24 4.2999997 12.28 C 4.42 12.4 4.42 12.82 4.2999997 12.94 C 3.6399999 12.92 2.76 12.9 1.9799999 12.9 C 1.28 12.9 0.7 12.92 0.12 12.94 C 0 12.82 0 12.4 0.12 12.28 C 1.02 12.219999 1.16 12.2 1.54 11.12 L 5.2999997 0.29999998 C 5.4 -0.02 5.52 -0.24 5.74 -0.24 C 6 -0.24 6.12 -0.04 6.2599998 0.29999998 L 9.24 7 C 9.42 7.3999996 9.48 7.5 9.58 7.5 C 9.66 7.5 9.74 7.2799997 9.86 6.94 L 12.16 0.29999998 C 12.28 -0.04 12.38 -0.24 12.62 -0.24 C 12.84 -0.24 12.98 -0.02 13.08 0.28 L 17.1 11.059999 C 17.359999 11.759999 17.72 12.219999 18.82 12.28 C 18.939999 12.4 18.939999 12.82 18.82 12.94 C 18.24 12.92 17.6 12.9 17.08 12.9 C 16.56 12.9 15.679999 12.92 14.88 12.94 C 14.759999 12.82 14.759999 12.4 14.88 12.28 C 15.7 12.219999 16.5 12.16 16.199999 11.3 Z "/>
</symbol>
<symbol id="gAA14E57E2DCC57A3F7809273EECD3C51" overflow="visible">
<path d="M 7.9104 1.5616 L 7.9104 6.6944 C 7.9104 7.7567997 8.128 7.8208 9.024 7.8592 C 9.1008 7.936 9.1008 8.2048 9.024 8.2816 C 8.4992 8.2688 7.8464 8.256 7.3599997 8.256 C 6.8863997 8.256 6.272 8.2688 5.7088 8.2816 C 5.632 8.2048 5.632 7.936 5.7088 7.8592 C 6.6047997 7.8208 6.8223996 7.7567997 6.8223996 6.6944 L 6.8223996 4.6464 L 2.4448 4.6464 L 2.4448 6.6944 C 2.4448 7.7567997 2.6624 7.8208 3.5584 7.8592 C 3.6352 7.936 3.6352 8.2048 3.5584 8.2816 C 3.072 8.2688 2.5472 8.256 1.8944 8.256 C 1.2544 8.256 0.72959995 8.2688 0.24319999 8.2816 C 0.1664 8.2048 0.1664 7.936 0.24319999 7.8592 C 1.1392 7.8208 1.3568 7.7567997 1.3568 6.6944 L 1.3568 1.5616 C 1.3568 0.4992 1.1392 0.43519998 0.24319999 0.39679998 C 0.1664 0.32 0.1664 0.0512 0.24319999 -0.0256 C 0.8064 -0.0128 1.4208 0 1.9072 0 C 2.368 0 2.9952 -0.0128 3.5584 -0.0256 C 3.6352 0.0512 3.6352 0.32 3.5584 0.39679998 C 2.6624 0.43519998 2.4448 0.4992 2.4448 1.5616 L 2.4448 4.1088 L 6.8223996 4.1088 L 6.8223996 1.5616 C 6.8223996 0.4992 6.6047997 0.43519998 5.7088 0.39679998 C 5.632 0.32 5.632 0.0512 5.7088 -0.0256 C 6.2848 -0.0128 6.8992 0 7.3728 0 C 7.8464 0 8.4608 -0.0128 9.024 -0.0256 C 9.1008 0.0512 9.1008 0.32 9.024 0.39679998 C 8.128 0.43519998 7.9104 0.4992 7.9104 1.5616 Z "/>
</symbol>
<symbol id="gF5F8064101DBF0FCB4BCFDA7012527FE" overflow="visible">
<path d="M 2.3167999 1.5616 L 2.3167999 4.1088 C 2.3167999 4.7488 2.368 5.568 2.368 5.568 C 2.368 5.6191998 2.304 5.6576 2.2015998 5.6576 C 1.8432 5.5168 1.3312 5.4016 0.44799998 5.2864 C 0.4224 5.2096 0.44799998 5.0048 0.4736 4.928 C 1.1776 4.864 1.3055999 4.7872 1.3055999 4.0576 L 1.3055999 1.5616 C 1.3055999 0.4992 1.1647999 0.4608 0.384 0.39679998 C 0.30719998 0.32 0.30719998 0.0512 0.384 -0.0256 C 0.8064 -0.0128 1.3055999 0 1.8176 0 C 2.3295999 0 2.816 -0.0128 3.2384 -0.0256 C 3.3151999 0.0512 3.3151999 0.32 3.2384 0.39679998 C 2.4575999 0.44799998 2.3167999 0.4992 2.3167999 1.5616 Z M 1.152 7.6671996 C 1.152 7.3343997 1.4591999 7.0016 1.7664 7.0016 C 2.1248 7.0016 2.432 7.3472 2.432 7.6159997 C 2.432 7.9231997 2.1632 8.2816 1.8176 8.2816 C 1.5103999 8.2816 1.152 7.9743996 1.152 7.6671996 Z "/>
</symbol>
<symbol id="g3976D55F213F07C6469FD06EC16139AA" overflow="visible">
<path d="M 4.9407997 1.1904 C 4.4672 0.704 4.0959997 0.4992 3.3536 0.4992 C 2.8927999 0.4992 2.3552 0.768 1.9583999 1.4208 C 1.7024 1.8432 1.5488 2.432 1.5488 3.1743999 L 4.9536 3.1488 C 5.1071997 3.1488 5.1967998 3.2256 5.1967998 3.3664 C 5.1967998 4.4416 4.8128 5.5936 3.0335999 5.5936 C 1.92 5.5936 0.4736 4.5312 0.4736 2.5856 C 0.4736 1.8687999 0.65279996 1.1776 1.0752 0.69119996 C 1.5103999 0.1792 2.112 -0.12799999 3.0335999 -0.12799999 C 4.0064 -0.12799999 4.6976 0.32 5.2096 0.9856 C 5.1712 1.1136 5.0944 1.1776 4.9407997 1.1904 Z M 1.5871999 3.6095998 C 1.8304 5.0559998 2.7264 5.1712 3.0335999 5.1712 C 3.52 5.1712 4.0959997 4.9024 4.0959997 3.8272 C 4.0959997 3.712 4.0448 3.648 3.9039998 3.648 Z "/>
</symbol>
<symbol id="gB7BB853387AAC07ADB7DDEF96856059B" overflow="visible">
<path d="M 2.2528 4.5824 C 2.2272 5.0944 2.2144 5.4272 2.1504 5.5551996 C 2.1248 5.6191998 2.0992 5.6576 1.9968 5.6576 C 1.6384 5.5168 1.3055999 5.4016 0.4224 5.2864 C 0.39679998 5.2096 0.4224 5.0048 0.44799998 4.928 C 1.1392 4.864 1.28 4.7999997 1.28 4.0576 L 1.28 1.5616 C 1.28 0.4992 1.1264 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7808 -0.0128 1.28 0 1.7919999 0 C 2.304 0 2.8927999 -0.0128 3.3407998 -0.0256 C 3.4176 0.0512 3.4176 0.32 3.3407998 0.39679998 C 2.4448 0.4608 2.2912 0.4992 2.2912 1.5616 L 2.2912 3.3407998 C 2.2912 3.6736 2.4448 3.968 2.5983999 4.1984 C 2.7391999 4.4031997 3.0335999 4.8255997 3.1871998 4.8255997 C 3.3023999 4.8255997 3.4176 4.7999997 3.52 4.6591997 C 3.6095998 4.5312 3.7631998 4.3648 3.9808 4.3648 C 4.288 4.3648 4.5824 4.6847997 4.5824 5.0048 C 4.5824 5.2479997 4.3519998 5.6191998 3.8144 5.6191998 C 3.2128 5.6191998 2.688 5.0559998 2.3936 4.5568 C 2.3167999 4.416 2.2528 4.5183997 2.2528 4.5824 Z "/>
</symbol>
<symbol id="gF8EC31AC53CF59E01ED9143906F6DA7B" overflow="visible">
<path d="M 3.7503998 0.61439997 C 3.8272 0.21759999 3.968 -0.12799999 4.608 -0.12799999 C 5.0944 -0.12799999 5.5551996 0.0896 5.824 0.34559998 C 5.7984 0.4992 5.7472 0.61439997 5.6064 0.69119996 C 5.5168 0.61439997 5.2992 0.48639998 5.1328 0.48639998 C 4.7616 0.48639998 4.7488 0.9856 4.7488 1.5744 L 4.7488 3.4559999 C 4.7488 5.2736 3.7503998 5.6191998 2.816 5.6191998 C 1.7664 5.6191998 0.704 4.928 0.704 4.1984 C 0.704 3.8911998 0.8576 3.7375998 1.152 3.7375998 C 1.5231999 3.7375998 1.7536 4.0064 1.7536 4.1728 C 1.7536 4.2623997 1.7407999 4.3519998 1.7152 4.4031997 C 1.7024 4.4416 1.6896 4.5183997 1.6896 4.6591997 C 1.6896 5.0559998 2.2272 5.1967998 2.7136 5.1967998 C 3.1488 5.1967998 3.7503998 4.9792 3.7503998 3.5328 C 3.7503998 3.4431999 3.712 3.392 3.6736 3.3792 L 2.5728 3.1104 C 1.344 2.8032 0.4608 2.1248 0.4608 1.2544 C 0.4608 0.2048 1.1776 -0.12799999 2.0736 -0.12799999 C 2.5216 -0.12799999 2.9055998 -0.0256 3.4687998 0.4096 L 3.7247999 0.61439997 Z M 3.7503998 2.9824 L 3.7503998 1.2928 C 3.7503998 1.1264 3.6736 1.0368 3.5712 0.96 C 3.2384 0.69119996 2.8032 0.39679998 2.4448 0.39679998 C 1.8047999 0.39679998 1.5231999 0.9088 1.5231999 1.3055999 C 1.5231999 1.8815999 1.7919999 2.4703999 2.7391999 2.7136 Z "/>
</symbol>
<symbol id="g68DDE7C8FDC8A226B6C32EAD39AF7364" overflow="visible">
<path d="M 5.0944 1.1647999 C 5.0432 1.28 4.9407997 1.3312 4.8255997 1.344 C 4.3904 0.7808 3.84 0.4992 3.2896 0.4992 C 2.3552 0.4992 1.5744 1.4463999 1.5744 2.944 C 1.5744 4.3519998 2.1887999 5.1967998 3.0335999 5.1967998 C 3.7888 5.1967998 3.8911998 4.7488 3.9424 4.3008 C 3.9808 3.9552 4.16 3.84 4.4288 3.84 C 4.6976 3.84 5.0559998 4.0064 5.0559998 4.4031997 C 5.0559998 5.1071997 4.3264 5.6191998 3.0976 5.6191998 C 1.8304 5.6191998 0.4736 4.48 0.4736 2.6624 C 0.4736 1.0112 1.3952 -0.12799999 3.008 -0.12799999 C 3.776 -0.12799999 4.4544 0.1152 5.0944 1.1647999 Z "/>
</symbol>
<symbol id="g570B752173035444311A253BD2376AD" overflow="visible">
<path d="M 2.1376 3.6608 C 2.1376 3.9296 2.2528 4.0832 2.3552 4.1984 C 2.8416 4.672 3.4944 4.9536 3.9936 4.9536 C 4.2496 4.9536 4.5183997 4.7872 4.672 4.4927998 C 4.7999997 4.2367997 4.8255997 3.8911998 4.8255997 3.5072 L 4.8255997 1.5616 C 4.8255997 0.51199996 4.6976 0.4608 4.032 0.39679998 C 3.968 0.32 3.968 0.0512 4.032 -0.0256 C 4.3904 -0.0128 4.8255997 0 5.3375998 0 C 5.8496 0 6.272 -0.0128 6.6944 -0.0256 C 6.7584 0.0512 6.7584 0.32 6.6944 0.39679998 C 5.9775996 0.4608 5.8367996 0.51199996 5.8367996 1.5616 L 5.8367996 3.4687998 C 5.8367996 4.1728 5.7855997 4.7999997 5.4912 5.184 C 5.2736 5.4656 4.8768 5.6191998 4.4288 5.6191998 C 3.8016 5.6191998 3.0335999 5.4528 2.2528 4.5824 C 2.2528 4.5696 2.24 4.5696 2.2272 4.5568 C 2.1887999 4.5056 2.1248 4.4288 2.1248 4.5824 L 2.1376 7.4624 C 2.1376 8.2944 2.1887999 8.806399 2.1887999 8.806399 C 2.1887999 8.896 2.1376 8.9344 2.0224 8.9344 C 1.7024 8.806399 0.7424 8.6272 0.2304 8.588799 C 0.2048 8.4864 0.2304 8.2816 0.30719998 8.2048 C 0.34559998 8.2048 0.384 8.2048 0.4224 8.2048 C 0.9856 8.1664 1.1264 8.1664 1.1264 7.1552 L 1.1264 1.5616 C 1.1264 0.4992 0.97279996 0.44799998 0.2304 0.39679998 C 0.15359999 0.32 0.15359999 0.0512 0.2304 -0.0256 C 0.65279996 -0.0128 1.1264 0 1.6384 0 C 2.1248 0 2.5472 -0.0128 2.9055998 -0.0256 C 2.9824 0.0512 2.9824 0.32 2.9055998 0.39679998 C 2.2528 0.44799998 2.1376 0.4992 2.1376 1.5616 Z "/>
</symbol>
<symbol id="g9662C1D9A80FEB5040A57FD9DFCA7985" overflow="visible">
<path d="M 1.216 1.5616 C 1.216 0.4992 1.0752 0.43519998 0.2944 0.39679998 C 0.21759999 0.32 0.21759999 0.0512 0.2944 -0.0256 C 0.7424 -0.0128 1.216 0 1.7279999 0 C 2.24 0 2.7264 -0.0128 3.1488 -0.0256 C 3.2256 0.0512 3.2256 0.32 3.1488 0.39679998 C 2.368 0.43519998 2.2272 0.4992 2.2272 1.5616 L 2.2272 7.4624 C 2.2272 8.2944 2.2784 8.806399 2.2784 8.806399 C 2.2784 8.896 2.2272 8.9344 2.112 8.9344 C 1.7919999 8.806399 0.83199996 8.6272 0.32 8.588799 C 0.2944 8.4864 0.32 8.2816 0.39679998 8.2048 C 1.1392 8.1536 1.216 8.1152 1.216 7.1552 Z "/>
</symbol>
<symbol id="g1CB3EC9D05726EBFDE8ADABEC8504FCD" overflow="visible">
<path d="M 7.1168 6.5536 L 7.1168 2.368 C 7.1168 2.1248 7.1168 1.984 7.0271997 1.984 C 6.976 1.984 6.784 2.2144 6.4128 2.688 L 2.0224 8.256 L 0.2944 8.2816 C 0.21759999 8.2048 0.21759999 7.936 0.2944 7.8592 C 0.8448 7.8208 1.2287999 7.3728 1.3055999 7.04 L 1.3055999 1.7024 C 1.3055999 0.5632 1.0879999 0.48639998 0.192 0.39679998 C 0.1152 0.32 0.1152 0.0512 0.192 -0.0256 C 0.7424 -0.0128 1.3184 0 1.6256 0 C 1.92 0 2.5088 -0.0128 3.0463998 -0.0256 C 3.1232 0.0512 3.1232 0.32 3.0463998 0.39679998 C 2.1504 0.48639998 1.9327999 0.5376 1.9327999 1.7024 L 1.9327999 5.6191998 C 1.9327999 6.0544 1.9327999 6.2464 2.0351999 6.2464 C 2.112 6.2464 2.2528 6.1056 2.4703999 5.824 L 6.9375997 0.1792 C 7.0783997 -0.0128 7.2447996 -0.12799999 7.4495997 -0.12799999 C 7.6288 -0.12799999 7.744 0.0256 7.744 0.2688 L 7.744 6.5536 C 7.744 7.6927996 7.9616 7.7696 8.8576 7.8592 C 8.9344 7.936 8.9344 8.2048 8.8576 8.2816 C 8.3328 8.2688 7.7311997 8.256 7.424 8.256 C 7.1552 8.256 6.5664 8.2688 6.0032 8.2816 C 5.9263997 8.2048 5.9263997 7.936 6.0032 7.8592 C 6.8992 7.7696 7.1168 7.7184 7.1168 6.5536 Z "/>
</symbol>
<symbol id="gD62975B7DE3250BE5F195D0E8335F60D" overflow="visible">
<path d="M 4.16 5.0944 C 4.8512 5.0432 4.928 4.8896 4.6591997 4.2367997 L 3.6223998 1.7279999 C 3.4176 1.2287999 3.3536 1.2287999 3.1488 1.7664 L 2.2272 4.2367997 C 1.9968 4.8512 1.9455999 5.0048 2.6239998 5.0944 C 2.7008 5.1712 2.7008 5.44 2.6239998 5.5168 C 2.2015998 5.5039997 1.7536 5.4912 1.3312 5.4912 C 0.9088 5.4912 0.5248 5.5039997 0.1408 5.5168 C 0.063999996 5.44 0.063999996 5.1712 0.1408 5.0944 C 0.8192 5.0176 0.9088 4.8128 1.1647999 4.16 L 2.8032 0.1152 C 2.8799999 -0.076799996 2.9568 -0.15359999 3.1232 -0.15359999 C 3.2512 -0.15359999 3.3407998 -0.076799996 3.4304 0.1408 L 5.1328 4.1472 C 5.376 4.7104 5.5168 5.0304 6.2335997 5.0944 C 6.3104 5.1712 6.3104 5.44 6.2335997 5.5168 C 5.9775996 5.5039997 5.6703997 5.4912 5.3375998 5.4912 C 4.9151998 5.4912 4.48 5.5039997 4.16 5.5168 C 4.0832 5.44 4.0832 5.1712 4.16 5.0944 Z "/>
</symbol>
<symbol id="gEFCBD5CCFA072E8B49E2065B449FDBBF" overflow="visible">
<path d="M 5.6832 4.9536 C 5.9263997 4.9536 6.1568 5.184 6.1568 5.44 C 6.1568 5.7088 5.9136 5.9136 5.568 5.9136 C 5.2352 5.9136 4.6208 5.6959996 4.288 5.2608 C 4.1344 5.3631997 3.712 5.6191998 2.9568 5.6191998 C 1.8176 5.6191998 0.768 4.8512 0.768 3.6736 C 0.768 2.9824 1.0752 2.5856 1.4336 2.24 C 1.0752 1.9327999 0.87039995 1.3823999 0.87039995 0.9472 C 0.87039995 0.48639998 1.1264 0.12799999 1.4591999 -0.038399998 C 0.768 -0.44799998 0.4096 -1.0368 0.4096 -1.5871999 C 0.4096 -2.7008 1.4591999 -3.0463998 2.4448 -3.0463998 C 4.1728 -3.0463998 6.0415998 -2.2144 6.0415998 -0.83199996 C 6.0415998 -0.4224 5.8496 -0.1024 5.4783998 0.2048 C 4.9792 0.61439997 4.0832 0.6272 3.6095998 0.6272 C 3.3792 0.6272 3.0591998 0.6016 2.7519999 0.5632 C 2.56 0.55039996 2.432 0.5376 2.368 0.5376 C 1.9968 0.5376 1.5488 0.7168 1.5488 1.2672 C 1.5488 1.5231999 1.6256 1.7919999 1.7792 2.0096 C 2.0864 1.8304 2.4448 1.7407999 2.944 1.7407999 C 4.0703998 1.7407999 5.1071997 2.4448 5.1071997 3.6992 C 5.1071997 4.3008 4.928 4.6464 4.5568 5.0304 C 4.6464 5.1584 4.9024 5.3375998 5.0688 5.3375998 C 5.1584 5.3375998 5.2479997 5.2992 5.3248 5.184 C 5.376 5.0815997 5.5424 4.9536 5.6832 4.9536 Z M 1.6896 -0.12799999 C 1.8304 -0.1664 2.0351999 -0.192 2.2015998 -0.192 C 2.5983999 -0.192 2.9568 -0.15359999 3.136 -0.15359999 C 3.776 -0.15359999 4.3136 -0.1664 4.6847997 -0.3712 C 5.184 -0.65279996 5.3375998 -0.83199996 5.3375998 -1.1647999 C 5.3375998 -2.0864 3.9808 -2.5728 2.8288 -2.5728 C 2.368 -2.5728 1.2928 -2.2015998 1.2928 -1.3312 C 1.2928 -0.89599997 1.3184 -0.576 1.6896 -0.12799999 Z M 4.0832 3.5712 C 4.0832 2.3808 3.4815998 2.1376 3.008 2.1376 C 1.9327999 2.1376 1.8176 3.0463998 1.8176 3.8655999 C 1.8176 4.7616 2.1376 5.2223997 2.8416 5.2223997 C 3.648 5.2223997 4.0832 4.6335998 4.0832 3.5712 Z "/>
</symbol>
<symbol id="gD5EEFB9760BC9A91B84F628EDDA52971" overflow="visible">
<path d="M 2.1376 5.0432 C 2.0607998 4.9663997 2.0096 4.992 2.0096 5.1071997 L 2.0096 7.4624 C 2.0096 8.2944 2.0607998 8.806399 2.0607998 8.806399 C 2.0607998 8.896 2.0096 8.9344 1.8944 8.9344 C 1.5744 8.806399 0.61439997 8.6272 0.1024 8.588799 C 0.076799996 8.4864 0.1024 8.2816 0.1792 8.2048 C 0.21759999 8.2048 0.25599998 8.2048 0.2944 8.2048 C 0.8576 8.1664 0.9984 8.1664 0.9984 7.1552 L 0.9984 0.9088 C 0.9984 0.4096 0.9856 0.1792 0.9472 0 C 1.0112 -0.1024 1.0752 -0.15359999 1.2287999 -0.15359999 C 1.3055999 -0.076799996 1.4336 0.038399998 1.536 0.15359999 C 1.6639999 0.30719998 1.7407999 0.30719998 1.8815999 0.192 C 2.1759999 -0.0512 2.56 -0.12799999 3.008 -0.12799999 C 4.3136 -0.12799999 5.8367996 1.0624 5.8367996 3.0976 C 5.8367996 4.6591997 4.6847997 5.6191998 3.5712 5.6191998 C 3.0207999 5.6191998 2.5344 5.4016 2.1376 5.0432 Z M 2.2272 4.6464 C 2.56 4.9407997 2.944 5.0559998 3.3151999 5.0559998 C 4.0959997 5.0559998 4.736 4.1088 4.736 2.8672 C 4.736 1.408 4.1472 0.30719998 2.9312 0.30719998 C 2.5344 0.30719998 2.2656 0.5888 2.0096 0.9088 L 2.0096 4.1088 C 2.0096 4.3775997 2.0607998 4.5056 2.2272 4.6464 Z "/>
</symbol>
<symbol id="g83A6AA7A836EACB3652229F4716CDAF" overflow="visible">
<path d="M 5.0559998 8.076799 C 4.3136 8.1792 4.3392 8.4223995 3.0848 8.4223995 C 1.7919999 8.4223995 0.65279996 7.5648 0.65279996 6.2079997 C 0.65279996 4.864 1.7664 4.2496 2.8927999 3.8144 C 3.6608 3.52 4.608 3.1615999 4.608 1.9072 C 4.608 0.87039995 4.032 0.3328 3.008 0.3328 C 1.8176 0.3328 1.0496 0.8832 0.768 2.1504 C 0.6016 2.2015998 0.4736 2.1759999 0.34559998 2.112 C 0.39679998 1.1264 0.44799998 0.79359996 0.6016 0.1664 C 1.408 0.1664 1.7664 -0.12799999 2.9055998 -0.12799999 C 3.4815998 -0.12799999 4.032 0.0128 4.48 0.2944 C 5.2223997 0.75519997 5.6832 1.536 5.6832 2.3552 C 5.6832 3.712 4.6591997 4.3136 3.6095998 4.7104 C 2.8416 4.992 1.5616 5.4783998 1.5616 6.5536 C 1.5616 7.2704 2.2144 7.9872 2.9696 7.9872 C 4.2111998 7.9872 4.608 7.1935997 4.864 6.3487997 C 5.0048 6.3231997 5.1712 6.336 5.2864 6.4256 C 5.2352 7.04 5.184 7.3984 5.0559998 8.076799 Z "/>
</symbol>
<symbol id="gDB4862E33098F259EEBBA99A57E5AFA" overflow="visible">
<path d="M 2.1759999 4.5824 C 2.1632 4.9663997 2.1376 5.4272 2.0736 5.5551996 C 2.0479999 5.6191998 2.0224 5.6576 1.92 5.6576 C 1.5616 5.5168 1.2287999 5.4016 0.34559998 5.2864 C 0.32 5.2096 0.34559998 5.0048 0.3712 4.928 C 1.0624 4.864 1.2032 4.7999997 1.2032 4.0576 L 1.2032 1.5616 C 1.2032 0.51199996 1.0368 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7168 -0.0128 1.2032 0 1.7152 0 C 2.2272 0 2.6239998 -0.0128 3.008 -0.0256 C 3.0848 0.0512 3.0848 0.32 3.008 0.39679998 C 2.3552 0.4608 2.2144 0.51199996 2.2144 1.5616 L 2.2144 3.6608 C 2.2144 3.9296 2.3295999 4.0832 2.432 4.1984 C 2.944 4.6976 3.4176 4.9536 3.8144 4.9536 C 4.3008 4.9536 4.6591997 4.6464 4.6591997 3.7888 L 4.6591997 1.5616 C 4.6591997 0.51199996 4.5568 0.44799998 3.8655999 0.39679998 C 3.8016 0.32 3.8016 0.0512 3.8655999 -0.0256 C 4.1856 -0.0128 4.6591997 0 5.1712 0 C 5.6832 0 6.1056 -0.0128 6.4256 -0.0256 C 6.4895997 0.0512 6.4895997 0.32 6.4256 0.39679998 C 5.7855997 0.44799998 5.6703997 0.51199996 5.6703997 1.5616 L 5.6703997 3.5967999 C 5.6703997 3.776 5.6703997 3.9552 5.6576 4.1088 C 6.272 4.7872 6.848 4.9536 7.3472 4.9536 C 7.8335996 4.9536 8.1152 4.672 8.1152 3.8144 L 8.1152 1.5616 C 8.1152 0.51199996 7.9872 0.44799998 7.3216 0.39679998 C 7.2576 0.32 7.2576 0.0512 7.3216 -0.0256 C 7.6415997 -0.0128 8.1152 0 8.6272 0 C 9.1392 0 9.5872 -0.0128 9.9456 -0.0256 C 10.0096 0.0512 10.0096 0.32 9.9456 0.39679998 C 9.2416 0.44799998 9.1264 0.51199996 9.1264 1.5616 L 9.1264 3.5839999 C 9.1264 4.7232 8.9344 5.6191998 7.8079996 5.6191998 C 7.1552 5.6191998 6.3616 5.376 5.6959996 4.672 C 5.6576 4.6335998 5.5808 4.5696 5.5551996 4.6847997 C 5.44 5.2096 4.9407997 5.6191998 4.2752 5.6191998 C 3.5328 5.6191998 2.8672 5.184 2.3295999 4.5824 C 2.2656 4.5183997 2.1887999 4.4288 2.1759999 4.5824 Z "/>
</symbol>
<symbol id="g793DBE65A5AEC1A16A65955B6C0E046" overflow="visible">
<path d="M 10.368 7.232 L 8.3712 1.6768 L 8.3328 1.6896 L 6.5664 7.0912 C 6.3487997 7.7823997 6.7967997 7.8208 7.232 7.8592 C 7.3087997 7.936 7.3087997 8.2048 7.232 8.2816 C 6.7072 8.2688 6.144 8.256 5.632 8.256 C 5.2096 8.256 4.7616 8.2688 4.3519998 8.2816 C 4.2752 8.2048 4.2752 7.936 4.3519998 7.8592 C 5.0304 7.8208 5.312 7.424 5.4272 7.0912 L 5.7216 6.2464 C 5.7728 6.0927997 5.8111997 5.9648 5.8111997 5.8496 C 5.8111997 5.7216 5.7984 5.6191998 5.6959996 5.4016 L 4.0448 1.6511999 L 3.9808 1.6639999 L 2.112 7.3216 C 1.9583999 7.7696 2.304 7.8335996 2.7519999 7.8592 C 2.8288 7.936 2.8288 8.2048 2.7519999 8.2816 C 2.3295999 8.2688 1.7664 8.256 1.2672 8.256 C 0.8192 8.256 0.44799998 8.2688 0.076799996 8.2816 C 0 8.2048 0 7.936 0.076799996 7.8592 C 0.65279996 7.8208 0.7424 7.8079996 0.9856 7.1168 L 3.392 0.192 C 3.4559999 -0.0128 3.5328 -0.15359999 3.6736 -0.15359999 C 3.84 -0.15359999 3.9167998 -0.0256 4.0064 0.192 L 5.9136 4.48 C 6.0288 4.736 6.0671997 4.7999997 6.1312 4.7999997 C 6.1823997 4.7999997 6.2335997 4.6591997 6.3104 4.4416 L 7.7823997 0.192 C 7.8592 -0.0256 7.9231997 -0.15359999 8.076799 -0.15359999 C 8.2176 -0.15359999 8.3071995 -0.0128 8.3712 0.1792 L 10.943999 7.0783997 C 11.110399 7.5263996 11.340799 7.8208 12.0448 7.8592 C 12.1216 7.936 12.1216 8.2048 12.0448 8.2816 C 11.673599 8.2688 11.264 8.256 10.9312 8.256 C 10.5984 8.256 10.0352 8.2688 9.5232 8.2816 C 9.4464 8.2048 9.4464 7.936 9.5232 7.8592 C 10.047999 7.8208 10.559999 7.7823997 10.368 7.232 Z "/>
</symbol>
<symbol id="gA11612CECC8CBEF18835767DAB11B2F7" overflow="visible">
<path d="M 0.5248 2.6239998 C 0.5248 1.3184 1.3952 -0.12799999 3.2128 -0.12799999 C 4.032 -0.12799999 4.6591997 0.1664 5.0944 0.5888 C 5.6703997 1.152 5.9263997 1.9583999 5.9263997 2.7391999 C 5.9263997 4.0703998 5.1967998 5.6191998 3.2384 5.6191998 C 2.3936 5.6191998 1.7024 5.2736 1.2287999 4.7232 C 0.768 4.1728 0.5248 3.4304 0.5248 2.6239998 Z M 3.0463998 5.1712 C 4.1472 5.1712 4.8255997 4.1728 4.8255997 2.3295999 C 4.8255997 0.7168 3.9936 0.32 3.392 0.32 C 2.0607998 0.32 1.6256 1.9327999 1.6256 2.9183998 C 1.6256 4.032 1.8944 5.1712 3.0463998 5.1712 Z "/>
</symbol>
<symbol id="gCEFEF3D67F35C6E83CC3757B1DD21B13" overflow="visible">
<path d="M 4.2752 0.64 C 4.3392 0.69119996 4.4544 0.7168 4.4672 0.6272 C 4.5056 0.32 4.608 -0.12799999 4.608 -0.12799999 C 4.7104 -0.1664 4.7743998 -0.15359999 4.8512 -0.12799999 C 5.1328 0.1024 5.5808 0.2944 6.3616 0.384 C 6.4384 0.4608 6.4384 0.65279996 6.3616 0.72959995 C 5.5424 0.79359996 5.4272 1.0368 5.4272 1.6639999 L 5.4272 7.4624 C 5.4272 8.2944 5.4783998 8.806399 5.4783998 8.806399 C 5.4783998 8.896 5.4272 8.9344 5.312 8.9344 C 4.992 8.806399 4.032 8.6272 3.52 8.588799 C 3.4944 8.4864 3.52 8.2816 3.5967999 8.2048 C 3.6352 8.2048 3.6736 8.2048 3.712 8.2048 C 4.2752 8.1664 4.416 8.1664 4.416 7.1552 L 4.416 5.5168 C 4.416 5.4272 4.3904 5.4016 4.3008 5.4016 C 4.2496 5.4016 3.7247999 5.6191998 3.3023999 5.6191998 C 2.4575999 5.6191998 1.8944 5.3375998 1.3823999 4.8512 C 0.83199996 4.3008 0.4992 3.5456 0.4992 2.5983999 C 0.4992 1.0239999 1.2928 -0.12799999 2.6752 -0.12799999 C 3.1743999 -0.12799999 3.648 0.12799999 4.2752 0.64 Z M 4.416 1.5871999 C 4.416 1.344 4.3904 1.2415999 4.2111998 1.0879999 C 3.7375998 0.6784 3.3279998 0.4736 3.008 0.4736 C 2.3167999 0.4736 1.5999999 1.2287999 1.5999999 2.8288 C 1.5999999 3.7503998 1.7792 4.2623997 1.9712 4.5312 C 2.368 5.1328 2.9055998 5.1712 3.1615999 5.1712 C 3.6223998 5.1712 3.9424 5.0048 4.1984 4.7104 C 4.3775997 4.5056 4.416 4.416 4.416 4.0192 Z "/>
</symbol>
<symbol id="g645CA8FA3D9155E2CBD9F8EED3C1540D" overflow="visible">
<path d="M 1.9968 4.7104 C 1.984 5.0944 1.9583999 5.4272 1.8944 5.5551996 C 1.8687999 5.6191998 1.8432 5.6576 1.7407999 5.6576 C 1.3823999 5.5168 1.0496 5.4016 0.1664 5.2864 C 0.1408 5.2096 0.1664 5.0048 0.192 4.928 C 0.8832 4.864 1.0239999 4.7999997 1.0239999 4.0576 L 1.0239999 -1.408 C 1.0239999 -2.4703999 0.8832 -2.5344 0.1024 -2.5728 C 0.0256 -2.6496 0.0256 -2.9183998 0.1024 -2.9952 C 0.55039996 -2.9824 1.0239999 -2.9696 1.536 -2.9696 C 2.0479999 -2.9696 2.6624 -2.9824 3.0848 -2.9952 C 3.1615999 -2.9183998 3.1615999 -2.6496 3.0848 -2.5728 C 2.1759999 -2.5216 2.0351999 -2.4703999 2.0351999 -1.408 L 2.0351999 -0.0256 C 2.0351999 0.1408 2.0864 0.12799999 2.2144 0.076799996 C 2.5344 -0.0512 2.9183998 -0.12799999 3.3279998 -0.12799999 C 4.0448 -0.12799999 4.6847997 0.0896 5.2096 0.5888 C 5.8111997 1.1776 6.1568 1.9712 6.1568 3.008 C 6.1568 4.3648 5.1967998 5.6191998 3.8911998 5.6191998 C 3.3023999 5.6191998 2.6496 5.2352 2.1376 4.6591997 C 2.0607998 4.5824 2.0096 4.5824 1.9968 4.7104 Z M 2.24 4.2367997 C 2.5728 4.6464 3.1615999 5.0304 3.5328 5.0304 C 4.3519998 5.0304 5.0559998 4.1088 5.0559998 2.6624 C 5.0559998 1.6128 4.6847997 0.30719998 3.2512 0.30719998 C 3.0207999 0.30719998 2.5728 0.3712 2.3423998 0.576 C 2.0864 0.8064 2.0351999 0.8832 2.0351999 1.344 L 2.0351999 3.6736 C 2.0351999 3.9424 2.0864 4.0576 2.24 4.2367997 Z "/>
</symbol>
<symbol id="g61B7E1470B16535C69F53F42DA9B40BB" overflow="visible">
<path d="M 6.288 7.76 C 6.288 8.912001 5.392 9.76 3.8240001 9.76 C 2.1920002 9.76 1.136 8.784 1.136 7.5520005 C 1.136 6.656 1.5680001 6.0000005 2.5440001 5.392 L 2.96 5.136 C 2.496 4.8960004 2.0640001 4.6080003 1.664 4.256 C 1.008 3.68 0.73600006 2.96 0.73600006 2.3360002 C 0.73600006 0.70400006 1.8880001 -0.16000001 3.584 -0.16000001 C 5.6800003 -0.16000001 6.7040005 1.376 6.7040005 2.592 C 6.7040005 3.5200002 6.3040004 4.3360004 5.4560003 4.848 L 4.32 5.5360003 C 5.072 5.9040003 6.288 6.7360005 6.288 7.76 Z M 3.6160002 0.4 C 2.8960001 0.4 1.8080001 0.896 1.8080001 2.3360002 C 1.8080001 2.8160002 2.016 3.936 3.3920002 4.848 L 4.144 4.4 C 5.136 3.7920003 5.5360003 3.0400002 5.5360003 2.272 C 5.5360003 0.67200005 4.3360004 0.4 3.6160002 0.4 Z M 3.7440002 9.200001 C 4.7840004 9.200001 5.168 8.512 5.168 7.7760005 C 5.168 6.912 4.32 6.1920004 3.8880002 5.872 L 3.3920002 6.176 C 2.384 6.8320003 2.272 7.36 2.272 7.8560004 C 2.272 8.592 2.7840002 9.200001 3.7440002 9.200001 Z "/>
</symbol>
<symbol id="g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" overflow="visible">
<path d="M 4.688 10.336 L 4.032 10.336 L 0.24000001 -0.94400007 L 0.896 -0.94400007 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
</defs>
</div>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(40 16.58)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="8.99" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.280000000000001" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.39" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gBFFDA84A1400D9E1136DF0DD93EA19F5" x="25.02" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEC3CC7DEE79E0AA801DFAAEF4B6C0B50" x="30.669999999999998" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g202CCBD46865F83C12D50E1B4FF9BBEA" x="36.43" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="41.35" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g5503E15E5E4E70E9E217A15BD1ECD752" x="46.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="49.75" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="55.379999999999995" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 25.159999999999997)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 27.159999999999997)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.64 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 42.31999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(393.5458818897638 10)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6D39B87B7095296261A07873F9B99896" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1B61845C1FB429ACDF5304290F5BF286" x="8.339999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC66F55FB8F08DA72FE76D3863D88042" x="13.511999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="20.003999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g48BCA4F06942DA5990D42018985FC781" x="26.759999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g45E4C10E27056C5AE488FE2D8290DF06" x="32.891999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="36.623999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FB89403B37B0F0F934DFEB7E5171B37" x="42.971999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFF269982F0E4C510F3A3BFF016D72390" x="50.303999999999995" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 10.296000000000001)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(6.768 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 28.488)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5ABA589ED074A65FC8C929AB4EB2344C" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 38.784)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(743.9997637795276 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g97A8E46F7A64F11D13C6F357868587EE" x="9.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.25" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.36" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gB844DCFB76B4CC44608DB013C9764E9C" x="24.89" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="30.37" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="35.14" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="41.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="46.58" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="52.599999999999994" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 15.16)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 60)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6C3A310EEC8A7EBBD176D179125951F0" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(9.528 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g2F0CE4BDC8DA4B92139017B781562218" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8D84A54D9303B24762DC3071B60ECD14" x="17.76" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3E9095A1FBD7854ED5F7B53469C97011" x="25.560000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g90B91206A818BADA9956CC42F47E57A0" x="38.064" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAC1066A28E7625F16F6C949E2F432C61" x="43.92" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.78399999999999 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g10BFE5E41011FF0F560FA08FAB260218" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(75.312 15.48)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(81.312 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gFC5C8D23DE5E426807758A924FDBA2FC" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB6675D993E92546012E46240B36958EC" x="12.096" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g9AEC0E315A165F115D211DDAB68AA0F8" x="23.832" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g767CEF02C917BBE3F159A8F04079F311" x="35.976" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g9CBC2DB69173A0577335373434CDCDA4" x="46.056" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2825DE3DACAF761B898A0442866AE569" x="57" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 39.48)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE7450862BF743B056E90C8779357A05F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="10.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g4EF2739944C6201AFAD05FE6C63B0B9E" x="19.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="33.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="44.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="53.379999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="61.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="76.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="86.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="97.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="102.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="113.28" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(232.56692913385828 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.58692913385826 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="8.940000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="19.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g98926218EB374AD77A2D864C6D10734B" x="29.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="40.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="51.019999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="57.339999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="65.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="80.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="90.89999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="100.97999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="106.39999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="117.24" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g757CB60871AF468909C575234729D90A" x="128.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="134.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="142.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="151.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF5D967C73B153E080367AE40708278EE" x="157.34" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 50.31999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 50.31999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="8.940000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="15.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="24.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="38.839999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="49.459999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="65.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="75.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="84.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="96.69999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="106.77999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="117.97999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="128.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="137.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="143.17999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="153.17999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="163.93999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="173.99999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="184.07999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="191.51999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="204.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="210.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="225.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="233.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="242.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="251.60000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="258.88" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="267.44" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 74.32)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC46470BA400E4AE9E0CCFB3B379C9D5C" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(14.44 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gC3F91E6BB9F8304E319658F9D45F8B38" x="9.719999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="22.759999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="28.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="35.98" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="41.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="47.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="56.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="71.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="79.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="88.66" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.04461942257217 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g92446B7A6A7F78674F0F5568B7ED0AC5" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(169.48461942257217 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA335A20E4C1D7F39210005AFF7F1A0EF" x="9.652309711286076" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="22.572309711286078" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="31.71230971128608" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="42.55230971128608" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="52.672309711286076" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="58.09230971128608" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="68.21230971128608" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="77.35230971128608" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="83.67230971128609" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="97.54461942257217" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="105.34461942257217" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="114.28461942257216" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(310.08923884514434 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g278A59F111DD0614EC58EAA01A502EFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(330.08923884514434 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="9.062309711286074" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="23.042309711286073" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="31.982309711286074" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="37.40230971128607" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="47.40230971128607" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="58.16230971128607" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="68.22230971128607" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="78.30230971128607" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="90.08461942257215" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="99.78461942257215" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="108.72461942257215" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 125.63999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="14.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="25.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="31.119999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="36.4" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(50.339999999999996 125.63999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g92446B7A6A7F78674F0F5568B7ED0AC5" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(64.78 125.63999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="10.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="23.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="34.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="44.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="55.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="64.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="80.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="90.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g21D1E528F66DB45787699F71DA377CC5" x="96.9" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="107.2" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 138.64)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 0)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDACA5EBB44D5F3DB530A1F5F650BFBAB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="10.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="16.240000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="24.8" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40.03999999999999 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C8BFD035DDE11C1B8F6EB4DD490B55D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(49.19999999999999 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="9.719999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="18.279999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="23.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="33.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="41.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="50.379999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="58.17999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="69.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="80.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="90.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="95.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="106.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="117.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="124" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(188.27999999999997 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g629AE7F75F47B1FD947FFA2989B5B47D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.88 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="11.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="18.479999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="28.559999999999995" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(247.24 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g92446B7A6A7F78674F0F5568B7ED0AC5" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 39.82)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 26.66)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDACA5EBB44D5F3DB530A1F5F650BFBAB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="10.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="16.240000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="24.8" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40.03999999999999 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g520D89691A96D56AE5196D136E86D2C6" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(51.63999999999999 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="9.719999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="15.919999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="25.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="32.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="38.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="49.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="58.519999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="66.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="77.63999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="88.15999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="98.23999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="103.65999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="114.49999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="125.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="132.14" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(198.86 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g629AE7F75F47B1FD947FFA2989B5B47D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(208.46 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="11.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="18.479999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="28.559999999999995" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(257.82000000000005 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g278A59F111DD0614EC58EAA01A502EFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 66.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 53.32)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="5.42" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(16.619999999999997 0)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6B54F166BDD11A6B5982665EE5474C84" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(16.639999999999997 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC2DD8543DFECD814014D8080F661102C" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(24.419999999999998 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C8BFD035DDE11C1B8F6EB4DD490B55D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(33.58 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5086E516F5DAE44F1BD2167760C4A5F1" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(42.47333333333333 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g629AE7F75F47B1FD947FFA2989B5B47D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(52.07333333333333 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g62484110D9EA4D906DF8002209024D54" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.40888888888888 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5A3E6390ABDCC3643B02834E2D933712" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(103.14444444444443 0)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6B54F166BDD11A6B5982665EE5474C84" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(16.639999999999997 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC2DD8543DFECD814014D8080F661102C" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(24.419999999999998 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g520D89691A96D56AE5196D136E86D2C6" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.019999999999996 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5086E516F5DAE44F1BD2167760C4A5F1" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(44.91333333333332 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g629AE7F75F47B1FD947FFA2989B5B47D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(54.51333333333332 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g62484110D9EA4D906DF8002209024D54" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(165.43777777777774 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="9.719999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="17.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="23.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="33.92" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 93.14)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 79.98)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gA335A20E4C1D7F39210005AFF7F1A0EF" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="12.920000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="23.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="32.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="41.31999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="56.559999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="65.69999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="70.97999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="81.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="92.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="101.03999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="106.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="116.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="127.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="137.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="147.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="154.8" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(167.6 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE451DF5392AF56A17EDB1EB9E2655F47" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.92 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="15.08" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(203.20000000000002 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C8BFD035DDE11C1B8F6EB4DD490B55D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.82)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g612BB0D9B453ACEC45B2B13686D7BB71" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.5 26.66)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="5.42" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(16.619999999999997 0)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6B54F166BDD11A6B5982665EE5474C84" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(16.639999999999997 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC2DD8543DFECD814014D8080F661102C" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(24.419999999999998 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE451DF5392AF56A17EDB1EB9E2655F47" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(33.739999999999995 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5086E516F5DAE44F1BD2167760C4A5F1" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(42.633333333333326 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g629AE7F75F47B1FD947FFA2989B5B47D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(52.23333333333333 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g62484110D9EA4D906DF8002209024D54" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.56888888888888 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gFF563528CC412172074F774399BF4710" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(103.30444444444443 0)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6B54F166BDD11A6B5982665EE5474C84" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(16.639999999999997 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC2DD8543DFECD814014D8080F661102C" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(24.419999999999998 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g520D89691A96D56AE5196D136E86D2C6" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.019999999999996 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5086E516F5DAE44F1BD2167760C4A5F1" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(44.91333333333332 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g629AE7F75F47B1FD947FFA2989B5B47D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(54.51333333333332 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g62484110D9EA4D906DF8002209024D54" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(165.59777777777774 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(178.59777777777774 6.660000000000001)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 1.52 0 "/>
</g>
<g transform="translate(170.59777777777774 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="10.08" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(188.11777777777775 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(193.11777777777775 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE1442E8CAAFDCA3BCCB763C26EB6A12C" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(198.67777777777775 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g278A59F111DD0614EC58EAA01A502EFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.67777777777775 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE1442E8CAAFDCA3BCCB763C26EB6A12C" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(229.79333333333332 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gFF563528CC412172074F774399BF4710" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(250.90888888888884 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE451DF5392AF56A17EDB1EB9E2655F47" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(260.22888888888883 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g520D89691A96D56AE5196D136E86D2C6" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 37.66)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g7CDEAAC4FEAEC30DB2F902B0A7AF7CE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.96 0)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g92446B7A6A7F78674F0F5568B7ED0AC5" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(14.44 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="4.3999999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="13.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="23.659999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g757CB60871AF468909C575234729D90A" x="33.779999999999994" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(54.18000000000001 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE451DF5392AF56A17EDB1EB9E2655F47" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(63.50000000000001 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gF5D967C73B153E080367AE40708278EE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(215.30692913385826 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g7CDEAAC4FEAEC30DB2F902B0A7AF7CE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(236.26692913385827 0)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g278A59F111DD0614EC58EAA01A502EFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="4.3999999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="13.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="23.659999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g757CB60871AF468909C575234729D90A" x="33.779999999999994" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.74 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE451DF5392AF56A17EDB1EB9E2655F47" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(69.06 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gF5D967C73B153E080367AE40708278EE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(494.80944881889764 0)">
<g class="typst-group">
<g>
<g transform="translate(0.000000000000014322751209022492 0)">
<image xlink:href="data:image/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgFBgcGBQgHBgcJCAgJDBMMDAsLDBgREg4THBgdHRsYGxofIywlHyEqIRobJjQnKi4vMTIxHiU2OjYwOiwwMTD/2wBDAQgJCQwKDBcMDBcwIBsgMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDAwMDD/wAARCAV0BDcDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwD3+iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKZLIkS7pGVVHUk4oAfRWNc+KvD1qxFzr2lwEdRJdxqf1NZ1x8RvBkORJ4n0vj+5cK38s0AdVRXFv8WfAsfB8SWh+gc/yWq7/GLwGnXxDE3+7FIf/ZaAO8orz2T42eAVH/IbJ+ltKf8A2WoW+OfgFf8AmKzt9LSX/wCJoA9IorzH/hfPgRf+X27f6Wr/ANajb4+eBx0m1A/S2P8AjQB6lRXlL/tAeCv4f7Sb6Ww/q1Rv+0N4NTpb6u30t0/q9AHrVFePyftF+FAMx6fqzfWOMf8As5qpL+0joA/1Wiak31ZB/WgD2uivCpf2lLDH7nw5ct/vXKj+SmqU/wC0rN/yw8LqPd7w/wDxFAH0FRXzZP8AtI64f+PfQtOj/wB95G/kRVCf9onxa/8AqrLSoj7Quf5tQB9RUV8nzfHzxxJnbcWMX+5bD+pNUJ/jT4+m6a6Yx/sW0Q/9lNAH1/RXxhP8UfHE+d3ia+H+44T+QFUpfHni6f8A1viTVX/7en/xoA+3KK+F5PE/iCQnzNc1Nvrdyf41A+s6pJ9/Urxv964Y/wBaAPuzco6laTzUHV1/Ovg1r27b791O31kJ/rURkdvvuzfVqAPvXz4f+eqD/gQppvLUHBuYR/wMV8E7jRmgD70OoWQPN3AP+2q/40n9pWP/AD+2/wD39X/GvgyjHtQB95/2lp//AD/W/wD3+X/Gj+1NP/5/rb/v8v8AjXwZj2ox7UAfef8Aamn/APP9a/8Af5f8aP7U0/8A5/rX/v8AL/jXwZj2ox7UAfef9qaf/wA/1r/3+X/Gj+1NP/5/rX/v8v8AjXwZj2ox7UAfef8AaWn/APP7a/8Af1f8act7Zv8AduoG+kg/xr4K5ozQB98iWE9JEP0YU8MD0INfAoZh90kfjVmHU7+H/UXtzHj+5Mw/rQB950V8LxeKfEEP+q1zUkx6XUn+NaVv8Q/GVuB5XibVAB2NyzD8iaAPtaivjy2+MPju3xjX5XA7Swxt+pXNbNr+0B41hx5v9nXA/wCmlvjP/fJFAH1VRXzhZ/tJaumPtvh+ym9fKmeP+e6t2y/aT0t8fbfD91DnqYp1f+YFAHuVFeVWX7QHgqcf6QdRtT3822z/AOgsa2bT4x+BLoZXXo489pYnT+a0Ad5RXMWvxD8HXX+p8TaXk/37lE/9CIrUg8QaPcjNvq9hKOxjuUb+RoA06Kgju7eT7k8TD2cGpqAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACszX9ZsdB0m51PVpxBa2y73Y/oB6kngDvWma+V/j38QT4o1ttH0yYnSbCQgsp4nmHBb3A6D8T3oA9C039obQbu/aG60y6srbDFJ3dWyQMgMoHGenBNeF+NPGuteLtQkutXvZWRnzFbK5EUS9gq9Px6nvWf4e0i817WLbTdOieae4kCABc4GeSfQAc5r1Z/2ddb/tryU1SzOmb/APXkt5oTP/PPGN2PfFAHiuaM19r6V4B8Kadawww6Bp7mONV8yS2R2bAxkkg5JrWh0LSIf9TpVlFj+7bov8hQB8KKjN91S305qeOxu3+5azN/uxE/0r7uW2hQYSCNR7IBUioq/dUD8KAPhJNH1Nvu6beN9Ldj/SpV8Pa2/wB3RdQP0tZP8K+66KAPhhfCviFvu6Dqh/7dJP8ACpV8G+J2+74d1U/9ucn+FfcVFAHxCvgbxW33fDOrH/tzk/wqVfh54xbp4X1f/wAA3/wr7ZooA+K4/hr41Y8eGNT/AOBW5H86tRfCnx1J08NXY/3ti/zYV9lUUAfH8PwX8fS/8wIp/vXMQ/8AZqvQfAjxzJ96ytI/966T+ma+sqKAPlu3/Z48YS/6260uH/emc/yU1oQfs2663/HxrunR/wC4kjfzAr6UooA+e4P2aZ/+W3iaP/gNof6tV+L9muwXHneI7l/9y2UfzY17rRQB4xD+zj4dX/Xatqb/AO75a/8AsprQg/Z88GR/fk1SX/fuVH8lFer0UAeaQ/AjwJH96xuZP9+6f+hFWU+CPgFf+YMzfW5l/wDiq9CooA4RPg34CT/mX4m+s0p/9mqX/hUngL/oW7b/AL7k/wDiq7aigDi/+FTeA/8AoW7T/vp//iqd/wAKr8C/9C1Zfk3+NdlRQBx//CrfA/8A0LNh/wB8H/Gj/hWHgb/oWbD/AL4/+vXYUUAcj/wrDwR/0LOnf9+//r0f8Kw8Ef8AQs6f/wB+666igDkf+FYeCP8AoWdP/wC/dH/CsPBH/Qs6f/37rrqKAOR/4Vh4I/6FnT/+/dH/AArDwR/0LOn/APfuuuooA5H/AIVh4I/6FnT/APv3/wDXpp+Fngc9fDVj/wB8kf1rsKKAOKf4SeA3PPhu1/BnH8mqrP8ABfwFN/zAwn+5PIP/AGau/ooA8zn+A/gOT7tjdxf7l0/9Sazrn9njwhJzBd6rAfaZGH6rn9a9dooA8OuP2bNLfP2bxBeR/wDXSFX/AJEVi3n7NeoLk2XiK1k9BLbsn6gmvouigD5Wvv2fPGduf9HfTrsf9M5yv/oSisO8+D3ju0LbtAllC94ZY3/QNn9K+xaKAPiC88E+KLIZuvD2px+5tX/wrIubK6tji6tp4T6SIV/mK+9qZJGkgw6Kw9CM0AfAlJX3Vc+HNEusm50fTpv+ulsjfzFZs/w+8IXH+s8NaXz6Wyr/ACAoA+K45JI/uuy/Q4qwmpX8Z+S+uU/3ZWH9a+wJfhR4Fm+/4as1/wB3cv8AI1Sm+CvgGXroQT/duZh/7PQB8rJ4m12P/U63qKf7t3IP/ZqsxeNvFUP+r8S6wn0vpf8A4qvpR/gP4Eb7tjdR/wC7dv8A1JqtJ+z94Kc8f2kn+7cj+q0AeAQfEjxnF9zxNqfH964Zv55q1H8WfHcR+XxJdn/eCN/Na9sl/Z28It/q7vVU/wC2yH/2Sqkv7OHh5s+VrOqL9fLP/sooA8oh+NHj2I5/t0v/AL8EZ/8AZauw/Hjx3GfmvrWT/etU/oBXfS/s16cf9T4ju0/3rZW/kRVGf9mpx/qPE6t/v2JH/s5oA52D9oXxlH9+DSpf96Bh/JxV+D9o/wARL/r9H0yT/c8xf6mpZv2bdYH+p1+xf/fidf8AGqc/7OvilP8AVajpUv8AwOQfzWgDTi/aU1AH994ctmH+zcsP5qauxftKrgeb4XP/AAG9/wAUrkZ/2f8AxrH90adL/uXJ/qoqrJ8CvHifd023k/3btP6kUAd8n7Stmfv+GJ1+l4p/9kqVf2k9M/i8PXX4Tqf6V5o/wS8fr/zAw30uov8A4qom+DPj5evh9z9LiI/+zUAepf8ADSWkf9AC+/7/ACUv/DSWjf8AQAv/APv6leVf8Kd8ef8AQvTf9/Y//iqb/wAKf8ef9C7cf9/Y/wD4qgD1f/hpLRf+gDqH/f1KP+GktF/6AWof9/E/xryf/hUHjv8A6Fy4/wC/kf8A8VR/wqHx5/0Ltx/38j/+KoA9Y/4aS0X/AKAWof8AfxP8aeP2ktCxzoWo/wDfcf8AjXkf/CovHn/Quz/9/I//AIqk/wCFR+PP+hcuf++k/wDiqAPYE/aR8PH7+i6ov08s/wDs1Wof2ivCbffsNWj/AN6OM/yevEX+FPjlOvhq9P02n+RqCT4a+NI/v+GdT/CAn+VAHvyftB+DCMsmpD/tgP8A4qnf8NBeCfXUv/AYf/FV88f8IF4uXr4Z1X/wFf8Awpv/AAgfi3/oW9V/8BX/AMKAPoSX9oXwYnKRapJ7C3UfzaqFz+0h4eT/AI9dF1OX/roY0/kxrw6L4feMHOF8M6ofrbOP6VctvhV45uTiPw1eL/vhU/8AQiKAPUZ/2lov+Xfwy5/37wf0WqbftK3n8Phq3/G7b/4muPg+B3j2UZbSYYf+ul1F/RjVxPgD42b78dgn1uf8AaAOi/4aV1D/AKFu2/8AAlv/AImmP+0nqh+54etF+s7n+lYf/DPvjX10z/wJP/xNOj/Z78Zs2Gl0tB6/aGP/ALLQBYn/AGivFrn91ZaTEP8ArjIx/Pf/AEqlP8f/ABtJ91tOj/3Lc/1ateL9m/X2A87WtMjPookb+gq1F+zVqJ/1viO1T/dtmb+ZFAHLf8L28d7s/wBo230+yJj+VaVh+0N4st8C6tdLux3LQsjfmGx+ldF/wzOdv/I1fN/14cf+jK5jxj8D73wvpM+p3niPTBaQDO6VXRmPZVAByx9M0Aa//DSWsbf+QBZbvXzn/lWbP+0P4ue6EkVppkUIOfK8pzuHoTuz+WK8jA9a7X4afDzU/HepNHb/AOi6fCR9ovGXKr6KvTcx9O3U0AfVPgbxDF4r8LWGsxxmL7VHloyc7WBKsM9xkHFb4rJ8MaJaeG9Cs9I05SLe1j2qW6sepY+5JJNawoAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoorjvif44tPA3hyS+m2yXsuY7SD/no/qf8AZHUn8OpoA439oP4i/wBh6c3hzSZf+JleJ/pDoebeI9vZm7eg57ivnPRdMu9Z1O207T4WmurmQRRIO5P8h3J7U3VNSu9X1Ce/v5TNc3LmSWQ9WY19H/s//DoaDpo8QaxF/wATO9T9xGy828R/kzd/QcetAHa/DvwXY+CvDsFjbIkl2RuubkIN0sh68/3R0A9BXW0gGKWgBMUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFUtU1G10rT57+/nSC2t0MkkjHhQKAK/iPXtP8N6PNqerTiC2gHJJ5J7Ko7k9hXyR8TPH+peO9ZNxcbobCEkWtoD8sY9W9XPc/gOKsfFT4hXXjrWdw3Q6Vbki1tv03t6sf0HA75PhZ8O73x3q+357fS7Yj7TcY/8AHF7Fj+g5PbIAvwq+HV9471THzW+kwEfabkj/AMcX1Y/kOp7A/WGhaNp+g6XDpmk2y21rAuFRB+ZJ7k+p5NGiaRZaDplvpuk2yWtrANqoo/UnuT1J61p0AJgelLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUVE7LGpZmAAGSTwAKAKGv6xY6Do11qepzLDa2yF2Y9T6ADuSeAO5r49+Ifi++8a+IZdTvCyRD5LaDORDHngfU9Se5rqPjl8RW8X6x/Zulyk6LZMQjA8XEg4Ln27D2571h/CrwLc+OPEiWuTHp9viS8nH8Cf3Qf7x6D8T2oA634AfDY+IdRTxDrEf/ABK7STMEbLxcyj69VU9fU8etfTg4Aqrptjb6ZYwWVjEsNtboI4416Ko4Aq1QAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACV8u/Hn4lHxNqJ0PR5SdIs3+d1bAuZB391Hb1PPpXc/tB/EYaRYv4X0Wf/AImF0n+lyoeYYj/CD2Zh+S/UV896NpN3rWq22nadCZrq5cRoo9fU+gHUnsKANn4deDb7xtr8em2SlIR89zcbciGPufqegHc+2a+vvDWhWPhrR7fStKgEVrbrhRjlj3Zj3JPJNZXw28G2fgjw7HploBJcPh7qfHMr46/7o6AenvmusoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArwn9ob4k/Y4pPCeiT/AL+YYv5Ub/Vqf+WQPqR19Bx3Ndr8YviBF4H0Ei3ZX1i8UraoTnb2MhHoO3qfxr5LlluL66eWZ3uLidyzMx3M7seT7kmgC34f0W+8Raza6VpcRlurlwqjsB3YnsAOSfSvsTwD4QsfBXh6HS7Fd7D5p5iMNNIerH27AdhXLfA34dL4P0b+0NThH9s3qgyZ6wJ1EY9+59+O1en0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUGgBKKSue8b6s2laKxiOJ5z5cft6n8BSk+VXZpSpyqzVOO7MrxN41+yTtaaWqSSJkNM33VPoB3I/KuQfxLrcjbm1GcE+hAH5VlEnJPX3peorzJVpN7n3eHyyhQppOKb89TodP8a6xZsPOlW6jHVZFGfzFd54a8S2muRkIGhnQZeJ+o9we4ryKtjwZM8XiazMR4d9je6kc1dGtLmSZyZhllCVKVSC5WlfQ9iHNLSLS16J8WFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFcT8VvHlt4G8Ntc5V9QnzHaQn+J/7xH90dT+A710HiXXbLw3o1zquqS+VbW67j6ueyqO7E8AV8dePPFl/wCMvEU+q6i2AflhhBysKDoo/qe55oAxr+9uNSvp729lea5uHMksjclmJyTX0x8BPh0fDGmDW9XhA1W9T5FYc20R6L7Mep9BgetcP+z78ODq90nibW7fNhbtmziYf66QH75HdVP5n6V9KUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVj+JtfsfDWi3Wrao/lwWy5I7s3ZV9STwK16+VPj38QP+Er13+zNMlzpGmsVQg8TydGf3A6D2ye9AHF+M/E194s1+61bUmy8xwiA/LEg+6g9gPzPNes/s8fDj7RJH4s1u3/AHSHOnxOPvMP+WpHoOg9+ewrgvhF4Em8ceJFimV00u1xJdyjjjsgPq36DJr67tbeK0tYbe3jSKKFQkcaDAUAYAA9AKALAHc9aWiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooqC7uobWIyXE0UKDq0jhR+ZoAnorlNV+JHg7SwRd+I9PDDqsUvmt+SZNclqX7QXg+0LLZpf37DoY4Qin8WIP6UAesUV89ap+0ncNkaT4fiT0e4nLY/AAfzrktT+O3ji/DLBd21ip7W8C5/NsmgD6yrM1PxFo2lLu1LVbK0Hfzp1TH5mvjLVfGXiXVsjUdd1CdT1QzsF/75BxWI7EtuLEse5oA+u9U+NHgWwyv9sfaWHa2iZ/1wB+tctqH7R+gRErp2jahdEd5WSIH8ix/SvnSy0+91BythZ3F0/8AdhiZz+gNdPpvwt8b6jg2/hy8VW6NMBEP/HyKAPVP+Glbfd83hmTb/wBfgz/6DXp3w98daZ460przTleGSFts1vMRvjJ5HTqD2NfKHiPwL4l8N3SW+q6RcI8gBRox5itnsGXIz7da96/Z28Eaj4a0q/1TV43tZ9S8sR27DDLGuSCw7ElunUD60AevV5x8T7gvqdtbjpHGX/P/APVXpFeXfEpWXxEG7GBcfmRXPiH7h62TxTxUbnK0CjrRXmH3gtdb8N9Ka61Fr+QDyrcEL7sf8BWDoelT6vfpa2wI7u/ZV7n/AAr1/S7CDTLKO1tV2xoMfX1P1NdeHpNvmfQ+fzjHKnTdGHxS/BFylpKWvQPjQooooAKKKKACiiigAooooAKKKKACiivLPj/46/4Rfw7/AGVp8uzVNUUqCDzFD0d/Yn7o/E9qAPKPj58QP+Eo13+ydMmJ0nTnIBU8TSjhn9wOg/E96wvhL4Fm8c+I1t3DppttiS8lHZc8ID/ebp7DJ7VyemWFzqmo29hZQtLc3LrFEg6sxOBX2T8OfCNr4K8M22l24Vpv9Zcygf62Qjk/QdB7CgDobGzgsbOG0tIlhggURxxoMBFAwAKs0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRXN+PfFdj4O8O3OrX5Vig2wQ5wZpT91R/MnsMmgDhP2hPiD/YGj/8I/pkuNTv0/fMh5hgPB+jN0Htk+lfN+i6Zd6zqdtp2nwtLdXTiONB3J/kO5PYU/XdZvde1e61PUpjLc3TmRz/ACA9gOB7V9B/s7/D7+yLAeJ9XhxfXaYtUYcxRH+L2Lf+g/U0AehfD3wjaeCvDUGl22HkHz3EwGDLKerfTsB2Arp6KKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoqlf6tp2nJuv762tR/03mWP+ZrmNS+KvgjTifO8R2khHUQbpv8A0AGgDtKK8l1L9oLwdbcWseo3p/6ZwhR/48R/Kudv/wBpOIZGneG3b0M10B+gU/zoA98or5h1H9orxRMSLHTtMtB2JR5GH4lsfpXO3/xn8eX551trdfSCGNP1xn9aAPsCqF9rWl2Ck3+pWdoF6madU/mRXxVqXi3xHqTH7frmo3APaS5cj8s4rId2dizsWY9ycmgD7G1D4reB9PJE3iO0cjtBul/9BBFc5qH7QXg22yLVdQvD2McG0fmzA/pXy7DFJM4SGN5HPRVBJP5VtWHgvxPqODZeH9SmB/iFs+PzIoA9k1D9pOIZGm+HGY9muLkLj8AD/Oua1H9oXxbc5Frb6bZDttiZ2/MsR+lYlh8FPHd4Ru0dbVT/ABTzxr+gJP6V0+mfs46/Ng6lrGn2oPaJXlI/MKP1oA4fVPil421LIn8Q3kaHqsBEI/8AHAK5i91K91CTffXc9y396aVnP5kmvonTf2cdChYHUdZv7ojtCqRD9Q1dZp3wa8DWGD/YwuXHe4meT9CcfpQB8hqrOwVAWJ6AVt6V4L8T6vj+ztB1CcHoy27Bf++iMfrX2ZpmgaPpQA03SbK0A/54W6J/ICtOgD5N0v4FeOb/AAZbK2sAe9zOP5LuP6V1ul/s23L4Oq+IYo/VbaAt+rEfyr6GooA8l039n7whagfbZdRvmHXzJgin8FAP6112lfDfwbpWPsnhywyOjSxea35vk11lFAEFvbRW8Yjt4khjHRI1CgflU4FFFABRRRQAlcv418PtrFosttj7VDnaDwHHdf8ACupoqZRUlZmtGrKjNVIbo8LuLC8t5THPazI/psNamieFdS1V8mFreDvLIv8AIHk169jHQUv6VzrCxTue5Uz6tKHLGKT7mXoejWui2ggtlyf4nI+Zj6mtMCjmlAxXUkoqyPAnOU5OU3dsWiiigkKKKKACiiigAooooAKKKKACiiigDO1vVbbRtKutS1CQRW1rG0kj+w9Pc9APWvjLxx4luvFviS81i9JBmbEceciKMcKo+g/M5NesftM+NvOni8JafKTHCVlvmU9W6oh+n3j749K8w+G3hO48aeKrXSotywZ8y5lH/LOIfeP1PQe5oA9a/Zp8DeXC/i3UogXcNDYKw6L0aT8fuj2z6173VXT7O3sLSG0s4lit7dBHEijhVAwAPwq1QAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAEE80cEEk80ixwxqXdmOAqgZJJ9AK+RPjF47k8beI3e3dl0qzPl2cZOMju5Hqf0GBXpH7SHxCMEZ8JaTL88ih7+RD0U8iL8ep9sDua8U8J+H7zxTr9rpOnLma4blj0jT+Jz7Ac0Adp8C/h83i/Xvt2ow50ewYNLuHEz9Vj+nc+3Hevq6NAqgBQqgYAHasfwj4esfC2hWuk6cm2G3XBbvI3d29yea2qAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiq80sdvC80ziOJAXZnOAoHUk9hWDonj/wrr+oHT9J1u2ubsZxEpILY67cgBvwzQB01FFFABRRRQAUUUUAFFFFABRRRQAUUVFPNHAhkmlSNR3dgB+tAEtFctqvxF8IaQSL3xFYBh1SOUSN+S5Ncbq/7QfhKyBFhDf6g3bbEI1/NiD+lAHrdFfOerftI6hLkaRoNtAOzXMrSH8l2/wA647V/jR461IFRq4s0P8NrCqfrgt+tAH1zI4jUs7qqjuxxXO6r4/8ACekMRf8AiHT42HVFmDsP+Ark18c6nrur6sSdT1S8u89RNOzj8iazhyfrQB9Uat8f/BlmWWza+1Bh0MMG1T+LkH9K5LVv2kZOV0jw+g9Gup8/+OqB/OvHdK8JeINXI/szRL+6B/ijgYr/AN9Yx+tdbpXwM8c3+1pNPgskPe5uFGPwXJ/SgCzqnx68a3uRbT2dgD/zwtwT+b5rk9T8e+LNUY/bfEWoup6qLhkX8lIFeoaX+zdfvg6t4gt4PVLaBpP1JH8q6vSv2ePCtqAb661C/buDIsa/koz+tAHzLLNJNIXlkeRz1LNnP50kUUkz7Ykd2PZVJ/lX2Ppfwq8EafgweHLRyOhuAZj/AOPEit+CDRtHZIbeKwsWf5URAkRb0AAxmgD41sPBHinUcfYvDupyg9G+zOB+ZAFdHp3wS8d3uCdKS1B73E6L+gJP6V9d5ooA+ZbH9nTxJLze6pptt7KXkP8AID9a6PT/ANmyyXB1DxHcSnuILdU/Uk/yr3eigDyzT/gD4KtcG4jvr5u4luSoP/fAB/Wul074Z+C9Ox9n8N2DEdGlj80/m2a66igCnZ6dY2K7bKzt7ZB2iiVB+gq3mlooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK5r4h+K7bwd4Xu9WuMM6DZBEf8AlrIfur/U+wNdGePYCvkz45ePP+Ew8Sta2MhOlacWjgAPEr9Gk/HoPYe9AHAalfXOpahcXt7IZbi5cyyOepYnJNfU3wE8Ff8ACLeEUvbyPZqWqhZZtw5SP+BPyOT7n2rxz4EeBf8AhLPE63l9Hv0rTCss2RxLJ1WP+p9hjvX1h6ADAoAUUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXFfFbxvB4I8Ly3eVfULjMVlEed0mPvEf3V6n8B3rq9RvbfTLKe9vpVhtrdDJJIx4VQMk18dfFDxndeN/E02oPmO0izHaQk/cjzxn/AGj1P5dqAOZurq4v7yW5uZGmuLiQyO55Z3JyT+dfVHwJ+Hw8I6B/aGoxY1fUFDSbusMfVY/r3Pvx2rzH9nnwANa1YeI9Tizp9i+LdGH+unHf3C9frj0NfTYoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoorz34yeP4vBHh8i0YNq96Clsuf9WOhkI9B29T+NAHnn7RXxCMs7eEdGmIiQj+0JEP3m6iLPoOp9+Oxryf4fwXVx420OGwLC4N7FtZeowwJP4AGsYma8ucDfPcTv7szuT+pJr6r+D3w1tPCGkW1/qFsr6/MhMkrHJgB/5Zr2HHUjknPOKAPS6KKKACisHxD4z8OeHcjWNZs7Vx1jaQGT/vkZP6V5x4h/aJ8O2m6PRdPvNSkXo8mIYz+eW/QUAey0zdtyWOFHUmvlnXfj94u1EsunfZNKiP8Azyj3v/30+R+QFcFrXirX9cZjqusXt2p/hkmYr/3znFAH2LqnjjwvpJb+0fEGnQleqeerN/3yCT+lcnqnx38EWeRb3V1fEf8APC3OD+LYr5OrT03w7rWqY/s3Sb67B7wwMw/MCgD3XUv2k7FcjS/Ds8no1xOqfoAf51y+p/tEeJ58iwsdOsge+xpGH4kgfpXNaZ8G/Heo8rob26/3rmRI/wBCc/pXU6f+zp4jmVTf6pp1pnqE3ykfoB+tAHI6l8W/HOoZ83xBcRA9rcLF+qgH9a5bUdW1HUnL6jqF1dsepmmZz+pr6A039m/SYlB1LXL25PcQxrEP13Gus0r4J+BtO2s2lveOP4rmZm/QED9KAPkcAtxjJre0rwV4n1cA6d4f1GcHo4t2C/8AfRGK+ydL8N6HpCgaXpFlZ46GGBVP5gZrWAoA+UdI+Afja+2m5hs9PQ9ftE4JH4IGrsNK/ZtQYOseIGPqtrBj/wAeYn+Ve/UUAea6T8DfA2n4MtjPfMO91Ox/RcD9K6/SPCfh/RwBpeiafasP447dQ34tjJ/OtuigBqqAAAAAOmKdRRQAUUUUAFZGq+HdG1a8t7vU9LtLm5tWDwSyRgvGQcjDdeDzjpWvRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUVz3jfxLZ+EPD11rF82REuI484Mrn7qD6n9MmgDgP2hvH/8AYOjf8I/psuNR1BD5roeYITwfoW6D2yfSvnHRdLu9c1S103ToTNc3TiONR6n19h1J7Cn+IdZvvEGtXeq6lL5txdSF2PYeij0AHAHpX0F+zn4AOlaePFGqQ4vL1MWqOOYoT/F7Fv5fWgD0bwD4WtfB3hm20iyIYoN80u3BlkP3mP8AIegAFdHRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFeb/G34hL4L0A21jIP7ZvwVgXPMSdDKf5D3+hoA86/aM+IH2+8PhXSZyba3bN66nh5B0j+i9T7/SvMfAXhS78ZeJbbSbPKBzummxkRRj7zH+Q9yKxY0nvbwJGrz3E7gAD5mkcn9SSa+tfg/wCAo/A/h5VuEVtUvAsl3IOdp7Rg+gz+JyfSgDrtD0my0PS7bTNNhENraxiONPYdz6k9Se5rSpMc0tABRRRQAUUUUAFFFFABRRRQAUlFYOs6uYWaC2Ybx95vT2HvXPXxEKEOeZpCm6jsjcYjvWXca/ZwyFF3yEddo4/OuaeaWT5pJXY+5xTK8GtnUpfw1Y74YFbyZ0f/AAkkHaCU/lVyw1OG8OFLK452t1rkPpVjSiyajAV67wPwPWssNmlaVRRnZpsuphIRg2jtqKQdKr315Bp9pNd3sqQ28CGSSRzgKoGSa+rPKMvxd4lsPCug3OrapLiGAYCDhpX/AIUX3P8A9fpXx34z8TX/AIs8QXOq6m37yY4VAfliQfdVfYfr1roPi38QLjxvrpMRePSbUlbWE8Z9XYf3j+g4rhGbJoA9F+D174S8O6i3iDxXeF57c/6FZxQtI2/vI3GBjoMnrz2FerXf7RPhSIYt7DVrhh/0yRR+ZfP6V812Vjd38vk2FtNdS9khjLsfwGa6K3+G3jS4AMfhnU8HoWgKj9cUCPTtY/aPuXQro+gRxt2e6nLf+OqB/OvO/EnxT8Y+IAy3utTwwN/yxtf3K49DtwT+JNa2lfAzxvfYM1jBYKe9zOo/Rcmu98Pfs42cYV/EOsSzt3itECKP+BNkn8hQB89yO0jl5GZnPJLHJNdH4f8AAPinxAQdK0O7mibpK6eXH/302B+Rr6t8N/Drwp4bKnStEt1lX/ltMPNk+u5s4/DFdSF9fyoA+bdA/Z11y5Cya5qtpYIescIMzj+Q/U13+h/APwhpwVr8XmqOOvnS7E/75TH6k16rRQBgaT4O8N6QB/ZmhafbkdGWBSx+rEZP51uAbenAFPooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopu6qGoazY2B23M6o/8AdGSfyFRKUYK8nZCbtuaNHNcy3jTTwcLHOwHfaP8AGtLStbstSyLeX5x1jbhvyrKOJpTfLGV2SqkW7I1KKKK6CwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCGWVIInlkdUjQFmZmwAByTn0r5J+M3j5/G/iEpaOy6RZZW2TpvP8UhHqe3oPxrvv2iviPtEnhDRZPmP/IQlQ9O4iB/Vvy9a8X8LeH73xNrttpOmJvnnbGcfKi/xM3oAOTQB2HwS8AN4z8RC4vYydIsCJLgkcSt1WIfXqfb6ivrJQqIEjUKqjAAGMCsbwV4bsPCnh+30jTF/dQj55CMNK/8AE59yfy6dq3KAFFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRUUsiwo0kjBUUFmZjgKB1JNAGT4s8RWPhTQLnVtTbEMC/dH3nc/dUe5/+vXxv4t8RX3irXrnV9TcmaduFH3Y0HRF9gP8a6z41fEF/GuvGCykP9j2LFbcf89W/ikI9+g9B9TUHwc8AyeN/EIN0rJpFmQ90/Tf6Rg+p7+g/CgDv/2c/h0SF8X6vEO66fE4/AykfoPxPpXv9V7eCO3gjghRY441CqqjAUAYAFWKACiiigAooooAKKKKACiiigAooooAhuJPKgkcfwqTXDO5aQszZLHcTXczx+bFJH/eUj864meB7edopVwRXzmcxn7rW2p6OBtd9xlFFFfNHphWn4ct/NvvMIysYz+PaswDJwOSeldfo9p9ks1Uj53+Zvr6V6uV4V1qyk9lqcuKqckLdWX6+afj78STrt6/hvRpv+JbbPi5lU8TyD+EH+6D+Z56AV2Hx9+Jo0a1l8NaFP8A8TG4TF1Kp/1EZH3Qf75H5D3Ir5p75NfZnjHReBPCWoeNNei0rThsU4aeYjKwx55Y/wBB3Nerp+zfL/a/z6/H/Zmc/wCqPnFfT0/H9K5/4c/FXRPAeg/Y7Dw5Nc3cx33N1JcqpkbsAApwo7DPv1Nbcv7Sd/n9x4atk/37lm/9lFAj3bRdE0/RLNLPSrOG0gRQu2KMLnA6kjqfc1pDGK+bJP2kNe/g0TTV/wB4yH/2YUz/AIaP8SdtH0v/AL5k/wDiqAPpfIor5rT9pDXwf3mh6aw9jIP/AGY1ZX9pPU9uD4dtCf8Ar4bH8qAPouivkXXfjR421a8E0epDTo1OUhtECqPqWyT+JxX0L8H/ABReeL/A9tqWoqouxI8MjKMBypxuA7ZH65oA7WigdKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKSlpKAOc8V66LBDbWxBuXHX+4PX61wskjyOXlYsznJJ5JNXdflabWrp26+YVH0HAqka+QxuIlVqtPZbHnVptsbT4ZpIJVlhYo6nII7U2kFcak07oyuem6BqaanYrOoCuPlkX0b/CtOuU8AIVsZ5D91pePwHNdVX2OFnKpSUpbs9Om+aKbFooorqLCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArzj40/ENPBeheTZMraxeqVt16+UvQyke3b1PsDXT+NfFNh4S8P3Oq6i3yRDEUSn5pZD91B7n9BzXxz4o1++8Ta5catqcm+eds4/hRf4UHoAKAM/M97d8b57id/dmkcn9SSa+rvgp8O4/BeifaNQjU6xfKDOevkr1EQP6n1PsBXD/s7fDnHleLtaiGOunxOPwMpH6D8/SvoCgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvBv2ifiMsUUnhLRpvnkA+3yofujqIgfU9T7cdzXbfGX4hReCdBMVoytrN6CttGTnyx0MhHoO3qfxr5LkkuL66LSM89xO+STyzsT+pJoAveGdBvvEmt22k6XEZLm4bA9FHdm9ABya+yfBPhiz8I+HrbSNNUeXEMySEfNK5+859yfyGB2rlPgn8PI/BmifatRjDa1fKDMSM+SnURj+Z9T9K9LHSgBAOKDRmigBaKKKACiiigAooooAKKKKACiiigBKx/Edo0tqkqDc0Zyfp3rZpvBFYV6KrU3TfUuE3CSkjgqK6240exuGJMYVu+04/SnWuk2ls2Y4st6tya+bWS1ebdWPS+vRte2pn6FpO3bc3KYPVEPb3NaervcQ6TeyWS77lIJGhX1cKSB+eKuAccUtfRYfDxw8FCB51SpKpLmZ8Gajc3V3fTz37vJdSSM8rufmLk859619L8DeKNWjWTTtA1CeN/uuIGCkeoJ4r6+m8G+G5dW/tWTQtPa+Y7jOYFLFvU8dffrW4F4x0HpXSQfIlp8FvHtwoP9h+UD3luYl/TdmtGD4A+NpD+8XTos/wB+5J/kpr6rooA+YU/Z28WH797pS/8AbRz/AOy1J/wzn4p/6CWlf99Sf/E19NUUCPmKT9nbxWv3L7SW/wC2rj/2Wq//AAz54z/56aX/AOBDf/E19S0UDPn3wv8As5z+csvifV41jGCYLIEsfbewGPyNe4+H9FsdA0i30vS4Bb2luu2NAc45ySSeSSeSa0aKAFooooEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLSUAeZ+JITBrl0rD7zbx9DzWdXfeKNBGqIJYCEuEGAT0Yehrh72zuNPmEV1GyN6no30Pevksbhp06jdtH1POqwak30K9PijaV0jiG53ICgd80IjSyBERmZugUZJrtfCvh/7F/pV3/wAfDD5V/uA/1rLC4aVeXKturJhTcnZGxotgthp0VuDkqPmPqT1P51foAor6+EFFKK2R6SVlYWiiirGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFVNRvbbTbKa9vpkgt7dDJJI5wEUdTVuvmP4/fEltfv38OaPJ/xK7V/wDSJFbi5kHb/dU/mefSgDlviz49uvHWvtOhePTLUlbS3PGF7uw/vHv6DAq/8Fvh1L4z1v7XfoV0eyYGdj/y2fqIh9e57D3Irnfh/wCD77xr4ih0uxDJHw9xcbciGPPLH37AdzX2H4c0Kx8OaNbaVpUIhtbddqr3J7sT3JPJNAF+GKOCJI4kVERQqqowAB0A9qmoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACsTxX4lsPC2g3Osam+2CAcKPvSOfuoPcn/HpWtPJHBC8srqqICzMxwAByST6V8mfGn4hP4113yLJyukWLFbdenmt0Mp+vb0H1NAHK+MfEl/4r1261bUz+9nb5UU5WJB91B7Afn1r139nX4c+ZLF4t1qDKqc6fE46nvKR6dl9+fSuG+DfgGXxt4gBuVZNHsyHupMff9IwfU9/Qc+lfW1tDFbwRwwRrHFEoSNFGAqgYAHtigCxRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRWZ4j1IaXprTgbpM7UU9Cff2HWuGt/EmqxXone6eUFuYz90j0x2oEemUUg5p1AwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBKhuLaC4XbPCko9GUGp6KTSkrMTRUt7G1tzmC2iiPqiAGrAXNPopRioqyQJWCiiiqGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFcX8TvH9h4F0ZppSk2ozgraWu7mRv7x9FHc/gOaAOU/aA+Iw8PacdA0ebGqXqfvpEbm3iP8mboPbn0r5t0uwutV1CCwsImnu7lwkaL1ZjTta1K61jU7jUNQmaW5uZDJI57k/wAh2A9K+iv2fvhyNC09PEmrwj+0bxM20bLzbxnv7Mw/IcdzQB2fww8E2ngfw5HYxgSX0pEl3OB/rH9B/sjoPz6muxpaKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoorzn4z/ABBj8FaIYLORW1i9Ui3T/nkvQyn6dvU/Q0AcP+0R8R8CTwlos3J41CVD2/55A/qfy9a8W8M6BfeJ9cttJ0yMtPO2M44Rf4mb0AHNUN097dk/PPPM/uzOxP6kk19XfBT4eR+CtDFxfxhtZvlBuG6+UvURA+3U+p9gKAOo8E+GrHwj4ft9J01MJEMvIw+aWQ9XPuf0GB2roKSloAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiig0Ach8RmxBZJ6u5/ICsHwnbpc69bpMgdVLPg9MgEj9a2viN/y4/V/6Vl+CP+Rgi9kf+VAj0eiiigYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRXPeOfFlj4O8P3Gq6i2Qg2wxKcNNIfuoPr3PYc0AZnxN+IGn+A9J86bFxqE4ItbXdguf7x9FHc/gK+SvEmvaj4l1ibU9WuGuLqY8k/dUdlUdgOwqXxV4lv/FOt3GrarLvnnPA/hjUfdVR2A/+v1r0/wCB3wlOtND4h8Rwkacp3W9s4/4+T/eYf3P5/TqAP+Bfwpl1WeDxJ4jhKaehD2ttIvNww6Ow/uDt/e+nX6RGABgYpiIsSKiKFRRgKBgAU+gBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiq9/dwWNpLdXcqQwQoZJJHOAigZJNAGT408TWHhLQLnV9RY+XCMLGDhpXPRF9z+g57V8ceK/EN/4o1241fUXJmnbgA/LGo+6o9AB/jXR/F/4gT+ONfZoXdNJtiVtIjxkd5GH94/oOPWrXwX+HknjPXPPvkI0eyZWuG/56t1EYPv39B7kUAdx+zt8OOYvFutRcDnT4XHf/AJ6kf+g/n6V7/UMEUcMSRRIqRooVVUYCgdABU9ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBoooA4z4jH5rH/gf9Ky/A3/IwJ/1zf+VaHxF/19l/uv8AzFUPAv8AyMA/65P/AEoEei0tFIaBi0VVm1GxgH768t4/96VR/WqU3inw/b5M+u6bH/v3UY/rQBr0VzMnxC8HRZ3+KNK49LpD/I1Wb4n+CF+94n0/8Jc/0oA6+iuLb4s+A06+JbT8A5/kKYfi94C/6GW3/wC/cn/xNAHb0Vwx+L/gH/oZYP8AvzJ/8TTT8YfAI/5mOI/9sZf/AImgDu6K4M/GTwCP+Y/Gf+2Ev/xNMPxo8A/9B0f9+Jf/AImgDv6K89f42+AkH/IZZvpbS/8AxNQN8dPAa/8AMSnb6Wsn+FAHpNFeXy/H3wOn3Zr6T/dtj/U1Tm/aH8Hr/q7bVpPpAg/m4oA9corxeb9o/wAOp/qdH1ST/e8tf/ZjVOb9pTTv+WPhy6b/AHrlV/kpoA90or58n/aVlz/o/hlMf7d2f6JVKf8AaS1p/wDj20Cxj/35Xb+WKAPpCivl+5/aI8Xyf6qz0mH6Quf5vWdP8efHUv3Lqzi/3LVf65oA+saK+QJvjR49l/5jfl/7lvGP/ZaqS/Fnx3Lw3iS7A/2Qi/yWgD7Kor4pk+I3jOQ/N4n1Qf7tyy/yIqvL458WSff8S6u31vJP8aAPt6ivht/F3iRh82v6r/4Fyf41H/wlGv8A/Qd1L/wLk/xoA+6KK+Fv+El13/oN6j/4Fyf40f8ACSa5/wBBvUf/AALk/wAaAPumivhX/hJNd/6Deo/+Bcn+NOHifX1+7repD/t7k/xoA+6KK+Gh4s8Rr93X9UH/AG9yf41InjXxSn3fEerD/t8k/wAaAPuGiviNPHvi9Pu+J9XH/b5J/jUg+InjL/oaNW/G7c/1oA+2KK+Kx8SPGv8A0NOp/wDgQ1KPiZ43H/Mz6l/3+NAH2nRXxb/ws7xv/wBDPqP/AH9o/wCFneN/+hn1H/v7QB9pUV8W/wDCzvG//Qz6j/39o/4Wd43/AOhn1H/v7QB9pUV8W/8ACzvG/wD0M+o/9/aP+FneN/8AoZ9R/wC/tAH2lRXxb/ws7xv/ANDPqP8A39o/4Wd43/6GfUf+/tAH2lRXxf8A8LQ8bf8AQz6j/wB/f/rUf8LQ8b/9DPf/APfz/wCtQB9oUV8X/wDC0fHP/Qy3/wD32P8ACpB8VfHSf8zLefjtP8xQB9mUV8bj4uePF6eI7g/WOM/zWrEXxo8eoMHXmb/et4j/AOy0AfYFFfI6fHLx4n/MUhb62sf/AMTUq/Hfx0PvX1qf961T+goA+s6K+UV+Pvjgf8vFifraj/Gnr+0B42HU6c3/AG7H/GgD6ror5ZX9oTxl/FDpbfW3b/4qpk/aJ8Wr96y0hvrDJ/R6APqCivmmL9o/xCuPO0XS3/3PMX+bGrsP7Sl+P9d4bt2/3blh/NaAPoG6njt4JJ53WOGNS7uxwFUDJJr5C+Lvjibxv4mkmjd10u2Jjs4ug293I9W6+wwO1b3xK+M954u0JdIsLE6ZDKc3X77eZR2UHAwvr6/SvNNLghutQt7e4uorSKWRUeeQErEpPLHAJ49qAO/+Cfw6k8Zayb7UoyujWTZlyMee/ZB7dz6DjvX1bDFHBGkUSKiIoVVUYAA4AA9K534eHw8nhW0tfCl3BdWFqBH5kRyWfqxbuGJ5OfWuooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAr5s/aB+JZ1e7k8M6JLnT4GxeSq3+ukB+4D/dB6+p+ldr8ffiQPDentoGjzAateJ+9kVubeI9/Zj29Bz6V81WFlcapfQWNjE01zcOI4415LMTwKANfwJ4Sv/GfiGDStOXbuO6aZh8sMY+8x/oO54r7E8MeH7Hw1oltpWlxhLe3XAOPmdu7E9yTyawPhT4GtvBHh1LYhZNRnAe7nH8TdlH+yOg9eT3rtqABRiloooAKKjkmjiXdK6oo7scVzmq/EHwlpJIv/ABDp8bDqiTCRh+C5NAHT0V5ZqXx88FWeRbS3t+Rx+5tyo/NyK5bVP2k4lyNK8PO+ej3FwFx/wEKf50Ae+UV8uah+0L4uuWP2S3020X/ZhZz+Zb+lc9f/ABe8eXpO/wAQTRKf4YI0jx+IUH9aAPsSm7vwr4iu/G3ii7/4+PEOqPn1unH9ayrjUr65P+k3tzN7ySs38zQB90zahZ2/+vvLePH9+RR/M1Uk8T6BH/rdc01frdxj+tfDBYsfmYmkzQB9uy+O/CkX+s8R6Uv1uk/xqtJ8SfBicHxPpf4XAP8AKviv6UfjQB9kzfFnwLDw/iS0P+4Hb+SmqM/xt8BRZ26y8v8AuWsv9VFfI6xSP9yNm+ik1Zh0rUZz+5sLqT/chY/0oA+np/2gPBcZPlnUZ/8ActsfzIrLuf2jvDkZIttH1OU/7floP/QjXg9r4L8U3JHk+HNWfPQ/Y5MfmVrVtvhR45uMbPDd2P8ArptT/wBCIoA9Mvf2lBgiy8NHnoZrvP6Bf61jXP7R3iOTi20jTIf9/e/9RWHafAzx3cY3abb24PeW6j4/75JNatp+zt4qkbFzf6XB9JHf/wBlFAG54P8AHWseOIrq41s24a1ZY4lt4tgAYEnqST0qP4ga5qfh7Qftuj3klncGVYvMTGdpBz1+grR0H4f3Pw/gltry+hvGvCHzEhULt4xz1zmtFvBtn4226VqNzPbwr+/3QbdxI4A5BGOfSgDwa78c+Krwk3HiPVGz1Au3UfkDisq41PULkk3F9cy56l5Wb+Zr6atf2ffBkX+ubU5/96cD+Sita1+CngK3xnRWnx3luZT/ACYUAfIpZnPzMzH35oxX2dB8MfBMGNnhjTzj/npHv/8AQiavweCfC0H+q8OaWuPS0j/woA+IaSvuuLw5okP+p0fT4/8AdtkH9KspptjH9yytl/3YlH9KAPg3a3ofypQjnorfgK+9xbxDpCg+iinCNf7o/KgD4J+zzdoZD/wA0v2W4/595f8Avg/4V97bVHYflS4HpQB8E/Y7v/n1m/79n/Cn/wBnX/8Az5XP/fpv8K+88D0pcUAfCA0XVGxs028b6W7/AOFSx+G9dk/1ejai/wDu2sh/pX3VRQB8PReDfE8v3PD2qH/t0k/wq1H8PPGMv+r8M6o3/bsw/mK+16KAPjKP4V+OpcbfDN6P94Kv8zVyD4MePpT/AMgExj1e5iH/ALNX2DRQB8nQfAbx1L9+1sof9+6U/wAs1eg/Z58YP/rLrS4vrM5/ktfUdFAHzZB+zfrzf6/W9NX/AHRI39BV+D9mqfj7R4miHtHZk/zcV9CYooA8Lg/ZssF/1/iO5f8A3LZV/mxq3H+zh4eXmXWNUf8A3fLX+hr2migDyKL9nbwiB+8vdXc/9dox/wCyVPH+z74KX7x1N/8AeuB/RRXq1FAHl/8AwoLwP/zwvj9bo/4U4fATwL/z6Xn/AIFNXp1FAHmf/ChvAn/Pnd/+Bb/40f8AChvAn/Pld/8AgW/+NemUUAeZ/wDCh/An/Phd/wDgW/8AjSf8KG8C/wDPldj/ALe3r02igDy4/APwP/zwvh/29H/Cmf8ACgPBB/g1Ffpc/wD2NeqYooA8ob9n3wX2k1Zfpcr/APE1H/wzx4NP/L1q/wD4EJ/8RXrdFAHkX/DO3hDteat/3+T/AOIqP/hnTwp/0ENW/wC/kf8A8RXsNFAHj3/DOfhT/oIat/38j/8AiaP+Gc/Cv/QR1b/v5H/8TXsNFAHj3/DOfhX/AKCOrf8AfyP/AOJo/wCGc/Cv/QR1b/v5H/8AE17DRQB49/wzn4V/6COrf9/I/wD4mm/8M6eFv+gjq3/fcf8A8TXsdFAHjn/DOnhb/oI6t/33H/8AE0f8M6eFv+gjq3/fcf8A8TXsdFAHjn/DOnhb/oI6t/33H/8AE0f8M6eFv+glq3/fcf8A8TXsdFAHjf8Awzn4Y/6Ceq/99x//ABNRv+zh4c/h1fU1/wC/Z/8AZa9oooA8Tf8AZu0Ij5Nc1IH3SM/0FQSfs2aWR8niK8U+8Cn+or3OigDwN/2a4c/u/E0g/wB6zB/9nqB/2aZT93xSv42J/wDjlfQdFAHzsf2arzPy+JoD9bNh/wCz01v2a9RH3fEdqf8At2Yf+zV9F0UAfODfs2av/B4gsj9YXFQv+zd4gH+r1vTG+qyD/wBlNfStFAHzFL+zn4pX/V6lpTn/AH5B/wCyVRn+AHjaL7g06b/cucfzUV9V0UAfHF78JvHNpM8T+HrmTb/HEVdT9CCc/wA65rVNA1fSsjU9MvLMg4/fwMg/MjFfdlN69qAPA/2W9H1S3n1fU7iKaHTriJI4/MUgSuCeVz1wMjPvXv1IBS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXJ/Enxha+CPDk2pTkSXLfu7W3zzNJjgfQdSfT3xXQ6vqVvpGmXOoXr7Le1iaWRvRQMmvjj4k+NL3xx4ik1C53R2yApaQZ4iT/4o9SfX2AoAwtZ1S71nU7nUdQlM11dOZZWPcn+QHQDsK+hPgR4Ct/C2lJ4q8QtHBf3af6Os5Ci3iI684wzD8hx3NfN6M0bKytgg5B9DU9/f3moS+Zf3k9y/wDfmkZz+ZNAH19q3xY8D6XuWfX7aV1/htt0x/NQR+tchqv7RXhy2LLpml6hfHsz7YlP4kk/pXzXBby3DiO3iklc9FjUsT+FdNpPw28Z6tt+x+Hb7a3Rpk8pfzfAoA7/AFT9o7XZsjS9GsLQHoZWeZv0Kj9K5HVPjB451LIk1yS2Q9rZFi/UDP61vaX+z34uugDez6fYA9nlLt+Sgj9a67S/2brJcHVtfuJfVbaBY/1JP8qAPBdQ1jUtTcvqOoXV2x6maZn/AJk1Rr640n4IeBtOwZNNlvmH8V1OzfoMD9K63SvCugaQQdM0awtCP4ooFDfnjNAHxlpfhbX9W/5BmjX91nvFbsR+eMV1em/BTx1fBSdJS0U97idF/QEn9K+uqWgD5s039nHXJsHUtZsLYHtEjykfmFFdFY/s3aWmDe6/eTEdRFCsf6kmvcaKAPKrT9n/AMFW/wDrhqN1/wBdLjH/AKCBWpb/AAW8Aw4/4knmY/56XEp/9mr0GigDjoPhb4Gg+54ZsT/vqX/9CJq9B4D8Jw/c8M6OuO/2KMn8yK6OigDIj8M6BF/q9E05f920jH9Ksx6TpsX+r0+0T6QqP6VeooAhjtoY/wDVwRJ9EAqYDFFFABRRRQAUUUUAcP8AEf8A4+rL/cb+Yqp4B/5Dp/64t/MVb+I//H5Zf7jfzFVfAP8AyHT/ANcW/mKAPQqKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAzfEOlQ65ot9pV0zLDewPAxXqNwxkfSvm69/Z88WxXrxWs2n3EGflmMxTI9SuCQfYZr6ipaAPn/AEH9m4na/iDXvrFZxf8As7f/ABNd/ofwY8EaVhjpRv5B/HeuZP8Ax3gfpXoNFAFHTtI03TI9mn2Ftar6Qwqn/oIq9RRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAcP8R/+Pqy/3G/mKq+Af+Q6f+uLfzFWviP/AMfll/uN/MVV8A/8h4/9cW/mKAPQqKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAOH+I/8Ax+WX+438xVXwD/yHj/1xb+Yq18R/+Pyy/wBxv5iqvgH/AJDx/wCuLfzFAHoVFFFABRRVDVtVstJtmuNRuUgiHQseSfQDqT9KAL9FcIfipoazbRBesmcb9i/ngtmup0TW9P1y2NxplysyKcMOjKfQjqKANKiivIvil4ou31ltKsrl4baBAJAjbdznkgkc4AwMetAHqTajZCbyTdwCT+6ZVz+Wat18x85yTk13HgDxzPplxFp+qytLYOQqyMcmE9uf7vt2oA9kooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKikdUR3kOEUEk+gHWpar3MInhlhb7sqMh+hGKAPItX+JeszXsg0tora1BIjBjDMR2LE5/Stjwp8THnuVtdfVEEhAW4jGAD/ALQ7D3FcnqPgbX7XUjaRWElym7CTIuUcdiT0HvmuflieCaSKQYeNirfUHFAH0xS1znw8vpNQ8JWE0xZpFUxsx77WIH6AV0dABRRRQAUUUUAFFFRSyCNWZyFVRksTgAUAS1BLcQwnbJLGhPZnA/nXlvjT4jTzvJY+H3MUC8PdL96T/d9B79T7V59NM80hklkeSQ8lmJJP4mgD6XRlcZVgR7Gn18+eFtevtG1W1ktZnERdVkg3HY6k4Ix0z6GvoOgAooooAKKKKACiiigAooqnqWpWmmW7XF/cR28Q43O2OfQetAFyis7SdY0/V42fTbyK5EZw2w8j6g8itAGgBaKKKAMnxHrNvoGlS3t1yE4RB1duyj/PSvN0+K2qi63SWFobfP8AqxuDAf72ev4Vr/GPTr+5t7G6tY3mtoC4lRATsJxhiB24xntXmUlndR2yXMttLHC7FFkdCAWHJAJoA9+8O63aa/p6Xti5KHhkPVG7g1rV4l8LdabS/ESWjti3vv3RB6K/8B/Pj8a9soAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAOH+I//H5Zf7jfzFVfAP8AyHT/ANcW/mKs/Ef/AI/bT/rk386r+Af+Q43/AFxb+YoA9BooqpqV7Dp1jcXdw22KBC7H2FAGV4v8U2vhqy82XEtxICIYAeWPqfRR3NeI61q97rd611qM7Suegz8qj0UdhTvEGrXGuarNfXTcucKo6RoOij/PWut+HPgldV2apqqf6GG/dRH/AJbH1P8As/z+lAHFtp94th9v+yyCz3bPOMZ2k+xrW+H+qz6X4psmR8R3DrBKvYqxx+hwRXefF29gtfDtvpkeEknlUqiYAVE9uwzgV5v4Vga48S6bEgyTcxn8AwJ/QUAfQVzcJawS3EzbYolLsfQAZr5z1G6e+v7m6lOWnlaU/ic16f8AF7X/ALJYpo9u/wC9uR5kxB6Rg8D8T+gryegD0DwH4Wstf8K6h9oUC5M+2Gb+JCFGPwyelcLd2stleTWtzGUlhcowPYg4NeufBv8A5FWX/r5f+S1598Q2RvGOpNDgjzFyR03bQD+tAHp/wy1d9V8LwiZt09qxgYnqQAMH8iK6ztXnHwR/5BmpZ6een57a9FbpQAtFY+s6uLX91AA8vcnov/16wJr+7mz5lwxz2zgfkK8nE5nSoS5Urs6aWFnUV9kdPcavZ27lHl3MOoUZqH/hILL1kP8AwCuWpa8mWcVm9EkdqwULbs7Ozv4LwHyHyR1B4Iq3XGaS7JqMBj7tg/Q12de1l+LliqTlJWadjgxFJU5WQoooor0jAKKKKACiiigAooooAK5vxh4ttvDEUXmxPczzk7IlOOB1JPOB+FdJXEfEjwhc+Ijb3enMn2i3UoY3OA6k54PYg0AU7D4r6fIcX1hcW3ujCQf0rqdI8T6NrBC2F/C0h/5Zsdr/APfJwa8W1Lwjr2nAtcabMUHV4xvX8xmsb5lfupX81oA+nKK8O8N+PtX0dkiuZWv7QcFJTlwP9luv55FevaBrtjrtiLvT5d6HhlPDIfRh2oA06KKKACuD+Jni698PyW1npm2OeZDI0rANhc4AAPGc13lc1418LW3iOx3SZS5gVjDIv0+6fUE0AcF4Y+Iupw6nDFrM4ubSZgjOUAaMn+IEAcDuDXsAPAxzXzLg8ggZB9K+g/B92174Y024Y7i9umT7gYP8qANO7nS2tpZ5PuxIzn6AZr5smkM00kp6yOWP4nNe3fE/Uxp3hK5VWxLd4t1+h+9/46DXilnbPd3cFtCMvM6xr9ScUAe5/DqA23g3TkIwWQyY/wB5iw/Q10dQWNulpaw28YwkSLGPoBip6ACiiigAooooAK8q+KnixnkfQ9Okwg4u5B3P9z6Dv+Vdr4414aBoE9yhH2h/3cAP949/wHNeCkvNLk5eRj9SWJ/mTQBa0XSrrWNRSysI98kn5KO7E9gK9PufhtaReF57azCzamVDC4k4ywOSo7KD0/nWv8P/AAynh7Sw0qA39wA07dx6IPYfzrqaAPEPDXgrWrjW7cXdjLa28MqySSSjAwDnA9SenFe4UlLQAUUUUAFFFFABRRRQAV4T8Rdem1nxDNEWItrNmhjT3BwzfUn9K92ryL4teH7TTZ4dTtmdXvpW82PPy5AyWHcZ70AY/wAMLqW18ZWcaFlS4DxyDsw2kjP4ivdK8H+HC7vG2m47M5/JGr3mgArgb/4p6Zbak1tFaTzxIxV5kIHTqVU9R+Irs9TmW10+6uHOBFC7n6AE183bs4J+8eaAPpKyuor60hurZt8Myh0b1BrA+Jenre+D707dzwATp7FTz+hNTfDp/M8F6Yf7sZX8mIq74q+bwxqvp9kl/wDQDQB8/W07211FPGcPFIsg+oORX0lBKstvHKn3ZFDD6EZr5nPSvo7QP+QHp59baP8A9BFAF+iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAOG+I3/H9af9cz/Oq3gD/kMv7Qt/MVL8Q2zqdsuekOf/AB4034ff8hefjpAf/QhQB346V5N8V/E073kugQKEt49hlbu7cMB7AcfWvWR0ryD4zWMNvrlrdRDD3UR8z3KkAH8jQByXh/T49U1m0s5ZFjilcB3dgAF6nk+w4r2XW/FWieG7JI0mikdFCw20DAnAGB04Ue5rwkilUdFVdzN0A70AXtd1e51vU5b+8bLvwqjoq9lHtXe/CPw4wd9du0xkFLYHvnhn/oPxrP8ABfw+ub+SO81uNra0HzC3PDy/X0X9TXReJfiHp2iL9h0eGO6niGz5TiGMDjGR1x6Dj3oA5L4pabew+Kri8ljdrecKYpAMrwoBXPbBFcf354r2jwP4xHieSa1u7dILmJd4CHKOM4yM88EivK/GHHijVB/08yfzoAs6b4s1PTNDbS9PdYEeRpGlX75yAMA9unbmsZEmuLhIokaWWVtoC8szH+tb/hPwbf8AiRPtEDx29qrGNpXOTkdQFHJ/SvVfC/gzTPD6q8MZmuQMGeXlvwHRfwoAXwJoB0DQo7ebBuJG82Yj+8e34Dit64kEVu8h6IpP6VLUF3H5ttJGOrKRUTvyuw1ucQ8hkdmY5YnJPvSUskbRMUkG1lOCDSV+fTvzNy3PoYpW0CiiiszQ0/Dtv5t95h+7EM/ieBXV1m6LZm0tBvGHf5m/oPwrSr7fLqDo0Unu9WeBiKntKja2CvM/FHxOaKSS10KEEqSpuZeRx/dXv9T+VekvGHjKN0YEH8a8X1H4a69BeOllbpdW+TskEir8vbIYg59a9EwJIPid4ghgKSi0ncnh3jIIHpgECqtx8RfEsvC3qQj/AKZwr/UGrtp8LdcmwZ5rS2Hfc5Y/oP61r2/wlXg3WrsPURQ/1J/pQBx03jTxJL97WLgf7uF/kBUDeKdfb72s3v4TsP5GvRY/hRpa/wCsv7x/oVH9KsL8LNB/imvn/wC2i/4UAeWNrusv97VL0/707f41C+pX7/fvrlvrM3+NevR/DHw6vVbl/rN/gBU0fw18Mr/y6Sv9Z3/oRQB4v9ruf+fmY/8AbVv8ab9quf8AntL/AN9n/Gvb/wDhXvhkf8w0n6zP/wDFUv8Awr3wx/0DB/39f/4qgDw/7Tcf89pP++z/AI035mfJy24/7xJNe4SeAvC0asz6eqooySZnwB7/ADVxms6v4T0G4z4c0uG7voz8szlmijYdxk/MR7ce9AGL4w8IXXh5Yrgv5tnNgBujI2M7WH9R+lQ+BdZk0bxHavG58m4dYpVJ4ZScfmDyKztW1W/1i7NzqVw80nbPCqPRR0Arc+H/AIYvNX1a3u2iZLC3kDtKeAxHIUepz19KAPcqKKQ+goAWiiigD5s1KLytSuYum2Zk/JjXtHwrm83wXZj+40i/+Pk/1ryLxWnleJtUj64upT/48a77wJrUejfDm5vZSP3E8gRT/G5AwPxJoAw/i3rP2/xAthCxMNiu1gP4nPLfpgfnTPhNo/27xI17IuYbFd/P988L/U/hXH3U8k9w80zFpZXMjH1JOTXt/wAOtEGkeGoVmXFxdfv5PbP3R+Ax+NAHUiloooAKKKKACiiigDx/4yak1xrsFgp/d2cW8j/bbn+QFU/hVoq6n4kFzMu6GxXzCCOC54X8uv4Vk+OJ2ufFmqyMc4uGjH0Xgfyr0P4MWoi0G7n/AIpbjb+CqMfzNAHf0UUUAFFYniLxNpvh5EOoysHkztjRdzkdzj09zT9A8Q6dr9sZdOn37fvxsMOv1H9elAGxRQOgooAKKKKACiiigArzD43TfNpUX/XVv/QRXp9eTfGxv+Jrpy+kLH82oAx/hPHv8aW7Y+5HI3/juP617jXjHwdXd4sY46Wzn9VFez0Acp8UtQFh4QuVDbXuiIFP15b/AMdBrw6u7+MWsfa9ah02JsxWa5kx/wA9G5/QY/OuEoA9t+E83meDIB18uWRP/Hs/1rU8aS+R4T1Z/wDp2dPzGP61zvwZm3eGrmL/AJ53TfqqmrnxWvha+EZYs4a7dIh+eT+goA8Ur6S0uMw6XZxHqkKL+SivnbSbVr3VbS1QZM0yJ+bAV9JUALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHnvxAOdbjX0gX+Zqx8OudRuj6Qgf+PVW8ff8hz6Qr/Wrfw4H+l3h/2F/maAO4rzH402chi028AzGjPEx9CcEfyNenVna5pFvrelTWF2D5co4I6q3UMPcGgDwnwxfWWna1FPqlsl1aEFJI2QNgH+LB7g16Tb+KvAumqZrGGFZRziK0If8CQMfnXBeIfButaNOQ9o1xbg/LNCCwI9wOQfrWL9ivG+VbO4Lenlt/hQB0/i3x/qGubrWxBsbJuCoPzyD/aI7ew/WuXsbK41C7S1s4nmmfhUUZP/AOr3rp/D3w81nVHV7pG0+2P3mmHzkf7K9fzxXqnhvw5p3h+28uwg+cj55m5d/qf6DigDE+Hng5/DvnXl9Ir3k6BCicrGuckZ7nI5+leUeJLhbzX9QuYwVSS4dlB64ya+jBXzr4khFv4g1KEDAS5lA+m44oA9S+Df/IqS/wDX0/8AJa7muF+DP/Irz/8AX03/AKCtd1QAlFFFAjC8SWpeBZ0TlOG+lc9XdyIGBBGQetZU+hWsjZRmj9h0/Wvn8wy2VWftKXXdHoYbEqC5ZHM1taFpZdhczrhRyinufU1ftdEtIWDMpkYd26flWmoGOmAKMFlThNVKn3Dr4vmXLAcOlLRRXvnnhRRRTAKKKKACiiigAooooAKy/Emt22gaVLfXSsyqQqovVmPQCtSsPxjoi+IdGksDJ5TlhJE5GQHHTP5kUAePeJvF+qeIXKTSeTbZ+W3hOF/4F3Y/X8qytM02+1S5W10+3e4lPZR0HqT0A9zXc6P8Krprr/icXUSWyn7tuSWf8SAAPzNek6RpNjpNqttp1ukEa9QvUn1J6k/WgDh/C3wygtttxrri4lHIt0P7sf7x6t/L616FDCkEaJEioijCqowAPYVNRQAUUUUAFFFFAHgfxCga38aampGA8gkH4qDWR9unOnLYb/8AR1kM23/bwBk/gOK9R+JXgy41eZdS0lFa4CbJYieZB2IzxkdMelcLpvgnxDfXIg/s2a3XPzyTjYqj19/wzQBL8OvD517XkaZc2dqRJKexx91fz/TNe7AVkeGNCtfD2lx2VtyR80smOXc9Sf6DsK2KACua8beKovDVkjbPOupyRDHnA46sfYZrpa8o+M95ZzXFpaxvvu7cs0gHRFbGAfc4zQBF4d+I+qza3BDqflTW9xKsZCJtMeTgEEdefWvXK+fvBFkt94s06Bhkeb5h+ijd/SvoGgAooooA8B8eWkln4t1KOQY3zGVfdW5H866X4X+LLDS7KXS9TlW3BlMkcp+7yACpI6dOK6n4g+EP+EigSeyYR6hCMKTwJF67Se31rxzUtOvNMmNvqFtJbuO0gx+R6H8KAPeG8U6Cq7m1ezx/12B/SsTV/iZodmhWyMl/L2EY2r+LNj9Aa8YPIq5YaXfag6pYWc9w5/uISPz6UAXPFGvXHiLUxe3MaRkRhFjXOFUEnv1PPWui+D0Fy3iSaeNWFvHblZT2ySMD9M1PoHwvvrjbJrU62kR6xRkNIfx6D9a9L0bSrLRrJbTT4BFEvJA5LH1J70AaI6UUUUAec+MPiNLpmqS2Ok20cxgO2WWXON3cKAR07mtLwN46i8RObO7iS3vQu5QjfLIB1xnoR6VwPjXwnqen6pfXphaayaRphOvIUE5we4Iziuf0m+k0/VLa8jOGglWT8jyPxFAH0lQKYpyKfQAV5L8bP+Qzp/8A17t/6FXrVeX/ABstGzpl2B8vzxMfQ8Ef1oAyvg1/yNU3/Xq//oS16f4j1eDQdGuL6c/6sfIv95z91f8APavGPAWsw6F4jiu7ncIGVonKjJAPfH1AqTxx4pl8R6kGjDR2MORChPJ9Wb3P6CgDAu7mW9u5bm4bdLMxdj6knNT6np1xpskUd0oV5YkmA7gMMjPvXQfDjwy+u6uJ50zY2hDyA9Hbqqf1Pt9a3fjRpxW40/UEXCMpgYjsRyv8zQBJ8E7kbdUtSfmykoH5g/0rO+MOri71qHT42JSyXLj/AKaN/gMfnXPeEfEEnhzUpLuKPzPNiaLaTgZPIJ/EVk3NxLdXEs9yxkllcu7nqxJzQB1nwo0z7Z4pW4YZisozIf8AePyr/U/hXtdcj8NdDbQ/DyGddt1dkTSA9VH8K/gP1NddQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAeeeOv+Q8f+uS/1q58Of+Pi8/3V/mao+Oz/AMT9v+uaVf8Ahz/rr3/dX+ZoA7aiiigAooooAKKKKACvn7x2NvjHVR0/0g/qBX0DXgXj5CvjTVA3Uyg/+OigDvfgvJnQryP+7c5/NF/wr0CvOfgqrf2VqLfw+eAPqF/+vXo1ACUUUUCFooooGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAEU27ym8v72Dt+vavnG+hvBqMsN4spvDIQ6sCXLk8+5ya+k6ha1gaUStDGZR0coNw/GgDjPhp4QbRoDqOpJi9nXCxH/AJYoex/2j39OldzSAYFLQAUUUUAJTJIo5VKyorqezDIqSigCl/Zen/e+w2wPr5S/4VaCqgwqqPpxT6KACiiigAooqpqsMl3pd3bwtsklhdFb0JBANAHnHxK8aW1zbS6NpbLOH4nmH3eDnavr05PSuB0bT31TV7WyhGWmlC/7o7n8BzVn/hF9bGofYV0y6M4O3Gw7fru6Y984r1rwN4Nh8Owme5KzX8i4dx0Qf3V/qe9AHVqoUBR0AxS96WkFAC1k+I9Gt9e0iawuRtWTlX7xuOjCtakoA+ftZ8Ja1pN00dxYzSqD8ssCF0YeuR0+hq54b8DazrE6q9vJZWuctNOhXj/ZU8k/pXuwooAz9F0q10XTorKxTZFGMZPVj3Y+5pniPRoNd0mewushZBlXHVGHRhWnRQB4Fq3gzXtNuWiawluIx9yWAF1cfhyPoa6fwH4AuWu4tS1yHyYojujt2+8zdi3oB6d69WooATHc0ooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA858df8jBJ/uJ/KtH4df62++if+zVneOv8AkYJP9xP5Vo/Dr/W330T/ANmoA7WiiigAooooAKKKKACuW8TeCNK8QXYurvzorjaFaSFgNwHTIIPT1rqaKAM7RdItNE09LLT08uIEk5OSxPUk9zWjRRQAlFFFAhaKKKBhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHnPjr/kYpP9xP5Vo/Dn7999I//ZqzPHDf8VFN7In8q1fhx/y/t/1zH/oVAHZ0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAeZ+Mm3+Irr2Cr/46K3Phyuba8P8AtqP0Nc/4obf4gvT/ALYH6AV0vw6XGm3Lf3pf/ZRQB1dFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUVV1C/ttLspry/mSC1gUvLK5wEUdzXA2Hxr8FajczQR3txEYlZ0eaEosuAThTnqccA4zQB6RSV8g+Mfi14p8SXcpj1GfTrLcfLtrVzGAvbcwwzH6nHoBXF3OpX9ySbm9uZievmSs38zQB9P6+27Xb1vWZv0NdB4M1jS9N0qRL/UrO1cyk7Zp1Q4wOcE9K878Ic+FdJ/684v/QRXmHxh/wCRsj/69U/9CagD6rbxd4aT73iHSh/2+R/41C/jzwnH9/xJpQ/7e0/xr4kPWkoA+1X+IvgxevijSv8AwJX/ABph+JngpevifTT9Jgf5V8W0UAfZr/FPwMv3vE1j+DE/yFRt8WfAq/e8SWn4Bz/Ja+N9j/3T+VP8mZv+WTn8DQB9gP8AGHwEv/MxQn6Qyn+S1Xb42eAV/wCY6X+lrN/8TXyULS4b/lhMf+AGnppl/J/q7K5f6RMf6UAfVMvx38Bx/dv7mT/ctX/qBVST9oLwWmdo1KT6WwH82r5qi8O63Njy9H1CT/ctnP8AIVcg8E+K7hv3fhrVT/25yAfqKAPfZ/2jPDCf6rS9Vl/4BGP/AGas+b9pLTFz5Hh29k/351X+QNeRQfC7xvN/q/DV8M/30C/+hEVdg+DXj6XGNCZP+ulxEv8ANqAO/n/aUkOfs3hlV/37wn+SiqE/7SOuHPk6Fp6f7zu38iK5+D4EeOpfv2VpD/vXSf0zV6D9nnxg/wDrbnSY/rO5P6LQA+X9onxa2fJstJi/7Yuf/Z6ozfHvxzISUnsYs/3LUf1JrZh/Zw8QP/rdZ01P90SN/wCyir9t+zXeE/6T4lgT/rnak/zYUAcVN8bPH8n/ADG1T/dtYh/7LVOT4t+PJeviO5H+6iD+S16hB+zXZD/j48SXD/7lqq/+zGrsP7N2gD/Xa3qTf7ixr/Q0AeNv8T/HD/e8TX/4Pj+QqCT4jeMm+94l1L8Lhh/I17nH+zn4XX7+p6s3/A4x/wCyVYX9nnwgv/Lzqh/7bJ/8TQB8/P468WN97xLqv/gZIP61D/wmvir/AKGXV/8AwOl/+Kr6L/4Z98Feup/+BI/+Jp6/ADwR6aif+3n/AOxoA+bz4x8Tt/zMWrn/ALfZf/iqT/hLPEv/AEH9W/8AAyT/AOKr6THwC8D/APPK/P8A28n/AApf+FBeB/8Anhff+BR/woA+av8AhKvEX/Qf1T/wMk/+KpP+Ep8Q/wDQe1T/AMDJP/iq+mP+FCeBv+fe+/8AApqX/hQngX/n2vP/AAKagD5l/wCEp8Qf9B7VP/AyT/Gj/hKfEH/Qd1P/AMDJP8a+mv8AhQngX/n1vP8AwKaj/hQngT/n0vP/AAKagD5l/wCEo8Qf9B7U/wDwMk/xo/4SnxB/0HdT/wDAyT/Gvpr/AIUJ4E/59Lz/AMCmo/4UJ4E/59Lz/wACmoA+Zf8AhKfEP/Qe1T/wMk/xo/4SrxF/0HtU/wDAyT/Gvpr/AIUJ4E/59Lz/AMCmo/4UH4E/59bz/wACmoA+aB4u8TL93xFqo+l7J/8AFVNF438VR/d8Tav+N5If5mvo4/APwP8A88b8fS5P+FRP+z94Kb7p1NfpcD+q0AeAxfErxrBjZ4m1Hj+9MW/nV6D4v+PIf+Zinb/eijb+a17NP+zt4Uf/AFV9qsP0kQ/zWqc/7N+hH/Ua5qK/76Rt/ICgDzS3+OXj2JgW1SGYDs9rH/QA1qWv7Qvi+Jv9It9KuF94XU/o39K6a6/Zpjxm18TMD6SWf9Q/9Kybn9m7XVz9m1zTpf8AfR0/kDQBYs/2k9ST/j98PWso/wCmU7J/MGtyy/aS0Zx/p2g38P8A1ykST+e2uDu/gB41t8+Uun3Q/wCmVzj/ANCUVh33wi8d2RO/w/PIB3hdJP8A0EmgD3ay+P3gi4wJ5b+0z3ltiR/46TW7a/FjwNeKDD4ktEz/AM9d0f8A6Eor5OvvCfiLTyft2hanAB/E9q4H54xWVLFJEcSxtG3owIoA+3rTxd4cvADbeINLlz6XcefyzWpb3dvcjME8Uw9UcH+VfBNSJLJH80bup9VOKAPvqivhGDXtXt8eRqt9Fj+5cOP5Gr8PjfxVB/qvEmqLj0upP8aAPt+iviyP4l+No/u+J9Sb/fmLfzzVqP4tePIcFPElyf8AeSNv5rQB9k0V8gRfGjx+n/MfLf71tD/8TVuL47eO48btRtZP961T+gFAH1pRXypH+0D42Q/M2nP9bb/AirkX7RPitP8AWWOlS/WJx/J6APp+ivm2D9pLXB/x8aHpzf7jyL/MmrsX7S1wOJvDEbD1S8I/mhoA+haK8Jg/aVsGx9o8N3Kf9c7lT/NRV6L9o/w62PO0fU4/93Y3/swoA9ooryKP9orwgfv2Wrp/2xjP/s9Tp+0J4KbqmqJ/vW6/0agD1aivLR8f/BBP+svx9bb/AOvTj8ffA3/PxfD/ALdT/jQB6hRXmP8AwvvwL/z93v8A4CtR/wAL88C/8/d7/wCArUAenUV5j/wvzwL/AM/d7/4CtR/wvvwL/wA/d7/4CtQB6dRXmX/C+fAh/wCXy7/8BXqSP46eAm66nOv+9aS/0BoA9JorgIvjV4Ck/wCY3s/3raUf+y1N/wALf8Bn/mYoB9Y5P/iaAO5orh/+Fu+A/wDoY7f/AL4k/wDiaY/xi8BoP+Rgib/dikP/ALLQB3dFeaXHxz8BRZZNRuZm/wCmdrJ/7MAKzZ/2h/B6Z8q11aRv+uKAf+h0Aeu0V4u/7R/h3+HR9Ub/AL9j/wBmpv8Aw0joH/QE1L/vqP8A+KoA9qorxKX9pHRcfutC1Bj/ALUiD+prMn/aVIfFv4XDD/bvMH9ENAH0BRXzpP8AtKakf9T4ctUP+1cs38lFVf8AhpDxBuz/AGHpu303SZ/PNAH0rRXz/p/7Sb5A1Dw4PcwXX9GX+taP/DSWj/8AQAv8+nmpQB7fRXz7L+0nIbtRF4aH2bPzZuzvI9sLgGvb/D2sWuv6NaarYEmC7jEibhgj1BHqDxQBp0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRXlfx6+If8Awiui/wBlaXNt1i+QgFW5giPBf2Y9B+J7UAedftDfEH+29RPhrSps6fZyf6S6txNMO3uq/qfoK8m0iwn1TVLWwtULzXUqxIAMnJOOlMsbO51C9htbSKSe4uHCRxryzsTgD86+uPhf8OdM8G6NavJbQz6yV3T3ZQFgx6qhPQDpx1696APCf+FH+NP7d+wfYYvs+/H23zV8rZn72M56dsZr27T/AILeBrS3jSbSPtMiqA0ks0mWPc4DADNeiiigDyK9s7bTryWysoVht7eRoo41zhUBwBz6Cui8LeGdB1bT2utW0XT724EpjElxbJI20AEDLAnAzWP4kXbr16PSVj+fNdX8P2zpEq+k5P5gUAXI/B3hmP7nh3SU+lnH/wDE1OnhrQ4/9Xo2nL9LVP8ACtQ0tAGemjaWv3NMs1+kCD+lSjTrEDAsrcD/AK5L/hVuigCutnap922hX6IKeIYu0Sf98ipaKAGKoX7qgfSn0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUlFAC0UlFAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVXmtLa5/4+beKb/fQN/MVYooAwLzwX4XvC32rw9pchPc2kefzxmsmf4S+Bbj7/hy0X/rmXT+RFdrRQB5zP8DvAcvTSpY/+udzIP61Rl+AHgqTOxdRi/3bjP8ANTXqlFAHj037OfhRs+VqWrJ9ZIz/AOyCqkn7N2hn/V67qK/7yIf6V7ZRQB4W/wCzVp5+54kul+tsp/8AZqqz/s1J/wAsfEx/4FZ/4NXv1FAHzvJ+zVe/8svEluf960Yf+zGqc/7N/iAf6nWtMf8A3xIv8lNfSlFAHy7P+zv4uj/1d3pUv0mcfzSqEvwG8cpnbbWUn+7dL/XFfWNFAHyFP8FPH0XTRBJ/uXMR/wDZqpT/AAm8dw/e8N3Z/wBxkb+TGvsqigD4qf4ceNI/veF9VP8Au2zH+QNV38CeLU+/4Z1dfrZv/hX27RQB8Ov4N8TJ9/w9qi/9uj/4VH/winiH/oA6n/4CP/hX3NRQB8Mf8Ir4g/6AWp/+Akn+FH/CLeIP+gHqX/gI/wDhX3PRQB8L/wDCL+IP+gHqX/gJJ/hR/wAIvr//AEA9S/8AAST/AOJr7oooA+Fv+EZ17voepf8AgJJ/hUT6Fq6ff0q+X62zj+lfd1FAHwW2nXyf6yzuE/3omH9Kia2mB+aGQf8AADX3uf8Adpnlp/zzT8hQB8FeVL/zzb/vk05La4b7ttI30QmvvMwxH/lkn/fIpVjQfdQD8KAPhaDQdYuMeRpN9Lnptt3P9K1rX4e+MroAw+GdTIPQm2ZR+or7WA+lLQB8Zp8KfHTf8y1e/jtH8zTv+FS+O/8AoW7r/vtP/iq+yqKAPjmP4QePZDhfDk4/3poh/Nq0oPgV47lQM2n20Wez3SZH5E19aUUAfKsP7P8A42c4ddOi92uc/wAlNWm/Z18XbM/btIz6edJ/8RX1BVDWNRtNJ06e+1CdILa3UySSMcAAf19u5oA+UPEHwf8AFmhWE99f29r9lt1LPKt0gAA/3iD9BjJrz/vXofxY+JV5441B4LdmtdGt2/cwZ5kP/PR/Vj2Hb8zWR8O/Aup+ONaFrYp5drHg3FyR8sS/1Y9h/SgCDwJ4K1bxrqostKQBUwZp5AQkC+rH+QHJr698HaDF4a8M6fotvIZY7OIJvIwWbJLHHbJJ47UnhLw1pvhXR4dL0i3EUMYy7fxyt3Zj3J/+t0rc9zQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRVLU9QttK06e+v5VhtreMyyyN0UCgDG+IPi+y8FeHptUviHkHyQQhsNNJ2Ue3cnsK+O/EWs33iDWLnVdTlaW6unLMT0HooHYAcAelb/xT8d3PjjxG922Y7GDMdpB/cT+8f9o9T+A7VvfAv4ct4t1ddT1WEnRrJwzKw4uJOoQeqjqfy70Ad7+zz8N/sFtH4q1iLFzOv+gxMP8AVRn/AJaEf3iOnoPrXuFNjRUQKgCqowAOwp1ABRRRQB5f4r/5GG9/3h/6CK6X4d/8g+69ph/6CK5zxb/yMd3/ALy/+giui+Hn/IPu/wDroP8A0GgDrKKKKACiiigAooooAKKKKACiiigAooooAKK88+NXj6fwN4fgk0+NH1G+kMcBkGVjAGWYjuRlePevnDUviZ4z1Ny1x4iv1BPIgkMK/kmKAPtKivhd/FGvyH59c1NvrdyH+tM/4SHWf+gxqH/gS/8AjQB910V8deDvin4o8NX8Mv8Aal1fWisPMtbqUyK69wC2Sp9xX15ZXMV7aQXcDbopkWRD7EZH86AM/wASazb6DpEt5c/Nt4WMcF27KP8APSvFNe8Ralrl0013O6xk/LDHkIg9AO/1Ndd8Y9T8y7s9MRuIgZZAOxPC5/DP5152ea+xybBRVJVprV/kfKZpjJSqOlF6L8y1aanf2Mge0vJ4SOm2Q/y6V2/hv4mXMTpBrqLNEePOjGGX3YDg/hivPunWj3FetiMBQxEbTj8+p5tHGVaLvFn0nBKlxCssTh43G5WHQjsam71zfw9Mh8G6Z5ud3lHGf7u44/TFdGOlfndSHJOUOzsfc0588Iy7ocKKBRUGgUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAZozSUUCFopKWgAooooGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFa5uobS2luLmRYoYVLvI5wqKBkknsMV8pfGP4mT+NtRaz093h0S2f8AdR9DcMOPMcfyHYe9dJ+0F8S/7VuZPDGiT5sYGxdzIeJpB/AD/dB6+p9hz5l4K8K6h4u16DS9NT5n5klb7sKDq7ew/U8UAXvhx4I1Hxxra2dmvl28eGubkrlYU/qx7Dv9M19a+E/Dmm+FtHg0zSLcRQxjkn70jd2Y9yf/ANXFR+DfCmneEdCh0vSosKnMsp+/M56sx9T+g4FdBQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXzF8ffiQfEN+fD2jy/8Sqzf9/IrcXMo/mo7ep59K7j4/fEj+wbFvDekS/8TS6T9/Krc28R7Z7Mw/Ic9xXzppenXWr6hBYWEJnubpxHGg6kn/PXtQBsfDvwdeeN/EUWm2u6OAfPczhciGPufqegHc19i6DpFjoekW2maZAIbW2UIij9cnuSeSe5rB+Gfgm08C+G47GLEl5Lh7u4A5kkx0H+yOgH49Sa7EdKACiiigAooooA8w8X/wDIyXf1X/0EV0fw6/48bv8A66j/ANBrnvFv/Ix3n1X/ANBFdD8O/wDjyu/+uo/9BoA6yiiigAooooAKKKKACiiigAooooAKKKKAOP8AiZ4Fs/HeirY3MzW08D+bb3Cru8tsYII7qe9eS23wI0/QXk1Hxr4kgi0qEFnEIMZY9hubOPoASe1d38SfjHo3hNWs9PCapqw4MMb/ALuE/wC2w7/7I59cV84eLPF+teLr43OuXrzYJ8uJeI4h6KvQfXqe5oAseOLnwlLdrb+DdOu4beInfdXU5ZpvonRR+p9q5Y1p22iahPpVzqsdtJ9gtiFkuCMIGJ4UHuT6Cs9V3H3PQUAb/gbwxe+MPEVrpFivMpzLJjiKMfec/QdPU4FfaljbJZWMFrEMRwRrEv0UYH8q4T4K+CI/B3hiJrmIDVb9VluWx8yg8rH9AP1z7V6JQB8/eMneXxXqZl3bhcMMH0HA/Sseut+Kls0HjCZyMLPGjr7/AC7T+orkq/SMvmp4aDXZHwWMi41pJ92IavaJpc2rarBYWwO6VsFv7i92/AVTVWkZQql3YgADkk9gBXsnw68Kf2HZm6vFBv7gDdx/q17L9fWsMyx0cLSdn7z2NsDhJYiouy3OrsrWOztIbaBQscKBFA9AMCrHSiivz5u7ufapKKshaKKKCgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACko71yfiTxnb6XK1tbJ59yOvOEQ+57n2FTKairs1o0KleXJTV2dZRXlD+OdcZyVmhUegiHH51f074hXkbAahbRzJ3aP5T+Xf9KyWIg3Y9OeTYqMeayfzPSKKztG1i01i386zk3Y4ZT1U+hFaNbKSex5EoShJxkrNCiigUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXk3x6+Iv/CLaV/Y2kzj+1b9DuZTzbRHgt7Meg9OT6V1vxI8Y2ngfw7LqdyQ9w+UtIM8yyY4H+6OpPp74r491zVr3XNUudS1KYzXV05eRz6+g9ABwB2FAEOn2VzqV9DZ2ULz3M7iOONBkuxOAK+u/hR4EtfA/h1IGCSalcYe8nHduyA/3R0HqcnvXHfs9fDoaTZJ4n1iHbf3S/wChxOvMMR/jI7Mw6ei/U17UBigBAMUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVxXxV8d23gbw49zxJqFxlLSA/xN3Y/7K9T+A710mtavZ6HpV1qepSrDbWqF5HPp6D1JPAHc18b/ABA8X3njPxFcapeEoh+S3hzxFED8qj37k9zQBi6jfXOqX817fTNPcTuZJJGPLMepr6U+Afw3/wCEa09df1iIf2tdp+6jZebaM9vZj39Bx61w/wCz98OBrV4viXWoSdPtX/0WJ14nlH8RHdVP5n6GvpYcDjpQAtFFFABRRRQAUUUUAeY+Lf8AkY7z/eH/AKCK6P4d/wDHjd/9dh/6CK5jxK2/X71v+mpX8uP6V1Xw+TGlTN/emP6AUAdRRRRQAUUUUAFFFFABRRRQAUUV518Svixo/gxZLSArf6tji2jb5Yz6yMPu/TqfbrQB2Ou65pvh/TJNQ1m8itLaPkvI3U+gHUn0A5r5y+Jfxv1HxB5uneG/M0zTTlWlzieYe5H3B7A59T2rgvGHi/WfF+pNea3etKf+WcQ4jiHoq9B9ep7mtL4ffDjXPHFyPsEX2ewQ4kvJlIjT1A/vN7D8SKAOWs7a51C8jt7SGS5uJm2pHGpZmY+gHJr3b4cfAQfu9S8bHJ+8unwt/wCjHH/oK/n2r0/wD8O9D8E2u3TIBJeMMSXsqgyv6gf3R7D8c12HagDwD9p67t9M0TQvDunxR21uXefyYlCqFUbV4H+8a83+CmhDX/iNpdvMu+3gc3MoPTCcj82wK+gfi98M18fW9q9tdraahabljeRSUkQ4JVsdOQCCPfiq/wAIfhWPAk11f315HeajcR+SDGCEjTIJAzySSBk8dKAPTQoUAAYAGBSmiigDnPGHhe38SWYSRvJuI8mKYDO3PUEdxXnknwx15Z9sb2jx/wB8yEfpivZaSu/D5jXw0eSm9Dgr4GjWlzTWpx3hHwHZ6FIt1cv9rvR0crhY/wDdHr7n9K7HFFLXLVrVK8+eo7s6aVKFGPLBWFooorI2CiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKDRQaAMHxjq39kaRJJGQJ5fkj+p7/AIV5GWZ3ZnYkk5JPc12HxPu/M1W3tQeIo/M/Fj/gK448j9a83EzbnY+2ybDqnQVTrISgUUVzHtnQeAruS28RwKh+WfKOPXgkH8CK9a715h8OLBrnWGvWGY7dSB7uR0/LNenY7elenh0+TU+HzqUJYm0eiVx9FFFdB4wUUUUAFFFFABRRRQAUUUUAFFFFABWdrOp2mi6ZcajqM4itbaMySOewH8yegHc1o18xftC/ED+3NVPh3S5s6dYP+/ZTxNMOv1Veg98n0oA4v4k+Nbzxz4jkv7gmO1jylrb7uIkz/wChHqT/AEArrPgN8Of+Eo1Ma3rEP/EnspPkRxxcyjnb7qOp9enrXJ/DXwZd+OPEsen24MVqmJbq4A4ijB5x/tHoB6+wNfYOi6VaaLpttp+nwrDbW0YjiQdgP5k9Se5oAvKAoAAAx6U6ikoAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoory349fED/hE9C/s3Tptur6kpCEdYIujP7E9B75PagDzP9oP4gDX9YPh/S5s6bp7/AL5kbiaccH6qvQe+T6Vx/wALfBN1448SxWCZSzixJeTf3I89B7noPz7VzNjaXGoXkNnaRPNc3DhI0XkuxOAK+w/hZ4Lt/A/hmOxTEl5NiW7mH8cmOg/2R0H596AOn02wt9MsILGxiWG2t0EcUa9FUDgVZopaACiiigAooqlrF8mnWEl1Iu4IOF9SegoAu0VxemeMpJr5YryCNIZWCBlzlc9M56iuyzwaAPJtRk87ULmT+9M5/U13fgWPb4fjb++7n9cf0rz2Q5lc+rH+deleEV2eHrMeqk/mTQBsVD50W4R71Vz0XIz+VVtb1BdM02W6bkqMKP7zHoK8unuJppmuJWZpGO4vnnNAHsFFU9HaZtLtWuc+cYl3565xVygAooooAKoatqdnpFi95qV1FbW0Qy8srYVR/j7VyfxH+Jui+B7cwzP9r1NkzHZxEbuehc/wL+p7CvmXxt4613xpf+fq9zmJSfJtk4iiHsO59zk0Aei/E7463Wo+bpvg/wAyztTlXvm4lkH+wP4B79fpXjMcc15chY1knnlbAABZnY/qSTXQeCPAmueNb/yNJtv3Sn97dS5EUf1Pc+wya+mvh38L9C8EwJPDH9t1Tbh7yVeVz1CDoo/X1NAHm3wx+A8k/lal40DRx8MmnIcMf+urDp/ujn1I6V75ZWtvZWsdrZwpbwQqESKNQqqB2AHSrNJQAAUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUGiigDyj4kceJn94Ux+tc1z3r0f4haBLfhL+yTfNCu10HVl9vcV5wxwSG+Vu4PWvLxEWptn3mVYiE8PFJ6pWYVa0ywn1K+jtbVSzuevYDuTU2kaLe6xcLHaRFlz80h4Rfqf6da9Q8N+H7TRLbbH+8mf/WSkcsf6D2p0qTk7vYnMMzp4aPLB3n+XqWNE0uHSdPjtYBkL1Y9WPcmtLvS4x0FGK9KNkrHw0pSnJzk7tiiiiimIKKKKACiiigAooooAKKKKACiiquo31vpljPfX0qw21uhklkboqgZJoA4D45+OR4R8MG3s5NuqagGjgweY1/jk/AHA9z7V8pW1tcX13Fb2yPNPcOERRyWYnAH1Jrf+Ini258Z+KLrVbjKxMfLt4j/yyiB+UfXufcmvUf2a/A3nTN4s1KL93ETHYKw6t0aT8Puj3z6UAep/CrwTb+CPC8NjgPfTYlvJRzukI6A/3R0H5967LFLRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFROyxKzMwVVGSTwAKAMjxd4isfCmgXOrakxEUA4Ufekc/dQe5P+NfGnifXr3xNrt1q+pvunuGztB4RRwqj2A4Fdl8bviCfGevm00+T/AIk9gxWDHHmv0aQ/XoPb6mq/wa8BP438SD7SjLpVkRJdP03f3Yx7nHPoM+1AHon7OHw++zxL4u1aD95KCthG4+4h4Mv1PQe2T3Fe81DDElvEkMSKkaAKqqMAAdABU1ACUtIazde1aDRdMmv7o4jiHQdWPZR7k04xcpKMd2TKSinJ7Fy5nihjMk0ixqv8TkAD8TUVrqNndHFvdwzH0Rw38q8F8Q69e69evcXkh2E/u4gfljX0A/me9ZiOUkDxsyFejDg19JSyCcoJzlZ+h4E85SnaMbo+mOorK8UWrXmh3UUQJfaGUDuQc1wnw18Y3Et0uj6tMZAw/wBHlc/NkfwE9+Oh/CvUPrXh4rDTwtR05nsYbERxEOeJ45jBweor0zw7f/2ho0MpOXVSj/7y8fr1rjvGVh9h1hnjX93cDzF9j/F+vP41b8CX3lXk1m5+WdSyZ/vAf1H8q5jpOZP3j9TXp3hX/kX7L/rn/U15ifvH6mu6ttSGl+DbeXP7xk2xf72T/LrQBjeN9T+1X4tImzFbcHHd+/5dKg8I6YdR1RXcZgt8O/8AtH+EfnWKdzSY5ZmP4k16d4Z0waXpccTD96/zyH3Pb8OlAGqBilo7VleIdd0vw7pcmoaxdLa2sfVmPJPoB1J9hQBoSOkSMzkKqjJJ4AHqa8O+KnxyjtfO0nwZKs83KS6hjKJ2IjH8R/2jx6Z61wvxS+L+p+MWk0/Tt9ho2ceWDh5x6uR2/wBkceua4bw/oepeI9Ti07R7Vrq6l6IvYd2Y9AB3JoAp3E9zf3bTTyS3NxM2WdyXd2PqTyTXsfwy+BdzqKxan4xElpaNh47EHbLKO28/wA+nX6V6H8LfhBpng9YtQ1Mpf61180rmOA+iA9/9o8+mK9PAxQBT0zTrTS7KOy062jtbaIYSKNQqqPoKuUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBoooASqk2nWc775bSB2/vNGCfzq3RRYE2thkUSRqFRQoHYU/FLSUA9dxaKKKACiiigAooooAKKKKACiiigAooooAK8E/ab8beWsXhKwkO59s96Qei9Uj/H7x/CvW/GviW18KeHL3WL3BS3X5I+8kh+6o+p/Ic18Y61qVzrOqXepahIZLq6kMkjH1J7ew6AelAGl4E8M3Xi/wAT2mj2gKiVt00mP9VGOXY/QdPU4FfZukadbaVpltp9hGIra2jWKNB2AGPzrzb9nvwSPDvhj+176LbqOqgPz1jh6qvtn7x/D0r1igAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvE/wBoz4hf2ZZN4V0qbF1dpm7kQ8xRnon1bv7fWvQviR4ytvBXhq41Kfa85/d20JODJIeg+g6n2r431TULnVdRn1C/kaa5uZDJK56sTQBP4e0a98Qaxa6TpkTS3NzIEQdh6sfQAck+lfZXgbwxZ+EPDtro9ioIjG6WTGDLIfvOfr+gwK4P9n74fHw5o/8AbmpxAanqCAorDmCHqB7M3U+2B6165jmgBQKDRQaAGmuE+MgY+G4MHC/aRu/75au8Nc18RNKfVfC1zFCN00eJUH94r2/LNdWDkoYiEntdHJjIudGUY9jwuk7YpT2or9NPgyS0ne1uI7mElJIWDqfcHIr6E0HUU1XSbW+j486MMR/dPcfgeK+d69r+FL7/AAdbD+67gfTca+X4gpJ041et7Hv5NVaqOn0auXvG9j9q0kzIMyWx3j/dPDf4/hXAW0z286TRHEkZyDXrjosqMjjKsMEHvXlOq2LWGozWrD/VsQG9VPIP5V8gfUFU8kk9TWlrN55sdnaKf3dpCq/8Dxlv8KzaUnJz97JoA3/BOmC81MTyLmK1Afnux+6Pw616GBWDo0Vt4e8OrNfzR2yBfOmllYKFz6k+g4rxr4l/Hd5/M03wWzRR8rJqTLhm/wCua9vqefQDrQB6L8Sfilo3gqF4CwvtVIylnG33fd2/hHt1PYd6+YvGPjDWfF+pm+1u6MpHEUK8Rwr6Kvb69T3NYrvPfXJJMk9xK3XlnkYn8ya9s+GHwLuLrydT8aK8EJwyaeDh39PMP8I/2evrigDg/hx8NNZ8dXavbx/ZdMVsS3sgO0eqoP4m9hwO5FfUXgvwdo3gzShY6NbhCQPOnYZkmb1Zv5AcDsK27Gzt7G2jtrOBIIIVCJFGoVVA7ACrNACUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFYGseGLHVtXsdTuJLxLiydWj8m6kRDg5AZAdpGevHPQ8Vv0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFeWfHvx/8A8IvoP9l6bMBquoqVBB5hi6M/sT0H4ntQB5R+0B48/wCEm8QHSNPlJ0vS2K5B4lm6M3uB90fie9ZfwT8EN4x8Wp9qTdplhie6J6N/dj/Ejn2BritOsbjUr+3sbKJprm4kEcaL1dicAV9j/DTwhb+C/DFtpcQVrkjzbuUD/WSkc/gOg9hQB1MaBQAAABwAO1PoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACq9zcxWlvLcXMixQwoZHdjgKoGST+FWK8A/aQ+IYCnwjpE3XD38iH/vmL+p/AetAHnPxf8cP418TvNEzDTbXMdnGePlzy5Hq3X6YHat34B+AD4o14avqcJOk6a4OGXiabqqe4HU/gO9cL4P8OX3irxBa6Rpw/eTN8zkcRIPvOfYD/CvsrwroFj4b0K00nTE2W9sm0HHLn+Jj7k8mgDXAAGAMAUooooAKKKKACg9KKKAPMvGXw6luLt73QvLBlO57djtG71U9OfQ159qelX2lTmLULaSBh/eHB+h6H8DX0bUU0Ecy7ZY1kX0YZFe3hc5rUIqE/eS+88fEZTSqvmg7M+bYo2mkWOBS7scBVGST7AV714H02TSfDNnbTqEmClpFHZmJYj8M4rSisraB90NtFG395UANWR0FZY/NHjUoctktS8Dl6wknJyu2Orj/AB/p5ZY9QjGNv7uQ+x6H8+K7DNQXtvHdW0lvMuUkUq30NeSeqeRVreFbD7frUKMMxp+9f6D/ABOKi1TRrzTrpoZInYZ+WRASGHbH+Fdf4M0mTT7R7i5XbNcYwp6qo6CgDxH9qHV9UbxNZ6SzyJpgtlnjQZCyyFmBY+pGAB6fjXmng/wfrPjDUhaaJZtNjHmSniOEerN0H06nsK+xPEPhnRPEtssGuabBexxnKCVeUJ67WHIz3wasaJo+naHYrZaRYw2VuORHCuBn1Pqfc80AcZ8NPhPo/gxEupVXUNWI5upF4jPoinp9ep9uleiUo6UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRTGYIpZjgDkk0AZfinxDY+GNCutX1OTZb265x3dv4VHuTxXxj4t8RXvijXrrV9RbM1y2Qo6Rp0VB7AcV2vx1+IR8X67/AGfpspbR7BiEI6TydDJ9Ow9ue9Zvwf8AA0vjjxLHHMjDS7QiW7k6bh2jB9W/QZNAHpX7N/gAwRf8Jdq0OJJVKWKOPur3l+p6D2ye4r3iq8EMVrbxwQIIoolCRqowFAGAAPQVYoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiszxDrdh4e0e51XU5RFbWqFmPc+igdyTwB60Acv8YfHsHgfw80kLI+q3QKWkR5we8hH90fqcCvkOea4vrt5Znee4ncuzHJaRyeT6kk1ueO/FN94z8RXGrXzbVkO2GLORDGPuqP5k9zk16b+zr8Oze3S+KtWi/0WBj9ijYf6yQf8tPoO3v9KAPRfgj8Px4N8PC6v4saxfgNPnrCnVYh9Op9/oK9JpKWgAooooAKKKKACiiigAooooASiiszV9TFggVfmkfoPQetZVa0aMHOb0KhBzdkaRx64rOu9YtrZtrMXf0Tn9a5me6mnfdM7tn34/Koic189WzptNUlbzZ6MMB/MzoW8RR9oH/EipLTXbeaXZKjRZ6E8g1zVNNclPNa/MnJ3RrLB07HfZBFLUFoc20e77xQZ/Kp6+wi7xTPIYtFFFMQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUABoorB8S62NMhEcGGuXHyg9F9zWVWpGnFylsTKSirs1rq7t7Yfv544v95gP51mt4m0pWx9rB9wrH+lefXM8t1MZbiQySN1JqKvDqZtK/7tK3mcksS76I9Usr62vU32sySjvtOcfUdqtdq8q0+9msLpZ7dsMp5HZh6GvStNvor+zjuIDuR+3cH0P0r0cJjFiU09JI3pVVU06l2iiivQNgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvEv2hviKNMs38LaNMfttyv+mSIeYYiPuZ/vMOvoPrXafFrx7D4G8PGaMo+qXOUtIT645dh/dH6nAr5Cu7u51C9mubqV57i4cvI7HLMxOSfqTQBa0DR73XdYtdL0uEz3N04SNf5knsAOSewr7G+H3hOz8F+HYNJsgGdfnnm24M0h+8x/kB2AFcf8CPhyvhPShqurw41i+QfKw5t4jyE/3j1P5djXq1ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJ/IV8q/Hr4i/8JXrP9laVNu0iwc8jpcSjgv7qOg/E967/wDaG+Iv9lWbeF9HmK39yn+mSIeYYmH3AezMOvoPrXz9oek3ut6rbabpkTTXV04SNQO/qfQAck9qAOj+FXgWfxz4lS0G6PT4MS3cwH3E7KD/AHj0H4ntX2BY2dvp9nDaWcSw28CBI41GAqgYAFYXw88IWfgrw5b6Za4kl+/cTYwZZCOT9OwHYV09ABRRRQAUUUUAFFFFABRRRQAUUUUAJXF6vKZtSlJOcMVH0HFdp3rkNZs5ILuR8ExSHcDnj6V4ecqbopx2T1O3BNKpqUKKKK+UPaCrGnW5ur2KL+EnLfQdar10Xhuz8uI3Mg+aQYX/AHfWu7A0HXrRj03Zy4mr7OD7m2igDgYpaUUV9yeEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaKKAGmvL9cuWutWuZGOcOVX2AOBXqBry/W4vK1a7TGMSMfzOf614ubX9mrbXOXE3silRRRXzxwhXb+AVYaXKSflMvH5DNcSql2CquXJwAO5NenaFYjT9MhtwMFVy3+91NetldNyquXRI6sNG7uaFFFFfSncFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAAayPE2u2XhrR7jVdVmEVtAuT6s3ZVHck8AVoXFxHawST3DCOKJS7yOcBVAySa+TfjN8RZPG2ti3sWZNGsmIt0/wCerdDIR6nsOw9yaAOb8deKr7xj4iuNW1FseYdsMQOVhjHRB/U9zk16Z+z18OjqVzH4q1qDNnbt/oUTjiWQH/WEd1U9PU/SuO+EPgCfx14gCTh00u2Ie7lXjI7Ip/vH9Bz6V9cWdnBZWsNpaRLDBAgSNFGAigYAFAFkUtFJ70ALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVxHxY8d23gfw69x8r6jcZjs4T/E3diP7o6n14Heuj8Q61ZaBpF1qmpzCK1tULse59AB3JPAHrXx1498WXvjLxFNq1+XRXO2CHPEMQ+6o/mT3OaAMS/vLnU76a8vZXmubhzJLI3JZick19N/Ab4cnwvpY1vWIcavep8qP1tojzt9mPU+nT1rhP2evhz/AGvdL4o1mDNjbP8A6JG44mlH8ZHdVPT1P0r6T9h0oAWiiigAooooAKKKKACiiigAooooAKKKKAE71T1G2FzZyRd2HH17VdpO1Z1IKpFwezGm07o4JlZHKsMMvBBpK7K6062ueZYgW/vDg/nUUOjWUXzCEE/7RJr5qWT1HKykrHqLGpLVamLpGlNdOJJ1IiHr/F9PauoVQBgdKUAAAAcU7jFe5hMJDDQ5Y79WcFWtKq7yPmTxr8cfFQ8T3kWhzx2FlazPEieQjmQKSNzFgTk46DGKfpf7RXiK3wNS0uwvAOpTdEx/Uj9K7rxv8BtL1/VLnU9M1OTTZ7hjJLEYhJEznkkDIK5PPU157q37PXiu0BOn3Wn369gJDGx/Bhj9a7rmJ3WkftG+H58Lqek39mx6mNllUfjkH9K6/R/i34H1bHla/BA5/guVaI/mwA/I18zap8MvGelZa88O3xQdWhTzR/45muYubaa2kaO4heF16pIpU/kaAPu6x1Kx1BPMsLuC6j/vwyq4/MGrVfA9pcz2sgltp5IHHRo3KkfiK6jSPid400kKtn4hvCq9FmcSr+Tg0WA+0KK+YNJ/aG8UWmF1Cy0++Xu2xo2/MHH6V2WkftHaNNgarot9anuYHWUfrtNID22iuC0r4zeBdSAC60tq5/huonj/AFIx+tddpus6ZqiB9O1G0u1PeGZX/kTQBfooooAKKKKACm/jzWD481G80nwbrGoaau67trWSSLvhgOuO+Ov4V8ZrrerrqX9orqd2L7dv8/zm35653ZzQB92UVx3wr8XReMPCVndm4WS+hRYrxBwVlA5JHoeo7V2NABRRRQAUUxmx1496ak0bfdkU/Q5p2YuZIlooopDCiiigAooooAKKKKACiiigAooooAKKKKAErlvFmgyXb/bLQZlAw6f3wOhHvXVUVhWoxrwcJbETipqzPIpI3hcpKpjZeoK4Ipv9a9O1DSLK/O66t1dhwH7/AKVFZaFp1m4eG1+cdGbLEfTNeI8qnz2TVjleGd99DG8K+HjCVvb5MSdY0P8AD7n3rraAMUte1QoRoQ5InVCKirIWiiiugsKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKK8u+OvxEXwloZ07TZv8Aic3yEJt628Z4Mh9D2Hvz2oA4T9oT4lG+uJPCmhzn7NEcX8yn/WOP+WQP90Hr6njtz5V4N8M3/i3XrbStNQmSU5d2HyxoOrt7D9TxWXbQT315HBbxvPczuERV5Z2JwPqSa+uPhD4At/A+gKs6I+rXID3coGcHsin+6P1PPpQBv+C/DOn+EdAt9J0tMRwjLOfvSuern3P6DjtW9RRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFNOF74Ap1eJftC/Eb+zbZ/C2iTkXtwv+myoeYoyP8AVg/3mHX0H1oA4L47/Eb/AISvV/7J0mYnR7GQ8g8Tyjgv9B0H4nvXPfCrwPceOfEqWoymn2+JLyYfwJ/dH+0eg/E9q53QdHvNd1e20zTIjNdXLhEUD17n0AHJPYV9i+APB9l4K8Ow6ZZAPKfnuJtuDNIerH27AdhQBvadZW2nWMFlYxJDbW6COKNBgIoGABVkClooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACqd/p1jqCGO+soLpSMETRK4/UGrlFAHDat8I/A+pgmXQIbdz/Fas0R/JSB+lcdq/7OWgz5bS9WvrInosoWVR/I/rXtVFAHzLq/7OniS23NpupWF+g6K26Jz+BBH61x+rfCfxtpeftGgXUqj+K2AmH/AI6Sf0r7KooA+Cbq0ubOTy7u2mt3/uSoVP5EVHHK8UgeNjGw6FTg/mK+8r20t7yLyrq3huIz1SVAwP4EVy2rfCzwVqysbrw7Zo7fxW6mE/8AjhFAHyzpPxD8X6RgWHiK/RF6JJKZF/75bIrsdI/aB8X2eBfRWGoL6yRFG/NSB+leiar+zr4auSW0/UL+xPZSVlUfgQD+tcdqv7OOtwBm0rWbK7A6LMjQsfy3D9aAN7SP2krB9q6xoNzCO720yyf+OsF/nXYaT8bPA+oEB9UezY/w3MLJ+oBH614Bq3wg8caYT5mhS3CD+O1ZZQfwU5/MVyV/pWoabJs1GwurNvSeFkP6gUAfbWna5omtx40/U7G+VxjbFMr5HoQDXzZ8bvhlJ4Vvn1fSIidEuX5UDP2Vz/Cf9k9j+Hpny1SVYMhKkdD0NbNv4s8QwWktmmtXxtZl8uSB5i8bL3BU5H6UAWvAHi/UPBWvx6lp5LKcJPAT8s0fdT79wexr6+8LeJdP8UaJb6rpMweGYcr3jbujDsR/9fpXxEYmWES/LgsV6jOQAenXv1r0X4B+KrnQPG1np4kY2OrSLbyxHpvPCOB6g8fQ0AfWRrF8U+IIPD2lNdzjcx+WJB1d+w+lbNeQfGC/afxBBZ5/d28Qbb/tMck/kBXdl+G+s11Te27OHHV3Qoua32Oc13xFqmt3BkvblimfliQ7UUegA/meay1llj5SR1PqCRTWpeRX6DTw9KnHlhFWPip1pzlzSep33w+8a3iajDpeqTNNBMdkcjnLI3YE9wenPSvWetfOmhKW1qxWP7xuIwPruFfRa/dFfF51h6dGsnTVro+qymvKrTak72HUUCivEPZCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKK5fx74y0zwTobX+pPukOVt7dW+eZ/QegHc9B+lAB4/8AGWneCtCfUr5g8pBW3gB+aaTsB7ep7Cvj3xFrd94i1m51XVZvNurltznPAHZQOwA4Aq54z8V6n4x1qXU9Wm3MflhiX7kK9lUenqepPJrt/gj8LZPFV9HrOtRMuiQNlVYYN24/hH+yD1PfoO+ADsP2dvhybSFPFusw/vpl/wBBiccoh6yH3I4Htz3Fe71EiLGiqihVUYAA4A9BUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUVleJNdsvDejXOq6pN5dtbrub1Y9lUdyTwBQBzfxb8fQeBvD5niKSandZjtIT/AHu7kei/qcCvkO+urrUr6W6u5nuLidzI8jHLOxPJ/Otnx34qvvGXiO41XUWxvOyGIHKwxj7qj+p7nJr0r9nn4c/2ldJ4p1mDNnbv/oUTj/WyA/6zH91T09T9KAO8+BHw6HhTShq2rQ/8Tm+QHaw5tojyE9mPU/l2Neq0vSigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKzde1DSbG0J1u6s4Lduv2p1Cn8D1rzD9ojx1q3hm0sNM0SVrSW+DySXCffCLgbVPYknk9fSvmu6u7m+nae9uJbiRjkySuWY/ieaAPefHHi/wCD2HEWgQ6xcH+Kyt/IH4v8v6A14hrt3pl3emXSNMbTbbtEbhpj/wB9ED+VLougavrspi0bTbq+IOCYYmYD6kcD8a9J8M/s/wDifUdsmsz22jwnBwW86X/vlTj/AMeoA8kAyQBzmvdfgb8Kb9NUtfE/iCJ7SG3YS2ls4w8j/wALsP4VHUDqT7dfSfA/wj8M+EnjuY7dr+/TkXV1hih9UXov1xn3rvhQA2vEfij/AMjncf8AXOP/ANBr2+vJvjBpMsWpQapGhaKVBE59GHTP1H8q9nJakaeKXN1VjyM3pudC66M8/o60VPpthcaldpaWUZkmkOAB/M+gHc191KpGEXKTsj5GEXN2judP8L9IfUfEi3LL+4sh5hY9C54Uf1/Cva6w/CGhQ+HtIitEw0h+aV/7zn+nYVuV+eZjivrVdzWy0Xofa4DDfV6Ki93qxRRRRXnnoBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUVFI6RKXchVUFiT0AHUmgDN8UeIbHwtodxquqSbYIFzgfeduyqO5J4r478eeLtS8Y+IJtT1JyATtghDfLCnZR/U9zzXR/Gn4gyeNfEDW9nI39kWTFbZB0lboZT9e3oPqarfCD4ez+OtdAuFkj0m1Ia7lHG7uI1P94/oOfSgDZ+C/wrk8X3C6vrKmDRYm+UdGumHVR6KO5/Ad8fUFnawWVrFb2sSQwxKEjjjXCoo6AD0ptlaQWFrDaWcSw28KhI41GFVQMAAVaoATFLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAQTzJBG8ssioiKWZmOAAOpJr5S+NPxGl8Z6v8AY7CQrotmx8lennP0Mh/kB2GfU12P7QvxL3yS+EtEnyg41CZD1P8AzxB9P735eteO+FfD994o1y30jTI99xOfvY4RR1dj2A7/AONAGz8MvBh8Vau0l85t9HssSX1wTgBeyKf7zdPpzX0D/wALJ0fTIY7LSdMlNtbqI4guI1CgYAA64+tY3i3QLXwZ4N0jQNMJ8kyM9w+MNO4UZdvxPA7DA7VxHFfS5XlVLEUva1db7I+dzDMqlKr7OnpY9Ti+K1qX/eaZOq9yJVJH4YrudH1O21iwjvLJ/MhkHHYg9wR2NfOleq/BiV20u+jY/IkykD0yv/1qeaZXSw9H2tJWswy/Malap7Oprc9FooHSivmT6IKKKKACiiigAooooAKKKjeeKP78iL9WFAElFVW1OxT795bp/vSqP61Vm8SaHB/rdY0+P/euUH9aANSiubn8feEbfPm+JtJXHYXaE/kDWdcfFrwLb53+I7Rv+uYd/wD0FTQB2tFeaz/HPwJB8q6jczH/AKZ2r/1AFZV5+0V4ThyLaw1W4Pr5SIP1bP6UAev0V4NdftKWo/49PDc7f9dboD+Smse8/aR1l/8Aj00Kwi9PNkeT+W2gD6Ror5Vuv2gPGsx/c/2bbf8AXO2z/wChMayrz4z+PLk/8hww5/55QRr/AOy0AfX9FfFlz8SvGlyP3vifUxn+5OU/9BxWbP4r8RXGfP17U5c/3rqQ/wBaAPuNmVfvMB9aja6t0+/PGv1YCvhKbVNQn/11/dP/AL8zH+Zqs7F+WJJ96APu6TWNMjOH1GzU+jTqP61A3iTQ0Pz6zp6/W6jH9a+FsUuPY0Afcp8V+Hgede0v/wADI/8A4qkPi7w2OviHSR9b2P8A+Kr4bx7UmKAPuT/hL/DX/Qw6R/4HR/40h8Y+GP8AoY9I/wDA6L/4qvhzFGKAPt9/G3hZf+Zj0r/wMj/xqJ/H3hFPveJdJ/8AAtP8a+JcUYoA+rvHeofDTxlp6Wmt+IrDMTFop4blRJGTwcHkYPcEYrn/AA5Y/BXw5ydSsdSnHPm3jGY/goG0flmvnGnIjN91SfoM0AfXafFv4eWESxwa3BHEvAWG3k2j6AJioJfjn4CTOzVJ5f8ActZR/NRXyklndP8AdtZm+kRP9KsRaHq8x/c6TfSf7tu5/kKAPpiX9oDwSn3DqUv+7bD+rCqM/wC0Z4XX/U6bqkn1WNf/AGavAYPBXim4/wBT4c1V/pZyf4VowfDHxrP9zwzqC5/vRbf/AEIigD1+f9pPSh/x7+H71/8AfmRf5A1kar+0RFfWz2z+Eo5YZBhlnvMgj6BK4WD4N+PJv+YBJH/vzRj/ANmq/F8B/Hcn37C1i/3rpD/Immm07oTipKzMq/8AHvnTeZa6TFbRk58tpmcfgeDWrpXxm1fRYDFpOk6TAzfelaN2dvqd36dKu2/7PPjGX/WXOkwf787n+SGtGD9nDX2/12taYn+4JG/oK6amMrVI8k5No54YWjTlzQikZMvx/wDGzfcOnR/7tt/iTVST46ePX+7qcEX+7aR/1BrrYf2a78n994lt1H+zas382FW4P2bI/wDlt4mf/gFn/i1cxuefyfGnx+//ADHiv0tYR/7LUJ+Mfj5v+Zhl/CCIf+y16an7NVj/AB+JLn8LVR/7MamH7NmlfxeIb0/SFB/WgDyn/hbvjz/oY7j/AL9R/wDxNJ/wtvx5/wBDHc/98J/8TXrP/DN2i/8AQev/APv2lO/4Zu0P/oO6j/3wn+FAHkf/AAtvx3/0Mdz/AN8p/wDE0f8AC2/Hn/Qx3P8A3wn/AMTXrn/DNuh/9BzUf++E/wAKP+GbdD/6Dmo/98J/hQM8kHxb8ef9DHcf98R//E08fGDx6OniGb8YY/8A4mvWP+GbtE/6Duof9+0/wpv/AAzdpP8A0H73/v0lAjy1PjP4/T/mPlvrbwn/ANlqZfjf4+X/AJjSn62kP/xNekN+zZpv8PiO7H1tlP8AWov+GarX/oZpv/AMf/FUDPPx8cfHo/5i0J+trF/8TUg+O3jsf8v9t/4Cx/4V3J/Zrh/g8TP+NmP/AIqoz+zWvbxO3/gH/wDZUCOMHx48d/8AP7af+AqU7/hfXjn/AJ+7P/wFWuv/AOGa2/6GYf8AgH/9lR/wzW//AEMy/wDgH/8AZUDOQ/4X345/5+7L/wABVo/4X345/wCfuy/8BVrr/wDhmt/+hmX/AMA//sqb/wAM1yf9DMn/AIB//ZUAcl/wvvxz/wA/dl/4CrR/wvvxz/z92X/gKtdd/wAM1S/9DMn/AIBn/wCLo/4Zql/6GZP/AADP/wAXQI5H/hffjn/n7sv/AAFWj/hffjn/AJ+7L/wFWuu/4Zql/wChmT/wDP8A8XR/wzVL/wBDMn/gGf8A4ugDkP8Ahffjr/n7sv8AwFWl/wCF9+Ov+fuy/wDAVa63/hmqX/oZk/8AAM//ABdH/DNUv/QzJ/4Bn/4ugs5L/hffjr/n7sv/AAFWl/4X345/5+bH/wABR/jXWf8ADNU3/QzJ/wCAZ/8Ai6b/AMM1T/8AQzRf+Ah/+LoA5hfj743X/lppzfW2/wDr1Iv7QXjT+KPS2/7d2/8Aiq6A/s1XvbxNb/jaN/8AFVG37NmqD/V+IbNvrbsP60AZkX7RPixfv2Wlv/2ycf8As1WF/aO8SfxaRpR/7+D/ANmqWT9m/Xf+WeuaeT/tI4/oarSfs5+KB/q9U0h/q8g/9kNAFlP2kNcH+s0PTj/uvIP6mpF/aS1X+Lw/Zn6TuP6Vlv8As7+MR9270dvpPJ/VKh/4Z88adpdLP0uG/wDiKAN5f2lNQ/i8N2v4XLf/ABNPX9pW5H3vC8R+l6R/7JXN/wDCgPG39zTj9Ln/ABWom+Avjlfu2tifpdL/AFoA7CP9pc/8tPCv5X//ANrq3F+0nYHHn+HLlf8AcuVP81FcA3wJ8eLyNOtm+l3H/U1Wm+Cnj6IZ/sQP/uXMR/8AZqAPVYP2j/DrHE2j6nH/ALvlt/7MK5n4rfGy38Q+HW0nwvHdWwugVupZ1Ct5f9xcE9e59OO9cDP8KfHVvnzPDV42P7m1/wD0EmsG88O65ZSvFd6NfwSJ95Xt3GP0oAh0mxk1XU7exgeKOS5kEYeVwiL7ljwAOpr7N8BaBp3hrwtZ6dpDxywRrlplIPnOfvOSOuT+Q47V8TujKSGUgjqDxXv37K8uqPBrUchkOkr5ZTdnas3O7b9R1/CkI99ooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvL/jl8RR4Q0f7Bpkv/ABOrxD5eP+WEfQyH37D357V1/jvxVZeDvD1zq9+c7BtiiB+aaQ/dQfX9Bk18beJNbvfEWs3WqapMZbq5cu57D0UegA4HtQBTiiuL67SOJJJ7idwqqMszsx4HuSa+tPg78PYfBGhiS4VJNYvFDXMg58sdowfQd/U/hXF/s9fDb7JBH4s1uHFxKM2Mbr/q0P8Ay0I9T29Bz3Fevar4n0LSf+QprFjae0s6q35ZzQBxHxotZjHp14FJhQvG5/uk4I/ka8zr0vxN8Yfh+ttNZ3F3JqcbjDJbwMwP0LYH6141rXjjQftH/Eks74QE9LlkyPpjP619TlWZ06VP2NXS2zPncwy6pUq+0p63Nv2r1P4MQSrYX8zKRFJKoU+pAOf5ivnu58btsItrUK395mJI/AVSn8e+KJrYWo1u8ht0GFhgk8pQPouKWbZnSrU/Y09b7sMuy6rRqe0qaWPs2+1Ox06Pff3lvap/emlVB+pFcrqfxW8Eabu87xFbSuP4YA0p/wDHQRXx3cXEtxIZLiZ5pG6tIxYn8TRBFLO+yGNnb0RST+lfLn0R9N6l+0P4Vt+LKz1K8P8AeEaxr+ZbP6VzOoftKTnI03w3GnvPclv0Cj+deVab4B8W6mAbPw7qUin+IwMi/mwArp9N+BHji8wZbO0swf8Anvcr/JcmgC3f/tB+MLgkWsWnWinpsgLEfizH+VY118ZvHlx115o/+uUES/yFdfZfs36w+De69YweoiieTH8q3bb9mzT1x9s8SXcv/XK2VP5k0AeP3PxK8a3H+s8T6lz/AHJin/oOKzp/FniO4/1+v6pJn+/eSH+Zr6Gtv2dfCaY8++1Wb/toi/yWr0HwE8Dp9+C+l/3ro/0AoA+XpNV1GX/WX90/+9Mx/magaedvvTOfqxr64g+CXgCLrojSf791N/Rqtx/CPwHF93w3bH/eeRv5saAPjgknqc/Wkr7Rj+GfgmL7nhnTj/vQhv51ag8CeEov9X4Z0tcf9Oqf1FAHxJnPWnRo8jbY1Zj6AZr7nh8NaFBzDounR4/u2kY/kKvQW1vCMQ28UQ9EQD+VAHw3beHtbusfZtIv5s/3Ldz/ACFa1r8N/Gd2B5HhrUue7wFB+bYr7VooA+Q7P4KePLkDdowgHrNcRj9AxP6VsWn7PPi+bHn3Ol24/wBqdm/ktfUlFAHzjbfs26q2PtXiGyi9fKgd/wCZFa9v+zXZj/j68Rzv/uWyr/NjXu9FAHj1p+zp4XjXFzqGqTH/AGZET/2U1pQfAXwNF/rLS9n/AN+6YfyxXp9FAHAQfBfwFDyNCD/79xKf/Zqtx/CfwLH08N2h+pc/zau0ooA5WP4a+Co/u+GdN/GEH+dTL8P/AAgv3fDOlfjaof6V0lFAHPjwP4TH/Ms6P/4BR/8AxNO/4Qnwr/0LOjf+AMX/AMTW9RQBhf8ACF+F/wDoW9H/APAGL/4mnf8ACIeGf+hc0n/wCi/+JrbooAxv+EV8Or/zL+l/+Acf/wATUkfhzQ0+5ounL9LWMf0rVooApR6Rpsf+r0+1T/dhUf0qVbO3X7ttCPog/wAKsUUAMVAn3VVfoKdS0UAFFFFABRRRQAUUUUAFFFFABRiiigAooooAKKKKACiiigAooooAMUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZWpeHtG1YH+0tJsbvPee3Rz+oNW7KytdOtUttPtobWBPuxQoEUfQCrVFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVV1C9t9Osp729lWG2t4zLJIx4VQMkmrVYfjbRf+Ek8K6no4kETXkDRrIeit1BPtkDPtQB8q/Fjx5ceOvELXCGSLTrYlLWEnovd2H949/QYFcXG/lyK6gEqQRuGR+Irtrn4Q+OoLxrYaBNKVOBJG6FG9w2cfniun0H9nrxNfBX1i8s9LjPVQTNIPwGF/8eoA8+1bxt4n1ddmoa5fSx9PLEpSMfRFwB+Vc+evPWvp/Rv2e/CtntbU7q/1Jx1BcRIfwUZ/8ertdI+HfhDR8NYeHrFHHR5I/MYfi2TQB8c6do2p6mwXTtPu7tj0EELSfyBrrtL+DvjrUAGXQ3t0P8VxIsf6E5/SvruKJYkCRIqKOgUYFTDNAHzZpX7OWuz4Oq6vY2g7iENK36hR+prr9K/Z28N2+Dqep396R2TbEp/DBP617JijFAHE6X8JPA+mYMPh+2mcfxXBab9GJH6V1Vjptjp67bGyt7VfSGJU/kBV3FFACAZ5NLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRTHlWNSzsFUdSTigB9FVRqVkxwLuAn08xf8anVwwBUgg9CKAH0UUUAFFFFABRRRQAUUUUAFFFFABRRUck8UQzJIij3bFAElFUpdX02L/WX9qn+9Mo/rVWXxRocX39Xsh/23X/GgDXornm8b+G066zbH6En+QqGT4g+GE/5iefpDIf/AGWgDp6K5CT4k+GV+7dzN/uwN/UVE3xQ8Or/ABXZ+kP/ANegDtKK4j/haXh//p8/78j/ABo/4Wl4f/u3n/fkf40AdvmjNcR/wtLw/wD3Lz/vyP8AGj/haXh/+5ef9+R/jQB29FcR/wALS8P/AN28/wC/I/xqWP4meG5Os86f70J/pmgDsqK5eP4geGWH/ISVf96Nx/SrMfjPw4/3dZtvxbH8xQBv0Vjr4n0Nvu6tZH6TL/jU6a9pD/d1SzP/AG3X/GgDRoqius6Yxwuo2hPtOv8AjUi6jZt926gb6SKf60AWqKg+2W//AD3i/wC+x/jR9rt/+fiL/vsUAT0VB9st/wDnvF/32Kik1Swj/wBZfWyf70yj+tAFyisqXxJokX+s1ayH/bZf8ai/4S/w6P8AmNWX/f0UAbVFYv8Awl/h3/oNWX/f0VDL438Nx9dWt2/3ct/IUAdBRWFD4x8P3EkccWrWxeQ4UFtv863aACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAowKKKACiiigAxRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVBfXtvYWzXF5MkMKfedzgCs3xP4js/D2nm6uySx4jiU/NI3oP6ntXifiTxJqPiK6M19JiMH91Cp+WMew7n3PNAHoGt/FW1gkMWkWhuiOPNlbYv4DqfxxWJ/wtbWd/8Ax5WTL6bX/nmuX0Lw/quuSsunWrOq8M5+VF+rHj8OtbOv+ANQ0LR5NRurq3kWIqGSMNnkgcEj1NAHfeDvHtn4gcWcsJtb7buEecrJjrtPr7GuwH0r5x0Wd7bWbKaI7XS4jIP/AAIV9H0AFFFFABRRRQAUUUGgBrnaN3bqa8I8c+JpvEOqyeVIwsYfkhizgHHViPU/oK9zuv8Aj2m/3D/Kvmk8DAoAX+dSQ3M8P+pnljb/AGHK/wAjXsvg7w3ot74U06W60y2mlkhDO7xgsxPvVuf4f+G5v+YcI/8AckZf60AeMx67rMX3NUvR/wBt2/xqX/hJdc/6C19/3+b/ABr1U/DHw63RLpPpMf65pn/CrvD/APevP+/w/wDiaAPLf+El1z/oMX3/AH+b/Gj/AISPXf8AoMXv/f5v8a9S/wCFW+H/AO9ef9/h/wDE0q/C7w8Ov2s/9tv/AK1AHlP9v6z/ANBa9/7/ALf403+3NX/6Ct7/AN/2/wAa9a/4Vj4d/uXP/f40v/CsfDf/ADyuf+/5oA8k/tvV/wDoKXv/AH/b/Gj+2tW/6Cl7/wB/2/xr1v8A4Vl4b/543P8A3/auS+JXhTSfD+n2k2nRyI0spR98hbI2570Ach/bWq/9BO9/7/v/AI0f21qv/QTvf+/7/wCNTeF9Oj1XxDY2M4zFLKA+Dg7QMnB/CvWP+FaeGv8An3uP+/7UAeOvqN/J/rL25f8A3pmP9aruWc5dmY+pOa9vi+HXhmP/AJcnf/elY/1q1F4G8Nxfd0qE/wC8Wb+ZoA8D2j2oyo7rX0NF4Z0OL7mkWIx/0wU/zFW49M0+L/V2Fsn+7Co/pQB84qpb7ik/QU4Wlw/3LeVvoh/wr6TWCJfuwov0UVLQB82rpOpP9zT7tvpEx/pUqaBrD/d0q9b/ALdn/wAK+jaKAPnYeGtc/wCgPe/9+G/wp3/CMa7/ANAe9/78t/hX0PRQB88f8Ixrv/QHvf8Avy3+FH/CMa7/ANAe9/78t/hX0PRQB87nw3ri/wDMHvf+/Df4VBJo+pxf63TLxfrbv/hX0fRQB80Pazp9+2kX/eQj+lRMAv3ht+tfTTDd1AP1qJ7WB/vwRN9UBoA+aQydmFGV9Vr6RbTLBvvWNs31iX/Co30PSXGH0qzb6wJ/hQB859ei5+lGD6GvoZvDWhN97RrH/wAB0/wqNvCvh9uuj2Y/3YgP5UAfPuKMV79/wh/h3/oEW/8A3xR/wh3hz/oD23/fNAHgOKMV7/8A8Id4d/6BFt/3xU0fhfQYvu6PZfjCp/mKAPnnhewo3r6ivo+LSdMi/wBVp9on0hUf0qX7Faf8+sP/AH7H+FAHzZlT3oCs3RSwFfSn2K1/59of++BXNfEvyrTwXfGKONDIUTgAdWFAHiB9xX0L4V+0r4b0/wC2588W6bs9enH44614Dp8RuNQt4QM+ZKifmQK+kkXaMDoOBQA+iiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACqGsalb6Rp099eyBYoVyfUnsB7k8Vfrx74seIGvdVGkwPm3szmTHR5T/gOPrmgDlfEWtXfiDVJL68JyeEQdI17KP6+proPAngmXXWF7fB4tOU8AcNMR2HovqfyrO8D+HG8Q6wkTgraQ4eZx/d7KPc9P1r3W3hjtoI4beMRxRqFVQMAAdBQA2ztYLK2S2tIUhhjGFRBgCqPijSP7c0O507f5ZmAKt6MCCM+2RWviigDyHQfhvrC6xDLqIhitYHEhZJAxkwegA/rivXqKKACiiud8V+LrDw2Ilut800wJSKPHT1JPQUAdFRWF4Y8TWPiO3eWyLq8ZAkicYZM9PqPet2gAooooAiuv8Aj2m/3G/lXzP3r6Xuv+PaX/cb+VfNHegD3/wF/wAidpX/AFwWt6sHwF/yJ2k/9e61vUAFJS1Q1XU7fTLYyzt3wqjqx9BUTnGC5pPQTaSuy9Rketebar4gvr9zmRoYe0cbY/M96z1uZwdyTSKfUOa8mpm0Iu0Vc53iIp2PWqSuE0PxRcW0ixX7tNCf+WhHzL/iK7lHV0V1OQwyDXfh8TCvG8TaE1PYfXnnxsH/ABJbA+lwf/QTXodee/Gr/kB2P/Xz/wCyGuos4X4e/wDI6aZ/11P/AKCa98rwH4e8eMtM/wCu39DXv1ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVwXxln8rw5bQ5/1tyuR7BSf54rva8w+Nk+TpVuD18yQ/wDjooA4vwVD9o8W6VHjI+0I5Hspz/SvoOvDvhZB53jS2bHEMcj/APjuB+pr3GgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigChrd+NM0q7vXPEETSc9yBwPxNfOs80k88k0zb3kcyM3qScmva/ipP5Pg+6APMzxx4/wCBAn9BXjWk232rU7S36iWVIz9CwBoA9p+G+irpHhqHcMT3YE8p78j5R+A/XNdVUcaBECqML2HpUlABRRRQAUUUUAFeRfGTTrpNXg1AIWtnhEW4dFYE8H0znivXajkjSRSkihlPBBGQaAPK/gvbXI1K9utrC18kRliOC+4ED8q9YqKKKOJAkSKijoFGAKloAKKKKAIbv/j2m/3G/lXzR/EfrX0vd/8AHtN/uN/Kvmj+I/WgD3/wF/yJ2k/9e61vVg+Av+RO0n/r3Wt6gCre3UdpbvPO4VEGT/h9a821PUJ9RunnmO1fuqnZR6Cum8fXW1ILVTjeS7fToP1rm9Dsf7R1GO2b7n33Pt3/AD6V87mNaVWqqEDirSblyFzQPD8mpkSykx22efVvYf41seIND0yz0mWeK3YSRgBSrHOScc5rpYYkt4ljjUKqjAA6ACluLeO6t5IZl3I4wRXdTwEKdFwsnJrd9zWNGKjbqeTV6jo8Tw6XbRy/fEag57cdPwrNsvC1ha3PnKZJCpyFkwQD+Vbw4H0qcvwk8Pdz6jpU3Bu4+vP/AI0/8gOx/wCvn/2Rq9A7V5/8af8AkB2X/Xz/AOyNXrG5wPgD/kctM/67f0Ne/V4D4A/5HLTP+u39DXv1ABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV498ZpvN8SWsAPENtu/Esf8K9hrwz4pTed40vMHiJY4/yUE/zoA0/gxDu8RXc3/PO2x+bD/CvYK8y+CVv+71S5I6tHGD9AxP8xXptABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHF/F9SfCWR0W4jZvpyP615R4YlWHxFpkknyql1ET/30K9z8WaZ/bHh+8sv4pEzH/vjlf1FfPrB43IdSrocMOhBH9aAPpqiuS8AeKIfEGnRwzuo1C3ULKh6tj+IeoPf0NdbQAUUUUAN3rnbkZ7CnV856rql/earNdz3ErXHmkhgxG3B4C+gHbFe3eCdSk1bwvZXU8m+dk2yt6sDg5/KgDerjfinq17pnhxWsHaIzTLFJKnVFIJ4PbOMZrsarX1lb31s9vdwpNDIMMjDINAHiPgzxHqWna5apHcSzwzyrHJEzFwwJxn2Izwa94rl9K8CaHpd+L23hkMqHKb3LBD6gev1zXUUAFFFFAEV1/wAe8v8AuN/Kvmg/eNfS91/x7S/7jfyr5oP3m+tAHv3gL/kTtK/691rerB8B/wDIoaT/ANcBW9QBwfjznVYgenlD+ZpvgNlXVJNzLuMOF9+RW34y0p722We3XdNDnjuy98e9cIsjwyh42KOp4I4INfM4nmw+K9o1dbnBUvCpzHrhpK84g8R6oiBRdBsf3kUn86gvNXv7zKz3DMv91TgfkMV2vNabV1F3NfrS7G94q8QMHW206529fMdPXsAf54p3gzVbq5uZba6laVdu9WbkjB5GfxrlIoZLmURQxvI56BRk13fhjQxpkBknAa5kHzY6L7Vz4arXxFbn6fgRTlOc79Doe1ef/Gn/AJAdl/18/wDsjV6B2rz/AONP/IDsv+vn/wBkavoTtOB8A/8AI46Z/wBdv6Gvfq8A8A/8jjpn/Xb+hr3+gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK+evGU/2jxTqsmcg3LqPwO3+lfQe79K+a7+UzXlxKxyZJWYn6sTQB618GIfL8NXEv/PW5Y/kqiu8rlfhhCIPBdiccyGSQ/i5/pXVUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFeX/EzwXJJK+taVF5mfmuYVHOf76jv7j8a9QooA+aLaea1uEntpnhljOVeNsEH6iuz0n4o6vZr5d/BFfAfxn5H/ABI4/Su28ReA9H1xmmRDZ3TdZoejH/aXof0NcTf/AAu1qB/9DmtrpO3zFG/EHj9aANtPi3bhctpExPtMP8KwPEHxK1PUomg0+JdPhYYLK26Q/wDAuMfgM+9Un+H3iVWx/ZwPuJVx/Or2m/DDXLiVftjQWUZ6sW3n8AP6kUAcfbwzXdwkFvG8s0hwqqMk17t4F0WTQvDlvaXBH2g5klA6Bm7fgMCjwt4R03w4g+yKZbgj555OWPsOyj2FdBQAtFFFABRRRQAUHpRRQBFcDNvIPVSP0r5pP32Hua+mJGCqSxwAM184avNaz6vdyWCsls8jNGrdQCaAPQfhL4jvJ7k6JcnfbxwmSE45jwR8ue45716hXzjpGr3+kTvNptwbeR12lwATjOccg1qp468TJ/zFZW+qJ/8AE0Ae81j6p4bsNQJeSLy5T1kTgn6+teWWnxM8RwY82S2uB6SQ4P6EVr2nxaulx9r0uJ/UxSlf0IP86zqU4VFaauhOKlozpX8DR5+S9cfVAf61NB4MtVYGe4klHoAFH+NZVp8VtKkAFzZXcJPptcfzB/StK1+InhuXg3rQk9pIWH8hXMsDQTuomfsYdjoLHT7WxTZaxJH7gcn6nqauViQ+MPD03C6vag/7b7P54q3HrukSf6vU7NvpMp/rXXGKirRRqklsaNeSfGLVp5NSh0lE2wwqspOOWYgj8gK9Ju9XsorZ5o7iKUqMhY5ASf1rjdQuWvbozzKm/G0fL0X0zSnNR3OrD4WWI1WiOE8A/wDI46Z/13/oa9/rzGO2hjvI7tIIxNEdyPtGQa6G18TTx4FxEJB/sdf8KiNaLOipl1SPw6nWUtY1v4gsp+DIYm9HGP16VYm1rSoP9dqVrH/vTKP5mtOZPZnBKnODtJWNGisZ/FWgJ/zGbH8JlP8AI1H/AMJj4d/6DNp/33VEG7RWD/wmXh3/AKDFr/31S/8ACZ+HP+gxa/8AfdAG7RWRD4o0KY4i1ezJ9POUfzq9FfWlxjyLqGTP9yQH+RoAs0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBFP/AMe7/wC6f5V80t98/U19NV83arD9n1W7hHSOeRR+DEUAe4/D/wD5E3S/+uX65Oa6GuS+Fcxl8G2it/yzeRB9NxP9a62gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAY4DqVIyCMEV4prHgHWbfVnisbM3Vs7EwyKRjbngNk8EV7dRQB5pZ/Ce2a3ia91CZZ9oLiJV2g9wCRk1K3wmsNvyandg+6Kf6CvRqKAPKbv4TXS5NpqsTe0sZX9QTWTdfDLxFDnyktrgD+5Ng/+PAV7ZRQB8/XXg/xDa583SLogd0XeP0JrLnsLuA4uLOeI/wDTSNl/mK+laKAPmNuOPu0gx/s19JzWFnP/AK61gl/34lP8xVWXw/o8v39Ksz/2xX/CgDwvwltTX7fG3ow6/wCya76Q7dzHoBk10uq6DpNtYS3FtptpDLGMrJHEARz2IrmevVc1y1t0e9lr/dv1GQSpLEJImDKwyCO4pZJFijLyHag6n0rpholhdaXHJpNtHasBuCINoJ7g/wCNc68bRSNHKpVlOCDWbhy6s66OJVa62kuhFHPFKu6CVHH95WB/lVbWILebTZxcBdgQnJ7EDgitzw9Do6TCO40+0SVj8soiAJ9if611S6Rp+MNZwsD2ZAQfwNaQhzapnHicXyXhOOv4HzqpGeOlJ3r6Qj0ywj/1dhar/uwqP6U/7Da/8+0P/fArqPCPmzafejafevpX7Jb/APPvF/3wKPslv/z7x/8AfAoA+auO9A46YH0FfR8uk6dJ/rLC2bPrCp/pWfdeD/D1zky6Ra5PdY9p/TFAHhMGpX1v/qL+6ix/zzmYfyNX4vFOvxY2axe/8CkLfzzXq1x8N/DU33bSSD/rnM39SaoSfCvRW/1d1fJ/20U/zFAHBReOvE0f/MTkb/eRT/MVN/wsPxN/0EV/GGP/AArrJ/hRp6At/a1zGB/fVTVeL4V2U4Jt9dZ8dcQqcfrQHS5zf/Cw/E3/AD/p/wB+Y/8A4mj/AIWH4n/5/wBP+/Ef/wATXUf8KjT/AKDT/wDgMP8A4qj/AIVGn/Qbf/wGH/xVAjlJPH3iaTrqTD/diQf0qB/GfiN+usXA+mB/IV20fwltB/rdXnb/AHYlX+pqVPhPpQOX1G8P02D+lAzz1vFXiBvvaxeH/toRUR8Sa4//ADGL7/wIb/GvT0+FOhfx3F83/A1H/stPHwu8PD+K9b/tsP8ACgDyv+3ta/6Ct9/4Ev8A40n9t6x/0Fb7/wACH/xr1kfDDw76Xf8A3+/+tR/wrHw7/cuv+/xoA8l/tvV/+grff+BD/wCNPTxBrSfd1e+/8CH/AMa9K1rwD4b0+yMvk3LNnCjzzyani+GPh+SFW/0tSQCcTY/pQU4tJS6HmieKtfX7usXn/f40/wD4S3xF/wBBm8/7+16OfhVoR+7cXw+sqn+lJ/wqjRf+fu+/77X/AOJoJPOf+Eu8Rf8AQavP++//AK1H/CXeIv8AoNXn/ff/ANavRP8AhVGj/wDP5ff99J/8TR/wqnR/+fy+/wC+k/8AiaAPO/8AhLvEX/QavP8Avv8A+tWRNI8sjSyMWd2LMT1JPJNet/8ACqdH/wCfy+/76T/4mqd18JLZpQbXVpkTuJIwx/MEUAZvwc1G8/tebTt7NZmEylT0QggZHpnPNet1h+FfDtj4bs2gtFLSPzJM2NzkfyA9K3KAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigChro3aVcD/YNcIK9DvY/PtZYv76lf0rgJIXjlMbowcHbjFc9ZbHtZbUSUos7Dwz/AMgeH6H+Zpmt6Ql/H5kYVZx0PZvY1a0eAwabBE3DBeR71dArXlTjZnmyquNaU4PqzzqaKSCRo5kKOpwQa3NA1zyyttfN8vRHPb2P+Na+taUmoR7sBZk+63+Ncbc28ttK0M67WHWue0qTPXhUp4yHJP4j0NTkCnVx2i65JZkQ3JLw9Ae6/wCIrrYpklQPGwZGGQR0NdEZqSPIr4edCVpbdySiiirOYKKKKACo7idIIy8hwqjJNSVj6iDe38NkOYx+8l+nYUr2Lgk3qMt7d9Uf7TeAiAf6qA9CPU/WporLyNVEkEapC0RDbeBuB44rTUcAUgosmOVR622H9q5u/wBTurq7NnY7VHzLu7kgZwD2rbvZhb200g+Zo0Lbf5VW0a2WKwgLAGQr5hJ9W5NS+xdNqC5pIz7Kwt7uDdD9otbmM8kuchvfsRWlpN2biw8yT/WRkq/1FXJXWNCzcBQTWXpA26I0p6y75PzJpocn7SN33RKuqoNMW8lj+9kBByWOcAD61TEl9Bc2sl1Njz5NhhAG1AR/OodBj+1tAzj9zZphR2Lnv+VT6/cC3urR252Fnx6kDAFSpO12bKmlUdNLXUs3l7M9wLWxCGUDLuwyqD/GpdHupbq1LzY3qxQ49QcUmkWxht98gzNL88jHrk9vwqLQ/lhufa4k/nVJmUkuVxRn+JC93LKsZylooZv94n+gqwhudMhWRZJLm1CguH5dBjqD3+lQKC3hq7uG/wBZcFmb2+bAFbyD/R1H8O3+lKK1NJzUYKNrpNr8h0MqSxrLGQysMgin5AFZemD7LfXNmpPl8SIPQHt+dJfFr69FjESIUG6Zh3z0WqvY53T1t03JhrFgZtv2lfTOTj86tWtzDdRCSBw6n0rD1zT9ltLISFhhjAijTjByBk1d8OJi1kkHCSyFlHoOn9Knm1sazpQ5OeLNIuBJs3DPUCsy/wA32opZBmWJV8yXacE9gM0muR+VLa3oJHkyjdj+6TzTtM/eatqMvoUQfgKbd3YmMeVc67fjcSyt3sb+SCIObV1DqTyFPQj8afc6lvma2sI/tE/f+4v+8f6VFrl1Oqi1ssmeRSx9lHX8TTtJurCOxRYZUUgfMpOGz3zRfWxTi2lN6v8ArUPI1Mp5hvURwM7RENo9ueat6VcveWMU8gAZwcgdiDiqd/ei7zZ2B3yvw0g5WNT1Oa0bSFLa3SGMYRAAKSIm3y2ktfQsCiiirMQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooozQAlRiNN2SoJHfFSUUDDiloooEJVDVNOh1CLbKMMOjDqKv0GhpPRjhJxfMjz/UbCexl8uUEjs46Gp9K1aXT2AGWiP8B7/T3rsbq2iuoTFMgZT+n0rkNX0eXT2Lx5kgP8R6j6/41yyg4O8T3KOJhiI+yqrU62xvob2ISQtkHqO4q3XndtdS20gkhcqR6d/auo0nW4rnCS/u5fQ/xfT/AArSFRPRnHicFKl70dUblFIDxS1qecNbpWVp/Or35b7/AMmB7YrVNU73T7e6IeVD5g6MpII/EUmXFpaMtFwBkkD3rLn1NpnaHTR50nQv/AnufWnpotsf9cZZh/dkkJFaEUaRIEjUIo7AUJXK91eZlS2H2XSbshmlmkQl3Pc4/lV7TnV7GB1OR5aj9KssARz0rNk0aLcxgmngDdVifCn8KYcymrS3uR6jM19MNPtz97mYj+FfT6mr0yLHZPGgwqxkAe2KWzs4bSPZAgUdznJP1qwelApTWiWyMvw3AIdIiyOXyx+pNV9Rg+1+IrZDykcZcj8a2Y1CIFQYUcBRwBVdbQjUmu93WMR7ce+c1DXQpVXzufV3LYHFZeijH21f+nhz+dav4VRt7FYbi4lSST9+RkdgQOop7MmL0aINfCppEwVQASo4/wB4U6fVbW3xEX8yQ8eXGNxrP1TSltrWIfaZ5P3iKEZ/l6+lbNrZQWo2wxKn0X+tJXuavljBa31f6FXTYZnupb24UI8ihVj/ALqj196TQRvS6l/ia4fP4cCtTFZbaXKjyfZLx4UkbcV2g4PfFNkcykmnpcreILhpozZWq+ZMw3P6KPf3NXtNuoDp8bxuioqgFScbT6GpLKxiso9seS5+9I3LMfUmo5dHsZpTLJbpuJycDGfrSs73Dmg1ydupWurxNRs72OFC0CIcS9mb0FJ4VbzbSaY9Xl5/ACtQwIITEqhUKlQAOlV9HsjYWSwls8kk0+XUftI+zcV3RUlbydfjaT5Vlg2Kf9rOcVel0+zmYvJbxu3divNOvLaG8hMcw46q3cH1BqgsWqWwxG8N0g+7vJV/xPQ1VgvzLR2ZowwRW6bIkWNfRRiq/wBt36j9liXdsBMr9l9B9arMmrXI8txFaIerK25vw9Kv2NlFZR7IRweWJ6k+ppIhpJXk7stUUCiqMwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoorz3x74/k0i9On6MkUlwn+tlk5EZ/ugdz6+lAHoVFec/D7x3eazqI0zVUi811LRSxjbkjkqR06dCK9GoAKKKKACiiigAooooAKrajfW2n2ct1eSrDBEMu56AVI8irjcwGeBlsZrnPiJpV3q/hma3sV3TK6yiMdXA6ge9AFIfE/wAPhypF5j+95Ix/PP6VMvxI8Nn/AJeph9YW/oK8ZisrqW5NtFbzvMMgxqhLD1yOtSvpOpL9+wux9YW/woA9j/4WP4a/5/Jf/Ad/8KT/AIWR4b/5+5W+kDf4V41/Zl9/z5XP/flv8Kcml6g33bC5P/bFv8KAPXZPif4eQnb9rk/3Yf8AEiq0nxV0Yf6u0vW/4Co/rXmUega1Kf3ek3rfSBv8KsR+EfEL9NHu+fVMfzxQB3//AAtnTR/zDr0/in+NJ/wtvTf+gZefmn+NcMPA/ibPGkTfmg/9mp3/AAgvib/oES/99p/8VQB2/wDwtvT/APoF3n/fSf400/Fuy/h0q5/GRRXF/wDCC+Jv+gTL/wB9J/8AFUo8B+Jv+gY4+sif/FUAdc/xch6R6PIx97gD+hqvJ8W5j/qtIRf96cn/ANlrno/h34nf/lwQfWZR/WrEfwz8SP8Afit0+sw/pmgDQk+LOpN/q9NtV/3ixqtL8U9eb7kNnH/wBj/Wlj+FmvN96eyj+sjH+Qq1F8JtRP8ArdStV+kbN/hQBmN8SvEr9JrZP92If1zUDfETxM42tdx47j7Oh/mK6OL4SS/8tNZX/gNv/wDXqX/hUkffWX/C3H/xVAHLaV4qZpPL1XA3niVVxj6gdq6iORZEDxOHVhkEHg07/hUcP/Qal/8AAcf/ABVXtL+HUumNmDXJWQ/ejaAbT/49WE6XVHqYfHuHu1NUVLrVNcFuF07UjC6jgSRq4P1JGa5m98ceMLCXyrq88tu2bePafodvNdlqOkXFjlnUSR9nXp+PpWbdQRXUZjuYlkjPZhWak4fEdVTC0cSuek7M5kfETxR/0EB/4Dx//E0o+Inij/oID/wHj/8Aiatr4PsJbhj9tltoj2CB8fmQcVrWvwvsrhN0GuvJ/uwj/Gt4yUtmeRWw9Si7SRz3/CxPFH/QQX/wHT/4mj/hY3if/n/T/wAB0/wrqP8AhUcP/Qak/wC/A/8AiqP+FRQ/9BqT/vwP/iq0SMEc5H8SvEijm4gf/ehH9MVet/itrC/660s5f90Mv9TV+T4Rvz5esD/gUH/2VUbr4UatGM217aTex3L/AENAGpafFqFsC80mRfVopQ36ED+dbNp8S/D0+BLJcWx/6awnH5jNed3fgHxLbZ/4l5mA7xSq36ZzWNe6PqVpxd6fcQ/78LD+lAz3W08U6Hd48jVrTnoGkC/zrTguYZhmKaOQeqMG/lXzZbwtNcRwqcM7BB9ScV2MPhO0VBuuLgSDq6kD9MVMpKO5vRw866bitj2iivn7VrTVNIl3x3dwbc/dlWRh+Bwaqx+INZj+5qt6v0mb/GkpJ7GVSnKm+WaPddf5exX1uFP5Vqn71eEad4k1NrW+e61a5eRIwYN8pJVs4yuT1+lVP+Eu8Q/9Bm8/7+GmipaQj8z6Cp2BXz9/wlniH/oMXn/fw0f8Jd4h/wCgxd/990zI+gKK8ATxn4jX/mL3P4kH+Yq/bfETxHb43XSTjv5sI/oBQOx7hS147H8VtaXrZ2L+4Rx/Wobj4oeIJf8AVLaQf7sZP8yaZJ7PRXkXg3x3rEniC3tdTuPtVtdOIsFFUxk9CCAO/avXaBi0UCikAUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiorm4itYHmuJFjiQZZ2OABWNYeL9Cv7sW1rqUUkzHCoQV3H2JHNAG9RRRQAUVxPiL4kWGkalJZJazXTxHbI6EBVPcDPUium0bVrbWtOivbEkxSevBBHUH3oAtXbOtvI0QzIqkqPU44r5tu3le5nedmMrSMX3dd2ec++a+l68l+M9vawahYNBBHHNMrtKyAAvyAM+vegDF+GCbvGth/s+Yf/HDXuteJfCSPf4zib/nnDI35jH9a9toAKKK5afx94ft9RazkvDuVtjSBCY1PoW/r0oA6mimxuHQMpBBGQRTqACiiigDwDxvf3d54ovvtMzMIJniiXPCqp4AHb/GvT/hZqc2o+Gh9qkaWW3lMO9jklQARk+2cV5Z43XZ4t1Qf9PLt+ZzXoPwWOdGv1/u3A/VRQB3wVd5YKBnqccmn0YpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAYQD1HFYuo+HoLgl7f8Acv1wPun/AArdoqXFS0ZpTqzpu8Wef32m3Vm+JUOOzDlarxzPC+6J2jb1BxXojKGXDDINZd7oFpcZKJ5DnvH/AIdKwdG2sWerSzGMly1UY1n4juoABcqJ19Rwa17bxFYTnEjGA/7fT86xrvw7ew58oLMvqOD+RrMmt5oTiaJ0+oxS56kNzV4fC19YuzO/huYJ1zDKsg/2SDUorzYcHIbFWIry6i/1dxIP+BmqVddUYSyx/YkehUhUEYIBHvXCf2tf/wDPy9I2rX7f8vMn4HFV7eJH9mVe6OvudIsbkgzWdu5HRmiUkfQ44rltW0xLQkx3EUvP3MjcKoyXM8p/eSyt/wADNMHrWc6il0OzC4SpRd+b5WGsqspV1DK3UEZBrAvvClrPIJLWQ24JyVxlfw7iuh96gur23tAv2iQLvYKoHJY/SsouV9Dsrxpyj+8RcsPh34dv4RNFLfDsQZV4Pp92rP8AwqrQ/wDn4vv+/i//ABNdPodg1laCNyC7HccdvatOuyN7any1RRUny7HC/wDCq9E/5+b7/v4v/wATXE/FLw9pPhTTbdbCW5e8uWIQSupAUck4AHqAK9wr52+MWq/2l40mjRsx2cSwKPf7x/U4/CssRPkps9TJsKsVilGSvFas4+O5mRwyO273O4V6voPw8XXdAs9SsdTMYuYgxjmhztPQjIPqPSuW+G/gceL5bmWe6e2tbZlU7FBaQnJIBPTHrzXv2ladb6Zp8FlaR+XDboERfQCscJGbV5bHpcQ1MNzqnTXvLeytpbY8vPwn1Vf9XqFmV/2t4/oayPFXgu78M2MN3dXUM3my+VtiB4OCc849K91rz7408aBZL63f/sjV3HyxwHgQLJ4w0tX+754b8QCR+te/18/+BBjxjpYH/PcH9DX0AaAFFFAopAFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDz34ztdLotqIN32UzHz/TOPkz7ZzXkwJVleMlGU5BHUEdDX0tNBFPG0U8ayRuMMjAEH8DXzbeJ5V3NH/cdl/IkUAfQnhi+OpaDY3rkFpoEZsf3sc/rUPivWBomgXV8Th0XbGp7ueF/XmqHwxk8zwXYD+7vX8nauK+MOufa9Vh0mF/3Vou+XHeQjgfgP50AcHLI00jSyMWdyWYnqSeSa9k+D3/ACKP/bzJ/SvGK9c+Ctz5mg3lsesNxu/BlH9QaAPQK8b+Mk/meJoIQcCK2H5lia9krwX4jXgvfGF+6nKxyCEf8BAB/XNAG78FoN+vX05H+qt9gP8AvMP/AImvXa84+CtqU06/uyP9ZKsYP+6Mn/0KvRxQBXvlkls544GCytGyox7EggH86+cL2zubK7e2vIXhlQ4ZXGDn+tfS9QT2sE0iPNDG7J0ZkBI+h7UAZHgGO8i8Jaemo5E4Q8N1CZOwH/gOK3qRRgUtABRRRQB4L8RxjxpqX++v/oC123wS/wCQTqP/AF8L/wCgCuJ+I5/4rTVPaRf/AEBa7b4Jf8gjUf8Ar5H/AKAKAPRKKB0ooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAMUYoooATA9KRkVhgjI96dQaAM6fRbCbJe3QE91+U/pVSTw3Zt9zzF+hz/OtvFGKThF9DWNepHRSZg/8Itb/wDPxL+Q/wAKT/hFrb+KeVvwA/pW/RxS5I9i/rVb+ZmBNo2mWUBkuCxUf3m6/gK5q5lWSUlI1jjHCqOg+p9a0PEzytqbrLu24Gz0xjtUGkaZJfP3WDPzN6+wrmkry5Uj18M/Z0/a1JXZl6nO9npE9+qB0iKrzwNxOBXAwXE1/rds87l3eeMewyw4HtXqnxUijs/BHkwrtUzxqB+Z/pXlvhqPzfEOnp63UX/oQraEFE83E4uVZ+R9ELgU0SKG2lwD1xnmmXryR20rwLukVGKD1OOK+Vb++vbu/luL+eY3TMd5djlT3HtjpjtUVq3skna9zpyzLHj5SSly2Pp3U9e0zTo3e61C3i2jJDyAGvl/ULpr7ULm6kGWnkaT8SSarMcnJBb6mivOrVnVVrWPtssyuOX80ubmb8rHsvwt8TeGfDvhWKG91OCK7mdpZkwxIJOBnAPYCptf+MdhZ3oi0mya/hH3pi5jB9gCM/icV4qAfRq1NH8OavrM6xWFhPJuON5UhB9WPAqo4iolyRRyVcowftJV60m73bu0kfSPhbXrbxHosOpWeQkuQyt1Rh1U/SuN+Nk37jTLfPV5JCPoAB/Oun8BeHh4Y8PQ6ez+ZLkySuOhc9ce3YVwnxmufM1+zgB4it934sx/wr1YX5VzbnwddQVSSp/DfT0Mn4Xwef41siRkRqzn8EP9a90rx/4M23meJLmcj/VWxx9SwH9K9gqjIWg0UGkAUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvnDxBH5evagnpcyD/x819H187+K12+KtUX/p6k/wDQjQB6R4A1WPS/hxLe3H3LZ5ePU54H5nFeU3VzLeXc11cEtLM5d2Pck5NaEust/wAIrBosRZV+0PPMPXoFH8z+VS+CtGbXfEVtalcwIfMm/wBwdR+PT8aAKer6XPpZtBcgK11brcBf7oYnA/Su4+ClztvdTtifvxpIPwJH9aZ8a7ZUvNMuEGFaNovyII/nWZ8I7nyfF8cZOBPBIh/DDf0oA9d1nUI9M0u5vZfu26Fz7kdB+J4r50uJnuJnmkOXkYux9STk16T8X9fUmLRbZ+QRJcYP/fK/1P4VxfhHR21vX7WyxmMtvlPog5b8+n40AewfDvTjp3hKxjkXEkoM7/VjkfpiukpiKFAAGAOAB2p/agDlfiB4obw1YxfZ0El3ckiLd91QMZY/n0rkPCvxI1F9WgtNX8q4gnkEfmIm1oyTgH0Irr/H3hX/AISi1gWKdYbi2LFC+dpDYyDjnsOa57wx8MpLLUIbzVrqJ1gYOsMOSCRzyxxxnsBQB6XRRRQAUUUUAeA+P23+M9VP/Tbb+SgV3vwUXGhXretzj8lFeeeN23eL9V/6+XH64r0n4MrjwzO3rdN/6CtAHdjpRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUGgCCe3huQBNGr4/vDNPSNUUKqgAdAKfQKATdrHB/Gd8eGLZP712v6K1ec+CU8zxdpQ9LlD+XNd/8a3xpGnp/enY/kv8A9euI+HcfmeNNL/2ZGb8lY0kDPeT0rm9W8DeGtXuWuL3SoXnY5d1LKWPvtIz+NdLTaTSkrMunUnSfNBtPydjxv4waBonh7w/aR6Tp8FtNc3G0uoJcKoJPJOeuK4PwPY/2l4t0y2IyGnVz9F+Y/wAq7b9oG7DanplmDxHG8p9ixA/9lrG+CNoLnxxHIy8W0EkufcgKP/QjXm1Ip1lFH3WEqSp5VKtUk22m9fuR78ttCo4jQfhUioF6DFPxRXpcqPg+ZvcQCvDvijced4zuxnIiEcY/BQT+pr3KvnrxbP8Aa/E+qTZzuuXC/QHA/QVRLO6+ClviLUrojqY4gfoCT/MV6XXDfB2Hy/DEsv8Az1uXP4AAV3IoGLSGlpDSAWiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV89+Nfl8X6sv/AE8v+tfQleD/ABKtWtfGd/uGBKVmQ+oIH9cigDm69h+EuifYdEfUJ0xcX5DDPURjp+fX8q808KaK+v65b2CA7GO+Vh/Ag+8f6D3NfQEKLDEscahY0GFAHQdAKAOH+M1oJPDttcKOYLgA/RgR/PFeX6Hqcujarb6hCoZ4CSEY8HII5/Ovd/FGljWdBurA4Dyp+7J7OOV/UV8/3trPZ3UlvdRmKaM4ZW4waAFurma8uZLm6cyTSsXdj3Jr2L4ZeHP7F0oXVymLy9AZgescf8K/Xuf/AK1cl8N/Bsl/dx6rqULLZQtvjVlx57djg/wj9a9gGcUAAFLRRQAYHpRgelFFABRRRQAVQ17UBpmj3l8f+XeJnGfUDj9av1yfxUnMPgy7C8GRo4z9CwP9KAPE55HnnklmdpJZGLsx5JJ5Jr0n4P6/aRQnQ5NyXMkjzRsfuvwMr9RjNeZV2Hwq0l7zxIL1sLb2Cl2boCxBCjP5n8KAPbKKzLnXdJswftWp2kRHVWmXP5ZrNk8eeG4+uqxN/uox/pQB0tFcwPiB4aP/ADE1/wC/b/4Uv/CfeGP+gon/AHw/+FAHTUVzf/CeeGf+grH/AN8P/hUcnxB8MR/8xLP0ic/0oA6iiuMk+J3hxPuy3Mn+5Af64qrJ8VdEH+rtr5/qij/2agDvaK86k+LVgP8AV6Xcv9XUf41C3xch/h0eT8Zx/wDE0Ael0V5j/wALc/6g5/7/AP8A9jUf/C3Jf4dHT8Zz/wDE0AepUV5S3xbvP4dHiH1mJ/8AZRUbfFrUW+7ptqv1dj/hQB61RXj7fFfWP4bKxX8HP9arSfE/xC/3fsqf7sWf5mgD2mivDm+I3iZv+X2JfpAv+FM/4WH4n/6CP/kBP/iaAPdKK8J/4WD4n/6CQ/78J/8AE09fiJ4nVv8Aj/RvrAn+FAHudFeLQfE7xFH982s31hx/Iir0fxa1Jf8AW6bav/uuy/zzQB63RXl8Xxcf/lro4/4Dcf4ipR8XYf4tIl/CYf4UAel0V5v/AMLctv8AoET/APf5f8KP+FuW3/QIn/7/AC/4UAekUGvN/wDhblt/0CJ/+/y/4Uf8Lctv+gRP/wB/l/woA9Horzj/AIW5bf8AQIn/AO/y/wCFIfi5bf8AQIn/AO/y/wCFArDfje3+iaUv/TSQ/oK5b4Xp/wAVrY/7KyN/44af488XReKks1htHtvs5Ync4bOcen0qh4L1e30LxDBf3aSyRIrriMAnJGO5FIbPfWpe3Nec6z8W9JsrRXs7a6uJ3/5ZMBGAPUnmo9L+MWiz2bSahBPZzqf9Wq+YGHqGHH54rOVaEXZs7YZfiasFVhBtP+tjgvjRd/aPHNwgORBDHF+m4/q1dF+z9Zb7zVb0j7ixwg/XJP8AIV5vr2oNq2r3eoSAg3ErOM9h2H4DAr2v4G6Y1l4Q+0SKQ17MZRn+6PlH8jXDS/eV3I+vzNfVcrjSe9kv1PQ6KKK9I+CGSPtRm9AT+VfNdxKZrqWU9XkZvzOa+itbk+z6LfTdPLt5G/JSa+cV/pTGe7fDaDyPBmngjBkVpCPqxP8AKulFZPhOPyfDWmJ0xbR/qoNa4oYBSUtJSAWiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVh+I/DGl+IYkF/C2+PhJY22uB6Z7j2NblGBQBh+HvDWmeHonXT4irSY3yOdztjoM+ntW5RRQAVWntLeeQPNbxyOvRmQEj6E1ZooAaABwKdRRQAUUUUAFFFFABRRRQAVzHxH0+bU/Cd1DaxmSVCswUdSFOSB74rp6KAPmUjBwRgjtR5jqpRXcKeoDHH5V75q3hHQtUlMt5p0TTHq6ZQn64Iz+NVIPh74Zibd/Z28+jyuR+WaAPC8D3P4VIscr/wCrjd/opNfQtp4f0i0C/Z9LtI8dxCufzIzWisaIMKoX6CgD5r+y3X/PvN/3wf8ACj7Ncf8APCQf8ANfS34UmB/doA+afIl/55P+Rp0dndyf6u1mf6Rsf6V9KbF/uilwB04oA+c4tD1ab/VaVeN/u27f4VZj8JeIJOmjXn4xkfzxX0JRQB4JF4F8Sv8A8wqUfV0H82qyvw68TP8A8uKL9Zk/xr3KigDxD/hW3ib/AJ97cfWZaf8A8Ky8SN/yzth/22/+tXtlFAHi6/DDxF3FmP8Atsf8KkX4Wa7/ABT2Q/4G3/xNeyUUAeQL8KNZb799Yj6M5/pViP4S3h/1urQL/uQsf6ivV6KAPMY/hGP49ZP4Qf4tUn/CpIP+gxN/35H+NelUUAebf8Kitv8AoMT/APflf8aY/wAIo8fJrD/jAP8A4qvTKKAPKJvhJeD/AFGqQN/vxMv8iaozfCvXU+5cWcv0dh/MV7LRQB4jJ8NPEq9IYH/3Zh/XFQt8OvEy/wDLgD/uzJ/jXulFAHhP/Cv/ABP/ANAxv+/0f/xVH/Cv/E3/AEC2/wC/0f8A8VXu1FAHhP8AwgHib/oFN/3+j/8AiqT/AIQDxN/0Cz/3+j/+Kr3eigDwj/hAPE//AECz/wB/o/8A4qj/AIQDxR/0Cz/39j/+Kr3eigD551fw1rGiwLPqVi8ETHaGyrDPvtJx+NVtO0bUdUV306yuLkR8MUQkA19FSxJLEySorq3BVhkH8KSCGKFRHDGsSD+FAAPyFAHzTrPh3Vk2s+nXaOvBDwsOPyrn2ilBw8bhumCDX15VO406yugRdWkE3/XSMN/MVyVMKqj5rn0GBz2rhaapOKaR8rW1jLKy7x5adya6vTfEWs6dBHBY6pcwxRgKsYclQB2AORXs154H8N3anfpcaE94iU/kRWRc/C3RJRmKe8h/3XDfzFaUqCp7HFmGZ1cdJc+iWyRwcXj/AMTR5xqRb/fjQ/0qxH8SvEiffnt3/wB6Ff6V08nwltP+WWq3I/3o1P8ALFVpPhJJ/wAstXB/34MfyatzzDIufiXql5p9xZ3dnauLiFoi0e5SMjGcZNcX/DXZ6l8M9Zs4JZo57SeONTI2GZTgDJ4I/rXG9qAPozRP+QLYegt4/wD0EVerO8ON5nh3TW7m2j/9BFaNAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAx0VlKtyCMEH0rh3+F2jtqX2jz7gWxbd9mGMfTd1x+vvXd0UARRRrFGqIAiKAqgdABwBUlLRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZ2q6zpulrG2p6hbWO8kIZ5ljDEdcZIzVq2niureOe3lSWORQyOhyGB6EH0rzv41+AdS8e2mmQ6VcW0BtJJGk+0FhkMAOMA+ldp4U06XR/DWl6bcMjTWdrFBIyfdJVQCR+VAGuKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiis7xBPLDoWoywMY5I7WVkcdVYIcEfQ0AaNFeI/s2eKNd8RXuuJrmp3N8LeOIoJmztJLZI+uK9u7UAFFFFABVPUNQtNNtjcahdQ2lupAaWZwigk4GSeOtXK5H4q+Grvxh4LutF0+WGGed42DzEhQFcMegJ7UAdFp+oWep2oudPuobuAkqJIXDrkdRkZq2Olcb8JvC154N8Hw6PqM0M06SySFoWJXDHI6gGuyoAWiiigAooooAKKKKACiiigAooooAKKKKAGM21SWO1RySa5//AITnwp9sFn/wkWlmcvtCC5QndnGOD1zXCftM6zd6Z4MtLO0laJdQuvLmKtgvGqklc+hOM1i/DX4KaJqPhrSNc1C+vjezrHdhYmVUTkMowVJPGM80Ae8UUUUAFFFFABRRRQAUUUUAFFFBoAzdT1zS9JeNdV1K0sTKCUFxMse7HXGSM1dSVJY1kicMrAEEHIIPevMfjX8N9U8eXGlyaXd2luLNZVcXBYZ3FSMYB/u16LpVs1nplnayYLwQRxMR0JCgH+VAF6iiigAooooAKK+f/hR4t8Qap8Yb/TL/AFi6uLBDdbYJHyo2tgce1e/igBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA8j/aD8Z674Pg0d/D96LY3LTCXMavnAXH3gfU1g3PxG8beNWj0/4d2rmO3hjF3qJRRulKjdjf8AKgznA6nrwKT9rP8A49fD3/XSf+SV6X8JNHtdF+HeiwWiBRPax3Mh7u8ihmJ/PH0AoA8T1nxN8Wvh9dQXOv3ckts78eb5c0Mh6lSRypx2yD6V0+q/GHW/FEdhpnw80t5tVngEl1IU3C3b+JVzgYB/iPHTvXX/ALQsMc3wq1UyoGaJoXQ/3W81RkfgSPxrA/Zd0y3h8F3uorGv2m6vGjaTbzsRVwufTJJ/GgDktZl+Nfhixk1fUb65NunzSlTDMIx6sgBwPcDivSfgx8RH8daXcR6nFHHqdgV8wx8LKpzhwOxyCCP8cV3uqwrc6VeQTKHSSF0YHoQVIr55/ZUOPFWtD/pyH/owUAdz+0F4x13wfZaPL4fuxavdSyrITEr5AC4+8Djqa73wVez6l4Q0e+vW8y5ubOGWVsAZYoCTge9eS/tY/wDIL8Pf9dp//QUr1P4df8k/8P8A/YPg/wDRYoA8T8OfGzWLDUNabXrj+0FhVksrRY1QySeZgZYLnAXP/wCurTp8cfEUZ1CIy6fG/wA0cCvFAQO3yn5v++jmud+Buj2+rfFyaS7jEi2Hn3SKRkbw4VT+BbI9xX1OOKAPnfwR8WvFGieK4/D/AI+VmR5VgeSaMJLAx4ViQMMpyMn05B9foivmv9qSGODxlo9zEmJZLT5mHfbIcfzr6MtJGltYJG6vGrH6kUAWK574g6jd6P4J1nUrCXyrq1tXliYqDhgOODwa6GuU+LP/ACTTxF/14y/yoA8n8OfGvUbHwBd6jrcyalrMt41vZxBFQBRGhLMFA+UFvqS2Ppe+Fur/ABL1vxpZ3viCO+TRXEhkDQCGH7h24GASM4x1rnv2aPCtpqutXet38SzLpgRbdXGVErZO7nuAOPds+lfS1AAKKKjuJlggkmcfLGpY/QDNAHlXxg+Lw8JT/wBi6FCl1q5AMrtylvn7ox/E5646DvnpXG21r8ctZgF8t1c2ySDcqPLFbnHb5OCPxFZPwQtB4x+LN1rOrKJ3iWW/2vyPMLgL+W7I+gr6gFAHz14f+L3irwr4hGj/ABGtZHjJAeVohHLECeHG0Ydfp+B7V7+txG9ss6SoYSu8SZ+UrjOc+mOa4/4k/DfTvHyWf225ms57QtslhUFipx8pz2yM1i/FV38FfBWXTbW6kmZIYtOSZ+GKE7TnH+yCKAOR8YfGnWta10aJ8OrZnDMY1uVi82WYjqUUghV9yDxzxVR7H462kP237TdS4G4xLNBI3/fHOfoK3/2X/DttbeG7rX3jVry8maBGI5SJcZA9MtnP0Fe10AeLfCv4zT6vq0Xh/wAXQJa6jI3lxXCjYJJP7jofut2GOCeMCvRPiLql5o/gfWdR0+Xyrq2tmkifAO0+uDxXiX7Tehx6R4i0vX7AGGW9DCUpx+9jIKv9SG/SvTfGGpHWvgVd6k+c3ekLM3+8VUn9aAPOvDnxm8Rz+GjYwodZ8UXd0yW6iEYii2rhiqABjndj8zx1de2Xx0ETai9xOMDf5MMkBYDrjYOv05NXP2VdHtmt9Y1p1V7kSLaoxHKrjc2PrkflXvlAHjHwU+K994l1RvD/AInCG+2s8FwFCGQr95WUYAbHOQB0NP8Ai9c/ElNWu4/C8MjaCbP96RHER907+W56VxkaJp/7UO22QRq+oHKjj78WW/MsTX0L4n/5FzVP+vSb/wBANAHyd8K5/HEEuoHwDE8krJH9p2pG2Bk7fv8A49K+n/h/Jr0nhOzfxYpXV23+eCFGPmO37vHTHSvHf2S/+P3xF/1yg/m9e+X1qLyxnti7J50bRl14ZQQRke4zQB4T4r+LviXxF4jfQfhtblkV2VbhIxJJPjqw3fKi+hI/EdKrXOlfHeBGujeXLnGTHHcQMfwQcflXoXhPwZ4S+Fc1zetrJha7QRl7+4jXCg5O3gd8Z69Kk1T40eBtNU41Zr1h/Daws/64A/WgDlPg18WdT13XP+Eb8UhDeureRP5flsXXlkdRgZwGOQB0wa7b4x67qXhvwBe6ppE/kXcUkSrIUVsBnAPBBHevCPBOtR+IPj9aatawm3jvb6SVUPUAo3X3r2f9ov8A5JRqX/XWD/0atAF34KeINT8T+BodT1q5+03TTSRl9ipkA8cKAK8+1/4q6t4f+L17p2pX+3w/aSndCsKFivk5Chsbslsd6639m3/kl9v/ANfU3/oVeSeLtLh1v9oeXTboZgudRhWQeqbVLD8QMUAdQ+ufF7x2n9o+HrY6VpUmTAoKR717He/zN9RgVkwfEj4ifD/XoLXxqst1bvgmK4VCWTPLRyL1P4kV9JRRJDEscahI1G1VUYAA6ACvHf2qYI28H6VOUHmx3/lq/orRsSPxKD8qAPXdOv7fUNOgv7WQPb3ESzI/qhGQa8F8QfFvxX4r8Svovw5tdkaMQsyxh5JVB5c7sqq/X8+cV6f8KA198J9EjY48yx8rI7AZA/Svn/wnrOq/Bzxxdx6vphkDr9nmQ/KXj3AiSNu4447HocGgDrLq0+OmkxPetdXM4HzMiSQTHH+5g/oK634LfFafxddy6Nr8cceqRIZI5YxtWZR94FezDrxwR2GK1tB+NngjVlCy6i+nSn+C8jKj/voZX9ateHvAnhEeIz4w0F2lupJJJfNgud8RLghsAZH8R4oA72iiigDA8aeKNO8JaFPquqOdkfyxxofmlc9FX3/kOa8RtPGHxV+Is80/hWFrDTkbAMWxFHsZH5Y+u38hUP7T2ryXfi/TdHLMtraW4mb03uxyceyqP1ru9E+L3w70TSbTTbK8nitrWMRxqLV+g79OpPJ96AOFuvGXxV+Hd3DN4qR72wcgYmVHRvUCRBlW+p/A17d4b8VWvi3womsaGxLSxOBG2N0UoH3G7ZB/AjnpXD+JPi18OfEGiXmlX17NJBdRlGDWj8Hsw46g8j3rkP2VtWkj13WNELkwywC6QdtysFJH1DD8qAOQ+KVx8RJ7CxHj6KRLYSsbfckS5bHP3OenrXcfC67+Km/w5D5En/CM/uRv8uHH2bjnP3vu/jWj+1h/yAND/wCvqT/0AV6R8K/+SbeHf+wdD/6AKAOpooooA8H+J/xL17wt8U4dOivzDosZtpJ4hCjEocF8EjOSM96oJ4s+KnxElluvCEDabpSsVQrsQHH/AE0flm9dvArC+OtidU+NkWnqSDdi1gyP9rC/1r6X0vT7fS9Pt7GxiSK3t41jjjQYAAGKAPne98V/Fj4fTRXHiPzLqyZgCLgJLE3tvXlT+Ne3+AfGNh400BNS0/5WB2TwMctDIOqn1HcHuK0vEGkWmu6Nd6XfxiS3u42jYHtkcEe4PIPrXz5+zdfT6R8RNR0KV8pPFIjDt5kTcH8t1AHsvxK8e6f4F0YXd0PtF3MSttbK2DIw6knso7n8K8f0/wAR/F/4gPJd6AXtLHcQphCQxDnoHbliPYmqPxeaTxd8boNDaVhDHLBYJ/sBsMxHvlj+lfSum2NvptjBZWUKQ29uixxogwFUDAFAHzvd+M/ir8O7qF/FEbXdo52/vwjxv7CROQ31P4V7h4D8W6f4z0GLVNNJUE7ZomPzROOqn+h7ir3iTRbPxFot3pWoRiSC5jKHP8JPRh7g8ivn/wDZpv5tL8e6nochIjuIHDLnjzIm4P5FhQB2P7QfjnxB4Pu9Hj8P3a2oukmMmY0fcVKY+8DjGTXp1ndTSeGYbx3BnazWUtj+IpnOPrXh/wC1r/x/eHP+udx/OOvbNO/5Ey3/AOwen/osUAeD+DvjhrdvZao+tS/2tfyCOPTrZYVXMhLZJ2gEgDHHUngdc1dltfjrqyfbhLNZq3zJbrJDCQPTZ1/BjmsL9mjR7bUvHVzd3MYkOn2zSxbhkLIWChvqATX1EKAPAPhh8WfENv4sj8MeOQWklk8hZZYxHLDKeFDAAAqTxnGeQc4rt/i3c/ECCbT/APhAYXkQrJ9q2JE2Dldv3/bPSvMPj6q2fxj0m5gQJI8VtMxH8TCVgCfwUD8K+lgKAPjPwhL4wTxtcyeGo3bxAfO81QIyevz8Nx1/+tX0j8Lrzxanh++uPiGpguYZWZC4jXEIQEn5OMA5ryL4Kf8AJeNT+t5/6HX0Pr+ntqeh6hYRv5bXVtJAG9CykZ/WgDwjUfip418b6/Jpnw7tWt7eMkh1RWkZM43sz/KgPp+pNR38fxw8P20moT3VzNDGC7hHhnIA55TBOPoK5v4f+KtQ+EXibULLXNKkYT7Y7iL7sg2k7XQnhgcn2PrXt+hfGfwRrGFOq/YJG/gvYzH/AOPcr+tAGf8ABb4onxus2nanFHBqttGJCY+FmTOCwHYgkZHTnivUq4jwf4A8KaVrDeJPDpZpbgPiSO43xEMcsABxjNdvQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAeCftZ/wDHr4e/66T/AMkr13wD/wAiL4e/7Btt/wCilrzL9pnQ9W1y30NdI0u8vzC85kFtC0uzITGdoOM4r07wVDLbeDtEt7iN45obC3R43UhlYRqCCD0INAHOfH7/AJJNrX/bH/0clZH7MX/JNn/6/pf5LW78bLG81L4aataafbTXlzIYtsMKF2bEqE4A5OAM1l/s86Zf6R4Ba11SyuLKf7ZK/lTxNG20hcHDAHFAHo19/wAeU/8AuN/KvnT9lX/kbNZ/68h/6MFfRd7k2cwHJKEAfhXhH7Nnh3WtF8TatPq+k31hFJaBEe5gaMMd4OAWAycUAWf2sf8AkF+Hv+u0/wD6Clep/Dr/AJJ/4f8A+wfB/wCixXnn7TOiarren6Gmj6bd6g8M0pdbaFpCoIXGcA4r0fwJBNa+CNDt7mKSGaKwgjkjkUqysEAIIPIINAHhP7OX/JV9Z/69p/8A0clfStfPvwI8Oa1pPxN1W61PSb+yt5bacLJPbvGjEyoQASMHI5r6CoA+bv2q/wDkadE/682/9GGvofS/+Qda/wDXJP8A0EV4V+0n4d1rW/EmkS6PpN9fxx2jK7W1u8gU7ycEqDg17pp6stjbKwKsI1BB6ggCgC3XKfFn/kmniL/rxl/lXV1zPxLtZ77wBrtrZwyz3EtnIiRxKWZmI4AA5JoA83/ZP/5F3W/+vtP/AECvbq8e/Zq0XVNE0HVo9X067sHluUZFuYWjLDZjIDAZFewjpQAVBfQ/aLOaD/nrGyfmMVPRQB8w/s33S6P8SL3TL393PPbyW4VuDvRwSv1wpr6erwj4ufCrVZfEDeK/Be43TSCeWCM7ZEkHPmIe+epHXPTOay4PjH8RdNh+yaj4YE14nyeZNZzIxI/vKCAT9MUAeq/E74h2PgG0s7i8tZLt7uRlSKNgpAA5bntyB+Nc18W5pPF/wSOsQWckGRDfiFyCypuwckf7LbvpXD6N4G8Z/FDxRHrHjiOay02PGRKvlFo858uNOoB/vH65Jr6HawtW046e0CGzaLyDDj5fLxjbj0xxQB5Z+zFrFvd+B5dMBAubC5YuvfY/zK357h+Fev182a38O/GPw38RtrPgQzXtjzt8kb3Cd45I/wCIe4B9eDVmT4y/ES6g+yWvhdY70/L5iWczEH1CEkZ+uRQA/wDap1iGbUdH0SHDzQK9xIByRvwFH1OGP5V3niTTn0n4AT6fKMS22jJHIPRgq5/WuL+Gvwo1zVfEn/CUeP8Acp8zzxbTHMsz9i46Ko/u/hgCvVPijaXF98PtctbK3luLma1ZY4olLM544AHJNAHn/wCyn/yKWr/9fw/9FrXtdeRfs16PqWi+F9Th1bTruxle8DKlzC0ZZfLUZGRyK9doA+aLr/k6Vf8AsIp/6JFfQvif/kXNU/69Jv8A0A14ddeHNbP7Ry6r/ZWof2d9uRvtX2d/KwIgM78bcZ46171f2ovLC4tmOBPE0R/EEf1oA8C/ZL/4/fEX/XKD+b17L4+15vDPg7U9YiVWmtYC0YYcbyQq59skV886BpHxK+GesXo0fQ7i584BGeO0NxHKoJ2kFeR19jzzXtmn2eq+OvhY9l4ngNjqOowSRyIYWj8pg52koeRjAPvQB4/8J/An/CzrzUdd8V6lc3UMU3lFBJ88jkbjlj91QCMAfpivadN+F3gnT8GHw3ZuR0MymU/+PE14V4fm+IXwk1K5hTRnuLSU5kTyWlgkxwHDr0P4j3FdOPHHxU8cIbDQ9BGjxSna92I3TYO/7xzgf8BGfSgDn9He2f8AaWX7GqLAmoyRqI1CqNsbLgAcYBFesftF/wDJKNS/66wf+jVrxXWPCniL4YeObC+srSbVRb7J4pxCzRzOVxIvGSMEsOucYNev/E8av4n+CIZdLnOqXiW8slnDE5dG3qzALyePegCT9m3/AJJfb/8AX1N/6FXml7/ydEn/AGEY/wD0WK9V+AOm32k/DyC11OzuLK4FxKzRTxlHwTwcEA8159d+HNbP7Ryaouj350/7ckn2sWz+VtEYBO/GMZ96APoavHP2q/8AkRtN/wCwkv8A6Kkr2OvJv2ktH1PWvCGn2+kafdX8yX6yNHbxNIwXy3GcKCcZNAG58Kb2DTvg9pF7duUgtrN5pCFLEIrMScDk4Aq3pOueDviVaXMNqlvq8VqVEq3FqRt3ZxjeAex5FJ8LtMmt/hnpGmapayRSC1aKaCdCrAMzZBU8jINeM3vgvx18LvE02o+EIp7+xfhXhTzd8ZOQkqDnI9R9QRQB6Pr3wJ8G6krPaQ3OmTHkNbSFlB/3GyMewxXk+hPrPwn+LEGjm78+2lniimVchJ4ZCAG29mAPHoRjOK6T/hdPxAkQwQ+EE+1dMi1nOD/u5/rUnw7+HHibxH4zj8XePImgEUqziGYBZJXXGwbB9xRgcHHTGO9AH0EKTNLRQB8z/tM6d9k8f6dqU6F7W7tkDe5RzuH/AHyR+depWXwj+HV7aQ3VvoivDNGsiMLqYgqRkH73pWr8UPBNr468PNYTSCG7hPm2s+3Ox/Q/7JHB/PtXjOj618TvhaP7KudIfUdOiYiMNE0sQ7/JInIHfB6egoA9Tn+D/wAPLaCSebQ0SOJC7sbqbAUDJJ+aqXwqj+Gs+sXVz4DtmS8gh2zSHzwFRiOP3hxyV+vFee6v4x+JXxHtm0bT9AeztJ/kmMMToGU9Q8jnAHqBjIr1r4S+BE8DeH/s8rpNf3LCS5lUcZxwg/2R+pJNAHD/ALV//Iv6H/19Sf8AoAr0j4V/8k28O/8AYPh/9AFcL+0vouq63oujx6Ppt3fvFcSM620LSFQVABIUGu++HFrNaeAdCtruGSCeGxhSSORSrIwUZBB5BoA6WiiigD5f+Nl//ZfxztdRPS0a0nP0Ugn+VfTME8dzbxTwOskcqh0cchlIyCPqK+Zvjbp66r8cLfTpJDEt59kty46rvwufwzWta6r8TPhVEdKk07+2dIhYi3l8tpEVc8bWU5Uf7LdO1AHv99dQ2NnNd3TiOC3jMsjHoqgZJ/Kvmv8AZ4gl1f4q3eqqD5UEM07E+sjYA+p3H8qk17xJ8SvibD/Y9poktnYyEeasMLxo4zxvkft7ZGfQ17D8JfAUPgXQjA7CbUboh7qZemR0Vc/wjJ+pyaAPGPiVJ/wi37QEWqXYP2Y3Nte5HePChj+BU/lX05BKk8KyRsro4DKynIIPQ1wPxg+G8XjrSo5LWRINWswfs8r/AHZFPWNvYnkHsfqa8q0TxZ8TPhvANJ1HQ5ryzhysInhd1QDskicFfYk49qAPozUr6DTNOub68kEcFtG0sjscAKBk184fs5wSat8Tr/VtpEccEszH0aRwAP1P5Uus6p8TPir/AMS+LR5LLTmYb0WNoYT3Bd35OOuB+Vez/C3wNb+BvD32KNxNeTsJbqcLjc+MAD/ZHb8T3oA8s/a1/wCP7w5/1zuP5x17Zp3/ACJlv/2D0/8ARQryT9pnQNY1y60FtH0q91AQJOJPs0DSbdxTGdoOPumvXbGKQeFIIGjdZRYrGUx8wbywMY9aAPB/2VP+Ro1v/r0X/wBGCvpCvAf2avD+taL4i1iXWNJvrCOS2VUe6t3jDHfnALAZNe/UAfNX7Rf/ACVrRh/062//AKOevpWvn347eHta1T4maVd6bo9/eW8dvAGmgt3dUIlckFgCBwc19BUAfM3wU/5Lxqf1vP8A0OvorWNVtNG0y51HUZWitbWMySuqliFHfABJ/CvnLW/C3jrwR8Rr3XPDWlT3iSzyyQSwQ+crJISSrKuSCM47cjIr1v4dXmv+MfCWpwePNMayeWR7bymt2hLxFBk4bnqTzQBoaZqfg/4mafM8ENtrNtbv5bfaLYgxkjPG4Aj6iuc8QfATwjqUcj6at1pcxHymKQugPurZ4+hFeb/8Iz8QPhPr9zceG7ebUdOc8PFEZklQHI8xByrD1/I4rUf4zfEC7Rrey8Jqt0eMraTuQfZc9frmgDD+Ht7rPw5+LaeGJLnzraa6W1uIhny5A+Nsig9GGQfzFfUleC/Cr4a+ILzxivjHxsrwTLIZ0hlx5ssnZmA+6o7DrkDgCveqACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBMD0pcD0oooATA9KMD0FLRQAYHpSYHoKWigBMD0FLiiigAooooAMD0oxRRQAUUUUAGB6UUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHzV8Vf8Ak4vSf+viw/8AQ1r6VrmNV8BeGtV8QRa9f6aJdUhaNkn86QYKHK/KGxxj0rp6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACionkjj/wBZIi/7xAqFtTsE+/e2y4/vSqP60AW6KzX1/R4/v6rYr/vXCD+tRN4n0BBl9c01frdR/wCNAGvRWI3jLwyp+bxBpY/7e4/8aifxz4TT73iXSR/2+R/40AdBRXNP8QPB69fFGkf+Bkf+NRP8R/Ba9fFGl/hcqf5GgDqqK5Bvid4HT/mZtP8AwfP8hVd/i34Djzv8SWx/3Ukb+SmgDt6K8/l+NPgKLO3XPM/3LaU/+yiqU/x58DR/dvLqX/dtW/rigD02ivIp/wBojwhHny7TVZv92FB/N6oT/tJaEo/0fQtRk/33jX+RNAHtlFeBz/tKRf8ALv4Zf/gd2P6LVCf9pTUG/wBT4ctk/wB65Zv5KKAPouivmaf9o7xK3+o0nSo/94SN/wCzCqE/7QXjSX7i6ZD/ALlsT/NjQB9UUV8lS/HTx2/3dRt4/wDctY/6g1Ul+NHj6T/mOlf923iH/stAH2BRXxy/xe8et/zMc/4Rxj/2WoX+K3jp+viW7/AKP6UAfZlFfGH/AAtHxx/0Mt//AN9gf0pn/CzPG3/Qz6j/AN/jQB9pUV8Vn4leNT/zM+p/+BBpv/CyPGv/AEM+qf8AgS1AH2tRXxT/AMLG8Zn/AJmjVP8AwJb/ABo/4WJ4z/6GjVf/AAJf/GgD7Wor4o/4WJ4y/wCho1b/AMCX/wAaT/hYnjL/AKGjVv8AwJf/ABoA+2KK+J/+FieMv+ho1b/wJf8Axpf+FieMv+ho1b/wJf8AxoA+16K+KP8AhY3jP/oaNV/8CW/xpf8AhY/jX/oaNU/8CGoA+1qK+LU+J3jdPu+JtR/GTP8AOrEfxY8dp08SXZ/3gh/mKAPsqivkKD41ePYcY1sP/v20R/8AZauwfHvxzH/rLmym/wB+2UfyxQB9YUV8x2v7RfiiL/j403SZvokin/0M1r2v7Sdzn/S/DcbD/pndFf5qaAPoWivFbL9o/QXA+26LqMB7+WySAfmRW/Y/HfwNdAebe3NqT2mt24/75zQB6XRXHWfxS8EXv+p8S2K/9dXMX/oQFbNr4n0G9x9l1vTps/8APO6Q/wAjQBsUVHFKkqgxSK4Poc0/PqKAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoorjPip42t/A/hmS+4e+mzFZwk/fk9SP7o6n8B3oAl8UfEjwp4XvUsta1VY7k8mJY2kaMdi20Hb+PNee/F74zSaUbWx8G3FvPJcQCdr7AkCq33QoPG7jJyOOmM1896he3OpX097fTPPc3DmSWRuSzE5JrodN+HviTV/DkOuaTp017aSSPDiFdzgrjnb1KknGRnkGgCvf+PfFmoOXuvEWpknslyyD8lIFZkut6tN/rtUvJf964c/zNe3fDL4GQ3OmS3nje2ninkYeRapNtZFHUtjuewzx3ruoPgj4Ch+9pMkv+/dSn+TCgD5MaeZ/vTOfqSaYST1YmvsWD4ReAovueHLc/70kjfzarC/DDwQn3fDNh+Mef5mgD4wx9aXH1r7UT4c+DI/+ZX0n8bZD/MVOngTwmv3fDWkr/25x/4UAfEeB60E19xL4N8MJ93w7pX/AIBx/wCFSr4W8Pr93QdLH/bpH/hQB8MUV91L4b0Jfu6Lpy/S1j/wqRdC0hfu6VYr9LdP8KAPhLa3oacIpP8Anm5/A194JpljH9yytl/3YlH9KlW3ij/1cSL9FFAHwlDpl/N/qbG5kz/dhY/0q7F4V8RS/wCp0HU3+lnIf/Za+5QMCloA+KLf4eeMZgGj8M6oc+tuw/mKvQfCTx3P/q/Ddyn++yJ/MivsmigD5Gg+B3j6X72lQxf793F/RjV+D9n7xrJ986bF/vXBP8lNfVVFAHzLB+zn4mfHm6ppkf8AwKQ/+y1ci/Zs1U/6/wAQ2Sf7kDt/UV9HUUAeAQfs0nA8/wAUDP8AsWX/ANnVuP8AZs04D974jum/3LdR/MmvdKKAPE0/Zu0Mff13UT/upGP6VIn7OHhwfe1fVG/GMf8Aste0UUAeN/8ADOfhfvqmq/8Afcf/AMTTx+zr4U/6CGqn/ton/wATXsGB6UvFAHkA/Z18J/8AP9q3/f1P/iKd/wAM7eEP+fzVv+/yf/EV67RQB5H/AMM7+D/+fvVf+/yf/EUf8M7+EP8An71b/v8AJ/8AEV65RQB5H/wzv4O/5+NW/wC/6f8AxNH/AAzv4O/5+NW/7/p/8TXrlFAHkf8Awzv4O/5+NW/7/p/8RR/wzv4P/wCfrVv+/wAn/wARXrlFAHkf/DO/g/8A5+tW/wC/yf8AxFNP7O/hD/n71b/v8n/xFevUUAeOt+zp4VP3dQ1Vf+2kZ/8AZKryfs3aAc+Vrepr/vCM/wBBXtVFAHhU/wCzVYEfuPElyh/27VW/kwrPn/ZquR/x7+Jon/66WZX+TGvoWigD5muv2cvEiD/R9W0yb2YyL/7Kaybz4C+OLYHybayuj6RXSj/0LFfV9NNAHxte/Cnx1aZ83w3eOB3i2yf+gk1g3vhjXrAn7douoW4HUyWzqPzxX3RRQB8CMjISGBBFNzX3jeaXY3v/AB92Vtcf9dYVb+YrGu/AHhK7/wCPnw1pbn1FsgP5gA0AfFsN3cwHMFxLEfVHIrTt/FniK2Ci313U4wOy3cgH5Zr6pufg74CuCd3h6KMn/nlNKv6BsVmz/AbwLJ9yzvIf926Y/wA80AfPEHxH8ZQ/c8S6p+Nwx/nmrkPxa8dRH5fEt2f99Ub+a17Xc/s7+EpR+6vNVh/3ZkP81NUZf2btCOfJ13UU/wB9I2/oKAPLovjZ4/i/5jgf/ftYj/7LVuP48+O0+9fWkn+9ap/QCu6k/ZrsSf3XiW4X/etFP/swqtL+zSf+WXif/vqz/wDs6AOWj/aC8bL97+zX/wB62P8ARhVmL9onxav+ss9Kf/ti4/8AZ62H/ZrvwP3fiO1Y/wC1bMP/AGaqsn7N2uD/AFeu6e3sUcf0oAbF+0h4gH+t0bTH+hkX/wBmNXIf2ldQH+v8OWr/AO5csv8ANTWTN+zp4sU/utQ0mT6ySD/2SqU/wB8bRfdj06X/AHLn/ECgDsYP2lrc/wDHx4YlX/cvAf8A2QVei/aS0M/67Q9RT/ceNv5kV5lJ8D/HseSNJif/AHbqI/1qlL8IfHkXXw7cH/ckjP8AJqAPaIP2ifCkn+ustUh/7Zo38mq5F8f/AAS/3n1GL/etv8GNfPs/w28awff8Man/AMBgLfyzVKTwb4oi/wBb4c1hPrZSD+lAH0svx38CN11C5T62kn9BUy/HDwCfvazIv1tJv6LXy1L4c1uP/WaRqC/71s4/pUb6Nqi/e0y8H1gf/CgD6sHxt+H/AP0HW/8AASf/AOJp4+NPgD/oPD/wGm/+Jr5M/szUP+fC6/78t/hSf2de/wDPlcf9+m/woA+tf+F0+AP+g+v/AIDTf/E0v/C6fAH/AEH1/wDAab/4mvkj+zb3/nzuP+/Tf4Uf2de/8+lx/wB+m/woA+t/+F0/D/8A6D6/+A03/wARR/wufwB/0H0/8B5v/iK+SP7Ovf8An0uP+/Tf4Uf2fef8+dx/36b/AAoA+ul+MfgF+niGIfWCUf8AslWI/it4Glxt8TWY/wB7cv8AMV8eNZXK/et5h/2zP+FRNHInDKy/VcUAfZ6/EvwU33fFGm/jOBT/APhY/gz/AKGfS/8AwIX/ABr4qooA+1D8R/BY/wCZn0z/AMCFqtP8VfAsH3/Etmf9xmf+QNfGlPjjeT/VqWPsM0AfWlx8cfAMWdurTSn/AGLWX+oFUH/aB8FJ0OpSf7tsP6sK+ZrfRNWuTi30y8mP/TOB2/kKvxeCPFcozH4a1dge4spP8KAPob/hoXwd/wA8NVP/AGwT/wCLpG/aH8Hr9211U/8AbFP/AIuvAP8AhXvjL/oWNW/8BX/wp8fw68ZM2B4Y1T8bZh/MUAe3XH7R3h9GxbaNqMue7FE/qapSftK2X/LPw1cn63aj/wBlNeWW3wo8d3H3PDd2n/XQqn/oRFXV+Cfj5v8AmCgfW5iH/s1AHcz/ALSsxz5PhhFH+3eZ/kgqay/aUiLAXnhl1HcxXm4/kVH864qH4D+OnALWVrF/v3af0zUF78EPHdqhZdKiuAO0NzGT+RIoA9Ug/aM8NPjztK1SM+yxt/7MKivv2jtBRP8AQtF1C4b/AKaOkQ/MEn9K+fNc0bUNB1F9P1a2NrdRgF4yQSMjIzgmqCoXYKqliTgAdSaAPsD4Y/E/TfHiXEcNpLYX1uA7wSOHyhONysAMgHg8DFd5Xi3wA+HGp+GJZtd1v/R57uARQ2v8SoSGLP6HgYHbvzxXtNABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAUNY1O10fTbjUNQmWG2tkMkjk8AD+vYDua+PPiT4zuvG/ieXUpiVtkzHawZ4iiB4/4EepPr7AV2vx/+I3/CQ6ifD+kS/wDErs3/AH0qtxcSj+ar29Tz6VxHw48H3fjbxJDp1tuS3Uh7qYDiKPPJ+p6AetAHZfAn4YxeK5pNZ1+Bn0iBikcTEr9pk78jB2jvjqeOxr6XsbK106zis7C3itraFQscUahVQDsAKh0XS7XRdMttO06JYbW1jEcSjsB/M9ye5rQoAWjFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaKDQAlNDA15d478eSi4m03RHMQjYrLcDqT3VfQDufyrh/7Y1NX3/wBp3gb189v8a9vDZLXrwU2+W549fNadKfKlc+i6QV4pofxD1rTmVbt1v4O4k4fHsw/rmvUvDXiGx8RWXn2TnIOHibhkPof8a48Vl9bC6zWnc6sNjqWI2dn2NsUUDpRXAdwUUUZoAKKKhnuIYVzPKka+rMB/OpcktwJqKwrvxRplsSBOZmHaMZ/XpWVc+NznFpafjI39B/jXLUxtGnvL7jN1YLqdlRXnVz4q1SfOyVIR/sKP65rPn1G8uBie6mcehfiuOebU18MWzJ4mKPTJr21hP764iT/eYCqM3iLS4ut4jf7mW/kK83UGQ8Kz/XmrUem30v3LSc/8AP8AWsHmVWXwR/Mj6y3sjsZfGWnofkWeT6KB/M1Wl8bw/wDLKzkP++4H8s1hQ+HNUlH/AB77B/tOB/WrUfhG/P3ntx+JNR9axkvhVvkHtKr2RafxvN/BZoPq5P8ASoG8aX5+7DAv4E/1qRPBsx/1l2i/7qE/zIqZPBsQ+/eufogH9af+3S6ibqsot4v1RuhgX6J/iaiPinVm6ToP+2a/4VpXfhjTrO3ea4u5wiDJOVH4Djqa5STZvPlAhc/KCcnHvXJXqYijpKTv6mcpVY7s2P8AhKNX/wCfpf8Av2v+FH/CUav/AM/K/wDfpf8ACoNDt7G6u/s95v3PxGynH4HjvXS/8Inp/wDen/76/wDrVdGOJrR5oyf3lRdSSumYP/CU6x/z3X/v0v8AhUieLtUXq8TfWP8AwrZ/4RHT/wC/Ov8AwIf4UxvCFifuXE4/L/Cuj2OMX2vxHat3M5PGWoj70du34Ef1qZPGtz/HaRn6MRU7eDYf4LuUfVAahfwc/wDBeKfrHj+ppWxy6jvWLCeN0/jsZB9HB/mBVmLxnp7/AHo50+qD+hrHfwhej7ssB/Ej+lVZ/DOqRdIA4/2XB/wp/WMbT3V/kHPVXQ6+HxJpUuP9KVD6OCP5ir8N/aXGPKuYpP8AdYGvNJdLv4f9ZaTD6IT/ACqqysp+ZWQ+/FNZnVj8cPzGq8luj14dOKK8qg1C7tx+4upkx2DnH5Vo2vinVYcbpEmH+2gz+YxXRDNab+JNFLERe56JRXH2vjbtd2pB9Yzn9D/jWvZ+JtMuMA3AhY9pRt/XpXZDF0anwyNY1IvqbVFRRTRyqGicOp6FTkVLmupST2NQooopgFFFFMAooooAKKKKAGFVPUD8qja1gf70Mbf7yA1PRQBSfS9Ob7+n2zfWFT/Sm/2Npf8A0DLP/wAB0/wq/RQBQXR9LX7unWY+luv+FTpZ2yfctoV+iAVYooAQDFLRRQAUUUUAFFFFABXk3xo+K0XhOF9H0R1l1qVfncYK2qnufVj2HbqewNz4zfE6HwZp5sNMkjl1q5X92vUW6Hjew9fQd+vSvlmeW4v7x5pnkuLidyWY5Zncn9STQA2R7m+vGkleS4ubh8knLNIxP5kk19HfBb4RpoaQ6/4mgD6qQGgt35FqOxPrJ/6D9ad8EPhMugRRa/4igD6q43QW7jItR6n/AG//AEH617LQAgGBS0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXjPx/+JP9iWb+GtHlK6lcpi5lRubeJh90HszD8hz3Fdf8WPHlt4H8OSXG5X1K4zHZwn+Ju7H/AGR1PrwO9fIeoXtzqN9NeXszzXFy5klkfksxOSaAJNI0271fU7ew0+Fri6uZBHHGvUk/09+wr6/+GXgm08DeHo7CICW8kxJdzgf6yTHQf7I6Afj1JrkvgP8ADceGdOXXdXhxq94n7tGHNtEe3sx7+g49a9doATPtS0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBoooASsnxRqY0nQ7u8JAaOM7M936KPzrW61558aZZE0mwiXPlyTktj1A4/ma6cHS9tXjTezZy4qo6dGU12PKmJJySST3PWm0tAr9NStofBt9Q7Yrufg80o8RXKBj5ZtiWB6ZyMVw9esfC7S49I0WTVL4rC95gqXOMIOnX1PP0xXi51WjSwrUup6WWU5SrprZas7+j8K5nUPGNpBlbRWuHHfov+Jrnb/wAR6jekhpvKQ/wx/L+vX9a/Mq2Y0aezu/I+ulWjHzO7vtVsrP8A4+bhEx2zlvyHNYV740hTIs7d5T/ef5R+XWuPjjkuJNsSvLI3YKSTWvZ+GNQuCDIqW6ernn8hXnyxuIrP90rfiYurUn8KGXnifVLrIM3kqe0S4/Xr+tZTu8shaR3kc92OTXZWvhKyjwbmSW4PcD5R+nP61sWmnWlp/wAe1tHGfUDn8+tSsHXqu9WQvZVJfEzgLfSL+5wYrWQg/wATDaPzOK07fwheSYNxLFCvoPmP+FdqTjgUV0wy2lH4m2aKhFbnOW/hCzXHnzSyt7YUf41owaDpkONtojMO7fN/OtKiuuGGpQ2ijT2cF0I4oYoh+7iRF9gBT+h4ooroUYroVZC0UUUwCkNLWfrt+unWDy5HmEYQdyxqKk1Ti5MTaSOV8Xaj9rvmt4zmKDjju3f8ulYQOOacck7jkk9SaSvkq1Z1JuTPNnJyeoquwYEcEHIPvXo2h6gNR0+KY/6z7sg9G7/415z/AErZ8Kan9ivxFKcQ3GAfZux/pXXgMR7KpyvZmtGdnY7zFFGc0V9KdwmTRRRQMKKKKADNMeGKQYkjRh7ipOKOKlxT3FZGdNoOmT/ftIwfVRt/lWbceEbSQfubiSI++GH9DXR0lYywtKe8UQ6cXuji7rwleRjMEkcw9Pun9eP1rIudNvbQkz2sij1K5H5jIr0uiuOeWUpfC2iHQT2PLoJprd91vM8TeqMRWzZeK9RtsCXbcKP7wwfzrrLvSbG8/wBfbISf4gMH86xb3whC+TaXBQ9kfkfn1rn+qYijrTlczdOcPhZbsPGFlNgXKvbt6n5l/Mf4VvW93Bcpvt5klU91Oa86vdB1GzLboS6DncnzD/GqMM81tLuhd4nHdTg1cMwrU9KsdPxGq04/Ej1oUVweneLbyEhbtVuIx3+63+B/Kun0vxBYagFEUoRz/A/B/D1/CvSo42jW2epvCrCWzNaikByM0tdpqFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFcf8TPG9p4H8OyX8xWS7lzHa2+eZJMd/wDZHUn8OpFb+uataaHpdzqWpTCG1tkMjsfT0HqewHc18efEfxle+NfEU+p3TFLcDZawZyIY88D6nqT3PtigDF1nU7vWtUuNR1GZp7q4cvJI3cn+Q7Aele9fAL4XLZxweKfEEH+lSDfY28g/1SnpIwP8R7DsOevTlPgH8Nv+Ejvl8QazCTpVo/7iNhxcyj19VHf1PHrX097UALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFZPiPXLHw3otzqupy+VbWy7mOeSegUDuSeAK0pJFiRnkYKijJZjgADrzXyj8cviM3jHWfsOmyEaNZMViwf8AXv3kPt2Htz3oA5bx74tv/GXiKfVdQJXcdsMOcrDGPuqP5k9zzXo/7PXw4Or3cfijWYAbC3f/AESJxxNIP4yO6qenqfpXGfCbwHdeOfESQurJplvh7ycdl7ID/ePT2GT2r6+sLK30+zhs7KFIbaBBHFGgwEUDAAoAsAUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUGgBO1cZ8WbYz+EnlCbjBKjn2GcE/rXZDrVLWTaf2fKmoFPs0ilXD9CDWtGsqFSNR9HcxxEFUpSg+qPnSpra2mupNkEbOR19B+NdDL4esUvZDFLLcW+792GG049/8itKGFYwEhjwOgVRXq5hxhRpx5cJHml57HyVPLpN++Y1joADh7p9zLzsXp+JroLi5muWBmkMmBgA9B7AdB+Fa+meF7y7w9z/o8fvyx/Dt+NdPp+hWNjgpEJHH/LR+T/gK+LxNXHZnLnxEtOi2S9Ee5h8H7PSOiOOsNC1C+IZYfLQ/xP8AKP8AE10Vj4TtYgGu5DO390fKv+NdD7DpSVpRy+lT1er8zvjRiiK3tobZNkEKRL6KMVKRRRXaopbGq0CiiirGFFFFABRRRQAUUUUAFKaSigAzgEnoK841q9bUNSllLZjB2oPQdq9A1FWaxnWP75jbH5V5kfl4rxs0m7RgtjlxEnpYnsrY3l1HboOXOPoO5/AVC/329ASK6rwfp3k2kt/KuGdT5ef7o6n8a5RjuOfXmvLqUVTpxct2c7hypN9S7Zac91p09xH8zQMMj1XBz+VUv512HgaP/iX3DY+9Lj8gKz9c8NzQ3DTWKGSFjnYvJU+mO4raeEk6UakF6lum+VSRe8Na+0zxWN0PnxhJPX2Pv7101cd4Z0S7a/S4u4nhiiO4BuCx7cV2VezgXUdP958jppc3L7wlFFFdxsFFFFABRRRQAUUUUAFFFFAFXU9RttLtTc3cmyMce59gO5ri7/x7ctOf7PtkWEdDJyx/AHArJ8W6u2rao5Q/6PCdkY+nVvxrFrhqV2pWifVYLK4Rgp1ldvp2Osh8e6gH/fQQOvcD5T+eTWxZapofiPEU8QiuW6BvvMfYjrXneacjMjh42KkHII6jFY+05tJ6m1fKqFSLUVZne6h4RlTLWM3mL/ck4P51z91az2k2yeF4iO5H8q9B0K7a+0e0uX/1ksYZvr0NW7i3iuIylxGJVPUMM1NTL4T96m7HxVXDqMnFaNHC6Z4kv7AhS/nxD+B+SPoetddpfiOy1Haqv5Mv9x+M/Q9DWNqnhNWzJpr7T/zzk6fge341zN1a3FnJ5dzEYm9/6HvXOq2JwbtPWJgp1KfxbHrFLXnmjeJruwKx3BNxAOPmPzD6H+hrtNM1W01GIPbSZPdTww+or18PjadfZ2fY6oVIz2L9FFFdpoFFFFABRRRQAUUUUAFJ05pa8S/aD+JR0y2fwtok227nX/TZUP8AqoyPuA/3iOvoPrQBw/x4+Iw8U6odG0mU/wBkWUnzMp4uZRwW91HQevX0rlvhl4IuvHPiSOwi3R2kOJLq4A/1cee3+0egH49AawdE0m813VbbTdNiaa6uXCRoPX1PoAOSewr7B+HHg6z8FeHYtMswHnOHup8YMsmOT9B0A7D3zQBu6bp1rpWnQWNjCsNtbII4kUcBR/nn1q9SYpaACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoorifix45h8DeGHukKtqFxmOziP8T45Yj0XqfwHegDz79oz4h/Zo38JaPNiWRQb6RD9xTyIvqep9sDua8O8NeH77xLrVtpWmRmW5uWwPRR/EzHsAOTVK7ubi+vJbm6kea5uHLyO/LOxOST75r6m+BXw8XwloY1HU4saxfKGdT1gjPIj+vc+/HagDrPAvhaw8G+HbbSdOQEIN0spHzTSHq5+vb0GBXR0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAU01U1G/g0+Ey3MgRew7n2FcPrfiK51EtHFmG3/uhuX/3j/SuPE4unh1rq+xlOrGG5v634qgtN0VltnmHBbPyL/jXGX17c38xluZGkc9M9B7Adqk0/TrnUpdlum4Dq5+6n412ekeHbWxxI486f++w4H0FeM/b42V3pE5v3lX0Oa0vw3eX2HnH2eFv4mHzH6D/Guv0zSLLTVHkRkyd5G5Zvx/wq8Bikr0qGDpUdUrvubQpKIpPP+eKSiiuw1CiiimMKKKKACiiigAooooAKKKKACiiigAooooAKz5tG06efzpLVGfOTxwT7jpWhRUShGfxITSZV1IiHS7koAoSFsAduK81PWvRPET+Xot23+xj8yK86rws00ml5HJX6I7nwSNuj5/vSsf5Ct2snwsu3Qrb3BP5k1rV7GGVqUfRHRD4QxRjJorJ8UXc1ppTvbkq7MF3D+EHvWtSapwcn0HJ8qL17eQ2du8874VOvr9BXH33iu+kmP2TZBGOgIDH8Saw5JHdmLuznuWOSadbW8lzPHDAu53OAK8Cvj6lVqNPT03OSdaUtIm1Z+K76Jx9p2Tp34Cn8CK6/T72C/t1mt33Ieo7g+hFedXtlPYzGK5XY4/Ij1BqbR9Sm0u4EsZyp4dOzf/X9KMNjalOfLV1XnuFOpKLtI9HoqCwu4b23WaBg6sPxB9D71PX0EZKSujtTurhRRRVDCs3xRd/YdBvJUOHWMqre54H860qwPHvPhybb/fTP/fQqZu0WzfDRUq0U+6PMCc8Dp/OiiivIP0MKfBE80qRRDLyMFUepNJXceA/D5jH9qXa/OR+4Q9gf4j9e1aU4ObsceMxMMNScpb9Dq9MthZadBbA58pAmfcDn9atUg6dBRXrKNlY+Dk+ZuT6hUV1awXcRjuI1kU/wmpqDUuKkrMhq5xur+FpId0mnkyx942+8Poe/86wYpp7SbMbPFKh7cEe1eodqy9Y0O11JSxHlTdpVHP4jvXkV8vv+8o6M56lHrEqaD4rjuSlvqG2KU8CTorfX0P6V046V5Zqem3GnTeXdL1+646P9K0/D/iWawKwXZMlt0H96P6eo9qrDY+UH7Ov94U6zXuzPQhRUNtcRXMKSwuHRxkMDwamr2lJSV0dYUUUVQBRRUFzcRWtvLcXEixQxIZHduNqgZJP4UAcj8WPG8PgfwxJd5D31xmKziPd8feI/ur1P4DvXx/d3Vxf3kt1dyvPcXDl5JGOWdickn3JrqPip4yn8beKZb8krZQkxWkZ42xg9SP7x6n8u1dn+zx4AXWtV/wCEj1SHdp9i+LdXHE045z7qvX649DQB6J8CPh1/wiekjVdXhA1i+QfK3W3jPIT2J6n8u1erUgHr1paACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAp6nf2+mWFxfXsyw21uhlkduiqBk18c/ErxjceNvE02pTbktU/dWsJP+riB4/E9T716D+0X8Qv7Qvm8K6TNm0tWzeSIeJJR0j+i9/f6V5x8P8Awld+M/E1vpVpuWMnfcTY4iiH3mPv2HqSKAPQf2dvh8NY1EeJtWhzYWUmLVGHEsw/i91X+f0NfS1Z+iaVaaLpVrp2nQiG1tYxHGg9B6+pPUnua0KAFooozQAUVCZo9+zzF3emealosK6YtFFFAwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAErI13XINKiIY+ZOR8sQP6n0FVvEuvx6bGYLfEl0RwOye59/QVw26e8uCTvnnkP1JNeTjMb7P93T1l+RzVavLpHck1C/uNRuDNcuXb+Feyj2Fa+heGZLrbPe7oouoj6M3+ArU0Dw0tnie8Akn6heqp/ia6E8VzYfBOb9rX1fYzhSb1kRQQR20IigQRovQCpQaSivYSSVjrWisLSUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKB1oooAx/F7bdDm/wBoqP1rgq7nxqcaNj1kX+tcOa+dzJ/vkvI463xHo+hrs0ezH/TJavGqulf8gy1/65J/IVaNe9RVqcfQ6o/Cgqpqdst7YzW7DO9SB9ex/OrQoFOcVJOLFJXR5URtJXuOK6DwRB5moySMP9XHwfcnH8qyNTAXULpVGAsrAfma2/Azf6dOn96MH8j/APXr5nCq1dRfc4ofGrnRa1pcWqW5ifAlXlH9D/ga8+ureWzuGguFZJF/zke1eoHrUVza29yB9ohSXHTcoOK9nFYKNfWOjOmpRU9epzngSOULcyEEQsVC56Fh1xXUU1EWNAqIFUdABgCnV1UKTpU1Bu5pCPKrBRRRWxYCqmrWKahpk9m4wJVI3eh65/A1bpaGrqxUJOMlJdDxe+s7iwumt7uMxyKe/ceo9RUIG59q7ix4Cj7xr2e7sbW8XbdW8cwHQOM4qKz0uws33WtnDCx/iVcGuJ4bXRn0cc7tC0o+9+ByHhXwczul7q0W1BykDdT7t/hXc8KoVB044paPpXVCKgrI8TE4mpiZc02KKKKK0OQKSlpKQ0FFFFAEV3aw3kBhuI1kjbqDXDa7oUumsZI8y2xPDY5T2P8AjXfUkiJKhSRQykYIPQiuTE4WNddn3MqlNTR5/oOtzaTMOTJAx+eP+o9DXoVjeRXtuk1u4dGHBH8vrXD+I9BawJuLRS1seq9Sn/1qp6Dq8ulXAcEtA5+eP+o9xXn4fETwk/ZVdvyMY1HTfLLY9NFLUFrcR3UCTwsGRxkEVNmvoE01dHYncWvDP2kvHP2KyXwnp0n+kXKiW+IPKR9Qn1PU+31r1fxn4itfCfh281i8P7u3TKpnmRzwqD6mvi7W9Vuta1a61PUJTLc3UhlkY+p7D27AelMZZ8IeH7zxR4hs9IsAfNuHwWIyI1/ic+wHNfaHh3R7TQNFs9LsFC29pEI1AHJ9Sfcnk+9eb/s7+Bx4f8PHXNQixqOpqCgYcxQ9VHsW+99MV65QAdaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAzXm3xu+IS+DfDzW1g//ABOb9StuF6xJ0aU/ToPf6Gux8U69Y+GdCu9X1OTy4LZSxHdm6BR7k8Cvjbxn4kv/ABXr91q+pH95O3yoD8sSfwoPYD8+tAGXFHPfXSRxK888zhFAGWd2PH1JNfXPwj8BxeCPDaRTqj6pc4ku5l557ID/AHV/U5Ned/s4fDvO3xdrEXqLCNl/Ay/0H4n0r6AoAMUUUGgBuRk15j8R/G0qzyaTpEpjMZ2zzqcHPdFPbHc/hXpjdGr5uvC7XU5lJZ2kbcT1znmvcyXDQxFVymrqPQ8fNcRKjBRh1I2kdnMhZi5O7O7nP1roPDfi/VNFuY28+Se1z88MjFgR32nsa54ADpRX2VbDUq0OSUdD5anXnTlzRep9H6fexX9lDd27bopkDqfY1brzn4P6x59lPpMp+e3PmR+6k8j8D/OvRR0r85xNB4erKm+h9xhqyrUlNC0UCiuc6QooooAKKKKACiiigAooooAKKKKACiiigBrVz/inXksIzb2xDXTD/vgep96teI9YTSrQkENO+Qi+/qfavPmMt3dbjulmlb8STXk4/Gey/d0/if4HPWq8ui3EjSa8uQBmSZz9SSa7fw/ocWmxB5dr3LDl/T2H+NP8P6JHpcIdwHuHHzN6ewrVrPCYPk/eVPiJpUuX3pbhRRRXpnQFFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAFLSClpDRgeN/wDkEJ7zD+RriK7Xxy3/ABKol9Zh/I1xRr5zMf4/yOGt8R6dpy/6Db+0afyFWKitBttIx6Io/Spa+ih8KOyOwlFFFUM801T/AJCl1/12f+ZrT8Et/wAThl9Ym/TFUvEUTQ6zdq3y5cuPoeau+C1P9tFsfKImz+lfMUlbE28zz4q1X5ncUUUV9OegFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJIiyIUcKysMEHoRXCeJNGOnS+bCu62kPH+yfQ/0rvKiureO6geGdd6OMEVx4rDxrR8+hlUgpI4zwprZ024EE7H7NKev91vX6etegKc15ZqunyafetBJyOqv/AHl7GoPF/wAQZ/DPgS4MSu+oMRb2r4yE3A/Mx/2QOPU4rkwGJlB+wqfIyozafJI8+/aN8cDW9fXw/p0ubHTWPnEHiSfof++Rx9c1zXwb8GHxl4xhguFJ02zxPdnsVB+VP+BHj6Zri0Wa8ulVA8ssr4UdWdif5k19hfCTwZF4K8KQWkiL9vnxNduO8hH3c+ijj8z3r3TsOxijVFAAAA4AHapKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooryP8AaB+IP/CO6KND0ybGp6gh3sh+aGHufZm6D2yfSgDzD4+ePj4o146Tps2dK01yoKniabOGf3A6D8T3rE+Efgebxx4njglRxplriW8kHHy9kB9WPHsMntXLaTYXOrahb6fYQtNc3LiONB3Y/wBPfsK+xfhz4QtPBPhmDS7XDT/6y5mxzLIRyfoOg9hQB0dtbxWdvFb20axQxKERFGAqgYAFT0UUAFBoooAbxmvn/wAZac+l+JL23cbVaQyoR3Vjkf4fhX0Ca5fxz4Ui8R2aMjiG9gz5Uh6EHqp9jXqZVjFhK15bPRnm5jhpYil7u6PDqK19Y8M6xo+Wv7R1jBx5iHcn5j+tZFfeU69OquaEro+OnSnTlyzVjr/hO7J4vQA8PA6n9D/SvageK8h+D+myyazNqLIfIhjMav2LHHA+g6166B1r4jOpxli3y9Ej67KouOHV+7HCigUV4x6oUUUUAFFFFABRRRQAUUUUAFFFFABVPULyOytZLidsIi5+voBVviuB8aaobu9+xxN+6hPz47t/9auTF11QpuXUzqT5I3MnUb2XULt7iY8t0HZR2FdV4V0YWsYvJ1/fyD5Qf4V/xrH8KaT9uufPnX9xCen95uw+grueleXgaDqP21T5HPRhzPnYlFFFewdQUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACq2pWS6hYy2rz3FuJBjzLeQxyL7qw6VZooAz9B0saNpcVkLy7vREWPn3kvmSHJzy3Ga0KKKACiiigAooooAKKKKAOX8eSjyrWL+Pezke2MVyiruZF/vECuo8Zadcy3KXcCNKm3YwVclcH09KytD0m6ur+NmidIkYMzMCBgHOOe9fOYqnUqYh2Rw1VJz2PQOnA6Ciilr6JI7hKKKKYGdq2i2mpEPOrLIBjepwceh9ak0zSbbTFItkOW+878k1exmkz71l7Gmpc1te5PKr36gaKKK1KCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDD8YWtvJo0t3cSpD9lUyeaxwAo6gn3/nXneq6fBqumXFlcKDFcIVz/dPYj3B5rB/aF8d/bLv/AIRbS5d1tbsGvmRuHcciP6Dqff6Uvw21j+1vDyxSvuuLMiJ89SP4T+XH4V4+YUOS1aO63OStG3vId8A/htNH4gudc1uDEemyNDao68SSjrIPUAdPc+1fQvWuQ8B3+5JLKQ8p86fTuPzrsK9bDVvbU1M6qc+aKYUUUV0FhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRUM8yQwyTTOqRRqXdmOAoAyST9KAMPx54psvCHh261a/IIjXEUYPzSyH7qD6/oMmvjbxBrV74g1m61bUpfNubuQu57D0UegA4A9K634yePm8b+I2FszDSLImO1Tpv/AL0hHqe3oMe9Wfgl8P38ZeIFur+P/iTWDBpyekrdREPr1Pt9RQB6R+zp8P8A+zrAeKtUhxeXa4s0brFEer/Vu3+z9a9txUUaLEiqihVUYAA4A9BUtABRRRQAUUUUAFIaWigCNl3Z3cg9jWc/h7RpCWbS7MknJJgX/CtWkqoylHZkShGXxK5DBDFBGI4I1jQdFUAAflU9IKKlvqykraIKKhnuIrdN0rhF96zm1+zHQSEeoFYTxNGn8ckjSNOctka9LWJ/wkFqescgHrgf41qQTJcRCSJtynoRSpYmlWdoSTCVOcPiVieiiiuggKKKKACiiigAoNFFAGT4j1EaZpkkyn94flT/AHj/AJzXnUMcl1cJGhLSStgH3Nbnji+8/UUtUP7uAZb/AHj1/IVL4IsN80t9IPlT5I8+p6n8q+cxMvrWJVNbI4qjdSfIjp9NtI7G1S3iGAo5Pqe5/GrDUUV7cYqK5VsdSjYKKKKoYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUVVuNUsbf8A1t3Gp9M8/pSW2qWV0223uo5G9A3P61l7SF7XV/UnmV7FuilpK1KCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACuF+L3jtPBmgMlq4OrXoK2yf88x0MhHoO3qfxrp/E+vWPhnRLjVdSk2wW65x/E7fwqvqSelfIvi7xFfeKteudW1I/vJjhEU/LEg+6i+wH5nmmBl4muZ+N800r/VnYn9STX0h4P+Ho8MeBC06r/a0xFxcsOduOkY9gDz75rmv2ffAO+RfFesRfu1JFhG46sODKR6DoPfn0r3SdBNE0bcq4Kn6Hisa8Oem49yJrmR51ol2bHVbaYHChsP8A7p4NepV5JdRGCeSNuqMV/I4r0zRLr7XpVrNnJeMbvqOD+tedlU7OVJ+pjh5bxL9FFFe4dYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV4F+0X8RMBvCOkTYPB1CVD+IiB/U/gPWu8+MXj1PBXh5vs7I+rXoKWkR52+shHoO3qcD1r5LlknvbpmkZ57iZsknLM7E/qSaAL/hTQLzxNr1tpOmrunuGxuP3Y1/idvYDmvsrwj4dsfC2gWukaYgEMC8t/FI5+859yf8K5H4J/DxfBeg/atQiB1i/UNOT1hTqIx9Op9T9BXpVABRRRQAUUUUAFFFFABRRRQAUh6UtFAEUsqxIzscKBkmuX1HWJ7h9sDNHH2xwT9TWl4nmZLdIlP+sbn6VzdfNZrjakZ+xpuy6np4SgpLmkK7PJ/rGLf7xzSUUV865OTuz0VFLYK3/CrM0c6k/KCCPxzWBXU+HrfybEOR80p3V62Uwk8QpLZI5Ma0qdn1NaiiivsTxgooooAKKKDQAd6huZVggeVzhUUsT7CpaxfFtx9n0OfHWTEY/E8/pmsq0+SnKXZCbsrnn93ObmeSZvvSMWP4mvQ9FtBZ6ZBBjBVMt/vHk1wejW32rVLeHGQX5+g5Nekk9hXiZZDmcqjOWgrtyYUUUV7R0hRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFADZZI4YmkmYIiDJJ7CuE1zX7jUZGSItFbDog4L+7f4VseOblktYIFbAlclseg6fqa4/vXg5hipc3soadzkrVHflADuetL/ABD5sEUUhrybs5Tt/CmsG+h+zXL5uIxwT1df8RW9XnXhzd/bVpt67+fpjn9K9Fr6XAVpVaXvdNDvoyco6hRRRXebBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAU2V0ihaSVgkaAszFsAAckk+lOrwr4+/EPc0vhTRZuB8t/MrdT/AM8gf5/l60Acb8YPH0njPXPIs3I0exYi3Xp5rdDIR79vQfU1X+E/gSbxr4gAnBXSrUhrqUcZ9IwfU/oOa57wvoF74m1y20rTIw007fe7RqPvO3sBX1x4R8N2PhTQrbStNXakQyzsPmlc/edvc/oOKYGrbwxWtvHDbxrFFEoSNAMBVAwAB7U+iiluB574nh8rWrlezEOPxGf511vgiXzNFVP+ebsn9f61znjNcazn+9Gv9a2/ALf8S2dfSb+YFeHhPdxkl6nJT0qs6iiiivojtCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKyfFOv2PhrRLnVtTkEcFsuTzyzfwqB3JPFaE8iwRPJI6pGiliWOAAOpJr5Q+NXxDfxrrZtrCQro9ixEA/wCez9DIR79B6D6mgDlvHHii+8X+IrnWNQbHm/LFEp+WKMfdQfTv6nJr1X9nX4dfa54/FurQ5ghJFjE44dxwZD7DoPfntXC/CHwBP458QLFOJI9KtSHu5V4yO0YP94/oMmvrq0tobS1itrSNYYIFCRoq4CKBgAD2oAs0UUUAFFFFABRRRQAUUUUAFFFFABRRQaAMTxJavNbrLHyYySQPSubrvTXIa3btb3zsRhJDlT/Ovms3w2vto9dGelg63/LtlGiinQxSTSCOJNzHtXz0YOT5Y7npuSSuyfTrM3t2kY+71Y+grskUKAqjAUYAqnpdgljBtAzI3LN6mr4FfZ5fhFh6evxPf/I8PE1vaz02QtFFFemcwUUUUAFJS0lAgrlvH8u2ygiH8UhP5D/69dV2rj/iF/y5/V/6VxY52oSM6vwMy/BUW/Vw5/giY/nx/Wu5rjvAi/8AEwn9ox/MV2XeuTLY2op+bM6HwBSUtFembCUUUUhhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAcx47j/ANHtZcdHZPzGf6VyIr0nWNPXUrB7djhjyh9G7V59f2VxYTGO5jKnsex+lfO5jQl7TnS0Zw1otO5XNGaKu6Rpk2qXAjjXCD779lH+PtXmwhKclGJjFOTsbPgmyZ7mS8YfIg2J7k9fyH866+oLG2jsrZIIVwiDA/xNT19XhqPsqaj1PQpx5Y2Ciiiuk0CiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiuc+IHi+z8GeHpNRutskzZS2g3YMsnYfQdSewoA5z4z/ABDTwjph07TJAdZvFPl4P+oToZD7+g9ee1fM0aT3l2EQPPcTvgKMs0jk/mSSasa1q17rmq3Gp6nM011csXdj+gHoAOAOwr3H4C/Dk2UMXinWoQtzKM2ULD/Vof8AloR/eI6eg570wOr+EHgCLwZovnXaq+r3ag3D5z5Y7RqfQd/U/QV3dFFIAooooA4fxr/yG/pGv9a2vAAxp1w3rN/7KK53xNN5uuXBzwpC/kP8a6rwRD5WiBsf6yRm/p/SvDwvvYxteZyU9arZ0NFFFfRHaFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRXAfGPx/H4I0Ai1YNq12GS1jPOz1kI9B29Tx60AcF+0T8RTHHJ4R0eb5mH/EwlQ9AeRED79T7ceteKeF9AvvEuu2uk6ZF5lzctjPZB/Ex9ABzVGR5726Z5mee4mcsWOWZ3J/Uk19VfBH4eJ4M0L7ZfxZ1i+UGYnrCnaMfzPqfoKAOq8DeF7Hwf4dttJ09SQg3SSsPmlkP3nP1/QYFdBQKWgAooooAKKKKACiiigAooooAKKKKACiiigBKint454ykqBlPY1LRUyipK0kCbWpknQLMt0cD03VdtrSC0GIUVfU45P41ZorCGGpU3zQiky5VJyVmxaKKK6SAooooAKKKKAA0lFKKBBXH/EIcWbf7TD+Vdea5jx9Fu02GTHKSj9RXDjVehIiqrwZleCGxqU49Yf5EV2XeuD8Hy+XrcSno6sn6Z/pXeVy5ZK9G3ZmVB+6FFFFekbhRRRQAUUUUAFFFFABRRXmfjPx3M9y9hor+XGpKyTj7zHvtPYe/U11YXCzxMuSHzObEYmGHjzTPTKWvn59Sv5H3PfXLN6mZs/zrS0XxZrGkzo8d3JNGv34ZmLKR+PI+or1p5HVjG6kmzzI5xTbs4tI9uoqpo+oxarp1vewZ2TLnB6qehB+hq3XgOLi3GW6PajJTV1sFFFFIoKKKKACiiigAooooAKKKKACiiigAqK5tobqIx3EYkQ9jUtFTKKkrMDF/wCEV0zfuKSFf7m44/x/Wta2t4LWIRW0YjQdguKkozUQo04O8YpEqEVsgooorUoKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK+o31tplhPfahMsNtBGZJXPRQK+TPiX4yufG3iSS9kzHaRZjtYT/AAR+p9z1P5dq6344/Eb/AISC9bQdGmzpds376VG4uJB6eqjt6nn0rivAHhK78YeIodNtQUh+/cTY4iiHU/U9AO5pgdd8Dvh7/wAJLqg1nVoc6RZScKRxcyjnb7qOp9enrX0rgYCqMKKp6Npdno2lW2m6ZCIbW1QRxqPQdz6knknuauUgCiiigApJJBHEztwEBJ+lLWT4su/sujuucPP+7H9f0rKrPkg5diZOyOEuZjNdSzN/y0Yv+telaDb/AGXSLaE9QgJ+vU/zrz3SLX7bqcEAGQWGf90cn9K9SAxXm5XC7lUZhh1vIdRRRXunWFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFQTzpBC8kriNI1LMzHAAHUn2oAzvFXiGx8L6Jc6tqUgWCBc4H3nb+FR6kngV8b+NvE994u8Q3Orai372U4RAcrEg+6i+wH5nJ710/xp+IMnjPXDBaSMNIsWK269PNboZSPft6D6mq/wAH/AEvjnxAFuEdNKsyHu5V43+kan1P6DJ9KAO4/Z3+HAu5o/FutQ5giP8AoETj77j/AJakeg7e/PYV9Edar2ltDaW8VvbRpDDEoRI1GAqjgACrNABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBoooASloooAKyfE1r9q0a5j/iCbl+o5rVNNlQOhUjIPBrOpDng49xSV1Y8psJzaX0FwONjgn6d/wBK9OByAR35rzPVLY2eoT25H3WIH07fpXb+GLz7ZpMfOXh/dN/n6V4WWy9nUlSl/VjkoOzcTVooor2zqCiiigAooooAKKKKAMTxvftpvhi8njOJGURofQscZ/AZrxAn/wCua9d+Kv8AyKh/67J/WvIq+vySKVGUlu2fL5xNuso9kFFLTlVpHVFXczEAAdST0Fe81ZXPH1Z678L93/CJQ7unmvj6ZrqvpWb4b0/+ytBs7HGGjQb/APe6n9TWlX51ipKdWUls2z7jDwcKUU90kFFBornOgKKKKACiiigAooooAKKKKACiiigAooooAKKKKVgCiiimAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAevYCvAPjN8WTqLTaB4YmIshmO5u1PM3Yop/u+p/i+nW78efiQymXwvoM2MfLf3Ebf8AkJSP1/L1rxvQ9Gv9f1W303SoDPcznaqjoPUk9gPWgA0TSL/XtVg03SoGmuZ2wqjt6knsB3Pavq34aeCbTwX4fSyiKyXk2JLq4C8u/oP9kdAPx71X+Gfw/sfBGl7V23GpzgfabrHX/ZX0Ufr1NdkOKYCUUUUgCiijFABXD+L7/wC06l5Kn93ANn/Aj1/wrqNe1FdN09pM/vG+WNfVv/rda8/gjkurhY1+eWV8c9ya8fMa2iox3e5zV5/ZR0/gOxy81644H7tP5k/0rsxVTTLNLCyit4xxGuPqe5/GrYr08LR9jSUep0U48sbC0UUV1lhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXz/8AtE/EYsZPCOjTY/6CEqN+UQ/mfwHrXa/Gv4jR+DNE+y2EgOtXqlYAOfJToZD/AE9T7A18qnz726wN89zO/wDvNI5P6kk0AaHhbw/feJ9bttK02PdNcNjJ+6i93PsBya+xvBvhiw8JeH7fStNT5IRl5CPmlk7u3uT+Q4rzf4dWGi/C3SP+Jqxm8Q3qBrlIQGaFeqxZ6D1PqfYCul/4Wvpn/QPvf/HP8a66eCr1FzQg2jlqYyjTfLKSPQqK5vw14x03xC7xWu+K4QbjDLw2PUY610QrCpTnTlyzVmbU6sKseaDuh1FAorM0CiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooNNLUAOoqJ5o1+9Ii/U1Gb22XrdQ/99j/ABoAs0hqs2o2Q63luP8Atov+NN/tXT/+f+2/7+r/AI0WA5bx7YYlivoxwf3b/Xsf6VQ8I6h9j1LyJDiK4+X6MOn+FdZqV1pV9ZS28l/abZBjPnLwex61526+XIyqytsbG6Mgg47g189jYSw1dVo7M4qsXCfOj1E9aKxdI8Q2UtgjX15Bbyr8redIqZPqMkdanbxJoK/e1zTV/wC3uP8A+Kr16U1UgprqdMXzK5p0Viv4w8Mx/e8QaaP+3lP8arS/EHwfH97xJpg/7eFP8q0KOjorkpvih4Ji+94jtG/3NzfyFU5/jB4Gi/5je/8A3LaU/wDsooA7ml7V5xN8b/BUP3bm8l/3LVv6kVTm+PvhRP8AU2uqSf8AbFR/NqAO58Z6a+q+HLu2hG6VVDoPVlOcf0rw/wDSupm/aE0Qf6jRNRb/AHmjX+RNcP4l+JWi6tdPc2vh24tJnOWIu12ufUrt6/Q17mWZjHDXhPZnj5jgZYhqcN0X67z4a+GGluF1i9jxFHzArfxt/f8AoO3vXkFj8QIbS4Ex0WK7K8hZ7htufcADNdC/7QGvhdsWk6XCBwB85AH/AH1XVmGbRqQ9nR67swwWWyhNVKvTofRQFOr5sl+PnixvuWulp/27uf8A2aqz/HPxo/3WsE+lt/ia+aPePpuivl5/jb42/wCf20X6Wif1pv8Awuvxx/0EIF/7dI//AImkM+o6K+W/+F0+Of8AoKQ/+AkX/wATSf8AC6PHP/QWh/8AAOL/AOJoA+paK+Wf+F0+O/8AoLQ/+AcX/wATR/wunx3/ANBWH/wEi/8AiaAPqaivlxfjX45/6CMB/wC3WP8Awp3/AAu/xuv/AC+2h/7dUoA+oaK+Y1+OPjT+KexP1tx/Q0//AIXv4y/6hx+tsf8A4qgD6Zor5p/4Xz4w/wCeeln/ALdm/wDiqevx78X/APPHSj/2wf8A+LoA+k6K+bv+F9+Lv+ffSv8Avw//AMXR/wAL78Xf8+ulf9+H/wDi6APpGivm7/hffiz/AJ9dK/78P/8AF0f8L98Wf8+uk/8Afh//AIugD6Ror5u/4X74s/59dJ/78P8A/F0f8L98Wf8APrpP/fh//i6APpGivm7/AIX74s/59dJ/78P/APF0f8L98Wf8+uk/9+H/APi6APpGivm3/hfviz/n10r/AL8P/wDF0v8Awv3xZ/z56T/35f8A+KoA+kaK+bv+F++LP+fPSf8Avy//AMVT1+P3ilf+XDSz/wBsn/8AiqAPo6ivnRf2gfEv8Wm6Wfwcf+zVMv7QmvfxaLpzf8DkH9aAPoWivAY/2htT/j0CzP0mcfzFTL+0Rc/x+G4fwuT/APE0Ae8UV4av7RP97wz+V5/9jUi/tEw/xeGJPwvR/wDEUAe3UV4p/wANEWf8XhucfS7X/wCJqVP2h9N/i8PXY+k6H+goA9morx+P9obRG/1miagPo8Z/qKuQ/H7wtJ/rLLVIv+2aH+TUAeqV558a/Hv/AAiWiCz06UDVr8ERnvDH0aT69h789qryfHTweLWWSM3xlVSVieDaXbsM5IGfU189+K9fvfFGu3Orak2Zpzwo+7Gg+6i+wFAGfDFPeXaxRI8s8zAKg+ZmYnge5Jr6l+EfgCDwZoyyXSI+r3ag3MmM+WOojU+g7nufwrif2efA6bf+Eq1JAznK2Mbc7B0aQjsT0H4n0r3CgAooooAKKKKAD60OyorMzYVRkk9BRXI+LdZ8xjY2r/KOJmHc/wB3/GsMRXVCDkyJzUVcyvEGpnUr5nBYQp8sQ9vX8a3PBGk4B1G4Xk5WIH07t/SsLQNKfVL1Y/mEK8yN6D0+pr0qKNYo1jRdqqAAB2FeZgaDrTdep/T/AOAYUoc0udkgpaKK+gOwKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAK5nx94vsvBfh6bU75gzjKwQhvmmkPRR7dyewrY1XULbStPnv9QmWG1t0MkkjdAtfIPxS8dXfjrxE92+Y7CElLSDP3E9T/tHqfy7UAYPiPXL/AMR61carqsplurltzHso7Ko7ADgCvafgV8PG0/Tm8Za3bjzViaXT4ZR90YJ80j1Pb259K5P4GfDpvF2sDVNViP8AY1k4Lgji4cciP6DqfbjvX0vr1u8vh+9trVdrNbvHGqcfwkAD+VVDWSTM6jai2j5+nmkuZnnmcvLI25mPUk8k0zNA/wB3acUV+oU0lGyPz+o+aTbNnwPK0Pi7TGjOC020n2PBH5V7/Xz54Rjkk8T6asfUXCHj0Byf0r6DFfG5+l7eNu36n0+TNulL1HDpRWZqPiLRtLUnUdVsbQL18+4RP5muU1X4y+BdPyDriXDDtbRvJ+oGP1r589076ivGdS/aM8O25K6fpeoXhHQvsiB/Un9K5u//AGk9QYkaf4dtovQzzs/6AD+dAH0VRXyxeftB+M5v9RHp1r/1zgJ/9CY1k3Xxp8e3HTW/K/65wRD/ANloA+vaK+MJ/ij44n+/4mvx/uOE/kBWfP448WT/AOt8S6u31vJP8aAPt+ivhSXxFrc3+t1jUH/3rlz/AFqu+pX7/fvrlv8AelY/1oA+7XniT70yL9SKry6vpkAzNqNpH/vzKv8AM18KPNLJ/rJHf6tUVAH2/c+NfC9vkTeItKQjt9sjJ/IHNZlx8VvA1sSJPElmcf8APPc//oINfGg56CnKjOwCqSfQUAfWd38cvAlvnbqk1x7RWsn9QKyLv9onwpFn7PY6ncH/AK5ov82r5vt9F1W6YLbaXeTE9PLgZs/kK2rP4c+MrzHkeGtS56F4GQfm2KAPX7z9pOyUZsvDlxJ/11uVT+SmsW5/aS1g/wDHp4fsIv8ArpK7/wAsVyVr8FfHtz10byv+utzGP61r2n7PfjKb/XTaXbf787H/ANBU0AFz+0H4zlJ8mHTYB/swMf5saybv41+Pbj7usrCPSK2iH81Jrrrb9m3Vzj7V4gs4/wDrnC7/AMyK1YP2a7UKPtPiSZj/ANM7UD+bGgDyif4oeNp87/E2oDP/ADzk2fyArPn8aeKLj/X+ItUfP/T3J/jXvVt+zl4ZT/j51XVZD/stGo/9ANaUHwA8ExY3rqM3+/c4/kooA+Z5df1ib/W6vfyf79y5/maqve3L/wCtupn+rk/1r6wi+B3gKM5/sqVv966kP/s1Wk+DngFP+Zejb6zSn/2agD4/Lserk/jSbj6n86+x0+EngNf+ZbtvxeQ/zapP+FVeB/8AoWrH8Qx/rQB8Z59zRxX2f/wq7wP/ANCxp/8A37/+vS/8Kw8Ef9Czp/8A37oA+L816N8J/E/2K4/se8kxBO2YWbornqv0P8/rX0Z/wrLwT/0LGm/9+RT1+HHgxCGTwxpgKnIP2deKxr0o1qbpy6kTgpqzPM/FOhQeINLktJsbx80Lj/lm46fgehrwu/s5dOu5LS6j2TQsVYH/AD09K+pfFGif2ZcebAP9FlPH+yf7v+FZmlQ6P/aAfVtKsbtXwDLPAruh7ckE49q8LDV5YWo6NTY5YSdOXLI+ZSIx1x+VCsv94V9ow+HNAUB4dF05cjIK20fI/KrSaXp0f+rsLVP923Qf0r3TrPiny3b7qMfoCaljsLyX/V2k8h/2Y2P8hX2wtvAv3IIh9EA/pUoJHTrQB8XQeGddnx5OialJ/uWsh/8AZavQeAvF0/8AqvDmpH/egK/zxX2HuJoyfWgD5Lh+FfjmbGPD1yn++6L/ADarkHwZ8cy/e0yKL/fuox/ImvqjPvSUAfMsPwJ8ZyY3rp0f+9c/4KauR/ADxO3+s1DS4/o7t/7KK+jqKAPnyP8AZ61o/f1zTh9I5D/QVZX9ne9/5aeIrcfS2Y/zNe9UUAeFr+ztJ/F4mX8LT/7KpP8Ahndf+hmb/wAA/wD7OvcKKAPEP+Gd4v8AoZ3/APAIf/F0v/DO8P8A0M0n/gEP/i69uooA8R/4Z3h/6GaT/wAAh/8AF0f8M7w/9DM//gEP/i69uooA8Pb9nZe3iZv+BWf/ANnUbfs7P/D4mX8bQ/8Axde6UUAeDt+ztc/w+JIfxtm/+KqNv2eNR/h8Q2n4wN/jXvlFAHz/AP8ADPGrf9DBZf8Afl6af2edZ7a9p/8A36kr6CooA+fP+Getb/6D2n/9+pP8KP8AhnnW/wDoO6d/36k/wr6DooA+fP8AhnrW/wDoO6d/36k/wo/4Z61r/oOad/3xJ/hX0HRQB8+f8M9a3/0HNO/74k/wpP8AhnrW/wDoOad/3xJ/hX0JRQB89/8ADPWt/wDQc07/AL4k/wAKP+Getb/6Dmnf98Sf4V9CUUAfPf8Awz1rf/Qc07/viT/Cj/hnrXP+g5p3/fEn+FfQlFAHz3/wz1rv/Qb03/viT/Cmt+z5r4/5jemn/gMn+FfQ1FAHzo37PviP+HVdLb/gUg/pUTfALxUDhL3Sn/7bOP8A2WvpCigD5ok+BHjJeh0xvpcn+q1C3wO8ar0t7FvpdL/UV9O0UAfLv/Ck/HH/AED7Y/S7j/xpn/Cl/HS/8wmE/S7i/wAa+paKAPlc/Bvx0v8AzB1b6XUX+NRP8IfHSf8AMDJ+k8Z/rX1bRQB8lv8ACrxynXw7cn/ddD/Wqs/w88Ywf63w5qI/3Yt38s19fUUAfFd/oWr6bj7fpN9a54Bmt3UH6ZArPZSr7WBX2PBr7k/Ue9U9R0bS9Tj2ajplpeKeomhV/wCYoA+QvBGpappvirTpdEkkW7a4jRY0J/egsAVI7gjrX2TWHo3gzw3ol19r0rRrK1uOf3qJ8wz1wTnH4VuUAFFFFABRRXOeJPEIt91tZndN0Zx0T6e/8qxq1oUo80mRKSirsXxNrwtla0tGHnEYdh/APT6/yrlLG0mvrpIIAXkbuegHcn2pttbz3l0kFuheVzk5/Uk16HoOkQ6Tb7VG+Z/vv3PsPavGpwqY6pzS0ijmjGVWV3sT6Pp0WmWSQxc92bux9av0oGKBX0UYqMVGOyO1JJWQUUUVYwooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiivIPj18Sh4asW0DR5P+Jvdx/vpFOTbRn/2Yjp6Dn0oA4T9oT4h/wBt6g3hrSJ86daP/pMitxPKO2e6r+p+grg/h14PvPG3iKLTLXdHCMPczYyIo88n69gO5rmGJJyetdJ4f8da/wCHNMlsdCu1sEmffLLDGvmucYALkEgD0GKAPsTRtMsfD2jW+n6fGlvZ2qBUXOOB1JPc9ye5rN1bx94S0kst/wCIdPiZeqLMHb/vlcmvjvVde1jWG3arql7eHOcTTM4/Ims1RuOBQB7n468b+Abu4luNFmvpLpuWEVviKQ+vzEEH6D8K4hvG1j/DBOT6HArntJ8I+I9Yx/ZmiX9yD/GkDbf++sY/Wut0r4G+Ob8AyWEFip/iubhR+i5P6V6dLNMTRjyRenmcFTLsPOXNKP3GTF8Rta0+eWXRXisWddvmLGryAezEHH4YrJ1Xxl4l1fP9o67qFwh6o07bfyHFetaV+zbdvg6t4hgj9VtoC/6kj+Vddpf7P3hC0wb17+/cdd8wRT+CgH9a4q1adaXPUd2dVOnCmlGCsj5ddix3MzE+pqezsLy+k2WVtPdSf3Iomc/kAa+ydK+G/g3Swv2Pw5YBl6PLF5rfm+TXS2ttDaxCO2hihQdFjQKPyFYmtj41074ZeNdSANr4cvgD0MqeUPzciuksPgD41uArXC2FoD1E1xkj/vkGvquigD5xs/2bNWkx9t8QWUP/AFyhaT+ZWtm1/ZqsVA+1eI7lz/0ztlT+bGvdaKAPHLf9nLw0n+v1XVJfo0a/+ymrsH7PvgtPvnUpf9+5A/kor1aigDzWP4E+BE+9p9zJ/vXcn9CKtR/BbwDH/wAwLd/vXMp/m1eg0UAcTF8JfAsQG3w5anH98u382q5B8N/BkJynhnTM+8AP866qigDEg8JeHLb/AFGgaYmO62cefzxWjDZ2tuuILWGIdMJEB/IVaooAaowMAYFOpKWgAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3dtFdwPFOodGGCDXnOu6NLpNyVwzQP9x/X2PuK9NqtfWcV7bNDcKGRhyP8964cZhI4iOnxLYxq0udeZw/hzXmsWFtdMz2p6E9U/8ArV2qyLIiujBlblWHQiuA1/RZdLlycyWzfcf+h9DT9D1yfTHCMTLbE8r3X3X/AAry8Pip4eXsqxzwqOD5ZnfUVDZ3cN7Cs1u4ZG7j+R9Kmr21JSV0dad9UFFFFMYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFDsqqWZtqqMknpVXUNQtrCLfcPt9B1ZvoK4rWtdudSynMcB6Ip6/U9648Ti4UF3fYynVUTR1/wASmTda6c2E6NN6+y/41gWNncX9ysNupdyefQD1J7CrWjaNc6rN+7XZCG+aQ9B9PU13+l6Zb6XAIrZMf3mP3mPua82lh6uMnz1HaJjGLqu8titoWiwaTANoDTN9+Q9T7D2rXoor6GFONOKjFaHZGKirIWiiirGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFfM3xw+HPiOXxte6xpum3OpWd+yuGt0LtGQoUqyjJ7cHGMV9M0UAfHWkfCPxxqjgxaBPbof4rsiED8GIP5Cu+0P8AZvunw+u65FF6paRFz/302P5V9D0UAeZaP8CfBOnBTNaXOoSDvczHB/BcCuz0nwnoGjqBpmi2FqR/FHbqGP1bqfzraooARVAFLRRQAYooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAIJ4I7iNo5lDIwwVPeuG1/wANy2Ba4sgZLfqR/En+I967+kIB61yYjCQrxs9+5nUpqe55Xpuo3GnzeZbMRnqp+6w9xXa6PrtvqICEiKbvGT1+h71Dr/haK7Lz2IWGfqV6K/8Aga4ye3ns5zHMjRyKeh4/EV4v77BStLWJy+/Sfken9KK4zRvE81ttivlNxH03j74/xrq7O+t72PfayrIvcA8j6jtXrUcVTrL3Xr2OiNSMixRRRXSaBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUCisfVPEdnZEpGftEw/gQ8D6ms6lWFNXm7IlySWpsO6oCWKgDqTwBXO6v4pjg/dWGJn6bz90fT1/lXOaprN5qBImk2R9o14X/6/wCNGl6Rd6m3+jx4TvK3Cj/H8K8irjp1n7OijllWcnywKtzcTXkzPM7SyN68/gK6DQvCss+2bUQY4uoj/iP19B+tb+i+HbXTFD482c/xt2+npWyBit8Nl2vtK+r7Fwo63mRQQRW0axwoEQdABwKnpKWvYSSVkdSstgoooqhhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJVPUNNtdQiKXMSvnoe4+hq7RUShGatJCaT0Z59rHha6tCZLTNxCOw++Pw7/hWLbz3FtNvglaJ17qcH8a9arK1bQbLUgWkj2S/89E4P4+v4149fLdeei7M5pULaxOf0vxYRiPUk3dvMT+o/wrpbW7t7yMSW8qSKfQ9Pr6VxuqeF76zy0I+0RD+794D3H+FY0UktrNvjZo3U9QcEVgsXWw75aquQqk4fEj1GiuN0/wAW3UOFvEE6j+McN/ga6Gx1vT70DZMI5P7snB/wr0aWMpVdnr5m0asZdTRooorrNQooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoqneatZWP+vuED/wB0ct+Qrn7/AMYHlbCDH/TST/Af41zVcVSpfEzOVSMdzq3dY13OwA7k8CsTUPE9lbArb/6RIP7nC/n/AIVyF7qN3esTdTPIP7vRR+A4p9hpN9qBH2eBin99uF/OvNnmFSo+WjH/ADMZVm9Iol1LXb/UMh5PLjP/ACzTgfj3NV7Gwur6QJaxGT1boF+p6V1ml+ELeDDXz+e/90cL/ia6SCCOFAkSCNR0VRxVU8BUrPnrP/MFRlLWbOb0jwjDDiTUGEz9fLH3B/U10kUUcKBIkCqOgAwBUtFexSoU6KtBHRGEY7IKKKK3LClpKWgAooooGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABWZqWjWOof8fEC7/768N+Y/rWnRWcoRmrSVxNJ7nEaj4OuI8tYyiZP7snDfn0P6Vzt1Z3Fm+26geM/7Qx+tesVHLDHMhSZFdT2YZFeZWyynN3g7GEqEXtoeZWesX1njybhgo/gb5l/Ktyz8YEYS8ts/wC1Ef6H/Gte/wDCunXBLRqbdz3j6fl0rAvfB97CSbeRLgds/K3+H61xuji8P8LujLlqw2Oitdd0+5+7cqjf3ZPlP68Vo5BwyHPuK8yurC7tP+Pq2kjHqV4/PpSW93cWpzBPIn+6SKqOZThpUiNV5L4kenUVwlr4p1KHiQpMP9pefzGK07bxjH0ubVx/tRnP6GuynmFGe7saKvBnUUVkQeJNMlHMxjJ7SKRV+G+tJx+5uYXz6OK6o16cvhkmaKUXsyxRRRWpQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUM21fmbA9+KNACiqtxqlhD/rLuFfbeCfyFUJvFOmx5CSPIf8AZU/zOKynXpw3aJc4o2aK5WfxiM/6NaH6u/8AQVm3PifUpujpCP8AYT+pya5Z5hRjs7mTrwR3jsF5ZgF9TxWdd69p1rnfcqzj+FPmP6cVwU9zPcHdPK8h/wBok061sbq7OLa3kkPqBx+fSuN5lObtTiZ+3b0ijorvxjniztv+BSn+g/xrFvNb1C7yJbhlU/wx/KP0rRs/B99NgzvHAp7Z3N+Q4/Wtyx8I2FuQ0++4b/aOB+QqfY4zEfE7L7hctWW+hwsEE1y+yGN5GPZQSa3LDwjf3GGuClsn5t+Q/wAa7mG2ht02QRrEvooxU2K66WVwjrUdzSOGividzE07wzp9nhmj8+T+9Lz+Q6VsqoUBVGAPSnYor06dKFNWgrHQoqOyClpKK1GLRRRQMKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAMUYoooAYUUghlBFZ13oGm3WTLaoCf4lG0/pWpRxWcqcJq0lclxT3OUuvBdq2fs1xJH7MAw/oazLjwjqEYzG0Mo9iQa77ikrjqZfQn0sZOhBnmFxompQf6y0lPuo3D9M1SeN0OHRlPuuDXrfWmSwRyLh0DD0IzXJLKY/YZDwy6M8pjurmLHlzyp/uuRVyHXtTh+7eOcf3sH+YrvZtE02X79lD+CY/lVOXwppcn3Ynj/3GP8AWsv7Orw+CX4kujNbM5iLxVqidXjf/eQf0xU6+ML3+OGA/TI/rWvJ4Lsj92edfyP9KrP4IX+C9b8Yx/jS9hjY9b/MnkqorJ4yl/js0P0cj+lTL4yQ/fsSPpKP8KjfwTcj7l3EfqpFRt4Lvv8An4gP5j+lL/b4jtVLf/CZW/8Az6S/99Cl/wCExtf+fWb8xWf/AMIdqP8ADJbn/gZ/wo/4Q7U/71v/AN9n/Clz4/sK9XsaH/CZWv8Az6Tf99Ck/wCEyg/585P++x/hVD/hD9T/AL1t/wB9n/CnDwbqGOZYB+J/wqvaY99PwC9XsWH8Zr/BYn8ZP/rVE3jG4P3bWMfUk0g8F3p63EA/76qZPBMp+/eKPohP9RT5cdL+kO1UqN4uvz9yKBf+Ak/1qu/ifVG/5bhf91BW2ngiH+O8kP0QD+tWI/Bmnr9+Sd/xH9BS+rY2W7/EXs6z6nJSazqU337ub/gLY/liqsk0kpzI7ufdia9Bh8L6VHj/AEXd7uxP9auQ6XYwf6qzgT/gAp/2bWn8cvzH7Cb3Z5lHDLKR5MLyf7ik/wAqvQ6Dqc/S0ZAe7YX+delKu3gDA9qfitY5TBfFJspYZdWcJbeDb1wDPPFEPbLH+n860rXwZaRnNxPLMfQYUf411NLXZDAUIdL+pqqMF0Mu20LTrXHlWkeR/EwyfzNaIAAwBinUtdcKcYaRVjRRS2EApcUUVaRQUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooNABSUtFABRRRQAUYoooAKKKKQBRRRTAMUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB//2bhK9z8AAAAAITqoPstd2R71Q4RzjV2WxA==" width="237.4047244094488" height="307.15198820722014" preserveAspectRatio="none"/>
</g>
<g transform="translate(53.52236220472441 320.15198820722014)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="15.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="25.119999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="35.739999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="43.019999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g18D1F1E967E0B15C3E9466BFBC921865" x="56.959999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="66.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="75.97999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="85.67999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="94.61999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="103.75999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="111.03999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="119.6" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 433.56299212598424)">
<g class="typst-group">
<g>
<g transform="translate(8 18.5)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAA14E57E2DCC57A3F7809273EECD3C51" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="9.344000000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="12.812800000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="18.5344" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="23.296000000000003" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="29.1456" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="33.8048" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="39.2832" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="46.1696" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="49.638400000000004" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="55.116800000000005" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="60.96640000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g1CB3EC9D05726EBFDE8ADABEC8504FCD" x="67.54560000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="76.4928" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD62975B7DE3250BE5F195D0E8335F60D" x="82.3424" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="88.704" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="92.1728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="98.5728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD5EEFB9760BC9A91B84F628EDDA52971" x="104.4224" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="110.7328" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="114.112" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g83A6AA7A836EACB3652229F4716CDAF" x="123.03359999999999" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gDB4862E33098F259EEBBA99A57E5AFA" x="129.2416" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="139.3536" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="145.2032" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="148.5824" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g793DBE65A5AEC1A16A65955B6C0E046" x="155.1616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gA11612CECC8CBEF18835767DAB11B2F7" x="166.3104" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="172.7616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="177.52319999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gCEFEF3D67F35C6E83CC3757B1DD21B13" x="180.90239999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="190.57919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="196.97919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="201.74079999999995" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g645CA8FA3D9155E2CBD9F8EED3C1540D" x="207.59039999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="214.23359999999997" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(798.4017637795276 8)">
<g class="typst-group">
<g>
<g transform="translate(0 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g9519A9B09125702A7696E3BE317A1C17" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" x="11.440000000000001" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.608 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="7.44" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="g5396A27CA60B9808846A090320835A9F" overflow="visible">
<path d="M 1.91 1.22 L 1.91 5.23 C 1.91 6.06 2.08 6.1099997 2.78 6.14 C 2.84 6.2 2.84 6.41 2.78 6.47 C 2.34 6.46 1.87 6.45 1.48 6.45 C 1.15 6.45 0.65999997 6.46 0.19 6.47 C 0.13 6.41 0.13 6.2 0.19 6.14 C 0.89 6.1099997 1.06 6.06 1.06 5.23 L 1.06 1.22 C 1.06 0.39 0.89 0.34 0.19 0.31 C 0.13 0.25 0.13 0.04 0.19 -0.02 C 0.64 -0.01 1.13 0 1.49 0 C 1.8499999 0 2.33 -0.01 2.78 -0.02 C 2.84 0.04 2.84 0.25 2.78 0.31 C 2.08 0.34 1.91 0.39 1.91 1.22 Z "/>
</symbol>
<symbol id="gEEE4EC0F13100E99C1017169F912BE3E" overflow="visible">
<path d="M 1.55 1.22 L 1.55 3.12 C 1.55 3.61 1.68 3.52 1.91 3.23 L 4.2599998 0.099999994 C 4.41 -0.06 4.5699997 -0.12 4.72 -0.12 C 4.8399997 -0.12 4.94 -0.049999997 4.94 0.14999999 L 4.94 3.3799999 C 4.94 4.21 5.0499997 4.24 5.66 4.29 C 5.72 4.35 5.72 4.56 5.66 4.62 C 5.3599997 4.61 5 4.6 4.7 4.6 C 4.4 4.6 4.0499997 4.61 3.75 4.62 C 3.6899998 4.56 3.6899998 4.35 3.75 4.29 C 4.36 4.25 4.47 4.21 4.47 3.3799999 L 4.47 1.51 C 4.47 1.24 4.44 1.0699999 4.13 1.49 L 1.8399999 4.6 L 0.42 4.62 L 0.39999998 4.5899997 L 0.39999998 4.35 C 0.39999998 4.31 0.45999998 4.29 0.48999998 4.29 C 0.87 4.2599998 0.97999996 4.14 1.0799999 3.9599998 L 1.0799999 1.22 C 1.0799999 0.39 0.96999997 0.35 0.35999998 0.31 C 0.29999998 0.25 0.29999998 0.04 0.35999998 -0.02 C 0.65999997 -0.01 1.01 0 1.31 0 C 1.61 0 1.9699999 -0.01 2.27 -0.02 C 2.33 0.04 2.33 0.25 2.27 0.31 C 1.66 0.35999998 1.55 0.39 1.55 1.22 Z "/>
</symbol>
<symbol id="gA419F36517085793EDBF3FE4736A2E59" overflow="visible">
<path d="M 3.04 1.22 L 3.04 3.74 C 3.04 4.11 3.1399999 4.2599998 3.46 4.2599998 L 3.72 4.2599998 C 4.35 4.2599998 4.48 4.06 4.68 3.34 C 4.7799997 3.32 4.87 3.32 4.95 3.37 C 4.9 3.86 4.89 4.23 4.87 4.7 C 4.52 4.66 3.8799999 4.6 3.04 4.6 L 2.25 4.6 C 1.27 4.6 0.69 4.65 0.42 4.7 C 0.42 4.23 0.41 3.84 0.35 3.37 C 0.44 3.34 0.53 3.33 0.62 3.34 C 0.82 4.06 0.93 4.2599998 1.5799999 4.2599998 L 1.8199999 4.2599998 C 2.1299999 4.2599998 2.25 4.14 2.25 3.75 L 2.25 1.22 C 2.25 0.39 2.1399999 0.35999998 1.53 0.31 C 1.4699999 0.25 1.4699999 0.04 1.53 -0.02 C 1.9 -0.01 2.31 0 2.6499999 0 C 3 0 3.3899999 -0.01 3.76 -0.02 C 3.82 0.04 3.82 0.25 3.76 0.31 C 3.1499999 0.35 3.04 0.39 3.04 1.22 Z "/>
</symbol>
<symbol id="gFAD9169AC3141E7FC4EA568E3BBD2E9B" overflow="visible">
<path d="M 1.91 1.22 L 1.91 2.09 L 2.46 2.09 C 2.84 2.09 2.98 1.76 3.11 1.39 L 3.33 0.78999996 C 3.56 0.17 3.8999999 -0.07 4.33 -0.07 C 4.48 -0.07 4.79 -0.04 4.96 0 C 4.99 0.099999994 4.97 0.19999999 4.9 0.28 C 4.54 0.28 4.35 0.34 4.15 0.85999995 L 3.86 1.61 C 3.74 1.92 3.62 2.09 3.49 2.22 L 3.49 2.24 C 3.83 2.36 4.3399997 2.77 4.3399997 3.46 C 4.3399997 4.29 3.82 4.64 2.6299999 4.64 C 2.3799999 4.64 1.81 4.6 1.51 4.6 C 1.22 4.6 0.79999995 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.78 -0.01 1.1899999 0 1.52 0 C 1.8299999 0 2.1599998 -0.01 2.48 -0.02 C 2.54 0.04 2.54 0.25 2.48 0.31 C 2.01 0.34 1.91 0.39 1.91 1.22 Z M 3.47 3.46 C 3.47 2.6699998 3.24 2.3799999 2.35 2.3799999 L 1.91 2.3799999 L 1.91 3.6799998 C 1.91 4.21 2.01 4.31 2.57 4.31 C 3.27 4.31 3.47 4.06 3.47 3.46 Z "/>
</symbol>
<symbol id="g7FD6A8241485CEBC032BD9E4CE659816" overflow="visible">
<path d="M 5.27 2.35 C 5.27 3.77 4.13 4.7 2.83 4.7 C 1.4399999 4.7 0.37 3.6899998 0.37 2.22 C 0.37 0.85999995 1.4 -0.099999994 2.75 -0.099999994 C 4.39 -0.099999994 5.27 1.05 5.27 2.35 Z M 2.74 4.37 C 3.6299999 4.37 4.4 3.55 4.4 2.21 C 4.4 0.97999996 3.79 0.22999999 2.8999999 0.22999999 C 1.93 0.22999999 1.24 1.11 1.24 2.34 C 1.24 3.6899998 1.99 4.37 2.74 4.37 Z "/>
</symbol>
<symbol id="gBFFDA84A1400D9E1136DF0DD93EA19F5" overflow="visible">
<path d="M 1.48 4.6 C 1.2099999 4.6 0.76 4.61 0.37 4.62 C 0.31 4.56 0.31 4.35 0.37 4.29 C 0.97999996 4.25 1.09 4.21 1.09 3.3799999 L 1.09 1.22 C 1.09 0.39 0.97999996 0.35999998 0.37 0.31 C 0.31 0.25 0.31 0.04 0.37 -0.02 C 0.75 -0.01 1.1999999 0 1.49 0 C 1.75 0 2.1499999 -0.02 2.95 -0.02 C 4.06 -0.02 5.2999997 0.5 5.2999997 2.25 C 5.2999997 3.58 4.48 4.62 2.81 4.62 C 2.1299999 4.62 1.77 4.6 1.48 4.6 Z M 1.88 0.76 L 1.88 3.98 C 1.88 4.23 2.1299999 4.29 2.52 4.29 C 4.2 4.29 4.43 3.12 4.43 2.08 C 4.43 0.68 3.81 0.31 2.71 0.31 C 1.9499999 0.31 1.88 0.48 1.88 0.76 Z "/>
</symbol>
<symbol id="gEC3CC7DEE79E0AA801DFAAEF4B6C0B50" overflow="visible">
<path d="M 4.35 3.3799999 L 4.35 2.11 C 4.35 1.25 4.35 0.31 3.03 0.31 C 2.04 0.31 1.8299999 1.09 1.8299999 2.02 L 1.8299999 3.3799999 C 1.8299999 4.21 1.9399999 4.24 2.55 4.29 C 2.61 4.35 2.61 4.56 2.55 4.62 C 2.1599998 4.61 1.76 4.6 1.43 4.6 C 1.0699999 4.6 0.68 4.61 0.32 4.62 C 0.26 4.56 0.26 4.35 0.32 4.29 C 0.93 4.25 1.04 4.21 1.04 3.3799999 L 1.04 1.81 C 1.04 0.31 1.77 -0.099999994 2.86 -0.099999994 C 4.41 -0.099999994 4.8199997 0.78 4.8199997 2.24 L 4.8199997 3.3799999 C 4.8199997 4.21 4.93 4.24 5.54 4.29 C 5.6 4.35 5.6 4.56 5.54 4.62 C 5.24 4.61 4.88 4.6 4.58 4.6 C 4.2799997 4.6 3.9299998 4.61 3.6299999 4.62 C 3.57 4.56 3.57 4.35 3.6299999 4.29 C 4.24 4.25 4.35 4.21 4.35 3.3799999 Z "/>
</symbol>
<symbol id="g202CCBD46865F83C12D50E1B4FF9BBEA" overflow="visible">
<path d="M 2.76 -0.099999994 C 3.54 -0.099999994 4.02 0.19 4.49 0.82 C 4.47 0.89 4.37 1 4.29 1.02 C 3.83 0.48 3.48 0.28 2.81 0.28 C 1.8199999 0.28 1.24 1.35 1.24 2.34 C 1.24 4.02 2.02 4.37 2.77 4.37 C 3.57 4.37 4.04 3.9299998 4.16 3.23 C 4.2599998 3.1999998 4.36 3.1999998 4.46 3.26 C 4.46 3.6699998 4.44 4.0899997 4.3399997 4.54 C 3.9599998 4.54 3.51 4.7 2.71 4.7 C 1.39 4.7 0.37 3.6999998 0.37 2.24 C 0.37 1.61 0.57 0.91999996 1.06 0.47 C 1.4599999 0.099999994 2.02 -0.099999994 2.76 -0.099999994 Z "/>
</symbol>
<symbol id="g5503E15E5E4E70E9E217A15BD1ECD752" overflow="visible">
<path d="M 1.9499999 3.3799999 C 1.9499999 4.21 2.06 4.24 2.6699998 4.29 C 2.73 4.35 2.73 4.56 2.6699998 4.62 C 2.29 4.61 1.86 4.6 1.55 4.6 C 1.25 4.6 0.83 4.61 0.44 4.62 C 0.38 4.56 0.38 4.35 0.44 4.29 C 1.05 4.25 1.16 4.21 1.16 3.3799999 L 1.16 1.22 C 1.16 0.39 1.05 0.35999998 0.44 0.31 C 0.38 0.25 0.38 0.04 0.44 -0.02 C 0.81 -0.01 1.22 0 1.56 0 C 1.88 0 2.32 -0.01 2.6699998 -0.02 C 2.73 0.04 2.73 0.25 2.6699998 0.31 C 2.06 0.35 1.9499999 0.39 1.9499999 1.22 Z "/>
</symbol>
<symbol id="g1E8994F5C297EC73FA26D93D22635023" overflow="visible">
<path d="M 2.82 -0.14999999 C 4.11 -0.14999999 5.16 0.9 5.16 2.19 C 5.16 3.48 4.11 4.52 2.82 4.52 C 1.53 4.52 0.48999998 3.48 0.48999998 2.19 C 0.48999998 0.9 1.53 -0.14999999 2.82 -0.14999999 Z M 2.82 4.2599998 C 3.97 4.2599998 4.9 3.34 4.9 2.19 C 4.9 1.04 3.9599998 0.11 2.82 0.11 C 1.67 0.11 0.75 1.04 0.75 2.19 C 0.75 3.33 1.67 4.2599998 2.82 4.2599998 Z "/>
</symbol>
<symbol id="g6D39B87B7095296261A07873F9B99896" overflow="visible">
<path d="M 1.86 0.948 L 2.52 2.688 C 2.58 2.844 2.652 2.892 2.94 2.892 L 5.472 2.892 L 6.168 0.864 C 6.3120003 0.456 5.856 0.408 5.28 0.372 C 5.208 0.3 5.208 0.048 5.28 -0.024 C 5.724 -0.012 6.384 0 6.852 0 C 7.344 0 7.8 -0.012 8.22 -0.024 C 8.292 0.048 8.292 0.3 8.22 0.372 C 7.752 0.42000002 7.344 0.456 7.14 1.0320001 L 4.668 7.896 C 4.488 7.788 4.164 7.656 4.008 7.656 L 1.284 1.224 C 0.972 0.48000002 0.612 0.408 0.084 0.372 C 0.012 0.3 0.012 0.048 0.084 -0.024 C 0.396 -0.012 0.792 0 1.152 0 C 1.644 0 2.244 -0.012 2.688 -0.024 C 2.76 0.048 2.76 0.3 2.688 0.372 C 2.232 0.408 1.668 0.456 1.86 0.948 Z M 3.1560001 3.3960001 C 2.892 3.3960001 2.808 3.432 2.856 3.552 L 4.08 6.66 L 4.152 6.66 L 5.28 3.3960001 Z "/>
</symbol>
<symbol id="g1B61845C1FB429ACDF5304290F5BF286" overflow="visible">
<path d="M 4.548 0 C 4.548 0 4.824 1.152 4.908 1.656 C 4.8 1.716 4.704 1.74 4.572 1.704 C 4.38 0.996 4.032 0.408 3.276 0.408 L 2.736 0.408 C 2.46 0.408 2.292 0.6 2.292 0.828 L 2.292 4.056 C 2.292 5.052 2.424 5.088 3.1560001 5.1480002 C 3.228 5.2200003 3.228 5.472 3.1560001 5.544 C 2.7120001 5.532 2.22 5.52 1.812 5.52 C 1.44 5.52 0.924 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.32 0.408 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 1.068 -0.012 1.86 0 1.86 0 Z "/>
</symbol>
<symbol id="gC66F55FB8F08DA72FE76D3863D88042" overflow="visible">
<path d="M 5.664 1.092 C 5.664 2.088 5.736 2.124 6.1080003 2.184 C 6.18 2.256 6.18 2.5080001 6.1080003 2.58 C 5.892 2.568 5.556 2.556 5.184 2.556 C 4.824 2.556 4.272 2.568 3.924 2.58 C 3.852 2.5080001 3.852 2.256 3.924 2.184 C 4.656 2.136 4.716 2.088 4.716 1.092 L 4.716 0.444 C 4.3320003 0.336 3.936 0.276 3.516 0.276 C 2.016 0.276 1.524 1.812 1.524 2.796 C 1.524 4.248 2.22 5.244 3.372 5.244 C 4.56 5.244 5.064 4.644 5.244 3.876 C 5.364 3.8400002 5.484 3.8400002 5.604 3.912 C 5.592 4.404 5.556 4.908 5.448 5.448 C 5.088 5.448 4.2 5.64 3.528 5.64 C 1.812 5.64 0.444 4.5360003 0.444 2.64 C 0.444 1.116 1.584 -0.120000005 3.3 -0.120000005 C 4.116 -0.120000005 5.004 0 5.796 0.432 C 5.712 0.51600003 5.664 0.624 5.664 0.708 Z "/>
</symbol>
<symbol id="g4C6038BE04CA3E1481E54A97A0E34303" overflow="visible">
<path d="M 6.324 2.82 C 6.324 4.524 4.956 5.64 3.3960001 5.64 C 1.728 5.64 0.444 4.428 0.444 2.664 C 0.444 1.0320001 1.6800001 -0.120000005 3.3 -0.120000005 C 5.268 -0.120000005 6.324 1.26 6.324 2.82 Z M 3.288 5.244 C 4.356 5.244 5.28 4.26 5.28 2.652 C 5.28 1.176 4.548 0.276 3.48 0.276 C 2.316 0.276 1.488 1.332 1.488 2.808 C 1.488 4.428 2.388 5.244 3.288 5.244 Z "/>
</symbol>
<symbol id="g48BCA4F06942DA5990D42018985FC781" overflow="visible">
<path d="M 2.292 1.464 L 2.292 2.5080001 L 2.9520001 2.5080001 C 3.408 2.5080001 3.576 2.112 3.732 1.668 L 3.996 0.948 C 4.272 0.204 4.68 -0.084 5.196 -0.084 C 5.376 -0.084 5.748 -0.048 5.952 0 C 5.988 0.120000005 5.964 0.24000001 5.88 0.336 C 5.448 0.336 5.2200003 0.408 4.98 1.0320001 L 4.632 1.932 C 4.488 2.304 4.344 2.5080001 4.188 2.664 L 4.188 2.688 C 4.596 2.832 5.208 3.3240001 5.208 4.152 C 5.208 5.1480002 4.584 5.568 3.1560001 5.568 C 2.856 5.568 2.172 5.52 1.812 5.52 C 1.464 5.52 0.96000004 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.212 0.432 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 0.936 -0.012 1.428 0 1.824 0 C 2.196 0 2.592 -0.012 2.976 -0.024 C 3.048 0.048 3.048 0.3 2.976 0.372 C 2.412 0.408 2.292 0.468 2.292 1.464 Z M 4.164 4.152 C 4.164 3.204 3.888 2.856 2.82 2.856 L 2.292 2.856 L 2.292 4.416 C 2.292 5.052 2.412 5.172 3.084 5.172 C 3.924 5.172 4.164 4.872 4.164 4.152 Z "/>
</symbol>
<symbol id="g45E4C10E27056C5AE488FE2D8290DF06" overflow="visible">
<path d="M 2.34 4.056 C 2.34 5.052 2.4720001 5.088 3.204 5.1480002 C 3.276 5.2200003 3.276 5.472 3.204 5.544 C 2.748 5.532 2.232 5.52 1.86 5.52 C 1.5 5.52 0.996 5.532 0.528 5.544 C 0.456 5.472 0.456 5.2200003 0.528 5.1480002 C 1.26 5.1 1.392 5.052 1.392 4.056 L 1.392 1.464 C 1.392 0.468 1.26 0.432 0.528 0.372 C 0.456 0.3 0.456 0.048 0.528 -0.024 C 0.972 -0.012 1.464 0 1.872 0 C 2.256 0 2.784 -0.012 3.204 -0.024 C 3.276 0.048 3.276 0.3 3.204 0.372 C 2.4720001 0.42000002 2.34 0.468 2.34 1.464 Z "/>
</symbol>
<symbol id="gA2769E14ED9B16297025579DD26D23A1" overflow="visible">
<path d="M 3.648 1.464 L 3.648 4.488 C 3.648 4.932 3.7680001 5.112 4.152 5.112 L 4.464 5.112 C 5.2200003 5.112 5.376 4.872 5.616 4.008 C 5.736 3.984 5.844 3.984 5.94 4.044 C 5.88 4.632 5.868 5.076 5.844 5.64 C 5.4240003 5.592 4.656 5.52 3.648 5.52 L 2.7 5.52 C 1.524 5.52 0.828 5.58 0.504 5.64 C 0.504 5.076 0.492 4.608 0.42000002 4.044 C 0.528 4.008 0.636 3.996 0.744 4.008 C 0.984 4.872 1.116 5.112 1.896 5.112 L 2.184 5.112 C 2.556 5.112 2.7 4.968 2.7 4.5 L 2.7 1.464 C 2.7 0.468 2.568 0.432 1.836 0.372 C 1.764 0.3 1.764 0.048 1.836 -0.024 C 2.28 -0.012 2.772 0 3.18 0 C 3.6000001 0 4.068 -0.012 4.512 -0.024 C 4.584 0.048 4.584 0.3 4.512 0.372 C 3.78 0.42000002 3.648 0.468 3.648 1.464 Z "/>
</symbol>
<symbol id="g7FB89403B37B0F0F934DFEB7E5171B37" overflow="visible">
<path d="M 6 4.056 C 6 5.052 6.132 5.088 6.864 5.1480002 C 6.936 5.2200003 6.936 5.472 6.864 5.544 C 6.4440002 5.52 5.916 5.52 5.52 5.52 C 5.184 5.52 4.656 5.532 4.188 5.544 C 4.116 5.472 4.116 5.2200003 4.188 5.1480002 C 4.92 5.1 5.052 5.052 5.052 4.056 L 5.052 3.024 L 2.28 3.024 L 2.28 4.056 C 2.28 5.052 2.412 5.088 3.144 5.1480002 C 3.216 5.2200003 3.216 5.472 3.144 5.544 C 2.688 5.532 2.184 5.52 1.8000001 5.52 C 1.44 5.52 0.948 5.532 0.468 5.544 C 0.396 5.472 0.396 5.2200003 0.468 5.1480002 C 1.2 5.1 1.332 5.052 1.332 4.056 L 1.332 1.464 C 1.332 0.468 1.2 0.432 0.468 0.372 C 0.396 0.3 0.396 0.048 0.468 -0.024 C 0.948 -0.012 1.428 0 1.812 0 C 2.196 0 2.676 -0.012 3.144 -0.024 C 3.216 0.048 3.216 0.3 3.144 0.372 C 2.412 0.42000002 2.28 0.468 2.28 1.464 L 2.28 2.628 L 5.052 2.628 L 5.052 1.464 C 5.052 0.468 4.92 0.432 4.188 0.372 C 4.116 0.3 4.116 0.048 4.188 -0.024 C 4.632 -0.012 5.112 0 5.532 0 C 5.892 0 6.396 -0.012 6.864 -0.024 C 6.936 0.048 6.936 0.3 6.864 0.372 C 6.132 0.42000002 6 0.468 6 1.464 Z "/>
</symbol>
<symbol id="gFF269982F0E4C510F3A3BFF016D72390" overflow="visible">
<path d="M 5.796 4.584 L 5.88 4.584 L 6.0360003 1.4760001 C 6.084 0.48000002 6.072 0.432 5.4240003 0.372 C 5.352 0.3 5.352 0.048 5.4240003 -0.024 C 5.844 -0.012 6.288 0 6.624 0 C 6.984 0 7.3320003 -0.012 7.656 -0.024 C 7.728 0.048 7.728 0.3 7.656 0.372 C 7.044 0.432 7.032 0.504 6.96 1.4760001 L 6.7200003 4.572 C 6.684 5.052 6.7920003 5.1 7.392 5.1480002 C 7.464 5.2200003 7.464 5.472 7.392 5.544 L 5.772 5.52 L 3.9720001 1.224 L 2.436 5.52 L 0.768 5.544 C 0.696 5.472 0.696 5.2200003 0.768 5.1480002 C 1.3560001 5.112 1.464 5.052 1.44 4.824 L 1.056 1.452 C 0.948 0.456 0.792 0.408 0.336 0.372 C 0.264 0.3 0.264 0.048 0.336 -0.024 C 0.576 -0.012 0.936 0 1.128 0 C 1.368 0 1.812 -0.012 2.052 -0.024 C 2.124 0.048 2.124 0.3 2.052 0.372 C 1.368 0.42000002 1.38 0.564 1.4760001 1.452 L 1.824 4.5 L 1.848 4.5 L 3.552 -0.048 C 3.576 -0.108 3.636 -0.144 3.696 -0.144 C 3.744 -0.144 3.8040001 -0.108 3.828 -0.048 Z "/>
</symbol>
<symbol id="gD77922058D8F1A3A631DDE5946887BDC" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z M 3.384 5.112 C 4.764 5.112 5.88 4.008 5.88 2.628 C 5.88 1.248 4.752 0.132 3.384 0.132 C 2.004 0.132 0.90000004 1.248 0.90000004 2.628 C 0.90000004 3.996 2.004 5.112 3.384 5.112 Z "/>
</symbol>
<symbol id="g5ABA589ED074A65FC8C929AB4EB2344C" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z "/>
</symbol>
<symbol id="gEDADDD9BA25BBB833C1F4B684DC50419" overflow="visible">
<path d="M 4.83 3.82 L 4.9 3.82 L 5.0299997 1.23 C 5.0699997 0.39999998 5.06 0.35999998 4.52 0.31 C 4.46 0.25 4.46 0.04 4.52 -0.02 C 4.87 -0.01 5.24 0 5.52 0 C 5.8199997 0 6.1099997 -0.01 6.3799996 -0.02 C 6.44 0.04 6.44 0.25 6.3799996 0.31 C 5.87 0.35999998 5.8599997 0.42 5.7999997 1.23 L 5.6 3.81 C 5.5699997 4.21 5.66 4.25 6.16 4.29 C 6.22 4.35 6.22 4.56 6.16 4.62 L 4.81 4.6 L 3.31 1.02 L 2.03 4.6 L 0.64 4.62 C 0.58 4.56 0.58 4.35 0.64 4.29 C 1.13 4.2599998 1.22 4.21 1.1999999 4.02 L 0.88 1.2099999 C 0.78999996 0.38 0.65999997 0.34 0.28 0.31 C 0.22 0.25 0.22 0.04 0.28 -0.02 C 0.48 -0.01 0.78 0 0.94 0 C 1.14 0 1.51 -0.01 1.7099999 -0.02 C 1.77 0.04 1.77 0.25 1.7099999 0.31 C 1.14 0.35 1.15 0.47 1.23 1.2099999 L 1.52 3.75 L 1.54 3.75 L 2.96 -0.04 C 2.98 -0.089999996 3.03 -0.12 3.08 -0.12 C 3.12 -0.12 3.1699998 -0.089999996 3.1899998 -0.04 Z "/>
</symbol>
<symbol id="g97A8E46F7A64F11D13C6F357868587EE" overflow="visible">
<path d="M 1.89 1.22 L 1.89 1.9599999 C 2.07 1.88 2.27 1.8399999 2.52 1.8399999 C 3.86 1.8399999 4.27 2.8 4.27 3.3999999 C 4.27 3.9199998 3.97 4.62 2.55 4.62 C 2.18 4.62 1.76 4.6 1.49 4.6 C 1.1999999 4.6 0.78 4.61 0.38 4.62 C 0.32 4.56 0.32 4.35 0.38 4.29 C 0.98999995 4.25 1.1 4.21 1.1 3.3799999 L 1.1 1.22 C 1.1 0.39 0.98999995 0.35999998 0.38 0.31 C 0.32 0.25 0.32 0.04 0.38 -0.02 C 0.71 -0.01 1.06 0 1.5 0 C 1.93 0 2.28 -0.01 2.61 -0.02 C 2.6699998 0.04 2.6699998 0.25 2.61 0.31 C 2 0.35 1.89 0.39 1.89 1.22 Z M 1.89 3.84 C 1.89 4.16 2.01 4.29 2.49 4.29 C 3.08 4.29 3.3999999 3.98 3.3999999 3.28 C 3.3999999 2.56 3.1399999 2.1699998 2.54 2.1699998 C 2.34 2.1699998 2.09 2.2 1.89 2.28 Z "/>
</symbol>
<symbol id="gB844DCFB76B4CC44608DB013C9764E9C" overflow="visible">
<path d="M 1.8299999 3.62 C 1.5899999 4.19 1.5999999 4.24 2.1399999 4.29 C 2.2 4.35 2.2 4.56 2.1399999 4.62 C 1.8299999 4.61 1.49 4.6 1.0799999 4.6 C 0.76 4.6 0.45999998 4.61 0.19999999 4.62 C 0.14 4.56 0.14 4.35 0.19999999 4.29 C 0.69 4.24 0.76 4.13 1 3.56 L 2.4199998 0.28 C 2.55 -0.01 2.6 -0.12 2.71 -0.12 C 2.78 -0.12 2.82 -0.04 2.96 0.28 L 4.42 3.55 C 4.63 4.0099998 4.74 4.25 5.2799997 4.29 C 5.3399997 4.35 5.3399997 4.56 5.2799997 4.62 C 5.06 4.61 4.8199997 4.6 4.56 4.6 C 4.19 4.6 3.9099998 4.61 3.6399999 4.62 C 3.58 4.56 3.58 4.35 3.6399999 4.29 C 4.18 4.25 4.23 4.13 4.0299997 3.62 L 2.9399998 1.13 C 2.9099998 1.1 2.8999999 1.1 2.87 1.13 Z "/>
</symbol>
<symbol id="gDAA1267270512376F631C9A10449D5F4" overflow="visible">
<path d="M 2.48 2.25 C 3.1399999 2.25 3.1499999 2.06 3.1699998 1.6899999 C 3.22 1.64 3.3999999 1.64 3.4499998 1.6899999 C 3.4399998 1.92 3.4299998 2.26 3.4299998 2.4199998 C 3.4299998 2.56 3.4399998 2.8799999 3.4499998 3.1299999 C 3.3999999 3.1799998 3.22 3.1799998 3.1699998 3.1299999 C 3.1499999 2.6799998 3.1299999 2.57 2.48 2.57 L 1.91 2.57 L 1.91 3.99 C 1.91 4.16 2.04 4.27 2.23 4.27 L 2.8 4.27 C 3.62 4.27 3.75 3.9399998 3.9299998 3.37 C 4.0299997 3.36 4.12 3.3799999 4.2 3.4199998 C 4.16 3.76 4.04 4.54 4.02 4.61 C 4.02 4.63 4.0099998 4.64 3.99 4.64 C 3.85 4.61 3.75 4.6 3.58 4.6 L 1.51 4.6 C 1.22 4.6 0.76 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.76 -0.01 1.1999999 0 1.52 0 L 3.06 0 C 3.46 0 4.12 -0.02 4.12 -0.02 C 4.24 0.39 4.35 0.94 4.42 1.36 C 4.33 1.41 4.25 1.43 4.14 1.4 C 3.98 0.81 3.6899998 0.31 2.86 0.31 L 2.4299998 0.31 C 2.01 0.31 1.91 0.42 1.91 0.75 L 1.91 2.25 Z "/>
</symbol>
<symbol id="g6C3A310EEC8A7EBBD176D179125951F0" overflow="visible">
<path d="M 2.328 -4.632 L 8.208 -4.632 C 8.352 -4.488 8.352 -4.056 8.208 -3.912 C 4.896 -3.648 4.728 -3.288 4.728 -1.2 L 4.728 13.464 C 4.728 15.552 4.92 15.912 8.208 16.152 C 8.352 16.296 8.352 16.728 8.208 16.872 L 2.328 16.872 Z "/>
</symbol>
<symbol id="g2F0CE4BDC8DA4B92139017B781562218" overflow="visible">
<path d="M 3.96 1.896 L 5.232 5.232 C 5.352 5.544 5.496 5.64 6.072 5.64 L 10.632 5.64 L 11.976 1.728 C 12.264 0.864 11.568 0.84000003 10.656 0.792 C 10.512 0.792 10.344 0.768 10.2 0.768 C 10.056 0.624 10.056 0.096 10.2 -0.048 C 11.088 -0.024 13.368 0 14.304 0 C 15.288 0 16.632 -0.024 17.52 -0.048 C 17.664 0.096 17.664 0.624 17.52 0.768 C 16.584 0.864 15.792 0.84000003 15.360001 2.0640001 L 10.416 15.792 C 10.056 15.576 8.616 14.736 7.776 14.736 L 2.568 2.448 C 1.944 0.96000004 1.224 0.84000003 0.168 0.768 C 0.024 0.624 0.024 0.096 0.168 -0.048 C 1.056 -0.024 1.488 0 2.424 0 C 3.408 0 4.728 -0.024 5.616 -0.048 C 5.76 0.096 5.76 0.624 5.616 0.768 C 4.704 0.84000003 3.576 0.912 3.96 1.896 Z M 6.552 6.7920003 C 6.024 6.7920003 5.856 6.864 5.952 7.104 L 8.064 12.4800005 L 8.232 12.4800005 L 10.2 6.7920003 Z "/>
</symbol>
<symbol id="g8D84A54D9303B24762DC3071B60ECD14" overflow="visible">
<path d="M 2.4 3.048 C 2.4 1.056 2.016 0.84000003 0.552 0.768 C 0.408 0.624 0.408 0.096 0.552 -0.048 C 1.5600001 -0.024 2.64 0 3.96 0 C 5.28 0 6.336 -0.024 7.368 -0.048 C 7.512 0.096 7.512 0.624 7.368 0.768 C 5.9040003 0.84000003 5.52 1.056 5.52 3.048 L 5.52 13.992001 C 5.52 15.552 5.592 16.44 5.592 16.44 C 5.592 16.656 5.4240003 16.752 5.208 16.752 C 4.32 16.464 2.4 16.2 0.696 16.128 C 0.624 15.84 0.648 15.576 0.768 15.360001 C 2.28 15.24 2.4 15.216001 2.4 13.56 Z "/>
</symbol>
<symbol id="g3E9095A1FBD7854ED5F7B53469C97011" overflow="visible">
<path d="M 11.208 9.456 C 11.88 9.456 12.264 9.744 12.264 10.632 C 12.264 11.088 11.64 11.784 10.728 11.784 C 9.672 11.784 8.28 10.992 7.584 10.368 C 7.152 10.608 6.6480002 10.656 5.568 10.656 C 4.5360003 10.656 3.528 10.416 2.736 9.8880005 C 1.752 9.264 1.104 8.328 1.104 7.104 C 1.104 5.928 1.8000001 4.656 2.9520001 4.032 C 2.208 3.384 1.056 2.112 1.056 1.632 C 1.056 1.176 1.128 0.888 1.368 0.528 C 1.584 0.192 1.872 0 2.352 -0.144 C 1.32 -0.768 0.264 -2.136 0.264 -2.544 C 0.264 -3.432 0.552 -4.464 1.2 -4.92 C 2.136 -5.568 3.72 -5.712 4.872 -5.712 C 8.208 -5.712 12.024 -3.96 12.024 -1.32 C 12.024 -0.816 11.784 0.216 10.824 0.864 C 9.8880005 1.488 6.288 1.656 4.512 1.656 C 4.08 1.656 3.432 1.704 3.432 2.664 C 3.432 3.048 3.672 3.384 3.792 3.672 C 4.296 3.432 4.8 3.408 5.544 3.408 C 6.768 3.408 7.896 3.72 8.712 4.44 C 9.408 5.064 9.8880005 5.9040003 9.8880005 6.984 C 9.8880005 8.328 9.216 9.216 8.4 9.8880005 C 8.592 10.128 9.384 10.56 9.624001 10.56 C 9.84 10.56 10.008 10.416 10.08 10.272 C 10.176 9.96 10.608 9.456 11.208 9.456 Z M 4.2 -0.6 C 6.048 -0.6 9.6 -0.672 9.6 -1.944 C 9.6 -2.808 9.216 -3.792 8.424 -4.224 C 7.6800003 -4.656 6.456 -4.704 5.544 -4.704 C 3.96 -4.704 2.88 -3.528 2.88 -2.304 C 2.88 -1.488 2.88 -0.936 3.144 -0.456 C 3.384 -0.552 3.696 -0.6 4.2 -0.6 Z M 6.96 6.912 C 6.96 4.608 6.288 4.32 5.664 4.32 C 4.176 4.32 3.984 6.096 3.984 7.32 C 3.984 9.096 4.416 9.744 5.352 9.744 C 6.48 9.744 6.96 8.808 6.96 6.912 Z "/>
</symbol>
<symbol id="g90B91206A818BADA9956CC42F47E57A0" overflow="visible">
<path d="M 1.176 1.392 C 1.176 0.48000002 1.944 -0.24000001 2.904 -0.24000001 C 3.864 -0.24000001 4.68 0.528 4.68 1.44 C 4.68 2.376 3.912 3.096 2.9520001 3.096 C 1.992 3.096 1.176 2.328 1.176 1.392 Z "/>
</symbol>
<symbol id="gAC1066A28E7625F16F6C949E2F432C61" overflow="visible">
<path d="M 1.2 10.896 C 1.2 10.2960005 1.752 9.6 2.616 9.6 C 3.312 9.6 4.008 10.128 4.008 10.872 C 4.008 10.992 3.96 11.16 3.888 11.376 C 3.816 11.544 3.744 11.736 3.744 12 C 3.744 12.552 4.584 13.656 5.736 13.656 C 6.96 13.656 7.8 12.144 7.8 10.704 C 7.8 9.096 7.704 8.064 6.432 6.864 L 4.392 4.92 C 1.416 2.088 1.008 1.416 0.936 0.768 L 1.0320001 0 L 10.2960005 0 C 10.584 0.912 10.872 2.568 11.04 3.936 C 10.728 4.08 10.512 4.176 9.96 4.176 C 9.432 2.544 8.736 1.896 7.656 1.896 L 4.5360003 1.896 C 4.608 2.664 4.848 3.312 5.64 4.032 L 7.056 5.328 C 9.912 7.968 10.872 8.544 10.872 10.776 C 10.872 13.272 8.76 14.64 6.288 14.64 C 2.856 14.64 1.2 12.384 1.2 10.896 Z "/>
</symbol>
<symbol id="g10BFE5E41011FF0F560FA08FAB260218" overflow="visible">
<path d="M 7.248 16.824 L 1.368 16.824 C 1.224 16.68 1.224 16.248 1.368 16.104 C 4.68 15.84 4.848 15.4800005 4.848 13.392 L 4.848 -1.272 C 4.848 -3.3600001 4.656 -3.72 1.368 -3.96 C 1.224 -4.104 1.224 -4.5360003 1.368 -4.68 L 7.248 -4.68 Z "/>
</symbol>
<symbol id="gFC5C8D23DE5E426807758A924FDBA2FC" overflow="visible">
<path d="M 10.104 15.144 C 8.784 15.336 8.28 15.792 6.048 15.792 C 4.968 15.792 3.552 15.456 2.544 14.64 C 1.656 13.92 0.984 12.816 0.984 11.64 C 0.984 10.728 1.224 9.576 1.776 8.856 C 2.88 7.368 4.872 6.552 5.9040003 5.8320003 C 7.008 5.064 8.088 4.104 8.088 2.76 C 8.088 1.584 7.056 0.768 5.592 0.768 C 3.984 0.768 2.328 2.088 1.848 4.272 C 1.464 4.416 1.08 4.32 0.72 4.224 C 0.696 4.224 0.672 4.2 0.648 4.2 C 0.648 2.4 0.84000003 1.128 1.104 0.24000001 C 2.4720001 0.24000001 2.544 -0.24000001 5.856 -0.24000001 C 7.32 -0.24000001 8.496 0.192 9.4800005 1.08 C 10.344 1.824 11.112 2.928 11.112 4.416 C 11.112 5.664 10.584 6.504 9.864 7.296 C 8.928 8.328 7.584 9.0720005 6.6480002 9.552 C 5.688 10.032001 3.984 11.28 3.984 12.648 C 3.984 13.992001 4.8 14.808001 6.024 14.808001 C 8.064 14.808001 8.736 12.96 9.168 11.376 C 9.504 11.28 10.104 11.28 10.368 11.496 C 10.368 12.768 10.272 13.752 10.104 15.144 Z "/>
</symbol>
<symbol id="gB6675D993E92546012E46240B36958EC" overflow="visible">
<path d="M 10.344 3.096 C 9.36 2.088 8.064 1.824 7.152 1.824 C 5.28 1.824 4.1280003 2.904 4.1280003 5.256 C 4.1280003 5.4240003 4.152 5.52 4.152 5.64 L 9.912 5.64 C 10.488 5.64 10.608 6.048 10.608 6.384 C 10.608 8.424 9.816 10.656 6.288 10.656 C 3.7680001 10.656 0.888 8.424 0.888 4.752 C 0.888 3.3600001 1.392 1.896 2.424 0.96000004 C 3.336 0.144 4.512 -0.24000001 6.216 -0.24000001 C 7.872 -0.24000001 9.504 0.6 10.704 2.352 C 10.704 2.664 10.584 3.096 10.344 3.096 Z M 4.248 6.6 C 4.272 7.44 4.392 8.352 4.728 8.832 C 5.112 9.408 5.76 9.648 6.024 9.648 C 6.672 9.648 7.56 9.024 7.56 7.104 C 7.56 6.96 7.56 6.6480002 7.512 6.6 Z "/>
</symbol>
<symbol id="g9AEC0E315A165F115D211DDAB68AA0F8" overflow="visible">
<path d="M 7.08 1.176 C 7.248 0.192 7.896 -0.24000001 8.952 -0.24000001 C 10.272 -0.24000001 11.208 0.264 12.096 1.104 C 12.048 1.392 11.952 1.584 11.6640005 1.776 C 11.352 1.536 11.112 1.44 10.656 1.44 C 10.128 1.44 9.984 1.872 9.984 3.048 L 10.032001 6.504 C 10.032001 9.96 7.896 10.656 5.928 10.656 C 4.176 10.656 1.488 9.648 1.488 8.064 C 1.488 7.392 1.776 6.864 2.7120001 6.864 C 3.576 6.864 4.2 7.392 4.2 7.968 C 4.2 8.088 4.176 8.232 4.152 8.376 C 4.104 8.616 4.056 8.856 4.104 9.096 C 4.1280003 9.36 4.32 9.648 5.112 9.648 C 6.12 9.648 6.96 9.216 6.96 6.168 L 5.352 5.664 C 2.832 4.872 1.056 4.176 1.056 2.28 C 1.056 0.624 1.968 -0.24000001 4.056 -0.24000001 C 4.752 -0.24000001 6.144 0.528 6.936 1.152 Z M 6.96 5.232 L 6.96 2.0640001 C 6.36 1.584 5.76 1.2 5.328 1.2 C 4.296 1.2 3.936 1.896 3.936 2.64 C 3.936 3.528 4.008 4.272 5.712 4.824 Z "/>
</symbol>
<symbol id="g767CEF02C917BBE3F159A8F04079F311" overflow="visible">
<path d="M 5.472 6.432 C 5.472 7.296 5.736 7.656 6.048 8.016 C 6.2400002 8.2560005 6.456 8.424 6.816 8.424 C 7.032 8.424 7.296 8.208 7.488 7.968 C 7.656 7.776 8.064 7.584 8.616 7.584 C 9.312 7.584 9.984 8.304 9.984 9.312 C 9.984 9.936 9.264 10.656 8.4 10.656 C 7.56 10.656 6.6480002 9.936 5.544 8.352 L 5.448 8.352 C 5.4 9.0720005 5.28 10.248 5.28 10.248 C 5.256 10.464 5.064 10.656 4.728 10.656 C 3.6000001 10.368 2.328 10.032001 0.744 9.864 C 0.696 9.72 0.744 9.264 0.792 9.12 C 2.112 9 2.352 8.784 2.352 7.416 L 2.352 2.928 C 2.352 0.936 2.088 0.888 0.624 0.768 C 0.48000002 0.624 0.48000002 0.096 0.624 -0.048 C 1.632 -0.024 2.64 0 3.912 0 C 5.184 0 6.168 -0.024 7.2000003 -0.048 C 7.344 0.096 7.344 0.624 7.2000003 0.768 C 5.736 0.864 5.472 0.936 5.472 2.928 Z "/>
</symbol>
<symbol id="g9CBC2DB69173A0577335373434CDCDA4" overflow="visible">
<path d="M 10.128 2.088 C 10.128 2.376 10.08 2.832 9.816 2.832 C 8.856 1.944 8.04 1.488 7.344 1.488 C 5.544 1.488 4.1280003 2.784 4.1280003 5.664 C 4.1280003 8.328 4.728 9.648 6 9.648 C 6.888 9.648 7.248 8.712 7.32 7.9440002 C 7.392 7.296 8.04 6.816 8.808 6.816 C 9.576 6.816 10.128 7.416 10.128 8.16 C 10.128 9.24 8.832 10.656 6.216 10.656 C 3.384 10.656 0.888 8.376 0.888 4.824 C 0.888 3.264 1.44 1.896 2.376 1.008 C 3.312 0.120000005 4.416 -0.24000001 6.12 -0.24000001 C 7.56 -0.24000001 9.216 0.768 10.128 2.088 Z "/>
</symbol>
<symbol id="g2825DE3DACAF761B898A0442866AE569" overflow="visible">
<path d="M 12.672 3.072 L 12.672 6.816 C 12.672 9.456 11.544 10.656 9.4800005 10.656 C 8.592 10.656 6.888 9.768 5.52 8.928 L 5.52 13.992001 C 5.52 15.552 5.592 16.44 5.592 16.44 C 5.592 16.656 5.4240003 16.752 5.208 16.752 C 4.32 16.464 2.4 16.2 0.696 16.128 C 0.624 15.84 0.648 15.576 0.768 15.360001 C 2.28 15.24 2.4 15.216001 2.4 13.56 L 2.4 3.048 C 2.4 1.056 2.016 0.84000003 0.552 0.768 C 0.408 0.624 0.408 0.096 0.552 -0.048 C 1.5600001 -0.024 2.64 0 3.96 0 C 5.112 0 5.856 -0.024 6.888 -0.048 C 7.032 0.096 7.032 0.624 6.888 0.768 C 5.88 0.84000003 5.52 1.056 5.52 3.048 L 5.52 7.968 C 6.528 8.592 7.32 8.88 7.752 8.88 C 8.712 8.88 9.552 8.448 9.552 7.08 L 9.552 3.072 C 9.552 1.056 9.168 0.84000003 8.184 0.768 C 8.04 0.624 8.04 0.096 8.184 -0.048 C 9.192 -0.024 9.96 0 11.112 0 C 12.432 0 13.488 -0.024 14.52 -0.048 C 14.6640005 0.096 14.6640005 0.624 14.52 0.768 C 13.056 0.84000003 12.672 1.056 12.672 3.072 Z "/>
</symbol>
<symbol id="gC1513612DA0E34F2B247DB2830CD7DFD" overflow="visible">
<path d="M 1.24 4.6 C 1.24 3.34 2.26 2.32 3.52 2.32 C 4.7799997 2.32 5.7999997 3.34 5.7999997 4.6 C 5.7999997 5.8599997 4.7799997 6.8799996 3.52 6.8799996 C 2.26 6.8799996 1.24 5.8599997 1.24 4.6 Z "/>
</symbol>
<symbol id="gE7450862BF743B056E90C8779357A05F" overflow="visible">
<path d="M 6.92 -2.22 C 6.92 -3.8799999 6.7 -3.9599998 5.48 -4.02 C 5.3599997 -4.14 5.3599997 -4.56 5.48 -4.68 C 6.18 -4.66 6.92 -4.64 7.72 -4.64 C 8.5199995 -4.64 9.28 -4.66 9.94 -4.68 C 10.059999 -4.56 10.059999 -4.14 9.94 -4.02 C 8.72 -3.9599998 8.5 -3.8799999 8.5 -2.22 L 8.5 8.34 C 8.5 8.62 8.42 8.84 8.2 8.84 C 8.059999 8.84 7.94 8.679999 7.7799997 8.46 C 7.52 8.099999 7.44 8.04 7.2 8.2 C 6.56 8.599999 5.7799997 8.78 4.94 8.78 C 2.5 8.78 0.7 6.7799997 0.7 4.14 C 0.7 2.28 1.9599999 -0.19999999 4.8399997 -0.19999999 C 5.38 -0.19999999 6.04 -0.08 6.3799996 0.12 C 6.8399997 0.38 6.92 0.42 6.92 0 Z M 6.44 7.3599997 C 6.8399997 6.92 6.92 6.62 6.92 6.14 L 6.92 1.54 C 6.92 1.18 6.8999996 1.0799999 6.64 0.94 C 6.18 0.7 5.64 0.68 5.3199997 0.68 C 4.16 0.68 2.4199998 1.52 2.4199998 4.54 C 2.4199998 6.62 3.26 8.099999 4.8599997 8.099999 C 5.46 8.099999 6 7.8599997 6.44 7.3599997 Z "/>
</symbol>
<symbol id="g8C7315D77A5D71E18736DE61553C419F" overflow="visible">
<path d="M 1.4 1.1999999 C 1.4 0.62 1.88 0.14 2.46 0.14 C 3.04 0.14 3.52 0.62 3.52 1.1999999 C 3.52 1.78 3.04 2.26 2.46 2.26 C 1.88 2.26 1.4 1.78 1.4 1.1999999 Z M 1.4 7.16 C 1.4 6.58 1.88 6.1 2.46 6.1 C 3.04 6.1 3.52 6.58 3.52 7.16 C 3.52 7.74 3.04 8.22 2.46 8.22 C 1.88 8.22 1.4 7.74 1.4 7.16 Z "/>
</symbol>
<symbol id="g4EF2739944C6201AFAD05FE6C63B0B9E" overflow="visible">
<path d="M 11.44 -2.44 C 8.88 -1.4399999 6.68 -1.42 6.08 -1.42 C 5.8599997 -1.42 5.66 -1.4399999 5.46 -1.4599999 C 5.52 -1.42 5.6 -1.36 5.66 -1.3199999 C 6.5 -0.71999997 7.3999996 -0.29999998 8.08 -0.12 C 9.8 0.14 11.179999 1.02 12.08 2.32 C 12.88 3.46 13.32 4.9 13.32 6.58 C 13.32 10.719999 10.46 13.16 6.8799996 13.16 C 3 13.16 0.74 10.08 0.74 6.2 C 0.74 2.62 3.12 0.26 6.1 -0.14 C 5.74 -0.32 5.4 -0.53999996 5.08 -0.78 C 4.14 -1.4599999 3.34 -2.26 2.76 -3.06 L 3.56 -3.46 C 3.76 -3.1799998 3.9599998 -2.9199998 4.18 -2.6599998 C 4.56 -2.36 4.98 -2.26 5.16 -2.26 C 6.54 -2.26 7.7 -2.6399999 10.059999 -3.6 C 11.559999 -4.22 13 -4.52 14.679999 -4.52 C 16.76 -4.52 18.779999 -3.78 20.039999 -2.6 L 19.699999 -2.24 C 18.38 -2.98 16.779999 -3.4199998 15.78 -3.4199998 C 14.259999 -3.4199998 13.24 -3.1399999 11.44 -2.44 Z M 6.62 12.44 C 9.26 12.44 11.4 10.24 11.4 6.2 C 11.4 2.62 9.679999 0.52 7.3999996 0.52 C 4.96 0.52 2.6599998 2.7 2.6599998 6.54 C 2.6599998 10.74 4.64 12.44 6.62 12.44 Z "/>
</symbol>
<symbol id="gD8CB364949770E6EB9E57283C62D30EB" overflow="visible">
<path d="M 4.3399997 -0.19999999 C 5.12 -0.19999999 6.06 0.19999999 7.04 1 C 7.14 1.0799999 7.3199997 1.12 7.3399997 0.97999996 C 7.3999996 0.48 7.56 -0.19999999 7.56 -0.19999999 C 7.72 -0.26 7.8199997 -0.24 7.94 -0.19999999 C 8.38 0.16 9.08 0.45999998 10.3 0.59999996 C 10.42 0.71999997 10.42 1.02 10.3 1.14 C 9.0199995 1.24 8.84 1.62 8.84 2.6 L 8.84 6.44 C 8.84 7.04 8.92 8.5 8.92 8.5 C 8.92 8.559999 8.86 8.62 8.76 8.62 C 8.66 8.599999 8.36 8.58 8.059999 8.58 C 7.4199996 8.58 6.7 8.599999 6.02 8.62 C 5.9 8.5 5.9 8.08 6.02 7.96 C 7 7.8999996 7.2599998 7.66 7.2599998 6.3399997 L 7.2599998 2.48 C 7.2599998 2.1 7.22 1.9399999 6.94 1.6999999 C 6.2 1.06 5.44 0.74 4.94 0.74 C 4.3399997 0.74 3.34 1.02 3.34 2.8 L 3.34 6.44 C 3.34 7.04 3.4199998 8.5 3.4199998 8.5 C 3.4199998 8.559999 3.36 8.62 3.26 8.62 C 3.1599998 8.599999 2.86 8.58 2.56 8.58 C 1.92 8.58 1.1999999 8.599999 0.52 8.62 C 0.39999998 8.5 0.39999998 8.08 0.52 7.96 C 1.48 7.8799996 1.76 7.66 1.76 6.3599997 L 1.76 2.52 C 1.76 1.14 2.36 -0.19999999 4.3399997 -0.19999999 Z "/>
</symbol>
<symbol id="g7FBC39AA6D9FB89D8B638A3651405A80" overflow="visible">
<path d="M 7.72 1.86 C 6.98 1.1 6.3999996 0.78 5.24 0.78 C 4.52 0.78 3.6799998 1.1999999 3.06 2.22 C 2.6599998 2.8799999 2.4199998 3.8 2.4199998 4.96 L 7.74 4.92 C 7.98 4.92 8.12 5.04 8.12 5.2599998 C 8.12 6.94 7.52 8.74 4.74 8.74 C 3 8.74 0.74 7.08 0.74 4.04 C 0.74 2.9199998 1.02 1.8399999 1.68 1.0799999 C 2.36 0.28 3.3 -0.19999999 4.74 -0.19999999 C 6.2599998 -0.19999999 7.3399997 0.5 8.139999 1.54 C 8.08 1.74 7.96 1.8399999 7.72 1.86 Z M 2.48 5.64 C 2.86 7.8999996 4.2599998 8.08 4.74 8.08 C 5.5 8.08 6.3999996 7.66 6.3999996 5.98 C 6.3999996 5.7999997 6.3199997 5.7 6.1 5.7 Z "/>
</symbol>
<symbol id="gB9C04FB79CAD4691AB5EC7F01BE2AD7F" overflow="visible">
<path d="M 3.52 7.16 C 3.48 7.96 3.46 8.48 3.36 8.679999 C 3.32 8.78 3.28 8.84 3.12 8.84 C 2.56 8.62 2.04 8.44 0.65999997 8.26 C 0.62 8.139999 0.65999997 7.8199997 0.7 7.7 C 1.78 7.6 2 7.5 2 6.3399997 L 2 2.44 C 2 0.78 1.76 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 2 0 2.8 0 C 3.6 0 4.52 -0.02 5.22 -0.04 C 5.3399997 0.08 5.3399997 0.5 5.22 0.62 C 3.82 0.71999997 3.58 0.78 3.58 2.44 L 3.58 5.22 C 3.58 5.74 3.82 6.2 4.06 6.56 C 4.2799997 6.8799996 4.74 7.54 4.98 7.54 C 5.16 7.54 5.3399997 7.5 5.5 7.2799997 C 5.64 7.08 5.8799996 6.8199997 6.22 6.8199997 C 6.7 6.8199997 7.16 7.3199997 7.16 7.8199997 C 7.16 8.2 6.7999997 8.78 5.96 8.78 C 5.02 8.78 4.2 7.8999996 3.74 7.12 C 3.62 6.8999996 3.52 7.06 3.52 7.16 Z "/>
</symbol>
<symbol id="g21D1E528F66DB45787699F71DA377CC5" overflow="visible">
<path d="M 4.08 -3.1999998 C 4.4 -2.6399999 4.66 -2.08 4.9 -1.48 C 6.5 2.3799999 7.3999996 4.44 8.44 6.68 C 8.84 7.52 9.12 7.8399997 10.059999 7.96 C 10.179999 8.08 10.179999 8.5 10.059999 8.62 C 9.66 8.599999 9.2 8.58 8.639999 8.58 C 8.04 8.58 7.4199996 8.599999 6.8199997 8.62 C 6.7 8.5 6.7 8.08 6.8199997 7.96 C 7.46 7.8999996 8.099999 7.7799997 7.7799997 7.06 L 5.7999997 2.48 C 5.66 2.1599998 5.48 2.1 5.3199997 2.5 L 3.54 6.66 C 3.1799998 7.5 3.08 7.8799996 4.2 7.96 C 4.3199997 8.08 4.3199997 8.5 4.2 8.62 C 3.46 8.599999 2.6599998 8.58 1.9399999 8.58 C 1.26 8.58 0.71999997 8.599999 0.32 8.62 C 0.19999999 8.5 0.19999999 8.08 0.32 7.96 C 1.12 7.8599997 1.38 7.68 1.9 6.46 L 4.16 1.1999999 C 4.3399997 0.79999995 4.64 -0.12 4.44 -0.68 C 4.2 -1.3399999 3.9599998 -1.9 3.6599998 -2.52 C 3.4399998 -2.9199998 3.1599998 -3.1 2.6599998 -3.1 C 2.3799999 -3.1 2.3 -3.04 2.08 -3.04 C 1.5 -3.04 1.1999999 -3.6399999 1.1999999 -3.8999999 C 1.1999999 -4.3199997 1.5999999 -4.64 2.1399999 -4.64 C 2.56 -4.64 3.36 -4.48 4.08 -3.1999998 Z "/>
</symbol>
<symbol id="gAC7FD886AB12F72ED3B61B0327264BE7" overflow="visible">
<path d="M 3.12 7.3599997 C 3.1 7.96 3.06 8.48 2.96 8.679999 C 2.9199998 8.78 2.8799999 8.84 2.72 8.84 C 2.1599998 8.62 1.64 8.44 0.26 8.26 C 0.22 8.139999 0.26 7.8199997 0.29999998 7.7 C 1.38 7.6 1.5999999 7.5 1.5999999 6.3399997 L 1.5999999 -2.2 C 1.5999999 -3.86 1.38 -3.9599998 0.16 -4.02 C 0.04 -4.14 0.04 -4.56 0.16 -4.68 C 0.85999995 -4.66 1.5999999 -4.64 2.3999999 -4.64 C 3.1999998 -4.64 4.16 -4.66 4.8199997 -4.68 C 4.94 -4.56 4.94 -4.14 4.8199997 -4.02 C 3.3999999 -3.9399998 3.1799998 -3.86 3.1799998 -2.2 L 3.1799998 -0.04 C 3.1799998 0.22 3.26 0.19999999 3.46 0.12 C 3.9599998 -0.08 4.56 -0.19999999 5.2 -0.19999999 C 6.3199997 -0.19999999 7.3199997 0.14 8.139999 0.91999996 C 9.08 1.8399999 9.62 3.08 9.62 4.7 C 9.62 6.8199997 8.12 8.78 6.08 8.78 C 5.16 8.78 4.14 8.179999 3.34 7.2799997 C 3.22 7.16 3.1399999 7.16 3.12 7.3599997 Z M 3.5 6.62 C 4.02 7.2599998 4.94 7.8599997 5.52 7.8599997 C 6.7999997 7.8599997 7.8999996 6.42 7.8999996 4.16 C 7.8999996 2.52 7.3199997 0.48 5.08 0.48 C 4.72 0.48 4.02 0.58 3.6599998 0.9 C 3.26 1.26 3.1799998 1.38 3.1799998 2.1 L 3.1799998 5.74 C 3.1799998 6.16 3.26 6.3399997 3.5 6.62 Z "/>
</symbol>
<symbol id="gFB78EB03C35D4F852337F4EC6AC104AC" overflow="visible">
<path d="M 0.82 4.1 C 0.82 2.06 2.18 -0.19999999 5.02 -0.19999999 C 6.2999997 -0.19999999 7.2799997 0.26 7.96 0.91999996 C 8.86 1.8 9.26 3.06 9.26 4.2799997 C 9.26 6.3599997 8.12 8.78 5.06 8.78 C 3.74 8.78 2.6599998 8.24 1.92 7.3799996 C 1.1999999 6.52 0.82 5.3599997 0.82 4.1 Z M 4.7599998 8.08 C 6.48 8.08 7.54 6.52 7.54 3.6399999 C 7.54 1.12 6.24 0.5 5.2999997 0.5 C 3.22 0.5 2.54 3.02 2.54 4.56 C 2.54 6.2999997 2.96 8.08 4.7599998 8.08 Z "/>
</symbol>
<symbol id="gE68C39294AA7FBA9B91EA2F8E9CC3997" overflow="visible">
<path d="M 3.62 2.44 L 3.62 6.42 C 3.62 7.4199996 3.6999998 8.7 3.6999998 8.7 C 3.6999998 8.78 3.6 8.84 3.4399998 8.84 C 2.8799999 8.62 2.08 8.44 0.7 8.26 C 0.65999997 8.139999 0.7 7.8199997 0.74 7.7 C 1.8399999 7.6 2.04 7.48 2.04 6.3399997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.71999997 0.59999996 0.62 C 0.48 0.5 0.48 0.08 0.59999996 -0.04 C 1.26 -0.02 2.04 0 2.84 0 C 3.6399999 0 4.4 -0.02 5.06 -0.04 C 5.18 0.08 5.18 0.5 5.06 0.62 C 3.84 0.7 3.62 0.78 3.62 2.44 Z M 1.8 11.98 C 1.8 11.46 2.28 10.94 2.76 10.94 C 3.32 10.94 3.8 11.48 3.8 11.9 C 3.8 12.38 3.3799999 12.94 2.84 12.94 C 2.36 12.94 1.8 12.46 1.8 11.98 Z "/>
</symbol>
<symbol id="g35631D62198EF939061DC90C9391724A" overflow="visible">
<path d="M 3.6799998 7.16 C 3.56 7.02 3.4399998 6.98 3.4399998 7.16 C 3.4199998 7.7 3.3799999 8.48 3.28 8.679999 C 3.24 8.78 3.1999998 8.84 3.04 8.84 C 2.48 8.62 1.9599999 8.44 0.58 8.26 C 0.53999996 8.139999 0.58 7.8199997 0.62 7.7 C 1.6999999 7.6 1.92 7.5 1.92 6.3399997 L 1.92 2.44 C 1.92 0.79999995 1.7199999 0.71999997 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.92 0 2.72 0 C 3.52 0 4.12 -0.02 4.72 -0.04 C 4.8399997 0.08 4.8399997 0.5 4.72 0.62 C 3.6999998 0.71999997 3.5 0.79999995 3.5 2.44 L 3.5 5.72 C 3.5 6.14 3.6799998 6.3799996 3.84 6.56 C 4.6 7.2999997 5.5 7.74 6.2799997 7.74 C 6.68 7.74 7.1 7.48 7.3399997 7.02 C 7.54 6.62 7.58 6.08 7.58 5.48 L 7.58 2.44 C 7.58 0.79999995 7.3799996 0.71999997 6.3399997 0.62 C 6.24 0.5 6.24 0.08 6.3399997 -0.04 C 6.94 -0.02 7.58 0 8.38 0 C 9.179999 0 9.9 -0.02 10.5 -0.04 C 10.599999 0.08 10.599999 0.5 10.5 0.62 C 9.38 0.71999997 9.16 0.79999995 9.16 2.44 L 9.16 5.42 C 9.16 6.52 9.08 7.48 8.62 8.099999 C 8.28 8.54 7.66 8.78 6.96 8.78 C 5.98 8.78 4.8599997 8.5199995 3.6799998 7.16 Z "/>
</symbol>
<symbol id="g22D858CFD6AD86697C1391C74FD687D1" overflow="visible">
<path d="M 0.85999995 8.58 C 0.58 8.58 0.5 8.34 0.5 8.179999 L 0.5 7.9199996 C 0.5 7.8199997 0.52 7.7999997 0.59999996 7.7999997 L 1.78 7.7999997 L 1.78 1.78 C 1.78 0.35999998 2.3999999 -0.19999999 3.32 -0.19999999 C 4.24 -0.19999999 5.24 0.24 6.02 1.12 C 5.98 1.3199999 5.8599997 1.4399999 5.66 1.4599999 C 5.14 1.06 4.54 0.9 4.02 0.9 C 3.48 0.9 3.36 1.5 3.36 2.74 L 3.36 7.7999997 L 5.44 7.7999997 C 5.64 7.7999997 5.92 7.8799996 5.92 8.059999 L 5.92 8.46 C 5.92 8.54 5.8599997 8.58 5.7599998 8.58 L 3.36 8.58 L 3.36 9.36 C 3.36 10.66 3.4399998 11.46 3.4399998 11.46 C 3.4399998 11.58 3.3799999 11.639999 3.28 11.639999 C 3.1999998 11.639999 3.02 11.559999 2.84 11.46 C 2.62 11.34 2.4199998 11.24 2.1599998 11.179999 C 1.92 11.099999 1.7199999 11.04 1.7199999 10.9 C 1.7199999 10.66 1.78 10.8 1.78 8.58 Z "/>
</symbol>
<symbol id="g98926218EB374AD77A2D864C6D10734B" overflow="visible">
<path d="M 5.62 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.7 4.04 12.099999 5.12 12.099999 L 6.62 12.099999 C 8.12 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.88 9.34 9.92 9.54 10.0199995 C 9.44 10.84 9.139999 12.759999 9.099999 12.92 C 9.099999 12.96 9.08 12.98 9.0199995 12.98 C 8.679999 12.92 8.5199995 12.9 8.04 12.9 L 2.9399998 12.9 C 2.34 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.1 -0.02 2.3 0 2.96 0 L 7.2599998 0 C 8.22 0 9.82 -0.04 9.82 -0.04 C 10.099999 0.96 10.4 2.28 10.559999 3.3 C 10.36 3.4199998 10.12 3.46 9.86 3.3999999 C 9.46 1.9599999 8.76 0.78 7.24 0.78 L 4.92 0.78 C 4.08 0.78 3.8 1.1 3.8 2.04 L 3.8 6.46 L 5.62 6.46 C 7.3199997 6.46 7.3799996 6 7.44 5.1 C 7.56 4.98 7.98 4.98 8.099999 5.1 C 8.08 5.62 8.059999 6.18 8.059999 6.8599997 C 8.059999 7.4199996 8.08 8.099999 8.099999 8.58 C 7.98 8.7 7.56 8.7 7.44 8.58 C 7.3799996 7.48 7.3199997 7.22 5.62 7.22 Z "/>
</symbol>
<symbol id="g757CB60871AF468909C575234729D90A" overflow="visible">
<path d="M 0.88 5.04 C 0.88 4.14 0.96 -0.48 5.12 -4.08 C 5.3199997 -4.04 5.48 -3.8999999 5.54 -3.74 C 4.88 -2.98 2.54 -0.22 2.54 5.04 C 2.54 10.3 4.9 13.059999 5.54 13.78 C 5.48 13.98 5.3399997 14.12 5.12 14.139999 C 2.74 12.099999 0.88 8.76 0.88 5.04 Z "/>
</symbol>
<symbol id="g67483374C2628B9150A7D3585AC4A61B" overflow="visible">
<path d="M 0.96 2.76 C 1.04 1.78 1.1 0.84 1.1 0 C 1.3 0.04 1.5 0.06 1.5999999 0.06 C 1.74 0.06 1.86 0.06 2 0.02 C 2.54 -0.12 3.08 -0.19999999 3.82 -0.19999999 C 4.94 -0.19999999 7 0.34 7 2.32 C 7 3.6799998 6.02 4.48 4.66 4.98 C 3.46 5.44 2.6599998 5.74 2.6599998 6.8399997 C 2.6599998 7.66 3.3799999 8.12 4.06 8.12 C 4.5 8.12 5.66 7.96 5.92 6.2599998 C 6.04 6.14 6.44 6.16 6.56 6.2799997 C 6.62 7 6.66 7.74 6.68 8.4 C 6.06 8.5 5.1 8.78 4.06 8.78 C 2.58 8.78 1.24 7.8199997 1.24 6.54 C 1.24 5.08 1.9 4.46 3.4399998 3.82 C 5.1 3.1399999 5.48 2.72 5.48 1.86 C 5.48 0.88 4.52 0.45999998 3.78 0.45999998 C 3 0.45999998 2.56 0.71999997 2.36 0.94 C 1.92 1.4 1.6999999 2.28 1.5799999 2.78 C 1.4599999 2.8999999 1.0799999 2.8799999 0.96 2.76 Z "/>
</symbol>
<symbol id="gF5D967C73B153E080367AE40708278EE" overflow="visible">
<path d="M 5.08 5.04 C 5.08 5.94 5 10.559999 0.84 14.16 C 0.64 14.12 0.48 13.98 0.42 13.82 C 1.0799999 13.059999 3.4199998 10.3 3.4199998 5.04 C 3.4199998 -0.22 1.06 -2.98 0.42 -3.6999998 C 0.48 -3.8999999 0.62 -4.04 0.84 -4.06 C 3.22 -2.02 5.08 1.3199999 5.08 5.04 Z "/>
</symbol>
<symbol id="gCDF8B867C9AAFA36255BC29C36465E90" overflow="visible">
<path d="M 3.5 2.44 L 3.5 7.7999997 L 5.3599997 7.7999997 C 5.54 7.7999997 5.8199997 7.8799996 5.8199997 8.059999 L 5.8199997 8.46 C 5.8199997 8.54 5.7599998 8.58 5.66 8.58 L 3.5 8.58 L 3.5 9.719999 C 3.5 12.799999 4.42 13.28 5.08 13.28 C 5.68 13.28 6 13.04 6.2799997 12.34 C 6.44 11.98 6.66 11.7 7.08 11.7 C 7.4199996 11.7 7.8999996 12.12 7.8999996 12.5199995 C 7.8999996 12.86 7.68 13.219999 7.2599998 13.54 C 6.74 13.9 6.22 13.96 5.46 13.96 C 3.78 13.96 1.92 12.5 1.92 9.38 L 1.92 8.58 L 0.9 8.58 C 0.53999996 8.58 0.44 8.34 0.44 8.179999 L 0.44 7.9199996 C 0.44 7.8199997 0.45999998 7.7999997 0.53999996 7.7999997 L 1.92 7.7999997 L 1.92 2.44 C 1.92 0.78 1.5999999 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 1.92 0 2.72 0 C 3.52 0 4.48 -0.02 5.18 -0.04 C 5.2999997 0.08 5.2999997 0.5 5.18 0.62 C 3.62 0.7 3.5 0.78 3.5 2.44 Z "/>
</symbol>
<symbol id="g560AC22EF992EFD90E66808483D7B3BA" overflow="visible">
<path d="M 11.12 10.24 L 11.12 3.6999998 C 11.12 3.32 11.12 3.1 10.98 3.1 C 10.9 3.1 10.599999 3.46 10.0199995 4.2 L 3.1599998 12.9 L 0.45999998 12.94 C 0.34 12.82 0.34 12.4 0.45999998 12.28 C 1.3199999 12.219999 1.92 11.5199995 2.04 11 L 2.04 2.6599998 C 2.04 0.88 1.6999999 0.76 0.29999998 0.62 C 0.17999999 0.5 0.17999999 0.08 0.29999998 -0.04 C 1.16 -0.02 2.06 0 2.54 0 C 3 0 3.9199998 -0.02 4.7599998 -0.04 C 4.88 0.08 4.88 0.5 4.7599998 0.62 C 3.36 0.76 3.02 0.84 3.02 2.6599998 L 3.02 8.78 C 3.02 9.46 3.02 9.76 3.1799998 9.76 C 3.3 9.76 3.52 9.54 3.86 9.099999 L 10.84 0.28 C 11.059999 -0.02 11.32 -0.19999999 11.639999 -0.19999999 C 11.92 -0.19999999 12.099999 0.04 12.099999 0.42 L 12.099999 10.24 C 12.099999 12.0199995 12.44 12.139999 13.84 12.28 C 13.96 12.4 13.96 12.82 13.84 12.94 C 13.0199995 12.92 12.08 12.9 11.599999 12.9 C 11.179999 12.9 10.26 12.92 9.38 12.94 C 9.26 12.82 9.26 12.4 9.38 12.28 C 10.78 12.139999 11.12 12.059999 11.12 10.24 Z "/>
</symbol>
<symbol id="gD3761FB0B01B207797C607CDFB6E3A0B" overflow="visible">
<path d="M 3.3999999 7.16 C 3.3799999 7.7599998 3.34 8.48 3.24 8.679999 C 3.1999998 8.78 3.1599998 8.84 3 8.84 C 2.44 8.62 1.92 8.44 0.53999996 8.26 C 0.5 8.139999 0.53999996 7.8199997 0.58 7.7 C 1.66 7.6 1.88 7.5 1.88 6.3399997 L 1.88 2.44 C 1.88 0.79999995 1.62 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.88 0 2.6799998 0 C 3.48 0 4.1 -0.02 4.7 -0.04 C 4.8199997 0.08 4.8199997 0.5 4.7 0.62 C 3.6799998 0.71999997 3.46 0.79999995 3.46 2.44 L 3.46 5.72 C 3.46 6.14 3.6399999 6.3799996 3.8 6.56 C 4.6 7.3399997 5.3399997 7.74 5.96 7.74 C 6.72 7.74 7.2799997 7.2599998 7.2799997 5.92 L 7.2799997 2.44 C 7.2799997 0.79999995 7.12 0.7 6.04 0.62 C 5.94 0.5 5.94 0.08 6.04 -0.04 C 6.54 -0.02 7.2799997 0 8.08 0 C 8.88 0 9.54 -0.02 10.04 -0.04 C 10.139999 0.08 10.139999 0.5 10.04 0.62 C 9.04 0.7 8.86 0.79999995 8.86 2.44 L 8.86 5.62 C 8.86 5.9 8.86 6.18 8.84 6.42 C 9.8 7.48 10.7 7.74 11.48 7.74 C 12.24 7.74 12.679999 7.2999997 12.679999 5.96 L 12.679999 2.44 C 12.679999 0.79999995 12.48 0.7 11.44 0.62 C 11.34 0.5 11.34 0.08 11.44 -0.04 C 11.94 -0.02 12.679999 0 13.48 0 C 14.28 0 14.98 -0.02 15.54 -0.04 C 15.639999 0.08 15.639999 0.5 15.54 0.62 C 14.44 0.7 14.259999 0.79999995 14.259999 2.44 L 14.259999 5.6 C 14.259999 7.3799996 13.96 8.78 12.2 8.78 C 11.179999 8.78 9.94 8.4 8.9 7.2999997 C 8.84 7.24 8.72 7.14 8.679999 7.3199997 C 8.5 8.139999 7.72 8.78 6.68 8.78 C 5.52 8.78 4.48 8.099999 3.6399999 7.16 C 3.54 7.06 3.4199998 6.92 3.3999999 7.16 Z "/>
</symbol>
<symbol id="g733371913480EE84B3609C9E9CD62F8C" overflow="visible">
<path d="M 3.34 7.8799996 C 3.22 7.7599998 3.1399999 7.7999997 3.1399999 7.98 L 3.1399999 11.66 C 3.1399999 12.96 3.22 13.759999 3.22 13.759999 C 3.22 13.9 3.1399999 13.96 2.96 13.96 C 2.46 13.759999 0.96 13.48 0.16 13.42 C 0.12 13.259999 0.16 12.94 0.28 12.82 C 0.34 12.82 0.39999998 12.82 0.45999998 12.82 C 1.3399999 12.759999 1.56 12.759999 1.56 11.179999 L 1.56 1.42 C 1.56 0.64 1.54 0.28 1.48 0 C 1.5799999 -0.16 1.68 -0.24 1.92 -0.24 C 2.04 -0.12 2.24 0.06 2.3999999 0.24 C 2.6 0.48 2.72 0.48 2.9399998 0.29999998 C 3.3999999 -0.08 4 -0.19999999 4.7 -0.19999999 C 6.74 -0.19999999 9.12 1.66 9.12 4.8399997 C 9.12 7.2799997 7.3199997 8.78 5.58 8.78 C 4.72 8.78 3.9599998 8.44 3.34 7.8799996 Z M 3.48 7.2599998 C 4 7.72 4.6 7.8999996 5.18 7.8999996 C 6.3999996 7.8999996 7.3999996 6.42 7.3999996 4.48 C 7.3999996 2.2 6.48 0.48 4.58 0.48 C 3.9599998 0.48 3.54 0.91999996 3.1399999 1.42 L 3.1399999 6.42 C 3.1399999 6.8399997 3.22 7.04 3.48 7.2599998 Z "/>
</symbol>
<symbol id="gFB54B84572F46C3C9CB2B1A90182D6B2" overflow="visible">
<path d="M 8.88 7.74 C 9.26 7.74 9.62 8.099999 9.62 8.5 C 9.62 8.92 9.24 9.24 8.7 9.24 C 8.179999 9.24 7.22 8.9 6.7 8.22 C 6.46 8.38 5.7999997 8.78 4.62 8.78 C 2.84 8.78 1.1999999 7.58 1.1999999 5.74 C 1.1999999 4.66 1.68 4.04 2.24 3.5 C 1.68 3.02 1.36 2.1599998 1.36 1.48 C 1.36 0.76 1.76 0.19999999 2.28 -0.06 C 1.1999999 -0.7 0.64 -1.62 0.64 -2.48 C 0.64 -4.22 2.28 -4.7599998 3.82 -4.7599998 C 6.52 -4.7599998 9.44 -3.46 9.44 -1.3 C 9.44 -0.65999997 9.139999 -0.16 8.559999 0.32 C 7.7799997 0.96 6.3799996 0.97999996 5.64 0.97999996 C 5.2799997 0.97999996 4.7799997 0.94 4.2999997 0.88 C 4 0.85999995 3.8 0.84 3.6999998 0.84 C 3.12 0.84 2.4199998 1.12 2.4199998 1.9799999 C 2.4199998 2.3799999 2.54 2.8 2.78 3.1399999 C 3.26 2.86 3.82 2.72 4.6 2.72 C 6.3599997 2.72 7.98 3.82 7.98 5.7799997 C 7.98 6.72 7.7 7.2599998 7.12 7.8599997 C 7.2599998 8.059999 7.66 8.34 7.9199996 8.34 C 8.059999 8.34 8.2 8.28 8.32 8.099999 C 8.4 7.94 8.66 7.74 8.88 7.74 Z M 2.6399999 -0.19999999 C 2.86 -0.26 3.1799998 -0.29999998 3.4399998 -0.29999998 C 4.06 -0.29999998 4.62 -0.24 4.9 -0.24 C 5.9 -0.24 6.74 -0.26 7.3199997 -0.58 C 8.099999 -1.02 8.34 -1.3 8.34 -1.8199999 C 8.34 -3.26 6.22 -4.02 4.42 -4.02 C 3.6999998 -4.02 2.02 -3.4399998 2.02 -2.08 C 2.02 -1.4 2.06 -0.9 2.6399999 -0.19999999 Z M 6.3799996 5.58 C 6.3799996 3.72 5.44 3.34 4.7 3.34 C 3.02 3.34 2.84 4.7599998 2.84 6.04 C 2.84 7.44 3.34 8.16 4.44 8.16 C 5.7 8.16 6.3799996 7.24 6.3799996 5.58 Z "/>
</symbol>
<symbol id="g3C2FFF86BC828E66F78F8A687CE12C70" overflow="visible">
<path d="M 3.34 5.72 C 3.34 6.14 3.52 6.3799996 3.6799998 6.56 C 4.44 7.2999997 5.46 7.74 6.24 7.74 C 6.64 7.74 7.06 7.48 7.2999997 7.02 C 7.5 6.62 7.54 6.08 7.54 5.48 L 7.54 2.44 C 7.54 0.79999995 7.3399997 0.71999997 6.2999997 0.62 C 6.2 0.5 6.2 0.08 6.2999997 -0.04 C 6.8599997 -0.02 7.54 0 8.34 0 C 9.139999 0 9.8 -0.02 10.46 -0.04 C 10.559999 0.08 10.559999 0.5 10.46 0.62 C 9.34 0.71999997 9.12 0.79999995 9.12 2.44 L 9.12 5.42 C 9.12 6.52 9.04 7.5 8.58 8.099999 C 8.24 8.54 7.62 8.78 6.92 8.78 C 5.94 8.78 4.74 8.5199995 3.52 7.16 C 3.52 7.14 3.5 7.14 3.48 7.12 C 3.4199998 7.04 3.32 6.92 3.32 7.16 L 3.34 11.66 C 3.34 12.96 3.4199998 13.759999 3.4199998 13.759999 C 3.4199998 13.9 3.34 13.96 3.1599998 13.96 C 2.6599998 13.759999 1.16 13.48 0.35999998 13.42 C 0.32 13.259999 0.35999998 12.94 0.48 12.82 C 0.53999996 12.82 0.59999996 12.82 0.65999997 12.82 C 1.54 12.759999 1.76 12.759999 1.76 11.179999 L 1.76 2.44 C 1.76 0.78 1.52 0.7 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.02 -0.02 1.76 0 2.56 0 C 3.32 0 3.98 -0.02 4.54 -0.04 C 4.66 0.08 4.66 0.5 4.54 0.62 C 3.52 0.7 3.34 0.78 3.34 2.44 Z "/>
</symbol>
<symbol id="gAA212A9DBB5FA7333A767E41B2F6A3B3" overflow="visible">
<path d="M 5.8599997 0.96 C 5.98 0.34 6.2 -0.19999999 7.2 -0.19999999 C 7.96 -0.19999999 8.679999 0.14 9.099999 0.53999996 C 9.059999 0.78 8.98 0.96 8.76 1.0799999 C 8.62 0.96 8.28 0.76 8.0199995 0.76 C 7.44 0.76 7.4199996 1.54 7.4199996 2.46 L 7.4199996 5.4 C 7.4199996 8.24 5.8599997 8.78 4.4 8.78 C 2.76 8.78 1.1 7.7 1.1 6.56 C 1.1 6.08 1.3399999 5.8399997 1.8 5.8399997 C 2.3799999 5.8399997 2.74 6.2599998 2.74 6.52 C 2.74 6.66 2.72 6.7999997 2.6799998 6.8799996 C 2.6599998 6.94 2.6399999 7.06 2.6399999 7.2799997 C 2.6399999 7.8999996 3.48 8.12 4.24 8.12 C 4.92 8.12 5.8599997 7.7799997 5.8599997 5.52 C 5.8599997 5.38 5.7999997 5.2999997 5.74 5.2799997 L 4.02 4.8599997 C 2.1 4.38 0.71999997 3.32 0.71999997 1.9599999 C 0.71999997 0.32 1.8399999 -0.19999999 3.24 -0.19999999 C 3.9399998 -0.19999999 4.54 -0.04 5.42 0.64 L 5.8199997 0.96 Z M 5.8599997 4.66 L 5.8599997 2.02 C 5.8599997 1.76 5.74 1.62 5.58 1.5 C 5.06 1.0799999 4.38 0.62 3.82 0.62 C 2.82 0.62 2.3799999 1.42 2.3799999 2.04 C 2.3799999 2.9399998 2.8 3.86 4.2799997 4.24 Z "/>
</symbol>
<symbol id="g713198A7DA4F5CD7D462D4529B1D64BD" overflow="visible">
<path d="M 7.96 1.8199999 C 7.8799996 2 7.72 2.08 7.54 2.1 C 6.8599997 1.22 6 0.78 5.14 0.78 C 3.6799998 0.78 2.46 2.26 2.46 4.6 C 2.46 6.7999997 3.4199998 8.12 4.74 8.12 C 5.92 8.12 6.08 7.4199996 6.16 6.72 C 6.22 6.18 6.5 6 6.92 6 C 7.3399997 6 7.8999996 6.2599998 7.8999996 6.8799996 C 7.8999996 7.98 6.7599998 8.78 4.8399997 8.78 C 2.86 8.78 0.74 7 0.74 4.16 C 0.74 1.5799999 2.18 -0.19999999 4.7 -0.19999999 C 5.9 -0.19999999 6.96 0.17999999 7.96 1.8199999 Z "/>
</symbol>
<symbol id="gC46470BA400E4AE9E0CCFB3B379C9D5C" overflow="visible">
<path d="M 13.66 13.7 L 10.48 13.7 C 10 13.7 9.76 13.559999 9.76 13.259999 C 9.76 13.04 9.92 12.92 10.24 12.86 C 10.719999 12.799999 10.88 12.38 10.88 11.78 C 10.88 10.94 10.559999 9.62 9.92 7.8199997 L 8.4 3.9199998 C 7.8999996 4.94 7.24 6.44 6.42 8.42 C 5.54 10.48 5.1 11.78 5.1 12.32 C 5.12 12.34 5.16 12.4 5.22 12.46 C 5.48 12.7 5.7999997 12.82 6.22 12.84 C 6.52 12.86 6.66 13 6.66 13.259999 C 6.66 13.639999 6.42 13.7 5.94 13.7 L 0.76 13.7 C 0.26 13.7 0.02 13.559999 0.02 13.259999 C 0.02 13.04 0.17999999 12.9 0.5 12.86 C 0.74 12.82 0.97999996 12.639999 1.24 12.32 C 1.36 12.139999 1.4599999 12 1.52 11.9 L 6.8799996 0.08 C 7.02 -0.22 7.18 -0.38 7.3599997 -0.38 C 7.54 -0.38 7.7 -0.22 7.8199997 0.08 L 12.759999 11.88 C 13 12.48 13.38 12.799999 13.9 12.84 C 14.24 12.84 14.4 12.98 14.4 13.259999 C 14.4 13.639999 14.139999 13.7 13.66 13.7 Z M 11.54 12.84 L 12.3 12.84 C 12.0199995 12.32 11.82 11.92 11.719999 11.62 L 11.719999 11.78 C 11.719999 12.219999 11.66 12.58 11.54 12.84 Z M 4.24 12.34 C 4.24 11.46 5.5 8.24 8 2.7 L 7.3599997 1.1 L 2.3999999 12 C 2.22 12.38 2.08 12.66 1.9399999 12.84 L 4.38 12.84 C 4.2799997 12.7 4.24 12.54 4.24 12.34 Z "/>
</symbol>
<symbol id="gC3F91E6BB9F8304E319658F9D45F8B38" overflow="visible">
<path d="M 8.96 12.28 C 10.44 12.179999 10.44 11.639999 10.0199995 10.559999 L 6.8599997 2.54 L 6.7799997 2.54 L 3.58 10.679999 C 3.12 11.88 3.24 12.139999 4.6 12.28 C 4.72 12.4 4.72 12.82 4.6 12.94 C 3.8 12.92 2.8999999 12.9 2.18 12.9 C 1.4599999 12.9 0.76 12.92 0.099999994 12.94 C -0.02 12.82 0 12.4 0.12 12.28 C 1.22 12.179999 1.38 11.84 1.92 10.46 L 5.8599997 0.22 C 5.98 -0.099999994 6.12 -0.24 6.3199997 -0.24 C 6.54 -0.24 6.68 -0.06 6.7999997 0.22 L 10.94 10.42 C 11.32 11.36 11.639999 12.139999 12.9 12.28 C 13.0199995 12.4 13.0199995 12.82 12.9 12.94 C 12.3 12.92 11.599999 12.9 11.139999 12.9 C 10.679999 12.9 9.78 12.92 8.96 12.94 C 8.84 12.82 8.84 12.4 8.96 12.28 Z "/>
</symbol>
<symbol id="g42587C4E387B2C5F870DA01C2914651F" overflow="visible">
<path d="M 6.68 1 C 6.7799997 1.0799999 6.96 1.12 6.98 0.97999996 C 7.04 0.5 7.2 -0.19999999 7.2 -0.19999999 C 7.3599997 -0.26 7.46 -0.24 7.58 -0.19999999 C 8.0199995 0.16 8.72 0.45999998 9.94 0.59999996 C 10.059999 0.71999997 10.059999 1.02 9.94 1.14 C 8.66 1.24 8.48 1.62 8.48 2.6 L 8.48 11.66 C 8.48 12.96 8.559999 13.759999 8.559999 13.759999 C 8.559999 13.9 8.48 13.96 8.3 13.96 C 7.7999997 13.759999 6.2999997 13.48 5.5 13.42 C 5.46 13.259999 5.5 12.94 5.62 12.82 C 5.68 12.82 5.74 12.82 5.7999997 12.82 C 6.68 12.759999 6.8999996 12.759999 6.8999996 11.179999 L 6.8999996 8.62 C 6.8999996 8.48 6.8599997 8.44 6.72 8.44 C 6.64 8.44 5.8199997 8.78 5.16 8.78 C 3.84 8.78 2.96 8.34 2.1599998 7.58 C 1.3 6.72 0.78 5.54 0.78 4.06 C 0.78 1.5999999 2.02 -0.19999999 4.18 -0.19999999 C 4.96 -0.19999999 5.7 0.19999999 6.68 1 Z M 6.8999996 2.48 C 6.8999996 2.1 6.8599997 1.9399999 6.58 1.6999999 C 5.8399997 1.06 5.2 0.74 4.7 0.74 C 3.62 0.74 2.5 1.92 2.5 4.42 C 2.5 5.8599997 2.78 6.66 3.08 7.08 C 3.6999998 8.0199995 4.54 8.08 4.94 8.08 C 5.66 8.08 6.16 7.8199997 6.56 7.3599997 C 6.8399997 7.04 6.8999996 6.8999996 6.8999996 6.2799997 Z "/>
</symbol>
<symbol id="g92446B7A6A7F78674F0F5568B7ED0AC5" overflow="visible">
<path d="M 13.059999 1.74 C 13.48 2.1599998 13.7 2.46 13.7 2.62 C 13.7 2.9399998 13.54 3.1 13.2 3.1 C 13.059999 3.1 12.92 3 12.74 2.8 C 11.5199995 1.42 9.98 0.71999997 8.12 0.71999997 C 6.68 0.71999997 5.68 1.36 5.12 2.62 C 4.62 3.76 4.38 5.16 4.38 6.8199997 C 4.38 8.32 4.6 9.66 5.04 10.8 C 5.64 12.42 6.58 13.219999 7.8399997 13.219999 C 8.74 13.219999 9.62 12.86 10.5199995 12.139999 C 11.42 11.42 12 10.62 12.28 9.74 C 12.38 9.46 12.5199995 9.32 12.74 9.32 C 13 9.32 13.139999 9.559999 13.139999 10.04 L 13.139999 13.34 C 13.139999 13.84 13 14.08 12.74 14.08 C 12.5199995 14.08 12.36 13.92 12.28 13.62 C 12.2 13.32 12.0199995 13.16 11.719999 13.16 C 11.32 13.16 10.719999 13.32 9.88 13.62 C 9.04 13.92 8.34 14.08 7.7799997 14.08 C 5.96 14.08 4.38 13.5199995 3.02 12.4 C 1.5 11.16 0.74 9.32 0.74 6.8599997 C 0.74 4.4 1.5 2.54 3 1.3199999 C 4.38 0.17999999 6 -0.38 7.8199997 -0.38 C 9.84 -0.38 11.599999 0.32 13.059999 1.74 Z M 12.3 12.4 L 12.3 11.54 C 12.139999 11.719999 11.9 11.98 11.58 12.32 L 11.74 12.32 C 11.96 12.32 12.16 12.34 12.3 12.4 Z M 5.12 12.7 C 4.94 12.5 4.7799997 12.259999 4.62 12 C 4 10.98 3.52 8.58 3.52 6.8199997 C 3.52 4.06 4.12 2.1 5.3199997 0.91999996 C 2.82 1.88 1.5799999 3.86 1.5799999 6.8399997 C 1.5799999 9.8 2.76 11.759999 5.12 12.7 Z "/>
</symbol>
<symbol id="gA335A20E4C1D7F39210005AFF7F1A0EF" overflow="visible">
<path d="M 7.14 -0.19999999 C 9.08 -0.19999999 10.86 0.71999997 12.219999 2.5 C 12.12 2.6799998 11.98 2.8 11.759999 2.8 C 10.34 1.24 8.98 0.62 7.12 0.62 C 4.42 0.62 2.56 3.6599998 2.56 6.58 C 2.56 8.3 3.02 9.74 3.74 10.639999 C 4.74 11.86 5.9 12.42 6.94 12.42 C 9.7 12.42 10.8 10.78 11.32 9.059999 C 11.559999 8.98 11.759999 9.04 11.98 9.16 C 11.88 10.2 11.74 11.16 11.54 12.259999 C 10.5199995 12.36 9.62 13.16 7.16 13.16 C 5.46 13.16 4.04 12.54 2.86 11.46 C 1.54 10.24 0.74 8.28 0.74 6.2 C 0.74 2.72 2.84 -0.19999999 7.14 -0.19999999 Z "/>
</symbol>
<symbol id="g278A59F111DD0614EC58EAA01A502EFD" overflow="visible">
<path d="M 19.1 13.7 L 16.279999 13.7 C 15.799999 13.7 15.559999 13.559999 15.559999 13.259999 C 15.559999 13.0199995 15.679999 12.88 15.92 12.86 C 16.64 12.78 16.8 12.54 16.8 11.5 C 16.8 10.5199995 16.5 9.099999 15.9 7.24 L 15 4.58 C 14.719999 5.2599998 14.259999 6.52 13.599999 8.36 C 12.9 10.36 12.54 11.719999 12.5 12.42 C 12.719999 12.679999 13 12.82 13.38 12.84 C 13.7 12.86 13.86 13 13.86 13.259999 C 13.86 13.639999 13.62 13.7 13.139999 13.7 L 8.36 13.7 C 7.8599997 13.7 7.6 13.559999 7.6 13.259999 C 7.6 13.04 7.74 12.88 8 12.84 C 8.26 12.799999 8.48 12.679999 8.639999 12.48 C 9.059999 11.98 9.46 10.8 9.8 9.8 L 7.3199997 4.1 L 5.96 7.96 C 5.14 10.3 4.74 11.78 4.74 12.42 C 4.74 12.639999 4.96 12.78 5.4 12.84 C 5.7 12.86 5.8599997 13 5.8599997 13.259999 C 5.8599997 13.62 5.56 13.7 5.1 13.7 L 0.9 13.7 C 0.39999998 13.7 0.16 13.559999 0.16 13.259999 C 0.16 13.04 0.29999998 12.88 0.59999996 12.84 C 0.9 12.799999 1.14 12.5199995 1.3199999 12.0199995 L 5.56 0.12 C 5.68 -0.22 5.8399997 -0.38 6.04 -0.38 C 6.22 -0.38 6.3599997 -0.24 6.5 0.06 L 10.26 8.62 L 13.48 0.14 C 13.62 -0.19999999 13.78 -0.38 13.96 -0.38 C 14.16 -0.38 14.32 -0.22 14.44 0.12 L 18.68 11.98 C 18.88 12.5199995 19.14 12.799999 19.439999 12.86 C 19.699999 12.9 19.84 13.04 19.84 13.259999 C 19.84 13.639999 19.58 13.7 19.1 13.7 Z M 17.42 12.84 L 18.14 12.84 C 18.039999 12.639999 17.88 12.24 17.64 11.639999 C 17.619999 12.16 17.539999 12.559999 17.42 12.84 Z M 12.38 9.4 C 13.12 7.14 13.86 5.08 14.639999 3.1799998 C 14.299999 2.28 14.08 1.66 13.96 1.28 L 9.9 11.98 C 9.78 12.3 9.639999 12.58 9.46 12.84 L 11.759999 12.84 C 11.679999 12.719999 11.639999 12.559999 11.639999 12.34 C 11.639999 11.88 11.88 10.9 12.38 9.4 Z M 3.8799999 12.44 C 3.8799999 11.44 4.8599997 8.26 6.8199997 2.9199998 L 6.08 1.22 L 2.2 12.04 C 2.06 12.4 1.9599999 12.66 1.86 12.84 L 3.9599998 12.84 C 3.8999999 12.719999 3.8799999 12.58 3.8799999 12.44 Z "/>
</symbol>
<symbol id="g3BBBD96D467CC564123619D79E97B4D6" overflow="visible">
<path d="M 7.8999996 12.62 C 6.74 12.78 6.7799997 13.16 4.8199997 13.16 C 2.8 13.16 1.02 11.82 1.02 9.7 C 1.02 7.6 2.76 6.64 4.52 5.96 C 5.72 5.5 7.2 4.94 7.2 2.98 C 7.2 1.36 6.2999997 0.52 4.7 0.52 C 2.84 0.52 1.64 1.38 1.1999999 3.36 C 0.94 3.4399998 0.74 3.3999999 0.53999996 3.3 C 0.62 1.76 0.7 1.24 0.94 0.26 C 2.2 0.26 2.76 -0.19999999 4.54 -0.19999999 C 5.44 -0.19999999 6.2999997 0.02 7 0.45999998 C 8.16 1.18 8.88 2.3999999 8.88 3.6799998 C 8.88 5.7999997 7.2799997 6.74 5.64 7.3599997 C 4.44 7.7999997 2.44 8.559999 2.44 10.24 C 2.44 11.36 3.46 12.48 4.64 12.48 C 6.58 12.48 7.2 11.24 7.6 9.92 C 7.8199997 9.88 8.08 9.9 8.26 10.04 C 8.179999 11 8.099999 11.559999 7.8999996 12.62 Z "/>
</symbol>
<symbol id="gA1481BA28623480CC7E6165783E2A864" overflow="visible">
<path d="M 4.06 7.96 C 4.18 8.08 4.18 8.5 4.06 8.62 C 3.46 8.599999 2.76 8.58 2.04 8.58 C 1.28 8.58 0.74 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.16 7.8599997 1.38 7.66 1.8 6.62 L 4.42 0.16 C 4.54 -0.12 4.7 -0.24 4.9 -0.24 C 5.08 -0.24 5.24 -0.12 5.38 0.19999999 L 7.3999996 5.12 L 9.46 0.16 C 9.58 -0.12 9.74 -0.24 9.94 -0.24 C 10.12 -0.24 10.28 -0.12 10.4 0.17999999 L 13.0199995 6.52 C 13.34 7.3399997 13.679999 7.8999996 14.7 7.96 C 14.82 8.08 14.82 8.5 14.7 8.62 C 14.299999 8.599999 13.86 8.58 13.259999 8.58 C 12.66 8.58 11.82 8.599999 11.219999 8.62 C 11.099999 8.5 11.099999 8.08 11.219999 7.96 C 12.719999 7.8799996 12.5199995 7.2999997 12.24 6.6 L 10.559999 2.44 C 10.36 1.9399999 10.28 1.9399999 10.12 2.36 L 8.4 6.74 C 8.0199995 7.68 8.059999 7.8799996 9.12 7.96 C 9.24 8.08 9.24 8.5 9.12 8.62 C 8.5199995 8.599999 7.72 8.58 7.12 8.58 C 6.62 8.58 5.96 8.599999 5.3599997 8.62 C 5.24 8.5 5.24 8.08 5.3599997 7.96 C 6.2999997 7.8799996 6.54 7.2999997 6.8999996 6.3999996 L 7.02 6.08 L 5.62 2.54 C 5.3599997 1.88 5.3199997 1.86 5.06 2.5 L 3.46 6.62 C 3.08 7.58 3.1 7.8999996 4.06 7.96 Z "/>
</symbol>
<symbol id="g1788914935A6D7BFA016214155630E72" overflow="visible">
<path d="M 1.9 2.44 C 1.9 0.78 1.68 0.68 0.45999998 0.62 C 0.34 0.5 0.34 0.08 0.45999998 -0.04 C 1.16 -0.02 1.9 0 2.7 0 C 3.5 0 4.2599998 -0.02 4.92 -0.04 C 5.04 0.08 5.04 0.5 4.92 0.62 C 3.6999998 0.68 3.48 0.78 3.48 2.44 L 3.48 11.66 C 3.48 12.96 3.56 13.759999 3.56 13.759999 C 3.56 13.9 3.48 13.96 3.3 13.96 C 2.8 13.759999 1.3 13.48 0.5 13.42 C 0.45999998 13.259999 0.5 12.94 0.62 12.82 C 1.78 12.74 1.9 12.679999 1.9 11.179999 Z "/>
</symbol>
<symbol id="gDACA5EBB44D5F3DB530A1F5F650BFBAB" overflow="visible">
<path d="M 2.08 10.46 L 2.08 2.44 C 2.08 0.78 1.74 0.68 0.34 0.62 C 0.22 0.5 0.22 0.08 0.34 -0.04 C 1.24 -0.02 2.22 0 2.9399998 0 C 3.6399999 0 4.8199997 -0.02 5.8199997 -0.04 C 5.94 0.08 5.94 0.5 5.8199997 0.62 C 4.2599998 0.7 3.78 0.78 3.78 2.44 L 3.78 5.8399997 C 4.22 5.7 4.7 5.64 5.4 5.64 C 9.04 5.64 10.139999 8.0199995 10.139999 9.719999 C 10.139999 10.9 9.36 13.04 5.66 13.04 C 4.9 13.04 3.72 12.9 2.9199998 12.9 C 2.18 12.9 1.14 12.92 0.34 12.94 C 0.22 12.82 0.22 12.4 0.34 12.28 C 1.74 12.219999 2.08 12.12 2.08 10.46 Z M 3.78 11.08 C 3.78 11.66 4.08 12.36 5.52 12.36 C 6.8999996 12.36 8.28 11.9 8.28 9.36 C 8.28 7.2 7.24 6.3199997 5.2999997 6.3199997 C 4.7999997 6.3199997 4 6.3599997 3.78 6.42 Z "/>
</symbol>
<symbol id="gF9DE6E66E5D3ACB0B17DC7988DD660B8" overflow="visible">
<path d="M 1.7199999 2.44 C 1.7199999 0.78 1.5 0.7 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.04 -0.02 1.7199999 0 2.52 0 C 3.22 0 3.8799999 -0.02 4.3399997 -0.04 C 4.46 0.08 4.46 0.5 4.3399997 0.62 C 3.52 0.7 3.3 0.78 3.3 2.44 L 3.3 4.18 C 3.6799998 4.16 3.9599998 4.14 4.16 4.08 C 4.38 3.9199998 4.56 3.74 4.7999997 3.4199998 L 6.2599998 1.4599999 C 6.8399997 0.68 7.08 0.29999998 7.1 0.06 C 7.1 0 7.12 -0.04 7.18 -0.04 C 7.58 -0.02 8.0199995 0 8.42 0 C 9.04 0 9.66 -0.02 10.059999 -0.04 C 10.179999 0.08 10.179999 0.5 10.059999 0.62 C 9.38 0.7 8.88 0.78 8.34 1.4599999 L 5.7 4.7799997 C 5.62 4.88 5.56 4.96 5.56 5.06 C 5.56 5.14 5.56 5.18 5.64 5.2599998 L 7.3999996 7.08 C 8 7.72 8.7 7.8799996 9.5 7.96 C 9.62 8.08 9.62 8.5 9.5 8.62 C 9.04 8.599999 8.48 8.58 7.7599998 8.58 C 7 8.58 6.2599998 8.599999 5.7999997 8.62 C 5.68 8.5 5.68 8.08 5.7999997 7.96 C 6.92 7.8799996 6.44 7.18 6.2599998 6.94 C 5.7999997 6.3599997 5.18 5.68 4.66 5.2999997 C 4.22 4.98 3.6799998 4.74 3.3 4.68 L 3.3 11.66 C 3.3 12.96 3.3799999 13.759999 3.3799999 13.759999 C 3.3799999 13.9 3.3 13.96 3.12 13.96 C 2.62 13.759999 1.12 13.48 0.32 13.42 C 0.28 13.259999 0.32 12.94 0.44 12.82 C 0.5 12.82 0.56 12.82 0.62 12.82 C 1.5 12.759999 1.7199999 12.759999 1.7199999 11.179999 Z "/>
</symbol>
<symbol id="g8C8BFD035DDE11C1B8F6EB4DD490B55D" overflow="visible">
<path d="M 6.56 6.5 C 6.56 6 6.8199997 5.74 7.3599997 5.74 C 8.08 5.74 8.54 6.3599997 8.54 7.08 C 8.54 8.2 7.3599997 8.84 6.16 8.84 C 4.7799997 8.84 3.52 8.24 2.44 7.06 C 1.36 5.8799996 0.82 4.58 0.82 3.1799998 C 0.82 1.22 2.12 -0.22 4.08 -0.22 C 5.14 -0.22 6.08 0.04 6.8999996 0.53999996 C 7.58 0.96 8.08 1.38 8.4 1.8 C 8.54 1.9799999 8.599999 2.12 8.599999 2.18 C 8.599999 2.3999999 8.5 2.52 8.28 2.52 C 8.179999 2.52 8.08 2.44 7.96 2.28 C 7.2999997 1.4 6.48 0.84 5.54 0.59999996 C 4.92 0.44 4.46 0.35999998 4.12 0.35999998 C 2.98 0.35999998 2.4199998 1.06 2.4199998 2.44 C 2.4199998 3.6799998 3 5.48 3.48 6.3399997 C 3.9599998 7.22 4.98 8.26 6.16 8.26 C 6.92 8.26 7.44 8.04 7.72 7.62 C 7.1 7.56 6.56 7.16 6.56 6.5 Z "/>
</symbol>
<symbol id="g629AE7F75F47B1FD947FFA2989B5B47D" overflow="visible">
<path d="M 7.44 7.54 C 7.04 8.4 6.42 8.84 5.6 8.84 C 4.2999997 8.84 3.1599998 8.179999 2.18 6.8399997 C 1.26 5.6 0.79999995 4.3199997 0.79999995 2.98 C 0.79999995 1.24 1.8 -0.26 3.46 -0.26 C 4.18 -0.26 4.9 0.08 5.64 0.76 L 4.8199997 -2.52 C 4.7599998 -2.82 4.58 -3 4.2999997 -3.06 C 4.2 -3.08 3.9399998 -3.1 3.48 -3.1 C 3.36 -3.12 3.28 -3.12 3.24 -3.12 C 3.06 -3.1399999 2.96 -3.3 2.96 -3.58 L 2.96 -3.6599998 C 3.02 -3.8 3.1399999 -3.8799999 3.3 -3.8799999 C 3.6799998 -3.8799999 4.88 -3.82 5.2599998 -3.82 C 5.64 -3.82 6.8999996 -3.8799999 7.2799997 -3.8799999 C 7.56 -3.8799999 7.7 -3.72 7.7 -3.3999999 C 7.7 -3.1999998 7.5 -3.1 7.12 -3.1 C 6.7599998 -3.1 6.2599998 -3.12 6.2599998 -2.8799999 C 6.2599998 -2.8 6.2799997 -2.6599998 6.3399997 -2.46 L 9.04 8.54 C 9.04 8.72 8.94 8.82 8.76 8.82 C 8.4 8.82 7.64 7.8199997 7.44 7.54 Z M 6.7999997 7.46 C 6.98 7.04 7.08 6.7599998 7.08 6.58 C 7.08 6.56 7.06 6.44 7.02 6.2599998 L 6.54 4.3199997 C 6.16 2.8799999 5.98 2.1399999 5.96 2.1 C 5.58 1.4 4.48 0.32 3.52 0.32 C 2.74 0.32 2.34 0.91999996 2.34 2.1 C 2.34 3.02 2.96 5.2599998 3.24 6 C 3.62 6.94 4.5 8.24 5.6 8.24 C 6.14 8.24 6.54 7.98 6.7999997 7.46 Z "/>
</symbol>
<symbol id="g520D89691A96D56AE5196D136E86D2C6" overflow="visible">
<path d="M 11.04 12.66 C 11.04 13.54 10.179999 14.099999 9.24 14.099999 C 8 14.099999 7.14 13.299999 6.68 11.719999 C 6.58 11.36 6.3599997 10.34 6.04 8.66 L 4.74 8.66 C 4.2999997 8.66 4.08 8.639999 4.08 8.22 C 4.08 8 4.2799997 7.8999996 4.7 7.8999996 L 5.9 7.8999996 L 4.44 0.16 C 4.22 -0.97999996 4.02 -1.8199999 3.84 -2.3799999 C 3.6 -3.12 3.26 -3.5 2.82 -3.5 C 2.52 -3.5 2.28 -3.4199998 2.06 -3.28 C 2.7 -3.1799998 3.02 -2.8 3.02 -2.1599998 C 3.02 -1.64 2.76 -1.38 2.22 -1.38 C 1.54 -1.38 1.06 -1.9799999 1.06 -2.6599998 C 1.06 -3.54 1.88 -4.1 2.82 -4.1 C 3.32 -4.1 3.78 -3.8999999 4.16 -3.48 C 4.7999997 -2.82 5.2999997 -1.88 5.66 -0.62 C 5.8799996 0.16 6.08 0.91999996 6.22 1.68 L 7.3799996 7.8999996 L 9.0199995 7.8999996 C 9.48 7.8999996 9.679999 7.9199996 9.679999 8.38 C 9.679999 8.559999 9.48 8.66 9.08 8.66 L 7.54 8.66 C 7.66 9.48 8.22 12.5 8.4 12.88 C 8.599999 13.299999 8.88 13.5 9.24 13.5 C 9.54 13.5 9.8 13.42 10.0199995 13.28 C 9.4 13.139999 9.08 12.78 9.08 12.16 C 9.08 11.639999 9.34 11.38 9.88 11.38 C 10.559999 11.38 11.04 11.98 11.04 12.66 Z "/>
</symbol>
<symbol id="g6B54F166BDD11A6B5982665EE5474C84" overflow="visible">
<path d="M 11.34 13.66 L 4.7 13.66 C 4.24 13.66 4.02 13.639999 4.02 13.2 C 4.02 12.98 4.24 12.88 4.68 12.88 C 5.08 12.88 5.8799996 12.94 5.8799996 12.62 C 5.8799996 12.58 5.8599997 12.46 5.7999997 12.259999 L 3.1599998 1.64 C 3.06 1.1999999 2.86 0.94 2.56 0.84 C 2.4199998 0.79999995 2.06 0.78 1.4399999 0.78 C 1 0.78 0.79999995 0.74 0.79999995 0.32 C 0.79999995 0.099999994 1.02 0 1.4399999 0 L 7.98 0 C 9.34 0 10.639999 0.39999998 11.9 1.22 C 14.04 2.6 16.08 5.2999997 16.08 8.58 C 16.08 11.54 14.259999 13.66 11.34 13.66 Z M 14.2 9.32 C 14.2 7.06 13.179999 4.3199997 12.139999 2.98 C 11 1.52 9.5 0.78 7.62 0.78 L 5.4 0.78 C 5.18 0.78 5.04 0.78 4.96 0.79999995 C 4.8399997 0.79999995 4.7799997 0.84 4.7799997 0.9 C 4.7799997 0.94 4.8199997 1.0799999 4.88 1.3399999 L 7.58 12.2 C 7.7599998 12.86 7.74 12.88 8.58 12.88 L 10.7 12.88 C 12.94 12.88 14.2 11.559999 14.2 9.32 Z "/>
</symbol>
<symbol id="gC2DD8543DFECD814014D8080F661102C" overflow="visible">
<path d="M 6.3599997 -4.96 C 6.54 -4.96 6.64 -4.8599997 6.64 -4.68 C 6.64 -4.62 6.6 -4.54 6.54 -4.46 C 5.5 -3.6599998 4.66 -2.34 4.04 -0.52 C 3.5 1.06 3.22 2.62 3.22 4.16 L 3.22 5.8399997 C 3.22 7.3799996 3.5 8.94 4.04 10.5199995 C 4.66 12.34 5.5 13.66 6.54 14.46 C 6.6 14.5199995 6.64 14.599999 6.64 14.679999 C 6.64 14.86 6.54 14.96 6.3599997 14.96 C 6.3399997 14.96 6.2799997 14.94 6.22 14.9 C 5.02 13.98 4.02 12.62 3.1999998 10.8 C 2.4199998 9.059999 2.02 7.4199996 2.02 5.8399997 L 2.02 4.16 C 2.02 2.58 2.4199998 0.94 3.1999998 -0.79999995 C 4.02 -2.62 5.02 -3.98 6.22 -4.9 C 6.2799997 -4.94 6.3399997 -4.96 6.3599997 -4.96 Z "/>
</symbol>
<symbol id="g5086E516F5DAE44F1BD2167760C4A5F1" overflow="visible">
<path d="M 2.78 2.12 C 2.1399999 2.12 1.7199999 1.64 1.7199999 1 C 1.7199999 0.39999998 2.18 -0.099999994 2.78 -0.099999994 C 3.06 -0.099999994 3.3 -0.02 3.48 0.16 L 3.5 0 C 3.5 -1.26 3.08 -2.34 2.24 -3.1999998 C 2.1 -3.36 2.02 -3.48 2.02 -3.56 C 2.02 -3.76 2.1 -3.86 2.28 -3.86 C 2.46 -3.86 2.7 -3.62 3.04 -3.1599998 C 3.72 -2.2 4.06 -1.14 4.06 0 C 4.06 1.06 3.6999998 2.12 2.78 2.12 Z "/>
</symbol>
<symbol id="g62484110D9EA4D906DF8002209024D54" overflow="visible">
<path d="M 1.56 -4.9 C 2.76 -3.98 3.76 -2.62 4.58 -0.79999995 C 5.3599997 0.94 5.7599998 2.58 5.7599998 4.16 L 5.7599998 5.8399997 C 5.7599998 7.4199996 5.3599997 9.059999 4.58 10.8 C 3.76 12.62 2.76 13.98 1.56 14.9 C 1.5 14.94 1.4399999 14.96 1.42 14.96 C 1.24 14.96 1.14 14.86 1.14 14.679999 C 1.14 14.599999 1.18 14.5199995 1.24 14.46 C 2.28 13.66 3.12 12.34 3.74 10.5199995 C 4.2799997 8.94 4.56 7.3799996 4.56 5.8399997 L 4.56 4.16 C 4.56 2.62 4.2799997 1.06 3.74 -0.52 C 3.12 -2.34 2.28 -3.6599998 1.24 -4.46 C 1.18 -4.54 1.14 -4.62 1.14 -4.68 C 1.14 -4.8599997 1.24 -4.96 1.42 -4.96 C 1.4399999 -4.96 1.5 -4.94 1.56 -4.9 Z "/>
</symbol>
<symbol id="g5A3E6390ABDCC3643B02834E2D933712" overflow="visible">
<path d="M 13.719999 4.54 C 13.92 4.64 14.0199995 4.7799997 14.0199995 5 C 14.0199995 5.22 13.92 5.3599997 13.719999 5.46 L 2.24 10.9 C 2.18 10.92 2.1 10.94 2.02 10.94 C 1.6999999 10.94 1.54 10.78 1.54 10.44 C 1.54 10.26 1.64 10.12 1.8199999 10.04 L 12.5 5 L 1.8199999 -0.04 C 1.64 -0.12 1.54 -0.26 1.54 -0.44 C 1.54 -0.78 1.6999999 -0.94 2.02 -0.94 C 2.1 -0.94 2.18 -0.91999996 2.24 -0.9 Z "/>
</symbol>
<symbol id="gE451DF5392AF56A17EDB1EB9E2655F47" overflow="visible">
<path d="M 2.48 2.58 C 2.48 3.06 2.58 3.72 2.78 4.54 L 3.76 4.54 C 5.06 4.54 6.06 4.7 6.7799997 5 C 7.44 5.2799997 7.8799996 5.68 8.099999 6.18 C 8.24 6.52 8.3 6.8399997 8.3 7.1 C 8.3 8.2 7.2599998 8.84 6.14 8.84 C 5.3599997 8.84 4.58 8.639999 3.8 8.24 C 2.26 7.44 0.91999996 5.62 0.91999996 3.4199998 C 0.91999996 1.38 2.1 -0.22 4.08 -0.22 C 5.14 -0.22 6.08 0.04 6.8999996 0.53999996 C 7.58 0.96 8.08 1.38 8.4 1.8 C 8.54 1.9799999 8.599999 2.12 8.599999 2.18 C 8.599999 2.3999999 8.5 2.52 8.28 2.52 C 8.179999 2.52 8.08 2.44 7.96 2.28 C 7.2999997 1.4 6.48 0.84 5.54 0.59999996 C 4.92 0.44 4.46 0.35999998 4.12 0.35999998 C 2.98 0.35999998 2.48 1.4399999 2.48 2.58 Z M 7.5 7.1 C 7.5 5.7799997 6.22 5.12 3.6399999 5.12 L 2.9399998 5.12 C 3.32 6.44 3.8799999 7.3199997 4.64 7.74 C 5.24 8.08 5.74 8.26 6.14 8.26 C 6.8599997 8.26 7.5 7.8199997 7.5 7.1 Z "/>
</symbol>
<symbol id="g612BB0D9B453ACEC45B2B13686D7BB71" overflow="visible">
<path d="M 1.4599999 1.68 L 6.74 4.64 L 1.4599999 7.6 Z "/>
</symbol>
<symbol id="gFF563528CC412172074F774399BF4710" overflow="visible">
<path d="M 13.32 -0.9 C 13.66 -1.04 14.0199995 -0.78 14.0199995 -0.45999998 C 14.0199995 -0.26 13.92 -0.12 13.74 -0.04 L 3.06 5 L 13.74 10.04 C 13.92 10.12 14.0199995 10.26 14.0199995 10.44 C 14.0199995 10.78 13.86 10.94 13.54 10.94 C 13.46 10.94 13.38 10.92 13.32 10.9 L 1.8399999 5.46 C 1.64 5.3599997 1.54 5.22 1.54 5 C 1.54 4.7799997 1.64 4.64 1.8399999 4.54 Z "/>
</symbol>
<symbol id="gE1442E8CAAFDCA3BCCB763C26EB6A12C" overflow="visible">
<path d="M 2.78 -5 C 3.04 -5 3.1799998 -4.8399997 3.1799998 -4.52 L 3.1799998 14.5199995 C 3.1799998 14.839999 3.04 15 2.78 15 C 2.52 15 2.3799999 14.839999 2.3799999 14.5199995 L 2.3799999 -4.52 C 2.3799999 -4.8399997 2.52 -5 2.78 -5 Z "/>
</symbol>
<symbol id="g7CDEAAC4FEAEC30DB2F902B0A7AF7CE" overflow="visible">
<path d="M 1.3199999 4.7599998 L 9.4 4.7599998 C 9.66 4.7599998 9.92 5.16 9.92 5.4 C 9.92 5.58 9.86 5.74 9.639999 5.74 L 1.56 5.74 C 1.3199999 5.74 1.04 5.3399997 1.04 5.1 C 1.04 4.94 1.1 4.7599998 1.3199999 4.7599998 Z "/>
</symbol>
<symbol id="g316778D5069ED68A0C52C06F0AD18D23" overflow="visible">
<path d="M 1.14 0.85999995 C 1.14 0.28 1.62 -0.19999999 2.2 -0.19999999 C 2.78 -0.19999999 3.26 0.28 3.26 0.85999995 C 3.26 1.4399999 2.78 1.92 2.2 1.92 C 1.62 1.92 1.14 1.4399999 1.14 0.85999995 Z "/>
</symbol>
<symbol id="g8D44D9C01F9AF6C3B1D634FDF54DE6FB" overflow="visible">
<path d="M 5.66 6.46 C 7.3599997 6.46 7.4199996 6 7.48 5.1 C 7.6 4.98 8.0199995 4.98 8.139999 5.1 C 8.12 5.6 8.099999 6.18 8.099999 6.8599997 C 8.099999 7.54 8.12 8.059999 8.139999 8.58 C 8.0199995 8.7 7.6 8.7 7.48 8.58 C 7.4199996 7.48 7.3599997 7.22 5.66 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.9 4.04 12.099999 4.92 12.099999 L 5.8199997 12.099999 C 7.94 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.92 9.34 9.96 9.5 10.0199995 C 9.4 10.84 9.099999 12.759999 9.059999 12.92 C 9.059999 12.96 9.04 12.98 8.98 12.98 C 8.639999 12.92 8.54 12.9 8.04 12.9 L 2.9399998 12.9 C 2.3 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.06 -0.02 2.06 0 2.96 0 C 3.86 0 4.8399997 -0.02 5.54 -0.04 C 5.66 0.08 5.66 0.5 5.54 0.62 C 4.14 0.68 3.8 0.78 3.8 2.44 L 3.8 6.46 Z "/>
</symbol>
<symbol id="g18D1F1E967E0B15C3E9466BFBC921865" overflow="visible">
<path d="M 7.8599997 9.7 C 7.8599997 11.139999 6.74 12.2 4.7799997 12.2 C 2.74 12.2 1.42 10.98 1.42 9.44 C 1.42 8.32 1.9599999 7.5 3.1799998 6.74 L 3.6999998 6.42 C 3.12 6.12 2.58 5.7599998 2.08 5.3199997 C 1.26 4.6 0.91999996 3.6999998 0.91999996 2.9199998 C 0.91999996 0.88 2.36 -0.19999999 4.48 -0.19999999 C 7.1 -0.19999999 8.38 1.7199999 8.38 3.24 C 8.38 4.4 7.8799996 5.42 6.8199997 6.06 L 5.4 6.92 C 6.3399997 7.3799996 7.8599997 8.42 7.8599997 9.7 Z M 4.52 0.5 C 3.62 0.5 2.26 1.12 2.26 2.9199998 C 2.26 3.52 2.52 4.92 4.24 6.06 L 5.18 5.5 C 6.42 4.74 6.92 3.8 6.92 2.84 C 6.92 0.84 5.42 0.5 4.52 0.5 Z M 4.68 11.5 C 5.98 11.5 6.46 10.639999 6.46 9.719999 C 6.46 8.639999 5.4 7.74 4.8599997 7.3399997 L 4.24 7.72 C 2.98 8.54 2.84 9.2 2.84 9.82 C 2.84 10.74 3.48 11.5 4.68 11.5 Z "/>
</symbol>
<symbol id="gAA14E57E2DCC57A3F7809273EECD3C51" overflow="visible">
<path d="M 7.9104 1.5616 L 7.9104 6.6944 C 7.9104 7.7567997 8.128 7.8208 9.024 7.8592 C 9.1008 7.936 9.1008 8.2048 9.024 8.2816 C 8.4992 8.2688 7.8464 8.256 7.3599997 8.256 C 6.8863997 8.256 6.272 8.2688 5.7088 8.2816 C 5.632 8.2048 5.632 7.936 5.7088 7.8592 C 6.6047997 7.8208 6.8223996 7.7567997 6.8223996 6.6944 L 6.8223996 4.6464 L 2.4448 4.6464 L 2.4448 6.6944 C 2.4448 7.7567997 2.6624 7.8208 3.5584 7.8592 C 3.6352 7.936 3.6352 8.2048 3.5584 8.2816 C 3.072 8.2688 2.5472 8.256 1.8944 8.256 C 1.2544 8.256 0.72959995 8.2688 0.24319999 8.2816 C 0.1664 8.2048 0.1664 7.936 0.24319999 7.8592 C 1.1392 7.8208 1.3568 7.7567997 1.3568 6.6944 L 1.3568 1.5616 C 1.3568 0.4992 1.1392 0.43519998 0.24319999 0.39679998 C 0.1664 0.32 0.1664 0.0512 0.24319999 -0.0256 C 0.8064 -0.0128 1.4208 0 1.9072 0 C 2.368 0 2.9952 -0.0128 3.5584 -0.0256 C 3.6352 0.0512 3.6352 0.32 3.5584 0.39679998 C 2.6624 0.43519998 2.4448 0.4992 2.4448 1.5616 L 2.4448 4.1088 L 6.8223996 4.1088 L 6.8223996 1.5616 C 6.8223996 0.4992 6.6047997 0.43519998 5.7088 0.39679998 C 5.632 0.32 5.632 0.0512 5.7088 -0.0256 C 6.2848 -0.0128 6.8992 0 7.3728 0 C 7.8464 0 8.4608 -0.0128 9.024 -0.0256 C 9.1008 0.0512 9.1008 0.32 9.024 0.39679998 C 8.128 0.43519998 7.9104 0.4992 7.9104 1.5616 Z "/>
</symbol>
<symbol id="gF5F8064101DBF0FCB4BCFDA7012527FE" overflow="visible">
<path d="M 2.3167999 1.5616 L 2.3167999 4.1088 C 2.3167999 4.7488 2.368 5.568 2.368 5.568 C 2.368 5.6191998 2.304 5.6576 2.2015998 5.6576 C 1.8432 5.5168 1.3312 5.4016 0.44799998 5.2864 C 0.4224 5.2096 0.44799998 5.0048 0.4736 4.928 C 1.1776 4.864 1.3055999 4.7872 1.3055999 4.0576 L 1.3055999 1.5616 C 1.3055999 0.4992 1.1647999 0.4608 0.384 0.39679998 C 0.30719998 0.32 0.30719998 0.0512 0.384 -0.0256 C 0.8064 -0.0128 1.3055999 0 1.8176 0 C 2.3295999 0 2.816 -0.0128 3.2384 -0.0256 C 3.3151999 0.0512 3.3151999 0.32 3.2384 0.39679998 C 2.4575999 0.44799998 2.3167999 0.4992 2.3167999 1.5616 Z M 1.152 7.6671996 C 1.152 7.3343997 1.4591999 7.0016 1.7664 7.0016 C 2.1248 7.0016 2.432 7.3472 2.432 7.6159997 C 2.432 7.9231997 2.1632 8.2816 1.8176 8.2816 C 1.5103999 8.2816 1.152 7.9743996 1.152 7.6671996 Z "/>
</symbol>
<symbol id="g3976D55F213F07C6469FD06EC16139AA" overflow="visible">
<path d="M 4.9407997 1.1904 C 4.4672 0.704 4.0959997 0.4992 3.3536 0.4992 C 2.8927999 0.4992 2.3552 0.768 1.9583999 1.4208 C 1.7024 1.8432 1.5488 2.432 1.5488 3.1743999 L 4.9536 3.1488 C 5.1071997 3.1488 5.1967998 3.2256 5.1967998 3.3664 C 5.1967998 4.4416 4.8128 5.5936 3.0335999 5.5936 C 1.92 5.5936 0.4736 4.5312 0.4736 2.5856 C 0.4736 1.8687999 0.65279996 1.1776 1.0752 0.69119996 C 1.5103999 0.1792 2.112 -0.12799999 3.0335999 -0.12799999 C 4.0064 -0.12799999 4.6976 0.32 5.2096 0.9856 C 5.1712 1.1136 5.0944 1.1776 4.9407997 1.1904 Z M 1.5871999 3.6095998 C 1.8304 5.0559998 2.7264 5.1712 3.0335999 5.1712 C 3.52 5.1712 4.0959997 4.9024 4.0959997 3.8272 C 4.0959997 3.712 4.0448 3.648 3.9039998 3.648 Z "/>
</symbol>
<symbol id="gB7BB853387AAC07ADB7DDEF96856059B" overflow="visible">
<path d="M 2.2528 4.5824 C 2.2272 5.0944 2.2144 5.4272 2.1504 5.5551996 C 2.1248 5.6191998 2.0992 5.6576 1.9968 5.6576 C 1.6384 5.5168 1.3055999 5.4016 0.4224 5.2864 C 0.39679998 5.2096 0.4224 5.0048 0.44799998 4.928 C 1.1392 4.864 1.28 4.7999997 1.28 4.0576 L 1.28 1.5616 C 1.28 0.4992 1.1264 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7808 -0.0128 1.28 0 1.7919999 0 C 2.304 0 2.8927999 -0.0128 3.3407998 -0.0256 C 3.4176 0.0512 3.4176 0.32 3.3407998 0.39679998 C 2.4448 0.4608 2.2912 0.4992 2.2912 1.5616 L 2.2912 3.3407998 C 2.2912 3.6736 2.4448 3.968 2.5983999 4.1984 C 2.7391999 4.4031997 3.0335999 4.8255997 3.1871998 4.8255997 C 3.3023999 4.8255997 3.4176 4.7999997 3.52 4.6591997 C 3.6095998 4.5312 3.7631998 4.3648 3.9808 4.3648 C 4.288 4.3648 4.5824 4.6847997 4.5824 5.0048 C 4.5824 5.2479997 4.3519998 5.6191998 3.8144 5.6191998 C 3.2128 5.6191998 2.688 5.0559998 2.3936 4.5568 C 2.3167999 4.416 2.2528 4.5183997 2.2528 4.5824 Z "/>
</symbol>
<symbol id="gF8EC31AC53CF59E01ED9143906F6DA7B" overflow="visible">
<path d="M 3.7503998 0.61439997 C 3.8272 0.21759999 3.968 -0.12799999 4.608 -0.12799999 C 5.0944 -0.12799999 5.5551996 0.0896 5.824 0.34559998 C 5.7984 0.4992 5.7472 0.61439997 5.6064 0.69119996 C 5.5168 0.61439997 5.2992 0.48639998 5.1328 0.48639998 C 4.7616 0.48639998 4.7488 0.9856 4.7488 1.5744 L 4.7488 3.4559999 C 4.7488 5.2736 3.7503998 5.6191998 2.816 5.6191998 C 1.7664 5.6191998 0.704 4.928 0.704 4.1984 C 0.704 3.8911998 0.8576 3.7375998 1.152 3.7375998 C 1.5231999 3.7375998 1.7536 4.0064 1.7536 4.1728 C 1.7536 4.2623997 1.7407999 4.3519998 1.7152 4.4031997 C 1.7024 4.4416 1.6896 4.5183997 1.6896 4.6591997 C 1.6896 5.0559998 2.2272 5.1967998 2.7136 5.1967998 C 3.1488 5.1967998 3.7503998 4.9792 3.7503998 3.5328 C 3.7503998 3.4431999 3.712 3.392 3.6736 3.3792 L 2.5728 3.1104 C 1.344 2.8032 0.4608 2.1248 0.4608 1.2544 C 0.4608 0.2048 1.1776 -0.12799999 2.0736 -0.12799999 C 2.5216 -0.12799999 2.9055998 -0.0256 3.4687998 0.4096 L 3.7247999 0.61439997 Z M 3.7503998 2.9824 L 3.7503998 1.2928 C 3.7503998 1.1264 3.6736 1.0368 3.5712 0.96 C 3.2384 0.69119996 2.8032 0.39679998 2.4448 0.39679998 C 1.8047999 0.39679998 1.5231999 0.9088 1.5231999 1.3055999 C 1.5231999 1.8815999 1.7919999 2.4703999 2.7391999 2.7136 Z "/>
</symbol>
<symbol id="g68DDE7C8FDC8A226B6C32EAD39AF7364" overflow="visible">
<path d="M 5.0944 1.1647999 C 5.0432 1.28 4.9407997 1.3312 4.8255997 1.344 C 4.3904 0.7808 3.84 0.4992 3.2896 0.4992 C 2.3552 0.4992 1.5744 1.4463999 1.5744 2.944 C 1.5744 4.3519998 2.1887999 5.1967998 3.0335999 5.1967998 C 3.7888 5.1967998 3.8911998 4.7488 3.9424 4.3008 C 3.9808 3.9552 4.16 3.84 4.4288 3.84 C 4.6976 3.84 5.0559998 4.0064 5.0559998 4.4031997 C 5.0559998 5.1071997 4.3264 5.6191998 3.0976 5.6191998 C 1.8304 5.6191998 0.4736 4.48 0.4736 2.6624 C 0.4736 1.0112 1.3952 -0.12799999 3.008 -0.12799999 C 3.776 -0.12799999 4.4544 0.1152 5.0944 1.1647999 Z "/>
</symbol>
<symbol id="g570B752173035444311A253BD2376AD" overflow="visible">
<path d="M 2.1376 3.6608 C 2.1376 3.9296 2.2528 4.0832 2.3552 4.1984 C 2.8416 4.672 3.4944 4.9536 3.9936 4.9536 C 4.2496 4.9536 4.5183997 4.7872 4.672 4.4927998 C 4.7999997 4.2367997 4.8255997 3.8911998 4.8255997 3.5072 L 4.8255997 1.5616 C 4.8255997 0.51199996 4.6976 0.4608 4.032 0.39679998 C 3.968 0.32 3.968 0.0512 4.032 -0.0256 C 4.3904 -0.0128 4.8255997 0 5.3375998 0 C 5.8496 0 6.272 -0.0128 6.6944 -0.0256 C 6.7584 0.0512 6.7584 0.32 6.6944 0.39679998 C 5.9775996 0.4608 5.8367996 0.51199996 5.8367996 1.5616 L 5.8367996 3.4687998 C 5.8367996 4.1728 5.7855997 4.7999997 5.4912 5.184 C 5.2736 5.4656 4.8768 5.6191998 4.4288 5.6191998 C 3.8016 5.6191998 3.0335999 5.4528 2.2528 4.5824 C 2.2528 4.5696 2.24 4.5696 2.2272 4.5568 C 2.1887999 4.5056 2.1248 4.4288 2.1248 4.5824 L 2.1376 7.4624 C 2.1376 8.2944 2.1887999 8.806399 2.1887999 8.806399 C 2.1887999 8.896 2.1376 8.9344 2.0224 8.9344 C 1.7024 8.806399 0.7424 8.6272 0.2304 8.588799 C 0.2048 8.4864 0.2304 8.2816 0.30719998 8.2048 C 0.34559998 8.2048 0.384 8.2048 0.4224 8.2048 C 0.9856 8.1664 1.1264 8.1664 1.1264 7.1552 L 1.1264 1.5616 C 1.1264 0.4992 0.97279996 0.44799998 0.2304 0.39679998 C 0.15359999 0.32 0.15359999 0.0512 0.2304 -0.0256 C 0.65279996 -0.0128 1.1264 0 1.6384 0 C 2.1248 0 2.5472 -0.0128 2.9055998 -0.0256 C 2.9824 0.0512 2.9824 0.32 2.9055998 0.39679998 C 2.2528 0.44799998 2.1376 0.4992 2.1376 1.5616 Z "/>
</symbol>
<symbol id="g9662C1D9A80FEB5040A57FD9DFCA7985" overflow="visible">
<path d="M 1.216 1.5616 C 1.216 0.4992 1.0752 0.43519998 0.2944 0.39679998 C 0.21759999 0.32 0.21759999 0.0512 0.2944 -0.0256 C 0.7424 -0.0128 1.216 0 1.7279999 0 C 2.24 0 2.7264 -0.0128 3.1488 -0.0256 C 3.2256 0.0512 3.2256 0.32 3.1488 0.39679998 C 2.368 0.43519998 2.2272 0.4992 2.2272 1.5616 L 2.2272 7.4624 C 2.2272 8.2944 2.2784 8.806399 2.2784 8.806399 C 2.2784 8.896 2.2272 8.9344 2.112 8.9344 C 1.7919999 8.806399 0.83199996 8.6272 0.32 8.588799 C 0.2944 8.4864 0.32 8.2816 0.39679998 8.2048 C 1.1392 8.1536 1.216 8.1152 1.216 7.1552 Z "/>
</symbol>
<symbol id="g1CB3EC9D05726EBFDE8ADABEC8504FCD" overflow="visible">
<path d="M 7.1168 6.5536 L 7.1168 2.368 C 7.1168 2.1248 7.1168 1.984 7.0271997 1.984 C 6.976 1.984 6.784 2.2144 6.4128 2.688 L 2.0224 8.256 L 0.2944 8.2816 C 0.21759999 8.2048 0.21759999 7.936 0.2944 7.8592 C 0.8448 7.8208 1.2287999 7.3728 1.3055999 7.04 L 1.3055999 1.7024 C 1.3055999 0.5632 1.0879999 0.48639998 0.192 0.39679998 C 0.1152 0.32 0.1152 0.0512 0.192 -0.0256 C 0.7424 -0.0128 1.3184 0 1.6256 0 C 1.92 0 2.5088 -0.0128 3.0463998 -0.0256 C 3.1232 0.0512 3.1232 0.32 3.0463998 0.39679998 C 2.1504 0.48639998 1.9327999 0.5376 1.9327999 1.7024 L 1.9327999 5.6191998 C 1.9327999 6.0544 1.9327999 6.2464 2.0351999 6.2464 C 2.112 6.2464 2.2528 6.1056 2.4703999 5.824 L 6.9375997 0.1792 C 7.0783997 -0.0128 7.2447996 -0.12799999 7.4495997 -0.12799999 C 7.6288 -0.12799999 7.744 0.0256 7.744 0.2688 L 7.744 6.5536 C 7.744 7.6927996 7.9616 7.7696 8.8576 7.8592 C 8.9344 7.936 8.9344 8.2048 8.8576 8.2816 C 8.3328 8.2688 7.7311997 8.256 7.424 8.256 C 7.1552 8.256 6.5664 8.2688 6.0032 8.2816 C 5.9263997 8.2048 5.9263997 7.936 6.0032 7.8592 C 6.8992 7.7696 7.1168 7.7184 7.1168 6.5536 Z "/>
</symbol>
<symbol id="gD62975B7DE3250BE5F195D0E8335F60D" overflow="visible">
<path d="M 4.16 5.0944 C 4.8512 5.0432 4.928 4.8896 4.6591997 4.2367997 L 3.6223998 1.7279999 C 3.4176 1.2287999 3.3536 1.2287999 3.1488 1.7664 L 2.2272 4.2367997 C 1.9968 4.8512 1.9455999 5.0048 2.6239998 5.0944 C 2.7008 5.1712 2.7008 5.44 2.6239998 5.5168 C 2.2015998 5.5039997 1.7536 5.4912 1.3312 5.4912 C 0.9088 5.4912 0.5248 5.5039997 0.1408 5.5168 C 0.063999996 5.44 0.063999996 5.1712 0.1408 5.0944 C 0.8192 5.0176 0.9088 4.8128 1.1647999 4.16 L 2.8032 0.1152 C 2.8799999 -0.076799996 2.9568 -0.15359999 3.1232 -0.15359999 C 3.2512 -0.15359999 3.3407998 -0.076799996 3.4304 0.1408 L 5.1328 4.1472 C 5.376 4.7104 5.5168 5.0304 6.2335997 5.0944 C 6.3104 5.1712 6.3104 5.44 6.2335997 5.5168 C 5.9775996 5.5039997 5.6703997 5.4912 5.3375998 5.4912 C 4.9151998 5.4912 4.48 5.5039997 4.16 5.5168 C 4.0832 5.44 4.0832 5.1712 4.16 5.0944 Z "/>
</symbol>
<symbol id="gEFCBD5CCFA072E8B49E2065B449FDBBF" overflow="visible">
<path d="M 5.6832 4.9536 C 5.9263997 4.9536 6.1568 5.184 6.1568 5.44 C 6.1568 5.7088 5.9136 5.9136 5.568 5.9136 C 5.2352 5.9136 4.6208 5.6959996 4.288 5.2608 C 4.1344 5.3631997 3.712 5.6191998 2.9568 5.6191998 C 1.8176 5.6191998 0.768 4.8512 0.768 3.6736 C 0.768 2.9824 1.0752 2.5856 1.4336 2.24 C 1.0752 1.9327999 0.87039995 1.3823999 0.87039995 0.9472 C 0.87039995 0.48639998 1.1264 0.12799999 1.4591999 -0.038399998 C 0.768 -0.44799998 0.4096 -1.0368 0.4096 -1.5871999 C 0.4096 -2.7008 1.4591999 -3.0463998 2.4448 -3.0463998 C 4.1728 -3.0463998 6.0415998 -2.2144 6.0415998 -0.83199996 C 6.0415998 -0.4224 5.8496 -0.1024 5.4783998 0.2048 C 4.9792 0.61439997 4.0832 0.6272 3.6095998 0.6272 C 3.3792 0.6272 3.0591998 0.6016 2.7519999 0.5632 C 2.56 0.55039996 2.432 0.5376 2.368 0.5376 C 1.9968 0.5376 1.5488 0.7168 1.5488 1.2672 C 1.5488 1.5231999 1.6256 1.7919999 1.7792 2.0096 C 2.0864 1.8304 2.4448 1.7407999 2.944 1.7407999 C 4.0703998 1.7407999 5.1071997 2.4448 5.1071997 3.6992 C 5.1071997 4.3008 4.928 4.6464 4.5568 5.0304 C 4.6464 5.1584 4.9024 5.3375998 5.0688 5.3375998 C 5.1584 5.3375998 5.2479997 5.2992 5.3248 5.184 C 5.376 5.0815997 5.5424 4.9536 5.6832 4.9536 Z M 1.6896 -0.12799999 C 1.8304 -0.1664 2.0351999 -0.192 2.2015998 -0.192 C 2.5983999 -0.192 2.9568 -0.15359999 3.136 -0.15359999 C 3.776 -0.15359999 4.3136 -0.1664 4.6847997 -0.3712 C 5.184 -0.65279996 5.3375998 -0.83199996 5.3375998 -1.1647999 C 5.3375998 -2.0864 3.9808 -2.5728 2.8288 -2.5728 C 2.368 -2.5728 1.2928 -2.2015998 1.2928 -1.3312 C 1.2928 -0.89599997 1.3184 -0.576 1.6896 -0.12799999 Z M 4.0832 3.5712 C 4.0832 2.3808 3.4815998 2.1376 3.008 2.1376 C 1.9327999 2.1376 1.8176 3.0463998 1.8176 3.8655999 C 1.8176 4.7616 2.1376 5.2223997 2.8416 5.2223997 C 3.648 5.2223997 4.0832 4.6335998 4.0832 3.5712 Z "/>
</symbol>
<symbol id="gD5EEFB9760BC9A91B84F628EDDA52971" overflow="visible">
<path d="M 2.1376 5.0432 C 2.0607998 4.9663997 2.0096 4.992 2.0096 5.1071997 L 2.0096 7.4624 C 2.0096 8.2944 2.0607998 8.806399 2.0607998 8.806399 C 2.0607998 8.896 2.0096 8.9344 1.8944 8.9344 C 1.5744 8.806399 0.61439997 8.6272 0.1024 8.588799 C 0.076799996 8.4864 0.1024 8.2816 0.1792 8.2048 C 0.21759999 8.2048 0.25599998 8.2048 0.2944 8.2048 C 0.8576 8.1664 0.9984 8.1664 0.9984 7.1552 L 0.9984 0.9088 C 0.9984 0.4096 0.9856 0.1792 0.9472 0 C 1.0112 -0.1024 1.0752 -0.15359999 1.2287999 -0.15359999 C 1.3055999 -0.076799996 1.4336 0.038399998 1.536 0.15359999 C 1.6639999 0.30719998 1.7407999 0.30719998 1.8815999 0.192 C 2.1759999 -0.0512 2.56 -0.12799999 3.008 -0.12799999 C 4.3136 -0.12799999 5.8367996 1.0624 5.8367996 3.0976 C 5.8367996 4.6591997 4.6847997 5.6191998 3.5712 5.6191998 C 3.0207999 5.6191998 2.5344 5.4016 2.1376 5.0432 Z M 2.2272 4.6464 C 2.56 4.9407997 2.944 5.0559998 3.3151999 5.0559998 C 4.0959997 5.0559998 4.736 4.1088 4.736 2.8672 C 4.736 1.408 4.1472 0.30719998 2.9312 0.30719998 C 2.5344 0.30719998 2.2656 0.5888 2.0096 0.9088 L 2.0096 4.1088 C 2.0096 4.3775997 2.0607998 4.5056 2.2272 4.6464 Z "/>
</symbol>
<symbol id="g83A6AA7A836EACB3652229F4716CDAF" overflow="visible">
<path d="M 5.0559998 8.076799 C 4.3136 8.1792 4.3392 8.4223995 3.0848 8.4223995 C 1.7919999 8.4223995 0.65279996 7.5648 0.65279996 6.2079997 C 0.65279996 4.864 1.7664 4.2496 2.8927999 3.8144 C 3.6608 3.52 4.608 3.1615999 4.608 1.9072 C 4.608 0.87039995 4.032 0.3328 3.008 0.3328 C 1.8176 0.3328 1.0496 0.8832 0.768 2.1504 C 0.6016 2.2015998 0.4736 2.1759999 0.34559998 2.112 C 0.39679998 1.1264 0.44799998 0.79359996 0.6016 0.1664 C 1.408 0.1664 1.7664 -0.12799999 2.9055998 -0.12799999 C 3.4815998 -0.12799999 4.032 0.0128 4.48 0.2944 C 5.2223997 0.75519997 5.6832 1.536 5.6832 2.3552 C 5.6832 3.712 4.6591997 4.3136 3.6095998 4.7104 C 2.8416 4.992 1.5616 5.4783998 1.5616 6.5536 C 1.5616 7.2704 2.2144 7.9872 2.9696 7.9872 C 4.2111998 7.9872 4.608 7.1935997 4.864 6.3487997 C 5.0048 6.3231997 5.1712 6.336 5.2864 6.4256 C 5.2352 7.04 5.184 7.3984 5.0559998 8.076799 Z "/>
</symbol>
<symbol id="gDB4862E33098F259EEBBA99A57E5AFA" overflow="visible">
<path d="M 2.1759999 4.5824 C 2.1632 4.9663997 2.1376 5.4272 2.0736 5.5551996 C 2.0479999 5.6191998 2.0224 5.6576 1.92 5.6576 C 1.5616 5.5168 1.2287999 5.4016 0.34559998 5.2864 C 0.32 5.2096 0.34559998 5.0048 0.3712 4.928 C 1.0624 4.864 1.2032 4.7999997 1.2032 4.0576 L 1.2032 1.5616 C 1.2032 0.51199996 1.0368 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7168 -0.0128 1.2032 0 1.7152 0 C 2.2272 0 2.6239998 -0.0128 3.008 -0.0256 C 3.0848 0.0512 3.0848 0.32 3.008 0.39679998 C 2.3552 0.4608 2.2144 0.51199996 2.2144 1.5616 L 2.2144 3.6608 C 2.2144 3.9296 2.3295999 4.0832 2.432 4.1984 C 2.944 4.6976 3.4176 4.9536 3.8144 4.9536 C 4.3008 4.9536 4.6591997 4.6464 4.6591997 3.7888 L 4.6591997 1.5616 C 4.6591997 0.51199996 4.5568 0.44799998 3.8655999 0.39679998 C 3.8016 0.32 3.8016 0.0512 3.8655999 -0.0256 C 4.1856 -0.0128 4.6591997 0 5.1712 0 C 5.6832 0 6.1056 -0.0128 6.4256 -0.0256 C 6.4895997 0.0512 6.4895997 0.32 6.4256 0.39679998 C 5.7855997 0.44799998 5.6703997 0.51199996 5.6703997 1.5616 L 5.6703997 3.5967999 C 5.6703997 3.776 5.6703997 3.9552 5.6576 4.1088 C 6.272 4.7872 6.848 4.9536 7.3472 4.9536 C 7.8335996 4.9536 8.1152 4.672 8.1152 3.8144 L 8.1152 1.5616 C 8.1152 0.51199996 7.9872 0.44799998 7.3216 0.39679998 C 7.2576 0.32 7.2576 0.0512 7.3216 -0.0256 C 7.6415997 -0.0128 8.1152 0 8.6272 0 C 9.1392 0 9.5872 -0.0128 9.9456 -0.0256 C 10.0096 0.0512 10.0096 0.32 9.9456 0.39679998 C 9.2416 0.44799998 9.1264 0.51199996 9.1264 1.5616 L 9.1264 3.5839999 C 9.1264 4.7232 8.9344 5.6191998 7.8079996 5.6191998 C 7.1552 5.6191998 6.3616 5.376 5.6959996 4.672 C 5.6576 4.6335998 5.5808 4.5696 5.5551996 4.6847997 C 5.44 5.2096 4.9407997 5.6191998 4.2752 5.6191998 C 3.5328 5.6191998 2.8672 5.184 2.3295999 4.5824 C 2.2656 4.5183997 2.1887999 4.4288 2.1759999 4.5824 Z "/>
</symbol>
<symbol id="g793DBE65A5AEC1A16A65955B6C0E046" overflow="visible">
<path d="M 10.368 7.232 L 8.3712 1.6768 L 8.3328 1.6896 L 6.5664 7.0912 C 6.3487997 7.7823997 6.7967997 7.8208 7.232 7.8592 C 7.3087997 7.936 7.3087997 8.2048 7.232 8.2816 C 6.7072 8.2688 6.144 8.256 5.632 8.256 C 5.2096 8.256 4.7616 8.2688 4.3519998 8.2816 C 4.2752 8.2048 4.2752 7.936 4.3519998 7.8592 C 5.0304 7.8208 5.312 7.424 5.4272 7.0912 L 5.7216 6.2464 C 5.7728 6.0927997 5.8111997 5.9648 5.8111997 5.8496 C 5.8111997 5.7216 5.7984 5.6191998 5.6959996 5.4016 L 4.0448 1.6511999 L 3.9808 1.6639999 L 2.112 7.3216 C 1.9583999 7.7696 2.304 7.8335996 2.7519999 7.8592 C 2.8288 7.936 2.8288 8.2048 2.7519999 8.2816 C 2.3295999 8.2688 1.7664 8.256 1.2672 8.256 C 0.8192 8.256 0.44799998 8.2688 0.076799996 8.2816 C 0 8.2048 0 7.936 0.076799996 7.8592 C 0.65279996 7.8208 0.7424 7.8079996 0.9856 7.1168 L 3.392 0.192 C 3.4559999 -0.0128 3.5328 -0.15359999 3.6736 -0.15359999 C 3.84 -0.15359999 3.9167998 -0.0256 4.0064 0.192 L 5.9136 4.48 C 6.0288 4.736 6.0671997 4.7999997 6.1312 4.7999997 C 6.1823997 4.7999997 6.2335997 4.6591997 6.3104 4.4416 L 7.7823997 0.192 C 7.8592 -0.0256 7.9231997 -0.15359999 8.076799 -0.15359999 C 8.2176 -0.15359999 8.3071995 -0.0128 8.3712 0.1792 L 10.943999 7.0783997 C 11.110399 7.5263996 11.340799 7.8208 12.0448 7.8592 C 12.1216 7.936 12.1216 8.2048 12.0448 8.2816 C 11.673599 8.2688 11.264 8.256 10.9312 8.256 C 10.5984 8.256 10.0352 8.2688 9.5232 8.2816 C 9.4464 8.2048 9.4464 7.936 9.5232 7.8592 C 10.047999 7.8208 10.559999 7.7823997 10.368 7.232 Z "/>
</symbol>
<symbol id="gA11612CECC8CBEF18835767DAB11B2F7" overflow="visible">
<path d="M 0.5248 2.6239998 C 0.5248 1.3184 1.3952 -0.12799999 3.2128 -0.12799999 C 4.032 -0.12799999 4.6591997 0.1664 5.0944 0.5888 C 5.6703997 1.152 5.9263997 1.9583999 5.9263997 2.7391999 C 5.9263997 4.0703998 5.1967998 5.6191998 3.2384 5.6191998 C 2.3936 5.6191998 1.7024 5.2736 1.2287999 4.7232 C 0.768 4.1728 0.5248 3.4304 0.5248 2.6239998 Z M 3.0463998 5.1712 C 4.1472 5.1712 4.8255997 4.1728 4.8255997 2.3295999 C 4.8255997 0.7168 3.9936 0.32 3.392 0.32 C 2.0607998 0.32 1.6256 1.9327999 1.6256 2.9183998 C 1.6256 4.032 1.8944 5.1712 3.0463998 5.1712 Z "/>
</symbol>
<symbol id="gCEFEF3D67F35C6E83CC3757B1DD21B13" overflow="visible">
<path d="M 4.2752 0.64 C 4.3392 0.69119996 4.4544 0.7168 4.4672 0.6272 C 4.5056 0.32 4.608 -0.12799999 4.608 -0.12799999 C 4.7104 -0.1664 4.7743998 -0.15359999 4.8512 -0.12799999 C 5.1328 0.1024 5.5808 0.2944 6.3616 0.384 C 6.4384 0.4608 6.4384 0.65279996 6.3616 0.72959995 C 5.5424 0.79359996 5.4272 1.0368 5.4272 1.6639999 L 5.4272 7.4624 C 5.4272 8.2944 5.4783998 8.806399 5.4783998 8.806399 C 5.4783998 8.896 5.4272 8.9344 5.312 8.9344 C 4.992 8.806399 4.032 8.6272 3.52 8.588799 C 3.4944 8.4864 3.52 8.2816 3.5967999 8.2048 C 3.6352 8.2048 3.6736 8.2048 3.712 8.2048 C 4.2752 8.1664 4.416 8.1664 4.416 7.1552 L 4.416 5.5168 C 4.416 5.4272 4.3904 5.4016 4.3008 5.4016 C 4.2496 5.4016 3.7247999 5.6191998 3.3023999 5.6191998 C 2.4575999 5.6191998 1.8944 5.3375998 1.3823999 4.8512 C 0.83199996 4.3008 0.4992 3.5456 0.4992 2.5983999 C 0.4992 1.0239999 1.2928 -0.12799999 2.6752 -0.12799999 C 3.1743999 -0.12799999 3.648 0.12799999 4.2752 0.64 Z M 4.416 1.5871999 C 4.416 1.344 4.3904 1.2415999 4.2111998 1.0879999 C 3.7375998 0.6784 3.3279998 0.4736 3.008 0.4736 C 2.3167999 0.4736 1.5999999 1.2287999 1.5999999 2.8288 C 1.5999999 3.7503998 1.7792 4.2623997 1.9712 4.5312 C 2.368 5.1328 2.9055998 5.1712 3.1615999 5.1712 C 3.6223998 5.1712 3.9424 5.0048 4.1984 4.7104 C 4.3775997 4.5056 4.416 4.416 4.416 4.0192 Z "/>
</symbol>
<symbol id="g645CA8FA3D9155E2CBD9F8EED3C1540D" overflow="visible">
<path d="M 1.9968 4.7104 C 1.984 5.0944 1.9583999 5.4272 1.8944 5.5551996 C 1.8687999 5.6191998 1.8432 5.6576 1.7407999 5.6576 C 1.3823999 5.5168 1.0496 5.4016 0.1664 5.2864 C 0.1408 5.2096 0.1664 5.0048 0.192 4.928 C 0.8832 4.864 1.0239999 4.7999997 1.0239999 4.0576 L 1.0239999 -1.408 C 1.0239999 -2.4703999 0.8832 -2.5344 0.1024 -2.5728 C 0.0256 -2.6496 0.0256 -2.9183998 0.1024 -2.9952 C 0.55039996 -2.9824 1.0239999 -2.9696 1.536 -2.9696 C 2.0479999 -2.9696 2.6624 -2.9824 3.0848 -2.9952 C 3.1615999 -2.9183998 3.1615999 -2.6496 3.0848 -2.5728 C 2.1759999 -2.5216 2.0351999 -2.4703999 2.0351999 -1.408 L 2.0351999 -0.0256 C 2.0351999 0.1408 2.0864 0.12799999 2.2144 0.076799996 C 2.5344 -0.0512 2.9183998 -0.12799999 3.3279998 -0.12799999 C 4.0448 -0.12799999 4.6847997 0.0896 5.2096 0.5888 C 5.8111997 1.1776 6.1568 1.9712 6.1568 3.008 C 6.1568 4.3648 5.1967998 5.6191998 3.8911998 5.6191998 C 3.3023999 5.6191998 2.6496 5.2352 2.1376 4.6591997 C 2.0607998 4.5824 2.0096 4.5824 1.9968 4.7104 Z M 2.24 4.2367997 C 2.5728 4.6464 3.1615999 5.0304 3.5328 5.0304 C 4.3519998 5.0304 5.0559998 4.1088 5.0559998 2.6624 C 5.0559998 1.6128 4.6847997 0.30719998 3.2512 0.30719998 C 3.0207999 0.30719998 2.5728 0.3712 2.3423998 0.576 C 2.0864 0.8064 2.0351999 0.8832 2.0351999 1.344 L 2.0351999 3.6736 C 2.0351999 3.9424 2.0864 4.0576 2.24 4.2367997 Z "/>
</symbol>
<symbol id="g9519A9B09125702A7696E3BE317A1C17" overflow="visible">
<path d="M 5.2320004 4.096 C 4.8 2.64 3.7760003 1.024 1.6480001 0.224 C 1.6480001 0.032 1.7120001 -0.112 1.84 -0.192 C 3.456 0.28800002 4.4480004 0.96000004 5.3440003 2 C 6.3360004 3.1520002 6.8320003 4.6080003 6.8320003 5.872 C 6.8320003 9.120001 4.992 9.76 3.7600002 9.76 C 1.664 9.76 0.8 7.728 0.8 6.352 C 0.8 4.9760003 1.536 3.7440002 3.7120001 3.7440002 C 4.1280003 3.7440002 4.7520003 3.8720002 5.2320004 4.096 Z M 5.3760004 4.6720004 C 4.848 4.32 4.32 4.3040004 4.0480003 4.3040004 C 2.48 4.3040004 2.128 5.84 2.128 6.6400003 C 2.128 8.400001 2.8000002 9.200001 3.584 9.200001 C 4.592 9.200001 5.504 8.656 5.504 5.92 C 5.504 5.5680003 5.472 5.136 5.3760004 4.6720004 Z "/>
</symbol>
<symbol id="g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" overflow="visible">
<path d="M 4.688 10.336 L 4.032 10.336 L 0.24000001 -0.94400007 L 0.896 -0.94400007 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
</defs>
</div>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(40 16.58)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="8.99" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.280000000000001" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.39" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gBFFDA84A1400D9E1136DF0DD93EA19F5" x="25.02" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEC3CC7DEE79E0AA801DFAAEF4B6C0B50" x="30.669999999999998" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g202CCBD46865F83C12D50E1B4FF9BBEA" x="36.43" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="41.35" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g5503E15E5E4E70E9E217A15BD1ECD752" x="46.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="49.75" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="55.379999999999995" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 25.159999999999997)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 27.159999999999997)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.64 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 42.31999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(393.5458818897638 10)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6D39B87B7095296261A07873F9B99896" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1B61845C1FB429ACDF5304290F5BF286" x="8.339999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC66F55FB8F08DA72FE76D3863D88042" x="13.511999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="20.003999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g48BCA4F06942DA5990D42018985FC781" x="26.759999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g45E4C10E27056C5AE488FE2D8290DF06" x="32.891999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="36.623999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FB89403B37B0F0F934DFEB7E5171B37" x="42.971999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFF269982F0E4C510F3A3BFF016D72390" x="50.303999999999995" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 10.296000000000001)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(6.768 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 28.488)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD77922058D8F1A3A631DDE5946887BDC" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 38.784)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5ABA589ED074A65FC8C929AB4EB2344C" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(743.9997637795276 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g97A8E46F7A64F11D13C6F357868587EE" x="9.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.25" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.36" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gB844DCFB76B4CC44608DB013C9764E9C" x="24.89" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="30.37" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="35.14" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gDAA1267270512376F631C9A10449D5F4" x="41.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="46.58" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="52.599999999999994" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 15.16)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 60)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6C3A310EEC8A7EBBD176D179125951F0" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(9.528 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g2F0CE4BDC8DA4B92139017B781562218" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8D84A54D9303B24762DC3071B60ECD14" x="17.76" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3E9095A1FBD7854ED5F7B53469C97011" x="25.560000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g90B91206A818BADA9956CC42F47E57A0" x="38.064" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g82ABC2E7771A896CA6A6993FF216117A" x="43.92" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.78399999999999 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g10BFE5E41011FF0F560FA08FAB260218" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(75.312 15.48)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(81.312 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1BED8054A02AECF3BF3EC56A671C1672" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2825DE3DACAF761B898A0442866AE569" x="16.944" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g841363B3896A8C79F18618DF16186242" x="31.799999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g841363B3896A8C79F18618DF16186242" x="45.192" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDD7DFDEC0D240E3DC5A3664E12D4BDDC" x="58.416" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g24FA36D774E663C81AD78F0ED3820373" x="68.664" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g42F794F2554BA43C69EE8F3AA6FD9BAC" x="76.392" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3E9095A1FBD7854ED5F7B53469C97011" x="91.176" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g42F794F2554BA43C69EE8F3AA6FD9BAC" x="109.68" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB6675D993E92546012E46240B36958EC" x="124.46400000000001" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g24FA36D774E663C81AD78F0ED3820373" x="136.20000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3E9095A1FBD7854ED5F7B53469C97011" x="143.92800000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2825DE3DACAF761B898A0442866AE569" x="156.43200000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g79601DAFF2C13DD0AF25B87F7A83C884" x="171.288" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g841363B3896A8C79F18618DF16186242" x="184.536" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g767CEF02C917BBE3F159A8F04079F311" x="197.76" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDD7DFDEC0D240E3DC5A3664E12D4BDDC" x="208.03199999999998" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 39.48)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g92446B7A6A7F78674F0F5568B7ED0AC5" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.46 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA335A20E4C1D7F39210005AFF7F1A0EF" x="9.385529308836379" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="22.30552930883638" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="31.44552930883638" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="42.28552930883638" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="52.40552930883638" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="57.82552930883638" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="67.94552930883638" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="77.08552930883639" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="83.40552930883638" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="97.01105861767276" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="104.81105861767276" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="113.75105861767275" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.53105861767276 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(188.55105861767277 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g7EBE636920865BE15FE72D33C3AE049" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.9910586176728 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g579F1BD1E42C90590E5C6584A163F6DD" x="9.719999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="21.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="30.400000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="38.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="48.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="54.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="65.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="73.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="82.16" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(343.0621172353455 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(360.08211723534555 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6ADFF08DD375E893907BE2D5FE0746BE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.52211723534555 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD5ADBDB4F1D8E002AEFDDEC4CBF7721F" x="9.719999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="23.74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="29.159999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="36.959999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="45.519999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="54.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="61.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="72.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="81.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="96.26" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="104.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="113" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 50.56)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gCBC8B237489E88077E829B631AC27C8B" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g46EE6FB315699AF9CBE00AD0EAD33ECA" x="7.34" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g8F63AAB7FFA6B186E1B4BC124750174B" x="17.22" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE9BB2E81A58B731A2047F77D70267173" x="27.299999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB88E546A1990E31D64B5C4B23478426F" x="33.739999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB416F8956A8016097936DBEC1F135503" x="51.839999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC81C3C15134AD04FEC0FE7FCEBE8BB14" x="63.459999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="69.96" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gED653E9CCAB5F6C6237350979071A74F" x="84.74" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 76.72)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 77.22)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDACA5EBB44D5F3DB530A1F5F650BFBAB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="10.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="16.240000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="24.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="40.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="46.36" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="57.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" x="71.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="92.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="103.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="112.62" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="121.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="129.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="137.98" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="145.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="157.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="167.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="176.88" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="182.29999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="192.29999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="203.05999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="213.11999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="223.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="230.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="243.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="249.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="256.91999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="266.99999999999994" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(304.82 77.22)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g278A59F111DD0614EC58EAA01A502EFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 114.97)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDE6529B954490BC6DD8A7FF7D66D28D4" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g46EE6FB315699AF9CBE00AD0EAD33ECA" x="13.1" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g911507D70DD1D78477F3BEDE827F51DF" x="22.98" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD9D3B6C4D6AB50B3CADCA65007C1BC50" x="39.32" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2EB1DC9A979CD3C8C9D80DB754EBF6AB" x="49.1" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g936880EEF467D45CE0F64A721CAEDAB8" x="61.06" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE9BB2E81A58B731A2047F77D70267173" x="69.62" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCD50B0C5537328D0484BBB5C5B7C30A" x="76.06" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1344FEF92B65FBC27D977C1EC5D9AECF" x="84.6" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE9BB2E81A58B731A2047F77D70267173" x="91.75999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7B316FC97C7634445DBF19AF1976B5C8" x="98.19999999999999" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(107.32 114.97)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE9B2270BB65CFFF96111DE686524B072" x="0" fill="#543795" fill-rule="nonzero" stroke="#543795" stroke-width="0.5714" stroke-linecap="butt" stroke-linejoin="miter" stroke-miterlimit="4"/>
</g>
</g>
<g transform="translate(0 127.97)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="15.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="30.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="41.300000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="46.580000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="60.52000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="68.32000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="77.26" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="82.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="91.62" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="100.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="106.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="111.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="122" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="137.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="146.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="155.54000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="171.38000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="179.18000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="189.56000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="194.84000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="200.26000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="211.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="220.14000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="225.42000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="236.04000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="243.84000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="250.16000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="259.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="266.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB91E67CF1B63A9F4CC30BB03AE35508D" x="274.34000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="283.74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="289.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="297.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g17AD34DB90B05275C6F1422A9B4B5274" x="307.09999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="317.03999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="322.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="333.29999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="348.29999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="353.71999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="361.52" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="371.59999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="376.87999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="386.0199999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="392.3399999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="401.4199999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="416.5399999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="421.9599999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="429.75999999999993" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="435.0399999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="444.1799999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="455.01999999999987" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="465.1399999999999" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.02 32.32)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 46 0 "/>
</g>
<g transform="translate(17.02 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDACA5EBB44D5F3DB530A1F5F650BFBAB" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="11.06" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="21.82" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="30.96" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="38.76" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g13CAD87D675A42FC6A129543D89F948C" x="52.7" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 52.32)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g612BB0D9B453ACEC45B2B13686D7BB71" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.5 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDACA5EBB44D5F3DB530A1F5F650BFBAB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="10.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="16.240000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF9DE6E66E5D3ACB0B17DC7988DD660B8" x="24.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="40.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="50.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="60.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="66.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="76.9" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="88.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="96.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="102.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="112.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="119.94" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="128.88" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="136.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="148" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="154.32" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(186.89999999999998 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g629AE7F75F47B1FD947FFA2989B5B47D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(196.49999999999997 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="13.940000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="23.080000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="31.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="47.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="53.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="59.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="74.94" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.82)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g612BB0D9B453ACEC45B2B13686D7BB71" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.5 26.66)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="5.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="16.62" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="25.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="30.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="40.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="48.339999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="57.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="69.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="76.03999999999999" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(91.12 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g629AE7F75F47B1FD947FFA2989B5B47D" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(100.71999999999998 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="11.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="22.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="31.22" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="47.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="56.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="61.480000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="71.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="77.18" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(193.73999999999998 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g7EBE636920865BE15FE72D33C3AE049" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(208.17999999999998 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="9.719999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="18.86" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="28.979999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="44.099999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="50.419999999999995" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(273.68 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g7EBE636920865BE15FE72D33C3AE049" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 66.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g612BB0D9B453ACEC45B2B13686D7BB71" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.5 66.98)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="8.940000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="14.220000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="22.020000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="30.960000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="40.68000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="49.82000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="59.940000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="75.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="81.38" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(113.96000000000001 66.98)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6ADFF08DD375E893907BE2D5FE0746BE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 145.45999999999998)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.02 138.45999999999998)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 46 0 "/>
</g>
<g transform="translate(17.02 145.45999999999998)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDACA5EBB44D5F3DB530A1F5F650BFBAB" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="11.06" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="21.82" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="30.96" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="38.76" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gCAFB20A65E8FBEFE071D9C4C8EE95E49" x="52.7" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 171.61999999999998)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g612BB0D9B453ACEC45B2B13686D7BB71" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(34.52 158.45999999999998)">
<g class="typst-group">
<g>
<g transform="translate(0 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="15.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="20.4" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(30.68 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g7EBE636920865BE15FE72D33C3AE049" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(45.12 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="15.62" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="31" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="37.32" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" x="52.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="74.18" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="83.88000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="91.16000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="101.24000000000001" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(167.16 13.660000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6ADFF08DD375E893907BE2D5FE0746BE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(526.9580052493437 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<image xlink:href="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAesAAAIACAIAAAAt+tMqAAAgAElEQVR4Aey9f3Abx33/vRb1fThqKALqVKMwLQUqk5Fa1ikw06pyh80A6vRbtp0+BDOJHrZTpWCnymiaOAFiSxYZywFoOaV+JAEV0ZZSywEbUpbCh1+DavtYbDolEJE2JUr16RfDsFQJm2ZID13ypGGG/EN/3IO9PSyPhwNwONwd7oAPhyMe7vZ2P/ta6I3F5z77WcTBDxAAAsYSSCQSCKFwOGxss9BaCRJAJdgn6BIQMDeBWCyGEIrFYuY2E6yzAAFQcAsMEphYYgQikQgoeImNabG6AwpeLPLQbvkSCAaDCMF/vfJ9A2jYc3gbaQgTqgICigj4/X5QcEWkoFAuAqDguQjBdSCgNQE3/6N1rVBfORIABS/HUYc+F5eAy+Vyu93FtQFaLw0CoOClMY7QCysRQAj5/X4rWQy2mpUAKLhZRwbsKl0CSSd4MBgs3f5Bz4wjAApuHGtoCQhwHEeCwaPRKNAAAoUTAAUvnCHUAATyIADLefKABUVzEQAFz0UIrgMBTQmAgmuKs9wrAwUv93cA9N9gAqDgBgMv7eZAwUt7fKF3piMACm66IbGyQaDgVh49sN2CBEDBLThoepmcWFrrGf+o+Y0Hnu47OztuoEAcBeI7O254uu80v/GgZ/yjxNJa9rZBwbPzgatAQGMCZZLWKv7wEf1l5lY0hmj96nrGP3KduU0ke3P7Oyh4C514D4Un8e+J91DwFj7JC7rrzO2e8Y8y9RgUPBMZOA8EdCFA0lqVZGrZwfv/E4g+pHNJIkD0350dNwLRh4P3/0cXrNapNDbNerrvoEB8U9s7WK/7FtDgI/nfvgUUnsTFAnFP953YNJveS1DwdCZwBgjoSIAoOMvK/G/UsVWdq+4Z/2hduMlc8sIM6pkTfi/MCFPLlJcgy6RSZ0uLXH1o6H2s3Ueuowsz8qotq+YXZvAtgXho6H1JB0DBJUDgJRDQl0CJpZaNTbNEuyuO30AXP0ADS9mEaWAJXfwAlwzE616+UVbeFXb1SeubP8ffSDrv5qAkK+IDS/jGQLz1zZ+zq0/oexQUnKKAAyBgBIFSUvDIzQUUiGOPbV4zysFH6MIM8fNGbi4YAd0EbRDPCf4uIivQCk+GJ1Eg7jpzm3YIFJyigAMgYAQBnRScmVvp+ulc8kt6aOh9T/edQPQhOY4/fKRTr4QZZfCWmhnl4CN814t4Mh6IPtTJQvNUK7DK93NOVtYvzJCZOOkdKLh5RhksKQsC2io4M7eS/vCQuCnoI8TqtlESmqYhX/9b04JDQFZllJ/kPQPBawkNbTNbVeSbCvaBKMeSveSZBygQJ19fQMHNNtxgT4kTYBhGk8SEiaU1YWYXiOP4s+5pdGVRqhG83xl13q3gn4O5ztyWjWfIl7jGksSLeKm6UxJLa9VtozhYMLso53v1xHsoEE8srYGC5/vuhfJAoPgEkg4TYYodnlTqxEi5npvfeCB+FJZvZ5i5Fdz0izc0lKSK4ze2to2W5INN3yXsuZb5cM1XsiXlrywmFRxXnu/4QXkgAASKS0CYep94L29dGFjCT9IC8c+evp1zsV+mPnq67+DItuwxJxK5yflyYKniyHVP951MjVr0PJ4jk+CTnARUFOB9KaDgFn1vgNnlSIBdfSIs5DvzQP0U+OIHFUeuV6ua88amWSxJ3dPqW88kVfxHiyZOHvO8M4SnBdp+2lGAA0t4LMzTW7AECACB7AQ0C2noW9h05PrOjhv5ulPqXr6BowCpiGh4MLC0uf2dEpuG449bzT3gYubBW6Dg2f/LwFUgYBYCwWsJPOcqMKCY/v/vw6Hc4sjinP0UfAJ6TMCJVd04vkW1eyen/QYX0B3X4CP8ZcjgXkFzQAAIqCAguC80jEjjl9WgQFx5JF84/iH+CEmPeKGfCgUe8B8q4fiHKviY8JbovY8xrp45Xb6yENQ9c6DgJhx6MAkISAno8vxw8BFZqK1w2us+x+AsSwXKdNbbN7e/4714X9p5a74WvjNl7a8GMK0JB6wGAmVEQJjNabKiTyIoqaA0JTRxXLO2XwIkxgw+Qife29lxQ4kx5i8DCm7+MQILgYARBFxnbus4+eUX1CiZhmvphU/XbnKGj0gxgqn+bQiR4Jl6qtV5/TsCLQABIKCegPBATKsHmOnCwXuflSyJBAXPaxRhDp4XLigMBEqTgLCEPcs+AOminOcZJd5nHSPBxdbyc3AlXwjMP9ig4OYfI7AQCKgkEI/HFd7pvXhfrxBsKp28IyWnPTAHz4lIXEAI3dHzoxfHBYmbhGMgAAQMIEA2O06muFLSlvsco++qkMFHZKl9TmNAwXMiEhcQvrXo8fyZfvRe/AAUXMwcjoGAEQQYhkEIRSIRJY3hHXB0Xdc3+AjvrROI51zRXt02gpMgUvnQ4yB4y3n6lhIsliiz9diIvtE7nXdBwS3xTgAjS40AQkhhjlkjZr49ONNhTgX3Xry/6eiIrgpecXTEd2myZAbbd2myQk9iuPKSgQUdAQIWIuBwONxutxKDzaPguj9T5T9IlETFKOFmhjICMZ0cKfxmPaDgZhhosKHsCLjdbpfLpaTbtaExk3hR2NUn+OOkkLSI2R0vfLrUfJNtKWFYxDLO07c2t7+rxxeXze3v4vdGEfsGTQOBsiWgfK818zzJ5DjOfY7ZfHRE4+TgRNavLG42xIUSf/go/vDR4P3/Gbz/P/GHj/TeVkJ4nql5OH8qGS8oeNlqCHS8mAQikQhCSEk4Ch9NqMskbn1iqCyakOM4YXmRHtNwxUtDVQwb2U1USK0eiONvEht/Pd13un46p1McOv4M1jbFFb8Iy30OxzKBgqt4P8AtQKBQAiSgUEk4iu7e58FHm9vfVZ5PSlgsrm2YMy9JejzDjE2znu47RK/xBtDhSRx40zO3/nthBp15gJMW8Jre+ubPNddxdvXJ06du4aeOmkC7slhxdOTpU7eIuwkUvND/inA/EFBHQGE4iu5ppvPM6cquPqluG3nqiHa+lIGlTUdHakNj2nrA2dUnzW/gPd3xnnDd07k9P1cWSVw8CsQD0YfqxjTTXczcStWxkU3t7xYq4n0LFS/drDo2Qp0/oOCZmMN5IKAvAafTqTAcxXn6Fv7Pn/0xoOqr+S9kJ3pU8dLN3LKY06qBJYkkaQKdmVvBcfRkQ4y8Njm7skgy7rrO3Nb2E4WZW9l6bATPxC9+oHIoe+Yqjo5sFck3eFE0ebdAJUBADQGv12u325XcqWNQWj7ZZcWmEpMKFXFevlEgHr33sbjyAo+j9z7e2jaKp96qvRZ8oN7Ojht0qlugSeT2xNLa06du4c+V70zk9+E3sITOTqFA/OlTtyROHpiDazI0UAkQyJsACUdhWVbJnXoFpRXw/DByc6HqGO9OUSeUfQubjo5UHRvRVr7xVLdtFLu8C9xLSO1WotlHk119Qh4k4Mn42ancRl5ZRGencOFA3HdpMv1rASh4duBwFQjoRYA8zIzFYkoaEILSTt5T+QVc1pvBL6b3vzWtxADZMszcCl5qH4ijk/dyixG14coiLh+I14bGtJ3ksqtPbO2jTx25nt8MlxomOehbqDhyPa+tRGUppZ9k5laEAJVAHH+POTuF3phF//SL9d83ZrFwv3STPF91n2MyrZgFBU/HC2eAgBEEWJZV+DCTWON/C28EjB/KSYRG3cu+BXFIg+oO00kljhP/zgRWoiz2vDGLvjOBS2aYUao2g9zoOnO7ohDnSbrlvDulkA+5LD1KfnoFryWcp3m/ysboRiLcyRQxwWuJ7B9yoOBZCMMlIKAvAYfD4fV6lbfhvXgf/98ufJX2lcVN7e9uPTaS/q1cuTHikomlNSHKMBDHX/lDt/Es++yU8HvyHgrdJq4Aot0SZ664KtXHwtMCrT7hqJrzK0Wzy6hqm8mN7OqT2DQbm2YjNxciNxfIscKhAQUvED7cDgTUE/B6vXV1dcrvJ5HFWMRffZhtqkvVR/aAn32LI9KUG5C9JLv6JHrvY9+lSeoiIHPJZNos9znGd2kyeu9jhcKUvSHZqzs7bmD3t2yXCzk5sLT5yHVP9x3ZRot+EhS86EMABpQvgbweZhJM1GuBJ7l5xckRFXv1IQlp0HVSafyICtsp9Mxpr+Cp/OnmJAYKbvybDVoEAgKBvB5miqmRHbywQ/nslFIdv/gBDirnp8P6TYTFRhp57D7H/F8v6TABJx97A0soENfJG14gJVDwAgHC7UBAPYF8H2aKW0osrRFnBfYvn7yHfpCQl3Ly8JDX7trQWCnlbqU0dE+aOPgIBW/t7LhBWzTPASi4ecYCLClHAvk+zJQwik2zvkuTeC+YVDAD3oQhdJsGopHz3ov3S1K7CQ3hGaZOLhQyDe/GgUB6PICVDGi+L0HB8yUG5YGAlgTyfZiZqe1kvHDwWiIZfOa9eD8ZPpxMXEde6vrwMJMxBp83Yld4ZdsYGdxxWFVvPHBoEQhsIKDiYeaG++EFxwmR8oUEnOS8N8/8X4YNC8zBDUMNDQEBGQKqH2bK1GXBU2S/hfjDR4XY7j7H6BJHKJH1QDz5taYQO/W4FxRcD6pQJxBQSoBlWafTqWSrB6U1mrscM7fS9dO5TJstJM+Hht7PN24PP9EN3tIljlAs4qDg5n5rgXVAAAjoSCA2zVLhxlPmMw9wPu4LM3izhQsz+Dg8ic/zj2R3dtxQnvHKiG2MBh8hUHAd3x1QNRAAAmYlwMytkI1yNre/g/O6ZM8aeGURXZghm+Z4uu8omY8b9iRT+YeKYUMBXhTDUENDQKAcCZBs3TjhVHhSPmJd7KkQH1+Y2XTk+ta20ZxxkIKCq1ihKm4u+zHEopTjmxf6DATKm0DXT+dQII59I9nn3ZnUc2CJ+FVCQ+9nASmk3i084VcmMwYfYZ9PIG7CtawwB8/yxoBLQAAIqCcgLLQ58V5+U+90GeW3ocgeB4LXNHXe1e9h5ub2d8ne8Opx6HMnKLg+XKFWIFDeBIR5sVYhIryIZ3Gn+C5N4uwCOjlS+L3owvEPTTikoOAmHBQwCQhYm0BiaU3Y6kwrSeXdKVvbRjM92BQ+MMKTukzDO+9uPTZiwiX1sCbT2v9PwHogYE4CvkuTm7XdK2fwERpY2pQ1Tzde16PHNJx/hpndh1PEUYA5eBHhQ9NAoAQJ6DgdDk8ms+Nm2jGSmVvBseTabiU6+KjipZsabmak+XiDgmuOFCoEAmVNwNN9Z5NWew2nPdXc3P5Olq2HNd5KdPAR/jwIxLP434s+0qDgRR8CMAAIlA4B3VN158ryqtlWooOP8OIjU67DFL9dQMHFNOAYCACBgggIEYR9C7o8URx8hOPKA/EsYSHrW4kWGB7+nQmyKXNBOPS/GRRcf8bQAhBQQCAcDue167GCKotQxHvxPnahpHk/NDyzqe2d7KHZya3fha2WvzOhpt2BJfQKYwn5hliUIrzFoUkgIEugNBKF49xVWsWAZ/oY4JdHyjIUn/Rdwo898dagP0jkoeNnp/AmR+b2fYu7CXNwMQ04BgJFIxCNRhFCsVisaBZo0TCOBtEpKJsKOh+RosTY6L2Pa0NjeFn/SzfRqw+zrezvW0BnpzandoLOFO6ipFGDy4CCGwwcmgMC8gQYhkEIhcNh+csWOWuYgitPURK5ueDowDouTMlDt3GEydkp/PsKg0K3iXCjQNx5+paFtJu8I0DBLfI/A8wsAwIIoWAwaOmOGqHgqtIEJpbWwvEPyQ6iRM1RIF7dNuI+x5BtoM255DLnmwEUPCciKAAEDCLgdDrdbrdBjenTjBEKzntRlM/B9emoWWoFBTfLSIAdQECrfeuLSBIr+JkHeTw5pN5t5QeK/eBF5GBY06DghqGGhoBADgIkHCVHIXNfdp6+ZZJYFHNz0sw6UHDNUEJFQKBAAiUQjiJkeVU+oc6/5Ob2d70X7xeIumRuBwUvmaGEjlieAAlHiUQi1u2JsCazZ04vR0rfQvY1mdZClylZrvJegIIrZwUlgYDuBKwejlL0vCi6j1ABDSSW1nrGP2p+44GtfZTGw5CDupdvNL/xoGf8o3yf0IKCFzAgcCsQ0JpACYSjeC/e36xHnm6SIvwojv/Tmrru9cWmWU/3HSLWm9vfQSfew+uexL8n3sPZCPigdU/3HeWhjaDgug8eNAAElBMogXCUxNIaViI9dq3Mmh9cOWQjSyaW1prfwLskY4E+8wBlz/nVt4DOPMCbYwTirW/+XMl8HBTcyNGEtoBADgIlEI7CcRzJSZJDrfJ9hnllcbPVJuCxaXZr2yhW5PBkHnt4DixhrQ/Ebe0Zd5WjbyNQcIoCDoBA8QmUQDgKx3Hs6pPqthGcVUrDfTJfulll1s0qZd835KFuxfEbKj/J+haeOnJ9a9to9v0lQMFl4cNJIFAcAiUQjkLAMXMrVcdGcEqpfOfasuX5dK8WSloixOQEbxX0Gcbv75w9USIoeHH+o0KrQCATAauHo9B+CSp2/GaBKkaydWfZ1YG2aJIDYafQE+9p8OnFi/jWtozuFFBwkww6mAEEBAIlEI5Cx5KIOHanZH+CJzvv5nfkwbN462TrTj4DSCytbW0bxc4T7TxIm45ct7WPyj7YBAWnbzY4AAKmIOD1eu12uylM0cIIZm6lug3vmYCzuSoXtYElnLD76EjVsRELOU84jvN038GPLtV9YmX6JOPXMfkuTaYPCCh4OhM4AwSKSaA0NusRE0wsrZHolIqjI+g7EznUrW8BvfqQbJTjPscoj4wWt1isY8F/osceF513kxu/pdMABS/WWEO7QECeQCwWK4HNetL7Fptmhe0rA3G8qcIrjLDNwg8SwsHJe3SzhWQib2tNvUl/Pd13cNy38q8amSbd6eevLG4+cj19Gg4Knv5OgzNAoJgEEolEyTzMTOeYWFqL3FzwXrwvuFb4VYhkLWJ124j34v1w/MP0mWZ6PSY8Iyxl6p7W4AFmuoIPPiJB4hJvOCi4Cd8JYFK5E7DZbD6fr0woxKZZiSpZtOPh+If4o+jKol4Kzm9OFL33sZgPKLiYBhwDAVMQ8Hq9Vt+sxxQcjTUCJ4Rpf0cv+eZn5RVpjhRQcGMHGVoDAgoIJPgfBQVVFok/fNQz/lFo6H362/XTufjDR6UxF1YJpeDb8ARc7/2Jgrckib1AwQseN6gACFiEAEltWt0mTW1K3NDkX0/3na6fzoGUqxhSDFCPKBSxT5zPlyK2DRRcTAOOgUBpEugZ/2hnxw0UiFccuY6zBl78QBrSd2UR9czhxHjt7/CbuI+Ght4vTRb69EpIjK63gqftEQoKrs94Qq1AwBwE2NUnJDP1prZ3sHCLJ3SZjnvm8F6XgfjOjhuFbyJjDgy6WyFEguu3OREZLFBw3UcSGgACpiHAzK3Y2kfxvFtFiFvPHBZ9S61oLyJ4IZQQ5uBFHANoGgiUEoHIzYWtbaNPFbLCe2AJvYh9L8FriVIio1NfwA+uE1ioFgiUHQFmbkWz/Er8eu7sWarLjq9ch7GC6x+L4jx9S9w4+MHFNOAYCJQCAXb1yc6OG1ou7+bd4uATz/7mcJ6+pVk+9AyPKCqO4mWrYjNAwcU04BgIlAIBT/cd7PvWMD0en6W6uk0+wWkpINOiD7qvyeQzFEq+DIGCazF0UAcQMA0BvdLj8Uu6wSGeZZyZuRXsSFHx0DjDjFsaOMQHg0tC9UHBs4wIXAIC1iPgOnNbr7XdnXer20YtmnbKmIGsDY3h9IoKFTmvYgNLFXIbPYOCGzOy0AoQMIJA9N7HeBp4YUYXEbmyiAJx/1vTRvTEmm0IX4D0mIbzkeDpGXdBwa35TgGry4MAwzCBQEB5X32XJrEHPK/JXV6Fg7fqXr6h3J7ilkwsrUkywMQfPtI7/Yv7HIO3p9A2RTjs0VPcdxK0DgTUEQiHwwihREJpODZeOq/JBruZZL17WnanGHW90+kuZm4lEH3oOnMbfx3J8Nv8xgOd0r8Qb7iWQSkDSxUv3aw6NiLrv4I5uE7vIqgWCGhAgOz2EA6HldQlPEnTyYVCNJ13pJh22/jE0lrrmz8nqo33Gu6exsle6Er3gSV8fPEDSfoXybNBJaizlyH7O6OT97T5MhTCH0Xp/hNiAyh49rGAq0CgyAQcDofL5VJihEGpOcy6RDMQfSjMuMOTipwYfQsk/YutfVSybYIS2tnL+N/CX1YKFfGBJbwXXdbEBqDg2QcCrgKBIhPw+/0IIZZlc9qhezwyPw3f3P6OZFFJTsP0LsCuPml+4wFWzBPv5b1FTs8cnq0H4l0/ndPWTkHEj99U9HGS7ra6sohdMYF49m88oODajhrUBgQ0JsAwDEIoEonkrDd4LYFVLF0LtD2TtslATsN0LcCuPvnsad7lrdp9NLCEpT8Qb33z59qaStwpOL7wB4n8xuXsVMXRkapjIzm/HICCaztkUBsQ0J6Aw+Hwer056y1DBSfyjcNvqLNb9ccVn/5F81hJZm7FeRqn6t1EdDx7jMqVRfSDBFb8QNx9jlGSxgAUPOf/CygABIpMQKEjRVDw7BqhWuBSN25uf1ey0VcR6QjOE4V5z1NdyDgd1i2HV+TmQm1oTHDTH7+Jzk7h3zdm0T/9Av/LvyQ+k6TX29Exlum5ZTpqUPB0JnAGCJiLAHGk5IxIKbcnmcInlqbLZ4hPXDZur/D3BDO34n9rmkzJBTUXBTsmkw4GryWUzLvFloCCi2nAMRAwKQGn01lXV5fdOEHBtZqQys5Y+WhCM2RHYVef4A0/g7cyTqhl7c95cmBp85Hrnu472VEXfpVdfRKbZslvIeGMoOCFjwXUAAR0JxCJRBBCsVgse0tbj43gbTBz6pTqAhdmUCCe7zwxu83qrgqRHhrmX6RMMqxfV2en3neBgutNGOoHAhoQYFnWZrP5fL7sdXkv3q84OqKjgp94rzY0lt0GA64K2wrr9Fk1sLTpyHWzRUxmogoKnokMnAcC5iLg8/nsdnv2wHBhNWDhgRl0Qio+GFj6Xy+M+C5NFp2L0E09JuCkv3J5XIvea1kDQMFlscBJIGA6ArFYDCEUDAazWMauPqkNjWmZlEOs4Lyu6fSUL0un0i/hrxq6JvDik6FL9lJIN8MMZ0DBzTAKYAMQUETA7XYrnYarXt4ilmzxMf8M0wwTcI7j8DNMnVwoqS5XHLluks5mf2eAgmfnA1eBgIkIKJmGcxxXGxrDCU6vLGrpED+OV3gXMgFfm7zsb9xTichP5Z7GzljuTAEy8AUneHhSy96lhHu9TpMtPZUBwZ8CBc9EBs4DATMSUDINZ+ZWqo6NYF+KVqt7Tt7Lnl8pJymm08lrd+UOp9vrdTt38Dpe2XIt551pBYwImhx8hIK3XGdupzVuuhOg4KYbEjAICGQhoHAaLmzWo0mCUz4neCHLzdnLjVi+KxsjC7RnMR8v4t4oPaP0wKCFS7zTX6lNxSsHCl489tAyEFBFgEzDc277cOLSMKquecr1fxc0E+dn34V5hK+1YP12+Blxb8cOYwVXMwk3SMH5qHCxxeY8BgU357iAVUAgIwGy7UNzc3PGEhy3uLhYW1tLXM5PffG0msRPVxYR7/suZPbNcRx73o3NcJ8XnN7swmQscnifDZ+UqHqW/oguGaTg5oh8F/Vb/hAUXJ4LnAUCZiYQDAazL9F85plniHxv/2TN1m8M4SwcrzBKn20OLOFcS3zKjsIj6i43EkOk/+7Y51f3JDOxtIZt0zQdyvoDTPpIE55kmvk/ANgGBCxNgGVZh8ORKVPKgQMHqF4yDJNMuxG8lsAL7gNxFLqNXn0oL+UDSziN9SvM5qO4pO/SZCGRJym8MR+ebVc63F7y0+IPR64xC+lRKJN+BzW68XLqdvm/uCNnHsjILtXfgg82mSkFozwF/izMwbPAgUtAwLwEotGobNLw06dPUyXs7++nHUgsrfnfmnZ0pHKcBuI4D3XoNgrdpnlNUSBe3YZXXWqX+YRMwXNJMne5EaXK8HekXlDzNxw4T9/Sa9USkX5zbwcqZgEKLqYBx0DA2gSGhoaofL/44ouynUksrSU37gpeS7jPMfQ36exWkdpUtv6NJ4mCu3PvMERv4yfj2RVc9/3k+PAbLb6C0F7pdQAKrhdZqBcIGExgamqqqqqKKHhTU5PBrWdoTnCO7Es9yMxQbP00f4PDnzX5CjO3oqsrvOKlm46O4ifwWoeS+QgUPDMbuAIErENgeXl5165dRL7r6+tXV1dNYrsQDI5Q5Z59xBW+b4/NVonc59fkLMRz9hz6zd/mPsfgdadaLVkS+80vfpBzf2E5y4tzDhS8ONyhVSCgLYGGhgYi39u2bZudndW28gJrW7jWub6cHlXabHv2HY4kZCpVMv8WbhNiCnVYW7+p/V0zZNCVwSN3ChRcjgqcAwKWInDo0CHq/h4dHbWU7dRY3mOuZPqdusN78T4Om9E2xyy/kKfwGMqUjbr/BQXXHTE0AAR0JXDu3Dkq3729vbq2pVvlCgJQ0trmN1obeeqIdr4Ufgeiwhagplmp8wlQcJ0BQ/VAQE8Cw8PDVL6/8Y1v6NmUbnXn4TuR2qBlDq++hYqjI0+fulXIrpVS+/R/DQquP2NoAQjoQ2BmZqa6upoo+P79+/VpRO9ahWAV+jnEL7bPGomy0SKyXw8ODy8km+6FmYqjI9VtI9aSb47jQME3vh3gFRCwCIHHjx/v3r2bCN/u3bsfP34sNryrq4thNqSSEl8tsePYNIuz6R4dUZP+ZfARSSFgudk3GURQ8BJ7M0N3tCSQSCSy70upZWN51rV//34i39XV1TMzM5K7bTab3W7v6uqSnC/Vl8zcytOnbglpA5RPxn+QwAtT+RQClpt9k6EEBS/VtzT0SwMCyS3N/H6/BhVpXUUgEKBuh+Hh4fTqE4mE242TAjY3N5v2Qyjd7ELObEj/8gqDc7xkkvK+BXR2iuQSqA2NRe99XEi7xb0XFLy4/KF1UxMgIpgzE7fBfejt7aXyfe7cuSytkxSGdXV1sVgsS7lE/k4AACAASURBVLFSusSuPvG/NV0bEtK/YNcKn/tl/V8+5yIKxJ2nb1koajDTGIGCZyID54EARzJxezwe87AYHR2l8n3w4MGchsViMYcDZ/1rbW0120dRTuMLKcDMrYTjH3ov3ie5X6rbRsiB79Jk5OaCJXKeKOk+KLgSSlCmfAnkzMRtJJrZ2dlt27YRBW9oaFDYdNKLQnpht9tDoZDCu6CYJQiAgltimMDIohHInonbSLNWVlbq6+uJfNfW1i4vL+fVOvWM19XV9fT05HUvFDYtAVBw0w4NGFYEAgzD2O12j8fT09NDHwBGo1GEUDgcLoJBoiYbG4XdbqqqqiYmJkRX8jiMRqPEqQI6ngc1ExcFBTfx4IBphhNgGMbr9ZJ5rt1ub21tJc8AyebCVNMNt4trb2+n7u+hoaECDYhEIqDjBTI0ye2g4CYZCDDDRASSnpNIJEICURBCdXV1ra2tCCGfz1cUK/v7+6l8nzx5UisbxDoeCoWK+PmkVY/KsB5Q8DIcdOiyDAGGYUKh0ODgoPhaIpEIh8NOp5MKqPELHcfHx2nrBw4cEJunybH4s4p+59CkZqjEAAKg4AZAhibMRSDpKpEIMZliE6G02+3RaFRicTIOj4RzGBxZOD8/v337dmLY3r17JVZp+JJhGJ/PZ7PhbYnr6uokfDRsCKrSlgAouLY8oTYLEHA4HHa7PRIR9m6MRCIIoWAwmHR5B4NBomKyUXdExOmNend1dXXV5XIR+a6pqVlcXNS7Reo+Sv8M07tpqF8dAVBwddzgLgsTYBiGyDRJG+J2u8UO7kQiQdwm6UrNsqzNZnO73cZ0vqmpifpPYFJsDHPLtQIKbrkhA4M1IMCyLJHppOc3qcjBYFBcKYkBTyZFSX+4Fw6HjRHTEydOUPnu7+8XmwfHQIASAAWnKOCgvAiwLEsDByUKznEcca0UK53I1atXqXx/61vfMufABIPBQCAwODiY/jlnToNL0ipQ8JIcVuiUUgJ+vx8h5HK5JDPrWCyGECqKgk9MTGzZsoUoeFNTk9KeGF7O5/PRjxmXyxUIBHp6esoq9YrhyGUaBAWXgQKnyooAmW7b7XaxXjc3N9tsNuNnl4uLi7W1tUQZ6+vrV1dXzTwWLMuSx780dh4hZLfbm5ubQ6FQPB43HqCZcelhGyi4HlShThMRYFk258SQPtsMBAKtra11dXUIoaLEY+zdu5fI9/bt22dnZ03EUYEpsVgs+ZzA6/WSBZ+kI3V1dSDoCuCpLAIKrhIc3GYVAh6Px263S5wk6cbTEBSn0xkOh3OKfnoNhZ85ePAg9UuMj48XXmERa6DTc4mgk7QzoVCop6cnHo8X0cLSaBoUvDTGEXqRkUA0GiWxg+nRgZJ7kqJDvAE55V5yoyYvv/Od71D57u3t1aRO81RCBd3n84nXuCr5cDVPL0xoCSi4CQcFTNKYAMMw5Ht9IBDIWXVOoc9Zg4oCQ0NDVL6ff/55FTVY7pbkoCRRB4NB8JUXMnag4IXQg3stQ0AcAG42yZiamqqqqiIKvn//fsswNdDQaDRKnOmDg4NF+YZkYF/zawoUPD9eUNqiBGKxGN0d2OVymUfEl5eXd+3aReR79+7djx8/tihhXc2mac3pNxX6gLTMNR0UXNc3HlRuCgIk6NvpdCa/s5Nj87hfGxoaiCpVV1fPzMyYgpeJjUhu+0l8L263WxzxQoL6adBLUR5EFwUbKHhRsEOjxhFIpo0liatok5FIxGazyeYgpGWMOTh06BCdVA4PDxvTaIm1QjTd7/e73W7yyJoi9Xg8ra2tXV1dJRyZDgpeYu9n6I6UAEkoKHGb0ABwktxKeo8hr1999VWqNa+++qohbZZ+IyToJRwOE02nhMlSo6LE+OsKHRRcV7xQefEJhMNh2eU5NB12UYJPhoeHqbgcOnSo+JhK14LkFs9k4ajP5xMvuy2NHoOCl8Y4Qi8yEkgkEsRJKpmGJ7NZBYPBokzKZmZmqquriYI3NDRkNB0uFINA8g0T4n/i8bj5415AwYvxHoE2jSVAHCmSEBSXy5WektAAux4/frx7924i37t27VpeXjagUWhCOYFkbgCJP72urs7j8SRjmUiyF1PJOii48pGFkhYmQBLp2e32QCAQj8eTQQvJnYuLErGwf/9+It9VVVVTU1MWZlrSphN/Ool78Xq94tRdZPiIrHs8HjJhHxwcjMfjxr+jQMFL+m1Ylp2LxWJkc7JkgirxZml0eT35H1gU9/dzzz1HWkcIDQ0NleX4WLjT6bIuiWgkg0tyv+j0DY9hmHjqJ/nhAQpu4fcTmJ5OgOT1JqHf5H9X0lsiLhaLxaLRqPFzJY7jent7qXyfPn1abBUcW5oAUXbyvDQYDCYfmbrdbr/fr6RTNM26y+XypH7o/qj0DZPxQEkbUAYIWIVAXV2deNPLZNB3Us3NYPzo6Cj9T3jgwAEzmAQ2mIFAJBIhXhp32k/yM4B/3C79J5b6wU/pzdAHsAEIaEKATMDp/Lq1tdXhcEhCUDRpKN9KZmdnt23bRhR87969+d4O5YFAJgKg4JnIwHnrESAKTkIFwuGwzWajYQMkNVJRurS6ulpfX0/ku6amZnFxsShmQKMlSQAUvCSHtUw7xbIsQqi5uTkajUpW8Xg8Hq/XWxQuTU1NRL63bNlCP1GKYgk0WnoEQMFLb0zLpUfUW0IyTZNuk8RVCCFxqEkRN55/8cUXqfv76tWr5TI20E+jCICCG0Ua2tGUAMlXFQqFEolEcpNit9tNqqd5wD0eD1lC3dXVhRBSGBigqY1cf38/lW9xXKO2rUBt5UwAFLycR9/CfadKTaJNJI8r6UycCKg4OsWwPpPPGGJAU1OTYe1CQ2VFABS8rIa71DpLNpWXLJcnnUwkEuFwOBgMFsX1PD8/X1NTQ+Tb5XKtrq6WGnrojzkIgIKbYxzAivwJkKSDZLpdV1dXFKXOZDVdkbF9+/b5+flMxeA8ECiQACh4gQDh9qIRIAvhOI6T3bGhKEkHCYsDBw5Q9/f4+HjRAEHDZUAAFLwMBrnkukgyn9jtdnE4CsknRx4Ykul5Ufr9yiuvUPnu7e0tig3QaPkQAAUvn7EukZ6SZTtutzsajYofYCYSCafTSdWzKMEnV69epQYcPXq0RIhDN0xMABTcxIMDpskRqKuro7GDkutJQQ8Gg8mrOqWFkzQneTkxMbFlyxai4I2NjZKr8BII6EEAFFwPqlCnXgRIiJ5+Pu5kCn+PxyNeDaSwJ4uLi7W1tUS+d+/evbKyovBGKKaaQNSLeXujqisohRtBwUthFMunD0TBZT0ksjGFeZFJZusna39U7Ka4d+9eIt/btm2bmZnJq10onInAwli4xemwVRK0lbY9+w5HGDZV+nIjPt94OfXaYn8XxsKH9+0R+oZQ5Z7GzmsLefcBFDxvZHBDcQk4HA673S6JHSSbYapQXtoX8vBTXQ0HDx4kGoMQGh0dpXXCQQEEFiJeW4pqpc1mS+k4Qo5jk3y9+ig4e+2Y1+s9do1+UBTQh8y3Th5zCJ3DfVuX8cbLebYLCp4ZMlwxJQGStUoi4mQnTPGDzXxtJ8mZ872L47jvfve7KaFBr7/+uooa4JY0AmzUS1Rth1c06V5LxMLeHXTarY+CT/qxtjr85FMizTKNTkS9yLbv8GX6hWLhmo9IemXLtbyaAAXPCxcULgIBlmWTuU1CoVBPTw9pnmSqoptetra2IoSUP71MpjAMhUISuXe73ZLdfEhbfr9fMt8XIxgaGqLy/dWvflV8CY7VE7jWwuv3Dl9Mpo4FZpLMU62s4NzamrRrwodWnp8doOBSjvDaVAQYhrHb7VQl6drLWCwm3qJQ1jOeqSNkGadE8clmV+leFLfbnSkt7dTUVFVVFbGtoaEhU3NwPk8C7Hk3hlqZ6xmlVMEXLh+W83/EOr1eb8t50Zx6bfKy3+t02PDPnn2Hw2OC+3ksjHfLceBPj0oHHnb8Ex5bN1/wy6dujExulOHJ8y1e7+HLC9zaWLhxj81mczgPK/fGkMl/vrN/UPD14YEjExKoq6tzOp1kvkxc1WI9VbfpZSKR8Pv9pE46E0/mUbHZbMk0h2IRJ+71ZH6VdDLLy8u7du0i8r1r167l5eX0MnBGFQGizLndCVIFl/d/CMK4/sCT4d0kCPHOdeKCJhfZ8/voVGH9IHUje1nwy4vuQ5XOTma9j7xBDn9EaADXkceMOubj/f7OzrweZ4KCr/OHI7MRIN4SKrLBYFC87U7h1vr9fjqp5ziOYRiysLO1tTUejw8ODrpcLpvNRg0Qt9jQ0ED+l1dVVU1NTYkvwXFBBATJ3Xc+1zM9VQq+0IlXfe3wxej0eeFa+LJogi7/OZDgb0MO/1jqvrUxItTOzkSqu8Qg/LbY0XI5scaxidgYvZgqlOnv2OEdeUo+XxMoeCagcN5QAgz/I2kyGAxS37Rkl4ZYLJbFPS2pJ9NL6k+nAebJzSLEzplMHxiHDh0i8o0QGhoaylQ/nFdDQNDB1Nw3cxWqFJwIpTuSsVpZBSeO+T3rYs3fTupan2YLlle6I7k+fNJaT83/3Tk/tyS3goJLgMDL4hAgC+IlS2mI2ySRSBBvuPiqy+UqJOs3nVbTeXdXVxfteVLQk/P9cDhMi9FLHMe99tprVL6/+93vii/BsQYE9FXwlJPdHZY4sVOWyyk448fz43WpTpWVfIaQl/vC+et3xM0/us39vSPVMv0LCk5RwEExCTAMQ0Q8EAhQO4gb2uVy2e128bNKkhpF7LCmt2Q5iEajpHLyeUC92zShSmtra5bbyaXh4WEq3wcPHsxZHgrkTUAIRNFpDs5xTKeTRCriRTT+y1Ihl1Pw1OTaJvkh9TjDgudaIuhKey445ivzjgXHDYCCK8UM5fQmQLfdaW1tpZNf4uhILp6mPhOiv+LnmQoN83rxKuzW1laXy0WfjpJ7WZYlV7Mv7JyZmamuriYKvnfvXoXtQrH8CAiLXXb4Rc8IZWuQCqac9nIcObtx6ebaZKTFybud8WA6WqKiWbNcLaSl9fgUIUyF/Dl8OeXrlhoka7XkZOI8mX47cnZXcqPwEhRcngucLRYBEtUnVlIq4h7+J7kJvUR/lZtKKhd/HojvJVGGSf8MTVorvrqysrJ7924i37W1tYuLi+KrcKwdASEoY8dhURyfXO1SwZTTXnkFF2pjmQheIIQQErmf5WohGVjSvSgSq6QGSS6nv2QvN/LTeNED0vRC2c+AgmfnA1eLQIC4v8WrLpOPOZORuTjA1uEIBoN0hp6vcWTtD0JIXLm4kkgkkunjobGRT8OB0JYtWyYmJsR3wbG2BISwjExPBNeE1TBSwSTaK41CFD4PMjllEp17cPj3+kpIOQUnASxinZftsNQg2UL0ZCo8cceGrwD0ssIDUHCFoKCYoQRkt90p3AKfzxfhf0joNw1ByVnz888/T2bfCKGrV6/mLA8FCiKwvqiej8pbrwvPmh2pR4ppgkk86CLhXxujPu+UgifGUut3SK2CYAupVjiOE9R640PFVDDhYRpMmLJJPJtIMyhVKP1vKhbR5s03EYqkLlBwCRB4aRYCslEiqo1LPq4U63V65UTcZevv7e2l8v3yyy/LloGTGhNgjuG5Mf+DcxJ6vW4nv1iSLNbk/dbpghnzEaeIbQ9eUbmPv8HR6MYnBQXnBbvSse9wJ/4k72zZI6yiSbmyOY4TvgEgxz5cx54Wkr2WrgNK3Rv2t7h5X3rqs4Hj0g3KBCXVhrCsyLbhZ19YZE2mGlLnQcFTJOBv8QgkEonkIhqPx9Pa2iqOMBE/2yzEukgkYrfbHQ6H2MFNK/d4PIFAIPlESxytSJsbHx9PKQlqamqi5+FAdwIL1zobU6otaPkOZ8v6UnbinV4XUGxQAs/R6Y/DG0kIjzJTS/RxASEUhRTbsc8fEz3IxJWIPj3E+cfTbiUpYdfvljNInhJVcGqq6CDnAwBxnaDgYhpwXAQCJLbE4XC43Xw6DITEAYUsy5LHjzT4L18TE4lEckdN2eBxWjlCSLbA7Ozs9u3byX8ul8u1urqab+tQvnAC7AL/w6ZWQ+askdyQrfxazjpJCZk6UrcuyFzLaZn2BUDBtWcKNeZFILmu3ev1EnciUVun0ympQXZ2LCmT6WUwGEw+/xRfTS6XHxwcpGfIiiH6kh6srq7W19cT+d6+ffv8/Dy9BAdAwCQEQMFNMhBlagZZm0OdG36/32az0ZcqoEQikebmZvHjpWAwWFdXR850dXXRTId0vX6mVpqamuhX2/Hx8UzF4DwQKCIBUPAiwoemORI4SECQuG+6cicajaqYepOsJuLPAPIhQbWYbHJPdoTIUv/x48fpLf39/TBUQMCcBEDBzTku5WIV2fcyHA6TA7GkejweFQsvE4kEeRYajUbpTDwajXq9Xp/PJ35MmmVTiP7+firfbW1t5TIY0E8LEgAFt+CglZbJbrfbzv+It1xQl/mEgklu60PqpDN6eokcZKmffJYQBW9sbJTcCC+BgKkIgIKbajjKwhiGYcj6eNJbGppNdz6LxWLJNZMqJuBifHRNkHheTwqQ+mWDT+bn52tqaoh819fXr6ysiOuEYyBgNgKg4GYbkRK3h8yO3W632FVNExMihOrq6nCeCreb+kDyIsKyrMfjIapNPxvEmWNJBitZ+eY4zuVyEfnetm3b7OxsXk1DYSBgPAFQcOOZl3WLyaWPktg+iiMSiZBkb+mzZlom5wFJn0KXX9JlOzRzbDINYSbXyoEDB6j7e3R0NGdbUAAIFJ0AKHjRh6C8DEhOrmmmb7IU0263u1yuTKqaLx1x/eReumxHnO8wvdpvf/vbVL5ff/319AJwBgiYkAAouAkHpZRN8nq9drs9EAjQNIFut5vkmVLnNqGwotEo+TCgnxD0EsdxJHNs+lohUubq1atUvr/2ta+Jb4RjIGBmAqDgZh6dErQtkUiQkO3kDsJ0w/hoNJr0fYtD/VT0nG5xmWmpDslKmF7zxMTEli1biILv378/vQCcAQKmJQAKbtqhKWXDJD4TouCSkyr6L/Z6K5zRLy4u1tbWEvnetWvX48ePVbQLtwCBYhEABS8WeWhXIMCyrMvlcrvd6ogkg1vEoSYKvd60rb179xL5rq6unpqaoufhAAhYggAouCWGqWSNDIVCdrs907Y4SrpN1uV7PB7xpJssmk/mzMo+rz948CB1fw8PDytpDsoAAVMRAAU31XCUmjHJh4rilZbp3Uu6wqk3PP2qwjN0a01xjDnJsmK32zO514n0EwVXnbpWoYVQDAjoRAAUXCewZVdtIpGQJAXkOA4hJBsZojmd9K01caJ+hnE4HLLT8OHhYTr7PnjwoOb2QIVAwBgCoODGcC79VoiGSiK73fyPMZ2PRqM2G94zK+eCoKmpqerqaqLge/fuNcY8aAUI6EEAFFwPqmVaJ3Vc0Gmv1+tV/YgyC8REIpHMXEhboSXpMnrxLj/0Kjl4/Pjxrl27iHzX1tYuLi5KCsBLIGAhAqDgFhosC5gai8XEE2Gyu4LmdpPpdvIRKF09T5vw+XxiA+h5erB//34i31u2bJmYmKDn4QAIWJEAKLgVR83UNtM0VYFAgM7KSTJC+m+68ubbJTrdFocSJitJPjgNBoOZ6v/qV79K3d9Xr17Nt1EoDwTMRgAU3GwjUgr20JU1LpfL6XQSbzhZPY8QKiR2UEwnkUg4nU6EEM1axXFcXV1dpuiX119/ncr3K6+8Iq4KjoGARQmAglt04CxgNg3yE0dqa2t3MtEgyRabzEkbCoU8Hk9y13lxTCFtbnR0lMr3gQMH6Hk4AAKWJgAKbunhM5HxyaWVg4OD8XhcbJNskJ+4gPLjWCxGkncntyoOhULiG8n6HYSQzWaTDUSZmZnZtm0bUfBMWVPEFcIxELAKAVBwq4yUqe1kGEa8B7w4SoQ+dZTVVoW9IpuiJcNakj5u4jmRCDHLsrFYTHayv7Kysnv3biLfNTU18/PzChuFYkDA/ARAwc0/RhawkKyMj0QiJImrJEqEPHUsZGlPXV2deFcd0pxCLo2NjdR/Iv5oUXg7FAMCZiYACm7m0bGGbWSCTL3PslEisrNjhd0j9VPxbW1tdTgcCis8evQole/+/n6FLUIxIGAVAqDgVhkpk9rZ1dVFQgbF9tFYFHGUiLhAXsfifeXD4bDNZqNqHo1GJe4Ucc29vb1Uvr/5zW+KL8ExECgNAqDgpTGOBvWCYZienh7aGMuyZPkMQtI3Eo0SKXDL+eT2OizLIoSam5tJGnFxrLfH48m05nN8fJzKd2NjI7UZDoBAKRGQ/scrpb5BXzQnQJ4iirP9idfvpDfn9/vFgpteQOEZ4l5PRpuIkwiSub/YGFrb7Ozs9u3biYLX19evrKzQS3AABEqJACh4KY2m7n1JyjFZLyN2Q1OfSXpuQg0NotHlg4ODZFeHZOi3+PEmbWt1dbW+vp7I97Zt22ZnZ+klOAACJUYAFLzEBlSX7og9J6QBl8sl2VSBKix9pKncFOrXJreQxFUIIUnoN437JuosK98cxzU1NVH/yejoqHIzoCQQsBwBUHDLDZnRBhPvsxK9Vrd+hzhDxNHiLpfLZrO53W6yJ7LL5aJT/kQikXSkBINBiehTKN/61reofPf29tLzcAAESpIAKHhJDqvGnSJuaEnub5q1SiymZP1OpqeLsmZRTzoJXJHEDpKmc+6XRmru7++n8l1I+LmsnXASCJiQACi4CQfFjCZRvRY/OZTkkiV2MwyTryMluaLS7XbTgBOn0ylGINu0uABtl8r3/v370wvAGSBQegRAwUtvTPXqUSa9Jr6OLJsqKDSIeNLtdnt6iDddJSR2toirnZ+fr6mpIQq+a9eux48fi6/CMRAoVQKg4KU6srr0i3o8xHpNY1EKX79DPOkIIbFnhvSE5JLNpOAk6RVCqLq6empqSpfOQ6VAwHwEQMHNNybmtkjs8aAPGDmO8/l8mrielW93STkdOHCA+k+Gh4fpeTgAAiVPABS85IdYlw4WEjuY0yCyx3xSlCVZZGVv7OzspPJ99uxZ2TJwEgiUKgFQ8FIdWd37pS52UKFZYs+MeKYvuX1oaIjK98GDByVX4SUQKHkCoOAlP8Q6dpB4PBwOh05tkJl+pswqExMTVVVVRMEbGhp0sgGqBQJmJgAKbubRsYBtDP+jn6GZFu8sLy/X1tYS+a6trV1eXtbPBqgZCJiWACi4aYemyIaR3CNdXV1ZnBiFmEjqD4VCPT09KppoaGgg8l1VVTUxMVGIJXAvELAuAVBw646djpYns8gm9w4mEmm328WreDRpVbwrG8l/kh4+mKWhgwcPEtsQQkNDQ1lKwiUgUNoEQMFLe3zV9I5l2bq6OqfTGYvFIpEIyQCeKRBbTQMcR+onU2+y5DKTszu9/q6uLirfnZ2d6QXgDBAoHwKg4OUz1kp7GgwGbTYb9WzQjICFL9ghFhDJFtcv3nYnu5XDw8NUvg8cOJC9MFwFAiVPABS85Ic47w4mcwHStTkMw5B9FWjeEqq8edebuiEYDNrtdvKKqDn10kSj0SzulKmpqerqaqLg6SvvU9XDXyBQRgRAwctosBV21ev1Ukmtq6sjWzpwHEc26ClcOkkgOQlisdvtYv+Mx+PJlPX78ePHu3btIvJdU1MzPz+vsDtQDAiUMAFQ8BIe3Py6FovF0vPH2mw2Wovb7Q6Hw4XvmkZ213S5XHa7XazX4h2NaaP0YP/+/dR/kmWeTsvDARAoBwKg4OUwyor6aLfbnU6nWByDwWByDk5uTiQSsgmnFFWdVog4TxBCdLJPolMyPc/82te+RuW7v78/rT44AQTKlAAoeJkOfHq3EUKS+TVxdzQ3N/f09LhcLkna7vQaMp0hod/Nzc3i6HIa5UI2bEu27nQ6ZZ3sr7/+OpXv48ePZ2oFzgOBMiQACl6Ggy7tst/vb25uFs+IaQmyrj2LvNKS9CASiYhzz3IcR1O/IoTEu+0kEgmfz+fgf4LBoKx8j46OUvluamqircABEAACHMeBgsPbgKM+DRqCIobCMAz1dYjPZzom+6LRfTVJ5ZFIJOn+DofDNptN8vQyUz0cx83MzGzbto0oeH19/erqapbCcAkIlCEBUPAyHPT1LtNpb85NcNbvUXAk3lczmdhE7N2mDXV1dWWvaWVlZffu3US+t2/fPjs7m708XAUCZUgAFLzsBj0ajRL1JA8Pqe9bdv8d1XTI1Ntutzc3N9N4RFKbOHNslvobGxup/2R8fDxLSbgEBMqWACh42Q291+tFCLW2tpKHk3QaznFcpv131DGi023xHJxUxbIs8bCHw2HZyl944QUq3729vbJl4CQQAAKg4GX3HmBZloh4puhAuv+OWNzVYco+rxev5RHX39vbS+X7ueeeE1+CYyAABMQEQMHFNMrluLW1lUikZAkP7X8kEskU20fLpB/09PSQk62trfShaL7z+vHxcSrf+/fvT28FzgABIEAJgIJTFGV04Ha7I/wPyeyaV6hJJkzE8e3xeEgUuWR+Tef1iUQiUw0cx83Pz2/fvp0o+O7dux8/fpylMFwCAkAAFLy83gORSESs19RVTQXX5/PRZ5v5oqHB4+K18rQS+mxTvOyTXuU4bnV1lUaOV1dXz8zMiK/CMRAAAukEQMHTmZTyGYfDIZFX6qr2eDyBQAAhRNU8XxB034ZMm0KQfTUzfUI0NTVR/8nw8HC+rUN5IFCGBEDBy2vQfT4fzexKey5+tinRd1pGyYHf73c6nUSmM30SZHo6SrOQI4S6u7uVNAdlgAAQAAUvr/dANBpNz39CEGi4ZzGd19Pl9bFYLMsGEVevXqWz70OHDpXXkEBvgUABBEDBC4BnnVvj8Tg1Nrn/Dg0UoSc1P6DLdjweD0mM5Xa7ZVthGGbLli1EwRsaGmTLwEkgAARkCYCCy2Kx9kmWZUOhEPVXUAeF3W73eDx2/sfj8YRCoa6urng8nj0+pBAWZHl9VKVWEAAAIABJREFUcpefTPuoLS4u1tTUEPmura1dXl4upDm4FwiUGwFQ8BIc8WRIn81mo7qcjP1IZv7z+/3JIEKHw0H9FfRAXFhzHMlwl3A4TI2R1L93715iRlVV1cTEhOQqvAQCQCA7AVDw7Hysd5Ws1skU78FxHInXTiQSybU2sVhMk2131GE6cOAA/RQZGhpSVwncBQTKmQAoeEmNPom5zpRshHSV7LaTvYwBUE6ePEnl+9SpUwa0CE0AgdIjAApeOmNK9pmUhAMmw0LS5+NOp7PwDYsLATc0NETl+8CBA4VUBfcCgXImAApeOqNvt9slUdgsy9bV1aXvjkaebWbyTetNZGJioqqqiij43r179W4O6gcCJUwAFLx0Bjfp1LbZbMlUJ3TzBJfLJfuUkiymp8EqRiJYXl6ura0l8l1TU7O4uGhk69AWECgxAqDgJTWgDMOQaJNW/kc2fyyZehdrAt7Q0EDke8uWLZkSpJTUkEBngICeBEDB9aRbjLrpUppkFHb640oSqVIMu3CbBw8epO7vq1evFssMaBcIlAwBUPCSGcoNHSFpAsUbw9M4QtWJqzY0kP+Ls2fPUvn+1re+lX8FcAcQAAJSAqDgUiIl85rEfdM0gSQjiiRSxbDODg8PU/luamoyrF1oCAiUNgFQ8FIe30gkQp5tJhfQJ6U8U2YSvRFMTU1VV1cTBa+vr19dXdW7RagfCJQJAVDwEh9ouoeDil3TNEHz+PHjXbt2Efnevn377OysJtVCJUAACHAcBwpe+m8Dkv67WIEf+/fvp/6T8fHx0scNPQQCBhIABTcQdvk19fWvf53Kd29vb/kBgB4DAX0JgILry7eca+/t7aXyfeTIkXJGAX0HAjoRAAXXCWy5Vzs6Okrlu7GxsdxxQP+BgD4EQMH14Vretc7Ozm7bto0o+O7du1dWVsqbB/QeCOhFABRcL7JlW+/Kykp9fT2R7+rq6pmZmbJFAR0HAnoTAAXXm3DZ1d/Y2Ej9J8PDw2XXf+gwEDCQACi4gbDLoKljx45R+X7ttdfKoMfQRSBQTAKg4MWkX2Jt9/f3U/k+dOhQifUOugMETEgAFNyEg2JJk8bHx6l8NzQ0WLIPYDQQsBoBUHCrjZgp7Z2fn9++fTtR8F27di0vL5vSTDAKCJQaAVDwUhtR4/uzurrqcrmIfFdVVU1NTRlvA7QIBMqTACh4eY67lr1uamqi/pOhoSEtq4a6gAAQyEoAFDwrHriYi0BHRweV7zNnzuQqDteBABDQkgAouJY0y62uq1evUvk+ePBguXUf+gsEik4AFLzoQ2BVAxiG2bJlC1HwvXv3WrUbYDcQsDIBUHArj17xbF9cXKypqSHyXVNTs7i4WDxboGUgUL4EQMHLd+wL6fnevXuJfG/ZsqVYe0cUYj/cCwRKgwAoeGmMo6G9OHDgAHV/X7161dC2oTEgAAREBEDBRTDgUAGB06dPU/nu6OhQcAcUAQJAQC8CoOB6kS3JeoeGhqh8NzU1lWQfoVNAwEIEQMEtNFhFNnViYqKqqooouMvlWl1dLbJB0DwQKHsCoOBl/xZQBmB5ebm2tpbI9/bt2+fn55XdB6WAABDQkQAouI5wS6nqhoYG6j8ZHx8vpa5BX4CAdQmAglt37Iyz/NChQ1S++/v7jWsYWgICQCArAVDwrHjgIsedO3eOyvcLL7wASIAAEDAPAVBw84yFGS0ZHh6m8t3Y2GhGE8EmIFDGBEDBy3jwc3V9ZmamurqaKPju3btXVlZy3QHXgQAQMJQAKLihuC3U2OPHj3fv3k3ke9u2bTMzMxYyHkwFAmVCABS8TAY6727u37+f+k9GR0fzvh9uAAJAQH8CoOD6M7ZgC4FAgMr366+/bsEegMlAoCwIgIKXxTDn1cne3l4q388++2xe90JhIAAEjCQACm4kbQu0NTo6SuV7//79FrAYTAQCZUwAFLyMBz+t67Ozs9u2bSMKvmvXrsePH6cVgRNAAAiYiAAouIkGo7imrKys1NfXE/muqqqampoqrj3QOhAAAjkJgILnRFQuBRobG6n/ZGhoqFy6Df0EAlYmAApu5dHTzvb29nYq39/73ve0qxhqAgJAQEcCoOA6wrVK1f39/VS+Dx48aBWzwU4gAARAwcv9PTA+Pk7le+/eveWOA/oPBCxFABTcUsOltbHz8/Pbt28nCl5bW7u4uKh1C1AfEAACOhIABdcRrsmrXl1ddblcRL63bNkyMTFhcoPBPCAABCQEQMElQMroZVNTE/WfXL16tYx6Dl0FAqVCABS8VEYyz368/PLLVL5PnDiR591QHAgAAVMQAAU3xTAYbMTVq1epfDc1NRncOjQHBICAVgRAwbUiaZl6GIbZsmULUXCXy7W6umoZ08FQIAAENhJAyTyiodQPwzAbr8q/6unpSd2h/m9XVxfLsvINiM6yLNvV1TU4OBjP+qOkKlGt5Xu4uLhYU1ND5Hv79u3z8/PlywJ6DgSsT4B+mcYH4XA4Z48YhtlwTwEvlHxgRKNRFS3U1dV5RD/Nzc2hUChn18qhwN69eynP8fHxcugy9BEIlDABNV6URCIRk/tRosgqUDIMI9eacC4SiQQ3/vj9fvfGH4SQw+FQ0jTDMF1dXfF4XKe+KLFBvzIHDx6k8t3f369fQ1AzEAACxhBQo+DGWFaUVnw+H9U4hJDdbvd4PGQKT5Tduu6aM2fO0K61t7cXBS80CgSAgLYEQMGlPMmUP+lQCgaDXq/X7XbbbDaqfVTWW1tbQ6FQPB5PJBLSKsz3emhoiHahsbHRfAaCRUAACKghAAqulBpR9mAw6PP53G43FURy4PF4AoFAT0+PCd0vU1NTVVVVxM76+vqVlRWlfYZyQAAImJsAKLj68SHPA2Q1PemdV1+vpncuLy/v2rWLyPe2bdtmZ2c1rd5qlcV8+PvUvvCC1QwHe4GALAFQcFksKk8yDBOJRJKPUmOxmMoqtL6toaGBfl0YHR3NXH20xWaz2VqimUuUwpXL/C4WDv9kKXQG+gAEOFDwUn4THDp0iMp3b29v1q4SbWu8nLWQwRcnz7d4vS3nNZRbUHCDhxCa05kAKLjOgDNXn0gkenp6Ml8v9Ep3dzeV769//eu5qjOjgmtvEyh4rvcBXLcWAVDwoo1XOBwmkS2tra2Dg4Pa2jE8PEzle//+/Qoq114tFTSao4j2NoGC50AOly1GABS8mAMWjUZ9Ph+JVrTb7a2trZo40GdmZqqrq4mC79q16/Hjxwo6maaW7LVjXq83PMZx3MK1zsY9Nvyzp7HzWtpTwIWx8OF95LrD6fVfnlzb0N7a5GW/cLvN4fRKK+BdJYcvL3BrY2G+mMN5+NrPLx/2er3OHbgTO5xe8oMLrf/kqJYvuHCt0+t02Gw2m8PZEplc40DB1wHCUSkQAAU3xShGIhGv10s01+Vy9fT0qF469Pjx4927d5Oqqqurp6amlPUwTcEn/Q6EUGP4sndDODxCyBkWhcCzlxsrcWuVNv4HH4sfFDLH9hBbyHW+KNrREl1PicM37PBH+OZIWYf/n/iYEfKK/iuqN3e1HMes11hJ2q10OnGfNhiojA6UAgLmJAAKbqJxYVk2HA47HFhl7HZ7IBBQsVxo//79VPKGh4cVdy+DguO6bO4wmVavjRFRrPTSkJVrLVgcReF5a5OR89dS+kyuVjZG6OR5IcILfmXLtZRlpGHczo6Wy4k1jk3ExoRPiDSbhHuUVDt2mJ/A07bXJsPu1EeR6KMgZQX8BQKWJAAKbsZhi8VidEre2tqqXMe/8Y1vUPnu6urKp29paknm4Kiy8XJKj3F1JKDa5hOiJdfO78PS65dNarnQ6cST83W55+1hz/PLoWjUi6Dgle6IuB2+aJpN/FlF1Qoiv7Ht1PcFUHAeJPxTAgRAwc07iIlEguZpUaLjvb29VL4PHjyYZ8fS1JIoeJrYRTbqrzDVdfjS3eOcpGjKIEnFpOF94TT95gSvNdV6oQIl1ZI2RDN94V7SWFqnUqbBXyBgMQKg4GYfMImOZ/KPj46OUvluaGjIv1dKFVxajo228O4KhCp3OFvCY9RfwgmT+JSH3EZ/eKd0ZYswjZdWKDJd9pKiasmd6Uqd6byoUTgEAhYiAApujcGiOm6329PdI7Ozs9u2bSMKXltbu7y8nH+v0tRSMlVO1ZhWTohVcZCHhQjZ9nUSn4ogtTSURIgoIX9aOmPCpFuuQqEx2UuKqiV3goKnRg3+lioBUHArjWwyuxZJquXxeGgKrZWVlfr6eiLfW7ZsmZiYUNWlNLXMQ8FJg2uJa34nr+M7DuMYxMljfOCH1AkitS6t4fUCspcUVUvc4On++UzKvt4mHAEBKxEABbfSaBFbw+EwCSEneyo1NvK5PngJv3r1qtr+pKll3grOtxz1Yg13dmJniiCjvJxnNiut4fWi8peUVEuedqJ95zd619kwfvAK0YTriOHI4gRAwS05gCzLJpcChcPhb37zm2T2jRD69re/XUBn0tRSkYKzY7GN63dINUIIiBAQ4l4PJhQMXGNZuuonreH1TpD7aeBL6oKSahOdfBz6jlTQDPb1UI99unclVTX8BQLWIgAKbq3x2mBtf38/le8DBw5suJb3izQhVaTg/F07nF5/OBKJhP2NvN9kPQQkFb6H11XyRSKdh737sMt8XUTTGl43XQg8RLY9bq/X7XR3CjmulFTLkm8DCNn2eP2dfrK+s9LtxsK+3vh6W3AEBKxIABTciqOGbRZvOe1yuQruRpqQEn9zmtiRcqk4azbm3yeEopAPk0qHNyJasclxaSVI0MplWijKr0XN4C1nxStC96QUnFNQLcdxiYiX/0Qhltn2+WMsCVB0HNMw3WHB5KECIKCeACi4enZFvHN+fr6mpoYoU01Nzfz8fBGNwXq6QH42ep3FNqVKLGQuIi6+4ZjcK3tj7mrXsty9oRV4AQQsSAAU3IKDxnEul4v6T2hQiiV7AkYDASBQAAFQ8ALgaXdr/OEj8W9iiT7nk2njwIEDVL77+/tlSsApIAAEyoMAKHjRxpmZWwlEH7rO3EaBuOxv8xsPesY/kqj5iRMnqHy/+OKLRbMeGgYCQMAEBEDBizAIsWnW032HqHbF8f+DwifRhW+inmfXf8MnUedrm9v/lZQJRB+yq084jrt69SqV78bGxiKYDk0CASBgJgKg4IaOBrv6hGj3piM/wao90IIGm7P99n0Zdb6GAvHqtpGv9t7asmULUfD6+vqVlZUspjMME43SFLBZCsIlIAAELEwAFNy4wWPmVmztI5uP/DuedOfUbrGyX/kbFOzD8/E/aUOVVcndfN5///3sdgeDQYSQJjv+ZG8IrgIBIFBEAqDgBsGP3FzY2nZ9U9u/oL4vZ5t0i4VbctzdgUX8S28MxUZzGs2yrMPhqKury5TLMGcNUAAIAAHzEwAFN2KMYtMsCsSxyzuvqbdEwQeb0YVvbnr+J589PU7c4tlNj8ViCKHW1tbsxeAqEAAC1iUACq772DFzK1vbrmsg30TQLz6PAvHWN3+uxG6/359MMwUOcSWsoAwQsCKBIit4YmlNEi1nRYhZbGZXn3z29HjFkX9X7zxJn4nz7pTgNbouPUv7HPhSstGBa0DA4gSMVvD4w0eZgqBdZ24Hog/jDx9ZHOkG84PXEth53fOsSt93unyTMyfeqG4bUfLhR3wpwWBwg1nwAggAgZIgYJCCs6tPQkPvV7eNkgBnFLyFzjxA4cn13zMP8El+bYutfTQ09L4SV6/Jh4BdfVLdNoLDSDIJserzV/4GBeK+S4oSNLndbrvdDo80Tf5uAfOAgAoCRih4z/hHSVHG6hy8hS7MoIElNPhI/ndgCRfgpXxnx42e8Y9UdMk8twgTcNXBJ9n1nY8TVzINTyQSCCGfz1coGSFbIST2KxQk3A8EtCKgr4Kzq09a3/w5CsQ3d9xCPXPyqi2r5j1zFcdvKH9kpxUObeupe/mGLhNwouz8NDwc/1CJzeSRZiKhyHWescIMGcMzlocLQAAI6ExARwXnH+LxST/Ck3lot1jQzzxAgbjrzG0relQSS2v4a0d3h/YulNTcfHP7v7rPkV2Fc7xNWJa12WyFTsOtrOCT51u83pbzitxOOWDCZSBgHgJ6KTiR74oj17FXRCzK+R5fmEGB+GdPW0/Ew/EPsYJf+Rv9FBydCaNAXOHHm8/nS/pSCpqGW1nB0zawMM//QbAECKgnoJeCC5mb8vKcZBL3ix+gQLz5jQfqe1mMO/1vTWMFT82XdTnoeRYF4rFp2b0PpH3WwBsOCi6FCq+BQJEJ6KLggngVOPsWC3o3VkOFEdBFJppq3n2O2dzxpi7CTT8V8lHw5K5juafhC2PhFqfDxv/s2Xc4snEXY3kFX5u87G/cQ+5xOL2d1/A29es/vPvi8OUFjluvfE8jLbV+N25P1k+/fp/Nlm4Ut97A2mREsN7hbKG2L1w+7PWSbTLxdp3khzdo3Ug4AgIWJaC9gjNzK3ju2Xm3IOeJWL7J8Yn3kvFzSkIvTDIS7nOMjo8xiYj3fRkF4pGbGyUzc//JNNzv98sWoVtSVtrwTyWfBbHS2bnuaJdRcOYYvyU8QuKbdrRE178W8O4Lhz+SKphKj1vZeHlhIeK1pV6Tv9IdLHMbJex8md4AsrVcwx2N+SRt4JbStv+URQIngYDZCWiv4J7uO5uPXM8WMpiuzkrOXFncfOS6CX0pv/jFL27evPnWW299//vfb2tr++u//muPx/OZz3xm0//zfd0VfLA5368mPp9PPjY80ekkyjaW2h5obczP7xPs7EzNjNMU/FoL1vnKxgj9DFmINPKniHjidz9xQOO69xwm0/OFa771DYht7jA/0V+bDO/jPzTEWx4rMUqmAU6wAu2hpgulxJWb/b8m2AcEFBDQWMFJCie8TkeJKOdbJjyp3O2roO95FPnv//7v69evv/nmm6dPn/b7/V/4whf+4A/+4Dd+4zfIxFH+3y926a7gvBcleu9j5T0hSzQjkYjkFqLFIsXjr48dxvvQ0/mqRMEXeNGvTG1bL9TInndjHlQrBQV3+Nfn8hx7fh/PrLLx8vpkXZgs23yxlG2KjEop+IYGUi3sO5+qH55kpqjC35IioLGC+y5N4viTLGt28lVtcfmBpWTohf+taT1G4Je//OXPfvazn/zkJz/84Q9PnDhx+PDhv/iLv3C5XL/2a78mL9A5z36x66kXrprKD064ORwOl8u1kSHj3yDV9OJG3ZMoeGSjVKdukpTaWIVQSFJGOCupUJlRGWbX0ptlzUiZDH+BgFUJaKzgOztuoBPv6TIBJ1J+4r2dHTdUw/74448ZhvmXf/mXCxcuHD9+/G//9m//9//+37/1W79VXV2dU5AzFbDb7U8//XRjY+Pf/d3fBYPBf/zHf3z77bfv3r37wls/0z0W5cI3VXwpCYfDaZs/EH0TnNm29R/iDHeGiZdko+6SVykP+Po9xINe2SJMpWWlc2NNqfGUFFVmVAYFl7YgqTvVJPwFAtYmoKWCC88wNQxBEU/AyTEflJL9eeaHH344NjY2MDDQ1dV19OjRv/qrv/rc5z736U9/OpMEKzn/yU9+8nd/93e9Xu9Xv/rVf/iHf/jRj370H//xH1NTU6urq5nGP3JzASu45jmtaCDKYDPqfG3rseuZDMh0Xm51D9G3SodbCNXY8OfwZcERvlEVBQWn4R0b7mnpjAn+C1np3FhTylJJUWVGgYKn8MHfciSgpYKn1rAs6jgH75lDgXj03sfT09PxeLyvr+/UqVNf+9rXPv/5z//+7//+pz71KSVynKmMw+FoaGhoaWl57rnnvve97/34xz9+5513PvjgA3Xvi2QyL6zgZ8L6OVIqjv67wuRWki6QsEJRrquoF0OhDm9J8dTLjbpLsqSsO7xTpSR/JbJMrm6sKXWHpKgyo0DBU/jgbzkS0FLBhURO6RNnbc8E4uiZ1kwqnP38r/zKr+zevfuP/uiPvvSlL7344ovd3d2Dg4O3b99eWKDBFFq+CXBIePv/p5eC81s9KA8lFHeMYRiEUDgcTp0kDyWRmz74S13Y8Feiu+RB447DYxsKSV9IZJlcltQk3CMpqswoUHApcXhdTgRKUMF/9Vd/9Xd+53f+7M/+7Mtf/nIoFLp48eK//du/3b9/XzTlNGiEBUfKhW/qIeKbOy5vPXZd4ZL69A5Ho1ExkFTc3mEaTJi6RVRKqrtCMKF7PZhQuGmNZVMxifICK62J3CdRcE6RUfINcNIWiK2iQJdU/+AvELAyAS0V3H2O2dT+ro4uFDKXD8SR+9lPfepTzzzzzOc///lnn3325MmTfX198Xh8elqXMJVCxrc29K4u03A+jlBhYkJl9jMk+htVOvYd7oxEIpGwv8XtxCEqNDBQqooce5mP/kZ4raM/jG/qPOzd56gUO2Skssxbk1YTfza9qAKjFCq4EOSIbHvcXq/b6e6EHFfK3hdQytwEtFTwVCaQDLm/tfKlWGp5fSpA/qSW0/CBlk3t/1Ibelfrt1Yi4sXqK/6p3NNIn0lyQn5wv1j82Jh/H5Z50U/lDmdL6uEnxxFvNv0UIDbL1ZRa/COJL89llHwDqTm4KJc5Xd6JTd0DCq71uwfqKwoBLRXcMD+4tRKk+C7hhUhIQ1/KK2+oCCJU/PZaYxfIz7onJPe9qXsWUitoct+SVwlVRsm0QOzUyUiZ9uAUENCXgA4KfkX3WBR1j+/0BZm5dnb1ydOnblYc1Wiz45Ov5ZULJbNdcAUIAAHLE9BSwQWPga7x4Hy6cGZuxVrg+Q0zr2MRv/h8Qe4UXr7VRRBaixhYCwSAgBICWio4x3Fbj41on5VQ7EA/8V5tKHv0mpJeF6FMYmnt6VM3sTvlVVW79gy0oOP/r35JBYpABJoEAkCgYAIaKzjOi3J0RK9wFD4vinVnoOzqE+/F+1jEv9Wbx1rNgRZ09iSev+eTSLbgNwZUAASAgAUIaKzg0XsfY4XqntZFxIuXm1DDkfS2n0df+VdMKdSHfvDNbNuw9X0ZnT2JgxEDcfc5xnK+Iw2hQVVAAAjIEtBYwZMJ9XFU+NER7dMTDixVHB1RuLGvbFdNcrKurg5VVqFnWrc89x9YxwPxipf+D1bzsyeF35OvoVDfUy/8M7n628F/V7iPmkk6CGYAASBgGAHtFTwVAa11inB+33qrz0Oj0SgJnLbZbCzLJrsTvJZwn2Ocp28RvSb/us8xjmd7Uf2foupPhkIhw94N0BAQAALWIqC9guP9GIUI6MJ2qRc/wORDUHTKDG7kgJGUUsk9430+X/Z2v//97xOt/8IXvpC9pCZXGUa0AYMmNUIlQAAI6E9AFwXnI6Bv4UeafQsaOMT7cJpW5+lb+tPQtwWWZenKxViM7kQj3+jw8DApvGfPHvkSmp7dmOhK06qhMiAABHQjoIuCcxzHR0CPYBHvmStIxHvmKo6O1IbGVKdw0g1d3hVHIhEiyg6HI+fNy8vLVO5zFi68gNzGPYXXCjUAASCgLwG9FJzjOGZu5elTvHtX9Rof3nny9Klb2bd00JeQdrW7XC4iysFgUEmtn/zkJ0n5//zP/1RSvpAyZOMe8KUUwhDuBQLGE9BRwclM3H2OwU/nXmFQXqvt+xZQ6DYKxL0X75fA7Bt/nvEpuYkiJxKp3d+zDvgf//Efk/I9PT1ZC2pwkXh4cnrnNWgJqgACQEA7AvoqOLEzeC2B12oG4ujkvdye8X/6BS4WiG89NmKtDFbZB8Xv9xM59nq92UvSq9/4xjfILc8//zw9qd+Bz+ez2+2idOD6NQU1AwEgoA0BIxScTMaFAJVAHDvHT95DZ6fQqw/RP/0C/776EL88eQ9f4kOk/W9Nl8bUm46S3W4nchyJROjJ7Ac//OEPyS1/8id/kr2kJldjsVhypzXl5mnSKFQCBIBAIQQMUnBiIrv6JHJzwXdpUpiS82JNJJtMun2XJiM3F0pMuzmOE4eBKx+t8fFxouA1NTXK7yqkJDzPLIQe3AsEjCdgqIJLupdYWotNs7FptjQeVEp6J37p9fI7CSPk9/vF53MeEwVHCC0vL+csXHgB8jxToZu+8OagBiAABAokUEwFL9B0q9yeSCSoEOcb7PGZz3yG3JszflwTGsTUfD9mNGkaKgECQEAFAVBwFdDyu4VMbBFCTqczvzs57vOf/zxR8O9///v53quuvNfrtdvt6u6Fu4AAEDCYACi47sBxKiv+JxwO59vYSy+9RO798pe/nO+96soTlz08z1RHD+4CAgYTAAXXF7g4DFxFoF5/fz9R8GeeeUZfQ0W1OxwOj8cjOgGHQAAImJQAKLi+A6M8lZWsHZOTk0TBP/GJT8gW0ONkMBhM5t6C55l6sIU6gYC2BEDBteW5oTaWZWkYeDQa3XBN8Qui4EZKKnmeqXDpv+J+QEEgAAS0JwAKrj1TWmNeqazoXZIDmk3ln//5nyWX9Hvpdrvr6ur0qx9qBgJAQBMCFlPw+MNHPeMfhYbep7+D9/8n/vCRJiwKqUTWMNdftJIZdCHxeV/60pdIJd/+9rcLsTCve8lnj+rvDXm1BYWBABBQTcACCs6uPukZ/6j5jQd09Wb6QXXbaOubP+8Z/0g1CBU3KjEMfeVt9Cdt33n7gYr6yS2nTp0iCv6Xf/mXqitRcaPNZlOewkVF/XALEAAChRMwu4L3jH9kax9Fgfjm9ndQ51108YMNCccHlvDLCzOo827FkesoEN/ZcSN67+PCueSsoWf8o50dN5QY9tRzeDNM1Ya9/fbbRMF/+7d/O6dVGhYgqbhUxM9oaANUBQSAQHYC5lVwZm5FkMiOWxtUW7z7muT4wgwW+kDc031Hv+Qq6gzb1KbSsA8//JAoOEKGDhaJg1QRw579DQdXgQAQ0JCAoaKg3O7ovY+3to1uOnIdz68lMp3zZfd0xZHrtvZRPbZFJobh+b6Bhn3iE58gIn737l3lDAsv6XQ64Xlm4RihBiDH9ZZjAAAaSElEQVSgHwEzKnjkJt4Ys+L4DTSwlLd8E33vW9h05PrWtlFtPSrrhuW1W4X4I6dv4SnesMjNBeWD+od/+IdEwfv6+pTfVXhJ2LincIZQAxDQlYDpFJyoJDrxnnr5Joo5sFRx/MbWNs1m4tF7H+MnqMFbxhv293//90TBjx07puu7QVI5bNwjAQIvgYDZCJhLwZm5la1towXNvsUT3oGlTUeu7+y4UbhPXHPDnuL9PAoNe/XVV4mC//mf/7nBb6Dkuh5Y2mMwc2gOCCgnYCIFZ1ef7Oy48dSR64VOcsUi3ocdMp7uO8qJyJbc2XEDO+VVO0/EJpHjvoWKI9cVGnb9+nWi4Dt37pQ1D04CASBQngRMpODBawnspuiZU+n7TldJciY8iQLx2DSreoD1Mqx7GgXiSjz1y8vLRMERQr/85S9VdwRuBAJAoMQImEXB2dUn1W2j2MucSYgLOL+5/Z26l2+oGzli2OYOvQzb2aHIsF//9V8nIj46OqquI3AXEAACpUfALAoejn+IJ+B9C3ooOI78UzbbTR9gwTDNvxmQDyTeMCVxKX/6p39KFPz8+fPpRsIZIAAEypOAWRTcdeY2foBZwEQ7+70VR677Lk2qGGOTGHb06FGi4F/5yldU9AJuAQJAoCQJmELBE0treALePZ1dhQu6euI9W3ve/gd29Qk27MyDgprO/rHUebe6LbdhP/rRj4iCf+5znyvJNyJ0CggAARUETKHgQgy4Ti4Ukb8i31WahhmW80Hre++9RxTcyK0eVLyf4BYgAASMJGAKBReCPbLPVQu82jOnIiLFMMOURKQQBUcIffjhh0a+RaAtIAAETEvAFArufwvH1enoqRh8hEO5A/HgtUReI2GEgg8+UmjYb/7mbxIRf/vtt/PqBRQGAkCgVAmYQsHd5xid4gg3fCrkr+DucwzOKVjg9D/n7coM++IXv0gU/NSpU6X6doR+AQEgkBcBUPBsuPBHy/GbJlHwjo4OouAHDx7MZjRcAwJAoGwImELBfZcmK46O6CuUA0sKnRXioTfCvaPYi/LWW28RBXc6nWIjDTtmWTYQCMAe9oYBh4aAQE4CplBwI9zN/JNMJQ8MxciMMIzP3KJkUc9//dd/EQU3eKsHCgT2sKco4AAImISAKRRcWPeoYd6odNfzxQ9UxKKYzTCq4D/72c+K8gZyOp0ul6soTUOjQAAIpBMwhYIzcyu6r+jpvJv0oqT3P/sZI5YancE7OCtMM/t7v/d7RMR//OMfZ7dcp6vBYBAhBI4UnfBCtUAgXwKmUHCO42pDY3hXh/S5s0ZnNre/6714P186gmH65Nsinc3LsNbWVqLgx48fV9GXwm+BzTMLZwg1AAENCZhFwYVnhqq3Vcsu9LwTXImvOZ2sYJhOHh7esHBc6Qqd7373u0TBvV5vuqnGnHE4HEVs3Zg+QitAwCoEzKLggr+i864e0/DNHber20YUeiokI6erYSh0e+uxPAz7yU9+QhT805/+tMROw176/X6EEMuqz7dumKnQEBAoeQJmUXCO43yX8FYMWu6DQybm/DNM5fPc9CHXyzB+Ap7XMtH5+Xmi4EXc6iEajSKEIpFIOig4AwSAgMEETKTgiaW1rcdGNF5BM7C0qf3d2tBYIVjZ1Sdbj41UvHRTy+3f1Bq2bds2IuI3bijaGqKQjme612az+Xy+TFfhPBAAAoYRMJGCcxwn5AI8eU8rX0rFSzerjo3km5Iwnb7mhqHQbRSIqzDM4/EQBX/99dfT7TTmjNfrtdvtxrQFrQABIJCFgLkUnOM44cmhJrnCT95Dgbi6B5jpyITVPWenNPh0KcCwZ599Fiv4b7i+4D8RGnqf/Hb9dC7+8JGKz4P0bio5E4lEEEIMwygpDGWAABDQj4DpFHzdIV7ITHxgiUxy/W9Na8hOcIgXaNgrTDIAXJ1hPeMfuV76V/SVt/EDA7nfnR03AtGHObONF8iELM4Mh8MF1gO3AwEgUCABMyr4uoiHbqt5sNm3gH3W2s2+xYiFrwjHb6ox7MqiasN6xj/a2XEDBeIVR66jzrt458+euXUb+hbwy+5pHFPPK7un+46uOu5wONxut5gMHAMBIGA8AZMqOPWJbz46gs5OKX2EeGUR8Q6KrcdG9NMvwSceiBtjGDO3Uvcyr93Hb6CLH+T24QwsoQszm45cR4G4p/uOuhjKnG9EElOYsxgUAAJAQFcC5lXw5Ew8sbRGHBc4c+HJe+iNWXkpv7KIfpBAvHeCOCh0ki06EtQw/AFz8h5uXXYt0sASMex/vTCCAnHfpcl8DYve+3hr2yied1+Yya3d4mVNA0sojKMzP3v6th7+cRJTGIvFKBM4AAJAwHgCplZwgiM2zfouTeJAQ94/gEUzdHv9N+UOrg2N+S5NJpbWDIOo0LDqthF1hpHJfsXxG+veErFGKznumas4cn1r26jmIs6ybHJdj9/vN4w2NAQEgEA6AQsoODU66RgJXkv4Lk26zzH0N/lIMHgtoblC0UaVHOhhmOCrOfGe/OxeiXyTMn0LFcdv6CHiTqcTXOFK3h5QBgjoR8BKCq4fBbPVzMytYOfJ8RuFyjcV8SPXP3v6dr4+nOxYwBWenQ9cBQIGEAAFNwByfk2wq09s7aP4UaSsb1357Ftckl/B3/zGg/xMyVoaXOFZ8cBFIGAEAVBwIyjn1YawdKhnLr9Hl2K9lj3mH2xqGKJDXOHBYDCv3kFhIAAENCQACq4hTA2qYlefVLeNIj0ykg8sbTpy3dN9RwMrU1VAVHiKBPwFAsUhAApeHO6ZWhUm4H0LGk/Ayay8e1rFVnOZTMULr3w+SJCShQ9cAgJ6EwAF15twfvW7ztzGDzBl3SCFnxxYUr2gX7Yb4XAYNl2TJQMngYAxBEDBjeGsqBUjtuU88d7ODs3S0pJN1yDFlaLRhUJAQAcCoOA6QFVbZTj+IV61pJMLReRIKW74vFo8cB8QAAJSAqDgUiJFfC04wQv3lmSpgQ8r1DAipYi4oGkgAARAwU30HvBdmsQpULLob+GX+hZ0ytpoIo5gChAoGwKg4CYaavc5Rpc4QonuB+J5bc5pIkBgChAAAhsJgIJv5FHUV6DgRcUPjQMB6xEABTfRmLnPMZva39XXi3JlEcEc3ERjDqYAgYIIgIIXhE/bm+FJprY8oTYgUPIEQMFNNMSCgmuY0EriAR98hHf5CcQhFsVEow6mAIECCICCFwBP61uZuRUcD57vdjzpMp3lTOfdrcdGtDYc6gMCQKA4BEDBi8M9U6t4K6LOu/q5wiuOjngv3s/UOpwHAkDAWgSMU3B29Un84SP6a+R2aBYaEhwSfnREy8zg4vk4v5wncnPBQkDAVCAABLIQ0FfB2dUnPeMfNb/xAGdMTW1o+f+3dzUxbSRZuAaQfFniIyfGueUykblx7Nw4dm4cnRtH+xAESFm1s4nkDETyjCDKjJSoWYkEDijmRm72xATDgsYJSeSMQOPMDCuvyFiNFAkfOPS6ftxut9u/XVXG4bUs6K6uv/6q/PXzq/de2U/GFvZ/+OUYnLytEUoeGhifeE6EGD50d//KbJrvTj1Wz+EEEAAE5CMgisGNs/NI4oiSNd5uJvYWs9KTP9DyMfvEc2jhPY7DR5j9xtIb4HE6/OqTd3g357UTziRO1jDjqb9ETDJN03RdF1Ez1AkIAAJNEBDC4NGXn5jQHXvbOk7T2gmKE2/ySOrW848gIbIIhfezPBl8vTgwtz0azTSZCl5uKeTwUgOUBQQAgS4Q4Mzgxtn5zafvsVit7XUmRa4XsZAeSV2f3wdhnAUpXHjPjcTv7KJIShywiqKMjY11Mf+gCCAACHhBgCeDG2fn1+f3MX0vHXZJPSuFwduvhme3wGA59Ay/z/hYFj44EB3NCvat9/IlhLKAQNcIcGNwSt84tN6TP7qkb2o1sVIYvLMzPLslTmDsGizJBYPze5jEf/ytezzXi+h+lu++PK4gaJqGELe55NoEJAICgEA9Aty+dUx5wmWH9fXiN7df+ee2QCfOJPEHB93YF66dDP4TK08kmA8mEgmEUDKZrJ9hkAIIAALiEODD4OEXeAvd7pUndptlSxK//er6/L64J++XmqlOHBuJty+Mr50gojkZnknL0Uclk0lg8H6ZUdDPrwkBDgzObCfu/dr9j/16Bt84xe8DKfLjxR/O5KGBA89GUkNz2+jhB/T0T3eo14vo5zx6cICNESOp0LOcNLepfD6PEIrH4xcfTOghIPA1IcCBwdkvfe72yxung3d2vr27A7oUOuGSh4b65B3+rUM+WEMS3bc+mNxJ+vBMWiZ3W1+Gsh5c0zTrEk4AAUBAAgJeGZwJ4GJ8CLHvTyQlyAlFArgimjDOzhMHn7XNvLKYVRazo9FMcH6PnpcT5ehMXJ/L7/eHQiHXW5AICAACghDwyuAsIKoAAZwqCgbv7IwtXBRtOA0SEH356dbzjzeW3tBP2fU0+vLTxru/BY1Qv1QLTj39MlLQz68JAa8MPrawjz3jXRXZXBIXsH9QbxUpxtn5D78cjy0QU/eKEgO7LGl7VlQAFEldmd26+fR9D6Xg3s5LRVGuXr3a2z5A64DAZUPAE4OLVaFUjFJ6u565/J//fXsXB2/BZL3w3j1IwHoRW8HH3mJz+EjqxtKbS8jjYBJ+2bgDnvciIOCJwVkgPS424E0E9h7t62icnVO5G3N3+89YifESSRxdhAGW1gdgcGlQQ0OAgIWAJwZPHHzG9g/ts1sTmm58a/D2q9CznNVjOSfZ4y/+uS0sU3cRIWC9iGMxRlI3n77vrf5HDla0FWBwmWhDW4AARcATg8vY13HjFGnY1kLmgCUPjeHZrW9uv3LXmTR+2dSsBxB79uvz+5eExHVdB6cembMU2gIETNPkweBtMlrX2eQyePb4y/DsFtaceN9x+KffqVr8Mkw1cMu8DKMMz3jREODB4MJMCZlIK5HBq/G5Vgo1AnXXrx9C4reef7xoA8+9P8Dg3CGFCgGBlgh4YnBpK5nhF4ctn4RLBuZfylezT3TiX711CjA4lxkIlQACHSHAg8E9hpNtKd7KskVhxpEc91WoPNrQ3Our/9rpaGD6LjMNjSLWsT43E0AIBWZkr2v33WBAhy8NAp4Y3Dg7x7YoAiivqsEguzuW/cgljMiNpTdDt19xUH9XiLv6FESXIiHKqwSUmjTBITRKKbcanrjm9yFy+PyBoBrbzJdYo7kwYfBwnzN4YTM8PuJDvmCszx+kyVyAW5IQ8MTgpmnibXnntqtUVU9eHlOICkICGKK9kwZmX8sPD5AvllJHp9GXn+yfjXd/C9o9wyODlzLha5S5EUI+v7/C4wj51ISB54AgBs89nlTVyccy6LSU01X8FiJHoN9fRRK+l9BECwS8Mjjb0ZHXul8d3Q/NbatP3rV4CB632YOIW5UlxoVywr3mi6VI4sgZBsCKB0BOvr27c+v5R77aeU8MTjUkCPmC4arQbRrZ1amgDzGuE8TgqxOYUCdWecyjJnUYySn6hvKPq+N+rA4CBm8CF9xqCwGvDG6cnQ/PpPFWXnXkyyFFovJBWcwOzb3m0OdGOKwUJIQHyBdLt55/ZOFn7+xgd6TlY6deaPkYb79571ea7cbSG14ieSAQUBSlrXnnzJSPBYlYOv6YCNu1t0u5bJ6k9DeD4xeFfzy8WRD2Y6IWNri6DAh4ZfAyRsyvh6/9xsYpWi8OTKel+fIIV+hvnA7NvRb6e0LfLVyZ3cIPEnvrZG3X98p6EcVzWPUfSXGJAaBpmq7r3XxtMlMjmMCvxShTN6rCyeCF1SlVVWc2HayfjKlOrUghE58av+bHRyCohldzVLVOKwiSxkeCKj2mVgtWB5hevlIwhunXdhibM6qqxjOmWUhMBQN+v//aRENtTMkoVDrqfBBblXAKCHSCAAcGp2I43nDAlSa6TiRRCfn+zG+EDFuSFRTl3EJApGE7E721PdSpImi9iNeiSUCuXrmPUkJDwVgtP9YNl5P4nNe0AKutqhUxVifI0ijWrTP1OlNgJENYm+E4LOVGdobp5WlBurw6Mkl18qQt2tREnDVAKqq2S7K4/nHvuGtWSAQEmiHAgcFN09R3sYoA781osZXHE6I/kRYORZJhu7YnYjHTODu/sfSGid5dw04Avz6/L0dT75iSVBHtD7XaKNlJfM5rWi1Nreq1Nycx947HrddDKac/tsvt7npwWsw3oVvlCjp5E/gmNyv9Z03hlddgLGOYJSObyVYE7Uoml//uHXfJCEmAQHME+DB4uQ2mS+kiDlQ96RCVcXB+r3nXOd6VxODxHIqkOHabVsWk759+9/r6XCkMkt2lpUvijAct2bchRE7ic17Tgqy6iixcejyOEBoJNw6t48bgBaKY96mJms4YjxUsZ1eqZsYxeE2yce01FbAL94675YQ0QKApAtwY3DRN5tD48IMnKnnyx+B0ejSakckj/cvg7MXJS/9DrO9vPn3fdM5wv8koVxCDm0zJHgg5lNjWc7gxuF5L1ZW8Duqll61/PFSKV/47qqkkw39AoFMEeDJ4lcTvZ9taSauXvh8doUjqu+/3ZNK3aZqMwUU7l2p7fH9YsG7H3np6ZTpGgVg9apvNlxQ7nWbN81N5tw3jOifxOa9pMzS1KiibRmKSrFUi5BsJTsYzllqEdcuFwVkdxCzdbz+oQn2S6XvcO8CqbfKv23JNqoRblxMBzgxumiY1rB6YTqOf8x0wy/Lx0F28jVnoWU4yfZum2acrmTeW3gyIcCLV9q7MbskchYRK1gCVVnYsTuJzXtPvME21MThOLmzGJgJ0LRLb9MXsWo/GDG7ZpzAzFfpvMpZkum73DrSmkm7Lta4ZclwyBPgzOBVplcUsiqQG5rbRo6Nm1hHrRUz0Uczdo9FMD/3Ova4EOiRZt8uB6TTHtVm2euxd/V3f1eXjsr5ephhuEFU1QoqbNbjtG+kkPuc1zUpTHQxOb5Xym+Eg4fGRqYxVsRuDkwgsrnVYxTw4ibp33F4znAMCbSEghMFpy/puIXA3g5kxksKe99F99ONv1c/9LLqzS+9emU1rm3mZQl89NsLDA/D26Blb2B+YFeaCRIIZyBsRtkLYcEWwRM23ncRHr222IWRcmYmgtdzoHOyEijncZrrowuAmtUSx87yzGnzt7JBbHre0bsu51QVplxoBgQxOcc0XS/HUX8piNji/R/ma/h2NZpTFbPjFIS+HQI/DyERaYeEBqM01L05kUVy4WP7Uy+Abp3jj5khKTkAxOnBVp3pslVc9sNQ87mfCcB3xMYs/Ra8UKWViVMauGowYmSTz32G1UsK2WZnQWhzrkVbVTq15yTAqkbaAwasDBWe9QUA4g/fmsTpvlXEi31VBGzkOzW1z9C8VHY4GbZxK357UWFUr7jU4JqGiquNWkEIWULaOwc1kiK5R+q8pqqqOE013YELBiRUZnBD2SFANx3Vdj4cnSGCpGrm98guAVKIEFRoysOIHhCpl9dgUbaFqNFPfoSYzL088SIkqXSEd9QVwp/FR51bapBq4BQjYEAAGr4LBrCE79Wm00XTDlVtiCc7Rv5TofISpUOgT3fv1yuxWFR0ZZ6WcPkld3C03Sd+1iaorO4sPXhMQKm8L9odQQNXzTDKuCNlGMjzOTFForT6SqeZ5bG8P7NtfiVJYV5Ras6xahjpuHaqp2H5BpXrryewnNpWOvQScAwKtEAAGryIkSgwXEOAFLxRrew1fGO28VFrmEeN/VIW7yVnJKJCjohtpkpXeovmr2g2XAqxKKzRJfRZWSaMbhUKTsvWFIAUQkIEAMHgNysxBhq+Bx31slsNRADdNE0ewEqbwYS8GwuAdOdlrmhYKhWoAhQtAABAQiQAwuBNdtuLKa0mTBI2Kp/5yNuPtGq8G8/LDbCSME5vCjl48Cjm8PRmUBgQAgQ4QAAZ3gmWcnY9GM9gjyTuJC4vPBQzuHDa4BgQuJQLA4C7Dnj3+cmU2PTidxjshNBJRW6Y/OECRlKCA4JjBhW5PunGKd4eIpDrSooAM7jKZIAkQEIkAMLg7usbZ+XffEwP2H3/rOMbL2gn1Mg2/OHSv3XPqxVzJBAb3PLBQASDQGQLA4A3xMs7OqX0h1qg8OmpLGF87wUHSI6nhmbTQCAHKYpb/lhqOXxWxt8Mz6YbouN1ACKmq6nYH0gABQEAIAsDgLWBNHho0xgtWqtzP4iguDv34ehH9+7/o0RGmVBJCQEJwLuH7Mm+cDkynO1UBedrpuMU4wG1AABBwQQAY3AWU+qTkoRF6lsN7Otfu+G6/DM7vhV8cdqQ4rm+ozZTs8RfctDiv+q6iuACDtzl8kA0Q4IUAMHhnSGaPv5TVI+W4fdpmvhxokJ4kDj7LIW57X0ejGRyP16H64HVJjCA7fShgcPsAwTkgIAEBYHAJIAtpgilSlo/5k/jaCQ3U3mm/gcE7RQzyAwIeEQAG9whgL4tju/W5bf4MTkLLdiqAm6YJDN7L2QBtX0oEgMH7eNhZRFy+zpkkrmwXdpDJZBIhFI/H+xhQ6Dog0G8IAIP324jV9pfFU/TieWRXna8UBqfT3e1TShk8mWQ7SNZ2E64AAUBACALA4EJglVYp9TzClo4OG0c7L7d5vnYyMLc9PJPuQn+Ct9YjMjgwuLShh4YAAay6BBT6HQEayAUbF3qRxFcKA9Ppf8yku94ySdf1skdPNmvfQrjfoYX+AwIXHQFg8Is+Qu30zzg7ZyEVH37oOAbAxin2OCU7TXdN3+VOappWXslsp7eQBxAABHghAF85Xkj2vh6qE8ebSv+cb9dAZfmYupKW3ZE87uEJDN77GQA9uHwIAIN/VWNuxQDAPP7wA3r6pzuVrxTQww+Uu0ejGS4hXFRVDQQCXxWa8DCAwIVHABj8wg9R5x3Udwvqk3eWxz9e54zu0w8+rwQGCM7vcdx6AgITdj5QUAIQ8IoAMLhXBC9s+bJyPHHwmXr/K4tZ+ikHq9I28/puwaPOpP6pgcHrMYEUQEA0Av8HWr4JA2WkpB4AAAAASUVORK5CYII=" width="222.56692913385828" height="232.08608496239395" preserveAspectRatio="none"/>
</g>
<g transform="translate(4.043464566929138 245.08608496239395)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="15.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="25.119999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="35.739999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="43.019999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g6636102111388326E3C89C955A433A6D" x="58.67999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="67.97999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="79.41999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="89.11999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="98.05999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="103.33999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="112.41999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="120.97999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="134.01999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="140.33999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="151.09999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="166.75999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="176.75999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="184.19999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="193.33999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="203.71999999999997" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="10.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="19.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="25.200000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="35.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="45.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="56.02" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="66.10000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="73.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gCDF8B867C9AAFA36255BC29C36465E90" x="86.34" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="92.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="102.62" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="115.06" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="121.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="136.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="151.24" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="156.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="164.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="174.54000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="179.82000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="188.96000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="195.28000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="204.36000000000004" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(75.42 65.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="8.559999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="13.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="24.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="32.26" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="38.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="47.519999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="54.959999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g316778D5069ED68A0C52C06F0AD18D23" x="62.75999999999999" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 433.56299212598424)">
<g class="typst-group">
<g>
<g transform="translate(8 18.5)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAA14E57E2DCC57A3F7809273EECD3C51" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="9.344000000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="12.812800000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="18.5344" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="23.296000000000003" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="29.1456" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="33.8048" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="39.2832" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="46.1696" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="49.638400000000004" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="55.116800000000005" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="60.96640000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g1CB3EC9D05726EBFDE8ADABEC8504FCD" x="67.54560000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="76.4928" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD62975B7DE3250BE5F195D0E8335F60D" x="82.3424" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="88.704" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="92.1728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="98.5728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD5EEFB9760BC9A91B84F628EDDA52971" x="104.4224" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="110.7328" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="114.112" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g83A6AA7A836EACB3652229F4716CDAF" x="123.03359999999999" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gDB4862E33098F259EEBBA99A57E5AFA" x="129.2416" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="139.3536" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="145.2032" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="148.5824" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g793DBE65A5AEC1A16A65955B6C0E046" x="155.1616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gA11612CECC8CBEF18835767DAB11B2F7" x="166.3104" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="172.7616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="177.52319999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gCEFEF3D67F35C6E83CC3757B1DD21B13" x="180.90239999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="190.57919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="196.97919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="201.74079999999995" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g645CA8FA3D9155E2CBD9F8EED3C1540D" x="207.59039999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="214.23359999999997" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(790.9617637795276 8)">
<g class="typst-group">
<g>
<g transform="translate(0 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g54C180954D544D3C78C9AD9E4F48A6CA" x="7.44" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" x="18.880000000000003" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(28.048000000000005 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="7.44" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="g5396A27CA60B9808846A090320835A9F" overflow="visible">
<path d="M 1.91 1.22 L 1.91 5.23 C 1.91 6.06 2.08 6.1099997 2.78 6.14 C 2.84 6.2 2.84 6.41 2.78 6.47 C 2.34 6.46 1.87 6.45 1.48 6.45 C 1.15 6.45 0.65999997 6.46 0.19 6.47 C 0.13 6.41 0.13 6.2 0.19 6.14 C 0.89 6.1099997 1.06 6.06 1.06 5.23 L 1.06 1.22 C 1.06 0.39 0.89 0.34 0.19 0.31 C 0.13 0.25 0.13 0.04 0.19 -0.02 C 0.64 -0.01 1.13 0 1.49 0 C 1.8499999 0 2.33 -0.01 2.78 -0.02 C 2.84 0.04 2.84 0.25 2.78 0.31 C 2.08 0.34 1.91 0.39 1.91 1.22 Z "/>
</symbol>
<symbol id="gEEE4EC0F13100E99C1017169F912BE3E" overflow="visible">
<path d="M 1.55 1.22 L 1.55 3.12 C 1.55 3.61 1.68 3.52 1.91 3.23 L 4.2599998 0.099999994 C 4.41 -0.06 4.5699997 -0.12 4.72 -0.12 C 4.8399997 -0.12 4.94 -0.049999997 4.94 0.14999999 L 4.94 3.3799999 C 4.94 4.21 5.0499997 4.24 5.66 4.29 C 5.72 4.35 5.72 4.56 5.66 4.62 C 5.3599997 4.61 5 4.6 4.7 4.6 C 4.4 4.6 4.0499997 4.61 3.75 4.62 C 3.6899998 4.56 3.6899998 4.35 3.75 4.29 C 4.36 4.25 4.47 4.21 4.47 3.3799999 L 4.47 1.51 C 4.47 1.24 4.44 1.0699999 4.13 1.49 L 1.8399999 4.6 L 0.42 4.62 L 0.39999998 4.5899997 L 0.39999998 4.35 C 0.39999998 4.31 0.45999998 4.29 0.48999998 4.29 C 0.87 4.2599998 0.97999996 4.14 1.0799999 3.9599998 L 1.0799999 1.22 C 1.0799999 0.39 0.96999997 0.35 0.35999998 0.31 C 0.29999998 0.25 0.29999998 0.04 0.35999998 -0.02 C 0.65999997 -0.01 1.01 0 1.31 0 C 1.61 0 1.9699999 -0.01 2.27 -0.02 C 2.33 0.04 2.33 0.25 2.27 0.31 C 1.66 0.35999998 1.55 0.39 1.55 1.22 Z "/>
</symbol>
<symbol id="gA419F36517085793EDBF3FE4736A2E59" overflow="visible">
<path d="M 3.04 1.22 L 3.04 3.74 C 3.04 4.11 3.1399999 4.2599998 3.46 4.2599998 L 3.72 4.2599998 C 4.35 4.2599998 4.48 4.06 4.68 3.34 C 4.7799997 3.32 4.87 3.32 4.95 3.37 C 4.9 3.86 4.89 4.23 4.87 4.7 C 4.52 4.66 3.8799999 4.6 3.04 4.6 L 2.25 4.6 C 1.27 4.6 0.69 4.65 0.42 4.7 C 0.42 4.23 0.41 3.84 0.35 3.37 C 0.44 3.34 0.53 3.33 0.62 3.34 C 0.82 4.06 0.93 4.2599998 1.5799999 4.2599998 L 1.8199999 4.2599998 C 2.1299999 4.2599998 2.25 4.14 2.25 3.75 L 2.25 1.22 C 2.25 0.39 2.1399999 0.35999998 1.53 0.31 C 1.4699999 0.25 1.4699999 0.04 1.53 -0.02 C 1.9 -0.01 2.31 0 2.6499999 0 C 3 0 3.3899999 -0.01 3.76 -0.02 C 3.82 0.04 3.82 0.25 3.76 0.31 C 3.1499999 0.35 3.04 0.39 3.04 1.22 Z "/>
</symbol>
<symbol id="gFAD9169AC3141E7FC4EA568E3BBD2E9B" overflow="visible">
<path d="M 1.91 1.22 L 1.91 2.09 L 2.46 2.09 C 2.84 2.09 2.98 1.76 3.11 1.39 L 3.33 0.78999996 C 3.56 0.17 3.8999999 -0.07 4.33 -0.07 C 4.48 -0.07 4.79 -0.04 4.96 0 C 4.99 0.099999994 4.97 0.19999999 4.9 0.28 C 4.54 0.28 4.35 0.34 4.15 0.85999995 L 3.86 1.61 C 3.74 1.92 3.62 2.09 3.49 2.22 L 3.49 2.24 C 3.83 2.36 4.3399997 2.77 4.3399997 3.46 C 4.3399997 4.29 3.82 4.64 2.6299999 4.64 C 2.3799999 4.64 1.81 4.6 1.51 4.6 C 1.22 4.6 0.79999995 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.78 -0.01 1.1899999 0 1.52 0 C 1.8299999 0 2.1599998 -0.01 2.48 -0.02 C 2.54 0.04 2.54 0.25 2.48 0.31 C 2.01 0.34 1.91 0.39 1.91 1.22 Z M 3.47 3.46 C 3.47 2.6699998 3.24 2.3799999 2.35 2.3799999 L 1.91 2.3799999 L 1.91 3.6799998 C 1.91 4.21 2.01 4.31 2.57 4.31 C 3.27 4.31 3.47 4.06 3.47 3.46 Z "/>
</symbol>
<symbol id="g7FD6A8241485CEBC032BD9E4CE659816" overflow="visible">
<path d="M 5.27 2.35 C 5.27 3.77 4.13 4.7 2.83 4.7 C 1.4399999 4.7 0.37 3.6899998 0.37 2.22 C 0.37 0.85999995 1.4 -0.099999994 2.75 -0.099999994 C 4.39 -0.099999994 5.27 1.05 5.27 2.35 Z M 2.74 4.37 C 3.6299999 4.37 4.4 3.55 4.4 2.21 C 4.4 0.97999996 3.79 0.22999999 2.8999999 0.22999999 C 1.93 0.22999999 1.24 1.11 1.24 2.34 C 1.24 3.6899998 1.99 4.37 2.74 4.37 Z "/>
</symbol>
<symbol id="gBFFDA84A1400D9E1136DF0DD93EA19F5" overflow="visible">
<path d="M 1.48 4.6 C 1.2099999 4.6 0.76 4.61 0.37 4.62 C 0.31 4.56 0.31 4.35 0.37 4.29 C 0.97999996 4.25 1.09 4.21 1.09 3.3799999 L 1.09 1.22 C 1.09 0.39 0.97999996 0.35999998 0.37 0.31 C 0.31 0.25 0.31 0.04 0.37 -0.02 C 0.75 -0.01 1.1999999 0 1.49 0 C 1.75 0 2.1499999 -0.02 2.95 -0.02 C 4.06 -0.02 5.2999997 0.5 5.2999997 2.25 C 5.2999997 3.58 4.48 4.62 2.81 4.62 C 2.1299999 4.62 1.77 4.6 1.48 4.6 Z M 1.88 0.76 L 1.88 3.98 C 1.88 4.23 2.1299999 4.29 2.52 4.29 C 4.2 4.29 4.43 3.12 4.43 2.08 C 4.43 0.68 3.81 0.31 2.71 0.31 C 1.9499999 0.31 1.88 0.48 1.88 0.76 Z "/>
</symbol>
<symbol id="gEC3CC7DEE79E0AA801DFAAEF4B6C0B50" overflow="visible">
<path d="M 4.35 3.3799999 L 4.35 2.11 C 4.35 1.25 4.35 0.31 3.03 0.31 C 2.04 0.31 1.8299999 1.09 1.8299999 2.02 L 1.8299999 3.3799999 C 1.8299999 4.21 1.9399999 4.24 2.55 4.29 C 2.61 4.35 2.61 4.56 2.55 4.62 C 2.1599998 4.61 1.76 4.6 1.43 4.6 C 1.0699999 4.6 0.68 4.61 0.32 4.62 C 0.26 4.56 0.26 4.35 0.32 4.29 C 0.93 4.25 1.04 4.21 1.04 3.3799999 L 1.04 1.81 C 1.04 0.31 1.77 -0.099999994 2.86 -0.099999994 C 4.41 -0.099999994 4.8199997 0.78 4.8199997 2.24 L 4.8199997 3.3799999 C 4.8199997 4.21 4.93 4.24 5.54 4.29 C 5.6 4.35 5.6 4.56 5.54 4.62 C 5.24 4.61 4.88 4.6 4.58 4.6 C 4.2799997 4.6 3.9299998 4.61 3.6299999 4.62 C 3.57 4.56 3.57 4.35 3.6299999 4.29 C 4.24 4.25 4.35 4.21 4.35 3.3799999 Z "/>
</symbol>
<symbol id="g202CCBD46865F83C12D50E1B4FF9BBEA" overflow="visible">
<path d="M 2.76 -0.099999994 C 3.54 -0.099999994 4.02 0.19 4.49 0.82 C 4.47 0.89 4.37 1 4.29 1.02 C 3.83 0.48 3.48 0.28 2.81 0.28 C 1.8199999 0.28 1.24 1.35 1.24 2.34 C 1.24 4.02 2.02 4.37 2.77 4.37 C 3.57 4.37 4.04 3.9299998 4.16 3.23 C 4.2599998 3.1999998 4.36 3.1999998 4.46 3.26 C 4.46 3.6699998 4.44 4.0899997 4.3399997 4.54 C 3.9599998 4.54 3.51 4.7 2.71 4.7 C 1.39 4.7 0.37 3.6999998 0.37 2.24 C 0.37 1.61 0.57 0.91999996 1.06 0.47 C 1.4599999 0.099999994 2.02 -0.099999994 2.76 -0.099999994 Z "/>
</symbol>
<symbol id="g5503E15E5E4E70E9E217A15BD1ECD752" overflow="visible">
<path d="M 1.9499999 3.3799999 C 1.9499999 4.21 2.06 4.24 2.6699998 4.29 C 2.73 4.35 2.73 4.56 2.6699998 4.62 C 2.29 4.61 1.86 4.6 1.55 4.6 C 1.25 4.6 0.83 4.61 0.44 4.62 C 0.38 4.56 0.38 4.35 0.44 4.29 C 1.05 4.25 1.16 4.21 1.16 3.3799999 L 1.16 1.22 C 1.16 0.39 1.05 0.35999998 0.44 0.31 C 0.38 0.25 0.38 0.04 0.44 -0.02 C 0.81 -0.01 1.22 0 1.56 0 C 1.88 0 2.32 -0.01 2.6699998 -0.02 C 2.73 0.04 2.73 0.25 2.6699998 0.31 C 2.06 0.35 1.9499999 0.39 1.9499999 1.22 Z "/>
</symbol>
<symbol id="g1E8994F5C297EC73FA26D93D22635023" overflow="visible">
<path d="M 2.82 -0.14999999 C 4.11 -0.14999999 5.16 0.9 5.16 2.19 C 5.16 3.48 4.11 4.52 2.82 4.52 C 1.53 4.52 0.48999998 3.48 0.48999998 2.19 C 0.48999998 0.9 1.53 -0.14999999 2.82 -0.14999999 Z M 2.82 4.2599998 C 3.97 4.2599998 4.9 3.34 4.9 2.19 C 4.9 1.04 3.9599998 0.11 2.82 0.11 C 1.67 0.11 0.75 1.04 0.75 2.19 C 0.75 3.33 1.67 4.2599998 2.82 4.2599998 Z "/>
</symbol>
<symbol id="g6D39B87B7095296261A07873F9B99896" overflow="visible">
<path d="M 1.86 0.948 L 2.52 2.688 C 2.58 2.844 2.652 2.892 2.94 2.892 L 5.472 2.892 L 6.168 0.864 C 6.3120003 0.456 5.856 0.408 5.28 0.372 C 5.208 0.3 5.208 0.048 5.28 -0.024 C 5.724 -0.012 6.384 0 6.852 0 C 7.344 0 7.8 -0.012 8.22 -0.024 C 8.292 0.048 8.292 0.3 8.22 0.372 C 7.752 0.42000002 7.344 0.456 7.14 1.0320001 L 4.668 7.896 C 4.488 7.788 4.164 7.656 4.008 7.656 L 1.284 1.224 C 0.972 0.48000002 0.612 0.408 0.084 0.372 C 0.012 0.3 0.012 0.048 0.084 -0.024 C 0.396 -0.012 0.792 0 1.152 0 C 1.644 0 2.244 -0.012 2.688 -0.024 C 2.76 0.048 2.76 0.3 2.688 0.372 C 2.232 0.408 1.668 0.456 1.86 0.948 Z M 3.1560001 3.3960001 C 2.892 3.3960001 2.808 3.432 2.856 3.552 L 4.08 6.66 L 4.152 6.66 L 5.28 3.3960001 Z "/>
</symbol>
<symbol id="g1B61845C1FB429ACDF5304290F5BF286" overflow="visible">
<path d="M 4.548 0 C 4.548 0 4.824 1.152 4.908 1.656 C 4.8 1.716 4.704 1.74 4.572 1.704 C 4.38 0.996 4.032 0.408 3.276 0.408 L 2.736 0.408 C 2.46 0.408 2.292 0.6 2.292 0.828 L 2.292 4.056 C 2.292 5.052 2.424 5.088 3.1560001 5.1480002 C 3.228 5.2200003 3.228 5.472 3.1560001 5.544 C 2.7120001 5.532 2.22 5.52 1.812 5.52 C 1.44 5.52 0.924 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.32 0.408 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 1.068 -0.012 1.86 0 1.86 0 Z "/>
</symbol>
<symbol id="gC66F55FB8F08DA72FE76D3863D88042" overflow="visible">
<path d="M 5.664 1.092 C 5.664 2.088 5.736 2.124 6.1080003 2.184 C 6.18 2.256 6.18 2.5080001 6.1080003 2.58 C 5.892 2.568 5.556 2.556 5.184 2.556 C 4.824 2.556 4.272 2.568 3.924 2.58 C 3.852 2.5080001 3.852 2.256 3.924 2.184 C 4.656 2.136 4.716 2.088 4.716 1.092 L 4.716 0.444 C 4.3320003 0.336 3.936 0.276 3.516 0.276 C 2.016 0.276 1.524 1.812 1.524 2.796 C 1.524 4.248 2.22 5.244 3.372 5.244 C 4.56 5.244 5.064 4.644 5.244 3.876 C 5.364 3.8400002 5.484 3.8400002 5.604 3.912 C 5.592 4.404 5.556 4.908 5.448 5.448 C 5.088 5.448 4.2 5.64 3.528 5.64 C 1.812 5.64 0.444 4.5360003 0.444 2.64 C 0.444 1.116 1.584 -0.120000005 3.3 -0.120000005 C 4.116 -0.120000005 5.004 0 5.796 0.432 C 5.712 0.51600003 5.664 0.624 5.664 0.708 Z "/>
</symbol>
<symbol id="g4C6038BE04CA3E1481E54A97A0E34303" overflow="visible">
<path d="M 6.324 2.82 C 6.324 4.524 4.956 5.64 3.3960001 5.64 C 1.728 5.64 0.444 4.428 0.444 2.664 C 0.444 1.0320001 1.6800001 -0.120000005 3.3 -0.120000005 C 5.268 -0.120000005 6.324 1.26 6.324 2.82 Z M 3.288 5.244 C 4.356 5.244 5.28 4.26 5.28 2.652 C 5.28 1.176 4.548 0.276 3.48 0.276 C 2.316 0.276 1.488 1.332 1.488 2.808 C 1.488 4.428 2.388 5.244 3.288 5.244 Z "/>
</symbol>
<symbol id="g48BCA4F06942DA5990D42018985FC781" overflow="visible">
<path d="M 2.292 1.464 L 2.292 2.5080001 L 2.9520001 2.5080001 C 3.408 2.5080001 3.576 2.112 3.732 1.668 L 3.996 0.948 C 4.272 0.204 4.68 -0.084 5.196 -0.084 C 5.376 -0.084 5.748 -0.048 5.952 0 C 5.988 0.120000005 5.964 0.24000001 5.88 0.336 C 5.448 0.336 5.2200003 0.408 4.98 1.0320001 L 4.632 1.932 C 4.488 2.304 4.344 2.5080001 4.188 2.664 L 4.188 2.688 C 4.596 2.832 5.208 3.3240001 5.208 4.152 C 5.208 5.1480002 4.584 5.568 3.1560001 5.568 C 2.856 5.568 2.172 5.52 1.812 5.52 C 1.464 5.52 0.96000004 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.212 0.432 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 0.936 -0.012 1.428 0 1.824 0 C 2.196 0 2.592 -0.012 2.976 -0.024 C 3.048 0.048 3.048 0.3 2.976 0.372 C 2.412 0.408 2.292 0.468 2.292 1.464 Z M 4.164 4.152 C 4.164 3.204 3.888 2.856 2.82 2.856 L 2.292 2.856 L 2.292 4.416 C 2.292 5.052 2.412 5.172 3.084 5.172 C 3.924 5.172 4.164 4.872 4.164 4.152 Z "/>
</symbol>
<symbol id="g45E4C10E27056C5AE488FE2D8290DF06" overflow="visible">
<path d="M 2.34 4.056 C 2.34 5.052 2.4720001 5.088 3.204 5.1480002 C 3.276 5.2200003 3.276 5.472 3.204 5.544 C 2.748 5.532 2.232 5.52 1.86 5.52 C 1.5 5.52 0.996 5.532 0.528 5.544 C 0.456 5.472 0.456 5.2200003 0.528 5.1480002 C 1.26 5.1 1.392 5.052 1.392 4.056 L 1.392 1.464 C 1.392 0.468 1.26 0.432 0.528 0.372 C 0.456 0.3 0.456 0.048 0.528 -0.024 C 0.972 -0.012 1.464 0 1.872 0 C 2.256 0 2.784 -0.012 3.204 -0.024 C 3.276 0.048 3.276 0.3 3.204 0.372 C 2.4720001 0.42000002 2.34 0.468 2.34 1.464 Z "/>
</symbol>
<symbol id="gA2769E14ED9B16297025579DD26D23A1" overflow="visible">
<path d="M 3.648 1.464 L 3.648 4.488 C 3.648 4.932 3.7680001 5.112 4.152 5.112 L 4.464 5.112 C 5.2200003 5.112 5.376 4.872 5.616 4.008 C 5.736 3.984 5.844 3.984 5.94 4.044 C 5.88 4.632 5.868 5.076 5.844 5.64 C 5.4240003 5.592 4.656 5.52 3.648 5.52 L 2.7 5.52 C 1.524 5.52 0.828 5.58 0.504 5.64 C 0.504 5.076 0.492 4.608 0.42000002 4.044 C 0.528 4.008 0.636 3.996 0.744 4.008 C 0.984 4.872 1.116 5.112 1.896 5.112 L 2.184 5.112 C 2.556 5.112 2.7 4.968 2.7 4.5 L 2.7 1.464 C 2.7 0.468 2.568 0.432 1.836 0.372 C 1.764 0.3 1.764 0.048 1.836 -0.024 C 2.28 -0.012 2.772 0 3.18 0 C 3.6000001 0 4.068 -0.012 4.512 -0.024 C 4.584 0.048 4.584 0.3 4.512 0.372 C 3.78 0.42000002 3.648 0.468 3.648 1.464 Z "/>
</symbol>
<symbol id="g7FB89403B37B0F0F934DFEB7E5171B37" overflow="visible">
<path d="M 6 4.056 C 6 5.052 6.132 5.088 6.864 5.1480002 C 6.936 5.2200003 6.936 5.472 6.864 5.544 C 6.4440002 5.52 5.916 5.52 5.52 5.52 C 5.184 5.52 4.656 5.532 4.188 5.544 C 4.116 5.472 4.116 5.2200003 4.188 5.1480002 C 4.92 5.1 5.052 5.052 5.052 4.056 L 5.052 3.024 L 2.28 3.024 L 2.28 4.056 C 2.28 5.052 2.412 5.088 3.144 5.1480002 C 3.216 5.2200003 3.216 5.472 3.144 5.544 C 2.688 5.532 2.184 5.52 1.8000001 5.52 C 1.44 5.52 0.948 5.532 0.468 5.544 C 0.396 5.472 0.396 5.2200003 0.468 5.1480002 C 1.2 5.1 1.332 5.052 1.332 4.056 L 1.332 1.464 C 1.332 0.468 1.2 0.432 0.468 0.372 C 0.396 0.3 0.396 0.048 0.468 -0.024 C 0.948 -0.012 1.428 0 1.812 0 C 2.196 0 2.676 -0.012 3.144 -0.024 C 3.216 0.048 3.216 0.3 3.144 0.372 C 2.412 0.42000002 2.28 0.468 2.28 1.464 L 2.28 2.628 L 5.052 2.628 L 5.052 1.464 C 5.052 0.468 4.92 0.432 4.188 0.372 C 4.116 0.3 4.116 0.048 4.188 -0.024 C 4.632 -0.012 5.112 0 5.532 0 C 5.892 0 6.396 -0.012 6.864 -0.024 C 6.936 0.048 6.936 0.3 6.864 0.372 C 6.132 0.42000002 6 0.468 6 1.464 Z "/>
</symbol>
<symbol id="gFF269982F0E4C510F3A3BFF016D72390" overflow="visible">
<path d="M 5.796 4.584 L 5.88 4.584 L 6.0360003 1.4760001 C 6.084 0.48000002 6.072 0.432 5.4240003 0.372 C 5.352 0.3 5.352 0.048 5.4240003 -0.024 C 5.844 -0.012 6.288 0 6.624 0 C 6.984 0 7.3320003 -0.012 7.656 -0.024 C 7.728 0.048 7.728 0.3 7.656 0.372 C 7.044 0.432 7.032 0.504 6.96 1.4760001 L 6.7200003 4.572 C 6.684 5.052 6.7920003 5.1 7.392 5.1480002 C 7.464 5.2200003 7.464 5.472 7.392 5.544 L 5.772 5.52 L 3.9720001 1.224 L 2.436 5.52 L 0.768 5.544 C 0.696 5.472 0.696 5.2200003 0.768 5.1480002 C 1.3560001 5.112 1.464 5.052 1.44 4.824 L 1.056 1.452 C 0.948 0.456 0.792 0.408 0.336 0.372 C 0.264 0.3 0.264 0.048 0.336 -0.024 C 0.576 -0.012 0.936 0 1.128 0 C 1.368 0 1.812 -0.012 2.052 -0.024 C 2.124 0.048 2.124 0.3 2.052 0.372 C 1.368 0.42000002 1.38 0.564 1.4760001 1.452 L 1.824 4.5 L 1.848 4.5 L 3.552 -0.048 C 3.576 -0.108 3.636 -0.144 3.696 -0.144 C 3.744 -0.144 3.8040001 -0.108 3.828 -0.048 Z "/>
</symbol>
<symbol id="gD77922058D8F1A3A631DDE5946887BDC" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z M 3.384 5.112 C 4.764 5.112 5.88 4.008 5.88 2.628 C 5.88 1.248 4.752 0.132 3.384 0.132 C 2.004 0.132 0.90000004 1.248 0.90000004 2.628 C 0.90000004 3.996 2.004 5.112 3.384 5.112 Z "/>
</symbol>
<symbol id="g5ABA589ED074A65FC8C929AB4EB2344C" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z "/>
</symbol>
<symbol id="gEDADDD9BA25BBB833C1F4B684DC50419" overflow="visible">
<path d="M 4.83 3.82 L 4.9 3.82 L 5.0299997 1.23 C 5.0699997 0.39999998 5.06 0.35999998 4.52 0.31 C 4.46 0.25 4.46 0.04 4.52 -0.02 C 4.87 -0.01 5.24 0 5.52 0 C 5.8199997 0 6.1099997 -0.01 6.3799996 -0.02 C 6.44 0.04 6.44 0.25 6.3799996 0.31 C 5.87 0.35999998 5.8599997 0.42 5.7999997 1.23 L 5.6 3.81 C 5.5699997 4.21 5.66 4.25 6.16 4.29 C 6.22 4.35 6.22 4.56 6.16 4.62 L 4.81 4.6 L 3.31 1.02 L 2.03 4.6 L 0.64 4.62 C 0.58 4.56 0.58 4.35 0.64 4.29 C 1.13 4.2599998 1.22 4.21 1.1999999 4.02 L 0.88 1.2099999 C 0.78999996 0.38 0.65999997 0.34 0.28 0.31 C 0.22 0.25 0.22 0.04 0.28 -0.02 C 0.48 -0.01 0.78 0 0.94 0 C 1.14 0 1.51 -0.01 1.7099999 -0.02 C 1.77 0.04 1.77 0.25 1.7099999 0.31 C 1.14 0.35 1.15 0.47 1.23 1.2099999 L 1.52 3.75 L 1.54 3.75 L 2.96 -0.04 C 2.98 -0.089999996 3.03 -0.12 3.08 -0.12 C 3.12 -0.12 3.1699998 -0.089999996 3.1899998 -0.04 Z "/>
</symbol>
<symbol id="g97A8E46F7A64F11D13C6F357868587EE" overflow="visible">
<path d="M 1.89 1.22 L 1.89 1.9599999 C 2.07 1.88 2.27 1.8399999 2.52 1.8399999 C 3.86 1.8399999 4.27 2.8 4.27 3.3999999 C 4.27 3.9199998 3.97 4.62 2.55 4.62 C 2.18 4.62 1.76 4.6 1.49 4.6 C 1.1999999 4.6 0.78 4.61 0.38 4.62 C 0.32 4.56 0.32 4.35 0.38 4.29 C 0.98999995 4.25 1.1 4.21 1.1 3.3799999 L 1.1 1.22 C 1.1 0.39 0.98999995 0.35999998 0.38 0.31 C 0.32 0.25 0.32 0.04 0.38 -0.02 C 0.71 -0.01 1.06 0 1.5 0 C 1.93 0 2.28 -0.01 2.61 -0.02 C 2.6699998 0.04 2.6699998 0.25 2.61 0.31 C 2 0.35 1.89 0.39 1.89 1.22 Z M 1.89 3.84 C 1.89 4.16 2.01 4.29 2.49 4.29 C 3.08 4.29 3.3999999 3.98 3.3999999 3.28 C 3.3999999 2.56 3.1399999 2.1699998 2.54 2.1699998 C 2.34 2.1699998 2.09 2.2 1.89 2.28 Z "/>
</symbol>
<symbol id="gB844DCFB76B4CC44608DB013C9764E9C" overflow="visible">
<path d="M 1.8299999 3.62 C 1.5899999 4.19 1.5999999 4.24 2.1399999 4.29 C 2.2 4.35 2.2 4.56 2.1399999 4.62 C 1.8299999 4.61 1.49 4.6 1.0799999 4.6 C 0.76 4.6 0.45999998 4.61 0.19999999 4.62 C 0.14 4.56 0.14 4.35 0.19999999 4.29 C 0.69 4.24 0.76 4.13 1 3.56 L 2.4199998 0.28 C 2.55 -0.01 2.6 -0.12 2.71 -0.12 C 2.78 -0.12 2.82 -0.04 2.96 0.28 L 4.42 3.55 C 4.63 4.0099998 4.74 4.25 5.2799997 4.29 C 5.3399997 4.35 5.3399997 4.56 5.2799997 4.62 C 5.06 4.61 4.8199997 4.6 4.56 4.6 C 4.19 4.6 3.9099998 4.61 3.6399999 4.62 C 3.58 4.56 3.58 4.35 3.6399999 4.29 C 4.18 4.25 4.23 4.13 4.0299997 3.62 L 2.9399998 1.13 C 2.9099998 1.1 2.8999999 1.1 2.87 1.13 Z "/>
</symbol>
<symbol id="gDAA1267270512376F631C9A10449D5F4" overflow="visible">
<path d="M 2.48 2.25 C 3.1399999 2.25 3.1499999 2.06 3.1699998 1.6899999 C 3.22 1.64 3.3999999 1.64 3.4499998 1.6899999 C 3.4399998 1.92 3.4299998 2.26 3.4299998 2.4199998 C 3.4299998 2.56 3.4399998 2.8799999 3.4499998 3.1299999 C 3.3999999 3.1799998 3.22 3.1799998 3.1699998 3.1299999 C 3.1499999 2.6799998 3.1299999 2.57 2.48 2.57 L 1.91 2.57 L 1.91 3.99 C 1.91 4.16 2.04 4.27 2.23 4.27 L 2.8 4.27 C 3.62 4.27 3.75 3.9399998 3.9299998 3.37 C 4.0299997 3.36 4.12 3.3799999 4.2 3.4199998 C 4.16 3.76 4.04 4.54 4.02 4.61 C 4.02 4.63 4.0099998 4.64 3.99 4.64 C 3.85 4.61 3.75 4.6 3.58 4.6 L 1.51 4.6 C 1.22 4.6 0.76 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.76 -0.01 1.1999999 0 1.52 0 L 3.06 0 C 3.46 0 4.12 -0.02 4.12 -0.02 C 4.24 0.39 4.35 0.94 4.42 1.36 C 4.33 1.41 4.25 1.43 4.14 1.4 C 3.98 0.81 3.6899998 0.31 2.86 0.31 L 2.4299998 0.31 C 2.01 0.31 1.91 0.42 1.91 0.75 L 1.91 2.25 Z "/>
</symbol>
<symbol id="g6C3A310EEC8A7EBBD176D179125951F0" overflow="visible">
<path d="M 2.328 -4.632 L 8.208 -4.632 C 8.352 -4.488 8.352 -4.056 8.208 -3.912 C 4.896 -3.648 4.728 -3.288 4.728 -1.2 L 4.728 13.464 C 4.728 15.552 4.92 15.912 8.208 16.152 C 8.352 16.296 8.352 16.728 8.208 16.872 L 2.328 16.872 Z "/>
</symbol>
<symbol id="g2F0CE4BDC8DA4B92139017B781562218" overflow="visible">
<path d="M 3.96 1.896 L 5.232 5.232 C 5.352 5.544 5.496 5.64 6.072 5.64 L 10.632 5.64 L 11.976 1.728 C 12.264 0.864 11.568 0.84000003 10.656 0.792 C 10.512 0.792 10.344 0.768 10.2 0.768 C 10.056 0.624 10.056 0.096 10.2 -0.048 C 11.088 -0.024 13.368 0 14.304 0 C 15.288 0 16.632 -0.024 17.52 -0.048 C 17.664 0.096 17.664 0.624 17.52 0.768 C 16.584 0.864 15.792 0.84000003 15.360001 2.0640001 L 10.416 15.792 C 10.056 15.576 8.616 14.736 7.776 14.736 L 2.568 2.448 C 1.944 0.96000004 1.224 0.84000003 0.168 0.768 C 0.024 0.624 0.024 0.096 0.168 -0.048 C 1.056 -0.024 1.488 0 2.424 0 C 3.408 0 4.728 -0.024 5.616 -0.048 C 5.76 0.096 5.76 0.624 5.616 0.768 C 4.704 0.84000003 3.576 0.912 3.96 1.896 Z M 6.552 6.7920003 C 6.024 6.7920003 5.856 6.864 5.952 7.104 L 8.064 12.4800005 L 8.232 12.4800005 L 10.2 6.7920003 Z "/>
</symbol>
<symbol id="g8D84A54D9303B24762DC3071B60ECD14" overflow="visible">
<path d="M 2.4 3.048 C 2.4 1.056 2.016 0.84000003 0.552 0.768 C 0.408 0.624 0.408 0.096 0.552 -0.048 C 1.5600001 -0.024 2.64 0 3.96 0 C 5.28 0 6.336 -0.024 7.368 -0.048 C 7.512 0.096 7.512 0.624 7.368 0.768 C 5.9040003 0.84000003 5.52 1.056 5.52 3.048 L 5.52 13.992001 C 5.52 15.552 5.592 16.44 5.592 16.44 C 5.592 16.656 5.4240003 16.752 5.208 16.752 C 4.32 16.464 2.4 16.2 0.696 16.128 C 0.624 15.84 0.648 15.576 0.768 15.360001 C 2.28 15.24 2.4 15.216001 2.4 13.56 Z "/>
</symbol>
<symbol id="g3E9095A1FBD7854ED5F7B53469C97011" overflow="visible">
<path d="M 11.208 9.456 C 11.88 9.456 12.264 9.744 12.264 10.632 C 12.264 11.088 11.64 11.784 10.728 11.784 C 9.672 11.784 8.28 10.992 7.584 10.368 C 7.152 10.608 6.6480002 10.656 5.568 10.656 C 4.5360003 10.656 3.528 10.416 2.736 9.8880005 C 1.752 9.264 1.104 8.328 1.104 7.104 C 1.104 5.928 1.8000001 4.656 2.9520001 4.032 C 2.208 3.384 1.056 2.112 1.056 1.632 C 1.056 1.176 1.128 0.888 1.368 0.528 C 1.584 0.192 1.872 0 2.352 -0.144 C 1.32 -0.768 0.264 -2.136 0.264 -2.544 C 0.264 -3.432 0.552 -4.464 1.2 -4.92 C 2.136 -5.568 3.72 -5.712 4.872 -5.712 C 8.208 -5.712 12.024 -3.96 12.024 -1.32 C 12.024 -0.816 11.784 0.216 10.824 0.864 C 9.8880005 1.488 6.288 1.656 4.512 1.656 C 4.08 1.656 3.432 1.704 3.432 2.664 C 3.432 3.048 3.672 3.384 3.792 3.672 C 4.296 3.432 4.8 3.408 5.544 3.408 C 6.768 3.408 7.896 3.72 8.712 4.44 C 9.408 5.064 9.8880005 5.9040003 9.8880005 6.984 C 9.8880005 8.328 9.216 9.216 8.4 9.8880005 C 8.592 10.128 9.384 10.56 9.624001 10.56 C 9.84 10.56 10.008 10.416 10.08 10.272 C 10.176 9.96 10.608 9.456 11.208 9.456 Z M 4.2 -0.6 C 6.048 -0.6 9.6 -0.672 9.6 -1.944 C 9.6 -2.808 9.216 -3.792 8.424 -4.224 C 7.6800003 -4.656 6.456 -4.704 5.544 -4.704 C 3.96 -4.704 2.88 -3.528 2.88 -2.304 C 2.88 -1.488 2.88 -0.936 3.144 -0.456 C 3.384 -0.552 3.696 -0.6 4.2 -0.6 Z M 6.96 6.912 C 6.96 4.608 6.288 4.32 5.664 4.32 C 4.176 4.32 3.984 6.096 3.984 7.32 C 3.984 9.096 4.416 9.744 5.352 9.744 C 6.48 9.744 6.96 8.808 6.96 6.912 Z "/>
</symbol>
<symbol id="g90B91206A818BADA9956CC42F47E57A0" overflow="visible">
<path d="M 1.176 1.392 C 1.176 0.48000002 1.944 -0.24000001 2.904 -0.24000001 C 3.864 -0.24000001 4.68 0.528 4.68 1.44 C 4.68 2.376 3.912 3.096 2.9520001 3.096 C 1.992 3.096 1.176 2.328 1.176 1.392 Z "/>
</symbol>
<symbol id="g82ABC2E7771A896CA6A6993FF216117A" overflow="visible">
<path d="M 5.952 13.632 C 6.96 13.632 7.464 13.056 7.464 11.928 C 7.464 10.104 6 8.64 3.792 8.136 L 3.96 7.176 C 4.464 7.32 4.752 7.368 5.112 7.368 C 6.36 7.368 8.112 7.008 8.112 4.1280003 C 8.112 1.368 6.48 0.768 5.592 0.768 C 4.656 0.768 4.152 1.368 3.8400002 1.776 C 3.576 2.136 3.168 2.664 2.28 2.664 C 1.536 2.664 1.104 2.04 1.104 1.632 C 1.104 1.128 1.368 0.768 1.896 0.504 C 2.76 0.072 4.032 -0.24000001 5.208 -0.24000001 C 8.04 -0.24000001 11.208 1.992 11.208 5.328 C 11.208 7.056 10.08 8.568 8.064 8.712 C 9.12 9.24 10.2960005 10.512 10.2960005 11.976 C 10.2960005 13.032001 9.72 14.64 6.408 14.64 C 3.912 14.64 2.904 13.8 2.136 13.104 C 1.608 12.624001 1.464 11.976 1.464 11.6640005 C 1.464 11.328 1.584 10.776 2.376 10.776 C 3.432 10.776 3.72 11.328 3.864 12.096 C 4.1280003 13.56 5.136 13.632 5.952 13.632 Z "/>
</symbol>
<symbol id="g10BFE5E41011FF0F560FA08FAB260218" overflow="visible">
<path d="M 7.248 16.824 L 1.368 16.824 C 1.224 16.68 1.224 16.248 1.368 16.104 C 4.68 15.84 4.848 15.4800005 4.848 13.392 L 4.848 -1.272 C 4.848 -3.3600001 4.656 -3.72 1.368 -3.96 C 1.224 -4.104 1.224 -4.5360003 1.368 -4.68 L 7.248 -4.68 Z "/>
</symbol>
<symbol id="g1BED8054A02AECF3BF3EC56A671C1672" overflow="visible">
<path d="M 9.528 -0.24000001 C 11.856 -0.24000001 13.992001 0.864 15.624001 3 C 15.504 3.216 15.096 3.504 14.832 3.504 C 13.128 1.632 11.184 1.008 9.504 1.008 C 6.7200003 1.008 4.512 4.272 4.512 8.016 C 4.512 11.736 6.432 14.808001 9.288 14.808001 C 12.6 14.808001 13.68 12.936 14.304 10.872 C 14.592 10.776 15.0720005 10.848001 15.336 10.992 C 15.216001 12.24 15.024 13.392 14.808001 14.712 C 13.584001 14.832 12.504 15.792 9.552 15.792 C 4.848 15.792 0.888 12.84 0.888 7.56 C 0.888 5.304 1.872 2.664 3.792 1.272 C 5.328 0.168 7.2000003 -0.24000001 9.528 -0.24000001 Z "/>
</symbol>
<symbol id="g2825DE3DACAF761B898A0442866AE569" overflow="visible">
<path d="M 12.672 3.072 L 12.672 6.816 C 12.672 9.456 11.544 10.656 9.4800005 10.656 C 8.592 10.656 6.888 9.768 5.52 8.928 L 5.52 13.992001 C 5.52 15.552 5.592 16.44 5.592 16.44 C 5.592 16.656 5.4240003 16.752 5.208 16.752 C 4.32 16.464 2.4 16.2 0.696 16.128 C 0.624 15.84 0.648 15.576 0.768 15.360001 C 2.28 15.24 2.4 15.216001 2.4 13.56 L 2.4 3.048 C 2.4 1.056 2.016 0.84000003 0.552 0.768 C 0.408 0.624 0.408 0.096 0.552 -0.048 C 1.5600001 -0.024 2.64 0 3.96 0 C 5.112 0 5.856 -0.024 6.888 -0.048 C 7.032 0.096 7.032 0.624 6.888 0.768 C 5.88 0.84000003 5.52 1.056 5.52 3.048 L 5.52 7.968 C 6.528 8.592 7.32 8.88 7.752 8.88 C 8.712 8.88 9.552 8.448 9.552 7.08 L 9.552 3.072 C 9.552 1.056 9.168 0.84000003 8.184 0.768 C 8.04 0.624 8.04 0.096 8.184 -0.048 C 9.192 -0.024 9.96 0 11.112 0 C 12.432 0 13.488 -0.024 14.52 -0.048 C 14.6640005 0.096 14.6640005 0.624 14.52 0.768 C 13.056 0.84000003 12.672 1.056 12.672 3.072 Z "/>
</symbol>
<symbol id="g841363B3896A8C79F18618DF16186242" overflow="visible">
<path d="M 0.888 4.968 C 0.888 1.824 3.384 -0.24000001 6.6 -0.24000001 C 8.304 -0.24000001 9.72 0.24000001 10.704 1.128 C 11.928 2.208 12.336 3.8400002 12.336 5.184 C 12.336 8.328 10.2 10.656 6.624 10.656 C 4.632 10.656 3.144 9.96 2.208 8.88 C 1.296 7.824 0.888 6.384 0.888 4.968 Z M 6.2400002 9.648 C 7.872 9.648 8.976 7.704 8.976 4.416 C 8.976 1.536 7.848 0.768 6.984 0.768 C 5.0160003 0.768 4.248 3.72 4.248 5.496 C 4.248 7.704 4.632 9.648 6.2400002 9.648 Z "/>
</symbol>
<symbol id="gDD7DFDEC0D240E3DC5A3664E12D4BDDC" overflow="visible">
<path d="M 1.152 3.504 C 1.248 2.328 1.368 1.2 1.5600001 0.288 C 2.016 0.144 3.552 -0.24000001 4.896 -0.24000001 C 6.744 -0.24000001 9.048 0.768 9.048 2.856 C 9.048 3.672 8.856 4.32 8.304 4.92 C 7.632 5.688 6.624 6.288 5.52 6.768 C 4.56 7.176 4.224 7.9440002 4.224 8.64 C 4.224 9.192 4.68 9.648 5.376 9.648 C 6.216 9.648 7.032 8.88 7.632 7.416 C 8.064 7.344 8.328 7.368 8.568 7.5360003 C 8.568 8.4 8.472 9.312 8.2560005 10.08 C 7.488 10.416 6.888 10.656 5.568 10.656 C 4.296 10.656 3.096 10.176 2.328 9.408 C 1.776 8.856 1.512 8.184 1.512 7.5360003 C 1.512 6.816 1.8000001 6.2400002 2.256 5.736 C 3 4.92 4.32 4.08 5.04 3.744 C 6 3.312 6.264 2.448 6.264 1.872 C 6.264 1.104 5.496 0.696 4.848 0.696 C 3.7680001 0.696 2.616 1.8000001 2.112 3.552 C 1.728 3.624 1.536 3.6000001 1.152 3.504 Z "/>
</symbol>
<symbol id="g24FA36D774E663C81AD78F0ED3820373" overflow="visible">
<path d="M 5.568 2.928 L 5.568 7.704 C 5.568 8.904 5.664 10.248 5.664 10.248 C 5.664 10.512 5.448 10.656 5.112 10.656 C 4.44 10.392 2.496 10.2 0.84000003 9.984 C 0.792 9.84 0.84000003 9.36 0.888 9.216 C 2.208 9.096 2.448 8.904 2.448 7.5360003 L 2.448 2.928 C 2.448 0.936 2.184 0.888 0.72 0.768 C 0.576 0.624 0.576 0.096 0.72 -0.048 C 1.728 -0.024 2.736 0 4.008 0 C 5.28 0 6.264 -0.024 7.296 -0.048 C 7.44 0.096 7.44 0.624 7.296 0.768 C 5.8320003 0.864 5.568 0.936 5.568 2.928 Z M 2.328 14.304 C 2.328 13.512 2.904 12.72 3.864 12.72 C 4.9440002 12.72 5.568 13.584001 5.568 14.208 C 5.568 14.928 5.0160003 15.792 4.008 15.792 C 2.88 15.792 2.328 15.024 2.328 14.304 Z "/>
</symbol>
<symbol id="g42F794F2554BA43C69EE8F3AA6FD9BAC" overflow="visible">
<path d="M 5.472 2.928 L 5.472 7.752 C 6.432 8.4 7.392 8.88 7.824 8.88 C 8.784 8.88 9.504 8.448 9.504 7.08 L 9.504 3.072 C 9.504 1.056 9.12 0.84000003 8.136 0.768 C 7.992 0.624 7.992 0.096 8.136 -0.048 C 9.144 -0.024 9.912 0 11.064 0 C 12.384 0 13.440001 -0.024 14.472 -0.048 C 14.616 0.096 14.616 0.624 14.472 0.768 C 13.008 0.84000003 12.624001 1.056 12.624001 3.072 L 12.624001 6.816 C 12.624001 9.456 11.496 10.656 9.432 10.656 C 8.472 10.656 6.768 9.6 5.448 8.688 C 5.376 9.528 5.28 10.248 5.28 10.248 C 5.256 10.536 5.064 10.656 4.728 10.656 C 3.8400002 10.416 2.4 10.08 0.744 9.864 C 0.696 9.72 0.744 9.24 0.792 9.096 C 2.112 8.976 2.352 8.784 2.352 7.416 L 2.352 2.928 C 2.352 0.936 2.088 0.888 0.624 0.768 C 0.48000002 0.624 0.48000002 0.096 0.624 -0.048 C 1.632 -0.024 2.64 0 3.912 0 C 5.0160003 0 5.688 -0.024 6.7200003 -0.048 C 6.864 0.096 6.864 0.624 6.7200003 0.768 C 5.712 0.864 5.472 0.936 5.472 2.928 Z "/>
</symbol>
<symbol id="gB6675D993E92546012E46240B36958EC" overflow="visible">
<path d="M 10.344 3.096 C 9.36 2.088 8.064 1.824 7.152 1.824 C 5.28 1.824 4.1280003 2.904 4.1280003 5.256 C 4.1280003 5.4240003 4.152 5.52 4.152 5.64 L 9.912 5.64 C 10.488 5.64 10.608 6.048 10.608 6.384 C 10.608 8.424 9.816 10.656 6.288 10.656 C 3.7680001 10.656 0.888 8.424 0.888 4.752 C 0.888 3.3600001 1.392 1.896 2.424 0.96000004 C 3.336 0.144 4.512 -0.24000001 6.216 -0.24000001 C 7.872 -0.24000001 9.504 0.6 10.704 2.352 C 10.704 2.664 10.584 3.096 10.344 3.096 Z M 4.248 6.6 C 4.272 7.44 4.392 8.352 4.728 8.832 C 5.112 9.408 5.76 9.648 6.024 9.648 C 6.672 9.648 7.56 9.024 7.56 7.104 C 7.56 6.96 7.56 6.6480002 7.512 6.6 Z "/>
</symbol>
<symbol id="g79601DAFF2C13DD0AF25B87F7A83C884" overflow="visible">
<path d="M 1.776 3.048 C 1.776 1.056 1.728 0.768 1.632 -0.144 C 1.9200001 -0.24000001 2.184 -0.312 2.448 -0.312 C 2.76 -0.048 3 0.288 3.216 0.72 C 4.152 0 5.616 -0.24000001 6.7200003 -0.24000001 C 9.384 -0.24000001 12.192 2.4 12.192 5.8320003 C 12.192 7.2000003 11.6640005 8.544 10.896 9.432 C 10.032001 10.416 8.88 10.656 7.6080003 10.656 C 6.864 10.656 5.592 9.816 4.896 9.312 L 4.896 13.992001 C 4.896 15.552 4.968 16.44 4.968 16.44 C 4.968 16.656 4.8 16.752 4.584 16.752 C 3.696 16.464 1.776 16.2 0.072 16.128 C 0 15.84 0.024 15.576 0.144 15.360001 C 1.656 15.24 1.776 15.216001 1.776 13.56 Z M 4.896 8.352 C 5.688 8.88 6.216 8.952 6.768 8.952 C 7.9440002 8.952 8.832 7.872 8.832 5.52 C 8.832 3.552 8.496 0.768 6.6 0.768 C 5.9040003 0.768 5.352 1.056 4.896 1.608 Z "/>
</symbol>
<symbol id="g767CEF02C917BBE3F159A8F04079F311" overflow="visible">
<path d="M 5.472 6.432 C 5.472 7.296 5.736 7.656 6.048 8.016 C 6.2400002 8.2560005 6.456 8.424 6.816 8.424 C 7.032 8.424 7.296 8.208 7.488 7.968 C 7.656 7.776 8.064 7.584 8.616 7.584 C 9.312 7.584 9.984 8.304 9.984 9.312 C 9.984 9.936 9.264 10.656 8.4 10.656 C 7.56 10.656 6.6480002 9.936 5.544 8.352 L 5.448 8.352 C 5.4 9.0720005 5.28 10.248 5.28 10.248 C 5.256 10.464 5.064 10.656 4.728 10.656 C 3.6000001 10.368 2.328 10.032001 0.744 9.864 C 0.696 9.72 0.744 9.264 0.792 9.12 C 2.112 9 2.352 8.784 2.352 7.416 L 2.352 2.928 C 2.352 0.936 2.088 0.888 0.624 0.768 C 0.48000002 0.624 0.48000002 0.096 0.624 -0.048 C 1.632 -0.024 2.64 0 3.912 0 C 5.184 0 6.168 -0.024 7.2000003 -0.048 C 7.344 0.096 7.344 0.624 7.2000003 0.768 C 5.736 0.864 5.472 0.936 5.472 2.928 Z "/>
</symbol>
<symbol id="gC1513612DA0E34F2B247DB2830CD7DFD" overflow="visible">
<path d="M 1.24 4.6 C 1.24 3.34 2.26 2.32 3.52 2.32 C 4.7799997 2.32 5.7999997 3.34 5.7999997 4.6 C 5.7999997 5.8599997 4.7799997 6.8799996 3.52 6.8799996 C 2.26 6.8799996 1.24 5.8599997 1.24 4.6 Z "/>
</symbol>
<symbol id="g92446B7A6A7F78674F0F5568B7ED0AC5" overflow="visible">
<path d="M 13.059999 1.74 C 13.48 2.1599998 13.7 2.46 13.7 2.62 C 13.7 2.9399998 13.54 3.1 13.2 3.1 C 13.059999 3.1 12.92 3 12.74 2.8 C 11.5199995 1.42 9.98 0.71999997 8.12 0.71999997 C 6.68 0.71999997 5.68 1.36 5.12 2.62 C 4.62 3.76 4.38 5.16 4.38 6.8199997 C 4.38 8.32 4.6 9.66 5.04 10.8 C 5.64 12.42 6.58 13.219999 7.8399997 13.219999 C 8.74 13.219999 9.62 12.86 10.5199995 12.139999 C 11.42 11.42 12 10.62 12.28 9.74 C 12.38 9.46 12.5199995 9.32 12.74 9.32 C 13 9.32 13.139999 9.559999 13.139999 10.04 L 13.139999 13.34 C 13.139999 13.84 13 14.08 12.74 14.08 C 12.5199995 14.08 12.36 13.92 12.28 13.62 C 12.2 13.32 12.0199995 13.16 11.719999 13.16 C 11.32 13.16 10.719999 13.32 9.88 13.62 C 9.04 13.92 8.34 14.08 7.7799997 14.08 C 5.96 14.08 4.38 13.5199995 3.02 12.4 C 1.5 11.16 0.74 9.32 0.74 6.8599997 C 0.74 4.4 1.5 2.54 3 1.3199999 C 4.38 0.17999999 6 -0.38 7.8199997 -0.38 C 9.84 -0.38 11.599999 0.32 13.059999 1.74 Z M 12.3 12.4 L 12.3 11.54 C 12.139999 11.719999 11.9 11.98 11.58 12.32 L 11.74 12.32 C 11.96 12.32 12.16 12.34 12.3 12.4 Z M 5.12 12.7 C 4.94 12.5 4.7799997 12.259999 4.62 12 C 4 10.98 3.52 8.58 3.52 6.8199997 C 3.52 4.06 4.12 2.1 5.3199997 0.91999996 C 2.82 1.88 1.5799999 3.86 1.5799999 6.8399997 C 1.5799999 9.8 2.76 11.759999 5.12 12.7 Z "/>
</symbol>
<symbol id="g8C7315D77A5D71E18736DE61553C419F" overflow="visible">
<path d="M 1.4 1.1999999 C 1.4 0.62 1.88 0.14 2.46 0.14 C 3.04 0.14 3.52 0.62 3.52 1.1999999 C 3.52 1.78 3.04 2.26 2.46 2.26 C 1.88 2.26 1.4 1.78 1.4 1.1999999 Z M 1.4 7.16 C 1.4 6.58 1.88 6.1 2.46 6.1 C 3.04 6.1 3.52 6.58 3.52 7.16 C 3.52 7.74 3.04 8.22 2.46 8.22 C 1.88 8.22 1.4 7.74 1.4 7.16 Z "/>
</symbol>
<symbol id="gA335A20E4C1D7F39210005AFF7F1A0EF" overflow="visible">
<path d="M 7.14 -0.19999999 C 9.08 -0.19999999 10.86 0.71999997 12.219999 2.5 C 12.12 2.6799998 11.98 2.8 11.759999 2.8 C 10.34 1.24 8.98 0.62 7.12 0.62 C 4.42 0.62 2.56 3.6599998 2.56 6.58 C 2.56 8.3 3.02 9.74 3.74 10.639999 C 4.74 11.86 5.9 12.42 6.94 12.42 C 9.7 12.42 10.8 10.78 11.32 9.059999 C 11.559999 8.98 11.759999 9.04 11.98 9.16 C 11.88 10.2 11.74 11.16 11.54 12.259999 C 10.5199995 12.36 9.62 13.16 7.16 13.16 C 5.46 13.16 4.04 12.54 2.86 11.46 C 1.54 10.24 0.74 8.28 0.74 6.2 C 0.74 2.72 2.84 -0.19999999 7.14 -0.19999999 Z "/>
</symbol>
<symbol id="gAA212A9DBB5FA7333A767E41B2F6A3B3" overflow="visible">
<path d="M 5.8599997 0.96 C 5.98 0.34 6.2 -0.19999999 7.2 -0.19999999 C 7.96 -0.19999999 8.679999 0.14 9.099999 0.53999996 C 9.059999 0.78 8.98 0.96 8.76 1.0799999 C 8.62 0.96 8.28 0.76 8.0199995 0.76 C 7.44 0.76 7.4199996 1.54 7.4199996 2.46 L 7.4199996 5.4 C 7.4199996 8.24 5.8599997 8.78 4.4 8.78 C 2.76 8.78 1.1 7.7 1.1 6.56 C 1.1 6.08 1.3399999 5.8399997 1.8 5.8399997 C 2.3799999 5.8399997 2.74 6.2599998 2.74 6.52 C 2.74 6.66 2.72 6.7999997 2.6799998 6.8799996 C 2.6599998 6.94 2.6399999 7.06 2.6399999 7.2799997 C 2.6399999 7.8999996 3.48 8.12 4.24 8.12 C 4.92 8.12 5.8599997 7.7799997 5.8599997 5.52 C 5.8599997 5.38 5.7999997 5.2999997 5.74 5.2799997 L 4.02 4.8599997 C 2.1 4.38 0.71999997 3.32 0.71999997 1.9599999 C 0.71999997 0.32 1.8399999 -0.19999999 3.24 -0.19999999 C 3.9399998 -0.19999999 4.54 -0.04 5.42 0.64 L 5.8199997 0.96 Z M 5.8599997 4.66 L 5.8599997 2.02 C 5.8599997 1.76 5.74 1.62 5.58 1.5 C 5.06 1.0799999 4.38 0.62 3.82 0.62 C 2.82 0.62 2.3799999 1.42 2.3799999 2.04 C 2.3799999 2.9399998 2.8 3.86 4.2799997 4.24 Z "/>
</symbol>
<symbol id="g35631D62198EF939061DC90C9391724A" overflow="visible">
<path d="M 3.6799998 7.16 C 3.56 7.02 3.4399998 6.98 3.4399998 7.16 C 3.4199998 7.7 3.3799999 8.48 3.28 8.679999 C 3.24 8.78 3.1999998 8.84 3.04 8.84 C 2.48 8.62 1.9599999 8.44 0.58 8.26 C 0.53999996 8.139999 0.58 7.8199997 0.62 7.7 C 1.6999999 7.6 1.92 7.5 1.92 6.3399997 L 1.92 2.44 C 1.92 0.79999995 1.7199999 0.71999997 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.92 0 2.72 0 C 3.52 0 4.12 -0.02 4.72 -0.04 C 4.8399997 0.08 4.8399997 0.5 4.72 0.62 C 3.6999998 0.71999997 3.5 0.79999995 3.5 2.44 L 3.5 5.72 C 3.5 6.14 3.6799998 6.3799996 3.84 6.56 C 4.6 7.2999997 5.5 7.74 6.2799997 7.74 C 6.68 7.74 7.1 7.48 7.3399997 7.02 C 7.54 6.62 7.58 6.08 7.58 5.48 L 7.58 2.44 C 7.58 0.79999995 7.3799996 0.71999997 6.3399997 0.62 C 6.24 0.5 6.24 0.08 6.3399997 -0.04 C 6.94 -0.02 7.58 0 8.38 0 C 9.179999 0 9.9 -0.02 10.5 -0.04 C 10.599999 0.08 10.599999 0.5 10.5 0.62 C 9.38 0.71999997 9.16 0.79999995 9.16 2.44 L 9.16 5.42 C 9.16 6.52 9.08 7.48 8.62 8.099999 C 8.28 8.54 7.66 8.78 6.96 8.78 C 5.98 8.78 4.8599997 8.5199995 3.6799998 7.16 Z "/>
</symbol>
<symbol id="g42587C4E387B2C5F870DA01C2914651F" overflow="visible">
<path d="M 6.68 1 C 6.7799997 1.0799999 6.96 1.12 6.98 0.97999996 C 7.04 0.5 7.2 -0.19999999 7.2 -0.19999999 C 7.3599997 -0.26 7.46 -0.24 7.58 -0.19999999 C 8.0199995 0.16 8.72 0.45999998 9.94 0.59999996 C 10.059999 0.71999997 10.059999 1.02 9.94 1.14 C 8.66 1.24 8.48 1.62 8.48 2.6 L 8.48 11.66 C 8.48 12.96 8.559999 13.759999 8.559999 13.759999 C 8.559999 13.9 8.48 13.96 8.3 13.96 C 7.7999997 13.759999 6.2999997 13.48 5.5 13.42 C 5.46 13.259999 5.5 12.94 5.62 12.82 C 5.68 12.82 5.74 12.82 5.7999997 12.82 C 6.68 12.759999 6.8999996 12.759999 6.8999996 11.179999 L 6.8999996 8.62 C 6.8999996 8.48 6.8599997 8.44 6.72 8.44 C 6.64 8.44 5.8199997 8.78 5.16 8.78 C 3.84 8.78 2.96 8.34 2.1599998 7.58 C 1.3 6.72 0.78 5.54 0.78 4.06 C 0.78 1.5999999 2.02 -0.19999999 4.18 -0.19999999 C 4.96 -0.19999999 5.7 0.19999999 6.68 1 Z M 6.8999996 2.48 C 6.8999996 2.1 6.8599997 1.9399999 6.58 1.6999999 C 5.8399997 1.06 5.2 0.74 4.7 0.74 C 3.62 0.74 2.5 1.92 2.5 4.42 C 2.5 5.8599997 2.78 6.66 3.08 7.08 C 3.6999998 8.0199995 4.54 8.08 4.94 8.08 C 5.66 8.08 6.16 7.8199997 6.56 7.3599997 C 6.8399997 7.04 6.8999996 6.8999996 6.8999996 6.2799997 Z "/>
</symbol>
<symbol id="gE68C39294AA7FBA9B91EA2F8E9CC3997" overflow="visible">
<path d="M 3.62 2.44 L 3.62 6.42 C 3.62 7.4199996 3.6999998 8.7 3.6999998 8.7 C 3.6999998 8.78 3.6 8.84 3.4399998 8.84 C 2.8799999 8.62 2.08 8.44 0.7 8.26 C 0.65999997 8.139999 0.7 7.8199997 0.74 7.7 C 1.8399999 7.6 2.04 7.48 2.04 6.3399997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.71999997 0.59999996 0.62 C 0.48 0.5 0.48 0.08 0.59999996 -0.04 C 1.26 -0.02 2.04 0 2.84 0 C 3.6399999 0 4.4 -0.02 5.06 -0.04 C 5.18 0.08 5.18 0.5 5.06 0.62 C 3.84 0.7 3.62 0.78 3.62 2.44 Z M 1.8 11.98 C 1.8 11.46 2.28 10.94 2.76 10.94 C 3.32 10.94 3.8 11.48 3.8 11.9 C 3.8 12.38 3.3799999 12.94 2.84 12.94 C 2.36 12.94 1.8 12.46 1.8 11.98 Z "/>
</symbol>
<symbol id="g22D858CFD6AD86697C1391C74FD687D1" overflow="visible">
<path d="M 0.85999995 8.58 C 0.58 8.58 0.5 8.34 0.5 8.179999 L 0.5 7.9199996 C 0.5 7.8199997 0.52 7.7999997 0.59999996 7.7999997 L 1.78 7.7999997 L 1.78 1.78 C 1.78 0.35999998 2.3999999 -0.19999999 3.32 -0.19999999 C 4.24 -0.19999999 5.24 0.24 6.02 1.12 C 5.98 1.3199999 5.8599997 1.4399999 5.66 1.4599999 C 5.14 1.06 4.54 0.9 4.02 0.9 C 3.48 0.9 3.36 1.5 3.36 2.74 L 3.36 7.7999997 L 5.44 7.7999997 C 5.64 7.7999997 5.92 7.8799996 5.92 8.059999 L 5.92 8.46 C 5.92 8.54 5.8599997 8.58 5.7599998 8.58 L 3.36 8.58 L 3.36 9.36 C 3.36 10.66 3.4399998 11.46 3.4399998 11.46 C 3.4399998 11.58 3.3799999 11.639999 3.28 11.639999 C 3.1999998 11.639999 3.02 11.559999 2.84 11.46 C 2.62 11.34 2.4199998 11.24 2.1599998 11.179999 C 1.92 11.099999 1.7199999 11.04 1.7199999 10.9 C 1.7199999 10.66 1.78 10.8 1.78 8.58 Z "/>
</symbol>
<symbol id="g7FBC39AA6D9FB89D8B638A3651405A80" overflow="visible">
<path d="M 7.72 1.86 C 6.98 1.1 6.3999996 0.78 5.24 0.78 C 4.52 0.78 3.6799998 1.1999999 3.06 2.22 C 2.6599998 2.8799999 2.4199998 3.8 2.4199998 4.96 L 7.74 4.92 C 7.98 4.92 8.12 5.04 8.12 5.2599998 C 8.12 6.94 7.52 8.74 4.74 8.74 C 3 8.74 0.74 7.08 0.74 4.04 C 0.74 2.9199998 1.02 1.8399999 1.68 1.0799999 C 2.36 0.28 3.3 -0.19999999 4.74 -0.19999999 C 6.2599998 -0.19999999 7.3399997 0.5 8.139999 1.54 C 8.08 1.74 7.96 1.8399999 7.72 1.86 Z M 2.48 5.64 C 2.86 7.8999996 4.2599998 8.08 4.74 8.08 C 5.5 8.08 6.3999996 7.66 6.3999996 5.98 C 6.3999996 5.7999997 6.3199997 5.7 6.1 5.7 Z "/>
</symbol>
<symbol id="g67483374C2628B9150A7D3585AC4A61B" overflow="visible">
<path d="M 0.96 2.76 C 1.04 1.78 1.1 0.84 1.1 0 C 1.3 0.04 1.5 0.06 1.5999999 0.06 C 1.74 0.06 1.86 0.06 2 0.02 C 2.54 -0.12 3.08 -0.19999999 3.82 -0.19999999 C 4.94 -0.19999999 7 0.34 7 2.32 C 7 3.6799998 6.02 4.48 4.66 4.98 C 3.46 5.44 2.6599998 5.74 2.6599998 6.8399997 C 2.6599998 7.66 3.3799999 8.12 4.06 8.12 C 4.5 8.12 5.66 7.96 5.92 6.2599998 C 6.04 6.14 6.44 6.16 6.56 6.2799997 C 6.62 7 6.66 7.74 6.68 8.4 C 6.06 8.5 5.1 8.78 4.06 8.78 C 2.58 8.78 1.24 7.8199997 1.24 6.54 C 1.24 5.08 1.9 4.46 3.4399998 3.82 C 5.1 3.1399999 5.48 2.72 5.48 1.86 C 5.48 0.88 4.52 0.45999998 3.78 0.45999998 C 3 0.45999998 2.56 0.71999997 2.36 0.94 C 1.92 1.4 1.6999999 2.28 1.5799999 2.78 C 1.4599999 2.8999999 1.0799999 2.8799999 0.96 2.76 Z "/>
</symbol>
<symbol id="g7EBE636920865BE15FE72D33C3AE049" overflow="visible">
<path d="M 2.08 11.8 L 2.08 1.9 C 2.08 0.9 1.9799999 0.85999995 0.94 0.85999995 C 0.52 0.85999995 0.32 0.71999997 0.32 0.44 C 0.32 0.08 0.62 0 1.0799999 0 L 6.48 0 C 6.98 0 7.22 0.14 7.22 0.44 C 7.22 0.71999997 7 0.85999995 6.58 0.85999995 C 5.54 0.85999995 5.46 0.9 5.46 1.9 L 5.46 6.2 L 6.04 6.2 L 9 1.66 C 9.5 0.85999995 9.8 0.39999998 9.88 0.28 C 10 0.099999994 10.24 0 10.599999 0 L 13.32 0 C 13.82 0 14.059999 0.14 14.059999 0.44 C 14.059999 0.65999997 13.94 0.79999995 13.7 0.84 C 13.2 0.94 12.5 1.64 11.58 2.9199998 C 10.679999 4.16 9.88 5.3399997 9.179999 6.44 C 11.46 6.8799996 12.599999 8.04 12.599999 9.92 C 12.599999 11.259999 12 12.259999 10.8 12.88 C 9.76 13.42 8.58 13.7 7.2799997 13.7 L 1.0799999 13.7 C 0.58 13.7 0.32 13.559999 0.32 13.259999 C 0.32 12.98 0.52 12.84 0.94 12.84 C 1.9799999 12.84 2.08 12.799999 2.08 11.8 Z M 10.7 11.94 C 11.4 11.5199995 11.74 10.84 11.74 9.92 C 11.74 8.54 10.94 7.7 9.36 7.3599997 C 9.7 7.9199996 9.88 8.76 9.88 9.9 C 9.88 11.04 9.66 11.92 9.24 12.58 C 9.74 12.44 10.24 12.24 10.7 11.94 Z M 9.04 9.9 C 9.04 8.66 8.82 7.8799996 8.38 7.56 C 7.94 7.24 6.96 7.06 5.46 7.06 L 5.46 11.86 C 5.46 12.599999 5.74 12.84 6.6 12.84 C 8.5 12.84 9.04 11.9 9.04 9.9 Z M 8.26 6.3199997 C 9.92 3.6799998 11.219999 1.86 12.2 0.85999995 L 10.5 0.85999995 L 7.04 6.22 C 7.14 6.24 7.22 6.24 7.2799997 6.24 C 7.56 6.24 7.8799996 6.2599998 8.26 6.3199997 Z M 2.8 12.84 L 4.7999997 12.84 C 4.68 12.62 4.62 12.32 4.62 11.92 L 4.62 1.86 C 4.62 1.4399999 4.66 1.1 4.74 0.85999995 L 2.8 0.85999995 C 2.8799999 1.1 2.9199998 1.4399999 2.9199998 1.86 L 2.9199998 11.84 C 2.9199998 12.259999 2.8799999 12.599999 2.8 12.84 Z "/>
</symbol>
<symbol id="g579F1BD1E42C90590E5C6584A163F6DD" overflow="visible">
<path d="M 3.78 2.44 L 3.78 5.8199997 C 5.46 5.8199997 5.8399997 5.52 6.12 5.06 L 8.26 1.5799999 C 8.84 0.64 9.7 -0.19999999 10.9 -0.19999999 C 11.2 -0.19999999 11.54 -0.16 11.74 -0.06 C 11.82 0.08 11.8 0.26 11.719999 0.42 C 10.82 0.42 10.32 1.1 9.8 1.9599999 L 7.2799997 6.16 C 8.139999 6.44 9.94 7.48 9.94 9.58 C 9.94 10.58 9.599999 11.4 8.88 12.08 C 7.9199996 12.98 6.68 13.04 5.42 13.04 C 4.48 13.04 3.6399999 12.9 2.9199998 12.9 C 2.22 12.9 1.28 12.92 0.34 12.94 C 0.22 12.82 0.22 12.4 0.34 12.28 C 1.74 12.219999 2.08 12.12 2.08 10.46 L 2.08 2.44 C 2.08 0.78 1.74 0.68 0.34 0.62 C 0.22 0.5 0.22 0.08 0.34 -0.04 C 1.24 -0.02 2.18 0 2.9399998 0 C 3.6999998 0 4.64 -0.02 5.52 -0.04 C 5.64 0.08 5.64 0.5 5.52 0.62 C 4.12 0.68 3.78 0.78 3.78 2.44 Z M 5.44 12.36 C 6.66 12.36 8.099999 11.92 8.099999 9.559999 C 8.099999 7.06 6.68 6.5 4.74 6.5 L 3.78 6.5 L 3.78 11.08 C 3.78 11.66 4.02 12.36 5.44 12.36 Z "/>
</symbol>
<symbol id="gD8CB364949770E6EB9E57283C62D30EB" overflow="visible">
<path d="M 4.3399997 -0.19999999 C 5.12 -0.19999999 6.06 0.19999999 7.04 1 C 7.14 1.0799999 7.3199997 1.12 7.3399997 0.97999996 C 7.3999996 0.48 7.56 -0.19999999 7.56 -0.19999999 C 7.72 -0.26 7.8199997 -0.24 7.94 -0.19999999 C 8.38 0.16 9.08 0.45999998 10.3 0.59999996 C 10.42 0.71999997 10.42 1.02 10.3 1.14 C 9.0199995 1.24 8.84 1.62 8.84 2.6 L 8.84 6.44 C 8.84 7.04 8.92 8.5 8.92 8.5 C 8.92 8.559999 8.86 8.62 8.76 8.62 C 8.66 8.599999 8.36 8.58 8.059999 8.58 C 7.4199996 8.58 6.7 8.599999 6.02 8.62 C 5.9 8.5 5.9 8.08 6.02 7.96 C 7 7.8999996 7.2599998 7.66 7.2599998 6.3399997 L 7.2599998 2.48 C 7.2599998 2.1 7.22 1.9399999 6.94 1.6999999 C 6.2 1.06 5.44 0.74 4.94 0.74 C 4.3399997 0.74 3.34 1.02 3.34 2.8 L 3.34 6.44 C 3.34 7.04 3.4199998 8.5 3.4199998 8.5 C 3.4199998 8.559999 3.36 8.62 3.26 8.62 C 3.1599998 8.599999 2.86 8.58 2.56 8.58 C 1.92 8.58 1.1999999 8.599999 0.52 8.62 C 0.39999998 8.5 0.39999998 8.08 0.52 7.96 C 1.48 7.8799996 1.76 7.66 1.76 6.3599997 L 1.76 2.52 C 1.76 1.14 2.36 -0.19999999 4.3399997 -0.19999999 Z "/>
</symbol>
<symbol id="g1788914935A6D7BFA016214155630E72" overflow="visible">
<path d="M 1.9 2.44 C 1.9 0.78 1.68 0.68 0.45999998 0.62 C 0.34 0.5 0.34 0.08 0.45999998 -0.04 C 1.16 -0.02 1.9 0 2.7 0 C 3.5 0 4.2599998 -0.02 4.92 -0.04 C 5.04 0.08 5.04 0.5 4.92 0.62 C 3.6999998 0.68 3.48 0.78 3.48 2.44 L 3.48 11.66 C 3.48 12.96 3.56 13.759999 3.56 13.759999 C 3.56 13.9 3.48 13.96 3.3 13.96 C 2.8 13.759999 1.3 13.48 0.5 13.42 C 0.45999998 13.259999 0.5 12.94 0.62 12.82 C 1.78 12.74 1.9 12.679999 1.9 11.179999 Z "/>
</symbol>
<symbol id="g6ADFF08DD375E893907BE2D5FE0746BE" overflow="visible">
<path d="M 1.9599999 11.8 L 1.9599999 1.9 C 1.9599999 0.96 1.9 0.85999995 0.97999996 0.85999995 C 0.53999996 0.85999995 0.32 0.71999997 0.32 0.44 C 0.32 0.08 0.62 0 1.0799999 0 L 6.7599998 0 C 10.12 0 12.58 1.92 13.42 4.48 C 13.679999 5.2599998 13.82 6.14 13.82 7.1 C 13.82 8.92 13.299999 10.4 12.28 11.5 C 10.9 12.96 9.08 13.7 6.7799997 13.7 L 1.0799999 13.7 C 0.58 13.7 0.32 13.559999 0.32 13.259999 C 0.32 12.98 0.52 12.84 0.94 12.84 C 1.9 12.84 1.9599999 12.759999 1.9599999 11.8 Z M 9.54 1.42 C 10.54 2.62 11.04 4.5 11.04 7.06 C 11.04 9.54 10.42 11.34 9.179999 12.46 C 11.7 11.639999 12.96 9.84 12.96 7.1 C 12.96 4.22 11.62 2.26 9.54 1.42 Z M 6.42 0.85999995 C 5.64 0.85999995 5.3399997 1.0799999 5.3399997 1.8399999 L 5.3399997 11.86 C 5.3399997 12.639999 5.68 12.84 6.56 12.84 C 7.8599997 12.84 8.84 12.16 9.46 10.8 C 9.94 9.76 10.179999 8.5199995 10.179999 7.06 C 10.179999 3.8799999 9.42 0.85999995 6.42 0.85999995 Z M 4.5 1.78 C 4.5 1.38 4.56 1.0799999 4.68 0.85999995 L 2.6799998 0.85999995 C 2.78 1.1 2.82 1.4399999 2.82 1.86 L 2.82 11.84 C 2.82 12.259999 2.78 12.599999 2.6799998 12.84 L 4.68 12.84 C 4.56 12.62 4.5 12.32 4.5 11.92 Z "/>
</symbol>
<symbol id="gD5ADBDB4F1D8E002AEFDDEC4CBF7721F" overflow="visible">
<path d="M 2.96 12.9 C 2.24 12.9 1.18 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.16 -0.02 2.22 0 2.98 0 C 3.72 0 4.56 -0.04 6.62 -0.04 C 9.44 -0.04 13.16 1.24 13.16 6.16 C 13.16 9.88 10.099999 12.94 6.2599998 12.94 C 4.8399997 12.94 3.74 12.9 2.96 12.9 Z M 3.82 1.68 L 3.82 11.28 C 3.82 11.98 4.52 12.259999 5.5 12.259999 C 9.82 12.259999 11.24 8.76 11.24 5.68 C 11.24 1.64 8.82 0.64 6 0.64 C 4.04 0.64 3.82 1.04 3.82 1.68 Z "/>
</symbol>
<symbol id="g713198A7DA4F5CD7D462D4529B1D64BD" overflow="visible">
<path d="M 7.96 1.8199999 C 7.8799996 2 7.72 2.08 7.54 2.1 C 6.8599997 1.22 6 0.78 5.14 0.78 C 3.6799998 0.78 2.46 2.26 2.46 4.6 C 2.46 6.7999997 3.4199998 8.12 4.74 8.12 C 5.92 8.12 6.08 7.4199996 6.16 6.72 C 6.22 6.18 6.5 6 6.92 6 C 7.3399997 6 7.8999996 6.2599998 7.8999996 6.8799996 C 7.8999996 7.98 6.7599998 8.78 4.8399997 8.78 C 2.86 8.78 0.74 7 0.74 4.16 C 0.74 1.5799999 2.18 -0.19999999 4.7 -0.19999999 C 5.9 -0.19999999 6.96 0.17999999 7.96 1.8199999 Z "/>
</symbol>
<symbol id="gB9C04FB79CAD4691AB5EC7F01BE2AD7F" overflow="visible">
<path d="M 3.52 7.16 C 3.48 7.96 3.46 8.48 3.36 8.679999 C 3.32 8.78 3.28 8.84 3.12 8.84 C 2.56 8.62 2.04 8.44 0.65999997 8.26 C 0.62 8.139999 0.65999997 7.8199997 0.7 7.7 C 1.78 7.6 2 7.5 2 6.3399997 L 2 2.44 C 2 0.78 1.76 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 2 0 2.8 0 C 3.6 0 4.52 -0.02 5.22 -0.04 C 5.3399997 0.08 5.3399997 0.5 5.22 0.62 C 3.82 0.71999997 3.58 0.78 3.58 2.44 L 3.58 5.22 C 3.58 5.74 3.82 6.2 4.06 6.56 C 4.2799997 6.8799996 4.74 7.54 4.98 7.54 C 5.16 7.54 5.3399997 7.5 5.5 7.2799997 C 5.64 7.08 5.8799996 6.8199997 6.22 6.8199997 C 6.7 6.8199997 7.16 7.3199997 7.16 7.8199997 C 7.16 8.2 6.7999997 8.78 5.96 8.78 C 5.02 8.78 4.2 7.8999996 3.74 7.12 C 3.62 6.8999996 3.52 7.06 3.52 7.16 Z "/>
</symbol>
<symbol id="gCBC8B237489E88077E829B631AC27C8B" overflow="visible">
<path d="M 2.28 9.559999 L 2.28 2.44 C 2.28 0.78 1.7199999 0.7 0.62 0.64 C 0.42 0.52 0.42 0.08 0.62 -0.04 C 1.42 -0.02 2.8 0 3.6 0 C 4.4 0 5.74 -0.02 6.54 -0.04 C 6.74 0.08 6.74 0.52 6.54 0.64 C 5.44 0.7 4.88 0.78 4.88 2.44 L 4.88 9.559999 C 4.88 11.219999 5.44 11.3 6.54 11.36 C 6.74 11.48 6.74 11.92 6.54 12.04 C 5.74 12.0199995 4.4 12 3.6 12 C 2.8 12 1.42 12.0199995 0.62 12.04 C 0.42 11.92 0.42 11.48 0.62 11.36 C 1.7199999 11.3 2.28 11.219999 2.28 9.559999 Z "/>
</symbol>
<symbol id="g46EE6FB315699AF9CBE00AD0EAD33ECA" overflow="visible">
<path d="M 0.97999996 1.16 C 0.97999996 0.39999998 1.62 -0.19999999 2.4199998 -0.19999999 C 3.22 -0.19999999 3.8999999 0.44 3.8999999 1.1999999 C 3.8999999 1.9799999 3.26 2.58 2.46 2.58 C 1.66 2.58 0.97999996 1.9399999 0.97999996 1.16 Z "/>
</symbol>
<symbol id="g8F63AAB7FFA6B186E1B4BC124750174B" overflow="visible">
<path d="M 8.42 12.62 C 7.3199997 12.78 6.8999996 13.16 5.04 13.16 C 4.14 13.16 2.96 12.88 2.12 12.2 C 1.38 11.599999 0.82 10.679999 0.82 9.7 C 0.82 8.94 1.02 7.98 1.48 7.3799996 C 2.3999999 6.14 4.06 5.46 4.92 4.8599997 C 5.8399997 4.22 6.74 3.4199998 6.74 2.3 C 6.74 1.3199999 5.8799996 0.64 4.66 0.64 C 3.32 0.64 1.9399999 1.74 1.54 3.56 C 1.22 3.6799998 0.9 3.6 0.59999996 3.52 C 0.58 3.52 0.56 3.5 0.53999996 3.5 C 0.53999996 2 0.7 0.94 0.91999996 0.19999999 C 2.06 0.19999999 2.12 -0.19999999 4.88 -0.19999999 C 6.1 -0.19999999 7.08 0.16 7.8999996 0.9 C 8.62 1.52 9.26 2.44 9.26 3.6799998 C 9.26 4.72 8.82 5.42 8.22 6.08 C 7.44 6.94 6.3199997 7.56 5.54 7.96 C 4.74 8.36 3.32 9.4 3.32 10.54 C 3.32 11.66 4 12.34 5.02 12.34 C 6.72 12.34 7.2799997 10.8 7.64 9.48 C 7.9199996 9.4 8.42 9.4 8.639999 9.58 C 8.639999 10.639999 8.559999 11.46 8.42 12.62 Z "/>
</symbol>
<symbol id="gE9BB2E81A58B731A2047F77D70267173" overflow="visible">
<path d="M 4.64 2.44 L 4.64 6.42 C 4.64 7.4199996 4.72 8.54 4.72 8.54 C 4.72 8.76 4.54 8.88 4.2599998 8.88 C 3.6999998 8.66 2.08 8.5 0.7 8.32 C 0.65999997 8.2 0.7 7.7999997 0.74 7.68 C 1.8399999 7.58 2.04 7.4199996 2.04 6.2799997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.74 0.59999996 0.64 C 0.48 0.52 0.48 0.08 0.59999996 -0.04 C 1.4399999 -0.02 2.28 0 3.34 0 C 4.4 0 5.22 -0.02 6.08 -0.04 C 6.2 0.08 6.2 0.52 6.08 0.64 C 4.8599997 0.71999997 4.64 0.78 4.64 2.44 Z M 1.9399999 11.92 C 1.9399999 11.259999 2.4199998 10.599999 3.22 10.599999 C 4.12 10.599999 4.64 11.32 4.64 11.84 C 4.64 12.44 4.18 13.16 3.34 13.16 C 2.3999999 13.16 1.9399999 12.5199995 1.9399999 11.92 Z "/>
</symbol>
<symbol id="gB88E546A1990E31D64B5C4B23478426F" overflow="visible">
<path d="M 4.56 2.44 L 4.56 6.42 C 4.56 6.52 4.56 6.62 4.56 6.72 C 5.3399997 7.2 6.04 7.3999996 6.3799996 7.3999996 C 7.18 7.3999996 7.7799997 7.04 7.7799997 5.9 L 7.7799997 2.56 C 7.7799997 0.88 7.46 0.7 6.64 0.64 C 6.52 0.52 6.52 0.08 6.64 -0.04 C 7.48 -0.02 8.12 0 9.08 0 C 10.04 0 10.66 -0.02 11.5199995 -0.04 C 11.639999 0.08 11.639999 0.52 11.5199995 0.64 C 10.719999 0.7 10.38 0.88 10.38 2.56 L 10.38 5.68 C 10.38 6.18 10.36 6.58 10.3 6.7799997 C 11.059999 7.16 11.92 7.3999996 12.24 7.3999996 C 13.04 7.3999996 13.599999 7.04 13.599999 5.9 L 13.599999 2.56 C 13.599999 0.88 13.28 0.7 12.46 0.64 C 12.34 0.52 12.34 0.08 12.46 -0.04 C 13.299999 -0.02 13.94 0 14.9 0 C 16 0 16.88 -0.02 17.74 -0.04 C 17.859999 0.08 17.859999 0.52 17.74 0.64 C 16.52 0.7 16.199999 0.88 16.199999 2.56 L 16.199999 5.68 C 16.199999 7.8799996 15.4 8.88 13.679999 8.88 C 12.94 8.88 11.259999 8.08 10.099999 7.44 C 9.8 8.3 9 8.88 7.8199997 8.88 C 7.1 8.88 5.66 8.12 4.52 7.48 C 4.46 8.08 4.4 8.54 4.4 8.54 C 4.38 8.78 4.22 8.88 3.9399998 8.88 C 3.1999998 8.679999 2 8.4 0.62 8.22 C 0.58 8.099999 0.62 7.7 0.65999997 7.58 C 1.76 7.48 1.9599999 7.3199997 1.9599999 6.18 L 1.9599999 2.44 C 1.9599999 0.78 1.74 0.74 0.52 0.64 C 0.39999998 0.52 0.39999998 0.08 0.52 -0.04 C 1.36 -0.02 2.2 0 3.26 0 C 4.18 0 4.74 -0.02 5.6 -0.04 C 5.72 0.08 5.72 0.52 5.6 0.64 C 4.7599998 0.71999997 4.56 0.78 4.56 2.44 Z "/>
</symbol>
<symbol id="gB416F8956A8016097936DBEC1F135503" overflow="visible">
<path d="M 1.9 6.18 L 1.9 -2.2 C 1.9 -3.86 1.68 -3.8999999 0.45999998 -4 C 0.34 -4.12 0.34 -4.56 0.45999998 -4.68 C 1.3 -4.66 2.1399999 -4.64 3.1999998 -4.64 C 4.2599998 -4.64 5.08 -4.66 5.94 -4.68 C 6.06 -4.56 6.06 -4.12 5.94 -4 C 4.72 -3.9199998 4.5 -3.86 4.5 -2.2 L 4.5 0.14 C 4.94 -0.08 5.3599997 -0.19999999 5.8399997 -0.19999999 C 8.88 -0.19999999 10.86 1.8 10.86 4.74 C 10.86 5.8599997 10.44 7.1 9.66 7.8799996 C 8.96 8.58 7.96 8.88 6.92 8.88 C 6.3399997 8.88 5.2599998 8.179999 4.56 7.54 L 4.44 7.54 C 4.4 8.099999 4.3399997 8.54 4.3399997 8.54 C 4.3199997 8.78 4.16 8.88 3.8799999 8.88 C 3.1399999 8.679999 1.9399999 8.4 0.56 8.22 C 0.52 8.099999 0.56 7.7 0.59999996 7.58 C 1.6999999 7.48 1.9 7.3199997 1.9 6.18 Z M 4.5 1.3 L 4.5 6.42 C 4.5 6.54 4.5 6.64 4.5 6.7599998 C 5.08 7.2799997 5.8199997 7.54 6.2799997 7.54 C 7.1 7.54 8.059999 6.54 8.059999 4.2 C 8.059999 2.52 7.46 0.64 5.72 0.64 C 5.5 0.64 5 0.76 4.5 1.3 Z "/>
</symbol>
<symbol id="gC81C3C15134AD04FEC0FE7FCEBE8BB14" overflow="visible">
<path d="M 2 2.54 C 2 0.88 1.68 0.7 0.45999998 0.64 C 0.34 0.52 0.34 0.08 0.45999998 -0.04 C 1.3 -0.02 2.2 0 3.3 0 C 4.4 0 5.2799997 -0.02 6.14 -0.04 C 6.2599998 0.08 6.2599998 0.52 6.14 0.64 C 4.92 0.7 4.6 0.88 4.6 2.54 L 4.6 11.66 C 4.6 12.96 4.66 13.7 4.66 13.7 C 4.66 13.88 4.52 13.96 4.3399997 13.96 C 3.6 13.719999 2 13.5 0.58 13.44 C 0.52 13.2 0.53999996 12.98 0.64 12.799999 C 1.9 12.7 2 12.679999 2 11.3 Z "/>
</symbol>
<symbol id="gD9D3B6C4D6AB50B3CADCA65007C1BC50" overflow="visible">
<path d="M 8.62 2.58 C 7.7999997 1.74 6.72 1.52 5.96 1.52 C 4.4 1.52 3.4399998 2.4199998 3.4399998 4.38 C 3.4399998 4.52 3.46 4.6 3.46 4.7 L 8.26 4.7 C 8.74 4.7 8.84 5.04 8.84 5.3199997 C 8.84 7.02 8.179999 8.88 5.24 8.88 C 3.1399999 8.88 0.74 7.02 0.74 3.9599998 C 0.74 2.8 1.16 1.5799999 2.02 0.79999995 C 2.78 0.12 3.76 -0.19999999 5.18 -0.19999999 C 6.56 -0.19999999 7.9199996 0.5 8.92 1.9599999 C 8.92 2.22 8.82 2.58 8.62 2.58 Z M 3.54 5.5 C 3.56 6.2 3.6599998 6.96 3.9399998 7.3599997 C 4.2599998 7.8399997 4.7999997 8.04 5.02 8.04 C 5.56 8.04 6.2999997 7.52 6.2999997 5.92 C 6.2999997 5.7999997 6.2999997 5.54 6.2599998 5.5 Z "/>
</symbol>
<symbol id="gED653E9CCAB5F6C6237350979071A74F" overflow="visible">
<path d="M 1.1999999 1.1999999 C 1.1999999 0.44 1.8399999 -0.16 2.6399999 -0.16 C 3.4399998 -0.16 4.12 0.48 4.12 1.24 C 4.12 2.02 3.48 2.62 2.6799998 2.62 C 1.88 2.62 1.1999999 1.9799999 1.1999999 1.1999999 Z M 1.1999999 7.16 C 1.1999999 6.3999996 1.8399999 5.7999997 2.6399999 5.7999997 C 3.4399998 5.7999997 4.12 6.44 4.12 7.2 C 4.12 7.98 3.48 8.58 2.6799998 8.58 C 1.88 8.58 1.1999999 7.94 1.1999999 7.16 Z "/>
</symbol>
<symbol id="gDACA5EBB44D5F3DB530A1F5F650BFBAB" overflow="visible">
<path d="M 2.08 10.46 L 2.08 2.44 C 2.08 0.78 1.74 0.68 0.34 0.62 C 0.22 0.5 0.22 0.08 0.34 -0.04 C 1.24 -0.02 2.22 0 2.9399998 0 C 3.6399999 0 4.8199997 -0.02 5.8199997 -0.04 C 5.94 0.08 5.94 0.5 5.8199997 0.62 C 4.2599998 0.7 3.78 0.78 3.78 2.44 L 3.78 5.8399997 C 4.22 5.7 4.7 5.64 5.4 5.64 C 9.04 5.64 10.139999 8.0199995 10.139999 9.719999 C 10.139999 10.9 9.36 13.04 5.66 13.04 C 4.9 13.04 3.72 12.9 2.9199998 12.9 C 2.18 12.9 1.14 12.92 0.34 12.94 C 0.22 12.82 0.22 12.4 0.34 12.28 C 1.74 12.219999 2.08 12.12 2.08 10.46 Z M 3.78 11.08 C 3.78 11.66 4.08 12.36 5.52 12.36 C 6.8999996 12.36 8.28 11.9 8.28 9.36 C 8.28 7.2 7.24 6.3199997 5.2999997 6.3199997 C 4.7999997 6.3199997 4 6.3599997 3.78 6.42 Z "/>
</symbol>
<symbol id="gF9DE6E66E5D3ACB0B17DC7988DD660B8" overflow="visible">
<path d="M 1.7199999 2.44 C 1.7199999 0.78 1.5 0.7 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.04 -0.02 1.7199999 0 2.52 0 C 3.22 0 3.8799999 -0.02 4.3399997 -0.04 C 4.46 0.08 4.46 0.5 4.3399997 0.62 C 3.52 0.7 3.3 0.78 3.3 2.44 L 3.3 4.18 C 3.6799998 4.16 3.9599998 4.14 4.16 4.08 C 4.38 3.9199998 4.56 3.74 4.7999997 3.4199998 L 6.2599998 1.4599999 C 6.8399997 0.68 7.08 0.29999998 7.1 0.06 C 7.1 0 7.12 -0.04 7.18 -0.04 C 7.58 -0.02 8.0199995 0 8.42 0 C 9.04 0 9.66 -0.02 10.059999 -0.04 C 10.179999 0.08 10.179999 0.5 10.059999 0.62 C 9.38 0.7 8.88 0.78 8.34 1.4599999 L 5.7 4.7799997 C 5.62 4.88 5.56 4.96 5.56 5.06 C 5.56 5.14 5.56 5.18 5.64 5.2599998 L 7.3999996 7.08 C 8 7.72 8.7 7.8799996 9.5 7.96 C 9.62 8.08 9.62 8.5 9.5 8.62 C 9.04 8.599999 8.48 8.58 7.7599998 8.58 C 7 8.58 6.2599998 8.599999 5.7999997 8.62 C 5.68 8.5 5.68 8.08 5.7999997 7.96 C 6.92 7.8799996 6.44 7.18 6.2599998 6.94 C 5.7999997 6.3599997 5.18 5.68 4.66 5.2999997 C 4.22 4.98 3.6799998 4.74 3.3 4.68 L 3.3 11.66 C 3.3 12.96 3.3799999 13.759999 3.3799999 13.759999 C 3.3799999 13.9 3.3 13.96 3.12 13.96 C 2.62 13.759999 1.12 13.48 0.32 13.42 C 0.28 13.259999 0.32 12.94 0.44 12.82 C 0.5 12.82 0.56 12.82 0.62 12.82 C 1.5 12.759999 1.7199999 12.759999 1.7199999 11.179999 Z "/>
</symbol>
<symbol id="g3C2FFF86BC828E66F78F8A687CE12C70" overflow="visible">
<path d="M 3.34 5.72 C 3.34 6.14 3.52 6.3799996 3.6799998 6.56 C 4.44 7.2999997 5.46 7.74 6.24 7.74 C 6.64 7.74 7.06 7.48 7.2999997 7.02 C 7.5 6.62 7.54 6.08 7.54 5.48 L 7.54 2.44 C 7.54 0.79999995 7.3399997 0.71999997 6.2999997 0.62 C 6.2 0.5 6.2 0.08 6.2999997 -0.04 C 6.8599997 -0.02 7.54 0 8.34 0 C 9.139999 0 9.8 -0.02 10.46 -0.04 C 10.559999 0.08 10.559999 0.5 10.46 0.62 C 9.34 0.71999997 9.12 0.79999995 9.12 2.44 L 9.12 5.42 C 9.12 6.52 9.04 7.5 8.58 8.099999 C 8.24 8.54 7.62 8.78 6.92 8.78 C 5.94 8.78 4.74 8.5199995 3.52 7.16 C 3.52 7.14 3.5 7.14 3.48 7.12 C 3.4199998 7.04 3.32 6.92 3.32 7.16 L 3.34 11.66 C 3.34 12.96 3.4199998 13.759999 3.4199998 13.759999 C 3.4199998 13.9 3.34 13.96 3.1599998 13.96 C 2.6599998 13.759999 1.16 13.48 0.35999998 13.42 C 0.32 13.259999 0.35999998 12.94 0.48 12.82 C 0.53999996 12.82 0.59999996 12.82 0.65999997 12.82 C 1.54 12.759999 1.76 12.759999 1.76 11.179999 L 1.76 2.44 C 1.76 0.78 1.52 0.7 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.02 -0.02 1.76 0 2.56 0 C 3.32 0 3.98 -0.02 4.54 -0.04 C 4.66 0.08 4.66 0.5 4.54 0.62 C 3.52 0.7 3.34 0.78 3.34 2.44 Z "/>
</symbol>
<symbol id="gCEA9C4D02BCE2DEFAC223AD31CCFFF9F" overflow="visible">
<path d="M 13.259999 2.32 C 13.36 0.7 13.28 0.68 11.98 0.62 C 11.86 0.5 11.86 0.08 11.98 -0.04 C 12.719999 -0.02 13.5199995 0 14.12 0 C 14.719999 0 15.639999 -0.02 16.3 -0.04 C 16.42 0.08 16.42 0.5 16.3 0.62 C 14.94 0.68 14.88 0.76 14.759999 2.4199998 L 14.16 10.84 C 14.08 11.92 14.179999 12.2 15.54 12.28 C 15.66 12.4 15.66 12.82 15.54 12.94 L 12.92 12.9 L 8.679999 2.76 C 8.599999 2.56 8.54 2.48 8.5 2.48 C 8.46 2.48 8.4 2.58 8.34 2.74 L 4.24 12.9 L 1.3399999 12.94 C 1.22 12.82 1.22 12.4 1.3399999 12.28 C 2.72 12.2 2.84 12.16 2.7 10.66 L 1.9 2.4199998 C 1.78 1.22 1.54 0.71999997 0.39999998 0.62 C 0.28 0.5 0.28 0.08 0.39999998 -0.04 C 1 -0.02 1.64 0 2.12 0 C 2.6 0 3.3999999 -0.02 4 -0.04 C 4.12 0.08 4.12 0.5 4 0.62 C 2.6799998 0.71999997 2.58 1.3399999 2.6799998 2.46 L 3.4399998 10.48 L 3.48 10.48 L 7.62 0.099999994 C 7.68 -0.04 7.7999997 -0.19999999 7.9199996 -0.19999999 C 8.04 -0.19999999 8.12 -0.06 8.2 0.099999994 L 12.7 10.679999 L 12.74 10.679999 Z "/>
</symbol>
<symbol id="gFB54B84572F46C3C9CB2B1A90182D6B2" overflow="visible">
<path d="M 8.88 7.74 C 9.26 7.74 9.62 8.099999 9.62 8.5 C 9.62 8.92 9.24 9.24 8.7 9.24 C 8.179999 9.24 7.22 8.9 6.7 8.22 C 6.46 8.38 5.7999997 8.78 4.62 8.78 C 2.84 8.78 1.1999999 7.58 1.1999999 5.74 C 1.1999999 4.66 1.68 4.04 2.24 3.5 C 1.68 3.02 1.36 2.1599998 1.36 1.48 C 1.36 0.76 1.76 0.19999999 2.28 -0.06 C 1.1999999 -0.7 0.64 -1.62 0.64 -2.48 C 0.64 -4.22 2.28 -4.7599998 3.82 -4.7599998 C 6.52 -4.7599998 9.44 -3.46 9.44 -1.3 C 9.44 -0.65999997 9.139999 -0.16 8.559999 0.32 C 7.7799997 0.96 6.3799996 0.97999996 5.64 0.97999996 C 5.2799997 0.97999996 4.7799997 0.94 4.2999997 0.88 C 4 0.85999995 3.8 0.84 3.6999998 0.84 C 3.12 0.84 2.4199998 1.12 2.4199998 1.9799999 C 2.4199998 2.3799999 2.54 2.8 2.78 3.1399999 C 3.26 2.86 3.82 2.72 4.6 2.72 C 6.3599997 2.72 7.98 3.82 7.98 5.7799997 C 7.98 6.72 7.7 7.2599998 7.12 7.8599997 C 7.2599998 8.059999 7.66 8.34 7.9199996 8.34 C 8.059999 8.34 8.2 8.28 8.32 8.099999 C 8.4 7.94 8.66 7.74 8.88 7.74 Z M 2.6399999 -0.19999999 C 2.86 -0.26 3.1799998 -0.29999998 3.4399998 -0.29999998 C 4.06 -0.29999998 4.62 -0.24 4.9 -0.24 C 5.9 -0.24 6.74 -0.26 7.3199997 -0.58 C 8.099999 -1.02 8.34 -1.3 8.34 -1.8199999 C 8.34 -3.26 6.22 -4.02 4.42 -4.02 C 3.6999998 -4.02 2.02 -3.4399998 2.02 -2.08 C 2.02 -1.4 2.06 -0.9 2.6399999 -0.19999999 Z M 6.3799996 5.58 C 6.3799996 3.72 5.44 3.34 4.7 3.34 C 3.02 3.34 2.84 4.7599998 2.84 6.04 C 2.84 7.44 3.34 8.16 4.44 8.16 C 5.7 8.16 6.3799996 7.24 6.3799996 5.58 Z "/>
</symbol>
<symbol id="g733371913480EE84B3609C9E9CD62F8C" overflow="visible">
<path d="M 3.34 7.8799996 C 3.22 7.7599998 3.1399999 7.7999997 3.1399999 7.98 L 3.1399999 11.66 C 3.1399999 12.96 3.22 13.759999 3.22 13.759999 C 3.22 13.9 3.1399999 13.96 2.96 13.96 C 2.46 13.759999 0.96 13.48 0.16 13.42 C 0.12 13.259999 0.16 12.94 0.28 12.82 C 0.34 12.82 0.39999998 12.82 0.45999998 12.82 C 1.3399999 12.759999 1.56 12.759999 1.56 11.179999 L 1.56 1.42 C 1.56 0.64 1.54 0.28 1.48 0 C 1.5799999 -0.16 1.68 -0.24 1.92 -0.24 C 2.04 -0.12 2.24 0.06 2.3999999 0.24 C 2.6 0.48 2.72 0.48 2.9399998 0.29999998 C 3.3999999 -0.08 4 -0.19999999 4.7 -0.19999999 C 6.74 -0.19999999 9.12 1.66 9.12 4.8399997 C 9.12 7.2799997 7.3199997 8.78 5.58 8.78 C 4.72 8.78 3.9599998 8.44 3.34 7.8799996 Z M 3.48 7.2599998 C 4 7.72 4.6 7.8999996 5.18 7.8999996 C 6.3999996 7.8999996 7.3999996 6.42 7.3999996 4.48 C 7.3999996 2.2 6.48 0.48 4.58 0.48 C 3.9599998 0.48 3.54 0.91999996 3.1399999 1.42 L 3.1399999 6.42 C 3.1399999 6.8399997 3.22 7.04 3.48 7.2599998 Z "/>
</symbol>
<symbol id="gFB78EB03C35D4F852337F4EC6AC104AC" overflow="visible">
<path d="M 0.82 4.1 C 0.82 2.06 2.18 -0.19999999 5.02 -0.19999999 C 6.2999997 -0.19999999 7.2799997 0.26 7.96 0.91999996 C 8.86 1.8 9.26 3.06 9.26 4.2799997 C 9.26 6.3599997 8.12 8.78 5.06 8.78 C 3.74 8.78 2.6599998 8.24 1.92 7.3799996 C 1.1999999 6.52 0.82 5.3599997 0.82 4.1 Z M 4.7599998 8.08 C 6.48 8.08 7.54 6.52 7.54 3.6399999 C 7.54 1.12 6.24 0.5 5.2999997 0.5 C 3.22 0.5 2.54 3.02 2.54 4.56 C 2.54 6.2999997 2.96 8.08 4.7599998 8.08 Z "/>
</symbol>
<symbol id="gCDF8B867C9AAFA36255BC29C36465E90" overflow="visible">
<path d="M 3.5 2.44 L 3.5 7.7999997 L 5.3599997 7.7999997 C 5.54 7.7999997 5.8199997 7.8799996 5.8199997 8.059999 L 5.8199997 8.46 C 5.8199997 8.54 5.7599998 8.58 5.66 8.58 L 3.5 8.58 L 3.5 9.719999 C 3.5 12.799999 4.42 13.28 5.08 13.28 C 5.68 13.28 6 13.04 6.2799997 12.34 C 6.44 11.98 6.66 11.7 7.08 11.7 C 7.4199996 11.7 7.8999996 12.12 7.8999996 12.5199995 C 7.8999996 12.86 7.68 13.219999 7.2599998 13.54 C 6.74 13.9 6.22 13.96 5.46 13.96 C 3.78 13.96 1.92 12.5 1.92 9.38 L 1.92 8.58 L 0.9 8.58 C 0.53999996 8.58 0.44 8.34 0.44 8.179999 L 0.44 7.9199996 C 0.44 7.8199997 0.45999998 7.7999997 0.53999996 7.7999997 L 1.92 7.7999997 L 1.92 2.44 C 1.92 0.78 1.5999999 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 1.92 0 2.72 0 C 3.52 0 4.48 -0.02 5.18 -0.04 C 5.2999997 0.08 5.2999997 0.5 5.18 0.62 C 3.62 0.7 3.5 0.78 3.5 2.44 Z "/>
</symbol>
<symbol id="gD3761FB0B01B207797C607CDFB6E3A0B" overflow="visible">
<path d="M 3.3999999 7.16 C 3.3799999 7.7599998 3.34 8.48 3.24 8.679999 C 3.1999998 8.78 3.1599998 8.84 3 8.84 C 2.44 8.62 1.92 8.44 0.53999996 8.26 C 0.5 8.139999 0.53999996 7.8199997 0.58 7.7 C 1.66 7.6 1.88 7.5 1.88 6.3399997 L 1.88 2.44 C 1.88 0.79999995 1.62 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.88 0 2.6799998 0 C 3.48 0 4.1 -0.02 4.7 -0.04 C 4.8199997 0.08 4.8199997 0.5 4.7 0.62 C 3.6799998 0.71999997 3.46 0.79999995 3.46 2.44 L 3.46 5.72 C 3.46 6.14 3.6399999 6.3799996 3.8 6.56 C 4.6 7.3399997 5.3399997 7.74 5.96 7.74 C 6.72 7.74 7.2799997 7.2599998 7.2799997 5.92 L 7.2799997 2.44 C 7.2799997 0.79999995 7.12 0.7 6.04 0.62 C 5.94 0.5 5.94 0.08 6.04 -0.04 C 6.54 -0.02 7.2799997 0 8.08 0 C 8.88 0 9.54 -0.02 10.04 -0.04 C 10.139999 0.08 10.139999 0.5 10.04 0.62 C 9.04 0.7 8.86 0.79999995 8.86 2.44 L 8.86 5.62 C 8.86 5.9 8.86 6.18 8.84 6.42 C 9.8 7.48 10.7 7.74 11.48 7.74 C 12.24 7.74 12.679999 7.2999997 12.679999 5.96 L 12.679999 2.44 C 12.679999 0.79999995 12.48 0.7 11.44 0.62 C 11.34 0.5 11.34 0.08 11.44 -0.04 C 11.94 -0.02 12.679999 0 13.48 0 C 14.28 0 14.98 -0.02 15.54 -0.04 C 15.639999 0.08 15.639999 0.5 15.54 0.62 C 14.44 0.7 14.259999 0.79999995 14.259999 2.44 L 14.259999 5.6 C 14.259999 7.3799996 13.96 8.78 12.2 8.78 C 11.179999 8.78 9.94 8.4 8.9 7.2999997 C 8.84 7.24 8.72 7.14 8.679999 7.3199997 C 8.5 8.139999 7.72 8.78 6.68 8.78 C 5.52 8.78 4.48 8.099999 3.6399999 7.16 C 3.54 7.06 3.4199998 6.92 3.3999999 7.16 Z "/>
</symbol>
<symbol id="g278A59F111DD0614EC58EAA01A502EFD" overflow="visible">
<path d="M 19.1 13.7 L 16.279999 13.7 C 15.799999 13.7 15.559999 13.559999 15.559999 13.259999 C 15.559999 13.0199995 15.679999 12.88 15.92 12.86 C 16.64 12.78 16.8 12.54 16.8 11.5 C 16.8 10.5199995 16.5 9.099999 15.9 7.24 L 15 4.58 C 14.719999 5.2599998 14.259999 6.52 13.599999 8.36 C 12.9 10.36 12.54 11.719999 12.5 12.42 C 12.719999 12.679999 13 12.82 13.38 12.84 C 13.7 12.86 13.86 13 13.86 13.259999 C 13.86 13.639999 13.62 13.7 13.139999 13.7 L 8.36 13.7 C 7.8599997 13.7 7.6 13.559999 7.6 13.259999 C 7.6 13.04 7.74 12.88 8 12.84 C 8.26 12.799999 8.48 12.679999 8.639999 12.48 C 9.059999 11.98 9.46 10.8 9.8 9.8 L 7.3199997 4.1 L 5.96 7.96 C 5.14 10.3 4.74 11.78 4.74 12.42 C 4.74 12.639999 4.96 12.78 5.4 12.84 C 5.7 12.86 5.8599997 13 5.8599997 13.259999 C 5.8599997 13.62 5.56 13.7 5.1 13.7 L 0.9 13.7 C 0.39999998 13.7 0.16 13.559999 0.16 13.259999 C 0.16 13.04 0.29999998 12.88 0.59999996 12.84 C 0.9 12.799999 1.14 12.5199995 1.3199999 12.0199995 L 5.56 0.12 C 5.68 -0.22 5.8399997 -0.38 6.04 -0.38 C 6.22 -0.38 6.3599997 -0.24 6.5 0.06 L 10.26 8.62 L 13.48 0.14 C 13.62 -0.19999999 13.78 -0.38 13.96 -0.38 C 14.16 -0.38 14.32 -0.22 14.44 0.12 L 18.68 11.98 C 18.88 12.5199995 19.14 12.799999 19.439999 12.86 C 19.699999 12.9 19.84 13.04 19.84 13.259999 C 19.84 13.639999 19.58 13.7 19.1 13.7 Z M 17.42 12.84 L 18.14 12.84 C 18.039999 12.639999 17.88 12.24 17.64 11.639999 C 17.619999 12.16 17.539999 12.559999 17.42 12.84 Z M 12.38 9.4 C 13.12 7.14 13.86 5.08 14.639999 3.1799998 C 14.299999 2.28 14.08 1.66 13.96 1.28 L 9.9 11.98 C 9.78 12.3 9.639999 12.58 9.46 12.84 L 11.759999 12.84 C 11.679999 12.719999 11.639999 12.559999 11.639999 12.34 C 11.639999 11.88 11.88 10.9 12.38 9.4 Z M 3.8799999 12.44 C 3.8799999 11.44 4.8599997 8.26 6.8199997 2.9199998 L 6.08 1.22 L 2.2 12.04 C 2.06 12.4 1.9599999 12.66 1.86 12.84 L 3.9599998 12.84 C 3.8999999 12.719999 3.8799999 12.58 3.8799999 12.44 Z "/>
</symbol>
<symbol id="gDE6529B954490BC6DD8A7FF7D66D28D4" overflow="visible">
<path d="M 2.28 9.559999 L 2.28 2.44 C 2.28 0.78 1.7199999 0.7 0.62 0.64 C 0.42 0.52 0.42 0.08 0.62 -0.04 C 1.42 -0.02 2.8 0 3.6 0 C 4.36 0 5.6 -0.02 6.42 -0.04 C 6.42 -0.04 6.42 -0.04 6.42 -0.04 C 6.44 -0.04 6.46 -0.04 6.48 -0.04 C 6.5 -0.04 6.52 -0.04 6.54 -0.04 C 6.54 -0.04 6.54 -0.04 6.54 -0.04 C 7.3599997 -0.02 8.639999 0 9.4 0 C 10.2 0 11.54 -0.02 12.34 -0.04 C 12.54 0.08 12.54 0.52 12.34 0.64 C 11.24 0.7 10.679999 0.78 10.679999 2.44 L 10.679999 9.559999 C 10.679999 11.219999 11.24 11.3 12.34 11.36 C 12.54 11.48 12.54 11.92 12.34 12.04 C 11.54 12.0199995 10.2 12 9.4 12 C 8.639999 12 7.3599997 12.0199995 6.54 12.04 C 6.54 12.04 6.54 12.04 6.54 12.04 C 6.52 12.04 6.5 12.04 6.48 12.04 C 6.46 12.04 6.44 12.04 6.42 12.04 C 6.42 12.04 6.42 12.04 6.42 12.04 C 5.6 12.0199995 4.36 12 3.6 12 C 2.8 12 1.42 12.0199995 0.62 12.04 C 0.42 11.92 0.42 11.48 0.62 11.36 C 1.7199999 11.3 2.28 11.219999 2.28 9.559999 Z M 6.48 0.64 C 5.42 0.7 4.88 0.82 4.88 2.44 L 4.88 9.559999 C 4.88 11.2 5.42 11.3 6.48 11.36 C 7.54 11.3 8.08 11.2 8.08 9.559999 L 8.08 2.44 C 8.08 0.82 7.54 0.7 6.48 0.64 Z "/>
</symbol>
<symbol id="g911507D70DD1D78477F3BEDE827F51DF" overflow="visible">
<path d="M 11.28 10.46 L 11.28 7.3399997 L 5.08 7.3399997 L 5.08 10.46 C 5.08 12.12 5.64 12.2 6.74 12.259999 C 6.94 12.38 6.94 12.82 6.74 12.94 C 5.94 12.92 4.5 12.9 3.6999998 12.9 C 2.8999999 12.9 1.42 12.92 0.62 12.94 C 0.42 12.82 0.42 12.38 0.62 12.259999 C 1.7199999 12.2 2.28 12.12 2.28 10.46 L 2.28 2.44 C 2.28 0.78 1.7199999 0.7 0.62 0.64 C 0.42 0.52 0.42 0.08 0.62 -0.04 C 1.42 -0.02 2.8999999 0 3.6999998 0 C 4.5 0 5.94 -0.02 6.74 -0.04 C 6.94 0.08 6.94 0.52 6.74 0.64 C 5.64 0.7 5.08 0.78 5.08 2.44 L 5.08 6.3799996 L 11.28 6.3799996 L 11.28 2.44 C 11.28 0.78 10.719999 0.7 9.62 0.64 C 9.42 0.52 9.42 0.08 9.62 -0.04 C 10.42 -0.02 11.9 0 12.7 0 C 13.5 0 14.94 -0.02 15.74 -0.04 C 15.94 0.08 15.94 0.52 15.74 0.64 C 14.639999 0.7 14.08 0.78 14.08 2.44 L 14.08 10.46 C 14.08 12.12 14.639999 12.2 15.74 12.259999 C 15.94 12.38 15.94 12.82 15.74 12.94 C 14.94 12.92 13.5 12.9 12.7 12.9 C 11.9 12.9 10.42 12.92 9.62 12.94 C 9.42 12.82 9.42 12.38 9.62 12.259999 C 10.719999 12.2 11.28 12.12 11.28 10.46 Z "/>
</symbol>
<symbol id="g2EB1DC9A979CD3C8C9D80DB754EBF6AB" overflow="visible">
<path d="M 10.2 2.6599998 L 10.2 6.12 C 10.2 7.7999997 10.24 7.56 10.24 8.04 C 10.24 8.38 10.16 8.599999 10.04 8.72 C 9.679999 8.7 9.28 8.679999 8.9 8.679999 C 8.34 8.679999 7.04 8.7 6.2599998 8.72 C 6.14 8.599999 6.14 8.16 6.2599998 8.04 C 7.2799997 7.94 7.6 7.7999997 7.6 6.12 L 7.6 2.4199998 C 7.6 2.22 7.6 2.02 7.62 1.8199999 C 6.7999997 1.3199999 6.14 1.28 5.7799997 1.28 C 4.98 1.28 4.38 1.38 4.38 2.78 L 4.38 6.12 C 4.38 7.7999997 4.42 7.56 4.42 8.04 C 4.42 8.38 4.3399997 8.599999 4.22 8.72 C 3.86 8.7 3.4399998 8.679999 3.08 8.679999 C 2.06 8.679999 1.3 8.7 0.44 8.72 C 0.32 8.599999 0.32 8.16 0.44 8.04 C 1.36 8 1.78 7.7999997 1.78 6.12 L 1.78 3 C 1.78 0.88 2.62 -0.19999999 4.3399997 -0.19999999 C 5.06 -0.19999999 6.52 0.38 7.68 1.02 C 7.72 0.52 7.7599998 0.14 7.7599998 0.14 C 7.7799997 -0.099999994 7.94 -0.19999999 8.22 -0.19999999 C 8.96 0 10.16 0.28 11.54 0.45999998 C 11.58 0.58 11.54 0.97999996 11.5 1.1 C 10.42 1.1999999 10.2 1.52 10.2 2.6599998 Z "/>
</symbol>
<symbol id="g936880EEF467D45CE0F64A721CAEDAB8" overflow="visible">
<path d="M 4.56 5.3599997 C 4.56 6.08 4.7799997 6.3799996 5.04 6.68 C 5.2 6.8799996 5.38 7.02 5.68 7.02 C 5.8599997 7.02 6.08 6.8399997 6.24 6.64 C 6.3799996 6.48 6.72 6.3199997 7.18 6.3199997 C 7.7599998 6.3199997 8.32 6.92 8.32 7.7599998 C 8.32 8.28 7.72 8.88 7 8.88 C 6.2999997 8.88 5.54 8.28 4.62 6.96 L 4.54 6.96 C 4.5 7.56 4.4 8.54 4.4 8.54 C 4.38 8.72 4.22 8.88 3.9399998 8.88 C 3 8.639999 1.9399999 8.36 0.62 8.22 C 0.58 8.099999 0.62 7.72 0.65999997 7.6 C 1.76 7.5 1.9599999 7.3199997 1.9599999 6.18 L 1.9599999 2.44 C 1.9599999 0.78 1.74 0.74 0.52 0.64 C 0.39999998 0.52 0.39999998 0.08 0.52 -0.04 C 1.36 -0.02 2.2 0 3.26 0 C 4.3199997 0 5.14 -0.02 6 -0.04 C 6.12 0.08 6.12 0.52 6 0.64 C 4.7799997 0.71999997 4.56 0.78 4.56 2.44 Z "/>
</symbol>
<symbol id="gCD50B0C5537328D0484BBB5C5B7C30A" overflow="visible">
<path d="M 0.96 2.9199998 C 1.04 1.9399999 1.14 1 1.3 0.24 C 1.68 0.12 2.96 -0.19999999 4.08 -0.19999999 C 5.62 -0.19999999 7.54 0.64 7.54 2.3799999 C 7.54 3.06 7.3799996 3.6 6.92 4.1 C 6.3599997 4.74 5.52 5.24 4.6 5.64 C 3.8 5.98 3.52 6.62 3.52 7.2 C 3.52 7.66 3.8999999 8.04 4.48 8.04 C 5.18 8.04 5.8599997 7.3999996 6.3599997 6.18 C 6.72 6.12 6.94 6.14 7.14 6.2799997 C 7.14 7 7.06 7.7599998 6.8799996 8.4 C 6.24 8.679999 5.74 8.88 4.64 8.88 C 3.58 8.88 2.58 8.48 1.9399999 7.8399997 C 1.48 7.3799996 1.26 6.8199997 1.26 6.2799997 C 1.26 5.68 1.5 5.2 1.88 4.7799997 C 2.5 4.1 3.6 3.3999999 4.2 3.12 C 5 2.76 5.22 2.04 5.22 1.56 C 5.22 0.91999996 4.58 0.58 4.04 0.58 C 3.1399999 0.58 2.18 1.5 1.76 2.96 C 1.4399999 3.02 1.28 3 0.96 2.9199998 Z "/>
</symbol>
<symbol id="g1344FEF92B65FBC27D977C1EC5D9AECF" overflow="visible">
<path d="M 1.26 8.679999 C 0.97999996 8.679999 0.68 8.599999 0.42 8.38 L 0.42 7.7999997 C 0.42 7.7 0.44 7.68 0.52 7.68 L 1.8199999 7.68 C 1.78 5.66 1.76 3.1 1.76 2.1 C 1.76 1.4 1.9399999 0.71999997 2.36 0.35999998 C 2.82 -0.02 3.54 -0.19999999 4.02 -0.19999999 C 5.12 -0.19999999 6.3399997 0.35999998 6.74 0.91999996 C 6.74 1.16 6.62 1.28 6.3799996 1.48 C 6.12 1.28 5.62 1.1999999 5.24 1.1999999 C 4.7999997 1.1999999 4.36 1.54 4.36 2.54 C 4.36 3.54 4.3399997 5.68 4.3399997 7.68 L 6.3599997 7.68 C 6.56 7.68 6.8399997 7.7599998 6.8399997 7.94 L 6.8399997 8.559999 C 6.8399997 8.639999 6.7799997 8.679999 6.68 8.679999 L 4.3399997 8.679999 L 4.36 9.36 C 4.4 10.7 4.46 11.62 4.46 11.62 C 4.46 11.74 4.4 11.8 4.2999997 11.8 C 4.16 11.8 3.4199998 11.58 3.1 11.44 C 2.76 11.3 2.18 11.179999 2.04 11 C 1.9 10.82 1.8199999 10.28 1.8199999 8.679999 Z "/>
</symbol>
<symbol id="g7B316FC97C7634445DBF19AF1976B5C8" overflow="visible">
<path d="M 8.44 1.74 C 8.44 1.9799999 8.4 2.36 8.179999 2.36 C 7.3799996 1.62 6.7 1.24 6.12 1.24 C 4.62 1.24 3.4399998 2.32 3.4399998 4.72 C 3.4399998 6.94 3.9399998 8.04 5 8.04 C 5.74 8.04 6.04 7.2599998 6.1 6.62 C 6.16 6.08 6.7 5.68 7.3399997 5.68 C 7.98 5.68 8.44 6.18 8.44 6.7999997 C 8.44 7.7 7.3599997 8.88 5.18 8.88 C 2.82 8.88 0.74 6.98 0.74 4.02 C 0.74 2.72 1.1999999 1.5799999 1.9799999 0.84 C 2.76 0.099999994 3.6799998 -0.19999999 5.1 -0.19999999 C 6.2999997 -0.19999999 7.68 0.64 8.44 1.74 Z "/>
</symbol>
<symbol id="gE9B2270BB65CFFF96111DE686524B072" overflow="visible">
<path d="M 5.5078125 5.9765625 Q 4.6875 5.625 4.0625 6.0546875 Q 3.4375 6.484375 3.4765625 7.2265625 Q 3.515625 7.96875 4.21875 8.3203125 Q 4.921875 8.671875 5.625 8.3203125 Q 6.328125 7.96875 6.328125 7.1484375 Q 6.328125 6.328125 5.5078125 5.9765625 Z M 5.5078125 0.1171875 Q 4.6875 -0.234375 4.0625 0.1953125 Q 3.4375 0.625 3.4765625 1.3671875 Q 3.515625 2.109375 4.21875 2.4609375 Q 4.921875 2.8125 5.625 2.4609375 Q 6.328125 2.109375 6.328125 1.2890625 Q 6.328125 0.46875 5.5078125 0.1171875 Z "/>
</symbol>
<symbol id="g3BBBD96D467CC564123619D79E97B4D6" overflow="visible">
<path d="M 7.8999996 12.62 C 6.74 12.78 6.7799997 13.16 4.8199997 13.16 C 2.8 13.16 1.02 11.82 1.02 9.7 C 1.02 7.6 2.76 6.64 4.52 5.96 C 5.72 5.5 7.2 4.94 7.2 2.98 C 7.2 1.36 6.2999997 0.52 4.7 0.52 C 2.84 0.52 1.64 1.38 1.1999999 3.36 C 0.94 3.4399998 0.74 3.3999999 0.53999996 3.3 C 0.62 1.76 0.7 1.24 0.94 0.26 C 2.2 0.26 2.76 -0.19999999 4.54 -0.19999999 C 5.44 -0.19999999 6.2999997 0.02 7 0.45999998 C 8.16 1.18 8.88 2.3999999 8.88 3.6799998 C 8.88 5.7999997 7.2799997 6.74 5.64 7.3599997 C 4.44 7.7999997 2.44 8.559999 2.44 10.24 C 2.44 11.36 3.46 12.48 4.64 12.48 C 6.58 12.48 7.2 11.24 7.6 9.92 C 7.8199997 9.88 8.08 9.9 8.26 10.04 C 8.179999 11 8.099999 11.559999 7.8999996 12.62 Z "/>
</symbol>
<symbol id="gAC7FD886AB12F72ED3B61B0327264BE7" overflow="visible">
<path d="M 3.12 7.3599997 C 3.1 7.96 3.06 8.48 2.96 8.679999 C 2.9199998 8.78 2.8799999 8.84 2.72 8.84 C 2.1599998 8.62 1.64 8.44 0.26 8.26 C 0.22 8.139999 0.26 7.8199997 0.29999998 7.7 C 1.38 7.6 1.5999999 7.5 1.5999999 6.3399997 L 1.5999999 -2.2 C 1.5999999 -3.86 1.38 -3.9599998 0.16 -4.02 C 0.04 -4.14 0.04 -4.56 0.16 -4.68 C 0.85999995 -4.66 1.5999999 -4.64 2.3999999 -4.64 C 3.1999998 -4.64 4.16 -4.66 4.8199997 -4.68 C 4.94 -4.56 4.94 -4.14 4.8199997 -4.02 C 3.3999999 -3.9399998 3.1799998 -3.86 3.1799998 -2.2 L 3.1799998 -0.04 C 3.1799998 0.22 3.26 0.19999999 3.46 0.12 C 3.9599998 -0.08 4.56 -0.19999999 5.2 -0.19999999 C 6.3199997 -0.19999999 7.3199997 0.14 8.139999 0.91999996 C 9.08 1.8399999 9.62 3.08 9.62 4.7 C 9.62 6.8199997 8.12 8.78 6.08 8.78 C 5.16 8.78 4.14 8.179999 3.34 7.2799997 C 3.22 7.16 3.1399999 7.16 3.12 7.3599997 Z M 3.5 6.62 C 4.02 7.2599998 4.94 7.8599997 5.52 7.8599997 C 6.7999997 7.8599997 7.8999996 6.42 7.8999996 4.16 C 7.8999996 2.52 7.3199997 0.48 5.08 0.48 C 4.72 0.48 4.02 0.58 3.6599998 0.9 C 3.26 1.26 3.1799998 1.38 3.1799998 2.1 L 3.1799998 5.74 C 3.1799998 6.16 3.26 6.3399997 3.5 6.62 Z "/>
</symbol>
<symbol id="gB91E67CF1B63A9F4CC30BB03AE35508D" overflow="visible">
<path d="M 2.08 1.9 C 1.4599999 1.9 1.02 1.48 1.02 0.91999996 C 1.02 0.29999998 1.54 0.099999994 1.9 0.04 C 2.28 0 2.62 -0.12 2.62 -0.58 C 2.62 -1 1.9 -1.92 0.85999995 -2.18 C 0.85999995 -2.3799999 0.9 -2.52 1.04 -2.6599998 C 2.24 -2.44 3.3999999 -1.48 3.3999999 -0.08 C 3.3999999 1.12 2.8799999 1.9 2.08 1.9 Z "/>
</symbol>
<symbol id="g17AD34DB90B05275C6F1422A9B4B5274" overflow="visible">
<path d="M 6.5 7.96 C 7.58 7.8799996 7.7 7.64 7.2799997 6.62 L 5.66 2.7 C 5.3399997 1.92 5.24 1.92 4.92 2.76 L 3.48 6.62 C 3.12 7.58 3.04 7.8199997 4.1 7.96 C 4.22 8.08 4.22 8.5 4.1 8.62 C 3.4399998 8.599999 2.74 8.58 2.08 8.58 C 1.42 8.58 0.82 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.28 7.8399997 1.42 7.52 1.8199999 6.5 L 4.38 0.17999999 C 4.5 -0.12 4.62 -0.24 4.88 -0.24 C 5.08 -0.24 5.22 -0.12 5.3599997 0.22 L 8.0199995 6.48 C 8.4 7.3599997 8.62 7.8599997 9.74 7.96 C 9.86 8.08 9.86 8.5 9.74 8.62 C 9.34 8.599999 8.86 8.58 8.34 8.58 C 7.68 8.58 7 8.599999 6.5 8.62 C 6.3799996 8.5 6.3799996 8.08 6.5 7.96 Z "/>
</symbol>
<symbol id="g13CAD87D675A42FC6A129543D89F948C" overflow="visible">
<path d="M 5.7599998 2.44 L 5.7599998 9.38 C 5.7599998 10.58 5.7799997 11.8 5.8199997 12.059999 C 5.8199997 12.16 5.7799997 12.16 5.7 12.16 C 4.6 11.48 3.54 10.98 1.78 10.16 C 1.8199999 9.94 1.9 9.74 2.08 9.62 C 3 10 3.4399998 10.12 3.82 10.12 C 4.16 10.12 4.22 9.639999 4.22 8.96 L 4.22 2.44 C 4.22 0.78 3.6799998 0.68 2.28 0.62 C 2.1599998 0.5 2.1599998 0.08 2.28 -0.04 C 3.26 -0.02 3.98 0 5.06 0 C 6.02 0 6.5 -0.02 7.5 -0.04 C 7.62 0.08 7.62 0.5 7.5 0.62 C 6.1 0.68 5.7599998 0.78 5.7599998 2.44 Z "/>
</symbol>
<symbol id="g612BB0D9B453ACEC45B2B13686D7BB71" overflow="visible">
<path d="M 1.4599999 1.68 L 6.74 4.64 L 1.4599999 7.6 Z "/>
</symbol>
<symbol id="g629AE7F75F47B1FD947FFA2989B5B47D" overflow="visible">
<path d="M 7.44 7.54 C 7.04 8.4 6.42 8.84 5.6 8.84 C 4.2999997 8.84 3.1599998 8.179999 2.18 6.8399997 C 1.26 5.6 0.79999995 4.3199997 0.79999995 2.98 C 0.79999995 1.24 1.8 -0.26 3.46 -0.26 C 4.18 -0.26 4.9 0.08 5.64 0.76 L 4.8199997 -2.52 C 4.7599998 -2.82 4.58 -3 4.2999997 -3.06 C 4.2 -3.08 3.9399998 -3.1 3.48 -3.1 C 3.36 -3.12 3.28 -3.12 3.24 -3.12 C 3.06 -3.1399999 2.96 -3.3 2.96 -3.58 L 2.96 -3.6599998 C 3.02 -3.8 3.1399999 -3.8799999 3.3 -3.8799999 C 3.6799998 -3.8799999 4.88 -3.82 5.2599998 -3.82 C 5.64 -3.82 6.8999996 -3.8799999 7.2799997 -3.8799999 C 7.56 -3.8799999 7.7 -3.72 7.7 -3.3999999 C 7.7 -3.1999998 7.5 -3.1 7.12 -3.1 C 6.7599998 -3.1 6.2599998 -3.12 6.2599998 -2.8799999 C 6.2599998 -2.8 6.2799997 -2.6599998 6.3399997 -2.46 L 9.04 8.54 C 9.04 8.72 8.94 8.82 8.76 8.82 C 8.4 8.82 7.64 7.8199997 7.44 7.54 Z M 6.7999997 7.46 C 6.98 7.04 7.08 6.7599998 7.08 6.58 C 7.08 6.56 7.06 6.44 7.02 6.2599998 L 6.54 4.3199997 C 6.16 2.8799999 5.98 2.1399999 5.96 2.1 C 5.58 1.4 4.48 0.32 3.52 0.32 C 2.74 0.32 2.34 0.91999996 2.34 2.1 C 2.34 3.02 2.96 5.2599998 3.24 6 C 3.62 6.94 4.5 8.24 5.6 8.24 C 6.14 8.24 6.54 7.98 6.7999997 7.46 Z "/>
</symbol>
<symbol id="gCAFB20A65E8FBEFE071D9C4C8EE95E49" overflow="visible">
<path d="M 1.22 9.36 C 1.22 8.94 1.5999999 8.58 2.02 8.58 C 2.36 8.58 2.96 8.94 2.96 9.38 C 2.96 9.54 2.9199998 9.66 2.8799999 9.8 C 2.84 9.94 2.72 10.12 2.72 10.28 C 2.72 10.78 3.24 11.5 4.7 11.5 C 5.42 11.5 6.44 11 6.44 9.08 C 6.44 7.7999997 5.98 6.7599998 4.7999997 5.56 L 3.32 4.1 C 1.36 2.1 1.04 1.14 1.04 -0.04 C 1.04 -0.04 2.06 0 2.7 0 L 6.2 0 C 6.8399997 0 7.7599998 -0.04 7.7599998 -0.04 C 8.0199995 1.02 8.22 2.52 8.24 3.12 C 8.12 3.22 7.8599997 3.26 7.66 3.22 C 7.3199997 1.8 6.98 1.3 6.2599998 1.3 L 2.7 1.3 C 2.7 2.26 4.08 3.62 4.18 3.72 L 6.2 5.66 C 7.3399997 6.7599998 8.2 7.64 8.2 9.16 C 8.2 11.32 6.44 12.2 4.8199997 12.2 C 2.6 12.2 1.22 10.559999 1.22 9.36 Z "/>
</symbol>
<symbol id="g8D44D9C01F9AF6C3B1D634FDF54DE6FB" overflow="visible">
<path d="M 5.66 6.46 C 7.3599997 6.46 7.4199996 6 7.48 5.1 C 7.6 4.98 8.0199995 4.98 8.139999 5.1 C 8.12 5.6 8.099999 6.18 8.099999 6.8599997 C 8.099999 7.54 8.12 8.059999 8.139999 8.58 C 8.0199995 8.7 7.6 8.7 7.48 8.58 C 7.4199996 7.48 7.3599997 7.22 5.66 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.9 4.04 12.099999 4.92 12.099999 L 5.8199997 12.099999 C 7.94 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.92 9.34 9.96 9.5 10.0199995 C 9.4 10.84 9.099999 12.759999 9.059999 12.92 C 9.059999 12.96 9.04 12.98 8.98 12.98 C 8.639999 12.92 8.54 12.9 8.04 12.9 L 2.9399998 12.9 C 2.3 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.06 -0.02 2.06 0 2.96 0 C 3.86 0 4.8399997 -0.02 5.54 -0.04 C 5.66 0.08 5.66 0.5 5.54 0.62 C 4.14 0.68 3.8 0.78 3.8 2.44 L 3.8 6.46 Z "/>
</symbol>
<symbol id="g6636102111388326E3C89C955A433A6D" overflow="visible">
<path d="M 6.54 5.12 C 6 3.3 4.72 1.28 2.06 0.28 C 2.06 0.04 2.1399999 -0.14 2.3 -0.24 C 4.3199997 0.35999998 5.56 1.1999999 6.68 2.5 C 7.9199996 3.9399998 8.54 5.7599998 8.54 7.3399997 C 8.54 11.4 6.24 12.2 4.7 12.2 C 2.08 12.2 1 9.66 1 7.94 C 1 6.22 1.92 4.68 4.64 4.68 C 5.16 4.68 5.94 4.8399997 6.54 5.12 Z M 6.72 5.8399997 C 6.06 5.4 5.4 5.38 5.06 5.38 C 3.1 5.38 2.6599998 7.2999997 2.6599998 8.3 C 2.6599998 10.5 3.5 11.5 4.48 11.5 C 5.74 11.5 6.8799996 10.82 6.8799996 7.3999996 C 6.8799996 6.96 6.8399997 6.42 6.72 5.8399997 Z "/>
</symbol>
<symbol id="gA1481BA28623480CC7E6165783E2A864" overflow="visible">
<path d="M 4.06 7.96 C 4.18 8.08 4.18 8.5 4.06 8.62 C 3.46 8.599999 2.76 8.58 2.04 8.58 C 1.28 8.58 0.74 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.16 7.8599997 1.38 7.66 1.8 6.62 L 4.42 0.16 C 4.54 -0.12 4.7 -0.24 4.9 -0.24 C 5.08 -0.24 5.24 -0.12 5.38 0.19999999 L 7.3999996 5.12 L 9.46 0.16 C 9.58 -0.12 9.74 -0.24 9.94 -0.24 C 10.12 -0.24 10.28 -0.12 10.4 0.17999999 L 13.0199995 6.52 C 13.34 7.3399997 13.679999 7.8999996 14.7 7.96 C 14.82 8.08 14.82 8.5 14.7 8.62 C 14.299999 8.599999 13.86 8.58 13.259999 8.58 C 12.66 8.58 11.82 8.599999 11.219999 8.62 C 11.099999 8.5 11.099999 8.08 11.219999 7.96 C 12.719999 7.8799996 12.5199995 7.2999997 12.24 6.6 L 10.559999 2.44 C 10.36 1.9399999 10.28 1.9399999 10.12 2.36 L 8.4 6.74 C 8.0199995 7.68 8.059999 7.8799996 9.12 7.96 C 9.24 8.08 9.24 8.5 9.12 8.62 C 8.5199995 8.599999 7.72 8.58 7.12 8.58 C 6.62 8.58 5.96 8.599999 5.3599997 8.62 C 5.24 8.5 5.24 8.08 5.3599997 7.96 C 6.2999997 7.8799996 6.54 7.2999997 6.8999996 6.3999996 L 7.02 6.08 L 5.62 2.54 C 5.3599997 1.88 5.3199997 1.86 5.06 2.5 L 3.46 6.62 C 3.08 7.58 3.1 7.8999996 4.06 7.96 Z "/>
</symbol>
<symbol id="g316778D5069ED68A0C52C06F0AD18D23" overflow="visible">
<path d="M 1.14 0.85999995 C 1.14 0.28 1.62 -0.19999999 2.2 -0.19999999 C 2.78 -0.19999999 3.26 0.28 3.26 0.85999995 C 3.26 1.4399999 2.78 1.92 2.2 1.92 C 1.62 1.92 1.14 1.4399999 1.14 0.85999995 Z "/>
</symbol>
<symbol id="gAA14E57E2DCC57A3F7809273EECD3C51" overflow="visible">
<path d="M 7.9104 1.5616 L 7.9104 6.6944 C 7.9104 7.7567997 8.128 7.8208 9.024 7.8592 C 9.1008 7.936 9.1008 8.2048 9.024 8.2816 C 8.4992 8.2688 7.8464 8.256 7.3599997 8.256 C 6.8863997 8.256 6.272 8.2688 5.7088 8.2816 C 5.632 8.2048 5.632 7.936 5.7088 7.8592 C 6.6047997 7.8208 6.8223996 7.7567997 6.8223996 6.6944 L 6.8223996 4.6464 L 2.4448 4.6464 L 2.4448 6.6944 C 2.4448 7.7567997 2.6624 7.8208 3.5584 7.8592 C 3.6352 7.936 3.6352 8.2048 3.5584 8.2816 C 3.072 8.2688 2.5472 8.256 1.8944 8.256 C 1.2544 8.256 0.72959995 8.2688 0.24319999 8.2816 C 0.1664 8.2048 0.1664 7.936 0.24319999 7.8592 C 1.1392 7.8208 1.3568 7.7567997 1.3568 6.6944 L 1.3568 1.5616 C 1.3568 0.4992 1.1392 0.43519998 0.24319999 0.39679998 C 0.1664 0.32 0.1664 0.0512 0.24319999 -0.0256 C 0.8064 -0.0128 1.4208 0 1.9072 0 C 2.368 0 2.9952 -0.0128 3.5584 -0.0256 C 3.6352 0.0512 3.6352 0.32 3.5584 0.39679998 C 2.6624 0.43519998 2.4448 0.4992 2.4448 1.5616 L 2.4448 4.1088 L 6.8223996 4.1088 L 6.8223996 1.5616 C 6.8223996 0.4992 6.6047997 0.43519998 5.7088 0.39679998 C 5.632 0.32 5.632 0.0512 5.7088 -0.0256 C 6.2848 -0.0128 6.8992 0 7.3728 0 C 7.8464 0 8.4608 -0.0128 9.024 -0.0256 C 9.1008 0.0512 9.1008 0.32 9.024 0.39679998 C 8.128 0.43519998 7.9104 0.4992 7.9104 1.5616 Z "/>
</symbol>
<symbol id="gF5F8064101DBF0FCB4BCFDA7012527FE" overflow="visible">
<path d="M 2.3167999 1.5616 L 2.3167999 4.1088 C 2.3167999 4.7488 2.368 5.568 2.368 5.568 C 2.368 5.6191998 2.304 5.6576 2.2015998 5.6576 C 1.8432 5.5168 1.3312 5.4016 0.44799998 5.2864 C 0.4224 5.2096 0.44799998 5.0048 0.4736 4.928 C 1.1776 4.864 1.3055999 4.7872 1.3055999 4.0576 L 1.3055999 1.5616 C 1.3055999 0.4992 1.1647999 0.4608 0.384 0.39679998 C 0.30719998 0.32 0.30719998 0.0512 0.384 -0.0256 C 0.8064 -0.0128 1.3055999 0 1.8176 0 C 2.3295999 0 2.816 -0.0128 3.2384 -0.0256 C 3.3151999 0.0512 3.3151999 0.32 3.2384 0.39679998 C 2.4575999 0.44799998 2.3167999 0.4992 2.3167999 1.5616 Z M 1.152 7.6671996 C 1.152 7.3343997 1.4591999 7.0016 1.7664 7.0016 C 2.1248 7.0016 2.432 7.3472 2.432 7.6159997 C 2.432 7.9231997 2.1632 8.2816 1.8176 8.2816 C 1.5103999 8.2816 1.152 7.9743996 1.152 7.6671996 Z "/>
</symbol>
<symbol id="g3976D55F213F07C6469FD06EC16139AA" overflow="visible">
<path d="M 4.9407997 1.1904 C 4.4672 0.704 4.0959997 0.4992 3.3536 0.4992 C 2.8927999 0.4992 2.3552 0.768 1.9583999 1.4208 C 1.7024 1.8432 1.5488 2.432 1.5488 3.1743999 L 4.9536 3.1488 C 5.1071997 3.1488 5.1967998 3.2256 5.1967998 3.3664 C 5.1967998 4.4416 4.8128 5.5936 3.0335999 5.5936 C 1.92 5.5936 0.4736 4.5312 0.4736 2.5856 C 0.4736 1.8687999 0.65279996 1.1776 1.0752 0.69119996 C 1.5103999 0.1792 2.112 -0.12799999 3.0335999 -0.12799999 C 4.0064 -0.12799999 4.6976 0.32 5.2096 0.9856 C 5.1712 1.1136 5.0944 1.1776 4.9407997 1.1904 Z M 1.5871999 3.6095998 C 1.8304 5.0559998 2.7264 5.1712 3.0335999 5.1712 C 3.52 5.1712 4.0959997 4.9024 4.0959997 3.8272 C 4.0959997 3.712 4.0448 3.648 3.9039998 3.648 Z "/>
</symbol>
<symbol id="gB7BB853387AAC07ADB7DDEF96856059B" overflow="visible">
<path d="M 2.2528 4.5824 C 2.2272 5.0944 2.2144 5.4272 2.1504 5.5551996 C 2.1248 5.6191998 2.0992 5.6576 1.9968 5.6576 C 1.6384 5.5168 1.3055999 5.4016 0.4224 5.2864 C 0.39679998 5.2096 0.4224 5.0048 0.44799998 4.928 C 1.1392 4.864 1.28 4.7999997 1.28 4.0576 L 1.28 1.5616 C 1.28 0.4992 1.1264 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7808 -0.0128 1.28 0 1.7919999 0 C 2.304 0 2.8927999 -0.0128 3.3407998 -0.0256 C 3.4176 0.0512 3.4176 0.32 3.3407998 0.39679998 C 2.4448 0.4608 2.2912 0.4992 2.2912 1.5616 L 2.2912 3.3407998 C 2.2912 3.6736 2.4448 3.968 2.5983999 4.1984 C 2.7391999 4.4031997 3.0335999 4.8255997 3.1871998 4.8255997 C 3.3023999 4.8255997 3.4176 4.7999997 3.52 4.6591997 C 3.6095998 4.5312 3.7631998 4.3648 3.9808 4.3648 C 4.288 4.3648 4.5824 4.6847997 4.5824 5.0048 C 4.5824 5.2479997 4.3519998 5.6191998 3.8144 5.6191998 C 3.2128 5.6191998 2.688 5.0559998 2.3936 4.5568 C 2.3167999 4.416 2.2528 4.5183997 2.2528 4.5824 Z "/>
</symbol>
<symbol id="gF8EC31AC53CF59E01ED9143906F6DA7B" overflow="visible">
<path d="M 3.7503998 0.61439997 C 3.8272 0.21759999 3.968 -0.12799999 4.608 -0.12799999 C 5.0944 -0.12799999 5.5551996 0.0896 5.824 0.34559998 C 5.7984 0.4992 5.7472 0.61439997 5.6064 0.69119996 C 5.5168 0.61439997 5.2992 0.48639998 5.1328 0.48639998 C 4.7616 0.48639998 4.7488 0.9856 4.7488 1.5744 L 4.7488 3.4559999 C 4.7488 5.2736 3.7503998 5.6191998 2.816 5.6191998 C 1.7664 5.6191998 0.704 4.928 0.704 4.1984 C 0.704 3.8911998 0.8576 3.7375998 1.152 3.7375998 C 1.5231999 3.7375998 1.7536 4.0064 1.7536 4.1728 C 1.7536 4.2623997 1.7407999 4.3519998 1.7152 4.4031997 C 1.7024 4.4416 1.6896 4.5183997 1.6896 4.6591997 C 1.6896 5.0559998 2.2272 5.1967998 2.7136 5.1967998 C 3.1488 5.1967998 3.7503998 4.9792 3.7503998 3.5328 C 3.7503998 3.4431999 3.712 3.392 3.6736 3.3792 L 2.5728 3.1104 C 1.344 2.8032 0.4608 2.1248 0.4608 1.2544 C 0.4608 0.2048 1.1776 -0.12799999 2.0736 -0.12799999 C 2.5216 -0.12799999 2.9055998 -0.0256 3.4687998 0.4096 L 3.7247999 0.61439997 Z M 3.7503998 2.9824 L 3.7503998 1.2928 C 3.7503998 1.1264 3.6736 1.0368 3.5712 0.96 C 3.2384 0.69119996 2.8032 0.39679998 2.4448 0.39679998 C 1.8047999 0.39679998 1.5231999 0.9088 1.5231999 1.3055999 C 1.5231999 1.8815999 1.7919999 2.4703999 2.7391999 2.7136 Z "/>
</symbol>
<symbol id="g68DDE7C8FDC8A226B6C32EAD39AF7364" overflow="visible">
<path d="M 5.0944 1.1647999 C 5.0432 1.28 4.9407997 1.3312 4.8255997 1.344 C 4.3904 0.7808 3.84 0.4992 3.2896 0.4992 C 2.3552 0.4992 1.5744 1.4463999 1.5744 2.944 C 1.5744 4.3519998 2.1887999 5.1967998 3.0335999 5.1967998 C 3.7888 5.1967998 3.8911998 4.7488 3.9424 4.3008 C 3.9808 3.9552 4.16 3.84 4.4288 3.84 C 4.6976 3.84 5.0559998 4.0064 5.0559998 4.4031997 C 5.0559998 5.1071997 4.3264 5.6191998 3.0976 5.6191998 C 1.8304 5.6191998 0.4736 4.48 0.4736 2.6624 C 0.4736 1.0112 1.3952 -0.12799999 3.008 -0.12799999 C 3.776 -0.12799999 4.4544 0.1152 5.0944 1.1647999 Z "/>
</symbol>
<symbol id="g570B752173035444311A253BD2376AD" overflow="visible">
<path d="M 2.1376 3.6608 C 2.1376 3.9296 2.2528 4.0832 2.3552 4.1984 C 2.8416 4.672 3.4944 4.9536 3.9936 4.9536 C 4.2496 4.9536 4.5183997 4.7872 4.672 4.4927998 C 4.7999997 4.2367997 4.8255997 3.8911998 4.8255997 3.5072 L 4.8255997 1.5616 C 4.8255997 0.51199996 4.6976 0.4608 4.032 0.39679998 C 3.968 0.32 3.968 0.0512 4.032 -0.0256 C 4.3904 -0.0128 4.8255997 0 5.3375998 0 C 5.8496 0 6.272 -0.0128 6.6944 -0.0256 C 6.7584 0.0512 6.7584 0.32 6.6944 0.39679998 C 5.9775996 0.4608 5.8367996 0.51199996 5.8367996 1.5616 L 5.8367996 3.4687998 C 5.8367996 4.1728 5.7855997 4.7999997 5.4912 5.184 C 5.2736 5.4656 4.8768 5.6191998 4.4288 5.6191998 C 3.8016 5.6191998 3.0335999 5.4528 2.2528 4.5824 C 2.2528 4.5696 2.24 4.5696 2.2272 4.5568 C 2.1887999 4.5056 2.1248 4.4288 2.1248 4.5824 L 2.1376 7.4624 C 2.1376 8.2944 2.1887999 8.806399 2.1887999 8.806399 C 2.1887999 8.896 2.1376 8.9344 2.0224 8.9344 C 1.7024 8.806399 0.7424 8.6272 0.2304 8.588799 C 0.2048 8.4864 0.2304 8.2816 0.30719998 8.2048 C 0.34559998 8.2048 0.384 8.2048 0.4224 8.2048 C 0.9856 8.1664 1.1264 8.1664 1.1264 7.1552 L 1.1264 1.5616 C 1.1264 0.4992 0.97279996 0.44799998 0.2304 0.39679998 C 0.15359999 0.32 0.15359999 0.0512 0.2304 -0.0256 C 0.65279996 -0.0128 1.1264 0 1.6384 0 C 2.1248 0 2.5472 -0.0128 2.9055998 -0.0256 C 2.9824 0.0512 2.9824 0.32 2.9055998 0.39679998 C 2.2528 0.44799998 2.1376 0.4992 2.1376 1.5616 Z "/>
</symbol>
<symbol id="g9662C1D9A80FEB5040A57FD9DFCA7985" overflow="visible">
<path d="M 1.216 1.5616 C 1.216 0.4992 1.0752 0.43519998 0.2944 0.39679998 C 0.21759999 0.32 0.21759999 0.0512 0.2944 -0.0256 C 0.7424 -0.0128 1.216 0 1.7279999 0 C 2.24 0 2.7264 -0.0128 3.1488 -0.0256 C 3.2256 0.0512 3.2256 0.32 3.1488 0.39679998 C 2.368 0.43519998 2.2272 0.4992 2.2272 1.5616 L 2.2272 7.4624 C 2.2272 8.2944 2.2784 8.806399 2.2784 8.806399 C 2.2784 8.896 2.2272 8.9344 2.112 8.9344 C 1.7919999 8.806399 0.83199996 8.6272 0.32 8.588799 C 0.2944 8.4864 0.32 8.2816 0.39679998 8.2048 C 1.1392 8.1536 1.216 8.1152 1.216 7.1552 Z "/>
</symbol>
<symbol id="g1CB3EC9D05726EBFDE8ADABEC8504FCD" overflow="visible">
<path d="M 7.1168 6.5536 L 7.1168 2.368 C 7.1168 2.1248 7.1168 1.984 7.0271997 1.984 C 6.976 1.984 6.784 2.2144 6.4128 2.688 L 2.0224 8.256 L 0.2944 8.2816 C 0.21759999 8.2048 0.21759999 7.936 0.2944 7.8592 C 0.8448 7.8208 1.2287999 7.3728 1.3055999 7.04 L 1.3055999 1.7024 C 1.3055999 0.5632 1.0879999 0.48639998 0.192 0.39679998 C 0.1152 0.32 0.1152 0.0512 0.192 -0.0256 C 0.7424 -0.0128 1.3184 0 1.6256 0 C 1.92 0 2.5088 -0.0128 3.0463998 -0.0256 C 3.1232 0.0512 3.1232 0.32 3.0463998 0.39679998 C 2.1504 0.48639998 1.9327999 0.5376 1.9327999 1.7024 L 1.9327999 5.6191998 C 1.9327999 6.0544 1.9327999 6.2464 2.0351999 6.2464 C 2.112 6.2464 2.2528 6.1056 2.4703999 5.824 L 6.9375997 0.1792 C 7.0783997 -0.0128 7.2447996 -0.12799999 7.4495997 -0.12799999 C 7.6288 -0.12799999 7.744 0.0256 7.744 0.2688 L 7.744 6.5536 C 7.744 7.6927996 7.9616 7.7696 8.8576 7.8592 C 8.9344 7.936 8.9344 8.2048 8.8576 8.2816 C 8.3328 8.2688 7.7311997 8.256 7.424 8.256 C 7.1552 8.256 6.5664 8.2688 6.0032 8.2816 C 5.9263997 8.2048 5.9263997 7.936 6.0032 7.8592 C 6.8992 7.7696 7.1168 7.7184 7.1168 6.5536 Z "/>
</symbol>
<symbol id="gD62975B7DE3250BE5F195D0E8335F60D" overflow="visible">
<path d="M 4.16 5.0944 C 4.8512 5.0432 4.928 4.8896 4.6591997 4.2367997 L 3.6223998 1.7279999 C 3.4176 1.2287999 3.3536 1.2287999 3.1488 1.7664 L 2.2272 4.2367997 C 1.9968 4.8512 1.9455999 5.0048 2.6239998 5.0944 C 2.7008 5.1712 2.7008 5.44 2.6239998 5.5168 C 2.2015998 5.5039997 1.7536 5.4912 1.3312 5.4912 C 0.9088 5.4912 0.5248 5.5039997 0.1408 5.5168 C 0.063999996 5.44 0.063999996 5.1712 0.1408 5.0944 C 0.8192 5.0176 0.9088 4.8128 1.1647999 4.16 L 2.8032 0.1152 C 2.8799999 -0.076799996 2.9568 -0.15359999 3.1232 -0.15359999 C 3.2512 -0.15359999 3.3407998 -0.076799996 3.4304 0.1408 L 5.1328 4.1472 C 5.376 4.7104 5.5168 5.0304 6.2335997 5.0944 C 6.3104 5.1712 6.3104 5.44 6.2335997 5.5168 C 5.9775996 5.5039997 5.6703997 5.4912 5.3375998 5.4912 C 4.9151998 5.4912 4.48 5.5039997 4.16 5.5168 C 4.0832 5.44 4.0832 5.1712 4.16 5.0944 Z "/>
</symbol>
<symbol id="gEFCBD5CCFA072E8B49E2065B449FDBBF" overflow="visible">
<path d="M 5.6832 4.9536 C 5.9263997 4.9536 6.1568 5.184 6.1568 5.44 C 6.1568 5.7088 5.9136 5.9136 5.568 5.9136 C 5.2352 5.9136 4.6208 5.6959996 4.288 5.2608 C 4.1344 5.3631997 3.712 5.6191998 2.9568 5.6191998 C 1.8176 5.6191998 0.768 4.8512 0.768 3.6736 C 0.768 2.9824 1.0752 2.5856 1.4336 2.24 C 1.0752 1.9327999 0.87039995 1.3823999 0.87039995 0.9472 C 0.87039995 0.48639998 1.1264 0.12799999 1.4591999 -0.038399998 C 0.768 -0.44799998 0.4096 -1.0368 0.4096 -1.5871999 C 0.4096 -2.7008 1.4591999 -3.0463998 2.4448 -3.0463998 C 4.1728 -3.0463998 6.0415998 -2.2144 6.0415998 -0.83199996 C 6.0415998 -0.4224 5.8496 -0.1024 5.4783998 0.2048 C 4.9792 0.61439997 4.0832 0.6272 3.6095998 0.6272 C 3.3792 0.6272 3.0591998 0.6016 2.7519999 0.5632 C 2.56 0.55039996 2.432 0.5376 2.368 0.5376 C 1.9968 0.5376 1.5488 0.7168 1.5488 1.2672 C 1.5488 1.5231999 1.6256 1.7919999 1.7792 2.0096 C 2.0864 1.8304 2.4448 1.7407999 2.944 1.7407999 C 4.0703998 1.7407999 5.1071997 2.4448 5.1071997 3.6992 C 5.1071997 4.3008 4.928 4.6464 4.5568 5.0304 C 4.6464 5.1584 4.9024 5.3375998 5.0688 5.3375998 C 5.1584 5.3375998 5.2479997 5.2992 5.3248 5.184 C 5.376 5.0815997 5.5424 4.9536 5.6832 4.9536 Z M 1.6896 -0.12799999 C 1.8304 -0.1664 2.0351999 -0.192 2.2015998 -0.192 C 2.5983999 -0.192 2.9568 -0.15359999 3.136 -0.15359999 C 3.776 -0.15359999 4.3136 -0.1664 4.6847997 -0.3712 C 5.184 -0.65279996 5.3375998 -0.83199996 5.3375998 -1.1647999 C 5.3375998 -2.0864 3.9808 -2.5728 2.8288 -2.5728 C 2.368 -2.5728 1.2928 -2.2015998 1.2928 -1.3312 C 1.2928 -0.89599997 1.3184 -0.576 1.6896 -0.12799999 Z M 4.0832 3.5712 C 4.0832 2.3808 3.4815998 2.1376 3.008 2.1376 C 1.9327999 2.1376 1.8176 3.0463998 1.8176 3.8655999 C 1.8176 4.7616 2.1376 5.2223997 2.8416 5.2223997 C 3.648 5.2223997 4.0832 4.6335998 4.0832 3.5712 Z "/>
</symbol>
<symbol id="gD5EEFB9760BC9A91B84F628EDDA52971" overflow="visible">
<path d="M 2.1376 5.0432 C 2.0607998 4.9663997 2.0096 4.992 2.0096 5.1071997 L 2.0096 7.4624 C 2.0096 8.2944 2.0607998 8.806399 2.0607998 8.806399 C 2.0607998 8.896 2.0096 8.9344 1.8944 8.9344 C 1.5744 8.806399 0.61439997 8.6272 0.1024 8.588799 C 0.076799996 8.4864 0.1024 8.2816 0.1792 8.2048 C 0.21759999 8.2048 0.25599998 8.2048 0.2944 8.2048 C 0.8576 8.1664 0.9984 8.1664 0.9984 7.1552 L 0.9984 0.9088 C 0.9984 0.4096 0.9856 0.1792 0.9472 0 C 1.0112 -0.1024 1.0752 -0.15359999 1.2287999 -0.15359999 C 1.3055999 -0.076799996 1.4336 0.038399998 1.536 0.15359999 C 1.6639999 0.30719998 1.7407999 0.30719998 1.8815999 0.192 C 2.1759999 -0.0512 2.56 -0.12799999 3.008 -0.12799999 C 4.3136 -0.12799999 5.8367996 1.0624 5.8367996 3.0976 C 5.8367996 4.6591997 4.6847997 5.6191998 3.5712 5.6191998 C 3.0207999 5.6191998 2.5344 5.4016 2.1376 5.0432 Z M 2.2272 4.6464 C 2.56 4.9407997 2.944 5.0559998 3.3151999 5.0559998 C 4.0959997 5.0559998 4.736 4.1088 4.736 2.8672 C 4.736 1.408 4.1472 0.30719998 2.9312 0.30719998 C 2.5344 0.30719998 2.2656 0.5888 2.0096 0.9088 L 2.0096 4.1088 C 2.0096 4.3775997 2.0607998 4.5056 2.2272 4.6464 Z "/>
</symbol>
<symbol id="g83A6AA7A836EACB3652229F4716CDAF" overflow="visible">
<path d="M 5.0559998 8.076799 C 4.3136 8.1792 4.3392 8.4223995 3.0848 8.4223995 C 1.7919999 8.4223995 0.65279996 7.5648 0.65279996 6.2079997 C 0.65279996 4.864 1.7664 4.2496 2.8927999 3.8144 C 3.6608 3.52 4.608 3.1615999 4.608 1.9072 C 4.608 0.87039995 4.032 0.3328 3.008 0.3328 C 1.8176 0.3328 1.0496 0.8832 0.768 2.1504 C 0.6016 2.2015998 0.4736 2.1759999 0.34559998 2.112 C 0.39679998 1.1264 0.44799998 0.79359996 0.6016 0.1664 C 1.408 0.1664 1.7664 -0.12799999 2.9055998 -0.12799999 C 3.4815998 -0.12799999 4.032 0.0128 4.48 0.2944 C 5.2223997 0.75519997 5.6832 1.536 5.6832 2.3552 C 5.6832 3.712 4.6591997 4.3136 3.6095998 4.7104 C 2.8416 4.992 1.5616 5.4783998 1.5616 6.5536 C 1.5616 7.2704 2.2144 7.9872 2.9696 7.9872 C 4.2111998 7.9872 4.608 7.1935997 4.864 6.3487997 C 5.0048 6.3231997 5.1712 6.336 5.2864 6.4256 C 5.2352 7.04 5.184 7.3984 5.0559998 8.076799 Z "/>
</symbol>
<symbol id="gDB4862E33098F259EEBBA99A57E5AFA" overflow="visible">
<path d="M 2.1759999 4.5824 C 2.1632 4.9663997 2.1376 5.4272 2.0736 5.5551996 C 2.0479999 5.6191998 2.0224 5.6576 1.92 5.6576 C 1.5616 5.5168 1.2287999 5.4016 0.34559998 5.2864 C 0.32 5.2096 0.34559998 5.0048 0.3712 4.928 C 1.0624 4.864 1.2032 4.7999997 1.2032 4.0576 L 1.2032 1.5616 C 1.2032 0.51199996 1.0368 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7168 -0.0128 1.2032 0 1.7152 0 C 2.2272 0 2.6239998 -0.0128 3.008 -0.0256 C 3.0848 0.0512 3.0848 0.32 3.008 0.39679998 C 2.3552 0.4608 2.2144 0.51199996 2.2144 1.5616 L 2.2144 3.6608 C 2.2144 3.9296 2.3295999 4.0832 2.432 4.1984 C 2.944 4.6976 3.4176 4.9536 3.8144 4.9536 C 4.3008 4.9536 4.6591997 4.6464 4.6591997 3.7888 L 4.6591997 1.5616 C 4.6591997 0.51199996 4.5568 0.44799998 3.8655999 0.39679998 C 3.8016 0.32 3.8016 0.0512 3.8655999 -0.0256 C 4.1856 -0.0128 4.6591997 0 5.1712 0 C 5.6832 0 6.1056 -0.0128 6.4256 -0.0256 C 6.4895997 0.0512 6.4895997 0.32 6.4256 0.39679998 C 5.7855997 0.44799998 5.6703997 0.51199996 5.6703997 1.5616 L 5.6703997 3.5967999 C 5.6703997 3.776 5.6703997 3.9552 5.6576 4.1088 C 6.272 4.7872 6.848 4.9536 7.3472 4.9536 C 7.8335996 4.9536 8.1152 4.672 8.1152 3.8144 L 8.1152 1.5616 C 8.1152 0.51199996 7.9872 0.44799998 7.3216 0.39679998 C 7.2576 0.32 7.2576 0.0512 7.3216 -0.0256 C 7.6415997 -0.0128 8.1152 0 8.6272 0 C 9.1392 0 9.5872 -0.0128 9.9456 -0.0256 C 10.0096 0.0512 10.0096 0.32 9.9456 0.39679998 C 9.2416 0.44799998 9.1264 0.51199996 9.1264 1.5616 L 9.1264 3.5839999 C 9.1264 4.7232 8.9344 5.6191998 7.8079996 5.6191998 C 7.1552 5.6191998 6.3616 5.376 5.6959996 4.672 C 5.6576 4.6335998 5.5808 4.5696 5.5551996 4.6847997 C 5.44 5.2096 4.9407997 5.6191998 4.2752 5.6191998 C 3.5328 5.6191998 2.8672 5.184 2.3295999 4.5824 C 2.2656 4.5183997 2.1887999 4.4288 2.1759999 4.5824 Z "/>
</symbol>
<symbol id="g793DBE65A5AEC1A16A65955B6C0E046" overflow="visible">
<path d="M 10.368 7.232 L 8.3712 1.6768 L 8.3328 1.6896 L 6.5664 7.0912 C 6.3487997 7.7823997 6.7967997 7.8208 7.232 7.8592 C 7.3087997 7.936 7.3087997 8.2048 7.232 8.2816 C 6.7072 8.2688 6.144 8.256 5.632 8.256 C 5.2096 8.256 4.7616 8.2688 4.3519998 8.2816 C 4.2752 8.2048 4.2752 7.936 4.3519998 7.8592 C 5.0304 7.8208 5.312 7.424 5.4272 7.0912 L 5.7216 6.2464 C 5.7728 6.0927997 5.8111997 5.9648 5.8111997 5.8496 C 5.8111997 5.7216 5.7984 5.6191998 5.6959996 5.4016 L 4.0448 1.6511999 L 3.9808 1.6639999 L 2.112 7.3216 C 1.9583999 7.7696 2.304 7.8335996 2.7519999 7.8592 C 2.8288 7.936 2.8288 8.2048 2.7519999 8.2816 C 2.3295999 8.2688 1.7664 8.256 1.2672 8.256 C 0.8192 8.256 0.44799998 8.2688 0.076799996 8.2816 C 0 8.2048 0 7.936 0.076799996 7.8592 C 0.65279996 7.8208 0.7424 7.8079996 0.9856 7.1168 L 3.392 0.192 C 3.4559999 -0.0128 3.5328 -0.15359999 3.6736 -0.15359999 C 3.84 -0.15359999 3.9167998 -0.0256 4.0064 0.192 L 5.9136 4.48 C 6.0288 4.736 6.0671997 4.7999997 6.1312 4.7999997 C 6.1823997 4.7999997 6.2335997 4.6591997 6.3104 4.4416 L 7.7823997 0.192 C 7.8592 -0.0256 7.9231997 -0.15359999 8.076799 -0.15359999 C 8.2176 -0.15359999 8.3071995 -0.0128 8.3712 0.1792 L 10.943999 7.0783997 C 11.110399 7.5263996 11.340799 7.8208 12.0448 7.8592 C 12.1216 7.936 12.1216 8.2048 12.0448 8.2816 C 11.673599 8.2688 11.264 8.256 10.9312 8.256 C 10.5984 8.256 10.0352 8.2688 9.5232 8.2816 C 9.4464 8.2048 9.4464 7.936 9.5232 7.8592 C 10.047999 7.8208 10.559999 7.7823997 10.368 7.232 Z "/>
</symbol>
<symbol id="gA11612CECC8CBEF18835767DAB11B2F7" overflow="visible">
<path d="M 0.5248 2.6239998 C 0.5248 1.3184 1.3952 -0.12799999 3.2128 -0.12799999 C 4.032 -0.12799999 4.6591997 0.1664 5.0944 0.5888 C 5.6703997 1.152 5.9263997 1.9583999 5.9263997 2.7391999 C 5.9263997 4.0703998 5.1967998 5.6191998 3.2384 5.6191998 C 2.3936 5.6191998 1.7024 5.2736 1.2287999 4.7232 C 0.768 4.1728 0.5248 3.4304 0.5248 2.6239998 Z M 3.0463998 5.1712 C 4.1472 5.1712 4.8255997 4.1728 4.8255997 2.3295999 C 4.8255997 0.7168 3.9936 0.32 3.392 0.32 C 2.0607998 0.32 1.6256 1.9327999 1.6256 2.9183998 C 1.6256 4.032 1.8944 5.1712 3.0463998 5.1712 Z "/>
</symbol>
<symbol id="gCEFEF3D67F35C6E83CC3757B1DD21B13" overflow="visible">
<path d="M 4.2752 0.64 C 4.3392 0.69119996 4.4544 0.7168 4.4672 0.6272 C 4.5056 0.32 4.608 -0.12799999 4.608 -0.12799999 C 4.7104 -0.1664 4.7743998 -0.15359999 4.8512 -0.12799999 C 5.1328 0.1024 5.5808 0.2944 6.3616 0.384 C 6.4384 0.4608 6.4384 0.65279996 6.3616 0.72959995 C 5.5424 0.79359996 5.4272 1.0368 5.4272 1.6639999 L 5.4272 7.4624 C 5.4272 8.2944 5.4783998 8.806399 5.4783998 8.806399 C 5.4783998 8.896 5.4272 8.9344 5.312 8.9344 C 4.992 8.806399 4.032 8.6272 3.52 8.588799 C 3.4944 8.4864 3.52 8.2816 3.5967999 8.2048 C 3.6352 8.2048 3.6736 8.2048 3.712 8.2048 C 4.2752 8.1664 4.416 8.1664 4.416 7.1552 L 4.416 5.5168 C 4.416 5.4272 4.3904 5.4016 4.3008 5.4016 C 4.2496 5.4016 3.7247999 5.6191998 3.3023999 5.6191998 C 2.4575999 5.6191998 1.8944 5.3375998 1.3823999 4.8512 C 0.83199996 4.3008 0.4992 3.5456 0.4992 2.5983999 C 0.4992 1.0239999 1.2928 -0.12799999 2.6752 -0.12799999 C 3.1743999 -0.12799999 3.648 0.12799999 4.2752 0.64 Z M 4.416 1.5871999 C 4.416 1.344 4.3904 1.2415999 4.2111998 1.0879999 C 3.7375998 0.6784 3.3279998 0.4736 3.008 0.4736 C 2.3167999 0.4736 1.5999999 1.2287999 1.5999999 2.8288 C 1.5999999 3.7503998 1.7792 4.2623997 1.9712 4.5312 C 2.368 5.1328 2.9055998 5.1712 3.1615999 5.1712 C 3.6223998 5.1712 3.9424 5.0048 4.1984 4.7104 C 4.3775997 4.5056 4.416 4.416 4.416 4.0192 Z "/>
</symbol>
<symbol id="g645CA8FA3D9155E2CBD9F8EED3C1540D" overflow="visible">
<path d="M 1.9968 4.7104 C 1.984 5.0944 1.9583999 5.4272 1.8944 5.5551996 C 1.8687999 5.6191998 1.8432 5.6576 1.7407999 5.6576 C 1.3823999 5.5168 1.0496 5.4016 0.1664 5.2864 C 0.1408 5.2096 0.1664 5.0048 0.192 4.928 C 0.8832 4.864 1.0239999 4.7999997 1.0239999 4.0576 L 1.0239999 -1.408 C 1.0239999 -2.4703999 0.8832 -2.5344 0.1024 -2.5728 C 0.0256 -2.6496 0.0256 -2.9183998 0.1024 -2.9952 C 0.55039996 -2.9824 1.0239999 -2.9696 1.536 -2.9696 C 2.0479999 -2.9696 2.6624 -2.9824 3.0848 -2.9952 C 3.1615999 -2.9183998 3.1615999 -2.6496 3.0848 -2.5728 C 2.1759999 -2.5216 2.0351999 -2.4703999 2.0351999 -1.408 L 2.0351999 -0.0256 C 2.0351999 0.1408 2.0864 0.12799999 2.2144 0.076799996 C 2.5344 -0.0512 2.9183998 -0.12799999 3.3279998 -0.12799999 C 4.0448 -0.12799999 4.6847997 0.0896 5.2096 0.5888 C 5.8111997 1.1776 6.1568 1.9712 6.1568 3.008 C 6.1568 4.3648 5.1967998 5.6191998 3.8911998 5.6191998 C 3.3023999 5.6191998 2.6496 5.2352 2.1376 4.6591997 C 2.0607998 4.5824 2.0096 4.5824 1.9968 4.7104 Z M 2.24 4.2367997 C 2.5728 4.6464 3.1615999 5.0304 3.5328 5.0304 C 4.3519998 5.0304 5.0559998 4.1088 5.0559998 2.6624 C 5.0559998 1.6128 4.6847997 0.30719998 3.2512 0.30719998 C 3.0207999 0.30719998 2.5728 0.3712 2.3423998 0.576 C 2.0864 0.8064 2.0351999 0.8832 2.0351999 1.344 L 2.0351999 3.6736 C 2.0351999 3.9424 2.0864 4.0576 2.24 4.2367997 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
<symbol id="g54C180954D544D3C78C9AD9E4F48A6CA" overflow="visible">
<path d="M 3.6480002 -0.16000001 C 4.88 -0.16000001 6.7520003 1.088 6.7520003 4.848 C 6.7520003 6.432 6.3680005 7.7920003 5.664 8.72 C 5.248 9.280001 4.576 9.76 3.7120001 9.76 C 2.128 9.76 0.624 7.872 0.624 4.704 C 0.624 2.992 1.1520001 1.3920001 2.032 0.512 C 2.48 0.064 3.0240002 -0.16000001 3.6480002 -0.16000001 Z M 3.7120001 9.200001 C 3.9840002 9.200001 4.2400002 9.104 4.432 8.928 C 4.9280005 8.512 5.36 7.2960005 5.36 5.1520004 C 5.36 3.68 5.3120003 2.6720002 5.0880003 1.8560001 C 4.736 0.544 3.9520001 0.4 3.6640003 0.4 C 2.176 0.4 2.016 3.1360002 2.016 4.5280004 C 2.016 8.464001 2.992 9.200001 3.7120001 9.200001 Z "/>
</symbol>
<symbol id="g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" overflow="visible">
<path d="M 4.688 10.336 L 4.032 10.336 L 0.24000001 -0.94400007 L 0.896 -0.94400007 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
</defs>
</div>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g/>
</g>
</g>
<g transform="translate(40 30)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(624.3697637795275 25.8)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6E7B5CC2B72AC8CDDEB63FB023F45240" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gAF2E61F9C5EC3B2D9B048D1511B1060D" x="29.2" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g385ED71BD3F10D2170A1311D8F1A15B" x="53.12" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g2192B3D4CEA94ECF87445F8EE62E404B" x="67.44" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g8F4F96B13A9D8B27A4F3C34609AEF61C" x="80.44" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9BEF8AB47349CEAA320776726D3DB3DB" x="93.32" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g5CEF84A95ABDCAB0EDEF87161576AC77" x="117.96" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 41.800000000000004)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g985B950D50769631420A9A59AEA7CEFC" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2F3EA0F52D7EBFDBD1E9205C07C62175" x="4.752" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAACD21C62EEBAEA5F571EAFD70656C36" x="14.384" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE307093CF7EFBC8D676E62CB78C07836" x="22.848" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA95D2B4A225624CA202B59CBD1BF487" x="31.024" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3B851FDBB4F3A7C5E304DE6F7DEA331C" x="40.032" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1BA4F60CE8E3A065D660EA7EA67004B1" x="49.071999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE3CB9A16B9DD884349EFEF95066B2206" x="58.288" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAACD21C62EEBAEA5F571EAFD70656C36" x="66.16" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDBEAA3BAB7923CD0435518D325CA6C53" x="74.624" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA95D2B4A225624CA202B59CBD1BF487" x="79.6" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2F3EA0F52D7EBFDBD1E9205C07C62175" x="88.60799999999999" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.24 10.528)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(102.24 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.9693496646252555 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.938699329250511 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.908048993875763 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.877398658501022 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.846748323126278 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.81609798775153 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.785447652376796 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.75479731700205 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.72414698162731 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.69349664625256 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.66284631087781 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.63219597550307 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.60154564012834 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.57089530475359 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(89.54024496937885 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(95.5095946340041 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(101.47894429862936 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(107.44829396325461 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(113.41764362787987 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.38699329250512 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(125.35634295713038 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(131.32569262175562 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(137.29504228638086 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(143.2643919510061 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(149.23374161563135 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.20309128025661 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.17244094488186 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(167.1417906095071 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(173.11114027413234 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(179.08048993875758 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(185.04983960338282 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(191.01918926800806 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(196.9885389326333 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.95788859725855 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(208.9272382618838 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(214.89658792650903 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(220.86593759113427 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(226.8352872557595 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(232.80463692038475 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(238.77398658501 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.74333624963523 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(250.71268591426048 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(256.68203557888575 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(262.65138524351096 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(268.6207349081362 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(274.59008457276144 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.5594342373867 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(286.5287839020119 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(292.4981335666372 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(298.4674832312624 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(304.4368328958877 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(310.4061825605129 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(316.37553222513816 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.3448818897634 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(328.31423155438864 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(334.2835812190139 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(340.2529308836391 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(346.2222805482644 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(352.1916302128896 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.1609798775149 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(364.1303295421401 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(370.09967920676536 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(376.06902887139057 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(382.03837853601584 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(388.00772820064105 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(393.9770778652663 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(399.94642752989154 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.9157771945168 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(411.885126859142 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(417.8544765237673 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(423.8238261883925 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(429.7931758530178 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(435.76252551764304 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.73187518226825 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(447.7012248468935 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(453.67057451151874 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(459.639924176144 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(465.6092738407692 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(471.5786235053945 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(477.5479731700197 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.517322834645 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(489.4866724992702 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(495.45602216389545 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(501.42537182852067 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(507.39472149314594 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(513.3640711577711 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(519.3334208223964 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(525.3027704870217 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(531.2721201516471 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(537.2414698162723 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(543.2108194808976 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(549.1801691455229 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(555.1495188101483 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.1188684747735 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(567.0882181393988 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(573.0575678040241 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(579.0269174686495 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(584.9962671332747 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(590.9656167979 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(596.9349664625253 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(602.9043161271507 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(608.8736657917759 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(614.8430154564012 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(620.8123651210266 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(626.7817147856518 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(632.7510644502771 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(638.7204141149024 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(644.6897637795278 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(750.4497637795275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="4" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 65.328)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g12DC86CA8D9D6E336118F1B6EDF218A6" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9C63C5DDFB4402181293B5DF9DB8FDF6" x="10.22" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gF73CF51A640CD9E8903A9C4D4B743CCF" x="20.006" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEC1365C4E13D8501FA131C6543C06A3E" x="26.796" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.60999999999999 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.196915517139304 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.393831034278609 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.590746551417912 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.787662068557218 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.98457758569652 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.181493102835823 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.378408619975126 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.575324137114436 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.77223965425374 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(51.96915517139304 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.16607068853234 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.362986205671646 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.55990172281095 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(72.75681723995025 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.95373275708955 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.15064827422887 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.34756379136817 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.54447930850748 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.74139482564678 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(103.93831034278608 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(109.13522585992538 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.33214137706469 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.52905689420399 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.72597241134329 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(129.9228879284826 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.1198034456219 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.3167189627612 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(145.5136344799005 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(150.7105499970398 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.9074655141791 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.1043810313184 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.30129654845774 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.49821206559704 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.69512758273635 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(181.89204309987565 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(187.08895861701495 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.28587413415426 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.48278965129356 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.67970516843286 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.87662068557216 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.07353620271147 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.27045171985077 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(223.46736723699007 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.66428275412937 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(233.86119827126868 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(239.05811378840798 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.25502930554728 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.45194482268658 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.6488603398259 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(259.8457758569652 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(265.0426913741045 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(270.2396068912438 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.4365224083831 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.6334379255224 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.8303534426617 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(291.027268959801 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.2241844769403 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(301.4210999940796 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.6180155112189 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(311.8149310283582 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(317.0118465454975 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.2087620626368 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(327.4056775797761 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.6025930969155 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.7995086140548 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(342.9964241311941 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(348.1933396483334 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(353.3902551654727 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.587170682612 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(363.7840861997513 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(368.9810017168906 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.1779172340299 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(379.3748327511692 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.5717482683085 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(389.7686637854478 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(394.9655793025871 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(400.1624948197264 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.3594103368657 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.556325854005 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(415.7532413711443 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(420.95015688828363 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.14707240542293 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(431.34398792256223 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(436.54090343970154 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.73781895684084 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(446.93473447398014 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(452.13164999111945 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.32856550825875 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(462.52548102539805 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(467.72239654253735 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(472.91931205967666 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(478.11622757681596 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.31314309395526 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(488.51005861109456 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(493.70697412823387 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(498.90388964537317 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(504.1008051625125 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.2977206796518 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(514.4946361967911 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(519.6915517139304 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(524.8884672310696 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(530.0853827482089 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.2822982653481 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.4792137824874 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(545.6761292996266 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(550.8730448167659 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(556.0699603339051 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.2668758510443 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(566.4637913681836 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(571.6607068853228 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(576.8576224024621 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(582.0545379196013 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(587.2514534367406 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(592.4483689538798 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(597.6452844710191 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(602.8421999881583 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(608.0391155052976 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(613.2360310224368 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(618.432946539576 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(623.6298620567153 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(628.8267775738545 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(634.0236930909938 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(639.220608608133 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(644.4175241252723 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(649.6144396424115 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(654.8113551595508 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(660.00827067669 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(665.2051861938293 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(670.4021017109685 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(675.5990172281078 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(680.795932745247 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(685.9928482623862 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(691.1897637795255 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(751.8797637795275 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g9696EE00168B299790D79B47B78C5F18" x="3.5" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 87.54000000000002)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g9C63C5DDFB4402181293B5DF9DB8FDF6" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gF73CF51A640CD9E8903A9C4D4B743CCF" x="9.786" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEC1365C4E13D8501FA131C6543C06A3E" x="16.576" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.39 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.1956278798483515 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.391255759696703 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.586883639545055 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.782511519393406 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.97813939924176 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.17376727909011 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.36939515893847 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.56502303878681 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.760650918635164 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(51.95627879848351 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.15190667833186 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.34753455818021 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.54316243802856 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(72.7387903178769 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.93441819772525 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.1300460775736 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.32567395742196 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.5213018372703 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.71692971711865 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(103.91255759696699 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(109.10818547681534 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.3038133566637 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.49944123651204 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.69506911636039 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(129.89069699620873 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.0863248760571 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.28195275590542 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(145.47758063575378 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(150.67320851560214 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.86883639545047 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.06446427529883 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.26009215514716 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.45572003499552 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.65134791484388 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(181.8469757946922 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(187.04260367454057 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.2382315543889 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.43385943423726 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.62948731408562 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.82511519393395 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.0207430737823 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.21637095363064 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(223.411998833479 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.60762671332736 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(233.8032545931757 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(238.99888247302405 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.1945103528724 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.39013823272074 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.5857661125691 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(259.78139399241746 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(264.9770218722658 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(270.17264975211424 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.3682776319626 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.56390551181096 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.7595333916594 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(290.95516127150773 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.1507891513561 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(301.3464170312045 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.54204491105287 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(311.73767279090123 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(316.93330067074965 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.128928550598 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(327.32455643044636 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.5201843102947 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.71581219014314 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(342.9114400699915 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(348.10706794983986 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(353.3026958296883 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.49832370953663 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(363.693951589385 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(368.8895794692334 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.08520734908177 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(379.28083522893013 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.47646310877855 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(389.6720909886269 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(394.86771886847527 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(400.0633467483236 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.25897462817204 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.4546025080204 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(415.65023038786876 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(420.8458582677172 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.04148614756554 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(431.2371140274139 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(436.4327419072623 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.62836978711067 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(446.82399766695903 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(452.01962554680745 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.2152534266558 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(462.41088130650417 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(467.6065091863525 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(472.80213706620094 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(477.9977649460493 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.19339282589766 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(488.3890207057461 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(493.58464858559444 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(498.7802764654428 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(503.9759043452912 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.1715322251396 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(514.367160104988 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(519.5627879848363 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(524.7584158646846 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(529.954043744533 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.1496716243813 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.3452995042296 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(545.5409273840779 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(550.7365552639262 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(555.9321831437745 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.1278110236228 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(566.3234389034712 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(571.5190667833195 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(576.7146946631678 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(581.9103225430162 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(587.1059504228645 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(592.3015783027128 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(597.4972061825612 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(602.6928340624095 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(607.8884619422578 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(613.0840898221061 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(618.2797177019544 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(623.4753455818027 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(628.670973461651 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(633.8666013414994 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(639.0622292213477 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(644.257857101196 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(649.4534849810443 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(654.6491128608926 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(659.8447407407409 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(665.0403686205892 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(670.2359965004376 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(675.4316243802859 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(680.6272522601342 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(685.8228801399825 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(691.0185080198308 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(696.2141358996791 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(701.4097637795275 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(751.8797637795275 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD0485EF23018DAF4BFC69AAD15075193" x="3.5" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 109.75200000000001)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g42427CF90B88C34047186DDCC0B8064E" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9AE4831982D6CA553E49B4F41E9A233F" x="7.574" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="12.67" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gC80234271A0A022352A099322F0FCD32" x="19.726" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g3649D621BC998C9216AD40BBEFAC3AB1" x="26.628" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gC80234271A0A022352A099322F0FCD32" x="33.026" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="39.928000000000004" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gBBFA548D7BC5ACA0036C5BF286E59830" x="43.722" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="47.418" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g88B62CE1F53AC1AE1D938018DA31319" x="51.211999999999996" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g5799677F1612AA2CF55B8D046D0457BF" x="55.635999999999996" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gF73CF51A640CD9E8903A9C4D4B743CCF" x="66.346" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gE2267284F842780DB4609789BADA809" x="73.136" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="80.304" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA0F6184C06096774B92DEFE1EDA388E4" x="84.098" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g1F652CD6CF98783FD5BC41E10F253E3" x="94.864" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="102.256" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g2027E4E303C701A0DF6BD0919BBDE7B4" x="106.05" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g88B62CE1F53AC1AE1D938018DA31319" x="111.50999999999999" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(133.434 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.214964099826504 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.429928199653007 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.644892299479512 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.859856399306015 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(26.074820499132517 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.289784598959024 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.50474869878553 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.71971279861203 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.93467689843853 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(52.14964099826503 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.36460509809153 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.57956919791803 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.79453329774454 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(73.00949739757102 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(78.22446149739753 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.43942559722403 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.65438969705053 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.86935379687704 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(99.08431789670354 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(104.29928199653003 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(109.51424609635653 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.72921019618303 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.94417429600954 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(125.15913839583604 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.37410249566253 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.58906659548904 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.80403069531553 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(146.01899479514202 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(151.23395889496854 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(156.44892299479503 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.66388709462154 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.87885119444803 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(172.09381529427455 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(177.30877939410104 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(182.52374349392753 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(187.73870759375404 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.95367169358053 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(198.16863579340705 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(203.38359989323354 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(208.59856399306003 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.81352809288654 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(219.02849219271303 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(224.24345629253955 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(229.45842039236604 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(234.67338449219253 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(239.88834859201904 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(245.10331269184553 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(250.31827679167205 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(255.53324089149854 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(260.74820499132505 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(265.96316909115154 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(271.1781331909781 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(276.3930972908046 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(281.60806139063106 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(286.82302549045755 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(292.03798959028404 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(297.2529536901106 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(302.4679177899371 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(307.68288188976356 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(312.89784598959005 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(318.11281008941654 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(323.3277741892431 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(328.5427382890696 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(333.75770238889606 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(338.97266648872255 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(344.1876305885491 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(349.4025946883756 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(354.6175587882021 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(359.83252288802856 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(365.04748698785505 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(370.2624510876816 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(375.4774151875081 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(380.6923792873346 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(385.90734338716106 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(391.12230748698755 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(396.3372715868141 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(401.5522356866406 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(406.7671997864671 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(411.98216388629356 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(417.19712798612005 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(422.4120920859466 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(427.6270561857731 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(432.8420202855996 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(438.05698438542606 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(443.27194848525255 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(448.4869125850791 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(453.7018766849056 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(458.9168407847321 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(464.13180488455856 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(469.34676898438505 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(474.5617330842116 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(479.7766971840381 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(484.9916612838646 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(490.20662538369106 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(495.42158948351755 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(500.6365535833441 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(505.8515176831706 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(511.0664817829971 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(516.2814458828236 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(521.4964099826501 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(526.7113740824766 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(531.9263381823031 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(537.1413022821297 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(542.3562663819562 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(547.5712304817827 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(552.7861945816092 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(558.0011586814356 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(563.2161227812621 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(568.4310868810886 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(573.6460509809151 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(578.8610150807416 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(584.0759791805681 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(589.2909432803947 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(594.5059073802212 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(599.7208714800477 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(604.9358355798742 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(610.1507996797006 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(615.3657637795271 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(751.8797637795275 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1A68EE8359C8016621D122AFF85D0AB2" x="3.5" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 134.964)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g41BD02C814E5F1F9CC57CE5A8E90AFBE" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g48ABC493FE7862658825720022C8179D" x="11.12" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g31FD4B68C132D0D1A1E4FD30ACE8848" x="18.016" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA95D2B4A225624CA202B59CBD1BF487" x="26.671999999999997" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE307093CF7EFBC8D676E62CB78C07836" x="35.67999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDBEAA3BAB7923CD0435518D325CA6C53" x="43.855999999999995" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAACD21C62EEBAEA5F571EAFD70656C36" x="48.831999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g99884B2AD96AC7B048FEEB28FC8E4747" x="57.29599999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g20DDE86F15DD9C8B9599512790FC45E4" x="67.07199999999999" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.74399999999999 10.528)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(81.74399999999999 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.939158605174353 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.878317210348706 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.81747581552306 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.756634420697413 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.695793025871765 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.63495163104612 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.57411023622048 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.513268841394826 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.452427446569175 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.39158605174352 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.33074465691787 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.26990326209223 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.20906186726657 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.14822047244093 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(89.08737907761527 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(95.02653768278962 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(100.96569628796397 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(106.90485489313832 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(112.84401349831266 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(118.78317210348702 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.72233070866136 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.66148931383572 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(136.60064791901007 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(142.53980652418443 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(148.47896512935876 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(154.4181237345331 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(160.35728233970747 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.29644094488182 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(172.23559955005615 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(178.1747581552305 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(184.11391676040486 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(190.05307536557922 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(195.99223397075355 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(201.9313925759279 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.87055118110226 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.8097097862766 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(219.74886839145097 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(225.6880269966253 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(231.62718560179965 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(237.566344206974 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(243.50550281214836 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.4446614173227 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(255.38382002249705 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(261.32297862767143 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(267.26213723284576 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(273.20129583802014 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(279.14045444319447 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.07961304836886 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(291.0187716535432 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.9579302587175 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(302.8970888638919 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(308.8362474690662 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(314.77540607424055 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(320.71456467941493 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(326.65372328458926 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.59288188976365 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(338.532040494938 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(344.4711991001123 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(350.4103577052867 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(356.349516310461 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(362.2886749156354 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(368.2278335208097 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.16699212598405 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(380.10615073115844 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(386.04530933633276 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(391.9844679415071 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(397.9236265466815 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(403.8627851518558 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(409.8019437570302 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(415.7411023622045 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(421.68026096737884 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(427.6194195725532 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(433.55857817772755 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(439.49773678290194 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(445.43689538807627 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(451.3760539932506 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.315212598425 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(463.2543712035993 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(469.19352980877363 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(475.132688413948 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(481.07184701912234 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(487.01100562429673 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(492.95016422947106 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(498.8893228346454 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(504.82848143981977 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(510.7676400449941 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(516.7067986501685 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(522.6459572553429 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(528.5851158605172 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(534.5242744656915 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.4634330708659 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(546.4025916760403 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(552.3417502812146 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(558.2809088863889 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(564.2200674915633 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(570.1592260967377 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(576.098384701912 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(582.0375433070864 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(587.9767019122608 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(593.915860517435 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(599.8550191226094 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(605.7941777277838 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(611.7333363329581 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(617.6724949381324 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(623.6116535433068 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(629.5508121484811 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(635.4899707536555 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(641.4291293588299 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(647.3682879640043 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(653.3074465691785 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(659.2466051743529 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(665.1857637795273 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(750.4497637795275 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gB81772063B54F81148CB0F3810A30A3E" x="4" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 158.492)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g54625A295C6156FB7E0CA1A81FF5B54D" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gCA97BC07D124B95C474D25CFC2493057" x="4.648000000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gBBFA548D7BC5ACA0036C5BF286E59830" x="14.378" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEABB154513753541217365D535D0C073" x="18.074" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="25.074" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gD8D2A5E78EA4643EEAAC69DB934A336F" x="28.154000000000003" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g202FAE631B7A80A660AEE76AD2161E37" x="34.664" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g176D627313BEF56D87624592E290FFD2" x="43.148" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="52.19200000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g77113E0CAAA23E0B77E89A338ACC30A4" x="59.248000000000005" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g2027E4E303C701A0DF6BD0919BBDE7B4" x="66.836" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g88B62CE1F53AC1AE1D938018DA31319" x="72.29599999999999" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9AE4831982D6CA553E49B4F41E9A233F" x="76.72" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9928BAA4F6AD9C2CD04BDE4A0594D984" x="81.928" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g5D527560B31964E4713419A527341CBD" x="89.362" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g88B62CE1F53AC1AE1D938018DA31319" x="95.354" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="99.77799999999999" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="103.57199999999999" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g77113E0CAAA23E0B77E89A338ACC30A4" x="110.62799999999999" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.71599999999995 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.195625116775658 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.391250233551316 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.586875350326974 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.782500467102633 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.978125583878292 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.173750700653947 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.36937581742961 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.565000934205266 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.760626050980925 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(51.956251167756584 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.15187628453224 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.347501401307895 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.54312651808355 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(72.73875163485921 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.93437675163487 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.13000186841053 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.32562698518619 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.52125210196185 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.71687721873751 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(103.91250233551317 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(109.10812745228883 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.30375256906449 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.49937768584014 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.69500280261579 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(129.89062791939145 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.0862530361671 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.28187815294277 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(145.47750326971843 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(150.67312838649408 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.86875350326974 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.0643786200454 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.26000373682106 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.45562885359672 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.65125397037238 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(181.84687908714804 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(187.0425042039237 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.23812932069936 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.43375443747502 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.62937955425068 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.82500467102633 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.020629787802 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.21625490457765 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(223.4118800213533 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.60750513812897 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(233.80313025490463 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(238.9987553716803 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.19438048845595 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.39000560523158 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.58563072200724 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(259.7812558387829 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(264.97688095555856 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(270.1725060723342 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.36813118910993 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.5637563058856 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.7593814226613 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(290.95500653943697 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.1506316562127 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(301.34625677298834 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.54188188976406 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(311.7375070065397 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(316.93313212331543 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.1287572400911 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(327.3243823568668 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.52000747364247 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.7156325904182 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(342.91125770719384 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(348.10688282396956 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(353.3025079407452 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.4981330575209 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(363.6937581742966 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(368.88938329107225 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.08500840784797 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(379.2806335246236 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.47625864139934 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(389.671883758175 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(394.8675088749507 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(400.0631339917264 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.2587591085021 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.45438422527775 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(415.65000934205347 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(420.8456344588291 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.04125957560484 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(431.2368846923805 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(436.4325098091562 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.6281349259319 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(446.8237600427076 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(452.01938515948325 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.21501027625897 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(462.4106353930346 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(467.60626050981034 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(472.801885626586 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(477.9975107433617 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.1931358601374 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(488.3887609769131 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(493.58438609368875 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(498.78001121046447 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(503.9756363272401 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.17126144401584 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(514.3668865607915 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(519.5625116775672 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(524.7581367943429 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(529.9537619111186 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.1493870278942 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.3450121446699 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(545.5406372614457 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(550.7362623782213 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(555.931887494997 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.1275126117727 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(566.3231377285484 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(571.5187628453241 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(576.7143879620997 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(581.9100130788754 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(587.1056381956511 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(592.3012633124268 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(597.4968884292025 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(602.6925135459782 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(607.8881386627538 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(613.0837637795296 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(751.8797637795276 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g68885674EB6A8B1A6039D4F45B463C56" x="3.5" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 180.704)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g54625A295C6156FB7E0CA1A81FF5B54D" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gCA97BC07D124B95C474D25CFC2493057" x="4.648000000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gBBFA548D7BC5ACA0036C5BF286E59830" x="14.378" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEABB154513753541217365D535D0C073" x="18.074" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="25.074" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9696EE00168B299790D79B47B78C5F18" x="28.154000000000003" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g202FAE631B7A80A660AEE76AD2161E37" x="34.664" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gF73CF51A640CD9E8903A9C4D4B743CCF" x="43.148" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g634FF9E9D0A0144E2AFDD807D5ECB7D0" x="49.938" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g3649D621BC998C9216AD40BBEFAC3AB1" x="56.196000000000005" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9AE4831982D6CA553E49B4F41E9A233F" x="62.59400000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g5D527560B31964E4713419A527341CBD" x="67.69000000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gD0DD0C2B056F25673B3EED0135505F92" x="73.68200000000002" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.71399999999998 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.20068611023622 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.40137222047244 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.60205833070866 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.80274444094488 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(26.0034305511811 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.204116661417316 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.404802771653536 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.605488881889755 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.806174992125975 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(52.006861102362194 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.207547212598406 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.408233322834626 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.60891943307085 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(72.80960554330707 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(78.01029165354329 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.21097776377951 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.41166387401573 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.61234998425195 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.81303609448817 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(104.01372220472439 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(109.21440831496061 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.41509442519681 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.61578053543303 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.81646664566925 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(130.0171527559055 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.2178388661417 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.41852497637794 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(145.61921108661414 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(150.81989719685035 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(156.02058330708658 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.2212694173228 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.42195552755902 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.62264163779523 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.82332774803146 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(182.02401385826767 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(187.2246999685039 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.4253860787401 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.62607218897634 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.82675829921254 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(208.02744440944878 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.22813051968498 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.42881662992122 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(223.62950274015742 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.83018885039363 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(234.03087496062986 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(239.23156107086606 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.4322471811023 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.6329332913385 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.83361940157474 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(260.034305511811 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(265.23499162204723 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(270.43567773228347 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.6363638425197 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.837049952756 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(286.0377360629922 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(291.23842217322846 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.4391082834647 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(301.639794393701 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.8404805039372 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(312.04116661417345 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(317.2418527244097 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.4425388346459 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(327.6432249448822 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.84391105511844 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(338.0445971653547 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(343.2452832755909 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(348.4459693858272 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(353.64665549606343 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.84734160629966 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(364.0480277165359 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(369.2487138267722 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.4493999370084 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(379.65008604724466 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.8507721574809 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(390.0514582677172 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(395.2521443779534 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(400.45283048818965 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.6535165984259 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.8542027086621 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(416.0548888188984 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(421.25557492913464 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.4562610393709 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(431.6569471496071 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(436.8576332598434 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(442.05831937007963 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(447.25900548031586 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(452.4596915905521 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.6603777007884 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(462.8610638110246 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(468.06174992126085 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(473.2624360314971 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(478.4631221417334 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.6638082519696 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(488.86449436220585 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(494.0651804724421 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(499.2658665826783 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(504.4665526929146 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.66723880315084 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(514.8679249133871 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(520.0686110236234 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(525.2692971338595 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(530.4699832440957 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.670669354332 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.8713554645681 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(546.0720415748043 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(551.2727276850404 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(556.4734137952767 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.6740999055129 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(566.874786015749 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(572.0754721259852 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(577.2761582362214 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(582.4768443464576 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(587.6775304566938 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(592.87821656693 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(598.0789026771662 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(603.2795887874024 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(608.4802748976385 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(613.6809610078748 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(618.8816471181109 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(624.0823332283471 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(629.2830193385834 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(634.4837054488195 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(639.6843915590557 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(644.8850776692918 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(650.0857637795281 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(751.8797637795275 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gB1BEBEB6281B0C94AE56C4BB0BF6ED0C" x="3.5" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 202.916)">
<g class="typst-group">
<g>
<g transform="translate(14 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g54625A295C6156FB7E0CA1A81FF5B54D" x="0" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gCA97BC07D124B95C474D25CFC2493057" x="4.648000000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gBBFA548D7BC5ACA0036C5BF286E59830" x="14.378" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEABB154513753541217365D535D0C073" x="18.074" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="25.074" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gD0485EF23018DAF4BFC69AAD15075193" x="28.154000000000003" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g202FAE631B7A80A660AEE76AD2161E37" x="34.664" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g176D627313BEF56D87624592E290FFD2" x="43.148" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gD0DD0C2B056F25673B3EED0135505F92" x="52.19200000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="59.72400000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="66.87800000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g2027E4E303C701A0DF6BD0919BBDE7B4" x="73.93400000000001" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="79.394" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g77113E0CAAA23E0B77E89A338ACC30A4" x="83.188" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEABB154513753541217365D535D0C073" x="90.776" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g77113E0CAAA23E0B77E89A338ACC30A4" x="101.276" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g634FF9E9D0A0144E2AFDD807D5ECB7D0" x="108.86399999999999" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gAAC2A4387B1619C03EEEB0968B96165F" x="115.12199999999999" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gEABB154513753541217365D535D0C073" x="118.91599999999998" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gD0DD0C2B056F25673B3EED0135505F92" x="125.91599999999998" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gC80234271A0A022352A099322F0FCD32" x="133.44799999999998" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gA4DE3951E8A0322DEC5E3569D1D30666" x="140.48999999999998" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g9AE4831982D6CA553E49B4F41E9A233F" x="147.546" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#g2027E4E303C701A0DF6BD0919BBDE7B4" x="152.754" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(175.714 0)">
<g class="typst-group">
<g>
<g transform="translate(0 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.1979427869681425 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(10.395885573936285 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(15.593828360904427 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(20.79177114787257 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(25.98971393484071 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(31.18765672180885 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(36.38559950877699 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.58354229574513 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(46.781485082713274 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(51.979427869681416 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(57.17737065664955 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(62.37531344361769 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(67.57325623058584 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(72.77119901755398 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.96914180452212 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.16708459149027 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(88.36502737845841 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(93.56297016542655 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(98.76091295239469 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(103.95885573936283 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(109.15679852633097 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.3547413132991 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.55268410026724 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(124.75062688723538 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(129.94856967420355 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(135.14651246117168 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.34445524813984 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(145.54239803510796 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(150.7403408220761 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.93828360904425 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.13622639601238 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.33416918298053 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(171.53211196994866 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(176.73005475691681 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(181.92799754388494 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(187.1259403308531 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(192.32388311782123 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(197.52182590478938 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.7197686917575 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(207.91771147872566 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(213.1156542656938 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(218.31359705266195 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(223.51153983963007 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.7094826265982 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(233.90742541356636 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(239.10536820053449 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.30331098750264 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(249.50125377447077 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.69919656143892 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(259.8971393484071 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(265.09508213537526 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(270.2930249223434 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(275.4909677093116 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.6889104962798 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(285.88685328324794 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(291.0847960702161 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(296.28273885718426 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(301.48068164415247 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(306.6786244311206 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(311.8765672180888 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(317.07451000505694 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.2724527920251 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(327.4703955789933 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(332.66833836596146 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(337.8662811529296 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(343.0642239398978 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(348.262166726866 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(353.46010951383414 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.6580523008023 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(363.85599508777045 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(369.05393787473866 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(374.2518806617068 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(379.449823448675 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(384.64776623564313 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(389.84570902261135 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(395.0436518095795 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(400.24159459654766 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.4395373835158 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(410.63748017048397 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(415.8354229574522 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(421.03336574442034 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(426.2313085313885 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(431.42925131835665 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(436.62719410532486 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.825136892293 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(447.0230796792612 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(452.22102246622933 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(457.41896525319754 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(462.6169080401657 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(467.81485082713385 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(473.012793614102 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(478.2107364010702 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.4086791880384 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(488.60662197500653 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(493.8045647619747 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(499.00250754894284 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(504.20045033591106 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.3983931228792 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(514.5963359098474 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(519.7942786968156 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(524.9922214837837 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(530.1901642707519 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.38810705772 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(540.5860498446882 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(545.7839926316564 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(550.9819354186245 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(556.1798782055928 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.3778209925609 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(566.5757637795291 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g47288CF7D8F788F93B1406172900DCDE" x="0" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(745.3697637795276 9.212)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD8D2A5E78EA4643EEAAC69DB934A336F" x="3.5" fill="#00000040" fill-rule="nonzero"/>
<use xlink:href="#gC9680074409574DDF948104B0C55D755" x="10.010000000000002" fill="#00000040" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 234.128)">
<g class="typst-group">
<g>
<g transform="translate(0 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g89D0CDE21020452133A6A28D357E8121" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDC8BE94E2F4CFB356B16F8B3BD0C3FF6" x="8.074" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE5D1277DA16394E659B333D1EA421088" x="23.628" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g6724C1A826126332467C6264F812F404" x="35.728" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFFAD8ECF2B9E19A17BA2A700D6B3A275" x="48.664" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7D577C5B3423E584E3CA9C0C61B45B28" x="61.402" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2C79506DA740817B2A33371C9D8B3CE4" x="73.986" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gDC8BE94E2F4CFB356B16F8B3BD0C3FF6" x="87.274" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2C79506DA740817B2A33371C9D8B3CE4" x="102.828" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g14B71EE4190EC9CF4EC86C87E0E47E9A" x="116.116" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD56DD9CEC6529211EE0EE20264633A82" x="130.46" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(143.176 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(148.676 0)">
<g class="typst-group">
<g>
<g transform="translate(0 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(8.783784299689811 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.567568599379623 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(26.351352899069433 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.135137198759246 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(43.91892149844905 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(52.70270579813886 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(61.48649009782867 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(70.27027439751848 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(79.05405869720828 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(87.83784299689809 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(96.6216272965879 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(105.4054115962777 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(114.18919589596752 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(122.97298019565731 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(131.75676449534714 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(140.54054879503695 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(149.32433309472677 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(158.10811739441658 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(166.89190169410642 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(175.67568599379624 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(184.45947029348605 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(193.2432545931759 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.0270388928657 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(210.81082319255552 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(219.59460749224536 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(228.37839179193517 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(237.16217609162499 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(245.94596039131483 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(254.72974469100464 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(263.51352899069445 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(272.29731329038424 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(281.081097590074 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(289.8648818897638 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(298.6486661894536 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(307.4324504891434 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(316.21623478883316 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(325.000019088523 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(333.7838033882128 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(342.5675876879026 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(351.35137198759236 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(360.13515628728214 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(368.9189405869719 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(377.70272488666177 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(386.48650918635155 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(395.27029348604134 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(404.0540777857311 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(412.8378620854209 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(421.6216463851107 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(430.4054306848005 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(439.1892149844903 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(447.9729992841801 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(456.7567835838699 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(465.5405678835597 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(474.32435218324946 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.10813648293924 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(491.89192078262903 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(500.67570508231887 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(509.45948938200866 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(518.2432736816985 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(527.0270579813883 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(535.8108422810781 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(544.5946265807679 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(553.3784108804576 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(562.1621951801475 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(570.9459794798372 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(579.729763779527 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gDC78B3846EDAB84D21B8DADC57D4B72" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(733.7737637795275 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)"/>
</g>
<g transform="translate(739.2737637795275 14.190000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g9395E96C48DADE2CF7A23A407777B6BB" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g9395E96C48DADE2CF7A23A407777B6BB" x="11.308" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 261.318)">
<g class="typst-group">
<g>
<g transform="translate(16 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gFBB69929369BF0EC60A13F790CB240F" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9A2E3AAC6CC7A3D99F4D7199A710CE2" x="10.336" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g20C5113AFEA5FF7C7B1ACED872A410C0" x="18.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD032B844D751F1F27806C7004D4F5D2F" x="31.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8EC8620411AE7F46663E6890D2DD9166" x="38.928" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g26508BD01E1C582AC0C2221BD9BE4224" x="43.263999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gACDA1EE5EEC178C67D037C3CDBE0EFC9" x="51.93599999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g6E07D235467580A0707E6406EB5DB8A8" x="59.199999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1E702B8726C96DD59806A35F3CC560AF" x="71.29599999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8EC8620411AE7F46663E6890D2DD9166" x="83.24799999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g94C24BD726F4D930F93182C299232222" x="87.58399999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g40BC2CA66BF08C308C98CB508D30B53" x="92.63999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g985B950D50769631420A9A59AEA7CEFC" x="105.24799999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g658214B515038ED3D9F63EA3005CE066" x="110.38399999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g16352873ECA67EAF163D6C6FB1F0EBC" x="120.81599999999999" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(148.576 0)">
<g class="typst-group">
<g>
<g transform="translate(0 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.9688258967629055 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(11.937651793525811 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.906477690288717 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(23.875303587051622 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(29.844129483814523 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(35.81295538057743 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(41.78178127734033 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(47.75060717410324 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(53.71943307086614 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(59.68825896762904 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(65.65708486439195 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(71.62591076115486 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(77.59473665791776 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(83.56356255468066 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(89.53238845144357 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(95.50121434820647 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(101.47004024496937 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(107.43886614173228 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(113.40769203849518 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(119.37651793525808 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(125.34534383202099 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(131.3141697287839 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(137.28299562554682 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(143.2518215223097 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(149.2206474190726 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(155.18947331583553 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(161.15829921259842 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(167.12712510936132 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(173.09595100612424 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(179.06477690288713 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(185.03360279965003 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(191.00242869641295 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(196.97125459317584 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(202.94008048993874 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(208.90890638670166 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(214.87773228346455 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(220.84655818022745 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(226.81538407699037 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(232.78420997375326 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(238.75303587051616 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(244.72186176727908 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(250.69068766404197 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(256.6595135608049 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(262.6283394575678 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(268.59716535433074 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(274.5659912510937 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(280.5348171478566 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(286.50364304461954 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(292.4724689413825 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(298.4412948381454 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(304.41012073490833 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(310.3789466316713 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(316.3477725284342 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(322.3165984251971 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(328.2854243219601 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(334.254250218723 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(340.2230761154859 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(346.1919020122489 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(352.16072790901177 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(358.1295538057747 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(364.09837970253767 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(370.06720559930056 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(376.0360314960635 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(382.00485739282647 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(387.97368328958936 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(393.9425091863523 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(399.91133508311526 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(405.88016097987816 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(411.8489868766411 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(417.81781277340406 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(423.78663867016695 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(429.7554645669299 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(435.72429046369285 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(441.69311636045575 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(447.6619422572187 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(453.63076815398165 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(459.59959405074454 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(465.5684199475075 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(471.53724584427044 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(477.50607174103334 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(483.4748976377963 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(489.44372353455924 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(495.41254943132213 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(501.3813753280851 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(507.35020122484804 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(513.3190271216109 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(519.2878530183739 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(525.2566789151367 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(531.2255048118997 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(537.1943307086626 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(543.1631566054256 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(549.1319825021885 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(555.1008083989515 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(561.0696342957143 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(567.0384601924773 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(573.0072860892402 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(578.9761119860032 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(584.9449378827661 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(590.9137637795291 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gD91DF12E6685C776523A4EFE671EF7FE" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(743.0097637795276 10.528)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="11.440000000000001" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 443.56299212598424)">
<g class="typst-group">
<g/>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="g6E7B5CC2B72AC8CDDEB63FB023F45240" overflow="visible">
<path d="M 27.76 13.16 C 27.76 21.119999 21.84 26.32 14.5199995 26.32 C 10.5199995 26.32 7.04 24.6 4.72 21.84 C 2.6399999 19.359999 1.48 16.039999 1.48 12.36 C 1.48 4.44 7.7599998 -0.39999998 14.559999 -0.39999998 C 18.68 -0.39999998 22.039999 1.0799999 24.32 3.56 C 26.519999 5.96 27.76 9.24 27.76 13.16 Z M 14.04 24.64 C 18.32 24.64 21.72 20.439999 21.72 12.32 C 21.72 5.68 19.4 1.28 15.36 1.28 C 10.96 1.28 7.52 5.64 7.52 13.16 C 7.52 21.32 10.48 24.64 14.04 24.64 Z "/>
</symbol>
<symbol id="gAF2E61F9C5EC3B2D9B048D1511B1060D" overflow="visible">
<path d="M 20.4 5.3199997 L 20.4 12.24 C 20.4 15.599999 20.48 15.12 20.48 16.08 C 20.48 16.76 20.32 17.199999 20.08 17.44 C 19.359999 17.4 18.56 17.359999 17.8 17.359999 C 16.68 17.359999 14.08 17.4 12.5199995 17.44 C 12.28 17.199999 12.28 16.32 12.5199995 16.08 C 14.559999 15.88 15.2 15.599999 15.2 12.24 L 15.2 4.8399997 C 15.2 4.44 15.2 4.04 15.24 3.6399999 C 13.599999 2.6399999 12.28 2.56 11.559999 2.56 C 9.96 2.56 8.76 2.76 8.76 5.56 L 8.76 12.24 C 8.76 15.599999 8.84 15.12 8.84 16.08 C 8.84 16.76 8.679999 17.199999 8.44 17.44 C 7.72 17.4 6.8799996 17.359999 6.16 17.359999 C 4.12 17.359999 2.6 17.4 0.88 17.44 C 0.64 17.199999 0.64 16.32 0.88 16.08 C 2.72 16 3.56 15.599999 3.56 12.24 L 3.56 6 C 3.56 1.76 5.24 -0.39999998 8.679999 -0.39999998 C 10.12 -0.39999998 13.04 0.76 15.36 2.04 C 15.44 1.04 15.5199995 0.28 15.5199995 0.28 C 15.559999 -0.19999999 15.88 -0.39999998 16.44 -0.39999998 C 17.92 0 20.32 0.56 23.08 0.91999996 C 23.16 1.16 23.08 1.9599999 23 2.2 C 20.84 2.3999999 20.4 3.04 20.4 5.3199997 Z "/>
</symbol>
<symbol id="g385ED71BD3F10D2170A1311D8F1A15B" overflow="visible">
<path d="M 2.52 17.359999 C 1.9599999 17.359999 1.36 17.199999 0.84 16.76 L 0.84 15.599999 C 0.84 15.4 0.88 15.36 1.04 15.36 L 3.6399999 15.36 C 3.56 11.32 3.52 6.2 3.52 4.2 C 3.52 2.8 3.8799999 1.4399999 4.72 0.71999997 C 5.64 -0.04 7.08 -0.39999998 8.04 -0.39999998 C 10.24 -0.39999998 12.679999 0.71999997 13.48 1.8399999 C 13.48 2.32 13.24 2.56 12.759999 2.96 C 12.24 2.56 11.24 2.3999999 10.48 2.3999999 C 9.599999 2.3999999 8.72 3.08 8.72 5.08 C 8.72 7.08 8.679999 11.36 8.679999 15.36 L 12.719999 15.36 C 13.12 15.36 13.679999 15.5199995 13.679999 15.88 L 13.679999 17.119999 C 13.679999 17.279999 13.559999 17.359999 13.36 17.359999 L 8.679999 17.359999 L 8.72 18.72 C 8.8 21.4 8.92 23.24 8.92 23.24 C 8.92 23.48 8.8 23.6 8.599999 23.6 C 8.32 23.6 6.8399997 23.16 6.2 22.88 C 5.52 22.6 4.36 22.359999 4.08 22 C 3.8 21.64 3.6399999 20.56 3.6399999 17.359999 Z "/>
</symbol>
<symbol id="g2192B3D4CEA94ECF87445F8EE62E404B" overflow="visible">
<path d="M 4 5.08 C 4 1.76 3.36 1.4 0.91999996 1.28 C 0.68 1.04 0.68 0.16 0.91999996 -0.08 C 2.6 -0.04 4.4 0 6.6 0 C 8.8 0 10.559999 -0.04 12.28 -0.08 C 12.5199995 0.16 12.5199995 1.04 12.28 1.28 C 9.84 1.4 9.2 1.76 9.2 5.08 L 9.2 23.32 C 9.2 25.92 9.32 27.4 9.32 27.4 C 9.32 27.76 9.04 27.92 8.679999 27.92 C 7.2 27.439999 4 27 1.16 26.88 C 1.04 26.4 1.0799999 25.96 1.28 25.599998 C 3.8 25.4 4 25.359999 4 22.6 Z "/>
</symbol>
<symbol id="g8F4F96B13A9D8B27A4F3C34609AEF61C" overflow="visible">
<path d="M 9.28 4.88 L 9.28 12.84 C 9.28 14.839999 9.44 17.08 9.44 17.08 C 9.44 17.52 9.08 17.76 8.5199995 17.76 C 7.3999996 17.32 4.16 17 1.4 16.64 C 1.3199999 16.4 1.4 15.599999 1.48 15.36 C 3.6799998 15.16 4.08 14.839999 4.08 12.559999 L 4.08 4.88 C 4.08 1.56 3.6399999 1.48 1.1999999 1.28 C 0.96 1.04 0.96 0.16 1.1999999 -0.08 C 2.8799999 -0.04 4.56 0 6.68 0 C 8.8 0 10.44 -0.04 12.16 -0.08 C 12.4 0.16 12.4 1.04 12.16 1.28 C 9.719999 1.4399999 9.28 1.56 9.28 4.88 Z M 3.8799999 23.84 C 3.8799999 22.519999 4.8399997 21.199999 6.44 21.199999 C 8.24 21.199999 9.28 22.64 9.28 23.68 C 9.28 24.88 8.36 26.32 6.68 26.32 C 4.7999997 26.32 3.8799999 25.039999 3.8799999 23.84 Z "/>
</symbol>
<symbol id="g9BEF8AB47349CEAA320776726D3DB3DB" overflow="visible">
<path d="M 9.12 4.88 L 9.12 12.92 C 10.719999 14 12.32 14.799999 13.04 14.799999 C 14.639999 14.799999 15.839999 14.08 15.839999 11.8 L 15.839999 5.12 C 15.839999 1.76 15.2 1.4 13.559999 1.28 C 13.32 1.04 13.32 0.16 13.559999 -0.08 C 15.24 -0.04 16.52 0 18.44 0 C 20.64 0 22.4 -0.04 24.119999 -0.08 C 24.359999 0.16 24.359999 1.04 24.119999 1.28 C 21.68 1.4 21.039999 1.76 21.039999 5.12 L 21.039999 11.36 C 21.039999 15.759999 19.16 17.76 15.719999 17.76 C 14.12 17.76 11.28 16 9.08 14.48 C 8.96 15.88 8.8 17.08 8.8 17.08 C 8.76 17.56 8.44 17.76 7.8799996 17.76 C 6.3999996 17.359999 4 16.8 1.24 16.44 C 1.16 16.199999 1.24 15.4 1.3199999 15.16 C 3.52 14.96 3.9199998 14.639999 3.9199998 12.36 L 3.9199998 4.88 C 3.9199998 1.56 3.48 1.48 1.04 1.28 C 0.79999995 1.04 0.79999995 0.16 1.04 -0.08 C 2.72 -0.04 4.4 0 6.52 0 C 8.36 0 9.48 -0.04 11.2 -0.08 C 11.44 0.16 11.44 1.04 11.2 1.28 C 9.5199995 1.4399999 9.12 1.56 9.12 4.88 Z "/>
</symbol>
<symbol id="g5CEF84A95ABDCAB0EDEF87161576AC77" overflow="visible">
<path d="M 17.24 5.16 C 15.599999 3.48 13.44 3.04 11.92 3.04 C 8.8 3.04 6.8799996 4.8399997 6.8799996 8.76 C 6.8799996 9.04 6.92 9.2 6.92 9.4 L 16.52 9.4 C 17.48 9.4 17.68 10.08 17.68 10.639999 C 17.68 14.04 16.359999 17.76 10.48 17.76 C 6.2799997 17.76 1.48 14.04 1.48 7.9199996 C 1.48 5.6 2.32 3.1599998 4.04 1.5999999 C 5.56 0.24 7.52 -0.39999998 10.36 -0.39999998 C 13.12 -0.39999998 15.839999 1 17.84 3.9199998 C 17.84 4.44 17.64 5.16 17.24 5.16 Z M 7.08 11 C 7.12 12.4 7.3199997 13.92 7.8799996 14.719999 C 8.5199995 15.679999 9.599999 16.08 10.04 16.08 C 11.12 16.08 12.599999 15.04 12.599999 11.84 C 12.599999 11.599999 12.599999 11.08 12.5199995 11 Z "/>
</symbol>
<symbol id="g985B950D50769631420A9A59AEA7CEFC" overflow="visible">
<path d="M 3.0560002 1.9520001 L 3.0560002 8.368 C 3.0560002 9.696 3.328 9.776 4.4480004 9.824 C 4.544 9.92 4.544 10.2560005 4.4480004 10.352 C 3.7440002 10.336 2.992 10.320001 2.368 10.320001 C 1.84 10.320001 1.056 10.336 0.30400002 10.352 C 0.208 10.2560005 0.208 9.92 0.30400002 9.824 C 1.424 9.776 1.6960001 9.696 1.6960001 8.368 L 1.6960001 1.9520001 C 1.6960001 0.624 1.424 0.544 0.30400002 0.49600002 C 0.208 0.4 0.208 0.064 0.30400002 -0.032 C 1.024 -0.016 1.8080001 0 2.384 0 C 2.96 0 3.7280002 -0.016 4.4480004 -0.032 C 4.544 0.064 4.544 0.4 4.4480004 0.49600002 C 3.328 0.544 3.0560002 0.624 3.0560002 1.9520001 Z "/>
</symbol>
<symbol id="g2F3EA0F52D7EBFDBD1E9205C07C62175" overflow="visible">
<path d="M 2.48 1.9520001 L 2.48 4.992 C 2.48 5.7760005 2.6880002 5.6320004 3.0560002 5.168 L 6.8160005 0.16000001 C 7.056 -0.096 7.3120003 -0.192 7.5520005 -0.192 C 7.7440004 -0.192 7.9040003 -0.080000006 7.9040003 0.24000001 L 7.9040003 5.4080005 C 7.9040003 6.7360005 8.08 6.7840004 9.056001 6.8640003 C 9.152 6.9600005 9.152 7.2960005 9.056001 7.392 C 8.576 7.3760004 8 7.36 7.5200005 7.36 C 7.0400004 7.36 6.4800005 7.3760004 6.0000005 7.392 C 5.9040003 7.2960005 5.9040003 6.9600005 6.0000005 6.8640003 C 6.9760003 6.8 7.1520004 6.7360005 7.1520004 5.4080005 L 7.1520004 2.4160001 C 7.1520004 1.9840001 7.1040006 1.7120001 6.6080003 2.384 L 2.9440002 7.36 L 0.67200005 7.392 L 0.64000005 7.3440003 L 0.64000005 6.9600005 C 0.64000005 6.8960004 0.73600006 6.8640003 0.78400004 6.8640003 C 1.3920001 6.8160005 1.5680001 6.6240005 1.728 6.3360004 L 1.728 1.9520001 C 1.728 0.624 1.552 0.56 0.57600003 0.49600002 C 0.48000002 0.4 0.48000002 0.064 0.57600003 -0.032 C 1.056 -0.016 1.616 0 2.0960002 0 C 2.5760002 0 3.1520002 -0.016 3.6320002 -0.032 C 3.7280002 0.064 3.7280002 0.4 3.6320002 0.49600002 C 2.6560001 0.57600003 2.48 0.624 2.48 1.9520001 Z "/>
</symbol>
<symbol id="gAACD21C62EEBAEA5F571EAFD70656C36" overflow="visible">
<path d="M 4.8640003 1.9520001 L 4.8640003 5.984 C 4.8640003 6.576 5.024 6.8160005 5.5360003 6.8160005 L 5.952 6.8160005 C 6.9600005 6.8160005 7.168 6.4960003 7.4880004 5.3440003 C 7.6480002 5.3120003 7.7920003 5.3120003 7.9200006 5.392 C 7.84 6.176 7.8240004 6.768 7.7920003 7.5200005 C 7.2320004 7.4560003 6.208 7.36 4.8640003 7.36 L 3.6000001 7.36 C 2.032 7.36 1.1040001 7.4400005 0.67200005 7.5200005 C 0.67200005 6.768 0.656 6.144 0.56 5.392 C 0.70400006 5.3440003 0.84800005 5.328 0.99200004 5.3440003 C 1.312 6.4960003 1.488 6.8160005 2.528 6.8160005 L 2.9120002 6.8160005 C 3.4080002 6.8160005 3.6000001 6.6240005 3.6000001 6.0000005 L 3.6000001 1.9520001 C 3.6000001 0.624 3.4240003 0.57600003 2.4480002 0.49600002 C 2.352 0.4 2.352 0.064 2.4480002 -0.032 C 3.0400002 -0.016 3.696 0 4.2400002 0 C 4.8 0 5.4240003 -0.016 6.0160003 -0.032 C 6.1120005 0.064 6.1120005 0.4 6.0160003 0.49600002 C 5.0400004 0.56 4.8640003 0.624 4.8640003 1.9520001 Z "/>
</symbol>
<symbol id="gE307093CF7EFBC8D676E62CB78C07836" overflow="visible">
<path d="M 3.0560002 1.9520001 L 3.0560002 3.344 L 3.936 3.344 C 4.544 3.344 4.768 2.8160002 4.9760003 2.2240002 L 5.328 1.264 C 5.696 0.272 6.2400002 -0.112 6.9280005 -0.112 C 7.168 -0.112 7.6640005 -0.064 7.9360003 0 C 7.984 0.16000001 7.952 0.32000002 7.84 0.448 C 7.2640004 0.448 6.9600005 0.544 6.6400003 1.376 L 6.176 2.5760002 C 5.984 3.072 5.7920003 3.344 5.584 3.5520003 L 5.584 3.584 C 6.1280003 3.7760003 6.9440002 4.432 6.9440002 5.5360003 C 6.9440002 6.8640003 6.1120005 7.4240003 4.208 7.4240003 C 3.808 7.4240003 2.8960001 7.36 2.4160001 7.36 C 1.9520001 7.36 1.2800001 7.3760004 0.64000005 7.392 C 0.544 7.2960005 0.544 6.9600005 0.64000005 6.8640003 C 1.616 6.8 1.792 6.7360005 1.792 5.4080005 L 1.792 1.9520001 C 1.792 0.624 1.616 0.57600003 0.64000005 0.49600002 C 0.544 0.4 0.544 0.064 0.64000005 -0.032 C 1.248 -0.016 1.904 0 2.4320002 0 C 2.9280002 0 3.456 -0.016 3.9680002 -0.032 C 4.064 0.064 4.064 0.4 3.9680002 0.49600002 C 3.216 0.544 3.0560002 0.624 3.0560002 1.9520001 Z M 5.552 5.5360003 C 5.552 4.2720003 5.184 3.808 3.7600002 3.808 L 3.0560002 3.808 L 3.0560002 5.8880005 C 3.0560002 6.7360005 3.216 6.8960004 4.112 6.8960004 C 5.2320004 6.8960004 5.552 6.4960003 5.552 5.5360003 Z "/>
</symbol>
<symbol id="gAA95D2B4A225624CA202B59CBD1BF487" overflow="visible">
<path d="M 8.432 3.7600002 C 8.432 6.032 6.6080003 7.5200005 4.5280004 7.5200005 C 2.3040001 7.5200005 0.592 5.9040003 0.592 3.5520003 C 0.592 1.376 2.24 -0.16000001 4.4 -0.16000001 C 7.024 -0.16000001 8.432 1.6800001 8.432 3.7600002 Z M 4.3840003 6.992 C 5.808 6.992 7.0400004 5.6800003 7.0400004 3.5360003 C 7.0400004 1.5680001 6.064 0.36800003 4.6400003 0.36800003 C 3.088 0.36800003 1.9840001 1.7760001 1.9840001 3.7440002 C 1.9840001 5.9040003 3.1840003 6.992 4.3840003 6.992 Z "/>
</symbol>
<symbol id="g3B851FDBB4F3A7C5E304DE6F7DEA331C" overflow="visible">
<path d="M 2.368 7.36 C 1.9360001 7.36 1.2160001 7.3760004 0.592 7.392 C 0.49600002 7.2960005 0.49600002 6.9600005 0.592 6.8640003 C 1.5680001 6.8 1.7440001 6.7360005 1.7440001 5.4080005 L 1.7440001 1.9520001 C 1.7440001 0.624 1.5680001 0.57600003 0.592 0.49600002 C 0.49600002 0.4 0.49600002 0.064 0.592 -0.032 C 1.2 -0.016 1.9200001 0 2.384 0 C 2.8000002 0 3.44 -0.032 4.7200003 -0.032 C 6.4960003 -0.032 8.4800005 0.8 8.4800005 3.6000001 C 8.4800005 5.728 7.168 7.392 4.4960003 7.392 C 3.4080002 7.392 2.832 7.36 2.368 7.36 Z M 3.0080001 1.2160001 L 3.0080001 6.3680005 C 3.0080001 6.768 3.4080002 6.8640003 4.032 6.8640003 C 6.7200003 6.8640003 7.0880003 4.992 7.0880003 3.328 C 7.0880003 1.088 6.096 0.49600002 4.3360004 0.49600002 C 3.1200001 0.49600002 3.0080001 0.768 3.0080001 1.2160001 Z "/>
</symbol>
<symbol id="g1BA4F60CE8E3A065D660EA7EA67004B1" overflow="visible">
<path d="M 6.9600005 5.4080005 L 6.9600005 3.3760002 C 6.9600005 2 6.9600005 0.49600002 4.848 0.49600002 C 3.2640002 0.49600002 2.9280002 1.7440001 2.9280002 3.232 L 2.9280002 5.4080005 C 2.9280002 6.7360005 3.104 6.7840004 4.0800004 6.8640003 C 4.176 6.9600005 4.176 7.2960005 4.0800004 7.392 C 3.456 7.3760004 2.8160002 7.36 2.288 7.36 C 1.7120001 7.36 1.088 7.3760004 0.512 7.392 C 0.416 7.2960005 0.416 6.9600005 0.512 6.8640003 C 1.488 6.8 1.664 6.7360005 1.664 5.4080005 L 1.664 2.8960001 C 1.664 0.49600002 2.832 -0.16000001 4.576 -0.16000001 C 7.056 -0.16000001 7.7120004 1.248 7.7120004 3.584 L 7.7120004 5.4080005 C 7.7120004 6.7360005 7.8880005 6.7840004 8.864 6.8640003 C 8.96 6.9600005 8.96 7.2960005 8.864 7.392 C 8.384001 7.3760004 7.8080006 7.36 7.3280005 7.36 C 6.8480005 7.36 6.288 7.3760004 5.808 7.392 C 5.7120004 7.2960005 5.7120004 6.9600005 5.808 6.8640003 C 6.7840004 6.8 6.9600005 6.7360005 6.9600005 5.4080005 Z "/>
</symbol>
<symbol id="gE3CB9A16B9DD884349EFEF95066B2206" overflow="visible">
<path d="M 4.4160004 -0.16000001 C 5.664 -0.16000001 6.432 0.30400002 7.1840005 1.312 C 7.1520004 1.424 6.992 1.6 6.8640003 1.6320001 C 6.1280003 0.768 5.5680003 0.448 4.4960003 0.448 C 2.9120002 0.448 1.9840001 2.16 1.9840001 3.7440002 C 1.9840001 6.432 3.232 6.992 4.432 6.992 C 5.7120004 6.992 6.464 6.288 6.656 5.168 C 6.8160005 5.1200004 6.9760003 5.1200004 7.136 5.216 C 7.136 5.872 7.1040006 6.544 6.9440002 7.2640004 C 6.3360004 7.2640004 5.616 7.5200005 4.3360004 7.5200005 C 2.2240002 7.5200005 0.592 5.92 0.592 3.584 C 0.592 2.5760002 0.91200006 1.4720001 1.6960001 0.75200003 C 2.3360002 0.16000001 3.232 -0.16000001 4.4160004 -0.16000001 Z "/>
</symbol>
<symbol id="gDBEAA3BAB7923CD0435518D325CA6C53" overflow="visible">
<path d="M 3.1200001 5.4080005 C 3.1200001 6.7360005 3.2960002 6.7840004 4.2720003 6.8640003 C 4.368 6.9600005 4.368 7.2960005 4.2720003 7.392 C 3.6640003 7.3760004 2.976 7.36 2.48 7.36 C 2 7.36 1.3280001 7.3760004 0.70400006 7.392 C 0.60800004 7.2960005 0.60800004 6.9600005 0.70400006 6.8640003 C 1.6800001 6.8 1.8560001 6.7360005 1.8560001 5.4080005 L 1.8560001 1.9520001 C 1.8560001 0.624 1.6800001 0.57600003 0.70400006 0.49600002 C 0.60800004 0.4 0.60800004 0.064 0.70400006 -0.032 C 1.296 -0.016 1.9520001 0 2.496 0 C 3.0080001 0 3.7120001 -0.016 4.2720003 -0.032 C 4.368 0.064 4.368 0.4 4.2720003 0.49600002 C 3.2960002 0.56 3.1200001 0.624 3.1200001 1.9520001 Z "/>
</symbol>
<symbol id="gD91DF12E6685C776523A4EFE671EF7FE" overflow="visible">
<path d="M 0.91200006 0.688 C 0.91200006 0.224 1.296 -0.16000001 1.7600001 -0.16000001 C 2.2240002 -0.16000001 2.608 0.224 2.608 0.688 C 2.608 1.1520001 2.2240002 1.536 1.7600001 1.536 C 1.296 1.536 0.91200006 1.1520001 0.91200006 0.688 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
<symbol id="g12DC86CA8D9D6E336118F1B6EDF218A6" overflow="visible">
<path d="M 8.652 1.7080001 L 8.652 7.322 C 8.652 8.484 8.89 8.554 9.87 8.596001 C 9.954 8.68 9.954 8.974 9.87 9.058001 C 9.2960005 9.044001 8.582001 9.030001 8.05 9.030001 C 7.532 9.030001 6.86 9.044001 6.244 9.058001 C 6.1600003 8.974 6.1600003 8.68 6.244 8.596001 C 7.2240005 8.554 7.4620004 8.484 7.4620004 7.322 L 7.4620004 5.0820003 L 2.674 5.0820003 L 2.674 7.322 C 2.674 8.484 2.9120002 8.554 3.8920002 8.596001 C 3.976 8.68 3.976 8.974 3.8920002 9.058001 C 3.3600001 9.044001 2.786 9.030001 2.072 9.030001 C 1.3720001 9.030001 0.79800004 9.044001 0.266 9.058001 C 0.18200001 8.974 0.18200001 8.68 0.266 8.596001 C 1.246 8.554 1.4840001 8.484 1.4840001 7.322 L 1.4840001 1.7080001 C 1.4840001 0.546 1.246 0.476 0.266 0.43400002 C 0.18200001 0.35000002 0.18200001 0.056 0.266 -0.028 C 0.882 -0.014 1.554 0 2.086 0 C 2.5900002 0 3.276 -0.014 3.8920002 -0.028 C 3.976 0.056 3.976 0.35000002 3.8920002 0.43400002 C 2.9120002 0.476 2.674 0.546 2.674 1.7080001 L 2.674 4.494 L 7.4620004 4.494 L 7.4620004 1.7080001 C 7.4620004 0.546 7.2240005 0.476 6.244 0.43400002 C 6.1600003 0.35000002 6.1600003 0.056 6.244 -0.028 C 6.874 -0.014 7.546 0 8.064 0 C 8.582001 0 9.254001 -0.014 9.87 -0.028 C 9.954 0.056 9.954 0.35000002 9.87 0.43400002 C 8.89 0.476 8.652 0.546 8.652 1.7080001 Z "/>
</symbol>
<symbol id="g9C63C5DDFB4402181293B5DF9DB8FDF6" overflow="visible">
<path d="M 7.7840004 7.168 L 7.7840004 2.5900002 C 7.7840004 2.3240001 7.7840004 2.17 7.6860003 2.17 C 7.63 2.17 7.42 2.4220002 7.0140004 2.94 L 2.2120001 9.030001 L 0.322 9.058001 C 0.238 8.974 0.238 8.68 0.322 8.596001 C 0.924 8.554 1.3440001 8.064 1.4280001 7.7000003 L 1.4280001 1.8620001 C 1.4280001 0.616 1.19 0.532 0.21000001 0.43400002 C 0.126 0.35000002 0.126 0.056 0.21000001 -0.028 C 0.81200004 -0.014 1.442 0 1.778 0 C 2.1000001 0 2.7440002 -0.014 3.332 -0.028 C 3.4160001 0.056 3.4160001 0.35000002 3.332 0.43400002 C 2.352 0.532 2.114 0.588 2.114 1.8620001 L 2.114 6.1460004 C 2.114 6.622 2.114 6.8320003 2.226 6.8320003 C 2.3100002 6.8320003 2.464 6.678 2.7020001 6.3700004 L 7.5880003 0.19600001 C 7.742 -0.014 7.9240003 -0.14 8.148001 -0.14 C 8.344 -0.14 8.47 0.028 8.47 0.294 L 8.47 7.168 C 8.47 8.4140005 8.708 8.498 9.688001 8.596001 C 9.772 8.68 9.772 8.974 9.688001 9.058001 C 9.114 9.044001 8.456 9.030001 8.12 9.030001 C 7.826 9.030001 7.182 9.044001 6.566 9.058001 C 6.4820004 8.974 6.4820004 8.68 6.566 8.596001 C 7.546 8.498 7.7840004 8.442 7.7840004 7.168 Z "/>
</symbol>
<symbol id="gF73CF51A640CD9E8903A9C4D4B743CCF" overflow="visible">
<path d="M 5.53 8.834001 C 4.718 8.946 4.7460003 9.212 3.374 9.212 C 1.96 9.212 0.71400005 8.274 0.71400005 6.7900004 C 0.71400005 5.32 1.932 4.6480002 3.164 4.172 C 4.004 3.8500001 5.04 3.4580002 5.04 2.086 C 5.04 0.952 4.4100003 0.36400002 3.2900002 0.36400002 C 1.988 0.36400002 1.148 0.966 0.84000003 2.352 C 0.658 2.408 0.518 2.38 0.37800002 2.3100002 C 0.43400002 1.232 0.49 0.86800003 0.658 0.18200001 C 1.5400001 0.18200001 1.932 -0.14 3.1780002 -0.14 C 3.808 -0.14 4.4100003 0.014 4.9 0.322 C 5.7120004 0.82600003 6.216 1.6800001 6.216 2.576 C 6.216 4.06 5.096 4.718 3.9480002 5.152 C 3.108 5.46 1.7080001 5.992 1.7080001 7.168 C 1.7080001 7.952 2.4220002 8.736 3.2480001 8.736 C 4.606 8.736 5.04 7.868 5.32 6.9440002 C 5.474 6.9160004 5.656 6.9300003 5.782 7.0280004 C 5.7260003 7.7000003 5.67 8.092 5.53 8.834001 Z "/>
</symbol>
<symbol id="gEC1365C4E13D8501FA131C6543C06A3E" overflow="visible">
<path d="M 11.34 7.9100003 L 9.156 1.8340001 L 9.114 1.848 L 7.182 7.756 C 6.9440002 8.512 7.434 8.554 7.9100003 8.596001 C 7.9940004 8.68 7.9940004 8.974 7.9100003 9.058001 C 7.3360004 9.044001 6.7200003 9.030001 6.1600003 9.030001 C 5.698 9.030001 5.208 9.044001 4.76 9.058001 C 4.676 8.974 4.676 8.68 4.76 8.596001 C 5.5020003 8.554 5.81 8.12 5.9360003 7.756 L 6.2580004 6.8320003 C 6.314 6.664 6.3560004 6.524 6.3560004 6.3980002 C 6.3560004 6.2580004 6.342 6.1460004 6.23 5.908 L 4.4240003 1.8060001 L 4.354 1.82 L 2.3100002 8.008 C 2.142 8.498 2.52 8.568 3.01 8.596001 C 3.094 8.68 3.094 8.974 3.01 9.058001 C 2.548 9.044001 1.932 9.030001 1.386 9.030001 C 0.896 9.030001 0.49 9.044001 0.08400001 9.058001 C 0 8.974 0 8.68 0.08400001 8.596001 C 0.71400005 8.554 0.81200004 8.54 1.0780001 7.7840004 L 3.71 0.21000001 C 3.7800002 -0.014 3.864 -0.16800001 4.018 -0.16800001 C 4.2000003 -0.16800001 4.284 -0.028 4.382 0.21000001 L 6.4680004 4.9 C 6.5940003 5.1800003 6.636 5.25 6.7060003 5.25 C 6.762 5.25 6.8180003 5.096 6.9020004 4.8580003 L 8.512 0.21000001 C 8.596001 -0.028 8.666 -0.16800001 8.834001 -0.16800001 C 8.988 -0.16800001 9.086 -0.014 9.156 0.19600001 L 11.97 7.742 C 12.152 8.232 12.404 8.554 13.174001 8.596001 C 13.258 8.68 13.258 8.974 13.174001 9.058001 C 12.768001 9.044001 12.320001 9.030001 11.956 9.030001 C 11.592 9.030001 10.976001 9.044001 10.416 9.058001 C 10.332001 8.974 10.332001 8.68 10.416 8.596001 C 10.990001 8.554 11.55 8.512 11.34 7.9100003 Z "/>
</symbol>
<symbol id="g47288CF7D8F788F93B1406172900DCDE" overflow="visible">
<path d="M 0.79800004 0.602 C 0.79800004 0.19600001 1.1340001 -0.14 1.5400001 -0.14 C 1.9460001 -0.14 2.282 0.19600001 2.282 0.602 C 2.282 1.008 1.9460001 1.3440001 1.5400001 1.3440001 C 1.1340001 1.3440001 0.79800004 1.008 0.79800004 0.602 Z "/>
</symbol>
<symbol id="g9696EE00168B299790D79B47B78C5F18" overflow="visible">
<path d="M 0.85400003 6.552 C 0.85400003 6.2580004 1.12 6.006 1.414 6.006 C 1.6520001 6.006 2.072 6.2580004 2.072 6.566 C 2.072 6.678 2.0440001 6.762 2.016 6.86 C 1.988 6.958 1.904 7.084 1.904 7.196 C 1.904 7.546 2.2680001 8.05 3.2900002 8.05 C 3.7940001 8.05 4.5080004 7.7000003 4.5080004 6.3560004 C 4.5080004 5.46 4.1860003 4.7320004 3.3600001 3.8920002 L 2.3240001 2.8700001 C 0.952 1.47 0.72800004 0.79800004 0.72800004 -0.028 C 0.72800004 -0.028 1.442 0 1.8900001 0 L 4.34 0 C 4.788 0 5.432 -0.028 5.432 -0.028 C 5.6140003 0.71400005 5.754 1.764 5.768 2.184 C 5.684 2.2540002 5.5020003 2.282 5.362 2.2540002 C 5.124 1.26 4.886 0.91 4.382 0.91 L 1.8900001 0.91 C 1.8900001 1.582 2.8560002 2.5340002 2.926 2.604 L 4.34 3.9620001 C 5.138 4.7320004 5.7400002 5.348 5.7400002 6.412 C 5.7400002 7.9240003 4.5080004 8.54 3.374 8.54 C 1.82 8.54 0.85400003 7.392 0.85400003 6.552 Z "/>
</symbol>
<symbol id="gD0485EF23018DAF4BFC69AAD15075193" overflow="visible">
<path d="M 3.01 8.05 C 3.6120002 8.05 4.172 7.6860003 4.172 6.7900004 C 4.172 6.09 3.3600001 5.012 1.9740001 4.816 L 2.0440001 4.368 C 2.282 4.396 2.5340002 4.396 2.716 4.396 C 3.5140002 4.396 4.55 4.172 4.55 2.5900002 C 4.55 0.72800004 3.3040001 0.35000002 2.8140001 0.35000002 C 2.1000001 0.35000002 1.9740001 0.67200005 1.8060001 0.924 C 1.666 1.12 1.4840001 1.288 1.204 1.288 C 0.91 1.288 0.616 1.0220001 0.616 0.79800004 C 0.616 0.238 1.792 -0.14 2.632 -0.14 C 4.2980003 -0.14 5.782 0.938 5.782 2.786 C 5.782 4.3120003 4.6340003 4.8580003 3.808 4.998 L 3.7940001 5.026 C 4.9420004 5.572 5.264 6.1460004 5.264 6.888 C 5.264 7.308 5.1660004 7.644 4.83 7.9940004 C 4.5220003 8.302 4.032 8.54 3.3040001 8.54 C 1.246 8.54 0.658 7.196 0.658 6.734 C 0.658 6.538 0.79800004 6.2580004 1.1340001 6.2580004 C 1.6240001 6.2580004 1.6800001 6.7200003 1.6800001 6.986 C 1.6800001 7.8820004 2.6460001 8.05 3.01 8.05 Z "/>
</symbol>
<symbol id="g42427CF90B88C34047186DDCC0B8064E" overflow="visible">
<path d="M 1.4560001 7.322 L 1.4560001 1.7080001 C 1.4560001 0.546 1.218 0.476 0.238 0.43400002 C 0.154 0.35000002 0.154 0.056 0.238 -0.028 C 0.86800003 -0.014 1.554 0 2.058 0 C 2.548 0 3.374 -0.014 4.0740004 -0.028 C 4.158 0.056 4.158 0.35000002 4.0740004 0.43400002 C 2.982 0.49 2.6460001 0.546 2.6460001 1.7080001 L 2.6460001 4.0880003 C 2.954 3.99 3.2900002 3.9480002 3.7800002 3.9480002 C 6.328 3.9480002 7.098 5.6140003 7.098 6.8040004 C 7.098 7.63 6.552 9.128 3.9620001 9.128 C 3.43 9.128 2.604 9.030001 2.0440001 9.030001 C 1.526 9.030001 0.79800004 9.044001 0.238 9.058001 C 0.154 8.974 0.154 8.68 0.238 8.596001 C 1.218 8.554 1.4560001 8.484 1.4560001 7.322 Z M 2.6460001 7.756 C 2.6460001 8.162001 2.8560002 8.652 3.864 8.652 C 4.83 8.652 5.796 8.33 5.796 6.552 C 5.796 5.04 5.0680003 4.4240003 3.71 4.4240003 C 3.3600001 4.4240003 2.8000002 4.452 2.6460001 4.494 Z "/>
</symbol>
<symbol id="g9AE4831982D6CA553E49B4F41E9A233F" overflow="visible">
<path d="M 2.464 5.012 C 2.436 5.572 2.4220002 5.9360003 2.352 6.076 C 2.3240001 6.1460004 2.296 6.188 2.184 6.188 C 1.792 6.0340004 1.4280001 5.908 0.462 5.782 C 0.43400002 5.698 0.462 5.474 0.49 5.3900003 C 1.246 5.32 1.4000001 5.25 1.4000001 4.438 L 1.4000001 1.7080001 C 1.4000001 0.546 1.232 0.49 0.36400002 0.43400002 C 0.28 0.35000002 0.28 0.056 0.36400002 -0.028 C 0.85400003 -0.014 1.4000001 0 1.96 0 C 2.52 0 3.164 -0.014 3.654 -0.028 C 3.7380002 0.056 3.7380002 0.35000002 3.654 0.43400002 C 2.674 0.504 2.506 0.546 2.506 1.7080001 L 2.506 3.654 C 2.506 4.018 2.674 4.34 2.842 4.592 C 2.996 4.816 3.318 5.2780004 3.486 5.2780004 C 3.6120002 5.2780004 3.7380002 5.25 3.8500001 5.096 C 3.9480002 4.9560003 4.116 4.774 4.354 4.774 C 4.69 4.774 5.012 5.124 5.012 5.474 C 5.012 5.7400002 4.76 6.1460004 4.172 6.1460004 C 3.5140002 6.1460004 2.94 5.53 2.618 4.984 C 2.5340002 4.83 2.464 4.9420004 2.464 5.012 Z "/>
</symbol>
<symbol id="gA4DE3951E8A0322DEC5E3569D1D30666" overflow="visible">
<path d="M 0.574 2.8700001 C 0.574 1.442 1.526 -0.14 3.5140002 -0.14 C 4.4100003 -0.14 5.096 0.18200001 5.572 0.644 C 6.202 1.26 6.4820004 2.142 6.4820004 2.996 C 6.4820004 4.452 5.684 6.1460004 3.542 6.1460004 C 2.618 6.1460004 1.8620001 5.768 1.3440001 5.1660004 C 0.84000003 4.564 0.574 3.752 0.574 2.8700001 Z M 3.332 5.656 C 4.5360003 5.656 5.2780004 4.564 5.2780004 2.548 C 5.2780004 0.78400004 4.368 0.35000002 3.71 0.35000002 C 2.2540002 0.35000002 1.778 2.114 1.778 3.1920002 C 1.778 4.4100003 2.072 5.656 3.332 5.656 Z "/>
</symbol>
<symbol id="gC80234271A0A022352A099322F0FCD32" overflow="visible">
<path d="M 2.338 5.5160003 C 2.2540002 5.432 2.198 5.46 2.198 5.586 L 2.198 8.162001 C 2.198 9.0720005 2.2540002 9.632 2.2540002 9.632 C 2.2540002 9.7300005 2.198 9.772 2.072 9.772 C 1.722 9.632 0.67200005 9.436 0.112 9.394 C 0.08400001 9.282001 0.112 9.058001 0.19600001 8.974 C 0.238 8.974 0.28 8.974 0.322 8.974 C 0.938 8.932 1.092 8.932 1.092 7.826 L 1.092 0.994 C 1.092 0.448 1.0780001 0.19600001 1.036 0 C 1.1060001 -0.112 1.176 -0.16800001 1.3440001 -0.16800001 C 1.4280001 -0.08400001 1.5680001 0.042000003 1.6800001 0.16800001 C 1.82 0.33600003 1.904 0.33600003 2.058 0.21000001 C 2.38 -0.056 2.8000002 -0.14 3.2900002 -0.14 C 4.718 -0.14 6.3840003 1.1620001 6.3840003 3.388 C 6.3840003 5.096 5.124 6.1460004 3.9060001 6.1460004 C 3.3040001 6.1460004 2.772 5.908 2.338 5.5160003 Z M 2.436 5.0820003 C 2.8000002 5.4040003 3.22 5.53 3.6260002 5.53 C 4.48 5.53 5.1800003 4.494 5.1800003 3.1360002 C 5.1800003 1.5400001 4.5360003 0.33600003 3.206 0.33600003 C 2.772 0.33600003 2.4780002 0.644 2.198 0.994 L 2.198 4.494 C 2.198 4.788 2.2540002 4.928 2.436 5.0820003 Z "/>
</symbol>
<symbol id="g3649D621BC998C9216AD40BBEFAC3AB1" overflow="visible">
<path d="M 4.102 0.67200005 C 4.1860003 0.238 4.34 -0.14 5.04 -0.14 C 5.572 -0.14 6.076 0.098000005 6.3700004 0.37800002 C 6.342 0.546 6.2860003 0.67200005 6.132 0.75600004 C 6.0340004 0.67200005 5.796 0.532 5.6140003 0.532 C 5.208 0.532 5.1940002 1.0780001 5.1940002 1.722 L 5.1940002 3.7800002 C 5.1940002 5.768 4.102 6.1460004 3.0800002 6.1460004 C 1.932 6.1460004 0.77000004 5.3900003 0.77000004 4.592 C 0.77000004 4.256 0.938 4.0880003 1.26 4.0880003 C 1.666 4.0880003 1.9180001 4.382 1.9180001 4.564 C 1.9180001 4.662 1.904 4.76 1.876 4.816 C 1.8620001 4.8580003 1.848 4.9420004 1.848 5.096 C 1.848 5.53 2.436 5.684 2.9680002 5.684 C 3.444 5.684 4.102 5.446 4.102 3.864 C 4.102 3.766 4.06 3.71 4.018 3.696 L 2.8140001 3.4020002 C 1.47 3.066 0.504 2.3240001 0.504 1.3720001 C 0.504 0.224 1.288 -0.14 2.2680001 -0.14 C 2.7580001 -0.14 3.1780002 -0.028 3.7940001 0.448 L 4.0740004 0.67200005 Z M 4.102 3.262 L 4.102 1.414 C 4.102 1.232 4.018 1.1340001 3.9060001 1.0500001 C 3.542 0.75600004 3.066 0.43400002 2.674 0.43400002 C 1.9740001 0.43400002 1.666 0.994 1.666 1.4280001 C 1.666 2.058 1.96 2.7020001 2.996 2.9680002 Z "/>
</symbol>
<symbol id="gAAC2A4387B1619C03EEEB0968B96165F" overflow="visible">
<path d="M 2.5340002 1.7080001 L 2.5340002 4.494 C 2.5340002 5.1940002 2.5900002 6.09 2.5900002 6.09 C 2.5900002 6.1460004 2.52 6.188 2.408 6.188 C 2.016 6.0340004 1.4560001 5.908 0.49 5.782 C 0.462 5.698 0.49 5.474 0.518 5.3900003 C 1.288 5.32 1.4280001 5.236 1.4280001 4.438 L 1.4280001 1.7080001 C 1.4280001 0.546 1.274 0.504 0.42000002 0.43400002 C 0.33600003 0.35000002 0.33600003 0.056 0.42000002 -0.028 C 0.882 -0.014 1.4280001 0 1.988 0 C 2.548 0 3.0800002 -0.014 3.542 -0.028 C 3.6260002 0.056 3.6260002 0.35000002 3.542 0.43400002 C 2.6880002 0.49 2.5340002 0.546 2.5340002 1.7080001 Z M 1.26 8.386001 C 1.26 8.022 1.5960001 7.6580005 1.932 7.6580005 C 2.3240001 7.6580005 2.66 8.036 2.66 8.33 C 2.66 8.666 2.3660002 9.058001 1.988 9.058001 C 1.6520001 9.058001 1.26 8.722 1.26 8.386001 Z "/>
</symbol>
<symbol id="gBBFA548D7BC5ACA0036C5BF286E59830" overflow="visible">
<path d="M 1.33 1.7080001 C 1.33 0.546 1.176 0.476 0.322 0.43400002 C 0.238 0.35000002 0.238 0.056 0.322 -0.028 C 0.81200004 -0.014 1.33 0 1.8900001 0 C 2.45 0 2.982 -0.014 3.444 -0.028 C 3.528 0.056 3.528 0.35000002 3.444 0.43400002 C 2.5900002 0.476 2.436 0.546 2.436 1.7080001 L 2.436 8.162001 C 2.436 9.0720005 2.492 9.632 2.492 9.632 C 2.492 9.7300005 2.436 9.772 2.3100002 9.772 C 1.96 9.632 0.91 9.436 0.35000002 9.394 C 0.322 9.282001 0.35000002 9.058001 0.43400002 8.974 C 1.246 8.918 1.33 8.876 1.33 7.826 Z "/>
</symbol>
<symbol id="g88B62CE1F53AC1AE1D938018DA31319" overflow="visible">
<path d="M 0.602 6.006 C 0.40600002 6.006 0.35000002 5.8380003 0.35000002 5.7260003 L 0.35000002 5.544 C 0.35000002 5.474 0.36400002 5.46 0.42000002 5.46 L 1.246 5.46 L 1.246 1.246 C 1.246 0.252 1.6800001 -0.14 2.3240001 -0.14 C 2.9680002 -0.14 3.6680002 0.16800001 4.214 0.78400004 C 4.1860003 0.924 4.102 1.008 3.9620001 1.0220001 C 3.598 0.74200004 3.1780002 0.63 2.8140001 0.63 C 2.436 0.63 2.352 1.0500001 2.352 1.9180001 L 2.352 5.46 L 3.808 5.46 C 3.9480002 5.46 4.144 5.5160003 4.144 5.642 L 4.144 5.9220004 C 4.144 5.978 4.102 6.006 4.032 6.006 L 2.352 6.006 L 2.352 6.552 C 2.352 7.4620004 2.408 8.022 2.408 8.022 C 2.408 8.106 2.3660002 8.148001 2.296 8.148001 C 2.24 8.148001 2.114 8.092 1.988 8.022 C 1.8340001 7.938 1.694 7.868 1.5120001 7.826 C 1.3440001 7.7700005 1.204 7.728 1.204 7.63 C 1.204 7.4620004 1.246 7.5600004 1.246 6.006 Z "/>
</symbol>
<symbol id="g5799677F1612AA2CF55B8D046D0457BF" overflow="visible">
<path d="M 2.8560002 -2.24 C 3.0800002 -1.848 3.262 -1.4560001 3.43 -1.036 C 4.55 1.666 5.1800003 3.108 5.908 4.676 C 6.188 5.264 6.3840003 5.4880004 7.0420003 5.572 C 7.1260004 5.656 7.1260004 5.9500003 7.0420003 6.0340004 C 6.762 6.02 6.44 6.006 6.0480003 6.006 C 5.6280003 6.006 5.1940002 6.02 4.774 6.0340004 C 4.69 5.9500003 4.69 5.656 4.774 5.572 C 5.222 5.53 5.67 5.446 5.446 4.9420004 L 4.06 1.7360001 C 3.9620001 1.5120001 3.8360002 1.47 3.7240002 1.75 L 2.4780002 4.662 C 2.226 5.25 2.1560001 5.5160003 2.94 5.572 C 3.0240002 5.656 3.0240002 5.9500003 2.94 6.0340004 C 2.4220002 6.02 1.8620001 6.006 1.358 6.006 C 0.882 6.006 0.504 6.02 0.224 6.0340004 C 0.14 5.9500003 0.14 5.656 0.224 5.572 C 0.78400004 5.5020003 0.966 5.3760004 1.33 4.5220003 L 2.9120002 0.84000003 C 3.038 0.56 3.2480001 -0.08400001 3.108 -0.476 C 2.94 -0.938 2.772 -1.33 2.562 -1.764 C 2.408 -2.0440001 2.2120001 -2.17 1.8620001 -2.17 C 1.666 -2.17 1.61 -2.128 1.4560001 -2.128 C 1.0500001 -2.128 0.84000003 -2.548 0.84000003 -2.73 C 0.84000003 -3.0240002 1.12 -3.2480001 1.498 -3.2480001 C 1.792 -3.2480001 2.352 -3.1360002 2.8560002 -2.24 Z "/>
</symbol>
<symbol id="gE2267284F842780DB4609789BADA809" overflow="visible">
<path d="M 1.204 1.7080001 C 1.204 0.546 1.0500001 0.49 0.266 0.43400002 C 0.18200001 0.35000002 0.18200001 0.056 0.266 -0.028 C 0.72800004 -0.014 1.204 0 1.764 0 C 2.2540002 0 2.716 -0.014 3.038 -0.028 C 3.122 0.056 3.122 0.35000002 3.038 0.43400002 C 2.464 0.49 2.3100002 0.546 2.3100002 1.7080001 L 2.3100002 2.926 C 2.576 2.9120002 2.772 2.898 2.9120002 2.8560002 C 3.066 2.7440002 3.1920002 2.618 3.3600001 2.394 L 4.382 1.0220001 C 4.788 0.476 4.9560003 0.21000001 4.9700003 0.042000003 C 4.9700003 0 4.984 -0.028 5.026 -0.028 C 5.306 -0.014 5.6140003 0 5.894 0 C 6.328 0 6.762 -0.014 7.0420003 -0.028 C 7.1260004 0.056 7.1260004 0.35000002 7.0420003 0.43400002 C 6.566 0.49 6.216 0.546 5.8380003 1.0220001 L 3.99 3.3460002 C 3.934 3.4160001 3.8920002 3.4720001 3.8920002 3.542 C 3.8920002 3.598 3.8920002 3.6260002 3.9480002 3.6820002 L 5.1800003 4.9560003 C 5.6000004 5.4040003 6.09 5.5160003 6.65 5.572 C 6.734 5.656 6.734 5.9500003 6.65 6.0340004 C 6.328 6.02 5.9360003 6.006 5.432 6.006 C 4.9 6.006 4.382 6.02 4.06 6.0340004 C 3.976 5.9500003 3.976 5.656 4.06 5.572 C 4.8440003 5.5160003 4.5080004 5.026 4.382 4.8580003 C 4.06 4.452 3.6260002 3.976 3.262 3.71 C 2.954 3.486 2.576 3.318 2.3100002 3.276 L 2.3100002 8.162001 C 2.3100002 9.0720005 2.3660002 9.632 2.3660002 9.632 C 2.3660002 9.7300005 2.3100002 9.772 2.184 9.772 C 1.8340001 9.632 0.78400004 9.436 0.224 9.394 C 0.19600001 9.282001 0.224 9.058001 0.308 8.974 C 0.35000002 8.974 0.39200002 8.974 0.43400002 8.974 C 1.0500001 8.932 1.204 8.932 1.204 7.826 Z "/>
</symbol>
<symbol id="gA0F6184C06096774B92DEFE1EDA388E4" overflow="visible">
<path d="M 2.184 5.152 C 2.17 5.572 2.142 5.9360003 2.072 6.076 C 2.0440001 6.1460004 2.016 6.188 1.904 6.188 C 1.5120001 6.0340004 1.148 5.908 0.18200001 5.782 C 0.154 5.698 0.18200001 5.474 0.21000001 5.3900003 C 0.966 5.32 1.12 5.25 1.12 4.438 L 1.12 -1.5400001 C 1.12 -2.7020001 0.966 -2.772 0.112 -2.8140001 C 0.028 -2.898 0.028 -3.1920002 0.112 -3.276 C 0.602 -3.262 1.12 -3.2480001 1.6800001 -3.2480001 C 2.24 -3.2480001 2.9120002 -3.262 3.374 -3.276 C 3.4580002 -3.1920002 3.4580002 -2.898 3.374 -2.8140001 C 2.38 -2.7580001 2.226 -2.7020001 2.226 -1.5400001 L 2.226 -0.028 C 2.226 0.154 2.282 0.14 2.4220002 0.08400001 C 2.772 -0.056 3.1920002 -0.14 3.64 -0.14 C 4.4240003 -0.14 5.124 0.098000005 5.698 0.644 C 6.3560004 1.288 6.734 2.1560001 6.734 3.2900002 C 6.734 4.774 5.684 6.1460004 4.256 6.1460004 C 3.6120002 6.1460004 2.898 5.7260003 2.338 5.096 C 2.2540002 5.012 2.198 5.012 2.184 5.152 Z M 2.45 4.6340003 C 2.8140001 5.0820003 3.4580002 5.5020003 3.864 5.5020003 C 4.76 5.5020003 5.53 4.494 5.53 2.9120002 C 5.53 1.764 5.124 0.33600003 3.556 0.33600003 C 3.3040001 0.33600003 2.8140001 0.40600002 2.562 0.63 C 2.282 0.882 2.226 0.966 2.226 1.47 L 2.226 4.018 C 2.226 4.3120003 2.282 4.438 2.45 4.6340003 Z "/>
</symbol>
<symbol id="g1F652CD6CF98783FD5BC41E10F253E3" overflow="visible">
<path d="M 2.086 0 L 5.0680003 0 C 5.446 0 6.734 -0.028 6.734 -0.028 C 6.874 0.67200005 7.0140004 1.582 7.098 2.3100002 C 6.958 2.38 6.8040004 2.408 6.636 2.38 C 6.3560004 1.3720001 5.8380003 0.546 4.354 0.546 L 3.4720001 0.546 C 2.926 0.546 2.674 0.81200004 2.674 1.526 L 2.674 7.322 C 2.674 8.484 2.9120002 8.554 3.8920002 8.596001 C 3.976 8.68 3.976 8.974 3.8920002 9.058001 C 3.262 9.044001 2.604 9.030001 2.072 9.030001 C 1.5680001 9.030001 0.91 9.044001 0.266 9.058001 C 0.18200001 8.974 0.18200001 8.68 0.266 8.596001 C 1.246 8.554 1.4840001 8.484 1.4840001 7.322 L 1.4840001 1.7080001 C 1.4840001 0.546 1.246 0.476 0.266 0.43400002 C 0.18200001 0.35000002 0.18200001 0.056 0.266 -0.028 C 0.81200004 -0.014 1.61 0 2.086 0 Z "/>
</symbol>
<symbol id="g2027E4E303C701A0DF6BD0919BBDE7B4" overflow="visible">
<path d="M 0.67200005 1.932 C 0.72800004 1.246 0.77000004 0.588 0.77000004 0 C 0.91 0.028 1.0500001 0.042000003 1.12 0.042000003 C 1.218 0.042000003 1.302 0.042000003 1.4000001 0.014 C 1.778 -0.08400001 2.1560001 -0.14 2.674 -0.14 C 3.4580002 -0.14 4.9 0.238 4.9 1.6240001 C 4.9 2.576 4.214 3.1360002 3.262 3.486 C 2.4220002 3.808 1.8620001 4.018 1.8620001 4.788 C 1.8620001 5.362 2.3660002 5.684 2.842 5.684 C 3.15 5.684 3.9620001 5.572 4.144 4.382 C 4.228 4.2980003 4.5080004 4.3120003 4.592 4.396 C 4.6340003 4.9 4.662 5.418 4.676 5.88 C 4.242 5.9500003 3.5700002 6.1460004 2.842 6.1460004 C 1.8060001 6.1460004 0.86800003 5.474 0.86800003 4.578 C 0.86800003 3.556 1.33 3.122 2.408 2.674 C 3.5700002 2.198 3.8360002 1.904 3.8360002 1.302 C 3.8360002 0.616 3.164 0.322 2.6460001 0.322 C 2.1000001 0.322 1.792 0.504 1.6520001 0.658 C 1.3440001 0.98 1.19 1.5960001 1.1060001 1.9460001 C 1.0220001 2.03 0.75600004 2.016 0.67200005 1.932 Z "/>
</symbol>
<symbol id="g1A68EE8359C8016621D122AFF85D0AB2" overflow="visible">
<path d="M 4.466 2.6460001 C 4.466 1.316 3.766 0.33600003 2.926 0.33600003 C 2.394 0.33600003 2.2120001 0.68600005 2.002 0.966 C 1.82 1.204 1.582 1.414 1.288 1.414 C 1.0220001 1.414 0.75600004 1.176 0.75600004 0.896 C 0.75600004 0.322 1.9460001 -0.154 2.7440002 -0.154 C 4.48 -0.154 5.7120004 1.1340001 5.7120004 2.898 C 5.7120004 4.256 4.774 5.474 3.206 5.474 C 2.604 5.474 2.086 5.348 1.8340001 5.25 L 2.114 7.5880003 C 2.632 7.532 3.0800002 7.4620004 3.752 7.4620004 C 4.172 7.4620004 4.6480002 7.4900002 5.222 7.546 L 5.446 8.498 L 5.348 8.554 C 4.55 8.47 3.7940001 8.400001 3.052 8.400001 C 2.5340002 8.400001 2.03 8.428 1.5400001 8.47 L 1.064 4.438 C 1.8060001 4.718 2.338 4.774 2.842 4.774 C 3.752 4.774 4.466 4.172 4.466 2.6460001 Z "/>
</symbol>
<symbol id="g41BD02C814E5F1F9CC57CE5A8E90AFBE" overflow="visible">
<path d="M 2.48 1.264 L 3.3600001 3.584 C 3.44 3.7920003 3.5360003 3.8560002 3.92 3.8560002 L 7.2960005 3.8560002 L 8.224 1.1520001 C 8.416 0.60800004 7.8080006 0.544 7.0400004 0.49600002 C 6.9440002 0.4 6.9440002 0.064 7.0400004 -0.032 C 7.6320004 -0.016 8.512 0 9.136001 0 C 9.792001 0 10.400001 -0.016 10.960001 -0.032 C 11.056001 0.064 11.056001 0.4 10.960001 0.49600002 C 10.336 0.56 9.792001 0.60800004 9.52 1.376 L 6.2240005 10.528001 C 5.984 10.384001 5.552 10.208 5.3440003 10.208 L 1.7120001 1.6320001 C 1.296 0.64000005 0.81600004 0.544 0.112 0.49600002 C 0.016 0.4 0.016 0.064 0.112 -0.032 C 0.528 -0.016 1.056 0 1.536 0 C 2.1920002 0 2.992 -0.016 3.584 -0.032 C 3.68 0.064 3.68 0.4 3.584 0.49600002 C 2.976 0.544 2.2240002 0.60800004 2.48 1.264 Z M 4.208 4.5280004 C 3.8560002 4.5280004 3.7440002 4.576 3.808 4.736 L 5.44 8.88 L 5.5360003 8.88 L 7.0400004 4.5280004 Z "/>
</symbol>
<symbol id="g48ABC493FE7862658825720022C8179D" overflow="visible">
<path d="M 6.064 0 C 6.064 0 6.432 1.536 6.544 2.2080002 C 6.4 2.288 6.2720003 2.3200002 6.096 2.272 C 5.84 1.3280001 5.3760004 0.544 4.368 0.544 L 3.6480002 0.544 C 3.2800002 0.544 3.0560002 0.8 3.0560002 1.1040001 L 3.0560002 5.4080005 C 3.0560002 6.7360005 3.232 6.7840004 4.208 6.8640003 C 4.3040004 6.9600005 4.3040004 7.2960005 4.208 7.392 C 3.6160002 7.3760004 2.96 7.36 2.4160001 7.36 C 1.9200001 7.36 1.2320001 7.3760004 0.64000005 7.392 C 0.544 7.2960005 0.544 6.9600005 0.64000005 6.8640003 C 1.616 6.8 1.792 6.7360005 1.792 5.4080005 L 1.792 1.9520001 C 1.792 0.624 1.7600001 0.544 0.64000005 0.49600002 C 0.544 0.4 0.544 0.064 0.64000005 -0.032 C 1.424 -0.016 2.48 0 2.48 0 Z "/>
</symbol>
<symbol id="g31FD4B68C132D0D1A1E4FD30ACE8848" overflow="visible">
<path d="M 7.5520005 1.4560001 C 7.5520005 2.7840002 7.6480002 2.832 8.144 2.9120002 C 8.240001 3.0080001 8.240001 3.344 8.144 3.44 C 7.8560004 3.4240003 7.4080005 3.4080002 6.912 3.4080002 C 6.432 3.4080002 5.696 3.4240003 5.2320004 3.44 C 5.136 3.344 5.136 3.0080001 5.2320004 2.9120002 C 6.208 2.848 6.288 2.7840002 6.288 1.4560001 L 6.288 0.592 C 5.7760005 0.448 5.248 0.36800003 4.688 0.36800003 C 2.6880002 0.36800003 2.032 2.4160001 2.032 3.7280002 C 2.032 5.664 2.96 6.992 4.4960003 6.992 C 6.0800004 6.992 6.7520003 6.1920004 6.992 5.168 C 7.1520004 5.1200004 7.3120003 5.1200004 7.472 5.216 C 7.4560003 5.872 7.4080005 6.544 7.2640004 7.2640004 C 6.7840004 7.2640004 5.6000004 7.5200005 4.704 7.5200005 C 2.4160001 7.5200005 0.592 6.0480003 0.592 3.5200002 C 0.592 1.488 2.112 -0.16000001 4.4 -0.16000001 C 5.4880004 -0.16000001 6.6720004 0 7.728 0.57600003 C 7.616 0.688 7.5520005 0.832 7.5520005 0.94400007 Z "/>
</symbol>
<symbol id="g99884B2AD96AC7B048FEEB28FC8E4747" overflow="visible">
<path d="M 8 5.4080005 C 8 6.7360005 8.176001 6.7840004 9.152 6.8640003 C 9.248 6.9600005 9.248 7.2960005 9.152 7.392 C 8.592 7.36 7.8880005 7.36 7.36 7.36 C 6.912 7.36 6.208 7.3760004 5.584 7.392 C 5.4880004 7.2960005 5.4880004 6.9600005 5.584 6.8640003 C 6.5600004 6.8 6.7360005 6.7360005 6.7360005 5.4080005 L 6.7360005 4.032 L 3.0400002 4.032 L 3.0400002 5.4080005 C 3.0400002 6.7360005 3.216 6.7840004 4.1920004 6.8640003 C 4.288 6.9600005 4.288 7.2960005 4.1920004 7.392 C 3.584 7.3760004 2.9120002 7.36 2.4 7.36 C 1.9200001 7.36 1.264 7.3760004 0.624 7.392 C 0.528 7.2960005 0.528 6.9600005 0.624 6.8640003 C 1.6 6.8 1.7760001 6.7360005 1.7760001 5.4080005 L 1.7760001 1.9520001 C 1.7760001 0.624 1.6 0.57600003 0.624 0.49600002 C 0.528 0.4 0.528 0.064 0.624 -0.032 C 1.264 -0.016 1.904 0 2.4160001 0 C 2.9280002 0 3.568 -0.016 4.1920004 -0.032 C 4.288 0.064 4.288 0.4 4.1920004 0.49600002 C 3.216 0.56 3.0400002 0.624 3.0400002 1.9520001 L 3.0400002 3.5040002 L 6.7360005 3.5040002 L 6.7360005 1.9520001 C 6.7360005 0.624 6.5600004 0.57600003 5.584 0.49600002 C 5.4880004 0.4 5.4880004 0.064 5.584 -0.032 C 6.176 -0.016 6.8160005 0 7.3760004 0 C 7.8560004 0 8.528001 -0.016 9.152 -0.032 C 9.248 0.064 9.248 0.4 9.152 0.49600002 C 8.176001 0.56 8 0.624 8 1.9520001 Z "/>
</symbol>
<symbol id="g20DDE86F15DD9C8B9599512790FC45E4" overflow="visible">
<path d="M 7.728 6.1120005 L 7.84 6.1120005 L 8.048 1.968 C 8.112 0.64000005 8.096001 0.57600003 7.2320004 0.49600002 C 7.136 0.4 7.136 0.064 7.2320004 -0.032 C 7.7920003 -0.016 8.384001 0 8.832001 0 C 9.312 0 9.776 -0.016 10.208 -0.032 C 10.304001 0.064 10.304001 0.4 10.208 0.49600002 C 9.392 0.57600003 9.376 0.67200005 9.280001 1.968 L 8.96 6.096 C 8.912001 6.7360005 9.056001 6.8 9.856001 6.8640003 C 9.952001 6.9600005 9.952001 7.2960005 9.856001 7.392 L 7.6960006 7.36 L 5.2960005 1.6320001 L 3.2480001 7.36 L 1.024 7.392 C 0.92800003 7.2960005 0.92800003 6.9600005 1.024 6.8640003 C 1.8080001 6.8160005 1.9520001 6.7360005 1.9200001 6.432 L 1.4080001 1.9360001 C 1.264 0.60800004 1.056 0.544 0.448 0.49600002 C 0.35200003 0.4 0.35200003 0.064 0.448 -0.032 C 0.768 -0.016 1.248 0 1.5040001 0 C 1.8240001 0 2.4160001 -0.016 2.736 -0.032 C 2.832 0.064 2.832 0.4 2.736 0.49600002 C 1.8240001 0.56 1.84 0.75200003 1.968 1.9360001 L 2.4320002 6.0000005 L 2.4640002 6.0000005 L 4.736 -0.064 C 4.768 -0.14400001 4.848 -0.192 4.9280005 -0.192 C 4.992 -0.192 5.072 -0.14400001 5.104 -0.064 Z "/>
</symbol>
<symbol id="gB81772063B54F81148CB0F3810A30A3E" overflow="visible">
<path d="M 2.3040001 5.4880004 C 2.736 6.9440002 3.7600002 8.56 5.8880005 9.360001 C 5.8880005 9.552 5.8240004 9.696 5.696 9.776 C 4.0800004 9.2960005 3.088 8.624001 2.1920002 7.5840006 C 1.2 6.432 0.70400006 4.9760003 0.70400006 3.7120001 C 0.70400006 0.46400002 2.5440001 -0.17600001 3.7760003 -0.17600001 C 5.872 -0.17600001 6.7360005 1.8560001 6.7360005 3.232 C 6.7360005 4.6080003 6.0000005 5.84 3.8240001 5.84 C 3.4080002 5.84 2.7840002 5.7120004 2.3040001 5.4880004 Z M 2.16 4.912 C 2.6880002 5.2640004 3.216 5.28 3.4880002 5.28 C 5.056 5.28 5.4080005 3.7440002 5.4080005 2.9440002 C 5.4080005 1.184 4.736 0.384 3.9520001 0.384 C 2.9440002 0.384 2.032 0.92800003 2.032 3.6640003 C 2.032 4.032 2.0640001 4.4480004 2.16 4.912 Z "/>
</symbol>
<symbol id="g54625A295C6156FB7E0CA1A81FF5B54D" overflow="visible">
<path d="M 1.5120001 -2.7020001 L 4.48 -2.7020001 C 4.564 -2.618 4.564 -2.3660002 4.48 -2.282 C 2.548 -2.128 2.45 -1.9180001 2.45 -0.70000005 L 2.45 7.854 C 2.45 9.0720005 2.562 9.282001 4.48 9.422 C 4.564 9.5060005 4.564 9.758 4.48 9.842 L 1.5120001 9.842 Z "/>
</symbol>
<symbol id="gCA97BC07D124B95C474D25CFC2493057" overflow="visible">
<path d="M 2.17 1.1060001 L 2.94 3.1360002 C 3.01 3.318 3.094 3.374 3.43 3.374 L 6.3840003 3.374 L 7.196 1.008 C 7.3640003 0.532 6.8320003 0.476 6.1600003 0.43400002 C 6.076 0.35000002 6.076 0.056 6.1600003 -0.028 C 6.678 -0.014 7.4480004 0 7.9940004 0 C 8.568 0 9.1 -0.014 9.59 -0.028 C 9.674001 0.056 9.674001 0.35000002 9.59 0.43400002 C 9.044001 0.49 8.568 0.532 8.33 1.204 L 5.446 9.212 C 5.236 9.086 4.8580003 8.932 4.676 8.932 L 1.498 1.4280001 C 1.1340001 0.56 0.71400005 0.476 0.098000005 0.43400002 C 0.014 0.35000002 0.014 0.056 0.098000005 -0.028 C 0.462 -0.014 0.924 0 1.3440001 0 C 1.9180001 0 2.618 -0.014 3.1360002 -0.028 C 3.22 0.056 3.22 0.35000002 3.1360002 0.43400002 C 2.604 0.476 1.9460001 0.532 2.17 1.1060001 Z M 3.6820002 3.9620001 C 3.374 3.9620001 3.276 4.004 3.332 4.144 L 4.76 7.7700005 L 4.8440003 7.7700005 L 6.1600003 3.9620001 Z "/>
</symbol>
<symbol id="gEABB154513753541217365D535D0C073" overflow="visible">
<path d="M 6.216 5.418 C 6.4820004 5.418 6.734 5.67 6.734 5.9500003 C 6.734 6.244 6.4680004 6.4680004 6.09 6.4680004 C 5.7260003 6.4680004 5.0540004 6.23 4.69 5.754 C 4.5220003 5.866 4.06 6.1460004 3.2340002 6.1460004 C 1.988 6.1460004 0.84000003 5.306 0.84000003 4.018 C 0.84000003 3.262 1.176 2.828 1.5680001 2.45 C 1.176 2.114 0.952 1.5120001 0.952 1.036 C 0.952 0.532 1.232 0.14 1.5960001 -0.042000003 C 0.84000003 -0.49 0.448 -1.1340001 0.448 -1.7360001 C 0.448 -2.954 1.5960001 -3.332 2.674 -3.332 C 4.564 -3.332 6.6080003 -2.4220002 6.6080003 -0.91 C 6.6080003 -0.462 6.3980002 -0.112 5.992 0.224 C 5.446 0.67200005 4.466 0.68600005 3.9480002 0.68600005 C 3.696 0.68600005 3.3460002 0.658 3.01 0.616 C 2.8000002 0.602 2.66 0.588 2.5900002 0.588 C 2.184 0.588 1.694 0.78400004 1.694 1.386 C 1.694 1.666 1.778 1.96 1.9460001 2.198 C 2.282 2.002 2.674 1.904 3.22 1.904 C 4.452 1.904 5.586 2.674 5.586 4.046 C 5.586 4.704 5.3900003 5.0820003 4.984 5.5020003 C 5.0820003 5.642 5.362 5.8380003 5.544 5.8380003 C 5.642 5.8380003 5.7400002 5.796 5.8240004 5.67 C 5.88 5.558 6.0620003 5.418 6.216 5.418 Z M 1.848 -0.14 C 2.002 -0.18200001 2.226 -0.21000001 2.408 -0.21000001 C 2.842 -0.21000001 3.2340002 -0.16800001 3.43 -0.16800001 C 4.13 -0.16800001 4.718 -0.18200001 5.124 -0.40600002 C 5.67 -0.71400005 5.8380003 -0.91 5.8380003 -1.274 C 5.8380003 -2.282 4.354 -2.8140001 3.094 -2.8140001 C 2.5900002 -2.8140001 1.414 -2.408 1.414 -1.4560001 C 1.414 -0.98 1.442 -0.63 1.848 -0.14 Z M 4.466 3.9060001 C 4.466 2.604 3.808 2.338 3.2900002 2.338 C 2.114 2.338 1.988 3.332 1.988 4.228 C 1.988 5.208 2.338 5.7120004 3.108 5.7120004 C 3.99 5.7120004 4.466 5.0680003 4.466 3.9060001 Z "/>
</symbol>
<symbol id="gD8D2A5E78EA4643EEAAC69DB934A336F" overflow="visible">
<path d="M 4.032 1.7080001 L 4.032 6.566 C 4.032 7.406 4.046 8.26 4.0740004 8.442 C 4.0740004 8.512 4.046 8.512 3.99 8.512 C 3.22 8.036 2.4780002 7.6860003 1.246 7.112 C 1.274 6.958 1.33 6.8180003 1.4560001 6.734 C 2.1000001 7 2.408 7.084 2.674 7.084 C 2.9120002 7.084 2.954 6.748 2.954 6.2720003 L 2.954 1.7080001 C 2.954 0.546 2.576 0.476 1.5960001 0.43400002 C 1.5120001 0.35000002 1.5120001 0.056 1.5960001 -0.028 C 2.282 -0.014 2.786 0 3.542 0 C 4.214 0 4.55 -0.014 5.25 -0.028 C 5.334 0.056 5.334 0.35000002 5.25 0.43400002 C 4.27 0.476 4.032 0.546 4.032 1.7080001 Z "/>
</symbol>
<symbol id="g202FAE631B7A80A660AEE76AD2161E37" overflow="visible">
<path d="M 3.4720001 9.856 L 0.504 9.856 C 0.42000002 9.772 0.42000002 9.52 0.504 9.436 C 2.436 9.282001 2.5340002 9.0720005 2.5340002 7.854 L 2.5340002 -0.70000005 C 2.5340002 -1.9180001 2.4220002 -2.128 0.504 -2.2680001 C 0.42000002 -2.352 0.42000002 -2.604 0.504 -2.6880002 L 3.4720001 -2.6880002 Z "/>
</symbol>
<symbol id="g176D627313BEF56D87624592E290FFD2" overflow="visible">
<path d="M 4.998 -0.14 C 6.3560004 -0.14 7.602 0.504 8.554 1.75 C 8.484 1.876 8.386001 1.96 8.232 1.96 C 7.2380004 0.86800003 6.2860003 0.43400002 4.984 0.43400002 C 3.094 0.43400002 1.792 2.562 1.792 4.606 C 1.792 5.81 2.114 6.8180003 2.618 7.4480004 C 3.318 8.302 4.13 8.694 4.8580003 8.694 C 6.7900004 8.694 7.5600004 7.546 7.9240003 6.342 C 8.092 6.2860003 8.232 6.328 8.386001 6.412 C 8.316 7.1400003 8.218 7.8120003 8.078 8.582001 C 7.3640003 8.652 6.734 9.212 5.012 9.212 C 3.822 9.212 2.828 8.778 2.002 8.022 C 1.0780001 7.168 0.518 5.796 0.518 4.34 C 0.518 1.904 1.988 -0.14 4.998 -0.14 Z "/>
</symbol>
<symbol id="g77113E0CAAA23E0B77E89A338ACC30A4" overflow="visible">
<path d="M 2.576 5.012 C 2.492 4.914 2.408 4.886 2.408 5.012 C 2.394 5.3900003 2.3660002 5.9360003 2.296 6.076 C 2.2680001 6.1460004 2.24 6.188 2.128 6.188 C 1.7360001 6.0340004 1.3720001 5.908 0.40600002 5.782 C 0.37800002 5.698 0.40600002 5.474 0.43400002 5.3900003 C 1.19 5.32 1.3440001 5.25 1.3440001 4.438 L 1.3440001 1.7080001 C 1.3440001 0.56 1.204 0.504 0.36400002 0.43400002 C 0.28 0.35000002 0.28 0.056 0.36400002 -0.028 C 0.78400004 -0.014 1.3440001 0 1.904 0 C 2.464 0 2.884 -0.014 3.3040001 -0.028 C 3.388 0.056 3.388 0.35000002 3.3040001 0.43400002 C 2.5900002 0.504 2.45 0.56 2.45 1.7080001 L 2.45 4.004 C 2.45 4.2980003 2.576 4.466 2.6880002 4.592 C 3.22 5.11 3.8500001 5.418 4.396 5.418 C 4.676 5.418 4.9700003 5.236 5.138 4.914 C 5.2780004 4.6340003 5.306 4.256 5.306 3.8360002 L 5.306 1.7080001 C 5.306 0.56 5.1660004 0.504 4.438 0.43400002 C 4.368 0.35000002 4.368 0.056 4.438 -0.028 C 4.8580003 -0.014 5.306 0 5.866 0 C 6.426 0 6.9300003 -0.014 7.3500004 -0.028 C 7.42 0.056 7.42 0.35000002 7.3500004 0.43400002 C 6.566 0.504 6.412 0.56 6.412 1.7080001 L 6.412 3.7940001 C 6.412 4.564 6.3560004 5.236 6.0340004 5.67 C 5.796 5.978 5.362 6.1460004 4.872 6.1460004 C 4.1860003 6.1460004 3.4020002 5.964 2.576 5.012 Z "/>
</symbol>
<symbol id="g9928BAA4F6AD9C2CD04BDE4A0594D984" overflow="visible">
<path d="M 3.038 -0.14 C 3.584 -0.14 4.242 0.14 4.928 0.70000005 C 4.998 0.75600004 5.124 0.78400004 5.138 0.68600005 C 5.1800003 0.33600003 5.2920003 -0.14 5.2920003 -0.14 C 5.4040003 -0.18200001 5.474 -0.16800001 5.558 -0.14 C 5.866 0.112 6.3560004 0.322 7.21 0.42000002 C 7.294 0.504 7.294 0.71400005 7.21 0.79800004 C 6.314 0.86800003 6.188 1.1340001 6.188 1.82 L 6.188 4.5080004 C 6.188 4.928 6.244 5.9500003 6.244 5.9500003 C 6.244 5.992 6.202 6.0340004 6.132 6.0340004 C 6.0620003 6.02 5.852 6.006 5.642 6.006 C 5.1940002 6.006 4.69 6.02 4.214 6.0340004 C 4.13 5.9500003 4.13 5.656 4.214 5.572 C 4.9 5.53 5.0820003 5.362 5.0820003 4.438 L 5.0820003 1.7360001 C 5.0820003 1.47 5.0540004 1.358 4.8580003 1.19 C 4.34 0.74200004 3.808 0.518 3.4580002 0.518 C 3.038 0.518 2.338 0.71400005 2.338 1.96 L 2.338 4.5080004 C 2.338 4.928 2.394 5.9500003 2.394 5.9500003 C 2.394 5.992 2.352 6.0340004 2.282 6.0340004 C 2.2120001 6.02 2.002 6.006 1.792 6.006 C 1.3440001 6.006 0.84000003 6.02 0.36400002 6.0340004 C 0.28 5.9500003 0.28 5.656 0.36400002 5.572 C 1.036 5.5160003 1.232 5.362 1.232 4.452 L 1.232 1.764 C 1.232 0.79800004 1.6520001 -0.14 3.038 -0.14 Z "/>
</symbol>
<symbol id="g5D527560B31964E4713419A527341CBD" overflow="visible">
<path d="M 5.572 1.274 C 5.5160003 1.4000001 5.4040003 1.4560001 5.2780004 1.47 C 4.802 0.85400003 4.2000003 0.546 3.598 0.546 C 2.576 0.546 1.722 1.582 1.722 3.22 C 1.722 4.76 2.394 5.684 3.318 5.684 C 4.144 5.684 4.256 5.1940002 4.3120003 4.704 C 4.354 4.326 4.55 4.2000003 4.8440003 4.2000003 C 5.138 4.2000003 5.53 4.382 5.53 4.816 C 5.53 5.586 4.7320004 6.1460004 3.388 6.1460004 C 2.002 6.1460004 0.518 4.9 0.518 2.9120002 C 0.518 1.1060001 1.526 -0.14 3.2900002 -0.14 C 4.13 -0.14 4.872 0.126 5.572 1.274 Z "/>
</symbol>
<symbol id="g68885674EB6A8B1A6039D4F45B463C56" overflow="visible">
<path d="M 2.38 7.4900002 L 4.886 7.4900002 C 3.7940001 4.774 2.6880002 2.0440001 1.7360001 -0.08400001 L 1.848 -0.18200001 L 2.8000002 -0.14 C 3.598 2.24 4.368 4.564 5.9360003 8.386001 L 5.7120004 8.554 C 5.474 8.484 5.1660004 8.400001 4.6340003 8.400001 L 1.75 8.400001 C 1.274 8.400001 1.302 8.54 1.0500001 8.596001 C 1.008 8.596001 0.994 8.596001 0.994 8.554 C 0.98 7.8820004 0.82600003 7.0420003 0.71400005 6.314 C 0.86800003 6.2720003 1.008 6.2580004 1.1620001 6.2720003 C 1.47 7.392 1.932 7.4900002 2.38 7.4900002 Z "/>
</symbol>
<symbol id="g634FF9E9D0A0144E2AFDD807D5ECB7D0" overflow="visible">
<path d="M 5.4040003 1.302 C 4.886 0.77000004 4.48 0.546 3.6680002 0.546 C 3.164 0.546 2.576 0.84000003 2.142 1.554 C 1.8620001 2.016 1.694 2.66 1.694 3.4720001 L 5.418 3.444 C 5.586 3.444 5.684 3.528 5.684 3.6820002 C 5.684 4.8580003 5.264 6.118 3.318 6.118 C 2.1000001 6.118 0.518 4.9560003 0.518 2.828 C 0.518 2.0440001 0.71400005 1.288 1.176 0.75600004 C 1.6520001 0.19600001 2.3100002 -0.14 3.318 -0.14 C 4.382 -0.14 5.138 0.35000002 5.698 1.0780001 C 5.656 1.218 5.572 1.288 5.4040003 1.302 Z M 1.7360001 3.9480002 C 2.002 5.53 2.982 5.656 3.318 5.656 C 3.8500001 5.656 4.48 5.362 4.48 4.1860003 C 4.48 4.06 4.4240003 3.99 4.27 3.99 Z "/>
</symbol>
<symbol id="gD0DD0C2B056F25673B3EED0135505F92" overflow="visible">
<path d="M 2.338 4.004 C 2.338 4.2980003 2.464 4.466 2.576 4.592 C 3.108 5.11 3.822 5.418 4.368 5.418 C 4.6480002 5.418 4.9420004 5.236 5.11 4.914 C 5.25 4.6340003 5.2780004 4.256 5.2780004 3.8360002 L 5.2780004 1.7080001 C 5.2780004 0.56 5.138 0.504 4.4100003 0.43400002 C 4.34 0.35000002 4.34 0.056 4.4100003 -0.028 C 4.802 -0.014 5.2780004 0 5.8380003 0 C 6.3980002 0 6.86 -0.014 7.322 -0.028 C 7.392 0.056 7.392 0.35000002 7.322 0.43400002 C 6.538 0.504 6.3840003 0.56 6.3840003 1.7080001 L 6.3840003 3.7940001 C 6.3840003 4.564 6.328 5.25 6.006 5.67 C 5.768 5.978 5.334 6.1460004 4.8440003 6.1460004 C 4.158 6.1460004 3.318 5.964 2.464 5.012 C 2.464 4.998 2.45 4.998 2.436 4.984 C 2.394 4.928 2.3240001 4.8440003 2.3240001 5.012 L 2.338 8.162001 C 2.338 9.0720005 2.394 9.632 2.394 9.632 C 2.394 9.7300005 2.338 9.772 2.2120001 9.772 C 1.8620001 9.632 0.81200004 9.436 0.252 9.394 C 0.224 9.282001 0.252 9.058001 0.33600003 8.974 C 0.37800002 8.974 0.42000002 8.974 0.462 8.974 C 1.0780001 8.932 1.232 8.932 1.232 7.826 L 1.232 1.7080001 C 1.232 0.546 1.064 0.49 0.252 0.43400002 C 0.16800001 0.35000002 0.16800001 0.056 0.252 -0.028 C 0.71400005 -0.014 1.232 0 1.792 0 C 2.3240001 0 2.786 -0.014 3.1780002 -0.028 C 3.262 0.056 3.262 0.35000002 3.1780002 0.43400002 C 2.464 0.49 2.338 0.546 2.338 1.7080001 Z "/>
</symbol>
<symbol id="gB1BEBEB6281B0C94AE56C4BB0BF6ED0C" overflow="visible">
<path d="M 4.578 3.584 C 4.2000003 2.3100002 3.3040001 0.896 1.442 0.19600001 C 1.442 0.028 1.498 -0.098000005 1.61 -0.16800001 C 3.0240002 0.252 3.8920002 0.84000003 4.676 1.75 C 5.544 2.7580001 5.978 4.032 5.978 5.138 C 5.978 7.98 4.368 8.54 3.2900002 8.54 C 1.4560001 8.54 0.70000005 6.762 0.70000005 5.558 C 0.70000005 4.354 1.3440001 3.276 3.2480001 3.276 C 3.6120002 3.276 4.158 3.388 4.578 3.584 Z M 4.704 4.0880003 C 4.242 3.7800002 3.7800002 3.766 3.542 3.766 C 2.17 3.766 1.8620001 5.11 1.8620001 5.81 C 1.8620001 7.3500004 2.45 8.05 3.1360002 8.05 C 4.018 8.05 4.816 7.5740004 4.816 5.1800003 C 4.816 4.872 4.788 4.494 4.704 4.0880003 Z "/>
</symbol>
<symbol id="gC9680074409574DDF948104B0C55D755" overflow="visible">
<path d="M 3.1920002 -0.14 C 4.27 -0.14 5.908 0.952 5.908 4.242 C 5.908 5.6280003 5.572 6.8180003 4.9560003 7.63 C 4.592 8.12 4.004 8.54 3.2480001 8.54 C 1.8620001 8.54 0.546 6.888 0.546 4.116 C 0.546 2.618 1.008 1.218 1.778 0.448 C 2.17 0.056 2.6460001 -0.14 3.1920002 -0.14 Z M 3.2480001 8.05 C 3.486 8.05 3.71 7.966 3.878 7.8120003 C 4.3120003 7.4480004 4.69 6.3840003 4.69 4.5080004 C 4.69 3.22 4.6480002 2.338 4.452 1.6240001 C 4.144 0.476 3.4580002 0.35000002 3.206 0.35000002 C 1.904 0.35000002 1.764 2.7440002 1.764 3.9620001 C 1.764 7.406 2.618 8.05 3.2480001 8.05 Z "/>
</symbol>
<symbol id="g89D0CDE21020452133A6A28D357E8121" overflow="visible">
<path d="M 2.508 11.506 L 2.508 2.684 C 2.508 0.858 1.892 0.77 0.682 0.704 C 0.462 0.572 0.462 0.088 0.682 -0.044 C 1.562 -0.022 3.19 0 4.07 0 C 4.95 0 6.534 -0.022 7.414 -0.044 C 7.634 0.088 7.634 0.572 7.414 0.704 C 6.204 0.77 5.588 0.858 5.588 2.684 L 5.588 11.506 C 5.588 13.332 6.204 13.42 7.414 13.486 C 7.634 13.618 7.634 14.102 7.414 14.234 C 6.534 14.212 4.95 14.19 4.07 14.19 C 3.19 14.19 1.562 14.212 0.682 14.234 C 0.462 14.102 0.462 13.618 0.682 13.486 C 1.892 13.42 2.508 13.332 2.508 11.506 Z "/>
</symbol>
<symbol id="gDC8BE94E2F4CFB356B16F8B3BD0C3FF6" overflow="visible">
<path d="M 10.516 8.404 L 10.559999 8.404 L 10.846 2.706 C 10.934 0.88 10.912 0.814 9.724 0.704 C 9.592 0.572 9.592 0.088 9.724 -0.044 C 10.582 -0.022 11.726 0 12.342 0 C 13.002 0 14.146 -0.022 14.894 -0.044 C 15.026 0.088 15.026 0.572 14.894 0.704 C 13.97 0.83599997 13.75 0.924 13.618 2.706 L 13.1779995 8.47 C 13.1119995 9.24 13.309999 9.328 14.41 9.416 C 14.542 9.548 14.542 10.032 14.41 10.164 L 10.142 10.12 L 7.7 4.07 L 7.546 4.07 L 5.346 10.12 L 1.188 10.164 C 1.056 10.032 1.056 9.548 1.188 9.416 C 2.046 9.35 2.442 9.064 2.376 8.58 L 1.716 2.662 C 1.518 0.83599997 1.232 0.77 0.396 0.704 C 0.264 0.572 0.264 0.088 0.396 -0.044 C 0.88 -0.022 1.518 0 2.068 0 C 2.728 0 3.322 -0.022 3.762 -0.044 C 3.894 0.088 3.894 0.572 3.762 0.704 C 2.508 0.792 2.53 1.034 2.706 2.662 L 3.3 7.832 L 3.322 7.832 L 6.292 -0.088 C 6.336 -0.198 6.5559998 -0.264 6.666 -0.264 C 6.754 -0.264 6.974 -0.198 7.018 -0.088 Z "/>
</symbol>
<symbol id="gE5D1277DA16394E659B333D1EA421088" overflow="visible">
<path d="M 5.434 2.794 L 5.434 4.334 C 5.8519998 4.158 6.754 4.092 7.304 4.092 C 10.4279995 4.092 11.572 6.05 11.572 7.59 C 11.572 8.228 11.33 9.13 10.582 9.68 C 9.966 10.12 8.998 10.274 7.59 10.274 C 6.776 10.274 4.62 10.12 4.004 10.12 C 2.794 10.12 1.826 10.142 0.88 10.164 C 0.748 10.032 0.748 9.548 0.88 9.416 C 2.222 9.35 2.574 9.152 2.574 7.3259997 L 2.574 2.794 C 2.574 0.968 2.222 0.77 0.88 0.704 C 0.748 0.572 0.748 0.088 0.88 -0.044 C 1.804 -0.022 2.794 0 4.004 0 C 5.2139997 0 6.182 -0.022 7.128 -0.044 C 7.2599998 0.088 7.2599998 0.572 7.128 0.704 C 5.786 0.77 5.434 0.968 5.434 2.794 Z M 5.434 9.284 C 5.786 9.372 6.424 9.394 6.732 9.394 C 7.942 9.394 8.492 8.602 8.492 7.216 C 8.492 5.984 8.162 4.972 6.842 4.972 C 6.402 4.972 5.896 4.994 5.434 5.17 Z "/>
</symbol>
<symbol id="g6724C1A826126332467C6264F812F404" overflow="visible">
<path d="M 5.368 2.794 L 5.368 4.554 C 5.588 4.576 5.9179997 4.554 6.292 4.356 C 6.402 4.29 6.5559998 4.092 6.71 3.85 L 8.118 1.606 C 8.734 0.682 9.834 -0.198 11.066 -0.198 C 11.88 -0.198 12.518 -0.154 12.716 -0.044 C 12.782 0.088 12.782 0.506 12.694 0.65999997 C 12.1 0.792 11.44 1.3199999 11 2.002 L 9.35 4.532 C 9.284 4.642 9.196 4.752 9.174 4.84 C 10.846 5.368 11.572 6.468 11.572 7.59 C 11.572 8.734 10.714 10.274 7.59 10.274 C 6.776 10.274 4.62 10.12 4.004 10.12 C 2.794 10.12 1.826 10.142 0.88 10.164 C 0.748 10.032 0.748 9.548 0.88 9.416 C 2.222 9.35 2.574 9.152 2.574 7.3259997 L 2.574 2.794 C 2.574 0.968 2.222 0.77 0.88 0.704 C 0.748 0.572 0.748 0.088 0.88 -0.044 C 1.804 -0.022 2.794 0 4.004 0 C 5.148 0 5.962 -0.022 6.6879997 -0.044 C 6.82 0.088 6.82 0.572 6.6879997 0.704 C 5.786 0.792 5.368 0.968 5.368 2.794 Z M 5.368 9.306 C 5.72 9.394 6.424 9.416 6.732 9.416 C 7.942 9.416 8.492 8.602 8.492 7.216 C 8.492 5.39 7.172 5.2799997 5.368 5.2799997 Z "/>
</symbol>
<symbol id="gFFAD8ECF2B9E19A17BA2A700D6B3A275" overflow="visible">
<path d="M 12.122 5.17 C 12.122 8.712 9.702 10.4279995 6.402 10.4279995 C 3.322 10.4279995 0.83599997 8.382 0.83599997 4.884 C 0.83599997 1.3199999 3.454 -0.22 6.424 -0.22 C 9.68 -0.22 12.122 1.562 12.122 5.17 Z M 6.358 9.548 C 8.514 9.548 9.042 8.14 9.042 4.862 C 9.042 2.068 8.316 0.65999997 6.534 0.65999997 C 4.62 0.65999997 3.916 2.112 3.916 5.148 C 3.916 8.448 4.708 9.548 6.358 9.548 Z "/>
</symbol>
<symbol id="g7D577C5B3423E584E3CA9C0C61B45B28" overflow="visible">
<path d="M 8.272 9.416 C 9.46 9.328 9.614 8.976 9.13 7.854 L 7.172 3.366 C 7.084 3.168 6.996 3.322 6.93 3.476 L 5.258 7.854 C 4.862 8.91 4.73 9.284 5.94 9.416 C 6.072 9.548 6.072 10.032 5.94 10.164 C 5.126 10.142 4.246 10.12 3.168 10.12 C 2.398 10.12 1.144 10.142 0.32999998 10.164 C 0.198 10.032 0.198 9.548 0.32999998 9.416 C 1.43 9.24 1.628 8.822 2.09 7.722 L 5.346 0.198 C 5.478 -0.132 5.8519998 -0.264 6.138 -0.264 C 6.358 -0.264 6.798 -0.22 6.996 0.242 L 10.274 7.7 C 10.714 8.69 11 9.306 12.166 9.416 C 12.298 9.548 12.298 10.032 12.166 10.164 C 11.682 10.142 11.286 10.12 10.714 10.12 C 9.9 10.12 9.0859995 10.142 8.272 10.164 C 8.14 10.032 8.14 9.548 8.272 9.416 Z "/>
</symbol>
<symbol id="g2C79506DA740817B2A33371C9D8B3CE4" overflow="visible">
<path d="M 6.05 5.83 L 5.566 5.83 L 5.566 8.118 C 5.566 8.646 6.028 9.196 6.5559998 9.196 L 7.59 9.196 C 9.24 9.196 9.768 8.36 10.252 6.842 C 10.516 6.798 10.912 6.842 11.132 6.952 C 11.066 7.898 10.846 9.966 10.802 10.142 C 10.802 10.186 10.78 10.208 10.714 10.208 C 10.34 10.142 10.164 10.12 9.636 10.12 L 4.268 10.12 C 4.268 10.12 1.98 10.142 0.88 10.164 C 0.748 10.032 0.748 9.548 0.88 9.416 C 2.42 9.35 2.794 9.24 2.794 7.414 L 2.794 2.684 C 2.794 0.858 2.42 0.77 0.88 0.704 C 0.748 0.572 0.748 0.088 0.88 -0.044 C 1.958 -0.022 4.29 0 4.29 0 L 7.942 0 C 8.998 0 10.912 -0.044 10.912 -0.044 C 11.22 1.056 11.418 2.486 11.572 3.6299999 C 11.352 3.762 10.934 3.806 10.648 3.74 C 10.208 2.156 9.152 0.924 7.48 0.924 L 6.5559998 0.924 C 6.072 0.924 5.566 1.166 5.566 2.42 L 5.566 5.082 L 6.05 5.082 C 7.568 5.082 7.942 4.884 8.008 3.894 C 8.14 3.762 8.756 3.762 8.888 3.894 C 8.866 4.466 8.844 5.126 8.844 5.478 C 8.844 5.786 8.844 6.644 8.888 7.018 C 8.756 7.15 8.14 7.15 8.008 7.018 C 7.942 5.874 7.524 5.83 6.05 5.83 Z "/>
</symbol>
<symbol id="g14B71EE4190EC9CF4EC86C87E0E47E9A" overflow="visible">
<path d="M 8.976 0.704 C 9.394 0.154 9.856 -0.264 9.856 -0.264 C 10.626 -0.264 11.682 -0.198 12.078 0 C 12.078 0 11.968 1.562 11.968 2.244 L 11.968 7.436 C 11.968 9.262 12.21 9.306 13.552 9.416 C 13.684 9.548 13.684 10.032 13.552 10.164 C 12.892 10.142 12.1 10.12 11.44 10.12 C 10.78 10.12 9.79 10.142 9.13 10.164 C 8.998 10.032 8.998 9.548 9.13 9.416 C 10.472 9.328 10.714 9.262 10.714 7.436 L 10.714 3.322 C 10.714 2.992 10.626 2.97 10.406 3.2779999 L 5.368 10.12 L 0.924 10.164 C 0.792 10.01 0.792 9.57 0.924 9.416 C 1.782 9.394 2.112 9.042 2.376 8.712 L 2.376 2.684 C 2.376 0.858 2.134 0.792 0.792 0.704 C 0.65999997 0.572 0.65999997 0.088 0.792 -0.044 C 1.452 -0.022 2.442 0 3.102 0 C 3.762 0 4.554 -0.022 5.2139997 -0.044 C 5.346 0.088 5.346 0.572 5.2139997 0.704 C 3.872 0.814 3.6299999 0.858 3.6299999 2.684 L 3.6299999 6.864 C 3.6299999 7.876 3.696 7.788 4.114 7.216 C 4.136 7.194 4.18 7.15 4.202 7.106 Z "/>
</symbol>
<symbol id="gD56DD9CEC6529211EE0EE20264633A82" overflow="visible">
<path d="M 7.876 2.9259999 L 7.876 7.15 C 7.876 8.998 7.9639997 9.24 8.932 9.24 C 10.604 9.24 10.868 8.69 11.242 6.974 C 11.484 6.974 11.901999 6.996 12.1 7.084 C 11.946 8.096 11.8359995 9.24 11.814 10.23 C 11.814 10.252 11.7699995 10.296 11.748 10.296 C 11 10.23 9.24 10.12 7.502 10.12 L 5.2799997 10.12 C 3.586 10.12 2.09 10.23 1.254 10.296 C 1.21 10.296 1.166 10.252 1.166 10.23 C 1.078 9.24 0.858 8.074 0.616 7.018 C 0.83599997 6.93 1.21 6.908 1.474 6.908 C 1.914 8.668 2.156 9.24 3.608 9.24 C 4.906 9.24 5.104 8.888 5.104 7.216 L 5.104 2.9259999 C 5.104 1.1 4.906 0.77 3.146 0.704 C 3.014 0.572 3.014 0.088 3.146 -0.044 C 4.224 -0.022 5.302 0 6.446 0 C 7.612 0 8.734 -0.022 9.834 -0.044 C 9.966 0.088 9.966 0.572 9.834 0.704 C 8.074 0.77 7.876 1.1 7.876 2.9259999 Z "/>
</symbol>
<symbol id="gDC78B3846EDAB84D21B8DADC57D4B72" overflow="visible">
<path d="M 1.078 1.276 C 1.078 0.44 1.782 -0.22 2.662 -0.22 C 3.542 -0.22 4.29 0.484 4.29 1.3199999 C 4.29 2.178 3.586 2.838 2.706 2.838 C 1.826 2.838 1.078 2.134 1.078 1.276 Z "/>
</symbol>
<symbol id="g9395E96C48DADE2CF7A23A407777B6BB" overflow="visible">
<path d="M 8.074 2.684 L 8.074 10.626 C 8.074 11.792 8.25 13.046 8.25 13.046 C 8.25 13.332 8.074 13.42 7.876 13.42 C 7.656 13.42 7.282 13.332 6.776 13.09 C 5.434 12.474 3.938 11.946 2.024 11.154 C 2.046 10.78 2.2 10.4279995 2.508 10.208 C 3.696 10.714 4.488 10.758 4.796 10.758 C 5.082 10.758 5.2139997 10.67 5.2139997 9.57 L 5.2139997 2.684 C 5.2139997 0.858 4.158 0.77 2.948 0.704 C 2.728 0.572 2.728 0.088 2.948 -0.044 C 4.752 -0.022 5.786 0 6.666 0 C 7.546 0 8.536 -0.022 10.34 -0.044 C 10.559999 0.088 10.559999 0.572 10.34 0.704 C 9.13 0.77 8.074 0.858 8.074 2.684 Z "/>
</symbol>
<symbol id="gFBB69929369BF0EC60A13F790CB240F" overflow="visible">
<path d="M 5.7120004 -0.16000001 C 7.2640004 -0.16000001 8.688001 0.57600003 9.776 2 C 9.696 2.144 9.584001 2.24 9.408 2.24 C 8.272 0.99200004 7.1840005 0.49600002 5.696 0.49600002 C 3.5360003 0.49600002 2.048 2.9280002 2.048 5.2640004 C 2.048 6.6400003 2.4160001 7.7920003 2.992 8.512 C 3.7920003 9.488001 4.7200003 9.936001 5.552 9.936001 C 7.76 9.936001 8.64 8.624001 9.056001 7.248 C 9.248 7.1840005 9.408 7.2320004 9.584001 7.3280005 C 9.504001 8.160001 9.392 8.928 9.232 9.808001 C 8.416 9.8880005 7.6960006 10.528001 5.728 10.528001 C 4.368 10.528001 3.232 10.032001 2.288 9.168 C 1.2320001 8.192 0.592 6.6240005 0.592 4.96 C 0.592 2.176 2.272 -0.16000001 5.7120004 -0.16000001 Z "/>
</symbol>
<symbol id="gB9A2E3AAC6CC7A3D99F4D7199A710CE2" overflow="visible">
<path d="M 0.656 3.2800002 C 0.656 1.6480001 1.7440001 -0.16000001 4.0160003 -0.16000001 C 5.0400004 -0.16000001 5.8240004 0.208 6.3680005 0.73600006 C 7.0880003 1.44 7.4080005 2.4480002 7.4080005 3.4240003 C 7.4080005 5.0880003 6.4960003 7.024 4.0480003 7.024 C 2.992 7.024 2.128 6.5920005 1.536 5.9040003 C 0.96000004 5.216 0.656 4.288 0.656 3.2800002 Z M 3.808 6.464 C 5.184 6.464 6.032 5.216 6.032 2.9120002 C 6.032 0.896 4.992 0.4 4.2400002 0.4 C 2.5760002 0.4 2.032 2.4160001 2.032 3.6480002 C 2.032 5.0400004 2.368 6.464 3.808 6.464 Z "/>
</symbol>
<symbol id="g20C5113AFEA5FF7C7B1ACED872A410C0" overflow="visible">
<path d="M 2.72 5.728 C 2.7040002 6.208 2.6720002 6.7840004 2.592 6.9440002 C 2.5600002 7.024 2.528 7.0720005 2.4 7.0720005 C 1.9520001 6.8960004 1.536 6.7520003 0.432 6.6080003 C 0.4 6.512 0.432 6.2560005 0.46400002 6.1600003 C 1.3280001 6.0800004 1.5040001 6.0000005 1.5040001 5.072 L 1.5040001 1.9520001 C 1.5040001 0.64000005 1.296 0.56 0.416 0.49600002 C 0.32000002 0.4 0.32000002 0.064 0.416 -0.032 C 0.896 -0.016 1.5040001 0 2.144 0 C 2.7840002 0 3.2800002 -0.016 3.7600002 -0.032 C 3.8560002 0.064 3.8560002 0.4 3.7600002 0.49600002 C 2.9440002 0.57600003 2.7680001 0.64000005 2.7680001 1.9520001 L 2.7680001 4.576 C 2.7680001 4.912 2.9120002 5.104 3.0400002 5.248 C 3.68 5.872 4.2720003 6.1920004 4.768 6.1920004 C 5.3760004 6.1920004 5.8240004 5.808 5.8240004 4.736 L 5.8240004 1.9520001 C 5.8240004 0.64000005 5.696 0.56 4.8320003 0.49600002 C 4.7520003 0.4 4.7520003 0.064 4.8320003 -0.032 C 5.2320004 -0.016 5.8240004 0 6.464 0 C 7.1040006 0 7.6320004 -0.016 8.032001 -0.032 C 8.112 0.064 8.112 0.4 8.032001 0.49600002 C 7.2320004 0.56 7.0880003 0.64000005 7.0880003 1.9520001 L 7.0880003 4.4960003 C 7.0880003 4.7200003 7.0880003 4.9440002 7.0720005 5.136 C 7.84 5.984 8.56 6.1920004 9.184 6.1920004 C 9.792001 6.1920004 10.144 5.84 10.144 4.768 L 10.144 1.9520001 C 10.144 0.64000005 9.984 0.56 9.152 0.49600002 C 9.0720005 0.4 9.0720005 0.064 9.152 -0.032 C 9.552 -0.016 10.144 0 10.784 0 C 11.424001 0 11.984 -0.016 12.432 -0.032 C 12.512001 0.064 12.512001 0.4 12.432 0.49600002 C 11.552001 0.56 11.408001 0.64000005 11.408001 1.9520001 L 11.408001 4.48 C 11.408001 5.9040003 11.168 7.024 9.76 7.024 C 8.944 7.024 7.952 6.7200003 7.1200004 5.84 C 7.0720005 5.7920003 6.9760003 5.7120004 6.9440002 5.8560004 C 6.8 6.512 6.176 7.024 5.3440003 7.024 C 4.4160004 7.024 3.584 6.4800005 2.9120002 5.728 C 2.832 5.6480002 2.736 5.5360003 2.72 5.728 Z "/>
</symbol>
<symbol id="gD032B844D751F1F27806C7004D4F5D2F" overflow="visible">
<path d="M 2.6720002 6.3040004 C 2.5760002 6.208 2.512 6.2400002 2.512 6.3840003 L 2.512 9.328 C 2.512 10.368 2.5760002 11.008 2.5760002 11.008 C 2.5760002 11.120001 2.512 11.168 2.368 11.168 C 1.968 11.008 0.768 10.784 0.128 10.736 C 0.096 10.608001 0.128 10.352 0.224 10.2560005 C 0.272 10.2560005 0.32000002 10.2560005 0.36800003 10.2560005 C 1.072 10.208 1.248 10.208 1.248 8.944 L 1.248 1.136 C 1.248 0.512 1.2320001 0.224 1.184 0 C 1.264 -0.128 1.3440001 -0.192 1.536 -0.192 C 1.6320001 -0.096 1.792 0.048 1.9200001 0.192 C 2.0800002 0.384 2.176 0.384 2.352 0.24000001 C 2.72 -0.064 3.2 -0.16000001 3.7600002 -0.16000001 C 5.392 -0.16000001 7.2960005 1.3280001 7.2960005 3.8720002 C 7.2960005 5.8240004 5.8560004 7.024 4.464 7.024 C 3.7760003 7.024 3.1680002 6.7520003 2.6720002 6.3040004 Z M 2.7840002 5.808 C 3.2 6.176 3.68 6.32 4.144 6.32 C 5.1200004 6.32 5.92 5.136 5.92 3.584 C 5.92 1.7600001 5.184 0.384 3.6640003 0.384 C 3.1680002 0.384 2.832 0.73600006 2.512 1.136 L 2.512 5.136 C 2.512 5.472 2.5760002 5.6320004 2.7840002 5.808 Z "/>
</symbol>
<symbol id="g8EC8620411AE7F46663E6890D2DD9166" overflow="visible">
<path d="M 2.8960001 1.9520001 L 2.8960001 5.136 C 2.8960001 5.9360003 2.96 6.9600005 2.96 6.9600005 C 2.96 7.024 2.88 7.0720005 2.752 7.0720005 C 2.3040001 6.8960004 1.664 6.7520003 0.56 6.6080003 C 0.528 6.512 0.56 6.2560005 0.592 6.1600003 C 1.4720001 6.0800004 1.6320001 5.984 1.6320001 5.072 L 1.6320001 1.9520001 C 1.6320001 0.624 1.4560001 0.57600003 0.48000002 0.49600002 C 0.384 0.4 0.384 0.064 0.48000002 -0.032 C 1.008 -0.016 1.6320001 0 2.272 0 C 2.9120002 0 3.5200002 -0.016 4.0480003 -0.032 C 4.144 0.064 4.144 0.4 4.0480003 0.49600002 C 3.072 0.56 2.8960001 0.624 2.8960001 1.9520001 Z M 1.44 9.584001 C 1.44 9.168 1.8240001 8.752001 2.2080002 8.752001 C 2.6560001 8.752001 3.0400002 9.184 3.0400002 9.52 C 3.0400002 9.904 2.7040002 10.352 2.272 10.352 C 1.8880001 10.352 1.44 9.968 1.44 9.584001 Z "/>
</symbol>
<symbol id="g26508BD01E1C582AC0C2221BD9BE4224" overflow="visible">
<path d="M 2.9440002 5.728 C 2.848 5.616 2.752 5.584 2.752 5.728 C 2.736 6.1600003 2.7040002 6.7840004 2.624 6.9440002 C 2.592 7.024 2.5600002 7.0720005 2.4320002 7.0720005 C 1.9840001 6.8960004 1.5680001 6.7520003 0.46400002 6.6080003 C 0.432 6.512 0.46400002 6.2560005 0.49600002 6.1600003 C 1.36 6.0800004 1.536 6.0000005 1.536 5.072 L 1.536 1.9520001 C 1.536 0.64000005 1.376 0.57600003 0.416 0.49600002 C 0.32000002 0.4 0.32000002 0.064 0.416 -0.032 C 0.896 -0.016 1.536 0 2.176 0 C 2.8160002 0 3.2960002 -0.016 3.7760003 -0.032 C 3.8720002 0.064 3.8720002 0.4 3.7760003 0.49600002 C 2.96 0.57600003 2.8000002 0.64000005 2.8000002 1.9520001 L 2.8000002 4.576 C 2.8000002 4.912 2.9440002 5.104 3.072 5.248 C 3.68 5.84 4.4 6.1920004 5.024 6.1920004 C 5.3440003 6.1920004 5.6800003 5.984 5.872 5.616 C 6.032 5.2960005 6.064 4.8640003 6.064 4.3840003 L 6.064 1.9520001 C 6.064 0.64000005 5.9040003 0.57600003 5.072 0.49600002 C 4.992 0.4 4.992 0.064 5.072 -0.032 C 5.552 -0.016 6.064 0 6.7040005 0 C 7.3440003 0 7.9200006 -0.016 8.400001 -0.032 C 8.4800005 0.064 8.4800005 0.4 8.400001 0.49600002 C 7.504 0.57600003 7.3280005 0.64000005 7.3280005 1.9520001 L 7.3280005 4.3360004 C 7.3280005 5.216 7.2640004 5.984 6.8960004 6.4800005 C 6.6240005 6.8320003 6.1280003 7.024 5.5680003 7.024 C 4.7840004 7.024 3.8880002 6.8160005 2.9440002 5.728 Z "/>
</symbol>
<symbol id="gACDA1EE5EEC178C67D037C3CDBE0EFC9" overflow="visible">
<path d="M 6.176 1.488 C 5.584 0.88000005 5.1200004 0.624 4.1920004 0.624 C 3.6160002 0.624 2.9440002 0.96000004 2.4480002 1.7760001 C 2.128 2.3040001 1.9360001 3.0400002 1.9360001 3.9680002 L 6.1920004 3.936 C 6.3840003 3.936 6.4960003 4.032 6.4960003 4.208 C 6.4960003 5.552 6.0160003 6.992 3.7920003 6.992 C 2.4 6.992 0.592 5.664 0.592 3.232 C 0.592 2.3360002 0.81600004 1.4720001 1.3440001 0.864 C 1.8880001 0.224 2.64 -0.16000001 3.7920003 -0.16000001 C 5.0080004 -0.16000001 5.872 0.4 6.512 1.2320001 C 6.464 1.3920001 6.3680005 1.4720001 6.176 1.488 Z M 1.9840001 4.512 C 2.288 6.32 3.4080002 6.464 3.7920003 6.464 C 4.4 6.464 5.1200004 6.1280003 5.1200004 4.7840004 C 5.1200004 4.6400003 5.056 4.5600004 4.88 4.5600004 Z "/>
</symbol>
<symbol id="g6E07D235467580A0707E6406EB5DB8A8" overflow="visible">
<path d="M 5.3440003 0.8 C 5.4240003 0.864 5.5680003 0.896 5.584 0.78400004 C 5.6320004 0.4 5.76 -0.16000001 5.76 -0.16000001 C 5.8880005 -0.208 5.9680004 -0.192 6.064 -0.16000001 C 6.4160004 0.128 6.9760003 0.36800003 7.952 0.48000002 C 8.048 0.57600003 8.048 0.81600004 7.952 0.91200006 C 6.9280005 0.99200004 6.7840004 1.296 6.7840004 2.0800002 L 6.7840004 9.328 C 6.7840004 10.368 6.8480005 11.008 6.8480005 11.008 C 6.8480005 11.120001 6.7840004 11.168 6.6400003 11.168 C 6.2400002 11.008 5.0400004 10.784 4.4 10.736 C 4.368 10.608001 4.4 10.352 4.4960003 10.2560005 C 4.544 10.2560005 4.592 10.2560005 4.6400003 10.2560005 C 5.3440003 10.208 5.5200005 10.208 5.5200005 8.944 L 5.5200005 6.8960004 C 5.5200005 6.7840004 5.4880004 6.7520003 5.3760004 6.7520003 C 5.3120003 6.7520003 4.656 7.024 4.1280003 7.024 C 3.072 7.024 2.368 6.6720004 1.728 6.064 C 1.0400001 5.3760004 0.624 4.432 0.624 3.2480001 C 0.624 1.2800001 1.616 -0.16000001 3.344 -0.16000001 C 3.9680002 -0.16000001 4.5600004 0.16000001 5.3440003 0.8 Z M 5.5200005 1.9840001 C 5.5200005 1.6800001 5.4880004 1.552 5.2640004 1.36 C 4.6720004 0.84800005 4.1600003 0.592 3.7600002 0.592 C 2.8960001 0.592 2 1.536 2 3.5360003 C 2 4.688 2.2240002 5.328 2.4640002 5.664 C 2.96 6.4160004 3.6320002 6.464 3.9520001 6.464 C 4.5280004 6.464 4.9280005 6.2560005 5.248 5.8880005 C 5.472 5.6320004 5.5200005 5.5200005 5.5200005 5.024 Z "/>
</symbol>
<symbol id="g1E702B8726C96DD59806A35F3CC560AF" overflow="visible">
<path d="M 3.2480001 6.3680005 C 3.344 6.464 3.344 6.8 3.2480001 6.8960004 C 2.7680001 6.88 2.2080002 6.8640003 1.6320001 6.8640003 C 1.024 6.8640003 0.592 6.88 0.17600001 6.8960004 C 0.080000006 6.8 0.080000006 6.464 0.17600001 6.3680005 C 0.92800003 6.288 1.1040001 6.1280003 1.44 5.2960005 L 3.5360003 0.128 C 3.6320002 -0.096 3.7600002 -0.192 3.92 -0.192 C 4.064 -0.192 4.1920004 -0.096 4.3040004 0.16000001 L 5.92 4.096 L 7.5680003 0.128 C 7.6640005 -0.096 7.7920003 -0.192 7.952 -0.192 C 8.096001 -0.192 8.224 -0.096 8.320001 0.14400001 L 10.416 5.216 C 10.672001 5.872 10.944 6.32 11.76 6.3680005 C 11.856001 6.464 11.856001 6.8 11.76 6.8960004 C 11.440001 6.88 11.088 6.8640003 10.608001 6.8640003 C 10.128 6.8640003 9.456 6.88 8.976001 6.8960004 C 8.88 6.8 8.88 6.464 8.976001 6.3680005 C 10.176001 6.3040004 10.016001 5.84 9.792001 5.28 L 8.448 1.9520001 C 8.288 1.552 8.224 1.552 8.096001 1.8880001 L 6.7200003 5.392 C 6.4160004 6.144 6.4480004 6.3040004 7.2960005 6.3680005 C 7.392 6.464 7.392 6.8 7.2960005 6.8960004 C 6.8160005 6.88 6.176 6.8640003 5.696 6.8640003 C 5.2960005 6.8640003 4.768 6.88 4.288 6.8960004 C 4.1920004 6.8 4.1920004 6.464 4.288 6.3680005 C 5.0400004 6.3040004 5.2320004 5.84 5.5200005 5.1200004 L 5.616 4.8640003 L 4.4960003 2.032 C 4.288 1.5040001 4.256 1.488 4.0480003 2 L 2.7680001 5.2960005 C 2.4640002 6.064 2.48 6.32 3.2480001 6.3680005 Z "/>
</symbol>
<symbol id="g94C24BD726F4D930F93182C299232222" overflow="visible">
<path d="M 0.688 6.8640003 C 0.46400002 6.8640003 0.4 6.6720004 0.4 6.544 L 0.4 6.3360004 C 0.4 6.2560005 0.416 6.2400002 0.48000002 6.2400002 L 1.424 6.2400002 L 1.424 1.424 C 1.424 0.28800002 1.9200001 -0.16000001 2.6560001 -0.16000001 C 3.3920002 -0.16000001 4.1920004 0.192 4.8160005 0.896 C 4.7840004 1.056 4.688 1.1520001 4.5280004 1.1680001 C 4.112 0.84800005 3.6320002 0.72 3.216 0.72 C 2.7840002 0.72 2.6880002 1.2 2.6880002 2.1920002 L 2.6880002 6.2400002 L 4.352 6.2400002 C 4.512 6.2400002 4.736 6.3040004 4.736 6.4480004 L 4.736 6.768 C 4.736 6.8320003 4.688 6.8640003 4.6080003 6.8640003 L 2.6880002 6.8640003 L 2.6880002 7.4880004 C 2.6880002 8.528001 2.752 9.168 2.752 9.168 C 2.752 9.264001 2.7040002 9.312 2.624 9.312 C 2.5600002 9.312 2.4160001 9.248 2.272 9.168 C 2.0960002 9.0720005 1.9360001 8.992001 1.728 8.944 C 1.536 8.88 1.376 8.832001 1.376 8.72 C 1.376 8.528001 1.424 8.64 1.424 6.8640003 Z "/>
</symbol>
<symbol id="g40BC2CA66BF08C308C98CB508D30B53" overflow="visible">
<path d="M 2.6720002 4.576 C 2.6720002 4.912 2.8160002 5.104 2.9440002 5.248 C 3.5520003 5.84 4.368 6.1920004 4.992 6.1920004 C 5.3120003 6.1920004 5.6480002 5.984 5.84 5.616 C 6.0000005 5.2960005 6.032 4.8640003 6.032 4.3840003 L 6.032 1.9520001 C 6.032 0.64000005 5.872 0.57600003 5.0400004 0.49600002 C 4.96 0.4 4.96 0.064 5.0400004 -0.032 C 5.4880004 -0.016 6.032 0 6.6720004 0 C 7.3120003 0 7.84 -0.016 8.368 -0.032 C 8.448 0.064 8.448 0.4 8.368 0.49600002 C 7.472 0.57600003 7.2960005 0.64000005 7.2960005 1.9520001 L 7.2960005 4.3360004 C 7.2960005 5.216 7.2320004 6.0000005 6.8640003 6.4800005 C 6.5920005 6.8320003 6.096 7.024 5.5360003 7.024 C 4.7520003 7.024 3.7920003 6.8160005 2.8160002 5.728 C 2.8160002 5.7120004 2.8000002 5.7120004 2.7840002 5.696 C 2.736 5.6320004 2.6560001 5.5360003 2.6560001 5.728 L 2.6720002 9.328 C 2.6720002 10.368 2.736 11.008 2.736 11.008 C 2.736 11.120001 2.6720002 11.168 2.528 11.168 C 2.128 11.008 0.92800003 10.784 0.28800002 10.736 C 0.256 10.608001 0.28800002 10.352 0.384 10.2560005 C 0.432 10.2560005 0.48000002 10.2560005 0.528 10.2560005 C 1.2320001 10.208 1.4080001 10.208 1.4080001 8.944 L 1.4080001 1.9520001 C 1.4080001 0.624 1.2160001 0.56 0.28800002 0.49600002 C 0.192 0.4 0.192 0.064 0.28800002 -0.032 C 0.81600004 -0.016 1.4080001 0 2.048 0 C 2.6560001 0 3.1840003 -0.016 3.6320002 -0.032 C 3.7280002 0.064 3.7280002 0.4 3.6320002 0.49600002 C 2.8160002 0.56 2.6720002 0.624 2.6720002 1.9520001 Z "/>
</symbol>
<symbol id="g658214B515038ED3D9F63EA3005CE066" overflow="visible">
<path d="M 7.168 9.824 C 8.352 9.744 8.352 9.312 8.016001 8.448 L 5.4880004 2.032 L 5.4240003 2.032 L 2.864 8.544001 C 2.496 9.504001 2.592 9.712001 3.68 9.824 C 3.7760003 9.92 3.7760003 10.2560005 3.68 10.352 C 3.0400002 10.336 2.3200002 10.320001 1.7440001 10.320001 C 1.1680001 10.320001 0.60800004 10.336 0.080000006 10.352 C -0.016 10.2560005 0 9.92 0.096 9.824 C 0.9760001 9.744 1.1040001 9.472 1.536 8.368 L 4.688 0.17600001 C 4.7840004 -0.080000006 4.8960004 -0.192 5.056 -0.192 C 5.2320004 -0.192 5.3440003 -0.048 5.44 0.17600001 L 8.752001 8.336 C 9.056001 9.088 9.312 9.712001 10.320001 9.824 C 10.416 9.92 10.416 10.2560005 10.320001 10.352 C 9.84 10.336 9.280001 10.320001 8.912001 10.320001 C 8.544001 10.320001 7.8240004 10.336 7.168 10.352 C 7.0720005 10.2560005 7.0720005 9.92 7.168 9.824 Z "/>
</symbol>
<symbol id="g16352873ECA67EAF163D6C6FB1F0EBC" overflow="visible">
<path d="M 4.5280004 5.168 C 5.8880005 5.168 5.9360003 4.8 5.984 4.0800004 C 6.0800004 3.9840002 6.4160004 3.9840002 6.512 4.0800004 C 6.4960003 4.48 6.4800005 4.9440002 6.4800005 5.4880004 C 6.4800005 6.032 6.4960003 6.4480004 6.512 6.8640003 C 6.4160004 6.9600005 6.0800004 6.9600005 5.984 6.8640003 C 5.9360003 5.984 5.8880005 5.7760005 4.5280004 5.7760005 L 3.0400002 5.7760005 L 3.0400002 8.656 C 3.0400002 9.52 3.232 9.68 3.936 9.68 L 4.656 9.68 C 6.352 9.68 6.7520003 9.04 7.1040006 7.9360003 C 7.2960005 7.9360003 7.472 7.9680004 7.6000004 8.016001 C 7.5200005 8.672001 7.28 10.208 7.248 10.336 C 7.248 10.368 7.2320004 10.384001 7.1840005 10.384001 C 6.912 10.336 6.8320003 10.320001 6.432 10.320001 L 2.352 10.320001 C 1.84 10.320001 0.92800003 10.336 0.28800002 10.352 C 0.192 10.2560005 0.192 9.92 0.28800002 9.824 C 1.4080001 9.776 1.6800001 9.696 1.6800001 8.368 L 1.6800001 1.9520001 C 1.6800001 0.624 1.4080001 0.544 0.28800002 0.49600002 C 0.192 0.4 0.192 0.064 0.28800002 -0.032 C 0.84800005 -0.016 1.6480001 0 2.368 0 C 3.088 0 3.8720002 -0.016 4.432 -0.032 C 4.5280004 0.064 4.5280004 0.4 4.432 0.49600002 C 3.3120003 0.544 3.0400002 0.624 3.0400002 1.9520001 L 3.0400002 5.168 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
</defs>
</div>
<div class="step slide">
<svg class="typst-doc" viewBox="0 0 841.8897637795276 473.56299212598424" width="100%" height="100%" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" xmlns:h5="http://www.w3.org/1999/xhtml">
<path class="typst-shape" fill="#ffffff" fill-rule="nonzero" d="M 0 0 L 0 473.563 L 841.8898 473.563 L 841.8898 0 Z "/>
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(40 16.58)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5396A27CA60B9808846A090320835A9F" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="2.97" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="8.99" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="14.280000000000001" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="19.39" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gBFFDA84A1400D9E1136DF0DD93EA19F5" x="25.02" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEC3CC7DEE79E0AA801DFAAEF4B6C0B50" x="30.669999999999998" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g202CCBD46865F83C12D50E1B4FF9BBEA" x="36.43" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="41.35" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g5503E15E5E4E70E9E217A15BD1ECD752" x="46.64" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="49.75" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEEE4EC0F13100E99C1017169F912BE3E" x="55.379999999999995" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 25.159999999999997)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(40 27.159999999999997)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.64 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 42.31999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(392.6158818897638 10)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g6F0940D406D545443F0C3F5AB20F1452" x="0" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g6D72A0AB4EFB019D977FFECF4A1600A9" x="6.95" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7035BD9A81EA6DB089327941BB80DFF8" x="11.26" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g7FD6A8241485CEBC032BD9E4CE659816" x="16.67" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFAD9169AC3141E7FC4EA568E3BBD2E9B" x="22.3" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#g5503E15E5E4E70E9E217A15BD1ECD752" x="27.41" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gA419F36517085793EDBF3FE4736A2E59" x="30.52" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gFF65128B49BB3276E17D04989ECB7ACE" x="35.81" fill="#54379540" fill-rule="nonzero"/>
<use xlink:href="#gEDADDD9BA25BBB833C1F4B684DC50419" x="41.92" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 8.579999999999998)">
<g class="typst-group">
<g>
<g transform="translate(0 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(5.64 6.580000000000001)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 23.739999999999995)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 32.31999999999999)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1E8994F5C297EC73FA26D93D22635023" x="0" fill="#54379540" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(732.4217637795276 10)">
<g class="typst-group">
<g>
<g transform="translate(0 7.896)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gF74D1E4498220F56E34936C81B24ED2C" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFF269982F0E4C510F3A3BFF016D72390" x="3.564" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD17E61D06C745FD691E5D7AFE136D0C0" x="11.568" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g48BCA4F06942DA5990D42018985FC781" x="17.1" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g4C6038BE04CA3E1481E54A97A0E34303" x="23.232" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g5490A23BDA1B2697F526AA72E92A878C" x="29.868" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD36D2D678ADE356EA3610170EDF710ED" x="36.444" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gFF269982F0E4C510F3A3BFF016D72390" x="42.168000000000006" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD36D2D678ADE356EA3610170EDF710ED" x="50.172000000000004" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g46E28FC12585DA626130081849FE40B4" x="55.896" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gA2769E14ED9B16297025579DD26D23A1" x="63.120000000000005" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 18.192)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g5ABA589ED074A65FC8C929AB4EB2344C" x="0" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(40 60)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<g class="typst-group">
<g>
<g transform="translate(0 15.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g1BED8054A02AECF3BF3EC56A671C1672" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g841363B3896A8C79F18618DF16186242" x="16.944" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC0E7F247CAD2177580FB7ED865B072E5" x="30.168" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g79601DAFF2C13DD0AF25B87F7A83C884" x="51.888" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g24FA36D774E663C81AD78F0ED3820373" x="64.896" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g42F794F2554BA43C69EE8F3AA6FD9BAC" x="72.624" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB6675D993E92546012E46240B36958EC" x="87.408" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gC80183FE843BD5B521235E3B107ADB69" x="99.312" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g5CE84699333B5C2123530E7EB1AB2F63" x="118.776" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g24FA36D774E663C81AD78F0ED3820373" x="137.424" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g10AC66E6714D96E9762627FFB6E156C6" x="145.15200000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g2825DE3DACAF761B898A0442866AE569" x="153.74400000000003" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gF2A450DA789E2AF150390BAEDFF9DA86" x="174.60000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3005F72D4AFC838AB38DA6C1497F98C5" x="183.98400000000004" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g63CC3E63B28F8D9D90BA6C1A685A1E05" x="200.78400000000005" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 39.48)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gA335A20E4C1D7F39210005AFF7F1A0EF" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="12.920000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="23" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="38.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="48.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="54.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="64.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="73.86" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(94.65999999999998 6.160000000000001)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 91.72 0 "/>
</g>
<g transform="translate(86.65999999999998 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="8.559999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="13.84" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="24.46" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="32.26" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="38.58" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="47.519999999999996" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="54.959999999999994" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="61.71999999999999" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="71.57999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="80.71999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="88.51999999999998" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="97.59999999999998" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(194.37999999999997 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="14.14" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="24.98" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(242.47999999999996 6.160000000000001)">
<path class="typst-shape" fill="none" stroke="#5437951a" stroke-width="20" stroke-linecap="round" stroke-linejoin="miter" stroke-miterlimit="4" d="M 0 0 L 84.48 0 "/>
</g>
<g transform="translate(234.47999999999996 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="0" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="10" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="17.44" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAC7FD886AB12F72ED3B61B0327264BE7" x="26.580000000000002" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="36.96" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="47.72" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g733371913480EE84B3609C9E9CD62F8C" x="54.48" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="64.34" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="73.48" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="81.28" fill="#543795" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="90.36" fill="#543795" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(334.96 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="10.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="21.259999999999998" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="31.379999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g5925E4E4FE8F59A76637BD462660B390" x="40.17999999999999" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 39.32)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8934F85724FE2A1B73A1C811C5B32995" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gC3F91E6BB9F8304E319658F9D45F8B38" x="6.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="19.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="34.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="42.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="48" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="58.62" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="66.42" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="72.74000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="81.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="89.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="94.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="105.38000000000001" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 65.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gC1513612DA0E34F2B247DB2830CD7DFD" x="0" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(17.02 65.48)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gFE29E79896646B3825DA2D41961151C9" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="11.76" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="22.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="27.799999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="33.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="43.199999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB8789F2F5F06048D4163694E4C0F3B6C" x="55.99999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="70.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="84.58" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="94.28" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="118.3" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="123.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="134.56" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="144.68" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g5925E4E4FE8F59A76637BD462660B390" x="153.48000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="168.28000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="178.36000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="194.20000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="202.76000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="208.04000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="218.66000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="226.46000000000006" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="232.78000000000006" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="241.72000000000006" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="254.16000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="262.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="271.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="282.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="288.82" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="296.09999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="306.17999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g42587C4E387B2C5F870DA01C2914651F" x="311.59999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="321.71999999999997" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(0 102.64)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD3761FB0B01B207797C607CDFB6E3A0B" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="25.5" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="34.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="39.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="50.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="58.760000000000005" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="64.04" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="74.66000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="82.46000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="88.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="97.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="105.16" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="117.96" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="127.1" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="132.38" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="137.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gA1481BA28623480CC7E6165783E2A864" x="147.6" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="167.54" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g5925E4E4FE8F59A76637BD462660B390" x="176.34" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="186.14000000000001" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="196.9" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="206.04000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="216.66000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="224.46000000000004" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="230.78000000000003" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g17AD34DB90B05275C6F1422A9B4B5274" x="236.20000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="245.98000000000002" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g67483374C2628B9150A7D3585AC4A61B" x="259.92" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="267.72" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="276.66" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="285.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="293.08" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3C2FFF86BC828E66F78F8A687CE12C70" x="301.64" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="317.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gF1C3ABAD267D886F542252ABBAAA32" x="326.53999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="338.46" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="347.4" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g1788914935A6D7BFA016214155630E72" x="359.84" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB78EB03C35D4F852337F4EC6AC104AC" x="365.11999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g713198A7DA4F5CD7D462D4529B1D64BD" x="375.34" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gAA212A9DBB5FA7333A767E41B2F6A3B3" x="383.9" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g22D858CFD6AD86697C1391C74FD687D1" x="393.03999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="399.35999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g35631D62198EF939061DC90C9391724A" x="404.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="415.61999999999995" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(465.13385826771656 0)">
<g class="typst-group">
<g>
<g transform="translate(0 0)">
<image xlink:href="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAB4AAAAQ4CAIAAABnsVYUAAAgAElEQVR4Aey9CZQtWVnnmzfz5s17q25NSg0UVZRFMYvSiiOOy6kf7Yy243rr+VyOIFrqw7bx2csBtRG1XcwCMvuAohRQQHxAqyitvAdSPOi65pmIkTgxGGNFnIg4Mbx14n/zY984Q56Tc9777ZXr5I59dnx771/EieEfX3x7rebEBJgAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmAATYAJM4BAIrB2CTTbJBJgAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmAATYAJMoGYBmncCJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwASYABM4FAIsQB8KVjbKBJgAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmAATYAIsQPM+wASYABNgAkyACTABJsAEmAATYAJMgAkwASbABJgAE2ACh0KABehDwcpGmQATYAJMgAkwASbABJgAE2ACTIAJMAEmwASYABNgAkyABWjeB5gAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmAATYAJM4FAIsAB9KFjZKBNgAkyACTABJsAEmAATYAJMgAkwASbABJgAE2ACTIAJsADN+wATYAJMgAkwASbABJgAE2ACTIAJMAEmwASYABNgAkyACRwKARagDwUrG2UCTIAJMAEmwASYABNgAkyACTABJsAEmAATYAJMgAkwARageR9gAkyACTABJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMIFDIcAC9KFgZaNMgAkwASbABJgAE2ACTIAJMAEmwASYABNgAkyACTABJsACNO8DTIAJMAEmwASYABNgAkyACTABJsAEmAATYAJMgAkwASZwKARYgD4UrGyUCTABJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwARYgOZ9gAkwASbABJgAE2ACTIAJMAEmwASYABNgAkyACTABJsAEDoUAC9CHgpWNMgEmwASYABNgAkyACTABJsAEmAATYAJMgAkwASbABJgAC9C8DzABJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwASYwKEQYAH6ULCyUSbABJgAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmAATYAGa9wEmwASYABNgAkyACTABJsAEmAATYAJMgAkwASbABJgAEzgUAixAHwpWNsoEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwASYABNgAixA8z7ABJgAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmAATYAKHQoAF6EPBykaZABNgAkyACTABJsAEmAATYAJMgAkwASbABJgAE2ACTIAFaN4HmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwASYABNgAkzgUAiwAH0oWNkoE2AC1ziBasW0Kq6VzK9qvK7rI7BfCgnNoUBsesmeV1VF6y6zithEVVW7rkL2d6255wpil/ZghFZfcl2qv0xmSZtitV3NipU5zwSYABNgAkyACTABJsAEmAATYAJXNwEWoK/u7cujYwJMYAYB0hNJAi3GRTEuciGhRNTRZhiaXzTdBLUlZq5N+4ADwtOfJCWLcCg/EznRnvntvEKSnmF8XrW6rsuyzPO8GBdUh/qzTIbWmpdBT1qm5lWeLm+tSIvTNVFCFfaQmWdzunx549PrHkgJdeBArLERJsAEmAATYAJMgAkwASbABJgAE9gzARag94yOV2QCTOD0ESjGRZZlo9EoSZJYSEmTRk3KmgQtGvJoWZZLDrUsy2JciBLzknkSQxc3tDf7SxqH0rpS/0njW7KJZfoPmy0O1FCr/LgWIUkLDyxmZ2n/WZIPhkN6Ou08NHzRDuXF+jNrii7teyNGZve2+sy19myTVlwyM7N1LmQCTIAJMAEmwASYABNgAkyACTCBIyPAAvSRoeaGmAATOGYCZVnGcex5nmVZ5pXJapLdJLdJXpP8JmVZtowGDftBEPi+HyydwjBM07QsS9IT52Hag/0oipIkgf15Zqm8GBdxHK/U/ziOkyRZkg/ZD8Mwmp/wXACPBNI0zbIMmjjURurtzEyWZXEcR1EkPFxoZ+lhQ57nZGRX+KThUmdo3QPJLDM6aqiqKtFhX3xmADuiNeSn64s1d83T8KkPrUxVVXmeQzHf1VqrQsvUgkXync/zHA+Kpj/xKIA20zJbdkGL/BUTYAJMgAkwASbABJgAE2ACTIAJ7J8AC9D7Z8gWmAATOB0EsizzPM8wDEVR5CZJO2kwlfANqnmet4zGKtpXrkywc2XZ5SVN01zXhX0S5upZKc9z13U1TYO1ZT4VRTEMI4qiZWS4LMvIfquraKtVCOO2bUdRJIanmNX3SRns67quKIo6P2lN0ptkWZbrukmS5HkOOPOMw77jOJqmLbavqioGouu6bdu+76dpusAstNdiXCRJQk8v8MRi8adpmq7rRlEEDZ02bmtbQE3OsiyKIq9Jrus6jmPbNp6UDIdDQ0jD4dA0TTws8X0/juMsy2aKvxgURNs8z5MkCZu0+BmDv5M8z8PTkcViLsaFpwthGAZNwkDoEybxaMf3/TAM8egCmxX93PUzz/M0TZMkiaIIreATg4qiCK3g8cYe7JN7/rywMNPltCkBgRZnjmVV++JDr2Xs00MCqtzKzOzVMnVmrri4EGaXqbNMzcV25n0rDm1enX2WL97iuxrftYeHan/X1nft//FW2E//l1l3QR3xK8ofLw1unQkwASbABJgAE2ACJ5/AyRWg6ZIOmZOPknvIBJjASSaQZZnv+7quS5LU7/d7V6ZukzpN2p5KiqL4vi86zM4caZqmjuOoqjoYDPpXJujbV5ZdXpJl2XGcNE1FmW/mcS/LMsuyBoMBeit+YjRiCeVlWfZ9XxSzZna+rus0TYfDIey3ujqv/4PBQNO0IAiWt9/v97vd7pX4r1hC02hRlmXDMMIwhIf4YjkmSRJd13u9XqfTucLilQvdbhcbutfrybKs63ocx/OYoLyqqjRNxf2HHlhI81Ov11MUxXXdNE1JQMeWFbcv8rTzqKoqy7IkSbQX9Xo92ppANxgMUAfwpwVu0T50STwd0XXdMAxd16Hyz/uERi9JkmEYcRwv456f53kQBHhsoGkaqfxKk+Qm4aEDGoWi7vv+Mo8u6rrG0xfDMCDHiz2HWUVR0Lqg1Rsr2fd933Ecv0nelUl8K4K+cRyH9hwAb33WQsrzXLSPVugTNsVF3/fF5zoty1gk83iGkaZpHMekv7c9/5uXFaDLJ0kyGo3w0It+WdNNwD6526dpiiBFu34mTcIxjcxSb1tCObzm8yZRyJoFvRIDzog2xTw1KlZu2RTrT+eXOaCRwenVdy3BSMV+Ik8rAvveXinAWsW4mGdfLEdlavcwMvTigvgIB+3OG+Dibkz3X7S8TF60IObRrlgyzUf8FvmZvaVqM7/lQibABJgAE2ACTIAJXIMEjl+AptsD0McibQm+gCMUnGECTGAlAqJYmaap53mapkFd3d7ehkbZ7/dJSRT1visVy55pmnEcL1bKSKM0TVOWZdHs4ryqqr7vU6AJ8Ya8NV54ECuK0ure4sWVBGjLsmRZbqnPixdVVQ2CQKTd6jYtpmkK+6KcOp3HcEiG1jQtDMNdzwXFuAiCQFVV6MuLmaDRfr8vSZKmaVEUUSdnZhD8xLZtWZa73S72H6jY0/0nef3SpUu9Xk98ukCaiyhbAN1oNDIMA12SmgSJGUp0axfCQ5Tt7e1+v++6LtyfCRFlaCzov6Zp2O1n9lksxNAefvhhSZIIPlmbmSnGhe/7mqbpuk49x0CmP/EEaHt7W1XVOI533XmqqoqiSJbl7e3tXq+Hn+20WSpZ1X5Zlr7vy7KMZxIzmbc2wWAw6PV6hmEkSUKblRTJqkkEqmWf3sCQ5yRJkvDoJQgCxM+hJmC5ZR/qv2maeHrRegOAngHQuHq9niRJlmXBfX5xCBf4zsP3HxL/rp+GYViWFQRBlmUzNy76j0EhOIzVJLtJTpPchSkIgiRJ5h2TRfuYPlSU46GP41MsF/NLhi3CJWue5+K6y+TpgE/XwK1tCpkeXvN5k5bRVakORo0dEpxF+yKf6W9pvz2QDJR0tDj9mc1J87YsukT9R+SfXV9hmR4IQIljh82WfcT6b/0G0ysTXkChR4ywIB4Kplvff4nY2/1bYwunl8DMA+zpHQ73nAkwASbABK56AscvQNO0V5gZzHXdMAxx0yJeql71W4IHyASYwEERoLtT3L0nSWLbtqZp5Pvc7XYlSRoOh67rek2C1gHhAyKI+BmGIbzJ5vUQLVKUA8/zHMeBpLL4Ex0Iw3A0GsGI+NlqDlEgXNcdrpIsy4KG2LLWWqyqKsuyMAwdx1nF/BAyVsva9CLZt217sQeu6Mc6HA5t24ZGCTLTlqHU5HkeRREZX6yRkRMuYlkkSTLTLBXS0wXDMPB0QVqY5CZBzcTTBVGPoE1M9uHha9u2oijQcNF/9BMevuInwoz0+31FUYIgmOnqKN6XriRA93ZSp9PRdT1JEtGU2GcxjwcAZpNWFaB39TYty3I/AvSu9otx4ThOr9fDMwPykYcQP+/z0qVLiqKEYUjxT1pbmfiUZSnan34DYwf55f94hqEoCpysFwvEeHfBNM3BYNDpdC5duiQ+IOl0Ot0mkXCPh3CXLl0aDAZ4OkIa6Mz+47BgmuZKj75kWTZNE4c1/EKJBhapUYTzpgdOg8EAvy15YVJV1bZt7JzT+yd+YpAXIcWKxzTxWYL4sxLz6Pyuew5+uUmSiPaXyUOdx5YlIDMHgrj2OEMt/4mwRfPs0yEIp8hiXIQrpmViUmFcZVkico6o+1M+n58WwKf+Q4BuPQTCdl/8Sa8ctQ6e2EvF/QfBkbCXorNRk8THDJh1gNR/PFOhX5O45x9UfvEFCY3ioJqbZ2d6j51X84jLxT3kiJveZ3Po+fJGxJFO5xfYocoL6hzqV9QByhxqc2ycCTABJsAETgiBEyFA4wre8zzcQem67nke3VfgzHRCeHE3mAATOC0EqqoajUau68IlEw7Og8FAUZThcIjIv7hHFe8bxbna6NY4yzKMet7tFg5TdMNJd/UtyzMX0UrrNnjmcQ/eWKPRCFPzZculUZPm9Zy2JvzUoBSgiSvdvOYuoTLZmZcR7VMcAJIhxAw6jPayLMNgl7lFgcaNKASIDjzv028SIhHHcbykAx1kUNd1bdvGs4p5n9CJEAN6QaCDFqs0TbEinl6Ypgkly9hJ1Jzneb7vu64bBAEiwxAfMSPaJ4HYmp8a9di0LAsDRHTvXfcctAI46OHiKB/iA4aVQmQgQDk5+cKxd+anqqrQ8T3PW+xKic7Dw9owDKlJ8hIJ7dq2PRqNRKlrJn+yD+kTrUx/4lvI04h/Ag/oxQI0DnR4twDxZ8gHv7eTUNLdSVCl8e4CPDdpCNP9JwFaVdX+cgmO9oZhLClAp2lKb4203koRxWI6hiOMD707Mr2LYhQYFI4hchPWBt0Xyc8bEN5dmOfBjd0GnwjO0+rn4sV+v69pGh5NofOEXbSM/Gg08jxvscHpb4fDYRRF2LjTAjc1R8fMmb+jBYWmaSIs1TR8cQg47MdxPGwi1+MIQ584vtEnjnNYjOMYz3VEa5Sn/iP0fxiGOHLi01sikf3WmRdNwD72nzRNW0Hz/TlpNBohuA3i25Bl6va8DD2MQYuLP3E0WACHWlm8aajafjLihtiPnQNflzp2BBDmdX5vTaPn82yK5bSfiIOdmRfXojzVpJJWBvZbheLBhCyImen680rEtZCfV5PLmQATYAJM4GoicFIE6CiKDMPQNI1uD64myjwWJsAEjp5AWZZhGMqyDDUEDoCY8Q8vnh9sl/Z2s0F9aF2LU/lBZZbp3jJ19tOfw7a/n74d9roHsn2znQSnTnJvXLLzxbjYMXDFf3oEQg82UELq1TL2y7IcjUZwo4zjOIoicqkkh8EgCChCMZSaZdRhah2BDmY+AHCbZDfJcRxI89CYltnrIJMlSeK6rmlOJHhnt+S6ru/7o9EIMhM9fBI3NPUcMh889BHG2royQZITlTjLsvCQDLEaSIOetl+MC2iUlmXh3YJp93/RlR4BQHAkbKnnrVGg/4R9OByqyyVZlin6+UybsIyxYG5Jy7IMw6DQ4bKQpCbBM5qUVgj0QDTNpGU/jmM8hqQrTLLZm5W63S6C2ywjQOd5DoF4lqXZZXgFx7btefYxIowCb/BQhCgMofUJLGgM6jzNWzBv/ydoSZJYljX90GJ215vSbrcL9/xdH91hzw+CQNien8tKO5Hu0X8alCzLiyf+pc5DgPY8Dxv0c6abPZAEdJTToqqqeHEBP/yWqzWMQ32jx9h4poXfkXNlotli7Sa5zWtVYtz/emHCuzu+73vzE45vfpM8z6PnUrtuXDy0xjOY0XIpa6a0XebkAt0cv196YHzFqaVZyJuER/t4Bo9jwkIql7/EBiIPgMWriF752IjTn6KFFr3pymKJuCLy9O28r6bLF5eQwVamtRawYwPR2Qe7q/gJI611abHVBC1SBdpeVCJmZj4yESsszlNzMzOL1+VvmQATYAJM4LQTOBECNN5+xavHuACVJOm0k+X+MwEmcLwEinHhui4i9kK8UBQFHou4dm/dfhxvb1t+JQfemZM22AMf4Ak32LrROuG93UP3oDQt6Q6/B/u0ihgVF9JG65PeM2jpSmRhcab1DsS0nkIluPmHtdb2xSI1BF0AHZueyk/UbkiswSrQX0i1mSnmkkYDB0zxZQLKt8IFBE0i3/xp2ULsP714gXcL6LnCgozv+2KICREOMaEjHp6LRFGESRrtJllXJlGgh4Lvui7i8uPIRk3MtJ8kie/7tm1D4oenra7rNNkm6drIIEATAjvseuSsqioIAoR4kpZO8IBe8IwHmxUCq+u6qqoubXtS0TAMTGI5r/+QkGju2V3DwvSE1O/3dV2n1y9E5tN5vNgx0363SZ2phOAwop7YMlvtJPTftm3agriJEDo7IzsYDFzXhfo/rbTCNv0AIdBTZBjsG/SsCHOi4sEPBG5ZljGvAP1aW52nRTy0w8bFhcr2rIT3FTAMvB+gadqST9eSJEFoeFVVp59LzSyxLMt1XbjPU1dnZrCLRlGE53b4kc78xK/ZbhKmV0UIlJlmqZCe23me5y6RMIVsHMczA5phs4rGSZ3HkVM8SM7M46GpGL29ZZOMtzIkGdO5qZXJdxKds3Z28Mn/lrXpRbEy5aerIeIlKtDOSfWRmbnWSoXL2Gk12lpcqTmuzASYABNgAqeOwIkQoNM0HQ6HmHyJBehTtw9xh5nAySQAxzTcE6qqimjCFGL+ZPaZe8UETikB8R77lA5hz91u3T/TIhkEHFHnFe//qdp0prWKuNYywsS0QZQgcu608Xn20RaNa9cMHhLQJxrCWmKXUIJv4aQpBvrJhITy0U6Cqz6JNaRlt5hQP6Fxk/QPXR7GYBn6DzWYJAkEPrG303lqDlEavKUTPPQxtR0ZadkneojfsuSkAqT0iaHhW5axiG2NfBRFw+Fwphw5s3A4HOIBg7gJZrZCHsqInCNfmaQmkXZMGbjPL1bniVuWZRQ9X9M0PFS4sp32kugevqsAjelhRQEaftD02XLbx6Asy1ocggPqahiGw+Fw13kFiAwc4cXgOfXCFEWRoijb29uXLl3qLp0kSfJ9f6Hhy18SfNy7zftE/0HGMAzHcaIo2tWvuRgXURRhVmesu/gT0j/mdajmJHFQFF3dNM2Z+3mrUJZlXdcdxwmCQLSzII8huK7r7JbgR+95Ht5KmXdMa7UFD/1WiBg8X8QDwqhJpKfjlR3xDSo65rcsYxFnLvKgn3d8xvGTHDvotznTJg2tGBd0TMaja2y0eWtxORNgAkyACVwdBI5fgG5NjkTRD68OvjwKJsAEjosAJlaCP47jOJjoD5ET+TL3uDYKt8sErj4Cc7SOz3mutQTo1vEHixACSA4Q7+HF1cW2RJJi+XR+ptY8s1Bcl+yjZstrb/HitHFYJpskQ4gtiqMWa+6aJyNiTWoRZsk4ldO4KINBQYlerK6SNbTYWhS7MZ2H6yXiz0yviM0NNQf7A2bAQ6+W+UT8h8Udg2XUgSsu+csvzkAqWuCeTOPFQNI0he+8P5W8neQ2aWdpEuBedG8ng5ShLQiBG+o8hcKAVzL83PEJJZFKSECHD29rQ8M4dgkIfKZpktyMTCsUDT3nRjnmmYCSOL19xVGkaep5nq7rUhONRBRqpTlJlmXDMPAAYIFxtDIajSzLUhRlnjQ8s1ySJNu2dzXecp8nU71eT9S6afpTCoNmWVYURbvGb8myzPM8WZYxY6qows/M93o9SZI0TTMMAxtx+pPg13U9Go1830fo/94S6dOf/nS329U0zbZt0U4rj0bxm7JtW5blXq+HBxjy/EQVLMtK01Tsecs+LeZ5HgQBJkaWphKaoj1TURRVVQ3D8DwPMeho7ly0RWaRIfd2/Ljw2xk2CRfVlpAwaYTneXiuQEe2mZbpyE/BZ/DGDJzu6QxI1Vod40UmwASYABM47QROhADt+74kSZ1OB6/1dTqdJZ+9n3b63H8mwAQOgwDdwMdx7DUpSRK8ODnvgvgwusE2mQATYAIggIPSvOMPyqF5kfJFAhC+nf5cla3YyrS16RKyT0fUxaKz+K04CtEy2TwhGZGJyJ+8+Q6pn7Q/zLRPvRIzM2vOLKQ9ByLOzDpHUIgxknckMq1PCjXbCn2zDH8MM89zCj6D6PNiAHrRD1TMLzMJIeCTgB6GIVxNvSsjQnjNlLD+ThBnZIIgoADrsIPPFvayLJMkwRzsM4NXTIt9cJ9PkmSBhzi1Ag9c27ZJfF8mA4Fe3IvIIGXwbZZlvu9rmoYgisjIzYSf0xqx3KThcLikBzReLCAP8WmDrZLt7e1eryfLsqqqC5jTEDBNiKZp3W63ZWrmIkLbQ8klI62M2G4cx5qmdTqd7e1txFgnjX46oyiKJEnb29uyLMdxjN/O9FFUbC5NU9M04bYlKv5ivtMksYSmPxUfcYlmKZ+mKQR0PB1Bn4mMLCTI3Hg243ke9kwRBeXJOJ5euK5Loja5iSAKOSnRi/dD0SDnmQATYAJM4FQQOH4BGi9wkeOzqqq9Xi+KolOBjzvJBJjACSSAi92yLLMsS5qEVw7pivYE9pm7xASYwAkhgAPIwXaGBMeZt9N0f97KoA+tQlpctYdYcVrUIIOtDNlH50V9edf8vFbI5oJMqxu0uGCVxV/BAh3/sYhV6CtRfaY8NT1zq7UaFSsvzov2W0ZavSIdarHBxd/ObOIICtErGuzMzLyeQzpfjJ3st4zMbKhVSJF8KVAGjIj8UUKOomRh152fpD2sInZvGjticaA/pMJnsxJJ+WRf7PO0ZZRA447jGNdCu34ivg3GOM8m2sXooHFjdtkFGr23I9OjJxjvPPsoz/Mc6rxlWZApF38qiqLrOqaQXcwc9uHe7jjOkgHc4Yg9HA49z5vXc/EHi9tbyPGihztpuGJGblKn05FlGdHbaX+bN5YsyyzLkiQJ88rCgviJgC1wPMdddqfTQfwZ2v9xVKxnpSRJIKB3u13I6JCz8dkTEg2k1+sNh0PE4N61/6PRCPFVoOnrum6aJp6vwEEeO3zrBYVZPeUyJsAEmAATOE0Ejl+ATtPUMAzMOW4YBt5C2vXNrNPEmPvKBJjACSAw7yL+BHSNu8AEmMAJIoBjxcF2aPHxR/xWzKMPYomYX7WH4rrL5Mk+KpOgsExmnn2yuSCzn3XnmZ22iZpi+fS4xG/nWaZysfKuebQ1T2AVV6eaYuFKeerhEWfETk6zXTyuZboq2l81L/ZHXBftiiVizb3lRWvLjEusM2/deeXiupSft5tRhVUzaJ22IAniKJkW6KnmSj1BFAjEnxktkYIgQHAJhIBYZlAIlBGGobtEQgBozE06zzhtF1SI49i2bbNJi9Vz+tbzPESHB7SZj81gvCxLz/MoJgwp3VKT5CaJvsmIw26aJuLb0Fabt1GyLDNNE9agZZPQTCHR0Qp9DgYD0zQRQmTX/sODm+LDQEnHbJmWZYmTVc7rYc2JCTABJsAETiGBYxagi3GBCFY4w1mW1e12VVWFx8Ep5MldPmACMy87RBeDmRXETlRNEks4f3oJ4IqW+o+Nu/wmpvpkgTNMgAkwgRaB5Q8prRUXLNLBZ+Y5S/xWzMOgWCLmFzQ38ytx3WXyZASVSVBYJjPPPtlckNnPuvPMTttETbF8elzit/MsU7lYedc82pq5M5DzL4xQzV1tzqtAPTzijNifabaLx7VMV0X7q+bF/ojrol2xRKy5t7xobea4xGtaagJr0WJLiNzV5nRD4iq75qdXF0vm9U2sc/T5ZWKSzOzVvJ/hzMqLCwksqsGJO0kS6OfiJH6tPCrkeU72xb2iZZbqxHHs+z7cz+M4hhF8YibVKIqCnRSGoe/7ENAh7mPvWjB8eKB7QswZx3FsIVmWRfI6HNV938eGoF2XOt9qKMsyhODQNE2W5X6/j1AhiKOiaZplWYhYTTE9WsdGWCYanGECTIAJMIFTQeB4BGg6ZxTjAvNj4O0kVVU/9alPua5b1zW/dHMqdqDD6yTtJGITCKqAt/zokitJEky5A7cL8RJHvO6hvGiQ86eIQDEuEBuO+rzSNqXK4h5CpjjDBJgAEzheAif5GCX2bT/5YyS865F/3rgOvM+thubZb1Xb8+I8+0dTvrduH3bf5vVKbHdenf2Ui/Ypvx+Du+7V1MqBZ9DtaWX8wBs6XQZpa5JaOo2I6rQy4khbX2ERFegrCqGOJqZXpwoU3QU1SXomU7SuWILpUhEKg6LCiNI5piRF2BZEd0nTFGFtFgjQaCLPcwjoURS5rqvr+mAwwAyWCBsiy7KmaaZpYlZSWJ7uOXX4GH8LRI8zTIAJMAEmsCuBYxagq6oyTVN8qafT6cRxzAL0rlvuGqyQ5zlmrEa8M0QN0zRN14xxl0sAACAASURBVHXDMIbDoWVZYRiSBwG5D7Qu/q5BdKd9yNiUeMBAW3P5QYmXp8gvvy7XZAJMgAkcDQHxSHU0LS7fiti3/eSXb/HAa+4qT8wb12H0RGxrnn2xzn7y8+wfTfneen7YfZvXK7HdeXX2Uy7ap/z0nrlSE2TniDPoJF2SUZ+PuBsnrblpDgSKNNmZGVpxQQaDnVdBlLxnNtEqFO2sui5MTYdboQt1aqvVCjUEn5IkSeCOHccxZGhZlkUlejAYKIqC0NvQoCl4CJqYtn/SdgnuDxNgAkyACYgEjlmALsbFcDgUBWhFUSAgTl+Qif3m/LVDADOcuK5rGAYFC8N8GjQpM2V0XXddl+Y3X3ABdO0AvMpGCo+M0WgUx/GSweLFy1PkrzImPBwmwASuAgLikeqkDUfs237yJ21cYn/mjUusc1B5sa15NsU6+8nPs3+U5av2/7D7Nq8/Yrvz6uynXLS/TH6Ztpaxcxh15vXtMNo67TZFVnRj0sqIdeblwWHBt/iqZXneomiHdOF5lWeW70eAntlVyNDD4RC3ewjK0e12B4OBpmm+74t+0OhSaxSnfVfh/jMBJsAErnoCxyxAZ1mm63q/3ycN2jRNTB/BAvRVv/PtOsCqqsIwtG1bVVWaAQNaMwnQeFGLZnnGG1uGYUCGbs1vjsuUXdvlCieZACaNgaMEZlPZNVyPeHnK+8BJ3rjcNyZwLRMQj1QnjYPYt/3kT9q4xP7MG5dY56DyYlvzbIp19pOfZ/8oy1ft/2H3bV5/xHbn1dlPuWh/mfwybS1j5zDqzOvbYbR12m2KrGYqudOO5OIqlAcHWmxlVhWRxdVXXRejOHABGm7RcRx7ngcZejAYdJqEOaKgQYsMW6M47bsK958JMAEmcNUTOB4Bms5zSZJomiYK0GEYXvXQD2qAV+tJF88eyrIU38YiH2c8qyAZmnYe+cqkqqppmlEU0XTYhOug+LOdoydQjAv4R+C4IUmS53kUdOXo+8MtMgEmwASYABNgAkyACTCBBQToHmQ/GdG+aGdeuVhnXn4/64pC8Ly82O6ubUEfKMZFmqZhGDqOMxwOZVmGBq0oCgRo0aaYF+1zngkwASbABE4mgeMUoMuyDIIAb9lAVVQUJcuyAySFmRP2YPDk+F/jzNp6No4RXX0nXcySUdd1GIaGYei6rqoqIj5LOwmu0BCge02CBo3v5SYpijIYDGRZtixrNBrBQ5Zw7WF/4FWOlwAixKVpCp8IzJfd7/cVRQmCgJ4xHG8nuXUmwASYABNgAkyACTABJtAiQPcg+8mINkU788rFOvPy+1l3nugslovtrtRWWZZpmmKKQsMwNE1zXTdN09Yd8Tz7YlucZwJMgAkwgZND4NgE6Lqu8zy3bZu0JAR4OljldzQaJUmyEm50YF436Dy3wOa8dResgq+WXBF9aJ2AdzV+KiqkaZokSRAEmqZBQZZlWZIkzDeImQbtK5NpmrguUZuk7CS5SaqqWpYVRREFFl8S8qnAdY10EtegQRBYlqWqqiRJNEH2cDhc9Qd+jUDjYTIBJsAEmAATYAJMgAmcKAJ0I7mHjDgQcfV55WKdefn9rDvP5rzyPbSV5zm8oYMgSNOUbuJmNiHa5zwTYAJMgAmcTALHLECbponpbuHEOhwOV8WEMxCthUU40mZZFoZhEATkVU3nLao/namqCk9up7+iyCEL7CDoMNZt9W2mQbGwVb8sSwzEb5Lneb7ve54XBEEcx6PRCPVba4kGd83vZ91dja9UgSZBDoJge3sb6rO0kzRNs207DMMkSfI8p0mWaQ7lMAwBZzgckhIN72lJkjBzBfvJrrRFTk5l/JAty9I0TZIkuMBLkoRI3/TrPjkd5p4wASbABJgAE2ACTIAJMIEWAdx57e1TNCVamFcu1pmX38+682zOK99zW1mTxBlfZjaB+3SxFTG/4OZdrMZ5JsAEmAATOFQCxyxAG4YBAbrX6yGc60qnh1ZlBI1KksT3fcdxLMvC53A4TNMUHFurTMOFEjqz2syznVgzyzK8HFSWZZIkURTFcbxkgFrROFw+wzD0PM+2bU3TVFUFKMipjuMgujGtNT2QVklZlpBuqVzsORXi5J3nOU72WZblTYLDtVjtYPN5nkdRhA338MMPk/uzLMuKoliWlSTJgj5ArM+yLAgCwzBIg4Z//WAwGA6HLcke6A52FGztwAnkeQ7fZ13XFUWRmqTrummavu/HcUzXo/P25wPvEhtkAkyACTABJsAEmAATYALXMgG6CV2QOUo+8CHDzXiWZXSDcJR94LaYABNgAkxgMYFjFqA1TZObGAsQoIMg2I+KNBqNXNc1DANC1WAwQBDhTqczHA6hBS9jf94Za975tYW4LEvf9yEZq6rq+/48g+KK6Bi59LYGAq/Pbrfb6XT6/b6u64iERV0STYl5TNpm2zbcRZMkIQKUqesaTt9Q8D3PQ6ADTdPMJtm2HcexWF9sYv/5YlxEUeQ4jm3bpmnSvIKDwQAxNCiO865t5Xnu+74oVmIHgxN0nudEDJldDXKFYyGAHTLLMt/38ZgK21GSJFVVPc8jX3h6X+Hw9s9jIcCNMgEmwASYABNgAkyACTCBk0mgdUs1c/GIe57neRzHfpOiKMqyjO8OjngTcHNMgAkwgcUEjlOAHo1GcpMQ1FVRlDAM93aegP+saZqY0hAz1PX7fXjCQr3VNC0MQ/j2LtNKnucIIQ1H5iRJ0jTN8xyCl3iWbSGO41hV1V6v1+l0ut2uYRjLO0HDh5di3dJAKDMYDCRJ0nUdISlIUW31AYt5nnuep+t6r9fb3t5WFMXzPFLDRQW2LMs4ji3LGgwGvV5PlmWKXyFJEs3mtwy3mT1ZUJjneZIknueZpqnrOp5JYFJKSZJM0yTP5QVGxK+KcQHVEuEaaH5LnpBQpHSS83gME8ex67qIBt7r9QaDgaIoFHYDey9+jHCNp6joJ3lo3DcmwASYABNgAkyACTABJsAEDpxAlmWu68L/TNd1y7I8z4vjmMMwHjhqNsgEmAAT2BuB4xSg4zimSAu9Xk9V1b3NJ5amqeM4iA/b7/e73W6vSd0m9ft9BK9QFMV13SAIaEq6xcjyPHddF87UOIeFYQhXXJK6RA0X1sqyNE2T5s2TJGk4HC4vQCdJQrFue71et9slUxSCA+rwcDgMgmCeAA2lOIoieI9C4h8MBqZpUmfEzqdp6vu+aZqkO0PyJpKSJIkC7mJ0K30Ln2XEzdiZQVCB2ihG3lhJ+0bcBsMw+v0+tEtZljVN8zwPw8fYV7K50qC48n4IYL4RBJ8ZDAZ4kCPLsm3b5PhcjAtSnykj7tL76QCvywSYABNgAkyACTABJsAEmMApIjAajUzTxL0D3q7WNG04HLquu/yb0KdovNxVJsAEmMCpI3CcAnQQBP1+X2pSv983DGMP84mlaSq6SUIwhXyJ+L/UBKIJa5qG4BW7bqooilRVhYoty/JwOPR9f1cBOs9zaNZobnkBGmGjHcdRlIn8CiVdkiTHccIwjKLItm3SoBVF0XU9CALMeTgtpKIkCAIE08CKg8HAtm16CIw6aNfzPEzfh0AH8IPG2Lvd7vb2dqfTUVU1CAI4UB+ggBtFka7r8OyWGm9rVVV1Xfd9H/7mdV3vQVjMssxxHPihwyw0dBagd93zj6UCbeKqquI4Hg6H+CEg7IwkSbZtj0Yj9I0U59ajIDJyLEPgRpkAE2ACTIAJMAEmwASYABM4FgIIg4l3f+GRBl83eocyiiJM14S7YOok3di2yqkCZ5gAE2ACTOBACBybAF1Vled5pA73+/3lPYURszjP8zRNPc+joA3QGTVNsywrbJLrulCypJ00GAzgybsYX57ntm0PBoNut4tQHqZpBkGwjAAtNwmRH5YcV1VVSZJAYoZm2ul0MCsjRcxI03Q4HFJsCk3TIAfPFN2wFqI5U39UVZ0OcjIajWzbVlUVkjfO1uT+jAxEQFmWPc+Dfk3n6cUYd/02yzJN0+ixAUan6zpiVcPLdQ9tYZUwDPEMHDuG6AC+B5u7joUr7IcAtggeNvi+L0lSp9PZblK/30ckFrKPypChaVNShqpxhgkwASbABJgAE2ACTIAJMIFrgQBuqB3HwZu1FIwR0wvJsmwYhuM4kKHhxQUsdBPBAvS1sJ/wGJkAEzhGAscmQJdlaVkWCdAQW8k5d1cieZ6HYeg4jq7rkiThvKKqKmRi8qQuxkUYhhSGAtUMw0jTdEETVVX5vo9w0r1ejwToOI4xm4F4lmqdqPI8l5skCtCLx1VV1Wg0gu9zv9+H7gYgonFRgMbsfJizEZ1pDQcrwib6Ayduir+B+ggzoqoquTz3mgDQpmk6jmOapizLUIf7/b6iKEtOqNjqzLzFPM/xnhQgY+ugFfS/GBfk4i2imGeQylE5yzJFUSDlwwecIpDQFqRVOHO8BGg3rqoqCAJZlvEsRFEUx3GSJIGzs9hJ2oitjFiH80yACTABJsAEmAATYAJMgAlcCwTKsoyiKAgCTC9EbmrwqcJk5pChEVpTvNOkm5FrARSPkQkwASZwLASOTYDO8xwhehF7QZblMAwXC7UiIMR4wkkFZxRMlIdpBqlmMS7EOMiQOHVdJ4WaaooZxHHudDqi9krxZ1tqV0sYXVWALssSftyGYSBSc6fTGQwGjuOARjEu8iYhIDWG0O/3MacidUbsP9xI67qGS7XcJFVVySYqtwIld7td+AhTaGmo/JjaUZZlXdfDMCSP7FaLqy5iqkCKNwLUCDkCx2faGeaNcUGLpF/DZxyhpdkDegGxY/+KrvnobQDTNDHTZpqmYsRnsSbtG2Lm2MfCHWACTIAJMAEmwASYABNgAkzgiAlUVZU1KU3TKIooyCT5q0F5QDRLclzj+4gj3kzcHBNgAtcsgWMToNM0hfgIT2FFURCSaZktkee54zjwnqaQFKZpTs9yCwmV4smisqZpLUfgVqPFuNB1/eGHH97e3oYsq2laFEVZltFj0tYqtLiqAA0VGPGX6dSIICE4FxbjIk3TOI7pES5OnAiJizrUOjIkv2I6RKlJmqb5vk+qLonLg8Fge3ubbMLVlAyWZQnvbMuyfN+HAzh9u+dMVVV4MIAtQkK/aZp4NjBzXKs2By97zOLY8oBuxQ5e1TLXPwwC2G+rqkqbNBqNROm5qiraaofROttkAkyACTABJsAEmAATYAJM4DQSoPsI3DKUZYmb6CiKXNdFUA7MdYQ56nH7ueuL0acRBfeZCTABJnBiCRybAJ0kCcRHuPSqqrqrtguIZVkGQaAoSrfbxVlEkiTDMGY652ZZFoahaZqIMoEW0daCTZKmqaZpmHmv1+vR3H3LSGArCdBlWcZxDBdjnAvR1mg0QvQJfCJMs6IoqqpCSIX78zxiOAFnWWYYBpRlSZJ0XY+iCP7L1K4kSYjvrCiKbdtxHJPGJ0rAxbhA8OsF0Fb6Co8QMEskAm33ej1d10kfX8navMotARrxuCFwzxzmPDtcfjQEsMtVVUU7NpXQT+9oesKtMAEmwASYABNgAkyACTABJnBaCLTuGsQZy7Msi+OYgnLA5avb7W5vbyuKEsfxaRkj95MJMAEmcNoJHJsAHUURtF04Mg+HQ6AUdc+ZcJMkMQwDvsmyLKuqahgGnHOn608L0Jh/YLqmWBLHMQRuCNaDwSCKIrHCgnye54qiQCbG6pZlzQtbgRDMiqJgyrVOp2MYBs1zSBp0EASYRUFVVbiNW5YFrRZa88z+JEmi6zoJ0IZhJEmCmlC06ew7GAzEx7/i+VvMz2xlb4VJkmiahmcPCD+tqupoNNqbtXlrIZSKJEn0uJsmuqRxzVuXy4+eAG2UBZmj7xW3yASYABNgAkyACTABJsAEmMBJJiDePojqM+VbMjQcoXDrfZLHxX1jAkyACVxNBI5HgMY8Y6IAbZomsOLkMQ9xVVWO40iSBAEavs8LQkMU4yIIAsMwKNwH5uKbZx/Rkz3PgzgrNckwjMUhO0RrEKCxOgRW27bnCdCYVxDicrfb7ff7juNkWYYzJd4bggc3SagYchzH9J6R2LqYj+NYVVXo+6qqWpaFECVVVXmeh6/gdo0AI+K64LB4W7TqL79YjAvP8zC9IdRnWZZd1z2o+B7Uk2JcILI2CPf7fVG4P6TRUeucIQILHpNQHXGXw6aZ+SnW5zwTYAJMgAkwASbABJgAE2ACTEC8cSDRuZXBzXWSJEEQuK5rmqbnecvc5i95L8NbgQkwASbABBYTOB4BuixL3/cxeWC/35dl2XEcdHTm8R2FCByBsBKdJkG4TNN05lp1XZdl6bouRU/u9XqyLNu2vQBKlmWmaVJ4EDRBCjKd2+ZZSJIEYnev14P467qu2D1YwOpBEGiaRm2pqhpFERyf8zyP49hxHKjnkFAlSRoOhxRJY14fUB5FkaIo6IOiKI7jJEmS5/loNBoOhzA4GAxUVfU8b7Gpg/02yzJ0ADtAt9uFAn6w8Tfquo7jGD7gg8EAu1kYhuK2ONhxsbV5BHb91cxbkcuZABNgAkyACTABJsAEmAATYALLE6Bbj5kZhIfOsozmmxGrzWwFFTiE40w4XMgEmAATWJ7AMQjQVVUh9ARkQSiDpIHO0wfLskzT1LZtBKyAvGuaZpIk81ap63o0Gok+sL1eT1EU3/cXrBKGoSgK67oOd2PxzDRvdfLt7ff73W4XenerOVq3GBe2bcO1GUKw7/s4sWVZ5vs+pPbBYCDLcrfblSTJdd3l41QEQYB3i6QmOY4zGo2yLHNdFxI5lR+48rt4/4uiSCQ8GAwsy0JoZtENdrGRXb9N09RxHODF3jIcDqmVXVfnCkyACTABJsAEmAATYAJMgAkwASZwugi0bttXWpw5UvJFm/ktFzIBJsAEmMCSBI5HgIaUDAEaonAYhugx6bOtARTjQnTpxax6YRguFk/FUA9oTlXVBVMNVFVlWRaFfpYkiQJo4BUeOoG1uofFLMssy4Lsi5AamNlg5qCiKKIQGbquW5YVhmGapkmSwGsb4Skg0A8GA8dxVjr5eZ6HIUtNEGTHcWBc13VM+ytJkqIoyyvaM4e8amExLhBEhR4/qKoKx2Rii8yqllv1obODHuR73/dbdXjxKAkU4wKvvKVpuvhne5S94raYABNgAkyACTABJsAEmAATuGoItG4qV1qchlCW5Wg0Eo1M1+ESJsAEmAATWIbAMQjQOIjbto1AycsI0Ai+YVmWtJMGg4HruguCb1RVRe7PNNldv9/XNA2nkJl0sAoJ0LIsB0GAmssI0IjpLPodK4oyz0fbdV2EYMaYMJUiRayWZVlRFMw6qGma53kzVeyZo0Ch67otATqOY9d1JUkicdy27VXNLmhxma9Go5Fpmtj0cO42TRMiuHhe30+vsOkRfAObXlEUwzAWPHhYpudcZz8ERqOR7/vD4RBB2IMgQKzz/djkdZkAE2ACTIAJMAEmwASYABNgAiKB1k3lSouiHeThBue6rud5vu/DAW4/96rTTXAJE2ACTOAaIXAMAjQcIRF9AgqsLMuLPaDTNLUsC8E3oMxKkjQajRb4UeZ5jqn2IMJSnGVN0xbI1kmSaJqGuMmY7g8Bl0l9pthP0/sHfHs1TaN4zXC/pebEExXmx+v1et1uF33DPIHD4ZBUY0VRTNO0bRuzLE63OLOEWoGjMcaCKNsI6wH3Z0SFTtN0ppFDKizLMooihBbBFJSIv4HJHxawXb4/ZVkmSUJ712AwwHZ0HAetLG+Kax4Igaqq0jT1PA+Bv7vdrqIoi58eHUi7bIQJMAEmwASYABNgAkyACTABJrAfAsW48H1fal4p1jRtOBwGQRDHcTEuIG2TcVHppkLOMAEmwASYABE4BgEa0+shmvMyAnRVVWEY6rou7yRVVU3TzPN8XkiKqqqSJDFNU5ZlcmeGsKvr+oIVR6MRwmKoqmoYhm3bQRAgdDLJo60zDVCWZel5HmY7hABNQ8uyDKIwScN1XUdRBEdp8s6WZVlVVRLKB4MBHJ9Jv6ZttjhDrZCPOc6Xtm07jqMoSq/XQ2iRBfL94ib2/O20AN3r9UzTRE/onL1n+9jucLMFSblJpmny9IN7prrnFTHFB0LK6LouSRLmDtU0LQgCfh6wZ7C8IhNgAkyACTABJsAEmAATYAJHQACTV2FKIdyw67pumqbrulEUie900s0s3Y8fQfe4CSbABJjAKSJwDAI0XmMxTRNT4SEERxRF86gV4wKBleUmwaE1SZIFE8qVZRkEgTjVHgm7hmEU42Kecg0Butfr4fGm67qiAI0eTgvQxbhA1GalSVKT+k1SFAXKNabXIwuWZaGCqI8jD73YMAzP8/Yg0lH3KNIFYj0Ph0OK/mwYxhGHfsbAy7IMwxAe0FDe+/3+QQnQVVXFcYz9Cs8ABoOBoiiapu0aKxzd488DJADH5yAIsEXwPKbT6fT7fcyHyVdmB0ibTTEBJsAEmAATYAJMgAkwASZw4ATyPPd9X24SvVotyzJkaM/zSIbGbTjdjB94T9ggE2ACTOC0EzgeAToMw+FwuIwAjYDR8EqWdxImBpwXPgIBo03TJD2X5Mh+vz8cDquqmuf8mySJLMskQDuOEwRBmqZwmp4pmSHWByJvyLLciM8STk79fl9RlOlTUZqmhmHAO5s8oLvdbq/Xk2XZNE3f9+M4Xsb3mWKD0I5I5zxR55UkSdM0RVGgAAZBMHMsZOSQMngwoGkanbwPSoAm32psgp09ZeJUbtv2HnT8QyJwVZqd3sPxs3UcBwFtOp0OQs3gWi0MQ3ot4LQAqcqa/sqiLovLiwv6T1gW1OGvmAATYAJMgAkwASbABJgAEzixBPI8D4JgOBziHrbbJASTJBnadd04jvM8P5Zb7BOLjjvGBJgAE2gROAYBmtxgocAu8ICuqgpqMkRhqUmKonieV5blTFURbrAt7RUrQoY2TbOu62kPaJwt4jiWZVmMy4xYAXCabq1VlmWWZYi8AXdmUpNJYFVVFTqUyD1JEkQkICdo+IdCLaU5Enc9geF0CIlctI88ZuGjUMuqqsqyfOnSJYTPnq5/BCV4gEyRRjAVoWVZLbAr9aQsyzRN4WmLTSw1IbpUVdV13bbtY/H1XmkIp7oydm88CMFAxAA4vV6v0+lsb2/3+31d13Fxhujtu+7eJwVLdVlrhu5cFnUxrkiDrsuqrqZ6WtWT8hJsrvicqsoFTIAJMAEmwASYABNgAkyACZxQAphhKEkS3/dN0yRXKniPYb4lBAjFm9P7ubE9oQi4W/shUNWTu0X87ccOr8sErgoCxyBAU0xnyIWLBehiXEAURuRiSZJUVQ2CYKYLc1VVo9FoOBxC9kIEBkVRRMfkeQI0ThVRFEmS1BKgoT5DDSfVjHw8FUWB7jwdb3owGMwUoEejkWEYmFOx3++jueFwGMfxkmesqqqgPmtNCsOwtWJVVXR2hMwtNanT6RiGMVO7P4L9Gd7i8HzH9ID9fn8PAjS2RTEuEE8cQR4wOyWioMiyrGma4zgL4rQcwXivhSZoW9BDmjRNbdseDAbdbpfmwDQMw/d9/GzpB3UK+DTXClU5cXkuxhX+8rzI8wL5clxM/ibhrutqXFdFKf7RCwokQp+CIXMXmQATYAJMgAkwASbABJgAE2gI0MvTxbiADG1ZFpzJoDlAiZYkCc5PcA4j0YApXusESH1unJbKax0Hj/9aJ3AMAnRd12EYImYFfGBVVY3jeHpT4HAfhiFEXhzWLcvyfX/arRW+0sPhkNxgFUUZNklVVcivg8FgsQAdx3FLgHZdVxSP4HmdpimiiEBlQ+gMvUmkrkJ60zRtelxpmmKiPLlJ3W5XURRxRGhxekWUwMPU933DMNBKFEWtk1xZlhg1xZgm72zf9+dZPuxyzOFAWxOSvWmaLfV8XjcwRuwVeZ6PRqMoijDVpLTj9ayqKuI+u647L0jLPPtcvgcC2Fcx3yDNL4qYOd1uV5Kk4XDoOE4Yhqdjc4hPp3cuF2YK0Fk2zrLxOM3GaZaP8jwpJn+jHCVFnl8WpssrHKH3QPjqX2WH8wxf8t0HX9Y1X8jtjolrMAEmwASYABNgAkyACeyNAN2E4tXbKIo8z7NtWwzKgXttRVH2PJPT3vrGa51AArg/+dxdykR6niyVdV3wrcsJ3GDcpSMkcAwCdFVVQRCIArSiKDMnIYTU6Pu+KFkOh8MoisgDmoTXJEmGwyHprQim7Lougk2TAD0cDqfxwouzrus4jqEpw46qqpZlUSxmmlfNcRxM6IfwAr1eT1VVp0m6rsPhGu6fhmGgOepnXddZlkE2hVq9vb2tKAq8kqelWJK/yQICWUBqh3idJElrUNMC9GAwQJiqmVp/a/VDWoQHtCRJ8GeHAD0cDrE1xZFSnuhRkAec+MMw9DwPjuQ09yNtNcdxaKsd0ljYLG0acoKGaz+eKnWahIA5mDL0uPzuV9tSJEALqui0AA31OR/laTIaPZKOHsmTKMNfmmT5KB2n2USDbhLtzPQTFruESUoX1xHrX4V5ATWNbsJ8cpG2k2i77BTgf1XxVdyVRHiJCTABJsAEmAATYAJM4OAI4E6HvG3yPE/TNEmSOI5937csC7IGhdaUJMkwjGO84z64obOlPRKA9Py5u5QdAbpgAXqPRHm1q4fAsQnQ5JWMEBxhGAKqqNFAgHZdl8JcKIpimmYURSTXok4cx4jDIDWp3+9rmpY0SfQ1HgwGhmFMi9ckQCdJIklSp9OBlNnv9w3DsCwrDMPRaBTHMaRnCMeQ2KA+W5bleZ7jOIZhINpyp9Pp9Xqe59V13VKXinFhWRYG1e/3O52OLMsQTKlvrV0MFrIsS5LE8zwMFuc527anA00gBIcYFQS+0qZpHq8jKgU5kSQJQUgMw0iSREREeYKArVyMiyzLRqOR53mYCAIDlKTJrI+YEUJRFMdxKI42WeDMoRJAXB38LrAhOp2OJEn0/AZbUPx1H2p/djV+OY5zWRbjohrXZV5NwIsN4gAAIABJREFUpOQ4GafZxHM5r5rCOk+qMEjcfwt13ej3P/Ophz79kQ//j3c++K7XvvpPX/S7v/drv/Krv/hzz/uF5/z8Lzzn/uf99P0//zO/+Ku/9KsveuF/ffkfv+TP3vzG97/vvQ9/6tPDzxqe52HeRejRaZpiDkbsz2BC+3wrs+tATlOFyyKy4BMgSs+Xr8zGk/jZTSqLybO6shxfHmPz2hqNt6irNM/GjUr9Of8C+pozTIAJMAEmwASYABNgAkzgIAiQt00xLugvz3PcmQZBABla3UmmabIAfRDgT6sNeDoXE5fn5jYFc9lPYjqWORWe1sFxv5nAvggcgwBdlqXv+6IALctyEAQk1NKAIFrZtk0CNCIrRVFEkiuCROOVf0SIpggMMAj9Wm4SgjLD2xonkstKR/OaPHyTNU2jifsQRZr8altBLRDFGLGG0zQtxoXneTTDHuIPILCG2BamQMSgEDeq3+/Lsuz7fr7jMkkExEye52EYmqaJbuA1H03Toii6wlWwWWemAC3Lsuu68zRusa3Dy2dZBsJSEzQDm2yZcBnFuEjTlJ4zyzsJ6jPkbNoWJ0foPDySJ8oyBGj8DPFcBDNqJklC+xu5+h5Xz3HqJ3fmxos5C8PwE5/45Btf96bXvvo17373u9/xjne8oUmve83r/uBF/+2Xf+H53/fsH/zKr/iau++695Zbbrv+/PVnz5xda9LZtTNb6xv4O7d2dmNtfX3tzPramY21tfW1tY0zaxe2Nj//llvuu/dx3/Zt3/bc5z73ZS972bvf/e6PfexjmqalaZrnOZEBEBwliBIOTcfF6lDanRag63JnRo6yrsdX/l3h/lw1cz1OJnes66KoR2md5pNX2OiPNehD2WRslAkwASbABJgAE2AC1zwBEqDhTUIz3+CWsyzLLMsQlwN+J1EUYdL1a57cNQqguTER1OdJdnKzU9ZZUWfl5K5HuNO5RiHxsK9RAscvQEN+hadwS4OGAE2SK+RjwzAcxwmCIEkSxGJWVRXuxtCLh8MhzVJYlmUURZqmyU1CBcdxaBo0EqCx/auqsiwLmiZ0Z/qkQiinkLnhHA01vKoq13VlWZaa1O/3dV0nJRQN0aLjOIqidLtduD/LsozQIniOCnFKDFlAYTfg8wv1GRofafHiLlxVlWEY1Bl0Xtf16WAd4lpHk3ccBxud5ofUNM22bczBSKAok+d5kiRBENi2jQgnspAgPSPYVhRFHHnjaDbidCthGOLRCGKvw+cXPzT6XWObTq972CU7V41VnhdZNh4lWZrmdV0//PDDL3vZy57xjGdcd911586du/PuO2+9/VEXLp6f/F23df7Cua2trfNbF7fO3XBu8+L6mfNn1jbPnNnYXD939szZ9YnOfFlrPru+trmxdm7zzObG2ubGmYkO3aT19UmdtbW1c+fO3XTTTbfffvuXfMmXfP/3f/9LX/rSj3/840EQZFmGaOb08KklQNMR47ARHYd9iMbQnbO6HtV1hvhoTSabeAnUk2JpUD+0XX9su/74v9af+Nf609v1R/65/sg/Z73P1FFW5/XkD++48aXccWxHbpMJMAEmwASYABNgAlczAdzCQH2mz9Z9DV5txJuOuLC/qi/jr+bNfRBjg29NNnGvuewOXdbVqK695i87iCbYBhM4lQROigDtOA74iYdyCNCWZZHrsbQz15ymaZj0T1VVzDwLt2Vd1+FKDM0rTVNxnjrEQUYQj+bl7p13vXc8oKuq8jxPUZRerwdHTjGcE1yeZVlWVdU0Tc/zRqMReR+TeC3tJHF6PYyLzkMIbL29vY1wH5CzbdsOwzBqUhzHURQlSRKGIUWyFtVnTdNc10UHqA+0D1ZVhdgj6DN6ZBjG8cbfQPcwBaUojkMfR3wV13U9z3N3kuM4pmnquo5XmkizxoMBOFBbzbyUaZpOcyAgnDlsAhCg8bsQHZ9b6jP9BA67P6J9HEkgPSdxmsTpG17/pu/49u+66aZbbrh404XrL26e35poyetra+c2zmxdt751y9mtmza3Lmxubq6vn1tbO3dmbWt9/dzm2a1zm+c3z25d1qDX1yc6c+P5DKF5IklvrG2cPbPepM3NzY2NjbW1iR69uZPOnTuHwh/4gR94zWteI0kSXmJoXc7iiHFV7tLNZVg1rovmLy8n7gATjwD4Bkxk6WriJVBltaXWb3/99o/+0Fuuv+MFZ+984fk7Xnj97b91+xe88Pa7fvGrvv7//Nn7XxVldVqyAC3u7JxnAkyACTABJsAEmAATOEgCdFlOl+vkMkLN7Pi7FKiDVehbzlxjBKA67wjQ8LqpxnUd1XXYvPR5jfHg4TKBHQLHLEBDUVUUxbIsdKmlT5VlGQSBYRjQKMkfmTL9fh/SM2bY8zyPHIerqoLzrOM4tLokSZqmWZaFQNI4N9AZAtMM2raNifJE9Rm6s67rkNjiOEYgV+p2VVWmaUo7SZZl27bpLfvWuEajkWmag8EA0/FBV0UECUdIhmFomkaqKwYL32q4T9LJT7SP8x9GAV9p4DohAnSWZXAAhzg+GAwwLkJBWjNmF4RULSrpyKuqOhwOfd/HK05XpVS38zs96f/pd4TgEq1tIe6cRzASuB5Mgjs3iZyLNe2zf/VX7/25n/v5Jz7xyRsb5/G3tnZ2bW1jc+vC5P+5tbULW2vX3bp27klrZ594ZvOOra2bL15/4w033HDD9Rev2zp//vx1W1sXtrYunD9/3SRdvHh269za2trFG28+t3l+Y2OSv+7ixfVJQI4z62c3kIE2vbGxsbW1de7cuXXI1mfOoPxpT3var/zKr7z97W/v9Xq+74MVostdZe/u4dKr8QeYqM9pPW7+ylFzFZbVdTSeuEDbfv1Zo/67D9X/+ZceevZ/eO/THvfKe+553c33vvOWJ3/ghnvfdeHO19/3xa//sZ/97w++z5HM+pHx5XfY2Pf5CH5Z3AQTYAJMgAkwASbABK5NAnSz08qINMSvxHIxT68jQ0k44rsksSecP0wC8IDOi2KEVsbFFUE36LZobh/EmXLmVuIvmMDpI3A8AnQQBHBqhraId/YBr3UUhiIMvZJEZFKf6ZV/uCRT5A0yVVVVlk3CvFJ0WtIuHcdJkqQl4KL10WhEmjV0Z0iilmUFQQBVCCcY2uAQuXRdJ51UURTXdfM8h83pcY1GIzgpS41bt9wkuHXjEzE0UI5PqUm6rgdBAI2PznP1ToL6XJYlhgB1HsSGw6Gozu+scdT/q6qC/o4NSp8iB/nKhDgbENNRzTAM3/c54MZRb7xZ7dFO2MpQ3dbOT+WHkamqCuotvA8Q4MLzvAceeOA7v+O777vvCWtrZzY2zm2evbCxcX5z/fy5jQubG9efmbg5r23c8vn3PePrf+hnfucrvuk/3/HYH3zWd/7sG9/yF+/967/5+w9/6IP/9/v+4sEHXvva17749//wl3/5+T/24z/xXd/z3V/7DV//xCc/9VF33L259aizm7dvbt1x9uznbW7dQN7Qa2fW1hon6c+VTJpf39zcFEvWz5579F2P+bZv+7bf+Z3f+ehHP+q6Ln7dmGW7eYhFVymnQ2ilPUHcxBhDMYmvMVGf4zqLq8mraKO6dka1ndRxXf9/cv2md+k//ry/efIXv/xxT3jj3Xc/8OjbH7zljndv3vW+m576j/d82cfuefrfPP2ZD/zpWxInnDg+J/kkoBonJsAEmAATYAJMgAkwASZweATo4raVEVsUvxLLxTzdjCdJInidOaRHH+V9k9gxzu+ZAO5xWqsX4yrLJ44yhlMrw9ofTfKPJJNaS93XsQDdAsqLVwuB4xGgKVys3CRFUXRdn4e0LMswDCmgBLRUqJCmaWqaZhgGBaMgIzh24zNNU9M04c5MIiaCdcBDefpAD8/rYZPsJrmuG8cxeTRTQ8hAgNY0rd/vo2+6rodhSAJ0qz68szGpoLx0UlXVcZzRaEQdpvMc2ScB2vM8+HETMdu2xWqUP+IMxh4EwXA4lK5M8vyEHQBO4ogvfMTdvjabox0MmZkQWnVocWblIygsy7IYF5iZ2jCMD3zgA8961rOuu+66JsTGJEhGE3bjpo2N81tnJn+ff9MdN954+9mLt/7sf/q9T6v1r7/47x/12Ofddd/PvuWt/xwm1XgSGGJcFeNynE1iQ1SXR5AVaZyn4SjvK+6H/l76wR/+zYsXv/zLv+z7v+TLvvGue++97Y5bP/+2z7/+xhs2z28hEMfGRuMQfXZ9MkHh+mX3560L121df8va+tZEj24Kb7zxxp/8yZ986KGHcPRIJylpHp5nTWTky3NWEGQ6FBwB2JlNtC65xI61+rYjQJdZnSd19khdhHX9SD3Rnb28/lSv/osPPPJ9P/u+e776ZWt3/PrNT3zlxS94w/V3v/3Co9914bHvOf/Ed1x44lu37nrTbY/70y94wu9953e+xP232gtGxST483jSMfEqjfNM4IQQmPmb4UImwASYABNgAkzgtBFoXeLSojgOKmxdA4t1kK+qyvd9cqobDAamaSZJkjdpuj6XnFgClyM8X55VsJlfvbkxgY/M81/wt4+570W3Pe4lX/3v3/GRh2o3rtOyYgH6xG5N7tgREDgeARoTA5IijOC/80YLJ2jolYqiSE1SVVXXddu2HceZliNbR/9iXARBoGnaYDCg6QpVVSUP5ZknCbQ7Go1wJqB5C2f2syzLPM/hZw13XdM04S49z3gxLpIkcV1X07Rp524EpgAieGEbhmHbtjjlYGuY6FhLgO50Ot0mDQYDCrQ9OSpWO0LazPEcZiEE6CRJfN8XZ5gk53FsYnySM7jbJExUeJi9Y9tXEBD3sXn7TKsOLV5h6AgXLMt66KGHHnzwwZe+9KXf9E3ftLU1kXe3trYQIqNxPV5fPzsJxLy1sXZ+fe36rfO333HvT97/m3/5d9pP/Pyf3/OkX3nal77ot37/XxSzdsLRaFyVRV1kxTgdk/o8+QEV4yyfhPL6rFe/5e3Sf/j23//27/iN/+dj7iNZrRjGP/7TP777PX/xyle/8jd/+7d+5md+5tnf++yv+OqvuveJj7vp9ps3b5hEhV4/e+7s5s1ra9evrV1Y27i4dnbigo2AHhsbGxcuXPjBH/zBd77zncPhME2TNPeLMmik2hEubwjyvI1yZLzFSygEdy7qalyW47LMJuTqcV0Vk/kEJ3n8Zc1I/Lr2y9od1w916le/Uf2PP/LA4//dH649+kUbj3vNuce/bv0LXrf+2Les3/3gxl3v37j7PRv3vX7rCa+4eN/LHnXf7931+F/8ufvfWNV14yfe6PInRG3kbjCBFoEj+x1yQ0yACTABJsAEmMBhEhCvvcW82Oa8crEO8mVZep7X7/dxq95rEt5yxsvWM53ejv2yf3ogXFI206HnJECX1URgrieT2/zBS7cf9djfv+HOt23d+udbt77hW777PZkwcXrLiadNUrykbH/Hy0zgFBM4UgGaDspJkliWRRGNNU0LgmCaItUnydLzPNM0KRTGaDTCo8LW4ZhWhNJalmWapp7nQepVVdUwDDEEx3TTVNKyTOXTmSiKIEBjqkPbtqMoEuNEi6sgUECe50EQeJ43HA5VVUXIYwp8LMsy8sPh0HXdKIpGo8tRhERT03lo0FmWWZYly7LUpHmQp1c/7BJ0Dz6qSZJgm8LZnD5t2/Y8L2gSJmOkmN2H3T22DwL0I2plTg6fJEnwO8LP3PO8Tqfz4he/+Hu+53u+8iu/8sYbb6QwF5j0byL7NmkStfnm625/9A2Pv/f6r/rye174W//pL9/3wQ8/5D7/tz5035N+/87H/Pb3/MCbPvLx0orqqCizqi7yuszqKm+uLybXFPlkgry0qvOJ9+6HH6q/5wf+/Cu/+r+9+a3/anqX8ZT1eFxlRZGV5Xg0ig3L+NS/fvofPvbhv/7Hd73mbS/5P379F3/6Ob/0tV/zozfe9IwLNz7p7PWPPn/jLWtra5vnt6ira2trt91227d+67e+573vshwpSvS6jpL0islaW5tm+YOVsBFbAvLKi7QCxOXxBM0kuHMy+SseqauoHrvVI/+W+VVdx3mapNUjyUR3/p9a/eFPlH/y5s8+67sfePqXvPmO219z290P3PLEvzp/37vO3P3Wtdv/7MJ9773xSX+3dc/frt30f6099lWf9/SX3/r0F3/RN7/4/t/8y0/20p3Zo+EYznE4hE3KWSYwhwD9WpfMzDEzt7iqipX+5hqa+8WSHd9ztbkN8xdMgAkwASZwoARWPVAfaOMnwFgxLuI41nW92+1Cg+50Ov1+Hw5nuAumYB1if+niXyzk/DESKJt3VLMdAboqxpM34+vaSeqnPvM1tz75nWuPevva5hvWb3rwptv/UDMnPZ23918ehSg9I7/y8Oa1MLt8dumifq6+xspD4BWuWgLHI0AjLrOu66qqIqjCgiNsiz35IyO+M001Joov04dmVA6CIAxDmrNuulqrLQhby1QrxgXUXrxKo6oqIhQjxvS0WVLG4WENIHDy9Zrk+34QBFEUxXGMOlhlpqnpQoi8o9EoDEO/SXijf7rm0ZeAJ9pFnrYpoveKMXyp8pLi+9EP59ppkbbFCRkydhvsGJ/+9Kdf8IIX3HLLLefOTVyJ19fXoT6vr69vbGxsbm5evHjxtttuu+OOO770S7/0+7//2S/49ee/4y/+1DIfqsrP5uPE8evn/+b7H//0F15/w3/56me++a0P/pv9SB2M66Su06LOx5c16EnU4Ykjb1wXcZ3WZVL/z8/UP/rcd9/3hb97//M/oph1lE8CHI/KR/JyNK6yqiqac3dVThTscVKFdZ245WeDMhtV9Qc/WP3oj77+7vv+l+/7ked83w//r1/+zK96wpOeuL6+fsMNN5w/f/5MM0vhxYsX19bWfvKnf/SjH/tAOrbqOo0e8cSDHjYKfa6+aVa9gJiu/7mrKPg7TwToajSq40fqUdQE2cA0g25aPZLXQVRLWv13/1L/+h998iu/9ZWPuueFN9/+kltuffPn3/qemx71vnN3vHvjMX9+9q4HNx/74PnH/fnZx7z1unvfceeXvfPer3nVs5/znlf+ufUJtf5XcxI2+pG6Tsajooybqz4WoFff8rzGtUdg+te7uGRVQiupz83hcdUWFvd3/9+u2h+uzwSYABNgAnsjsOoRe2+tnMS1IFkgYGAURWKU0V6v1+/3MfWUruuI/4k4nzSSfVzzkw3OHCSBopnP5vI7qnVZl0U2zsd1/Q+fKm95wiu37n3v+t3vO3Pnezdufted97wqfKRO04k8PfPvcrdYgD7I7cO2ThyB4xGgJ09+msjOvu8vcOxdIHjhKwqLsaAmIYezJGb3osJdM3SUFwXu6bWSJMGMiAiaYZrmgmARsIlJ0khLwljESRHFFsX8dOvzSqjz8yocffkyW2pmr2a+iDSzJhceFIEsy+I4xlOQJEnSNF3153NQPVlgpxgXf/Inf/KMZzzjlltuufHGG0l6njgUN3P9fdEXfdFzn/vcP/7jP/7Qhz40GAzidJTmo7SYRLSoai+OQ0Utfve/fvgJT/mDz7vtRU97+p+8+A/Vz2h1kE28m+O6SIqqqCYRN6piPIk2PB7XdVCWQT2u5c/Uv/fHDz/ta37va7/9D9/5QScq6zCvsjrJ6qCoU2gxZTmGH3Q5CSA9HtehO/ZHdf3QoP6R/+3jT3nKK77xW375v//DJ+LROIjCj370o8997nNvvfXW8+fPr62tX7x48fz58xcvnl9bW7vrsTf/8q/89Cc++U9JEkZRNDl6FJOj6LwjxgJiV3418/pnlUJcJO2sUY3rcjwqi7goo3GVZXWdlLVf1E5eG4/UH324funrhj/1Sw898SvefPuT33DdXa++5XFvvfVxf3nzXe+9/tb3nr/1L8/d8bZzj37T5h1vPHvHq2/9wjc+9Rve9n0/9/f/5RWXPvAvI8WfPA/4rFcEoyKtsibqMyaYzpow0Ds9mH1Fx98ygWMncOUv7ziWVkWwah9ZgF6VGNdnAkyACVyrBA77jHRyuZIADQ0aXmiWZSmKQm+HS5KECJyIOBpFESkGJ/Du/uSyPpKekQd009okHmFaTO4i/+j121t3v3zj7vds3vs3F+77m61b3/7vv+sD+bgeN69xzvwBXO4vC9BHsuG4keMicGwCNLkAQ0OZOf4FYiUdfMXMTCNiIdqalmwobrJYGfll7FdV5XmeLMu9Xq/b7Q4GA9u20zSdtjZtc8EYl/e/ntfQCSxfMF4RNeVP4BCuvi7N3CjFuMDkn5qmIeS67/u4+jkhBBC+5jd+4zce//jHr62tnT9/Hv7OCPp87ty5O++88/777//bv/3bLMvwjsVkZsJx3kTfmkxCXNX1Z636j17yL0/+wt/5hm9+3+Of8pof++kPDbRJqOJ/i+tHqokAfXnWvzqpyrgqyqoox3WcVeUoq1/35s7XPuuVj/nC5//+a/9Zi2srqe1Hgqi0xvW/1fXE/blx8UOw9aoosnQc13UVFnXHqn/8/v/x6C94/Z2Pfelv/+5fm87kWIFoQoPB4BWveMVP/dRPPfOZz3zKU56yvr5+4bpmisKJnn7my77837361a/yfZ8OZZShn8yKD6tmXv+sVNjsDjtrTKJi50WVpUWe5E2YDC+s//Uz9T99sn7Or37wm5/9wF1f9Cc3PvZPt+78s6073rH56LdtPvpttz/5/Z/3+L+87q4HNm9/7Y13v/QJX/a6b/m+D/7wcz768rel7/9/622vHhb1I2Xtx7Hrh+EjUbPd8klotQqu1ZPHAgf3tzOSiZB9UGZFm2J+eftYa3F90fJB5Re3eHjfLjNesfVV64vrTucPil7LzvEfOFsd2nVx1R6zAL0qMa7PBJgAE7hWCex6CmpVuHo4iVfsdNGOYKG6rmMWKMTzlJuE2KGI7Ql/rJk3blcPoNM2EsSALnBjOQnVWOR17VX1T73gIzc98S3n7nn/+t3vW7vzwese84Zf+x1t4pvTpNb+jcXL37EAfRkE/7s6CRypAH0SEJLWTL6cOIgv0MF37Xae57ZtS5LU6/U6TTJNc2ZQkV1NiRVa56er+2QjDhbbQiwRsXD+wAngR0HXQHVdp2nqui6miJRlGZdBnjcJ/nDgre/NYJqmSZK86EUvuvXWW8nr+dy5ydSCZ86cufnmm7/u677uXe96F8J0tGK85BP12AvHeZTVb3x7+rXf8s5HP+7lX/DUV3zTd771I/9S+2kd5pNgGpP4G03EjaaHSV0ndVkUVe0mpR3XD/6N+Y3f9cf3fPGv/cTz3/1pq3Iux5rIs9otarfa8YBu1NKJgYkrdFUHcdmV6j94WfCkp7/1UXe/5Ht/6L0f/+QkfESWV9RVPHkyTbPb7T77e5996623n1nbXFvbPLd58cKFGzbPbt1///2XLl0qxgWecu3v9zLz+mfXQtHteZIvisvXU+EjcV3XcVIXZW059aWH63e8o/6Jn/n4fU95/efd+ae3P+4vbrr7bWs3vnbtutdfuPud193zwI2Pf+vaTS+6+ISXP+bLX/cN//Gd//vP//Wr3tL95GfqYVpb+QSlX02ibTSzGY7qcTZxIm/impRFXZWXJ1Mt6/Lg/kQP6n2ZFd6um7ePz7UvrIs66NXc+s3wxZ4fVH5xi4f37TLjFVtftb647nR+ZXrzNvBJK9/1h92qsGr/D1uAXtX+6vXF647d86vy4fpMgAkwASawQ6B1wtl1cWe9q/d/nudRFNm2jXmh5J1pnMgb2nGc0WhEjnRXL4kTMDLc6KzUkcn06HU9mYB94oET1vW9X/3Krce+7ezdH1i/+/0b9zxw9o4/eM/ff84i7fGfKzrI3LSGvbhk1bZFa1hXRCZ+O8ljsKu2wfWvVgLXogBNdxUzN6oow82s0CqsqipJkuFwOBgMMI1Ar9dzHGcPUh11bEGm1fpVuSgO/6oc4EkbFF4Bo0cyWZZ5nocQ7QhDpmmaYRhBEOxhrz6MwWLijje96U1PfepTSX1G0Ofz588/5jGPed7znnfp0iX4FJOwSxHG8zILsv+fve+Aj6O4/l/pdFXNsiVL10/FvWBsijEEsOndoSQEAqEmIZQ4jd7B2Abcq2T13mVVF7lR3G1sMNjGtoSq1e9Od7qye7s7//+buVutTpKxE+BHgu7zPnuzs7NT3raZ77z5PpvNg8q3omtv3xKdkG26ND92xofLU890M6iXAwYNBw9Ew27EeQDk5AEB5RieB5y1D6Hibd13P5Y/KuGvj/yt/NOTyIpQK212IpZGbg8QTlgFAJrxAFTuAcNg3sMjuwMVFFhnTC+IUadMmbUqNfdclw1Z7ABA0+CygiFUPKyHpRmXy+VyOBwlJRUP3PeHiHCTVBollUVQAEZTjzzyyLEvvyC6HZIz/YLVLvR/LjpAwB1Cke1kWcKA1mFDvW7U1o0+3e9c+NGhex+snjw9J3jUxtDRRWGRlaNiqpVj86mw9fKYjcGGxDET1yfMSb387qw/v38wtda95RhqtyGrA1ldqN1KO/ElACeDwC1NI48deRwQ4KAjw3Jgn+yr9GAM8d+LETIUAv9ePt6zcAWHvRS48sPmTxo3CFkeLr1Q4R88MFyJP168uAkXUsrFpj9/nt7ciFPN8299tx+c8l/xE1f4QsIX26iLBXx/7Pwvtj7ivseFhC+2/iPpRzQwooERDYxowKeBC/kKidP4zvuf/icmQU6n02KxtLW1NeBfI/4R54S9vb1ut5t8of6nNfHjNk58Y5Gwf3liNNX/2KB9ArFyHDaR4RjO5ULos1MoZnqGXLdJot0OALQpN2rKyrpuWH2Lvdf0910HZfeDRPhDwNgi6jyRQxYqpB98VDhEVvr6JeDxamOhEz0CQPvp55e+OwJAwx3gB8BdyE0h4NQcx1kslubm5vr6+tOnT589e7atrY3MT15IPuI0IwMeog2xHsT6GQn/SBogCmcYxul0Wq3Wrq6utra2pqZm/BkwAAAgAElEQVQmsgqsqamps7PTYrGch9b8R6rYcNm63e6vv/563rx5UvyjKIr4HpTL5bNnz66oqOjo6CBPKMswRAi2y7AswwIzl9WFtn3a+7unPzPMyImbUx4y7sNn3qqttyILQr28w4FoFwKaYbzl4bMJOChiEetE6OA36IGna0dNWDz++hWl+3vbEepGqAv1OWHG2+1BfSywdzCIAwoOnmd77VYO8S7ENnWxlTWu63+VbYhKmxyf+vrbO082eqw06rC5nSzrYoEeBNhCXG6PmxbmA1xO7qsvmp564pXgkLjQcJNEFkZRlDJYdff8exoaGsi7y49Bfii9De5riXtcwx0dOp7nWY7zMB431NXttDNMFwtKaHGjr1vR2syuP/zl84kzk3UTM4LVGRHG6tGm2jB1dVBojix8Y1j0OnXCqmlXrb3shmXPvVFbtNN67Byqd6JOhLp4H5CHjQg4DsydGTdiaR4xDuSxIM7Ocy4PYlyId2LBdCoET/RwaGhhkUeQ4dLgeC8uyeLZBtG2/3ScD8xFECFm18IuDkDn0yfnBzqFfAZU26+qAzMnp/jVxzNUGiFzoTJCQDh0UQHhdDSwOHH8cGFxQYMr7xcjTkzCfgn8di82vd/pfrv9uTGI+14Rq+KCbfB9N/nFP6WDzxj6+eyfmOkf3vx7KQeX6IsZOr+LBXx9NfXl2v9/cfmziB1SLrY+Q2bCIlbcJxGH++s7EhrRwIgGRjQwooGL08DQ73nfd2Hw0aFzF8bjZPng0In+22J5HpZF2u12s9nc1tZGDKLJWMxut9M0Tb5E/zXNIljlD1pdcn94swQI1O+GGbowIZGvoy50XKHH7ssEnztMnQeU218IBwZLHPYVxCE373Ai9MFGiyo2U66tkWh3YgA648bf19i8p7jENe7P5t8PDYaDxTHDhUl5wzQVoHJBT14+yYEoNuvbHVxvBoy4YC2xEyFmxAJ6sIJ+4TEjADTcAMQFbWdn53mIm8U3CpmfJDFut7ujo6OpqamhoeH06dP19fVms5msjhGfciFh8cBmuPCF5PPfnkbc9v/2tvyc6y/uvvA8T5xgiG35CaF5S0sLQZ//vWmVH1wDxPx54cKFKpUqPDycGD4TDugnnnjim2++EUp0O11iANqDZ6ZdHHKw6Osz6Ll/7Yibnjzpqkr1pUl3/7FqzxnUySErcjhQrwugZM6FWBcYNTMsYgkbMA3wNHp/dVP0+I91l65Ymd/zbS9g1m1ML5A4I5oGa103j9yIxwA0YnhyOkI9TrTnkPOuewomxCZNMmbOv7X82HEaOzT09HIeJ8e4WDf4uQY4EfEAsjLOPtblASd+G1M/v+a6P8WOu3HmlXeqRkXLgoOpACowSHLLLbfU19f7WUALzR8YEPpVAwLeZw0xUGFvD0RI0A+MstAuIkDCwuLehMWOLL0gnb1o32mUs4N+7t2Ds+/MCdd/qBy7JnhsZriuNHriFioijQpNGmXM0k5IjZu25vrbs598oaZsi7mxCwp04kVqVsRbUF8fcnE8ZM30IZcNth4n4t2IpxmwfWZ7ec7B8Q4PcrsQ44TJABbWukE7hToD8xoRDtGDhUVuP8FphJZCB1SMKuJwP0bpQYwHaMFZkub7AGg/rHZwzhyBm8WwuABAiwLiE/srM2QCjJlCX++84g+tDmqyuESgP/nPRJzbkPX3i/xh0wu37pCBAUUzyOMHOtOIG1L8kokV+H1INNysw/1YxPsJubOHST94hmPAkyB+Kv698DDl+j1x/XlfLOD7Q6UfHjj2zgJeYEHD5yPulfSHh9fPyJERDYxoYEQDIxo4nwYu8LXMcR5fSnj3khzJW5iEBXMNYopxviL/q47xPA+rIWnabrcT2yCLxdLb20sWd4o18DNulq97IMY/MVGy0FmHziqPaLzk0YWtfTDN3ve3iWTtS+crqL8T5Dsy8J+k8w1k+jvDLDZh8Y0m8DnDoLL95XpvRpKYg8EBDCYgDxdy9SH08F+PU1F5Uu0WiXZ7kH6r3Jj26vKz3R5SIegJCh5IhNr3V3ZAT5FUhaC9/Um8AyBvk0lm4jQEPhaAY9JoodK+5mHTH6LzAWVCOSQH4jnJ70TxFRUOeeuGn1MyUmQ4sAHiODJWE9d9JPzL1sAvDoAWLrfw7uZ53mw219fXNzU1Wa1WWiCHF5IOChCrQxJttVpbW1sJAF1XV9fc3OxwAAvqyG9EAz9nDZD7X9iSmfbOzs7GxsYzZ858++23J0+ebGpqam9vN5vNTqeTpumfQ9+Opmmn03ns2LHZs2eDITD+URRlNBpfffXVr7/+mtQTqooF0TzH8JyHZVjeDUAy6qFRfQd6a/Eh/fglE2YUx4xLvu03RdsPsnZAQnls++xyI9oNaDKDAw4a2d2MlebhxGWpJ/RTl4xN+GDBa581diMbiwA75mk376IxAO3haQ4wK4CkeORkkdPNu1iEvjyOnn56q1G/ZELcuhuvyasqY6125ECOXtTbh2xOvo9mnYzHzTE804e7JzA7jk6eQ8tzGmbMWzT+8n++/XH5p0caHnn6WUV4KADuKmVgYODChQtbW1sBEOI4oWs+8MYTOjb9XvV4jIzjbj0PW87FsQ7ezfJuHjE053GxrIvhHDRyuJHDhfpcyO5CvQ5ktyF7l8fd5UYWFp1oRBXb0Psfdzzyx+PTrq7STikI0SYrY1KVkeljDKWjdWWKMWmBEQt1U1ZOvz7x5t/mvLhob3LJ2S+b0NlO1McgF41cDODBpNNEIw/D0cDs7AG8k/eAYNYTjmc9gI+DFTqBVftbhNk4/LpBPAaRWeAG4WkiHAceCz3IxcJ8AOPDoEkYtgQ0HGom35u5L0/IlrCOECTaAyA4wQH7u72kfsOBtr70/mC3OJ6EfbCmgI8PGRhQul+hw8HQvmReqHdw0TjGv0X9evd10r8vRoyQiis/eG6AHCXpxSmHC4tzFoeHSz9cieJyxcA3hP1QZr9d39XpP8t31cSgtv9RkaoHqJflEcggAHo4SBTH99/A+J70zo4IEyS+GvbPH3zf9RpQJZjdGeIngnTxa4S8TIRXCsd5vk/gDUnEByuw4kzOF8ZrSvrP4gcYPvsmhwZECgoUnyUO+94JRJlDnytk4mcNPfBNO7I3ooERDYxoYEQDgzXg/+URv4HJ94JlaZalxd8OstJOiMSnAM7l91EiFhikSLcbzDgGF/9fF0PaSKotwNCElM/pdJJmXpT3F0FpP60qyKADo8rQMcdWsD6Ms9sGJjjEOLabBlOeDryctAehLjd0WmgPw3GEaa//opP6i+8nH7ApxAlNxCWJxwf4iC8d6eN5sNkBzWALmwHEfmAK5AN4fVmS/hvu/3o7S97SCfUzGaZ48WUwadJNy1EZdlCRmxTGWpVu25jY9L3HwQSKVITDzbezHpuH6eNgfa0TIRfLguWRC7qDvh8Hy3HhYB/eAuEhjXiro9dDE7jJN4rymt1wpI0024fHTchBw0Ph5h005ANzOKAaFkPuDI/AsQ5P41HWIBhaDED7qgP/glrFkTiMy+Y5ZHe4fJpALnzxxZYLg04bifjFaWAEgIb3Wnd3d0NDQ2NjY0dHh8VicQF1z/l+gtM2mqYFR20kh66uLoZhhkGCzpfnyLERDfyUGiDdETK77na77XZ7Z2cncaRZh3+NjY0Wi4VAz+LO0E9ZySHLcrvdK1asCA8PJ7QbFEVFR0evWbOmubmZ53mHw+G1CPawAD0DaMSzrMvNu6y0x86jdgdKK2meeuUKw4R1o2JWXHldXkG5uRlzclk9dhfPujnWhVwuwF5dbmR3I4sb2cGxHoc2ZH87Zc77Y+Jef+SZ2jPNuMPCIMbjJl1nhnMxnIt0oBHHYxilz4Pcdg/qtKClH7caNSvijcnj41Yueu/L9jb4JPfxlj5k7UNWF2+j2T7ICgiP8bQ4Qk0t6PVlx+Ov+Vgz881Xlh461gjLmRp7uu757XxFmIqYfs+YMaOmpgaIO4btdvu6W9Dl8E63i9AiDvr3rJ3zuOAgnjuHdNgYgfR3HLjvgzlIUKMTnexA5Z9Zlqw/c9dDmyfOzAuLSVPHbwnX1Yaoa1XRVcroMiokIyA4OUJTMO7S4mvuzvnHBwcq9qFjLehUN2pngS+73cU5PQh6fKA9QHCB0JkDZJfAgQSMI/UGLJrjaA/jZmgn7XbSbjdDC+JiWcxewgJk7hMn43EyHgfNOBg3EXyWy+lxuVi3i3W7YcLAK7TXsyEg3j5Yth+ww/P2gG8SBIrA2TSisSk0Q7Y+S2Qv1ChAt0PlJs7ZGyYYMcEKRegk9CCJt0Xcc/NeOOEKigJET/3Pivh6D1cHnMaL254XTO7P9sJC4sLFYb/6k7uJFrWCJCCn+CUeclec+YWEB2fid5a3fX6xF7iL9ezVJ76UAgbtB0CL8XGS3juMIdDzYOxWDH0OhEoHoM8+AJrck14L/eEA6CHviiFb+n2AOKzwEIsYPrj4cD8wLSDUfgExbEHCYv2MANAX9pCOpBrRwIgGRjTwU2rA//NC3t7ibwSJQdB1hjlOkdUz7Pp6Kd46kzE4wzDEG7nb7SZG0IK/8Z+ybT9GWQJeTFpKsGaO42j8E7zFCK4IB4/RxDmIwz9GbYfJk4w4MJch4KUEzAVUl9wNdhZ10ii1zDz/yfJr79sUNydTEvvR6BkrH33xs51fIDsHfQuLlQYzFNFvmLIEbHPQcQEp9TfShVrgkQexTiC216RTKtyug3KDCHJ04CGC6ZKzgYERBo1ln7oCRq8NMe5VmbaPGleriimdemWxlYGjYJ/E0XaatzLA2EigZ7IVQFtfARhtRg68WLQPwZiJUEKCzTiuDBgag9sh5ORhxawLNwpqSX7k4TG7eTuCXKwcVMDpRp4+3AGHOoPlD42FjIOEc3EOggZ9OZ73n5gQkSRODlkZ70jHjat1fs2eN+ORg/9rGhgBoAGA7u3tbWxsrK+vb2xsbGlp6e7u/l4uDkJZYLVaW1paCPTc2NjY2tra29s7gj7/rz0l/6PtIfdwb2+v2Wzu6Ogg6HNDQ0NTUxNBnwmm+bO6nxkGfPM98sgjcrmcANAREREvv/yy2WwmV8lutw8AoGnEeng36nGhrm6Ps8OFdh5Et95bOlr3QezEtTOvTl21sbX+HLK4oHfEIg/D8mArzQP0TKNeGvW4gTzD4+JQXln3VTcmRhhemjt/w/b93Lke1GF2MyxP0GeWpRkOhHSpob8EHQUbjVBrD1q5pvmSafmXTq3VRCY//vDnX34FYG8f1+tCFhdPOzkGzJ8BgHYyDGvuARqxxnr08usHL7k6Uan9+/1/yT74HWqywfR3L28/fvbI7GuvDAySyGQylUr12muvsR5gKR3mPiVffAGAA+wPd1bcHEfjfj4NAL2bsfciiwV1W1CHGbV0o4YuVNeJznSiMx1o30lUsoNOLOz5xztf3vFg+bhZ67XjEyN0abKILGXEprGmPaN0n4bqdoVoqkO0ZaNN+ZNnb37omcbFSezBJnS8G53uQ2cd6Ds3auVQK4vaaLBDt7iBidtGoz4PiJ2BsJ0BEdwPMriDxJDZfx7mABwc7mSRrtbAfpvXfAAnduGtGzOQuXF3zYX7Xn08svF8L8tZPSyRXpbrZTkbz9p41sHzDsQScfEsETcHcxJunsZQNU3DtISDRk4sfS7UR8Oui/GKQFQCi86Ah8Ur0Akb0h5ZwGLJIjcxOOjr5wp9tgsIeHv5/ffC4HN8HWjhljhPQHS20AsVB7x9cZLsPPkIrfRLI8q/Pyu/NEPu4hPFNbmQMCniQlIOWa/BkSQrn0J9145cdMCgsXENbH2zFF4aEB85TL/9NQFSyXQIzXOC4JUAvA9mHRJ0Bk4YIjRQBoGI7zRfrbzDAHIfCqsJhJSDk4HvT+9SBLIggWxJWcLsi1sMi4vxYg/v8Rcx3oDDMK72PSH9AYiFJQte8ZlLw/tKjHdjnIJoRtCAX8CnN7BrJrjG4K24/uKJJXF4YD79o+H+x2wk9MvTAHkf/PLaPdLiEQ1cuAbEX83+T7nIBsLjNeDwuBksNOMizkVIgGy93WwP67cQk6Zph8Nhwz/BCMPtdv9M/KVfuJr8UvZ/Y3heQJ+HDIhTkkwIZk2sUghZB1EaSelX0I+5S+x2XbgX7+3eEV/lfQgdb0UPPX9o7MREmSZJqkmlItdQYzfI40oCNPkyTU5UQnJSFu1mUZ8dFqLynNgC2ndHEczXR8PnbQiJ9HXMhm2d91wfa7MXfcXdVABQidn1MDCs0IH0609imxGOB3S4D4H587NvHpZHZ1DKMpVu2+jY6jBt2mPPHSRG0jTjcDlpsELGgxQXDxbPbmGkwyIny7MYKCZxYBiNGJoH62kzjbpcqNcDxeOfi0N2HuPYeEhExjq9CDlcfW4Y2fqYmE/1oNqvUOnn6PAp1NoBIxaWJ0Y/nItnMQDN4kWlUCsSGKiI71UrsYzGJTKAqpfsoJenOXIrYNTmxsZGuLNMqj2y/aVrYASAhveazWZraWmpq6s7e/ZsXV1dU1NTV1fX+V2ucRwnkG8QwK6hoaGjo8PpdA6PBP3S77aR9v/cNOByubq6ulpbWxsaGs6cOXP27FnicpBw0fwM72Sr1Xr27FnCv0FMgB999NGWlhaapt1uN2GpFvzysR5gDwYjWdTdh3rMCNVb0LMvf6GOWxk7Zf1Vc9M/WnO2qxeZ+5CLZTzIxbB9XnCFc7kBfe6lAYZ2OXhUts05984szbgPZ89Lzq/qqu+AHkpPrw3AbrxyUACgPWCw6yEcEjRinTwqrOi99LLU8ePLJyRU33Dd1uJCrr0H0cBibAVqC552w2Q4AtsNcOuHbH3om1Po7y9+Mf2ypLGmxbc+WFxzyNmGP+edbocL2Rxs59N/fkIikRDvi7/5zW/Ioo1h+tykuyZ0/fsBaAJzcR4gV6HdaOH7m955b+ebC3e/8f7eF17e++zLXzzz8rFnXvr6/qc+m3dv5cQ5adETVodoV442po02ZgXH5FAhGaO0W6NiPwtT7w7TfRqm3xmi2xKm23T1Hd88+XfnkiSUVIzWl9rXlzdvqGhJLG8p2ePM3NKWsflcyU7L1v1M7T5mxz73zv307oOe3Qc9uw66d+537Tro3nXQvfuQa/ch1+GT6PBJdOQUyBen0dEz6NhZkK/q+uV4PfKTr79D3zSiE03oZDP6tsUrp8+hM23obDtIXQeq70IN3V5p7EGNPajJAtJs9UkvarX2S4cNdfVh0NyDbABhg3WDIDafZUIf7nf2YaTb4QsP3hWSCQEbTuzAJxLoHPBBPERjSUd5SHRQsArydcihQyp0jn1mJuKD4vCAd5HoLHEO3jA57fxpvLYY4hKGCn9vJiSBd7QyVA5+nX4hw+HT+qlliAYKmQiB8+cmPor79yTCd5X6oVQfa4cYgwYwGtuCiLdeK3sPwMceEPxwCnCqDyT1ZzAXg6Q0MNcTOR8ATaZzhNtMmBkgblcFPJoEiFGMsHVhZ6qYHJ8U5KaR21cohqQxARGsWMATNm7kGSicGwkC82CewZzrHjxjw3n+DQCagO+C0jAVST+lxmDomcT4dAvgvlif4vAIAD3gdTGygzVAnvoRZYxo4JemATHoeV5YkzwipPMpfGr6u6BkwpJmHE6nzQYsx2aLpcdi6bFazVarubfXQmI6O9vb2lpbWsHTUl1d3enTp0+cOHHs2LH9+/fv2LGjoqKioKAgOzt706ZNhw8f7uzsZD3scBi0MKjxa8LP7QqKqzck7ixEilOSVhDTIrvdbrPZLBaL3W53uVzDjA5+1Hb7vLdj0JEArw4EVBuL0jtGTV0bPiFfYaqkwooCNNVBxvLQybWB+m1U9HaZ/tPI8TtG6dbvPYw/yUMC0EDowcFSTQZyZ31T+oQRD1o1nEGOV0e4Tt4uNFl5iP0Hkkn2/v7nQP2I+ocAU+POOYdLZ3AFXLzXULkHoXMsMs1KVmoKA6O2UiGlCm3F6HGFH6cjG0K9CHU70TkL2n8cbfkc5WxyrM9se33R4dcXHX518eFXl+xdmvzF9gMdNga7xIGxJgixjN55GD383Lboie8bp3y0aOkJq5W01TkQgHbiQmjaCUe7+1D5busDf65Rz1xDaRaHT80MjFwUk/DRglcPnG6B4QyMVjjeDYZPDG4N5mIkyDgCZNyF1eyBp5nBjINYez78e5COIKLPjV5872CwYWHE+PSxEzf+ccE2pwdOxWcOPGNk75eqgV8uAC1ccZ7nnU6nxWJpbm6uq6sjMFxDQ0NbW5vVanU6nS78c/t+ZAmMzWZrbW2tr68nFqMNDQ2tra02GwBSQs4jgREN/Jw1wPO81Wptbm4WmDcI+ix2cDG4c/N/2yKGYY4cOTJp0iSKoiQSicFgKCsrg2lkbBnhtX3mOLIQz814XAyye5AV2Ts5V7MLvb/+iymz0yKNq2InL1mZ1NDTBx92lkc8cnOsHQydGezEmKcBj+ZchMNq5+e919+bI1W/Zpzy0Yb0nj4WaLRoYGxggL/C47V67jf34zgHzfQ4PD1udLIJ3ftQhT4+MSom7co5VZl5ru/OwefcA193zgXmtL3gt9D32mAQOtOE/vbqrrH6ZcbxGbf+pqZ6L+pBqNHG4ELBrbDF0fjGmy+pVMDCIZFI5s+fb7OBX2XBE8vAa0TGAOKRgBiMdrlddpZDW2tPT5n2r9HRr8SYlmrHpUToM8MM+WGG3DBjdogpPSQ2FcSUHmzICTbkBeuLlPoSpb5MqStX6qoVmhqFZos8pkap3Rqs2RysrsJSEarJ105L0V6yWjdjnf7SDaZLN2qnrouesDpm/Gp1wpqY+NVRsSvHGJbFT0+Lm5YaNz05dlpS3PTkuOnJ8ZdsjJueFDc9KXbahthp6wSJn5GYcGnShFnJky5Pmz4n65Krs2dck3vptXlXzCuafVPpNbeW/+q2iuvvqhHkpl9vu+X+HXf+btc9v//s/sf3P/DEgQefPvC7Px585Nmjjz3/5ZN/O/7Hf3zz7CtnXnitbsGbdX9/u+GlhS0vf3Du9Q/b3vy44+2VPe+sMr+7uue9tebFG/uWZjBrc/nEYpRaDpJWidIq+cwalL0F5W9DJbtQ6WeofC+q2IeqDqDqI2jzUbTlGEjtcVT7tVd2nEA7T6JPTqNPz6DP69HeOrSvHuRQA8gXjehoA/qqEX3zHTr5HTpVj842oO8aUXMzOteM2ltR+znU0QbS3YF6upDFjKwWsBDxSh9yOoGum9hmO2kg2rbjKRSy7WMgBljJWdyhxDchGMOzyE0I8HzIKKFAEfBRYrXr9oAJgxseDBDvLqbT9vAwECDwK7nPfFAsMNIJoCmNxwtgV4vTu1lfViwkE3LwjlaxUxo3x7s5npCrkDCN40kaWJqI6+/yeEshaynF9fGrlQfxNM95rdo51ofz8gT2dQNpONjtElPdfvt1WKFILELIEGTAEwZWNLyHsLvAfBIgyCyGngfYvAs1IaMenCMS2F18Y6B+c2YMpDI+rTs8yOGBl9kAwQY0XmX7bPBdDJDRE3sWMOwRrgUJEAC6D/F2xPWBvT9HxAngMhjvYJSZH3LrRDxx/ulEjAvEjYWEAZImDPgEgHaDD1E/4ZxIELD3uVgAWmxhTa4RuV7ey4fxbi+CT6h1RFbYg8yvvVeZ8OoI7DqEyt9v2/9uh3sDfj+3L+OAO/KXuTPEo3nhisDvLQFfEAJeJMI/H/E31f/YRe0PUecfLG+oyBD5X1T9LiqxuObDhS8qwx8wManPD5jhT5DVz7TO5NXn9w4UgF2RXgCf4+CrItDX9iFkd7o72zvPnvj24N792yuri7Jzk9esXbbwg7defuWf//zXgldfe/mtt95YuPC9JR8uWr5i6YqVyz76aMlbb73x178+/+STj993331XX311QkJCfHy8Xq+PjIwMCwsLDw8fhX+RkZHR0dEVFRVCHcS1IhYqJEZg0RS/xsWJhRz+bwN+1fveXaG2brfbarW2419LS8v3WtQJJ/5nAdEd632Fegk3GITO9dncCNV1ozv/sEs5ISN4eg1lKg2Kq5YYK0Mn1FLqApmpKlBTq4j7XDbuk0BDFTUq88EnDjsxobe44biGxHIZGJthQhuh/V+hZ/+1f22atf4cmAoTs43ztMVudzn7YNDFePBEOEJ48Svru6v9jTtw9wznR9rF4VVmCPU5kQ2v4zTTqIdBnR7UzqFzCLXyaGkWoqLWUVFF1NitgcYDVMwu6cTdVz/aMvXuWuO1WaOmJo6amBo6ITs4PlcRnyOPy1bE53gDsWlh4zfGTHn/2GnoFSMeOWwOmws0seMoSrgqm4paJ1XnyiNzI9UrysrazWZsI887OKAtsdOeXrzYErBemkFHv0IPPbZPNzFDacwKMBRT+s2UvlKVkK+KTVXq0hOuzMnf7uhkkNkDSsMfDIZDPBgsI/TJIfT4s/tuuLt8wWvHOu0IasDQmDOxH0YeEoXmETp6Cqk0S4I0RZS6hIpOGW18r6kdrGqGTH+eKzVy6H9YA790AJq81whcRcC4+vp6YgddV1fXgImhm5qampubW1paWvGvDf9aWlrq6+vFRtMj5Bv/w8/J/2TTCIO5cA+3tLSYzWbCoXye2fX/c1UcOnRo/PjxBH6dN29ed3e3HwDNeliGYWgP42Q8dpYze1AXh5pdqGhX52W3LVdEvzXpipS3Pjp2ugU+sb0uGxDMAfDshD4FA44YOA5AqB6r2+lExw6gp56ukhteo7T/eu7Ng8dPA/UzLFwivuxYlx8ATawXrbSnzQYsFo8/VxM7dfX0q4pipyW98v6Zs+2wOItYF7p4HgPQPR5kd9m9HidOnEFPvVBmmPxBqHrFlNmFyaXOdjfUs8MO088MsHi5XO5zTzz+sBRbQFMU9eKLL9rtwFL9bwHQcD09LMotOGIc9y/T5DURpnVhcblKQ41cv11u2CY3bJEbq+SmTVhKZcYSEEOZT8plhkq5tumKJhgAACAASURBVEqurZHHeEUZU6WKxhKzSanOUWrSgnVZwbqsEH1emCE/3Fg0ylgabigL0ZYFa0pFUhysKQ7RlYToSsL0xSG6ohBdUbC2MFibL4hKk6tU58ijs4goYrIV0bnKmDyVJp+IOKzS5AdrC5UxeYroXEgZk61U56g0ucE6EFIZDLLne6F2Q26IMRcj7DkqfZZKn6UwZMj16XJ9utSQLtenyg3JWJLkhg0qY6LKuF5lWqsyrVYaV6hMK4PjVqgSVoVOWBU2cXX4lNWjpq6NmL4uYvqasbPWqa/coJ+z0XRtyvgbsybfnDXt9twZdxbMuqd41j3FV8wvumJ+0dX3lV1z/6brHiib90DpbQ9X3P1o1X2Pb37wqa1/+HPt43/e/tQz2//03PZnXtj5l7/ueu5vnz7/j88W/GvP31/e+49X9vzztc9feXvvG+/vf3vxgfc/OrJ4xbHFK79YsurIh2uPLt3w5fKkr1cmn1iddmpdxpkNWXWJ2fWJOWdT8htSC7/LKmnKLm3Or2jNr2gtrDhXXNlWWt1ZWt1ZtrmrbHNX5TZzVa2lentvzU7rlt22LZ9Yt33au+3T3u2f23fste/cZ/v0kGPvUebAV+zhE/zRU+irM+jrenTiO5Bvm9HpFnSmFdWdQw2dII1dqKnbX1p6UKsFnbOitl7YnrPCbpsNtdtRRx9IlwO27X0Q2WZD53q90o4jOxyow4G6nFgckLjbBQKMOW5k8fQLmKuTjjkHj56dB7HhJYuwalFkez6AsIXg8hiad2OHmW5mAExP40PgSNMDAmA6XnoJAC42GCHbfqMvDMSTxC4PkIgLsL6LAT4+77SBBzl94h3B4TEBgd0Hb+EdgsWJydDtrAcLN8iQ2UsaCDSB2GDfioCNXSx2n82+mI6QsMALpvoDA3wf4NH9AjbUvNcFIc1zTt9SAGLaP3jrxPMHwjyHN0BmQQA4BjNqjDgPZsYeECPGoAn6LMaLSdiHPg9FM+3j+sBXUrhEvoDXkam4RI4HOyu+X8SX6kLCMAoTZgG/NzAclvfzjP+/6yAQzf+b5YtOFl/BHwmAFhfhb6knvqwX1hi/3AbvXlg2/3Eqcc2HC//HhVxgBmIlwCmkPsOf7J9++JQ/3ZHvq/NPV5MBJRH0lrA6DB4pkAWI+ATe4bCCOM1dPc0nTh3esq00I2vtuwtffPpPD1839/LYOHVYuEKpksoVEqkUCOXgJ1XIpAq5XElEGiSXSGSBgTKKCqKoAIoKpKjAwMBAsvyRoqiAQJBACSUJoqTSAIVSdtNNN1itZocDbDKISQoMB7CXFHEPWag5CRAoQNzOwTHioz9NmNThwrekVsSorru7uxn/zpw5U19f39ra2t3dTcZ3PxrULrpjyQOF1+QR2g0zQkea0bz7tgRGpwdP3U1pyihTsWxCkWJ8ZsikVGX8hjFTC+Wx1bL43VRCDRVbFWTcNiZug4tFHtol1gBuIwGgoW/kdKB9X6KEy1eOGrcxekrKrHnLvvx2ENAJ71hwZg4fboRdzrDAZdHHIzOLOhnUQcOKRmwVBHg0Bkk57JPPS0FBAGhvPK6BywPp31uy59ePlN716LbbHt156x923vzYzpsf33bTEzU3PfZpkC5NqqtQmbZLjZ9QkZ9SsUeoifsDJ+2mJm6lxtdQ8VsDE3YGxu6ijLso/Q4QIw7DdgdlqJLHrU4tOQsV5xFL83aG6ebQr/9yOHhStSxhR5Bhtyxq1xhNzqq1Z8AQHJzV0Hhxpg0bR+G6I5RRwIRpPwqOyZKrKyjNZkq7g9IdoPSfUcbSgNgyadxumWmTeuaqPaeBpNJnBOUBKw2Eyqr50boPwnQbw005o+OSX11U7yIpCLEccRDfD0T3PxAcQn0sWpFyKlSXETB2pyp+v8xUodAs/fwo9I0JtN+feiT0C9bACADd/2ZjGEbgdCbgsoDN1eNfA/41NjaSAPHVRl7uxPfgL/hGGmn6f58GOI4zm81NTU0tLS0dHR2EdkPcG+t/NnDoZ9LCEydOzJw5U6VSBQYGXnHFFfv37xc6mmI7aIYF6l6Lx9HtQe1utOsomnPnhqjxb864MeXj1NbjDQBCOZG113EOcAQwDsTLrAkAjU0yLX3o0CH0/ON7xiesko57/dYFpbVfObtd0H3hOURSg6cUVrCkg7Xz2O6PcyP0XSd6+a2j06/ImHR5lnrSR8+88cn+Olh7RSiJAUtCLhr1YrjMzjhciEPfnkJvvlM3flrKKP3K+NkZ68vYMxY4Baa28Tw/67G1tp7MzFxrMmgoigoJCdHpdEVFRU6nk8N230NdI/FQ0B/scNgAvkcInaijH3mu4Lr786fcmh41Kz0orjjQtA3L9kDT9iAjkW0SU3lAbInEVCYxlQUZy4MMlUGGaqmuRq7ZIlXXyNVVcs0mubZQrsmRqTOl0VnSsUVBkcVBUYWBUYXSmEKFrlhhKFMYyuS6CqmmIkhdLonZFBhdFhBVCjK2ODC6JDC6RBJTGhhdFBhdFDC2ECQ6n0hgTIFEXRikKZJqcT76coWuWqHbrNBtlmtrgtSVkugKSXSVJLoqIAYkSFMDoq0K0lZJdTVSXQ1OX63QVcu1VaQCUg1Gzw1bFMatCuNWuWGLVAenSNSVEnVlgHpTgHqTRFMu0ZQFqbFoNwXpSqX6TVI9BCTaogBNYYCmkFLnBWjyA7S5El1ekD5faiiUGYtkpgJ5bKFP8uWx+XJDllSfGaTLkOozpfpMuSFLbsyQG7IgRpMaGJMcFJMkVW9UqJOVmhSVLjVEmxqqSwnTpYRqkgUJUW8M0SSGajd4RbcuFEuYfi2IEWRU3PpRcetHx4JExidGxidGJSRFjdsQM2GjelKSbtJG/eRk47RU47TkuGmp8dPTxl2aMe7SjAkzMyfMzJx8ee6UK/Omzs6fflXejGuLLr2ucOb1RbPmFV95U+nsW0quuq14zu0l19xZhqXkmjtLfnV32a/uLrvuntLr7imdd1/ZDfdvuvGBipt/W3nbQzW3PVRz+8Ob73p02z2PbZ//+I77n9z9wFOf/O5Pnz/8l32PPb//8RcO/PEfh//0z0PPvHTk2Ze/eOGN439966sFbx//+7snXvzg25cWnX518enXlnz79rK6d1c0LFzTvHhd68cbOz/e2LksuWtZctfKDOuaHPuGfNfGYia9nEsv5zLL+cwKNm8zyt+CimtR6U5UvQdt2YtqD6Kdh9GnX/bLnq/Rnq/R3m9A9p9Ch06hw6fRkTPoi7Po2Bn05Vl0/Cz6BqPq3zag042ovgXku3MgDW0gje0gTR1eaWkHWr3WDnSuHbV1gLR3oY5u1NmDOs2oy4LMFmS2IksvstqBZsfuAHP1PuztlKDPBPL0skSzgFD7QFCwPRlCPMjBgBDM2oHHVE4ysvIgGwPSS4OFjtXpFbMTYPoOGrXhQVeXB5k5ZOFBrFgIG4wYaBaoZoYMiFM6wc261wu7G6/rHPIUIdIhSg+m69i2XbTlaOQR475e22MfcsCzAAQLP0jptXceCmX2smq7eE4sDp5z8LydiG+eQpiw6IUY3kVAcDx8hbc9DGI9HExCCiJ+xX5/mMO25nbEO7DYwRi9n9HHL0xcwBIrwv982z8hgo3dicsk/48CHomTlIMPDc7BL+X3t9+HBl5ESkKWciEnivyV9ecvihQDjYPDg7+f4jSQIVmpQLaCi1pRpBfpFMr25ijOhpjnDaRLIuZnOLFw6lABv3zI7lAJoR5+iQc3ToghKYXdfzMwXD3E8RebtfjciwmTBSveZSsDT/RTy2AdDpngP1fRebL1OyS+icgh4pLYa5eJp77EaSD8E/1wRcDickgAWlwJs9l8+PDhHTt2LFmy5JFHHpk3b15CQlz4qFCpVBIoAdQY/yQUJaUC5BSloCiyVeBwMEUFU1QIlmCKCpdIxgQFjZZKQjEY3Q9AC0i0N7tASh0TsfTjDwrys3fUbj169OiJEycaGxs7OjpsNhtN08L3goxu/HdFgJrf8EfYFbfxxw4LhV5ggNSH9bAul6ujo6O5uVmwqCOYRmtrq2Bm9CPA0ORBw7UQ3nLYuseG0Oen0OTrsxS6QoVpN2XYRplKKe2G4Klrr3+k8r3U1pI9aFUxEz4lPyCuijKVUBPBUDc0fmN9M3ZDMYADGs8n8UCB7KGRxYluuH972JTiwPEVlDpFFfvRa4uPuzDdsPepwOgz/t4xiPe4MRlJrxvtP4l+89yeqTeXh0xKpgzLx8/Nfyex87tesFcAbmbEwaJYCAIG7XuDEKeFnBsPGZML2oLVL4fHpiniSoISSgLHFUkT8qQJefKEPHlcGTW2Imzc/oDommDT59SonQGG/VR8LaUtp3S1lH4XZaylTFsp/VZKt9kr+q2UfluAoZYy1VLjasNmpe36ykHz3kY4Wf6sBUnGracSdkin7qFMO+S6TyNNBes21oEJEbBbcByycEBwwvEMoi1o+Ufd4cZUiaFYNaEmKK6aMm6h9LWUbgeIcSuWT6jYHdSYxAXvNdrAwMLjpvvIE+Dm0c13bB2tLQwxFVHRWVREpmZyott7e7kR24d4K7ZYALso4Ue05EbIzKDbHsyJ0OUHjt6uij2gStgq0S3d9Dkg/pgxRThjJPCL1sAIAN3/YiceZnt7e7u7u9vb25uagHDqLP4RrFmAoUmARNbV1bW1tREnvMPRTv2ib7GRxv+MNcAwjMVisVqthCaMGAj0PxIDQz+HdjAM09nZefPNN1MUFRYWRlHUQw89JDgeFOiYCSOzi+dhVRSNmnvRgtf3j41/6arbE9/ZcOxQI2pzuS2ebidqZ1APfOKBiQMLDVPHHhYwnbMN6K2360y6DRHRH1/5QFL1KbYD2w9Cem9/iCV4BEes9nBPyYk8dgRozvqsUzPm5BsnF8XOTLrtkdzNR23nPMgBc8seGLJzyM27aGRnwYUdzSLUcg4tWdoxYVpuhHpD1Pg1byW2HOsA9NnmcdvdiGEQ43KzdG9VecH4eG2ISkFRlEqlmjt37ldffeVyuYiVx1DXyNd3glGKP6DAOO2IYx0u2o2ABPloKzrShu7882ZlXKrcWCEzVcmMW2SG7TL9bpn+0yDD7kDTFiq2MsBUThk3SUzlEhNg0FJ9qVxfKNdlKnWpKl2SSr8uRL8qRL8C4NGY3JCY4lBNsUpdqATvInlB2rwgTUGQpghEV+oDc0uJSbXctElp3KQylSmNpUqjz+CamF37jK+l+lKfbArSbgrSVhDBMHE5gZuDtFWB2iqJroYIwZTxoQp8inAWANMANMdUUDHlINGVVFQFFV0ZEFMlUVcHYeNuAnBLNVVB6kqAudWVolIwxq2pCeyHuatkeoDFlfotSv0WlWGr73TA3AXBZuNVCn2lQl+pNAAyTjBxIQEJBKnLBZFqKuTaKqWuWhCSCcHxJWNLpNGlkphSApRLNZukmk0KbYVKUxWsrQ7WVoboqkD0FcG6cqW6VB5TIosuDIrKDxqTJxmdEzQmL2hMnjQyXxpZKI8qkkcVSCPzg6JyZTH5cnWeSleoNBSEmIpCYgtUplylMUdpzFEYshSGLLkuE7b6dIUhQ2HIUJpAFIY0IjJdilSbJFUnElFokhSaJKV2o1K7MUSXFKrfGGbYGGZMDDclhcV6JcSYGGJMxLsbvDB6PATCY9eFGdeGx64Jj10Hu/HrI8YlCjJmYuKYievHTkwcO2l99OR1YyetjZq4OnLCqqjxKyLHLx2T8PHohCVRCR+OHfdR9PiPYyYu1U5epp28TDf1I93Uj4wzlpkuXZ4wa8W4y1ZOmbN+6tUbZly7cebc1Dm3ZV93d8FN95fe8WDlrx/Z+utHtt77h233/mHbb5/c9eBTux/502d/eGbvHxcc+cs/v1rw0sl/vnbqtbfrX3+37o336t9Z+N3CxU0ffNi4eGnTkmWNy1Y3r1h3bk1i24aN7amZXWlZXRk5PZl53fkltvwye1GFq7SaLt/Clm9laj/haz9hsfC79iBBDhxFRPYdRWI5dgIJ8nUd+roOQHPAzRtBTjaB1LWD1HeANHSh+h6gwq83o+8s4Nf0nBN1ulA3A2JmQawekF7OJzzqxQg1walhi2kcLeAQdaAg/DrDCLidhRk+G+fFtQm6PXhr93kWJf5FvVseObA4OfDpLogbg/ICQO/xwLhL2BUCgsNHD55H9LKy+LxA+htcexEIgK8Bv/ZZSvuw7P6YfqiC5YD/UXit+q/WFR0S0gwIcNjbPObc5mjgYRL4ToCM0U/oAW4gvYbsAyOBthLTdHtHyx4fuOwHFvu//MnQepjqDpn4/JEDGomzHfw5EoarJPHgBP4x4j6I/zG/fYA8hnU16YOwBTxPqIlfLn67YmgQ6izCmr1U76KY/ptC0IU3O/9sfFoXx3uTCqcOFRCnJ+GhUvXXQ5zer2XC7oWkERKfL3D+qpCj5zt/qGMXkuegNF6fqdhSwA+DFjdWCA/KwB+7F1IOVcULjRMyOX+g/+LhapHEYh4liMYOYgd05/D9LM75Qqt1cenOD0D39vaePHmysrIyKSlpwYIFer0xcsxYpTKYCpBSgXKQAKUPVlZS1Gip3CRVJQTK4iiJkQqMpQJMIJSRomJ923iKSqCo8RQ1DsfEUFQ0FRgZEBAGsHVgAEWw7ECfeXQABOSywDER4aPDR+n1+ssuu2L+/Huf+eNfPly0uLi4+NChQ8ePf9nefs7DY08tHCdMI7I+txlEI+SFL37/kPDF6es/Sz249OFiSDnEOJ24ajebzW1tbX4gBqEMbW9vN5vNdrudME78Z3UUn00eJN/UF9njgYGlB6HL7yyJnL6Zit4coNmliNsSHJ87ZvLSzBqu2Yl6eFiM1YHQFffuoOIKKWMhNXkzZaqKnpbeixemwkPs+/nK4xAHq1Bzy51KfVJQbC0VVUrF11DRiXc8vMvBgJ2Q6Ckm7hA9NO5OtJjR7/5cHRL3ocSQQqmLqdjtVEItpS8Mnpw99Ybsdgb1Qd6I91gxewyN3/DkseQ46HFwDh5W2i1cWRdhWiPXbaL0OynTdip2G2WsoQw1GEfeFaDfQ0XtkIzdotTtlGg+p0ZvoWKKguIrKfUWEE0xpc0nEqDPCdBnBRrTpaYUWVxKUPxGyrj6T++esBDWZ9xgB4e+bEWB4zIDpx6hxn1GabcpYz9Xj8+t2dHnZKBuDMtzvIPjMHiOAH2ePL2UiilSTvmMis4PiN9E6cuwlFD6cgC+DTuo2E8o064A0/bYmXmE6oTxAGm01YW270GqyCTJ6HIqskAZX02N3RSsW93QhRwAvbMYgDbjFXT+ALQHq6wHoWnXJyrVOQFjtlGRO5XxW+WmFRV7gW+aHqZn4LusI/+/IA380gFocql9bzb4J+4L7HY7gaEbGhoI0XMj/jXgHwGgSUxzc7PdbqdpeOx/hBlFUsGR7YgGflINCE/ET1rqBRTmdDqtVuuKFStCQ0OlUilFUQqF6onHnzp27Cuz2cx4nA6nGXNgwax3j4M+24I+P4LuezjfOPGVu3+fXrj9XDPPt6EeG+p1oF4nbwNHVXg5F+DOLsQ4ANSwY2Kv9z6wTrq0mgr9aMq8rJIdbedsvBMP2TEALVp/zQJmzbLepVtW1tnNoaq9ttt/VzY2oWSUqfDGhypqjwGu0GTuJEaCHi9xLfDbQkURanSgJWn142bkjFaDLerrK+rq3agLoZ6+Ppal3U6aY/iGs2eWLHx3QrzJa+sRQBlN+qrNVT3WHjfjolm3B3CR4X6kM9i/9Q7IYRANtKY0BxrxIOA9yCv77rKrMkdFJRsmVI7WlYXpqoI1tQrNriDdJwGGXQGG2gCYP6+g9EWS2KLgiaVRlxZrZ6dqLl+qvmShYcbC2BkfxE9bNG7SxwnjVsUaNxgMG/Vx6dqEDPWE7OhJedFTCsdMyo+YWDBqQn7EuOxRCVlh8ZmhcWmChMemRcRnRMRnjB6XGTEuc1RCRlh8Zkhclio2UxmbrYzNVZlAQmILQIy5IcbsEGN2sAFIM5QAgoPINRkybYZMmyXTZsl1uUptrkpXqNLlY26NjGADkGwotdlyTY4gMk2OTJMjVWfLYnKl0TmymFxZTK5ck0OIO4BLRJ1DSD8gXp0nV+fJNAUydZE0Boy7ZeoSmbpEHlMkjylSaorlMSWKscUYyS2SRhZKIwuDxhR4JaowKKqQGIYD/gsCMdKxRdIoAJFl6jIwJNdVKPSVUl0FEYm+IshQKdNXKw01SkONyrg52LRFZdqmMG6V6TeDyTZYf1dgcBwQeamuChDzmGrp2BpZ9GZZdLU8Bqi6Vbpt/WKoVei2An0KFgyab1MZdih12xW6rVJ1TUBMBQi2AQ/UVUj0FRLDJrB8N5ZjK/hyiCHSH1+OmeaKKG1hgK4oQFcUqC+GCQNDsVxfLNeVynWlUl2hTFMgjSmUROdJ1blSdS6ZmZDq8qW6fLCRAby7CEuB0lCgMhYq9PlKLVwO32XKlWi8ItPk+SRHqsmUatLh0uvS5JoMuSZDqUuXaVLlMRul0UkKdXKwJiVEmxqmTRulywrTZ4QZUkKMG4MNiaH6fgnRbQjWrlVq1ig06/xEqVk1WILVa1Qxq4NjVhIJVa8KiyGyYlTMx6PUiyM0S0ZrPxyjXxJpXDzWtDjS+MEYw8LR+ncjdO+Ead8O1bwTqnknTPt+uP6d0YbXx5heiUl4WzvxPcPkxaapH467dPn4mSsmXrZq0uWrp12VOHVO8vSr0y69NmvW9XlX3JAz5+bMa27LvPaO7Ll35829q+C6uwtu+HXxTfcX3/pg8R0PF9/zh8r5T1bf+/TW3/x5x++e//z3L3zyyN+2Pfb3zU+9tP3PL+9+9uVPnnvl8wWv71/w+v5/vXXoxbePvLLwOJZvXl186vUPT7+59PT7y08sXnnyw7WnlybWr9jYsDK5cU3mubVZrYk5bUm5bRsLO0AKupILu1OLrWml5qzyztyKjvwac8Fma/Fme/Fme+lWR+lWR9k2Z9k2Z/kud+VuuvIzz+Z9aNtBtOMI2n0Uff4lmKLvO4kOnAI5fBYdqUPHvkNfNaCTLejUOXS2DQD0hnbU0IGa2vulpQOd60RtXSDtPT7p9sV0o44e1G5GHRbUaYVthxm1d8O2ywIfALMdWR1gGG4HV7BeEUzFbS4gTHew4L29j8XE27AMlnXQrJPhQNysWNw0x2L3iQTv6n/PDv8+5jyIoxHrxrSKDGYNZwFZ8tk8wZmQj+9Tw7PA502EjIZhHtQDBmbgM4jmvQ4MWLzEmJCLe7z+LgnIMmxdfEVAWXiFMnBMYTtvzIzJMyx8IwZWrT8z0lhShBjfhxg8khe04QfxkCygxIHQD2k4qYMYHiJhL6JIThYjbkIYE3RjbKUfj/bNMIvxvMFhIQshIG7mAPRZwJ3F2KAQJk3uP/k8te1PJOhJCBDEX9gFQlUQUQSEiUaErf9hIXV/SQNCQltJX2TAse/dETK/wMD3ZnieBIOLwPrxws2eAVM1fpFEJ4MzGC5GrBNx+Dy1u6hD4jyFsP+FI9Nc3ssruCGA68yz2EWxdzWdbyZJjLhdVG2+PzHP8wzDOJ1ON/gigR/Nui02S31DQ1tnx8HDX2Rk5bz/weIFCxbMnTs3fFSoQilTKWRKmVwulQXJFJQ8mJKFUcpIKlhPyUxU0DhKMo2SzKQkV1FBv6JkcwMVN0iUNwepbpWH3iEPvUMZdrcybH5w2K9VofeqQu9VKkEUyrvkyhuliquCFJcFyKcCbC3VUNIxVFAYFSTzMnEESgIkQQEBEooKkklV8iCVNFARFCCTB4DFRmhwyLi42FmXXfLQo7958fV/pedk7Ph0t7nX1WN1O7B5Z6/NKUxMkclIYd7Rxw4sjI0g8P2K+6lSCNUiSyHdbjcZKxE7aLJuW1jY3dDQ0Nzc3NHR0dvb63Q6WQ/7A7WFPE64zfg15ei1sSyysWj+k9sl+ozAuFpKXy2Nq5RHpV51XeHOXazba1ULH9kOD7rrmf3KS8ooYz6lL6ZiCgyzUm0e5HDb8byw91KQlgKjBgduMf74zy3U6FXKhE8CTLsDTDuDtBXX3LHLARbBRPVkYsaDVx2hZgeq+QL96r6tSlOa1JAv0VdQ+m0YPt4BdsemzUFxWdfdu6mXQ30uzuPpQsiFnQv2v/nxJDhQnFndKH8Tp4hapDKUSgy1VOxWylgVZKhUmDZT0eWQp+azQPUn8phahXqbMm4fxp1z5fEFEk2uXJMVbFwbbFwZGPWxUr88avJq3azll9yWeMtjOX96Z8fb6w/tOuRpasKfLM67ZtbFobRKsyQuizLtoUwHKO0nwQmfKqIXt9uRCyoJKH+vzW23gV+ONYkdkcYUqbaU0pZQ46qp6OyAuCJKlxkyIZeKWR6gTpKbtlLGT6iEHZS2Wj5+7+i4VLgQACaD2no86PEXv5Hq8gO0tQG6mkBdhcpQMdq0qotcLA/2kM5ZEWcl5wj3OLn8LoQ6WaSKfyfIVEBpdwTq9ytit6mMy7buBwvoEQBaUNdIYASAhnuAvNGECU+8+gL8mDmdzra2tpaWlqampkb8a/D9zpw509HRIbgcFHwajNxSIxr4H9AAeSJ+oE7JD6kPYqN94MCBW265ReIjQaaowF9dM3fh+4vqvzvd1d3qdNp67eBg4tjXfUuXHbv++jVq7d+unvdR6ZaOU52edtRjRi19QCFrcSG7m6dpHkyeifRYWLMd1Z9Dr7z91fRZlRHanJiZ6QtTW89ZERmBs/ht0Y8KYKtiHmBs5KBZFyaZrT1gfejZraPilweNWXPJtRVZNa7GPmDecCEXWWAOXGMc62Q8bjec2Meg1M3mKTenqGJWquOTnv7HnuOtYDJA4GSmr4+n3Uf273v4/vvjdbpQhVweGEBRVGysceWalX2uPoI+Y9hB6DwP1rn/SMsHQMOl5nD/jqZpp9PZa7eZzeijRScunbpxdOSS0IiV8rCN0lEF0sjqwKitgZod0ggPogAAIABJREFUQYadEsNWibGS0uQFT9h07YN1L61CS/PQ8jz7uuKuzIrOnPJzmQVNKan1SRu+27ihJTWpKznZnJhiW7i87Z2VHW+v7Hp9Rcdry9peW9qCpelv75xc8PY3f33z6xfeOP78q18+98qx51459ucXDz+9YN+Tz+97/IV9j79w4L4ntt/3+M75j++6+9Edd/9+550P1d7x4PY7Htx2x2833/Hb6lvvr7hxfum8O0uuu7Vgzk25c27KverG7KtuzL7ypuwrbsi5Ym7uZddlz/pVzsxrMmb+KmXGNckzrkm+ZE7KzDnps67JmHlNxiVz0qbNTplyedLEyxMnXLZhwsz142dsIDJhxgYi46evnzB1w/gp6xKmbAABf4ngMjF2KohhSgqWNNOUFNPkNNPkNMOkdP2ENN34VN34dO24NE1Csjo+KSYuMcq4frRxXYR+/Sjd2gj9+gjDWmE3XLsuNGZNsFokAIMCBipXr5dq1svV68F8WJ0UrNkYok0O1aWFGDLCjJlhxsxwQzaIMY9ImCE33AiM2yG6gmAt2RYGawtVusJgXUmwrkSlLVZpixW6YgCC1fmS6DyJOh9LoURdHKQpkWiLiAggcqC+OMBQSOkLQHT5lD4ftpoiEG0xpSsJNGwKMJUHxlVQxk2UoZTSFxEJMBTDuboiibZAosWW75oCqa5QritV6ktUxmKlqVhpLJWbwOBdri8O0gDRSmBMQWBMQUB0buDYXKheNADWMnWRXFMs1ZbiGpYEAZxdoTRUEVHoy6XaUjIlIIkuCBybHzg2XxJdgGHufJmmQKErVWlLg2FOZVOYriJEvynEUAoVMIBTTaIZpb5EoSuWa8FanwjY7PsE5jM0/UJmOPAkR7ZS6xWVLtcr+qxgfRowqOjTQgxYjClhpmQCeav0G1T6DUptolwHotQnqwwbg41rw0yrwmPXhcevD4tdFxa7IcS0Pti4VmVYo9StxbJeSK80bAg2rg41Lg8zrQiJXRESuyrEtDbEtFZlWKE0LJXrlsj0H8sNS5XGFYrY1cq4tcq4VcHxH4bEfxBmWjTKuChC/0GE/oNw7aJR6g/CYxaGxyyM0CwJ1y4J134Upv0oVL8sXP/hGP2iKP3CsYYPxpoWR8cuiYn7UDPuY+34pfoJSw2TlumnLAeZvNIwZZVp6trY6aviZiyPn7l8wuWrJl25buqVG6bPTpx5dfLMq5NnXZMy61cbL7s+9fK5aZffkH7FjRlX3pR55c3ps29NnX1r6lW3pV11W9qc2zOvuiN9zt2ZV8/PuObXmdf9OnvufbnzHsi74YHCW35bcuuDpbc/VHLnQ8V3/b5o/qOl9z5W8Zunqh98avMjz9Q++pdtjz9f++Tz25/55+6//GvXC698+vc39r307sFXFh5+5YOjry358s2Pvn576Yl3ln/z7ooTH6w5tXjd6Y+TAE9fnda0Oq1pXXrjhszmpJzmlLz21ILu9GJzVpktv6qveIuzrLavcpetcre56hNL9Wfmrfss2/dZdh7s3X3Yvueoa+8x995j7v1f0gePe774hj92En15Cn19BuSrM+irs0CMLsipBnSqAZ1sBPm2CZ1uQmdaUF0r+q4NfdeO6jpAGrpRYw9qMXvp0Qk3eosVONA77Kjbjix27PIIM7cQ8haHG/zYutxAUA4kLSyM5B08DEnd2I8QsYImwCi2XgSUi3jp9BDYF28ZFnjJCdG54JIUjMo54NMUhJiTk60QyWB3poJ1tLDQBojIBUoWPEFL4xW4DP60CUbkYpCVYHHQJx8MtGI4G/ivMAoP8D1G8MGIHJZW+4brgz99Q8TgryHAR/6fRQD8eQG2Jl9GgsV7yc0JLOXzIDrU+b5MhyjWP2qI0n1nD3NIACu9miLJBN0LNu9CjKBmcd9AyNy/Qhe/L2R14YH+Qi78nCFTDtSVuMlCWHweLtdPgcPt9tdxQEic3QWH+9GrgRUWMhBq2x/Asz9kNgeQZxbxA1h/IIZlEYPRMfDgi3P2PTbee2NAzf/DHcK5wTDeBfTt7ecOHz5YtbnitTdfu/WOWy674gq1TiuVK0PCRimUoWCbDKwawQEBYRJJBBU4lgrSUorxVOhlVPj1VPidVPgDgaOekIx6Rh7xvGL0AlXkP0Ki/hkW9RJI9MtYXg2LfjU85rXwmDfCxr4eGvVGaNQbIZEvh4xdoBr7rHzMk4HhD1Ih91CqGyjZ1ZR0FiWZRAXEUpSWotRUQDRFRVIBoykqNCAgRBIYIpWEyqQh0iB5P3l0IKUIk8Xoo+Mnjp99zXV/+9erZZu2Hvnia5ZHdofL4QY/dgzLMqyI42mg41kyRPoPtfoDni4M2YgVHSEbYT0sTdM2m62rq6u1tbWxsZEYzwmLuQn7osViITD0D1gfyArj8x6EXnj9i8jJmbK4LZRmKxW7mYpOuvrGyvrTGDQFkxwnT7t5BB78Yq/OpOKKqLgKKjov0JD/u+cO94GxjgWzYPkD0B4elmo9tqAmKCZJGftpoAEkSLP1mts/c/UTPeBRFH75OTyo8hiKvCqJ0qYHmKopYxVl2AJIsW43ZfgExPhZgKlaZUz8YFUT+Nmmbfj5Ak/JIvEQJmSGR11m9OSz+xVjPwZng9rkkKmFckOSTJeimlBFjS0G7FWzQx6zFZzixG4J0udGz0i/7PZNj/395CuL2pLzmYqdaN9xcDneZgMGrm4P4LbdCNnwHDBwVWCX0AjPUrt49GFyYxAA0J9RxkOUcU9owvbZt5RYGeQGojWavN95DqVnOsPUyxSmauXEvfJxtdKEIokhUZWw6q21ziONQHhd/gmKvbyI0qZR40opTU6APm/CFWlOB7n4LjeCdcERk1MoYzFQdmh3BOoqFOrUx//6hQ1fMW/FGEzEgUFrv9vGjdA5BiniF0rHF1PGXRLTQZlxS6hx6f4TIxQcfqr6pe+OANDeO0D8+hZuChJJXnsMw7h9P8GhgcCEJZwunDsSGNHAiAZ+cA2wHpYsHNu7d++VV14ZEhKiUIDHksAAhUoVrjHEbNi4oaGxu77Ok51x5oZfrRxvWKSPej0+bsGiD3d2O8BPcYfL5kLuPtTjQF0uEAsev3tdZpl5dLIdrUwx6xNWj4leHWNc/peXdjdYwA6ODAP6n3SvtRiMe4ESmkc2mra40PEz6Jl/HoielDwmITEm4e11GXVtVljMbsMz2Sw2sPagLg/qojmbw8k5LGjfAXTH77ZIYhbGz9zwpxf3fNsJ5tJdDHaiwrrMnR3LlywxxMSEKxQB2BWLVBIQHTVm6dKPsHkZmKIQ9JnsDqNzYbTjDfiG2dAgYe7NZrP1OZ08Ql2daOnSrx54sGjWlcmauOQITZ5iTJksqkoWAy4HlYYqhb48JK6SispSGYsnX/vpi4vY6s9Qiw1ZGOBQ6/Mghws5HMiNyUNoD0ZGPMjKAktZN4O6aKBGMXuQhfX6iHNy2CsIDWzXhBvX7UY0DTm4nECYa+sDi0WbExxPO7H3RkBenP3i7oPr6nSA2LFYe1FXNzrXhhob0dk6dOYMOnsGnfkWfXuSP/kNe+JL9ptjni+POr840nfwkG3/AcuePd2ffNq+c2fr1q1Nmzc3bK5q3FzVWFPZWFX+XXlRXUnet4VZp/IyvsnN/CYv60RO9omMzBOpqd8kbfxyzbovVq46smzFoQ+XHVz88f5FHx5474N97y7c+877+954d8+rb33y4ms7//Hylr/+q/r5v1c897fyPz1X9vRfip/4U+Hjfyz4w1O5v38i+8FHMn/7cOb9v0u/77dp9/4m9f4H0u+9P+3XD6TNvy9t/n0Zd9+bftf8tLvmZ9x5T/qd96Tfflfqrben3Hhz8vU3Jl53Q9LceUlz5yXPnZt63bz0a+emXXt9xpzr0uZcm3HltelXXJMx65q0WdekXTIn7ZI5GVOvypw8O2vSlZkTLs8af1lG/GWZsZemGy7N0F+SrpueqrmESHrM9LSY6WljLwGJnJE2Znr66GlpEVPTR01OC5+UHjwhRTU+VTEuRZGQJo9PlSWky8dlgCRkScdlycZnByVkS+KyJLFpkti0QFNqgCElQJdM6RIDtYmB2vUSDYhUt0GmT1Tqk/5/d1+mh104pEuS6JJkuo0yXYpcnwr0HZpUaUyKDLZpMnW6XAN269gIOk+iySV0LmCHDuAy4OkKHQDrKm2xUlMoVxfIYvKl6nxiYQ2Qt15kha0tlfokSFPiJfjGNN+YgrxETD7uYyHPBUA8OluQgOjsAG22RJcjMxXI4goVCcWKhGLluBKRFAWPA1EkFCoSCuXxBfL4AllcfpCpQGKEbZCpiIg8rgQkvkgRV6CIw2li8yTGfCJBOH95fJEsrlAWWxxkKoJ4U26gMTPIkB5kTA00pQYa0wON6RJThsSU4QtnSUxZQbF5ElMuJDZkBxkyg3RpMk2qIjpFGZWsjEpWRYKERqaEjU0dpckiEqbJJRIRkzk6OjN8bEb42IyImEwi4TGZvmRZYeQUde4obd4obV6EPjccS6g2KzwmMywqPWxsatjY1PDotPDolHB1arg6dZQmbZQmLVSTGqpJDVGnBKvTsGSEaDJV2kzs/DMLCF5MOQpTlsKUpYzNJgG5MSMIOA1TgoypQcZUqSnDdzRDgVlfMP1LmtKUpjCmKE1pclOK3JQiNSQLW0VsmjIunezKdP+Pve8Aj6Ja35/tJT0hZftuKhAgVJEioqgIyrVg7wUVu2JBRVRA6YQECOll03snIdTQe+9IC4SSEFK37+ye//87Z3ayoN7rvc+v3Sv7vM/kZHZ2ypl2znve7/1SIbOoKkOsSZeq0z21WZ7aLKkuW6qDeAu8klSJOgknGk3w0CV4hq3yCk/wDFvhHQrwCVvpG7HKN2JVQERCYFRicP8URXSackC6dmi2blhO2MiCiNEF/R8sj55QETOxavhja+59cu2Yqevue3bD/c9vnvDy9kde2/3o23smTdv9tw/3P/Hxvqc/OzT1y0MvzTr++g8np80588GC858tuTwj9vJXsVe/ibs+a1XLT4ltv6xun5/YsSy9Jzaje6XeuDrXmF5iy6pw5lajgjpwPC9dj0o2Aso3o4otqHoLqtmG6negtdvR+h1o4w60aSeYumzdibbtAuzYjXbuQbv2oj0H0IHD6PBxdPQkOnkWnfoVnT6PzlxE55rQ+cuM9TnxPb94FV28ii5dAx36lRbUfBNdu4Wud6CWTtTajdrwa7XdjNrNIBAjhVsmptBpQV02MGnpwdmfDE7ojnbTqMuO2q0MwP7FBjO7MZNuoOHFYcKqMzJCTNsh3giABa+MCQHJ3IA76rQFdOUOO6boHMhmR1ZI8umEV63ZTkTrRrMdw2o0W823fYxGCwvgoYxmq8Fix7AaLACjFVTwFqvDanO6a9X/4LX7W4b6Ni6D8IwuQp7wj/gFfRu/TNbNvLjdqBCSfYp4z5hpGHRg4T5S4LZaZndYovMOwpr9lxRu/+HvcrW/Pb7fmQPrcWdU2UPAin/G/IwVj/+ZAptk1X1hVxOHqWHCyZKZ7ouxZfxV7+n47fLsVtgC+9t/VGDsWVzCBuYcuZ2g3/q5u58yq+uHkPDLimwmZDVCS8duQpBfBNSKAEifjZckRwFVzwzd/Ddoc00GI22zXbpwrqaq4o3XXurXN9xDyuNwKbGEy+WxVswciuPL44dw+Goev69ANFQsuZcnHS/VvCkJ+9Qz4nsv3S+eqjgPebKnPMtTnkvgLc/xVuhZeCn13qocTwwc2aZnwtoUmcTRi6dMEihXC5UrxMpYYch8fsD3fN9POF6vc6XP8iWTOcIxFHcQxYmkuGqK34fi+3KEvhRPSoFbB0UJOTwxH7jo3n2Gne/Tp8/QoUOXLVt28OBBhJzg5men7wDbTu7tBfzRbf8/Pp/dJUJAuzt0k6jurq4uQkMTOR3LQZMkQK2traRj9c/vuOu26/0lGYIEWS5CqKKhTRg8xzeqhgos9R20Vxi6TjOscut+wk4jpwXRFtDUGxwotcxAKdIpZb0wcjMVlOsfmVu2nlznxt8qoJ1OGJIxONFz06s9NblCVSMQ0JpGvqJ27GObzXZCfzucyGajoSdiMKBr3WjECw2UJovyz6ZCa6jQUkpXTqk3UMqtPOU2DqTm28xTNwhlZQHquC4j3E34Nu99RJAHF0LI3APvIEM3hPgkZ13+aNbuR1+pfOTVyre/3vnWN4c/XGTjhxVSmmqecq1YvtZDXhkYnl+6Hl0zw50LKYtc2S8YLptGZhsk/CADtKTegOeFfNBwJ1stIHB+f/Y2XmgepdlGaXZRmi1e4VXfLbqGDcB67NC/hM/+Ayi8b5GXcj1Pt5PSbucEVPiqMh+cWrb3HPS5jHjTJic6ehU99l4ZPyJOHJUi0s3+YdluCxDQsL12G6rdhiRaPRaRrKcUW/iKSt3wzC2HgSXvsGH/MWYMmT31pMC8IYCAtiJR2CJBRDml2SyOOMRT1fqGLT/XCkPjvUMDZI/vTv/CNXCXgGZOvvvj+4+uB3YZ9wXYmaTg/tXd8t0auFsD/0010N3dvXPnzpdffjkgIEDAF1EUJRJ6iD1EFJen0cSMGfWaIvDZmMhvxwyOjVJ98e47KcdP9nRbkcEB6X0dMLRsNkPi3xYzumkByw2rEY88X7Gh7Ib20ZOqfGQJQarFz79Wefgs6rTCUDTRPrP3OxFBQzeYdjicZhrRZhq1d6Ol8Vf6DU6X9csJ6bcyNvlocwu0LRDuMxiRw+I0O1G3Hd0AApo2GXrQ9SY084udPkHzIoanvfv1pm3H7K3QmjB3mDvWb2qY+9MPI4YM9haJ+LiFL6AoWWCfgdH9Cgvzb7a10Iju6unEWhiSQtGVx/h3Kv2OtgKr84IDYpODk0BLg5EGDroNkqdt241+iW1+7o3dkcOKNANKvVU54pAsD9B4FkrkhVJFqa+mOjC0Wt23bMS4qo+/OpRXduvURdTcAgQ0tLRoq81htjvtVickaSZ9J5PDZqDNPXS3wdFjonvMDoOVNtiR2e5ksoeBRA8ykJmdVhOirTgu/fZDYjvDrKiPPb47FnRFqUN8OgacS9KhhFAyV9+fdCjJal0NTwhvtzIGrbQJ0SbkNCCnCQCx81h5Z8fid6b27YyO3grqCZAlGszIZOkFtDJtyGKHqcnFs4PfixF19SADRnc36upCnR2oox21t6FbN9GtVtR6A7VcByb92jV09Sq6cgU1XUIXL6IL54FSP3sGnTqJThxDR46iw4fRoUNo/360dx/atQ/t3Iu27UVbd6NNu4CBWrcd1W1FtY2oaiOqWO8oXecsXksX1Tnya+15a+y5tdbsaou+ypxZZUot604u6V5d2Lmi4FZ8ftvynLbY7JtLM1sXpbXOT74+N/HanITrcxKu/7jqxg8JN2avbPku/vrMZVe/WHJlxuLmTxc2fTL/0se/XPzk53Mfzf31g59Ov//jqenfn5j+/YkPZh0DfHv0/W8OT5955L2vD7/71YG3vjjwxox9r3625+VP97708Z4XP9r7wvu7np++87l3dzwzbcczb22f+ubWJ17d8rdXGqe8tGXKS1smvwh49MXGR57f8tCzmx94auP9U9bd93jD2Mlrx0yqGztxzehHakdOqBoxvnzouNLB40oGjC3sP6ag75j8vqMLI0YXhN9bGDayQHcPxogi3Ygi7fBiwLBSAt2QEu2QQm1MgTYm7+9DPThPGZMbMkgfOCDTr3+6b780n/5pvtHpd8Cnf5pXvxTPqGSPyBRpRLIkLEkcmijSJYpDkyVhadLwdI+IDM/ITM/ITI+IjNuR5REBkIZlSsMyJaEZYl26SJsq0KRgJAm0qwXa1eJQWBVGqiQsTRyayiyjThMAMljwVelCZbqHKtNbpfdTZftrcvqoc/wUel95JqaG9b5ygLdC76fK91Pl91EAApVFfRSFfRSFAbKCAFmBryzfV5bvJcsFhOQTeMoKCaTyQqms2CO4yCMo36NPnldgvldgvndQgXdQATjCB+d5BufBVyEFsExwkSSkxENe7iGv9FRUgTu5ulqsqhKqqwSqSp66kqss56jKKWUZRwUFjrqUAMT18hJKVoxRQslLOYoKrrKSq6zstYXB5jBcdTVXXU0pKyh5JSWrAIRUMIbvMkhVypOtAbd3nLBUoFjbC5y2VKCs5cmrOLJKKqSMIyvnKUB3T3KQuk+F6iqxtkYaWisJWyMOrRWE1vB11dzQSo6ugtKWgqmlugCgyqeUGKpcSpNHaXOp0BxKl03pMiltBqVLo7QYmhRKm0ppUzm6NK42hReaKtDBSRepU0TqJJEqQahcJVDEC5VxDFSxEk2cRBMn1S0X65Z7RsR7Ra3w67vCv//K4IEJsgErFQNXqAbGhQ1OiByyKnp44qCRqcPGZg6/Tz9yfM69D+SOnpA/9pGC+x8tGj+peMKU0oefKJn4VNmjU0unPF/1txcrn3y5cuprNc+9Wff8W/UvTGt46Z11r07f+PqHjW993Pj2p5unf7n9/a+2ffjNto++3f75D7tm/LTzy7m7Z/6879sFB75bePC7hQdnLTr0w5KjP8Uenxt3fF78yQUJpxYknFqYeHJh4vFlaadi00/H68+syj2bVHQhqehCSvGllOILaWWX0subssov6yuuFNTcKKxtKa+/VdXQUb++p35D19r1XRs29Gzc1N3YaNi6zbh9h3nXbvOefZY9+wx79hkOHjQfOmQ7fNRx5Jjz+Bl04iw6eR605+euoIvN6NJV1HQNXb4O7DmDViZ36NUW1NwGuHYLcKPDhXag14Fh7wLc7GbQ0YMMViYLKMkFeufUDhHiBAYXn04KRjwia6KR2QmwucTdtAOblmBakZTJ1F1s7k4S/w6L+Xv+3zZscsKambCmLv+thX9E0f5d3pkk+GQIoDuXJG9vth5YdhgO0w2kRUDmuP/kTyzPNBaseCyDndoQ0MEsNexWYOlmQgezy7C+9OzwAONy77J6dz+BcECsotnh2hAmoC0WaE/1YKmEHRpRrpgDcnTkSCFEz+lmx/KvGkSwTdw7IiC3NW6ZPWvWkJhBXh5SLw+pv683j0P5+vpyODwBXyKR+ok95DxRJEc4mCMcxRU+6B/0mm/Qu/6BH3sFzeTJf6aUcXx1MiReVpWCiEHRIJatE4U0gDlYcA2BJIRJcUFyY4g0tSJNtUhTK9SCuQFfXcNTVXNUlfAiUJRxZKU8WalAVsgPzhIFJYn7LPPoM8+zzzdS/w8EXq9wJU9Sooco/kiKP5jiDwDTD66C4gVSfH9K5Cv08JBIRTw+hBJSFCXgcaRioUAAnPTo0aPnz59/7NgxG/64c9CMBBf/+b/W33c/a+77yZaJhK67u5vNcUUE0SSXVVNT082bN81mM9sXuL0d/Xf++23L2+lwWHEjF93oQeHDFwZHF3MUVZSiRhJeI1FmZJQD+wzWQTSyGBkT4V9bUfT4IkpeTsk2c1XrJOoCTcyKmyaGp2aPwt0IxQ5p5NFTb1b6hpbwFJv42i2QL11ROfbx9VaG5oRxLzA1NsGz+oX3NlPhOVR4HRXWQEWuoSL0VFg6V5vPU1cKlQ1C5Uaeej1HsV4UvFkWWlFcae8xQ//gjkyzsONk780IIl6Z7iQUWq2wsVsIHWtDoohMSlvMVVeL5Gu95KXysFUdVkjNh3BKeeCaLQ47Bo29s1j3RIedtpktdosV/K0tVjDUQOAHYkTo6ffqgYDWbgEXDs16z4icogZyXsx2qAnwHHv86fWewZX84B1Un3WUem1IeNHrb+9u62aq0UbjLg8WMncgVL0HLc/r2HYKElPjDxxujwO9/dkJyl9PKSrBKlqxma8q/PCHgyRNSCdtA3NtYkFPMyw/rgPWcpu2IXTNgsThsdzQSkq9RRJ1kKOoCIhc1maBlx1JmUG2d3f6F6+BuwR07wVwx+u294u7pbs18O9WA+SF/e+21//c/tJ2+vz58ytXxg8ePEgsBos3UEMLPQQ8Hx430M+nX0jgcJ36/tH3Ph0Xl9F89WZHV4/VTpvtzm6zzUzbrKCjBRG0BfV0W80dJlBdVe+33TM1nR+42Eu24v5Hs9ZvM4BdBrLawQOT+TB+O7TDAR0Nu8NupWmzyYy6e1BJSfeEB0tUoasCwxf+GH/6wnWgGp02YFCxxbTRasdtEHygRiO6eQ2VZHWNHpYQLJ81/YuNjYfbrlosN4ytmYUZTz79XEz0sEBfPwmPx6coMYcjoChlYOBrL7147Mhhkm7R5rDaHLBvLAf9z9Wgy32IffThQ4MjpQlJakPdNtRhRSevoLy6lq8XHhjyQFbk8Bw/7WpvZbI0KN1fVeKjLJf2weJHRU6wSh89uOhvT6yLi7t25Ahwo90GZKGxlADbjJLmGvE4strMVpvRRhscQMqzboYk6szshKF/k4OYryKzxUEzQeVO6H2BawqmjkmnmpEMuB28i0NmFiPOJzBlO3YuN1VQr2MBO1khm42S/AsbwqlObCTfJBbFkNhMiwOajjilpN0K8es05qIZm1YSqU2WhCk+UzaHmdDxv01x5h5gC61mGurNQiMzjSwOgBnndjPYQV3OwAbmLWyKtt8WSCY3ZupAPU5AtxvIHDJ1zwJHVIdkSnbDfer+rRHvFZkSbeMd0247xAe2mxHEH/SgW52orQOb895ENzCut8JwxeXr6OI1sL453wxU0bmmXly4hNxx/iI6exGdOQ+8EngdnEVgfXACHTzK4PBRdOiIY/9B+74Dtr37rbsOALYfsGw/YNmy39K4z7x5r2XTbvOGnRg7rBt2WBu2WdZuMddtNq/ZZKpe31PZ0FVRd6u8prWsugVQdbOkoqW4/EZByfW8ous5+Vez85ozs69kZl/NyLmamt2cqG9elXVlRcal2LQLS1POLUo6M3/VyXkrjs+NP/pT7OEflx36YenB75ccACw+9N3C/TN/2fPFnB2fzd7+0XeNH8xsfP+rLe/M2Djt8w1Ojx7lAAAgAElEQVRvf7b+rU/Wvflxw+sfrX3l/dqX3q19/u2a596qfu6t6mffrHr2zaqpr1c8+Ur5lBdKJj9X8ujUwkefyZ84NW/i1LxHnsp9+MmcB6dkP/B4zvjHsu+flDPu0dyxE3NGP5I7coJ+xAP6IffrB4/LHDQuc/B4/eDx+qHjs4ffz2DI/fpBY9KjR6X2uyeFRdTI9Mh7UvuOSO03PDV6WHq/wamRg5LDB6boohN10cna6GQdWNCkhQ5O1w7O1A7O1MRkaWKy1AMzlAPS5dEZ8ugMWd80WWR6SESaLDITEKHHyAkJzw4MywrQZflrMv3UGb6qdC9VqpcKMlJ6yCE1pUSVJlIDiHKZr4ECX5VKAHw6Jt+FylSS3FIoTxPK0yTyTIlcL1VkS2Q5ElkOeLVjsA7vguAcflAuLzAH27sXeshLPRXgxOKpqPKSVXoG3wavkGrP4EqPoApJYLlHUIVHUIVnSDlAUeWpqADnFlWlVA2QaAAkgapQW8nXVbpI53KIYNWUUuoSSlMEfjUESibvECUvoGQFVEg+TBWFHGURONVoysHHBqj2SjdUc4B2qeaqa3mqWq6ykqOo4MhKKVkRAUdezFcWC9SlQk0ZX1sm1JUKdaWiUKYgDC0W6RhItMUidaFImU+M1InlPbjey/OIjYxImStW5QsVeoE8iyfLhPgDeQbYqauy3CFUZt4BsiRMFWlCJQxyEAgUaewcEJurMz1D9V5h2d4ROT6R2X79cvz66f36ZwZEZ/QZkBk4KCMoJjN4SIZ8WKZiRJZqhF5zT7ZuVI5uVE7YvTnhI3P6jc4fMLogZkzhkPtKho0vGfFA6T0PloycUHbvw6WjJhaNnpQ7dnLeuMnF4yaVj5tUft9kgtKxk0rum1w67vGyBx4vm/BExUNPVk6aWvv4s7VTXqp/4uX6qW80PPd2wwvvbHhp+obXP978xieN02Zse+eLHdO/3j195s4PvgZ8/O3ez2ft/+qHQzPnHP5+/vFZC0/+sPj0nNhfFyZcWrS6aWFi0+Lk5tj0q3GZN1ZktybktiUVtqeVdGWUdmeWGfKrTAXV5qJ6e0mDo2YTqt2M1mxBDVvRhp1o4y7UuBdt3Yt27Ed7DqK9h9C+I+jAMUaKfvQ0OnYWcPQMOnwWm7r8io6dQ0fOo6MXAUewVfqRS+joZXS8GZ24hk7fQGeuo1/x9Mx18E8/fQ2daQacvQx+LxeuMUbqQL63goC9+SZTuOpi3q+7CPeWTkbbTuTtN3tA4Q4idyxpBz07zqFscIB60eCAcfUuG4NuO/wL7wISDmVjmHoc2I55FSuymkHZS4MEkiF6IZeGBdnMDGA+K3Vnmzgk4bMD2gAEhFAm72sygsxYqxBa38WWkOFmK2ZvzQ5kop0m2mm2O8125lXLiLSJPZrDYqCNBkcPBiQLMTm72SOm4Q3cY3N2WR2dtKOLdnRB+i8M2tFjo7tttMFqgwLt6CHzcfpqEBhi8seMBQkuVtyBj5MMaEODhRkGd4K0wQ5D+HaT1dZjsXVarN2gwrdYLGbaagGZP3JCs8Nmo00mk81mczjsrsg2cPUlH7dm0T8ukp+4mroOi8VC2+lTZ87Mnj178ODBgYGBFEVxuVyws+CIuZQnRflyKIWAGyHhx0gk4wXeLwj8P5T0+coz6Cef4GXewat9gjM9g/P48hJKWQEPLgZVkDJaVsMM+8ka+CH1AlkdQLEWUkar1/DVa9x5Z56ajEdWCpSQR5onr+DLqoQhNcKQKomsUior9ZQVesvzIcgmJNkzcIVHwBKp/0Kp/3xpwFzs3fEJxZ9CCR+gRKMoURRH7CcQi8RSiUgi5ouEHA4w0Rwel8sHC2lPb9+x948rr6rsNvQQm013MppUjqt24e8/rtb/qSXc9+p3y7SdNpvNd5hynDt37sKFC62trWaz+V88HObGI2Q0NPgtTmCfP5191j+yUBJew1HCyys4uvibhefasKDHjG9ko9naY0NtVvToK9v8+q8RhjXyVJt9dJtlUbk1mx09LkUNjPC4Puxx2R3Qbbj/iTzf0DJOyEZBaCNHU89TFL3ywQk740njtCNLu7PTilBqHhLLMnj91oEHiKyW0pRQskXRk/LemX1q5GNVHkp9n4h1HEUVV76e8t3G8Sx+ffp+EMVgwpQd1sIdDUxAk0S/cKvasAc/3LdkSKzNgap2IYEumdLlQ6p25VqpsviZVxvbDSSfhJUGThs/zuw0jtAho04uWQzWxJDjheAHu5l29HRa4EhD743javMpzQZKs5XSVkvCV53vhEheQgMbnOitTw77a0o9tY085RZKs16o07/ybn3LTYgidX0cLAFsxQ8jI34SuecOMjtReEyuRNFAydZQqgZxZKP/gJz9F0FiTXIg9Z5jpt9Fzj07BQL62FUkDkvgqisp5WZx+H4qpMQ/cqER3SWgXefh7l9cA3cJ6N4L4V988vau4G7pbg3879eAw+GwWq1Go5E0Scnb+n9/t/4b9oBoExwOe1dXx3ezvtHpNCIRSKG9vfylEj/wfeN7UxRfIpHw+NSQodHLYhdt2rTpyuXr1290Wa3IYLF3mm/eMjTT4PQAn/rNPWOfTqECvwiMSIoYmppaeO0aHjo2ox4szmVaQG4EtNVBG2mbyWZzGrrQjkb01ONlasXSQNkPb31We/QKrNNgMUM4sB05HWaH0wwND7CnsN5qt/Z0ou2bDFMnp2uCv3jl1cK6Te1rtu9+4f3nKODS4eMh9IRmMWafvUUiZWBgZmqKzWKyW813ENAsB/3Pnm62MccWkAOoVofdCqm0adpEo1YDfcsO0VstDnShC8XrWx5/pWzEhCzdwKQAVYKkzyoveRbYDavLvZW1Aco6v8C8IFni0BHpn36xu7Leceg4pPwyWJDBiEwmiCYD9zA7BDkCAW032SFwGLQ/riYcyIKcOPbajnqwJ4fZ7KSNbn04lq4GvtiVwIppGOHheDLSj13UQPPOdlbdC4zEzMVluzbvJEIqctKwcNthcdAWByGRgUG2OI0WJ1iMWBj0WIAoB1oYC92AoSXSN5sTuqkA8CZhYIegc4IeO2NA0oP5YRNm1y0O6BSbbQ6jxWkGILsFAm8Bpl5AcxCDfGXHi1ktUMFWXLa7ynfMJEsy31rh4gfYnQDstQfkOQjWicybxkoPhxG5wekwu4BriCZ8e+8gDXOr0JCb22qnLTa71U7bbE7a6qQtboatpO/mBI89mgZrWiuNbDbXPlnhUrFZGRCqgsbp2hiNGR5RIFH2IBaxMgcP1xjRrdlhdAFWi68wixN4fIANmawgiiEw2YCDsOELiahbSAI0RsBmh+EFArIViwXa9ARmC+Sv6zaiDiPqMiMIsyADAzSIHw02mNNtha/cQZLdkTndFjD2JfJJkx07+dqQER5QMB+SpRpRp8ENPajThY5uRNDeBeT+zXZAaxtquYluYGln8w3UdB1sE85j3+HTV8CD+OQFdPwcEFuHzqC9x9HOQ2jrfrRpL1q/C9VvA4F85UZHab2tuM5aUmsprjEXVZrySntySgz64u7Mws7U/M6k7LaErNb4zBtxgNaladcWJzcvSLj888pLc+LO/bDs3KxFZ2bOPzHzl1Nf/3z6q3mnvpxz+ssfz8z4/uQns45/OPPoe18emvbZvrc+3fvGx7tf/2jHy9O3PPfupmfe3vT0m+v/9nrDY6+vnfTKmkdfrn345ZqHXqx9+IXah56vuRPPVj88tfqhp6smPFX5wBNV4/9W/cDjVeMnV42bVDnu0eqxj1SPebjq3ocqR06ouOfBshEPlA65r2jw2OKY0cUxYwoHjSoYNKpo0MjCmHuLYu4tiRlZNnhE6eARpYOGlwwaXjJwWOmAISX9Ywr7DSqIGpgfOSAvIjo3vH+Wrl+mJipdGZWmiEwNiUgLCk3uE5YcEA7wCUsE623tSqE6nqeO46qWU6pYSrEUpurlPHWsQBcnCo2XhGIrj1Cw9vbWJfloU7w1yT6aNG8twFOX4aXTS3VgA0IsR7AJCbYi0RSI1PkidT5fnSvQ5IjUOSKNXqQBBxKXCQkUyEziT8LDvjccZQZPlclTZfLVWQKtXqjLwR4sep4ii4ArT+fK0/nKTFAmqnPE2jxpKDifiDR6gToLAPNh0wJVrgvZZKZYUyDRFkt1JVJdiURbTCBWl7AAb3dtKVkAL1MKX2mKxJoi1/KFEi0D4rgi0oBxChljEGtSxRrQ8ou0yUT9LVGlSBSpYnmKKCRVLEsTy1PE8iSxfDX2Rl8p1cRKNbFe6gSoVW2Kry7VNyzDNyzDR5cO0KT5aFP8NEl+2tW+mgRv1Upv1Uov5QovVZyXKtZTTbDUQ7XEQ7VMolzqqVzmqVzirVzkrVzgo1rop1ror16EAebp3qpffNTz/XWL+4Qu8Qtd6qtb7Ktb7K1d4K39xUvzM5n6qH/2Uf/sr5nnr5nnp/sZY76v5hc/9VyACr7qo50bpJsbHDovJPznkPC5IeFzVVHzNP1wFt/Bi/qOiO13z/LokXEDR8fHjFs1eHzCsPEJwx9cfc8jifdOSh41OXX0Y2n3P5k1fqp+wvO5j7yYN+nVwkmvFk5+reSx10uferPy6berpk6rfOadqpfer3vtow1vfrZ52owt73297b2vt02fuXX6zK0fzdr58fe7Ppm9e8acfV/9fGjmgiPfLjw6a/GJ2UtPzYk7PTf+7LyVvy5YfWFh4sUlqU1L0y7H66+vyLmWkHcjsbAlufhmSklbWumt9PK2zMoOfXVXXp0hv95UtN5atN5assFWssFW3khXNTpqG511WxwN29C6bc5125wbtjobtzu37EDbd6JdO9HevYB9+wAHDwIOHYI4HgZH0OEjENlz9Bg6dgIdO4VOnEHHzwKOYjr+6HlEcPwiOnkRnboEOHMZ/XoZBjLPN4PH+oUb6GILOt/KeKxf7kBXOlFzFyIe68RAhpDsxEbmphEkgbewYrHdDkZh7XZwbyNGMZ1WCInrtkDTBAaAsUUMUbLD4Dl22TDRt0njmbcMjoUiUVBWGzjD2LE/DMRLWSAiz3xHvJQVPNmJM7vVBq9C4scBrJQFArCgZYM/NuwGQ6LN8Bvcii0L7P9saxCoLBwPx8p+u7u7Dxw48MCEB6WenoSlJU1TjsibEgZRlIqi+gnFD3pIp/p4veXp/bkoYJ4wOE4ckigJyYAYl6Ayj8AaUVA9R7aekq2n5A0c+RqOvIajqGIgr4E5snqerJ4vb+DL63jKtTxlHVddC+NtmjWkwFVWE/AVkGAZIKsSyGsFsjomtbKsTiqr85BVe8grvWTlAHmpt6zUO6QcpvIcb1mil3yxh+JHL+XXvqrpUv8JAo9oSqClRCquOIQjDqCEXpDJEOcw5PKFHB4/IiqyZk0tsVF2J6BJ5bAN5v9TvIH7Xv2dsrsa+vr168SFo7Ozk01qxVxYf/4PQ0DbHXYz6HJwI3zNVhQyMI+jrOWHN1J9SgTKwsEPlLSb4d4xI7h3IDAUpDno7S+3CLTpvLANlHodJav0UeW/8s7OHjt8BSQn1vW7+GecYRYfG/C3CN3/tyJvbSUnZCNHvZGrq+Mp82bMvcr4NENb0taD0PYzSNYvRaSopbTrKE09pSjlhaZ+HXfpMnal6LCjaZ+c9pBlUgG5Ym0jP3gPP6B20KiSLhvcziz77Io2wLQraSbC9g24GW4jM+wIdTrR8myHWJdJ6QopXSWlWvf/X6ALVl5pN0EPB99iNHRaoL3rTkA7YGWuwTQ7HmDDjXCzlTZ02cCXOWTISiC1teso7SZKVxoxIacJq6acmEROr+oI6JtDBVX69NvD06zhqfQTX9l4pR00QMYeTJqDdtt1PL1nlmQ5BBqdyKT3HkLqqGJR8GZKsYXSbBREVM5cYbjlhFOGMzs6nHhIjyGfmdEyln2GLy0IbTuFRLpEiDyTbRCG7qZkBaqhyztxuM9dBXRv3f/lS3cJ6L/8JXC3Av6DasDhcBiNxvb29paWltbW1o6ODqPR+M8HVf171AjxizCbzZ2dnWaT9ddff/1pznf3jbvH20si5Im4lKeUHyLk+lAU5SkVCrCHBZ9L9esb88Jz782auSIpsXzr9t2Xrly6er2l7RZ4BL/34RpleGzfYXnDxunnxZ89cwO1Ye/mbqC27FgEDRQbNH6A7HQip81uvwniFAM6fRR9Mu2gKjA2Knzp2+9VHTxluNLZ2e40kNc7BFgBg2W1uXI9dN5Cm9aeffX5RbKAZ4YO+vRvT89RRo6hRBQlpAQelFBEEYc6EQ88N56YPHnRLz8buzppG4xlE2mMwwG7xIIohEij88+fv982UgkBzYhvQB8Ex0pkyTed6IoVXbag07dQXkPztK+qHpqapR0430u9mFJlUaoKrmqtVLvBU1nroSjm+q8MidR7yhPvm7xtxvfXkvX0jr3o/CWgbKEPBuIFcDYzA9XGOB66bCKBLcR8oA1C+YAYtYMC2ulkeVirk2H1mZyQ0ExlAY0hB2gMAESYzNYSJkpB1NybU97p0iwDL0pUzGD6RurTnVglpD9NAweN2WGjFZmtsP8EQB5iWOxwwZjBhANT1XdOmbRhYGFtBec3BsDWYgAj7zTTDqMNAM4kvfvvdsaZfcNzSIfT1flknExgwON34XAtgAtOGA1wB84vbrdD//gP4TpXsACUnTQGoe3dprTdabPZmLEi0vYkJwo7p5OTxEYsE6YYdN/YqwR63S72mS1AkDNRrLva0uxa3S97fIfCRUH82fE+9nZdGP8cfCM78TLsFUNqlYjWzbTFTFtMDpvJYTM74QqEAQzMaNtdUfOQzw3vDxHjEw4drgAMciDuUzKfUNvswsSYxWKH697KGrm4WG82OxwhwSHeAdu9g8yf6PdJ5D5+JjnwjtnxemB57AZD+A4rJt+tmIWHEFnMvwN7bgJ0mhnqnBDoRNXO8PWEtXdNgV4h8kbs1Usce8G9147HWKyo3QL2Rm0mBFSOCcrtFtSFR2lAEYnNfw1OPPZCg1KyGzv/dtrA/7cTEz03zajVBIlibxhQSze63omudKDLt9Clm+hCCzp3HZ29is5eAabpZBM6cQkdvwiU+jGsiCei+EMn0f6TaN9xtOcY2n0U7TiIth8Ann3LPpCdbtrl2LSD3rDNtm6LuX6Tcc26rpq1HdX17dV1nVVruiprOsuqbpVWtpVU3Cwuv1FUdr2g9GpeSXN20WV9YVNWwaXMvEvpORdScxkk68+tzjyzMvN0fNrJ2LQTy1KPL045uij5yILkwwsSD81PODxv5cGf4vb+tGzfD4v3zV607/tf9n03D/DtnP3fztn/9Zy9X8/Z+9WP+z7/Yc9Hs3ZOn7l12tdb3/piM8aWt77Y8uaMxjc+3/zqJxtf/mTDCx/VP/fBmmffrZk6rfLJaRVPvF3+tzcrHnu9dPLr5ZNfLZv8WsmkV4onvVL86MtFE18qnPhS8UPPFzz4bN79T2WPfSJz9JT0eyenj5icNnxSCoOJicMnJg57ZPWQCasHPbBywLj46PtW9BsT129UbN+Ry/uOhHyS4cNXhg1bFTokIXToyrAh8WFDl4cOXgYYGh86dCWDwfGhg+N1MXHqAXHK6HhZ3/iQqOUhUcvlUUvkfRcp+y9VRS9TDYxTD4rXxKxSDVih6h+viIqXRy6XR8aHRK4MiUyQRSXLohKV/VYocXJLZb9YWT9YQ2BUbJ/IZb7hS3zClvrpYv10cf66BN/QRF9dsm9ook9orE/YYm/dYi/dAk/tz56qXzxVizyVS7xUS71US4FWVsV5KJd7qlZI1Su8NPFe2iWwsHaRt2aRp2qRh3KhRLnQQ73IS7vEM3Sppy7WQ7vcQ7lcIl8hka/ykMd5KBZ7KBd6a5b4aZb662L7hC4PDF3hr43z08T6aWL9tSv8Nav81Am+ygRfJeSV9Vct91ctC1DH4sJyf0WsvzzOT7bcWxbrEbIMViiP81Cu9FCu9FSu9lSt8lYv99Ys8dYs8VIv9lIvhp1XLZLKF0hkv4hDfpbKF3kolnool3so4z1VKzyU8bA/8gVe8sVe8sXeiiU+ylhfDSbQlUCaA3WuXkaIeKk23kO7XKpZ6qlZLNUsFasWixRL+IpFAiWGerFAvVgcukwSFicNWyUNW+UVkeQZkeAZsVIavkISFifSxgo1ywTqWIE6VqhZLtKuIIlMxbqVYt1KkXYFgVgXz0KkjRNp48i/ktAVktAVXpGrfaMS/PquDuibENw/Kbj/6uD+q2X9VysGJCkHJmoGpmhj0iKGpkcMTY8algG4Rx91j77/PdkDRmXHjMkdPDZ/6P2Fw8YXjZxQNuqRitETy0dPqhj7eNUYjFFTqsY8XTN2au3459c++OK6ia9tnPja5kmvNU56rfHxN7Y+/sbWJ97c9uRbW598ZwfgvZ1PTt8+9cNdz36054XP9r/4+YFXvjj6yhdHX51x9PXPj74x49gbM469+eXxN788/tbM4299c/Ttb49N++7oO7OOv/P90Xe+P/ze7CPTfzz6wY/HPp5z4rO5p2b8fOarn89+/cuvMxec+3bRxW8XXfxu8aXvFl+avfQyRvMPy67+FHdtTvz1uata5iW0/pLYNj/p1oJEwMKk9oVJ7UuSOpYkdcSmdmF0LE/ris/sWZFlWJljWZVrW51PJxU4kgudaUUoswTpi505Rc7cIrqwhC4upkuK6LIiW3mxvbL01v59Nzu6nO0d0Cy0QCo34vhiJgPJ/2xr8LcE9PqNG8fcdx9PIODwuAKBgMfjYRqaR/mqKM++lOReyuMpadDXHgFLPPxTJH45oqA8YUg+JO+VlQhlZUJZhTCkii+r4cnWEOqZB+Ua4KBvA3zLVdRxFbXAPqvqeCoQzPLVa3hKoKSJUJovryPLcBW1fEVtr1eSYq1IvlakqBMp6sTyWrGiGqNSKmfgoazwVJb5KEt91SUB6tJATa6/Mt4jaBbPZxolmUJJR8GxeMkpTx9KKOHxeFwul8Pj8kVCXXjYunXrEELuBDRhQt1bzu4Nj//dsvte/cMy8YY2Go2dnZ0kD+G/QqYT7pEYMDAiEmjZmxzoufe2iSNyKXUNpd7oFd0YPCC3rAEyuNB2yMEOlsMmYIhfeK2hT0Qapc6ngvOlg7dQgauGPZR1tglXJFg4gxyBBu6T0Tewx8UQ0FPKvDXVnJCNVEgtP6yGo8yK0zvsoGwwOaBRgzoRenXGFq58FV9dw9Fu4GhreJrEOcmtJGaCnK+z55G3fDEVkEEFVgnkjYLgSm9VwvELsIo7CGj3f/EaoG9H9NbE+troQK9+eFKqKwP3Ld0aSrtRqNPvuYQ6MFcN1xJupzFKZPJjWKnT1WWxIYcTukAgy7A7HFYzDf7MJ28gadgqSltMadeCCDq08LEPG6/RjPJ6bxOSjUrkRRVSkWspdbVAkzPo/vRTVyBIpdPgdkkS8phtMTO2GRbMoWP9BUJLll4IVJQIA7cJtYc9ovdIBuZVH0VdwE/D0jiQ1YpjMi34UIgNB0tAw5FYEKrajvjqZL62jgpcK9Btp0JyBzyY3oIHHu4S0G7n469evEtA/9WvgLvH/59UAxaLpb29/cqVKxcuXGhqampubu7o6MCpq/+TjpI5FlasAWkm8Id2GM/+erSoOOfdt6dp5P2EnACKEvMoAZeipGK+h0SA5RtCiShQxFMF+ESF6voOHBgz6dEnvvpy0fTp8VFR7/sHfBbZf/7n32w4dwNijm456DabpcthxQQ00ZU4WMbK6aSt9g6r1W7oQPELT4cFL+4XumratLoDR1Cn0WFFph5kbHcaDE4bNLegTWGnLeaenp4Tx3/NSCuNjnpAxInwkY7gc/tRVBDFk1ASCjhoHiXgUb7enKAA0WsvPVtaWHCr5QZ0Lmi7obuzx9CFIBwNiDJ3XvK/loAm1iIQAGqn7SBIdnbY7K2Wnqvm1uv2DjOCZMpnr6NjF1Bh1fUXplcGDUkQhqdRskyeosgjtN4zrEGorqBCSiifMkFghTgoM2p4yYOPVXz1/eHCUsPGHdart8DwpMcJWSmIJ7Nbw47QkiTzOz5Oh8NGgwaZ+F2Qo3YdL43TWrg3AsmamIBaQum6mFmWT4YCafCxIat4hUABE3KPzGdbvVCwW4ndCk0z7LCLOya9PpZ1tNiBOAVZMSNhJkJmPMXZE3tFyu4CZHJEsAMOKyGgaYfRQRuJGPl3prexxoxmmYgmXPJks9Nh/A1Y8bKZrPN2lplllm8v2BxQMQSkspkpuxiTFowkB2OncAnZbCwcdroXLk0LuKEwrV9o5BIml0x77zUXTezEG2S8TbD/DCv/B2KWuV4gcpm2WexWM3Z6Yaa0zUTbTA67GQGgbrFgxwxT2kjbDQBHjwsgXSfEKaicnd1mh8HsMJkdJpPdbLERWK12m9Vus9E0GZqi7bTNDtulbZbfHjUTuGC32OwWi50ZXcA2haQLA90m0gmEXhY+ZPJkIzQ6sY1x15mzUSAk+BoPw2AtDo5jcHVpyFgMBGWTu4IZnMGzQWuD5Xgg7qZxt8c1mMNQ6kyFM79leXZg3vHN6wodYG5kIuIx4z4NsX8hIkHgte0Og90Bke9YJwheOrgTQ9YA+nRXli5i+QIdHayIt2GJOrDz+G5nYtedYE3DhuG7r4oNdGDNc8mohsnGCMwNVtRjA0DBghOfsnJ4PC5ksiCjCYI2jCZQuEMABxk5w3vC3OqsTw7xdnf712BjBJLdbpvoxlx/pxF19KCOTkBbByjWW9rAjuYaRnMbunoLowNddaG5HTXdBCHn2WvozFXAqWbAySvoRBM6dhEduYQOX0BHLkL5+CXAiSZMyl+ER/TR8+jQr+jAWbTvDNpzCu0+iXadcOw6jnYdRzuP0QTbjzq2HaG3H3RsP+jYsp9u3GvfvMe2abd940563TZnw1a6fjNd32irb7TUN1pqNhir1nVX1HeXrukuru4oru4oqmovqmovqGjLLWvJLgjF7DwAACAASURBVG5Jz7ueor+SmNm0OvPXVWlnVqaejks+GZd0Oi7pdOzqU0tWHJ+/7MjcxQd/WnDgp/mHfpp/5Mdfjv4w79jsuYdnzTnw3Zy93/yw6+vvd8z4bsfn3+78eOY24lHz5mcbX/9448sfbnjpg43Pvbvh6Wkbnnp77VPTap9+u+qJNyqmvFb62CvFk18qeeS5ooeeKXjgqbz7nsweMyV7zJTc0Y/njJqce8/knBGTskZMyhjxaMrwicnDHk4Z+lAqwaAHUweOTx5wf8qAcWkDxmX0vy9zwNjMgfdlY2QMHJc26P70mLEZg8akDxidNmB0WvSo1OhRqQNGZ8SMzR40OmfgSH30cH2/YYDoYenRw9L7D03rNzg9KiYtclBq5MD0yIHpEYPSw2LSQ2MyNQPTlANT5f1TQ/omh/RNDOm3MqRfPCHZA8KX+oct8wtd2gtMuHtr47y1wJ57q+N9lLE+ylhvxTJvxXIveayXLM5LhkltoLZXEGpbql4lVa2WqAFQVq8QqVYSCNUJxDVeEJooCE0UhiULQ1N5tyGZF5rMD0vlh6XzQzMx9DxdJkedSakyKFUGR53J1WTztJDdlAVXk81R6zlqPaXKIgWuOpcLav18gQZE9wIVBtHUqxk7F+LiIlFmSZRZUpVerNZLNDkiVZZQyXi/MPYvikwRIJ2Y7RBTF54yjadM46hSKFUypUihZEmUIomSp1CKVEqRCjlv5SlUSBIVnAhfyVbDt4okSp1CqVN46lQw9tFmCrSZoLjXZEIKU61eEpotCc2WhumFoZkCbTpfkwbQpmAkCTQAsTaZACfOXU2y6ZKEukJVsliTKtGmS3UZnmGZXuFZrLM/8ff3jsj0jsj0icryicry7ZvtH5Xdp19un+i8wAH5QYMKgmMKgmOKQgYXEwQNygsekBsYnRMSnasYkKOJzgsdkBs5KDdqUHb0gKwBAzIGDkqPiYmf8kRiataRmnVnL7fYe8AxgAlmIu9BQtUxzeU/94f8xGq1klx2T02dyhfxPf28vANAyUFxRVxRANcjkvIeQ3k/Rvm+Rvl8IVEmimRFouA1wuAGYUgNSefLk1eAycYf4XYOmlLUUIoarqIWoHInoOt5SjDlwOLoBr68gatowBw0MNFYK72WnRLvDgEY99diVIuUGIpakaJWJKuVhNSJguqlQQ3S4DqvkGoveaG3MlkYPIfyf4/yeYryvJ/yGEyJtRxhH6yGFnv4+FIC4YiRY879egk3YVzj6LjdwtKg/wpp++fOxb+wlPte/cMyWT850VYrhDz+C1t0GcYQHwiiVIHVrNmAAvtmUtp8KqyektcJwysfennDlS5mCxaEuh1o90E07uE8j5A0r4i1VGg11beMG5YYMSZp9zEIRyMfEh9gs5GmHVQ9e1zQPEDovr+VeelAAU0FlAnDK7nKhMK1QMsiiCswdSKUt8HBUy3iqnOpgAJOQBkvMPGrBRdu0ajFYMU7DYM3Zgt679M9/JAUSlbNCV7LDa7wj8wvWQ/OQm4dk96yS6kMG2Kbbk6s1DEhNPrReom6mhNaS4WtpTTrhGHJN7FIudXaYXBaCAHNtO7I2omeCSzcbRAECSGoWOgArTq7mbaZEdp9DlGqlZSulNLWUZp1XJ3+k/mHb2EdsgWhd348LRqQz49poDTlwr5V/v0SaxvR9VtwctztNeB/4k7oUoFgVtmG984J2maEnn9juziomB+8gxOyh/LPH/xECcQIwzdAQOM2qe03BDQ5V8zabQjlrEGQd0RXT/mvEWq3U8H6MVNyr/XAeu4S0KSy7k4RQncJ6LuXwd0a+A+pAbPZTNjnc+fOnTlz5ty5c5cvX+7o6PjX46r+z1dMb+OPaa/ASKzFAgkZfj3btHBB7LChIwMDg6VSKYkcxAZ2QqnEz8c7WCKGJjWXovgcIZfy5FL+HEpGUUqVZtxjT737w4JVG3fu3XFo/8kLZ27carnW0tze1UbT8CKmnQxlY7Uhg8nW0Y5yUk/FRH6rDfn6i08b9x+mQdNntXeYum5037ra0XLxevOly807tu/Kysh4/PHHwyMjKIrL4QopCrZLEXClPJGYwjJtT09p//59P/34/ctN54k0lSWSQK0L7QBol7BwEZeQCe+/4oyB/NfpsDLcHJgXmy1OGIcHOEwmpwk0oTQkXgQCyAEygbottz6dvXn4w5nB0ekidQ5fW0tpaqmAKp5ikyCojvLL5fiulgYsC5AtCVItDlH//PHM44VVaO8JdKYJ3ezEVtE2LOfEdhk9NrrDaO42WyyQchnstwlsDrDbpmkQ+OC2GjbYdrqmva1B0rxiplBpLOXGLnx7gayNWSeuYYaFwz+8TSCMvSkYRhvri4lvBpmyKmYIrnM7R64yI+jG/7qX4WwyVDi0QW0s3Qyhtn8W2CuDOGb82SmsnN3WbYcJ7DajayYa594py0TbCPtMhNIsE31HAbPxWMBMrF3YS5rZnJNmxwBIAQQivTPZ7gamqB3Az5KRJ9wVgd/iM0UufOaHxDoTRguABe6FzW7BFDDDvLNkPTDRdA8AG3oSW0/a0WXHFuQOYpOCLT5dScVgyAHz1EbaAQAfc5ctCUNwM2eNGJi4tPusbwq2OCdG54y1jNMCKeEh0tHMeNGQOa6p+2UGSzLLEyMWA5bXGHCWTDwFyxzw3ANA6kycPdNt671rgPW47iBccI3WwCgI3iVwYwfgwQxiaQr0Mt4B9xsHly2uG8HdKty1BmLs7vJLhVXdZkFDtNG923I6zL0XPxbjw3PJhdvuF5yyBzPAcFG6eoVEk2TF/zIDJqTsBGabgXuUABnycRuZsOJBOOaaZSIUcOCszQ6bZJ8rdxTIAAwz0w6BGASs2B9CM2w4QhhPgTeygiEkC1bbToh+dupO9zNllxkuS7v/bsE93xlTxiGxxD2A8RDAz3PiV8NMaazKp/H4KY1HCNgpq7InUn12SbfCHQp6IuEnwnwY9iA/xOMfZKZ7rAAZLSB+9z006nKgDidqRwyYshO1O25DG0JtCN10AcoO1GJHLVZ01YKuGFBTF7rYic7fQufaAKdvoKPN6OBFtOcs2nEKsP0k2nkC7cTTHcfQjmNo6xG0+QDauAet3wkeNWsawcq5agMqb0DFdfbCanNeuSGntFtf3J1dYNTnWfR5lowcU0aOKS3HmJxlWJ3etSL51rLVrUtWXV204sqC+Es/x56bt+zMT4vPfL/47HcLz86cf+KLOUdm/HTo09mHPp514MNv97731a53vtjx1mdb3/x0y5sfbX71/YaX34MMkM+8ue7p1zZMfWX9ky81PPnSesCLG6e8uP7xF9Y99tz6R59b98jUtQ89tWb8lNpxj1WNmVw5clLlPRMrRjxSPuyhksEPFQ+cUNL/weK+4wvD788LHZujGZutGZurvS9PMzZXPTpHNUqvGpWjuDdbNiIraEiG/6B03+hUn/7JbGJVn34ZXn3TPCIgb6o4NBUnO00WaVmAX4okNIuFNEwvDcsBaHOl2lyJVi/R6sXqTLEmXaROgwKBJl2izRTrGCKY0MHsVKLVS3XZUl2WZ6geG4jnSkKzxVq9SAMMskCL7WWwVwww3ZocgVYv0Or56iyeSs9RwpSn0pOvhNo84mDDEOKqbL4yE0PPV+qFCgBf2QuyGDjeqHMkunx3iLV5Avh5DgPMtvN1BVx1LkeVQ0CYer4ujwVL2fN1BUJtgVBbxNcW8TTFPE0xX1vC15YIQ4sxCoXaAoEql6/MESr0Irleosz2UOq9VTm+Sr2vIt1fnuqvSPaXp/aR6wNClvvJP8wpu9BuRUY8YgcROZDgjbGB/mfbhITjQwhlZWV5eHtwBVgVIaYoDw9KIqNEAynBI5T351TQMr4qFSpBUcBTlAHXLKvBjHMFT856Pf9RwWXBwXpxKKpYnw2ushoLn+swm4ynrtywPOU6jF7emRDWIJoGrTQjnSYCap6KMNGwBlBMyxmIZLUiWbVEVo7TaGdD4gFlIgQlqOdRPs9SnvdQQjnF96CEUorii0T+CxeuNJt6eTx3BfQ/W7f/Z5fvbWbh0p/aT1b2Shra0AXDbySr02JBz7+5T6wu4UbUYQK60is6r6AR+GJi3QC88HoUfm+xSFlOBdVRQWupsFpKlzj4gWWN23tg62TliLQ6QXCDX/e37abVAcrcqDGrJNpSjmIjFVztO6BaoFpwsQO8yxwIXbWjMxbU/4ksSpPMDauXateptWVvvLrLYIYdhfzx0NLGjnAIldeYfMPSKFk1FQhKfEF4wezEbgMmTHtZYrd/3dudbHWZELrShbw0y/iKSm7oel7ERkpdPfGNg6RjZnMQyptdnCngo4L1OQAQn0mIXpcCwGFDqHQbopSrcTbjWkpVJ9CkVGwww6JW1LgV+UakU0GFVNg6KqyKUq36cXWL0eWR4drGnRv97f9WhC7bkF9MKuRtVjRSfdb6aLJmL95BIu3I8mStbP/qtpUQAttp7epCC1Z3SXS5PM0aKqSB6lNP+ae+/F4965d426/u/vMXroG7BPRf+OTfPfR/8xropV8RMpvNbW1tTU1Nv+LPuXPnmpqaWlpaTCaT+2L/5kd85+7/7qHZaKcJhpnBf9ZgstStXffT3HlPTX02IFDm49tHKvUUCsQCAU8o4ooklFBACbhiPiXlU1IuJoA5HA5HKOCJhOC/LBTIlLKYmIEPP/rw088+8+67786YMSMhMSlhdUrC6rSEhIzMrKK5PyU9NO7LPt5PR0d98NnneUtXFCyMW/XNjz+++8mHf3t26tiHHogZPlToIQEGXCAkwYwUlwPWziSdi1jE5fNEEnGwLOThRyd+9c1MvV7f3NxM4uOg4QXhZ70k3f8AAY0JUNCEAlxeEFbaZKVNNjsBSDhpGiTh0HjCjSaDBe08jFbo25796IBmbAUlT+aHl1H+BZRfsTC41ENe6q0s8FVCD8pbmS4NTpaGJAwcU/rC27u/nXs6MbV5/WbHidMgA7zRDgH77VbUYYbkdR1WMLYArof5gNSX7BvwUywTB9bNLMfENpAwA3Ubv+Zi7np/CHMwa8bIJd3WY8fcnAVzi25ErYsCI1wYy98RMo6VZrtoc5Y//wcFN9aVyXh4uzb59wwx/iw3/fdY7F4CGnPrvf/errD+/Z35MzvAKI6BTOw9ZQjKAEhXA7bXLNzOqcWd3yRsH9sPwc8Cl07G1RciHRSmi4hzOBHBNVjK9H7cTwQQmoRExlNW/gwFQjc7nIyKnHCvhJXuNe/GdCohZxmbbHsPshshRTq4ZvcAGAqYUMOELCbJIBk7CpeTIPPVbWwyYzLozuG6XcPAKf+GfXbf3B+WTcjpAmMwboOcX5D2iwWJzXTbBISFuIGsnNkBsljvt65sl51OiILtdP3QtbfMr7rdvnJfrBs5u5HDwHie0zhbmcN0W032bp1sFDaEt0X+NeAtknWyU3b3YA5enp3zmwKs34St13EaWbeHcO+titzqqtciyDXecEfFQvVi0prUMEtau1f4HStxHzPApL87dU4Idzzoxb4g8B3gFi7grp3HCQhgnNIFJnyY9AxJd5edkj4wuaFcxwuRCiwzfkeBWf6OTbtZxNy5PJsGFrvxwM9du0XsMcFGhhDimCgnl1cPQgQGV4GdQwpdCIKdCU/dgcvsVdWJUIejF+3EMYZGHS4wFxCNOl0A234rg3YLRHQTtBtxLj4cH9FtdRn+WsFgqseKrdtNqMuEQO2OX2GgtbcDP9hjh7y+YCKMrYQ7rOA1fMsK2ZBbTeiGEaY3iQExThTQSXbAjNeDU7neNKHWbkgPeOUmamrBiVuvonPN4Hp8tgmduYROXcTZWc+gg6dgiHfnMbTjKNpyEDUeQBsPoPX7UcM+tHYvWrMX1exC1TtR5XZUthUVb0ZFG1H+OpTXgLLrUGYNnV5Fp1XYk8ssiSWm1cXGVQXGFfk98bmGuBxjbFbP0oyuxekdC1M6FiS3z0tonbPyxo9xN35Yfn3W0mvfLbn67eLmbxZd+Wr+5S9+vvT5nEsfz77wwXe/vv/t2fe+OfXuzBNvf3H0jc8Pv/bpgVc/3v/yh3tfeH/Xc9N3Pv3e1ife2Trlrc2PvbHxkVcbJrzc8OCLax98Yc0Dz9fe/0zVfU9XjHmycvQTFfc+Xn7P5NKhEwsHP5Q/YEJu//E5/e7LiRiVHXZPZuiIDM2IdPXwNPXwNNWwVPWwDM3wTO2IbMA9WQSa4Zm64Zm6IVkke6p6SKZ6SKZqcIYKp1HVxGQpB2XIB6QF908JjEoM6psc3D9F1j9d1h9yq5JCcL+0oL6pAVFpgX3TA/oB/KJSfCOTvSKSvCKSJOGrxWEJotCVBOKwBElogjRstWd4oldEkndUsndkqmdYqjQ0RaxNFqmTBJoUnF41na9KJ3lWhapkApE6BUzP1UkSdZJUk0zgoU6UqsC8xVO1wlOZ4isv85VnBmi/XZK4/5bZRUCDEuFfJ6DNZjMxnRg6dChXwKGEHAjLEwkpXgAlHcoLeF4YMouvzOQqK/nqGiYnam92wT9inP9ofi8T/fcIaNA1A7DeeR2reuYp17IENOMWra4G+swFlonmqSB1IQuBvFIgrxRhSGSVkMYwpNJTniuR/SIImsbxn0B59aWEATyJN1/ko1JHVpRXgfTETlutVqZ1gZ+Md3ZI/t3+dz3e7/z7p47D1ehiyGJoi4Ea2GFFFy+j0EEFHPkaStdAaaqokLyRz25pQajZBhqZNgtaqG/1i0n17ruBUmwXhh3ghm+i+uYMmVp06iKmnglfixt3mJMFQzy24cfuq9mJrlmQasRygbqYq9wgDlvPU2X695/fgSAVqhmhGwjNK2imQhdRqlxeRKNUs0anjj+6BxvtMS9BJ3kr2czozK/IW5PAV6+hAuv4qgZKV/zEZwe73Rhn0qlgBdGYimWpd4YvNyG0/oDdUxdHycu5oRv54Rs56uLPfr4BCxOXN6ay3HsojN2f60gdsDD+HjKRQDeWNiOUXocoTQqlLqdUdZSqTqRZvbYRzDWsBvTgA/kiSGi8ltJtoELzp36x9xpuuf7Dk+h+AsGyBKHaY4jfP5NSlVOqDZyAMoHvvB37YSvgaOd6Td92BHdug+ir0fvfnpaGFVOaWq5mExVczw1I+ujLLUCxuy6SO3939/+/ZA3cJaD/kqf97kH/m9cAeQeTlhBthxTYra2tLPt86dKlK1eu3Lhxo6en5z/VAJqcwN8loBFCPUZze2d3D1bRdpstJpv9UvPVAwePpqXrn3/x1ci+fT28JTwx1j9zKS4l5FF+XMqby5HyGO9lnPsPc8RYOs0V8CU8+AE4M3v7+nj7enn7evn4e3v4+AolARyugscNpSilb0C0wCuEEggpkQjWSiDAnhp4RWTC5fP4IqFQKBQIBCFy+UuvvlKQX7Bv376WlpaOjo6eHpAAmEwm2s5YCjidLGUA7q+sQ7Fbh51Z4L/iunYQJSNLCBJ6zkU930lAw2i9DTLL2XH+tFtmdPgSyqrveGvW1v4PpAf1z/DRFEgVpRJljVi5RqCsFqhLRdpSsa5CpCqVqAt8w3O8NYmKvknRIzJH3J/1zmc7fo49W7sZAsZPX0PnbqGmbvCB7TYiu8UO5BjoFoCDRi5JptNhBOUFqEdZdSDLRIP3tpt01JW3D9M6rP7UVWDEm27rga2wYCsECr0cNJPqh20WkwJW8bqckV1SYlZT/LuFXmNinAjod5f5w5lutsus/UVv4bYdcLd7ZsqYK3dpS924YHzIRkK8ult5EKbVfc7fKRNxMUPRYg0sUea6qh2oVbIJZkO3q4PdFgM+mnRymBa6++Xu4qJJc5n1dGZZPsaThdFnu6w63EcJ7lSsE4m6q1qwL4p7hTD7jDW8TmcPC4ejy0H3wPG6ZvZyxJh1JR7IOF8lyVrJuiL3FlyUNFx+Lk0x2FHczjbiXhmWzLuxxiwl+ncLbL1AATv7ufWJfo98dMWHIkx/u90X7kfnsnfuPRBy+ljF9B376T7AwJaZZQgbTqYk9SSUb+d2nYwAHG+XcPq3TV2st4tcdjL09+0XlevGv21QitDxROQM9UM+bqwpeeTimFkYRIHLGD8r7mDYSZIi12OEGetitkietE5Qhrn99g/HDJhV4W3BGsj1cEfPvDd+wyXcgrOJP673BeN6D8fi7HW8ueOku85U72gH7O3vhSaQH7quInIt9dYYs9rbiWnWot21t3h5t2XIjrme49iOCTnNCAYiTMjmAm1iRP5Y6o9PwG+JaXI+SEQACQqw4JBj9m1BCuSUwNuCaOMdTrBtwS5LYE2Dnd9pIgDDjx3inwkd7ttd4G2ENcCnFnLpOuGeN7nE5kba5bQOMRSQtdboALiPLxmwMXqXDWiULhs4pAN5TWM4YWG3KAl4IELcO7vbLgN9chRMijwH5Moz2oD7Juiygj0oKRtJFuDeDFi9A7lk5SYHbBqIdQuTfA9SA7uh24w6Tai9B7IN3+qGQocByPdOI5TbOtGNNnT9JrpG0qJeR1dbUDOeXmtFzTfRZZwo9TzYyzhPXaaPX6IPX7AyuOQ4jHHoov3gefrAOcfeM/Y9p227T9l3nbDuOmEHM5kTjp3HnDuPoe1H0LbDzsbDjk0H6A37bA17LGt3WWu3Gio3d5Wvv1VS31pQcyO/+nph1fXcsqs5pc36ouaMgstpuU2pOZeSsxgkZjYlpF9YmXIuLuls7OpTS1eeWLTy5PzlR+ctOzx36aG5S47MWXz4x4UHvv1l79dzds/4aefnP+z49PttH8/a8uGsxg9nNb737aZ3v9n41pcNb8yof/3zupc/rn75w6oXppc/M6146tslT79V/OTrxVNeKXr85eLJLxRPeq5k4vNljzxb/vAzpQ8/U/rQ1BLAU8UTniwaNyVv9OTseydmjZiYMfyR9CEPZ8Q8nD7wEcCAh9IIBk3Iuu/x+uHjs6a8lLTlYHunDZmd4FRmd7Mp+KMWsvub83fLO3fu5HK5QEALhGBJwZNzJWPEvq/6yOb4a9NB3KqsJOD86+zzbaz0bwloRtRMpM3MtFf77KKh3YXP1Tx1pQvlPLU7SvnKYhdKBYpSgaKcJaBFIRWS4ApJULFHULZXcLyv/GuvwKcFnlEUXyyQQk7wAQMGnDhxwmQyEXMS5mXgdGtz/G4l/p+fyR7IHYU/teN38JfwG0h2Z6dRXNJpTsBKKqSe8i7k9GugVBnfptiaEWqywZDYU69s4aiSKHWJOGI7FbSeH9xABSS8+s2WVgSPC0TDIDgku2FIXXhFkNfuHTtpdqITrchv4HJKVcDVbpCEb6RCkkY+nkVMj692g543eHgKPzKPF1lPhdQK5RkzZ+2wQy5Qp81hZl7l+A1oNsITXjs0Wxy6luqzRqTZSKlL+j5a/FsCmm0lweG69pBUlwOPic5POeYZnkyFlFKa9YKwtUKdPh9bgpDcjL+pWFgf6dO5enbwL3krEwLaZDX1ONCibCM3NJ1SV1Kq9ZRqvUC7etthZ48Z1dUgmSIpMGqrR9ReSl4ru6fg4E0Ygv0zdiruJ9CJI+Zmp3RSoRmUrIyS1wpCSrXRyV3gUMIQ0IwFCVsFjIU0e0zgB+1A9C0L6ndfpii0jFLXUX6VfNl6UVDKTwuPWWk4la4GPPuru4W/bg3cJaD/uuf+7pH/u9eA0+m0WCxdXV03bty4dOkS0T43NTVdvXq1ra2tu7v7P9h8g5y7321eW+200Ww1WWw4FBEW7DZbiMjLYnV095jbOrsKywve/ehNTYTSxzeIS6m4VBiX6sPjevJ4Qh7+uNPFQoEnj+vJoSRcjpjLFYJtBwZPREl9JF7+vgKJJ8UVAThCkDYL8ZQCdw+KB+CJhEIPCV8CYme/gIDIvn2H33PP7Nmz9+/fb3c4jBaz1Wo1Go0WC04mY4FPe3s7vKsxKeYiDoDy+H/sfQd8HMW9/1wvOvV6/VRt01sggZe85KXxyD9ASICQCiGEvJeevJAEXkgg9BbAgDG2sS03WZZlWZZkS+6VThxawNhGbtiyZZXTle3zf7+Z3b29k06WjQ22NfeZjzQ7Nzs785293Znv/Ob704YpKUra+O3xuKUpAS3ofCsQ0FJyFAKa2tGJHIwuhoiQXL+CD/D4hX/hvz35wTU3rg2d85w7PMURnmmJzDdHGszhJuRrsYdXoKIFnpr2/LqW3KoGd2imKzAlL/y0vezeHN/fLvrSvK//oONPj2yb14UXrxX/8S7etQ8PDIEqK3juE4hxnCKLCrgrlIk/aRpJs18mU2md5aFEniYdoHNAemS4BTTQEXp+HRAj+6zagKeGxqopoubLUWd7s5HReoY0O3fdWncY45zKr0pYZPH+l2KfgbI3Xj2tBI2AVWlWcHioOUU0RlJtp6ojmtyErjsxSkQ3VwedCmLvTCl+w8JAmgW0MX1YPMPOPX0GoN39tDd0DFXFdK2puv1zmk07FqmjUU0sJSVxk8bOp2jolMk2BUdHQG+vnqLbdOvN0fUfMiJ6hvRISvvB+GPXzIJ069fskhBpdLOeLcUVajwgTCDSQurGBq1I8lPSfiZpdC38TNLrbDyEUzRaWb96qtoGWjOVmFXeItUWtUztuqroh4Fc1klhjf8lPK+Wn3J0anP0pmnEq2atrBo+AxAa+JTAVQlovQdHuy7BSrtu5hVpusZBk6rqxukZkRHrnyKFYdO9gQimyzS0CwFYfQFDa4hk4NP1niZdAP2VudKg1Z/2bGYrUrhpBt06pCNGjpif1FZlgym/Spy7JnisB6PsPvgqIBKkRoYaqOokBCmBxQQWOUNIShwvcQLxc0t83tIlTKJengG7agjPkW0NHBAkRLkIKwJ9CMuyTFaLYZnCOD0nO2igVgJwKPAjE7HCKzInA1EInnUlAdTiSVx/HNH0hMjToGeAbOALAgIPrzxKAFB+ANSH1CukCGQwSKSKRqIiCjJP2yuArBYEUQF9LUFM8EJcC0O8oAZB0qbyYAAAIABJREFUiglSlIQBUCVS+mXQQRnUF5lkDNtEaB5eHCQnxvXSOD5KQozjEryQVOWPYE1dXcwBwz9RoWr+1LsD8UvMc7B/hI9jPqZwMUUYlPko+RuTpZgMK05JgifFGSwESb9zhMQ3asvoCwxUXobeSbCiIIDkK0je86qWWsrVroDF9MCRzAniuiHlbpgIu8coI084/SER1hJiCni2GBCB3KdhgMMDXOpwkAPL96gmQE9J/CinGsv3xfDhIdwbBVGy/f14fx/e24d39+EPDuP3e/G7h4Bue+sQfvOgGt7qwS+8i9e+jnccAiP6IQnuK0FSwMGy4aO9Fcf6n2oBz5071+myg/6G1YnMQYQu8vp/VVZxf2H5VE/5PKtvkcm/5LgS0CNIcBwLAR00ctCUjFZpaGugSQ82f/MIBHRpU05pQ27JzILSJ4oqfufM+xxCDpPdBiAgdMkll+zduxd+bIbPWDE9WfMZmpIWHVN9jfyldoKkwB6RSy+fag3MQcE1prrVKLIIVU1vfxfvwvjPU/5VUTfZVTHLHOxAvhWouNnhb8zzTrnjb+9T9TFaDDzJVM1hIHmpkBZRzEirZELBL3Vja+1jKLTQWrkaeVvdoRk/+EVXL7GzHsD4N/ftA+2dmg5rVSfyLrroq+1D4JMZHpswzJPhh0KVaiQe1hIuu3KVLdBqKeuyB9ehcEvNFxdFFZV0BZeA9GFK/qrNTR9+ihgkQb5/22p33fOoYjHytzuqlnqqnnl1O0xR4L08wge+yCCg4QqwCQjeJUTvMXk4ie94ar+5aoYp2Ir8q1Fwpbny2a17YDTwpSuWFXoXocI2W2Rt0Vktf2+QPyQroJyEB/pBi3KUD60+NVqmBPS1v9mK/DOBgK5ocYUWXXfzy70x0AShFtAjE9DqBZSBZBxjfFjA7Zv7UdlfreElKLQi94yXbP4uZ8XUvz+zI6kS0LwRwlGqx7467RFgBPRp38WsgacbAtRrRDIJ7uz6+vr279+/a9eu7du3b9u2rbu7u6enZ3BwMJlMnvbsc7Z+pRZJ6QaPREpM4yZ5jKNCnJPxwoVvfPqi35Xmftdfev3ZZ19+znkXFRQV5+XlORw2i9VktpksNpvD4XI68pyOAhLyXK5cm5MMSC3IZAPHgfZck8WlUtJATGsfq8sB1hM2S15Bft3EiVd8/f/dfMuPb//fO5qXthw4dBD2M5GZGG2FPoPVp2c03cAUqNSzcbAyPJ4Nk6NJp2OlFL+g8a1A3FEvavQvJfSA3KRKFYToFGFurCSJVeQQxvuH8Ft78PyVu/7wxKb/+P788KefcVRNLj57qbtyhc3fZapoReVLkHeROdhojSy0hec7wuCJyBmaaQ/MsJQ/g0qesPmeDpw795KvLf3KtZ3X3fzyj3+19Q93vz113r5ZS95+Z3eyTwSlW+pEg0q9UtM542AxI64CbhhNZmTIONTyqxvljD2iETpGfjDFmIzO12ikjJGnU88llJZappZN7460/OQS5Kt0EoqM01NcXnohaSUMb4JIdiga/xpZKhpPmwcc6UAngrURv8EAEyYAYwzqiotBYZoSO9ScUf2rObFLSmDzl9Alm0k8IUIKDUBdEQoi9VfEKT5LZxWH45N+A9BaQRP0D22vfmhcJDPeWvpeTj1i/Db9pw0PM0kN4IqPhuGCvZTZH/NfzcAUGCv14unXpYqEIzxKic6ysb7wKzEep5cDJRievio1NLz+xhTSCv2sVA1VsyPD3E+7btpETq+AVq9UUcar6DeMHjHY1BrrqYJAeiFFgRM2HbqGSjfqF6WOTLVLq3azWj0zgFIPDZlHzJit/mmKzQacdcRo3Wg2qsmcuoW0m2rE+qeuSPsuHTe1wJFwU2lA/asRIwacs+bXRTiG3Qy0bpltJ83hJaxLT0NLye9a19aGCF1qEiRwsastS/GEECf29bCfZliQORDt1gPlLGWJChNRmSyDRhA8eymzoK+3GO8NPT7SwyRzadm4JJbxtEx7yKj7GLSd0mlMOBHHJ+5tYYmRBKI6DqtuOqMNLDARYKLbaSBOluXIX56HhcnUE5LGdSe6emn0xaH/Lob9XlQSQ0o9DgBrzX2BulqgHYLPDerviyw8wkCDsuzkF6Ub4Km/F4LqyD8uSUmtqwHtpG0YysytP4u1COykIQLuQAZpQSb+V8EFq/Ys1iXaaaJILAWM+eXs2jX6k90YoUAnBXhdxagYiwjU9mESenkMQcC9Clg7DoFQkciLggzrG8S8H2BS746jGftBXuqPbsqUKXaH2elByGI3ofPyPT8OVTzpLZ9T4l1Q4FvkCLRYgq26EfRHiLSmDJ+pE0LyN516Nlo9a1rPaWbRmdLPqvJGep6UonSgA9wS+tuc/lanv9XtI6GixVPRmOt7vtA7vbhkTlnZZKfrOoRqkdlDR/V2u/3uu++mNiL67+5osT1t82vkKq/g13dgT/UD1vASS9W63As3osjcmivWztiAz/xapyX4lLnieXP5IuTrtFetyq9pOuMzs9dswQliZqv+GHVeW3sNytpDQH2PaiDGMV76Mkbhp1Gk2VqzzhHqKp8w/57Ht1IHyO8dwkUT6i3edktopau20xme9lyjGAceOY6B36XLyTDMhqVZYjfzvV+9awu2OLzrLL4NKLzCVv1ET1wdGyUEUMYwBq0Wqf8ixvsF7P/UE46aOY7alcjX5qhsPPPzs/vJi3M4Aa09xNLGLYSk1YYP9IqyeHAI//bhnabK6eZQGwquAieEVTN2C3heO++dMNdW1pZb85KrZtnlN3YdIPtjRKJYkqpZlhh1GkhfpQkBtK3KzpvqmNSBgsuQb7E7Mv/RaSB9rq5p6c9M+mykp4HRM5ZhSRak2XolfEjBV9w03xF+hlbV5F/pDHS6yp5qWDJI3buTV3lGT2apH0s+3RFgBPTp3sOsfacjAjzP9/b27t27d9euXd3d3TvJp7u7e9++fX19fXSb2OnY7jG1aXQCmpIKUUH6x1uHfvqTxaGK39eE/nTT92ZtfnHn1rfeXrtpw9Tp0268+cbPXPbpotKi/MICt9tjszpMyGaxON3ufLfbY3XYHS47qHFYiFIH+DEkBLQdmXOQs9DmKfGEayLnXnTB92764cOPP7Zxy+bX/vH6e9vf37NvL91Nxgl8LJHQvU7TFQVqQnXKEdBAt9HpJmxSFokJrUA5aOpMLU6GJtsH8Ys78bOLd13/s7YJn3nOf+a8wpoGV3ieNTDHFmp0Vre46pZ5zuhAgYbCc1bmn7UCldabQw2WcKM5NN8WnmMNTnOEphdWLSyvayoMTvVPfHTip++8f8qGPVEY9+g72HUO2jhSPF7xjMm/dpjBFxjJaGM8I5t+aMxjjOsZMiLGPBnxjJzGw4ycIx5CfkIf6NNzGoEhuHGr/tHGVeqOUHRHe25afkJVE5ZB5dRIz+udD6ajZDs7bGqnAhe6XjOZxcd4TINuQQmRJOaShIw2ElWj8s7pjLlBxIDWllbOWPPhdyAdw1NuReM6VBvJ4ZmJ5A78yKhxnk4aarynEeCjihtnPmmTK0MdjHmM8Wz5s6XTc4+qejSzXpf0h782TdW/poY8Oj9lTKdxcn5aNbLx+JRp1VhXtRp6Lxj7i8Tp8y9bw486Pb2dGUcj1t+IaqqP6Jka1wl5dLrMcAulyPThiGnnpsrUln8ymN8Tckh1LzRKXatdmn2+ZhuXEl/SzV71iKguv5ElupE4BN12WCst4/lHD1M4gc2c2qnaTZi2KKJyMVqFj7r/9RP1BQA9JSOSujfSLN+NtdKyUBUvnctWmWVCN6fbX4Nklcrup5xbqky00UcmJZp1zlo33yY0haTR7pRTNWKXSUATylThwbZcIrbqYK5OAw98v2o8Tn5o8ODVWRvSlfS3qPf1CO5G6a84tQNDAQe/mmvTZKakT4bCj0w2dsB2H1if0G8kalSuGBwLpBhJuJtgv5FhI4Ki3h6wQiBphv/qzirYODLqdiJZAaNtngRqIZ7EySROxnEyhuNxPBjH/QmwsY7DHn+yBQBMxGH56RgJaKr/Vl9fjxBy5liQOc+MPpOf8/NQ2TR/6aKy8sUF3qWOQOvJSECnM84GFhsobJvmydAGBDRw0CMR0NOBgC5eWFY61W6/DqEJCBUik81uc5rN5vPPP39wcNBoBK39vNh/QEDGOK7gGe3YVjnVFGk3RdaAE8Kqhm/enkDhaa4zO5APZBks4XaTr7H8zMb/uWf/INEmwljmB/rEgX719w0Qpx7VsCWT0Jaqj3X6fAMHEXhGF0aR2Si01FqzzlO1Ni8wddmqeEzG+xP4lj+9UjixBZV12iJr8yYuveE3/+hXC4lpQ3eOmCkIEpY4PiZi/Nv7DtlDSwkBvQmFVtmqnn5zpzoq41RiOO1pntHrAsavduOcCU9aqhYUnLsJedtclXOvuWX5gAgL1Bm/R/oop400vmdVK2HD14qiHE7in9/7rqlyOvzogl0ovAJVzdmexF/9XqeneknhpJfdteuQ9+8v7ITZEHlC6oOUjDqmHVIgJSJTKGN8MI4LJk211naiqhUo3OKpmjNvKfSDSKZ4+ltRfYLTlwRZBJRhnRLY58MYP9ucsIfus4bmmgJtKLDS5F/pDq3MKZ+8fLUoEKqaLDwzAjqtI8btASOgx23Xs4afqggIgjA4OLhnz56dO3fu2LFj586d3d3du3fvPnDgQF9fXzweH7e2z7RHjdSPcWoOb0xFnar2J/H7u/DNN7VGAn/84hfuW7fhYJTHSYXvGxqMJhM8jN/x4YHD/9j6Wn39rLv/9tfvfe87V3/jys9//vMXXXTRpy75TE3dBGQ2havCk86deMGnz7vs85f+2xcuu+4H1//+z7fNWVS/4eWN+3sP0EJiHHh0GeWj88469UznDfQUo4WUcZiSLT7Khcb8FRkrEWHZNMtZMoHX7MXAGlrbOA+mBITISxCBTjB/JjYIsBWaTnRFDLtTB4iiZT+HN77a88s7Or74zfrA2fcX1T5SWDc9t3q+K9zsrGrznLMq/MXXQl980T6pMfyldWX/ttR1bn3+RfW5k57xVD3rrKi3F8zLKV5QFq7P9f7pa9dP2TMA6/Z02qWzzzo/QEdxx+uv8b46WeJjNB8eRpJmq7/OeWREsuX/uNPJBEW7+YEY14xjVDs5o5GmwYpZN9wzGkIC206oCNXckVAnKvlyfNs1/A7U5wcZkeE5aUpGNv0wW/7TKT2T3TPyaxoTaEQpW9vpA9D4LYXRmGKMZ8uvg58RMZ77UeKjP6iNJR+h/gSo4fkzqq0fGnOePHEVDQMfkcYBZFQ0/d4Y/c5Rv9XgzihpLIcjlE9LO4ZqDD8l1c6MhzHVGkljXRVQh6crjmAjbAz0yZhBzerPN6qVDyJaIzdYV3TRKGWVTNbT03+BUAj5Si0uo+aGa0CHQk7yoTVXH848DBsgiNAinbwG9RL6xKelaP2W+m8onV4+tXCSoVaklqppxWiksCYTZEjXSWfK4BOQ6X50sgypvVjpsojaaCP6NE5rBnHthLFECGFNrqsjw3HAPnMJnEwABx1P4FgSLKQTwNHBUgsZDKmCL8dOQCeTyRdffDE/r9jpLEUoaDFdlp/7o5D3EX/57IrSJYXly52+Np2AphrQqhxHsMU0UshuIn0iLaCDbZoTQqDLwQGJFhyBVkeg1elvcfpbDBbQTbkV8/Mr6gtL55WVP2p2fgFZAshcZDJ5nA4P3dmYocKRuvnGb0z9OdIF4CjGt9zVjSIN5kgX8nai8hZU2YpqWlBVMwoscZ69xVT3kr12eeTiWTOXJOm4HTZDCENkIJcgty9MvuDRSksUQaKCPuxSBDR8J8YwvncORtWLka/VUrUup3JdUeXU7g9h79uaf+CCiX+3hBtR8WJU0Zw/adby13BPUl2aga0JoK0RJQGsoZPcYFTAkxdgR4RYQHu3oOA6W9WU9nUHaS2GbfCCGmR8OAzkOwo+bQo1In+rOdjhCE1/4NkdUUJA6yun9CztIQb/tQEtRNQ2Gr4WBCGm4B//eau19nlLqAnUSyIdqLKpaQu2+KaYIsvMVZ3W2gXX/s8rhzDo8KhPIXUHTEYd0w61i5DpLsYvvIGdkSmmyi5rzWr3hI6Cqlmbt5L3ClV7Io8y9RGsP+JkGSuwyhjHuEfCM5aJjsiTntpl5kCryd+JAivNgVW5lWvz/c+8+iZsnyHLyUmVJE+rCzsYjwgwAno89jpr86mLgKIouuzGrl27qO0zZZ+j0SjHcboWoXHr96nb3mOouXFsPzIBrYDW3tpNhy7/6tOfvezhhYu2SRj3RGNJnOyN9Ue5GKfw4E1D/dCXLc8LQ/39hw4cOLBrz75Z9fNv+O73n5v+/Ls73tt3cO9gMhoXEgmZS8hcEmxVBAnLCTEZFzgqcShIRvdFmBeFBM8JgmBU3jhFCWiyn1VI4lgCgtErlEBmSvEkjidxMsaDQBgvxBUc7Y/3cRi/8Db/zIJtv7xz06VfWxC5YJbDOwWVz0T+OaiywVbXaK6ZO+E/N13yna1X/nbfjX8b+N5tH1z73//6ynVvfPaK1y/5941nnj9v0gUPPPDEK4dioINGZ+R0skt7nw6tju9f430FcW1Dblok2wRzxMyqr5GRpqVHm384E52tJqOmZxAG+mFm20ct5IRm1voUButkmpLG3KQP5VM24EZFES2u2nfTuY3eUuNddLwaotVZnRrotrr6MF6PDM9JU/QMGZFs+Y863UgoGePZiKmPMX0Ems/Q58aWUnCMKcY4fZwbU46Qn1xleP6MLtAPjTk/Slx774z831jyEepPsg7Pr1c4I2LMefLEVRSMBLSx3h+xotpL/iMWA2SEfk8a4zTxmEvXSQvd/CztoZXioMmODbqFJY2AVtflNF4n4+GmFq+mpvPWALLhKa/zwKBEZUg39oUaJ9+map4hKm84hIViYhRMZdZVD6t0d4766DY8z4kjsnS6e/gvOhvSms0j1UoyiFOlSVeNnK4x+7RKqhU2FGiAgTY36/OdVmsErIZjrqWoLUkR9NT8nEidCBzmKQfNE1EUCRPBelUHhGxvINjSk0d+joyaKolSX1/fued/yu4sR8hvsZ5VWHBlJHBbwPsYqHCUL3X7Wm2BNqsf6GOTfynyLx2RdzYFW2n42AloYJwzgs4+2wj7DAS0r83pa3N7O9zeDldFh7ui1VXWWOhbUFg+tcR/B3JfgGwFyOIxmZ0mE7gf93g8ra2t8PvWPqOiOE6+hIeffoMPYvzZ725G4VYUXo1KO1DVWuTvcExYg4JLHBOWmUIN+Wd1/PSuwZ4k7o2B6X5SAsaVjw9gzCUG9xNPeISgpA988miSNLer8AMSJfVJSwjo30+OAbvtbUPBNRbv8qoLmno4kNi49fZ3c2rqkW8hqliI/DNv+uN7e2KQzuvjdiCgwdsrXVJKJPv6EnjxWuyJLHJ419iAgN5gq5z2fMNOaBp9TajWvqlfud7BdF/G/+3Fu+2xXktkjiW8zFm90hpa7gg+vWR1PCbAZEF/ItKzVP4anuc8WVlLwQgZKKDkvyCCa6Af/uGf1pp6siW0FUXaUGXrf3y/1x5pRVVdppomU+gva94Cel09ly4oam83mjz8r3YRWLDEGDe07HUEpphCK+01q/MmdRRXz9j+IREr4STVLoO+KfS/VGVKgesexvjp5njuGU+ZQk3U8BkFOlGw0xzsyq1cWxR+dttuEN8nBDTTgB7eFeM0hRHQ47TjWbNPUQQURent7dWp5+7u7j179hw8eHBoaIgSmuAGR3PzcswD0FMUHL3a2viQWKlQbo5uLKUW0Ap+872+W//7sXPO/tk996z98BBxQy8LMSlOA6ckOSVJ96sSExjNSZrMw2hAEBOcRALxIKRoGySVOKeGJNVVpOzzKJqwdJFAr+3J0V90WJL6q1k6G6dnqSqTqR24tyITJBhPaWeCQCbdOirISTDOgd2mcVkaEsTEkCT2ifggjw8k8Cvb8NNzolf+YPVZ/7644qyFpvIZKHey3T+7sG5JycRl4YvWnvvlLbfc0ftUI+54CTevxi+8jdvWJZd0frDzgBKVYPSjc4ijbMDXB1v6TTJSZAy5dKJBj4xU0CmUpvVXamA9esrRNi11r3wSXuONbaEMwPCU4enGPMfW3mxnGUsey3WPNn+264493XjFbPFspZ3o/J/UdbO1K1v68arn8SonWz2zpZ/o646l/Mw8+vP2OEYyr3Fijj96hcf0bIbKZ+tQmk45U50KgQj5qGbL1HhZNkpGGBejtHRjc/RT9Ijx2yPG0/A21j3ti+N7cLTvIxWikSqhF2X8UpVDOWLb9Qw6dIaIXrIeoTw4sZFMuQOhiWSENlJPGas1hjhZGVXtu0VZXrNxPbJakdVtdhQjFLQ5Ppub+0Nv+b0V3pk5pY2W0qVW7zKLdxnyLwPR2OBSFFyCQs0o1GwK0tBqCrSpAZho1Tg6JfocMJg/B1rNaRrQY9B9poIb1MzZGE8ZPoOZthbabIFUAAkO3wqHr8vpXeWsWOOsWOes2OCuWGMvXFwUmOurfMSW/y3krkEOO3Igsx2ZzIhw0OaurlVAQFO3bGOAdJxkUR8vxAtf8fkzUbAdBVYj7ypUsgJ5Vzmr1tkCjfbyx370661vduNDCSCC4WYnVD6WJZGPE7euINenQEhQShdjHB8Aq+CdH+JDMWCek8kkOQ0ctMcw/tavX0NVi1CwE65VuvQL33l3WxKveg+joofLz98IN2Tl/Jwz/v7aPpgmcMRUJSUHT50qk2cgxlyUw29sxwXBmTm+lXbfC6bgRmdk3i//sBauSrcUEB16EHNPf8xGozFBIDQ6xlfe/CryLnSGO1H5MmuovXTStP2D1PIXbgTjA46sWcpYHMLCENkpqlouq8Q0zUpOURQpruBrfvq6OdJoDjeZw80o3IbCK1wT1qNgBwp1osCUb/+0ntiNY9B1NA4rs99/NJdALsERtaVp9e/lhKZagyttkZU5NUuKq5/pS8DCKjh+TV+k5AbjUoyHsgl13a/gXz34IQpNQ96FyNeKiO0zIaA7UKjDE+osq5p6YBDKIK1Tm5i9auyb8YIAI6DHS0+zdp4eCEiiNDAw0N3d/f777+/cuZOKPieTSUo66/6+9GHr+LSD1pufsnzRCGhQ4VDw7LnLL/23G+64Y+6ObqIXK8pDYiImDyWUWEKJjUJAy7JotKomjnrAPw+P4xweggAc9FgJaHpP6rWlkU/6Rs0YJhH/RZmGQqkqU4RTx2kkoyyB/2d9xVwlihUMJjxxLEUxHpCBht4Xw+8fxK3r8a/vfP8bN7446dL5FROm5QWm5vqed5XXl1Q1mgofc3nvP+dzs2/69doZDd079uO+JI4KypAkJxWFjiyN+3Mz26AN/rJjS8+gVTWePewMOm8cljxSgrEcY3ykvJlp2epztOVkljv82FjiWOLDSxg9Jcu9MfpJx+1bY4uMI3Nj+ujxo63K6L9i47VGrw+97tHmP9raDs9vvGK2+PCzhtfWeO7xyn+8yjHWzRg/2vKN5xrjR1tOtvzZ0o3XMsaPNr/xXGP8aMs5EfmzlcnSjxkB46N4lDgtf3iG4dcdS57hZ32yKcY6j6UmNP+IOfWijN+Okt+YTY/rhYwlQs1vj3iuZiWqZxxThBLQsKdNlnlFjgvcrT//KTIjm8cF7k1MYWS+xGL9pivnd+7iJ1zlc10VC+3excQCuh0FlqNAOwq1mEJNplCTOdBMrJ6JibSBfTYFW044AZ2FjDYS0CTeQVShV9l86xzeDY6KTc6KdY7ipuLA1MLgb02eS5G7AjkRJaAdDnA87nZ7du7s1tdvxoTp+MhE3x0SIaCtlU8ifwcQ0KGNyLfRM+kFu7f+q9/c2NCEOQHHBZwg1KU6JCdbKxRJhCAnCQE9oOCEpOAk8UwoSfgPf1pdPem3ze29AzHMcQmVxyUa0P/27RUo3GgKrQTSs6Tx2t8ObsP4Kz97GfkbUGEzCrZaa5//64yD/YRBFWSeblzQexB+cYSAjvP9GOP9h3Gxf7LH1273bTYF19sjC771/WXJuLbFktM2kmgqF6ADImNBkATw04eTCj77P5agooW5lesLqjfaQ8vqLmvsI2bJlHM1vmEhRZFBu4IS0Kpsjt44I1mrDIn4mlvfAuPiSBMKt6BwBwp1odAqc9VqVLHY6n+wa+1+rOBkjOMSfBrPneX2o5vwNHUmhVPAw+wzM97MD093hLrs4Q5XpLGocso/3iHn6xbQlHqn9tJkzw/GeMeH+KvfX2+rWYAqmlCo01zbYa9tBwGWQCcKtaEwbDKoPW/e4RgUxbjnLB0yTpMZAT1OO541+xRFQFGUZDLZ09Ozb9++3t7eRCIhiRL1YmfUczCOZU/Rlh6XaqcIaG3LpKjgaBy/vrX7+VlL3t3WM5jAnIJjopiQ4pRETihRSiIbLKAFWea1MGYCWpaOaAF9XNp4vAvJGCaNeDjWa9IttBr9C0URr/ISh8UEEQ6LYfCbcUiEv/vieE8Mv/went/R98d7X73i+pbzLqsvjUwuCU7PKZ2ZXzbHU/Rsmf/RCy5+ZO0mPpqEUaqgetbKtEoYsdKjjn7oGWMgoMfa9OEWD3qlxlJEtvrohYzamrFcQctjLHEsce28U+P/EVtEmzFKtuPbzlEulPHVESs2Yv6PXtuMYkc8zHaVETOPcqcebf5P6rrZ6pkt/XjV83iVk62e2dJP9HXHUn62PCydIcAQOAICR7FMniqJEtDg30OWQRpAkd/d8d43rrvGVehBDheylgAHjc5Gpi9Ycm7OKf1Lru8xZ8VUh3ehtaLdVLHWVLEWrJiBem62Bpr0YA5SPppS0h8XAU1paONf1TK61RxqMYebiSVpCxiThlaYA6vM/nU2/4oC/4L8sr+5ir+FXBORy4OcyGI32Ww2m9XhdLq/+53vc5zAzJ9Td4wWo+8RCcuDGJvCj4NZbni1KbwJFa/XYVxxAAAgAElEQVSxhFp+/oetMEDnVYNZsISVtTePRkBjkbjkUGIYlDEEHuNDSXxYxDf94p3csskF5Q/++e6tPB1J0FOJX5nwxfXmUKsl1Gmv6rJEltxdj5/pxJbaKaZgq71ynTnQkn/G9K09uJ+YP0tynO4VUAno1CRZinF9GOMBDkfOeMbjX2r3rzeF1lorF5z9uWf3HSKNFGOYk0Hvj+64NHDQ8KtRMC8ofQlcduazqKzZHVhVULnB4lvymStXRollstba4eSwiGURwKEBQBIFkLsnF1AZW5WABuq5agmqWobCK0HhxLfSElqO/HMuvWqJhEHGQ0gKEi/JxNmfxmRrPWT4T9ln3ZNAUgFfr0McvufhDYXh51yhDnuk1VHZmB9+flYDBsylfrBCp+wzqVIS4wEiu/H3uUO5dc8g70zibbIdlc92Tao/7+svA1cO1tltpki73bvk0i+vGCTLCaMMBQ0VZNHxggAjoMdLT7N2nk4IcBwXj8fJWxyaJYmSIAiju7M7nZo/9rakEdCEgxYxaFENDIlxTuFkKSHyCUmJiSKnxHk8JOIoj4d4nBRkowSHTkCDQ2BqAU13sxIFL4MFtG7+rLHPeqekRjtpNsJjb8rHlnPEwVJG4lgro40VIb9eBAFNJBy0nMBynAzqYhj38rC2PkD24L2/D+8fwEs7hd//+eVrblh+5gUzqyY8X+adHAg9XFX1P23t+2PUPgInJQjgu0Mvf5RI9nrTk+guMWMB2c848jfGcozxI59paM3wKulFjaWcI+fRixtj5Mglnkw5Rm+UsabZchrzfPR4tqsMT6fXGp6eLeWj123sV8x2raOt29Hm/6Sum62e2dKPVz2PVznZ6pkt/URfdyzlZ8vD0hkCDIEjIPCRCWiytw+8j+3vPXD19ddaPDkmZyGylyKzD6FqZLrQnntVXsV/FfjvzPNNzqmY4yhfai9vt/labb4WNfibbf4mm7/JCny0zj5nIaAN+htmf5sl8BEkOIykszGeRkA3mcPEnjTSTExKW1G4zRFqKKt8yl14C3Jegpxe5LAB+2x12C05CFlqayds2riF50VGQA+/9+h7hBLQYAEdWWmKrEHBDebKV8vPWbG7h6hY9GOZ2APDvQlK9eQkXVweHJaLWBYUReEVcC2+cxBffetqV6TB7l2SUzZ18nODQ8R0WndFGpOxIzjZEuq0hJa767oslYvqN+Cz/t9ma/V8VLQYlbc7wwv++nRiCOM+EfMSJ0saAW2cjEFckjEPlHccf+oLsz2BRXb/WlNopaVyYUHdI2/the0EWDoMXGwCQyAixrTJFAoZ3NsoPQO4eOIUe7DdWtxmKVyGihu+dMOWWHYCmhLB4EebKBjyEuzNJd5iBaqzT2evGCtxgVhAR5YC+1y9HEVWovBaW3g9Km9yVT9339SeBLD3xDIZnAIaZg/Du4p8CY4fNcPuhAx0f1LEd967qiA01Rlot4aXWCOLPJULb3/g4KCIRVDPFjCZtwoY9xIuet0H+IY7NuScNcc+oZOsN6yw1y1B/sevuHXDup3YFKkH8+dQhym83FK+6IprN0ZVgeqRKsTSxisCjIAerz3P2n2KI0DfobQRuu1z5ouVHJ/iDT1u1dcGSfDqxfDWl6hkc1KRkorEA48ZI+xzXJDjkpSkhiDaX2oBDQQ0dcOjLSMrHIxdQIJDhJAkXmJEkk8VRFEkGUY4RODP2GvHrWEncUHGUZpeTQId2NfwIBINgcM8CWIS9M6UuIyHBBzl8EACHJX0JvHCtp0PPfPSzT9ruPzKB++6e8nuPTDY4uUBGQ/JIxHQ+rXGHKE1HbG+Yy4jM6OxTGM8M1/2Y+NZx7du2a95+n5zsqF5tD16tPlP355kLWMIMAQYAgyB44kAfb+oEhxABwqxZHQgPjiYSH7161fb80tBkMLisbmLLc4Sk91vcp3tLvhPV+EPnCW/dZXf4yh/ylG2wFW2NKeiI6eiw+1d4arocFR0OLxtDn8HUb1otQVaLUaNZiNBnEY6ZyGgjeca42nldFhGOtQkOFotoRZLqNkSarKEGy2R+dZQvS0y21FVn1sz2ZJ/I7JfiswhZPEghKxm5DTn5DtLQhXh56ZMO3iwNx5L6vLExxP6U7ws7c4BC2gU+rvrzM2oeCmqWImCmyyB6T1RnIwOYS6JhSFZiROilbjNpOwztF1WJDotwwNJ3CfgPowv/8GW3AnNKNzhql1eUDnt5bfUiZvEYUUA53jL1w55Kqdbw6ss4XZ7dZsp1Hj5T/pt1YvNoRZU0moLtlRdNHeIGEoTm2ui8jHiDBnYcPgkMf757a/mBObY/F0otAJFmkyhp+6feZgQziIQ5jzGnCImBIkc6fa81CZp7Zb+vKonHaEOa3Gbx78KFS342o2vGQlozcoZJwQ5TvhiGeOogGc04zM/v9gVeOgnv90M9eCJXqREPRhB3eIC/vL1m01VbcA+V69EVStRZLW7ZgvKnZY34aF3DwIywDvTj9Fhr5aW8V/rLzBrTkoCRzw7PvjoC4XBaS7/cktkialysSXU/Llrt/QTWEQscEqS0u9v9+Bb7tyZe9Zs64TFKLAUlSwz+9cVn7HBE5l128MHDmG8bCu2VE0lOiFrULDLVLrgF3/Y1U8kODKqwQ7HOQKMgB7nNwBr/qmHwMjv0GG+B/Vsp14LT0yN6UsXdLuIyJ0g85SABgJU4UVYAwYdZ0GOC3JyFAIalLskMKNOSJjDMg/7xdIIaBE09FIfRkAP70/qKpNgBHqDehDkpCDzVLoE/kIf8cBKY9yTxNs/VN54L/rOtsPxBJZlnrjMTshgmZBpAT38ikdK0e8OfVR5pDOO/L2xTGP8yGdqOYxn0bj2Dft/9AicbGgebY8ebf6jR4idwRBgCDAEGALjEQH6fjES0DAqVmAX/sYtr3/9mh+UeGtt7kJkdVrtTovNZbKUIhRB1gvNOV9xFH/bXf7rXO/jBf55RcFFRYGl+f62PO/ynIouV3nnyAQ00MRGornLEhgeaIaROeVhRDPNrBeSdq5OQDv8oEvr9rW6A42uwCyn7xmb7xFzxV/tFT9DzouRJYBM+QjZEbJYkc2GnOdNuHDRvKbB/qgs4USc7Lwbj3fHaG3W7hxNgqNyFQqudE54AZV3miPTtx3CCfDQwmN5SIQNpnHwSa6yz3AqYZ/BzhjcDGK8+V+47rOzcmoWI/9yVLEMBeZcfcsLCQy+4uNcEksw6ZIlPGv+bk/l89ZwlyW03BrpsFd3mEOt7rpVqGyRKdDhqV3wxOxojEzWqGN08JCe5YOxwmN8kMP3Pv1+TnCGzb8ChTpQpMVc0/Bv16/ZS4xgeGKnfDiKB3nMS6kNl8SYCQ4pAW0PttvKOtwBqMZl16wZIFbbGj6Yk4B95qGt8IkL+NHn3i08s95a1Y58CyZ8ul4QiFwIGELLVARSJ6DN1ctRzUpUuxpVr0aR1ah8lSu08AvfbuoFI2XD5ygJ6BiXhM5R8PRZ24p805zeLnOoFUVaUFmDNfz8c0tBHRFj3D2ApzftvuHnq2yBh/MmLnHWbkD+9Si4wRZZ7fI1lYRnPDFN2BPFhzCes67fUv00Cq9AoXXmwCpr2dxHpkiMgDb0EIuqCDACmt0KDIFTDIEs79CsyadY805wdan5LdW5gx1PCrhboW96UREJAQr6G4KsWkDrXxFamSd7x4B9PjyIewZwPyfwWBAxZ7SAZgT0yH1It4XSvzD6VP22U4JepelhNxoNPGhEi0NYGhSkaEyWYmR7GnSfjJMJURZVswWiK50aDtKh3sgVGC2VnnesZ6dKNpaTLZ7KfaTY8BKOdAb7niHAEGAIMAQYAgwBhsDRIEBHG3TjP1hpgAfppIz5GAeOTz74gLv/wbmfvuwqjydgR3l2lGtBBQgVIVQG2tDOiabcz9kKf+go/UNO2T253ifzvbMKvYuLvB15FZ0Of5sl2KqFNtUIOtBh8a+y+NeQv6voX5BjNoZglxnCCi2kDjW2Gljm1LdEzdnsXwchsEY7t8Nodu30rSgoWVNatKq0tLm0YmZu8b32/F8j5w3IfhmyFyGribDPbqepMM9WfNVXv7Fp1XqiwoAFQaDO3o8G1HGRV7tzgID2XdKAgsvNlWtdE7egQJupZvZfZxzcLYBqcBwULGDDKCWgQftCBsNkykEfHgL68oH5yfwzpjqqF6Lyxaii1V63uuDc+S92430cUWAWgbsVeJg93HnfRk/lc9bICmu4yxpag0rakHcFKlhkr1qBiuZccvW6/Qm4ErCzAvkrgbTyiPNkTuCTMnhE73oV54Sm2gLgPQ9VtjomdThr599y+762zXj2EvzDX22tOPfJT185tY9LzTiGE9CW8g5HcBXyN9d8bmFvHCYsusgzlcfgJBxLyn0x/LPfv5gfeQ6VNgDfHZrzpRtW9MXBRTsoXkgwLeWJcTO1gLbUrEB1a9CEdah2HYqsc4Y3ecLz73pm24fEL2PqPjPOs1KpaTGtv4johyIDSDJ+/Q1c4J/h8K0i1t9tqKoDFT6fP6Gx7rL28IULcgJPoKLHbb5ZqHSBLdCRU72lsPYVS2G7q2j2FVe2v/IK5kXYjtqL8T0z37FUTQECOrjBHFhl99Z3bQaqnX0YAhkIMAI6AxB2yBD4WBEwvg7HeGHjKWOJj7HYcZKNWMtKhICmb18McQVEM0RZpla3YISbhYCWYDgBxtL7D+Idu/G+w+C5gnjXEGQlKStxUeEZAT3yvWQcGKUIaDI0pGNEgew+4xXCQfNYIAS0OCiJ0bjADUmyPoaRRAUGgNrneNC0xjK0co/lv7GcbPGxlzu8hLGfy3IyBBgCDAGGAEOAIcAQODICdLRh8JsiSWC6Cuqt8SQejOIkh1/funf6tEVXfeX6M0LnmZEbIRdCNpDmgEgpQpMQ+iyyfA3Zv+vI+21+yX1l3iklvpk5gfmOYKMj2OQINDsCrQ4/iHI4fCscvi6bn4YVNv8Km183Xu5KN47WLaB1o2aIwCkGtQ1CQ3eZ/KvN3rUQfKuB3QarakJAa8obbn9TWUlzsKghWDolWHF/YeGtzpwrEToPyHQbQlaEkBkhZ1343Af+8ljv3l7g4TFOxOLxePzIII7LHOTOgTF9FOPLrluLKpeBlzz/ClSz3Fwz3/vpmf/sxQdl8O8Sp/4AFZhHiQoE+jk8iDe/ib98y4qcc2eZw0328AqLb6m5rMFcOmXJJiCvBYwHBBzn4ASOmBXf+osOV+VUU2SZKbTSGlqHSpc7wmvzajbn13ZYvI/NXKLAfEKU4Exe5aBHJqBlPNAfox4OPziM84KTHYFWYgXcjrwtuWetya1ZavHOdFfWe2oXoLIZnrpHN742oDoBItMQ2ICp4LVbDudVPWmNdKCKdiDEgx3F58zdFyVOFcn1QWpZuz261h/48lVPBs6cYyprskVW26vbnNVPNq0DojYZA40RWQKHhDwGm6c4h79y/Xp7bTvob9SsR1XrUXitp3JzXmjGOuLfUSuV/DfOs9K+SB1kzCuAH1fANL2Atj3YgQJtKNiGalbaqlbZq1bZQ6vc4XWO4BpU0o6KWize5ZbyDuSpLwlOf+SxwX7ipzGegJYOYnz7029YqqahUBcKrbMEOnJ8U7d/CNtURfA8yT4MgRQCjIBOYcFiDIGPGQFKH1OxBipKQH3WfczVGIeXI9sMYdVXhNVpIralwDsYxlDwoXQ0/KUxsJKGdF6CXHhvD/7L3eu/+rVZ3/7hqo61OEGZURjwJIj5rkR7VjfyTUXGIdajN9m4X4w40ICNckQ1W5GIapvMSxJPDNXBGICIlYEVw+ilpn9rHG6lfwNH9FuabowPzzk8xVjy2OPDy2EpDAGGAEOAIcAQYAgwBE4KBIitBkfGyDCABUNOGhT8zhvvzpw++8qvfSPgjxC61gpWw5Y8q82LTAGE/CDNgc53WD9fnH91WdlP8/335/inuHwzXN55rvLFrrJl7vIOd3lHjrfN7WvJCSzJCSxxBZe4AkudwaW2YIst2EJdF1oDzXAYAPFoCOQr+heIbAiQWQ/mQKvZ32b1dVh9nTb/Krt/vSOwwRHqclS2501qc9UttNfMslY8kl/wp3zHj5zmq2zmz5lMZ5isAWTNszicyIRcHmcgFP7+927qalvd/f4utSdUDy6a67w0+9eTorM+6UrI5G6R4wq+66nD7pr5rnNeRIEuU2SZo7Ixv7bh8u+89mY3PhgDU/L+BIzkOWIQHcVAWW56G9/6p+1W32N55y1BvnmoZLG5pCWneEFVzZyZs8Qhnngmx+AYJiniWCIhEcL3uu922iqnosoWFOoyhVab/W3uUGeuf31JZOHN/90ylMTRqAyu+TIsoIcbQctYFkHyPKHgAQl//YYXiqrbUPlCa1WnObzOHF5njaywR1pR+Tzkne85c2Ve3ZP7DgPesiwLAtmIScb+7+/GuTWTTVUdyLcMBVej3KWuumX/+9TAEJljJDHul3GfDGT6b+56u6Tu4bzKZ03+udbwUndkmdP37M9vf1m3sFE4LAuUgAY1yDiPr/vJZk9dEwgrh9eg8DoUXOMMLC8MPx5XQNYDPkbeWY+P+bb4P4tyBeP/fWhfbs0slDcNlS9FgZVwrcgKFOlA/k7PxJdyazejkqWe6pUWb5OtovGyK9asfomIq8iYT0A1OIz7Mb7lL6+YI8+jYCcKrLb5m844b5qsAAHNSwmCxJjrxDKe7ggwAvp072HWvlMEAVmWOY6LRqPxeFxKyQucIrU/1ap59AQ0iHVQ62aM8fLVOy6+9NG80nsKyp655tvr9/aAKjQsWzMC+hjuBANzCwsA6hoAXZdR/9JlAM0r9NFew3CBEU6l39IvjPERsg5LMpY89viwYlgCQ4AhwBBgCDAEGAIMgZMFAZmwz2C4mBEwxpIoHTx4sLW19frrr6+srEQI2W1O8NtncjrtRS5Hud3ss6CADYWdjk/Zcq4xeW5Cnv9C7t8UVDySV/FUfsW0vIpp+b5n8/3PFASm5AWn5Aan5gan5oSmukPTcsIzcsIzXJGZrghYnroq59LgjsyFw6p6d2SuJzzXE57vjkDwhNWQE5rnDs5x++tzAnNyAnM8wQWe4Jy8yPOe6qdclQ8g7x9Q4S3Ic63Z+UWb9QJkqkUmHzLlIPoxoQlnTPjO937Q2NjU3zdIZTdSXaFgRZGIBJ8RjNT34zxGQUlivKsf59U9ibwLUUU78i22Bprd4faiqqXBSXP/5y97Ozfjf+3GHxzEW97Ec5cNPDR9zwWX1wcvnm8Nzkf+pSB8EVhq87XkBxvyix9Y2IDjg5jjQDQa5DsUzCl4MAF26EISn3HOE+bIc6iyGfQrfB3mQGtB9QpH6SJv1eQXXhgAQ+kEDzeurn9BJThGIqDB4lgE/jSq4PmtuHzS8w5/gyPUZQ9usAe2wN/QKpN/MfLNQsGn/+fR3X2aSz3VvTxxo9jTh2svXQB++UKdjjNeAYnk0ApHZNp//fmt1a8L7+zDXa8of3ni3eIJD+bWTrcF5ufUrUD+5pyaJXk1z/3wl1v+zwVi7yAe6BOEBLDPooiJQ/shSUomJfzj3//DUzvPHGxCYJ682uRf6Qw0X/KlxgRMl8SR2eejsdKRFWj+YQVfeHmDp2o2KlqAAutQcAMQ0MFW5G83RVbZq9scofmOwJSC6sn3TpaiGA+RS0i8ogigS5nE+ICCr7il0xyaCwR0cKUjMPfrVzdhYu3OgXd5ZgQ9zp8Tac1nBHQaHOyAIfDxI6AoCsdxAwMD+/fv371794EDB+LxuMy2q5zInjBaPRu2HCoa65lmAa1KRcOQAFyy8BjPWrC15qyHy4Mz/NULzr5g2o7dOBZXYNSgMAvoo+42o4yMhv/I/1W7csMVxjYVMObKFqeF0m8NF8ga1csRNQ0RGtHTR4lkLZR9wRBgCDAEGAIMAYYAQ+ATR0DGKfY5ozIcx9GZy549ezo6Ov74xz9efPHFhYWFTofHhFw2c6HTVmE3+8wogFAAmX3g3M9chUwT3UVfcBb+p6vwm87CG1wFN7oKfuwqvNVR9F+2op/Zin5hK/mltfS39rLfOcpvs3v/ZPPeYffdafX9lYS7rT4IFv/dVt899or77BUPkPCQs+wRV9lDOWX35ZTe5Sm53VP8+5yiX+eU3JpT9v2c8uvd5Ve7vZejvAuReyKyhZHdh2xlyFqErB5kdeYWFVldtsoJoRt+eN38hfM/2A1Wz8kETz3XYZmOOoF6hgCCDtmGdhkIjaNDHREe48Mi/tEfN+eeuQD5W8EW2Ntu8nc6w52W8kUlda2OsudcvmfsZU96As8W1swomFjvqJqLvHORr9VRsx6VNBae0Z4fmRM686mO9UBWwuRLBt45SYQ0eJICHRTH4Ql/MVVOR1UtYBcc7EDlrZ7qpTb/329/eNth4jhPoYrLeuXkETSg6eZUBUQZeR7zcWKR/eM/dPnPXJjjW+n2r3P7trgrXnX7Nti8DfmTnvrZI6/2YByDkqnhMfWAjrEi8wL+4S+22QKtyNtln/AKKunInfiCuaTFXDTd7Xs4v/ohT+XjzsiUnOr59spmc6jVVtmJilpQ6VPf/13nIKhj40MDYAMtcAmFbMwV4TpRDBNP/KcH9rgrn7eG6s3BJpN/pdXX4fbN/dkf3orBGXJ2AtrQ+LRMmTenTGzS+xTcsgkXVD7k8M1z+FaZ/RtAD7pmOapbgaqaUOiZnJr7fnfva+/vh9P74vBLSErELaeE4xz00fv9eMLnZ5lD81GgEwU7HKHpf/7rPzEhnklPMgI6E/nxfMwI6PHc+6ztnzACoOnA89Fo9ODBg93d3e+Qz+7duwcHBwVBMBJzn3BFT7vLG0lnY1wjPnUCGpQ3qKNCHvNU4jkp4ZkL3grVPZFX9nyxb0645tF/vk0AYgT0Md0nxvtcw3/k/x8LAT3GNtCBXQb7PGzAO/JcZYyXYNkYAgwBhgBDgCHAEGAIfAIIGOmrES+fTIKqbTQaHRjoe+nlF6ZPf+4nP/nJeedeFAzUFuaHct1Bp81nMxdTZWVkMoNShykXmUqQJYjMtch8FjJdgCyfQpZLkOUzyHIZsn8OOf8dub+IPF9Cnssh5FyB3F9DOVelQu41yHMNyvkWcl8HwfVtk/M7Zue3zc7rLI6rbPavmq3/brJeiqznIXsdcgSRvQLZCpDJhkxEL8RMqmM1IbsZ2cwTzpr4X7/87/aujj09+/qj/YIkSQpOcIIgSIIgSSIEKsqnYIER0CPeBvQ+Abt4YkT87iF87uWNnrpGU6ANVXSi8k5LcK0zss4ZWmsqX+EMrXaGVjtCXe7KFfZwh62yM6duvWfCJnukLb+2Ia/qyW/dsvaND6CoJHCrclJOgCtMjYCmFRAE/IXLnwWph3AbCrWZgq0W/2JL+VPnXz5VtU6m9r8ZEn/GyQaJEwJaUmReVsC6KIHFQ6JwWMY3/+KlIv/UwuDcwkBjob+lMNBQd/GCWR34AAZPiUOCQHwnYhncBIpARiuyKOBpc5TSmgZUuAiVrLBHNqGijrzAJndZp8PXnFuzrOiMrpy6FY7KdhRYgiqaUdkCU9HTdz5yqJew3qC0zkscxwkiNWPiRDxACGhFwvj+KYfckcmO0LO24Fyrr8Phbc3xT3l8el+MyGGnccu6/gYgYPwFp32R0Y8yUanu5XGvgBuX469etyo3ONUdnO2IzLBVTXFNmnLBNcvunzX4zwPAiMNPXohjLMSkOCzUKPjAvsNxDscw3roPe2qfMAcbka8NRdod4Wdm1O+lDDmQ9FAf9mEIqAgwAprdCgyBTwYBRVESiURfX9+BAwf27t27ffv2d955Z9u2bdQCOoOANr43P5nqjo+rGnGmcUpPi+AXj1PAywKXEPHshe/7ap7MKZldFJgfnvD4rn0wjAG34eA0XEy9ZY1vfBofHzAecyuH4z88xVi4cXhlTE8bkKUNwoxnGONpZ4/hwHju0cbHUDzLwhBgCDAEGAIMAYYAQ+BkRUB3XSOIHAkJjPGOHTumPjvt1pt/8f8uv3ZC1fl5bm+Bp8RhdSMggEGrg3gs9CCUa0IFyFRkshYja6nZXm4Cw+RSZC5CljII1nJkqUAmLwSzLxVsXmTzmW1BZPEjVAzOA5HXZPaDngYqR6jcjEAAxGHx2i0lNku+zZJrsTiR2aJKbSCoSKS28rs3fu/RJx9PCCIvSrwoCZIiSIrqGIb6g5FAaUQSNfPnESQ4jGO/k7WTTny9VFqRcL4JQkMv6BI81Q+4w02FdS9YKjpRSbs9sgFcBfpWoorlqHiJtXK1s2odKlqSU7PB6utARY2ldYtyg//74HP/+jCh+ioUYHehwmMwsgULaAVo6CEBTG5jSfynv26yVcywBtaikiUuX2NBeE5F7f2vbAPmWjQ22TgLM6Yb46DxDfwoTOEwjsm4j8Ovvo1nNvTd+cC/7nt8V8tK3CfhPgxhCCu8xAHvrMhY4IloIIiDSxIeiONv37y6bEKTqaQtJ7TJE9iY51vlLG1D5UudNZ25Z6x2VnXYI63uqlZn5RKb/4nJcw73E+Hnfh4urbOzEqb+P6MikLpgi9+yAZvK70AV9+RVz8qrXG4tbcgPPrLhNdxP/WIab8OxtNfYdi0uE9x0be6lG+L3T/vX/c/taF6P39iP98TBRjtBDKV5w65PsAMn/c6JuJ/HM5diW+BZkCvxt5oiS+3BR15+Q7sAWU5IHbDYuEeAEdDj/hZgAHwSCCiKwvN8X1/f3r17d+/evWfPnl3k09PTk0gkYPEdVt1THyMN90nUd7xc04gzjRMCWiIEdEIBiTAhKeH6pg+8Nc/kVswv9M8L1T3RvRfcszAC+qPfJcPxH55ivIpx3GVMZwR0GhrsgCHAEGAIMAQYAgwBhsDxQ0AnoCWJl2Ueg40wh7FC3dgc2Nu/ZcNrSxZ1PP3E9Ntvu/MbV37zovMvCnjD3jJ/SWFpQW6By5XjcDgsVhPYRiNkMpnMFgQyL7kAACAASURBVGSxmsxmM8S1D0mzWpDJQihskxlsqS1Wk9WMLGZktSC30+x2Wq1mZEbIgkx2ZLUjux3ZnWZXjt1T6CkoLigO+QN1NVVXf+PKe+/92/Tnp7382ssJMcljkRP4UQhoOgdT9TcYAZ3lztGYUzoeByL1YBI3dHI1F8ywlz5bVN2UX70MLJSDrbaqdnt1m72m1Vm71FG1FFXMRSXTXf5pRZVP//T3W9/ZhXf3A/sclQcELIkwp4LA6wQ05bhlYG2HePz172wsjswtCExxF9991bdaN72M+4mfw7RqjoWQJVLRxBk9eJn/P8kLnkhORwU8kMRRIg8NxDQEJYkFkF0WtaA6rpGAv5bwe7vwpZc3FlXW5/ianWXNruL5bm+jPbTMHmlzVi1yVdUX1M5whx+76uaX170BFs6guYGxCAQ4+ZDaSgqWsCCCh78E+R6/ewi7a37rDN3hDDyWE1xYXLmgou5v+4fgXPgYJ0JjaS89a/hfAi9x9g4lD2Gwd+ZIDSjpDNNcw1lav0NSUsL9HL79wX67fw4qW2SKtKNAIyr/S/dB/QTjqXoii4xfBBgBPX77nrX8Y0BAp8+M15Jlmdo+79u3b+fOnTt27Ni1a9eePXt6enqi0ajOPuvnZkSMRbH48UUgA2oFfI5IYAYBFtAJBceAgBbxnMW7vdXP5lY0pBHQBgkOtVbGoQCNH9/qnnalDcd/eIqx0cZxlzGdEdBpaLADhgBDgCHAEGAIMAQYAscPATo8k2VZknhBBPNnWYlzfJQX4hwnJBMil1R4Dmw4BweHdu7cuXXr1ldffXXx4sX33HP3j35045e//MULLzq/qipSWlzkcTvddpvLZnWYTU6LxWWz0kOSYnGYLXYTspuQhQTVltqELDY12B3Ik2stLM4JhrwT62ouPO/cyz79mSu+evlPb/np5MefalnSumnjlvXrN+7Y8QHGoLBBMeiPDXBinJdivBQT5KQoy8D9kQDSAimHdSkj6HS2L+sI9PhhfFKXpLWfms/yAJkIPCylJt/bg//8wD9LQrebcv9UUj01v3KGOzwlt3pq8RnTPNWPu0IP54bvueQrz//qfzduP0B8AFJBCWixIhP6VSQ0NI/J4gYhajmFB4VkjKMcHuDxO9txY/PB9evh3oOP7opFZzuNszA1U+Y/WGCgLaDkKxhEw61N6VaZOJfnJFo2TAlhXqjxzoaIesleHv/4tg15gfudZY/keB+uqJtZPmGZwzfb6X+wtO7Ob9y0cMWLyhDGHxIxC1kBPWtZt9km1yQG2dBIGYuCBA4VBzH+0Z/bSs/8Y+nEh/Ijz+b4H/rVnS9R42NBIOy11hPpc5/Mlh7hWAONKnJIhH2OYdUgXaObZVgUkHmyNJAqLyHgQRF/5Rsb3P5mc6DFXNmG/AvO/koDkYiGcrXTU6ew2DhHgBHQ4/wGYM0/sQjo9Jl+GUmU4vF4T0/Prl27du7cuZ18du3atX///r6+vmQyqYmOqc4v9BL0iF4Uixx3BHSQ9QghoAURczoBzUl4bvMeX83UXF9jnm9OsPbvH+yGIZfuhFAk9tBQN+PQRx3MHPcqn1YF6rCPEjE2WB90ZQ5ujMinmQcYzzDGjaWOJW4892jjYymf5WEIMAQYAgwBhgBDgCFwkiJAx2nETBi8pRDL0SS12eQ4judFKkgHzvskiZc4QeYlGB7LRExZ4rjEzg+2r+hon/L05Ntv+/1/3/LjG6791te/8pUvffazn7/sss9+5tOXfupTF19w/kXnnXvB2WdfeM45F5571oXnn33h+WdfcvEFX/iPz/7n17549TVXXHv913940/W//s1P73/wL9OmT17WtviVVzfv379HkpKCyKl7SQlhCCQj+ahqA7IU4+MJISbIcUGOEx/jImx5ZAT0mG83beybIqC5QcoPCxxO8hjHBdw7iKfNPviHv75zy29eu+oHnZ+/ev73f7n6v27f8vTcvg2vq1eKEs6aE+MSENG0tISMEzIhoAWYXBFtDQW83omYk7HCSfAvQZYSJA4rCRn8FUoYx4mUhsalps3CsrRrGAFN+WXCneIEL8VERTRMSUZknyVZTMrSEOWsYxi/8yGub8W/u+ufN/5i0+/u2vfnh3qbOvGePmCxMca9cZCqTiZELAGRKyQIA06rB+w3QEAIaHkofkjGyr4k3hbFX7zuKd8Zd5z3+Rm3P7x9T5TwwjIUojnMJMilzX2yNFgFRTIYNJPTFAVrtDvonIjikCRyGquvIUoIaIkH1lxNgvWAIQEPyjh85rwc3/K8CetQYLEtPOePj+wn7YUM2o8vW5VY+rhDgBHQ467LWYM/HgQMrytFloFNhr02ghCNRnt6enbu3Llt27bt27d3d3dT2+f+/v54nOo5QQWNp9NzP55qs6sYEIDBFfEDLpKhTZKsBIuUgK6om5Lra8j11vtqHtu+G7ZLYUUgK+WCCEbT0IFkHKGMZQBkuCiLnkIIaMPvFMd9ClWeVZUhwBBgCDAEGAIMAYbAMSJApyogSqBKF+ib9YFxoiMkUvTwwZJudCpiBby6ySKfiEUHe3s/3L1r5/Ztb73xz3/+47XXXn3xlZc2v/ziplde2vzaqy/+47WXtr7+8ptvvP7+9rd7Du4ZSvbF+UFBihHuW6J6BkQJJMNhYGbrjLXR/ZCr0y5ClRmnYNrJhtZoSeP8vw6j2tUpOxuZuMMBFlWQMS/ipABkdEzEUQlHZdBZjkvgM4enaxEqQamXBwQsdahDkmRKyBKhZFqymkJY2mG2PjKZdh1t3xipW5iv6/dnJneadm/oZ2FREaIYGirHic1yP8b9GA8S6caYguMKTmqNVattqCGd5qe1P4UJCGJAmTI+LONeBR8m5Q8phHLXracNpR0pKmjGzQkNO4H8djSSWetHWp8spcnaghOvYHwogWctPuDxzkCeVlTebvUtKolMXbNR46hhb0SWYljyeEWAEdDjtedZu08wAsZXFOxQE6VkMjk4ONjT07N79+7t27e///773d3dBw4coNQzz/NUN43Wy3g6I6BPcF9lKx5evhoBTWXB4hjLvIznLdnnnTDVE1iY453trX70/V0w6KAEtAhcNCOgs0F6mqUbh4ujDtVOs3az5jAEGAIMAYYAQ4AhML4R0KYqlFLTFRDUoREZPw8fJukpNH+KgAYaWlaDokiiIooKL0lJY1BkXpF5WUkSvWnqvE2hBrKyDFLUejBqN2v1JP+JvIautqFH1DyMgB7zLa13pMrRppGMlKCUwZ5XhkmRIBMyWiGkswJ64ZKmHpHtgrR8ym4TPlihd5TxulqebGUc/3TjvZQyMALCGtSqZczzRDA6SjSUY0TAmvK79EeSclM/rGrGdqVIaoKqpABrP6gQUpuUnyQ3/bAyxpIAxlKkDFBsJydolLPOp9OqaMlZCqVWWXEZ454k/u7Plnl89XmhLfbgOne4KTzxsT171fOIqIl2qSxlseTxhgAjoMdbj7P2fkwI0FeUDMu0mOf5oaGhvr6+AwcO7N69u7u7e8eOHd3d3VT0mVLPaa+0j6mO7DJHRkAb7lACOkkJ6AUtH/onPusJLsjxzi6rfuS9biCgybA4zsPgA/bxMQvoI4N7yucwDhc//mHwKQ8fawBDgCHAEGAIMAQYAqc0AsRKZvhwaKwplCmm1LMg84LM8xKXJIFTeFERqRSepDo5pLS1RPg3ypDJsiyCyIcWaFGjE9BU5Vlnn6U08nTE3mBjvBFhMdq5Z2TQbIe17aCUiDTeFhknjHJoPOsk6gmdsYX7R62jREhn4rQQU0kavfKjNFD/Ss9spPVBXEQBr4BRwhzHCdut4aufOsYItYBOv+PTj9SmHIGAppx7nMf4g8O4pOZvnsBCm3elq3KTp3LBld+dy2llgiXXEYoaY81ZttMHAUZAnz59yVpyUiFACWVq1JxMJg8dOrR3797du3fvJJ9du3YdOHBgaGiI53nNz3KKgj6pGjLOKzOcgE7IuGHp/sCkqbn++a6KWSXhB97ZjhPgfoNXZEZAj6v7xThQpPFx1XzWWIYAQ4AhwBBgCDAEGAIpAk5n4sYY0Qloyj4nJS4hJmmIC4mkxHEKNewQJFAjEBUsyDJYRtP8xAUip7PPksQPI6BT0yuIUQeDw+ygj9SFbIw3MkIfDy4n6Wg7jYBW8dHFKZLHRBMbWwolEhpXJpbjcaLFEdesqo+VgJZk4qlotNNpJY7MGssy5hMYL+rCtrKH3aFmi7fdGlzpqpz2wNSXVdeQpCgmwTHyj2ccpzICehx3Pmv6CUaAuhPEGHMct2/fvu7u7t27d+/atYuKPkejUUEQqLyGPjg6wTVixR8DAvQ9nLKAjkt4YeuB4JnPeXxzc8tmlfjve2sbENCw70+Ji+pAGbqUaUAfA9zsFIYAQ4AhwBBgCDAEGAIMgVMKASN1dnRxykETzQ2R0sqcwgPvLHHUe6Eg66bQEngyVKU20gyfdepZI6D1qZVGOtMEAwFtJKNPKajHXWWH308nLQQyEVSmTjkFsghzDFWl7dVPhDIVovFBSG3qlXE0Blk/Mz2iK1vTfQSDHLDESQmcORJtEFKkkVXXrJjTi4GjRALOlYlF9jdu2uTyz0UVi6yRDhRYYo883CPimEIcOcqa0PTwIljKOEaAEdDjuPNZ008wAlT6mfoe7Onp2bNnzz7yOXDgwODg4IiKzye4Rqz4Y0OAjgREsuosxwTcuOxQ5MwZnvJ5eaX1xRX3vfmvEQjolAqH8V1+bNdnZzEEGAIMAYYAQ4AhwBBgCDAETlIEhpOEY02hBDSR2gB+mQRZUr2wUF8saX+Jz0MQgFZPTBffYAT0SXqDfIRqDb+TPkJhJ/ZU6jKRasSkpJyP8pq0vfpJeplGOWn927FHKDnOgRdCoIcPx+FUSjIT7vkoCGjKZUsY/+sA9gSfREUNtsrljrrlKDT7W796kTgGJQS0SmEfA1s+9maxnKceAoyAPvX6jNX4lECALrTTqiqKwnHckPaJx+OCAOuN+kdfptdTWOTkQwAIaFjsFfCitr7KM2d5yhcAAV127xtv4wSHYcibsoCGATQdGZ98DWE1YggwBBgCDAGGAEOAIcAQYAgcLwSGk4RHl6JJ3gHXLJFgTDHGdXEPOszO8lefWo1kAT3MGvp4ocDKYQgY7/vjhYaxzGNmc2ViSDUEUh5KHONFbQOf+dxjc5v6eOIrUvWpqF8puwQHZZVjCh7A+I7H37J5pzoiK1FJMyqZaap7+vmV+KCot5teE1wo6UkswhBgBDS7BxgCJxYBKrIBa4yKQuWeZVnWE+m19VHSia0KK/0jIQC6XjLGA0m8qK236qzn8stnFpZMLy6/6/U3cDypEdA4yWOeWnAwAvoj4c1OZggwBBgCDAGGAEOAIcAQOAUQ0ImrY4wYKWZGQJ8CHc6qeAoiIBAOOk78GV7071PLKp8qqX5w6RosiMSvJ/3t6jt3Uw3MZKMFjIcw3hPHpWc87Ao3u6peQIVL3JOa88686xD5KqnoptVJuoE4VRiLjXsEGAE97m8BBgBDgCEwCgL6axjepCoBvWpT4qzzn6iqnVHqfayq9q4338Y8jxVJVOS4qBLQ4CyF0tDGkfgo12FfMQQYAgwBhgBDgCHAEGAIMAROQQSMo91jjxtpaGNct3oeHjFYQOv2POrO/1MQRlZlhsBxR0CfykLJ8SFRwXjda4L/7KdQyRTnmfNr/6Nhby9OJrAo4VgSizJVvKHV0H0gJYm6tUQ1O4ZE3K/gPz6wHxVMR2UrUcFK5O1yhqfd9rdVMQmnDKDhh0ifBse9UazAUxgBRkCfwp3Hqs4QYAiccARSb20QvKL6We/twjf+ZEnNxLtDVbf/8McNB3qgForMK8qQiOM8TursMzhL0d69bPfRCe8sdgGGAEOAIcAQYAgwBBgCDIGPGwHjaPfY40bS2Rg3DKUzC2cE9Mfd1ex6JykCxp+GsYr6VFYBjlnEnISbVx4umzTFWd2CfHPME2Zf9v8atu/BMQnHMY7LmFdkUpYsg+kVNWFOgnY0pjLUUHjbRuzyPWPzdqKi9bbQS0VnbSyZ8OSeA/BVNClwEqkAWwky9gOLawgwAlpDgv1nCDAEGALDEUgt3oITCEpAxxT80hvSQ09sfnjy5jffhXPA6EKOK8ogIaCpBIciYgjG4YAxPvxSLIUhwBBgCDAEGAIMAYYAQ4AhcKohYBzhHnvcSDob46MQ0Iavxo7Z8BqO/VyWkyFwciIw/K6mKQrR15BUj4McTGY5jIvDjzj8jSjUjDxPOytnBs5/vnEVPqzgqAwctKiIMhhU8QIWKesswyw4IeNegZx+xXVrPaFGu38tKt5gD66z+Z+787FdPX1YkBQJ44E4cXF4cuLEavVJI8AI6E+6B9j1Ty8EMsSdT6/Gjc/W0Je3SJxuyxLGPMaDIryeBwQ8yMOrGJwdy3FZHiQW0LoGNCOgx+cNw1rNEGAIMAQYAgwBhgBDYFwhkI38Orp0I+lsjBtY5lEKHDvgwwsZ+7ksJ0Pg5ERg+F1NU2CeSoJqkBznkj1R/NTMWI73KWewwRxoQeFWa1Wju3bKDb986ZX3cFSA/bycBMbPYBNNgm4IPYTxtT9Ym+ebj4oWWQNrLb4NqGRefvUD7x8CA2kQpDw54WG1OmkQYAT0SdMVrCKnAgLxeJzneb2msiwLgpBMJoeGhkAxCR67UkqBTBXg17OzyKmIAH15qwS0jGUeKzFFSGA5gcHmOalInBIXpKgsxRU5KSq8qIgSViRi/swsoE/FLmd1ZggwBBgCDAGGAEOAIcAQGDMC2civjzN9zJVVdWmNdRv7uSwnQ+DkRMB4PxvjmgQHbOWFIGEpSQyqbrv79YqaenewzVyzChU3/H/23gM+juO6H1/0QrA3lMOhkVSxY8ctdhL/kk8cJ3GcxN1OXBLHjv1ziRM7iRMnf7c4rpIsWb2QEimJEiX23glWUd2WHMumSBThUAhc4VXc3fb3+8+8u8fB7t3iwE5i9nM4vJ2dffPmO3O7M999+6asfWtt2xMtr3v8g5947rbbx7uPQNyEiAVBDU5nIWJCEmBLN/z5R3bPXvxk/aLuyqZD5c37lUXrq1rv/PdbXhxOCdGfr0yEpFVXBgKSgL4y2kFacTUgYNu2nt8w6kI6nQ6FQkNDQ5FIRFVVSUBfDc14Djay6M95D2jdAF1lSzWkM5DOQlq1s7qVNs2sZWi2aViWIQnoc4BYniIRkAhIBCQCEgGJgERAInB1IiASXpdLLh05t4WlnytzSgSuTATcvRpTBAKac9A2sMlsTIOICt/98XCD736la6Pi36osOVjefkCZv3WWb8fi9s1zm5Z3vHnlG9/16B9/bNsHP3f4A589euPvPz6v4775bevqFx6qWfhcedOxMt8OxffAn312bxIgxd9TuDKhkVZdUQhIAvqKag5pzFWAgGVZ6Acdj8eDweDAwMCpU6eGhoaSySSLA2xZ0gP6KmjFkkx0vELE7uImu2erKmT5R2Puz5bNwl0ZNkbcsCyLE9CmCaaMAV0SzDKTREAiIBGQCEgEJAISAYnAVYxAMfLrUqaXDp/bqtLPlTklAueEAPLA4qnuFPHolGV3r8aUPAGNjv+2brPlBjMGQFyDrAWPbTcW/e4jSudqpX1b/eteUFqOVPuemtn1lDJ7nTL3YWXhqormNTUtT1Y3P1G1eHV142M1zZtqGw9XLn6mrOlYmX/D7Dfeue3nkOARpnHpwSkbLk+YZghIAnqaNbis7nkjYBpmIpGIxWIDAwP9/f19fX29vb39/f3xeNzBPst40OcN9uVV4CCgwUVAG1nbVk3QiWw2QBLQl7fNZOkSAYmAREAiIBGQCEgEJAKXFoFi5NelTC+9xm6rSj9X5pQITB2BHNec73gTdlEbHpq65rNn5JU7I8yIBLQBtmpDxoQMACRVa1xjuZ8fhk9950Tt9fcrrY8qizZXth9R5u5WFu9X5m9TFm1XGveUN++v9nXPXnZ0RuduZe7amsXdNY37q1o21LTfue1FCNks+jObJ581RkoSgaIISAK6KDTygETAjYCu68lkMhKJDA4Onjp1qre3t6+vb2hoaGxsLJPJSALajdjVlSIueOIeCPCjhgGqAarGProKhgYs5gZreu7wzENwaNxRWnpAX12NL62VCEgEJAISAYmAREAiIBGQCEgEJAIXDgGLuwezbwPsLNgaWHxOyRa21yBHRueCPV64UklTYWKaUnUeD3o0C9uf0j725QP1XXfXdK1XWnYo87dXdnRX+PcqLTuVph1K046y5u1K05byxZtnNO6a3fjYez9y4PgvIWWCZuZjVeaWOcSiifgmS6QgEWAISAJa9gOJQEkIWJalaVoikQiFQmNjY+j43NfXFwgEotGoqqru+BvSA7okZK+kTJMR0GCBZfAoHJyAVlXQNNAMm0V/xjDRPAy0JKCvpEaVtkgEJAISAYmAREAiIBGQCEgEJAISgUuPwFl/Zw0gyz62xT5OAlq7OD7ERDVbebJ7AgQWWLqVztrmuAnDSXixD378UPat7ztQ0/5Ajf/+Kt/9yuK7lIV3zFzycI1/eVnj3crcW25427pb786MRFkEDwPZZx2YF3RhAnpC6oSy5c60REAS0NOy2WWlp4gAxn2ORqOjo6ODfOvjWyAQiEQimqaJcZ9FeYrlyOyXGYHJCGh8eM2WbsDPRALaAsOSBPRlbkJZvERAIiARkAhIBCQCEgGJgERAIiARuIwITPAANizQLMhyd2HG2fKPZTH3JdzIA/qCx7HwIqAtAMOyVFvL2jby31mA6Dijxs+k4YkdZ+5dM/o/d73y9R8+/YX/3PutW3/x4IYz249ZcQCVf86Ms1pZrDI2+1g238ESqf6SgM43svzPEZAEtOwIEoFJELBtO5vNRqPR4eHhQCDQ39/fyzdkn1VVdUfeIA56EtXy8BWGgCcBzV6XAv7Mmt2nTVUFg4fg0HQry5YeNC3bZCGgLUt6QF9h7SrNkQhIBCQCEgGJgERAIiARkAhIBCQClwYBImCBsc86C9sIaYBx/klzX2gdfZ4ZQ2twh2jjIjhBT0JAa7algsVDgeRw0TNpsO3xRIZR5nmzzmQhqrJ1C+M83jOrCF9zUGP+V2Ay+lm3bdO2TV4FDDtyFoJLA7ks5apAQBLQV0UzSSMvAwIYUkPTtGQyGQ6Hh4eHBwYG0PEZI2+EQqFsNktcc0HhMtgtizwPBCYS0Mg4n71tcwKaac+a+ripGQCRVCKRTap61jS1iQS0aYJpgm3yN6xIxXmYJk+VCEgEJAISAYmAREAiIBGQCEgEJAISgSsbAaRemTezhexzwrZjAIMZtvzfmAExgDENkhbofPLJ6egEo6Evrbswd1+2NPZqL7plGzzYpM4cmzXmp21xeywbTB5tw7CBPuj0zMh1RlKrBlvb0OD+29ID+srunJfbOklAX+4WkOVfqQig43M8Hh8dHQ0EAr29vaf41t/fPzo6mkwmvX2fkY++Uisn7SqMQHECGl+MMpGDxh1c7dcE0C1NN1TLMHn8DfSAlgR0YYRlqkRAIiARkAhIBCQCEgGJgERAIiARuGYRyPn+8hAXkNUAwhacAfjp6tG/+vyBN71nzRv/ePkdjw6FM5A1GEXNfaMvFwFt6KAZLIQzX4/QMtiqghpS4/mwzjaAZdumwX2cOcnBSWZGrtuMgM5CJgvjuiSgr9kOfSErJgnoC4mm1HUtIWBZViwWGxkZEcNuDAwMjI6OZjIZrGlBr2cx8VoCZDrUpRABjWwzezGKR+9ij3ZtYLfbWBbOpLWENo4e0Dz4hoHf3P1ZekBPhy4j6ygRkAhIBCQCEgGJgERAIiARkAhIBEQELLDZ/NEELQ1wWoc/+8zq2dffO+f6jXOu21zetHxG092f/PyhcZ1FeOQEdJoH4hA1XHSZe0AbnGxWLVB5yA2DxXFGJ+bcvxz9bIMONv+g0zNnzjWws2ByAjqjI5d+9iwZguOit+DVWIAkoK/GVpM2XwoETMMMh8OBQKCvr6+/vx+p53g8jo7PaIHINReUL4WhsowLh0AhApo9u8bIXCIBPXIGXvgVHH8p9evXspEUu9MaFgaAZhy0JKAvXJtITRIBiYBEQCIgEZAISAQkAhIBiYBE4CpCgKaQdhrgQ59/YubSnylzVygLtyotO5VFm+v8O2b7bvv5K4Zt2zwER/YiBICeBC4+8zXY27yMfVb5VNcyWTgOtuG8mC+AZJmAVIdpg2paKc6Y6xZoGuhZ9lGzoJo5AhpfEib2+dJGFZmkxvLw5UdAEtCXvw2kBVcmAqZhRqNRdH8OBALBYDCVSuk6D7zPLS7IODsSr8yqSauKITCRgGa0cn4hBcZBIwFt23ZGg027Un/8vjVv/L2H/vqzu1/qZWtKGCxSVi7yBi7CgJ2hWFkyXSIgEZAISAQkAhIBiYBEQCIgEZAISASuOQQsG3TLMgBg5/7wzNbba5q3VDVvqfTvVDr2Kr7t5Z37q3x3BxNsAsmYW1u79AQ0x9ziFmAM6BxZnJ8R2wbz4maO3Caw6M8s7jOYqpngvtIQz8R45A5L547eAgF9zTWmrNCFQ0AS0BcOS6npGkIAVyDMZDIYADoYDGqaxp9P5irpIJqL7V5DkEyLquRvt2z5wdy7R7nXiPAhNlvpFwCGRuDj/7B5RtNNTcuenNl82zdvfmEkhUs16LjwoCSgp0V3kZWUCEgEJAISAYmAREAiIBGQCEgEJAJOBCxNT2PaqtWvzWx6rGrx8aqm/eUtu5SOg0rrXqVj7+9+8NlxfM+WRXi8XAQ08OiSE/yUcSKMpuWDQ+fibvAlB5lDHgvMweNG64yexkiVPJy1Ewe5LxGYgIAkoCfAIXckAux6atsWv35alhWJREKhkKZpAGAaJqYXo5vd6RLPqwsBTwKah9lgkTaMgRF470c3zmtfMat19YKOe/7te8eH4sUJaPkG0tXVCaS1EgGJciEB/wAAIABJREFUgERAIiARkAhIBCQCEgGJgETg3BGwTBaVghG7O3elGpofrVx8vGrx8crGY+UtTymtB8t9W378AKQNfNv2MnpAF64hfw+YB5nMrU4IWR4oJA2gAkR0PQNs8svZZ+AeWpeRQC9cBZl6ZSIgCegrs12kVZcTASSgkU3O8s2yLF3XNU2zLMvNMnukXM5qyLKnjkBRApoNHnIENIA1OAof/PS+8gV3zutaN6v1rs//2+6ILhDQNkbJMrFjsIEHfaZukjxDIiARkAhIBCQCEgGJgERAIiARkAhIBK4eBBiFm8okAWA0CA2++yubuqsWH6ta9Ezl4uP1vn21TQ8efQmyuLo9vnw7wQv5SqkovgWc5VGfkwAJgBjAoZfHEzYMhBgrrbNJssGWKGSTZblJBCZBQBLQkwAkD09DBJA3ZEvK5Tfbtk3DxA+meZDO4qFpiN5VXeVCBHT+FaM8AW3b5lAI3v/3+8oX3dXQ9mR94x2f+eedwXE3AW2DxT8iIsREX5EjDNFSKUsEJAISAYmAREAiIBGQCEgEJAISAYnA1BFAD2jdtiCjw19++uma9g0N7d0NvmP1i7rnNq9938d2GtybmH1hHOapl3ERzxAmrUiSh03IANz+yOCcrm8tuvFni7puvntlzAAYxxWybPUiGiNVX0MISAL6GmpMWZULhICbgM4T0VNzfxZjRl8g06Sai4uAg4BmheHdF2+8LDA06wunI/CBz+yv9q1o8K+ra75TEtAXt1WkdomAREAiIBGQCEgEJAISAYmARODqRiC/ws7VXYsSrRcIaBNuWR1ruPH++o61NU1r6xasnN/4o1//BlQDdDAtGGfzTbNEtZcsmw02jyBiM3o8qrGYG6ciMKfzB+Ut99W1r6tesGp24w9//mtmD1sry2IBS+UmEZgUAUlATwqRzHAtIODNBYs+yyQT6SwKdLRE4VrAbjrVoUQCeiwKH/yHA9W+FfVt6+qa7/7MP+8OjrNXj2zgixDmQnDk+sgE/ISHyRPS5Y5EQCIgEZAISAQkAhIBiYBEQCIgEbg2EcBYDhjzOF9DnBnl966t/5bJJoa6DYy6/VUcqq7/9/rrbq1pu+kvP7X1pVfA4o7DBiOgM9wTWud+T1cOBjpAHGAcw1BqAIMJ+NYtQxWNd5b5n1QWPTHDt3Vuy+0/uPVYIg3jCZaN0ehykwhMhoAkoCdDSB6/JhBALtBdFQ8eWeSdSfbIX/CQu0SZciUjUCIBHYzDhz53MEdA++759FfPEtAsWoskoK/kNpa2SQQkAhIBiYBEQCIgEZAISAQkApcaAYMvXJfnoK91vxwTTE5Aq1mAMwC3bzr1n7f/csczEMpCJh8t2QCbuUGzhf3UK4zBRQKaxbBGY2MWLHn7amXhamXmo7Vd3TOad89tvvuJTUPsKHtXmLliyU0iMCkCkoCeFCKZ4apHgKhhy7JMw8TlBLX8pus68cu4xqC465BJVYnCVY/dNKtAKQS0aZihBHzk84eqWpbXd2ys89//rg8uH0syD2iw+MKDFpj8nSXsJPiyWX6YMc0AldWVCEgEJAISAYmAREAiIBGQCEgEpgkCE5ya8xOgXDBDA9iqdYUIaOIuRVa6mHyVIInzSmAhHNlaQVn+0WzmFG1yzhZ9wjlGE1C75PUrArStsxktb7DoOAxFoabt3sqO/ZXtR2r8Ryrnb1vUfn8gxI1ls2BrIgFNOi95bWSBVzYCkoC+sttHWnchEMD4G6ZhZrPZZDIZjUYjfIvH48lkMpPJiBy0bdsO0lncLZF3pmwXwnyp49IhUCIBHU7CR//v4Qrf8trOjfVtD7zrgw+GkuwFKm8COj8Eu3TVkSVJBCQCEgGJgERAIiARkAhIBCQCEoFLi8BED5xpTUA7gSdoSHDmuNT7RBZPFHCPE9CpLGw5ABX+hxT/wbLWIzW+wzULN/7+u3dm8cmBZeFMWDBcVCUkS3HaIyAJ6GnfBaYHALZta5qWSCSCwWAgEBgcHBwZGQmFQtFo1M1Bi4yzQyZmuURheqB77dSyFALasqzoOPz1F49Wtq6o7dhc27aiGAGNftA0tpAE9LXTUWRNJAISAYmAREAiIBGQCEgEJAISgQkIoFNvztmXU5d0GP2AtUk8oCn7JAJOsCbJdHkPFzPxypsbimSxKOfwMwAyOnzpX5+uaHlYadyltB6satlT1/T41/6zX0UC2iQCmipXQM/lbQ5Z+hWCgCSgr5CGkGZcSASQNRY1WpaVTqfD4fDw8HB/f39fX19/f//Y2FgqlUL3Z9MwTcN00M3uXeSdUfN04KC9F28UEb4q5EmbjMfqMvPf/I6Kd8/cc3uLMdSWFU/DJ750rNq3oqZ9U137Q+/64MrRGH9FyTLBsu18CA43AS0acCUgJvbnK8Ge87GhlHcXHPqpORzptEsZShToRLYOh7CJ6aIsZJmyKOopJk9ZqXBCMZ1iOmYXU0gmTXgVpV0SKKeHUIp+jzwemvGQx7lkp0ee89E/6bmlZCjFNrEipegslkfUU0q5xfSI6RdDp6hflC92WRdD/8XQebVjcintF8u6GLLYvudznSxmm6i/RLmYKkovUQ9mo7NKF6aknzKjftotfeAqnjKpPGktHOW6ZxDuFLHQSfW7q+kosUQNxbKhMRiKkAwrltltjHdOHBQhAt45qWgSvPPTURoEUsoFF8ikKQmlmyGqLf2sKy8nEtDahFjPzErkJTH4BoXbmMR8m8V/IEKTPHkstuDO2Q9DbhJFl+kwmu4u3F0ld55LmyKSxaKMVtjs0YEFb/3Dx6p8TyoLd5S17K/2b2/wLb97VSbnAW3yxwosI33cei5tnWRpVyoCkoC+UltG2nWuCKiqSrE1cKyTzWYTiUQoFBoaGurPbyMjI9FoNJPJ4E1LVdVMJpNOpzOeWza/qaqKzLU4XHDIpsEiAmM92Np0nOMu/RtHgd4wqKqKGbAshwHuXQRETPfQj9ksFreKbeJZpcgems/zEJZ+DkpoeOqeBmCKYRuGbRABzZrPRUDbtp3MwN9+6Xidb2WFf1O1b8Wff2z1aAgsA8AwbP4Uw7AszbYMy9JNUzN0Vdc0Q9cM3bBYohgh+pzrcg7Vp1OwUJpmUPolELx7zvkYgD8xXdjE35pYrndnRhvE/MV6iztdPKuYfDH0u3ETS3fbWSxFPEuUvfXTVU7MRr81sRWwXFEzyuKJKDvyTJqhmB73ieejX7SqmOYS9XufPulR0ZKC+ItmUHOLZ01ahJgBT6QrhqhHlMVTvGXxLG/ZW0+JR7GIC2i/o9wLrt8bk2JHHVZ57BbT4J3uodBxqJgeRzbcpcwFjxZMpFOmJBRUdf6JZEPpqugUx3WSfqoF++pU9WN+sazS5YJl4elkpLc2vM+69eBZ7nS6L5N+b8G7dPGooyy8YIoZPAoSs4myQyfuYgZcbEa88XnIWLSoGeWC+inRsqxJJyCl6CGFIvjkizOpBsxA6OGux1k0DxLLdcik063NneI+F6F2pF+oXbKNquwhuK11pzgMc+gX8xeTRQ1iHjFdlMU8pcjiuVOTiXjkp6XTyUxmnK4JqqozljK3UVYS8kfyE0/aZzbnT8SLp7sWlPkKF4ijzVfosttL+BcUdLDgl69A/fxb69u3Kwt3lrXsre3cOLvz9hMjLLA129gsmJPPhQloUe1lr6w04DIjIAnoy9wAsvgLi4Cu6+FwGINsjI6Oxvk2Ojo6ODg4MDDQ19fX09PT19c3PDycSqWQRMY7YiKRGBsbG5lsG81vwWAwmUwWnCTQ7RCHJljBTCYTiUTCJW/RaDSbzV3SPSDSNA3tT6fTGNja+zslbKbBVhXw3mjZRlVVhVNLEkvRj6VblqVpmqqqeXrf+V/lGy4bqeu6OD72tp/00yke40XLspCAzn1zpphpYOsq4LrEzAMaCei/++Lxet9KpWm90nj/2/7gZ2NhsPXJCWjdNHXTRBqa+okHf4T20zBL3MXlNIluFWc4pWtGhaV/i5pRLuVch/2TnlK6ZlSF+rFlHRZiIrU+aUaBOoN4Ful0qJ3UbDHDxdNPmt02exsgHvWQz00/XQnxciTOwLGLiv3T3VJue8gMRxuJ+umQWLpbVcGUc9PvjblYkId+Mds5yyXqxz5M/V9EfkpFe+gpHROxRLf9om3nplPU75AvuP0XW3/p+JwbVlK/owUL7orYliIXVFIwUcQfr43ndp0sqPz8E4uNSeieWCxDwaILQlcsJ13Vz7kI95VELAuNEVO8Zaoy3WXOQUPpCOANrpS6l5LHu2oX5KiIj4h8MeUlmk2IiTop0UMJHcLM7mXn88vPa/SLIyebYjaL6aINpcjnYD+pxXO9vzEzWkgnEgii5dS1vBU6jor6Hdq8dpFpRIaV5bNoPsgmSswUULM4A7WBLcVnAuh5AU8+q962mH+PqYOusQ/z9eEbe9l04ovL52jt2aIuqXS1ENB8VUETIAMGrNsIizs3NHR1Kwt2lLfum7F0/e++b+NrMYGA1j0IaGxoZ/teUtBlYVcMApKAvmKaQhpyIRDIZrOjo6O9fOvv70c+ub+/H1PwG9lnvMtimaZhhkIhpKd7PDfS09fXNzo6mk6ncewi3vgdMgBomhYKhQKBwEDJWyAQCIfDyC97AKPrum3b2Ww2HA7nfbu9/osEezKZpDGBdxGpVCoWi+W591L/p1KpUvRjdJRoNDo2NlZM9RjfgnwL8U30Xvcwng18ePSVRCIRj8cTk22xZAw/iVQ8o6mGZbGH7fTUlq3vy55Vj2fgM198dqbvkXLfpgrfg3/+odWnT0M6YWWTiTQn55PjqXiafWLjyVgyEU3EY8lELJlIpJKJVHI8k0mrWdGBxaMKZH8ymUQP/Ww2q6qqpuUG0Lqua3xDBj+TySBfLzrge+jH/plOM8PTk2345AGLwL7nrZnwR+OdDxZc+xm+Ye1KtB/xwUjuiIP4jVAgYqhW0zQiQ2moLf5msUaYghkwP2UuKJBOEsRsHvo1Tctms45htHhuMdmtU2wLsv8c9Is9E/WImovho6oqLvTqaNVMJkM9FjstVrZE+4nLduvHxkV8itnptryY/dgKovFu/d42i2VhTrSNuoSHMNVakH58IEeaHXqIeDUNE3t+iT9bmqziVJb0oH6xlNIxEfHBKwOaXaJOrELpZAEZhnXBjjRpWcWm7g7j0ZWPMpeOD53iUOjYFd/n8LaZqlmiZiyI9DuuPKI2tzwl8OkRqcN+ooR0volXAwcIHrvYGfDX6v07FWvhoVA8hOCI95GCMtlPlzWqi6itoIxWITL4K9B1HS+V4iUom82K9pfSxKRZ/HE5lJSyW8zsUn5HpJ/6AF2msMrFKkK/I9F4sf84ZIIOBfEsssFRFrUaneLQ6bFbTKeIFeZBJWQeFur4LmYtahB1umXTMD08NsTfhaZppf9ssXFpSIndHn9fxb7xtoL1ddvpSEH9OCah3u7QnM1mxbdRs9ncULmUBwBkP/2IUHnB3y8l4s/WYap7F73O8WXZUnxwaLiOTSB2HkefxLJs29Z1XVXVdDqdTCZxshLnW6z4lslkNE2jPkOluO3HPpNOpxOJRLTkzaHfrbZoig2WzedLjJzMaiqjMbu3ahsfDT1zdAgsSGfQ8RcJaBVAzXPQNOPigg22ARaGjEbK2gRTBT3LyGjX/YsF5Shm0lk+vFiOKaVP4FFFMlmQJ+RxahfyOQ9dpv2JyPOpr8Xgx8cD42DAF77y6oKlBypb9yste8tb98xY+sR/3DoQttwENPpCG8L8GZXgYwYKliKWeJkqLYu9TAhIAvoyAS+LvTgIkAf0AN+G+Nbb23vq1Kne3t5AIDA6OppIJBwDMlVVg8HgwMCAg6ruFbY+vmFCX19fb2/v4OBgOBzOZrOojW78ooC1zGQyo6OjaFKJ3/39/cPDw7FYzJsvwLtvMpkcHh5GC72/hQr1jo6OohO3d1OoqhqLxcbGxsRzS5ExxLYDandZuq7HYrGRkRHEvyB9joCj9zoW3d/fHwqFcODl1imm6LoejUaHh4cDJWyvDb6Gn6GRwTPxmGboLF5GftiCSxQCQFaFL3z5qXkt983rWrdg6fLv/ODn/a/B2HAsdHpo7DRj0UdGR4fG2GdwdGRoZDgwPDQ0Mjw0Mjx8emT49MhoKBg+E0mn09i4BQejVAVd1yORyNjY2HB+GxoaGh4exr6N33hkZGRkeHh4ZGRkbGwsEolkMplSHgBks9lQKDTIN1GnKJN+fIARCoVisViJ+rF9g8EgGjZWZMOnC/iNS4OWOHEi/WNjY6KSYDAY4ls4HI5Go7FYLB6Px2KxaDSaSCRwVE2DV/dvFlNwyoG0PE4JUEksFosIW4xv8fyWTqeJ5saJWTH9SDrEYjFSXnBegDGFUvlNVdVJJ2NYIunHBzBYfXcRpD+ZTOJzCEdIH+qNJKB+nNLgYwNUkseA/acZFKqlWaWqqiIgBft/KfqTfMtms0QAIdM96TWH2FWcaeOMV7QfLSf99LwHH72U8miE8Kd3OxClgt9E0NNLOYSzW0DN2K90XcdzEVtsO3oEhRNsnDAT+HTDcmt2pCB5JHIo9NALGQQsmsBBTtD7hiUWgcaTEm+mANkWXLMBm09UJcrYnZBDpGdOqJzKEgka0X7sS2LnFDWLMr61g/kJZ1TlKEvUj5cFUY9bRvsRHHp4QxXRJ25YNKbRMwa3TncKPisS9XvgT/rxIQ2yhAVRwkQAcNuP+ukpKbEz2OfxUoyPvujnSUU47LdtG2maWCyWSCTod0rtS2VRpZAAFe8pBS87WJBlWdlsNpVK4YULr7tECdHFAe8LmUwmlUrhjw77g3jxdFhOu9g/iSbDnydqdnxjpUQC18NyfK6Dl330G3Bf7cWUGL8tEobibYVMFQVseqTJstlsnG8xzw1vPfiEeKr6vW9bWKxDP14YxYIccBG/ie1LRdA9HfEhZPCiWso9F4Gi3pJMJtFCEXBRFmFLJpN4Zbbzmwg7ydjzE4lEOBwOhUJFBlMTkiORSDKZLOWeS6OdaDTKh07syzGmcu+Gw+F4PI5XBrKzmGAaZiqVCofDo6OjOFhlw2XXhkPZYb6Njo7GYrES8dd1HcMt0oB/0LUF8tvAwABOCePxOOovZjam67qeTqfRV2aIby7dBRJKt980THyTlUb7PSVsFEySZhPYg9x10XU9mUwGg0GKRXmqhG14eBhnE5O6QzlLtMEwGYVpQlbnNOSXvrR5acetvsYfvPHN//naMGQ1yKi6xSZYBanJnD6Lc5VjQXj2edi+c/zb3z50620vP/b4yPZd0XEN0jpoJvCwhoZtaWBNTkAznyK+kcEWul7boNssxrFmQhY/FmRt0PiH3LPRCUlwS0I1IplMsp0LSIEJnI7np3OXYl4vykrGXD6BXNGRFEZvZfYIwQDTYv7pbDr89j/aXdO8r9x3oMzfXeHbM2vp6kf2mCmANMeQ5ebxuvHZgyu0iGkwaNnLwkKQaHLyunxVlyVfDgQkAX05UJdlXjQETMOMRqM4Cujv7w/wDTnZoaGhSISxfjg9wHEqjk0xbHQ4HKYbPw59xG8ccGAKymNjY/F4vODD7fwYMveUT1XVUCgkanPLqBO/0X7kyr05RJwPqKoaDocHCm244mJvb69ITCPJG4lESiEjNE1DArogNeyRGI1Gi43q0GxsAiQQcXFID21Yud781t/fHw6HdR3f5vLqT7quB4PB/v5+77EcKj7ZexI//YH+SCyiGfk4ZfyOjGMFFudKh5tuPtm15GeLGn/8xjff9vRz5qmeRH9P/2s9r/b39Pb29p/q6z3V13uyn316+/scn/6BgaGRYfRAx67iqAAm4iRK1/Xh4WEMIIONSK2ZB4P9x9phCgaZKeXpgmVZqVRqaGgIB6JiJ3HIYtPgqD2VSk3K9KF7cjAYDAQCZLZDM+1iE/f19Q0ODmLncUwdHSjhbiqVGh0dDQQCuLKoaCcqxIA8yNrjtGRkZCSRSIieOwg4foul6Loej8dHR0fRPR/nRUNDQ4ODgwH+QgMKVASWEg6Hsec7psFu/ZqmxeNxZOdp0kX6A8KG1wTME41GseeT2aLNokz68YJD1gqKz4qDg4P4gCEej+NkBn+hjlqQftu2M5kMTiZDfBsZGcEJKu7iN6YEg8GxsTGc0Mbjcbysnaf+cDgciUSwlHA4TE9HKLK/Nz44GY7FYjiTD4VCo6OjouURvlGNcMI86UNH0Y8plUolEolYLIZ8AT0UIZvDwhYMBsPhcDKZpG7vth9TkP9N5TfUjwhjEYhMNBrFuE94CGsn/myL6UcGMJ1Ox/NbjBNVuIdMDXEToVCIGgKf7ng8F8QSUX8qlULzEGf8jhbaiG2JxWKiTyh1RRJIv2VZyWQSEUDNAtKFxdHRUWzcSQlQJFgRdtJF9hPm1HMQn2AwGI1Gvafx1CKqqiINhOcSRG54sLhwOBwMBvGJNaFRUKAxTzQaReNJubcQDofpAQDyxWStWxDtx1Koz2OHoXphjbBT0VtZFt/caiklnU6P8SeOpIfQFn/CDpl+XKQHBQdQRGOJ1y4M0YYXgZGREbwpINUXiUSQChcfUIlFuPUnk0m8dolFkLViXUZGRkKhUDwexyfW3k+/iNfG28rw8HABSkxIwjvX8PDw2NhYOBwukTpPp9N4T8f7Hd6wBK05kcbMgUBgZGQkFouJtxIHJuJuIpFAy+mGKw6PRRkbAu1Hz5KCPUdUjk4qaDnzFeAb3XMHOCmJFcCb5sjICM4dHByuqFOUU6nUyMgIGwXmJyABzw3DA46NjdFtS9TmkC3LQnAGBgbwRBzh9xXZ+vv7BwYGhoaGaEAldkuSsRS8c8XjcSQo0eoBvonDKoccCARQv/eVDYswDTMWi+Fov6eHjZU9/E5o0D48PJxIJHDM4LDZgQ++bDowMNDT03Py5El0POoVtp6enlN8O3ny5IkTJ37zm9/09PQg+JOOZjVNQwJ3cHCwp7Tt5MmTPT09o6OjmUwG9XvYj/eskZER7zZ1NHVvby/ZT8ppCCHiw5ZPzzcuQoJN7P4WAGPduJSXccWCSNZY0GDIgjmcgc/+6/E5HSvKFz5Q0/pwTdu93/jJAE6PkezEU1TLRNYzZVpZ7g5tAASC8O1bxt790edntz3Y0PJg7eIVdY1MmOm/608/ceDBTZm0CZkMgKmBNQ6WztjoCRubt6HzEH2bwAIhmpwR1nTI8DPSNmNR1+6CO1fC1/479vF/PPmP3x3+xi3Dmw5BhHPkYZX5+cbVKCNPaVlEVg2cGpLPL9tlbDijWTPZ1BlmDg8bopkwbqbZrm5iCp7pImqBrRZkZzU9ZfGAIxk1RyZMqBntiG7EYkbUjk8BKDPbLbbZfNFIzIBcci5nVB/PAux+Wm1oe6jSd0hpPVjedrC+cd+CrofOcPY5nuegbYBoCuLjMK4ystlAWt9gtL5mQVpjNTdBNRkEyEQ7yOhitsn0aw0BSUBfay06zetjGmYkEsFRNTJEKI+OjhIfijdpHKfigBhdh2gdwoJxCPKTffY/yV+PErls8cbvkNEnBb1RYsW3KN8ifMP5Nj72LziSoFYmhxQcleKIWfymgbU4PcARfDKZLMVbTdf1VCoVj8dFDaXIHvoRIgI/k8mgE25gsm0gv+GQdNIhIzIFkUhkcHBQHFQVk0/1ncLPwNBALBkzbCOHv0BAWwDpDBw9Yn34Q6t+583f++zfrXr5fxOneoZ7e070n/p176menlN9J3t7Tvb2vNrHPkhGO74HhgaRIEYoqEELCgMDA738EQIN/fMwnP2Ph3Bs2tvbOzQ0RJPtgjopMZPJjI2N4TQgUHw7WxJ/UQDj2EzaObPZLD4Q6unpOXHixEnP7dSpUz09PTglCIVCON8jO90CBp/BpwsOfAgoUcAq9PT0DAwMIBPk4QFNHNzw8DBOYxwzjr6+vgE+WUXoEHmc3gwODmL8GXG+bec3sSKqqkYikaGhIbxM4c8KL1yi5TQhwWkV6heVizpFmfRj3R06xV3MgEVHIhHkEMWLZN78s4NXfNrX19d38uTJ/v7+oaGhgYEB8eKDMtETqByDF+F87ILoR8tpzjkwMBCLxdB+t80iOJqmhcPhwcHBPv5GC7YC8hH0jVNlbNxTp06dPHkyEAjgc0fxKRoVhIKmafiiKz7UxPk8KnFjTvbjExScrOIvi9SS2fTEEd/SxbsGPjcN8A27EFE/KGAXRc5C5EAL6qeicbKKnRyV042VuigZj8Lg4GAwGCSakswmAUsE7oKUSCSQ3BH7DCGPAh7C4gKBQDAYTKfTCALaSZpRwEMA7M1cfLFGpKtILnj/wt6bTrP5oaNnOkopGFYrMHFzIIO7o6OjtG6wWyfCgr9ruiy78ReNp4bAfjU2NjYpDYS4ZTIZ5BDJ6oIGi4mBQIA6DzrkOlCiXwQ+msLbCmlAC2kXeyPVBQnBSCSCj9bE6ATihc7mG9JweGGhfkIXSfyhub/Rfqw+dSFU6GgLTdMikcikD8Xpt4yPLvDFnXQ6jcGCULNDv23bmqYlEgl8JQ7HIXRlQBDo9SYkYfG+2dfXV2Ljop8mPpDzZvfwhT+87SJNKTpROjChXdu2R0ZG8JqP3W+g+IYc4iuvvHLy5MmRkZFSCG5d10OhELYm9RnqpW6hv7//5MmTfX19oVDI3SEd+ANAMpkcGhpC9hOv/PT8Hu/pWDQ2Dd70T5w4MTjIBmyoza2TwAGAaDQaCAROnDiBRGcp36g/lUoVvKaJynGC09vbe+LECbTNc0iVO3jq1Ckx8CCiVLAu+L4dDcOIrvWuRU9Pz8jISCkEOr2iipr7+vrcDSqmYBcdHByMRCKlPABQVXVsbAzHJNhF6QpDAuof4BuOG4PBIBHEItoOWVVVXCsICWhxzIna3N/40yaCGK/wNt8cyvFQMpkUpyqOMWfBXQQHPdDFS6VbPwAkEglyf6bLl0NAm2mKNDIygh4JBRV6Jxo8MkNzmfO3AAAgAElEQVQEjH0vJ+rbbqtp29Hwum6lbUt5187X/+n2mJZjcc+OKbmjtMpJ0LFxSAHc8eBvbvy92+s7Hi5v2aEs2lvedKSi+amK5qOVvu5K/86ZN2yubPnxrfcPMoKZhR7OMPYZXabPWsZY2Dz1DNxb2jDB4J7XuUzjNux6Sv/kl7o73rxyTseahs6dDV37ZyzdN/vGnWW+B6va7/W9+f6Pf3XfiRCEbBhJZhlfnFsWiFucI6CJTM679PJ1gbCM/l/Dzp3xgdMQy9Pjls7qTeectRdAVXOeVSZAJMH8soVtwo6QznrQxF0yEl2bnQfd+5qpUqJhcspYB9XgtDuLAA1f/eHLte2rK1q7lbZDZf5DtU373v3hVwZ1CAP79CfgxT44+At9+yHr8S3ZO1cM/ejWX33tG/u/+8Pj9zzwy137TgdGYZzXzGDsc9YElbHTLGQKMvA5vpxskMK1jYAkoK/t9p12tXMQ0Oh5gZ47NCtAUHAQ4DEUc2CH+cWzxMG0eNQhox56PVkvsml8wzdGs9ksvqBaCsGKUynH4IxsoJhoOKMT53XoSuaopmMXles8ynBsips3gYgWUnH4Xl5osi2Y30pcpBGpBHqvbWyy7XTw9Ong6VAkeCZ+JpVJ6pbGBy5nRwkme/LNYnIEo9DbD4+s/sVzL4QS4xAYeW1o6NTI4KmhwMBgYHhgaHBgaPC1YfYJDA+5P6eDYzjfcOBAgIjCyMjI4OAgTRdxxtgjbDQURoZoaGgImRpRSUEZ58Po5OsdfwZdaZANGRwcxCF1QZ1iIr70R5NtNykgpmARIkEsqnLLREATxTk4OEgcEwlim6NHFQaHwde9Pa4Atm2n02kHAY3jcpw4oWMpOSIhgD09PUNDQ+hnio3r+BYromkaxofBhVJxjoSz+oKzgqkS0MSkoBO9Q6e4O8A3LBo9rIlOEmc14gzZQUCjBve3WApO+HGySmTBeeqnEpFHGBwcTCQSpXiIOwjogg5rjqcL2Lj07gJVwZ64eRDQ2OFFTEjGX7E4kyet1Gfoao/uyRScB59RoQZ6FQCRIT4Ff1nBYJA4yoL6iaGLxWJI69NcVNSPyh3fw8PD4XDYYzKPJeJkGx9q0oUFVQVcGzWB+FyN9BAyKCA+REDjZZMQJkG87JCM+lOp1LkR0A4oCu6Ojo56ry2M9hckcAsqpMbFpimRo2RRpLJZkYAmkAkNtzAwMIBhrxBe6vzi75cupyKBjpYT+A6B6oUxzfCXS3rsQhsR0PSbLcV+BwEtKnb0IrpsOkwttjs0NIQcdCwWQwJaxES8ZnoT0PRboIKQakSCdWxszPvpBf6skICORCLeYc2wCAxPh1eGoaGha4OAFlsWZbF93QQ03pWQfcbHkNid8MfV19eHBC4++iLlok5RxoB46AFN7egt9PaygHjeVwYsAns+PjQN8M1bMx7FXy4OyOlnSxUR+yc6yeL7aqh/oIQNV6zBXy7aWeybngvincWb16ZHIziaLcUDGl9ZGxsbQ5qVHi3QYNlxL+vv78c3TfGJdTGzMR1/WdFoFEdr4jjNfbXEFNRf8E3ZgmWl02l8EwujkjgexxbcxWtOKet2AEAqlQp5Rm7JT7DYf5yNxePxEqPtuWvE3Z+Zm+v37j/W0H5PRfNWZf6TSsf28q6dStOPg2nGmIqkY1pNozdsBuCFHviLvz3c0HGbsuBOpWmj0nq4suMX5W0/L2t9UWk9rrTtL2vfqbRsqmp+dMain+zYDarGHhvbIq880SAsiAf7MDTQNE56pk146RR85dsnaprvqG5eWbbwifr2A9XtRyvbj1R2dDM7WzcqTZurWjdVNN8367qbb30iGGY+3Yw65x696ObMded8ubnMYoLw4i1IJ+Fb//nK9cseWdCyoum6+778racTecPQJPzOp7H/GZWRsmt36v/23ydWbtRH46x23F6MVeIimllhOg+ijXG0z85YufJcMA2m2l1YPg054KwG8SSkUiwjK8xmJHEoA0mAo6/AnOvuqW5fW9a2W+lgHHRl+5GPfg3e8sHDne9cPWvJ8lntK+taHqj3LW/oWDmzc1W978HaxgfqF94/c9E9C1vuaO74/q33noxpOWA0GDdg3GQEtLs6IhhSvmYRkAT0Ndu007Ni+AAfRwbo0xEOh8lVWRxyoUyjsUkFkcAVaVy3TncKTgwwvVi7iGdhLLZS3JNRM7LMBa/jOKElT0+a13mcQhaSSZQyJaFE+1GnuFgN8t1a8Q05fO93UclUnPIViw7pCBaZ0TIZLaPqWc1UdUszWegrfHjO78cWe3dIN82sqWs2e4loLKJnNMhamYwRVdUzejamZtLs+YHKPuP8k9FU+mA6fuOQ16NXYDezbRtDTKLPY5Jvqck2jHFMIBQTbNvGYKDo14/K3d8JvsX5FuMv4ycSCfGZRzH99ACAAixGim9RvoV4gGl06PBQi4csy8pkMhjlABWHXRuqpZfxQ6EQPr2YlIBG9/l4PE6xIxyj80gkgi6u9CYvkt30Ijz9gkRBrBS9642BLGjW4X51eohv6BDq1i/qFGUKwYFRPvB0VEUOQaKAMxwkcPHSQVcMqgLpF0NwBINBjOqIReA3OSeK761jyMJJY2TjlY1CfDj0YxUc3+hTSd5MZHDBCyOSaBjScXR0FJ9hOBQSUAG+IduF+lEnaRbLwheZMUYtvvgSDAbJq7FgEZiIpRDHV/CugY2iqipqFgloolEcBPQA35BMwXfJiSkgs8U2paqhn6bYPSaVKSwVKXQIWCJWjTys0cJJv3FVYe/ndogPEdDFvL2QHXB89/b2joyMoH7s9kQjirVAfIijpE4iPgYrCFQgEAiFQkgzuZHHItB+fLSGYbtIfzGdAR4LCNEr5V1ptB/DdqEHOlkeKLJh0RSIoBQCGpcWoLBC2P8LVoES6UV+uvIQSg4B31XHn23Ba1rBegwNDcXjcceL8KgZwadvvGziBc3jB0uHMLgNekBjGGjqOW79xEFj1BQM7iRe+R1YYcArjOSLt3WPkQ9efDKZDIXgICPdAhZEi0bQiiNumwkZ/OVSCI6CT3zFgrB1AoHA8PBwNBoVnTZEnQ6ZQnDQjbUg9YaW460Bx/nuu5W7LmIIDnyELDYB3sHxRh/iEZCRsMOeg9rcOkX7bdvGJ/rBYLD4YGfCEXSRobuJqM0tY+fEqC/isIrGOW4BIxehKseVzV0XUX88zpbNmHTDGMpuU90pGMOabl4xPpiMF98wQyqVIoLYzm9u5dg5Mfp8ige/ShTaknyhCwztneIbOSd5NwGOlmlNBYzbjq5CmSIbLu7tdk8uVpCmaRiXP8u3IlonJKPxjguOh35xKlRsjiVii4tAFlMo5nTLJjAiNQbwpW/vqmi8c9bSQ4pv+5w3HVfattS03xbR2BkiI6oZzD82koatB6HzrY/Nu3Gr0rq27saDlUsOV3Y9Xdn5fHnbc2VtTyv+Y0pbd5l/v9K8t8q3a07r5s4b7h0JM5day+b+QW5TeAqSqhoYWU7WagCrNwe63vLjhvaHGTm+cKvSuEtZvFdp2l/dfrRmybHqJd1VnQcrW59SGg/Ude1VWh6qWXbbDx4+HePhJrIsFmO2UEhoFosDn2RnUtDdPT5r/k9nNe2sWrSroW3r/Ovv+dJ3DkUtGOfxRrD6YggOCyCVhfse7Z3ddXND10MzOu75+396OpXhLt62wb3D89mZr3eO9kYkdU6OpwDi/JPiuyqL/5EneUW48yhhGo8RAk9uivz95/Z++GM7/vqTOz/2yb0f+eShD3/y0Hs/vvWd79va/MYNFc1rKto3K+07GQHdcURp2qc0bleaH69esq22/WCN72hl06HKpu5q/8Gatu6qlgNVC/dUzd87Y+HOOY2bFrUu/8ind53RmCe1CmaWCOi8v3jeHPl/uiAgCejp0tLToZ44sscQY8g+h0IhMeQlDlBwAIOA5Aczpf6n0Zv7fu+hAsstvQncqoqdK+YsJY+YX5SLnUvpmNlRazpaUJiS/oIaLkgiTemnpA1vyQIBbbEUmxHShm1oJlu/2QBbsy3+MtG4zZ4Qp/ntnj3Cz5/OniHjhin5dNsQe5JlFcOKZss5JfmzxPxuOZ/rrNq8FQX+U2ZvAdlwx7MBR39AS7AMUcanC7SOVsFRLz5UwCWqKDqzx6iXao1PazRNczxLoF1amQ1fLIjH46lUCkftWCn34xmHchyy45SAvjOZTDIfiocW1MLJAxF8BeCemGQaJhLoiUQC50Ko0zHxi/MF/ZJ8o8kYGelGCQ/RmkK4zlKKxw7y1o9moMOLqF+UxfYVFyF0T/nQYDKbDMBIqZqmiQ53VMSk+h3gxPJPRJLJJDYuqcX+ORHyCXu4lBzGY8UnF0gMRIWNqAJMo8hCZHAxAR9g4FJdDrWkUxRCfMPgLSIIjvbFaTB2eMRcDMqMSsS64GOSMF+KE1eL8n6xBotDDlSEWoCEhZamjZ74RCKRRCJBS2kVu+uJ+jEMMVlI0YFJpyhEIhFkOhDwCQ0p7OBRfDSF+kkJgoO8kvgwCeVwOOyIMU0tS+opBSNTxfiipvRwizBxCLH8WnmpVIrwIVVi+5LxmqYhTUOwO3TSLrUsXkDIvZ1sdgtIU6ZSKbRctJ/kMA+wHolEonwFV2RtcHlVb4LY4hu9BIAUkNiRYq4NF8HD0Gf0XBChcBiPRdNlM1aIwKJGIehwfdF0mj0bpkU1RNjFUhAcfNxbUH/ctSE4ePHHNRUdd0bSj5XC9+FwnUO67NPVUsQKwcfLGl02RRrXgRJeHHARQjGGeyEijqWR5Xg1Js1kcDEBmwA7djHlmI53HFqEELtHMXzwokHv7SF/RzcOgki8pyDspazFgsoRIhyTEIeIrUDfjhs6cnB0ugNzB0R4FL/10rZS1ialUmjAo/GNxjne4ytyH/bGH83Gm0tptudyed9TyHj6/dJ40juaPPYEzCwCW+zHiwXRBYoqKwqox53TW6dYBbKEEosJoiV0lmgAmYGJaKcjp/eueIr4sxJNIg0lNlPBc0vERzzXBMaYpgE++oXN9f5VVS37FP8epW2X0rajyv/TsXGWN6FmkPoEnnMkBbc/NF7beJ+ycK3SuktZsl9ZdqCi62DdkkNlrdvK/dvKWrcpLTuVxn31Xc+WNR8pbzpUs7h7ZvPKO1YNR7OcgDYLxKLgVhncozedNNQMQEiHOx+JLFh2S/miu2Yt21/h31/btb+yfZey4MkZnbur/dtr/HsaOo43tD8377qfK/N3lLVuK/OvK2t/tLLr5h+tfO0MQMi2Q1qMjKeKW6BbLMQE20wTvv5f++tb72UhRFq6ldZtFf4HXveuuzIACcswAEw796EZombDsRdhwfU/VdruqLjuyfLWDfO77j36LHeKZlwtX8CQK7csHmDZNtnCiTYkTXhsG7z7E4fb/nBz+Q0PNLxh5ev+YN2TO0DlbPtZO/NcNBmMgg4wGIOlb71rUdvKeY1r5i5+bHbjmtmLNjQ0ran3r6hpW1XVsqe85bDSvlvp2Kl07Fda9ytNBxTfASa37Vdaustauqv9B+o6jtZ1Plff8UK9/9mGluNzWp+tnrN9XvOW+rm3/eSusZjJ+kOaeaCnTUhbGAn7LIvuMEruXssISAL6Wm7daVg3ev0wxJdtoUijeAMWR5AIDt2YSxTc45gSTyzx5l1MW7GmFPOXkkfML8rFzqV0zCyObyat0ZT0Y0F0ioizOMDCDGTVpAIpnNRaVEWDAGKK8x7QAgHNbvuaYRvswwYY7C0lHiBL40+n2TtZGLhDePEp95yfewQw9rlEApoqiBUhWMR6lSKTHreAyDj0U0EegsjbijZgEWIKKiG2t3TBo9Xc+ouZSh4fOGGj+apohnhuMc1ifpRx7of53cCWkoIEqKgHtYn2iLJomyg7yiIlSBAjaY566JColmQ8ihyQqF+UxfbFE93IYAqppeuGO0XUjHIp+ovNjd3lOpAptotAOebwWAp2G/omjsZtuUcKTulJSUEBO2pBJaLZBee0RNmICKAqwhx3RVUFZcpGk393K4v4U10wcdIpbin6C/YoNANt9r4yYE5HnGLSWbBZMRGvaVQEmiqWReDruo4/W6q+yAS5ZcyGpZAS+l1QQ2CJiDxpLmgwHUXqECsrsjmk0y2IzzAm7fOiZjSYWELCRxQwD73SRB2S8PcQsOEQH9TpMB4P0WWNXqQQb0bUb8WCSDO1JgliEaQfH7UiOISAqNAho34sWizLUQuHbdTrSBueS7sOGDHdQ7/DftJP5nkLDmtFZM5TdvQQ6vnuEsWcF0om41GhNwgO24rZQDodQrH8paQ7VLl3qX3FHlK6LFZctIcKcugX83vLBbWRWhJIP2rDs+jopEIppYh5SpfpyjYlG6aqX8wvFiSmT1UW20U8t5h+Mb0UuZjOUs41wdQBxgE+8rnd9b41VS0HlNZ9StsepX3n/NcvD2eZjozFXidlTHQKEgDfX9FT57urbNGGqs6DyqItSuNapWOtsuiBKt+97/nsC1+7Jfb+L71S1/6QMvOxOV3Hy5u7y5oPlTcdqWlZ946/fDyUAc2AVKIYAa0BnEmoY8wpW4Nv3dw7o/XW2Us2KIs3Kwt2lPl21XRuVBrvaVhy34zO25e+Y838JQ9ULbhvjn99g3/T3KV7K1u2lLVuURgJ/ljDdbccPcV8jnT+yUPBqsE9k3SDRU5m5Hs2C3/96U1V/ocZXevvVtp2KL4V7/vcAUbC2iyDm4BO2/Dxf3pp9hs2Vf3WxvIbtld3HpjbtXrrviRze2bRkpmbN95HGGWvq+Mmm39uPZB+53uenNP5cIV/i9K6W/FvVfyb5izbXd/0s3/9n+PaBDvz9k78rwM8fRJmdN3c4N+gzNpat6i7btGhmsVHqpr2V/g3lfu3KS1PKy3PK+3dSsdeRjq371P8+xX/Xlap1s1K0/qKlvX1nVvmLNtdvnBD9aItM5q3zGndPKdl7bymVfOa7/zDP30yqjLEEtxpnL9CnCegJ1oi96YJApKAniYNPV2qKc6syBVInFU6gBBvrhdbdhRdcLeYDQUzi3x6wdkUnlVMp5heTD+li5lJpqMFBcrmYZvjRPEUD9lxlseuqMQjGx1yENDOXe4BzZ7qWxZbxoKv8Gti0DHMmntDKhc5uhgBjTS0aJsokzGiIGY4B1lUVVA+B53FTkH97qPiQNlDFqkEj55Tun5RIU3VHAa4tYkpmJnOJQHTMWdBVCdNFEs5H9lRkKiKjBetFTNMVXa0r4NSIXBE2Euc0qMlpesXyxJl1FP6lFIs0YGkY1e00HGo2K5HH3acQjndLSLmpGxi4gWUp6pftLYUM6aq363TuxXIHveJU0ohPaLBmIgPIfAHVWLfFjO7TyHDUL8jAx2dVChos/ssyiZeE9zZaIBB9mAK5iQlxQSq8pQE0uZtj3jZmbQWBVUVTMTSReXihcVDpjqS/aJAZREBh6qIIKarpXhW6bKoH88ie6YkiF2ddF4QwbsuYhHeOc/tKOl3nF4MHEe2gruk0yEUzFxiokOVexf7TzGzJ00vZgYVhBlIT7H83umkzS2QflGDO9v5pIiapyqXUu5UdRbLL5ZVLM/5pBfTL6aXIos2lJJfyGNZLEgFW0vwA5/prvetq2g5WO47wJygW7dd9wcb4rmV9iCaZOsumAD/fstrs3/7sZrrN9Rcv0fp2Kb4nlSWrWp404qv3zo4mGFE9oDGSOqtx+D6N22a37a90rdJad2mtO4t86+r9t/86hjzPaawHugGlLOHkcOGaoRUi0UFufehRNX82+paNzdcd1Rp3F3WtLth6dbqtp994EsH1xw0IzxsyFgGxsbhtvtH3/6utfPaVtU3bahq2lvZ1F3esqumfcP7v/yLYWAcNFu2L+dTzJyeOQGt6pAxwErpLJ7yb7/jrqqWTUrLM5yA3lTWfP+P7o2whRZti9hnFBgINiRtmPuWR5Vlu5SlO8qX7mro6p7dtvLeh19LqUw5f/OWOUEblpXSzTQ39YF1Zxqvv3VO2+PVi7Y1tD1V7T+oNG9RFqxRFqypb9sws2X5v3zzRC6INNOQMzeHTP6fCjBgQv3rfjBj6dpq3/7Kpv2M32/pVnx7lfZtSvsOpfUpxfes0naMx9/Yr3TuquraXNv1RF3Xg3Wd99S13V7Xekdt0111i29vWPiTjuvveee71nzgo9u/+JUj//2jXz6xMTwcAnTRspijlmpAxmIJGPRbnGrnDZL/r3UEJAF9rbfwNK4fvWvpgYF4c73YsocZdKiYDZTBIYj5HYdoV8xTTKbMxYSCJxbLjOniKd456ah4iodM+ScVRCWTZhYGLjmHZfGuiDIbKDACmrPPBhickmaLEuJCvkxiN1lvD2hJQNMMxy3QVBxZj2KtJrYsym5VmCIqJAbBkdmtTUwhPXQ6CpiOOYvZ6Z0ulnI+sqMUURUZL1orZpiqjGXRWR5kDZY41XJL1+9oDtol2y4en+IA/ALuisaTLOqnRFHAViBXTRFz8dxSZIdaakQxvRQ9xfKIekg5UZziUW95Uv2icof+YueK6WLplI6JpI3SSxFEhQ6ZThfTKXGqAirxOGtKvwuR8xI1i6YWlB34l7hLqgraj0dRFf3ecRcPFTyr9ETST8pLFKh2ZL8okAEimBhLoeBvVjy3FFnUj/nJnhIFsRTSdgEFUb9bFgtyHz3/FNLvUFUMHEe2gruk0yEUzFxiokOVe9fRf4rZXyy9mBlUEGag04vl904nbW6B9Isa3NnOJ0XUPFW5lHKnqrNYfrGsYnnOJ72YfjG9FFm0oZT8Qp4cAZ204P2fPlzr21DRcrjcd5AR0C2bfucv9nAHaMiAlbRYOIa7HglUdz2gtGxQOrdW3rC95vrNyqLb/ujT3QdeZRS2CRABKwlWikfq+PFtyer591X61nECeleZf0NVyx0v9zPeNz+Pw8V78uGSuXdyWh8fN+HIc9C85IE5HdtrfIeVxXvrl+ytarz39b//yJrdjFBmIZg5Lcp8dXVImWxG93efPzq7aWX94h3VLUfKm45UtByo8C3f+CJjw/MENC4DeJaA1kEPp2EsCfPavl/J4m88o7R2M6K88ebNexntarLXZ22Rg0YCOgFQ98ZHlaatin9XeWf3jCVHZ7Su+v5tv46lGQhsgslqxqSkweJr/899fZVNP6poeqSmaUed73Bt67FqX3dly5aKlo3Koo3lLTvmdh2Z5XvglQCZWjhGiQowCvCD1YH6zh/Pu+7ROt/KOt+jNb5HK/2PlbevUdo3Ka0HGQfddoytANmxubpjdbXv9ht+/9GPfeHIf/zoxPJ14xv2w/FXoGcEgmcgmWLe6Eh16/yfDpDRmdeWxSqumuxhAQuWnQ8DTrNtoQdJ8ZpGQBLQ13TzyspdaATO42Z8oU25HPqmNHE9HwNFnFE+H20X7FweqYrZY7Fg0DweNHtkbdsm2Dp746q4BzTakGOx2dIcE6pYooV0Ton5p5qN9E9V8C5oStrI7a70zob6PWwgAygPpbgFykOWiClXkUxVu3g2l95G52bDuenHip9bifKsawCBi9oBsE+eW8/ESwpdWM5ZyZXcRud52ZkUk/PUPyl059l5vO1H5fQAY6plUd0nLWXSal7GDFOt9QU3lWC84JovgULkoLEKyBRTdaYkFDN1SkooczFt7nQ6xbsPu0+UKQURuILxZAS0BpC04K/+9mBd68ZK35GK1kMV/t1lvrXv++yzyE5m2dwJVu2HsvabKzrWNtx4qGLJroqO9cqi27/yzVNJFTQzF+lCZXEkTIvFnYCRJCy6cWVF6zbFd1jxHa7y7ViwZOXB59khzdAt5gOkWTwWYh406//3sE4DjAG84d0bKpvX1nUcre88rsxfX994xx/8yU0jpyGjMsIUXYnAZhyvmQ+ykTbhd975eEPTmsrWvcqifcr8/XXtGz797ZdPc4cjnosvrccLs8A0QNchqwMcegXql93B4le0Hlb8+2r8a1735nvtnKM0qwt9TA6HaUPgDFR33cMDKx8qaz1W3fFile/J797Sk8x5QGfB0sCCdIaR42v2wpylD5Uv3jzvxpcq2w4oi7coTduVlm3K3DV113ezINr8U+l/+HPf/MU4MMdjU03nMZnw3wKIG3A6AcdfNv/lv3Z99FOPfvLvt3zmiwc/988vfu92vfPtOxgn3npUmbm5un3H3GUPf+7rJ85okDBY7OlxGyM7s++szQJgmzw8JZsmM5+tHKpU2QkFy53pioAkoKdry8t6nxMCV/DN/pzqM8WTLtmQUcQZ5SlaenGyIwHNY26w2yp/gMuoZPZoOcOGIoyAZh+3BzQaJAlod8s6Us6BnZm0h1AR1C0oxS1QHrJETLmKZKraxbP5Yl8Qzk0/Vvzi1Vpqns4IYJ88t54pCehJe86kwF7sy9p5Xj287Sfjz60U8XQPJL1t8Djx0hw6t7pfQNsIxguo85KpkgT0JYP6qiiIOvOV96vPEdAJE/7iU91nCei2nZX+xz7/jRMI71gGjvfD3LfdqzStbLjxkLJ4Y037phrffV/55qupswvnoWexbTEu2lY1GB6H+a9fXtG6Q2l5qrzlqZqWHfM77//5q5BhcRHPLsbDCd5cM2ps2UD42m2/rOxc1XDDM8qC7pq2Q1WNj/zBnz3Z22ODZifPJM7ywczFmHHdFqQsSOk2rH5Snd/xoNK0sWbps8rsvTW+LQ033hLMEdDjPNI1c4bO+1+bJmTTAMt3Q+Wy+5W2LUrrAcW/r9b/yEc+vl7NsDUDiY3NzQrzBPRgBOo67yxr21vhO1LB/KZfqPBvuu3BMPoRMxbdzrKTAV7pg/Y3P1q+eH2t7zll/tFy/w6l9THFt1xpuV9pfrRm2W6FpexS/LuU9jUL3nBPIAUpdDtHQ4VvfBjAxicsNgiMqzCehazKvJhVk/lxv+/TJ6rbdygthyrbj8zo2Fa76Psbd8O4AVnuyaxzitkES7+ktygAACAASURBVGcxqtlSkGCx73wdWU/IrTcoFCrFaY6AJKCneQeQ1ZcISARKRoAIaDv35hS+SGUz9nkcIMtHI+yVojzRzB78ilv+fozjB/GIlCUCEgGJgERAIiARuMYRIM7oGq+nrN5FQIA6z5VHOF6E2kqVVzECzIdYB4ia8J5P7BMI6O3Vnat+cH/MNBhHmQH4nb95pPq6lUrH9qrOgzX+XTOaH/jXb72a1BgZmrHYHArDNBgsaAMnoFUYTsH8161klKvvaHnL0RrflrkdtwXOMFegfNANAi7nD5S14fCvoXbJT5W2J5WW/WxJvflbqhbdsvcpFhJiwlQN52lME2OfWSRrG8Ip+P2/3F7ZsUVpOqjM2lW2aEPNsts3P8ts4+5HGeYHzWeIyEEDWEkT/uXmUxVLHuLxK/Yp/gO1/lX3PDhg6HgW8bNMMLjdhgVnCejWQxW+Y0rT0cr2tWt2IBlvA8adtmD4NHziH56q960sX7RdmXWgtvFwWeOjVR23vfNTm//mv55rf+cTStP9in9TjoBuWzdz6f2bD0JinGCZIKDhREPjMYNXLGbAazFoe+sGZdH68rbD9Z3PVCx+omnZzWNx5pxucpY5rwvDnpytF7qTi9NekvOnyP/TFwFJQE/ftpc1lwhIBKaGAL8/2+QBbbNhBL8FZ0wrYVtpsFVGTds8theLszFhVJN/Np67PU+taJlbIiARkAhIBCQCEgGJgERguiIgCejp2vJXXb0ZrYoE9J9+fG+tPxeCo7Jta82S5cs3QybNYjX83++/UH7jXeVdG6o7D1S27q1pXv2v3+w9k2J+uAaPsDzO/Xos9nqpaoEKlq2qMJyEuTeuYqEtfIfLWw7XtK6b1fG9GDnZIs3J52sW08R466QFf/53R6s7n1QWr1cWbKtuP1rfsfG/bhpLmqBrHFvkeM9SpEhApy0A3YaoBv9+U7/iW1Oz9PmZXS+ULdxU1XnfD5aP8JNUZqltOqZ2ZzLwoS8/Vdb+MPOA9u9hHtBtK55+KdeOGIiDSkMCWjdtTkDfwzygW7srfEeUxn3VHav3HMezTM4JMyb+nhXjMxbfM6tje03zvqq5exa27Wy64f6V2yHKQzk/dQqa3rS8rO0x5gTt36X4N9X6V331Wyc0A0zN4RbFNNuc5c/oRtbMe1qzlEwKzoxm4VdBqO14SFm0VmnaX9l0qGbR4+/58AaVvwTMzaJK5AT85468IebLoSD/TWMEJAE9jRtfVl0iIBGYEgL559sYA5qetOvmuG7GLTNlWxonoFmIZ7ZWIf+IN11RnlLJMrNEQCIgEZAISAQkAhIBiYBEQCIgEbiyEWAEtAEQs6DjrXcLBPRmpeknW5+FtAEPrztTdcMdyg0blLY9ysJt85Zs+9DfvpA2YVxnC7xr/MXSFA9uaIKms6UKszaLnAy/CsDMJSsr2raX+Q9VtHbXtj9+/f/52RnGT4Oq6jzwMI89zPxzGaOaNOCOVWO1bQ8xIrhtHyuuef1vvWsPW9LQzr+yijM6mqQxOjlrsQ/jr+MW7H4JZv7WRuY9vXhfxeJt9UvWfPX7vZyA5lyri4A2AH73/TvL/E8qjesV33albceS/7PxTD4CM3kHUyMmEinNME8MQG3HXYp/T7nvQLnvgNK8c8Z1q375Gs9lmZZuZy04EYD2NzxctWjtvGXHlFkbZ85b+6a3bXi5l7mTR2y2NGJQgxWb1fqlDyv+bUrH7vKOXbW+De9+3z41FyaEyswJWGmkjPGbMdWgZmE8AbDmEFR3Pao0b1YW7a73P9XQ/Nj/971f5h29tZyHem52zDQRhA7BWarcn94ISAJ6ere/rL1EQCJQOgJ5Atq0+fDI5Etd2JYJqg0Z28paRtayDIv/GZYlCejSoZU5JQISAYmAREAiIBGQCEgEJAISgasdAds2DYC4De2cgGYrELZ2V7Ztruq649U4vNwPi2+4qfz6NUr7dqXzSFXLpj/70PFElq1il2bss50FO8M9fnUwTEjpkDDZKneMFt35FFT5H6xo2660dZf599d2rPrwlzdFOZvMvHlNFYwM86DmTtAqwBkNfu+9Gyv8GxT/YaX9gNKxbcYNa+7bDBGD0dxnY0aIjCk7Fxf1sZgftwUHX4G66x5R/PtmLXu6rnVfpW/dZ/7tVYP5E+PihTb7n3O7ZhanNeh4y+rK9h1K6w6leaPSuf4D//gSMsAUV4Q1cf4sVdV10/75Cahtv0dp3Vfh21feuk/p2rvwLY8GNTbJxLqH0/CP335lhn91ZfOuhvajVQvWLWy8c88eZqsGcEZnlVUBes/ArNevUDq3VtxwUGncNqute+nrn8jk6W+qNPYxrDejnvNrBvKa6xpkYgD/vSJZ1vW44tuiLN7T0PZ09fwHNuwYz1c0Kwnoq/13ernslwT05UJelisRkAhcbQjkBwrsyT5nn9nzcVNVzYRmJHRz3DQlAX21tam0VyIgEZAISAQkAhIBiYBEQCIgEbhACNg2iwEdA/C/7e7qto2MgPbvr2zfOPfGFadS8PffGFGa7lU6tihLupXFOyp9q44/D7YF0Sz6PtsZYOsJ8gDQWRMSOsQYAW3DmSh8/YeB6o5Hytq3K237y9p213auuHP9cAxgPPde6hmww2BhZA2IGbBuB1Qvvr28bZPSvk/p2Kd0rXvrx/b0qUyjajH+OccC4xRP/OZ+0CZYEQ2e6YWK9rsqO/fOWvZ0TeuBypZtn/mXQUZAMy6WnyPMEMGGX78KczpWlPl21V13TGleV7Zs5W3rmZOyxaOLGKyufMufBZz/PfRcor79nvIcAb2n+sb97/jrQypAWtMx+64jUNN6l9K4uqp9f03zvnn+x2+9PWBZ3AqAjJ2xwU5qxmga/uSzzyvzH1a6dikte2e3PTdz/vK+vrNNi6Qz7p8loPNsPHefMjXQYwB/9aWnlPY1StsOpWlf1eIj81ofHhhj7cIZ7zwBnVPMNKE266yQY/jPli0liQCAJKBlL5AISAQkAqUhwAcKmsbuvGx9DBMefvzZXQdOneiJxpK6bpqmqVl8Y+7P0gO6NFBlLomAREAiIBGQCEgEJAISAYmAROBaQcDWAc4A+N62vLJtc5n/UBknoN/6/iP3boWKzscb3nBQadnKQiS3rfrJSsMwQc9ASmN+zmmwsmCaNtK0mgVpHoJD0zN2Jg3veO/m6qUblM7tSudupWN7bdedR07ws7hfLthRsCNgM29jA2A0A3/58UNzuzYzCpUR0LvKO1fcvSFzOsN8qgutW8jhpyDNbB1CLarDzwdBaflpVdcepXFP2eJdte07/+W7EQtXSGQzQhNZaCwUANZvT85bskZZuHv2619Qmh6vveHuQ68y526Tx6rOEdBYisBF7zwUrW+/q7x1V5VvV0XrtvIlmz/93deSAKoJyRgz7F0f6K7t2Fx7/aHy9j01zRv+8L370yqS4BCKhDNGlIcMseMGfOcBTWl/XGleX3/DM7VNz9TMefBAN2ex897LOQacV5ctGck/SB8bnP1nMT0Arv+TjYp/I4sl3bJXmbXpxrduSjPW3i6BgCYymrP810q3lvW4IAhIAvqCwCiVSAQkAtcmAvlnubx2AgEdzcJX/n3TjW++9YbfvvOvPvzg/54ElS3SrBmWhQGgZQzoa7NDyFpJBCQCEgGJgERAIjBFBMQF9EqRp6heZpcISASuLASyAENpqPD9jC0Y2HqQhWBu3/DuL/a0/ck+xb9Wadul+LZXND/wle88rwKYnAFlS+wYucsD8xa2GLtK9Khtwosvwfwl9ynt25Qb9ytdW8qu39r89oeSBgsfoYHGKGVcfwfMLEAcYN/LUOe/u7Z9t7JgT1XH0cq2zTf83pqszhx0dcah6hSOmaZ7OZ9oZGSBhaFOWnD4f6F+6X1VXXtmLH1m5tIjdR1rvvHDQfTQzpG3OV9mxnyrAN+46eVZHeuUhfuUlr0Nr9vW/o67IybzWzLYwoiWZlsmhu4wbWBBPjSTvVgLdz5+qq7r9sr29bX+jdVt65Ulq//nESNmQUYDy4Cde2D+svVK0x6l/SizpOW+F16BrMloevaxTZNVmnllj9uw+QWo/a3HlbZ1Svv+ysYjdQsevntFgCHJcuYRzvcXRJi7g6PfOQMnBvD0IFT4H1BauhVft9Kyc27n9s/986tZGzRmrAbAPKCJyEYA0Yuae0CLiFKufJHy//RGQBLQ07v9Ze0lAhIBTwTo/sly5V+V0gGe/mWy641fn9V4e+3cu6/77Xs37BjPsnUzDGKfJQHtias8KBGQCEgEJAISAYnAdEEgT3qU+n+64CLrKRG4RhFIm/Dr01Dpv495H/sPstX/2jd99iZQWpaXXd+tdHVXtK17+59vOh1jpCmnme38EoIksHTLYly0aTOy9evfPjZv2ZOKb7fStq3irfuU61Z87ae9GRa02LCZo7DOKGxGRltJgCDA9x4cqWlbVdt+uLrjRWXOtuqmh7/9g2FOnILF1jbMmq5gERMIaDsLYCV1WLvPUBbfVrvsYFnrkUr/7mrf3fetTjkJaGZsjvj+2JcP1PnXlzV2K637Z964/j2f2hQ3WMQPwzY0MAzLYn7PGHfZUoExzLoG8L37flPXeWd1GyOga9ueqLpuxUP7IWpw5tqE3/2jtcqixys6jyqLdtVdt/Vr3x1K6GwtIts2HZ9xG14YBcX3E2XphvIlByt9R+qb13zrR6+k+QKPdAkW+x2f7VqcVmbRSzSAEMAjB9IVvtVK0zGlubusZevcrsdvuiueNTltzwloDLWBeiQBLeIpZW8EJAHtjY88KhGQCExrBPIEdP4/f3fJAHj+FW3ZW7+1uOvBmYuXL3vTvU9sirIn2+wRvu345M9kgyvxM61hlZWXCEgEJAISAYmARGDaIECsR4nCtAFGVlQicE0iYEdVOPwrqO1cIRDQ2+p+a7eyeLXSvLusdYvS9OOdz0AwCSpzdibSWRA49Wxx7x/TgmMvQdON987s2MK8gFt3K/6Vc9/+0xdG2NKFLCoEY2GZLzAR0KMWvOMDj9e1Pzmj62ll8VFl0Y65S1Y9/0tOr5pggaEz1+Nc9AlRYBw0TthsAyy2BuJ//Oik0ry8eukRpaW7rGVznf+WF37Dz2RZeShobqTFvYLjADf84QNVTWvKm7uVtv11N6z55u2/iRpsLUHDNtiH+yznCWgdIG3xFRf/6Xsv1rWvqm7dXevbWedfO+8NK54ZgIjOXKofeDjTtPQRZc5KFrTEt67xLU/0Rli30djKgabjMw7Qk4byZTeVX7dB6ThQ1XZsVufmv/lCd1xjHst0BRa7HVY3v/Qio9aDNnz1Jy9UtjyuNB7hBPTGeZ0P7n8G0gY7ih7QSEBPnNuyPYuVg6s45tZyzAMq5s2XKdoh5emBgCSgp0c7y1pKBCQC54RA/laZ/88HN1kDnn5JX/Lb35nf8WD1/Huar7vl/kcDWbayhJN95q9GTeCd84rOyRp5kkRAIiARkAhIBCQCEoGrDQFiPUoUrrb6Oe0Vq+k8xvdtG2PWFjzolYiavXLIYxKBy42ACWYkA1uehmqRgG7bUXPjYaV1e3nrnvLGB7/y3/8b1CCG6wUWIaA1i/G0wJZ8h7/9518psx+sbN6lLN5dd8NhxX/PJ76xYzDLHJoZ75xndW3b1rkH9LAGFU3frW/fPHPJcw3XvTT3+kOdb34ka4PJYzdzF2RL5J1JPhswgkdt1gHe9cG9s27YoXQcVFq7K/wb5nT+T9r6f+y9CXhcxZU2fLXL8oKNZVtLd2vzgm0czDIJX5wQhg/CZDIJCSHMTNYvyZDJJOEn65BJBkhCBkjCYgK28b4v2PJuy5ZseQOMWcIaMLYWa2ukVrd7Vffd7/mn6nSXSr2p5Q3Zrnr6aZ1bt+rUqbeu+t5676lTNGxIlKuOBmJGAvo0wMiKh7Mnrssq3SfZ6/OnrVhe5/ebSECruqWb/R7QAKZh6jIAhCz49k+PFlasz7UdLCxvHGnf5LhuwYcKuFWye+HMG1eOsq8vmrJn9Ky6gqkLn90Mp02yOaNO+O94AjoCcNwHU29bnjd1g+Soz3IcvOKqupu+vNWjoMd09MeJv0aiXSa/SUTUAXp0+Px3d+aWr5dKD0pl+3LKn7+y+ul2DwRVwnozAjouhgkSzQPZ5/QcNG+FkC8XBAQBfbmMtOinQEAgcAYIxPhi+tciAbI0zVAMOPYuVF3zcGHJvLEVq0um/HHe8tYIEtCUocZ7O7pC843GtNHbO39CyAIBgYBAQCAgEBAICAQuUQR4QjYT+WxgyER/JmXQBr4kbjTN5wxVZv3Ciqgw6TevmQSBsyzTNA3diMtnCoUgEBhWCKgAz202ciufIx7QdhqCo2Jv4bSX86sOjKneetX/WevVoc/CeBhGKg9o1YSQTByVG4/B+Ku3SCX1WSWNWSW78hy1I6oe2djYQalQi1DK0T39CIWqgd4HsGSLMrJi3sjKOmnc3pFTX88q2/Cd+95QADQa7TgaAyOZBzShvAH84bBukeCLfzsBWeP+IlXulqa+mH3VUal44ee+UdtngkbjU5OisSDKBtlBEQ68AUWOuTmTnpcm7ZFK6nKqF77UBGQvQdB1CJuWbBl61O+a8sdKRA3J4PTBXf/2QoG9Nrv8SF7ZoZHlG7/4zb0eBTr88D8L2kZWLiysrpPK6oum1V5/55JTGlGIzSLny3+rAG6AW761uXDKOqliH4ngPHFt+fVLfUCiebAfEP5qIaxzNM4kEVWAAKHRH8q11WaVHZRs9bmONbfctcurQp9OYp1QjlqN9ZtYgp/YX979mRHQfINCvqwREAT0ZT38ovMCAYFAegRi91T6lxLQhk4edP56HKpmP1JYsmBMxaqJU//4zApBQKcHUpwVCAgELgsE2NzmjP37LguYRCdjCIjrJIbEJf6X/2XIRD4DOAzdQIoW6VrWiqZpKpc0TSMeiBmkpDYgEZyUMk6VyTeVVGeaTKbT0A38YA7qZBVJ/AGyM5hIAoHhgkAY4E/LvVEC2rGfxICuaJDG7y2o3DfKNv/ppf4+g/jS0m3vUofgoJypOwyz/36TVLKVxCMuPZhXtiN74rxv/fQFsgseiZ6s6WANJKDNPoBH5nlH2VcXOfZJEw/lVx+TylY/+MdmxSQtMr9d5vUcJyCIYQO8YXjsaRg/tUEq3yPNeCVn5tHs6uXz17lk3IOPOl9H2WTqrB22YP0eGOlYmFdSm1VaL5Xvk+x/ae4DvyUrIJtW2DIHEtA6hINyn0z2/fvYTavzHLXZ5YcoAb3hV787HjagxQOT5ywpml6bP7Vx5NQXsssXrD0ScNK2kHKPcb6xCSvd1tAH8PWfNeRXrcytapTK66XyTeM/tuKkGyJ6WgI6eu3oKsBfm2CU4/Fc25as8kbJXpdbsey7v3jltEbChdAQHCbuQMiQTEZAYx51OB8uV6WwY1ggIAjoYTEMwgiBgEBgeCIQu5/Tv5SANkmsZ3jzBNRc/8fCskUjbSsnTH4sKQEdNz3Ad+QxhcOzu8IqgUASBBKv5CSFMsg6V3oyaOpSKPKRE3M4Xvx3elj5kkxOX2XQs0zPR47GoKZ+JAUuAVgugS58JEN/0TXK/y9nImfYQZ4OjsQST9FalhWJRMI0oaAoyqAENGsdr0/mfWzohjZYYkwxEuJxbTHNjCVnFDOy53z1OE6ZtY46eVWmaSqKwucIWSDw0SIQ1OE/n2jNn7ws27FDihLQ+6XxDdIVq2bOWRKme9mZlEjFIBsJOxCS8MYAcDoCd//w7cKqrVLZHhqMuDHPtrH06nlvnMT+mQbZTtDkCWgDCAH9g1+eGOXYUlR+qND2ilT2QnbZ8nVbZVkhk7hoxAkqxFGoBhAuOAJarxJ2K9B2GkqnbixwvCDZD0pTXpCq6sdeu14D8IUJka2h4zD1BMa+hE14bEFkpGN13qQthZUHJPu+ohlL3MSh2K8Q92dCQBNPaCMWb1kHLWLpFomtXFz9RH7l+qyK+lzbwTG29X95tkfV4YE/eYpqlmddtTt7xn6pYuPt3z0WBPBRf2WNxt9IJKDREfvBp9/OLn0ut2K/VNEoVe4onLqi4Q0Ip/CAjro/07BAJsg6wOINoTEVC3LLt2URDn1XbuWiJ1b2ejSIUK9wCr2Z1gPa5FyqGd4f7SUpWh8uCAgCeriMhLBDICAQGIYIxPjiGAFNVkCaOsA7zTD5hj8Vli0aYVs1fvKTT6/o6CPPEtEdMPjJVVynYgrjssWhQGD4IoDX89nbl+b/4uyVs8k838qg8pDaHVRbYoGh6k9DVQxJ1TkpPNTuYHmeTMGcszGGt+Fs9FyqdS8B9tYkc1iRBkeA/3Hg/8viZCQ9B1eXUCKO90x1qGlaHCuaoCl5BrogD0beElflzPUz9tnQjUgkEoglWZYVLgWDwdiZgN/vD4fDcYEs+N8ZXkbaOvE7RnSn+8uPC6+TRyfEpd5kyUVTTywFAoFIJII0NK+H7IOmG+FwWFGUzNGL0yAOBQLnFgGvAj946J3c6uWEgLbvlxwNUsX+3Opj0thFf1rYRVhgk9Co6HpskdkR9YM2gawzpbkWcWyG3z72nlS8SConnrxZ5fXZ5bsKHEsefqbLp0DAC5aqGWQ7QXojiQWRIAysCV/59uujHbsLS/ePrnpVmnQor2zF4VcgIsfY52hhFjuiv/cGIaBVv0HCg/z6T235pZulSUel4gbJvmfkzLpf/CnojUBEQwKa3r84ArrPhJ/9rntE+bqCsm0jqg9JZXur/37HhybIEFIx/oap9hPQ2E2q4+0WGFU5L7dyU1bFnlz7vlH29Y0vwDsnoXjyPGniEql6lzR5W8GU+ZtfALdODFPAVCzVIEixmWVUMGgMjefWdEjjns0pPyBVHJSq9uRUr13TQGju2M8Ro8Bjt+AYIACKDvDzh5tG2FblltVRD+hduZXzNx+y3CppOuZQ1R9BO5ZDzxE9aAlCiiE4UBbfAgGCgCCgxXUgEBAICARSIkBvoSYNF6aTZyKLLNvULPhbK0z5uz/nly3KL1lzZdW83z5+so+sI7Oi91z6FIX3+P63yme430xK28QJgcAFQAAv40R/qyE1HXveHfB3SBrSF47+r9FCA9pIe5BeJ3/2vOpH5chW8B5zvAEXWE4LW5IfsjTlz8ZyhgwKZ6Pqkqwbhw+7hFJRh3H5w4S8RgIaacc4C/GQJ/L4nEGvCgxKMCRCVpZlTdPOABlDN7gYDylFv98fDAaxlcyvSeQWOa5ygMjY1SBNPp8vGAxmzkLKsux2u3t7e72DJR9Nbrfb5/Nl7mwbDoddLldPT4+bJs9gye12B4PBDMExTdPr9XZ2dnZ0dPT09DAK1+Vy8bLH42Gtu93uQCCgacRzcdCkqqrb7e7s7HQ6na1cakuROjo62traXC5XJBKxUiS+UTS+tbW1s7MzhcoB2c3NzU6nM+n4qqoaCAR6eno8Ho8sy4m3bN4c3gYhCwTOAwKE0/zf1aJ3fH9/lmNpTsXuLEcj9cNtlOz78hxL3nMS3pQm1QTdQPqYHpPN3CljqYRBDkPt8zBizOM5k3ZIkxqzqxul8eukSSu//N3XgwYNwUyfRwwwoxpijydkM0ADbrvjpaLSuoLSHdKEXTllR0Y61r71PuF+sZ0Y8Ywez7GaeJLM3Ij9+4/CKNtz0sR6yfGWNH5/0cyDJdULPnifUL4x322VkL1k7keSCRC24JYvNeZO2DDCUZfvaJDs9dd/+UiQxOtQVVBNUycBoFmEZNyqnvLttS9CdtXK3Mq6XMeBfEfDiMqNb7vg2//53hXTlmXZV0uVWwpnbvinf9vmp6E/cJMhnYQSSkJAk+gYALsa5PwrFucUH5EchyX7bqmy9t8f6Iz2nhhrAPTRTwSs6O9hjDa2ZIDbv/GSVLJdKjlMPuV7ciqfeb0DTuug0G5qYNAPaUilPtGGBaFQDAkLwIj6R1NbcKNJBEl8CwQEAS2uAYGAQEAgkBoB+oxhRvfz5Qjo99th2scfzy9blDdp7ZWVi3/7eCsloMnmMPSZhrzGxyQI6NToijMXAQJ4GfMc0BmwM/zUl6eQeLW8zJc/3xidQXeGZNL51j8kY86sMD8cF7I75+Tay6TL7NrjW0xKhvJXLxbOUD97tcDaSiPwgKfXjxyrpmno7pmS+Ex2Ap1A0+vHs5qmRSIR3xBTJprRcxO5M6QIE7+dXOLPZngpGroRCAR6e3vbk6U2mhi12NnZ2d3d7Xa7vV5vhvZrmuZ2u5PpTpLX0dHR1dXlcrk8Hk8m+i3LCgaDLpfL6XR2dXUxJLpjCXO6aEK5vb0dOcpM9Jum6fF42traGAJpBMSqqampra0tQ/s1TXO5XC0tLc2x1DJYampqcjqdkUgkE/vD4bDT6WxqakKtDJ+4XnR3d8d8iHu6u7u9Xq+qZkSIBAKBzs5O1M/rRCgSv1taWpqamjo7OwOBgJUi8f1yuVytra0nT55sbW1tyiC1tbWdOHHC6XQmvmBQFMXr9SLMTqfT6/XKssy/feHN4W0QskDg/CBAONyZNy/Nr17XT0BX7Muy7/j0XS/5aQQJMj8ia0qjfrvoEm3QUy4vBMKwZx+MHPlne82hIvvh0dNekcq2SWXLJn9qQ7MbZJxs0croQ0044BiNjAT0x2/enVu8ZVTFzitq9hfYjoxxrDvyKu0rcdE1YgS0RgNpxGrGsDBUcHvg8189eEXNztzKF6TKY9lTX5LKly+YHzADoIdIOco6D9hhDwno6z6zPWfSpiJHfXZ5XVZVAxLQYdBVyzQJc2ySyB20nmVGGdsIwB/Xg1S5Mbtyf67jUL6jIb9qy8pDUDRjSa5jRWHNlsIpW6Xyxw6/S+oZBDcy3zQogjyAUdkCTYMPTkDRuMWFk17Mrjgk2XZJlTs+9ZWDFkAkxFjoCCWgg8Thm/YGna4ArJAFH7/joDSpTio9SD7l9TmVT7dFwA+WQm3XSNxtTaeQE7Y5hp9Gd0JaHgAAIABJREFUNm+EcJAUMqIxVFTKmUc5+hjA4u9ljYDwgL6sh190XiAgEEiPQCIBjW/FW3pgxifnFpQvzZqwelzFoqQEdHQ1Ga5p6l/ZlL5BcVYgkBIB0zRxMyWNpmScEsnDszjzxDlnSo2pT7BdmxRFkWWZrTRmc1q2Hjy1jv4zaAbSZEwbrhfm1knHi7hVVL+WwSR+gp1eHkxT/Pn02hLPxtcf7Bi5SCQ3eeTjEYkd49BnTiAyLhWVx9QM8hedUhM96eJ6w3OgOLhsxXooFEKvTLb+nQnBYBAjscZp4w8RWBYX1R9LTEkaAf1MMwnvYJpmOBz2+/0+LnkHS36/X5ZxKSpvchKZ6e8YYspQv6ZpoVDI5/O1DzGFQqFMLiFN03w+X09PzxDVtydyZIno4G8aEqxtKRKyq/jNF8nQCTcSiXR3dzc3Nycyn4mU4smTJ5ubm9vb27u6ujKxHwBCoVB7e/u7776bCT5IZXZ0dDidzkQ0kub09PSgVdiFOJvxELuGMrKZbrc7qba4TFVVe3p6mpubMyA/m5DcPH78eHNzs8vlilOV9DASiTidzpMnT56IpZODpePHj3d0dGToBB0KhTo7OxGf1tZW9h/Go4T5nTR1dXV1dHS43e4MPaCHSkC3t7e3tbX19PRk7gHd0dGRuQd0V1dXS0tLb29vItqqqvb29iIDjiPldDp9Ph/GG2H3a4umxOoiRyBwbhEwLDgdhhGVD4+YsjXHsYd6QB/MqqjPr9h070Mk/gZJxHuWfhPiUweQTSDb3+H+fuvq4IryZ0cWbxlTeih/0p6cki2F9g1l1yzZ9SpxwlWT0K7ICEf7IZvw8Vs2505YRwnoA7mljQVlq2t30bPIlkY50/7pGSPCdYAeF3z/R6+NcSzOr9icXbNbqtiWO3nr7V//a5BSz3Ig2krcHySgy2YsLijbkle2K6tst1RZf92XDoYAwqCqFnHVJr3mCGhKIoNfh2/95pTk2JRXua+g4mBBRWNB5Z6pt7wqla7Kr6jLd2zPsS35zn++2yuT0B+UOk9LQAMYKvFHnnL184WlDYVTXpQc9ZJ9+5gp891e0GnISGIDcZ7WAIL0QwhiDCUCoHlVqJ6zSSrfnWXblWWrk2z1uVXPdmngAyVCPdRpNxTCP8eoZwAS5fr1dvjCPTvHT/3DZz6/UI1yzmHS+wGDEwebOLzsEBAE9GU35KLDAgGBQOYIpCKgO71w9afm5tuWShNXX1G56EHqAU1e93Ie0IKAzhznMy6ZoRPcmenH+JJDqotkHOP7Ugk84ci6gDNDdpjYrqZp4XA4GAwiwRdKkcLhMEbAxG9Gowyqn4SX0UgITlVVw+Ewqsf13X6afDSFQiFsIhKJZBhxEptWFCUYDDJVHo8H5bjvQCCArCUuV8cmmPGJ+CBBqaqqLMvBYNDr9brdbo/Hg9am+sZWcKkypE0Ii0wT0+/1euM0M8bSQ5PP5wsEAplwZKZpqqoaiUQQHK/X29vbi6E/03zjkvlIJJI5x9rb24t+k7zXJPJ6id9Op9PtdodCIYxIgPgn4oT5hm4Eg8Genh700+S14er4jo6O9oEJOTifz5cm4gEqR3zC4XAcqZT+sK2trbu72+fzqaqaeM3wHTF0w+/3u1wuZG3we6CxSY46Ojp6e3tlWU6vHACQwO3u7k5vcOLZnp6eQTloy7JkWUaCOFFD+pzu7u5MOOhIJNLT09PS0pJeW+JZv9/P45xUxl8b5E/bkiVUG9c6FvR4PIOCHw6HMcpBc3NzooWYw1+uJ06cQAK6s7MT7ceLMKnxZLpumqFQiHfCxb6k+uYJ7lQ64/JdLtf777/f1NR08uTJplhi1ypmIKnb1EQ44hMnTrS0tHR3d8fpSXpoWZbX60XalOlMJbS0tCDyTqczk8HFi7+3t7e1tRUBaW1tTTbI/Xnt7e1IEA965WN3VFV1uVxtbW34zgCHErlm/tvpdDInaPQOzpCAHmoIDo/H09vbGwoRjgqvnMRvfiDQbdnlcuHPfu9gqbu72+/3J/3NRyjQkxrfKOCV3NPT4/P5kBDHpgf9r+EtFLJA4EwQoKTk305A9qQ/5Fduy3HUZzkOShWEgC6o3PLLRz29GGVHo0RylFElP6gqpUJPA/xhZWvR5LnSmCXZE/YUT34lb8Lm/AmLiic/s3ST0qNBiFK4jC/mBWatasJtX9lRZF+ZV7Ixa8I2qWSvNGH5glU01gTjTDF8Ba1jUp0Kpb9DFvzgvrdHT1qUX7Y2u6JWKtuQXbV61JRnth2OqtdlSqgyByMAne6maNEQHEVlfy6078wq2ZVVukey1117x4E+4mOsEwIa2WckoEn8ZvRihtMy3PyNFyXH5tzKvfmO/fTTIBVvzC7fNXrKC1mTNkjjfvt2G2HoDdz4j0w3raQBoBnVG5bhtjsaCQV/1SESgLt8R4Fj0VMLukIB8PtIR0hMEJ0E0FAtE4OIxGJZ654IFM9aKtl3So4t5GOvz6uc3yWD19AilHsmX5ZCzAcIU1I+2Ad1R+SyTz5deM1yybFCKv3tq++gY7UgoNlVKYQoAoKAFpeCQEAgIBBIiUCMgKaPN3StFCElAVxB+NhNT+SVL8kq2zCmatH/999v9FlkvREhncliMIt8cD8N7gEl2gyJ2YUMZDROR8rmh36CeSOmX/GNkyI0gk2QMmmNkX2Koqhpk0YTH+wyk4ZwKyEk++L2EYpz10TCMRQKsZlqhvrD4TDz500qIPeKHGggEBiS/kgk4vV6/YMlH01+v9/r9bK1xsx+XmCDYpqmLMs4TfXQ5E6dcBqLk+FgMIjzVV4tk5l+ZLI8Ho/L5cIV6KgeydCeWOru7saJPcbc9Hg86GDF9KQSTNOMRCIejwcjdbpcLqaKZwqY3N7e3tnZ2dPTEwwG0RWa2cwLrDnkQHt7ezs7O5HmYN5wSYW2trauri6v18sIeqYqTsD/KQTf6XS2tbUhEZOoFnmcNrqevaWlBZmUQf188b2Cz+dzu909PT3oo9dOU1vqhG59Ga4l1zQNaaCmjFNzc3NHR4fH40nD1LCBQI4SkeG5wlQ0HC7Jb2tr6+3tTc/RYxORSMTlciEmPMg8pYhQYRmMxIr62f8vpEimaWLsVH5AWVtxAhuQlpYWXGiflAxi9BOy516vt6uri7c2E9nv92dyccqyjOw5sy1Dwev1DnpxAoCiKN3d3cePH8/42okWTD+y/Gh4PJ6TJ0/yV0tzBon9cvKqEmV0wn3vvfcSXW/5HmGD2M22traOjo44p1ErlvgmDN1QFMXn83V2dmZgcvP777/f0tKCnCCvJ41sWZbH48ELBvlZvFA7Ozu7urrYrzEe4rul7u7upE6ySVvBFyQ8C59Kdjqdvb29Pp8vFAopihLDg/xNqhkzLctiNKt7sOT1evGeO+iVz1rEO5efrmDwD0wBmoLBYCgUwnu9LMuZ79SHHYw+q5FYq/2Jtc4Lacr31xyIFZ8/VJlvGrn+YDDY3d2Nv37Nzc34xqK1tbWrq8vn8+HDGGslrro4FAicSwQsElV401Z3bsmTORW78x0Hch2HpKoDWZX7pTHrv3ZfuzcWAZr44VJOWDHBS9cUBQB+8uc2qfJJqezZkR+ry6/eO8JRN8b2/NjSPz2ztM2nkSDLfk3FSBTRyRblXJGGpr0gMZBVC376+3fHTF6SV7pBurI2u7JBKl/9hW+8GJIhEo721TDBigXjCVvgVsEL5HPPr14dV7O2oGybZN+UVbW1cPLunPJ5TyzvwnokhgZG/eh3ngZVN9Ct++ibxijHk3m2HTmlu5GA/uJ/fEBdto0BBDSZJBoGGDRSBXT64Kpbt0uVu3Mce3Lt9bn2+hzb3qzS+pzy/QWV+wodKx98wulja66ivDluUMTT7zE59pP8i982FzmWFk4mjtiSvS63YuuVU1b9fi7sfRkeXwxf/MbLV9Y8dO8fGlwmjeNMwk1aOhgGHZLCqqel0i1SRS352OvyHEuOvAU+BYIG5ayDQVLWVNADuvc0PD7XeWXNU/kz1knTtkk1OyX74y5CTBOncMLqs7kwE87lBSd0XWQICAL6IhswYa5AQCBwIRFIRUCflmH2zX/KsS3KKX+eJ6DJTAwJ6OhuznR1Ene7tQxTich9URfPIHMv9Q2WMum1ZVmqquJy7PQTPWQw0WcTPWoz2Xoe9QeDQaQp07hnsi2AcMqKfoKDznwM3UBvtVR+TIydxE2BkMHE5a48WZAKK6afRYpMJaAB6LbpcrkynGwrioKugm0ZJyQjEJ/0E11cyI8EJe/HmtgFhh6u7XW5XJnoN3TD5/OxeJRMLXIcjJtrb29HngW5m/b2drfbHQ6HU9FwbCzQVRCnx+gni+alYuKQjerq6goEAqqqMnD4gUbiQ9M09H32+Xzo5Mv4xzTjgCS1y+Ua1EMWPaD9fn97eztO6dla+Dj92Be0HD0WOzo60P40HA3qRw9i9BdGjpW5DfLEHJORTXM6nWmCmVo0YZhdl8vV1NR04sSJuC6kwh/1d3V1pacRcdxlWe7p6UllcKom0I8yDcGNHqbIgfb29vIEYhzyeIgG4PXZ0tLS1dXl9/vT4IM0MXu1gxX5y5snKFHm2+3p6Ul/5eNFiy8Y3G53KhxS5Wfi3o4EN148vP2ZyPhqJ82Vif+8GEO5q6urfYgpcw4RI/nyN5TYC690f9NfOWg8uyd6PB683/HfPi75acId9pCvTPObg8rxP4tx0KEMErK3mVjOmsCrNBAI+P1+PrgNrkRh71NlmvjXtLyG9DJGccG3EXyv42RDNzSa+HyLpvT6cS0R1lVp4u1EGfM1Tcv8suEbxSaYYWhVnG18ZtwpXhWTsUx6nawwDhNvRmJziY2mKpNJPt80ax1d/jFgDr7na2pqwreVTqeTf2E86D9+nH5xKBAYAgImmDLMW9BSZFuUW7E/334o13FEqjogVe/Pnnwgt3rltiPgVUDVSAgH04SQRqJqdEZgVYM556vbJMeivCnbpKmbpCm1km19XsXq4qqnn99i9cUYWMWI+vnEEdDUQpO6VZMo7xsbYVTN3KKK2lHVBwtmHsibWiuN+t2RYxCWwReAgEyYbytCAjrrlBAPALzRCV//2Qv5FU+NnrYvv/pFaeJ6ybZKKn/ugb8EvAbZ2NA0VRoGORb8mDRJYiDrFuqAI6/KRRVPZtu25ZbVZZfXSxV7b/76q4yA1nF/QM0kwTgsEkZZBU0BszsCV85aXjDtULa9LsdWl2PflWOrk4p3F9UcHDO9rurG9S0fxuCXQySIBw2YQTcoipHOJIt9oqGl1+2E7NJHc6o2SZX1WY59OY59BY69I2zbsyYunzhz58QZ+8fPWDf9H57tBRJT27II+6yDZoBiADg+sV4q2Uo9oLcRD2jHioWrfb4+6KNYyQGV2kC2gnR64b7/enucfUGBfaNk3yxN3ilVrf7eQ81BEuSDhOMmI8ImwkyIdUj8vQwREAT0ZTjoossCAYFApggMIKDprZ1MDABCBlx3y6M5tkVZtk2jqhb9+AH0gKbe0eQBIOb+bEZfQ+OzPnMyRYqQJwrbB0uZWGzoRigUQldBRlQlFZDyaKOpu7vb4/FEIpFBZ8XoZOp0OnFik1Qzy8QmMB4lW2iP06pUfYlEIiyeI9I9ab7RC7WZxutEV0FUnmZahX6aLJ5mJhzNyZMnu7q6wuEwU55Kv2VZ4XC4o6PjxIkTacyOO3XixInOzs5QKMRmuYkEK8KFBDS69yIdTEdvkC8kuJFAZ00k7UscAd1OY1kyZ95ErLAjQyWge3p68OVBe3t7Kt4N8/FC6urqwigQzPhEfHgC2ufzMRcwxqEnFTo6OvDKH5SAZjF2mdd2UoXd3d2Yj16KCF13d/egNCLqR9/wzs5O9CMedK16S0sLgp+GIEZqG2lcn8/ndDozJ7jRgzu9BzQjiEnsP7+/ra0t7vLGw8SLB/9tPR5PJh64eP1jJF989YJDzF6KoIBvp/BH1el0opPpoCFi8H/BNE3c6o1xoInEJ57qpQljvASDQSTLUv0mICuE9ofDYc8QUyZMHK50wYUjjJ3MUMgcfMuyQqGQmllCnnFIMegtywoEArzZ/G9UKjnVfYTPxyU7LLIQ2sa++RBJ+AvDXzCDtsvYRuSg+XbTyGmuljS1Ek+dKz2oGaHgf2aTyvyw8vgkmpc+h6/Ly+lrpTqLGti/WyIyfBNMTqWN5WNJhgOrmKgfq6Qpn6ounz9UmdnJC+yNC94K8Y0ye+bB+NTsnWiqjvAKhSwQOBMETDDC8Mv/PDquen1exeF824tRArqmQaraKV21rahq2e+elLvdhOkMm3DKB+sOwz/d+2pO9cL8yVukiRtyJu+VKmoLZu3Im1lbcNXTy7b6gwqNV0weO6IWIftMPIn781hgacIuuwFGTfvjlZN3SJN2SlVbpMnr8yY9d8e/7FOoB3OQzthQl2WCNwjPrAyXzXp20nVrsipXSVX1WdNekko25X9s/V33H/UDBBRa1or5bMemd7EYypSHBmg44htR+WSWfVt2OSGgc2r2X337njCAYkW9tomXkm6BqVmg6KCooEXAPNkLuZXzC6e9kG3fSwhox7Yc+47RUw5Lk9ZnVz/78BJfH/baVEH1ksAZgxDQJLCbCdAdgpJr/pJbtZ4S0I3Ztv15pfuKSuvGVe8snbFPGrPxyikbb/tubS/l7MkrVcKL6zrIYQtu+ueXpdIdkmOvZG+QHA0F9o233La1L0RaJhS0BXIEFA1WPG9Mvm55gW1x0ZSdhdP3SZM2jpi56apblraFIUC5ZxKsw9QJOiIJBGIICAI6hoT4KxAQCAgEEhBIJKCxSFCFG2/7nxFlfykoWzmuau5P//tYhK5dIm/lLRqaKzaZwPJIJSDN0dXVxVz5mmhCgoZRt0mFBNOSZKiqiltRDbpcGlvEkJFdXV1utzsTAhr1t7W1vf/++xgrM43l6I3Y1NTU3t6eIQHNPIixbnqCEhlM9HMMBAJ8lIYk0NAsXAiMBB86sSaFGttFArGtrc3tdqMTZWxIUz5GYbxIdL9Nb3wbl9xuN0YiTj/RRT9NPhBB+2Cpo6Ojs7MT7WdcSSKBi3Dh2xG3243uySx0L7qBc/b2i3jlhMPhQV9dIFOJITjQO767u5t/DZMoY0xPl8uF+hk4qew3dAO3kkOataurqzdtwhjHmcQIRhpX0zQM0+ymifn4s0YwH8OeuN1uDOuJwUAR4VTfpmkqihKJRDD2SyAQ8NHk9XqTMpZeGuMlEAjgQnhGCSXqR/dYREyW5RBNSPPxMk/8oUOlLMuqqvJkXKJypHuY5zsSH2qypCVLuFsmq55UP2OUeCFVScxn14mhG+g4n55kYf8XaXh8vkW+KzxBnL4VvP6ZbZkLfNNJ5Ux2EUxaETs+qNlJ657DTLw4E8eXxzlO5qlSi6ZU9uBZhAgxx7pM4bkioFF5emPQSISd/c9mUiURHL6/qIH/VeTPnnMZm0v8PucNZa6QIRD3b5VoZFzOoE3EaearJ62bpnyqunz+UOWkNuDVgr9++FKto6MDQ0Kz5S+tra0Yv37Qn99UTYh8gUB6BEwT5D745nf2javZnmt/Md92NNd2MLdyl1S9VZq2S7p6f351Q1F57ciyv0y5flX1Devy7HNHzFiWM21dVuXu3MqDBZMPZ1fVjZq+N6tyWeVn1qzYD84+suugHI6QPwBqhIRCTkZAo4MxKWsAnAb4xi+OTJi8Ib90q+TYJFXVjqnePta24GcPvPNeG/TqhCG1APx9sHK9/+bPb7qieuGIqjW5NRtypuyQSrdJFdukikVf/tkrrSbQmMnYaeLvzHXfoAR0dMMDWYNd+08XVP5Fsu+Q7Lske13OlMbyT246TfyWSIRrw6JkuUFilDACWgc4/Dd95LSlUtV+EqzZUZft2JHj2FbgqLtiyob/c9fm0wB9xPHaAiMCoNAYj+SxgjhkU/qdzVWZAKYRoeExvvKD/fnVi7OqtmZV1OfYG7PL9uVM2lVo23Ll5B0jyzcWlT617SXwWBgHBQziC66bYAYV+MYP38sueT7Htley75fsDQW2bZPsy7/0lcbt++GdU/DK27B0bfDGmzdcWbn0yppdUsn2/OmH86ftKZ69uXz2UwfegAjFhfqsm8QfO+XMicNSiJcNAoKAvmyGWnRUICAQOHMEYsuaTLrNIECfBj/6yfrKmqfK7PPslQ/9+oH9ZPNmsh1DxCDrkzTcWcKIroICRVPbOsmmVaFQiEVKTcp+YibjQNvo7jrt7e2Z2M5vuBTnHph4iE20t7e7XC6MDzjobAQ5Powy0dzczGxrpymuCfQDRR6QhfHlJ+o43eL7pWkaC2KI5CkfcyNOxhjBuM8Ysudp7Me2UL/X62XOqkldWTGzq6sL44fgKnt+csjbjDKeNXRDlmXc0CzRgzIxp7e3F5fEYvwTZCV4KiGOHkIO1Ov1ulwujKTM2M9EAZ00/X4/gsPbz8t8X5BDxH32kPrkOVAmu2nCXf4wADRTyGvjZSyA8WH8fj+Spxh/JpCQMGQn224RaVCeXGDNMXwwh23SiFFlgikSrq/HkWLu1ThvRz285Ww+z6grWZYTTI5moOXIwaLTJc9Rxqllh5ZlMeVMYD6biYwu0meZcFioGaFjXBtDkqHHLDkD4SNUwl8Gg8ppusbqpinDnxpqeb4uk5mSDAVWMU44J/jH6fyoDjOEghU7GzuZkgyFVG0xHj/DgYhrLpXaIeWzlyhp7oBDUpi+MOtC+mIX/iwzjAlnbwNTFSek0hxXLOlhqrrnMJ+954hEIrj2BR87MQrTiRMn2tvbcQHKOWxUqBIIMAQME1x+mPPZTUX2XTnlr0j5O7Im1Y2uWXfTv74vVW+TqvdJFfsk287sii251bXZ1Vtya7ZLVdulss1SOQk6MXravjz7Fql42a3/etStQ8iECNkoj2z6qmnU+9bETf/IDn44z0IelpC7hOvU0aM3qMPfTkFJ1dyC4jWjqvYUVDTmlOzLmrAjp2TthKs3XP0Puz/9tSMVN24unrk+r3JpweT1WdWbpPINUnltVuX2EfbNxTWLf/zgsV4T+ogTb4TwvZiQTu33gI75RAOEw/DCq3DFtBXZk/dLVXVS5U6ppl6qevavvYThlSkBTfYRIqtjdbpzoakBhMBc33gqf8p8qXKvVNVAPhV7cx27y2YeKiz+856jJIgy8XjG4BVmTBjg9003KaKdp1wv0a9qZDr6WjNUfXJR4dQV+VN3ShO3SeU7SaTpio1ZJc+OsT26aE0oHI3CjX3TCL1Ou7ZjKxRPXDCirDa3okEq2yNN2l5QsnmUbVOhY2WhYzn52NeNKN1SUFKXO2mfNGGvNGGbNGl+9bW/fek1xRskoTmoLnRZj3mts0tECJc3AoKAvrzHX/ReICAQyAiBKAFtaGTnPVzi1bD/w29+fdunbpz/3f+3tmH/h6pJYlzp5HYfTCSgw4rc1tnR1NQUCoU8Hk93d3d72tRBE1Ku6ByaiZn86ku2ljyN4Ha7/X4/7vWXSQxoJONkWWZunoym9Hq9vmQpGAwqioKBHQclWHHWFA6HcRO8VDQfy0eekefjUqGE80BcKI3OQYm8XlwOutOib3LcNDKxFSzAmD40adBvxlRmiA/jFzRNUxSFxvxM/sWiaiIBGmc/f5jYFwxsigQo3wWeG2X5GTpgYouIP15vjAYdVEBw+GKJ9mMOuhKjnegwnhQdBk4kEsGLMw3pz9piBuCeWokxTNm2nKwKLyTFmbHeGCiAccTsP4U1GidkoplXjtUZMkwbrydRTmXzucrnWzwDnXz1QeU0+jOkDpkG1hbLOQOBKclQOIMmLroqGULBip3vDrKG0lwhZ0NAnyv7M7HzXLXFflXSYHIO2zpjVYjJGVdnFXlseZkViBP4MqnkuCrn9hAbZb/wlLAjTwuBQKC3txe9oXEbAAxvxR4qzq0ZQttljoBmwqleuLJmfoF9f275G1mTXsiauNE+e9n6RiiavlGyb5HsdZK9PqvyAPH5rW6Qquol+z7i/Fu6WRrz3MiKpROvWvzQE0pPECI64ZpVSkDrpqnHLm7m5UMJaG47vigTS8IkWwCnQzB/sWdi5XMjbZuzSuulksNS2UtZ9pdIc2W1UtkmIlS9KE0+IlU0SLZtUiXZeFAqXjDe8eST85yeCLgjqg5BC7xkwz0SuJly3cgFRylhPCD0tBKB905CXtkzkm2PVNUoTTko2XdLVfO3vxmNR0H3LyS+AZSAVoF6HFsA+9/1Z1X+SarcJVURDjqror6ocnv+hKd+80irJxJ1TyYXFTpQx+jc2N8o747sOyWgDQCNbP9ngc+ChrfghjtWF0x7XHLMlSYvlirmjZ+96MZ/Wtv4CmHBuWQR92rQDN2KBEB2wzVXPyvlPZZVvj3fsV8as524sdsOZtsOUJ/o/ZL9QFbZwezSgwX2/TklWwoc6z7z5boTp6iRVGksNErMhYtrSYiXOQKCgL7MLwDRfYGAQIAgELtNpkIjevs0TZ1wQ7SUBnCyBQ4eUU51kGOVfAydPCxF6DYOFt1NmLzqBgAkoE+2NIcVWdU1RYtjO+MPkeBDwoifxlBlg3yx8qnKsSkK21OIxa9IVYXPx1gNbKk+8omMfeN7wthJ1iI+OjILk05ikUbUNI0vllRG2o7XydvJy3EGxJ5g0/1FBjaOmkQ9vGaUz0B/nOa4Q9bfxLb4FlmxpAJfN2mBpPjztc6VnNh6OugHO8dr49EYrF6684k6ec382TOTUyGJ2tJZluwcb0Mqzbz9yXSQPF5Popxe89mf5Vs8A2189UHlNPqH+l/A2kqjc9BTTEmGwqAKL4ECGULBig2HLjNjMryKhlo+wz4ytRmWF8UyRIABGyekqh5XLOlhqrrnJB9bTPzBx50ScHkWhi9juzefk3aFkssWgXhykTrPqibsexlyJz5X4DicXfpqUfXL+eUrv/j/drsBvv3fbeOu2VSt81DuAAAgAElEQVRQvV0qqcu3HyH7E1buza7cK1U2ShW7CmqeL7lm6fd/+dqxdyCokDgaKg0JoVOXZySg8dsAg31o3AniUBz79E/pNICgDP/+08ayazdJ5duk8sbsypeksoNSxcGsafXZM/ZLU49KFS9Ltpek8sM5pbtH2jfZZ228/paVOw9EXGHi+0ypYsUAhfzIM+9j0k3+wAASc0I1NavHA+OvmldYsy/X8Zpke00q2ZdfvfzZjd0BIE7BZIcgEjdDNUE2iWezDyCggRIAmHHzuonXHiLBN+y7Cm277bNqv/TtjUFKIkedrfEii3Lf0Ssuhj+bclo0wLVGqWRDjcUH8QAsO3TqD+vefmjxB4+v69r3BvgMCOuEMTfDZDPGWJKBWKXIET3ghlVrPCOr52Y5NmaV75MmHJBKDufYDtOQ0HVSxS7ysddJjm3SlQvG1jzzg5+84g+QwNB9fVFlMdtIl2Pz7EQh1rL4ezkhIAjoy2m0RV8FAgKBZAjgjgoGXXcUN2GIFWe3zOhDh26RJ52gTN5G+2Qiq2CooOl0TwmegMbVYUhA97h7YwrJUrI0Cc1ghTMR2Dpc1oU0+vEU7xE5pBaZwybqybBuooWpJu2DWs76mEpDHGJYflC1iQX4hpgcp5w5hSVWT5qDeuKUMOVxQlyxMz6MU8sOz1jhkCqy5piQFJkMM5kSNvqYk2H1pMUSdWIH+fyzkVPBdWaW85ak0szbn7TLgoBmEKXHMO4sAz8uf0iHTEmGwpCUX6SFM4SCFRsO3WTGsN+i9FYNtXx6bewsU8tyhHBOEGDAxgmplMcVS3qYqu45yccWk/7g49ovjD3l9XoxMBpetxlevefEQqHkEkOAzY5Iv2LcqGrAU0th3NSdhK8sPpRbVj+qaskf5r3frUOHAbd+a8+Eq5dnjVs4xr5llKN2VOWqETVLchwLx31s5Xd+1XT4b+DV4EMfyHSnPcMiHtCxD/GATkZAR8/HWM5+p6LTAcKGRgC+95t3iq/fkF+9oWjKnqzy7VL5dqmilkR5duyT7I2SvS7XtjF/4rOTZy36/WPtHj+0u4hzsAxGnxWh3kUGibKITHB0IhhPQFtm2NTV0wG49rYV5dc3FJYdlEbukYo3j6ma//unXg2qNIYHoYdNg1DrYRNCQByjAwBm0IIlm7WaG9eOrHh6TMW84qp5//aTV3oV4ts0gH1OuHoQf3R40qMhOIj7MyWgFRM0GfQIxcVDW+pSCavOJYNsadjvCC3TUn5VDxgqcTz/j9++PXLmEql4eYFjb75tX76tPs++LcdRm125IbtqdXblkoLKuTM+vXjJ+oBugBImihXcrTE2GGghbZFdLLzA2SLEywYBQUBfNkMtOioQEAjEIRB7VKKbVpC3xwYknS/E3/0ty8IVYYoF5AOqQl4ko++zohMamjyp6ISS1nWLfCJqRDUUzTDYh62yT94kzY2zd9DDNKqSnuJnKXyBQRvCAkOatPD6eTlVW3yZVHKquqnyUQ/f6/TyUNvNXD+WjLOTNReXf4kdsm6eE4EHBxXimJ6Ncl7nhZSHan+Gtp0xFBnqF8UEAgIBgYBAYJggMOgPPotClvgOcph0QZhxUSDAk4jRWBAk6AVJvjD8+686sm3bpLLGkVNfzyndOdL29J6jSgTgZJAQrs+s6/mXe/bPuX3t5/9593d/eujnDx/d2BD8oBu6fIQsDlF2NmKSGRZZXZqMgKb7veOu7wbQvfhMSvBSXyLitswCNgMoGuWgn9vd93dfXDt2ytycCc8U2VcWVa/Pc2zIrdgqla0cUTN35i3zfvn7g54gIXz7QkhhE/drDUwVdPpRNWILiZsRI1dxGkkmkRZELFMGzVA1eHxJx8QZzxQWLxpdumZ81bLPfXWnN0x8n3GeqYOmko2EwibILKCHRnnf0wB1LyprtrQ3Hg30mSQcRj8znOKaiI0CHwO6n4AG0Kj9BNUw/ciUnKbjRXdTtCz08aY8t0lX8wbp9o0hXNobBvj9srbKTzw3qnLBGPvK4uqNxTXrRlYslSqelWy/+8Q/LXtq4QeyRmAy2JaIKUyNgRYzuf81QcoK4sSlioAgoC/VkRX9EggIBAZDIEpAk9hhKlgkgvNAPlI3Sbiv6HYMVBljiPANvAo6ZZ9DCgR06KMcdDwBrZmqZqqKJvMENInCoZBw0pZhQup18IN1IP78oBOPuAJ8d/lT8XqTHWdeni+ZKCfTTfISSybmpKqbKh818L1OLye2iDlnrz+pHtZcKv0fVX5Sa8/YGNbNcyLwZqBCHNOzUc7rvJDyUO3P0LYzhiJD/aKYQEAgIBAQCAwTBM74B39ILgXDpLPCjI8QgeQ8YozavOWfj5BNBUvrcisPFlXsGeN46qSTePwGyZ570KuCRyab8oUs8OngVSFgEGa3T4tyx7pBoyPjd2YEtAFkQz+Ncqix7e8QngiAgqyqMwJ1L8AvHjr+rf949a7vvviNH735/ftPPbY48uJxcOnE8zrqwEuIdLK01aRWqGDKoMuEho5GBIlxqYyANsmWe6YBlIpVAOY/7/ncXbU3fXb1/zzZ5faDrkOfXyPGEW9jTSYdDUUJaJ2S5ZTYpg7ExN1b1omfUyYpNgoDCGgahQNJeLrlISXIDQuMaAyQgYr7nawwhkkEiJM02fhQA3D2gcuAU16o3QuPPtX7q9+e+tVvT/3hac+8WvPVDkKRR+J3gSS88oDUrz9mbJR6xsMBZcXBZYKAIKAvk4EW3RQICAQSECA3RfLi2iRPFZYMoFr9y7t0i7zx5uM4M1bUJEvASDXVMhXCQcsKhBI8oA30gEYCOvpNPaAVk/hBR62h7VtGchI6weJBMs5m4sHXHaQZejrz8nzJRDlVW4klE3NS1U2Vn6jhzHLOXn8qDcMzH1E6t7adGfKJtXirEs+eWQ6v80LKQ7V2qLadb/1DtUeUFwgIBAQCAoFzi8BQf+f58ufWEqHtUkWA5xGZxzGhHXHXGwu8CpRcv0iq2SxVbM+q2ltUsWf6320MG4SvDFMCGsN1uEKmWwa/QSjpPvIhszLyIsTQyNSKfNCx1iKBjYmrLnEJwk+iBzQS0DKJm0G4bAOJ0NhSV5zvKXTu1d0bJUlVGqiijzDBpG0TQDEgEDDMqOMx4aANUFUwE9yH+RjQpOuGRXtPCWi/BR6LcOtoCVFmGqAHCAFtMALaZ5IA0CFCbpP5ImndBNAiIdJFBAi3KsRQHykupthY8AR0tHfRGtgxdNqmUaxjVaIt0q0LoyE7KBeOntHEGtOE6K5HAH1hCAaiKgNBRJi+MzDCCvFZxzgfSNxzftvYeszfi3Yxrv0UHRPZlzQCgoC+pIdXdE4gIBBIgwB5XFANM2yQ9VDkQUGh+13QqBpAn31UGRSVbCUcfaGLT+ocAU0epxTCX8s0+nMkFgMao3CQEBxxBLRCQ3/JOnxwwt3dFdYwFpeZ3OE3je1JT/ETibORkyqPy+T1x52KO+RLJspxhdlhYsnEHFY4QyFRw5nlpGouc22pNAzPfOzXubUtc6zSl+StSl8y87O8zgspZ24hlhyqbedb/1DtEeUFAgIBgYBA4NwiMNTfeb58nCWWZWGwuLh8cXiZI8AziAMIaJ0wj7oBr7wH2Y4/F8zaJ03ZkzulPqe09h+/+pJKUTsdDqpgRXRypBBuV5PJxzQAvDSEsGWqYERA76OfCCGjTYNcipR65i7XaPwNcoZSqUhA0w3hkemlEzekPi2LTPLMWHBiyh7rlPPFyrpFfJKDMsgaiZWhyJap4xkScwO9qpFN1mhjtCssBnSMgKZ8salBH43uHDLUkKb0aTiB1AnXbBAmnTonRQziAU0DQFthSkAjqAZFJUiAGUgcp7rkYmPBCOgordxfPkFPrArx8aYfg0b7UKj7eMxdmS8UyyM6URvVLsth1QwCmDoEDfIGAfVhiBKuTr/IlPJCv6VCunwQEAT05TPWoqcCAYFA9MYco5PB1GXNCOpg+CLQ0gXHXtdPtpLgZd6IGSZvvMNh8EXIyjCNe+ghIi5lit28gcaP1gzCYEfot2KAhh/dUjVTph9VBytE95RYtfb9L33x4YZdXaAAuX2nCD59vgeM79T5bkvoFwgIBAQCAgGBgEBAICAQuCgQiEQiXq83EAjIsmya0Qfni8JyYeQFQABJRI6Ajl4hJsCqre786uVSVaNUczi7ep80ce2Df/b5SFTh6PpRk+7ERzll4v1L51Ak+AbhdAnVrJHwD9EPKcr8nQlTTQ8HdpDYQh12iQZmUmIZ9Fvm6c9Emfphsw0V8TzRxJccqLn/LNLAGIOZmUFxwfkiK2kSIprMHXXC3xLbcbdB5HfNqA1I+PYTuAOa5e3BtvgcJhNV7BNTwM5SAY0x0IJYEa4WXx3l/kKk7sC42CxAdqxQCvtjp8XfyxEBQUBfjqMu+iwQuGwRYDddggC5KZIMxYCT7cb9/73trn9Z8517ti5Z9VYIX19DKAzuCJw2QOG5Wo6AJltK4H6DlG5WYuwzCoSDZgS0YqmeUNgnw+794b+78X/sth8vnnecLFqiVsTpx8PzPUx8o+e7LaFfICAQEAgIBAQCAgGBgEBg+COgKEpPT09LS0t7e7vL5QoEAmTbEuJJKpJAgCDA5lOUTEYOleT+rx/wb/70Xm7VeqniBanyBamyPqt02ZJNEFLAAk03CeManTvR1Z/o2ozaEFlGN8cJyD5HvwcMArOlnwRnCvlz6eUBKhnrGuOEozQu7fiAkvQANeM/SKpWsFb/mxymOVq5nwHmNSS2xfSwYmkI6P7mooqwEhLiTEFCqVStJs/n9aSSk9cUuZcnAoKAvjzHXfRaIHCZIsBujKT/sRe5igH1B33TP/bflTVPTCx9+LZ/fO6tDyBoQRjCETitUAI6zkc59t6+Twe/DkEd+mK+z1HHZ94DWrdU3VJVi+zn0B2En//m6OjiX1RUPPTcM82yF6wweShjSZDCDAohCAQEAgIBgYBAQCAgEBAIXEgELMsKh8MdHR0nTpxoampqa2tzOp29vb3BYFDT6E5tF9Ia0dYwRoD6HRO3ZCLoMtD4y7fdVZtbuUmqPCxVHZSqdubYnnv5A1AtUiITApojt9mkLVHgQeHPknz+OHOZ1xidIeI8EVXE5owDisUOMmklVpb+ZQQ3q8npZ3lMGFCXHrBTvNN3NBxJYun+HKwnCOh+RIR04REQBPSFx1y0KBAQCHxkCLAbNrGAvnw2dbLHxObt7pqr/jB+wvwxY5+54cblr7xNeOUw2V3QRzdnTgjBQYKRKQYp5dHJFhpBHWRKOhsG4KefidYt1QBNsUiUrN1Hgtd8akH5lGccVX9evOhDGpEMHxiimAgC+iO7OETDAgGBgEBAICAQEAgIBM4/AsPcm1hRlN7e3tbW1jaa2mlyOp1er1dRyKJARIg9sp5/wEQLwxABspE63cudENC6FjIs8EbA9rFncis3SxUHSRSO6s25lU98qBDPaBIhmvOAhhQe0JkRyDE0YotZY7VIPpvrDUmIaaR/GUHM/JQ5gnhASXowaEPxVdLqT9QWX32wPiaWj+WgbhYogzUVO38mf5mSNMKZ6BV1LlUEBAF9qY6s6JdAQCCQBAF2byTn6IEcMRUdDrxkTfvYE5PK148rfn6SfX7DYTgtk/0xdAibVtgiMaDJJhgkRTcMNDSjL6ydVi2vavrDasAwyOLEWPwvg4SNJp9oUA4aIQu8Gvzi98cmVP9lYvXSifbHn1vcQ03k9rRIYrLIEggIBAQCAgGBgEBAICAQuEQQIE+Lpslo3GHYK9M0w+Gwy+Xq7Oxsa2trbW1taWlpbW3t7Ozs7e0NhUKqquIWhSZN+ICM38OwO8Kk84AAZZ+tfl9ay5RVE156G0bYnsmt2iFVHZCqG7Imb7jmC7WnAfw05CDOkggbTSlQtrsgzs5iRrK5WmrhrAlcbItvINY6/ZtW/4CS9IDXw8sDSvI6eRkrYE5abbxmlAfoz+iA15FRhQwKnQ+dGTQrily0CAgC+qIdOmG4QEAgMHQE2E2SVKUHckSNaPBuE8z5v4snVKwbNXHTuNJFzyzuc/eBCjrdjlmmG2JwBHSMgw4rZLkZAIRlHR+q4gho05INIDsLG6D4ZXirGa69eenI8gVXVq0aOfGR+ctccnQt41mG30IrxLdAQCAgEBAICAQEAgIBgcDwRcCyLE3TVFUd5uEsLMuSZbm3t7ezs7O9vb01ltra2jo6Onp6eoLBIM9BI6U+nFn14XtNXJSWmTSWs0q/6ZzKUsIaPL1CGVGxOreyLqtyv1S9N3vymtvv2esG8NMJk4UBI6KstQXkLQzZdhBnZzEY2FwttTBEAjemOf4v38CAc2n1DyhJD3g9vDygJK+Tl7EC5qTVxmtGeYD+jA54HRlVyKDQ+dCZQbOiyEWLgCCgL9qhE4YLBAQCQ0eA3SRpVfL2XtVCEcM61QP/8r0NxVOWFJWtGVn67Lf+40AvIaBV0HXQdLDQA5py0CZ5UCIfA5QIeHrJR4nEttSgj1E0Cgd6QGuKHgKwVKOvpUP+1cNvjq95doRtWXbxs9WzF29tIJtyiCQQEAgIBAQCAgGBgEBAIHA5IGCapizLoVAoEokYOkYmGKb9tiwrEon4fL6enh6kodEburW1tb29vbu7OxQKoQc07wc9TDsjzDq3CBDC1ARLpWGfiWpNjwRVuPPfXhlZsz27cm+UgJ6y4vuPvNkLENBA1cg60aj7M4k+aIFpWBaJW4ixpAcLLMHmcJzXDs/kxjrIl0M5dib+L18y/hwe8/q5DXviCvN6eHlAsThViYex0ryG9HKsRuZ/eX2Z10osyevh5cSSIkcgEI+AIKDjERHHAgGBwCWMALtJ0j7qALIFfbKh9ATg3l/vvHLqooLyDXmTnpv5yQXdfWTHDNCAxOEwKZtMo3CQt/zIMuvw6mswb/4H8xa88+prukEDaZBv8nBFAkDj9s0RLQgAQV179W/y9I8vGmlbmVe2anTN4i98a+87bRDmHqIuYdhF1wQCAgGBgEBAICAQEAhcGgicTawJt9u9b9++TZs2vf7667IsnxkHfTYGDGkITNNUFCUUCnm93u7u7o6Ojvb2dqSh29vbnU6nz+djUaGZ+zOaxw6H1KIofBEggJGROQLaJLMlLaBCzSfWF06uz6s+kF3dKFXtkaoXPbS42QsQ0qKrRcnyUwPAIOzzOSCguS3lGW5srscEdipOYAXSzcZ4pjiufuyQ18PLsfP0L68nUeaK8hrSy1ylDEVeX4ZVkhbj9fBy0sIiUyAwAAFBQA+AQxwIBAQClz4CeNcn/SQENEBYM8N+FZ5c9MaEKWsKSurGT9lZWPKHPS9pMj6PyAoYsmnJpqmaJsnS6Dv8U21w57/Wl1QvtE1f+O0fHQoEiEZVIQViBDR5Alf0kF+Tmzzm/yx+b9xVa6UJm0ZPqR0//ZknVzd1BEG99OEWPRQICAQEAgIBgYBAQCBw8SGQikg1TVNVM3qC48M9G7rh9XofffTR2bNnX3HFFXv27MFgypnjgtoucLALEiRBNxRF8fv9LpfL6XR2dHTwrtBut1uWZaSbGWKJQubdFCWHOwKMgDZ1sMjUSKNzqg+cUFC1QKpoLJh6NLvqsOSol+wL61+BPo2s+FRUk3jwGCbZi1AzqTtPdLXoUHyfke5MjlBGVGj/NDCqhK+VRDtfnpeTm3BWuYmWJOakboAvm1iK7xkvJ5ZMzOE1J8qJ5UWOQCAdAoKAToeOOCcQEAhcagjgo0N0FZUOJEBzRDX6ZBPqDninXLdjRNm+K6r3FJY99dj8kx09IPtN1ee3TEZA64Rf1sHQ4K13oGrmipwr1xaUrZ31qTXtnQQqVdWBROPQDDAwUkdY9fk0/dU2+ML368ZfvVsq3TGqevWN/7R+72tBj0YocJEEAgIBgYBAQCAgEBAICASGFQKMO2ZcKlkDZ5qGbrAIznho6IahGxpNGBZZ0zR0HPb5fB0dHW+99VZjY+Pjjz9+6623jh07durUqQ8++GBzczN9pIxuMaKqqizLfGBoFtcClbMmNE3DFplhF8bX2LIsVVUDgUBPT087FxW6qamps7MzEokgL69pGovLcYEtHFbXzyVuDHLQpgkW8WlGAnpjQzC7colkP5hd/WJW5SGpoiHHsfD9duhTIKKCZtC9N5GA1snqUhLhkO7ZLghovFoSyd3EnNTXFV82sRSe5dtJLJMqh9ecKKeqJfIFAskREAR0clxErkBAIHBpIjCAgDYtUCxQVCNiArQ64VO314917Brt2D7SsfC7Pz1wqocEdyaru8ywaYWpB7ROFktaJH9/42n7VUtHlm0ZW715xo2r33iTsNqmAbql64SDjoaKjujePgvmb2i3XbtoVM1WacL6kRVPP7PG3+kX7s+X5iUmeiUQEAgIBAQCAgGBwMWOAE+eoowENLLPiqJEaAoGg0jIHj9+/NixYzt27FizZs3ChQuffPLJBx988N57773zy3ded911V111VXFxcX5+flFR0Sc/+cmf/OQnTzzxxKJFi9avW//888+vXbt2zZo1DQ0Nx48f7+7u9nq9TqfzjTfeOHr06LvvvutyuRRFYXw0eS5NSBcMbU3TgsGgy+Vi4ThOnjzZ0tISoCsBkYUXBPQFG46PrKEoAQ1IQKvUo+c/fnMou2qlVHlYKj8o2Q9I1XuLpj13WoWQDBGDBDYkl62hk/114glo3JcwujvhoHx0IgmamJMSmQQv5sS6LCdeSULd+AJDP2ZtZSikbiETBVgbS6bW1H+G6eQHSB84QP2lhSQQyAQBQUBngpIoIxAQCFxCCMSeHqhvi24Y0Y3I3V744lf3TKjeMKp860j78uv/7+Jjf4OOD2XDUAn7TD6yaeronCKHYcvWU7ZpS6SRK6TilTNuXH3osB908milmWqUgI5uSKipAP/y/b2jbPOlcctGOtbe8Nl17znhtExcBiBmzCWEr+iKQEAgIBAQCAgEBAICgYsYAXRtjqN5+f4EAoE333xzzZo1jzzyyA9/+MOvfOUrc+bMmTFjxsSJEwsKCiRJysrKysnJyaJpxIgRmJOVlSXRlJ+fX1hYKElSTk5OdnZ2YWFhQUGBzWb79Kc/feeX7/zmN79555fvvOGGG2bNmoU599xzz2OPPbZ58+bjx4+HQiGkwnnzeNvOk0wecWNe3qqqBoNBt9vd1dXV2trqdDoxJgm6ZgsC+jwNwTBSi/OX2CxGsyBowt/945KsinVSxQtS8X6pfJ9Us+OKj813KyQEh2wSAppEMkT2+SIhoDEWYz/ssf7255y1xCjeDIXUDWaiAGvHd2swnXHssyCgUwMmzmSAgCCgMwBJFBEICAQuUQQsEwzd0jSy/rFPhj/PbS2rXjSmtHZU6bryGXOfWtZy6kPzvZMndAjrENJBJuQyvWsrCrz+JlTPWlVQsrmgfEPl7KUvH1NNFciTNxhkdw0yOaDRoDV44eVQ1dXP5F65SBq9ZLR9wS8feafDD2Hc+RyfFi5ReEW3BAICAYGAQEAgIBAQCFx0CGCcDTQbgyCrqtrb2/vXv/511apV999//6233jpr1qyqqqqJEycWFRUVFBTk5+fn5ORIklRUVDRhwoSqqqo5c+b86Ec/mj9//s6dO48cObJnz57a2tply5Y9+uij999//z333HPXXXfddNNN11133bXXXjt79uyrrrrKZrONGjWKkdTZ2dkojx49ury8fObMmTfffPNdd931wAMPbNiwobW1NRAIGDp5iGUI8zLLPCcCizeCxLehG7Is+3w+t9sdCAQwMjWjnpm/NmPJz4kNQslwQWAAAW0aJrS54cqpf5Lsz0cJaPs+qXrjP3z/RbcGEcNQaJBoGgCaeUBHNyG0LGOgR+3gROrgJeJg4q3lZVosvbYBmvi6vDygEHfAl+Flrkj61hPPclVjbkyomUw7B/0MqJ3BwaAKM+eyM2hNFLk8EBAE9OUxzqKXAgGBQCICFomSYeigaYZhqBEFXn4Vaqb/ZWzJxnHl2yZMee6Xf3jzrVPy+6eaFcI+RwlovBWrKiGgK2etGlG6BQnol44qhkzobIDokxR5DNAhEoIHH3zRPnnpmNKNY8vXT7l25fN7/F4NSEHcB1HEgU4cGpEjEBAICAQEAgIBgYBA4CNCAGlTZFFlWT5x4sTq1au/9a1vXXvttTabbcqUKbNpmjFjRnl5+ZgxYwoKCvLy8oqKiubMmXP33Xf/7ne/27hxY1NTk8fjCYfD6B2MBK6iKMFg0OPxOJ3O9vb2pqamEydO/O1vf3vttdcaGxvXrFnzwAMPfO9737vtttuqq6sLCwuzs7NzcnImTJgwY8aMm2666eabb8aAHpMnT54zZ86vf/3r2tra7u5uWZYRKrZFIXbhHOLHeOc4lhljUsdlCgL6HCI/HFVFSU/qbmPppgGHXoMR9qck21bJ8YJUckiyN0gVK77/SJPHBBlk1TJ1E3cgFAT0gPHMhOLlywyoPIDU5kulkgfUzuAglR4+PwM1oohAgENAENAcGEIUCAgELn0ETMsy6Mt28t7YMsHUCWtsGGpfH/SF4TO3rCgYvfTK8t1jq5be8Z1dh971HXd2yoR9DugQ1kyZuDWbgAR0xdUrKAG9sXL28hdfUg2ZxICm5+nqJIvsynHyHfjMp1aOK10y3lE7avySr37zhaYPgUaWJjH8yLYd2qUPuuihQEAgIBAQCAgEBAICgXOIAHOtjfP55fPPjIRF395wOAwAXV1dmzdvvuOOO0aNGlVYWHjrrbd+/etf/9znPveJT3xi9uzZNpstJydn3Lhxc+bMue+++/635JtvvhkMBjFMM+ssBq/AbQaRjMYN/VBmxZggy/LJkyfr6+uffPLJr33ta+Xl5UVFRWPGjJk5c+adX77zvvvu+81vfnPvvfdOnTq1oKBg0qRJd9xxx6pVq8LhsKZpcd1nOs9eiNOMmzQm5Z1ZJl/l7A0QGoYfAplzuB0AACAASURBVNTXxlJNA+atCOeXLcou35Vb8XK242hWRb1UsfDpHZbHApUs+zRMQxDQMZ9lbiB5KjcTmasa0yY8oAeAIg6GOwLDl4A+syeG4Y63sE8gIBD4iBHgCOiYJaYBqiYHQ/qHLvjJz1+smbmzdPLBkbbV1//Dxl3HQu93+yJWH09A60Y/AV1Yvi3PRgjoF14kHtAWWYpkAGiGIZtgGgZs2QRXTV+Tc8X8Kx3rK6auXLgi0uGFoK5Enxqi0Tpipoi/AgGBgEBAICAQEAgIBAQCgyGQitzk889gOokBN9Bb+Z133vn5z38+adIkDKwxe/bsa665ZtasWTU1NQ6HY9asWXffffcf//jHAwcOtLS0IGGtKIosy7hfCEZqVhSFEc0Z2oOhlpHFdjqdr7322vp16x944IHPfe5zVVVVNptt9uzZd9999y9+8Ysf/vCHn//85zHn29/+9ptvvolNMxAGQ3EI55lOJjCiOZXASsa9JBhCq6LosEaAEtCgGibc//vjBSUL82y7CqtfLKx+Madyq1Txx51vgw8IAW2auqUTAprbhFCE4CBDmwnpzJcZcDkID+gBcIiDiwOB4UJA40tUXMKDtyj+jiVuWhfH1SSsFAhcBAiYFmimqUadoKnBmmYEQ36vv++td93rNrnt01bnj9uUO2HDuMlL1+wFpwwhQ1UhoEJYBdUAUE2IqPBBK1RcvaKwfFtu2fNjK+YePKJoCtmEkEY501Qt7JbDb7fB9+9/b2z1qryJyyZNXlVe9dgHLaCQraJVE3APBwYZ/xDBZHZWCAIBgYBAQCAgEBAICAQEAgQBnCci78kQYdxxXBgKLMyKpRdQiSzLhw4duv322/Nowt0CMQrzl770pV//+tdbt249duyY0+nEbfcM3cBprKEbaNWQGk1jEurRNM3n83V2dm7duvXee+/97Gc/W1JSUlNT88lPfvLHP/7x/ffff/vtt1dVVX3mM59Zs2ZNogt2Gv1DPYX2xPWOz0wqIyb8FoVDbVeUH2YI8KSorlnwiwePja2YW2BbJ03YlFW6pahm5TX/sPQ0QAhAt1Qa/RkJaJPS0MRLB0yyJjUhBvR57mjUX/g8t3JJqefHGuVLqnuiMxcYgWFEQMuy7Pf73W63z+czdNyfK/p4IQjoC3xZiOYEApcuAlEC2jRp6GULNM0KBvt6e3t6PadPtp4+cFT77J2HcotXX1ndIBU/9/X7jr7fA37dUiHECGjFoAT0KXDMWjbCtj23bNOYyrkHDkc0hbzHpgS0oluqAnDoOFxz+9aiqufzSlaOLp37gx+/4PIQ4lkFxQDdAFPD7QpJLUY688KlOw6iZwIBgYBAQCAgEBAICATOCAFkORnVi5S0qqqKomiadvYEtNvt/sIXvpCVlVVWVnbLLbfcc889DzzwwKpVq/bt29fU1BSJkFBqiqIw9vk8EdAszAX2Fz2pNU3r7OxcuXLl1772tZkzZ0qSdP311//4xz/+2te+VlxcPGfOnAMHDpy/uTPPL7Oh4zNTycFYCoVCqqqePwuZVUI4nwjESEm6pY1mwRsn4cbPLRxpeyp7woL88vl5tgdW7PL1KBCxgMy5dDI9sujbGUFAn89xOR+6Y2Pd7659PloROi8XBIYLAW3ohs/nczqdra2tLS0tPp8PR4Ddwy6XARH9FAgIBM4vAiQEh2nqihKJRCJ+X9Dj8fb09HR2dnZ29ZwOWq++a37nvtdHVSy9omanNHbexJl/PvIe+DWyfEwFWSWsMci6FdHgg1Ngu3ppjID+S+NBWVPQdBWgzwAlDPDk6hNFjrkj7JtHlK61TVvSeBhU+gymgq6RjyCgz+9gC+0CAYGAQEAgIBAQCFx6CCAzi/wvozIN3VBVNXFPPJxOZg6CpmkHDx4cO3bs9OnTa2trW1pa0EFKlmXe5zquId69d6gtprKNTYRN01RVNRgMMs2Gbjidzj179jz66KM33nhjeXn5DTfcUFxcLEnS3Xff3dzcjKR8Ks3nNp/ZmUZwxlJ3d7fP58Nw1efWDKHtAiJASUnKPpt0OxsF4FQIvn3fkSLbQ+Ov+vXPHjkiA4Qp7Ux2vKEhB5F6jr03iro/Cw/oCzhqZ9aUIKDPDDdRKzkCw4WAVhSlp6eno6OjpaXl+PHjnZ2d5y+CVXIkRK5AQCBwWSBAbqKGoYb6Al6v1+VydXR0tLa2NjU1fXCytamt90QXPLPWM376M/nlKwsdqwvKHl60yeOTQQdNBVWxVNUyw5oS0dUT7WCbtXiEY0dW2cZR9rn7D0QI5UySDKBETKXND3d8rzav5NmRZbWjS1fdfPsuj5+E3lCJB7RBCWhdeEBfFhed6KRAQCAgEBAICASGMQI8b8gHuGDc7nCznSegFUXx+Xw4kezu7g6FQhgHI859OPMu/C/dfN99940dO/bee++NRCI4J0V2W1GIrwFyzSggm4Yxo89T/A02OqqqEu+JSMQ0yYo7y7IURXE6ne+8884DDzxw44035ufnjxgxoqioaOnSpbIsXzAOmlmYRmiOpZaWlq6uLq/XGw6HE12hmYbMx0uU/CgQGEBAKxaEwZQBvDqccsMrH0CAss8f+rwGaGApYFhANyFEJ2i6RkEQ0B/FuJ1Jm4KAPhPURJ1UCAwXAjoQCLS3t7fQdOLEiY6ODnbXxPtQqg6IfIGAQEAgMBQEyE1U0xWf73RnZyeyz83NzSdPnjx+oqnHE9ABDr0PV9/23IjKpQW2NWOq5n/zR/v7LLJ0TLaMPkOOmEpQC8kgt/TAjDnrpfHrpJJNI8rn1m7rpfulgwWqX+7uCSqNf4WS6Y+OLF05uqy2cvrax55wBWXQqJsA5Z1Vg0aUjsYbEiE4hjKKoqxAQCAgEBAICAQEAmePALK0jKtlwStiXopkHpamFSRekQ+NK2aaJu6/h17JGBkD9ceV1DRNoUmW5VAoFAgEgsFgIBDweDw9PT2tra3vvPPO4cOHd+7cuXLlyqeeeuq//uu/fvSjH33nO9+56667/v7v//6GG26YOXPm5MmTp0+ffuONNzY0NCCtyajMzOeS2JG2traPf/zjxcXFK1euBAAkfJGAjuspj9v58IBmLwMQsVRjYZqmx+M5duzY9773Pdwy8Utf+hJuioihQuIA/0gOm5qampubW1paWltb29raOjs7u7u73W43xjNhHYwbtczH7iPp1GXcKG4/GN3PxrCIe03Ein5k4moD/z97bwIW1ZWuCyOEsRmboQgURRibyQaVK6iXQa/jIzF0YtRHjP4Y9ZKoR422469Gf6ecqLEdYguYFsUBxRbUo2iOA1wUvYpyVPQAVdU1do1dY2rYNe2/q764zj7FII6IrvX44Kpda6/h3XvX+ta7v/V+VvvSxkSSetJqtCs+W2yk1fny2klpezGcMAIYgfcFgbeCgDaZTFKplO1ILBaro6NDKBQaDAbqT9T7ckHwODECGIHXi4CdgCZMBplcAoI/TCaTzWYLhUKp/B9qHWEiSb6VHD/3sOdHu90+rPBl/GX4hGMt/2kx2yMHknqrSW/Tay0aC2ngyMnU3JMuoVUDPqz2ou86WSvV/GK3oaykWWnS/F1LLt3Y7B+1xz/y1G+jTsWlHPi3n0md3Q3g138W0uD4Z3UQ0FTdZ2r+9WKBa8cIYAQwAhgBjABG4P1EoPM6C+hUpCwBsCCOFX1EUsvAh6ICiLyG41ar1WAwyOVyPp/f3t7+6NGje/fu3blz5+bNm1evXj179uypU6eOHj1aVla2devW1atXL168uKSkZPr06ZMmTcrPz8/MzExKSmIwGOHh4WFhYSEhIYGORKPRYmNj/ymOkZaWNmjQoOzs7JycnLy8vPz8/HHjxn36h0/PnDkjEAjEYvEL7KYFB2cul5uVleXv719dXY3cnN8GArrnG5UgCJlMtmHDhoCAgPj4+MuXLwNdTmV4e67htX4LXuocDofJZHI4HN7TJBaL9Xo93I3InZx6L3VHu7/W3uLKn4UAIqDtHLTNSlqsdplCsz22jc1qFws2/7risbPPRrvooD3koHPCBPSzcMbfYwTeNQT6mICGHyGNRsPj8WA2YrPZTCZTKBQajUbqT9S7BjweD0YAI9B3CBAEIZfLBQIBvPcSCoUajcZsterNhM6xZey7qtbAlH0uQeXe9MPhv/vh4LEWwr51jCRsViNJGGwakjQIFGR6/klX2qkPImt8GHtP1so1v4DBZbOSJPcf5OBRRwcE/Nk3vDqEcWRC4WmWwO4OYCINwEFjArrvrj9uGSOAEcAIYAQwAu8vAkAZQ9w8wpFMjgQ+vMC0EgRhcCQkkkDlAY1Go0wmY7FYDx8+bGpqunTp0vFjx8vKyvbs2bN169Zly5aVlJTMnDlz2rRpkyZNmjBhwtixY/Py8gYNGpSYmMhgMGg0WmBgoK+vr7e3t5cjeTiSv78/nU4HR+YxY8Z89tlnxcXFS5YsWbVq1Zo1a1avXv3NN9/MmzdvxowZkydPnjRpUkFBwfjx40eNGpWTkzNy5MixY8eOGTNm9OjR48aNKy0tfYG1JDC2CoVizpw5fn5+69atU6vVwIp2R0Cj5SrVZxwOvoE7DBpCPbSYLY8ePUpPT/8nkuXl5ehNwBvoyTObsJgtOp1OLpeLRKKn5DOPw+Gw2Ww+n69WqwmCwAT0M2F8mwqAMoMjvKDVYmedLXY3HNJq+zVYHXg226ykzVHG7v9sl90A0pn6920aFO4LRgAj8HoR6GMCGiIqyOVyDofT0dEBDokdHR0SicRp89TrhQHX3t8QQEYwyvS3EeD+9hkCNpuNIAiVSiWRSMRisVwu12g0RqPRbLVaSKvaahZbyTt8ctDoY67Bf/ahH/swqfyP66/rfn2rb7aSZqvNrvIsUZJDRh/2oP/F66Oj/jE7q85KVVo7SW0iyX/oyQv/R/e7rGNetGMegUeD6QfWbL7/dzUQ0DrQfXbobxgsDmuN7Fp/A29J67ObBDeMEcAIYAQwAhiBdxUBm80GdKper9dqtaB3oVKplEqlQmGPzNzR0XHnzp2rV6/W1NRUVFTs3Llz7dq1JSUlU6ZMGTVqVFZWVkZGRmpqalxcXFRUFN2RaDRaaGgoclX2f5oCAgJ8HSksLCwlJSUrK2vMmDGFhYXFxcVLly7dunXrrl279u3bt3v37o0bNy5ZsmT27NlTpkyZMGFCXl5eenp6QkJCXFxcbGxsVFRUREQEzZHCHCk0NDQ4ODgwMNDPz8/X15dGo9Hp9JCQkLCwMDqdvm3bNuSa/Vx0sMlkIgjiyJEj3t7e+fn5XC7XaDSC0gioiFBrgzyVBaYeed33DwwQOgwaJiRJXr58OTIykkajnTp1iiRJJ82Q192lHuo3mUwgsQJ3mlQq5fP5EIWlvb2dy+UqlUqDwQDBCakw4rVeD6i+BV85nJ1tJge9bLWzz3apDbsjtP2vY2co0NIkacYE9FtwvXAXMAJ9jEAfE9AWs0Wr1UqlUiCgQRmqo6MDwkf0MTa4+X6CANVG6Sddxt3sSwRsNpvJZAKRQb1eD9KEVqvVbLUSNqvBYiFspN5Erl73OCb5yG/oR34TdTBrQnUz00EuWxWkjSDtsQMJvYn8dO7x4JTv3cM3pA7fd6JGoNDaKWaCJGVacsP2xoTsSo8PD38YeyYyft/RGqnCbI9OaCZNZrsngM1OZNtDEjriyGACui/vCNw2RgAjgBHACGAEXiMCQPhS3VQt5qcBICjNgkuy01egjwzUJ6WscxYFwYPyGo1GKpWyWKzW1ta7d+82NjZeunSptrb21KlTlZWV5eXlu3fv/vbbbxcvXjxr1qzPP/984sSJOTk5SUlJMTExQPWGhIQEOVJAQEB4eHhsbGx8fHxsbGxSUtLQoUNzc3PznqbcpyknJyc3N3f06NEff/zx5MmTi4qKZs6cWVxcPHPmzM8++2zcuHG5ublDhw4F8jo+Pp7BYERGRoLCBo1GCwsLCwoKCg8Pp9Pp0dHRiYmJoLAxbNiwvLy8jz/++PPPPy8qKvryyy+XLFmyevXqDRs2bN++vaysrLKysrq6+uLFi7du3Xr48CGXy5XL5Yg1RmIOzpB18xncwJubm+l0enh4+PLly0HCwmq1gjgJdd3xqvLd9OUZh6me7CRJEgTR3t4+ZcoULy+vQYMGPXr06O0hoAEo5OBsNBqBAYDNiO2OxOfzZTKZWq02Go0W83+Ta3gGEPjrvkTgVy0OB7lsv852Dhp4Z/CQ/tWdBj5YYeHz64enzHRfdh+3jRHACLxZBPqYgDaZTGAh8fl8CI3LYrE4HE6XESreLDK4tf6EALL/+lOncV/7CAFYQhgMBr1eT41X7uCg7aywPUAzQV6+TKYOKvcOL/ekV4akHN5ZoVYQpFYns7PPZitpJcwW8nyjfOrCkyM/K1v7r00qs13i2a5zZiMFMnL6vFO//d2Pv004GUT/y7D8yvsddvaZsBPQFgoBba/IHsgcE9B9dDPgZjECGAGMAEYAI/CqEEAeqSgenZOZ0dmXEyzYLjuA+GhUCXizWswWpVLZ1tZ2+/bty5cvV1dXl5aWbt26dfny5fPnz58zZ86MGTM+/cOn48aNGzFiRFZW1tChQ9PT0xkMRkhICKheuDuSt7d3QEBAaGgonU5PTU3NyckpLCycPn36vHnzFi1atMKRvv7666KiosLCwvHjx48ePTovLy8zMzMjI2PIkCHDhg0D8eWcnJzBgwfHxcXRaLSAgAB/f38fHx8vLy9oBbQ1vLy8AgMDGQxGcnJyVlbWqFGjJk2aNH369K+++mrlypXffffd3r17Dx48WFlZWVNTc+HChcuXL1+7du3mzZu3b9++d+9ea2srm80Wi8UqlUrjSDqdDnwIAGqCIICyRLoiSMn6eQlokiRNJhOPx/v0D5+6u7tHREScOHHCYDCAJondYnsNqcsb4JkHwaMCwiQaDIYHDx7MmDHDxcUlOjr6wIEDYrEYxv42OEEDZoiARi9jNBqNWCwGRzTYDM3n88VisVqtprpCPxMKXKBPEXDobjjkNeBC/9oZCGrz6wd7Gceqx77wcfrXp53HjWMEMAJvFIG+J6BVKpVYLObxeCwWC6KBiUSiN4oBbqwfImC1WlWOhEyr/zbh9cMR4S6/MQSQ1YvWh78uThw+yVZ77AyD1UzebyEnTq4KiDnoHlXpErpz1Od/bf+7Q7/ZYLPH1XD4LulIkqkmmQpSTZIa0qYj/2EgRTrScvc/yMwRf/akHwhMPBn60Z61mx8pTEBA2yykBf49NcLs1hgmoN/Y1ccNYQQwAhgBjABG4HUjAEQz9S+1RavVajQawQVHJBJJHEnkSHw+/8mTJzdu3Kirq6uurj548OCWLVu++eYb5EQ8YsQIEKaIiooCr2HQo6DRaChYH3guw9+QkJCoqKjU1NQRI0aMHz9+2rRpc+fOXbZs2cqVKxcsWDBjxoyCgoKRI0cOHTo0LS0N3J8jKYlGowUFBQUEBERGRkZFRQUFBQUHB0PNoaGh0dHRMTExsbGxUH9BQcGsWbMWLFiwatWqLVu27N+///ix43V1dY2Njc3NzQ8fPmxra+NwOGjIEolEKpUqFAqgksE8A6fdzkw9FUBQrKYegTwQsk58K6KLO5fvfATaBYnIvXv3RkZGenp6Dho0qLGxEThojUaDKnyFmc496c0Ri9kCyhsKheLIkSM5OTkDBgzw8fFZtmyZXC4HRh749N7U9lrLAFZOBDS47Wu1WpFIhDhoFovFZrMlEglVwvu19g1X/koQoD4OwC9DtU5cc5cfX0kHcCUYAYxAv0CgLwlosBL+GedBIBBwuVyYb2DbVL/ADnfyDSDgZIAi0TqVSsXhcLhcrkajQV4PToXfQPdwE/0RgWcQ0Farzaa1Wq16E7l8Y6NP9M4B9J8++KjUJ2ZTxRmRUEIaf3EEdrbYd5SZHRELFSZSTthUNrmWFOpI0S828q/njB8ll/p8dMyDfvCj1J2N/5dUm0ilSWN+yj5b7MGikSMAJqD7432E+4wRwAhgBDACbxQBqpkHZMcbbb7XjUGgYyaT+ejRo5aWllu3btXV1Z05c+bUqVNHjhzZs2fPli1bUDy9mTNnTp48edy4cVlZWcnJyQwGIzw8HNSNg4KCQkNDIyMjY2JikpOTBw0aNGzYsNzc3OHDh2dmZqalpcXFxYH+cnR0dEJCwpAhQ/Ly8iZOnFhYWAiSGikpKdHR0ZGRkWFhYX5+ft7e3r6+vqCY7OfnB77PcXFxSUlJaWlpoHcB0fzGjx8/ZcqU2bNngyv0+vXrN2/evGPHjgMHDhw/dvzs2bNXr15tamoCx2SRSCSVSmUymUKhkMvlSqVSrVaDmC/ogYC3sslkokKINEOolxUKUI9Q89TTkScyZGAt4FQAfez93YKas5gtHR0d06ZNc3Nz8/PzGzt27KVLl1D3qFwbylMd1dHBXmaoXQWvCBgXOt45A+too9F48+bNb775JiIiwtPTk0ajrV27tq2tDfH4YPSicXWu580cARw6E9CwKxHkOMAdjcVi8Xg8iUQCAVrgxDfTSdzKyyBAvdW7ZJl7OPgy7eJzMQIYgf6FQF8S0GB5SKVSLpfL4XBYLFZHRweXy1WpVP0LRNzb14FAZ4PDzgnq9UqlUiKR8Pl8MFBkMpler0e7tF5HT3Cd/QsBpNBH7TbV8kaSecgop9pMNnsQQY2NNBIkebnJEJW1zyVgq0vYblfG95Nnn+eLScL4q7+yIxwhabbZBTnMNlJv+0VrU8p1Go2Z/N//cuc34X/2iD4VkFQ5atJPYjmpN5Okg32G+Bs226+Bop/uQoNdap3/UgeB8xgBjABGACOAEXh/EUDTN7h2IjILIQIFCEcCyxB91TkDzBdVqAGOgEspVA47pajnGgwGcJ158uRJQ0NDTU3NTz/99MMPP6xbt27x4sXFxcUgdpyfn49o4oSEhKioqLCwsODg4ICAAB8fH29vbz9HCggICAsLi42N/aeP7ejRowsLCz/9w6cTJkzIzc0dMmRIUlJSVFRUcHCwj4+Pr68veBwnJiYmJCTExMTQ6fSwsDAIweft7e3p6enl5QUl/fz8/P39g4KC4uLiBg8enJubO2HChKKioq+++mrFihUbN27cvXv3oUOHTp8+feHChStXrjQ2Nt65c+fevXstLS0PHjxob28Xi8X6pwlRyeB3DJh0/ku1qRA7jK4RNUM1uqjY9jJPPR3lYVFJNfZ6WVt3xcCN+tq1a6NHj3Z3d/fx8Rk6dOj58+c1Gg1IXpAkaTAY4HTwRAadbioOqHvPzKBuoNvSbjWaLagJKABB/IDKl8lkJ06cKCkpSUpK8vb2dnFxKSgoKCsrEwgEUBgeB2rTqJU+yVB74pS3mC16vR4CYAqFQplMplQqtVotOEH3SW9xoy+DQA9cc5dfvUxb+FyMAEagfyHQlwQ0qHSJRCK2I7EcSSAQ6HS6V2hA9K/rgXvbHQIWs0WtVoNMGDjLwyY+mUym0+kwAd0dbu/JcWTIUscLlvev8hq2X0NgwKIIFiqdFgkWG2m0kb8AAf2LieQoyc8W//sHv9vtkVrpEV+ekXv83xvsKhxgPFkg6oaJJE32kIJGk8Eh8UwKleSwUWe8Iypco6tdPtzx1R/r/qEmwe8Hsc+YgKZeKZzHCGAEMAIYAYxAzwh0N6ejs0A2wWg0EgQBVgFBEBCJDj6ikhazRafTqdVqpVIpk8lEIhGXy2UymY8fP37w4MGdO3fq6+vPnj17+PDhnTt3btiwYenSpbNnzx4/fnx2djYE0IuJiYHoeeHh4VQdDGCZvb29XV1dXVxcPDw8/P39w8PDk5KSwDd5zJgxw4cPT09Pj42NpdFovr6+wBr7+fkFBAQEBgaGhITQaLSoqCiIgBceHg7aFwwGIyYmBryVBw8eDEH5pk2bBhrKW7du3bNnT0VFxZkzZ+rr6+/du/f48eO2trb29nYOhyMWixUKhVqt1ul0CB+EBgSvMxqNwMVTNZSpVD6YTJ15Z3SEalP1CQHd2d6jjvF587Dn0mAw3Lx5c/To0X5+fq6urvHx8du2bXv48KFardZqtRCcENWMblGAAvUH2ag9ZFAlkIGqIG80Gqm+WXK5vLW19bvvvvvss8+Sk5O9vLxoNNqwYcPWrl177949pVIJJi54QCNnaqf6++RjD8OH8cIDq9frDQYDuiExJ9AnF+slG+2SZe7h4Es2h0/HCGAE+hECfUxAEwQB4QeBg+ZwODKZDEwZPN/0o9voJbva87W2mC1arVYmkwkEAg6Hw2azgYBmsVgikUgmk2m1WrTYeMme4NP7EQLU2wa8cuAvNS6N03IIRtetBWxnnxU2Uk6SepvNZrCSWpL8y1VT0NDdH6Qd/s3Aar+o/Ss3tP3DYFfe+DUZSLu0syO8oNVCWkh7FbWXybC4fZ70SpfoEx/E7vrLSYFaS5oMdsEOm5VEHPRT32ewxzr7Pv+3yB1P28P/YwQwAhgBjMB7h0DnaevFIKDW82I19O1ZVIIP5UHkAfk7W61WjUYjEAiYTOaTJ09aWlrq6+svXrx48uTJn376adeuXdu2bdu0adPq1au//vrrmTNnfv755wUFBVSPY/ApDgoKCgsLCw0NDQsLo9PpsbGxSY4Eofx8fHzc3Nzc3d19fX3DwsIYDEaCI8XHx8fExISHhwcEBHh4eLg60gBH8vLygoh/oMg8ePDgrKys3NzcMWPGfPzxx6B3sWDBghUrVqxfv37Lli27du06ePDg8WPHa2pqLl682NDQcO/ePTB9pY4kcyQkeQHeGMD8ApWMLhZwqcDoIaaPIAhw8gW+EukFw1kIXrCjeiaUEd+KKNeey7/kfUg9ndo0tXU09pfMABl67dq1+fPn0+l0Ly+v8PDwoqKigwcPNjU1qdVqjUYDEa0BMaoKB+oPtcPd5an9pNq3NpuNIAiFQnHv3r0zZ87s2bNn1qxZgwcPDgsLc3FxCQ0NzcvL27x5Z3O5XwAAIABJREFUc319PcTWBr9po9GIJDioNfdtvruxU49TLygc702fATEqbr05C5d5fQj0wDV3+dXr6wmuGSOAEXjbEOhjAtpgMPB4PCaTiQhohUKBJH3fNrDecH9g3n2r3l2/JgSQ5YHqhyMEQWg0GplMBoIbLBaLw+HweDw+n8/j8TgcDp/Pxx7QCLT3LUM1TJHIoFarZbPZICUPq6nu7i50/L8yvxLQCtJmtFntLDNXaeGbyfyZx1wYPwSk1vpGHRmUe+Tuf1IIaCNJ6h0EtEOXw0CQAhm5ZM3/DY0v96Gf+IBekTDiyM17pE5PGo2kFRPQ79s9iseLEcAIYAReBQL/NU89zb1YrU/Ptv//YjX0+VkGg0EikTCZzObm5mvXrp05c+bQoUM7duxYs2ZNSUnJ1KlTJ0yYMHLkyGHDhg0ZMmTgwIFJSUnR0dERERGhoaEBAQGenp4ulOTm5ubv7x8VFZWRkZGdnZ2ens5gMPz9/QcMGAClXF1dvb29QYsZYv0FBQWB3AGqxsvLC/SUo6Oj09PTc3JyCgoKpkyZMmfOnG+++WbLli379u07evTouXPnGhoa7ty5c//+/ZaWlocPH7a2tra3tzOZTLBmwVmbIAhw/wQ+Ua/XgyQI4ouBTTaZTAZHAo9mKn1stVrhK4IgTCYTVAinw7mwzoIagKnszWWFm4fKD3aZh2JvMwHdyyFT/YhJkuRwONXV1YMHD3ZxcXFzcwsLC8vNzZ0zZ86+ffv+SU/LZDK1Wg0eVFRYqE9cz3nqJTCZTFKptKWl5eeffy4vL1+2bNm8efNGjRoVFRUFN7CHh0daWtqiRYtOnTolFovBBjYajeg2eDsf8N4jgNDo5UCoNaNzcaYPEeiSZe7hYB92FTeNEcAIvGEE+pKAtlqtOp0Odr0BAS0QCFQqFbKx3jAWb2FzMKG+hR17rV0CyTONRiORSIRCIQSo7OjoaG9vB91nPp/PdeiGc7lchUJhMBiQyfVaO4Yrf3sQoNqadm9lg0GtVkulUpFI1N7e/vjxYz6f7xTuxqnzqAbKcStJEo5/VvvaiSRVhFX6C/lT1X/6RW7y+vAn36gjIbE//Kmi7R8EabCShMVoNT31gDaQNov1Fz35NxGZP/HQB8F7vcOOhUQe/HTyub/xSL2JNFiMFru6dA/WV5dfUXqHsxgBjABGACPw/iEAs1WX3pTPBYZTPc88F1E/EOsM1BgsZgtsk0eE5jP9JMAzFNVmtVqNRqNWq6WG9Ghvb3/y5MmjR4/u3bvX2NgI8he7d+/etGnTkiVLiouLP/nkk7y8vIyMjOTk5NjYWJCnCA0NDQoKAoWK4OBgNzc3xBpDxtvbOzg4ODo6OiUlBfSUAwMDPT09Eb8MZGJAQACdTo+Pj09ISIiLi4uJiYmNjY2Li0tISEhKSkpPTx8+fPj48eORhvLmzZv37dv3008/nTx58tq1a62trU+ePOno6OBwOAKBQCwWSyQSuVwO7rFgoyK0AYeuLBBU5O3NoG47+UcD5QrfUntPLd9dnlr+ufLUPlDz4IMMVYF9CHHLm5qaTpw4sW/fPqFQSPUQR3emU+tQJ/WgXq9vampatWpVSkqKu7s73Dzh4eHDhw+fOHFicXHxihUrtm7dWlZWdurUqbq6uitXrtTX1zc1Nd27d+/BgwfwygHd57dv375x48aVK1fOnj1bVVVVVla2Y8eOtWvXfvPNN6D3MmTIkJSUlLCwsAEDBgDlHRcXl5WVtWjRoqNHjzY3NwsEAlCd7nIIXR6kDucdy6Pxdr4P37GR4uFgBDACGIF+jUAfE9AajYbD4SAPaIFAoFar0Ta6F0YWLCGnbVAvXNtbdSJ1fn2rOvaqOgORBiE0JdJ6pipvcDgcxD4LBAKtVtuD+fWqeoXredsQgAcBVsJ6vV4ul8N+W/gxYTKZQqHQYrb00G20FuqijMMzzK6nYbVodbrbd6T/838d8g8v84s8FsjYn//Jgf8Ukay/C9U6sclKWE02krCQhMVsJFRa8ucmS3pOqW/EIVrMWVrYD//f+gdyGUmYTUbSQJB6h191l0Rzdwe76B0+hBHACGAEMALvDwIwW71CAhqJ9iI7mQomEmSAjBO/7MT0oarAEoNIYjAjt7e3P3jwoKmp6erVq7W1tZWVlXv37v3uu+++/fbbpUuXFhcXT5ky5dM/fFpQUJCXlzdo0KDY2FhQVQ4NDQ1xpNDQ0HBHCgkJ8fb2dnd3d3NzQ9yxq6urp6env79/sCMFBAR4eXm5ubmB6gVkQCIjMjIyKSkpMzMzNzd3/PjxhYWF06ZNmzlzZklJyaJFi1atWrV58+Y9e/aUlZVVVFRUVVXV1dU1NjY2Nze3traCgDLIXGg0Gq1Wq3Ik0P81GAydJeAQG0tFleoRjMwPZNI7lXxrP1J7TvXzRUN2GhG1fHf5Fx4s3IqdW4S72mazyeXylpaWM2fObN++fdq0aYMHD6bRaHl5eQ8ePADt5p7dFKBj0Arc5+BorFAozp07V1xcHB8f7+np6evr6+Li4urqGhwcHBUVhaS64U0GnU5nMBiJiYmpqakpKSnJyckpT1NycnJcXByDwYh0JAgp6evrC+rhLi4uvr6+UVFRWVlZBQUFc+bMKS0tra+vf/z4sUKh0Gg02FsL/RZ1vgecjrzwPYZPxAhgBDACGIFXjkCfEdAwbSgUCg6Hw2Kx+Hy+SCSSSqUqlQq0tF5yqFRDx8l6fsmae3k6uIq8jJwIbJSDeMdqtVrlSEhrjPqGv5ddguVBLwtD/3tZ+GWKITcE0HqWy+UikQiUwSEuJSgq8Pl8gUDAdyTgo9lstkwmA9MfZOxephv43H6HAOjigeMzbKRgOhJos6hUqhe/KxwENFDCOqPhHypy6/a/BYT9KTDitG/EYY+wP564KBZrf/nFIjKQUsImt5lVNkKvMxAyLfmvBzpCf7fTL/KIV1BZFOP7xgbSqCdNFovBrgJtxAR0v7vNcIcxAhgBjEDfIoAoMCrlB1buc3UM1QNsWg+1IROaWj/sTlMqlUKhsLW1tbGxsaampqKiYufOnevWrfv666+nTZs2bty4ESNGDB48OD09PS0tLSkpicFghIWFgaqyj4+Pp6enuyO5ubl5e3uHhISEhob6+/t7eHiAULK7u7uHhweU8XAkLy8vb0cCSWUkfOHu7h4SEpKWlpabmztp0qQZM2YsXLhw1apVW7du3bt374kTJy5cuAD+py0tLY8fP+7o6AAlNz6fL5FI0IZLpIPs5M0ARjhIWEBcPoQ5ZJxgpGLVOY8gRZnOZfrXETQQpwx1FE5fdfmRWv658tT7GV6WGI1GjUYjlUqbm5srKiq+/PLLQYMGBQcH+/j4REdHjxkzZvny5bW1tXK5HBoSCARO/umdO4BagdUKMJsgkXHt2rVVq1ZlZWV5eHi4uLj4+/snJSXl5uYWFRUtWrRoxYoVS5cuXbRo0fz58+fOnTtr1qxp06ZNmjQpJycnLS0tPDzcz8/P29vby8sLMc4eHh6BgYEMBiM3N3fu3Lk7duyoqqq6e/cu6HtQ6XJMsMIuaqVSCXQ8AgfdY50vJT6CEcAIYAQwAm8DAn1JQFvMFrFYDDHlgGoUi8V6vf7FaSOShJ19arVaLpeDgINQKJTL5b2vFqaul7w2VqtVq9WCr4TBYOjliJA9AbsdtVqtRCIBsWOOI7FYLC6XKxQKlUolirzXZVepEzDUZjQaqfFJqAWcaoAw4tB5oKHRvO5U8pV81Ol0gBVoPcNIEcXMZrNhS6NUKlUoFGKxWCAQwD3D5/ORvzyC7pV0CVfSLxCw2Wx6vV4mkwmFQh6PB3cF3C1yubz3z10Xg6UQ0BazRa0hr9aTyb8vjUqo8w2v/jC5dOa/1ArUpMaq+IUU60mxyaowmY1qg+3vKvJ/r7jlEf6vPpGHAyLKx4w/9re/kYSRNFutBtLOQVuxBEcXcONDGAGMAEYAI9AtAogC64Ey7vZkyhdQD1iDarVaoVCAbhWLxWppabnjSDdu3Dh//jx4K2/evHn58uUgrDxx4sS8vLyhQ4empKTExsZGRUVFRESEhYWFhIQEBAT4+vp6enoi7+MBAwa4urpCjD43R0Juy0Afg2MyROSLjIyMjY1NSEhITk4eOHBgZmZmdnZ2Xl7ehAkTpk2bVlJSsnz58vXr12/dunXXrl0VFRVnz569efPmw4cPQT0ZfBREIhGSvFCpVGAkI9sVlgYgrAzmIhi6RqNRr9cTBAEgAeMMkm6gj4y+oqBIIkoaeYgDE40MUcAZmdndZah19sd8b8bVXRnq8e7G/kznIfRcwKuRjo6O8+fPb968+YsvvsjOzgZn5Ozs7NmzZ+/du7ehoaGtrQ0WEVeuXPnhhx8WL168bt06NpuN7pPuekI9DvcS2mCnUqnu3LlTVlb2+eefZ2ZmxsTExMfHDxw4cPjw4RMmTPjss8+mOdInn3wyevTo7OzsjIwMeCsTGBjo7e0dGBgYExMzdOjQCRMmzJ07d9OmTVVVVQ0NDU+ePJHJZCACjvyB4J7UORLqALVvyMve6SBEI4QbG5DvXKDfHbGYLSqVSigUwtJYIpGo1WrwSep3Y8EdxghgBDAC7xUCfUNAw/xnMVsEAgFQjeC6qFAonssOQNYeXDNqzDpwrAbhYDabLZVKOxNSXRpA1LkZqFu0RZH6Vc93iVarlclkUqlULpdrNJruDIXuKoEX+CKRCMkfAz5MJhM8OIRCIWgfOyEAFaJxkaTdUNbr9QqFQiQSoVPQGoZ6OlqZqNVqiUQilUphCMD8GgyG7nr7MsdtNptCoZDJZAKBAKh28E/hcrk8Ho/L5QoEAolEAnvN9Ho9OEHD6wqBQADHqaN4mc7gc99+BNC9jfb5QkRKRECjF04vsEXAafgW0mYh7Q1aLKRWRxZ/+fNvaYf9wmqCGIeShu650KiUEaSRtGhIudaiIUhSYyL/g0UOGl3pF/sX97BDYbFl/+/6ewIBaTKRFhtpIG0G0oIJaCeQ8UeMAEYAI/A+IAAmFhop1Z6k5oFCAnWpzrvWgCE1ORJYPk7nkiRpNBoVCgWbzW5paWlsbLx06dKZM2cqKyv379+/ffv29evXL1u2rKSkpLi4uKioqLCwMDc3d9CgQUlJSbGxsRCpz6F+ERIYGOjvSL6+vl5eXh4eHp6enuCb7ObmhpyUQe+Cyi97enqCFkFqampWVtaoUaMmTZpUVFQ0Z86chQsXLlu2bM2aNZs2bdq5c+eBAwcqKytPnz598eLFa9eu3b17t7W1FUJ9AKGs1WrVjqTT6YxGIzDIEFgPySwgSCEDgCArF6hh6l/0FZI06XwEKumMrVNb1Baphamn95DvsjZ8EBCwWq1wnzsBAvEY4aBSqXzy5EljY+PBgwdnz549bNiwxMTE+Pj4zMzMT//w6YoVK06dOtXS0gKriVu3bh06dGjp0qUTJ05MSUlhMBjJycmzZ89ms9nPtUajPndo9aHX64VC4cOHD8+cObNp06aZM2eOHz8+MzMzw5HS09MzMjIyMzNzcnLy8/MnTpxYVFS0dOnSTZs2lZWV1dXVPX78uL29XSQSabVadMNQb0uUR9+ipp3wgZciTgdJkkTvSKg1QL5z4X5xxGq1qtVqgUCAQgTx+Xy5XK7T6Xrp9dUvhok7iRHACGAE3j0E+pKANplMyL0XYnfA1NtLlGHiRLuugGYVCAQsFqujo4PJZIKCMJC2XC63c7Q66jSMGqW+cgdtWZlMplQqNRoNxBdGJbvMgCyAVCoVOBLQvs/Fqms0Gj6fDz4dwM6zWCxEQEOezWZLJBK9Xt+lCQLrHPDvUCqVIpGIzWa3t7cLhUKdTgcLGLBF0GBBeVmhUAiFQuDuqVQvh8ORSqXPZaJ1CU7ngzabTSwWQ6RBriNxHInNZvN4PJFIBC+04USTyQTENKABHtD4dXdnVN+9I+hhh+fdZDLBSxrgnSGEKZvNBvMdxQGHs14Yjf8ioK2kUknWXTLH/e44jXHRI7iClrh/3vKrXA0ptZFaO7NMqk2kTEeeuWL98Pdl3ozjLkEHQ2L21VzQW0nSbAEC2s5BYwL6hS8HPhEjgBHACLz9CIABBrMPODFQCVPg1KiuiGCGIYIJBgh2Gng+OlmeBoNBIBA8fPiwvr7+/PnzR44c2bVr18qVK7/88suPP/44Pz9/6NCh6enpSUlJIC8LnHJAQACSv6CSxUjOwukguDC7urqCLAb89fT0DAoKio2NzcjIyM/P//jjj2fOnLlw4cINGzaAb3JtbW1DQ8Pdu3cfPXrU2toKIddAZE8sFoOMgEaj0el0yLMYBg4emkiQjQoCGKvwFdqT92KTO7ooL5l5+2/Cd6aHThcaXsyo1Womk3nu3Lnvvvtu8uTJMTExbm5uEAmwuLi4tLT07t27CoUCdtnW19fv37+/uLg4OTkZ3qmkpqbOmjVr586d9fX14Cn/XHA5EdDoI3hhw5sS6OGtW7fqHenq1auXL1++fv16c3NzW1sbuBDBUwD3P/rRQD1B6zgogP5Sb11U2CkD61Cj0dh5hfhc9ThV+/Z8BBCsVqvBYJDJZMgBhclkstls5IaCaei355LhnmAEMAIYASoCfUNAg4uHwWDgPA0o19HRIRAIkElK7WIPeSRVgbbhg8sweMiCLy3icLlcLoi+gcY0dRanTtIoTxAEhMLjcDhCoVAmk0G8ux76Aza0UqnkcrmgHcHlcqVSae/HpVargX0GZLiOxHEkxLJB5RB/D/XWqVdgZGg0GqFQyGazgYXn8XharRY6SbVCLGaLTqeTSCQcDqe9vR3J5AF00C68WH7lHLTNZuPz+TBM+CsSiYB6ViqVBoOBOkCCIBABzWKxhEJhb66IEzL4Y39EAGxxWHsYDAbQoKQ+7DweTyaTIYMbPd0vM1hUicVG/mIgfzGSU4tuB3544je0Kj96RUr2kQtNpJ4kpWaSJyP/JiIlv5BLNzZ7M3508TvgTjsyOP/0Yxap1pFmG2kmSYPjn9Xeoe7iDXZ5/GVGgM/FCGAEMAIYgT5AAPFH1AxYXzqdTqVSyWQy5Bzw+PHjBw8e3L59u7Gx8eeff66pqTl06NDevXu3bNmycuXKuXPnTp06FRQw0tPT4+LioqKi6HR6eHh4aGgoMMvu7u6ISqZmXF1d3d3dPT09vb29AwICgoODaTRaZGRkTExMXFxcfHx8SkpKZmbmiBEj8vPzx48fP3Xq1FmzZn399dcrVqz4/vvvf/zxx0OHDp06deratWvNzc1PnjwBZxEejycQCMRisVwuV6lUEJsEOGIn5wYq9FRzjnoc8kDKdz4ORxCMYLt2VwwffycRsNlssEi5efNmaWnpokWLJk6cGB8fHxISEh8fP3HixG+//fb06dP37t2TSCRyufzhw4enT5/esGHDJ598MmjQIAaDERsbO2bMmKVLl5aXl1+9elUgEBiNxpfBCtmHkEFVwU0OAnFGo9Hpdu38igWWw+h0lKHWj9ZryGffqVF0Fto/AUfAZoZH0mg0wo4KqI1aP/X0fpFHw7fZbBqNBn5LORwOOCfB6lssFms0mp5/c/rFYHEnMQIYAYzAu4dAnxHQsHcGnG05jiSTyXr/uhKMUZIkDQaDQqEAXWDOUzobKoSPPEcCF2BwxJBIJCCgTJ2GO19arVYLCiEcDofH48FZz2RgLWaLSCQC52voRu8JaK1Wy+fzoTkul4uIb4VCAdp2IAmNZJHVanV3kysMTaVSCQQCJGcBjC2VgAYYQUgX0XmAVZsjARkN7tgCgUCpVD4Tgc5I9nAEPKDhGgmFQnAYVyqVTs7d0E+dTsd1JHBvB8Xw5/Iu76En+Ku3HwH40ZBKpXw+H210gMcEhRxE23JtjvQyg4Ia7J5opMVMmv7xC3nyPPnRwGMfJp4LjT3PGFj7/yzpuPaQ3HTg/rw/nv/jtzeu3iOHF5wMSPyrz0fnvGgHv1xwnyMiTaSdfTY7vKQJB/eMCeiXuSj4XIwARuCdRwD99iLa0en33OnjWwWIxWwBBYx79+41NDTU1dWdPn364MGDu3bt2rJly9q1a5csWfLVV1/Nnj17+vTpkyZNGjNmzLBhwzIyMuLj42k0Guhd+Pr6+vn5IWFlxCmDsLKbmxvVYdnd3d3f3z80NDQ6OnrgwIHgmzx16tTi4uKFCxcuX7587dq1mzdv3rNnT2lp6U8//XT06NFz585du3btzp07Dx48aG9v5/F4IBknl8tljqRQKLRarV6vNxgMBEFQ3bTR1UGw9/JygGMmcshAZ4G7N9W2hK1OVPk71BbO9F8E4IrD8gT+9jwWi9kilUpbWlouXry4adOm8ePHxzlSampqTk5OSUnJnj17rl27JpFIuFxuW1sbODvPnDkzOzs7Pj4+JiZmyJAhkydP3rBhw8WLFwUCgUKh0Ol00CiS8uj9wpPaW3T3wkH4pYL9DV3GHIIC6CwERXeLOCiAiiHQqMep/UF5oJtJkhQIBBcvXrx06ZJMJgMJDiCg0YOGqkLn9pcM6rnNZgNFe6VSCRugQRce1uBCoRAFCgJqnnoi5PvLkHE/MQIYAYzAu4RAnxHQFrNFJpPBG0vgN5VKZe/tAIIgQBtOqVSKxWLkNczj8YDHFIvFIGQskUiAnm5vb4c5icvlQtQRZN1S3yrD1TWZTHK5HCmEMJlMUBx+Zg8tZgswuUhDowcCmjr/GY1GqVTKcSRgn/l8vkqlAosB9mCCmQVlBAJBDwQ0+JLI5XJQyAUvYyoBjZqGHUxAtYPnOLg8Iy9y+Ai0uEwme+WEL+hlA8Ou1+u1Wm1nRxgQg1MqlSDlBtcRgEVbWd+lxxKPxQkB2Oug0WhQWE4mk9ne3s7hcEAi3Mmkdjr9ZT463JLNVlKvI0m2nJyx4Lo//WAg/dwHwUd/m3Dyy9X/iP+fJ1zCtnrRd/6v6TcjB1d/EHEhJK4hklH6/Xb23x2B1s2kzUzaCJIEAvo5VThepu/4XIwARgAj0M8QAOMEES7onWJnBgGVgVPQX7DoTCYTOP11pnhgQgG2CP4Ca2MxW5AbL9QGLoQEQRgMBgiYDO/1Hzx40NDQcPr06bKysk2bNi1evHjGjBkFBQXDhw8fOHBgYmIiyF+Eh4cHBQX5+/v7+vr6+PiAkrKrq6uHI7m5ubm4uLi7u7u6urq4uLi5uXk7EtWd2cPDIzg4ODo6esiQIWPHji0qKiopKVmxYsW2bduOHDkCPPKNGzdaWlra2tq4XC6fzwcbGDb8daebTAUZjb3LDICMsO0M5iu5vYCeo1aFWqQexPl+igC6muhlA9KlgRFBNEiTyQQ3mEQiaWxsLCsrKykpGTJkiJeXl7u7e3Jy8pQpU9asWXPmzBkWiwUMMpfLPXfu3Lp16woLCxMSEvz8/KKjo8eOHbto0aLDhw+z2WxYU1CXe06/G89c1j0Tc7h70eODBks9ER10ylDLOOWdSnb+6FQePiINaDabXVBQkJSUVFpaCj9rSqUSIgNBSVRhl/X0l4NwRxkMBpVKJRKJOBwOiHAyHXIcAoEAVKHhLVrnXzMEwmv6ZesvMOJ+YgQwAhiBN4lAnxHQJpMJTRUQwValUiEWqQcIYLaASVQqlQIjCYwth8MRCAQqlUqv14NpYjQatVot7HPs6OjgPk0EQSBbwWlCgqa1Wi0SJgY3bZFIBALKPfQNXjJzHKkzAY3muc41GAwGGAv4AsMqQi6XI7YXBJ1BTwPqh5F2N2UCLQuqGjBocBRFEhzQGYvZAu+NoV0YKagZqNVq4K8RK83lcl8HAU2SJFiiMBbkHQMoIdBMJpNCoaAGKpTL5XARoUxnVPGRdwYB4AvUajWPx2M6EmwEBiV0p/VDdw/Fi6EBBLSZ1OhJk9hAllb9PTKp9Dfhx73Dq0J/92++cac9PqryiftryO8vBv/+tMuHh11+WxfE+Dkx8c+XL5hNjiaJXwloOw1tJa2YgH6xC4HPwghgBN4HBJzYHJPJhKSQjUYjGG9UHNAPPjjYgtMumEBAKFOJZqhNp9MpFApwXOjo6Hj8+HFzc3NjY+Ply5fPnj178uTJioqKH3744dtvv128ePGcOXOmTJkyceLEESNGpKamRkVFhTsSyF8EBASEhNjj9Xl4eCA/ZRcXlwEDBnh6evr6+gYGBtJotNjY2MTExJSUlIEDB2ZlZY0YMWLkyJEFBQUoNN/KlSu3bt26e/fugwcPHj92/MKFC/X19c3Nza2trWw2G6IxQ1BrtVqtcCRk6DpZTWiXGwwcMX1USwnyYP0iY7jLjJOFjNCmXoKXzL+OOl+yS/j0V4sA9X6DOwrdV7C6gS2nLS0tNTU1W7ZsmTp1amZmZnR0dGJiYnZ29rx583bt2nXp0iUejwdPbnNz88GDB+fPn5+fnx8fHx8eHj5o0KDJkyevWLHixIkTjx490mg0YBnCU0B14UcdgF5Rn4sXGzW1HmqeWhv1ODVPLeOUpxbrMu9UHl7RobdoKpWqqqoqLS0tMTFx/vz5DQ0NarUa9g0DH41crzrX0++OIBpaLpfDShYclWABy+Px5HI5WvijGwAhAPD2u1HjDmMEMAIYgX6KQJ8R0ARBAJkIcgogT9wbAhpFIVMoFDDNcB0JhINVKpWTLW40GoGHZTKZHIdGB5/PpyphITMIzUBWq1UqlXZ0dACJDF7VSqUS0cE9XGyL2cJ5moAWR6Qt1N/Z1DYYDGKxGJh0+EsVuwDnX5vNBlYXDIHL5QIB3V1PYFDAvAM+QEDr9XrkRmQxWyCCMLDPPB6Pz+dLJBLYsgRkOojtQqOwf60316i7Xr3AcQQaQRAIAQiSDvJeyIB4gcrxKf0FATAuNRoNSITDI6lSqZDo8+sbCBDQBpuCIM0qG8mSkFNn/59A+n7vD0uDYqtcgss+iDzuzqj+IOqEG/3IgMhjH0Rc+m3MuVGjT/D+ZhffsDkcnwm7B7TFTFowAf36rhSuGSOAEXgHEOhMQAMxClYN4pTfDhTKAAAgAElEQVSp7x1NJpPBYAAnR9CK7ejoaGlpuXHjxsWLFysrK/fv3799+/b169cvWLCguLi4qKhoypQpH3/88ZgxY3JycjIzM1NSUqKjo8PCwoKCggIcKTAwEOSVvRzJ09MT/JRdXFy8vLyCg4MjIyPj4+MhHF9BQcG0adO+/PLLhQsXrlq1Cqjk0tLSioqKqqqq2tran3/+ub6+vqmpCXHKUqkU1JO1Wi3E5QN6HfiyzoYi0MpgEYEVB8YwKgmzJPUGACQR2+L0ldO3XbLPyG8UWWKoOWptL5l/HXW+ZJfw6a8WAbh/0CMMGaSg2NDQsGfPnhkzZgwbNiwhISE2NnbIkCETJ05cunTpuXPn2tralI705MmTM2fOAD0Nys5JSUmjRo2aN2/egQMHbt68CdtG4ZcBHgdoiJpHjwNaO0DfXma8UEPnv9Q6O3/b+3Z7fy481IhzV6lUtbW1WVlZQUFBo0ePrqqq4vP5nWuj9rO/5y1mC2xSgdU0m81msVhMJpPH4ymVSuCgOyPQ+2vR3/HB/ccIYAQwAm8DAn1GQBuNRuBnEQHdpWyWE0ZgMYAzLIfDgakF3EPkcrlWqzUYDGBewIk2m81gMFAJaOBheyagTSaTQCB4/PgxuGZD9EKngHhOHUMfEQENSs0cDqdnAtpitoDWB1WpWaFQIDSsVisEskDiAxwHjS4SiTQaDWrXKQO0NRDQnKdJKBQaDAZYuhAEAZM0CpaIXhGjxQA0rdfrVY7UJxH/wCyA6NLgkQ1vHfh8vk6nQ8Yl6rMTDvjju4EArB/0er1Go1Gr1aBNCU8x3M+vdZhW0qq3qAnSpDbbAwhWXyBTh/7ZK3SrL73UL/bkBxFVH9CrfWLP/iau1ivmjDv9rEfonxctaRLwSbHcYnUQ0A4VDpOZNGEC+rVeKVw5RuCdQQDmPurfFxtadzXA8Rer87We1ZmABj7FYrbo9XqpVNre3n737t2ff/751KlTBw4c2LZt27Jly+bMmVNYWJifnz9o0KDk5OTo6OhIR4qIiAgNDQ0KCkJ6ygOeJldHcnNzc3d39/DwgL9+fn7h4eGxsbHp6en5+flTp06dN2/e8uXLN2/eXF5eXlNTc/369du3bz948ODx48dPnjxpa2uDUBk8Hk8sFsMOvM4yYk6IgYUG4wKnbJjOwJKh2jOIUYIt5KgeZMTCDIhERaAAuuiovFMGClDJOExAO0GEPz4XAtSbtvOJ1PvNYrYYjUYOh3PhwoX169d/9tlnSUlJvr6+4eHho0aNWrBgwZ49e+7cuQOBPQwGQ3Nz86FDh5YsWZKbmxsUFOTt7U2n00eOHLlmzZra2loej0eSJKyYLGYLGIeoA91Rz9S1w8v/EqLHzSmDuoEeUqcCPYOGTu98FhxBBagZ9BWsmwwGQ0NDw7hx4wIDA728vP4pFsRkMmE9i6qlvsyjVtVP81arFaQdRSIRxFUCnoHL5SoUCoIg0MCdMv10vLjbGAGMAEag3yHQZwS0Xq8HBhl0mvh8PlL662FKBj0+tVotFAqRSDGQvCjcMJpRwIdXp9NJpVIul8tkMsGpWSwWw/KgswkCTRMEwefznzx5gghohULRQ6+oVx0IaNBNhr8ymawHr2G9Xg9SJEBAAwsMNDq0CBw6CIlwHZEJuVyuUChUKpXdBXGGFYvRaISYDJynSSKRgMeoxWzRaDQg6AEENERZRNE5YEQISeR/RB3pm8ybTCaIlAh7ZtlstlAoBF3sXl6XN9lb3NYrRwBuaVhLoB+KV95K9xVaLVadmTQZrKTeRioN5Iw5Z4LpawKj/uQdWfkB/a8f0P/qHlXjTj/rHlXjFXv6t3E/nrtoUSpIndEeftBMkhYbaSGNFtJoJc3AQfdaiKP7TuFvMAIYgXcUAZh8nXz04OBzjRjVA1VRiQb4Ie2yNtgUDzpm6D2fU8nez7xOWswmk0mr1crlcrFYDKHD7t6929DQcOnSJZC/OHr0aHl5+c6dO1evXv31118XFRUVFhaOGTMmKysrISGBwWDQ6fSIiAgajQYiGH5+fiCv7Obm5uHhERAQQKPRoqOj4+LiUlJShgwZkpeXN8aRJkyYAKH55s+fv3Llym3btu3Zs6e8vPz4seN1dXX19fW3b99ubW0FGWWxWIwkL+CtJwCCFC0AUidYev8RJjWwQp9rUqNeU3SHoHqgA728Ok5VQSVOf6EM/O396HDJ9xwBkE0Hh1OQ0NHpdDwer7Gxcf/+/fPnzx83blxKSgqDwcjMzJwyZcr69etra2vv37/P4XBEItGjR49Onz69efPmmTNnZmVlxcbGxsTEDB06tKSkZPfu3ZcvX2YymdR3Nt2hjZ4y6m3cZb67GvrvcfhxgOXn7du3i4qKBgwY4OvrO2bMmNraWtBjhGVyD0vUfjp8cJ8CJUmQ00Trcdgkje6BfjpA3G2MAEYAI9CvEegbAtpms2m1WpgPgIAWiUSIY+rZdNbr9SBYwePxgINGjr3Ul8xwVWCpA7H7gIBmsVhyuRwtxpD5Do0Cw6XT6fh8PvJqAfXnXl5mREAj6WRorsvTQQQD3tACESwSiZCECCwDTCaTSqUCwh10byGwb3cWA7K3YBQgg8Vms6khDWGPKtX3GXHT1H6iGbrnK0I95TXlTSYTCkAHt41YLO5hp+pr6gautk8QgPuQ+qjCkTfUGZt96zNpM9lIkz2WoI3UWciqWmF2zg7aRzvsBHRkjZ2Djqz5bVKDPc84nJZ/9P5jUqcnCRtJ2Kx29vlXAlqPCeg3dNVwMxiB/owAzOPASyJC8AV+91A94HWo0+n0ej2ydoCPtlqtBkcCwMAKcgIP1UMQBPCwThYIolCNRqNMJmOz2c3NzfX19efPnz9+7Pi+ffu2bt26Zs0akFSePn16YWHh2LFjhw0bNnjwYIjaFxUVFRYWFhwcHBAQQA3ZB/H6vLy8AgICQPVi0KBB+fn5BQUFU6ZMmTdv3jfffLN+/frvv/++vLz8xIkTNTU1Fy5cuHLlSn19/c2bN+/evfvo0aP29nawghQKhVqtVjmSVquFuIIQlRqYZSpHj0xKELtAbstOY3fCqpcfkamGKu+loYUmRLgx4CM6iD72phvoLHSPdc6gCnvZvd60i8u8qwiAtwrQmvCrIhaL79y5U1NTs2LFinHjxqWmpkZGRiYmJubn5y9YsKCsrKy5uVkoFEokko6OjuvXr5eVlS1atGj48OExMTFxcXEZGRmFhYXr1q07efJkc3Mzl8sFBx14BtFPWXd4oru3uwLv5HH0XKPfbYPBcPv27ZKSEl9fXz8/v5iYmLVr17a1tcGPv9OPXr/GxOl31Wg0ajQamUwmciS1Wg2DfT9vjH59ZXHnMQIYgXcJgT4joNVqNQoRABoXSOGuZ3ypghUQdZCqROE0qRAEodFogLBmsVjgAa1SqZAljcojO8ZoNCqVSh6PB/wsn89HM1YPHYN6wOoCz27koK1UKrub3QmCkMlkHIekBhDxEKQYGoJXuBCckM1md3R0MJlMgUCgVqt7Xv/ABKzRaICjB8ZWKBRCEEWr1QoYcjgcUH8G9rnz6JzA6VzgzRyB4ajVarFYDB7QHA5HKpXCnlN0Kd9MZ3ArrxyBZ15B6n1Izb/ynnRdoc0h5Gy1kHYm+VcOWqoi/2XJ+ZCIDT4RlR9EnnWl17jSzw6g1Xl9dNEn4fDslS1yHWm2gQC02WylEtAE4qDtvPaz/3XdKXwUI4AReBsQeObP14t1EhEHVEIQmRm9rxPVg9QeOlsjaIcTFAY9ZY1GA/ysWq2WSCQikUgsFsOL8CdPnty+ffvixYvl5eXff//92rVrlyxZUlxcPGnSpGHDhqWlpYGKa0xMDIPBoNFoISEhoaGhwcHBIILh6enp/TT5+Pj4+/uHhIRERUWBmPKkSZOKiooWLlz47bff/vjjjydPnrx8+XJjY+OdO3daWlqePHnCZDKBrpI4kkqlgn46xQMAB0yDwQA+mMAdO6lYUGEE2r07d2/ERKMJiHrui+VRVQB77y8u9cQe8r3pVQ+nd/lVb+rEZd5bBMAm1+v1ECfzzp075eXlX3/9dVZWFo1G8/Pzi4uLKyws3LhxY3V1NYvFIklSJpM9ePCgtrZ2+/btkydPTkxMhKCd2dnZX3zxxbZt2y5fvgy7SG02G8TQA3jhqUF+Ce8t5l0OHD28sKzW6/WwZhQKhWvXrqXRaLBTZNKkSdevX9dqtcjtqcva+tdBNHbq1An3pEajeZdG2r+uC+4tRgAjgBGgItA3BLTValWpVFQCWiaT9UBAozWe0Wjk8/lIGYPP54OiExoSmnvgCLgYi0QiLpeLCGgIXgcFUHlowmazgXcwx5FA7AJ0k1ETXWagHpIkTSaTEwENQmadz4K2xGIxx0FAQ2A9qggGUq9GXDafz+9NLESwzNRqNYyazWaDwgbYGQaDAXYkwRglEgkQ0132EMaF8O9c5g0cgT6oVCoIQAcvBmQyGawY+7Zvb2D473YT6MHpYZjoJnTK9HDKq/wKCGiLjbRaSJvRRpo0BqPRTP77v+t+P+RPvpE/fRBZ4xpV/UF0rXtknUvocfqQyuN1pNZip5YtdgFoRECbnkpw/KrC0Qv22foqB4LrwghgBF41Aog9fLUVQ7Wv1gMabSRisViPHj26fft2Y2Pj1atXL126dO7cuVOnTh06dOjAgQO7d+/eunXr8uXLS0pKpk+f/sknn4wePXr48OEZGRmJiYmRkZGhjhQWFkZzpPDwcDqdHhMTk5CQkJaWNnjw4GHDhuXn50+YMKGwsHDq1KkzZsyYM2fO4sWLN2zYsH379r179x46dOjs2bNXr15tamq6f/8+k8kUiUTKp0nxNKnVaojORxUlA1oBQhEit2s4CDRxD1ujkJnXS7Ohl8Ve7NJTp7Pn4tGoJ/aQ702veji9y696Uycu834iQBCEUChsamqqrq7euHHj559/npGRERMTk5SUNHHixAULFpSWljY0NAiFQg6Hw2Qyr169umvXrpKSkqFDh0ZFRUVERKSnp0+fPn3z5s1Hjhz5p7subHMEMOE1EgIWjH946uFGRV/hDHpbBlAgph6UJ0Ui0bZt29LT011cXHx9ff8Zy/Gnn35CMYeo6IFWMvVIv8ijHy64PeAv6Oz38AKyXwwNdxIjgBHACLwzCPQxAQ3UKo/HUygUQEB3ds8BrOHVulwuB9uF40hO5CmaeNCyAbx9QeOCxWK1tbWx2WwIXke9hHAiTNtarVYgEADLCWJk3Uktoxqo7Wq1WiCgwe+YxWKpVKrODss2m40gCGpcQQ6HI5FIoKTBYFCpVCh2IjD1AoGgB91n1BkYBQQCRh7QXC5XKpVqNBq9Xq9QKHg8Hupkb/y7qZW/+TxcTRTXGBy3QdikM7Bvvnu4xRdAANnEaOGNnlmojfpMUfMv0NYrOAU4aDulbCZJQqNTG02kUk6uWtXsH7XPhVbxAaPS46OqwMSLrsF/zsw7fOs/SKMjXKGFtJht5qcSHBYLaeod6Uz1jH4F3cdVYAQwAq8PAfgRg7/UVqjcNCKUEWdKLQl5VAYoVKcK0beIdkFR40CyWS6XM5nM27dvX7lypba29ujRo3v27Nm0adPy5csXLFgwZ86cL7744rPPPps4cWJ+fn52dnZ6enpKSkpSUlJ0dHRISIi/vz8IX/j4+Hh7e3s5EugpJyYmZmdnf/LJJ1988UVJScnSpUs3bdr0ww8/lJaWVlRUVFVV1dbWXr58uaGh4datW83NzSB5gQJa6PV6nU5nMBhMJhO1z9Qff+qP/CvMdwb5rTriNNLn6hs697nO6qEwqtAp08Mp+Kv3CgGCIHQ6nUqlglHDYk2n07W1tV27dq20tHTWrFlJSUkxMTEhISGxsbGTJ09et27dlStXOBwOCEDfunWrsrJy8eLFI0eOTExMTEhIyMjIyMvLmzNnTnl5eWtrK6yD1Go10ndGdyMVanTQyW6klsF5QABhBRMHSZISieTo0aOJiYkuLi4DBgyIj49fvnx5R0cHrKcQpE6XoB/hCUN++Q4j6F6+KlwDRgAjgBHACFAR6BsC2mK2KJVK5NjL4/HApkETJLWLkIe4eaDAwGKxgIVE7sBonkAZOAu8fYFsRQQ0eNNQm0DTFWzyQvobPB5PKpU+c88OatRkMsnlcqCeEQHdpWKGzWZDEhkcRwKJDJIkCYIQiURsNhvhw+Fweun7DIMC7wAQEkEa0EBAQ/xGriOYIYfDocpnUwF5q/JgDymVSj6fDz0XCATgV45Mpbeqw7gzz4tAZxFM9Ew5ZZ635ldWHpSg7QS02WolftGRGgV57x6ZN/FSaPIpT8YRl4gKj4ijvpF/Wrb6lt5IEhZ7ObPNbLbaHaef/rNgAvqVXRFcEUag7xAAW8XpfTkESUbrdugdEMfUknAuhOYDmVS9Xq/VajWOpFarlUqlQqGQSqXgLdjW1nb37t1r166dOXPmyJEju3fv/vbbb7/++utp06aNHz8+JycnPT09Pj4+2pHAlzAsLCwkJCQoKCg4OBgy/o4U7Ej+/v7BwcF0Oj0xMXHo0KGjR4+eMmXK3Llzly9fvnnz5gMHDlRVVV26dOnmzZstLS2tra1tbW0QEoPL5YrFYplMBkrKRqMRJKFNJlOXlwIBApjA23EECCagX2Z2Q+d2ifwLHEQVOmVeoCp8yruEANwP1BERBCEQCFpaWg4ePLh+/frCwsLU1FQfH5+0tLQRI0aUlJTs3Lnz+vXrILAuk8lOnz69devW4uLizMzMwMDAgICAjIyMT//w6aZNmy5cuCAQCKBy0COGePJwhHorUjvQ3XFqGZx3wpD6RlMikZw7d66goMDb29vDw8Pf3//zzz9vaGhAgpZobYWg7kd4dr5je9l5mJphhkIDR1D0shJcDCOAEcAIYASeiUAfENDgy6xQKBDHCjrLPXtAEwQhlUqp3K5QKNTr9TBC6lRBnXuUSiV4TENbbW1tXC638zYcdIrNZgPeluNIQHQ+083WZrMZjUadTgchd0EpAryMWSyWTqeDrU/Ui2Gz2WQyGcRFhLZEIhGoLkokEjabDZLQQJ0/F/sMrVjMFrlcjiQ4OByOTCZTq9UQHQhg7OXoqN3ukzws3cFxG0RRpFKpWq3ujTRKn3QYN9ozAuhxAz7CaDSqVCq5XK5Wq2HtAQYfFHP623PNr/9bu2+yzWaxmkm1nNSoyFWb/k5LPu5KO+zy24rf0CuS/kfZhauqX4ykQ+nZaueg/xsBbcME9Ou/RriFfoNAf1/awbtecOx1Ah24V51Op1Qq4Y3y48eP79+/39TUdPXqVZC8OHLkyMGDB/fu3btt27aVK1cuXLhwzpw506dPnzBhQl5e3tChQwcOHBgdHR0eHh4WFhYaGhoYGAg8cmBgIFDJQUFBISEh4eHhDAYjNTU1Kytr5MiREyZM+PQPnxYVFc2dO3fhwoWrV6/esmULCF+cPn26rq7uxo0bDx48gA1eEolEKpVKJBKZTKZSqTQaDegmw6ConAV1gGiJTj3YswmHSmICGkGBMxiB/oIACh5TV1e3Y8eO6dOnjxgxIj4+PjIycvDgwTNmzNiyZUt1dfWNGzdAI7Gpqam8vHzDhg2jR49OSEiIj49PSkoaP378ypUrjx873tDQwOVyYew9OB5RzT8qUN0dp5bBeUAAYeUECEEQN2/eLCkpiYyMHDBggIeHR15eXnV1tVartdlsaMMK4mSdTn+XPgJE1BfD1Omvv1sp79KVwmPBCGAE3hkE+oCAhrfcEHyPxWIxmUw+n6/VantYvYCUM3J/ZrFYVE4Wza8oA1XpdDqhUAhkLngTt7W18Xi8zuYOrIiADpPJZOBmCxEOu/Rfdrr8MD+BWzfinQUCAXhSG41GJwIa1J/5fD6TyQRvbmgLaRxDB0C7WSQSqVSq51XjspgtUqmUw+GABzTsa5PL5QKBADDncDjgP97dCtNpjH34EQhouGHAaxu8uZ8pjdKHfcZNOyGAnk14+uCaWq1WrVYLN2p7ezuLxQJRHXhe0CnUjFO1b/4jCvJu0pOEgayoIumpR12DDg8IPOJPP/iHojqpijQSpNkeahAT0G/++uAW3zoEOj+/cAT9FKACb13Xu++QxWyBl+j37t1raGioq6s7derU/v37v/vuu3Xr1i1duvTLL7+cOnXqpEmTxo4dO3z48KFDh2ZmZmZkZMTHx0dFRYWHhwcHB3t6esImaDc3N3d3dw9H8vT09PLycnd3d3Nz8/Pzi4mJSUtLGz58+IQJE4qLixcuXLhixYqNGzf++OOPlZWVNTU1dXV1169fv3nzJoTpg7fsMEWC37HBYIAwfTqdDtQw9Hq90Wg0mUzdLa17tgrgLOpfsJ1AZ7M7b2iEJSagERQ4gxHoEwTgGXymbw3q2927d48fO75kyZKJEydGRESEh4enpqaOHTu2pKTk4MGDDx48EAqFIpGoubn5woULW7ZsmT59emJiop+fH9DTs2bN2rRp0/nz51ksllarVSgUYAHCug9+PVBb1AyaGpx+qbo7Tj0X5wEBwMoJDcDfZrPdv39/w4YNYWFh3t7eNBotOTl51apVra2tSI7DCXmnet6Nj+hxMJlMekcITdCr7P0D8m7ggEeBEcAIYATeGAJ9QEBbzBa9Xg88L5ChPB6vZwIaAgMCLQuuwTKZrPM6h2qU6PV60FBGQhbQlkAgQMUQyoiSNplMKCogONtqNJreTEJWq1Wn0wkEAubTxHGEFuRyuSjEPGrOZrMhB3BwRuY+TdBbOFcgEMhkMp1O18NCEdVJzcBsCgNBBLTYkcAfHOLIgwfx229eAP5wNTEBTb3Q/SUPTxw8ZfA4wPZznU4nk8n4fH5HRwds9AYhGjCO387Rod8Km5kkjOS/XSIH/o/Tbn6HQqP/LSTywKkzpNFAmvQ2i9nmpHYKJ9psFvSve2/ot3PouFcYgedGgPrsA62JjlAfEERKotnWaU0IChVardZgMBiNRvgLNRAEgRQeqP1DE73JZAKlC7TqRvIXWq1WrVYrFAqZTCYWi+Gt8MOHDxsaGi5cuFBVVVVRUQG0MgTlKyoqmjRp0vDhw9PS0hITE0H4AuLyBQcH+/v7BwUF+fn5eXp6uru7uzqSm5ubp6enj4+Pn59fYGBgSEhIaGhoZGRkfHz8wIEDs7Ozx44dO2XKlK+++mrVqlXbt28vKyurrq6+ePFiY2Pjo0ePhEKhQCAQCoUSiUTpSFqt1mg0otEBqvDz0su/6NxXNfujCkHhmnoVOudR4VfVeucm8BGMAEagOwTgAYQtGnq93uknF2QAZTJZe3v79evX9+zZM2vWrJycHAaDERYWlpKSUlRUtHbt2pqamsePH+t0OqlUeufOnZMnT65YsWLcuHHp6el0Oj06Ojo/P3/16tXV1dVtbW1yuRx1Bv3UU3+soEuoDM68bgRA9Q5+rlUq1f79++l0+oABA1xcXAIDA7/44oumpiaYWFFP3offbYvZotPp5HI5n88Xi8VqtRo2TOP7E90GOIMRwAhgBF4JAn1AQJtMJnB7hBB5HR0dPRPQ4FksEAiQXzDymHaCAE2QRqMReVg7EdBCoRDet1MXP2h20ev1EIGQ60gikahzxEJqo1AJeDRTYwYC2Q0uzLBLl8qpwV42qpwIKISAQzTEP0SOz9AcGhq19S7zqKRIJKJ6QMM6lsVidXR0cLlcuVzemcHvssI+Pwj2sVgsBmSEQiH2gO7zi/JcHUBcEti7aA+EUCjk8/lo0wDcls+UXH+upl9HYfsjZrXrOptN5LVG8veZf/YL2x/K+Ets8o6btxwNmkmrqUsC2ozYZ5utBz3o19FrXCdGoA8QoD77iHFGGbQM7rxJCE3Kz9VpgiDUajVIXjx69Oju3bv19fV1dXU1NTUnT56srKwsLy/fsWPHxo0b16xZs3Tp0pKSkhkzZhQUFOTn52dlZYGYMoPBiIiIoNFoQUFB/v7+EJTPw8MDOGVYpbu4uLi5uXl7e0OYPmCTs7Kyxo0bB/IX8+fPX7Zs2apVq9avX//999/v2bOnvLz8xIkTly9fvnXrFoTpg51PUqlUoVAAt044EuKUUcRCq9UKkQkBOmoBdIRK6PScR0YC1Qp6Lpy7K0ytmZqnlu/uOLUMzmMEMAJvAAH49YCGlEplR0dHc3NzeXn53Llzhw0blpyczGAwUlJSCgoKVq5cefr06fv37z9+/FgsFre2tp44cWLFihWf/uHTgQMHMhiMmJiYnJyc2bNn79+//+7du48ePVIoFFR2G/3sd/7Jwr8Jb+BaU5tA8zJoTeh0uoqKitzc3NDQ0IiIiMjIyDFjxlRVVcHEBDKSaOH8ymcNasf6Nm8xW7RarVgsbnckiHkA2oDgB/YOj71vkcetYwQwAu8bAn1DQGs0GolEApIaIMGh0+nQ9OZ0DSAoH8fhUMzj8fh8vkwmQ2YNtTAYMSRJqtVqPp+PvIkR1ctisUQiUXcNkSSp1WqhV1xHEovFSGaa2hDkYQoH32egR7lcLhK2Bk9taA5Wg6gGq9Uqk8mQ+AbHkbhcbkdHB5vNFolESqUSaW7AhIfsM2olFrMFHLuobkcIBIhfBB7QXC4XIvgxmcz29napVPr/s/cd4FEcadojCUUrGqVVXEWDkFYgaYUEKwQcAnFEY9IBggOHEzb8gNZrg/cAw5J2McHCoAUBS7SNMUuwFiM4kOGIR1wQ6BQ90ROZqOkwM93178xnavtGwSJKwl3PPFJNT3WFt6u7qt/66v1IkuwuQynMVoFTANnKDhLQsCMYlvFb7TAYTD7yXBHAk12b1WaxWMDwWSwWw24BuKYymUyr1RIE0fW7pf0WYxDLIKsNiX5AxQuPxqetikj8z/9Y8LVKj1jwU2i12Ww0fB5Jcdi9F7LIgj/I4dLw0V+7uvSjz3O9GnzmPAIvDgE8SrZ6X7d6kFs5YKjB2R1BECqVqqam5vr161VVVSdOnNizZ8/mzZtXrK1+rzMAACAASURBVFhRUlIya9asCa9PKCwsHDp0aE5OTlZWVkZGRlpaWmJiYlRUVGhoKNgm+/j4+DqC96Pg5eXl5uYmaBFcXV29vLwCAgLi4uIyMzNHjhw5derUuXPnLl68eOPGjbt37z58+PCJEydOnz59/vz569ev37t3r6amprGxUSaTgZ6yyWQiHAHqDwMZDNAwJcDgAKEMDYcVa3DuR9M0JmsAKzgdDuK/7dPNLX+FTOAvF+2nj3Nz5sa5Obd1nJuGj/MI8Ag8JwTwYwceKUajEdjklStXjh8/PjU1FVjI7Ozs2bNnb9u27dy5c+B0tKmp6fz58wcPHlywYEF6erqPj4+/v39SUtLkyZNXr1596NAhoVAI/uQRQrDLBB4+sHgG+1RaPo7g6YcfC8+p1Xy2XARwH4DLgRAiSfLq1auFhYVwWT08PJKTk9evX09RFLwF4wv0k6M2t6DuFWdZFqzQ6uvra2trMQ2tVCpBCRMvCXevdvG15RHgEeAR6GoIdAIBbbPajEajQqEAieT2CWiGYYxGI6QUiURisVgulxsMBjwE4gimlWmaVigU2AZZJBKBKz+ghtshoFmWNRqNwNtKpVKlUqnRaEwmU1vcJXhTBKeFIkeAQoH4BgJaoVC01LYGgeaGhgahI2DDXrlcrtFouDbX2Hq65djPMAx4b9Pr9SRJYgsySIkQciKgwc4U3B6aTCauRXZX65RO9YGtgiDnDWSlWq02mUxtWXDDdaFpGnxwg/wlVzCa22ecyuK/PicEoCdjl1wikQjWQrA9vl6v53o/f07V+MlsuTcavpWczsJpbAwyEujG3eayvfcPHhPdqDbQLHqo0llJgrEC+0zabCTD0D9+WJJFFP48op7tjPUj6plxKov/yiPQPgL4BbL9ZJ31K7zoAp1KEARIXmg0GrlcLpFIQBKqtrb25s2bVVVVR48e3bt3b2lp6apVq8A8uaioaMLrE4YMGZKZmdm7d++EhITY2FhMKAcEBPj5+fn7+/v5+Xl7e3t6enJllL29vTHdDOIYoaGhYY4QHR3du3fv9PR0UMAoKiqaP3/+smXL1q9fv2vXriNHjpw7d+769es1NTVCoVAikchkMoVCAVMC4GJMjgAb2PGAAkMP1gOBMdppnIJFOGBkwHex2WwGSQ2nqQJmajDR3DKC0zxWBD/BcM2fVffg5syNc/Nv6zg3DR/nEeAReH4IkCQpFArPnDmzc+fOhQsX5ufnxztCSkpKYWHhxx9/fOzYsVu3bmm1WpBHO3To0Nq1aydOnJiamhoREREdHT1o0KC5c+du3rz59OnTMpkMyzWwLEvTNCy8geI8Vy6prccU/0x4fte61ZydCGiKouBVt7q6etasWUFBQV5eXpGRkdHR0fPnz6+vrwfTEHyZ8Ov2Mx9BWq3tCzvIsixFUSqVqqmpqa6urtYR6urqmpqapFIp9qyA6/OSNR+3i4/wCPAI8Ag8bwQ6gYAGTlkul4O9cPsENLj6EYlEYC8skUiUSqXRaMQvdTAiAkzwvqfVauG1FhQw8B5/0KMARph7FoYYCGiQ4BA6glQqNRqNrY4x4CbYYDBIpdL6+nqoHlh0gsE18MtqtdrprRIhZLPaFAoFUG/QNJFIpFQqCYIAwSlulbBtFNQZ/4W9xipHMBgMWCcaEmACGthtocN+HCj4pqamrq9ygBEA9LjSKEDTm0ymVltB07TJZNJoNCqVSuMIarUaaH24jhhADBS3LD7+nBBgGIYgCNBWA+q5trYW5HdgVtfWMs9zqk/LbJ06htNXbvp//sQgG4OsLKIZ+8fKIhuLEMOyNMFySGeGJR99zCwiHn0ohGjHh0tAc8vh4zwCP40ALO3ARlru632rwxbOruXTD6s6gNExZNhOJlhC1GAwKJVKsVhcV1d3+/btCxcuVFZWHj9+/MsvvywvL9+8efOaNWuWLl26cOHC4uLiOXPmgIzysGHDBg4cmJWVlZqampCQEBERERISEhQUFBAQEBgYGBAQ4OvrCzbKXl5eHh4ebo7g6urKtVT29vbu2bNnREREfHx8eno6eOqbOHHirFmz3nnnnQULFixZsmT9+vWfffbZjh079u/f/80335w7d+7q1asPHjyQO4JCodBoNAZHAL9DQA1jQyd8s2Ponj4CeXbE7s+JJuBeX4jj6j1B5Okb8vQ5PEG1H+uUp68hnwOPQHdBAD8uWn1u0zStVquvXr168ODBjz76aOTIkf369UtMTExKSsrLy5s7d+6ePXvOnTt3+/ZtjUZTU1Nz6dKlTZs2TZ06dfDgwdHR0WlpaVlZWaNHj167dm1FRYVEIpFKpQaDgSTJtp5FXNw6/uzinsXHnx8CuLfApbFZbeBcQSwWL1++PD4+PiIiIjk52d/ff/DgwceOHSMIAkyduOyz09P4+dX2xeQMS8gEQWi1WhCxrK+vBzvoxsZGsVisUqmAqef2+RdTN74UHgEeAR6BlwmBTiCguYbGTU1N7RPQDMNotVpMQONFSGzQymUVYekSs8/gt0cqlYL6xJMR0AaDoeX1xkbcEkcAMYGmpiaZTAbG2tAuoVCo1WpbEtAWi0Uul9fV1QkdvHBDQ4NIJNLpdC1fevHoDnWAr6C8Aa/9UqkUXCW0ZQHNJaCFjqBQKLqR+TOgx5VGAeN0nU4HfAE4p9Lr9TqdTqvVKpVKqVQKLZU+ClyreZh1AZKtTtNbXm7+yNMgAOqlsCoAqzv19fWwP0AsFoMxO/jDfJpSnv5c6BJtvSZx83/UeezuBG12LegfD0AEMTbEWrDJs4N6NjPsj59H7DPBIiCgefaZCy0f/wkEHvW9H//j1KAdDF+BkgZrWafXJHj6wU9gqAuDDrDJTotADMPAg7e6uvrChQsVFRX79+/funUrmCfPnj37jTfeGDly5LBhw3JzczMyMlJTU8FIOTo6OjQ0NCAgwMfHx8sRPDw8BAKBi4uLl5eXj4+Pu7u7m5sb/OUSyi6c4Orq6unp2bNnz/j4+MzMzIKCghkzZoCd8qZNmw4cOHDs2LHKysrz589fu3bt7t27sAzc2NgIq7k6nc5sNpMkCYQyGOhxOV8MHQwxGFg8Xj+/0QHK4lam1bJwMkjJrTCu7dNEuBl2Vvxp6t+RczurXXy5PAIvGAHgzkiSBOUf/DCnKKq+vr6ysnLr1q3vvPNOenp6YGBgUFBQ3759p0yZsnnz5osXL4rFYqPRqFarr1+/XlFRsWTJkvz8fF9f35CQkNTU1KFDh86bN2/Pnj21tbVKpRIsmsGzKwwibd2JXAQgDXd+1ZGzuDnw8WeLAJeAxlcHuo1Opztw4EBGRkZQUFBUVFRISEh6evq+ffvwa2Zb1/HZ1vDF5waYQLk0Tev1ekxDg0KmSCSSSqVarRbbP+Fu/OJry5fII8AjwCPQfRHoBAIaIWQ0GjFL2NjYKJVKsdSy05sYENDgrlAoFIK6otFoxFtW8dOfJEnseLC+vh7EyMBHMxDQYHDdEQto4aMAetPwBgukLfgoUKvVmGiWSCSwm1itVuPhCkhwoVBoNBrxCy3uJTarTSaT1dXVgagIrKyCKHNHXkppmtZqtTKZDHh5mUzGFXQGQJwsoEGHBP5iqHF9uniEoiidTgf7tUHMWiqVymQyuVyuUCjAuaJYLBY5Alw6rPoNEbFYjGVbAB/8t4u3vbtXDxTSNRoN3O9YowbuLKPRCCKnTnd9p7QaugR3Yu1E3uFa4c6DI0BDPyKjbSyyPDJ5JjH1DBGsv+EgoHn2GYPKR9pDAHdOEHDAf7Emg9OaItx3er0e1uRA8aa2thb88l27du3q1avffffd119/vXfv3rKyso0bNy5btmzhwoWgpDxkyJCMjIzExMTY2Njo6OhIRwgPDwe/fL6+vl5eXqB3galkzCO7urqCtbK7u7uPj4+fIwQEBICuaExMTGJiIshf9O/ff8iQIePHj585c2ZJScnq1avLysqAWT579uydO3dgZIQRVqlUwl4WWHckSRK7SeACB8td+HkCEfwVth/BgA6Qcs99YXF8NfEDhFtDXI32f4Vk3DSPG8cFdWLkcev8uOk7sWl80TwCnYUALBzeuXPn8OHDq1evnvD6hF69eoWGhiYkJIwYMWLu3Llbtmy5dOlSTU0NeK+prKxct27dnDlzhg0bBptRBg8ePG3atBUrVpw4ceL27dvglobbHO4CJ3emxL1Duem5cW6alnFuSj7+/BBoiTwcgbkETdNff/318OHDe/bs6e/vHxYWFhUVtWDBgvr6evxK2/K6P7/adkrOsDAPr5/1nCASibRaLWgGtjp2d0pt+UJ5BHgEeAS6EQKdQECzLAvKFUJHaGxslEgkbTkhBAmOtghoPF4C+yyRSPDufolEQlGUzWrTaDSYnQQXfy1fSuGCsSxrMplAOhnqhiWnDQaD0Wg0GAxc6hnMnJuamhQKBbgJ5hLrsF5qMpnwaI27BcMwQECLHQEQAFERzH9B0/ApOGKxWAwGA3jka2hoaGxsVKlUeDEW741yIqCFDlNrsNfGlhE4z86KtNVGqA/8StM0mGaAhrWIE+AaYRNv+AoC3PC3qakJCGu5XG4ymfB1h5zhb2e1/WdSrsVi0Wq1EokEfHpAjwX2mSAILmv2AqZx+Lq3Cj78im9AHGnZT3A+OMIloG3IZvsnAf1P22cHAQ0a0D/6IeRIP7daI/4gj8CPCGDLZRBTJknSYDCIRKI7d+589913J0+ePHr06Jdffrlz587S0lKQvFi0aNG777771ltvgYxyYWFhXl5eZmZmr169YmNjIyIiwsLCevbsCXoX/o7g5+cHwhc+Pj4eHh7u7u5Y8sLV1RWsk4FodnFx8fDw8PLy8vPzCw8P79OnT05OTkFBwdixY6dPn/7WW2/Nnz//ww8/XL169caNG7dv375//35ssAzayvAQ4Kok6fV6giAoRwApKnx/AQpOj4iWDAgWD6FpGtzzwhyg5S2MB0qnPF9Mh4P6dGSx2QmBltXDCZ4g0jK3F3/kCar9WKe8+BbxJfIIdAoCFEVJpdLq6upvv/1206ZNM2bMyMnJSUhIiIqKysjImDFjxtq1a48cOXLnzh2wxbly5cr27dvff//90aNHJyUl9e7dOzk5efTo0QsWLNi/f//169elUilsTQObFYvFAgr+ZrMZNtxg05yWRCTcpG3h0P4t3NZZ/PFni0A7VwEcSFoslitXrkyePLlnz55JSUm9evXy8/MbO3bsjRs38PT4J0exZ1vnF58baJobDAaZTNbY2AjC0PB2jzdkc19kXnwN+RJ5BHgEeAS6IwKdRkCDQSvIYojFYiBqW85aMAENpqz4iQ8W0DA2wO5+iUQCjDB4otdoNDA0wuqlyBHAhrqlOwW4ciDrrFQqwVJY6AhgbAtmtmBJja04YbevQqGAyiOEuMQ6aEDD1A1Ga9w/WJZVKBRgAQ3VFovFXMPkVt+KoXo6nQ6MSYFdBe4bK2Lj9+qWBDRO30UGy1bbCBAxDEOSJPDOKpVKrVbL5XIuAS0UCkHPGhPNTjS00EG4g728Xq83mUxYswUgwteCjzxXBCwWi1KpbGxsBMVniUSiUChgdzzezfdcK4Azh2cL906ElyjYuEpRFFZRx6fgCMuyVoax2GxYuwAYLjtfZqGlP8ikP8goC22x2ewfhrYwJG1rpm3NNsZsY8yMw/cglnu22WiGsSJkl4uGIhibQ7eDcRxjEcv884PrwEeeOQLtPIIeqyzMe+IXcnjIgDUuVmeGHthy3ysuC8yWlUplU1PTzZs3z5w58+WXX27btm316tUffvjhO++8M2nSpKFDhw4YMCArKys9Pb1Xr16JiYngPAo4ZX9/fx9HcHd3xybJLi4uPj4+ISEhYWFhAQEBmFOGBG5ubqCSAWbLnp6e7u7uLi4uAoHA3d09ODg4OTk5Ozt7xIgR06ZNe//999esWbN169a9e/ceO3bs9OnTFy5cuHLlyu3btx88eACbmUBUB+5u3OT2I2DQDfcjaGUAaFz77nZedNvKvOVLMoaaG4HTuUdeQJxb5xdQHF8EjwCPQPdFAIYYbv1hrQ6O6PX6O3fu7N27t6SkZNCgQWFhYb6+vgkJCYWFhQsXLty1a9f9+/f1jtDU1PTNN9+sXr168uTJiYmJnp6eQUFBaWlpM2bMKCsrO3PmTH19Pbw6wUonRVHwQG5HHhAes9wHmlOcW20+3sURgGuHh06EkEgkWrRoUXBwcFhYWEpKSlxcXEZGxr59+8xmM8yguJe7i7fuyaoHPIPRaARyAFu51dbWNjU1qdXqLvJO/WSt48/iEeAR4BHoFAQ6gYBmGEav13MJ6H+McKCQAC+ZXCDAghLIR+yIFju+oGkaCFlMR9bX14tEIrVajVlmg8GAJTjAo71arYbdu8AFwPAJhdqsNm7dhEIhFC38vwHYcKFQCIJoMAwDV46lRaC2YJvMpb2Am1Cr1cBfi0QiyFuj0XANmbkggAM3vV6vUqnEYjHsBOKWzmVScHMUCgUQtZA/ENA6na6rDZaYASQIwmQy6fV6pVIJvDxedQAbdqGDVoZGgS0tJAD2WSwWS6VSuVwOm7V1Oh3wzgAIl17kwsXFmY8/cwQsFotGoxEKhXBjarVagiBavsw883JbZohtSDGTBVsTaJo2m806nU4ulzc2Nt6/f/+uI9x2hOrqarhPZXK5yWwPEonkzp07Z86cLd+xa/Xq1e/Nnzdq7JhRY8e8N3/eX/btdXz+8pd9uw5+ueevJ746c/ZvFy+de1Bzp+n7OrVGrnmoUmvsvkbB1zZeN6JIG0XabNZ/8s6Yg27ZkC54pDveUOByB1+ClutSWEnZYrHgt3F4jMBP3HMRQuC4RuEISqUSNqk8ePDg1q1b169fv3LlSlVV1fHjx7/4/Ivy8vJNmzatWLHigw8+eOedd6ZNmzZy5Mi8vDyQUU5MTIyKigp1hOjo6NjYWPgaGBjo7e3t5uYGGhfAEYOqcnBwcHR0dEREhJ+fH6aeXV1dPTw8vL29fX19g4ODY2Nje/XqleIIaWlpOTk5Q4cOHTNmzOTJk+fMmTNv3ryPPvpo/fr1e/bsOXr06Llz565du1ZdXQ1iVvBoBWcDZrOZIAj4C8s20CHxuIPJdzjyBH/x2287kSfIttVTOutu4lams+rAl8sjwCPQ9RGA1W68cxGc6Gg0mrq6uhMnTqxbt27GjBm5ubkRERExMTEZGRmTJk1auXJlZWVlfX09uIetqqoqKytbuHDhiBEjkpKSYmJievXqVVBQsGTJki8+/+LGjRtisRi/fcC6KexEAYlnPGXiPrU6Hu/6CPM1xAjAZcUjL7yAy2SyDRs2gL/KXr16hYeHx8bGLlu2rK6uDk7EnQHn8zJF4N0BzAtMJpNCoQArtAaH9yZYsHmZ2su3hUeAR4BH4AUg0DkENNdSuKmpCUv0wjDGbTawusBWc61ccRyo54aGBvBBBILIsGgPuZlMJqlUKuIEiURiMpnApoA7tYJyzWYzV4VD2FoQiURgyAk7heFEm9UGAh24KLVaDT85tYtlWb1ej3VFgIMGh2yg5owJDpqmsUNeTMICAS2TybCsBJTiVJZSqQSuFloAPhKxdjb3lBcfx4CAprZGo+HamIOHOkwxQ/1FjwJ8xWsJRqMRnKKAAR3MEri7s6EsXOKLb+zPuUQw6gQbdlhigQvBve9eDH2JCWiwzYRFnbt37+7Zs6ekpGT69OkFBQXZ2dnpaWnwSUvp06dPn759+/YfkDswL2/Ivwwd9/r48a+PHTRoUPqv+sXHJQf493RxcRMIBD08Pdy8eggEglcC/R0f31cCfXp4CXwDvSKjQhISo/v2S83JzSoo+JeR/zpiwusTiouLd+7cffv235UKtUKuMTfT0EMYK7JYWLsLQ6v9YzeP/tFCusv1IO49BcB2uSq2WyF4wOInBk6LLdy5q3TwjNJqtVKptK6u7saNG+fPnz916tSRI0f27NmzZcuWVatWLVmyZOHChe++++6bb745Y8aM8ePHFxQUgKlyRkZGWloa+JQPDg729/cHUjggICA8PDw5ORmsisLDw4OCgnx8fLCFsouLi7e3t7+/Pwhl+Pn5eXl5Ocli+Pn5RUREJCYm9u3bNzc3d9iwYWPGjJk+ffrcuXMXL168cuXKDRs2lJWVffH5F8ePHz99+nRVVdWlS5du3Ljx4MEDWKk1Go1ms9lksi+vgJt7kK3gIoDxcYoAXHAQwIQ4dAmnTtJ9vzq1+pl85aLxTDLkM+ER4BF4KRGAyRKI7wmFwuvXr+/YsePdd98dMmRIZGRkWFhYcnLyiBEjFixYcOLEibt374LRzNWrVw8ePLhkyZLRo0eDb9g+ffoMHDiwuLh49+7d165dAxc1LZX0YXDEu0+4T6oni7+UF+VlbRT3EuNNiiCEeODAgZSUlJ49e2ZnZ/fr1y8kJGTKlClXr14FR0dwIhcWblbc490uDg3BdwRBEGAKJhaLlUql0WjEi0Pdrml8hXkEeAR4BDoLga5CQOv1esxJcbEAk2RgkIWOANQzNn1tcATMPmO1MmyqZjabwY+t6FEAqpcgCOwADQYYKJeiKNho09jYCNlinQcwiJZKpUqlEkSruVW1WCwwLEE5YrFYo9EAucbNH/wgQa2g8pAeWiQWi1UqlUajUalUYEwnk8kkEgk2xG5sbGxqapJIJHq93skEDyqDywKXjJipF4lEoBb9Yvg+LjIt42D1bDabgdYBpWYwVIcVBcel/tH8HF9rOCh02EHL5XKDwYBZEmg1/osX8HGngp9a1oQ/8lwRgM1r2G16J14XLgFts9rOnj07efJkT09PrFTg6en5irent3sPDxdXD0EPN4Gbg192FQhcBQK7IgEEFxc3D3cfN3fvfx50cSTpIRD06CFw8xC4u7l4uvXw8HL39Pby8vHy8np0qv2/i6td2cDNzcMeF7h7efqOGzvp68Mn6mqFGrURsXYtjh+p5y5JQHMfaPh2A5N2fDM+1x71bDPH40t1dfXFixePHz++f//+0tLSlStXLliwoKioaNSoUYMGDQISOS0trU+fPvHx8VFRUWFhYYGBgV5eXq6O4O4Ibm5u7u7u3t7eQUFBERERvXv3zsrKGjx48NChQ7Ozs+Pj4/39/XFn8PLyCggICA4OBic/Xl5ebm5uYNcMaVxdXcH5T+/evfPz86dPn/7ee++BnfKBAwdOnjx5/vz5q1ev3rt3r6ampra2trGxUSaTaTQak8lEkiR3dABfOrA4h//ijQhcSIF9YBiGoihgpfFICjcvvIY5XWtI73QQd4/uHuHi86ziXEyeVZ58PjwCPAIvHwIMw0gkkuPHjy9fvnz06NGxsbH+/v5RUVE5OTmzZ8/euHHjxYsXwbm6SqU6c+bMZ599tmjRooEDBwYGBnp6eiYkJEyfPn3t2rXHjh2rra3Fls54IMDydNj8hft0evr4y3dFXuIWcS83d0AHmayjR48OHTrUxcWlf//+BQUFHh4e/yCjjx8/jjloLjLcrLjHu10cGgIzH5gAg2E4sM8tl3C6XQP5CvMI8AjwCLx4BDqBgAZff0AKg4muWCzW6/V4uZWLAggfg2Wx0BGADsZbYBobG4GRVCgURqMRhgfYRAZxiqI0Go3o/wa5XK7VauEtnTtMAjFqNBqBSsaZi0QicEio0WhAAAQyh6pCnKZpYK6hnlKpVK/Xw09QBG4XwzA0Tev1eqlUiosAAWsw/oXKAjiYfgVmViQSyeXylj6pcea4LGg1JqCBEOeyEviUFx+B/e9arRZ3AyDZAQQg2TErjX1IArBCBwGtVqvxvPnF158vsVsgAN0MmyfQNH3t2rW1a9fm5OSA4i3+a5c1cBH0EAi8erj4urv7efp5u/u5uXm5e77i+UqAu7ev5ysBrwS86uET4OLq5drDy8XDW9DDy04nO4hkF09BD293gZu/QOAjcOkhcPMSCALcXMM83SNcXQPt/LSLQNBD4OrxT9ZaIHDx9vDu4eIhELj3DAh3d/MLD4ubNHF6WVn5oS++bKpv0Gt1iEUw60UIdfreBXiwAI/PXUiAOIj2ttUruEZVkA+sDHHTA0kKm1ewJzrQvoCnFuiWYCtdkiRBCwJEe0Qi0f3792/dunX16tWLFy9WVVWdPXsWCOWysrJNmzatWrVq8eLFxcXF06dPHzNmzNChQ3Nycvr169erV6+EhITY2NiwsDA/Pz/QOgwODo6KioqPj4+NjY2MjAwODg4MDPTz8/Px8fH29g4ICIiMjExKSkpPT+/fv39ubm5aWlpkZKSPjw/ml+39wmHCHBISEhsbm5ycnJCQkJycnJ6enpGRkZ2dnZ+fP3z48AmvTygqKnrvvfeWLFnyySef7Ny588iRI5WVlZcvX37w4IFcLpc5gkKh0DqC0WgE3+uY9MfXpdUIF2E+ziPAI8AjwCPQ6QjAih2s7cEAihCiadpgMMBOSr1er1Aozp07t27duuLi4iFDhsTGxoaHh/fq1Wv8+PGrV68+dOjQ9evX5XK5RCK5evXq/v37P/zww9GjR/fr1y82NjYpKWnIkCG//e1v9+zZc+nSJZVKZTQaweAGryBCuVwTDcxNdzo+fAU6FwGYSzjVATY5Xb16debMmd7e3ikpKYMHD46JiUlOTl63bp1IJML9p/0tUE7Zdouv3Pd9qDBAhFmLlgm6Rbv4SvII8AjwCHQWAp1AQINcJigUYwJap9PhR3lLLEAWA3Q26uvr6+rq8F8wGdbr9SRJwoItzKjw4i1soJbJZCJOkMvloBONxaCd3t5hz5FGo1E/Clqt1mQytUPgUhSlUCiwprNMJgMvDThn3C44AlvqQCoU08SYbhY6AhYYAU5WKpUCb94OVpA5Qkin02GVD7Dd1mg07dQfV+8FRCwWC0EQGo0GKHhQ24DrW1tbCyw8XCO9Xm8wGHQ6Hcg4AE8N5D6+xC+gwnwR3RQB6PA0TdfX1y9fvjwzM9PV1TU03zNLnQAAIABJREFUNBRTz25ubh4edntkCK+42zloLxc/d0Ggq5uvwNVH0KOnq8cvBIJIgSBIIPDv4Rnk+UqAxyvebj4+Ak9Pu9Wzq0DgBsyyu0DgJejhE9DzF31SBqWnjUpOGP5qYKp/QEhI+Kthkf6vhvkEBvn6+Pi49/D0cPfy8fTxcPN0mE8LHFm4CwQeAkGP0NDw7Kysuf9RfPbsWaVSCQ9MkiQ70dQCnirY2x5E8KssvG849ZBW196c0uCvTtN3m9VmNpvBfeXdu3cvX7588uTJr776ateuXaWlpWvXrl2+fPmHH344f/782bNnT506dcLrE0aPHj1s2LABAwb07du3d+/esbGxYKHs7+8fEBAAf3v27BkTE9O7d+9+/foNHDhw2LBh+fn5mZmZqampycnJUVFRwC8HBQWByiHoYyQnJ0dGRoaEhIB6hqcjeHt7+/j4+Pv7h4aGJiYmZmRkDB48eMSIEWPHjp02bdr8+fN///vf//GPf/zss8/27Nlz6NChEydOnDlz5sqVKzdv3rx7925tba1MJtNqtTqdTqvVwlMO1DC4spsYH24Egw8MAlyatv5yT+TjPAI8AjwCPAKdi4DJZIL9l3iIhPk8wzByufzatWtHjx5dsmRJYWFhYmJiXFxcSkrKkCFDiouLt23bduHCBdiXeffu3YqKipUrV06aNKlv377R0dGJiYkDBw6cOnXqqlWrDh8+XFtbCxN+WP0Fd4IwZOPFy5YjSOciw5feRRDAb5G4PniOZzabGxsbS0pKIiIiUlJSRo0alZ6eHh4ePnfu3Dt37oCdBEmS4NWp1WkJzrMbRZwmqODoArcOvnaj5vBV5RHgEeAR6HQEOoeApmlapVIJHwWJRNK+czyGYQwGA7aEFTuCRCIBHQa8Rxi8irXEFGwKRJygVqt1Oh1BEPhcGEu4AwnM2/A+tXY4XyiRoijMJstkMiC4If+WVYKCgIOWyWTAL2P2GfPRQNBjvWMn0eeWgyIeFxFCRqOxJQGNrUFxylYzabXCz/Yg+KIExGBKDc3EvDPWbYDNXxRFmc1mg8Gg1+sxU9NZlX+2UPC5PT8E9Ho9TdMHDx7s1avXI5JZAG7cuBy0XUfh0c+uAoGfV0TPV3v7BkbF9cqOSfoXD89cX89xAkF+bNTwqf/2XmnZ1k/LNm74bPMnpaVz3p4/YdL03CG/6d2vd3RCcmJK+pvvvvu3ytP2FSAtEjUg6feIIu3tMzRrH9Te279/7zvvvJOcnBwWFhYTExMcHOzp6QmG1I/KdxEI3HxfCYSvKSkpO3bskEgkYAvciRy00zXCj0enByOelOOFQEyY2qw2kiR1Oh3I09+9e7eqquro0aM7d+5ct25dSUnJnDlzJk6cWFhYmJOT06dPnwRHSEpKSkxMjI6OdqKAsbc9cMTn7+8fHh7eu3fvQYMGjR8//q233iopKVm4cOGsWbNGjRqVm5ublJQUEhLi5wiBgYE9e/YMDQ0NCwsLDw+PiIgICwvz9fV1d3fHIhhubm4+Pj6RkZFpaWlDhgwZN27czJkzS0pKNmzYsHfv3mPHjp06dery5cu3bt2qrq4Gf+hSqRQUMIBEdkIMcIBHFljAOVkMQXrYHwOW4MAXgHU5dyTC1D/Xfg0jz4041YH/yiPAI8AjwCPQ6QjAAAomzzKZ7OzZs5s3b3777bcTExNdXFwCAwOjoqLGjBmzZs2akydPNjU1gTMbUHYuKSkpKCiIjIwUCATBwcE5OTnFxcU7duyorq7G+wIxy8xtKR6Lsfmz0wjCTczHeQS4COC3LdCE+Yd7CZg+TZ06taCgwNvbOy8v79y5cyTpmO8i9HL3Me4sixvnIsbHeQR4BHgEeATaQqBzCGiLxaJWq7HeAigac7nRVqtrMpkMjgD8I5gEchle7gCJ48C0ms1mlUolkUikUqlcLgcSs1UJDu6EDLO0rdbH6aDZbJZIJKANIhKJNBoNRVHc6jmlh8zB1FqhUIDKs+hRwCS7VCpVq9Xg6ADGuZb5cI/gNARBSKXSpqYm0LKQyWRgZo4T41ETH3nBEZvVBi4WlUqlSqXS6XTgUdCJ0oJawQo8kNEWiwX7mXzBdf45F4e7VlcDAV6rQF3dyS7+4sWLM2bMCAwMBHkEFxcXUNrlctACgcDb2/sXoWHxv4z915GD35wz8w9/+HRH+fGqqzW1EmbfV015+Z8UDNrXN3nl7KJPL16qtSIbjUwES5Asa0PIhhDBUEaLgXnkNJBi0P/+r+kPyw6PL1w3a+qntTUmi9WOmc6og5228JeiqJMnT/72/UXvzH1n8r9NSuzdS9DDV+DqLxC49PAMshtFu3v28PQQuAjS0tOXLl1aV1cHdkzchxtci+d9LwMrSpIkPISVSqVYLG5oaKipqbl3796tW7cuXrx4+vTpioqKI0eO7Nu3b+vWratXr16yZMmCBQveeustoJUHDRqUnZ0NPvciIiJCQ0N7OkJoaCjoXSQnJ6empvbt2xdEKvr375+RkZGSkpKUlAQ/ZWZm5ubmDh48eOTIkZMmTZo6deqYMWPy8/MzMjKSk5PDw8NBT9nf3z8wMDAgICAwMDAkJCQiIiIuLi4tLS0rK6t///45OTl5eXmDBw8eNWrUlClTiouLFy1a9NFHH61evXrbtm379u07evTouXPn7t27B3pHMpkMHlBqtVqr1RoMBvDXBx5o8XMJVghgTME3CPe6YEYe30cQgePwZMODID4RR+B1DpuwYX4BJ2g1gmvCR3gEeAR4BHgEnjkC3AdvRzIHJ+QNDQ23bt06evTo0qVLx4wZk5eXFxsbCyal7733Xmlp6blz5+Btorq6urKycuXKlW+88UZ2dnZCQkJcXFxOTk5RUdGGDRuOHz9eU1MDGoYg1YWtargMIHfgwGMHJHjc+nekjXyalxIBPNtBCGm12q+++mrw4ME9e/YcOXLkhNcnREZGZmdnl5eXg8EEt/txe9rLgQz3ruHGX47W8a3gEeAR4BF43gh0GgENCshCh56vSqXCAhrtNBhMBvBECh76QOPCWXgYgFd6blYMw5AkaTQaDQYD4Qh4Sxo+C0eeYLBkWVar1Uokkqampvr6+oaGBnASiAkFbmWc4piHVavVmkdB6wg6nQ4q3D6R7ZQhfKUoSqvVtuR2W03ciQe52q9O7GFbtcLToJZMXFun8MefEgF8d0AE7hF8pzxl5k95OixIYG4XdkIolcpPPvkkMzPTzc0NrInBH6CPj0/Pnj2BdPbz80tKSioqKiotLb1y5cqNGzeEQmEzQTVbkNGGjCw6UaUaVLA97BcrXvvlhhH5Oy5fIFQaRCMrjUwUoinEUCyyf+xxs8X+seqaGYMRla6v7hWzOPWXi4tnfU4YEUEgykJTVjNtsStp0FaL1dHXrQxjpkidqVmlN1f9992vvr7y9n+s8QtIFQiCfV8NtYt7cELYL8LnL1gAxlAURcFrJNwL+HJwLxMXVfAGCcjAiXgtB9CjKMpgMEil0urq6itXrpw5c+abb745dOjQ7t27N27cuGLFit/+9rdz586dOXPm1KlT33jjjbFjxw4fPnzgwIFpaWkJCQkglOzn5+fl5eXt7e3n5xcUFOTv7w9yFsnJyVlZWfn5+SNGjJg4ceKcOXPmzp07e/bssWPHFhQUDBs2bOjQoQMGDOjXr19qairoY+Tn5w8YMCAzMxPyDw0NBU7Z19cXFxEQEBASEgJGygMHDiwsLJw4ceLbb7+9aNGiZcuWrV+/vqysbPfu3V98/sWRI0cqKipOnz594cKFW7duCYVCkMWErdCkI4DZMh5fMLxcGLlxDHWrB/GvLSM/mR4StDyxnWvdamL+8ciFmo/zCPAI8Ag8WwTgwcsdf1vmD7oEDMNotdr6+vqTJ0+WlpbOmDEjIyMjOjo6ISFhwIABkydPXr169fHjx8FHek1NTUVFxSeffDJ79uycnJzY2Ni4uLjs7Ow33nhjxYoVlZWVd+/elclk2O2N09CA6wMRvLqJqWd+vGh5mfgjP4kA7mbwYmswGE6dOjVjxoyYmJhBgwZNmzYtOTk5MTGxuLj49u3bkBt+0cZ9ktv3frLE7pgA5l3QTAyC2WwGEXburIwb744t5evMI8AjwCPwxAh0DgEN9nRGoxEMymDX2E8+i/G4BSMZ/opP5B7BB1uFBjY1Y4rB6UTuV+7pbR1HCJEkKZfLRSJRY2NjbW2tUCgESr2DjCoYb3IpISceBNtlt+TWuTXkxnEO+Fzur10t3g623KriZHg/Oz7CTcbHnzkCgDOoKIAZrE6n0+v1JpMJyNBnXmLHM4TOgO2gEUL/sM+dMWMGMM7gDg4TuUFBQYmJiUOGDFm3bt39+/dB1MVsNtufCYg1EGYGIQIhHYP+/j0qnLwzOGplz9A/FBbsPX3SqtejZsJOQFOIpOx/GcfHSiEzhQwkekgwlFqLjh2Rj8zb3Tfxk5lvHLh9BREmIKBJymriEtA2hGiWMdKkptmCEBLK0H9VGQ//VTqk4P2hw9/KHlQQFBkicBW4enu6OeygBQKBp7fXP9zllZWVyeVygiBMJhP2LITn923d71qt9saNGxUVFWChvHLlypKSklmzZo0fPz4/P79v375JSUlxcXExMTERERHh4eFhjhAREREVFRUeHh4QEOD7KIACcnBwcEJCQmZm5rBhwyZOnDh79uyFCxcuXbp0/fr1W7Zs2bhx4/Lly+fNmzdjxowRI0bk5OSkpaX17t0bPP7BG3VcXFx0dHRwcDD49/Py8vLx8fHz8wPJ5pCQkJiYmNTU1AEDBowdO3bWrFklJSUff/xxaWnp/v37T58+ff369QcPHtTV1WH1HqVSCSIY+MGLxS5a3Vfh1MfAey2MC04/tfza6pMHH2wnws2qnWSt/tTyKreaDB/klsXHeQR4BHgEeASeIQJAycFk22KxwFom7M8DHzBGo7Gurg5G3g8//LB///5xcXG+vr5RUVHDhw//4IMP9u7de/v2balUarPaampqvvnmmwULFowYMSI+Pj4gICA2NjYrK2vWrFllZWXnz59XKpVgjAIKddzXHEwOcscIpzhPQD/DS/+zzQo6FTTfaDQ+ePBg9uzZQUFBWVlZixcvHj58uLu7e35+fmVlJbwFm81mbj/EkxNu732ZwIQG4iabzWbY4qxUKrG3KpzmpUfjZbqyfFt4BHgEniECnUNAQwO4hFFHmoSf1PBkx1/xMNbySPvZQnqss9HWV5xJO/kbDAaRSAQ+A2tqahQKBWZA8OlPHGmn3CfOs6ud2ME24mRt9YGu1q6XqT5gRWswGEDNRuQIcrncbDZ3hWbCy5Verz9z5sz48eM9PT3BVBZoaD8/v4yMjOLi4oMHD968edNmZaHO9ndFkmKsNvsiELIakd6MKLHZcKuJmvu7S7G9t4bFre+f/+e/7Ltv399qQwaSpRBDICth56kZApkI9BB/mhnblWumKRP+kpqwbvaU47duEAyya0BTFKKsZspmoG0UbbXYPyxjceSgs5LKZvT3WvT2vOO9U5cOGrI59zdLT1SKJTri6v0bH61aljd0sJeP3eWdt7e3m5sbNGfKlCmXLl3iurbH891WCWib1fbgwYOCggLwzhcaGhoTExMfH5+YmNirV6++ffvm5OQMHjx42LBhI0aMKCwsHPkojBo1aty4cVOmTJk9e3ZxcfF77703f/78hQsXgrbGpEmThg0b1r9//z59+iQmJsbExISHh4eGhoaHhwc5QlhYWERERHR0dFJSUp8+ffr27du/f/+8vLzhw4ePGzdu2rRpb775ZklJyfLlyzdu3FheXn7o0KGTJ09evHjxzp07dXV1jY4gFAoVCgW4gTU5AtYZhIsIQwD3DRyOWCwWrImJuyiwzFh/GR9vORBwf2oZx88i7k/4YDuRx03PzarlVeb+2jLOLYuP8wjwCPAI8Ag8QwS4BDRs5qMoiiRJgiCqq6u//fbbNWvWzJw5MzMzMy4uLiEhIScn56233tqwYUNlZeXt27dlMlltbe2pU6e2bt06e/bszMzM+Ph42NMzatSof7hN/uabb+7du6fX68FIhXIEbEDDfffhDg0/GW85UsCRZ4gMn9VLjAC3t1gslurq6mXLloWGhkZGRhYXF0+aNCkqKionJ2fHjh1SqRQ23uE+ye17LyVE0EBor8Vi0Wq1YJfW1NQkkUhUKpXBYOBuYcSAvJRo8I3iEeAR4BFoFYFOI6DxzKnVarV6ED+m4cmOv+KsWh5pNR98ENLjrzjSVj5tHadpWqPRAAHd0NDQ2Nio0+lwrXC2Txxpq9z2M+SexY23f1Zn/drBGuJkbfWBzqr/y1ou1+KeZVmz2Qz6v+AeE2ZUOp1d2rgTA/QKkOCoqqpKTk728PDAJs/BwcH5+fm7du168OABRVEmkwkhRJjtEhZQZ8bCMhbWZrVRLPkQGRXIclNk+u0fzvTLOejf85PkjM07DykfmhCLEGFjCZvNwT4zjwhoA4HUDgLaRCNGZ0b/+fvK3kmL584+dfMaIml7CZTFatffsOkom462EbTVQtpsJMvSCJkQ0liQzIhm/sep0OgVccnrEl77zz+sOy+SIRohgm1Wm1R3a+6t/eOfwsOjXF28PD1esYuH+Hi6uLjk5eXt3r0bxB+xZRP3vuBeEYPBIJfLDx8+vGXLlj/+8Y9r165dunTpBx98UFJSMm/evDlz5kydOnXC6xPGjh07atSowsLCgoKC/Pz87OzstLQ0YJbDwsL8/f09PDw8PT39HcHHxycgICAmJiYlJSUnJ6egoGDSpElFRUVz585dunTp5s2bt27dWl5evn///mPHjlVWVp4/f/7y5cs3b968f/9+U1OTXC7X6XRmsxle18Gg22QyOfmGhXVKrls/uHD4ooONM0EQXEt8zMLj5zDwzuDKD1PVYBaN03AR+8k4fhZxU+KD7UQeNz03K7i+3KvM/bVlnFsWH+cR4BHgEeAReCwE2h8dnAholUp1+fLlzz77bOHChQMHDoyOjg4NDU1JSZk0adLChQv3799/+/Zt8KZ+8eLF8vLyefPmjRgxIjExMTQ0NCkpafTo0fPnz9+9e/fly5cVCoVSqYTdorA5ErwOOFUenvnccaEj8ZYjBRxxypz/yiPQFgIgiWkXlKPt01yxWLx///6srKzExMR33323pKQkOTk5Li7uo48+qqmp4fZJbt9rK/NufZx7S9qsNrBOq6+vb2pqEgqFYrFYIpGo1WrYdolb2v5zBifjIzwCPAI8Ai8HAp1GQD8NfC9gAMNFdKSeZrNZJpOB+nN9fb1YLIbNdx05t4NpHqs+3DzxiS/Z8Paytot77To9jqUtwPrGZDIplUqhUFjvCA0NDUKhUKlUdroFNMuyYBJ74sSJpKQkgUAALgddXV3T0tLWr18PjuMogrSQlJWiGavtR4ISWewdyS6AgbQaFWmzPETo73L0hy01wdEf+wb8cXDBN/v+alCTyMwggkVmZCMQ7fgAAY0MSGdGBj1jFGuahRL057L76Skf//uMIzf+hyFpO2fdTJspq8nOPjNKilHTtmY7AW1lzfbcEInQ9zpU/P7FzLzKtIzK6IRPSpac1VOIoCmWaGYJPUImPak2kpaKigvJSTmensFhEcFevi4Br/rbzaJ9fTd9uhnwhy0XmFp1YmBv3rw5ZcqUTEdISEiIj48HtY2oqKiIiIgQRwgNDQ0JCfH39/fx8fH19Q0JCYmLi0tPTx8yZMiE1yfMmjVr4cKFq1at+uyzzw4cOFBRUXHlypX79++DK8K6ujoQr9RoNFqt1mg0gq0WbEZu6/WDexd3PA65cdO3vFO4v+I4lsKEI7h7d6NnI25LByMtkeGP8AjwCPAI8Ah0EAGnnZowwuK/RqNRpVKJxeJTp06tW7du7NixaWlpkZGRcXFxKSkpU6ZMKS0t/YdObkNDg1arFYvF33333caNG998882+ffuGhIQEBwf37dt34sSJixcvPn36dENDg1OtWn3O4zSt/vo0B3HOfIRHoH0E4BYAywAwyadp+tq1azk5OUFBQYMHD16zZk1eXp6fn9+oUaMuXbpkn2hbLGD/0X7OL8Gv+B4E71NqtVosFjc1NTU4QmNjo0gkUigUOp2OJMkOar69BLDwTeAR4BHgEcAI8AQ0gnEURNxg2ODuxcZItRWxWW16vV4sFoPH6sbGRqVS2er+7rZy6MhxPJ51JDE3DT6xG5Es3Pq3FX9Z29VWezvxOJ5CiUSihoaGOkfA7DNBEJ3etViWNRqNVVVVffv29fT09PX1dXFx8fPzmzRp0rlz5yiK0ul0FGWnnm0WC2O1sTaGZW0/fhhEkSDHwSCEVDT6dJ/ol6l/8nl16cgxFcdP2l0RmpCdLH7EPpMOAtrq0N+waq36h7TZaEN136NPN9alvbZywpj9587a2Wc7a283mrYrb1C2h5iAJm0WwmZ3cviQRvUKVLL86q8G7u3z69NxKYcmzz55rwGZaGShtajZiMx6hChts1qiaP722/tZGf8W3DOrh2eAt6+XQCDo4enhHxjwy4T4ffv2cb0LYraXe48cOXJkwIABWVlZ2dnZQ4YMKSwsnPD6hGnTpr311luLFi1asWIFKGAcPHjwm2++qaqqunHjRnV1dUNDg1Qq1Wg0Oofet16vNxqNWHgav4HgfcG4aLAshocqV4yIW6Unjj8xAQ0VxtQ8RDrxznqCoh8XtCcogj+FR4BHgEeARwAQAB0noNjwWGYwGO7fv3/x4sXS0tI5c+YMHDgwLi4uPj4+MzNzzJgxy5Yt++qrr27dugWrsxcuXCgrKyspKSkoKEhJSUlKSurdu/fo0aMXL15cXl5+7tw5lUqFc8awP+6j/pmkx6XzER6B9hHg9je8TU0qld64ceONN94IDAwcOHDgxo0b33777cjIyJycnH379hmNxvbzfGl+xeDAZJWmaVh/AgKaS0NLpVKtVgt+Sl+a5vMN4RHgEeAR+EkEeALaDhFN0zpHAJ8JePDoCLNG07RKpWpyhMbGRrFYbDAYfhL3F5bgsdrywmr19AW9rO16emSebQ7gdVCtVoO+OfTzpqYmmDbRNN2Re+TZVskpN+gJly9f/odfQS8vL3dH8Pf3nzdvnkwmQwhh6wwwNHCkt7HIYkM2G4tsLCJoAiErQkiqtXxVYfxV7qfRr/3h9alfnb1E/6Cz2z4jO/tsIOzGzmYzos3I6vhrNiOzzmqmEGoQoj/9sfrXqTv7p+849KXCSCAGIYs9U9aKLBbWZGENFqSzsAaSIUibjbAiI40af0D/78Mb4fF/yh5y9NdDvyx44+DFalZvQWaKtctSEwRDELSFfGiy/KBC/2/B3tzs95d8cCw3998Fglfdvf0FAsEr/n4ubq45OTmnTp0CWDAFjGlW2Cmp0+nq6uqAU5ZIJEql0mg0EgRhNpvBjSSYKoM9C2Z4uVADm4yPwFcgmjvO5HJv2yeO4+rhHHCtcAT/5BTpyLk4ky4YcWrOT37tgk3gq8QjwCPAI9D1EQBNZzzDYRhGqVRevXr16NGjH3/8MThUCA8PT0pKys3NLS4uLi8vv3Llikwmk0qlly5d+vLLL9esWTNu3LiEhISAgIDQ0NCcnJzZs2dv2rSpqqpKKpWq1WqTyYTzB0B+8pH+XBN0/YvC17CLINCyH8IiCsMwjY2Nv//974ODg3Nzc8vLyxcvXhwREdGrV6+KioouUvnnXY2W4AAHLZVKwY4Hc9BAGmg0mq7wMvW8YeHz5xHgEeARwAjwBDRiGMZoNEodQavVYvdWMIRgpNqKYP0NoSN0HZ9sUGHuQNhWE7rj8Ze1XV3qWlgsFp1OBx6cGxsbm5qaRI4gk8lAerjTawsvbxqN5p133vFyBHd3d4FAMH369Orqaq42CLfDWFmrhTVZEWV1EM8k09xsI/UWdPq8ov9vNoZFfTRuyoEb1UhpQBSLSCtrQzSFFGYka0aGZjsBjcyIMSPSjBg7r2xC2/8sSUteF/eLVX/eolZrkcnOL5PNNrPNzmuzFsZs/7AmC0MC+9xM2/nsjz6uTc3c3yf7UNyvSkdM3n36BqFDSE6YSCsimm0UZaFIG0HbuezSsjvDR5TOmH7o+v+gee99EfTqAIHglR7enr5BAQJXF4FAMHbsWKFQCBcFc9C4yaCgAo6MuK+7kKCtiwi/WiwW4KYxfd9W+o4cx1V6mkhHSOS28u/IuR1pSGelaatdbR3vrHry5fII8AjwCHQ1BFo+J1utId4WSdM0SZIgnbFly5Z33303Nzc3KCjIy8srJSVl3LhxH3/88ddff33nzh25XC4Wi6uqqrZt2zZnzpz8/PyQkBA/P7/k5OQJr09YvXr1/v377927R5Ik1y8utgltWbFOOdIqGvxBHoGWCLTaP2H3sM1qUyqVZWVl8fHx0dHRa9as2bt375IlS65cudIyn5fySEtwwFWJ0WhUq9UymUwkEoGHbfAaJZFINBoNSZLc+flLiQzfKB4BHgEeAUCgWxLQz/bi2aw2lUoFwwDeDtNyQ1zLQlmWpShKrVZLJBLg5kAF9Znrb7Qsmj/CI/D8EAAnbyRJKpVKiUQCos+guSGVSsF3XBfp5HAP7tmzJyYmxs3NTSAQeHl5xcTEVFRUgGs7LkoMspO5DEI0okmksyKjFZHNqNnAkupm9F/nqYLC7b/85cfz/t/569WIQohmkJW1MnZJDAWFRASSNiOjkbURDm0NGiEdiRoa0YY/Kn6VtCUjZdPmT+7U1SM9hYy2ZhoRNCJsiGSR1cKQjg9tsbHNBDKYkFiKPl5xK/VXu5JTD0Ymbxr2xr5j53+QEawOEc324uw8dzNpN702WtC5y9SY8V8PLzxy6gz6807pr/svT894OzA0WdDDxe/VQIGdf7aHv+zbS1loJxNmmAcDCC2J6Y5MdiEHrj11R87iwv7M49zJ/eNm/jTnPm5ZfHoeAR4BHgEega6AAPfJj4dC7NwPxk0sKmXD3EpjAAAgAElEQVQ0GhsbG69cuXLw4MFly5ZNeH3CwIEDwR9vYWFhSUnJrl27zp8//+DBg9ra2ps3b3711Vfz588fM2ZMampqnz59oqOjMzIy3n333V27dt25c6e2ttZgMHD3DOHKdAVk+DrwCDw9AtCl4c6Crq7T6Xbv3p2amtqzZ89FixZJpdKnL6U75oBvdlDBJghCr9fjdyugocGdO3gm7Aj50B1x4OvMI8AjwCPAReDnS0BjGoVhGKwwIBKJpFKpSqUyGo3tDwPAfCkUCpFIJHQEOFev17d/Ihd9Ps4j0AURoCiKJEmtViuRSED0uaamBrzMaTQas9kM3tjxvKqzmmAymWxW271796ZMmeLi4uLp6SkQCLy9vZctW6bValutFRDQNmS1IvNDVvkDoZKZm7/X2I6ekowZv3fgb8rW/OnB/TpEOFhnK4NYhmaRjkFyGv3QjJQmxmywIbmesTskZJD4B/SXcrJ3/Ge/Siz73cKrdfXISDFGG9FsF9iwf6yo2W5nzVotNpvFxlosSKNGP8jQf370PwkJa2N+uaVP392/KSz/61mtjEDAPhOINLN2FltvQSYW3a5H7yz422up2z7bjk7+Fxo8fMvQ4es//7ph1IR/d3vFy83Tw8XDbvHt4uY6acrkhqZGiqLw2zW+QFj7GH7iHm8VJe5BSMwT0FxM+DiPAI8AjwCPQBdEAE/sneqGBzI8CGJrTYqiLBa7J2KLxSIUCisqKtatWzdu3LikpKSgoKDQ0NDs7OyioqJPPvnk/PnzIpEIDFYqKytXrFgxfvz4lJQUf3//uLi4Pn36jBo1as2aNZcuXaqrqwMPY1AKdnjrNDo7VZL/yiPQTRHg3l9Yrk2v1586dWr48OHz58/vpu16+mpz59t4awVJknh3qdARQN5QLpcTBPH0hfI58AjwCPAIdHEEftYENFh6sixrMBjwppiGhgaRSAQaqe2YeVIUpVAoYOQQPQoymexn4uS3i3drvnpPg4DZbFYqlSD63NDQ0NTUJBQKQXYD85vcSdXTlPU054J4Tnl5eXBwMEg/CwSC6OhoEESmKMr5/gVfg3b7ZcaITDpkUSIkNKIte+rT+69J7bdm/eb7cod+uwUhikSsXcWZQYyBYR7StmbCSjbbaJMV0Q4z6v/9Hu3Zr8zJ3P5a3Po5RX978AAZSWSyEs0sRSPaggw00jo4aMLKWq0MstqQ1YLMBvTZxsaMtN390g+l9d0xqHB7xXmd3M4+W5qRmUDIzKJmZP+oadSgRKW7hfEpq6fOvrT9L2ho4V/Ts/+0Yft1uQnt3HcoIjb6R+NnhwpHeETE2e+qCIKAd13uBXoaAhren51ye5qr9vTncivzuLk9zbmPWxafnkeAR4BHgEfgRSLQlv0HPPmB/wWCzGKxgDWiXC6/fv36wYMHFy1aNGzYsPj4+ODg4MTExGHDhr333nu7d+++ffu2TCaTSCTnz5/fs2dPSUlJYWFhQkJCSEhI7969R40a9cEHH2zduvX69etYXgOPudjwGfwlcAegtrjyFwkXXxaPwDNBgHt/wV0G8jImk0kikajV6i7lG+mZNLmDmTjd8vDVZrVRFGU0GrVaLYgcNjU11dfXNzU1aTSaDubMJ+MR4BHgEei+CPx8CWiGYcDqASFEUZRWq5VKpQ0NDfX19SKRSCaTKRxBq9WaTCb6UQBFVJIkNRqNWCwWCoUiR4CISqXiVy+7783A1xzYRr1eLxKJahxBJBIpFAqtVms2m1uVd+jElygQZ1ywYMGPPKxA4OHhkZWV1djYiBD68U78kXRmHbIZDGIRYpENIaWNeojQ5Sa0trz2tV+v7dVv9bZd4nqxXXmDRAbacRZrRchGI5sJMWaGsdJWC2EzN1uQhUViGVr/SUOv11bHRS2fOO6LM6cphJDJYiNYgna4H7TYlTTsBDSNKBpZaQZRNrsqx/o/3c/q9+c+vQ8mJm0fPv4vB45/b0TIgKhmuyg0STGIYJERIQIhGYn+pxaNmXTstfSdazcQr085k561be2GutofkIZGt+4+GDt+nJePt8DVxd3Lbvr9akjwqrVrzGYzT0C3cyNzXwbaScb/xCPAI8AjwCPQjRDAzE6rdYZfMQFNEERdXd2JEydWrlxZVFSUm5sbFxeXkJCQl5f39ttvb926taqqCnz23r59+6uvvlqxYsWkSZOysrKio6MTExNzc3OLioo2bdr0zTff3L9/X6/XY+cxCNn9yrScFzntIoL6tFpV/iCPQLdDgHt/wV0GCzwIIZIkYRmmrcWhbtfYx6owINPyL/g4pSjKZDKBMHRTU1NDQ4NCofh5AvVYqPKJeQR4BLo7Aj9fAtpp/gf+1sRiMYhBCx1BJBJJJBKZTKZUKlUqlfpRwPpNokdBLBYrFAqu07Pu3jP4+v88EQCzYplMBm6a5XI5vFzBlKjlLKrli9YLw41hmNu3b/fr1w8T0N4eniMKhmu5FgTgZ9DOJZsRawURaNKCtCy6LkYffiKMSN0Uk76y7AuRzmq3PiZZmkImC2uwMQaWNSDGgGxmxNKIpVmrnrYpjSRhMqM/b1Wlp+yJCd/4m9yNFRUPWWTnlymEKMQ8IqDJR+yzhbVz0+h7OVqx7uZr6TuDwrfEJJVl5n/6l2P3mvQmPTI1o4cUMlCIthPQDHpoZaRmRsWg/3j/+Gupfy75nemDD/WZv971u9/9T8P3qJlBRovZhtjSTz+zN9zVrYeHl2sPD4Gr279NLzKZzCyDLBab01Vg7XIirXyckrX1tROvcltVenQcK3t3MPLoPP4/jwCPAI8Aj8BLhAAYiBAEAVu1nFoG7l6uXLmyY8eOpUuX5ufnR0dH9+zZMzExcfjw4UuWLDl58mRtbS0swJ85c2b79u3z58/Pzs4OCAgICgpKTEwsLCxctWpVRUXFgwcPlEqlxWLBvnmdXiicioav3OlTqwn4gzwC3RoB6OFAQDv9bWthplu394krDzNqgMtmtZEkaTAYlEqlTCbT6XQ8Af3EwPIn8gjwCHQXBH7WBLTTRbJYLBqNRiQS1ToCmEJLJBKRQ+UZFJpAjkD4KMBPwD5zLSCccua/8gh0IwQsFovZbNZoNCqVCnQMMf8IEyanv53VNIZhrly50rt3b0xAu7u5Dc0f/FCltleJYW00i+xWzMhOPSMSCGjWikgKibXoPzfdjO+/7bWBu9aVN1XLEGlPYbIwZhtjsrEPbUjNoocs0iHGbHdbiGiS0NO25ocGdHD/D4Ny/5IYvSM1qWx7WZ3aITfdbAECGtE2h/dCZLMiwooIEtmaWaQh0epP7/4qd6d/eHlY/L6MQWU7Djc0Gsw6ZDCihwTS0XbJDppi7RbQSgqprGj3kYa+v/lk9PhLHy2xDhx4tGh65a0biLHZbbhtyMKy7Ndf/zWoZ4jA1c21h0cPDy+Bq1vBiJFGYzNPQD9yNtkqJd1ZvZUvl0eAR4BHgEfgOSJAEASYW2IGB+T1amtrDx8+vGTJkvHjx6enp4c6QkZGRlFRUWlp6fHjxxsbG8Vi8c2bNw8dOrRixYopU6akpqZGRETExcUNGjRowYIF27ZtO3v2bFNTE03TJElSFPUEkhrcidNzRIHPmkegkxCAHu5EPeOv8GsnVa2rFwsG0SRJ4p3ZXb3GfP14BHgEeASeAoGfLwHdKmgWi0Wv14MetNAhryEUCkEMF5zVNjY2AhMtdASRIygUCp59bhVP/mB3RADkCy0WC+UImH1uVQ6Y++sLbizLsqdPn46Otkshe3h4AA2dm5v74MEDqAlpbkZ2BtoKyht2XpJFFhrp9Gj7HmG/vPWvDVyzZmdNo8GuuWyyIitrtbE6BukY1mxjzAxLMqzZ4YTQBBlKpGjfvu/zcssSf/mnlNc+WfHxHZEEmShEWBDF2gloO+NtQ4yD9WZZmw3pSWSRGNCOLxW/yvvcL2LnL+KP9h341/LDkiYj0iFaj0xmZKUQTdslO8wUsrs3tCB06pJ26Og//6r/rinT/t6v78F/HfX5f19AzUa7LDXV7KgLi+7+vbp/7kCBq5u7p7drDw8Xtx65A3+j1xlZBtG01elatGr+zDJOqbrj11ZZ5nYOdsc28nXmEeAR4BHgEfgJBIAURgiZzeaGhoZvv/22tLT07bffzsvLS3SE7OzsN954Y9WqVYcPH7527VpNTc29e/fOnTu3devWoqKiPn36REVFxcbGZmZmzpw5c926dV9//fW1a9fUajXXpNpmtVks9jXgluEn6sf/zCPwUiPAvSMw74wj3F9fahievHGtqvdwswMMuUf4OI8AjwCPQHdEgCegf7xqXB7NZrWBBSgw0dgbG6hzABMtFArFYjGoc5hMJu7p3bEf8HXmEQB+GRSEseccbEkE+HBnkDjeWdCxLHvixIng4GCBQODl5eXi4iIQCDIzMysrKx+J4TiUN+zGzXbpZ4Ts7DBJohu3UfbAP6bnrl255XL9Q6TnNIBFRjvjzNA/bq1FFgaBOAcyW9CBz7V5v9kRE7UmJmb5+x+cu/vAbuRsIJDd/Jm1f2jWzj47xKMRy7JWZGtG6Ph5Ov1fdvr+cqt35Pa+AyrK97Pf6+wqz3pEmxBtRohkbZTdAtpEISvBou+VaPHK76IT14ydcClnwOHE19ac+FszQTrsehEyax1m3QzSaLQTJk4WuLh6+bwiELj08PAqGDHSYDAxtmcvwcFBqKtF2+GaW/2pq9Wfrw+PAI8AjwCPwP9BAM8uOk64sCxL0/T9+/e/+PyL999/f/DgwcHBwb6+vhERETk5Oe+9915ZWdmdO3cUCoVMJrt+/fquXbvef//9nJwcHx8fb2/viIiIvLy8mTNnHjhw4Nq1azqdDmb1mG4GHo1lWZgb8JrO/+eC8V94BJB90osD5p1xBP/UBd+Xnd50uuzFBDC7bPX4ivEI8AjwCHQQAZ6AbhMoEGbSarVqtVoul0v/bwDPbEajkSAIPHR1wWG1zebxP/AItIYAzBHxy1VrSbrQsQMHDoDts4eHh6urq8DVxcXNdfW6tTqjAWrJICvjMEq2IUTaLBo9+u6/rcNH/jm135oNn/1vvRxpzITNobABDDVCJINMDhbeLqLhCKTJYlGTaN9RYuDgQ5GxpRExaybP+Or2/9pNnpsZG8FQhMVq14Bm7UrQFhuyWW0IWazITk8fOqHpX/C5S8hq3z6bfz3uy6N/Q2o1MluRlrBLezg+jBmZCUZHIbudtQWhoyd1v/5Nae6gv/Yf+NdfZX66bbfwodFeEXshFspiQixhJ6NNJnPxu/MEAhd3T2+BQNDDw2vy1H8zN5OMvQI/+l6EBrT31+GVsb0EXf23Vlnmdg529fbw9eMR4BHgEfiZIwDbsPDUGtBgWRZUnsHSmaZpo9Go0Wjq6+vPnj27efPmt956Kzc3NyEhAVwFFhUVLV++fP/+/deuXWtsbKyurj569OiKFStmzpyZmZkZGRkZExOTmZn55ptvbtq06fTp03K5XKPRcGkybhzzaHh2xP0V4j/zq8Y3n0cAI9Dy7nje9wjDMCDLbrFYJI+CTCZTqVRardboCPAA0el0GoerGDC1oWna6VGDW9GlIrD6BQtgXapifGV4BHgEeAQeFwGegO4QYgzDgPQbQRBmRwCpJmCcuQNth7LjE/EIdG0EcJfu2tVEFRUVoaGhdld8juDi5uri5vovwwvu3L1LMTarXbLCTunSyG5xTNjQd5cMM2adiIr9/e+WXf17reMnRo/loe0SHSzLMFaHETH7iIC2n37gb6acUUdejdwaGLohO2/LsdMPjQwyIoKwyztrSIYgrSxps7PXFMNSLG1Dth+Mtu+uocH/+rl36J/8kz7LLTq085QGBKMZKzKY7WobQEATiDRadc020kijvz9gphX9Nav/3t/k/y3917tXbbjfoLC7TqSRxcJobVYjSyEb+aNB9weLPwI/hN6v+P6Dhv545R9o2l75x9DW4AnoLt7F+erxCPAI8Aj8zBCAnVhOjQaZVNoRZDLZlStX9u7dW1JSkpeXl5SUlJCQ0KdPn8LCwgULFmzfvv3ChQs1NTXV1dVVVVXl5eXFxcXDhg2LjIxMSEhITk4eO3bskiVLysvL79y5o1Qq9Xo9QRDYggTPf7gRnoB2uhz8Vx6BdhDg3jvceKunwIITd28BTgY/4XsTH4cI9zhN07D3sb6+fvr06f379x85cuSE1ycUFRUVFxevW7fu22+/vXbtWmVlZUlJydGjR4F0xprLWMDHqYiu8xVW4CiKArF7iqJo2r5Zs+vUkK8JjwCPAI9ABxHgCegOAtVesp8cXNs7mf+NR+BFIfDyrZzfvPn/2fsO8CqK9f2TnJyWRgLpOeekI4SawJUmIEhRaYogNuQvClcBryhcULyickFAaZcWIQktQCAECCEkAaRKKFKCtJhqKslJOTXby/x/s5MshxAQVEp095nnZHZ3dvabd2Y3s+9++34Xu3Tp0oSAdtKoVn2/1ozZGIF6JgB0La60gMzj+LjXk/XBi14au//sdWDiAAdowNlglEIG+hRzPOAF9pblAfzLQY1kAudOnTP3fWmPZ9tNge23d+6xMelAbYUV1FEYASWeSwlQTvBWgmUJFmAc1NOoB1QloA79bHh2RIJPyGqf8FVPD9+afAEvxAXnaIpiMB4nAM5CV2aU6lnMTDGlBjDj0/SOndcOH3E6rN3aN9/LvFwI9akJAGrxCoqvZlkjS7EsCUcMVk9MmfahTCZzkDu5uLXS6oNS0w6wDM890HQUuko3KwWNmGn730c1TJs/zz2cmh9oV/O1S1slBCQEJAQkBJ4QBBABLbolchxHkiSKKHjy5Mk1a9a89tprERERbm5u3t7ePXr0ePPNN7/77rujR49WVVVZrdaCgoKdO3fOmTNn2LBhYWFhGo3Gy8urd+/ekydPXrFixaFDhxCLjWGY/SeMYtvtp/RiXiKgRXykjITAbyIgXjhNMnc7sEkxUQxQjD0jCgOiBxkkuWOxWGpqakpLS3Nycs6fP3/ixImkpKSFCxcixxSlUqlQKORyuYODg1wu12g0zs7OCoXC2dl56NChqampZWVltbW1iMNFfO7dzHsStqMmW63WmpqaKmGprq6WJECfhK6RbJAQkBB4UAQkAvpeiDWZBN+tqP0/zruVkbZLCDxeBJD3EIZh6J15k89IH69tv/vshYWF/fv3b0JAK5zVA18Yeu7nS0YhNqgNgJtWcCUPjHl9l6//F52j18VsNNoE5pcF9ZCAphsIaKjCIQh2IOaaB8BKgJ+vscNHrwuN3uYZtq3zM8lffZtbSwArz9bh1VamnAQlFCSgzThHYjyoF5IJgGO/1A97L96x9b+9gpcNGbsn/SwoYUEtYHC8mrNWMxhPk1AwmgQcJfDLFsBWWMHBH/FOUYuDQ9YFBX//8mvJp7NBLQm9pM1cvYWuraeqadbK0jRLQdr4+vWcF4ePhPrXUAPasU/f/pcvX0HdCgDHwcSwDUmgmG8jk5uQtnf2gH1plL+zzKPc0sTg3736KG2WziUhICEgISAh0DwCIr/c7G6e5wmCqKmpKSoqOnHiRGxs7NSpUwcNGhQeHu7j49O+ffsRI0bMmjUrPj4+KysrLy+voKDg1KlTq1evnjx58sCBAzt16hQUFBQVFTVq1KjZs2fv2rXr6tWrRqMR0Vii2yNFUTabDcMwe0dC+ym9mJcI6Ga7SdooIdAsAqLnsngFocydhWmaxjDMZDIZDIby8vKysrKCgoLLly8fO3Zs796969atW7Ro0ezZs6dNmzZlypSpwvKhsLz//vtvvfXW6JdHDxo06Omnn46IiPDz83N3d1er1XK5HIUll8vlzs7O7u7urYTF1dUVivXJZCqVKjQ0dNiwYTNmzFi3bt2ZM2dyc3NFMvpOI9EWsS13K/BQtyMC2mw2l5eXFwhLUVFRZWWl1Wq1v32JNjxea0UzpIyEgISAhMCdCEgE9J2Y3LYFTTpv2yStSAi0NARomrZardXV1QaDobq62mKxINUzcYJin2kpjbPZoFjzF198gSaaPj4+3r4+Lh7uDkqFm5fn3EULCAAMOFmFgWOnuXcmp0d3/z4i8tuRryZcyoOBB22AoQDBcwSAqsk89H8WYhUyLKi12cqMNhMAh86D1yYdDe4Q36XHYb/QdVNmnb5RAiwsgJLNbB1BGyi2juKNkIDmrYQQUdBAgYuFYOx7x7xCl+o6f/vyOzuPXKDyq6EjM8bzNMtyNIw5yNKQgKagDXw9ACYADl+1vjQ+9anITX5+Mf0HbD9wtKrCwkChD56v52mSp4R+4SiKsdkwi8W2Zk2MVquXyRzVauc2rb3j4uIwmw1wrKBEjTOQPDfjwGyDvzg8lhV8naE8ByK9CYH6Fny/m2GY0SZWOMyejH70o8Oea2aEdwX2v/Z77yf/6O2XzighICEgISAh0BQBjuMIYWm6AwCz2Xz16tWUlJS5c+eOGTOmW7duocLSt2/fd955Z/ny5ceOHbt+/fqNGzcQNz1z5sxRo0Z17NgxMDAwPDy8f//+U6dO3bZt29mzZ0tLS81ms+hQiab0iB0TOWX7+c8fyd/ZEGmLhMDfEwF0HYltR6qVyMvYZDKVlZXl5OScPXv2yJEjW7ZsWbBgwbRp0956660hQ4b07NkzOjq6a9eukZGRERERgYGBbm5uaJJv/6tQKNzc3Hx8fPR6fbt27Tp16hQVFdVNWLp37967d++nn366X79+r7766uzZs5cvX56QkDBv3ryAgADksIKClstkMuQZHR0d/fzzz8+aNSsjI6OoqMhqtVIUZTbDCOX2Kh9Nbg5i6x5NBn0IYrVaKyoqchuXoqKiiooKk8lEkuQ9TBUtfzSmSmeREJAQkBC4NwISAX1vfJrulW7iTRGR1p9gBNBDF0EQFosFUc8VFRX5+fkVFRXohXmzD2BPcINuM40kSZqmExIS/Pz8kL9Dn759w9u3c/FwlykcQzq0S844zABw8QYY/tL69h0XDX1xp5f/1K8Wn6ihgBUGAKQoQHEcBZWieZqH6hsCRcsBigVWFpwrAGOmHfLtuCX6udO6pzZOmJx1pQhU14N6FiM5A8PUMbSFZnCKxQneXA/lOJgaClzKB29PzQwMj/HULhk0Ju7Sr/BcuBDcECN5kuJolqeFWIVQLZpjCZ41A1DCgCXbSrRPfd+1W3pkx9j4TdXlJqgxXc/TOMviUN8DKmtg9QQAwGqtT0jYFhHxlEzmKJcrHRzk48aMM1RW8RQJOBIAnIfhD+sJYK0HVgv8JaEL9G0EdGMEREhGc7Dht4UtFBnnOwno28rd1h8Pa8WeVrannlHefu/95B+WlVK9EgISAhICEgIPioC9H7TZbM7Ozo6JiZk8eXL37t3d3NwcHBwCAgIGDx48Y8aMffv2lZWVYRhWXFycnp6+YsWKCRMmREREeHt7t2nTpm3btmPGjFmxYsWRI0dKS0utViF0r8AfsQyLopPZf/glTn7sN4oz/N+XedC2S+UlBP6SCKCLq0nTeJ6vra29fPly4vbEOXPmDBkyRKvVqlQqRCs7ODg4OjoqhEWlUrm7u4eHh/fs2XPw4MHDhg0bNWrU2LFj33zzzfHCMnHixBkzZixevHjLli1paWmnT5++fv26wWBooqgjPgGhu0FJScl33333wQcf9OzZs127dh4eHsgbGgrZOTggMrpVq1bdu3efN29eeno6ClSIOGj725R4c2jSwIe3is6IoiziOG40GktKSpATtOgKXV5ebrFYxLvZ3e5vD89IqWYJAQkBCYH7R0AioO8fK/giVFwe4DCpqITA40CA4zj0XVtVVVV5eXlpaSn6uu0vQ0CjR8q8vLwRI0bIZDJ3d3ddkL7fgGcdlAqZwlHm5NAxeuDqmJ/GT0gMC/v3vz4+Ofs/P/Z+9rO9B38101DXAhcIaAYGDESEMA3FkDnITNvM4EYBmDb3tK5HzFNDjgf23PPi63uvFQIDJhzImWiulmfMPIWzFEsxNMFb63ncSIKf88D/++BoaORK3+D5YyfuPpvDGDlgZnELVW+zAZsNkDTFAIziq3G+pp4kLARrJAgDDnZmYk9Fx6jdVrdtl7gmtryiDuo+V1ssiH1GBLTFVs9wICc3/4svv9bpgtRqZ2Hi7ti6VeukHbsahhiHA5hYwPEs9LBu0JimG/lnoYkMd8sJ2t4DWuSdxQwioJv8intR5mEPbtQrIvVM3eEELe6SCOiH3RdS/RICEgISAr8fATHaGJLCIAiiqqrqxo0bu3fvnjNnzsiRI3v27Nm+ffuIiAgk2bxu3bpDhw7l5OSUlJRkZWWtWbPmgw8+GDZsWJcuXUJDQ7t06TL65dFTpkyJj48/depUcXExhmEEQaD36zzPk8KCwouJs3eUuRtB06TYA63+flykIyUE/kIIoFc+qEEkSZaXlx89enTu3Lnjxo3r3r27p6enUqmUy+Wurq6enp5arbZLly6DBw9+8803P/vss0WLFq1YsWLDhg2HDh26fPlyeXm5yWSiKPQJYANGLMM2kWwWr9NGGbrb0ER7YUwXgsBxvLy8/OzZswkJCYsXL54yZcrAgQODgoJatWqlVCo1Go2Dg4NSqQwJCXnjjTeWLVt29uzZ2tpakoShV9BDh3iu287xMFfsv9hgGRbH8dra2mJhKSkpKSoqKiwsLCgoKC0tRVghO+2DOj56mx8mHlLdEgISAi0eAYmAfoAuFO/g9t+5PMDxUlEJgUeIAEVRJpNJFAtD78mLi4srKirMZjOS4BCfwVri2EZzXIqi1qxZ4+Pjo1arHZ3k0d279X6mj8JZLXNyVLlou0a926XT9P/OP1FYDM5m0zv3XS4xgOp6GP2P4CmSJwgOJzicATQFaFbw7iVM4MY18PnX2V2f2RA9eL9P1JbOQxP3/8iQAodLA57izCxr5Ol6nqI5mqdonmDZegZcywWTPkiJaL/MP2j+m/9MPn2VRUrTVtJMkDYou0EClog8wN0AACAASURBVMMYUEeAcpyvtBDmOhttMPM368Dw0Xtaey8NDt08c1ZRQSmwUjAsopUghdiG0P0ZeUAf+uHIy6+M9fHzl8uVCieVo6OTwkn15mtvMSRDWDA4uDiW5wDLAoYBBAPqWWDjgI0XBEAExQ1KEOCgABS+FhPyjb7L2OSFdrONxblGwWxO8Jq+5RBtP4R+d745G+wJaGS+yDg3yUgEdHP4SdskBCQEJAT+bATsb/IPWrfNZsvLy0tPT1+7du3777/fo0cPvV4fERHRrVu34cOHz5s3LyMj49q1a//3dvn/4gzv3bt3/vz5r7zySvv27dHn9v369fvggw/WrFlz9OjRwsLC6upqe36KJEkcF1SnBPdn0SXQ3mB7QuduBZqUv5/VB8VBKi8h8FdFgOd5HMcvXLgQExMzdOjQ9u3bu7m5qdVqX1/f6Ojofv36vfPOOwsXLtyxY8fJkyezs7MLCwsNBgOGYbSwoFg1IjjiRwzoMhQVdewfxpGDcLNqyHBqzHHN7rJYLOfPn09KSpoxY8aAAQN0Op2zM/LtkCmVSm9v7w4dOsyaNWvv3r1VVVUEQdjfB0TzHnamyf2KpmnEQVdVVVVUVJSWlhYVFeXl5eXn5xcXFxsMBqvVStO0vali/mGbKtUvISAhICFwPwhIBPT9oCSVkRBoAQigGQb6Xgzpl5WXl+fn5+fk5CD2uaSkBLHPJEk26xMk1tACWts4oaRpuqSk5Pnnn0df8Gk0mo6dO+mDg1zcWslkCoXKb8gL46/mVJEcqLEyNTbKiEOxZ5xlSY4leQpnCIyuJwBBA9bKs0Ya/FoF/vXv8619Fg95/ky/AYfbdl2+LDa3Chd9hjEKYCyHNVDWPE/REK2iX8G/p//s3ebrtpHz3/vX7iM/3axjIcNLiaQoAwDPAGDkQBUD6khQhzFmhgc1teC/886HhawKDYmZ8P8O5xYCGwYYDtLhOI5TFMNwACOoOpNl1ZqY8LZPwe8EFSr05aCLWuPVuk3avlSWhkQ4x4LyGrwGB4ey8CmzDk6eeWrOd0Xf72J2nwBHr4Czv4BrZaCoBpTUgkobMDOQmDazoI4CRgpYGcFXmgf1NLDirLmewnCoJy0sDAyX2JCQAzJnP+8XP1EU32f8jow4P25Sc4MqCiTkUWzIP80DWuwZIURjixjykpESAhICEgKPHwF0u7anbpvYhAgj8WaO5J5ramoQ1/Pll1+OGDHC09PT2dlZp9MNHDjw448/Xrt27ZkzZ8xmc0VFxcGDB1esWPH+++9HRUV5enq6urqGhYUNGzbsq6++SktLy8vLE10Rm5z3/lft/+P8Wfn7P7tUUkLgr4qA1WrFcTwnJ2fZsmVt27Z1cHCQy+Xu7u4jR4785JNPEhISrly5gvyXKYpCF7I4Y7yfK/FBcUN13s9RGIYlbk+cMWNG3759PTw8RMlpR0dHLy+v999//9ixY0gBAzkXi/e3+6n8D5YRkRGxoihK/Mi1rKystLS0oKAgLy+vqKioqqoKyVijwuKxj9LgP9he6XAJAQmBvzYCEgH91+5fqXV/FwREjwD0fZbRaCwrK8vPz8/Nzc3Pzy8tLa2srBTDD4qg2M9LxLy498nP8DyPHnQzMzP1ej2aL2pcnFUatZNK6egEA2GrXVRjXxv9U/a5OquR4jkLTlhwAqNogqUJliRYkuQJnCMZobU1DPjsm1OhkSuHj7z4yivXO3SI/fecY+XGBvYZAxTOkRRgoB6cwIjyHDBZwM0KsOK7kqjIDeFBy6Z9vP/sVUsdC/laigec6KTLAsATAgFdw0L6t77OauQB2LKh8Lm+63085708KvXYKQoT6GyeBSzF8ixntdZXVFRu3JzwwrARbbx9HZ2UamcXREAj7bzp//oo75dcnuUAw+EkX42BKyXgrSl7Atr/1yN4mZt+lXPQMo1+sS56dcf+6/u/tGP4W3vfn316xryL81b+siahYtchIvMsOHEFXCoCBdWg1AQqrVBppA4HFhJgLMBZKCBNcEDwwqYphqZZVmg/YBtFidDYEz/6Q99WP+iv/UT59oHHQXnu+yOghZL2xPKd+Vt12++7tVXKSQhICEgISAjcE4EmShro7i1+k4SELyiKIgjCZDJduXIlJSVlyZIl7777LnJ21mq1Tz/99MiRI+fNm7dr167Tp0/fuHHj4sWLSUlJc+fOfemll6KiokJDQ8PDwxE3HR8ff+jQoaKiIovFghwk0XTlnjb+xk5xwvMnZn7jlNJuCYG/NALoPlBRUbFu3brnn39eo9F4enr2799/5syZSUlJBQUFBAGjmKDJIbqQm9VWvvcl+aAQPtC9AglVZ2VlxcTEvP3222FhYRqNRiaTubq6yuXyyMjIjz766NSpUxaLBTlePDJKV8TE/rUfz/M0Tdtsttra2vLy8sLCwry8vIKCgpKSkvLy8urqagzDULAc0eXoQdGTyksISAhICDwMBCQC+mGgKtUpIfBIERB5WJIkUbzB0tJSxD7n5eUVFxdXVVXZbDbBo/Y2JTVxTmOfeaSm/+GToRkYQRCxsbGhoaG3fBbkMoVCLnOQqTVOCoW89zN9kvek1BrNgoQEb88+s5AoBjgNqoxgxZrr+tD/vPp61uQpefrQxdNm/FhQB12D6wGo56GiBc4AkgVMIyNaj7EmI9i+ge3RKSEyfPnib3Ou/spUEVCvg+QBzTTKVyAaGkpdkEI1RgbgGAFO/1g/fFB8oNfno0ZsTUqutNHATGA0A8Mi4jaquqomNTXtrbfe9vHz17i4alxcG1vn4ObmplKpxox+5ZfrNxriB3KQR8dYkF8Kxr+7z0e70N33exffTa6BG1x0G12DtjvrElR+sQ5t/ifz/E7u+51L0P+82q7VdokL77m588CtvUbtHDEx7f/NPDZrUfai2KIt++szToNLuSCvHBQbwE0jsNKQjzYRvBmnkBoJxXMkTaEFPUvc+Xv/NPQfJKB5AMNINpsafagh4WxPOt+Z/8ODUapAQkBCQELgr4+APQFN0/DfACKdEZ2E4gSeP39+69atn3766eDBg8PCwgICAiIjI4cPHz5z5szE7YmXL1/OycnJzs7OyMhYuXLluHHjOnTo4Ofnp9Vqe/To8cYbbyxYsGD//v0FBQW1tbU0TaPv65HLpEjB/BGg7ec8f1b+j9gjHSsh0FIQsL9e7G22WCwXL1585513/Pz8vLy8IiMjv/rqq1OnTpnNZp7nm8QFRZSo/eH21d4jb3/I/eRRVb9ZUtToIAiCoigkFZ2RkfHhhx/27t3bw8NDoVA4ODg4Ozt379599erVZWVlJEneZ+W/efbfLNAsIKLzB03T6NuRImEpFJaSkhLEQYvs8yOjy3+zOVIBCQEJgb85AhIB/TcfAFLz/yIIsAxrtVpramrKysrQa3D0Jry4uLiystJms6GZSpP5R7NzmhaHCHrotVqtK1euDAkJcXNzc3Z2ViqdHOUyB0eZUuUo8LYOXm38Pv/8y4vZl6tra5DvM8GSOI/jfD0AoLoOJKeUdeq4YED/pE8/K3+q45JBw9cdPsdYACgnaSsAFraBgCZYKKzBc4BngdkCDqRU9ese21637H9LC0oqQA0BnXVxAHlqXuQ4EWENCWiWh3vMDODzc8GnH/8Q7Pufrk8t3LGjTBCYoKtMv1ZX11ZV1O1O2vvW6xPc3T2UCrVM5iiTOchkDo5OSrkCBg13dHQcMWLEtStXOciFw4XjOJJmIL3NgwOHmNffPhoUvslHv93db6PaJ8ElIMVNf8A9KK1V2AGP8DTX4N0K/60y742yNhtk3vEyn3Uy31Uy32/lAd+o9d+o9fNd9AvbhC8Jj17d/dm44eOSJk8/9N+ll+ISi/YfrTt+wXbxF6agHFSagbEemHBgxoCVADYS4BRMBAkIClAkDPJI05CFhwmGeuRploWJo2iOYlkhMSwiqe0IaCRJLWLH8dw9ZDcaPcx5GvA0xzF3ctAiAc1BArrZ1BB+ssWNfMlgCQEJAQmBR4+ASEAj9hmF9sIwrKam5uTJkytWrHjttde6du3q7e2t0Wi6d+8+duzY+fPnp6amFhYW1tTUXL16dfPmzbNmzXr22Wd1Op2Hh0dQUNCAAQM+/PDDhISEGzduVFdXo6hfyF/SZrOJ4rB2/yluRSD4HQg0O/n5gxt/hxnSIRICLQ6BJpeJaP+mTZt69+7t6OioVCrfe++97OxsNDVFBTAMs2dCmzyMiA7FTSq/c1U83X1mUA2/WRjd09ANB71RQ27OOI7/H4c+ffr0kJCQVq1aubu7q1QqT0/PSZMmnT9//pFx0HfiYH8TRh8gImFoMfAP8j3CMEx8Y3cn5r8Ji1RAQkBCQELgYSAgEdAPA1WpTgmBR40AjuMGg6G4uBipgCH2uaKiora21maziUHhH7VZj+R84sTRZDJt27YtOjra3d0dSkJDJ2gHuVOj37DMUaV06RLV7ev/zjt15nS1yWilMQLQHODNFJecer1Pv6/7PrNt+r+Kh41I6dJ93vrEnFIrqAWggjKaWRpnebpRCQJn+SqrBWPAvr03n+v3XYR+xsbYkqs5tJmCYh0UADaaxaC6HQ0JYshVC4/KMEIgBSBRimEYSFhX8o/23/WJXrVw3gWLDZQZjHmleXsPJM+fP2/kyJFebXxUKo1SoXZwgEIiAgctc3CQOzo6RkREzJ49u6ioiCRxGjpb80KdFMGSRrreQHHVBCi4Cd754FRA8Eq/oA2egds8A5PdApLVvjsUvokqv12agGR1YIoqIEURkKoKTNPo05yD92mCk1T6BMfAWEe/DQrfRLVPkrN/kod+p6dui1vgeveANa0CV3qFrArtGv+PQbsHv5I27PX0198/Pu0/V+Z8l7dsU9WGPdYDJ8CpbPBrOSivBDU1wGQEZhOw2iAfzQhCyxwAVrK+1lIDSWmoWk0wPNoDB4rALCC9aQoGieQIlqnn6XrAUoChAEtDQRNOiLHIsoATEs9AZW2eARwNWIrnYOKExPAUJL1hREaWhS8LWEaIzsgCqjExgi87w97uGf1Ixqx0EgkBCQEJgRaDAMdxyPsYhftDL315nrdYLBUVFWfPno2Li5syZcrAgQPbtm0bHh4eFRU1bNiw2bNnJyUlHTt2LFtYUlNTP/3001dffbVPnz5t27aNiIjo3bv322+/vXz58uPHj+fk5NhstmZ5FvuNfxYB3WKglwyVEHiSEEAXI7oMEbMJALBYLOvWrdPr9RqNplOnTkuXLr1+/bpoNZqiP/lX7p33GWQzAADDsKysrDlz5vTq1cvT01Mmk7m5uY1+efTp06fRxxliYx9XBhmPwv9UVlaWlpaWlJQ8xsCJjwsH6bwSAhICLQIBiYBuEd0kGSkhcC8EOI4zm82lpaUoDnJBQUFRUVFZWZnJZEKhkMVp4r1qabH7RAIaAGA2m0tKSubNmxcaGurq6qpQyJVKJ42wKJxUDg5yB7mTs6urt6/P4Bef/3bl0hvFeVW2mpRDx4eO+GjAoAVLv6uZ9N65nn2WrI27XoUBGwBWwNQBMy+40dLCLwNAbT1tpEHm8dJRw9c+22vp5viiigpgxIQ4fgDgPBDckiEvLCSOYygSxzAblI1jWYIF/Okff3156JpQ31kzPzr000/kmQs3vl48r2e/HgHB/s5uaui+7eiocFIJ7s+IQHdQqTRarX78+PGHDh0qKysTHEaQ+zO0juEZAmAWUFfLmwwMX4WDmIRfho6KC22/OKpnQmi79fq2cT6h61oHx7prYzV+G5ReGx084z2CUtyC9joHJqsCk5QB29S67c4hO11C92gCM5S+BxU+6UrvNJXvfo1fqnNAmspvr5N3kpP3dlXANlXAZrV/nEYb4xK8zj1ibevIVb6dVmm7rg6L+l/vQZuGj06eNOXY7Dnnvo8t3plcczyLvXwDaoP8WgVumkEdBiw0wDnI1NOCQzjFAJYDLA/FUBgYqpETcGM5juEYCvpOk4JQCo3YZxpwJOBxmABlR0ATgMF4jhBpaOQNLbDPkIAW+GiChVIiGAsIgX3mWEEl5Za7dYu9CiTDJQQkBCQE/nQExK+8EQGNfOiMRmNubm5SUtLChQvfeOONjh076vX6sLCw3r17v/vuuytXrszKykIBkA8fPhwTE/P+++/37dvX19dXp9NFRkYOHTr0k08+SdyeeO7cufLycpvNhsy2J4DukRcd+v70xkoVSghICNwbAXRhigQ0ImfXrFnj6+vr6OgYHR2dlJQEPSzsljsJ6CfTFffOe45dI2DWYrFcunTpiy++iIyMVCqVCoWiV69eWVlZOI4/IS3ieR4FJ7RYLLW1tRaLRXQ/Qq1r0iJpVUJAQkBC4LEgIBHQjwV26aQSAn8mAhRFVVdXFxYW5ufnFxcXl5WVVVVVGY1G8SPWJ2Ru9Ge2+fa67BuI8ufOnZs5c2ZUVJSvry9icGUyIRy3QgWdoh3lDkqFzEkmd1E7ubVq7R+hC+nzxtuL/j1rX6eojyZMirl4najBgQEnaxkrAWlSyCmTgBGCEAIzBfb/UNqt1yfRUV8sX3LNagUElG+G240EZaUojCZJmqBogiAwDLPieD2Ux+BZgrTZcOuRYz+OfmlKG/dhndv984Vh0zp0fUauUkONDfvFUaZQq+QKhcwBZrx9fYa9OGLL5q1msxl1K8/zOF4vhN2DBDTNUSSw1YObVlBhBnW1HGHmQQ0OLtzgj52hvt+Ys2jF5Zmfn5w07YehL+3oN3RHtz7b23fb3LlX4lPRW7TtY73CY9qErm8VvN5FH6PRxWn0OzW6vchLWuWfqg5I1wQe1ARmqLUHFIF7HP12OvpvU2i3q/QJ8sANct1GZchmTegWlW6DOuB7tf8ql4CV7gH/a+W/qnVgTBtdjFfQSp/gbzv3Xj94VOLEfx2dPe9CYiqxJ5M5eAKcPAuu5oGCElBZDeqswEiAaoyusmA3jdYaG2FjIEnN8IKUBw1oCoav4aG8thVA33QjAJjgcU7xHMGxGMdigCFgOeTlzMDYjIDjofIJDw/kgIUDJhbYBCdo2Kf2BPTtY0pakxCQEJAQkBC4hUBVVdXp06dXr179+eefDxw4MCAgwM/PLywsbMCAAZ988snOnTsvXrxYWVmZk5Ozb9++hQsXvvrqq23bttXr9QEBAb169Zo6deqiRYuOHDlSUVEh0iK3am/M3UkD3W1L4xHSXwkBCYFHhABik1mGRa+mKIo6cuRISEiIUqns06fP4cOH0aVtb02zBLT9pN2+8GPMN3ufsbcHfflRU1OTmpo6cuRIDw8PjUbz0ksvXbp0iaaFAOL2pR9THsUEQjFg7Z8BUesek1HSaSUEJAQkBG5DQCKgb4NDWpEQaHEI8DxPkmR1dXWpsFRWVtbU1FitVjQf+vvMOdAclyRJgiCQRxWGYdeuXYuPj58wYUKvXr0C/LXOzq5yhUKhVjlpVA4qucpVLVMpZE5qmZOHTOYhk7nLHIJbtYnq2Xfcv2Yu/Oy/3322YMHS71cm79936VLur8UGM2apsRlzS6ritx3t+ezMgKCJs2cfKSwEtSZgwUGdjTVYyZp6S42ttqrOUFldaTDAdOZMVnp6WvyG2CVLvv33p7PfmzypQ6fO3t6hMpmfTNbWQeEnkwkqIYiAdpQ5KhwUaoXaBSpwtPHxfrpXz88+n3MgM6OsrAKrh9FRbDYb+g66wQmaEzyFOYYENgJUYqDCCqoswMQLgiEWFthoUGMGdRZgsgFzPSi+Ca7lg6yfQOYxsHFn7ZoN5QtW5P3nm2sTPzw+ekJ63+HbO/WLC+wc06ZdjHvoapeQGJegeJegzS76BI12i6MvTCrtVpV2qzJws0K3xTk00Tlkp0qXpNIlOwfvbRW2v03Efs+wfe46qOCh9tmjaJPs4LFZ5v59q6BNHvp17rpVbrolap//tg75NrTL2k49459/OfWVNw6988HpD/99ata8gwtXH4tPurH30M2Tl+hrv8KWmHFgJUE9CQNFkkIQSJIHkIuGChsNDDLDQT9pimGh6IYgpy14UwPACCEdoVd6PQ+sHKhjYbIIHtAN7s+i5vQT+ETU4m5HT7jB6H6IHiNFU6V+F6GQMn8HBJoNCHG3hhuNxuzs7K1bt37zzTdjxozp2bNnSEgIChU4ZcqUpUuXpqWlnTt3rqKiIjMzc9WqVe++++6QIUM6derUvn377t27j3559MKFC5OTky9evGgwGJCrIMuw9/g2q1kaqNmNd7NZ2i4hICHwkBBAM210/fI8f+PGjUGDBimVymeffTYjIwPpJjc5dYsmoO2NR9rQGIYRBFFQULB48eKOHTu6u7tPnz7daDSiVj850wkUXkW06n4eBsXbbJMelFYlBCQEJAT+XAQkAvrPxVOqTULgUSOAXndjGGYRFpvNhuM4mh2KYT0etU2P/Hxo2nS3CCcYhtXW1mZnZ8fGxr70yqiIdqFtfFupnB3V7mrB59jBQeEmc3KVazwclB4yJ3eZ3Bmy0gq1zMlJ6aJxdnUPCuoQ0bZzp66dop6OjujUzUv3DyeXZ+WaIf/o8WHPZyb0e+7FQS8Mfua556J69oyM7hDeMSy0XUh427CItmFhYSEBAX6tPNxUKoVKpXJ0Ussc5Y5KmaNSJpOrHeS+SmWoQql1cFTKHCD17KRyauXp4dHas9s/uv/ny7lpaWl5eXlQTJqmWYZnGXF+iFhTqJwsOEHDXxZG+8MpYKMARgFCCP7HMkCQr6ABSUI3bVxI9TTAGBhTESUrC6wsuPYrf/VX8HMxuPwrOHUN7D5GLdmUP/vbn8Z+kDL0je1RQ9eG9VgR3DXe76l4N/0qhc9SF+0qjXaNRrvGWRvnErhDE5Ck9E1y8t7hGZLhEZbpEZbpGnpAo09V6/c6B+91Dd6l0e9UBSQ46za7Bm110cOMizbBLWCHq/8ON78kd78UD/8dnroYz6AlrUOWeQUv07WP6dBj24AXD7702o+Tp/88d+GvG7Zj6T+AC9fA1UJQaACVVmDAQR0D3aExAOoBsPEAE5Q9xAHIwpCPVgrUYHyphS4CkIY2k6DOxlVb6Foba8Z5nGBJkqcYHsp1s0BEGGbEeh5J5j6EQJCmyyOx5i94EugLz4uqjqiBLNTJkRYJgb8RAihyoOjAiHgKgiAQBMiBsby8/MyZM6tXr544cWJ0dLSnp6eXl1dERMTw4cMXLFiQkpJSVFSUm5t74sSJbdu2TZs2DTlEu7q6durUqW/fvh988EFcXNyZM2fKysqavO/5TaBvuwXfc+U3q5IKSAhICPy5CIgENBLfmDFjhru7u06n27p1q73Ks/306W4X8Z9r2EOqDRkvNg3dNkmSxHHcbDanpKR06NDh/8Kef/PNN1arVXzmEpv8kKx6GNW2RJsfBg5SnRICEgKPAAGJgH4EIEunkBB4iAiI8zxx9iBuESdDD/H0T0bV9m1HeVGiTkQDiqPRhA03Gy21J0798M8p/wwMCpU5ubq4+ylUXnKFl1zu6Sh3dlKqNS6uru4eCrVK5gjdkhVOKiEGoByqZDjJZEpnmdxX5vCUzKGzzElwYXZydFDLnJxlco1MpmpwaLaX05DJZHInB6XCWaX0USjayOQymBQyeIzMVybzbd0mQB+i6xLdpU+/Psv/t+LwkSMmq4ViaBTeBEW4boi619BUqCkhaCXfIqAFlQkY3A8lQfIYOgTTHEWxOMlgFEsSLE2wNM7RBM/CBAiYeIrgWYznMR5ggqswxkGmth5KYAMjA6pIcBMDpRZw7AJIOgCWfV/56X9vvP7Pwy+/fWDQy8nPDE0K77optONWbbvNfm03e4RucgnaKA+IdQyMVQVtVOg3yXzjZd5xMq8EB6+dDl67ZN67ZH67Hfz3yAP2yf0POPkedPI9ovY9pfY7qtHu1+h2u+r3OAfuUfomqX13uAUku2t3eug2euhjPHTLPXWL2v1jXbeBGwePTRr97u5Z32Z9E5sdv79yzwk84ydw4hq4UAx+qQTldeCmERjMoNoKailgZFkzT1h4zMri9SyB87jAxlMMDEHJ8FB9GnACESnESrxFQj/a0W1PQCND7ji/REDfAckDbLBDrx5jMZwjaQYdjq6qB6hKKioh0GIREP8nohawDIv4FOTWl5aW9tVXX41+eXRISIi7u7tWqx0yZMicOXPWr19/5MiRvLy83NzczMzMJUuWvPPOO926ddPr9a6urpGRkePHj1+4cCHiplGdJEk2YZ/t3Qnt/2sjS+y33E++xfaAZLiEQEtFAF2Y6AvLvLy86OhomUz24YcfGgwGkaUVL17USHG1SaZFQNDEZrSKaGgAAEmSn332GXo5d/bsWRjlhWHtD3ny24juyU3+KTz5ZksWSghICLRoBCQCukV3n2S8hICEAETAfsIn5mmaJkmyiSAdzVE4RQIAzpy9PHTwGyOHT1q4IG78G7P1/oN6Rr3RtdOzYaHt27T2VSqcPTxau7q6ymQyZ5Va5eQslyOZZgeZo0rm5CpTeMgUreGvE3KjRty0zEkjUzk7OamcFAq5XAmTo8JBrpSrVAonhbvcMVzp1NHFNbRVm0CfwIDoHk+//tbEf386d3183P701Os512pNtaJLJklT6AFenPKKwZdQeD1EQDf8Cvw0D+WqaRi7j2twlmaFsH4kMBGglgAWAmCQd+agjjJMLCA5nuRYkqdojqA5jOMxjqN4GvAU4GjACeEBRR9RHsBDTBjkdstqQX4ZyL7Bnb7ApmVatyVVL/s+9z/fZn/01U+vf/RD7zFbw/uvDfjHGt+o9d4dN7Zuux3Syv6Zzr7HVf4nHXWHZMEZDkEZMn26LChNpktz1KU76tLlQfvlQfuVwWnKoHRlULpCmyr32+Pou0sZsFOtTdLoE12DtrsGbVUHxcsDYhwDVip0K9Qh/9OErtSErmw3YF/nFzP6jDs15O2zb029+tHnhQtXGWO2YfG7zbuPUad+Ab9UgfIacNMAKgygooarpyECq3mIrQAAIABJREFUDAA0gNgxgvvz4/aAZgTdFPTbhI8WVu0o1Dt3/5Yvr/0Rd7tv2Jexz9+t/JO23d5mlLe3kOMYlhWkGm9WMiYLMNRBlyUAAI7jt90oEM53/tpXJuUlBFoyAkge1GQyZWdnHzx4cMWKFW+99VbXrl3Dw8M7dOjQs2fPcePGzZs3b/fu3adOnbpw4cLx48fXr18/ffr0AQMGREZG6vX6Dh06jBgxYvr06Tt37jx9+nRlZaUoOYoImibRj+3ZZ/s3xCL3If7vvs9MS4Zfsl1CoAUjgP5d7t2718fHx9fX99SpUzQNHSbs5qjwIkYtvNvl3FLafzf7OY4jCCI7O7tTp05yuTw5OdlqtbYsApplWPT5rNVqFZX9Wkq/SHZKCEgItFwEJAK65fadZPnfAgHp7fT9dPM9JohoEoxgpCiKZlmWBzjJX7qU/585q9P2XcZs4Mih/FFD5yQlXK6upEtLbubk5F++fGXr1q0zZ87s1rWLd2u/Nu7B7uoghaO3TOaicfdTe3gpW3s4uGlkKrlMpVC5qt1bK2SOMplSpnGTtfJwa+Xh5uLu5uru4erh6dray6211t3zKfdW3dxcnxkwYNqSpduOn7pQVFZYVl1Uba61ErhAGDMUS9IctBAjiXocp9nbPClun9zf8oC+jYDm4XaBgOZ4DvAcdO5lOI4EFhLUCSLRDQQ0itJHNrhJQy9plsNYzsZxJp628rgQ/k+EnicZ2sLQFpazcDxGcxgs38h/MywgKUDSkPymAKjEQbEZXK0C54tBVi7YfQwsWlf90Rd5r0683HfIydDIFH3k3tYdE1p13iykBMeQ7x2D18tD4hXBm5XBO5VBu1XBKQrdHpkfdJRWaVM1+jRVUJqTdo/MO1HmkeCk3SPXpzgF7VOF7lOHpSpD9sh0O2Xa7TJdomNwkmNwkoMu0clnq8p3s4tuo0dIfHD0lrCnN7Z7ZkPn/rHDx+yeNOXI/G+vx24qyzxGZl+HlHSlSYh/aAXWemDDQIN3NAcoDtCNGtNQvAG+6BCSAMudTOc9tohA2mXuLG7PPjfJNxa+3QBRArtBkMVur92JxGxjJUJTxK23Z+zL2OdvL/XkrtnbjPLQVnR/EF40wPcMP2cbPvl488iXFyxbc/RyLs4AcLOGsNUzLMOjLuZZjmc5AN/DkEJCLynEFzFPbvsly/5uCNj/77v/tptMphs3buzYseOLL77o37+/l5eXWq0OCgoaOXLk7Nmz169fn5+fn5eXd/HixYSEhHnz5o0aNapdu3atWrXy8fHp16/ftGnTYmNjjx49WlpaajabReFXpOZBUZTo+Iz+bd3jt+HaFEy3b8v95O+/vVJJCYG/DwL2186drRZ54Tt33ecW8alk/vz5Hh4e06dPN5lMUA9OWO48u/0W+/x9nu6xF7O32T5PCkteXt7gwYPd3Nzi4+MxDBPnG6jkYzf+3gZQFGU0GsvLy8vKygwGg81mE2/dqCH3PlzaKyEgISAh8PsQkAjo34ebdJSEwCNCAEk8//Ep4yMy98k7DZoFopmxaB2kpniBj2IBxwkZGjr8CtScsJNlOIZiaRImAtw4z7827Lu+3f+5asX+S5dLj/14bsfund/Hxyxe9u3iZd9+u/TbxUsWfrdk3rIV36xfv3bLlk379u0/kHH4h2Nnjmf9nP1LVXYOM2/xlc5R8wYNmZt91URwAGNrKXCTBgaGp1geIPXhRvMQcYbYRKiw0ZhQUxD1jMreotjQ+q3JscA+84KQAw9lJhh4IsBCppsD9gkpezQSBAxU9oCbBOZVNAHWK1Lbt3yrWYGWbQAT6usKfLfgxEtDz2KYKB4yuZTg1222gaJfwflrIPl46Zq9P3+28uik/6S+OCHhuVe393pxa/SAxLCuW/QdE/3bbvcL3+kdkuSpTXLx2S5vnSDz2iILSFSG7FGHpapC9jvqU2WByTL/HTKfBJlfgky71VG/3a39Pk3EbmVoklyf7BSYqgpMVwWmqQNTNLrdGv1OF32iqy7RXbvNPSDBPXCzR8BGuftyb31853+kPDvkh39Oy/v0s9Ily+vWb7ClpIPM4+DkeXD+Osi7CX41gAojjOJoNAGbBZA4oEiA4Vw9yeAsL4RDhM3kBGraSFBWmsUBJOJNGGGlGJKFGh93LChCJNPIb7MAlmrwSkeO6YJ6teChDitr9IlGPSJUiLoIgSwqgjc5kTAexPFzZ+bWiGocY3eWuXPLrVHW5HSPaRVdBXf+MvCJGI5mlgVQ+hlqqMNtIDUlr3OHrwL0i7xCvxv29qHNqZbiGhjNkoLfD7CwFRTPwQ9pLTyoEZIJ0tDcbS+EbqHQ6Of1mJovnfbvi0Czg1AUbhKnDSh0bVVV1fXr1/fv37906dJx48Z16NDBw8PD09OzW7duEydO/OKLL5KTk69du5afn3/kyJF169ZNmTLlhRdeCA0N9fX17dix49ixY+fPn5+SklJYWCh+bt/4j6PpX2SYSGGg1SaFxDJi/9k3537y4oFSRkJAQgAhIF5r9lcQuvRYhm32owTxRnGfGKLyHMdNnDhRpVKtX7/e/tTovPdZVYsuhnC4ePFinz59NBrN7t27xe+oRPCf8AaSJFlVVVVYWJiXl1dcXFxZWWmxWNCXo+g1wxNuv2SehICEQAtFQCKgW2jHSWb/jRBAXkUPOkf8GwF0z6Y2i1sDWcUJBBXfyEEjElEg+3iOsiegl3x1pHfnzxbMPWitAxYTsNUzFE1wPCHwVSwLIEknqF4I7BUA9TiJkTzBAoIHFgpsTip9ZsDmqKdX79xTVmsFFIwIWMmAchZUA8AiY0TlDaE1yBQoTWzHDKI5LTxXY4vRoY1rALo8N0mQAmjcKOYbSGdENd/+KxZG5LV4CNqODryzzC0L7pmDHtkMT/EcAVgrALU8uElCd+nrZeDHbJB5EqQeApt3sN+urP7s66IPpl8ZN/7H/oNS2nXf2Pqp1a3afd+q3fpW7Te5PbXVOSzBMSBe5rfeMTBWro1zDIx18I+TB25S6LZqgpOcg/eptQdV/kdVAT+oAn5Q+x9SB2Q2JP9DcNX/Bxf/I64BR118f1C1ydB4prq12dPaN9k3MNE/aHNg+LqnomJ7DN7+3Oik51/f8caU1BlfZy1acXldfO7u3eWnTxHXb4CSSlBaAyrMMBCilQNGChgwmMw0sDLARII6HA4jCgCcBzgDCBZS8KLPuD1FL3haU7xQ8PZfxEfTjeyzQJ2KBLRA/bONLH9zBDQcG3aD504eWaRTm911j43is1UzzPo9+/8h7Wy4mhs98sVVyNojAprhOPjszRAcA6+dg5k3u0WtCnsq0S040UkXG9Yj9v3ZJ09fAnVmwBIQb5bioVI6V8fxBg5UcnwNz2HoAr/VeLvcQ2qYVK2EwL0RQByBSCqhVZZhUdgAnueRp/PRo0c3bdo0derUQYMGRUZG6nS6jh07jhw5csGCBcnJyVlZWcePHz948OCWLVtmzpw5bNiwiIiIwMDA8PDwAQMGfPzxxzExMadPny4pKUFfl4uujk0IZftVdHGIBDTK2BcQP9W3b6DdJXVfWftjpbyEgISAeKGhpwbEOKPrjqZpgiBEmYU/7tpCUdTkyZNVKtXcuXMtFkvLkp74U4YKEhpKSUlp06ZNYGDg5cuXxY8/xPvXn3Kih1cJSZLV1dUoomxBQUFRUVFpaWlFRYXRaCRJstmnp4dnjFSzhICEwN8HAYmA/vv0tdTSFoYAz/M0TWMYZrVakUSpNBv4s7pQ5KiaZIT64TZBxYJiWQImGpw+WrtvR0l5EbCaIFvN0jD2CEHaKBoqJrMsAcszFENSFE3ASb/ADOIA0pFHz9QPGrY8ov1/5y/ONWPATAKcr2eAEYBaAMyoRYI3ayOdh0jGhqbeMtCeTGzEAe1tXLPjmkWO+NY+u5y4904mWtz1pxPQFlu9DSNwisRo3ESbzZyVEJzOaynWzMKAhxgQwh6ywEoDMwGqLaCyFpTVgF+rID297YDpi2XZE2ceGfDytp5Dt7bvtT6oy+qw7pv0nTZ4RaxvFRTnqt/sErhD7btD5b1b453h7HfU2e8HIR2C2tMwpasDUMpU+R1U+//gHHi8VdAZT/0Zt8Afnb2PqdpkqL1TXQJSXAKTVL6b5T7xCv9YZ22cmy7WUxfrF7ReG7JeFxaji1j+7PBtw8fv+n8fH5v25cUtB8Du4+DYFXCpCJRXA0MtdJeuswKj0Nf1LKjnIDFtJHkjRZtpqh6GQMQYyEvjLCAYgFPAxgAbC2BZIQYkZK1vKT8IERKhi7WYUCcJ66I7eyNPTTWS0pRAgEPvaaQMftvvLbf624lmQUP8tpJoy23lxWerxhFrN7QeR1bEhWsE4ZaAiUhAQ8KLo3iWwevZKgOI31DfPjpRGRCn0m9vFZQYEpnYb2BS6j5QbYBvmCiGpVkry0HNGZSgNrrwwkm4DG8hgHKPo9XSOSUEoLYMIkFE30ak6WkymfLy8tLT07/66qtXXnmlY8eO3t7evr6+UVFRb7755tKlS0+ePFlQUHD27NkjR44sWbJkzJgx0dHRnp6eHh4eXbp0ee+99xYsWJCZmVlZWYk+rgcA2Gw2hDjLsFDMqlHytQmtjFabvS6aXjbCun0vNlvgHhvtj5XyEgISAk0IaJqmKQqGEqGERXyBZA+UeP2iC81+173zNE2vXLlSrVa3a9cuOzv770lAYxg2YcIEjUYzadIks9lMkiQKzyjete6N4ePdi54xrVarwWAoKirKyckpEJbCwsLS0tKamhocx8W3m4/XVOnsEgISAn8xBCQC+i/WoVJz/goI8DxPkqTJZDIYDKWlpSUlJQaDAcMwmqYlDvpP6WB7ygq5QaNfkeRrQkDTOCCtgMLh9/yiEHCDWgUPv9uHB/KAISkMs2IkRgIOB9ANtqIOjHsr7qnI2R9+nF5UBm23klAXgwUWgX3GUXOgw7MglwFXH4yAvg0Pe/q4gaW8bX/DiljsURLQ0G8OAJplrQReh5nrMKOFstazGA4YEjAET9WzRD1LECwpyKJAR2mSYxkAZS5sNHQkt7GQpLbSoKwOXM4FJy+AFXFFC1bmf7bg+r8+vzZ6/MnnRv7QpdeekMjE1gGxHgEbPQI2ugduhpobAQlugdvdAre7BO5wCUxyDkzWBCQr/fcqfFOVvhkK70x5m8NKnyMa/xOagGNK34MKn3QnvwOqgEzoSe2X7uiVKm+9V+W1T9Fmj4P7TpnrBo/QTa6hazVBK5XaFXL/Jc7Bq7wiN+ijNg4alTZ2fOYHn5yePe/CstjcuF2/phyvO5pdfzEf5N4E5VaYDDiopYCFBTYAMB4mgW8WhTZ4pMfS0H3It9nO8VkYHhyAWhLIx5rgeLEOAgACAFJIKA9p6EZxDzhQG9JthLIdBy0WaJK5rbz4bPWEE9Cw7RxgkPJMIwHNWUzUpWxsfZx1wj8Lg7tl+nY47KFPd/FO8grY3KHjpi/n5tz4BeqAQ30VGJyTIHmM5DEKUJRQlURAN3dHkbY9FAQQN3SPqu0JaJqmKysrT506tXr16mnTpg0cOFCv13t6eoaFhQ0fPnzu3Lk7d+48fPjwmTNnTpw4ERsbO3Xq1L59+wYFBfn4+ERERAwZMuTjjz9OSkrKzs4uK4P/qwiCEONzIn9J8QPz33SCbpbMunXjsMvZt85u831l7Y+V8hICEgL2BDRinwmCwHEcwzCbzVZbW1tWVpaTk3P16tXLly+fPXs2IyMjcXviunXrVjcuCMN7PGiIb7wAACdOnNBqtWq1esaMGVVVVeJFK1aCtvxV+4UkyQ0bNgQEBOj1+qNHj6Lbtfgu8MlvO/r3QZKkzWarrq4uLi7Oy8vLz88vLCwsFpaysjKj0YgePO8xJP6q/Su1S0JAQuDhISAR0A8PW6lmCYHfiQBBEGimWFRUlJeXl5ubi0L9oFfrv7NS6bC7InA7HS04liJJDZalYGJYloZezxwjJEGzomFy2agkzUPNaPjhM8WSOEdW2uqsPLiWD/71capeP3Pcq1vPX8ZwgQikAENBB9h6DhAc5BDh+SCr2JR6tjfXnpNG1trv/f15kYlukrlbjfbF7lbmbtvFY6HmNZSlhr9CjMQGoQSRDecZyK+iQHBQt5fl4A8DaAaQgpYFyQGSg7wt5KN5KIJhZoHBBvLKwZmfwcGTbFKqaf22soUrbsz++tILY3b2f2Fb12c2tO26PqzzRl37TT6h8Z76Da30W121O50Ddij9dih8dqoC9mi0+9SBqQrfFIVvqjog01V3uFXIMfegI666wxrtD+rAI+rAI0rtEUVgpkKbqtDtUej2OGmTxaTQ7REkp/dq9DudQ7aog9d4dojR9Y5v/9zmHi/ueH5c2ttTT0377NJ/FuUuXV+xPYU+mAUu/QJulIDCSlBmBDUYMJKQXq8XEhSPbnwZYe/Z2/ieghc8nTGet3CciRPY7EbqWSKgRXYeyo8LCuQ0xzFwnNHAUge2Jlzv0Wu9tz6+TViqe8gBz5AM7/ADTq3iXdp8H6Df0G9g8p79ZM6voA4DOPTKxzBAYYKaClT0aG5Bd4OGe8LdLgBpu4TAgyAgKmnYH8QyLEEQJEmijRaLpaio6Pz580lJSbNmzRo2bFjXrl1DQ0MjIyMHDx780UcfxcXFpaenZ2VlnTlzZtu2bR9//PHQoUO7d+/eoUOHyMjInj17TpgwYd26dcePH8/Pz6+trUUsg/0YR9/yoy32I9x+zN8tb2/5/eTvVs/dtt9PnVIZCYEnFgE0sBFrbD/IRYMR29vEC1W8JBF1aLFYTCZTdXV1RUVFYWFhTk7OhQsXDh8+vHXr1tWrV3/zzTeff/75tGnT3nnnnVdeeeX555/v3bt3VFRUx44dO3To0K5du5CQED8/P19f38DAQK1WW1hYiOwRbRCNRFvQuyhEShoMhrFjx8pkMp1Ot3Tp0urqaqvVemdzmm2aWH8LzeA4npGR0aVLF7Va/eWXX6IvRRA4qL+a4PZENVPsEXRjZxkWx3EUjbCoqKhQWAoKCvLz89GzJ0EQkv/TE9WDkjESAi0dAYmAbuk9KNn/F0FAfOQjCKKmpqasrKxYWNBUoLKy0mazSTOAh9PZv0VAswTL2VjOhj7DF5yjuYbJpT0BTUOylGJYXHDUNXHg64Ung4I/Gv7Chp/OASsBKICRwEICCwPqBfkFGsZG+/sR0CITDX19uQZOv4F0pgFPC+wzIqA5CorychjH2sTEchjLYTSH0byNhHrLJgICyyHB5Xoa2CjI4dpIKIJRbQUGMygxgF9+hU7TO1KJpTE33//4zIhx+7v129y5d0L7Hlsjum3xCl/VOny1e/BKN/0al4B1LgHxGr9Nap8Ejc8Ol4AU96B09+CDau1BmU+arHWKzHOvIvAQpKEDM50C05wC0+T+BxwCDjj4Z8j8j8EUcFimS3cI3u8QslsWvF2m2yT336gJ2Oiq3+gREh/YMcG/XZxX+Bo3/beewYvCotcOGr33jSlH/j0/e8XG4vQfQXYe+KUM5JWB0mpQaQa1GKgjgYmBycIAqyDVQQjDBsbNY0moA8ML0sUNlwcKT3iLhP17e0DbE9BQlYTCwDfzM4LCvvQMXOmi3ewclOQekuQatMMlcIdzwA6PgL1tAhLadY6Z/+3VX6sgAW2DnyrwVkEihuKBEMaTQ7/iTVt8nJO8hB7OLVqq9TYEeJ6vqqo6evTo2rVrJ02a1L17d7VarVKpQkNDx4wZs2DBgoyMjJycnBs3bqCQgxMnTuzYsaNSqfTy8oqKiho+fPjnn3+ekpJSU1NjsVgoimoybpFnnMhNiEqyDf/1BFvsx/zd8rcZfR8rd6vnbtvvo0qpiIQAVKp5ZCjc7VzoakIj2Z5QRtvvNA9p6VgsFqPRaDAYysrKELl85cqVixcvZmRkxMXFffPNN7NmzRo/fvzw4cN79+7doUMHPz8/jUYjk8kcHByUwqJQKFxdXQMDA0NCQvR6fVBQUNu2bTt27NinT5+XXnpp6tSpX3zxxdKlS+Pj49PT069cuYIYZCSwY3/dNbEQRTplGXbTpk1eXl6urq7t2rVLTk5GH0mIdwz7VqPamtTTglbFvkM62pcuXRo8eLCrq+vw4cNv3LghviqwZ5/vNhgee6vFnkUdhH6Ry7zJZEKDDTHRBQUFxcXFRqOREJY7/1k89rZIBkgISAi0RAQkArol9ppkc4tHoMm8hOM4giCsVqvRaKyoqCgtLS0WltLS0vLycoPBYLVam8wIWzwET1ADmiegb2kuA5wDNRy4ycOweVZI50FFArhASQ7ImELumaN5ngE0BTV9Kyxg3baCrk9/+dzg5Tt3ldFCyDiKr2ZADQPqBAKatj/r38EDWvAsF3hT2HIBPhQdUfB3bvAuRz7mDMSV4yjI+AMLB+oE/Gs4AF19OV5Q3IbzfeSOygjPQixFchQNVRIYFtA0TBzfgCsHiUe+nuPNFFSXNpPw96YRstInz4P9R8nVW/K//t/592elj5u067lRm/o9v+kfz8Z17bkp9KlN+vDt/uE7vUKT3IJ2q/V7nbR7HPz3OPnvVQemOgekaPz3qAL2KP33OvnvlQfsdQjYLws8INPul2n3ycMzZfpUmfdOmfsWdfhBVXCGk36/kzZZrk1U6bc7hya6hG13DktQh2xUBccrAtcrAmI02hj34DiftglPPb2n15BDL752+s33s6fPzZ+/8ubaHfU7DoHMC+DH6+BiEbhaBvKrYCBEgxlY6gFOAJICNByGALqKN2R4AUPiMRDQ9i77d7nS7cf//eTvUg36hECs4Jb6M9KDFj2gBcEcHgaCBOD4ibJJU5K7PBMT2Cm2dbsN8sBVrmEbXUO2aYKT1br9ap8kT+/1kR1jP/wk6+BJusIG5XJMAFgBwAFHQSXphiSS0Y13A75hzImSKXc3WtqDEBD/FSIMG5D8q6PzoM3kOI4kSQzDrl27tm3bttmzZyNlZx8fH51ON3DgwBkzZqxZs2b//v03btw4efLkpk2bZsyYMWTIkLCwMK1WGx4e3r9//48++ig2NjYrK8tgMCAvxWY1YcV+QUbejUKy76+75R+0G+9Wz922P2j9Uvm/FQJNhs2jaTt9xyI6LCPxdCSIgZjl2tra6urqkpKSq1evnj179tixY2lpaYnbE+Pi4lauXLlgwYKZM2e+9957L7300oABA7p169a2bVtfX1+NRuPq6urp6enu7u7h4aHX6yMiIjp16tSrV6/hw4ePGTNm3Lhx48ePnzZt2pw5c7777ruYmJjE7Yn79u07cuTIuXPnioqKamtrLRZLTU1NSUlJbm5udnZ2VlZWZmZmcnLy8ePHUcgZ1A5RUOJO9BAHbTAYPvvss1atWjk4OHTo0GHXrl0Wi6WJRI99R9xZT4vbQpLkpUuXxo8fr1Qq27dvf/z4cQBAkwc0sclPZutE8+zfNYo0tMViKS8vLy4uLikpKSoqys/PRxw08nDnuMbP8J7MtklWSQhICLQEBCQCuiX0kmTjXw4B9O9fbBbLsBaLxWAwlJSUFBYWFglLcXFxeXl5bW0t8n1GhcV5g3islPnDCIjs1a3MLfaZZ/kGArqKB0Y7Ahoq5wrsMwl4kmMIloKiCTQJCBwkJJUNHrm2c9Tc+E2/Gq2gzkYDQDKghgW1LDAL7s8wUCFKDSwppAQatTiaNsl+R8NBTYv8rvVbzsiIC278vVtl9uXvVuau2xsabMfaIx7/DgKagZH1OOhNDrVKLILvbx0DaWgTpKQ5Ck6UWeg63eA3LWQgmixgCEBiUNgECm2zFEXbaNbM8nUMfIVQxwOMAzTBQy91khPETwTISQA9iw0YuGkGuaXgcg44dR4cPg7WxdV9t6zq3//JnTT95+deSe88YId/lxi/Tuvdgv7nrlvjrlvjql3rrF2vCYxVBcYrtRudtJvl2gQHXYJD0HZ58G6HkL2yoFRZYIrML0Xmv1+mS5Pp02WB+2SBe2SBybLAJJl2h4M+ySkkRRmWpgo5oAxKV+nTVUFpzsF7nYOSXIO2O+s3uuhj3UO+b932e/8u69r23dRtWOKz45JHvrPvvRlHPlvw0+rYwsQ9lUd/tF25AW4aQGU1qKoFhjpQYwQ1JijyQvCNSdCHJoTQhCwPncKg2DQPhT7EhOSnWSCoQtvLQN+mAd3w9gVWcPtbhVtdbz9gb20Vhzx8gLFfuZ/8rWrumruzGmEoCa8kWEALrzV4iubrLOCnK+TeI9iCmOKJs893GbTRo+0S73bxbiEJCt9tjp5bHZ03aNxjXL0XPTs8cfsBosQGA4bWCd7QGHSF5nDACNrlHNPYkIZvGaCau126q6nSDoiA+O+sSeYvj06TCcDd2stxXG1t7dWrVw8dOrR8+fLx48dHR0eHCcvTTz89YcKEJUuWpKSknD59OiUlZevWrV9//fULL7wQFRUVFBQUEhLSs2fPSZMmLV++PDMzMzc312w2o0gS6HQi9d/s2cUekQjoZvGRNj7hCIgDGFFs9x7tf2JbCIJAgssWi8VsNhuNxtra2oqKiuvXr2dlZaWlpW3dunX58uVffvnlhx9+iJyXBwwY0LNnz+jo6E6dOrVt21av1/sJi1ar1ev1ISEh7dq16969+/PPPz927Nj33ntv9uzZS5YsWbdu3Y4dO/bv33/8+PFz585lZ2dfv34dhY+rrKw0GAw1wlJeXp6Tk3P27NlDhw7t3LkzJiZmwYIFs2bNmjx58rhx4wYNGtS7d+8ePXpER0dHRERotdqBAweiryKQr6sIY7MQoZtDZWXlN998o9PplEqlj4/PggULqqur0a673T2ara1FbCQIYu/evaNfHu3l5dW+ffu0tDSklS8y9SJiKPNkNsreSPueQu7byPu+pqamoqICEdD5+fklJSX5+fmVlZWovU9muySrJAQkBFoKAhIB3VJ6SrLzr4OA/f9+MQxxVVVVcXFxvrAUFhaWlJRUVlYajUblHDlBAAAgAElEQVQMw+wj/zyyafRfB+7f3xKugYaGTBzZmGi0UQwBJ9B6FMdRLAMZOUsduHgee/312C7dPl+6ItuMQcqTgPHzLBQUUbAxgIDUKs80DAOB822OtGqew/v9rXmCjrTXNIaoCUnAAzHgDdDcokGh1zN0fKaQ/omoFi36TTcw44hA5QRiq4E/RR0H4/wJLw+MPDCykG3GYTg+eOIG+hVGrBMC9kHGVtDnJlhAsAAXUj0HKutBzk1w6prtQFbd0tgrs+afenXyrn6j4jv0Xf1U7+9D/hHj3+l/rmGLVEGLXUKXuUascYmIU4dvVoVuddAlyHw2yXwTZLpd8uB9TsFpTsFp8qD98qD9DsH7/j973wEX1bG+vdQtLCxIW7fBLkVqQDQqGutVNNeaaDCJ7Vr/luSq0atevdGYa401IqIIClKlSFMUjRSjolGQqwihhiqwIOyybC/zfXMGTo4gxlQ12fkd1znDnDkz78xpzzzzvCTHCySHJPjLScZQ6SQSJ5bEDTPinTJ2CDPhRZB5URRuLM0xHttiaY7R5vwohmMUgxdtxY22YkdZccIpNrvMmNsFvl+Pm5n04fLsDV88PhkrS88F98rBgx/Ao0ZQKgT1UvBEBVoxFBUxWHQYeNoq1bYpoIi2DFOVVgEg12gUKqVKq9RAwnA3yqwFarVOqdHAXsCQXGz25UfsGoHYvSBgOOZ6krRwWgFTZMYiPekYaRgq2fyY86fjz4zlPhcKoSitFtYV0uIxb4QqtU4NVdo1GrEGjoNmJZzWyC8BX52smvnRJRv2Vw7O0Qy7KDPWBTNOmhk30cLhnPOwuE+2V199AMragQjzHAq9RwKNGHSJddBNG8SgdQDpyUAY+o9b7f2MGX7XHSRtSVxYjVQjkfBlr1OjxcgoM/FPOBLU6wn44l1iCX+aOM47w1tEpJWpVKrm5ub79++fO3du48aNY8aMsba2NjQ0ZLPZEyZMmD9/flxsXElJSW1tbU5OzvHjx5cvX+7j48NgMMzNzV1dXWfMmLFz586MjIyysjKcl9drYTiyOX7250b69stzs+kT9RZ43SyAhm5fZI34/oznQcRkJRbQmgBiNtQ0VBSSZVcoFEgNT6lUtre3NzU11dXVVVZWPnr06MGDB/n5+RkZGceOHduyZcvChQsnT57s4eFhZ2dHoVBIPcHAwIBMJltbW7NYLIFA4Obm5uvrO3z48ICAgPnz52/bti0oKOj8+fPXr19//PixUChUKuGkO7ppoPogIfjOzs7W1taGhoaqqqqHDx/m5eUlJyeHhYV9+eWXK1eunDx5so+PD4fDsbKyMjIyQic3MTGhUCgWFhb29vYcDofP5zs7Ow8ePHjixIkLFixYt27d4cOHFQoFOuPLdCvSo5dKpXGxcU5OThYWFubm5rNnz05NTUVPB5VKpVAoZDKZXC5Hd7m+5n2ZE73CPOjxhyoQGRnp7e1Np9P/P+U8KysLNV+lUqGR82YB7n3v8HjX6HQ6hUIhEomam5uRIgdyR9TQ0CCVSl9hX+hPrbeA3gJ/DgvoAeg/Rz/qW/EmWQA94/HleG1tbQ0NDZWVlWVlZaWlpeXl5ZWVlY2NjZ2dnUol9ICHv0Yjytib1NQ3u649AHSP4AbhdQ2q72LQsxQB0BgMBTm5ddWKTZ+FDhmyZvfenJomqE8sB1I5aFXArQNDn9VqHdyIwOtfCYBG8CDCKxHkq4JYMNqeYdr+aO/uSwBz//gj+kzYJVKzYbzXnEF3+TIMP2zXAZEOCip0AR2Cp1Ua6N1QpQEaDSRVY6iqDrpJ7EalIdEdQGQWY7926nRiDMPu1EB9kNJGcPsRSLmuPX2+dfeJ0n/tvrv0X9fnLE+bMOf821Oi3UaHcfxODvAIYridYLiFWricpQui6Pw4mkMCjZ9MdbhA5iaZcOKNWLGGA2OMOHEmvARjXrSxAwKgzxjzok14CWTOBQo3jbBlUNmXqaxrVFYOdeC35pwcS8dLNE6CCTOSyomgckONBx4jWe8lMb6wdA1xHB41fFbG5CVZH6y9unznt/85Vfz1+crka0+u3Wi9Vai8Xwpq2kGtGDRJQasctCtBpxJIVUCu6vb3qNQCuRrIFPAbEoFZ8EtYAzcI7UKsGOdP4xEI+xJQYBxQRhg05skPwc04+owiL4dBP3OxEE9DuNsQk3uGCZRmUeuUCp1cpuuS6CRinbRdqWiRasRq8FQOGoTg8lWwbn3hmIAL1h6n6W7nDFlnSZahpuxIc36k59i0tf+tDLvQ+KAeIvUdADRpFU+1KqgNrYXTU2oNdKr5ZwWgCaYFSqUSd4LX0dHR1taG7+KrtonfsSgRB1gRdIIwDuLcKjrFj9d8T4x46j9NHGFJyDLoF/l+KC0tzcjI2LNnz8cffzx27FhXV1cmkzl48ODFixfv3bs3LjYuJycnOzs7Kipqy5YtCNvi8/murq4BAQGffvppUFBQenp6TU2NTCZD9sMt1mPOZ/7H//rcyDNZsZ3nZtMn6i3wWlkAXVxI+AKXv0CzYggoxO9FvaqtVCoRbVmKhdbW1ubm5oaGhvLy8jt37ly7di0tLS0uNi4kJOTgwYM7duxYv379ggULZsyYMXbsWF9fXzabbW5ubmpqSqVSLSwsbG1tBQKBj4/P6NGj33333cDAwMWLF3/yySebN2/eu3dvcHBwVFRUWlpaXl7ew4cPGxoaOjo6RCJRR0eHGAsIWS4vLy8qKrpx48bly5eTkpJiYmJCQkJ27dq1du3aJUuWzJkzJyAgYMiQIU5OTvb29jY2NlZWVgwGw9ramsvlenp6Dhs2bNy4cTNmzMBPvWvXrpCQkKioqOTk5KysrIKCgqqqqvb2dnTHwA3Sn4nwDH0jUqn04cOHGzdudHZ2JpFILBYrMDDw2LFj9+7dEwqFMpkMgO5nB94Lv+Asfc/7e6SgIYTTg1DNc3JyNm3axOVyLS0tFy9efPv2bfzBR/xM6zXV93tU77cqs+8dvm+KSqXq7Oxsamqqrq6uqalpbW3FW/1bVUNfjt4Cegv8BS2gB6D/gp2ub/Krt4BWq0Uvu0KhsK6urqqqCnGfkcMH9DKKPs7R3DvxnebV115fg27cDWHQSNUAkkpVSlBfJ9u7K2LPntjvq+Q6AFqlTxXQh1yjArQoQIcSyJVArYRkUhyAhoIGz2Bq3ebtQ+z8k5j9lwDQfV+LsRQNRktH7OZevzhjXfEjuv0MKo2lP4N3Q/QZqVLgtGgMUtUpgU4BtHKdRgG0Kgwkhb7oAFTxhiC1GsK1MgXcOuWgQwraxKBeCIorwK0H8ivfdiRltZyMLd9x+O6iT9OmBMaMDIgeMjrObXA03yNuoGOsLSduwMAoK+Y5+MuOseLGWnHizVkJVOZ5KiuBzEqicC5AAJqXgm3JFB6UojblZZhyskw5103ZOabsHJJ1uikny0xwDcp3CC6aOiQbsKNJAyNIrAgS94yBw2kS7wTJ4RiJd4TkeNiIf4g15KzzO/F+k9NHzbwS8OH1D5ff/fTfZdv31J6JkqVe1N29D8qqweMKUNMInkqATA3E7UBFZL3oINKKNk0PebkH50UTBN3cacSgxn+JuDBkPePbS0DPz1wjxIJ+ZGn3lEIQwSBk1GqABjKggRph0DJdFwCgQyYWyZQSFWjrhBfYUxG48xgEXap7b9Ml5vAgmkuIKeesoU24ofVJG5dQj1HBH61JDUupfdwK6lVACKA8tARqQ8O5CjUAuDUI5+3G3/8El69GrZHL5RKJpLKy8t69ewkJCYcPH05KSqqoqEBuDHQ6nVQqRat5ioqK7t69m5eXd/Xq1fv379fX1+Mzr4hIiFweod839AP+1/SpSqWSSCRCobCxsbGgoCAiImL58uVjxoxxdnbm8/m+vr5TpkzZuHHj+fPnb9y4kZmZGRkZuXv37rlz5w4dOtTJyUkgEAwdOvSDDz7YtWvXxYsXq6qqhEKhRCKRy+U4+k+s3nNvocQM+rjeAn9iC2i1WgQro/kz5NlPKBQ2NTUh8vLNmzczMjLOnDlz6NChrVu3rl69GsG7o0ePHjp0qLu7u0AgcHBw4PF4LBYLQb12dnZo+mfYsGFTp05dtWrVjh07jh49GhYWlpSUdPXq1fz8fKSMgVR0GxoaWltbRSJRZ2dnR0cHcvdSVVX16NGj3Nzc1NTU0NDQvXv3rl+/ftGiRe+/935AQMDw4cM9PT3RqdHZmUymjY2NnZ0dh8NxdXUdOnTo5MmTAwMD16xZs3379uPHj0dHR2dkZGRnZ9+9e/fhw4fl5eW1tbWtra1IfgfdadHdoFd3o68SlUrVK/3Fu+golAfJj9y6dSswMNDa2pqBhZEjR65YsSIoKCg/P7+yshK5s3txma/DX5GnQa1W29TUlJmZuWXLFh8fHyMjIy6Xu3Xr1uLiYpFIhOqJ0GqcJ0T8WHvurfh1aB1e8+c+F/BElE2j1kgkktbW1ra2tl5Lcl+ftuhroreA3gJvlgX0APSb1V/62v5JLKDVajs7OxG9ora2tgYLdXV1LS0tSKgR8Q2JPoJ6vRP8SQzxpjYD4UtqJNuAQU8QgNaogFQKlAqgUEHJZw0AEl2HDAgR/VkBJEqgfB4ArXkGXOu2yV8BgIYA7zMA8TOIMD7k+4tAeW4d6OqzyXr0Unqhz93yKUTuObHoHgVkCEM/qy8NGdCI6wv1o1VdCmWLTiOEfGiggkAs5tqOOJYh2KkFSg2kD3ep4CbTAgWAVNlWMSgpB1e/AbFx4NAh8Seri6f+PWNKQNrwYZEenie4jl+xHQ9bM7+2YoYwWKHmrDBzzlkz7lkzh0gzXpQZL4rqEEPlxVF4iRRumin3kin3sjE3i+xw3db7nt1b9yn8b2hOOVTBNYrgCtXlmtmg6zTXqyaCDEPBBWPnZEOnBJJDDIkTReKcI3FiSOwoI06MGS/GghtlwTxtaXfCjnOMwz/i5HrY1XP/xKlnFyxP37H3QcjZH65e7bh9S1L8CFRWg3YRkCpgi5UaoNRBVnjfDTHHEW1chal4vAiD7sGN+4K20OaYYAeOd0OKcV/p6b5H4hh0d+FIiwMyoNU6pUorV2q61FBqBcalColUIe1SKDvlKplK26bUlUk1FRpwtQR8srPIZ1ySFe+MAe24JSuSYnPIzukgc9AO33H7QpNrbn2vfYo5J+zCMGhsJkqHAfFqDTSPGrrJ7GkdcXi8JvGf9Xnc0tLy4MGDhISEo0ePzpgxg8fjkUgktLJ7wYIFcbFxycnJkZGR+/btW7ly5cyZM1kslqWlpaGhIYlEYjKZS5cuTUtLu3//fkFPKCwsfPz4cW1tbUdHR2dnp1wuR+u+36APeLwfccYcnvLiiFarbWhouHbtGsKUPTw8qFQqg8EYOnTowoULDx48eP369UePHt26dSssLGz58uXDhw+3sbGhUChcLnf8+PHr1q07f/58Q0ODQqHAXxIQAtLfeYk3OjzeX2Z9ut4CP9cCr8+g0qg1CoUCgbytra2I5FFWVlZQUJCbmxsfH3/48OHPPvts4cKF77777rBhw5hMJq5QQSaT6XQ6g8GwsbHhcDgCgcDDw8PPz2/MmDFTp05dsmTJli1bjhw5EhMTk5ub+/jx49bWVoRUInMhzqxUKm1vb29ubq6rqysvL3/w4AGaiktLSwsODv7iiy9Wr179wQcf+Pv7Ozk5WVpaEtU5KBSKlZUVk8l0cHBwc3Pz8/Pz9/efNGlSYGDgZ599tm/fvoiIiPT09IcPHyLn5FKp9Lk8YsRcUSqVSPsCh5VRDfGlJzjBBQHTciy8fNcjU6MKoKlERI+VyWShoaH+/v5GWEDqHzweb8GCBYcPH87IyCgvL29sbJRKpWjYvPwZ/7CcjY2NJSUlZ86c+f91trCwIJFIVCrV2dk5Pj4eEcbR+lQc0P9TAtBodgG1FPUv6uvXttf+sOGhP5HeAnoL/EoL6AHoX2lA/eF6C/wSC2jUGqFQWIOF2traxsZGoVDY0dEhkUjwpe5o8SDCCNDzXv/U/yW2/u2PwTElhEkiQV2oO4xgR6g4q4FitwqgVQC45L8bd4Z/xzi2UOoBCR93/z4PgP7t6/16lNjLergXN2I6ir9MffsehVJwOYifUT6xLCKtFgdPMUQV6kjAjlXLgEYONEoovKKFstP9qf8iyBQWooOoNNKn6BYSUUNOtVYFiykpAfl3pGmXas/FlW/fdWPD1rxln2TNXXpp+MSzXiPDuF7HbfhfD+CHWPJPMxzCLAXnrF2TLQXJpqw40oBokmU0yfq8EfMCmX2RZJNozL5o7pw9wDPfwuUOTXCL7HjN2PGiqXMq2S2F4pFE9ow39T5v5B5n4BJrLEgwE1yw5KdZOqSa2cXSrCPsHOPs+FE02xM0u+NW3NNM5wh755Ms1yOOnocH+QUPHXtuamDWR8vyP91S8Z+9PwRHNZ258CTpm67MW7qiGlBcByqbQG0reNIJBT3EGOwOhYMAkChAq6gbp9dgMzZ472rUOqVSjX8So29g9NmM8DV0JyTwpXWYKXt+id2G4jj6DOWY0UWKIHE5dCiqk2q0Eo1WqtHINZofNY50WqVOCzOooRtRdRcmGS5Sg8xvNMv+77aXR6wzP4XNSrK2ibKxD2M6nuQOOjL671Fffl15vQBUPYWK0gAAsVYpBVIZ6FCBVhVc8aBAMxkaOE0Bq/K6BZVKhfsUEgqFOp1OJpMhkUepVNrR0fH48eOMjIx9+/YtXLhw5MiRNjY2FhYWCFbAwQUGg2Fvb29lZUWlUnEoh2RoYGhshDYSiUSmUjgcjoeHx9CeMGLEiPHjx0+fPv3DDz9csmTJ6k/WbPjXxu07v/jq0MEzEREZly5+V3C/5PtSRB5sa2uDEqIqnUapQRxG4i8S9HiFT8m+ADT6dEeoBPp0F4vFVVVV+fn5CFMeO3asQCBgMpkeHh7vvvvu5s2bIyMjMzIyrl27lpCQsHPnzvffe3/o0KECgQC5E1y0aFFQUNDNmzdLS0s7OzuJeMebCNm/bheCvj6/xgL4a+oLZOLQ5YmkMNDFi27vaCQTJXTReMbrg6NgSEpYIpGIRKLW1lYkvlxcXHzr1q3MzMz4+PhTp04dPnx4165dW7ZsWbVq1bx586ZNmzZmzBgfHx8nJyc7OzukUGxtbW1vb+/g4ODj4zNq1Cjcud+6deu2bdu2Z8+e4ODguNi47OzswsLCyspK3Bk4YviKRCLkV7C0tPTWrVtXr15NT09H/v0OHjy4c+fOTZs2LVu2LDAwcPLkyaNGjfLy8uJyudZYsLOzY7FYDg4O/99/3dChQ8eOHTt9+vSPP/545cqVGzZs2Llz59GjR6Ojo9PS0rKzs+/du1dZWYkw7udOFuK3Hfxu0PcbgXhXJMbxQ/pGcMv/ZESr1SJhLtTvxLPrdLqCgoKtW7d6enrSaDQSiWRgYIB+bW1tJ0+ePHfu3C1btpw+fTonJ6eoqKiqqqqpqUkikeB4OqoYKhNfNIPkO3B9FdzfABo/vaxE3EWl9WoRMiCC6Ts7O2tqam7cuBEeHv7ll18uWLDA2dnZyMjIxMSERCI5OTmtWLEiLy+PaEOiwAvRjMQ8vc74Zu3iwjV9L0mibXs1Cm9+r3T9rt4CegvoLYBbQA9A46bQR/QW+OMsoFQqES+jpqamurq6oaEBTarj71W93mzwJ/oLnvp/XO3/6mfqhXhBc0CGJgZAI8Im+lXqMAxaq1PqIFdUiRAziEHrAWhkQwQT97InvvtrxhmCHX9e+fiJccgYpeAAtAYSniGADH9QH2u0P4LKOE0XQBXqlwxIhgJl1kAHgKBLCUQy0NIBqp+Akmpw5yHIuwcyb4CULLDveMO67Q/fW3hp5LvRHiNPO/mdtHc7Yul42MbplDX/zAB+BIMfSedGmfFi6Dwo32Fok25ofdGUmUHhZtAE6WbOKVSXRKpbAokdZuwUazc0y2X8Pdu3shnOVyjsVBov3cDmvDkvzdwhxcg2isqKp3Hi6Y6JFG6sOT/GyiXWQhBtIYg2sg0xsQ+lssLNuSEMp6/svPY5vn1s0DunPEafHjUjcc6yb1dsvHPodHFkYvnVG+L7/4NSHhXVoO4JaBZC6rRUCdcHyBSgSwo6u4BCDlQqaEK1BiiUQKbQqdQ/Wg7rCHixQEK5Vo1v3V4QEYqPzN4tdEHsQ8SfVmKeD5FfSakOdGmBBAHQWrVSq9ZoVTpId4f9qARaKUZo7tRhmuBKoJIDIJKDih/A/q/qR79zgTUwgm5+hm4eYWUbxbAPtxOE87xOjZuZsGpb1rcPQXMXpMR3QlEOeRdokYHW1x+ARrbu5Vaora2tuLj44sWL69evnzJlir29PY1GQ1zmHjdakPuMA9BI9hThC3gGAyNDhD4bGBmiuAmFTMECuSeYmpqamJj8WLKhAcWMbGnNYLKZPD7X2dXF6y3viRMnLlq0aOfOnadPn76Ufum7/O8aGxsRzw49DdHDkYhW/DiAXl0MOXFCbsqKiooyMzN37Ngxffp0Nzc3e3t7Ly+vgICAlStXBgcHZ2Zm5uTkpKSkHDp0aMmSJcOHD0cr7v38/GbPnr19+/aMjIzi4mKksIGAACLYQWw4MsWra7T+zHoLQAsgXA9/iX3BsEQMXIQqwjVkao1IJGppaWnCQmNjY3V1dXFx8Z07dy5fvhwdHX348OFt27YtX778/ffeHzlypLe3t6enp4eHh5OTk4ODA5fLRfoYlpaW1tbWPB7P29t71KhRs2bNWrZs2bZt244cORIdHX3x4sVbt24VFRUhnys1NTX19fUNDQ1NTU1tWGhsbKypqamqqiotLb17925WVlZ8fPzx48e3bt26YsUKhCz7+/v7+fl5eHi4uLigs9vb29va2jKZTC6Xy+PxBAKBn5/f5MmTFy5cuG7dui+//DIoKCguNu7KlSu4OEZ1dXV9fb1QKCQSmbVaLe7nEB9PL7AhnuePj+D3XhTBK4m6HnVofn7+v//9b29vb9wTo6GhIZlMplKp1tbWtra2Tk5OI0eOnDNnztq1a48ePXr+/Pns7Oz79+9XV1ejeUc0v4grR/+yZqIxiQpB+ocNDQ1lZWW3b99OTU09duzY9u3bJ06c6OXlxWAw6HS6gYEBws3ZbPbMmTMTExMlEolSqSS2tO99+E92N0aNRSxvvLFEC/TtC2TnF+fpe5Q+RW8BvQX+ahbQA9B/tR7Xt/e1sIBKpULL9NB7dnt7O3qzIc7n4897Pb/pteizF1YCgWBaTTcsiQPQGO4MqZVowxjQ3YBajxAEJEG/sOw/2R+JEOHPA4h/whA47xXm+70AaCT/APFlYjtQHK8AMYLlI+RFBGg4QJBEAxHdJjJkdcjtoQ76uOtUQfeAwi7ILG6RgQ4tBDqL68GN/0njM384HlW6dlvOopVZk2fFvj0u1G90uNvbp9iDvrbkfm3DjbEamGjOjKczE+icZEuHdCvHDAY3jTYwiWx73tg23oSZYMJOIjteIAtSTJxSuP7fDZr4eNCk/3FH3SDxzpC4p0i8E6bOZ2zeymC4p5O5CSTrswyXdLpTCvSgyDtPc4ymC6IYLvGWrgnmrvF0lziGS7yVU6Qt/2t7h31Mx/0sx/3evqET/nbhH/+4t2lT+anT4sQk5Y2boPgxKHkMqqpA8xPw9ClUXhZJgEQOZEq4yVVwAYEKE7iBawiwDVtGoES/mMdIFfpFXhB7JgRwwyLzqlVAiblUlKuAVAOkatCpAZ1qIIH6G1pIf9ao0cIErQ7GlACKukDashw6qdRIMGb7EwVoVoDkq5KZ89MdPU9b2J8kW4bS7eMs2IkDHONZHvG2zqE+o6J3B7UUVoEaMWhWg06glkKwXQPBbQjIPDsjQRwhxPhPDPHf/s/IFy56HrW1tT18+DA0NPTTTz/19va2tLSkmtEMjSEFzMLCwtDQECLOJibGZIga9+DPRgYGBlQqlUwm49Bzd8TQgGRsSDIx6t6MIP0NBsiMNjU0NjImm5KppkYYv6z7T8YkA7KBEcXQiGJIgrQzGAww9JpEgoebm9E93Nxnz569efPm06dPZ2ZmImRWqpCqtEq0ugCtMkHxZ6/S3956eInEBzcilXd2dhYWFp45c2bNmjUjRoxgMpnm5uZIQGPTpk0xMTEIAktKSlq3bt3YsWNZLBaNRmOz2f7+/suXLz99+nReXl5dXR2C2nGEDp2R+HlPjOP10Uf0FviDLUAchyhOrAC6QBDxWSKRiMXi1tbWxsbGqqqqkpKSgoKCGzduXLx4EeG827dvX7JkydSpU5F7PUtLSzRTRaFQaDQanU63srJis9nu7u6+vr7Iz96sWbMWL168ZcuWw4cPx8fH5+TklJSUIJEHnDyLwG6RSIRw7dLS0gcPHty5c+fmzZvXr19PTk4ODQ3dsWPHypUrp02bhuaB0KlNsUChUMzNza2trVksFp/P9/T0HDJkyKhRoyZOnDhnzpzVq1fv3bs3PDw8IyMjPz+/trZWIpHgFkCALI5+4i5Y0doIXB8Dz48MiPjFLxB2x/O/qgheT2LvEyuD+h0AUF5evnnzZn9/fw6HY2try+Fw0IQB+rW0tKRhAU1N2tvb+/r6zpo1a8WKFVu3bt23b19YWFhCQsLly5dzcnJu375dUFBQUlJSXV3d2NjY1tYmEonEYnEnFiRYkEqlnZ2dQqGwvr6+oqLi0aNH+fn5OTk5V65cSUxMPHLkyKZNm+bNmzd27Fg+n89gMBDNufuRQyIhiFwgEHz44YcJCQnIITzC03GqNUJaiZ9peLw/axAt80bE8f7Fm/aTX6N6APqN6Fl9JfUWeOUW0APQr7wL9BX4y1kAvQfjDp1kMhmuJobeU9Hvyz/y/3IWfP0aTACgfyRq9hCfMfQZ8z2IuJzPYUC/fi363WpEAGOh27afIZHx01VCWB7M92sBaGItiRjxjwA0EYMmYoi94s8A0EiJGAkEQwnlHgwaSnhoofC0Rq5RdCmlXUqpVGluzV4AACAASURBVCWTa1RyjUqqhFuXWi3Tqrp0ii6dQgqUcgwhhXxbDRApoa50cxuoawLV9SDnNki5LAuNrN9/pGLL52WrP3085+NvA6Ze9h0e6+wZxuQFMR1P2nBD7fhnbQRnLRzDSPZBJGYQiRlMYp4isaJNXdNMXVNI7AgS86ShINzS9zx7xGV7vxxrz2wzp0sm3FQ7n5yBg/O4w247jvjOzOkSTXCR4niJ4njJ1DHdiJdKGphIGhhHZUfTWRFkuzBT61MUm1CaTRjVOpxme9KKfcyWf4TlesTB49DYd2OmzE4IXHJx0aeZ/953a/+JgrDEH5KuPL1RCB5VgYY20NgOWjAicZsCPFUCkQqINUCiA1JMeBppakC/fz9uiBHdDT0jIRzMyHINZJajTaaBIhtSrQ4DoDEJDp1Gi29AC31RqrFTdEEus6YV0rVBKwD1cnCjGKz4V67z4JOmVkfoA+PNBqbTuemWjpdoA5PorGgT68NvT0z+77Ef0m5I68SwzmjRA+za3gC0Cuh6NmyEwBH7LEb906P9V+dQKBQNDQ0lJSU3b97cvXv30qVLR44cyWAw0He4kZGpCdkMxU3o3fiygYmZCdnc1ISCA9BWVlb29vb4URhmTCIZkkjGJJIpiWRqBKFkU5IBhWRiZmhCMzUwNSEZGpEMDQyMsWyGJESRNqIYG1ANDc0MDKgkEgU71tiAZGBoYGRsYGBkYGBkZGRKNSWTTUxRlahUqkAgmDBhwrx58z7/YkdC0vlHJY+qairbxe3dlHncsN2RZ3oBxwh+tRW7C5DJZPX19Xfv3k1LS9uzZ8/cuXP9/Pz4fL6Dg8OYMWMWLVp08ODBxMTEnJyc06dPb926NTAwcMSIEYg76efnN3fu3H379p0/f/7+/fvIXRjCO4i62HhV8cr3iuAZ9JG/pgVwwKjXwOh9//lNrYMkMmQymUQi6ejoaGtrEwqFzc3NjY2NtbW1RUVFyMNeVFRUcHDwvn37kD7Ghx9+OH369PHjxw8bNszd3d3BwcHOzo6BBXt7e4FA4O3tPX78+FmzZi1cuHDlypXr16/fsWNHUFBQdHR0ZmZmbm5uQUFBWVlZfX19S0tLR0eHVCqVyWRisbilpaWmpqaoqOjmzZsXL148f/786dOnDx48uHnz5tWrVy9cuPCDDz4ICAgYOXKkj4+Pi4sLk8m0sLCg0WiWlpZMJlMgEAwePHjMmDHTp08PDAxcvHjxJ598sm3btn379oWEhCACdW5ubmFhYVVVlVgs7qWAjF7mcQOj93w0jYS44YhPil7ylT1B1SfgShR4Ua9h5AXjDaHnSGUFaVyIRKLi4uLk5OTPP/989uzZfn5+Dg4OOG2cw+GwewKHw2EymZaWlnQ6nUqlmpubW1paIlVuFxeXwYMH+/v7jxs3bsqUKXPmzJmHhY8//hhF5mNhARbmzp07c+bMiRMnjhw5cvDgwe7u7lwu19LSEi27QdOohlgwMTGhUCjIu6OPj8+MGTMOHDiQkJDQ2tqKzI76i6g0ogegn3tXIa5pwOVZXsOhq6+S3gJ6C7xaC+gB6Fdrf/3Z/4oWwKeIETsATSn3BZ31APSbNTiIn3w9Ws9I8RnXfe7mbPbA0D/+9c1q6W9RWyLAS4z/FmXDMohlEuM/o3ziYb3i/ZZCRJ/7ZOrRf0b8ePz3Rz916Cxo8PyoN4ELT/SOdOu6QLVxNeb3EpO2kMpAp7R7q6zWVlYBtJVXge8KJBmZFWdjHm078O3ybVcnzT/nMeGwk/8R7tCvbbyPWrgeMxecpfNj6Pw4Ov88lZdIZieYMBOgtDTrCpl1xXhghoFdkrnTZYZLJsPtipV7Fskigia46DT6wduz6t5+r9pl/D0rn8uWb10ycowd4HOJ7plKYkeRBkaS2FEGvHgjfqKJc6KJc5yJS4yxc4SR8ylD569JrodIzodJLkEmg0IYvqfth4Q5vXPWd9K5ce8lTv04fc3Wx59/VR8UJYu6CL6rBAW14FETKG8FjR3gqQTqSkvVQKbCeNMqIFfroNF0apmqSybrVCg7NeourUaq1Uh1kIhM6A/oN1IJ1FKdqkun6gJqOVApgUoDlHASQKvGJEF0QIn5V5RhvialEIwGbUqocx0aJ5o85zrL7YKxbQLJOtHA9gKFl0LlJtPZKRbsRHvBOc+hUWs3F13N1XaKgUyClanSadVKSLKGjGg1ZFdDrY5OLCIDOgXEo7W/10oI/EMRreyWYSE/Pz85OXnDhg1DhgyxtbWlUqmQnYz5DDQwMDA1NTUyohgZWZOMLUkDaFRHK6tB3LcnBYwa/wHT/i2yqTmJRKLRaE5OTsePH09LS9v15ZdOfIET39HNXeDrJxjiLxg8yuWtkR5vjfB7y/8tga+1y+ABgwYLPAZ7+w4f6ubtyeGx7Vk29kxrG1tLKp1iZGoEAWu09VClIYptYkoyphgYmhoZwc3E0NTUCGLQZBNISqTT6SYUspGJCY1OZ1hZ+o0YumLN/wWdCMr6JrP+SY1CLQXQptCqCpVSoVAgOxBv1L3ihCHy/ChuSRweEovFJSUlWVlZhw4dWrx4sa+vr52dnb29vbu7+wcffLBnzx6k6BofH79///6FCxcOHjzYzs4OST9Pnjx5+/btqampDx8+RB4FEQyF66H3qgRe/144CN6KXvn1u38pC6BhgL839trFRyzRJvjIQUfhh+Cvo8TMGrVGJpMh535CobCpqam2traioqK4uDg/Pz81NTU0NHTXrl3r16+fP38+8u/n7u7u7OzM5/NZLBabzeZggYcFgUDg5eU1atSoadOmLV269N///vexY8cQuJyXl/fgwYOSkpKKiora2tr29naxWNzW1oZA7fr6+urq6rKysocPH+bn56enp4eHh+/Zs2f9+vXz5s2bOnXq6NGjfXx80Hl5PB46KYfD4fF4XC7XwcHBxcXFx8fH399/xowZS5Ys2bRp0/79+6OiojIzM2/evFlYWFhcXFxeXt7Q0NDa2opmg3BD/awI0XrEOF5Ir85C6Wjm6bn9RSzkNYnjbcHvjfD1CwsIf8TbiFqk0+mkUmlDQ0NxcXFmZubRo0cXL148duxYDw8PPp9vY2NjjgUGg2FlZWXTE6ywgMQxkJsBQ0NDEywYGhr2Un9CStMGBgY4uGxkZPSj0BOmRo0W9JDJZFtbWxcXl2HDhk2YMGH79u3JyclVWGhra0PEZ9zNIN47xCb/ZPw16aZfXI3+GthfgRq1Bk0Ctba2ikQiqVSKDNhffn263gJ6C/w1LaAHoP+a/a5v9au0AA5Ao0c7ej/rJbNFfGn7yUVPr7Ix+nP3WID4oqYHoHus0t//vRBdfLe//D83HS+wV+TnldPrYHy331JeCoDudkMItaR7uJn9FtjzB+Lo6nVzeMEuwhHQr0gkQj5Ou1SgVQ1adKAZgCdqcL8GZNzSHIyo+mxXYeDy3Bnzc8fNvDwiIGPQ0PMugxMcvBPYHslk+7MU5jkaN4rGjSSzw8nscLogylwQT3NIovEumPHT6YIMulMazekCWZBMFiT7zij3/6hpxEctg979nv5WNsP3xoC38239v7MfdddiSI6BWxqJH0MSRJKcwkkup0jO4SR+LMkhjsSNJnEjDR3PmHBOGtgcIJnvZTicoXNCKQODTOz327kHDxoZOeb9izOXZm0/UHw0tOx8elvWt4pv72kKHoGyWlDfAtq7gEgKOuVQxAO6fNQBpRKoFNDNI1BBn5GKLiDrBPIujUKmlEu7VIqubpBaLdeqMYeEGgyz1IHuaQCg69bPAWoF7CwIQzeIQFEFWPzPh05+SQNcLlgI0ii8ZCo3xYx1mT4wawAry2ZgKpsXM2pU4snj9Y8KoJK0TIYd3NObADK527VArIURhD7DHv7x779pDCciadSa9vb2rKysnTt3BgQE2NrakkgkCoWCPtQRs5hGoxkZGTEYDGcX90mT53y0dM3Gr77YHRUSf+O7pG9KP9sUN4Axik5nGRoauru7R0REKJVKAMBTYevtm7du5Gbf/Pbq7buZtwovFpbl3C+7db/0QeH3RQ8q8gvLb959eOd2wd28O7ev3riefiX9QlpSfHx0WPiJA0f2btu5ZfVnqxb836L3FsyZPGf6yIAJHsOG2js60KysjSlmRiZUQ0NjpMKBKmlEMsBYbHiiMZlCJ5mYGlPJFpbmLm6C+YvmHv56//W8a03CRplSpsYuEhxWI14yxCvrZayO8kskkqKiorjYuO3bt0+ePNnBwcHGxkYgEIwePXrp0qWHDh3KzMy8fv16RETEpk2bxo8fb21tTaVSHRwckL/BEydOZGdnC4VCAIBUKkXqouhB/zJ10APQL2mlv2Y29IaJj3bESZTL5QqFAo0xlUqF4sg+KD+Sg0B+9trb22tra0tLSx8+fHj//v28vLyLFy/GxMSEhITs2rVr3bp1H3744cSJE729vTkcDpq7IpFIpqam1tbWHA7HyckJuRsdPnz4qFGjpk6dumzZMgQxx8TEXL9+vaioqL6+vq2tDT2SlEqlXC5HBOrGxsbKykokjnHjxo1r164lJyefOXNm79696LyTJk3y8fHhcrlIqNfAwACJY1hZWTGZTOTfz9fX19/fPyAgIDAwcPny5Vu2bDl06BDyK1hcXFxfXy8Wi5HwBU7U7cVcRpdYL/CReK94mXh/ww8/Fr8R4SnoKYDSf78nQn8V+wXpvWqOjyg0qPAG4hE0GpVKJXoqoVmNlpaW+/fvJyYm7t+/f/369QsWLJg5cyaaSBAIBCwWy8LCAqlzUHsCmUxG0iimpqboTxQKBUm1oNU5ZDKZjgWUk0qlWllZcTgcNze3kSNHTp8+fcmSJZs3bw4JCcnKyqqursbXoaIhgWr4KwfAG9GDL+50Yv8S4889CjkxbmxsrKioqKysrKmpaWpq6ujokMlkKpXqT2CN57Zan6i3gN4Cv8ACegD6FxhNf4jeAr/WAsQHOf5m9oIIMf+vPbf++N/HAsQ+eh4A3e17sIf+DFf64xuORBJVgH+far4mpRJbTIz/VtUjlkmM/7zyiUei+M87/tncBF3aZ//wEnvE0fWCG0V/f8LPoFSrZCq1XAsUGLG3UwdBULEGiHSgUwfaZKDhKSipBYXfg8wcaXxq67Hwsp1HHn26rWDBJ/nvfpw5clqCx+hwp2En2d7HbFxPWDpGMrjx5qx42sAEM9YFC046nQN9HpraXyazvqHwckiMdJJdlrlzvuOICu8pjd5/L3OacJc5/BsL3zT3qXfcp90eNP3moGm3Bwy/RHsrxUAQRxp4znJQmqUg2YITR7aNMGCEGVidNrGLoDAjKMxzFOY56sAYGjvC3i1ioPtJlmcI1/OE58iIYX+LGz8zZercS6s2/W/r3uqgsx1RqfKUb5TX74IH5dCX4xMhaGkDHSIgloAuORSYRr2pAECmVciBXA6kcsioFitBhxI81YB2bINW0eqkWq0Sss8xI+owZepODahqBF8FVb0z+YKNQzidG2PGSTbjpFmwrwwYmGPHum094IatVaaAHT91YsbuXf+7X6htegq6VFAHRAFLkCqBWA2kap0SKkRrMc+kPbX6NSMNjRPU3TiupFKp2tvbKyoqIiIiFi1a5O7ubmNjg5BcQ0NDOp1OIpHodLpAIPD19Z04ceKmTZviYuOyrl2tqKlp7hI90XR+L5blFIHl/8x0ctwqYC+zs/F0cnIKCgpCOqdwKY9KpVGpMBC/S65s7dI0SUGrHMp6K6FQjBJ0yoBECeQ6nRKoVRDNV8s1CoVaCh1Cgk4t7BbJU3lHdZvwcV3DnceV39wtSrmcfS4++fCxE9s+37Hy/1bPfv+DMe+MfsvTy4HDtbJgmBiTDQ1NDY0pGHHayMDEnESiGJiYQeFpCIaRLGzMfYZ4L1w87+CRg/l3bz9pedIubldpNCqNBq0+6PZh2X1pEbX4f/o2XFpaumTJEh6Px2azhwwZMn/+/O3bt4eGhp47dy4oKGjLli2zZs1CnD43N7cRI0asWLEiJCTk2rVrpaWlYrEY6W71WvyEX6T6iN4Cv8wCaFEdzqNHETkWEHm5vb29paWloaGhtra2urq6tLT09u3bmZmZCFzet2/ftm3b1qxZs3Dhwvffe3/y5Mn+/v5eXl58Pp/NZtvZ2VlbW9vY2HC5XE9Pz2HDhk2cOHH27NnLly/fsGHDF198cejQoYiIiJSUlGvXrt26devBgwcVFRXNzc3t7e0ikQhRp5uamsrKygoKCrKzs1NTU8+cOXPkyJEdO3Z89tlnS5cuDQwMfPfdd8ePH480E5ydnVkslpWVFZ1OZzAYTCbT1dXVz89v/Pjx77/3/rJly9atW7d169bdu3cHBwdHRUVlZGTk5uY+ePCgsrKypaUFzbniCstIDBo9IhUKBX4N9mdqdP8kPnl/bvwFJeNFofrguzgAjVL6K+H1Se9Vc1QxlPjctxGkodyr/rgWNjpQIpE0NDQ8fPjw5s2bly9fTklJiYqKCg0NPXLkyJ49e7Zu3bp+/fo1a9asXr161apVK1asWL58+dKlS5ctW7ZixYpVq1atWbPmUyxs2LBh+/btBw8ePHXqVHx8fFpa2rVr127cuFFYWFhZWSkSiXpBohq1RqFQoKkafNa2v9k+YsNfEO/V0jdut7+m9dcQmUzW0NBQXl6OMOiqqqqamprm5maRSCSXy5/b+/0VpU/XW0BvgT+xBfQA9J+4c/VNe/UWQA/vvvUgPtSf+5bWK5GYv29p+pTXwQLEPsKR5T6Rbg+EGAytB6B/W4CXOAr6lvxLYL2+pRDP8XPjPQD0zz0O5ieOrl43h5fc7WYkaYBCoZJJFSpNN99WCzQKIOlSPRUrRRKVRoaJWkhUEC7sUgEZJkMh1oEnXeD7JlBQDW6XgLRc7fFzDf85ULLyX0WB/7gzalLaIL9zfM8IjmuEreMZC3akmV0sg5NKZ6eRrGLNOGnUgRdM7BIN7WJNBkaTOefI3AgTXoSNdzLarN9KYXhccBp9e8JHjXM/1by3XD5hdqPn8Pts1yscz2+4Xtd43t9w3vrG3CGFxr5gZI+Vw4owYYeR7INJ9sFGrBAyL5TMO0nmhJA5IVTeCXPn4AFux5xHhXlNCB85LfJvs6OXrcvduP27/cfKT0XUXf1WV/g9qG8HzV2gXQ2R5g4d3EQ6IMJEMaRAq4SiJjI1/FVhWijQuahCA+U+utRamVYBdTk04GknOBfX9t5HGVaO+ywcQujcKDo7xcAs1Z5z34FfZmf/nZ3tZSenCx5ep6fNioo4/8OjKvBDK6hvV8mAVgbkmHNFNdJBV+t6q6H/klGCrX3uJeCAvN3Gxca9++67NBqNRCJRqVR8zTKVSuVwOP7+/suWLYuMjLx//35HR0d7e7tMJgNAp9DJNQA0KkDOQ+m0D+N9hpwUcP/rzl87/+MNV65cEYlEiGWJDVCgUSl66qxS6ORdOkWnTiXW6TrVIP+upKQENLeCLrW6QyUSqcUSNZQ4V2nlSrVYphF2qVslmk6RRtWuBjVPQVGl5GFVZ3OHVqYGco1GIpV2dHS0trbW1dR+l38nNip69393LVu2Yvq091xcvSws7I1MBpgzHA1NBxqZ2JBMTE3pJiZmxghhJ1NNB9gO4PDYGzZ9lnghoeFJo1jSqVRDDJoIQGNrEXAGeu97BX71oVXkiB964MCBTZs2HT16NDIyMjw8fOfOnbNnz3Zzc0Mg3eDBgxctWvTll18mJSWVlpZKpVKkf4K8PsrlcuIS+144SI8Z9f+/YRYgjhP8tvyHdS6Cz6RSqVgsbsdCU1NTRUXFvXv3rl69Gh0dfeTIkS1btixbtmzmzJnjxo3z9fXl8/lIhNe+JyB9GCaTyefzkQrz+++9j3zBHTt2LD4+Pi8v7+HDh9XV1fVYQF7gxGJxR0dHc3NzTU0N8vl2+/bt9PT06OjooKCgHTt2LFu2bMaMGSNGjPD09ETTNlwul8fjMZlMe3t7pM7BwgKfzx8yZMiMGTMWLVq0fv36Xbt2hYeHp6WlIdwQiXI0NDQ0Nzcj3We5XI500tFYQY855O0QCRAj+6N04kJDdO9CGD2SYiZekuiZ22v1Id6/Lxnpb/gSD0fjhJiCJCxQSn8lvD7pvWqO90L3+wZ+GUClsecEdHivxR/4sXhpiLOPdMZFIlFra6tQKGx5NgiFwtbW1vb29o6ODpFI1N7ejlQgcLI/XlW8WOKETa86EOuKH/gLIsRy3sR4f03ury1arbajo6O+vr6urq66uroCCzU1NQ0NDUKhUCQS4Xro6BLrrxx9ut4Cegv8uS2gB6D/3P2rb90fZwGVSoW+KvGlRr1eXvurSn8P+P7S+ytHn/76W6BHBRiJMHTTMHuhnK9/K/Q1fFUW6O+e8DLpQKuDA47gs0+HYXA6rVKrkWi0YshF1UCKikqjwzaNQqdU6ORyIJcBqKcr6dnEGgjdPlWCp3LQJoWuAps7Qda3sqgLjf89eu/TzXkfLsmb+VHe32ZmvvNuis8759yHhTv6nmC7nTRnnmAMjLDiRls7xDKdkwdwz1NtzpHMzxpaxBlbJBkPSDaxTiJZxFLtk5mCy76jCibPrZ+7qnPO/7WPmVM6bOoD74DbTmO/4YxIcxyXPtD/vJl3uKFzsOGgk4auoYauYcYuZ0xcooydzxk5RRrxz5o4hpMdTxvzTplyT9G4J83YIWbsYEuH4AEOx7meoZ7+sUMnxs1Zfn315wX7w5vPXlQl5oL0OyC7GNwtBz+0gCdPgbATtEshYVkGID1cBEnRGrFOJwMwsbUTCnvItKCgVPvfr2+5DP8vdeDuAY6xNGa6vVO+g9c9O+dvLNlxxozj5ranrLnB9IE7/vZezKmElsdPQJMUiLVqOVSA1nRB8ypkQCaHEDfUge51Q8B3f3LU4f5/EOkPeeVKSEhYuHChubm5oaEhhUJBsCzaHTZs2KpVq4KCghAKg6/BR5iOUqMQiprEanCjULViXbYdez+Hc9h/2OHPt6R+d7cSSSqjb3v4pIOOHNVdkrauznaJRA4AEEogob5JBC5nP5kzO2juB4crf5BLVBo5bKlMAbRKHYCq3Tq5CnQogFgKNJ0a0K4EGTnNsxcc/OeW8O9/kMnUaMCqtFo1BHDlCrUCKqUgU0i75Ddv3w8JiVm7bs+Y0QusrUYwGN6WVkwjU+jh0JhsSjKAHg5Rk0kkkoW11ewPA8+ci3xYXCJTaHBEBLOwFvTIhOt0RDY0wHZ1CEhBApcikaipqenixYsHDhz45JNPxo4di/yY8fn8SZMmbdy4MSoq6t69e4jzhS/lRoAXDoGha/Yn+1Sf4Y2wALE3cawT72u8CYiEiw9glI7DbXh+lIKuR1xJAykDoPmkpqam6urqx48f37lzJzc39/Lly0lJSWFhYYcOHdq8efOSJUumTZuGXFza29vTaDQTExMymWxubm5ra8tisbhcrkAgGDFixPjx46dOnfrBBx+sWrXq888/Dw4Ojo+Pz87OfvToUUtLC6LqKxQKKTYDhODswsLCO3fu5OXlXblyJSEhISws7MCBA1u2bFm8ePHMmTPHjBnj6elpZ2dnbm5Op9MpFAqVSrW0tGSxWE5OTt7e3kOHDh09evTkyZNnzZo1f/78tWvX7tq1KyIiIi0tLTc3t6ioqKGhAa2reJmHGn5VEq1EwDy7oy9ZVF96JrFb8U78DSMvqNhveJZXUlTfpvWtBnFuhpi/bw/2SkHXEbq14g+vXnl67RLLx2uCEvGcz82DZ9ZHXtICKpVKJBI1NzfX1dVVVVXhVOja2trGxsaOjg4cgyYOgJcsXJ9NbwG9Bf4cFtAD0H+OftS34o+2AP6mgk6MQGe5XN7a2trW1tbe3o78VxAx6P6qiBf1kpH+ytGnv/4W0APQr38fvc41fMlbxHOzPQNAY7TbbgBao9ZqpBottmkgugdlCrRKlVaq0okV4KkCPFWBDiwuUQCJQidV6OSQBaxVdanVXWptp0rXqQJdGkgKlupAlw48aQdlP4D8IpB1U3cpVxV1oWlvcOG/vri1cl3Bx/+4O2na5eFjEj18zzm5hzN5wVZ2x+05MTYD46yY5yxZUVbcaAt2JGVACH1guCkrzIQdRuGdNWKdNneNtfe94DT2G+9384YH3vWdfcN96nVBQNawj/439KNHQz96PPTDMvY7uXbDsxm+l828UmnuF2juF8zcLpi7pxhxYsj8BKpjEpmbQONdQGRqKjua5nCK5vg11fEw2eGAjdcJxxFnB/89ZdwH6dPmJfxjTfrm/97ee7z4TOKTpKvtOYW6+9XQBeL3QlDVBupF4KkUMsRFclDXCkqfgNjLbR+tuWHnFm5gFU5mXbByucQZnOUTcMN7fDaNFW3Bi6fzIs0cvmb5HX7//xLDE0oeVim7AGiRgw6g6wRKCejqguVBbBVHnHtFfnJk6nQ6fB5UJpM9evRo69at7u7uVCoVeWpCspgCgWDKlCmHDx/Ozc2VSqXoKPwzXqlWKVSYJKsUijsXFis/3fAty3HvIK+TM967cCq0tKUZQsgoIMgMQ58hAK3TSlG6TApuf6c4EVock9j80fzw8WP2HDl0u7EZ+XVUIABaoYO8crVOqdKJ5UAq1oCWTnDhcuuUWcdGT9x37FRReY1OBa2h08LjMAeTGq1WrUF4gVqr1WBTKjoA6urArp3J7i7zPpr7xT8WfzJ+4hgHPt9ygBWZSjEyMYHODLFgQqOQjA2olpZjJkz66uDRO3cLWp+2a2D5QKVVKjUKlUqFtUit0/3oEFKng2fE4ePCwsL169dPmjTJ3d2dz+e7ublNnDgR4fjp6elVVVUdHR1o+TZCDPEDcZgDRdBF+pN9qs/w5loAh1fwHtdqtQqFQqlUoj+hcYUaKJfLEY8Ykf3RMvYHDx7k5uYmJyefOnVqz549GzZsWLVq1aJFiwIDA6dNmzZu3LghQ4a4ublxuVw2m81isWxtba2trdlsNrapPwAAIABJREFUtqen56hRo2bOnLlgwYLVq1dv3rx5//79p06dOn/+/MWLF7Ozs/Pz84uLi6uqqhobG4VCYTvGG0Wu4fLy8jIyMqKjo4ODg3fv3r1x48alS5fOnTt3+vTpEyZMGDFihI+Pj5OTE5vNtre3Z2KBzWY7OTn5+PiMHTt22rRp8+fPX7169bZt2/bt23fixIlz586lpqZev3797t27xcXFNTU1HR0diG6MXyO4rX4T6vFzn4Avn4gPud/7In1BlfA6vKGRvk17cUOI+XvdKn+TXWL5eE1QIl7+c/PgmfWRl7eARq1BkjstLS3IZWh5eXllZWVVVVV1dXVjY2NnZyfxkn/5kvU59RbQW+DPYQE9AP3n6Ed9K/4gCxBfUBC4jE6MVPba2tqQ4lVlZWVDQ4NcLifm76+KxDwvE++vHH36628BPQD9+vfR61zDl7k//EQeDM/TaYEGYn9Q9kENgFIHNwVhk0Har1oGpDIgVgCJDmaCfvywA7RApYRoo0YNCbsQJER/hrLSGtCp0EmhdocKHqHEyMJSHWhXgVYpaOoADULwQxOoagBXcmWxSU0Hjz3ctuP29Jkxk6ZEjxwbPnjESRffr/neR9iuB2wEh0i2eww5QXSns+ZOsVTeeTI7wZiVbMw6T3aINBWcNeZFGHGiGB6XGR5ZDPdrDPfrnGF3/KaXv/epbMV/wZIvNO+ta/L/8N6gyVk2Q+Kd/3bVeXyujW8mc8i31h43aI7ZRqw0I26kEe8U5EoLztGcYylOcSbccybsMCrvpAX/pKUgZIDTSXvXMJb7Wa5PBH/o2dFzLk9fkrd0U/Gm3VXxaSD7JsTZa5pAcS34QQQu3Qb/2itk+cST7E4Z86KtPFMYXtGuE64ELK4fNPa25aAUG+8UmnM4zeErnvuXK/+ZlXpFWtkEGmWgDQARxKBlSowBjUjqvdBnnK77gvGp0+mUSqVMJhOLxenp6WPHjkXemZDsBolE4nK5CxYsuHjxYlNTE/rqRvmROoRSrVKqVQCOB21nl6RVqMq/rVi6+KLboFPOrsH/3JyTkS1sl4JOGdQOQnzhHu6zFmLJGiVGFgdaBbiU9mTmjDOuzrtGvxPl7bX368MPGutgxRU6IANKGSR9wzgaeHIgl+p0IhVIuVI/7J3dPn4Ht24viUsQNTRBf5IYIi/HBqkKG3Ww4hCNBjpITtcBmQZ8m/fk/WlfDPP97FJaQ3u7pknYmHXt6tb/fD5pyiRXd1eKOb1bGNoAc2RobEwiGVoMYE6aPDUoOKS0rEypVhHlcXRABVnP6EqBl1M3AI3gwtDQ0MGDB/v5+S1YsODIkSNXr15tbGxElC4lFoj8VoQ+45ckjnTgM9Mv6E39n3C79WcKPAOOZfSN9Hfs75FOrA8+aYGqhEjNSqVSKpUiDYHGxsby8vLCwsLc3Nz09PTw8PC9e/euWbMmMDAwICDA39/f1dWVyWRaWVlZW1vb2toitJfFYiHBCmdn52HDhk2fPn3BggVr167dvXt3dHR0Tk7O48ePKysrEdkQyRQ0NDTU1NRUVlZWVFSUlZUVFxffunUrLS0NgdqfffbZggULJkyY4O3tjTQxbGxsGAyGubk5g8FAihyINO3i4uLp6Tly5MiZM2euXr36888/P3bsWExMTHZ2dmFhYVlZWXV1dXNzM1JCaGtrE4vFONWR+LaMM7t7dQGyGH5pEI35B8d7Vex33e2vab/rSf+Awvu268Un7Zv/90vBa/KCU+B59JFfZgG0HksikbS0tOD3H3QLKi8vr6+v7+zs7Ct688vOpT9KbwG9Bd44C+gB6Deuy/QVfpUWwN9X8HdlxNeQy+XNzc1otVFtbW1JSUl1dTUmo/mjeGt/9cbLfMlIf+Xo019/C+gB6Ne/j17nGr7kLeIF2TQ6gG/d6sMYttcHfQaYTrFSBt3lKSH0DDHAHhga4nUaoFPDrRuWVqgULVpdK4RSgRQySqGSshoT8VDCX6BWYli1QgckKiBSQGARlqqFJ5ApQFsbqKwG/ysB59NEwWdrtv737rL137w7L/XvC64Nm5LoPjzCyfec4K04nnsc2z3WzCGI7hLMGHTGyi3GlHPWmB1jzI4zZp034SSQuQkUhzgqP5rEDGZ4RXtMvv7OR/enf1K7YrduxS4wfVXHqMDGkbPbRsxqHz6rxWX8XYcxOczhVwf4XjHlJ5EFKRSnVLpLmvmgVLpzIsUhzpQVQ2bHU7nJ5vwLZoIkimOUKee08cATJnaHqHb7bBz2OXkdGTbm1PSP4lZtyd9++OmBM2DRxjZ7n3SSTbghL9ZYEGnunegyPn/6SsmQGRXcEbcYnhnWXhes+WGWA7/ie339z/8U5haBOhkQYoaTYzb59QD0li1bvLy8TLBAIpEYDIaXl9fSpUvv3bsnFoshxKxUEp0sQWFitUoFFVgg81cJQJsY1NeDTRtyuMz/+PqE7j9cX9EEWpVwFCh0SpmqCzlmhJMQKGB+/XQ6XZsY/K8YzFt03mfoCb+hUZ5ewTt3Pq4uA1IJkHQCqQIooP61FpvhgNomMgC6tKBTAy59I54yI9Tb7+iatcXrP/vfWz7/OX3mTocYKNUqNSTWwxGq1cmhZIdWKdeourTw3MIuUFCsXLYkZNhb//zPpkt1P8CZFQ0cWZBI/kPdDxfSktb9a8PYieOYjgNJVAPIhKZSTMwYJCOKoRHN2JQ296N5WdeuCttalBpF94XTPwCtUqlqampSU1MfPXqEO2BUKuG6AfxbWqVSSaVSlNjrStQD0D/r7opbr7+j8Ay9In+wuih6G1Qq4boBqVQqkUja2tpqamoePXqUn5+fnZ2dlpYWHR19/PjxPXv2rF+/fsGCBQEBAX5+fgKBgMlkMhgMChYsLS3ZbDai1Q8ePHjcuHFTpkyZPXv24sWLN27cuG/fvsjIyIyMjFu3bpWWlgqFQrFYLMFCW1tbXV1dcXHxvXv3bty4cfny5ZiYmFOnTh04cODzzz9fuXLlvHnzpk6dOmLECC6XS6fTjYyMkCgH0sfgcDje3t4jRoyYMGHCtGnT5s2bt2zZsrVr127fvv3EiROJiYk5OTlFRUVNTU1SqRRXEUGDGVkeEZlxSYS+WhZ4D6L83SsnsB1UIFqB0asfX9UuXts/INJfG/+AU/+up+jbrhefrm/+3y8Fr8kLToHn0Ud+sQXQjDi6K7a1tdXX11dWVpZjAYm5Nzc3o8cornv+i8+lP1BvAb0F3iwL6AHoN6u/9LV9ZRYgvqngn5HIM4ZUKhUKhZWVlWVlZRUVFdXV1VVVVUKhEGd/vLJK60+st4DeAnoLECyAeLUoASpCE/Do3nGgw1xlQreZ3eLR3aRcHc5/JchFdHOpe1BqSNjtw+HVaoFSCzFnJcaYhW6J4KYDWoyRrdEAlaY7h1QL2dRNSMrjnibrG1FKWlNkVMWhI3f/s/NG4MrUCR/HeU0M5g454Dj0OPOt41auXzOcgi0cz9DYEYa2p0lWJw1twsmsGJpDEt0xmcxNMuEkmDokkx1TB3hc5b59x2dy+cjZ9e8EVo76sOydjyrGzq/64DPJrH+2/X3lk4BlNX6z7nsEfOsw8rKtb6qlW6KV+wVrrwsDPBPpLlE0p0i601m4OYSb8U6bsU5TB4bS7E7TmWctOHEMXrKVIMPSOZPhfNXc5aqp40VjXoapQ6aV543x8zr+vlw6ZFYlzTXNhBNP5sRS2bF0dthbY8//a3fx3XII73ZqgQpo5RqFGmiIG9GShM7sHZXJZMXFxcuXL+fz+SQSiU6nGxoaWlhYTJgwISYmRigUIoourraBFCcw0RWo+q2ETHb4r00OSmrBpu3XXV23Tp586kx0VUMH6IITC2qohQEHhkqjlWq12B5E+2B/KqE+C7iaL//7wjjO4MMuI+P4Q07sOPSgpQPIpJD2rFRAAFqOdFqgv0edSKfsBKBBDC5cUf59VubQ4Remv39j2qwrI/xPbN6Uc69AI1cAlUbXA0B3aUGrGmrCSKXQcyaUhimqAss+SXZxWL9wTkRBvkImxaQ6gBw5GFRqZACopCrF/8oeJl2JXvjph25D3zKkWZBMzUkkspGxmYGhKdWM7urm9tWhr76v+B4JW0ulItQmSILW6TC+Nf7M16I3AWR64ltBr84gQtIIDyVmxom6vY7S7+IW6GUufBdlwHeJAsp9cU/czng2vHwEeRCZucQ/EeMIXZXJZCKRqKWlpampqbGxEfEMCgoKsrOzExISgoKCvvjii/Xr1y9btmz27NkBAQFjx44dM2bM8OHDPTw8uFyuvb29DRYQxDxkyJAJEybMnj176dKlmzdv3rt3b3BwcHh4eHJy8tWrV/Py8vLz80tKSpDzroaGhrq6uvLy8vv37+fm5iYlJYWEhOzZs+ff//73ihUr5s+f//5770+ZMsXf39/X19fT09PFxYXD4dja2trY2CAXfy4uLsOHDx83btzMmTOXLVu2adOmnTt3BgcHR0VFpaSkXL58+ebNm4WFhVVVVW1tbT1CNHCoP3fo4sYnWkkf11vgt7IAPsB+w8gL6oaf5QV59H/6ZRbA7yFyuRxh0IinhWDoysrKpqYmtGao19KHX3Y6/VF6C+gt8KZYQA9Avyk9pa/nK7YA/o6CvmTQLhJ9rqurQwuLcAa0SCRCa29fcaX1p9dbQG8BvQUIFkBQJp5AvK29fBw//GdGtBiPWoJRpKUETjUmL4Hp+Wp13cxoRLZWQrUPiF0qpHCTdwGJGLSJQPkT8KgR3PsB3KkASdnyY1F1a7bnvb80xX9K1JDxMZAuPfiMvfMJO8Epa37YAH6ElVOMJT+W7njOzCHSzCGSxjtrwg4zGhhuYB9O4cZauiXb+6Sbu8YyPOPt/JKZw9KHvl80fXXrPw+CPVHgP6fA6r1g5iet73xcwh99GW2Oo66whkAuM5Ufa8qKMWXG0wYmmXFS6NxUGg9uVF46hZthzE4nDUwnMdNI9qkk6hljhzSKSwbJLs6Am2rISTdmZZJZqWTbMzb8oPHTYk6crah5AqVLdADINSo1UKmBAvtFAhHdgP5zbY767vHjx4sWLTI3N+/WPCaRbGxsvvjii/LycsTPfS4ADSW/NTq5RiPXQby2Uw0Kvwcr1id7vb3tk7XXsvN0T5WgSS7rAnIpZKtDhBrqJmuVWh1ibGvlXSq1DNbr5gMw+eN4W58DVj5Hvf8eu3JHflUbkCiBQg47UaUAchUEoLt0GPoMNE/U8hYtSMjqmjQjmeN4Zsz4m6PHp3v7HvnP59+VlUE7QGEPoNFApQ2FBsiQ50sZpFNDmv0TKTgQUub79t5pU059dwOI24FMAdFqNZBqNUCj1qm0cLYD43SrdEBeKSz/5vb9rf8Nch/8DolkRCKRaXRLMpVGIpEMTUgfL/gYaWcplF1KlRSX4CAC0Pg1gnoB38WBzuf2znNRvP5y6tP72ravnYkpxDh+LB5BLAGckP7/2PsO+CqK9e2TRgqBJEIKqaRCApEWqVKCREBEUEC4gCBNQeSKgiDyp16aUoUAEkLvEAQSDAgixdCUJiWYSippJ6ft2V7e75sdWI+hXNtV0NnfZjNnzuzs7DN7dnafffZ5NbUylutqaEuixHEcRVEGg0ELn3X79u3Lly+fOHFi//79a9asmTVr1qhRo3r27NmqVauoqCh/f/966uStTj4+Pr6+vv7+/qGhoVFRUTExMc2aNevWrduoUaPmz5+flJR04MCBs2fPZmdnFxYWFhUVFauT9nJ6bm5uQUHB9evXjxw5smHDhsWLF0+ZMmXUqFG9e/du3759WFiYp6ens7Ozm5ubl5eXjzrh7fr7+0dERMTGxmKKuW/fvmPGjJkzZ8769evT09MvXryYm5uLnTEqKir0er3FYsGxQ7V9x1y8dnLQpM01KCFbnHHatgaSJgj8UQg8eKT9/pzHtE2r/DFlyFe/EwFZlhmG0ev12BEoPz8fq6ELCws1EbTtQPk7N0dWJwgQBJ5wBAgB/YR3EGnek4IAvkbBl+aYXMajKWafs7OzsftzeXk5Zp8xT/2ktJ60gyBAECAI/PUIyCqBieXSmq73Z83CuQL2CxZkjpexmlUQJGQSobp+MCKYRTBLYBLBwKuzoC45yC+DjKti6tfV67fnLl517YP/OzHs3dQer+/q0nf3c903x3bZUDf0P3UbLqwTvMg1YIWz90YX7x21/Xa5+G13rL/F0XuTS/A214Z7nUMO1wo56hLxlWvkEbvgvfVafvVs72vxb+aPXghoXqS8tVB5aVx+z7F53Uf/mDDyRsdB37XqfSayc7p/3P76MXvqx+x/JuaAV+OD7uH7XcLQ7NzwC5eGaS5hhx1C0nQN9usCvrAPPOgYcNDZ/4vaAXs9/bd5eK+NiFo7bOiBlL2FDIdIXhHxrSYRrCIwqnXPIwlo/KJrRUXF+PHjEZdqb+/k5KTT6QICAhYuXJiTkwMA2A/KVvt8L43YZ6S2pgTOwEtFevjhRxj73qHwpqPHf7g7qxAsApgkoEGmgWWxAlpBNhdoKFRoGShRETkOzCa48D28/vZp79jVPi1WN4hb9PbM9Dw9VFsUSQCJRTN6liBKjMxZgDEBWw3SHU7+4lxFn+Fp9YIWh0ZtiG2x5YUeu9dvqigoAaMZxWQERHYzEopwKUjI9FlkgKeBtQCYZNj+RVXCy1s7dl69c+cdjkNsNSeZRTCKQKHmSUgNzUuclactAsUAV8FwBRUorOKRb669P2V2m/ZdPTx9XNxqu9R21ul0LrWdhg4devv2bQulp6xGdNSJ6m4ix+l7wucaVIX28b8S0PgQ/7Xlf/bD+Id90DTLNcC3RdL2egwfz7iwRmTgTI7jaHViGMZisVRWVhYXF9++ffvSpUvffPNNWlra7t27k5OTlyxZMm3atJEjR/br1y8hIaFly5YBAQGenp7u7u5ubm4eHh6+vr6hoaHR0dFxcXE42l7//v2HDx8+YcKEOXPmrFq1atfOXenp6efOnbt582ZxcbHZbDaZTMXFxVlZWdevXz9//vzJkyfT0tJ27dy1evXqhQsXfvTRR2PHju3Tp0+XLl2aNm3q6+urWnG4uLq6enh4+Pv7h4SEREZGNmvWrGPHjgkJCb179x44cCAOKrhw4cKkpKTU1NSzZ89mZmbizWEzd7zE+455do1c1g5UfBGLeXntyMLsPP4KY2t7xD6Y1lYkCYIAQYAg8HgENA66vLy8pKSksLCwoKCgrKyMoijtvKSdZB5fFfmWIEAQeNoRIAT0096DpP1/BgK2g6IkStrLmMXFxfhBLmafKysrWZa1vV/6MxpHtkEQIAgQBP4+CMiqwzSy5ZBAFBWe460MY0FUJPCCZOWQbQOaJMSHirwic7Kay/OMpHAK0tgyMgpwx0oohKLeCjfy4fwNOHpeTDlhSd53d9mG7I8Wnhs7NaPX61/Fv/RVXMeUxq22BTZK8gtbWzf4Mxf/z2v573LyP+gUdNAx5IBjw32ODffYh2y1C95k13AjmkOT7UKTvVvtD+54uFmv0+1e/679oO+7vvHDy2/nvPZu8YB3y/u/U/Ha+IrXxld1GZQV++K5Bq2+9Gtx1D0yzTkk1TE4zbHhYbugL+yDUhwD9zoH7NXV3eTyzA6PZ3Z51Fnj6f7Rm2/sKi5GLVepZ73KQT+OgNZsFufOnRsWFubmhvS8Op0uPDw8OTnZZEJuEhRF4bdc75HOtv8kiZMVHhChf9cM39+UBw/fGv3spEnT9569ZjQgy2YwirxZoawoIiWKM8hLKAChICiyworAWgXEjF+4BKPezfBvttmp4Zo6UYsHTUg7l2ngAVjGBBynsKCglRVe4hiFUQloRQ/w5TVTvwn7QlokRrTcEtFs+bC3j6Ye4/NLwUSp8QmBZeRqAaoFxcwpPKsoDACFvDvApMCXJ7h+g3a3bb8ycU1+uR70JgqQMblBhGoRzCqVhhxmOAEpoAHAJEDeXUj8/Pq/J+09e6lMb5YPp5+e8O8Po5vGOjo7OtSys3PUubq6Dh8+/PqNSwoIGgGNAhI+MOE6bbNxzuOXv7b842t7Wr79bQ/jfzkBjQNpWiwWk8lkUKeKior8/PzLly+fPHly//79mzdvXr58OXZDHjx48CuvvJKQkNCxY8e4uLimTZuGh4f7+/v7+fkFBgbi+H6NGzfu0KFDz549Bw8ePH78+Llz565evXrXzl3YreL48eOnT5++cOHCjRs38vPzS0pK8vLyLl++fPr06cOHD2/fvn3p0qXTp09/5513Bg8e3KtXr65du7Zv375Vq1axsbHR0dHY97l+/fr+/v7BwcFRUVEtW7bs3Llzv3793nrrralTp86dOzcxMXHbtm1paWnatm7dulVYWGg0GjWr8Qd7H0f90uyVcQGciX/xeF1FUXAYQI2sxyVt2Wdcie2lrO2hq6UfbAPJIQgQBAgCj0IA3z5bLBaj0VilTmazGT8Gq3G2eVQNJJ8gQBD4eyBACOi/Rz+SvfjfIoDFIIjyECUcYaasrKygoCBfnfLy8oqLi6uqqliW1R7k/m8bRGonCBAECAJ/NwQ0TbSoKl45CRkvcEhpq9CKQikKBciLmEFaWEUAEBUQQBEUGcWmw8UQK6qIKCSehKhSXq2CFpGG1iKDRUEMJiYxLQDlNGSXwrnr7NFvzanHqZUbct7+4EhCvx0t4/c07ZQW1e5gaOtDzoHr3II3uIfuqBu+R1d3ja7+RqfA3e7hBzwiD9cOPegSfMApIMUl+IBb8BduISmuwXtcQ3a4hiCraLfwTa37ft/9zZyhH9ETFkKLXjf9mn+j892lC9hrH5JiH7zbMWinS9Bu98A9dfx2+gbsCw7a4u01/Y3B2ysqkPhZdVSu4sHIIzdsJP3Gs22f4+HGYrFs3LhRo57t7e39/PzWrVtnsVg0IgkPYZiHwgpHTefIy8j0udgMX57SvzJgRWT0xH9/cDC7AMUGtCK7DIEGmlLMNCKgRVFBwAKAwCg8j7hdGuB2IYwYd8Y3MtGr8S738PWd++49+b1s4mUFDKBUg0gBBwoLssgLMm2RGKMgl1ngq4vW9v03u0Ut8Ij4rH6jhWOnpF/MRHWLKCqmLALLI7vnMhbKWcWAdNOKZAUoZaUKBq7chsFDD8c2Xbh48dWSu+g4UIXSJgCjAgYFrIg1Vp1dGE4wUhzFg56CdZvuRDeZM3zU/qu3OBMNJgq5kO/em9KhUwfM2ut0dnYO9u9MGHOnKE+WgGMRVacalSMzaFvk//bpP3B/MV+pmWJrzHINDDEByvM8p041xLmKotA0bTKZ9Hp9RUVFYWFhTk7O9evXz549m5qaum3btmXLln300UeDBw/u0qVLdHS0v7+/m5sbfhvAzc2tbt26np6e9erV8/Pzi4iIiImJadmyZZcuXQYNGjR+/Pj58+cnJycfPXr06tWrhYWFpaWl2Oi5uLgYW2RgL45vvvlmz549SUlJ8+fPnzBhQp8+feLi4oKCgry9vT09Pd3c3JzVCculfXx8MMUcHh4eGxvbvn37Xr16DR48eNKkScuWLduzZ88333xz8+bN8vJyTAdjkTIWLGu/TfyzrbHU+N+H9pHtt7ZpDW2cqdWJP2LNuJZZgwyyrcc2rdVJEgQBggBB4DEIaOeNGud5HAwZn3m0Mg89sz2mcvIVQYAg8NQhQAjop67LSIP/AgTwkCkIgslkKisrKywszM/PLygowO8QFRUV6fV6fDf+FzSObJIgQBAgCPwdEKhBQAs1CWiZ/ol9liU1fqEAwCgKJYNZBqM6m0WgRGBF5N2LQhqiiIfIjQHRmjzwPDIypjgw88hegudBoRWVaRWQ24VVBkqCvHL4PhPSTsGWgzB/VdnUeXkjJ17pP+Jch5cOx3VNi2l3ILzFF/7RKfXDUuoG7HPxSXHyPlDL52CtBgec/VNcg/e5heytHb7bLWyHW9gO19CdDoHbdA226ny32fnvtg9C7LNd8F77oL2qAnp37cCdIdEH2nU50fPloxP+fTItrZITgFNAjdhn5JGF8iMJaKxrvn79eo8ePdzc3Ozs7JCVhIvLrFmzioqKEE0sCLakUg0CGn9FcUg2fOx7pcera8MaTxo2Yuv57xFja+F5RuZY2coCpc40CyyPaV0JJAYYKzAc3LwDk/9zJazVpsZt0t2DN3Xu+/XRU4j3RxQwlCM6WKGAB4VTZJEVZBYA4XwtEwaPPuQQ/B+3JonBHVZPWXb1egnqQkqyWDk9NpgWwchBBQvlVqXarLAG1H1QJaMtTpl+sXGj+ZPez7h1E7VBpeaRs7Q6WxXkGS2gSmQeuUgryHs67Uto33Fjl/i9S5eXZt9Bqm1WAlYEimav3bj22oC+zm6Ozq5uzq4uvv7PzP7PjCuXb37z9TmLxaL6W98LyPZ3+JH9gn3AHPFvoAPwitpjjwd5BCzIxQceJl6xRzPDMBRFmc1mo9Go1+vLy8uzsrLOnz+flpa2ffv2tWvXYn+MCRMmjBgx4rVXX+vQoUN0dHRAQIC3t7eXl5eHh0f9+vUDAwOjoqKaN2/eoUOHF198sW/fvoMHD37rrbemTJmyZMmS9evX7927Nz09PSMjIzMzs0ydcnNzb9y4cf78+RMnThw6dGjHjh1r165dvHjxtGnTxo4d279//xdffLF169aRkZG+vr54Q3Xq1MH+GJjFbtu2LQ7uN2TIkLFjx06ZMmXRokXr1q3bt2/fsWPHrly5UlRURFEU/iWigJ8//0lirhlz7lpQUNvf7IPpx/eL7be2aa3bcaZWrW0ZLZMQ0BpcJEEQIAj8fgRszzO/JP37t0hqIAgQBJ5kBAgB/ST3DmnbE4QAz/MGg6G4uDhPnfLz84vUqbS01GQyEfb5Ceoq0hSCAEHg6UZAVn0PJJXEvMckYj5RzVcUlVVU1bKCCAyP2ORqDqo4tDRyQDHAMiAziK5GZK4iAggyiKI6yyDKigiyABKHlohTVdBSEiVeFBhBRrHyeLCGsVCSAAAgAElEQVRyyIaYFlFcPgMDlVbIKYLLt+CbDDh0BJI2C/MXW8a9V9hvaI5f+AHviC/rRX7pGXG4bmiaa9ABp4AvHPy+0NXbr6t3yNHvS+eAdOeAw06BqY4hh+yDD9oHp9oHHMZBCGvV3+AdtubT1cbvMyH/rmr5LAEHmCtnVcacf5QCGgBYlh09erSfn5+dnZ2Dg4OXl1ePHj2ysrK011ptSSXMdqlRByWcz3FceRWc+B7iX9sW3XL1GyO+OnuRNVrASLMKyLzE8JKKh8xyCs0hNpySFRoJsnmwGODHbJj16c2QFonRnb5qELu/Xff0Lbsl9dEAUjIrKPqglQFkSwW8Isk0MksRILcQ3n77VHDkKufIxMBum+bsvP1dhaQHsEgWXkaeIch8WQTkvgJGVjFQitGksHoAM0CBCZauyYprvXDc2ENXroKZQvyypCCFMp6QD4ciqBy0lVcMiO9m4dsM+NfAb7t2PTlw0JXXBhzYvOtaYTljYRExzQtI2pyZ9cNrA/o+U9/HsZaLzk7X5NnGXTr1mPT+jJLSIoB7Iuin+yf1a1r/mwlozXz5fm8osizzPM+yLEVR+LXr8vLywsLC7Ozs69evZ2Rk7NmzJzExcd68eZMnTx41atSAAQMSEhLat2/fsmVL7I8RFBTkr06+vr7e3t4BAQExMTFdunTp37//uHHjpkyZMn/+/FWrVm3fvv3AgQNfffXVqVOnzp07d/HixatXr2ZmZt66dev8+fMHDx5MTk5evHjxjBkzxo8fP3z48P79+3fv3r1t27bNmzdv2rRp48aNAwMD69Wrh0P8BQYGhoaGxsTEtGnTpnv37v379x89evTUqVOXLl26YcOGffv2YSL70qVL169fz87OrqiooGlaEpFby0ORxjhwHIcfGmllZFnGj4Xw0vbX+qi0hu1Dt2X7rW1a2yLO1Cq3LaNlEgJag4skCAIEgd+PgO155pekf/8WSQ0EAYLAk4wAIaCf5N4hbXsiEMBX+SzLlpaWZmdn3759G8crLykpKS8vRwopQXjoncAT0XrSCIIAQYAg8LQhcP8WBXHQSMp8b0bkIiYc0RKRnJIInKpoNqrUs1lln2kG+J8IaFlB+mfEPvNoiZholVQUVXMFGXkTCyynIiTIQHGCgWX1HGeUJFalpoEHQPJaEaoZqDDCnbuQlQ8nTsOqtTBkxK1mbY/U8d/s3mCnq/9u54C9zv5fOPsfdG5w2KXBMbeAU3WCzqA5+Bu3wKOugWkuQYecA79Ac8BeV/+97v5b3fwXN2y28MxVKLMiBW8VbWQVnhFZZG99f9b8N1A4PHXCIw7DMMePHw8NDcVRB3U6XatWrU6ePCmJEsuyPM9jGO+vJCMBpiQJMs8pqH5KkMr1wq1s6NU/uV7AlNf6p12+CmV6sHLIWwMF8BMEiZeQdYbI8JKVl02sYhCBBk4AHgxVsHZ9kV/EvGbxh8I7pNYNX/HJymIThcxRODMCWVKAAYkCUZRlSVQECZlGF5TA3P9cDw1ZXt93ecO2axbsKs3igAVgVaUyAI0MVe4R0KLamyZKMZsUXi+Dnoe1m7NaPDen72tJtzJRj3E8MtpQcMBArImXFVlUFdfIyITmFLidBWPGHAkOTHq9f1679l/Etf90X9otE4dspq1IkA0WK0WxhqPHv2zXvpNOZ+/o7Ojs6uJk7zV39hJ9dblqPq7aeTxtP6Lf3N7fRkALgkDTtNForKioKCkpKS4uzs3NvXbtGjZiXrly5ZQpU15//fUOHTqEhYXVr1/fxcUFW2S4u7t7enr6+PgEBASEhoZGRUVFR0e3aNEiISFhxIgRU6dOXb58+a6duzIyMgoKCmiatlgsZWVlxcXFOJJVZmbmlStXsD/G4sWLJ0+ePHz48F69esXGxmIjDgcHB51O5+DggIP7+fn5BQUFhYSERERENGvW7P//ZLAF88SJExcuXLh9+/Zjx45hcwzMF2M2VvsRaeSsLbxYzW0rZ8blsb67hp0IADz0+ZDtJh6Tvn9uRP9t24DTtt/aprWSOFOr37aMlqnto+23D6a1OkmCIEAQIAg8BoEHzx6/JOcxFZKvCAIEgacaAUJAP9XdRxr/ZyCAr/JlWa6qqsrPz8/JySkqKiovLzcYDGazmbDPf0YfkG0QBAgC/zwEHrxFsfVBxoYdqjpYUD2jtaVkKxkWZMSfSsi+g1MdhkXVJFrmRYETeFbiVKZUVhDRKPMgcgprYaqMVJWFkXgFKs2QVwHX8+HoWVicVDFzSdHAkd+2jj8Q1Gibd/DuOr4p7n5f1A7YWztgt3twSp3gQ+5BqW7+qbV8Uh3rpbp4H67td9TN97CbX6rObbtzvb31glIDI9KCo/eExW6Nap7c+LkVz7/02YqN13KrVGdqGRhZYCXUMKxTxktMwGN6yNZGg+O4UaNGOTs729vbOzg41K9ff968eThWgWYji8nEe+tKiiBJKqtLVctGC8C5TBg94cumMbPeejP15NeM0QiMIHKSmRdYiRWRgJwBhRckgREkCyOZrRJt5USzUeZpWLmmqNOLKa0Tvopqn9Ks+46Fyfm3C5GmmONAEkCSkTWzyixDlcWiABgZyCuCefNvN4r8zMfz084dtm3bV3jXhNww7vO7MsgcSKwi82qEQ5oHWkC9BhZFYQF27bG+mLDx+Q7z9qXkmCgk0BYkSRLQSooAiiSi5koK8ApLW1mGZyXIK4HZ/znXvt2GLh3PdOl8OjJmwYqk67SM9owHYASZE0Re4miOKikrHjX6HUenuk7OdXQ6OxcnvwMpx3mBUm2uxb/Bjw+LbTUvZrxHNX5i2m5KosRxHD7YOI5jGAYzvwaDAVsw37hx49y5c8ePHz9w4MCGDRuWLVs2c+bMyZMnjxs3btCgQV26dImNjQ0ODvby8nJ3d/fw8KhXr56/vz/mfDt27IgtMoYPHz5p0qTZs2cvWrRo9erVe/bsOXbs2KVLlzIzM7Oysm7cuHHp0qVjx46lpKRs27YtMTFxwYIFM2fOnDRp0siRI/v27duxY8emTZsGBQV5eHi4urrWqVPH09PT29s7ODg4Ojo6Li6uS5cuffv2feONN955553JkydjrfS2bdsOHjyYkZGRlZWl1+uNRiNFUdpLbNrvBf+CtOXjyVnbb3EaA6vhqSU0wHHN2sdfm9Aq/A2JX7utR5X/DZsmqxAECAIEgccjgE84mvWl5pKP/Ysevy75liBAEHgqECAE9FPRTaSRfz0CiqIwDIPDrJtMJpqm8e0Zlor89e0jLSAIEAQIAn8vBB4kPmwJaLyvD5b5eQ4K38eDwqg8okUGs4hmkwhmCSmOKQCTgmajBHoOKikoMyNLaBMLt3Ih9Tj1yao7I9/7rk3CwegO+3war3cPSnTxW1s3ZLtH8IG6gYdr+39VyydVV2+HznuTk/9Wt4a7PSL31gnf6RywwdlvvWfQJr/w7UHR28Oe3dWoxc7nux8ZPPra+9PuJG6gNu02HTjCHD1DnbiozywVjTKK5meVJUxA86LwKAIa04iYEzx27FhERIROp6tVq5aLi0vnzp0zMjLwbduDxJkoAzLVliUWKCvQepC/z2ffmvKNf9j0oa9vO/s1RZuApkROpHjRKPK0RkADx4mCmZPMtGC1CJKJhYoK2Laj6vnuKb7RG2O7HPGJ+Wzi7As3C9TYiSKNSGEFqcxROEEkbQYjJwkAFSaYMfvc888nBwbMe7VP6v69lsry+8crEi8D4o5FESReRi7eZh65qZgFEMySbBbg6k0YMvBwfPvkTck5lZXAS5wARkniBR4kFj06kCVaEk2yqKqa1YqrLbA88WZcmzU9XjoeH/91i1ab5356Ja8MQc3dV5fzEseJNC8xNMeu/XyLh0egTudmb/+Mk53vsiVJFF2tgEXdlftNfcL+a/fqNThQTKRqClzkgmIzKQqKr6hNLMuazeaqqqrS0tLi4uKioiL8vldGRkZKSsq6devmzJkzceLEYcOGvfbqa/Hx8XFxcbGxsdHR0eHh4UFBQT4+PvXUydPT09fXNyoqqlOnTq+88srIkSOnTZu2ZMmSNWvW7Nq56+DBg0eOHDl27NjJkyczMjLOnz9/7ty5I0eO7Nq5a82aNYsWLZo6derYsWMHDhzYo0ePTp06tWvXrnnz5tHR0REREaGhob6+vp7q5O/vHxMT07p1665du7726mvjxo2bNm3a4sWLk5KS9u/ff+zYsYyMjAsXLly7di0rK6ukpMRgMDAMo4U3xD8NvO81yGL8Ufvt2CZs4f35GQZ9sv22Rp02qKPkg+v+tpwa1f6qj79tiw+u9as2SgoTBAgCBIFfggA+o+KHoLaxZ6uqqiiKqjGW/ZIKSRmCAEHgSUOAENBPWo+Q9jy5CGg39jhh+5bik9to0jKCAEGAIPB0IvAg5YFzbPfmUWW0fFHlQPUA+VbIrIRsPWRXwY96uF0JN8rgSgFkZMHJG3AhF76+Anu+gg37hKWfV70x9uSzbdf6Ryzzjfi8TsDnLg2S6zTc5R66R+eVrKu32SPysEdkep3wL2uHHnYPS6sTkVY7fK9zww0OwSvqt1jboO3KhvHLo19ckfD61rEffr1qS+Hh00JOJRSYoZwDZCUhgV6AKh5F/7MAGHkwsKKJFylJZBWFkyVOVr0ypHtLWwU05rCw18GsWbN09yd7e/sZM2bg27MHiTMckpGTgFUUGvhqUb6aK43/8HCjZp/0fGXbsWOlRr0s8IAsNwSWFyhRMEs8haw2OEERLLxoZCSzRWKMPFTRkHoE4jrtrR+zNfT51GdiVo1+/2x2DnBWpH1G7LNKdIuIjmZ4ZAONxMt3ymDT5uoWLZeHNJw2dMTubzKMJgaVv6d/llSjC0Ray4okygotIlTKOTCWUUazBFcz5fET9r7Yde2KT7PvFgLPgSQqksQKIoPk7QKHZpmWZMrKVyKIAEr0sPcg36bT1rDITa/2vxKfsHfStLNZRYgQZ5BmGvlZ84jppnjZgjhoUdq9O93Ts6FO5+jg6KHTeQ4bOrayqkSQTL+HgH7wiLU9en9PWrtLx91te1uu8ctaJs5hWdZkMlVUVBQVFeXk5Fy9ejUjIyM9PR0bMc+cOXPkyJE9e/aMiYmpW7fu/SMLmVd4eXn5+fn5+/sHBgaGh4dHRUU1a9asS5cugwcPnjBhwvz585OTk48fP37z5k0cGyM3NzcrK+vWrVs3b948e/bswYMHk5KSFixYMH78+IEDB8bHxzdp0sTT0xNvwsnJydnZ2cXFpW7dupi/btKkSdOmTVu1atW1a9e+ffuOHj36448/Xr169b59+86cOXPz5s3KykqsWUa+7epk60dhSwc/xpfZFvyHksi29dimtXOLlrAlnR/f49oqvzNh2/hfm/6dm9ZW/7XbJeUJAgQBgsB/RUA7G3McR1FURUVFcXFxvjqVlJSYzWae54ka+r/CSAoQBJ5kBAgB/ST3Dmnb/xwB7UpaSzxqk9qIiO9ztPI48ai1SD5BgCBAECAI/DYEapxmtY+2tWmZNRIaYcQpkKWHHSeLRs042Lr3Zx1f297x1b0dXk3p8OoX8QNT2/XZ06TrpogOSXUjFnlGLfFuvKpBk/X1wtd4RyR7hSS5eCd6Bm2y91rt7LfBN+aga8g2h4CNDoHJrmEbPaK3esZs8myy3qvJuhYJX3Z9/eSQiZffnXdrzvqc1YdKU69x35VCkRnKLFBuReERDTLimimQrSCUWMuqBT0DHFalmjnGaLWIoLAKmmuwz4Ik1SCgkSWFxVJRUdGnTx87Ozt3d/datWoFBQWdP3/eYrFge1lMSgqCgC0XRFnmFWBl1cxagYIqmPfphfDGH3frvuVgKiMDmMyVJhMK2YfYPIEWxWpJqFYEiyRaBNnAyyaLxBhEJBL/Pgc69/sqKO5g7Itnnole233g/q8zwFINEoOcN5DbNrASCqZoEcHKg8AClFXDxq25nTutbRQ17403t1y6wVZxSLJstJhpKysLSC+t3J9lWRaB5aRqHsFGcQBZhfDhx4datJz89pi9uT8CbUWBBiURNVWQrIJkkkSTJFokiUX2KaJRBCg0wuHTQtfeB5u03J/Q62pQ+Np3Pjh58QeFRybTwKEYkyhwJQ/VqiCe5QWF42Dtmn1enuH2Du6OTu5O9l49XnzNaKz6PR7Q2mWD7RH7R6UVRcH0K8MwFEVZLBaz2WwymbALc1ZW1rlz51JTU3fs2LF+/foVK1bMmjXrvffeGzJkyCuvvNK1a9fWrVtHRUUFBQXVr1+/rjr5+PiEhoZGR0fjyHsDBgwYNmzYhAkTPv7444ULF65YsSI5OXnXzl3p6emnTp06efLkkSNH9u/fv2PHjnXr1i1dunTWrFkTJ0584403+vTpEx8f36ZNmyZNmgQFBXl7e/v4+NSvX9/HxyckJCQmJqZt27bx8fG9evUaOHDgmDFjPvjgg7lz5y5fvhzH9zt58uTly5dzc3MrKioYhtGepjwUN1mWOXXCVDtyOVePeXzYa78C7SVujY/WukY7UfzyRI1TjVaVbf5DW0sU0I+CheQTBAgCBAGMgHZG5XmepumqqqqioqL8/Pw8dSoqKqqsrDSbzSyrxjcmqBEECAJPIQKEgH4KO400+Y9AwPZW4cH0o7aASz54F/Go8iSfIEAQIAgQBP5kBDCXhOknWoLr5dB3/M4GLT+p13i1R8NtHiH76oTsrx20p1aDzU4N1jsFJDkFfq7zWlQreLVr6DrHBit19Za5Bq71aJhUN2itb3iyX+S6gMZJDWLWhLdZ36jz+tZ9tr/45v7xCy7/37ofV6dW7jvDXLgOuQVQbQYzC7QEjIJMHljVgEK4b0PBAnDKvZlXJbXYduK+A7KixtJTeOVevMUHRyVt9MFgnjlzJiYmBmtI7e3tExISKisrFUVhWVazVsC8myBJrCRYeN4oyBVWyC+HOQsyYp9d2OulnXv2GKrNwCm0ABWSTN9TzoqMIOsFuRJRz4qBVQxWsJrVnfouG+IHb/HtlNJy8K3wNrsSeu++eAFKS4AVVQdtQUE+3AolIP0yxSms3iLSPHx9gnu134bY2Fnj3/3i24tl1RxvkQ1GroyXOB4xhpIkKiqnrCBds6iIsmyhjQASrSgGChYtzWja4v1XB3z27VmL0Yj01YLMIrE2z0uiRZaNsmyUZEqQJFqBKkEq5eHwd+ygCccaxGxo1eVMw9id7RN2fn2Wr6aRJQgPPI8IaEoloKsExQwAogCFd+R/DfxQp3sGBaxzcrbTuTZ/tm129o+CyKiK6occwrZ9ZPu1lo/9UrRAEfiwxCVt02rIRxQiEtOjeC1MK9M0jdVemni5uLi4sLCwuLg4Ozv7/Pnzqamp27ZtW7ly5ezZs996663+/ft37dq1VatWjRs3Dg8PDwkJ8ff3xxSwbYi/uLi4Xr16DR8+fOLEiXPmzFm1atWOHTuwRcbRo0fT09MPq9OhQ4dw5TNmzHjnnXf69+/fvXv3jh07tmzZMioqKiwsLDg4OCAgwM/Pz9fX18fHB28oKCgoLi6ue/fugwYNGj9+/IIFC5KSkvbt23f06NELFy5cv3791q1bWVlZRUVFBoMBu5nZkr81jnNbYH9hWsNfIzJs638wbVv+UavUKFPjI24YzvyFjSTFCAIEAYIAQeChCODzMHbhMJvNpaWl+fn5ueqUk5NTUFBQWlqq1+vxE3fihPlQDEkmQeBJRoAQ0E9y75C2/Q8RwLcKtrciWDj2+FuIGncd2sf/YUNJ1QQBggBBgCDwaxCwDV9jFSHLCEM+TPOIWODgvdoj8IiH/2kP/9O1G5xwa3C0dsCXnqGHPKNSXBtu0Pl+qmuwsE6jZZ6NF0d0SGrba098333D3zkzdfbN1ZsMKUeUa3fghxLINcFdGcoBLQsFKGHASAHPgoIZZQU1FNPKj1oihwhtRmWxYbIISNqr/Fefa4xEWloaNoDGHPT06dMtFgsAaLHjMA2NRLKiYGEZCZDP9bV8mPXJ+eCIDzrFJ6akUCYKjBZBACMmoLGAFPlaqAQ0r+hV9tlkBqFKhnNZSv+3ttd7dm6Tf51xb7v1uZ6bd+2vYpl7HcMDy4oKLyi8bOFlEyszFhYYAY4eN785cn+LlrPGvL3z6k2lipYZoFmoYJQKbHzBoxZKAgqQiGcQRDBZeUaS7uph9drrbdvP7dpj/hdfFuktwCH2mUabEGhBZGSJkmWzLFGSxLKKYlHgLg8FLLz5f6fCOq1v1v3riA5ftOy+/YuTUM6gRwKiooY3lGVR4XnEkhsZiRYVKC2E2R/vbRLVx9HBX6dzwJB2aB+fk5MjSfyjDr0HryK0Aw+zxliNayu/ta3K1jUC50uihN84zsvLy8zMvHbt2oULF06cOHHw4MF169bNnj179OjRL7/8cvPmzb29vR0cHOzs7Ozt7WvVqoVD8NWrVy8wMLBx48axsbE4BN+AAQPGjh07ffr0pUuXbt68OTU19fz581nqdPny5dOnT6enp2/fvj0xMXH69Oljxozp1atXq1at/P39HRwQCNgZw9XV1cvLq746+fv7R0VFtWrVKj4+vk+fPiNGjHj//fcXLFiQnJycnp5+9epVLFu23U0cFRMfjfiKy3bHHyR8H38NVqPmh37ULswerNz2kk9zUcOSAk1YUKOM1mbbamukcTN+f8sfujskkyBAECAI/KMQ0E7d+LksRVEaB52Xl4fV0JiGrqqqslgsgiD8o/AhO0sQeNoRIAT0096DpP2/EQF8q2B7p8EwDFYq2d4d1ai9xl2H9rFGMfKRIEAQIAgQBP4qBPCJHd+6sDJUyJCRAx8uzI3vfaF+QFp9v5PP+J+o53+qnv+ZZ/xPuPvtdfFbF9gsqdHza18Ytmf0nOOLd9/ad7byWincpVXPCh6qLaC3qEHxRBS30ApgVhSzjMSxwn2PhvtaZsw/i2jfNQZaZaVVolnV4CIlrhalDwfqw4JpmzpssNMGGnxXhr/ZuHFjcHCwk5OTnZ2dTqebOXOmXq/H4lkkKsaEnyDwPM8wKMJehQku3gYUdTDiw64vrU7aetOocsfVVLkg04LMShKPEEPrMoJk4hW9Kn+2WIAzANwsh4+Wftsq4fN2fQ9Evbwj4qXE+Ru+L7YCh7TejAH01YLeyom8oLCylZWRrQfDwpXvYdzbx6IaTZ72f8d/yBT1FrAIQCMBskEEA6KSRQHPnKzcmyVgBbRuaYXy5ZGibl0T27dftjLpUqkJrchBtWrZTAmyQVKQ8FmSkImHICFvDaMCP5TBhyuyfOJWRnU/GPbC3pD41Wu+LL2LzE+AV0CReUUSRQl4GXhUG2uV4E6RtG7VtbgmE4P9erg6hzrWcsEEdP9+g0pK7tr0w0/JGj2CKWaO47Af8X3sBY7jWJal1YlhGIvFYjAYKioqSkpKsrOzL1269NVXX+3duzc5OXn58uWzZs2aNGnSmDFjBg4cmJCQ0Lp168aNG4eEhPj5+dWvX9/b2zswMDAiIqJly5ZdunTp1q3byy+/PHjw4DFjxmAV84oVKzZu3Lh169YtW7Zs3bp1+/btmzdvTkxMXLx48cyZM3HNQ4cO7dWrV4sWLUJCQjTxcv369T08PLy8vAIDA5s1a9a+ffuePXsOGTJk3LhxEyZMmDZt2qJFi9avX7979+709HRswVxcXGw0GimK4jhOu15SFEXbfVt8fkINQJZlTM1rmRrRoNHBeF2twG9I2G79l6RrbOKXrFKjTI0ayEeCAEGAIEAQ+M0I4BMsXh0PMRzHVVVV4ReAsBcHZqILCgrKyspMJpMkSr95c2RFggBB4E9GgBDQfzLgZHNPFgL4dp3neZZl8bs8tsPeg22tcdehfXywJMkhCBAECAIEgb8EgRoEdK5ePH6ZHzTm6+CojX4N9vv5pfkG7PMN2OXnv6dRTGrHhBO9B51I3GxKPQ2XCuC2AUmbqwEMAJUsuqfB7LEEEifSRlpfTVVaeIMEmHxWVJrZdi81RfPPCWhUCw6IiP05MONsyz5jVhr7QttWCNpAY0tAL126tH79+k5OTvb29jqdburUqWVlZSgyjyghHTInKZwiccDSqKoKAxz6uvLFgdv8msxr3mlF4pa8civ2CTEDMMjRQkL+D3hd4DhFsCqCRZAsrMSZ1aiJUz75JqLN/Oe67X+h/9dNElZN/Swjx4xqsILZolRWCWVGwUTzEisqrMQxkmKm4M4dmPN/11u3+nTU6O3fXWVEAIugVDMsJTIC0DJYJeB4iRNkXpB5HhlBgwgCJ0sMB7wIP/wgjxyxqc1zC1cm3rlrAKMg01DNwl0kf5asgmxAHLRMq48ZFE4EiwyVMizZWu3ZdGmjl460GXzW89n/vPfptz9UonbSSP4sgsSCiAhoTkGhCGkAiwTHT1PPd1zSKPyDwAY9dDoPREDb6+zsdePGjjdUm37WE/c/4B7Bd7zYiJnjOIZhzGYzpphLS0uLiory8vIuXbqUnp6enJy8cOHCDz74YMSIET179mzTpk10dHRERERoaGhAQICvOvn7+wcEBAQHBzdu3Lh169bdunUbOHDgW2+9NXXq1IULFyYlJW3fvj0lJeWQOqWkpKxdu3b+/PnTp0+fOHHi4MGDe/bs2aFDh5YtW0ZGRoaGhoaHh4eFhQUGBtpWHh4e3rx58y5duvTt23f48OFTpkxZsmTJjh07jh07dvny5Zs3b2ZlZeXl5eFAghUVFRq/jH2WNa4ZP9XgeR47L2M36hr+y7iwLMuYgtcK34fw3n9CQNcAhHwkCBAECAL/cATwCFsDBEEQKIoyGAylpaWFhYV5eXm56pSXl1dcXGwwGHie1wapGuuSjwQBgsAThQAhoJ+o7iCN+TMQsB3YOI4zm816vb6srMxoNHIch90YbW/4/4w2kW0QBAgCBAGCwB+EAGa1sAKaE+FattjvzQ0NguYFB2/w9lofHLAxMGBem3afjRx5eO26wpu3oNoIiPSUkJ16AokAACAASURBVJwZU8IMoiwlVpF45E6sSCDZzooi1ZiReQaeFQHwjNarYbWhcdOIa5VxxL6f/DeQBcdPdDZe92GA4FuslStX1qlTBxkWq24J/fv3LywslETJZDCCLCMjajPaB84KV27Aqm3WRp02uYbMb9Rx9cINP1bIYEKiYJZBYmRaRDOLgv+JMkKBlVQra2Q9YTCzRQZYkny9ftS0Di+nd3v1u7iOKZOmnb2aKZcaqkWwsoqJVSyszLAShyTMgDTRtAi5OfDxlPNNImeOHrH72k2rpOrEGVlgFckqsTximFkRWEFGvh0iil+IwJfBrABnpuH2bRg3em/ndgsWf/rdnULUKXrawoCBUSp42YIYczTzgiRxKLIgctMwA2z7Uo5ovznqhfSeE4p94z5/892Um9lIFWViaUGmJZkCkZIlJPe2oqCDSBb9XSYMGJHWpN16/8iP3D1b6XR2brVd7B109b09T506xXEPebFXe24tCAJN05cuXTp+/Pju3bvXrVs3c+bM0aNH9+7du3379mFhYV5eXq6urk5OTq6uru7u7nXr1vXy8goLC2vSpEnLli07dOjQq1evAQMGjBo1CquYExMT9+7dm5qaevjw4bS0tF07dy1fvnzSpElvvPFGjx492rVrFxkZ6ePj4+7u7urq6qxOderU8fb2Dg4OjoiIiImJad68eYcOHRISEvr37z9u3LiFCxcmJycfOHDg1KlTmZmZRqOxhtDY9lLnCUk/7JD/7XmP36nfXi9ZkyBAECAIEAT+XAQUReE4DgdhLioqys3Nzc7OzsrKys7OLiws1Ov1LPLiuvfG2Z/bNLI1ggBB4FcgQAjoXwEWKfo3QAATE4KA3o1lGMZgMJSUlOTl5eXk5FRWVrIsSwjov0Evk10gCBAE/skI1CCgr94Wu/dZFhY+MypyWZNGn732SsqiT74/8Y3JbEYUrCiiGHSgOjgrMkiiggS5EscpLKewoiKKiojZZ1sy6769hgKyUpN61jjo+4XuM8v3LDlkxBDfY6xxGi/vF1O77tEENM8jynXXzl2BgYE6nQ5bcAQHB+/fv1/rdN4IRbfl78/yny691v21PZ6NVusClkQ+v2He+sJbRsQ+m4CngGZA5EBEdLCiqlk1AtqqIJ8REaxW2LznTlzXlS3jd3Xrdz46bs+wkWfPnwOGBpqjJDDxkhXFEpQ4VhL0FE0jawvIzIX5867GNp49bMi2c2dpfDvIyBwlMqzCcwqSPKszK8i0ascsqry/pMYGhMJSmPjegebRM/49Lv3GLbAKqE6LQFtlipWtGvWM2GdZYRXFqlLJ+78Wn395f6sXT3Qa9ENwl/3PD9z31Qm9jJ4pA8eaJdmsukXTksQyEmVRBCvA1VwY8c6p0GcTA1usrNtwrM4x2N7e3sERWZq8/HKP3NxsDU/bhHYYAEB2dna7du38/f09PT1dXV09PT2Dg4OjoqKw0LhPnz7Dhg0bO3bse++9N2XKlBkzZkyfPn3q1KmTJ0+eMmXK5MmTJ02aNHHixNGjR7/++uvdunVr27ZtbGxsZGSkv7+/lzp5e3v7+fkFBwc3bdq0ffv2PXr0GDBgwJgxYyZNmjRv3rwVK1Zs2LBhz549R48ePXPmzLVr1/Ly8gwGg+YDrt2KY3+MJ5991hpsC/jvSWud9dDE76mZrEsQIAgQBAgCfz4CmIbW6/VYB52dnX379u2srKz8/Pyqqip8gfTnt4pskSBAEPjlCBAC+pdjRUo+xQjgew8cZAa/xVNVVYVfki0oKMBv8ej1eqKAfor7mDSdIEAQIAioCCBPAFBEWRZlmZegygh79uf8a8iqiR+kpBwozc4DWoDSCsnCIrthUUKzLAHyEBA5QWR4Cc1/MQH9sK7E1iI43s6pU6datGiB3Yp1Op2Tk9O7775bXl7OWGRzGezadHnosPWdeqxr3G5LYLPtzzTeGNVx86INd340IKWwHiQL0CoBLXMKMkTGCCgigCChSH8ssqgADg6n6l8d9EXT1psHjs5s2Cyp28s7Tp4FyorCCKLgciDgEILIdkMWKq0SC/BjLsxfcLZt60/6vrzuxIm7ouopwkqclacZkeVqEtBIyMxKHKVQJokx8lBugEWLbjzbeOGwgQdPHlesHJh4xD6zwLKyGoQQxSqUMIXNyRItowKHvqb6/OtITOv9rwzLiX3hcPDzy9d/qS8tB+TSLSuKzN6PVcgLkkJJvAhwLRum/SczpsXGZ4IWPxP5YS2fl3S6ZxwcHOwddPXqea1bl8gL6k4+0BEalYmdu1auXDl37tzp06djOnjNmjWLFi2aNm3auHHj3njjjX79+r344otxcXGaoXO9evV8fX191CkgIMDf39/Pzy8kJKRp06Zt2rTp0aPH8OHDZ8+evWbNmh07dqSmpp47d+7mzZu5ubmFhYXl5eUGg4GiKJZla1heauQyDoQoiZItmYtV29quaLtgW0b79lEJ27X+F+lHbZfkEwQIAgQBggBBwBYBQRCMRmNpaWlBQUGOOuXl5ZWXl+MbeduSJE0QIAg8aQgQAvpJ6xHSnj8MAe0GSYs0iJ0KaZquqqoqKirKz88vKCgoVCdsIIUdD7UbOVzDH9YgUhFBgCBAECAI/O8R+BkBrYCFBSsH5VVAsYjBNDNgYSRewfpkGQl4BZYXaEGy4lkjoFWDiF+sgEaeG/f9N3DisQpoLIJ+pAL6YSjdizGocos5OTldunTB8mfswhEZGblr567KcktlKXw0ZU/z52d06rer08CzQa13N35+8+Lku3oRscpGkCjkzMHQSP8NnMrq8jYsvCwoMo/ckm9fhzGj0qOarOk96HKXV050fGlH2tdsNYVMQ8wWJC0WZWA4hWZFVhKsEpgUyKuAJZ/9+GyzOfEdPz15wkpZgKJpXuIYntHY558roBEjzMmKgbNUs3KVFQ4ftT7fdmWPhC2pB1jKgoTp1VYGeWgAsgbhRMSQ3yOgJYmT0LOE76/D628cCgpf+8rAzFcG3wh+dvnc9TdzTWCigDaLMlJXM2hGnYJqKDXLdwywYl1li7bbQiKT63hP92g4VOcYqrOvq9PZOTs79+7dKzfvR1kWJVGiKNVF26Y78IUBNnjBBO7ly5ebNWsWEhLi5eVVp04dbLjh5eXl7e3t4+Pj6+uLbZ27du3au3fvQYMGvfPOOzNmzFixYkVKSsqpU6du3rxZUlKCX8ACAC2GIXLlVqP24fCGWqhD7MiMv/2FDDJWQAuCoK2lXSDZ7Nl/SWqr/I8S/2Xz5GuCAEGAIEAQIAjcR0AdoCmsJyspKamsrDSZTAzDCIKAB6n7Bcl/ggBB4MlCgBDQT1Z/kNb8UQjgscc2FJUgCDhGEB6rcPiC/Px8PGiZzWaKonAEA0JA/1G9QOohCBAECAJ/CQIaR4b8NGQLIxtVt2KT6vkgSgpIKOodKwMlAyVIFkm0yBKNgtpJ2F/43lJVUWMttajViVi/e3Ya2ILDxohDM4OWVVOP++Xu22v85PJ8rwKbLxBQj3Uv1KK9ybJMUdT/JzE9PT01EbROp0tISDj+9bdWGq7+yKZ/J8xNvtPpXwcbx69ZuP52bhUKuMcoDKNYOKAYFJ6QpxWV1ZWQ8zOvAK/ICqAAfUYLZOXA5A/PtHguqc/Ayy/0Pd+845ZlSXfy7oKJEXlR4EVBBhBEYDjJQiGlcDUFxRZYknwzMmZR5y4bDh0o0VcCovklXpKQ4QbWPmsKaEliJZlGQmYRKA6qaLmgEg4eNrzYY8VLLyceOFhtZdEDA0YARgQrA5yAfKM5QSWgZd5MWay0xPHw/WVp2JtpoRGfjRxTOOTNnKgmiR/OvlhsQSyzhQZBkGRJjZUILAYXxUIESEq5+1yXHY1it8e23NCg4Qf2Hq10Oledo4udg2PLli33peyhaZMgcuiS4CFRIX92RMuyXFBQMGDAAOy2MXHixFmzZi1btmzjxo27d+9OS0s7d+5cdnZ2bm5ueXk5TSM6G7PG2vLxt8q2FzPa0/SHJh5fj+0qP9sB8oEgQBAgCBAECAJPDwLak1dJlBiGoSjKYrEwDMOyLM/zGgH9s2u2p2fvSEsJAn97BAgB/bfv4n/oDtp6gOL7LpZlq6qqytSpuLg4Nzc3KyuroKCgqqqKZVmsMxIEARcmg9Y/9Lghu00QIAj8LRDQzuEqoaznlFIe7gpypaQYZYVGIQRBkMEsgxEtFRp5OYjI1gAZcSCH4ieagMbtvHLlSps2bZydnTUO2s3d/eW+rx47c4EF+PYG33XAwuiOH63dm5+thzIr0norokkSkXEzq/CsorDyPQIa6aBBZkA08MgcOacMJk0/3r7z+gFDL74y5HJw7NrZy+5czwWKVyi2EunERQ6bb3AKa0FCajRtOVTaImFZoxYrVq0pq6gEiQOEsSTVIKAFGVHSKgFtFmSaFcHCIFX1l8erO8YvbtV67oattwvuIt9nHhRGUhgUrBDNiH0WAPcOj2474U4ujB6x89nYxLfevjPoXz/ENF03fMSXeUXIQQR5W4uCokiyggloFE5QYlHAydQzXKsXE33ClgVFfFbP/9+1PF/QOT6DMLS3923gv2bNmntOLMLDwxnZ8rz4cbXRaCwvL6+srLRYLDRNsyyLbVIw14zLYIhw2napHagPJvAqDy4fLPn4HNsa8KWRbQ5JEwQIAgQBggBB4ClCAA95+IYdXw5pS9tHrbYj41O0d6SpBIG/PQKEgP7bd/E/dwc1J0Qcqh7bbuTl5RWothvYf6OyshIrkjBM2rhFBq1/7nFD9pwgQBD4GyCAYgOiWUGmA5QgmbC6WZF5RWYBhdiz3GOfgUJO0Yh6BklAs+rw8CsI6PvjhYR4bZvZRtxcQ+6M8K2R9d+EtmgVzB5q45TFYklPT2/SpAkmoO0c7HVODjpnp/iXeu459PXF7/WLFh3atOVUWTVYVcU2cBxy3WAFiZcECcm/MQHNy0j1jDXRAsCtcvjPqu/DYmd37ZEy8p3rUW2Thkw8czEbDByIQItSmaAFHpStPJg44GkaTp4WuvXf1ajDytkrbmQVAcMDcpRWWWTkHHKf0MfezYiAlmkBqgXFTPOSgYIL38GQIftim82fM/+7rCIwiQqlGHkwIcm2LLCylZUZ1XxDERSzoFAAkJ8jLJx5Oq7pp4P6XRz3dmHrNhv+NXT/lR9AbwQeadwZBRhZoSUZRSBE6MlgqFQyLli7DdjSIHZpYPQKnetwnetzOjdfnYuzrpaufgPfRZ8uNhqNiiLxAnpK8ajfwf0eRweXJsWqUVgSJSzFss3XelCr4S9J2DaJpAkCBAGCAEGAIPAUIaCNm9rl0EMTWrFHDdNP0S6TphIE/k4IEAL679SbZF9+hoDm+IzVScXFxThSQVZWVm5ubmlpqV6vx7Yb2mraAEYGLQ0TkiAIEAQIAk8fArYEtMQKIocFMkgRK/P3CWgKaZ8VVnX7vcc+P0UENABwHLdixYrGjRvrdDpEQDva63S6WnXcnm3RZtumI5fPF+nLrJKo8CDxwCMCmhGAlRRkw6xwarhBDplvyIhEBtYCUCpB4v6b0fGLuw388r0Pc2Nbruw38kD6WaWcBuT6DCAKRkStIgMTiVEYC1hEgO8uK71fXd+49aJ/z8zILEHsPi+hGIUgoFmWRRsCGjP7tKBQAlSzstXCQkERvPvOiVYtls+dfyMzD/IrBAbZe5hZqGJkFN6QVUy8bEIPBiSJU2hOlu6WyZvWX3m+xbxXux34dC73XIutvV7ZdDKDL69G3Dfy9RbNkmKUlGoBjJiwZhgovCN/POOQb+SHnqHTda7D7Gq/pHMM1rnUtnNzdqhd671Jk/MLirB4WUFNf7gfSo33q7SfBrZXxlcRWiZ+bIBXqbG0vcz4k9O2zSNpggBBgCBAECAIPEUIaCOmdtv+0IRW7PEEtG2xx5d8iiAiTSUIPMkIEAL6Se4d0rbfhYCiKBzHVVZWFhYW5uXlYckzXpaUlBgMBpqmcUwePN7UGIG0j7+rEWRlggBBgCBAEPjrEFBvS1A0OTxj9wNbnTI61eOAgBKKqieisICyLIuiwosKjz2gcXksqUa0pDbb7NdP7s4/ZdqonLVVHs5q/rTO41OYxMT3WjjaO03TBw4caNGihWbE4eTmotPp/P0aTnh3csa35+7bQeANyyLHI59EEYmgEQet8Ga6nAVzqdV4xwqbjt8JT5gd88r2/u/daNE2Ob5z4skznIVHphY8IFGzzIEk3eOWZYAKFn68Cz0H7nH3fXfkO8lXMvUygIVlJLzrkgKyoLqg0JzCIu4YGT6bOajmwAgAVlbOzYNpH33ZrMknH7x/6XYuVFnBwoNVQf7SLND3Ag+qpigGE2OiRBnAyMLK1Reebzf/rSFHPl9ieeWFQ107rN+3v5yWgJaBVSRO9bMWwShClQxmBWQZIDdX+GRBavPYMfV9+zvV7q5z7KDTNdHZBel0tXV2dV7uM/Didz9YGUyzKyp9/viuQMeJdrOqXTBoOQ+ujMtolPRjSj64LskhCBAECAIEAYIAQUBDAA+p+HJIW9qOxbZpba0aCe3BsG1hMjrXQIl8JAj8sQgQAvqPxZPU9qQggGO+G43GgoKCrKysnJycfHUqLS01GAwURWG7Z9sxpsbYo318UnaJtIMgQBAgCBAEfiUC+LbkJwJaQlYMD844dqBKQCP2+akgoO8zy0DT9IULF4YMGeLn7+9a2821tpu9owPmo1u3jlu4cP75i+eMFiPDM5zAoniAAsuLAlITyxKnsCKYRRAsChy5UN1j1OaIbmsGzyl87rX0rj227N9TXVmBEBfVGblqiMg8RACgASwK5JXD6PePPRM+q8frO46ezOYEFkCg2ErM0Ssyj0M7CrItAU2xSN3MygBlZbB08ZnYmA9GDt9/4yYYrGBV/UCQgzNYOWDvEdCSIkiSBFCq54uMsHbHpcat3uvTf8enC0r6vfxF5zYr1yRm3a3EreJZYGlVwAzAqBEHGStPFd81z56TFBP9Sl33OHf3Fg5OETpdkE7np9P51PNp8q/B72bllFtpLeIgJqD/y7MCfJGAj0ftgsH2ouIxh6rtuo8pRr4iCBAECAIEAYIAQeBBBPAwqlHPOGE7FtcYZzHXzLKsyWSyWCySeM9l66E1PLg5kkMQIAj8UQgQAvqPQpLU88QhwPN8DQIax6DH1PODzX1w0KoxdD24CskhCBAECAIEgScZAXwa124wJAUeOmPt828joG10zj9zdv6Zz/Mfp4DWhipbBS4ghW/u4sWLExISXFxc7OzskCmHnZ2rGwpRGB3d6OPpH527cLaguIATWIqxYC9mTuE5BVHGnALXflRGT0iLjFv17hxD91GXG7ZdsyIxp7oSKAvqXgkYJJhWvaRlxD7LFQyXdRcmT78aGLnohVe3pJ2mqymQQOJlC82bZUBacjXSII39N5D8GYmgeQ6ZnqCggkVFkLjias9unw1/Y/Opb+/yAOw912iJB4qHah6MqLwEaBVFMYlSkQXWHcht8dK8519ftHhj/oi3z3Z8PmnRp+fvFCPLZxYkGigaaFoBGpmEMACMDFR2UeacT+ZFN2vh5FpXp3NBSwcXnZ2LzsHd2d1v+IiJP2ZX0CwSuNtM0qMsOGzK/JTUOuUXEtA/rUlSBAGCAEGAIEAQIAj8egRsR97HpHHFiqLQNI1fjC4uLtbehMYraleJv74VZA2CAEHg1yFACOhfhxcp/RQhgC049Hp9iTpVVFRg4bPt6za2u/Ooocu2DEkTBAgCBAGCwFOEQI1bi4eyz5Jyz3wDKZ/RXcg9BbQs/yILjntuE6prgy0Z/b8moPFYJggCz/MWiwXF+hOEgoKCWbNmxcXF2dvbu7q6enjWwVJoJycHHz/vN94cunvf7sysW/dJYZ5TeADQm+A/874NDpvZb/D5wW/d8Gm66O1pp7LzwKAHo5mVQJDAIoFVBIEH5K5hBKnQBJ9vv920xWct2iYn7SqpZNFBIcg8xZgYwSoqospx34vlKMiq/wZmkwVgeRQNcfe2qpcT1r3aOznjLGoDJZkUAA5kHsmfWR4ZaJhEsHIKyyoKLYGehY2peeGd5rbom7RoT8XrHxyObDV/7PtfFVehTVMyUkvTYNYIaBbo3Lu3Nuz8/PXhr3r5161V197BVaez0+nsdToHnc5Jp3NyGDJ8dHGZkZfQkwOb6RcpoG3Ko/iQ2mSbT9IEAYIAQYAgQBAgCPwvENCG3ccn8KZlWTabzeXl5fn5+bm5ufn5+YWFhVVVVRzHkSfH/4veIXUSBB6FACGgH4UMyX/qEcBBCDmOo2maoijs+Kw94bQdq576XSU7QBAgCBAECAKPQMD2bP8oAvpePigS4hIlbQbszYGXtipmnFa3aEs626Z/1pwH130w52cr/PcPtvulDW2yLBuNxqtXr86fP799+/a+ft72DjoHRySI1ul09k52DrUcOsV3+mj6h5+vX3P+u4y7ldUMCxuSL7Vt/cmLL+x+c8TFZs8te2nQsrPXLUYaBfSTECacDLQIVh4R0GAFuVKEbQcKX+j1eaNn567dWFZhAbOATKJFRFUrvChgB21REbWZB55XZFZA1HNlOWzbUPlS160vdFi7Ifm2oCDeWfWGppD5hoRiGPIgqpbOFlYxUYJgpGHvIWj1ws6mPbe8vbh45Ly7YZ3XDnpvT7YeKIAqzmwUDDIy4QCjYCrSV53+7uKSVSv6DnrVwxtR8I610axDcnCdzkXn5qULifR7f+pEtHcK4tQl+Z56XcX9VxPQ/723SAmCAEGAIEAQIAgQBP4iBDQFdFFRUU5OTnZ2dk5OTlFRUWVlJRao/UXtIpslCPzjECAE9D+uy/8hO4ylYVpUenyjjvfd9qb9H4IG2U2CAEGAIPCPRcD2nP9PIKBlWWYYBtPQ69atTUh4ITgkUGVeVfa1trNLbWedgy4wpEHXhM5D33xr2Yp9ca3GdGizaNLES/GdEwcNTTr9fbH5njsiOmrUGI2CCIIICgeI8N19PK9L7zUNwj6cMe9cVgFyiLYIIIKECGgF/YnAikAj9lmWeQWLmnm0LgsWM5w4AsMGpLeKXr56WUFhCdAScCByQHPAIgU0JqBR2EOeVUzVFoOJgq9PcAk9DzVpve/dhdXD5xR7t97Qe/w3By+aihFFjiYa6IKqgoyrZ9duWTdo5LDoVs1dPT0d3NwcXZ1r1XbWOd4HwFFX+xn7DvFxW3Yl5xRmSyikospB33cXUR8hyKqc/WeWHP/Ynw/ZcYIAQYAgQBAgCPwNEBAEAYugCwsLcWiogoICLUaU2WzWjKH/BjtLdoEg8MQiQAjoJ7ZrSMN+KQK25IK2Ds7URGH4o/YtSRAECAIEAYLAPwQB2zHi70pA2+6jNvAxaLIajdXr168bOnRww/AwR+daDrUcHGrZIQ+K+5O9s3edus0bRb4RGfZmWMjA5StSS/UGWjTRAscLiiYNlmQUWdAiwLErYvzrScFNZr/5TvrVHxUDC1YBrByvyp8FpCZG/ssUmhWRR+pmJHBmkPQZeAVOnxbeHnEqrunqRXMyc7OQrLqa5hHvjEIWApqVn2ZGEM0WOLyf6tF1U1xc4rQ5Zf+erY/utrtZ7+Td5wU9QDkrFlaZv7uRuW7rznEfTI5t/ZyThzvyv67thKw27tltOOrskfjZ3tElKKTh6LfevnLtB+y5oeq7kexds7eWQVbF0L/OA/of8lMiu0kQIAgQBAgCBIGnFwGWZc1mc0VFRXFxcWFhYUFBQW5ubo46YUcOmqYJDf309i9p+VOBACGgn4puIo18HAK2N95aOZyp3Yfjj9q3JEEQIAgQBAgC/xAEbMeIfxQBjftXUSRZFhmGOZx+dM5/5j3X9rnGTRp71vNwre2ms0PCYDtHD53OU2cfpNMFubg2jGsdP/bdkXMXTNuxa9eZb7/7MavIQonI+FmdsvKk9/7vK//oKa8N3Xs5E8w8GDjaSBusgllEUmakgJaQFNqMCGgkf0ahAP8fe+8BL0tWlYv3DWfu3Dt5mJyHLGkGHRAVEwiiCAOTQB6oPB4i4EgQEVHeExCewkjODqLMiDgIhgdINPFHVCQ793JOh9txOt6uru5TOez/r+o7vc7uSl0n3XvC2r/+da/atWvttb+9u2rvr1at0vDxxNe/5dz+0k9d/8g3vfL2rwx6wrSEbouxZRmuG/DOIKCDGNBWsOmKZU3885cHT33C+3/00e964+u/8/tv/t5DH/O2G372g7/7rn//+D+V3v/xv//tP3jzL77gpT/0o086ct4VhX1HAsZ5/8HCQeLX9wURN/afXdh/9gUXP+AXn/PCu+/+G00XysgCUR5aGxLQwp+GT2ECeqWv+YcRYAQYAUaAEdhNCLiOa5qmqqq9Xq/VajUaDXDQiMhRrVabzeZgMHAdl6mD3dTv3JZthQAT0NuqO9iYtSEg0wrx60Q8Z23auTQjwAgwAozA3kUAhGTe9q+tdF6tecvJV8O0YyzHXdbNpXLprz/1ydtf9opHXfe488590IX3e2jwPr59BwsH9hUOFg4cKiwcDj4HD+2/5NL7P/zhj33Sk2989nOe+4d3vP6Tf/uJT37yi29+08dvuOH2Z9709i9+cez5YmIKzV7W/b7pdU1XMV3V8kame0J3e7o9Mi3PcAIP6IkQA03857fES178Dz/0g7//6lf/zde/uaxbwghiPQtH+I7wAw/owPfZC99AaASyIz7/2dZTn/QH1//Ay1/0K3f/2q/+yUMf9otnn/9Tj/rB5z7s0b9w5YMfc+7l155z2ZWF084qnHZO4bTzCgfPLRSOTD+HCoUzFw5dctrpFz/kBx73vOe95CMf+WSlMtD1AB4EfXb9gHUOoQuifk9xQ0864Tskp3n8ywgwAowAI8AIMAI7HAFMlizL0jRtNBr1+/12u12r1crlcrFYLJVK5XK51WqpqjqZTEzT3OHNZfMZge2IABPQ27FX2KYMBFzHtSzLQ85XIQAAIABJREFUDJNlWXSLMk43x3My1PIuRoARYAQYAUZAQmBtlPLaSkvVbIqI613Oq56iToQQd3/0C4/8gWdeddkTzj//kYeOXBwQ0IUwUsXBMHBFYV+hcMb+/eceXDjz4KGDC4cLZ5x9+IwzLj24/6r7nfMjz3jqq9/xx5/60Ac/9ZnPf+mrX//X483vqXpdBL7OZvCSwsDj2RbCtV13YtsgoL/6dfM3XvHph//A773kJX9XbwWNDgMtB+GhDdc0fUtZHjW6rWJt6evf+fcv/vMXPvqxT7zrXZ94yANuO1j4kcsu/tlLL/6Jw2c8rFC4olC438EDF4Us80IhiCSyvxAEeD49zDn70BlXFQqXHjx49XnnPmph4f4HD159080v/PO7/rbZOjGeBF7PpiksOySg/SBUyBS3wNdp2hGzBDRlT3fzLyPACDACjAAjwAjsXAToTVGIyDEYDNrtNlyhK5VKvV5vNpugoaW5wc5tLlvOCGwvBJiA3l79wdZkI+B5nqZpg8Gg0+n0er3xeGyaJq4i02Vk8JuthPcyAowAI8AIMALzEFgbpby20vPq3vT9vu/brm/ajmZYqmoPeuJNr/+rn3rcq5/4Y6/7oYe/6JW3f+gP3/zRl770NT/+kz/9qEdff+nlVx4+ct7CaecdOHjO/oOn7Tuwv1A4LWR7DxQKZ+0rnL+wcPG+fWefceaFD37owx77I4+98aaf/+UX/OLtr3jx7S9/6e0ve9ntL3vF617/hre8/a0f+rP3/8WnPnrPP3zqo3/92ef+yh0XX3rbtQ943itf/Zcfu+c/3vXBv3zjW+74P3/w+6957W+/4jdf/oIX/s/nPO85N9709Cc95Uk3PO6HH/CQh51x9iWFwrkHDzxo375rDxy8qHDg3ML+CxYOXXL6oYsPHDjvwMGzDpx25r5DRwqnHS4cOqOwcHbh4AWF/VcUClcfOPCoc878yQvPe9KlFz759177kXbXdoRwfCt40yESHJ9XfJ9X5w5TzJmAniLBv4wAI8AIMAKMwC5FAASCZVmgoTudTqVSKRaLlUoFPtHtdtuyrF3aem4WI3DKEGAC+pRBzxWvAwHTNBVFabVa5TB1Oh1N0xDoeXURyQT0OpDlQxgBRoARYARmEFgbpby20jMVnYwNz/Msx9VN2wmjOTum+MbXzBc+964ffOirXvfq//efX122dDEYuMer7S//01fe9vb33n777zzxic+8/tGPv+jiKw+EQaL3FS7dty94v9/+g6cfPuOcQqGwcOjw/oOn7T944MDCAt5teGBh4eDC2QcPnr9w+vlnnXfBJVddeOWDL7vmYQ+85OqHnXb4ukLh/qcdeeR5F113xdWPuejyh1xx7bUXXnzBocOnBToX9q18Dh4oLJxWOHiksP/8wv6LDi5cHrDPhcKhM88sHDh9hQTfd2j/gSP79p9WOHBa4eDp51xwzVkXPPis8x9xzrk3nHnGjz320S990k++/rofeOkb//dnF48Fbxd0hWu6iuUPfRHcsQ7CbsTY59lb114QFyRw0RbBixc5MQKMACPACDACjMBuRAA0gmVZ4/G41+vVajXQ0EtLS7VabTKZzE4PdiME3CZG4OQiwAT0ycWba1sjAqCVg2d1PU/X9eFwiGdklpaWjh07Vq/XJ5OJ53nEPq9RPRdnBBgBRoARYAT2BAKOJxxPmJZnmqJ23HvHW770+B967atv//uJInQ9iErhCWF7lmlbphmEqtB1UakM7/7oF37lef/7QVffeMkFj7/66uv2HzztwGkHFk5fOHzGkdOPHD6wcGjf/tP27T8tYKIXCqGv9JFC4exC4ZxDhy4446zzzjjn3IXDZxf2nVMoXFIoXF4oBBR2oXCoUDg9OIReFhiQ0OHnQEBGF4IAIGcvnHZFoXB+wEQXCguHz9x/8MDC6YeOnHnm2eeec+0DHvRDNzzu55/+zP/xS7/25j/6yO+89s4nPOGl1z/q+b/ynA++5AX3/PxP3fGyX/3kN78mllXhBC9GXLa9gScUzzciBLTw/NXP6ihgAnoVC5YYAUaAEWAEGIFdiQARCMFTYrYNqgFvJqzX671eT9d15hl2Zddzo04hAkxAn0LwuepUBHA9wD1JfGua1uv1Go1GuVzGKwIqlUqn0+ELQyqIvIMRYAQYAUaAEZgiAB/tgFt1RWlJfdEL3vrr/+uj935TTFShm74r3IB/Dt4LaAdew2G4ZMcWJ7riA+/6t0c95H/+5u0f/uQnv/wXf/mX7/vgu//wrW961W+/8ldf/KuPvP6Rj7zuuuBz/SOvfsDlV15z2SWXXnPRRQ84sP/iI4evObQQhGwOSefzDiycf+DgGfsXAm455Kn3h0x0YWHhwOEjhy644PwLLjj//AvPP+/CC/YfOHLRhQ+54H43LBx88L4DFz/gwY9+zON+4pm33vJrv/6/fud1r3zHe976Z3f96Wc//7n/+Po3aq3OsiGUsbjnr7/+hCe+6FWv+sg/fmH0Wy+/55ef/e7/+FdreSQcS7iOcD3N9RVPTHxhMwE9HQ78ywgwAowAI8AI7GkEZAKaAkPj/YTj8di2gzlD8CjUNO1psLjxjMAmIcAE9CYByWo2FQG6Bti2jYdiOp1OvV6vVCqlUqlerzcajeFwaBgGrg3T6wI/K7up3cDKGAFGgBFgBHYLAkRAeyJwcP7SF79777etZUVMRsI0gjfyhQS05oplV5iucF1h67r40md7v3Trh57+5D/47N+XlpeF5diaqU300XDcG4xa3/zu17753a9+87tf+eZ3v/Lpz9/zsXv+9F3vfccfvPktt970wgdf+8SFwnVnHnjsNVc84YlPuPXGm57+Mz/3o0992k88+SmP/7mn/vRTn/rkZ974tFtvvul//OKzf+WXnvt7r33Na3/3Nb/zu6/5nde+4RW/cceLnv/uJ/7Eax547S3Pec5vfvofvrx0vFhpLqp6U9XrY727bI40UwuCWWuWMjE9ISrVE3/76a+UqupIFY26XiqeWF4OOHTbEZZrOsIIgm9M2efA0zv4SL7PkFc7mj2gV7FgiRFgBBgBRoAR2JUIEIFAgud5ruPatu06rueFkbjClqPArgSBG8UInGQEmIA+yYBzdWtAwPM8xGMix2e8mrbT6QwGA9MMXihEFwy+MKwBWS7KCDACjAAjsMcQIALa8TzNsDQ98A7WNaEtBwS044mQd152xdgVuit0R2j9wfg3f+ODP3z9iz/4nn9p1nxNF7qlB0GxhGN7muWNHTHxgo/qCMXyB7ZQPBG8sae8pLz8xe957MN//cmPf+0/fbE6HLpCmGOz5gnFtIe6OfCDVwK6vuuYuqYvj21T9xzLdS3bFke/4z/3lnf9yPW/+ZpX3VMq67otxubYEhMRHLLsCt32DDeglwMa2XSFZrmG42uWPTaCWUHgvx0mV9i2ZzihT7fvu8EkIYz+zAT0Hhv43FxGgBFgBBgBRiABgQiNQOGe4/lxniGek1ABZzECjEAMASagY5BwxvZAwDAMRHymVwHA97nX6w2HQ9M0cVsycoXYHrazFYwAI8AIMAKMwHZAgGjnKe8qPMd3HN+xXdcOwm0Iy/Ytxw0zLVcE/sL4BBSzY7/vfX/+3vfcHUSFtgL3Z8vV8XF8i0qGhDWY62VX+K4r7vnY1276hf9908/fcc9dJccO2O2wsOZ6E9fTPN/wPEt4bvCBXZA913fEPXd9+6anvOHtf/hPS0cRQEMEOoPwIF74ccJo1QG2XsBhC8fzbBf2O2FJH8XCtmghqy5F3sAbCKcvIZzxg17tLvaAXsWCJUaAEWAEGAFGYG8iQDxDpPmUT5w1FcjYRWVYYAT2MgJMQO/l3t++bbcsq9/v1+t1RHwulUrVarXZbPZ6vfF4jBcPUoRoPtFv345kyxgBRoARYAROJQJEQAePkoYfzxW241u2Z9DHcgO34sBf2Lfoo5kT2zOUyYllY2w6muloxD5brk7FHN8KeWwzjN2hB/GjXdHviK/8U/srX1b67SDkNBV2XcN1A/Y5jYAWjmgdF9/46uS+urD0QJUbuGYHIaqn9getQAoIaOEHZLq3YnYYOSR4n6IXVBuQ6aFtq+7PcIIOvsPEBPQUS/5lBBgBRoARYAQYgRkEiGSYyZ0+ge15nj1NFK+DDolz0xElvMkI7E0EmIDem/2+rVs9Ho/7/X6tViuVSpVKpVwuV6vVTqczHo8R9Nl1XHzAQfOJflt3JxvHCDACjAAjcMoQWKVtpx7EnitcYoQjTLScbzpBrGdPOMQ7E2EdoapDL2Mz9IMOg0f7wvKEZghNDzhgyxeWcKAZBLTvWcEnCIsR9YAWrjAmYtQXthFAFjLFbhjB2QztB4cuRBhmAwS05znhJyC1JQI64NmnHxee0fiemTPIkaBX+4g9oFexYIkRYAQYAUaAEWAEIgj4vm9Zlqqqw+FQVVXDMDzPm5lgRA7gTUaAEQgRYAKaB8K2Q6BYLIJ6rk5Tq9VSFEV+3yC5P/O5ftv1HxvECDACjAAjsF0QWD8BrdvLrrA1cyKECw46nYC2pxx0wPk6vmP6lu4YumMYrmkJJ4jeEfpWzyegQ/dmVXE8J6DJgzcHCt0Xy77QvSCSR5SADl9ZvEpA+0H8D3hABzw7XqUYfvvEQc+sD+cS0NulH9kORoARYAQYAUaAEdhGCBiG0ev1Go1Gq9UaDAaj0UjTNNdxt5GJbAojsP0QYAJ6+/XJ3rZI1/WlpaV6mMrlcqPR6Ha7o9FI13V6kkVePUbkvQ0et54RYAQYAUaAEZARIM4WAZRXvkMn6CASdMbHdDTydI4H6Jg6F5OX8argCMMKHKAn+JjBpgEOGsE3ZA/oFT/oMAb0yqsCHeE7wnedoNgK+xwQ0EI4Kw1becvgtJle8DLDGX/qFZo6aDv8vlEUWEwPC3/90Jka36s7CLTVLJYYAUaAEWAEGAFGgBEgBAzDaLVapVIJlAWChSJSKJVhgRFgBCIIMAEdAYQ3TzEChmE0Go1imOD4rOu667gRT+cI70ybp9h6rp4RYAQYAUaAEdhGCBCXumYCOo10XvFlXg1wYUu+xgENbQnDnCWgQw46cIKWCWjhBSE4YgR0yCaDffYMBN/Ad+j9HCJ7kgjobdSLbAojwAgwAowAI8AIbCsEDMPodruVSgWPbtdqtXq93m63x+OxHCZ0W9nMxjACpxwBJqBPeRewATMImKY5Go06YVJV1bKsxKD+xDhHhBldvMEIMAKMACPACOxpBFIJ6Clr7KY7QQeUMTydw/AXDr4zfJ+xyxGuKTxNuJrva8LVhWNOo3CEITVs4dvCs8Wq17Mry4E7M30ChnolrXRj1FtZyMdOQ3REW41jkTszHLI8oGcK8gYjwAgwAowAI8AIMAJAwPd927ZVVe31es1ms1wuVyqVarVaqVTq9fpwONR13bZt4jEYN0aAEQACTEDzSNheCFhhwm3DyFl7ugjN+t1ejWFrGAFGgBFgBBiBU4lAlIpFSApinzNjcWyEgBaaLzQv+OhChBy0ZgnNDWI6hwR0wEEHvHOqB7Tr+a4XvIRw+llBkQnoUzmcuG5GgBFgBBgBRoAREL7vu45rGIamaYqitNttuELjMe5qtdrr9Uaj0WQygTsdhRJl7BiBPY4AE9B7fABsl+aDVBZCuE7g7rRdzGI7GAFGgBFgBBiBXYjAKjFNcTBIgB/xCjUsxVOexktePXbqcewgPkbIbjuOsEeG1p9YphCGEH3DUOyRKU4IobvCjNQy1bAKsXyTWay8JBDqV8skSQn+zUnFcuaFL0PMWZaLMQKMACPACDACjMAeQyB8DbIHGhoPcDcaDdDQpVKpXq+3Wq1ut6soiqZplmUxxbHHBgg3NxkBJqCTceHck4wAEdD8oMpJRp6rYwQYAUaAEdh7CKySyMQIkwBSeB0EtAiOtCxhT1yvfJ/9D1/ufOLvjpea9rIvTKFqXifwgA5S4Pg8pZ6jxDET0HtvNHKLGQFGgBFgBBiBHYYAEcqu45qmqes6InLUarXyNFWr1Uaj0el0VFW1bXuHtZDNZQS2AAEmoLcAVFa5dgSIgKZT+dp18BGMACPACDACjAAjkAeB+QT0lCCWwyRDXj12WsYR01KesGzhjU1xxzv+8Wd+5sPXPeqOl9z+qW/+t2EL4QonsCx4xskTgRzokXXB7iQC2g9coeckaJpTKPdu9oDODRUXZAQYAUaAEWAE9iQCmLEgdqjneaZpjsfjbrdbq9VKpdLS0lKxWCyXy9VqtdPpjMdj2w5uw+9JqLjRjMAKAkxA81A4eQjgQRXUR4xz4ubJs4lrYgQYAUaAEWAE9hwCq8QvOT6TMKWVUWZKLRPHPBOUA2VkAtqxhTjeEDc89veuueJ9D7n2Lx593dv/6hMtAOwHxX1Efw5rCXSRL/RKGYmBnobgYAJ6zw1QbjAjwAgwAowAI7DNEYgQ0J7nWZalaVq/36dwHEthqlQq7XZ7Mpm4jrvNG8XmMQJbigAT0FsKLysPEPB937IsPJai6zru+0kLzKjIqDECjAAjwAgwAozAqUYgTj3Hc6ZEtueDoPYCdll867/Fo6//oysu/MtLz/3EtVe984N/0hxpwnCCy/0K++wGnHIQjEP4TvCiwVVWe6bVcoUzO3iDEWAEGAFGgBFgBBiBU48AuAzPC6Y1nrcaFbrb7TYajXK5DFfoVqvFBPSp7y224FQjwAT0qe6BXV0/bgNOJpPBYNDpdJrNZrfbBQdt2zbeNxiln/mxlF09JLhxjAAjwAgwAjsEAZn9TZND6thzKURG4NHsiW99V1x33Tsvv+CTF5/7N1df9d4P3HlfQEC7tudZvmf5rueHETh8T7gi4KCZgN4hQ4LNZAQYAUaAEWAEGIEZBGQCmmRE5EBU6Eaj0Ww2FUUxTZNDcMxgxxt7DwEmoPden5+sFnuep2nacDhstVq1Wg3vhK3X66qqxklnOedkGcj1MAKMACPACDACjEAaAmmks5zvBU7MAQHtIqxzQEC74lvfEddd9+7LL7rrovvdddW1b33fR4qKJXQxckXwPsJg9eUGoTcC4llKoKGRMbtHKsQiI8AIMAKMACPACDAC2wYBmceIyLZtm6apqioFgGYCetv0GxtyahBgAvrU4L4XarUsS1GUVqtVLpcRhn9xcbFWq43HY2p+5ByNTdrLAiPACDACjAAjgFBOWzplPzlXn62rBQ9+bvZQkYlm0o3MgCtGzGjPcwL22bcDZlnYIKC/+R3xiOvfe9Glf37eRR+54oF3vO/Pjo9sYQjVFWNfBJG4Auo55KBJLwTwzgjN4QYRvJJT5Ki1biYrlXLXqpDLz0VAQne+OFdbvMB8pWGJ+IE5c3ac/sgJc679OXGgYidZP9W7iQJhklPnmsrjpWQ5Na+j2JqM2Yj+SEdnqyKr5h5FJbMVrnsv6c8prLWinGqp2F7TH2kv4ZAmRMrvuM20diHf87zIuweRH2+mrCe+l3MYgd2BABPQu6Mft0Ur6GTqeZ6u68PhsN1uw/GZ3J97vZ5t2zBXPsnK8rZoDBvBCDACm43A3AXJBivMqV8+29BZa4NVb8rhccNy5mxK7dtZSUBHOq7nrcEpVoZubtPWoX+uzngBhAVE7Kn43o3kwP6NvNaG4Jo1A1wz8kj2KVwzEdCe54Qfy/Etz3MsR/zXt8SDr3vvkcs/unDxXZc86IPv/chQtYQlHF/oIiCg3YCAlvltUh86RiMuR+SbjIQwa+oatiJ60jbXoJGLZiKQhnB2fqbKmZ3ZejL2zmhJ38jQkL0rXeXMnmwlGXtntMxugP2Ur4nISfxGFbMKVm/+RPKxefL1J5oRz0xsS7wY5SBgqwwU7YoIsmZZjhTDpuu4iDSYuDdPJqpINGxu7Zuon8xItCRekVw+zc5Ifk7N8brScmT9cXvy5KRpRj7rz8aH98oIyKNFzk+U8V9IHKKJ5TmTEdihCDABvUM7btuZTUtr13Enk0mv16vVavB9rlQqjUaj0+koimJZFkxPPL2u6TS97SBggxiB3Y5A/G+bv8W0zCMl+Y/NUxL6aVVMteRc21D5PHVtRRnCZ33K89uPkok0RBw9GEPK84BJ+tdxVB79hI+sX26O67i0+E9rESnJEGT9iTKBk6GEdkWaJg9X2Xg4MlN1dHi2IF9/6VgSso8l73KUny1MDHHg7Ox5DhjnkID2w5IoQAGc/dCrOXCC/u5R8YjH/umZD/zEoWs+df7973zHnepAE7rtCN+cIaAFHKm9UH1wjyFoSzQyx6xR060kg6f7Zn+BNu5h5HcVX4d+jL3sb7Qxv3J0kNzFO07/bG/k3VoTRHmV7oFywI2G2dwWy+XxH5H/KZETF50uTrL+jBNm4l8j/9+c8IGLoh1LhAaVXJ+Q3YTIaMdmJDOjXrl8XI4fKJeJ743nxI2XNUTkdVzF6BSdeHKjwRYfjXFTN56z1bXsEf00KjbeIztaA+Gwvn6nw3c0CGw8IxBBgAnoCCC8uR4E4H5FQY7g+Ly4uLi0tFQulxuNBt49SP5ZdD5NFNZjAR/DCORDAGM1X9n1lFqf/jW5dgohIkskTNkx6Y/swuYG9cORB7UYhmFZljlN9DbRuWBhgYG/vGmalpRgpOu4lmXZti3tCTZzeozSAsl1XF3XNU0jPaSfVpKJZx5kzm3IFhUg+yOLtwxT5V3EC6SZh1X6mpblZBLmzdn4rFW/zBrITU6zn/KxFpUPiU/rYbnruKZpRsqTnjQhUl4GmWRqbOSZyjSdyMdRGOQ0FKm6uBBvV7Z+7CUjSUg7yvd927aBJOE5W5gIaPJ6lhyVZ4tOt8BBi298Wzz4+g8cuupjhcs/fuTK9/3R+/r3KWKkaUJY4SfwZl9xaF8hsX16jeFUVa7fnCgBjVwaZwutST9hPlcA4LNVZW3NVRgpsN30Z7Utc19O/DN1JO9c62UxWUt67tZZnl7nzB78wdc0B8AoorMBNmeUShu4z7d1+sEIY76BmUD8JIkcefBLBs4XcSCRnmn65QLUrSRkVJNHP2CMXxeoUWn6USBtr5xPl3L0rPyd0Yr8+mn6AW1kebaGSLHsTRqTOSeEsknZmhP3yuilyYkHzs1EQ9J0yvlzVaUVkJVkyGmH58nPUAvk5ZND/i7LVivvpb+q7/uY6keWFfH5Pw0hWU+aTGpJT5pA64s0/TKekeoiOvGAuFyezuHyKi+ihDcZgZ2IABPQO7HXtqPNtm1PJpPBYNBsNkulEthn+D4PBgPDMMjojOkOlTmFwrrNy38gri6b28at0JloISay+RsbV5J9LD1LTtMLeYFB12B5L2XG64rnuI4LChWTBnlVQ1XTYoMEmjJmGy+EiOtHFeCbaLZBtRPfCs1z9YN9nswmXdfRKF3Xx+Px7M4JqNg4FIk5WPLFNaAKTdPwGo3xNCEfNFaiQjkTcynTNCNGappmGAbyI7t0XTdNM6d+vG8a7z4dDoejWFJiaTwea5qGKvL8iWzbBsiqqsrq1TBBPfKRM5lMTNNE74t5CYNH07TxeDwajWRjoZNyRqMRDBiPx4ZhEI2YOH7QLigfj8c4UFGUYZgGYYLcD9NgMCD0oB/2Q09iI9CzGB6y/sFg0O/3e7GEivr9vqqqsB9LlET7USOerRkMBt1ut9PptGdTJ0zdaer1esPhUFVVTdMATtraAMphPy5hvV4vrr8VJrnOfr8/Go00TZtrOarwPG88Hnc6nXq9Xq1W67OpFqbGNLVarX6/T++rgYaMb4S9UhSl1+u12+1WqyWb2mq1ms1mo9Egodlsdjod2G9ZFk6nSf0bcMOe55imrqpKf9DtdO4L1N/XwKfZqjdb9Uaj1mjUgmY1qsfr5Vq9WKoMv/I1ceVD3l648M7C+R85+9oP3fGhYW8slk1L+LbwTd934eYcBIJ2XFM3RkOl2+60Wq1Go1FrNqqNerUVCPgEm406bTbva+FV8hmYEAGBO1IAp9MJqgAOzTChRsIHe1utVmTeklERjUxSTkrShHa7PRgMaHBmKMcJfzwe9/v9terXdX0ux4qRPx6Ph8NhZOSnGY/RNRwODcPAmEkaOattMk1zNBphZE4HePQX/4ZGo0EdMRwO6YG5VV0xCTSBqqo59aPidrs9mUxk49POPOvT3+l0tOBeSxDFImbyagbuSOm6nt/+ZrPZbrf7/f5kMsHdL2rFql5JMk1TUZROp9NoNGZPOQlb+Ed0u10anNk9S/+sbrebX3+v11MUBdOSbP2+7+PNXb1eT/7Pwk76xkCl8x5dVujMnFGLbdv9fh+jIm3AoyIMToCvqurcwYmpsq7riqJ0u12Yl1YFWgfl4/GY5jyJltONTNM0J5PJaDRKuyzKV4F2u42enUwmmed8QfpptjMKE+YMdE3HhZiulVCOCzpdbbPttyxL0zRFUQaDQeTk0263cU2nb7qm67pOzkzSSF8VyX7ggzmPmp4mk2CSbBgGTaTxt4Xx8b8w6cdUELM1QBT/VhQFs7XJZDIej3VdtywrrnPVerGKv2EYOCoyG1Rmk6qqaALpl7XFZVDDpmkahqFp2mQyUVV1VuXK5BDTwtFohHnyZDLR9eD9DXGd8Rx0LuynaecoKUG5Hqa54FBF4BzQcFqVTJISrS9onk/jk7TJAhqIy3qSvmge6ad1CumnIQQBI4cAxPiU1WH5Q4sL9CxgR39hTUoaZLNZZgR2FgJMQO+s/tqm1tq2raoqltblcnlpaalYLFYqFayiVVUFBQMXaTBNUwfK1V/5HimdtRMbjJM4MXc4LxuZae6UBRVhygjNedSiTsxa5q70qC246uNyS99amLAJWf42TTP7kuN5Hl25TdPErEK+sGXImLUQAmkVId/zPE3TMKNKn9FF99AdCDAdBEVccB0Xky2oGIWJyLLIJAmbg8FAURSKLR7XKedYljUajbrdbq/X6/f7YN/AuEFPvIrhcDgej9G/mFjICiOyrJ9oN9BinU4nkYzr9XqTyQRT6rn6OxjLAAAgAElEQVSjyDAMIu9IwEqg1WphDUD5ELCYTOtW2X5wZGQ2CVhjgLQCbrRLURTiQGVViTI6Fxpk8Pv9PpowHA6pRyBg7guOMlGnnGlZFkLPY9HSnCYsL+v1OhbJ9N1oNLCqocWwrC0u27atKEq73YZimUSph4nysc6s1+vtdns8Hssr4bhaykHwIjApIGKoCuinzWazCeKs0+mMx2OsJ3HahLa4DPBxFBCo1WrVMCFGf6lUqkxTrVYLeMBaDfYTwU2mxgXTNHu9HkEN5dCHWEylaSqHqVqtVioVMDVzCW4hhGEYnU6nUqng8IzvSqVSrVZhiaqqoGlw5oksDKgVvu9PJpNWq5VocKlUilRXqVQwnEajEemXMSfNJGia1mw2i2FalNJSmJBPcqlUqtVqzWZzNBrhzJD9/8XIbzablUoFqiIGYxP6l5aWFhcXS6VSs9nE1ZlgIWunQkBA+75rmnp/0K1WK+VKsVRaKhYXl5a+j0+xuFgsLpZKS+VKsVwpVo4vVWtLlaryuc9bj7jhw4ev+fjBaz557gPufPud6nBZmLbji1UC2vWF6wfrbV3Xu90uxsnS0tL3i0vHFhe/XwwEwqRYLCLn+8WlxVKx0WiAI05EBn2Bb8xP8GAWqigWi7hHjrlKsVgEPsXiSn2Li4uVSmU4HE5xSPil7vY8bzgc1uv1crkM8Od+l0qler0O++ee8/HPwv9l+h+a/9toNGjwJFg/zfJ9X9d1TN5qtdr0BJD8L6N2YfCAw6XBQ4BMda/8apqGf1YaPmiMvLdcLrfbbV3XI6rim7CfOpcsTBQwlhYXF8vl8mAwkO+70ICJVAH9rVarVCph2Ej/3VWRNCOrUqkoihJRFd/0fd8wjMFg0Gg00PxVjZJEfwEIGDyY85DZJERqMQyj3W7jNeA0vKGHvoEVDSlM3VVVpctWRCc2iZpvt9vVajVNOf3FAGCxWKzX691uF0xl4p+XqgMH1Ol0qtUqHZ7Ys6i9WCwCnF6vh7s7BAsJpByCpmm1Wg0649cpwgSXABSr1+v9fp/mtBGF8qZlWaqqAp/4RYRO0fjTVavVcrlcrVYj19wMiAzDQLRDHCtbK8uoiGrp9XqGYch/W9lmWcZlBZMZzBnq9XralR3G12q1fr9vmqasJ002TbPf70Mnruwwm5AhAcZjWoJreppOyvd9X9O0breLievcGwCgvLvdLp02aczIAunHbDDjvkiz2cS0Dadu+GP1er2c4OCy1e12W60W9GR/VyqVZrM5F3zccQS1Tbcu5FZQR8era7fbvV6PEIgLAEqEk4bxeEw3FWgI0Qw2LmC2qSgK3V0g2KkiWb+qqgCn1Wr1wtSflxRFwX07ecIZ/38hR1XV+HpkkJ76/T5uigcTpvCFJWQ/CaD+wTPgpmzEZLrTBnwwz6c1F276ZuBDQLHACGx/BJiA3v59tK0t9DyP5kARFgOXk840gfLrpiT4RBiGQVNeutJE2k9+fHDYAW/VzpGIB48opE1cFSzLmkwmw+GQrm0ZPgu0q9/vyw4RdL2RlZM8Go2Iw5pSZCu/pFB2YcP8iWisxIkjEdCe5ymKggDcNHvLFiqVSrfbhf1psAMcePj2+33cZqAFTLawuLjYaDRA09At6LSKbNvudDo1KVVzpHa7LeNPUMsCZhWGYYDpKJfLtNgGY5VWD9YbuOpHJhakn5pjmibpz4ad9lar1eFwCAJdvg0jK0d4CsuyBoMByC955GCygnm8nA+53W6rqgqag+wk5SRgvt5qtcrlMib6NEfETBQLD/gBUS1E4OIeCfTHp3RBoFfPm0wmzWYTYXnkEY5hD98uOR8OQYqiwA+alMf1Y1Y9Go1qtdrS0hL+MmQ/CXKPQ242m71eDz5HBEVcwJxSVdV6vY4ltPxXJZlgQTOPHTtWKpUGgwEGfzb4lmV1u91KpVILE6aepJkgoioqlQoxKQg0IeuXsQLPYppmu93GEr1cLtfrdSKj47CAwMWSCeuxbJoMg6dery8uLspMBFiUY7OJqJWjR4/W6/XJZCIzQXHwkTMej6vV6tGjR4k6pNMONQp/ZACIcyCYApy+5FpkrHBaUxSlXC4fPXoUaqkW4iboDwu4sObHeg/6ZcwjrfA8bzAYFIvFo0ePgu7ESjvCSlBHoK5isdjpdPL4meK0U6lUlpaWjh07RsajLWgCaoTmpaWlo0ePYnASGRGxOdxEdAzfso1utw2ueWnp+4uLx+hDTHTAG4dkdLF07PuL/c993iEC+rwHfvgdHx4rmrCChZnle4bnOY7ngYAGk9Xv96vV6gq7Ua1WqtXj9drxgO5YTcg5Xq+VKsF97lqtlnbrEX2BHncdV1XVZrMJLoz6F+NwaWmJuC0aUSDoO50O/bNELNEQ8n1fURQ4tldzp0ajMRwO595axq2Xbre7ikIOqVqt4u4F3ZaOmb+SgTvKIFgxGulPJBMQqBONA1VUr9fBUdJTRARIpC5d11utVq1WkxVmy7g1mIepwa2jZrMZf6pAriJif71eHw6HuJpjkNC0KmI8LluNRgMnGfrbZgu1Wm00GsWvUxHlcG/HaR/8XdrwoTMDgQ+mhoxPtB8ENwhcurIAisRvQgwcKDo0rRXkO48JW/YkSra/2WwSAR0HhHJg/HA4BEGcjQ84PpRpNpu4tTO3f3HNBTtPRDnOlhnXlEajkefxC/yzer1etVrFPb/IEKILCs1FcROiXq/jfTmJfSrjo2lao9HAGQxK0sYP8qG/1WrBIye7f4UQ+OfCbJnil+tCz9IFa3FxEdf0tGEj2z+ZTDBnkM88skIZIsilUomu6aQqUcAdd4Avs9tp/1y6/QB84v8swEV1WZbV6/XyLIVwax+Trk6nk+fBFCEE3XcE8vV6neZ+iQL+vLi7QEbGBTxVAMdz0J2474gHpGieSXNm4qOpj+QTfkQ/QeT7vqqqtVqNZjjoVozDxG/0S7PZxIQQqkghKqJN3/fH43Gj0YAqABKZLUc2gU+324W7T6J+1IK5LpzqclALK0UwIRwMBljEZY8fzMar1WrESFzI0Cj6xloAHg/j8ZgwpyZQDguMwA5CgAnoHdRZ29FU13Gx9KLZCVY+uDCAkqbJCtaWdFYlARMLeGPJTE3iDAYEcb/fb7VaNOlMm1JQ/uLiYiQOdRxNnM3xuCgcgujwbKFYLFarVUVRiKOJXxjktgyHQzAFtNyluS8qkifrcP0ol8vgiGlKiiqoFcgXQmBWRAuJPAIITVzYZDtJOW5oo3Wu48Jhp5Y7YfqlqiqIHvkeg1wFZMuy4LBDy4C5QqlUarVacxeraBr8EOPz2oycarVKNxjmEtC6roN8zFAY2VWtVnu9Hgh06kcZGbCfVphAQANSeZxkyLVabTgcovsiwyZSC1zVsEqJGClvynXB+wAELg37xFEkE9DguGs5EjhoRMnI1m/bdoSAnt78Wv2VLYdMBPRcD3rQWCCg4WzejSXUhLti5XI5PwGNf65MQMd0BxmyfpmABs0kd66MFWTLsjqdDi3jO51OL0zdbhdTW3nJAVca+OxrmkZnNnnARGTTNEk/4YxhEzl/0lgqFovtdpsIUNn+iHJ5MUzLdaoFy0taQNJKCafNyK0RGRmqBb7/jUajVCpVwxThU2phipxO6Z8r64RMmiF4nkfrMTBxUJjGymEv2Y8zcKJm6CcPaKyCIhCR2y8u04uLi+DZW60WhRCBntj3CgFtO+bgRC+khSuV4yU4O09dnkuV4ysfFAi8FSujZALa9j3fmBLQgfuz6wcu1vDTBG++OOW2ZQ/opTCRB/TR7x8rFotkf8zsQKd81wHBTzBgMBoJKIwWzCUwkPANminnYnswGJTL5cXcCSMfK+248ZEc27ZzMh1ACYQUokykEdDyWMJNWdm3UR4wxTBBM9qHOxygmXBnEYttWac8Z6AzD1Tl+ZZvyiZeTWSIcE2nuwiJ+iP2g8bKICjltuCyWF1Lgvv5XMuBnqqqrVYr272auEv8taFf5jhoZigjg8sKPB7yMGUEXa1WU1UVIGS0Ag4ow+EQz3akDX/Mb/G/K5fLuLjgwZ2ItZFN27bH4zG9VCZNPw1L3J4k9/m5+OCaJS9MalKS1xeEzLFjx8rl8lyaD+Nf13V4+FLbce2Tr1yQMbiwYkLnykuhCCy0SddczNlAc8dRkvGnay51bkb/ZhPQgEq+JoLKxH07MjJNwISwXq8fO3aMLCdTI5cwQgzXRNyUTdOM/A0S0PLJIREr27YHgwE8HujEKwsYM5hRYEXc6XRw0zHbcuzFUo6eLWi1Wp3MBBfvwWCQvRTC7V5EhpEJaHg393o9mmdSbSBJaVqV85qoqiqtXqk3Mc4Tv/EfyU9A4+5Foqq0zEajgchj9FSZH6ZId2C6Ox6PcU2s5UuwnwhoaI5/oy4ioKu5EzDsdDo0GyflEft5kxHYEQgwAb0jumn7GglSBl6TeGoYnAWeuDx27BjcrGqZCQ4I8BnJvjBgPj2ZTPr9Ph43jq+UaKYoC4uLi81mU9M0nLITAcUuhJxDSDsiSrIFzJnApEBz/MJAkzzyUCa3i/iURbYclAFmXcSRxfVTi+hB9ez1mFwFHjfOdtghD2jMuur1OpE+2eBgb7PZBMEtMymECRlPBLocImBuRXiQP6cHNB43xpIjwjFVkxJ8gSke5VwCGot5sr82m1DDbF7woD3pTySgZdDwrDpu+MuMIWRaDMi7Wq1WHg9oWgxj8EcUQjMsl/nKbrc7HA4R6ZiGZWLP4vbDKIx/ErntT5txt194WM/1gBZhohAcvTC+Sj+WZFggk/1zxw+81ZQwniZitgxjCfUOwpgwiKTR6/Xg8ELgwNTEb03T+mFYGLQ6pj4I0ooCiqIgJmy/30/0ZqLqIKA6TdMGYYJ+ZZqgcxDGawZmwzCCNr7zOGlCv67rOGSqeCbMNKqm734YdwVOlPIIT0QGmaAR0zq3LwWbxiKq2WzSfUHgEPmW6/I8D4MTFgKHyHpMdoeB/zj8KGX7UYWsGbJt23iwZjCNd4kFXkQnPQGAuDfx02ZcM/65hmGoqgrlaRDJ4ONvm/ZXndayQkD7vqvry4MTvcGJXn/Q7fU69OkPuvRBgcGJTrdvf+4L2qMe875zrrr7jCv/6qIHvP+9dw5Hy8K0vJCA1kIP6FUCGlE4hsOhEoYmHwyHg+HwxEg5MaKhFAjIOTFS+ieC2OKIfzI1deYXvUAMFMLsok8BO432QRhVvB8+P4unbrvdLgJwy8+6zmgPN6ij4Y2Vdk6I/4vxYC8ep42rjeSAL0CYztFoFo4ZbKIbozBwpyUF+I5oxqC1bRsxtYC8rGUkJeSjLRhj9M+CWn+aqBaKd4lZoqIoau6EsGDoPjBxpFYWAA4CmGaHBRuFSW4Fzjw0QhIJXNKPQUKMzFwBT9Wk/bkwm6J3V8iRdtNGCw3X3jThmp5tP665iFQLBLK/5f5BsFf0qkhPCBSAEwvgjX+jUWhCLwwAjfgb9P9KVx/swSOJuKrGlVMO/lZ4yp5iKGfjA/d5JYxBjCbI+JNmJQzjOwrTYDAAdZ7HeMRvGQwGnU5H9lqNz0NoRler1TqdTsRJMwMfmjPIlsdltA4hEXBrQb5mpenHagWzMooJRneqcPcUD651w6B26AJEP0/TKecjigXuhUcmIdNhHv3tdrsUEE9WFZfh6ot/Lo29qDppGxOSXq9HwWdo8PhSoorg4Y6Yb/EOjedUq9XBYDAajfJMNfHPxUspEECcrt1pAuyf65uPBxcsy8I1cTQa4WFieczQ2QZXTNSIk54cgiN+fgNOGFq6roMTx8ihYVNNSVjHUfyTxPEZ0b/Wp44QX4Xwh7Z4K8Dwapq2JgIaT9VgtoyRQ/pJkENwyB7c1dwJjnoYhKSWxiQLjMAOQoAJ6B3UWdvRVLz1SwnjouK9Ogiij7cREnlam6bEEzpubrfb7TyudlgvDYdDeq1KLYxkWg4TTuN0t5ycCxqNBp7bwqUlDUqsN/ASM+iPTyPiOTJHiYtZ4oUBuxDVrt/vR6JwxNXKORRJFpYn6scueHAjfoisAQQiTXMju/BcWPxKLAOFSuGTglmdTJ1kyJ1OB08Ukra4/cihGwyYFeWZNWICifgkpD9NwNxrMplgsS3PrjDHQo78DUKN4gnSMpUMprqQgzdvqOEb6mhKR9xEvMZE/aRTFqCfFqu0VqSF93g8VqSV0ihMeIsFHiSXtaXJwQvBwjfb4OUhaAipAkOETXxrmobXqpDDTppm5Nu2jfBz0D8O0yRM9Ao7VVWRTy8nMabv2cvAHxNW6CdwIFAthA8VWKv9wIfMgwAl+OtBM97zg7dyZ59zZLjwBkgrTDI+afoty8oTnZn+19Bv2zaeI8G5GmMbXi0Ukh/rE7z8JM9KG62Aqz69ulMWMCO3Z5NlWfmVy0CtQ8bfh6BYh4a0Q6BzKzSn1bjd8oO2e77vBp3supbrGoYt/vMb7vU3vPX8C9573jkfuPrKt77tbcc8V1i2CAhof7ISgkP47vSDDsJmXKbuSxTkxWq8QOSkES+wkZzsqvNozuhNHC4/M5RHoVwG/7stRYDGv1wvZNS7kdrp2ESU4jWuKYeUr+moTSlMVZOwDrUbOXYd1UUOQY9EMte0mW3/xv9ZW60/u7Ebt39L9c81b26BuHmYutCEJ14gkoOb+pgmyVMD6JFnI5jqGOGrqumOVERbfBORCaEfOhO/UTWiO1KQwLnNzx5dcWMQlYKWEnP1E1OM1xHRlDUuYJ6G2/94cXHi2ZJqxDxQng3SC8DH4Uuq41UggiXwl5UnNhMVAUnq1kTkkSnjn39CiDdL0SRTz0xGmLBUke2Py2gRIl+R8aAd5NcyyTL8Y9AWDP7I2KBaMEPGFZMuzRDIfLzAiZYY5CZVC4kOxFiHLxqBT/pZYAR2EAJMQO+gztqOpuIMaFkWTpf0skHcXI3c+ZdfdAAmlL7xzpA8LcSUQtd18gkazXMLGo1G8lU/oxZcHsBhaZpG14BsARwfXXjoMh+hJGidRi9RlC9vGTLmYXBzIyV0mYw0J1JpZG/aJozPPhY14mJJV748Ag6RYaGjyB7Kka/KyJRz0uRsy+VaSCZBdkfCbEbuC5rfYEqRNrGg1pGFdKCsLS5TMQocltiWuJHyE4IRqwhMEqix6xBICQmJSsiGxL3IJA1rFeihP6oFGuS6ZJ3y7BDsLS1dIj7sdBRplnWmyZjO0jetoFAX5qNpx+bMJ+WwHAuwNP2JY4YqStxL+tMe2MSyJ/+tC6puewrU0VtkXiLIW1TXdlQLV+nAMk8IxxXi3iVxw+Ne/5D7f+DcQ2+67H6/9Z63fdvUhOcI39NCAtoKroPCdzaDgKbOTRTor524d4OZdObfuB65WzGcNqhzlx0ewWfjrdvSgbFx8+Zq2On2z23gBgtk47NZ/9wNGrmXD99IF2zk2DyYb4V+vK8eU/08+uUBTARlXKApIt4HnsHhouH0bIqMg2EYsmZ5Co18WiTKRyXKaBrNtOXz9ibK9EAwdCZaEsnMUzsOgS+UfDit7BIFuWS8Z/PUS2WgimpRVbXf7zcaDYoPlvO9IKSQBUZgeyLABPT27JcdZhVu1ZIvHsgy+NmBkqZzunyals+zuFblbDZOzTiE+Ds6XycK62AH4qZm5KRdm+UWwQZiny3Lojv8GYLs5IjpiHx5I/2R9Srlb6Ig91ciyImZOEq2WYaRzMOYocKUv7nCOoYBDJBtlmXZPMqXM3PKcsNlmQ5HZjbCVPiUCHmaT2XWKuDPjubHj423N+JtAd6fJsSRP0tEYVxbPCdyIwFnIdwbo7riR60pBw/rkTYYj7MB6Pg1aYsXhn5YHt+LJ0Cxd93/mkS1nLk7EVghoD0ioNsnxI/+5OsuvvC3Lz7v9x7z6Df8zT0NXROeG0TzFmLsC9P33ZNDQEf+4Ju7mXZp29xaWBsjwAgwAozAjkZAXs2ttSGROa28SbNEijwzV7lMbaMwzWllzbIcPyStFlwTabq+RRMe1L7pykkt2Z/WzHg+GbOJc2ZEkhmNRojp1263R6NRhHCgellgBHYQAkxA76DO2tam0rmYrCSWh1gzkIy0SQJRIXRshkBKZOp5E0/3dO0k/dkCtSLx8iw3hCBah5C2yiX90EnGrLUK0pMhkM6MMhm76HBZoPLUrWiCXIYaRQjHc3IOAFJL9eYU6MCIIB+OXXLO+uREPciUG05yYvn1Vb2Ro2BGdkdQmbUK1FgaA7KGuNnyXlmWS8r5siyXYZkRYARyITBDQAc8s+GL93/4G0/5ufdd98jXvfiFdxcXV9T4QvfFsi90V9iucLM9oOU/JsuMACPACDACjAAjsIMQyDV/2DaFNgLspjcCxoAhgcsaXtmNisjUTa+XFTICJwEBJqBPAsh7vQo6S6YJcAoGtZQHLJCV4IUjhFSew+eWgZ0y5zVXTmva3Lo2sUCaDXnyc5qRTS/mVJJWLMJBR3o2u1PSdGbkEywZZeRday0vH7spcho+m6J8mysh8EnY5gazeYzA3kIgRkB7QrRPiK993f30Z7pHjwrPE8IPIPGF6YplNyCgTS/Mhte0/D0DHTSv6J/ZwxuMACPACDACjAAjwAjsSgRoyUMC3NFkp7Rd2XBu1K5HgAnoXd/Fp76BdN5ME4jeRYG5FjMBnQhRGrx58hMVxjOJgM7ZU3ENGTkywZqtP96iDLWbtYsq3SyFET1z9cv44C+TjVJE/47eJHBI2NHNYeMZgd2GQEAuB9Gfw+/gJ/BzdgM/aMsTth8yzWGbQ8dnPSSgdU84Mu9M8gw4TEDPwMEbjAAjwAgwAowAI7D7EaAlT2QBKOfvfhS4hbsRASagd2OvbrM2ySfKPPJc86EkQlsjc+6x+QvkMXVumfzVbbzkXGMyCqy1dqha61HZ5ePmpZXPXzJNww7Njzecbgns0BblNDve8JwHcjFGgBE4KQiAfV4loE1faF7AQWuesCQLQtLZ8oQRfpxEJ2ipeOg3TRz0zA7eYAQYAUaAEWAEGAFGYHciIK99iPSIPB+8O1vOrdrtCDABvdt7eBu0Tz6B5pHnmgwldC6Wdc49Nn8BWe265fzVbbzkuo1cB4mJujZus6whbr+8V5bzl5SP2gVyvOHr6LudiEO84TuxFWwzI7B7EZghoF3hm0LYM60NA3AIXyKgrVAOgnNEPtHjmICeQYQ3GAFGgBFgBBgBRmCXIyCvfYj0YAJ6l/f63mgeE9B7o593XSvlk7Is77qGcoMYAUaAEWAEGIHtjwDRyMIVfvh2QeEFjLPrBwyzG/LMrhC2F4TlMMJv9oDe/t3KFjICjAAjwAgwAozAqURA5jpk+VTaxHUzAutFgAno9SLHx51SBOSTryyfUqO4ckaAEWAEGAFGYM8iAA46aD4oZ1d4bhDo2QrjcFgiFLA5JaATOOgZ+Mj9GS7UM/t4gxFgBBgBRoARYAQYgV2OgMx1yPIubzY3b5ciwAT0Lu3Y3d4s+eQry7u93dw+RoARYAQYAUZgeyIwQ0CHG9405kbAPtNHYp9BQHthMOiVcBwzbWMCegYO3mAEGAFGgBFgBBiBvYWAzHXI8t5CgVu7WxBgAnq39OQea4d88pXlPQYDN5cRYAQYAUaAEdgmCCQQ0K6wXWE6wvCFSZ8w0w65aSagt0nfsRmMACPACDACjAAjsB0RkLkOWd6OtrJNjMA8BJiAnocQ72cEGAFGgBFgBBgBRoARyERglX5eLeb5wvZ8w/U0RxiOMDw/+ICAnn67rnBTPaBXVbHECDACjAAjwAgwAowAI8AIMAI7GAEmoHdw57HpjAAjwAgwAowAI8AIbAcEJALam9rjeZ7leprtLtueZnua62muazi+5fgWE9BTlPiXEWAEGAFGgBFgBBgBRoAR2P0IMAG9+/uYW8gIMAKMACPACDACjMCWIjAloD0hnPA1hMHLCFcJaH9i+xPXNSQCOvB9xoc9oLe0a1g5I8AIMAKMACPACOwVBPD+jLTWTveSs0BaQc5nBLYCASagtwJV1skIMAKMACPACDACjMAeQgAEtLfyskEnaLkvHFcYvq97pulrrjfxHMNzLM9zQg9oJqD30PDgpjICjAAjwAgwAozAyUBgSjGjLk8IN/wEm9O52qx4MoziOhgBIMAENI8ERoARYAQYAUaAEWAEGIENITBd1Bie0CbGMOCfbaFOhOKLgS90L3wJoet4juu6lu1Zlgg+ju84vuMKnz5TPcEqiRMjcKoQkF/0lEc+VXZyvYwAI8AIMAKMwAwCIKDDb98NJlMDzwj9AqZUdDjBImKap1sz6PHGFiPABPQWA8zqGQFGgBFgBBgBRoAR2O0IhMSx5wrDFYbhusery3f92fc+enfpq9/3Wo4whHDd0P3ZsVzXsD2DCejdPiJ2dvvykM5ymZ3dWraeEWAEGAFGYDch4IfOzoiIZgsxNr2RthIgzQ13+cFtfjv8MAG9m3p++7eFCejt30dsISPACDACjAAjwAgwAtsaAU94rnDswK9ZTCzxf9/yjw97yP+5/wN+/2ef9aHP/ruy7Ajfd33P8j3DExMn+OiOMMMY0Kvuz67w2QN6W3fznjFOJpfzyHsGGG4oI8AIMAKMwLZGYIVQ9oTQhOj5YkkX/3BMNHyhuisPl2GmFbLP1vStHdu6SWzcLkKACehd1JncFEaAEWAEGAFGgBFgBE4BAr4XBHx2LOEYQhRb4qef8s6LL73jwsvefeEDX//Hdx7rKkLTNN8zfH/iCdUJPstMQJ+CjuIq8yGQh3SWy+TTurZSG9EvHwt5bXXPKx3XjxxPShupN01/JH+eman7I3rybKbqmu7wfX8qBr8ZOlFMLiAfyDIjwAgwAhtBwBW+8EN2WRHizn++57KnfvHip/+/B90qPvtdMXSDgNCIAO2vxIZmD+iNoM3HrhUBJqDXihiXZwQYAUaAEWAEGAFGgBGQESACWiwL8Y2SeMSPvOvCqz929mUfP+fKO97w9qWxJXBVf7oAACAASURBVEzbEb4pxLIvlt2AfYYHtO0K1xNe+Fl9O47sBz311JGrY5kR2CoEZFpQYlPniPJRm2IZFFKt+fXLJfPL+W3O0Ol5nuu4dphcx/U8jwqvVT/K0+ERgbQR5ysXoL2JAkpm65e1xeVEtUII13HJnoDemU1xPWk5afo5nxFYAwKzr6FLPjBPmeQjOXdbI+A5IctsCfG9/r9cc1vtnNvaZ95WOv+2L115s/hcKZilUddjgjVz72xbN42N2wUIMAG9CzqRm8AIMAKMACPACDACjMApRGCFgDaEGAvxn2XxoB/7wFnXfurIZX971hXvecPbjq8Q0MISQThoyxOOI2xH2G7wYQL6FHYcVx1FQKYFZynErC35qKjGdW37vg8+V64VtWTrQxn5KMiyhXE5W6e8N02/XIZkqohytlRAdVtdRaJ+9Jfn5XUljMBIQMkUdmJFnMkI5EKAGMaM0tMyfJc3A6St27V1sAcvHnSFUIR4/xcX73ebcfA2Z/9tyum3FS96tnjL50TPC+KfIbnhawmZgN66bmbNMQSYgI5BwhmMACPACDACjAAjwAgwAmtAwBdhCA5DCFWIrx0X1/74+05/4D0LV37qzCvf9Ya3l0IC2pq+8CbQi1UPFmB5vtdgyxYXPTkk10moZYtw8n0/4gq6RRVtkVqZCozTuGk58lGbYlgiAY3ADtn6gT/ckGVryUIrTLQJISdzCqts2zYMQ9d1M0yoJdEqqiVxb0YmHZgmoFL4WVMzUThDLRyT4aYd8dFOqyien6afTLJt27Is27Yj5rmOS1VHdsm1pOnnfEZgDQiAXJ5SzMkHhns96XKcXGwduVK9W0ezrsOuvIdMkQluKEltSTt8rW1E+fW9AHD1HhcMS+OOHSGa4r9//OWNcwIC2t1/m3rotqWLQwJ64AkriNIRfGBKmpK0BnM+I7ABBJiA3gB4fCgjwAgwAozA9kAgz7Jz0y2lFSM00yYJm16jHFZyrvJTgslcq7jALkXA90N3ZkP4EyG+VhbXPv5dCw/6i/1XffzIVe8IQnDYwrQD32fhO4g9iEXvtkUj418MDm6tjopr+j+CnNpccCJmy/ZTY1GG6DwItBf2zG2I53lg32Q9oN4Sv6mWNbU3UVViJumXm5xdl+u4aAJo3OxvqtS2baorQ79MEEMzaZAFkJggiyHPjWiBBhI7bBgGCGJSAj2TMGEXGWCaJuFDQrwVnucZhqFpmqIoqqqOw0QVgZWGfk3TwFCDh8V3hmaqy3VcwzBGo5EyL41Go/F4jNrRRkBEquKC67i6rquqOpymjEpGYVJVVdO0ueDj6mxZlqZpo9GoH0uDMKFamC0z1Phb4TtuNucwAmtGgNhJmWQMecZVBtMLKEg3vDPsbtab6OR6Q510s3nNTTglBxAtGyKzQkCHQKWZAwp3FdW0clI+5j9WMCUKXwqYzv+SctK/IsziLOmeigNLfKHxjYtu6Z6x4gE9OHLb1y6+WXwmDMGBUvLYmB7Hv4zAViPABPRWI8z6GQFGgBHYGQjkWRluw5ZgwUbLflrFbZappDBRiIS8jPg0bZYNsh7P80BzyJkRmZgmec2caL+cCSV07KaPh7UqpD6NtI42YfzcYlQ+LhCSMg5pMsX0jOtJy/F937Ks/A0H+GnakE/mCSGMMGWXp6PANOU3BiFNXSd4TpMqTSQowy5wPM/yPMdzgyc7v31MPPSH3374/h89cMVdZ139x2985/eXHWG5erDa8uwgWkf4AKjh+JbjmraV52NZVh4nTZgq/zEtyzJNE1hlfJumKeuXmwyZkAQ7Cf4O3+Dd9PREZBxcg2WF1H2U6fs+FGZYG98VsZ/UkgBeGAPANM1EY0EdglUcj8fYnEwm4MsIgexRZNu2qqogB8fjsRqmUWZSVdUwDDpfkc2yQPgIEbzQEgRlptbVnXn0U12u445Go+FwqORIaOZkMgENikuAbCqpJcE0zcFg0O/3B4PBUEqR2obDIYr1+/1erzcej/FnJJQitWDT933TNIfDYa/XQxXgPamufr8Pzd1uFxwpCui6jm4lPRH9sB+d2+l0ut0uVdELE+zsdDrtdrvVarXb7U6ngzLD4VDTNNu2s0eOEMK2bUVRWq1Wo9Gopyfa2263B4PBaDTSdd2yrGzXe4CjKEqn02mEKb2GerPZbLVa9Xq91WopipLxz6WeFULout7tdqvVaiWWqmGqhanX6+m6Lo8WGXZZIcuMwJoRkKlJ8JeuEE7o5+wFdOcq1xzyqgiMZW8KAU2EZqgZddlyjbBtzU06WQfI9k95edlHGHAG1kwbEieI59g6vQfgIh4ZSk8J7hn9U/oejtLoNaKhV5yXp2YkVDoW4i1fKJ97a//wrZOFW/UDt1bPvvW7T/lt0fCEGRRfUcUhOBKw46ytRYAJ6K3Fl7UzAowAI7AjEJBpx8Rl5zpaIS+oNkunbAZ0gn+E4xhkfMdrT8uRdcoylZcz88hkGGlIW3WDJsteM8drJLXxXYk5VD5NINzIzjzjAWVysnvgy8AhEoGSaC1luo4L3jCRKUMmOQzC6c8wDPgtkpIMwfM8MGumaWo5kq7r4/E44gpHiCVWpGmaqqq6ris5Ejg7wzASVSFT5n+FEOPxuNfrEcE0V1BVFTSlPBLSqvM8T1EUsEhtKQ2lJDfLdS3PsYTlu6b47n+Lh93wtsPX/Pm+yz961jVvfeM7jy67IQHtmcIxTNNe1m1lYp5Ql/snhp1+b+6n3QvYLkVRDMMADZdmNthhXdcnkwloxF6vJ5mfLLZarU6nMx6PaYjKfwrARV1g2/ZkMhkMBt0wEePWSk/tdrvX6wH/tDFDtfi+r6pqt9tNtjUpN2J/Iji4d4X7KKPRqNPpkL2kEjnNaaICzWaz1+vZtp2oOZJpWVa/3wfBN5fmIwaw0+lMJhP8f3GKiKgl3FzH7ff7tVqtmjvV6/XBYJA9cnCjRQhhmma73c6tOyjYbDZVVYVDK7GKsv2y17OiKNVqtVgslstlmaWM1FipVMrlcilM1Wq13+8TAU2nUMIExiNf1/VOpwNtNSkB6lqt1mq1ms2mXF29XldVFdoiJ3+5FUIIy7IGg0Gz2Ww0GtNhMqNKVksy8Jl7N851XFVV6/V6sVgslUp0eKJQKpUWw1Qul9vtNgh0P0wRm2nT931d13u9Xr1eT9QZySyXy8eOHSuVSt1uF+x5tn7DMIbDIexH/5ZjCd3abrdxx0XuSiiX+5QsZ4ERWAMCMgENRpWckEPScdWFViKgpyGBQ2p1DZXNFpUJXH+V7F6tkWybPW4bbU0pXTd0Tw6uecQxTxnhleZIe1aJ47ktmTo7Q38AOw6eEtOBAsAYAmiHZiB+2eqdA4Jxqi2h2hO+eNGH24dvOXH6rerCrdrBWxfPv/W+3/oT0feDN3GQfzfuEmToSVDNWYzAhhBgAnpD8PHBjAAjwAjsDgQia87NWgLRgip72RbHMKcB8Okj90bZJ9GyLJCecIzC87lgN+AKSgu/eO3Igc3goSINoV2I5wiF+CZKlPSntd33fdu2x+PxaDSCAx0MjnzrYYIHpWEY9NBuTogMw4AT4jgzKYoyGAwURSG3rLn2u46radpgMAAB18lM4DEHg4GmaaZpgqNJQx75sBz603TLJFej0eh0OoqiTCaTbM3YC1e1RqPRbrdDkmfOF3z6FEUBjUJDIq2uyWTS6XSazWa32yWWLUOoVCr1el1RlDSFxDFhTE4mk1arVS6Xq7lTu91WVTWn/aPRqF6vLy0tFYtFIijb7bbEPw/xj8OfKySgXeEIzxLfOyoe/pi3H7k28IA++9o73vTuY5onbM8QvulYmq6Ziqp1T4xa3UGjdV+lWi0fr1Sq1YxPKeDiykTzZUBk2zZuFYAgBtE2p2tLpaWlpVKp1Ov1QHDLRH+ko/G3VVW12WyCPQRLWJyXarVat9uVAx1EWoGK0MuKotRqtblmUwGyf64fNJxMu91uuVwGzVcqlcCSUXOINCN6FGwgcZQRyyOblmV1u10QbaRqrgCOOI+f+2QyqdVqi4uLS7lTqVRqtVpzzwzogvF4TBzivF5d2V8qlTqdzjoIaBl5Qps6olQqoYJKpZKfgNY0DYMz94mhKp95IpOBeOeCgM6vnAj6LSWgDcNA92VcGfFsQa/Xq1QqcYK71WpFGiUT0Hk8oImALpVKOJ9HTvi18K5JuVxutVqywWQ5hAjmvMkIbCYCMkccEtAIwRFUQUzrptCRRJKSWhKmJO9mtmuTdMFGon3DR8BCZKYEMeAir+RVUnh9Bnihc7ozrULuHYmAjnqRTz2ms+q8z2o87pW9hZtPnH7r8FDgAb14/q3inm8Gr+nQPd/1cFdi5S7BpvR4ljW8jxFYRYAJ6FUsWGIEGAFGYE8hQOs0rHnmEo7rAwdud7QyB/NInr+y5zJRtxDIvIx6Ec+RnvKOUKxwKaVHpBGwUtM0PCtNDk0Z+hFCAY9747HlQSxFHnMGm2yaJulPW1JiMdzv98Fswpsy7RuPJDebzX6/T89iZ1iOXYZhkLdXZCUc2QQbValUOp0OXPnmjgc8SF6v18GhVDMTmLJqtdput0ejUR5XSjgON5tN6I98y2QNaj569Gi5XAYHnYa5jBhc7RbDVMuRGo1GtVpttVqyq13GKO31evBzrFarOdTX4DHX7/dlIyOyTIyCg1tcXMyjvFarHTt2rF6vj0ajnAR0s9lErzWbTeCJb3INxt0XuqmTk4B2bV3XTHWshwR0r9FqgoAuH69kfBZLxaWlJfhpZvuxwhd+PB4Ph8NutwtSaS6NCAIXbonoU2omtR19Yds2AuBCOVwpiQhOE5aWljA4cxLQqqo2Go3ImM/YLBaL1Wq11+tZlhUZM/FNy7IwOGGtrJYYTyBGzVlcXKxUKsPhMPtxDUBnWdZwOGw0GhiZieEI5P9vpVKBW66iKHnODOPxuFarlctl6M/zXa/X2+027h7FAUEO/lxwwsV9C2iuhiliMDLprw0nXNy9SPSAxn0FVGSaZq/XoyASkVMx3VSr1+vgK6vVFYIYIWIwMiPDEvpx0tZ1HbEjoKper6fVRVU3m83RaCTjENePvZZlwX2e3J/zCOTeLke5gcLIt2VZCMEhqyVMZAHtQreOx2Ncc4FARCdtUnwSACs3v9Vq4VEJuIcj/ka73cYdytFolIeAphAccA+n+3aIWAJt1Wq1XC43Gg1cR2Tb0jCnMiwwAmtCYOVaNn3H4ApVKlOcri+8YNwFaokdzkNu5rEDLLOsNjhPTT95NJyKMrCX4mK7wg/OWlN+lvaCvY2GxchpMIEAdf40RglFhtaEmAgxDr81EUTMmEZIWfUlD+uCgmi1KFTWv3HRLcP9N/UP3aKcfpu6/+bvXXir+N5Y6EIYrue4qwT0ZvV41A7eZgSSEWACOhkXzmUEGAFGYNcgkOh2hEUsVq26rpODLWKPwutW13UjlsA3zV1GAj1wrOPxWAnTKCkpijIME8rg1UZ5/ODgyjcajXq9HsWj7E8Tomf2woR1ILjd4XCIqAhEEGd0NOJdwoM1QqNUw1QLEz3PW6vV4CJKfpQZyl3HHY/H9Kw3VKV9VyoVcGSNRmM4HOahaTzPA8e6tLR07NixNGdBYprgUVir1QaDAQUiWFmZJDXDMIxOp0MPiUceJ4/wNeVyGRxcs9kEzeRPU5LuIE/TtGq1evToURwo02QkE0EGD8SlpaVKpQKOb6p+um6IVQOOL+5HGbGcNsHRE0c5V/9gMGi1WqVS6d577yUlGQLYbdxgiBm7kkGV+r4/HA7hu33vvfdWp0l+bF8GB8QiwI943qXV1e12j4ap2+3K9cqyfGxA/bhemgf0xBemb/jCdG1dMyxlop9Qx93h8L5up9FqVhv14/UaPrWU1Gg0KHBqmg2IW22a5mQyUVWVnKBrtVoG8pXA/TqIojAYDMiDWK5ClsnDGg8NgIZGRAKZHYvI9XoQUhbsvwxaRMbfzfd9TdMocgjFwcgQKMRHnjMDHrwgy2WmL9IQ2tVqtbrdLm59ERpx47ELp02clrvdbs4QJQgTTHcXMs48pmn2+/3uNITx9JSf9YvHOyaTSTY+4KBN08RlBRpx4QCHGL9BiADEuAmKJ1Qybt0BH9w3xfjBtW+QkqhJiqJomkbDg7ogghLZj8GfrVyuE/rRobLyuH7cgMGDO6McCZHEMZegmPuRkSNv4qkmenCH7iIrswk14/WAmJPQzCQDf5wfEJyHgmJjSqBpGiIsQRhPE+5byw8GZesPeDzPw01rdZqgWVEUeKaXSqV6vT4cDnEqpuYT8pTDwp5FIJlYXAscIZnp265rOUEYCTq1ulMyNfh3e37wQgbHDz4bZiF1XV+tyPNd2w6mBKc04VHIjZjg+76TsuAJnIilsFTzm0q8s3wPIGKc7oquLkoTsWiKey3xPVMcM0XNFW1b3BdESbJCAp/uF0SOXtl0Qub64//+7SNPE+c8Xzlw8/Dwbc2DN06e8npRdwM62/Jdx1+9IZE6TU5Wz7mMwAYRYAJ6gwDy4YwAI8AI7EgEvDAhpCM54YKolWkOcuEhod/vY7FK09mM9oNj7Xa7cDiqSQnOR1LGqthqtTRNy6MfLyzCC4XgskTGy20hRyf4wfX7fU3TyA9UpCTLslRVBUFMjGdEIFYL8SiXlpaq1Wq320V4xxTFK9mIQYxgnRG18c1isbi4uFgsFulB9WzlInxD3WAwqFari4uLGQQ0YiyAhi4WiyCgKVJwRi2u4w4GA/g5Rth5goWEUphkD+i5i224b4MCq6WkqpTg9AcnUAxvqiJCo6BR0A8HNyLaIqOIhhO81PEqsLkEBPSDA2q32xh19A9KE0A903u0yHhowzdl+r4PJ18M/k6YwI7hpgtRV7KA+Bu47USqZP2ybBgGjo0Q1nRgBFXfzUVAe75hObZue5plL5vWRNPUyVidjJWxis+UtJn5BYND/9k0G9A0cs1GdG+Qg6PRSElPeIkZsZOyflmmdxvKoc81TUMw8SlnlfALpozOujLOsgwCMRJZSM9MuEVomiZGTspKeaUS6LfCRAHWM+Kf0z1I0h/p9ETjKSA73b7MaMGa7KfqEOkbDUFfyPGXIjKK4Skc0pAt0HsmoRzkZuQZHbleuUDa+QHg0zNAdI6iQWWHiRqVWHVEebw7KNh0RE8Ek/gmXXDlAS/rJ/tt2060LYIPbaKl1F5ZZ6QXaPzLh0SelyK1ESTlTbkJkSrwSBYKUC0wKfL0QKRMTv2RsytZAla61Woh+gcCCiEmFTTDTpSP2Myb2wqBwCV26w3aOAG9EkcYoZ17lui6YiDEcuhXO/QD71rFCvxqbT/4uAGviUrX3bqVf1DAaIceu2NX9AyheGLsC8UUqi7s1YjH665lfdjbdhhyIv/BIIvl8oYnVFsM3QDDpilOiOBzny16bhBSOSlF2ygT0JCBuOsHHTGyhSJE1RSfvtd8zV3/dcOv/etlN3/9qmd/9dpnf+Ehzy49/63iXytiuFLTnJ4yheh4J172oe8d+Llx4cZR4RknTr/12OlPF6+8W/SCiB+e7Qe+76HXe5LhnMcIbC0CTEBvLb6snRFgBBiBU4JA4hqPFnKyI5KqqtVqFd61pTAVpYScyHetVlNVdW674P4MjrIURlmFYmgjz1mpthURgQKIDMqoCM96t9tt+DDWpCSTzrLcbrfzENAIvgECGlobmQkuluRHGVnKpjUBUSyazaZsYaIMGxCCYzKZEFmQphngK4qSyM7LvCrJIEb7/T78BMF0pOlHvq7rw+GwF3qghxRo6hdq6Xa7o9EI7DytzNOqIJqDPOiVWBpKCTyjruvk205VJP4d4GeK987JHNwkJYEpQ89mawYHARqOqDccnvEdp55Ri4wP1QsaxTRNWT9IJStMdizJ1CTpSUSGagTXgzLyISRTyXCt6wrPFa7vO+K/j4mH//A7zrz/XQtX3n3etW/7v+/+vu4LSziuMAMnaOE7UtjDOUup1ToCiaomYXZ/8hYVzhDkIzOK0a5IeSKzMgT5kEQZyhN35czM1kDGk5BTLRXL0I9dxJDSIWsSMvRn6KHmZAgZh29kF9VI/U45EEg5NvOcV0kD6SRUaRcJpJ+ENBpX1ibLUIXDSS0JslrioGUWeK5MdcV1kvJI7XRIHoHUJgqRKtaxmaiWMvMrtG272+3iZi0CLuGRKbomEgj5dXLJrUOALkwyjegFb4Tzp+EQNrtyifTcKDmIqA66ED1PHNPF274gnvee/uNe9f2rn/eV8572+Uuerv3GneILxSDOwzQh/IPc2OmeNfyuuDy7IuBSa574t4H4dFl8oSruVcXQD3xv6d13a9CaWjQnSvKEPPnugYR8cmVeSDd/WxF3/pv5gvcOfvq1/3XxLV8992nfeODz7Bd9UHypErDSsykDz1Wz0U2OEEMhSkL8/t8VH/6r3z37GUtn39w457beOc/unx18euc8u3HWrf/14F8S/7gY3CpwgprovZKz1YZby0KU3K898vmVhaePCr8wLjy9f+iW/7zfM8TfHBNjYXq+403Z57kNT9DOWYzARhFgAnqjCPLxjAAjwAhsQwSwOoJhnueZpqmqKpyXJ5OJ/Jj5cDgslUrwkCUumBjnuCsuIi30er25rcZL6hDskjxhyVWWBNpFdeV51Rhqp2e94cFKXCr8VcGo0jf29nq94XAo05QZDbFtezQadbtdUhIR5BqHwyEFgJbJvgz9ruPiWW88Ia5kptFolNMxHDXSs8yIr0LOjBkcKCKH4PBsahJl8Cw5NMNHEuxn/BuVyjcV5i7gCUMSMpAENUkFSDkJtEsWyPWMioHvSKRU8GwpqH8qn4FSxi7Zhogsa4YsF5D3yvkRWS5GslyGMtOMRAEcIheOyJJOT7h28PFcENCP+OG3nXXtXYeu+NgFV7/jre8sGcFDn54rfFf4lu9ZvsDH8YLM/IveiAGJ9sfLIEeydo6YpgH5GCRUJuLBGmH+MZbkQzLqJp0bFNKqkO3fCLWXqJ+Ug6bEJkqutTmJ+k9hZpzSlVtHhiU2M7KXzjAy/vKBVD4iyGVkOVIMm3KBuTJpSCwZ2Uu3sRNPkomZ1FLSTzojAhWgQ/IIdFSiEKliHZuJailzrkI6R3meNxqN8EwMbslTWC24QuPW6VyFXODkIJBIQDuepwdxK8I4CKAC8fq40CZwjonMIAWjoDJ4rVxwHAVAQGSGcHOVo8zZWiiBdjv0dB4I0RCdl3/w3x/x/G+dfWN5/y8MCjcaB28zDz+nf8Zt1Uuf+/nLbhQf+rLoB+63eKVeLmIdlGXESD90eYZ7dcv17/7XpZe+47MPf85nTn/Cdy657SsXPeOfH/lLnTf+hei4wlphTtfw7j4nbI4iRD/8qCLwOA49u6mPVkAiEGwhNCFGInD6Lqnia8fFvyyKb7bEcS2gepdDa4VwqS2JcKM7zFDPdwaT1971mctv/K/73VQ/71m9hZv1hdushWeNT3/W8TNu/swFT/U+/lUxgrf5ii2IIr0ytwn1y5WsuIIbIVNf98Qf/t1/XPuc9mW/fOK0W+zTnj0sPM06cJt98Fl24RancIsXfG6un/es9u/+mczjp2KoCvHpyjfOe8bw8G3uwWeNCr/QPnTz/3fxTeJ7tugKoYb+7+OwXaPwWwkZ8GH4PQrxMUOEgWfOEcjFGIHcCDABnRsqLsgIMAKMwA5BgJZGWDYbhoG3+lSr1Uaj0e/36UVYnufhhU7FYhFEcHX6wjT44SZ6/TabzeFwSMuqNFRAgBKB25lNcjDNXpgoB4uxDNqRqnYddzKZIGy0OpvoMXj4s2qahmCOk8lEjkcZ8SyLtEVGcq6MR7zzOLhFauHNRASolxP3/v/snQl4G9W5948kS5Z3O7GdPewUSLlAL1+h7S1dPijkZrGi3TshgRsKLVC4bL1AWBMKFG6A0jYpZacQKAlQAglbIGQhm7PZcWwrliVZq7WPZtHMvN93zpHHiuOEkAUCzDx65NFo5iz/GWvm/Oad/3vwhXRnHXwd9dujqoAEEg8SC1IWJGjfA1N++Agqf6Kg8rkxE//80CNunFNeBlHCLxL+nPMfzB+SjdAeZXx4fAyEvgXH1ZH8W42wg/ZdpPxI7rv4u/XpIAp/0/U5wuP/IMooh8hhVKGoqswopR31mcNuHr1FynFcMpmMRCI0y2VXF86t2t3d7fV6Q6FQLBZTbMSPesvVAo9EAeUWKSsKHA4eJQQzyhEjC+ywTJ2CeZBZQj65/c0NhJz3Mi0qg1EqPyCy2EQ4Pxz18IyYpUEH54yEjTXCAvQDPPrhrhObe8tte9G0UKE1XdGUKW1kSxoDaHq8wNqPZvSW2zZMdsDydmAw0cU3ifdv9qBqOQXyzIslogEvS9ghPc1CVIIuCR5cuW5UXc/4pvbRtq4qW3+JbcBoixTbO3TT9px2RfbuVyHEYYM4DDmHB5LTi4Fh77h+fxI2RbPz/rp1onPzyU3S/a+DV8KZ9Einh3C/gu8TGUyZ3QAv7cqYH2qrdXSNadpT27haf+nOyZczLX+CT4J4H2aBpZXRWwh0nphhcJIo8wKWIw3QK8Ddb+6e1OQb29xfZg/pLWxJo1DSxOvsssYOWgevd3grHeu/1wxv7oSkcqRgQp67x0DpfDa3BN9vkIGTCK2OAI5KtvzRN7qh32BOFTv54sYUMqdRXRbZoKhVRjbQOLLICoamPca69ssXQkAAEbgUQ22gxbynwgb3FQ7WllqeCJfYg+gyMDQKJS2BqiaY8RBsBugF6ATYyMDqAVjaAS9sgyWfw+Nr4PoX4boX4foX+VtehH+sx6z/i/MZD1WozqkKfCkFVAD9peRSV1YVUBVQFfgGKECHedTFkmVZioDdbndPT4/b7R7mUExdLGgmpfigTWp0cIqNNNEnRg9RCJqzKJPJUH8AGgk7LBo3/6v9Q2X3r0gZx9LgbhoXnG/ROAwrK+NSZYaakNDoKmWhUqxSfL91CAAAIABJREFUY/5XXzivbKXOfO0K0J115M3I3+lHXtq3uQRZIvQZj2ElGfr64fRz5leMe7Ks+m/fO3PJ4iXBjIgHe9gcUsLjmiyJelaGmgdURgXQB5TmML/Y/1fuMAsaaTNa+DGtYqRqj69lB+n+Qb46vvpwgNYc4e/qoXT/MKrI/5U+jM0P0NeRFx9G+comShw9z/PUvcrr9dJQ6O7ubrfb7fV6g8EgxdCHotXITVSXHgMFFKyIn9eRJGwlkQRYtnn3f/8p9tcV+COAlMUBtSkCoIlHwr7tEAFYEVgCTZVvRICMhE+NyuIjudWakXL2xN2Sz7GgZ3xTuqQhhaaCrkGqmh0pdcSqmgJGa8pgj6IZUTQ9ZbDvRpdFzA9A/AsANGXNBLQTRE3O3LlQ7qyIu+BKwCpX6Fd37jbMiCJTFE1N6W0JvY0psPEaWxpNy2rt0SJ7++lXwMpOLBcrSxmiGg0AJ71WrgeUGYyJRYAPd635fmt/dSNX6GQqmz+qmg7PrYMExrgiwaS5wG1ijwIJHtPnd3Z7nQ/uGlMfK22UCppB2wqaJg6Zw8jUXWhpm/Jf8Op2YPHVCCXR9K44vbOQo/DRDA6g7pVjcx/3jmlK6axsgZ3X2RlkiaG6uMHGFzeCrgGQAzQOptDhKbN56+6GwGCnSMOHgtxphDnl+7SdDICHT9363O5TZ6dLGhg0jUVmDllZDY6AThsdIa3Jr60bMFjZsqZEoT2ms3TUOlw3PQUhXhxIygwHDDloIhJ2WaEvTwbL4uPg3T3bR1nSGouALFF0GaNz9KKZMGORfOmCnvOv23HOvK2nz90yuWVTrX3LKOvW8lk7S2btLbN7y5yecufOWueKk6yB+1+GFEhxjLnVSVXgqCugAuijLqlaoKqAqoCqwNevgGJhHA6HvV4vdSh2uVx9fX2hUCg/xRxdU8yKdJg07HHy/Z+oVaDtoXdyWCxz/gPaytiMhpAobfjC0ZeypiAIHMflP+eutJCuM+J7Pq3OXyG/U/nLD2U+f1t1/tuhQP5+/3b06Jj0AmNiCWQa/oUBdHcf/GrGoyef8b+jahec8r35z7zoimXIQE+GLDaD/qYC6GOinlqoqoCqwLdXAeUkQq9MlHeO42KxmMfjUTJk0BABn88XjUZpwtVvryrf5J5lAXpTsHDF3tPnbh9lWX+is++3T2JvBxbHtLLUoVcmf0hmP9xVSQZewt+FZehhsSlzBwfdInhkiMg4+xyPGTSNacV/lDuvh6gTro5gcQBY3dtzwXW+Kme8xJnWWLB7g84RKXXsKTbtLK3rq3IMFFgEbMtQl0DmtMbSflILhHPBuQey4BAAg82kwk8pt6URxzEG5+L701rfyXNDZQ6uqAGKcHRwSmdN6W0pvY3TYgANCNPbTu20jPlB+MCP43CjAEyu15T8KtxZmcGoOg7tly/cVmnmypuFAoc0+oo9Y5zcDU/jSiUcYjwUuJ0l+D8OsHj1RxNsuyvtbp0pW9oKBS0pNF1AJtDUS0WXp4qavUbHulNaYfsA3phWRh3BSCg6TvMnEWeMzcn+i27xVDckRzWnDHYX+lkUmVKlDbGqJl+Fo9+AeTEgh6TDQdADqG5trRkzazIpXci5ZCjGKzT9RQJgBxOwLeic0BgptmeRGZCZQSYGWQDZGa3VXWHffULzJzV1wZ/c3FZl7hxt7xxlW3tqo/D6OmDwfQ5gBHizLXnVkzHzAqYu94peNl+0/zHxn/fsPX1uqNCa1drB0IgdPLT1SXxXwBQpsPkq6nvK7b2lTnexw1No9xudA8WN8eLmaJEzbnAk9I5gkcM1qcXb/BD4+SFzmEM8DtXVVAUOTQEVQB+aTupaqgKqAqoCx70CyjiHwlyWZcPhsMfjUbyVe3t7lbENHQXRPuXTWGV0RGeUMpWZw5CBbjtiyYdRGt1EaU++JWV+FcoKI84caM389oy44UEW5m+rzn87FMjf3d+OHh2TXuQAdC6zoAg4COnZV7rsTa/+5Bf/e91/L+/x4ZFmRuKyeQCaDszoOO2ArVLG4UcSF3bA0tUvVAVUBVQFjq0C9CSSf8mhzHMcR12hXS5XJ5lockKPxxMKhTKZzLFtmVr64SnAAWwKbx1tyRidSWTyl9o/HG+GD3uBkZJZLhf7nN3XQlcAbIvRK8Bz63tmzX9/gnndZMeGM1o+OX8uvNUJPhlimEFTSjlkdnHIZz3sF5ERIMzBp73vTWncW2aF6qtSOmtUaw4XWt1Vjvgld8Hdb8HLHfDwmq6CGWmDHdNhzD3tO6ssQBwphrws9pNFIPQZR8PSpHn0tE2tmVMQvWFxZ7kFipqgcm4a1WV0toCmzlNm6xxl21Vt66m0pQz2JJqWRNMyevsudOnWGuv7kyzRO56HsAgC7qQs4+QQCrRVZnBAd7f02elNoTIHaB0JNCOsM3cU18HC97BHBAHQuYBlSp/9AA8s23XWXHeFM6CZxRU2yoYmSdsoIKeA7GlkSSKrYGgeQHU7y+3h+1/DmRLp01i8jBMkKxUnAN7t3v5vV/YWmqJoJo4ZL7K7jKbucY2pX82Hu9+FJW1w58pQGUbPKb2NNThkQ8OuMQ58H4JMSsg8LRIvo3uXJZ7LffDeJHNnucWDZoiFDaBxSsga0pr6ii3+0Y27xzXE6x+GpbugQ4IdHGwR4Ik18SufgGW7hvZMf2LpySZXbYO/FLeNvmLFDvpKGh343oPeCYWNLDKn0EwJ2eNoqqhxDqBZYY01rnMmNI4osiY1Dt7YIpRcnipqpAA6UOzYNaFBvOMf2OREnVQFjo0CKoA+NrqqpaoKqAqoCnyFCuRjMkmSaFBwLBbzer0ul6urq4s+4BkIBJREdsM2+ULPivz1vzA8ef+uKw+fDqto/zW/1BKlVcqIblj5ygqHOJNf+yFuoqyWv606ryrw3VSADrJkgAgDu7rgs42Zbh+ksWFjNiOnafrBLMjKa4QsOvnQ+UDz301x1V6rCqgKfAMVUC4S9p/heT6VSgUCAXqpRq/WaBboUCg0LOftN7Dr3+Qm5599lH7IOHR373892lVh5Uh2uHiBdetoCzyyAqLE1ZeuSQBkFttxkLkUwKvb+35+2wbjNE+pI2ywhw12T7G9p9yO43nnPAm9ubhbGs97oEhkpRUYBJNUiLklrICDhTuS7p/d3Ftu6y8wJQrtiSJHV7Fp00mN8NQnOPWcADAgQhDE6QsixfZMaWNaY5GRbdco6xcC6Fxo9pATB4Ag4gJ7WLjmmcikOWmjQy5wQmHTAJrmRzN7axp80+6CB9+EF9bCA8u6xzX6icUEaB1MgS1aaAsW2daPt8F7u/CtaYAMuSSgOYrzSTSOu17p3VqOcycCMrMI8/T2cjO81I4BtIgDt7HoWUJ1AwD3LmuvwTbNidKmlMHJaxwycuKw5YJ6puxysfq/OENrGtXHkb13VOvy7zWBD0dQ44higaRFpsQ/JkO3OHDJnZ4yW0BnihdYmQKbv9yxvOwS+MtqvEkcIASwnQHTw/1l9n6jJVHkYDVWDKD9eCwyFMk+tMPwHP53ZgE+9e7+yfV9tY3piqY+NC2EZkJJy4DG1DXavvH7V8Ci92BrGILEizpJwP8ASaUYIfWyMsggMCx83rPmREewyBZCdUkNzojIFTqjaGYQTWUNjjCaymltWa2d1+AIdF7nHEAzsvrGCJomGJr5gkZB3yroW/FMUWumoCGAZrk1db2FZneZY/v4xvWX3QgdcQgm9znG9u2L+klV4EgUUAH0kainbqsqoCqgKnBcKEBHNRTCCoKQSqVolpuenh6a5cblcgUCAYZhKJ8dRmnphvsPjQ6y5Mt2+0BFfdlyhq2vFKsC6GHKqB9VBb5KBWiYDx0N4nEuk41zwGSx42UGJAZSLCRYHBjN87Kk0Ocs5FIR7tPU/GH/geb32UD9oCqgKqAqcPwqoFyoHGiG5/l4PB4IBDweDzVM6+rq8ng8mUwmf5Pjt4ffypbRsw89tynByDJAN/vuWQ19JVZsboCsSZ21vdICD66AEDZJHjZlOR78LDy7ZsuJzf5SZwSZBGQDZAdkZzX2lBZbVXSOtsuPvIWxpoj9qahxMOHWwwob4eNQOEhnotN2994SSwaZmUJHpvaK7mqH5xe3wio37I5h7km7EJZg7uKA0TqgMbEGRxKZNo2xUgsOWvXI9VK3jeyg4zJlvkFI3LAkPHkOr3dkDc4EMkf0lr4qh+ffroFFn0CPiOOLeZxsEd5w99U2RtDMNJqRRbYssskIpyiEf+2CFAbIGZy8GAdB05cSiIw1+fvWPcY6UWsH5Mhq7cES+9axdtiQwg4eIqH7EkkVyAI88dGGCc6BAgsga6bAGdLbIiX13YWzOsY0bxvXuGW0o7emJV7cyhdenim63FXeuGbKVdCWhjQB0FkZM+gMj2OufRBr+mNvuS2OMH3GkHfCbN9Pb8ZK+ngMvGn70hC85I6+EmvAaA0XWlPFzk3j7bA3hff44CpKR7CqVP84BEz3Bce2ZEobo2hmosgxMKqpq8q2cYId7n8b9hLrD5mkbFb2tjho54Jv75OHyACgX3hrwszOwpmJ0ga+uJEvbswYnWmD3Y+mRpGJK3Ri7kzoM1NgixTY/EX2QHXLziJTR7mjvcKxq6ph1+jGnTUN68tmba5x9pz9G978CFz1N7jrbfjLGvCTOycZjpPEkY8HpW3qjKrAYSmgAujDkk3dSFVAVUBV4HhSgA5RqBlFKpUKhULUeYPG0fT29gYCAeVxzvzxzGHPH0bvR6zrMMoZtonSd4VBj1jRIS4cVrj6UVVAVeALFaCjLJrznYZu0eEqh6OekxnwsuBhIUwANMtDlgBo/OTryAA6v758AJ2/XJ1XFVAVUBX4hihwKJcfkiTRlNF+v9/j8fT19YXDYZ7HMEvZ/BvS3W9LM+lpjJ7eCD1MplOQkqGD++QkR8BoFUjKuFChFbtYLFwBgREANERlWPTBtlpbf4E5jmayaBYUNEvInkV2jjBoBlkCxbZ146zwry5MPxV4qSDvEeWkZ0blqyDH3/L8RuPUpM6axan2LvONbtjww3mwM4W9kklRTColszz0cX0/+A1b1hRDdSmD3W00K0kIGeKnnBfFrZROSlBO83QNPwv3vr5jYkOwzMEUOaNa896CmW1V5nDjw7DeR60tcHJCRoCEDL0QtT8YGd0URpdldDgmV0bYoINEQJPiJBkk5TAf8uLAAHr+sj3FppTeBkUtrMa6t8TimX4XeEloMLXY5oj182vbP6wxeUodoG8AZOcKG/01LW+VXgr3LoMdaXDJ8KePN065ylVeP6B3Zopa2g2z3jutETwYXuP6CNgVB5LgF+C2f2wrmRnQmRgtjn3uqbR9+O9XwHo/hEQcZk53Mo+jv/eefXVYY8ro7SFU5610DNgWwt6ElM1JSP2pafZBvFGWGGk/sWqbYRqntUXQNKbQ4UczNxVNS9/8LHSzEAF8lZSRIY3/67P5yXOUQ1GUCS8ne+RvH60+raGjwuIvsgaKbdHKxmhlY6Siod9oSVc0ZXQ5AB032No103ZOau6++Pb4jX9PLHid+dMqeGUTrNgNmwdwQHcEM3fwZsEvYo/ymKx4c6dAGvl4yDs01FlVgcNQQAXQhyGauomqgKqAqsDxosBQ+AMAHb0EAgG3293T09Pd3e1yuXw+Xzwep1kHaaOHrvKOYO4w+j9ibYdRzrBNaLEKfR4W3D1ipQdZOKxw9aOqgKrAFyqQPzIlPtAyJ/OslGbEKCMFWOijAJrDEdAsD/z+APqAUTYqgP5C9dUVVAVUBY5vBQ5yyUG/os2XJInjuEQiEYvFIpFIMplUskPnr3Z89/Vb1DqF+kk5hiuCjBnxDm7zJGe4EAPolM7qL7LuHG0dAtAKOBYBfAy8uL77xNaE3sEgs4DMWWTPap0ZrYPRYADNYWPiWV70q0CFM+N4hNpK4BjbbA7IHlBNGTDopC4cAxy8sXn3SS0RVMcic9bgDJfY14wxw/vduLXsYKI/6lPxt4+3jbIQTo3dG9rHN8CLWyANDAkjZqijxYFqHbyxDHEQ/rrys9F1kYqGZLEzWGB26WeuL50ONz0PnSyksEEHDQTGJZGEftE7nu+pcSY1uOqM3i4WONpH22DVrlzzsoSrDmLoofpjIM9bvLfMiuOaK2ZH0YwdRTPgkbexA0aGIF2eJDNc1fvp6c3uqvoBNEvUOGM6y95xLe0/+R18Hsd0NUXsLCIAayOZOX9pO3n2xrH1K8Zb4PH3MShnQRJIWDErYxWeXbN9gtODpid11oTe5iu1rT/RCdtiEJdhAPs7ZxPE5bmfhac/6RnTkER1kt7pRTM2V5ngpTYIYCsV2ml6S55XosY5gM7MvyaZ4iVO0DakUV2ysmmzcRr8z2s4vSMAcCLOJJmV07EEyTLI7ePKTa+FCIAWWA6v7+Vg2fbsdU9nrA+FfnUna3kIbn4Nrn05dtrVHjQjo7OxyMxpbf0lNrjyGfg0jsOr+2UcC58h+D4pQ1qWEwI7wPAJjLyxSYgMrCimMxkJIC7z7MGPB7qN+q4q8OUVUAH0l9dM3UJVQFVAVeC4UYACaFmWk8lkOBz2+XzUSZCmU/f7/YlEIj+d+hcOhA5xheNGgFxDDrHZX7ja8dYvtT1HRYH8+zSHUuCIx8mhbPhdWodi59y7BBJ54cFmVs5mZV6QGEFOkVeCgwQHKU7GnhxZmQLo4Q/bKsV9lzRU+6oqoCqgKjCkgCzLNIcHy7I8zyt31ukpaWg9de4rUCAfQBOOiutMAmxht413RAuxlQSntYWLiI3yH1fCgIgfNMwSJwdexobLn4Q2n9AUKW+CyivlktYoMoXRrKSxMVzckKqcnURWWdecRtaM1sFpcb4+6BZwgK0gS1kxP5Zin74qN2WzEj7dDgiwLbXhjJZIqYNDJk5rC5Y5Nky0w7Pr8bcATCIpy/hhI5zncE1o95QrdxdMjyMTIFtIa3pnognak8BhLHmQCGgJIJnlMhKJ/g0K8PKWtWMtkVJsfBxG0926mRtLpmfn/RX2irjXjAQ8Bqn4YKbWE0kRXlyza4yDL25MaC1pg50rbcJOGnsY7NFBA5CVKwClgzLAAERm3OMvd4T0NrHscrbAuWdCC6zYiaOJaSRyPw+7xejP7wqWNCQ0DkbjjOnteya0bJ+zEEIyRuG0fInMMMS7eW1PbNl6+HwvDk4nzRM5XoozeM9uiLWfOy84qjFb1pzR232ltnWnNsJLmyAgQQqnUcb9AhIo/kHvrn+7yq2ZISArFDYOjGp6b3wduAEiXCaToWYmuF9kF1FPFXwz4Nm1a2vNidIGKGxKozpvTSPc8QpOQZkhItDjTZRl4nshCLSHZOfna4LzQA4S86SMexGSsWd0UMbR7p1c/Ce3hjUmSe9Mo5kMsmwvq4OVLgjwuBZs7kGkEwi+p5orhZOq8N0WkhPyix9QI+urb6oCh6GACqAPQzR1E1UBVQFVgeNFAfqQlizL8Xjc6/Uqsc9utzsQCKRSKRpBQ5s7IlY7vIXHS/8H23F4vdh/q8Hy1L/fHgVoAsz8fX3wvh2jhJkHr/Qb+K0yXsTMGT8wmmPQkghCFlhBYkSJEUVWkHjyYgWJ0Gc5K+ZlHMovhc5/A6VQm6wqoCqgKnBMFDj0M9cxqf67XOh+ABpfb8dl2JjZMcaeD6C3jbLA39ZDChiOBMCmSUrAARAbn4iPmZPUOMDQmtDagiXOjYUzghfeCv+97LNRln69HYyXMzoHp3UAsrnLbPBmO8bAAtAbD8quH74TKDEUATtCDAD8eomvtimls7LIEjPad4yxw32vQz/2TsArihKkCWB28WD9Y6jCGdCbmSJnRmfbU2mFxR9DgKPe0wfxgB7yYehPQBcfufiOTvQrSe8UkCWBzH2jnX3T7sT4NSoCK2JKSwA0SHIusJaRk0+9s73amjE6kzprymBPlDf6LvwdBBRAjHPrUWK7z3sYPP9xU4SkbUwVNXJFTdsmN0NnMoODg0n3XSD/5jlPeQODHBxyJgobese2+Or/AEEJG1mM+GgVBrj7RPZKGQ5nq/DJcO2zvtENMb0V+1mjuo5qe/K25zC3jRP6zEk4XnsgA73cgG1hX5Ujo7dLemfMaO8Y64RH3wU/DrUWsyLNJIlrz+J9kGtFHOC2f3RUWJLFTknv5JDVNaEZ1nrwg2FK1Dy+BpKVew84wl0iyiiMOLfrScA4teOQyLyAPayxxUoYdn3vipTBDhVzcM5GNGPLODv08pTXZynolrDrCDYeOcCkHHhfNnTjAOWpi1UFhiugAujhiqifVQVUBVQFvkEKKAA6FotR+ux2u/v6+ih93sdDLP+a4ojnjzeJjrhDuQKOt36p7TlyBVQAfeQajlRCPjqmABo/PkoeHuZwpDOwksxKEi+K+EUxtCRhY0Ml11B+vvv84kacH6kN6jJVAVUBVYFvswL51zbf5n4en31TqCgld7KMXYkJgB4wYo/djM4WKLatrTbB293AQi5qlSOZ9/62rqPKLpZdzmicKWQXSlraK23w0k6cnS8M8Il/Q9ksD5qeKnBktA6JAOjM71/AQBknUsjf7QqezNNIJqslZXhn184TmoIGS0hrChbZ3FWO7l/eDJ2JXIAw9owgtiG9Mjv7CXexJYnqsmXNHjSjq9ScaVmEY4SzuHyaWi+vgpFmeYA4JK/5y95ROHshDgBH1iCauWWMDdb6ISYBh8m5SEzLKTzFQbwi3mrgf57bUW5iCmxMgS2mt/aX2WHOXzGAplkjaG2UrtLTP2XEQYxTw4XWpLE+bnBEi5zuH/4OYpBhSHRwGOCpTe0Vjr4iR9jgTOsbwrVXBBx/wF4TUR5DcGoSTfbdSP0ZXMaJeM03t2+f4BwwYIeQpM7q05uSF98FHTg8PBf7zJM4aI/km/PonhpHCM2UDQ1BNHNPjUP+7dM4cV8mV2Au5Fk5eGiPwhC++I6A0Zo2OhitlUPWnbV2nP5REIhxGdlWHjJ8x/D3EAG0RAKieRmSPOxObhxnwwDa2MQgSx+ajtMn+nMeMjgFtDR0bA32f/jf/INv+HfqZ1WBo6GACqCPhopqGaoCqgKqAl+TAgqAjkajfX19brfb5/MFg8FkMpn/AFf+9cRRmf+aunvAao9Kp9S7/QfU9xv1BT0YlCZ/WQBNg4/yNx9WoPLVd3smnxLnA2hehpEAtCgKIn6sWAXQ3+3DRu29qoCqwJdQIP/a5lA2+7LrH0qZ3911FIaoQMw4wOdMWy123uC0GKd6ymzv186EtSHgMEzMBfBuiH40yd5faOM1Drn0Cjea5TthLix1QT9BgdSOef4KT1XzQKGD0Tl4DS6nZ9Z8nA6Ow5XR27TDrj3wR+LPgK/8UwL0S3tbH3JXYRw8UGBxV9ix+cbiT4DFHBMbNXAAIQE6Obb18c5RtrjGDAUNUD3XVWXfdv7V0AsQ5YacFij/HXFn06/6M/DilnWj6jxouoAsPDLHjPa9k1thaQdE8WaSJGHEmQegcaAybgPEr3xid1FdWmNhC+wRvaWn3Ar3voOtnEmM8D5mx/TKAof0Avhh0xhrQmvhChsHdLZebR1j/yPEQE6LGJ3vSLdVOzPls/1GZ38pps/d510HPQBhfPs7F4BMQqWz+Z0SZZkXQMhFdeM4YA4gAMErF3WWW+SyFrGwwa+t657QBC9shwE5F9DNSBCVoE8KzXtix0nN2PBEa2OQxV1m673s97A5AiGMn2nWUNoDXCc9frCpN66i/aSWhN7GFDqSGksczdhgnAqdKcy+yfdEwX3uPRwigM6hagygAd7vbp/YGEWmKJoaRyZXsRmu+iu+q5HFpuH0Gkz5ichXJX9eWUEdE+XLos4fRQVUAH0UxVSLUhVQFVAV+KoVoHCN53mO42JkSiQSqVSKugd+1a1R61MVOA4UwIgzK+ZfOotZMd8JXcyK+bdnhjVZzIriYB5zPIIYnIat9p3/mA+g8bxEEuiQR2p5kTBoGgFNop6zWRr8fAgA+jsvrCqAqoCqgKrAFyjAstjtQZKkRCKRf7IbPF8N//sFxalfj6jAiAB6dRgD6BI7W2BPG+x7K+0rT7ZhmEsBNADsiaTn/Gl3iTmms2X1jSmDs73GCa91QjdD7RhEGSAiQpvwyTiHt8yZKXCyBfb+MvtnpzRgfupjgMcYlwWcKWGfnSvm3C04SYQYD6/v3DreESt2gNaRQDO2aS/ru/xh8AoYdwIJLo4CbEiA/VFXqUWoao2hmRE0M1hibz9jDrzXmfNrzhKTh8HuD8HTwSX4r0QobXdm7SR7pNSBLaSLmqNo6u6iOli8BjwsZrgidprGZtPY05m8aOh2GqAL1oyzeQqx27VY4EiXNXbUOuCVdpwhUMSrK5n6MA6mW7HkeartkR01NlZj5XXY3Dk45nL47fPgYSApw15Z+u1z4erZKWT3I3N3qWPzKbPhpe0QkSnUxuVQp2Pl5gHuSX6UNbY7xiifAfjHjnVl07sLZkRQHW9s6C23tV92K74ZQD1MMiKEJPjQ13fRzdurrT2Fdclip1DSFNaYdkxsgM8DeF9I2PCa2loo10Y56QYBdMfJrSkDPmZSenwzoHOUTbpnKabwdDOepIuUyM0DvOVgY2mT89+VCgbTY+ICeJKW8MHlbWV1QklTEtVFC4k7+Z/XYgDNY+wuHsRbnNaovqsKfCUKqAD6K5FZrURVQFVAVeDYKEAHGTSuMP+dLj82daqlqgoc7wpIksSybCaTEQQBR+XwfD5xprdtaB8omxbIJEmSIOSu0Smkzr9eP977/FW3L38MhDMQipAlSdzxWHIEAC1j8w1ZJC+S4oZGeO1TyuBA7KvuilqfqoCqgKrAN0oBjkzJZDIUCtEn3va/GqRL1KvBw9+xIwLot1xba6zhEkwSE4X27lH2totvBA9BtKwI4Qys2LlpYn28pDFT4BQqZ7uqnDD/behiII39KTICwY0JCXzQbX3AVeVM650Zvd2e475+AAAgAElEQVRfat860QmrQ+DH9hEjAmjckSzk3I3jMGBZMFDdnEJmucAZR3XYiXjpRgxnWeJBkQR4bceWyQ39ZXahpCmIpvr0pp0V5o7zroYPfRAmZs3UeoOehsn5l7LQ4YrhGGGh79on3FUODlkZrTVV7AyWOby/uBV6WdykrIzv3NMzuDhorEFRchzgX77tpbMCOrNQUA/6hj407bPy6bDSAzG8gUiy+tEUiNhZg2rOkvDt1a7do2wSsmWRI25wdFc54YF3MS/OArzh2jW+JayzQ+ncWFHjxnIzPP4JRsY87n1uGvK2GFwyDEDLOFkiRvbORf0FJh+6LG2wxw22z6vq4J9bIMRBPIPpcG8K3mzfddpsX6ktiGYKZc3Jyqa9ZVZMn9/sgSQIopif1U+5qsG1KodQGNw/udGtmRHVmlmDI6G3eSrs742aBn9djaO5EyRkO4N5/NAth3zonD+vVEAUlojeNNK8s+7OznKLWN7CaK3R8obPKmfAR0EIS8AIIEhfbO2i6KTOqAocSwVUAH0s1VXLVhVQFVAVOMYKqEOLYyywWvxxoYAykD6U1lCOTBO5cBxHH4oUs6LL5dq6devmzZvXr1+/hkybNm3q6uoKBoN0HRpQpoQ/K6lgDvRfdqDlh9LIb/46yhgIz+wPoEXgZPwSchHQGEBnaYiURBapAPqbfwyoPVAVUBX4ehTgeT4ajXo8nt7eXq/XG4vFWJalN1yVWATlvDmEtL6exn5ja1XooXJzNA7w/JZttbZgiT1lsOMEdNX2zE3P4BR2PCGpvaK/+eHNRTODBVa+uNlVbO2dcTf0YUaIb9JyBLgCYIqaBPjfVR3VzpTBmTLYgyV2HBe8ZCPGslkc+0zMMfA+3Ec+GSBOkgpu8m+qsQgl2Oo3gcw9aJr//96Ocw9KxIw4AHDX8s7R9qDBMoDqMsUN/nLHrhOb22fdCbvjMMBRk4qcW7GCjJWaKO5UPiYB3tqzcZytH80QkFUqbe4f1bBi9DT4wA1pDEzpISdi2kqUoiiaFjIAcMXiLjQtoXek0SwoagkaLJtOaoRtLCQwn1UANEOieHEJOI0hQEqG1zZ2VVgBWSVkj+ntW0tN8OxWbLXsExL/+UC8tCWApqcLGz3lDTD379hcm8GlcUqz6UWK8hHP0DYNXr3g3MkAGwL9E1olZGXRTF7v8BVb+y65HZuKYNaPbUDgD+9urbEOVDfzxoYEumwATd9baQ9Ovxs2BPBOpBM9VIgA++Y4HFwhDvDA2z01zrDOzCALVF+ZKG1wV9g3jrPBQ+/iOOg0WTP/DkA+dM6fH2y+Em6Okz1yAC7po1Ode8usXKEzpbP6yx0d58yDbmLDwhHUPuT/vN9xNdhM9a+qwFeggAqgvwKR1SpUBVQFVAWOlQL5Awxl1KGAs2NVq1quqsBXq4BynB9KtTgLOcvKsuz1epcvX37//ffPnj374osv/ulPf/rDH/7w3HPPPeuss0477bRTTjnljDPOOO+88y688EKTyXTbbbc9/fTTzz333MqVK3t6esLhMMMw1MqD1j6s6i/VpGHbfis+KmMgPJMPoCXgsyDwILL4IWI8WuTwwFIF0N+K3a52QlVAVeA4UEAQhFAo1NXV1dnZ2dXV1dfXFwqFEokEz/P5p63v/HnqyHbVvgAas8E4wJOrd9RgAJ022NNGR0e1Hf78IQQkbPiQAnixrfPk1r0lNp92VryyZfeJl8PydrwVAEez7tIWiQAJGd7cuaPWmdDaWIMjWmjzjHJiZ2SysrLjhgNoAEgQR4hH39ldZmaRBYqaApo6d00DPPAepqUpgJV7Oi+7bZdxBpS38sgSRlN7C03tp7TGrnkK2sKQwriSsmLqfYEhLMnXl4OfCuukNJkHCELC9mCXbnoczZCQLaG3bR9l4ee/gnl3BtNnarGFm6oAXpmUyQJ4YN2oWSE0izc2gbFFQo7M2Dnt/3E9dHIUuYqEO7OE3vMU9HMCFjMqwl8/wG7RyAoEQG+oMMFrXbCXg3+17yy3M8iaRo5ARTM239jMQgoyKV6g4cAH3O1K+8gFDC+Bl4MH3xwY1QTIDpqGBDLvrXbCwx+AT4QgD5+4vK0Pd1Tbo0X2KMJJFGH0nP7qRrjiKeiWIY4fmMNVZWUQctYfNB45Z8ehKCkTvrxH7PyPG9xVjgCazhQ6BlAdjoM2mnfU2Nr/703w4md41yeJEFkixL63HvBu2u9Fdx2OHE8DrPZvnOz0FVuZAlsUzewusyTmPA5egLhEmoezGuZPBxRJ/UJV4BgroALoYyywWryqgKqAqsCxV4BeUhz7etQaVAW+BgXo4U3vr9DqJUliGIYaa9A8nHQ5HQyEQqEnn3yypaVlypQpEyZMqKqqKi0t1Wg0CCGNRqPT6eg8ypvKyspqa2urq6vHk+nMM8+cMmXK/fffv3nzZlpy/iAw/wp+2PzXoM5xUaUCoHkJB1axMuHOAwDbQpnulBzDI0yR5VJSVpQEMl6VsyKI5IVDvQ7Yifzx2wFXUr9QFVAVUBX4bikgZsV4PO7xeLq7u7u6urq7u3t7e30+XzQapVlA8v2j1PPUYR4c+wPoJMCCtzuq7X3amSmdVSxw9NQ44Z12iMvYRcEjR350sxfNiBU7IlWNWwxT4ZZXoYvFOJXw2KFm0JL9sLHKnEAm0NZzWkesohl++xJE8er5gbD7bAUAMQn64fMfXOkutjAIv/oLTG1VZljqhq0CLHhnS7XFpZ8J1XOhqIlDVp+ubtdps+He13GYdgKjUuWcS2N16XsuGppCZwV0DqTwPeQlH24ZY4sbbCwyZ5EtVdqweZITRxwPCDhOmZVEEv+N20ksoHMNDqYx/bzzn67Khoy2PqtvzmobUmjmHoPJPRfnEsRhzqSnWUKNFRcLPivgr0JC6v5X91RasxhAW+MF1g1jLLAmCVv53f/5P4GKRiibyxlbtlTZ4Y12bP2cwtHUtOFDitE25bh4/vUEmc/I4IH2C64NYB/t+gF0WUAza8+kVljuh06A+ct2njp7t6EuU9qcRGautCVc3bp+vAPufA06WeygLeIgaby3+NzepTCdYn1MpmUSRk07hlk8CxsGNpza0lVkDqFZSTRLMDQmNbZEUb2von7PyXOCloXwSRDcWYyhiTj7HDaDjs+53mX3PaQSAI9/vKPSPFDiYA2OEJq2o9IsP/Eu1pmRMSLflz7nX9PuK5f6SVXgmCugAuhjLrFagaqAqoCqwLFWgI4ujnUtavmqAl+LAvTwzj3jSTIEUmMNegGtXEYnEonu7u733nvvlltuKS0tNRqNWq0WIaTVaveHzjqdrqKiYtKkSWefffYFF1xw8cUXWyyWSy65pLq6WuHUlZWVU6dO/ctf/uL3+1OpFO07zkJP2qBGmeUdDBRASwK2gWZE4GWADe2Buxd//NuH/vXMBy5XGo9hk6molOXxS+KzMi/iPPQiNeLIK2rf2fwB477fqJ9UBVQFVAW+gwooNFnMiqlUyu/3u1yuPWTq6enp6+vz+/3hcFhJRq2sr8x8B0U7zC7vC6Axt00A3PqP7lF2prKZ19kFZMER0FsC2FIjBfCnD/qqHBkSKtupn/HxJCs2mojkKqdnM0pIcy4NEdh58uVxVAfICdr6TGmzaH8MIgRrDgYp79NyWkREhE/DO09t7TfmAHREb0lNuQ6W7Amef8POCjNT5EyhGQlk7kPToyddFb90Pry+C5s8JGmgrgyinAO1hBezJHyWJSgVg+/BhsqihNPr+cBrf8BVYeO0NhnZMjqbr7YJHvkIehn8cFMGW23lADTZcAhkDwC86900oTFS1CCj3ItFpq4Sq//mJVhJwuUlAmlpe6hpMyuTi4iAwN77akeVldVYJWSN6a2bJjpgvQiPf75jXGOmtBnKZndq6uLOx8Av42YIubDu/dg97c9I7ykZVod6Tp8bLHLwOmcGWX1oZviMa+EvHZH/uH17la0bXZZE5gi+o1C/vdzsvvj38HY33qEc8GmOpZQ4m4PFw0K5SWj0IICmkDpLDpJPgv3T79leZYuObvWiaRFUx2kdmQJnoqh+76j6D8bMcrc8Ah/0QnscH1Eidm4RREKQcx7bg0cE7dDgJ+wZ8tvn3MWWZLEzY3TGC6zrKmfC6h6IctgLLYv/+2lOS/V3QNFMnfm6FFAB9NelvFqvqoCqgKqAqoCqgKrAISmQj33zN0gmk21tbYsXL77uuuumTp16wQUXfP/73zcajQghvV5fXFxcU1Nz1lln/exnP7PZbNdcc82CBQuWLFmybNmyjz/+eNOmTVu3bt2+fXtHR4fb7e7r6+vt7X3llVfOO++8oqIiPZk0Gk15efkFF1zwyiuvBAIBMStyHDfMalO5mldQeH4Lvxvz0uBjpxIB0FmPn7v2pmfHff/OslPuOPPn972xOoTHhrIoZVlJZCRIZfGLIRgaM+gDqpQ/ZjzgSuoXqgKqAqoC3xUF6BmH3pEVBCGRSHi93q6urj179vT09PSSye12BwKBRCJBXaHzT1Lf4fPUlz9CFABNzlH4casoiHOf8lY6+IqWJKpjkaX3zKtwkKkI0M52/PDaXu2MLLJlkGnvKAf85WMI46eBpDhOjEfPZsMAtO9H/z2AzDyygaE5aax3/eC3MHCg+GdShCDCgARL1u0a5wwaLCzCr7TGAhc/nqlojhtsETQjjmawBkfQYNkx3hm99RnYy2JSnBZAxGGw1I0hB6BJUG2aGD/QKN58/2JMcrMA7/VtqrEMGDF9BmSLFtqCP78Nu1rHCawmWDNn5UF6OASg+yFyyT1daBqvbQCUe4nI6qpwZP+wDIs2CKAVZExbxYGE72IHRfbeV3dWWRJaS1Jj6Tda2iY64V8x+MW9XdqZvA4T242TmmGVD8IkAJvaVoxgU5F/GbHvfEKGxRv21DgiRU5GY88iB5ReDtMX+yrq95bZXQUmxtgY11iDBlvHpBb27qU4oDtKaH0SxyfnchzmpMSHAOXMPJkZwsX0Cxbw3XnqShYE+MPbG05tcdc29xusYQN2uE7oHdEiZ6e+zl3b3DnaCVe/AJ9GIIirk/G+I8dY3rXScLORAei/6JZwoTVtdAwUWAZKHDtOaQGPBBEGiyni3wAVQH/5nwB1i2OigAqgj4msaqGqAqoCqgKHp0D+OIGWIGZFnkyCIKgjh8NTVd3qm66AAqDx846C4PV6ly1bduONN1500UVnnHHGmDFjysrKdDodQqi2tvaMM874+c9/brPZFi5c+NFHH3V1dbnd7nA4nEgkGIbJZDI0gFrIm6hndCwWu++++2pray+99NJFixZdf/31Z555ZhGZqqurL7vssqVLl/b19Q1L9KRYrh/P/540TdAxa6ECoEEEVgTw+OAnP7uv9pSnisb/aeyUhY8/18PQoabISFJCgkQWv5gsXlkF0N/0/061/aoC310F6DUbxouD07HWgtajPBLEcVwsFvP5fL29vS6Xq6enh7739vb6/X7KoGmTBhuYB7GOdVu/6eXnA2gZ8EM7YUjOWhAssQ9oTF50SdroSP1qPoaDcRnuXd5RZc2UNvJ6hxfNCP7kZujOYOA4iFdHANADEPnPewN6awpZofjyhN6xabwzl/5ucKthEgosB1EZ7nyto8IyUGDhkUXADNqcRnUJNINDpgSaGS9raDNOb/+3q+CV7RhnZ8ggAmSChgmAFvAxgGsglJRGQNOI3XwAjav2s/JVf41Xt7AaK2icoHG4y2zwp9UYrJMW8iDzOF8ihtv4v4AmWRQAB1wv+rBrVINoaJExfXYSBt0MyOGuqseu2RGSaXCQFyvdlAB4eR8AjXFqgcVbZGmvscMTu7rQNKGsNYXMewwm9ncvYBSeHITBpEkUCOe9y1IO/u9Ln0GGmAx3Lt9jmBktdKSRLYscMTRNKGoe0NnCRsfAqJZozeXt5dbe82+Apz8HN49dPrK5OGvaYBGj3dxLsWOmCH6QS5Me0ihpZZ+mZOgTYHm7x7rg/fJp26tse0tsA3p7psDJG5sEQ6NU0BgssG4e64B7lsNO8vhdhuwsRSbiFM3iZSSIXQYIw/YJTqbAljbYQ1qTt8jS//Nb8d5PC9h/QwXQedKps1+7AiqA/tp3gdoAVQFVAVWBnAL54wq6SBCEZDIZiUTC4XA8Huc4Lt/xVhVOVeC7pkAgEHjwwQd/+ctfjh07tqioiNo4n3TSSTNmzLj++usfe+yxt9566+OPP+7s7IzFYgoUoGP1g7zzPI5n4Xn+9ddfv//++1evXh0h0+bNm2+++eYxY8YghAoLC8eOHWu32z/44ANBEDKZDKXhXwpA05tJkiSxLJtLX5NHLigmphYfgoDz2+T/vyv4WOEIdH3lGKDpp5SPyowkSRSaK0uO+gweNOKXJAEvybBju3zOeQ9WjnupsOaVUSc//shffXEWsnh8xoKUIhHQTBYyWZyWCRtx7DMI3W+QOMLg8ah3QC1QVUBVQFXgcBXI/02m84db0hdvl1+XJEk0RiGVSoXDYZ/P53a7KYDu7u52uVw+n2//OOgvrkNdgyqQD6AlAFaAILh/eP1AiYMrbYkZndiJ+NcvYMrsErrO/nVIbxMLG9JljRurzfByGw7yHUSiI1P/OMA1z7iLbTGdLYWsKa19Y5UZungcsKzAyv33RT/rmzG/t9DEaLE3hYSsArIyWmtUa04aHd3GurVjLfDEh5gRp8mJWcKFDZHlITI6dOLFtllkomsO1elKfTa6LqOz4UyA+saM0bl3yjzYlaQuIQRjU/6K0TM206DNTgI8v2NzpbVPb48iewo5GWSHormgbwXk7Cm3wzNrIUSMnoeagOukTcuCDJwEIann6sd2VmH6HNFb/IUWnKTxZwtDaBqDTFGNdc+Js2G1Fyfuo7kLh1kkD/WBXlLQz/teXsTk6GXzgwZLQo8BNItsSWRKYb9pe6i0fnuxaf0JjXD3P8EDxEkZBzbTS538nUPbTPk7uYzMYgqflTMcuesuEjhOq82tShqcAuxb3ZOE1zauufDXu05sDVQ1JbS2DDKDpl4uaBxAMxNF9e7qpozpD/B+P+5mmhQ4KFPOukSSMF/OyrCme9cofCSkdNagwdJdbIV5T+cOAOIpjjG8NHSfTLmeHNJJnVMV+KoUUAH0V6W0Wo+qgKqAqsAXKZCPn8SsyLJsIpEIBoMej6evry8QCCSTSZ7n1euGLxJS/f5bpYAynl+7dq15lrm0tBQhVFNT87Of/eymm256/fXXt2zZ0tfXl0wm6VMC9B+E/jcdBDorXymezhzHJRKJVCpF/Z0pzw0EAsuXL6f1lpaWFhUVnX766Q8//LDL5aJgN98M+uC6C8Lg+OHg65FvD/JvrggyrBiFR9MVKLymC2m0dz7OHrbtEX6UQOIhy+PhJ65kRxucfe7/lo97rbD6jVEnLn7kz+EYQwE0DxIjyWxW5rMgZDF9VgH0EWqvbq4qoCrw9StAzyMKHT52DVKqGHaOE7MiwzCRSMTr9bpcLpqcsKenx+PxhMPhTCajbHjs2vZtK3kYgE5y4IftJzalShuiRc5gWX336Hq4eyV0ASx4s6PCJhqbJZ0jNnb29stuAReLUx8QNwZun6jZPJHiAP/zz65KR7DAyugcjMa+q9oBqz3YUTpnIZy3MpnF59c4bDt7bqzYwZHsfICsHLIGC8zuKseOyY2pyxfBah90J+iWlHnS91xZBIbmluCwbsKpAzy40zAw6KRMOy4AvL11W6WZpAG0SXqnr8LBtC7C9s1kIuG3BEATuImtimXAqHRteH2VJVnWKlT9V7r48pS+KaGpD6M6UdcoIcfuolnwtzUQwN7EIo6exi9cHnnLEXBWguAQgI7pMIZOlTYMaEwcMnHIOjCqBeYsgS4mF2OeD5lzrVP+5H9H5wffB+Ses6+O6SyMxp5G1iSaldLamfKWQHXLZ6NnxVsX4ZSAnizejxT3ZvHfYSki99E2TbrvimOT6Fgat4D4dOQ6pRxOdBuaezEuQ5cgz3999QnOzpr6WGmjYGjkdU4e2XhkiqBpLm3d55Mb4aO+nNPLIICmZeMqcO5nWX5l7W6SsJHRWkOF1s5yG9z9Nt4XRGKg9PmLAPRQXwZvSCgiqjOqAkdRARVAH0Ux1aJUBVQFVAWOSAE6nOA4LpPJJJPJWCwWCoVoSEtfX18wGKRo7IjqUDdWFfgGKiBJ0qpVqy666KKKiorzzz//2muvfeONN1wuF8tia0WWZTmOoyHDYlZUZhTEfJAZZUxO8QHVhud5WiAtShCE7du3P/LII1OmTCkrK0MIVVVVORyOt956y+PxKNR7RGSs8F/q8sGybHd395tvvrlq1aqVK1f+/059+OGHq1ev/uyzz9atW7dx48a2trb29vauri6Xy9VHJp/Pl59RSukLbfmIOzM/KDu/VXT5iJt8mYV0kLLPuwRZARgBWLxUhG1tcPY5j5dPeFY/5sVRJz31yF+CQwBa5CVJykpAh51qEsIvo7y6rqqAqsDxqAA1iaI/zgf5ZT4qTVfOWcMANK2dZdl4PB4Khfr6+hRj6L6+vnA4zHHcsW7bUengcVSIQgxlQoSTAuyI7RjvTBQ5+gzmvdWN2DHj77vh7fDGyY2h0S1hVMcW2HdWWWDZVgxGs7gr1Kt3ZKCXAHj8k91jGt06U8bYyGkdvWNb4Jk1OU+JkYQQBQFC8qe1Jr64kXBhHAGd1FmDY1si0+6G97sxpozn6DWlpUNmxLQ7pCnUpxgz3yTAXoA7lr524iz4+zqKLDFnFQEY6Pn9kl2jrAyygNY5oDFtqbbAi5uBpd9jfEwJMk/6mkmxmE1vjgdMC3sLzVA2txdNC+odoUJnwtgI5VcKyAmaelepLRcBTQA0cfAgbSJvOQbKyRCSaQR0QotzLfLIksURytMEZEkaHb6Tr4LXenJOIPkBySOIdjAA/XmthdFaOWRnkDmrb/ShmYGxl4cuuxuW74SACDHi2kzdpakm1Pg5v6mD6Byv3JFlf/fc8rOb4IX1MCCIONcyloZ6Q9OmDXk3067SGwBRgABE7njxg+o6T1VjvMCeQnUSdgZv4Y1NPUbzqvEm+CxAUDipG+dBxIcYnjICpCBw/8u7K/GtCFZjDRdad49ywPPbISJLJI1hLunkQQC0jIOjc+Ln/FnwXh5aQutS31UFjoYCKoA+GiqqZagKqAqoChwlBSRJYhiGjh/8fr/X66W50ZQYlmMXw3iUeqAWoypw1BRQjvYVK1acccYZZWVlF1100cqVKyORCMMwtBqO4/Lro48kK5T2C2eGDchpULPi3UEeqOSpV0YikVi2bNmll15aWFiIENJoNKeddtqiRYsYhqFB0Epr89tD5wVBePzxx5966qlFixb97ne/q62trampOfnkk0877bQzzjjjrLPO+v73v3/uuef+4Ac/uPDCCy+66KJf/OIXl1xyyWVkmj59utVqbW1tvfrqq6+77robb7zxlltu+f3vf3/XXXfdd999CxYs+OMf//jUU08988wzL7/08htvvLFq1ao1a9Zs3Lhxy5YtbW1tO3fu7Orq8nq99PbVocdrK73Yr1/KqGRoZh8AnYVtW+H75z5ZNvFZ/dhnqQVHLEMioLNZyGYlEc/TcdzxDKAVnKRIcaCZfCSUP3+g9dXlqgKqAl+LAvTfU7lFd4RtYFk2TCZ6f1E5ceTf9qNOTcrPwhHWmF/FiABaEAQaxBCNRqkxdDeZvF5vPB5XH6H7cvrnA+gsiRRe0b53cmtUY92rmemubtoyzgnLonDFi57RTeFipwfVdaJpYuMiiEE2wWB6d/AJW1W07ZzU3K03MYZ6Dtkj4+eI9/4TGyjvc11DooNpY7ISdETWVpvYAju2xSAWHAGjFf7rGdjGQELOpBlO4DlJJN4P8nD6TNojEhMIPJsG8MCA5cGdY+vbxzfBba9hpEt5K4d9Jz433dY5ypbWWMQCRw+a9sE4E3RwkMH3j+nhx8sS9YDGW3G4tIDpAVeVM47MoqHJa3TsLKiDa1Z49FaougoDaH0ztuB4YQMG5YMAmt83AhrLxskQlPZe/Vh7Jc5AKCCLRF5Q2AJah7/UHjIvxO7PAwcIFD+g7NgpRMJ3yUXs/RWSt462ZJGVxzYmdihu7THMgtY/gxsgwGFnayIGNa/I7cxc5kH8VW4JxfxZgF5ZmP3U+vK6bSe2iP/zKk4eOHiVQ9MQ0kaxCjim5FoGQRAlRoCEgOn/h95Uw2Nd45qZmjlxVAf6FijEx5t3fEvqyichKGLfMpneHcCB8nhK8RAFz7xFe8usWRIOHyq0t1XbYVUQQllJkHGEuYSNqqlVN/51ksiLHlEC2XEciaQm/cVlkr4pV3i0HvVdVeBoKaAC6KOlpFqOqoCqgKrAUVCA5pMJBoMUPbvJ5PF4gsEg9d/YDwYdhUrVIlQFjkMF6Bg+k8msW7du6tSpGo3mJz/5yYYNGxQseKAh/f4rKGuOOJPf92HgIP8ryqbXrl3b0tJSW1ur0WgQQqeccsrDDz+cTCbpYCx//fx5QRB+/OMfjxkzZvz48aNHj66oqCguLjYYDDqdTjvSpNt3olbXyrtOpzMYDEajsbS0tLKysopM1dXVEyZMmDRp0sSJEydNmnTaaadNmTLlnHPOOffcc8877zw6c+GFF15yySVTp06dPn26yWRqamqaPXv2nDlz5s2bd+ONN95xxx0LFix45JFHHn/88SVLlvzjH/9YunTpypUrk8nkYF+U8cjg86g5jIx5skheAJIkwtY2OOucv5VMeFU39sXKUx95ZPHeHIAeLCgrASfJnCQzHMtwrCCKgiimMxmGY+kuoEHoCi6n9xWUvSMIArXtlmWZJRMtON81e9geoUfFYP1AI+Xp8cCybCaTUSy5lXWGVaosHzZDC6HlK2Br/yNt2FbqR1UBVYGvRQH6yzAsvTP9JaGJaqn7GU0DkEgkMpkMzV7Lsiz9XVIwbmdn5/XXX2+eZb766qsXL168YRMsVpoAACAASURBVMOGRCJBn11T7pLStLfKT5nyI3aEfd//F4b2S+kd7UU4HKYXk4FAQH2E7ktrng+gecDpAf/ycd+41qTGli6s9+pmDZxwNTzWmR4/r19nZSpm79bP2nXWVfBuHw4rpn4UNHT6QJg0BfBh/7qJzu5ia0LvyCCzv8juM90HQYBgMsc3aaOzEmR4nLWXl6A3s2VyQ0pnBWQBkoSwo8IC21IwQCyKSewy9kOWiSEGjZdVOkK+jbPsQDqN43Lb+YjloR26Gf2Fjs0ls+D+9yBCmSvgYFsvrDwNZx3M6O0Jva1/TPPmH14NLhmSBF+KspQVszgDMeGVDECPyFzxRKCqIY5mCsgeKbB1nzgbbloOd3+621AXNzigfC7om/aUW2DJx5DCweEU3ua8yXKhvQR+8gBBabPjro4qbG+dRVaR9DSNZoLO2VFlhRfXYf5KGLGyW/dRTFm67wyJY5az+DEsCfxSR4UNkF3EHN8hFNS31zhhbVDxTsltShqWD47plRD9FrNjBmC3yLY+2VFbv7vMunG8E576FB8D+dNgHDa9eBr6hi6niJqGNDMAf1u3eqy1F82UkQOQPYOsqarmD2tmwmYfTSqoWJcwHAsxHgKw7Ue/DeltgGwCsvkLbZ+PscP6JERAzuBkj7KE7zWkAOIkdINLMTJPVI+mcGcDAs5sGcdLDkXDocarc6oCh6WACqAPSzZ1I1UBVQFVgaOtgCRJlD77/f6+vj7X4ERjn1OplPKk/9GuWS1PVeB4VIDaa/h8viuvvHL06NGTJ09++umnE4nE/nx5WOuVcfiIQ/T9Fw7bfMSPlEXiuByOc7lc8+fPnzhxotFo1Ov1o0ePnj9/fjKZPIjBBcdxS5Yseeyxxx544IH77rtv/vz5t99+++9+97urr756zpw5V1xxxezZs1taWpqbm51Op9VqNZlMM2bMmDp16q9+9auLLrroggsuOP/8888999wpU6acccYZp5xyyuTJk8ePH19bW1tVVVVeXk7NqQ0GA8XiCCGtVqvT6fR6PUXZWq2WfqUhE/1IvyokU3FxcVFRUXFxcVlZWVVVVXV1NaXY5llmj8czqMkBATRJPpQbiWIAvRXOPPfvxRP+qRvzcuWpDz2ypAsDaBEEhhc5/h+Ybb/66hvL/vnmW2+/887K91d9uvazDRs3bt3W1rYdTzt27Ojo6HC73ZFIJEmmVCqVn7aRhvgNQ8aU7NC9z/M8ZUaU+9CwwcFeYJtqupoSTkj3r7KysiZdbRhWVr6lM3QdxUlcIdEH32pYIepHVQFVga9SAZqXVRCEQCDQ1ta2atWqZ555ZuHChbfffvtNN9107bXXzps3jz50cuutt95zzz0PP/zwE0888cwzzyxduvSdd95ZuXLlhx9++Nxzz02YMEGn0yGEqqurzz//fKvV2tDQcM011zz44INvvPGGcvdO+cFRfnOOsLP7n8hoFcpyeseUZVn6UB3DMGr4wpfWnLou0Ox2HEBATv/+JVdlA6epF4tb0sVNfqMTTr0prq/3oelBnX3X6PrMjc9BexKYwSBTGndKY4r3rz4N0Cm+f7LTXVXPFTYKyJYpbe7+3lWwkYEkyCwPKQ4YCSNCkQRB8xJe2JPcOMEe15jFQQC9bZQFtocxnsa8Gxsp7Atm8yyoByEvLtMl7J1xb1dNc1RjDxU6t586F97eiwOTidMxhqrbmU8n2frL7EyBLWN07i6q6770NpwjMZU7ymjgMo5WTgHslWNNfwydfCVOo6dvzhQ428utcMsr2CD70Q07S2ZFCmxQ3Jo1OLuqbMx9r+JoX+JNIZDO4aIGswjibnAAfnGr/a7dlTkAnUVmBpk4rY3RWtdWzYQtXhrcrXQoHwrvr7SyBKNbSaL3vKFfxF7JyC4TAC0XNrdPbIZ+3CAaFoy3Ig3DGSixJQl11MDvuYkB8DLQnU3aHumfPLcLTeutafr0zFZY44cBvBNyrcrrnbJwCPXSb0l/JLqjvSIs69pSZupDv4KCJtDU88aG3Se1wPuduB3YxgxPWZKDFDuueKH9nF9jhTGAdgT1jg21NgygY4CPHwKgM+SeQq7ZGR5nbkwDfN7XedOfnv9h42uWG6AfR6IPdW2wi+pfVYGjroAKoI+6pGqBqgKqAqoCX1oB6rwRjUa9Xm9vb28PmVwu1zD6/KXLVTdQFfjGKkCHOAsXLqytrdVqtSaTac+ePYcCBJURvjIUP8jMIcozDB+Ew+FHH3104sSJNCr5hBNOeO211xiGGTG6jYbaUVpK5zOZTJxMqVSKhtelUqlEIhGPx8PhsN/v93g8vb29XV1dnZ2du3btamtr27Rp0/r16z/77LOPP/541apVK1asePPNN994441XX3315ZdefuGFF5577rlnnnlmyZIlTz755MMPP3zPPfdQknLDDTf85je/mTdvXnNzs9VqnT59+iWXXPLTn/70ggsuOOecc84666zTTz/95JNPHj9+fGVlZWFhIYUp1GOkuLj4F7/4RW9v76BKdDBFHyvNkqd4+cF3ZYRNIqAHAbR27D4AGgAGApGzzz67vLKionr06LG14yZOmHziCad97/Qzvz/l384799//z/kX/PhH//Gzi3558cVTp02z2G2Oeqej3ulsaGhubr7iiivmzZt3ww033H333Q899NCjjz76xBNPLF68+IUXXli2bNmKFStWrVr1ySefbN26tbOzkyZujUajqVSKOnrT6EUaMa3Mcxy3/50DOrob7HXuLz0GFNCcPyOQiS6h29L3/ANvWGnqR1UBVYGvXgH6XywIQiqV8nq9S5cuvfrqqy+88MLx48eXlZWNHTt28uTJ9DmSE8hUUVFhMBhKyWQ0GgsLC4uLi6uqqiorK8ePH19UVER/KpU7f3q9HiFUWlpqNBpPPfXURYsW0T5SHEyTClAQPOLJ4tAFyf9tOcg8fdSD/sodeuHqmlgBigUVrskC9Im7Lfe4ShxCQaMfTRvQ2aLGBh+qY5ADyuZGihrWjXHAahL+zIr4jC/lEvTl0KrCShV9WYAg7Jp5h7vCCcZWQPVZfaPLaIbbl0O/iBFhClsDwx7irUxoZiaTgT2xtWMtQTQzrcHOyAKy4Ijg93Zh1CiAzAsUQCtn6xzopN0BgnsDWdiUaLvwN1vLLL0FlkRhQ3uJNX7Tc+AlNRIujAn1h32fjjUHKpwpZIbCJo/R7J56B+wVgZUzIPPEhQOyMgQ56JaZxkd7yq0ZoxOQPa2x7NRPc0+7E/wAHgGe3rKzyuLX1mV0Nq7Q2VvT4GpaCEEZSFhujnjmIVr8ryHkAPSeSmxqnCVOIwKyZvT2gN7c/8vbIJpj8kMYV1H1oDPYrp0waBwBHZB2VuYAtIwcWX3jzlonbIpQ/5MhFItbivcGS8wqiKszOTyw5QgPq7zdP76xvdQcq2hOlDdvH213XfcUDn9OYZMPharnN4ruIGoGTfk7dV+WBFkSiFNGCht6wD3v9lQ62AKnjBwJZN421g5vtsEABzy+vUGDoHGxaQA3fH7mbF+RncWpCx2RAsfW0TZYk8Qx+4yEnUCIIQtkgU1zIktuT4Qk+MeObae3bq6oWzeq7o0TTfBeB0bsypS3R5Rl6oyqwFFRQAXQR0VGtRBVAVUBVYEjUkAQhHg87vf7ae7yPXv29PT0eL1e+hQnjX0+ogrUjVUFjicF9h8wj9i6Tz755Ec/+pFGoyktLV20aBEeemGLBzzll7D/tvnfHnx+/20PsoTGyVL/h76+vgcffLC2tpYy6NbWVp/Pt38I7cFLo+By/3eKMocRCrrasIXDypckKZVKJZPJVCrFMEwqlaKG8oFAwOfzeb1et9vd09PT3d1N0faOHTva2tq2bNmycePGDRs2rF27dvXq1atWrXr33XeXL1/+/PPPr1ixIhqNDtaiDGkpg1boM01BREeCBwPQbIJ1dfb84Ac/GDNu7IQTJ4+dOKFmTG3V6NEVVZWlFeXG4iJjcVFJeVlJeVlhkVFboENaDdIg/BqcqPeI0WgsLi6uqKigxiOTJ08+6aSTTibTKaecojhrn3322f/+7//+4x//+OKLL76UTNOnT3c6nXPmzPn1r399ww033HbbbfPnz1+wYMGiRYueffbZl196+eWXXl66dOm77767evXqdevWbd68eceOHTt37uzo6FAyQ/7/qPz8ye/3RyIRxWI7H0PnH3uDGqp/D0cBRUnlf/9wSlG3+c4rwPN8MBjs6el59tlnrVbr+PHja2pqfvSjHzU3N99+++333HPP/2PvTcCiOrZ98QZklKnDGMbLeFHgqeinqA8cnqJeFQk0DQrqcYjX8Y8mXmM8L0a9GvXF6RqHaxyOcYgxmqNRr4oecTiOQdEoSBgDNAR6sEd7Huqf2qu72HYDQcUhya6vv+7q2lWrVv323rV3/fbaa3366acFBQVcLnfYsGFRUVFOTk729vZelhQQEBAaGhoUFOTl5RVKJXDln5CQkJycnJWV9de//jXzvUwvLy94syQlJWXnzp1FRUXl5eVyuVwmkykUCq0WWzBazeTkCCeZjvcVqdZxBoTQ63QsltnaioAVAa1CqA5d7/N+vQtX1y1P7z71qfNEiX2OlMVRs3KaWRN+9pqEPvgGSZFBrjEZjNhJFPG0C24WbAloLUJNWt2677Edbrd85DBZwUpXueSV+09EG8+gomq081JFzqpTkVnatd9hnhEhncGAGlU3Iye1uHCedMPR+XSsrJ89OGjzWSQ0IjUyKc3eo+lXa9zSgJBAjU2jf9ajvTeuh+VWu2c3sDIk3SfXeUw84zsB3WnBXVBWvtgUVmlCJ0qv+E1o8cqVsdKRfa7Wb3pt/wLsH5mygEY6E1KYMMV5hfdz6uJSx7Ea51zkOElul/WQNapm2BL0QIYrSI3oeGnxu9k/d0sXszIUTtxGv7yy1EWoBjPsaoqhNdsJWyygCQH9IPvTKi+OjmKfjSwO6j71iV1GAzsHfX4RSdqkdlv3Xnu5ZwhovvEHv2y1HZdy8ZGtYGU+cElHmwsx+d5KP5slgTW8uViLcLhFCUI7rt6PmFLvlfvEOUfmObneN/9CaDa6XocHBpjDbrD43yBakb1j5qiN2EuGORko4TyEvnzQ6D/lCRUdUe2R/0/2eHSnEUnUSN96QuMm1JFZFJtf48mV22WrWTlPHHKwa5GrcvQEu+Awu6LWUQy63ICfajQb0bYL90Nyf+mebfCe+uTdaWcislCZHGmoG2yLIi8IMWnOZBgE2kGAIaDbAYYpZhBgEGAQeF0I6HQ6uVze0tJSX19fXV0NZo88Hk8kErXpmfR16cX0wyDwShCAe2dCJLXeSpueWZ8Z9IZt27Y5Ozs7OTn5+/tfuHABDMeAgO4MDd3l2uOli95AiAOhUPjRRx+5u7uzWKzExMRbt25ZOYVoTwEyZPpY6Hmo0F7zjsvBxI90QbTtuFUHW2mDgkUTWToRU2jImAlopDe74HAJ+TvrXbMFtFSJjHpk1KGWJv7t27e/P33q8JEjXx06uPdv+/5795fbd+74Ysf2LVu3fr5p49r161atXv1/P12+dNnHH/7Hkvn/X8G/z5n3/r/Pnjlz5vTp0ydPnpyTk5P5XmZ6evqYMWNGjRo1YsSIoUOHDho0qF+/fn369ElISIiLi+vRo0dcXFxkZGRAQICnp6ebmxuxYXSkEjgb8fT09PLyAifaPj4+fn5+QUFBgYGBflQKDg4ODw+PiYnp0aNHYmJiUlLSwIEDhwwZMnLkyLFjx8K79lOnTp0+ffqsWbMWLly4fPnyT6m0evXqzZs3b9++fefOnXv37j169OgJSzp16tTZs2fPnz9/6dKl69ev3759u6Sk5NGjR5WVldXV1TU1NXV1dc3NzQKBQCQSSaVStVqt0WjgG/aRlTG+1f4FQ8uO37WHMGVgjEmny23PqRc7JuHYI23BBlOr1cITFNIjZMhfq4HQD0jYZGWBTuTDYyHytwM5dJlM/s+AgNVEajQa5XL5qVOn8vPzAwIC+vXrN3369LVr13711VfffPPNpk2bpk2blpKSEh8fHxERER4eHh0d3adPn7S0NC6XO3/+/FWrVu3fv//06dMXL14sLCy8cOHC1atXb9y4ce3atevXr9+7d6+xsREhVFVVNXbs2MDAQE9PTwcHBy8vr+jo6JSUlKysrCVLluzevbuoqKi+vh6ep4KnKfrRS5+6X/Jg7kJRf4ajxXqMhDWGG5OnCFWaikKy+a45xm55crscmV3OU1aOkpWjsp/Ic+beDJqIyhGSU/ap2D8CvlWAhJloYk9KbnPAPfRTZDh8vdQ/V2Ofg+wnmlg5RlaO1Cmnyof7KIBb/Q73Z2/uzwF5N3pNxzwjpCdG5fRtvwRMFjhiAtrAynrixHn8v2ahezIk1OolCkwN67HxNZCtuJGRoikr1eg8T5+5qZqd22iXaew+TcPKbXTi3vzXaej4Q1wHu3fA3Ct2gvHUhK7wLgVM4HvkiFhjdCyO2D6zPiAPnahDPA0SqLCNNg+hbbceeWdKu+fqnXIN9txm1tjmoKl1/2cp5pfFBuwVRGpAtehMUPpP3TOEDplPnDi/eHBLArLRkYeoWY1MyKiiGHNKYTNlD7H/Woy1f/m83iPbxDJ/dCwOv1vmA18OOluHWdQXTdgtipGKiixE6kn/1dDtPSHr37QsDvKY0eiRW5wwE92VmT04m7DJMLZKJnsNUSj9rEEnK9DEHcb4xY1OnBa795D/v1d151wI56KjJThUIOX12wA7HYdnNCGV3qjQmp7q8DMAkPaMA2wcsVCrpWyTTQjxTGjvvebw93UeU2X22WLnnHqXzOsxeZjyxrsIm59TUQVNBo0W76l6dDoh/ydvrsQhW8nKxkEyPbhoZzGSId1TPSiDWz6lDOpvCE1Tt5f6cyvcM3/pni21w7u14T++xJQ6DhCNfanhmzlQ/kVBZtoxCHSAAENAdwAOs4lBgEGAQeCVI6DT6WQyWUtLS11dXW1tLfjfqK+vl0gkarW6Yx7hlSvHdMAg8AoQIEQSWXUTMprem0gk+tX5pr29fWxsbFRU1Pnz54HDsm1lXuPRG7+yPJ0R0Gq1Fy5cSEpKsrOzCwwMPHbsWCdPWPOq1GSij4Wef5kRdTkBTcOyAwKaYp/xsspsAf2vvf9mS0BbGdTg11r1OqVGrVAqscG2Rq3SanQGHNcIv6OKHTWaNDq9Uq19qtKAQbdEIhEKhWDQDdbclZWVZWVl9+/fv3v3bnFx8a1bt65Z0uXLl8+fP3/q1KmTlnTs2LH9+/fv3Lnziy++2Lx58+eff7569epPPvlkyZIlBQUF8+bNmzVr1tSpU4HjHj9+/KhRowYPHkwccIO7kpCQkICAADab7eHh4eLi4kQlFyo5OjrCX6C54fEJlLi7u/v5+YWFhUVHR8fExMTGxsbHxyckJCQmJvbq1at///6DBg1KTU0dOnRoWlraqFGjxowZM3bs2IyMjOzs7Nzc3MmTJ8+cOXP27NkLFixYvHjxJ598snLlys8++wxc0+7Zs+fI10eOHz9+6tSpc+fOAbt99+7dhw8flpeX19TUNDU1CYVCqVQKBpj0w5i2f83ZjreCixudTgd7RK1WA7MMbwaAa902JcBRDcd5x0c4OYZtdYPeoQI5ZWyrtamAbTWm5A+MABwkJGApQojH423evDk6OtrX13fo0KGfffbZF198MW3atP79+7PZbFdX1+jo6IEDB6alpc2fP3/Pnj1Xr14tLS0VCATkIIcwp+BJSaczW0PaYvjgwYODBw8WFBSMHz8+LCzM3t6exWK5uLh4eXl5e3v7+vqOGTNmy5Yt165dE4lEYBBNnsSQo7rjc8S2U9sSkEC+bStYlZCa5PQhGauaf4q/VgS0HKG7T28FYDYQOeQ9ZeXI7XLUQEB3n1ruOwmtPYcaTEiNCWjMbuqwkbsB/FRgU2iLNwY6lQm+GKoUtyPym52zlQ45ehb+aO1ylN2yFY7ZKodsqVN2s19+44SV6IkFdTVCWy7c85rAd8pSs7KMrCyFA+dH1/FP8zejSh02bhUiXFmCsJ9liQnxdahWjR4o0IeHf3gnU9o9D7nPELH+Dbn8hc/KfOQ7EW39BwjX6SjfF/iNJiO2XK7QFgZhAlrNynrCGvvELkPomVsano/23kB/v6/79OiDPrMaA/KFrPF6VoaelaF0zS3zyHiUshD9IERPDEhD+SF5akBNpjsjFj3yzBA6c8TO2XynLJ4XF72/FzUhJKNuGlQaYMxbCWgdQgLU9P6WJnfs19jEyjayslG3SU88cnEsvlLNM84iLMB08reVgBYjtOHCj94cuctEZD8RuU1ttn/v54DJTydtQSVS1KjFpL8WP1TA5OwTrBJ2KnLrF82SQz8EcJ8452hZ2G6az8rguecU+UxA+/6JmnTYgwd1Q4QdOqtNZrtyNUJCA471p6DMzMHYHCIbqihqWEmV8036v/9QPvGzm/4clddU5DhZ7TTxl+45tz3Ho/WnkBrJ9RrwfwIENNIZsa36L6bbE5aVs7ky++ynFAEt9MhTjV2LqimdWyirZxxsEIc3fJT47794cAWs9CbHjDrnjHK7Mbz/vRgfITqklSspP+KgvoUo7ySsTDUGgU4jwBDQnYaKqcggwCDAINDVCNDZZ7B94/F4DQ0NEokEv77HJAaBPyICwAvASr7NxTYseqVS6Weffebg4ODm5ubs7Lx9+3a5XA6+LK1avfxCvfMwE+YLmjx+/HjgwIEODg5+fn6HDh1qU47tGp4oTKSREUGGVGhTYMeFdBLhZeS01UuHBLT5JVOjwYju/ohi+vzN2coCGqLrGA04dg61wAECWqXVqLQajU4LcYEgPL3ZBudZJQBJgIh+/AB3Q7exJXgShKEO2ReELdVoNFKpVEQlcMDdSCUSCRYeDVZWVpaXl5eVlT169OjevXu3b9++fv06+OMuLCw8d+7cmTNnTpw4ceTrI/v379+9e/cXX3yxYcOGNWvWfPrppx999NGiRYvmzJkzffr03NzcCRMmpKWlDRs2bPDgwcnJyWC4HR8fD1bbMTExYH0ZGhoaHBwcEBDg5+fn7+/v5+fHZrO9qOTt7Q1W28BnWVlwh4WFRUZGRkdH9+jRAzjuXr169e3bNykpqXfv3n369Onfv39KSsqoUaMIwZ2Xlzd16tR58+YtXLhwyZIly5YtW7Nmzbp16zZu3Lht27Y9e/Z89dVXhw4dOnr0KHDc4Gv7zp07JSUlD6lUWlpaVlZWXl5eUVFRTaUaKtVRqb6+vqGhobm5mc/ni8Vi4MHBS4yKSmDiraUS3TQb9hrZ1+R4JnMImFeTJp18AoSY9GdCAM76srKypUuX+vv7Ozs7h4aGDh06NDw83MfHJzo6OjU1NScn59NPP/3mm28ePXokl8tNJhN53glvDGg0Gtq7IJhWJBBC3qA3aKhENplMppaWloMHD+bm5oKzpoSEBHiw1LdvX39//5CQkNmzZx89epTH40GgaTJxtflQlvTYyQycL+Ss6bgVCcRKHFXDWUaEdNz8j79VhtCZusd+uTIWB7HylCxs/qylaGieW64gbRXlm8LiJ1htRFqj2UuvkbJHbpOABttkBWqZsbX0HW6LW47MEX8U3cwEtNg5u84z+05UHjpfgxlhSFqEbrQ8ipsucMTss5GVpXLIbvHNf+jLaew1H318Ep2sQ2csn53X0YeHWlI+rvCb2OCU+dR5opKVrWFx5XY5PztkFvtw0ZfFqNGEjWRNSKM1miMYakyYuW5EpSMW8z1ykH2OyiGbzxqvYk9p8cqt8uHWhUxpCJ1ay+Y2uXE0npM1LI7cgVPrP6mZ8xkqk2COVWU0GYxKRFkai4yyTw7dd0+XOXPV3fOkdpk6tzxJ+PtowwXUYMQGvNhbBfjLpoI3YitjE3qCRPN3/tKdRkA758v8pj5Mno99VRN78Oc/8rAzDao3TA0/1px9N0PuP0PNykZOk5+y3pOw3mvqnlP8L/lo2XfofxrR1Sfosgh9V43+6zr65H+a+33YHDGL554jdOKqnSaq7HOesrIbXbJ/jPoL+tsdJEJIQcVwBHciYFQuRKjWhH4yYDq4EeHHAxKEa7ZQjp4r9OgnhM43oc2X0YKDdyMmPwycWNJ9QqVDuoLFwUbxzpN/CZham7MGNeHdhJ1kUPw2ZWNNDV5lQgID/9PDFewcJStbZp8tsuc0szIesEZJR/wnOvAY/VOCbsjRhst1gz965MURuE9UsDIN9ji2ZJnd6CuhHHSuGrVQrqX1RnxrZMLMOZMYBF4dAgwB/eqwZSQzCDAIMAh0hAB4axUIBGDHV1tb29DQIBAIpFKpVqsla5iORDDbGAR+PwiQQ5qQR20utsHjOZiYFRcXDx06lM1m29nZ9e/ff+vWreXl5batOrnAfhmoCPUAfSkU+P1PPp//Kz0XEhLi6OgYGxt76tSpNruwVY+UEHqUPqiXpB5AOP27Ta1eqLAzBLReZ0LFD1F0Eiag7QOP+EZ+vnVXlVyJjAb0VC7VqGVUhHvK7omygNbotFq9Dsdzt4Snh7+4hFolwjcBrU3NAUnYBHm6wwdCU2q1WrVaTSZYkGk0GjUabGGtVquJhSM0J/VtO6X3CFuNRuz3E5JKpQJn3BBbUkoliUQiEomEQiGfz29qagKP/+Bz6eHDh/fu3QPz7YsXL549e/bkyZPffvvtoUOH9u3bt2PHji1btqxfv37t2rWrV69evnz5Bx98sGDBgvnz58+ePTs/P5/D4UyYMGH8+PGjR48eOXLk0KFDBw4cmJiYGBcXFxMTEx4e7uvr6+np6eHh4e7uDqEmHagEltp0I25XKrm7u3t4eFi5KPHx8fH39w8MDAymUhiVwOl2QkIC0NzJyclgxz18+PCRI0eOGzcu871MLpc7adKkadOmTZ8+/f333581a1ZBQcGHH34IPrjXrVu3YcOGTZs2bd26defOnbt37963bx+4GxmhRgAAIABJREFU5AbK+8SJE2fPni0sLCwqKrp69epNKlXRUl1dXUtLi1QqlclksBMRk14ZAsTnCZnSwSz9lXX4UoLVarVcLq+qqiooKAAWGHw6xcfHZ2RkrFu37uTJk48ePRKLxTAPqKk3zyBvZeNMZmmruYj+cAtMByDSKUIIyOuGhob9+/ePHDkyJCSkf//+y5cvP3DgwJo1azgcTnBwcGBgYF5e3o0bN8CPfHu9vAAKoKeVtu3J0el0arUaXmtQKLCXX9CECGmv4Z+lXIbQN2XlgXkiVgZiTQTbZy0rh++Ycy8oDx0pxRwuuNnFZq2dJaD1RoT4SnS24h/REx/55tR55tR75DR1z+G7ZvM8sst8s4vCs9HX97CB6hONWirHaKsRqlFpFu37uTt2AG1gZWkduL+4ZJWxRvG7ZYq982oCJv0YiD14lAXkVPjl1LNzhC45cgeujDUBOU3WO+bJvab86M39R1guOlOPmVDq4bFeY9RqKAIa7HZlJlSverrym0rPLI19tsqRa/Sa2sIa/8Qug8caIWFNUDhxJS5clc9UnlMG/5288uA89MlxHDpPpNIp1UiLqWcVMuJYfwoTOnr7lsc4mWuOxnOy3C4LOecLHTKxI44tFyhLbezXGLPCxGs2FYCx5aO9PA8zAa1nZRsdcp68O0224EtUp8GGyS+aWgloNUL12l8W/Hc5m6tyyUPOkxErF7FykPu0Kta/NfhNLnuH+9O7+WUBE8ve4Za7vVdjly5gpWuxT+rMp6zxTx1zm91zq9m5t0Jy0ffV2D4agviRGyUlwlbeX5fUZ68tDMv+3n/8reR5vLnbdZ+fRv91Qbvi2JPZO/lZ60pi/vIoOP+RF6fcYXwTK13RDT+EaGaNF7ImPHHOafGfWpLwPnqsQEYcYZIMmsR9xkedxICO3C7zxWy4xAG74FB0y1F7TPmJNbbCM+eHgNybPpwKzxyR5xQ+a7zBYaKRla12ynnMGn0nYhL6Rx22724VjA9k8ExN+mIyDAJdiwBDQHctnow0BgEGAQaBziJgNBrVarVYLObxePX19Y2NjUKhUKlUAgFHX9p1ViJTj0HgrUQAVrBAz1lF1NTpdAqFQiAQFBcXS6VSWLGDH1vgoKuqqj766KOQkBAWi+Xu7p6QkDBu3LjPP/+8qqrKlh0gNPFLwmC75KZbVgLdUFdXt2TJktjYWA8PD0dHx8GDB9+7d6/Nfsn6X6MxRweiVyN0Az1DFHixeeDFWtG16jBPVlfPZrDJD7Zp1iL0QykK7rHNNfykW/DxgMA1Xx/4RSJF2HrdoDQaFEaT0mhSG5DOEiTeYtjVYa/MRjoCcDapVCqpVAo+SSDCZG1tbWVl5ePHj0tLS+/fv19cXHzjxg0SWPL06dMnT5787rvvjh07duDAgZ07d4KZ9ooVK5YtW7Zw4cLZs2dPmzYtNzd3/PjxI0aMGDhwYO/evaOjo0NDQwMDA318fFxcXOwtyc4OR4e0s7ODAvgLJcBuOzg40AluZ2dnV1dXIMEhtpsltCT+tbOzc3R0dHNz8/T09PbGbgqCgoLAmjvKkmJjYxMSEpKSkvpRacCAAampqUOGDIHvkSNHpqWljR8/Pjs7Oy8vLz8/f9q0ae+///68efMWLVq0dOnSFStWrF+/fvPmzdu2bdu1a9e+ffsOHz588uTJ8+fPX758+ebNm/fv33/8+HGNJQIwMUoFm1DAH79Wr8evlsNTDbpTeDhtySZ4hkH/pjck5WRugRmPLpD4GyETAv0YgK3wyMSqnPwlNCLpmj7PkKiqdBPyNmcPeKwCYsn8bFWTTHSk9zeVsbo0VFVVTZo0CQ7UiIiI1NTUJUuWlJWVCYVCk8kENvjkvouOD4AGJc87OqtdptPpHj58uGHDhp49e7LZ7BEjRhQVFfH5/GPHjoF9dK9evTZs2CCRSBQKBXkGaYXwq8PTZDKp1WqRSCQQCMTUOwrwQI6uyfMi8Oq0fZ2S4SKHe1Qg9D9VRT7jZT5/Qd2nPWH9mxb7gOb+EjQT/fcNbEQMsXh1FJenQ0hP+UgAG2d4+8f8klCr+vh6iUxIrkbNOnRHWD3ukysBGT+G59334zz05fwzMPPnaRvQP+ux8wfw2KBBSGswR/+70VD8bnYjayyflYbcJouds4Wu2TJH7LhD4sIVu3JFbvij950udcoWsCYIHTIF9hliV67cY3J58OSfFmxDPzZj9hnIR2AcgdQ0UH4nNHgIqBkJ/vfHMvd8hT1XweLI7LOldhyDx190rpPV3XLldtm6d2ZUeGbfTpyJdvwD2/aqLOSlisrrsWtjzJgL0ZWATIXfDLnXFIkjV++cr+qWK3LNfRzxlycrjqAW7LoEvxbV+l4B7l3+t0stoTMRi2ti5WrtcvT23Dt2I9HuIiQ2Yt3aTFaOU9qqQ25cMM8q1aGfVNeCshq6TVDac1C3SVoH7lO7LKU9R+XIVThxZY4YVWk3jsKBo7TnKFiZalYmYuUoWONkvlN+COT8lLsa/SjBY39K4WagcAMSV4LQvts3/DIeeEyo8c7+yZvzkzenkvp+6Mt54Mspe4dT5cXheWTznDKeuGRr2VMFrAnIe5rWLtvQPf9npwmVMdOVH+zDLLYc29HjEJR43sdfcKDhHEbYhO633A3iKtwnPXXMFbEmqLvlqrvlPnXMlTnnKv1miLpPfOKQrbDnau1yDN1y9C6TeO/kPv4/i1FRDfbToqVcxFiwYghoCxLM76tCgCGgXxWyjFwGAQYBBoHOIKBSqcRisZDyzqlSqYgDTavVS2dEMXUYBN5yBMhKXq1WC4XCa9euHT16dPr06b169fLy8jp27FhLSwvlRRhXBDbZoDcIBILr169nZGR4e3s7ODh4enoGBQWFh4dnZGSsXbu2sLBQIBCoVCpYKneJLR45++iUEPBEKpWqvr7+iy++SElJ8fb2joiICA0N/ZWVW7VqlURCBYjpxD4A7omQC3TKg0BEdOiEPOsqRLL1hq75T5Zvz2ZMOI67ERm1CN2vQn7RK7uHHfQI2v8vwcu/3V+twJZbJsw+G2VGhDlohoB++b1BDhLCM0IJnAVQSJhHrVYL8QzBBhxoRLlcDobDEomkubm5qamJz+c3NzfX1tbW1NTANzgeKS0tffjw4Z07d65du1ZYWHjmzJnjx48fOnRo7969O3fu3Lp168aNG1etWrVs2bIPP/xwzpw5+fn5OTk5HA4nPT199OjRI0bgWJGpqanJyclJSUkQKzImJiaaSlFRUcBx+/r6stlsb29vT09PV1dXR0dHOklN8oT1dnJycnR0hL8ODg5QAf7Ct5OTE4Sg9PDwILEovby8fHx8goKCQkJCgoODQ0NDwWkJ3Td3r169evfu3ZdK/fv3HzhwYGpq6rBhw0aPHj1hwoRJkyZNnz59zpw586hUUFDw8ccfr1y5ct26dVu3bt23b9/BgwePfH3k22+/PXHixKlTpwoLCy9evHj58uVr167duXOnuLj43r17JSUlDx48ePToUXl5eVVVVX19fV1dHRh283i8lpYWPpWEQqFIJBKLxcBOwu4Dnhqmi+c9kDozPwAjSe5JrDpqUwI59p5Xn1da//79+1lZWSwWy8fHJy8vb/fu3VVVVWCnDJcMMv3Szybb/PMqSSSQhhqNRigUnjp1aubMmfHx8XFxcYsXLy4pKamqqtqxY0fv3r1DQ0P/+te/SqVSwoa3iTMR2IUZg94gk8kaGhqqqVRbW9vc3CyVSunPdN/O/duFILQpqpWAViFUq7k+dH6xZ0ad43vS7nk1dukVPpN4E9ageuqtHswOYzbQRH2MBrOfB/xYFqhVOrtKdQYuoHFWRRHBlVr03SP0/06j1SfQlzfRPxpQM+VBWEexuhqKZ9QaMQdtRNib8PGyin+d0cKehOlRx2xlN/xROWSru3Hho7HPNthzkUu+xnOywCu3yotzx23sHf9stPo0EpgMcg1SUkwuNgk2E8fUZdz8FzuzforQsbJbAdlV3jnNnhPF3pOl3lMa7DN4jplN3XMa/CY/DMpDH32LGii3EnrMimKK1ESNSGkGRKfWoRYd+s/TxW7pLez8J845T50nPnXM1blOrvaZ+Pgv/w/jpn6WfYad8c+q2+7pKlamySlfjl0tjyl7NxedeYDEasqJV1t77LkIaNgjfB36uuTWu5wmrxyRQ2YTa6yyG4Ubi4vwB5tgI+x3haNncQSsUXzW2CdOnOrumdeDOWh7Eaae5dQBABiSbyPlNnrhgVo2V+DM0bjnP3HiSBwxi620xxn4K3HIktplKu05T1mZzawxfNfsGucJosCppT4c1cRN2Pi9UYfEWuxQ23xkmQ8jM9Tk8b0Eoa2XS/25Pzu9V8dKU3fL1dvjj7FbnrFbntYOOxbXumDD85+7Z5W8k6l5fwf62YikmNfWwl6DHWfe+e0C3BboTBmDwPMhwBDQz4cXU5tBgEGAQaALEQCCAN7yhvUklJCly2tbfnThoBhRDAK2CJAjWSaT3blzZ9u2bZnvZcbGxoLBY3Jy8qRJk9LT00eOHCkSiaA53VZaq9XW1dXNmTPH19fXzs6OzWb37ds3MjIyODi4R48eubm5R74+Ul1dDZ4xgH2z1aGTJXAO2lZWqVQlJSVr164dNWpUcHAwm82Oi4sD/xujR49+/PixldkdXYLJZFIoFNevX//mm28uXLjQ3NyMfR7qDcT4kZAgkHm7Z4BneWe8TqE+2NIJeyfUIlQnQuMm7fOJ3uLs85/9eq+8/g8BXmKrxUaDwmRUmrDTRxVDQNOPkC7Jw1lm+9154XDw2xrnEglwZAJ5rdFoVCoVeBsARwcCKkmlUrlcLpPJwOWIQCCAoJHwrk9VVRUEjbx9+/bly5cvUqmwsPD7778/duwYONHesWPHZipE5Jo1az755JNly5aBH+158+bNnDkzLy8vNzeXw+FkZGSMGzcOLLUhUGR0dDQ4zvbx8fH09HRzc4Mokfb29sBHQ5RIR0dHiAvHYrEcHBzs7e0dHBwIbU1obqsMMet2dXUF/jqUlkhoSuK3xMfHx9fXF1x4BwQEgCPvoKCgiIiImJiYuLi4hISEfv36DRw4cPDgwampqcOHDwd2OysrKycnJy8vb8qUKTNmzJg9e/a8efMKCgo++OCDxYsXL1u2bOXKlauptHbt2k2bNm3fvn337t379+8/fPjwt99++9133506ders2bMXLlwoKioCy+7S0tLKysra2trGxkY+ny+RSKRSKbxxRXYuzEhkria23vQSkodWpAmZsoi0N55Rq9W/jnfmzJksFissLGzNmjUVFRXwno3JZNJoNBD9D64XcORbzcMvMxsDIHQQiOV4TU3N/v37U1JSAgMDBw4cuHnz5lu3bhUWFg4fPvzXZyEHDhxQKpXE9Jgu4dXldTqdXC4nBHR1dXVtbW1TU5NMJoO4C2/h/n11aIBky4XNwsRRHjbkx6+fS5xSHJR73497NTy3+f8exrbPKovrZxoBjWlo/EzW/DFra2ME3VquMiKxDj0x4g9EvZMakcpoNgo2UbygnvrGRtBGfKFVInTywY2oSbVumVo7zJNq7LEFtMyZK3PmPnXiah24ehZHzkr/hTW+0jPrduQkybyd6I4Im1TLTUhlsSImnKklBiHWyoQ0OqpCoxIVVZdkfVr8v97/p2d66TvcnwLy7vhyqlL/Q7/iOLpSi9VQI6QxgeW02ZeDnrLRpUyq5WoNeqJGtYbHo5fV+ueLXHNF3ScK3XKFLjkl7+ZKdxViCfpWArrVAzFP+zBmmsSRq+qWq+iW88Ql+4fQHFSt6shDxHMR0IC+1oRNqgvLb/eYUuc3qaHbBIVjKwFtModA5BhZHB2Lw2eNEfhPLo7MUy49gK5WozqpWXPyjIEogKggkBsu1PjlSp2y9fZcbEDtYLakBhpabcfR2Ger7TD7jP2ceE3+OSDv1r/kCudsR4dvoEYq1qIBIZXOpNVBTEsD9aIZPDLA5DPVnTkjRcKP9hUH5Ta4ZiuccrUO5o/ajqtkZeu6TVT7zigPzvvhf8/X/O0SfiTQrEBS7EtbZtQ+Neko42qMiOVhhPnYZH4YBLocAYaA7nJIGYEMAgwCDAKdRQDu6eFNXrKuIwsP2wVMZ+Uy9RgE3j4Eampqtm3bNmzYMAgDBdaI8L4/MDu+vr4xMTENDQ3gqgLCxAFFCwRudXX1nj174uPjPT09o6KiFi1atHz58vT0dFdXV09Pz379+i1fvvzBgwcdEMGdQYUwERBRCjOnKlVxcfG0adN69+4NVpngWACYpnnz5pWVlUkkkg761el09fX1me9lent7x8TEpKamfvzxx4WFhWDxbcuAkNU+mRY6o/nrqkNfmJO8HoydjNSqU/AUnSpqnrbg4rQ5F45/W69RIBk2gdYZjEqTUWtCKhPSMAT0S+4vODZsjxByWaF7vqY7EyC0Gl0BIod+3SHHITlESRN4R4EEfoTLFtnamQxxJQzEHHDZQGi2KQ1scqVSKTDaQGrX1dVVV1dXVVWVl5ffv3//9u3bYF987dq1CxcunD17Fnjtw4cPgyvtjRs3Aqm9ZMmShQsXvv/++1wud/z48WlpaSkpKb169YqJiQkLCwsICPDy8gJ/I3QamrgZsbe3d3R0JP6yIQPfzs7OQHADrw2UN/jdtre3d3Z29vHxCQwMDA0NjYqK6tWrV//+/QcMGJCUlJSYmAiGsREREX5+fuCtG6YamCFBoMUDCibNITk7O3t4eIDfEuKkOzQ0NDw8PCYmJj4+vlevXklJSQOolEylgQMHDho0aNiwYWPHjuVyudOnT1+wYMEiKn344YfLly9ft24dxJ+E4JMnT548e/ZsUVHRjRs37t69+/Dhw5qaGoFAAI8ftFoteYLemV3/quuoVJhVaWxs/JWst7Ozc3Fx2bx5M/H8btU7mfDbZJ9f+H6MnDskAy/3wCmDuSmpdOHChfHx8SwWKyMj4+bNm4WFhUFBQb169aqpqSFG0Fbavoq/xAm+WCxuaWlpbGzk8Xh1dXX19fVNTU0CgQBo6FfR9dssk1zbIINnSKMJyY3oZxM6VII2XUQ3BBRTTNn9avGVD2yfW78t7DM2gobUHgENWw0mzCcaTAYdZhuhTKXXtjrktZCbJoMRu7AyISQxovtyVHCwzBeHK6x4B7uNLvXnlvpzH/txK3y4NT45xS5jqhNmo4UH0G0R9lMsMmDOVIMfHKufKLEQPfWhCEiwRQYuUqPR4a3gdfoJQlca0H//E33yHfryB1TYiB5rUKMeGZBBjysRzxNmuOCHUl1lMOiUWiTUox+ERbH594Mm/hAy8WZo7p3IyWjndcoHtAa3N48YabUWZlxoeDJjW2XwlMeuGc1B04p9M9Gyb3B9fC5ZalP/Wr8sEBFprZssObJnsRh8X2JAeiOSmdB9KfqPQ9dCOD/Hzqx+h1vvhT91nhjYnz04P3tgBxr8pIVo7h50T4K9phCfakYclZSIJRlsP14iKwrJagjMr7Mf3+TGgQ+vO87wunPq3Dk1npxfgqcWu4ypCp2MsjfjmJAPlNjqGbtAIccNNV4jnksIAW3eRsFgJv1VJlSrQOtP346fUfJu7mM/86fEI+OBV2ZFYP5PCbPRruuoVoueIqNKo32K50nwHAOPNgAhhoC2HCnM76tCgCGgXxWyjFwGAQYBBoHOIACLH3KvSdYqpKQzQpg6DAJvEAGTyQQmk1Y6qNVqHo93/vz5devWjRs3Ljg42NXVNTQ0NC4uLikpKT09PTo62tPT09fXt2/fvgUFBSdPnqyurhYKhfDaL+Gn4KSA1btMJrt79+6SJUvCw8NDQ0NTU1MXL168YsWK3Nzcvn37BgQEBAcHjx8/ftWqVadPn378+LFIJNJoNB1QwyCWWCKrVCq5XC6mnGA+ePDg6tWrX331VeZ7mT179nRxcQEWCawmg4ODORzO3r17S0tLgbkgFAxRmACi1WqLi4snT54M71n36NHD19fX398/Li5u1KhRa9as+e677+7du1dbWyuXy9s799vkDUkXbzKDl0Bg+qxH1CL9qQ7xpaiyFv1YilQqpNEinUFqMEmMRi0mdLAPS53Zbhqsp9+k9r/jvtu7XkA5nEHEVTHxxUEOJNL8JSEgctrLtCf/eeu3J6eDcrjCgi8djUajUCgkEgl4zQaLbAgFWVlZWVFRUV5eXlZW9vDhwwcPHpSUlNy9e/fOnTs3b94sKio6c+bMt99++9VXX3355Zc7duzYunXrhg0bVq5cCS5HFixYMHPmzMmTJ2dnZ48dO3bo0KGDBw8eNGhQcnLygAED+vXrl5SU1Lt378TExB49ekRHR0dGRkZYUlRUVGRkZEhIiLe3t6urqxOVgLZ2cnIifkVg2nF1dfX29gYzavCI3a9fv0GDBg0dOnTIkCH9+/dPSEiIiYmJiIgAi2yQCdLc3NwgsCRxsR0REQExJMEXSmRkZFRUVEREBKgXFhYWHh4eSaWIiIjw8HCo36NHj9jY2Ojo6ISEhOTk5H79+vXt2zc5OXno0KEjR44cO3Zseno6l8vNz8+fPn363LlzwXB76dKlH3/88fLly1evXr1x40Zgtw8cOHD06NGTJ08WFhZevnz56tWr165du3Hjxp07d+7evXv79u3KykpwlwG72OqAaW+/G/QGjUazdetWLy8vd3f3Dz74QCwWk6kehJC2VjLb+0vqv0CG9AgZwnTLZLJLly69//774GZ90aJFeXl57u7uCxcuhLNVrVbT9XmBrjtuQvSBYIlqtVqhUIhEoqamJgiODX54mpqaRCIRMRjvWOYfb2srnwjXLrkRG8yKKPtWPb6AAX+LKTyTxTyVakPMn1sJ6A7RIR3ReMfWBtAReP6lrKsx6Ym990pNqNmAKpXo3GPx+mNlszdenbDk3pTVdYt3CVcfQYdvoWv1qJnSVm6E6IjYgNoiyGzvCqQjdWFWU6Qk5qC1Jjw2HfVfR3HWCkqOFGHmXUUzWzZR13OLELghwKOg6FGzhwc95Uf7JwX6/seWL05p/34Hs+FSynoafE9bKGVgtPHInyJ0k/fj5LWnIrNvDpir2XQKVUiRGhn12B9FKwNrpvUBdLNRcAcEdCummDfHJwEu0RqR3ID1adCYjt588p9Hmj7Y9eOUNf/M+Kh69mb58sNo3w1UWIV4RiQyYp/LBvODBnILQ999kMfQSREqEZqWHfk7O+1KKOdGEOfWu/j7H6FZF2JySkZ++Mv87Wh7IfpHFfoF4YPqCYUSxShTwFPqQWxGCwEN+pu7sBhBm2/BlNSueYLQiWL93kvN649W/HV3w+pD6Oht9ECKajRIaMSoWtxt43iTyOyCgxx1DAFNP0KY/KtAgCGgXwWqjEwGAQYBBoHOIkAIaPoyA/KdFcHUYxB4EwiQI5bQr0BDq1QqkUhUVFS0cuXK9PT08PBwFxcXX1/fXr16DRs2LJZKoaGhbm5uAwcOXLFixdmzZysqKmw5YlgVkF7oJwWfz7969eonn3ySkJDg5+fXs2fPnJycBQsWLFy4MC8vr1evXkFBQYGBgX379s3Kypo9e/bixYvXrVu3a9euQ4cOHfn6yJGvjxw7duzEiRPHjh3bv3//rl27tm/fvoN663/NmjVLly6dM2dOTk7OgAEDwNUGmEC6urpGRUWNGjVq1qxZW7ZsuXTpklAo1Gg0cAoD2UfXlr5P5HL5rzaYYWFhHh4ebDa7Z8+ewcHBffr0GTx4cEJCgru7e2Rk5MCBA8eNG/fhhx/u27evuLhYLqfi3VOeOoA+U6vVGo2G7pST3sWbzJsJaFiGmxXRG5FcjkQinUan1xhkOlOLAQmNRr0RL/gM2I7HvG5rXUa9ySH8sfo2r6j/WIN6sdHAKQmnp1WoPcJNw8sWxJobqhE/JGq1GuLUQQWNRqNUKiUSiZhyygxuRsBHs0gkamlp4fF44Dsb7LLBdzYEhLxy5cr58+fPnj174sSJI18fOUilAwcOgB/tLVu2rF27dvny5cuWLVu6dOmHH344a9asKVOm5ObmZmVljRs3btSoUcOHD09NTR04cGD//v379OlD6ObQ0FAwmnZxcaGbY7u5uYFFtouLC5vNDggIAMvrhISEPn369O3bF/jr1NTUwYMHJyUlxcbGAuMcGRkZHh4eQqWIiIi4uLiePXsmJCT07t170KBBQ4YMGT58+JgxYzLfy0xPTx87duyIESOGDBkylEqDBw8GjygJCQk9evQAet3f35/NZru7u7u5uXl7e/v4+LDZbC8vLxJzMjAwkMScjI6O7k2l5ORkCO6qVCrhAKCbJLd3SOh0uqKiop49e9rb26empj569IjM0vTmbV5i6HM4Pd9eX50pBznkNQK4YsJRZ9Abmpqa9u3bN3ToUF9f3/DwcGdn59GjRzc0NADz3lU6tKknCCf6wGmi1WqlUmlTUxM8m6murq6pqamrq+PxeGKxmP48oE2Zf5xCmi1t61UKCvUUM0tF0VVTDKrWYklK7GDp7HMnJ2RwYUHoP0IIEkjhMS/F55rJWizZQD3SBdPlp5QvaQn1raK4Y7EBx9lTYSNfrcmoQkYNMuqNlOtnKlIijT7H1C2IMVPGhFw3mmlqzOoCFiZzSSsLDCbQz1LJwESTEeE2SoREOPKiOVwhqWEmkfFYCXRYGxkOYIjqTKhWh/1dUIbSJhM4OKGAIbsJNCN/LXQ2Qa/jDHhYNg9HR3HfEooOFpkwKfwEIZEJ25trMHoqZFJQH5WFBwdUrL6xmbbWiMNXChDiIXSLj67z0TU++icf1VCDElDHjcSEFJRPFYuK8EIZdVDhcxTLodhnMpNYKlK/sFPAql1L7SBzZEIKbQVCTTIkVJsdVUNLvGexMTUJmUk/2Fr31zPdMH8YBLoMAYaA7jIoGUEMAgwCDALtIdDx3Sd9gUHPtyeNKWcQeIMIENYGLCshspnJZFKpVAKBgMfjrV69OiEhgcVieXt7BwQEeHt75+U3RFbOAAAgAElEQVTlDR061MfHh8Vi+fn5xcbGLlu2rLS0FEzS1Go1kAJtmlHTzwhYHqvVaiAjdDrd48ePV61aNWDAADab7evrm5iYOGTIkDlz5hQUFOTn5yclJfn7+7tQycPDw8vLC1yyEn+s4J41MDDQ39/fzc2NvGsPL9q7urr6+vqGhYXl5eXt2LGjsLDw1q1bdXV19NBMxJEorOHp2lrtI7Vaff/+/bVr16ampjo5Obm6urLZbH9//7CwsDFjxowdO7Zv376enp4ODg5eXl4hISH9+vX7+OOPL1++DM49jEajUqmkx1q0kv8W/IXVMXYGSb2PqzOZZEaTUGdq0aFGAzYcEmLq2bzQsV6pvQX6Myr8kRFo89ykz2bEVNyKoyTPlgg6JpMJ5j3y5gTZRDIdXPTJKyN0QhwsXoHjBuHkbQwIC9nU1ATUNuG1gdS+efPm1atXL126dP78+e+///7o0aN79+4lNtorVqxYsmTJ3LlzwdlRenr60KFDBwwYkJiYGBcXFxUVFRwc7Onp6ezsDJOSG5XAEBs8fri7u/v6+gYHB4eFhYEFdFxcXI8ePeLj4yFIY0JCQk8qEfI6Li6uV69e/fr1S0lJAZ46IyNj0qRJ06ZNA3/WixYtWrp06Zo1azZs2PD555+vWLFi0aJFc+fOnTVr1rRp07Kzs8ePHz927Njhw4enpKTcuXNHrVbDE0pAjOxKgrZVprKyct68eSwWy87ObunSpeDFGC43VjsXGhKBHWSsunixvyAfLhZ0CSaT6eHDh3Pnzg0LC7Ozs4uNjT1z5gyEDKWrRG/SJXm6PqAVfAMH3dLS0tDQUGdJtbW1DQ0NYrH4bXwI2iVw0IUQphUelVqxmeCR2ULXYvfFmKLFjB5J8Jd80y949H7MeUo+mBqTZ7M0L8pULWoDyME8LFC90L7VOppixsFDsI6yjwY2Eb90ZDQZgDzFHDQO2QBuF6CCRbiSol7xVdqECV3i1hmXtPZi6d3CGpu1olrhNjTQzBd8gqcWUQEgqDp0spiGMMEQexrRGIxKnUlDuQ2h+4kgIBIhZmqcIEJqdJghilFjUiGj2qDDhgVKDVLqkIbax/B4wczXYy7YgK2GTSrqAwbjEBKQvpfNAwdMFEYkMSCFCfPvcovdt45i4cUqpDEiyo0JXVEQZcs+4xIyZJKB2nDE4GPDhGWqzY9JzEcLvHWG78+MRj12gWY0GvX4oLUGjuxAuj5MnkGgCxF4ewlouEXowqEyohgEGAQYBF4bAmTxCTdSHU9orTdbz+Zem7ZMRwwC+CbZJpFCOj4QmYq8satUKhUKxblz59avXz9mzBjws8Fms5OSkiIjIwcPHhwVFeXl5RUZGTl69Ohly5adPXsWwgzSuRsgX0h3Noo8UwAeY2GdrNPppFLpgwcPDh48WFBQMHDgwNjY2LCwsKioqL59+w4ZMoTD4UyjUn5+fi6VcqiUm5vL5XIz38scM2bMsGHDevbs6enpSSydExISMt/L/OKLL65cufLw4cOmpiaFQkGPGYgQ0ul0ZAigTJvUBn1QEG6Uz+eXlJR88803H3744YQJE/r37+/v7+/t7R0YGJiSkpKWltazZ8/IyMiEhISAgAAfH5+oqKicnJytW7ceP368pKSEz+eTfun75bnyAOhzNelEZVie4hiDGu1TjVqm0/+iN/J0qFFn+sWAmo1IQiOgYTlL1mudEM9UYRB4xQhYnRfPzDsWl6yggtFohCdh4CSBkJuwFSZJmNaIJTW5K4DKMJ+Qx3jEjbLtEAlhTSTAhAM1wZCW9AszM5DXUqlULBaLqCQQCJqbm8G9b0NDQ01NTTWVysvLHzx4cPfu3Vu3bl27du3ixYunTp06fPjw/v37d+7cuWXLlvXr169ateqvf/3rkiVL5syZM2XKFA6HM27cuLS0tNGjR48aNQossgcOHAjORvr27du7d2+wfY6Li4uOjga3HmFhYWBPHRQUFBwcHBISAv49wBMJeP+gOxUZPHhwcnLyhAkTPvjgg4ULFy5fvnzjxo3l5eX0adYWKyi5fv16UFAQ+Ojfs2ePWq3GbmypJ5305gRPqx3d5t/2+nqucpBMv16QyVyj0Uil0u3bt/fs2ZPFYk2aNKmmpgbcOsFF5Lk66mRlK33IiwJwqQJvVM3NzeASuoZKYAcNr/4QADvZ3e+pGvCSxLExRY/C5QqPArZS1qtain1GlBdgcuQYkMHqQy51rbwkHQ5KPhXmELOBeIqg+FAwUDU3AV4QWgF9TG1oFWjEtyVytUqmUsrVKq1ehwlcSFi0EenxoaehjKBxoL92CGh8tuDxmEMKK6lhQhluQvfdAaOyUNW4M6DmLaM1I0ZIXj3FiVNK6SkH2a1cqllR/EOD0SRXa4yUjbkUIY1O+4xbZOiOkLDWPKpl7DTJbWQtqiLKphtIZlKt1dEHQnBSYOrW4goDOGgIwQg240QYyRBReAoy6PBO0eqQmvpQ2xRSmVarVWk1TzVquVoFdLC5FcbN2vwZn3RkyFYZ0iuUGzFkuC8tRXBrDAadTm0yKJEBX32oINjEozTRE546PKMG2cZkGAS6CIG3lICGWzf6XUIXjZcRwyDAIMAg8GoRaL1zorwQQogeWGqSTX/ku/ZXiy4j/ZUgQD8yrfJ0poMczAihlpaWurq6EydOLF68uH///hEREeBdNCUlZeTIkYGBgWw2G96tzsrK+vLLLy9fvlxTUyOVSn9zAESBNmuSrVYZg94gFAofPHhw/PjxzZs3z5o1KzU1NTQ01MfHB1ym9ujRIzk5ecSIEWlpaSNHjhxBpeHDhycmJrLZbHt7exaLlZiYOGXKFHCv0dTUJBaLbR2DdF4rUpP+9jes8IGZMugNYrH4/v37hw8fXrlyZVZWVmRkpKurq7+/f1RUVM+ePePj48eMGTNy5MiwsDAwJ4+LiwM3HceOHausrJTJZHCnRPqCTJuFsAlwg91Kx9BKwm/+JSudZzP4zV69Sas36XVGrR6p9UhpMCoMRqXRpMbvCVs8D1Lyn21qXj12btH4m/oxFRgEuggBOE3aFPa8ZxC9/ovlO1aDvrUz8un1bfNGoxEzIyqVQqGQyWQSiUQkEgmFQshAKEgej1dTU1NeXl5aWnrv3r07d+7cuHHj6tWrhYWFZ86c+e6777755puvvvpq//79e/bs2bVr17Zt2zZv3rx27dpPP/10yZIlCxYsmDFjRm5ubnp6+pgxY9LS0oYNGzZw4MB+/fr16dMnPj4+IiIiMDAQXl4JCQm5e/cufTqlj5Gu/969ex0dHVks1q+OmE6fPq3T6eClmfbq09u+6jxdB8iTHo1Go0gkynwv093dnc1m/xoWUiaTwVZy00iak1YvmSECrTIkNKhYLCYuoSsrK6urqxsbGyUSCeGgrUbxkvq8Lc0JZ/qsMW/r9Yni+OAaZiYEKdWNyAgfA8JUJfmQcqOZYX52oDT7X7IBOOjWHsmGNjOEi6RvBf0MFEOsxxbQYL2LwxfSL7+0tqCwxSjWPBasMwEEGEpoTmto7pZeDQ8KSwA6G1uJ42wro/oMkWpuT1cLD91szE3x3riKLVDWOmAJgDYZBZWh49J2Hvpue5ulFG6uoCY8EQBCnlgN0wcA+ra9B0Ftim3XG406g0GPPZRh0r9tNcgw28xY1CO/5HQmgANvrjEaNEbcF51kI9MLAZwhoAmSTOZVIPA2EtBwzgBfQ06PVzF4RiaDAIMAg8ArQkCn08lkMj6VpFIpvAFKbgjoF/tXpAAjlkGg8wjAkQmkJP2bGDuDkR04P21ubr5169b69ev79u3r6urq4+Pj5+cXGRk5b9685ORkiJQVGBg4cuTITZs2NTY2ajQkUninNOr47KCfRHS1CaWr1WrBQ6tAILh9+/b+/ftXrFgxd+7cMWPGJCQkBAYG+lLJ398/KCjI398/MTEx873M5cuXnzt3rri4WCwWd6yA7RhsVYISUpOuJ4HXqg4Q6KWlpV999dXMmTMTExPBlyv4S42Li5syZUpGRkaPHj2cnZ19fHw8PT1DQkJSUlJWr159584dGZVUKhWIBW/RxLYONKGrAXARZV7gXossk4i9DCzAKLMqk9ZkxOsci7tJIt/ifwM0osug5wlyTIZB4FUh0PnT3OpUfVUKvahcUM9WSXp5e/nO9Elv20F9eLQGzkPgUSXMQuBUhG7uDVcTtVotk8nEYrFAICDuhsEuu7y8/NGjR/fu3bt169bly5fPU+n69esnT56kxxJsnVUoFem6HT9+nMVi2dvbBwcHHz9+HDhrumVl5/c+XWyX5NvDE6BrampKSkoCVyceHh779++HWd1K+S7Un65Pm3mNRiORSIhz86qqqtra2paWFoVCQd8FXQLO2yXEmkt9lhm05QEp7Wns8/MQ0O2PnNCXnbpGWmhNszxogwlok8lgJqBhL8NgwNvys51DG2JibenWdrztllC2zeaHzZbmZvAwA976MWsLdUALm/rPKtf6z7Z38zYs4QUIaLoSrb3Y5KgbHnwjY/Vpk4C2qvO8f5/p3Ha89BKqKl0+8f1ilQGaG77p5zvpi9zRkQOPbGIyDAJdhcDbQkDTV7kQbId+VevCC21XAcfIYRBgEGAQaBMB8A4pk8mam5vrqNTS0gKeW+lLiDbbMoUMAm8EAbgNpdORkIdyg96gVqurqqrOnj27evXqtLS08PBwFosVGxublJQUHh4+bNgwb29vcLuRk5Ozffv24uLixsZGRAXQ6/IrOGhl9U0/uYja8Hq7VCptbm6ur6+vqKh49OjRA0t69OjR48ePKyoqampqRCIR0LVwN/JcOltpQv6SXQklbcILtzqkJkJIpVJJJJKampqioqIdO3bMnj17+PDhERERbDbb1dU1LCxs9OjRI0aMGDRo0IABA4BSZ7PZiYmJ06dP//LLLy9evFheXg6W5sAyE+F0NV4dAQ1x24F6Nsc7ojxjwtKIKENl6MulzuSfbc38YxBgEKC9rm41a5GJqIPMC+MHfREP2uBmhDwFtJrryMwD1cBvPnhzhpowUQMxbVsOM7NOp1OpVKAwkU8fGn0s9+7di4iIgOejO3bs0Gq1RGFoQq/8mvPt6Qwen8+dOxcaGpr5XuauXbuCgoK4XC6PxwOfyzqdrr22LzMEusw282AIr1Qqwaiivr4erpjgfIY0eRkd3t62hOOzVZFsIhlMSmLqk7J91uuwBTT9Y7aGbtsC2la+TQn9Gmmz0VIAylj+mVlSioAmtK95l1EsMXZd/YwxNHQC7DP5pvVMBttBxpqbJXIor9XtEtCkl2frk7FYZWwVoCrALsDeRvDHYn+NVaI3sJL1HH+Jlq8h84xatupDiaWSlT5WvDP5yxDQFsCY3zeJwFtBQJN7Jp1OJ6aCSoOzRXJVIxXeJFRM3wwCDAIMAu0jANOUQW9QKBQikQisRcCcp6mpiSGg20eO2fIGEIDLKyzjCXVLVvUkA9UuXry4cOHChIQEiJgXGBg4bNiwPn36uLm5+VOpZ8+e06dPP3/+fEVFhUQigfHAmlmj0dB9JXfJUOn3Bra3B/AMG4y11Wo1uO1Tq9XgTJO8vg3l9GBK7XnbsO3CahRW+pC/pBqUEFRJhh70DF51B32gPqJ8DvL5/NLS0kuXLu3Zs2f+/PkpKSn+/v7wanlcXFxYWFifPn24XO64ceMCAgLs7e1DQkIGDRrE4XA2bdp08+ZNoVBIOG66GrYEtG2kNaJ/mxn6aofYPoMLS8oxolGFzB8twgHr23qjky6jM/k2FWEKGQT+1AiQCcdqpqKXt5f/TeDoDWEmIdOXbYbw0YSJJs7HoCNibAQOr0nvoLnJZAISlrwCSypQb/JjgzzQh3RNV49e+dd7sNmzZ3t5eTk6On766acikUitVisUCiuI6E1eW75NncHfhVar/eSTT8LDw1etWlVVVTVo0KBhw4Y9fvwYrk3kBReQ0FUK0/VpLw/qgScTsVjM5/NlMpnVi31dpc/vRg6dELRQgYR9fpZ6Bhr6bSSgDSZbAprO/0KednW2HbVtyTMEtJW0DiygoReb+u0dEG30i6v+OQlo2h6yPHSgHvwT3plkGAK6vQOKKX+dCLwVBDTcSUil0vr6+oaGBh6PBzHfyUIRbnrIdfF1AsT0xSDAIMAg8JsIwOwE7DOfz+fxePX19bW1tdXV1fX19bD4Af7rNxdOv9kXU4FBoEsQIFdYYh0Gi3y5XK5UKgUCwZkzZz766KPo6Gg7Ozs/P7/AwMCEhITU1FQfHx8Wi+Xr6xsbG5ubm3v06FGBQCCXy61CPIGS5ML9Olf+hAchp5vVXQRoRd9KZ0wIVU1X/iX1txJFFKATwfQ86Ebna8C1SF1d3bVr1zZs2JCRkREZGenv7+/j4+Pu7u7n55ecnJyRkZGUlOTn5+fo6Ojl5eXn59erV6+pU6fu2bPn0aNHIpFIKpWqVCr6IwECArDhVl47OjjSbBc8dF+Nahwd3qhCJjUOFo+jFgEBDa0sYtuU0UGhpR3zyyDAIPC6EIDplFwvyFxK5iiryQ0eZZGJhWSsqpG/zzsO0tAqQ5cjkUgePnw4fPhwFouVkpJy7do1MLvu/PxGl/Ya8qBYZWVl3759+/fvX1FRUVtbO2TIkKSkpLt372q1Wng5xhbz16Ab4Az7HZ7vQvjNX+nyN6LPaxhyp7poiwC1sJ9mI2jy1yrTKfldVaktPcHVb1vX2rbK6ISyrTTbEnp92/zz1m8Phzbk4KpWUJs9UGM16A3aE/rHLydMtKE11iM+xcnIGRccBAom8+oQeCsIaHi9VyAQ1FKprq5OKBTCkrjNG5dXBwcjmUGAQYBB4MUQMOgNSqWyubm5oaGhrq6upqamsrKyoaFBLBbTfSAyc9qLwcu0enUIAO+JENJoNNXV1fv37y8oKEhJSfHy8vL09IyLi4uPjw8LC4uPj/f39w8ODk5OTv7ggw8OHTpUVlYG9s5gzkbM1uj3snSO4NUNwUryyxPQZCz0BbZVL8/1l44DyZOAhNBLmwQ0qUy6M5lMKpVKKBRWVFScP39+3bp1M2fOHDZsWExMjJeXl7u7e0hIyNChQ3v37t2zZ8/Y2Fjwdt27d+/09PS5c+ceOnTo9u3bPB6PvM8OdoXQOwyc9NVBpr11KhhBEwJaRRHQVhy0RWx7Mtort7RjfhkEGAReFwIwBdn2RqYmq8zbQEDrdDqJRHL06NHAwEAXF5esrCwejwcUqhUH3d7obMfb5SXQNXkcKJfLV6xYERUVtXTpUpPJdPXqVR8fn5EjRzY2NgIB/aYIX9CT3LtCBi769Otjx0jS7wq6HMk3I5DOZ0Kexn6CBbQtGQolr1XhtvRkCOjXugveps4YAvpt2ht/Xl3eFgJaLBY3NDTU1NTU1tbW1dXx+XwgoOF6ZvX9591dzMgZBBgE3jQC9OmI6AKUUEtLS21tLTjIq6ysrK+vh0DhVjfudAmQJ3KYDIPA60EADjxgGw16Q01NzalTp2bMmBEaGhoQEMBisTw8PMaMGRMbG+vh4eFFpYSEhJUrV169erW6ulqhUOh0OnA0DHbTxIEDObxhIOTv61x/QqfEUo+uAz1PPzEJ/Uoy9K3Q6mV2Db3f9vK2i3mrmlYKGPQGlUqlUCgEAkFZWdmVK1d27do1Z86c/v37Ozs7e3h4BAUFhYaGurm59e7de8iQIQkJCe7u7l5eXuC2u6Cg4Pvvv6+pqSG8BgQNI4QI6a5NNdojiWkEtEmF7aBNaoQoAhq/gAytKMntCeignGjEZBgEGAReEwJw+rfXmdXk8AJ/25PcXnl7XdDrw7sjCKEjXx+JjIz08vLKzc3l8XjgRplw0Fai6BI6yLd3LWuvvD1RhKnX6XQKheL777+Pjo5OTU2tqqoSi8XLli1js9mfffYZ3YGb7TWiPeFdWG6FErGFty3vAAHbyl2o4ZsR1RaxSxhnhoDGbHybnzZwa6emuXk7u7cNObgm2QUkY1GD3qAdmX+CYoaA/hPs5N/BEN8KAlqn0/H5/OrqaoaA/h0cMoyKDAJ/bgTot9GAhNFoVCqVfD4fDJ9hKgNXQuAjj85ktUmK/bkRZUbfZQjQV4YdC9VqtXw+v6am5uLFi0uXLk1MTHR2dnZ1dWWz2Z6enj179gwPD3dxcQkMDExKSlq2bNm5c+ekUqlcLgc3lMRmFhachLS1PTtsSzpWrEu2Qqdtnmt0fYhBHLFEJgMBX8zkzIVWL6Mbvd/28rbkglVN4PqVSqVGo6ErAw46VSqVTCaTy+VNTU337t3bsmXL1KlT+/XrF0AlNzc3Hx+fhISEUaNGhYeHe3h4hISEsNns4ODgtLS0jRs3lpWVtbS0KJVKeGODcDTE7ypRBrpub8lIEdBGygIaPUX4o6Y+WmSkgjLhNSWV2hPQQbm5JfPDIMAg8NoQgBO/ve7ItPDCmfYkt1feXke29Y1Go1Qq3bt3b2xsLIvFGjt27O3btwkHbTvf2kpos8RWAdtJsgMqlsgEX08wqz98+DAtLc3f33///v1SqfTUqVN9+/ZNSUm5f/8+qQ+9WF3X6FtfUd52vLbQkTrt6WCldmfwaU/U21JO5zMtDgwI6ckQ0Bba1+aCboUbhs6mzjMl7ezwNuTgmmQXkIxFPr1BOzL/BMUMAf0n2Mm/gyG+FQS0Wq1ubGysrKwE4qaurk4kEtFD8fwRLlS/g4OBUZFBgEHgNxCAm2z6zbdBb5DJZE1NTeDxGaIOAvtMXOva3nkzc9pvAM1sfiEECAFNWtM9KoDBrE6nq6mp2bt37+zZswcPHuzr62tvbx8ZGRkUFBQYGBgbG+vl5RUdHT1hwoT169dfvXr18ePHMpmMMLP0gx9OB9IXWYTTS95UnqyHScZWE8Iyi8XimpoahBA91hPwAvST11bCy5cQ9drMPK98OAB0Op1Wq9VoNCqVqr6+/tKlSxs3bpw7d+6oUaPi4uLc3NycnJx8fHyio6P9/f0jIyMjIiJcXFx8fX0HDBgwderUzz777PTp02VlZTKZDByzwE6nQ0G0pWuIg9tjX89GHdLqEZIbUB0fVTcivgIpEWqWiXRIj6MRmsD1IN0pdMfrT7KV3huTZxBgEHgbESCTg1Xm9esKCkgkkj179kRERLBYrOHDhx89ehRMoYkPIqLnc2lIbwV3dFBiNVuCTNhEl2/QGzQaDbhuKysry8/P9/b2XrBgQW1t7alTp1JSUuLj4w8cOKBWq4kEcoW1lUaX/IryZLzk9pWU2PZI1xCuSuSbtKJnbCX8fksI72mTaWVVX2x05EJoeYj7W2I6wbjSZULeQtfSt/xWRx1tp8ux9NCV9duT1Zm+2mv7tpTTsXspneBIoInoAB3GBzQNJyb7qhB48wS00WiUy+X19fXAPtfU1NTX14vFYrC+IdenVwUAI5dBgEGAQaDTCMCMRDg4eHGysbGxurq6qqqqhkokjCpIbe+2u9N9MhUZBF4EATjwgEWVyWRSqVQikRw8eDA7Ozs6Otrb29vLyysoKKhfv36enp52dnbu7u5sNnvQoEG7d+8uKSlpaWmRy+W2psHk4G/z6gyFL6JuV7ch6pFMBz2cOXMmLy/v7NmzpI5GowEymr7mJ1u7MEPUazPzAh3BfocHBrD7NBqNTCYTi8X19fXFxcV79uwpKCgYPHiwu7u7vb29i4uLu7u7t7d3z549Y2Ji/Pz83NzcgoODBwwYkJ6evm7durq6ujapZ1CYriEsaQxIq0NaFUJHT98u+OjYxKm7Dxy9L1QhmVGrR3otQ0DTIWPyDAJ/OATanMoIa/l6hkvXAZ6inTx5MjEx0dXVNSgoaN68eefOnUMIkfgcOioR7pj+/kdnFG5zdDAVwyQM8slzXFJfLpdfu3Zt/PjxISEh06ZNu3fv3q5du+Li4ths9ueffy4Wi8nLLtDEalyd0a2r6th2TUqsuoCBk+eg5GJK6ttmrCT8rv/a8M5GSwlDQHdAe5J9TiddO1OfNLTKvExbK1Fv7C8di5dSgiGgXwo+pnHXI/DmCWitVisUCmtra8H/RnV1NZ2A7voRMxIZBBgEGAReFAE6uaPVamUyWWNjI4meWltb29zcLJPJIGIMdEK/1X7Rbpl2DALWCJAVrPUG6r9Wq1Wr1SqVSiKRlJWVFRYWFhQUhIWF2dvbe3t7s1gsT0/PyMhIDw8PBweH+Pj4lJSUrVu3lpeX0y2myfqZvizvmIBuU5m3v/DMmTM+Pj6jR4+ura0VCARCodDqHSw4i9/+gRC6nOwm0NloNALVAhXUarVAICgpKdm/f//kyZP79OkTERERHBzs5OTk6uoaHx/fq1cvLyr17t27sLAQvELTpzKSp2FiNCK9EakNSKFD+jq+hjt53bshCzy9ZyUPWXr7R9FThJ5onmiRgcRefzYoPX2p1V6e1huTZRBgEGAQaAcBqwkK3G5cuXJl/vz5fn5+Li4uUVFRy5Ytu3DhgkgkkslkGo2Gfkm1am7bCalA55eBciVcMzy3g6nYoDfAVsgoFIrm5uaamppVq1b16NHDw8MjOTl59erVHA4nODg4Pj5+9+7dfD6fsM9EAdIvXVuy9S3JmEwmMM4QCoXNzc0CgUAul+t0Ori7ILcTv4uxvACkFrqZ8M4kwxDQnSGFba/+L7ATiFuPF2v7trSiY/FSOjEE9EvBxzTuegTePAGtUqmam5vr6+tra2t5PB5DQHf9Tv5dSQTK422+tfpdwcko28UI0AlopVLJ4/EqKiqqq6vr6uoaGxv5fL5CoSB+/aDvP+pNdhcjy4hrB4E2jx9YwrXZwmQyqdVqoVBYXl5+8OBBCEnn7+/v6ekZExPj5OTk6+vr7+/v4eGRmpo6f/78vXv3lpSU0B+ZgCcKOudIVowk06ZWberzNhfSXXDMmDEjMDBw69atO3fu5HA4V65cAc1/dyMFhYH7sAUfXHNAuVKpBNP4urq6ixcv7tq1a9GiRePGjYPIk56enuHh4VFRUQcOHBBxKwMAACAASURBVFAoFO0ZQdO60COkNCKZERPQ6Oa9lp69F3p6LYuO3hYT/9Hhvz+WmZAaaRgCmoYYk2UQYBB4JQiQeZsQxCqVyqA3CASC7777Li0tLSAgwNnZOTY2dvz48atXrz527NitW7eampqEQiGE2IVndbbKwcM8iP4qEomam5vr6uoqKysfPXp0//79u3fv3rlz5yYtXb9+/erVq5cvX7506dLFixcLCwsPHz68atUqLpebnJwcEhLColJoaGhERESPHj24XG5RURGPxyMuoeg6kHG9zaskk8mk0WgkEkl9fT1412xsbBSJRAqFAgLewoh+F2Ohg9/JPENAPwsUnURlCOhnsfmtf3Tsfqtu+9vb8sTSwZ5gXHC0DyWzpcsQeDMENFx14OoOAXPqqNTQ0FBfX9/Y2Nhl42ME/d4QgNDVHbz+BgcP3FMCG0IOp9/bWBl9f5cIwPGmVCrB73N5eTk8PBMIBMA+/y5HxSj9ViJApjurKRGsqOgqG/QGrVYLD3TPnDnD4XACAwNZLJaLi4u3t3dERASbzfb19fXy8goJCfnggw+uXLkiEAgkEgldiG2ergB9vv29z7qgP6zhYVwlJSVxcXF9+vTZtGmTh4fHvHnzRCIRAEKvbAvRW1hiu3dsS4ja9IdqarWaz+f//+x9CXwUVbpvJyGdhWw9SQADSWS9ROSNiBdQrwo+RH0s4abTCS8h+gD16ahXlLnqDHdEfTo6D7c7jjgqel1wRJELok9FroIMmyMCAoIk3U1Xdbe90t3VnepauqrOm1Nf+lB0FgIC2ap+TThdfZbvfOfUWf7nq//X0tLy0UcfPfLII5dffnlxcfHGjRtZliW21R0DH9iPUAKhGMIANCshtGNPtOrSFcOHvVZ20ZsXj/0/b75//ISAoijOIyGhJGQJyZgCWkEynvMVJYUPmkinB3QN6BrQNXD2GiCHphAA5mWHw/HOO+9ce+21I0aMyMvLy83NLSoqGjt27KxZsxYvXrxixYo//vGPa9as+fjjjwEy3rRp08aNGz/66KNN6rVx48a33npr5cqV9913X0NDw0033XT11VdPmDChvLzcZDIVqldBQQEETCZTcXGxyWQqKioqKCjIz8/Pzc3NysrKyMhIT0/Py8sbMWLE5MmTb7zxxgceeGDdunVer5ewP519tXs6pSAI4XDY4XD88MMPR44csdlsNE37/X6GYeAkgMyqXcxNPV0JvXxdAz2sga4B6C5AZCy3FneGqO3soE+pHomPPXngTxvVeHdSaTPqOr42ph4ewBroeQA6Eok4nU5H8qIoiuz6BnC7DNyqt7eAlmU5FouFQqFAIBAMBkOaKxwOw6tzA1dfes0vuAYAChQEIRgMulwusH2GdwzBoPKCS6QX2G81QMBBeKuXWCXLsszzPMdx4GguGAzSNL1u3brbb7/9sssuS09PNxgMmZmZeXl5JSUlBQUFI0eOnDlz5rJly7Zs2RIIBBBCUkIi3o26UB9sDmXNBXfgbxcJe/lP2lpA5WKx2NNPPz106NBFixbNnj27rKxs06ZN4KWKRO7llSLinXXriKJIXvoG+7XDhw9Dh+keAM2qRtAJSUE7dklVVSuHl75XNvTDyjH//sbaQBAD0DyPBAElEjIA0BiD1gFo0nB6QNeAroFzqwEYDDUzWFtQURSfz7dhw4YHHnjgqquuKisrM5lMWVlZYI8Mf9PS0tLT09PS0rQ3DQZDenp6RkZGZmZmlnplq5fRaMw89crKysrJycnPzwcwuqSkpLy8fNy4cTNmzLjzzjsfV6/nnnvuvb+8t2fPHqfTSd5D6viQ79zq5TznJssyy7I+n89utx9Tr6NHj1qtVpfLFQgEGIbhOA5eFjzr2eo810DPXtdAz2ug9wLQStJXZQrcrEGxe159ugS9WAM9A0AThUgJKRgMUhTl0Fwsy+o4DlHRgA2AKXQ8Hg+FQkCzC24qCd8uRVE0TTudzmAw2A/sBQZsQ/e5ipPRieO4cDgMZqQsy+qdsM81Ze8XmADQxHkRIXeOx+MMwxw8eHDdunWLFy+eNGlSbm5ufn6+yWQyGo35+fnZ2dkVFRV1dXUrV67csmWLzWZjGIZUGTgxydeuA7BFbP+361S9+VdtXQCQQAgdOXKkoaGhqKho8eLFI0eOvPrqq5ubm+HACeL35hqdE9ngWALIOoGsA6hR4eSjqyLaNiHYYga/vymhHTtR1fjnLypdd9GQTSNG/fmNta0BAUUUIa4BoBUZqYrVLaC7Uq3+m64BXQNnrQEYutsD0JChIAjRaPS777579913n3zyyaamppkzZ06dOnXSpEnjxo0bM2ZMVVXVL3/5y8mTJ0+ZMmWqek2bNu2KK66YNGnSFVdccd11182cOfOGG26YNWvW7Nmz582bV/PPNWaz2WKx1NfXL1my5P7773/sscfAnnrDhg2bN2/etm3bgQMHQqEQDLZASUEG2xQCt7OudY8nhB0cx3HBYBDYNX9Qr+bmZoqi3G53MBhkWZYwO/W4wLoAugZ6oQY6A6A7u99BFQgiTAIdRFJvaSKkWkDL+B23tguCMkKi+pFVU2v4jeSgiZ5Mpv+va+AUDfQwAC0Igs/nc2gumqbhPeJTxNS/DDwN8DwfCoXcbjdFUTabTYs+AwZN/rpcrnA4LAhCP7AaGHjt3PdqTIBmWZY5jovFYhzHnRGc1/fqrEt8QTQAzELacUwLQIMIsizDqe3nn39+1113lZeXZ2Rk5OTkFBUVAZtkTk5OcXHxddddt2rVqubmZo7jWJYlxIuKogCEDYauYFitLbHDisIevv3fDiP3iZvaugA2EY1GEULr1q3Lycm59tprGxsbs7Ozn3jiCUDtIX6fqNrPERL6m5Y/Wnunq34CGw+1bACgt+9E46peKhm6oWTYJ8NGvvb6+0JIQFFR4lFCQEIC93VAnzuwgNYK8HOqo6fVNaBrYIBrAIZuLQANp7nEJx6QQgAEDMzOoVDI4/HY7XbgL6Zp2uv1BoPBiHpFo9FYLMaybCwWi6sX+PuNx+Msy8bjcZ7ntd72wPcgvLEEMUk0eIGJvHQCLQVDbl+fccgMC866fT4f8EEfO3aspaXFarXSNO3z+cDgLIVhbID3WL36ugaIBrRAMxBikDspccjX1IAWFNas01KjaSk7Uig4ZEWRZDkhYeMCHiEWoShCEfXTipCAf2pbHIJZdNeldFCwfmsgaqCHAWiO49xut81mI2BiKBTieV6fjQZaZ9QutqSEFIvFwHuyw+Gw2WzN6mWz2RzJi3QYuOl2uyORCHl/baBpT69vT2mAbBV6SgC93P6kAdipQo2A05nYQ4miGA6Hv/nmmzVr1tx///3gThDeCy5Qr7y8vCuvvHLJkiUvvvjijh07yJ5Wu/EmYcicOBske8X+pMzu1IVUXFEUAKApirrvvvtyc3MbGxvLysouvfTSHTt2AGNJdzLsH3EI0Az6OSM4GPZIkoy270SjL3klb/iG3PJPfjH6z2+s4+Mc4uLyzr/t2fG3v9oczYLIIaTwfJzn45LEqTTQCBx8kbdMQJ/YUFr99A/16rXQNaBr4EJqQDvOdxiGmZG8ZgTnsuSrlimiw+Q/5yaZlIktcP9YVWonESkhxePxcDgM+33Y0LW0tFAU5fP5otGovuu/kI+DXlZf1ICEFDFpapzA7M6obZEvSq2S0FYjsFPWkmOQqmpB4fZhuEP+pgDQCkKihOICiiPk5tBuJ/vEB4mnN6BPDiG/glolOSG1oXY6AE0UrgdOp4EeBqBZlqVp2mq1EjwxGo0SA8PTCa//3k80AOstYJ8Ezg0wfHY4HHa7Hc4nbMkLugr8RLqNw+Fwu90Mw6RsXPuJgvRq6BrQNTAANED2bMC3C0u6eDx+9OjRF1988ZZbbpk8eXJBQYHBYAACSqPRaDKZJk6ceNttt61bt27v3r2RSATAZRhOgTlBu8UlO+2Un2ALPQB0fEoVtcABnF+yLLt3795p06ZNnDjx17/+9bBhw5qamliWJYD+Ken76RfSD0E/3QegwTYHIRkD0DvQyEteyy7/yHjxpvwxL/3HhzzPISGq/Mv9Sy8eW3n9rGvuufeOV17509fbt/r8bkHEAHQ83tqZRnUAujPN6Pd1Dega6FoD2nG+t4W1szORrftDbtcV78FfSV0gANWMx+N+v99qtRIM2m63e71e8OWjW571YHvpRfdyDRDzZxTjUVjAZsheCXlkRLPoRBzFOCRAFLUesBTT8mC0B52hwgR01gZSAGiMdouIlVFQCf1h3ReXLvxbmWWrac6ua+5GVhGj0uQimZA7ekDXQCca6GEAOhKJUBQFALTD4aBpWj8I7aSl+vNtRVFEUQSrZ7fbTasX4M7QKzwej09zeTweQKgJAG232x0OB7zP1Z81pddN14Cugf6uAUG9pIRkt9s/+eST2tpak8lUUFCQkZGRnZ2dm5trMBiMRuPQoUPvuOOOnTt3AuLMcRzBDRFCwLMBxETaLS4BoLXvCBPbq/6u2tT6pWySwSScYZg1a9aYTKZZs2ZZLJbc3NyNGzeCN8LU9P39u1Y/3alrFwD0G+vbAOg51fOy8o15RdkZWQZjVnppafG11/7T3ffc9fbbb3u9Xi0vKvRVYv6saLZX3RFGj6NrQNeArgGt91TtgNZLwtrZWStSX284bV1IGDwTer3elpYW8EzY0tKiY9B9va11+S+cBkSEmsPoC1u06fnjl99DX34vuvt1tMeHYipmLOJFUts/lZo5uSQ7VcD2YDQBjpM/AQf0yWSigloR+mjfN2MXOn+xwDWo2p49//vyBvTuPtSKudQgJhSnr9RO6k0Pda6BHgaggcsSbFsdDofL5dLNnztsLDJ/90v9EM4NmqYdDgelXlartaWlxeFweDyecDgMNKbwZhzP8+Fw2OVyURSlxaBpmg4EAv1SRR32Cv2mrgFdA/1MA+Fw+MiRI++///6vfvWrcePG5ebmZmRkGI3G9PT0nJycysrK6dOn33XXXZ9++qnf7wfAFBZ/ZAlIFELe5NVucXUAmuhHC0zATaJDq9U6a9as4uLi22+/fcyYMdOmTTt27BiYSJM42nz6a5gsPLpZ6+RuB1tAb9uOKse/kjn8PzMqNuaPW/X6h3EujvhWdN+vH7jiysm5BcbMnLSMQQajcZDROCg9w5Cfnz9q1CiLxfLUU09t2rTpwIED0WhUtT3HZK1dW0B3U7z+2kx6vXQN6BroQgPacay3hbWzMwaPZIzepAxoIHMXFeyFP3WmZykhsSzr9/sdDkdzczPA0DabzePxMAyj+/LphU2pi9QrNAC+/twC+sOmvaMX0qb6UJYlltfgrVi87fLF6LPDiEdClG1bg5GlmIpHpyLCSZQZ1ysFek7+pHVCmJBljGoH0dGFvz9SUCNkN7Qaan4yzLWVLkC//wTF1FFLhaCx/48OS+wVGtSF6F0a6EkAWlEU8EsANAsOh8Pr9Z6Td3BkWQYyTfAykTKXn3ULaCfU7mRyesfxXeYCdsE8z7MsG41GGYYBJxgcx3WZ7hz8CL6wYBkElnTnpF06lEwUxUgk4vF4aJoGNJlSLwh3tigRBCEcDmtTQS8Ch4Q6Bt2hqvWbXWsA3HZrLUPP1dDRdbn6rwNQAzzPC4IAMxR4Ijpy5MjLL79cXV196aWXmkwmwrNRVFQ0cuTIefPmrVy5cuvWrQ6HA7gptRvXLuYm7U8k3M20A61dyPMej8c3bNhQUFBwxRVX1NfXGwyG5cuX61SV3e4PKgC9DVWO+/OgsvXpI/6z4B9eXr2ObWWRGEdun/dv+795b907//e53y9ecsuUKVcUmQqysjLT09MNBkNmZmZOTs6QIUMmTZrU1NT02GOPrV+/vrm5OfmkiHGW14oBVDPnb32iLUsP6xrQNdBXNACTHbiQ3bVr16pVqyKRCJkBIUBe/Um53yNfQbFAgg9+rYGREjaSZG7qK/rvQk5ZlsGKyOPxAAxttVqBRFHfu3WhN/2nAa0BHqEwQv+++ceLGsJ5CwI5lhPZllCWxVFg+a9h1a1Pf4gtlHmxvYqSWLTmlw5BZ+3N9hQccYSOcF+PqrfnmU8Mwp+fss2HimrQkx+jsIIXYGpyHYDWaFkPnkYDPQlASwnJ7XYDma/VaqUoKhgM/sxZVpblWCzm9/udTielXk6nExwbnkYTp/7coRjaxcqp0VO/iaIYj8cjkQh4+E39uZPvZNEDyC+ZoYGSgqZpp9Ppcrlomvb7/d2hpAQoTVsXsInrkF9MSkgw9wMMJwgCy7IcxwGrMmTVieBncxsk4TguEAhQFEUcDAKODL4pIpEIz/Na+bUlSQmJYRiPx6O1gwYy6Fgspo2ph3UNnJEG4AAGfKPr0MYZqU6P3F4D0J3adyRFUSKRiN1uf+eddxYuXFhQUGA0Gg0GQ1paGiBxJSUl06dPf/bZZ5ubm7WWy+ATqTsgMjGCJpMLBLqTtn1FBtSdWCx2xx13FBQU3HnnnVVVVWPGjPnqq6+A22Rg0nF0u/VlhBKSjLZuRRVjX8646MO04esLx//51Q9aY60owaEEUniFYwUmHAt4vS6admzd+uUf//jC1KlThwwZkpaWlp68gHOmpKSksrKyurp65cqVNttxKaHIEsI20cm3PrV9u9tC6hF1Dega6LcaIDY0sVjs008/veGGG3JycrZt2wZ7q86mRe1I0iNh2IJRFPWb3/zm448/TqHV6metpSiKIAiRSMTr9bpcrkAg0L/r28+aT6/OhdYAi5BN2j3h1tbChSijIZZpiRgtsUyLO8+ys6wWvbVbZeHogArj3ADQJyS0yfptSY0rxxzOwB8q1/y1aS56/wAKqDYBSdPpDoq70JrSy+sbGuhJAFoQBJqmKYpyOBxWq9XlcoEb+q41R3YdKdEUReE4LhQKuVwuh3oBbguGtF6v94wMhzsspZsAtCiK4XDY6/U6nU6/38+ybIe5pcgPCyYw3OZ5nmEYn88Hh8PNzc1W9YK6tLS02Gy2YDAIMERKPtqvgB0LggBqAT8PsAIj6zASH0ytEUIcx/l8PrvdDgU5nU632w1IdHsMhSQ/i4CUkCKRCE3Tzc3NwLYBpxE0Tft8vng8DsV1CJdDcbIsRyIRl8sFmoF2pygqFApB3cki8izE05MMEA1AJyE9iuf5aDQKj0wgEIjH4915fgeIrvRqggbIwAJ9o+seApHBVJNTr1gstm/fvtdff/3uu++eNGlSVlZWdnZ2ZmamwWDIy8u79NJLLRbLm2++eeDAgXA4rCgKy7IwMmsP5LQyaMPaNtLe705Ym3Ygh4Hrqbm5eeLEiZWVlY8++uiQIUMWLFgQDodhpiYQxkDWUid1lxESUgDooqpXXlkbi8aQlDRfllEioQjYXaEkcBwba2X8fr/NZvv0008ff/zxurq6q666avjw4Tk5ORkZGQb1ysnJGV5WPmPGf7/33vveffe9vXv32my27iwaO5FTv61rQNdAv9WALMsOh2PVqlUTJkyoqKh44oknnE5nLBYDCxvYXHRnTryQcWBf9t13302ePHncuHGPPPLI0qVLW1pazu3Oq1c1OXiwYBgmGo3q/Bu9qml6WJgkoNnDYvSe4mMI7fAeGr84kFEjGcx8uiWeYRHSLN5cyzdjF6JvAtgtYfLiEeJUK2aghO6YgkNr8pwS1lpAA6btV9Bjm5qLav2ZZtaAP8cHmzeMMSMfMG4oqVQeSUn0/3UNdKaBngSgOY4D9Nlut8MLON0xLIKNX8p8zHEcYL7ACwzZOtQLqITtdjtYDXeNFBA1gYGYKIrBYDCgXsFgEGZHWI6QmO0DLMt6PB4AcJ1OZzgcBjC0fUztHZiGwW7a7/cDjA7CAxDscDjATNjlcoEpNLxcps0kJSwIQjAYBBvhlpYWEIa84kQqAgsylmUBDqaSl9PphBMC0B5BhFNKOeuvsiwzDON0OgkLGNgvh0IhlmXhvTNgU+kCaud5PhAIAHINglutVqfTCbg/1LGbjX7WFdET9mkNkAcBOmQgEIAjDRiUYrFYymjTpyurC39ONEAGFgJAd2bmTIpTFCUUCtE0/cILLyxcuHDcuHH5+fmArGVkZOTm5k6cOPHuu+9et27dgQMHIpEI0EFqeZxSxjGtDNowKZGcMmp/7TqsTTuQw6AlhmFWrVo1fPjwG264oaGhobKy8u233wa1dHEsOoD1hm2fERIQ4iQFbd2GLh77fM6Qv2Rd9P7Qf3hx9dpwqwpAi7LAK2xCSai0grIgchzH8nycvGvFsqzP5zt06NBHH320atWqe+655+qrrzaZTEajMSPDmDe4IG9wQWGhaeTIkTNmzFi6dOnLL7+8c+dOr9fbTc3D6i7laepmWj2argFdA71NAx3usPbv33/bbbcVFxdPnDjx/fffP3z48PPPP//2228DgRWZuLueEC/wr0SxL7zwgslkyszMzM7Ovu222ziO69+rUFHE04AOQJMO0M8DAHfKCIkIw6atCMXVhQPQHJNf4Ws/10W3q9eK0Pex3RcvOJFtQVm3JAwYfU4YLFS+ZcsVi1FQVWAyMx4h/lwB0ECrEUCo6U/u3NpwhrnVUC0bLPY886Hb/oCbj28zu8YYNNg/Ezg7KY/+v66B9hroSQA6FosR8gSbzeb1ertDKwEMWQRFRQjxPB8MBgmDsEP1YudIXuDhsKWlhaKoQCAQi8U6XKxoVQMYN2GHgJxcLhdYn8GKRBtfG1YUJRwOUxQFTn7Bh55WWm1kEga6Z47jOuSUsNvtgDjb7XaHwwG4ME3ToVCI5EACRDxFUaLRqNPpBFKL5uZmh8MBBlxaYAL0GYvFwuGwz+draWmxWq12u52iKCgIgG+KosLhsCiK53bbBtbWVqv12LFjYAUPbigAcSaHDRAgddQGpIQECod2pyiqubmZoijADUEbKX+1yfXwANcA9A14CiKRiNvthkEJfHODJf5pR4wBrsOBVn3SZwgKCQMU8BS1n8UYhqEoav369XPmzCkqKgKLTqAXKCwsHD169B133PHpp58SXKz7YywZ2c60CUjC7pd1pkX0g/hSQrLb7fPnzy8pKVmyZMkll1wyatQom812bn1L9ANF4SrgPUgC4bdAwwjFJIQ+/y//iIt/U1j0Z1Phq8OHr/iPN4+LHBJ4JKOEhAQJYQ6N5CUpStsHIVlRJDjOAe/EPp8vEAjs3bv3+eefb2hoGD16tNFozMnJycrKylSvrKysESNGXH311b/73e+2bt3q9/tjsRjP8xzHtX8Y2x9pJ2XA//eTttCroWtgIGlAEARCuweWNB988ME111xTVFRksVh27NjR3Nx8zz33ZGZmzpkzB+iVe7967r///vz8fKPRmJmZ+fjjj5Mz6d4v+dlJSMbhs0uup+ozGlAQSsiIlxAno7CMHDL6yo6cMl478EkEE3BMHc3UNmocITf6yfJ7f359zHATymxA+bf6DXP2l9aeWPUxhvLP6XUKk4akoFZ0ZOQt0Yxa9IslIcNcZKj/aWiT8OZXGHFOJBdOBIBOaTgdjz6nTdNvMutJAJphGAA3ASP2+XzdAWoBqyXsxkC7QdM0ZAImw8BZYbPZCDODzWYDO2JgmuZ5nmAH7dsSLIIZhgFDSId6ud1ueBkfpsn2qeAOmLkBqQig3i6X67T1khIS0G4EAgGn00nsed1ut8/nCwaDsViMYNMgD5gztxeDiAcEo5AbyENRFDGahmigzGg06vf7gYcLTJ4p9YKCQBi73Q40Jud2kwZvl7vdbgDZw+GwIAhaIIY0U4flgvyhUAhs3imKomm6paXF5XIBmxippjbQXmn6nQGrAegYoigyDON2u202m9VqhaHD5XIxDHPOD10GrKr7TcWhz8DQ1P5sjHA9BYPBnTt3vvnmm4sXL544cWJWVhZAz1lZWaNHj77xxhuXL1/+4Ycf2u12YBaGoQ8y76auyLDWzfgkGknY4bhKoukBKSF9+umnJSUlVVVVjY2NRqPxgQcegLeazqil+r8m8R5EUNHnEwgxEkI7/hasHH1P+dDnK0pfvHTcis8+9iGEIuFWGe8+Baw9GSX74SkAtLoHxQqDhwvgfo7jotFoMBh0OBwfffTRI488YrFYrrnmmsrKytzcXHiTIC8vr6KiYsqUKbW1tU899dT69ev37dsXCAQgK4QQMX4kADd5ivXW7P9dVK9hP9WAdhYLBAJPPfXU2LFjhw8f/thjjx09evSdd96ZNWtWeXl5XV3drl274vH4aXdkvUFPf7cHamxszM/PLykpGT58+J/+9KdoNEpWF71BwnMrQ3IuSIJZ5zZ3PbfeowFo4WAUebjE29s+GVf3RYV5Y1WdtPpLFFVtohOq7W6K+bPeL0SVVuOlL2wFtYLBfMIw22uY6ylu/Hj4POWblnPevKcA0LyEDgVayhp5Q22rsY4x1AgG8/68eehbZxvzRpsJgmqIACm1xuw6AH3Om6dfZNhjALQsy7CXAODYbrcT49zuKFaWZY7jYrGYz+cDF3YENgJjYbfb7VEvt9sNjvvsdvuxY8eOHj1K03TXr9UDAB0MBrXO8dxut5bVoTMhFUUBRghAsiiKcrvdp7WgFEUxGo0CbTSgqGDprPXCx/M8sEI71AsAaO3Ci4gEN8EWm6ZpiG+z2VIAaPBEHIvFQqGQx+MhhBuOU03IwSDUarWeVm9EgO4HAEGORCJAu0EgmPbbws5qKooiuDEEk22gLvH7/fDCGlnTaAPdF0+PORA0IAgCwzBer9dutxM6cqfTqTtFGQitfxZ11No7w0gFeBZMSTzPu93ut956a+bMmVVVVUVFRYCOpaWlmUym2trap59+eu/evcFgkE9ecJ6qPXg7C6n0JOdJA3+fhR9++OGcnJympqYpU6aMHz/+448/jkQipL3OU7l9LFu8P0wgxKgYNAagHR50y22vT5zw7Kjy/zPnf/y7tRlxMbw/6T4ArdWA9hnheT4Wi3m93oMHD37yySerV6++mBcN/QAAIABJREFU//77p06dmpeXl52dnZWVlZaWlpubO2rUqKuuuqq6uvrxxx/ftm1bIBBgGIYsxuAphkYk6w1tiXpY14CugV6uAe2+gOO4I0eOLFu2rKys7LLLLnv77bePHj362GOPjRgxYuTIkQ8//LDL5UIIxeNtbD+9vGocx+3evXvatGnFxcXl5eVFRUXPPfecdgTr5fKfqXj6Hu1MNdbn42+lv6yopctvbc6uPlpo/rpqITrGYC4OXl1KyEhSz7Sxp4g+X9VzUQGA4FuYlnFLfIbZAcNcKte8Y3gtevlLLfvzuSgJ53ESgJYRYkT5rW3Hiuv4dMsJQ/WJQeZgRg19+b3oRLI0clqQQp9CoGcIJKPr/+saQAj1GAAtJSRAfFTvepjzgWGY7rNcAewI7MZAMQHcEV6vF5YXxONTLBYLBoNOp5OiKCgL+Bm0C5eUriDLMsuyWtd2drvd4/F0B4CWZdnr9YJlt9VqpSjK4/F0fd4OVsB+v59wazjVKxAIaF8gjcfjYCkMZt1OpzMSiXRYC7ipKIrf7wf0GeShaZp47IHJnuf5cDgM6DPEBPjb5XIBcE/oCACAjkQiXdclRZOn/QoANM/z2mxhZ9jN5QiQeFDqBWcPYLgKRWszIeHTSqVH6PcaIM8I2D57vV4YH5qbm+Fhh9cOwPy5w6es36tIryBoAMBlbR8gADQBs3ie93q9Vqv1s88+mz9/vslkMhgM2dnZYPJcUVFRW1u7cuXKI0eOcBwHZPrAMgQnqWTi04GwXtjrgIjj2muvnTBhwiOPPGIymaqrq8FLgSAIpA/0QskvqEhtADSrsnDEJCSHefS378Xlv/vr7/5t5+bP/VICiyMICRWATuDp+HQW0MRyGSoC9sskrH1qotGox+PZsWPHq6++OmvWrIqKCkLTkZ6enp2dXVJSctlllzU1Nb33l/eOHDmidchMFgbaZzxFdV38lBJT/6prQNfA+dZA++cxEAjs37//zjvvzM3NnTFjxrZt23bs2GGxWIqKiq699to33ngjHA4Hg0F42agPDdo7duyoqqoaNmxYfn5+eXn5hg0btEbQMHadb21fmPw7G4e1ba09hrwwUumlnC8NnJDR7z9tMVmchjk/GW4KZ5gPDLFEXv0MA9CcagettBFEs0ku4/MlSR/JV8ZE2TIKiSfu+NPh8sZdhXP3XboErd6O3PI55984BYAWEfKJJ/7t7RaThTWYo2lmd0a13VSH/nUtBqABFif4sg5A95Hu1BvE7DEAWhRFt9tNgFq73c6yLNlRnFY1QNDsdDrB8BlemQcjZW1aKSHF4/FQKATOCYFNwuFwAD+DNqY2LCWkUChEqCeAEDkUChEOaG3klLCUkAiHBvgM9Hq9giCkRNN+BVeHYKoMZrwejyccDgPjB4kJlCBgMA6U2SyrcXpK4qkBgEgA4gfA2mazeTweQLRhpgeCRa/XS6sXQM9erzcUCkWjUZZlGYYBShDQgN/vP6M2OlWijr+Bsbl2hQF7TrIW6ThZ8q4gCGC+Dcwh4MMwGAxq4exkXP1/XQNtGiD9nxzAUBQFY5Hdbne73QBPkMUu6Y0Q0PU4oDQgiiIZwGGGIh0DTu927969atWq22+/fcyYMRkZGenp6VlZWYWFhb/85S9vvfXW1atXf/PNN5FIhKTqoheRnjagNNzLKwso89q1a8vKym688cbq6mqTyfTMM8/E4/GUo9NeXpHzKx7eh8iqxRKHnRAi+QSbCMRQIIJORJCQwMTPgDgDAA3CJDs8puBI2tyctLyBxYB2WZiMj//vrDosyzqdzs8///zpp59uamqaPn36yJEjc3JyDAZDRkaGyWQaO3bsjTfe+OCDD773l/e2b99us9nIwTwhw9FmDqsp7R09rGtA10Bv0ACgsX6//8MPP7zmmmvKysoWLVr09ddfr169etKkSfn5+QsXLvzqq6+0osJLD9o7vTkci8XWr18/fvx4o9FoMBguueSSLVu2ACsRrChgSOzNVfiZssFQrygKEFFG1CsajcJ+/Gdmrie/8BpoM2f28I5/WubOnJ8ovCVkmJfIbrCNaEJfWfszAE1Q2rNVuiLJiJXRN1TLY29yb29FP0awtXiQPR8m4ifXYRxCLnTc/DhVWBcxVEuDF1LZNTvLatGnNhRqOypoI+KACnbx92wrrqfrlxroMQBaEASwSgaqCrvd3n0/v6Iows6fGDUDIBuPx6GRYMMAFBPAGwi+xQBmcjgcXU9dHMcR6NahXmD+3B3zNFEUIQngWQ6Hw+fzaQ2ZU7oRuAoE5mIArCmK8vv9WghVUZR4PO7z+cCjoFU1rAaXgCm5ka+wNPF4PFoi7FAoRPZyUkJiWRbOAAh5hc/nAx+AJB9RFMGEnODv5KefH4CVE2hVmxvch7/a++3DoVCImI1T6uX3+wla1D6+fkfXAGgAWNfD4bDT6SRDELyvQMz8yTBCHvzu9Eldw/1MAwTqgnEYHLVzHOf3+1955ZXp06eXl5fn5OQY1QvgrXvuuWf9+vUtLS1gckW6HCFtIHlqddX9cU+bSg+fbw3AcezfJ9OmpiaTydTY2Dh69Ohx48bt2rULfCCfbwH6Rv5tAHRCdUkjCijRKkuMhJgEak1gQDohAwAtyUiWk+93Jvt8pwB0St2T8fH/KT/BV/K+Aiz/wuGw1WrdunXrmjVrli1bduWVV2ZnZwMljsFgKCkpueSSS2bOnLlkyRJ4YT8Wi7U/1yd5dliiflPXgK6BC68BRVGAsi8ajb7xxhsVFRXAs/H1118vXrx42LBhVVVVzz33nNVqbb//6mz0uPC16E6JsVjsrbfeKikpycvLMxgMkyZN+vzzz4mlTndy6NNxYNMKPo3Akgx2rLqlUR9rVgK/wtR9JHS4cmE8t6E1uz6e28Bm1R8oqUUHQ1oKDjjQ7p0UHITo+AxagWigG2k6zl9BSFRQTOZ+oFBYQK3n2vOgRrCTADSLUIu8a0yjp2gBm14rZNY7Ciybx9WjQ1HMuCaqlgNdgM7anzT560FdAz0GQHMcBya3YNLrdDrhleTTrgyAsMLj8QDzBrF91qLPgBwpisLzfDQaDQQCBICmadrlcnXxBhYctNI0DWa/lHoFg0FIclrxBEGw2+0OlUYZcggEAl1AovF4HOoCptwAWKcYaPM8D2QahI7Z7XZr38Nq34+lhCSKosvlslqtIIzb7SZ+ooFjBAg94FeXyxUMBuG14vZ1hNza329f7hnd6Wwz2dn9lMyj0SgwPjscDjDi9ng8Z0TkkpKh/nWAaICgzy6XC9yTwqGOz+cjjwB0whSGULg5QLSkV1OrAVEUgeL54MGD69atq6ury8/PJ97PSktLp06dumjRoo0bNxKiADLswx1yjKHNVhvu5rinTaKHL6QGvvzyy/z8/Msuu6y+vt5oNN57773ksOpCitFLy2rbXLXtmySUEJDIIV79xAUUlxCvKKlAM9xpf7+zOv6cZ0RKSAzD7N69+4UXXmhsbJwyZcrQoUPz8/OBNrqwsHDUqFFz5sx58sknd+3a5XA4QqEQOKHVzgKdCabf1zWga+ACa0AURb/f/+ijj1ZVVU2dOvXZZ5/dsGHD7Nmzi4qKrrvuunfffRe2PMTs5gKLdw6L+7tB0ooVK2CkysrKuuSSS8Csu4ud7DksvWezIgB0OBwmNmdWqxXcIJ13J+HdBw27H1OjUIIz9k+aY6ITJfmCk6LyO0cRWvvt/rx5UsEt3rTqSH6DL8dCT70f+U51QqhVSscnzliVJ6FSolgoV01yyq/JTIjaSQoSOFkmyYTUIhlJVllBRMINksw2+Xsn/2vkOUUqTXQimKRqQoKfkgkB7MUYdFwVM8a18pwm9fkJRhHaTH+dd7Mrx8wZ62OGGldpo6tpJXIpmHsaJO5cV+dHJj3X/qCBngGgAUSm1AsAaACFu4Pv8DwPdq8OhwPQVWKeTM6EySuTgLQCvTIUd1qvgGBeDbbSACUDrzTAr6cFYXmeT+Hu6OKclpBv2O12AKB9Pp8WWQYrHnCHCATWNpuNpumuzZ/B2zvP80BRAvis1+sF14uKooD5niN5URQFdQSIpMPt1mkrfhZPQ2ebyc7ua4sg1M9QO2hcn8/XVxyMaOuihy+wBjiOC4fDQPLeol4OhyPl9EJr/kygQ+iZF1havbge10A4HD5w4MDq1asXLVpUVVVVXFycq14VFRWzZs16+OGHP/7445aWFrJTwmtiWSZvscALs6QXdVad7ox7naXV758nDWiN1lmWfeKJJ3JycubPn3/99dePHDnyk08+OR8z43mqy/nNluxAcDH4SwKJCcSrBtCtEopJKK4gUaXaAEHwxuU8AdDwxLUVI8spbQReZ51O55dffvnCCy/cfvvtN998c2VlpcFgSEtLKykpKSsrmzZt2i233PLUU09t2bLlhx9+gLfH4BHujhr1Z7k7WtLj6Bo4aw3Isrxjx47FixeXlJTMmTPn5Zdffvzxx6dOnTp8+PB77rln69atxPAZxvCzLqg3JJQSUjQaffDBB+HMOzc39+qrr/7222/JijRliOsNMp8rGciyKhKJgLMW2J47HA5wFX5+N33twMcO6gVxCBLXQYxObxHAEcdIlgU3SZpT4pC7HQVOSZjMraOIF+QegM7Y7TD+tP0nqxTPASQ89M7x/Fopp9FlmG3PmGsdXIPuW4MCKqZL6LhOBXbb8klmS+pwstYQXwt2J4vFkUEhSTAXCjl5X1PyyZskSTtJRJVuDFsgQ3FqQZKaSRuEDWlBOPh7atEnkW5Sk6S0gD4LahFtwiTzb9NkQkGCrHBCPCEIWILzcrWNKhGEnv3yx19YXOnz2EEWxjDPW7EYrf0OBWUE1ulaLUH4vIijZ9rfNNAzALQsy9FoFHh7wYTZ6/Vqd3qdqZnn+WAw6HK5tJy/0Wg05YgbXpmETFiWBZpj4MSgKMrn83WxkRAEIRAIAIgMHsnC4TAeZDp55VMrKryjTVEUYWoGsFh7TE1WDAihaDQKJBgApoMnRpIhwPQ+nw9+BQCapulgMNg1hQjAHyzL0jQNtB5Op9Pn80WjUUEQRFEEBB8MtIE3ORwOEyG1e6fu1JoIfF4DWr1JCSkcDmtZs6EWsViM0KKdV2H0zPucBkj/gVccAH0G8g0YE+DpgHqlPAIpX/tc3XWBu6MBgIxhxCOsR36//7nnnps+fXpZWVlmZqbBYCgtLR0+fPgNN9zwzDPPHD58OBAIiKJIDu3A2JmYPMNEow9K3dF/74xD3qYirFbTpk2rrKxcvnx5eXn5jBkzUtYevbMWF14qdcOlcj5jwg1JZeA4uU9U5dHuzFJ++rnywgNIVi8pAzg8reRRjcViNE3v2bNn/fr1Dz744BVXXJGTk5OZmWk0GvPy8srLyydMmDB79uzHHnts9+7dkUiEHPATKVMQrpTitF9JEj2ga0DXwJlqgJgWIYQ2bdo0c+bMrKysm2+++d13321oaMjNzb3ssstWr17t8/lSDAjI6S8ZE8606J6ND2ZJVqt12bJleXl5xcXFRqNx7ty5drsdIRSLxfpovbqjVbIkk2WZYRiv1wu8i/AONJhPRSIR8O18LvWghdJSID6CuBH8kcxmSZCxQ3ixfX1JOowiJjFRgmPCr/A1+WP7PNrunEJYQUBYFbjsNM15/SGJzHIApMqq7XMCoShCx9H+yXcGBtchYyM3uPGY4eYjpXXozf0oqMaRMaorqybA2KFEEpYV1DtYSwn1VrJRTgK+asI2RBjCybTtb7bpM6koAMahrJORoQFIc2tKFFXBsHcvNQettG12ymAmjTnJkmbdqqCkxVMCpCkgnYCweTGRByJjpYDcCQXhj4xkpe2TlI3kc2YBUkdVWF5NLCckzDotIHT7q/TgWn/6/J8MN0QMc34YWo+ORjCxGlSfpD1VhpQKdvOJODOx9dh9WQM9A0BLCSkSiQCACAC03+8/LQAty3IoFCKwI0VRLpcrEom03wFq9wPguw8AZUBjA4FAFwA08F3A3NbS0kJRFJB7dGdiA8iYpmmttXKKhCQfKSEFAgGCpNvtdpfLpT20B0mAIgDAYqfTGQwGgYS0614H1NIAhTscDpfL5ff7GYaJx+OxWMzj8VCq1zUwHw4Gg1qHh0TCrovoqV/BRB3IN6AWYBVOziHIWrOnJNTL7YUaABQAT5eKEolEyCmRw+GAlwO0MEHX4V5YO12ks9aAdrJACEUikUAgsH///vf+8t7ChQszMjIMBkNmZmZpaenEiRNnzZr1xBNPHDx4EIxuwIcqQJOQD0G1yE2CYPbycfWsFdi/E8JQAI0ry7IgCB9++GFpaelll11mNpsLCwtfeuklwrXSv1VxFrVL2YGcmkPKj+dle9L1SA7PJjkuAtK2UCi0Z8+el19+ecmSJVdeeWV5eXlpaWl2drbRaBw2bNhll122ePHi999//9ChQ/Bym6BePM/D6T4sP0iHIasRkORUDejfdA3oGuiuBoD0mXhfmDFjRkVFxdKlS1esWDFu3Lji4uL6+vodO3Z4vV6g5u9PzyBhgDx48GBDQ0NpaWlFRUVWVtb8+fMdDgeYHHVXj30tnnYMF0UxGo16PB4gybSrF+zrPR5POBw+l9bQp6JpxIQ3VX8AHAMs2C5JauQuvpN8VOyVYNBaY1hANjubKQkAjQtJzq7wfxfFnt+f1LoAkIqBWtBSBKGv/T9WNsWMdajgNjl3oS2renuZGe0JoUgyThJ9blVxWNAGRwBoLe8wVCCJI+NS4JNSMXK//a/qnVQAmmRIQG2Sg5qzlGIBnUTMASXHbQQ5APospoLmmiZqa6s2edUuBHA2q9YdsmprdAK+Sxh3xuhwEoDGixm12VPq3d2vGrXwqrA4YUJWBBH5Fdc1D9Lp81qz6/msBScM1ZFrf4vcfBs9CNT0VOVAock+SDpjd2XR4w0QDfQAAK0oCmCITqeTWCUTK+POlumAqAJnq81mo9QrEAgQxFa7vSeZ8DwPFsRkoqJpWuvxvH0zg8U0ANBWq9XlchGAW1tE+4SAbcViMSC+INzW0Wi0w4QQkzBN0zQdCoUgW57nGYbx+/0AkxGC2nA4nEIP3aEYcDMcDhP1ejyeQCDAMEw0Gg2FQpAtpWLQoMMOJewi8576iZCWOFSWbViFOBwOwOVBKrJe6Skh9XJ7oQbImAAAtNfr9aiXz+cj9iOwYyH9p7NAL6ydLtLZaQA4mhiGiUQioVBox44dK1eubGhouOSSS8DhT3Z29sSJE2+//fbXXntt3759BGYiRs0EX4bO0yEA3VdG17PTYf9OBYMAwTKkhPT3I/NbbrklPz+/5p9rxo8f/8tf/nLfvn39Wwk/v3barUgyN+29n7V1SmbYwf+djeFwPyUBvDkHHgKI75CdO3e+9tpry5Ytmzdv3vjx400mU05OTmlpaWVlZXV19fLly1evXr1r1y6PxwMLRSkhESS6/YSSUqL+VdeAroFuaiASiQiC8MMPPzz44INjx46tqqpqaGiwWCwVFRWXX375c88953Q6YReWcuqTMgh0s7jeFo144vF4PGazebR6DR06dNGiRXa7vTtmSb2tRt2UJ6X5gI2EGFHB1h7+EmsSsmfvZhFdRAOTUwIHk0mL3GnDGVWAsA0l1GB5XeR8Eiol4B1Alm2muRithY+gWsICFHuSd7ijrNsEIFKqqGjbTQIUqgnP14zbTirAUjFYqUKrmLOCQeiFr52DaxPpdchgkdLrrPnmb29chgmg423RCOwO1tNEDzgfYgVM9KapL5RCWu1k3YlgpyLLJCaBU6EsHJ3kT84V4A4Up7S1Tps8pLVUD8vJNjx5EoCjnZqcSHQyQGRTGw4oOHAVtAmhdBWATsgyhxQO050pEvbxjAv5+RfYl+N8FCS1cuhoYHdFvSe9utVYJxXd+lO2GS19D51IlqPVUlJRpEFAD+SrNpBMr/8/cDXQAwA04TXuPgANtMU+nw/MgcFomqbpSCRCToZTNvnwFfzUQXzAlGmaJu4K2ze7oigMw4B3PkCQfT5f+2id3QGUXJucoigCb2lTKYpCAGKHerndbnC/LiUkoMgAseGv2+1mGIbjOHDVqM2qwzBYixMAmqZpv9/PsixQ38J9u93udDq70EaHOffgTYAOCa8IOLEEFrAUThJYsvSgqHrRvU0DpEsAuwLLspx68TwPbkwI+tAeNYC05G9vq5ouTxcaIETMHcaBd3G8Xu/TTz89Y8aMoqIicC1YWFhYVVV1xx13bNmyxePxwHv3CCFRFMmAKaoXgE3E3lkHoDvUc9+9CU89AaBFUQRHdhUVFRMmTJg/f35WVtZvf/tbhmH6bh3Pk+Tq1q5tUyR1sEHSbkYgfO4FIYN2ZwHAi2EZCa0MQsCaE4AMaHSn07lr1661a9cuX778+uuvN5lMBvUqLi6eMGHC9OnT77333nXr1nm9Xo7jSIdJwcJSatihVClx9K+6BnQNgAZ27dq1aNGioqKiyZMn33nnnWPHjjWZTPPnz9+5cydE0G4DO3y4tBH6llZFUQRzq1AodPDgQbPZbDQaL7300oKCgsbGRrvdnoK6plS/b1VWK21KRcCCDQ4IAYYGF0pWqxXMucCmBJZk2nzOLiwhxMsSxvVkhHiEWhG20g0lPxGVUIJrMxk9CTt2pzCC3MlKG8KI2Z3UIhi1FCjoBMJgXxihmIpDt/E7dFIAQTAx34WKYiYxQZwA/6qWlcRFO8nlnN0+ZY6XZQkpGIAOI7ToNTarHhnqeMOcVsPcH/Nrgo+uQUEJJdpQXVE1doa/WhATS6bNVAJUWzoJ76o3AOxta7iU2hAVgX6S+WHlqCAyQNKqrhCS2tR1Mg+SHMqQFRxHlHFaYuwMYLSWfAPqoMWRIXwyXzVEMldrAdng6spyWw8hOSRkRcKrjARShJ8BQCfkUyBrwpLSdldGKBxHf7XtKpkfMVoYQ82JbMvhvGr079tQCEk8JiBpu0hnVr9DE52UP6lkbdMlU+r/D1wN9AAALSWkeDweCAScTidhcYIdPsw07VsDOKOdTmdzc3NLSwvx16cljkhJBa9rgfs+AkCD59wuIAlCiwEHqsDgnJJzh19FUeQ4LhKJAEU1RVHkSLZDIWVZ9vv9QO7sUC+PxxONRjmOCwaDWhIPYDdmGAagDe1k3KEkcBMqQtQLNsIsywaDQfCsCA4cQqEQoX7uIrfe8JOUkGKxGID7UAWapl0uV3cYsXuD/LoMPa4B2HsAbQLgAiASGLECAA3AgfYpax/u8YroAnStAW2T8TxPIGPYurAsCyPJnj173nzzzYULF5aVlRkMBqPROGLEiClTptx2221r1qzx+XynHRvb9xkt8NS+L3Uttv5r79RASnfC+zhFef755wsLC+fMmXPFFVeMHDly27ZtOgatbT5QmhZ+BQxawhspuGCz08NbEmB+7+xcX9v0pEYcxzEMs2/fPqDpuOaaa8rLywsKCnJycoqKiiZMmFDzzzVPPfXUl19+6Xa7w+EweUsvpl4wDQmCwPO8Vj/ty+q7YFmyifX/dQ2cAw0oihIIBL744ova2tri4uLJkyebzebKyspLL730N7/5jdvt1npuJ+VpHyhys+8GCL4M48aOHTvmzJljMpmqqqoKCwsXLVrk8/ngUBzq2OHY0nerr21NWMPH43F4UdjpdII3F4d60TQdCATAWuus60vGXowryjLiJcRIGDn9xo/+8Kl/3uN7Rzbu+4dbg/9zJfbG9pOEsWkVM20Pup1GBgCFCQwoIeRHqEVC73yHlq0J/I9Hrf/tru+G1H5X2eC1PIX+sretLBVbTs2ZwJcwqQrqZCuQrFX0WZQwdQP2BYw/qTmcz++iJGGtKggd544OqUdpGIBG6fWsYb59eBP6+DAmPMYYu8IiKS6LvCwRq2SOjSfiPG4FgqpjwhH1K0Kdmf8TqEfCSzaVK1mLkyooEeflOI/iAoqLSFQPGGKCxAsqtYWK4CdUfLm9nkDVQMQsykhMSgrKFhA6IaKAiAISCgiIkXHmwJicomEiDwmoEdraTO0beNuiakLbXnJCdauhuiJEAibiaLe+Simpg6/4SEWWWJEXFJmTxLgsAuN2DCmtqj01EhXk49HLXxwprWOz6tn0Wt/guu8qG9CP6gFMKw/m7Zoe1laKDkB3oG79VjsN9AwAHYvFfD6fFoAmtBhk3NeKCn7zHA4HQZ9pmmYYhowv2sgQhvd0wMUfeUknhVKjfSpRFL1er8PhIObSYJXcPmb7O7IsRyIRqBQkh+kwxTgXEgqC4PF4oCACdns8HuAYaWlpAZoReKUoGo3C61cpiEZ7GcgdKSH5fD4CQFMUFQwGI5GIx+MBy+7O6LNJDr0qALp1u91WqxV4q4EBHNYZHfaZXiW/Lkxv0ABeg3R0kceKoIcdxTp5rzfURZehCw3A6SPLsgT6QeoileM4p9O5ZcuWl156yWw2jxkzJjc3NyMjo7y8/KabblqxYsXmzZutVmuHR4ZdF0c2e6QLkcDJftMNN7ZdlKL/1FMaIEzBsL2HY4lAIGA2m4cMGXL33XcPHz685p9rYJruKSF7W7lEaeRBSKjWOgnY2GCDJTAQ6mEAGo4TOltCaB9eCAuCQNCueDwO5gI7dux45513li9fXltbO27cuLy8vIyMjIKCgqlTp95+++3PPvvshg0bjh49Gg6HCYqU0l7kEJSMJFBcSjT9q66BAaUBeF7C4fDatWunTp1aVlY2YcKEkSNHDh069IYbbti0aZPX64Unpf0Zkvbh7U9KA46gUCi0ffv26667rqysbPTo0SaT6d577w0Gg3DiRXjtyfDb18cTbWuSSoFVeCQSAc+EVNKzkdvtjkQisPzrbGzvTpfAwCXEiyLkROKK97++uO740MYT+QuYrLpAVi1dvGBnWe2J376FPDLi26x3UzDo0xREwM2YiAkoaBH9++bvr7irZcxi19CFnpzacIaZNZijGbXOwrqdpfMjy15HtIRyd3nCAAAgAElEQVQ4/GqR9mr7CtMpgUfjEvYgBx7lVEpfzOorYQT6AgHQGlxVSIgYfZYR2u48XlSHDHVSeh03qM5vmHOo1IIOxbFdeRwhVkGMiE7wKCRhso6oagwOZuBgA661JiYqaBWQj8MnBGA2HpFRKI7bQy0wgX0aqlAy0Q/Yg4cFnL8foSMhtL0FbW1B+72IjmM7d0U9T0haSZNyIEP8FSymsdWzguIyljyGkFtEuxxozfbosxs8D78e/O1bwjMfobe3o900lo1RcFtoW47ohwTU39tM6WXsZhCzMMdFnJBFKCKhiIA4SU7gD7a85tTSpTMDoKEd2irFq11QRiik9mBWAtNmLCYrI1pk/2X18SLcUkJGnaugznrDw8iu6pnF5uwdWuTrALS2w+jhzjTQAwA0uBEAABq4IGiajsVisBPoUFBBELxeL0GfHQ5HIBDoAn0GuAFc/BH0Gd7T8Xg8HRYBN3meh9NUmqbdbrfX62VZVhTF7pjCAXk0sX0GK12KouAFf22hxFchYMFaCeEOoM80Tft8PpZlAX3WLrDIZAzZtl9bSAnJ4/FoAWifz+f3+8HnIeDRne2FtKL2hjD4PgZo3m630+rlcrkCgQA4Pu4NQuoy9H4NkKfmZwZ6f011CbUakBISnESuWbNm2rRpBQUFBoMhIyMjNzf3uuuue/755w8dOkRcmPLqddoBX5t/97uTNpUe7isa0IKD8GIvrD0++OCD8ePHT5gwYdasWcXFxS+99FJfmVLPo+aT+yhQmihJGHdWP4KCXxft6wA0AMSgQK29oSiKkUjE5XLt3bt348aNK1asmDlzpslkSktLy8zMHDJkyOTJk+fNm/fqq68ePXoUv2mdpIrujLSn/aJO22o/B1XR5qOHdQ30Zg1ICYmm6ccffzw9Pb20tPTmm2/Ozs6urKxcvnw5GPy6XC6GYXieh11Sb67LOZQNDtdlWf7qq68mTpxoMBjKyspycnLuvPNOiqJgeCG0YASu7dPTk3aVpa0RvMLCcVw4HPZ6vbABpygKtoeAKvyc0RLDcEEefW4P3fRoy5AFgYIF8cw6Lq02Yph/Im1+a36jq6DuwBALenw9RkuBlqGLlob5MSWCjFCrhJwc+uBQ9ObHqaGNgaIGelC1N7PmxCBzLKM2nmFhB1n4giZPXt2xAjP6zQcYzQQMNAkedoB6CzK2KQ4IKCyhGJe0mcXWsj8XgE6C5looVStPW/0A5tTqhEfIrSR+/fZP+Rh9bjXWhXLq/Pn16Kan0GEF2RT0E0JHBPS1G310FL27D722E638DK1YL9y2Ci1bg57ZjP6yG7lYlMCaFjFeLTNxFn9hEXpjt+u//2Zrybwdl96K3tnZ5s8wSYyBAWhszqy2EbBsRBFyyOiZz4790/3bS6u/L6v/YWj97qJ5P169FP1xM/JJgF+31QX+S6k4YNAxEXlF9B2D/vVd5z8utVbccthkPlJkPpI3vyWvhsq3HP9F/b4Sc+Cfn0Rf0biTcMl+kswNY9nkkwSgT5J9SwidkNG+MNp4FH0TQC0siiqIl3gZf7D5M4+xdXKdIrCam/YO0IQk4JaEUEzBfcmP0DEBfRtGP4jIrZLAYMeREgqJ6Jhku+p+T15dIh0D0MeL6qSH1iC3ggF3SRVbm3syrAPQSU3o/3elgR4AoME2GU4sCQANhsadzRPxeNztdgOThtVqJYB1ZzWTEhJQOWvhYAJAd1YKuE4mALTL5QIAmrDEdlacLMtg051SHNjqaoFjyAGIR0EeQg9C6K0pinK73YFAAFz6AvwNgAhs6shAQyoCd7TiybJMqKgp9XK5XE71oijK4/GQ19K1qXpJWFsd0JXL5QKY3qH6HnQ6nX6//0wNFXtJ7XQxzrkGCEJEnogOi9A+OD8n3GHm+s0LowHt4NBZiYIgwPgWjUZ379792muvLVq0CN6Rz8/Pv/zyyy0WyxNPPLF3716Ak2APA64IO3ubr7OyyA6nOz2qi0z0n3qtBkjLkg08mMH+fanQ1NSUmZk5d+7cESNGXHnllceOHUt5ZarrEanXVvksBYMNJ95WYQftCfXFZV7B+yP8wV7jCQCNzbHUD2xV4O9ZFvszk3UxpJCmJwFSFuA7QCgHL8WT7gHrz0AgsG/fvtdff/1Xv/rVjBkzxo4dW1ZWVlpaWl5efu211z700EPv/eW9vXv3RqPRWCzGcZwgCACskLI67DxkEUgk0QO6BvqrBlpaWpYsWVJcXFxWVjZ8+PChQ4dec801a9euBdfuYOIKbhjg2emvemhfL7CDZhhm/fr15eXleXl5mZmZRqPxoYcecrlc7S2g+7p+tKNiCgANQ6IgCNFoFCzbnE6nz+djGOasR0usQBEbeGIKgg+/2z50vievLmiYFzfMEw3VvKE6ZpgfTTNH08x+w5xARs3fhpjRdwGMyiU6ReVwbgRzhBaFGbMVYeD10XWHh9UHc+uChtmJ9Dom0xLOxV9PZFuYTIuQWS8Nqm81VLPptXtLzcibBFJVDBhc9gFkCWGMycYQ8iLulc3xP3+OdlgxbtuqciWrYKXWAvrk7AvyqMgutgKOqVgkn5yoifBqgICMJ5MDsAtM2WGEAgj7FfQhFFQZG2IIHRfRZvf3lY2BHAufjut1ItviyKxGda+Gbnr0+A2/2TrcvGu45bvyBYcqGnfmzd5XNL9lWIO7fJGrtPF4yYLvh1g2jTIH3/oCBVgM1yBZxZ5V9PkvO3cNqXFnzg9nmO2Fls+qFiCbgFFpddXBYW96SQBaUCsVQOjd3Z9VLWgevchZWMfkNcQyakVDbSK7IVjYsGtIzaHb/oC82KodG08DjAsYsYqnY60rqml5BCsZvfjFfw2Z5yxp8BnmoaxGNPgWKb1OMJgVgwUZ6lH6gsig2iNZc/dcvCD2r2/i+DEVvYU+QA4SkocToEURS64WHJLRhn3bxjV8XTB785C57iXPo21WFMIW0CySMPuH2HaoAM8IyTX1eAD4srFGJNwTEghRAvpgb3DZ6n3Tl24tr9013LJnWO2nQ+fur1uBNu5DNI8cIton7y82nzDW4hpl1LUU16HXt6OgjJN3fpG+QQB/uKP923lq/ZeBooEeAKCB0Nnr9dI0DQC00+kkAHT7NTf46wNqC0B4PR6PIGjoz09tLFj9ezwesPYlfBoA9Xq9XrJPIOlIofCOts1mc7vdwWAwGo2Cs7L2VswkrZSQWJYF42KwOAao1GazAc+y1mQGUomiGAwGHeoF0aBeVquVoii/3w/+BkVR1E60MLjAHQjjY8yERABuuAlFEACaMD6rpTmgoGAwCDZc2iSkRj0eAKpWMEVkGAa4SqD5gHkjGAyyLNu+HXtccl2AHtEAAaDPrnTyNJFx4Ozy0VNdGA1Ac0NZiqIA+gNfRVFkWTYUCu3atev3v//99ddfP2bMmCL1qqqquu+++955551vv/0WBlhBEABF0nYA0pfObmxMyUrvURemS1yYUkhrwtQTi8V27959iXpVV1fn5+evWLEipF4XRp7eVYpme6Ya+XCtfMLtj+//wb3n4HFnOA67V1YQJRn8tYNHIu2WRBvuXZXrTBrt895ZHI7jHA7Hl19++cYbbyxfvryxsXHy5MlDhw4tLS0FwugHH3zwjTfe+Oabbzo8/QKiedL3CKRCiu6sXP2+roG+pQHSycPqtXnz5hkzZhQUFIwaNaqoqGj8+PFLly49dOgQmaO1+6P2+6y+VfezkxYOwN56663KysqMjIySkpLRo0c//PDDgUAA0HliwJSycySqPrtyeyoVGfRSAmAHANpg1AuMxGF3DJG7JXMSBMQswLyIvf+9vf/7X5hp4/xWY500qF4wmBMGC8ppSqRjO+homplNr5UNtZ6cWrr+94iSUDAeb1WBz87Lg3kO/86LiOFRcwz9y3vs0MXRNDPKXyQaF8QyLaEsizvPcthkPphf7c+vj6aZJYMZGeqUtLrDJjNa/w0Gu0WUYFgk42NdTv2AHTQGzjmEPMjfsPK7IbWOsqbvh1jQ059ho2BRBhYOeC0JTKEhbZu8rSoTCIPQjwL6LooOsRg+ZgkfBQGhMSwrqSCpQNBUWS3XKypvfx3+Xy8wsx4Vbn4yPvvJyLwnQ9VPxmv+EJr6659KGj3p1UwmtukGy+5wZq0/q9abjT+BHAxJh7Lwh8mqa82uZ3Mw24k3s8abawkUNXxf2fjjspeQh8cQKlAjI4T2eD6rNB8vqotnYkNd3+C6QxNvR1udKCQjCSsHU3EA6RdS0edmXvyX178bZrEXWn4ajEuMGXFCzEmN/SLWerLMzRVN/jv/hLwCEjFg34Y4J/1WtGG7P4bQVrf7uodcZbfY0ueEM2vZ9FqUtRBlNykGi2iYnzDUyIZaLq02lGUJ5ODPsV9YwgufQ3YJxeB8QwWyodcl+x4YdwsAQMcRotDuyf/7h7ya4OD/eXzQvO+LanZPvRP9EEOsHEcyj2RBwd4dyUUOOU4BoCUF20pjKmoFY8ctPHpsvfPSX9kLLcGyRb5fNP6UbXZnzvdm17oL65tL6/eOqHfPfRRtCaMX9lrzzSFcF3wK8oXhWnQookLjHUPQ2jVc+3Dnz4T+y0DUQA8A0IqiRKNRAIgJAA0Gax3OExzHga9bR9L6NRwOdzZ9EvNqIGqgVE4owIUJAN3+9WqSGwGgXS6X3++PRCIAQLdPAtM50IkQ9Lk9AO1yudpXShRFv99P2DYAp3a73VAivE2WsrQiX8n2A2bcoHqB/NqCFEXRWg0DCg/IOEVR8L65Nn4v6ftQTVhGBINBj8fjdDod6gW6pWk6Eono0HMvaa/+IQY8CL3wcegf6j0ftQBHgiRnGAADgQBFUa+88spVV12VlZWVm5tbXFw8cuTIJUuWbNq0iWVZMJsCQIdAzySTcxLQ9iW9R50TlfaeTMg6gYgky/LatWsLCgpmzJgxbdq0sWPHbt++HfPiqU6JB9Y8dcomilNNrdCr/7GrbuEzs6ofeeXdPZ7Wtp0RNhHDZkQiUohtVV/dqmifd9IrtAEClkFMjuP8fv/Ro0e//fbbhx56aObMmSUlJUajMT8/f+TIkZMmTbrrrrtWr15NmOJgmNJmSMKkaHJHD+ga6IsaADoaMrqCddG77747YcKE7OzsoqIio9E4ZcqU1157DRz/pJjmaDdHfbH6P0dmcJ4UDAZXrVpVVlZWWFhYVlaWlZX1u9/9jqIowKC11tBk0CDa/jmlX/i0Wvk7C5P+oD2T6GZ9yTyEobpWhNbu/a6w+kTafDa9VhncFM9tcKTP/bGo9lBRDVVY50ifG86s5Q21yICRx51Fc9E2D+ZY6PIi3g/wFj7AoBBi7n2VHboYGRYgwwLOUOPPrz+cV33wonr0u0/QW/vQ89v4f3yotXChNAh77RMNtceK6/jXt6CIaqCtvm5EAOiTmCOD0L99YB/ScMJYi7IapayG0D8uQw5OauUIAA3AZQIpAlAkB1UOZUpkX9j01T8u2XZx3dYh1X8d02D/XyvRX53oJxEFuBTQEaDSk2QRmEsEIUp6f1T1seI6t2F2PHtBLHeBP7/ek1cXyLFEBtWqCD7GZNn0tr/RNHNrmllU1Yja/lpkg5kzzOMM1aKhlhtUF86td+diFux9o5tCL2zElBRqVVvjKl/zm98cKlsQzMUgspJWF8yt21ZajX6UUQTD5W3iJVRwPIYQJQZufe7osAW+HAyCxzLxR8jACQGAlgxmLq3Wn2k+MLoJ/b99SoDB7CW4tZIoNhgn+yW02fHjhNt/MtYwhrknDLNjhppoRm0gbb4/08wUNDoNc0M5dUxWXdBQjfH0TIuQhv/aShdIS9/E5wdxsY3F4pS1E66ZmPxgW+mPWg6VN0VNtypZTUp2ozu39puRDeivHhTF6DOLMAydCkCfPCZI9kWw13ZHkS2G1n574Lqlh4fUeQyzscIzG5VBC/h0C5dWK2TUCZn1bFb9icH1PwyafbxkAVr8friwMWaoSaTXRbPrvx+5EPN1qDbxnHrwcLLLqUWRJ6jDQFIa/X9dA1gDPQlAU+pls9mcTicA0DBzpLRMOBymaZpYCns8npS3XEl8LfpMURTwOBM7awCggTiMJIEAzGQIoXg8DmW5XC6fzxcOh2OxGCDC2gkMTHTj8XgoFHK73VrmDQL1Ao+z1+sFpFhbopSQ/H6/1WptUS+Hw+HxeMB3REop2qkUwtpJl2VZwNlZltXehxKJO0RH8gLSD6/XCys8bVla8XoqLMsygEQMw4BvH8DogcmEpmmv18swzMDa1fdUY/TNcoF7QWsS2zfrMaClPu24BMMvQDMsywYCgZ07d/7xj39samoqLy9PS0srLy+//vrr77jjjvf+8p7T6QRtgmdCkjkMmANa0Xrlz4UGQqGQ2WwGP4RDhgxZsmQJcJJyHDewpqo2+x2875CQLCrou/3ohhtfLyldUTx0xS+nPvH1XjEqIR5xCRRXGQTjAwSAJhg0Wc4BeXQ8Ho9EIvv371+zZs0DDzxw9dVXT5gwYdiwYSaTqby8fPr06Y899tj69eu3b99OUVQsFktxRkKWfOeiF+t56BroSQ2AEyCEUCAQcLlcK1euHD58eE5OjtForKysXLx48ZdffinLMuxcYINDnqb2O6OerMmFLZthGLCO8vv9Dz30UGlpKWDQOTk5q1atCgaDgD7DYolorO8ufsig1/0A9Bay8OuifSR4c0fF/jDwt6n524ssVK7ZbZjNZy0IZNW6hi488o93o/f3ooMM+s/m3Rdho92EiplyabWO4gXo/27GNrOdX6JK2yCq+B0GNUMSevBd97AmbPtsqEeG+oBh7tExi9DyteiHODquoqsehF7Z15xdHcrBFr6csf7wkLrYf2zBnvrgUh3QcYAjAyuxhNDR0PfjbqUNs2OZltY0cyK74a+5N6FmRuEETEahGk0LapKEajyLaYXtCnr8o7+V19uHNx3Lq7EOrrHnme15Zndxw57i+eilbehgABtWqzBsG+wImCzBIBWVXOK/7P81vIbKNaOchYrBkjBg1BUbdBtuPGGYg4Hm9HolDRsaxzJqoxmqFbkhFYBGafWKsUHIbogYLd7MGjrXfCB37nejFu6Z+xDyq+hzq1p9cBW44sOWIQtCORiAltLrPHl1f61qQh7VpWHSehsb7YYQOsoHb3luR/5sR14tNnxWDbH5dAtBnxMGC3b5mGYOZ9buLzbbf/MaOiGihGoBDZAqILkuAW12/HBx0zHDLCG7AWU2SIPqI2k1dPq8YwXm/SMW7L54AXX1skMjm743zj5mmAUW30ymJWK0+NPn/zh0AVq9HfmVU/igCQytArtgzI59JD7zxcHiunBeo2hsVAY3uQvr/zrhFnQ0jqLYu0Y8CUBjkmv4kHxSYGgeoZ9k9Ot3mkcvOlJkbhk012OYw2LT5lpc65wFrYMb4tkLhMx6cVA9Z6yPZtczOfWtgxtQyW1wxze4rnX+U/i1ALnN+L3NWaKmw3eIO5Obmoh6UNdADwHQDMO4XC6HegGnc2cANLgfpDTObf1+fzQaBU4MmISgGcGzH2H2ALNiLdM0sYCGY2Ft45N8UgDoUCgUjUa1ADTsJTiOA8e7FEVZkxeUSNM0oeAATwgw/2mL0wLQzc3NNpvN7/eDs0HIX7tcSFlAgKg8zzMMA2s18MIBr5OTiiCEiCQO9QL02W63MwwDbIPdmZK1Yp+PsFYGnufB6jmFO4WmaaBD6fAF1TOVSlvimabV4/cqDUBvhwaFx9/n87lcLo/HE4lEzklv6VX1HQjCdGHxB9UH+2VZlmma/vjjjx955JHZs2dXVlbm5eUNGzbspptuWrly5ebNmwF3JqZSJC3HcV3wKQ0EDet1PIcagFONjz76qKqqauzYsTfeeGNxcfH7779P1hhkjBow846KPqsvev7nJvG/TXp92EWvDyl7veziP2zagoIcapWZBDZMimBbqQFgAa3tbASJhm4Tj8eBvjYej8disXA4vHXr1pdffnnp0qUzZsyoqKjIy8szmUyXXHLJzTfffMcdd7z44os7d+6MRqNk/Qa9S1tE+/DA64HtdaDf6XUa6HA8jMfj+/fvb2pqys3NNRgMBQUFU6ZMWb16NbjDicfjHIcBMPIcEUQVbF1JV+91tT2fAoESpIQUDAafeuqpysrKkSNHZmZmjh49etWqVYFAIMUCmujqfAp1vvImTXwWgdPKJBGwkkfIhQ6PW8QUNHrTqsPZdT8Nmn84rxq7wmsWkTeOgnFMTPHMJy2F2KQXGWqFNIsrq4atewZ5krhwu/JkFX3mAOBWEGIk4bUvvi+qiRnmo7xFcUONzzAX02s89zmysXh6ZHkhIWL6iz/tdJY0BHIwkhsz1u0fVidv+AZjlzySIyw4oAMHv23WszxC//ntkWILhhezG9hBGIP+m6kaI9rYAPskAJ1AKjNyq4Jcivi/Xzl+0UJ3RjUqWhwxVDOGmsigWiYTG8Z6M2t2Fldjr4ARFX5u+6P+R1w5AO7ZipADfTHKYiuoVfJv4Q3z44b5bUbBWXV8ToOSje1tZQPO9sQgs89o/inbTOeaHXm1jrxa52D8cfx/9t4ETorqXBuvmZ6evWeBWdgJCFzF5K8kXtTwqVevC1yWGWd6mw1ENAnZXMgXk/BdUWM0XteoYIzKVcFEBWJUrkG5UcQFENkZhtma7uluep1ep6urqqvq/efU232mpmcYEZW169e/mdPVp87ynlNV5zznOc9bQqQqthXN3TexyX7ZncG598GPX4TbXoQXPobuOIgg84qREfi2RdibnvKPWhTNJSLFiWyjrdR4pPFB6OGBCHXwyiNDQcZ7AH7ywuFqs71IHx+xqDff4Ckw2HVEiKNrhNFSbnSUGF0Fer+2PpRVF8mqbyvXH7j590TuA4C4+0tIRMVCBGKELa5dExsdeYT7HGfqohp9r85sHd3svuIueGIL7IsTAZMjpBfBXy3QuNJSSvQ3UM5bzDEdza3bNqUJPrQTfBnRWewtyVX85DlSvyCIt7/cM3pRqKiJzTGHmBrfuJs/veY2sEsQlWSRkKA5xa3kEAA0powwNHFHCcFfvGD91uJAgfFo1gJfgcFf2nhUZ+wsrD1UVn9gQtPe81oOTGjqqDT5iwkJGr1fyvlNpBflmiP5JkupAZa9Qnq+ssENqeV09QFrQLHmIQOD7onMiXPaAqeGAR0KhSg/t7Oz02azIakZ35TqBuE4DvU3UMsYdSoQFMZRCIWf4vE40maRg2yz2TweDwKaKPSBdFq3242DGMyFXo4BCkBblQOxXSSeoKMqJK2gowNMtrOzE8nOXq83EAjQeqGgczCI3mrJmInWS0yIHo+ns7MTSdDd3d0+ny8ej2OctEFV2oZxZP8Fg0GHw2FTDqfTybIsXkWzAAAUr6Aa0Ojk0Gq1ok9F9e4k9VUnLUwHEOi9OhqN+nw+LDMuFVitVsT2UXZDrUxCWwQTUZeZJjt8QH1JJnwmWgDbF7s9z/PRaNTtdlutVrwf3W43rmmdiVU7Z8vM8zze5sRPBs+jTj1aA8WdkSF16NChFStWTJ06taysTKPRlJWVXXXVVQ8//DDyBOm1dKKV9ihAVPqcNXKm4l+vBWRZ9ng8d911V3Z29rx58yoqKi677LJ/dlHsq2l9j379estwmqSmiEJKAkhxZSfuK3+LTrtoZVn102VVfxw7aeW6tyAqQVAISMTtelBhmyVS06/Bs5XTpE7fYDFoZ6AQEi6/CYLAsqzFYnnllVdaWloqKyuzsrIYhsnLyysrK/ve97538803v/HGG+3t7WlraUTQU3EKoi40zYUG1L9mwhkLnFoL4IxGkiSWZffv3z9r1qzs7OzCwkKtVlt3Y922bdto8eichfbkwQEa+RwJqC2A0Pzy5cvLy8uvvvrqioqKsrKytWvXqiUr1dh92rXniMXU1VS/dZDYS9jLUR6Ogs34O2epKc7UxXOMkZImW2Vj0PQw8apHvLelPNq55M+r9SGmJsEYiIfAosZE7UNgjxP4sH+6358hAtAEzkSN5mc+2DvO7NbWQfFiOcccLmk6OLEZXtxJiLG8LCqazgTds0TgRy96isw+4vlQH8ox7hrbAB0RQumNi+SjlIegB4QAqygHswCv7zxSRjQlErlmVmuMMLVE0+NwiGStFA8JtmSTVoCDrrjzpkcPVRLximC+sS/XGGHm+ZhroXhhX66RkHbz9Lb8Ostlt0NnDGIS8CpZZNSjoM7mOPJu7/uvDbvGm31ljZF8UyDPYC2o68ivsZcabZoFXJ6ZiJaULI5qDRZmtrOq+aPy+fsu/Ymj5WH27r/AU+/Cuj3wiRO2OQjGelQi1vDJBPT0K8hvTCk/2hD/OhNHLlvmydHHcxuEnAY222Qdswie30IEoHkCzoogQ4iDHpH75cuHKo2BAqOLmQPlNzuyF7Tqatu/fzu8/DkcZmFfGH775p6JTZ4RTVEt8ZHYU9UET20Cv6K/QVQnJGBFoo5xINR7zXJXXn2QqYkzdSFmnldn2lpZI939GjiVoU2fspQRA8Ir75XBJsMD71knLvHmGWOMIcjMdTFzj+iMcNc6Mg6ClIQ20slTGHSyir3gq32wO/fGUFFTNMcUyzH0jGkJ3vMKeEWIkcUDVFBJtX6qD2DPRjp8TIQIDx3hgPEhW2WjJ7c+lmcKM3V2Zp5r4pKtEwyJe1+Hvx8irhHRaeQ77fZ/vd1RQrxfslqie57IJr3Iysw78q3F8GorIZIrJqFtrr6PMJwsfOZfxgLDWuAUANCSJFFVje7u7o6ODqvVijuw0vYYopaix+OhGheojIFbXOn+VkmSQqEQpVTblMPlcqEvArfbTTWgu7u7XS6XGplCzBffxGoJDqty2O32YDDIKwfHcaFQyOl0UoIzSkPYbDZUBZEkKRwOpwHQ4XBSEQozwrZABjQiZRQWRxkNHEPQUcLgtkPVabvdTuUpfD4fNYU6fhoATTWUcYqiLo/6qpMcFnNTMPcAACAASURBVAQhHA5T3jqFy62K3jfqqGCje1OHTzn8yhFUjlAoFA6H0Zt8LBZjWRYlYsPhcDAYDAQCfr8f1VRwgnea1P0km/osyw7vEVQPxC6ENyZ2oX9CQup1prOs7md3dbBNceENlxbC4XBnZ+fGjRvvvPPOyy+/vLKysri4eNy4cXPmzFm+fPnf//53lIakZqGUH/k4DnpVJpCxwIlZQJblXbt2XXzxxdOmTbv66quzs7MfffTRUIhM9tKWk2l/PLGMTuerUq7bJR6kPiBKmGvejJ138bO6UX/UVT8/etKzBIAWIShEJLK9OapMlAfPXOiZ07muX0/ZaGcYHKCraOFw2Gazvf322/fdd5/BYJgxY0ZVVVV5eXlFRcWkSZPmzZt39913v/baazt27HA4HIFAIB6Po/fmtK0k6iy+ntJnUslY4CtbAGcuPM8Hg8H169dfc801xcXF1dXV3/nOd+6//37KFhIEge5DVffkweGvXKIzLAG1BQh2Go0GAoHbb78dvRFWV1f/00Xu66+/7nQ6CcyVEOmesLTl+TOs2l9TcenLZgBqFgXp7tc+K5gLpYuBMUWZ2jbNXAJTtvMgQG88KhKndjILMgRl+9W/cmXXxLP0Qo6JLW7i5j8IEUhwQ6twIDhMMGVWhN3uQ+cv4StvJo74mPq+osbdugXw+CY4KkKciDKzSi4QEaG1b9+EFmHEEg/zH0LRQlexGRb9ETwyURDmFPQ5obCYRQUWxzz6AF7baSknusa8xkgw9DQAmqK4YQ6CEL3jhQPjGj1FROIjmmvk8sxybqPia7E5lkcQ5ECeIaIhytew5hMEH+MxNonLJpQ3OQUjEwr26hDg7S5Y+gI7/wGp7hFoeRqW/Alue90xYbGXqYkwC7hsQ1Cr7ynSQ/3j8FkMehTcNqwsXMdSSiic4jdPIn2cNDhVllC3vgjggX3jmuO5DTHGIOe1hBn91vw58JEFFFYeQZ8FGfwyPPvhwSmLenVmSWuGooVebf3BUSa46zXolIkx/TEC6Ft4+FvHZ9OIz8ZDIw3b/6UFdrnJeUGMcYr4CA/gkuK/WdtRUt+noM+xHENoREvb5EXwtzboCKFECQpPKwRhpVEiMtgAVmz0jGiBgoWgbYaim3xZdXun3ERo2lg1qmxCq4l4tA/s/+eXLtIEpoiGCLC0VZlgwy7o5YmSmUCMkxRRoRIctFtjCzkj4AP3z1bZKht7mblhZgGbb/YVGfeW1iZ+8CwcYImkBqtgysQ7h9IE+7gjl/zMpiN0e15r4jVGobDJnl/30cgFsD1EQHORxKT5DA6omygTzljgWBY49QB0Z2en1WpFoDZt0IyvTI/HQ9Uk7Ha72+0OBALRaDQejyM0HAqFbDZbR0cHko57enq8Xi8CxxzH+Xw+yoC2WCzIF04zB77FyapkPE71pinB2Zo6KPTc1dXV3d1NM2JZFlNAYJ1G6+npoXLVatCTSnAgWGaxWBDpxtEYJkX/0qJyHIfDC4pxWywWh8OhxtNp5MEMaIvFgjLKiHGrY56SMO5CDYfDTqcTSesUdMZAT0+P3W6nchwIuKPlkSJtsVhsqQMvwXTwVxoHmdTd3d1Dyn+fkrpnMv3qFkAAmud59GhKu1BPT4/H40lDJL96dpkUToIF1Ns4xITo8/na2tpefvnlpqamCy+8sKKiIi8vr7q6evbs2U8//fShQ4dQzp7jOHy6igmR47i0/en0QXqswEmoVyaLs94CkUjkpZdeGjly5KxZs6ZMmfK9731v+/btKEZPp/p0dRm76xlik8GTCzyTXvwU/TkRBykCZFLz0t+kyRetKaj6c0H12tFTVq3fCH0ShPiEouBIN24eb/rp+Z3534d5IuHoCAeECEajRkdbW9v69esfeeSR5ubmb3/724WFhRqNpri4eNq0abNnz168ePEjjzyydetWlCyLxWJUM/fM7HtnfhtnanBsC9DHYE9Pz4MPPjh58mSNRoPv961bt3q9Xuz/iD6jxiB9lg5z7xw7w7PwF7Ud0CGhmBD/OTG85ZZbqqurv/vd7xYUFEyfPn3Tpk3oH4UuiKovpA1xFhpocJUowKfAaEgERp9vBFGLAmxq2zXW5M2uhbxmYIyB7LoDE5pg4wHwEsxZEEXUOiDIZkCGX6+zFNaFs+tZjcFXZISbnwUWiG6GctCXHC0FOcNJ0B6O3f5C1wijWNTsY2ZH8k09VU2xm58Gl/JuRIa1KEOfDJZE4hdr9xXUBLVGWXdTpHRh+5gW+HMreAXgVegzYtBEW0OBg/sA1u/cM4p4wIvnEFWKKALQbQoDOgXnksguHp7bsn+s2Z2vD+cRAJoA1llEmpkraIxk1XN5ZqIOnGtkNYbOUn33LY8SAixLKpQ0GuXtIpCKdQ5yBIqNKAvRbhksLBwIgxUcV/zSU2RMMAaeqfNr6joqTfDcTrCxEFcuQ+97nExMxCsfQYKkwjVRIhEobk4p5gmAzthuXS1kN4iaBl7bEM0x7ZnYAh6ij8zLij05gHXbt33L7CzU84VNfUxNgJnXWlQDj78DToEkygHwMrASkeR2S3AwAOt3wLod0BbAhuMTZAGMhEWAtw59Ms5g1db0MXV8lqFXZ94xzghPvkvqG+WJSZUD+xXpJKIMcZn4ZtwXbxvbEtaaEtnmADPXw8zfN6GFe3dv8gIKQOOACK2qwOsHJ98UzjMHsvThbEMkq9429RY4FCI8dFYGjlCeSS796LMKGE4oBe7h5WUvW8Yv9OTWB5kFfJYhWNr02RgDrNlF2pHA6ygNoyxjYGl6ZXjr0N4qQ6CAOB6M5hqJ+81i/cffMkGHIp+W4vifu6O3/mbLhE7cAqcLAI1SFWoAAuuEahU2mw3xRPQriPgy8luRPIsUaXRUaLfbQ6EQKloIghAIBCwWC9KNEbGNRqNpb1x8GZNXA8c5HA7Mi0pAUGZld3c3imYg2E0FOnCGEAqFfD6f0+mkbg+pc8U0zBfluihCijxfj8eDShrqxsSCCYIQjUa9Xi8Snzs7O1HQ2WazIc0qrTqYwmAGtN1u9/v96vRPVRjdRfr9fmw+RJltqcOaOhB0xma1Kpxo9d9UdFsqOvmPmL5NEQ3HCNgcNpvN6/Wq52OQOc5kC8iyjErodIEKmxv9eaIHsCHvizO50mde2WXlOM5y43ICx3EWi2XDhg16vb64uJhhmPz8/IKCgssuu+ypp56y2+3Ut/vgZCkvHl8lmPvwfwcnkjmTscCXtYAgCK2trfPnzy8pKamtrS0vLzcYDJQBTe8C2hW/bPqnLv7xTjGUeJIAiTgkkgzovyUmX7Qmt/r13FGvVk998vV3pD4JIpwkyiBLyY9SryGzOHU1Plk5086gDmDmOFCRFUkNxJHpuwzFCvx+v9Vq3bhx4/333z9z5szy8nKGYbRarU6nq66uvvzyy5cuXbp69epdu3ZFo1F0h0BzGaZ+wwB8w1yV+SljgROwgCAIPM/39PTccsst2HunTp16++23d3V14Soy0nWx5w/TM2nHpvfICRTmDL2E1h0lIlHPBKlU9fX1BQUFN9xwQ1lZ2Xnnnbd79266IDrYmGdo9U+k2AMBaERRFaEGBYzrZNuuv8td3ggaM8vM72VqOssN8H/Xgo+wSQVBIEgFBftCMry6Z0d1vVNb25ur31s4Hx58G3oF3AxEOcHphewV4M32T8rmH82tI2zckptbmWuPXH4HHCZgKBFllhRgMSITBeEntuwb3WAvNPqy6hzMXFtFc+TmlXAUIKwgm8h6FhXokPKgeYXEun7n7tFETwNlkZMAdHtKggMBXA5gi+3jqU3OQj3oFrFaIk9hLzUeqjRC40q48VFbdZOjoD5cYGK1BMU+WmR4//wmolbRR+rEKx8SUhDtJPRKvAJKMi/ERYGjcCwhfQMcFrdOMnlLCQc5wRhcefX7pi2C/SyI5Mc+hfc8wFYEhE0CrCjqxSnOGzFOUuNEBPjQclgRGwHdLSGmLlzcnNA/Dl5gEzx5ILAAXfGPLv2BrbLRzcxO5Df68vRdFSZ44B1wi8jmxvLLERZiyspBWCBXsQRQjgkcS4YqyqGoi1hr7tmfNy+QXccxejbf3DW6SVjxGsHQExDHhJS4OKZJQsMJxdlgdxzu/p+eIqOf6GLr2WzT7hH6jt+thV6OmJLC90q/kVGcTABwwue6Wl7bEGDqejWGHmZu8Jr/JLg5gauIVAu6lCQyLInkw4BYHT/E6yAPf/j7npH1fm19PNfE5puDpU2HxjXBa/vBJUOYE+JcCusnSUWFpEIMeGD7GEOwkLgijOWZYtn6I0X1bdffBR1x0lQZAFppscyfr2iB0wKAtlgsPp8PUdq0MYQkSTjURrgWsVpn6kAdZMqERSqxz+ejchZiQgyHwz09PQgZd3d32+12r9fLsiz6DlabD1/eKK9sTR1q9BnxUIQ4nU4nkqyxwLIsx+PxQCDgdDoR/bRYLG63mzojUmckSVIkEkFglAKmKG+N6iK4VUoQhHg8jqxnRNm6u7vb29vRbyEiqmqZVHUWgxnQSNlGRjY+qNLin8yvsVjM7XajodR/U1bv/482x++2gYc1JdOBpxF9xvbCn3qUA2nU2F6UUnQyK5vJ65uwABVvwcUn1MNxOp2BQADv7kxbfxNmP/408SFD/w6+EH/CbS4oAf/JJ588+eSTtbW106ZN02q1ubm5U6ZMaW5ufuyxxz744IOenp7jbNM0mo86a1qetBeNOk4mnLHACVhAEIRNmzaNGjVqypQpV1xxxbhx49asWTN4TZ12+xPI4mRdQmcwxxlIlksieou8IksZF2R49Y3weRc9lzvqz9rRa6vPf3z934WYDDGuH30Wk5NImsvJqt/pnQ9FkYYcEtOT9Cnn9/t37tz53HPPLVu27IYbbpgyZUpJSUlhYWFpaenkyZPnzZt35513Pv/88x9//HFbW5t6w5y6c3IcF4/HxQQR98RlvMEoVeaZeXp3nDOgdLiygg4e4vH45s2bFyxYUFZWptPpamtr33rrLYSead+mb3zsll/49wwwwTdTxDTLiAlx9+7d8+bNKykpufLKK0tKSqZOnfree+/hPY7PEPokObfua+SWKpiiqLA/eaLuKxHw0M4mblttH7vQz9RIjAGKFznLzZY5ywngS0hrRGFfbWdktu5Y8KvDIwxHyoyfXHQz7CfUVJGgl0RDI4EyGtjilNPqEDsu+alTW+tl5oo5JihbYq1shLc6yKYhUeHRxuJEO9gmwiPvdY1ucWvqoOJHvVpzd1btjvFN0Bon9GdUS6BgOn2FJhC8huhTbx8aSYSMEwz5RJnaI+ffmgSOZUkRB5YhBt2zf+MsN/OFxDFgX1Z9e3Fd5CfPwmcu4krRysOfPt051mjXES1gmSEuENtGmWGjBQKyKAhxRaWaYMTKizzF/U2ixojC96PSIYCdsc+r9b1FJjGvMZ5rOlxUa6m9h4gmi4SCjL4Z+xNRjIbWVjRPCE8XacX9NxCKav91T3t5g8Q0QO4iL1Pn0jXBnRuIkkmfgtL2gXjzKndFs4OZIxW39OWb9lfoQ799FTwCgX1po6S1UcqzIiGUI/7MAzg5+fGNu0YZvNp6KFwsMvWOvLqef/81UU8WCCSb5L33ly8VwloFAd5x7B3b4i5o4LLIx1LSsLt+BVFejiTlTEh5lKwJAA24kLC7s8QoM+Yoo/dqDfYRZrj/7xAmcjrJhRBcfuCTchz9Bked8dcP7hvfaNEucDFzxGxjqMhMuM9/3AI9LOm9OALDXqQwqd2RYIxsA5DAyYauW8EWNvYy88Rso8jUBaoXxVb8BXwSuVDRRREVaJ52vVRtB/2nvTQ53hsUIXPiXLXA6QJAezwebIK0d6Esy5FIBJm/iNUi0qTWZ0D3ep2dnShkgSp4+HJFtgj1+EeharfbHYvFcIStbnoUHqVSzlT2oaurCyHsnp4eBLjV7l+wzIIg+P1+qo9hs9mCweBgmBsLxvO8z+dDaRGrciAebbfbnU6nz+fz+/1er9fj8bhcLqfTabfbbcqBka1WayAQGJ7PO5gB7XA4ELDGx7q64iczLAiCx+NBhRNsU9qyFESm9HCsL9adAsp21UFxfLpUQFtZHd/r9Q65GHAyK57J66tbAOfGKMiOXgfp0hSuMahn0V89u0wKJ2wBfMioZ5JI0uE4jmVZvBl5nvd4PFu2bLn33nsvv/zyCRMmINlZp9PdeuutK1eu3LVrF33eDvksHbJ4aQCKOg6W6tQ+ANXlyYTPDgvgGCASiTz00EMajWbmzJk6nW7evHkWiwX5p1hN2v1O71rTOcVxBpK1kUBS9s3GAWKSDOv+2jv1ome0o9dqxqwdNf3xde/xHADLK16BEmTuIxLfzKIsH5Mrdnpb6ZsqHe0kaYPhYfITEyLLspFIxGazbd269bnnnlu6dOmll15aXl6elZWl0WhKSkqmTJkya9aslpaWJ5988tNPP6XP1cHJpu0jwWd45pk52FCZMydsgWAw+MILL1x00UUlJSWTJk1atmzZjh07UIlRPWZQ3wvHEz7h8pwFF6rtAwDBYHDbtm24Heeyyy6rqqr6/ve/v3nzZuocJS3+WWCB46oChcNS6HOSuJoA2Nx5eNJCX1ZtmFnAa4xsacvuinr4nw6i/kBk3tIPQjvlAf6+Z8cVP31rcj288jHYIlgGXgFnEYDuB1V5AEcMnt/SXd3Yl1Ufz9KzWqOVmQeLngW7QrnF9y0AWAV45B87Rxpd2TfGmDqpaLG3pOXA+EXw/GdJmFON5dEaSYqjPE6GMHBPvN1ZbpAY8uGzDKGsusDVyxVkkRSZ7YtBiIfXt7eNMosFTaAxx3OMPbm1CdNjcISXnIr0hES4w901K7rLDLEcg8wQONtRZoLHt4BbkBIiD0SrWnmRk9LQaqKZ1JISxCYhgL8cah9hCOYTVZC+XOOBsjrPr1YTQWGJgK6Cit2MNlSbe+iWTSgQ7fMfHi42JpiGRHajN1vfWWKGRz8iUHsfgCsOr+5sLaqRNCY+y+DX1LUV1sCytQTwlgiuTMpMbU7zoPZUjIxIOukDO30fTDH3VDXJRS2QRaQ8dhXPh9cOQJQUHvFxmkZ6QFLUSDrh/dFGe3EDm93AMw3Ooob9/+cOIg8dShqQ4NC0PDIxmvSHTdZi4kwynmV0FRi3FcyB11tBgEicTS5vIACtsKFFZc0jmbU3Cg7Z8r2fugr0XqaGyzMLRc2HdXXwxGawxCCuCHekSqnUkayXsJIQSXDELFFwzryDyzNHmAUSowem7uiIRvjTPyAkofA0KqFjYWmRU+kN/D/QngN/y3w7py1wagBoRHipwILFYnG5XMdqB0EQ0JGgGmHEMIUpXS6X3++PRqMIsCKOTJ9f4XAYNSusqcNms/l8PvomVmeN6nvUqyHFRm02m9vtHlJbFlfpOY5DlQwsm8PhoALQ6vQxLMtyLBZzOBw0/VTRyH8qfGxTHRROdTgcoVCIUgMGJ45n0gBoq9VKUX66AH6sa7+582JCDAQCVNQ7DYDGdQWHw4FK36FQKBqNsixLBeCoa7J4PI6eBiORSDAYdLvdCEo7lMOlHG7l8CgHapV8c/XKpHwSLID3ZjQa9fv96HSUbkpIQ59PQmEyWQxvAVk5cDKJzBEyuFKc3YfDYY/Hs2vXrvvuu++SSy5hlKOgoGDs2LFXXHHFY4891tPTgxIr+DxnleP44Rg1tSftKiwV/h2+/JlfMxY4fgvgbnEA6OzsvO6666ZMmXL55ZePHDnyiSeeiEQi9GVNu9/xp3wqYqqnFcgFGvyXxFEQZ0kVmwDQCpkpBhKs/2vvtP8vCUBXf/uJDf+b4ACEhDJJShD0OQNAD9m4tJOkPbuGjIwnJUnieR65F/iwxeHo3r17n3jiifnz50+cOLG0tFSn0+HOkpKSkosuushoNK5bt85isciy7Pf7cfOQoBzUjytFAzPPzGHsn/npOC2ABPxgMPjAAw+Ul5fn5uZecsklL7zwAnKih3fcqr4vjhU+zmKcldHSbIJSk5988smFF15YWlp61VVXTZgwYdasWbt27VKzNOhVZ6VNhqkUqiXHUflBBOgRQj9c2V1A0GcvMzdc3Hi0ugWWrobWEET79Q2oucjDmTCJFRatAODhCKzJEtEFouSg6DiT9dUUS5TE7APYHzl46U97Ry+OZNULuWZHXt32kbWwxUvozwRDVGDKwwKseLtrZFNvXoOgWyQUtAQYvXXczfD0B+BSVKox08F1k0EWFYJqEKTH3u4uS9KfWY3Bk1sPt/wJQhJRKgYgPvessP17P/SOIOgzkbouMPbOuw/aeAIG96V0GOIAz209PIIA0AmG/D2qMyYWrwRbDBKE6D0AME2VB02U+pb6HwL41fqjOmNYa4gwtazGQIQ+1u0gVU7hvKmoKRCWCoyIKl1jFH9ATFMRG4n9bsOh/DqeuIvUezTGg2Um+JuNVDIGcBQ+ntoUGtECec2S1uwsNgT0vyeca4Se0YyYVH/eSnlSJylHHiLA3/liZxWRsIjnGDlmfrDYHF/0FEmN7Qff1cmow4TRHFP0NP7lFgpAHy1s+GTaTdCuoPMJYvgBNHARwAeenz9rJfA6AaDthcZPJprgIJE2EUQR1+2J9cSkHIeoLAkQOn9UgAD0/fKlttJ6oqzCzHcwcz2jFsKPXiBdKA6kf6oOOoQjG1L74qQ+n7k6JrTEcgwsU8cxtQJT215SD+914r2Ag7dEqm/j5ar0BgYzAPRAe2S+UQucGgA6Eok4HI6uri6LxYIgstvtxjKlPbxw20soFEJpC1Rhpsg1qiG73W50A6hOQf2eYFkWyZJIsMXLHQ5HJBIZcoiPWyAjkYjX6/X7/cFgMBwOo5TekCw8ZFKzLIvEXlQC8Xq9sVhsyPiIj6gZ052dnWgNq3KgWSi4ZlW0JhBg9Xq9xyo2bVQMoHM/itHbbLZAIKmpjwVIi38SvkqShOIb6Omxq6sLq4Z1t9vtHo8nEAhEIhEEnQVBQL+UaVx1ytChXislSUInjZFIJBwOR5Qjqhwx5RieLX4S6p7J4oQtQG9SMSHiYoPNZutSju7ubpvNhrrPqHBHI59wdpkLT8wCFGXDy/EJrAagI5HIgQMH1qxZ85vf/Ob6668vKSlhGKaiomLGjBk1NTUPPfTQli1b3G63mBBxbQmVlPARiqkdf8Ew/uCrjnX++FPOxMxYYLAFeJ5HUr+YEDds2FBWVnbBBRdMnjz50ksvbWtro7cG7X6DUzidztD5CKFUHeND4gwGoBVZSMKAVgPQWWPXVk1//I1/SHE5A0B/cTvTTvKl3mW4Nk+ftzj4QZndWCzW3d29YcOG3/3udzU1NdOnTx81apROpyspKamqqpoyZco111yzbNmy1atXb926FWWsEKKi6DOV4xhcehyMfamiDk4kc+bsswB247R6oVb+T3/606qqqqlTpy5durStrQ3jhEIhvGRwr1PfEcOH07I7p76qLYPzHaRYvfPOO9OnTy8sLLz44ovz8vJmzZq1efNmdN2Mty1Oo+jl54LRkNaKDthIfSMA/7DvGWfuzTfIWcZEfmNs3K2fjjXAFheEFUB5gPYGNdUAFC/MscSecREiPPFoJyT1i5PUYAmI+76HNx0e3ejNI5rLQWZBV1Ed96NnwSYTTeeYDH4AC3hrHvBN+mGftjGR3ehhaiw5td2jb4KH3ge7BL2KWjDqbwzVTgR85AG8EjzcD0CHtYYjOj3c8zfo5VBtmMRZvq59JHEwKGYT34NtFUbY6iK4bTiFPssArgh0cLurifhGLFsfzzV5ioz2q+6CzjCpHcK4OFhQWQKt0186hOkDIBseI07tNPoQUxPL1reObYS9CuyjujbJ/8U0qWdFdK6IbUa3S0kKkBqB4LL/PpxfH2dMIeZGV65p90gT7IhDL6GBw69f6y4zRDR6KGjuK23+vLIedvgJV5kT46JAoFsKZ/cXtx+ARlWNpCdDDxyctrg33wCjl7JaI1Qv3a+rgY88RJICbYplVqejDsvKyGi/4Lrm7p4icyzLzDFmV755c1UdAaDDIHOyoGDUiEGTSzkAF1jqfttTZBQYYyzL2F1idDc8hJA3QYopjK4IhYBAVjuIhjgAHI3Cuj0HvnOrV2eScxtJZ6taRBquQyLo86BjQNmjIvgg8dt1B4triBdKRh9javqYmt26BXAwTC4XSS74wQsHXD4ocVIi+hn8a+bMOWyBkwpA08d2LBZzOp3oGBC1idEJId06jS1CcUaO4yKRCNIeUQYa0VjUTR7SqSBtU4omo787xKCRDjwMQxmVSTnloK9nmmZaAIf+0WgUGc20RoiIpUWmX1E2GitFgXU1yxuxY6vVarfb3W63z+cLhUKxWAxZgTSdYwWCwSDivJhmT08PbnA7VvyTcB7Fr9FPI6qaWCwWZHa73e5QKMRx3BdaG8tJ+5K62NjWSOFRg9dp+LX6kkz49LcAjpJlWcaFKPQpik8PlMRB0efMHPgUNiXejxRoiysHliccDre2tq5cuXLhwoUzZswYOXIk7grX6XRms/m5557bvXs37oChiaBYh1rmCNfMMMIprGYm64wFhrSAWh3yn/t4lixZUl1dPXfu3MrKyh/84Ad0pDHka2vIBE/pSfW0Ih2AliChfCj6PIABfSwAuvKCR9/cAmwCJPTMLinqGzhZIlX9ginMKbXG6Z457VR0/KyG8HB0St2KRKPRjo6O99577+GHH25qarrwwgs1Gg0+kIuLi0eNGjVr1qzFixc/9thjH374od/vVwuX0fV+MSHSFX3kiKjLcLrbK1O+k2IB7IQ0KxwbvP322yhMfPXVV7/55ps2mw1duKf1WPpV3a+OJ0yzO8cD6vcRAGzcuHHq1Kljx4699NJLCwsLr7322j179tDRGs6VhjTv2WpGBDOTor28DEfYsOGhwznzoGwx5DT6mes7i+sS975OpISJPzqBqESnDjQUsQzCagrALJJ1WpmXCLqUtgAAIABJREFUSSTFD4JEHMRJckIicrkkMgfglF3/sSI4anEvM49l5keZ+e4JN8MWJ3hECAgE/H29bd+3Fnbl3ehlbkxomyJMnbe44dCkm+CF7QS87lOtBatB21QjKZxuomwFdi78i9VHyojnwEQ2YTe3VjfAmr3kNYvI5Z7AwYkLvdl1vJZ4mXOOXwzL16EIdTIxsvRMZIXBI0fm3u8pICIeQmFTMN944LyFhEWLIsWprIf7n5D43jD0ws7RhmiukdUY+rLqIxq99/u/hCOKYom6LlShWz0GSQtTNDMO0J3w3/LMkUJTIrsxwtQ5co0fjzIRUQtrHHb59482BZgFULzIytxA1Ktf3k0g/oTMJwROEvvB7v4C0KRpQCGV9wry05uOjDBBtknIMYXzjB25CxKNTxA7BFSuB/vTGWQPQlIG2C+6//3ensLGWFYjxzS68s1bxzdANxAdEmXkFFNA9eSKhTsOB/kPJ5rthYT+HM02tpUb4el3wc0rzHPyZwAJWsLTSkaWeNd1v2ovrvMyNXJ+U1BTv7usFv6nHXolUn05OWajA6/k8EsG4CRwc2CFjyYae4r0CED3MXV+ZsGBCU2kE/JEvQTRZ8ruH2L0Ru03TGCQkTInzjULnBoAOh6Pu93ujo6O9vb2zs5OdNanHj3jIx4f+DjqxT2GLMuGlINSXNUCi7Tx1FAUhsWEGI1GPR4Piiz7/X6WZekLmF54YgGES9S6Ijab7XhUMqikQDAYRMIyVeSwKcc/PUQ7HA5kPaMMRf/L74vKyvO8WrrE6XTSafAXXfpN/Y4MaK/X63K5EFjv6upCZDwNbPrCEgw5Whrm5BcmmIlw2loA71O1HHx3dzf2H4/Ho/aqdKqo/aet6U5OwdTPW5xPchwXCATa29vXrl1rNpvLy8sZhtFoNCNHjhwzZsysWbMeeOABteyS+uFPH/h03Sjtvj45lcrkkrHA8VtA3UUBYNOmTRUVFRMmTJg6dWpZWdmGDRuQjEajHX/KpyKmesL39QDQFec/8taHZGsyAaBJ8sQSynZlrN8QU5hTUfEzMk/aqdRP0RRakv4fOdG4y8Ttdu/Zs+fVV1/9yU9+MnPmzDFjxpSWlmZnZ2s0Gp1OV1VVNXPmzEWLFr366qtdXV2BQCAej+PlQ46caTHOSCNmCv11WwBVXDBVnuetVuuqVasmTJhQWFjY3Ny8fft2AKDKRcfqurRTHWfg667EmZqe2lzIpnrzzTe//e1vT548ecaMGRqN5tprr/38889RtRKnlnTclXbtmWqCYctN33AEtIsA/E/rZ+U1oVyDkGvmNUaxoKlrbDP8vZWgzzwQQFlSoGXlaYr2IclTtFR5pyVA5kBKYtACQW/7GalEBFmGzZ1tUxZHCs18lkHOMfcyNexlv4I2ATwADtn6s6d3VRnd+cZwtiHI3BjRtfjG3nJkxs/hHTs4FUwS127xhTwU1inizqMEgI1zLX7MVmrkNeTjKTJ+OLIWdsWSysg9ib5fvOwedVOEuTGWZ+oorO2e/Rvo5IFIOyhH0jWf8oIOyMIPnz2i0/s0dUKuOZZjaBvbBK3hFPY5rJXxx4QMARb2+vZWGaJaA6shUh6EA97yNDgVyRKlMXBJ4DiSU0VhAbqko3UP9RSZRU1TjNHb84zbz78ZugD2Rby3PddTpJcZA8vUWgrr+n70DBzhIU5kjnki/5Vqvn4iMV1SSIKmEhHyVg6r0HXDr/3FJmBMksbkKzJ+rJsL6w8RkrX6GKpR8HeiqxwhEhy7zv+hraChj2mIMw2O/IaD/3obgcsVAFpISXAkk/QmYJN95yiTs4CgzxGNcW+FEd47BGGFu62gz6g9TVpNyZosqEgAfhHWbNtboQ/lGtzMDZF80sTw85fAnWTlo3h0GnxMEpGAaHccYeH+dw6X6b15+qhGTxjQ2XpXdk3PpXcQ+F4g3Z9XGNBpKagtkVybGQZ9PratBqST+XJWW+DUANAIRCJfGD0Hqt95g8PqQXQasxV/6n8lHLu1xISIesEIPQ+zqfDYaQz9C+LIyDjuUnRFEIBOw2WGvBhLjtKooVAokDqCyoFqEqhHMeTlw59E2rjf7w+Hw7FYDMcZw1/yjf6KpO9AIOD1elGG22634867L5sv2u34/37Z9DPxTx8LUACaZVl8aPT09LhcrkAgoFa5oZ3h9Cn52VGSL3yO0Qgcx1kslvfee2/lypVms3natGkFBQUMw+Tn50+fPr2lpWXlypUff/yx3+9XLxzio1j9kFc/1Wmz0sDZYdVMLc4mC9DOibtw/H7/Qw89VFJSMn369IKCgrlz5yLXj0YjU4bUcfrZgU7PEzj/RswY+VdqBrRIHAomtSCVeZxKV1PRgEYnhFlj11ac/8jbW6GPp6qBpPLog12pfgaAPvFekOpHx/WfspgJJ4/j4vE4qpZZLJbNmzc/88wzS5cuvfbaa6dOnarT6bKysvLy8srLy6dOnfpv//Zvt91226pVqzZu3Giz2VAfiT75v1R/Tivoidc8c+VpaQFkCyEAjR3sww8/NJvNkyZN+s53vvOf//mfdrudakTQjpTWK07s62lpj1NQKLX1iEcxxZXOiy++OGHChMmTJ3/3u98tLCycPXt2a2sraksOHn3hmVNQ9JOZpaxgfl6A377RPsIQzq6PavShHL07Xw9LXya4MCgvPUGSRWXJVGVWLGYSsVUQQMKAVoA58lQkssUyC+STrJBbYu95dW/hfCJnUWD2FRh6yk1w97uwk4VX9x6+/Lau0U1WZkE42+BhaiJVSz4vvdFlfAh2eIl2cBykQDzpp48C0KmE6btTwdIliAtgl1pvuMumI24DWY3BrjNsndxEgE6/8lnftnW0qUtzI1vYbMuav2OcEf63I4kYIgqZWiQmPgYjMjy2ad+Iek9ufR9TF2NqiVjH+93JwiTrNuw/GYjAyCuf7qkkto1nkb/WEgM8+gF4RRAkgnsqIs/JbBVoFem99C8dkfQbHBS3jV1w+Pu/OKKt5xhzjNHbCk37Zy2DgwAbunZ8q9mtrYOcxniOcf9oE3xO3IyJQhJ9TqaDKhv9bO4BiKmEbScBrDvUOaoxWEjoz0KOyVFm2nHJD8CncNKHqjptEdr4kqAIPXfBlrGNFIDuyW8ImB4HhyLLrTDXk5ramGYIYOXHB0cQ34OhHPL5rNoIR4j6Nv6u1kcTlIEagcsFgCPcJ5f+oD17bh9TE2Lm9RTp9/zrUjjEkqbkCQMaEqQfp8HHJFEJIMhBF7dvYlO4uJF01BzShaJagz23Vmh4XIGwpaTStOLDY+h2QUB8gC0ViDztzFCmy5w7pyxwagBoNDHP82HlQERY9WxPD9K3I/6Ag138ixsMcf2c/nqsJlSvyR8rzgmcR39Zfr+fSl50dXV9Fb0LrE7aivQJFEw92TiBy7/2S9BQ4XAYGd+BQCAaJR4R8KCtnjox3H8a+TgDw6WV+e30tkAaAI2iz4FAgO4OTusDp3dtzrzSqVGGIUsvy7LP59u1a9cDDzxw9dVXjxkzprCwELd1n3feeXq9fvXq1a2trSjWn6YgpJYupc95DKif6uomHrIMmZMZC5xCC9D+SXeU+3y+uXPnTpo06eqrrx43btzjjz+OI5bBvfoUFvsYWdNpBfrFiStTk2TclO4zkeAYGoAmtCFekmCd4oQwd9Ra7ei1o6f916YtwHJIO5JBIpqaGQD6GPb/cqdp3zuegJq8jGJluGSCqhqCIPh8vtbW1vfff3/t2rW33nrrtGnTNBoNwzCoGV1WVjZhwoSrrrpq6dKlzz777Pbt21mWxe1rNPdhSk/jqAPDxM/8dCZagOd5ZAaICTEUCq1evfqiiy7Ky8u78MIL169fjxsxeZ6ne9fUehHqjnEC4TPRXN9EmdWmw6UmAAiHwytXrkQM+tJLLy0pKam7sa61tRVfSWmjL/z6TZTtdEkTeb4RgP2xf0zQ23WGMFPH5pvt+XX7RhnhbQtBfhGVU9BktUlxSIykXQoH8oQwSzBohKETqa/J+lrFHv39nTnzeY0xqNW3Mtc4Kpvgv7vhZ2t2/8sia4nBr6mLaIwRXcuhgtod4xvg0c3QIRAKNsJ2XGotWFAwcQV9pqrIyOIVCCIqk31GDtj5vR/YFQCayzbYdIY9Vy+Dwzy4ZXCD/8b/so5s6dWYwvlNh8oM0R+uIuofRD1aOUQlI5KiIigckeHPu3dU1h3NrQsw8yLMgoPFNbB+FyGGC6myJWt4jH+K+HXi/vUHRyYBaF+eXrFwN4QUoQ8lY4SC1XRkrB0hoCtZDQajSQN1wN4LfmDNqY8xphij7ykwHbn+bvhMgptXtxfrBV1LFPWv798IYQiJHHKfBwDECOgny54Gkcq9sQhRPV7xjie3nito5LWmeK6po9IkPvwmUSxJkZHTat6fJGpM488hgE2OPRMWe4taYoyJY8xdxabIXWsIkM2CmJBpR0qmFgX49V+txUafRh/NMQW1xk/GGMHBEvGQ1NoDZoToc1LQvA/g+Q/3TWxyMQsCzGwuz3y42sw/8iYxNdElV5RhBLJAQvtwvzWISozALl/rqGwSckyxnCQAHdYarMV6uPMVohUjiHShJQ3CHmCEdEOmuor6/IALMl/ORQucVAB6eAOrn+8Yk54Z/kI6r/tCoOQL0zmxCJIkhcNh6iYRNWrp6OrE0jxbr8KxKboZDIfD6iajzY2Bs9UCmXp9WQtgJ8HVi7RO8oVfv2xemfhpFkALI1QRj8cR9Od5PhqN4jLSu++++/vf//6CCy5gGCYvLy8/P7+0tHT8+PFz5sx5+OGHLRYLLsWhm3u670R9jw+e+QzfrGklzHzNWOD0sQBuh8I5/7p166ZPn37hhReOGTNm5syZuA8JBbuOhbmcPhVRSoK+25V9qKntxsp0hULPAwIEp5Z5kMgEXJLguf9un3TBoyMm/K1k9OsXXPDoO28HieN2MgMRiM8dAnsQzg0mqARPs9qfgcUZ/smpHm5h5YaMjz8JghAMBh0Ox/vvv79ixYorrrhi3LhxhYWFeXl5WVlZ+LQfP378rFmzbr/99jVr1rS2ttrtdqrzRlWnqScV5EMMmSM9eQaa/LQucur+ojfaFwS+YmVQoQUTYVl29+7dS5curays1Gq1c+bM2bVr15Dp09YfHBgyfubkCVsgHo+vWrVq3Lhxs2bNmjlzZmlpaXNzc2dnJwFaJQn5QOrxmLpFTjjT0+vCFHhH3kToGPDl3ftG1PsKCNzWl29qK9d3NT9IBBMoMXYg+/lY1REIkCiHlU+fApuSmJIiIuzn4GB8+7fMvTn1MkOo1l5tPUz6mT2/7qB27tGKJoJvlrT4tfWd5QZrzT3wziEiy+AIE4yVJ2rSPNHnVT4INCrvSzXyKFBF4IgMFvjfqgVHi0wJxiQzJnuxyf3jZ+AoQA/AuoM7S+rYgoXANEYKW7aM1hNPegAJViDrxsj4/qeLQir3EQD4X9enFXXOnDoxtznC1O0trBGefjcpTkKfL9Sqg60TA+hMWOff21lCaLyxLKO90EgY2QfjRBKEwDdoJ5JnPwiLQwWFoR5TNcWA5PsAWuXPxjU4C8xsdkOcMXcxNUL9E7De1ZZf62VujGQZnOVNjgW/JXWPQ0gUhOR4I/kYTOZOCkBrMjAgiOCSoPbRCFMLec2JbCObb/6wcDa83w4xRex7QIGSX1AZg9QLEWKslUeEh9+3VS3iim9KELjcsLusDjbuJ82akNHXerI8mIyT4w1/sDPzY0ydqGno1Rph4R/BlSA7zlLWxrL2490A0AvOuSuiY5b0Evpz7ZGsebsvvBl6BOgTCPqckAgJOsWDRhg66bcQXXH+tb1tfHOfrgm0jUif57INgTxDd3Uj/OED6JVlkeRPO5vaWAMsoQaajxUecEHmy7logbMEgD61TScIgsfjsVgsNpvNarV2d3fb7fY0ot+pLeHpk7sgCLjxk2ygYVl1wehYR30yE85YgALQqNtA+8nxBDLWOzELpE1C1Lw5v9+/d+/eZ599dunSpTNnziwpKSkuLs7Pz8/Ozp48eXJTU9MjjzyyZcuWSCQSj8fphZRlo241LJs6Lwyr4wwOn1iNMldlLHASLID9HHnQ/3SVvGTJkvz8/BkzZpSXly9fvhxn+MMgcSehhF8mCwpAK7tRldmG8ichAn4GAdCS4meQCGbCXzcePf/ih7OKnige8cfRI3++fUssHCRMH0UqkyMy0BkA+ss0xvHEHfy0TDtzPInQOCgVHYvFJEny+/07duxYs2bN3XffPXfu3PPOOy8/P1+r1ebm5mo0mtLS0vPPP/+666674447Xnjhhc2bN1utVuqokD7Vacpq1oi6hOoImfBXt4AaIDie8FfJETEUJNF7PJ6XXnpp1qxZY8eOHTduXHNzc1tb2zCJq/uAOjzMJZmfTswCDofj0UcfHTdu3PeUg2EYbB18N0WjUfV47CxsixR4lwSgfQC3rz1SVB/KNci6hUGtfmdFHbz6KcHY+oE+JZyyRb/ZaVLKKTEFQAdBjiCYq5B4pYQIIQnete0fbYpk1QNTH2OIF76oRh/Orvdl1TqyF3hGNB2pbvp8jBHu+RvRygjIICjiVgrcjMgzKRIlAytwc1zBZ/EcYoKkUiGAz6OfVNZ6CggADYzJWmKClf8LtgR0QW/DE1159QECp95kKTDC7/8HHKICPBOmL1lqRmUH5BsLQPzOfRreMdZs19YltE19jOGArs67fA0hTXMq2HagKZImQuSxlwDiey+4xVpMhIxjWcYjOuOR+vvBJiv5JeNitskviRTGqWQyYAdWMobyrw/goPjZuAaXroklriPnh0sWQcNzsOilvhE39TILglrjrvI62HAQXALw4OuLIsN68JNQVRPVj7Li188De8vr+pgFoGmUNKZYgXnflIXQ5pPFfld+6kJJSpmT/i2RAY1cbi84//3/+XRNvMYM2mY/U7O1uhYOemXFIXPa2jBZCQiC45Jf9DGmBKMXs8z+AjP87M/gkUkT4yeVaxK1Rz+GW7u7pi6JFzURwe6S5rbSevh/6+AoaVhZVABoQoJWxKAFosUBoiwQXoByWMXQdSsCJY0Ebdc2shqi38JlG3rzDe2jG+GZj8FHyNeDqehoslRxlP+0kMMEBlyQ+XIuWuA0AqBPofkpWePEysBxnN1u7+rqstvtPT09nZ2d4XCYIi8nlubZehXZeJsQEZ3PYPRnayt/vfVKDfySbkDo1+MJfL0lORdSQwQNb1LqnYZlWdRtf/rpp+fMmTNu3Lj8/HzkwWm12urq6tra2r/8+S8ejycUCvE8T6FnKpGEpktrsiFPpsUZ/PVcaIVMHc9QC1AAWkyI4XB4165dlZWVVVVV48aNKy8v/+CDD9Al1JkwyccpIW6BpXMcSZm+xEWIi8ALkBBAUmbKRJGDzOLQQboyd+60wk1L3xg/7alxkx9d2PCy3wlcHARBzADQZ0rfps9eFExAhDEej9vt9vb29vfee++ee+7BvfyMcuTn56Pi/3nnnXf99dffcsstTz311Oeff07Fsij9/0zo/2dKKw1XThWaciyO34Dzw6X1Rb9FIhEAiMfjO3bsuOOOO0pKShiGmTRp0kMPPeT1egVBSGOcfFF6md+/fgug10e/3/+Tn/xkzJgxN9xww/Tp03U63aJFiywWC47cUKly8B369Zfm1KYoKVieF2wzb/fl6aO5xqCmvpu5/vNxJrDxhLuaAlXpyy9ZXjWmNrAKYoqxG1MQ1OSthWrFz2xtqzCGs+slpp5n6lmmro+piTK1UY3+qM74aVVd6Od/gs+c4OKSvGCFPouv04SCHKLfP17JArHoGPE6SNBjxAQJ2ilK4BPgHdueSr03z8gxxgRjPFxmhI8chFL95469pXpnjl4e+UNfYeOOsY3QJRJcmyVVTfJ2EXeXlUQTin+8Dvj8/MWOfAOvMbPZpiMjGtpM9ycVkBEpVtlqgD1kEOMJglpu7d1eqbcXJgHo7hIj3Pc3kgLXH30ApkrljdNN3x+fhPoA2sSt32pwlBIAOsDUSiN+AKaXeqpvipUtCmqN7dnzw/9xP3gBAglIQCzOH+t5eEwAmgfYfGj/iHrIbRKY+kSuOVxg8l/7n+AmsuADS0O+YcFRJQV/TVYxArDJuq/SFMtvSjBGIafBmlfrrX8AgoqQWUr+hCYo8iK4oHXiYj67EYi8tcFT1gz3v0dUvGkD0dg0EILgg6/vKamJ5ZnEgiZ/sWn/t5rh0wBZkyA1J7rkRJ08oTDqeeInk4QlmTSEF+C+Dft1NRGNPsDME3JMfbnGvlzixDJQYGyrMsF/fw52opiKcDrtctSktBT9JVTfKYPDAy7IfDkXLZABoEmrcxwXi8VQivoEekEkErFYLF1dXS7lsNlsalG8E0gwc0nGAueIBegUlwYGV5z+dAKBwamdwBl1vvRySu+iZ75sQJ0shr9sCl8lfholmSaFS0Q4FWFZNhQK/RNEW7ly5YIFC8aNG6dRjpKSksrKysmTJ1933XWPP/74oUOH8BFKhkbKClP/hjKarsrrGq04/ki/HmdAlWQmmLHA6WUBvK3QVbKYEOPx+MqVK7Va7YwZMwoLC+fNm+d2u3meHzy9P/lPgC8yHM4scH8n/YsbOHkReDGFPvMgJkAUyX5OMbXpNJFQJjXvb+efesG78jn3vr1kQhvDLU8yp0hwEBlCVRmGmM6pfs0ET6oFaG/EAA5osQSoGY2SSjzPOxyO7du3/+lPf2psbLzsssvGjBmTl5eXnZ1NIelRo0ZdffXVd9555yuvvLJ79+5oNBqLxTiOQyxsSFGmIatK3w5D/po5OaQFKDpwnIEhE1GfpPcs7SH0V+wSGzdurKmpKSws1Gg0M2fOfP755zmOkyQpHo+j7hCNnwmcEgsg7ycUCi1atGjMmDELFy688sorS0tLf/nLX7pcLireTV0QHf8dekqqc+KZJpQ10+7YgTHmqEbfl2uMFJp9JWbvvy8HJ09c+aUEfNPfTGooTZ093mMKcotawwrqp8RgAf5zfXcZEd8QFQA6xtTLuoWO7AWdI43d378D/noInDIEUmpXCk4YF4negZxIOltA7I/AzbKCFscVBPafKSv1SHJ7EyK4OXjlQFuF0ZtH6MbxLGPrCCNs94IDeq9e4SpqdDM3OnP0H+b+Bzy7A3ohGozxgsyJA5itpNAIpkYAXLDzez9yljbEs4y8xnx0RPPu7/+cuM5DlZKUykRKw1hlEQSgvSKs/Ki1usGdnyxPR6kRHn2HAOIpAJo+nfovpkbuPzUo1AdwSHh/osmma4hmm/nsRqloMdS9bM26MZBnCo+8aW+VCZ77jECrqoEGzUsdQIA2/a8kyZ4QvNu6p3hBlJkXY2qEXLO/2ARNT4En6aEwrUxq5ByBWlJFAcAO0o9f9I9anMg2Q06zL6uudbQZXt0PIdK49KGaTA19Oe/v7Ri/mGWMMmMOZxt6Kltg1XZCSD8WAJ0AcEpdjQ8cLqrl84lc9UHmemftfYRQTzRVpCQALSmgMydDXAGgBWUZ5igHr+3fUjYvXLEwotF7cuv9xaZAgTGaa4znEAD6UKURXtkPlmAGgE5r8czXr2KBcxeApuMnWZaj0ajf7w8Gg7FY7MvScjmO8/l8XV1dFoulp6fH5XJ5vV58Z3+Vhslcm7HA2W0BOp8cMnD61B2Lh4ARoqs4oaJ0Hjp6QLYv8keQQTyMF1Ca7ODqf6N1p/lSCEw9LUR5HFxRe+utt+69997rrrtuwoQJKO6cn59fUlIyduzYhQsXPvPMM59++qndbqeWSavI4FpghMHnM2cyFjhrLICdHB8C+GTo7OycP3/+qFGjLrzwwrFjx77++utpFDP1jXP62QGnaTjLlKMx4pgpGO1jE4RMxIMYZMMpt0sEgyZOakBIgMADxGSIiBASIMIDJ0AiQSZBiutBTgaOBBCAxqnmwJoPnBwqvw0VbeBFmW8n2wLYdSVJ4nk+Eom0t7e/8847jzzyyJIlS2bMmKHT6SgMnZeXV1ZWNnXq1Nra2p/97GdPPvnkBx98YLPZ6NuTVw5EpfE9iz+lLZSqbxZ67cmu9pmTn/o+Op7w8DUb/HDD+Aguf/rpp8uWLZswYYJGo9HpdDU1NTt27GBZVv24wxSGzyXz6zdnAfXtY7VaTSYTwzBXXXXVhRdeWF1dvXz58q6uLvXI9myGock7CeCD9gNldRyjj+UYgoUmR4kRfvt3sMc4Nk7h43QAenDzoJy0ABBm5QgLRLlBJmoFSDgFIosRbXjUWaiPZBH6c19WfW9OvavYeGjSQlj1D0JrDRP9DlIeyixVciE0W8UFIklKOSSWI77vHAL8edtb3205+pvVECUlVVi3So4uHu59q7vM4M0z+platrDZOmYRtAM883Fb9SIHc2OYqQtU3XLwut+Ah7CpY0rOcSmpVzxgx5OkYNxW2ap/wF2xMMbUSTlN7kLTtnFmaJMhomx0wjKrEF61eeQEEM91v/iLraK5V0sY2QIyst9pJ/i1AkCrQdtkHRVLRIUUPq1OUR0mEhz8B+ONPUXGPsYQyyIAd0RDlKbF0sWHC27cf9UysCrVU181VFjtWpmGQZJAgNCqje0jDJDTyDK1sTyTt9QMd/6F0LeHPcjoSCYDHmLWEMAblo/z5kYLmiTGBHkt9hLzvitvh9YI9JE7Ukkp5WQD1xPiABv3W6oXyZoWjjEGCsyHq5tg01HST4YCoAkdKiLDzsCO8xc6iw1CjonVGDrLDfCHd0nvSvVgfAWQHhVXaO+igj4HBGhj945v7C0yRTX6UJGZCG7c/7GrmDCg4zlGf6HxYJUZXm0jFVEO+ipJfj/+f3Rd4Rgd5vhTysQ8CyyQAaDJ6lM4HHa5XB6Px+/34wrwcTatJEnopwUFoG02m9vtRsm840whEy1jgXPTAjgUpjAoDZxuUxScANNJFAawycSEiB6WUmMI8jDByTOFZWm9BrcynVoGa+HWAAAgAElEQVTTOCeh7pgpLTCtCMp9dnV1vfvuu7fddtukSZMKCwtzc3Ozs7Nzc3NLS0vHjh173XXXPffccz6fD70R0jpisdP+DlnftHwHx8mcyVjgjLYA3gW4FoXr0JIkrV+/fvz48eedd96YMWOuueYadBFB5/bqG+e0rDvOoqRAqI/QwmQ46kqgfx0OEjyIHEjKJ8ETkFnglQ8LCRakmExc9cRExe0N2UdMsMok8YYA0Io/dzonSc74k9KK6ZOcDAB9ijrHFz60EYCm/ZnjOI/Hs3fv3k2bNj344INz5szRaDS5ubkIRmcpR1lZ2cSJE2fMmLFkyZJVq1ahYDS+W+PxOBJB8FUVj8dZllVvGjjt75dT1E5DZUtvouMMDJXGgHNiQmRZNh5XqJoA6Is4EAi89tpr3//+97GJi4uLly1b5vF4sOHo2IlyaQekmPlyEi2gvndYlrXb7TfccENVVVVtbe2UKVPKysqWL19OOVjoUpLe1+rx3kks8jeWFScCK4uvbD08wiAoALSvwNBRpoenPwE3GderbfUFhUCyK9UmUMA18thE0QMA8MqS/lG/tj6u0J/7suqP5tdbL/gBvOcEt6gA1qjDrOLqIiCZQJGE1HlZQYSDAI+889Fk867y2venNSIrltC1Ecr0A/zohZ4ifTcz28Us6CtZCJeugE9g6+SWrkKzULwkxOg7qlrguY8I5C0kAWhOHgBAI5+aEIdZgKPQ+7Pnjla09DG1iWyzJ0d/cFQDvH0EwgRjJRCzyi1euqEkAD/EG//gLm2KaAj6nGCMbeVG+NxPBDR4go1SaWvqIbDfG2F6cgO/RwH2cVtHG47mGfoYfTTbGM0mjO94llEsXLinuBaefJcYJyVxPPDiAd8o6KwOgCgBB31Pb+wuM4CmMc7UR/JNR0c0wrK/QO+Ay4f8EhVIyxIbdiRE01OWnLo+Rg95i2L5TQeqzPLTm8AvkYV40moDH8+iIq2y5tPuEU0y0xhjDD5d054xDbD5KEHthwKgieKrX4C3utvGNvXmG/gsot3cWmGAzR0QVWSblevQfyDJkSi5yCRbFsDCd9esCFQvijALokzd0YomWLYWPmJtpUZWSz6+ImNrdcMwAHQK3x7SDANP0sFeBoAeaJhz81sGgCZP7WAwiPLNDofD6/XSFWDsE8nH+lAdhOd5VH+2Wq12u91ms3m9XjWjcKiLMucyFshYIInV4qAWiben7QAX4SSe5xFuRmEKjuNwz6mYEHF6jI0qSRJWJ64cMeWgIpioACuoDqz1yaw77qFG0QyUHurq6nrjjTeWL19+0UUXoVMprVabn5+v0+nOO++8WbNmPfnkk/v376cTEqpjqx6jp4UzXTxjgXPQAngX0Js6Ho+jj+I777yzsLDwggsuGDly5L333ovr3Oq7Hi88LS2GADSZjgX88PEH3IbXOj7fe8TfF0wAmTzxchKAVvBoIQ5CHDgW4izE4hCOQ5CDMA/RBMQSMp+QeYUlTSU7lK2sZDaCuRAH7ZLCrBpIBUvN0U5LA2UKRdpPktTKS7g6G4vFIpGI0+n8y5//8otf/OLKK6+cOHFicXExIpUMwxQXF1dWVo4fP/6KK65Yvnz5hg0btm3b5vP5qA8VuopD7yn1iyZj+eO3wECQIw3zSH4dPrW0xXhZlnmeb21tve2220aOHMkwTF5e3sUXX7xq1apgkGzWVi+xZ1pteNuenF/VrYCrCK2trddcc01VVdWSJUumTJlSXV39/PPPu91u9KObhj6fVUsIvARBMfLkW4dHELQulmNwFxr2ltbCunbwS6JANvEQX3AIDw7CywaAbshA5pQL0GMgSutSANojw42P9mURAWhg6gWm3lJcDw9tJA4AFZpvVKHJole/pDtBfCXyilwv2Swkk0lEXBFlvm+D7fwftGnmWksMrvn3Ei0LMiIHIukLRBnDf/3drrx6KzPHm13nL2qA/1gJt647lF/Xw9T6NEZ7oTkw53dgVXwPcgSDlkSFrosMbAWJ7i8DB4Tt+8R7R3TGPqYmzuh9WXXWkU1w79sQJujlMQFoumAcgSOXLestaohpiFNEiTEdGmkCuyJlrchXq1WtleIQKJw8j/okAtFaBejhUaU6/R6JAOziPq8w9GoMcUYfyjEGtQR9FhhjlKnbV22G7uQ6GShVI8ke41DjzjRMRjwscE9utJQSAJpj9OECk72iEf7vX5JSGINTw4esUvy4KBJ03wXSb17rqGrpVarfx+i7mLmc8XHoUMjMRE6FdrLUEzpBcOHow29268wJxtzHGNylTZ+Na4D3jxLfj2icAf1POeni4elP7aXGqNaQYEiX3l1tAKey+J+C4LGfKog/0vMBusLhxU+26mr7ihqhdLGNmdN9/q3wmRe2ebtGGBPZBID2DAtA47htGNsqhcv8yVhgCAtkAGgySAqHww6Hw6IcCCLj+icaLG3gS60oJsRgMGiz2bq7u63K4XQ6M+4HqX0ygYwFhrQATktwfoJgaCwWC4fDyJcZZr1nyNS+lpM4sB4+Kbfb/Y9//GP16tV33XXXihUrduzYga6ZXC7X/v37t2zZsmHDhpdeemnlypUPP/zwvffeuyJ13H///Y888sgzzzzz8ssvb9q06cCBA8FgMBwOoxQmfbx8vYN7auQhK8WyrNPp3L179zPPPNPY2Dht2rTCwkKGYTQaTVZWVmFh4fnnn3/LLbesXLly27ZtHo+HCl7jBAbhBlpgPJn2d8h8MyczFji7LYB3gfqmJlPCSGTz5s0XX3zx2LFjJ0yYUFFRsXfvXtSJpjHVt89pZiJFbEMGjoM33jg6+4bVl8z8L33j77fvs4sAfWKclyUFg06wkFDQZwJAcxDjIBqHXg58HPgSEEwQDDqekBOoFq1IcIhk7ks+inK8FJWIb0MhCUUrc+oEpLQlU1O708w4meKQITQSY+lrQo1Eo5MVnuej0ajD4di2bdvq1auXLVs2d+7csWPHUiQ6X/FqW1hYOGXKlJqamrvuumv16tWffPJJOBxGzasz4U75xjuD+imB4cFZquOof03BG0NDz8PfXjRNmiDLsoFA4Pe///0VV1wxSjmqqqrmzp27YcOGQCDAsiyOcIYcKtBEMoGTbAHajjjtRS8F27dvv+6665AH/e1vf3vs2LGPPfaY3+9Xy3an3X0nudhfe3ZkliEA9Are+145NJKgzwhA7xxRC5tdBF6U5LjCQyVZK1RRJAXTm64fABQUNWQfwKFwx+9ebnvwZbCECWCqls7wyFD3aCQFQItMfXtJPfzxHwTdjvIxLh5RgGV0XcgrehokfdRxIORkBYYOCkQD4bcbWqcuduXVO5i5XRUmYdlLRAoDEVai6kso0t3fWerX1ofzzNGiZkdWLcx5JlzS4s66UdTdHK289cDoFnj6Y6KMHFc+HAGRE4rUB5FkUALokDCZbAzg9T2thTdGmPksUxdi6nqLm6B5FUkBweOYYoGoIqmhvLAJrEofKFH4fFJLtKApmp2U4Ng/0ghHFYkKJY6glALdGQrY0kTMBGCvr/OHj22e3vTh7DsI8xdFSFJSJCRiBGAnt2+EIagx8IwexTc4huTSV9wSnPPbJF9YWUTod7E4VGeioLM6QIwSAz4FQAuMvi/f5ClrJBIcKQY0VrQ/STUZXADo4eDlPR8Wz3Xkm+LaJihY1Jtn2l1tgk12IEotRKpFuXbgs5nol0Hvr9dYikwJxhzLMrrKmrZ9qwm2HE06qKS27c8Y4CgP97xztIj0ZASgd40ywFE+uaGBjKpIjgjxk3xxaeHJ9w6W14dy9H1Z9b48/cEqI6zdC4447HS2VRjF7KQER9fIBvhzvwSHOltc+0hKkKuaPS1O5mvGAoMtcO4C0Ih/4V+WZb1eLzoS7OzstFqtbrcbB75IcqRvXwpUCYIQDoedTmdPT4/FYkEM2u/3q5HrwebOnMlY4By3gHoEjAyaSCQSDAY9Ho/L5QoGg3QD4Mk0FBI9aI6SJNFihMPht95665577pk9e/bEiRNxK7FGo7n44otNJlNzc/Ps2bMvvvjiadOmVVVVlZSU5Ofn5+bmFhYW6nS6/Px8dMek1WqLi4srKiomTpw4ffr0a6+99tZbb121atXevXsp1QsBKVqGrxhAPpoazQ+FiIIXx3Gtra1PPfXUlVdeiX7qGYbRarUMw1RUVJSVlV1//fWvvPKK3W4Ph8MUVlA/ANXhtNYc/PUr1iJzecYCZ5wF0u4CeoM///zzxcXFl1xyCcMwer3e5XKp+WXqq06zKicBaK8fFi55pWjMg7oJKyvP+939j+1BjcaEJCUkiYcEMqBRgkP5G+ch+VGgZ16JKJGHEkGcFT/yIpmoy6IkCiwnBAQ5mgAR54oc2ScqJxQxTVkiE+MUFH2amSdTHIX+zPM84s7qnqwO0xcHccskCG63e/v27W+//faPf/zj8ePHazQahmGys7M1Gk1eXp5Wqy0pKZk2bdrll1/+4x//+MUXX3Q4HCgojBtx6G2FECe+PdXvu7OsWdSWHBymAAaKz+ItmZCIgyv6oXGGCQxpNMxObXCO47Zs2dLY2FhVVVVeXv7/s/cd8FFUa/tns9ndbLLpvUNIkKpe4KLc+1mvBS8lIdmWAhHbFfUWyx+9+nkRr9jw2lBRmopd8VqwgIiCUqWFUEJIsqSSnm3Z3ZnZmX3/3zlndzIpYBCkyMxvfrtnZs+c8pyZnXOe857npV2ImTNn7tixA4guhzQd2u7SMkt/lcNnEAFKQDMMs2XLlj/84Q85OTkGgyEhISE2NvbZZ58Vx8h0xds58rYaNJwcQDvb+fgHFXF+qYHWMOOuBD18VUftTCm5Su2gPX5yFTOG9E8Gc3kMA24WmwHXADy46mBa8U9hUzemFghPfIKZYvExA2zQ6jU926LKZ4kFNIsKDkcUwNNfYhVmsnkA5+nxSznjS/HmA8HmwRRlNzGUPgJw14qy6PwqrK1xfYM679vUfDjoBo+PBeq10IeFgMtth9JLbMF6pxpr+NK9DeV1ofxmNOVoYunRooVYGZkhIgyU7faSFy19w5JPKovh5ywBoMJZHmu0YwtoA4OwK8JDMSbY1gFtPGaKaxmcoIWwxt34Nc0CeVlTw1srbIqd4Q4tcQZhjWZnkHFXghF2NfEebDXrJTiRuoKbIfwzB9DIwif7f8ouORSlPxpu3Jph8m2qELw4OZ7jMCB0twFs8+yN0ncE6d0o34MMHmTgkcEeZKiINMCLG/32wiQL2oK4RuLlfhtt2k4Y7wD77G86XLhugFV7KiILOKQXkMkbZO7WFNb97m/QTFuIoEgt5XHh8EwFZq05BhukdwK8vuVAnKEBTWlFuV5dqQ3l7wvJhae+xEblAjjxnzPdxHuFBBiARr7K/ESDrtCHitzB5vqowk05M+EgdzwC2gNw9ztNkSa7Cps/M0GGsgQD1Nj9t6ubAaxJLfhz9ADU8a5bXt6pneKOnCmozA6UVxNrghfWQaUN17/GuTvOAGE38uqSJvTn1vBC+OdnIqGPC80GFgWITeivi/wlIzBYBM53Apr2ingvb7fbGxoaKJVcHdgaGxutVqto1iGC6vP5HA5HQ0NDbW1tXV1dbW2txWJpbGx0Op19TD/ES+SAjICMAH77k43KVng8HofD0d7e3tLSUl9fX1VV1dDQ4HA4pEOdXxs0qaUwteSiw+Pm5ub169c/9NBDl112WXZ2dlJS0vDhw7Ozs0eMGEFHXNReWKlUqlSquLi4iy666PrrrzeZTHfeeecDDzzw2GOPPfXUU88+++yiRYtefPHFhQsXzps375577ikuLr7qqqtGjRo1dOjQrKysESNGmEymZcuW7dmzp6sLeziWakyfTN0puU//kViWra+v/+6775555pnJkyfHxcVRWpyOGyktPn369EcffXTz5s20gfpkLV1LK/IIx7eAHjCdPsnKhzICvz0E6J3f51MQhIaGBrPZrNPpxo4dm5iY+Pnnn9O6n/UaqQIZGkNbOxTd/LEq5WVVxofh6Uv/9WStgwceSy/gYQ01ghbZZyIGjVWh6e71efFO4mIeWQDsXsnr3wUvz/MeVrC5vA4vYNloG0fc5PA8C9himlpmicO1394981uqUZ87v/8hrazP5/N4PHTuubGxcc2aNQ888MDUqVMnTJiQmJhI50TpdG9oaGhqauqYMWOmTp362GOPrV69eufOnY2NjVTHhmEYsddN31O/SRqawih9+dJwgF8mS/AxFeJjQPD4sDI7XZrA+gQ6i9Ob5Ojhx6TnB7wPpagKgnDgwIHly5ePHTuWOiWOjo5OSUm5++67W1tbBUFwu91SwTE6PdCnqzBgLvLJM4UAfXxWrVo1bty4rKys2267bfz48cOHD3/rrbeoTIfoIFTkoKUP9Zkq9snki4lIL7aAhmXfVcUaWaXobI1YgBICmOoVUBq6h76kuWInCGTrBPh4T/PkfzUlzWxA17LRpT/F5sHr27AshmgU6iO2uve+bdEVuBBW4XChgurwgvoZj2FDYBsuScCLIA74N+pmoZtwoEd98O2R6ivvq4gsaFMVMNoia4ixPE4PSzZCO7aP7iGgrT7YWF+ZXGQPKuhWY2LdE2xkVSaPutCpNrsiZpUlmOC/+zGT6AoYBlMHw5RGpEa5RJeZKjL7C2OFA6Nu61Qa3EFYRsOHTEfDTGWX3Q2vb4E1NczDH+wcdfNnqXmwrhJsWMIDa4nwBGHACh5lqcXOYJM9yOBQGLqRYU+sAXa3E30TzAbjjWolY2+NPrB44MVvfkjTW0Ly2NBil9a8P7sUyhpxhwEA09Aig2wD+MmzO0bfGowJaI6wzwIydAQbtiQZYFMH2IEnLeX1m3oTeMXLf5aAplrMH+7YHTaNVRiw/0Bk5hXmyvhCqCYyygRFZ4CAxvPoWHqFTCN0AqzYvDF2Opa2CJllQ/lH1fr92jy443Xc6GTq3oURGsgC2g1QBxXX/bNFiwnobpXZEmnakFMCBxjcahSunhuFnKH24HM/bIo02dSYffYiogGNpXQAW9DjCRMeullwC5jFruYP3/BgbXIJFz6zC91gU+Q3JZTAP96Ceh66feBiocq2UTfFjvQupalLobeGFnqnPQ01HDaxZ8g92c5j94bV3bCpSiT6/aLnUiv1QOnkbxmB/gjIBDR+k1LKqaOjo7GxsZ5sojV0ZWVlTU1NU1NTG9layNbc3NzY2EjZ5zqy1dbWdnR0nE7irH9bymdkBM4JBCg3arfb29vbm5ubqXh6TU1NdXU1ncU5/c8R7+U5jhMEoa2t7Ycffnjsscf0ev2YMWPCw8OpsuHQoUOvueaaiy66KDY2lpLO1JmSVquNi4vLycmZMGHCZWS76qqrrr/++mnTpuXl5RmNxqKiotLS0jvuuOOBBx6gmhyPPvro448/Pn/+/DvvvHPy5MnDhg2LiIi4/PLL582bt3PnTqfT2X/GizbriY6rKYwNDQ333nvvH//4x2HDhlGFDbrqOTw8PD09vaCg4M033ywrK+vq6hLHjVTGWhzVi2PIPqNf6SDkWOFz4oaUCykjcAoROM6z8NVXXw0fPjwtLW3EiBFXX311S0sLnSLqM7A/hYU5FUlRThhaOqDwlo+VqZiAViW9Mvffhzvc4PZ6sC0zXsOLjaC9wJGd9wLmjolNdA8NjSMQq0w/pYWNoL0+3it4WUFgGZ+rm2c9ADsPtu8+1OEFcPICgzWjeWx3JltAn4q2PA1pHOv+F89LyyCuKaSa0e3t7WVlZe+9+96CBQtMJtOIESMiIiKoQbRSqQwnW1JS0rhx40wm07333rt8+fI9e/b0eTP2OZRmd+6EpbQwDlPJGukr2G/mDJh+Eu003eBzgdANvBsEt987qEBXEhAaGhMRx9kHxEfEUxAEp9NpNBpTUlJSU1MTyXbppZcuW7astTVgzNkvCbHdxXT6RZFPnGEEKNH83rvvXXzxxWPHjp0+fXpOTk5KSsqyZcuonPexvICei21KnQXix8ApwLfVR6KMgLDagF1jtEQavLe9Bm2EFgxwfIFv0kY+YjjcDdDCwT47/O2NQ5kzKzXTu7RGt9JQF2ksm/4gNHBEHTnQpj6ALh8s2VQWp7cHFfCowB5UUBdagEWKX96ErX2lm8+vPIWZPgeAhYdDAP/76e6MkkPh+V1Rxd7IWdZQ076ofHj8K0xzs9goG5OynA9Thw6Aj3cfjDd2oTw/+0y4dXdokT2iuDm2GEpfoea3mI6keVFnC9JPAZPnAeNcUjgG7DNfqI0w2VUmVoF3m9pkiTYfiDNVxpprY4vbIoq3xea3P/cZtGKharxwSeS1W8Ay8vZ2lOtQYgtoLzJW6wywbCMuKktIavp/1A1Qz8FeN9z7TkV6yZGwgkY0zR5R3Dr0Frj7TWiVoCQyyHaAXZ4tCfqjakxAC8hI92at8eDEv0ETgB33L+hcA5WeEI7554er2dcCWgBwcFDp3huVD9qZoCgEZAZkbgw3w/9+jNMHcHPeHrkSAHe3Czo8eFLh/608GFfg1Jkh+ibQlHQqDRVx5r1TH4L9Nkoie7GvZXHr/ZfcjQnoHRfe2hJs5BAm7it1+m+zzLC3+3gEdLsAD3/eFKqnGtA+ZKiKNsDGWtzKLMnLyWHuuJqBlzZUZpUeUee2qQqcaiOnNleH5LbMfAbqfdAlgJPFptzdcGjYzS51YafGZNUVd2pM++JMsNqCa90EcKAb35YLv9ubVvJTTim38gdsCE+1YqjbTMlbRqykHJAR6IOATEDj3hEFhWEYq9VKjTGpUTNVhbZYLKKPwVqyUatnGhZ/tduJqHwfgOVDGQEZgYDhM33WqJkMne+hDxp9lOiCg9PPPjsc2LVwZWXlwoULp06dOmzYMJVKRVcEU642hGwIIa1WK57X6XQpKSnZ2dljyJZDNmolnZWVlZ6enpSU9H8rGSMiIrRarVqtVigU1GiaGlOPGjVq4sSJV1xxxbhx41JTU4OCgkJCQn73u98tWrSourp6QA6aDj4HfzdRu5WvvvqKVic+Pl6tVoeHh8fGxl599dWLFy+2WCwcx7ndbqfTKf4NUjNwyojRvH6x+bOY5uDLLMeUETjXEfAde2tra7v33nsRQjk5OUFBQfPmzaM6m6IR9FlZdz8B3dqJCWh1+mJVxoeK2BfumXeg1QHdnm5iyNyLgCaU8cAEtN+iGXzk38zPofE8y/hYt8AwAF0s/Gfx+tc/+MkpgIPzeXiGBw6zbzIBfVbeHP0Ldezbv+cXkUill9M3BXUIIXYAnE5nTU3Nhg0bHnroIeqlQKfTBQUF0alfqtcRGRmZnp5+zTXXzJs376uvvrJYLP3Lc5wzPQUioePEPO0/9aYkBiKgBaJoQ1fP0yXzxFrT5wbBRQhoJkBA0zjUIJo+cgG7aUxdSXM6TjUZhnE6nR0dHVOnTs3MzBwzZoxOp7vqqqv2798v6pVRz8biQjeamhTk46Qv/3QGEeA4zuFwsCy7Zs2axMTEMWPGmEym9PT0YcOGvfPOO7RBqV2C2Lhis57BYv+yrKmJKr7WLcDWRktSsU9hFBAWz23W6vcMLYG1VZhQs2PpDEwEe4nVp5vIZFgBax/vd7qfWLVumLE5vsQbPhNL6EaWNEeYfsougR8t4BDwJX5egVBxHSysqfwu09CsKWBRgV1laAzOrdXqt6WY4KO9OBc7SdxOpKDbAUtzNAMcAfjPhl2phXXRhY3KGUeD82zhRR2RReVx+vbSZ6GOuAskVrT4/5MlBHQ3wOsbymMKbCjPE0zMnwkBbQvWN0aZynJmweYObK9KLI7dbr8OsZ9vFjnoAE2Lq0BrYQN4af2m2BktoSYmyOQOMmHDWJTfrTI7kb4JTbaqjIeG3Mi8SWhloiTSw0G3QO3Ee6pJHI8Cc/1tGmPNDQ9DFY8J9FonHCUm0xYfvLFjR87Mg7q8xqDpVmVBhzK/Jspw4PK7odzRmw4PyGg4AcqZ71L0TWEmDzIICCfuRcb6MGN76fPYz2G3/wahXiUICyv9t5OGcUxCQPdQ1P66twMUv9wanC8EFwPCHLRdY94alQerKjGV7yQ3CdULtwNWD9/a3Gl48lB0fjO6HrQloClyhJgOhM7YMf52+MEC7R6fgFd3AUBHa5u/fD15kiIRAvqHdNNRlM8gfSeaURNh3JBhgt3O40lwNHvgyTWVunyb2iAgAyDD0TCDd+5b0ELEQGwADQJ8sNNa8qwls7Q7xAQIT5m0qPKPxJgaJz8M+6xkTYATWB6T443ujj/N646dXaOYXhuU24im1eqM38bnwyOrYdGPrr+9sWFI0cG4IqvKeDT5RvaFrzAOlIDmiGQ5Mbmm+AbqKH/LCPRF4LwmoPuCQZTpqCaAaJgpZaKpkSbV56ipqbFYLHV1dfX19S0tLV1dXXQOuX+a8hkZgfMcAdpVpWNOlmVdLldXVxed6aHPUX19fVNTU1dX14DE66lFjxaDkqoA0NLS8sUXX/z1r38dO3ZsVFQUQkihUIgsMw1ERUWNGTMmNzf3ySefXL169Taybd++fceOHTt37ty1a9eePXvKy8v37dtXXl5eVla2m2y7yLZ9+/bvv//+s88+W7ly5eLFi5966qm5c+cWFRVde+21EydOHDNmTGZmZmxsrFqtDgpsV1111TvvvGOxWHAHkWzUOkyUuRxk17+iomLhwoV5eXlJSUlRUVEjR47Mn5G/cOHC7777rra2VhxIUEBEG0wRHzGXkwmc2raTU5MROKcRcDqdZWVlY8eOTUhISE1NTUpKWrt2LR4Ik0mgs7VqmIAGgDYblP71q5Ahr6GYFeFZr9987/bGLnCzbjxu8WIlDuJgkOOBowQ0MYLGptB9duqEkMThvD7W62OJrbTgAehkYc0PzgmXPfCfxdusHDg5bGHN45ENQ30Vnq0QyeU6AQTEOU76ZqFXSt8y9B0kfno8nvr6+q1bty5evPiWW2659NJLs7KydDqd6MBQpVJFRQWXZSAAACAASURBVEWlp6ePHDnSaDQuWLDg888/r6qqam9v5728z+ejPvFoRjTZ/pmKBTiBmvzSqH30ssVkMDI8y3IezsvwPNZMpz/Rk2I0EsDMkHTiio72Rd1njucZjmU4lvVyHM/TT/GQ4zHLIKWh/XaUvfOQHtFZ6urq6jlz5lx00UU5OTn33HOPxWKh8/dUCEXsRYhg9glIE5TDZxUCdGGi2+1evHjx6NGjL7vssltuuSUnJ2fEiBGrV69mGIb6ERX7jWdV4U+gMIQaY6mFr9cHFdauy//J6ErcKJ9VGpvR9IYY8+b4PHh1G+z3YD7RDtDGQrUNG37u88Cbu+GulT8l6euG3WwJzXegXFAWOZT66vCCHWNugm9qMGHde2PsTmx5aoPGOYsORen5iFketakdTWtC0yzBeUeG3Aw3LYX398OGZthkgzXN8EEtzP+WnfKkJeuWo3Ezj6ApQuRsIay0U2moDzPuGzoTHv4AmgVMc7sEYP1PGLaAdvnACS0L3tsblW9DeW6lwa3EagxupaFTkbcjfJqw6GtsnCsxJu7FfIqWxVLq3AdOlwc6PVDN/jdLXxE6w6bQsyElVpTnU5c4MM1t7tbNrIs0H77sPjjC4cQDds14aovHlLp11guHww2dGmw6DQhT2K2JN8KMZ+G5jfBNK2x0wL/XNP5xbmXKTGvS7BZFbjua6lQZOsPNu9LNsK0Z9z5YH/iwfmMvaImUxOqM/KboYm+QGQgBzSFjVYQR/vMVtPgobS3SzOTagNB1r5oTalpitNuLObUBvL7jcFqJXVfiQ2ZQlEDsHe0hptbRf4XXy7H49VHCO1ew8Ek1mF6sijHXqnI7UC4brAdtEacxNsSYt1x8K3x3BBPPPLYN53gfkbLAzjNI+2E/GD35d+O5h+8TZhxFeQzK70C5TZGFWxMN8FkVNhsnTHnP9AY5YXe7cDdsH7MtxdAUqmcVmIB2Kw1VCWYwPQ/3fADFixouvaf2gltrY822MDOL8iG4BMJnHwrLq7/xGTjCQAcDbv+9i986DoC7366MMDREmDvCCm3BRofS2KkyNmuNe9B1jXGldeGmhlBjq9a0NWYGfFaGG50jzc0SY3wJ2U8KKH/ICAyAgExADwAKAHg8ntbW1tra2oAcdHVVVdXhwFZBturq6qamJqvVSl2jDJyQfFZG4LxHgA75qMyFw+FobW2lCjZ09UB9fX1zc7PNZhPZZ3HQcjLI9emsiDqGHMdR9cmysrLnn39++vTp2dnZ6enpV1xxxaRJk9LT06mdMkJIrVaPGzfu73//+9tvv717924pI0xrRMt5rELSX2mtWZb1eDwMw3g8HrvdTsn3AwcObNiwYcWKFQsWLLj99tsnT548dOhQkfI2m81LliwpLy+nSyA5stEBXp+qHasAixYtio+Pj42NLSgoeOWVV9auXUtlpsX4ommzOI4Vx/xiE5xkQMxLDsgIyAiwLMswzMqVK9PT03NycjQazdy5c1tbW91ut2hFePahJFACutMJc+Z+jwno5He06UvyZ39dj4UcvUTNeQACmsUqHAOzzz5MUuOdsM8sA14XGX412OD2e1an59zz4muVDha6veDi3Dy2EOsm1py9dCnPPqDkEg0WAelrhV4jPSO+hqQ9B8p/tbe3V1dXf//99y+99NKdd9552WWXJSYmkhVKISqVKjQ0NC0tLSQkJD4+/g9/+ENRUdHDDz/8/vvvWywWp9MpTZYSapSe7qNQPMjX689WtReL0Tu2+B6nBeC9vMvloosh8DyOj+d5lvMyLOfBKujk2QqQ0T7KU+BFA4QTFNET06TEtMfjcblcLsbjZhnKRFPSmaq8YhqEGlD3pqF7F7PXEcdx27Zt+z+XFWlpaePGjVu+fLnI71NScjC9iF4pygdnHwJ0tuall17KzMwcOXLkrFmzhg0bNmbMmPfefc/lcrndbnqXnn0FH3SJAgQ0JtsEHzR54J8fVEUbmtAUXlvsDjF3aQyu+NkHdXnbc0pqi57gHv/Y99wX9vtWNBgWlI+8qTymoCnS1IimOdVGj9qEvbeFmCpjja3TH4XNLVBjAw/XjdnF3puThS4e/rtrR4a5UZPvUOodKNeJ8hlNcUeQ3pp08ybdtE3Jht3J5v0xxqoIc0OouUWl70T5HoWRRQYhqPAomlITYdySboYnPoMmH7jwnxmWVmAELJjAE7NTtw/cUP7353fppllRrkhA21WGI+rcyj/8A4v2skIv7lJkZ6kKs8hB40faz4iyXh5zi+28b+n330RPa46fdVRjOIpyXSHFzWh6rWpGRRxhn7+2YJ+EbmKXTWhev9PgboD39+7OKGnV+vWjvcjoUBjaQ82VseaDKSWVSSVHYgqbwkxtKkMHmo7VQnRFlkjDT5lm+GgfZkKxaTZxXExeEj3IugHqYeOlt1uizVxwoUhAH4gxwqflmGonvhB7/odx7U6AgMbOl30CrtERrrXwqX3KKUyQCRTFDMr1BRcfRXnVqbMar3zQMee1rVf+/dss8+Ehs+0RMx0oD5dEaea1hfbIQku0vmrSP2BrOxzuBAfLcF6B8/mwzbdAJtXpe68fAV0L24aXNqjyPUhvR3mdYYX7IvWw6EdcKdouval41kuo/8PO8ukPVkTrHUq9Dxl8CqNbV+yIL22LKW4I07eEGmxhZkZb5Ak28pqiTrV+j+oGLDhTj2ckuC4HCLjFqKII7nMt2/JjTN7hkBndupnOICNH+H1cteBSDzIzEaXNsTO3Rc+Aef/FKVDzeWxq7reApjy5n9rvaTM5JCPQg4BMQPdgQUPYoY6Xp8sAfT6f0+lsbW2tr6+vI84Ga8lGbZ9bWlroqqW+ScjHMgIyAhLZDfpAcRxHn6a6ujqqsV5TU1NXV0fZZ1FxmL6Q6efJoCiu5KWJiAl2dXXt27fvoYceuvLKKyMiItLS0qZMmfLII4+UlJSMGzcuOjparVZHR0cbDIaPPvpo8+bNlB4S3YXTukiHsqKKpZgRHYlRg2Xxz0T8lZ4XCWV6nmVZi8Xy9ddfv/zyy7Nnz46NjUUI6XS6iRMnzps3b8+ePaJAM40v/TwWYvv371+6dGlzc7Pb7aZGZ8e6ilZHms6pCktzlMMyAuc5AlRovrW11Ww2h4aGXn755eHh4R9++OFxnu4zjxge6uA1ozY33P/YLk3Gq6HD/qtMfOnSySssbcBjApooQAvYzSCllSm/PBABjUlnSnwR6tnjBQ8LrAtYB7G5eedzy6gJC2KT71u0uKHbg2UqXVw3j9edOgBLC8gE9Jm/HU5JCaTvF5qg9EyfMI3AcRwlv6hSh9PptNls9fX1W7ZsWbBgwVVXXUWdA4eHh0dGRkZHR8fHxwcFBVHl6MzMzLy8vOXLl5eXl7e1iQufeyyI+7wBT7KOlPIQh+R9UqNdHVoLuiBMfPwFQeC8DMO4GbabYbtZzsV53Tzv4bxuu6Oz6Wid5Ug13SsrK3bu3Lnxxx+++Xbdl2u+XrN+3eaftlVaqptaW452tbdYO6zdjk67raWzvcNmdXtZWhjskJAwziL73McOuk9RxUOWZSsqKiZNmhQVFVVQUECdFbMsa7fbMcvNMLRX05/KH7ApxWTlwFmIAEO2J598kvrLveOOO9LS0saPH//RRx/ZbDaxoy4tudjK0pNnbZga5lKLU/xu2WPbceHN1eEFVpXepTE5Ub4n2OgOMdeiyQ3qvKZI09GYotaoogZ1XgOa1qEq6EJ5vrCZ3iBjt9pYFTxta7IeXlyDSeEOLBolMre9qu/hwcFCK7B3Lj0Ya2hR5nkUejfSs6pCR2hxoyKvO3Z2R1hhm8bYrja2BenbUEEnyrcHYad/XHChQ2FoS7n5u7E3whcVmJB1YtKZpdLPAuH7OGJ26sHSvY2PvrU3Kt+hKBAJ6FatYVt8PnxaAc3Eh52UuxQZ5z4BsRpUjoMj1sQOEF5Ys3nszVXppQ2xJZZoc1XyzC2pJnjoQ+yergsbKWPBZSJAQllxfGz3wp6O9WNKm3VmHzKzSjOrKvSqih1KY0uIsS2iuDOssFNlbEMz2lBeM5paq8nbHjl92//cCbuaMQ1KiUxOwCpEZCOnyAeDtUoqSp48oMtnlWbATgKxkfXeeBOUddFrfVI5EUyynwABzQcESKDZDpsbtkTntaEZoL0RgkrcKI/RljRFF5eFTMcq2PElDdHFjSGGTpURwmdDcDFoZzUpp5XF57fOWgjbW6GZA2vA8txL7KCxzbN/p/r+PRbQLkysl11xT63OyCpMHDK4FMZ6dT7cuRKb5A9EQOOTXgA77357w0/DZzaF6pkgLMThUOpblHmtWoMjZmZ3ZIldY+xWFFiVBUfCCramGe2PfQBHnGAliiA4BbzihqEuEjmsQ/3juFuPhBs70XSPAhPQVOQEUBFoZ7dpjLuTzfDCWiwX4yZm7xQvAU8ViOyzTED33K5yqB8CMgHdD5KBTlCTSafTSe0UxP7WQHHlczICMgIYAbFXStlbu91O53KolI3FYmloaGhra3M4HGKnVrykb1dj0IhSi2NqBNTnIrvdXlZWtmDBgkmTJmk0mqysLOowcNKkSWPHjs3Kyho7dmz+jPwnn3xy27Zt1dXVdG0p9VB6QvaJtPDiYEwshlg7PM7kOJZlKSElWiLTYXBdXd3GjRuNRmNCQgJCKCkpafz48Xfcccc333zTX+NSzKU/YuJcGiXE+xh2iYURc5eeOVVhse5yQEbgfEaAzgDRBxwANmzYMHTo0IiICDrXdRwXXmcYNP+4FHtrtzMw//k96owXIkd+jqJfzp6wqPIoXsiKCWgiF0AJaDIUxiocLBmYdBMlRjfhsL3AcYKHENACFt8Ajxc7XPc4wdsFUNEGM255O330fxKGPL7olSaXG6+7dXMOH9h82PLHDdiyTB7RnOE74pRkL32/0ASlZ/qEaQSqQyXmjmlat5tl8RJ0lmWtVuv+/fvff//9OXPmXHvttTk5OREREeHh4QkJCdHR0UqlMjo6Oi4uLiMjY9KkSffee++qVasOHDjQ2toqvv7om1R8QsWMfkGAMlxUl5muS+6TiNPp3LNnz7tvvf36suXbN22pPHDw+/Xfffj+ByuWLnvmmafnzXv4vvvvuXfuP+6d+4+5D973wEP/7965/zAV6S8aPzY6Ljo0PDQkTKMKUSnUeEfBQXgPQnhXKlQ6bWJG2ugJv/vTlMlTC/KmF+TPLJ314IMPvrzopW++XlNz6DDn8jBuj9j3wJ2EAA9CvJL1Kan/0Ofz1dbW/vWvf3300Ufr6uoAgGEY2qOg7eLxeMTOTJ/mkx4OnLp89mxCgKqpdHR0PPTQQ1FRUddee+2dd94ZHx9/+eWXr1mzxuUiJKakwOdi+4pPKLHtBXhzy9Y0Y124AVLmcMEmCC5i0XTAQrp5PmzQWuBA1/OoAIKL+GCTPajAFl7UnXrLzojpnQVPwCf7seUvZWwxeYffUL3eUjzhZVkeS0lU85XXPbA/Vt8Som9Bf3YifbsivxlNg/g7vchkR7meYLMVFdiQ0RZs7NSYumJLqyKMe+NN7psXQx2ZpHUJwOFnlrgeJe4HveSV6/VhqaouFtYd/Cm75GhccZPO0KQz1IUbdiUZmIffA4sb7HhuQdJ0JNiHeqaHIgFNym61O3FUBuAoDzu64KUf4bE18J8N8OpW2OOBShdwIHB++1lRhIP3gcPDYIRtAO/u2pto7tCarSFme5ChG81gkQET62h6G5rWiWbYNWZr5MyDmmm7kgzOv7wCFVhToscRIm4wvxF0T/lZgA5o/H/Ld2mmsUqzD5kEhN0klmWVwiE7JmSlFtB+3vZECGhiLO/PzgbwxFfVGTceCc7rQHkuZOhCeVzyX9rDi+26EldIsR1rYd9Qg67hE2/r0hqbYou2JM+ARz+CRsHPzwLweB6QMMVe4lY2wEH3JaAZgBZfuX7+kZhCLriQV5gdKL8+eIYj/2lMQNOmIe3iL1vg3sOHrUyF6dGyOH2bRu9WGrASSwi2erYF69uV+c2agvrQgvKYgkN//Ad8XI7tClgB60HRqQOSHOWgcRCbru/+MSq3Ua23qrAEhy3YaFUZ2zTmxrjSHSlmeGcvNJNLA/obPuy+8gT8CvSUXw6dlwjIBPR52exypWUEfmUEaK+UDudYlu3q6mpqaqqrqxPZ5+bmZofDwTCM1FS5D0n6C8rIcRztY1FSW6R6Dx48+MQTT1xyySURERFDyXbRRRelpKQkJCRcfPHFt95669KlS9evX19VVSXqVEg71jT8C8pzopfQ8TDHcRaL5c0335wwYQJVutTpdFFRUXfcccemTZvEND0ePJKUllP8aZAB6bXS8CAvl6PJCMgIDAaBPjyX0+l85JFHEEKxsbFxcXGPP/44HkT0kTgcTLq/dpyeYRvYWHhqyY7w4QtR8orQjE+TRyzbfwSP8nwCC7zHJ2DJWso+g4/x+Xhrt7einv/vFs/K9Z1H3H4/9oyXLB4mgtGcz8n7Or3QzeGBJCxe7Uka/2pQyoshSY+/uLgac9gAnM8uQKcPusBHVqz+2vWV0z8LEJC+iY71UEjjiF0IQRDsdntTU9O2bdtWrFgxZ84carSLEIqKitKQLSUlRafThYeHDx06dPLkyffdd99nn31WX19Puw2/nID2EzfY+lnAtvrYmqzD2+0iUy888ByDzfmamxq++PLzO++ak5M1NDI0NCc17fejRv9+1Oic1LT4iIjI0NAQrVqlVSIVQsFIoUVBYQqFNgiFKFCIIihUGaRTK8JUSKPAEegejJCSRA5GimAcQGoF3jX4UxmsUCtQKEIRCP0uI+t3GVmzZ+jfXbrM0d7h6OwUvCyAz+G0YY1pvh8zFbgTxD6JuGyLKoeITUAj9pkLP1bDBVKVv89GBMS29ng8/7dgcc6cOZGRkVdcccVtt92m0+mys7PXrFnjdGI6UnR6JN4G51aLUw4aU8UMQLMPnluzKTG/Xp3nCtJb0Q2gLAJFEeGgDT5kcKN8J8rzoAJsUhpdtDO+YP8ND8CHO7H5p4OYfwYsbV2YKMWpihw0lqiiL3cBsHBzlbPz9pc3hE0+GlLgVOpdwVir16MwupDBE2z26kptatNRlGvXlbSl3LwuZnpN8VPw8U7oJOIIActSH1ZxwDvm/+g/j5hlGyc88/mX6XnfxE3dkK7/Ypgelm/E71cGl0ks1aBuPsJy+oHCRj1kStlBCGUr+aS+Ez3+lFkyRRxgIwMgCOSqVui4e+ne7Fm12vxWdIMX5fMo34NRzecjZtl1RUfDjQfjjfvHzYFXf4BaHzQzQDoAhHc+htmvl4D/+obD8SZPsJFTm9uV+dUhubbCZ+AoI3KqIjB+oPoQ7scBQkrycgBNPLz2/bqUvMa00u6IWS41Nty2hhZaQ8xWpcGBcu1oeosityJk+o6s4oabn4Ufa/HMhI3DFDzZsFAGhpFIphCDblq2Pp84vtVnXfBBRaSBCTJ1olxP4s0HwnJrcx+huiL+5MSvwJyBv7yH3EcNj1fGm1qUeUyQgUG5XpTHB5vq0A1Hkku2ji6FV9ZjF5eOwB1FDLL9iZH7wz/P7/FBgwcWrv4hw1AemtegM1VFmbZG5W0dc7P74Q9gZzu00hYiUjbE8BmbWZDbpAdzsZByQEagHwIyAd0PEvmEjICMwEkjQHul1AjX7XY3NzdbAltdXV1jY6PNZutvVnyqurB0fSuthNPp/Pzzz6+++urIyEiFQkEdFoWGhmq12nHjxv3rX//67rvvampqxEEs7SxKe9Vi+KRR+fkEOI6jihkA4HK5Vq1aNWnSJK1Wm5CQkJ2dHRsbO378+DfffJOuI6YYisX7BehJr5WGf76gcgwZARmBQSMgPlyUpgGAmpqaCRMmaDSa+Pj4MWPGlJWVSf+CBp3wrxxRMpju8sDrn1cmj39WkbYsJH11TNaK1d93Y+dAAguCqy8BLcChKuc9//p05LWLM6948X9f2VbRBk4vsJzLx2PVDsHn8YLTw7W22Zo7AKq74ZqbftRe8E5I1kfqpKeffnan3UoUGLHIZTu2gPZxJzh6/pWRkZP/1RAQHxYaOKF8qIAA5dGcTmdXV9euXbtefPHFadOmpaenazSakJAQrVZLJ6EVCkVQUFBqampubq64uugXctC9CWhCD4EDvDbwubADz44aS9Ubbyy/5pqrVSqlLjQkRKkMQigEoWi1JlqtCVcodcrgCI1GF6oO06p0KmVYkAJzyAiFBCGtUqFVKkKC8KEGIa0qWKMKDlIipCCGz0FIqcA7toRWBmhowkcHByEtYZ9jkCIGKcIRIaM1mtjIiMcefaSxqZ7zYt7ZxWCz1mNx0HT1BmWfRWExaRuJDSQ9+Qt6I2I6cuBMIUAfHFFErqGh4eabb46IiDAYDKWlpXQ1HrWBoAbvtJxiu5+pYp9YvgEKEi/f8fmAIw79jjDw1o5DE+48lGiuizTWB+c6Qs1Wlb5do2/WGauiDeUxBWWReZtiprtmPg9v7cA+CW2EwiO0H54rJUQ0pV97EXAkOx6rPxCqzilgNnnJpl0jZ1elzzwSZ66NMFhC9dWh+qooU03KrN0x+rLU4h0ZxW35T8K6erD4Z4b84rw+yvD51Rtosn5aGf/kAycP7YB99729DZZ+Dwed2GyW9dPBJ0ZAB5h0v1xJgP4Wv6XMKUWAFrJn2QftP/DEi0QjBy+v/XF48eG0kiNRxoZIoyXaWBFn3Jti2pRc0HLDPFiyFcpdUMeBlczaUSeCNA//RHhPOxMwSbRadkOmoSbKcFA7fXf49C1ZRfBRObh6OguUQO+BKND6fj66J8l+IZqpOJfg5KCFg60ttr+8fHD4LRVx5l3a6bvDcvdF6g9GGQ5H6csj8g5lz3bMfA6+rMQzEwQ1H4tJZ6yNLKYT4GrxsxZAWAxgG2ksPg1Q3rE+w1gZa96jnbotOnfTBSXw+UFslTzgRm5CrPEhAJY1rxbgmW82Z5r2xBbUp8xsTJlVk1LivO4ReO47OMxBq4D9VQ54KxApcOJVmmTDAL5Xv6mBV7fDgnXw1DpYvh2T1y0Adh82eye3PX2OCPssE9ADNo98cmAEZAJ6YFzkszICMgIngwDtyFIDZKvVWl9fb7FY6uvrm5qaWltbrVarx+M55UMUcaRE/RkyDHPw4MH77rtv7NixISEhGo0GIZSYmHjJJZfMmTPn/fffb2xstNvtLMuK1A/tSdMhqNirFgMnA8ggr5US0BS9ysrKKVOmREdHjxo1irpMzMrKmj9/flVVldPpFDWpxUKeclQHWXI5moyAjMBxEJA+oXShxvvvv5+ZmZmYmBgVFXXXXXedjUIcEgK63SV8X+4Zec1S1ZDlIemfhaW89vjzu7s5wBZeAqaVCbfO43GJj/Px8NWXDeMmLVQmP6O74LWxf1q4ywI2Bnie9QmsT/AImI62e9jOVqvjqAceX96kG7ZUnfFJ1LA1cUMWv/FGpcsBbtZNJCU7fYA95EhW5B4HZvmn8xcBsQMgsqVUOdputzc3N+/evfu9d9+bO3futGnTRo8eHRkZqVQq09LS4uLiRowY8fnnnzc0NFAfxX08NxwH0H5vW8wkCCDwRAjT7vPYgfly0/r5Cxf8/g8TEUKqEJVOF4oIdRylC4sJC9Mpg3XK4BhtaIw2NFKlDlcpoxVBKQgNRSgHBQ1HyhwUlI0U2UiRg4KHI3U2UqUjZSIhlCOQUqtUhigUYUihI+SyljDUagVmooODCFuNEP0pLDhYG6oJ0qkJq61EGkXSkNRb/3r7d5s3tNo6HJyLxfKtA2x9UBUVvcQ/tAGukU+dmwiI/XbaB6ZL8e64447MzMybbrrptttuS0pKuvjii9euXSs6zu3fWz6rq075R5Hwo2XleHAJmFBuB/h4l+fBt3dOnLN/9C3lOaW7LyjdfNFN26bdb/nnUvhsF1TZMdOMhaUEzBIGdIIpyymSsKIdKE6e5Oh/sgjBB3aimFzjgq8Peh9b1Tz72bbC/7QW/afxpufr/7bY8dxq+KIcE38tPqzaEbCf9adAkyb8oVgJGsBZsZxgc4GTxRc22bGVq8/PEYqRB9M6YuQ+AXptn5PiIS1aT939XDm5yEdIVSchND/ZZZv/nnPee+2Pvdfw5HsNr3wKZc0Y/GYPtDFYF4IBn4vhOVJzmjpttUDRezhlHsAO8MmuDX/669cXmHZddy+s3AjtWIXaSxl/Qsn2EOg0BSkHHUiz77ckR1oEHEEA6HBjVLe3wrIfWv/fCsutzx+57YWOB1YKi76G1eVwwIrpXSfg24nleY6j9u99EycpibiJAXr/4IbmiHDH1oYDd76w9n9uq73jRdhcj2tKdEX6p4ZbmaSJvxiAdgZaWGhkoMoBu5thTwvUc9gKvsGFY/aFo296PQS0i8UL33BqXnzPuwAHsNi0D3fmsItGnBhNT6yFGOibrnwsI9AbAZmA7o2HfCQjICNwKhAQLSkYhmltba0jW3Nzc3t7u9PppMIRpyKfXmmIWtJ0heC6deumTp2q0+kQQmq1Oj4+/sorr3zuuee2bNnS2tpKGXA6mqJ96D6f4vhKDPTK7Nc5oLhRK2y73U7FrA8ePDh79uyEhISJEyfef//91157bWRkpNlsbmpqonYo4hjg1ymUnKqMgIzAySIg/o1Q1Vqqmjpz5szw8PCQkJDRo0evXbtWzEOcEhPPnLEAHolh8512N3ugFX6ft1KdvUyd8Ykq8dWb//aVw0V+5D0+nqjJ+nyEfON8Xnj/7aYLRr0Ulv5BeM6quBHzv9+NRy6EgPb4BJeAnRM5WZ6xc7BpP1x0zZuatLd1GV9HD/ls+MXLNm/Cpj4M2w3gFvBwx43Hfj2SkGcMDDnjsxAB+mSJr2/ey7MsS/WpqK8F6rUFD9EFwWq1trS0bN++/f3333/ggQeuvfZa2kPIyMi4//77u7q66IQ0VZk4VmXFZ5lmKonmH30LIHR7utd+v+6iCRcnpSeHRGDSGSFMax1HAQAAIABJREFUCisQ0imD49QhsUp1nEIVgrCRcjpSDUWqHKQaiZQXI2W+IuEvuuwHh0x88sJrHht5Fd0XjLjq6RHX/G/ypbO12dNQwv8g3USkuwjpLkS6bISyEMpEKA2hRIRiiNVzBAkkkvNDEbpQGZmOVFFIGRkSEhyEQrRqhFBkTMTw0Rfcdd/fd+7b3UNhkPpQNU+xIydy+jIBLWnu31qwDwFNZdarq6uLiori4uKMRqNerw8PD7/kkks2bdrUR7Wm/4rGsxQdcVZV8AkCng7FXjq95O1CjU+7ABoBjgBUAdQANnbuIuwb0SbgeB5rKRBPa7iCAe6PPvkiCUsP/RFIHBrT/4lJRkJkt/swOXiYhWovztRGdqp3wQPLeqmCdA+SAWJUpPnEAE7S4zeXpjIpwOFKuTttICGse5I6dkhM82QCItfJE/LZLWAv9Njpg5OHLgE7LbT7sENFN1YOPuYWqK80ApbAJv5UMb3rETAx2uqDOh8GsJUBF57+owQ0Lb/IkPoToWkOlLI0F2lYALC78TIRryAAK0A7C00sttSu6YY6Bpq9YMWdFJEgpi8IaQpi+DiQUgIaT2r4fODhMCwdPiz90UZuleOgJKZO7zQAnmGB4cAbOBYjSLhvybleQVpCjvfn53Fh8Sgfw2Ov0AIITr83RYHHM5biZED/evVKVD6QEeiHgExA94NEPiEjICNwKhCghjPUQVAb2Ww2m8vl+pXYZ8rV0mFnY2PjI488MnToUIRQSEhIRETElVde+dZbb5WVlYk1E8eQJxoQU/hVA6JPJOrwZ+vWrUVFRUlJSVdfffUbb7xhMplSUlJuuumm6upqWgxxaf+vWio5cRkBGYGTR0Dkxfbt2zdixIi4uLjo6OgbbrjBarVS2aLjDGBOPvcTSYEuHsXeahxe5ogdrpz5YcgFSzRDVqkSl/xp6pudXSCwAF4v1aQkxjA+7JCIg7eWdwwbtkKd8Kk24/OUMS+s3YoHhniIJrhAcAk+D0t46E4PzF9UkzBiKYp+Nybr2/DUJXfcu73Tig2reYEo6FL1ZzqyP5Giy3HPHwSkL/F+pPAxYXC73U1NTYcPH37llVfMZvPDDz/c1dUlzun2s272p0PzormITo/FPNzu7qajDWu++vLS8eNC1SrKOwchpFUqQxFKUIXEIBSLUCpSjlToRiLNOBR2OYqcgmJvRGn/jpn4wdj8NReb1o8xbhxl3DhKT3YaNm4aYdyZbd41zLw9x/zDSPMPv7/p0zHGpRnXLYz/471Bw+egoYUoeQqKvRSFXoxCR5D9YhR2KVL9QzPi09+XrL/y9ufTr75JM2yqNj0bqRKRIgrz1MoQpRIhlJ4zZNUXn9idPR6hRUIf/yNxXM/u5XkvXu/gFYiO6VmoXC82hhw4cQT6cNB0sY7dbi8oKMjIyLjtttumTp0aGho6derUbdu2cRxhFUkudN3hiWd4mq4QuUiRI+YJn4iXO3h5/wtX8GHOjiXaDm5COlPDT0aqoRCQJKYpDkRA91pJINKd+F1K0qcqwDwJe3zgJjyskwgjePAKogEJWZoMzbNHz6E/eFSIAycu+HhMr7O+Xo5GpURh/6vpGWkcaXjw8XHMANFPhRp6qiXiQNHwEk3kAZhSwpUGzkuL0QOvV/BDyviwTXo34aMZ3sfjv6aTdIjXkwuttkhYU91w3CcC7CiZEcDDYx6cwf4hadb43REo+bFAG/A8zRRX1ovZXnwzMGQfDPtMUqRA+cEXy0ywpHc+vXlEPMVi+C8MHNPIVFOFCo7TT9YvPo5tzOne58JAAoFv8f7/RYAEUpG/f4MIyAT0b7BR5SrJCJwlCFAyRfRdIx0lnvIS0uGix+PZv3//HXfckZqaqlaro6KiLr/88iVLlpSXlzscDmkXWVqYEwqf8pL3SbBPYagtJMMw1dXVd999d1JS0vTp01977bW8vDy1Wn3XXXe1t7fTODIH3QdJ+VBG4OxEgA7yWZZlGOaxxx5TKBSRkZEpKSkvvvgiwzB+86UzX3SRfcZrSp2Cp94Npf+7STtysWbohyHJKyZd9caB/SDgwTmxOKJDTDwcwQT0m8ttQ4e9rU74PLQXAc1hAppnBR6P17oY+HEvXGP4PCprpS7tq5Tha1JHPPfDDsDu4n0MHd4Rk2oy/j/W+tMzD5RcgjOMQJ+X5iBLQ0Wu6GyQ1Wrt6uqiXpHF9QcDctD04aW8lRgTG+V5uaqqymeeeXrihHFaVXCkCtPPYQhFkz0ZobEofFrSiCsVcdei2OkoqVg15C/aC/6VcMnyUdO//n3pF0NnbBpasC/bXJVTcjir8FCG8VCGnuzGiky8V6cZG5PMTYnm2mRzdZp5Y9h1m+Km7Rhi3j36xp/G3vjD2JnfXFj8ycWFL2T86amsP/07B++PZ17xasa132QVlF9Q+l3E9eVjbto64eblOVMeSJ9kCB92CQrPQookpEzS6jSq4NDw0Pvvv7+yspLWmlo6+z9lAnqQt9S5H01KQNPHij4mW7ZsmTp1akZGxl133TV9+nSlUllSUlJbW0sXFlBr6LO59pQmk9JqeOYU2wZjrhaEHlXln69FgFqlJCNNWUx/YOKSXkIp14AKMNGVwvQrXj9EpnPwGQlpKC2JP4HAm7BvLgHLVnwJJbixJpbAgODGDlF7aictrTR9aVgaRxqWxpGGpXFoGP8qMo8S9lOKPw33xJSm2BthujijTy44OpkCY8GHWdHAjJnoIvVkCOieWkhKJVr74hkCwggHvgPoUzKdtK/Yjv1bSpLkwMFfcImYEC1S/xREuQzRHlxaR2mYJkXToZEpm8+Czw2+bvIp0tBio4gF6BsQbwOZgO4Lzfl+LBPQ5/sdINdfRuBcR4D2j2kttm7deskll4SHhyOEUlNTH3nkkf3791OihxorsSxLHenQDl+fgetgDn9tuMQyiBmJo9yGhoa77747IiJi8uTJn3766aRJk2JjYz/++GPa+z/7xwBijeSAjICMAF7/y7IHDhwYM2ZMVFRUbGzsyJEjy8rKPB7P2QEOXm5KzMCsAtgdvKOFh6ffbw8d/YpyyLvqlBVjxy1d/Zlb8JBxPFZ+FgfHIgH9hjrp/dAh76aNfWrdVs6FR0UMZqx5bDzDerFY4lNLKuMueD44cUVIwqq4rDefWHSoiwEvHt45iW0Yh/8PBTKA7j+oOjtgkktxbiFAKTZq6UzJVp/PxzDMYNZmkWG8z+vz8jwLHCt4WTfrdnHuuqP1Dzz8z9FjR8XGRmOpDYRigtXRCEUhNFGXcAOKnT/0svevKl31x5lvDLvhvYzJnw6Zui47//thBRsyZ2zJyN+Voa/IMFsyipqGlDRlFDemGeuT9bUpdDceScF7bYqxPhnvtSlGS7KpMtl4KMV4MN20P8O0f4h5X1bhgeEzD4yYtW/krPIRM8tHzCzLKdo71Hwoe2b1sJnVmUXVmUWH0s37M0y7sws3jS1+J3Pyv6N+P0s5ZBRC2UiVFhyKzbTVmuuvv95ms+Hl/DzP8djYmVLtwGFDUYEccrzfAppSPOdW68ulPT4CYv+zTwAADhw4MG3atKSkpFtvvXXq1KlarZZy0JT6O36yZ9uvVGyDBWJ+ywmYtCUcNCGFieUpYRj9rv8CpfeSX4gUR+BUgHsUmbhjvqYwqerPhfcT3z7w+IDBBDS1U8Z/R9KEJGkdg5f2F0OkF+kfFG47Hlvj0o025eAJ2T5FEA976tw7JEaQBnAUkXzsx0EPEFN6SrwwUG36I2VFaaNgA3ZCPXvA5wGspkIFVZgTJ9x716bvkZeYIGPdb7L7O2fS0tKZeuqGUpyGP2m+1d/4lIs/kdSolAeZX5HUheiP0/uEll3y2wBBf+40LcYHpCPmIeyzm8AuOsD8mdSkTTlAPvKp8xcBmYA+f9terrmMwOlBQDSpkPZoTz5raWqCIHg8nq1bt44fP55KOiYkJLz22mtNTU0uF5bucrvdDMPQkkgv/AXhky/58VPob3VFi80wjMfjaWlpKSoq0mq11I/imDFjbrjhhq6uLuzLntT0+InLv8oIyAicPQjQuaWvv/46JSUlLi5OpVLNnTvXZrOdHXqaAlnRij0H8YSA7gT472aIGrMwaMgKZeobQ0a9vvi1NoYB3kvGfIHlmiBwvBfeWNGVmbMiJPF9Xea7aWMWrtvKUwJa8How+8yB2wsVjfAnw6qk0W+jmKW6lLf/8KdPK2vxoFXAS1u76dAcs8+B/expOLkk5zoC9NVPp6X7K2n0r50/PjG1kxLQ1m7byg/evnD8ReHhYdjbBCadlakKzRCknIDC/6xKeuV/jN9ec/sPl8zePGHW3t/fvGdU8b7sourhpa0X3laXPfPIkMLqFENNQn5tgrEh3lgfl98Qr29K8u+NSfrGJGNjkp96FgnoI8kGS6L+SIqxYWhJc07pbt31+6Kn1CTpa9NMtSnGunicVEO8vi2l8Eh0XlVMbm2KsSbJWJWob0wv7hxxW33OjRU5M38aOXN1TsHC+D/+CanHIFUKUoUpVFFRUSOGD99fvo/jeUboYZ9lArr/LfGbPHOsLjHtXm7YsGHChAlxcXG33HLL9ddfjxD617/+Re2gz43+p0iHESoZW0Bjv7l+Aprwvz6s5BsQjKASCGJD01+o90GRHO5DRYrnxavEAMWWChfgvLz4FYeduREpai/W/hUtsgPO3cSLjxsQCWhKy/LgJ6ApDS3+dw2SNOxfo+OTjMeLLwFcLOQAEIkmzzQtkW8diICmpCjhe7Hts4fwodiiiPD4lIAWjb6lZTsuhP1+DJRBJKAdAQIaz03QAot2wgR3PF8vEtD90juBEyRrP0oUtUBhBpMIle6gBHQP1IEmpGd6zg+Uoj+uj5gUYEUafJdSZW1K9/vv1cC1x0tNvAFOpAqBhOXv3zICMgH9W25duW4yAmcDArT3QyeoRWPekyxYnzR5L19TUzNlyhSNRqNSqeLi4l566SWHwyFm+ovtnWlG0s+TLPnJXE5NJp1Op8FgiI2NnTt37l133YUQmj9/PrVaOpnE5WtlBGQEzggCbrf7zjvv1Gg0ISEhv/vd79avX39GikEzlQzYKAFtF8DKg90puJwAXR74458XK4YsQqlvRGS9XTxn++FGcPnAzXltnXY8dMdCGQIvwOtvdA4d/npYwieR6Z9ljH7p263Y2xCAl+U8LAd2Hg/WHnqyLjrz1eDEFREZ70alL3rsyRq/6CE2RuN44LHRFqEI6OcZhEXO+reHAJ3ZpUu2/UvgSSUHnAOmkb0+rHfOCSznZTxux3fff1NQXKCNDVMEYavnWBScoQgZilTjUNjfkye8lHHNV0NzNyZP25KRt2uY8cDw4soRxZXDTIczTVUZppoMQ02GwZJuqE0zUAPnuiRDfaKhLiG/PtHQn3em7LP42ZBiqk810L0hzUj3+lRDQ4qhPhlz1o1J+vrEArwn66nddG2KsSHF1JBiakwtontdWtGR4Td9MyT/RpQ6FKE4dahOp0sMj5py1bUHD1VYux3+Rmd5LItDjaCJ+jMl0WQL6N/eQ3GsGlFbeJvN9sknn4wZMyYnJ+f++++/+uqrExISHn/88aqqqmNdeHadp3QYsQal8gKiDgYO0C1A1YlHx6qC5F15rCh9z/e9hJSHrAgiirrk4eJ4v+kyHXf0TeLYx2LimCCVbPQ5/ZmnNUD1isn3hkE8HQgcI75YhgEv72Eq6eXST+mVgaYIZNbXLlwa159mQNhEBJPWVxpTTG1QAUkZaCKievKgLj9VkfrhfKoSPlY6tLK9fiXPCxVC6SXxcayySZtVGu6VqHxwviMgE9Dn+x0g119G4NdGQNIRwsFTkp04dKTdYqvVOnv2bIVCodVqNRrNLbfc0tTU9NsjoCl0giCUl5dffvnlSUlJBoMhOzs7ISHBYrGcEmDlRGQEZAROPwIbNmwYPny4RqNJS0vLn5Fvt9tP1V/lidZFMmDzW0ALmC52ucGLTWEYePCxzYq0p1DKm6FDP5pw/ZcHjuKlqTaPg2G7sXKGFxsHcT5YsbI984LlYQmfRaV9mTH6lQABLbBezs1Duxf2NsHluWujh36sy/ivKm7xhX9YsnkbWalLbIt6xswyAX2iTSjHHxwCtGcymLhifwNTz2RnOM/69WtHjr0AqZFSrVAjlKlQj0Ehl6GIUt3wF0f8ef2EG3flFB+IzTugvcGSZqodVtI0YlbDsOIjQ0yWdMw7izsmoFP1tSnGI8mGuqSCuqQCkWU+TqAhBXPNdG9MM9KdHhLGWV+frA+khsM0KUpAH00pak0q6koossUXNWpn7Ar98+ohuX/RDL9QGR2j0EQq1DEhulGjRnV0dXEusuKc6UVAY89mgVXYWExA3s4PBEQO+r1338vOzo6Pj583b971118fGRn5yiuvWK3WcwAGCR3mJ9qoYi/9PMEKSN6Vg7pSGr+37azfnxvrExiB9/AcdR5IXX36yzmoHDBRS7eeF6hEAPp4T2s/MvFn8j1GfGkdpeFAuci3pBX81DI9Qy84bsq90qEHND6doyaq0NK6H7MMAyQkn8IIiLeQCIcUQxr2/9SvpXqdp79KP8UU5YCMAIBMQMt3gYyAjMCvjoCUgz4lmYkDQt7Lu1yud955JykpaezYsRMnTgwNDV23bh0VRP6NWUCL0PFefuPGjYmJifHx8ePGjdNoNCtXrjxrfJeJxZQDMgIyAj+DAFWl93g8zz77rFqtjo2NTUxMXLlypdQk82eSOKU/SwYbAo/9u7vIjv0CegHcDKzZ6I0ZuRglvRU65LPIrNfe+AITD1beyQo2PHYh0pmsD5b5CehPorAF9IuUgPaBwILXJUAbA8s+7YrKWhyW9rEq4aPw1Ff//uBGu4eubMWDSNHHujyYPKXNKyf2SxDo6W/wmIC2urqWrFyCgojiRjBSIjQEBY9DypuVmUsy/rRpdNFPKZjVrYrMb04tbs++sX4I5p2JvXOBJb2gNq3vTgho/ZHkArrXEsVn/2cy9jrY6wzRhvabP6cV1KcVNKTr6V5PDmtT8ul+JHnGkeQZJOxXlCZXmerSzXXpZkpDH0TXNMWay2Jy1w83/i3q4otQRARSKJEiNja2uLCotbYBXCywAt69flVZKQF9pubJfkkrytecNAKUg+a9/IoVKzIyMoYPHz5//vybbrrpww8/PEd9kJzM2ETyrhwUstL4AxLQWNTYJ3h4jhGwAM4vIKDFckjfm9KwGKFvoB+Z2Itq7Bs7oO8sOS+tXf+wJGLgWpojjSqlKSVTWj+TjlRmOkBAU8+EYpWlKfQqg3wwaAR+FsO+nHWf1hQPB52jHPF8QEAmoM+HVpbrKCPwqyCAHV1QHzXUg/OxMzmZTt6AqfYMCL18V1fX7bffrtFo5s2bl5aWNmXKlObmZrvdLmWffxsSHCIUDMPY7fYXX3wxISEhPDw8KCho9uzZvJdwP2IkOSAjICNwdiNA/8cAgGXZw4cPX3fddUFBQVqt9pJLLqmvrz8j5I5ksCEQu0cPj/0F8lTzsMMGO/bBFdO/0ma8F5m9Rp22VH/H140M8c/DdIAgiAT0q2+2pg5/LSTu44jUjzPGPPvtNizB4QOBB+y2sNkF/3y6KjTzNXXyR9FDPssau2LrXmhsdzNuD9Nt47GsNOagxWEkDUjKdna3q1y63ywCAiewn3z536xRWSgEUX+DQ5EqNzT9P8OvWXdJ6Y/D9Hvici1RM5pC89vCC1oSjE3JpiPJBTXJ+TXJeZYUPyNMmWLxk3LEvyYBnU9dGtanYsUPC3Z4aK5NL2pIK2rPmF0ROq0m1rArzbAqp+AvEWOGoBAFrhlKSUh8YcFT4GT8BDT2BYp7VTIB/Zu9uwdRMeyUUhA6Ojqef/759PT0yZMnU/2Nc7T/eTJjkxN9H0njywS030UhBUXkKCXsM7XGlYJ2PKKzNwGNB6cB18ViCoO4u+UoAyAgAtgXfxJ3gJPS1pSGB0hbPnX+IiAT0Odv28s1lxE4GQQ4jnM6nVayuVyuUyXuPMgi0V4jpb+bmpouvfTS8ePHr1y5MjQ0dP78+Q6Hw+PxnELS+WQ6qYOs0QlFczgcHIfdEt99990KBR4tTp48ub6+/oQSkSPLCMgInFkExD8WOlu2du3ahIQEpVKp0WgeeeQRp9N5+r0RBgYbArZ4xLtARBWxwySWBzcLdg/8/f7ymMzXUew7mox3h1/x+ufbweoD7LyJWEALAB6AxW+0pOQsVsWuCktZlTH26W+3e10+/DsH3lYHbN8Hl1y3KiL7vZCMj8JTlt101zZLM1jddobt5nmPX/2ZDCBFiDBZT9aH0s8z23By7ucVAuJUkM/Hu1yO6XnTQsNDNaHBQQhlIjQz4oJFWddtHD9703DT7qGmA2n6qkT9kej8hvAZR3W5RyOn18XmHonLrU+aUZeYV5c0oy5pRn1Kfn1KfkNqgbiLuhmiXIZffyPJXJ9k7q3FgSU1/PobJIXGNL24iwk2pFL1Z6q/EYifgmWjazPM1Znm6syiyiFFB7OKKoYVHxxSuDNFv2/srW9n5/4RRccjVVxYRIhCOW74qK1rv/M53J4uOzY3lBDQdH5IROa8uh/O88pSrtlqtb722msFBQW053n6X1VnSSsM8D6ipBstnzRMzkjfYn3ClDNt62i31NbWNtS3tLdZHXY3y7Be7peNsPqk35crlJKD0rCknL1AlsaRhiXx++dIzwwqHZqmJGr/1CQ/9rakHkR5el0rH5xaBKT4Hyt8anOUUzvHEZAJ6HO8AeXiywicXgQEQeC9vMfjsVqtTU1NtbW19fX17e3tLMuezoJICWiLxZKZmWk2m5999tn/Mx78+uuvObLR8kj5i1MSPp3VPE5ebrcbAPbv35+Tk6NWqy+77LLKykppfHlkKEVDDssInIUI0H8kca0GXcwRGRmZlJSUnZ29detWahx9OkseGPIJArZnFjCl7AMvD4wXPBx2NtjtgdffbM8avSwi65PQnNUoceH9z1W1c6SM5GIBsLHzKytaE7NfDY75ODT5w/QLn173E0sJaI+P7fbB06+0Rg19DSUtR8lLMi989Yv10OkEl9fGCb3YZ76XLyWZgD6dN4KcVw8CdKobAJzd9nXfrtXpQtXByugQdQYKvjFyxBf/c9Oe3//lwPDSqiFFloyimnRTTarRkmisjdM3xOY3xeY1xObVx+U1Js6ge33SjMbk/Mbk/KaUAnE/zQS0JcNck154KLNwX3bR3pyi/cOKKrNm7k0w7Ljw5seGXzcxJDESBYUp1YlhkaV5hv3bdmIsBPAyrNDbCaHczei5S86nEHXdabVaW1tbAcDtdp+3d8IxCVZ6PwyCVA28c6EPAV1tqalrbKA0NMMwvwBhMWUx0OsmPS5ReMx69b+KJCpmMWBgUPkOAqtBpXOM8vS6Vj44tQj0vyv6nzm1OcqpneMIyAT0Od6AcvFlBE4jAoIguFwum83W2tra0NBQXV19+PDhmpqalpaW0ywAJyWgKyoq0tLSSktLn3jiCZ1O9/333wMA7R/3cQb9WyKgqQU0x3Hz58/XarXp6embN2+m9aV3xC/orZ7GW0nOSkZARqA3verzORyOsrKykSNHIoSCgoIMBoPNZjvND7Jk9BggoAVMQLM8MDx4BLeHg6YGuPbPH6mSlmtzvlZkvntpwdcVjTgC1t8QgBfA7YVXVrQnZy1TxnyiTVnlJ6AFbAHt5NnKRvjT9NVI9zxKXhoy4tU/F31woApcDHCChyhv+MfhdDQu/dOWlE2+eWQETisCdOrd6/M+8cQChFBEUHAyUubFZC0d9uftOUW7o6c3xZo7YkwdMabmBGNtirEmvfBwZmHVEHN1OnYG2BSXfzRhxtEEPwfdlJSP934ENBXK6KX4fCIa0A3pelHWoz6tIJAaFoD2a0YHJDhqM8wNKYW1yeZDmYWHhhZVDSmqTS85EJZbkVX61SU33ZY8PhYpNEFKNUIJoRHPPvo4XvvACQKRX8DStBKFHPpUntbGkDM7owj4fD6PxyPV3OA47jQPAc4oAL0yH+D+lxKp0jC5TvoWGzAsWkBXW2roXtfYYLPZ+nLQgyD4+qffq+j9U5CU9pj16n/VIOo1qHwludP4J19+aQq9yiAfnFoE+t8V/c+c2hzl1M5xBGQC+hxvQLn4MgKnEQGeCC43NzfX1dXV1NRUVlZWVFTU1NS0traeQQvoqqqqsWPHXnHFFS+//LJOp/vhhx98Ph/lZ3+rBLTY9ee9fENDQ3p6ularXb16tUhAU5vK03hryFnJCMgInDACUnaVEs3Uv5NCoYiOjg4JCVm6dOlpHthLB2x+C2hKQAsBAtqLq/nAIz+FZi1R53ypzP4qLGfZx9+47N2EgPZhi2kPC4uXt6dkLQmO+Vibsir1wmfX/iTYvNiNoYOHtz87kjh8MYpailKXRIxc+K9nNngBeA5A8HmJq0Ms5xgQgJZCJC3bCWMtXyAjcBIIsCw2/i0/UJ45JF2rUUUrgrOR8qFh//P9MMO+qNy25JmtEQWduoLOCH1TTH5NQn51ZtHhrMJDOYXVWaaGFMPRhILjEtAGagEdoIwxhf0LnBAOnoCuSzc3JZrrE0yWtMLqzCKqB10bWXAw1rDn4ltfyLlhgiZBh4ISQiPCFaorJ1y6d+sO4PAKfqrCIT6ePPjXJZwEtPKl5xgCLpdLfFuJfexzrA6nrrj0rdQrPSmRKg2TSNK32IDh/gR0zRFLY2NjV1eX2+3u0eIYBMHXP/0BynmMdI5Zr+PG75/jCaQzCKxOtPzS8vS6Vj44tQj0vyv6nzm1OcqpneMIyAT0Od6AcvFlBE4jAi6Xq7m52WKx1NTUVJHNYrE0NTVRSeLTWBCcleiHsLm5eerUqRkZGc8991xERMTbb79NJTh+gQb0aa7CL86OWmNRJ5C1tbUJCQkqleqhhx4S7b6poxiRu/nFGckXygjICPzaCIjPKcuyTqezo6OjqKhIq9WQ0JStAAAgAElEQVRGRkZeeumle/bssVqtv3YZBkyfEtBYhYNw0BwPHM97BCzx/P0eiBu/BCW9rhy+Tj30rbn//qnu/7N3JXBNHVv/hpBVwiIhCdkwbGUtqDy3FrU+rfq5s+P6als/tfZZtZ8Wfa7P1vrqVte6YFG0Ampdn+tT0SdFnyBWRMpqSIKEECEL2Zf53s3gbQRxqRvqnd/9wdybuTNn/jO5OfOfc8+pbanDZrMZTWDjxqp3wnd6cg9RWPt4oRsvFwOlw01HlRyMGLvLM2AHibvbxWddaO81hWVaNHyqI8qhw4k0aiiNJxyBDoUA/EktKb1NIpGoRKIXgrzn2nlj8If/8R5+1z2ulpkkYcbd8R5zxwdln8vYYyr5SVWC5DtdkiVdUuv4ibWcuBYXHKx4CTtexkmQcRJquYm13MQWb87cZAnvMcf9ktgtj8lgVs+OTEvlNYKUGr9UMT9ZxkqUsRLFviliXqqYlyrlptayxlZ5J97mpZwNS03q5O+LIF4E1M+1kOmz8btVLcOBhhG12u3o0aEGCBfm5SBgt9sxU1zsl+vlNP3mteJMjzrnTRazsrFRJpPB1VZlZWV1dbVEIqmvr1er1UajEVvdtITye3Zo2pC/j6nyacu3V11Hq6c9OfHrOAI4As8VAZyAfq5w4pXhCLyhCFgtVq1WW19fX1NTA6nnioqKmpqahoYGaA3xkt8ThzBDHlaj0Xz11VdEIvGzzz5js9lTp05FA7WbTNAIGlORnyTzuowe7Dh0THn48GE2m02j0Xr06NHQ0AAHAlpAY11+XfqFy4kj8BYigH1PzWYz9O1+6dIlPz8/oVDo7u6+YsUK+H03GAwv+TH7OwFtR8MRmq12s9VqtKJWzBWNIHneNdfQTMT3ZyJ3z5/6b7uYbzA6jKNtNpPZCPZnybr9aTPZYx2Dty0oZsOV30ATAHKj4fJ1EPX+FsRnMyPogLvw+8/m5koajCinbXMYPzsCFb6FcwDvcgdHAG54QwKaRnJ1R5CeiNsqfmxh5+F1jLhaZsIdn7hqdkIVp+WoZiegp+zREt+Een5i/X0OGmOfWxHQj2WfJTzUkvqpjocS0FJ+ikSYKuEl17ASalgJaIRDbqqE6yCgOeNqWWPveCde8U+ZyYwWIURPhEBCEDbDfd5fZ5o0GodbeJSAhhx0Bx8yXLwXgQD8tcIIUHj6Ihp6G+p0Jp1b5S02m1qtxjjoqvsJLrvgHgCqD7wqAvdVtdvetHhe8rRXP34dRwBH4LkigBPQzxVOvDIcgTcRAbPZrFKpamtra2pqqqurKyoqKisrndUgaI/88rsO14Q2m+3w4cMsFisyMlIoFIaGhtbW1mI2whi58ySZl9+FP9aiMwG9fPlyIpHo5ubm7e198+ZNSFE5//1jTeB34QjgCLxkBKwWq8lkstvtWq123rx57u7uJBIpLCzs1q1bJpPpFRHQLXEI0VCEjvhjJrtNZTaYAcg4Z+X03ImwMonsfVSvJYv/XihtACbUXFpnMlnKSu1z5px590+bI3tv+XZr6R010AKgAWD1jgpW4PeI1w6PwEOeon/8fMbcjNLWZpSAtqJ20Lj580uedXhzT4IAVDZu30YtoOlUMhVBQhHi3M5Rl9jDqzvHoUwuM07qk9DmiJP6xNWx45T85BYO2mH7DC2gndnkl0lAywQOApqTKGYniH1bCGiUg/YdV+vgoK8KE1e8MygYITMQhEoguBFdRw368O6dO8Dawj7jBPSTzJk3sgxOQD/HYW1FOrc6NZvNTU1NMplMLBbf55+r4OJLqVRCO2ibxQpsLYubZxLsaQncpy3fnnAdrZ725MSv4wjgCDxXBHAC+rnCiVeGI/BmIWC3200mk0qlqqurgzpQpSNJJBKoAL3y7kJTX7FYPHDgQDqdHhgYSKfTYRxCzDndk1DPsMwr784TCuBMQI8YMcLDw6N79+4Igpw5c+Yl20g+ocB4MRwBHIFHI4Btp5nNqK+KGzdudO3aFXGkuXPnajSaR9/+Ij51WEA7CGiHR2ZIQFvsFr1VawagUAZG/u9pZkiWi1eGNy89vNvG81csjWagt+qMRr1RD34rBcdOmU9dstdoQCNAj2o1GPfZv9z9ttK4OSTOj90/3PXrHVCvNqPcs82GE9AvYhDxOp8LAjCwBCSgaXSKK4JwEWSye/Axv+HFnDgxK6nGe4yEiTLRLZbF7ERHJq6GFSdlja5jx9XzE+Vc1O0GZJ9lnIRXRUCjRtC8ZNRAmxXnTEBLuOOkvuPuMlMLhUk/dI+PQKh0BKGRXF0RpGtIaNnNm8BigebPz0JAO+tjz2Vo8EpeJgJw+B5tAQ29w/3urbgd+Z6jsgpbfO1cz7VinFudwmeOWq2ur6+XSCRwCVZRUVFVVQUNgPR6vdlgtFmsUHl4pm/W0xLBT1u+nTnwyiy425MHv44jgCPwUhDACeiXAjPeCI7A64MAFvPKarEaDAZo+1x9P4nFYqlU2tDQYDAYXm2fMGXLZrOZzeb9+/ezWCwXFxcEQT755JOmpiYoIVbsSTKvtkdP3jpU3E0mU25ubkhISM+ePVesWEGn03NycuDwPVb1f/K28JI4AjgCLwcB52dUY2Pj3r17BQIBg8Fgs9mHDx+Gn74cSdq24iSb1WbXAQDumcAP++oCu+1i+/9M9trl47d1RtqlWg3Q2VvutlmBzghUJqBzsM8KAM7fNgmj11PYP7oLDlDYG5dsuFOmAHrUAtoGbBaUg0ZzjgTXt63+thULv4Ij8FIQMJvNJpOpqqoK7vUyyFQuQh7g4pMTlXQj7C8Vvkl3vOJkfhPEXSaIRePudEmtEiRX8pPKuHEVvigHLWPFy7lJcm7SgwR0spTbcrwYC+h2nUqLuUk1D1pAS/lja/hjxb4ptZ0TCn3H7IudFIXQqQhCJrsSEYRBJm/5/nsU6Zaggw6uzPnr+WSj4PQY+T37ZLfipToKAr+PnP3+s/5B0aBOjmmhkEiF3yCj0QgjlmMBS5xvhaYVNptNr9fb7XadToctNDC3cpD7hnc5v+lociRYrbOEMO/cyuuVt1qsOp2usbGxvr5eKpVilkASiQS6QIQ71mazudWuAAbC69VfXFocARyBtwEBnIB+G0YZ7yOOwFMgALVDu92u1+sbHXEwKioqSktLy8vLxWJxfX29VquFGs9TVPoCimLaFVRzVSpVUlISgiA0Gi0oKOiXX36BNoNYsSfJvAAxX0iV0Mn1fxeDixYtolAoO3bs2LBhA4IgOTk5arUa+r92VtNfiBB4pTgCOALPFQHnZxQAQKPRJCcnu7i4EInE4cOHy+XyVivM59r4YyrDZENNIAFqo220grzrlg+GZbtztrtzj1BZu2IG7zl4Tqc2AZMdWM3AZAQ6A9CYgR6YG4FBDsD3+ytYYduQzhmdu2RFvJ+VfcFQ04x67UBdb9hNKAf9CAL6MQLiH3cQBN5kHypyuXzGjBkIASG7kryJ5Eik0998e1350yeFnsOkPklS0USx/0RxwHh4VHdJrRAmVvETajjxUh+Ug6518r/hsIB+NQS0mJsECegaTqKEkyJ1OICW8sdWC8fe4abIPOIKmCN2vDsmCqFSEQRxRd/C4DGZX82a5ZhhTmaabQhoaIlpNpuhLSp8Cw2bl9gz5BU+xzBh8MwfRgAbx6cyYcbIZQAAXGVgAsCP4GldXd3GjRuXL1++c+fO48eP37hxo6mpCUY+1Ov1BoPBZDLB8Ccmk8loNGJXoFSQp8bYakxUrK3XNANJ+aamJmgNDT1ySCSSpqYmCKbJZHpT+/6aDhkuNo4AjsAjEMAJ6EeAg3+EI/A2IgBj9xkMBqVSKZVKIftcVlZWWVkpk8leyZvgDx0GTLOESrDNZrt48WJoaKiLiwuVSp00aVJ9fT1c/ziXfHT+oQ112ItisTgqKiomJkYqlc6aNcvNzS0vLw/qoB1WZlwwHAEcgfYQaPV0slqsly9fDg8PRxBEJBKtWrVKpVI5l2mvnhdxHWsX2BxWb1a0Ea0OrN9c/07UPobvz0TmPhfemo/TrlTLgd4IjHpgNFibjaZmk9ZgV90zae7oQMJfD9BE2wk+mQzBlgFJB4qVQNHCONsASkSbALSCfhEdwOt8YQjcpyRttpZQkg9w0Jgjl/vF0ELtHGgNjzweuPGJOvQASfqAYE90+4OFrBbrqTOnvTksxGEUzEMIwxGfEzETfmWNkfuk3OWOlfLHygSp2HG3y9i7gmTU5warhYPG/G+8EgIaGlxLfJOwQ8pNrfVFDyl/bKXf2CoeSkBf9x7xHSc2EiHREQRxQVyICIfp/Zfx49CNIucRwLB9ECVM72q1C449Q1pl2tyNX+jQCDgPX1tB4SYE5IitFqvZbFar1VKp9MaNG5cvX87JyVmxYsXixYuvXbtmvp8geYpuahqNlZWVo0aNCg0NDQ4ODg0N7datW2xs7KRJkzZs2HD27Nlr164VFxeXl5dDN4CtTGEwN1ZvHgENv1M2m02n0zU0NEgkkqqqKrFYrFAonC2gMQ760WPUdtTwKzgCOAI4Ai8TAZyAfplo423hCLwGCEDTFY1GI5PJKioqIPUskUgUCoVarYbBlztCN1opWHa7/b/k+OLFi+l0dNHE4XC2bNmCLYScCz8i3xH61VaGh5qZNDQ0zJgxg81mb9q0SSwW9+jRIyoqqq6uzmazvbgxcoaurZz4FRwBHIFnQaDV9wuuNhcsWEAkEhEE6du3b0VFBSwDtwmfpa2nvReTDeWg7hsqW8xAJgfTZxWzu+R04h9xFe7hx+z4IUvSpAfNBpve3Nxs0DQbVSabRtlsLleCsA/Wk/npVEEWhbtiatq/7zSjkQlRUhBlsiytCOi2HOXTyoyXfzkI3B8pmxVYLXaTzYYG0sQYE8dFi9XhRtxqB1ZHnMn7tzjTmagflocdFhvADtRLC3Y8Ue8wkhSV6A8S0PCFMNip8vLyIUOGEAgEOpXMRkhRCOkfXQZcDRl/mzmmwnP0HffRYsbIGo9RtcyEu5zkOuG4Wr9UKT9J4psgYcfDQ8ZJkPgmiLkJmP8NKbddXxkS3u9W0s4+o58k39atR1sCWsZJqWWjh5SbWtFl7G9+qWXMuH/7jpjrHvUOQqI4fNDTGXQKyXX82FSjXud4AeL+CGDYOkYCU1RMJpNSqaysrLx9+3ZVVZXUkWpra5VKpV6vfyXk4O+PryeaNHihRyGAgYmNeKvSVou1oaGhpKTkzJkze/fuXbly5fTp0wcMGBAUFBQQEODhSLNnzy66n65fv/7LL7+cPn06Ozt7y5Ytc+fOHTlyZExMjJeXF4yCQCKRmEymv79/eHh4z549Bw4cOH78+LS0tB07dhw5ciQ3N7eoqEihUEBb4LYkbCv3FK2kfb1ObTYbNA+SyWTQCwdUBuDCrW3f2xuj16vXuLQ4AjgCbxgCOAH9hg0o3h0cgWdFABoRGI3Gurq6ysrK6upquVze1NSk1+vhu29Qoeloag0MQlJWVhYfH0+lUmk0Gp/Pz87O1uv1EBFnpbm9/LNi9/zud5YQ6pTwfUOdIwEAsrKy3N3d+/TpI5PJVq1aRSaTFy5cCF99dda220pkNpuVSuWlS5fKy8sVCoVOp8Nc9UHfHW1vaWVX4ryAbFsYv4IjgCPwXBDAnmmhoaEIglAolClTpsBv64vbZHqM5CiLZwEob6wFwGQFQGUAWYebomOyuUH/JAuPkUWZ78RuyC02q22mZmudxqhq1uutFtBsAln/tPMit5N5uyiCjICe27dnN6gMaNxBNLUQ0BZoAX2f30I/xfKtMo+RE//4pSDQalAsdovJqjeaDWar3Wy1W2w2s9VqsVvMNpPJbjPZUR8rFoBy0OjhoKQfxjhDGhojnU1WdKbBw9KqRXja0lfIh7Y7Zdpjn7Eq24UMC3GG/sKazRv+sZrrxSS7kuiISyBCH0kWbgkYVtR9Shkr/q7bGJVXirZzaoNnUi0zqZqfXNElpaJLSrkA9Xoh46CHxDepipdUyU8S83/nnVuoYR56xZmYlnKTa33Rw3Ex8Ul4Z6yMMwH90PolvkkyToqMlXzXJ7mGnZzv9T+FASmX/OMPRSYMQrz5CAXd+HIkMtl16tQpjk0F5y/lA4hBp71ms1mr1a5evdrd3d3Ly4vL5UZERAwePHj8+PEzZ85MS0tbv359Tk7OqVOncnNzr1+/Dt273b59WyaTYZ4ZTCaTXq83Go1QmYEqBzSqhXmz2Yy5X3Au01YvdValWuUfkB4/eSQCEFg4uHr0kd7y5IY3QTPnioqKo0ePLl++fObMmcnJyf369RMIBBQKxcXFhXw/wTAt3t7ewcHB3RwpJiame/fu4eHhMOABLEAgEKDvKRKJRCQSXRwJ5ikUCo1Gg5uyRCKRQqH4+fmNGjXq008/3bJlS15eHuaVAgAArYOhm45Wow9PH9npDvohdEii0WiUSqVGo4Fur1u5tXHubAftBi4WjgCOwFuMAE5Av8WDj3cdR+BhCEC20Ww2NzU1yeVyhUKh0WiwlUBb/f5hdbyCa1Awq8V69erVkSNHQvW0R48ex44dg+oaNMhyVsva5l+B3O00CWXD1l3OsFst1uLi4kGDBrHZ7L1792ZlZfH5/Ojo6CtXrjiv0NqjifV6/bFjx4KCgjgcTo8ePRITExcvXrxz587Tp0/n5+dXV1fDqC/QKx+MGwNflMTeqXRuBcrZTifwyzgCOALPhABkvrKysthstpubG51OP3LkCACg1fr/mdp4qptRAtoEQJPj0FmBrdkOqurA3IXF3IAMV+5BF0GOe8j3i7YUVzbpG61KnUVlshr1BtBsBPP+LmWHZpO5+1x8f+CELz971WawOKjnFgFauESMDrQCnIB+qrF5BYUdgwX54t95X4vDP7jebNNbTEazwWTVG2x6o91ktFlRDtqGss92G2jz24GNPJZB+Wpo/mwFFnhgn7XKoJ1vsXGGLDc0qId+XdCNjfbRwWpqtwj2awgJ6OL8a6P+PJjl5U1HiN4IMRShj6aKNgcOu9V1isxvgpQx5i5lRKNHUp1XQoVvQqlf0m1R8m/CFgK6lo1y0I8moDHiuBUTjTHLT5jB6oGktvNpyxXfJAkrWerj4MrZSeXBEy8FJpzt89HydwZEIQymKzSARhloKo28YcP3Gq3Khm4itEYM6ic2m+3WrVs5OTlbt25dunTpgAED+vfv37Nnz4iIiMDAQA6H4+npyWKx2Gy2h4eHp6cnl8sNCQmJjo7u3bv3oEGDxo8fP2vWrMWLF69atWrnzp0HDhw4depUXl7e7du3YeBrpVKpUqm0Wi30BYxtt0PbT6i4QuUE01ig1gd1IWeNqM3ca3fo3+YPIErY7gsGhdlsVqlUlZWVN27cOHbs2OLFixMTE0eMGNG3b9/g4GBPT0/INjMYDCaTyXIkHo8XFBQUGRkZHR0dEhLi5uaGEc0UCoXBYHh7e/v4+Pj5+UVERHS9n3r16jV8+PCJEyfOnDlzwYIFq1ev3rVr17p16yZPntyrVy8Oh0MmkykUCpVKpVAonp6eQqEwKirqvzYo33777eXLl5uamqC/aWz98obNAfhcwpQBbLxaZbCBwzM4AjgCOAIdBAGcgO4gA4GLgSPQgRDAjKANBgOmujlzoB1I1jaiGI3Gy5cvx8bGMhgMBEGCgoIOHTqkVqtfawLaarGq1WpozfFfx9zjxo1zd3dftGjRmTNnhg0bRqPRNm/erNPpnKlhZ1W7FUgqlWrTpk1z584dMGCAUCik0WheXl4CgSA0NHTAgAHjx4//6quvtm3bVlhYCMO/wGphkHEsAswj6m/VHH6KI4Aj8IcRsNvt9fX106dPRxCEQCAMHz68rq7uD9f2rDe2WEDroBG0FRj0wGoD4FyBpfuft7r6bqbwf3Lhru+bcODgJUWd3qoDagD0GpOluhYMT/m3G38/lXfY1Xdzr2FbfqtDicjfU4v5KkpuQeq57V+M93oEm/h7hXjuxSPgsF+GHDEam9JiRw2VDdYWf95GYDPaDUa7wUFAG8w2kwW1irahuoQNO5z4TDjAKDntPNQtfjmsqPeHFhccbTcn7vcV8s4GAHT3D4PD6trx+YMuI6BLjieZS/DHDnVoa7Wiv4ZG07EDhzxIVG9XGgNBfBAXf4Q+lO63/d0xv3SdVOyXXMYYcddtTL1X0h2fhDLfpN8EKeWCFAknRe6TomCih4yDnrZihOGpmJ/sfDy0jJOV9KNsotve27pmBwFd45NU45NUyU2+E/7J+XeS0nskDO3EEyBkN6IrQiYgZJSAfrfru1cLrt5T3UNH8L6nlPuYt/zXaDRbt24NCwvj8/kikUggEAiFwoCAgKioqAEDBsSNiZsyZUpaWtrSpUvnz58/Y8aMSZMmxcfHf/jhh7169YqOjvb392exWN7e3pCkZrPZPB4vMDAwOjr6vffegyauy5Yt27x5876f9h0/fjw/P7+kpKSmpkYul2s0GoPBoNfrdTodVFkxVg4Kh73F5czNtZIfP8Wwwth8SOUbDAaIp06ny8/Pz8jIWLhw4dChQ0NCQry9vSGVTKFQRCJRnz594sbEjR8/ftq0afPnz1+/fv2uXbv2799/9OjRc+fOXb58+caNG9nZ2cOGDevWrduAAQPi4+M/++yzRYsWbdiwYd9P+y5evFhcXAwj7FU7klgslkql9fX1DQ0NKpVKp9Op1Wq5XF5QULBjx46JEydGRUW5ubmRSCR/f//+/fsPGjSoW7duAoEgIiLi888/P3/+vEKh0Gq18CvsrLXCmfBaD/pDu+A8wx9a4LXuMi48jgCOwJuBAE5AvxnjiPcCR+CFIIC91fVCan8BldrtdvgW59mzZ8PCwhAEodFoQqHwm2++gdfbKmdYHzsUww7lxNa9UPu3WqxNTU2TJ08mEomTJ08+d+5cv379aDRaWlqaWq2GNHFbT3AtC34ntOEVo9EI40zm5+fv2bMnOTkZGpW4u7tD66TAwMDIyMgRI0YsWLDg9OnTMpkMMyzCWnlCBfcJiznJiGdxBHAEWhDQ6XTXr1/39/en0+lsNnv37t3tect54ZC1GJmaADAAoLUCrRqoVQDIrWDZxmt036WdRbvd/fcwAjfMWFZQWgf0DucazXbwr6uWPoPPIoxMMvtnqu+GL5blSpoc/jcwDhonoF/44D3/BmwoKWy13h/J2nrrr8WgoAhUSECdCqiMQG0GGitotgKDDRitwGRHTZqtDuvn+xx0OwS0kz8NyHg6E9AP8NMPmDfbbMBkQ1szAKC3ASNsFmOuHRDY7MB837b6UabRGF7YD7HZinLQNptNc68pdUSctwvVDUHo6EHkutCHu4tWBw+89Ke//BbxUalPXFnnMb9xk27zkkr5yZV8lHRuIaBZqTXs5Go2ahPdiiN2JohrBCnwkPJT4OFc+L5x9FMT0NX85GoHxy3jpdT6pspYyWJmQhUr4bYgOV+UsD8iblznYBFC9EAQEpGA0FyRTiQi1fXTqZ/cU92D7rwfSkBDFaW0tHTlypUzZ85MTEzs379/9+7dIyMjg4ODWSyWm5sbhUIhkUh0Op3L5UZHRw8aNGjixInz5s3bsGFDZmYmNG5dtGjRrFmzPv7445SUlOHDhw8YMKBnz55RUVFBQUECgcDb25tOp0OjVzc3NyaTGRER8eGHH06ePHnhwoXbt28/ePDg+fPnr1y5AnlM6KMAuo97w8hHbHI+e6aV6ouxz9DtG/Q4fPHixe+++y4+Pj40NJRGo5HJZBqN5ubmFh4e/umnn65atWrdunX79++/efNmQ0ODWq2GhurQOwp8kQ7+ZkHnKlevXr127VpFRUV9fb1arTYYDNCe3bkvmBiYig7VTrPZDAcUACCXy8+ePfvNN9/07t3b09OTz+ePHDly+vTpU6dOjYyM9PDwCAkJWbhwYVVVFRz9t2EOYGsczObGGVU8jyOAI4Aj0BEQwAnojjAKuAw4Ah0IAUx9aaWVdiAR2xcFvi0IX1G/cOHCoEGD3N3dCQSCj4/P5MmT8/PzoSk0avqEmlKhfzHttuP0F1LJsJdGo1Gn08H8tWvXpk+fTiaTBw8e/N1330VHR3t5eS1YsOD27dswDgnsTqtOwdf0oDu86urqwsLC4uLiuro6yFnDkCZarValUjU0NNy4cePQoUNr166dO3cuXEOGh4d7e3szGAx/f//Y2NikpKTFixdnZGScPn26qKiooaGhlakRfOcRc+aIvb8JHdW1P3T4JzgCOAIPR8BgMDQ2Nq5Zs4bBYNDp9NjY2PLy8ocXfdFXf7chRT1BW4FWAzRNwNgAbL9KwbhPTwhCthNZ21y46Zyo9K05zdJG0GDQNdnB2oxqT9F2hvCfrt7ZHvx1R86hL0ejj2CsQicCGtKLba1cnWnHF91RvP4nRMBmRTll6Jnl5L9q+g3ICA7Z3uP9zGmz/7Nhx92DJ/VFZUCuBjo70NtBsw0lo/VW1BfHk5geoz/lwG4CFst9c3k7Om3s9z1ymB0OOlAT6fsepaHbFmhEbTUDixmYLMBsd8wzC7DqzRq9RWkBTVaUGNdbHLEvW+Zh+x3GuDBoBN1sNFjN5pL8gsExfbwQsgeJSmW4EYlEbwSJQejT6SEZAcP+FZSYF5jyn9AJtyImVwZMqOIkVXmNueM+WimcIOWn3OYl/Oo7uoqXIvZtOSTcVAk3VcofK+WPdc5L+WNlvJbjPunc2kk0vC7jJ0m5iXcFydjRlrauEaSIhSk1jjrrOWMbWKl1zNSazonl7KQCUepev/+Z5h4WQWB4IAQ3EgkhIAgRobjTB/3Ph1cLrgIAmg3NcL8B23XAMMMUKnjFaDTK5fL/Bmy8cuXKmTNncnJydu7cuXbt2sWLF0+dOjUxMXHgwIG9evUKCwvj8Xienp7e3t5CoTAkJAR6XRg/fvyUKVNmz56dlpa2ZMmSFStWrF69etWqVV9//fXixYvnzZs3ffr05OTkIUOG9OnTp1u3bj1yMwwAACAASURBVKGhoUKhENLTXl5eQqEwIiIiNjY2ISFh8uTJM2fOXLx48bZt2w4cOHDmzJm8vDzMdFqhUGBuPXQ6Haa3wF7AcXfewm97BUPgNc1gxgFQFTQajVCj02g0t27d2rNnz8KFC4cPHw79ZpBIpICAgH79+n322Wc7d+48duzY9evX6+rqnMPDtILOWcHG0MN01MeC9tD1CLwIKwEAaLXa0tLSzZs3JyUlhYeH8/n8AQMGTJw4cezYsV27dhUIBH369Nm6dWtDQwNUg1uJ5NzEU+UfK3wHKYBFeekg8uBi4AjgCOAI4AQ0PgdwBHAEHkDAWQN74IPX4QQquFBSm81WXl4+adIkDw8PIpFIp9NDQkKWL19eVlaGdQWaZmA+BLHrrzZjtViN9xNklg0Gw7FjxwYOHMhms0ePHj158uTAwEAWi7Vo0SLIPjur1Jhyjw0lNDBRqVTbtm0TCoXR0dGjR4/+6KOP0tLS0tPTb9y4odVqsS7D1tVqtVQqLS0tvXz58sGDB7/77rvp06cPGjRIJBLR6XR3d3eBQBATEwNfjF25cuWhQ4cqKyuh/2hYFeafDoMXCgbNqJ0DB2HCYzLgGRwBHIFWCJSXl3/44YcIgnh6es6aNauxsfEV7JlhfDHKHuusQGcANg0AjcCotIGMn2TRPbdT+NupokNE/r6Ifvuv/mo3AiAzgL8uL2L4/0jlHe7Eywnqll4qRt01tGafHdbQGMuME9CtJkCHPYUEtFytm//3bLfOCzr7/ujTJYPB3+jjv/6dnukfJh6ePCt3xabSrBPKokpQqwFKA2jQgUYT0JhBsxkYLWhkQug52mBGDaUNZqA1oIfejE4ylLm2Aq0F6B2bFnYAjDZrs0lntOgsdhPkoCEBbUHZarsJWA3AqgcWHbA226zNVqBz2EKj9tdo8EOz2a62AK0J6EwOtyFPS0AbrGaUpDPZTv904E+BYQwyFXElIAji7uIqQEihCPE9hPwZLSQ9YtS/Bk7/V4+PzvmNLuDFlQtQ5lfCS672TSwVJJbwEyq5ya0IaJSD5qbKOCm17IcdjmiEMCZhrW/yXc7vB3qRmyjjJEjY8VKfOBkrXsKOl/g+xMhawkuWcVLqWKgnkDpmcjU75VcuypUfjR47zT0sBmF4IwSKC9odIpnoSnENDg0+duKozojugpusxvYI6MdOTrvdDm1X1Wp1Q0NDnSOVlJT88ssvR48e3b59++LFi6dNmzZixIiuXbv6+fkJHQn68eDxeAKBIDw8fMCAAUlJSTNmzFi6dCm0dz516tTp06fPnj177NixXbt2bdq0afny5VOnTh02bFjv3r0hMc3n84VCIaxTIBCIRKKQkJDu3bsPGzZs8uTJ8+fPX7t27f79+/Pz8ysdYbdlMhmMz4zx0dg+ettHLrwCda3XV5Mxm80wUp9er29oaLh48eKSJUtGjBgBXbQhCOLm5hYbGztnzpzTp0+LxWKlUonZNUMF77ET4I8VwJTYtsg7V2gymbRabUVFxf79+z/55JOQkBAY/TI+Pn7gwIEikUgoFK5YsaKioqKt3YlzE0+VdxagY+ahEo5Zo2MGOh1TWlwqHAEcgbcHAZyAfnvGGu8pjgD64msrFB56BVPCWhV+LU5b9Ugul69YsSI4OJjiSN7e3rGxsenp6VVVVQqFApoGoGZNZseSsgP00GAwYF3Q6XQqlSo/P3/mzJl+fn6enp6xsbHDhg0TCARhYWEbNmxoamqCDDU2ZJiNCXYF9kmtVptMpuLi4mnTpvXs2ZPL5TKZTC8vLxaL5efnFxUVFTcmbv78+YcOHbp165ZUKq2rq4MGQdDxtNViVSgUYrG4tLT0yJEjy5cvT0pKioiI8PLy8vDwcHd3ZzKZgYGBPXr0+OijjzZv3nzlyhWpVKpSqdRqNQxnD1/nNJlM0LE4dNQIYX99l20dYL7gIrwtCDQ1NeXl5XE4HARB/vs6wrlz5+B3/6X235k1Rp39WgwANAOgAqDJBhqU4NP/PdPJbwMt+BhZdN47+OBnsy5UyUClEgyccLxT4G4Ce49XQGbqp3l6IzAb77OJD9SJEtu4BfRLHdNnasxmt1sdLDDqCvxsfnXPwWtF3bYxArZS/dIpfrsofruofulk3mYKdy3znfXv9t87OOX4J19eSVtxa9VWyZbddTuzGrIPa85cAnmFoOAWuFEGympAZS2okoE7daCuCSh1oNHoYKttoNmO0tN6I2g2AI3e2qw36k1Gk8VssUELaKsFmA1A1ww0artWbTeorUBlAk060KgBDQ2gqgLcKLRUVhp1RtT23gLMMEbhkxDQ2A8ruo0KgM1iBQAYFU3nDx8fPXAIzRX1lNwJQdwdfz0RxA8hRCCkwQTWXGHvvTFJp7uO/c+7E6/7JZVwxlT6jLnjmygTpGLss9g3BVo9S7iptb6pdV4JCo/fjwbPpAbPpHrv5Ls+yZCYlrNTFazUBvRIhoeCnaxgJ9b5xNf5xMu94+qZ8XdZrQloKTdZxkm665Mo75wk90yo84iv8Bpz2XfMkZCEJV36DiZzQ4kMT4RAJxAoJFeEgLhSXINEXbL3ZGqb1dDLijP7DK+0mjsQJfizDnlJ5+1nGEYCuwWyY1hhjMe02+11dXX5+fl79+5dtWrVjBkzkpKSBg0a1Lt374iICD8/PyaTyWAwKBQKmUz28fGJiIgYMmTIxIkTFyxYsG3bthMnTly+fPn69etFRUUFBQX5+fmnTp3KyMhYsmTJtGnTkpKShgwZ0qtXL+gbRCgUenl5wfiuFArFzc3Nz8+vd+/ecWPiZs6cuWLFChgO8ezZs9DldFVVVW1trUKhaGpqUqvVOp3O4EjQBBjbdH+9FBuoKxqNxsbGxtzc3Hnz5gUFBZFIJBgeUCQSDR8+fOfOnTU1NZDBxGwIYDcxfRUb2eeYwfTY9lqBmGMt2my2pqam8+fPL1iwIDIyEu5bREZGent7M5nMGTNmFBQUaDSatlYazg09YR5rtGNmoEm7RqOpra2tr69vbGxUqVRGI/rswxOOAI4AjsCrRQAnoF8t/njrOAIvFQGoV8EmMR2rlQTY9fYUvlblO+Ap1JIh0QkA0Gg058+fnzZtWnh4OIVCcXFxYTKZffr0WbZs2f79+2/cuFFfX99Ki32FnYKxdGpra4uKinbs2DF+/PiwsDD4jiqPx+Pz+TweLyEhIS8vD5otO48XzD9Ut4YXdTqdUqmUyWS3bt06cuTImjVrZs2aNXLkyJ49ewYHB3M4HB8fn4CAgNjY2JSUlLS0tE2bNh0/fryoqEihUDhrrlaLVaPRKBSKoqKi/fv3r1y58vPPPx8yZEhYWJiPj4+HhweHw4mIiBg6dOhnn322efNmWIlUKjWZTFASuNqEeZyAfoXzDW/6dUHAZrM1NDTMmTOHSqXSaLQJEybU1dW97Kc0RhajqFmswAa9QcOIb1Y9uHTR9k6fzWT/dPd3LhFZB0Oj03MOgWIpeKffT52C9iHMrZ0Dfvh+2z3U9tnWxgLaMRI4Af26TEg4XHbUwQXqUrnJcE+ht1361bp8U817I890Dtzjys6gcXMovtmurD0knz0kn90MXqZnl12eATs8Azd7B21gBq31DfneN+R7TshqVtB3nJDv/KLWhb+3rcfAXX8etX/E2GPjppz9dNa/5y678ffvy7fsrt11QHHgaMOxU/cu5Omu3jCVVQOZAuWXNSbUklprA6gxvh002IDcAu6aQHUTOFdg27K79q//d3V00pGobmvejV4+b/7pO1J088RgRw+THZ2Jj07OP6wtm9ZmM3qLFYBmY+m1ogWzvgzkCtwRIhVBHVe4uiB0AsETITARJBhxjUYISUTuIp+YH3gfHBQMvhgw5mpw0q2wSb+KUm51SSkVpvwmSKkSpIp5qBeOu5xUNIAhfYy8E3rcdRtTyxgjZYypcR9T64vaR9f6omUgAX3PJ7mRldLASlb6piq4yXd9E+XcJHjc5SWJhSmVfinlfsm/dUkuETkOv6RfhQmF/PgrvDF5vNGnhKPWsWLHuggiECqXSKW4EFxIKPtMo5DoDHpwaHBOZqZBpXKAY7/viRt1+d3WBcdDAYRPJ6iPQRfAbR12YfoApDWhj2CTyQS5bKy8Xq+XSqUFBQVnzpzJzs7eunXr8uXLZ82aNXbs2CFDhnTv3j0oKIjP5/v4+HA4nMDAwK5du/bt23fUqFETJ0784osvli1btn379qNHj+bl5eXn51+8ePHcuXMnTpw4ePDgrl27NmzYsHTp0tmzZ48bN27gwIFdu3YNCQkRCAQwHKJAIAgODo6KiurTp8+gQYNGjx49adKktLS0VatW7dixY//+/efPny8sLIQ2DSqn9FBMnv1iK5Xv2Su02Wwmk+nq1asrV66MiYlhsVguLi4EAkEgEIwfP37r1q0VFRXQSgO6sMAG5dmbfmwNzp1trzBWBhaw2Wxarba+vv7cuXNpaWnR0dHQCzmCIF5eXsnJyefOnXsuHHR78nSQ65iWXumw65dIJLW1tVqt9hXsW3cQRHAxcARwBDoMAjgB3WGGAhcER+CFIeC8fLJarFhoEcgGvmwK44V1s23FNpsNrmpsNltjY2NhYeG33347aNAgJpNJp9MZDIa3t3evXr1mz5791Vdfpaen5+bmVlRUqFQqg8EAWVGsTmwRZTQaMRvePxwKDFtcYZ6RTSaTUqmsqak5f/78d9999/HHH/fo0YPL5fL5fC6X6+HhQaVSSSRSv379MjIyysrKoPNlzGEfpoK3l4EBSeBfWAbmdTqdTCarqKi4evXqwYMHly9f/vHHH8fGxjKZTBcXFy8vL5FIBOP8TJw4cenSpQcOHCgvL9doNDDeIww6D+2aJRLJlStXTpw4kZWVtXjx4vj4+JCQECqVSiaTuVxuWFhY3759P/roo6VLlx48eLCsrAyz9cbYf0wwCDu83mogsBHBMzgCbwMC8EuBbdgUFxdHRUUhCPLf19LT09MhAti3/uUC4jAFdbBwqDkoAMBg1zSCnH8quNHf0rvsIXEOMAXZ7w/+z9KNgN/9EMLZhXhv9g3fcuxfwOHyx+wgoR8iMsZBt8o8pCh+6RUj4LAetqEcrgVoDAC1r/vtDpj15U0We61IlOnnlyUQ5PD5+/mCI3z+MS73sJfvQTJ3r6twD8kvk+6/1y0wu1NAFkX4E9Vvn3vAfoZ/DlWYSRVmMkR7GaJMuvBHOn8ng/+jl2B3Z0GGl2B7eM+fw3vlhPf+KfL9n/40KCd2xJHBySdGTDyVNO30X7688Nevr8xbVzx3/e2pfy+I++uFP084Fdx3r29Uhptop5vwRw+/HTTOquh+mTv3gzU/1GUfUTXqgd6KRkN8bMK+YlBfsrYQ0HZgtgGDWa1QXj53YfTQ4TRXcicqDXXH4cZgMhidEAIdQRgEghdC8EWQAATpidBHuHKm+EQsFvQ5HfvJ5ZjJV979S8E744uFqWW+KWJWyl3vlEpksMx1hMIjqZEz4S5nnNR3XA1/vFgwvlo4tlo4toY/FqWh2Sl3fZLrmKhZtJybgnrb4CdXCZKrHaRzdZfUcv/U24GpRSGpBaGp+e+O+3f3Sef/NOlEt7H7/pS8SPT+X7zeGYIwPyAwuyOeQoTkjiAuiIM7pxIRF4RCch00ZHBxcbEFfVXBBgHCFEUMiseC9rwKwBax7WqoGFgtVoPBoFAoampqysvLS0pKLl++nJOT880330yfPn3UqFF9+/YNCwsTCATs+4nJZLLZ7ICAgJ49ew4dOnTKlCnLly/f99O+8+fPX7t2rbCw8ObNm6WlpVVVVWKx+MaNG2fPnt2zZ8/q1as///zzhISEvn37RkVFBQYGBgQE+Pv7+/n5CQQCPp/v5+cXFBQUGRnZq1ev0aNHz5gxY/Xq1Xv37j116lReXl5paalUKlUoFEqlEhpNw9e/YHcwMDGdELq2gMbFUEmDJTEwsVvgFXiKffq0GavFKpfLDx8+PHDgQB6PhziSp6dnTEzMpk2bbt68icUgadXu0zb0SsqrVKqLFy8uW7YsJCTE09MTneMEQtyYOIlEAuXBOoVN71ci54to1GqxQiK+srKyoqKiqqqqurq6qalJpVLBDZ4X0SheJ44AjgCOwJMggBPQT4ISXgZH4A1BwG63w5DWcrlcoVBoNJo3fjMcqvVw/Ewmk0qlunHjxoEDB5YuXTpw4EA+n0+lUqFW6u7uHhAQEBUV1a9fv/j4+MmTJ3/xxRfffPPNpk2b9uzZc/jw4dzc3MLCwtLSUrFYDGPXwGDfcDkBIwc6r5GwPPzIbDbDiILq+0kulxcXF+fm5u7evXvJkiUJCQk9e/YUCASQtPX09GSz2dDHBZvNDg4OXrZsWUFBATYXIb2OmQ87a9KPzmM1wOUN3JOAJLJer9dqtQ0NDWKx+PTp06tWrfroo4969+4tEAh4PB6Xy/Xx8YHO9ZKTk1etWnX+/PmSkpLa2tqmpia9Xq/T6eDfxsZG6EL6l19+Wb9+/YQJE957772oqCihUOjj48Nisbhcbo8ePSZPnrxmzZrjx4+XlpbK5XK9Xg99Q0N/kVqtFroBwV7jdZYcz+MIvA0IwO8y9jAxGo07duzw8PBwcXHp06dPbW2tzWYzGo2w2KsExG4BNtRRrFIH/verk+7+6xGPdBfPn7y6HAvvf4Uk2IOw9yLsLe/235v7HwdPibrusDxU4Fa8M3b60ML4xVeOgN2Ghgq0oO4uVA3aRhsAJ4+rJqQciO21vk+PLb1jtvXont4jZk+P7lndumaFRe8RRmeyo3d7h2d4hu0i8n8gCXdShJkU4U8kfhZFkEPrcoAiyCGw9yCsvUTfLCr/5068Y27cY3TOURr7EIm1n8TKJrH3kdiZJM4uCndXJ79ddOF2imADvcv33hE/MLtu94jcQX/nB9eA7URRuqtor2uX/UThz0TefhI/i+GfwxBlRrx/1ou7MazrpmXf5t1VPD0BbXe44ECt+O1oBEazFZitdpPZqDfsztgVGhpKIpFQH8pEIoIgrhQXhO6C0AhECkJ1QTwQxAchCBDXMITcD6GnIJwv6eH/YPbe5PX+Pp+BZ4RjrgakFgeMLxGNu9llbFGX1CL/sYUBYwuDxhUGjbsemHozILVElHpLmHzLN76YNeYmc/R17xFXvIf+wh6W32XMf95JvhKWcjk85d8RKbnvpvy77yfHe43LfHfUptDBfw/s9xknahSRE4NQBQiRSSB6EVzdEaK7C7kzmd6Z6kYjU1ASmoxEd49evPBvcrkc3R03me0ms81ixbaBnVWLlzbxMHIWqlKYruVMGmISYlJptdqqqqrr16+fPn06IyNjwYIFn376aXJy8tChQ7t16+bn5wedb5BIJDKZzGKxIiMjBw8ePH78+FmzZi1atGjbtm0nT568du1aSUmJRCJpaGjQaDRqtbqqqio3N3fv3r3r16+fP3/+lClTEhMTYTjE6OjooKAgLpdLp9MJBAKZTGYymcHBwTExMUOHDv3oo4+WLFmydevWAwcOnD59Oj8//+bNm5WVlVKpVKlUarVao9EIjUKwLsAMtH7AXJS0/dQZh1aftncKVSxombF79+6QkBAajQa9mvB4vKlTpxYVFTU2NkJ7f0yMV/8r015/2r8O3xwqKSlJS0sLDQ11c3Pz8PCYNGmSUql8rfvVfo9bfC1CxaCxsVEmk4nF4urq6qqqKrkjqVQqvV7/Mi3ZHyEt/hGOAI7AW4gATkC/hYOOd/ktRcBut+v1eqVSKZVKq6qqampqFAoFFmXljQcF09FhkL2mpqaqqqpr167t3LkThmXv1q0bi8WCS0cymUyn06FnQAaDwWKxhEKhv78/fBOzV69eAwYMGDly5KRJk7744oslS5asXbs2PT191yNTRkbG1q1bV61atWDBghkzZqSkpHz44YfdunXz9/eHbiuoVCqFQvHw8ODxeF5eXhQKhUql+vn5JSQkLF269MaNGwqFQqvVYraQWI+c14RPkodkVitWF1tawNUOpMs1Gk2DI5WUlJw8eXLbtm1paWmJiYn9+vULCgqCbvUCAgJ69+49evToL7/8cvPmzUeOHLl8+bJEIjEYDJDahlXV19ffuHHj0KFDmzZtSktLmzRpUu/evblcrpubm5eXV3h4+JAhQz7++ONFixbt2bPn4sWLVVVVer0eTkuMfcN698ZPV7yDOAIQATjnsa8AAKCuri4hIYFOp5PJ5M8//1yj0Tg/E17dd8QEbPeAw6/u8X+rPog/5t5lp5tfFpGTSeTuRtjpJOEBku/2YePP3qpCXRfYrFrcAvrNmOTolENZWJUFNN7TiU1Ad69ZX3/Peldhk9XbJXVAfBfU1KE+natkoFQKTuUb9py4t3Jb6bx/FKR+fmbExBM9hu4LfW+3d9AGD9FGunAdXbi+k2iLm2gbRfgDhb+dwvuRws2kcPdSfLNp3AM035/pvJ/pvAM0bhaZgzr6cGGmkzi7aLw9NOE+qt8+kjCLJMyiBOynBh5w7ZJNEOxDuHsR370UQQ6V/7O78BSl889URhbDY31sv00ltwFqyf+4hH2t4M8u9tdutWEH3D2VSCTr168fMGAAg8FgdvZydUGIrgiJiFCIKAGNHgjiiiAUBPFEEA6CdEGIQWjoQteeCONDkm98J9Ekt+CZnaOWCGPXBQ9OjxiVGTIq+50xPweNOeo/5oRozFlR/Hn/hAsBibmBSReDky6EJP8rIuloRNxPYSM2ij5Ywuz2pWf4zM7h01jhSV7+HzJ8/+Tq/g7i2gUhcQiunV2InVwIri4IQkQILqirEDLBxQW6DUEI/v5dpvzvJ5cv5Rp0zQAAdFvLatM367D9LWcQMPXjccg9h88hAY09AzEaGppCQ6lgM7Ak5oIZaxsLgahUKsVicVFR0cWLFw8fPrxz584VK1Z8+eWXH3300YgRI7p37x4QEMDj8aArD39//5CQkG7dug0cODAhIeHTTz+dPXv2unXrjhw5kpeXV1hYWFFRIZFIampqKisrS0pKrl27lpube/To0a1bt3799ddz5sz55JNP4sbE9e/fPyIiQiQS+fj4MBgMT09PPp8fERHRq1evgQMHxsfHT5s2DcZCzMjIOHbsWF5eXklJCTR0aHKYrGJmyJhN9GPH4rEDBE3I9+7d261bNxKJxOVyaTRa7969t27dKpPJYP3wHTvsXUlnqDFsO34G/j7K5fLTp09PmzaNzWYLBIKpU6cWFhZCYF/TfrWHPDY3oBF0Y2OjXC6Hs7TGkWCUF7Va7bzB0F5t+HUcARwBHIHnjgBOQD93SPEKcQReMQJtdSmz2azT6ZqamhQKRW1trUQiqXKk+vr6t4GAhoBAHbTV2EAbAa1Wq1AoCgoK9u/fv2XLlq+++iohISEmJkYkEjEYDPhOIoIgLi4uRCLRxZGIRCI0nCGTyTAD+WLawxJklp1LwoiI8Ap0t0cgEGDNZDIZ2mj079//yy+/zM7Orq6uhitA6PQZe0MT6wumbj5hBrsRZqAlNeaiEfMKAgCABtHOSqrdbse4+yNHjixbtmz8+PHQRNrDw8Pb25vL5YpEot69eycmJqalpe37aV9lZaXBYEAdZjremYVTsa6urri4+OLFi1lZWV9//fXQoUPZbDaCIHQ6nc/nh4aG9urVa+jQoYsXLz5+/Dh0OeLcu1ZdwE9xBN5UBOC0x8gX2M0LFy4EBga6uLi4u7ufOnUKriRhvFBIwTyWfXgBcJmsltrGpnI9sMl1YP531RTfVS6+2xCfHQRBJjXwgGfwSQpn6+SZV2QNqAtoo6kZJ6BfwCi8/CptDjfQeitotgJVY7MYoL44lEbQZARqvb252arTWpq1NoPWalKZDSqLVWMFaiuo1wDJPSBuAKUScKUYXLgKMvZr1my/m/Z1yf/+39X3h2W++/5Wdsg3ZM5iKn8dmfcDjZ9B5//UiX/QTXDY3e+4l/8/vfyPuQl/dmXtQTrvJjL3kVjZBJ99LpxssvAQWXgI4eUgnCyEk4MevgddeYdpwqNU7nEa65ynb15n71y+4FBk9NpfbwE0fuLj0kN/fVoRo9Cm0mw2q1SqsrKyrVu3RoaHElGr4paDiKC0rwsJcaURSTQilUikEghuRFeGK4lBIHZCCAwE9RztgyAChBCEkMIRcizSeSDSeRjiPRrxTkS8UxDv8QhzPMKciPhMRHzGIZ0TEc8RiNtghDYAob2HUGMQciTiEoxGQUTYCGpw3QlBUHts1BgbQW2xGa4EdxLCIBM7kSk0Kmr4jCA8JitpVNylcxeU8jqU4rT+/moC9jxxRgDmH4fZc/u8Fc4YAY05WGvVElagrVl0q5LQqbFer1er1Q0NDXV1ddXV1deuXTtx4sR/gzzPnDnzv/E2Bg0aBA0FOBwO15F8fHzYbLZIJIqMjIyNjR03btz8+fPT09NPnTp17dq1mzdvlpWVVVdXSyQSmUxWV1dXX18vk8lKSkrOnTuXlZW1evXqOXPmJCQkvPfee6GhoSKRiMPheHt7e3p6enl5+TiSQCCIiooaPnz4p59+unz58vT09NOnTxcWFlZWVioUCr1eDx3BPSIMoLPa5txrbOxsNltRUdHIkSM9PDyg6cOoUaPy8vJgtA/o9BkuEOCvDzYBnGvrmHlMVGzmwB9HAIBcLl+0aBHUNocOHXrmzBmM3MeQ6ZidenKpsF5D7956vV6lUtXW1lZVVVU6JalU2tTUBBcXT145XhJHAEcAR+DZEcAJ6GfHEK8BR6BjIYAtGDCx9Hp9Y2NjXV0dNNaoqakRi8W1tbVqtRpTy7DCb2QGU8geq2KaTKb6+vqKioqCgoLz588fPHgwPT195cqV8+fPnz59+rhx44YPH96/f/+YmJjIyMgIRwoLCwu9n8KcUmhoaHBwcFBQkL+/v1AohF4soCMLuJKBQQX5fL5IJAoPD+/du/eQIUOmT5++cePGy5cvl5WVKZVKuBiAYmMkVKtVB/z0Ufyg8gAAIABJREFUD/xFl5p2OzQjwoyGsFZgBnvd1fk6JMFhvES9Xq9QKG7evHnw4MFVq1ZNmjSpV69eQqEQeq9msVgikah79+6jR49OS0s7cOBAQUGBWCyur6+H7jWgT22FQlFeXp6Xl7dr164pU6bExsYGBgYKBAImk+np6SkUCqG/jnXr1p08efLmzZswEr3xfoIEN+S4sfcK234RnCF6I+c53qk3EoFW8xaSAps2bWIymQiCTJgwoaamxm63w2cF/J5it7wEQGBbNrvBartrBXUGoFNbwNodtT7B66miHxFeBsL7EemCGp8Kw/f/7evbChXqekNnMj8B7/cSxMebeBYEbADAOJQGgMbzM9vtVovdAg+z1Wq0tRwmq9FkNZptJvSw2s1WNIRli+twAKwODttkBU3NoK4ByB2HRAZ+KwPXboAfssGCdSD5M3nUgPzOQT93EuwnMvchjAwy+wCFcxDx2uMdeJLGzSFz9tC7/OQV+rN76EGqfzbRL8eF/zPiexxh/wvxuUjwyaXyzroJztHZl9xZ//bl5bE4e5PGHyupQFv/wwn7AcVIT8iKQgviirLfdmzZMmLwwCA/AdvbneAwPUbciIiHK0JFKC4EdxdX1AUYgjDIVJoLyRUlqBEvCt3TlepBIHsiJG+E7INQfNGD7IsQuQiB63An7euwnuYgCAv16YF4IwgTcfFGXDq7EL2JrkxXUmdXVwaBwEAJbheqK4FEJLhSXKmenTr5eKB0OIVApJDJZHKwKOirL/7v1/xCvVJjN5hQjyIPQwN7njhn/jBof+BGiLOzEoJ5gn4o0/pUcrY8we7X7rx7Z7fbtVqtWCy+efPmuXPnMjMzlyxZMnXq1OTk5OHDh/fq1Ss0NFQoFHI4HE9PTxqN5u7uLhKJYmNjk5OT582bt2bNmszMzEOHDp07d+769euVlZVQ+YGBRgwGg0wmKygoOHnyZFZW1po1a9LS0iZPngwdWHft2jUgIAD6YfN0JBiTo0+fPhMmTEhLS1u/fn1mZuapU6egTgW96ul0OhhdA1OEMLSdMbHb7Wq1etu2bV5eXgwGg0qljhs37tq1a63KwEowVQp+ilXYwTPO4+gs6n+9qcyePdvNzc3b2/vDDz88d+4cxkE7F3t9887zGW4kGAwGtVpdX18PzY+gV+jKykqJRAJfrHxLVoKv75jikuMIvGEI4AT0GzageHdwBADUyzGlXK/XNzQ01NTUwBgU0BeYXC7XarWvlzb5LEP75Ao0xsbCjMlk0ul0Go2msbFRoVDUO5JMJqusrCwrKyt1pJKSklv3U0mbVFxcfO3atQsXLpw8efLIkSOHDx8+dOjQwYMHDx06dPjw4SNHjpw4cSIvLw96A4TOlDUajdFoxEbw/rLogf8Pfem+1eLhJZxC62lIIkPvz9DBdUlJyeHDhzdu3Dhv3rzRo0f37NlTJBJ5OZJIJIKxeubMmbN27drs7Oy8vLza2lq9Xm80GrVabVNTk1KprKioOH/+/ObNm9PS0iZMmPDBBx+IRCIPDw9PT8+AgIDBgwdPnz79m2++SU9Pv3DhQmlpqcFgcPafCEccY9WxqY5h8izTCb8XR+BlIuA8aeG75ACAmpqafv360el0Npu9bds2uPuCPTScb3nRosK2bHaDBdwzgwYj0GrMYP32GnbwOrJoF8Lbg/AzkS4H6NzD/qHZqzdUN2qBAaDmsjgB/aKH5gXX7wg92JqAttusAB5WC7Ba7CgzazWZLXqzVWO1qa02tQ0edp3Z2mw0aYymZrMNfUUGJW3NQK0FTSqgM4DSUpCzv+Gb7yoSPv01ZvgvXiF7ydxtZO4OGj+D0WWfV2AO4vGDCzuDGXqkz6jfJs8DUxeClC+0/VMqOgXto4iyiMIDLvzDCOcUwspFmHmId54r+xydd76T7zkG+xTT97C796rla341OKJo/mGg4A8Nxj5Dugdjc+xWi0GjNuu11/Ivb9ywekziiNCYiE6CzgiDgDBQD9GocTQBQXOOREQIFBLq/gs65HVB3WM4kosjSqAr6joDNWSGpy2fOUhrF4Tg6jB1JiNEMsGV4kKm3L8XBhhE3+FyNEYhcrrw+g/587xFC37M3F1ZfaepUY1uRVscLq0d7DP29Hh05g+D9gduhDg/oAPZbPBtLSwMhnO1zpI7X3+qPKY3tr3LYDDI5fKbN29evnz55MmT+37at2bNmgULFkybNi0pKSk2NjYkJITL5XIcicfj+fv7h4WF9evXLzExccqUKfPmzVu7dm1GRsbx48eLiopkMplcLq+vr5fL5bW1tVKptLy8vKio6NKlSydPntyzZ8/69esXLFgwderUuDFxH3zwAQynwWaz+Xx+cHBwZGRknz59oLn0vHnzLl26BABo+3Zjy4PaASIAoLy8fNKkSWQy2cvLK25M3NWrV2FwaWfoMGyxTHusbluIOvKVkpKSuDFx6BeQTB46dOjFixc7srRPK5vzQMOvDHwuGY1GlUollUqr7yfIRIvFYqVS2XbH4mnbxcvjCOAI4Ag8IQI4Af2EQOHFcAReGwSg8gEd72q1WqVSCQlTLA5yXV2dTqd7M/TIJx8VZ6261V3Oa0iorkE/yI99fxO7ERo9QbrTeS0K1T5npxaYh2XIIMNTGMYQjgj8i1n3YDU4L72c+9IR8tCSGkoCiTDo0ANOQqVSWV1dff36dUgoT506tUePHm5ubtDhBpPJFAqFffr0iY+PnzNnzvbt22/evKnVaqF3FBi2UaFQVFdXFxYWnjp1as2aNSkpKSKRiEAgkEgkd3d3gUAQHBw8ZMiQWbNm5eTk3Lx5U6VSwfiQ0BrIZDJhaGNwtZoD+CmOQIdFwHnSYhSzTqc7dOgQlUr19PR87733ysrKoHd72AvnW15Av7C4gGjGbrc67F5NJqA1Aa3RbtCZwcZtUnbQRlfRPoR/AOHvQ7r8zOAcDX4ne89PSq0BaGxA/2zE3wvo1FtY5QPj6PCIAq+0B4XTp3bgMJWFVywOO2idHQ0sqbfbTKhbZAuwme1o/DqLwWbVWq2NVpvcBupsoNYGaq2gzgLuWdBtCJMJWJttVpUJ3NMBpRb8ch2s/UH8P/E/9Rm4OyhqC1O0wa/7YUbwTyThTlqXH4ncLTTRVq+wdHbXnQP/cu1vP4CfLoIdJ8Ds78DQyZLA9y76Rp+hig6hUQcFRwncY0TfkwT2GQLrX4jPOaLPeRr3HEN4hMH/sUt4+sd/vVhRB3SOefiH90LgF8351xn7yYbMu8lssNhNjWql2tB4t6m2Xn+vqLpkS9bOj+ZM7fXnWG+uD+KKuHm4MRgMNzqdTqLQXMluJArNhUQmuLg6+GgKjUpyoxEYNIIHneBBd/V0c3WnU9zoVDqtE41CJ5M6ubrSiEQayYVGIVLortROJAqDTHWndvKk0xlUCt2VSCYwmZ3fe7/37C9n/bD9h9LK32rk0iaLwQRAg8XYYDHes5mbUQrabkXfiXrS1N4seRHXnWVyRtv5unO77V13LvOEebjnd/9tK6PBkWDAQMwOALq5g7vv0NmdTCYrLi4+deoU3IZPTk6GrLS/vz98OQxG/oA+2wQCQZ8+fcaOHTtnzpxNmzYdOXLkl19+KSgoKCkpgVEKMetmnU4HIzwXFxcfOXJk1apVn3zyyYABA8LCwgICAoRCIY/HmzlzZkNDg1qtbkUpQkwgena7/cqVK127dnVzc+vbt+/Vq1fha2TOuLWXf0LcOnIxu92emZnJZrOpVCqdTp85c6ZUKu3IAj+VbM4D7fxlgR45mpqaIAcNbZKqq6uhKbRKpWo1YZ6qUbwwjgCOAI7AkyOAE9BPjhVeEkfgtUHAbrebTCaVSgV9z9XU1JQ7UnV1tVwu1+l0GIvx2nTpmQV1VqbbqwwjlJ0tayANDdU4zKLWuQZ4F6bWt23IbrcbDAbocaKtw2XozsLkSHBtAyt3dsqMrXMe2opzi68qD+MNYh4DoU20s2cM6CIAWjfLZLKysrLTp09v2LBhypQpH3zwQXBwsEAg4HA4fD4/KCgoOjp6xIgRc+fOzcrKunr1qkQiUavVkIyGfj8kEgkMILlw4cIRI0aEh4cHBwdjvhSjoqLi4+O//vrr7OzsoqIiqVQKwXRGz3kE8TyOQEdGAPtSwwkM93g0jgRfJabT6TAaIbaVhd3yYvr1AHHpREAbTMBktFkNZrB5Ww03cD1NcBBhH0U42SRhVmffXaFhG//5T6XeBJotqBeOP8z6vZhOvYW1PjCOjyOgob2zBbQMHXYvZJ8NAOjsQG8HRpvNhE5Uq8P82Wqy2nSo4bNVabcqgK3BZrtnBFodMOgA0AKgNIFKBcgvsZy+bJ39t8JBIw+JItdyAr9jCP/RSbCazF9H5G3oFLQT4W2mdNnK63EgZkRu4l+rl+8Ee3LB5n+Cmast/ScWBv/5eKegnR4hP9H8dxP4GS6CHKLwMFFw3EFA/5PIPk5knyCxTlCZp9xYBzv7/eAtWrRiU0WFHGgAML4YAhruSRuNer1Jr7fq7MCmMqo0Zq0F2DRAr7br9MBcr2vSWPW19+QFvxZeuJh7/MjR3ek7N65dt3H12u9Xrlr97cp/fL1i5Tcrvvnmm6XffrNw5dfzv10+79tlaSuWfbV8yYK/L1m4ZPHihX9bPD9t6byvFv3f3IVzv/zbV/83f8Hc+QvnpS1OS1ucti1ja/ahrNxfcm/evqHTaQwGndliRK3RbSaD1Yi65Lab7tnMSmBpAnYVsOuBzWKzYY+Ox2Ze5hfGWRj4GHT+NYefOsvjXN75+rPnoQrXaksbe3MOBqKEW/KQs4bKNrxLqVSWlJScOXMmMzPz22+/nT179sSJE+Pj4/v16xcWFgaDH7q7u1OpVA8PDxhLY/jw4RMmTPj888+XLl26fv363bt3Hzp06MKFCwUFBWVlZRKJRKlUqlQqqBEdPnx49+7dubm5AADoiMO5vxATDL0zZ86wWCxvb+/t27dDm31nM2dnAFvlnet8TfMGg+H27du9e/cmEAgIgnzwwQdVVVWvaV/ait1qoLERh0sVk8mkVqvlcrlUKoWRCaFxklQqValUcCZgI962cvwKjgCOAI7AsyOAE9DPjiFeA45Ax0IAGtVqtVq5XA43t8VicWVlZU1NTV1dnUajeQvZ58eOENS3nH0iY0pbqwymmT1hBt7uXBgK0/YKZkcMlwFwBfuI1h/bqZdZAM462KlWMsNTzDAc9gsS7tBmU/n/7H0JWBRH/vZwDJecMsPAMDPciIgRj1XRaNQVj/VKosb8c5hPE7NGzSYxbtRk1ZiNV7yIcsip4IUYVNB4xiurqFGjwSuKEM5wjXMy03fXt9WFnRZQMdEsYtdTD9RUV1dXvVXTU/3Wr9+fVnvr1q2CgoKtW7cuXbp06tSpw4YNi4qKQp55NBpNdHR0bGzszJkzV6xYsWXLlu+//76iogI5XjObzchx0KFDh7KyshYvXjxjxoyhQ4eGhoa6u7t7eHj4+/v369dv8uTJH3/88fr16w8ePFhcXIxeNX2whXuTVwRaHK8/E2HxWiIC/IxF9AcAoKqqasSIETY2NkFBQfv27UNfQyGP8LhB42lHIR1JsYCkAUkBkgAUwQKMBKmZZd3+kuGn+dbL95hctS+qx76J/3csKaWopgYwnKXl426YWF8rEfhtBNHOwYP/AoblIg1YUiD3jAEoo4KihQFGLlI0Cx36EQxUg8ZY1krTBNR5JjnOmgAURjdQZgPkfK/Xg+PXQPpe3YL1JRNmnIp6Pjuk+66O/tmygN0dNdtdNRudgxMkASskIV92iF47+O3T76/Sf70LbPwOfJ0L5saz4z+43XfieVnXI+7hhxwCt0pUyU5B6Tb+8RLXBW5RG33/cjBk8EX7gDwHzV5nzX5n331S+e4Osl1K392hwZvem3X02JkGMwNtny0AWuJTkIOGxr90i/rHrcC1xR8++CWFYiQ0R8VTBLT1JuAXRBB5vezGdQLNQONxQUT5FMMQLGMFjAUwVsBid62VYXsh6DSgKPiXge8i0HAQGGEUbC3A0Yd3Ca6zFGAJlsFBYyRYSEA3tkT4g3efdCuAeSJF7tOclrSrH/f1W7z0Xczgf2EBYX6LaZqi0QLm+vXr586dO3r0aF5eXmZm5rp16z799NNp06YhmenIyMjQ0FBk3axSqUJCQrp27dqzZ8/+/fuPGDFi8uTJ77///sKFC9esWZOdnX348OHr16+TJIlhWJOlvrBtNEVv3brV2dm5S5cu586dQ6YVTdY8jxu8tlIf4mExDFuyZAl6Fa979+6XLl1qK+17HO0QjnXzNPIHjkyUSktLi7iAhDiQT8Lmpzwjc+NxYC/WISIgIvBwBEQC+uEYiSVEBJ4iBNA7Vmazua6urry8nF9YVFVV6XS6Z9P2uTXDJ1xvIWOWFh8YmjxgCM+6XxrVIzyK2tM8pwkBzb/JK2xJi2e1poNtqgzqBW80JHzvD8Ow2tra27dvX7p0qaCgID09/b333hswYIBSqbS1tZVKpW5ubnK5vEuXLkOHDv3www+TkpJ+/PFHJD+NVKQJgrh48eLVq1cPHTq0evXqCRMmREVFOTk52dnZubi4yGSy0NDQAQMGvPfeexkZGdeuXauvr0fe2wCA+ul3LddwYauaDGKbAlNszLODALr/8DcEpOO/fdt2f39/Z2fnl196ubS0FE1j/kbxuMH5jb7kiDtkDwsJaI6DpgmovwAsFEhIuRQQvDgkZJevfHdYSM6uXaCyGtwxAJLkpBsYzu70z6CMHjcAT319v43gg6lndLQlAhoxt9DrIIoMsDAAg0N6l4DGWUjsWjiKmuIQI2hgNIGaKlBUDL7KqH5x5lFVn7iOXVY7qFc5+Cd2UGW6+W5z99nh6ZvjrtzspNzgGpYQ+865FbvBnitgXyHIOARem1MUMiBb2TPTp9tGr8h097BM18BcZ81OO2WyRPGVe3icum/ai/+4tD4fzFgOggd+7xCQ2yFon8R9s6c6z1uzy8c/KyQwafXyihs/Q9qWY10x65MhoPlvHyKgWZZmGIpiCYolGMjxthj5r3XLCcRB44Ah7rLPjZQQ3CHgCGhOeBuN2gPY5we8eIBmRtuf4Dy8TRJPqOVNrtL8o3DAhEeF+c3TzRk9RIwKX4lDaZ1Od/369YMHD27atGnZsmUfffTRhAkTXnjhhW7duoWGhvr6+iJfzc7Ozm5ubh4eHj4+PqmpqcLX6RAywrZZrdbly5fb2dn9l8IuKSlBBPQTArANVotW1zk5OSqVSiKRhIWFXb58uQ2283c3STjWLaZRzRiGabXa8vLykpKSyspKnU6HYZjwhUvhub+7MeKJIgIiAiICTRAQCegmgIgfRQSeYgQQ+4zeriovLy8tLS3mQnl5udlsFioRP8WdfDJNFy6zmj8qCHOEJVuTRucKS6IeNM8REtDCKwrT6Kwng8H/slbeclPYCJqiTSZTXV0dstE4ceJESkrK7NmzX3zxxejo6JCQEC8vL7lcrlQq1Wo1kpDOzMw8efLk1atXb9++XVdXh5RAtFrt2bNnMzMzFyxY8Nprr/Xq1SssLEylUsnlcpVK1a1bt3Hjxs2bNy87O7ugoKC4uFgoU9NkN6K94i+EXUy3WQTQ9ONvCOiOUVxcPGXKFIlE4uzsnJqayisCPZm5ikiqRt6ZpyBZgN81gqYJFlgZ8J8fLF17LnL3XOznHzd4WNbFK0DfAAwNSHaDhf8YJCLcZsFurw0TENDctgHaPLjnLyfqfZeeRvOIZqEhMzRu5iLFUZyNw3j3X6N+MEevApyB/LS2AdyqBBevg+w88MUa7bg3T0b03yaLynTrvK1DyDaPsGw7eUIHv3h50NfqsNV9B24dNHznR58W7zwEDp4HO0+ArzLB3xdUdR38rU/4Zs/Ajd4hmbYdv3ZUJLr6p3UMTHXTfBX2lw1DJ+a//v6xr7NrD10Be86DD1fe0fTbaqtKcNRsk9ivlwXtlWtyZP6pAwbnxK27dbsUNBDQcpsjoAkcUDhnkY/kj/+gBTRCSviXV0j/faQz/01HCcRbI+Nl/tsNeUyGZmkKmT83bhs0DslvY32vEfTTPbeFCAvTT6hXwku0mBYOk7CAMP8BaXRKi41H6yLElqLdR36ViON4bW3tzZs3jx8/vnPnzuTk5OXLl8+ZM+edd95544039u/fL3RkjSoXtk2n03344YcSiWT48OHFxcW8ckiLzWh/mehp6MKFC+Hh4ba2tuPGjSspKWlP3RSOdYtpvrMkSRoMBq1Wq9frLRYLmgn8dBWey58iJkQERAREBP4gAiIB/QcBFE8XEWgrCCDdZ5PJVFNTU1xcXFRUdPv27eLi4vLycr1e31Za2VbbIVxm8WuvFhPCkq1Jo0qEJREGzXP4R4sWryusp62i+IfahYgzoVkQknvGcWiMjKa3wWDQ6/X19fXXrl07cuTI7t2716xZ89Zbbw0cODAiIkKtVru7u9vZ2UVFRb3wwgtTpkxZuHBhamrq7t27r1y5YjAYcBw3mUxlZWVnzpzJzs5etWrV22+/jRz4yGQyNze3gICAmJiYCRMmICf1ubm5ly9ftlqtqAH8kLWyn3x5lGjlWWIxEYH7IYAmEn8rQMbOOI4fPHgwKChIIpF06dLl1q1byJC/+esa96v2UfKFBHSjASyAigs4C3AaCnFAI2grC4oqwdcbLoybsPXlSdt37P213gKFF3Bo8syJOdCc/bRoAf0o0D+msr+RkveQzkIy+l4C+q48BRKUoGhAQa0HzoQd6WsQd8U4kEGxhYEm8GYSbN9VtSzu+hvvHH9+WL6qy1Z5+A6nwEw7TbpUk+EUmOkUmOkSlBHSe2fsKyfmLKlI2MrsOgp2HwXJ28A/l9T3HfltSM8tsrAURdgmb/90O+fV/sFZMlWSs9eS4KiU4S8dnjrr7Jq00uz9urM/gxIjKDKBrO/ol2ae8olO9eiU4aBKd1RudZRvclOkuHRcPnLMnh27LPUNkHq2sKBKq+UIaArnZDE49YpG/3u/D+Qmt3r+4+MloPkvvqB+RPpDC+u7GwZQheNeuvm3Eb+b//t62VbO4rvfJPGE2tfkKs0/ChdswqPC/Obp5q3lLaCRyxAkhoCKIUeIvG9n3uUGz0qj3wKr1WoymSwWC1q0NLmEsG0Gg2H27NkSiSQqKur06dMkSQqXXk1ObH8fkX/sixcvhoWFOTk5JScnGwyG9tRN4Vi3mOY7i9x9I0/dfGaTbWxUA39UTIgIiAiICPxBBEQC+g8CKJ4uItCGECAIQq/XV1ZW3uZCWVlZZWWlVqtFbiXaUEPbalNaXKg9xszW9Ls1l2tNPe2pDL8aFj5uAQD0glBcXHzq1KlNmzYtWbKkX79+vr6+Ei64u7trNJrevXuPGDFixowZCQkJFy9eNBqN/ANbbW3tjRs3CgoK4uPjJ02aFBoaKpVKJRKJk5OTXC4PCwvr06fPu+++m5aWdu7cOa1Wa7VaCYJAch/INKnJ9ws9yPF8epMBbU/jIvblz0egyXRCk41hmMTERDRvX3/9dZPJhMzfmhR+HK0VEtC8HXRjAhHQFPRmBowkqLWA0npw61egp4GRBQ2AxgBGMhaWITixBtEC+nEMyCPX8Rsd+WACGokX05zgAwX/AoPFwtkLAyuDG0jLHUyPAaKGMNcAcBuA2ywoA+AnHdi4n3h9VkGPF7K79M30DU5w6bjeoWO6X+eDjuocScckiecKj5BVisglw97ck7CbPl4CTleDA7fAl1vBC29dChl81L3zDpeQHJegXLfAfI/gQ57q3TKfZKViTXDQqojOSz/59NSRk/StcqDD4ZaGFYBKKyhrgBd9fkK+nWqto2azrWyPg3y/h39+R3WWj/qr9+cUFN6EshucerKJAFYC6pXTFPyLU3DjhKYbrbdZWI6Pj4it8OsmPFWY/8fTwpr59DPFHvK9biOJ3z2mwvajSvhdw+aE9f1yhFdvYsTAL0WEZVDaarUuWbLExsZGoVCkpqby7qOFTWqvaYZhMAzDcTwxMdHNzU0mk+Xm5qI1YXvt8gP61WRRzU+h5nPmAZWIh0QERAREBB4JAZGAfiS4xMIiAm0aAeTSpK6urqqqqra2Vq/Xm0wmtLJs0+1uM41rvuR6vDmt6Whrrtiaep6pMuhNVQzDTCaTwWBAenbnz5/PyMiYNWvWpEmT+vfvHxoa6uPjo1AokBuf/v37T506de3atbm5uQUFBbdu3dJqtUajEfHRubm5y5Yte+ONN2JiYrp27Yr0OmQyWZcuXcaOHfvRRx+lpKQUFBTcvHmzuroaCechwJE5CXq8EUrp8Q+Wz9S4iJ197Ajc7/5QUVExadIkOzs7d3f3ffv2IQIaKXv+Pvv9+7T8oQQ0pPZwwJhYVkuwNVZQgwEdTZsAbgEYBiwkgzEUxhHQ0LudSJzdB+cnl838ZiortHoWpjkLaOg6D0aWgBHqaVhpWo+TJpLFAKi3MFoc1GPgag156lew7Uf6g8TzMZMz/fqv9Y7e4BKcJvVLdg9IdlMluqtSvTSbPIOzQvp+G/v6T1Pmlm3cC/adAft+AEn5xCcJv/z13W/lfROcnkty6bZDErxZEpjlHrlL4r3BJXBbSM8jfQYdn/b2pdXLK04eBVWVoLoWmHFgwKDsNANAlZm9XE4vXH8uZEC6RJUkUW+xUec7+X4vcc5z9EzrHJ2emFFbXAUaKGCmAAbPqyOAgYAZ+F0CGprtiwT0k5tw7b7m+92TW5MvBEdY/n50c/N84Vk8e8gXEx4VpjEMy8zMdHd39/T0fOutt2pqagAATUhYYXlhO5/2tMlkMpvNmzZtCg0NtbGxcXd33717N4ZhT3u/HrX9aHxFAvpRcRPLiwiICPxxBEQC+o9jKNYgItBWEOBpOPQKHmIf0Eq0rTSxbbdDuOB+EunW9L41121NPc9mGeTd28IF5E0FeTW8du3a6dOnv/nmm3Xr1n3wwQcTJ06fN2i6AAAgAElEQVTs27evQqFwcnKSyWTh4eExMTFvvvnmhx9+GBcXd+jQoeLi4vr6ep1OV1RUdPHixdzc3HXr1n3yySejRo0KDw/38vLy8PAICAjo3bv36NGjp0+fHhcXt2fPnsLCQovFAgBAPujRa61NHgUfdVyE8+FRzxXLtz8EhPOBTwMArFbrjh07goKC5HL5yy+9jBQtEQ3Nb36g8n8Mk9YQ0CQOCAvAjMBqBkQDoM2AagC0BdA4Q5MMwVAElHC46zOtfcgC/DFUn9zZaLy4+lkoCCFEHsl2c3br5L1/aWT+TAGaACzGRQugTRRuYiB9W20Ev+rB0VPUgiWnJk7Jixl7QPmXnc7BmzqEbOsQkm3nn2Hjl+IUmOQctNwz/N+9/5b5zifnVqZq9xwDJ85DkY25a8pemnmqx+hvgvttUXTdZKeIt1GkKLrle0RtkYZ87RiyUhEdN/L/7Z+18Ie0bP3x0+DXKmC6AxgS9oJmgNEKDZ/1BKjSg+PnmQnvHPLunC7x3ypR75Oo9kmcNruq/uPSMXtg7J7cA2QlJz8GtUEYnID6zwYUKchBWzkOGrLPIgH95KZgu6+Zvw//joQQnN9xepNTeAK6SX6TjwAAi8Vy9erVMWPGSCQSlUq1ZcsW9CPyAN/L7WOzkKbo2traNWvWREVFoZ9LtVp98OBBYceFg9KO08JZIeymMF+YFpYR0yICIgIiAn8EAZGA/iPoieeKCLRFBNC7/7z1JVpAtMWGtr02CRdbTyLdmh635rqtqefZKYP2XZCoHxKMRvIa/PMSn4D8BUUjncTq6urr16/n5OTMnz8/NjZWLpdLJBI7OztESUdERHTv3n38+PHr1q37/vvv6+rqaIq2WCxVVVW3bt36/vvv09PTJ0+eHBER4eTk5Ojo6Obm5uXlpdFoevXqNX369KysrBs3bmAYhjy6CMe0NeMiLC9Mt+ZcsUz7RkA4H/g06rLFYtmzZ8/UqVPlcnliYiK/8/E/IqAtFmAmoKEq1QAwC6AxlsUZlqRp+KgvEtB/0jT9TXADEv0sCeAgYFy0MADjSFgoQ8FRsUiYgjd8hlbPGCdzYWVBAwtqLOBXC9h30jhj7rd9/vp1cNTyjuovvdXrnH03eWh2ewbs6eCf7azc6KTcoHwu6y9j9v8rwZJ7FpyvAMevg13HwZwvCp8fmhYY9ZVryJcSvwWekQm2visdlV87qxI6hmWoumf4dPvyhdc2rcz69WIZuFEFKu8AMwYICpA4IAlun4Jzg1hjICgAaq0gaUvRX4am2MrX2PrusFUflGiOSIL2SzQ5fhE7Zs8rO3sJmEhQb6XK71QRgMQYaPXM6W80UMB0l4BuZJ9FAvpPmo/t8TL8ffh3JIR4/I7Tm5zySAQ0SZLbt21Xq9WOjo4DBw4sKChAqyO+STQF79XodwRdiD/09CZ0Ot2KFSuCgoL+q9L2+eefDxgwICYm5tSpUyIBzY9pk0nFf0SzC71QxRcWEyICIgIiAr8DAZGA/h2giaeICIgIiAiICDzFCPCbNMiZj1arRd7kN2/e/Nlnn02ePHnIkCHdunXTaDQyLgQHBw8YMOD1119ftmxZbm7umTNnrly5UlJSUlZW9uOPP2ZnZ69YsWLq1KmDBg2KjIz09/dHWh9hYWFjxoyZP3/+5s2bT5w4ce3atbKyMuQLkX/asXKBh5JXu+YX/fdL8KeICREBhADDMAaD4fLly927d1er1YWFhQRB8DS0cBum1YjdS19CzQNhbKoBDQDDQGqZogCJAQsGGnBoc4pZAWVhWZxzVkgxgGsSxdIUZ5DbOMFb3SSxYOsQQELGsCzDOXyEZDILGhhgpICeAncIcAcH9VagNZJ1JkpvARYzgxkZAgNQW7kBwKIEAPUmcPVnsG8/G5dU/8q7p3sMy/UMWesevM5OsdI9MM1eEa/olO0TkKUMyujaZ3PsS3n/+Kxw3aaG/1wGB86AlL3gk/XE8KkF4YOzXUPivMJSOwZldVCmuwdm+HXLcg1a49Nltab3sj5j4//++aGkvJ+P36q7psXqaSggjhFQMhw2hQLcP+i20oRZLQzQEaCwlJi/6piqT5xdQIJD4FapKsc1JE+q2uYatrXLC9tWrr98qwSQADpChNseLEEAimIJGoo+k5wTRYIBFBfhjL0LqHBuo/TdI+J/EYE/F4H7/e43z2+xXXyx+x3FcRwAoNPpli1bJpPJnJycJk6ciLwRotfIkFc6noAW7mK2WGdby2QYhl9lobaZTKbvv//+7bffVqlUsbGxO3fu3L9/f2ho6MSJE69evdqkcFvrTltoD8MwZrPZYDBYLBbeN3hbaJjYBhEBEYGnDgGRgH7qhkxssIiAiICIgIjA40GAt54muIDjuNForK6uvn379sWLF/Pz81NTU+fOnTt+/PgePXr4+Pg4OzvL5fLOnTsPGjTo1Vdffe+993hKupILhYWFe/fujY+Pnz179ujRozUajSMXZDJZt27dRo4cOX369OXLlx88ePDmzZs6nQ45MBSSg8I030n+eZJP8IfEhIgAQoBhGIvFYjQa165d6+zsPHny5Lq6uj+ZgOY4aEhAE5BCtBKQhrZaAYWxLMFCzg+aPsNAMYxIQD/JmfsbAQ0ABJ7g7J0bCGDEOerZzNbcIaq0+K86ymACuAkAHQXqcXCHBFoceo888h/D2g1XJ725c/CwLZ0i49UhyQ7yRBtFiq1fioM6WRqYKFGucQ6N7zP2yMx5ZXHJTN4RcPQMKPgJJGyyvPNBwejXjgT2ypY9t8M5OMNBneyoSXEJ2uQWlOmmTvYJXhcdk/bm9KNxGeXfnjJfLgO/kqACw7TAqAeGBsBCt4AkRzsTBKDNNFNnxn/VY3oDCSq04OB/7rz0VoI8Yp5d4HqJ/2Z7dbaNz0YnZUrH4PUv/7/j2/NMv1ThFtJqwhsIQOEsgbMExVIUS911q8jNQW6zBO6GiAT0k5yGYt2/DwH+h/6hiRbr589q8ajQiLWoqGjOnDm+vr62trajRo3Ky8tDyxKCIHgRP742lGixzraZyTCN20t1dXXx8fGDBg1SKBQTJ048dOiQTqdbunRpQEDA6tWrtVrtM6gB/UhDxrKs2WyuqqoqLS2tqqrSarUmkwm94ddcRfqRahYLiwiICDyDCIgE9DM46GKXRQREBEQERAQejgDighmGMRqNlZWV165d27p16+zZs2NjY9VqtYODg1QqdXJy8vX1DQgI6Nev39SpU9evX19QUFBaWlpbW1tRUXH16tWTJ0+mpKRMmzYtKirKzc3NxsbGxcUF+ULs2bPntGnTtm/bfvnyZYPBgGEYeurjfcfx7CFKCJ8DH956scQzhgBv13/r1q2RI0cGBAScOXOGn0Itbmw8DKHmNqHCnBYsoBEBzXBG0CSgSEARkIxmccAQLGSduQDZZ5GAfhj4j3pcODS/nXs3F1qm44DAoCtIzAIsFqjTzVgAMACgo0GpDtRhoLAUbN9b99m/f3xpUn5kdGpAcLI6KMtDnuTssdZVluggT3RRpXiGJ3l1XhM5PH3Wqiv5V0DBr+CSFuy9ABbE6f722jl5UJq7X5Kzzyp3VbK7/04nn11OPjnummw3dbJb4Iruw9Pfm3/8+5NMRREgzMCoBRZTY1MbSCMGjBZgxliCYKH1IkNhDKMn6NoGqtYCCDMLfR5mZNd2jVnl5r9AHpbYISDTUbXNRbmtY9AWdZcNH3x66exVqBlixFhoNc0SOqOOZAiSeSgBfRekewz8ecvo38AUUyIC7QAB9EuBOkKSZEVFxRdffKFWqyUSSUBAwPLly69du2a1WpH5M/rheBrXHmh3v66u7sCBA6+99lpAQEBYWNjcuXNR7w4ePBgTEzNw4MDLly8jcbZ2MLJPrgs0RRsMhtLS0qKiotLS0oqKipqaGq1WazabCYL4XauLJ9dYsWYRARGBto6ASEC39RES2ycigBAQf+DFmSAi8CQQYBgG0b78VwyZRaNXOK1WK4ZhvIkHegmxvr6+srLy9OnTmzdvXrJkyTvvvDN69OioqCh/f38vLy83NzeFQtG3b9933nlnzZo1mZmZe/fuPXXq1MWLF8+cOZOXl7d27dq333572LBh0dHRwcHBCoXC39+/S5cuI0eOnDNnTnx8/P79+69cuWI0Gs1mM2KlEW/XmofA1pR5EjCKdbYdBAiC2Llz56JFi4qLixspX4bhp/ejtPN+xBzKfxABzcs8E5wjO8g+c1aoiHoWCehHGYXWlIU6GyzAuUhCch8KdjbyqdxYUCRgrABKOZtoYKSBngZ6BpTpwA8/gyNn6NTtdX//8GTPgUnBkXHefit91ckK9UYP31S5OtOxY1wH37WqqI29h3/36vu3v9oEcs+AA9dA1vdgwcYbby46GPNqctCAVV6d1noEp7qpNrqrMz0CN3QMSpZpMlWh2c/Hnvx/M29+sbZm13FwrQZUGkGDCQALlJemGwjaYgaEiaUMJKklGAPJmnEWIwBBMhjJWEjWiAEzKl5wHSxadS28e3xHZVwHRYJvcLabX5az9wafwLTn+mYlZeoLb0HHgrUmnAbAZDGarSacxAgaJ2hcaAGNrJ75v/eqyjSZ8K1BXiwjIvA0IYBWCOh3AbWbZdn6+vr09PSYmBh3LowdO3bdunWnT5+uqKhAPxxtcF2BmvQA6YyqqqpTp07NmzcvOjpaJpNNnDgxNze3vr4eAHD48OHY2NiwsLC4uDiLxcIbSj9NA/nntpVlWYvFUl1dXVZWVsGF8vJyREMbDAbkcPvPbZF4NREBEYGnGAGRgH6KB09s+jOCAL/yQ4wYz4U9I90Xuyki8EQRQHSz8KVU/nL8V09I3qFMnhEmCEKv15eUlFy7du306dM7duxYtGjRG2+80adPH4VC4eDg4Orqqlaro6OjR48ejfQ3cnJyzp07d+3atQsXLuTl5a1fv/6zzz57+aWXw8LC7Ozs3NzclEplZGTkiBEj3n777S+++GLHjh03btwwGo0AAJIkhYbSJBf4xydeQppvHt/yFvvC91RMtDME0HCjR2shB81Pg9b1twkf16qPPLWH9DZowFCApWGkaUCzrDDyzYEmq2IQIICgFmTcPwkhBSTDYiywMqyFYTGaJuC9goLqJyxUUcYp6G8QyiJTAFSbQXEN+M+P4Is1l//+0dGYv6aHP5ccELZVpsxx89rdoePujv45viFb5MHxLqpFXQcnjZ9+OCGXSt8PLteAby+Bf6fR735R2X30rrBBW7yfW+fROV4iX22niHdWJbkGJtkqlnqErQztv+GV6UeXfV2661vschG4+guoMgItAcycS0MowExDWRCSIWgaI+kGkjaRtIlmLChSLCyCMzTG6VCbANh3EYx4Y09Ir00u8g0dvDa6y7Nkflt9/DL9VPEf/PPH/d+RFhLgnLozSbMERfLUs9ACGs29BzLO985wJGNyj5jJ/YdBPCIi8JQgwN92kbtm5AnDZDJduXLlww8/DAkJcXNz8/HxiY6O/uyzz44cOVJWVmYywVcVcBxvTjUKa3tcAPDrlgdUiEwHkGK11Wrl1cwIgtBqtbt37541a1ZUVJRGoxk5cmRKSsrNmzdxHDcYDJs3bx48eHDnzp3nzp2L9mgfcBXxEI8ASZJGo7GmpqaysrKsrKykpKS4uLikpKS6utpkMjW3g+YnRmtGk7+KmBAREBF4FhAQCehnYZTFPrYHBNBvv1artVgs7aE/Yh9EBNoRAizLkiRJEASGYVar1WAwVFZWFhUV7du3b9GiRWPHjo2MjESeCX18fORyeUhISO/evV955ZWlS5ceOnTo4sWLV69eLSwsLCgoWLFixauvvtqzZ0+FQuHt7e3p6enl5RUUFBQTE/P2228nJiaePXsWOTM0m804jqNVvtVqRW6F+EdK3oW98DEApdsR8GJXWkCgyT7E/5CARmQ0xz6LBHQLI3X/rN9BQFsYYKTZOzRjJCkchxQ01EC5o4O++LQYqDJAZefDp5l/LbsQE5sU0Hmpf/jKwMhEVac0uSZd02mvi2yHY8c9fqFHVF129xj67d8X/pL2LTj1CzhfDb67Ab7+hp3wjwthg7Z4Rq63VS1zCYmXKL6S+Kx0DUpzUaV5h2wMjE6P6J88+eMTX2WVH70OjZ1NJCBoSHmTABCA5hwAQqNsinNHSbAMzhIkYyEYE0kbaMoEKAugME55g2K5MlYGylJ/nasPGJji89xWJ98sB8+tMr9dvupt3j7rBgzanbWFrq6FPeV2ORo9C7I0FHi5q/gMtz3QPHwE6hnZjosE9P0nqHjk6UWAXwbwqk1IbQNZE2dkZAwePFgmkzk7O0skEqVSOXr06M8///zEiRM6nQ7HcYIg+MUGAoH/xXksVCOqTbhuaRFq9OIa3wDUqpqamuzs7Ndeey0iIsLT03Po0KGJiYk3btxA7Pn169cXLVqkVCo7d+4cFxeHfCS0WLmY2SICNEWbTCZkB13CheLi4rKyspqaGsRBo4nEDwo/iC3WJmaKCIgIPLMIiAT0Mzv0YsefGgRYliUIwmg0VlVVlZeX19bWNln8PTU9ERsqItC+EHjocxfDMGjrqLa29vz589u3bV+2bNn06dOHDRvWu3fv0NBQBReCg4P79es3bdq0Tz/9NDExMScn5+DBg/910b5ly5YVK1ZMnz49Nja2R48eQUFB3t7eMpksMjJy7NixH330UUJCwu7du8+dO1dRUYFxgbdRQrRjizR0+xoEsTdNEeCf+vj5KbSI59mHpqe18Pleg9CmCrmtPXqv1bNoAf0b0PciCB3i3S/+dk6zFDegNMNiDKinQTXN6knKajRgWAPQ14Oim+DwUTY5Qzdr9rnRE/KCI+P8QtZ6a9b4BG7wUqd2UCS4+q/3DkkM672x7+g9k/95dcEG3a4fQN6PIOsYWJZFfbSyNnbySUW3eJeQeCfNRknHJKkmQyKLk/iuslWvlnVPfW74jjFv5s9edHZz/p2Cn8EvZlAPgB6AOhIQAPqcpCkYWaGiMgPt4blDNM2YaVrH0jWAqoOq1ATUDKcpUHuHNeGg8CaYv+xnr26pNiFbJYrdEs9dzh2/ceiQFNVz84wPzxz/HtTUgTt3AEsikpsCOPS2yNJCl4N/gIBuBrWYISLQ/hBAvwjCBcPly5fT09PHjRun0WgkEolUKpXJZOHh4RMmTFixYkVeXt7p06crKystFksTxpnnjv8ISnwl/A9Zi7WRJInYcLPZXFNTc/jw4YULF44YMSIkJCQ8PHzSpEnx8fHnz583Go16vb6oqCg5OXn8+PFeXl4jR47MyMgwGAwtVitmPhgBmqKRHXR5eTnioEtKSkpLS2tqaoxGI3o/j1cPf/AIPvhC4lERARGBdoyASEC348EVu9YeECBJ0mQy1dfXV1dXl5eXl5WVVVZW6nQ6guAMnNpDF8U+iAg89QggohmxvfwjGXqzleAC6iFJklYu1NfX37hx4/jx41u3bl2wYMEbb7zRr18/X19fJycnBwcHhULRo0ePYcOGjR8/fs6cOWlpacePH7948eLJkyc3b978ySefDB061NfX193d3cPDw8vLKyQkZODAgdOmTVu1atWBAweKiop4//VIsaeJDeyD4eafGfiOPLi8eLStISAcQX7o0UzgD7WuzfcSpCIB3TrUWlMKDcRd23AkUcLQ9xLQNGgcLjh2NAPVNO5KlaCBoRuNi6HnPSsXLSyw0KCBAIXXqI2bLr/7bvrwYeuCQr8OCMpQBaUpNSkyVYJMvc43MNEvZEMH+VdBUWkT37nwVQq1twCcLQUni0HmCTBtyY/Dp+0PG5Im67Ze/lyac3CCxHe1xHetszpF3mmro3KtZ1hc77Hf/H3xlfQD4LtCUFQNqu4ArRVKS9fjUGnaCkAdZgCA5mIzPBABDYlplqEwljIASgtIHSKgGYrAKWDEwJ6DlomT93moV0l8UmzUezoEHnb1z/NSbRwYuycxo7beBLQGYDABi5kTvKYoQIgEdDOoxQwRgUdEAIlaGAyGGzdupKenDxs2TKlUOjg42NjYIIkwlUrVp0+fd999d/369UePHi0pKeFFwNCl/uDK4aEENE3RSHDDaDT++OOPGRkZ06dPj46O9vf379at2/Tp0/Py8srLy+vr6y0Wy5UrV1JTU4cOHRoREREVFTV37tyzZ88i3x5I1uwR4RGLA4IgzGazVqtFj6XFxcW3b98uKSmpqqrSarUGgwEpogiXHCJqIgIiAiICQgREAlqIhpgWEWgrCCBdWmT4XF1dXXo3lJWVVVdXI58PbaWtYjtEBEQEAOSKmtt9NBJI9/5DYu5IsgPHcQzDzGZzdXX1lStXsrOzFy5cOH78eCTZodFoVCqVXC4PCAhAkh0LFy7MyckpKCg4f/78vn37Vq5cOW3atIEDB6rVag8PD6VSqVarfX19+/fvP3v27P++S3vy5MnKykr0diQyjkbPiizLoksTBCF043NvSxs/icP71CHQ4jgKM1vXo8dDQN9f+qB1rWh3peC9ArAUwyACmgIsF6GtMCePTEJNZ4ZimcYDgGABCQW0eSQYjuTFADABUMOA2w2gsA4UmcCeU8zHSy7GTswJ7fZ1eHRKcOdERUCCf+A37rItHTyTvXwT/IPWq0NW9RmY8eY7B/d+B64Wg2tl4PAZsGEnM+WTK+HPZ3XsnOQamuwUmCTxWesYmOwSmu4avtGrS5Zvt1R11yVjX9+2Nv2XoxfBlSpQgoydWWC0gAYLa7EyFoywEriVwjDGirMWClhYqMxMo2kEhTLuMuYEJ8QBO4QsoymAG8242cRQcGfdgIG0rcU9BsTLgr529U+T+m2TuG9wD9kU2D313Tmn/vMTJLb1OHS5SEHVDRQolm6MDAMtoFEUWt/ffx7eb57zeIsJEYFnAgH+pRnoxJRlMQy7efPmpk2bJk2apFQqJfcGFxeX4ODgIUOGvP/++3Fxcfv27bt+/bpWq9Xr9RaLBXHEAAC0E4/oSFQtfxX01UU79839cAiJbBMXcBy3Wq06na6wsDAzM3PGjBkxMTEqLsTGxs6fP//777+vr69nWVav1x8+fPiLL74YMWKEWq0OCAiYNm3avn37kBPCZ2Isn2QnGYbBMMxkMtXW1paVld2+fbuoqKikpKS8vLympkan05nNZqQKjVYdT7ItYt0iAiICTx8CIgH99I2Z2OJ2jABPEDAMg+O40WisrKwsKSm5fft2cXFxaWkp2mHGMEy4MmvHgIhdExF4FhBAlDSSbzabzXV1ddXV1ZcvX967d29iYuK8efNefunlfv36hYaGyuVyb29vJAn9yiuvzJ07d/Xq1SlcSEpKWrt27Zw5c8aPH9+jRw+1Wi2TyXx9faOjo8eMGfPBBx+sXr06Ly/vxx9/RE5jhLwzb8GNbiz8jUh8eHhKp1+TEWz+sXX9uh8x97jyW9eKdleKZSH7TNKcVnGjcDFAfho5AhpnAc4wBHdbYBmSZTkbXwgDB7yVAXdIUENC6rmwDuy5iC/dXPT3L394bkRmQJ8M15B1zgHrbGQrXVWJsrA0n06Z8pAsRWhW79ijUz8oW54A9h4D566A4z+AzG+s//z8zMS3dnV7PiEwOl7RKcFdneCqTHL22+ARkObkv85Jtar78NwxU0/OXl66drP2cgko+hVUm4CehsS3AUa2gcUZKMBMApZkGYJlCCjizMJIQ/YZpzkhaE5yA4pBkwBggCW4SHMdInCAWyHVTlDAhIGzP+kWfXUwvOdiJ8UCeXiGV8hm98C0jiGJoyZ/tyHHeK0KaClYiYG0EOA3oplnnJskRAK63X17xA49QQR4api/BqIay8rKDhw4sGDBgl69enl6enp4eDg7OztwwcXFxcPDw9/fPzIysnv37uPGjZs/f35ycvLOnTtPnz5969aturo6o9GI4zhvKM3vwfM5/OVQA5CNM3qRi6Zoq9WKXho7dOjQihUrpkyZMmDAgMjIyK5duw4ZMmTWrFm7d+9G1jklJSVnzpxJTEz8L93cq1cvf3//Xr16zZ07Nycnp7CwsPnl+OuKiUdFAC0qMAzTarXl5eXFd0NpaWl5eXldXR3ygSyuIR8VWLG8iMCzgIBIQD8Loyz2sa0jgH6h+TUZMo3k2Wf0s47eb9LpdBaLRcgctfW+ie0TERARaAUCvF4H4oL5Ry+SJDEMq6+vv3Xr1qlTp/Lz81etWjVlypQ+ffrIZDInJydvb++AgIBu3boNGzbs1VdfnT17dlxcXH5+/okTJ3Jycj755JNBgwZpNBpnZ2c3NzeVShURETFw4MA333xz2bJleXl5t2/fNhqNyIkibyLdhK9sRfN/KyLujf2GRRtINRlK/mPzpjUnlR/dYrRpHQ9z/ta8Fc9EDhoF+MIEx8uivywDOWgGaiND3pYCGAUwksFImiZIQJLQoyBNQWPoojvgUjXYeND49mdneo3KCRmQ7RGZZuuf7Bm2x1G1zd4v0UG9yjnoS3vVvMC+68b+/dCSrLpvzoGCCiiysfkQ+DwejH+3tPfIU4rIrR3DstRd9nXw3ezgkerileTqHefps9JP81WPfslzFlz+5gB57ga4WgHKTaCegYyzCQAzZ3zdAIAZ6jdTVoogKZymCY4xhwQ0jAAacdMw4jQUBTGjyAAzw2mE0KCBAlYrazVRpImBdWpxcOYK+HzN1f4jMsP+kuga+KWd32KJ7N8Sv8/7jt2yPK3iUhmknitNkAE3kdAYnADUQzno1hPQzdW3n4m5KHZSRECAAP8DIUwgO2XkzeLSpUtZWVmzZs2Kiory8PCwtbV1cHBw4YKTk5MzF6RSqaOjo4+PT3R09PDhw6dNm7Zw4ULk3OLEiRNXrlypra3lVQT5BQ/JBbR+YBgGaQ9ev349Pz8fec4YMmRIQECATCYLCwsbM2bMokWL8vPzb926VVlZefny5ezs7MWLF48fPz44ONjNzU2j0YwePXrp0qWnT58WWj2jfgl6LCb/EC3TV1gAACAASURBVALIR5Fer0dyHKWlpSUlJcXFxeXl5Xq9Hlm1i2vCPwSxeLKIQHtEQCSg2+Ooin162hDg9/wRCWW1Wg0GQ01NDe9luLS0FClvWCwW9FrT09ZFsb0iAiICD0FA6EAcFUXsM0ojn+9IrwM5Ir9+/fru3bu//PLL1157rWfPnkou+Pr6+vj4qNXqrl27jhs3bt68eampqd98883WrVu/+OKLcePGde3aVa1Wq1QqX19fhUIRGhrar1+/GTNmJCUlnTx5sri4GMMwkiSFz58PabfgMG8/JTxdfPwQIPRnJ5sMBP+xSTuQTW4T/rgtENB8g9vZLEIaODhOEhTN6UggC2jonI8CJAVIHBA4YHhNZ50Z/FwEDh3BM7b9Om7als7D4mTPrZF1TXcO3Oio2WyvyrRTZnmG5XfQbJdHbewam/PG3B9Xbsf3XYKyzkdug5TD1JRFF6LHbPWMTHAOSnXUbHYJ2imRp/l02eui2uamynSVr+vSY/Ok10988ulPJ/8DyqsAVNDgHAlaATCyFh2tZSANbrUAs5lqsJC4hSBxksJJCu6WQQKaYhD7zBCI9qUBTQOSgeyzngZ6BhgZYGEARgMrDfsIpasrdaC6ARw8d+fjJd/F/G2LonNaB2WqvNNWz4i1HcIWhryw/ou0su+vQeK7DgM6ChgoeFYDw2rNRpGAbvItFj+KCPxBBND9tokyBi+mgSyIGYapq6tDjgrff/99tKjw9/eXc8HZ2Vko1GFjY4NIaiQR1q1bt8GDB7/yyivTp0//9NNPV65cmZGRkZOTk5ub+w0XcnJy0tLSli5d+t57702YMKFfv35qtdrBwUEqlapUqlGjRs2dO3f58uXp6en79++Pi4v7+OOPJ02a1LdvX6VS6ePjExERMWzYsE8//TQnJ+fWrVtIAATpftAUjXOhnf2U/MERfyynkySJVKFramoqKysRDV1XV0cQ8D0eEfDHArJYiYhAe0JAJKDb02iKfXnqEUC+Herr66uqqpCLYfQ2E/IvjON4c4rqqe+z2AERAREBDoHm74cKnwaFHl2aPB+azeby8vKzZ8/u2bMHqXC8+uqrAwcODA4O9vLy8vT0VKlUPXv2HDdu3MyZM+fPn7948eIvv/xywYIFs2bNQs94QUFBMplMpVL17t173Lhxb7/99tKlS3Nycs6dO1dcXNzc2b1wxJCAI8pBr3HcTwtbeJaYbgsIIAFeAKCQLkGR6CMU6qVpkqahtEKj40Eo1kvTBEFiOG69a/FKQdtcCkeZOG7lD/HO8kiGIGioAizoLMOyNOIr+edStG+BylgsFpPJhORo+PnfLmloq9VqtppwFsOYhgbG2MAY9aThDqbXkQ0WwBhoYAHgl1pw4gcqfWv1zI/ODv/bvqDQNP+QDJfABLdOm2z8UtxDt3t2ypYqE7wi4qNH7nrt4+srNrMp34L9heDwNZBxEHz0lf6l6YWhA7eremd6RaY6ByW5BKfZ+qXY+ma4BGW5hyU+F5v9t8n5b374bdrOX0+eh74Ea7TAQgCMABgJbbBxirPHZlictRDgDgFqCHCHZI00DbepSJImSZqhYKRpgqYJJMTMkdEM1LBmaRqYaEgd60nWrNWZGjBgpUCdDtwxgmu3QNKmX6e+fyriL6kdg5I8AnbYy3PsZd+4B2/pPW7bv5Iu5//UcF0HfRtaKS7SkHpuYGiMpa0MjrMEzhIkA6/LXZFq/le0gBZ89cSkiMDDEeBvtvwyQ7j24PeY0VGj0VhUVHT06NHMzMzPP//8vffeGzVqVM+ePcPCwjQajaenp4ODg5CPtrW1tbkbnJycPDw8FAqFSqXSaDRqLmg0GqVS6eLi4uDg4MgFJPTh7Owsl8uDgoKioqJ69OjRrVu3iIiIkJCQgICAqKioESNGfPTRR+vWrTt48ODNmzctXEAtRN15eLfFEn8AAfQKHVKFRs4Ja2pq9Ho9MmX4AxWLp4oIiAi0TwREArp9jqvYq6cOAST6jN5jQqLPJSUlZWVlSEsL+RBrzk89dd0UGywiICJwPwR4Po4vwBNwwkcp/vkQPQryzgzRBhVyYa/VaktLS8+dO7dv3764uLh33323f//+KpXKzc3Nw8PDx8fH39+/a9eugwcPnjx58uLFizMyMjZt2rRgwYJhw4bJZDJbW1upVOrh4RESEoIo6blz5+7bt6+8vBy9J4txAT2Xovc2UDOQmTYqg9osbDnfLzHRRhAQEtBIkpigSJ6JpmnCam0wmQ0Gg85g0On1d+rqaqqrq6p+raisKq+oKCsvLy0r+6W0tKS0tKSyqlx7p06nrav5taqioqzq14q6upo7hjs6o+6O4c4dwx2T2WCxmCwWE4ZZSArnmEGWJEmLxYIcHly+fHnPnj3Hjh27efOm0WhEvnbRlsZTMYv4L+ZDBxd9cyHUgGI5d3xWTtqigRNWrjSBojqQc7j67dl5IyZkdeq1MvS5eGVosk9Altx/pywg1ykg3TEw2c4/QR6xceCLJz5daco9Bo5cBJd+BfsvgzU59P/N+SFycHpg77SOnRI7hmV0UKe7ajZ6BKV7haXaKpY6qpZ1GbTjzQ8uJmzRfXcOilrUE6DWCuqt4I4F6K3ATAGMZfmIMyyMLMaAOwyU4tAzjJGhMCiwQUCJakRAM1SLBDRLgwYaGAjGZDIT0CKaBFX1IO+w4f05R/oPTgntnKwMzOro/42rT66r7y5br02qrvkj3ji96xSUt9YCUIU3wD0M0kpSVoK2YjRuZXArC+U7cBZD7LNIQD90yokFRARaiQB/H2v+C84fQglUYRPysbS09MKFC3l5eWlpacuXL58/f/7MmTOnTp36yiuvjBkzZtiwYYMHDx4wYED//v0HDRo0dOjQ2NjY4YKACvTv379nz57RXOjOhW5ciImJGTVq1Pjx4994440PPvggLi4uNzf34sWLpaWlJpMJ7YUTBIHjOFqKoJzmK6tWQiEWeygC6LeMdyOJXtozm81I9bv1yLe+5EObJBYQERARaPsIiAR02x8jsYXtHwHEGen1+oqKCqSfVVxcjBwK19XViexz+58BYg9FBFpCoMnz3oM/NqHq0Aun6G99fX1paen169cPHjy4Zs2aqVOnDho0qHPnzsHBwf7+/j4+PkFBQT179hw9evSsWbNWrFixatWqTz755OWXXu7Zs2d4eLhGo1GpVP7+/mq1uk+fPlOmTElKSjp27Ni1a9dKSkq0Wi2SBuK16VmWRUbQ/BOs8Hm1pY6Kef8bBJi7ts+cBzxAAdCAY1W1NRd+uvTd8WPZ2dvWrFk1Y8b0F18aO3Bgvx49nwsODpTLvd3cnV1dnVxdXVw6ODm7ODo5Ozg5O0ildnY2EgcbiZuTo7eXh7+/X3BwYHhERJfobv0GxIwcPeKNN16b9u7bM2e9N+efs5cu/TIhYf3mzZt37tyZn59/4MCB5UuWent5SSQSZDEXEBAwa9asCxcuIDH0/x0BLVQlue8Y8V9MwLAwPixA2VNoLQztefUEqMVAiRac+xkcOgfWZWpfefdYt+ezVJ1T5SFZbsoMR58UZ9+0Dsp0D01Wx9Bt3p0yer+482/v5K/aojt7C1z4GfzwE9i+A3w87/qQlw7II5O8I5LtfdfIQjPc1EkdVF97apJcFEn+4Vu6D9w1eNzuRV/f2nWCLKwGxVpAw+EHNAlwHNo7Wzn7YhNLNgCLuTFiZkBYAGUBFA4owOKAweEJFAWlNQi2MUINEQrZPkMJa4ZGuwucBTTLCW5YAYCqIscPWD5f+NNfx+QEdIv31sR1ei7XxTXVxWWrh1u+TJEnD0jWdF0167OCS7+AGhxoCai2wQBofQ8IAlAYQ0FRbJzFcNbCWWRjFNto+yy0dL5f+q45v3BMf0uLGtAPm7bi8WcFAf6G9uAEgoNlWQzDrFYrvwDgX4FC920Mw3Q6XUVFxc2bNwsLC69w4RwXLl26dOPGjaKiott3Q1FR0fXr1y9dulRQUHDixInjx4+f4MLJkyfPnj1bWFhYUlJSU1NjMBisVisyykEeC9FFeSaUX4GIa48nOmsRvGigheATBMHPh9Y0gLeyb01hsYyIgIjA046ASEA/7SMotr89IECSpMFgQD4cysvLKyoqKisrq6ureWZHtH1uD8Ms9kFE4BERePDjH7/0b/KeI/Lqg24ayA4Isj8kaTQazWYzhmEGg6GqqurSpUv5+fnx8fELFix4/fXXBwwYEBERoVarFQoFso8ePnz466+//tZbb02dOnXKlCmTJ09+8cUXe/fuHRISolQqFQpFZGTk8OHDZ8yYsWTJks2bNxcUFNTX1xuNRvTswbPP4qPFIw77n1ccWUATFHnHoD9z4WJKxsaZH370t7HjQjtHdnDzkNgIX56W2NhKpFIbqdTGzl5iawejjW1jATsbidTOztHWzsnOzsFG4sgd/e10G4mN/T1VNflgaydxdnB0sJfy+TY2Ni4uLq+//rpOp7v7WPtwYvcJAPcbQfmgyiHvTPPqE1A/5J7IIHKTBlCLhATAykCrYCMJiuvAdxesCVt++fCLc8P/b1d43xTvsPWysDRH32R5+E53TbbEO03qm67okh3aL3/kW4WfrQMbD4C8c+DYdZBzFCyOuz115vGBg9Mjw9d06ZKqDE12VSV6BKR1DEx38lnTwW9lcPekv76YP39x9foU8tAJ8NNtUNsAzCx0+meiSNqqB1YdwMwsgdMUS0EviAwGcKjy3BgtZoBZOA4aEtAMCy22KRayzyTXExLuYHCxOQHN0dDQTNpKA5phwI/nGob0/SIqcpWDfKWTJtNDk+vuu8dLlu8t36dQ5Cv9N/Z6PnFl4uUbv0LBDgsL6o24Bbc0ss8EAUiCoTAo/cFgJCMkoCEHfT/SWZh/z5g0GSLQOEZCGvpBIy4eExFovwi0ZuFxv96jN6LQTRtJYfBEJO9onWeHmxOXOI5bLBYMw5BJLFrM3P0JoNHLVWhVI7SZ5dcY92v5/Vor5v9BBPhVKC+/xg+ucIAeehV+BB9aUiwgIiAi0A4QEAnodjCIYheeegRIktRqteXl5aWlpWVlZdXV1YjHwTAM/So/9T0UOyAiICLwexHgn6larKCVq3y+EqGGIxJA0Ov1NTU1VVVVN2/ePHLkyKpVq5Bkhxdnkerq6urj4xMaGtqjR4++ffuOGzduzpw5y5cvnzdv3tixY318fCQSiZubm1Kp1Gg0vXr1euWVV7788ss9e/YUFxdbrdDyEQUcx/mNNGQi3fwx8m5Z8f8TQQBtVPCjAACw4JaKqvKMzRtj/zZCIrWzd3KWSOwkEgcJRx5LHTvYSR0lPMsslbi42kodIPVsZy+xs7dBNLQtd449R0fboDM5ItlWKpG6cAKgNhKJbWNhqZ1NB2dHiQQS1nZ2dja2jVy21M5GamcntXeE0dZBautgZwfj0e+O11TXAQDMZoymAIosLx1yFyeWZZv7O+Kc4NHor5BY/H3pxkuxnMC1kGDm9LEBTbAMxjIYwxANVpLmSuHcOQygrMBiZiwYADUW6EyvqA7s/I78x8KLfUZtC39+i99z251VGRL5BhtFinNgultYmkdEokdknGvEkm6jtsyNr9uwF/znF3BNBy5Wg4RcMGbKTz2HHgvosj0kaqeP/yZXj0Rv700qTXZHZaqnKkEWsE4evOKVaSfWpNWeugYKS0CtHpgs0PcfTgGCATQLeXAOQgZAKDkjY47e55ChaEBBuvduvIs6DW81yMSbYWEtjdQzqhFS8PdElgRQxdoMAAFYgDeAo99WDH3+XwrfD2384hw7fSvxyHVWHXP23eep2akMS+o/PC3vsKFSD6nnBqj4AVtIUjgk7aHBNc0R0ARNQw6aYgk+soCEkUVm103/3ks6350u0CsZL1QuyBSTIgIiAvcigFYO9+aJn0QEfkOAX1v+lnU31crVqdDlgzjf7oIn/hcRaM8IiAR0ex5dsW9PCwI0RRsMhoqKiuLi4rKysvr6eovFIqQJnpaOiO0UERAReOwIPGB93/pr8ZXwCf5cnpJGvLDVajUajbW1tSUlJQcPHly1atW0adNiY2MjIiKCgoKUSqW3t7dSqQwPDx8wYMDUqVM//vjjt956a8SIEd27dw8JCQkODkZlgoKC+vfvP23atHXr1h05cqSwsLCqqgopA2IY9GBGEETrn0/41oqJR0UADSuvFW42m0mSrKmp2blz5z/n/bNHr+42jnaQdraV2HPUMGKPveV+Xt5yhZ9vQHBAWESwUunj7e3h4mrv4NjIPvMEtJ2NxF5i4yCxk0ocpBJoxmxnK7F3dHByc4cEtIONnYOdvWOjKyp7W4mdjcTF0cneFjLWtvbwNEhnw+AgtXeW2js72Dk62HFMtL2jra19n94x0/8+a97cf6WmZH6zM//0qfPXrhbpdWaT0YpZKRyHVnEIE5wLNMVRpZC5bGSfoQVuSyauj5TZyNmiKwnpS46AZhmCZiwka8ZZrIEEOgvQ48AKAA6gpXOlnr1VA87dBql7fn3jo73dhyeqe8QrolI9wza6BG5xCchxCcx2DdrqGZEVHJPTecj2MX8/PW993f5CcLAQfHcd7DwNFifXDf6/HT5dFwb3ifeL2OQdsM3DL8PDN9XTJ8XTZ0NQ2Na/9M/vP2znlH+cSdlmPXkJ/GIAdVRjAwiW429plqRZhuY45+ZzqLFHkI9mIJHcyPYLMeRvHfcw0YiMpu9HQHMmzBzbXVsOvvpyf/8Xlnceku8X87006IBb2GFbWbosPHHiu98ePENU6mGDiXvaxkCemEEdIDiZaZGAvgcg8YOIwBNFAH3rn+glxMqfagT434Xf1wt+/YlOF+fb74NRPEtE4OlCQCSgn67xElvbPhFAHgh1Ol1NTU19fb3VahV5mfY50mKvRAT+RwjwDwlNEjxbh9qFHAohIo8gCOTWvL6+vrq6urCwMD8/PykpaenSpVOnTh04cGBYWJhCofD09JTL5SEhITExMcOHD4+NjR02bNjYsWNHjx4dExOj0WikUqm7u3t0dPTIkSPffPPNxYsXZ2VlFRQU1NXVMQxjtVpxHBfveH/OvDAajVqtNj09/cUXX5TJZBIbia29HWSc7SVSV0cXD2fXjh2ie3eNHTXk+SExUd06dYoMCwhW+6n8vLy83Fw9nJycHBwcpFKpnb0NT0Db2knsbSWONk5OEm9nG5mj1MlB6iSx7SiRuEns7R1cpS5uLi5uLrxmtLMLtIC2sZNInSVSV/jX3tHB3sHFzr6Dnb2b1K4DNILmgq2trY2NjYPUydGhg52ti0Ti4OHmFx7avW/vQWPHTJg188OkpOT9+/fX1tbq9XeQY0wMw3COk4ZvbT9WAhopTTDQhrgx0oBAkQBQlRgDFguwNADawvHOFgB0GLheDPYeoL9YcuW1d451GZbj0iVRol7jFbXJLTSjQ0C6kzJFKv9a0Wl9SO/4Ce8eWp5WnbzH+v1N8J+bIGU3+PDfFZPfv9Z3WJ4mKtkrIM5NucZd+bWXJsFbva6jerVP4HLf4MV/HbfpH/NPbNhSvue48Yci9loNqCFAAwB3ANABoGOBgWEaaMJKYRTDUAzT7PFeaMvdmEa8PLJnFnL090xRSLvfNYgWkNeNFse/5XCGxhwBbdYDbTW4dgt8uLS0Y7dNToFJjsq1QT0TP/j8wqkrwMBC22cCQP+HSGyFN3OHbaYZlkY9IBiGQPbOaHzvtXFuoTuCAoIeCLcQBNliUkRAREBEQETgSSNAU7TVaiW4gF72he+lNN77n/TFxfpFBEQE/scIiAT0/3gAxMuLCKAfXYZhkO9m/uG52YOiCJWIgIiAiMDvRKAJ74w+8gKLfKXIaWFzRhg5SsVxHOk5EgRRW1t7+/bt8+fPp6enz5o1q1+/fh4eHhKJxNHRUS6XI0WOyMjIUaNGffrppx9//HG/fv1kMplUKnVwcPD09PT39w8PDx87duyiRYvy8vJu3rzZhArnmyQmHhcCer1+586dvXv35oVT7KRSVw93iRRy0DJ/n4HDBkZGd/IL8HFyd7B3sZHYQu1mjh12srNzspFIbW0dbG3tbbkgJKClUjsHqZNU6u3o4Ovo7OfkHOjm1svNPTq403ODhr0w6bVXpk1/Z968T5Yu/XLdurjVq1cGhQapg2TeKom3ytZbofSWh9vYe9nYe9hI3SANLW0koCHTbWdnY2MjtXd0dOggtXOzkTjbSJwlEidOJ8TBRiK1sbGTy+UxMTErVqy4ePFieXm5VqtFNPTjIqABABRL0JzfPZ50JgGGwUhggIGSygDoGRi1DCisAD9VgPRddRPe+aZz77WhzyWqw5K9g9IcQjOknbLsglMlfmvtFKtdVWv/8tdv3/vkl50HwOUScLMGnLwM1qTVvjb98F8Gp0f336QI/NovKFkRkNRRuc5HE+/ms8rNZ5VvUFxQl2Vj/m/76uSSIwWgsBReuhYHRgCjGbAmQBkAYQCYCWANUMEZw1gCZ4lmBPR9uVoh6SxM3zMPEYEr/MurKgszOQ+CUOSDBiwF/RDqTGDVxjLvqMVuQfM6x3y1YXv17Vp4pokGDRSFToV6G3RjdTQLWQlOK7YpAY1oaAG/fN8e3S0j6AG6kiBDTIoIiAiICIgIPGkEEMuMvJJotVqdTmcymcT34Z407GL9IgJtCgGRgG5TwyE25llEQEgMof6jxy1xK/hZnA1in0UE/kQE0K2G9xGElPjQlphwA0x4j7pLBjHI9TwyYMFxXKfT3bx589ChQykpKbNmzYqNje3atWvnzp1DQkI0Go1SqVSpVN27dx8/fvy4ceO6du0aEBAQEhISFBSkUChkMplarR4yZMjMmTPXrFmze/fuH3/88fbt23q9nr8NotdEmjDj/NE/EbOn4FI8LGg7k2GYysrK/fv3D3j+BX+lGlof29hwkhd2tlIbiYONxE7i0tHDycMNmkJLHeydOthIO0gkdvZSd07S2dHJ2cvZycvL01flHxgSEtarV68XXhgwZsyoVyZNeO+9v3/2r/lJKUnpWzdt3LE577uTZy4Zv048H9X1g7/9bXFRsZ5iGJPF2IA14LiVpgmKpWAENA4sP//6w7EfjmbvujBq3GcK/5jnh0wc/+pbL8SO6NQlSqVRd3B3k9hIpFKpIxc4MtrBQeri6NDB0cHNydHTwd5TInGRSBw5ZryRFo+MjHz11Vfj4uL27t1bXVdttprQgFkJK0FDTWaSIR5VkQMAQNBWksFQVSSnZUECUEOZoJUxABUEqMTA2ZsgK8/w6aqfh089quiV4hS6SiL/t63qa8fAZIn7altlvH3gSq+ua3uP/eZvb3y7PKFu73fgzCVw+CTYuB0sWnZn3KvnevY74KveotLkKPy2uXumuLiv95CtU6jjVSFxoV1WDxu3/Z8LLyVlVZ36CdyshXSzFQAjDYwMMDHAxJINkHG2WDjSmfMcSGMsjbEszkDxDehj8EF+HIXsLewo+nzf6d6EZW7xI18l536RpaC0B07Dxi/8umD24r37T94x09AlIw5tnymMxjm+GxAkS1NQKgTKVXMENHcLgvrOgCUB26j4fLeN/GXuJlpszIP6ft9eigdEBEQERAREBB4XAvxiEsfx+vr60tLSiooKrVaLxNke11XEekQERATaOAIiAd3GB0hsXvtHgP895lkDngBq/50XeygiICLwv0MA3XOEt6AmadS0JpnNP6Ji6DUOi8ViMpmsVmtZWdmxY8e2bNmyZs2amTNnjhkzpkuXLl5eXs7OzjKZTKPRhIWFRUZGdunSpWfPnkOHDh0wYIBGo/H09PT19Y2Ojh41atS777772WefZWZmnjlzprq6Gkn9CsXxObtISIWjhPAW+r8DtU1cmYfCbDafPXt20qRJSqUSyjzfJZ+RcTEkoO2hMbGtixRKaNg6S+y9pU7+dg6BEonGvUOnnt1H/XXIpGnT/pmyYcv2bTsPHDhw6tSJmzdvlJaW1NZW6/V3SAq3ElacJUgASg3GchP47gwY8NdV/Z7/4sxZwooDU4PFSuAkQ0DJBhbKYhCAwqFfPoIBVIXeeuQk27vf0r+O/Ozwf0p0OHul+OcfCi9+d/Lo1u3bExISZsyYMWDAAF8/Hy8vb7cOCkept4O9p6PUQ2rnZmvrIIUi0bY2NpyCNadd7ezsLJFInJycVBr/wUMHffzJ7CPHjmj1Woql9CY94qCRxrHQtvcBaW44GZLBcJKAQscs9M2HW0EDASpw8LMF7LuEL910Y9y03D6jspRRa73DElxDNtpp0p1CM+00ydKgZFvVeo/OGS+8WvDJakNSLjjxE/j2FNiwjZy/5NpLk7/pF5umDF3jG5zs6Z/eQZbp4r3FXbbNTZbp4rkuMDRh6Mid//zsatJG7cET4MxPoLgWaEloZ20GAOOEPqwANLDk/2fvPOCjKPr/v+mFEBISaiABQoBQBBEQwQJYQMWG7RGVx0cfnsf6qD97L0gT6b1JURABEcEK+qgoKApSVEqSC6lcruTK9pmdme//P7vJeVIUH0EBZ1/zuuztzc7OvHdzc/u5732+OjV1ptsR2ZrJDLsgkxKTElsu5/kCeed/6dqsV2/raznPj7rH0UTeI27nbXEbDUotxCBIoCIEfh1qVfsi4KmW6/I32kHOvLfMLkKAPip/8YIgIAgIAqcagUh8la7rHo/H5XKVlZW53e7q6mq/3++kquYTgr2caoMT/RUEBIFjJSAE6GMlJeoJAieIQLSac4IOIZoVBAQBQeAXCES/C0WvO7tEbznienTL3HvXLo4G6nh3KIoSCARKS0u3bt26ZMmSRx999KKLLnKMIJKSkjLsJT09vXnz5v3793dSGmZkZNiKopSWlpaTk9OjR48rr7xy8uTJ27dvVxQFIXQ0y46I9hrdq7/UukPA+YnrpEmTGjbkoc3JyckJ8UlxcYl2rr+kugjoeL4hJkniSQjjk+Mb5CSnd2+UPSAv729ndLlz3Zqqd1YVOMUBJwAAIABJREFUfbahzFDq+FFQTOw3zLBp6tgysWUibBCCMEVBA7YXw8Brpl181Rst2vzfpBmf6QTUuqBhsNVHri5azEJcfbY0gFoCeyrhxpv/m18wY8b88moZggABKyATWUWKYWiGpvOvYwn1eDw7tu9/4pG5bVtfnBDXNkbKSEhKiU+R6nruXCj1jwnJ3HVaiuHP4xLjkhskdSjsMGf+HF/Aq+iyiQ3gOQmtQ+KgD3kaJUlblIftItkw3R6T2PkOZR98vgn+/eQ3va58I6NwfIP8l9PypyW2mpaYMyel5cIGzV7NbLWoQfOpjVq/cvVtX7y8QNuyD3aUw6ffwexlcO0duwv7v9Wm18qkVrOlJlNT2ixJyX0jrsWSuJZzk9vMTG43IavrxItGfDB6/sHdpXDgIPgUbk8RwBBmoIClgKUCaPUCNI9xJqZTbLmZYEIwRZgaTiEEOYkHf0VQrot4/qnWT2tH/OeJFpqPUMHZ2wLgxfbKcGw0KGLUoBBClsGIHcKMgBjALwqLK9SEq88/E6C5AwdfCPAI6Ohy1AjoI/RHbBIEBAFBQBD4kwlEC9Ber7e6urqysrK8vLy0tLSsrKympkZRFEeG/pM7Kg4vCAgCJ5KAEKBPJF3RtiBQT+AXNJG6uyv7T3118VcQEAQEgT+OQPS7UPS604PoLUdb/9UYZC4hWYR7IGAcDAZrampcLteHH344adKku+++e9g1w84+++zOnTvn5eU1bdo0MzMzJycnPz+/sLAwNze3efPmubm57du3z8nJyczMbNu27cCBA++9996JEyeuXbt2x44dfr8/FArpuh5tJ3KM+JyeR4JufuG9+hgb/OOrHd5nRVFWr159ww03xMbGOp4btjwbw7MN8jjoOMeEIzY+LjZByu/csu+APvc+9PSiZZsXv17Wu+/orme88PK4fU89/GH/Xvc88X8LayqBWlxE5ibDoNqOvkApjz1HyAIGIQV2F8F1f1/XqNWolu3GXXvzih9LUdC0xVoASnniOF7f9gE2uEcE901WAKbNr8zJnXdGj7fvfeiLHaVQEqwNcRXaXiixdNs0A7OwCroJkyZ+2rfX3Zddes/U6UvHTBh7/a2X5XVKa5wTIyU5jtCSlGAPTuKP3MNaklLSEh0ZOiUtudfZvSZNmfj5l/+tDflsDZpGRGfHLdpiXJWOLrYMbSEwKEBQhj37YPmyyofu//jCATO7dJ/WqO0sqcUMqeWUlPw58XlTpZbjG3aY1b7/mguv+vbBp4wJM+HDL2HdpzD/TXjoxQPD/v55u+5Lcru+0aRgaWru/JiWc6ScOXFtF6V1Wtqs69K8XksGXP/uP5/+Ztba0Mf7YK8KZSb4DFAwj3TGAHZXTSdRn0oM1aIGIQbBBjGRXTDG9hc/jFiMWoRaiFoGtfjXA87l8SuC8vEUoKmjOwPPKcgLA9P5BsIxYMHU0LGMWZir6MwAywBscYdtizo2HT8J0LZ3tPOe45wXIUD/8W8v4oiCgCAgCBwXAhEB2jCMYDDoJLguLS3dby8ul6u6utr5LIcxPvyDzXHpg2hEEBAE/nQCQoD+00+B6MBpToAxhjF24vVO86GK4QkCgsCpTCBaXP5N43DE5aOFJEeactp3hEvnXREhhDF2foy5Z8+ezZs3v/nmmxMmTLjzzjuHDh3apUuXjIyMuLi49PT0Vq1atW3btnnz5s2aNWvfvn3Xrl3z8vIaNWrUpEmTwsLCSy655B//+McLL7zwxvI3fvzxx1AoFLl1URRF13kgbcTaiDHmWFc7orOtotbFU0cTcNYjnT9pV5w7Ooyx4/iMMXa73WPGjGnXrh23dE5IcCKDY2LiEuJTJCkmLjY1NiY5OSmtWbMWI/5+y9SZ47fu+rCocrcnBJ9tJn37zuvS7dW/jfjynPNmdmw/8l+3Tfvuq5AWqhcCQbfAVAFUsA2FCYT8PMh53wG45V8fNM1bnN50QZsOE7bugFqtzsqBAWYszJjC5V4GFmAdDB8yfDqsXk86dp6T3mh2XttXh9/+9vYSrkoHIWCATsAEagIhWki1KJQHYNFb+8674ImRd8z5/sdQSON6uE/x7ivfu3LdqkeeefSsc3smNUpMzkiSYqWEBrHxqbZ5tSTF8ShpnmIxJo4L8VKslN8h98XRz+8r3oMpovV2EwScqGFuUR0tQFvgeBFDWIWvv4URI9bld5iS1Xxy09wZjdssjG0yPyXvtbROs1M7jT37+tevfejDCWsCs96Dd7+Feavh3meVS4fv6XzOJ606v5fR+q20Vm8lNXsts/3K2BZzMjq9KrV6KavX5LNuWPnvl75ZuObApm3hcj9UBcGtgkcHP4KQBRrlyrfJrTYoAoLBsnhyPssCbujMI53t4vzgwBadifPIa/GCACNqkWMSoH8lotn5/wGIrvZzV+WomHFqBzE7ocyIcpsNW4Ou7xYBzK8K4G7O3BaaELBss2fKLU4OX6LPyFEFaKdjUf+ljuAe/Rj1olgVBAQBQUAQ+KMJOG/vEbu2cDgcCAQqKytdLlexvThx0E5mQifrdeSz3B/dV3E8QUAQOGEEhAB9wtCKhgUBAGIR0zQVRQmHw7quR7uXCjyCgCAgCJxUBKKln9/asci+v7Bj5N4jEnQcyWQYHe1CLBIIBKqqqoqKinbs2PH666/fc889jkN0Wlpaenp6ZmZmw4YN09PT8/LyzjzzzF69erVq1SrBXtLT01u2bNmlS5cbb7xx2rRpu3fvdrvdTmQ0QkixF4RQdCcjnYmsRMZyKt757Nix4+qrr3ZEZ+ex3iWZy7CSFJuRkd2+fYfRL431emtMJJskqFoenyx//kVt585P57R8ZcBFG9t3ndal50sTX/7SVLjmSFFEgDYjArTFzTE4SE8Anh67s2n+K5k5r7XpsGLuYjVscOcFLgkywqgBrJZBkN9z8lxz3ALjoAxf74CevWc1aTIlP3/xxZeuLyrnFhNBYAEIGtzyAgPFYLcf0uDtz8L5Pe/rP+CRTV/4LADZAG+AusrlIldYMQEBQ2C+89Hay669tGmr7MbNGyU2jLHjvKX4lLjEBklSnO3HESPFxEvJDbgi3+OsHuvee0czNedK4MYgThwxrU+TWJ8s0QKmYh6D/NrrB7t2ndAmf26D7CnpuVNTc2ektVlacO7GfzxZM+ddeG8XLPoY7nllW6/rFmZ0mpiRPy+9zYK0nFel5OkNmr/RsMUaKX1+w9bzU/MmNT9jRt+r35i6Wnt7G+wMQrECbgVCmiYbZlg3VBNxcxPKMwc6Js6IcdsKy4ZNeSg08EDy+ov16Oqzo0Hbj5RLxb8SAR2tLEf/e0SvR9c5guBLozRoR32OaNAGD4Lmp5WfWUdE5nba1NadHadnx2BbCNDRwMW6ICAICAKnEYHIh0DnK3PDMDRNCwQCNTU1FRUVLperpKSkvLy8urra4/FEkhOeip/ETqOTJoYiCBx/AkKAPv5MRYuCgEOAWMSZWT0ej9vt9vv9hmEIDVpcHoKAIHByEvg9wquz7y+PK7p9R0CL7OXEUDs2ApE3ScaYruuhUCgQCFRXVxcXF2/cuHHu3LmPPvro9ddf36dPn8LCwubNmycnJ8fGxmZnZ7dr165p06ZpaWlZWVktW7bMzc3Nyck588wzL7/88pEjR06ZMmXdunX/PyPf3r17g0Guh0bHRNcLevxvdD9/eUQnz6umacqyvGrVqu7du8fExDi5+HjIr23BIUmxSYkNOheecccdI998840S1z4Ak0LYfkSIQokLbhuxtkn2MwUdpnfoOmnIdUtXrguqKigBHoiMTTspHL8LNIkdBG1x0wSGGA9Xnv36gQ59ZjfpOLtj36X3P/19dRBkzOVOAphSq16A9lmgIbCCmhZCUO2Dm//+ZssWL+a1nvDvuz7/ehtXnQ/4wGvweGqDO3XYRySAMHz9Hbnsb0vanvHIynV7AiooCAIybNsGN14/a+TIBaUVXOxWQdZAYYC37/lm4swJFwy+IKtlk9T0hlyG5hR4lsLY+MSUBmmZWU0kSUpKSS7sWjhqzKjyqnIAZjFLR7ptnfwzAZrYEdAMwBOCb7fD9dcvO+f8BedcuOiW+z+5/6U9E5bC2EXw4Djr2n+Xdh+0sXWPN9LbzcjqsDij9VsNm63OyHkzp2BlTsGi3I5zep2//JoRHzzwwqZFa6u/OwA/HIRaxn2ckR1LrlHQCbMtNYjzyJV6VhfjbOflc2yc+eVmgz1eAnRUfHC0uHy0yzq6TpQAXd8KJTye2SkW4S7bTuER0Lb0/KsCNN87OsbZWXcioK2fu6MQLsXXHxloXWi23fPI1p/XiK59tBGK7YKAICAICAInioDz4SrycSvy+y3DMAKBQESDLi0traiocGToUCiEUJ2R1InqlmhXEBAE/lgCQoD+Y3mLo52mBI4oWGCMvV5vZWVlmb243e5QKCQ06NP0EhDDEgROeQJHfB87xlE5+/5y5ej2I3cgjuDrPHXcMCIpaBz/oogeTSl1jDtkWfb5fMXFxVu2bHn77bdnz579wAMPXH755e3bt09M5J6/TpR0enq6JEnNmzfPy8vLzMzMyMho2bJl586dBw0aNHLkyOeff37ZsmU7duxw/JHqIkntfkT382gjOpbxHm3fE7Hd6/W+8sorhYWFkdjnpKQkx4IjLi6uT+++zz076vvdew0dhWUfA5WBHJKrArLX49crquHOf6/r3nVOk6zRObmPX3/L4i3fczsIWeZ+GU6UMJcVKbWdE3TGLTIwF08ZfPAVLbxgUlaX6RkdJg0evnxrEXd2rtXBAkaZYRsSI6A8uNmCIAKDxy9rMHbszk4dRzfLfupvN67dtRuCKoR0CKhcSnY0Vsc52CDgDcItI1fknfHUc5O2ezSu2GoIPvvUvHHYiq4dn5k/f09JGWMACguHCG9fZ7JP8R5wl7313tqbbh3Rqm3beiBxUkxCXEJKbHxycmqD5NQUKVZKbZg6/pXxpeWliJhHE6BtDZpHYiMLftwPX34DX2yHeStqbr7v/bMvXdO+91vZ+cszcpa1aL82s/XytJZzM3LmJjaa3SBrTkHXZRdf/cHzE8oWr5K/2An7DkJFAPwGyBaEMQS5uzVfdKvOosIRnaMfHYeN3ylA/6IFR0SqrRdwo2Tluv5F//lFAbpeej5cgLbIcRKgD9Ggf1mAtkPFfyY6R402elRiXRAQBAQBQeCPIOB8cIp8zR99SIxxxI6jpKTE5XKVlpaWl5c7985Cg45mJdYFgVOdgBCgT/UzKPr/5xOITKiOhsLvVBHy+XxlZWURW6vy8nKPxyPLcsTTKqJx/PkDED0QBAQBQeCPIhB56zt8JVqVPmT98MqOwZGmabIsh0IhWZZramq+/vrrefPmPfjgg4MGDcrLy0tNTU1JSYmL4y7ACQkJLVu2zMvLS0tL4+npUlKysrKaN2/evXv3O+64Y/r06Zs3bw7Yi+OY5EjSkayGER2cK6T1UdIOs+i+/VEU645DLGIYRjgcfvjhh9PT0+Pi4hwJ3rF+TklJyc7Ofv7550tLSxm1Y1N51zUKYRMHwPZxdnvgwfu/zW8zs3HGhNw24x5+8oN95UxlEMKGgQHZ3sPEtuql1HLSCTrHDlnw/tfBjv2nZXadmd1zevuBU9Zu0apNCFLuEI14RjmDUcSPyheLQICAEdZg8eK9HfKeK8h7+d93fPL9bv6agesKwtx3AgNVCbhlqAzCDf/4sFPvKXc99VFxLffBAICd38EF/WYWthsza2p1jR/8qqlQTWFhp+hMtouqMx2B9cHHG84fdHFMQgMpJik2PjkhKSUpJTkuMS4mnttxxMRLKWnJ02ZOQ8QMysFIBHTEdLjOLMKWMW1+3P3DF4ZLh81p321KaqM5TVq8l9vus9z2GzKyF+cWLG7bdXqP82fc/eiXc97wbN0Du8rBbYCfgWxHOluszkGDC+1R0bmMcnfsw0tEeia2AwrhQeG8K85T56pz/k0Yob9U7KrOXjbCyEOUJHu4uHwsW+yW6luJtuCIXo+24+DrdcLx4e0fRS6OcvaIbrb+sM5eTms/689RmrMPH0EgVgQBQUAQEAT+MALOzHXEw5mm6ff7q6qqysrKSktLXfZSXl7u9Xp1XRdGHEeEJjYKAqciASFAn4pnTfT55CLg/IbIUUMMwzBNMxwOu93u0tLSoqKi/fv3l5aW1tTUOOpztKryC9PwyTVC0RtBQBAQBI4TAed974iP0W+Ph6wfsX70Rqd3xCKOa4fX63W73V999dX8+fMff/zxW2+99fzzz+/atWvz5s0dY4qWLVtmZWU54bFpaWmZmZmNGjUqKCi4/PLLH3rooSlTpqxdu3bz5s1FRUWKokSG7rzPOwJ0RIY+vBuR+id6BWNcUVHx4IMPOp4bmZmZjtqelJRUWFh4zz33bP3mK02TeaStrttRzBaFMIWwY3/s9cJzz25r03pa8+azO3edO33OQa/MzQwQmLXKQURMjAmxmJ3aDhGCKEWWbV3iCcP31TD0jlVSixcbFs5q3nf81Lery00I2GKr7gjQ3LvYAGIAQdQyMNV0CzZ/KZ/d6/k2LZ76122ffL0FVM02VgDGj2WZPMLdwhrWEUCJF8bO3tes8+hr7/x4exUEAXwafPxfddgVr/U7a/qsqe4DpVySVpkjQCuOAK3ScH1RZEMPa/RAmfr007NTUwsSk3JiEhpyO444W32Oi42xS0HHDl9s+cJiCNsG0BH1mSdNZLxwIlw2VYDbZoA/BDfeOq9V7nONs2dmZi/u2GXt4Mu+vGnEN2On1Hy0Gb7dC1UyBCzQ7dp2wkaigKaDxpuyeB7GwwXoI2rQQoB2pGohQJ/otxHRviAgCAgCfwwB5/PS0Y6FEAoGgzU1NVVVVeXl5S6Xy0lLqGmaEKCPBk1sFwROOQJCgD7lTpno8ElHICJA67quKIrP53O73c7E6fyMqKqqSpZlhNARJZWTbjyiQ4KAICAInGAC0aLtcVx3TDww5sGylFLNXmRZ9vv9RUVFX3311fr16xcuXPjQQw8NGTIkPz8/LS0tNjY2ISEhKSkpISEhzl4SEhIaNWqUn5/fs2fPiy+++IYbbhg9evRHH31UXl5u2CbF2F4i7+fR/T8WbP/zfdQhd26GYZSUlNx3333NmjVr2LChIz2npqY2bZZ9yy3Dd+7c6fXWODHLpqlrmmaaOmWGBWELuNVyOAwTx5ec2W1ui5wpvfsveXWF2y1z2TRsEG6PzUVhHRMVLA0sAyyDWgb3SgaoMWhRLdz1bHHDggVSi1cadRv/1NwdZSb4KcgUNMbtpS0KjFhANaDh6urvA0E3oVBdCX+/cX2XtmOGX7ts74/cl8FioGo8VS+ygpgGsKUjC4d1LaDDsnW+jue+2PWSMe/vhjIMIYD1HwYvuXByx7ZPL13kq/HZ6jMGGVkqQSrRFMY16Hr1OawSg3sPI9ixHW68dm6XDve2zhmWlt5FikuT4uOl+Fj+GJcYn5gqSdJNt9zoCxy0GLJz9pGIBm0L0KwukpYnOzRNbFGAdevLbr1t0b33fzJjrvujz9mWnbC7GMp9ELJ49HcIQy3ihiMhi6kMG2AgMBG3zyb81PPIXVYXBew84Yc5QgR0JPA5suIE/UZHQNddEk5Cv6M8OnVEBHR0yPSx/J+KOoKAICAICALHl8AhH2MOb9zJFx0IBDweT0VFhfMDYuej1+GVxRZBQBA4FQkIAfpUPGuizycdAUopQkiW5WAw6EjPxfbicrkqKyuDwSCx+J1nRLBwVn51Gj7pxik6JAgIAoLA8SDgvPsdl8dDuuO0SSk16xeEkFPHiV92viasrq4uKiraunXr9OnT77vvvoEDB7Zv3z47OzstLS0hISExMTE9PT0jIyMtLS0uLs6RpNu1a9e3b9/7779/6dKl3377bVVVFbHIIXHQh3TmiE//53f+Q3asrKy8+eabHa9nSZIaNmyYmJiYm5s7Y8aMUChgItXjrQQnoBnq+mkxiycDZODxw9q1Rof8cbmtXu4/YPG6jTwq1wCQMZEN7k+MCcNEJVYIsAZIZ1glxDCBygAHdHjg5W/S2i1pXPheWsHUq+58e0c1mMDVZ52CaSfQ49HWlsGYwliYgqIaUHMQHrn/i4KcUddc+sb3O8FbCzrh7hyUS+EKgEJYLRegMasNw+4iOGfwhI7nvvj654FSC1w6rN544NwBT/fp9dSiBVUH3eBXsQqqjDXZ0DWEdctQaViBWpUFdRI2LcVEgAns/gHuuXNTYf4rl1284uw+o1rnDU7JaC0lxEoJkhSXKMVy9TkpOS0mXvriq08xNcAOyOaUmFUX/kzrA5YZBYZN01Q1nhoxGAJZ5XYctSaPi5Ypl5vDBMIEFIsXnTCdEJOhel0b27o2481w22qnXR4OzRjh6vDhGnS988bpJUDX68DCguOI7w5ioyAgCAgCpy+BQz7GHHGgzue3yEc1x4LjiDXFRkFAEDgVCQgB+lQ8a6LPJx0BhFA4HA4EAl6vt7i4uKioqLi42OVyVVVVBYPBiPxxiFRxLNPwSTdU0SFBQBAQBE4YAedd8fDH43hAp3FKKbGIE8uMMQ6FQsXFxRs3bly6dOmLL744cuTIAQMGFBQUZGRkxMbG1ieyk2JiYlJSUho2bNiqVas+ffrceOONDz300MyZM9etW/fDDz+EQiGnn85Xko4AjhDCGDuHc/IoOhOBUzN6pL86RudbTK4OY+z3+5966qmsrCxHgE5KSkpNTb366mFffrGFD8rSeUAx9fNCQsRS+aFtHT5kGCqGjz+FgQMXt2oz+pq/rfnw85BqC6IKoQYhyMLIItgyEQ0RSwaTOzQzK6TjUIhy9fnZRa70HjMyO7+X3nbFrf/59MvdlslzAxIeccwdJjTuw8FMRg2M/Zoe0EyoqICxL5Sc0WHijdcs+WRjSNbAoGBC2ASFAqg8IBsQUR0CRcVw9bA5PfqNHTt7X5kBLg3mrKi6YPCYfgMeWL5qt2pyrVxlpgp+HWp04kXYwJZp2E8RD5WmzOBD3fI1DLvxozZtFzRrMrNr4YL+/ac+++KaGfPf7DPwnLg0KaFBw8SULElqIEmJsQkxt972t0DYD1zzJZbt8c0744ikTj47LhrzYG1dwwjx2GrTAoPwgRiMmEwzQTGZYTKEGDcfcQw0LMb/Olq2c66jznK9FMvFaDsW+uePh9WP2rV+Nfr6qat/eBx0feUT+jd6MIebZvx8ZFEdiZahozYfvuq0f/j2o235rfWP1o7YLggIAoKAICAICAKCgCBwvAgIAfp4kRTt/EUJOEJDOBz2er01NTXV1dWO7UZZWVl1dXUoFIqkrnK0gyPcLv5FyYlhCwKCgCBwKIHD3yHrZLVDKx7/54wxjHmIq6IoHo+nuLh469at77zzjpPVcMiQIQUFBY0aNXIComPsJRIrnZube/bZZw8ePPj222+fMGHC5s2b/X5/RHSO9txw1OfDQ6ej6/zC2BzRnDE2ZcoUx8M6MTHRkcWfeeYZT40PIQtjLh9jItsadKDu0ZZ3ia0R/7AfLr9iWUb2Y8NuXr1lF3eNAACVIN1CJrYbsCVsREOY2AK0SSjRMDffgPe2Q4dLlid3WpKcv6z/lRu+2AW1Guim7XlCuO0JhTCDIGMKN4LmufbA7YVx4789+8wpg86d/cnGUG2Iu1HoREFQY0KtaVt2IAAF88olpfDYo5927PzUw89+vrcKahAsWHWg/4WTOnZ56LWV35dUmQq2BWhQVfDqUIHgIEM6QyYhfsS8AFQ2MDHgi8+t8y5ckZ07J6XR5KYtp1446I3160ltCDwBvHPfrguG9E9o0LBR49ZpDZvHxCZLklTQqV1ZZanFLGzHZdedAkcedbRMLkAz5+sEThgTTOoLRZgpmIX5I+VGJY7ubKdt5AI099ygdZf2kU4uP4BzkOjHY7nyD/9/cY71s8cjHfK4b4vuuRCgjzte0aAgIAgIAoKAICAICAKnAQEhQJ8GJ1EM4U8jQCyiaVogEHC73RUVFVX2Ul5eXllZ6fF4FEUhFr+jdpbDbxSP5fayfm/xVxAQBAQBQeCEE3AUXsc0KSIKE4v4/X6Xy/X111/Pnj37n//853nnnVdYWJiZmZmQkOC4SMfExEiSlJiY2KhRo1atWnXr1u36669/4YUX1q9fv3///mAwGA6HNU3Tdd0wjENSAvymuQAhtH379vbt2yclJSUmJsbGxmZnZz/xxBOR7zuJxe2X7cLqQqHZQQQ1IUPGAHv2wn8e+Lp5zpMXDZ277yBUhXnsrUqQZhom5sHaTiZARHRbgA4RrBPbU1u14NsiuOimt5JazU/IWXDudetmrayRgVtPaKZhG1VQ5hybYQa6xSwVg6cW5i4oa1/w8LnnPrthY62s8cBhwgBTDYMHgc8EbvkRQjRkQI0fZs0tKuj06LAbFpe4wVUDC16v7HrWk736PrdmvT+MIIzBp1GV5/dDKgRU4OMCJIOh82JiZFKNwNe7YcgNG5Kaz01usaBr/9eeGP3jD/u4JKtrPMJZMw2v33PDzbckpKRJEj9rsfFxjZs0XvPOmiNcXlEhus43CsQi0aXeWcuy7badeOcjz/ZHaPywTdEy7mEvHtuGqA7XRXAf236/s1Z0z4UA/Tthit0FAUFAEBAEBAFBQBA4LQkIAfq0PK1iUH8QAYRQIBCorKwsKysrtRcn8Nnv9+u6fkgnjnxLyr0gxSIICAKCgCDwZxL4BQmYWCSSAMf50lHXdb/fv3fv3g8++GDevHmPPfbY8OHDzznnnNatWycnJ0csO5zA5Ozs7Ly8vP79+48YMWL8+PErV6789ttvKysrMcZOHHTEmsmRMn+ZArFIcXHxoEGDGjVqJEncEiQ7O/vuu+8Oh8OKojDG7JQDjGBwCqOgGyEEBw3wqgR+KIb/PPBlh8KXbxqxZtN2FmRQKdco1NCwaWKk67ppmnUaNOEOE4ioBjF1iwczb/0Bht6dUaWlAAAgAElEQVS8onHbVzJbL29WsHjWyppyFWoJD3KmYBFsAkZgUWaBxcN5WcCw9pTCwqVlbQuePPeCScvX/MCAe1aY2OJfzTKTQi0FHwLFBBo0eST1Ox+gwUMXDLhk+tc7Ye8BmLFgZ7/zR18wYMKrrxWZwG2mTW6+ASowGXQZQir4DfDbArTJnT80Du+Tzejim9Y27TG/SbelXS58a/JrgYowD5rWdZB9yLLrAMD3e3686rprk1J4+LMkSQnJSaPHjQ0r8hH4O5KundbycA26XoD+6e/vmeujZdwj9ORYNgkB2qbkkDwWYKKOICAICAKCwKlOIBIxED2QyHQcvVGsCwKCwJ9LQAjQfy5/cfRTm4BpmjU1NS6Xq6SkpKysrLy8vKqqKhAI6Loe7bwRmf+OuHJqIxC9FwQEAUHgFCcQyRD7q+Nw3sOdAFhHqHXkab/fX1JSsnPnzvfff3/y5MnDhw/v1q1bWlpaRIyWJCkuLq5hw4ZNmzbt0qXLkCFDhl0zbObMmeXl5c7RiUWQvfxyH2RZXrZsGQ/atZ2pk5OTh10zzOv11nWGILtvjLs+YF6AgaxqOg36Ndkdgkee+ii/49PnDZq2YVPQLUOImCrIusVjnxFCTmi20xTvFVDkZCYEqFDgzsc2FfSY3m/Q+zl5C8dOCvkR+C1dBc3gPs7cThsQMAsotSzAAaZWqbBola/wrAmtCp4aNWmbWwEEFgLEjSksBAQBUYCGKdMMC2QLNnzB+g2cecbZr8xcWlFZC8tWa2f1ealL18eWv1FRE4SAwRP9ydTO+MewynSVu3DIJtOoRYDnO+R93fcj9LlgSmLbJ6W8h6+8b83He6DKgBBXvW312gDQgfEki1wH9wQCAy8cJMXGxMbHJaUk/234cK/fdwT+9QJ05Ez9JDYfae2IE/0R742PcCyxSRAQBAQBQUAQEAR+CwGMsWEY0b9dO9pELObi38JV1BUETggBIUCfEKyi0b8IAdM0vV5vWVmZy+WqrKx0Ap+d+Y+nLzq25S/CSgxTEBAEBIFTlED0e3m05Ohs5xnk7JSGjjBtGEYgEKipqfn+++9XrVr18MMPDx06tHv37vn5+VlZWYmJiZIkJScnJyYmdu/efeHChVu2bHG5XHbkMom0c7R7JLfbfeuttzqmH5IkJSUlffbZZ4ZhcNXYMglBvFiEEu41wQiYJk+XBwABHSZM+7Znv9EXXzFvxVrfQYWrzzpTEU8fqCPMXUHqDY7r1GzEeLhxCGCHGx4Ys6tZ4fiCnvObthr70CP7D1SATHi+QQOCJoQx1QhBYNkCNFADWADgg+3hsy6ZlZ73xAPPbiqpAT/G/Fi2AM0tQiwE2OBB05hoOux1wU23r87OfXzMFO/BECxZKXc7Y2zv3i+veTtQ5eVOEm7VJzMsM8IfweRJCJmuMl2nJrOjm5UQ7NsLV1+zuGnbx1v3fuHusZ/u8kIQQAHwq5hg25LaqDOmxphQ26B6xep3Mho35SHQMVKzlk3fWvuWbSfy8+tUCNA/5yGeCQKCgCAgCAgCJwkBxpiiKMFgUNM051dczmezwz+tRT6znSQ9F90QBP6aBIQA/dc872LUx4EAYzwfkSzLTvpBv99vGEZENXCmvWjZ4mjrx6EroglBQBAQBASBE0bgaO/ejl7smGk4dSJbnI0IIU3TQqFQWVnZli1bXnvttXHjxt17771XX311QUFBZmZmRkZGfn7+wIED7777bo/Hc7h30yFj+vzzz/Py8mLtJS4u8ebht1aUV9UJx1yANggxKEXcY9nOaxdWwbCNmJetcp11ztih1y1b/k5tkECAMBVUC0yeNA9pdjEss84DmttAY6ba6f62V8P9r3ybdca0zILZLTtO/MddG7btAERAQ5iAYTLNKZhqPKKZGBTAq8GGbWbfq6fnnjvx0pFvbi1F1bIBADLWEAOL98wWoA0KOg9JdlfCmAm723Z94aa7NnyxG2YvhH7nLu7dZ+rry/0m4+4ZFmAZ/DKRbd3ZUZ9NlcdBY5USGbOqAOwogmG3Lm/d8fFOZz0+ceE3+93MAAigkAkKoiFiyYARtZ1JABCmmsng290V1990d0w8NzNJz24oJUqDBg8MhAOayUdBD0Ff/6Vy5J72aFfFYfuJDYKAICAICAKCgCBw/AkwxgzD8Hg8VVVVXq83FAopioKQ82swnrDh8Pvx498J0aIgIAj8FgJCgP4ttERdQSCKAGPM+dF0JKmUE/4WuTuNOHse7TbV2R7VpFgVBAQBQUAQOOkI/PJ7uPMqpZTrtvbieDU4gcTOYJzJwqkQCoUqKip++OGHL7/8cuHChbfffnv//v0vuuii/fv3Iydc+egA5s2bl56ebqfOi4mNTVy//gMAIBbDloktnVCNUIUyjYJBud8yyCZ4ArB2vXzugJe79n5m0Zs1jmtzGLAOmskMHjeNFLuECVIMQ8OEIAsbFniCcFCF8Yurs3tMTM6f2arH4uv+/u6OPcAdM7QwAVM1Q476bICGWRhoEAAhBt/ugetGvpPR8Zn+f3v17W/0CgVhHu1smkBNArwwjVCNG0vrYMqwalV5z7PHDv/nx1v2wuvvQO++rxd2mvrmSsMbgLAFOhgaBBUWVKgWCXy2V7gALVOoDsKGzcqAK2Y1bHXP2ReP31EEIRNCOgLABvIB6JpWTVCQIZ1ZgC2QCX+tzAP/eeTVgk6XxiW1kqS4mCQpLkWSYqUVq1ZEjJgPOQ+RE334DW30FXLIXuKpICAICAKCgCAgCJwIApTScDhcUVFRUlJSUVFRXV3tyNC6rmM7f7Jz0Og52lk/EZ0RbQoCgsCxEBAC9LFQEnUEgUMJ/MKN6C/fmoop8FCU4rkgIAgIAqcOgej38OheRwyCIxWiXz18nVKKEM/7J8tyKBQKh8MejyfyteXh9Z0tTz31VFJSiiTFSVJsclL6nh9LTINEBGhMZExCBFTKU/JhCyCgwdfb4Job3m3b6elZr293BXnMsQagAjHBMhlyBGjAASAHGT2oaLWYEMdzotaA1R9B36EfN2i/NLvrkr5D39j0HagYuGwNtVyFJgETFIOXMOZ2F9iUDW8Qbrvn3TZdZ/a+5PXXP6x2IzDsEGYLVBM0gwKPWYaADCENoLoWPv8Gzjxn1HmDZ765Ht79DPoPXtDv3KVvroCwAUEECgurzKcSTSFUsfi+KqgKC+uAuPMGEI8MX3wNw0esb5b7wHmDX/7v10aZl6PikeBEA55zkJiKTFSDanZEt+0F7VLg8Ze2dur2TGr6ECmhY0xSelp2WkIDbsUx/NbhOjKPGAF9iLNW9JfNh8/7RzuDYrsgIAgIAoKAICAIHBcClFJZlisrK4uLi10uV2lpaUVFhdvtjk7IFLlndz6nRT6kRX61fFx6IhoRBASBYyQgBOhjBCWqCQI/IxA9mUVmMqfG4dNbpMIRV37WrngiCAgCgoAgcBITiH4bj+7mH3MnM2LEiIT4pNhYbiSd0ahpSXEFo8AoOBHQmMgarlUMr2bJtnMFfLsLLh+2vPvZM16avMcV4NKzXbhfhsGISQkhiCEdcAisGso8iKiqaSDgFs9vbzC7nDM/Jmt6SpuFl9z60TubwWNHLZugYKg1bfdnW33mGrTJNMMwfB64+/53C3tOPXfwmpXvQ6mHG2gQBowRwqOxgyozw0wLgNsPwVqAXZUw4r7323YZ9dIr7hkLlQGXze3Zb+z8V2sDIb6jR/Ur4FbBoxJDxaByZZ2oIKs8JaGuAfEo9KvvtJtufjs397lrb1i2bSd4Q6CY/HBgKYBUboCNeApCS8fMJIC5scaPXhg1f3/rTuNa5D6bmHaZJOVy4VmSpHgeWd67b+/K6iohQEdf22JdEBAEBAFBQBA4OQkghAKBQEVFhcvlKikpcblcZWVlTmYmTdMcF47IvXnkm2Pns9zJOSLRK0Hg9CYgBOjT+/yK0Z0oAs68FYlWi57GouWJY1k/UV0U7QoCgoAgIAicXgR+JkBnZJcUlzkCNCImzyVIVETlkOELm3rAgL2lMOKO91vkPf7QMx9XhutinzXg6vNPArRFGMJOwRgzoEFkejVY9X7FoEtXJGe9nJ0/t9/Qlcs/dusAIQwYwKTMZMhkhsGTEGoGt8hAPF2hAS+M3dSmw4TCHvMXvBGudaKUeYpGLkIzLkD7VAiEwOeHah+EfQAPvPR+o5y7Hnra9eEGuGTwO/mdHl+0rOygDwjwAwWQX+G7+FVQVWbqhOkU6xDSwa9DbQij8oNw402LmjS/6/aR7+7Yzc09kGVbX/OTjoEQrj5jBAQBWJQi3UJ+DSbN87Y7Y15uh6kNm94rJZ8tSdwDWkriAnRMrNS2bd6OHTuOdtVEz+mR+9jISvSrR2tBbBcEBAFBQBAQBASB40gAIeTz+SorK0vtxZGhy8vLPR5POBw2TfNoJpnHsQ+iKUFAEDhGAkKAPkZQopog8DMCzn2mEKB/BkU8EQQEAUFAEDiRBJ599tnk5GTuVSzFJiWl7NmzzzSxaZo6Mi1mIWIaxGTAHTGKK+DFsV91PmPUrXe8vb+auzlHYp+d9H1OBDQmBGOCdYIRIMxFapnC3goYdsvKnLYzs3Jmnn/ZivVfWApwJw0Fc1sPi3Gp12DILkRj3PJDtmDWov09+k3odtbsaXODIcz16LoFc/mXMR43HaKeENT6IegBGD37i3Y9n7x2xPoVb0O/fivzckdNmfW9bEEIgcZTJxqM20aHVQioEFJBNRhRCdKZrHMlnJQdRHfdvSo//5F/3f325m2gWdy1w0SADMCGiWTZFqQJWAb3m3YUbQs2blV7nrM8u/mc1u1fzs75Bw9/jklqkJGW36FVekaiFCN16Nh+27Zt9V0/9G+0xBzRnSMr0a8euqd4LggIAoKAICAICAInhoCu64FAwMlGWFpaWmwvpaWl1dXVoVDIMAz+FXv9Erl/PzF9Ea0KAoLALxEQAvQv0RGv/ZUJOJPUIZ6P0UDqZzH+N3q7WBcEBAFBQBAQBE4Egddff71JkyaOY4QkSTNmTPP5PQBgYp79jwL3qfAb4A7DmFf2FnZ7ceiwadu+twAgTC0n9lll2ImAjgRBIwubGIV1TcYkYMHOUrjqbx9ltZyb0XRe/wvXvLMxoAPPaYgpwtRAjCInxSHjJh46bxv8Crz2pqdbzynnDHz15Rk/VgWA+zUTDRGT/+4VA8WMMgOzcAB73XrQg+DTHfjCK5cPvHT96FdCl131do+zJk6ZubcqACoXkEMI/BjCJi+KztXnAE+ZCFTBpgWmSklFFdxzz5L8dg/cfsearbsgZIFCeCWLAiNgu21QLpljYJTbcACAArBpl3LWwLHpjad07LT6oiGLmrS8QpKyJEm69LKLe53VOSU1TpKkbmd0KSkpOZZzF/0ZIPKB4Vh2FHUEAUFAEBAEBAFB4DgSoJSapqkoit/vr6ysLCkpKbIXR4MOBoOKomCMI9KzmLWPI3zRlCDwmwgIAfo34RKV/yoEKKWavTiRTZH7zOjxRzYKAToai1gXBAQBQUAQOEEEduzY0aNHjzoBOka66KILKivLFU2jABoiYYN5ZKgOwy13vdG6w7PnnD/lsy0y90sGGkYhgyGdYoNx/42IC4ezhZtk8MyEsKcSbvjnyqzWs3M7rCns+dqGTaBRCBsytQi1uGE0psikzGDMAMOwv3zVTdjwMRQUjurSfdqoCUV+FTyyqrKgynwyt87AxAKCGLEIJkQhyKdDZQCuuHFFTtvpjz2tXXnNR1nN7h49Yev+Ct4BjaceDNglZEIY1QvQMg0oRDaB+hXiD8ETj647o/DRG69dvH0HD75GdudVBsh2xOaDsYBvxUApMgECBL4thYtumN+i45imObMvGvz+zSMWxiV1kKSGkiTdNmJ440YpDtXhw4frun4spy/6M4C4lT0WYqKOICAICAKCgCBwHAk4k2/kd0imacqy7PP5qqqqysrKSkpKiouLy8rKqqqqPB5PIBBwXKEj0/dx7IloShAQBI6RgBCgjxGUqPbXIhAKhWrsJRQKRf9mJ5pCZPYSAnQ0FrEuCAgCgoAgcIIIuN3uf/7znzGxUlx8TFy8FBsnrX/3HQJMx9Q54g9F5N4nvmx35oR23Z4fN32HCWAwEjIDMgoYxOT2zZRHLjvFkaF5eDCAzGBnEdz18Me5hZOat3/1nMHrZi6v8JogI4tgHXhDQDBgAiYzTFAMCHNPDARffwNXDV2f22rcw09tqq4FWWeK4TXAGwa/G2QvmCYlzORx0BiDXwafDM+9WFrQ4dW/Dd979bDNPc+e/tIrW0u9ECAkSMKI5w3kkrXF7TQUk/tqBDUIaxC2IFSryVXVMG1yce9u4y8dNPfbb0C3eGizCsTuILOAp2T8uQBNdQaltXDr/73buHBmfPNJPfstXvy6P7/zYCm2gSQl5OXkd+/SNTUxIT5WSk1K3rBhA0J2XPevncLozwDO+q/tIV4XBAQBQUAQEAQEgeNGwJl8IwI0/6obc18yRVE8Hk9ZWZnLXkpLSysqKqqqqgKBAEIoMn0ft36IhgQBQeCYCQgB+phRiYp/AQKM8SgthJDb7S6zF7fbfbSJKjJ7CQH6L3BpiCEKAoKAIPDnE6CUrl69OjevVWqDxKTkuJTUhFtuGX6wxh9WuP/G55tqrr9xRqv2o1p3Gjdu6t6iKm6FYYcFm6alIGJiwjBhBiEGBY1xx2cVwPGQ2lsF9z31aZP2L8Q1frLwnHkLVikHZPDbaQmRJv8kQFtgMo0L0AxpBKpq4OZb3myTN+6xx/f+WAyeMCFUsywfYn4ZAh6Q/WBYlAICbIFhQa0GK9eibmcsHzRg6yUXfda569RHn/6izMvBhligFoW4x3RdwRao3AOa1WqgqKCpINeGYdrk/ef1mTeo36yvN0NtmIc/+y1d5YHSJgKLHCJAI7Asbg/92EubWp8xrknXRV3OX/3Wh/Cv/8yIb9AsISU1NSWzTav2aSlpqUnJifEJVw69wuv1U3JMJzr6M4Czfky7iUqCgCAgCAgCgoAgcDwIOJNvRICOviXXdb2mpqasrMyxhHa5XGVlZV6v1zS5OZizHI8uiDYEAUHgtxEQAvRv4yVqn8YEGGOGYYRCIa/X60xXLpersrLS4L8zFhPVaXzmxdAEAUFAEDhlCGCMLx18cVyMFBfDI6Bbtmj16qtrTB3WvV07sN+Uru3Hd2g/5qUXfwiEQNWAcE1WxZaOLRNbJrEYwXayQYvrvIptU1EZIAdqYeRj37XoMjuj47gzB8+aunSvH4PfoioYXLY2TGbyGOO6CGhLkw2e6rCsDP7974+bNH1o5J3vFx/gZh0mUAsMQhVMZIPJGijcf9lWlA2GfCZ8shU6dp/X48wPLh2yrSB/4l13v+eqglqedZAaPPaZ1yUAFCjh0rFuQK1CvbWmL4CwbMDixXu7Fozu1W3iBx/InlqoVcGjWBpYKmg63z0qApqAKVtEB78HZswqadHmxca5Y9ucMeHNDXThym1JGa0liTs+J6c2SGuQnhCflJiQnJ3Z5P317+u6TixSP+fzv6fMlSE6KggIAoKAICAI/MUIHG2+ppRijMPhcGVlZam9lJeXe71ewzAcJ+i/GCcxXEHgZCEgBOiT5UyIfvyJBJwpStM0J3FBaWmpy+UqLy+vrKysqakRAvSfeGrEoQUBQUAQEASiCZimue2brWf16N44Iz2jYbokJXTvcdFjjy6/cMDL7VuNat9q9HOPbwt4wO8FjAlXn2mAYJM7OGOdWgb3trAgoPEmA4QHQZf64Ynx29r2WpiWP6XzhdMXvVvj0cCvYg2QShXT0ghBxCLE4tHTmHBBVlbB44axo3Z16jj6xptW79oPih1PjXiUs8HzDRIVE5VQhRCDx2YDD6EuN+GuJ39olDMjt2Bpp84Lbv/Hh/uLocrPFWdbfbZwvfpMuZkzMkGxw5/DGnCt+fU3DvTrM7Zn17HLlgQCMmgEag0IICKDqQPSwTK5Zs1zEPLFPmjQBzMnl3TpNKFTl3mFPWfOf8P72XfywKuGc7vnuLi4pOTUtLTYeK5ExycmT3xlctAfskcqBOjoK06sCwKCgCAgCAgCJymBIwrQ/FNA/WIYRiAQqK6urqmpCQaDmqY5P24+SccjuiUInO4EhAB9up9hMb5fI+DkGwyFQj6fr7q6OvI7ncrKSp/PFw6Hj+YB/WsNi9cFAUFAEBAEBIHjSQAhhDEGYCtXvNGiabMGydzFODGpdWxsl+ysa9q1eeilF3fuL+ZuFBQgJB/E1Iupn1qIFxokLIipYTjiLIWKMHx/EEY+vqVtn5nJbZ4uHDhh3ttFRW6iGzwIWbeQTrjbBmZhp5igmJSpGnhqYOL4ki6dXrru+sW79kONARhAByMiQBOqOQVTwwm1PggwYUV1Tq+5WZ1mp7V87OqbVny3C4K2h4bOA7EtBBEB2gBQKCACKGi6daDuWnjrndp+50zr0W3srBk/1Ib44TTGQhYLE6oyrpWbvBgWmIQXYlHQFXhntV6YP6V51vizes9f/Kbi8sF9z76c0rSFFCNJSUnxySmJDRpIMbFSbNytf7+tuLjYuWW1KD3iDe3xPJGiLUFAEBAEBAFBQBD43QSOOF87s7njq4kxRgjpuq4oiizLQn3+3chFA4LA7yIgBOjfhU/sfBoQQAgFAgG3211dXV1RUeFyuYqLi10ul9vtDofDhmEIAfo0OMtiCIKAICAInAYEnEQFAPRgVcV/7rk3JaFBQlyj+IQWkpTXKGvQI4+u99byAGeDEAoaom5E3YTVOgI0V5+h1gRFA2IA1CAoC8NDYzc36zazQbtJhQMnLt9Q41YBMWAGIqphmpjnLeRpAP0m3zFoMs0gUFYB06bszc157MwzR2/8PGxyI2nTh6tN0A4XoE1mEIBqCu//ADn9pzTuPrtB+5fOvOilTTv42QjIEDKcCGiMgNjmGzxamrAgtQ2dw0gNGfDNdujdZ1TjxneNGb1L0Xn4tq13g8yYzJjGmB3+bCAeFW0SYBYDZMHHG+DsnrMK8mZ2LJj+7IvfuUMw+/V34zIzpYQ4KTlJiomJT06RJP7YqWu3Gq9f0XhYOCaE2LbYkXva0+CyEUMQBAQBQUAQEAROSwKRyTraMisiQDvqM7YXSimxiPDfOC0vAzGoU4iAEKBPoZMlunr8CSCEQqFQdXV1WVlZub2UlpaWl5dXV1eHQiHTNA/5Ne7x74FoURAQBAQBQUAQOGYClFIenww0WBsYfNFlqSlNJKlRTGKeJLUeOOTOfS4tZBg6DZrUY5KDiHgwDTge0BYYABiBFgLDS6Fchacn7crrOTm+5ZT8vkvmrKyo0XjUM0FhMDSqm8ikBsEGCxngN8APwFQMQQXmzK44q+fEjp2eXLysRKWggaZB0ICgne2P+29EFxOoH+CHANz+zO7G3WcnFYwaeMuyjTv1AAYNg4HBZNz3GQFBQGwDaAZgISsYVlQDQ1iDL7+qveKKaa3z/j163Cc/FlsKBp2BTuxi+37oPPiamnb8NQX+R9Vg1ZueC85d0ix7dLu24x585PMfXbDu4y1tOvdISM+IbZDKLThiYhJSUtMzMoffMqK0rAK4+wd3F7EorTPxqL+pPeYzIyoKAoKAICAICAKCwElBwNGgnZnc0Z0BHIuu+tld5Hg4KU6U6MRfjoAQoP9yp1wM2Jl+iEVM0wyHwx6Pp7y83NGdHd9nr9fr/ELHvs//2Vwl6AkCgoAgIAgIAn8iAcacQGGKTX3EzSPS05rGxGdJUiNJSpdSsrr1Ofv74u8JqBTCADJXn0kIExURXaVhH6r1ETUAsNsD/3rmg5zuL0tpj3Xqt2L+Kiiu5pHIxNSYqRBTs0yEMI+k5gI0C6g4HFQtXxAWLC7q1XtK8xYPvzj2q9KDoAIzIGhCGDMlWneOrJsMqg2YttLdpNvMxoWzz71h+TtbcJCCaltRc78Mbg9NTaCIceXX1tZNYNhxjq6ugrvvfbNDp//cctuCH0tQ2OKm1QbUC9BcerYiArRp72Pq8MF7bOAFCxtnPJue8eid//mouAo++WrXWeedzXVnSeKpG7kHhxSfnHLn3fcWlZRqBtJNTGz/aCFA/4nXtji0ICAICAKCgCBwXAgcLkA7ptA/yc9CgD4uoEUjgsBvJCAE6N8ITFQ/9QlQSh3p2efzVVVVldcvlZWVbrfbCXzGGDvqszPcyFx16o9ejEAQEAQEAUHg1CJQF/LsBD5HPcKXmzZNnDDz4iHDJCnJllYlKVHqf+H573/0IbZMAOYkA+SGGiwEoCMgPgo7q+E/o7a27P5Kg7YTcrrPnLTA45N5aDQPRVaB6KBjqloWwoAsojNZZ6o3oPoD8NbacLfuo5q1evCe//twdzGEMGgUDMYwNQjVGDUixRGgLTBMAtt+hP5DlmTlz+o5YNUHW0EGO9TZAmIRTA3Ekwdy9dkRoLm8Tgm3wjChshQee3hT184v/P2OJTv2QBjx2GeDuz/zYuvOhg6aDtQuls6gNgCuIrjhqi/y28xt1vKJoTfMLXbD9+XhYbfczvnEOwJ0jBQTm9+p06TpM9wenz8QMrFl22LzIGinRCb96J/0nloXjeitICAICAKCgCDwlyUQPY/X5yPkf6O3/2XhiIELAn8iASFA/4nwxaH/HAIYY0VRvF5vRUVFaWmpy+UqLS11Ug4qikIsfut7yBKZqw7ZLp4KAoKAICAICAInmMCRBehwyM9NojDs218x4p/3NMzOkuKk2AaSFBfTslWbcWNf8fsD3PbQ0rkATVWf7tEBvnPBHQ9vzjtzVkLzFzr1nztjea3fgIBij8B2VrZ0UAhVCEIWRhZWmSlT8GuwfOXBs/tPa9ry4aHXzt5VBAoDDbgAbaf8I9QybBcNBJbFiEUpsii1CE+HeN8Dn7ZqM7rXea8tWUV8Jo991sKWGdYsHCY0jMAwGUKM3xOCZQFhYDs4uw7Ak8/8t1XeMz37Tv7gczlEuOkS/Z0AACAASURBVOjsqM8qJbaNNdYgrIOiA+JiNAPdgo0b9GFXrmyWMaVd3qxLhs788EvP+Fmv9xo0SEpOleJiklJjk1NiMzMzr7z6mlVvrXHOmkXBVxuwKA+fFgL0Cb6SRfOCgCAgCAgCgsAfQSBy8+6EQkc06Ojth/fDybQRsew4vILYIggIAr+TgBCgfydAsfspSaC6unrv3r2l9lJWVlZVVeXz+TRNi456PiUHJjotCAgCgoAgcPoQiJaeLTtEmW9hjNQX7lthESircj/13PNJacmSJCWlpSWnNkhPz/jHbXeUHeDuxooaxoQbLu/cA9fd+t+cgkVpOdNTmz0xffHugyGQbT9lg3C5GVnEIESnWGc6IrU6lgMW1BLY8A30u2RpRovnzug9/sMvDtbqtvoMxGCEZ+0jiFoILMqTAyLgjwCmCUE/LF8S6NLhld5nzfroYytgcBHZBKDUYlSjtJZy52gFU8NiFheAEcEhRTahxoS7nv6mRY+pTbqNGf/awYMWBIAf0QRqMH5QgyHEzTc0j+EmgGXGyg7C6jW+CwfM7JQ/rlPbyRcOmD1m4rsXXnVzeotWMakpSWlpdvCz1KlDhxlTZxbtLwHgujMmzCkW5XZbx3iDevpcX2IkgoAgIAgIAoLA6U4gWnSOXj983MQiQXtRFAUhhDEmFhG/hToclNgiCPzPBIQA/T+jEzueqgRM06yqqioqKnK5XE6+wWAwaJqmUJ9P1TMq+i0ICAKCwOlJ4JgEaErAxJZsmI888WRMIvfiSEhKSU7mqfY6d+66ZPFrlZWVCMGuXXDFFUva5i9tU7CmffelL8+u3FtuGAzpTD+8GFRFNKRgszIMn+yEc69aldj8uey2T776ZqVPBx2QBobBg5cN7r9BjLoIaEwBcQNnTaeWBZs+gb5nzurVbeqKZUpQ4Q4fdrZAhMCwQKFQS6GWUY3vwGzZ2v4BUnkA7nzhk9QOY1r0XXjPKz+WUfBQCDNm72uZYCEgGKjB0w0iAJDBrAzguYu3d+n2UNu8Bxs1vC0z/YZ27a+VEptI8bHc7TmGOz5LUsyA8wd++fmXumJgg2vkhNmaeb0GHVGfxU90T89/JjEqQUAQEAQEgb8kgWjROXo9GoajMhuGUV1dXV5e7na7A4GALMumaQoBOhqUWBcEficBIUD/ToBi91OPgGEYwWDQ4/G47cVRn0+9YYgeCwKCgCAgCJzmBBwB2ol9/umxPvyZx0E7sqmDQdXNOfMW9Onbj8dBJ6WkpDSQJCkzM+uB+/9v4fz3rrl0Ws+uczt3WNu5cNXzL7s8KgQRGGDoTDZYSIefCk88SFWTMo1CkQcuv2VFWuuxTQrGzFtV4jN5JLJRrz7/JEATDagCVAMLKAavD776yrpiyOrO7SePGbMjpHGLDIVqJhgmIJP7PiMEYZ4p0bJlZMT9LyiFCj88PH5f1hnTGnZ9+ZanvtqnQI1ly8wA3Cea17a4ZQdYmFs/o1rd2F+uTZrxYe9+96c3viwmoY8UWyAlZkopyVJcrC07x0jx8Z06d330kceD/hBXugE0WZNllWvQFg8hrytRCvTRblBP88tNDE8QEAQEAUFAEDjtCETP6dHrzkCdLc5HgHA4XF5eXlxcXFpaWl5eXlNT42SHEhr0aXdRiAH9aQSEAP2noRcH/rMIONMMsYimac4Xm39WT8RxBQFBQBAQBASBoxM4VgEaIR4L7Pb4AGDn7h+GXnm1JEmpqWmSFJuYkBwTE9ckq3PTjOvO6jyxScOXnn+q/EAFV3VttwxqcAE6oENdMSFosIBBTM2CA27496OftzlzclruqOtGvrO3hnjMgGYHPpuMhz87AnRdEkKmcGMNwrXhnTvh1ltWd2g3eciQN/a6eLrCgCnLNGAC16B1bqYBCBClCLAFJhi1XBj2qPDstO25fZc17Ly4/02rN/7AnTd0AE0BQyU6MnXLNowGK6AEASCohz/6dMsll/87o3E/SeokxXWWpGZSfKqUzPMNpjbm+rskSRmNs5Ysfk1RNO7yAQAMuOGHHW3NaL36zOXvn5bDb1CPfo7EK4KAICAICAKCgCBw8hKIntOj150eOwZcGGOEUDAYLC8v328vjgxdXV0dCAR0XY/8VDq6BWf95B256JkgcPIREAL0yXdORI9OMIHoaUMkGTjBsEXzgoAgIAgIAv8zgWgLjkPX6+Og65yLeUJCnv+PMQp+f+CB+/+vsFOXhHjuyBEbnyhJqZLUMj2533m9H/vhW8BcCdYsCqqJDKpbgClgk2k6USwwdaIoCHwyPDlqa4uCSbFZTw+8fvF/d5oWj32WuYEGQxazDin+oD8oh00C3+8ht932Udu8yU2aPTNvsfugArU0LNOQAYrJCzIZmLYWrAQNLRAAxoOmK2rgqUmbWvYaIzUel9Fl/tINVrXBo62RhS2TmpqlaVpYCQXlYCAc2PTll68uXnzZlVfEJabFJzaR4lpIsS1jEprHJmVKsbFSrCQlSYlpcTHxUveeZ65es5ZRiBQeBG3HQfNHysXouhL94SBq/X8+eWJHQUAQEAQEAUFAEDj5CTi5BxFCiqLU1NSUlpY6GrTj2FlRUeH1ep2oNUc6EFZdJ/85FT08aQkIAfqkPTWiYyeKQNR9Zd19e/SWE3VU0a4gIAgIAoKAIPDbCBwqOnPFtL4cTYDmltAm9zj+7yefDRlyWUpKg5QGackpDSWpQUpiTqqUf1Hf6yeOGecq2h0OKzoGDWGVIINgYjdtUkIBVAyLlx3s0GNii8J5Hc9ZsPg9z0E7tSABxTqiAG2HBmGA6hp47LGNPbotzs2bfeHQRdtd4CdWiPl53DR33rAfGViWDcIEU7ZME/aUGv95dkWnQS9KOfe36rNw9hqokHnGQkyYpsk1Xn95ZfW6d9dPmzlt5J3/vHjIxRmNMxukN4yJi5ek+JjY5Ni4tNjY9JjY1Nj4xITkhHiei1HKapY58MJBGz/51MRWRH1m1FafHQ1aCNC/7WoUtQUBQUAQEAQEgdOQgCMFUEoRQpqm+f1+x4ijuH4pKSkpLy/3+Xymadrf99cZoAkN4TS8GsSQTjABIUCfYMCi+ZOPQPRUcfj6yddf0SNBQBAQBASBvyaBn+TmiO4cWYkI0M6vR7l/hG1nDAAIWYaOdM0M1IYmT57atGlzSYqJjUtNS2meHpfTLDmvRcOmuc1aPv/cS9/t3lcb0jWTOTHBAGBgXjZ+cnDw0JVN2k7N7vTys7NL9oTADzyLIKWHBj47cdCIgW6BLwDz5wZ6dlvctfPKFrkvPzr+v6Ua1DJdA41HPTPbx/n/sfcmcFIU2f5vdTe90k2D0DTDOsgyrMM6gHBBdFjkgYCyOaLyXP9uPBUZRb0I+mbU+aPodf0L6nUGueO4fNTR53rF5Y7b1RH/ynJ7qZpaum5VV9XUOrV2VeX7V/6oY3RWZXZ200B3c86nP9WRkREnTnwjMjLzZGRkOhVPSakW+SOAcqv+74b0+uv2Dpr6/8xY9S8/mf7rq+96u94l2T3xpqb//vd3P/6fux795crzB/x0aL+BZ1Sf0ae8sqysd2lJSQmW18jUq7CkqLCiqKispLiipLissLCwuLi4qqrq/BWr6v6rQZKkRCKp4YDO+vOl3OsBxJyePY9rzQSYABNgAkzgdCOQSqUSiUQsFgsEAna73Ww2G43GxsZGOKLNZrPH44EPGot28XXC6dZDuL7HT4Ad0MfPkDV0MwJqN5l8CulmDcnmMgEmwAR6OIGOOKATiWQw+I9UMvOFvXRKikbi+/f/cezYcdV9BxQVVpQZepcZKvoUVPYv71da0ruq38BLL/8f/2vvvu8PG+uNdl8w+Y+I9N+O+NX/47G+A24eMmrX5Vs+/t/2zFrMgXQ6lmhJtWRm/SgW32hJt8RTku2/0w899OWksU+cv/irKZNf/PnMhz89EnGkU0F8dTAlxZNSHD5oeeELKRJJeIMvv/If5y6/pfqnF0xceFvRoBVDJv/qgsvv/tUVt0yfOaO6oqLA0CuzmkavQkOZoaisV2l5SVnv0uKy4uLi4rKystLS0oKMFBUVlch/ReXlvcvKKhbMX7jrfz4U8IeltBQJxzL+9dwlODAJWgCsdm3Qw7sYV48JMAEmwASYABNoTSDZkoxEIh6Px263WyyWxsbG+vr6hoYGs9nsdruj0Sgv49kaGG8xAb0E2AGtlxSn65EE2OncI5uVK8UEmAAT6EEEBC/psfm6rSqHExl9QS/ZkozFYvTF9lQqFQ6H6+rqXvi3P65efeGwmqGVhRUGg6Es86k+g8HQq6y8ql//2nETfr70vBW3br3z4Yf3PPLwH3429ryfDrvk3IW/fe89n9ubKa4lLWVut1rimUnQmcnW6ZZUKpZKRpOJzF9c2veH78+e9+CqZe9eeenhSeMfufe+v7rDUnM4EIhFgtFIMJoIhFs8Xn9dg/HDj/7j5Zde2/+H/dddc/2oUZMq+w4vKP1JUfmwwrLBhuIaQ2EfQ1Hmw4m9CgsLMw7ojBSVlvTuU1VUVFRTUzNx4sRJkyYNGjQIDujMIteFhZnfIsPYsWOvuuqqL774IvyP6I9rPbei1XqD1uKgGeCt9/MWE2ACTIAJMAEmcPoQoMsnSZJisZjf729ubrZarSaTCfOgrVarx+PBktD0ZcLThw/XlAkcJwF2QB8nQM7eVQgkW5L4fG1clkQige8DaNvHDmhtPryXCTABJsAETjWB9jmgFTN54Y+ORCKReMzj8bz1xp/PPmv+wL61vQpKSorLDJkP9hUWFcvfKiwuKC2vqOg9oHfFsELD0LKCSVPHrb9z695HH3rxg/f+8/PPvqn/r6PNLrvX6/F4vfir/5vR4XE1mE0ffvTN9GmbZv/izrdek/6vpc9MnLjlwUf+/eEn//Xhpx7ZesevN115xcLFSyZMmTJo8NCa2kF9qvuX967uVVJhyPqXDQZDSXFZVWV1RUUlPM7FvUorKipLiiuqq/uNGDFy7ty5l19++fbt25cuXTpw4ECDwVBcXFxUVFRYWFjUq6CwyFBaVrT6ghUff3IgGo3G43G9TcYOaL2kOB0TYAJMgAkwgdOIAK6mEolEOBz2+/1OpxNToRsaGkwmk9Vq9Xq9mAot+qxPI0BcVSbQIQLsgO4QNs7UxQhghpff7/fI4vf7Q6FQLBbjx5JdrKHYHCbABJgAE2gvgTYc0JKUZ/1iTIiOx+OJRCLZkkyn0/GWRCgcTqVSAZ//xf1/WrZsef+a2so+fTPOXPnDfUWlhsLizExig6G3wVBrMAyt6DWxpOCnlWXDM+tgyFJcXFQry8BBtQMH1f5k6JCfTRg/dPiQTK7CPlV9xxoKhxsMgwyFgw2GCkNJkaHEYCgwGIoMxRVlFX2qZR2FxaXlFZV9oLCgoKi4V2lxr1KDobC4V2nfvmcMH/7TiRMnz5s3f+nSZVdeefUdd9y1dettF16wduzYcfKKz70KCjJ+54KCgsLCwtLS0gkTxm3c+KsvvvyPcNgvSenMAiHpZDyReT1WBg16KszZAa0ChqOZABNgAkyACZzmBOgbG8mWZCgUcrlcZrO5sbGxrq6usbHR6XS244H3aY6Sq88EsgTYAZ0lwf+7M4FYLObz+ZxOp81ms1qtdrudnkl252qx7UyACTABJsAEOuKATqfTmPscj8cz3ud4PJbIzAvGq0LJlqTf73/vg3+/85/vmjx18uDhgwoyrmcIHNBnGAwDDIYzDIaq0l41sgM6s8xFUa/MisuFhYWFvYqKiot7lZYUl5WWlpcVV5T17tunqLe8rEdpacbpnFnmoyDjgD4mBbIrurCgqFevkrLi0vKysoqKiso+ffr27XvGkMHDNm26/Df/73233vrrW2659fL/+8ply5afdda8UaPGyHOiC0uKy0oyyz5XYMXn0tLSvn37Ll++/LHHHmtoqPP5/h6NheTPM2Y+kyj3GAU0lV7EDmgVMBzNBJgAE2ACTOA0J0AOaHycMBwOu91um82GGdAejyf7qPs058TVZwLtIMAO6HbA4qRdk0A0GvV6vQ6HA88kGxsbzWaz1+uNx+M8A7prNhlbxQSYABNgAieaQCqVSrYk4/E4PpVD91HYpDWj0+nkgY/ev+qaS0aPHVpW3ktel6O0wFBdaOhbVHBGcVF1Sa8+su8440guKIBrGROlCwyFRYW9SnqVlRdXlPUqL5X/igtKiwwlBZkvB/bqZSjKeKALCkt6V1X3r6mdfda85eevuuba6+/85+27dz/y8MP/cumlm2pqasf9bMKwYSP69OmL2dDl5b3Ly3sXFvYyGAoxRTrj5C6rKCur6Nv3jHnz5t9//+/q/qshHo8Hg8F0Okl/KSmVyiyTnZkUrgsvO6B1YeJETIAJMAEmwARORwJ07UTP9f1+v9vt9nq94XCYHdCnY5/gOh8fAXZAHx8/zn2KCNBaS9FoFI8ijUZjQ0OD0Wg0mUx2uz0UCvH6zqeocbhYJsAEmAATOPUE8CEEcjQnW5Lkes45P7ZEYz73323vf/D2li1br7z8hrlzFtX0H9av76Cqyn7l5b0NhoIKWTKLNZeUlJaWlpZXFJeWFxWXFhT1ynz+r7ikqLg0s1lSbCguyvzB+1xUUlRcXt13wJkjR0+ePKV/TW3vqmp5lQ9DYWGv0tJyLL4BRzPiMVEa06YLCooqe/cZOnT45MlTNmz41YO7dn/z9bdu99+TLel0Ssq++ppSOKAFN3RbrcAO6LYI8X4mwASYABNgAqctAdEBTd/YwAUVPd0/beFwxZlABwiwA7oD0DjLKSaAWV34JoDL5bLZbGaz2WQymWWxWCx+v5/nPp/iRuLimQATYAJM4JQSwJ0SOaARQGRru9JpKZFMhdNSTJJaki1Jj8d/6If6Tz7+bN++/du2bbv44ovmzJk1ePDgkpKS8vLy0tLS4uLiwl5FvUpLepWUZT5gWFxiKCopLKooLKo0FPXJ/BVWZOY+9zIUlBbBVV1YmFm7GX/ZRTkya3pg6eeiopLCwl5Y0aP/GTWVvfuMHTtuzYXrfve7Xc//6x8+/vjThnpjIBCKxRJpzG+WpGgks7w1KsIO6NYNyltMgAkwASbABJhAJxDAVZP2bycUwyqYwGlDgB3Qp01T96CKptPpWCwWCAScTqfVajWZTJj4bLVaXS6X3++nm9IeVGmuChNgAkyACTCBdhDQ44CW0ySTyXgi+Y9E8h+pVGad6FRSSiSSma8XJuOJlkg8EZYkyfN318efHHj22We3bt16/vnnjx47ZuToUWcMGNi7qhpToYuKy4t6VRX0qs44oHtVwgFtKDo2lVme3VyIrwiWFJdhkY3+Z9TU1NRWV/cbNGjwjBm/2Hjxpbf9etuBDz82/80aiyVisax/OSWls3/xeEuyJbO8RjyOtZ4l8j6n00nMfeYZ0O3oJZyUCTABJsAEmAATUCGg7XrGXpWsymh6gVu5g7eZwOlEgB3Qp1Nr94i64mNKgUCgubnZarUaZcGyG4FAIBqNsve5R7QzV4IJMAEmwASOl4B4aySGRb3y66UtaSmR+cusp5xZ3SKdceK2pFLxVDqaSkeTSfqLy/EtmE9tNBoPHjz44Ycfvvraa888969P/q+ndz/82O92Pbz5plvkv5tuvOkGyI033rh58+YtW7bs3Lnz0Ucffe65537/+9+/8cYbX375ZV1dndPpDAaDWDMEduKlV3HZEHEGN8KoRbZeiq8OZmdKi1U9lkFeIFpcfAPh3JQcwwSYABNgAkyACTABfQTgYs7raKalPOhSR59KTsUEehoBdkD3tBbtwfXB2v/RaNTn88H7bDabMfe5qakpFArxdwB6cOtz1ZgAE2ACTKC9BLLO2Uw+MSzqwU1RxvV8zAEt+6DT6az3OZxKhzNu6FQ8+9ci+6BTdKOVbMlMl04kk4lkMpaIxxLxjH9aynwNMCmlyYksFopwKpWKx+OxWCyRSJA28SZNdDrnZm8dww7o1jx4iwkwASbABJgAEziJBHChldfF3NFrm5NoPRfFBE4KAXZAnxTMXMhxE8CyG8Fg0OVyNTU1WSwWsyz0ycH23KYetzWsgAkwASbABJhAlyeg5nRWGC4nS4prWWSWszg2/TnrgJanQos+6MwCHYlEsuWYw7ollUpKmcUx2pRkSzImi/jGUu69GU7reW/k8hXBDuh8VDiOCTABJsAEmAATOCkEcNGFq5dEIoFH7HFZMs/pEwm6sNF9bXNS7OZCmMBJJMAO6JMIm4s6DgKJRCIQCDgcDovFgmU3zGaz1Wptbm4OBoM0oOu82T4OQzgrE2ACTIAJMIHuQUDnOVHTAZ1ZguPHv2PzoDOToNPpJCgkEoloNBoKhyPxGHHJnQGNidLksBY/Ii/ekuWG9dWCHdDEngNMgAkwASbABJjAySaAyxW83RUKhbxer0sWj8cTCAQikYj8etixN9L0Xduc7CpweUzgRBNgB/SJJsz6O4dAIpHweDxYc6OxsdFkMtlsNo/HE41G8QgRt6wYynlA7xzorIUJMAEmwAROFwJKB+6xRTmwNrT4m1kn+tisZ/GcKzqO1eLFNPrDorZ2tEbuKs/aMe1QzUmZABNgAkyACTABJqAkgCuWWCwWCARcLpfNZsOcOafT6ff74/HMp547eFWjLIq3mUC3JMAO6G7ZbKeh0fF43O12m0ymxsZGo9Fos9lcLhe9vUv3sTygn4Z9g6vMBJgAE2ACx00gnwMaC0OL3ufW60SL51w6EdOLpdgrxncsLJbSjmpqu5tz97ZDNSdlAkyACTABJsAEmICSAK5Y4vF4OBz2er0Oh8MsC3wXwWAwGo128KpGWRRvM4FuSYAd0N2y2U5Do5MtyWAw6HQ6HQ6H0+n0+Xy5jxDF0Tzv92dPQ25cZSbABJgAE2ACOgiwA1oHJE7CBJgAE2ACTIAJMAEVAuSOgO/C5XJZrVaTyWQ2m202m91udzgckUiEkkENNlVUcjQT6FEE2AHdo5qzZ1cG3yGMRqNwPaOymE5Fg7gY6Nk0uHZMgAkwASbABDqPgD4H9LH1N3gJjs4Dz5qYABNgAkyACTCBHkFA9EXE43HMn8MioiZZjEajw+EIBALxeJwmzLEDukc0PldCFwF2QOvCxIm6MgFxoO/KdrJtTIAJMAEmwAS6AwGsT6F0SUsSYvLXQDwXn4hw/lI5lgkwASbABJgAE2ACXY9AOp1OJBLhcNjtdjc1NZnNZpPJZDQaTSZTU1OTx+MJhULxeJw+zsxu6K7XhmxR5xNgB3TnM2WNJ58A3eue/KK5RCbABJgAE2ACPYsAO6B7VntybZgAE2ACTIAJMIFTRADLcdjtdktW4Im2Wq0ejycWi5Erg+ZEnyJLuVgmcMIJsAP6hCPmApgAE2ACTIAJMAEm0H0IsAO6+7QVW8oEmAATYAJMgAl0bQKpVCoQCMAHbTabLbIYjUar1erz+WKxGM+D7toNyNZ1GgF2QHcaSlbEBJgAE2ACTIAJMIHuT4Ad0N2/DbkGTIAJMAEmwASYQJchkEqlQqGQy+Wy2+34MqHRaGxsbLRYLB6PJxKJiD7oLmM1G8IEOpkAO6A7GSir00+A1jlKp9PJlmQqldKfl1MyASbABJgAE2ACTIAJMAEmwASYABNgAkyg6xNIpVKxWMzn8zmdTvigGxoaGhsbbTabz+dLJBK0FkfXrwtbyAQ6RoAd0B3jxrmOl0A6nU6lUolEIhaLhcPhQCAQDoeTLcnj1cv5mQATYAJMgAkwASbABJgAE2ACTIAJMAEm0MUIJFuSkUjE5/PZ7XazLFar1eVyRaNRdkB3sbZiczqfADugO58pa9RDAJ+FDYVCbrfbZrNZLBan0xkOh3ketB56nIYJMAEmwASYABNgAkyACTABJsAEmAAT6BYE4F9OZQWeEIfD4XK5/H5/JBKhSdDdojpsJBPoAAF2QHcAGmfpOAEMu5IkpdPpSCTi8XisVuvRo0cPHz5sMpn8fn8ikei4ds7JBJgAE2ACTIAJMAEmwASYABNgAkyACTCBrkRAdEAnW5LxeDwajYZCoYgs8XicloHuSlazLUygMwmwA7ozabIuNQK5oy28z3a73Wg0HjlyBA5oLH6kpoTjmQATYAJMgAkwASbABJgAE2ACTOCUEEin06ekXLHQrmCDaI8Y7sq2iXaeqvCJ4HMidB4PnzbtER0jWJU0lUolW5L4JhZN1zseGzgvE+iyBNgB3WWbpmcalkqlotGox+NxOBw2m81qtZrN5sbGRpPJxEtw9Mwm51oxASbABJgAE2ACTIAJMAEmcIoIwKUl/nbMEDjLjl9Px0pHrq5gg5r9Xdk2NZtPZvyJ4HMidB4PEz324AhKpVLioYSMFHk8NnBeJtCVCbADuiu3Tk+zTVx2w2g0NjY2ms1mq9Vqt9u9Xi9/hLCntTfXhwkwASbABJgAE2ACTIAJMIFTSkDh52pzhqaasXqca2p5Oyu+K9igVpeubJuazScz/kTwORE6j4eJHntyj8fcmOOxgfMyga5MgB3QXbl1eo5tiUQiHA77/X6Xy+VwOKxWq9ForK+vNxqNDofD5/PF43GxtjQKi5EcZgIdJtDhS23tEqmjniD92qWfhL0nul6sX7sRuzsf7drxXibABJgAE2ACTOAkEBCvVxHuWKF6nGsd06w/V1ewQc3armybms0nM/5E8DkROo+TCV29qx1rnXU8HqednJ0JnBIC7IA+JdhPr0JTqVQsFvP7/c3NzVZZLBaL0Wg0mUx2u93v9yu8z6CjNmSrsROH8uynZbX+i+nVdIrxYnotvdl9YnpRj1pYTA8dtBQUv4yjBk1PvAiWwnoyaqQhPWoBRd50Oo0PTSjiO2sT+hOJBHUVNcNwlZbtpK3e/MprDKWna6m8yfJGKmzQTiPuVWSkTTGNGEYCMYbCbeallBqBztWPxsLR3SbVDtgP/WhiDctR3w7o1wCltiudTuMrK2oJTkJ8J9aUVOUNHH9d8qqlyPbq2nMkIgAAIABJREFUp4xtdrb2aub02gSwnuMJwi6qFZtYI6xtrcZeDZ3iLg0N3WWXSFXDZhpdNdIcz64O6MeZmj5dhXZRs6G761erV5vxYnfVaOtceogBN5y7xV8NVXlNEvW36TijlkXpeRXmjUylUjjtRqPRmCxxWUTLO9YTRA2JRAKbuPjMawk+O9+m/YrWoYon8knegrQbQqE/r4bjj1TYoCg0d7MDJYIkfgk+XfwrFAKj2l5FYmzm6hdbPDesqHJenWKkaDPKysUixoh51cLQg71i3rxhER0tuKymmeKpmoQ0lUrRXkUAaah0xV7FJilEelw55JJBjPhL+sk2hWbeZAJdlgA7oLts0/QQw1KpVCQS8fl8mPhsNptNJpPRaLRarXoWfdYY33MBtStxbnaOOX4CdB7NvUZRxNBJtM0Tp3iKbW+YSqHLL2igmpLBiKFNMaMiLNog7hLjSb8ioICgsQnNCmsV2jprU38p9ImMZEtSZ+mERWd6PclIpxjQk7FdaUTlbfZSnZqhE42r/8JXp3Lc5ol9uLPM1m+AIiUZkGxJxmIxBdK8mwoN2pukv81kdKiiUO30tFdxThGbjxQqAvr141EBlZXbfArN2GyX/kQioegPyK7xK9qjHYZmDVV5d2nrFPeeHP15IWtEihbqCeeFoBGpUyeGYnhmNM4jubv06BfTiP1HAwudYcW82mHxNltbM/YSNG21tFenfkKEwUTnkCL61No0XtRJtRAjyWYxoJ88TiXIq2ClUUrX1J971ItMFGEkphZUC8BJSuSpryJGoZM2U6lUIpGIx+OxWAyuW43DDTqRlwoiVXkD4tUULM/bkRSVyqsqbySdc6EWekRfLmmmPpNXjxiJc5aoBGRyf8U0sVgskUiIenLD1BvRmclmNEGufjEGcy+gU63Di/opjI8SRbMSEYTg4KFOrsF5Y8BHUBMJ65BoNErTR/KqpUhYLrIFB8TA5txeRPHUM9V6vpp+kXZuuF2Iki1J0VqyLddsilFrU8KC0Ria4/E4PRRJtiTFtqAw2iSUFboUJz6iZoRBBhOJUAQNDtnu0+o/ysKzH7F/5mqmCz8oj0ajkUj+bpO1V/k/r06OZAJdnAA7oLt4A3Vv8+LxeDgc9nq9DofDLIvRaGxoaDCZTM3NzYFAALf3NLLT+YYuEGOxGFxdGicGMMI8a0qmM9BevjrVUrLj0Z9Lg0CJ5+x2lYV5EPhVs41O3jBAWz/2kqmUWH9AzQyKz2sP7VULiAYoKqK4msFtAG4zqCwQzvurKJEIiCUq0kiSpPNmOC/JXG25MeLNktjKijCunOj4ooCCSa7+RCIRiUTEC1+6mFMEvF5vMBiMx+MiEG39uEwMBAKtruDUN+LxeO4hkGszxZD+gA4JhULRaBT6xSqQttxAu/SHw+FYLEYNLd645mpGTIf1qymkeLRLu/TTmExKNALpdDqRSESj0VAoFAgE/H5/my3QLv3JlqTyYjxnOxgMomi/LLjZQ8tqWI5dpD8oC4yHHrVf/fpxvwF7T4T+dDqNd4/I1DbhBwIBnfyhHM2qRy2lUehXGxk6rF/nszFcMIRCIV87pU1PCnoOOSip4joDOu1PtiSxrFk7zfepASezEYBrJhgMtle/Qo/aZjweDwaDXq+3vfoVz4Ty6scrF/r1OxwOt9sdDAYx8ufVKUZCv/7O43K5fD4fTqB6zrnt1e/xeOjI1elMicfj+u0/mfq1r9bQCjh4A4GAR58Q/3g83qZ+wMedS7MsTlkcsthlaWotfr8/EonQY4B0VsQ+I4bpzqi5udkrSGutP255vd5QKISrU+3+j3uESCSCxvV4PE6nU81y1MVut+PSC2REOxVh8j4LJnvRAm5ZXLIAGsL4dTqdgUBAe+QBM/gQ/Vnx+Xxe77EixKZ2u90ulwsF4TcUCpG1eQsCGcwKt9vtBBeNi19RoU0Qv98fjUbzqqVCacBPJBJi3UWdamG3263nG0h0ThRMs1llQQwqRc1KASgnN3G2e6ZF42F/LBYLhUK5+lGK2i/0gw+UKzTTZjqd9nq9os2i5dQoioAe+JIkJRIJdHvR/rzMxSPa4XBEo1F0fu2Di865VquVishljsMNv06n0+VyBYNBPdf58XgcYxrZ7HA4xL5KDaoI6LxmoFbgABPoCgTYAd0VWqHH2hCNRn0+X1NTk8lkqq+vb2hoaGxsxPTn5uZmj8cTkiUoCDwFvqzgqoueEGpcAeDcIDoa/DqE0GtoRulICYP1/yKXtnKyQZIkUbNAJYjLO/z6BSHbdBYhXhiJOsVwQBCyTUM/PdBOJBJ04tQZ0D7fo/SoIKL9esLiZAq66sqtSzqd9vv9drudrio0AiIrnfoTiYTH48Gsf1z66PzNNZVaRAyQfj3Y7Xa72+0OBAJ0VaR9yShJUiwWw2OkJlnEqx/xYgvhhoYGq9WK+3kN5mR/NBoFfJPJlKstbwzuxyKRSHv1m3SI2Wx2Op1+vz8UCp0I/U1NTR6PR+GG1mhokY8O802ifoKsFkilUrjTttvtZvn1lDaLAByFG1FDv9frbW5uttvtVqvVrEOam5v9fj989GpqKT6RSIiHbd4bJIvFIlbN6XT6fD7ccpAetUA8Hhf1w3xtRKS/TU8lHuo0NTXRaNMu/fS6vZrxeP1IZGLRIcRfo0/iiVooFMKwRkXoaF4z6SdPXF77U6lUMBh0uVwWi6Vd+v1+f5vkJUlKtiQDgUBzc7PJZCKzjTrE6/Xq1O/1epuamkT7gZ+qkzcQCATIU5CXDCJpTBbtp4qoBSwWSzQa1VCLXbiTdzqdtFoa+nyjDmlTOTpPOBzGmmwK+3G0WlTEarXqhK+mPy+Zo0ePNjY22my25uZmPfrxXKepqQn9RXtAMJlMdXV1WHHO6/XSYatxfEWjUY/HY7FYcMHcpv7Gxkar1epyuQKBAGbb0cGVt5RIJIKebzQaRSAoSIzByAn9OKfTVM10VnJbHPChBw2q0KnYNJlMsB/XJKLxufan0+lAIOB0Ok0mU0NDg0IVbVIPMpvNjY2NFovF5XKFQiF4mtKCKOxPpVI4chsaGurq6rBaYG4vJf04wG02m8fjicViuCaHeoVm2vT5fE6n02w219fXk2ax54sjA5rAbrfjGYb24ICJDrknXNFanG5QhM1mg/3wEWsMDqgRHprabBm/J3SaBRE7KkWj/zc1NUUiESKQGxD145ybtwhSSwF8T6ipqUn0QefVj6aPxWJNTU1EOG+fJ+UI2Gw2PT5iUT+d06kgtQDaXW0tSrEiqVQqFAq53W7xekYcgmCtpbWYzWa73R4KhajnpLMiKqdzel792idGvM2sPbLhQE6lUnAIULfPa3PrGljcbrceHzSdE8VzLjWEGEBbUCk+n4+GTQUTcTMWi9GRi7wwXuz2ufXCyKbTfrfbTYckOobJZKKzrtjWVKjZbNbu+WIVOMwEug4BdkB3nbbogZZEo1G32417GDqB4VoT1/rkySI3Ex734frGbDbDEyFe0uHUmQsr2ZL0er2is0A836iFcbOHU2/2pJz5L+rH08VIJOJ0OtWuIdTivV6vnhMPfHxNTU0ExG630wkm95RmyQpNK9C+ZMeJExdq9e2RYDAIGiIcBR+0DsibswLjqdHFEyeSoAY6n9wmW5J0FydiUYSzhWf+Qz9NeNHmE41Gm5qajh49Shry2k+1wG1Dc3OzHv3pdDocDuN+g/RrBI4ePYq3BPTfbMMNZDabyUIik7cgk+mYm1LEIqmLy+VqbGwUr3qxkI6ifbGJ491qtfp8PppWIBak6D/xeByjhMVioeNUcYGI1sRvgyy430hnRd12KRgM2u32xsZGjDyiZjU4cIWj82dLaDUmiMX5/X6r1YoHbIRdI2A0Go8ePWq32zHsEBlRpxh2uVxms7mhocFiseRVazQaGxsbgQW/NpuN3i8RVeWGky1Jj8djs9kaGxvhhcHFLvTkHSrq6upsNpvOS95kS9LlclmtVm1ngdgQhw4dslqt4XBYz9OpeDxObiDyFOSlRJFHjhxpamrCsIzGzcVCMbFYDP2Z7gHyBhTjP9xMdNoibYoAvs2Lw5bMU4z2IhmEjUaj0+mkCXeoguKYQkHw4Yqa9YQtFovH42nTDYdHFy6XCzdI4lCgXUpjY6PP52vzDYNUKhUIBJqamnJ9cLlMxBij0Qg3kIK2YhMXDDhy0aboP1BlUReTyaRHfzweb25uxitfqALCeAyftxdhjIWDG82qsFncjMVizc3N8GG1S38gEBD1iGEqFI/z7XY7fHAY3GiEEY0XzzhAp+HDorLgSUHj1tXVEX/SLHYnMaztQBftDwaD0F9fX98mn7q6uoaGBqPR2NTUpKdxE4lEIBCwWq11shAf2hRHzrq6uiNHjtTX15vNmacvWBUn7wFLfGKxmMPhqK+vP3LkCGwDGailhhBHaRiPztPmOSUcDpvN5kOHDqE3Up9UaKZNXPDY7XZRP1mbGwgGgzjNYTSjkZkaWmxThPEAwO/3k/EaiMRzLk5/UAKDReUYneBHdjqdcECjn4j6EUZ8KpXyeDwmkwnwMZqhb1NFsEm/RqOxrq7Obre3OWzipI9bFVyQ48oEqsSyFMrNZrPb7RaH/VzsaflbIxgZmpqaSKc5ez2MGEtrASKr1Up3K+msiEVgBjHeZ8KCirAWtMWwGAPlR48etVqtbV4z0PtSpJ+aEvrz9p+GhoajR49aLBZ0HtFmRRiXo5FIRHwuKFpLxVFD40LXZDJR51HopE2aYY27CboksMiCzbz80TpwQIt9kjRTAOdcPDqiMU1kotZ/LBYLzrnt0g/NNAioBRobGx0OB+aKiQevoixczmHGgMg8r80AhV84cCORCJQTDUUgnU7juR0alzRY8gn2omi64NHWj5t0j8djt9tFlVCFGLEuCJtMJjz6wowHBROptdA5nS4C0f3ytjX1VavVGgwGW2viLSbQDQiwA7obNFI3NREvstHqz/Q02yILnsqasxdGirM1nR7w5JPu5NNZyWWSSCTcbrfOSXbQj1/FJS9KyNUfCAQUs0VEJWphr9eLtQhyFVIMbsW9Xi/O9+JZn25jiI/47o/oZtI48VNDYCaIWEqbYZ0OaHIQi9colnwCUHRu1nO9jkt2m81GvSWf4h/jxEqJax2gZfErCZJIJPx+v8ViOXLkSJv2WyyW+vr6w4cP19fX42aVfKxq+uPxuN/vt9ls9fX1P1qpHjp8+DBcgWazOe/3OQXbM8FYLOZ0OhsbG2EV3QyDA12miAGaMCV2G4Va2oxEIg6Ho6GhAXfyhFdkJYbJ1ejxeAiOWJDiIiwcDsPTgTsx6huYbZ37i7Kamprw9EWhjcymQCAQsNlsdI9NF3PixSK6JX4R73A4dDqgvV6v2Ww+evRofX29CFktDGex3W6nS+rcPknGS5IENxZcALk0MH9WHF1NJhNmY0G/qCo3DDcZ3lCBl4TGHJGJGD506JDFYqGRIVenGBOPx+FAb2xshBdADQvFNzQ0OBwOPcaj8zscDuqTegJGo7G5uVmPm0mSpEgkYrVaSa1FRShBY2Mj3DQY9jU6J5wFeN2V+ryeQFNTk9frpZENnUcsiMLpdDoYDOK5BeGFv0Y0WBHGDPc2R2acVrxer+IBs1hQ3jCeXmBkUJszhUph5NF41pVXv9Pp1NO4cHDj0QsNDlCo3Qo6J8kmEgnMo2wTuMjfarX6/X5aRUE8lBThWCyGR0d5IahFQr9CFW0COzZjsRguqBQPt8ShPi83PQ5oOLhpEmtePXlbwWazacyjJPuxcg4e+tKAn5cJSjHLYrFY8Do2AVELwBME/QoguZsYURuzk3DbHBlwwYMZ0DAvr+UUiQriihoXnG16UuAjw2VAm8dvrn4aYdT4RCIRm82GSd94+pi3NQk+5npbrVaa/k9NmbcImg4CN6t4BFFzk3IEMGzSWgEK/agRIjFsYp6m6DdUPICnGuHBOdxMeh6aJluSPp8PrxyJD73U9OO+AzOUtTsPHLiRSMTj8cCHK14YWFqL3OWP/cDHR5NkiYMIH5F4a8ftdpMbTtQjhqk0eNP0fPIH9ofDYZfLRfNkibNaAHxcLlebV8s46eCCkybJwk40NNksBsxmM82A1m5f6A+FQnjfS0OnqN9qtTY3N9MTd3CW8oninAsgYK52h4i5XHq857jLjsfjinO64uDK3cSjESxepHGdj0OMXtY0Z+/9gUK0XxHG3H/M9dEYebA+id/vx4s11BVF1BTGXgCEA7pN/bjahH49d6NkgM1mwzldw3i0djwe93g89OhINFKt82OMDYfD0MC/TKAbEWAHdDdqrG5mKs4H4XCYVjVyOBz06hNO6nQSolOORRYaeTHVi6YK0uktlwXWf6BBX3/ghDqgXS6X9iULzvqJRMLn8+mc4SheAeiZAQ1PB3yg+rEgJbmZiHxaFgX/dDqd+4p97p0YYtDE+G3TzUEFuWRR0ynGi/rJTaNhPxajxOvG1A9Fr5MIHLeRmKrmdrv16KebVXhmRVPzho1Go8VisdvtTqezzUtqSZJgv8PhwOI2VAWaTZwbwGIgip5PqBWBqLyQjt1uNxqNoioqSBFAT8CcCD0OaPJRijOgcfua96oLTliXy4UlOBTW5m5ihrXNZqPXI0Q3rvjOAcLYi9dp0dvz9nkqKBqNYiqi1WrN1ZYb43A4mpubfT5fOBzWoz8QCOBmkm4pFcAtrZeYaGpqam5uDgaD+Ogf2Zk3QAsRYNqISMasIhbLsTci9by+QPqpV9DLLmoB3G/gyMprsxiJdzvUVOWNx+cH9BiPWw6Xy0UdA7dz4l292BY4Omi9TnR+tbsOLGOKL/S63W6da/LAOxwOhzVehMeAD0qRSMTlctEyoACS2yfFGJ09ByflYDDodDrF7G2GaQkLWsZdcRRgE2dGrJKRtx3VIrHSrhp26jx0M4+XrmA2dGq3hc7FW+jzy/r5uFwuLKCv+Fwn2SwG4MP1er2KtVCbNQWrEIh6KEwz+IAOPlyv16voPArsYIUyXbLocUCTs4AOLpG8Rg1oRgKZTQHRfixg7ff7dcKB5eCv5+mFaL8CSO4mupbT6cSic/QiPFmeNxCS17fxer1ut1sDSHNzs9PpbG5udsvLauG5Ha528qpFJJYQ8coLcHdAv4Zm7EokEsFg0CNL7nK9iuq4XC632+1wODweDzlYaRDIWxaeHnk8Hp/Ph+UmxGFH0ZfQgd1uNyZpKkYb6EckRmxcU2HlKFSBuofCcmCHGTqXCcawiWEfI3Nzc7OGfuzF1QL5yPIObqhCsiUZjUaxdLtbFlKuCFBd3G431rCmufmESISPyEQiEYvFAoEARh6N40ssDudEPedccXVvslA7gJVn9Fzt4LjABa0vn3hVJBAI4LQiAskNo/+Ew2GPxwP46Pwiitww+Ovv+aFQSFwXW8XkVtHBYFAbPrU43k0R9VNF1AIejycYDOZ2ntxeSg8YAoGAAr9fXQBf4w6OGgLfMgkGg36/HyOn2+3GIaz4RV2oLWgJjlybSTmW7cLnTKBfoVOxSbi8Xq/OWxWc030+H+Vts//4fD58ukD/rbRYIw4zgVNIgB3QpxB+zywaZzKcienDaPgyAAZoXHXhepH8HeJC++Tkslgszc3NGLtJIfTnssMMaKzZT9pIlVpA5xIc6XSa5lyIHoc2wx6PByd+7RMbLnkxrYCupHPvZMQLa9z46XRA437D5XKp6VSL1+OARtXwbiDO6OLpU3FWxkdR6A4fVy25rSnGQL/P59P5zRmxdD0OYlxYhMNhn88Ha8VrN8V1Ei4O8M2iSCSiU78kZRaCcMlfIspVKMagaCxAHI1G9TigceMdi8UikYg/Kz6Vj7eggrhZFe9nNPonDj24WYOCBFQEz5wwT40OW+3Lx0gkglZD9UUg2Qr9+B/fPdOYByflCD7uERIk2PrDdD9q9/tROtwoaUFytP4YEY1GvV4vWk0oJH8QRwq8hIJ61SU+JEnC18bC4XA0n+CT2VQYVvfW6YZD54/FYuFwGBrC4XBEEEWB2IOP2rf5aA2A8NkfGIlvgis+jKnY1H8nD+PxUrDCTo1NOFh1Go8JXwqz460F9lOJ2mMaucngfk0kEvF4PBaLIbsCRd5NfIFT7DkIU3fEaRdHNPwFpIeM1AjoIUOlx+NxDVV5d9FsHTUHNAYNVEdhP1VEIwAXj8aARqDgRkSXhqlQ27p5lVvwjJMSjUCyJUktmxeFIpJKFyeGq1UErUwclFaqbCN9XpvRM6llSb9oJBVHAZSTkAUNqtMBDU9ZWJZIJCLyJ+V5A2p32nRkof+g55BmFR6ZaLQRdQM1/SI0jN7RaBSjpYgoNyxqpvOgqC03jKcjGGYxRGjbjzGB9Kj1GSSAGygej0Nzm/pRtLYDi4qmItD5wT9vO1IkLBE//0idUKFW3MR3/KAklzmN2GhfNDGNzLn6EUMjD17nh2cnlzxZHovFaK/OlqUqUBOTBjI1r376wiFpUASoUjhycUhqNC5KQen0OBM6SZVYBEVCP5ktWiuGSTO+najdJ8WCSL+oTS2MzkOvjGiXgjYSSSoGDYxgub96zok47+BqB1ahCUQO1ChiAJ2zzTGf+MM8bCKsaOVcVm2OacQBI5toDA4KFIew4hcfAaL+T3bmtgWUAwgNbjQKiUzEMGAq9IsdRuy0sI2woO+hxbE8urgLpUSjUVwto4hczQr9YAU99CuWqygCm7k0cgvCyIxRhQjQgZY3gGTalucWxDFMoCsQYAd0V2iFnmYDnYFwq0bnNkxLwVU7vEhwYfll8WXFmxX4HLFYZ5unH5z4yQuj4WBCcfiVsqJxeqDqdCxAlmeLyvMfmsVzmP6LNliubX+eIvVFwTBqRyIg5qZICoh7c8M4H1NldebK1aMWQwo1Amp52xuvVoSaHrX0euLVdCJe1AC2Gl2CVFHn1EgsaqaMuV1CTNZmWNRz8sM0IomXjx22uc2MlKBjNUX2duXtQImURaMntMsGMTGUi51NLE4RFjOqhcUsamnyxissyZtG7Nvina0GGdEeOvooUlEKdb82UyoyYpPUKgKUGDdasBbMaVcnBhSl699ErXG7Lp4LSAMl6LC1UKUzO5Wr0b46VeUm64BOnfbkPZpyDciNUesSCmiwXDRGfzi3UEUMDgH6Jc2KZHk3ReeImICUoP+Q00EEJaYXw2JeNf2K9FCrxzNFyklDbgztooBaM1GCDgeAvcPZdWZEHU9oLcSWIqRqR5xaPFWHNCAGo6jYeTQ00C4KkNpOCUAtLNRQSAlEM6heYqSGkjZ3kTFtpjyeBO21FtXU7m+E4ngM08hLNmikyd0FtyxGLY3+RsZrkBHTkEKRic68uUa2GUOaYUPe9IoBn9JQXooRA1QRMTI3rFFubmIxRuFzF3eJ4Q7rF68ntWuKvdppRJMQbm/6XA0cwwROCQF2QJ8S7D280NwBUTwv5obphgG3o3imR74hPa/2YIhXYM0tKDdGkSXvZm6ujsXkVX78kW2etHKbQ3+hajUVNeSmEffqCUODnpR60uTakxujR4+eNLmateuill5PvB572ptGvN5VyyvaJqYR49sbFvWc/HB7rUV6NTv1a1PToB2vXXrevGRS3r0akR0oS0MbduGuA4M8GaYRaFOh/gt6ParypiHzxAPkeAZSsRQRSAf0k22KABVBN2xiAtrbWQFReeeGFV2lswxW0yMar5bmZMbrtId6jgJXm71UTT/iqaakR+yuYl49YdKmCIhliXoUyfJuUsXJQiQjPYr+314+avpFY0T7xfi8YSRWWNWmBkXtRM1UUwqIe9sMt1l0mxraTKDwNGnUpU1Vagmo7noCakrEeDU9evqPmFfU2VlhnfqRTHF+VLNfp87cKiCjeJh0evu2t//orAvxya0UYkQ9amG1vArslF3kr8irSCOmxC4xPSVW0Bbj9YRFnWJYzCvGtzcMPbm5SL/GLkojBoClzUd9Yrlidp1h6s+55iFG1K+WRoxXK1dMI4Y19KuponhRD4eZQHchwA7o7tJS3dtOGig7K3AycXRHmzuLj1rdRf25acS9esLQoCelnjS59uTG6NGjJ02uZu26qKXXE6/HnvamEctVy6uWRoxvb1itrJMT315rkV7NNv3a1DRox2uXnjcvmZR3r0ZkB8rS0IZdZIzOQJsKFXd6etK3N42aqe3Vkzc9lNNtlVhW3vSKSDG9GKZkpD/vXkp2nAFR+QkNH6edbWYXjW8z8UlIoNMeSqbttsg1mDLmdWRopxfz6gnnasuNEfXk7s2NUUsvxovhzuKTa4n+GNEeMayhQdE6YkpRA8Li3q4QPgkW5hahEaOHiVp2Pf1HzKunrPamaa9+Mb2a/WKadtmDjOSww2a7NLSZWLRNj34xvYZyjWMKuUQ9amFt/bm5RP6KvJQYacSU2CWmp8SKWojxesKiTjEs5hXjOysM/Xm1iUVrhPPmzRupoaTNXXkVdiBSrSA1VUifd6+aKorPm4sjmUAXJ8AO6C7eQD3EPBooOytwMrl0R5s7i49a3UX9uWnEvXrC0KAnpZ40ufbkxujRoydNrmbtuqil1xOvx572phHLVcurlkaMb29YrayTE99ea5FezTb92tQ0aMdrl543L5mUd69GZAfK0tCGXWSMzkCbCtkBnZckccPeE+ogUDRBXns6K5LqdYICop0nqIh2qdVpDyXTdlvkFk0Z8zoytNOLefWEc7Xlxoh6cvfmxqilF+PFcGfxybVEf4xojxjW0KBoHTGlqAFhcW9XCJ8EC3OL0IjRw0Qtu57+I+bVU1Z707RXv5hezX4xTbvsQcYTen4RbUNY20IxvUZKjWMKuUQ9amFt/bm5RP6KvJQYacSU2CWmp8SKWojxesKiTjEs5hXjOysM/Xm1iUVrhPPmzRupoaTNXXkVdiBSrSA1VUifd6+aKorPm4sjmUAXJ8AO6C7eQGweE2ACPYcAXTF0INBzKHBNTjMhF7JYAAAgAElEQVQC1NtPs3qrVpeAKAKqGdq5Q1TbzqycvJsROAltTUV0MzSyuWS8wnFzkutCZpzkck9VcaeWdifWmhqum9boRNh/InQqmqyb0lbUQvGkNncvYkSeYlgt/WkVDyCnVZW5skzgdCDADujToZW5jkyACXQJAuLFZXvDXaICbAQTaD8B6urtz9ozcxAQRaCzaiuq7SydrKdrEjgJbU1FdE0C2laR8afWpUVmaFvbY/aeWtqdiJEarpvW6ETYfyJ0Kpqsm9JW1IId0LlA2huDztbeXJyeCTCBLk6AHdBdvIHYPCbABHoOAfHCvb3hnkOBa8IETm8Casd+Z1ER9XeWTtbTNQlwW2u3C/PR5sN7tQl09/5zIuw/ETq1W6H77tXDSkwjhrtvrdlyJsAEmIA2AXZAa/PhvUyACTCBTiMgXly2N9xpRrAiJsAETikBtWO/s4wS9XeWTtbTNQlwW2u3C/PR5sN7tQl09/5zIuw/ETq1W6H77tXDSkwjhrtvrdlyJsAEmIA2AXZAa/PhvUyACTABJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEm0EEC7IDuIDjOxgSYABNgAkyACTABJsAEmAATYAJMgAkwASbABJgAE2AC2gTYAa3Nh/cyASbABJgAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmEAHCbADuoPgOBsTYAJMgAkwASbABJgAE2ACTIAJMAEmwASYABNgAkyACWgTYAe0Nh/eywSYABNgAkyACTABJsAEmAATYAJMgAkwASbABJgAE2ACHSTADugOguNsTIAJMAEmwASYABNgAkyACTABJsAEmAATYAJMgAkwASagTYAd0Np8eC8TYAJMgAkwASbABJgAE2ACTIAJMAEmwASYABNgAkyACXSQADugOwiOszEBJsAEmAATYAJMgAkwASbABJgAE2ACTIAJMAEmwASYgDYBdkBr8+G9TIAJMAEmwASYABNgAkyACTABJsAEmAATYAJMgAkwASbQQQLsgO4gOM7GBJgAE2ACTIAJMAEmwASYABNgAkyACTABJsAEmAATYALaBNgBrc2H9zIBJsAEmAATYAJMgAkwASbABJgAE2ACTOAUE0ih/LQkpU+xJVw8E2ACTKC9BNgB3V5inJ4JMAEmwASYABNgAkyACTABJsAEmAATYAKdSgBu5ZQkJSQpLEk+SXJLkkeSApIUP+Z0TqfTUioTTkmZPxYmwASYQHchwA7o7tJSbCcTYAJMgAkwASbABJgAE2ACTIAJMAEm0EMJwKMcTEhRSfrC9t38m74ctNa3ZIf0yhEplqlyKBRKpVJwQCdkpzT7oHtoV+BqMYEeSIAd0D2wUblKTIAJMAEmwASYABNgAkzgVBFIt1NOlZ1cLhNgAkygaxFISVJS9iubk96rHrMNuDjae2Og8uK/DtkgfVgvBRItgXDGYHkGNDugu1bbsTVMgAm0RYAd0G0R4v1MgAkwASbABJgAE2ACTIAJ6CbQTv8zL2WqmywnZAJMoGcTSElSPCWFJOmpTw4Pv8Rdvi5cuDZQvK6+9iL3zXuk/05J/5AHTNkB3bNJcO2YABPoeQTYAd3z2pRrxASYABNgAkyACTABJsAEThkBdkCfMvRcMBNgAt2aQEqSYinJHG365R2Bmk3NhmXJXhvSVZeZ+6z7dPIm6b/l+dHkfcYi0PwIr1u3OBvPBE4nAuyAPp1am+vKBJgAE2ACTIAJMAEmwAROMAF2QJ9gwKyeCTCBHkogJUnRtHQ48HX1yoBhZdSwJl6wLmxYY61Y8/XPLpMOx6W/pzJrdODzg3BAkz+6hyLhajEBJtBjCLADusc0JVeECTABJsAEmAATYAJMgAmcegLsgD71bcAWMAEm0B0JJCUpIkn/3nC0ek3UsCpqWBOW/1o5oOXPDmZ+2AHdHZuYbWYCpzEBdkCfxo3PVWcCTIAJdDYB0enQKbpJYQe0pdN5XkqEwg5o4yxMgAkwASagkwAN3RoBKZX+8U+nXk52fATotEjtcnz6OHfnEKDmoEDn6GUt3ZFAiyQF0y17P2gYdHHQsDpUtBZ/f6ta+/Hky6T6uORPZfzOoqQlKc8Fr5iCw0yACTCBLkGAHdBdohnYCCbABJhAzyBA9050l9tmvcQsGuE29eQm0NCm37xctRzDBJgAE2AC2gQ0ht8fnc6ptJSU/1pS7D3R5tlZe3PbpbM0s54OE8htFL5E6TDMnpAxLkleKbjzj3+r3eg3rAoWrQ0WrQ0Xrv1b1dp3p10m/S0uBXOczeyA7gkNz3VgAqcFAXZAnxbNzJVkAkyACZwEAnQT1d6yKGPeQCor2Hucyin7ybnBg82pVCq3atlqZf63t2q52qhexx9Ip9OpVCrZkoSFClCKojWKIz0JQZItSWhWqNXQ08V3oZrUmh1oSsqr1hMUzNU2uzio08E8NI3YoOjwOALi8XgikcAvHV9iYjGMjOIv9uo8cNSSKbordOYtRaEBGek3b2vSXkVeMXE0HGmJxCRJCgeCiXBUiiWS/4hm3NDsQBExnciwOIB0Yjmi2txwJxakoQrlaiToOrtwsGAckCRJPHZEel3HYLbk5BGISpJDsv7qfnv1hqBhRUj2PicMa82Vaw+v2ynZk5kFOkTJcUeLOznMBJgAE+hSBNgB3aWag41hAkyACXRjArhrEp1oGm4I/fVMp9PJlqTgw0yI7hIxTO4b/eWSzbmOGGgmpw/p7Nxb3FxtuTHtYoX7WEKRy4cqoqGWlMBfFovFRK8ZLBR/qTgKiHsVBcG7LTaozjC1iHYV1PTH4/FYLBZtLTFBRDNEbhph4iOoybAiEXWKYVEnQUNA1BmNRiORSFi3BIPBQCDgl8Xn83m9Xg/LySLg9Xp9Pp/f7w8EAsGsBGShFvH5fG632+VyNbclznxit9ubmpps6tLU1GS32x0Oh9PpbG5udjgcyEK5rK3FYrGYzWaj0djY2Gg0Gk0mk8VisVqtTU1NVqsVe02CGI3GhoaG+vr6unxyVBbsqZelobU01jcc/f7Qf333g/FI3cEvvz5y8Ht3k+PH8SHFfpQfYXRiCANLXoU01CMNNnHCzfukkMZeMYAhVxzTcsOKUU5jU/vcQQ9HyQCxXsgrxnTZcCKRiMUyT2IgIC/WvRvVJVsJ/t9JBMKSZJGMv7zdWbEuZFgRLVgbLVjbYsjMgI7sfFFqTkmJ1gXxwNmaB28xASbQlQmwA7ortw7bxgSYABPoTgTo3lW8+Uwk8vuLxfvP3JsujVsvtcQUL2qmaYakEAHxhpk85uS4JO8hBeBeJG9gKBSCfwneJfEX8aFQKBwOR2SB8xBZ4Bz0ygK3mMJphQQ+2XWY13vocrkcDofNZrNYLIJfyAQXUkNDw9GjRw8fPvzDDz98991333777V//+tevs/Lll19+/vnnf/nLXz755JOP1OXAgQMffvjhB7K8995777777jvvvPP222+/9dZbb7755p///Oc3BHn99ddfe+21V1999ZVXXnlZkJdeeunFF1/cv3//vn37/tBann/++eeee+7Z9svevXuffvrpJ5988vHHH39UXR5++OHdu3c/lCMPPvjgrl27fpcjD8hy//3333fffb/5zW/uueeeHTt23K1Ptm/fftddd93ZWu4QZJuK3H777Vu3bt2yZcvNN998U2u58cYbb7jhhutlue6666699tprdMtVV1115ZVXXiHL5ZdfvmnTpstYThaBSy+99JJLLtm4cePFF198UVY2yLJelnWyXHjBhatXr17VlqzMJytWrFi+fPkydTnvvPOWLl26ZMmSxYsXL1q06Jxzzlm4cOHZZ5+9UJBzWgv2nC3LAlnmyzJ37tyzzjprzpw5Zwkyd+7cOXPmzJ49e1ZrmTlz5vTp06dNmzYlK1NlmSbIjKnTZk6Ztuifzl7wizmTzhwzbdzEOdNm3L/z3lgonGpJ4lSX16vYnc6CXcxWOinT0y+cnbU5IxedUpE4VxV0JluS2to6jIRO1ilByCrEJRIJYWe73yXqsG2dkjEUCn355Zdff/11JJKZ0SpertBlSacUxEq6GYF/SFJj8qsJmxzla2OG1fGCdfhr6LdOevmg5E1LLZkK8Usj3axZ2VwmwARkAuyA5o7ABJgAEzhNCdCNXGfVX3GDCu+tODNUDEej0UgkQm5Z0YdLYb/f78vO4sScQafTiTl99nxis9nMZnNjY2N9ff3hw4e///77b7/99quvvvrss88+/fTTjz/++MCBA++///7bb7/95ptvvvHGG6+++upLL720f//+P/zhD88999wzzzyzZ8+ep5566klBHn/88UceeeShhx7atWvX/fff/9vf/vbee+/duXPn9u3b77jjjttuu+3WW2+9RZCbbrrphhtuuOaaa6688srLLrts48aNGzZsWLdu3YUXXLhq1arzzz9/+fLl58myVBY4iRYsWDBv3rw5c+bMmjVrxowZ06ZNmzx58oQJE8aOHTt69OgzBRkly2hZxgiCZCNGjBiWleGyjBBk+PDhw4YNGzJkyODBgwepS21t7cCBA2tqagbKUltbO2jQoCGCDBVkyJAhgwYNGjhw4IABA/rnSL8cQZIBAwaQfpSi57empmbAgAH9+vXr27dvtYr0laVfv379+/cf0Fr69++PvEiD3+rq6j59+lRVVVVWVlbIUt4eKSsrKy0tLRGkWJaioqLCwsICWQztl4KCgsLCQlKiUwGKQ8bi4mLKjnj+PdEECgUpygriULTBYCgoKMAvmimbKs9/QdmxIBIVFxeXlJSUqkiZIOjPlZWVVVVV1dXVffv2zT0uBg4cWFtbO2TIkKFDh44YMWLkyJFnnnnmqFGjxsgyduzY8ePHT5gwYeLEiZMmTZo8efKUKVOmTp06bdq06dOnzxBk9uzZc+bMmTdv3oIFC86VZZEsi7OyZNHi8365eNm5i8/7p4X/NHXmkKp+k0eOWb/qwn95cHc4HJYEwYlJiOBgxwmk5feH4vF4NBoNh8N0wsW51efzeWQRZ+XTrHk85hTnvB89evSwLIcOHfrhhx++//7777777q9//etXX331xRdffK4pX+iTr7766ptvvvn222+///77Q4cOHTlypC4rmKRvsVhsNltzc7PL5fJ4PH6/PxQKRSKRWCyGp90nyBve8TZQz2m1WpcsWTJ37tzPP/8cDwbI70wB9dy8p+cS+IckHYn9+6BVTaUXJgxrU4Z1CcPaaK/1P9Ssk974TvqHRA5oxZcIey4RrhkTYAI9hwA7oHtOW3JNmAATYAI6CZDrmSY6JVuSwWDQ7XYfOXLk4MGDP2QFt5dff/31V1999eWXX37xxRefffbZxx9//MEHH7wvC6bKvvvuu2+++ebrr79OLt3nn3/+6aeffuyxx3bv3v3AAw/cc88927dv37Zt25YtW+CfveKKKy699NKLLrpo7dq1omd20aJFZ599NmbeYardjBkzpkyZAm/smWeeOXz48MGDB9fU1JDrsKKioqysrKSkJNfppnDiKNw8cOXAhwh/juC9yQTLy8srKioqZSG3JBw6fWSBQ6cmR+D5hI+VHLhDhw4dNmzY8OHDR8gyXBby+IwePXqsIOOyQg4g0Qc0RZZpgsAXNFOWWYLMbi2YqDh16tQpU6ZMnjx50qRJE7MyQRZskbMJBSl+JwsCDXBRwTk1NSsoAmnJbwWTYYDoyYLlM2bMoCrApYUJmHNlmT9//oIFC84555xzzz13yZIlS5cuPe+885Zl5TxBli1btnz58hUrVixbtkycE3ruuediTujCrCxYsGDu3LmzZ8+G3x+2o76wfOLEiePHjx83btzYsWPHjBkzatSoM7MycuRIePyHDh0Kn35tbW1NTQ083dQ/y8vLxT6m8ByWyEJua/ThvE5GMSWSKfozNqFK/EVG/CpKp030fHTyCn2CxMh4Mn/pSKfjF8cpWS0aRhXMGxDJiMQonOvEh+MYCeAIVtSdCiI70S6FsohNRi2CoQZmU10qZcE4g9/+/fsPHDhw8ODBw4YNQx8cNWoUfMQYHKZMmTJjxgxyBC9evHjJkiXLli1bsWLFalkuvODCtWvXrl+//qKLLrr44osvueSSTZs2XXnllVddddXVV199ww03bN68ecuWLVu3br3rrrt27Nhx77333nfffb+TZdeuXbt373788ceffPLJPXv2/P73v3/llVfefvvtDz744ENB3n///Xffffe99947cODAJ1n5LnMi+fazAx8f+c9vv/vosytXrx9XO2zkGbXzz5q7cOHCRcuWXnrVFbf+euvvf//7b7/91mKxNDQ0eDyeSCRCb4T45LVNgsEgXijB+yXRaDQWiyXl2dOpVAoPNWOxGJx3kiQlEolAIOBwOPx+fzqdfvbZZ3fs2HHw4EGPxxOPxyVJSqVSicSPb7NDIb21g8VwEokETpR4gIriEENOw2RLEg9cyfuZSqVisRgesgYCAY/H43a7fT5fMBgMyRIIBLxer1MWj8fj9XpdLldTU5PRaKyrqzt06NC333772WefffTRR++///6bb7750ksvvfDCC88///zevXufeOKJRx555MEHH3zggQd+m5V77733zjvvvPXWWzdv3nzdddddffXVOMlu3Ljx4osv3rhx40UXXbR+/fo1a9asXr165cqVK1aswGx6DJx4ILpEEEyipzFzwYIF8+fPp3nxNBF+hizT2xIkU/vFsD9z5sxZs2bRmD9v3jyM+QtkWbhw4bnnnrt48eKlS5dieF+5ciV16Q0bNlx88cWXXnrp5Zdfji593XXXXX/99Zs3b77pppu2bNly66233nbbbdu2bbvrrru2b99+991379ix47777tu1a9fDDz/82GOP7dmzZ+/evc8888yzzz77wgsv/OlPf3r99dffeeedAwcOfPzxx3/5y18+//zzL7/88ptvvvnhhx+OHj1qNBrNZrPVarXb7fCGox2xDpLP5wsEAnCL4wFANBqNx+NY3iQSiQSDQZvNtmbNmvLy8jlz5nzxxRdYbYlcz/wkRjptJSRJbxz565mXWHutailc7zcsjRouDJdfdKDyPOmIX4qmpWRm/nNKyvyxMIFuT+D4J/Pr0aAnTXtRijrFcHv1HH/6Ti291dgCzeLvcVvLDujjRsgKmAATYALdjQBubFKy4BZakiS/33/HHXfgrnL69OnkdxszZgzNqx0yZAhmoeK3T58+5eXlpaWlFRUV1bJUyYJ5pvC7wXUCZwrctf3796+pqSE3ypgxY+A9we+0adNmzZp11llnwec4b968s88+e9GiRXApwuG4cuXKNWvWrF+/fsOGDRs3boQb5YorrrhGlmuvvRZ3nrj53LJlyx2y3Hbbbbfffvvdd999jyA7d+6855577rvvvodkeeCBB+6///7du3c/+uijjzzyyMOy7N69+6GHHnrkkUeekuXxxx9/4okn9u7d++yzz2LGNOLx+8QTTzz66KO7d+/etWsXtN13331wEfzmN7/B7OkdO3bcLcv27dvvvPPObdu23XbbbViQ4ZZbbrn55ptvuummzZs33ygvxXCdLNfKggqqLbNwqSyXXHIJAvi97LLLLhVWBtiwYcPatWuxCMDq1atXrVpFngg4as8999yzzz4bjoZZs2ZNnz59ypQpkyZNmiDLxIkTESCfLNyyI0eOHDp0aE1NTd++faurq/Hbp08fTCsWPXRwz1EMNktKSkR3P3pR7i/6Enpa36ygO9XW1g4ePHjo0KHDhw8nn/4YWcaOHTtu3Dj0Lri8RScIXB5wds+dOxdTOM8++2y4uRctWgR/B7wzcHmflxU4QVatWrV69eo1a9ZceMGF+FuzZs3atWvXrVtHnj70UrFdNm3adPnll19xxRVXXXXVNddcg/ZFv73hhhtuvPFG+E1uysrNN998yy23wDl4++23b9u27Y477rjzzjvhTNkuCLoW/e7cufPee+/97W9/+8ADD+zateuhhx5Cr1b8PiLLo7I8pkNwFDz55JNPPfXU0ydR9sgCP9EzzzyzZ8+eJ5988vHHHxdNRi1QI0U1aRMHNQ5SHKH33nvvPffcs3Pnzh2C3H333Vhl5a6s4IC9/fbbxWP2FkFuzgodxTfKcoMs119//XXXXXetvKzK1VdffeWVV15xxRWXC7JJFvGwhd+Q3qJYIT9WWbp06eLFi/H+xEJ5kQ3yD4qewenTp+NhzyT5UdOECRPGjRs3ZsyY0aNH41EKHqIMl2Xo0KGDBg3CExQcXv1aCwb88vLyqqoqGthxnGKzb9++NTU1mEw9XH7fYpgstbW1I0eMmDV9xuyJUxZOnL5o/PQ5oybUlFYWGQy9yksN5cWGyrKawYNqa2tHjRo1c+bMdevWbd68+Z577vntb3+LV08wct5zzz33ZuWJJ554+umnn3322T/84Q8vvvjiq6+++uabb2K9oM8//7yhocHlcsVisVdfffWWW26577779u3bt3Pnzr59+y5YsODll1+2WCwOR2b5abgIyXFMXulUqpVvJ9mSxCRiPKm1Wq319fWHZMHbNl9++SUezb777rtvvfXWG2+88corr+zfv3/v3r2PP/74ww8//Lvf/W7Hjh14CnvTTTddf/31V1111SWXXLJu3bpVq1YtW7bsnHPOIQ/vzJkzp8nrmUyaNGncuHGjRo0aOXLkqFGjxskyZsyYsWPHTpo0iZ4jTpIF4zPG5HHjxk2aNGnatGkzZsyYLq+OMk0QuIuxC3tJ1cSsQOfkrEycOJGew42VZdy4cePHj584cSJNjZ+qLkLheYLopZMnT0YVxsuCyqIsxS/KnZKdj0/Z8VSV7JkiCyJJs6iKninirIHp/6NGjRotC14FoGc8pHbq1KnTp0/Hk56FCxcuXrx4+fLlK1euXLt27caNG6+66qrNmzdv27Zt+/bt6MBwcD/11FPPPPPM/v370Vffeeed995775VXXtmwYUPfvn3/z0PQN998E99aEH3QEstpSCAoSb//8rthF9tKVscMa8OG5VHDhcGKi478/BqpOS21pKXMsjfppJRuNUidhqC4yj2DQMecp2IuMZzLpFOdp63Ui+Vmw628t61Sn8iNbOmdUgaqcGx4Eel1UinsgO6UZmIlTIAJMIHuRAC3N6ID2ul0BoPBp556asGCBXPmzJk/f/6iRYvOO+88uHovuuiiSy+99Morr7z22mtvuummrVu3bt++/d57733ggQd27979xBNP7Nmz57nnntu3b9+LL774yiuv/PnPf3777bfff//9jz766LPPPvvqq68OHjx46NCh+vr6BlmMRiO+cNUoi1UWoyw2WUwmE1IePXr0B1nq6urq6+uPHj1aV1eHlHV1dYdlgRfghx9+OHjw4DfffPP5559/+umnH3300YcffvjOO++88cYbL7300h//7Y/79u17/vnn9+zZ89hjj8Hx9MADD9x3331333337bfffvPNN98oO3yvvfbaK6644uKLL77wggtXyrJixYrFixcvWLAA82SnTp06adKkMWPGjBw5EstZDBZkiCBDhw5FgkGy1NYeW9pigCD9ZWnt58lsIR5zafELtz55eLMO2L7Ii/QD5HUw8CvmQpoBAwYMHDgQ62mIk3YHDRo0ePDgIfJr+CNHjhw9evS4ceMmTJiA2+zZs2efddZZZ8s+Wdxpw99KM86uuOKKa6+9dvPmzVu3boVj9I477oCj//7773/wwQcfffTRxx577IknnnjyySf37t37/PPP79u374//9sdXXnnl1Vdfff31199444233377nXfeeffdd99///0DBw589NFHn3zyyaeffvrFF1989dVXf/3rXw8ePHjkyJGjR482NDQYjUaLxWKWxWQyIYBf9CWbzdbU1OSQxel0Njc3u2RpVhGnLEiGWWxerxeTFt2yeGTxZr8y5xfEJ4sQcSyIeNorfpguKAtmdyJ1QBbMjhRnd8ayEo1GMT8uLEskEolGM9M/4bBICIJHSu39xWiQlkXSIel0OpVKYTZf/CQKKkqfRxP9hmQ1aiGOb3lpQJUCoCIl5sBmG6HVf7VKUyJFk4VkERsX8yLFZsUiCeI6CWLHEOOxeAJWTpC7tkvs2ogRf5ubm51Op8PhUHyT0CYLjhocU0b5g4QYbI8cOYLFFg4ePPjZZ58dOHDgvffee/vtt994442XX3553759e/fufeyxx+Dr37179/3333/PPffQPNwbbrjh+hszf5s2bVq5cuXUn0+Z8bOJv/qnJb8cOWlYUWVtSWWvwkIDpKK4tLICwdLSUoPBUFlZWV1dXVpaWlBQUFRUVFZWViFLuSwVFRVVVb0repeVlPQqLDJUVfXud0Z17aCaoUMHjxkzZurUqQsWLDjvvPPWrVs3ZswYOMcHDx582WWXrV+/vk+fPsOGDbvwgguvvfbaAwcOSGkpnUyhLdxud1NTU2Nj4/fff//pp5++/fbbL7744p49ex566KH777//3nvvveuuu2655ZZrrrkGjuOVK1diCYUpU6aMHDkSr+bQkF4lL+yDFX7wjk55eXl1dTWmsQ8fPnz06NGTJ0+ePn367Nmz58+fv2TJEjxdWLx48cKFC+fNmzdr1qxp06bhdIMFUsaMGQO37IQJE6ZMmTJt2jT4XsnxC23wjeLZ7fLlyy+84EI8D8NT24tkWb9+PZ5qrJafROJh5MqVK8/Pivio49zsuyN4PDk/K3Pnzj1LXig8d1nwWa1ltqbMmTMHT53xCHBBVs4WZOHCheecc86iRYsWL16MR9HLly9fsWKFfJY+ZjZWuFqyZMmiRYvwYGb+/Pnz5s0766yz6PQNfzQeycC5j0fsWEuqf//+ffv2raqqqqiooOWVSktLy8rKysvL8UZUdXX1gAEDcNofKMuQIUNGjhwJd/bgwYPpFFxdXY1uIHfezE9VVRWe0+BEvHHjxg8//HDDhg1lZWVjxox56623AoEARlf9ozENfT5lSzUAACAASURBVBzosgREn5QYzjU44/QJStKDbx0ctN5RuuYfhlUthtVxw5q/997Qcsmj0t8zfmdRcjWcFjECxPQJmAmekDIfejyt/fui2/G4u5TQXPl0dcCtiVZPyUuhS3kWRP+xREpJifOZoB33ozZFOtHydGZfSsq8n5DM7TxiSoWSTtkU20u2BMbAclX78xWtrIJCc1Z5vqx649gBrZcUp2MCTIAJ9AwC8LBkztfy6pDYvOOOO3bs2GE2m/1+v9frhV8DXjm73S6uBXn06NFDsnz33Xfffvvt119//cUXX3z66acH5C/XYUWOd+Rv1r0ry5///OfXXnvt5ZdffvHFF/ft2/fss88++eSTjz76KG7p77777m3btuGt4Wuuuebyyy/Hjf3555+/TJalS5diRQ7MCJs0adL48eNHjx49bNiwmpqafv36VVdXV1ZWlpaWFhUVFRYWFhUV0QKpJSUlFIm39UtKSugekibxYYHUfv364aZx4MCB4kTaMWPGYArthAkTJk2aNFmeojVp0qSpU6fOmDGDZs7OzQreGj5b/urXueeei7vlJUuW0A3z+eefv3r16gsvuHDNmjWYMLVp06arrroKzv1bbrll69att99++/bt28VX4HfJ8uCDDz788MOPPvroE0888dRTTz333HNw5u7fv/+VV1557bXX3nwzMwdQfGX4m2++wZoqhw8fbmhoaGxsNJvNmP3ndDrdbrff749EIng1uM0ejhvjlCCiBzB3r+jOQ6YO31SLBYl2UqEamrELBogm0UefyDZKgwDFa5ROzgLRKjGc10tLjlTYAKvw7j9+xUlwaqWLpWiHNQig6DZrqq3/JO8l5qiXgk+blW3XZ9Oog1GXoEIV5QIC7SUHPXm647LAQ43nB/QIQeyWiraAAZRAsVdBXqw7DED3E1sZGigmby1ILZWed4igvDibwF+fbEm2pFKxVDKaTESTmdpLscTH730wa/qMZfPPWTvz7BVjpv+suO8vRozt369fUVV59bBB0xfMveSSS26/ecsD/7zzvm3bL7tw/a3X3bjzjrt23HnXOeecM+PnU8cMGDyosLzSUFhuKOyVGegNY8eP/cWcX6xYteKyTZcs/uW5CxfMn3fW7Nm/mDll8uTRo0fX1A4sq6qs6FPVr3//n0+cNKh/TXVx2U+q+69efv6vt9w6e/bs8vJyg8Ew+xeztmy+6cb/cd3Vl11+2a82rl69etHSJXPmzIHbd/z48SNGjBg4cGBlZWVJSUlBQWb9bizhXVBQUFJS0r9//2HDhsGPPHfu3HPOOWep/AXIBQsWzJo1a+rUqRMnThw9evSIESMGDx6MB5DwV9bU1NTKS2/DazlhwoTJkyfj7R9MYMfUdTiXMW8dU9dHjhw5XJZhw4Zhunq/rODZZP/+/QcNGoRnnwMHDsRjSxRXKwsMoN/a2lrxASQWiUIR4i/c35gRPH78+AnZZcHxTgnNp56hLjPbEmQll/qk7Jx9eTJ05ofmX2P+PibvD5NlqCxD5Geo9AiYIhEzaFBmij1VvCYreBxMT3yFp8MDsIjWwIEDgW6QLFhnaeDAgVTc0KFDzzzzzDGyjBo1asSIEUOGDOnfv39VVVVJSQldluDKBJcl6EjFxcV9+vSZN2/ezJkzy8rKqqqq/s8rR6+99hpWfaGRRBGQWE41AdGnQ2FVo1o7npTOndbZsFcKSNIdf/yvM9a5S9cGDOdLhnWxwnW26vXSjtclXzqeTsEHLaXSmT91Ids60ZHaLk+WumnKPS3H1rVWxh+zPC37g6OSFJakkOygD0pS5Fie1AlwFrfIDkT5W49Zk7RId3Q5lNZ9I1tS1/jf2m+bysBOJ2XT0EszTZOSpLjcEP/INkpIbiM47wWHr1a3oYJQbzBBXpG56AaFx5n6N+0SyP1YIvTDJSwrpHxC8tZB+bE0Bt5kptaZVw3yH0TZFsxcC8kH47FkyECFkoWtDWjDElguQmhtZqstsYisVdRSPx5HWQPIS042kMlJSYpJqZiUkls8fexrp6L+VgV3ZIMd0B2hxnmYABNgAt2UQDqdxhvHkiQ1NzebZV/ktddeW1paWllZuWzZslWrVq2RZdWqVStWrFi+fPmSJUvOOeccfCVv3rx5c+fOnTNnzsyZM7E4A1bqGJuV0aNHDx8+vLa2FtNvMZOosrKySpY+WamUBb5gTAjCnN8BAwYMGTJkxIgRY8aMmTBhwvTp02fJy3HMnz+fnLmYl7169eq1a9euX79+48aNWMYUa5higva2bduwwiNe4n7wwQexqgbWeXz22WfJdfvCCy/s37//T3/6Exy4r7/++ptvvvnee+998MEHNA/3k08++fjjjz/55JPPP//8q6++gkv3yJEj9fX1RqPRZDJZBKG5t06n0+Vyud1uLAQJPw5cQtoupO7StcS7YtFmxIsxbYZJVZsp8eCE0ucGtDXoTE9uNW1tuXtz9SMmN+WpilGzsKvZear4aJcr0tNOeWr3dqA1O9znUVPyU8MHHWmJR+VJQKFELBmLv/HMvnMnTB8/bOTk4aPGVw6c2WfIxdPOPnfMlJ8MGHjBr9a//v+9abNYA/bmsNHectj66VP733rkGdtfvpUcvr+bbGaz+ch/fvv+A0/984ILti5de+Oq9Recd97M2TMn/mLKyIljBwzuP2jgGYP79xtUXVVTXVnbr9/k8eMmTZ4w/Gej+/10yOipkyZMmTxu9JhJQ0aOKKz8iaGkX2HpT4dkpj/P/ad5Q4cOLTIYflLdv7qgpMpgqC4oKSsrKyotMRgMpeVlgwcPHj16NCYaT5w4cdSoUYMGDerbt29lZWV5eXlxcXFhYSGeaGKyNtaVGjFiBN4ggcMUPtPs6XEs3izBzGWc2vBmCc5uy5Yto8eTWF3qsssuu/rqqzdv3owHk1i/eOfOnb/5zW+wqM6DDz74yCOPPP74408//fSePXueeeaZ559//oUXXvjjv/3xT3/600svvfT666/jhSQs+PDee+/hwfB7srz//vsffvghzm6ffvrpX+Rljr/IJ19//fX/z953wEdVpe3fZDKZ9EICAUKxwVpXV/0su59ti+IHKU6NaSyKrnXt6OquBVddVMpSBQSpiyKIIlJkqYbQ0ggppJJJnZlk+sxtc+99///3nsllCEVEXcvO/eU3Offec095zrnlPOc9z0tefNXV1fK6o2/8Q+atz+VXXvIU/Kmurq6srKyoqCiXt8P97igOyFtoSUtDtn3yVlJSsnfv3t27d5PlUF9+ierkmzdv3iRvn8vbxo0bP/vssw0bNqxfv/7jjz9eu3bthx9+uOZfa1atWrVixYrly5cTnZ8FCxbMnx+U+pk1a9ZMeZs+fbqi4TN16tRXZdfEyoT6Qw899MADD0yePHnSpEkTJ04sLi4uLCzMz883yU6JiQx3VlbW+PHj77777t///vfjx49/5JFHiJjV8uXLe3t7yZ0V+rXwU3n+kJL/XH8Jp8PLzBsnU599XrfCEQVYFJdXNtrX72FVkHkcmcY6lfoh8RUCCBwgFM2xxhsdVK4QZYKofG9cXnW6HjY0AqrZB7cgMXQ6aoxwssSMd6Alr1JWpZTnFiBpcjIReeKK803tRAoyjeyViWVC+NI0Tc4GRNEHAieJ4Oagw4/eF5slqPDDEQaaBegUgMGIktwWJ5HFoamfIRxA4lR0s3RAVlvyOd0YEStJWNbgZcH6KSTpKfUlsLDI2aHR9DcrRj9ReIYy/qCHlSrLXHAAJBokRkaI0M5YOAbAwoMDoJ6DMi/+NQN0yZS0mw3akPeLlQ8gcElvx0SUjEh1gzeYBOyJhhB4XmA5ECT8lTe80QQZ7kC/vfHJTXNS+sot138D8vJFwdzlBE9yCBEQgRfEgCCAFJD/CA1NbjxSgJNoWdmiC48AgCBLtLMAXgk8AvgE4EQ8SAokgynIXYWT+y25SZWy8wx7krQOjxd6Xdg5lQQGIHlSeZRIcooko6A5tiTXWQCPx8PJTekQ2YBcElYU6ADn5VlPgHWIrEvi/CAwEt56AorNo+ZP8O876rFhAjrYauF/YQTCCIQR+C9BQDFS6+joyMzMHDt2bEREBLGQSu7f0tLSMuWNmAuNGjVKEUMktlo33HDDrbfeetddd+Xm5hIJ5okTJ06aNOmhhx56+umnX3755b///e9vvfXWtGnTZs6cuXDhQqLOQQQ6tm7dumfPngMHDlRVVTU1NZllp/ad8tbV1UV4WyKD4JI3ol2gLD9Xdr1er1/e6JM3cjD0FOHciWEpnLyFmoErI72Towzc6//4D34wKLsnfZqcfFFoLorV7Vnin3z1j3QvtOKhRTyPeilJhaZzprAS+bSBM11Fjp96yWnjnzcZd2r65Mhpc/lBDp6phD+2cv4g4HxtpqHofW3kHzDCebTmefd5Us0BBDTLcwEAJ0fTHPvF+k8vzxg5NiVjeGxypibppqEXF9/0h/EXXH1NSuaC2XN9LMNxXMDtBxcDDs6y9cDud5Y4th32lNQcXP2ZYLaBi4bjtn8/+/bWh6dCgwW67PZ2c01t1a6S3StXLv/sX6sfNJr++tSTzz326EP5+ca77/7dr3/zP7+65hdXXj7mysuHjxyRGBM7Mi7l1guvuDpxaO51t1yWOVqjjk5KSR6cMWRwWnqCWpNARaZS6hGapAtSh1AUFRsfp4mNUanVcQkJRGbhoosuuuyyy8iqlxtuuOGOO+4gM7V6vb64uPjhhx9+9tlnX375ZeKwkSgOLViwYNGiRUuWLFm+fPmqVauIRLUyu7lnz559+/YdOHCgvLy8urq6oaHBbDZ3dXWR9SjE0SLLskTChaZpYiZPtGLISyrUql2xZCeB0PeLsoqCXKVcS2JyHEeM8RUVGnJtaCcfEP42XXpAUmfZDS0tCZ+pc4YmEnqVAgX52iHVHPDLyFsoAqEpkFc2uZwsXAj9HZCU8oHB87zieZJ8gZz63UJEeIh3Spe84IzoO5nNZo/H8/+dT6SkpPx/kZZFixZ5vV6GYUInrRU0zgTIt2mg8LXniIBCQBMOmpcJNJZmkC/zCWii65DABdAL0M2BTSZJvRLQIjGhJJcTSkghi0IDWIxesN88hVYbnVS2j9JCbFFfcv6eC4xQQ4MH+SCyBSmwk8tNkgrySv2s6EmM1flSSKKcGoOsmQQBEfwCeAX0iEhoeIUHPLk857InykwmITeD8XkRCV0RwM6gpXOFTZr+edVtT5aNLd43OLc007BzbH6l/mVYfxisPAjfjPkNkpgi4MvFB2AX0eTcIoIFoI2BDhasAlhYcJ8gQLFUBFmFKeyvmEJAMyFonwR4f8yf2H+FF5a5UxZwMiBIr3MSTgnwANV90sxN+29+uPSi/JL0nEPDDYfHFLXr/w4fHoZGF2JLLMnlmg/AROnzJwhogi0B1CdBtxesHNgBm6OTwVuJk282Pxec5iH0KmH9Q6ytB+KsVEQugXJRsHUDItAceDnwi9iZWQk4mUHG8kkBUeQk/DsbAS13jRPPZC8HNhZ71OdV/MrdYGbAH8I+k2rLVHDo/JAAEs+woo/Bkjg5cAiow+MD1Hzv5rDidi/pg1i7097C5KAC68kENF4V+uQiebMyBe4HcALi7AZw88AjTPLNjhXH6ZkwAT2wS4X3wwiEEQgjEEbgmyPA87zL5Zo+fXp0dHRCQsL/H1p/+umnpaWlu3fvrq6urpe3tra2zs5Oi8XS19fn9/vJaE3RaiBzxWSEzMi+3ckyc0VtQPHgRGIqu0phJUkiozvCCw8YNpNBlzKMDD174jXfn5bCfZDxdv9hIMeVgpHUQgeZSli55LSBAdEGFIDkosQhAWVgTHZDK3L2upy2AD/Og0odTwVkwJGvLb+S1NfGDFtAnwtEZ4mjQH3awFkuDJ8a0Pd+zICQxv1GJfym9+yAxJXHIHmqk/Eh5/R8/MHKURnDIylKE6lKoCJuvfjKB26bYLz85sn/e/eeVeuBFz0MjaM7HwM2P1PRvOmdhfSBeqi3HZqz+ujarTgENXsPvbmk6tWFzGelYPPh6CjAee29wNC8uevYh5tKF6/sbWvxOKy+9vb2QxUdVTVt1TX1hyvLdu6d9+pbq96YeWz99hV/eWvZGzOOHaww6PTJ6WnqhNioWE10ROTFg4ff+aubLk4aHEtFJKg16fFJd952x6uvvvrP+XM/WLlizdqPNmzYsHnz5p07d+7bt6+8vPzo0aONjY2tra0dHR1kutTlcp36dgt9f4W+lc6xXRTieADIZDf0fReauHKWNOW55EWSCn0UnDZHJeXQeg14qX3tLnkRn8tvKNVLyHHy0iQ34FlKqJw6lxqFxjkTyXsuN4VyrRKZHFEKMyBAMFeobYXLJr3IarXOmzdvyJAhF1988Zw5czwez4DvFqXYA5IN7/6nEejnd4K0GiPTWb0AB2wwY7t9wtTmXz5ceWGh1/QuLD8IZhEpJBaZI7QolDeFiVasMzEpQpb1QH26UaQMTirbQo2TYgrMycZa3StIEtGyQSIR3yCUUwgbJeskIOk34C+Y5bfGiJX1FQIgoVGnj/BWEtglcErIjPtDKNj+Op5rnv3E3In4NEC7BB8ccNzz5pHRBeYRxX1phfZ4U3dU7vGICccT9TWpuq9Ss+D19eANksMnrj1TSOEivRz08mADqOFh4UHx3lme215qHFW0L3ZczSUT4U+L4cMq5KPlFlFu7f6m6089BNZQ5M/dFFq5KtiL+hP+Uf0nhDCheZG7d7LIii4t6ch9rXSksSGz4HiKsSNe3xGjNcdom2NymlINhwflwjvbcA5GNpjH5gnBitRO6f+4S3aUPsABWEVo4oW/fchOmlt1+X0HxxTaDG/BioNgEcDLS4xsB63ApyhdDAAu5NZQzpDbLWgUTLLmZf0QC0CXCH0iuEWcSWIFIiYWEGUSVr6ePH6DSYUkfqL5RDmpkvZdVxZVjsiryDD0Fc/AORKFFyaBk+55wFcGj/MoCJdNgGoPfN4Ms3bCcx/CtF0wey8c6IUODu3NQ9NRIFVKQgL9u0pWwQcLic8CdPNQT8Paapiyuvuuv7Vf/0R9ZsG+lCzXve/Civ1I9/vwRc1IAiuinBoS0MqfkqkC6HkFwhbQ5wVb+KIwAmEEwgj8lBEQAoLFYrnllltiY2NHjhy5YcMGMrRTBntklEgMrxRTLEI0k+EQiXBaDMjoi1xFLINCx+cKT6F80ilHQjlcZdClRCMlJIkPEMk9bTFIfHyJnuyrjWRHiHJSi1BBWJJvaKYkndDPjgFnz5Q7Oa5kR1JW6nV2iuHsaf5Izioj4QGAhGJ1jkVVkjqX+Erk0wbOnsKpl5w2/oAanTbOaQ+emj45ctrIP8jBM5Xwx1bOHwScr800FL2vjfwDRjiP1jzvPh/6hFSmFQWW83Tb3ps244LkwfERapVarYlU3fGLax64bcKkX9/11h8fb99dJlvPCTzDIlBexnGobus/FvbtqgCzu2L+R63/2gZmN9T2mBd+tu3Pb7k2fAWOgGh3gYhDN8HrgU5r/dovvpw6gyuvFV124P1M6/Hqz7Y4qhvAw4LFc3zHgX3vr4WjHa5tZV/NW+Vu7qB9/rIjlR9uWPf081NuuP76Ieq4a4dfdN9duQ9p82+/+Tdxak0cFZmZnFZUVFRycL/d7fL6/USNl7wvlBeZKIpkRlYInDCRUx7pA95oBFjlRaC8vJTUcAgsb6TDKLa3ytTsgHdHaEsRwBUz3tB32andj/QKkhcpT2hSp8b/YY8o95ry0ldK/rUFO1P/D8VWefuHNoTymaHkpUCklEdpX+XUgPKQXEgKA74olAIMINlJC5Lu5Ha7/7+x/HXXXTdy5MgXXniBpmmSFCnn1+Y+oDDh3e8FAQnQBJhwMYQ7swnQIQX+vm73aANqN8ca/FEGVpPXGaurGpnvfWoJdMoGhryE7XgKQ0T4KCwq4dTahKOaCUDpvZTWF2PyqvRViTns7E1oosidTAYplNOZ60kkJs58/pzPkCX8rGyu3OiCjVXw3nb7i8vtLy63/nV5+yvLYWMllPcgb+uUF/bLGhcnKZKcJSuEVD5N9B0cAJ/W2PPfPZph7EkweuPyIKYQVPlAGThKy1J6JsrYS2U5Y4zHrnoQic5+au4sOQRP8bJhKQ2wo43+04Ijo5E/7Y7K7aUmuKnxPKWnY/LMiYbSTAMsLYW+oADuCQqPcKkSGrigKbpwgnvEZu3fI6a6Zy8MqTGZKiBc4dnj/4Bn8T0XEMHFg02CL452PTCrZFD2seis7qhcj0rPUnouwsCpTXRMnjfa2KfS8mmT6sbeBz39oiTC1xHQEgDLYwdA5QoAKzjf+Gj7pfmVg/Xdg/K7VDl9ccb2VFPpUB3M3AzdWByO4waysWfgRhVyG+UxZDVnvJCRMyIrFb6ohmUl8PdP+edWeN9YC0t3wVet0OJF03ivCIxIjIIHfOoEOdmQTLFLcKhAsulSU+NgkyepoIMadzhdCyUtaC3OC3jvK6wwWTFAiHBOLowHYE9z+3OLNl+gOzBYW52U2xiTY4031mmySkYZrX9eAK0cPgHIyoBQTr//eXJqDwne+6RnsnLPt4D09mfNv51yIDWnMUXfpsm1R+mkCKOozutJMNZcVNz95/nQSgONAtDB7oyXy71dCqntqZl9kyNhAvqboBWOG0YgjEAYgZ84AmQMI4rivHnziEucN9980+/3KyOc8wiEDsxODZ87YKHXkmKEHlHe/UoJB5xVMgo9Hho+bZrKVSQQGj/01JmGmqFxBoSVpJQCDwgoEc4j8QF5hXfDCIQRCCPwgyBAnmPkzYKakAyqcjIM89rLr6goKoaiUtWxw1PTf3fV9YaLrnvs+ruWvvimr7lTHo+BaHXhgtMA2Gqbt89a2rluF5Q0fPXu0oMLP4LmPugF64c7D0xd5N5yGPrcXreT5RlaZFkI8E5X35f7d7z2T+fBI+D0gtsr9FgPrfmkavUG6PGAD3q27C/950qos3Z9vGvH6/PhWA/4OJbnfAJHB7gAzXZU178+6bFLI5JGU3E3XXz5kw8/+sAf70uPSUhVx8bFxd186y1z3ptPc6iDQVBVGFvCh546lRj6PA991J/L8XOPc95NrGShlO2n8t4hBSZG0EotzgMHcq1SfYUaPhWHr82FRDiXMgyIedoyKEVS5jAAYP369ddcc01qaurzzz9vs9lC8xowHRJ6Khz+jyEQnOyRABw0EqD/busZ9/KxQYauOL0rSs9TesA/dB7YlWA4NNwAf9+AUrl+AE4IklD9ZA6xMEWOTpKAEVBx4qClNdkAlMEfqXdFG5xqfVmGHioteGHgZAJ6QIWF/kQDEsaUNzSuPK+NzIsEL5UATV+dABuq6McXl1068dAQ3dGk3JbY3NaY3GPxudVJuWVp2opR+fDHhbDLCj3IPDuAd4DEnSBmv6YcuHRGAqhh4KElLSOK2uP1FrVWSJkICZOAMgbQH6OOo3RIRqvzGUorqkwojd0jC9R+XS4yESlj0gUwfVtZhr4xOtum0TtVOi+V66OyIbbYQ433Uzl9Km1tfM7WkVrYWotNFkAh4BNknMz3SYIoBlAmGKtEmjAg05ryjOpJ9exvk5MOnlJaxTReCQyI/wPsiv29iOXBJUK1H55Y0THmAXOczp6YxyYUQnwxqPL91DieyvFROUJsAa3GiQGPSn9oiA4NzBWL3dOBIOtaYBSUxeBlAtoBsLm55Y4ph4bqj6Xoe2L1TrXeH4l/TrW+I15fPzQP3t4CohxfTpOISfQz/ydAIskqpsbkRLAdBQCzAB9XM39+f+doQ+VQY0Oa8XiKsS3J0JpsaEzR1w7S7x+mdz+yAI640cCfxuSD1vPy8zr4YFfsghVVHC9Ir318ODnbEqP3qvBRUJWu75y6Evwg+Bg6IHfv/jkMLJIgoewGB1AjwkPLakYXHowbfzRF25Sg7dHonCodE6H3Rxl6ErCElpuegc1msLGnvrNI7RSwFTRwggQLKZ+38PBRVestzzRnFtqGFLVETuiIzm2JnGCPMXiobIgwMZTOHq3vvfAB/rH3oZvBCpNqn0Jwf/v5kjABTZos/BtGIIxAGIH/FgQkSTKbzdddd51KpfrDH/5gs9k4jgsdAn3TMHkTn+n33GENTYGUIfRImIA+dyTDMcMIhBEII/CfQUAxyVQ46Pr6+ieeeGLYkIx4TUwSpb40PfN3V1w37pJrXh1fVDpnFXh41u1lvX7UfRYBOpySuXff8vVN/9oKFR2tH2w6OGslNPdCp7937e51D73StX43dLqA5zwC7eB9XXYL8Jy74fhXMxZ7dh4Gtx9oBsw9e5esPrDiY6g9Di6J3lW19/WFzk9Ketft2fbKHChrgV4GaCSgkX0mXoxsdOWCtS/+1qC/5pYUKiIxQj3+d3cW603XXXk1RVFJaakZw4b+6ZGH9+zZ43Q6GYZRDGaVwAAxpdC3Veg79FyOn3ucb9+moXl9+9T+AykQMM+bgA6tb+i4nRwn3xUDaqFcMuC4sqtcqxw5U2BATLKrdI/QaYzQbx4AoGl68+bNN998c0pKypQpUxoaGkjhye12dlP3MxUmfPy7QkA2U5YkjkcDyV6A93btHqlvic0VkoqZCIV9RgJapAxuNbJaBy8ugC3NMgEtIt9GKByZ2SHsJbI9EoCbgT4O1pU3pRoClIFWGZCATi44ctVklILlhRNr4cWgcW6wjwmy9aVbRANSJ0CPiKLGHiLGcRL5d+7kEZl+Q2bQy2JS5VbP88t3jza0DM5rocZbInJcVA5P5QaoXIbS+iJ09ojcDmqCWZVdkWGABdtRCFvmoP0gBJeKnFSQk1tDAvDxYKH55bs2pd3dlqD3qg08pQ9E54nqPI7SeqjxLmqCO1LXQWW1R+VYo3UWVa5NrSsdosWaBpACFJDDx+3kpHEPlxcIAHYauoS+P809MtQoZT7ER5k4tYmJMvqjDF6V3kaN56NMAUofiDT2/HlHbQAAIABJREFUxRlrRha0PTQL7W1ZkcWlN3LKhHOUQGGfZVUKBuxgmfOpb+4m6aNSFPeQrW3FgIAM4GmKg2lxHj+Zfw0KpjCAxrYEqX5C87R1ObV239cRXlb6dolgE2Fd+f5LCizphV6VnqFyQFPAUFo/NcFHjfdR2b5oY3e0tiNG2xuL5v/dicYvM3NRMeYMDGZogVHRhWxegOUlh0aaWmJzu+L0vRq9R6UnNxRPYcCj0lujtJWjC2BfG5owB/CWIa78FMpVSTnIa8vsNuZAMkF/gABH+oQnl5Wm5zYNyXMPu8+tMXIqYyDSGKAMXISBpfAWdqr19enGTSNyYOU+6KBBvtvw3hFF5dUvWzTLkx+kV8jd3fL7lzwphf5INAz3qvT1qXrL80vABaKPITcCKViwnLwsvvyvA4eG6vuS8+3RehuV0xmVY1FrnSqdn9KJlF6iDJzK6I02NlO/bb3iIeiQ9XxOUR0h97XyGxBFYp4v0iwqO9uAe2PdoSG6vuT8QGKRh8ql4/I9g4rMiQZzjJaLK4BIk0jpBErnj9S3XPoAHLUCL+IjjhfQ+F1E+BSQz/0ZojTHgECYgB4ASHg3jEAYgTACP2cEeJ53OByPP/54TEzMDTfcsH//fr+8ylgZESk2OOQz7tv/njuaZ89LIaBPGy00l9NGOO3B0KtIODTaqWe/0ZHQpL42/I1SDkcOIxBGIIzAjwSBUAKapumKigqj0RgdERlDUSmU+tJBw69NG3n3qCunGiYf27gL+vwsz3nkQTaOjhw81HQdeu8j85ovYX9rx5JNFXM/hDoLWHj6y4qP7n+xYvYa6HEhVe2jAf224+icrzn+77cXWvaV8R3dot3Bm7vKF6+pWbaeqWsBRgyU1h7+x/uetXttq7bvfWORc1cl2Lwovcoi9YxkgY+DDqfny/IvHppqXvhZ5cdbnr//kV+kDh0Sk/jLK6405pn+L2tCfFIiRVFpqam/uvqaaW++1draKi9BFmmOpTmWC/C8IPACyiMGxJPcE5FH/Znep2c6HvqCOHucb9/ooXl9+9T+AymEFlgJn3u+yiUDqBxy/LTpKJec9qzyKXKms6HHB+SipEwCpK0HHCSXEwcbW7ZsufPOOxMSEiZOnNjQ0EC4j9D0w+EfBAFBNnUFVoQaByw5WJaS0x2jo+Py+6jxXhWyToQ1C8gW0G61wRJnaEjSoYhtr+xMTCGg+4mcExIcLga84PrHx0eGIHPNRuKvJb3QVzgTzYl5Ptij+mnQICskydxlD4M2px9Vw5MrnXe/5rz7Nd+zy8AHgodGG16Wkx9WZPHJucKG7DPOhwCsOHzkkuLKhOwWTY4tMpeLyXcjKZzrQxZS54vQuSmtO1LnjTY61frmqKwjQ40wbRPhoE8Usp9pHJi9KHs/swL90qrSTEPn4AJvQr5MBeZCFFo6+ygtnVDQkWg4mqJ1/O8Lhy/ILxmmO3hhfkmm3v7EIrAj1xZKQPfjenI+foCvzO3aqQ3D8m0avS/a6KRyrFR2Z1ROc7y2OVHXmWTspLJAnQ/RhXx0Xs/gwn2XFsFxAD8S0PgAUbyx9Vck6M+Qhp7JsypH5DWOKPxqtJFbsBXnABS67uRSBP34oYoEQK+EiiXNIhywooG8TZa5kDnoYEMrBO7JiXz3ewpFG5q0zPCiesyzqxpHFfUkGH3RSNb7KR2o893UeAd1Nx2X35lkrEnTW377YskoY3VSbtdFkw+PKep9filOWpBkSXvIoA1AJbgbAOhm4b091RcUdiYZPUkFNs0JApqlkMz1RyIB3avSNg3JO5rzEpbKS9jlMyGNx3nSDjLpK/s6Bli8r2y4sTZqvDVaZ4tEAQp/FDK8QqSRizB41QYiKoLZJRU0DzLuH2GEZfvBSpMnfyj7HCSgSa+QKVroFuqHmEBdIFL6gFzspmS99bH5eOMzeC/55T8faVa/7Kr0lXV1Fxbb04vohAJPjMmp1jsitY5IJKDdkToW08HiMVFGH6VtjMvtfXQ+HGcGOHgkt9hAo29RQvZZkHP58/LOwQW9Kq2HyvFSE6TofFtkboM660iKtj7d2BI5wSFPI/HyvVw+RM9sOoxlZDhkn+XSkjY8/Z0V2mfOLRwmoM8Np3CsMAJhBMII/CwQEEVx48aNgwcPHjp06IoVK1BFC4Bl2bMPegcMkL7R7rnDdvZkybv/THFCczlTnFOPh15FwqFxTj37jY6EJvW14W+UcjjyeSMQ2hDnnUj4wjACYQTIAxlxkHUwCRVbeaTq5t/8OjE+IUkTmx4Ve+WgzFFU9C3Jo967/1n7jnKwehiXp8/rDqAUoTzIbumtmbd2z9QFcNhsW7X96OwPoaodOYvytpV/eqli5ipo6oUA+P1+yeNDGzchwPU6SuesKJ29HPwceLxgc+x+b3nVwjVw3A4uzn+4dtfLsx2rtsOWqiPTV/VsLAEXsSiDoO2zD13MMyW1Gx6beujFeVDrgDZX7aZdz+mKrxl+kSYhLmn4kPvuu++FZ57NGJSeEo80tCZSlZuVvWXLFrvLyUkiI/CMwLMi+udB94koyooH0eCofzvT+/RMx/uvw/9nj/PtO15oXt8+tf9ACqEFVsLnnq9yyU+IgCZS0TSNlEdpaem1116bmppaUFDgcDiChOC51z8c89sjoGj7ygwaWcXP+xl8Ui092DHmAU9SAcQUMlHGDmpCS5K+Jg3X3R9L0dtj0ITZE6GzR+lsGj0KcRzsQtox0G8B3U/MnaB1vDzYoevphbXpaPtMqwwOjaFxsAmmb4d29LWn0KyyWWJ/OiygX7gPD1fe8VTFqPzGuFxLnMEai77gqib/A3k6mfUkfByxGD1XVNws+EFasrM0PRdVBeLyrNR4OzUBhjzYq9F3x+ja43TmOPzt0eisVHYvleWLNsLgydYo7dEMI8zbjobbsvdFpAMHsI9EdUSSOTkL9Dwyt3wI+rJzxhi5uAJOZeyl7raotQ3qrJYRRfbfvgRz90G1CLUitABsqKl86B3/rI1oEOrHx6as54BaGSfkMmSJA6ypCGDzQ6Wt8n8ePj7I5NYYpfgit8bYQN3dkFlg/8PL8PJnsLwGXt9+NCmXjsmDqIIAZfClT9yVPB72WsAjyo/6EAJaUeD188CBfe7GyuGmPjUyhuZUU9nvnoI+1OrFW5h0ngH0rgTYeWqc0vTPq8c9v2dM/s4LjRvG6I898C7saIYeATuJwin2d5JzbbLzixdSwmAriTLD2wWOyXPqU/XuWJODymIjDX6NqVel7Y031qvGH8vIc/3hFZi5Gyo5qOWgEWBZRe/k2fD+brDKszRB3Yr+jhrSBbA3CgIXkGc4uln4sLxqZL59UKGVymLiC3pi9S1JKIVRn6pvS9DbNMF5HV+00ZZeeHCUCbaZ0cI6SDB/XZ3JlFEXDe9trxtR4IvPd1NZdupOSJzkpHIcsUZrvLE33tgdb2hLQhUdf6RelGeP+lTa9nj9V6ON7KrdYPFAQOIFdE6o0NAnpiUIAW1mGlP0AWqCKLPPPKU/nqjveHAWGunLbRqQ5x3wo8QPYAbPfXOODNK1R+W4Ka0YV8glF9sSTc3x2rokbfUgXWOSzhWF+tpMlJFWGUCV50kqODQ6D3Z3gUMKPkb6q066yYmbjLDRbh76oPPphdXx2WwkLqrwU7reiFzbkKK9KRPgpQ2w5DAsONg95kF+6GQU8qayGUpXka7rWbEN+H7tDjmLgen353t+/8ME9PnhFr4qjEAYgTACPxkEPB4Pvuz8fgBoaWkZN26cWq2ePHlyT08PGecoEhynDtVCj5wp/H0AQfI6bcpKMU579iwHz5LmWa769qeUAg8IfPuUwyl8UwRCm+CbXhuOH0YgjABBgHhLE0XR5XDyXlrieKfPs2DZkrHXXElRlOzNj7ps8IjRlKbwguvXPvwKs7cGelmgBeAFziePyQECHb11yz+vmfMRVPdYN+4rW7gWWhxw3Ak1nV+9u7Ry0TqxshXsbMDt97rcaMjDSdDt3P3B2m1zloDZxnZZmZaO6vc/al76CTR3o3+kox3Vby+1Ld4kflL61Uv/tG7YDZ0OsnLWJQ/+PAwNfX6o6Tr4xvsHpi6CQ63Qw0OZedfrCza8MvPfq9ZNfvKxtLGjE6Njbr/quqIc/S3X3TgybUhspFqjjr70isuffn5K/fFmD8c4aa8E0OdyBp1yiQIhoAkDoiwDD33anF843N8UBAbQx8rxn2LgLJ2BzOuELkQDgPLy8nHjxiUmJt52220lJSVh/Y3/aKMTBo0LetWTrYEl2udHBYCtjdXDTOhyLa6gj8ryxuW1Dy8qveFBWL4PjrpgY4M5o4CPMrGU3kPl2KgJRwcb6Hc/RbNQXrYMVRidfnNarJdXgCb66O+fbUtC9tkfZeiON1SNyIOPa8EqEM2BID/Ii2iCjeytLLvx10+q0o2dw/94PN7QrTHY1AanytCjMXRc9IDw3GqwSSzNEY1iWiYGMRHCOYbmriBLfCGiJAjA1M+ODLu3WZ3bG6GlYwp86jxXtKkr1tgwtLB6zKTKS+8vueDekmGGo0PyepMLvbEFloh7rFSuO1LnTMhrziyE3X3Q1+97LYSAJjnghAorqxA8uqx31P2o+RtjtEXm8qkTLdSEvrTC/SOMtofmwvYmLIlbpkSdssaIV6bwSGUCKL4hoNi0RCxMkdSU0LctcEhMY7UqHHU3PmZWZUNcMUp5qA2dKabyiwph5UGosCCVaQXogT79W10JBlDnc5Tel1R8aLAB6jBfwhsijU8e+grPh8ok7m0j9OZE2e1kJLbXrkwdHLABi3INIMgSDeRXcbTYycNbm8ozTU3DC1qTDe3x+vZ45FuPpegbRxTCjF3Q6gE/j/2EuKpT+G6lgb7zQD8BfaKJ0EAb4OGlfaMnW2L0fSqtLTLXl1jQQ2V3D8qvGlPsfHQBbKlDsRe7AHYebBxYeWxruwgeCWhZP5oIEJOpDzLv0s9Fk7lbh9eNC6HWHq0YZuxINloikIrtU+uOxmYdvvI++NdBOOKFdS0Vg9AbJ0tlBSKN/pSiY4MM8NpnWLwB+uJKl+6vDuJE5qCdwL38Ic4TJOfLVKweIkwQYXJF6Y8NMlSMyi8dafz30Jwdw3LrhufjJEpUARpEq/T2KF1LimHT8Gwod4BfYqTgyicy6R4koBUJjuP+mjS9l5rgVQX1Q1qS9OZH54AFb15ciyC7XMZmPeoEw8yelLw2Ta47IT8QaWQorUNjKNPcXXv7087nl3nfWNtheKM9Xi9o8q1UlitCK0Qa3ZS2PdUEL63DHntyr1C6JB7nZV+FdhraOemZFWVJ2U3U3Y5IfFJ1ROfuTRoPL30I3fIN1cvhFM7MEktqPgKCKwAKj4+aSH9SCrQ8N9Df006k33/k2/wPE9DfBr3wtWEEwgiEEfjJIEAI6Llz5w4dOvTWW289evQoYZ+VidzQMY8y2DvLSEk59X1AQBI/bcrnne9Z0jxtRt/VQaXAAwLfVfrhdMIIhBEII/CfRECSJLIYHJcRe/weu3ParBm/+NVVyD5rYtKjYm8aOfaKuMGTb7hz9YMv2T8pASuLYqmcgKPxgOy2q4+pXrO5fMZKOOayf1JyaN4aurwJejn2QEPJzOUVi9fxR1rR55WXxdGUIOGAyivUf7J91/xVfFMH2H2+5vYd769q+Wgz1HWCh4dWa+8Hm9gPtonr9lW+/UHLqi/guI2MPH3AOYBB11AsD7Vd25+bvnPKDChthlYn1PZUTlu+669zvKW10Odt6e5Y8cnaCbf8dhBF3TTmij/eYyy6x/DLsZclxMVRkRGJg1Kyddq5Cxe0tpvJKB1NoXlOkeMIE9DfXydUvkm+vyz+YykP+BII3SVlCD1CTJ6rq6u192hVKtUVV1yxYcMGhmF+ToD8x5A/z4xEmediRGB5MveGj6ODlv1XTGyPygFNoRBl8iUXlsWO9/5xNrTw0EMjKWwHeGJNe2Q2F5Pvk120NSXrvc8tQ5UMQuwQRieUMgMAjwCdUPKLwu541N/wRxnMiYaDl09E89IuBp2hyVwuVoQ8g3xoS9v0wPTuCx5wq01WKtdG3WNXGdyRBh9l8EQYfJp76y78I3QhlRkQkTZn5NpgCkrWA3AhnDsDaMa7eE9ZuqEvNs+tNvVRuV1UtiNjUnnyPehpcF4JlPmgNoA1OsLCvK9arn+idWhRG5Vtp+5hIw0eKsetMULuu3CcBWagwSYAuAQWn8kugGkbHSPuZyk9E2X0xuU5UwtrY7LQgPqZj+CAE7pl/V0ZNkROkGlZ2TqTQKg8eDmQfLi8Rn7wE2KdEcDuBzu48qebk41ClAkoExdh6IjXN137KGxrQ+ELkooHoBPoxxcfT9TTKPqR06Mx7Mo0gBnAg6+gIG4DCGgHwKaOmkFGewzKBwcoVEDen6GDEhswMgGtqHYIcolZABvwL64+mqK1UFli8sQe6k4mAjVbiHgLKvAOL4StjSh7wkhYk5N5xgFt9Z3tKpbaxFxeQJZfen1d3+jJ6AkzQtur0XclmxoGGfYlTYDnP4ZyL3RJOHlAo2cFRuCBk418SWmVrqVYQIf4CiS2ucFJAgA46qi6uMgaa6ATCtiEwh4q+2hslsswDY6hdTlYGTBL8M727hgdxE3yUzoixsIXzMI5A3ku5wRpHppvcOpIBJ+AFPnHZZXDTd0R2RBXJEXlQdJEiyr3WHQW5C+AxWVw2AsdAA0C1PMwd3fvr560JOc5Yo1eNXLQvRp9R2Zx78QZ6JoP3Xui5AvZBhLQZroqXe+gJjjVqCLNROibkvW2l5ajJ0MBcNkW9nsRzILrgbmYBXW3PSLXm5DvjcvrSjZ1XfsELNiHJemTZ1laRfjrJtew+xxJ+UgfU3o/leuONXG50zDCyVsQBAIuJ98GVgnmbq8bbLRH6/nEImuUtjVO+1VaNizYhdy9A43ScHMDLDrcFqsVKB2g4od2f/x4ONSODUq2085RBc+d578wAX2ewIUvCyMQRiCMwE8FAb/fzzCMEBAOHjw4dOjQSy+9tLq6Gr/iQpYRKa/S8Kjmp9Ks4XKeBwJkYB+6yD00TM6eR7LhS8II/PcgQGQiCAft8XiaW1sm5GRTapVKpRoUl3jt6DHZV910oybjuf/NKZ+zhj3QgD613AL40R0TOgC0uaGX8eyoLH1jMeyoh41lJa8vpPcchU4PHHc0Lfp0619mIPvsYkUaBZfReokXoZfx7T267pUZcKwLPCzY/QeXfVz9yVbw0+DyQJu1Zckn5jeXweaqiunLW9ZvB68odveh9LPA+QSGDjAggv9IS9NbK3c/8Hdh51Fkn7vo6iUbvvzLTDjWC1av6PBiRgCNJWV/u+/RXyRnpFOaG6+4+oVnnr3jjjsoioqNj4vSRKcNGfzUM09v2/4llksQaJpWVBFCecPvJPzf06nCNQ1FQOk8SBJKEpFKq6qquvPOOyMiIi6//PLNmzdbrdbw11ooaN9HmJgS4iNIwqcQuuRiBSTdjjOd4/5mSS9kEwoFNF3MMcfpGo1ToV225xUkgefRJrTcuyctuzcl30PlBCh9Z6zOcu80aENaDR80CgGtcMFkYX6Vd+fQ3K4EtIBmI1EToMX4dySMLAxmLZNCwctlTVnfQwsqk3KOU+Ol+IlW9NSn9eNC+yAB7Y++99iwQlhVSoQ4WJQMQjoVN4WtU7BT6EI0HwZYXbF3mKEhQe+NL3RROXRMQU3k+PpfPgIrDkFbAHkrhwROmZpFDZAAHBdajG9aBxWBqkCKynNQE2xU9uHkbNhcD05RKbySG84uujg40Ndy+YOuKD1QRlGd16vRH44ed/y3zyMJa5WlKmiZZxQlAhgWWwZBgVAhoAMgEZ6TZIG1xJcFcM+vrEnV0anFQZndOJP1qsfgkBOVmol5LPqCk6CB3/OLAmtKvhBl8lD3HIvXHst/C+l1P+aItsgka0XCWwCwCbCssn7IvWcioE9yXSiTfYHHl9TG5/gSC/yUjqf0XirLT+UQApp4rqujxjXmvEwmKgJo2a1UV0HuewgoTU9mOBws7O46MrrAHq3nKK0/Um+JMxyKHV/568dgTzt08YiJ7DVRYHEKtr9BTikY6WOk5fo7PNo+k1kYFqCVsxW+eyw2x0XlojfIpMK2tDzvvdNxysQjAiPgn1OAOroyKccVoXWq9a7EfEucoeXGJ7B7CAgOacMT/Vnp2KSfuyXY3Vk60tiXnA8xRSIKl+d0xOv3ZuTC2ipoYaGdQ6EYh9yTPQI4RDjON5im1g/N641FSWinSufKmLRzaC7sbJJVnEWZbRfxgwHnFfr9EAJAm58Q0A4NiudwEYaWFAM/bwvpQsSVH/QBN3l++5CCnsgcD5XLU2hkfXSwQXh6OZh5XCsmypP0TgYRPg5dWa8e1UxwRWjJvIgvxtRw5YP4QDh1I7MjpMe4ABbvrbyw0Dq02Bdj8lHZFrV2R0YOLNopP83ki8lsQbcAD77fGZXDUnpQ5fVSWfWX3g/tsng0eUooz4pTczzfI2EC+nyRC18XRiCMQBiBHysCZPRCLJpxkCx7EWlpabnpppsyMjIWLFjgl7dQ6i1MQP9YGzNcrjMiQDwynWUQTjgyhmH8fr9H3tzyRsJeeWMYhmVZnkfLJnLjnDG/U07g+srwFkbgvw8Bp9OJQ3uPZ8eOHf+XNWHI0IwIihocm3jT6EuN19468erbPnjwL4feXOL8fD90u6VeN/gF4NALluShobXXu60c2eftNbCr6dDfFni+LIdOL7T0Na798stX5zr+XQ4OFnwsy7IBUeQZFvo8UGXe9sqc3h3l4OTB6tq17MPKVZ9Cc7fk8YAoHlmxvnXuh/yyL6tfe696xad0czsOsQQReC7AMRLD4FrsdmftwvWf578gfbgPLDx0ehrXfvnpS9O7P9sLXV5c+e5hwOEFNwu9/r0r1/914sM3XXz5oJiE0aNH508syissGPOLsWq1Ojk5OS4u7vbbb587d25ba6vA82JAHv+ekID+Gh1nhV782sB/X88K1xgRUDoG+TAjRziOq6qq0uv1MTExY8eOXbFiRZiD/r67CzF95mSGK/iy5wG6OJi+pS5J61XpIXWyL0Jnj9bb/udpOOJEmknZ3DyYhaP/90JTgtZFZUGkqTNW1zDuL4SADpLairmochUPsLq8cnRBVwKKR/NRpqZUA/OP9dDhR5UhXHLSL2dBA7RzHQ/NbhiWb6GyWE2BnbrHTI23q40+ysBQBpYyMpTBQWUfS9T3PLkYzH5gkQQOiIBU7gCSjhSAsJC8zC32QNv/PldNjevRGNyaPFZT0BVrbLr2cTjgRv4RlfyBcfs9Hh8rU8NoiyoAtAiWXz7BxRVJMQVuKturNlQn5lgenQdmFo27T/1i6mHgxfX29KJApBEi82i1sU6TBQ8vhSYJegVMEGU0ggSjAhIJKKymQkALcs0wE7l2Xr8fpwGWlpamZqMpelxBOzXBOnxi3egi+LwNTdSVDdflACwqrcgwOBPy+Og8b3TekYw8WF8J9gBwmG7QAppIhxCOT5Bp99l7Tk9A+/BGJl5q8TOVlcDOW15fXZmU00tNsFMTBE0+p0LPckwEig6j78ooI05UUFkHhuphbQXYmQCy3+hv4FTklLJ/ZwGFgwYAswf+vKJNneOl0PDWG21sSNLBw+9DmzwRQrREzqVMod2sP/2gy01BtvN9+ePy5BwudaKPynZRE9qjcxv+5zE47EC+H2cYZAoZCVmw3fGiJUbvTMjrizN2xuqCBLR8NwwkoEXZZJ6wsW4W2tjm25/tTJJllCPzGConkPmg9dYXYL8D+4CHk6wu7DAAAZp1Mf6AKOJSAweUXT3ZnGx0RaMRtC+58HBydveTC5Ct9sjqN2jxfQoB3eqpTNM5qAmuaNRwD1BIQMPqffhk4OVFAH2S94219al6GzWBjkPDZ5taVx4zHubuBTPWw8vjYi3ktVkBZUx6GN/b648M0rGx+W6EKMuj0jddcWYCmkyaMQDdcGhsUS11lyulkEksdFC5rUPy4Z2N0INW2G6WxsUcnITm2Edc5UORLufjClBxPi5XemgxqpMRDWhC4ivtKDfLt/8JE9DfHsNwCmEEwgiEEfhxIUAs1IiBM8uyNpvN5XIVFhaq1eonnniCSD+zLBsqvqEQ0D+umoRLE0bgdAiQ8TnP80S+nIzPSURRFDmOc7lcjY2N5eXlJSUlW7du/fjjj2fOnJmdnT1+/PiXX355/vz5s2fPXrx48YoVK5YvX7506dJ169ZVV1fzPN/X1+dwOLq6upqbm9va2sxmc2dnp9PpJDZoQkAgVDUJ8DzPMEyYhj5dE4WP/UwQULiw0PqwLNvZ2fnaa6+NHTs2PiY2XhU9Mi7l5uGXFF93x+O/mXBw1sqtf53FbC6Dxl7kcwUcDQoemvP4ocfl+6TU/O5HwpYK2FlbN22la8M+6GXAybV9tH3L1LnmkgrUvmQEHH3x8q+DgSbrVzOWOb8sAzvHt/Rse2/ljoWroaMPHAx09LV+vuvQux841+wof31R0wef+WpbZb0NkRfl5a4+Glws1Pcce2f12oIpHSu2QjcLDPCVLeteerd+7Tb0UuiV/3wCMt0CuPbX7pqzom7jzreeeP53t96enjlUk5Z8/S2/Li4uzr57fJImNi0haUhyanpi8p8m3ld54DDj8QIvsF6ZfJLA5/ZIwokluqETvQqY5xgIxTwc/i9EgHzLKZQ0wzBVVVUFBQVxcXGjR49etGiRy+U6yxTsfyFi322VFa0AQTbYRGbIK8CKgwdSc8yqbD7KJKpMloicI0MMsLEVOvGBQ0g2ZFppXETveXWNOaPARt3FUvrWBF1r4T+gS7ahVqISLli2cpUEEXp5mLWjNsNkSzS5I3VMtOlQ/ATY34nsLRHuoGVyzQ/QKcGflrSkmCxqPR1TYKe0rdT4phSTeUhRN5XrpLKAygMKCU1LckHDuJeg3ge0bIVM+D+FUSIEEwGF66bpAAAgAElEQVSOHPQDNDLwt/WtqXl0FP6h/kZsnuOGKXDQhRrWjCzTIFuxcnJFZWeschJ2gEWHKhNQVQD1rzV5nSmmLy/QQ5UbbCwEkPo+Qb4DQKt/f+IEf6Sej8L6WuONlRcWIsvpktOVmUVCRZ6lZRUmmgSCMQXAF4QNyi4u7I5BP5BCysTeeGPtqEJYshc66CCeRNPDAXDQXjvmfmdqsVuT51Qb7YOKd2TcgyB7eRBJY6LNN25El1mQG9smwKxdtemmXo2epfQ8he7yUOXgsBuBQrofaVq0iKcBVpWXZejtiXleSmuhJqC1L3WXJy6vnbrLqdL5oo2yYniOP1LfN3ySteAdNEKXGUkvz54L2SsX7jx/gtApUDZ59sWO80XomChjn0rbnWg8fFEBtotbFheWS3PeReIkETuBB+CL+sPDULREFmXWor3w4Dz4ohGsrCRJDEjIkDJyB7VJ8OqmrtS8nsgciyrXnGjwGN9BI3G5h2BJyI1HOjAhoEUJXT5YgX/lo6pkVK5gooxOKsceb+q8+jGc4bBL4JdkXlg2YQ7gryA7sUTdcJcEi/dVDzN1R6N7wF4q63iKcevFBjjGgkM4YQFN1J8VDegWd2WaTlTnedWonyNShoZBBviiGpwcWn07AN7efGS4qTsqF2ILObXJkpz379TxsLoCdWY8cmHkmeygVXVAAh8Pmyv3p2QHEosc1AQsSURu16+fOb0FNADK07s46AP62WVtwwq7qHFsQqE93lQfl0P/cQ600bgmAFAchmVZWXHezzy5pH1ooVtt8MSY7Jn37Ryhg81NKOdN9LX7pw3IpE7w9zx72YnLwgT0CSzCoTACYQTCCPw8ECCWoYSeI8TZu+++S1HUr371q56eHqLdSdM0y7IDxsY/j+qHa/HzRoCMyRXaV5luIWT04cOH1/xrzZQpU+64447U1NSYmJjIyEhcPh8bSwKRkZEqlYqSt8jISI1GExERkZKScuedd06bNu3VV1999NFH8/Pztfdo9Xq90WjU6XQTJ06cMmXK8uXLS0tL+/pOSK+JosjzvFKSnzfs4dr9FyKg3GvknUJmd2iabmpqys/PT0tLi46ITIxQp1PRV8dn5I6+Zrruwb4NJbveWGjduA+aesGOjAMOv1muu9UsOryB+o6qN5b6l26Hfc173lp85P31SDR0u52H61c98Vrjuu1BUoCsaQ3Ig89m2663329avgkXOzfbts1dfnTDdrqmDXpc4JPYg/Wlb79vXbn1+KIN9cs+BXMf+HGZuh84WmSB58DLQTd97N2Va/VPuVbugA4v2iIds3zxxrwDSz6Gbtk6mxHQQaJPAAfrPlT/1T9XWDfvr/lwy7rZi48eqX73vbnDrxijGZxy0QUXPvHgww8XTcpMTB2dlpGs0kRT1C8vuXTaK1M7W9poZ5Cd4BlWDAjkb8As7znyzkq0/8IuF65yKALkBhzQH2pqarT3aCmKuvDCC2fMmNHbi4uxOXkLvTYc/k4QIIRpUAZBkMAOXb9/sSsOV+VzapOf0pmTjfDONlQD6OMg6PBO5sXQtx4Hm2uq0lENtk+tq0zTcbM3gU2W6VCYPjlA9mThDoApa5oHGdm0SX6NqU+tQ2PYjn7bYQnwMeUDVFWevq0lxeSicoToQi75jz2Di/cPuod5cCHMKnFe+2xntF6MKmCpbKDudScUHhhdAPUB8CIBjeQ4cQencNAKUpIsjuAF+KKt8YJJ3ug8oPKEiLzeuLyjmYWw8khQeZZwrwFMh5a1OiTipE+Ud5qkmhsf60kyCVEmPsrUl2AqG6yDz2RKC70FIq+FtCEpxt7W2sRckTI4qWxHrBHNRad+jrnIiSPbJQeVAioBghjZDcWSsOuYvuzb0PXnRc2J2FKeCJ05Iqs6KRdeWgtmmhCXAkg8keU1Q5vxre70Ij66gI7Ks8QYa4cVwKxd+HqS7VZpmXpFQpgY/xIOGgB6JZi1qzrVEEpAl40wQTVL6GN8/flk7ZSvWvcP01vU6AjOo9L3pRU2DysoH5kHxplw79z6dKM1WsepjDSVzVJob1t52SQ4jpOaPM/TnGwVq1T+uw4Qq1meaH2IMnS7mqvjswOUvo/KssQZ6lP1MHUjtgu5E74dAY3VEdBEt+aWJ82JyD5LFArONKiz4PUt0M55e3o52aVkkICWALpo+KL1yMh8e2KemRpflpQN/9hE9LuD9tShBLQEOJcjSninbGmu+MVE25Aiv8Zko8YzwyYfSMuF1ZXYcIxM+ApSQCadMb4YdGWJ3DcjQSfU3/JUA3W3n8r1UNmWGP2BwVr4pBYVpXlZfyMgW0CjKrT8hwJezqpUrRSVR6uwRgHKUJdmgOo+cItgEeGzuuphJmnYgxBb6KCyemL1BwdrYf5OaPWDT04BraT7BT1EOcyJ3OeHDw3RcXEFDmoCF5PfHZXr+L/XTtWAJp0iONWxuqzu4olt1DgPNYHV5LXE5tbd+Bi04jQaLhcga7aw9wLM23lgqL5To7VTObbI3Johxs5H56KVt0sMrmkIE9Df9e0WTi+MQBiBMAI/TwQUApplWY/Hs3z58sGDB1922WW7du0iIxm/309YM4WA/nkCEa7VzxGB0DE5mcn3+/1Wq/XAgQNTpky57bbbUlJSCL9MUVRkZGRaWtrFF18celCj0WRkZFx00UUjRoxISkpS+GiVSpWcnJyZmTlmzJirrrrqV7/61dVXX33JJZcMHTo0PT19+PDhF110UUFBwcqVKxsbG/1+/4nPuJ8jzuE6hREIJaBpn18MCB6PZ//+/QadXqOOjoiIGBSTkEnF3pwy6ombxq+Y9DzsrK2ctbp5zTZo7UVDG5l9Rqu3gAA0Z69t2fXe6voPNkp76w79c1XtR1u5XhfwwO6r2/H6/Ko1m6DPT/f0HSmr8Hq9fq8syuxgmz7eXjZ7NRzpgqOW+vfWd3y6BwU6elzQ4xH21++btrhn1Vbnmh0VM1eAzQdMAAQRdZ8llg4wnKUPXKJj0abDT77buGA9tDig2wPtzoq5H9Yt/Qy63YLdAxySxXgvMwIcMR+asaL+g40Na7aWzF9tLatj/HS7q3fvsar7n3psRMbQaIoad+Mtut+Oy77lt5cMyRyRlJas0qTHJPypaNKXn37e2dKGUqH0CQIaaeiQTWESzzEQ7oFhBJSuQuY7PR60q2xsbLzvvvvi4uIyMzNffPHFuro6NGcLb98DAgoBjbypHTx/XdU0NF9MncREm5hok43KEca9AXUePMuIIt3fCsRRHgdgkewTpjbHazvS87+6JB8tEAWZ4CNsXz+5E6RTeQE84ND/oyPRwMQX+GPzOmK0x299lpBNROICedVOCVbWNgwttKj1QnShm8pppsZ/NdIEKw+DmUOz0AaovLDYGp/HUAaILPRH31uWfA/stYOnn4Am+YXaPhPoCAHdIXn/701bpFa2oUYCuiEtz//6OkzZLZOUstkprmtBp3+SF3k7mY8jiRz3wLubzKloHo5iyjGmhgQtvL2d0IWybDWaUOPGACzd1TAYTVO9Kr0t0VSVrkdbcpn2xQiKxz8S/+RfxQJXIaAJu00cLSL5+HFN3fB8h8Ygqkw+SlsVcdeRu6ZAox9Zc7TBlevv4aGd8zy8sDmzuDfaGIjMk6ILLenFlsIZqBAtW53jGh6ZaQyS5oQcJyCcjoBuvPwBaJKVo0mBbV5oZW33zzqensfFFXgprSs+rzbDRP9pAdS5UX24jYMFu4+nGBlKh/4qI3SuaENZhh621mBvQcpbJIU9GYDvbI9IzRBVZ8zIB9KSnXVpSKE6VbruRCNOIXzegu1CSGpFa/jULnSOhfIBPL2yIuJOolMBlKE73tB+71vYOjiNwQS1lQmxKwBOZlug9d43zYkYc9+lRVDnR3USuRPJa51koPpzR28TEgqJmLNf7c6c2JNgtKhy7RG5x4cVoqCNF5Dw5ZDhJabWtMx3B+RfjvDRnAQ2gX55TUeyESi9QKFK9bEUPby1GcVhAiL+IQ0ti6sw8q8AUOs4MkgnReUFIo2cCv9qhhhRW4MFqGVb/vfp9uhc0BQyVLY71lR9UREsKsG5K68szR6QE2H7OWj0vSwBDdKqvXUjCvwak5fK9UUbzXE6/r55KB6iTCCRALlfAMAmVf/PIx0xWtAUQkSejZqASzQ+r4MO2SZfUflocsKcrfsG5zZHZdmjUOLDFpl79MIiqLAhikRuXrm1+hdqBDPtx/m8/4ctoM8buvCFYQTCCIQR+PEioJg/b9u27corrxw8ePDMmTPJohu3203c2hDjLDK8+fHWJFyyMAIhCEgSzt4rvBjDME6nc+vWrc8888zo0aMTEhJiY2PVanVsbGxCQkJ0dLRGo0lOTk5PTydG0KmpqcOHDx89evTIkSMzMjJSUlJiYmJUKlVERARFUenp6bfffvsTTzwxb968zz//fPv27aWlpTU1NQcPHly3bt20adP0ev3YsWOHDx8+adKkffv20TQdUrRwMIzAzwoB5S4jDCqIUp/VtmDuvKsuvyJOrYmJUGmoyNEJaddFD37kitt3PDcdNlfueHFW/ZLPoN0JNFlHCshBo56GyPc4dixbW7dxp1TfeXDZ+rKl66GP8Xu9fV2WzW/Or1ywFnr97i7r7LenF+YXLFiI24q5Cz+ds2TfgjVQa4FaW92CdWgH3WTDdbU0QFlr3TsrOpZsPDr7X3XvrYXq4+BlGL9PEDhGQPYZpZ/7aPfGfRXP/bPqrwugwYpaH83W8g82lL+3VqxsBb8o+Jgg+8yhCseBGSt6Vn1p3bhvy1sLPKW1yHQHRLIAvKun59MlK8f/8qYL1EmXDhqed3d2sdY4LDktloq8bOSFQxNSxg4f9bdnn6+prEKTN9kCGiVEeHS9SPwxkElfhU88l8DPqj+FK3NeCCj9hJc38vHGMEx1dXVxcbFarU5NTX3yySfNZjN6sPOHihCfV37hiwYgoFBsXoAd5r0j9LbkvEBMPq0yWKN1dYONsLISLKzAyiRYoJ8UVSghL8DG+v3XP7B2+Hj4uDKYdoh5L9JtiiKzLNzRfvPT1ihtF3WnPQrNq1GP1YliuMiFiijrASW2w0m5zpg8OqaAT5x4nBrfNPqPsK4OCWKUdw2AFZinVzTGaSFhEkTe66C0PaMfgFU14JaZ337W+wSBFaQVZfvWDj/M+3dj+r2QcD8hoJ0xeSWj8qBbJryIjz/ZIFtE7k9yBwnoAATkJ6UkS2dsqGhKM0oR+EerjV1xenhqTVCSQmYMgwS0D+z/WHt8GGoRQPrknlg94rmgpF/qQq4OybEf1yCA8j/lmMKSnURH9oIv9y1vKqpRByiDi8qtTtfD+grUT0Az3n7D5k6h/N6pFYP0PZH39FG5TpXBPqj46KWTocaPFLaApthB74dEhyUgs9KkBUFWMZ6xqyZJ36vRMxGowtEVpz/2myehR7b0JsV1AawsL0kc36PRodZzXN5+6g5kn9tE8MgMt4dF73P3zm2j7nJQ2R4q1xWhLU/IEudthU4/6iSwiml9KADfWZgQ0EHiXgRwS31vfNiSkc9EGWHQ/Z2x6CIPFuwFF3ZAQrwjLkGT6XMrBhq8999Lfgl2Nx8YrO2msmiVgYnQu9WGigwD7GlBXlgWLiEEdHB8KshksYODLdX7rppUMqYAlu3FGwHVuXFFU7A7ScGbCVNw0+ADz8ItO+Lv6tHo2iOzXenFx6Kzjt38RFC8gtgayybPNEiEgCZm10ECOiBhBTfXtw8pgIg8Xiag7cMmwV/Xgy04ryxz0HLZWJk7FgFqkIBG9jnC4IvQ+WJMR4Ya8d7pEPk/LWwdks8mFKLbSY2pKi4L3v4cu7qDR9kxQTZ85oO0OGJFVoB5ARbuaB89iTiodKr1TakGeHYlVv9UAhplZzjf/M1VQwy02giUyU/ltsfrhfvm493novGbBN8TAs5pzd66c2huW6zWgd1e15uSX5aSA9O3gVV+lCmJKw8o0s7Kk43snu9vmIA+X+TC14URCCMQRuBHjADR2aisrLz66qsjIiLy8/OJ4zUiDK38Ko4Kf8RVCRctjMAJBIhfQaJ6KYqixWJZunTp2LFjNRoNRVG//vWv8/PzH3/88b/85S8vvfTSiy+++JK8vfDCCw8++GBxcfHjjz8+f/78tWvXvv/++9OmTXv22Wfz8/PHjRv3m9/85pprrsnMzCT8dXp6+jXXXHPXXXc98sgjs2fP/vTTTzdv3nzgwIGGhoY1/1qTk5OTlpZ2ySWXLFu2jNijETeGxBw7rMhxorXCoZ8OAqcqyQbHfrJLNKvV2tra+vxzU0ZljohRqaMpKp6KuCwtcwyV8Pgvbtv/zEz+X3vLX11U/s/VwlEzeFiHrFTjZ3ElK47irHT9Zzu/XLLGVt24c+W61/705NuPPz//5TdfeWrK/Yb8v058eP2sRUe/OvDV9p25Wu3Fl196y12/H5I5fFTG8Fsuu2bd9AXc4aa6BesaV27m26woqeEXoc1lmf6R7Y1Vbf/8qGz2Sk/FMehz8SxNi+xxRw/a+YkC2P3+Tft3Pf7m5sdeD+w9ipy1nelct2vjC++6yxqgz4tJ0Sihg+LUx23l7609+I+llrW7tr+zuHXrPhRt9HDg5ySGA4YHJ9O5ufTvOZP+/AfdRZqUBFX0rbfe+udnnrrmumuTY+JuvOLqa8denhaXeMstt7y/crnZ0kUWTdNOt8/tIUJYaJ8knfBPqBCLZwn8dLpPuKTfOwJkZZvylvH7/S0tLZMmTUpISNBoNCaTqaGhgbglQPedspOP0K71vZfvZ5lBv8c59J7qA3/RLMuQoi5qPCRN8lLa5kHGzofnoKkgc5L15UlIEELWIyve0meIRuxJkekEOE4fSMpyU9mcytir0jYNyUN9jx5e5GViTgDU4X1oWUdasZXS9lG63uTiYxc/AIsPgwUNV7EkfpkCXlPemGjgKD2nvrebyjWn3guvbARPP1WnkEoyGe13+QTi6I8FqOEqr3qwJUYraYqAMtKRppYRE+HdL4OCEv0EJEmAQz5ccIMgSQIIPFZAlMDNQElbU5oeKPzjovR9cUaYOA+fwP0bcsdyUh0vLW1JMfiobFaTZ4/W9yQYbeNegQ6a4zha5FFAWSF8Fb5ZvpQUoD+94P8TURiAjw42DEYTbIgwBSKNnqQC4R5ZNZgWaRZlnRGLMkev4e1jg0xu9b00yk1oO9KKa296Cnb3yFauSD3j7ICcWVC+WikPkTGxA/x9W3Oc3hWNUhJsJDqd6316MRoLkyYDgG7hq9HGJuou9DGYWNSTktdy6zPQKeKLDN8/cql7GPigrHqQzqLW+iJ0bkrbmKLvfnA2sqUOHrwsluP73AiemImsLtL10tLWZAND5XBqkz1K1x1vsN71MjT0MX6aRcFvuQ0IAnKpQic1TlvMgNOLU9E4PQvQA95nljYMy++iJrio3F6NvioxB/6yBq16ZcDJpIPyK/uAlOcMGAmcEjjQLhjkeQTS3xULaFIL9MrgEKAdjlz/cEsKutdzaAxtSYZtQ7Phg73gB4njod9pMBF9JiocxJtlQOajkfL3i1Da2TAMiXivCucYmuO18Pgy6BMDoshJotDvL1aez5Dv0J21Vel6NhLZZyuV3ZNgBO1MqBVh2YGDiVl0arEQX+hLLkRJk6dWQI8s9BGQ7xqZgA5+dAky+8xLSMcLwE5d25yoQ1eQVFZPZE7d8HyYvxs7mNJm8gwWgssCtEulNz10LFEbSC7mIgzWWMO+4XrYY4EeFlgRp8Z7nNAJ8MLqY6OLnKmFTpWunfp9j0ZXf9FE+PAwAhuqua5k0T93cNrGPY+DYQL6PEALXxJGIIxAGIEfNQKSJLlcrs2bN19//fUxMTF/+MMfWlpaFC9qYfb5R9144cKdFQGiQks6M8dxc+fOHTFiRGRk5C233DJjxozy8nJC8RAngRzHsSxLtKGJWDOx5SS3ABnJ+/3+3t7exsbG/fv3b9y4cfny5e+8885TTz2VnZ194403jhkzJiMjY+TIkTfeeOPNN9+cnZ1dUFBgMpkyMjIiIiIuvfTSN954o7293Wq10jTt9couY2SaSaGczlqb8MkwAj8KBMhdc1q6SpIklmV37tw5ceLEUaNGqVSqKCoiVR07hIrOpFTP3Jy199F/wNrD7f+PvTOBb6pK//5t0qZJm+4tBcoii7jgguI4LqPOOCo4XWlWaEsFFVdUGERFQUEUlEUGURRFEXFYFFlll0XZoUBL931Pm6TZk7vk3jzv/7knDRFwXEeZ1+QT4yVN7j3nOefem/M9v/N75q8tmvMR1JpQrgXQ5fYv9vR02cDkPLNu++b573+x+APt3++/LC4lOVzRV5nQWxGXHK5Iksj7xSRdkdZ/QM+0a666OlIhl8VEDb1xWO/+fcMlkihKenliz8mj8nfPfhdKmnEcDuCsaq5dtb151oqO2Z8Wv/Gx90wtoc80zziA6WDtPAhCR1fr1m8OTJm/b+Lrvm9KodUObjAdKtn8/Hzv4QowOxEre8Rsh5wPHJxl54nKJZ+7Nx4pWvhp+9cnMOWXgwUXCx7RRdrCdX1d9MXk18s/2uQ5Xbvp/U/u/NMtcXFx11x3bX5+fl62atRf70uLjh/Yo3ffvn3jkpNUeu3OnTttnSYcbPMInTmOI9NU5BJEpn6DA37R7Uuic4QKcWlEIHj2gvQf3stbrdZx48b17NmToqj09PRTp04FjKECST6Cu9alUZX/nVKgOa4PZZZmFr4qq+5X4IzQ0BR69RqorOO9NXAGDbgR2XQDmoBw8LyN/1RnYitM9KSHm0rjcj1UllemN8bovo3LgO2NYkIwUbHbBfDmntJ4jSlqjF2eZ4opOKzIhLk7Uc/oFItBgBwHsLumNmk0R2md4bpW6aimGB08tQps3QCaFI7QJS8Aw/sYkedZAd460JCcZ5LruPDRAqWtp9JL/zIZ7Q5EBBrgUWSDw8PyLnSz4MArAmgAcNBwqLEqUQWUykepPFJMLQgTPgBnIEhiMMRdtL6xpjw2l6Zy+eh8t0LvkuvKkjXmWZ9hqlhWBGqMWK+L4dcL30Oq7BPl2SZoGzvfEKsDCgG0S65r7VMI7x4Go9hOXiLTLjt90xONsToHlQvhY93S0Q1xY05d8wjSZ4MA9Dm+5xMuZsGBttc+BMT//LxNobVHoGEFI0HPX/uiTYCLZ8QC2sH62tqymBwnlcNLtCaF5lgfLWwsA6fAYCo4fKBbhIWBEve3fTVtUWq3BJ8NMerajOnQJOZjdPzXAfS5/im6PLfPXVMZk8tSuaDIp2U6T4S2LFHd9sJyaHZju5CJme4+H9wrLi6Q9WEfQwAtiNMk+1t3p2R29hxrj9QyijGNSvXW3llw3IgzKCKgDqDn8zZY7Gc4ox14sgFLcRGBk5IAy6OxydKjdSl6k0LjjMBnVaLmWPpUaHALZgcj8IQ1X/TVC5j/EKfk3QIcbS3vPcYl0zpl2q5oXY0yF546B6AD2Bo/zIvh2FNW3EPjlqhdYSoDlVUTp4YHV8A+x/HB+eakfEFZ0BWWU5+gbciYgRTY5c956O0G2WSHuDdiAO3wgREq7nuuPVoDEj1I0FH96GV6ONSJiubguJNVFDaApQdKeulaFSqnTGuiMosiRlomfQCNDMbWJVroVLtN+jdqeuitEWpQFDilalvy2EOxGbBoV2CKyMuwaJsWPKvQ3dbn+skv2woB6F8Wv9C3QxEIRSAUgUssAj6fz2Kx7N+//6qrrqIoatiwYfv37w94BQTT55BU8xJrulBxflQECFymafqzzz7r27evRCK57bbb9u3bZ7f7k4ARshysNwzeL3GnIe8Q1WfAM52Y0rAsa7VaGxsbz549u3fv3s8++2zmzJkPPfTQPffcc/311w8cOPDyyy9PSkqiKCoqKio+Pv7WW2+dOHHixo0bW1paOA4XVJJV0sEHDW2HInApR+D7ALTD4eA4bsuWLbfcckuUUklRVJhcJgmXRlNhV8oSlj/43DeTF8Dqo51z1xa9+iGUtoFLAJrjRcWYf8DiYE5s2f24Jl/9txGD4nvEUVI5RaVEKmMo3EkMJU2URSVHx8bIFRFSabRcER8TO7j/gB4JSfExsZSECpNiBtE4SjJd+2DbvpM+m5vvcpxYu3Xn7HdL5n58fNZ7zLEK6HIJHg/abgiMi6e9Pq/P5oDS5s/GT93wyHTYXwrVHdDh9uwo+vrlJQ0b9qGbpJvlOQ6HWDQPJsay88TxhSudGw6XzV3ZsnIHtNoEixM8LM+waCXpYKHCfHzmMkyZ2GIFByvY3K3VdTOefT5ZruyrTPhT/yHTxj9+//Db+ioThg4e0r9P354pPa698uqZz02rOn3W62F4jqNpOgSgL+VT4NIvG+HIfmRF2JZo9lJXVzdp0iSKolJSUkaMGLFjxw7y0y4EoH+VNsWrhBt1hXXZL1dI0zlKBZTGReWir/GUz6CVAzvmHiSPgJfGefT5h+kNMUHwAHxyoCFZT1PZ7nBNZ8+xB68phDoBjCy4fViMjcXFgx7ojBltpFTNktz6tHGW/MXIKO3dvtIEQDMAxZbatLFc+GhLmLpTpmmJVNP6RWBBZnXuEQBM5OhOHuo518jZnTKNEF3IUNoO6r6G1AJYcRj37z2fd4n4S/AieBPpMwJoEV463XC4PgCgnRGqhmgVTPoUzOKvI5HV+wPCCnDaUNo3j4vO98j1tEznlenNEarm/uP4grdhnwHqaHD4CLcOmF7gP78noALKhUWh9RHjwV4qsxJ9qAWprjNG13T381DFo8a2zQN1ANM31fR/oDl8lEeig4h8C5VbF6+r+cd0OG5GTifmSSR8j1gjkFe/Fwcpihd42gvtXih8z6gcbZNp3OHIoNGtYusZ4NCfBFwcHDUd76ujk8e5qWwXlVsSnQWLd2BTsggf0VMOfDTPgQdZdsVdk5uj0cqDDlM3R6uPDC2ECgaxIC0Kg8+13K+/RaTt2GcEYeMAACAASURBVD0ILC5qK+2bJygLmEg9G4FCcrM0tzpFx41+C/Z1QIuAYlsRBNNi1wtWzX5v58f5AUTDnWMXFEdnmaO0trBcA5VR0UPX/JRoakyLUPWnVM5PnIkiO7hzdwiunDmNVIYzAmcFPFIxGeAXp1D+zAseEALMN3h+jqihkbwKov+yS4AjrZWiApqVau0K0c38aQTQ/iSHYt5C/DAxCREAdpSV9tC6JdiC5ghVCSq7d0De8pY4rT1Sa6FyWsOziwbmQ4WYD5THnJwk8rRoP026BMHQXvBh59/RdDpFbYnUQEQeSMd0xugq7pmKyx3cYksFGDRxljeA8e8vNlDpzgiNhcpqpTIxhenRFuzPTkCLno+PYcpBhcpOZfGUykzd1xmeeyI5Fz47AZ0CfgzAZferB/wnWtDpFhzgn9JKF/lsCEBfJCiht0IRCEUgFIH/0QgQ+nzq1Knrr7+eoqiBAweuW7eOWFLabJg/ggBoMoYh9O1/tKahYv8xI0A6rcfj2b9//7BhwyIjI++9994jR44AACs+fvy0CgHZBDoHB5Pw6MCvUvIncmZVVFQcOHBg586db7zxxvTp0wsKCnr37k1SHcbHx2dkZOzatYucaME7DG2HInCJRyBAtQLKXFJgq9W6YsWKIUOGpKamJqYkR0TJqcgIWXjELYOuXj9r0cGX34XPj3re21E7dxWcqMcBt8PDe3kPyxitFhqxK/PZkmX/+POd/Xv3iVXG9IiKve2aG/RZudqM7D8Nvf7vt95xeVq/3kkpKUmY4TMxJfmmm26a88qso3sPfPzO+3qVJj41JTolgaIoGRXWK0xx1+Brx6v1rz07bfEzLx5897Pts9+2HioGow1ohvMySIs50fcZwFlU+dXk17c8Oav6061QZ8TVuCfrdzw2GzXazRZcC8xwaIbI8uDimW/Ltk+Z591+avuUeRVvr4NaC9ad5Xlxl+BmwcJ+O+3tb55bRJ+qBdpH2xyiKQfv67Qtf+WN6+J6XxmdMrzXwEn5Dz6hHzsgMXVQatoNl191db+B/ZNS0/92745NW6xdFjI1dWGcA9eZi25c4t0mVLzfMgKkhwS6EFE6+3w+t9vd2Ng4YcIEuVxOUdSNN964Y8cO3ssHAHTo994vaSY8cztp+KquJE3PJY0DSgOU2inTHuung287wSiKOkUeGlCFXgjgvoeXBpULqR9yZGb25x09CmgRVranFdbmz0E3YQsLdh80QXXOzJp4nU2mc8jzSsOzt/VRw9EucAHP+nwoyBV3Qqx8m/nKyx5gFPmmsFxLpK49PNc2Ypbf/TaAkYjymlBzDsDEQbGrIq2Aj3lAUIx1h2ntkfoTPXXQBohHuw12A8hL3I2AmlQ+AKBFUwaHBw7W1ySg/FmgVLZI1dnYHJi2BgwXMyjvAn7yJyWJqirqfrdCD/J8X7gelGMbI7KrBhbCjPXQIGD2wmCTkyAiFhRB3BQAHCwNrQ6Y/kVlTK5doePCdWyErilBB7M3IbZrA9hc1nrH8+beD9rCtU4qm6FybTJdeZKuQ/cm1PHovOFGsErMNxAOinQx8IqH6bZM4dwstLBM9pu2mHxbuNohVbtkWvQyPmXw+xi0e9iH3rWnPchE6t0StVWp92S+jsUgieZEFwgefGhq4QNo421Pvt8Qo+Yo9JI2KNS7kzKgSCSVP8lt+byg/JR/BroGiO1SlqiuDUv3yPWYzk6iY6XaBiq9btB4mL0FfY0dIoEWFerBADq4h5DO5S+CD9DYqsJ5rJ+uQ47hslA5nTG6g/20UGIGsweFzeTLFz2F/vObgS/iqgWAAzW1A8exETohQs9INPYITVFPDdQz4AMb7RbnF7pVx0G3XgKgcZRB/JdtAhwSLTjC1GgjHq4ujcvlJiGARvfnQJ8I+DXTAFvLKnro3BI1G6axyTTliix4/ZhBoXbJdUYqw6BQH0/Ihk9PQbuH4zivKOgmANol5vPEQws4zcGKpQOzD17Z2qbU2CUqQapjqJyqyCzL1I9wHoXYjpBaYzpEETHXQ1FctpPK5Sg1Kx/TptTU3jbJ31IGsP1zeVkvvSM2z0ll8pSKidQbk/Pbbnwa/n0Gmj1gZ9DVxOX30z7Xa7pPN3Koc+//sq0QgP5l8Qt9OxSBUARCEfhdIxBY9U/AgcPh2Lx589ChQ0nKtdmzZzscjsCI5bwNctv9XYsfOngoAj8hAiQDIcuyTU1N99xzj0KhGDFiRHl5OVqfiZaXhCafB9F+wgHEjwb9HP3eTWK12dnZOXPmzNTU1MjIyL/+9a+pqak333zzrl27CGz6qccNfT4Ugf9GBMiw4cLXwLECrjXkBkFynXEcV1ZWNnHixH79+snl8ri4OGlEhDQiIj4mVn1f+jcrPj/1/uctH2wxfrCtY8UOOFSF+f1cHPiA4Vg3Q7Msa7NYP3xn6Q2XX5UYFUNRVHyvHsvee7/keFFzXX1jvf95pujU8SNH9x3Yv33PrmNFJ+sa6l1WO+/wuIyW5rr6IydPfLVv96NPP1lYWDj8iqGJYZFx0sh+MUl/7j04/Zo/vzTu0dIDhzxWq9vtcLsdPEO72jtQrVxlOPjq0n2T36z7eBNYHOjacarpyLMLq+Z8CqdbwMNbHXbG7sSEPAyYj5ZufXFh1+p9pXM+qV66Hkws2NB5w0dj+XGFdaPl+L9WHZz7ofdYNdg5t8nqj1u7zVNUs376gi1z350x9rFhvQemRcbm35/94sNPjrr1b1cn9L518FDtvenDBl+Zmpj80gvT9u/fT2x5fD6fx4ODz++9uAT9IdBGoY1QBMjamkDvCP45BwDV1dWPP/54TAyeazfeeOPnn38eHLGAL0fwm6HtH44A0Qi30PDs2uYoFSQ8iJYOlAq3X/kCmlmElaL/BqFebLddBLneBhOzHz4WA9AqtOfPqw1L56lcH6Vp7zXWNnM1mr06WBQwLvy6RDmKTZ7gluU5YgqPp+hgQzkYEESxxKeYMGjE0DwYwHbvTLsy3xyuscl0VqmmqKcOWTZ+2ucTrZXRM4A4GhPjg1YvPfPz8hS9PVLvlud1Reqao7Xw4mZ/bsPvA9CCALwAvBcEr48X9dBdDPz7SH2C2hem9krVpmg1MtlFO8ENjIfGIxLHEhIyK+ZDa3rm3aMpua2RuZiNUJYnROidERqTAn17rbdMhTd3Qb0PMbRbTNkH8AM/sVqZ9tuntFLpDqnaHa7hovIM/R+EPe1QA/D6zsYrH62n0jupkR5K7aYwOKWJWnhzG6p6nWIoOfB5/Z4bAcZ4boOIdAmDBoBGxnHPzA4qG60MqBy7QoczE02iCtvlg69KKgeMtckQIDaFZVak5cHqs0CDxWjyZ5kTk+ChAhpEq423d9TEqb0UPrtk6hOJObChGhXZQW7LP9yRfsYnSFsE+K8L9dvQzLb/c9nxHipDpIoL10FEniDVeaR+P2XTLVPQGbzJBxZBcNEENDs5Bk2nujFy8K8OFn1MsI6OF1bWJIh2JRQKe4vjc30vrQEDzTjd/piQWAd/+Qe3AzM8JOeEGyyz1zQl6HyUBiLz3eGaVoUKJq7ELiTO0TBiIS8aJ0Tw5LxwA3T5YMXBmp5jHFS2QKm7wnJKe+rQqsIi+FXPxKyZAGi32EWX7atO1TulaAPtidB2hufCgInWCLVFkttGpZ9WZsHir6HGgW0qtiqxM+FFmO8KdC1SMgcLLXA6RZzYCMP0lZiaMiEHtpwFByricd0FiQwvuoWwIMzZUJWIsfVSyNwrkrUwZR3UA6woqhn2eKky2xqX1xWWY6QyzHFj6gaMa9W+jhM8ZtGOnBXQbsjDdffMoIbsnmA7Nz9x0dj9lDdDAPqnRCv02VAEQhEIReASiwBRcZIl/yzLbtiw4fLLL6coSiqVPvzwwxYL3m+DByrB24GRTEgKfYm1aqg43xsBQRAMBsMzzzyTmpp644037tq1y+12B0bXvxmAJhM/Pp+vo6Nj+vTpMTExhYWF06dP79u375QpU4LNQL63JqE/hCLwm0Tg+8Zu5x2c+BQT23SO406cOKFSqVJTUynxoVAoKIrqk9pz8rgJTQdOHlyyquaTrU0fba36YKP7eBVYaEQDHtGwguyX49d/uvqqywZJKCpcERnbv/eL818vr6uxOs755JAP8uBjvZyD9tjcTpfHg5YXXv8wB/P8eDmzxeKyO77etiP73pHRYRFD+w/KT8+5tt+gXomJfxp+wxsL36yqrWKcDnC4cdzY6ihd+Om+yW8ee30ZtNhxeOb0Vi7698Fn3oQDFWCiBUFwcgyWtsMBtabTS9c1/Htn1Qcbq95bD2UGpM9i1kHUOPMA7fa6j7ZsmfiaZe8p6PIAzbndoojPxUC9+dSSNcfnf7LnzQ8ajpzesW6D5p7746mwvw2+dnrehKcz9eo//y3njntuuPyqv95+R1JCwg033DB37tyKigoyPXYeTAy+Fwdvn9dGoX/+wSMQ3DfO+y0HACaTadKkSRERETKZ7P8S886ZM8dgQOIYyF74B4/ez6k+uXoa4GQfnSNK75XpQZbnpHJKElWwrQzpM4Ft4v+JHS1BheR7PxlAd0DRsIc7InJFnbW+NSWP/2gvsionwHFD7RUTnDK9VzLGKtFVJo72PrUSnTEELIUDxKtmd348zFjYBYz2rc6Y0V2ROnuEziPRnU3WQZm4uJ718V4fIzoYo3CSSCldALVseeb02gS9U4ZPg1J/PH4UbGlGbCd6jFx4K8HDo1RYEC0NvOD14g7bGfqlT5vi1bwEMxAaYtTblffBrkZkmoIo/mW6RcVoGM1gPthW2vXSqsNpmkal2ipVMRIkaF4KzRPskdoyWUb1zRPhoyPIiN3iMd2iAcRFW9TJQomlrk8BHaa2UtmQ/JCJyvQMfgI+Kim993nE68p8L6WF8HxPXGFF1KjO25+HL2swwjxmrmV8+IqK5CCFa4A+E8Lvp+AkHEaovPwht1TMc0jlmJW6prumoi7eyYERWh96y9ir0ESNFOIKG1PGcE8th2YBOu0Mw3RjPrTgYNG9RLSl3nq2Ot6fvNEhVVfEqTC9pPU3AdCMiGZJpdCIgcNsde0sO2PNiTRtS4zGEabyUhofpRHEdjFJc4siRpb++Un45IiYTA9rgCuRRHpPMHQwjPY7YhtgT19VpwJ34qU0HVGag5fp4JsWcAs4K0GclH8WgA4UHLtZF1TkzKimRgCFwmG7QledooM1ZeDE7smICumLs1RyxpK1DC6AdoF+6bOqJK2FyvJRGmuEel9cOuysBxtq15FBE/MNgqHdPrRif2NTVZLWLlHRYSKDlmoweyGV6YrLL6dGGv4+DSpE+tztGu+HyOIpTFydgVjOeAHlzwu21sXifpxSnJAwxum7RryM814uBP3YaQLVtrFggtLMaTUJaHhNADT6vSyvhrHLDsrua5JmdYXleKLGtIZnn5LdfyBNBfO24ZIIB2bCREcRlFH7cNKd8HSy58BrN4O+6Dn3M94MAeifEbTQV0IRCEUgFIFLKAIEwFkslg8//LB///7omBkXp9PpjEYjkVwFD1SCt4MHM5dQfUJFCUXggggE5kisVutnn32WlpYmkUimTZtmsVjIn4L9NH4DBTQ5qMOBw7nDhw/ffffdl19++dy5c2+99daCggLy/gWVCL0RisDvEIHACEJc6YnDXfI8ryhIBhiGmD5v3bp1+PDhMTExSUlJSqUyLCwsNja2d+/eb86YBc3WhjW7Tr21yrB274GFK2xnahgP7fJxLMvyLtrnxlWcnM3ZcLYi85a74sJksvgYWa+kx6c/12Az0gAOH0f7eEbwP0Wdmb8gBDczAu/kGDvj8cNo1u+uyjrcOzZtuecvdw3q1z93VO5rc+c8/vQTf7rt5rSBfSdPfga1z1Yaas1VS9bue+K1o9OX+MqbMINQVUfLiq92PTrL/uW3YKVdHo+NZ3DkaeegytT8zoau5Ts6N3yz463lYHDg50XtM0JwDwsdzq5tR3dNnNO1eh+YPLTDaWHcbuDdTid02mtXbjs6/d3Dryw9+s5qp8HkcDhKj5585dFn0ijpAEp2T9pVz6kK80dkDUpNu+u22++4444+ffokJSVptdrNmzebzWaWZYPvv9+3fV4bhf75B49AcD8J/i1HwmK3261W65QpU2JjYymK+r/XV155paamhiTgDQ5d8H7IdvBfQ9vnIkCI48pvjifl8CkPuuQ6V/SYdlmuPfM1MAVUl4hnCcilxY2AHUEAZ33HiODc3v1bRGaNYKyKP9RbbVegyBooPWYwO1iPALoRPI+8XyfPpSk1T2lbZdqTtz8DVRwYOafVbfOilBnX7XcDaLxoOgEmftoUozNGah1SLUNpKxK0sL8BC+oF2sMSsTZ+hQBoADht39Nf2xatYyQ6t1RXH6c7POxhaES3WZ8H6xR8K+neRlorEmhR2Cz4sBZ1nuJ7JrXGovyZDle3xqqPX1UIlRxhx0i4OCR3PPhwLhCAo0WabOa8K/cX3TiBEDQCOtkwDR2mBuVYq1RVK882/20avH8Q2nxoixxEEAOgE6vT6YE1J0qV2V6ZnonUc9EogIWMD4yxeXVhWQ75aDOV6aFyHTEFx5LVzn+uQLwugM+IGaS9IoVDMxMv8ugLGbRX9AKhCZAnYtt2OJowyhuRBxH5Hiq3PUYLT32CEwN2Ab4sPZycY6CyWCrXE6E9EDUSTrRhfAIa227tvB/O8gBl1ooEP4B2S9QtcVp4dRsmTmRF+fAFPSfQKBf7y095L0gBLRo1I9v0sRz2bBMPqw6eHv5oQ7wWIykyaPSjoLI9UWMMkuyzkRld978CK48RfTF4UT5OWoT1+xpjW+FotEuAdeWYpDHCT7Hr4jVnR00nHQPPkQDVFUQKGzyB8x+3A8XHOjsBStxHL9M3UiPRaEKiqaBGnL6iEBqwJ3f3WzE4F+6T2GGQWSUXQANfkT6tNC7XSGWzlMoWM+b4kAI875znfkcR12YsOe0DK1inLK+IU1mpbJpSoQ9GGOqRTVRmZ4yuvE8efFKE0wnBD1J0HrF5t6MJdj08K492Hr1qbEs0qvitEeq2KHVpggqWHAQf8BzHBgC0/ycSQA33ZVpmZaKmS44zN4xEA6kPd0ZrO6Mx9aVHmeeKHtMhzanrnV+nnQ0HGhGXewBYpM9+AM2KAFo8N/2nV8AmPgSgg1sttB2KQCgCoQj8wSNAELPRaJw5c2bfvn3DwsJIbrQnnniiqqqK9/I0jZqviz6CByF/8DCGqn+JRwAFI+Jj8+bNN9xwA0VRV1555ZkzZwRBIAk2SWrBQD//JYPq4PPi+7bPk5UtW7YsLS3t/vvv79Onj0ajsVqtZPHBJR7VUPH+CBEIjLj+M4D2Abg8HovF8sbrc2645tp4hVIRLpNKpRRFhUsktw2/edvqL6DV2rX1SM3bn3ObTxyb/0nXsTLwsHbgTMDSPOfp+r/ltSw4+c5TFds+WHVNcp9YiSw8XnnfaNWxyrMe0eLQRDsdXsbJ4dPB0nbG4xH8ejJcGu5FPO0BARPy+ASvhwGaA5oXbG7O6XHbHV9t2qzXaMNkEffnZK1Yt2r99k0jc9Kvu/qqd2fMhoq2rjVfb3vk5Z1PzoZvy8DowNJ+uvOrwhc6PvoK2nCuyMA5u2gEDdDq6Pz31y1zV5uWbjn87mpTcTUK8VCDxqHpswcTD3qOVmx9dp7l8wPQ4gYWuuy2DpeN43mmxVi+dkfx3E8Ov/B21Qcbod7k70Umx7FPN76VP1E94MarJHE3pQ6YOv6xh/T5Vw+6vF+vtDtuve26oddcddVVQ4cOffnllw8dOnThtYX38ue9+Ufon6E6/vgIBHePwM2OpD0gpi4syxoMhhdffJF4cfTs2XP69Om1tbVkxjRwoOD9kO3An0Ib34kAg2rKzmc/rErRGaksb0yBKVpblzoGVhShS2t3GrAAgCYL6oP3EAA4wW9efNsFsKulbtB4h1zHUJlA6Yqjs6DWgzRz4e7KfoUuZQFEjvVIRpck6LxLv0ZIavNzYQfH+/00RHiK73oAZmyqi9WaZFp3mJajtNVxWlhfLIqlwe2i/QCaYGsApIfrSk/3Hm2J1HkpBNCVibqzulfRQNYnZtv7fgDNgcCCl8cCicctce/vkWmO8iugGxLUxgcXQQMLLh/r6LZZEPAK70bhNFFXA+cWzWdPmpjHlxX30LQp0eoBiWfMOIjIF51PNJXUvSeSc5tHz4FvW7DAjNgAYsH8SnS0MWE8L3zaGKvhJVoHlYMMWqZ3IRAc5QvPM1HZzpQHm5LzK4Y+Ah8chhaetCPH8bzX5xVQ++yfTCAl62bbBEYHPE5EQCsWvaTrePwoRqIDeaFboq5J0MBbe8EkQCvTdP/0ammGXaJyRmgwDeO0z8GKcNvpdvMch9HqlsGSUxghYJW1JNlvwUGHaztjdDBpNRh4XJHzHeTu70GBm/vFe9SPf5c4ivBiW4uQ3eXDKiLodIiLfk5bvY9/cDZF0x6N7ULLdHzkGJDgTAlL5daGZxb3z+t4aBGctqBtBY12LTzWzw+j8bcHw4IZ7Jo3jHF6nFSgMFMfJmxceRCs4owJj+ppEH2xz7teBdeDVNn/ToAgi9Mo/rPPBvDRscpUPR2DfuIeqaY+Qduong2tYsUC+wp8N3gDTwcfFt0nguwyvmhgfrUsy0LlWKn0zsQ83E+LAB4E0KR2BLJjwkAalx20PfhWlTLXgpMcORylYijEx13hqqPUPe6H3hHtv7tLQCawSH/jsdP5UzASJN3kgSmfnoy8vzM81yXTmiLVlfHqohsnQDUPDHYcP4AOdAsTAxvLD/VWN8ai9zQbhogfYse7KZWTyu0KVzVG5pTEZBf3z4PnV0Mzj7byOC0gYCYMbzeA5lD+jFkxRXNqP9kmERej0r3eo7sKv+D/IQX0Lwhe6KuhCIQiEIrA7x0BhmFaW1sLCgqSk5PDwsKUSiVFUZGRkVKp9M4771y/fr3ZbPavGhZ904IHLcGDkN+7HqHjhyLwnyJARtetra0qlUoikVAUNW3atLa2NkEQGIYh3tAcx51nwfHbDK0dDkdHR8ett94aFRUll8tffPFFh8MROOn+U61CfwtF4L8ZgcDolMh6/OMln+AVx7voTkEMJQAYgXdzTHFV+cSnn05NTI4PlyspSk5REvFuosrI6iytgWarbduxsrkrTUu3lL75qW13EZiwn7t4UUGHAzYWbAKUtuxf8NEnU18b2qNvOBU2bPiN3xw+5GER77I+AbGyOHLjxGE+eRUFU/7bkVfAD5wbZOLiVgETBopP1uU5fujIP5+ZpIyLvezqwXOWLFj75brMv/0969qbd8xY9PVTrx96fpFQVAM17dBkNa7e82XOU81vrIIaI3jB6HG006IBiJluWr2r4s1VxiWb9j33FmJ0ixN1eTSPT0wFJkCNcfusJQ0b9oFZxCK8z2w2IzVgwLmz6OT0pUenLGpcKtJnF+f36zjTsO+FhcemL1kx/tlXH336sl69Iikq/e6/vz9vwcjb7ugTnzi4b9+Mf4y87757omKirrl+6Kp/f9YmOiSgINtudzqdwVcwcqcO3aP/m+fH//a+z+sbLMuSPsN7+ZaWllmzZqFvu/gYP358VVUVANA0zXt5m812Ye/6be6V/3sR9wAYYM+N46rl2W5KZacyzXFjDvXXoa2q5xyAFlXFhL+K6IoALLG2fnUzEb0GtIoXDYQVYNHe6hSdU6YFRQGjyG+9diI0ATRwzfe+VBs5yi0b7Zbn1So1tjFvIcmyeQm7Ja4CuG+CEUX1JOqmF39TFauxRqD8mQ7T1sRqbc9/Cg1uZNNibj3CoJFcE2fcaesrZdnoJkHpnOG64hSd8M4u6ESs3O2KdNFyI8Bzgs+NklkaDDTM3lorz3RRuRCmZ6gczEC46hA4fOARZbzdPAtzD5D9BQggZn5D4g+H2tiJHxb31LZFqc1UloUaSVPpoBxnixnTkYDPsrQxsLYCkSIPVos9YJGBta5iW9JntkpHgTTfF11oorJAOY4P04PiAbdsdHVU7qkrxjlmrIUqNxpliPwucKNE7smLIlByT+sGxBhnHpzOc0kU/SXnAI4ZTiWqXagIzrJGjS7uNRrW10Izz3y072wPvSkMMxx29hp35JoHodKLxSPNRLh/t10LYmnyjgFO9ETLFEeYxhOVb44e3XH3S9CMLJgkrPN/vVuOSoCgvzDivn/+C2mFYJov7guxOM3h8qAugL11jgnvHE/IrpdmMpF6D5XlpkYKUp05Stsaq22P0Z5N1cIHR4io3O50BJZb+YGyGUqueUjo8ZCXygVKa6dyDyVlQ6UNzU9wNgGNT8hDzMl4kaqI2fmQvWKVyanVPUNAliDg+//nGPPS+uYEnS1cDYp8K5WNwuF3dmLwxSmSi+w38BY5F4i3hkmA2TvqI7KQtku0DKWuStJ6l2xHA2hx0jwwVUG8d/CXQwe0qV9rVKrtVCZN5dKUyhGmQvhLZRztqYYzFvyBRBIgXoBy/Y3oFadwOjjYVFraN8+u0DlF+XwjlbFHOQK2VeAEUjdtJwzaf1GhAV7fViHPckjVAuUX0SMBl2hMVEa9POfkgLy6vDmwrw7jQ4vEmRWAEYAWEEPjj0I0tvb5kD6L1zawusSDdZ+wrIjI//M1LBDIH9wIAegfDFHoA6EIhCIQisAlFIHgmWGGYUpKSgoLC2UyGUVRcrk8IiJCIpEMHTo0Ozu7X79+sbGxTzzxxJkzZ4gekySbImOPgE1BaOBxCbVuqCj/MQJr164dOHCgTCYbPHjwxo0biQyZiEeIg+3vAqDRxtDhmDRpUmRkZExMzKpVqwRBCAHo/9iSoT/+FhEIjKsvBND+Nb8AdqdDALA67EePH1OP1iUkJPSMTYinpP0j4/oo4nr1SJ0yabK3wwpm1v7VsfJ5q1r+9cXx6UtNXxyAVnRYdnOM37+SEdBVucZU9+n2iuWbPn95YV9lwsDLBny28lOXTV56MwAAIABJREFUHYcxgpf3n56ibowM3gIAOsCgvQKOQgPRwdsTLwheP4AWx51gbutYtmzZlTddl9iv58OPPpT1179frUh8+rZ/7H9+IbP9BLRZweRhNh/ZMX568QtL4EgtSpO8IkZhWKCB3n/2+Mxlpg+3H5+5rHPzITA5UfTE8Kh9Jt7QHew3b3xY9PEGXxOqm8kyI2enGYxOy56iitc+qX31k4o3V8HpZkwc7xHXKZe37p06v37+v7c9+apl57GOyppNG77MHDmiV3zCsIGDZ0169pH8gt5JSSkpSfeljxiZk95rQJ/+gwaOUqk2btxIrmCIhLz8eQya3J1D9+hAfwhtBCIQ3DeCf9ohmfH5amtr58+f37dvX7lcnpCQMHbs2LKyMlye7nQGUPV5ewj+bRk4yh99wwVw2npoSL5BoRYojYvK6kzMq8x4EXXBooKQQDACoP0ISVR+kisViZ7/fXIV/j4zDkEEr0+uaE7QoYWrfIynx0O+rHlQBbD06+Pxo1qpbEaRb4gd/W0/PRwwIKjtzqQWsLXFw4n7R3zqBvj0zNk4tS1cK1DIoBuV2qr7piG5duAFFqf2RKIkslZAPPfIx83hozwSHRuGCujiFB2sPgr2c1fji3cGH5JLN/gY8IGLgQpb+eACZ6Qa5AUIwuLGVQwshAoLXtQZDmXO3TzLDxADdykxyaF4mfZhYQwAX1a1/v2F4wnZLYn6rnCVncq1KLT2SK0vDF9P9x4Ni/agia2IbolCGe0XWuHY4LEmmRYkeSbqH1ZqFKco6KRy6uS5lf0KhUc+hENmaOXxk8T9Q6yfv1AEQBMPXAIrXTwq0LsA2jlwiCJvMcLYpj6RFX5ZXJ6ip8O0LKXpUubtSsqCo26ogppRs+pkozhZnj224GzfAuFfO6AN5y+xtKSHEIW1eGAipsX26IDqG57sikQAzUTmuWLHll71MIYC9afn83pS5os3ys9996L75LFxBXTksHLY878oa/nb8yXJamNyvlWqslHZ1ghMlCdQ+FrevwDmbMSgiZ0Mb+Cirhn/WW4tGVjAx47lqGygtCZpbuNf/gldCD/JtDQB0Be1CCMV+lEAugvgiRVtSo1TpuUVeRYqq7SHFtYcwVPmx9FTXHrlBahnD8akW6gsL4UyfDahECFyvZgcQtxPAEDTRFrNoFVO7V+ntCk1biqHplRuEUAbI1TlkZnw9EpocpK+ivw6CECfizmeI6L184Hm/UPG1IZnMpR42ZHrjlB3G/LmYT8UKTqx+iGiaRFo+xBM/3NNiyyH6abPePYlPNgsySpLVLePmA7rzkC7D5rNwHAMCAyI3JkWGbTowkGYgFekz+LqDgAri3p2o5iRUpwbIqb3pC1+4WsIQP/CAIa+HopAKAKhCPzWESAJoHkv39rampOTI5FIevbsGREREQygZ82a9frrr993331RUVFDhgyZNWvW2bNnnU5ngNCFAPRv3Wyh4/2yCNA0PWHCBDLXkp6e3tzcTKwtAxMqv1ffdjqdDodj/vz5Mpls2LBhZJwfGsz/stYOfftXiAAZ2JBXohPygi/gv+x0uz0sw3t5g8Gw8csNd912e4+EpB7KuIHK5GuS+wyI7zHsqqGLFy+2G83QavMdqS6bu7LlX198O/2dxrW7fdUGIgKieVx2gPS2wyEU1Z1avLrk3XXQ6p4x9rFoSpp+//3mTqPTZhe8vNDtL9GtiiKqMjIYJwt1z/kqBiqPjCxgUIhSaBHmCDjl8/muzXdk3JuSmpwWlzBIEffPTL1x3wkwuKDD5dlTVPzUgpKJC+BAKTJi8HEC6zXbod0h7Ck59fKy1kVfHHpxSd2aXbgQFT1JeZYVMyi6GLa6tWTJ2tL3vrBXNQHv4znObrej77ODg8M1p6a9e+a5d+r/9TnUmMEsKgldPJyoq3/7i6YFqw+9uPjMii/RzYP30RZrR3Xt/BmvoPa5d5o6O2vSpKfTczIGX3dl36sHjczNuPPeu+OSky6/YsjUqVNLSko8Hg/6aHv5wAUtdI8OdIPQxoUROA8fk25DPkb+ZLFYli9fPnDgQIqilEqlVqstKytjGIZkDbloT7vwKH/0dxwAX5w92VvriskDid5N5TQk6/nX16MBtNePUgOXWX+sCJO+KLb97p/OfYRsdUHrHVO7YvTOCFxE355cAI+thtNw9NqHWuNGe6Ly26nsorhR8K/dCJJ4cNs8iMlEOSYtiiL9VJTszQuwq/VIfI5Vir69HKUxRGpO9tZDCTrYuroJGBFRItq0gkuzoD1S4wxHAO2ldOVJOvi6FrHdD+hGEUCjtplHCsa+sLJE/g9X2CiILuyk7m+J0cC09dBGexnWX18ShEDUztsIKFuNTjCyUO+GDaf23f5oZa8xpmitTYamHF4K06xVy0cdGVQAnx2Hdi+6VHtFmbYToAV2puaYFXqaGgVRhWxUQUfYqPJ4TXnmdPjyNHI6B1bea0AaiKhRZMLiC859ekXbYnRUII5MAoAZmGdW7Bz2gP3LI8juRfiIIREA7MDM29zcq9BL6YDSm+S6g1c/AMUA8w7XJo02UjkOKrdVrmm4cyrU0uAWETtxjibi80Ddye2ZBzCCJ3deJ1oo6FhKzUYVnOith2qneJsUvx74SvCGP7K/9skaaClScJxpADC7wcRCEwMbTh+87bG63vmO+HxbuJoOQ+cQp1TdljRmV69sWHcSDCzqpkVDYXGKF2B72alklTtc46Gy6DB1S7Qa/rkazLgki/h1kAvXdwB0QB0fJND2z+gEVTfgAY1/6gKnbn6TPNcTNYYLRwVxVa8xsLsGp2R+HIDGO3gX0NNWVcWqmEi9kRrBJhS29imEGRsx3aKLx/2IMSGya78C2gNQyZ24vKAjCh0wXGEqVxgyaEOk6lBKDuwz4MqDgNVJEIA+Vw9eJNnHWzszZrYn53WF5TiodKB07bLcfYP1cNSAKvHupWOky5ATn+N56ALhgXfaotDxQxATRXqkGoNSezA5G97ZBa3iNDnh5l6e9XIobEf/Dbxv4Lo08f5BGstFzmUXwKbSvUPG0M8sR/AtXmf82vNzJf75WyEA/fNjF/pmKAKhCIQi8LtEgJjesixbXl7+8MMPFxYWyuVyhUIRbMGRmpo6dOjQxx9//IUXXkhLS0tKSrr55pvXrFkTzOyCBzC/S0VCBw1F4MdHwG6333777RERERRFjR8/3u12B5Oa87Z/g74djJhtNtuECRMkEsnTTz/d1tb24ysV+mQoAv+9CAQPUQMjXNYnEAbtBR+x4Hjrzfk3XDl0QGJqkkQeTVE3JPT5c5/Lb7/hprPFJQhe7bTtm5LKJZ8b39tyfPrSxrW7ocnss/kXI6P1KMshnK2zNn689cSClZjcb/fREdf/OYqSZqZnNNbXE/kzcmSfj/fyZHjZrXgSR9bisL8bTOO5G4gJ/iMYQJM/eH1ut9sieI5VFk94bEKPuLg4ipr50BPQYkYsXtVZ9OqyA+Nehg3HwGATTT3Fr9kEOFhdMn0Z9/He8lkfmdbthyYLSp5ZZL4Mx6JJpcl5bMX6HTMWQ0kz5/S4fJybY1xWu9Bp407XFb3wTv2MjypeXQFn2giX8RjM0OFsfX+z9e3NJTOXVS5bD1YPuDxAM8Cw3pbOygOH57zw0sg774pXRvfp03vy81PyHn4gdXDf2LTkEVkZBePH3XTzzTKZLCMjY9euXXY7ysaCL2W/wXUsEOrQxv9WBIL7BukzgXfI1AXv5RmGWbZs2ZAhQyjxcccdd+zevZto7UMA+kc1tw3g7f3l8SouOh8i8mhKVZ6kgY0l6ForYihyXSVX2h/eIYGP/vX7QZc5Yr9ggqI0nVuhd4drzBGqiqhRMOtbmPjF6dhRjqg8V+ToSsWo5ntfggqXfxU/EUMKyIcJh/oOXhMAihy7E7PMYuI4ntJYpZrqqFz4dwU4/UpclACLTwTQFmgf8XIAQPsoXVWCDk4a8RP+BBzngPt3akpUw7wPrD7YWHF2QB6T9iAoxnhl+saI7KOX6eGYBTz43e+41gbfnC7cJgcQAF07LBx6ULy4pihN15ygsyt0bAQ+XcqC4uicrYO0UO0FG1JypJh2H5xxHh1SaFBojdR9QnieVaoxxI6G/KXo1+EC8PhYl1gft6gAFw9EZjXx7iSSUFbM04t/sQtghvIH5jb0G3cySd302r8x1iKOxxdM0AfmScs7+zzkpbRAaTrCRtmy5sABpkqp9iU+5JPld0k1pT308PYBMPt4WpyyuED+jKEJ3J5NAE+sNCjQs5uhst1h2oq+Y3EaAC0qRPZ9Yay+T1P/nUb6Wf8IAOgL+zcPYGah1QevbqoZ8mBLnNYp03olWkaiccXk1fXO/6JfFpTY0HFCzGuAaSftACu+ORGdYaWyHFSGQ6rGHJvLjkGXn/t7Rf8N4gJxbhVUMIAOZCYMVpGTxsPeha7VBEC33T+jQYY5Et2Uyi1R1/UpgGOd2PriqfcDsRB8WOwNpQd65aKMWqo2U5mGeP23/bVw2o2K4O4pi+BVXLhjF0Ax/W1CpkmBmTMdYei/QVOqpihVQ9bL0CbSZ1ZsxIs6pwjiqoU2HzN1ZV2SzkRl+OR5XpneLlGdictxvLYOAbrorhPQTwf04GhxZuStuXM6Y3D9BBuGT5NCUz1oHGxr8p/tOM+OVwhsTEG04ODQ3Iz24dMfcAE9oHFKvssHH36zt3dua2p+0cB86CSRFcP7A+H7sX8OAegfG6nQ50IRCEUgFIFLJAI0TbMsSzD0iRMn+vfvT1GUTCYbPnz4119/vXjx4jvvvLNv375kyHHNNddMmDDh9ttvT0tLoyhKq9Xu3bu3qamJDPJpmg6kd7tEahcqRigCZCBN4kC2BUGw2+2ZmZkymUwikUydOpVYpgYvPf6NwQ1ZmM+yrNPp3Lp1a58+fZRK5bp165xOcW1nqBVDEbgEIkBGjgFKggaDYtI/j8BZnPbi0rMvPv/C4N59B8T3iKOoNEp+Y0KfrKtufixL11JbL3h5utMCjabqFVtK3lh5dPq7jat2QF0nKsNYBtPg+ATGQyPDbbLZPtmNZLaoyXWq5vP5794//DalVHblkCFbNm7yMixH+xkG78VBfmDJLcHQ3TA6ANB8KBQKPAVk0ChvwxRRIBou4yBQADDYzYeOH776yiuUFDV74mQwuqCyo/r1FXsffbX8vXV8ZTNpAZfNCk4vFHeYFm+0L9pkmLfOve4glLaBneE5DqeyyOecbOe2I1+/+q79eAXCkgAx4XxwtqVq0drjk946MXkRfFNNlm+Dgwajs2bNzro3PjO/valsyRqoagMOfG5RGe31usrq97y3snTPN+2V1bOee35A794JiXH3pY+Y+cbsv6ff12fQgNvvurNw3Di1Wj1gwID+/ftPnDjx2LFjHR0dWDsvj94jQndKpnOxwa1LoGeFinAJRSC4dwTDaEEQaJpes2bN8OHDSWqQa6+99pNPPrFYLCzLkrV0v/F98xKK2o8pihVgxoaGGDUn0zNUNhumKUlUwd4anHIT06wFyGHgGntur6h2/O6pKoiomABojkMczfO0Bb2MUFZZ1FHaQ8uF6zxSzPPWmlIAb5yujRxlVugtVLYhUnO8Xx5srgKzeHkkh+nWURIu6r+OkT95AWq9uwfpW2VqntLwlIamNJ3hak61EBpdHOeH1UTCid+wQNF1E84H0IdakNnRPtqOM44Xwk98ixYReAcNpU77X15wxeV75HpHmMol1xUnqjwLN6HiGKPlp6x4Yb9wR4F3AnyWOFSQbGtOgA4fHDQYRr7S2vsBJ/oqpHsj8hwJhccTc2HJfhSkcziNSQD0gQGj2xRaWqyyTaYrV+bCNhMSQHHaFKNEynCuqfAtHvCCe+49N0AL73xgcWufQoNkVFmi1v3ODqKeJuQfI1PtbtLMqY3IQQAtf4CLHwdjPoRH1loUekycKBndFq2rz5mFtidusdbEqyVwDHKPC75JmwFmfdUQg4UHWaGTUpclamHZN2gAQnToXh9rdfjc4v1UAJrcawI7/G9sBLcX6Wekr3tF5NopwFFj9S1P18dpGMUYL6VxUypL7JjjPVSweDdYgkTfNuAWbalMRDjLh+vM0tyqJC2sKQPruYR+eGsT73jnA2hSLwHPJo/LjaGwcwh8nQBOYizul67jF82+kj89Xh+R5ZRpnVSOW6I+E5cDRwyoXicK3uCwk+B3x422OVAX3MpW/WVSnSLHFKk2UOkuua4hNQ8+O43yZ5L3Mkj+HLgCIGHf3nImLseiwOM6JVqnBPN/YvLP5Yfxrx48lb7T+b1YI87iwB9RAkALAy9uaI1HF3g2TOOV6Y0RqrKYHJi0kvi2e8XJoKA+in2QA3AzNHRwlbc/Y4ofEwDQjbEamLMFteriT7XgihKlP43OObyLZxFMB1+oOgEWf13WS9+oyDWk5Df//QU0ugk4xgR/sjtuP+P/IQD9M4IW+kooAqEIhCJwSUSgrKwsIyODuD9rNJozZ86g85vbbTQa169fr9frSU7CqKio/v37X3311bfddptCoYiPj3/44YcPHjxIEDZmH2H8dOCSqFWoEH/4CFw4nCaTLgsWLEhJSVEoFAsWLHC73eRjwePnwHbwHv5L4aRpMTsZQHl5uVqtjo2Nvf7660+dOoWOBKFHKAKXTAQCI3+fOIiwMx438FaPc/ve3aNUqgRlbFpMQk9Kfp0yNeeKm9RDb1305PO2ikYcDgH46juLP9547LUPi+d9atj4jVDeAjaPjxfcwGOmGi/rc3jAAZ4dRSUvvg+bT7P7zu5a8snXK9Y9os2nKCpWGaMalVtactbtdHI0Q04ZAqCDExIGDKADpy0OhwLPIADNu/CkY12e6sqqLVs3zX7jtdEPFiSmJsWER8x9YjKcqK5etPrr8TMa/7WWLm8A8FkYh4t1467KWurnrLLPW181/cP297fA2TboYoDhWC/HeGjBw3gMZtOpikOLVkJRPVhpt9Np9frPcF9tR/GCVYcnLzzy7CI41gTtNH7XyYHFU7V2Z/GCVZWvr6xY8ClXVA1O8U7q9fpYxtNh3P3+yoovd4LRwTUanHXNR7fvfqJwXO8eKddeNzR/bN6ERx8dMHhQnz59cnJyJk+erFarBw0aNGzYsAULFrS3tAaQ/UUZ9CXTuUIFuSQiEDhxAvdEMjVLbkY0Te/cufPKK6+kKCoiIqJnz57z5883mfz+5oGb5nk97ZKo2O9eCAvAixtaYtD5gaayeYm2OD4X9tWIwAiZV/fk2TkNazAeAqZbcukBaKPhjLFrwfrSGR9AiwNYIBMArMuDX7ZxsKUEs5xJkD05ZdrO+Py2aJ1JqhYtjEdWReb4XlgLdQxyt8CDUKVuJPSdQ3MALb7SjJdqo9S0CKA5SkOH60t6joYWAIu4mF+kV34PaDvU3zm1IwrTD56z4NhwCsETzXM0h2tRRGkwMSP28yzyP7MAdRz7xAfmpHxfuJ6mVGZpbmV0TkvWK5jzUBSmnuNfwUAzUP5zV3sR1AYwdKBKHCJyqORto95okqtdlNpIjbRH6JqS82HSKuhEAI1FtfJw2nlgwOiWKK2b0giS0UZJ7tlkHZwFVHGKVfXrZAMxFKMnEBcRwYdp2RwCmAQos1XpZp1VZHpjCmjZ6IqeebCnFi2bRISINJgBqIeDVz/QGa33UXo3NYqPGwdZSzuSxzrCNGjKkTihosdo+LIYOhg8tMeLr6IM2t8tgkkoAZldAB+eqEjQWsLUvvA8R5imJCKzRT0HPRBQQO4DJ48s0gU4BcLijCyZGAjU5lfcONdkAWQfoK0B2bUXUH5+ym7NnN0WhWTZQ+W45LqaODX72LJzkyUsfiwAoLuokR1UZkOvfNjW8sMAmlRJpM+46fCBUYBSm2HeulPPvwNV1m446/NL182+xr8/3xiZY5WiA4Zboi5L1sCmM6hnRxU5Mm7x+Z2JEDRjIdNFtZb6Z96pTtU7pGo7ldtJZXUk5zfcOQWaRRfk7ikfXmyQ71hSWAGWF1XG5FrlWjelosOQPjuk2jPJWthZg4VkkAQTwo4FQK2x2H4cYNlaGcOk9xsSdRCZR+zmuai80oj0TvXr2PoiIj5v/iKwgoEooNvun2GMQwMfNkzDSDRViRpYdRSnTAInEelv4s5Y0evZAwLSZ684mYZNKeBqgxdWV/Yv6FRoXHH5TQPGw4tr8NQjp2RQetVf2NNCAPoXBjD09VAEQhEIReD3iYDNZlOpVHK5XKlU3n777SUlJSaTiaxxDpDlgwcPjhgxQi6X9+jRg6KohISE4cOHDxw4UKlUJicnT5s2rbkZNWJkMebvU43QUUMRuCACwcNpMjwmOf1qamruu+8+iUSSkZFRU1PDi66ygfFz8Ng7eA8X7P5XeIP38h6Ph2EYg8Ewc+ZMpVKpUCiefPLJkPz5VwhuaBe/dgQIg/Z4WRvtpsFndtrXbdowIisjqWePWEVUHCUdltS34E93F15/17fvrBIajegjAQBGe9263SffWFE879Paldug1QIMWjm7GJrInxEom5y+3SXlsz6i1x+Gotavnpt/+qMNYLDt37pj+HXDYpUxFEU99cSTDbV1mF+P49BqWfQc/EkAGkdrPD59NFtbVvHmrNduvu6GHnFxiqhISk7JEpV333prydqv6t9ctWf08xVzVniPVYLLw4LgBpZzuaCypXrxmornljbNWFG1cA2crEP+4uF4jvMyLLhYX4vZV9ay463lDd+cBBuNiiSALlbUy1V3Nn+4pXjmh3snzTN/dQiau9Ag0slAY6dxx+Fvpi5oWrT2yOvLzPtOgtsLHMuBwHI0GG3H12zasHAptHSB08ecqWnYeRBMLkdlw+KXXx3co1dMeET2PzLmvzkvIyMjLCzs5ptvnjlz5tNPP52WlpYQG5d1f/r+3V8H1G0hMvhrnxD/v+0v+H4X2CaVDKx127dv30033UR+ByYnJ8+fPz9k+fLD/eD/yMtLG5piNPYIjVvMnFYem4sKaBcHwvkAujulKoLQcw8Ph1cME8Crm0oHjj0dm72nZ3bH/M+h0z+BjQ3EAZh5ZuHmqiQtK9XyEvE1bhwdM7ad+odTorWFqU8naaDGixiL2AcHE9tuKPYdYshgHj/+1S/PxqntEg0r2kDbqZzKeK371S/8QLMbQIvmFeDWLjTH5tPheq9E7wnXn+2h73xrIyGn4h3kewC0lUZoNe2LxpQxtmg9ojcqt0Wee/CKfPRcdvqnEv0Q7EL63M2gyU0qYC+A1Ex0uCakD2f1u1lnSZLWKdMziny7YnS9PJcrfBf10V6xMhYfAdDN0QigvZS2K0J7NEUNBy1YZZH7ekU5st9DiszKooYbW5NzevAzzSxsrWm8bXJ9gpZJGtdJZTZQ6TD6HbTeFo2syaHQ9+SMa0+PHEdMgY/SualciH/QGKk1yZA8esL1hkiNb8wS6ALeIU5MdtfN//VzXSRottUG8LXxZLKmTYEM2iEfXS3NOp6igXUV0CHmMOwCaBGgkQXjd3ho8M5+xe1AoxD7FGxE4mIsom+/1MIL2JlPWip66NyROltYriVS06jIhUc+QGU6eSBjBffiLWXJGrdEbaFGmqjM1tR82NoClh9SQBNejKDdB0YP1Akwa9PB1NxD8Zl7+2v4NzaCkQcPZocIWHC49QtaotVdYTmsVOsKU1Wm6rve2oCTBxcF0NgHfIKHwQwTdnA+u6LqsrHGGB0XroMwnUWhPdArF744TTA3dssg+fN3JhK6cLKqIVplidTwkWM4CruBMVJ7qLcWThmJBJ5hONLT8KwnvNstujM7wP3Y+w39CpukWTYqB6R6kOXZFbryQYVw1obJAEWt9IUt67/mCAJYgBv7tkGpdcm0dDi+osD8zc0IoMkSLzJ5IDaI32UbAys2KE4yCWDioJz2PfpBcXQWk/awMVJdGZ2zZ7AOKsVJr8CZ292kFxbmJ70TAtA/KVyhD4ciEIpAKAKXRARqa2vHjx+vVCrlcvkdd9xx6NAhRnyQFWREWEEwtNVq3bp164gRIyIjI4l/rlQqTUtLI9u33HLLvHnzKioqHA7Hd1afXRK1DBXiDxqBwBA64LDBcZjrjKbphQsXxsTEJCcnT506taKiIvCBAKPBX8jfffzyIAb2F9gVTdNut9tsNi9evPjyyy+nKGrAgAHr168PyZ8DIQptXFIRCIwkq5vqFy15+/IrhqQmp/SKSxqSktYvPGbU9bc9dnf28Y/Xg5EGowMcLDj5+i0Hjs5aduyld8ve/dxb0ggeHHxjmhwe1XBohWH1cMX1ze9sgM2n4HDt2Q83nF66Duos0Grztpn/Of7RK/sPjImJSerZ4x9ZmV9u2mg0Gp1OZyDjjYCGmzj4JAtviTLIvx3AK2TYKSYy4sHXZTQ98tDDfXv2vvnG4Y+OG6fOzIxPiB3Up8/XH65ybTtWOmXxoYdfhf1nweTysYzJYuTdbjC7Or7YW/b6x+Z/bTwzY5nnwFmsg6h9xrPVw4KV9ZW1HHl/7enPt4tDWB/r8ng9DJbE7Oxave/IU/N3TJjZsW4fNHTg8NvhBhbsB0/vnfFW07xVh6bMM+87Dm4U13GMx2rt8hjNbXuOHHhrOTQYocPBnKjc/sbS9m9Ogt0LZhqq2pY8O33E9X9KjY4bft2wpydOfOapp/v37nPdVUMfyC+YO3O2OjP7iv4Drxty1bPPTK6urCK9CNfMitYll1SnChXmEolA4A4VvEGmZsV5H04QBKvVun///oyMDIVCERcXd/XVV7/22mv19fWBGdzAPZTs5BKp2u9cDNGCoy5e0yXXOKhsnlLVKHNhRw10ceA9H8gSGHSOtLIAnQwYATadPK2e0dhnrFGS41SOOZuqhQ/3goXHJHgi/0Eu1iFYJ39Yn4DwiJXi00JlucO0Niq3gbofdb6ztoGBR+gZOAw5UjcQDFhk+CPGYl5B2FByMkndJUX/DQ6fWnN8wfaeObC5nKBhgu1fAn0bAAAgAElEQVR4rw//+ehHpuRCT7ieD9O7IvRVSfrOp95H8aMdOVvwhRovg8SA1glQ5zRM+aCm55g2Kr0rHLXPneG5pxJzPfM3QqsHXD5BTBjQDcnF0gXDrG5VJikJyefmJ4kimz5nEkLIexnTdd0kp0xvCss1RIqu1k+sQABNvKotPjjr3D5kdF2s1kVprFS6Kyr/iCId5u/GhmCw2AJxbiBhIiUhTA3Rsx2dOt49cLS3xhCrs0tUDrmuJUZzoqcO9hjQUKL7gbF3AWypLe5X4FIWMFSuixrlDtOyUQVovEBpXLFjv1X8A9aVgZlkzu2uuAjSvzNFQagu2bcLoBZ29dXUxGrbqWyHfLQ9tqBaPqrqusfh44OwpcQzY/WuP43fduuDsOE0So+/E9buwv2S/3c3B9kH+dnAis4x5xJdiu1CeCZGE4W9ACVuy3VPOyM0VqnKFK2tVGR7J7yPCmiyCwaDbluypbgHuioLUp0jTIUeEZ+WgQWvN8G9ixhEnJtNCfTzNg/sqqr86z9b+40zx42plmYc6q2GT46ittriIFwYi20F/rEPmuK0ZipLkOrclKqlV4Fh0vvQIuaB9F6ggCY2L17MXuhZuOlUssoq15qoTEFZYKYyW9LGwnv7cfZC7GLBYRH1yOLeUFWNhuAw7v12ucom0wiKsQyFFhwdcu3xVC1sq4F21M573Ohdhmpmrw88om16Ow/HWhseXngmJrueutcoybFHaBxSdR2VXnXZWNjRDB78hUTGNXiUoAeZoxGnacTUmk990qhU2yNQ/uyM0NTFaxr/MR2aRYm6W5y96HYg8V/hcVJfvJ44AQwclLob7n6uXJljidQ4o/Q1UTlI3t/ZCVVmYMUjB58sQcX4eZshAP3z4hb6VigCoQiEIvBbR4CwLafT2dnZ+eSTTyYnJ0dERIwYMeL06dNEH4r5nbqfZNRBXjFxsdm8Zs2azMxMYgwtlUolEglZj0lR1MiRI1euXMmyLPHiIIJocs/7rSsZOl4oAt0ROG8sTeSTdXV1f/3rX2UymVKpVKvVe/fu/b65k8DXu/f3K/yfjNXJb8HW1tZ58+YNHz48NjY2KipqwoQJLS0tv8IxQrsIReDXikD3eFnw8hzPe8FXWlUxcdIzgwYN6hWXdEVU8lWSuFtj+hTedPfL+odrdh9Gg0KLG8eTZtq1+9S3UxfVvvpJw1vruNN1ZMG4R+BYn4B3GRcNDo4/XnPmX6uZ7UVQbSt+Z+2xpWug3YlopsZUvW7X9kXLv3xvxdiHH6QSo2S9kuQ9ElRazaJFi06cOWW3271WJ3A+s9mMXupOGhc+nxsZ+vXOwcMtGodR/Iy5r/Xq12d0ft7+/fu/WLdGOzJ9eGLa0geesX+848CEV/c++mrHZzuhiwYnw5utKEl2g23r4cqFq9re31j13nrngRKw0OD1eQTODajJxsrWmb9ZvPLQZxsdTQak6j7w8QJnc4KTM+06UfbSsuJJi1s/2gZmDtwMirAsDvuxks0vzG1d/mXpax8I+8+A1ck6bbzbCU4neLx8Se23b37A7DwJnaxxx+Gdc95hztSgYTTjgzZ355o9Sx94pmrjno/fWHTXzbf26pF6/z33PTV+wni1vmdkzB3X3Ljk9XmvPvfiyDv/lpbc46477ly+fLmpy9xpMXuR+oj/dXcP/zCy+5+h/4ciEBwBnODxYicnty2n+NiyZcsdd9yRnJwcExPTs2fPxx9/vLGxkYgPnE5n4KYZ+vnnj6QN4IMj5b3HtCk1donKQ+U0hGfBlFWYfs0t4A9mwedjOa+HEYKttzhRkGsCqPTB4ytqeuibJVkGKssRm9cRp6++5Wk0k+UQutE4Ayem2mviT/7lydZYBND2SJLSTe+gsv4fe98BJkWRvt+bA5tgyWERRcUTz8QZf57e/Q9PT4F1d2d2YAmC4TCdihEQQYKApJW0ZEmSkRxXMmxgI2yOzOadnDtNd3//+7pme4ek3hlO76afeWZqOlT4qqq766233q+V+ltNTLI26XMERu1tnugI7KigUdeBhph5ohfbBBe6JFiDk2n/ZBf1AlBqLkDTHKmp+uMHKEwsb3hbQXd/AF+eLuussQUli1Qy65/cGp6MwOs5E0jA0h6hDhQNcMm8T6eE+cm3NGvmFPXUNATHs2EjzGHq8sDnS3uOgDmHkaLLIdAmw4uID3tRMDFhnmFvyHqR5zgFJ8sxss80NI+DQQJpHQ8nmu3x85o6DIeO4+nwkbYuYy91SYYtJQguM/LHhs7ual5eVB/3kp4ayvipuaDhlvDhTQ+8C7lWzLC8OeRzMah4ImSQMA67ytlhX9RGJ9sjR2F9hae0Rqfk3zIKvs4GQ5u0GkFGRRnXW5tzscNQW8RImWCuZtFzIH7cVHJVWILuzRXQJCtmkJoijFcZq1SqTr6jK9OtMsZpgeZ30qr6jGn1e8EVkOzwV1uC1LrI4dU9Ukp6aMojEy6HPH8xNh6m7wEL8C4Pj95TsH/rpx3qlS/HyVfBK4PyTjI9QIu8nWNwBlpJSJClUQ5VmZ+ZpvUfAuGjjNRQW49xpb1TYEcpKplwcjNgJHBKsDfvYtfEVup5moq3U/EtMRp4byvQwNk9fHTkIMs1QkBVT8YYEadSKjiYsPFSnxHVHRJ0wYm6wITybprC5GkI+zplVXTSKSRSL1mV3TRmaihQKjP1rDZoWHa/EXCk2iNfI0hWs4WUAN8BHByyyy8auJeX53R43hyikoJHSKEplvDk4o6J4oQNiFzfaJOhdQn1KzgBu5sOWh7/2BSkdoYMZ8NGOvxRf8MUpLkSoTH9aSqU4YyFyOPpEu0Gp4jzBxUifJGe3ynB2mOcqUOyI1yDnShElU8NrnnsXTgv+zrm2576xAdjW07a3GG2/WcA1mVre4+2BanclIoOQCeEVR1VsDwLmuQOe7V+B84fSSLQAjSyUGiX3ttY2GdEc6cRpuAkV0iyNmhYftwIfup2zGSbhI5n2qm97tuS/rd+fQD0v2U230U+C/gs4LPAL2sBhVnJMMysWbOio6MpinrqqacKCgrw7VF2naGgz2TUoWDQFouFsKFZlt20adNDDz0UGxsbGhoaFBQUFhZGIOmIiIjBgwcfP37cYvE8mImah28c8svWsy+1dgt4D4YVRUuO4zZu3DhgwAA/P7/g4OAnnnji4MGDHMe1cwR+Bga0kifSxQAgOzv7rbfeCg4OJv4/b7311lOnTimq0Mr5voDPAv9JC8hYqsTxwAtOms4vuvy3Ic/7+/v7UVS/DrE9KOqZmNve/79hS19+/8qxDNA7EFzgJLDwkF9XPGt96eRV2R8shtx6XAHKizzPoxaogMoVOGar1mXMWu3adQGqrOcXrD+3ZBNozSiO3GB1nig4OXsVkqadfElt1ay1y6L796GCccqzW2RM3759P/zww0tnM3HMBuBRrfGMONvYSbLghkeuUR5/2UA6V3H5oT//8fcPPbh4zcoJH334+zvv7EEFzU0Yp120LXvMtPzX5tau3gNWt2SwSFY7mOxgF/njeRc+TrVsPHZx9mr7mcuITbslRkD0mXZzYKOhwZK7bNvx2SsdNY2sA4fBKMrBIDBNn7p89oNF59+Yy+24AFcsQEvoXVCQLPklGUvXuw6cvfDpIss3p6GykYAItMUErBvK6o5/Mt+49Vto4pwn8k6mrqULKkFvAzsNJpfz6MWdr0wuWfcNlDe4apqq84teGzU2JjC0X6dub6aMnfnOR4Pibh/Quddrw0cf2bnnvTff7hiBk1sffTKpoLRY57Da3SwNIjGVcnv8TzYwX9q/YguQFqIQnElORVEsKip67rnnQuUtMjLyueeeq6ysJK+RSqPyvfh5KtYOcE53vkdiU3QyE5zM+aks4cmXe2lgezGSImkZnbFyCCfZBbxzmngZKqWhzCF9vudo9DMNkSqg1ECpXGGaioiE3H4pcKYVrHijI0xPBIcYgAJr4b2vtES0A9DQYayLSrB2SEEG5YES0HHAAmdn0BGrgoF66bte1RIVirER4OPdtRGqRmoIhI4GSi1SKre/pqyzRlj5LegJs1G+tNEJeY7sW0aaQ5KBSnZTybagZG2EmklcAFdkkNHKoziyTQb4nIBC0ouPH+s5rKaLRks946QSuNAR5dRfK28baxq/DOpFoNslSghpmyBgbpAQuHcw6HeRKCkTXRGCTyu+zjiZYmyVk6vj4Nsr0vS9OXeMq+s6xhqgEQJS3FEvVkary/78IRQzCFASkQiXBE5glh/L75RkpOJdMunbTSU3RQ83jEiFSy7EoM0AZhHpzCY5bOAQZTtZy7y/Ka/XcGu3l6SQUTSV4ApNKQ8elh83EtbnoMgD2RTDSjLBfG56cYcXLOHDXX5qHnFn/Ebl3/CUwj4j4bINLLLuM2Kj8qPNM1XgDfl6oc9I4pXALgnrT+V1T9b7J9gDMDb8BCQ7Q5NtIWp7QFJjSEJO5wRYeETB0z15+3d/CNgsSRLqINsYlJkmExJOmd1M6kWhWqPPOwk1i1sYlNU+Ue38cEN2vxH1sSiazFNJztDkmtjkymcmQrEDNYU5EWFlTsR3hvPVF3ommUMQIYXQkfX+Q3N6qWFfETLlUaPDy8iEmWuVoMEFxWZu9u4zd6aURiVUUYPN/gmmUFVpRPzRfkmQWYdT47JkVvv8hhOgSsq6RWMPTQZKLfmpzf4Jxj4vOVXzoNSF9W5gwSpgilYRWhl007clJ/PuMdooFR+soamhYpCmiXq+MHKY8cVF2M6VWYobWhihXBEYAer5ygGvOoI1dMgoe4DGGogzB9YAjSFYUxeqrrzrNdiUA1d4NFozQJ4BthYYn/usIipRDB8JlJoP1tjCkusDh+WGPVf85LuQY0RhE5yVlxvPdbCvN56MNWgXIFNXcNdYfUiSm0piqSRHQJJddgQKe4qxzesl0IlgBJwV0PNgFMAi4czN8vSL971c1X1ES0giXuKX2BKSeC78GfuEtdjZnfI0Gyk4abbX5eSGVvnenT4A+ntN5DvBZwGfBXwW+LVYgKbpBQsW+Pv7R0REPPLIIzk5OS6XS2FlEnSM/FXAaIViIEkSz/Msy5rN5tTU1EceeSQmJkYhRAcFBRFpjpdffjkjI6Ouro5lWQWM/rWU35eP/yULeA+GlbE0EV9evXr1PffcExwc7O/v379//ylTpuTn51utVu9mrywo/vE2I5MxDMNYLJZTp07NnDnzscce+6eMJnHyGR0dvXr1ap8nzx9vZ18MP70FJJA43mmzHz1+bNgL8bGxsbf26hNF+fekAv5AxbzU/9E1f5+oO5GLjn1c8iCKBqi0NczZWvFhWv7Hy6zHcqHVgdRdRAoQekb2E8dDq/3bL1aXrdoDufX67aeyv9zMljfgwNUmWDNLTsxZZT5dAAJyjG0sbeHoi8WFXy5c9PxDf7wzultEUEin6JgBt9z2t8F//XzBvMOnT2gb0BWBZ0NaURsDWsB+DwAtrP2KWTdpxrSg8NBet/aN+/1dHXt0vb93v9RX3q37+kjNvM2VE5aUfbqKK6oFCTinU7TZocUCedX5n62EbzJr0nabDmeAATnInJt3CByugbXRoDW2HMo4NnUJFDcy9TrexbgB+Yyodp1dUztx9cUXZ15ZuhsakTiHXgFtLnNeUc66bYUrNjev+aZh3TdQWQ9Wq8w2BIl2QrMhZ9nGywvWQ06962Dmt0u+qj5/EWgGnDRYWCarZPvb086mfgXaVnBxotEu6qyX9p94K37EUw88PPCW/sOfGTrjrffHPBt/V5fef7xv0ITxb8z4dNqwYcO6xfW+6w/3p25YXapvsINIVuG3r1m+mv/YZkff7/+6BZSHpvKKyLKs3W63Wq0XLlwYPHhwWFiYv79/ZGTkkCFDLly4QNO09zP3f918pPwugCa4/NhbreEqyU/NUklGaqguTFXWXQNpGVANoOURITIAEorrUD8B9lTCh9vOdx5WGD5EG4EYEPhp3JTqSmTS5Qdfg6xWXHXByGvw5TUfiLpxAMe0RXEphg4e/Q23vxpCx1gD1VVRauG1tQiwOt0IsdHow05q+9y4jsgNgaBFNsxV0b3jGyM1dipBojQigqSqxkhN/pMToNaN2DfZRKQAO95cY0DYDknQjsBkQ7imNEYFL62Go41Qi54GoYiBiy6Yc9T+3MzSqITm4ASTXzxNJQCldgdrrnTWID28VS6g0A5AKxgmSv+7ZdFbF6CiSJ0EBRYosSMuZpOlMayA4XIGjZljg3UXYcp++rnZJd1HlUaqa6OG1/kn2KgEjhrujBhzue+LsLcIi8AisRSxawIQl1rLbh3bSv2NphIECicAaP/klk5jKvq9DBP3w4EmyHDASR18UwGbCuGzfWVPvp/VMfFK7KimqBRTeIrLT2OlkvRRKYg+rzyNiCGBRuXHIGGW47SBDeDdr2ui1C0hKnsAEp95Ss34oepCbmwSzD7kYY96pJ+vB6AV6Fkxj+ziTQCocJzvGO/s9KIhGEFM5NL6qYxBiYaQJEt4ckWPEdlDP8YmR6jobRX4Y35xtQTPIybrAGgW4IoEeRYourpeTACVLpR0yLPA+iz4dJ/u0fcLo+O1XUY0d05pCop3UEPcVBIdkYLKxQcu40sFJ7oBfQOi8LEoQhPT+KePdYEJEDoSWbpBamevly/1TYElZ6GChwYBGcpmQES4xA4VAJuLpDHLrtzzWnlMUmOUuiUsydlpdB31bHH40Lwn3oLTtTjZA8C5vRjZZEqj2mF+bTl7y2tAJYF/iptK4DuMrI5MhDc3Yb03AQpJNwAUsLDktH7o9MzI5/VdR+EME5XgooY1Uc/X9hrlfHU5GlmeJregaW6+oRNRDsocBV3UXOhIJijFHqAxBqpMQWpLoMYaoGGCUhqpF8rCEou7jGi9842yrsNLOiU19hxdGfB8s99Q1l/FYLqJreGqkriR2lFzoaAJJ8udsnT41cRnJROs57UD8XFsnowAZqgZN78mCqcBeBmDNlBDDDEjsiOHwCurYFsxnGqBbAcca4LtFTDzYFP89Jw7R1+Mja+MSmwKiqdDNXxgsj4oMStqCEzZgUroLhEEnCdD7rNbTsbnhFCpAF/AZwGfBXwW+G+1AGF9ktI5HA6GYRYsWBAbG0tR1ODBg/Py8nDxstdGVlx+BwCt0KhFUdTr9WvWrLn33nuDg4MjIyNDQkIIGB0cHHz77be/8847Z86cuSGmRoYoXsn6gj4L/CwW8B4MK2FRFAll8uDBg0OGDImNjQ0KCurevfuTTz65b98+sqKf4zhFRubHM7l4ntfr9bW1tenp6R999NF9990XFRXVq1evBx54wM/PLyoqKjU11Waz8TwK4/4shvBF6rPAv2KBa27RLM2sXLny0ccfi4mJ6d2lW6x/aFfK74HAzsnd79nxxjTDqXyoN4LJhZgIC1Bnr522vui1BSWTVrKHctFvjw0dEgosJ/AIQOMw1cWfXbm1aOUuyK1nDuYULtnmyChB9JmRoLo1a+1O/ck8FPGw2Q1Om9XloJ0ukWYlg63xXP6xVZuHDX6mcyd8ikWEh3ft1XPAPXePfnHM0qVLC/PyjS269oLKSLQkSQanbfP+3Z98Pv32O++IDg0PCw4J6RIzfPTIU+u2mg5eyJmxMu/TtNNvfg7Z1cDKwyNJQpimujVzzuqq+ZtLPv+qdO03UNmEkosM7+BZ5D7zADoX5GvPfrG25VgWAkCsaDUYGbsDD+XUlMxYd3H0dPuCPVBQj0cB3DaXWFp3bv6q/GUbM+atyJ6/Ei5Vg8kqWk2cywq8C8zW4l2HGrcchlytbsORzIVftWZf4i1WAElwOOmskp0TZhz/YgVdVA1GK6MzAi1y1U3fLtlQtf90waGTb6aMvbN7nzu793lpqOrLydP/754Hukd1fOb/DV6wYMFbH0wYMOi+mFt6qcaP23HiiFMe0rcD0DK3TrlDKoF2S/pC/5MWIC1BQZ+JcpTgFsh7Y0FBgVqt7ty5c2hoaHh4+ODBg/fs2aM0HhL4nzTb1YXmEGdseXdlVXg8QyXYqKFMoBoix5hDVJc6DM29Y7Tl1aUwa480Y5dt/PLmpz6u6j+uqs+o8rBhpuAkG5Wgo56zBiNpuix8mHvkYjjVgGgpLp5vA6AJvuMG2FZ0qVOiJULj9kcnhIK/2kbF62JGnr5FAyUcYp3KJvwrADQtI+P7yvP6jyn2f84QkEQHIjezIkp18J5RUOYAC48eCMkmApyqv9QFoWfOD1U4TAEqfVTKlRhN5S1jzUlzqp+dVHTvq5d7aYrChliiUyB8lEglQdAIIWQEHaq5EqPmX1wKVTxYOafAEWdr5FtBWNHnmSDLMJ+tbn5v1bG7Uw71GpZ130vNI+dZP9tqmrHVMXWre/JW24tLSx55+0z3pNzoF3SdRplDkh3+GjZ4FN1hjC00xRo0vDl8eF5MEqzKQbwSgBckIkTsGRHZUM/a0eMVR2AyK2PQbkrtopKh51t10SNKO48412FIZsfEoh4pV+LGlkcm1QbGG1HEWc2Fj3HHvuroNK4qSpNzi8x91rWpdciCC0QIWEa8URHFPm5ZbUdNfeALNn/U13bLAHRNlLr4b5MRydVzvNUl4+I3ZEATAFqxjSAikCizbRtZWHK+rNeo8hi1NgIR7dagpCuBQysiEkp7jvj296Phsh6fSiJS4X+aTQLkKQsAp6t176769q6UYz2H5fz+pZYUrBfDzK32aVv5T7Zaxy0ufvSt0z0SLnYc1hCpMgUmOv0S+cBkNmIkHZHiCtMYojQFsYmwqQBs4KZZtywyw3keWDKl/ZMdrXHjmqhnGCrBjcB6YmtAfElk/Ml+asNry9jpO6wfb9C/usSqmnupZ7I2VmOJTmEjRroCUQCnxX+YqcfYy50SHSkLocSBEz+M0nbxn2dzY9XAmbpLfUaY/OIlSiVR8TQ11BakKg8eUnHL6Lo/f2xVzc3uN+JibHxxx8SKoCH6kCREw6khTipBH5lc2jsFlTdK7MCDjJ57HBC2JXDdrwDoPCPPVNpFwwfjBIbFP7klTF3fQd0QrtGHaFx+Gjs1DAJHi9RwEWdENByVaKKeEzqM1FPP0UFqc4iqmHr6Up8RzvfXQx0WiihuYUo3GVW066QrBG0LiyIn3ZMsQQhAizIGzQQno0/IiKQLUc/n35JS2m90Zdyoyi5o2+ZOI4wdU+xRKabAxGbqGWNQojYk/kz4M/DJdtAK+DaobArxnzgtVPb/iICPAf0jjOe71GcBnwV8FvgZLEDoloqABpFmFkXx2LFjRHnggQceOHPmDBlOeKfvPd7wpoJ6DyrIaEQBqTmOW7RoUVxcHBETiIyMJIGAgICuXbtOnTq1uLiYwHkkIUVP0Dc+8ba8L/xzW8C7DRMuP8dxBoNh5cqVf/zjHwMCAvz8/CiKUqlUW7dsVZj7xHWh4BZYliUyHYrTQiXDyhIBURQ5eSM+PG02m8vl0mq12dnZc+bMeeyxx8Lk7bbbbhs8ePCf//znrl279u3bd86cOd4rD7zzqSThC/gs8EtawPvm3Njc9MWC+f3vQD+ZwYFBUVRQnF/4ff4d37j3L5tHvu88kgtmRmI4h9nq1luhQndl0Y7yN1OrP1xpO5SNDCZaAE4Q3QIrCvKAD8DkKNx19MzSTVDUCmeqz328WHvoPIK2ZhbqLfs+XVS//yw0W0SadUHbJegXiIM6c/Hu49m7Dutr6xenpt5///2B/v4dAoI7+AVFBod2Co985P4HX9SkLF+0+OSRY3u371y2MPWd195Qv5D4+7sHduvRPaJjdHR4RO/AiOQ/PbNz9y59UwuXX5k7c1XFjLXnP1hgSM+GVrNI07zTieIbWuPhqakF89Zfmr22cuVuuKJDbFqmSdlomTSlo7kzxTvemXl58wEwYslsDjuS6JwSVBprZ2/OeG1O89K9cKkJh552FmwcNDkK5qwtm7OuOm37vilfOIvKgGXB5gSrHVUxeLfuzMWMBauh0tS6/mDewg1CfpVbZ8J65zlbbf2ZRWt3vz9LqmoCixMVQhwMtNhPLd+cvW4Xep83Cvu/XDNGpenbu0+vDjFDHnly/iefvTZqbJeYjrfddtuHkyceOH50yHBVbN9evQf0n7lwXpOulRfwtia6Be9nuu/+80t2tF9/Wt7twTtMnoyXL19+/fXXw8PDg4KC4uLiBg0adOzYMUI7IOuHfv0F/FlziJAWAnMSVDnK7xhnpIa5/JMYKtGNKhZqa2BSa2hSXbS6uhN+6qLVhg5qW1gyHZHChY5wo/hDIuuv0obE5906EmbuQcalpU3TwGsxu9lhQyLn5/sqe4+0RGg4P5WDGmKmnjVQw/I7q6T1Z7GMRHaHeEtrR9puXnovcq1kYUDvhs2ZGX8Yr+37Ul20pjxGfab/SHH3RUIg5XkZxSMyGWaARccKeg53haYApbH5q6zByUzwcDp8ZGu0pjEmWR+ZbAtLtlFDHdTzEqWCiHFG6rn64Pjs3mqYtdcjVI0sbQQzr/l47Mnw0MwduFNd1iulPCZJG5HUFJ5U3yGpvJOqqIuqvBMK12qjkps6JOvCklFRN0gjhI6C0Bf5wBR3yGhTyPBLHRKan5sJF/TQhDAdz/BEZxhTJcZhATL0eXe/rA1LslIJQvBIF6ViAtGzojlMYwjXYMwhyY5g3OMMGc4EDwf/4eA/UqKQuFrSI8X99nqolcCAgh6IxJEPUT1QRJz/ufRl8s6qbiN1HTS0f7KDehYotRAw/HKsGjKaEQO1cyhpRaxwAwkOpZI8AdQ/Jq70HBIUm8Uvjx6/M+V87AsFYUO1sSkFEUMLfzfONXUrUlO9wcGbt4J/4Ygo86mbuMO3q6t6plRFJzV0wObdFO6pl9JYVUUnVW20qiFS1RquMoQkuQJVQsgICE4R/NVuf7UlVF0cMazxmSlwuALBdw5YGuFhbFukfISbXGjJHzS+JUZjoJ4hczkslWQPwAZQFZ1UGTMFZigAACAASURBVJNUE4VNoiUsiQ4fYaficcrHL8lKxZuCcWdOp3j4fC+UWLDpOmXzooFRSN2jESJDpRIKXgF8eaK8GwqDOKlnGSrB6ZdoCkR9ifpw/DSHYlgXnGgMStRTQ4WwFIZKbAwcltFHLczdC3Wy7Licd4+n0O+wJicLxWzJqY4dzgVoXJTKGKgq7ZAEL2+D8TvLOw3XBagtOMORLASkgF8KUMMBScqJRupZIzWUjRldGhGfdd9L8HUWms7IgOzmmQPJw7tWWopXHjy3AbnNyzcGed2YSYKPvy7rmGSgnkf2N8LQKiZQbQ1W6cJUjWGJjSEJpkiNqUOyLjjRHKbmO47hA5NxAil8RFV0Us6Dr8JmdOqI1vQCvom3Q1YWHPLKwo8K+gDoH2U+38U+C/gs4LPAz2cB4hMG2Wdu4cKFCw8//HBwcPDDDz98+PBh4nVQwc6886CAywou5j3w8B6skkEIAOTm5n766adPPvkkkRQICAgIDQ1FhlpExBNPPJGWllZaWupR6pT1psmFP6HEgXf+fWGfBa63gHcbVsKkHRYWFq5Zs+bpp5/u1q1bbGxsVFRUUlLS5MmTMzMzW1parFarQuQXRdSxJRvLsjRNkwkVoplO07TNZnM4HHq9vrCwcOfOnVOmTBk2bNhtt90WERHRr1+/p5566oknnnjwwQfvuuuuuLg4tVq9ceNGg8GgdDSlc5EcXl8K3x6fBX4ZC/CCYHPYa67UfvTJpDt+d1dwZHhwh7AQ/4DOVPB9YV3ffODpfe98juhzox2cHMMwDqMFWDBtP53x5ryyiSvhcAHoaWB5sc2rLVk9w9ldV9Izs9O2iVmVkFV9fvJS56EcaLYi97neWLj1YNGmA1CFLGae510gugDdoIGThwp9/vLtO2ctLj+b7TJZzWZzUVHRmmVprw5VD4zs1oMK7kQF+FFUCOXfOTK6T9fuv7vt9lu694qNiIoICO7ZIaZTQGhH/5CBPfpOGfdGU04xsKJQpy9esSPv07SSGWsaNh+RdGbRzYEooK+/WpN27b7yZdsvLdxYu24flDa4TRZJ9vWFuXI4kDt2uiTj0+UFq3ZBjQ4YxHARmOYl0Nqbl+/L/cfCok9XQ1EToupkJGbgmjYcbZizGXZlXl6wns4tFcxGUXABy4DdAQzfeDLzxLRU974LLV8dOD3tS+uZfGgyAS3jBHrr6VWbv52d5rpQBGYnEs1YCaxs/eELRev3wcVqqDBot6efWb2t4GLuoaNHxg8fPaBTz4G9+n3yzvvjRo3+wwMP9urVa+jQocuWLZszZ85Dgwb16Nrt+eefP3z4MLn5kBua911IuUP61mT8Mt3tV5uKd0vwDpNJVpfLVVVVNWHChK5duxK/IPfee++mTZtaWloIv+H69nP9nl9t2X98xgiKikCPA10RXopJaIlQO4JUjF+S4K8G/2TBX80FJTuD1c5gNR2AyraosEwlsf4qW5CqJQIhOevzM+FwNcpKOD3uvDw4qQwgCQBOgYM6g3HShpxe6tbQJMYPP6bgpPIOCdYxiz0y04KMQROZYw/y9J3la0OsCGFRdPHIoS7nIC1Demu9NHE7HCrHQskbx7mJWIYbKaUA9Wz9P9Iquo90RY22BqMTPKA04J9CB6ltQVgu1l8FVDIEpLiDNU1B8SWdkooeegN1ZptFLKMi4iyjwQQTVr4R1eJEOFuRc2tKSwhqShDhYJRuCFA5glSuQIyf80MNEIlK5imVg0oyBal1HUbURQ4v7pCY1V0DM46giq5LTkDmg3vAR9kvm8c8NQ5YffZI1LNXItXN1DA+OIUJ1Cgfzg9FrrEUVDIEj3JSSRYq3uCX0BKhqe3/CsxLl2cLJLxRE1wel8jISimcB5vDVJwA+8rOxWlqYpJtESOtgeom/xeqO2pg8m4wAO/yQp8xf98hweGpLQ8AjUM+OfJKM1QLsC4LPtkN0w7A6mzINGI9yqjkD2kF39lErj4o4hogOFORf0uKPijRHoAiwjJ82V4vdABWDWnkHJXooOItAYmGMFVDh6Rs6k9lt46BRafQVSABx0XgBYEjPjaViQEAqHfBhoycXmpj7MhmaggTqHbLehGoPhyQ5PLHdN1UkkAlyuoZyUygutlvaG20Kid6qPDCPEhvgVLZTZEEeC+SVxKgerWsi45F8k6rGZzj07KC/moJTzbK7GaXPyojO+SEXFSii0IGtykw0d5tbGOXlMtR8fl3j4ODlai8wcuiW7KRvJDYq42m/KNFMAE7c/eVTsM5v2SGUukCk2p7j4Mv8+ACl/fAG+URan1Qsj00RYgcZ6GG0HJrd0amlPk9W9ZZndkjCabvgyoOWli0nluUBFEAiZY/WNFt3VlJsD0gA+4Ctk1ZK8MpQYmtNn5aVSzOkBEeNOeHGLQzGPuvNVhl8Is3UsMcQSprYFIL9bwxXN3UUVPURcWMXQqXrdAqv/MoCciF5+Ubgw+AVqziC/gs4LOAzwL/zRYgwBnLshkZGQ888EBwcPDjjz9++vRpMgYQ3CiQeX35vYcZ3x3mOIQeUDyKYViWzc/P/+ijj/r160fkOAiltGPHjhEREU899dTXX39tMBjIsIQAf0rk1+fBt8dngZ/WAkpj8w6wLOtwOMhYuq6u7siRI2q1mkhkhIeHd+vW7eGHH546deqBAwfOnj1bUlKi1+uJUIaih07as9lsbmxsrKurO3ny5MKFC0eOHDlgwIDu3buHhYVFREQMGDDgj3/84+OPPz5gwIAuXbrExcU9+eSTaWlphYWFKD/HcQrurARIJn9aC/hi81ngeyxARinyEMzFsxcvF4waNza2e1cqJCC0Y1R0185RYeExFDVpyMj9b8507M8CAy1ziAREBOyC7WTB2QkLTv9jruloNhhcIIGdY6wgOEEAXkAqtI2vOnjm2MzlUG6E/Ibs1E01e09Bqx0Pufj83UezNu4BvQt0NnQ3JG/o7s/lslXUFczdcOjNWVk7DwIvMAzjkjfJ6qrdd3pFyjuf/lk9U/3K+2PHvzRytHpYwpCnn7m1V58eHTtHBKEyVC8qbGBw7OMdek0aNqqhsBSMdtAxlev2F0xJy/9kmXbzYbG6CXU1kAgFUKOzrjrk/HKv8+sTl5ZsgctXgJV0VqNRdCGLh+XAxvLZlRXT15d8thZqDAhGy5gISjybGdibk/HK58cnzIPcGoR+CPpscRn3Z5R8tta54JtL7y9q3nMCeJF2mWnJSQsucDrcRdUVy7eJG7+lVx/Kn72KyywCK4sCjm7RVVlXsfqboxNmC/lVYKFRnNotQb3ZeSo/d+UOKNVBDd245mD69GVwRY85AdBX16V9NufRAfd0j4h5dNBDn0ycNHp4Sr/uvR68dcCMt95fN2fR5Nff6dW5a79+/SZPmVJaXma2WTk3otBEd0iZGCa3I+8b5ve0H9/h/zoLeNe+EiYNg5RVkiStVjtlypSoqKju8nb77bcvXLjQbDYrz0rFKkoMyp7/7oDM+5OQXWiyISY1d192t8QiarA+KNEdOYoPTOYCEI8msKxDRmY5P5WBegZh2biRZx58CbZk4YWoxiC7WZPJs2g0GSYTZSzRIyKwK+vwLYl1oQku/yRrsKoiKvHyn96HShk4JiLRXBsP+gZv/dfVgxdiRQtyCiKA0Y3wlh3A5EZvscrmBsEtoRCHW86QG7HdlvfWFg14uSl6uMNf7aaSuQCNISSpPjzxSodElOKlEqzUkLqAodm91a3TNiGzm0Z/ZXg7JTRtj0CAkkY7MCiwHFRbL/YfqY9MNoQkWQMREGT8kjg/D7iJxOo2dFikkvVBqvyg5/JvH6cdPo9dlg5aCUFYC4hWhuXdgmxSDwAtF0FCISY5P01u+OZyxt1ja4Jf4AI0XIDG7Y8fASW5EYDm/PADIaOM/knaqOSKAa8iNH+2CbQcWoluA9OJQzy5RKh5IaeITzg31qxr7t6svinFndQFvVPODHwRVp9Bx25mGX1WcHcMfD8A3QY0ykZDRFje0ewEg4B8XqTZivhkoQVMWm4GPxkMLYHEcFBlzb1tpC0smZUFHIiOMOenurpqVCBPtBgCEgoDnim8bVR98ufisqNQzaAcikyelfnIKPrs3QpEt1wvTkBN7XkH8u8c09xphC1IRRBhUzBOujhk4Nst83aRVR2Q2BCpKuszMv/xN2FjJhrWKKJZ5GJ7+oHszFN+9rehzyI4eLl5tzrABMKUbZndEnVhKj4w2R6A8hSmYPx2+nkA6ObQxOJbR+/sn9D6xQ5oYNEtoY0Hs2fFV1tnbW/J14TkKXYBjFCkml4XreEpNU0l6YNUhdFJkG5FB55Ha050TyoPTWwMVtsjx7T4v9ASpq6NVhX21uQ89ga/cD/Uy93ccyNAYJ2RBII+Mwqw3vZ21566ssfTBWQGNCfhKi4to399WW63JH2IRwyaDlBZQnGJRkuEGgnsiEEPxfmDLqOyeqpqh38OB4qh0oJtjGxc201DXnvBy42x7dhP8+tjQP80dvTF4rOAzwI+C/zkFiD4slarffrpp/38/O6+++6DBw8qtGiCnV2fqDJI+N4AudZut5MhK1HX1ev148eP79q1q7+/f8eOHQkMTXQ5nn766f379xuNRpK0Ev/1efDt8Vngp7WA0ti8A4S/jC+I8kYCmZmZr7zyylNPPdWnT5+wsDA/Pz9/f/+goKCBAwe+/fbba9as2SRvGzdu3Lx5865du9asWTN58mSNRnP//fdHREQEBAT4+/tTFBUUFBQWFhYTExMdHf1PoeeYmJhHHnnk5Zdf3rVrV0NDA0G9SUcgqXt/k0z+tBbwxeazwM0s4FkK0zYgEQHSL5x55oWhIRHhIRHhHbp0DO8UHRMZ1T0kMu29qcdnpWk3HoF6O9Cci2UQfQZwpuevT37n2zdnMwdzwIFayQzD2ETOCLwdBNSvsAktRzJPzUiDkyVQ66rdcLhq2zGwCMiYMzJ5O48cXrwOIVRCf6N53irz62heajBWbz++Z+zkypV7wIHaoCzPIQvYzkFpY+bnay5+tio3dbP7slY02q0Go66xqaFWe/FC5oHtu5ZNmz1z3FuvDBo87ZmURcmvN6dng4UGl2Tafrp08ird/O35U1dIl2qBcdO0080xUKejD2Xrpm9kF+09NzFVzKsCNzB2mxW4JrfNzjHotanemjtvQ8aEhXCqFIeyLI8KGwwO753ni3epJuR+sASKGsDOExdAotVVfzbv6AfzhS2niyenufddgIo6sNtZt0MCt8NkAL2let03ltUHxPXp2R8utKdnQ5MRkWuagyZT5qqti//2In8kBwnRggQuBmws+21+5mdpkFkFBrBuOXV5wWYup4rw2rCKWQmM9LEVm16497GuVPC9vW5996XxqVNmqh/+07DfP6p5fPCOtLXLFqYOHDgwtmuXhx5/9ODhw2Zbu/9VMjOtaA153zBv1n58+/9bLeBd+0pYKSxpJJIk0TQ9e/bszp0733333ffdd19MTMzSpUurq6uvwaCV85UY/rsDBD/04EJu2Wne5lzd858V3zG2vMeImhhVXaRKG4W6BDUxKBxR0UlVGquq6juaUc2HTbnon5AAssRFWBtUikbzAqAR85EAGhg+9cCF20Zc7qW5fPuY4mc/hks2lIDgZeSRSEC0QVTfb/Y2AFoSUQTCs0ngtDk5OUqnKCCfEd29YmYECfWHMC0Zo8bzDQDrsy7cMbqoc3J5jLoqJvlyp8SczgkZXROyuiRUx42+MuAVeHsz5LvAAZ67PSv7Y7wJAE0KjTGLEuj55rELszoOq4xB7YWmcFR7MIWqzCEqQxhqBbSGowRHQ0RyeadkdtgXMP8EXDAj9Ixe8mRvg3KRiDBJO1FdBqCR7k2ATxMDOgGqJHh7y4XgZytiNdUdNXXRmoYojTYquTY6uaJjcknn5PyYhJp734SPdsA5PbQA6GQOr1xxOPlAYpctg1aS0yVMcawNGw9aBs4aYGUWLDkBeSZEYBE7liv7xwDQckIcAW3lMDYTQUT4nuU9yh5yUm0Hf+wvvgeYhcZxC3NjhmkjELskH1OoyhSK9dIarmqKwDZfG60q6axihs6GL47DOR1c4cAmVw0+vAScdQaBk9D9oGdiQK579O7Li1g1JhZqadicpX16Um63pMudk8o6JpXHoASHNgLbw5VI1OIo7TkiJ05jHT4fdhRDI4BRanfdKTdpRZfY4w5B+S9XE6kpRGN1AMtPVj3wRkHUsEsxCeRTHJ1QEZVYEZVYGpN4vkei+Ol2KLMjpR1QOQQnqjmZjy4blVTjzeyLYwELCy1w+v6XGyKSOUpFU0ktYerzXdVQKavuNPGQ64LJe21D5lbd+w/T05/By2uQZb+7BIn8rRy4eLuzbT0C9kqBBpFuk8/2zDG0vd21Z+OabIkePjhNo9MOqLDB4uM1f3irpBMatioapVRKOquKuqkvdVdXxo06G/z05V4aR/J82FuKXkPli3ie92hPu+Xik8bvbU9Pbtpz8W+HfAD0v20634U+C/gs4LPAT28BAiVIkkQkL6qqqoYMGRIaGjpo0KDdu3cT2EshPt9QgoPkSRlsKCd/937vkrhcroKCgvfff//2228PDQ0lkFxYWBhFUXFxcf/UOkhLS9NqtYQ9TVb+kkGvTzfQ24y+8H/KApIk1dXV7dy5My0tbdSoUffdd1/37t1jY2PJt+Jvk3jdVL79/f1DQkII6Ny1a9fevXvffvvtTzzxhEajmTp16ubNm/Py8vR6/fWFItCzd48j4evP9O3xWeAntwARlsFlu4T1A+K6TV89+OfH/aJCQjuEBAUFBEWE+PlTA2K7p737yZFpS8q+2g+NNmAkJ8vgsMcpQq62etrGgncW674+BVdsYBPAwQPt5nlBxzgtLhc4hdYzhWfnrnHsvgBZDRWp28u3HYXSRqizQSPr2nXh0LtzjOcKkfuMEIDEMIxnhqbZZll77NToqY1rDkJFC8tzNhyAyus5s+vKPl2T8+GSwkVfc9VNwPACy7nbPsgqMjuE3OqMaWlHX/3s+Pvzi/adkAw2sPN8ZoVt4V5Ymt4ycxMcyYNWG7BuEESwuOwHMyo+W0Mv3lf26SouswQcLPCcXaBNEm3mnS6bHVrspanb9r461XayAFne6FKRB5pHJD2r9tx7C/f/fZr9RAHQKHuN+XRxprP52Qu+Mmw6dmn+hqJ13yBt3GhG0WfcJDC4GtbtLZ68lF59KHvKUueJPLAxvMUqOl1g5/Q7T+4Y93H1hv2oUgKAELnRLlysKJmznv76JJSZ67ccz1m0CS7Xgw0ZWyyITpoGi6v6wJmjE+YWzlj7yR8Tk+546P6ufTVPPTMladzkhDGP33b3ff0H/OONN7ds2/b2+xNuvfP2uwbe/dZbb2VkZBCZFKLZhUN+efPdl+Sa8n1dawGCJpNFPACg0+kWLFjQrVu3O+64Iy4urnv37u+//z7hQRPBN2W29ZpXymvj/S/6TxAenpBNRQkYEQwc1DrgaHHjlPUFQybmPPL6uf4jjvaKPzFwVHHCp84Z22FfIVQ4QC8hEOmSId0buu1qA4UJwoMAtBvALEGZwXkoh/22EJpoeXpMTpsT8K7pzSZtw5fxwu/+iF4pteWElIsVBV4QEHiWnQIih1QWNHCLIu6kJSRu13NwqoZfuL/p9aX1o+eZxi9jp2yFpcfgWBlU2JH47JKXiRB0mcRLikSgR++8KWgpWhKggadn77r48GvFd71UFJdyqTviYgU9kzPjkrN+P06rniXO2g2HKqDMhaCwQZakIJRkLwiMJCjjwrL+AIEgOSwUnoVLW2T6uQGwUg6UiF8eNU1YVzvyi8rkz+v/vtg4dYuw7jRcaIAGN7KqSZUR0BmLhXFiayfQHrqL9FSCrHiAcaM/T8TEZZzRJMdA+LltpsbeQIxw036hWE0J3PTU9tgI8Vsx6Xde8UMOypofclOpd7mWHT77xOu5vxt7sWtiRvizOdFDz3camt5t6J7eQ3VvLudTD8AZLdY+aeQO+WkuM7JJzbNiO/rs0YCWZx1Qzovn0Rpu+RI7QJ0LDuTpPt+Wnzgl/Q7Nyd6J5/qqcx58tUQ1rW7iGvf2C1CkQyq6Q4ZHWbmlESO1AdDt0s+KneXmIcmMXWyDbgH9T1gA2dNHSmzzdl/5x9LqMXMbxi6wT1gLi47A0SoodUCLBGaUxhLQXyJWqbJ9b62gU81WF5xtOts7qTk0kaESnZSqOkLVOnoR8tbJBJIDkB6uA09jNsl/7XL3kcslyX2QNG3vDtTe2L27Emnn17QrBX/He7qIb3EWgAYBztbD4qPGN9NqXphW+eyk+uGzje+u5pYchmOl0IDKIdjyZc1urBechZJffpT7hmyI9npsu5147OOdK8VkPyzgA6B/mJ18Z/ks4LOAzwK/lAWU93ubzZaYmBgcHDxo0KDs7GyyxvYHyl94Dzu9M36z/decg1qZMgw9adKk6OhowgkltFCKokJDQ/v37z9x4sT6+nrCyCYO3NpxB+/ofGGfBf4TFiDDZqPRqNVqa2pqTp48OXfu3FGjRj333HOPP/74Qw899Mgjjzwub0899dSwYcNGjhw5fvz4d999d/r06atWrTp69Gh+fn5NTU1TUxOZa1EKofRQsscH9CiW8QV+YQuQG2/bTKTIs/TqlSvuHXQfFR1ChQV0jIyICQ7pHBnZMzwyffHaS2t2Vm8+AjUGwWAjcBKOjmot+Z+tPjF2umHFYSjTIaBg58HlRtazzJ1zGG3GyzWH561p3HESig2GdUfzvtiA6LOeQVzgeFH+J2ni8ULQuYhgBc/zOCznRHBJ9LcFB4e8Y52zE4pbwMHRInKjEBcua70ydX3ZG4tq5n4NOTVuI+bHjY5COdqNH2RLtdi0q/dffC/1/NvzbXszwMqBG2wXig+8MRNWpDdNXAsH80BrBYecVTsLVbrcyUutqd8UTF7WtPUY6KwgiU6BsQq0nXcJLhfYpStbju19dSpzOBeMLtGNXC3sy4wE5a0XP1566o3Z9LcFqCIi64SAg6aLqo9MWdi47mDBvPUXUtfby68AywHjQgCa48BgNW5PL5+2svGLzXmfyuhzgxEYFp0TGu1iXtXhN2fUr9oLVnTkyPEMOkisbilavAV2ZUBmXfPaw3lLtkJZE9LoaBzzYmZorjnz8tm5a3RL9ua9t9i0/XTVtmMTk8b+LrTz/UGd3/pLwqqZ8//8+B9jOnV8+P8eW5a2/OutW//0pz917Njx3nvvXbx4cWVlJcdxdrvdB0D/wj3xN50ccTSt0+mWLFkycODA/v37x8XFRUdHJycn19TUKBMbxD/2NY+/33TBvzvzBHvi2qiIblFEPIvANDYZTqoDqJagSkRybquMPzJtICWBIK8Bib4jPUTlRCAr3wmaRkBGgisRBIigP96gz78dlgFWrMo2KNMTFiQPj0SU8B7OoDoT6Hlo5KCOh3oRi2mWAUFvOrYCfpH8KCihd/YUtJTsdIhITy5nINMMR7RwSAvnLVDIQgkHlRyKEugEhMYYGa/0colG4iZiIQTlJoAdQnVe2SBgMdob8Wl58sAOqMStAyyCTga1EX2TwNVGbJZrR4H/ZAKvjGtfDUCTqiC4IpkXQEugs8q2qid/5fK2A4g3rXoF4VQCNz315zsgANiBaLUAwql1LBLwz7TC0XrIY6CQgRIGqhjENO1yMb2yQvKtgPKkUgj9WQGIcbqL+MslF5KakuQ2bxHwRaIeoBpAK0O0FrneSQPD2CUPiE9aznVJkwwou8lfXkZ3OXRSKTtdYCQk+VoB9CKiwHq5DehFMOPqLpyGp3EhgFsGoBUhChLnNfErCbUHdCxsKcjrmqQPQgDa7qcqjlFZP9uO5pJvF6RpyNPzclORr5RE1NdQPiSVm6bl3ZWus4MnJ9dMe5BUaXl2RC8bth5Q3Fwv28EhF5mcQ+5pJG28ISBO4J0f73B7qUk7VzJ21YHv/+MDoL/fRr4zfBbwWcBngV/MAsrLvdVqfe2118LDwwcOHHjq1CllP8mJgiP/rBkjMHRtbe3o0aNjY2MVGJoEgoODu3TpMmXKlKKiIr1eL7gFlmWVNZvXZPhnzacvcp8FvsMCSmeRJAkhLlm1mZzv3UpJ2HsPvl9JEuH4K+eT2LyT847fO+x9ji/ss8BPbgFRRBd/BIO22WxNDXUL58/r26dXUGgQFR0S2iki0i+gl1/In265q3jrwaqv9mUu/EqsagE3mG1WTzsvadIu3HHqtc/zlmxnShpQXFIEgXELnMALkshLYHe7ShvSv9xYu/s0lOlqvj56fsF6KNBCkw3HcvlNpfM21209jjABiyKiDpCsvKx0YeDgfNWZt+fVzdoMmVqwcbJKsSBaXaBjyxdsLXpj4cW/z2HSC8DKIyQNqEHJcZwZOJvI0S1G46n83MnLcz9Y0rTtBBIPOWALak5/sNC2/ODliWn1q/ZDs00GyiUwuqBKd3HWKufygyVTV1VuOig16jm7nZU4F0+zLC04nMh33ptzdNzUpp2nkMXMC06JRy/zDloqa7y8fMepianG3WdxOOqQRbGtNF1QmbV0U+mKHRWrvzk4/UtoMksu2mwzI7AgCtBodJ8qKJm+snXxzvOfLanZfQwsDLhYBKYtTsiqOvrGjJLl20FrBLtLYBmQJDA7Szbs1W04Apla28b0rGkrIU+LVyElXJa25ACqW7Pnb2hddyRv4jL7jrOgNUOj+eiX6z74m+bRyN63+0U+/rv7pk+Z+ur48cEdwvr16/fa38fv379/1qxZcXFxffv2HTly5PHjx8kiXG+3hN6TZD95O/RF+Ju2gOAWaJrGSSMAu92empraq1evyMjIjh07hoWFxcfHZ2ZmOhwOcp8hp/2my/svZb5NBhqRKeTDCqIsIyAhPZmWPy6ZnOsCxDFZPCoJ+LkZZHbT1L2phUpYAXcIAqT8/SkC+AggwsRXf+M7D3jKiydwsmwCAaqIEggjor9WO8EhuwAAIABJREFUBVtVcnvTsnkOiDJlGGmwBLpyiaiVbOLBIhPGLTILFWWORZwHxWeKhAkRdEyOg5iB8K0V9LkdgPbKwFU7SQ4JaI1a1W2kWqKkLEtgK5d6Y21KcljYNgUVspNAqwrA6inR1aa4Pqob7RFFuOaDqf34j1KiHxLAqpEVMzwnE54yLcPNhCGLRpPApch8C4jsk3YoX6MA90rOvUzU/l7cPr0ho5zYGIhmN64A4MHEYSptKs8goeoI9qarFLSvLZCS4vUBPBUVUXjJxbotDrC4wCUgdx19/cmUakn+dpOZGMwniURJQxkRXLNfOQEDZoAZ+4o7JhqDUFfaEqAqiFXB9nyUDZHLwsuJYE7kqRQFdPYOeGf+qshv1tm9TlL6Iilue1aVWiHCOCygJomVw0l3715E2q2cEKkq2bXnjRuhV7IymK5k76oD3//HB0B/v418Z/xWLKAsKPtXM9x+a7yRS7d/NTbf+T4L/BgLEOUNmqY///zzzp07/+53v9u7dy/P8zRNK9qOv1iLJQmR1DMyMl5//fX+/fuHyFtQUFBISAhRLejfv/+bb755/PhxnU73i+XtxxjZd+3/iAXIdAhZk05mRxAFk711kW8Fv2MYRL9uaBYC83k3bOWVlJx/zSHl7w1j8+30WeBHWuCa5odClDZbcXHxy6+M6961c2hAAKrKhAaEdgjp4R8y/PePl36159KSLWdmLINLV0AAxkWjTgbLQWWr4esTR1ImXfgwlS6uJwux7SChLqhbYhF6kJyXrhR+tb9syzGod+oOZ2as2GbNr0RKr56lzxQVzduk/eogGBj0U8iwJsZhBN4hcCjTWdhQOndT0cx1UGZGfIHhkTxockGVvmLpzsz3Fl2emCbsy4EGm6SzygMzSZAZ0A4BhTjs+ZXZX6zP+3Rl3qy10GADBoT8mtK0Xc2LdtXP316ZthuKG1B5g8RZ1lS9fGfV7A0107+qWLQF6nSoas25bJzT4aaR+2xwQXb1qdFT677YBrV6N80yAi/I6LOtTNu458zRiQtbD1wAI490PwsDJhp0dPWmgyVLt5n2nStc/w1dUgtWVIh0uGWtRCcNRXVXUrc0LNxSMGNF47FzoDMKZivQLFidYrE279O0sllfQVmT0KRH9BmAbWgt33/izJyVkFGpXb03/eP5wskiZHALILlYsDJgQU9El5Zsq1666+xHqa1fp0NRExjZhpM5p+etrdh4cOG4d4f/39N3dOvdr2/fUWNGT/pk8l8HP923Z++H//DQsiVL/0l/HjFiRFxc3D+f0bNnz66qqvIB0D+yo/0vXC640SkoeVCSJ6DD4Vi3bt1dd90VGxvbuXPnLl26PPvss+np6VarlbgP/V8wi3cZiRRDuxqDQrMVZdDKLSLBVkZUlUc/3qIVXOZqUNI75puFCeh2Le7mHeFPEr4Odyb5J+gzh1RQmRCK7gkRkiaYlCfPaIT24n4HXOUNqykwGWlpaCUFWCQsV+UMkgxhdLbDaTczmAcpw8M3sTbingRwJHG4Ua0YIcibnH9tSj8gD9de8kP/X2Oha0zwQ2P58efJWKXEigIrCoS/3G4b0t5EcNMe35WiW2ifZWlL+/qStGHQ8uSN3F7IVCgvoPwLaVRtV7f/IpmJ58jL+fcA0G1ZVJImKbbHRdYVeVqX3CvJMVFSRgdkh9Ka21F1OXLldeu7moAFYPzqqvB4mz8C0KYA1cUuKsjW4cQ5g6CzW4a7PQxoL9bzDQFo78xj+Gad3es877yRsCyHjn4gSf49ZpQvEVh5hRkvq354RdKGSLd3dsWq3oGrrvDO21UHvv+PD4D+fhv5zvi1WUC5HRDGJXmSERlEMrdG7iM3zLb3obZVq3iicuvxPuGGMfh2+izwk1vAI5cpx0sA6EWLFsXExDz22GNnz54lDZ48tq/Hwn7yzHxHhGazubKy8uOPPw4PD4+IiIiMjOzTpw/x2xYQENCvX79nn332wIEDHMexLEsmhEhxviNO3yGfBX4OC3jeuuQbutJ3SPdRVMu995Ow94Pg58iVL06fBX6kBZT3HxKPzYbiFXl5eX/5y1+iYyLDQoJ6d+kSSFEBwQERAYHvDRsO+VeaVh04PWmx8UwBrjNlcHzr4lmQwL4vO/3lGenvzOPPloENQRQjrs7EcbrNYnfTPNj44i1Hi1Z8A2UG5nzZkZnLGr7NFkx2FCxucNWu2le2ag8qJyKai6NWRhJwtMXzcMV4ZvbqorSdwsUqsMsao1YX8pRz6ywrDl/6YGn+J2m6gxlgZHH1qwtp1zjulVWLgZMqD5w+9cmSkjkbj09cBMWNKAli4aqX7jIu29+8+mBu6maoaJUZTLIQc3lD2cqdhjWHLKsPab/cDhU6cDFOgWF5xsm5dC4Lzj8dyzv3yoycCalwrgx40S7xOHg2u8AqVm05+s07swwHMsAuYUI2DhnZJqF64+HapTsg/VL63BX2oipHq06SBE6mqiHeVN509uOFhROXZn78peN4DtgYcLuRZ+1gobThzGdLLy3cCBer0DeRg0buM4Alq+jI9MX0t3m1Xx/OWLyBuViGK51pQC6Sk8fvOnP1ou11X2wrWbS1aN1epIOZeSioz5ixCg7ln5yypGLvycrzuV9Mm/mHBx70Dwx49NFHv5g+673X3vz9HXf16Nw1ZfiIffv2LViw4L777gsJCYmPj9+3b5/VitrT5Ftwy4LXV7/u/sjW6Lv8t24BwS2QJUFkeRB5F7XZbLt3777nnntCQ0Nvu+223r17P/HEE7t27SKFVXz/XjN0+q2b4qr8ewMr3mEZdPZAw8oF5AQP8CMTZcke5YR/MUBenj1c0X/x2n/7dAW3agMNkRLLtCkSeASoCfiOSBW+KymotHLJ9wZIBDTHErhTicGT7TY8sb0U3sa/5ug1h9onBq7D7EjZZIXr9phJ6Hq89zui9ZZVuf60X/Oea4t91f+2qvdUqDKd4DnphuUiwK58Brlc+VaiVvYQGytv16hkI4q8IHheZkj8ymXkr3gj7vM1ZyqX3DxAmtnNj3sdUYQ+vPb9oKCADOiK+15rDUqAiNFOKkEflHihZxJUucDuBh5FNggA7a1q4Q09k/BVaXmXlISv/77qghv88WDQMrEdq8C7g/Dy/MHVQs/e9aUwp5V1BjdI4Bpw/MZn3HSvD4C+qWl8B35bFqBpmrwVKfe4G+afHAUABfJjWZzQuwbXu+G1vp0+C/ysFiAjAYfDsXbt2ri4uM6dO+/atUuZX/EGy5RGfg0Y8fNlT0mRDDlqampefvnlXr16URQVERERFhYWFBREUVRISEh4ePiQIUOOHDlSX19vt9tZljWbzb9YPn8+C/hi/m1ZQGmxyliO9CAFfSb0Cu9u5T1/6Wuxv63q/l/LLVk1z7Ks3W7fvXv3ww8/TFFUYEhgRER41+joQIoKCwp8VT0cKppdBzMvTl3pPJSDWKcE4GDAxYGLazibd/DvM4o+WeM+UwYmN8gra/UgGUFyshzYOTAxGZv3Zy7dKmVWw+Wmoq8PNqdnQ50Rl0Xr7flLtxUt3gZXzOg4z43QMwrF8oJNbxSazaeXbkqfu8qaXQpmmqw5xaW7NWbbisOnR0w5+8Yc894LeAgART8YBK9dINAiDwI0ncotSP06d0ramfcXQmE9ugc0uPI37iv8ZKVj1dETny0zZhQhAi4C2F1gtFds3F80b0Nz2p7MT5ZA/hUwujiecYgMevyjGXDS0GSpW7C18J2FcLoMdDTn5i0cjSu7682WozkHP5h3acVOuGLE1b52GswsGPi6TUfzpq1ybkg//I+Z2iPn3Aazg7YzIHLIEheh0VK16puL7y3MmDDfdSwHaluBRd1lsNHQbC9buu3bj+aLeVVgZTEVBxZTqGw4PXel7XBm+bbDh+avsOeXg96KZefkJbpugFaH9XB26YfLTV/srFi9F2oNyNoubbyyfI9t7bGCmWtrNx/F5epmh8tkPXHihFqtjomM6hHZ8fWRY1d+uXTIM892ie08aNCgWbNm7d27d9y4cT179rznnnumTp1aVlZmsSAKL4oiyyLJ3Hsp1f9ax/GV9xoLkOcjeSwSfSpyArmx9OvXLzIy8q677uratesDDzywd+9eq9VKVhFd87j8b3tiesM9BJghe9pYw6S83pCNB99xtwHQ1xj61/2XFITAx0Rsg6BXKFIke/LzuGVTMCwEDxGv9Jb6/V70mZzglq9SvhW483ooGG3mXRE/EIC+5hLvSiKqEaQuSFncXqzY65NTovJuA8rO30rg+9peW+17AGhs26RoSqlvFAPeOm4kFeJ9LjnBY++2l3ICQHvIudfAvt7pCrLijcKRV6ztncD3hQkAreTzpqdjY2gr9U1PuskBFw/V9KWeyXSQWgoe4fRLbA1KKH/gdWgW8OUHlaXbP9fjzp4916y/J4UlCSoFvyZwk+x47yY91CMAQhjOHlt4+q9371OsRAJKd75xx7w+b94J/4CwD4D+AUbynfKrtAABji9fvnz27NkfjnDxPE+4ma2trXv37k1PTydItA+A/lVW8v9QpkRRJKPEdevW9Za3I0eOEGG+tqf2jX9/ARuRhAlUR/qL4BZsNltWVtakSZMGDBhA3BLGxMT4yVtwcHB4ePijjz46Z86c/Px8Hwn6F6gjXxLXWMC7t5Cm692Mvfd47/e+6poIfX99FvgVWEAZI+BYmaadaSuW3X//vWHhIZGRHULCgv0DqACK6h4Z9eFb/zCXVZuPZJ74JLV2yzHU2ZRH7yzNOJv0tqzS85+v/vbteXCiDB2guxA0YUXJBTKU7GRcNU11B85mLt7MZ1dCteHYl+tK9p6AVjvShGuNhqPZJ2evgkt1qJ4BgHM5bgFXNDtQmkO79/ShL1a6q1s4k41nWHCLiLS20pZdZwvfST3z6qyaTUd4LapkIBVAXorrBASgJYazFlZlzV2XO311/pz17pNFYGJBa2z65mTe7DX29ceK528s++YY26KnnehkD4x01Yb95yZ/2bhyb9aMFYg+2zhLc4tTQAY0os9mBspNVbM3ZL07H9IvgUVErjEnAM1Bg5G9WLnz3Vml6/a5yxoA1QUYxmoHA2vfl9mYugt25dR+sVn71X5XhVbgWTmHqNQJFtq641TOO/NrZ21o2ngY9TpYTnS6oNUMTa66lXvOfbSQ/TZfVrWWLe5gxGJtYdo249ZvW3edPLZiQ0txudtgBppxOBzkPRYsHORoSz5bW//BqvrPNsLlBvToeLmhYvmuxnnbL01KK1m9B2r0WINOzwro1tbWpQsWPTnwgZ7BkQ8OvPeTiZPee++9e+65p1u3bmPGjNmwYcP8+fOffPLJ/v37//Wvf12/fn1TUxMxOJlCVm50pD15DnmPb5WzfYH/agt4T9ASjrzicpDjuH379g0aNCgiImLgwIH9+vXr37//6tWrtVrtDTHo/0I7kR6h3HSlqxbLkvISZ3ftEA+5RD72XcDNTYylJPUfCShl8fCd2zLZfpdoNwjeQhT+8g/MLYG0FHEPj6y2DL0pjMu2NL1+r8GdvY780KCCm0sICSoIO95RFVLzdXH9wEL92k67rhzfv4MUgdQmos+I+cpqxbL6NrEYYcJiXDd/TJB4bpYeiZ98u2UStEfWxvsCpToIItw23/MdiXpffU24rVwEB8Yy/Sybk4c9OUUxCRCg4alEl39SU1C8M3EuGGWVaS/0WbGA8vz1DlyVN6/biKfsVx2+8R/vpug5g9hTbuaePXLMJF2SH++4vGPwDnufc1X45o3hqtNu9McHQN/IKr59vwUL/FPQc9KkSSEhIRRF9ezZs6Gh4TtyTSarlfeqHTt2REZGhoaGRkREpKWlkQtveiP4jnh9h3wW+IksQJjOixcvjo6O7tmzZ3p6OspNOhwMI3sokulL3k1UCf9E6X9/NN6TNKy8oa4ly1ZXV0+cOJH4q/Hz8+vWrRsqkFJUaGgo0ej48MMPS0pKXC7XzdK4nkpDOuzNzvft91ngey2gdBBlgE32eFOeb3YO2f+9SfhO8FngF7cADgo4Hh8K2obaRYvnx/XuHhEe7OdPde/VNRAXogTc07//2i8W8toWrqj22KepOYs2QJ0ZBGCNVgReGYEtb7i4cOPRCXPhVBno3OCUHGa74JYEtwQ88pFBb689nnFs+mL3qUtQ3npu2caLOw9CswnZwU1209Hs49OXuQtrhTo9SzOMhPobeKFLALPQtO1E+qdL7LkVXKvZ7nTYWFp0MqB3iaeKsz9akvX2AuOG42BiWYfLxLksiDuLBPUGThArmrLnb8idujJn2qqm3aehyQFmrvXAuawpS2HvxaLPV1sPnQcDQt4s4xCMJuuxiwUzV+u+Opw1c6U1PQdsbqBZB213iKi/gVzvVkb/5e698f9oXXcIWmlw8ZyTBicHbuDyqg9NW5yVugkqdeDinTa73mLmTDYpu+ripGWwM7t86lrD+iNQ2gQMCoXyOHqVBUxyKi++t7Dg3YW2naeh2Q6cm3baWb0J6k2u3eeKZ62lj+dCnd7N0DRHg4sBK3dh5orKBZvpXedOz16hu1TGWK0CyzAuZ6vJgErcJpfzfPGpCfMrJq8ueXsxnKwCHQdGoXrprvyPl+W9m1qTugMzaZVLxIuM3QEMDy4ejK7DKzcNffSpiPDwqNiOI0eP2rlz54QJE7p17vK7227/7KNJZ44cn/LBx3fdOaB3XJ833ngjNzfXZrPZnQ53m7orISG2D8t/xGDyF+8IvgR/Ggsoz0dFn4rneY5Dl6Esy7a2tmZmZj788MNhYWF/+ctf7r///p49e6ampioYtPJUJfEoj9SfJnP/8VhIj1CQGBmAJqiZhyX6/9n7DrgorrX9hQ1LCTUWvGL0atSrV70a9Wqif1tuTPlSzI0a/ZJobmLMZzTFFmtsiCJiQbEBgjQFxQJoUCxIL1KkI7v0XpbtO21n5/3n7NHJCOo1iUnU7Pz2B2dnTn3m7Mw5z3nP85poOkxo3pe0/Tmt4Iv6QwI8OXuX4IaJ/+38lLgjAP0AC8quTehkAf0TkiaCDF+9H1o4N+HVrvnf7wxKhW+l4H6xOK877Pb90j4d54W4dQ3jNmI68p4ENG1i7W/3AQGbj1AVHDgfwYm7gjz9isxy7xDQuP/8FA9nYcr29jj8EVhA/5YENNqJBfXrgxp7zTOKZhGid9Wi92usZsDiIFAgZ4dIeJxDKhycEbl74D8chwy8hZ+fQBB0V3TyTte9K8K9vpg8pqISf/q1CvAU3h2MLa6MMCccp+tfYZy7wr9izGAmoO9C0vzlCUJg7969EolEJBJZmo5169Y9gLTClzDHV1RUhBOKTb56Bg0a9AS12lzVpwkBvCUWW53QNB0YGNinTx8bGxsvL6/29na8Z5bXirn9Mv5D28/LpuPKCLm8mzdvLl26tG/fvlZWVv3793d0dLSzs7O1tcW/UFdXV3d3d7xZAdt8aTQmEzaTGA6vitDVLvVxaPUfCrm58EeAAO5FD//3ERRpzsKMwKNGgCRJhULeLm8lCU1dfdXSNUvtnK2txaJnRKK/vtAXLfqJRSNHDos8GgBtaihtzN4demNXCJQ0sk0KRCurGWgjoYEsPnL2wlIv/aWb0KAFFUPrKIoxoM20YNIj7qCI7FtXd/kT6cXQoGkNu1TsH0XUNiGj3SY15FUk7DnampJL1bfRGr2OY9TAyLVIhxoM0BqfleR+WHM5F1HVjJEB0FMktKohq6JoY0D2ch/ZwdNQ0gAqQkeRCmDagNEDaBkKqSpXthZ4BMk2BGav8pX5R0OrFjpIyJUV7wplTyQw4VcrD52Em1KktqwjQa2jiitydgYoj1/O8PJrvpQCTQrQkqxeT1EEDayirRWaFFURF4/PXVp9MApkLSBXkySJtxlxZQ1p3kGFh06xORWgotGLGIxahUpdUHF9rU/HgVjZluC6IzFIaVprAJqmdTo0hW3TsVfyzs1fnbV0V0twHCutBz1pIAk0P9SxjT+kxH3joYhNBR1BGBEPzml0UNlcERJbszOcOXa1+vCZjmvZoKU4mmIZijFQJiVZgAbipkdg2dbgrO/20+ezoY6ENk4VmSjbEHhrjV+t7xm4WQdaI6dHqqkITwMQ5fX6tBJ9SvHZnYeunT2/be+uoRPGWkisRo4c6b1n99aNm9/656R/uLgt+Ne7iZHRQX4Bb733bs9erlOmTDl8+HBtU4MWOCX6MBpgadOU+HZXfeiJ7u345n9PBQJCDhrT0FiLA5/XarUJCQmTJk3q16/f5MmT+/fv7+rqum7dOo1Gg60KsJgVL2nV9T37BIMkpFcEv46f+B0TocnztkKK54lrNW+D/BMRzBsIP0RjupJW9zuD8//1WN0v/3ue51uAS/+pjXcuPDjVnVh/mv+4t5vsZ3lkbjdeSED/UjzwU+IuApTPljeCFmYu+PUJT//xYQr5zah6f0ul7XsGyw/0ohly0Yym7h/BwXRQdFHeMDWbBZYFE/UMDBjZnz54kRv/FT55HrqRne/U/RPyMTsF7p9CcEVYN2FYEOVhgmYC+mFQMsd57BCoq6uztra2sLDAVLJIJPr4448fUEtMQGP6bNasWXwqien4nV09PKCe5kt/KgRomuZXTQICAnr16mVlZbVu3bra2lrMPnclZP9YfPjaCquBfYEyDKPVajMzMzds2NCrVy+JRIJdqFtYWNja2lpaWkokkhdeeGHRokXh4eFSqVSPmILb8usMw/Ac9D2nMcLizGEzAj8XgftNibuex2d+bv7m+GYEflMEsI9lvoiMzJSP5839a79ezvbWLhIrJ8kzSADaVjxu4j9vpCQhy9/S+mvf77+5JxxyKqGD5GiTgCcJUK1pDrsaMX+tNPACNOpBw5A6imAMlMkXDdemBQXL5lREb9nTGpcGtQr1pYzyQ6eM6WVAGEBN6K7n5fqG119JhxYFrdGTLKMzSXagaRbJtSbfvOzl33IpExrUyAiHYSmCBA1FJhffdD+as3Rv/kZ/5FHQAKyOJFlGCWwHsIhU7VBBk7rq2IWS7w7mfOmtiUgEaTs0qtrSCq9vPdjkH9Ny4HSe+2EorYMOLTLEJowgbSo5HCH1OZ7nFYDY5zYl6EmG0DMUgaSfaRoIQ+vVrKil7iX+UXCrCfQmEhmA0RLqfFl+0Ln8Q6e4LBnSvqCQQySEbYMiwdO/5cj5pr2nG/xiobAROSREiq4sylBtAFlH+bZjVz/f1B4UB0V1qEQD8psIpKE1JfeHrfurIy9BbRsNbD2pQEZIcp36YlbVnggi4GLFjlCky9GmA/1tApqjKVAR0KTN2xGcv9E/bc1+SCqDRrRCIA+5XOUZXuUZXumDK4nMrzXtyKIcGCPUKmojLuftCE7xDCg6n6BpVzRrlZeyUv/90RzJs7bdevZ49+13fLd5rflk0dR+f3+535AvPl0Qceqkt7f3uLFj+7r1mf3h3JNX42ooVQOjadKrTA2407Me20n+nQqa//8WCHQloPF4jGEYPOTTarUZGRlvvfWWjY3NpEmTRo4c2bNnz6+//jo3NxfZ53Ecb5rAGyUI362/RZ1/pzyF9Irg14FZG1wHIW8rPP871fCRFiNko1DGfPMfohRh2geH/xACml8zENZN2CzheRwWXjWH70JA8Fu46/xDf8HPh7skOHCe/G3oVESnrw9d0G8eUQ8gNeYM+aTRfjZn8xElmiW3mlnV6yM4LQWFyerZJMHBCz2bhGtMBDRyEGEmoH/z+2MuwIzAI0bA09NTJBJZWFjY2dnh/f4PJqD54vPz83mjaUyKSSQSMwHN42MO/J4IYGMThmEiIyMxabts2TJkhWaS3ehExf6eFfu5ZRmNRoIgsMSNSqWqqKjw9PTs3r27paVlt27dBgwYgH+kIpHIysrK1dX1zTffjImJwVbeePZiJqB/Lubm+A+PwMPQyk/JhPnhQTHHfKIQwMaGBKG7ev3ym+++IbESuYos+orEAx0cHS3Q83XK1JcL83NAq4dbzdlb/eK+8yYzyoACikA2uoghkhsU5zICZ3wjOxANbQbgQEdQWtZAcpyR4YxyHag4KG3JOxzRfDUL6hW6mJSE7/eQmUVQ14qY31u1N/eGVgRGQ7MKSIpkGT0g54HItrqVYDLKz2/eL425TrcogDLx3XoGmtR0UnHFluDMBdsK1h2GW3KQa0k9ARRjNCDRZ5JjaaUGmtQVATGVXsfzvvOt3B+FlDdogDp91o6gxtA4XUxKyub9kF+BstVqQN4BJVVlWw4r956s2ntceuwstGvAaNRTeq2BIAwkR5LQoe+4cuPq2t0p245AZQtyuojUogigjdCkLg+MSd3qh2yflcinID4M5Q3F+yLb/S6oQq4UeIdBhQLaTd4aDaaN2iQNzUR7WPzVJR5F2wOhqB5ZZ1MGoCjQkZoSRNkXR1xgG9vAYKDBoCN1xjYFlX3rlmew5vCFMu9Q7cUs0APyUkgi82fEPuspUHMlAeeufLMj8bs9ivhsaCFB2gap0psrfW9tCbrq6QcNCsS20xxoKaJVgXwktmipqLTy9QFxn29G0t56hjAyJMcqKH2rXr0v4PDQ4cNEFqK/Dh8yY9bMfZu3/3vydGdb+0mTJoUcC/4hJnbB/E+cnZ3d/vaCx8G9eRVlKobUMsiw+vaBJ/mP7VT/TjXN/x8tAsJ3H88gYwkObCSBaeiqqqoPP/zQyspqzJgx06ZNs7Oz++CDDyorKzmOoygKOyzBY9pOomqPtrZ/eG4//V5MVeEZs07n//B6/s4VEOLw8OHfuZLm4h4tAvyN/rnZCp85P61zCI2geTvox/ytpAO4UJHlOrPFbrZBMlcvmtluOzvPdTakKUB1W3njJ8eDqNm3bZ85TEBzDNL3wp8HWkDzUPOBrpjzl/7rs0gYUxjumuc9zgjviDB8j6gPOvUbWkDf01aOXyZ9UKX+BNfuCc6foN2PrIn9+vWzsrKysEATL0tLS7FYvH5ADaBXAAAgAElEQVT9+gejiqUMNm3ahM2frayssD7A0KFDH1m1zBmZEfhvCPC9FAvCaDSa06dP9+nTRyQSLVy4UC6XYyf1tz07mWYD+FX93zL+w64Lq8caWNwuhmGys7MXLFjQr18/GxubbqbDyclJJBLxf995550DBw7U1dXhHHgO+nGz+/7DkDUX/IgQEHbR+2WJ4zxMzPvlYD5vRuC3Q4BhGI1GExl5Ytqrk11cHV0d7cY59vjPixP+JrFzs7Ze+OGcRmkZ29wK0obSvaFXl3tRaaVIB8MkrdGuU1NqLRTUn/3KI2tnOFRoQI1mKFrWoAOOYTmgOFAwcKut6tiFquBYaFLpMwszPI9ARhkotIhpVZD5h0+kb/ODHBkSMqQpkjOxzxQLahZuVMV951168hJV06LsUCjUKlZDgMYIGRUlm45mf7qtYl0ApMmgVk7riJaOduQGkDLJRpMsV9XaeCYx/3u/Bu+T2e4BUN4OKsRoVwWeR2bISSUZewKVyTmg1CIzZJqG+tbC/cFN7oEtW441+J+F8gbggGVJDUtojSQyf1aThvSSuBWeJ79Yr7uWC+1qRqfTM4RWrQQlLT11OcH9kPZKHiiQ7TO+X3RFY9HRc4rDF6jAK1e+261NLgIlzXZoGJ0OMcUUDY2KluPxZz5dU7g3DNk+K0jkY1BPIfK9ovnclj2F4TG0tM4ECyK7AUB/oyxjy+EGrxOlG/waoq5CdSvITUIlFAWkKa2SajubfGWpV8amw+qL2YjvlpNMRvmNLf7pi70KPILY6la1XMFSNGLesV5pOwkpZbJ1AVVrAyoOnIZqOaMnaTR9R34g1VqNQqGIDo2YMGqM7XNODq7d33vtTX9vn2+XfNWrR88Bf+mzesm3ifFXdu30HjVmtMhK/K/XXzsTE63V628bgON6380+m5+HGJWn+6/w3ccT0DRNY1cfvB00AEil0k8//dTNzW3ChAnjx4/v1avXzJkzU1NTaZpWq9U4LY6PDQuEOT8dGGKyRtiWrmeEV/88YSGN9fDhPw8+T19LhXf557burieDkMQUZio8f/eLCW0RFiod/9ziH1V8I4AawPN8Q/8Frc+8rxO9rxHNqLd5P/65t6CYBM19CGgT9WwmoB8xAc1zK7xuaae7fD8Cmu+LneL/Rl9pmlYqlbm5uadOnZLJZLybL2Fx+CUqtI0VhrFsqzD+fw2zBpbHB5sK8l//a1pzBCECVVVVWPdZSEAfP36c9zEojMyH8RL90KFDcSqxWIyZ6FmzZvFxzAEzAr81AvwzED8kIyMjhw4damNj8/bbbxcWFgqfnJ1G8L91xX5x/vjpLUyON4yzBpYgiMzMzKVLlw4ZMgRvOHB1dXVwcBCJRLamw87ObuzYsZ6enjU1NSqVimEYkiQZhunKQf/O7whhc8xhMwJmBMwI/IEI6PX6uro6f3//Ef8YZiUWWYtFg126fTZqwr97vvCG22DvxUsb8wuhQwOV8tJ94Sf/b21DbCLV2I4cA3ImjVKKU5XVnVzlVRoW11FSDXoDMjGmOY2BQTLNKh3oOChvy/Y9WRV4HqQKY3pZ3tFT2qQ8pHdh5JjWjuaoa4U7gw2pxdBBAGNgjLSeIhGprWagsD7j+4N5u8N0FQ16rVYulxsJClkl12lrPUIKFnrmfbMLrhaAGpn90ixl4AxI10LPAAPQwdRFJeS4B9RuC6/efZLNq0Tscwdz48jJG7tCiPNZ+fvDZafjjW1yo1KJCN8GeW1QdNn2QNlGv6odwXCzBmXLGtQcqQOaIHRIIbqiLWfT4TML1jZdSDEZaxtBRxiNBk6l0V27meR+WJFTZmxFngyRN0KShSZlacj54p1h6kMX8tYdolJK6OoWA0FRYGSAQxLPKkPHqYQfPllb7HnMUFiFRDAMBlKhRMnrlQW7QioCznHVzUDTOpZEcicGCtrUpV4hjdvCyjb6t564gsyldSQQJuts2gBKHcgJTfyNou/989YcvBVyHqrb0M6nisbcPWFXvtlR6BVKJBWBErntNajRX6NCC+0k8UN20ff+sk1BmesPggz5TuRo9MZkKZpUmNjtRkXZ6csxOw4d2ub9zxGjeto7/XPEqJWrVu3bs/fDV9/+17Ax/3p5koe7+4mQsP/77PMXh4/424CB3yz5Kis9A89ohJMULK3Av3b5wB/4KzAX/VsjgO8yb7+Mh2G8yAbuJBqNZsmSJc8///zkyZMnTZo0aNCg6dOnR0ZGYq8eJEnSNBJVFx585zHPeX/rO2jO34zA74aAkCu+q9CuxHEX+vih4nfN565kj8EXtHgP+nk+zc5zFZbvGyRzdaL3213nV72zEWqMoLsPAS0wgv5JANrI3iHVTbgK225qqBDtP4B8F9bnfuGfeUN+LQHd9XVCUdQ9+Vz8NgJA/jzw640/Ixzo/Mz6/5Lo2EZvwYIF1tbWIpHIwcEhJyenU0N4ghiLk+LXp7Awfts4TshxHKZOMHvSKSbeykQQBM894VT8V2F8c/h+CPD3KOJEBE9AW1pa4t39UqmUj9A1B9zl6urqsHCHxZ3jR+VEDw+PrvHNZ8wI/EYI8L2Upulr165h2+epU6c2NDQQpkNYLj8T4FMJrz4m4a6PR1wx4fOtubl58eLFvXv3lkgkFhYWPXv2tLe3t7a2lkgkDg4OlpaWzz///MqVK2tqatRqNJGmKIp/UwhnL48zDo/J7TBXw4yAGYGnCYG2tjalUrl58+Y+ffpYW1v1dHZ4/ln72WMnvtd70MuiZ2PXe13d61ebmAFKptrnRNTcb0uCTiMnhAySV0ZazHqjrqz+pPu+q7uPsdJmljQY0ECcY0lDh1qjVmuRBbG0OS/gbNauMChqgbLWSx6+isRcqG9HyXWkulCavvUIJJWAggADYp8Zo0kcWWeEovqY5Z6ZHgFwq5VUadp1JhpUS0O1oupIdMZn7qXf+sD1EmjWAUkRRvShWST9Dwo9dDCqC5kF24PLtoVkrtoPCcXQogEdW33ueuKWQ5BQnL4z6Lq3P7SowWgAkoAOXX1YbOm2AF1QXM4GX7ghRSbelEFrJBVAtqnkyKq6oK5i94m4z76vPHwGGpWoIJWOlSuBMbZkFVxYvastOpVpViDvf4iAZqBFUxZxEWluxOSU7QzXnM+ERhWrQ6IlHRylpk2+B1NK4hduSl66E7KQ9bderwHgDBoN1MqL/E7lewdDaTPQnNFoMAJH6DSg0hWHRNduOZb5qXt78EVop5B3RMpknU2QqFwlzSYWZq73TVm8o2rPSahWgpyAdn2yX0TCBt+k9b6Ifa5XYuUQFF9DQwcFmbJbW4IqNwUlr/Zhb8jQSdM01EBQhFKNTKTbCdm5hKQ9wYb8KkOLMjMl7f3Zs56xlrg4Ok0Z9/KmxctWzf9iQM/evV26fzZr7tWomIgjga+Mm2BraTVlwsTAwEClUkkxNIumzMjGHc9x8DRN+ApG9TEfTykC+Ebzw06+lfyElzEdUql09erV9vb2w4cPnzFjhrW19fDhw6OiovCQj5fj4EXkhL2Iz9McMCNgRuCJRkBIid7VkJ9LUN4vftfzdxXzGHwxAjTSGX3ntFvPoq3mKERv6i1n1fb4sOXLA9BkBKR9dvcHPWFNEhwce9sC+qGdEArRNhPQ6N7zdIDRaCwrK1uwYIFIJJowYUJ5ebnwKu4mWCgKhymKqqmp4bsPP77hz/xGAYZhaJp+7733MGuJecglS5bwxWHbPV7SlK8YfiXz0fiA0WiUy+WFhYXnzp3z9fVdvXr1Z5999sYbb4wZM6Zv377Ozs68+Kmdnd3UqVM9PDwoisIEt5Cg4TM0B+6HAL4XADBnzhxMQOO/IpHIzc2NoqgH48lxXMSJCLFYfId8vv0/KSnpfiWaz5sReIQI8B2YNbB6vT4uLm7UqFFIu3PKlPT0dIIg8EZaPppwZY5/0j7C+vyeWWk0Go7jysrKlixZMmjQIGtra0dHR2dnZxcXF1tbWyzKYWVl1atXr9WrV6elpdXU1Gg0GjyB4R/CQmT4yvNX+TPmgBkBMwJmBJ4CBGialsvlMpls1apV3bt3F4lE3bs/5+bkNO35Qf/uP2L24FE3j57IPRBaFnQGZE3U9byEBRukHoFQ0Xi77UYACuhb9Wn7j5/d4CMvrES2zwZgDZyWNdAAarWWU5LQpC07eaXA7ywUt0FBXaJvcFbQKWhSIU5Tz7A3yrN2H4MMKdQjRQ850BqgjQYaWDBkywq8w35YtqM1MQ8MQDG0ikTmuqBimoMu3vhmd8n3R8hzaciomWKBQtSzjkMfhVqFqO28uqy1B4rX+WV856O5lAN1iC9WV9Sn7AmG9Erl6eRMnzColSNhZQBo7dDHZ0m9Q5R+sTc2+kKOFBrlQBpohpQDIqCNBAGylo7dUTf+4168MwSK65A1NIBeoUAaygXVcZt80g5HQKOKUWhQhiQDKppJLrmxyU977Er+tqC6C6mgomiNXklom1h9B0uCVs/mycq2BmYt300kFXANbYxOx7I0kn5uV3fEpCS7H9Tk3YIONWjR65tRqUFLtcamJC/dWfTtno4D0VCjAB3FkYh9ZimTHTQJkFst8wy5/oV7qU8kVCqhRQ/Vitawyzmb/C6t3aO8fhPa9KCmTEbiHLLR1gEUtZa7B5esOFDuHowitKhQ/Tk0BWNITOgTdbHJKXuCtTdlQEOHWqUCo1TTtn3/nil/f9FVJB7Qs/eKr76N8g9e9N7cMX8Z8M7YSQc2bU+Kjlv9zbIhAwcNGDBgyddfJaUkKzWmJQRTB8K8IU9H3vP9a4po/vP0IHDPu4xP8v2BNbAVFRWrV6/u1avXiBEjPvjgg549ew4cODAkJKSlpQVbodE0zW9lMxPQT0//MLfEjMAdBISU6J1zpv9diWN85q5Igi/3i9/1vCDRHx/ECl45daX95jGSuZzkQ6PVXJ3FzDKnmcZdsdCBRl9mAvoBt+nXWkDzlN+5c+d69uyJxQ1EItG4ceO6EoL4JQQAfn5+2AJu5syZFEV14lY6fX1A7f/rJZ6b4PNkGAaz5Nj2GbPDM2bM6JRVa2vr8uXLP/jgg2XLlnl7e587dy4hISE6OvrQoUPr169ftGjRrFmzpk2bNmTIkG7duvFixDzXzAcsLCzEYrGVlRUWfLCyshKJRK+88opSiYbaD5aM6FQl81d+9NOvXz8hAW1pafnee+/xPtDuCRRadTKwy5Yt62QBbWtrq1Ao+G58z7Tmk2YEHgkCeJ8EmqYyTF5e3ujRo62srF566aXr16/zyhtCly9PDQGNN52gncIGliRJqVS6bdu28ePHYyEOBwcHLIYjEonEYrG9vX3v3r0/+OCD5OTke3LQ/L3AT3X+Ic+fNwfMCJgRMCPwFCBAG5is7OxPP/3UycnJSix+7tln3WzsJz4/4IOhY/8z7OXqqB8SdhzK3R8C+TXGxPzsrYfLtvhBjdakF2xE5rGkkbpVn3/8fOyGfYqUYiA4UkcBzRF6ysQTA6uhQMPJYpMvewYQCcVQ2JB+JFJ6MRGZJyt1QDH6ssq4TT6K6BRoo4AyKoFuAVoPNJA0yNpL9588u2ADeeUmqGm92sTqGjho0zacvl6+4Wj6Fx7MDzdAi2yodSoly1CMAVlAkyylam2npQ1ZO4KqdkXmrz1EnkoFJUAb0Xyz7IdDIUxyiTo6vcjvNJdfAyoC0cdqgrlResP9kCLwQpl3sPJCCjQhUQ6OJCmGVHHoL6jptoir5cv2F3yDyGIgjaxCZVCpQalhpfWZe4Mrwi4gQ2OCQarKAEBw7ddyU9bsN55IrfQ6Xh96SVtep+xQdKhVSprQ4d5TJy8+GJm+fBd3IRuqmoFF5kza1jZgOOnFxIsb9jCZZUDTcqWc0elAR4FcVx9z/ZZXSO7yPc37oqC8Azp0yC0hc4eA1pBQ3tJ87Icrn2+65RkMt9oQPi2UJiajeJ1f9irf1rgMaDPdQSMgoUiCRXezuEHmGVby7X4kpX3xJsj1WpWaNB2IfdYjieqyGGT7TGfLDI1yvVbbolEi43UAlUJ5fvvBhaNf7efYva9r78/enb33u407l69756UpQ7q7zX797TNhEYFH/D/66KPnenQfNmK439GAqqoqkiT58baZgH4KniQP34SHIaDxLuf29nYvLy83N7cXX3zxo48+Gj58eJ8+fby9vVtaWvD01mwB/fCwm2OaEXjiEPizE9CU6e0cV1jy3Cxw/pyynE1ZztaJ3i949l2IyERvdvpuAvr2ZNVsAX27pz8yAlpICGL6taSkpBPBimm+2NhYW1tbCwsLGxsbsVi8ePFi4a+OZ4qFJ39NmN86hHPetm2bRCLBu78xXW5nZ+fj4yMsQqVSDR8+nCeRsY873EBsNMtfenBAaGkrxEcsFi9fvhzzUMJyzeEHI4AHxLW1tRKJRIjnj2F3d/f/qsr9o+LBpEmTOhHQ48aN41cCeCbrkXfCB7fLfPXPgADuVJhoTk5OHjBggEgkev75569du4aZWfy0xCKMwq7Ih59ElHCrcROEE1q0q1ijOXDgABblsLKysrOzszYdNjY2+Llqa2v79ttvx8bGtre3C5eI8KwGeyzsNDd+orF6Eu+vuc5mBMwIPHIE8D48gqYS0hLfnvmuzbPWDs/aOds/+5xINM2u98qxry+e+BrImptCLtxwPwQ5VZBYdPmLzZc+3whpt0BtMJAEksjQ06CDsuNxgYvWtV7LQRbNOgNLGoADlV7frtMSFAMU1F7LPrnWm0wtAzlbcvJS/O6jICcVzc1oXNTYFr51V9XlVGjoAK0BKIOaIpAzPJIBOdUWfuWHhZubIq5BgwaRpAQNtBFadR2R1zK+8spe4EGFXoNWPTAsRxNGIw3A6kgNxZk0KOrl2YdOtJ9OSly3vzXsMjRz0MzCzbq4Lb63TlzUXbt5fvN+IleGBKZpFpGwKSXJq3bXHYxK+H5P+8V0Y0WjUa1hKIJjDQAcpdWAhtKfTru+0CN2wUbIrQWSM1A0YoQ7CKhW3vA9nuwTAo1qoGiapZAJM2OE8pbcbQGGyGSZZ0hTSBySVEbO/DgDZ0AizgDQ3FF0OCr0w+Xyc6nQqCXrWhGkGgpUlC5PdmqrT2tWMagJLYP4bKRqoibhZl2he+D1hR45Gw5Dfi3iu5FHA4ZlGGA5RksABZVHY6M/XZ+y4SAUNoAGQM7C+dyi1Ycu/mejOjodtEYkkM0Y9R0qRm/CSgOyg6erNgZlf7EDLuRBZQenJ3QcxQFodWrQk9BB1EfGn1qyseV6NmhIvVqFVLaNLFKpZqEt6WbuRr+MdQe+fWP2kO5urhY2PSxt3nn19YvRsfPnfNjdwemvbs+vWrkyIyPD72jAwMGDRCLRO++8c+HCBdyrCYLAWzb5d6sw8Mh7vjnDxxYBPJXmR3F4wkXT9K5du0QiUZ8+fZYsWTJw4EBbW1tvb2+9Xq9Wq7EjJd4nIe45j20DzRUzI2BG4I9HQGj1/MDa/N4yFGh40OVQQN03B6WOM/WimWrLmRqLmWD3SaHDDLhSioYKt50cd0l124GikMDv0poH24x3zfIJPPNoCOiamhohISgSiSQSydGjR4WsAQYHk4CYYuCt3rAWBxZK7sRZPypIsfrH+fPnse4zXzS2R+5Uypw5c6ytrS0sLKytrcViMW7az6KeMYFyPwLayspqw4YNPO/ZqXTz1/shgAdAsbGxVlZWwv5maWmZmJiIaan7pcV0P/Z+Jrwvq1evxjcCSwTwY+sH5GO+ZEbg5yIg7FeXLl168cUXJRLJgAEDIk5EcBxH0zRPp96PUX1CF0X4hvMBo9GIDaLxA18mk23btm3MmDHOzs6Ojo48+4wXirAox5w5c86cOVNSUoK1BXnwsRwhn7MwwMcxB8wImBEwI/AEIWA0GmmabmhoiIw6NfLlsc842jh3cxrWr/9frewnOz//5eCJ4fNXstllVafjyw9FwrUCuFqUvnbflUXuyNy4Tg4ERTMm4pKC9mu5Z1d71Zy9Do0q0NJAGFiaZRiWpg2IMmZBl1uZfuhka3w2VKlLT8UnHA6HWgWywKUNuta2q8cirgaeoNo6wGAA2gA0Mhw2yNUgaykLjLn4rWdjyCVoJoDgOA0BKhL0QJzPyF2+J2exlzbgApQ2AcWavA7SRjBoCRVl0Bs4mmhrzQo7m+Dl579wdcAXawoDzzWcS2o/n55/6JQ0+HxHXGb87qM1CVlMXRuidWmWLqnO3360cc/JmzsCboVFG0zss54htEYSgFPXNyE9iqzywrWHr3y2uSUmFbSIJEcHyUGTtvRodNHRc0jfQ00ZaGQrreno0JZWyfzPyv0v1Ow7Wbg3zJBdjrwmGliTrCCLlDQ69JVnrpz+YiNqY4VJA0RHI4q5gwRp86VdAU2pN1GrkZ4zQbIMoVTTt+pzPI6WfO9fsj0EsqsQ+0wxJMvoWOT2BgGuZYtPxMV8uaXIOwxyq6CDQa4gsyrL1wf8MHvVrQNRUNWOtz2xDMORiNDnqlrrQy/JtoVWeoS2BcRBRQcoCMZA6VBKMKo10KYpPXEhdvk2TfwNkGuAoZU6FSLQDRy06+ik4vxtQeXrA3JWH6iJTrwRFTd34vTh3fv8xc5p3Ogxa9euXf39umGjRvbu3fvjOXMjwsKDgoI+nj/P2dl5xIgR69atk8lkuD5CXzjm9+zt3vUn+yckoHEfwGM5tVodEBDQp0+ffv36LVu2bOTIkT169Pjyyy8bGhrwGO+p2cn3J7vh5uaaEfgjEHhcCehObPHtKXkryP53W4XDTJ0FYp91FjMNotkFzu9DjWkMdk/OGoHaKTP+qwBwMwEtAOMeQd5jclRUlJAQxOoWhw4d6pqmvLxcJBLhyCKRCGtT7NixA90Qo1Gr1XZN8kjOcBynVqtHjBhha2vLmy1LJBJHR8fCwsJORbzwwgu4khKJBEsG80l+VkBIdArxEYvFQUFBnQo1f30YBIxG48qVK4VgYvdl2F/Zg3MoLCzEt5VfS7CwsIiPjxem4sfWwpPmsBmBX4MA36nUanVOTs6LL75oa2vr4uISGBioUCjwa0xIQGMbEz4VH/g1dfij0vKVFwZwZfCKETYJr6ysDA0NnTZtGlbhwAuEeJcMfuT26NFj+vTpvr6+tbW1Wq0Ww8X/7YrYH9Vec7lmBMwImBH4NQgYjUaFQhEYGNj3r/1Ets+IbMSOjva9xTZv2vb5qv9LJ5dvhbJG9fXsxF1+3E0plLXUbT52fd73DScugZoGI4fIR4YGBiCt/Mo6n9rzyVxVq4l9phmWYwFIAsk3g4Jhc6vz9p5oi0qGRlKbU3F1XzBVUIXYW50RNGzd5bSbZy+CXEWDQQ/I8SAioHUMlLd0BF8+O3/tjYNITxkVhOQsaGhQwuWC6i3Hrn22sT0oDipaoE0JFGXgDEZAHx2JfPc1tzWePxO1/ZuVn05943+GjPlnt76T3Aa/3OuFueOmLf7Xe3nB0dGeBzOjLxHNcqCMxmYlNKnyDkfc2hOeu/lIlk8INCiMao3WQLQDkn5G/gBbVZBWfnP9wZTFO+oDLyC3hAyLzJ9pDmRtykvZqQfCkciyhgaC1urUtE4HrcofPA+U7Y8o3HEsxydUlVkECg2pUJJI/tiIvAgSBupq3tXlXnm7w6BeiwBBHgspRLI3aJJ8Qm6ciAWSQzoVAIROj1w+1utveBy99KVHwfZgKG9DIs56tEKqAFpuIotBRRkv5/+wYFPCmr2QXYlmoO0U3FLmfOd77cP1HQEXqbI6oBh0g1jm9nao2rbKU1cqtobc+GZ3ZdB5aNKCmkD+eTka2TjrCFBSmivZp1d4FEZcgEa5pl2OnDuqFaxWBxRAfm3t1rCmTaEF6w5rz6RBnVaekh+61jNg5ZaXe73gLBL3Hzxw/jdf+oYHLf1uxUuDhv3P2Ilrlq2Ij48/fPjwW2+95ezsPH369MDAwObmZuxcvev2rF/Tz81pfxkCf6AtgnAUx4fxbjY/P79hw4a5ubnNmzfvtddec3Z2/vLLL7EvKCyzKYz/yxpuTmVGwIzA04/A40pAI48Ypg9l4o/ByKEF8g5IefXbckdEPdMi9NGLZraNWYb2Nj3o4BnnTgFBGjMBLQDjHkEsV8oaWA8PDyEniCmDjIyMrmmOHz8ukUjs7Oww0YBFMF555RX8Tu1qMd01h4c/gxds+fhr1661sLDg1RvEYvGPRPnu3bspyrTbjo8HsGjRIp4ct7CwsLS0/Fm8Mx/5fgT0e++9h50zCMo0Bx8Wgddffx3fHf7WzJo167+OyVgDGxQUhPW4+YQWFhZYjLvTEv1/ze1h62qOZ0bAZFKFF8CkUilW3rC2tt61a5dKpcLw0Kbjnnp5/Kj9Ce2TwvoLw7jhrIHVaDTY+yI2Z46Kiho5ciT+gWOlJmwKLRKJ8FujW7duPj4+UqlUrVYLTXKEluPC8BOKm/l3Y0bAjMBTjAB+GPL72YUt/fG9sGnTpr59+9o+a2fjaGdjK3GxtBogkiwf/sqtPeFQo6RzyuPc99LJ+VCryNkZUPDN7urtoXCrHok8GGmC0CGPfzXy8yu9KgJjoUZONrQBYbJ8NhXDEQbQclDYELd6r+Z4EpTr9MmlIRu8WzOKEHtLcqBm5Jez0nyC27IKkV4HGDqAvq3p0UpV+cdEf7SmeGcYjUoErUqN5CwIjsuuSFrkkfPVzsIdx5ADQI1e29FuNBqMYMQEtAHRpnRKepL75u8H9OzVw1LiLBL3sLRxFFk4iSwdRKKeIslIh17/+dc7SRcvI5MUAhG++cFn0z39Kw5FXd/sC7JmQ2sHQRMKIFsBST8DSdE55QXrDiZ/tjl/ayBUIo9/hh/tFHQkyPWK+Oy4TfuZ0jrQIwZZK1fqFQpjmyIr6FTitsONoXGp2/00OWVI7Ro4tVqpViqAZYFmqcKKxO923fIKQVQyhShhUoG8C1JVzUk+IWkHj0OjwkhQKlKvZyhkB12rKN8Tmbxkx40NhxG5LNdzeiJHiDAAACAASURBVAoohiAIFUdrWRpIlsqR5a05mLjQQx6bjqhkLQfVylL3oOvzN9XvjYJGCiiOZBklTegZykBQbJOiKS69yDvs1qZAZFItbQENyRgQ+0wjP5IsGEAVf+P0lxsqw39ga1uQ0jSL6H5KrQa5GtrJsv0RLZvDGtcHGaKzoFoLFapi/zOq+Jwcv1Oh63csnv2xvb29yFI0YtyYjRs37v/e453RE52sbKZOnRoZGXnlypUlS5ZYWFi4ubmtXr06Pz//nhz0o52yCX8Fj09YOG75w9vLr7X/IfgIoeDDeAZNUVRwcHDPnj2dnZ0/++yzGTNmODs7z5kzJzs7u+v0ik/7h7TCXKgZATMCjy8Cjz0Bjdfc0buAAdBC5MvzC56bqRTPZEzsc4vTXPjyKHTc1/jZhHwn3pn/KrgtZgJaAMY9gphFpWl6zpw5QrIVu5Zqb0e7yTodmZmZIpEI62DwxK69vT1WQcUvqk5JfvFX7HcOJ79w4QIuDlPeWF7j/X+/f88S/f39sV9B/JdPiMWgsSNBS0vLnj17Tpw4cc6cOStWrNixY0doaOilS5eys7OLioqkUmltba1UKk1OTg4KCtqyZcuHH344evToH6n2jRs34iqZmZFfcGdpmuYpPL7/RJyI4LPiRzad4GUN7IoVKzABje3uRSLRlClTcMJOjFWntHzm5oAZgV+AAO5dN2/enDJliq2tbY8ePdasWcPr4mFxGKG7cGEfFoZ/QdGPZxLcKLzrhadgcIA1sC0tLcHBwa+88oqrq6u1tTV+3kokEivTYWNjY2trO2zYsE2bNmVmZsrlyOZLrVbTpu3h+HnOT9KE6PGFPp6YmGtlRsCMwJ8HAbx4xu/hAECGrQCQn5+/cuXKF154wdbWViyy6OHs5CqxGyl57stx07OCo0DWAiklebtDOuLSIbe63S82YbHHzZ3H9GlFoCIYnQ55VFbpoaQhcbt/6qHjdEktaBjQUrSOwG8coEyzpzplyq6g5vDLUKzQn0q99L1Pc0IOkByyO1aQtZfSo9fv7riWCzojqSeajQSN6WAFS5xISvnKK3WrnyKtCAyg6VAipQiCQ9rHniFXFrkX7jimv1EGFCJ81ZoOmqUqayqycjKycjIys1IjIkJXrVo+c+YMtEtSIvlw5uyL0bHBRwKWfrnkpRfHDO7d9zmR2FFkOXbs2E8WfHb98pWEyOhkn5COs6lZu0J0qcWgQz59FJS+ldGrWJPAYnVbyYFT2V/vLlnnB2VtoDWyDEMRJFPXVnE+6aLHweoLyYhBJhhkv6xFhuEl5+Jv7gtrDr9UHfaDJqMIVDrgjAaKRuugHPIaBLK2lG3+ZbuOQ1EL6O9MI/WMrqoxJfxcypEITtoMWtMGW+xInDDWXUhNXbk3c6UPm1gM9UowAmFkKIrSqTXy1jZDmwpKGvN3hiZ+taP60DnQcKCkQAOyI+fSF2xr2RUFJY2okngSin8DNNd4NSt5+e7SDQHFu8KpzHLQsSxlWgYAMBm5A3U17+LXHnXHLkC9GmiDAVjGSCNfiKQRqttK/KPS1u/PW3eo1f8CVKmhSt167FL9vtPayKQrG31VedLmImnk4cAZk1+1F1kMcX3+35OnR4dGrFq+wtXVdeDAgUuXLr1y5UpwcPCbb77Zo0ePSZMmHTx4UCqVEgSh12MHloBnbfxL9qn88eLW8aMUrOVIkiRN03jJHA85KIpqaGi4fPnyyZMnQ0NDw00HDpw5c+batWuZmZmlpaV1dXVqtZqiKJycRwxrWeCveE8YSZJ4YV6lUmHDcyxngRPyExZcOq4kn9vvH+BHXHFxcRMmTHB1df3kk0+mTp3avXv3l156KSEhgTAduGK4tl3//v7VNpdoRsCMwF0I/AlIz7va+3O+dCKJac5oNLDoxX2tLMltpuq5ebTF7A7JrOJhn0M5C/LOhq0/p6g/S9xfpQGNR88AMHLkSCEBbWFhMX78+K6WxVhH7K233sLWx7ylsLW1tUwmw+/dR8L94Xcbb2VM0/To0aPFYrGQ+HZycsrJybnnfS4uLsZKHTY2NjzLaWtrO378+FWrVkVGRspksk4r4bja/DAFZ8u/YrG7hk5N6/T1njUxnxQiwHFcc3OznZ0d1kXBzJRIJOJFVHiLSIy8MC0ATJ061dLSUiKR8DIs7u7uOA5/p/hAp7Tmr2YEfhkCHMcxDFNVVfXaa6/hbR/Lli1ra0Oaknxn4/stP44XXuLDv6wCj2Eq3CL+adk1gGnoM2fOLFy40N7e3sXFBb8sxGIxdl2Lf8XDhg379ttvExISlEqlRqMR6lQK8+QBND9yH8POYK6SGYE/IQKYcsIcFs9kpaWlzZw508XFBQ9W7aysnxWJhto9t2LajBtHIgzldW2pedk7AxXhVyC/vu5oTOpXnpmrfHSphdCiAMZAazRAcaCgywJjsvaFt+SWUnIV4l5p420LD5IFFQVKtjA0tuxYLMhUcLUk2z2g6VwSkn7WM0AZ9QWVV/cEVpxPoisaQYsmUSyAjqWRP8CsyqQvtpVtPEqklwLJ6doUiLFVElAlL/AIyl7uU+x5zJhepiyRRYaE7D/os233tm9WfPvB/84eP/GfQ4YPduvj6tqrW7duTs4u9iYHvG5Lly5NSUy6fi0h+dr1mNNnQgMC13y19J/DRlpZWXXr2WPksOH/njx9+7wlxSGxUKOCBhUQpIbSaVnaABwyMW5QSo/GpC7fc2OFD9yoA5XRqNCyOhIYUKQVRa7ZURh1Cdk+EzTidhkANS09HZ+8/Qh9Ni3p+33a9CJQIPaZYkh5axvyoGgAprj22qYDqZsOGZJLQIGsofUUidQ8WjU3Is9f8Qtnq1uBAYIgaOBaFfK8rOzdazbN/PtL8/qPi/nOC2rk9WWy81fj9wUHlN4qQ8bROg7K27PXHzr/yfpb+09BhQKpSLdq609eu/y1Z92OCEivQosERo7uUCOFDSRDDR0Zxdc2HWjwiixe50enlyFVbhYYCklOs3o9KIma2OupWw5W+59DNtpIJYVFBDaaDxuhSS0NjsnbfjRr08GGsHi41Q6NVPupxLLNgR0HYn/41lObXARyPaLjWzTlPyS99bcx/Z9xdHvWeezfR+zYtj0oKGjKlCkuLi6TJ0/evHnzpUuXtm3b1qtXr759+37++eepqal40bfTb/ZpfbcKF4o6NdloNDY2NgYGBq5bt+7jjz9+7bXX+vXr16NHDwcHB2zp4uDg4Ojo2K1bt379+g0bNuzll1+ePn36+/9+/9NPP92wYUNAQEBCQoJUKlWpVASB1ofa29uvXbvm6+ubkJCgVqv5FXq+XDyYxBvm8PT2sRrbGI1GiqJycnJw/5k7d+7MmTPt7e2nTJly8eJFoxE9hfhGdR3r8s00B55oBITraE90Q/6MlTcT0Pe/63d1bJajwEgZWeSQuYODgNTaiSvK3T5K6z0LYkqhxQhqtMp4/8zMVxACv4qAxhDq9Xp7e3shAS0Wizdt2nQ/gENDQ3nqmQ+Ehobi+I9kHIMH99iT+I+60ps2beJ3cPPc965duziOIwiia4larVboC0skErm4uKxatYrfanS/puHz2IcMv0iOPYzxreta3INzM1/lETAajfHx8Xh7PubyRCLRkCFDMKQ8q8WPyfiEAEDTtKOjIyag8aKCnZ3dzZs3O/GA90wrzMccNiPwsxBgGKakpGT69Ol2dnYODg7z5s2rra3FvU7Y9+5HmPId8ml6bvA/VWGru4aRfyelMisra/bs2XZ2dnjzCl58wptRsFS0i4vL/Pnzk5OTsSQUnuEI9UyeSgx/Vic0RzYjYEbgsUKgEwFNUVR8fPwbb7zh4uLi6Ojo5OQkFoudn7EZ9IzD//2/N64fDjUWVkNBzcUNe2qOxUJRqyEqNfEbz6SVuxTRKdBOAGngWANo9FDe3nEysejoOUVOGaknFJQe6RQbWJozAou0NaBGVRF+sTDgDJQ2QDNZejCqPjwemjSgZZALuzZt6oHwyphE0FFqrUatRUKGiIHVM1DSnLv1aOqKXcbLeciAlwPQkYjArVdIg6KvfLb56oIteXtD9yxa/tbYlx2trfHY3sJa7Ojs0M3VxaW7k8tzDvb2NlZWFiIL0XPOjn16/2Xo34aM+ceocaPHvDZl2hvTXp0+eeoHb8/4x8Ahz1rbSCwsrUWWjpYSNyuHmeOmXjkaASoS2RSzNMUg73wgayXOZ+V8sydriTcklYIWgGQQ+9yi1GYWp2w7IjsRBxo9xdEURaC2t6jZtJKrq3exZ9LyNx5pO3kN5LfZZ4ImKLUW2T7n1ZXviTy3cCNyIahm1HKFCuldcFRNi+xcQuQ6L/pWvbKlray6IupCzNLvVkwe//KoAYOfE4ldRda9n7H/W6/nJ/+/SYOG//25vr0dXLvv3r3bWNcOUnW7z7moV79QHDyPaHQ5AZXt7efT477ZnrLOF9Kl0KzlSOSFGHl3bNVAux5KGnM2HW7wjshcucd4NR9Je7MccBxQFEeSoCThYu75T9dn7guBqlZko603APJYyCKeXWHoiEm5vnp34Rb/ttBLcKsRVBwkl0u3hrR4RuZsONyWkk+3KJAFt56FWkVuSHTkhl1x+4NG9O7/rFhiZ23zxRdf/DjM3rx584ABA7p16zZr1qyEhISEq9fefO313r17jxo1ysvLq6GhgeM4rVbb6d36NI1S8ONCSEDzrauoqDh9+vS4cePs7e0dTIetrS3eocVPaSUSibOzs4uLi4ODg62trcR08PZMYrHY1tbWycmpW7du/fv3nzBhwvz58xctWvQj6Y/nqoMHD16xYkVGRkZzc7PRaNTr9VhJGdeKYRjeFFpoDd3JLur3f+JhijwnJ2fq1KndunWbN2/eqlWrnJycBg0aFBsbayagf/87gku8izv7LSpxh7g0mhYsTathv0Ux5jx/YwTu3MffuJgnMnusAX1765ORo4FDwyraiIZVTRQ0sJBVD5V6IAEt8yPNM6zV8UQ29vep9CMgoIuKirBUBc9Bi0Siy5eRiFunA78d9Xo9Jg54j3AikWjdunWYOODf8Z3S/rKvWq1WJpNJJBKs/owHB9bW1pMmTcI735FBgaFzR2loaODdJGIFUisrq6SkJH7bFE3TwtEArhumPHBYuKOK37SFL+ER2y9rzqNK9WCQ8YYv3Bx+fPmzisZc0sMneXhMdu/ejW8iXkiwsrL64osvcEG4UL7Cndook8nw4A9TVxYWFq6urrzRvTDVgyvTKdsHtJHP8wFxzJeebgQ4jlMqlTNnzsTrJfPmzauvr8frWJ1+X0L6le85nQJPDVa4XcImdw3jiR9BEKyBpSjq+vXrq1atGjRoED/B45XcxWKxi4tL9+7dZ86ceejQoZqaGoqihBnyxT01AJobYkbAjMATjYCQgGYZ5tL5C+NGj0HidRJrayuJtaXYQiQa22fgytdnZfiGatOLmBu3UnYGaGLToKCRPptWvT00bZm3NDgGWnWg0hvVGobQg96gOnE9Z/WB1vgs0CDj5XagdJTJ6tDAAsFCK0Vczis7cgZyaqBKmbg/tOx4HNSqoEOP3RJmB58ribgIjUokoAEcybFg4EDDQk5l7tajCd96dpxLhkY1mnTpCMRgVrdJg6LTNx6I+WyD3wdfvfKXgYMdu7tK7F4eO3bivya/Neff36z41nuPd3BY0LHQwICjh31993ru2Lp588Zvv/36m68WL/xswaz3Z874n7enTpz00pix/5o89Z+jRo/5x6jJ419+e/rr777+5qihw6xFlr0cXUb0feG1KdN8/Q9fTU9ubm6mmuXypJt5O4IzF3tBdA7UoQojotwI2szii+t339wbCrIWVq9FYsmUHrQkm1ZUuitYe/Ri3Z5I+clryJ7agGyfCQOJbIcpgCp545HYa4u2yaOSoKodkbkIBIbjuMrErBPrvRIOhh3esP39ObP7jBgiec5RZCW2Fll2l9j1snYQi0TPWFqKrMQO3V0sn7Vx6O4ycOiQk+HHudr2Sr/oS/M3NGw/Dtn1iOOmOSiqi/nOK3zhOuWlbKhXsh0avEiAPBq1UVDUWOcbJVvvl/n1TnVMMtS0AEVQtI6jCWTgTEDrmetX5q0vWHdQmV6I7o4WCWJwGh2yfVYYIKfqyirvzA0HyvdFQHETcoVUUFfpdbxx2/Gc1QdUcVlGucbkoRGgXt5yOSv3yCndlTxVYr730rUL5nzUx7WXra1tnz59Vq9e7efnN2/ePLe/9B4yeLCHu3vMuei9e/cOGTKkf//+CxYsiImJkcvlwiEKb9z6RP8whZXH3C7+qeL9voWFhd7e3hMmTHB2dh48ePC77767cOHCpUuXfvzxx8OGDbOxsbG2tra0tLSxsVmwYEFFRUVLS0tpaWlCQsLJkyf37t27bt06rI88ceLEwYMHIw3uOweeomLLJ7y5UywW29vb9+3bd/78+Tt27PD394+JiUlPT6+qqlKpVFhhkmef8cTktsyOsA2/exhPjYuKiubOndu7d+/Zs2evWbPG1dW1f//+hw4damlp6To2w73od6/pn6hAXj2gU+CRQYCJS5NeEWvioE2Pz0eWvTmj3wkB7o4SlPn+dUFcSEBzHGcAzoBkoI1AsiiuzuTbGQD5nzAfD4fAIyCgT58+LRaLhU4IbWxsmpubu1aAf0euWrWKpxExLThmzJhHS0BjspvjuNmzZ4vvHNiGztraOjc3l68efh3yX3/UakhMTMRkuoODA2aOevfuLXzTPzwLKcz28QnjZWoMEUVRPxqJ47rxq/3YZJiXqRWOMh+m7fzYCNt4CpfrMeOPweQBefjxx6effop7Dj9E8/f3x6Xg+yisKp8/AERHR+OE/NLCK6+88vD2AjwyeDDKJ8QybRRFKRSK2tpaXAdecYWvjLAm5vCfB4G6urrZs2fjScXrr79eWFio1+t53c9OjxS+t9wv8DThdr823u88AFKczMjI2Lx5c48ePfgFRRvTcWcSJ7KxsXn11Vf9/f3r6uo0Gg3eA4W9Jz3Mg+tpQtjcFjMCZgQeTwT48QPHcSqVao+X9+jBf3exsnV9rvszIgsbkYWdSPSS26DD36y/utOPSy2B3NqEDfuaTl1FhjbpsrxNRxIXIrVldX45skQGDvmdYzlFWkGldwTE5kELARSjArYdaMLIoDkSYqNJ7YWs/J2hSCu5Rlt26HRF+EVo1SIemQVoUJb4nYnf5EvXtqIXE4ACOx5kAArb5J4RFz9cnbstABnwshwYSNBpoU1bcyz64oL10QvWL31lxl9tHbtL7D6ZPTciLDw7K6tN3t6mkrfJW9VqJUHoKIrQU3odqcOfxuafDqngkN05KqSytpbWrPSM5cuX/6WPm8jSQiQS9ezXZ/iYF1evXh0dcaout7gsJkEafB6K6lkd2aIxcdDVzRl7jmXuCABZE5KYQLLOBiAMkF9Z4XO8be9J2frDUp/jbE0jMig2aTiyBpPhcCuhuZyb7R5YFxwPDVokgkHoNRxrJKgrkecWvPn+q0NHj+rzgr1YgkxSbEx/JVZIydrG9lmx5FmxxPYZiY3YSvKMlZ2VdTcn57/2cntr2vT/GT/5raFj3+47YufcLxP9IipLy5ur62J2Hg78akPt9WyuVQUaktUQlFZvUGpBD1Aur9oZrt53rmCVT/uJeK6uGcCgNSIXioROhSyd425kfeWZ9KU7l3ATSXuzFGGkGOTm0QgcGDNvZWw6eHmFV3nAWWhWg4KGan3LvnPZn27LXLSDSS4BAkgNah1UtupTirN8wvTns6CwvcgnovDkxbaSipOh4dOmTevm4vK3gYNef/ON8BPHA4/4j/vHi3/p3vPf784ICwuLj4//5JNP3Nzchg0b5u3tLZPJhFqLvCrj4/m7+7m1EpqwqdVqHx+fF1980draesCAAdu3b79w4YKHh8d77703dOhQJycna2vradOmzZs375133vH19W1sbOSLYw0sTSORca1Wq9FolEplbW1tYWFhUlJSdHT0nj17vvjii/Hjx/fo0QNPVbG5NPZVg71f4I1fPXr0GDp06Pjx46dPn75y5crY2NjGxkbUgU0HNnUSPlvwaIqvxm8dwMXxk6DS0tJFixaJRKJx48Z9+eWXw4YN69ev36FDh/CkCVdGOAb+rav3J88f2yYzJpV7xqRI9GvtlHnSWRgwW0A/0f0ME9C0qX9weBH2iW7Po6w8v3iDM2XRAMLIsaa9Zfw1M3H/cyD/tQQ0x3E7duywsrISEtBDhw7l/VR0qgx+RV2+fFlo/ow56PLycswkdkryy77iF9v169exZPAdCloskUg2bdokHFh0zT8sLAxXCYsFi8XiN998sxMz0jXVE3eGH7jcr+a/chu7sA/wDjQoitLr0bZQXGhX8/P7VQaff/HFF4WuIEUiUV1dHW95IRzNdOKbvLy8+C38mK7auHFjpzgPLpofXWELcQDIysr6cRg6duxYBwcHOzs7zIm/9NJLwcHBD87KfPXPgEB7e/sHH3yAH3QvvPBCfn4+Xn2538+q0xOm69enCbSurXvwGb7tGo2mvr5+2bJlffv25fc04GVCXhS+W7duf//738PCwqRSqXB6/LN+73yJ5oAZATMCZgQeFQJarZYf/9TW1q5du/avbs+LRaJe9s4OEhsnGztXif2bw8cdX+OZ7HUUMqWQWpa45UBHTArUqKFSlbfFL+s7n5LtxyCnArSERq9G0sB6kiqvTdobyF7Mg5I2tCfUxCCrwIhc9ZEMGIDKLI9fsweSpSBVNkVcS90eAHVIYQPJVsg1BWfis3eHQk4VaCjCyKg4Guk+62koa65e51/wH4+C9b5Q3gwGTq/XUKQWlFriWnbuxgNxC78Pmv/tXyyt7e1sPvvPp9UVlRqNBltBMgxDknqaIY1GA4cmaiaeFNGfdzz7mTA1MSMcCz998GwOb1IsKSuNPBM1+uXxzq49RM9YiMQWYrF48AsDV367rKagFOrk0KrREUgcmW5XpRyLilrpwd4oB4UGWCPo9dChhsqWy6u92g6ckW30a9h1HG41s3qtBiiKoZEHRcoISlpxNTd2lXdlWDw0Uxi9JkJbVlPt8d06V5G1g0jkZCF5RiSys7ZxdHR81tHhhSGDBw8ZghUYrK0Q+/ysWOJkY9fdwambnYOzxNbFytZJbO1oKXlObNNTbNtDJP6bS6++f3H7ay+3VwaN9F22oTKnsKW2XitXkioN0rPWs1DV3njiStlG/0r3Y4rweCirBVJLAKUDA+KXWSOZVpC+ZFv+sl2Qdgvq5UBSJEtpAHHQaIG2QJa13f/s5+sLfE8wuVIkqKKgdYGX8z/fkb9kNxeTDS1aoJAnQ+CATi1NXLff+EMu5DYmrNkrC7kANe2gZ+kOdXlJ6ervVnVzcbGVWL84ctTW9RtPH4+cN/dD1+49+vTps2HDhrS0tO3bt7/88su9e/eeNGnS+fPnGxoasLVKV2ueR/Wr+T3zwUMRPEmkTEdubu77/34fK2Z8/fXX4eHhS5YsGTFihJOTk0QiGTJkyKpVq/Lz87VaLXbSSFHU/YZ5eJKLbYBw5hRFEQShUqmam5uzsrKCg4OXLFkyefLk3r17Ozo62tnZ4S28eP6C59oWFhY2NjYODg6DBg3auHFjVVUVfqTgv9jJIT+g+t2gwyXyBDQAVFZWrlq1yt7efuLEiRs2bBg5cqSLiwt2gsJXjw/8bvX8cxXEs8MmahgT0Ggnholj/FV0GZ+zMHDHghaBfNdj/s+F+hPZWsw+s6bOYbjtN+FX9ZAnEoWHrTS2SsSk08OmMce7G4FfRUBj9nDu3LlC9tnS0nLZsmVdyU3ehhRXYNKkSZgH5G3ZvL29H+0GIqPROHr0aAsLNGDljwkTJvAGv3dD8dO3NWvW8Aa2mD/asWMHP27A78ufYj+xIY1Gs3379jfffLNv375OTk5vvfXWmTNnsO0zHvo/YAj14Ebze9ZwbiEhIe+999748eN79+5taWnp5ua2ePHixMRE3hr0wbnxVxmGsbOzs7S0xH1GLBa7ubnh+8JTz8LbxCcEgE8++QRbtWP5F4lEkpGR8QsIKTwqvXjx4uuvv47VqLE/NF5VBvfqvXv34poI62AO/3kQUCqVa9as6dGjh6Wl5ahRo3Jycu6pvMEPvh8m8DSh9zDtFcbh246F+1kDW15e7unpOXr0aJEIGT7j3x0Wg8IPbZFINGXKFHd397KyMpVKhXMQ5ikM8/mbA2YEzAiYEfjFCPDk6T1zwJ64MAddXl6+du1abOWAN+PbiK2ek9jNf/WddP+T+b6RcLUYkspu7gsriooDaSPI2qr8zt74xrtowxEuqxx5/6NpQqcBgqLKaxO8/dsvpkMrAVqG0RIGo5EGjgAjbWCoNiWVI8vaF95xKQsKm4nIZOn+U0SuDNQmKWc9XZmYddEnUJFSiDz1KfQcSZu867CQU9G4Lyr9860Faw9AQTWo9cCQFKnV1TU0XU1J+84r87udJUGnNn6y8C+OTq+9+q/SomK8yCoYWRk5DlnacRxr4AyMkTZwBgNnwHQzTz0bjEb8YVgWf2gDQxuQ/AVrYAmCuHblyuJFX/bv169bt27vz5718uRJA4cNffe9Gc23Km9bcCv1sjPXzn6/uyk5B+QKQHoWgOQpiiqqjp2R7Q2t2h1a7XsCihpArutob+YA5Fo1o9JCGwkZsvRtAZVhF6FeDe060Btk0kp3752jxo17zsax97PPOYisez7rMnXipDmzZm/cuDHi1Mmy8vLMG1kHDx7cvn37fh+fA3vR54jvwcAj/kcPHvbbdyDQ99D2DZu/X75q6eeL/m/uvP/MmP36uIk9rO3tRJaOIqt+jt37P+c6dsjwue++v/qbZSf8g3LiErLCoq94HEpcs6d4fzhUNYNWw1AaLashgaZVcsi7Vboz8OoSd0i/BU0dQNFAIoFrkqWApKCwvnxHyJUvt6ZvPaIvkKHWNykN1wtufeVzodADngAAIABJREFU6/92t4VehnYaaECEu5bUFVbmegbV7ToJCTKZb1Ta4QhtZQNHM1qVmu3QAAONdfXno2OmjBnvIBI72dhN/9erEceP79q1a9y4cX369Hn11VeDgoJOnz69ZMkSNze3wYMHr1mzpqioSKlU4vuOX6z37P9P0EmNxrQ8Y2DPnTs3ceJEW1vbcePGzZ8/f8aMGa6urg4ODiNGjFi8ePG5c+cqKyvxLqtOjgExFXtPhqITRFhnjKZpPHXSarUKhaKysjI1NTU4ONjDw2PBggWvvPIKL9mBndnY2Nj06tXLwcFh4MCBe/fulcvlmP7Gs29+ePO7Yc6XiBvOcZxer/9RLnzjxo3PP//8/2fvO+CqOLb/LxDggtSgaASxm0Q0MSYv9Z8X9Zn2S4w+sT3U+CzJ08QklkRNsUYsUdGAmoBiFLFgidjAiIgFRFBAqVKlSr/9bru7e/6ZPbBeAQlGTTRhP3wus7uzU87Mzs58z5nv6dWr14wZM958801nZ+dJkyYVFhZiweSn/rBy/o0yMmdUEAgijN5YWSBEtawEFt8raaCFNcErzTNtw6DvlXzvdzrmrSZ1FRrInhxO7iRtTdmkCdrGriYiubMLdwVAE+YyQejXrx8u+BEZVCgUBw4cMLc7wxKhS0AZmA4MDJTplTHw8ssvI14pT17lwB3VSd6CtGHDBltbW3RJLAPQKSkpiAzi9KLZlH19fRFPRAs7hUJx+vRpc2Tz9xWs2bzu90XE/ZvmMnfuXFz52NjYKJVKBwcHW8lvzPTp0+XIsoZHhnfxfZMjtBCgabqoqGj8+PEyMotKe2RrQWV+cHAwWkm3Up45OTlyarhJbezYsUajUZ7uYDryoGBe2ueffx57Kabg5uZmNBpbzrfZu0ePHn3rrbcwKdmhpaxKkYGwzp07/8V2I7bQ1m23mkrgk08+cXBwsLa27tOnz8GDB+We2ehVatRXWz5tmsvDe6Xlmja9K+u05C+IVqvVaDSlpaWhoaHPPvssrs1sbW1xy4uMRCuVStR4xcXFoT9YcwoUbA7UtD28wmwreZsE2iTwgEigZQAaC0lRVGpq6ogRIzw9PTt06IDzB4VC4WRr9/UHMzN/jj7x7SbmSCJcKktY+kPxnhNQUAnXSpP9d2Su+Cl1XkDl9khggNZpGb2OIArl6vTth/LDjhNfgkZi+8yAoOdZBgSO4/S16qorOSdWBZXsjYZySn3i0vkFARCXS5zdGVhgxOsJqRGrN1efv0KIOIycUEsgSHIUVJV+v+/UfxZkL9kCiflgAkGr4Sg96PXlMedPLFh56uMllTuO1F2+8rhXl07t3SKPHeFoBgSCOpn5f0d5yDZyN1upNaZVBIDmOELWrNUX5+YvX7K0d4+eT/T3njJzxju+oy3bKb/3X8/XaAHgQsj+o1/7V0QlEEJGnqUFA8lJbSjZc6xiW4Ru9y+p322BtEIw8GAk5tI6nqpVqcQaLeSpsr8PL90eBeWUWK2vq6wN37lnyGtDnBrapZtH14+mTf9p60+JFxL0er1ap0VwnNiYq1RGo5Ey1P/ROj2t07MGijQKMeIQOD1Fa3SUWltbUl6anRdz4Ejwmg3jfEZ39ezSzsLa5RGlh7NbF+f23Zw79HFyH/7USz9+8nXSpjDCHyKYQGQYVkcZVSKlozJzU1b+GD1ziSk2FcpqgaZZvYbgzvinZvL8d8dP90v7dov+5CXSfEYTpBWlrfop+YNVwk+xUKgClcSzZ2TFwqoL3+8kkPSFktLvD2Rs2mcqrZFEpeN4noBHNTqgeH1JZeBCv8/GT+ndrYfS3s7NzW3y5MkRERFfffVVjx49PDw8Jk6cePr06SNHjrzyyitOTk6DBw+WvcxxHCd/ppudRd/sBA9YCBePOP0g7xHDbNmypUePHkjujE4F3dzcJkyYEBERcfnyZaTUoGka62u+6dN8X6b5CsV8KoizGnmdhVyFaBZNmR00Tet0uoqKipiYmJUrV7q4uOACpGPHjn5+fsHBwU8++aSTk9PMmTMpikIiDvMZ1B8mYzlTrC8KEADKy8vXrVvn7Ozs7e09Z86cN954w9bW9s033/xVA4cDhfzgH1bUv0tGMqrYMADLALQRgCKbTu7lUT+k4z9eJGRNAmnbe5lHW1r3QwLYPTgAA4AaoJZ4PwBJi8sI+FVos2dvRu5tA1czQrmTS3cLQOv1eqVSif6gZAC6oKCgKceF/JXF4pWUlKC7BgR5bWxsLC0tKyoq5AflpsVAayqFIx1OBfR6vZeXFwKCMo68evXqltPBFPr27YswJZbKxsampoZM0R6iA4WG8wAZkUd8PzU19bnnnpPXPI0Cv+7wWrZsGdZUbrJGqFmzcsAc5eZbu3atq6urLHlbW1vEu82zs7e3j42Nbb2lcEREhLzLHk0A1q5diwB004+c3H8wfWdnZ+yl6Kv6pZdekr1QNlsdnD7KtyiKqqmp+fjjj2VNBmLo8t5/8/1xDg4ONjY2er1eloacTlvgLywBiqJYltVoNB999BF2VHd39/DwcPk1RKBT7pl3GvgLi67lquFAhOJCYcogMhrclZSUhIaGvvDCCwj6y8tFO+nA1Vrv3r1nzpx59uxZrVaLKz15+YcL5qZjSMularvbJoE2CbRJoJEEmgWgcQ6G5F0Mw5w5cwbV2E5OTmQHVTv7di5OXbp02bR8NZ1dcnJ1cPHOExCVevbrwKyfDkGZDjJv1O45Vei3I2th0FX/UDGrGAS+WlcHRhqqdDW7ovM374cqI+gpQRCMIKhBrAWOAeCMtDa7KDpge8GBGCij1Ccvn/ffbrqQDRRAHQ1qBnIrY9Zvu7LzCGh4E8XUIwgsgEbQHLuYOtv/wofL6cgkqDQAywsUZdKomezC1FVbDk+al7lptyk9P/bIESdHu75PPG5iaY5mtOr6vSaNxHKnp2gcTUZ7Ew8cz+qMIEBdZfVPW0OefKpfd+8nxs+YZvOo038mjDdVqkt/PnNk3pqc/SfhhhZoVltXZdSrmYrKsuOnE1dsVodGnf3KX0zKBj0HlBHAxALH8oyg0kNBVebm/amrd0BWLRigpvjGt34r+z7h7eLyqEKh8Ojd64tvvjmTkFCt1uhoRiYJMQkCx/OsieN4Xv4SkUky3/yfYCLRRJYj6gGKMzD0nsMHX3rueZdHlP/5v+ERITu/mTbT27VzNwuHVzz7HNsUApSZbaJRDxnX0wPDfvnsW+3R84QV2qAHowFoIzAM6CnQ8OXh0Uf+t+jiwo2QlEu6gYqCElVBQHjMjG+vBeyDShZUlK5GBRwPNOSHHMnz3wtZtYkbdiasDzWk5AFNjM0J0M9woKNBy5ku5Z0LCE059EtVXtGhI4dfGTLI1c3Nzs7unXfe2bhx47Zt2wYNGuTq6vrqq6/uCt15/szZL7/8sn379p6enjNnzszLy6utrcW1BuKhd9r0f2J8eQnJcVxNTY2fn5+zszOuIl1cXPr27Tt58uSUlBSNRkNLhznOLk/zWpjXYRx5JoOdp4X4ckxzBfzFixcnTJjg6upqYWExefLkgoKCrKysoUOHurm5BQQEaDQaFLuc7B8sT7nMcgA5RoKCgrp27dqxY8e5c+eOGjXK0dHx1VdfvXz5slqtNrcc/4NL+/fJDonIeRA5iYtDB/w9B6CJMAUgA50IgoknrEttxwMvAaI2FoGM/7UUXK6qmLbhTLcxldM2QDVRT5jpkh/4mrQV8GGTwF0B0AzD5OTkoP0yMl0oFAovLy8Z8TT/3MpfI/m76OvrK2PWCPj6+/s3EqAcudH1lk95Ez937lw0UHV0dEQwaMiQIa0BBPV6vaenJz6C3Fu9evV6SF9CnLUglsqyrEql2rN7D7JYmAPB5mG0g05OTpZB56aNeDvho9l7bW3tO++8gwKU4VoZiTbPy9LScvjw4a0HoNeuXYv9RDY9Tk5OlkG9pqXCKgBAWVmZ7CfTysrK2tr6o48++k0AGnsLzhGDg4Nx2x3WSO63slW1UqlEbyFyBSmKak1/a1rstisPrwQ0Gs3SpUvReWmXLl1CQkJaMISRB7dWBh5esdx9yWUR4XAkr9wwZdzYXllZuXXrVl9fXy8vLwsLCxyCLC0tbaUDR4COHTtOmjTp4MGDarVar9fL+ycwwbsvZ1sKbRJok8DfWQL1Fr9mZl8ySsUwjFqtDg0NfeKJJ3BGhDMZZ2fnfv36/bQpiC+uTt4RURh2golKTl0Tei34EGSXQyXN7juf8D+/zFkbitftgbwq0BMrX6NeCzdUGT8dSl2zHdLLoZogv8T2GQSd9AsAdYWlp4P3ZOyOhHIjZJSe3bizMjYZGIBSFdQyUFBzYlVQ7r6TkF8FGpoySR4LGREqjPyJ1PjP1yfOWmvYG0vQZy2FngyZ7MKEDduipy8pXBcGGYV1eQVTJvo+Yms5ffqHZEJFM3qNZDp11z0AAWiTIMgjs8gTMLq6ujrkp21PPfuMUwc3hbXV6BEjC+OSD36+Mm3zPj63HCiemN3xJtAZ8qPPxS7/vibs+OXlPzIxl6GKyIcDkx5YSqTAxEOlPm/vL78sDoTkIqigQcV+OWdep06drS1tbKyVL772WljEzyWaujoTW8fQGo6lTCxBnEE0B6BlDBo/TPKvTCqCAZb4KxKAFYATDCJXxxpTU1Mn+ox58jGvxR/N3rZ8XfDCle8PHebt3mXUW/9XUJhjECkjZwCGhqKKjPU7oj5aUhR2DMpqOUpv5Aw8YwSa4mvVUEtxx5OOf7jo4EeLqLNXCX+IioJKw9Ufw2M+XVEWFCFklICGFiiJa0VN5R89WxJ8BM7kXt/9S+zmMLGwCtRkmkrzEgBNcWAUb8RcCp3+dcFeCc3niD17Umrytyv8+vTpY2tr6+3t/cEHH4SFhS1durR3795eHp4fTJkaFRV16NChUaNGde/evV+/fhs2bKisrMQugMrju+4O9z0BebGAk/ba2tqvv/7a3d3dysrKzs5u8ODBS5cuvXLlikqlQn/IjZTWcrvL6yZ5xtJs4E7jmyfCm3idTrdx48aXX365U6dOU6ZMyc7OTkhIeO655/r165eYmGge+Y9Xq2Pu5nLAyqrV6vDw8KeffrpLly6zZ8/+/PPP3dzchg4dGhcXh4C+7Fznvjf23ykDHEgJLbiaUMoQy1Y1oZS/94eaAZVkP0sBoUW6H1nc+0L/XVNEk+eG2hP0mWwLgrIp/hcd3q1qN+Zq57GQXAGM5GSvIVrb/zYJ3FsJ3BUAzUv0WOifV6FQIDg4YcIELGLLn1jexEdHR9va2spI5a/cHf369TOHes2/o79ZbUEQkEKLoqji4mKECO3t7ZGo18LC4sSJE412SDVKE2ce+fn5SqUSlwf4O2rUKBlSb/TIQ3EqF37fvn24UR1bSoZKmwaGDx8uk6hgO7ayLUpLS5999lmFQuHg4IAmz+g0Q85CNhzGK7a2tq2X4ZQpU7Dk8q+sOW82EXnudfLkSRkKx+66a9euRjbO5imgrlhGqD///HOFQoF9CdNBM2pEnC0tLZ2dnbt06eLs7IyVsrKyQiYTuQDmibeF/6oS4Dhu3rx5Tk5OVlZWLi4ua9euRWZA85HQfF5u/k61JvxXlVtr6tVIPrJBEF5HfidMR6fTJSQkTJo0Cb8sCoXCzs5OqVTiO4vUHA4ODq+99tqOHTtKSkpkLibzjcOtKVJbnDYJtEng7y6Bhq3NKAdEn8mvcMv6G0+0Wq2/v3+PHj3s7e3t7OxsbGwcHR0tLS37Pf5k9KGjTFHlhZD9lzbuYU+mJvvvzA45TGDl/GrqeGLmp/6GpbtvfBsKsenAiMCyYKCgzqg7duHkN/41lzOAZlm1xqDTMJLXQWJ6xgpMUWXS/sj4HQfhWjlklUX/sLM0MY0uqwatZPtcaszaGhETsIO/XgUm0Ko1BFpV66FUB5FXsj4LuPThqhs7IolNMcsTN3hqGgrrcr7fdeLDhRkrQyC9GBhT6qWLHp4dnV3aHdi3l+zYZViGqvcvfZcdQwagJcyXoBmUwLEiEWRNTc2mwI1ej3l0bOfs8/ygg8sDIldshoIaQmlNSwtphledvRS7PFD/c2zCsoCSPZGg4UCnF4DXAqcCSgAeajTqownxy4KYpFxQM/qKujO/xLzUd+CLTz7zWPtO/Z56eve+/ZUGnRpEDYAGRFpiwySAOEhYsoSMN0KZzU9ZUWj0Z5JMpAVBoATOIHImQYj55eRbL7/W08X92+mzj/y4IyM6bpLP2C49ux47f1INFDHUTiuoDjoY/cHCK2u2QUklgKA3GbSikRYooCmggTueFDd5ydHRc9Qnk6BCRSBpPVt54HTkp8vjVgTxKXlACQa1pBLQ0ZUnE+NXh0BCXu2xhPPfh0J+JV2jJnAqTwBompcMtLMrj32x5uiKTfqMQqBFoDiT1ggAtVXVYWFhr7/+upUVceTev3//VatWHTx48N3/e6dTB/eXX3557Xr/K2lpX379lbe3t7u7+4QJExISEmiaxkXZ7WbC8mf9LnvLvXqc4ziVSqXRaPz9/dF0ydHRcdWqVVlZWSzLIiN5I0j9bmZ0cvVbH7ipjxHF1NTUyZMnOzk5vfHGG9HR0QsWLLC1tV2xYkWjIt0r4bQ+nabVQdTeaDQeOnTopZde8vLymjFjxpdffunl5fXMM88cOXIE1+9/MQy6/htwK9jXejHey5gigIqFIoCVR4yfboX1kYRmwSTZQrcum2Z39tQ/Kg3WJMFlB+hPt8LhNKgRkYT/lq9g6zJqi3XfJWBOzCJlZmJY8v9a9fke42rajdEohme5jYboLDCwbS1435vjb5zBXQHQgiBs2LBBRjPRXhhpLsz91zX6HOLHCWXev39/dA0n0yOkpKTI3rrQJ6F5/Fa21JQpU9AuGw1MbG1tp0yZQjYnGslc6nYH5hsXFyejpRhYuHBho+XE7VJ4MK8jpn/s2DE0121Uu6anVlZWSqUyLS0NZ43m+99bbou0tLQePXqgKkKmpLCwsHj55ZeDg4Pj4+N37NiBvBwyKm1tbV1eXv6bcsOSvPzyy9jHEEXq378/+pK+3exWTjYoKMgcgFYoFJmZmfLdFgIURfn6+iJ7NdpUWltby0kpFIrBgweHhYVVVVUR9aFOd+TIkQkTJqxZs0Z2c99C4m23/mISWLlyJYKev24jWLJkiUyB1wZA331DN1rSyAA0rseQUgMHOrSGFgQhOTkZd6oqpcPOzs7Z2RnVSDg6WVhYDB48eN++fTJnlLyd4jeHlLuvUVsKbRJok8BDLAGEFWTIWfLvhCtx8mvi0aBBAGAE3sDQap12jf+6Ll26tG/f3t3d3dnZGZ0/v/nmm2W5BaBhi47HJazZbjyaGL0oMH3rIcgsAz1AfnXaulDK/1DyND84cgkqKV6lIQA0C1WR8cc+X6k+mWSsrdNxRp4na0gegKDPBgE0QtHxuLjNu+iEbCinogO2X9x/THejmnBZ6Bgoqrm2JeL8yi2GtAJCmizvtL2hhaSS7C+DokfNL/ffT1BmAIEipMlQWFuy9fDJGUuuLvsRMspBLzA1NQd/Dndzc+7ds2v8+XMmliZ0GcK9YfyUAWhG4BmBpwQO5a2ljBRFVVVUThg91s1S+Z9/DD6xPoSg5DV6YqNNM4TCuKDiwqofC4MORM9bmb8jAio0YGRNOg3FG1VAGYBjNarai2kx3wQYoy4Te3AeeNr07ZeLBz7Wa8Gkj7p26Dx48L+u5eZTADUmRgugEk0anqMEghrjfBg/QOaIs2zpLOPOqAzAX7yIcYhPRkJPTQwSo34+/I9efb3du+wLCK7NKfpm9hy3Tu3DD4cTG2e10Rj2y5F/f5y4YD0xhGc5I2cwAm0QKZaniAbiYs6pj5cfHP4JsVLngSgJjCyVmrv/g6+T/bZAWpFQWgWsQEhRDEz5hSvR3wRo958r/Pn06eA9+tQ8UFGVdTUUiMTZIyvxb2i5lI17Y7/9gckuIS3OIBc4UHUaQWOsKSjZuWHzxP8b0f3RjnaW1s7OzjM//WTv7j2LvlnYv39/d3f3ESNGREZGnjhxwsfHx87Orl+/fmvWrCkpKflNlrwH4WuL4DIAaDSa8PBwR+kYO3ZsVlYW7tHENaC8AjIHoxtNTu7rKQ6Y8oI0Ly9v6tSpdnZ248ePDw8Pt7a2njx5ckVFhXkZ/vgx1jx3DGMZcC/IyZMnX3vtNXd3919dEb7//vtdunTp169faGhoWVkZeul4EPpDK4V2E55DUM9EmJUJka5BcvOHtxuw25uRW5n6vYqGxM8F+oyhn2d2HJvt7HOx27iUT/3rHRHKOlRp6CYKNsy3ATfHjxqOWs2XiAOo5QzfH0nqPDq9w+iox8dCcg3oyOjxp1W5+YK2XZUk0ASARgUvtftsescxJptxnMInv/1YAkDTPCuSLTtt7fiwdJ2Gweb25cX3miEG76CRfinyogpkBkH06yaJGv6PafG7BaDnzp2LpA0yGW5kZCROzprFneUvE4pn9erVCEDL2Ognn3yCMDEiC43i316o5A7mmJycjKCqTN3VqVOn2traltFneQq+ZcuWRpjsrl27UPvdcu4P8t2TJ0/a29ubWx+jA+Xw8PDy8vKEhARLS0sXFxfZZvDX5li2bJn5lEtuiNtNDqqrq9HRH0L/CENbWloePnwYJYP4/uDBg9EUES2RraysWsOvjZm6u7sjco3qipH/HtnE5XozjSCK4pw5cyzNDltbW5qmb1cR8yQ++OAD7AxOTk4YsLS0tLa2dnBwmDBhAs5NMb65fOSweVJt4b+kBBD01Gg0a9as6d69O1razpkzp6CgQO5gd7SH4C8ppXtYKfnlwoAM7su4gIxNcxyn0WhiYmJmzZr1q8UWNg1S5djZ2dna2iIw7erq+uug5OfnFxcXp1arGYbhTTxFUQzDyC14D8vfllSbBNok8NBLQF7C3QpA8xIETMiCTTxN01qtVqvX8QBXrmVOnDbFub2bhZWlrZ1SoVB06tzZrp39/z6akZ6eDkauKvrStY37jTtjM1buqDp2AW7oQc1xGcVx60JKtx/PWPmT+sAZQpRBCQRn1NHCxWunlgQUHo2FGg3LMwaREXmTyDIajYaYSJfTFbujz6zawsamQyFdEXby0vZDfFmtUasDkwiVxuv7oi98tw1Si0AjGSzzIqEnZgDSyrIXbT05aVFecATkVoFBIG76dCwU1hQHHUr8MiB57XY2PoM4MKzVg5Fa9MXnlgrFe8Pevl6QByAKJsmQiqxl5L/f2dS4HOJ4XrbPVRt0DEmWHKWlpTNmzHCwspn69nBDZiGYgKpTcSYGKAaS8zL8dxZt+Tn3x/D04L0EfdZL1ylGoCgBwKDTaJOz4wN2FETEQg2pPq0iNsLzfacNfLTr5Df+/XS3x8cMH5WXk0+on0XOAKJO5PQcQ/P1ALT8rcFvUAOsLOLijQUR/0zSWq7Rr4zvmIA8zVHG8O07nunZZ9DTAzPjElYv+Kbbo+2TDkVCHVe4ce/xcXNzlgbDhUyoI8QhFG8UBBMIPNAmTVJG8sqtZ75Ye33vCSiqJC6iWBZKtecXBSb5BUNiLuh5MDCcSgdapvZC+umVwdV7TheFRh1dF1ybkc9U1Bq0ujqR0QFPgHstByo+ftOui1v2qZKyCHhkIooEoj4BwUQxoOezD5xM8g+N+HzVphkLZo6a4NjOwdbBvl+/fqtXrNzx0/bJkyZ5eXg+98zAVX4rTv1ycmNA4Av/eN7Dw+Ott97au3cvskLr9ZIjRABUGKO5a6MP+p/1zUVbFgCIiYnp06ePg4PD2LFjCwoKcIkhG1RhaeU+jaVtVAX5bgsB80daiNaaW2VlZZMmTbK1tR0/fnzXrl2HDBmCk89GRW1NUvcvjnmzsiwbHx8/aNAgBweHESNGzJkzx8vLa8CAAYsXL8btaAzDyAj7/SvS3acsALCihNoKIqOV+naFDkpFiCuHHWehXAAcDiWVHBnQ7j7L35cCB1AnFn7+Q2qnMTqXCXS78RVdp6ZNXknczdGSq0CTSN53k2jU63GMJarEhoOV9n+w0qeteVjKAFAgJD4zLc36nXyb99I9fSEwBmqY+gRkgLs1gYZM2/7fRwmI9dMU4nIWDx6gjK6bvy3f0YdT+LCKkResXoccPdlHJfD0vXZW2ZBr2/+7lYA8zSIvptSanLRVq/n3FHMTgYxLKhC/O1zkuxK2nINK0h8oafMcLRJqeGSHbymRuy14/fN3BUDzJt7X11dGLTGQl5dnbkdm/qE1D6MutKCgQMYrEeDz9PRUqVTmts+t/45SFGU0GkePHo0ApVKpdHR0tLCwCAwMbA3giEVCvgVzDDo+Ph7Lc49k/ocmgyhMz549FQoFYi6WlpYODg4+Pj4cxyEoLwjCunXrEJ6W6ZXHjBlzOxVCsxUYMWIECg3ZwK2srPr165eWlsYwjFarle0Lhg8fLmdhb2/fqVMnc9KVZlNGA4SqqiqlUokMzqi0mDVrlqx1uN2D+OyIESPM8GfLXr16yeVp4cHAwEAbGxssLRpOogxnzJhRVFQkP4jeSORTDMhdvdH1ttO/ngQ0Gk1gYCBqR2xtbceNG1dWViZPuM0R0rZecfet30iGt/s64AvOSYdWq83NzUU/7BYWFvguOzo6ypw5qFXq0aPHsmXLysvLNRpNvfXirfvo777wbSm0SaBNAn8FCbQIQNM88eomT99Tr16Z8P5EVzc3QgfUzl5pb0fMNWxtAjdvIoiwCNWXMtM272P2x19e+EN1WDRhk9DwUFB9cmVQ0U9HUteHXtt9HLSsUKchXgdrddzV/Mhv1mX8dIgvruSNRkogADTLMyLLAMODhmNPpCQtDoKEfMhVFwcdTvt+D5teRBgq9DTU6IznMyI+X5W+/TBUUyS+CMTrXbUerpYlLwm+MMc/2S8E8ipBTYGBmFpDOZX9ffiluf4X522g49KhQg0UB2od6HTTJ71voVCMGzOyquIGZdARWmpy3LIt3GyVAAAgAElEQVQs+n3N3QiAZjiWYhkjx+hoqlal2rZtm1e3ru2UdmsWLia8ExKSSzKqM6Z+91Pd5sPq0KhrwfuhTMWX3CBm0QxDfmmGNxrV+UUXfghLDdkP16tJBQVg67TAwg9zFw9w8pzx3n8GdnviwwmTNdUq3iTSPMeAQIvECpvjebSAbg0A3Qh3lk95CXcmnyeyqifdyKBRr1vu91g7x/97+dXBTw0c+vRzJSfjqfDTp6cuvPjFWjifSbB+mmJMhHmD1mlJI1YZzn4XfHL+mvIDMVCpAdZErgtwJSDs9OdrCPpcS4OeYWtUUKWFG/qU9WF1YTH04Yu/LN1YfSmTqdXodDqdidEAMS0npahhqVOp59duq7qcRVQRnAiCyEpGnMQSuqK2KOLM1XVhkZ+uuLJ2J6SVQJn6wJYdfXv2trGwtLe2Hecz+vjBCP+Vq4lnxXaOo4aPOHTwYPz5uJkzZ7q4uHTt2nXhwoUlJSXypAi7hPwpbxT4fR3m7p8SRVGj0YwZM8bNze3JJ5/MyspCGBRtoczNCBrl9TvKb/5Io9Tu9FQQhJSUlNdee02pVPbo0ePpp5/Oy8uT07/T1P6A+CzL6vX6tLS0YcOGubi4/POf/1y+fPmTTz7ZqVOnRYsWVVdXI+j/sGDQpFcjkFfJwuk81YzNZ/q/v++JUbA/kexLwOFQQoUYaWT8AyTcOAsWoA4yfZdn2w83KnzAcUq67buab/dCnQCEV4a87PjHcZwJK9MAlos0y0njANsCsKUFOFOV3WNSySPDbzwyotDdF9bFQJUEQLcGdDaP07jobef3QQKNAGhBJF/5Wsh8fZ62wySwHFurGEa0CCU80LxJ8lopT2buQ2nakvz9EsCZVv3uBOk94lt4T+V8DGLO6rDYLqOyOoy52Hk0LDsA9ZudgOFYGsDYmkTk1O4icLcA9AsvvIBooKWlJXHnbWeH2kv5+3e7AJaZoqjhw4ebo71KpXL//v1oLWv+bCvriGy/yPuMYOU777zTGhtb2Zb2nXfeMS+PpaUl+tN4KD6HTaXEm/ihQ4dijezs7BAdfvfdd0VRNKeJUKlUaLMsE6o8/fTTiN6atwKGG+UiCMInn3yCfNkWFhY2NjYODg49e/YsKCgwSofMRcBxnLe3t6yxcHR0HDNmDLZ1ozQbnYqiGB8fL/O0KJVKCwuLLVu2yBB5o/jmp4Ig9OnTxxyARs+HqCYxj2kerqysdHFxMdeOWFtbv/rqq5cuXTIvsOxfyPxZc4mZX28L//UkgOizvb29q6trhw4dhg4dmpmZKS+0ZPRZ7qjNvkF/PbE8IDUSRZFlWTRn/lVdmpubu3Tp0gEDBiiVSicnJ6VS2b59+w4dOuCghxc7d+68dOnSo0eP1tTUUBTV7Av+gNSurRhtEmiTwJ8mgUYYtETBgRbQHICBJ+SJWr0uOjr6X/8c9Ki9Y4/HPN0cnIh/Wmur3k95L/tuJdn2WKXRXsyK9Quq2xMbvywo9Yd9BH1Ws1Cqyd584PLioLIfDiWu+wlUBpFldEatqNFBoeqCX9Cp70Oo/BLCw8CxtGQBbRAZYgJcreNSCy6s3GqISIASuvZYQnzAzqozKYTBmRKglhABH561IifkMNQxxCRPAJ5hQU1cFOav2Bk/Y1XUwg10ZjGJbGQJO0e5lvkpJm9mQNzkJXD8MtTREiU0J1IG1qibNPE/llaKVwe9cubsaa1WbdRrJSPoewlAsyaC5hsZYqqs1mlTrqR+OntWrz69be2Udu3sjxw/LBCAmAWOhWrd9R3HytfuLVux89raHZB2nVRB5IFheGK/TH6Z0srTW8J++X4rlNbyNVpjnYY1UMAKVE7pd9Pndn/E5a2nX+71aOfp70/j9IxoIra6HE+gZ/yTAWjz7zhCyfgrA83SPtZ6lNk8gvnkkMDQEnFKSUH+/96f5KiwcFYo3n9rWOa+yFOffJvydYDhXCpoib9BljNSIkWJFGswcAXlpduPn/9yQ/6+E8S+mwcCSVcbsncdOzZvNXvmKmhNoGdMOh17oxqKNKn+YTeCjkLEpeOzV9FxmcTOXRB1JsaA6DPDQbWeTsg+tSjQeD4DaE4SmUiLvFaCHkBF3ThGVCNXvglK/G67MSmHmEtXaAuPnt3x1cpxbw7z6tj5MUfXf/TxDvRb/XPono+mfuDZsdMTffp89dVXUVFRW7duffHFFz08PAYNGrRz5061Wk1YsClKq9U+gLOjQ4cOOTo6enp6kn0J0iGjz+YN96eNOU0ylg23AwMDUbPu7e0tW0A3if7nX8BGx6VlWlrapEmTnJ2dhw4dOn/+fOwnixYtKi4upmm65QXan18TIKqk+mIQt640bL8Y39M3yXV4Qkefo/184efL9bCOFMsIhFGpAdf9Y4vPEWKQyjnBufYjdIr3uHYTiIu52Fwwcrxk7Yg2j7SMj9cxkMdCmhYqJPIlkYwxLVlWagBCkzMfG1dpP7pSOSqvky+sj4FKyfGpObjcmvAfK5i/aW63AtDE2p0GyONjvEbpHp1IWY0ush5uHLMWbvBgInwsnNwx/qbyenCrjfQ4nGTRXq/3bxiTmim0fMsg5q4Ou9hhZKnNiErncandJ8CpXII6EyIIgZcUTn9Mo98VAA0AnTt3RvIN/H3iiScaQS3mn23zMC7sBUGIiIiQLWcRJXzzzTdRdubxm5Fmk0uCIAwZMgR932GaVlZW586dQ1dgaNTW5KGbF7BIvXr1MgegHRwcMMbNj83NJ+4sdPcp3Fl+Uux58+Zh0yBAjLTFFJL6NSSH2PpLL72EFUeKjIEDB5rL3zzc8Bz5bzQaDx48KLeglZWVg4ODq6tramqqHA2zE0Vx69atyKSMtC1WVlZbtmxpjVgEQQgPD0c42NraGps4Li4OradbTsFoNNrb25sD0LNnz5YZV+RCYkBOatq0aTItDNbOx8dHrVazLKvRaFiWxe6EIL5Wq5XnqeaGEnJqjXJpO33oJGDe/811UWvWrHF3d3eRjsGDByckJHAchyoK8/VVo1Hxoav+X6DA2ChqtfrKlSvr1q0bNGiQq6sr7m+wsrJydHTs2LEj6s9cXV29vb2nTp164sSJysrKNgz6L9D6bVVok8C9l4D5ilpKXTZIEQG0lHHXrl3PD3zWXmHlamnrbmXX/dGOHdza/+vNN46ePEGmLkau9kL62SWbK7ZGXl21o3SPZPt8QwvlmuSQg4X+4XUbj5z5Yq2QnAcGykAbRJoWr1ekfR+WuXGvMZewM3MUWTSwPEFXKYFYQFMZRce/3VgXEQ/lHHUq9cLmParL2WAUTJVqgh3n1CT770zyD4UbRlxWirSEPpeoKg+cSfp0XfysdcUxxHDPVEuMgqFcqzuckP/Zxqv/XcHsjiVP6QgGyjNGwUQzrOHjmf+zc7Bxc3MePOS1E5HHVbXVIi+h2jeNoH+n1GULaASgAcBAUXv2hb87/L3HPD06d/G0d3B46tlnLqZdpgmQSkg2ru89kbY0uG79watfbWJiLoOGEnU6jbpGZIlkiCkzxeQcjz0fvFtzNQdoE9l1zosmrVFbVJ58NPrIpm3/G/4fF4WNveKRiWPGG9R6g9aAe2hwdmduAY3zAaybOb7cMgBd/5Rkb4hhAQSWI9h6SkLC4Gefd1YopgwbeXBlwKkv1winUkBjABPLM0bORNBnzkRxVXXXI88dm+1XGhoJhZUEYdfTUF4H8dknv1qnPpEIFTrQM0ytylBVDeV1xTtPFG3Yb9oTd+XbkPK9MVBpBD2j0hJnlYRWm+VAzzFJudHLNmVtjYByrQlELdlxL9bqtToTo62uLYmMT/YLub4iLH1ZCEGotQKoWePVgoSNuypOXSpPywkN2jqo/7MOCkU3pcuU90bvDt4WtGnzm6+/0atXr1deeSUoKCg6Onr27NkeHh5OTk6zZs26dOmSVkss5c0nSObzq9/ZY+76MZVKhR7Uv/zyS3Sah5TEjab0D9qsHjHoEydOeHt729raDhw4MDs727x/3rVg7mUC5tLjOC4jI2PGjBkdOnQYMmTIkiVL3n77bS8vr6lTpyYmJj74GLTIcsRrKwAUU/BT3JWeE/OcRxV18E3wHAMbTxL8ziAQfhuB7I7nCJsNCf4Jh0mClA6k5HYcV2k1Is323cIRS0AFHM2wEgBtAFFP/qSDA8hWRzw++nBPn7SFwaCWzGMlDPq2NNAagLUnMx8dVedIMOiszr7wfZsF9J/Qzq3NUtadIyIpiASAPpIT9+h7ZYphNRYjsjqMgYBYqCVK9VZZ1LY247Z491oCUguSjRbETbNEPc9KYRlrbpohtmgNMFM3FXXwLVC8Weg8Ovm1zyBVhf4wQHrZcSrb9Ol7e+WuAGiO45CjAPFEa2vrt99+23wm0UJY5okWBKFjx46ILVpYWNja2lpaWmZkZOCyX06hhWqzLItUEocOHUKsEM2xbWxsZs6c2cKDjW4RWwcTL5sAY1Ldu3eXAQjexKNPZ9TfchxnDkXhjArj5OXl7d27d9WqVV9//fWe3XtUKhXeNf/6Nsr9Hp7KuURFRcke8xBqsbGxSUxMbJQX1mLx4sXIwoGO/oYOHSoL3zyAz8pZ0DSN/B6WlpZ2dnZWVla2trb79u3DKTv+4iOFhYUYE1vZwsLC2dm5UUlud8qb+JUrV2KLYI2USmVVVZW5Efftns3JyUHTaRmD3rJlC1m8cQ27DhqelHF5rVaLKDz+KhQKLy+vRgp5lAmSgzfakom3GlJt+//QSwAb1Hy9hFUKCwtr3769m5ubjY3Niy++mJKSgteRPtg8fhsA/UB1AmzQQ4cOvf7665aWlugtwNraunv37g4ODtbW1kql0t7e3tHRcdiwYVFRUUajUa/Xoxtb8w0QD1Sl2grTJoE2CfyREmje0Ldh6r9ty9Z+jz/Zvp1TJ1tHN4W1p6W9q8J6ku+EOo2aAH8CQH5l1tYI1bZfEr8IuLZxP/Hsp+agls47dPrM8iB2z7nYWWvUJ5MIdQbLEtvnnBuXN4Tun/OtKa0QWJaWgFUBBIFglDQIgqHkRlzIvsqj8ZCvgficM+u2GVLyxCrJSNYoQIn26vJtcV8FQpkGtBSS/IKRByNoIy5cXhx0fkHAjcPnuCo18CLhBq1m4efLWTP8EyctY3afhQo9sDzL0QxHMwzF82x5afH4/4xzVNqOHjG8V9euT/Tpdejgfo2qjuVoQTBxJmKRLU8UsV2IORXPMxzL8bxEQNF8c8keCDmel8lMYs+e8e7fz9nVZe4Xn3/y2WcdOrrP+/rLWoNaT+nUNyoyj8Uk+QWz209dXxFqPHIBtLSJmIaTP61aRfg3iqoy9x7fM3+lNimb5CpRpAgao6lSfX7/0f2BW7iymshd+zs5kH1v/xk7luyb4ViEv2XzZ1NzpEzm3aDlcH1tUW8hnfDAMwwxM6wpK3/zpf/noFD8+5VBGxcsvhGTCOWk2IRWhSgZTAxl5FWa7H1RB77wi9m4XSwhjq9BR4GW5S/nHv54iWp/LLGdNxLeWYmtxZQRfvza+r0QnX154Q+l26OghgMtx3MczRPaDUO1CrQ0lGtjvgk4t2gTZJQCMdIUVITDWjo4MF4tOL94c87qsDNf+LMxaaARiHe1nNqL/qHlsZeFchUYGDCwhWcvzRv5/uNWzm4KRc8Oned88tnJqBPz5s3r2bNn165dp0+fHhUVdfjw4aFDh1pbWw8YMCA8PFzelorzcPwi/7kz571797q4uHh6ekZGRrLS8YBDz9hKuHw7e/Zsz549bWxsBg8eXFRU1Oi9w5gP4C/DMDqdbsOGDR4eHgMHDty4ceOYMWOsrKwmTJiQm5v7wHFxEOSuYXwnOgppCVkFEHgm2WNssfOYQgefS4+N5haEEQJovSARK0sYnqkFBuX73yxEHcpABaT3nZrXZWLWsK/hfBE0kAHxEmc9BaIBJCboarHg44CEx0add3j7RF9fOJUPWqnw0haf5suqBvhkW47DyJp2Y0rbjUr3Gg/bEgjiTkaim/wehNuj2T8cNM1GxeZzuf1VTOD299vuNJGAeUMIIjHO3xxf0GGcynLkDZuRZ7uNgaRa0BJuGYQrUffQJucmcvxTLxA2Z0mlxfJkW1INQFo11LGEIe02mq6bLUgDVAE9KyTXyaeu3dg819GmD4MIGbSerX9JJbXZ/a7eXQHQZWVlyJ6JoK21tfWMGTMaQS3mE4tmw4IgfPXVVwgBIMeulZUVqqCx8q2ZlFAUxXFc//79EZ1EpLJz586/6XjQXL4cx5WUlOCz8m///v0RrGwW6xQEQaYATkxM3Lhx4/vvv9+7d280nrW1tUXKCycnp7i4OACQIU7zfO95WIZInnnmmUYA9MqVK5sa/xqNRt7Enz59mnAU2hGCwl/97K1du7bZ9kLwHV11/Tpv/vjjj1FW2BMcHR1nzZqFhgMyBo21fvfdd1ExIHNAb9u2rRGC36woUMP/0UcfYUaIknfp0oWiqJb5o3EShii8jD5bWlrGx8c3FYJ51rGxseYAtIWFRUBAAE6G5GgoHLm3y9fbAn89CaCCQe7P2Hm2b9/etWtXfF+8vb3PnDkjVxxjtgHQskAenID82qIGlKbpI0eOjBgxAgdtHPocpQP1cEql0tXV1dfXNyIiorS09I8ZwB8ccbWVpE0CbRJoVgK4+bHB62DDhJ8grIKqrDIkcHNfrx6OFtaPKBSdrB08rB37OLl/MHJcaWERZ6SBAW1SdqxfUPbaXbl+oVeXboW0cqjjoY5TnUm9GrhXG36W2ETviybGrcT6l4Xi2utbI47P8qOTskHP8DxrBPLHiKzIMkx1nVBadXLz9uzDp6HcCJcKz30Xcj0yjlg90wIYeCjSJK8NPffFekjIAw1FsQxh0qBFqKJM5zLPz153aubKssPnCOjJSwhLHWOKSrk+94dLvksI+pxRCgyn4RkDTwBoliPAblVR8bhh7/Xp2DlkfcCqZcse79mjZ/duARv8a+sIiyuASKJJRhs0Teulg2IZkzTnI/76BAG9rptbEOMCydz8GeNczUj/5+BBXbt3X/Xd6uiYmOeef75n714pKSnqulqgGPXlzFi/H0o2HUxbGqwNjwWNCBRNmQgGLdI0rzcQIVzOi/12U1XMZcJ2LYKJYQkKX6O/9kvc4e+3anOKQc/eyC30efc9S4Vi8L+GEJ+HAnGByJrqWTiwwE07g1zm3wzUP2sGtXACK6EyQkpCQn+v7vYKxdvPvnhqz36hmqDPCOILWp1QWQcauuJ00vYpX5xfu7U2I1c0SrvjKRPkVZxYtOFKQBhcqyBLR4omoLCGYVNyk74PFY5eLtl0qGRHFFRxoOGAIugzAaApFlQ05FUnrAqJ+3ojxOWAhuVNvBo4vcRSDVpGF3sl8dstSQs2pi4P4ZLz4YaWGFDfoDICw6/v/gUqNLrKGtLv9SybXnRw4boVYz587/HnOts52z1i89ILL+7cuXPjxo1vvfVWhw4dXnjhheDg4MjIyPnz5/fs2dPDw2PixIkpKSkqlQpn6eZrjaYSvk9XzFFahmGmTZtmb2//7rvv6vX6prbP96kMd5ksTk0BIDIyEjfvjvz3SJ1OZ161u8zivj6OC8CKiooNGzZ4enr27t176dKlH374oaur67Bhw86ePYuWW61ZJ97XcpLEzZDnm+It42FdVJbn+Lr2E4vtfVLa+8CSA5BHkY0CrEDGUl5CdVnJBPrPIeCQBEMcjQLsT4eNZ6AKQC0Q4nuypiUAMWLQOpEjFCHZxshuPkUdfPMcRsZ2GQVXjMRXIW5ruZ2I60Djs6rY3qfadlSp85i4jiMhvpZoqsR6wvt6GNoc9DQP47gpX7ldLre/bj7wNhPLbLxt5u7f+RJKRhBBBTBnT5XjWL1iZEm7UXmjlkK+EYxkVMY9Pb8h4b+zDO9P3W8DIN+amQBgFKBYDRqAHKrm4807+4w4P28DVNH16p8m0U0SoUr9OFSpgyK+5q3FBXYj9K4TLzu9B8eyoJbHvXH1MPStKdzzs7sCoM+ePWttbW1lZSWje4GBgbdzbWw+w2gUzsnJQfoqpVKJOKaXl5dsoIqRW6g5fgz8/PyQ49jOzg7tsnfs2NHCU01v8Sb+xIkTMvSMgSFDhuAnULaZpSgqKysrOjp6586dixcv/uCDD1555RWZ1xgpJmS+CxsbG7z1wgsvIOQhe4JuWoB7dUUURYqiZPINGYN++umnZama58UwDAIrr7/+ulKptLOzc3R0rKysbNRM8qkgCMhBcfLkSTfJtQ4CN5aWlr/6MiZmFHq9jNbxJp7jOB8fH5loFQU7depUnFXIGO7Nj7pZ4XCCxXHcG2+8gWzj+Pvqq6+2jD5jGqIoBgYGyv0TA2q1umXV+rp168wBaIVCgZi1+TQIS9tsmc2K3xb8K0igEQAtCMKBAwd69uxpYWHh5OTk7e194MABuZ7o/g7t5c0xaPn1aeszsqz++IDcCpj1r+pPjuO0Wu25c+cWL17s5eVlb2+PRByOjo6urq5OTk62trZ2dnadOnV64403QkJCysrKcAfxH1/4thzbJNAmgQdBAo3QZ7QP0muII7jSzNyv/vfJM52693Xt3MOh/cuP9+/l2rHfY103LV9dnlNg0OrIYr5YXbw9stA/PH3RlpqtxyFPTaySBeATsq+s2U5vPZG26MecsGNQIaHPAkButX5v7PlFgaqoBLhBttMBx3ICAaBpkdXV1dEFpZd/2JO+9SCdWSzmVyas21EaHgPlGkLlDMCnF6uCIpNmr686Eg96YnpMi7xoZKCaoo9dyliy9dh/F+b8eFCoUNfb9+k5Y9TlK19uTpyxumxTBLF9ZjhWFAw8y0jQM0E5jTSoDfMnTn1c6fqpj29E2O7Q7T+99MLzPbt3mz37s/j482p1HWdiqqurS0tLc3NzMzIyMjMzS0pK9EbkGiTQZbMYtIxHo/WxAFBeUfHRzI/d3Dt88tlnZ8+f+7ePT4eO7suWL6d1erFKZUjMTFr2ozYk6sryLfrjCVBhILU20EAR9FkqJ2VIzLywMljzSxLZpioAAWGNFJSrVPHp+xf7qy9mkkaRNiaHh+3q1rOHV++eew4frKP1lEDgWkYgTghZUai32r4VKzFfnN8ufEunbQBEpMikgUqKri9esMDZytpFYTVn4hRNQTEwBH02iIRZhTYaiKrgdPrhSQui5n2nS0gH2iRVjYGyuoQN26/8sJdPvw5ayiSaTCxNHA8m5Sb7bVHvOnVl7c78sCjIqYRy4jqS4ziDKAHQJoCrxTUbDqV86q87ehFqKGA4SuBUjJHUUc8a4zOLloUWzNqUPDeg9lgC6hOglssMOngxcJc+NQ9EqNOojVqdobjyYsj+4n0xfHz2wWUbxvzrbVcHJzsbWycnp+nTp+NO0B49enTv3n369OnHjh07cODAe+8O8/LwHDpkyI+bNpeUlBgZWv4u/8GzI1wQ8Sa+rKzsvffec3BwWL58eW1trfkO3T+4SLd0ld86kbfn7tq1q1OnTlZWVrNnz5Yv/tbTf/59eUml0+mCg4P79Onj7e29cOHCyZMnt2/ffuDAgRERETU1NTiR/jOLa8ZaUI8NsQBlDKyKSu8wusx2pLbDpJSOown6rAJCXsQKYEILaAmANkn2w61Cle5bLRmRgMJqgEqNYKBFliPs/wyPulPCJM+zZAvFgbT4DiM0LhMqXMZdHTQbSiXuavzCmUHwt5SyFrKe/ajcflSVjU+l+8TkXhMhB0CF9rMEwSRvkGw53jD61acgCxaHzkZ3b8mmuROpSDJFtWyoezOqnH6Twjcdq28+dc9DralXa+Lco4LV90RZ5pV83ZCvtbZjaIVPgdMo2BxDME2yf6kNgL47id9pm0rxcXr526MFC6SZKgG+OXC1i+/1juOvdhoT7jUMjqbVEzrfWnak8+bMmejLKbisies2tsh2RLnz2JTnpkOhiM+2xPl+a7J3c3ZXAHRYWJiNjY3sfU6hUERGRnIcZz6ZaE0YAAYPHqxUKtE2FhHbQ4cOychvCzUURdFoNFZUVCD7sGzDO3jwYK1We0dTh1/JQH744YdGAPQrr7wSGhq6aNGiiRMnPvfcc+7u7hhBBkPlU3TiJyPyeN3Kygotdi0tLRGZaqEu9+QWEoOkpKQolUosjAxAX758Gb/3TaFbNBVPTk7u2rWrq6trZGRkCw2HRtAA8Pbbb8u1Rnz54MGDWAtzAHrEiBHIrCLLtn///qWlpUajEdFnGYNuKgHZycYTTzwhy9zCwmLs2LGtadxfH//qq69krYClpaWtrS1WFtn9zHOUJ0Pz589vBEAHBQU1Mn7E3FtTBvMs2sIPowQaAdDnzp3z8PDA7RrOzs4XL17EZQxuC2gKPT8UGzkfxnb5HWWWhzWWZdVqNQ4FtbW1uD1FFMUNGzY4Ojra29srlUobGxtPT09XV1eFQuHm5oZMU88880xYWFhJScnvyL3tkTYJtEngYZcAjiHEhheIix5cLWClkk6fmzpyrJvCqq9Tx+c6dn/eq4+rwrr3Y10O7d0HJkFkOU5PgVG88v2e8sBDuX6h11btJOizWoQyFXc1P2r+qrLA8JLVockrgvjCMkpdByYTVKjglysnP1xSsvsE3NCAkSaIJMcKJoJBE+d7GmPC1r3nlm2Ca9VQrNqx3D9jdySU6wmoSvOgZrJ2RSbOD6T3xYGWr6uuqZ+/qSi4rrkwPyDh07Xpq0MhraSBlIODa+Xxn6+Pmbyk+IcIKNIIJr5OZAyiZAtsYgj6rKdBTasvpm/83+f9FPZdFFbD//X653NmvfbiiwqFwr6d8p+D//nf9ydM8P3PpAkTR430eWPo66++8sqgf77m8++Rn33yydKlS8+eP1dUWj+EyjJE+EDuHoR8QxBAEMPDdj3q7NK/f/8NGwOfe/EFpaPDOF/f2qpqU7XGdCX/8uoQ9caImoCfC0IioIaGSgmgN1AEeqZo0NGQWXL0qzXZWw5CmRaY+jRCj0oAACAASURBVGUdp9Jpk7KPLgusPptKYBdWJIg8gPpG1VuDhzrY2w8bOaKwoowSCCxLi/UAtAnNIAmocRNSkTpAvb/BpqAGXpErRWaMZs/i9VMnT3j36aNQKDycXY+F7SH6BROBng0iw/IM6WEZRXGfrr48ex0k5RJ/kiaRUG1cr7oQtPtCwA4orAKKpSiDmjWAwEN6UZJfsHAgvjwogqDPJWqyP5cjRt/EmpsjdtCg5cr3x57/71LYFksWsXrGwNAqxkiMMziASipz3a6aRTuvzdwAv6RDsUqt07IsmxV+Isk/VMwug1o9qzPyOgpU1In1IVeDD8DpjJzNByIXB2z6evmiLxb07d3Hwd7exdHp2acG+K9eExMdPWHCBAdnJ49uXv4b1ideSPh20RKllbW7q9v06dPTMjPk73KjGbW8NGh0XZbnXQZwYyvDMFlZWc8880yPHj3Q/eDDBUCLorh582alUunm5hYQEHCfZHWXor7d49jEuCbdt2/fgAEDbG1tP/jgg7lz5yoUiieffDI0NLSmpkbuIbdL5z5el0FMiUKIDEoiQDUDB5LPO7xdZeNjcByf8+hocX4Y5FNoe0i8lfISAE2QaAmDvpMt7fIw0rLlMVZZjvzbiBXR+BF/qjdl1TA8ITgFOoD5uyq9phiUY8vdfNXzt0MJRbRfWHgZwzWH1UwC1EB851G19mOqHhl5w2tK5uvzIF1HtqEQqEtkGwHQN/NuCJlXwDzlhvu3/d8QGQFoVrLubPQRQbUiguw35XMrzCfn3zgjTP/WWpPFoERJghmhurRxCtIjmB3ptzz5iuGnQy7DzXJi+nIfa3iWb5hdyInzkjzxtL6ocgmldM2nIjejmcdpqEt9MeRIJUxW14nGR0brrUaltR8FiZUkfRP5qJEWJDWWFLQNjzcW1O86vymB3/U4gQd/74N/3HMo/Fbmh33gVtoT7DakqvI7KEh08joJet6ffO31+dfajaAdJ+itR1c7jyP7D4LPkBe5yUFU/g1/AECmgjyQjRGhiRXdp5U9MjxR+TYsOgB1pH/zkh7tfkv4rgDoZcuWyQA0You5ubm/Q/vKcVxQUJA5kmthYfHSSy/JRsdNJHnLBZqmZ86cqVAonJycLCwsEC+4ePHinZaEN/FoNSzjpIg7mJ/KYXMwFO1q8QqG5WiyI7thw4bJ0wI5cEs17uLEPEHEwsaPH48AmUxv+vHHH99FDs08euTIEXP/k7/6exwyZIhMi4E0IGVlZa+99pqFhYW9vT2SFdjY2PTq1QtdFCKuhxOLZjJouITc3C4uLuYynzt3bmv0EwAwdepUxJ2RDsXDwwOBZjTVb8ik/j9Kcvr06diCsvLgxRdfRFNufFamAm/0eNvpX1UCqAjR6XRHjx7t3r07KpZcXV337N6j0WjQoF52WGRu+CyH5Qm0+dv6VxXXA14vbE0cf3CpyXEc0j6yLJufn+/n5zdo0CB7e3u0gO7QoYNSOhQKBcLTzz77bEhIyJUrVyiKwhQe8Cq3Fa9NAm0SuHsJ4DBOQBNpVYkjiV6j1as0pyKODXnmhSfdPPq6dn7D+7nHnTs+ZmU/+B8vHT1+rI7WawWJrq9Wd/1QbMri4PxvdxB+3stFUFQHapa5knN2XfCN4EPMvtPx3wVBQbnIGEEwEWPe5IJjHy266r9dzCsHvZEgjYKES5pMYGRARV/feyJ2UQCklkCx7sKPe89t36+6ViTqKLK9Wk9XXkz/+duAlNDDYjGBntUGHVGl61nIrkxeuS3u8/Xpa3aaLuUJRRJvBsUzVwuvfL8nZW5A1rJtkF7CafRq4GqBo0ysYCLIBavWQI0BUvITVm25tGrr6ncmjuv/Ul+vbr17dH+mZ5+eHR+zUj7i4ObkqLRtZ2mltLLu2tnzpeee/8eAgc8PfPalgc/179mno4tb375933777a/mLzh+5GhOTo6RY9Qmmqx5TISkGP8oiiovKT2298ArfQe4Wtp2du/Ys+8Tbl09fKdNTr16hVAYF1SlrAq5sX5fwfLtRT/+DNdKCasGy4PJxDGUYGKJBIqqUtbtSPILhiI1VGpYnVFbqwI9Z8oujdsYVns2FQwccDyxTAcg8LSB/3z0JHeFjZOt3ex5n2fm53LSSkzPMQaeZUXpe27i6zEFqT8hBtHUmhvXjPIan8SVkOubeIQg0kZDeWnxJzOmuzk7ubu6rli6pLSwEN0SsmiVrTFAXlXyyq1JXwfyvyTDDTVXUQsaGqqpmv2nj8//riYpnapT6QX6hlEFINIlFTkhh1Q/ReWuC0sP2E3AYh1L6sUR6m1SBqMINWxN5MWDny4vDTkG12qIByqON/CsgaHJurOgqmjToao1+zO+ClLtOg1FGtCwQq0uN+7yxZD91CXCzEtQNi0jZJRcXRdWF3ICzuVdW7cn4YsNcYs3X9kXBRo6MebsV7Pm9urcpb3SoU9nr/fH+gZu3rRold9Lrw92ecx90KBB+3bu+nl3+Dif0W7uHZ58qt+PW4Jra2t/XYLJdh5or9NUef+b6wWpTVr7gwA0RVERERHu7u79+/fX6UhPwG96I78vrU30fsbD2aM8mcT1iFqtnjFjhqWlpaenZ3R09P3M/z6mTVjXGQYxaA8Pj2nTpn355Zfe3t5PP/10SEiIXq9nGKap7dR9LJCctAwOEphWQp9pgCLu4muf3Og4UWs3NlUxhPVdD2UC2RHPEWYhHCiIHTTFk8HWyBEYmhfJ6CQdRoYmowFSOMkwjwTwmSR8iQZiiaiX3AeaU3fIcTEdjvgeEzFR7vaQnNgAPN18vAFMlHFAMj6UM+o3FnNukxk735zHfOF4BlHOmRqiYvqyNLAENA/Zmuwek/T246qtfS46DTOsi4ASHYGtJd4RwikriMQeXCDdthnEFodILMfNrDD12//KuKo0GhGj8yYANKksClnyBFlf04byyzgyXpeH6/osMRoAsRPHgxdZAyXypHHRbSMrgbMM+U6TEZEm3y2e5yTnrtIjBDPkBemTRMqCORLlhNRqdbSeMEFxkoqCoIOSokKiwEJ9gEHkNJKLWvLZJR7meEryEMuSFpcQbVl00uSCBrGG1pOuJR06lgSIzhuA00gKaV4SCN7GCmLlM1QXlG9R1mMqlaOKX5krmT+TnVKkghJZFnFWbLylJ2Aav/lrjolTJpYSONQW0CLPSgj7b6ZwuwgynHq7CHd1HYWDfUzuGb+lQ8KIt+Tb+v5cPz0gDYRTDlYaHkinkf06YxwOoNgIP2fBfzdfaT+qzGWsqf0Uymq0yXJMieV7SV3GQkxpswD0LQXDE1HquJXAj/HPUrxV6/5+avcJcL6YuDKWRoqbw0UzD9+DS3cFQE+ZMkXmXEY/b0ajEQHQOyqa0WhkWdbZ2dnCwgJpNNAnYWZmZr2UxNs2I2/iL1y4YGVl5ejoiGQgCoVi3rx5d4o+I4Q0ZswYc+y4hbA53CybGFtaWuJ18wcdHBzee+89lUqF306GYX6HiFojTxnYSk5ORuoPxE/t7Oysra0LCwtbk0hr4mBGPj4+5sbvlpaWR48eRXpcRJ+PHDni6uqKcWxsbNB+sHv37r/udkdptxKAZlm2qqoKCbVlDHr16tW/qZ/AciL3tLW1taWlpZWV1cCBA7GOOHVrVF+c2O3YscPKygptum1tbbFfffjhh7KEsZqNnm07/QtLAC36z549+8ILL6BS51dvdX5+fubo8+1sn5suov7Cgnooqma+fpM1BBjAhmZZtrKyMiIiYtKkSbgvx9XV1dnZuX379qhTbN++vVKpHDBgwLJly3Jycqqrq81d1D4UQmgrZJsE2iRwpxLASQsZ6qU/ANCqNRXl5RtWrP6/517pZu30pFPHcYPeGuDZ01lhNXH4qMvxCRyAhifcx2yl6kbkhfMLN+X5hZYHHoKLeVAtrRXzb2TvO35lY5j+wOlLawj6DCwHHA16I6QUnpqzkkDSeWWgMzIMRfMMId/Qa8mytrS26mRCwtoQSMoHlXj1p59jv99xIyHtZMTRlatXfTZn9n/H+E4ZMmzkUy/P8p2ybOHioJ3bw49GXEq4mBt78aJ/6IVFm+OXBcHVUoIy6Fm6SsVer0zZciDq8zXRH6/gfkkFSlTrtCrg1MRnMwc0xxkMZCFaUH1p3fayoIgzC/yztxysOXP5ctSpnQGb1s9a8OXk/2343n/JimX/eOopN2tbN0ulz5C3Nq5Yc/b4L2UFRdeupEdFHAnwXz/jf9OHDhnSu1uPrp0933z9jUVLl+w6sO+XM6dzsrMT4y4cOXho+9aQhV9/PWH02Oe7PdFRYdPN3rVPZ69xE8Zv3L614AZxlwe1+ktb9l9ZElSyds+VdTsgu5x45ON54Ag9BfHsJ4J4vSJnT2TW5nBIKSKguUkEVhBUesitiFr5Q+HhM4SlRMIFyOScFcAglsdeXjd51vPtu9opLOza2S/yW5ZdVECBoDMxt+xdlfoNgqTmLgrNYWjzdWt9N2tYxxCkQsI1ygoLFy9Y4Obg4ObstGDeF+lZ6ZSJdAm1jtDEgYE2ZRZFL1gb900AHZMCVQbJ6yAFaqH2QOylb4NM59KhTsuCqY7VaWkdXVZ5ePn3hUE/564Li1u6iUu6RtBnjiAgPEdIVKgqFZQZmajkY3NXRy0J1CdlEwiMayiWCFCqLt0TXbRyV8Kna6/viIQCyUiqzijklJ9cH5J//BzUSiB1rVF7MSsz6KAp7CycLTGFxGQs2hI/b0PaxnAoqiH4uI5Wl1RE74sY86+3nRQWj1opnx/47Oo1a34K3zVywjjPzh7P9O238IsFEfsPfLdurfeApz29uoz898iYmBidjihIcB+nvI3y/s2gcC1G0/Tp06c7dOgwYMAANCN4kAFoWXEua76zsrL69OljY2Pz6quvVldXN7u0qe+BD/w/vV5/7NixYcOG2dvbT5s2bfny5f379+/evfsPP/yg0Whk/cQfXY8G1JK8LyYRGICgM5c8xlTaj65xGpfadTxcVIOG9FOy00XCKInDUlYg7PN6pt6MkZIcEkp8M/Xll50TNryCOBwRNFMCoIlu6PawMmJTRG9ElGcNAKdBcluKGTQkK6N1TRGlelgWbxTSOd3eN9iMqVK8d7XreMjTE0NYQeAQC5MxMqnY9UkZBThflNXZ16Acq7IdndDRB06kkWHHRLBXBsgfAWFNBH6W6ZXksZEUE0+wHA0FrpdPC/8abEsFCZxFtK5R7epPpfQRCW16RVYB3FIkuaYI/VazSGlNisMKDMeiz0YCzkro/803jpW4R1QSiCjVTALdJQtos3Ykr7BcNZon8C7C0BIGTbTaEuooR5EDkl1qPS58sy71UHJDmjRPIEseiPKD5iXlB4gaYz2OKRcDK4xg58mcK/bDjHbj8pxHGT7cDAZgRQHR53r9AWFWFUEtEA4rFoiDTSN6mZSLdpuAIJIyUCLp0FRDt6ak7iqZ+t7msd++jHbAzG0E9dvPtzKGDNO3on82Q1vR+v4sdzlJLKwkKqL6QIxYI22EAiAMP1naurlbr3bxLbAdrnIZf8PiPc0jo/h2E7SK90rsfbj/biQk74ZWVk+KpgM4VZnjMb7CbtT1juONC0KhjGyZogTJU/OdpHSnce8KgH7xxRetrKyQMcPCwqJr1653mj3Gx0nABx98YG1tbSMdiJyilWvLULIgCEOGDJENjRUKRc+ePVGJfaeFEUXR29vbHDtuISwjoXIchOARuET818PDA71XIV6JJrR3Wqo7jc8wzLvvvitTf2DxZs+eLXsmvNMEm42fn5+PTrrk6r/44ou4lwoni0uWLEHuVFtbW+whLi4ugwYNysnJMZ9DyEhQs7mQt08UeROfmJiI4pXZnMPCwvDu7R7E66IoPvHEE1hIxJHffffd2z2I5edNvOyLUlZpIAz9zjvvFBcXoyTNa9FyGdru/jUkUFZW9uSTT1pbWzs6OioUikWLFqH5DL7XLaPP2LV+s7f/NQT1sNRCbg7zFR3Lstis+FUCgLy8vP/P3neARXGt7w8gsHSQplhy0cRoEm+M8eamt19ujDcWAksRUBNLbowx9n6t0SixRlGjiIpCLGBDYkEFbAjSu/S6sLtsrzOzM/P9c+bgZGOsibc9f/fh0bOzM6d858wp73nP+0VEROCNNGdnZ3t7e19fX7ydhscpBweHxYsXNzU14X21Xyaj/yuGeJLPJxZ4YoGHswDuKzA0hhnB0vaO+fPn9/H260EQb3UPnPjuyLcHDvFz9Vg8b4GiRYL4tgAmgxHUlOViaeXSuNrFcaUr9kBRK3IKRwIoDBXHzhTtSLJkFaQuj5FfvwkGPZBGMJFQ01qyZnfG/O+0pbeAY0yUibaQQFHIgxxCvkkqv3r/10tNBdUgN7ReurF56twp740a4tu3t6+/u6cHYWvjZGvvTzgEEI4+3ZxcRE7O3T18evXw8/J+zrf3sG4+Y/yfm/f3CPGwd157fsjn0RPOHT3x0w8H9kxdnLF6p/laBShI0CEsA2sxcxQv3WAB6NAUbEus2nqo8Ns9rUjhQQUKI0h1xhvl59fE1qdmgMGUfzM3dv2GmDkLQ19+53kH7372HhNHh6755/KDCQeyrl8rLC6qKC498eORWV9+9dwzAxxt7bo7u/2pR693Xnntw9ff/sugwQHevk629nYEYUcQngQxxD3gy6CIrBNpyJEhzcMrNGTvS7kSs6cyJiH3291UTQvyNMgyHMOLI5vMnM4A7SpVcubVJd9T+dXoSKnegOBpPQWtquxtiSUJp9iWTkZn+tX54oqO47O/vbhhz/b5KzzsRYStjWdPv9VbNrSqOzUMSfKrZh4aQB4UcT+PVDJZlmYYDD1bA9DWDioFuEHYtzCptcXXcsZ+PMqFIEQEsXj+PLlCZmDMHSa1TKOw6HSgNUOT8uam/ce+WKo5cwORu1nWJFeAgYWLZdfmbWw5dgkoQGLQAKRWC+2qws0HClfuatt18vLKWMO1UtCSQLHoqB+FSHlavQ7URja9+NznK1OmrWTKmsFMq3XaLvY3B9CiUCVlVC3bUx2TWLrjKNcg4zRGUqEBierKmt2Sw5dAg+AIaFJBmaT4+0PS/ecguwWS89vnxTX/c2/V7hNUTRu6X/h06otSL7zz9OA/iTzdCaKHk/tnEyakpp3+MeHg6y+/4uIoeuPV12J37Uy/nDnykzH2IsfBgwfHxsaqVOiVwZ5mEJ2QwUsKnj95e8wWUvjjAewHorS0FAOd58+fx+KNXe84K1TdH0/qMcSADdBlEd6DBU3TW7ZsIQjCx8dn+fLlwrzlMST2b49CmDvl5OSMHDmSIIgRI0bExsa+8MILPx9dXbp0KUYD/v1l/BXYpyWhE0r/8mWDa0ino7jEZTRy7iehMP0Zgc4UIskiAJrkAWhezQB0DEKFZCxiNePPbXJuFzx9G4nFP3ZBkLcZpHdthV0XdWYE7Z0uh12X4GotOlOPOcu3Idrb6f3q/zvZnJiY+lNlnsdouX1Io81I+f8tQWgXYmGzOh517MLCMNPYwsOdFh6RPJxT2D1YbS/WOoUXPBUJDXoepgegkNxH16kR9hcA2prIhRIQwH1BZOBXOb3fF8wUNgrZs0aRBdltfFEAXn9tZx6aR2W5i4VZQGpFJMCqY2efDe9cfQjkACoT1lAS8HQEr5s5kFNQqYFLbbAtE3ZkQnYbqNAwjUUPfokcOaW8nQMSgXx45wBFImDQPHyN8F0zgyYJGhYRWg0camAkYkkjLw7AGXmMEtlMIGhygEYNCpCKghTQU1Le4wIJaCjnaeAYJEU2xdZGaDLA9vO1HmKta2S+bwgcyAUSse/NXfA6z8vWc9AJUK6HjFY4UQFFKtTM7g1B/9L00ISBhBoznKqBb1KZaXuUk7bChtNQgrY2f5X5+9XzXX5jb6PZ1ps0eKMFl1GwvHWjuEtEt2tD+AkfQcAbOugiLsyDoGQhP788iJ8V4n3oAG7VeAuqy2OGmZd7zqgj5x+oevqzdp8ohXOY2iOq1SeywmWMrvfkauJvRqeIMvcg+P4cqn2rTagHJ2sCqKXV4evlPtHtLqH5A8ZDLjotp6SMVmI9D47md9zxyAC00NY5jvP398c+A/E6/MMPP/wdORAW7devX8dIJZbfJQjC09MTu+wThqXfxh8XF4dha+wNz9bWNi4u7re3PcwVlmU9PDwEWQnMwv4toxmjmdYAtLOz84ABA4KCgmbOnLl169bU1NS6ujq9Xi/YCiOejIV5vCiwUCgBoydJsqCgALsEFP4lCOKxS2ht27ZNgJ6x1sfq1atxVZaWlmJnhsINmEI4ceJEIZ/YILcnk+h/oSx3BDAV4uTJk9bV8bNCy/nz5/GdeCp2x1PCV5Ik3d3dBQCaIIiJEycKv1oH8MISs6p/Pgu2cOFCnCIWuRZaRUBAwLp16/79EyDrrD4J/3ssYN0s8/Ly3n//fUdHx379+tnb20+ZMgUzTR4SfX4CQP97quyRUrHuf4QVnTDWcBxnNpvxV71ef/369c8///yFF15wdXXFck/29vZ44CMIQiQSDRo0aOHChZcuXaqrq7OubiFLuDkJiQrXnwSeWOCJBf6bLYDfWcw3tOZmshamorh0xrSvAnv2FhHEqKde/HzY317p3vf5Hn03rt9AWWjOTLEGnp6mIVWp2bmzN1fM2Fq5cCd3qQw6KYTbdupLDqdlbdil/+nq+VWbytPOgV4PNIn+rW3NXv/Dyc+X0JeLgWNVlMaM5IAZhD7rKVCZtHkV13YcbDl7tSW7YN3M+cN69xvg7tO7m+voN977euq0NevWJv6YtHFdzNaVa7evWjdv2ozoyKghf3nZ1cujm62tPUEEELZOBPEnG1cngvB0cLIjiO4i10A3n8FOvjNHRuSeOo8oTvwaFcOXQNLoSqsif8/Ryh+OVu84WrBhPzSoELNJZSKvlV1ZvVN69BI0KPWVDT/u2FWVkwcKnfRczq7J84MH/fXNpwb5idz69es36OUhA4e++Oqrr7768rCXX3ixv3+vgf59ehCiAY5eL/s91VPk7uPi7u3q7ufs3tfB/b0+gya/OvzHFRu11c3AAG3kjanQVZ3KKNh00HQ8u+C7faqsAiSZzFEsa0EYNHY82K7SXMo/P2ut9NAFUCM2NGUwGGRykOpu7juWu+sI0oM2IeUNndmEiqnnoFqet25v9nd7oVmhamybN3tOn36BhJODo7fHqLGhB1KOJKedSk47lXL61Im01PSLF27k5lRXV8tkMiNpvj8AbY1Eo40DhepG1pWFX8188U/P9HJx9xO5fBYxtq2xkaTNOsak4cyootUGaFBU7Uo+PnWZPDkDpLcZTWqT5kJe+herajf9iAjRNMOLRDOgNtUmpFZ/Ew/JN8o3HTReLUUvFIV4+ljVhK8+Sp1XlTF3Y9rEZR2p18AEJorU0GbEpWAAWhUdJ68UL9pRuTTuVtxJS1Urqm6S1rdIryaklP+QAmUS6FCjlW2VtHjDQWXiJchthWN5+dM2VE3fUr1qP9TJ9DLkvg+lSFKgJU15NQW7k0+t27E06vOgl9/q7eje3cH51ZdeXrFoSdL+A1OnTn3m2QHuvt4zF8w9kZa6bOWKQYMG+fj4TJo0KSsrC61ZeOIkppRaD6nWE7M/3m9g6kBTU1NISIiTk1NoaKhKpcLEF/yTkMTjTVeI9pECQl+EZyw0TUul0g8++MDJyWnIkCHNzc0URRmNRmGa8d+Q50cqIEmSZv5TVlY2YcKEwMDAoKCgLVu2vP7664GBgTNmzMAHo63Xko8U/x+6GUNZZoD9V0p7hkudQxu8wmDOYag3g9yIyM4UDzpTCH1GU0f8FeNQ58vzJ357bsQMOFN2L3joF3AQ81JNvEKrHiFkvyCYQgFYHgJmABQc7L18pW/ojb7h+WHLEJ5o4KFBzJ008UCkinc/aPo1X5ThmZI6nmutAWgHWJZc7x2ud41sFQXDl0lQwyCnhSoWoY1KQMxKCUAHH9axyIGhmQEdcLHnCt1GKx3EKvfI/IEToIPfpkI8cQatjxgG6W8gMjiHmLAkh45c4BU/a6WPjG37C3IplPMBAYyjopv0PEhnvs3Wxkl0JXQbZRTASBxA4kNo75DBQtV3JGVBZ5fMcenZHqMqXYPOBYrhmgRUDML3af7PwqFCqQGqdPq1yaefCc32Car0DSvpEXamdxCS15fflu/AMeMaUehRdbaYNMeuQXY9NKi76hcJlfB/FG8fGQn5bXC2Uh+TAnsvw5VmaDQjdxFmVCSGh1/NfLHQl04e9G8x0YevtczZ1TQuRjo2Rjl9l/6Hs9DGIDgZbUugZPFg1AWqYuK8AkyLDrZ4has9oi72CoZCFZBoVEe1aOHQyCjnoETd/vWOC/3DrvUMyfT4+OaQyeSW02g3xVodxsp62Ooolk6AH/M7w9aV9Y6s9w5v9gi75SmuDBx/9e1pqEWhFo9aiMBDt4rjwUH8lnRhrcjjBU+yNvL/mvhWbeRbuIFvG3r+RdDxptDyYQO/ccG/XHyTRSliE3UVy8JHpb/9CH5KdzseHNDyv2puR8jDz5ia8OAC3OMOnAe81Y12O0wA+W11X2y+0D+swj9c5xlNu43r8Iwo8AqCafshTQ4Ru9ucQjQOocVeweyPaGRH1fzwHySoBbD7cpHTyLZuY251D4Xlx0BBaczGu3Q7Dx/tQ9z5aAA0HvNwtAqFQpA1wOq6v1tlGIv8AsBrr72GkT68sHd2dk5MTLyXVi9N0wqFwt3dXSQS4fttbW1HjBjxQGWGu5qF4ziZTIYRcKz2gAFcHBaJRI6Ojq6urj/rF48ZM2b69Onr169PTEzMzc3t6OjAisAPHPLxAuZfMSEQQBMAmDZt2h3I76JFizBM9sAc3tUyv71I0/RLL70kpIKB2uzsbJ1Ot2zZMixQgEFnbLefhcJXrVqFZww4D5jgYD2n/G0q+Ar2aYmdQwqgv42NDVaRFoDsez0ul8sFkAhX7oIFJZrrCQAAIABJREFUC+56Mwag8bwT19QXX3whEolsbW0xhI01rDHaPnTo0E2bNrEsa72jcMds9a6pPLn4v2IB3FAZC2M2m1tbW7G/zaeeesrNzS0qKqqqqgoXxPqdepjw/0rx/z/J512rTCg77hPw8IS3D6urq5OTk4cNG4Z7Px8fH2dnZxzG/Uzv3r2jo6MvXbokkUj0ej1FUULHInRW1okKaT0JPLHAEwv8d1pA6AcoisIn9HGfcOnChb+/+4EnYR/o4DHUpcect4NG93ph+ICXLh0/LVMpkFCjwYzkCNSUIbO4ZdPR2qXxRUt2wvVaxCE1ADQpWk9eLvpun/n4lVt7UiqOpgHifnI8xExLjl9MXbBWkX4D5GqGNJIWI4JW8WpbZYSK5vObdl9JOha7fPWov7wRYO/c37/nzH98cSQ+IeVA0t64Peu+iwkfGzF69OgP3nznzaGvBPbp6+/j6+gkQhvq3ez9XD0G+/d9/U+D/j709Rd79bMhCEd7Bw8PDycnJwcbW4IgBg4cuHHjxpLCIsTgJm8LmBqZ2pTzl5ZvLY09VLbrKNTKoNOEpC2kutLvE1vjU6FRTebdOrdxV+HRNARPaEnTxaL89QkZMXExU2Z9t2j5gnnzP/3qi5DJ40MnjQ+Njpw2+fOVU2ctFU/cNHbavk/n75g0N2Fj7PqYmKVLlmxfsfaf74oPRMw6v3iz8WY14tVyAAYKTGDJrmqMPUbvTq9dc0CdWcB1qtEpOYZitbouiVWaY65XpM1dW3zwJEjVCKXV6VilBlrkJftOZm3cqyqp5ZliXctk6NRBVnXR/Ngry7ZDM2L9KVhzi0J26tyZCZMmOro6d3Ny7O7r49ndy93by8vXp7u/b5+n+j4/+IV333133LhxS1cs33cg4WZBvlKDdDNohjGYTEbSbKRJM0OTwJqB01lImUZVUFq8ffv2SeMnvPjMIHdbB0eC6OHmHjzi72X5+ayFYoDh9WX5l6Cuo2b/qZSpS8u3H4YOA5hZk0GHSPE36wqW7WyKOwmlzWCgOIpUmrUow+m5Td8f4fZcqFsZz14uAyXSwkbOKgEoikLqrhaAW9LLK3ac+WpNXXwqyPRAc6yFQesRlqPaFTX7T2fO3nB9/paaPaegXYsQFr0ZFLqaM1eqj19CeDQ+FVwvy9+TUrP/NNxsIpOvV8zbXrVgZ2nMAaiWmdo7kQYjUvtAWy+gppSJl3Lnbb2xLr7wwKn8U+k7vokZFjjQz965j1+P4E+C4xMPJB47OjoyrHvvHi8OG7pq1aqUlJRJkyYFBga+8MILy5Yta21uQRVKsxaSwrNrPHRiMVlhGP2DnYawIlu6dKm7u7uvr29cXJxMJsNzP6PRaDabhSXeH0zrcT2OeyQA0Ol0eHHk6Oi4detWPOW4A4AWDCWU9HFl418XD85qfX391KlT+/TpM3z48GXLlo0ePdre3j46OvratWtC0taLX+HiYwwIEAzKEuYs15M33v6qynlMi1f4qYBRUGlGgLKJl7IRZHyxo1FEd+URw2pt3rPjG/wii3zFZ/8cDZ1dsbI8SiawFTH1EvVKFgAFlE7fDMn5CKdTm7rcn+KC4X6LZpDIrxkgszXnTxFt7mEV3T5O7xcKtTToefyJ44mQ7VD/j82Xn41CzNNGM5hQc6DNJEi0iOBcQ0MlDdU0VNBw3VTeJ0rWLVhNjG4iPoLpp2HcLlK8ofX1OfWDpxb1CLvhNKLEMzjd/aOysBXQRCP9KD0HSpDPjy9xGa0UhVbZj4S5h0CJ8NwuPi8Sn2aRJ1gDj0VKOJAzCCm28MRSdGCEQRDbH/lgW9Z3wqlSOJyH4hdQX4zk4UHTzBNuMcavZxCMyxsJqSFZ0CEL4TX5JS9mhCpe/MuUevcwqSispOdYSCxBJGiSz7zGhCq9jYbYy/kBYU09o6ttP1a4hncQIy1u4yR2Y5r+9Jlq6g4E/uIP5rXiXrTO1Dp6xQ3/kPM9P4F92WCw2pJA0hkA9Rz91Z7rAeJCz6BKV/RX0zsa5iSi1G/Di2h/Dn8sAI0Mu+Jo0Z8nX3f6qNDmwxYXsdwnutk38rr7yNznJsAPV6CZl3/BeyFdKDzSD0F2aKCqPpjf6RlZazfy6l+mIOq0EfHWUSPha42buf9Wn+gG52CZZ6TMJUznHNEsCi4LHAe7Lgtaw9iAXfnhBx1E+W/iYP6hYo+gauIjuaNY6SDWOobpXSNbiJF53YNUyxNBwfu/ZSgj/yI8EmoqpIUCSj10MFBHQ6kZslVwph5OVsGZBrjYBhfa4FIHXOyAtAY4WAhbM2DlMfjnEfjnEcM3R6DWiAjmgOQmUDy4JeKakpsQLFtlRKTvC21wQQIXOuCiFC7J4JIc/aU1w6Fy2H4NvjkN85JgZgKsSoVjZdCgBQO/6fKrLD7El9tHAbo2CRAFngMFK117OLOPuN4zVOYWrnaNULqEl7qMrvloEZyv5xU5zDB6fQPxkcEmJNv+Q6jVoVfvkV4pDlCP0Qltr8xqF4Wo3CNbhs1ALU2gyQsccCHwEKV5mFt+JwDNcVxBQYGgh2BjY/MzDfnbb799mCTveg9JkhzHWfNqbWxsRCLRX//6V60WTbDu+pk6dapIJHJwcMCKE05OTqWlaOf/d+yO4hJh2NTGxgafsMbIQlhYWHx8fGFh4b0QRgFiuEsXZpVvoY+zuvaYg1qttk+fPtaAiIODw5UrV4QplJAHnNXfl3xLSwtWIcDH0u3s7Pr373/69OlXeR/oghtGNzc3BweHoUOHYrYyPumGtxMEQwmBe+UETy/Wrl2LCyX829rK6wBaHz+5WxQ1NTU4kwIffM2aNXe7EV3D9Sjssvzsl2zRokVoSebgIDwuZMDR0TEwMDAuLg7PULG09//QDO9eRnhyXbAAbrFarfa9995zc3N799137e3tIyMjZTKZWq3GyvV3vFBCe75XQIj8SeC/wQJ3raY7MiYwHxF5jf/odLq4uLjnnntO6AB9fX2xp1O8y+Xg4DBp0qTi4mK8jrU+MIEP9grp3pHWk69PLPDEAv9tFsBvq3WuaJo+cODA0MEvEgTRg7B73bHHvDfHBPd5cfoHwe2FlaRWTwKrMfJuf1iA0o7qmMTKJbtzZ282pRdCux5UJHSaIb8hZ8UuOFvSuO1wzg+JIFch5Q2DHpplLccvnP3n+s6z10CuBrORoo0MYwYT77eK4rjGjuRl64+v+T7s/4Z7O7v4OIhCh//96ymfjx4+/PkBA329fZycnFw93AkbwtnZuXdAr2effmb48OETJkxYvXr1nj17srOzi/MK6ssqJdX1Jddzl85d4OnihjouW6LrDwHSdm4+XkNeRhvttdU1tJk06vUVV3JubIiv35586dudUNGMtCAkKlCYb2w/WLUrGWpVUCu/uv3AjT2HQaYDPWUsqb3yzS554oX8rUklh8+AQk/pjHqa1AJd39mB4Foz15lZmPnNzvqdJ64u32G4Usaq9BYTCRpzdXJ61pyNmdPXKVKzQUOTeqNZpwctQ1+pyJgRY9x5tnjaRmNSFrSrwWJhLQiKBZ0RtEZQaena1qyVsR3Jl0BlNCn5Y+QaA7RrWk5kZK3eBUVNoEGsZ7Q9QDIIaW3sLFy4PXPyKsirB63ZwpMF1RazmaErKyvLSkpnfPFlgLevh8jZ2R55BCFsbWzsbG27dckPEgTh5e098PnnXn/zjUlTJicdOlRdV9suk8rVqrrW5qzc7B9Tjy3+dtXfw4J7Bvb17O7l5iByJmwdCcLP2f3dt99qbms2kkaTyYCWvywDNAUqXdPxS/ETZhVsS0RCKGaGUWkQhbBRcXXuhvwlsVDSiIRljWZdpwL0RlV+xU/Tv6H2XmhYk2A+dg3kJoTvsAzJIce6vPsvgEZ55ZbDl2esz123FyR6pPFp4al8FAdGpjHtyo15W6qW7Sn4LgGaeflpANCYK85k/fTdLqiRgZJEjbam4/z6uLL9p6DJCFnVxf/cVb80/saczVDaAgZGr9KYKIS5I/qzkatPOtewYn/Not3Xvo1Dch9yPSiMZ3YdfKXvABcbe4IgAgb0m7lyScqFM0tj1gwc/Lyfn19oaOixY8e2bdv2yiuv+Pr6Dv/bh5fOnDMpNXwR0FuIlgM8tCcMoI9xyl1WVjZw4ECRSOTv7x8fH69Wq7GHYWHP6V+NdVr3MPcJcxyHgWYAqK+v/9vf/kYQxNChQ69fv46XIcKWOV7L/CtsdZ/sPZafaJrWarUURSkUiq1bt/r5+QUEBKxatQqz1MVisbDSNxqN/9J6QYf6eY2dLlajBeBgXnH/cW3uYcUeQfDDBYQBqSmsjYDcDN5GMrHeMepejGD47lidWwhpGyp3FOc+Ew2SLvECpPFgdVye4oFZi9YIraaGsd/efP6zo4Fj4GIdmAAd1MAfjFIh7iq/LyilTZO2o8hdozs8I8xTdyFo2HQbfzICJObm/Cmi1S20wGNM+fwdXUinmYUrtblBi4r+MrV6yNSKoVNrXpxa7i1WeY8zEiEgGkc6RhjcohAa5T2uvVuQ0kGstw812YdpuolvuQSl9RdDDYXovTpEiK6PWlvrGqwUhZa6B8HWTFDx7G/LbXhUz4KUhYx61dQd6S9NuDhipvFgJsKgsbj1beeEtxnJj9J8cCmNiIXd+t3hS89EXH1+fM2aA6CgkNnxbgGS02aRcr0aoEwBZ8uVO07DhSqQ8g/zWiVoTk7TQsX9kgMDQDPkDJjQ7hiqcgyv8RkL+0sQDZynB6NU2gFWn6jpHS0ViTUuEe3dglpFwQrnMHCeAITY4hBR2D0Yfir9hXjM8JWtBcWKxEKHEUoHca1nOD3rAHSSPM0dQGVGAPrFhpo3ZtV1D6snPlITY0AUDY5RGptghEEfyYcOtIuAMokdWuo4qDNppsRW9o7q8ER+IJUOYrltUKej2OAR3emInNRl+wTBulSQmJHN0ZYA8ofJcUhLGkXVCFf7hOo8oxtdQmRf70SGMnNoiFQD/FTeNmZlc98J7Taj9fah7Q7BbbajzUQIZRfW0m1Mwztz8VaK0M90mQ7Ts1sZ3eTY+oDoZuJjtSiszT/6VvfQRpcQuaOYc0GvT86b0xCbXk2yiKbMGXjFj0frzzGjnAS4pZLM2X1z6JSSwOjK3lElAeGF/qFFvuJCn5Aib/RX7CMu6R6C/jyDS7uHVHQXV/mE5fYOO//XSZDbBhqzmevai0XGMXHoVMGxvFufrjv/dNj1AHGBH4oK/XUPLvYKLvEMLvdCkVR0F9/yFFe7Bte5BNeJxtS5hRQ8FVn79Tb0Xmhuv7C/tKcHhe4AoGkW7V50QsaoOWV9o6Reka0eYbe6h+b2DoOtWch07bw0uRxahs2Q2gVpuonrnp0Mzabf2R8qOFh9ptEzTGsb0hQwDnI6QKrr2igScGch8KCiPOTvjwZAY5AO01cPHjwoANDY+V5iYiKGbB4ybevbMI6jUCgw3ofZpph9fOPGjTsMir+ePn0as89sbW0dHBxEItGcOXN+tzIvy7JHjhwR4EWcAW9v76KiojtSF5BK4VWxHuBx2LpoQli4TbjyGAM4k6mpqRgtFUSx33//fVxfeA//Drzs92Xg6NGj1vIUdnZ206ZNw+olrq6uQgacnJwEujGeyeHkBDtYB+6fkzlz5ghVgwNGo7CxeM9HOY7Lzs4WWikmUMfGxt7rASE/1jWekJAwcOBAvDOBBWcERNvV1dXZ2fm11147cuQI3pywRprulcqT6/9DFqiurhaLxb179x4yZIi9vX1YWFhpaangjPuOt0loP/cJ/A+V/f+rrFpX2V0LLgxtgh92iqIO/XgoOjo6MDCQIAgn/uPs7Ozk5IRPgfj5+Y0fPz4lJaW5uVmv1+O9N9xRCC3nrmk9ufjEAk8s8N9pAZZlJRLJihUr+vXrJ7Kx8ycc3+/eb9ngjxYMeG+1eLK+tpXRmUiSxA7o0XqvStq+7nDrovjcmZsUx66gOb2ZAx2jzSiq+mY/vTu9Y9uxq2t3Km/V0AYdq1KAxqg/fS112rKafcehWQZmo4lB6DOLfNOxYCaNNc1nY+O/mzzj3cBBT7l3R5v83ezcRI6BXj6D+wb+ZejL777/3uTPp6z7LubM+XM3cnPqGxsUKpW0U96pVKjVaq1WazQa0RBmoZFKKUBpVUXsrp2zF8yfMGniqOCgV9547elBA339/bo58vvuzqI/DXxm4dIl5y5dKMvMbtqXmrNyZ/P5a2hRrTGwzdKqvSfKtx/mShqgXtZ69ELx3mMg14CR4urbL3+/r35PavPetPzth6FGxjTKSLka4cv8Zj/Zoeg8l5u9Yqf0h9NZC7fUH70AKlLRIQMz05lyOWf+1gtf8+gzv45Tq9XIpVKZpOKbvfTu9KJZW9p3nYZWIxgtSBSbJBnSbDGbQKWFNnX6up15cUfYOgmYedESnREt7HNr8tbt0Z3LBw0HOuQIDDnvYjhLg7TuSPrp6Wu4K5Wgp0wWSstSGgatihGTl6LBSBWkZx1cvy0ldk/Cxtj502dGhIS+8sor/v7+vXr1cnZ2trO37+boYGOHmOPdHB26+/oE9On9VGBg/4ED+jzdz83fx9Hbw9HX08bDmXC0c/Vw7+nl091O5GsrChs5Jv1GlpxD7pxIjqftkRZOppJeLzy1IAahzxIlcKAx68BigaqOwuU/XJ29vjP1KpCUhjbqjFoEuN+srV6zD+Ivtqw92HksE/mvNzFgQWQyGjiThUJEvzppy4/p16avr/hmL1R2gI5iLQxiKVo4aFVAdk3Zqnj5isTimVuguBk0JOI+A3TeKDuzfrc0uxQh2lIT3Oq4vCPx5u6jiOF1o6lzffKtOdtLlsdBYQtoGNCaKJ0ReeK10EynVn36Rsu6Q5pvjzatTTLerEbvsoGDelnaprjytMyY5aueHjSQ8HBy7dfr1REfHE47eezUyfDw8B49egwePHju3Ll79+6dNGVy3759n+0TuHrxsqKb+bSZ7II5GIRBW38eV0fBsmxubi7Gvt3c3IKCgs6fP9/W1oaXTg9MRcjSA+/8gzdgdWwkOaDXr1692sPDw8vLa8uWLVgxDGsEYVsJwNC/LW9/sGi/fRxrjGzYsOHpp58eMGDAwoULQ0NDPT0933rrrYyMDDyt+u1Tj/cK9i/Ng8sAUlYlXlfjHtLmGd725lyoN4GJIU1m1JeyCNdDLvd4iV4T8AAficRzq8JXVTuONncLUzqI8/tHQ8dd1HM5HoxGOdcAxGVedv6oxS8qJyAUjpWD2up+AalFLlUBjhfe8A9ReEQqRaHX3D6GQjmou/yVob6rk6YWJVb5hevtQ+vdxbWL47oAaCOoFu7P9BpZ6xzU3q3rz+Q1XmUbDPZRQIQAEWYigrX2oY3Ex23uYRKviA738Db3sI6ACQX9optm7YBGI3qjlTQ0cTkvT2l1EatdIyoHTIQMCZKJoBCnGI0RRg6xXBcfyese1OQqbnQYU+0ecuW5cVAhB4oXaearClNO7+Nu8e4VivBHhD7DDVn2oPHNvpGl3UNufLIIyT4YeCyf99kHagYph8w5eNl1REOf8aXdQwp7hmn+sR3dhnaKb4P1v01DD1BkvtEzrM3uE7Xz2Ar/sXCgBD2FGdYSgFkHG3qNq+s2qt0trNI9uKRPZMu7C+pe+EJiH8TYhhmIUXWiMeqZcdBMon0GnI4FqTO3R69v9ghTOYZWe4VTsw+AjESKEWYKVX2GqtI3osVFLLULUtuFUKJIHRGkJ4Jp56hK16CGsd8iaipmuCMMGnGfa4OWV3qHdjiJOz0j69xC8nyC83qFFXmHlDh8rHWP6rQLbrIfk90rFFKLkX4IAGoYfBeKNrQNHOTprruP1DlH1LuLYfclUPJEZAULR8pv+oW0eEe0u4Q22I+ucBlT2m8c87dVWp/xGiJIbx+a4xsMecjzjbAm6jKhCYm06L+OK/QMqrP5uNk55KZfCGw6A+VmKIYiX7GMGN3pGZk15DOEomqRXZAvA+TOEXVUv62H+10hkT2v/W1mYd/I1u4If9fah6pFYSonZF6FfUinXTD+QxIxjvxPjqFKB7HCPqTFOSTPY3THF9tASZsZGvHBWV5ZRcXBufpzvYJK/EJvdRvZ3i1IahfU5hjcKgpuF4V0OCLld4V9iILH+tWiMIMo3OwQTjpGaB3DakRjMnoEwf7roEEHd+6X87v+xiO8XVs3eIPBCPnLdx3sP7r0vdn04iT4MQc1eJLfBVHTiATQDmV9o+SO4ma3UGPUZpDzuyl3jfz+Fw0Audqy3pEq2+Amp2CIOQVSGk1WBdDZOnD/qB7610cGoHHMNE2vWrVKgPYwJJeeni4MjQ+dAeRrAt+MA1FRUfgsM4aAbW1tP/vss7symocNGybwlEUikbu7u16vZ1n2YaDJ32aPZdmNGzdicBPjjARBYFVrLLNg/WII47oQjzDA44Bw3Tog3GN98fGGP/vsMwGoxZVy4sQJnMQdwMd98vnALN0BB2NvhLjWhBrp169famoqOtpgQgsI7NcLx4yTxoAOVtgQbCs0hjvyMHHiRKFcDw9AMxYmLS0N709gwVZbW9uEhIQ7Ihe+ChWEs4HXaQAgk8lmz54t7HZgx5vYvBhpsrW1FYvFlZWVd+mLhdifBP7XLFBdXR0VFeXq6vrSSy/5+/u/9NJLFRUVHMfhDgE3EqHNPGTgf80G/7/k17r67lVmTIXGtS8sShUKRXFx8YIFC/z9/XEf6O7u7urqinsJd3d3Hx+f995778CBAw0NDXiEwvgLTvFeaT25/sQCTyzwX2UBFkChUTdJWufMmRPg5+/p5PqUk2dI/5dnvPD+ysEjri3eBm0a0JMcReNDUSjzNdLabcn1M7fXzYjVJ1+DVi0r04CRgVZt8eYkpM+YmFXw3T66pIbVaoAygYUhs4szZq0ti9nLFdWAibJQRjNrQvRnGmGCFpnyevKpT//v46E9nvKxsfd3Qe5w33r3ralT/3EkLv7mxYzq6mqpslNvNKq0GiwEYbJQZobGTrFwn4OmXgxjYCidhVTRJiOwJmClaoVMpWhoaiooKrx8+fLZs2c3btz42eeT+z+HfDjbOjk+1b/fP8KiS3Yf5a6Ug9JoksppmbIo9XzW2h/gcjnITA2nM/N2/AilTaAnyab2/D1Hm5PO1uw5dWNjApQ0Iwqt0sjpTKyJBCMFZqDyavNW7CYPZBaviGtMOAOdZk6mARraL+XdWh5/MXppx48XQGY06vXITyADVFlTzZYj7esO1y6Oa9p0FAGpCiOYKV4z2Yz0SRgOOtT5Ww5krdnZlnUTaF62gqbAaNHdKMv8Zrv2zA1UKVINGEiLiTRqdaAxd/yUnTpnneRYFlfTwdC0lqV0lFln0HdxWcycrqLh5Ja48nOXtXWtdIeK7FCo6luvpp5bNX9xbGzsjvi473ftWPXtmunTp0/5dOL44LBP3v3wxb5P+zg4u9jYOzk4Eo72hIMt4WTv6OrsJnJyJWz72Ll++PyweRM+rymrMAA6fYwcgLH8YlVjhlut52J25u86DE0K0BpYC0WTJmiVt20/XjT3e9NPudAi5wDazYinrM8pr1+1z7wuuX7hD607jnO1EjCaaYOBos00cAYGIQxcc2dbUvqNeVvy5m+Dm4iJbNbpBfTZlFl6/esNVbNjG5fvh8xq0HGgNoKW1JXVX9iyt+NiHu8Ci4Naec72Q2VJaVDWBvX6lg1HqmfF3vxqg/anXOTnyojEQDkjiXx26SlNbmXVmoS21YmSDUfhajXih+oZqJYXbDt0aN63upI6k1Jz7KfUkMnjCQ8R0Y3w6uX/xbQv09LS1q9f//rrr3t4ePx91Mgf9sRt27btw9ff7uXhPTY0LDk5WdLRYWFZjuH/bg/Yj7GL4DhOoVCUlpauWLECn6zt379/dHR0SkpKeXn5vdYmeDT/94/per0+KSnJ39/fwcFBLBZLJBJhiWeNPgtb3f9z8w1cHIyzKxSK+Pj4p59+2sfHZ8KECZGRkX5+fu+++25GRsZjbAAPjkpNQa6krG9Usyi40DMI1qSCnEKoGY8EomUsj+tZbgPQ6PUjOWhjWqNjGpyDLQ4Rmm7iosBokN4WG8Bo8m3MDXUBFoByXebTETV2IzVukWW+oXCyFkFOwkeQyzUDtLGyf2xr6DVO4ixu6BEFK06iTScGQSpdqIoe1NGbmlzF4Bh9q9tI9fenwMiZVVp0rmLftex+kfW+EXKPCKlHhNItQm8nBqfx4DRBRwTVOwUVuI7KdB5e+Mz4+vfmy0O+hcm7YHYSrD0Lp6oQC5j3sAcqGprgcq8QqUjc7hJa/MqXSABExaDjGhZE/QY5aGfENfaMNjpF6IjRNBFC2YRWeocqNx5Dz2Iz8EA0xduwK9tCYe8f4AAdtiABEosL3UZrHcMkHuHXX58KTQwST8BOY3UAFdqOzzbV+IabnCMpuzADEax3jij2EStWJSGSL+p+b1fAHcnpAK4rr3l/IukWrHQZW9qDl+BQ8Oh2C0MvTKx0D5aKxG3+0fkBYTDzABSYoIqCbA18stXgEmkkgprsx1x58TNkLl7DHyVDATRB0ZAp9bYjlY7hRe6fwA/Z2NkjomkXKjufm864fap2jaoTjakNiNK8tqD1hS+LPYKkPtHFXsGpQ8d1MZQZDvmYbaVMs/eW9oqQuYR1evIuBGcdhIsSaAQoZWF/WUO/ia1uoZ12wQ1eYQ3ha6AR7UdiujeDN0h0HByranhqgsoxFLmwu9GGak0JkFZd2jNc5hImcRZXugffGjYN4nJQtAUUTDzQRIzU2oZU9Ixo2nkSDGjOgyyHCbwkr7USk9Y4cEqT/Ri5T7TkrflwU4vQzE6AOsjxRlzdFoegpuh16AoNrIlkbjs8FLCgO6rirl+RUjONziud/HPkzR7iKtFomRtSZm92DqlzCa71EFd3D63xDa/xDa/3Dq/3DK12D7nlhkzR4h0h8Ypo8o7I9w2pCl0JnSj/Fh4BR+1WxcE8+7A9AAAgAElEQVTZ+uv9I8u9xXK/cQovxD6u9Yso7xFe5h9W5osacJWXuMpLXO4RXOo2psjx40rHURLvSEmPcaU+4qv9IiCeF2Km79my7lqcX10UmqSFV5eWcEhERUKjLR+K/41kQcc3/lLVrT7RErsx1d5hSLtZi3qAX0X1kF8YgAa6/qPFco8Ipc+4W8MXQjW/yWSNOwvhh4zzQbf9TgCasTATJ0601uQlCAJTlR+pAf02e1lZWZ6entjzG1YQ/tlxXEtLyx13rl27VtDkFfjX+B6s5nHH/Q/8yrLsjBkzMNH1Z81iHOfDq1r/wVI/MHsPcwNjYfr37y8AtXZ2dm5ubtijNJYlsZ6X3J6/of8fJnLre95++21sKJyWQHnG+IuNjc3ChQut779rGO9VYMqwMLcTAnc8gh0iC0UjCOJhuMYsy+7duxdruWCU3NbW9tCPh+6I3PqrtVkEc+Ebbty4MWLECDc3N3zWHjd+R0dHd3d3jE37+/vfP3LrhJ6E/zstgHdE9Hq9RqOZOnUqQRAffPCBra3tSy+9VFlZSZLkXTfD/jvL8iRXj9cCSDuPF4z7bZ+JRfZnzJgxaNAgfDrEzc3N1dUVb1PZ29s7Ojq+8cYbp06dqq+vxx0LzhvmKz3efD6J7YkFnljgMVrARJEkyxg4OremPHTS+F69ernZ2Ad0cx0/+O1vh4za+WbUzQ0JCKfjMTi0JAZgdCbo0Gt2n22cs7N2zg7DgQy4JUErRgtAvfTWnuPs6ZtwviRz2VZJdiHisRp5/LGu4/yS9eWbEyCvGvQmSq+hDQYEsCIlYYA2deOZK5HDPw7w6u7WzT4wIGD29OkXzp9tk7To9BpALqk4jE7g0994UUfx60y8uBKmNxb+ogk4PbB6HoAmgRXuwaYjTWZJR8et+trDx5LffO8dEdpst3neK+Dod9vJJimYOGlO2eHVWxTZZaAGy9nCs/M3UAV1oKRAw1UlnancekR5KDN/S6IhtwrhjyaaRAIBfDF1FBS21K8/RO9O1+8+V7HrGBIk1dNI5OFmbf6S2GufrahZvQ+aEP+XAlBpVdCslB84J/nuUMuaAy3bkpECsplS69RatYplLSRYGKMRVJQiJTNnyTa4UQN6i1GlYhh0yFieV7Z/wTfFSacQ9IxF22iOaVOAhpGfzTkxZZku5RpUd4Ae6fWbGVqv0SJvh+hgMM0VNqSv2l6UmKq71UwbzaTJDEbGVN50fMXmpoxcvdGoQARs6NRpaDNJd6igUQEVHbr0guL9J/MOnc44emp3/J4lq1fOXjB/8dezF4+dPPf9kM2hU9PX7mrJLSW1eoNWh8zC8vqkFoDazqyVO86u2GZpkCIHX3ghqWCVBy5cm75efSgTtIhuqaSMZqMJJPqGTUcaZu+QLIovWb2XKazHIIBEIdeSaF8B1WNTJ1ypypyyOmPiSoQFS42cmUK1bzCBwgQFrZ0bU/RrjhZ+tbHzTA46Ws6hTQ6o7cj54cdbaRlISkVBQpWk7OCpnLjDCHWqkbWtP9S2fF/JoljZ4YuoyvQk6Pg/VFWk+Ur51cXbcmdvvr5wqyyrEG0SqEzQopV+fyLj0xXVPyRDiwKJVps0DdKWbzau7TfoaTRi2hLDhg45evTw5SuZX8/6WuTu7NbdfebX088dPTF9/KRn+gZ6enrOmjO7qbXFqNfjM53Wo7DQsB/XW19QUIBdqTs7O4tEooEDB65Zs6apqUmhQF4Wf5uKkIE7Ar+9849c6aLiAmg0mh07dnh7e9vY2AwePFigaVurCOJpxr80P3+kLA98Fucf+94gSVKlUp06dWrIkCG9evWaNGnSzJkzfXx8Xn/99TNnzmDOGXbJ8y9S60YdF8krBaxMrvePbPOPPvtsODSyiNnKo73WbQLjv5h9izDWDrpp0sYW5xCOCDUSIeq3FoGSlwnFaM4dhugww6LDtd5hzcQIqX1wvlsQnGpAcKrwQZogPAdWC3Ct83r/6CLio2a/cRmDP4VmHqviHaghsQcSQX4Vf/5C6zRWQ/y9xi0UrkuAAgapzQO0GrU7z9VGrM1/bXpV0ArjJ99RHp8CEUoR4grnT2DLObhaCw0GxF9W8IgkDqg4tEdF8c4DARCIfFlW3DtC5hRa7Rqsmx2PIEUVjXKoMkODGb5KkPec0GkTZLYRg+t4cIo2EKPruo3KfHECYr/yPmUR8ZQHZikBNxcKe/8AErmmESAbc77eO1zrGNbuFnb9xYkIBNcBElJQ09AOpvFbK1zGyJxCWY8J4DpeRYxknKIkrqFX+4RCngYN3PeCQAwAV2RX/cVtonCZ09hs90/gXAeK2QCwODm720ftNqMVfuN/6jUGztRAC42qycT7cjxUW+MeQnlNaHANOfF0CDRQCNXF1a0HqIVMnyCVe7TcMaykdzSUA8h4xFwGkogNlTajVA5j67zHtn60HK60Ins2kfK1R073HHWhf5hsYwqS4MDqwC1mw8rDFc98Vu04WuU7Pt9fDGeq0f2CrzwZwFX5zQHjWpxD1K4RN5xGwIFChK7ypG+sj42Kszm92Ecscwqt6BWJ9FtUAEnlxX7hKu8JEpfwQv9wZl4SEhvBBZcBHKgo8xCr3KOLvcTq70+DHE1OOAtoFRr0jsgBkktzfMUdrhEdtp80PvM5XG5FiZoAyZ7EF0r8os1EiNQrEnamY1we7wFg+rN1r36/ymeQPbvOBRig6vsjp96YdOaZsNaglZ3jNhpnxlMrjhjXnzD9cI47ko2o3/uuwPZ0w8aTnasPwbZzsPcG/PNI9vszfnrnczhZwG9XMHjfCM0YSKRsnjNpzfFnQ4tfndb04WLJ2HUdC+Nl65PpfRmQdA2O5UNqKb3ngnnXecOOM8atp2Hbedh9pXN2XNLLkWmfzIY6PejYR9Zitm7/QoeCd7eMHDpMYEavHj5mgf41M8gEZyurfMLaiFFVPSJgby5qaQ9Spr2LYXHj1ALsTC/pHiL1ic7sFQLXZIifjrsz4V8Bg77XW3OX2O956XcC0AAwYsQIawDaxsbmt1oZ90z2vj8MHIg4F46OjhgFdnZ2XrJkifUTeXl5+AaMKv4sc/z+++9bc2ytb37IMMuyISEhGFe15z8/YwcrVqx4yMcf9rV5yOge/TaSJPV6PQZbMVBra2v717/+FbdFAUsVAtbzkkdNLTAwEAMrGHEW5CkIgoiKipJKpdau+R4mcrPZLCh944zd8dQbb7xhjT4TxMO2202bNuHNDKwSThBEUlLSHZFbf7U2i2ArzHzEt6Wlpb366qvu7u6Y6/2z9LmAvxME4erqumbNGtwUOY773YIw1ll6Ev53WgCDjBKJZPLkye7u7k899ZSdnd0LL7yQnJws0Pn/nfl5ktZ/jwWsO4e75ookybq6utjY2A8//NDV1ZUgCA8PDx8fHyxMZGdnJxKJRo4cuX79+vLycmHAwk0O73zcNdonF59Y4IkF/v0WwIddzGYzyTKt6s6kMyefe+uvhIOtLUH0d/L6M+E+47n3Dnw4RbPnHLTpKKkKeEIWpzMhQmijvHbf6dal+yv/sdGUkAGlbUjZgARo15TtOda456Qu5UrWmp2NaVlkB+/thQWoaM5aE3v5m23GrEJQm4BlzCYdazKB3ojUjRW6jtQrG6K/HDpgoKuH6/Dhf7tw/qxKITcbEUkWiSAj3gvCxhh+GYMxaAw0U9b0Ip6jh9lPZuBM/J9ww68YOyyS3KUsaJWnUqmOp6QEjx7j7erex8v30zGhJ3YlpGzeVXIiHRQkU1hf8F0Cd6kMVAxXJ208nH516XbV3vOX5m1UXshHjgotnNZkVBp1LAByJ9isqtt8hN6dbthxpjLmIFRJEEnWAqqsopJVuysXbq9fvR+uV4PSwNAkw1Cm1g75kUsdm4+2xfzYtjWZu1YBSqOFsygZYxdxGJ1bN9Qn/nR88hLLmTyQkaxUidhRao2+vuXU1t15R1KhQwkWi4olu8iHKsZ8oej8rJhbGw/BrU7QUsBwNMOYKFKr1iA/kBoTW9uRvWE/crjXIMeSjpRax9VJL6yPqzmabq5oRoA18p7EGkwmZPc2DVytbow9VhST0HwoHclWmNEhcbVSBXpKcrngxrr4szPWXl+1i7lZi4QyWA7xwUkarfEMDJRLcr/bf2l5rCmnilLr0ILcSILUqD1w6WTw7OqYRJCYkcALOjXKgppU/JjRvu5w+/IDkk3JbEE9aEmaplUksrORRH7zQEcZzuZfnh5TOGer5uAllD0TZk8BAoWLmiuW76maua1u7k5tYgbIeJRLZwKp9ub2xIqEkyDVIrM0KPNiE2uOnoNGJVRIGnefqPvn7ptfxihSMqFBCnrEJUf51JHoOHC1rGpDUtmyuNx/7rBcq0R8f4oFuVFx4lr2lG8VG1KguAWURmBYE2UymA0KtSLtp1TxmNHdHUVeIlGvnj2mz/762E8n45P2fzDib/7e3d98/qXtq2M2frvu448/9vbzff+DD/btidcqVBzDYieBZrPZ2q/M4+olTCaTRqNJSEj44IMPevToYW9v7+np6efnFx4efvTo0fr6+jtOnVvPDazDjys/Auotk8mampqmTZvWp08fW1vbd955Jysry3qpYh22zgkOP678/NviwVv7ODmtVltaWvr++++7ublNnDhx5syZzzzzTP/+/RMTE2UymZClf1VJKYBaJu/Pk5o9wkq7h3QuO4igOh7tFZK2BqMxqIpe7U66Y25cm3sYQwSThNjw5mJQ8SxUKwAabVuyPKxcqsj2C1Y5hbEeE6T2wbf8o+BQ5S8ANCaZ0oA0lGuNsOR4oVuQxCnspstodns6QorxeQp+CCB1ZpBBXo9wynmcnhAXe4mhHchOxKZGGLTKDG1G5HGu0oyQ62s6tdd4hhDr7MIkr80DKWciaZJGQs5oTOFRL4ZDEgmCwAiCyLQcHCmv8A+XOyI2KIIUdXwpSEAaHTGpNZ5io1NEi+1oXe/J1Y6jld2jSccImUNIYf9xUGzswh//CABNMQiAXne+2StcbRfS4R5e9t5s5PvOAMhBogHYtScquou17lENzogSW+sd1uAcrLQJMojCbzmMgph0TIK2rsFfwjqALNmNnmHtzmMlThGZ7mMgl4YyAxzIzfYYo/Yar/Id3/biV/BTDUJXsegHOifFQrq0rle0zjO6zi0k4y+ToIXfqMB1pwXI0eX4ihVOkW2i8Ia350M1D9pKAVadLuwR2eQgrnUJoz/bCbeQm0fWYEZdqMwEGfVwqgxB1RZe1bqTgrTqrD7iOrcQTc+JhT4hcLYVZAg+/eXPDFCvh7WnWn0iGZdopVsETE2AJj1D07haUUnVwH69t9o7rNVFrHxtPgKa65jaQf+QuUTInMLrA8bD4hRosAA6s8TvF+gBTjeUBkR1OkfkOvwd4i9j+jByaGiyoNqvh4YRS9t8x3U4hRW5BkFSJXTyeVbSUGdpfnWWwju6jfi4vE8UasAABpOpXaMQ0OeHRdJuA9BdGLSOhSYS6mm0J9TCQjsLchbULHKEqKeQI2gjIBBcboY2LShZJHWi4LcKEJcfEPecJ8Kb+bMLyOUAkpcBpNxSS0MtCc0Uis3AR6hjUGxIMwVAz6KpSyf/Ksk51JY6AZr1aOjX8PsEj4jSCrAzeuuESuLfu7t05ry+PCRm13UPk9oF3eg+BnLUoMMshEdMGDd6GuBqfVb3UbXOQUW+YtiTw29X3M4Jzo91A/vlVfmdoYcF8n4b/fPPP/9bAPq3tz3qlZ+xy+XLl2N0D+Ob9vb2ffr0oShET0Ddn4UZPXo0xqYx18zR0bGiouJRE7rjfpZlX3wRuZQR4rS1td2zZ88dt/3XfuU47syZM4IDQBsbG1tb27lz5/52SxxPUKxbMy7Uw775AAL92cHBATvdcnNz+/DDD/F5KOyy42EMhSeOLMvOnDnT3t4+KSlJmGZZP86yrODvS4ChrW+4T3jp0qUEQdjZ2WHEnCCIgwcP3ud+4SfBPsIVnDe82X7w4MEXXngBZwaLe2CYG18RMO5HBeKFtJ4E/oMWUCgUU6ZMCQgI8PLycnBwcHd3P3HiBK7KJxX6H6yX/3jSQp9g3VVad1m4a8WqhWfOnBk+fLi9vT3W4sD9JO4f7Ozs+vXrt3r16urqagGG/o+X7kkGnljgiQUECwia7zzZiFm3Z3vfoc8TDnZ2BNHH1et5wn3ZoA/j3hmPZCKaNaBnWA3PPLGwCLarlkv3nr36VUzVsj2yfeegQoKIohaAdq3yxJWbq34wncsr3H2k4dxVxIlWaBB41yC7uWlv6tzVuqx86OhEzuiApYw6hiYtGi1IVIrM/JMrN80cE+Ht6jpw8KDCwnyOsXCMRa9VWygzBqAZQCweTGR+IAAtYNPW6DNeB6J+zMLwgDavAMiif41aXYdEMnfu3IAePVxs7Pt4+b477NX0A0fJnOq0pZtbz2Yj54oUlP94JnfNHkNi5vW5m9UpV6BFA2bWzNAderVCo0ZG6DCWfn+oeu1B1Z5zmf/chqBYEpBMZ4mkfG1C7rwtBSt+gIIGUJOczgBmiq1plaZkNK47qNp6onDlLsipBoWR0xl0tBH52mN5Np+OUmTm/zhpgS71OkgNSIRapQWtCRpl1/cdyT56ipYpLWYTBYzCwlMWDSwUt+Yu2Ja/dCeUtCDVVAtCnxEXmWV1Bj0isCuoy5v25+w8DPUyoBjaTILWxNVJC75PurktiWqWUTojOq5r4eETIw1K0phRnLdkx9U5m2r3nYYWLaIP4/WxloYWfcvu1GvTYnLmbzVdLsMiniaWphme5mzmoKyl4Js915fEItawjuySlG1TK49fOxu1uHrFXijrAKWpy+Vau4a+UlGz5oBx17mKjUlIuJlDQpykVo/2PygWDBSozFxubcnCHTe/XF8dmwwtavQBBi2LSRpKW0tW7imdv710yS7Z4Qxo1YCRRt66GlWNCWkZq7dDnRw12mZl+b4TNUk/QWUrtBok3yeXzfm+6Zv9LbtPco0dYDJzRpJFmucIg+ZqOgq3HqqJSby17qDkNH8GmeJB+TJp1qwNNxdvh5tNPFJDgtoAOiNjNOqUSpNSRUpkG6bPGxaAXCkQIrsBf33xm63rr2Zf/X5dzOvPDn792cH/mDBxx44d8xctHDBw4DP9+n855fP8m3l4SYgZNsLQLLy/fzCAD2gyFkahUCQlJQ0bNgyP3ch3YkDAz16pN27cKJfL8YQQ7VHxLedea6s/mBmB+tDS0rJ9+/bhw4d7eno6ODg8/fTTaWlpOA+o9q3ycIfyxmO3zx8v0UPGYN0P47ouLi4O/iTYz8/vgw8+mD59+uDBgwMDAxMSErAddDqdUFjredpDJne/26RGSKko6BFabftxjncQFPCQtxXOI0BGGEXCusYIReokjetPtPlGsUQo3S3c/O4yBCgjX5o8ssMDOgiApgBaSenMXbe6hyptgjqI4UpRaL1vFGzIhA6+lxCgHwYQstbE5Pce20yMUtqFlgZEQQt/WsRaR1lPQ4kyz1usE41tsQ2CiFhESTYhyJwjGbTjZeZxNB0PgB4tbfaJVhLBzW7hMO8IaBEKJ3zuAKDxqRr0qxHg27Ra7zCFfUilbxgScMBu7rQAR4pvBoTKfaJrHEZffSoMjlTDRQXSj7Yf0+YYjOSDj1dCJw+785agb3slFBJ9cABrQN8GoBXEGCTMHRWDUHUtDzJmtBS/OKXOLaTRM+yc3yjYlgUXWpWRG5qdQziXcXrXSOMn64AEPb9xe5fkdACXZAV+YVKnsS0uEZcDwuEmB2nS/Gcn1zl+IvGKOufxEZzkuc86QHt1aOhlQUHDZXVDjyidc0STq7hi5GLE9eaHHZSEDuBUXWHPCGm3sDrnMOPs/Qj9bwE4XJrvF6HsMaXWPULx9zXQyKFhEQlDcKi7NjOgZdAVEpCEFxKmgc4xq2udg0jfiXU+4bAyBSGq+IMUnfitEWzTa211PuGsfQTrOq5x8FRoR4/jk1KoBcqh/e0Fco8IJPs7Ph6uk/rxWxu8Itp5fWqYn4IQVX4UM/K1jXD25Koyn3CjKKrSNRjOViGgX2gqjXpYe+am5yd1zuI89yBu1XGEySLwl4Za2jg1Dvnu6/ZxSUA4rD6B3gKGs7D8XIcn7eI393YxHvx/1xvHOzxAd/OoNA/Qcwh35j80TeNDM79ExwB/3IpC2ycGnnuPDIU6bzz/QU2fYsHEI84k/5LyNuARZT4a/D7gGPGePwWIdoA3IbRMl5dIkr4nuf6X3NwjdNshIf7Zuk8TwjxTm6PXnWjwCJU5heYGRkIdOoSEzXKPeO9yGdEChK00GVQO+aLC5qNbLkGWz7YjHF/ozqz6q65NjrtE9miXfj8A7eXlZQ1AEwSRk5PzaInf7W6WZWtra62X63jg379/P7b7gQMHMP1ZmBDMnTsXj0x3i+9hrzEWxtvbW4gT+z9MSUl52Of/0/fRNL17924h/xgV3bt3L54S/fZfoRELSlvClfsM2xhtwWAuVsrGYHRUVBQe/vG/ev6U3MOYhLEwYrEYa63MmjXLGs0RHqdpuk+fPng3QiggvvM+WcWPz5o1C/tjFB7fv3+/EPN9AoI18D34Kw4LmVy5ciWWixH4+Fi8xcvL62EUQu6T+pOf/lMW0Ol0a9eutbe3DwwM9PX19fT0PHz4sLWs/MO37f9UEZ6k+y+ygNAn3NHt4DUS5kviF5+xMFju+cKFCx9//LGHh4dIJPL39xe6Lx8fH3t7+969e69du7aqqurJUYl/UZU9ifaJBf6gBWpqar7fEev/bD8bNycPe9Gf7N3f6P7U2F5DjoTMbN52DNF78cqHYtG7T3PQrlceyboweWX2zI23dp+ADhPCNxH3WatOz89esAUuVtxKOFV6/BziwCJsiQWlWXYyI+XrZdWH08DEID1oHpxAbgktFGgMUNmaPHf1iXXbBvv39vf1/nr+LI5jNColAMtaKF7kGTGFaZbCWs+CBAdW4fhFWwOhHl3dmPCTNWD9CwOaBzsQz5Smu9h5iN3HdSoVMevX9+kRQBCEi439Cz2fmvzmiMzvExC71gDyi/l5sYcsZwvrd57Qpt5AND0dWryagGtWylCZJOqWhLNVaxLII9euLt8hPZfDr6gBGjWt36dkfxmTOTMGKjrQRa3BpFRBp8585mbevC3mPedy5m9R/5QNEjWwoNNrFAak34nQeaURyiVn5sVU7UoGiQ5IFl1UaECuaz2VeXFTHHRqwGJplraagTVzDGI3l7deXb7j3Ocr4UIZmIDUIg+xJE11zSopGhS6vLjki2t3kVUtwIBKoaD1JtCyRbtTMpfFQnkb0KzGbNQr1KRcjda9ChPk1Retjk//fFXbrlR0A+ZeocPyHNSrycSs3Gnrs2du1B6/DlI9WDjKQmuMerS4MzNseYvkxwtHIueiXwGU8k4TRaLmUdJ2afq63HlboVACcjPTqUXSGTqSvFpRvjZBsT21bM1+tqgBLUQBNGYj2gWx8G1Hy0CdpmXbseKZW2q+SYDKNp20U2JQy1kzGmsk6rrYlKK520qX7DKcvIEAAgCLQgtaWp+eV7R+P+TXQbsBbrVe2ZVYfuQnqJdDk7px94mCad+1LouXx/8EHQaLTmeieEVvAwkGEtRk1b7U7GU7rizY0pBwBsElnTqQGy25Ndfmbr40bS2UtKH2YCDR8t7MIOEO/OnUam6Wn1m3/fz2fVM//azPs4GEl0jk6x72ySf5FzO3L10zZUzYi88MeuWVVzZ/vyV+397/e/c9Txe31/76alJSUkdHh9mM/EkKn644//B/eIjH28OMhZFIJPv373/++ecDAlDLt7W1dXZ2Hjx48KJFi/Lz87H3P2GRJWTmjnnCH8lUTk7OnDlzsMSira2tq6vre++9l5WVhXOIpeGEDNwLfX6M+fkjZXmkZzHnTFhzYQ20goICsVjs4ODw0UcfffXVV4MGDerTp8+OHTvw5PxfYX+U53YTLEmpdg9pdgtte2s+AuZ+/emCw7oAK9Tbof4dUWJN1N5LDb3GUTahjGMk9f4K9CIIdwsQtgkgqyW955gau5G0S7TSJogOmNLmOw4WnUQETDMfHX6KApAYYE9WpWeoSRSl8fkUpsQjwuZtAnYXHmgCOFFc22eCrJu41jMc1vIUaQZoI++YFMHHDDrUj8SdaFj/U6NPVIftJ5W+ERCfBwp+bALQ6g2/ZUDjPUuUHAnw9f46txCpzZiygAgkdmzhGbhF8kv+YxpcQ+rdxTefioCsNvRTIwvfnKj3jZA4/z/23gO+iirtH78kpJJqQghFEMuuhfd10X3VdVdZfF3LSgnpkACCwiKCICgIiFSBGDohSJUSaQEpiUAIkAJphPTee25yc3P7nXZn5vn7zEmGayiC7v7V98d87ic5d+6Z0+bMmXO+z/d8n8As19Gw4xq0oko2keCQpa1/3Kg/9U2QaKdrExrcg5WKUU3eEzrn7EJOaxsFrUL96GWVg8JLPQLyn5gEJwqhkUf3j3m6on7Bnb382hSjCp+YDAYsgoyg/ig/PUCCssh7fJvT+FqHwIaXF0IG8K+vqfYKq3YYl+8TAgezoVGS12DRjaxoZtBO2c5AfFN93wmdvQPqXAMbJkciNCyDl0aA/dn5PiEtNgHlLsGw/RJUC3CDrnllYUuf8TW9/LIenQwp7UADx+EtwASlHsKyLEVR6NdOT6MQ8NHsUq8go12Qxm1C45/nQAWF94Icli7IGL9ZRKg0qJ6aySoCRPsJ2Oz1OGORmNKAMGsLlA0M09kH1fUJgM8uwudJ151GN3qMT+v1Bsz9FsosYAZOY2KlGiCmqwfYmlLo7Ace76uG/guyWrpMDoiti1DNZg4Nr3cLafAcf/2JyVBqxJdLhwhVHPOv3bn9Qmp9JhQ/HKabtRN5ymakk8qDkvzYdlfjPv6j/pUZnUCgALqEIxMsmhiBGBAYAW3z5FHr1GlRBZtM2+RMLOhaAKn+xGJDGxgAACAASURBVKjcbX7hpYoj11mGaKUHkSSIVnwLaovJyaBEBtkVQVwIyk/3zRj3FpIBaCkFuXGsA/jwtvLG+ftqnPyULsFlI+ZBiQF32t2pP98hZ/QVKvdQDTDhm1u8JiidApV/W4CmL9IU8niFSm/dnzskeO+nfz4AbY0+E3Tv2rVr957xnWKSd2dwcDBx7yav2MeMGYO+xQ0GeQZAmK3PPPMMDoPWPeBOSd/1vF6vl0myhM3aq1evCxcu3PWi39CPvIWPiIiQm4sA0FeuXLGelFiH5X4sA9BEjZQAKGR/mTw0yK9/lmU1Gg253TKt2M7OTqPRWO+Dky/s0UCEji2fZBhm9OjRpMy2trY7d+68rcAux3Genp6EmS73OoNB2kkk277kRK0CgiDMnDmzBwM6OjraKsrdgnITyYEesSmKysvLGz58OJmPOjk52dvbE+mYdevW9Yj84OtvvwU0Gs3HH3/s4uLi6+vr4eHh4OCwfv16Ig4j94E79e3ffu0elPA/0QJkTCNsLKLVw1t4649Go4mLi5s/f/7DDz9MVHqIJLSNjY2Tk5O7u/uwYcMWLVqUmppK1rG35UTL3e8/UYUHaT5ogQctgOsRC08kRDmOIxOMqqqqWbNmPdTX27aPo6OtXX+F3QjHgXMfeyX67ffKD8RBs0ZrMnTyNK4SGWmfqVFgrhRmLt95dfG28m/OgsqIk3VkLYH+bEbJqn1w5Jpm77mUqANEIwKJus1a9fdpcZ+uLf7mlNCKLCbRTIlmSjCZgbOARTBXNlxcs70t7uqxTdsf6efr5eN1+vszqDzAcYKFJ1Rlsu6yCAL5yMOFjDJ3UXvuCkDLV+E7Dtc/iFYLFv7mBmxpgWfSG2b964O+Tq4jnxr+3MOP93P1mDt1Ol/eDBUdpVuP6b9Ly9txvPb7VKFFw2kMxLQmrfYAOo3V311p2BwLR9JSP4/SXryBxOdWA9Tp6nafrVq2r2hhtPH0NRQatggWmgIjTWWWlC3frd9yqvjLva0nr0CLRuKa8EYLxXA0WCxI6KtRXf1kffWmI2gMEAFoBhVLWCg8En96SSSTUwEUozFqNZwJl3IWEVr16V/uPj97DTrQazaAibUwLM+wHI28Y/Sn1KYr+y4xMWKXUNyIgKkgiU226kt2nsxYs8eSVQlKPcfz6L/RbEaQiQWoURWu3Js0dQUKZeQ2It+N4pFTbBSgTEXFJBdOWVvxcZTmfBZyn2mO57gux00cDyqj+WzmlTkRDYcuQE0H8qxZjtMYoKot//OdeZ9s45KL0dGfgUVWl5ZRJ+Wmfrqpcf2xqo1H9ZdyiTYID6LZbEZStp7imjugTtux9XTZvCh0PJhbj4Q5nu0CHVoMjQfOF32+q3DRjvq9cdBs4A2YI+jZjoyiS9u+YbLLQWmG0qa0vUevHz1jaVGByqD9LjVn4dai+Vsq1h3AdjZRDENRLAWchGG1GptiEmrXxuR/vrN03xlo0oLagJTA4qasdfsufPil7uQ1UFG4ODfTEr/MAjRj0mmBFaik/IsLI69vOwTVrbrm1oNHDr3lP6q3Q2/v3g4jH38m7NW3jm/dtenLdUOHDPHu329cQMCq5SsWzJv/p/9+9rHHHvvggw/y8vLI6k8W8ftPDGWiiM1bWloaHR39xhtvDBkyhCxb7OzsnnzyydmzZ584cUKlQi0dIqhlrb9Hll1knXXr7JEArMgh7+Yvo1K6hI9UV1efOXNm8eLFgYGB3t7eTk5OvXr18vb29vHx+fjjj9PT02WgWRY+tn6Ebxv+TzTOfzpNUk3rXH7YNavT6WbOnDl06NBhw4ZNmDDhueeeGzRo0MqVK9VqtfUa1vqqXxpu5zvfXFbZ650GzxD4cC/ogBHu6O2LwDWYI6EXJlVkuI4y2ga2Kd5sGjYTmhgcVEmk7v8gADVzT47N2+32Qe0KP3h0TmOf4Ca3UM1bKxFRNUrAFrlEEhpun7ip2mFck2JsZt9AON/YJdNB4CrsiBKqtDWh3neS0in4xqDxcLYKYWWLBKSRvwRktgA0QWvoV5W9Rqts/PMGjIdsE3I5uw+5pDIG1QVOA0C1oebV+TUOY1t7++lHLkXpAxQSgYb3N1a6BTT2Hpvu4w/x1aAmCrYAcYVXnd9q7D22zjsUPj8J9cY7QL/ded/L/xYKZu5tcg9uUYyq7x/OfnUa8fQ2EXYn5fUNrHLxR7mPiLOoumCW6m4EY/DGJs+wdqeQnIfDIP+meEvP3PQAZ5tLvMa3OYVVKsbBxP2wOr3BLbzJZXyRTyisk+Q7iCQ3aRqGl8SIAFafL1S8oVaMLXEcrfv8EGYtyevje9AIsD013zOwQTG21D0EztVBPcCihHrHUMrp3Rqfd+HbXLzd3U1M4D65YGaGxl1TDWx94Gqtcwg4hFd6BKIbww7pEgJ3Smg6LWWFuHcHmF9dQin8wWlivncgVKMQVhchW2+Bq8113mE6xbhW11DYUqWy8W9zDM5396en70TitqkLeLaQEnGYWnvAunKncWqbwNrHp900w1hQzcO0MrbQDR025vb+Jyz+Dn9tZOCSknp7Ta1zYLtHeOXQyZVjv4AqSRODwyGqC/PttovfOkLKdb9TwGg20zxHQFFi9SHoM3kIeAB8rVu5OrMGqYlemTTbkeYGPzaDWAS0WBPtEbP0nieGClQws3Bmpmvji1wwYrDHCYN8WAXlc/caIFW6S2wzQIPYERpR13tMU59A9bRtqEMCYKCp2xtU7pCUIN1kmsDWOoCVZ2s8gnT2QZWDJ6KEi4yky8+/jEHfIcF7P/0zAWiapnsAggqFIiEhgWRs/ea796KQmByH9oTjx48TO7OMqDo5OeXk5CxYsICQo2Xt3fj4eDQTEYPG/WZmFb+2tpbkRWBosm/63wKpW2Xynw0uWrRIFscgd6e0tNQadLYOy/dILhMBfwmbr6amZsWKFWFhYRUVFfL+L7SbsazRaCS3RlZBsbW1lQHrW5OV0ye3icRkWZam6dGjR8tUdxsbm7Q0ZH/ceoii6OzsLEPPJNDS0kJme9YjS49rf2AuTJs2zbqj/kDbiYyM7BHtTl9JXciv1mE5viAIFEUJgvDmm28qFAo7OztHR0ei9Dp16lTSXHLkB4HfbAsQ+0pHR0dERETfvn0HDx786KOP/rAHYsWKFc3NzeQ+yh37Lv3tN1vBBwX7z7UA6Rjy0EqgZ/KVrC1lMLqkpGTdunWDBg0i4+cP5g1ZG1qhUPTr12/GjBnFxcU9xCXlkt92CJJ/fRB40AIPWuCXtwDxZEVkxLKzs/38/AgTws3D3aO3459sPD9+5rWDoz5InBvBlKE/NJVAt4k0CimgLqegTcrLXL7z4px1Zd+chSYNcoeRm8pASUvW59FwKke15WT6F1FQ3Qo0i/hyu1bILD/10cqCXce50noETyUAGhgLLopEgGZ18q6YplNXoKJ14Qcfurg4D3186PWc60gXsPBIT+Y4kcf1lTXr2fptRTDomwA0wgn4u4xNywxo66sI+tz1V96ALaBOBQBkZ2e/9tdX/+jpOzf8vef/NHzk//yl8kRi4YYY1e5zBZGHru46yrQgP1AE6ORpibongpHuyChKXr2T/za1cePxlpPJ0Ih6hVDWpj58pWL1gdxPt1lOpYNOBB4Yo0EwmTsyCvI2HeS+uVS8ZEfLd1egvg0YlrMwOtqAu50lBpNY2pC0antp5EG4UQci0AY9QZ/rv09NjNypyyySPMUzBsZECRJNScuXf3P2yoKNulNpSJc2StCzxPLmdEagOaCE6riU82t3GK4VQzOSrEWahU6mPvby5c+3MlcKoR2d4LEgIgDN0Ejm1bIle08nTl1etWwfos86Hmnsui7ne9zJjJyZ60s+3IRS4E2YIGvhkLdrZlDyQm1suJCeODeiY38Cos8aM264ZkWhtClj3d70WZHiqSxEn00sQuEiQG59zpd7myOOZszfhHB2i1aQFsnYE0ySYKjWDG3Ga2t2Ny3aWzxzI1KqpQJLXiwBGrWqI1eyF20vWbG3bucZVE0x8xaGtejNUNNxZuXm1tQb0KqDBm36toM3Dp8GlQHUeqG4vmjN3rJFOypW7IGcBtB3oc8cQyFvukHTejChZNmemmX7GrefQi68QRKcadBU74+/tGCj+tQ19MDJCpyFQZeNLMszkvHATBvzKtK/iLq6cKOYV411N5rra6vLi4sily57qf/Q/3J46Ine7uNfffPE/piL5y988NEsH99+f3z08eVLln6zZ29wcLCvr++zzz4bHR2tVCqRSi6xoX/5IGCdgqxhSJYbZrNZq9UmJibOnj3by8vLycmJLBs9PDxeffXVNWvW1NfXy2scMgEg3h2IcZoQeHuA0dZOIHgLX1NTs3///vfff//FF1984okn3NzcbGxsbKXDxsbmtddei4uLq69HowKZWpDHVgajrZ/iW8PWVfu9hEktbi1tbW3tmjVrvL29Bw8eHB4e/tprrw0ePHjSpEnt7e3EfHjrJT//jCCCEcr/MFXpENA8aDJsSQY90Dxq6d726DpPaIw0BzXGTN9AnX2QuXdQ0aAJRHxABqAl0NYCBeqCx95t6RNS4xECn6fApwl5TmOqeo8tGjoZSs1oxST75HmJhZprrhg2o8M5tNk1tCUkAkpNNzm20sCLCKYW1B/tbnwoTOk2/uoz70I1D52shbHgq0pS6uAJOmZC3d5rT0xstPFr6e1f/fJ8KJVYvd0Vs8ad5DCORSz6x8t9bGKzU0CrazAsPIV04E6AfWnJD43udA2tdwuClSehnkaqJjnylFl9/XV9Qjv6ToR/7QVlVzvdqRm7i3DX/yqef39Hs0eIUjGmakAYHMkEpQgVXNnrC0p6vVVs907t+DXIQeYA7XOoOgzivJiqfuEt7uNzBo6Hi+VdrO1bM9EDnKgp9ApV9ZnYoAiAmWdLfCZW9fIvdwlm/rUbhT6k4+a95tFvLTRyfOimFudAvV1QoZsfOn5U0XjvROkWmQAiE4rcA1t6B5Z5hML3dZDHKR/9UGMfVqp4Bz44Au3Adwv1E3Cb7Gm5WToK4HzlFbe3DYqxeoV/9f/MRhGPLkRZuvdSYxsBcW8E+DuExj/NMtugE8hsb3/Q4OuFJoCslofThRVuQSZFYKtDEIzcqFS8qfOYlPXsNCgxY5qiBNmTGmLtAEpMGYPHN7iGmPpPE8ZvRQlpUjIKoB7KXv+s1jmws8/46oGTINkMpRY4Xlj5+PsNjoGtvf1LXPyFj/Yh4N7JS0xhiW7MERmrm2PVzZreQwgHT55nRfR+0dXJSB8lUDIKmPD4jmat7C6dZjDQwKH1iCPAOsGtCcp+MyGr7C0issVpyahsYNDoq0Ujd9eHFqXNBDxwP0K68frujm+V1j0HfxKANqGMdcF/vd9m59/kHqz77AC0oY3DzKEKx30d3UOCJBGzJ7PMM9DcOwilXbJbgJGsSvKTTwI/WbZ7y/5nAtA6nY7IDVv/PXr0KMn0ZleyMjvcW3lwDkFeq97e3tZwqkKhCA4OJhifDIAGBgYyDEOIY/eY/p2ipaWlEWKvo6MjoQ//W6Sl75Tdf+J8DwDa1tb2JwFo61mRXKTly5f36tWLeGL84osvrNnlBJ4mYKu1hSA3N5fMz+RbL6d220BqaupLL71Epm7EoV9ISMidkBcAIFKq1hh0SUkJgQJvS5ommQqCMGnSJJnYTlxWLl269LZF+tknBUGor68ndXF1dSV+IB8A0D+7PX+VC/V6fXR0NKGZDB8+3NfXd/78+cTIQTZYyB37AQD9q9yg32ympGPIALQMPVv3ExKHLDvJqumJJ54gwJaDgwMRIHJ2dra3t/f09JwzZ05KSorBYGBZlrfw/0FNw99smz4o2IMW+FVbgKKo5OTkESNG2NjYoFHZzm7gI4N9nN0++tvovSFzEj/dAGVIC+3o6NDxlAFXIQBqvTElP3PFjpQ5EdXRsVRhLcryWjjkj9Spk1dEG44kW77LLNxwkEopgDYtrkwMZrakLmnRxvwNB5iKBkFvAIYBnkfusyhJc1Qr8/edLD/8PTR0VqdmvfP2m4reimH/9XRZeQnxzUWAclRslradygLQ1m+rnwdAyylYI9E8iFoLbRA5A0tv3R7lZO8w7IknH/H0effVt+M/jazdeEyz58K1Nbu5RpXBYOikjbj7FlitBV3ndeZWZG2Joc9ktu44VbkjFpo1KEJa2aY9crn0k201S3Y17DyFSsSUtOXTTIPaVLDtcFPUydr1h2sPxgsqDcsj9Nxp1ploiZ5HoTx08cZDSQs3cDmVYGJFluHNZmjX0dfLrn61u+X7q0CjTDZNm3mOQXeOzZ2Gb5MyP96ojE1C8rWEPuNuXEFEWq6Zg0atIaUwfuU2fVoxqmp0GEBtxFX3jfrLy6Lqv0tC8i+NazwLgMGCG64tTR3aizfOfbQm49PNzPc3EGPgENIFIw3NOv3p9IpPovM/3KA6lgTV7UChsjYlcBTLiDozNGtV5zPjPoloOZwIZW3oGFBySMiWN1VGfpsy/Uv14SvQhCg5+iqkOWg1NGyObVqyr/LzPe2HLvINKoqijAgDs4iSmzn8NGtaYpMKl+6qnhdtij4HFe24WuZF/KmN0Xx7JevTzdmLt6FciVLPm82oG67TQ6u2cufJgo0HobYdmrXlB84U7fsOGlQoaF7cVLXtWMWKPYg+X6tC2VZjFwCNTdpmhNSy+pUHm5bub9oUCzU66NQDxUBNm+p06pWPI8xn06HTJPIWDgQGLKgSw9EszwDDQlVrwheb499fKl7IAT0tUEj8R4o0LRjzKtaFTv+by4CnbT0ed/Z61GfAquUrkq6lbtqy+bVXRgx9ePBfX/pLZGTk58u+GDJkiKOj45TJk1NSUmQtrH/j4CED0PI2UGS1CugCsaOjY8OGDc8//7ynp6eLiwtZPw4cONDPzy82Nra2tra6utpgMFgvoOSCEYp0R0dHS0tLbW1tUVHR/v37p0+fPmzYsH79+rm5ufn4+JAZQq9evVxdXQcOHPjSSy8dP35cre6SerUumPy0/mRALsD/jQBN06dOnXr66acHDx4cGho6fPhwb2/vKVOmNDU1/XsriBQ3DaR7jmnvE1zsG4IO33SSb767A0xdqI0Iemj62yftvf3NDiGZnmOhTQKIZCiHQpdo6mnbK73Hl7sG1ry9FEoBLnZe7etfYz8uw3UMvftS1yZ5gpFpAHZer/YMNTmHN/tMgl2pqLTbhaVhvTF1C8r7Zo6YU+8S3OQZVh6wEuNoGIGT9nNwIArEiAe4ByW59cZQ9BpX6ThO88HXSH2VrHWkDa2hJ/kM5sEAFKoz+/ornQKr3ANhbSJUGKGGKxo6sdM1tNXenxu9FqqMwEkeF8mVTUyObxDdJ0zrEqoeuRh1OaTjJl529/bsin7zKlYUwAB0+OY2zwlKm7EFPkGQo8Jkv7pQ7Buie2hilvsYuFaP+rwEDUSjKMC21LKBE1V9J+f2DxX3p6Iuczfj+Ec5GACOFF5/KFDrNllnNx4mxhbYji5xDkjo5w+VDLabBDCS9sELLRIiWaBN9xzTZutHOU+ofGwKqKRIkjQ24t8/eIn8PLbMM1jjOqnqoQmQqNTNO1Dv+269Y3DawPFww9zFZJfKQRBSa1lvPN3GcB/trfUMpnsHt3iGGpYfQd+Dt5SfcNwZjoVmJufhUINjiME5tPip98CAUtU0L6lt6cGy/WKJd4jWNkhl4691Hm9wlMjdV5uxTUjGXSRhqYlaefOK2GLf8W3uYcUeQbAxCQzdALQB4Pv6TN/gCruxdX2CxDGRcN4AUw4W2I/ucA7V951S9vAkWBWPKihmQPQWfXSKKB7FiChc1mUM+VHz38cXTE3oUmFGoSfp0+UnUAJViXvAJhZ9Y+okbN4gdE02unU6cB4neZS46ViUFVHNmXiYRJlv6UKd5M9QK33V4u2ARiP+ZJSIxDcvlop/P/35p+vbA/Y1ApQJGf0CtI7Bda6Bli3xqGotooHhp5O6UwwjQHJbrneAyT640tkP4ovwMee6t2nIY0GPktwptZ86f98ANFlXq9VqGQUmGDSRUCAvaeu34E8VoOfvshrmtGnTiKIugfacnZ0VCgX5S84oFArZ9+Btl/09k77r99OnT8sZ2dvbozMMR0cZgbrrpb+JHxmG2bZtm9wyDg4Otra2iYmJPZAR+at8j+T9TaIoZmRkPPXUU4SVTGY/sbGxpHokPgnLrg5lbHfNmjWyl0jrmLdtms2bN5PikdI6Ojq6ublVVVWRyKSEPS4ketPWAPS1a9dIZ5NdkfS4hHwNDg4mDi1tbGxI4OOPP75tzJ9xkmDfFEW1tbUNHz5coVC4urqS5+KBBMfPaM9f6xKWZXfv3j106NDHHnvs+eefd3V1nT59+q1uteVH5tcq54N8f4MtQHqFPK6SwJ3GQNnGVlNTExERMXr0aGdnZ1tbW7LIdHJyImY/sog6ePCgUqmUe92d0vwNtsmDIj1ogd9RC1g/WR2daoPJePj4sZde+autnZ1TH2dnFxfvh7yGePSdNy78wLRFmWv30tdKoFWPAKLAcwKL6321nsupvL58R/KsNXXbY6FMCUaWMiGbtbOsNndnbPO+c8zpzOJtx+jrZShNoKeR09pmuLbpm7SlkkiCgeIsDMdQZj0KFmPrVbXWHjmfu+EAFCu56+Xfbds14pW/KWwVz/7XM8V5ubhTkGNZC8dauC7lDcn9oCz3LI8bMjMap+6CtNK7Bwa0fHnXVd3aHSaeNQNvBr5O2Tzi9dccFb3+aOv++f8G53+xqzM6Lnv5Lihq5jSG5k6VGQQaEQ8zbaagVZe142jdgXPKmIsIfRY2QLsO2vSmcxm5S7bmzopoiIyBsiYwmCmVWlLJ0N3Yeqh+y7GqtQdqd59iCqsBndUzSkanpfTA4XpbqGyqiIlP+XyL7lwGqHUMQzEUCmKYr5clR+ws+zYe0zfoupbmIkBjJ3cpN2XGmvI1B9E1Ig880yX6jK1t5kAvUEmF19btaYy/xte04U5nM6IbcKM2Y8XOppgE6GRQGQPXtsgDx0Wenmm+kJG0aHPih2uQa9ygA47X0WaGonE1m12bvWDbjalrNNvjoEENLC9QDLYGQhUC0qvz6s98GlF3OAHK20ArIciMyJQ3lR+IS562unHdEajRYDpmycKh1Nd8e6Fo3rayudtUu8+BkjZp9a1mncHC4I5jlsOVvJY1p5UUrN6XM3+rZs8FqEUdDKRa62lopyCxpPzz3enz1hdvOaxPL0RtcQCGNgLF1xw7l71hHxQ1QWlT9sHvKk8kQEkDtBmgsL5q27Frc78qX7sfkkqgVoMIu8EsUBRqpBgoS3pZwYo9xR9vK/wkikvMR1DGItKNyoa45KMzl7bHnIN6NfCcHigzsDRwtIgANLAWaFBlRe6NfW+RMS4dlAaGMiOjjGMRm6hVF399/PySDVvCP1z3/tw/D3jMVaHo7+oZFBS0a++eq8kpcz+aM+ypp4c99XR4ePj69evDQ0IfHfjwy//93IbVa+trawnjuMf4Y20P7vHT3b9a47xyTBmM5i28TqdLSEhYs2ZNQECA7KvG3d3dzc3tjTfemDdv3sqVKzdu3BgdHb27+9i1a9fGjRsXLVo0ceLEf/zjH0899ZS7u7u9vb28fJDXcb6+vn5+fmvXrs3MzGxvb5fluRiG0ev1pKbWj+pPhuUq/J8JiKIYExPz/PPPe3h4jBgxYuTIkS4uLhMmTCguLv631VGUsOYqfabn2FbHgBzfIDjfgCMDASBvmw0BaGQ2pR7g/Z0VirdVijH5nv6QgV5DETQkEXQAF1qKh0zqHPh+jk8wHMxA1LIOSl7/DLHjh0IyA5dCE4tAGLmkA+DdnfTAf+n6hBU/PBGut+NWEk5C9LohUfzaDPGDxjU5B9d7hRlWxUIrC0bpzSJ5qOMln4WIW+oB9mUXPBSkcggudBlHrT+L+N2tOBqpkQSo4dBHxHG/Lyn2Dam1HV3SLwSOVEE1GObtrXYc26J4J8fTD+KqoZOhBLTYkd0A0AGZXn7m3kHtitEFD0+AJh4o/PXmcZ+AHZp4aTAFRaq9wtvs/HO9A9ChXxtUPfdhlYt/+8NTYdZ+UEpblEgeIoCKh9jyksGTtL7vFfuEsl+dxdbmuoHUm0WRWmZ/Tranv7bPRN5xcqddaJvPlGteAXCogMDEDAhm5Csj/RZbkkFDArXoUMPgyY02Y1BVee63EpIr4ZqEAW0Ecc7BOo9Q7qH3WtzHw7nOq8+8W+MzKe+hENh6BVnValkuGotEcOQuQJHcgg6oeP7Dxt5jwWNKrocfpNaQot8edNTRUGm+6vK23mVCtf2YlneWoZS59P7BkVwPhuXHagZMUivG6e1COvuMb/CZCKvOIUZMeNekf4pgIbcp3xDnO7bNe1KDc9D1p6ZAnhGo7nbTAnyZUOM1vkLxz1LFP+HTC82PTVc5BFPuk6vcgtMGhaAHSCNAOxrXGWPXRh/EoFE0WZqZWLf8/YYZgBYONwrsugw7pM/Xl2HXZXFnouXrBEv0BWrtCeOyI53z97TO2t7+6R5jxAmIuQYXi1EkRCeh1bjDAEsizaCk7Ds5yFPCxQp2xwVL1Hlu2zl2azwcyoD9abAvFfamMJGndauONi/cUz0nqn7Odv3aWIjNgox6tPRQtzxB91uj28aXn0ECBOsALjWXPz6l0zGo1MUPDqTiOGDBzW14tdWjJOPGt021KzKJb0JQO93Hv8MpqMhpNOxPxc6AJOgfY9CkJHdM7l5/+JkAtE6n6wFA29jYrF69+rbv/nsti1U8QRCKi4vt7OzkLU5kCxL5S0QVli1bRsY18lcGUq2SuY+g7MHP0dGRmLIdHBz+/Rt57qNE9xeVmIIJlkHQczs7uzlz5hA6uWy0JwFym2Ssn6bRM8nMmTOdnJycnZ1lbY3XXnuNoijewlMUZT2B8/PzIyRoe+lQKBRDhw6V4xBVL7GBnwAAIABJREFUCuv4ck0SEhJGjx5NoG25/9ja2sbFxclE5tveR6KIYk23P378uAxAy+nfGvDz8yNdyNHRkcDlEyZMuDUaOWM9e5PPcBxHqIjyGXn2icsWszk/P3/kyJFEoI14I7SxsYmNjbWOdqccH5z/VVqAEFiItobZbD569KivdLz55psuLi5Tp04l6LMsnmC9COmx1fFXKf+DTH9TLUDGDVIk6/CdCmndnZKSksLCwtzd3WWpemJmI2PdW2+9FRcX19GB+9kJvYthGGuTmzxk3SmvB+cftMCDFriXFtBqtRZB0FPmjz77xPePjypsFfYerm59vWz7OPZ3dj81f+35GSvjZy7nUgoRQaZRSQA/ZNmZXV34eVTRnPXFS6LEvErQmxmjwdChBi17/etj19cfgIT8rFW71RezwUQhS9fMQ11n+ebD8TOWmS5cxym+ieY5xsyYUVcXRKAspd+cKlz3DaTXQlLJ1eVR6Tti3g8OUygUzw97Njcrm+M4ysIiaC2IxO1Nt7YnLj9k1FiW5ugal+4KQMtQNUlBHlvkANKUWEHT2s7xPMUyUyZP9lLYjnvoyax5myzRFyqW7mEvFyJxGGlegpljUIHEzPGVLVfW7lIdS1LFJp9fGQXVSmjXg44ypeYVrtpZsjw65YvNgPIjUmMajdCsbtx2rG1dTHPkEdTWqNeCgeZAUIlmFas3cxSSZ2vbavae3u7/r/KTCWCgVIbOTlqPToZaNWkbv2mPvwZ6mmdoE0+jVDRtQWWPw6kJ4xcWr4/hcqqt4RVctzM8qFkuuTjrq/31sZdxZW6kJUAH4EZTyicbS7ceg3pkZ6OvQgHxd4QbBIDCxoSPI76ftrzzSBI06sGAfqKwSxgYyKvPX7g9Y/LK+pUHoUAJZtbES2LTJtqo0SGvKr8lc+Wu7N2x6K/PyCHbmgVoMqoOXjw/Y2XxV4cgrxEMrLFdjdhGO9W6/0L5in0ZsyJVe89DjRpEMImcFjgjzxLmOzBCa3xa4kfrCj6NQveYrXriPog1UUKVEm40lC/elT93c8oXW4W8aujQWjrUWA9VZ/uxi9nrdunzy0CEypPny06cM9Q3gN4Eter0VV/nfLHj4pw13NUiUOoltpqAyDVtAYo1F1SlLd1eveZQ9YajpvM3cNVNCaBn1OkFRz5bVX40HpQoOSIILAMsI9I8cCpdO5iM0G6q3Hr4TNgC6rtrQAksWNqBrmc02PmV2oao2IJFUYkLIpvjU0FDndkXM+rJP3soFC629s8888z8Tz+5fPnyoX37//mPNwf4+v7txb+sX7Vm7SeL33rq+RGPDgseNTYpKcloNBLeMVG36CGRfC+jgXUc8r7ueoKsf5BgNbLS4S28Wq0uKipKTk5esmTJgAEDrIkvZJ+Th4eHl5eXm5sbsTTLS1qyr5fQnsiy6JlnnpkxY8aJEycKCwtpmibCHbcauclctMeMVH5abxv4cfF/x9/ITZGn6FeuXHn55Zc9PDxGjhz5j3/8Y8CAAX5+fjdu3NDr9YIgyIb/n1lh5FcClOmve45tdgpI6+sHZRJ8i51bws7IXxkekh2ISaCgkWMQetuaVOoR0Nk7QPXI+8b1p6BekrMn/uJ+cNA3+evy3mOq+gRXvvwpSgB3ioiK7kit6zex0nbMtT9OglQUA+wCGevYGz7BSptxyr6TxPd2QjOLgxVBDLshS3wYU1oTPN5p7xNa6hXC7EtCWJm4vZViWiS+JqK/HTx8drrJIVDTK7C8fzhcqkYglaRGKoIyuhIftpuLi8VgUeIDohOr+4e1e0zIGRgCGQKcaEzu81aHWyjCYevjoZlGSyFpdEJxVYPm5YWdilFmRUChdyDWUUa65da7n5uEe03MUPDMexqPMKVLsPalBVDIwqZzZQPDaj2DM/8wGYo50HfRvbtYtmoR0owFgya1OoQU9x7LzD2ImLXUhF0lJe0soM0TVn9f7hGstgkEh4lGRWCFS2Bd0BqMLw3zFALQKBNsoKXvFoALDdd9A1vcQ1q8JqQ/HAwFkiXSIiDGykvIoEbUB0WoXEMoW3QgCTNOZ7uMLfAIVI5ehcRzSYi3q8Wk0tykVxPQX8NAbkeeb7DWMVipGGP+32XQYh39x20n6TLDlvP5jqPa7PwrfcJgWyryn0ksowg6qAqNaPKcSCtCzbbjGz3Cbvx5JpSx2FWkg5CDEYU24Q4AWHKyvm94k+KNDp93mdUnod0Clu772wGdb6zQuYY3K0bTrpPaeo1T2fi3KEaXeYdWvBsJpToE4tFFsHTH0XECDyyPngPJQ9SV4f3/IxD55ZKUP4aVeQcXuo6VP1W+Eyr7hZb2DS71CirzDq7yCa3rF9Y4YGL9gInV/cOKfYKz+gWkPTYBDmRhT0b2OqK3OJ4zArSxHauP3HgsPNf+7SI3v3zXsbmuY7JdR1cOCq/oP6HMJ6TEO6jYK5B8ijz8S53GlDmOKe/jd6NvwPW/z4G0RpBcTtx/fXpe8aMO0ON51AB8X1swJKy1T1C+ux/EFYOGwweTF4GTHCpaJSaNEHemRsuAshGgCs65vlHdx/+G2xhhyzkE6BnJKQiJQwokx7fK4mcEfw4ATaRvZQCRLJV79eo1e/ZsGUb8GUWRLxFFkcwYXnjhBZkkK7+tbW1tnZycbGxsmpqaGIaxfsvKKfyMQGRkJMlLngfY2dnJEO3PSPD//0uysrJky3mvXr2I4kROTo5sNiczGFIwAivj26ejY+HChcT2TrwvEhTVx8eHCGsQmNW6OhEREbI6Sq9evUj4nXfe0WjwnSrNOG+OibyF/0HuOScnJzQ01M3NjQDcxFOfQqHw9PSMiooiWC35e1vk2t7envg8lDHobdu2yTiOddl6hIOCggjeLaPef/3rX3vEIV+7LLTSnJI4lb5tSayvzcrKWrx4sQz3kydCoVC88sorpNEeYNDWzfXbCTMMYzQaycT98uXLTz755MCBA0eNGuXs7Ow/zr+trY3AfPLslognyAuAf9eY89tpkAcl+SUtQPoDScE6fKc05YGLvEkZhklISAgPD/fw8CDWMmIqk5epP+zMPXHiRFNTEzEHEntYj2XnnfJ6cP5BCzxogXtsgZq62o8WzO//xFCFo63CVvE/L7/kZO/wzt9GJmzbf3HG6tQP1mpOJkOtChmpLAuIbNKgo6GkpWzZ18UffqVctR9SSoHiGJMOvQi2qtvPZWSu3Ws8mZa9bl/V4QvQomV5Rq/VgMqsPJwQP2VJ656zqJmL2oK0habMjFkQLMCLjVezLy3fCpeLoUxXveFw/uZD5utlkYuXo1i8d9/z588zHEtZWBrVD6V1k7SAkjDoOwLQXfTnO2tA/zQALYhIWGMFs9FYmJ8/4vkXH1e4fPmivykqvmHVIfg+F9Qs0LzGqEfMheNRf7lOXb0/vnrTMTE+5/q2b9XpRQinGlkoqivZfLBk5Y70ZZs7M/PB9MPOZB4sHNS1UglZTSv2GSKPNW//Dq5XghbX9pTAdHAGDWcSLCxoKCql4OysleV7vrO0qEy0ScXqRQBTLfrNq4lNgNp2kaaNAn5EvEc8pFUVfbw5fXYEf6MaZTqt3AShl0WNGZrMWev21R29CJ2caJDQBLUZSloK1uwvjTgEdXrQMLhg5hGARiFsi8iWNKQt3X5h+gqU1yhoAD3DGSmcA5tZaDIUrj2QM2tDzbJ9kNMM7RTDsTpc1rD4q5aGem3uuv2FW45YKppxuctKMos6MH2XnvvZ9oIVe6j0UrRz4D53Hpq0TEJuyeKd+fO2Nu88C/kNmAIvmkROLwHQaI3Q6tU5ZUWbj+Quji5bexCKWiwMawTBRFEYuVSVuzi67vO9BYt3QGkLaClRpwOjCdrVnVcyLi38ClIKQW1I/+5szv5YqGwGtQbUutK9311f+XXSwg2d8Wmg0uOyVhBQuNzMgIFhi2qLd8WWrNqXNDdSHZ+BRhSUnaWE4vpTyzZc2xXD1zZLLCwLsdUIiDOziD7XtjTtO33u3UX1W45BTScgkMUrgW23GMBEV8TE53627eqHa9SnU0HNgJZrTMw89em6LRNmvdD/sb5Orh59XF8b8fcjh2JSLl6OXLXmz08OG+LmPcMvdOMHC2b+M2hIX9/HHnssIiKisrKSeAYihltrH+n3OBrI0X4SgCaEBlnZmbhq7+joSEpKmjBhwogRI5555pk//OEPQ4YMGTBgQN++fT08PNzd3fv27TtkyJA//OEPw4YNe+6550aPHj1r1qxjx46lp6e3t7frdDoCPVvPFuQpKHn7y1+tZ6R3D8uV+r0HSLPIU3SWZUtKSmbNmuXm5jZ8+HDik3DkyJGXL18m4uC/qL5EbqK0C4BO9/aDTB3hzOIiUcagZQhVJhx2swYRd0tqSXT6h8EtrMUztHZSBMJ5Og5HfhogpbHQEwnI6Q6jYOMVBEy1LF6SoysdMrmlT0j1I1PM8/ZjFSwSzTapsdQrxOA+qcg7BNZfxKTIISGLxBKJGOLJsjT3sR3OoYVewXCuULpWKhCPgGyXgK2INFjqH6uM9qEG22DkX1cYEW+Sq0DQZ1bCRpkuCByX9wwSjQ3z9tZ4hXR4TGh6fg5kA7y+psJhTL1bUOULs6GBFdp13SXr/q8G9p01asVYo8Kv/KEgSKnH6hP5CAKLdoGj3fHv/h8d/PLQzBU/Phk1PbzCIXwPZLIJjwfX9Qsr8wmhlxxBkrUJi43iJSRxHUAuW/zkv5T2IfW9AzQB66EOayeRVvHteVPLpBPg48MNriGdinFc7/HtitE3XP3g+yoss8TbZgAMwBt5yXSqp0EJ+tFfNvYJrFa8jWrU6+Lw1rAg8hIaKL15oUOk/CO0ziEWRZDYO9Ti+V6Lz6TswWEQW4JIX3fD377eFoBODhKri70Cdb0D2+z8IWRzl5zLbS+g0b1k3ZuLlR6h+r6TM4eGw9V2tIWQ22hChayy/13c4BgMDu+qFP45HoFwNBdhZengpHuOsiEoFwZwsTbHN0TrEqa3Cyn2HQ+lRjAgmN2F9aig9fl5JofxaoWf2TFMZRfU4BpSMeRd2J+PIuDdPQdvA9EbZiS/lGiz7O4At63CT57kAcwifTT1qq9/jc2oVscApUPXp9Xev8XOr9FmTEOv0Q22Y5rs/fBXp0ClU2Cbc1CHW2i7x4Raz+CEIQGQ3wJ6CkFbi4A3yyyAGsomrS118WMcQnX2QR0Oga2OAah13ieoxTmwydG/0d6vydG/ydG/xRkT1DgEGe2CGEVguz0aqKpnbwMdj/T8X3zID2JXStYYtAbg2/zCgaFKtxDccHC+FLScZIuSFLfM6NCiS0LEIODLVMNgHW97kGRFSUikGlIHBdb1CSjw8LdsikN0Xurg2A1ItG5e/G1Tuq+T9w1AE4iZ+IWzBoUVCkVgYOB95X1rZOs3vSiKUVFRstywdV62trZESKHHu/bWBO/9zMKFC8myX3aLZ2tri06ufycHwU+HDBlCaiGb311dXQ8cOEAcK8s4LwHWExMTp02bRsh3CoXCzc2N4Nc2NjaPP/54bm4uTdPEdNzDrtDY2ChHJmg1uXDQoEGLFy/Ozs4uLS1VKpWZmZn79u1bvnz5U089ZY2MkxYmsPWJEydIA98duLkVgF60aBHpLXe5P7yFnzJlCrEoEG54r169Bg0adJdLCHqu1+sJj/vWmAaDgXggefHFFwlTXq4aafkfAGgy6bn12gdnflMtwDDMxYsXhw8fPnTo0L///e/u7u6vvvpqUVGRwWAgWwTk+X2PgPWw85uq0YPC/CotcPex69Yiyf2HCLmSYZm38MnJyatXr3722Wet95cQd7uenp5vvPHGjh07qquraRqdL/eAoW/N5cGZBy3woAXupQWIXSc3N/e9GdN7uTsrHG1tnFCZ3dXe8cNxEzq/u5a+cOulWWtr98ahKq7GgBgixaKigJkGpbE48pu8mesK5kTApRyEXAVWZMxgFtm04txNMXC5uHlPfNWBeF1VoyAIWoMWaAudmHN14cayqKNQrQITzTEUMAxnMqGsAc2qruVeWBOlvpgFFWpl9KnmnaehXgUUe2jPPvSF2N/nq+itJh4ZtbQoyo5wSIAss5HoIkhE6G7nhF1ACXEneAcJDmsA+k5hsm2ouro6eKy/p8LmDd8nqzccrVp7qPFoIsoBs7i8adeoccZoZMWy5qaYhNao03C2sGLtIc2VXL5ZzWt00NSu+vpUw+q9Gcu3tCVeBQvD8SbgzHx9k/nsteIlUWWLo1LnR2iTcoARaR2iGDRtNpgl+rOZhrSy1KVbs3YcttS2AsMYzHoAkWpT5R08lbPrGDSqBL2B4brpz3oailQli3d8P/dL1J3AHbaC5OhPEptmBdBQlpLG/K9jS/edsVQ0W1Q6JG7TPFR15Hx14OqyaESfO4y4cmN54CT0meaFnJqyr2IuTfqiKfo0tOotFMNx6FqQNhhBaWhcdyRvRmRN5BHUCm/XI1uZZ4082gxQeqWFqtxz5vTSjVRxPTIETRILzCBy53LSPtmU9Xk0l1oCWqqLtmnkILUsZ2FU1dK9dZuOQ2EjtOsFjRE4XN+inLTAoTx0gyZl5Y6CFXsyl+/sTM0nWpaYgoGH3MaKJbur5kfnLYgynMkQ65SiwcAadYgFV9RfWL2p6XwS1LcXHYi9sSvGnFMKLRpQsy1Hzt+I2Bv74RfNp5MQaEBcRhB5C6pn6M3Q2Jmzdk/hF18XrNjTdiIZ9BwaFTQUV9p4cdW2zKgDhqIK4BgAnhZMFPrWpEVBMthUNld8fez8jC/KN8dASSMYaQEEg7SVgOrUmM5lZc3bkDw/UnU6FVGAVi1kN9RHHlVtOXV1/sZrmw5M/fuoR5w9vR1dHhs85N3QsEuxZ5KOn/koIHz0n15+/annPpv24aJ5nwwfPrxv376jR49OSEiQ97DK79yfpJVYjxhk8U+eBRK2/lXegGt9kizEyC4l4mudpunGxsbMzMwLFy7Ex8efOnUqVjrOnj17+fLl1NTU/Pz8lpYWo9Go1+s1Gg2576TAPczM1rX4eWHrov6uwz0AaFKXoqKiBQsWDB48+Omnnx42bNjAgQNfeeWVxMTEX1pTQgQt12c8hAzovL6BcLYazMAI/E2rHsKLErBn/bf7BEKWDZD25ES1+4RGe7+rz0yCehFdgDIA7dAybWtV77HqPuPTnpyCftv0ErxrAmgQNGMiSh39Wx6alPfkNMhTI0bZAuZ5+8tdAxudgrIeCYerKgIpYh0lgLWroxoAtibnewa22QXmeQVBdiv+2k1tJvobCDRaEEfO8w019g7R9Q4ufnwKtAPHkxeIlOCdAGgaJT5yX/u42jVA6xkO/1wH2/LVnmGtrsHpPv5wsgRUt6BvgkSanrG32SmgQzG6xiOI+jIWFZkl2i8p/P3dKXJfcpRlD4fr7INaXIJg2jGYfbLYJ7ihX1j6wCCotECHhWDcooCwO94jE0A1VL78aZvT+A7nCeXDP4IK3LMj6QaLlARAE4wUtMBO2NTs4K/r5a+3CWh3DWn9+2eokqHnQMSWoyVJZwrdCwrIRF56rL5/eIdDoOqhsPwnJkGOGjV5ORFn+N17j6wBaLAJ1SnGKgdMzvjrTKiReMcSPHgHjFCCbjUiHMoodB2rUfipXUJg3jFQi6yIKic3m1tmpxoA9t3IcxrV6RjU5jupYdIGpJzrMKIJhTAQnr7+9LR21zChz5T6XuOUb65EO6KUPY9ONxF2lnSa8MZR726vcvJvswssdfGHz6QbJ92trtKqoGDwRF3vYI3Cv8UpuGBQOHx2DAr16P5RcsCIcVlJKIa40yROEk/lJM9aByrp/P3d+5uxUWPKBHnjV1x7JCS3f3CxT9enqG9QoXdgvqd/rodf7kP++d6BRf2CS/qHlvQPLeoXnOcVcMNjbI772It/DAU1CDoz2S6Gdwqt+gAXSrMfDSu2ewcNKh6BhQ8F5HkFFPgE5XsH5j7kT8LFviEl/UPLBoZVDgqv6Rta7+BXYP/O9acmNyzaA0aRskjzoZsl/TkheTghXhVv9g1REg/ZcqW0b7DWPSzTZRQkloFR2nFAFGHMEoW/VUQflbkGiK+FU/lojL/tQS5BMz5AtVA0fIbWOaTeLYjbHIf9QM5VtrHdl6HotjlKJ+8bgJZRPy8vL4Ih2tjYEIxv5MiRd87onn4h9kyZN0pRFAFSXV1drQFoe3t7IvBkbda+r4nFraWZMWOGjFQSSNHe3l7mDt8a/zd45odbs3TpUmtEmFTEwcHB09Pz7bff/vDDD5cuXTpr1qxXX33V29ubbPqW48iK22+++WZDQwOhD5BqyneEfKUoau7cuQR+tf4rQ7EEQJE5yzI1uFevXoTCrFAoHn300bi4OOJAkgB8d7qDvIV3cXGRuc8kMH36dLkr3ulesCw7c+ZMmdKO3oRsbX19feX48hyOnKmqqpo6dSrRYBk6dOiIESNmzpy5YsWKxYsXT5069a233nrhhRfs7OxkoJlIxLi4uBASNKn+3r17CTFfzuVB4FdsgR63WC4JTdNpaWkDBw50c3MbOXKkl5fXk08+WVxcTJy/kWg9cGf5q5zmnXqsnMuDwP8LLUD6w73XtEf/IeZA+V3T3Ny8fft2b29v4vDAycmJjGD29vZOTk4vvPDCoUOHGhsRzOqRDimA9ckH/fPeb8qDmP/PtoAgCMnJyW+++Sa+wW0VHv3R/ZennVPEnM+gsLlm5YGUKSuqvj6FGgtaE+o/UBKP1UyDhq7YFJM5N6J85deQUgRtOmBZg1oJrMV46caVTyKp79JrdpzKjNgHpc2tDU2IP3K8uaAq6YutDfvOQoseAIwmPWVB+jMYzEBZ2PKGS1/tNF/JhSZd/r6TRZtjkAXM8upOVVl23t+ee8HZxSX03YkmnqV4npG4KdYY9L8LgCa60j1gaAuIRo5RaTXvTXu/r5Prk73cNgbOyFm1p3THCaZWKfKC2qjH3epEmaRZ1x6fjlISF0pyP91WteU41HQg97amOe/rw20bvs3/bFNz3EXQa2lKp2qtB6WKSr6RvXCTOupk7tpdTHohKDVA0QxDCYLFYjCgKISZZUvq4uesTlu5gyqpBV4wmvS02QRGqjjuUurmb1C5WASNXmPiadQaNtLQTtd/FXNlxiptWkE3BU7a/2tmEYbWIxm5/lhixcF41Pow4uKcN1DQSdUdPH965gpjSiGYRN5EI7WZw13D+NHzjdtPXZn4hWrTSchtAjOrZSkTQ2OCZrHsm7MFH23Knr4OUssQqgBQWyiDBV0FIrStY9tPpiR+vpWtbEYwGnDpi8v+3PrMBVsvvL+8/EAc6ND9rImhuXYtlCnLVu2vWbbvxsrdqNGsMdMGo4VCOjZ+GE6qBZf91f60BZsvLdiov5IHnRgHH2cdBaWq1k0nquZHFy+IRqZ2uxkbAXVCeGhrvxi5tfrwKWjTlx45XfZNLORWQocJdBb21NW0TyIvLVxfHfM9ilNbRBphYuwUkvgG5H19NG/J9pyFW5uOJEKbGYWb9TS06FO3HkxYuZXKKgI0G/AiWIyi0SQYEX1madDTyoPfX/xgefKi9eiS0WwRabS+YOc30/rsksQZK9NnRyD6rGWgTWu+UZ7x2bbm1THly/bSJ9Oh3gC1qguHjr/2wssKhaK/u9cLjzy5ctqcb5ZHbpi35K9P/6m/u9erf3tl6dKls2fP9vLyGjhwYGRkZFVVVQ+t5Hsf6Mji/+4AtIw4yzQdjuOMRqP8QmekQ86ULHLlrwTFJiIb5KQgCAzD3Ha22ePl/jO+Wuf7ewxbV1kmnsusOBS/MRiioqKeeOKJQYMGvfjii0OGDHn++efj4uL0ehxsif3svudFIqCEQqX+mvfYJkf/Uq8gOJALBhyt7wZASxgND2BgadS+aIfmqRvr+gRonUMyvfzgcC5irxTAqbIbQyeq+4yvcQuGLVcQItRKHEzCZP7yXLZnYItbWKFnSNvMHVBmgUK4+mhYmd2Yxn6TGsethkqJK33rvfyBTvvF6WrPUKXNuHyfEMhVIdGYlXBKiY9Lduoj7FusS3F4q1Mxrl3h1/bKImhB1Ix8MFWi9WxAl4aEzyudE3HIqhMThgTUOIw1uYfD9KP6/55Le0+pdQ9i5+6DBh5hRxm3IsXjeATQvzhZ5RXcohjV4BrUHLwGmiSY8yZ6emtN7nyGANCXKir6T9DbBLQ6BsDafKVTYLNHSHn/CeL8g9As6U2wEs5OADyL1OZtUP7PL1pdJhj7TMrpGwpFiLbS+EsXAG2RYGjQgP6tFR22/ubeQWq7gEq3ANiUIjOOOQl9RhBfL+k1bUvK8w1u7xPcYDsG728M9hAwsYJFsllaAdAmv7WdjkGsIgAUwbzDhLr+4exXp0EtObuTWqxHs92sPydhjtsTCvuM6VCM1rqHwaqL0In9kEOYV4K5CURImPKtUPXM9M4+IfWKUaVDJ8HlOvSYR/E0z+t4iSpbA9d8Q+h+/zI4TyxyD4adWaDDdmA5kWJ4M1qvpabrAH7h4SzXsfWKMW3ek2r+/hnk6rHrSvt2ukqrgqseY00O4zUK/xqPEDhaTuwovAUfA8aARlaRsiBMLmlPQyvAoZy4PwZ/OywIbrRhar/kYADKdLDzMuzPgr3dnyPFcLgIYvLhUB7+PVIEx0rgeCmcqYGDubDxInwRq/vXdtieAG347ibumnFwsEjovA4gthB2ZGKz7MyEXRmwOx2Ol8DRIvg2H2Ly4HQVfs5U4+e7CsxlSyosOlr5wSaoY4DF9+UvqZN8rbRjAR8mGYPuejx1ACtPF3n46zzCsx3fhu8rEcrXS242axmIK1ItOVA0bulZ31EpXig9f35oINRqyejXcwy0BqArucZXF1DOE1rcQ+jo8+TW3KyJbN6Qy/cLAvcNQMv7WV555RWCuBEHcQqF4qWXXvoFJem6lKyryRdRFKdNm0ZykZUx7ezsAgMDCSR6p0X4zyhGeHi4rNJAcrS1tTWSs6jBAAAgAElEQVQapWncz0ju17hEFEWj0fjoo48qFAqylZvoY/SAbmX81N7enoCtNjY2BCz+QYhj+fLlZErUtYq4XUVYltXpdIMGDSKAsqxeStrN+n6RAsikclIwV1fXwMBApVIpp2190+WTcoCiqMcff7xHLV577TUyF5Gj3RrgLfyiRYvk+hIox1pZhaQgw+s+Pj6k8Pb29nZ2dtY+D+XuJ6cmV5PYSBwdHZ9++ukbN27cWowHZ36VFugxVZUHXCLqXVhY+MILLwwYMOD11193dXV94oknLly4YG10IVz4n1wG/CpVe5Dp770FrDunHJY7myAIDQ0N27Zte/XVV3vsNSHuCkeMGLF58+bKykoicUiWr8Qca53Iv/H9+Htv8Aflf9ACPVqAwBZms/ngwYMvvfQSEQfr19/XxcVl6JAhu9dthBJl9Yaj6e992bj+GBQ1goYCE4PoM7KDGGjWaI5dynxvReGnm9WXMoneLkJ7LM/lVVyYu8b8TULHjrj8rw5yxQ1d9CQzB3Xq04u+yow6BNWtAkUZLZSZoxiGQsFoHqCgrnhXrOZSNjTpqs9cTtiyByqVYOLbdRqa56BJvTL8g/69nJ7/4zNHDh8jG2VpATdMyxj0rQC0PLzcxEp+igFN0GeO50mAtBvDITBRVlU5YfJEd08PT4X98jcmZC7fWbD9GNR16I0GlUBrkMoqrd9MYtPplMTFm6kTaVXbYou/PgGVKmjSQHlr646TZcu+LlgZ3XwygW5pZmg98AwYaUtCZtPmb3V74rNW72hNyQK9EYmzFksX4k/x0EFBdnXKF1tPzllpzpA8jAkSncciVJ2+lBkdo8+vAJ2Jocwm1iyAwKu1UKUq3RST8NGXbd8lgcaATHOi24su+yTMQ22u3h9/I2I/Mos7KMSJjCwYhfrvr307fUnziSTk4XLSx4JLMHOnDjSM6vS1xIlL65bth2tVyHGT0kR4Wm2u/Sb+ypyIuOnL9Wcz0O+fALTIawRGy1KIPus5bUp+0ld79GnFQPEiy6FPQhYgoypr4bakqSvav7kASi3qddBmJNpXqlXRCGcnfxTRmlHIcZyGMRssDO7tRRycAaUOGtSlB+KqvjyYtXBb+clE5OCbWFQRMbFQ3qLacqpyblTmJ5vpy/nYaWkGkzWy0NhyZff+rG8OQ1Gden9c6fp94o1SxJFVJvZKbtL05cVLoppizkNFC17FMDqeUrF6bacaKEF/LuPKnLXJs9aUbz8GajM+FGYB6tXNx69cWh4lljZIOi0ULVAmMFGiSbDQwHLQpq3afyp15qri5V/T10vAhPqwiH+xPNAilCkLNxxMW7Cx5dsL0KYFygIaVnUq+cbSHbnLdrUcvQxVKjAIYGSNGl1KSsr8D2b90WfQIBvnR3q5BL448tDG7WePxs76YOaQIUOeeuqpadOmzZ49+7nnnvP29p40aVJsbCxFUQaDQRTFO21tlAcHGX27bUCOZh2wVvmQ543ycyfPPK0vufuvd4ppfRUJW8f8PxwmZKMecxu5vtaYviiKTU1NS5YscXNzGzBgANng+/jjj0dFRaWkpNA0bTQaZQjm3tsQt00YIPsR5C/XeQTDyjjQijgmC9JwZ5H+WvcYCX0mqA4O1JyAiO3xG6Vu/ozThCbXIJi2C8mhlSbDO2tUnhNVLuNzHg6DfANoBDBK7uoECZmtFC8/Nr6+b3iJ7ej8gWGw8jKsuFzmG1ZpOybXwx9ichAXlkayLreocqNoAN7brfQIa+s1rmRgOOSrcZzhMbJowZcVkqFJgTObr3uM61SMU9sE0qPW3RT0kAFkBqCahc9jOxfsBwrTwKFQy8O19tR+fjqPcI3CD4YvKrEf1e4xIX9QKNSIoBXxtYTCx1KmJCNO0hv5Nuf6gKB6u7FKl2BU085n0RGctMefxJJr8NMBHgmbwoHkKp9Qo8IfcfD/3cw4hCpdgq8M8IcagHYiMSyVWAbOaJSe0M8/WOMYyDhOahowFfbkYTkBN8eIPKKGFoktDVrIGxBi7h1E24d0OAWVeQbCmQZo5cDSpaWLqZs5NCREpVb5hGqdQ4zOoRV9QyzrTqHLR1qwCALH84gwWAHQhrFrOhwCaYW/oAjS9fIvHzoJKsx4EzkcD4njwdvX3SL5Rdx1ucjDv00xSusSCv/aD20Cz2EPQMRGEljAZSyDKGT7uxvrXQK1doFl7gGG96OQu01j3SwCtHfqEFi8qi3oH2bsM8ng/X7So2FQIZC+hBILuOlF+rSCuOZMwSOTmjzD2vuEXnX6J1RLTHYpKYKNYmk7IP/hCYxLeKdibJlvKNoVJK+YUp26aoMANFGzqaTh6/RMt9FFA0JPPBEAVZIAyu3rfLezpK2w74iSNUAn2Ug6JQTW+q9aBLWAuupaCcHXSX/1UmMaJIOE9LSS93iXCw2yR8AgxTRIT6JORMuQ5paPVgBd94eEDQJqX3RvQbtbBX7yN5S8kPSXBRGHoO4DdcMEEdnKS4/nu/t1uIVqBkyF3UUQnQ4fHWga+VmK2zvZrqOL3f1r3AJbXIJUDoGdvQMy+/pTF3PJvPdHWIcsrIGECIBipu7Psw2OITUeQXAikzybXc3S3VDdBfml/+8bgCa7hkVRnDNnjqurq4ODA+FB29vbz5s3r2sq9ktLdfP6yspKa1zYwcHBw8MjIyODLLZl1a17f5HcTPrHoaCgINmDn8yZbW5G4f/fxUHuC8dxx44dI04aZYGIHtBtDwiVAKmOjo6vv/56ZmamjMbepdZky2pycjLBXmXQlgRkZFYGba3P29raRkdH415FWno3dGdz21kamcwBwGuvvUaox3Jdhg8fjpZYyx02FEjJiqK4YcMG0hrWuh8qlcr6QkJhSEhIcHFxIYi8o6PjbQFo0qQEuJdZzw4ODo899tjGjRt/9Eh31+vB/1+rBciYQOasZLgg3Umv1ycnJ7/wwguurq5vvvlmv379nn322ePHj99qbbKe75LUbv37a9XuQb6/6xa4tSPdegYAamtrY2JiAgICyDYLMqKSAc3V1fUvf/nLypUra2pq2trazGazvHWXMINu7b2/6xZ7UPgHLfBvb4GWlpYvv/xy8ODBxDjt5uLa18PzHy+9kvl9IrQa8tcfSpkdkfvZdshuhE4KhQ4I91lPgcrUdCj++ifrS+ZvhnPZYDBzgiRmyVlAqctbv08VfdoSk1S2/lv2WimCdAIgylbXkRax+/KyrZ3X8sEiGniqU6QMPALQqOZR11a08zjKTNdrm85dTYk+yJbUIauaQVVlQ4dGfelGdPjcV/s97qxQjPjb369ev05LUp6MtNjH9b5EOu3aaNy9/pEHlq41MFGiFFDskjivk9y+41f5Q5bNrIVjLRyKTbOMRRA6ddojx4+9+PJfnOwdHvbsu3b6x+W7TmWv28cX1LNtmnbO3AqMARUlRFAZqMyy/E3fwoX8up1ninbEQp0aOhgoaa3aeLhh8dd1S3cqTyRwDU00o6doHcoKF9fXrt7T8VVM9udb608kcKoOE21Avq3AIwBtYqFZC3X66jUH4qcs6Yi/Bs1qxKZx/U9r8suTN+5RJqSD3mRmzGbGbGGluWWjum7HyeNhn1QeikegFkAS65AkOGhJMkJtLj+bdGl5FNyoR/S5w4Cyy2YwJeWfX7q58VQy1KmAQxABl+ycYOjQQJuu+VRK7HtLylbth4tF0EJJhDERFSQ7mdZTKSlzIhP/tbr9bBrUd0hwD3prpCwsQ9F8h77xXNrFL3e0XcxCh36chEp0GqGkuW7DsfNhizv2XYDCRp6RGIiCAC268shv8+duzl+43ZyQw2oNLSZtp4iNjHv/GQ5MiGq1H71y7ZNNl6atbD90kW9QiUiGA1S11nA1++LKP43O/WhjR1w6tOmQEi7wyApv1lQcPXs96hsoqa898F32yii4XoVSIZ0myCpPX7QpY9ba2g0xUNaC3hTNDM/QPIDGqBXbNS1xqcVf7s3+dPP1tbuhSmnS6tVqNRj5tguZl5dFGRNzET5mWc6CADQlmlBcBQAa2lRnkv8/9r4Dvooq7ftCSCUhhBBAmgLqWl/Xsq7uvq7u+6krnzRJlVAWUFaxIIJUKdJLQi8mECAQCC3SYiD0QHrvvfd7c/u9U+/MPN8+c26GKyDCrruv7pf55Zd77tyZM895zpkzc/7nf/7PjQVhBYu3w8Vc0FtA4HkDCulisKas6rwluy9+tKL2YDyorSjkIgEVn5axcFvi7PVFESfZ8iYwM8BLJq0exWdo2tqkPrR+G6pCq5wGu/Z66bGn1i5fkXT12t69e1955ZVBgwb9nQ61bNmyiRMnPvHEEyNGjJgzZ05+fr7ZbCZ85HsMcxxRxDvTP9YFKXeZApU67vmxs+5nv2M+d6bvJ4df+zHEpYrc823rpAn6TwaDtbW1iYmJCxYs+MMf/kBW9Lq4uPTt29fFxcXX1/fpp58uLi6+bVb+xwaejk5D0ExE9m7tK180uoxr7hUkTd0FWoGT5FuYoM+2H0pwyJinI/qKvUFeW+GgEGOPgHrVW/leY+FiM2y93Pbwh+1uQYWe78HSM9AqI4DIQZWZpzRAG7BLjlU/NKndOaCtd2ib3+T2vpPbeoeqvd5HuYwcnR1Wlg+3D4YJbtgB/Hvhup7va7sHFA2aCMVGoGQki5MUAJqTZHQ4sznd5z1jNwxCKI3ZiAxKZbMBKgLn6soCVxYMnnjhkSBopRmZF4t37rGi3D7jrV6hXLdAs1two4d/bs/RsOw0tEv4sEO9BVlawdaJ/yIDWoR09ZVHAht9gg2eIU0PTYK/7YFmGRiVEctbGJtiwz0SPIBesGw6XdtvAu0UqFWNNfYIYN0nVHkHwIYEaEMeqx0xcwTOZAAatl5q6TPZ5jq5wSOYfS8cI++1S5aELMirx2lI5FaLUEeX9A8WnYL5HsG6nsF1D02ELAE6QGjV0waTHUvtANh4oXLopCbVO/ru42t8g6XP96EHTDQnYYhCGjW5fgBAm0av1jj706pxvCpA5xKgfXMJNCJ9GVvIvQFopNOL8F128YBgtWpMo+pdmLATYWUAG75EMIj4I4bIg1rklh4tf3xaR8+g1p6BN4YFQyFFQu2Rpz5WnwmgkMt+8kO91+R29/fho2goF9BfAtg6KJxYrbdg5ktOZgwKKXMbV+sR0PDoDNiebAey5YiUt+YMOuCS+1tWt2CLc2CRXyAU2LmbnAzwWmkWQy9Y5IbdIMCa+Bu9RzX0D83uHwAbz0IjA8ytvu0eFX7bTwSAtmt2Kwxhctc5/rfJQflscvu/LQv5663W0Tk3r5SLkOzl21GydY6pyMS8439OElm49cdJmBF0LlK92zXvY58EDEXjaieyKSwDq1x39RRcq4dpkXW9g9qdx7e6jC/zGFvpF1zvN6HRJ7jVK6jdI7DRw7/efXx9r8AGvwnNAyenPDcNcuvJs88RAbPPNBAvmAHy2Nz+ge3O4wv6+ENmI7ZMbBRYQZ23030Yf3+HPBgATdoIyTkjI8MxvJubm1teXt49aLP3Z89djiLiGE5OTs7OzpMmTaqsrCQHkcZwq9lKt1rRXXL5qV0LFy5U+LwKY/dXAUATDzhOAu/atYtweAmpRwFtHROEm0yIz08++WRcXByB5xSo7h761wRplSQpISFh2LBhBIYmnGsFa3akDyuA/qxZs2pqahRdtp+qE/ydvB/Mnz9fEfQgpZg4ceJPAtCiKCYlJRGCtru7u5eXl7O8Ka2UZE6g8IaGBoLsKBMejkVQwHQC37vKm0qlev3112OPxCqvs/dw2v0UtuuYn9ED5L4gvQS5O0hI9KKioj/96U+urq7vvPPO8OHD/fz8oqKiCC36tqs79i0/lr7tlK6vXR54IA/cu12RDoqiqLS0tIkTJw4cOJDoCJFutnv37r169RoyZMiKFSuamppMJhMJLUtiqHa+LOHnnVd5ICO7Du7ywK/aA8pwwrEUWq12zpw5vr6+RErLxcWlj3fv0W/+RZNfAe1s/cHzR6YtTFy0GbJroNWMRCcUPZDFN4wCl5h985NVF6ctps6ng45ChVzWChwNWmNlxAntru/gRMaNeeHtqGIMyCGlJajWa08kJX29lb6WD606YFmaQ/TZSABojSll56GCvSegVi+klKRtP2hJLULkmjCIKJHKrry6YHPc35bt+XL5H55EmfjhTzwRF59AiFOcHKickzplLuUCK3c9GQjdAqBlDJooHhIMWoGeScImiqwoMAIC0CSQTklZ6ZSpU318fVXduw3y8lk6bor1fHby5mioaAMOBJbTiowWHYRqmIbU4tQN+7TRF4UzWbnbYqG6A+Wha/Ta7aeaF0QaVxys2RAN9ch9pjDunAmqWqrCD7SvO1j7TUTVjlioauFpi4E3CyAIAodRB800FDZWrItOn74SjtyAeh2YKYahRJoWiurOLt/UdCkVTLSVo3QCxfKyNrfa2nQ08cInK9NXRUh1ZLGdRNNWRNt5Hsw8tNFUYs7l5TvU13OR284JMsxtFq4WJc8Ka4g4Q9QzOAnhA8SgUQMajJdyzs9cdeKvC7msKsSszQLyyKw8NBrE73Nyv9p+9W+rG/cnQAeDlc4JIm1nHIttBn1e5ferdzacScJfjajjj0hrcXvDhqNZH62v3HgYmgwCy9nxHQOTF3myYNHujC83t32fCmozWDmeYbFeJKwaBKB1LCRXVs+LyP1oY/Gmw1JJE7CijWZRE5MGTezVgkW7c+bvqItOACNNi7yVo4DjpJpmXUJy1qqdCLvH3chZs1ssqkLsQ2eFVmv1N3sKvwgrWRsFGeXIsKaRnA5W2ibZgLVBannKrA3FC3cWb4gWSxtAtgcAWm/kHp+/rvhIAug4VIiWBIGneRst2KzAWMHEGBLTshZtzZq/mb2QAY1ajDnJMygn3WqACn3Jot2nx31uPHIFTAxqrTAAWdXli75N/tuq/K2x5qIaXOYuIlxGc6zaqLeazFx1y9FVW+L3xkwYOdZJpfJycevp5BIwdtz6NWuTkpIWLVo0bNiwbt26+fv7r1yz+nev/N7Jyentt98+evRoU1MTgaGVl3bHPoHcFLcteVagjHugY8q99rMD0I7m/f+ZvhOA5nlegVEsFovBYEhISAgLCxs5cqSfn59KpXruueeGDBlCojo7OzsT9MDX1/fcuXMWi4Wmacf6+kmvom6wxEMHz4VsanIbr+4ZVPG7T6GNwakehTxInjHKfxlOJGRhFPCQ5R3AAroxq9qdxwvuodaeE8xPfF47aEqZ0+jiXgH5L3+K8J9VPo2I5NpktI4GyNG1PvaRUTXe2DNU5xpscg62uIc2OI3jxocjpEhskNFbsiYGASMRFTP0ry409ggyOQfnDAiGYj0C0Ail2wHoW+HfcpuTfd/Tdwtg3SeWP/JXhBcJ+9UGUM7A8YqCEX8t6DmueeBfC/8wCwnUABiFtZWGtfFl3v6s+wRwmahVvVXvPDb3hRkoOGuSLSelILRrGZtB2qZFhAax5r3llb0DLJ4TDJ4hCEHebCLL/FEz/icrw/EADqCVbf4yoqpfiM1tAvScrFaNbvIKTH4kGCnbRhFhM1n6mYCT9vvXKqA4RlJrc7+/MqrgRtXYCs+g/CETL/Ubl/3U1LqpYdDCoh0WDtIbK/2CoVuw0CPY5B7c4BMMm1NQvBv1i0VooqGcg7kxpQ9PavEO7ug2rsFvgn5WJLRKoGcAlyVJVpBMsqwHPnxxikKCDkkBoJluAWqvYJhzFJUTyHIQuers9ehYUpLGGHEcpDcUDJuo7jFe18O/dHAoFBiABZuJ4gUBn78mDhp4y4KDF/u8W94nsN4zIN1nLJwqwUtYOlsJgWyNAFrgNsQXu49nfD9s+M0nkI+C4PjGYpQVV5KNHSNXlPQJaukZ3O4cUDtoCkQkQ4vMMqYwK8TVZYPRug4oGjbJ4ITtobpPECyNw2iWAIwgIPpMlDfaAG60CB/srvENrvMKyHoosG7KRmSUUyLYbt2Rd5b7zj0EenbskG9ZQiZgHP/LYULJYOrOrG7fQ06UyyUvGMAyykLotybslZl7MnmPOSuRSDsHW4577Ajv7Vf68e8EyxQlnmFREMzIIPPaDFAjQGI9bL0O03bXPPtxRZ9Aq/dEg2qsxSOE85licAtq7j6m0mlUec9xZX2DigZPyB4xMemZyU1Tw6k1JyChFOooXCB1780EsCe7yH10rdPo7GGh0CgvGsMuQS5jJ8h6y9v3zu2nfn0wANoxt79TbhctWkQ4oY8//nh6ejoh4Toe80+mCVAo2ITDhw+npqaiChuAIvykZK60XGXPP5C4ePEiwUkV/NHZ2fnXgieSJzQpNYFTT5w4oUwCO+LOSlqlUv1dSjsgIODSpUskfIrj6fhyfM9NwanVavWiRYsUyP6uAPTTTz89e/bs+vp6Jdv77Qs6bSC0bsX47t27Hz9+nDSGe/COJUmiKKp///6O5k2ZMsVxEZYC01AUNWPGjLva74hEu8jbG2+8sXr16pKSkk4DESinaYwb86BFU3LoSvy8HiDdAlkkQQBoEinb39/fw8PjrbfeevLJJ/38/Hbt2mWxWDA+PVGudDBC6VjukXA4vCvZ5YEH9sCPNS37kjoAvV4v2ATScyYnJ3/00UevvPIKgaGdnZ2Vp9Uzzzwzb968tLQ0i8WiUISUzu3OqzywoV0ndHngV+sB+0BFDt5NXp3Liksmvx86sF9/J1W3Xr16eXp6Dh465KMPPqzLyIdarfbI1VMfLr2+JtKSWYYx2RhZbxdXEHM4wLtWdPWjlQVzN4vn0jH6ECuLDSDziCk5dArBu+M3r8/e0Bx3BYwygcXKg4Zhz+ckzl5vSkhDzprJSlFmlkXaEs3RYKWrvruUsz0GSpqotOIrm/c2XUlDEisr4MitwwIlbcWbDl/4ZHXamr1Qoz6658BTTzzdw8Xt0ceeHB/0fuyJ7wpKyrFwCglIHnUTNPnW6AgleTv/HDDoOw+TBDsALfC8wPPHjx9/43/+3MPVxb2Hy0Me3guCphVujb329XYmtxoFJqwMxTJmG2KjyHqr77i56UDDvnhz7PWEOeu1l7OhxQytFu3Z1JrFkS0L9zSujYbkIrCaTJyRp03Q3NYc9V35kt0Naw5UbzkM5c0gSAaLjpHRZ0T8rTQ0aBojT1/5cDm7/xJUGaFZhyM6m8jUtSRv3l9/LBHZuzbBYKNMEgM0anPrT9/MWLIjbdlOKasSrPKCWABB4BBKpnno4CCvOW/tAcP36aCnKRPKWgAPdFLR9a82FS6JhNwmiWIbjR2Ev4arXykR8hpzVu5N/nITpGLB0QZWDtpjEqFKX/Tl9rSpqwrXH4QGI1C8jeUwFgjD4ZBPj2oYSTsOmVNLEKLFIFCcoDMjEh2flzFjbfGiCCholpjOmEUGpuFMUurqPakLt2vjbiBczvLWdi2eiBWCG1A8l1qWvzSydu7u0gW7UaGC4nGgbGVBS+kuZOTN3pL7aXjFjhPQahFF0UoQDkYwp+Snrf1WiEsy74/PWbaNvpIBej2Cy3Xaqk0xGTNXF87fimLTWhoQyEb0GSw0cKI+pSB/6bfVX0cWrIiE/HqkJIsisIKurDZ+Y0TR4XjQyC1WkAepHA0sDbQVjFYoarixICzpk5VVm2Kgpg20eoGyIABtZaHFXLYy6lLIfPXOUyjSIkgIQLdZc7+JyPzbmqoVUbasKrCwHOIbrMwSBJ5hO8prr4RHlR+KLzpz5XTUoahdEe/8+c2B7t69VN2HDRj00Qcfnjx2PPZIrH9QYN+H+j/7/G+/nDtn9OjRjz322KBBg2bNmpWdnf1jGHQXAP0L7OPvCkDzPN/Y2Hjx4sVvvvlmwoQJzz//fL9+/fz8/J599llvb+/Bgwd7enoq4z5vb+/nnntu5syZNTU4mXHblPxPFtkOQLcz8EVMoweKOKf4joV6yn6igkETmLUTelboz+R3XAhgBdhytcFvAusaAi4TzaoxZqegdu/Qy73ehS2JCMIaZZFcJZ4sxrkTUGTj4wP6gR/oPEONPYKYbkEW99ByrwCIzAIjLmMhYBzhGd8qSwc0PP2JpUewyTUk0y8QCvWo7IGCzrhShpM1nO0B5/Kbr/R/T90jQK8aV+kdBLuuI9TVCpDSCp8eKOgT2NY7tNojIGNQCJyvA6Ngk58ziDJ/sq+xZwCWxXOqXjWqvHcAbL1gDzonyH0jiVHQCa3ah8YNFoi4mtZnrL53aLtqdL7X2LYl0YivyWc8GADNArTy2QFLqvsGSz0n2VSBrarRN71HwfYr0M6DhZVom8hLBCclkwFWgwU7ZA6ggskYNKHdNUTtFKRzfV/j+X6dV1COzzhYeBQaaHzs6lhIKK7rGwLdg61uwVrP4OZeQWleo+CbU3AiDw4mC6tOlvzXjPqBk6o8xjV5BxV7joWZ+6C+U0wEQXhUlLY4AtCCBFpJO251q5s/pRpn7ebf6BuCEsN6WWS8s/IccdXOffZPnmKgxnjz6cl1XgFaj6Ai99GWTyOhQRaXYAB1P5LrK99bljUI7Sn28b86YBysioMWATtnphOA5iT71KmAMTCNry1t7D6+sXdoy+/nwb4suFAL2680B2+sfGJGo9+kJs/gMrdxhQPeh03XoYbByQmrXcpDfnPANoUG60CasrPNM8jgEaztNzn3kUmwNwPR6hYeJVb0AJdrWj/ZndBnZEkfFIUo6Dkm80+fQR0PWsSpCcGWjFNuK/Jdv/4AgJYhYwUsvvN4pVe/86e77PkhAE0apHy5ewLQJLwzas78AIy2w9Cded7lcnfuIv2FwtduZ+FSsWHDyZKQFTeenZIxOKjCN0jrE0p7TGBVAZRqlE0WcmntNqbJZVzjgInMX1bA/BNwuBguNEIBjTdyi4AKJBZ5idydl7ttjxZsgeGaPqEVzqMLfzcT2lj5rbkTgO5smv/7ADQxu0XelCKQEa/y9Z9M/IAl/sO87gE7/vDA+/1mNpvnzEzvfGAAACAASURBVJnj5OTk4uJCREVefvnlexhwv/n+W467631rMplOnjy5cOHCP/7xjz4+Pr179+7bt++wYcPeeuutmTNnXrp0qaGh4eeyzmw2x8TEzJgxIzQ09N133x05cmRISMj06dM3bdqUl5dHgvLd1cj7NEAUxRdffFERFfniiy/Iidiz/LgKB5kkX7RoEYGVnZycXn/9dYvFQkJ8kBzIMeTRyLLs+vXrhwwZ0q1bNzc3N6UluLq6Dh48eNSoUStWrLh48eK9/dYFQN9nnf4bDiMvmoRHzzBMVVXVW2+95evrO3r06GeffbZfv367d++2WHB49vN2XP+GonVd4j/YA6SrJG2STOuSCRIivp+bm7tkyZLnn3+eMDfJmozu3bt7eHg8+eST06ZNu3btmtlsZhhc1UZiNhBUmmR75///YE92Fa3LA3YP2IfpeEdcTr3x9ut/9lI5ecqIlbuL6zP/9WzEvr20zgha2nQ2JWX2xkuz17YnZdOtagTgeM5kMtAGA5htcL2oeO62vJkbGr89hcoSoow6sDSYmcaD5/K+3i7GXm/de7rs+Hlbi4YTWINBB1ZRSCk5++Vqddw1VKJgkITLigKKPsmcprIzV8u+jYPsJltqWdzaHRnnLpq0esQSJZlvVqdt2xKXOXNjcXgsFDWDVTBpjVe+v/ju/3nHx7O3c3eXoY8Me/F3L38waeqWVRtSLlyzavQgAkVRLM9xNt4mokakYGVEK4NwBoltJY8aJUG0Rz8jCpUITyNFTjRSZrNZr9dX5hZ+PuWDx0c86uaBoVCf6D/km3FT6/fHZ66JQpUJjUVgOTPHWHgWbCLXqoUGfdauo81HLgiJOWnr9uguZUIHhVBmfn3uuqimrcevfxXGZ5YCxdkkjhNoMFtaT19q23y0dU1M9qpIPqdSomirwDACK0kCordaCrQSdTz5ytTleYt3Q2EzQgMmXLELFW3XwqIaz96AqnYwcxLDsSKqKgMPxoSMjC83Z83bDjm1YBVFG2pW4IuirOOMJqXXZny9S3M6GUyiyWSS4wdKUK1JWRV5csZSKaMKOiiKZ82Aa6ix/YgYJLDkm6i8udutp9PAKLImC6LSFplM10SlLNmZ/fHGmlUHuaJ6iWI5jsMAZYDccBnsaM/acKDxyEXU9CAAhdYMas4Qey3l43Xpc7eYLueCCGarvGy52SRcL878JvLivPDyI+eh3QycbDwrYPWxOCLGCsqtLFq1r3xRZOaCHfyNErBgtCtUiWk3WS5n53+9u+zjMPXaI1BYjxRmMrkugi2/OnXNbvZkUkvEd9eWbalNvAZ6HRawWduw+7trM1ZUhseIN4tBY8azAJgOA0LzFA/FLcUbDpUtj0pbsN2cVAgaC9LGWYCi+ozdR2rOXoVWPbLIBQFVPjgOGBosFArIlLelz9+U+eXGwnVRUNVuU+sYyop8atTl0BRHnrj40Qr2xE3Q0KAxovSzlq7bezpl9sYbX2ygzmeCAWvWKnBmm50ToymsvLwpqiXyHB+Xlrk1xpxdYahrbiyuWPXXT1/oOeCxnn379nB/7cXfxx4+nJSeun7b5v968fk+fn3feeedmTNnvvHGG0OHDn3ttddiYmKamppIz0Ces8pj0b4IwEGghgy273/IrWTVNRYgHv5n/hPCGcdxikRedXV1YmLili1bxo0b9/TTT/v5+Xl7e/fq1WvYsGFDhgwhDCES954IK6lUqocffvjChQtGDIyJUrnk1UippvsxD6tSw8PWpGLndyn3EBTQSG0CGfyVb2iZCi1Thy2yYKysg/ODjLEfoQEyjSWPTW3tMY5TjQFVoFU1psHDv+D3nyBOJIvq4p1B/pQGJyEcXPSXhU2DJjeq3mZ6BLV4Bl59OBDq8UiGYShZ/xYvJvdV5GzQQ8UzMyweIR2uAZWPTYOrVbgMhYBJAkJpJOAenmWF6jfmNrv7G7uNZ3tNqvIc3/7MJ5Y/LS7yC9T0Ce3oGVTnFVD624/oyESZ2izZlw5opKbffaHr4d+m+ovJObCtdwgVFAYNMtfVfhW5ICSteIIoGmig/f31pb6BDU5jynwCon4zFpFT+eHTCXApJ9wzwSKHN+ntLyp7B+hVo8Bjirr3hLKRC6GWBSs+2mws9ooEfyT6VOgBWkDQVA9iWHzhb6a3e4fqVONpn7/meIyqCvgG9YiJbEQHD5FX6n1DLE4B9b0CYcI+tVdws+v4Nr+Jdf1Ds93frfIOMHlOMHuE1HsG5A+ZAEuOIfiOq6Fu2Xwrrp3MocWr60H8fF+DT7BFNd7sFFDePwQutYEetafxxPtBKnmg155MGxykHTClucdY9cApllcXwId7bRO2SGPWl/QNrPUY3+IR0NwrKMl3DJzIQZo8lkh+9BO0mDQRXq4gDcAnMa0+k02eky19phV5jS/oE1jX5311n0m13cc2+YRmeIw+N3Q8nM5HEBkZ9AIu3OHRYJsoMiAx2FViYF6IKy4ZFtriE6TvNaGux5jKXv6ZfoHWd9eq31hc+PDkIu+AZr9Jbb6TmvtNzu4bWPb2QqhDqrUkq6Nz8vS5XT1M8YODJ2/5VE4pU+3KjIVCcr9rE/rHumLlFiT3Fnk03PafdCOOfGf7ntssvs+vpOx4m8jTRRUd1VM3XukzKq/X2LreQW29QzRewXr3IF23cUbVONopkHYK5JyDdaqxTV6BRU9Mg+sdKGijBRS81oug41GzRZH0ue1mdDCJsliwWikJSs3FQ0LbncfXeowXP4wANS5rI77Fxik7V3kgOmTwDyb/cQb0XS9o75vu+tuvYWd4ePjQoUOdnZ2HDx+ekpJyD3DzF1Wae7d4nucV6vGdZv9jd6YyKe2I8ZHMyRsDuagyT/BAD/s7jWQYxmg0zpgxY8qUKbt27VKa2b2NVyCYVatWjRw5ctGiRUS1ww43yivTlWspBQGAtra2vLy80tLStrY2wignhSKXu7e3lQy7Er8cD0iSVFNT8+qrr3p5ef35z39+9dVXfXx8duzYQdRgbhuB3LtR/XIK1WXJf6oHSA+jdFNKglChSaPlOO7QoUPPP/+8r68vmTF1d3d3dXXt3r27m5tbcHDw1atXzfJGvERRlNIJ35b4T3VjV7m6PHBrUCciQxkAjhw9+tQTT/ZSqUa49n6p/7BhXn0fHzYiPiEBfaWjuOsFSXPDbs4NM8ansi1qmqNZieNFjraaJbUeChpvfLEhY8bqxrBYqDcAY8MDZDEB/bXMomW74Ux2bXhM2YHvbC0aq9lIsRRQDJtRdm359vLoM9BiBNaOPttEkTNToDE1XEy7vHo3pNdDSvXJxWHll1LMHXoTS5twCAJcuz4pbF/OzLDyr3ZBThNocXWwaEGp4quHvpv81rghPX3dnFxdu7n0Vrn2V3mM6N3v6SHD33j1jzt37tQZDWaGVkZo6ApOlEePZE0phrX5e6BmzsYzDMNaKFzsiVH4eKHD1NLYFB4e/uSQYX2c3HqoVH3cPAd5+37pP6ntyKWbi7aXRp9D9i7FUSxjEThckW2gwSQV7TudvSUGGqis8ANFB07JWhM2NqPs/Nz1bVHxheEH2dRiqUMHIk9ZDMDZdOdvlK/f3xF+vGL1fihtYVvUFoxkyFJg420sGGlQM0xc6oXJSwoW7UYlbo0M0VICaOjSfWdurN+L6LOJA5qzsahQAZRgSy1Lmrc5ffYmOJ8HPIpj2leEID4rO6O87eai7R2Hr0CTCSwsos/4zkdVRJ05NXuN9QYqnyCILIlkKbRkpKCsPWd11LkJCwzRl6DRCLKSMJ5lEqCo5cb8LUVfR5Z8HQm5zWBmLQJH/vAAEaDFeGnjntroBChoBKuAAaxoFvlo8bmpH65J+SKcTcwFPVYrBiS08FCuT5+37fzMVWWRp/h6NaLAEspuYJBDRsAcTDzUaq6v21O8fO+1T9YiXK6xsBYKx8BmzpJaUrT+QN7crTWLIyG3DZ0jAdKQNSZos2aG7adjr4gnb15bspnOLrUZdYzZAIxQcez81Y9Wps/aaEuW0Wcrypgwaj0IwOvNUK9t2X6qdum+yzPXQFoVUCKt1iOooRdSNu69uvZbqFMDg4LdkiQD0IKAIhsaRJ/L1+6rWxGV/lUYZFdAWwdrMjEMxdIU6M0t524c/dviim9PQIsVDFYUWO+grFdyvv9kxY0Fm/ikQtSDtnAC4vlYv3I1GU99s6V4+zH4LuP7D5dz14pwXbmOthTXnvpq3Y3VkQHP/uGhbu5uKpVPL+8PPv4oPS8nMTFx+tRpKpXqqaee+uyzz2bOnNm7d28XF5dZs2YVFxcroWjIiEbhyjkuslbG23eFNtCqH26Oj9cf/tL17cE84Kjv3NzcXFhYGB4e/uabbz7zzDMeHh5+fn4DBw4kWLOnp2f37t27devm4uLiJW9OTk5Ed9HFxeXll1/Oz89nGEZZuftgdUSAMBPAsZKC3uMx0JzneIi8hlRQGXJU+libjD6bZabpXYrKoqYzPye61jsQ3CdJqnEWp4CCgcFwNI8gcXYArpM7LXACT8lrbnQC1PBN/quKhobm+4zPfnwyveEUAoJ6muZYq8xJxcvJkggEVwQD1L48y9wrVOPsn+4zljtwFbFRPYPy6zaU+6dl6BDn5HQShF8oHTihtcc4cJ9IqfwxoJ9LkK6Hv9kjpMxtzI2B/rDnOhhF2nrrHRI0UnJf1Fy2OAe2eAbmj5gElxuJkgYBOe91s1gBqnjui33XhwTED/PXbD2FQQtRYucBNsyfx2h4+R+sS+k1SuMdUus27nrvURCXiwxuHgV5cVAvoCYCgoZEn4oAwTa52poFy5q49Men3HT/v2VPTIdvTkMdZ1dBsQjQLujn7avvFWh0CczxHgvrU+oemliqekfj7G92C1b3GK/1DNb3Dm3oH5r/1DQ4XoxTCHoZ2lYKgYCdzIdFeqz8zBXRYHrugTT3ka0u41u9gtKGBkMhAx0MLs0hair3xKCxN2dEaJEK/Zem+oypdR7DeYTavCZ19AqpVo3Uqsbqu49vVI0qdx9bPHwy7E21i7SQJ5FDR0aUSbC9mQBOlacPm1zq8p7GNUTTK7TNM0TjHNjkPL7Uc3zOwxM107ZBhoY0dXS5rH4jD0lsNsnGgcRh9Aj5wdQk2OZHZ/Z7r9ZtjK6HP+UarFaN0/YItPScaHIN0avGt6rG1noGpg8M5hfFQrWNkOUZ2QQMoKEIiN03AE2kREhLcyicUgG3Ej/LoN6x0/jJ9K1r33+KILykJDhhAvpj11Men1jafWS783idW2CLR0CN+7jafhOK+wW1Pz8LQnbA0kt5fgG1D0+53n/ckf8KwtUSLSZeb5Y4/gdTGopL72qMvJ4MFbf0AFvPtzw8rc3VP8dzNOxOBi32bcSiXwEA/bNU811d9C/dqYiHCDZBK2+4HuSnZCj+pSb9LJmTm0TJSsFtyZ7bbiHlsH8s4QjgOuagvNjdZozjMfdOE84ywbIftIGRi3IcZ2f6yFcipv6YPYRVTU5xNEySJCKu6rizK/0L9wCpZb1eP2nSJFdX1z/LW69evaZPn64I7BCAjxz5Y63iF17MLvP+kzxAGqGCOysJUkbSjZMXwba2NhKl0MfHh8hxdOvWjQzAvL29p0yZcuXKlfZ2DFNCUZSSj2MH+KA96n+Sn7vK8h/uAccXehEsFLUpLHx43wEPd/d8SuU1dvCzH786cmHI9MLMHPQDJUBhY87S3alfhjUdTYRWPc3RBuAMwDESZ9MZoFqd+9XW9I/WFG86BDVqvk0LIOqMOhBFoaohZUOEKep7Y+S5gu0xUNMCLIvUNL2ZL67LDY/O3XwQpW8phrPxFAgsyIwnCydWtOR8e1y8XAjZzVnhBwviEqlmDU6T83LAw3ZjwZH407NW3/hkHVwqgVYGNFYwcmCBpu/TLq389vsl2yJnf7N67tfvvfXuiwMe/W3vIb4qp16q7t1VKk9PTx+/vj4P9eszeEDfoYP6PTx40CNDRwwb/pshwx7vP3iE38Ch/QcOemjgwIeHPPX8c2+NGvn+xND5X82LOxR79XR89I6Isf93lJ+fn5Ozs0qlesTD5/88+tyqv36as/9U+vp9BXvjEBoGJN+xvIw+0xw06NXxqSkb9+nPpmZsic7YfQTZvvU66UZx5opvWyPP5K2LajxxGSiJpy2ol03bDAnJxQu2WMJOtIYfg/Qq0FsZhrJikD2bHlgza4UWfUvc9SufrE39chOitDqBrB8HDVt15EJS2D4+rwZMMveZ51ieM7Sqpcq2yrDY7ycuaj98CWU6ATo4yg7dMgISlis0BTuPVR5KQPY6I+KKZgCxXqM/fDXx0zWo2W3lUUOZcKWRHshCg74jIv5s8LyyXSdtZU2CmdaZkEppUWtBw1bviiudt6tw7g7T6VRoMwssZxLxzyJwNE3bNMabO2MyIo4ZS2pFI4UcYRuAxkJfzM3/OCz/4zDtqWTkOCOtWyYUFzaWrjpwc+a6nLCDdF41MLyILDEBBTR4eZDfaoEaY/m245dnb0z7JkKfmAVtKARLqNZ8Xk3+5sNpC7aWro+G4lbooHHWhOaAFqHJkL8tpnR9tHToStGKiNb4JNAZrKyRM+q155JvfL4+44swKu4mGiOjzxJF44laMzQY9YevVn6xo/jTzca4ZDAKVpMZ38YNTNmZq6dWbaWLqs11yCa2gWADGYMWBDAaoaatavW+ollhGbM3QEYFMJzA0xiY0Gy1qXWt17OSlm5r2HcW2dYGMwbhNDKQU5eyZPv38zfUxV0Giw0VYyhZdZ1CJRNbRXPimt1FW2LFc9nFYTFIYG/SI72rvKV07+nmbXFVYbHJO2JiN+9+6alnnZ2dXV1df/+7l6N2RVy7cHHR/AUvvPDCoEGD/r4Ics6cOW+88cawYcP++Mc/7t27l0QV4jiOPB/toaVkBjQn/1c0oBWc8d7dZteb5L39c5+/CjZcI2IwGK5du7Z9+/aJEye++OKLAwYMUKlU/fv39/DwIAobvr6+JEQzCfCjUqkeffTRESNGeHt7v/TSS3v37h3/3nhvb+9Ro0ZlZ2cjC5mWVU0dKumn7SHQKAeQa84eMVHjhQq2TVNlCWaJEJdv5WGTcVECit3aS1KSTHOuYmqfnCH1mWZzCSl1HW39OgbnchjkGZI/gvcQMJo1yUIfcp8POoCb1ZZvz1evi4F2FKRhLRSqdMh/pJXeEuLQAkzfo+81wegSWNAvsGXTCRQCwqKj2oMkIW6IYhpWBvvJalYzdXPLgEmm7v58z4k2r0m816Q294DyhyY0v7cCrtUgpCtPxxHGK2oNd0g5T09r8wxq7TamZuBE2JsMjWiqCUPK4rGMLKmBl7sTWCY3kpbHMHdaERdYIDVd3nvnwbLJt/0jRGrMmQKIzz05dMyNoYGnHvWH6GSEXI24+I8FpOjeetclKJoCBHPyuXqAJhsKQRR3gBpVmBC2EySc5GuVct6e0+IR0KJ696r723DVBGFXEweMqRoYWusdWOUblDkgoOjNudrlMVBqwFK0WcCoBD3stFchtCr4qBFgb8pVvzHlD03IGRDYNGEdNAGYedTY/SkAWiBzBkTLpUnM+7/zCwYGN6lGaVUjW1UjLR4huh7+DW7jM/zGt08Jh0IDSjkretIO70KSHLsY1bmJipQe4Hh23h9nl474IN3nvSzfgKwBwUnD3q+euB6+y8M209maCZjTOY7AntIem84mL82hUAmkbXp4ybDQBg9/tWoM5fK+uVugRjVarRrX4h5U1u/9vJc/hTOlWEcGHnPm0ED5ExP2CRgFLf3xxkA4uSQAxm0AdKfrf4WfSh2RBACk1158JKDSL7hx4KQsr9EZwyZUvrsYIq5BWjO0ibhuoFVo3HmqeM6OmhXR0pUinMih5YcmITs7epKk7+oV4mcbQB2f8dqn5e5jW3xCLg71h0o5aqii9K1YpUDSd83tQXb+zAzoB7n0L/RYhcD7Kx2ZOzxYb799FZVbArjf6prlcx6oPghKS1BdZVaZ5KDA3OQYslOx6oGugh2yJJFXw9uucp/5KBRsxQwlQUy6LR9Hm5WfFL8Rjyn7uxK/TA84ViLDMDU1NZMmTfL09Bw9evSbb745cODADz/8sKamhtzpOP50fE158Hvhl+mELqt+vR4gXVPne96tTyX2DlnJQZ5QDMM0NDQkJiZOnTq1X79+JPAskfhXqVR+fn6BgYGHDh1qbGy8ldEPwxL+eh3VZXmXB+7qAfsjW3mhl0lZS1Ysf6hf/wEq5xdc/EKfeDVoxEs7/zafK2+yGSxgYpm0ssxvIpM+W2s8dAlKG8GC3GejDEALAieVN1buPpH2+YbKjYf4gmpBb5Q4VtehBo7TFJZnRhyuiTypi04o3RoDte1gQeUNiWHEwrqa/WfS1+2BvFqw4k4Gh71yUDtONBfVnF+7W386BfLayrYfrzpyAYfTVhbjy0kAzcaWc8k3V0eem7VGe+QqVGhxoGYRoKbDerM05Zs96Uu+TV25F0rUqFbZZi49enHLlC+/9J/0wXvBKxcvDQoK6vtQf5feXiqnzsAWLk6D+w94fsQTU0b5TxnlHzzO39/ff+LUKX8ZM+rpF347cMjgAX79vFzcXFUqV5XKWaVy7e7k5ub2xMPDd89ZdnDW8rrjlzJ3xpYdTmBKGliW1QnIfcY1ghQHrca6uKvZW2Loi7lV0fFpOw9BRStYRDGvuiT8UMOWY6UbD3bEXUOvGmmWsYDFAjnVzWGHzasOty7fZz2TAgYWbDZaZBkQrBJr4qysVm+6WXT6s1XHpiyAayVILms34iBVxxgTs0si4jAMoB5D/KHaMo8kaGjUp286+N3EBe2R8VCLismtjEkPcvRIK+EOCwWRJ0v3nYEaZBYLVgbP0tHVsYkJU5c27ToNLRgG0I4+E5Cj0dBy4lr8pEW1YUfBIIpGqt2g1VKyZnS7MX/X8bLV0UVfbueP3IA6PZgZ2obos1VAq5hG9dXI2Iubo7iSBlZrxNAjnCzTnF2TuWT3pZCFTPRVUNOikeJ0JhQbabaUbT9+89P1KfO2ULIOBs2xWpExoE94XPtsEqBU3fjtmZKvI69/vr4k6jRWPQDC6AJAvbY2OiHu4+VJK3dCtaz1oTejDgYPoGXrouOrwmKo/YmlKyOFxCxQG0BvEHX6hqspqQu3pn2+QRt7GdopsDICK+s+W2kEhhq1mtirzeuP5n200bonEeoMwMkhyASpJjHl4uao1rR84ESJY3mR42QAGiU4WAEa2jI37cubHVa/NFI4nwntBooymjgzwlM6K5Q3nV68seFAPNToRIMJb2ErC1VtNbvjzv5tadnheOgwCxTFUFZsXRYOJ110XO6ekzX7zkFCfsriHbVHEqHZhIiPia+Kji9Zd7BwcUTO8khsFVpL4tn4zz/+pK+Lh4dKNcC911v//frqlauSk5M/+OCDp+QtNDQ0JCTk6aef7tev35w5c5KTk2maJs/H2wBomd9n5y92AdB37WwfaOd9jgQd9Z2feeaZfv36Eei5V69e7u7uzs7ORCaRQM9OTk7dunXz9vb+n//5n0WLFp07dy4hIWHUqFHe3t7jxo27fv366tWrfX19X3jhBRLx6LaRr2LSjw75yUhaQiXyGy990OAd1OQVmPe7j5H0ymKf1AnQ/bQnsAnpeIjOKXxkYprXKE3gWlADcg8RDL79T+QlgbHhBQhCi2JQgCLyel65JOmliGo0r1iCix4AYvIyHw7JHBiY8/osyG5C+jMPeFPL0fBsOLaWUMmdSHiUW2De4fwRk1L7jc/o7581KMg2cRvsTcN8iKyEXEg5mBwSisEowfFC9V+WZg0PheWnoJkHXMVhxxxE+SR5acndfSKiujWWiuM4A/BmOU4uLg25HbT40dNl9qvMm9ZwUGiC78sgvRE0MgfZhpFjSfDYW3WtQMBKQs4blxNZ8Rkhg/I4EYAPNQMHDdKFEYFq98AO14DkoUGQx2LIwe/y2XkHYXY0rEmA+Gpo4JFBLIBFb7y75bchgKgmDlDJnntl2uXfTT/0+Dg4kw8aRPjsQPE9UELZWpwAEHibicIpgQoKws/nPjY5zX1kste72QODCh6dzEzZDt9XIxNW3iRWwKaimCGXXZDwVYImADS5sBGgnIcjhbDzOhzKhcRGyDFCo4AEWB7nR2wi8LxAnNk5jsCeEpuQIOHkAZk/0NHQJEDk9fZxq1IH+Of2Dcz2Gpfm/m7xw5NhagScqkHdGNk2bE0yioyRKWSc/EEZ0KTlK22e1Kq92L/eD1IMBeqlAc5Xw+ITMD8WYvIg14TyMh3yW4Q8aYUFxTAk8v1ORKoEeaEbetOh3pX0XT1DLmcEOFaYO3RCjevYQq+x1qWHMWihXSde7m8cGufP5e1/FoAmbfGuhera+b/lAWWe6k4DHJ+1SvrOw+5/D2kAdz65f5bMCTh4Z+YPZN5dD35Q85Tj/xlj7mpJ185/hQdYJKAxZrO5o6MjNDTU29v7lVdeGTt2rEqlGjlypEajIYoEZIZDacNKLf8rTOrKs8sD9+8BpSnelnCc3iMzKGSBOemXsrKypk6dOmzYMBcXF3d5I4tSnZ2d33jjjRMnTqjViLwom8lk+scm9pQcuhJdHvhf9oDDa7FiCVndwnEcS+MouL2qPmTM+O4qlZ+r53/7Dpvy7J/G/ealk+G7cUCOQ2qJz6nOmbPtUshCzcELCBarzWBhAUMEWjmBBa2pYmvstY9XnV8czpTWyVcRUe6W5oCFm9ujy3YcbYw8nbo2kkopAgPNG4w4iLVwdRFnrny2TsypQfBURBiLAzDyDPCirqRm/9wVxZFxkF7bGH2+Oua8UNSAurqMADoL6HlLQtaVr8LjP1/XcvQa1Bhx1EEBaBghoyZ3zYGKJftufroRMuqRTESBrbi5JDw2efGuhPA91Rl5jNFsMJuyi/KTMtOWrVn15G+fVbk5d+/evb+L5xNe/X7be9C7L/4xYPTYufPmLVy6MDog8QAAIABJREFUZMmK5f5Bgf/19DPdVaqHe/sNcu012N375cee/mzy9BNRBw2F1TfD9umOXa+LTsiIOGYtawALI8rijzpBRhiMgvFSzrXlOyG1Sns29fKGPYg+qymoU19Ys6M87FDJyr2pqyOgog3LhVAjJZbV1a+O1i872Lxsf1tUPIYQlCRB4CiepkHSGg1Mo5pNr8j4etfVWevbzySDFVAHgxPBxGmS8k5+uQZ3amjgZOavKCGA26AvXBt9cfryil0nocUCFGfhWZPIyURBXlIboYPOPnz25MotLemFWBc2gekwoELizbK4aYsrw2KhoAUsAqtFhQ2008KDWYL02jMff3N5+Q5QMzaNkWEYq4DCI2CgS2LP3/gyPHP2Zu67NKg1Ye2yfIfVZIdddEz78WsXFm4yFFajmIoVxaBtGiPUamp2xsVPW1q26yRU4NoU5NyxPLSb2/edv/Hx2uRF280Xc6BRK1oxtKMe+BpdO83J4qrNlOlYUtXqg6WLIwvXRiN1kZM5jIwEBql8z+kjf13w3fz1VH2LSNMIM9EcMKytSd0Ucz7rqy1cxPcly79lr2QjntuuhyYtVOgzvtpyccbyim9P8DUtPE2ZOYbiWYSDLYJUq5ayqrPn70j7dGPmsgioNRBBDGD4pozC88u31xy+gDobPMdKuErATJnAJuMZFU01Uaezvt6RNX9r28HzQEkSw5hZq5Wxgplm86vOz9vQcvgC1LQDKwLHiVYKGjVFB07FTpufv+UQzkYwrFViaZFFgExLgwny952q3HcWUmtSluxsOJwITQZkKVLQ/l1SzsKdUsyNmwu2IY++gxa1ZrCBtaE9ftOevzzy7FA3byeV6uWXXlq/fn1jY2NERMQLL7zg6en55ptvzp0795VXXlGpVL/97W8jIiJMJhORCZaX6SNFtHOB+YMB0Eov1JW4zQPkZUYURTJBSNO0Xq93HFJ1dHQkJyevWbNm7Nixzz//fN++fT08PHr16uXq6kqm0dzc3Dw9PYcMGUKm2J2dnX18fF5//fUdO3akpKSQOPAmE05pNDU1jX9vfPfu3V988cWUlJRdu3a5uro+9thjMTExiowAAJjN5k5ADT8dX7duGU8AZhnVtaw+XuobqPUJzfQZC6cqoUOWqieRAG6d8KMpvD1EAK0Epca23WehxowQNs1KCO7ZN0cb0Dko44BiDhzBl2VqsQBgAckKEis/wWQKNT7KcCMYLi9jUmk1kFGDICktH6eoY6AmhJwzIy8rYUTU9jEIqHPdxkMrj0iuVgS9JMcuk48kODjJoVP+AsHEjk7wSzaSoIpE0FkBB29zhyg/BxGLRwgSidgUCPJMDxb9toPv9RWlA+TjceJWJl13XhIjH6A0BP45bnb/EPzMQRIXSUsyJRwN4EV0V64p+RGMPajrO8k0cRM0AnrDKuFDwSBh2oTwtyShCDIqYyig4Y9bfAt1TSnTfZcMuQ0kJgRxp902Uss/kglpiTLmKxtjkEAtQZsE5XqoM4NaBsTRFTI0jzHx5OxISTtLbZNVL0yEHk24xISHbJJ/MMs6MqZOl8pTI6IsrdTZQsknAtDYOAUJV+cQDJoTcbWN0YbvKk0s5LTBlQooMiLHXC9nS92KNUlwZ6LNfQt9doTL79kWiOHKpCAp3I+47Vewu7NyZFOVd1oS8tEo32JmeVZH7gV4uXLMyiIDXr6jHN1lbygPUnA1wLSIJq9AY++JOQMCIU+D0Y/lCKJ23ypWPUiu9z72nwWg751716//Kx4gHe5dL+3YFyvpux75QDsf7LHxIFnfoywPks3txz5o2ZXj/3Ulvd3Eru//hAdQ2pLjOjo6Fi9e3L9//1deeSUwMJAIQOfk4IJrUo/KVM2Pvnr+EzZ0ndrlgX/YA44djmNayZA0XYI+k50Wi4WM6/4+Eps3b94LL7zg7e1Nlql6eHi4u7t7e3uPHTt2x44djY2NLIvKmriInmV5nu/q1hTHdiV+ZR5weC3GeCkiRh8iISjIauub15Pe+u/Xfbu7+aic//vhJz986a157wTnJly1GSyoisAC1Oqrdp68Nu2bqhVRiD53yOgzrv1ngJekmtbKA2cSJy/OW7yTKa0TWIYWke8JFhoaNJUHzlRsjW3cGZe5dk/b5Qxo06MYLoN6tXVX0q8v2AKXinAML48NWBHFfBGb1lMXdx2siL0ABS3Nhy8WRJ7kixuQA0sLCFFTACXtaV9tSf1yU83eeChTo5EU4LiuSlu29UTxkqii+d9CQjG0cKjLUWeuj07M+HJr9tcRlswyBOAAKJYhFCEjQzW3tuSkZ+xdv/mjP4/5y0NP/s5jwB+HPvFQ334DBg8aNGiQh7PrsAGDhvcdEPr26DWfzI1etenoxp2akmrosECrJW3zwbpdp1r3xGdvibFmVYAF1SoJ0w31cyWAvIaCjYeMccntJ69fC4uiMsugzczmVxUePH1t9e7isIOZqyOhsh35d4wNZbjbDFV7TtYujKif9616bzxUq0GQWImjOZoDG6KfAkBefcG66O+C5zbsPg21yJgiS9nMuZUX1kU0n0uGyjagRATrcRW2CFqu9djV7K+2N285KWRWgZ5mWdRiZkVZuUKPoQQbLqSm7j+J6LOZYUUB2wYDbHpF4pyNCZ+vgdRKUDMow2KV0WezvPg0t/7mou3FW48K5c2IVekMWHfInYbGszfSl0fkzN9h2H8RilpwQTEjmbR6A21BENPINZ+5kbU8UrhahNA5gKAzI2Bap8/afOjSx6trtp0QS5skI4UBEk0W0NGNcdcuzliR8dU2/fkMzM3I2GjWLPFGECw8i/LcHWxLzMWMr7blfrW9Yn0Mwg2MhB6gJWi1VEWePj9r7c3VkcbMYr1Wg9CtIEhGM5iptps5GasiNDtONW2IMR67DI1qlLzQUUJmRcXSyLQPV2WtjIDyFuA4M7BGEC0Ch7MvbRYmueTmkp3ps8Lbdp6BwiagULXc3N7RkVv23cpt9ccuQVk70JwgcBwCz7JnTBSozeX7Txcs2lm0YEfLge+huh0oRhka28oarqzZXbw9FkpaQG9GzifNCC2ahnPXYz75OnPrQamgFiwsb2NNIAPQVh5qNDXHL2VsOaSNu1G6+2T5/rNQoUZnqi2QXV+0+oBwKKk27KguIZ3wwZEeKAHiRNdLjny8dOKbo575zZNOqm6DBw9+6623YmJizp07N2vWrEGDBj333HNBQUH+/v7Dhw9/9NFHJ02alJ6ZYaQstMgr6PM/wID+lfWf/xvmEoyYXJll2crKymvXrs2fP3/kyJEjRox47LHH3N3dCdbs6enp5uZG5DWcnJx8fHyIBMcrr7wyffr08PDwnJwck8lEoGcCjNE0LdgEo9FYUVExa9asbt26/elPfzp37tyePXsGDhzYv3//9evXm80oI8NxMoIoh7J3BNfIG9ctxxBQDGeYAM4XFw4Kae4xtkD1NkzbjQRhWgIasV+CQCpN/dbpDik7LkS6ZrmjJp3bnVcnNthhYgwPi0AtfmXxjwOJANA0op9Ew0O+Ax1hUDlkHMokkE2xTE7Yc+YlfMYJqJhskWOu4lBIsDOIEVuU6dKYEGQIW5amxaIS+Fguzy3sj0T6JdK8Mr55VxyMlB7NkgFoAWF0kWhS2yUd7Bbf84OUVGZ63jKg0647AWh7zuRtgZwgl8Ke7HzJlhFVGe87VpQ3IMjYM6TFJ4RbGIP6JyxWAZEuIYA1LdeCRVHGUMDTuxlOfGP/hRFxYQcjT0qLkqILQn69q9McsyRY+a22wQlkGRALYuecmYwLOwLQpJzyf0FCuN4qV5Aj757Ui12awx60mZCTEZtHDPoHm00SZJUkbJzycxYFplCCSQ6nKFcu+4NZAfvkhIwcKzIgBIBWzMBjSB05vNc5ll1J/wCA7qxK5ddfXUIpTuftar/hCEdC+U9eD60ymE/mXLC1kMrtnHt64LILsiLK+dI8X3+DR3ClyxgqdDNoJAwscStvOVdy4z/wBX70hC4A+kdd8+v94fbHp0NJOrvZH3w6/P6LS96jLP9OWxV//Tsv2nWtf9gDDMPo9foFCxb4+vq+/vrrn332Wf/+/V999dWcnBxF+tkRfe4CoP9hV3ed+K/wgNLh3JZQrqW0XpLAFwV5Y5G2SVMUVVpaum3btueee87b25uM4nr37u3q6tq3b9933nln3bp1bW1tJDdHDrWSf1eiywO/Dg90DlTkEZOEI0959hEDl4ni8VNxv33xBbduTgNUbv/t8/CsP4xaNX6qOrMQec0AoskMOk6MvZHxyfrklbtthbWIzbEssBwBkaFBS0ckFM9Yn/NFuPVCJi4ZBkHHmHiaYsvqNaeuZ83fKuy7XLj0W/xVa+KtVlytamGplJLvl27RX85B7QikI+EQEed7aEYyUimHTlUcS4QyTUPsxbRtMQj/GWkULhABucO59WVhhwvmbK/dEItYm0UWDrbyUK9F/eKlUbXLD1Cn06BKC2oWtJLtRPrND9emf76ZOpWB67tljowgAxM0iBi/Dtd9M1JubeaaqORlu/bPWHh++4EDBw7sO3zoRPTBHctWLZnxSUJktCY1vyTuwsXwSENqIVLA1LTm4MXGdbHGvRdy1+yjbhYLDRqbiEgBjnk4EToYMb2ycMMBSMihL2Qlrt2pTS0ANcKv5UfjS3bHqo9dzN99BIprUVaYtyFJqlnfHHW6aUNMzYr9BWujZB4rDRzHsog+4/JpG0pJ1Gw7cXH68uINhyCrBsyI5mOf1qy5sSW6OuY8UmI5WZiQkVUpdACJxd9PX5a6MtKWVYWWS4DkX15A8IURoMlkupp3fdtBY24lOgfjugNYOT6vJjXswJn5GxvOJIGWAT2F6LOAPyEzulidu2bf9dW7oaxRHgvaBIoCDhuGMb2oeFFE2Zc7tNEXkRds5JH2RfEYr0+mTrd/l3T6o+VNsZfALBGZaZSSKG3W70tMnLwkfckuKasaWJEXBJalxVYtE5+RPnfTpVlr2k5fh3YDesKKwS/t4QdRTMRAJebkLossXbKnaNU+yKmFZj2i+YwEtXrjkStnQudlffMtU1AFHM9ZjCDxAk/T7e1Q13Zl7Y722MTklTva45OgUS2ajCjQnF9btf1YfOj8xu0noLIV9GZOh1rSPHIlRdBTbHpF3oq9BQt21WyMheQKaNEjsMtJxqKalC0Hy/afxXiYWgtwnCTY7LEHzTQYOfpa/vU5Gyvm7WzacASjCxopvCnkOmHU2rIDp7M2REFRPZgZmyTXuNasvZx5Zdm2pHURVFE1VgGDALRVwv8AUH82qebQebhZVhJ1Ov/QWb6qBSdjtJzpfFbekgjdrnPpS3aVR59D9JlCyWycWrAIUNhcsigifd626hsZZ86dDggY793bS6VSDR/+yIqVy1NSbu7dGzl69Ls+3l4v/va5MWNG/eUvb/n28/t7X7Fuc3hzh9rMMZyMK3EgkcE/AYl+HV3iL9tKSZLIHGF1dfW5c+eWL18+cuTIJ554YvDgwSSccu/evRW+c69evby8vDw8PDzl7d133120aNGxY8cKCwvJJDop623z8TRNk0u0tLTMnj27X79+v//97y9cuHDu3Lnhw4f7+fl98cUXJpOJjAXsQUodwLW7jDoJ/1dCAYGWV7409gwxuQdn9xoD3+UjU5hGYAbxXvnPLqdwn7WAIC9ivsrm+MqHXZUgg86E08rJaQ5xYUlCPFSm32Kv1sn9le80guL9iAEErbIDsogsY1Yyoi1S8lukJKBIFIbFE2UAmpEvSmBRB5Sd3BG37gtH9Pm+gSry1OZkNrcVEfYH2Tof/XgOMayz4I4+VNKdXHL5YDkooJ3PTZjUBGonZHaNAAuO1vQO5JyDqzzGwf4bstQ3OpxsBAImaK99YuCesKkC/9pEkWWR8I42CzK1XG45ClP53uUnGDHdGUMSmwdBmclpIq6nwcxJ8EOZO28XVlYskJVe5Gq3g4uEiUxATAXatqPb5DhBbmq22wFonHYkDdLWGXtWxDAAKOyMhGgZXieGoYcJlk0Y/ehFJdArCRFJLiW/W9zbB/ZfFcQWv//6AWgF6lUqisz4kOklcoMrMLSSsHc1nTfCfd92P/QwrsuDphlbynwCWr2CioZNgiQNMhscWuYPT/jZvnUB0D+bK385GZEu8q722LvPH37c9chfyM57lOXfaaHisH/nRbuu9UAeUNQJkP1ksYSFhfn4+Dz55JMhISEeHh7PPvuswn3GNwAJuXKOm1LFXWzQB3J718H/Cg84tkbHtHItxwZM0gzDEB4QOYbE8Glubt67d+8LL7zQrVs3Mqjr3bu3i4uLt7f3008/HXsktqamhsRWvU2Lg1xUuVxXossDv1APyC/fpNMmg2FcByCBxWLZHRHRp7+fs5OTr8plmMr9iz+O3hb6mazvzJp5yiowoDW0nbiUPv2bgi830dmlrE7LCSwrIakTMWgeWo9frvgorO5v4XAmE7QMazHbcTETbbqSnb54O/ttQtXyvabvbiJkiXH5KF6tg9r2uHnrUKK3xQisKHG8/eZCCUgh8+i51F2xUNxed/B88uZoc24lWDg7T01LSbm1SQu35S7aVbgkElKqcFiISsBG0NO1J6+kLNmZ8cUm84FLGDGJxgWzVEJu0rRVmX/bYIi+Au0SwnBmBsFugTfQFiQUixJiuCVt6SsiG7aezFkdVR2biOxRsjVrb0TE5B45A21WU3LBlc17+bwqaNQDBc1nbjRtONqx/nj+0kh1XBK0mMytGjkIlawaoWcgvbpo1T7u+E24UZ6/+2jLhRSULmkzqs8llew8ojuceH3Fto60PHIdrq0daLH24NnqlVGt62Py1kVBZbvYrkOwlZbhaVHAAXkHUxudcP3TdVc/XgPZDSSQIBIMddTJdTtKD8VDpRp4QHfxAuI9ahHi0m9OX3Xlo9Wom2zigRNRkZOTlYjlwIMdCennl2xpuZgus7AFZBNbOFDT5ZGnzs8La4xPxv0iUBYLbZVDftGSlF+fv3rflTkbmMwynFdgaZ6VRS0MjFRQe+aT5SWfbDaHn4J8DL6HsqqId8ujPx2jvZZ7eU5Yy/7z0EYBI5JZB9CY1WdTUj9elz5zPeK5Gkqv6RB4FrnG1ZqcLzclTV2mPnoZmlE6vL2jHacxOJkszwlgFaGsPf/riIaVhzK+2gZp1aClULicRe6zIfbKpY9WXP5irXizGGieNxmAoVEfxmrla5tOLVxbe+B0+tb9LReTEQSXRG17C9B8y4HvU7/YiHMAuTg9YDVjWEUbIwcpkwCajDV7z1asik6atdF2tQixZpoTrYxUq765/VD6poPQxqAPcayM0AMC0DYBNGbuRuHNhVtaNx/Pm7cNynVgwNkKlHIG4Nq1lYk3MrcfgpxqxOtZFucbOA4q2zPWRF5ZtAkKG5ATzXESSnrgH1Bs9XdXy76Ng+SquoPn0/aflJq0uEqABSatLHnZLv3Oc2UrD+RFngQdgzMNADrKjELbjYbinceTZq6Fa2VAYV4NDXWbN2x4fMCAPj16qFSqV3//8sm44ykpN+d/NffxR4f3H+A3ceKEiZMnDXpkqLO358TpUzNzshkGQ5nJq/gR3SN9C2Hv2e+dzmG//ev/rx93fT+5hzOMRmNCQsLixYvffvvtfv36qVQqNze37t27E/SZvKU4Ozu7dG5OTk6vvfbapk2b0tPT9Xo9ABgMBjLRTlYkOKLPgk1e3CBf3mQyMQzT0dGxfv16T0/PAQMGREVFnT9//tlnn/Xy8goNDW1qwvv3xwDoW69ABOvCKGmA8gubrzQMnmxwC9L3n3LjuamQ3YFdsRVJ0ITxiTNmP7Z1thkigszZeLzTZdqoMhhx9KcdB+QkebmDDATLnGXsbWzYOB0nSAhEjFfuTNE2WR9fNpxoVTvAW47XQTSQRhoyWqGg4T8AoOVbwJ6x3NWRdf924JvgvwRkvB8YTD6GGENKQUDVBwOgHZ1sJ0TLZZc6ceIfFJFAn3bn/AC+RBScILky3A8AzazVf327W4Cte1Ch6yi4XIEaG3JvIJPB7XoddhCfoL2kZjvr19E0BVt03Ok4zOz0g1JvjgfeShOb5TlCSSGM2y0nR0mA+iE2BKDtmww3yx21XHCH6sceTW4TtwBoeSrCUboEGwCZopDRYqWJkoT8kJK1PgSi0IHtmMNnjywaI4DIS5xNsBEb7B0o1gLZCNhNYOhOoBuvdv/brcmPzuZ0/+f+Mo9UWgIpGgGaFfRZmaXovL87C3Gb02772nnU3T9xtRBA5LXrQwLynd5pGDYNNl6AJrkG5X+3Zrbufv4/tbcLgP6n3Nd1cpcHujzwC/EAAaBJgM0dO3YMHz78+eefnz59+gh5S0pKwiXD8uvmbc9R8rXziY2fv5ASdZnR5YF7eEDBoElCWVLq2LyRHCBJjY2NBw4cICo0ZLCnUqm6devm5eX12muvLVu2LCcnx2w2sywyzsxm5PGRNQH3uHrXT10e+EV4AEeediYRC6KBRmi1vrZ29uzZvr6+KpXKU9X9Ne+h818bl7hmN5VdiRGfLDRyrSyU5kLyzQUbMj5dCxdywUBZzXq9RWcDwcSZbTpda9zVlNkbS+ftsEZfgkYj8HJ8Ip4FrVEoqC3eEK3fdaZqRZT22BVo0oAooFwex0OTIe/gmYKjCXRFE9A2XkBODyXhSAz0TM2Z6ynro2yXC/WnU66u2NVxLRcsnCSIVppGELPFnLXhQNnC3XnztjHJRaA1ActSej3QNlNqYebqyBvzwst2HEXtYAOH4OzFosK5O5I/Wq/ZmwgVOsRBGDswYSc+2yTUMq7SFG08VLP+cMHaqNL9p6BVDyYrsDbQmLK3HSrYdBCKm6lr2em7DlbHX0FerZnruJqVt/mgZW9i2fIo5lIealDICItJ5DQmA6p8aLi2baeYiERIqS3adqTs8FnooOH/sfcd8FFVafs3CWl0pAoiIsInlkXRRVe/VXfXdfXbgt+qgFh2ZV0buhRBegslQEIIKYQ0SIOQ0JIAqYT03jvpyaRMZjL1ztw69877/7/3hjFSbJ+66s79zS85c+eWc95z5s45z3nO83Tr6Et513YGUSFJxVsP91/OEs0mg1EDegMMmnRJ+RU7j3Xtj67YeQyBXZUeucY0P6S5bOBgkGMSizM+3Ju79hDktw7JXgsACkO5V2SV70no0oAVOJLCYTYjoNbzldb21YHlqw9TScXozUXxVo7nLLi4HhnlPJCFDbkHwzXpZchxNvN4FmMFNd/oF3f5Hzt6wi9Bjw5YPMXI0pL5I0CH9prvqfPvbpFY7WbAddYcSjhrTFDc0rM/qm9nRO++aMiqByOOBDkz4rY8I+km5zaWe4S2BF+AfhqhUgAEtQ101/ms9FX7yzYcgSu1MEihiSVFI/pc2V2/JSjnzc3KI3HQ2g8mM8OaGFxVbwVRRODTZIXa3mbP6L4NYTXve2ljs9B8T+Z8kWC4VJy3zjvt0wN09TUw02g5aDCAiQS1BhSDDSGx1b6R+fuPlUWeAY0BwEqaDECzTGlT4ScHOvdFCZXtNsxDAKtJo5cY6LreoMS6rSE5m/x0aWWoDGNiQLDySl3t0fjyAxGIPusYnmI4C28VLDxL43oCM80UN+Rt8u3ZH1O7/RgUN6OgOY/a0GbGbB3UK06nVR2JtrT1YcPjLQhYcwIotL3BCbmrDwpXa3C2hmSAYVH6xkSDjmo+n1G6KwQu15LH0wsOhJPdSpPBiG2mU10XdkF38qo56mrNoRjqmoIymcwg6DlkbwMDxYGxJ1fu6Dh/FRQaEAQ9qbcCDzp9pn/4a/c/NnvseCeCuHvW9Hf/+ffY6Khzcaeff/63U6Yh/XnZ39/63eI/3jn77oUPLziy94C6uUOeV0AVFEDBbVnk54a+4o1wwI/isfgDZUIOha0LLfcc5LlwWTZHFEWTydTb29vQ0JCUlLRhw4YXX3xxwYIFI9EhkpAlwhwcHNzd3eU9Y8aMcXR0dHV1nTdv3t/+9rfQ0NCysrK+vj65PMP7Nl8nLZ+lVqtDQkKmTp06f/78qKio2tra5cuXjx49esmSJQUFBRzHyWJNNlMNW3Hk0iHuLKN1KOYOoIGutw60jnxZ7/SKesY7yhe3QyMFAzi44KwSuibg36+sAGTrDkk8D29QX0h/zlMejpDKcJ18K4k1PMTkvemWN7RMGd666aghaPVmxeTr2fsctB06V4JZbWDm5ztvd4Obb/nFPTYs8oYMf/Gor3png4Bvd6CNJT0MjMVjh4PXMu9UB42z3qJGvKYl/lg3dQnO7Nrwd7mMtuq13fQ20PPt8nLz/q9Tdvnmtsmw65kfohVLBfkc4ZWqb1hRbRVmuwqyp4fam9yJut74EEqWX9IU49D1bUIZcsIGT9swZRmjx/tK0Rg6XrroUCftOjX7+tyePMP3hb/Ds3lzlIb2SPGXj5Tvddsjf2of2KZGhsfBlv6OS4M/awCN+vx7lja7/qVn0nLhDT8YkDR9pOYoZ+brtMxvlzE7AP3t4mY/yx4BewR+LBGQO45DC3UpKjg4+K677nrwwQc3bNjw4IMPLly4MCsrS+ZKCJZhS92+2IG9/tOL/38sBbPnwx6B20fgBgB6eAOW08NP5Tiut7f37Nmzb7zxxpw5cxwdHR2kzd3dnSCIhx56aOXKlUVFRXq9Hh3GGPQZu/kiwy9oT9sj8O+PwLBRn4XlTBRloqjm5uaXXvjD1DsmjXNynUg4PTN5zr7/ebsy4DQqMCCV0YpixEZKX1BV5OGXtnIHpFdCjwEo2syQtEDpdCpgKFVxVf7mIxUb/NqOnoEeI2gpBM5oBgxmaOwpPxCu8j/f4RmlPZ0J7SoQBBYsDGkCxtoYl5rmFWpq7bEyHCtaKSsu4SdJM5j43tzqggPhkNkAOU3Z+0NV2ZWgJsGCXzfBzIBJqAqMq94ZWrzGm0ksBBPHkEYrwwBJd13ObTgaV7TVv9H3FIqwSzalAAAgAElEQVQmo54ykFnVZWt9r7y5TRF8Cer6wSQNkXkcUspLg4dqp1nZFp5UuzOsaltw0/EL0KbEIhjMoNSWBp+sPRQFFX1Q1nll++GexEzQIDDdnl2Q6xWqPZ1Z5xWtPJOFKsx6xFiR2QSA/GItU+wT1X/oDFxpazgcg7TWuk5QM5BV2bQvFGJz27YdHTyVgp51PE1RBqCF7jNpxbuCegPPl3oco65WotAExSBezwmokqznoIcynMsvWe+Xv8obDZp0VlBToGNBI7SeuNjkfRJKuzBctm2QgcK2/l3Rle/u15xIw+NJHlDQHtFkRBUGjXxVe9qeo53xGdCpGaKwmgXo1HSEJEa9tqrZNw7q+4ARTRRF8SzFS9LeWqMmITd91T4qpRh6tWBGbRCzlbbSZujS1u881rTmcNvmIESflWYwI96N3GGWA4pnqtvTPvVqDzwHTUo08aNYrFYBdAV16Wu9itb7sgmF0EuizAvHgSBCa7/S63T265vaPE9AYz/ozQJlEtDaEQf/WFAzQGlb8bajin0n6z8+DLGFaF9mYK0MB1oTe6X66qoDV9YeMGdWIPosWoBH50xEnxkYOJFYuuVw+lbvkrBYUOs4jQYvaDBzlS3nV+4o3eQHha3AIm7OSwgMfsoDNKsUYRdbt4WXrfU1ppQJ7QNYBJyWZMriLiV9uh+K20DLiGaGYhkzy7AsPdjfj9HuVefuCWrbH9W8O5y7WAJaVFbhRY7lGdFMNV6+Wrj7GJS2iVqDxWpBbQ2LCN1axanUK6s9ucQinODRM4jIUywytWmxP6Oo6kg0XK6F2IK6vRFQ2YX6tzQj9ulqTl1qibhIJRXXeEXTOXWgM8krvFHyW0O1JWRd2nYYFxloKQyUKCCZWhCgq//S1v2dsRcjdux9/L657gThNsLhv3/5y/0eHjUV5X5+vnPunzdpxrRFv33mr0tfe3jOvPmT71q//B/VmfkajYYWsZYFQO2IG/qQ/+G/kjewj2U2sRwljuOMRmN1dfXJkydlv0fZUXD06NHu7u4y9IwThKNHT5w40cXFxcHBwc3Nbd68eRs2bEhMTMzJyenp6ZFRbGyB0qT4DcH/Yhf+Fu/kEwFArVanpKTMnz9/9uzZe/bsqays/OSTTyZOnPjSSy9lZWVJi1ewz3NLNrSEnUlPV4sEzfAAZX2ls5bR0/6hdn21Y8ry+ufXIQYNYFRL3zIZ07Td+/aJm/tsN+y5JSh8wzFDMNzt7/KVn9xwwRve3uL0YT+7t/j0m++y3fGbn/oNz7ie8y9gajZgWla4oABKVe1TlwsjluqIv7Q99AFocWJriAoqh1u+zs1/v2F2vqvDbQG8IXEL7rMNy0RwUSI4D4HC8loW+QKfA9DXYWgJ15a4zF+AoW+4n+3t8CNtO69Pt9jAbhvbenhieAZvG58bAOjr0iu3Pf4n9cH//Rv95cUd+hLIzV4pKNcE98x4u8ftr0V3LIbULux1XN++75zYAejrkbb/t0fAHoGfbATkLi/DMIGBgTNnznzwwQdXrVp13333zZ8//8yZMzZy9C26qNd3DfuVtAPQP9l28J+U8eEt9nZpWzwElDDFMRLDMJWVlYsXL77//vudnZ1HjhxpU+e4++67t2zZUllZSUubPNizz8fYYmhP/LgiYBs3yl5JHPq51ZRXPvOb5xwdHZ0JYhrhsGTsPO//XlrkFQEKvZXjhyTzDCQ0dKes9bj4/mYyKQe0JqCx021mDYiW8hZo7M7adjh3o0/zsTPQowWSRlDMSIOWhEZFu+/prr2RXQdjFGGJ0KUGTtJc5FhQUc2xqTkHwvTFDRaWI0FAUUv5x4QCpqg5Y2uAMS4P0uuz94UNFjZYGY6ThKDw4j26jpjU2i3BlRsDr0UmIhCMK7oRjGPLGkt3BlRu9a/xiUD4WGtANLy0tWRbwKUV2yv3R1hqFKBnkbuKIA0+CWSjJHzbremPzazyCKvfG1G0Lwz6tKjMSLLQ2k+mFVf6nIDcOihqLth2xHQxF286aICu3vTDwU0Bp5uPxheExSMBluJ5hjWyNMlIDFMNVRefWu4bA5eqVGHJmfuCoLoNlBSbWlS644j5RFLX7jBFQCyit2oNmIzIaS1rLN17rOFQdMGeYz2p+QhnS1xXVhRQFcLEQadWvFRVvSEod+V+zamr0KVDvJjiwSjoz+cnfrjLkt8IeklkWR48CQCl3X3e8fkrD/QdS4LGASyspPuKtFwOTfyY6vbM3UdbT1xEr7xBihEQQ4Q+qu9ESuK72zM2+/KNCuBQ6tTAULj4g+JgkOxMzr3kcaQnMQuUeqAZTqBp3gykCdp7y/cezV+9r2CrD5Q2g4EDMysaKM5M48oqiocGZdG+sMx9wZbaLmCsKJHBWBFYr+ur2R+Z+a4HF5sLXXowWzizGZH8QdM1/1PF7+zs9TghljSCIAi0ESwUiMi0Z1lJDaNpoDngTIf36bItR7ujU6FdI0mscGBkLA2KkrWHct/16IvLwMwYKUSfUTGWAS2ljr5Uu96nctPhAv9wGBxkTFqW1CPCW9Vd/MnBon8dVCUXoDCLCKKBEuV17yxAP6WPzCj/l0/jlpC+kIsoIWJkBJ5ndMbu1MLE7YfVOVWgJi00a2YRgKZYhpG01EFNZh8IrtsTlv6Bhy4hD3XMKQ7FNBjGrOgfyCrL8ApWZ5VhSCV9Z4qlgLFQl4qurPbsjk2FLi0YJPTZLGmSKNRUaVPaziM4DZNaV+UZwZW1Ailgu9VQ5vz6Eu9IJrM692B4d3wmaHi0jpQ3nUmfVXX6451FASehV29lOK1BP6Qr0tJT6BfedvoiNPcY8yuOb9rx0V9eWTB95kRn53unTHn9L4svXjgfn3Dmr28ucb9j3H3z5i7988vPPrRwjvuEPzz+lLe3d1tPt1Kt4jhOBihlhdwhnVzpS/czY+ENxfNr/BsOQMtdBcEikCTZ3d2dmJi4adOmZ599dvr06a6urrLChpO0ydzn0aNHyztHjx597733rlixIi0traurS6lUDtd3lpctypG/GSC+3n+/xX/5YFsHhqbp5OTkmTNnTp48eefOnd3d3Rs2bHBycnrggQfS09NlpPvm6+PpiNANY5JaAbQixFWXzlqmmLhMM+GNnknLkQddo0bx8W+13a7/9nUA6G91w1ucdLs83OLQn9kuW0fCKk0wGABCrraOe9Xiskzn+pr2pZ1gBEZimiNsbQOdh6eH7/x3BOe2dTe83d4iPURtllr4kJjSEPcZl35cfyEbWtqGw8py+nY3Hn7ksGNkySabcJPVKgg4N4iqHcNZ8LfI6Q1R/VkD0DeU9Tt/+zlcrwcIyC6dsLjD+S9Nk5aIHmdAKaKQEP6oSa/vGQuxA9DfeeXaL2iPgD0C33sE5I6v/NOGzB4DihjGnoqdP3/+tGnT1q5dO3/+/NGjR/v6+qrVapn+fIsu6rBdw34lv+eH7vceG/sN/iMiMLzF3pwe1rSR1yMzmuUErk8HSE9P/+STTx544AHZ88fNzU0eFs6bN2/16tXJycl9fX22E/8jAmov5E8nAjfiAizPkVRCbPyzTz5FEMSkUWPvJJyXTF8Q9pu/1W4JZkqageJJC0uDKJjMbH1bo3901pq9raHx0KkUdRqK1tGMwWzS4NCova/e60Tm+zsrPMOQOYuiomYUNxgkoVunjklr+NSvfeOxzqBzKCfNCaIoMTrNrPFqVal3pPFKJahMrCgY0I1HklnkgC1uzdl5jD5TBGmNFd4x185niRozCoZYGEESm1YlFZRuC6pZH1C3N8LSrADRijAlALT2NwfEtuwJr94VpM8olojDnLGsrvFAZM5He2sOxZCFDcKgyUyzFNrHSSRlCYNGaUgD13nuar1nZMPu44V7Q1E92SBdU2+x5NbVeJ+A6l4oa8vdd7TlxFnoN0raFIZMn6CaY7FdoQmN4ee5AZ1aM2gRRc4qopi0IILG1J1ehMaJuU18ckVj0FloVoLSBAV1uRsPkpGXu3xjOv1PQUkj2hMBgHIQOpR1RyJafE8W7j5myKkEkpZERVhgBItEqQbaaqnqqt4amvdPT6QP1yjAyAEjgtLQlpCV/tkhNqUCDLxFYwQRWBPFGk3of3i6IOONLcUeIVDdjSWnBbCIAi+hzxSvL27I9Y0sC4iFZjXoeIvaoDUaEBXNaqzZHHTlMx+xqgNonJCQfMNEDJeRh3rFhc0Hy2IuIFJvokiV0syZOIqEfs3gmfSiTYdyNx5UJKRLchYgsAxnptGajxaY6vaK3WEZqw9AixIQs+V5E41Mom5Th//ZjPf3oJ9kRQ+YEZ9CM0MDrUvIyf+XZ80qL8hqADPDs6QgUkizE3gQBJNWy/WrexJyCjyCr37mM3A2G9Q0xkQy7equaUw/GhW/YuNARDJ0qbBcegNwkgItRRoSsto8ghs3+DZ4hoJKBxwFIgsUDQ39VVsCi1Z4iGcLYNBo4STdZIqz0JJxpcLAZdZXrfNv2xLWFXjBUtKCRHsrCIPGxrTcpG2H1SnFQFlFGqniJgFFxqWFMhYw0d1nr5R7BDftPdHqHwctfThhw3FAMVxnvyqnPG7dnq6Eq2CgRTMlUBRrNFpJM9PYeWXdwd7gBOjWYt0h8VlCnw1s1+Xc7APBfEoZc6GgdE+YNrkYcT2KBz2nyigr2BNiPl/YEnGxITYFeg2iUm8laVRWGTRBnSJ/V1C5VyQ09sqjaF7kgEXJ7+pjMVXeYdBjGEi6WnAkTJdZZKlp8fpo9e8feexO95HTXUc9Mf/BzzZ9dvxU5D6vA//9q6funTL9pUW/fut3f1ow494pU6a89e6K/KJClXJAtKAwt/x1YKzXGzCaiQ3N/djgzp/Oo/Rr5VTub9986HAAmmXZ1tbWuLi4Dz/88De/+c2cOXMcHBwcpU0GmmWOs8x9dnJymjRp0tNPP71q1aoLFy40NjbKQvk2lF/uwHDXt28BQMs+hHLnX9YW02g0aWlpixYtmj59+rp16woLCw8dOjR9+vS5c+ceP358cHDwlgA01ukQaRDr2URRONvXzVl2xVfMXKYcv0zv/GrfzHc6PvbHZSg4J/MFfu3NQbt5z839N3mPHYC+OVbf/R4ZgJaHfSyA2mpaH9E68mXOealqzFL6bT8ghwDoG29tw51tiRuP+IHe3679SM+l62DiLWDd2wDQNuhZTnyfAPR1DNoOQP9ATeULtynqKJ21TDvprfaxr6r+Zye0UZLZ5vXVHrJs/PVH3xdO/I7e2AHo7yiQ9svYI2CPwA8YAdSQsuBIz9bjj4uLmz179qxZs/z8/ObMmePs7Hz48GFbd1aG0oajcjekh/+E/4DlsN/KHoHvMQJyI5fbtq3By4NGlmWNRuPg4KC3t/ejjz4qm//If11dXWfOnPnHP/4xMTHRaDTK3zKWxfXt32Ne7Ze2R+DrReDz9mwRUP1AtKp6+7wOHJg2bZqbm5sTQdxBEG9OeTj8+RWX/r7NnFIORpaz8Aikao2g4+r8Yy6u2NQWeBpaOoE0AoeiBya9BkTRXNecu+9o3gcenZ4RUNaChn5gteDHZhgg+QuF/bujdDuiOnZHmMuagEEjNYNBBzqjtqQufWeAKa0C9CLip1bgOAsYWOAAWrXXjl/qi7kChV1N3rGqpCJRY7aKaH4FnGAZ0HMVbRXbgys2BBTtCoZmFQwaBZ0BFT+6VK1HTletO5K//hCVVoYCFGYBGro7Iy9lvu9xzTPCXNIEjEjzFoPVogGLCVDNmDfRvFIHNJCZVU1H4sjj6Vc/8zGWN+NYlGSg3wB5TSXbAiyJRdDLXQuM7YpPgV4VgqotPal7jnSEnqs9eLzsYDhd0SzzYBibRAPJUjXtBX7RdHolZDeUHInpTcxFh7ouTYvfKfFsnir0fINvBDT1ov7voB5Rm1ZV+Z5jPYFnmg5Fqi5kW9v7LRyDI31eBJo3qnXAAVndkecVUbI+oMM7Hur7wWgB2gomIFPLMzb49J3Lhn4jozMiSZkVENdWGyujEtP+uatkvR9T1ITEXg6dHsEimlQa0OA8QebuoxX+sVRNOzBW0cwAL5r71GK9Infl/vxPvAYzKxAIZjnGKpBWnuUlP71axbk1u2vCzoARVSNorQ4QeLJYVRplfGrlzoAra3a3nDhrammzItpvFZE8bcGC9BjqfGMS3tkEuQ2WAT0j8LTIIwO6m6w7EJX09y2tPqehj0XBaEYiF9GCOrmg8BPP8o/3i5dLsEYAGFpSF7EKwDNAmUGA2uTMy94hUev2eL798Yrf/vnJBxY8uuCRXz75y/kPzb9v1qz7Z92z/p8fkN19gk4HLCXqNMiApgzQ0t6yN7Tyo72thyKgpg1oRjRoQWcEE1R5hKS8s7UnNBGMVmAFxiqZHPISZ1NFildqC1cfKvnoUJvPGWyERh5tBlEDpD11k48ypQgUeiDRipBFZefrKJsIAznlRbuCqrYFNR8+hV8ZM2vhGLNBD7RFd6UsdatPT3Ie9KG5IkWRooVDoLlT3XT8QldMMhoPGhlgOCAl+0ez0HExq8DnBJdWLqSUl+0Po69Uoda5FenwxoL6Gv/TVHy+JjK95tgZrqEbLCIt8gxFozx3w0DG6gNNnlFQ2QMqUqRZjmcoowEEsS35av3RGMiqhisVhXsC6OxyqG3rPJee4RdafOHika3bn73n/tEEMXbs6CefffpkVHRextV3l7zxu0eeeP2ZP7z1Py//4Q9/GDt54gMPPLB7+87+bsl2EsAocmYQhlZUyCZmCEMP70Vi+us9z34CR4miKK8yRKVjjkPVIAmLt1qtNE2Xl5eHhoZ+8MEHjz322KRJkyZMmOAsbbZZbVuCIIiRI0f+/5D6+PgkJyfX19cPDAzI0PPw2Nn6KrbEzdCw7aMvSQw/Sx4yUBTV3d390ksvubi4PPvss4WFhfHx8TNmzJgzZ87OnTvlmuB5Xr6mLUvyflkfGKcVsUEC9IPhw6ONd73RSbzU7rr4yr1LILMVnwAS4vcTqFR7FuUIXAeg8VHIAgxCy4ubFC4vm12WdIx7DfangEFkpcldm3LxTyZyNmT8KxNfgVV/VyW+BQqO4jpfApJf/+gLOZCerEPzPNerD7+V9u3LIyDLh8ui9iqy1TO6dsayFpe/ZE99GU5XAAs4Ty/H0yY0LteNrf18+fW/4ad2APobBsx+uD0C9gj8aCJA07TVamUY5ty5c7NmzZo9e/bmzZsXLlw4cuTITz/91Gg0yh3Q4d3Q2/VWbX3Nn9Ow4UdTUfaM/HsiMLxV39DyBYsgW8kbDAalUhkSEvLMM89MnTrV1dXVxcWFIAh3d/fx48e/+OKLOTk5g4ODMvosz+j8ewpjv+t/agRszdg2UEGhCY4jSVIURZVy4JOPVro6Y6N1IRwmEs6/GT/7/NJ1FWt8qZRy6McZFANDod9dP9kWnnD5w+01B8KhvBloM0plWBgrSQLDWa51NoeeLdzgU7rqAGRUg9qMPy2yMbuRoa9UZK7YPrAzsn1PBLRqgWbVBg3HM6LeCC39V71C6iOToH0QyXHIZ2WQ16njoa6vITih70Qa5Lb3Hk/tjc6Adh2q2aL0LoCOoUqb0zYfrt4QWLTeF7WDdZLMhY4ELd0Rm1K50b/yU1/6cgl065Cc0qXuDEtIfW9H8We+kNcAlGBmGaOIALTBajHLYgqMCAYrFLRkrfVu2x+T+cl+KGkHs8AbTECiAV3ZvlB16CVo0unPZteFn4EOJXoSmpj2hIwiz2O9x85VeoawhfWg0rMgGgEd8Yx6A5gFU1XrpQNB5tw6KG7L3BWIMG77IHTryg6f0EckszFXyjyDjJnFaBNnNCNS3DagO3G51SNUf/xyQ+ApaO4HjZETWNnrD4mrpJUsbGoMS8rbcSzrsyN8diPCOrSF6R6kytvytgUOnMxAIQhGHJr9Yq2gY9tT8k+t25u7PRDLpUNwGaExnrdSLIp7dOsKAk+WBcSaChvwrQywUjy0KHM8gtL+uYs+X4jKGACchWcECX02s9AycHVPUIlvJNTLWsOUhSSB5vg+pSIlp3i7b9mWw+3hZy11LUCZeJGx4KyEFW301FTz0fioV1aqIlOgjwSLlbSwLM9x3aqmI3GpK3ZUeUZAXR8oScRzaZSEFipbS/YEp7yz2RCZAoMUGEiBpUSRA5HnaZNOrRzs6sw7n/TRy0tmEG7jcDbFaSzh7D7ChRjhSDhjEydcHPDlTBCjHJ9+dtGWDWszks4PtLe0VZUl+Phefm9zx/7jUHENSMpq1GEzU6j7T6clvrtVeeIyyp1LVsxDADQjIOZS2VW1Jaj4owNt3vHQpAE9j3MnZoBOQ4f/2QrP44g+mzggGSsjcZ+tAmfhRZ1pIKe81Cei0yf22oFIKG2BHg2qluMNgKy8lrk7oP/cVRSxMSP6bOYohjSCieuKSS71DIW6bpw8oDnE5a0I/RgLa7MPBGvOZkFJR+2RGNWFbOg2gEm0GiimQ1keeFofm6U/ebXaOxpqukFPG4HXiHg7tq6reGdw3KtrxIvlYAQwsWgrx3HAWNRlNZm+IVB2DTLKszcdRGnyVpUuNe/K4WBtaQ2odWxHT1Zw9GuLnhk7ehRBEPffM2fn2g012YX+O/b96dGnpruMWbhw4eJXX5kz+96ZU6a9/7cVV69kahmTwYoaO0gRl2dp0CMOlwjYvBPkRxZ++jPaOI6T5exkQnFVVVVUVNSaNWuee+658ePHy90GfAhL/QeCINzc3FykbcyYMVOmTPnVr361c+fO6upqtVotN0IZerZF6PPn/A2dlVupM990yFfvkK8vWITKysrnn3/ezc3tzTffbGxsrKioePTRR93c3FatWiULgLAsO7wqr2vUohAw+gjIlW4CMABsii27Z3nJ3UvLfrMaqnVgZGUAx1Yoe+LHHoHrFYY/yfgjCwWzlqpdXzWNXNY4eQmEF4GB564D0NKENBoL/zQ2G274lYmfHABtg5vtAPTXb4s2AFqU1GbyWnJ+8be8e5dptkeDFoAVSAuLAIgsDj60skeaAbC1n69/r69xpB2A/hpBsh9ij4A9Aj++CJhMJsQHABISEp555pmJEyd6enouXrx4zJgxH3zwQXd3N/YSh2223u1XJn58ZbXnyB6BbxOBWzZ1+TsxfKLFarVSFNXX1xcdHf3yyy//f5FEmQotL6EdO3bsn/70Jx8fn7a2NplGNPzcW2brKw+45Vn2nfYI3BCB4Q1YQgGGzORESc2cJMna2toXX3zR1dXVkSAcCOLhyTPXPLM4de2BS3/fpoxKAz0r8LzZyiNRumNw8GzOpQ92lO0LNlU2oigBcDRjAAvDD6ig36CKSa7f4Fe/zhey66BjwEqaKUQGLaDWU2llzbvDG9b7t3hF6yubrByrJrX4EclAl7b5SGxnWAJ1TcGbaFYUZMsyo0INrYM1Qee6AhMhrak/IKnRNx6aVKgXwQAMmqFXJ1Z11B6Iqt0S3LArHHKaEH0WrICOdqLyVFrtrpDSTX7qmDTQC2CwQJumPzK5fJV36b+8VOeyZJ3oAQtlEiwsb+E4i4W1iDSLarllirr1gWqPkwMH43XnckHNon6uBaBDWRpyuikiAeqU+qi0pqB4uqUTwWKSVyfnNQWdHoi4VLcvlM4oBT3F0xTNsbwgaDQaBNObVTXHzlRHJ1FFjbkHw/sv5EC3HhSGuuD4Fr9TlpOZdR7BTE6FtacPBM5CGqC1Txme1L0jtNfjxDWfKLRqNDKAUswsJwsHUxzUqdq842s3BeevOzKYWib2ITbKm1ho0aRv8as+Gg+demRDcyLiyDyqZJD59cmbfZK3Hm5JzkX0T0Kfh3SfKUFs7uuNv5p3MNxc2w5GVGdmeU40UNCtafSLu7rGqzMqBWVVUOiCZ1GxQ+L59hnrgs7k7Q1BTRUTS5sloq6JgR6tOjU/ae3uZq/jzYEnxYY2MJtwukLksOo5ARr7qXN5ccvXKqNSJIIwI/s0coOGpvi01Le3NWwNoYoaMZ96GqWKVQao7SzbHXx5pUf36WTo1YDZzLAm9WB/w7XakxdiPQ7ufv2vL//qoYcmu44cRRDuBDHR0W2Sy8jRTi4uI5wdXJwJdydipBMx2pkY50qMcSQcCWIkQTgRziOIObPu/PV/P/a/zz/7r+f/mOjh1Z6Tp2lr1St7xEH1QFpu4md7kdzdJZkx0gwvSPRnRgCDABU9Cp/4itWHyzYFQr0StDwMmFBMoLL32qFYRJ/reoDmaA49FVmaoST+r0VjVCQXVO0Pb9sX2bIvAvKbgGQRfeY5oDmxtjPPJ7woJBbbOclYSJJiKUHgRK2h9kxy2f4wyKoDLYPiIQwLNIsa0A3dBV5hqlMZkHet9khM/4UsrCkdgyrkWrYgKLYtNNFwOjt3V5AhuxpokRF4A2qLiHRzT33IuXN/34xelM2DYAWGotHwQGMQrilygyIH0wqYnIqKgAhF3GWobDefzri6/VBnThGYKWz8Sm1LfGrM9gMbP1v/8MJfEARx96gJTz/wyOo3/xGx1+eff102Y8aMCZMnvfTCH5589LEZd0y+f968zfs88uor+xkjBcKQQPB/BgBttVqVSmVZWVlUVNTKlSsff/zxGTNmuLq6yjYSzs7OLi4ustoGqvA7O7u5uT344IOvvvrqnj17CgoKBgYGWFYCOG54yl9/O/xp/52kh3X/P0/KfZjq6up333133Lhxzz33XFVVVVFR0bPPPuvm5rZs2bLW1lYbZ0Umvcqwo4TeYL5k/Bl/ikhA4KaDhlo19LKgEyRw+np57P9/EhG4jmAiAG0GSOvKH/NHrcurRvelNbPfhLQOIPE3XW6QFpyRRQD6p4FB23DDr0zYAeifRFv9LjIpTZ5LFyI56DKhsbDZCqah6VTsgkpLeQSpnX8XN7ztNewA9G1DY//AHgF7BH78ESgrK1uwYMHkyZODgoJee+218ePHL1++XKlUykyNz3ud4k3LI2/fw/3xl9qeQ3sEvo6oI/AAACAASURBVE4EbtnG5S/F8NORLwZA0zTLsr29vVlZWUuWLJk6deoNuhwPPfTQjh072trabiAuDb8Urk+Vtht22t/aI/AtIiC3JVHSO+CsokxAkzloAlira2sXPv6Yg5Ojk5OTO+Ewd8S4yI+2FW0NTHx3e6NfnFjbDSxyn1FjQQA6tSL7X5756w9BcRMYTVJmLIxJi0i0YrD3RFLDzmO1630hoRhaB5CkbDTyZrO1V83m17UciKpY61O24QjU91g5VmHWoA6oIAAFPTEpjV5RUNoKFGfgGYPAIgBtAaHfUHg0rtYnFi7W9Picqz9wEko6cHxrlQDofhLaB6sPn6z41A+Z2ijLyyN4IVrBzJFXKyo3+ue9v6fJLxZ6SDAKoKJN5/MKVh2sWOdrjs8GhUakaRIEEkSLCAJjERgL0JIkQFNfn/8Fw6EL9Z8G9AYlQq8JJXR5gH5945mU5phL0KxSX8gu2hcCjf1oaQjAZVc1HjxBxqSXehw1JhdAnw4YlqSMLC2xWU0s9Bsbjp7pDE6E2t7CY6dbTqZAiwY6DXVh58r2h1kvl7QcitKczUSZbAAUMzGZlWcyytb7tG8Lrt8eBKXXgJIEn60i8BxDmS00C/2G3uBLdasDij/0MsflQ6saRah5AA3TcPRc/vZjYr0CGKt5QIM6yxL32ZxfX+1/+vzHHu3xGeYelclk4iy8/EJ6u5pRXSpM3e6HmC9n5QUB650Xod9Y4BuV89nh5oAz0DHIDejMRpKzIoJpZTjQonh31u4gsbgFWLCSZqNRj+IbOgbq+/K3+tbtC23wjeBL6sBkAgslWhkU9hYsMEjRZ/NyPtqL6HOHBlhEJCgTtit9Yf2l1Z4Nm4PhUhVoJDtBHrAWGhSFniEX39nSH5YEikFRr0/PTFm7dd3jTyycfs+dzne4O450ciaQ2exIEK6ODq6Eowvh4Obk7Ors4uzs7OgsEZ9dCMKVINwdiJEOxChHGYAe4YDEaIIgRhDEJIJ4aPKUh2fNfOyBeQ/OvefhmXf9ftbc5Y88FbP3UPHltIHOLguH+gmoZ0IKoBbqPMJrPwtMe9/DmotOj8h9plE3pmpPePZ6H0NGBeL+HKMTkVbM0owFAKuvsbdoR1D//lNV647ozmSBTuJ3Ywg4sbG74kh08mZv7lo30JyFJHmaQmDaInYWV2QejTRmliNb3Cyhz4wk/XytJ2NPQN/JVChqLTkQ1hJ9CXQsGFlUs1Eay08m1YZfgPKeykPRvRfzUbSE5c0sY8Gl29BxNjNxpUdXUAI0DkKfEbNAoTmk0NFfFBjdczoFartrj8d1nU2B5j7r1YparzBDSh6YKN6oB61Jl1OWtP2QtbFboKiCgrz3Xlk+f+zU8QQxy3XcM3MeunIm0fuwz/N/+ePI0aOfXPTESy/8YeHChWMnTvjdn19Kys4YNBtFi4AC4rxoY0APZ85+iyfej/MUnucbGxsjIiLeeeedJ554QhY7cpA2WeXZ1lWQwegZM2asWrUqMjKyrq5OXj7FStuXl+6W3ZX/y87h/X9b2mq1ysu5dDrd5s2bR44c+fTTT6ekpDQ2Ni5btkyW5igqKpKFOGQAmrOiDr4gdW0QoLFKj2q5MCaJv//lBbN/+mOOwHUAGontZoD9iU0z3hh0+muPy8uF89+GGgOYBCNNDbUEOwD9f6pK2xq2LyS+8Oa65sYNO79wWxlPl3ddrz55OcoXDrO/uSkCom0NhzRSw6CJ11d1yJ4lkuWkvOZDroKbrvGd7bAD0N9ZKO0XskfAHoEfIAKyGp0oiiRJlpeXL1q0aMqUKRs3bnzvvfecnJxeeeWVkpISmWcxfCTwlb3YHyDn9lvYI/BvjMANX4EbcjL8U3moVlJS8o9//GPevHnyitoxY8bIhOipU6f6+vo2NDTo9XpZWp3neaMRRVp5npc1OuwM6BvCa3/77SIg65XbfPCURh0ndaAVyr7jUZFTZkwfPWGc+6iR7qNGPnf/I2U7Q/Q+F66u2NXoEwsdg6LOxFBmo0YCBxt6Sj/1KV/lTZ7NBRUFvMXCUSxjAmRK0vTFgpz3d1VvPNIXmwZNPQh70QIYKeyYl3XVbg0qWHWw7kCEUNoMZgvPIqSIHFgL9MdmXvxkL1XQgERd2XHQwgMn8Epdd2ZJkVcUZDbzp/JLd4RaK7uQxWwFg1INnCh0IqG4ckdI1Tr/Xr9z0GWU7PB4MDCW3IaGXeG1q3wV+2OhqhPRwG49m1JWuf5Iyjtbq4PjQKkHE2KIOMlqBbCIPMWwosCRFOj4tohLDbuPtx082RCeACoaaImqpSR7kwurj52BvGZVdHrl4RjUsB40Izxa1Zmzcrcl+HLtZn8yKQ/0JsTIBREVDHhONJLQoy4/fqb5aDwUtrWfSCw+EgmtKrim6glN7PQ9DSnVVV4RXYlXwIx+dHh6r2Ywo6RmZ/Cg77m6faFkRgnoJIFjSTsVoR9OhO7BxrCE0jWHq9b46mOzoFWDxTQJMEB3x2fmbwmA0g455zKnGHGBFk25R+iZv29qi0kBhQ5EMLMML3IURfIW1qrSac5np6717LicDWaaRU1okTcYQanvPJWSudmnyDscGhRgZGmOVQOLkskiqk90J+Zk7w81lTahLgeNytTYUGnBWtZStT+8wyvqylpPqrgWzIjFC8CbrTTDmkBP0RmlSW9vVASes15TAM2KFg5hVi3JFDfkrfW6+o8dkFEHSpruV4HValFpQWWuPxZ/9p9bLn+4s/Jw1JFVG+fOuMvV3QXFNEYQDiOGEDxXgnAjCKcRDg6uTg6uTo7ODog7j5CgZaeh/yMcCScHwkmCqt2dkCg93oEYJ504QkKnxzoQ40Y4uEhA9ghpvxtBjHYa4ebkNOPOaYsWPb5q5UcpMaf7kwtbgi9krfXO2+xvyKxESjLNI2Gcg7qTl3L3hpizqkHPGPVoXqkBzkRRAomeftCpqdoSNLAzunaVryos2dLUA2ZJ3trEQYu6zu/01S1+UNYOArBGE23hkI/Mg6VNef5wSG9pHZLxOSuKb1Ac6Cjo0VWEnOk9mQ5NmpaIi80xyTBAWTRGFGnhoPLkxezgWLGqo9IvVpmUj7MjJgazoTMBKZpyak++vQ7NDK+poFdv0eqNelQdETT66tiktsgkyKzrCz5fH3EOtUdyGxt8Io2ZSPBHaXeGgRpF4fYAMa8elEZgLZxWnx4avXPZP341cea9DiOnEE4P3zvH++iRs5mXP960dtb8OVPuvftXz/x68Yt/nDJuwsz77t2xb09rc4uV4XgK6WOyHJzN9e7bPfH+LWfJj9khbq8E6wsWgSRJlUrV1NQUHR29YsWKhQsXTpo0yc3NzdnZWaY520DnsWPHOjs7T5o06b777nvnnXcuXLjQ1tYmdwlsE9LfqEswvDfynaflcYHcyeF5fteuXSNHjnziiScyMjJaW1tXr149cuTIBx54ID09XV5hiVN0EgBtkc6R6YEyNIMzhrIktARJD9Wd9MT9t9Sj/abfJgIygik5vOLKD8+EuruW68Yu7538Rt3iLdAjgEmgzZ8D0EOVfh0n/TZ3/LGfcwP2+wM16G8Ad94AQA9/+2OP7Y8lf0OVKmJ3byjyQ18Em7jJ955VOwD9vYfYfgN7BOwR+E4iwPO8TNLkOBzSZGRkvPDCC+7u7mvXrv3www/d3d1///vfKxQKG/p8s7fJl/Rlv5Mc2i9ij8CPNgI3NP6vk0+r1VpWVrZ69eonnnhCNq93cHBwcnJydnaeNWvW22+/nZKSIqsl2oZqsrbjNxptfp2c2I/5z4yAjIwgm1VE2zQtRRoYakCv+XD1J86j3R3cXEaOHYPzji/8sSIyYcD7TOW7+5t2S6q7GpJnWOAtwIhQ3VG8JzjnE0/LhUJQGFHpgqZAtIBVQA2N7Jo2zxP5H+/tDIyDZglKYwVkEw8YoLxt0O984Xt7ag9GMPl1aHBHMZzZLNI0MMJgdnnmZl/TpRJU8pWGoyxIbnhaU3taQYpHAJ9UofBLaPQ6BQ1qYEEgWQTdTBz0aGpjk7N3BOZv9u8OToS6AWRu8gCMlavrajoYU/qxd83Go7is2wwIjeU15a31Svv71p7wJKFLCYD0XmTk8cjhRZwODf00oKN7zmfX+5ys2R/ZEnFR7FIjT4/iYYBUpxTn7gqCGpXu5NUar2ioVoDODHoz1Cuaj8SKERmdHuGD4RehVQkgMoBCCgg960lQG5oSrxT5R0F5V390Su6BEOjSg8KoPnO1bV8kpNR1+MTWHIsTuvoQzjNJkH11Z9n+sP7D8dkf79Mn50PfIMZZ2qwcbzVQ0G/si0mv3Hy0fmOQwv8ctAyClkOvuXZNT0RK0vs7IbMe1BywPAVYTBweVSsaDp1Men9n07FzlgYFmBAmlpE+nGDQGZsuZpYfCNeczwadmUGVCKlCjBZtYt7VNQcuf7Jbn1MJlMVKsSae7QfEoEWa7S+qvbw3UJ9TDSSHsDiD1HWwAt+oqPCOUB5LqPcMt2RVgVIDFh6sPGXS87QJKI65UnZl9d7a/SegogPMrIg2SiJQDF3cULDNP2npOrhcjYreJotoprC1WKEhMSPkn+uX3/Poq7MW/MJ5wmiCcHceMcJ1hJOLk6sTMcbBYRLhOJUgpkuviYTTKIIYTRB3ODpPGeE8kXCcSDhMkj66iyBmSq+7CWI2QcwlHOYQxHyC+C+CmDX0cphMEGMJYjxBjHVwcCcIVwfC1YlwGeHk6ESMcB0xduxoJ4KY4DBi4ahpf5758LsLfnPZ86ipvgNbIILCfHdmydkdPj2XC2CABF4YZExmnB1Af0v87nRoWo9d0HmdHdgZrQtOhspuFHhB4jEPCn39kdOFm/z1F4tAwwMPDCktNbCI0Km+7B1Sdj5VGESSMqJ4DIeNoVdXFZPUGnkJGtTXTiTVRybRVW1D2tBmTpFRXOAXLZS2tp5OKwmOQ+NBedwsAGhYa25j7Nsbyj2CoawDTCIwFrS4FCxWA1l/OTPbJwyKWsnIlMaDJ6CplymuK94fzFwpg34t0p/1Oqq541pgHLpx9pFAWkCEisTUAr9IZUK2/z/Xer636hd3ziQIYtb8OS8t+9/4hDPeh71ffn3JuEkT594585lHF93/8IOuY0f/+c9/vpKSplUPSk3up/TH1h+Q3SBkUrCMF6tUqtzc3LCwsA8++OCpp54aN26c/Ovv5OSELq9OTo6OjjL67ODgMG3atOeee27Lli0XLlxoaWnRaDQywitfajgL5OtHx5a37zshiqLRaAwICJg9e/Yjjzxy+PDhjo6OQ4cOTZ8+fcGCBcePHx8cHMSZdUHAl2ROaOvbyFxC/joQyUmqqljGHw7A+foRtR95+whcp9Dio4UGKFZWvbCudNayhAl/gPNVoAP0/pUmHyTb2S8IQP9A0Ozt8/79fPITBKC/n0DYr/q9RsAOQH+v4bVf3B4BewS++wgIFqG+vn7RokWOjo6rV6/euHHjrFmzFi1a1NfXZ+v1ygQHuf/63efAfkV7BH7WEZAHpaKI9l+ycXxAQMDcuXPlBbYEQbi6uhIEMXv27MWLFzc1NalUqiFK5s86LPbC/cAREK/bT8minDRNt7S0PP/SH8ZPnew2YSyqPo9wWP3+R9ChM5zOvrBkXenGACa/AVhEvlijCbVl6xRth2Mvvre9OTYZutUo5kBSAmVCVFSt44rqyj71Lly5t/90GnSrkJLJ42gTBYt7jB3B51NXbLuy2pOtaAaN0WJAUQ6zQQ+MAGWtWVuPIHBmsCL0huixQPGsQNIDZQ1ZB8MgrdZ0IrPp4ClTbgNwgLaECNIJ0G/SnM6q3BVa7BmedyQKMT4DAwYORYRVXGPgmbJ1fkWfHoa8JhjkUC26uqN8zaHyjw4gB7m1Hy3XwILStyJPWzjUtmYEa48GOgYHEvPztwS0+MUX+EVbO1Sc1ogqB4Msn12PVnip9XC+vPFAtFDUDIO0WaXmFQM1/qca94SXbjnSciwOatrBhALHJotZtHCgJy0NXQOphWXh8XBNqb9YUHokCjpUoGG43NrsjT4Qk60PSCjeFQRNfSCKKGigp6C+M2u7X29wQvmOID69Ajr6UWnXyluQUw0optGqhstVbWuP6jxim/ZGQpUCqccsEpzVUekZ7+6C9HoYFECpF2nWZDKhxIHa1O1/LuntzXlHokzNCow2zWMVAFg4BiiWzK3O8PBvPZuG1HV5pygAB5DTXPzBvovLP4O8a9CnlbBgFAJANQmONTV2JXgGKrLLQUdbBYwnogmMAL1kT1Rqq3fM1TUH2k5fRmY3idLPAk9jon3AermkfoNf2XofZMTrKaSKgwiilWnsrPeOOrd8HRmfDQMM8EDr9cChBsWZY2FPzrn/DsJhhtvoCS745MTNaej/WIKYgVAy8bzDxNWzn/B++q9vTX34KWLMI4TDHxymPEmMeIoY8TQx4hlixAuE+2vEpA9Gzft04oLNUx7dNmXhrhmLdk57fPf0xz3ufGzL1EfWTX347TH3/pYY9wjh+sCIkTOIEVMdR0x0GjHByWm0s/Mod1dXV2f5rqPcXceOHTvKzZ0giAUz7n3ruZdSj0WDgekorIz5bF9Z6BlQkRxJaRkTiYIjVkTnDRx06Jt9TlPHM7oPnh44noLy0HoJfeas0EOWe0Um/XMHXKmHfgr57CYOa9wKwqDxalBMblicQaFEbjoadQqigRL6EX3uPJUGJe3dsemZ+4LhmhLUkmGjkVOV1MfvOsxk16lOpObvChoorLXoTYjuofauCGXtqe/tyv7XAShpQb0U3C0g+GemtZVNGV7BkNtgOpvbfOQkNA5AfXf64eCezAIY0AHLo/Rzny7nUEhL2AXo0OJ5JrotI//yTl/+QmHzkdiikFi2o+9cTMxvf/ec9GPnvGjOfy39zQtpSZcO7PN85L8emDRm3At/fOmx//7V5KlTFi5cuH/vvj5Fj2zN9wM/Ib/F7YZm9aTlSjZlDIqiFApFfX29v7//O++888ADD8i8Zpns7OTkZLMWlA2K3dzcfv3rX3t6ehYWFvb09MiusBRFMQwuzpAXQg1Hn2247bfI8Lc+5Svxa/zGMwzLsidPnpw2bdrdd9/t4eHR29sbGhp63333zZw508vLi6ZptDm1IAAtJ2z5Gc7Z/DxtB6BtAfqpJKQqG/KWNFtBB/hwy24BlYBzwGhBOCSMO1Sgnznl1g5A/1Qa7k87n3YA+qddf/bc2yPwHxUBmqY5jmtoaHjllVdcXV3ffPPNHTt2TJw4ccGCBZWVlXIoZMzCDkD/RzUMe2G/8wjII0b5e8QhyAImkykgIODJJ5+UXQrlEenIkSMJgnjvvfeSk5P7+vqGU6GHZ0m+2r9lFDo8G/b09xEB2zh/+MVtPLjhO79pWn6Y47Cf560cn5mc+qvHFzm7uaJKrpvz5Lumr1mzBlRGa2Zd1krP0m1BUNIGRk5gJSByQA9duo7g8+ff+qz6UKSlo58c1LBGI7CslaXATDPFdfWHIqo3Hmnaf1xs6ECo1CIgadrEgELbF3E59b0dVz/zZvPrgEZyJcmaKZMRBKBKmyo8w2q8I0FJIR5MsxzHIfJC0mKfrjAkbuBkBmQ21e2NghoVaJFcSTGcIMHBTHJ5xYaAlr1RZQGxMEAyBhI1ZJUG6KN7g5PKPvMv33LUmlmHMhcqE2jZ4oNhhSs9OzyjEKG2WC1Wi44lZfSZtkgl1VIwQGvO5VZ5hNXuDMva6o8WfJw0pGasUNl19TMfJj7feqEk71Mfc0IR6nLoaKF7oCE+uSMgvutIXPbeALjWDVo98BzK2YqImYLaMJBamOcZDC0a+kpF3sFQbWoRaFm6sL7i4Ak4X2QMTa7yCIGqDtkO0WowQGNXpW9EjWd48a4gOr1cMpFD/V+OZ4aMBzUmKFW0bQ4Fn0tdW8LFrHrQcIieG0RIrS5e40PHZIMaIXZeR9J6I68jwcDqs6qyP95fuMFPV95ES6LVVkoSDkb0SNSW1F3a4j2QmMsjNxwsjKS5zFrNmRUVn3gVv+NhisyAFhU2PI6zUiyea0Z94bqzadeSslDPhBUYgUcmo0UApaHjxKWaHaGlm/xags+xzZ1gNgOKroii2YTs9Yslee9sK13pKV4uAQMjsAxLU0AxTGNn56mU1Pd26CNSEX2WUFkzR1VWlr/71lv3jJ94h6PzWFfXMWNGObk4Obk4ubs6TxrheidBLCTG/GXsrPemPhz69NLoXy6Jf+TVMwtePf3Ikl2jH93iNP/g+CfOP7o0ceGypEeXpTzyesovll24b3HS3Jcvz/3f1Hkvp8/736wHl2Te/2rWg69efeCV9PtfvvTA4vgHFx//xZ/3P/i7dXN/9RTh/hjh/gvC/X7CfTRBTHFynTRqtIsD4ezshNIfzmjc6TjKbQThMIFwuJNw/vW9D7730ivH13tA2wDwoDXoFZTeLNP7zSIMcnxa1bUd4c3bwqoOREKjEgWjJeY+9Jv6IlMvf+DRH5sJKmknxaNQhhEbW2FMwhX/SCRZW6w4ZWJiwcSLfbri2KS22DQhu16XUlLgF42i7T16JFmTaBlaEHiSy2/kM6rbAs6aMypxnka0ovejmoQaxZXPfC5/4MFcKkMDJUmWmwMLMBzV3FUWca4t5rLyVBp+Q7NrobKjKDCyLfkqYuiCRMbXmxvCzjSHnsXvVJ8WDBTX2Z/nH6k/m03FZLYFxIuN3aAzgigM9vdvXbP2F3fOnOM46m7C9ZVnXzgdGhF7Imrp0qUj7xg3+8H7H31y0cxZd8+cOfOdv/0tISFBr9d/00fc93G87YH8JT+4pmFbUVFRWFjY22+//dhjj40bN44giHHjxrm5uTk6Orq6uo4ePVpmQLu4uMyZM+ell17avn17fn6+wWDQ6XQ29S2GYeR+ArYXaRuejS/JyfcRAfmaN2Tg5rdyPgFAo9GcOXPm7rvvnjp16saNG9VqdXJy8mOPPTZ16tSPP/6YoigZfZb//lvK8v1FyX5l+Qlng13xOUOh8ga+zJIoE7rgSo6jMvRsB6C/h0bz+RTOV158ePyHp7/yRPsBP6YI2AHoH1Nt2PNij4A9ArePAMMwVqt1YGDg97//vZub24oVK/bu3Tt37tx58+ZdvHjRhnzd3Pe9/SXtn9gjYI/AN4tAc3NzXFzc4sWLJ0+e7ObmRhCEjERPnDjx+eefDwkJUSgUJEnK7GkkbLLoXsVxnOwLahsEfrO72o/+sUbAVqHDh+Xo2GNBN5Mbci0/nG9mxskXsX1qkszcAMBoxAX7VqvVZDIF+vo9dM99DgTh4OJMuLs88czTqampYKDZqvaK3WHVO0OZzGqgQeDRoAx5smpGHZV6dZVnhU+kUNcJlCTUK3ICzwJrsdR2NHlG5K3cV3swgi6sB5JBDV8AVqMDFcVfLk1+/bPiNd6DV8uAsTCUWcsYe3kDL3LQpa3cH168+xhX1ABmXrQIFpYTaRZ5nZ3qwqOxnZHJkFJbtSd8ILUY1DRoUFSX1OqB5IxncotXHWrYEVbtHc1e6xFIGv3cTCy0qVpDEhrXBZav9NZfLgYNCxqkYCuj0q6sOlDsGU4XN+FCYF6gOZa2cCzP8TxvFURk7Kpoc0Zl5krPzn0xlbtCUSeXFpHmyQhsk6LiYGRvYIIqOj1zV2DfxXwYoCRjN1J/Nrdue2ivb/y1wDh1fiWYaQArxdOCgNg9KHUDOeXJ+wO1lwqgsK01ML4jNgUUBvZqddGuIDYqk43KrD0URRbUAsWCxSLoDNCjaY1MavWPK90Z1HA0Dsnm0mZmP4elDEUNCp948tCF4nW+fEY14s46BvmnJe0F73sO+l6AAQ6zR3FWhkMxYlKwXKnNWeeTu8GXTK+QlTdQt4GXuORG0Zpbn7rBqy46kevs53ikwaL+Bi1ATU/ZZnRx7DoSh0Ry6ZpAS5oPOgYalRkHQq4l54hKPViAN5hos6TawUBd9MXKXcG1249VH4oEpRlYydcRr2sBWuCKGho3Bma/vY1KKUYlB4bmWYRnQaXjkgqK1x7sCIhHWNZo4ZUaSqfbsn3Lg79cQDgSExydJxBOsk+gI4pjON1JOC0iRq0d8V+BY3919p4/X5rz18z7l+XMXVY49/WSOa9Xz3mjfs6bdbPfqL1nec2spfiauaRu1tL6u19rv//t1rlvts15o23OG+33vdn2X2+0zFveNv/N1vvfaJ23vPX+N5ofeLthwYrCBW+nPbQ04eFXQ+a8sG3K4yvGznuGmHg/4TqBIMYQDmPd3dxHu7mMcXMa5YIaII4OoxCDJiYRjncSrr97+PFjnofMAxrBIvRYTCqeElUG6NKrzuWU7gju2S9R1xt6xT4dznMYeajsNp3OyfxgryLsIt+lwpUH0oZtmxF7kwuzDobpypvwIgD6ATUzqAelvvlMeuXROGgYIDOrMg+FmyrQBBI0JjRC7DNlHzquPJMFV5tqvKL7rpSAjjIZjJyZBrMItT09ARcS/rGtPSELa5YTgJO+1BYRmnrKA09VhMS1nk5J2e1rSi+Bqu5KnxMtZ5JBaxKNBuAYUa3pzsirOhKJcyckajezZdcqD0cZLuSpTmVU7g+HkmbU7UE7TR2QNJldefz9DR+99NdFd917B0HMHjXxXys/PhEbsz/Ad+EzT029Z+Y9989dsPDRu+666+GHH/by8uru7uY4jmXZWz4A5ch8r39tz1Lbk1n2TZGpvjbItbW1taioyN/f/4033nj88cdlvrOLi8vYsWMnTJgwfvz4kSNHukqbi4vLo48+umLFitDQ0La2No1GI5fuy0tx88P/y4//t3wqZ1IOlGARCgsLf//730+YMGHNmjVVVVUpKSl/+tOfxo4d+9prr3V0dEhzWPjgtYn7yb9N8un/lvzbb/p/jIANdJbFNETJIVharCRJq1ikGS+c4EKX0c950LcBPYdfbXj6/5hJ++n2CPwsI2AHoH+W1WovlD0CP7cIyN0+hmFee+01giCWvyOySwAAIABJREFUL18eeyp26tSpTk5OiYmJw9FnWQrA1vn+SfSDf261ZS/PzzQCNr1ImqZzcnIWL15sW5nr4uIybty48ePHT5s27dChQwqFguM4+dsnr8yVQ2L7Yv5MI/QfUaxbDrnlnTbOss2OcrjD1fDo2I63TRnaPqWkTZYlJUmyq6trzZo1IyThUfcRLo6j3J58/rm6a41gAa6hO2nzobwdRyG7AfQC8FYGrJyFBwaYjKq0j3bXHDjBVLUAbxVp2sIxyJA1mtn6jhKv8IbNQY3bglHceUAPvMCZzWAVgbLwVypT391ettqbOpcHWjTQs4DVDJwRWMFk7o64dP5vG6wlzaBDWhwt8gi0GRjoNeYdDEf/w+Tqgi0BhrTyIbkA2TaRAzK/vmZzUMP6wOz1PtA0ADqaGtQjG5cFY0pZ6ebArBW7qOgsJA7TVjAInfEZ59/eVLwlUJddhbRQVsD18jyaJ7I0A5JiBADwRc1Fu4KZ8Izy9f4D8Vmg4RAWtAIY+MrQs4PRGZBRn+4RaC5rBjUFKhIUGm1Gef/hsxqfc+1+cUJ5C5C0mTGrKL2OJYHnQACyqC51jz9bWA9NA6V7Q0xnc6GfgdLWsn2h/OlcSCiv8wil8mrFfg2aMQKAlm46fqF0Z1D1ntDiPcHQ2AMUQ/IUi+N5XLwMZp5p6L646VDPwdMNO8L6LxUInSoElI2CtaglfdV+hU885DSDAUVF8LnBcMCBIbu6YKNf5if7+y/kYOYBUMCBE3FNdL8RmvqytvtdCzkHXSrkrQNoSR0ixYNsu1dM8ScHS3YEIveZ5Ib87igOGW1d+pagc5WHY9hrPQjfo0w2BwYajEL/hZyy3cF1O4Kr94VBu8qq0g0RZhkLaCno0pZ7nahYfYg7mYXos4VH1QcLB2aGKai59PZnNZv8oFxSUrZY25uaFr/44rjxY2S9i8mOLlMJh1EEGgbeRRALCLcl7rMP3/3b9Dv/XD35r3XTl9Te+VrDjGUNM5Y1zny9ecbrXXcu75v2Rt+0N3qnLVNMWaqYsrR78hJMTH2td9qS3mlL+u5cKr96pr+mmPFa98wl3TOX9Ny1pOeuZd13Le+4e3nzPcsbZr9eOWtJ/qy/Js9eHDv3T6G/+N9VUxc+T9wxE4FmYjTmx2kk4eTm4OROOI4inMY5uEwknEdLOR7p6rZo4WORMdE0tiNG6FTpUkqu+cV3+p2t2Bki6cOYyIFBbGYDlJBYdvHNTc3/j73zgIviXPf/CFJDDVVqrAHLNV69luRY4j/GeKLBihpjjMbkJFGjRhN7iaKIFJGqokaKCioWUBAQKVKl9w7bKMsu26dte/55d8xersk959xycpOcfT/vZxlmZ6c80975vb/5PmHJ0NQPKpCRqFsF4TJkVHdBxb2DIYOZZWgvkErEK5cj+3lx4r1nIVehiiN9WvMo5JKopl3NE6K8glIaekT5Z+LqolPgWXtDwFVeYpaqV0jqCtpfYm1bzJ27H+3vuHAPvfqg1vcQ0CBQdF99wIpJlT8qLQq9wn9UCC29nVfvFgZdUNahgxxUKPEgt7A880wkXViLMnDiNMXqq4u8MXQ1Q36nMPdYBMKqkAAKQiYQomOJO1QefKUn/qGqhX33/MUlr00Za2xjbm7uNGH0/tPfpxfmfrZnJ4Zhzq4uU6dOnTRpkqur66pVq27dusUwyv9X3gLRXxX/zgHmess0g/VdevrfSiSS3NzckJCQRYsWTZkyxcbGxsrKytTU1NjY2MbGxsnJydra2sICgVkwDHNxcfn000+zs7O5XK5MJtMbnJm5/fWm9V//Vr8+/7cDw1dSq9Uy95qlS5eOGDFi4cKFTU1NFRUVS5YsMTY2fu+992pra/U+aL0GbWjP/N/uwf/h0vUyMZqPrrscB0TdYNDeatT3rYNvqHXqM+pS177Ii/tLC9bP7aWBX5rWMM4QgX/2CBgE6H/2I8Cw/YYI/GYjoG8dMuqzXC7ftm2bpaXl8uXLo6KiJk2a5ODgcPv2bZkMaQRMi1/f7Na3C/Uz+c1upmHFDBH4fUWAeRDVarWDg4OFhYXr1q3z8vJiWBzMoyyGYWPGjAkODq6trWXMsHoupP7E/H1tsmFtmQjo1Y3hj+L6q65e71DqAKMkSRK6QlEU478jCIIZYNijzKd+MhzH5boqkkrUoBWKRCVlpbfu3F67fh2GYZY6ocTW0eGjnV/mVJbgOK7o5NXH3Lqx5UDvo2ImE6BWq1WoaZVYri1sbglMKD0WjQAaUhxASxAKjQJHgnJLb3v4zaq94cW7gyG/AWU8U6qR1KggQKCgixsrj0QX7w5WZlZAvwxUagp5n5C1ViOVsbOLH351nHslDeQUoSIVoFaoaSQiD+D9KU9rDsXCneresymCjDIYkOBSmYLQESGkFNTzOs+lVO+JqDkUK8mpApkWRBTi5w7KVRUdjUfjGvbFtMTcgW4h8oHyZXhxU9b+sKyvA+VpZdAnAyliRzDirJJECfTQq8FiNXShtG8DF9LbTyXI7hRBnwTkBC0QIcTExVtVp+Igt77gzMXOzCJkxBYRMEgo8xvz94Q2Hrz4bE+YpKAaQRIAJGqiDxfJVYRWpiBbWcXBl3sTMqCsvSbmZteNDCSXN/Obw280no2HJ43dZ5Pk94vQytMqLU1pBoborMraA1H4lceVx2JVRY0gkA6RUgloxUjRB6CUwqqWkrNXO8KSG05caY27T4qkqJNATFLFzY2nrhV/Fw6NPBiUqSmaUNFytU6AbuQ+PRTxaNsJ9vVMJPiiopXKJUqKAKEE+onn5xMyz8cpOjlAq0CrQd5nUgU8hfCHzOfbz1YfjtbWdKI3qQkaEClbl/6RTzVdTC05HgvtIpCqQU5pSRL9ijOkzqnuOHSx7duIzrAkbWUrkDiSwNVqoNRIfW7mtl9MLfgulP9DBiJsoN2qgzlIZEMZRRnbv686HgNlrSDAxdzeCwmXX5s8wd7WGkGeRyDReRQ2wgczmY5Z/T/MfrfzGz/8y/KCOVtKx61td1nNtlvZY7+yx2FVj9Pqbhf/7lFru0etZY1ax3Fbj6r7WpabP9t1DVM5o/w5o1Zz3dZw3db0Dqs8JD0jDZrltY7liQRoVD3Qzzle63vGb2yftLlx+mf5k9envb4i6rVFH1n7/GnkqLGYuSdm6YRZ2GFmtthIa8zY2tTc3srG0szczMIcM8Ze9XD+aveOpupqoqazPCSeFX2vKvAqOtcGpJQcV+IkCAh1cUvJvoiqU1eomi506CJAM4lSYsoo6nl79ono6oQH0CuiZTqPuZyCXrEgt6os8jqUdShL26oTHghr2kANyDctkANH3JGcVRp8DWp6Oy7ca4hIhqZejYKUKXSu6j4x58bjJ/tCCoPjoHsAUG+FQtc9pIF+EZFbURcYB/eKudG3ZbefQnN/6w93n4XFQTMLBBLEDZcR/GcVxSGXlAW1qCdGoQSuqPZqam3wNUivqAv6gS6sBzEBai3KwElrgScuiU0qibsJHBHgAB39N78J2L/i4wkTfTFrU8zS+M8b1gRdigoID5kzb66FhcX48eOnT59ub28/ffr0wMDArq4uHMd/fQ1af4lmRFK1Si0Wi9vb2ysrK0+fPr1ly5apU6eamJiYmZlZWlo6Ozt7e3u7ublZ6YqdnZ2np+fkyZM/++yzlJSU5uZmoRAZ4ZlUw8wt4Of9hcz4P8AnY2QRCAR79uyxt7d/5513Hj9+3NnZuXfvXg8Pj+nTpz9+/HhwcJC59+njwDRp/gCb/8+1CS+9nTUsFaFSJ0CrdVcWvQaN8qZqtSrQ0rqkuoxj+qWIvaQ76/99aTLDv4YIGCIAAAYB2nAYGCJgiMBvKwKMYsU46ZgkIWqV+kdg3Z49e8zNzVeuWJmYmDh37lwbG5szZ8709yPyI0OdYxJVvdQuNAjQv629a1ibP0QEGJ4G8wqqRCKprKw8cODA6NGjra2R6c9IZ1Y1MzPz8fHZvn17QUEBsmoqlXr12XBW/q8cBb9+GJmLM4M8RnqxXC6TySQSiVAoFAgEfD5/YGCgt7eXzWa3tLTU1NSUl5eXlJTk5eU9fPgwMTExOjo6KCgo8KfyxbDirytr1vqvWevvt2L5+8s/WLDonRmzZ5lZIci4ubWV6SsW7q95xV27KlAgLgcIZY23swpOxPbdK9DyJQqpjFAhfAQhlmo6+ov3RxR8FUg/rQWBAmhaJpeQMikMSYEtkt59VncwuujrIH7yE8SclRFKhUKLE0Co1c/bnh2PytwRAMVtIEPmShpUhIaiFQplv1BR3Xb3QBDrygPoHJRLxQSATKtUkhQMkVDVzY25D/drWvdfFFx9TDaxQQuCISFCiGgAOgfbw1MqvgmvPnZJlFaCxC9aiwRcBWjK2qsCr+ZtPdF7PhVYEtA5TumqzsKTF+9tP4FwHHwEFCbEUoY0rVAj/gYotUgcr2Q3h93siUqtDLjMSnoM3YNULx/kSEZvTc7IP4gyqpUEXmpMeQRDuEYoAwGhLG2rOnmZFZxcd/qa+HEFiAlaocCVSINGdBG1WskZyIu6Jk0rhjZR66XU8vB4RKPmSlsvpTaH34AnDWXfx3b98AAGdbotgGZgiJ2e3x6cKL+U0RwUry1qAimNggkwqMUl6Gkd5G2cyou3ONH3WMHJ9aFJwJUiRgoANHCen76C/OAl7YAjRzelRJoisj+L6baYO4++OFEXeQNlPtSJBWpQ4nIx0KSym1t5/lph0IXe+hatVi0WD4FGpxQLKfHVzMrtZ4t3nkUuXTGBMgRSOge0ggYJ3Z30uOLsNQQKp3TqggQnRWJQ0JqSlvbT1/oPx3Xtj9E+qQaBRA0qRE6haTQTjrgn8VHqF0daopKhnoUs3QSh1dBamUzTya04GVu4+wwU1EGviN/cvv+7b53HeiC8MobZWCBE0SjMaAyGvYPZbn91Yqj33LxZHxeP83/u7Nfq6Me29eu19uPZLufZr+A6rGQ7r2a7rukZtYbl5s/yWPuiuvm/GOPmz3JbzXJbzRmFKiNA941a0zdqzYCbf587o0GvY3uv53ht4Hlu6PfaIHRHlefq3+Gyssl1RaPX2jafTaUTPix486tLviv2O8352NLnT5j9ZMxiLGbmjpnZG5nZWFhamphZWVkav2I60sZ8hJnxsncWXdofUPfD/da4+72p+SDQ9amotCiGVYgwjlz/LXzkX9alAgSZEgiNoLK5/Oy1+qgU4ElAg1g6pEwOIkT0fnbqEv24GorbimKul93NRKZphRxx23lieUnT8wsp8LxLcKeAcyMbmntBCbhArJTIQaYeeFyW+Mm3hSeioWsAZfSUi9VqEhcJkbu5tLk9NEF89RE7/KbgSjrU9opu55ad/4Gsa0NrhZOgIKGdW3D+ykBaPvDEyOIop5sTHnCvPYLijueBcaKscmDxKaEIvQmh0oCY4D7Iq4y9ifz1GgA+8Tw6iXU7V1HbmZqa+mf/lZZm5iONjMZO9Pnm0P7LV6/s3LnztbFjRnm4j399gvfo0S4uLitXrCwsLPz1NejhArRUKi0tLY2Kivroo4+mT5/u4eGBYZiTk9Po0aMn6cro0aPt7OysrKycnJyWLFly6NChhw8ftrS0SHWFYPrPdBwtkiSZOziK5x+3qFWoY6mlpWX//v22trZvvvnmzRs3BQLB0aNHvby8xo0bl5SUNDg4qH/W+L8Crfxx98CvtWXDMRrMMCMYa9HprtZVFdKaUaMVvcSjE6BpnQCte/kFTfZS0SvOLw28NJnhX0MEDBEwCNCGY8AQAUMEfnMRYIh1jGWSUbgIgti7d6+ZmdnixYs5HM67775ramp67NgxkUik0WgY4OxLLjyD1PWb26+GFfpDR4BxWgUHB9vZ2TE5i4yNjU10xdLScvHixU1NTRSFknPpX1n4Q8fjH75xzCVO3xPw0vK0Wi1jQ6ZpHS9Yh2NmtAmmb09/mR3+CM18RZKkVCoV/VSEQiGfz+/u7q6trc3Pz09LS0tISIiMjDx27NjOnTs/+uijpUuXzp49e+LEid7e3q6urnp+KLP3mc8RI0aYmZnZ2tra29vb2tpaW1tbWVnZ2NjY/lRs7GxfdXJEvRcjjTETY3Nba3Nba8zUGDMzwYywEeam1o72e77d29PeCSibH6HIrck4fK4vtwKG5H0iAY+SypCAqgQRXXjq0r113/XHpkFHP3KwkjRyN+MUdPcrMyvKD0QUHYsqCr2CAMRM+iGUcAyAK6yNSHp+6pIgpxyk6Cu+StZLSzSgAbkK6npSdh5/djYOITKEUhxonQ4HgGuoZ03PDkbC/crq7+PyAy5qW3jqIRkCNCMOBgmdotbg6+0n4wu/Ce26lQNSSiSXSkidIbR1oCMwseTLMy1nk6BNl4tPAVDSkfV14L3Nh+QZFcATqSlarqQkagpXUjIVJQBaAWok9nWL2wN+YJ281hSaWBSTKO5kIbWUVCGnc0Fd0cFzUNBQE3O9/vo9GCKQC1hBQzWrMSSpK/hmxYm41tQcREVAx5DOycscPYOy5pSM1sQ06BZ3X8/ID7oIlZ3AlnQmZxYGx2kKGmrDE2suJANXiOKpVIFYIc2tfLo/tCs8+e6O49zcUhUfacFonkoaqbQkTbP5lRHXGfW5PTwFGngg16GreaL6E1dur98rKW2SDQgo0OiSPQGiZNRxuHHpRduCOkOTVbWdSG1HRa3R0KCkgNA0Xkt9dCCIfN4ENKECDQkkAmKIVJBR1bwzPHfdfuJxBfSJgaQQUURBAKWFPtlgRvHDfSH8tGIYohBQW0qiboAhqaK6rTX6Jj86tXxPMJ5aABIlKNW4XIqg0hIF8MSc+MxH20/lBMRQdYgDiwpjl+vqLQqLy91zhkovBo5Q2NK2fcunTjY2GIbZWzMoC8wewyZjxh+PGPWDz5K8OZseey+pGb2q021Nn9OaQYdVfMdV/U6och2Wc51Wcp1W8lyRuMwIzVwPf477GpbHmh73F2OQ9Oy2kqk819U819W9rqv7XVYPuK7tc13Lc1/H9VjHcV/LdVvb57aOqb2j1qKRXus5r21gj/mIPW4je8zHLI9PWl02VjquzXVelTNxY7jLwg8xj6kIAI29imFORqZOli8gDJgJNtJs5GtOzjvWbKi8lwVsAfICD8hADlDPK//mXOG2M9SzJhCTCNCMaDVaFFuetCDkatb+MKjo0jnlfzrGqljFh6IgsxZqB7IPhdenZAr7+Xy5BDHflTBU0fwwKFZcUCvIrkg/EKqp6gJcjRJRKtTQJ8fTy3P3hJScvAA1PQgVTRCUlkQ9RBQFjd1l+4KJi2n1R2OQCbqWJX1c+uhoiKSsTisYAh0lBu/ouX8yrDr+DghE6GRXgvBJWdmZOGV6+eNvzzZeTwPk0dYiR7yCAA2w88szA6OJsiaksw/K2uLuNkbehHYkfIMWWJUN174N+JO9tzmGmY40WbRo0bXEhPuP0t+YNQMzwl6fPBFlJvT2cnNzCw4O5vP5zFX6P7tW6w6p/84H0x2o/6V+/jKZrKWlJSoq6ke7xtixYxmehrGx8bhx4xYsWDBnzhxnZ2cHBwcMw8zMzJYtWxYXF9fQ0PCjzKo3fwxXsRmxVS+56pvW+uX+AQb0N1PmDshYXgICAjAMc3d3T0lJEYvF0dHR5ubmNjY2MTExDA+aMb7ow/4HiMM/3SYw0vN/FKCZRgEjQw9XmZkx/5n6/PeGbvgS/97fGKYzROAPGAGDA/oPuFMNm2SIwB8jAggGSdM8Hi8gIMDKyur999/PycmZP3++k5PTrl27RCKRQCBgOKGanxV9K/nXNwn+MYJv2ApDBP5LEZBKpUyywa6urmPHjvn4+Jibm1taWhobG5uZmWEYZmdnt3Xr1ps3bnI4HMYXxsyf6Tr6Ly3rn23i4Vezn1/QlEolRSF0LqMRMBMz700zBAwGqSyTyQYHBzkcTktLS319fUVFRX5+/oMHD5KTkxMSEi5duhQSEnL8+PHdu3d/9tln69atW7Zs2dy5c6dOnert7e3g4GBpaWlubm5qamqkKyYmJtbW1g4ODi4uLp6enuPHj/fx8Zk8efL06dPnz5//7rvvvvfee4t1ZZGuLF68+P3331+6dOmSJUuWLl26atWqNWvW+Pv7r/mprF2/7r0/L3FycR5pZvqKnc2Mt+bMeGuOhZ0NZoRhJkaYqfEIYyMPJ5ctH6yJPxJUdzn1wbYTgjsFSEwEEINSrstVCEJccCs/+4sAJOkOKJHlWaVC5kcxAXLNYEZxw+krzUHxVReTgc1H6AaNBk2jUAFX2JT8qDAgVvOsEeRqLUlKgB5Eufx06mc16+nuoKJjUQj9zJcqFQqJlkQOWQC6qrP+/M2ha9ldEberI26q23tBRmo0GlwuRxJnxyD/0sOyHSFF34Sxr2epeSh/l4DWqc+D8udhCRU7Quv3RiFPLluE5tcu7A5MyvrkKHIK98m1JC1WkUINKQIEppCraTEodfAKuvtKetO3kZLI+6Vn4iR1bXKFWKkh1b2DUNHeduoKpJbWnLvWnPKQ7mQjWjRC6w7xLqZxwm6VH47hpuRqekVIIkemYxIp1wDQO9SamlUcEQ+1LOGj4qdBFxV51dDSP5D+7GnQRWjkNsbfr4u/p6jveHH24ZS0oqkh6BonLLnidJwgp1zB6SNJXEorcAp/YQ/rl3ak5jadjpdEpVcdvQiVbODjIKGAho7krIzNR8nUEhATOGho5DjTKjmDwMWJ5MKnfznVFpiIXMxynatdIUGCv0alZnE77mTePRDY//gZyEi1miSAVqoQ11udVVW5O7T6yyAyMRdZXAmUcxIJ0FoAAYHn15adu9Z5Mwu4EqCARjudQmyNroGKc/G8mDtl+8K41x8haZVWA4mraBKlnOLLuLdykj7aWxWSIKluR4I1gFqh67doZFVFJTzeH0RnPYcBvOtp0afLVzqZWdqOGOky0twEw8yNje0xbOFIxyOjZt6fuDx//Mpa3/XtEz5keazpd1olehXVfqdVPGdUuU4r2c6oviRAszyQAM3yQKBnJEbr1Ge26wq26wrOqBcCdK/r6j5GgHZFsI4e5+UsJ1TZzitZLshSzXLz73Hz73BZ3u7s1+7sx3byH7TfKLDe2Ge2pt10eY3V8tJR/k99NjyYuWmb9cQVZp7/hll4Ikg0Zo5hZubGJq+MtLF6Zfzo165fS0CZIXENyACqOTUnLhd8foq6XQxSdCChlphShyvp4DfE3r752SGoYqGjmtQiWrRKO1jbVhmeBAUdUNjRGnW77tIdvJlNadQKUGsUJO95w+1TEURZy+CTyluHQ3iPS0FI4FIdXU1AQ1l38a7QqqMXEVFHpkI2f5JALHANBXxJ14UUbnACEZfeHHINytvUpU254Ze4ucUwIFQq0BxIPr8g+U5u9FVNS49aOARSGVHZXBuRQKYWNZ9LaricCv1ipUa3y3ECRDJOWfXd8AuK6jboGQQK2On51ecSoJYFCi1ICJRNkSfpT3ka/8l3H7/57r+4ehtj2GvObl9s+yrkQtRfvts9avxoKwe7sePHubu7u7i4bNy4MTs7m3FL6LOV/E9uYXp1mOliZEy7apWazWaXlpaGh4dv2rRp+vTp5ubmZmZmjGbq4+MzYcIELy8vW1tbc3NzZ2fnt99++/vvv6+srBSLxXK5nOmwZAwfehF2uPSsF6D1bW3mRvM/2ZDfzm+ZbWE2jdlSPp9PUVRSUtLEiRN/jGFYWFh3d/eP98oxY8Y4OzufOHGCy+UyyXJ/fkf+7WyXYU3+RgSGy8GaFxho/U/0RmZmjN4ZPVyV1k/89w4MX+Lf+xvDdIYI/AEjYBCg/4A71bBJhgj8riPAWPO0Wi0jaQUGBrq6us6ePTsjI+ODDz4wNzffuXOnQCBgJmOefPRtYv3AcMnmdx0Nw8obIvDbjwDzyMr0BjEPsWw2++aNm/PmzWPc0IwJC8MwBwcHPz+/mJgYHMcZQ7T+Kfq3/yD36z9yD9caGKVe/6jMxI0gCOZ1aZlMJhQKGX25uLj44cOHSUlJUVFRx44d2759+4cffrhs2bJFixbNnz9/5syZU6ZMmTBhwpgxYzw9Pd3c3BwdHW1tbS0sLEaMGIFhmImJib29vZub29ixYydPnjx37txly5Zt2LBh8+bNW7du/fTTTz/66KM1a9asXLFy2bJlS5cuXbx48dtvvz1v3rw5c+bMmjVrpq7Mnj17zpw5b+nKm2++OXPmzMmTJ/v6+vr4+IwbN87Ly8vV1dXR0dHhp2JqampnZ2c00tjK1gYbgWHGI1A1wozNTKdMe2PSG1PNjIwdsBGvY1YbJ74V+P6mS2t3cFNytVwh894/Okf65Yq7JVWfnek5dg3a+LrxakSWUBAgxPGsipozV1gX7jZcvCWubkHv5UslSHtVAbCEPYmPcr+PlJc1Am+IsT/L1ASp1fGdWwfYRy5XbT0FWdUIPSGjASeRzCqXKhvZtZHJrLi07gv3m+LuQZcAkS40WmSSUpBUXffgzafVeyLKd4W1X03TdvO1ag3jfdb0ilov3SveFZq//YwqsxpkGoSEbheLL2SUbznVF3pb28QFWiOjSbGKVKhphU59RrxppRoGpNLMiqrjl9pO/ZD+xbH+J+WgBg2hIAYGoI1XcTJWeSWTffpqY1Qi0dCKFDqKhvre/nO3Bs/fY4ffbr/8gDFyIgC3lkbx0WjUQnH946f3Q2N7s0t60wvTjoa2JaRBh1D+pLIy+gZUdOBPqwtjE/tqm5h0f6ACZWNPxbl4dvANbmgyKykDpCqQ4Vq1iiAQ8wTEOPDEPalPm87dhOvFvKBkIrsaOGKtQIqyLxY3Pfg2SHivCPpwLU4p1DSupFAmQJacTC4s2hH88MsT0mcNSCBGRUOLhtByu3hNiampp4J5RWWgVFFDg0oNiVNykCugrqv+cOyzT0+w4u4DD4nLGhVNaXUCdK9YW96WH3SxLSUTODrEtoJWDAhR7sGeweZHhsV/AAAgAElEQVTwG00Ho7q/j5MlZ4OMVA0JlFKxmsKR/VkoRYnp/nIi49tgSXkzqBBeHAmIEhJYIva1hzc27xXdL4BWtrC64euVa90wYycMe0VXnYxM37B0XGs1NtZ5bvkE//ZJm6qd3691WNI3Zj3HdUWf8wq+44p+pxU8lxUcnZrMaMps1xUst5Ust5U97qiyvVYzleWxiu21muWxClXdBLrPFywO5IPW5STkjEICNKM+o0+XlSyXlWzXVYyfustleaeTX7vzii5X/x7X9WynD9mWq1gmfiwTP47lKo792u5R61snfPLkteUXneYecPiXP5s6TzG2tMUwM4SyxkaYGY+dNjnl7h3UtdAy0Ho64dbq3f1J2cCWMDRstKMkJLQMin/IfrYnTHArH+WNlJO6TJu0ksXPOHe5/VY2tAx2X0mvjLiuauNpJTgj5QiqW55ExrfdzVWWt1dF3mTdzyc5fFBpNSo16jup6m0+dKlgRxCdXQMSQksogCRR+kdQKrmclgs3mgIusM9frwuKG8p6Bo2duWGxvLxiIGgNIkdrabmkJvfpvQtxmgEBiCRAa7TNPeXBcdLr2UOXH7GvpqnaOMxhhrorxApFU3fO5aTeslp0QA4RUMMqOn0RWaElJLJja0DNE/ZkFGUcDBPfLSLzG5L3n5ln5+2NWdq9Yj35zZlbj+yNSI5/b8UHrzo5ujo5e3t42tra+vj4MAomc3PULe5vf/z1G6L+W4FAUFpaGhsb++GHH/r6+trZ2Zmbm7u6uk6YMGHs2LEeHh5OTk4mJiYWFhZWVlazZ88+fvx4RkbGwMAAk8uB+dTbeIeLzvrm9C8O/Pp3w78dsv/uFPq7qn5LmT0lEomysrKmTp1qZ2d3+vRpmUyWk5Mzc+ZMOzu7bdu2dXd3M3Rshk/y31244Xe/gQjodeFh66IXoPWKs35g2FT/xUH9gpgXe/6LvzZMbojAHyYCBgH6D7MrDRtiiMDvOwJ6QVn/GiAAhISEWFtbT5o0qbu7e8OGDWZmZkuWLGFe4Wc+DQ7o3/deN6z9HyUCevVZb/KiKEqpVGZkZMyaNYuRNZGQoZM4MQzz8fG5dOmSRCIhCEJv4GVSNjGP1r/y8y2zuL++0F/frM1cDBnmMkEQOI6LRCI2m83QMJKTk0NDQ3fu3Ll27dr58+f7+voyDG4Mw4yNjU1NTRkTnKmpqT7sI3TFzMzMxcVl8uTJ77zzzrp16z799NN169YtWrSIUYoZ17O9vb2ZmZmpqSnzaWJiMnwmRkZGprrC+Nytra1tfip2dnaOjo6urq7u7u5eXl6enp4euuLt7T127Njx48dPnDhx6tSpU6ZM8fX1Hf9TcXZ29vT0tLCwYAgemNEIzGiExSuW5pYW/zLtjfUfbdj39e410+e/P2riZ5PmfzJu9nwT1yUekwK27+2sbgBcCX1SKGrP2XK85qsQyGoC9Bo9EKBCDl85AV38osMRrUHxud9HkjXtQKpUMhkxJEIoWK6Ek5xVdFKXPY8vQYZZNYDiR+yTAuQ41LObTv/wdM13kFwCAzrPrAqAopUSKfQKs45FdkWn1oUm5Z+Jgz45iAglTkrlMpIkSd4g79bT5wejmw5f6gq/hVDOKsBxHJ0dcpr9oCBvx5niL89IbxcCR4ZUNgokibn5nxxvO3IZahD6VqaQy1SUXAd9pmmUnU9LK0GqpIuan+4NVaUU14XEk4X1CBtNqICk6daempCrAxG3m45EdYYnQgsXhBINKQOpQhD7gPXdhfrvogXXsqBtEPgyWoa0P24vkt6UBF6S/eTotp1XA4Kvnw47+/mut171XOA0+nl86t1T56naDlFx3aOQC4LKRlFvHzJ9D4lBIK24llp1PrH8WHRnzG20LJxGoEzQKhUKFPqeAfaDvNpz1yGtsv7IJfxOMfSIQEyDTDNYUJNzNLI76TFKrkgBiRMUQaKfDykhoz7v42NPtgfKsqu0fIlaqVRpVWoKRzCNAVHf7ce3vznGynuGhEKUfU5JUnKQyYAn6rh4u2h7IDcqVVnTAaRKo0LCOtLWSVpd2X5vz6mymCRNMxvlJKQ1oKBUA2KQ0OUXUyq/O99+MGbw8n3oQskkKFpGK3FE/hRJ6cq259vP5m06oilrBwkppYg+iZCUyICEoXuFdz47xEpIh64BvKNn7eL33IxNnbERbpipM4a6ScZjph9aj/vh9fcbJ3/c7rqy08mv0+GDDvs/9zgu47kg3Xm49NwzasW/V530zAjQLK/VLJ0GPVyAZr7qcV/JyMoMEprrhrAbCMGBBlCKQp6HP8pMqBvm6lIUcj38+177sG/0Ro7X+i7P9R2j/Ntt/LrNP+CYLBsY+YFgpN+A6bLeV5Z3Oa5oGLfu2fSNCTNW7hw9Y67Zq16YsZWxEWaMYSbY7Plz+yubisPi0z451HcxHR3VahAPidBNTA3oFMhrr9gRKrueB52iF6kFCY2WLUg/F9d0Jxt6ROWXb+eHXiVru1AfBk4iOIwSss9d4d7Nh9bB1sSH9VfugYCixTKUbFMoU9V21x+59ND/O87ldJSiEydlchFyzFOUhs0T5JU2nL2siM+sPBmtfVoFte1ZodEtt9OhT4BefVCSoFK35D97cu063s0GtQpwQtPU/XD/GcWtp+2hCcUnYtE8abV4SKh7VYKCXklzSkZbZj6y3pNq6O5/cjxCkVMJfCm6jMgpkJDcwqq0gCho7AcuCZXs1F2nKqJuBn68/VVjc8x4hImz3dSFbyWn3Tt68vuxY8eamZhaWVn5+vo6ODgsWLCgvLxcf3/863f+l/AaP5+Ypuna2tpz584tX758/PjxpqamlpaWdnZ2EydOnDZt2tixY21tbZl+X1NTU2trawZnzGKxmMQqzAz1ujMjQ6PdqFLrq16N/cWBv36v/PkK/5bHMNsyfDMZXznzlNHS0rJgwQIrK6sNGzYMDAy0tbXNmTMHw7DFixfTNK1/cmE2UN8x8FveXsO6/UIEGGl42Bc/F6BffPmzKYf96G8NGgTovxUhw/f/JBEwCND/JDvasJmGCPymI6DXWfRrSVFUYGCgu7v7tGnTMjIydu7caWNj4+fnxzSg+/v79U1nPYhtePORaVD+kZrI+sgYBgwR+A1GYLhq/NLZJ5VK79275+fnZ29vzzwSjxgxwsjIyMLCYubMmSEhIfX19Xo3FsPxUCqVw0/wf/T2vvT8+dITOMOjZ/R0tUqt1BUGEMQo5oxbiplMqVQOpyrrLcz6H1IURZIkA8dglHc9c5nP57NYrIaGhrKysuzs7Dt37ly6dCk4OPjAgQOff/65n5/f3LlzJ02a5OnpaWVlZWRkxOBNGI3YzMzM2FhnVvzJbW5jY+Pp6Tlp0iRfX19PT09HR0dra2tLXbGwsLC0tLS2trazs3NycnJzc/P29p4wYcLEiROnTJnyr//6r2+++eb8+fMX/lQWLFgwf/78efPmzdWVt956a+7cuQsWLHj77bcXLly4aNGixYsXv/fee+++++7ChQvnzp07c+bMN954Y8qUKYzQPGnSJMaON/pnxdvb29PT093dfezoMVOnTHFycLSztnF1ch4zZoybm5uRkZGrkzOGYY6vOvzpjRmrps09uOTDA+/4b/R50xszdsWMX7d3fWfyjNMbt1Wdv56z9fsnn51QPKpAUiYic4BcIVXjOPAlz85fqz19uepUHPdxESAbowYIJARDj2jo8qPyAxFkWRPy22oBaBpJz6BBglTPAHEzr+jLU/0Jmcg1jCOUrRopbVptR291ZBIr/HbPuVuVEdeVjWw0NxXKWYRmIqfFRQ1Vp66UfBPWF/cQajg6iVlNCsSAazRVXU/2n8v85Cgr7BbS6YQ0DBKDmWUPNx4s/+actrob+iUIx6HS4krkDqZplJoPqbQAUNLeGnydTMirPXUVsaqHCBAqQEoBm990+XbrkdjGfRGchHToFSP/JqUGsbz3UUH9vkj2gUudZ5I0eY3AJ0ChVBEUr6+3q6c7IyNjz9e73pw+03qEie0IUwcjc8eRFg7Gpr6jPGLOBKf+EH8tIirs+MnAA4djzoYEHDocdebslbNhscdORe49nBF9pfTGPVF9G0gUlFQKWg3yPtNq6B0aKqzOPRklu1PUHJHSGJ8G/XLAtcCTUI8qn+wM6r76ABpZyM0NQJK4ViIDEaXOqmIfvvrs04CWH9J0KAzkEFNpVUDiICL4958+3h/IS80CWq2lCWR8Bt3iOns7QhLyPj+O6MCNbCQiUwQFKvRDAGAPZp6IeBp4QdvKAaEMZBSoAHEkpMq+ewXlR2Obvo9jXbij7eCiNVcjmgcStXFCkVdd+m3Yk7X7VEl5wCdUBKVB8HoFCHB2emHO/pCacwnQPdBb3/LN5q2mGGaGIde+renIVzBsKma557VZ8RPeL52ysXnc+i4PlDCwz3nVgOuqvlGreKNeQJx1TufVPe6/UF+YnXWWZ70P+t9N0B6rkAD9H+gcaznuqHI91vE81+urXnpGOGmvtQxLmu3pz/Ja1+m2ppvJczhqHcd5bZ/T2j6H1QOvrmY5LW9yX176ml/1/C8z/vRx5MTFa+3GIKw16tTCHK2tT374edK2ww2xKVDfoxHJlWq1GgAlGJSqpZkV99fv40c/UJa26WgVJDqMW/tbbmYi9VlId6Tmlsbdkjd2q4cQGUOr1mg6+pvj08vDE6G2V3q3uDI8SdnMQS8lKDVAaoEt41xKS/v0aM/FByCg0HGuIDTo9NSCghal5zeHXCUfFFWcvgiPK6Gxvy0muTYqCR1aqEeHBpzgPynNOhXBzSmCIRmo1DSLV3PhRv2ZK4rk3GenYhCHR6VR4zg6eikVCPCG8KTa4GvAFcGgBPrEZQmpz+NTUdZQUoX6SGgQ5deUXEiWFzYAXwn1vPzgK83x6cCV1yVnfLV83QcLFtlYWZtZWTp7uu/at/fsudCNmz52dnZ2d3dn+vPmzJkTHh7e2dnJSL36G+XPb3BarZa5OzDtWz1hqb+/v7CwMDg4+NNPP33zzTednJzsdMXFxWXcuHFubm4/Zuc2R8kvUR+khYXFG2+8sWvXrqKiIqlUOvzGxNyzfnG5+m5gpkU9/OaoX2H9wM/n8Psd859tKZOW0M/Pz8jIaO7cuSUlJf39/Zs3b3ZwcFi4cGFOTg6zyUyzwSBA/34PgJfW/G8I0MOl5L8uSf98yp+PeWnZhn8NEfijR8AgQP/R97Bh+wwR+D1EgFFnXpAEdTTPuLg4T09PBweHxMTEL774wtbWdunSpWVlZUwbUe/X+EX1Wd+AZib+PQTAsI6GCPy+I6B/In1pQL9VIpEoPz9/x44dVlZWxrrCyBpGRkY+Pj5bt26trKwczobW//BXGBguEzPWJ/1CGUGZuc7oFQH9t0zPmX4a/fjhA0qlkiRJuVwukUiEQqFAIOByuQ0NDdnZ2Tdv3Dx37tzBgwc3bdr0I+P+rbfemjlz5rRp0yZOnMhc/czNzfWp/JhwMZ8jRowwNjY2NzdnQMyOjo52dna2trYM0MLR0dHDw2PSpEmzZs165513li9fvmnTpl27dh0/fvzMmTOhoaGRkZGxsbHR0dHnzp0LDg4ODAz8/vvvDx48uHfv3m3btm3ZssXf33+5rvj5+b333ns/Pma/9dZbs2bNYtZt7NixXl4oxZazs7OTk5ODg4ONjY2VlZWlpaWZmZmRkRHKJWhkZGZmZm1t7ejoOGbMmGnTpr399tt+fn6bN2/+5ptvTp06FRkZmZCQkJycfP/+/YyMjNycnOzMxwvnL3BycPz6y201zyuzH2V+vvnTSeMm2JpbmiEUNDbW0uENG7f1b8zbv+LjnWs3zZkw2Qkz88BMV7tNOTzt/ah5G7J2Bw1VtwFOa2UEEEogKBDKCqLi66JvFp+I5ac9gwEx2jVKFdJnq3sG4x7mfX4CnjaCQq0hUBY1lValoHEtTYFAwU/NK/j8ZMepa9DMBalOngZAcAYAfmpef2SqJj6/I+QmXtwEAxJQaUi1EqdI9ZBMU9NdcvJSyb6IZ/sjoI6DnL+kGkgNCEgo78z/Nixn2+n2iFvQxEfqsxwGH5U+2n2mYGcw5DUjxq5O59aSNEFThAp5n1UUmoOqnlV3LE4Ufr/iQDTnRjZyZZIqpPH1SjsT08qPRVbvCRu6nA5turWVI1iELL8y68DZqqOxTad/gKJ26CXkjd0tJZUpSdc/+OCDGTNmeHt4mpmYYhhmYWRihhmZYCjQtpaWVpbmE31en/D6uLFjR3t6uruOcnYf5epgZTXe3WPKmLET3D3GOLtOnfD6ji+/yM3PFRNSuYpQqiiFQKjlDfblV+SeuUDnVHVcuMdJzgEBDkNyEBLq5x1VB6IrvotEOF0pQaopROtQkkjZbxf1habkf3xMHp8LHDGogJTIVASFdGGchrKWp/uD267ehtZuwJFGTCgVyKcsULRE3aj4OujZjlNDuRVoSgCJEv1Be7CH/zTo4tPAC1RVG9BaUjCE+gaEchAQfRkltaeu1hy5WH3mCnQNAE2rtLRaSQBNgkolKK2pCYh79pcA0aWH0C4EXI2I3pQWpCpNDevmzoBHR8Ohe5AWiAJOHLexQGKfraXlSB00eRxmvNVi3C3f5c8nb2wcv6HF27/DHUEwet3WcN1XcdHwC8JGl8fKLo/VTB0uQyNTs8cqfeV6rtZX/UgEg9ZRoX/6fCFAMxo01wNlI9RVf0aDfimZIdcNJTbs8FrT7r2mxXt1i+eaTrc1bOeVAw4r+19d3uO8vM1jVfO49ZW+6/MmrLw26f0VTuM9RppbGBvbGpss8vDJPnsBkWpIlVqlltEkqVWjw/t5Z86uoOrv46CWB7gGcZ9lSlUTpyLqZsuVB8CRcrPLKq+mUnXd6j7Ri8SSCiU/o7TqbDw8axcm55WcioNaNspCic5DgCFKciMv85OjbVG3EVFHQiFst4JAxBWRRFpeX37sPDssMee7oIGbWdAt51262xKbDJ184CvQESUQq7q4OUExA2n50NkHQ8iY/yQiriMmmbqVX/J9JF5SByqNRqNChnqCggFJ842HdSHxUNeHSOUCWcGVm1V3HsGALmkhrQIpoaroyD8TN/ikEjhSaBdWRlyviU6BWq62llUQl9ySXcR6Xn/uZOBYL++RRkZ2dnb/NnvWiYCA4ODgOXPmWFpaTps2jentW7VqVX5+Po4jwsx/plfqIf5M21gqlVZWVl6+fPmrr76aOnUqc9V1cXHx9vYeM2aMrS0iO5uYmJiZmVlZoQSY3t7e27ZtS01NZbPZAoHgpXd39Pfo4fcp/bD+W4MAzYSCeTBpaWnZvHkzhmFvv/12WVlZV1fXrl27TExMJk+enJqayjQhGKqYPpKGgd91BAwC9O969xlW/jceAYMA/RvfQYbVM0TgjxwBffNObyQEAKlUmpmZydhG8vPzAwMDLS0tvby8CgsLtShLOTlcfda3lf/KwB85goZtM0TgtxGBXzwBmSdYxhnEmJqVSmVbW9vatWsZmRJpN7o3hUeMGGFlZbVjx47Ozk6pVArIb6jLQPWrbN1LArT+XQq9OsC8ZvuSuxnlmsNxiUQi0pXBwUE+n8/j8VgsVktLS1VVVU5Ozu3bt+Pi4oKCgnbv3r1u3bq5c+eOGzfOxsZGj8Y2MTFhMvsxfBITExPmTWoXFxc3Nzd3XfH09Bw9evSECRN8fX2nTp361ltv+fn5bdq0affu3UeOHAkODr548eKdO3dycnKqqqpadKW2tra0tLSgoICBQYeEhBw6dGj79u1btmxZvXr1kiVL3nnnnfnz58+ePXv69OmTJ08eM2aMk5OTpaWlPseg3lhtZmZmYmJibGzM+Nb1E5ibmzNOaisrK1tbW3t7e09Pz+nTp69atWrbtm3Hjx8PDw9PSUnJzMwsKCioqKjo6OgYGBiQyWQIPqx9QUDUarUEQUgkEpRLcEh07mxIXEyshC9QK0jZgEAxKGqvrv9y4+bxozxfGWFiYWpmY2Zhj5l4WTssXvjOji+++mrNR/Ocxm73mf/dpEX+LpPfetV7o/+6ew/T+thcwNXarr6mxAflpy9VBv/QcSdLwx5AMAeVComJXIUsNPXR+ztEt/NAgBNDoiFcQoJGCVpaTUH/kOZRRcHnJwt2BkEdF+nLJIUcvkoVqID7IK/tTLw8Oq396BUo0pkZZYQKQEaTEoFQUNpQsi+i9puI6mOXoJoFchqhbGmd+lzJq/w6rHZbaHtQErBEIKMRw7pjsHh/RMHOYDyrCnAASo10ZwVOKHCKIAkVLdEiDRq4wpLAy8LAlIGT1yvOXIX2flBpgKRhQCG6/6xwT1DtsZjO6GSo7UIinVSGbJuVnZXHoniX7j46FVlw5WZ1SsYPR85sXLDE2dhiJIa9amtnZ23z+rjx8/40d8m7iz3c3J0cHK0sLU2MjS3NTZ0cXh1phNlYvTLr32asXrniyKEDF2KiUm7euH4jMSzm/O6j+95dvcxhnIeJs42T72vfBB+v4bZLcN1p29Dx4ES44vFz/GFpc+wd6MVBoUTe1Yqu0sPR+V8HIR2cVBMqUqBWiJQKWqEArkibmNe8M7wtLBlaBpCkTmtUBKWWETAo0VS3PdsX0hB0FXp6UT+QQq4iFbRcAux+aWJW057wgr98L77zFETIGEuBaoiWyTWkZkjCiX90Z9M+JExTyG+mg1MDiDVQ0lV7IKb5xNXS7y/ila3IC6/+SX0eHILG7pIzF/K/DuyJvo20aYJWK5VoTQRKqO0rPBzzPPyGqKFTJhCmpd/3mjDazNEaafYjMUdzy1EY9pGx512XRfXuq9vHbGj3XNfhvqbDfRUSeb1Xt7+2ClWvlZ2eqDICtF56Ho7U6HVbpa8DbqsH3Fb3uaPKSNgvPhm8xotPhODQgzh47uteVAbE4eGPdOqf+NG8USsHdV7sLq9VzaNX1Y9Z2eC9qsVzFctlueDV5UO2Hwjtlw/YL+91XM1yWtnhuLzce8VF3z8vthiF0hKOGDHDY0zZ/QxQoX4alJVLpSZJkuru7w5LqdgboSpvB0IzJEWnMwzI8s5dKz+fBK0CZWHTw4AoYUkDyFFqR1AA8Cnhw9KyoKtQ0gW5LYVHowcLakCmRD+ktAh0/rSmfFdYy9HL6AUCBaBDSEqBjACJgqhtLQi91BaeUH08qjb4KrQJiZSn5acv4BVNL34+hEMb73FwTGN6NuC63qZBRV/qk6bwBPXtwqe7A4WPnoFADjIc9XBotNA/NPS49MnxCGjrR0B2lvD5jft3zsWq+EOEWIwOUaVKyRl4EnJZnF0JbAEooDo0seRAJGQ3Qq+67ebj6tTHgKtVYrkWpxorqnd+8pmHjYMxhrk7Om9Y/2FcXNzGjRvt7e2dnZ19fX1tbGx8fHyioqIYELP+Yvjzex1FURwOJzU1dc+ePTNmzGDS+Xp4eDDNY0dHRyY3rJubm4uLC4ZhpqamkydPPnPmTHNz8+DgIEPbYNTnl2wZ+rb3zxeqv5UP/0o/8qWB4dP83odf2jT9v0yKCybXQmBgoJmZmZeXV3x8PI7jAQEBdnZ2EyZMuHz58kvvZf7eo2FYf4MAbTgGDBH4x0XAIED/42JrmLMhAoYI/I0I6Ft4zHRarRbH8czMTBcXF09PzwRdcXd3/5FVWlRUNBxdp59eP4e/MvA3VsLwtSEChgj8jyPwiyegRqOhaZqBTjBIDZlMxgwUFxcfOHBg4sSJFhYWGIbpnbP29vabN29++PBhfz+isv465SUBWjasyOVyPp/f0dFRW1tbUlKSm5v74MGDmzduxsXFhYeHnzp16uDBg1999dVHH320dOnSefPmTZ06ddy4ca6urjY2NqampiYmJubm5lZWVg4ODu7u7uPHj586deqcOXPefvvtJUuW+Pn5+fv7b9myZffu3QcPHgwICAgJCbl48eIVXbl69erNGzdv376dmpp67969tLS0hw8fpqen3759+/Lly1FRUWFhYQEBAbt27WI8y8uWLVuwYAHjU548efK4ceMYugWjX48ePdrFxcXa2lqvfTNmajMzMzs7O3t7e0tLSxMTE72+zCCk7ezsPD09x40bN3ny5BkzZjAu5i1btnzzzTfff//9uXPnEhISHjx4kJ+fX1FR0dDQ0N7ezuPxhEIhjuPDewppmsZxXC6XDx/PCP3MLmYkVz6vF5FhAWixDFRawOnqwpI715LuJyUf239wzry53mPHmGFGNmYWVrY2bm5ub0+f/fWf/Q8vWL1/zgf/Zuthg5mYWFl4+45ftfSD5ODoyugbVYGXm4MTys5eVnZwQUFocQJZGpt624MS6j4LHDybDG19oCAoJSlR4hKtDnNBa2T51SVfnm7eGwlFrcjAK1WoSN1vRbgg7VltQBw//DYnKAke18MQgOhFOk2VFKdbuVXnr6Osg0evqJ82gIhGYBatBuVn6xQPhaY2fR7COnIVSrsRJUAF0D1YHXHz2Z4wyY08pLKRGgSfpkhKSaPeDopWUwjBAXKal17Ucf7WYNCt7rM3iYp2oIAWS0BOkfl1WV+fyt1zpvvqPWhmQb+AFA8BSVK1bTXnrlUcPB+zYutflq5aMn+Bm4WtHWZsjmGuFjZjPbyWL/sg4MSJ56VlJE6IxeLw8PDTp0/v27dv+/bt58JDA04cH/Oat5PDq2NHv/bWnFkb1q/bs3tnZOT5tMcP67paWgScTtlAQUvVwbBT0xb9CXN6ZaH/sicFuRoF3ltRL6ts6b775NHJCOQNZ4uA0EIXv/F8cv6eUNmDUgQOBlAALaYVcrEIeof6U57kbTrSfiwOGrkIhCKnVGI5OipkJDRyik5GVZ6IhaZeGBQCqSNvqNVaTr88u7x597nqzwIESZnQM8DQUWSUgpRJAac77ubc++ww90oaDKJ+LCliRqNC5tY2H4mThj9oDrimKmxQ8vgkIVOqCMQLHhyCui527J3HWw9XnrgIzb0I+ICA1oBwEJ2y6tPXinWe45EAACAASURBVI5fhDo2PSStqq/+09tzEXfjJwDHKMx4AWZx0WVei8faDsulPW7r2txWd7uu7HZb1framubRa1p/JkAzTIzh0jNn1GqUVNANwTqYygjQjAbd64Y81Kj+B/V5jV59ZkjQf02Adl/OG7V80HXFwKgVLM8V7a+tahz9QoDuGbWCrxOgRXbLB238+qz8+m1XDLy6utV9debrq7ZajHPRYUacrazT790dEA9KlOh8BkKt7OpvS8lC3uesWhgi1RQtk8losawuOaM4LB5aBkWZ5fln4ngZJehVAKEcMWwkGjq3vvxkHALmPGdx49J1GSl1sjWu1HKFZGlL3uHIwl0h8JyDoDG4BqnPEgLEBAwpmhLv1UUmtUYl1ZyNg+IWIr24NvQHVUkDOqHEEtTh0c5rTbxfk5AKUt1+V6jFGUVVARcUidkVhyPYSQ+BLwa5ApHcCQr6huRljYVBl7SlrSBGlOeejMLMc5dEje0gw+X8QWJQqOjmZsb8gBJjCjXQJ2+4/jD1L8cgsx4aRexrGfkXrmt6RYgQTeuOF4WSX954+MPP3pk8w8vaYZStg+/rPkePHt23b9/CufNfc3W3sbJ2cnJydHTcunVrVVUVTdMvadAURXV2dmZnZwcEBCxfvnzChAkmJia2trbOumJmZubk5MTQjMaNG2etK1OnTvX3909MTGSz2WKxGMdxrVZL0+gywhz5DH/jpds089VLn/ppho/Xj3xpYPg0v/fhlzZN/y8D3dLhfSihUBgdHe3p6Tl16tTY2NiBgYErV65MmDDhx4S6kZGRjKv99x4Hw/ozETAI0IYjwRCBf1wEDAL0Py62hjkbImCIwC9HgGnYMY4MvdmQkaWys7N9fX0tLS1DQkIiIyNdXV2nTp2anp7+izPSNxB/PvCL0xtGGiJgiMCvFgHmrGQWN/wM1Z/4BEFUVlaePn3a3d2dIRozuAkMw5ycnN5+++24uDiGXMHMhHmWJknypcd15hrCvKrMPHIzgGalUqlfB72FWalUUhQllUp1rmURA8To6OiorKzMycm5fv16TExMYGDg/v37N2/e7Ofnt2DBgpkzZ/r6+o4ePdrd3d3Z2dna2tpcV8x0xdjY2MTExMLCgnEBu7m5+fj4zJ8/f8OGDfv27QsODr569Wp6enppaWlNTU1jY2NLS0t7e3tbW1tzc3NDQ0N5eXl+fn56enpycvLly5cjIiICAwOPHDmyY8cORlZeunQpIyszPmU3NzdXV1c3NzeG/ung4ODp6enj4zNt2rSpU6f+aMXy8PCws7OzsLBgkNCMcuHm5sZgoBmPMyM9MxAPGxsbd3d3X1/f2bNnv/vuu2vWrNmyZcuuXbuOHDkSGhp6+fLl1NTUrKys4uLi2tpaFovF5/PFYrFEIpHJZBKJBMdxvcbxv3NoqbVAKUGpUSvIutKK3IeZPU1tpEjK5/CaGxpvJad8vH7D62PGYRhmZ2dnjGHeNo5/ch338Zvv7tr6xUebN40aP/oVOxsXU6vlY//19KyVsQs25u07B429SEOUkaAAbWl71b6oVL+d7MhUaOoHOXOwoE/08r8G6Nz62gMxZZ+eUlzLBZZAq9bIaBLdnqS0IKOs5fiVgVM320/G4/dLgS0GQi3DpQpSAUIJ9Cm6zyZV7g59fjSaLqxH0ABKR4OQyYCvGLqeU7bheO3nQUinG8BR/kMBXhlwOX3TIfHdImBLAEe2Xwo0BGgo0Kg0GjWlE8Tb+gSpeZ2hN/ov3K8LS5AWIXQAqfOMQ1vv8+OxObsDaxPvq3sHVTIZkl+1KmJg4F5Y1J7/5/fJuBn/NtLuFQwzHoHSyHm6ur4+bvyOr7ZlZz4WiXS543QQAJVGQ6vUlFJF0JQakG7FYbEfZzyKjYzY/tUXCxfMG/Oa9ygXJzdXZ3f3UW9Mf2PZyg8iL0XnFuW1sjqau9u27fna1Np8xqwZyTeStDgl7eXn3LrfWV6DRHaUeBC6b2QVHIqWPywHIQXIbYyDVqOVoeyL6tRnhZ8dL99/Dqo66SExjeRJneYLQDd0Z+0Jqj97DSU5lJGAE0ASKOvgkJzMLGs8FNWyI0wRlwk9fIQyIHWxkuOIwJBaWrkzpD/lCXCEoEFUaJkS4Q5UFW3PT1xoP30td/spbU4t9KCkdmpQI6AHQUA3vy82teyjo/0BiVDZAUNSFUUrSR1NXEBWBsff3X6Cl1+pGhAregfPnwmyMBlpZIyNGImZGGOWI7CJmOkZp1mF7n7dry7vfXVlm8eaZvfVbNdVPGeEbO7yWIm4GW4oeWCP++pOTwTf4LijhIE/1bW9o9b2uq0ZVhkf9PAxaJiZHk086t+Nz8M0aP0MmVSEq3keqDLKNcdjBcdjxQsV2x2BPro8Vnd6+Hd6+He7reI6rexzRCCOPseVPFf/bhf/Lvd1TaPXF/is3W3++miUGBSzsrUKCjuLUzgllyEHMXuIG3M37dPDA9ml6t5BhusNfNnzS8nPIxOhvB2qu/PDLnPS84Er1OIUJccRDqWFUxBylZ9aALWc/OAr1TEpCLIxRCDvM6lV1nTl7QrO/zqIyKtFPHQFBTiJzi8xATxR990n3dfu829m1cfcgDoWVHbVxFwX5j3XMb5l6CDhCHpSs/OirpGtLPSKAKlWFzeVHYmiUgrrAq90xqdRjd1KhYLU0mrQgIKEOk7J8WhlWQvwREBq8TZW8pGz+PMW4AmRTi1TQQsn+3T0QPoz6BgAkVp8t6joYOTgzafAIfn3CtMCojT9YpUUR+ozY9+Wa5vj08vCEzseFuxZv8XN1PpVcytbe7t333039nTIgc+3Txw7nhGgjYyMJk2aFBYWJhAI5HK5SCRqa2tLS0s7cuTI+++/P2bMGBcXF4azxOR6NTc3nzNnzscff7xo0aIJEybY2dmZm5svWLDgypUrtbW1fD46ERish75drb8DvoSWYqY0fP49EWAc0PpIyuXye/fuvfHGG46Ojvv37+/q6srIyJg+fbq9vf2OHTvYbESi1zO+/575G6YxRMAQAUME/tkiYBCg/9n2uGF7DRH4v48A05LT61BM8w7H8cbGxunTp/8orISHh+fm5vr6+lpZWSUnJzNOul98JZ+Z1c8//+830rAGhggYIvCfRED/LIe8rjRyzO3cudPT05PJ1GRkZDRCVzAMGzNmTEpKSkdHB0mSapWa0IF6CYLQi55SqZQx1SqVSkZ9ZuzMOI4LBAIej9fd3d3Y2FhVVVVSUpKTk5OUlBQcHLxz5861a9fOmzdv4sSJ9vb2eh4Io8zq9VnGEcygJywtLW1tbe3s7BwdHUePHj1lypQZM2YsW7bsq6++CggIiIuLy8vLa25u5nK5AwMDEolELBazWKyamprCwsKHDx/Gx8eHh4cfP358z549W7du9ff3X7hw4YwZM6ZMmTJ58mQfH5/Ro0c7Ozszvmn9ahgZGVlZWTFA59mzZ7/11lvTp08fP368i4sLY1i2tLR0cnL68X2RMWPGeHt7e3h4uLi42Nvb29nZ2djYMJkGXV1dfX19Z82a9d5773344Ye7du06evRocHBwbGzs7du3Hz9+nJeXV1JSUltb297ezuVyBQIBQRDDM1YxqOvhO5OR+/WvdTOqx/DdOnziv2uYScujAUSWUKqBUmpJWsDrF/YOqBUkovciBVGjpuiBvv6HD9L+svUzVydnhAExMvEytRn9isP41yf86b13tu3b8+HGj2aPnfjJGws22vgenvjud29+EL39oKyVjdCupR2Vxy7W7Y7oPJ2oregEuVJFIcCFGqUso0FMaOrZJfsiyr44I4x8AO1iUAJfLukTCdDSG7mlh6N5p68XfRHIS8xCkrGUBBo5eQmFDPplrWFJtV+ebdkXrSyoR7kBSVohEWtJUsXl8+/lF+wMqvgiCLJboA8HhQbEdM3Ve/c2H2o5mwSsF+qzXEkpQI3rBGitWgMSBYhoeFzdceKK/FJG7p6z4pJ6wCmKwFUymaK8qehkbNZXJ5uikqUt3bpdoMZxmUzIDz12fKb3mNdNrbywEbY6NrGxqfGkKRO/2PZFY1vLkASBsPV5PhFIAbS0FiiNltYi4Zu5I4NGjSqSg7V9PM6T7Mff7f1m9coVk319HF+1NzMzcR3lvHKl37nw0MJn+YcOH7B/1Xbs2NGJiYkEgSzVL2TkbiH/Ru7TvaGcG0+gR2dxBS1QFOAUkpqfNTXtCe84FCvPLgexTKYmRECh/IEqjbqdWxwRn3swDMraQU4CynWnRYL+/2fvOuCiuPL/AFKlSm8aEI01Bs3FlpjoX3N6mkSlWi65eMYSNYklxhJ7FyyxodhoUQFRVEQEUUBpUqVKZ5eyu7Bs39mZ3Zn5/e/tmM1GTc7LJZe285kPvH078+bN982+mfm+7/v+xHJVQWX9vqjqL77u2H8R7teCTKmmSSBJVTsfBDLlrYeFC3eKj1yFLkQ6K+VSdAoaSt3UUXX8UsnWkygWZdwtaBai5qO056hRA6+n4kBU9uJtj1cfhYwqNHigJmmaxsVSEOINSZknP1zFTysAEa6RKlvKqyf+ZaylaS9rKzNzI8waw1wxoykmfa71f7/SbXab4+xO56A6r6Ba7yCua0CnS0CH2+x29ycr1z2Q5aBbPAPb9OlmLaGsxz4HfevC8d8Q0E/Y5+8T0AFcT1Qm3y2A5xrIdQ3iuAU1u6O11TWQ4xLY5owyWzxCG71C6/vNqeg/5/7LIWvNXvbDjFGQUzOjWcGzUWxPiRIaOqXXc/OW7anefZ7hCpC5DUlRrbySU5eytx2DMg40i+4dOF2TeAuZmXRJGBVJ4wQjkNyNvFibcBvqBHVXMu8cjVY+akKNJcJBBWQ15/KaPYlz1tA3ihH7rCIYlYpR4nSPBDpFojtFeXsiuaevlOyNhMLHzMPa3KPnubeyUYxBiRxEYpAoejIL74RFAKcLEdYkqB81Fu48RV/ObT2R1HD+mqaiGUQyitKyzwCqBu79rcdkCVnAFSGxPKcr59yljuwi5BMiwlHkzNqOspOXeImZwJEh25D0orRV+1ojkoGrUt6vuvN1VPejelyhVBIqNGyG0yBjyLzakvAYKO+AOsH1A5GF127Pnxno6upqaWY+xMsn5J0ZRw4eGj9+PIZhjo6OFhYWtra248aNi4qKWrVq1dixY1mfDdacyszMzMHBwdnZeezYsStWrIiIiAgJCWG9/p2dnUNCQvLy8lgXI10fq6Oe2cRTz8a6zQyJF0eAvf3p392EQmFxcbG/v7+pqWloaCiHw6moqPjrX/9qZ2c3b968yspK3dvNix/FsKUBAQMCBgT+PAgYCOg/T1sbztSAwG8FAfZJjn0+ZmkOgiBycnImT57s6Oi4fv36oqKigQMH9u3bNyoqig3rQdO0XK6dlvtbOQlDPQwIGBD4bxFgWWO2lMbGxj179kyePJm1G2aVXzY2NhiGjRkzZvv27WVlZTiOkySpUqlkMplQKORrl4aGhqKiotu3b8fFxen0ywsWLAgICJgyZcro0aMHDhzo4eFhY2Oji4/H2hbb2NiYm5sbGRnp/JfNzc1Z6wkHBwdfX9/hw4e/+eabM2bM+PDDD1esWLFhw4Zdu3YdO3YsJiYmOTk5PT39xo0bsbGxp06dOnjw4NatW9esWfPxxx8HBwdPnDhx1KhRw4cPHzJkiJ+fX79+/diQfaw2Wd8Ew8zMzNbWlg0b6Ovr6+npaWVlxVYJwzDWwYPlvt3c3Dw9PXV+0EOGDPH39x87duzkyZPffffdefPmLVmyZO3atVu3bj1w4MDp06cTExNv3bqVk5PDGkM3NjY2NTVxOJyuri7WiJm1tNZRyWwrsPQ9m2Znpei3MQv+U2K6H6c8nmJA9D/ql4woZnZFMmSGIdWgpjQ4wZBqDU6olSpKjchicY8IebYC8Pn81NRUNIoweqybsaW3FRIDWjjYuvTzevfdd4MmTV309rtLR075cNA4H8xysLnjgpGTLv5zw72lu+8u2Fa7KxryG6FLDoSajfLHqLRa3cqOuoOXCr88mr/hGBS1gtaEXCwWa8RyuqatePvptv2XSrZGtl++ByIV3oPoVEpN4BoVzu/iJWbmfrb//uKdcLMY0ZckqVYo1GIJCMTcmzl3V+4rWBmOtM/tWqINB17ivavLt+cejkHsG460z8hCmiElQMmBRq4dBLKNptNLH60/JjmaXL3jDOK1tdwZQxKyyobSLSfvf7yj5vAFvOgxiGVAkjK+oCT7/ppFi/xcXZ16mTr1MrXDsJecnd4YM3rb9i2l5SXdImQLi9hniiLUJOKatQQzBYyGRsw/hYyun11oLRONYJfJJZWVj27durlt+5bp06f27efl7Ow46jX/+fPnTp48ydXN2c/P79SpU8h/Vg3AlSov596avUZ0/AY0dCNvBJIChkGrVAUF9XXbIstXH4SMMpAolIRcDoyIxim5App5dWevXlu1i6nhoPBxSvzJxSEUgUBRuPtkxeYTRRu+RoB0iCilUqmUob2kJGRXpS3d/nBrBFRxgUakNbqa+D3QKeNeSCvadjJv87HGS7cQOylXgUbLPotlIFRUR1zM/Wxv9qe7BCkPoEuK2HOKQvJnFS3IKLq6Ibw4IRX4EponBgl+OSrO1d7R2dkRw5D22RHDXsZ6fdHvLxl+s2vdA1u0TG6TZ3CLRzCy1HAJ4LvM5rkiBXST1+wn2ucnVht65PILENDfaqVZjfNz5c8h+tuw2ufvK6CRg0ene1CXa1CPS5DQKZDnFNTuEsR1D25xR0w01yWk3S2U6xLS6h7a5Bna5D2n0nfOvUEhq82RAtoEw4yMsWlTJiP0WoXEraKMlXtyNh2BSi6ItVE623oeX0otOBYLFVyo5RWfScg7Fw/NfOSs0i0FGQmdkpKzSfXf3IKa9vas4ruRF0WPGpB1hgQHuRqaBOUnEr5ZuKHm3DXoJkFJaEgVTuIEgayfO7OKUlfvaTuW9HjfeeZmIVTzHh6Nvh9zieZ3A45GJoAvQezzrqNEYTVy2pGooLSlePup5vAL/HM3i47FQacEeYXjJGpfJQmcrryIuJqYa/CYB+0ipqGjJDKecyMLXZwyHI0S1XbUR12rPpOEpizwVXCv9vLCTSnbj0KLiC6ov3coqqu8jlKolEDLGDXyDupWQgm3cl+MKqUI8hvLTyTUX84AvqT9ceP546dGvfKqkZGRZW+r8ePHb9y4cf78+SYmJvb29uwA58CBA83NzVlPZ3Nz8379+r3zzjsLFiw4cOBAVFTUtm3bpk6d6uvr6+LiMn78+C1btuTm5rLBEnS9NDtupHN8NhDQz3ZkPy2HvSfqE9DswHlOTs7sWbMdHBzef//9wsLCoqKi4OBgCwuLadOm5efn/4/jWPy0UzPsZUDAgIABgV8FAQMB/avAbjioAYE/LwL6BISOAWlra3vvvfdMTEx27tyZlJTk7+/v5OQUFxfHwvTUjPs/L3aGMzcg8AdCgGEYgiBYTpkkSVbd3NjYmJSUNHz4cDakEoZhDg4OrJuEn5/fkiVLTp06tXXr1uXLl8+cOfPNN9989dVXBw8e3LdvXzc3N9aVwsLCglUQm5mZseLfV199ddCgQS4uSDCLYZixsbGlpaW9vb2zdnFycnJ1dR04cOD48eNnz5r98ccfr1mzZsOGDZs2bdq4ceOqVas++eSThQsXLliwYN68eTNnzpw0adLYsWNHjBjh4+Pj5OTkoF3s7e2tra0tLS1ZM2tWwW1kZGSiXcy0C0us69TNrHcHYk0dHPr27Tt48GB/f//Ro0dPmDBhypQpM2fO/OCDD1auXLl58+adO3fu2bPn0KFDERERMTExiYmJKSkpd+/eLS4urq2t5XK5AoFAKBR2d3cLhUKRSMQ6Y7B6cJaP0PW6rDJLdxExDMMaXLKb6duY6EJHshuwgtnnchw/TnnoDv1sQlcNlNAnoBnQECg4GEPRSAjMyp+1G1BqNYrpB0AQBI/HS01Nzb2bdSbs8Jyp79lao7EKK1sbs16mrmbW432GLHh7xoEV6+ZNfc8dM59q67th0OS9g6Ymzvys+lgCtIrIbomGphXUE5Nl6CI7jyVXbzhVtv0MlHBAQoOcAlwNcoKp55Ueucg7eLl6y5nmuDTAn9RXAwxDaUCOd+eW3113IPXjzUxqMbSIACflUjFyySAZsriucHdkykcbBWdSnmifVdB1v/z26rAH2yJUtVxGSahVT9hnMajlWvkzqGkUDO1hc8Xmk/KTN6u3RCI74w4pgkKjAZGiMSHt/oo9nLALUNKAlJ5ypaijM/bI8dF+g9wtrUy11sRWZia+Pt5r164qrywXy5DqGSdxlmLW8c5PEgxin79dabZBWe0zapgnOmhQKp/EBVWpEOcrEgnz8h4cO3Zk4qS3fHz69e3nZe9ga2xs/Oqrr8bExIBUJb5XdvXjzdVfHIeH7aACoVyOKDOaAakSqjmlW0+kzP+iJTIJCV0BhLhIxUaA7BQ1X85I+zJMlVOBuEJggMRRsDihCGpaK/afK153OH/T12RWGaI1CZKiSK1YG6CiNX/DkZQlW+iyRpAoGvgcDbJvJqFN3H4uRRiZUrMv+v6uk5o6LrIXZ/XdYhk087sT7+SuCctduU+UnC1t5NAaEjUwgfbGK5pvbD5ceCq+u76VVODIZkENO7/Y0NvErJd5L0dHu94Y5o31esvM6cTId3P8Auu9Qxs9glo8glu1K9c9UCuCntXuOqvFfVaj56wGz4BGz4BWj0Cue+B3emeWfX6ag37agkOfXNbz3HiKida34HhWAY0IaL5bULdLUI9TYI9ToKBPYKfzEwK61T20xS2E6xbKcUUEdItbSItHaHW/0OxBIassB/VFwRYxC0uzzxcuQsL8goZH2yNz1h5AdiUdIhArQKoS3iu+vf0IU1QPHFH++YTK5NvQJkRgCpExNyiYivhbBUe/oQvqibKmWxExbUWVaKBCw5AyJfQoq5Mz03dFtF3JQr8+EtmqsOM7oMBlj+pzD0c1HLxQ+MVhxTcZUNHZfO5q0ZmLslYOukJEYsQaFz3OP3henl0O3Th0K6CRL43JkJ+8KYxMqTt9haxuQc1HkOhCl5PQhi6zquhkvKQOJBpoEz+KvloSGY9M4bvEIJJBpyQvIi770Fl41AJCEh42FK09mrJgszynElqF13Ydq0/NAblKQaiUADjQjEQJXPGjsNjuM7fgQWPJwdjyk4nAUyLzHzkhbuCGb94eFBTkN3gQhmHsjYmNRsve3RC2Fhbe3t6hoaERERHp6el1dXXl5eWbNm0aO3asra2tm5tbQEBAQkJCY2OjzoeKnR3I3kN1j9P6I4L6vS5qCMPynyOgw1C3q+6V5F9t8eWXXzo7O48aNaq4uLi5uXn16tXGxsavvfZacnKybntDwoCAAQEDAgYE9BEwEND6aBjSBgQMCPyyCLBPcrrnY/ZgQqEwJCQEw7Avv/wyOzt7/Pjx1tbWhw8fZp+tf9kKGUo3IGBA4FdCQDezVUdr6qS1KpXqxIkTQ4YMsbKy0qeMdeytk3ZhNcKm2sXe3n7QoEGjR48ePHgwa+XBxgBkZWU2NjZsECediHj48OGTJk2aoV2mT58+derUyZMnT5gwYcyYMcOHDx8wYICXl5eTk5O1tbWFhYW5ubmlpaWFhQVrymFmZsbmsKYcNjY2rKTa1tbW2traxsbG29t74MCBI0aMGDdu3IwZM+bOnbtw4cJly5atWbOGtb84ceJETEzM5cuXb926lZmZee/evZycnLy8vKKiorKyMpZWFolELEGvUqlYNvlZ+pgVZ+l61B9P6F6kde/PbMs/m6+fw9pn64hs/cZiSWq2Vrpd/vuriaXF2QJ1+j59l4/v6s9oaVJczamqO30iIigg0NnRycbC0grDrDEj1952/oOGfrp02Zblq9ZODJhvN3jPKzNCrPzG23ovn/PhxW++aePz0LAHAyBQtUXdqll7Ivuf23uuPACuGMU9IwCEShBRgqs5hZsjcj4NaziaqLVvprsIeSel7FSKQK7E75Tc+3xf8c5ISUoetPaAlNB0i5D2WUVAM6/mUNzND9d3nEoGjhQh06OERmHOrshbGw/RZcg3Q65UytWEhCJY9lmD+FYKNKAprK/aGtmxJ65sU0TNkYtQx0cR0hiAHkXF6cT0L8OqTiZAowDEOM7vknXy16/4zMnI1M3YvI+xqb2Zubur84cL/1H4qFhEyAjQkKDRMGilgGFX/QhLSO/7fQ5aeyFpGIa14HiyLcNQupVGXh1PVrlcfu3atdmzZvv5+bEjMSNHjmx9VFN35d6dnaegqAU65Boaemg1O5QAAmXV8UsX5n/eej4ZOgTAUEq5mFQrSbUKcFJ0uzBx2eaOGzkMV6BQKXpIGRLAylUghdav48uW7Ctfdbg75QHdJiCkUgooNTAomlwlN2fdwfTPdqvvV4JUqVApnoSU7FLiN/Kr1h/vPpxUtv88WVyHrD8AFBIxJZKAUCW7nluy5vCdRVvrYq6DXEPjuFpDyPkCUFDkvcr09Ycqo64hgwiCkqlwMS7HcXzT8lXsGJeRMWZjZOKDWfzN3D16VEDBoJDGfqHNXiGtXiFczyCWZea4BbS4z2p2m9nuOqvTZVa7SwDHTeu87B3Y6hHc7hbMujl3uM/Rrs86QX+nkv5h0lmfg9YnoIPbvZ5eOz2DWQJa5Bwkcg7i28/ucArkeoZwX5rX7DWnyTO01XNOqzvioLkuaK3zDMl9OfRz84EumBHWCzO3MTu/PxwetZWu/zpj6Q7Ir4cuBZAMIxDV3M66uH43lDVDp7Qh/X7iweMdJZX3Licf3LrjyL79VXmFFckZSdsPSwtqBFmlD88ndT4owwWoi0M/bRWp4goklU28slpxHQd4YpASaHSHYUCugQ7F4+PxLUcTHm48Kr9wFwpb+AmZuYejgC8FtQbUWufw1p6C/Wd6knOhU4qcxztUkktZNRsjqdjs8rAoWW4FBLN9gQAAIABJREFUSBQKZD5D01IZCHHBncLk7YehThv3UsHwEjPz9p8RFlSg4RwVAx3iipjktAOnoLMHxCqo5lfuPHN78XbmWhHUicvOJGWevkjwELfOV0hIYNRyHDqlFTHXkZ91EUcSm1myPxoaBIwAeVhrhNLsuKSbkbGSdv6VhMT/e3uitbU1ey9zcXGZMWPGRx99dPDgwfT09O7ubpVK1d7eXlBQ8NFHH/Xv39/S0rJv376ffPLJ3bt3u7u7Wb8pXWerS+gGCHW3AN1XusR/3zP/yUtg7zs6ew2aplUqFY7j27Zts7Ky8vf3T09Pb2pq+tckJBsbm3/5dCUlJf2ru3juLexPjqTh9A0IGBD4kyNgIKD/5BeA4fQNCPxPEWDpEpa2YBmNmpqaefPmubq6Ll++PDc3d/z48a6urrt27RIK0cP9c32f/6c1NhzMgIABgV8Gge9oRL3yGYZh5V04jstksosXLr733nuOjmi2u84c08jIyEe7GBkZseyzqakpKzd2cHBgpdAuLi6urq4eHh5eXl4eHh6urq6enp5eXl7e3t5eXl6enp5ubm5OTk62traWlpZsIchQWKuM9vLy8vPzGzx48PDhw0eNGjV27NhJkyZNnz49ICBg7ty5ixYtWrly5caNG7dt27Znz57w8PDjx4+fO3cuISEhNTU1KysrNze3oqKipqamtra2rq6uubmZy+V2dHQIBAKpVCqTyVjfava9VMfnPksukyRJEAQbI09HzetBBSyzoGMc/m1Cx0Q8hfyz+fo5zxb7lOT5FyGgKYrlSVEsvm85U/0EW0Mkp9UGLSSkcpVE1t7CSbl67a9vTxro0dfe0trT09Pc0sLT0/MvA4cunfT+mjfe3/pW0Dy/0eP7DupjYe03cEBQSPCl8zFtD0qrTyRWbj5du/4U53Ai1HSAClA8NBygA2+LuvVwU0TBxuOtZ29ALR+UlFQq7ZQINcCoJBLe/ZKHm4+nL9oqvpkHbT0gJ1BYMwUJQoWsuPZRZMLtxVvbDsVDZQeICGTNwRGWhcXcXXsQGQpLkNJWjMulNCljvtU+M4CcZ+sE7edSxEeuio8lFx2Ighou2rejBySULKMoY21Y3ekrmloOOhZNV5eXzw8K6mNpZYNC4mGuNrZvjh0TdzG2U9LFV4gIYHDQ6DhofQz1OWh9AprdhuWatQT/cwhoHRPNMBRBEDKZrLW1NT4+Pjg42MbGxszMbObkqY9T72tqOgiuENQo+qOc0iBld5eyNeZm8pLN9acS4TEHgJLTSlKtRJJkOdF8M+v66t3cC2lIVKsipIxKpFZoRwgU6qTchvUnKz8JaztwCTolim6hWCFB0QUZGjiCir3nC9Yc7ErOgU4RRaiUalxN4NAlkd/Iq9hwXPF18qMNx6G6A0RKSq5gSILsFgFfKk3Mqtt2Jm/pbsH5VHVDG1KXA5AKBYgUzKPmij3Rj/ZGQ6sIJLhKiRM0RTI0jRMb5n3sjplqp2j0sjbp9ZKxxXQz95iRiIBufmlOm1dou2dos3cQCjPojuIQNrnPbHJ9r81lZqfTzA6n2RwXZMTR+OsR0DoLjh6XoHaHWW3Oga1eIS2+8xpemtvQd06zFyKguS4hbc7BHU7Bde7Bqf3eXdjrpT7IqAjz9XR/ePFKza7TqfO+6E68C00CNKaiJB9n5906HcPPLQWusORa2o7lK9csWBQ8dfq4V/3dnZ1sba0H+fiM9PB9Z6B/4OiJoWMnL54yc8ey1ceOHI2MPnchIf5MxKnwr7Zt/mTl4g8XLF+8dP1nqzZ/uf58zPl7aWmlSanZ+yPrjsVX7ot6fDwesirFN3Kzvz4PrXx0/Ws0aPiBj9TK/GsP4BEX+DLgiETxWdVbzijPpBdviuhJy0e/HY1GRREyuQQYkBZWZX99/vHtHOTIIZA2pmY9PHkRKlo0HV3I27q5q+FCal5EnORhFSgpaODV7Y3OWbCVvpQLjcruy9lVF1IlDVyFWKpCIzSAHORVjCy7ouJEAhS31p+7XrwvinlQCzIK5CTTLU09dzElIlr2mENLlFKhqK62dtiwYebm5tbW1h4eHocOHWpubpZKpXw+v66uLioq6r333rO0tHR0dBw1alRYWFhFRQXytNHGC9X1/7qhR/2+mk2zPfaz+bp9DYmfhoA+vOyNG8dxdpD42LFjgwYN8vLy2rt3b319fXx8/NChQ4cPHx4eHi4Wi9nZXfot8tMqYNjLgIABAQMCfwwEDAT0H6MdDWdhQOD3gcBTBDSfz1+2bJmFhcWMGTNyc3NHjBjh4uKyZs0akUjEno+KDW3/+zg5Qy0NCBgQ+G8RYBhGLpez408sT8oGnX/rrbdYNbSpqam9vb25drG3t9cR0KyjhZWVlc7HmRUpW1tbs5msLYatrW3fvn1HjBgxYcKEd999NyQk5OOPP165cuWWLVvCw8NPnToVGxt7+fJllkouLCysrKys14bmEwqF8m8XiUQiEonEYrFSqSQIQmdSwZLFuvnRiJvQUOy3T5ECPw7TCyqL9V9on6WJn83R316/As/m6+c8W86zOfrb65f84unvkaHAaJ636pOnuiOyltDsgQipXMzvijx6/JvT5/bv2jN6wvheluYYhtkam1lixj59XOdMnHZgzab9G7eOG/W6jY2NjYWln7XTJ3/56+WAlbkLdnKOJsGjNuQJQDLIl7ZdBqnlpZ+GP/h0X+vZa9DCBw2tkkhEXQLkOCzGIfdxxme7ry/eLLv9ECklVQTgKhReT0xAvbDz+JWbf19XvDMSylpAQYGUgE686cz16//YKIi+DXw5kLSGVElVMrkGZwliRIDiNNTxer7J6DwQrzh2vfHABWgRgFSBTlBGwfWirMU7ak4m0DUcoBhSraprrPto0QJjUyNLK3Nz016e7m5r16zicFpI0Mg1OIUCDIIa6GcV0PpeHKwCmtKS+XogUxRQNNC6VZ901k/r/HNYb+4VK1Y4OztjGLZ2wTJhQ5taSVIAKopCwtI2uTI5P23ZjpI9Z6CuA3C1TCmW00oNqYRusfRWYerqPY8v3ERQIy9qRgYaOS6DHpXqam7LV6cb1hxr3hMDj7sQn6gmRYQM8eONPG70zexPdpHX8hHjLBXTtAYUOHTJyIySurXH1QeTa9YdV17PYw1MlFIJiKTQKoSs6sYvjtd8Es49mgjVXNBQUlKh1hDo0Fo5benuc1AvonlihtKGoNDQGkGPsKBi/aTZ/piNJYZZW5n17mXsZdJrioXLmddm5gwObngplO8WInAPbegbVN8PiZE7XQLaXWdxXGdy3GZx3Ga1uAeg1ROFIkQO0W5aIw59Cw73ENaa4/uGG9/pmp+X/x8ooNu9gtngh3y3IL5bUIvjrGbXwMZ+ofV+8+p859W9NLex39wWD0RAdzgF8/sE13gGn3Z7axbm6oJhNhj2ppfv5dXbb/zjS3l8Js3hE0IRdEu594uuHI2szsrl1zce2rHrLy8P9rJ16Ofk/NaYMX+b+o69o52RuYnWwAPzcfOc8pdxvrbOdpiJs619H1dnUztrCxvURdtaWtmYWdj0MrcyNTe3tjK3tXZwd/L29hz98pB3/cdsDl0QvW6nuqa17V7hnaPnJY/qKALZQ6slUqqjq/hcYsm5RGjpQj+95i5xWlH55kjlmfSCjcc7k7KAJ2ZkCnRVAMh6eoR1zdf3HG3LzOe1cQFAmldxc88xTmW1Ui5VdAuBL+n+JiN/y3F43IFCEXaTlWHRKbM+Vxy4AoU86ZXcytgbKKIpjeYuIKt6ZPPCkNWcjK+OwM0yaUxm2b5oaOhCNiBqULcKGm/mJO05JqvnAgUikUgkl/7jnwvMzc3t7ZFtvY2Nza5duwjtEh0d7e/vb2dnZ2trO3vW7MuXL7e2tqrVavYuoxuD1HV9bD+s+6gbVtTP0U+/eG9s2PK5CLBg6m5/LOA4jqtUqu7u7ujoaF9fXwcHh88//1wsFqempo4aNcrNze2zzz4TCATs+IGuOZ5bviHTgIABAQMCfxIEDAT0n6ShDadpQOA3gcBTBPSmTZscHR2nTZtWWFg4d+5cExOTgIAA3bPar1JjVtege5T/VepgOKgBgT8nArrfnVKpRO/1KhXDMFwu99y5cyNGjGA1zjoXDjZhZGTEGmJYWFhYWVnZ2NjY2tq6uLj4+fm9/vrrs2fNXrp06ebNm8PDw8+cOZOYmJiRkZGXl1deXl5fX8/lcvl8PuuYrD9P9t+Cz7pS6HZheWfdXqxjxg8pl3XnqP9GqnunZcvU30ZX7LMJ3dusTg2nX86zaf3t9Ut7Nl8/59lyns3R316/5BdP6xPQz2WfNd/XQeuO+N0haAA1zee0NVbXynrEBK7KLy3eEx4WMjPA1R4p6DEM621h6e3mMfu997dv375qzeq3x7/5ikvfz8e/u9h++J5XZpxftF5UXEv1yECKI/6osJGzO6b4k31NR+LhcSdoNFKFSKmUAEWhyHgP6+4u2VHwWZj0ei6yAlARhFpFqQnEXIvo5iPx9/+5vfqrk0iSKSHVXD7wJXh66eWFm/hRadCEHJlJjVpJKGWEgiWgNQypdTpWym88qP7qBHMuvXLTSeJOKZAMjaMgbPx7Rbc/2dF+/AqSnSpUhFqlBPJw5DEz+95mvc0tepv38+0XERkhU0oJhiQYki/uwmnkb0A+z4Lj+QT090B+IQJaK5F+0gisnUJFRcWkSZOszC1GDh2RfvO2iqIQ+0wBiCko6XiwIuzelwegqAGBRtGERolIcpGYKKm9snSzIDYNmvhIKK1dcI2K7BYxOVUlaw63bT5bvSECHtaj4HIypVqhUMmkIFYKr2SlLNxUd+gCNPcgSxON1qJbTkItr3FvDL4/qXnNcTo5HwQ42SNGOmuSgvYeyK9vD7vYvSW69svjyEdboiBBIyMU6Nu2nqrIxFtr99PZ1dCjphUqivVYEKmU9ysehp9fOXLKaHNnawxzsLEyN8OcMGxSrz5nR76fNzCo2SuE5xLc6RbS0DekoS9yz+h0Ceh0mdXmggjoZo9ZzR4BzR5PPKDb3b4loD2CvjXi+M6C43lE8w/R0P8BAd3mFdzqFcT11JLjnsEcx1mtroGtfUNbfOc19ptb741iDza7h7R5zW1xDmx1CS7yCd7i8pc3MHsXDHPFsHf7Dv46YGHZ/rNQ2kj2iKVikeRx86U9h68eP31yb9iMKVPsrKxcHRxGvzJi/apVRw4fXLdurZO7s0lvM5PeZsaW5v18fMb4j3K1sTczMrZzsHdwd7HqY9evv69XX29HF+c+dvaWxqamJiaYmTFmamTv4dTPF4W5NNdy328NGTFv6oyvFi+7f+EKshEHRiQXA0nlxCam7j3OVLep2rvQIMcjTu3RBOJCdvGmCP7lLOCIQYNU7cjIBUDa2vbN3sP1t7KQObVS1VPbmHskuvFappDPIxgSVJrHSbezNx+Bhy3AEQEfF8Vl3P5gY/PmM5DLgbSKzB0nHt9+AEoSjdkAoB87ASDA7x+M4n+TAdeLq3dHQ3YtdOEglIOY5GYUXFy/t/FmDoiVtIbqEov2HAy3tbczMjJiR0+XLFlSVFSkVCq7u7v37t3r5+e3cOHC/Px8VvLMmt3r7I90nR6bYPth/Uz2V6Ofo59+8is1/PupCOjDzo4r62zEVCoVpaHS0tJGjx7t6Oi4aNGirq6u9PR0Np7NsmXL+Hy+fls8NW3oBe/4P7Xihv0MCBgQMCDw20LAQED/ttrDUBsDAn9gBHTss1wu/9ds9JUrV5qamv71r38tKytbvny5k5NTcHBwfX39r4uAWq1mvadZKwCZTKYL7cISRirtolOj/Lq1NRzdgMAfCQHdaxj7XtfV1ZWcnBwSEuLq6mptbW1mZsaqmDEMMzExYZXOnp6eU6dO/VdnsmvXrhMnTsTFxaWmpmZnZ5eUlDQ0NAgEgu7ubrlcrlYjqZr+G+BPSP8Q1PpF6W/D5uvnPJvW31f3UvrsZj+So1/Ci6d/pEDdVy9e2k/bUncgXUKfhmbVu/o5+mndLt9LsFtQDApgyCDDYVKjrqqoPH0qcsmSJX1f6sfq5TEjzN7VecTY15d9/tmSDxesn7twxV+mzugzYCBm87fXxm9etTb/+u2ezJKivefKNh6vQl6u7aDEKblMjWt9nAEgs6x47aH0xZvbom9AK09bB1pNk91CgaZNIE3MevDpvuItEVRWBXSIkVYaB03h48L9UU2xt5h6HhA0DrQMaDmtkmtwBYNiAyoYHICS3isq3nRUfCjx8aaIrqt3gdut7uCBUKQorbuy9UBZfAp0CCmlsk3Q0U1IuRLBnI8/1LpBYEOHDn7wIEcql+AkrlTjLOmsDbjGsO7P33pAIzKYXfXx/H76O9WzTv5MI2Gw/vo94HUfSFLT1SWMjf3GxMTMytxq2rTpXWIJQ1AgVpN5dbcXb09fslN8rwx4UpCRgGtNfkkKL6jO2xPZGpcKlRwUrQ4A1BQ6mkgBVa2Vu882bT9ft+Msnl4MJKWgVEpCiTTOnVL5jbzYwBUV+6MQbU1SalyJVORyFTTwSveebdkbW7n2KD8iGRqFIFUh5w2ZDHhi+n4V71BC/YaTVVsjoaQZKaMBZEAQUil0yPgJmVl7TsqySqGRD3KS1CCuCUlrK9ofbzuTGLIy8+CpmWPfcDAz7WWC9TI3tsGwtzGbCO9JpW7vdzgFtnmEcLxDW70QKdzhFtjuEtDuEsB1DWh3n831mN3ijqIRtnqgNEsxPwlFqBVBf0s6s4TyD9HNP57/HRn9rAE0kj97BXO8QzneoW1eoZ0eoVKP+VLXOXyX4DbnwDbn4HaXEI5rSLN7SKvvB+Vegc3+iy+8NG26mbszhrljxs4YtmL81MKIOHTNK1QgUXCraiO27d6wYMn/DR/pYWXjYGY+3M/vg9DQD+bOeWfy//Xv7+Pdz6uPq3b4xwSNAFk72Pn7+8/42/QVK1ZEnDqVk5dbVF5aUV31ID/v2o3rcXFxny5bHhgYOHb8uKGvjvB8ycvZ1cmmt5W5sZG1SS8zDHMwNh3k5hk06Z1j23ZV5hd1N3EVzR1FV9KgXQKcbkQHc4WF+2N6ou5UhV3ojM+Cph4gkZ2OWiJHrSyS3T0dVxafQnQIQKGBRrEgNq06OhmZ56g00CXhp+U9OHAWXUsSCuoEoriM3I+2Vn9+GAo58LDxUeTlxhvZijYB+4iIBgvRESU1EZerDn4Dd6uKD8cpMkqhWURxukCq5qY8yNgX2XGnkGzh0woVgauOHj1qZ2fHBiRwdnYOCQkpLy9nuUv29tTW1sYqanWzanTPn7ppMU+N/+lumrrfoCHxyyGgf6djfbfZ9xr2iUWtVnd1dX3wwQcWFhbTpk3Lzs7Ozc19//33vb29Z8+anZ+frxtg/qFBhV+u5oaSDQgYEDAg8NtBwEBA/3bawlATAwJ/ZAR07DPDMCiMz6ZNNjY2/5oIf/fu3U2bNtnb20+fPr2kpORXDzyoe5qnae2s2++3CauPJkmSpaFJkmQ5o+9vZfhkQMCAwH+FAI7j3d3dhw4dGjVqFOvRbG1tbW5ubmFhYWtr+/e///3cuXNhYWHDhw8fP358cXExK2Rm39Wfe2DdW6L+C+R/mn5uyU/x2vrbsOXr5/x4WkdA63qhH9+e/fY/PYsXr9VPK/nF93r27PQJzu/Fv/s+9/lEH/uD+6Mq6H+J47hYLM7MzFy3bt1L/X3NrVFkS8zUxNra+uV+vrMmTNm/bO2hzzdMGPSqu4XtEGevGQNGHgtYemHO6seHL8CjVhCJASiaUiIrCxUJnO7KnZGFK/erbxVqqSsSKBKAVsqloKbJ0vqKHadzV4Y1Rl9HIc6UGhRFrY5//ct9TbG34DEPcJrSUHItAc26MzPAyAgZpVFwi4rz9p6Eq/nNu89T1/OB2w2dQpCqVQWVD4/GViekEh0ClVIhIxRI+wkgl4rfeOsNzASzsDSLPBmB/G3RwlBazw2d7cb/koCWiGUAUFVVM3LkaxiGWfa2Tk1LR9zfY0H29lNJ/9jAjb6lFYxTiPJDZtkyaOxM23y48MB5qOaAXMs+MwzIlNCtgIauqvAY7r64vM/DZNdzQUYp1bhcawwCckKTVpyxcEvxpuPwsEHB7dTKzzWItuaKak8ndZ65XrsninPqKnLuFqtY+wV00Oq2R3vO1m+KrP7qJJ1dCUKZRCWTaEXioCSJO6V31h9ov/UACKAFEsBJSq1G1t4tEsH5tOxFO/D4LMmj2rCd2y3NjSwsjXtZmlhh2GuY2WbbERUD53T7ftjV/0PBS38XuM3luYS2OQdyXGYj9tktsN19drv7bK0LByKgW38bBLTAKajbbjbP6j2e1XsC2wCBA/J9bnYNrvGde79/4K3BgZtd/+KHGTsb9xpoZTfYzObMyo3iwkfI94ZQ8Wrr1/5z8avePt5Wtk5Gpi6mFt52fQa4e9qYmVmZmb4ybMiCBf/YuHnjhws+dHBysHN2eHvK5HWbNiZcTnzcUC8UiZQEahR2lAgnCblSKZXLWD/xmpqalJSUk6dPbti0fuas914b+WofWxtrU9PevXo5WFj0wjAnC6vRg4ev+mhRSmy8pKkNXSoqAIU6+WBk67nUkp3nmy9kMLWdyMad0uqUJTjDFRTEJBWcvgQ8qVrQw7TwGg9d5J24igKHdiugU8K7jdhnVUE1iHDoUlIpD4s/Cy9euAu+uQ/NivJzSQ0p2SRHwKjQmAQA0BIl9BCC67lFWyM1VwpSNh2qv3YPUeHtYhASZFHDrU2HH51JgtZuwClCrszOzn7Ju6/WOtzM3Nw8ODi4rq5OpVKxpCQLhVKpZKnJFySgn+ro2EIMf385BPTvbk+NBLC3b0pDcbnc+fPnW1tbv/766zk5ORwOZ/78+aampmPHjq2oqNAZcz0VSoEt+ZeruaFkAwIGBAwI/HYQMBDQv522MNTEgMAfFgEd+0xpUASnY8eOeXl5DRo0KD09fffu3SYmJhMmTEhLS2OfzH4LKBAEUVtbu3nz5uXLl69bty48PDwmJiY7O7umpobH40kkEt07gy7xW6i2oQ4GBH5HCDz3jUsoFOI4fvv27blz5zo5ORkbG7MENBuB8N133713757uHHEcZ+ci6A9c0TTN2l/otGP6xK7+C+R/mtYd96mEfjn6Xz33BPU3eCr9Q+U8tdlzP+rv+yLp5xbyVOaLlPPfbPPU4RCn88z67DY/lsMAMEjn/uw27IBiB493Py93z769r/mPtDO1cOxl6dnb3grD+rt6zpsdFLZj91fLVs71f+uToW/vHzVzz6j3D4QuyU+6zmtrlRAiESkCQgGtXbVHYq8v+0qZloe8ILRMHKmU4bjWprmOX7TtZMaynW1nryNbYTWAWAGdooJDUfl7TyP2WU4DTqnlOLpKGVpr/UyqNTioFMTjxvsHTopjb/JOXm6JSYaaJlAzIFNDVs2D5bseRyYhYoukaRxnSALkOAgJaV7FxFdGWpqYONvaPszLJdUqQCH5aPavPu+sS+vkz0/5O+srnX8o/f3GeRbjJzmUBgT8no2btmHGJubW1nOC52g6RKUnElM+39cYdwtZ66oohqJBTYJADDWCe5uPpe85xcstB/xb9hlXKTv40NLFP3alaW1E/boI8vIDJEqVKghcCUBTIom0sKpk/dHCz8OhuBmkGhBKgNQAoUFM4vmbrfvj5JfuVUbEQ4sQNRPyk1aAXKluaMvfFtG4O7pq11lR8n0QE4xMoVApUPPJlERFY97+M4IU5LHAqFSMigRcDQo1tIoUF7PvLt7VFpMKbUJGJqt4XPZ/0962deptZI6ZYdhLGBZi5pk8IrhuxEJB3/niPsHiPqH8PsEcl8Bmt9lcd63Rs0dAh0cAV0s9PyGgPQPaPFHmExG0h07ajFTMXE9klKG/tmm3f87f73YMavP4NwporQgahUlkV45bUJvjbL7le90W7wltArrtgwUOiIAu8JyVMTQkvO+Ed7A+fqa93Sws+2KmQa+NbyssBbmS6OBlJSdPHz/BzaK3u6W1u6W1s7mVk4WV/4CXQ99//6svvog5e6byUblMLiEIvKqqIjx8f8Ll+Nq6OvYSITVq1gEGPfIBQ2rUbM6Tb0mSnbBCASWSihob60tLi++kp0WdO/PZimV/nTLZ093Nw83F3NSst4Vlfx/foIDAtNTbwo6urmZu+Y3Mh8ficw/G4lVckJE0sskASoZDm7Az6e79XSepR83IQFyE11/PzNsTCTU8NEGhWyFJySsMOysurkYjIp0SRdrD5q1nH368i0rKhTqRMDqt5OtYdStin9GAhJoCCQ5yRp1fV7T3HC/iev62Uw9Ox9MCCSlTIv66sDX/i8P5e89qyptBQYNcVVFe7uXl5WBrZ9YLha+cNm1aQ0OD7v7FMAwbcpZ9BtaF6X42oU96Preje/IjNPz7ZRDQv9/pt4V+mtJQYrF4y5Yt3t7ednZ2ycnJEonkyy+/dHZ2HjNmTEZGhs6eS38vtuRfptaGUg0IGBAwIPDbQsBAQP+22sNQGwMCfzwE2Kdk3ZP0wYMHnZ2dR44cmZmZGR0d7ejo+Oabb+bn5+M4/uStQ6N9afj1gBCLxTU1NWvXrvX29vby8urfv7+rq6unp6ePj8/gwYMnT568aNGiY8eOZWRktLe3syqGF6ys/sPrC+5i2MyAwB8VAXY+wVNnx+VyDx06NHr0aGtrazs7OzMzMwzD7LTLJ598UlhYyBpDs3HPdEFKdQS0zhtH/7f2c6Wfqqruo375ukydMlo/58fTP1TOj+/Ffqu/74ukf4kyX+S4+ts8W4f/loDWlsiOd+re7dlbD3sbEsuk3T1CHo9XV11zeMuuya+87tHL2rO3vWUvMwcHh8EvDwqYPG3XRyu+fHPm2dnL/uk7xsfc5pWXB8yfFxJx/FBNVSnF4z0+m3Bt+VfdKVnQJWMkEhJ5OEsYXIHI0/qO8t1nkuevRexzvQBxzTISmnm0KO41AAAgAElEQVT55xNyD0fRJQ2IilJRtERJyXBEbmpohtJo1dNUZ0FxbvjJntibtbtPPz4cA3VcEMmhXdR1+U7BJ7vad0dDUSPScsqQNzpQDHQpoZBTHxa76M2prmZWLg4OZ8+dxklcyz6Djm5+NvFLE9BqNWL/5XLVpYQrNk6Oxr3Mpk74v7KrdxI+310beQ0ESkTKa2haQ5E9YlVNS9HeczlfHZMV14GU1cMyFKGiRBJlbUvN2SudO2JavohoO5YEHUpkzUGSjBIHOSEtrCo6FJ21cj9kVoISkJJaoXXfFuKdCXeatpxp2XY+b9cpuqoVZNpiZUrEUAtlucdjH22PzF99oP1CGrL5VuBaRhuQoUcTP/vQ2fLYZOCJCbmMBoYiSMQ+Cwg6vTwpePWjneeglgtKpVQhxBnFrcyUgUN8Lc2NzDDMBcPe6O28acCE68MCy/tMrzd+R+AQ2tEnsNk1sMldR0AH/TAB/YSD1rfg0Kee2fRzqGeWkv5PCWiPkE6PUIF7aJfHHH6/+TyvOUKnYJFdYI9toNAeKaCrvYKvef3t7IiZQfa+nhhmjmHWGDbE1vFO1Dcgk/Gam07s3vN6/wFultYYhvUxtxgz7JXPFy85dfjrB5mZdRUVgvY2FApSQ1JqAscVcoVUKhVrR0eAVT3T7CVA0xq9AXxk4U5RugwUvpUm1TRJqlUEwTYTjeOKZk5zXkFu9IWYT9euDv77PBdvT3Nba28/v79O+9v1xCRxHUdV2qypaqeFClxJaEMEAoiVVUnpaevDIbsKxCR0yTozC8tirtJljcBXgEyjKKotDDvLPKiGLhn6zRbUFa4/cm/BFsHhRKgVCpLuFe48BaUtIEfMOK2hgKSRtrqWVxYWwzmaVLT9dEN0CkgpZPfBgLKyuXhTRMbCbeKbBSClSb6os5kzZcoUy95WvYyNexkbjx09Jicnhw20y/aBlIYiCALHkUu17lH5uQm2W/vxXvTZftWQ83MhoI+87hbzVEImQ7NAOBxOWFiYr6+vn5/fkSNH+Hz+3r173dzcfH19jxw5wsYu1t+RLfnnqqehHAMCBgQMCPyWETAQ0L/l1jHUzYDAHwcBkiQZhjl79qyDg4OPj09ycvKRI0ccHBxeffXV4uJiuVyue/zSvYH8LCf/bGksE6F7jlSr1QzDtLe3X79+PSwsbPXq1bNnzX7ttdcsLS0dHBwSEhIyMjKSk5OjoqLWrVs3c+bMoUOHmpiY2NnZDRo0aMqUKcuWLbt69SqPx9qAoirrU9I6DSabqTvoU4mf5UwNhRgQ+H0hwL51EwRBaShW/5WZmRkSEuLs7Ozl5cVOVbawsMAwbMCAAfHx8Twej9JQOtL593Wyhtr+7xHQkTVsAlFaFFoRQaCmqG5pxZ0H5/cdXhw838UB2dTaWFj2sbC2wLAhrt6bP1h68etTn3y2zL2/t5uN9RBbx7mvjTvz2bpL63eK8soQGapCXDBFkSqVEvHCHbKS/edvLdlaExYDVVwQ4tCjBLGGG33zwe5T8qpGkCkpgtQQJEWQlEIFDJrCr+kRg5pmHrc+PBrNO5csPn8jZ104PKgEiRo65ZCUn/OPr/JW7YdHHORBzICGREbGFE8IjwXSXRfLF+y6sXr3O8NGYhj2tzmz80oKZUrkUi1TStU0+Sz7rGE0/ykB/UOqZ3ao4HttqpWfq3ANQwOhokrLKr19BmAY9nq/Ydf2ny44Hk8UN4FcpaG1BipqBjqkZZGXb64P0xQ+BgrUCiQhl8lkKpmc7hDVR117vCdKeeRac/gFaOYDqUGRGLULU8N5sOHr6//8SnGvFLqVT9hnCQ7tYmViTvmqw4LtMeVfHoXaDiAoSXcXEowTNHSIi88k3Nt6tGDj0YIdJ6GBB0jprdEwWh9qBVX2dWzt6SRQkhSFQjiqaZJWqKBDCjdK0z/cfGd1uDK3GhGohLxbLpQQEgD1N+dP97OzN8IwKwxzMzEdY+m0b9g7WX6B5X3e5b30UYtzYIN7IH/gP5AZtHtIp2dwp2dwm8d3oubveUB7oIiFzyOgQ7ieT9TQ336r2+ypxHfaZ1YHrZM5P5VAAQ/7INsNrtm0DqfALp8Punw+aHMO7LR8n2P5bq1rQP7wvx/2mzzZzNXJCDk3mxuhE9z66WegUHI5TStXrfC0sXEwMna3d5j93vvHDh0uKSjktbUrxFI0NIIGIGiGoRiG0jLMaLSB/UhpQ1yyVw6b1s/Rv6K+fUD6XiE0rVHTpIoi5BpcolaK1LhIjcffuj7/k49tPN2snZ19ffy+WPpZW0EVuioISqkiZSoCcA0vtzxtfyRRUoeGbRhoz3r44EQskkKLlNApgtza2xsOdNzJR84wAiWUteZ9Hla25uuqg7HQIoXMiuzNR9AlisJ5ogWJ95UkcIX1sandp1I4hxNbLtxGQnscgCeD+u609Qdj5q+GrGpolwEBlEL1zjvvWPZGtj9WVlbjx4x9mF+AZNQArOQC4aVd2IdkXWelI6DZnGf/fosS+v+kcoZ//0ME9PF/Kq1WqwmCUCqV6enpw4YNc3R0XLBgAY/Hi4+PNzMzs7Gx2bp1K/uywLa+bvf/YfUNhzIgYEDAgMCvhoCBgP7VoDcc2IDAnwcBgiBIkszIyPD29u7fv39sbGxUVJSXl9eAAQOuXbvGqhfZJ7CfERP2eZ3VIcrlclZdolKp2traqquri4uLExMTd+/e/eGHH06YMGHgwIFDhw718fExMjLCMMzJyWn48OEbN26USFhXTVQvsVjM5XIrKyvT0tL27ds3YcIEOzs7a2vrvn37vv7665s3b87WLqxxx+3bt4VCIUGgtxYcx6VSKRuxRPcWoXviNLw8/IyNbijqd4SAbtIxADQ2NkZERAwfPtzS0tLIyIi1ezYzM/vXDNZXX301OTlZKkXMmu6N/Xd0moaq/loI6PpYttfVEdBPOFCSJrslIMFFTW13r6d+sXTFQFev3kamZr1MzU3NPBydJ0+eHLx8waaDu79avmLWsNf+r4/Xl1NnLZo4LWpf+ONHZV3dnU/Oi6SgXdxyJjnz091Z6w5CdSf0qEBKQBO/4ULq3XUH8HvloEQ6XAVFKigS15DovsCqMwmAxs7WmBtNRy8SCXdrD5yHglrokEFtuya1sHTBdu76k5BdAXI1ovYAaA2JzDdaetpOXMmf81X18gP0vYrYsK+RpbWN6bhJb6Zn3pZqnaBJivhVCGhCRbEEdCdf6DdomK2ZzVjXlzO+jpOXNoGYIBmafBLyj34Uefn66r2tVzJBIAWaxjUosIKiSwRSUnC7sHznaenJlLq90cyDaloqI4FCUmUFDm09+QfPX/9gXf3hi8CTAEGChkKx4OS0KqOk9IuvxWEJFV8eZTLKQSChCBVJEaAioEPMS86qPBxXdTC2/EgcVdoAQinQlIoi1ASu4vKKYq60xtyEonogSSUgAhpIEmhg8uvzlu6t/OI4FLciWpOh5RqFgpQjX2GVXNrUdGbjdh9TKwtjrI9t7z4YNs7I/sSgabd8Z9a9sqjGe06ta0CTGwpL+JsioLnuKOQg3342z2Zmp2Mg3yO03TO0zSOk3XNutUdgivf0E4Omzbbz8cJMra0tMDQCiIXMmN7yuEbAb1+/Zb2tQ28nC4vZk9+5kpBYXl4ulUqVSiV6jNGyoNof3XfUM8tB/1wEtIbRkKAhQIOjlcaBIQBaxV1JGbeDPvrQyd3dwsT8vTcmnz94oqO1XSqWMVJC2SK4czKu7U4h8gEnoTOnOPVQJD+7GGQa6JZCMz9vT2T9uWQQSBmuAMpaG/fHPly8u3T1YSjjQlF9fvhZ2d0SmsNH14OWKUaG4O3inozigp2nq3ZFlew5p67iaH/yDNR2PT5w8e7KsMaYVKa6DT00cnn//Oc/jSzMMFMTrJfx8OHDb9++zbLP7KOpvkJC11+xEe0MBPSvdeN4wePqt9dz0+wzf1ZW1vjx4x0cHIKDg0tKSm7dujV06FAXF5dly5bxeDx21EG3+wse2rCZAQEDAgYEftcIGAjo33XzGSpvQOD3gQDDMBkZGUOGDPHz87t06VJiYqKPj0///v0jIyNZAfJPmK7+b89cN8GfJMmOjo7c3Ny4uLiNGzcGBQWNGjXK29vb2dnZw8Nj4MCB48aNmz9//tq1a3fv3v3mm29OnDjx4MGD+fn5VVVVjY2NTU1NDQ0N1dXVlZWVFRUVpaWl5eXlbDwrR0dHExMkETIyMrK1tfXQLg4ODiYmJiNHjrx9+7ZEIiFJUqld2IiFBgL63zacYYM/PALsqzV7mpSGysrKCg4OdnR0NDU1NTMzs7a2trCwsNMuH3/8cU1NDTuQo1ar5XL5Hx4cwwn+XAjo3ur1TTlY81kCkAUzGh0US1GsOTGJV7WGr9zw0buBk8aMd+3jZGtuiRkbGbnauA/xXRgYuO2jxQcWf/bp9NnDHVz6WtuMfmX4vj077t3LFDa0QKMQMh5lfrr73vqDZHEd4rk6RdCj4iVmpm840HAlA9RIKM2X9SgoUk6RIiAljNbsWEqAkKw/Gd+6PwaSC7PW79fkPwK+CIQK9Y38/OV7ChfvgDsVgNPI4gMtDJAUNAt7Tlwr+OeO2q2nIacauhUFd+/Z9bHFTDEru94TJ799I/W6HJfpK6BZEpDlo39eBbS+ahXxjwyocQoYwAmqQyCcOOkdW8wydNhbsrw6kJEEoEBxaAypU9p5NTtny9GW2JvQyKNEEhkQEiCRoTYOkN9YtPZoe9jF8p2nRbcLQUowJEEDTeBKeQMnN+xMwoJ1ZYdioFMBXWKNSiuLluFk1qPKnWcgIbd40/Hmi7dAQhBSqZJAlDHwxeIbufX7YrqPXCnffQYvq0dYajRqAlfjSoLXVRx3Nfvr83QNBxn7kkgBjfypFSSUcos3RdxbuhtSy6BHDQqSdcfWqsIZkEiBy7uz6+hnk2a85OpiammCzKB7WY7CrL7ye/P60OCiAfNqvUJaXQPb3YI7PUJ1CuhWj0B2/R8roFlZNNczpMUjuMUjmOMdyus7j98nkGczU2Azk+MSWPBSYOpr87b4TRhtZOdj3tsMw/r0tuyFYf79/Qqz7uIMfjnjet+B/Vxc+8yZ+X7Rgwe8LoFEKdcFC9X7lSHVs/76cxHQrGKdpaFJhtYAIyVwBQoBClyB4Gxc3Lhxb9gaWQzz7B86Y3bO1TRhbnXS7hMl6Vm0UAYSgqpsKTh9qfbaHbpHAhIFVHHyD0dVXUwBjhDNV6hsrdh88vEXxx5vOQ3plVDOKzoU/SjpFoikajT6QYqBUqoJ6JSrU0vyVh0s3xz58GAMXtIAYiXgDFTyJWfSsj/Z03jsMjR1gwinRfKNa9eZmJthRpi1o73/669dvXpVpfxWyM8wT4Ww1u+v/tP0z9VnGsp5cQRepI3Y2V35+fkBAQF2dnbTp0/PysrKzs5mPy5YsKC+HnVHujAVL350w5YGBAwIGBD4/SJgIKB/v21nqLkBgd8NAqWlpf7+/vb29nFxcfn5+QMHDnR0dIyLi9NNOWTP5GfXAkskkhs3bixdunTChAkDBgywtrY2MzNzdnb28/MbPXr09OnTg4OD58+fHxgYOHPmzNDQ0Pfee2/w4ME+Pj7jxo2bOHHim2+++a/oiGO0y8iRI/39/ceMGePv7z906NBhw4bZ2dkhaZB2MTc3t7KysrCwMNcupqamJiYmw4YNmzt3bnh4OBv52kBA/26uV0NFf2EEdNrn1tbW06dP+/v729nZ2djYWFlZsSEHra2tTU1NT506pVQqWc8NtVrNhu7Rl4z9wtU0FP/7RkCfINCN/LHXj4IipTTirZ7cdLpx3v2y5MOn6+4XNZZXXUu4PHHcm05OTpidOWaE9XNwcMKwycNfDVu7/sy+sOXz/z7Q29MYw97wH3n08/V1e6OrvziasXQHnV2JZvFLVCBQdqXmfrNgbff1+9AhpHEc16iUQOK0WkIRQi0BLerqBjFeE3Pt/vqDkPzw0fojHRdSoE0IEpJ74+7dtftTP/6KvHofeAog1SKR4ElLSEj6TnnN2mP1G05Cfj3IKcBVHV2dK1Z9iplgvi/3xzDs5SEvZ9zNoIFWawh9EvAXJaBpFE0OrYRKS0Cr6Q6BcMzoN3wdvRJ2HAOOjKYQt0xq1CBSdl7NvrVyLz8hEyQ0iBW4QiaicTmtApwm7ldXrI+A6JyyTRGKtIcgVIBSpZJJkcy5R1F3JSN+yVcFe09DEx8kCjlfQCuUtFiqrGzM3nBYfv7244NxiH3ulgFBKEitX7ZA3H49q35fjOJEyr1F26G4BdS0jFAQBE7JFdAl4WY/vLk/gp9bily8GRppzEkSeSwIycd7Y1PmrW8/l4rGGJQ0MIxaQ0ikQtQWuBp4PY+iEvIOnBbnly9f8jFmhrm59DHFsN4Y9gpmttjy5avDAytHLmx4+e/NfUPbvELbvZAFB9c9kOv+hIDmej7x0OjwCOp0f7JqjTiQ7UarV5B2DWn1QmmuJ/Lo6HRHf3VmHfo+0frhB3UWHJ0eoTyvOawFh46AbnILbPYKaev/d8HLC1pdA2t7T6uymVbkE3zr7YXLvEcNwyzsMKR7tuhl5Grd28/J6XZ8PAB0y4XjJr+BYdhAX5/SwkKCQESqBoAAWkWp1RSlo5z1rzo2zRLQSNiLBgRQlMyfZsHBlvZE2q/9oMBxqVymVJHamkD2/QeTxr9thmGIhnb3WTV9XmHcDUaiVLZ3QbOg/FxSXWIaKBhkUlPXcj/8TEd8BnRK0MBIZWvFodiqL481bYyElGKoErSevFJ97grIVWKZWKAQKYAS0iq1RA5VguYdMbx98TlfHMKL6oGPvMWBj6svPcj6x9aqPdFQ0go9ONCQEPuNsbGxSW8LzMLUb+jg23cz0ZVDM7QGBeFk/dn0H3r1+6v/NP377ql/n7V/wTYiSVKlUnV0dCxdutTOzs7Pzy8jI4PD4cycOdPJyWnmzJk6B0L9i+G7e9PvExxDrQ0IGBAwIPAjCBgI6B8Bx/CVAQEDAj8dAYIgWA1yeXn5+PHjvb29Dxw4kJ+fP2jQIFdX1/DwcNYTQ+eD9tOPpLcnqY2f3tHRkZmZuXLlyvHjx/v6+rJklqmpqZF2MdMulpaWjo6Obm5unp6eXl5e/fr169+//4ABAwYOHDh48OAh2mXo0KEjR44cMWLEqFGjXn/99ddee2306NHjx4+fOHHi22+/PWHChMmTJ0+dOnX69OkzZ86cP3/+okWLgoOD33rrrWHDhjk5OZmamtrY2Dg6Onp4eLz++usbN26Mj48vKyuTy+UsMqxiSKcB1zsPQ9KAwB8WAZZKFgqFN27cmDdvno+Pj4V2sba2Zn+SLi4ub7311r179/QhYGezsj8Z/XxD2oDAv0WAZQpYDhpZuLIuxIBihslIFY7j3Jr6lOhLOZdvEB3dyJ1ZoRJw25MSEqfOnO7i5dbb2MQcw6yMsIHenkHTpodv3X5w375Vi5a81X/IWybOh4b8Ler10Dsrw+BRG3QR0NCtvl6Usnjbw4MxIMBByY6bkGqKIhhSQamEGgVO4oBrGm7cTd/7/+xdB1wUV/4fQGBZulRBNGKJSow1xpx3xpjES2IsSWzRGM9oTCy5aExi7IqKGAVRmgiiAioiWBEpgohU6b3DwlJ2l+1lyu7s/v73dnSPtPubS9Pczmc+y2N25s1735k3++b7vu/7C6ezKluDL/aevgFVHVDb3RN1rWhP8LXt/l1p96FHgkLzqQia1EfSE8rgXk3RthOpG/aLruaAQAkUCmKoAM2VzJRnJ48b+qz32g2fuLg5T5g8ob6hllAp1XqW8BH9hxx1+yugGcr4h5/9dc1M+v/9VAOKBahnfNHVIHS6w0FBbEv2EOdB/KZOBLgWSJkKJCSZV5eycX/PuRQ98achlVLEyYEalAQ0C9oDL6qDk/mHLyJxNFcIGi2lVCLnjS4x3KutOBBZHX4J2hEdL8FloNNBr1hX3lJ1PI5/6kbnyat1MddV9e1qpVJO6jXjSlKUnFe966TIP77myxPE1Tzgikk1IWeixZE6cVpR1emkttxiQirVAI0jnluL8wTQJuRGXi/acLg37Co0diNmXasFLa1VqgAnQSYHLq/1QnLWwWC8ogEAGlrrX3vnDZbVACsMG4hhwzCzCZjVm5jTLufJt59f2vLCWs7wD5rd3uW4vNvluqjbbXHnoMUcj8WMDrpz0MIu94U89yUCN7Ty3BH73Db4+2unJ/q2z3WJwG0Rzx1x0J2eiKFu81rUOgR9MnQ28ncetIRhnHs8lvI8lvI93+/xWMr1eJ/r8X6nx/vcwct6PNDa5bms1ev9xtErc0ctSZu8/Ojo12dgTl6YmQ2G2WLI+9kOw14aNTYx8gxyj+EL4qNOszDM0cIy8Xy8DAVpBKVOrdSpca0a11AETZNaHalFHusPmWjdo7+0BrQ0aGmmGTKttT9591Pt9zv7aHXIWfq7C615mCdDbXcLBQCQl5P/8kt/Y5tbDWTbe9q5LP37/MqMHGjlN0Vdrw27rKnngpiEFkFheHx5eAK0iNEoSKesLzq15pvw0q0hRHwO1PYJkwsKg89DQzfgaiWOq4CmARD73CpoPXy+aWvE3c/8FRllaARIjEOHTH2jOGfl3rKvgjXFzSAhpJ29SbEXB7u5oxgGA0xH+IyJv5ooUaLYdKBDLtJaDY0cgfQBSH60+t+t6I//96MHGjc+sQjw+fxt27YxcQivXr3a0tKyceNGCwuLqVOnpqWlMf0iwxwv5pI/sXUxFsyIgBEBIwK/BAEjAf1L0DMea0TAiMBPIsDoFouLi2fNmvWvkGJ79+4tKCiYNWuWjY2Nr69vf2/lX1HSKBQK4+PjV65c6enpyfDOjELZzMwMSVHMzLy9vWfNmrVw4cJVq1Zt27btyJEjYWFh0dHRCQkJycnJmZmZd+/ezcnJycvLKyoqKi0tra+vr62tbW1t7ejo4HA4nZ2dXC6Xz+fzeLyuri4ejycUCiUSiVi/KBQKmUzW3d1dVlZ28cLFNWvWjBs3js1mm5mZMRJpNps9bdq0TZs2BQUF1dfXM31NWkP/JIjGL4wI/OkQ0Gq13d3dgYGBkydPdnJysrCwcHBwYOzUWSyWmZnZp59+2tLS8qert7FCfxgCzMs8Q0AjtlPPhyJGSe/LrAGdQirraGjua+3UihWIbXy0NLU2HTy4f/P69ZPHjTMzwaytzJ1sbLxcXV98YcqOL744uc133xvvh/516dZhf53jOvqfr793Pzi24dTV1DV7U9cdUJe3UjwxqUa2G2hklCBJNUHruUzASV5BRfHpBKjurI++Wn78HORUQ2VH1+lrtTvDrv7j6/ort0GhAhxRzzRJ6AgCFLimqq1oT+jdz/wE13K0TVwgNDqKJEEjVavkalVgUIC9g+3cuXNWr15lw2Z98vFqoYAnFPC0Gur3IaCVegKawCmFVJF0/cbQ4SMcbRzGPjNKyhMBrkEGHQKVpqjp2ucHG8MSoIEHpE5DETJCiquVWplU18ytCohRRt5Whd9qDrygq+tAbtc6HWi0IFJpcmvyvzia92UAVLQDocGBRvHdxDJo7KkIiu0IuVwfEHv/UIS8sgkRxABKqQSBfLe4ZFeoNjKtZXuE/GwacMQgxwkdpQYt4BRd3V5w9HTvjRwQSmk9+4xU6rgS+mTCS5k3V27rOJEAJW2o8EgpT6NghgoccBp4ooabGSl7A1W5FWiAQSFVKSSdLY1zp013x0wGYaYeehrXC8P+ijn8g+19cugrt4a8VT58cdPQJRyPxV3uP0JA97gj6pnnvqTnxwhozmAUYLDPdYnYeYnIdZHADUmhuR7fIaAfqqQHoUwYqrrPdYnIheGsl/S6Lu1xf7970Ps9g5f3PrOyy3tl8zPLiocvufHsOyGj33jb1G28qY0LZj4AwywxzG0AyxbD/uI9OjUhiRJJgKCaC0vmTHjR08Tyb8+ObyqrUqvVmn4ENEGr9ezzjxDQOlqj+80IaINxAUNAE7RaByBTKBMTr7DZNi4ubtOn/83Jyn7J32Zf9QvJP3pWV9AEPTLgyWsv3i6KuARNvWiIqEPacT6t7VBc2ZYTbYGXoKy791JW2oEwsrINZJRORaIwucj9Rgtd0tLA2NYDMfkbjwiTcqCJB3IKhITySn7+xiP5G4/QqeUgJUGjzbqVOtzN08oUucl7DR0Sde6sRCl/GChQz6QzZDpDoD962Hzn749Tzt/d+p0DjP88DQjI5fLw8PBJkyZNnjz5xIkT5eXl27ZtY7PZY8eOjYmJYd4FCIIwxrp4Gi6msYxGBIwI/PcIGAno/x4745FGBIwI/GcE2traJkyY4ODgsGPHDoFAMH36dDMzs40bN6IevT46H3P49+ad/ec8f/RbHMdpDd3a2rpgwQK2fjF9tGAYZmNjM23atMDAwOTk5Orq6paWFj6fL5fLGY22oQyMuLJ/D99wLoa5oDW0wVeaiYfWnztm9AvMDgylLpVK6+vrd+/ePXnyZEZ8zRhGm5ub29nZjRo1as2aNSkpKQKBAL3hGGloA9zGxJ8UAYqiFApFZmbm8uXLPT09XVxczMzMbGxsRo0aZWVlhWGYo6NjQkKCUIgmuX/PH/NPComxWr8TAsyDXc8+6wlo/QcNwDhBo0JodKDRUXKVWoGmz6Ogf0goreP39iilkoa6mmMnAv8yfdoADHO0tXFwtHOytxvjPOit0ROjNu9KOnTi3Vf+PsjE6jXboX4zFkfM+7Tveh6IVRJc0QdUH1CkmqJJilApgdYCXyJ+UHN+z7eCzAf43Yq0vcehlgslLTlfH6naHVa2M7jiRAzd1oXmBpEE4q3VBOCErrXnzsHQS6u2Kq/nAV8JhAaQjpLSaii1UgkqqjQ1c+7LszwcB65fvXr2yy/bs9mnT55E3rUK2W9NQKPWqpeTqwFwBVFaUPzKq69hGGY1gLVy0XJkjytGbtdQyb3zzbHCQ6eRpsyu1YUAACAASURBVJjUgZbWUCohLlbgyJD3fsiZksOne2NuZ+w5DvVcUJIocqMGQK7R5Ncmbz54+R9bqYxSFDtOiYh5ZNPMFef6n2oNT+qKTk7dHQQNXFoo0alwkOMgJTXFjeVHzpJnMnqPxFf5n4H6HpAT6ChkoIE0sKk7A9sSM4AvB5IGteah+YZIxk25n7f5SNn2ELy0ETkF6/XyOh2NtNgKEuQavKTu9rchbWn30Le4CjRqkCrp8sZrm/atGTV1JMbyMmO5mQ5wwkztMcwNw0Zj2CbPibHPvnXV6ZWaIYvaBi1qH7Sow31RlzvSPjOmHFwPJHz+3mpw1ejW08oiF0RAi10W9bl+RwTNSKEZHTTXY4nAZbHcfpHSZqHSZqHC+l0Z+x2RzTsShyWSgUtFTks5zguLnedmec5Ne/a9xElLVgwY8hxmNpRlbWGCsawsMAxjY5gXZrbihZmFl29QakKukgnqm+MOBkwdOHgQhv3j1bkowKYOaA1N0Ej+TGppUktrtGikgNE8M/2lh+YbvxIB3b9jZkj3J6Af3oQa5GwhlyvXrv3UxcVt3779KxctH2nt/PHsBXQ7H91OXdLyy7czoi6qu/pATYOMUOfU3tl8pORAVPb2E3C/Ce43F+wMFd/IBzEBGh0tx9HtQQOIiZ6LmflbT2RuOcpLuAtcZBwPPLkwvTh/U0D2Jwe5V7JBqAI1XVxc/OqL0zEMG4BhQ9w8Lp4/T6opnb6NoAcKrX246j2gf6fHn/E0TwACKhWaIoLjeFZWlpeXF5vN/vzzz7lc7qlTp1gs1uDBg+Pj45m2I5VKCYL4FaU5T0DtjUUwImBEwIjAvxEwEtD/xsKYMiJgROBXRKCxsZGhgzdt2vQvEfGKFStMTU3XrVsnFAqZ4X25XE7pA4v/8pPKZLKbN2++8sorXl5epqamjOp52LBhCxYs8PPzy83NFQgEBpr7IROhPysTbdzwVf+S9N/te9uZf5kZlP37iFot8vVjXoq0Wi1j/SYUCmtqagIDA+fNm+fs7GxhYWFpaenq6urm5mZvbz9mzJhFixbFxcWVlZX9kIb+3vtV/2IY00YEnjoEuFzu0aNHJ02axGKxGM/0MWPGeHt7Mw129uzZmZnIJZN5LBgJ6Kfu+j7JBTaQVoiD1ofL+5HSIpYIzfRHXz3UK+oYCadMJhGLhVVVFSEnjr/+6iw3dxdL8wHO1jbWmIn3II81K1ceOux/dLfv/rdWHH51+RznUYtffGXvjl33yov5egIa1yACWovjICdUBTWFx891JecocyofHI+R3S7SFNXlfRvRdOB0m9+Z9qgr0M7X8PvUpBLXIPYZ+W/IiPqz165u3NsSmwxtAiBoIElEmOq0QJAgVtZcupUfefHuxaQxXkOn+PgsfucdFxenGa/MqK6rRkQ2MhBA/hu/kQVHfyTvpmW++dobluYstrnVSM9nYoIjkc68j4C63vt+p+/vCoXyTkZTjFq6WkWpVRqR6EHM5dKQGM3dyuyjkS0ZuYheBwAViWw6arvvbD16YdXX3YmZwFMi82C5khBLQKzkJmQ0BF3QppflBZ5RPKhF8Rv1WmUUbq6gPn93iOJchjQqpfLQaajjAg0IMdCibFt7K0P1Lh9dYkRKEhpkAK2iQEZBRXvuPiQzp7MqNSIJriWRfYSaQobaOA5KGuq5eSdj2u/cR4cgrbUSZLg2t6o+4FzOZv/ULQdXzXh9pJOzNYZZYZiVpZmDjZWzidlQDJuFsX0HT0t+ftG90YuKRiyqfGZRu14NzQiif0hAM+xzh/uiTjfk2tHrupjvvEjgsrhPr4DWW3D82x6aq3fk4HosErgtkQxcrLBF1LPQegHPen6H9dxW+3ltbotbBi9t8FpaOnxp+vj3T4584yun8YvZQydhNsMsrU30j2BHFmu0nfOiUVN2/n1xacwVFEsTQNjTk3r2Qsz+IzOGPuuKmflu3AIqNVC0SqWiNGq99hmZbzwioBEH/WhBdPSvpYA2tN+fSvQPbKtW002NLT4+4yZNmpIYc3E422nnqvUankTd1deckZ8XexVvRgM8oIP2gvKi/ZF1vtFZu4KhuA0edDSGXBZdyoY2vfsN8hkh0QiKVAslbYVfn8j+5+H6U1ehSw5CHChQFdSl7wjKXHugLTgReqQakqqtrX1z9t8HsmwsMWyE++Co0HBChTMaauR/rUXmGwYC+kd7nqhgxuVPigCjvJHL5bm5uT4+PnZ2dp9++mljY2NUVNSIESOcnJwOHTrE4/EMtWdkMUyDMt4tBliMCSMCRgSedgSMBPTTfgWN5Tci8GQhwJCwHA5n7ty57u7u69at6+joYIJvLF26tL6+nnlPYHpU/8EC7/+tlYEgFgqF0dHRQ4YMYWgsDMOcnZ0/+uijmzdvNjU1CQQCwxmZDhxzYH9u93E6dj/12vOj2x+9gCHPQv0bsU6hUFRXVzP2IC4uLiwWy9PTc8qUKdOmTRsxYoSzs/Ps2bPDwsL4/IfBphglNaO5/l5RH6e0/y96xh2MCPymCBiGdtRqtUKhkMvlKSkp8+fPt7Ozs7W1tbKysrGxGTx4sLu7u6mpqZOT0+eff97Y2PijN/xvWk5j5v+jCDAcNMMyP+Sav4OE4cH+8GGuQSykjiLFYnFzc3NC/KVN//zc3cPDysEOCR1ZZkPHjJwwYvTmGfOPLVn/zer106a+6OzsPGHypJWfrAk7HckR9KLccQpaeisDYyTn78CDthy/k9LkfGVGSfr+4OZTV3qOJbQdvQC9OEhwnQrHKVxAyZD8WUn3JeemrvPtiU5mOEF9QXXIypokoU/Kv1eSueeEJqea5vT679w92M3V1d3F1m2g/RDXDzas7lIIJRRO0OqHzKBeianRavVR4IDU0jJcJZRK0A6PSHcGCKYJM2mCICQSCZPWaAEn1d18QTOHw+3uIXBKKpJ1tXPbahoTYy5Ofn6SpYmFjSnLzoS18u1Fgrp2nC+FLmllyOXsb05Qd6tRwDe1RgeA1MhqFYjl9YkpD46fFd/IyT4a2Z6Wq5XJNQQOBIVkpw38mqMxNz/d03vpjl6qrAW5CnGCPaLOWzkNgXFUwv38o6e7sopAJGOodmRuUNdRGRijvpBNxmVVBcQQhbWgoh76aNMAbeLG09c7rt/TNfWi0IIUCkmHxNECFeQ11G8NfbDxW/HtAhDKcA2hAI0KkHM3cu0gSKjvvr33eEtmHshVCpkEGUNTAGWchp0RzTsiyvyiZLmVwsa20MDACd4jnMws2PpOiQsLhfUbiGFjWPYvWTp9PGRSyJQFKVOWl3i+22Q3v8Hm7Tr2W8gfw21pl+sSjvPCFqd3Gwe+U+c4v37ggma3ha3ui9vdl3S4Lel0Q2R0j8fSLq/3ucM+6BixkvPsqs5nVza5voMoZos32rBXOdgsvvkcpcv7+Ig1vSNW1Q9fXv7s8tKJq3JfWnNu5Fu+9pPWWnr/3cT1ecx6OGbhbWY9UO/1zMKwIRY2cz3GBPz9g7DXVuTsOqFr6AQpoSppyImIq76dde/KjeFug6wtLb788ktSS1M6rZzAH9lu6AwENK1DMwcMbQf1VR45Tjwc12HuIX3wT8Nuj7b9On8Zv/J/6QO2b9/OtmS9P/89B8zMb8OXgENTet7tmEvdVY2g0oFEjRc3FR+LlZ663bT/HJ1dA9XddUfiOqNuovESGQEK/aoBENNwr6V11+mCjUdaQhKhTQgiAnqk2prO0uPnU784XB+cgAhrHaBJeG++bW1ibjXAwppl5efn19HRwfQAaUCW2MxiqLixL/frXPInPpf+V5y5B4RCYUdHx+LFiy0sLGbPnp2dnZ2WljZt2jR3d/dt27ZRFMXMiWQewoZXgCe+osYCGhEwImBE4LEQMBLQjwWTcScjAkYEHhMBtVrd19e3YMECKyurf1ktd3R0bN68mc1mL168WCBAIWIMdPAv7FQx0gCCII4dO+bq6spmo3c9S0vLOXPm3LhxQyxG4h31o6V/R5/pCxrOzvz7/9aufw/y/00bXjMM2ep0OrVaTZIkl8u9efPm2rVrPT09nZycxo8fv379+lWrVtnY2NjZ2S1evLikpITxHyAIgqKoh68s2u/E3zFka0wYEXgyEaA1tMFmp7W1NSIiYvz48U5OTvb29qamps7OzowOGsOwMWPG3Lhxo/9j4ee2zScTAWOpnkAEDMH0UNmYWfFalECWGwAa0DGrnpzV9f9E9BlNg/45TGnUJE5wudx7ZUUff7XJ2dsLM0NEoz1m9ry50zvj/3Lw4MGQs1G79u4ZO3rMAMxk6GCvefPmnQoOlVQ3pew7zg1Jgipx2c7Q8gOR3Zcy7vlHiK/dF1/KKtp2AvKbQIQDkj7jJIkjza5crsqrvrDq64ajsVDZiZxCAOSkklITWq0G1JrW7II7R0/BAw484GSeOBPjHxgXHD7Ky8vKhoWZYp7PDjsZd7pPKSO1yNmamZRDURRDQFM6LUGrVWpSpSYJGqlZlSQhw9E8ce2jX09mKJQgCIVC0dTSVlD04HLSlZOnonz9Dn2+5cuVq1Yve/+Dd95e8NdJ08YNHjHQxMpmgBXLzHKog9uKN9+tzMgFFWj58qKElFu7TkBFD4jUICMVErGKVKm1BFAUP6sw2/cEpJeUHzvblJgG3ch+B7kG41poE3OOX7q+/OvW0MuI9UPBDZG/Myhoyb2y9J2BRGxmxd6I5sQ0kOIAOpUaF8vEBF+YejhcEJemTczL3X4csc9CGYAOp3ClQAwSqu1cSvqOIG1zL5Ba5LtC0chumwR40FK69UT56oPU2TvAl4rkYgVopEDJgaRoEmhazenN3B/SfO4GMuLQaGQSMTJnqODkbw1q3xnZsDMC2UmLlEBROlpTVfRg6RtznDAzNoY5m5hZYZipGWZlY2Fpgtlj2BjMYqnlkGvjFhY++37xqPdzPeYXuc0vdVtQ5fFenedi4fPrup/9qPmZZbUeC2sGoS1NXkubh7zfNmRp+zPvc4Z/0DZqRcvofzSO/UetD1rrRn9QN3xp/aB3a5znVTnNLXGec9/5jRT3v6dOeP/m9JVnJ73rO2T6QsztbxhrNIYNxjAHDLMzHWBjbm6BQmuaDMCwqR7Das7fUMVl3vlwZ+W2EKjmIY6Vw6+Lud4QewPaeGkXElzt7a3trL/atV2jbzr6eIM6NY3Y5yeQgAaA1NTUYV5DnK3tPCxs0yPPNyVm3Ak+J2tBWnjgKRT3qm5v9u86kVT8eSCkVEOztDjkYq5/FPBJUBDIAEFJgJQAKQ11gq4956rWHqk5dA66kPAZBAroVhQEnMv6MuDOlqNUfj2oQSzoW7psGeO8gWHYjj27e/r4KpJQ6g3ijAT0E/hz8LsVqf8rA9OlB4C+vr7GxsYPP/zQysrqpZdeKiwsLC8vnzZtmqOj44oVKzgcDjN00X+S5e9WYOOJjAgYETAi8JsiYCSgf1N4jZkbEfjfQoCiKJIkt27damVlNWXKlPz8/M8//9zKymrevHldXfo5j3oC+tcimCQSSVxcnI+Pj7m5uamp6bhx44KDg7lcLkEQMpkMTRGlqP7UM3MxmL7gzy1D/x7k/5vuzxoznUiGLjfcDQKBIDs7e926dSNHjvTy8nr99dfXrVs3Y8YMOzs7Hx+fsLCwtrY2hobuz2UbzmvIx5gwIvCkIWBocTqdTiKR5OTkLFu2zMPDw97e3sHBwdnZedSoUUOGDGGxWC4uLu+9915ubq5cLmdqgeO44SY35POkVdBYnqcaAYZrRnTsdwloNXIx1jGrgYk28NGIgNabRKN59Pr6q0jkE8GR9d29e3fnZ1/MHDV+gpOXPYY5DGA5DnJ9dvL4D1atDAgI2PPN9ndffcOL7fBXr9Hrp7+xZ8a7wlPJyrDkxi9DOAfPlR+Phbx6SKtE7HNRC4g1oMDVJFqRl7GCkBRWX/ls7/3dwdrCBuT/ACAHkiRxLY6TMllPQ9PNkChlTiXUi7VX8ksOn4ZqrvR+RfCmbR+89paLlbW1pcWwYUO3fPVlRFRkZmZmcXFxdWVVY319Z2dnr4DPE/XxpWKhQiZSycUKmUQplxNIK62maZwipVJpX19fXl7exQsXd+zYsWLFilGjxz7jPcLdY/BAZ1f3wV6DvIY4ubnb2tg72ziyMVM7DBvnMvTdt+Z/9dkXsccjJI1cUGjUncL6pMz74Zd4hbWgoCmJHOm2FXIU2q6bryqtKwmLU93I7QlPagy5CJ1i5Iah09sJcySc45eK1hzoOHAOipsRHw2ATLS5QqqgtsjvlOhcauvh2L7YNJCQtEJJAd2nEBNyWerZC/nhcX1Jd9O3BwjTi5Cxhn5cQa8Wp0TX8iqC46niZqT9BhQ0DykNaR208LqOXMxato1z9AK0oJHyXq1SDpRSR6o1JMhVeHlTYUhsw5lrUNmOrj+pAQWpLm2q2BvRsCey7vC5lrhb0CsCikLxD/X3FtEnyrtwZf1r88Y7uQ+yYsTQmK2dFcNBjzBjT8AGLBgw6J/uEw55vxw2/PXzo96+9dzi3HHLK59bWfPsisqRy8qGLSkeurD0mcVlQxeXP7MErd7IQ6Ns1LIHY5cXjltRMG5F9sQVqZOWXpm0KPb5+aeee+uYz+z9o17+augLnwyZ8Lq91yjMfBDydMaGYqZD9KsbZjpAr8u2tGG5D3J98+WZ5w4FQB2Xul5QtOZAxYYjkN8MAhI6JVVx1wtPXoDGHmgXJgaEurKsbVmWX32zFUXk04EGJ7UahJ5Gq6X0wmfGNR0N6PRbfmcF9L9bN0BXV9fLf5lug5nOGOaTHRKbczhKebcCeHLgCpVF9Xd2B3OPXW7Zd5Z7PBGKu6Tx2YVBsSBSkCQppwgVqSegRQRUdUnOpBet8Ws7GKut6kDjP1JC29jdEHI5b1PAgy1BUNAG3XJJe9eGDRscXZwtrVh2DvaLly/jifrQkI9GrSIJSqM2EtBP9a/GLyx8vwaBklqtliAIpofT0dGxd+9eZ2fn4cOHX716NTs7+5VXXrGxsZk1a1ZFRQWzj+HwX1gM4+FGBIwIGBF4QhAwEtBPyIUwFsOIwNOKQH9q9V/+G9u3b3dycnrjjTd6e3v37Nnj4OAwadKkwsJCFBpGH2fPwKj+wk6VSqVKS0vz8fHBMMzU1HTmzJm3b9+WydA8XIIg/gOazHl/HwKaqSyj7mS6koxFCRONRCgUZmZmfvzxx46Ojq6urjNnzly9evXEiRNdXV03bdrU1dX1o0S2kZj7DxfX+NXviYChKTE3quHUjMl7TU3NoUOHxo0bZ29v7+jo6ODgMG7cuL/97W+GeIP+/v5SqRQpGhUKptn+3FZpOKMxYUTgMRH4N0VlIKCRmQVyKjYQ0P0TGkBS6IcEtFqr0WqR9pMgVSShAi3SC/fJJcX1577xC/jsmyVzFwwdNszUytLCwdbRxdnHx+ej5Su+3bH3pO/hrYtWrXrurzMx+2+GTo977aPCT/2qdobDvRoobHrge5JILgKeCk3818ufEfssxaGm8+ZXh6595qvNrwehkhEmy0mUAAWpbOm8GRLVl10CjQLV5RzOsXiol0BmdaF/ZO+17L6s4oNr/zlp1GgMw2xtbT08PIZ4Dp46abK3p9dzI0f/dcqLr8185d133l28dMmH/1i5+uM1u3z3HgkKPBMbc+X6terKqqT4hC8/3zznzTdHjBjh6elpZ2NrbmY2btz4OW/N/eLLrwJOnIiIPL1v/4G35s0f7Orhbmr9LMtlzrMvnN1/jFPXQin1OmVE4sprku8l7AzszigGHagJtRpAINE7NffJtOUt9w+Ft55KFMVnVB+PgfJWfb1wkMgBB9nl7PRVuxp3n4KKXuCKgCCRLFqukuRVVh2P64q41h4U3xaSANVcdBRNA+hkAkFG9IXciAuyu6WFIbGca1kgkNMkIVeraDUJOKhuFhX7RvalFoEYR1bSQKuARgpoEdkWk1z6RWDTnkgkM1dp+CqJDLQoOqGaBJkK2vnp/uEl4RehgYu00motul14qqbwyw07I+p2RbTG3QK+lCYJGaEfSyNJIClQUm3Xsy5uPXg1+KTvF1tmvfSipRlmimF2tlYDHWysB5jaYpgThrlj2PMYeyJm8irGXoS5r7X03oQN22vhE+T00qnBs66OW3jluUWXx7wXP3bBhTHzY8fMPTdqzpmRb+23nbDPbsIe+wnbBk5YZeW90NrrdbbbNKuBI00tnzG1GGI6wMXExMrMhM0aYG05gG2CDKnZj1aWiYmtrfXchfMvXLog7eoBgVJ1I7/0y6DSz45AajVIAVr5D0Ljso9GIvaZr+KlF5zautfT2s4UwzZ8tlGuVJAKFSGVg9pAQGsZ8w1mhoGha4f6Kr+vBQdjLKPWjwAUFhZO8hnnjFnuXPZx6ren2pOyoEUMfAKaBQ8CY3jRt5sPxfKOX4WiLijmVgbEQR0SSRAAEg1SQKPGyCOIpPy8df51O07BvUaQEEg93SMrD09oCYgv+SpYcSEb2uU6rvDjD1cNdHE2Z7Msbdhz311Q3VCnBZAp5AwgTGzG/ykLju/cA/3GJB7zKf1f7/ZrvV/81wX40QP7o8G8MfXXNUskkrCwsBEjRgwePNjX17e6unrZsmVsNnv69OlZWVk/mqFxoxEBIwJGBJ5qBIwE9FN9+YyFNyLwxyOg0+kYoTFFUUFBQRiGTZw4MT09PTo62t7e3tvbu6amRiKRGEbyDYrg/4JIZbpxDMtcV1c3a9YsBwcHDMNWrlxZX1//+Fj07w4+/lGPv6chfwOD/MMEw0ozn/8SPsycOdPR0dHHx2f37t0vvfSSg4PD2rVr29ra5HI5Q9w//tmNexoR+K0RMNzhjEchE5CTJEnG1Z2iqOzs7IULF7LZbEv9Ymtr++KLL06aNAnDMDMzszFjxpw/f55pyAxbbShw/5wNG40JIwK/IgKMhPnfCmj9/wZimtbbcfT/RN8zbDWNyGg1TaORElp/mBSHHrws4nLZ+ZtEJ5/P519Nufn+hx+4DXI3xCQY7OY+7+9vfv3RuvPb/fa8NG+P98v7R776xcTXD81bWXn4zJ1tAfXnk4EnA7GeuxTLUIxBABAQtf5nH2w7QWRXQreI0A/VoHLgJPThUNOdF3hGnvYAOuRUWkn1kXPwoAPKurO/CRRfuANcsvdCRkl0Umt13T+/3mLCsmCxrRys7b0Guo8e9MzkYWOnPjN2tLPXtLHjvZxch7q4m2IYi21lzmYxNlZOA6wcMXM7UwsnGztLS0sbGxsHa9vXZ8zcsHb9h8s/fHPuvOmzZg0eMtTCnDXI02vScJ9Pp7218+XFJVFXoFsOOiBwSoOrQUYRFe2Xdx3j3HkA3TJE7FE6iYZQqEkQqaC6s+TE+baIK+Tl+7n7w8UltaDEkbC4mw/1XE1mxa01u+5/eVSaUQxyipJI1Uol4BpZUU3qzkBBTGp7eFLxt6eRGBkHILVUjwD6ZPWJqeVHzsL9xgfBsc03s1AAQwCVTI6st/tw5d2Kq5/s6UvIBgkaDe/BFWpA0meQ60SXsjM3HCo/EAkNfJCSQJD6yI80pSZAqoRGXkV4fGpABNGqJ7tBS8pkuk5+9YkLLf4xTTuj6g/FQKcU+TboaL5KJpZJQYYDH5emlaR8dbjqdBKKjqjVgVxenHFn2dvzHCwsLc0HmFmYOQ60t7aytNSHK/Q2YQ9GZLTJs+yB7piJF2bijZmMxExGo9VsJGY2HDN5BjMZqt8+XP/VSP2nN9qIWGx7DLMyM7FkmZlbmVlYmiJnDTPM1BwzG4ANMMXMzVCgwQGWA9gsi48WLy3KzpYpmPtNAXW9TTujMpZu641LhQ4J8FW9t/MyfIOhnAM8laaq7frhkPTI2Jcnv4Bh2LzF73D7eghChXy6NagV6BXQDwloxrVGp0UqduZJjsZ2DGu/NvwbPedp0Clpii8VK0ki6lTkM64eQ1j2lw6e6MwoBDkNCh1Ud1UcjW359rziXGbBvgio5ENKdfI6X0FWqa5PptXQuFaNxneEEhCr6azq9JW7C9cfhux6ZM0hR4bs3JjU6t2RDf6xHdHJ0CyAbnHwtwE2Njao7Vixxk+aWFVbo1AhHxvG6MYwla1/lQ3pfpD8eZJM7b43nMwQr9+jX7VaLY7jTOxuxqQOx3FE/+sN6AwxvZl+slqtZiZZMhbJ/Tlc5rWCsdx7wiNJMOB872IrFIrz5897eXk5OzsfOHCgs7Nz8+bNtra2Pj4+6enpjKSGqdd/8d70vXMZ/zUiYETAiMAfjoCRgP7DL4GxAEYEnm4EGI9IADh79uzgwYN9fHxSU1PDw8MdHBxGjx598+ZNphvKdBC/12X8uTWn9AsA1NfXL1myxMLCgokiXVZWxmiKH5OrNfT+f6POnCH//nKMH3bHDbvJ5XIej7djx44hQ4YMHTp02bJl06dPZ7PZW7ZsaW1FujADhj8XMeP+RgR+CwSYW9cwrGJoRyRJNjc3nzp1ysfHx8HBwcbGxtHRcezYsTNmzPD29sYwjMViffzxx21tbQz7zJjC9y+hoVEY8uz/rTFtROBXQ8AQh/BREEIDUfa9xMMzIg4aEdCMkhE0WlBrNdy+jsSsoqBY6BCDSk1p1L0ycUtba2Ji4o4dO6ZPn25mZmaJOEbMlW23bPKMg28uD3tzVdicjxaOnPSilevG52fumPXepWOhtWVlMolYLhIhdS2uhV4l58yNsp2hkFEJrTzkvEEqUZBANQUCKbSIGoLjxZeyoEkCaWUtYZfhXj0Uc6qD4rqibkBpjywm4/6uUMm9CqB1DV2cHXt2P/fsGG8nj5d9pqyeu2Tlm++uX/jhjk83r353yRsv/u2FoaNczdl2llYOtnYD2bbezu5jHdxfHTVh/ozX5s2aPdl79KShI4c5uI5wH+ztPuRZ71Hjxk+cMnXau+8s/PyTjYF7DqWePJ+06VDjqRtQ0w0iUq2iCL0CWl7DyT+ZILpXBb1yUKiBBB2OlKX6wiHPtgAAIABJREFUSIy8B8Hn205dh1tlNUfj8HuVpEBE0xQll4NCo0wpyli3P3fLUTqjDAR66hlAJ5VDG78kKIYfmyqISys9HosXNyCNKqEBXANcYVNCarF/lCbubsu3se0JaVRTJxCPBhr6ZFDKydoZyjmTDC19oAaeUt6nU/dIxCCllPfrbqzefX9zgCK9GNHZOFI9qzV67bNcBV2imtD4wm+j1HUcUBEUIMMOkOF1F5LbQy83+Z3tDb8BFVyQoaBhcg2ppCkkqSYBsmsvrdpWejwW2vjIY1qnBaFYVt9y92z8qb1+UYcDXp320tjhw62t0L1haWlubzJgkLWtra010khbmJgNMLE0NWGbmFhjZtbISNqMZWJmboZWlomZfruJLfbvlW2CiGYUD9NMv1piGAsbYGnKtjCzNjVhYZi1qdlQL88NW/6ZknFbIRIhCxElCWKVto5bcuTc/Y8PyiNuQwsPpERfdkn24Qjt3Spol9F5tcWnExrScnBu77Kli1l2bLdhnpWNNWggRO+U8uQQ0FotosKZNg0AxRVlY54dzcKwWc9NrryRiaycJSS08DrOpnQEXeaHXq/YGwlFHKjobQ6M7zqfDjyZjlLTarVWQ+tUJFI6l7Rlbjmau+Ew3ChFMQYBgCcT5VQUfn2i4J9H68MSNRVtIFKFBBwbPny4jb0dZoJNfmHKrdTbOEVqtOje0+o56P6/kv1/3Zj0r/Y0e5IyYljm/hqL/r/mWq2WoiiGaGYGsGUyGYfDycvLO336tJ+f3969ew/qF19f34MHDx47duzcuXOJiYlpaWn5+fl1dXVdXV1SqdTAXDMn+g949j/7H47TDwvDDNvz+fy8vLy5c+e6urp++umnVVVVgYGBQ4cO9fHxSUpKYsh3iqL+8PIbC2BEwIiAEYFfjoCRgP7lGBpzMCLwP42AVqtVqVTx8fHe3t5TpkxJSUlJSkoaO3aso6NjUlKSgWYyCB9+2P16fPhoDc10Ww8ePGhqamppabls2bLq6moAwHH88Vna/q8Bj3/2x9+zf/6Pk2ZyFovFFy9cHDVqlKOj47Jly2bMmOHm5nb48GEmFOHjn924pxGB3xoB5q5mXq2Z1z/mOZCZmbl06VJHR0dbW1sLCwvmmTBkyBA7OzsMw0aOHBkaGsrj8fo/BPqnf+tiG/M3IvBLEOh/2zMK6JbiiswT5xQ51Sg0mQzHcSTjlSnQtBW5XJ6fn+/v7z979mwWi2VvZultwn7Bxn2627DNcxad3rRrx5z318+a682yc3EaOOmvU3fu23XvbiYpk4EEF168k781SHIzD8TIgBhJg3UUqSZ0UrmsorE0OK4hOB5q+FDSURd0gbxRAK3y3rjU9nPJ0CBSnk5tPHgGCppBSKhpWkQoCKk8dO+ht559YbKd1wuuw4daDbRj2TgNdPFy9RjrOnQsy/V5m0Fz/zJzz8Yv0k7G3j8VH7rum9LLtwUtHbya5tJTl48v2xj8+Y7866ltVQ0ttY3ttc3t9S1d7Yh1hQZBtl9U7tEYaO5DGmcAkkQCUqjqTt0dUnUpDXnm4rSOQPwsrSRQdbjSxpjk6hPxkMup9o9rjEsBEQmUnixWkbKimrI9J7M/2a9JKQauFChajasQZ90jaTp7vSc6WZ6QnXc4kl9YqYdFf1S3qCcl9+7uE5BVyz2eUOwXCXVcEOuPQv4PQHcJCwPjqoIvQ7sQCGTAKiIUQpVcqyS0hU1ZXwcmrdsrvJGPROgKAlWAYZ9xEnqkeSfOXf3msLa0GQRSXCRGNiA08JPu8iJv8CJv1IfEq4ua0CgaSeEaCqf0xKVQCaUtBV8F5WwNwmvbdASBYhiCVt3dW3v1dmFYHBQ19t7IuRMYyckqqMjM2bN92+DBHizMxNaCZWZujpmZWJiYskzMLE0R3cwslqZ63hkx0RYsEwtLU/StYaM1ZmKNIbaaZYJkzkj4bM+ycbJjmyDbjedtnT78yyzfjz/LuHylq7uTRJdEp5ZIoUcGFdzS3RHXln/TGpoEEgCFtiO3LG1fCGTVAkcJHGXl0XMdiXdALFeRqpTsDBv3geyBtqHhITqK1OI4aJC3hEanoXTIUNuw/mwFtIE2ftQ4mRGgR/897l8U7g+FqKTKm+v/8srLbEvWpBFjEiPOavlSxD53yVvOJncHX4X7nKL9kXRqOVQJedG32y+kQReadoDm4uhvGBBT0NjXcuxS5mf+wsv3oJcEJYASyKyqot3hpbsjyo/EQKsAcDo6MsrC2goNrLKtXNxcb95KlisVShxX4nrP8n4E9E/1Ax+3bk/VfgYC+oc/7kw4bpVKJZPJent7y8vLz549u2HDhunTpw8fPtzOzs5Efw+b6hdzc3MrKysHBwcXFxd3d3cvL69hw4aNGjVq/Pjxs2fPXrNmjb+//+XLl8vLyzkcDp/Pl8lkP4z7wiD/xOLHYMWoTEiSLC0tfe+990xNTd98883y8vLLly8/99xzw4YN27t3r0q//EIRzxOLg7FgRgSMCPxPIWAkoP+nLrexskYEfn0EVCrV9evXXVxcPDw8kpOT8/PzhwwZ4ujoeOnSJaEQRa4nSZKROTB01Q+7pD+rTDiO5+XlMdbPr732WlVVFa2hxWIxw00/Zlb9XwYe85CftVv//B8nrVKppFIpo+9OTU2dNm2anZ3dRx995OPj4+7uHhcX97PObtzZiMBvjQBzV/cnoNva2oKDg19++WVHR0dnZ2crK6sxY8asWLHipZdesrW1NTMzmzhxYk1NDQAwnhuMKfwvfBr81tU05m9EoD8C/W97NHmcInvaOsTlTdCrQApfFanByYfWHI9CEQiFwpaWlqioqGnjJ3mZWzujKIUWbhbsyfaDFk+YfnKv35cbNkycNgVFMjDDJowZ8+XHn+bFJV3dfECZUgR9SsaYQk4qSTXiRqFXVBxz5e7+UChogazq1C8OCS/egfJuQVxaY1gC1PHI28XVfqchuxaa+aBEXDApUwgqGq8dCu24mXtuy4GvF67a8enmLV99vf7zz/33+V0Iiriw51jG8RjgCpFBQU1XZVRS3aVU6FGAQie+X3Vp9fZ7O4KVxY3aXgktUupkJKhoxLaTQNZ13dkVmrzlSGdKARCAKwhcRYKcwqs4GTtD7vudppp7Gcdk9OusoRC9yyPgTmXhgUjIb20OSHjgdwY6JdAnB7neNpojzj8YgZw3LmRCHwVCpVapAlqrbua2Xk5rDU+CO9VZO4LqL97SiqQSuYTQIT2g+EFNjt9JPPE+efk+Yp9L2xDbqNBLrUkaBLIr34blnTgPTUJQIc9iPUEOQNBkZVuh76krq3d1JGYhhSwAJZHqKBLhjJMgI9vjU1O2H+Wm5oJCo1emk3hHT9ft3LZv49RRaamb/KCKAyotULRYIRMrZIgol1BQwUnbfPjmyh2Q26Tq5lH0Q/fq3vySpF2HNXcr5Tfyyo/HEjlVaGeJEkhSKZHlp2Zu+mitu5ML25LFfqR6NhDNzBZbzMIas7A0sTA3tTDTq6HZmJktZuaAmQ3ETBwwE3vMxNbEzNHWxsPLY+zw4ZvfXXp2887Mw2EZh8OK468TXTyZQkoiNxkUSQ/qBN3Hk26/v61mbxRU90KPQt3cnREaQ2SUQ6MMeHTdyYSmqKvAlRBSqUSjkumIV958zZxl/sLkibVlZch3+xEBrdGh1O9PQH/v50OJoxCaD+qqln+yGo13eg+POhJEdPLRNeLJuVeyW8KSIKUi6/PDnJjbUMOnEvOrAuKghQ8qpH1WIydxvW65TcY/k5r3dRA/Nh15kghxUAFV3Fy7P5pz6Hz+3nCo6ABce/78eScvDzNbREBbWrGiok9L5LI+kZDSqDVarUwhJ9XUj/o+9+8T9n+8/GnSBgKaGZxWKBS9vb11dXUFBQUJCQkHDx5ctGjRhAkTnJ2dzc3NTUxMzM3RUIupqSmLxWKz2Tb6hc1ms1gsCwsLJsb4o7EYM2ZnZn8zMzPGNWj06NEffvjhoUOHrl+/Xltbq1KpGEOwn7Kt+N6d88cib/AxY3Dj8/kbNmywsbHx8vK6d+9eQkLCsGHDHBwctmzZwuPxDLM8mZ37T6z8Y2thPLsRASMCRgQeHwEjAf34WBn3NCJgRAAhwPSeDVhkZWWNHj3axcUlOjo6MzNz/PjxHh4e4eHhDDll+KQ19C/vdlMUxePxPvzwQ3t7e8bfg9FTGDSYfwJ1gEKhyMnJGTdunKWl5dtvv+3p6Tl16tTCwsI/QdUM94wx8VQjwHg1Gm5ImUyWlZW1YsWKwYMH29jYmJiYODs7z9Yvzs7OJiYm9vb2mzdvrqmpUSgUBgrP8EB4qqEwFv5/DQHDrxgNOhLQrH9k9YBYSC1jyoGYSq1hLx0TYFMiEkeFR5wKDNr4j48m+fg4sa2HWNs7YQO87AfOf+ONzZ//87N1n85/9fVxLp7PmztueHXeurkLo44E1lVXCaRCUkf1iQVAUbo+SUNy1v3gc1DdAzn1lUfPyRNzoIavupZXeywO7lZTaSUpOwOkmSXQJQKNDimOlVpNFSfvxPnW8+l9Nwvvh1yAdhHZI5bLlRSlofsU+ZdupQScxotbgI8DjygOuVh1+irwFKAEbXrF/c0B9zcHwN1aEOCqLgGoEHeJOGgCoEPWGJuaui2IvF8PEkpH6sk7AqCUU3w4pjrqOjT0UiIZE36N0uhZXzWIk3Javj0Pt8q6z9xG7HN9H2KoxTh0S6Gml+8Xf/8f+2pOJqJ4jPJHkYT7pN03c8qPnBXHZRTuC68Ij4cOAbLIloskEhGnojr925PSpBwiIac2ILb3Rg5IKSAfmm9oOYKqyKT7356WVreTfcjyWIOYc0ClbRBWHjh75eO9FWGJ0CUBNegIAvkaE2rEsIup9qSs+zuO9yXdBZ4EqX3VGhArxWlFBdtPQEx2x4FzgqvZICVpJaFSk0qSQGbTKi20iIu/Dr6zep/sSgH0qpALA04AoeNnPXgQHAuFTdq7VflHT/em5YMCmXkAodbgpFaqAommKTX/rP+J62cungkK992y/aN5S+a++MoLQ0cPs3LyNLd3MWE7Ypa2mKWFmaWZuaXpAAurASx7bMCLbiOm2HnOcBvxxpjJa95euHvD52eOB9cWPFDUtLRGXKk5eLo19HLlqQR1M5dWqZSgFQKB/Mq6pLqY+7WfHmvwi9PcqQEBQL2gOvpa24U0aOgDLtF+Ljkv6Kyytg2UuE7viq7RaVJTbj3jhszNv9r4GaexEbToomu1GpqmHnKOeh30QwW03gn63wbQD6/JwwfGv1uIToco8Uc2OMzXj6mAZjJhAtiSJClTyFMzM+Ysec/W09V7zCj/g369dS1ajgC6Za3X7uYGnIWC5tLj5yuD46GyV369AAmZyztAA3K5XE4xAn4dyEF+NiPjo70tkdfRKA7yfaagU/rA77Q46Fr51yE913NAIM9ISX1u8kQLB1uMZc6ytTkSGPCw5PouL4MGY2HM9IH717d/+il9fvYncBlLDUNlhUKhQqHg8XiZmZlHjhzZsmXLhx9+OGfOnHHjxrm4uDACZxP9wjDOFhYWjF2+qampra2ts7Ozp6fnyJEjBw8ezGKxmD2ZHSwsLMaOHfvmm29OmDDBy8vLxcXFxsbG1NTU4LbPkNFDhw79+9//vm7durCwsIqKCoFAgC4vRTFcLeMZ2P8S9K/LH3I5+hdGKBTSGprD4Rw4cMDNze1f71ahoaFXr1596aWXPDw8Pvjgg6qqKsbq2kBb9+eg//C6/CEAGk9qRMCIwFOHgJGAfuoumbHARgT+eASYXg5FUcXFxePGjXNyckpMTCwvL3/55Zf/JUzw9fUlCMJAPRsS/btZ/10dKIpKSUnx8PCwsLCIjo5mFNaMlPJ7gUf+u/yfkKMoirp06ZKHh8esWbPefvttV1fXPXv2GMxMnpBCGovxP4sASZI4jjNKnI6OjmPHjk2YMMHV1dXOzo7NZs+YMWPx4sWTJk2ysbFhs9kTJkxISkpSqVSG5s+8ARr46/9ZGI0VfxoRMNzGGtCpQIsDcoIGRG6gBdHQlBb6DbYydSRxoqeDK+0TqGTSgpycvdu2TRo12s3a1gzDnK1tRnoOnvvyrF1rNxzd8OX2ucvmj5niYGHpPMhl5huvHjr2bWVNpY4gQCRrSMu5c/w0tImhlpe//yT39A0o7dSkFBfuPwkP2iGrqiI8vi+7BO/oAYpCfJBUBU38u3tDm0OuKK4W3t4bCnU9Oq4YxIROqQYpWZmcff9MElndCXwKuuRFEZcqzl6D1j7oEEJVJ+fwxXurfaXx2dApBwooid7KmQa6TwG9ip5bhfGb/CRpZSCmVX0yVE25GpoF+QdPFx46A3U9oNIRBIGDltDRpJoCUt1XUlfkH00nFkBGTe7+CCq/EVqFyMdDDdDcxwm9mvb2ZsGhS1DfDUpKq1TRYiko6b6s4gcHT0FmbXfk9d5Ld6BNCDLEFNNqsqeu8dbxSGXqA7hdWnn4DJ5egsSqagAViSI6isi6S6lp24+R92u1UkJGkhoAlZpUq2ngq3jBN+58uLfgSAzKUAMakiJJHGmfAaBDLLtdfHWjrzDxLtR0ggJH9GivGM+vqTx8Rhp+o3LLcc3lXOiSgkyFXFc0emNWGoBPNpxIyF9/mDp/D7gEKoyMAClBlTSWhV5AltYV3Hv+Ea1JGUhvjlOg0XOvGgARLrlXlX40uvRGpk5C0EpKK1bRrQK8uCVxW0Dkpzsiv/CN3R+Udv7K9UtXLl25En/lStLV69k30jh3HlRG34jfuDd67bbkwEhZPQdJqsVKEOEdiXdaj8SpzqRVBsZoq9rJbj6lJhSgkapkgIPgcnbxav/yTwIgrxVapdBB5PhHl4VdgtpeUEFTQnraoVBlWaNaIlUoZTodrUKRFZXV2bkfz31vmI3jMwOdD+7e3dLUSKkJnU4/9qCXJjDjDT9KQOt+goB+6HphIKD1CSYi6HeP+E9PC61Wy+PxQsPDnhk5HLMwfWb82KjYcxKRGCRIvNyVkn//aDTkNtacSqo8dx2Zlec15fpH8TOKkSeMFqQqhZQmSZIEOa3MKLu+cnvNwbNI5iwiEAEtVJWFxDf4xzbviRaeS4deefrNlIkTJ5qzkH/3v/jTvb77RFKJITLew2fBd/8YnhvfS/ynWj3B3xEEIZPJmD6AQf/B4/FKS0sPHTrk4+MzatSofznIWVlZWVhYsFgsGxsbJycnV1dXNzc3T0/PYcOGjRgxwsfHZ+rUqbNmzZozZ878+fPffefdZcuWLV++fOXKlZ999tnKlSunTJni6ek5dOjQcePGTZs2zd/fv66ujsvlcjicrq6u7OzswMDANWvWTJ8+3cvLi81mm5ubM1fEysrKxMTEyspqyJAhs2fPDgkJKS4u7u3tZcbOGa78yUG3/y2h1WpJkqQ1NJfLjYqKYlxHdu3aVVVVNX/+fHNz87lz5zKBYZjZpf3vOiafJ6dexpIYETAiYETgpxAwEtA/hYxxuxEBIwL/CQG5XJ6amurt7W1jY3Ps2LG2trbXXnvNysrK19dXKBQa1BD9O+H9u1n/KesffGcY1e/q6po2bRqGYWvWrJFIUDB7Jn8D+2zQAvwgj6dmA9Onx3F827ZtHh4e69evf+6550aNGpWbm/vU1MFY0D8vAsz9qVarJRJJRkbGBx98YG9vz2az7e3t7ezspk+fvmDBAibeoIODw/Tp08vLyxmu+Xv6oz8vQsaa/ZkRMPyKaUCn0K+0flIQpdd+AqUDUmcgoBkgVCqVhqRATWtxnCYJQqUUC/hlObmBe/fPeGGqrYmZBYa5m1qOsXWeOWzMR6/OCd/nt2LpUndPJDX1cHV5668zjny57c6p2Ot+J1T3q6CiI3NnUEf0DagV6FJL724LhNxGqOqtj0yqvZoGyPGB0gGQQilwJQ2R1+qOxKnj8/N2hovvVoKAQLYeMjXdKui5U3r3WAzU9yILZhHZlVpw9/g5ZX0HqABa+nL3R9xbf6gn4iY09oKCArVWTZC4gkD0boeYl1580ze0N6sMBCpQ0WoVhdjnFmnliYTotTuggY9kxkhrjAh6pY5Ukzje0pm4L6D1QgqZVpK+7RgUtyJfXTEBMjV0ygQXs7I3Hy3eEQZFbaDUAUkjXlJJa9PLir4IgPM5ijNpFUGxyNyZJwGhFBlAC2X5EReE13KgjFsXdKHj/G3gShBTTFE6vhh6pKJrefd8w3vvFIOUwPXO1IjQJNV0U7fkSm7eP3xb9p0VlTWCDiiKQqSPWu+8IabIrKrsfx7mhF5Fymg5jlaBHLJrir4KIuOy2oPikdtJiwBwrUYqIxV6mbOMgpY+XvTte58dFsWmAUeB4hlKKGgXEjlVKfuOC2/lQUHj/W8jC0JjoaUHaZ81GhSuENHWCmVuze0dx0tPX5NyBUKFolssUktV0CDQ3aqo33um49uEBweidRWdQAKtQ7Aho3EAUABU9DT4n8/fFFB/9Dx0K+guIcqQJ5FmFBfsC+8Mvlx6KKozPQ80OpVCptFpaJKADj7crS/+LKBgQ4A8IRfENODAi8ssPxKHKiUkuu+WXDsc1lNQASSN9mcWMS7KrbjpF9x47c5X730w0NTc1d7+5Zf/Fpdwgcvvximc8d/QE8e6HxLQzJaHWen/GNrRQwLaQDbrCWhar7k2bOt/IEr3U0wTBNHX15eRkbFs2TI7B3trB7ups2acT75KgU6roUFG9uSWZwVGy24VESkleYdPKwrroFmQdySal1pIi+RIvkCigHhClRzUNF3JSd8RdHvHMfpBM7p8IgJa+1pjbxfvPVW8I6z55FUQUOV5hVOmTh3ItrXEMDvMZPncdzltbUwYEkOP9Kf6vYZaGxLfr9pT8j+jemaM73g83u3bt/fs2cM44zF6ZEtLS09Pz0mTJs2YMeO999774osvzp07d+/evcbGxu7ubhSMVL/86EQonU7HkLA/BQYy0lGrGeKb0b83NTVFRkauWbPmL3/5y5AhQ1gslrl+sbGxwTCMmYa1atWq9PT0vr4+giCYbsxP5f87bzfcDMybDoMJc0cVFhZOnTrVwcFh/fr1ubm5K1assLS0fP3116uqqpi5NQb23/Duw+T2O1fBeDojAkYEjAj8LASMBPTPgsu4sxEBIwIIAa1WW1xc/Prrr5uYmGzbtq2goGDOnDl2dnbbt29nuqQqlap/F5xJf6+b9fhQGgjooKAge3t7FxeXrKys/ocb3NAMnbD+3z5daaayJEmWlZVNnjz5ueeeW7t2rYODw44dO5gIV09U1/npwtZY2l+OAJKJAdTX14eFhU2cONHd3d3Kysre3n7ixIlr166dOXOms7MzhmFeXl6+vr58Pr//GZl2amjO/b8ypo0IPBUIGH7FNKBT6leNnnp+SECrdYiDfqSAVqvVFEUhtoUJbsaYzDL1JCmNSNLV0HQhMurjhUv/NspnIIZ5YObDHZyf8x7+wQfL1n6yZtWyZX8ZM87DjPWat8/KqbP2vbMy3S+0IuJSyYlYqOklbxSUHoxUXs2FrKq8I1H1CbfVrd3oRMzSLWm+kFp//JI6qYATlNQafQtJm2VqkGtASPIzSm/sOdGXXgoiGkjoLKm7d/oSWdkGchoauqsC4u5sPMSNvAltUpBTNKnXU2u1hEyFXDgquBn7wusSMuj2Po2MQB4LBECPknMqOeUz/767FYjjRhw4aLRaNY1ITA1flBZ8ujn+tii1oDjsQvPlDGSygdOIgO7Bu+PSc7YGFeyLgOpuEKsRhYosNqR4YW3F7pOayLS+oKTCXSHa8hboFqGjNCCvbr4XFlN76jIUtLSEXa47mQBtAhAraZVKI5eDmBCmF93aerTzchaIkEid1OpNqEk18BSyyzm5nx4qXX8UshtBRXUrJQo1SavVQCDfZ2lGacG+iOajF6FBjKhnHTL7oPNqCzcf1Z7NbDoSWxVyEdr5IMPR/oTePYMEqOfzY9OTP9lX5hcNtT2IxJciP2j1vaoHhyKbz92ABp7gWk5O0BnoFCEGVaXnkCkdyGlNUVPxsdjayOt6pblOqFIqSQpklCartml/rPzYzeqtJ+n0KpCicI4ETcuAVmppIHTQo+qNTiv+MqR4WyiUdKKggko1yElZflXm9sCeU9dLD0aKbxdAr5hSKpU0oQUtis1YxW3edbr408OCmDsgQpbHrZkPakISobATONLevIrkE6dFFU1aiQz01w4UKqBBnF16c08gfrcCKjuSD4eueH2Ol6PTAAwbNtRr9ap/xMScfVBe2tnbzdDQGr3VCY3awXdWdFkZ7lgH+hahQ580ChSJVubjhwS04RBDQovyYVTSRaUl32zfNmHCBAzD2OaW48aNi4w528nvpUkKRIqqaxk3/cPI+7WCa7kp3wRIbhVCizA7JLYpIR0NVwAodWq1itCpkA6aX9F473BU9oEIvLgJjaDw5dAjF1zJqTwQXbQtJHdPGNRwOQ+qZrwyE8MwK1NzR8xi5ZsLBI1tlBKXyNEkgP8dAhoAOBxOUlLS1q1bZ86c6ejoyPDOTk5OCxcu9PPzi4mJyc7O5vP5FKWfH6Bv04YPQ4/9h52BH27pfxQTQKL/FiYrRghMa/6PveuAi+JM3wNIDUWCoAHLWU+jxhIvRnNpnlFzMcZLTC6nRi+WnDHJGaOxJRasIKIoIgKCIBCpAkqkSe9SpXdY2la277Sd2fd/345u9szd/3K5WJLs/PjBt8vsV56Zb/ad53vmeZne3t6MjIwDBw688cYb48ePt7Gx4XyiMQxzcnIaN27cihUrrn5ztba2lqbp/6ctQxMPoWD4TjHuD03TXG6Y7OzsZcuWWVlZrVmzJjc3d+fOnSNGjJgxY0ZCQoJMJjMQ0GhuGW0PodumJkwImBAwIfCjETAR0D8aOtMHTQj8uhDg4jz0mCJJCoXCl156yc3Nbf369fX19atWrbKxsdm+fXtnZ6fBnswoFvqn4o9AjQvL+Hz+kiV1LslcAAAgAElEQVRLrK2tP/vsM4OAwlDbL4B6NoyFo/jlcvmxY8dcXFw2bdo0Wb91dXVxwhPjPU1lEwIPGgHuro+z0cBxPDMzc82aNW5ububm5o6Ojs7OzuvWrfv000/HjBnD3YU+99xzSUlJXK+4GySDqMf4FutBd9tUvwmBB4cAi1g2Hcc+IztO/e3/Xb5NT6Ldf6rfY4ZRlxABB8iBQasDWtdcVHH8s12r5r863cXDFjO3sLCwcbAfPXr0+pXv7t/82dG/bf/wxdcXjZw8FsM2zVm0e/G7SZ5+HVczKg6HaK+VwR1BjnfIncQMpNYU6r0ylBqQ4eIbJeUHAqG0p/bklabABJT9jwL0o9CJcmrSDl+QZ9dCtwj4Ck1917Uzwb1VDUhY2yHtCUjKe/8r3rEotqYLcBY0lI6gGJpmcRI5KPdIq85elSQWIT5Uh0yAKSUBGugOT/92y2FJfD4oEGHNkJSOINRivSC3X5rld2kwqxTqeS2XrnXHZeCtfQgBkkVEbUpl1Y5z3247QZQ2IyIbpQLUIY12cXP5kRBpdI4yriB//3mo5TFifZY/LUCroPpCbI1fNNzu6bqcmnM0ELpl7ID0LnOtBSK79uYe35bruaBmtHIF0hpzG1/BpFW2bw8o/cATMutR2j2CVANDgRYoCrHzjfzcz336zichlwYpSQ0pkOK7hld3IgKSKxVROZV+UUxLPyFH+eWQX4caR44r/QqIL019b+e3h/yotl4Y0iCcxQrokdw5fWUoMg1aRIKUgmK/cG1tB8gIIBmkiCf1uRx7FFUnwsq9wkCIeF7kQI1ToKaVla1Vx0IFZ5M6vaN12fUgI2kVrmNYSksjQh3lXiSbIm6kfnw4f+85tqoTZKSOQkbbyqKGiuOhbHxp84krvOgMZDBCIt23mFCJBELgKSoPBqWs2SOPzAYxDQqmP68y+/wVaOiHfhLyW0u9QvtulSOeGpHCOsBpoIBt6sv0Dm6NzUADSchL3OU1kF8Vesz3adfRbha2zubWbs4uLy177ZPdO3JyciQSiQhXqpFBDaNiKKWOVutokkXpH5EkmWbunvYc6czNAmRcgzStyFFdB6yWUapVUpVCjePoI9zG6Cg1rsVRnk8EhU7X0t+z/fD+ZxY+5+bhbjXM8gkzy/nTZp46dLSnq0smEAEF0pzqrAP+eHqVrrQt7WiAOL0cuhW1F+Iqg+KojgGtDB19XK1hlDioWeiS1Z69eu2L4+jQaxEzDXK251pu1ZFLdYculRy4ANU9rYUVbyxdhlmYWdqh5HiLXny5sbYO6aa13/3oGBalIUULTv9r3Ht34I/HHy7+R7NTn4glMDDw5ZdfdnBw4CTGGIZNmjRp3759WVlZfX19nEjCwI3+ExBGLx70yNrb2y9cuLBgwQIDP45WKezsXFxclixZkpCQwD2saejG/Vdswz8eUYFlWY6G7u/v37hx4/Dhw5977rmYmJjTp087OTmNGTPGz8/P0GdjTt8IY1R8RN03NWtCwISACYF/i4CJgP630Jj+YULAhIAxAgqFgnssrqen56233nJzc9u4cWNXV9cnn3wyZsyY9evXi0QiA/vMffC+MIh7aVznf1VOTU0dMWKEk5NTRkbGfToIjrH9H+v/rzrzEHZmWTYvL49z01u+fLm9vX1CQgKOo1uvh9C6qQkTAsYIcGcdd0c3b948Lk+9ra3t7Nmzd+7c+fHHH9vZ2Zmbmw8fPnzNmjUCgYC7U6X0XrQGXdgvbIYa42Mq/woR+JdfcP/2+syRznrxJuKntIh0Q44ZEnnNrYKLh73rMguqswu+3r132ozplnY2GHrA33KKo9vyWQt2rVq/66217057/sM5r842d/6928StL72Z8sUJ8np54/m48qBYTecAoi+HVCi1nYKWFtaVHLigiy0RhKWVeoWSle2IXSV1KL1ew0DyV2dEabdhkAQVSMoaEo+ek5U1IjPcfmXv5Ztpfz0weCQKbjWBSIU6iVNA0DqCAhUJvfKywLjyM9EwQOrZUj2FqtThaTUZn3h1B6VAuxg0FElTWooADYGsMJRMTWh8U+g1qO9tjUot9b8CrQPMkBL5U+Ogzakv/tuJvM1Hh9LLQaAAnNYqNKxECUL8jm+UOrYAT6/K8wnlZ5Qhea9WT7z2K9ojUqtOhEG7ksiuLfCLgLpeEGpouYrECVDgbDu/2CesMyYTZBrQAa1WI7mxXt0MRS3VO/xqPjxOBWUATwUK5LWKCE6aAh3gJU2Zu3zrj4ZBQSvyudAha2YYVNWfiyHiisThGTf3nVZWtwHBKEhcqaPRGFUEKLRQ3NK4w692z1mmpRcIEllXyzW6zsHigMiu8GS43alJLc084i8prEbErobSUTQSXGtoaBXe8Y8pORYC9f3AAKFUIbcTLUBDX9HxkB6/+NYTkerkUhChh06GKA0Sk2pZRDSLFEPp5d9uO5G585QyuwZ5jKg1KAsiX1YfGK++kjMUkoYOR6cEnQ8aWi1ToFNOomq/mJSx2bP3Ygo0i6BLPFTdevmrE0NFdSCigKdqOBWluFYMEhJoQKkRcRKkONs6kHs2ovd6AfAJflpplncwebsN2bYIlG0puZtfXj7NceTwYTZPDHfEMGz27NnvvPOOT6B/RXN9n4CvokmJFheRiE2Wy+V3yVkti2homtFRNPohKMApFtdLG2iK1fPUOEUit26GYVlWq1/P0Gf4RB/RKJQdza0BAQEvLl08bLi9taO9rZX1iGG2i595zufL/byqBrRQgZYNenIPBUBGHTSIq8/H9F3Lg368Jz67LjSJbeojRXq3FnTodSh1JB9vPR2TvHG/prABZLRe/qyBO71FR4IEwanZX/qShY2DpXV/+dMq5OdgZWnn6DDK3T0jK5O76P0aCGiNRkMQBE3TOTk57777roODA2fxbGFh4erqum7duoKCAu7pKIJAWS6Nk/79d9fJ//mLhKNiDfS3QCC4cuXKunXrJkyYYGVlZUha6O7uvmPHjpqaGpVKpVAoKAol0vyfG/+JK+DGQtN0X1/f9u3bXV1dZ86cGR0dHRERMXbs2OHDh/v7+0skErlcjuP49580NUVcP/HxMFVnQsCEwE+EgImA/omANFVjQuBXgIBKpRKJRJ9//rmdnd2qVatycnI47fOHH35IEARJkvc91PYv484fh5NKpfrss88sLS1ffPHFzs7O72cwM7T14+p/PD+F4/ibb77p7u7+5ptvWltb79q1SyZDz42aNhMCDxkBgUCQmpr67rvvcjJnKyur0aNHL1u27KuvvnrllVdsbW0tLS2nTZt26tQpoVCoVCq5NSFDvkHD9HwM7/EeMpKm5n69CNzzrkWzgNUhpSTNygaFlTkFgpZOkGl0SlwkEObm5/n4nV7+1orhtvZP2Tm5YFaT7FyWTJmzavaL+1dt+PMzL6x8ev4LT45b5v605/J1fu9sKfSPpIUyRL8iQg3wsuayE6G6lAo8Kq/NLxbq+kGs0iEvY1pQ0lB+JhrPqAUhAXwN3O6pOhnRnpgNYgq6VILg1IK/+1R7hkBlF/D1ZCilJ6BJBtQkiFT9SYWZhy6wrXzQ6HRa1Bb0q+iMO7V7L3adikMsql7+TNIURSMCGnpEzdGpxf6XoZ5H3izLOXJO1dhGioaQ+FeohILWxq+Db/31oDAyEyl8Naj/iH1Giumw5ouJUNJR5h/dfj0PcdMEYp813Xzh9eKGU1GQ38rmNzZeTaPqe2BQBQqaJkhKjcOgMs07qPRyAohVnAk10ilLlSCUMdXtrccul3x0VOh/DRoEKEMgTgHLoh8NKb/dUHY4OPXjw2RhIwwiITkiglskTX4xvLBUZUppwbFgaXG9ZkguJTVqhqK0NE3iIMfpW9Ut3hHlB/21RXUg1xByOWhpdlDYmZxVG3SVqWpR5VeXnAhW51aDRI5spmkGUa4UA4OynsupqZ+fQEOgANHKuN50+E5vm19s35n4jpPRg+HpiETWIqSFNEp4iEpSUppRUfmlf9WOc6LkIpASOEsPaZQg1tz2j+44n9B26mrr+XhoEiBJO0ErCVwhk0OvZDA2J2OzZ9epGJRpcIjWVXTknbvSmVeOck5W8Rr8Y9vCb0C/fuwUcpJBjtKd4prghJaYdGgWsFWdOQGRLdkliCWXE6AGKrf+0oZdB9dv/dt7aye5j7EdZmVvZ4eZm9k7O02fPv0vb74d6OcfEBH6TVpKRXVVT09PZ3dXe8/dH6lKIVUpZGqlUqmk5SqtPp2jGsdpgmT1qwIksEqKUOAanCIpLU1pkb67rrHhtN+Z1994Y/KEiTaYmZOF9ShH52muo//+h7dDtx9qzi9DB05EwJ3egpOhSABe0tnsH9cflwN1fDK5rCkwQXynDVggOAsU5KNNAx+XpZTkb/NRJRYDX45WVjQ6ZX5d+YHArtOxzf5xkluV/Jrmte/+2d7e3szK0uoJ2/FTJiVcS1RpNOIhCQM6Y7u57yugfzGXO4FAcOHChVmzZtnZ2c2dO5fjc59//vmIiAilUskZxHGDNahx/wkZ4yBAX34IyBhyd0ul0tTU1P3798+bN8/gEG1tbT137tyIiAg+n89ZKj+ELv2IJrioCcdxf3//KVOmzJgx4+jRo2FhYU8//bSTk9OOHTtEIhHH+BsANwb7R7Ro+ogJARMCJgQeKAImAvqBwmuq3ITALw2Bffv22draLl26tKGhYfPmzba2tvPmzaurq+O0DwZemAuYjGMgQ/lHIKLT6aRS6YIFC8zMzBISEgwxpXFV/0v9xvU8bmVfX99x48YtXrzYw8Nj9erVEonkceuhqT+/eAT6+vp8fHxmzJhhZWVlb2/v6Og4Z84cX1/fzz//3NnZmfNYXLZsWU1NDaNlpFIpZwHPTcnvq3J+8XCZBmhC4F8jYERAo9nBsMgmGScpmRI5OSD6+K7hgFAqaWppjoyM/OvaDyaO9HCztBuF2fzGwuEPk2b9Zf6iL/60duuyVX+a/vwHv1u00HHMwqcmbV6zLvlaEi1XwYCsxi9aE50HmY13joer0yqhTUAJpKRETnTwM3zD+HH50CaHQTV0Syu9w6XROcBTglgHyVX5Hx0r/uq8Pj0gi/pDo+4BSYOaAgU5VN5YcPIy1A0AAWqFGiUkVOp0aXcqvjhXst0P6pHBNIsjTTHyl9AQICdaIq/nHvKHpkEob8n3PKcuqNGJhwjZEGgoaBW2Ho3IWLOvP+g6oOUqZLwAGprtERVfiqsKjod6fvnZqJqo69AvRfujXGO62ri0PM8LUNoFt3uu7fXhZZcjhS8JoNAnPZQoCwOisryDZXUdSDLMEMh6AydAKIe2wYaAmJyNB4V+8XC7A+WX0yA1MRomzkLrQPJXPkmfHhYk5CFtrxRHvyVs3YkI8aU0XXb9t4fOKUsaQSCXKuQKliIYlLkOyZ8beNUHL2Z9fESQUcR1ksY1hFBYGJtYEBgBTT1US/etoPC+pBzkOMzqcJYkkNUEDTg9UFKb+qWPOqsaFATNMJxVrqq1t9A/sicgqXJ/YFtgInTJkApbh4YoJTW0VIk45W5Vye5z+RsPQ2IZCHGkTwdQiqWl56ObfKL6LiQXHrxAlLciE2oNjcsUKiky8u6Py0nZdKBwx2m43YMMuIWqjOOB/OtFaKS9sqqz0Xf8Y6BlACgghFKQ49o+MShhMDanwisMavqhovPGYf/evEpQEVqF3qCjQ5z5lV/e8WBJXbuY11+cke1z5PiixYvH/macu9tIB8xigvVwV3ObJxwdnpo4bsGCBcv/+Maf3l315p/v/qze9OHqTR9+8NHGjZs3fbph82cbP/r444//tvXjz7Z+suPz7bu+2rvb88D5kKArsVczb2WVV1ScPe+/48udv3/5JXsnR3Nzc2d7x7EOLmOtHJ/3mByx70TyLm8koh+UI4K+W1l3JnowNgd4yF685nQUNIuhvCtvj588oxJwWoajxQm0KUnol0Np+41tx0XxeSDVIfZZjjMt/QXHgvv9Eqr2BlQHxfNKala//76Fg63FEzbYMHM3D/fImKv0PT/3XzABbbxaLBaLjx07Nnz48Llz527evHnOnDn29vYrV66sqqoSi8V38dS7YAOAIUmggQ81WOQZAnXjyg0f/8kLhvCDq1mj0bS2tnp5eY0fP3748OHoKRP9tmvXrt7eXkPrht4a3nnkBS5RKkVRiYmJY8eOdXBw2LhxY3p6+owZM8zNzTdu3EiS5L9D+5F33tQBEwImBEwI3IeAiYC+DxDTSxMCJgT+CQGdTsepm2Uy2bZt22xtbZcvX15fX+/p6eno6Dh58uSmpiZO+4BuqLX3si8Zh5n/XP6n2n/YC0bLdHZ2uru7Ozs7l5eXf99/w7iFH1blz2avgoKCqVOnTps2beTIkW+88cZ9Wd1+NsMwdfSxR8BwQ6jT6ZAqjaZJkpTJZCUlJevWrbO3t7fSb25ubkuXLg0ICFi/fj3n+Ozm5rZ///6qqiquBsPNm2FW3vfOY4+EqYMmBB4MAvcIaEPCKL1XrL6te6axjN5XmnOX1oKO198XezVmy4cb50ycOsrS/ikLO2fM7GnX0Svmvfjlnz747I33Jji6jnJ0Hv6EwzSPcYdWbUzafrzhRARkNdXsD5ImFoCEADkOcoLqFtyOSELZ/1oFMIhDtyLf+1LPtVzo04AUyG8ryz/2TlmzR1XVhqw2KORjSwJL6BhOWD1UVHft0JnBglrtgFQhU2pxGuQMFHc0fR6Qt/ogW9CCfBvQY/cUyTKIs+4SCG4UZh/y0yTmQ72wKyihP6MQxFJgWCC0IKTqvcOvr9vHC0yGXjkyplCTyDFDRjXEpBX5hkNlT1VwfEloPNUxgAhBkgKCEeRWfXvAD6mzm4TZx4MaolJBoEL0Mc0i3rBf1p1aUB4UCw19eh2rTgY6xGzTWmgb6ApLSd3wdfORUCjtABULpBYZQ8vVyGejqrtwn3/yZ0eHCmpBTiKXEhKAp+RFZfWH3UQS2uCklsQsUHHG1ug3OmAkC3W9bT6ROVuO9F25CSoNA1oFoRQPDnYUlUUd8+GVVvRV1Pgf8PTc8unVY6dDDh4/c+RExDdRoSlxcek3rlwI9tzwaZJXQM31rLKyspyy4sKcvM47jdeiYnJikgezyitC4nVtfFAxOiUSBSO6U6tDHtmNooYd5wvXHVLFFyG1MgNI9y3FBzLLbh8PpRNL672vEEWNOoJSUgRy3pAR0KuQJxVfW7snb4evIqcGFCxI8Bvnw3ICIhHB3avqu5ZX6hsB7SKU2BAtBei17VJKklmBMkMWdkFhT83R0MGbJYgNRwsSNNT0VR69VO4XKatoBpLW0KRIIlaolD0ifl5BfmpYtOcHH+96a+2rE2Y8M2HKKBdXR1s7q2GWmKUFZo5hw8wwC2yYo52zx0iPyRPGT5o4yX3MONdRLi4ujsOdRrt7eDzl7uo+avhI1xFPjRwzbuyE34yfNX3G2Kc8LDDMyswcw7An7RxGOgx//ulZfjv214YnF3uHooWWPg3SwgvJpnOxkohMaBQLE/OrTkciwv2O4PapiP6UAkQ3663b9X7b+uSZVT3pX54aiM/VCeX4kBw51TQPlPpG1HhHtB27wgtMFuRX/33TFszBxuIpZ8zKHDPHtu38QiSTGiysDQS0sfaZ84BGZ5fh58FcUR5orYyW4WjNvr6+ffv2ubm5LViw4Pjx40uXLnV0dNyxY0dra6ux/QjnWcwR0Mjy+95miATuKzzQzv8/lbMsW1dXt2/fvunTp1voNzc3tzVr1jQ1NbEsi+M413lDRPT/VPUw/6XT6bistjk5OdOnT8cwbPXq1fn5+e+8846Njc0HH3xQXl6OLnj6zLfGUD/MTpraMiFgQsCEwA9BwERA/xCUTPuYEPj1IsCJGZVKpY+Pj42NzYsvvpiTk+Pl5eXg4DBz5sz6+nouVmO0DI4jG797Mec/Z2AxioZ+BJQsy2ZkZLi4uCxevLirq+v7caFR9Y+diduPGK/hIxRFKZXKZ599lsv08vrrr3PuuoYdTAUTAj8tAtzDs1ydfX1958+fnzVrlpubm5mZmZ2d3axZs7y8vDw9PWfOnIlhGKeHSkxMFIlE3Kw0JBs0UGxchb/UGfrTgm+q7ReOwPcIaMN3GcdnMYCoVEZPANL6lIFqhlISeF9fX15W9pG9+5c8/+JTNo7OmJUzZjnJzuX1Zxdu/uuGFSvfmjdvnscTw9dOW7h1wsLDv3vr+t8O3TrgD618xCbrgOIJU8+F1iakA08GCgAx0xGe2hGVxjb1IUVtXlPuZ17FH3vp0mtgSKVlEfvMsoiARr4HUhXTNpB69HxvapFOoAQaWBUFUkqb09jiGV601hPib4OQ1BHI+hnXUjRBAk5pKlvyTlzUpt+GOn6Xz5XO4AQQDbG4Gkm8+6WDwSn5W462+URDoxA58CI+Vwd8BT+n8ttD56Ckoz86syoiGW/tQ36+ADhf0l5QUXIxhsirhw5Z4dkrtdE3gCcFDctKVYgwZaApNv3mwXPC7ErEIcoJYHQo56KWptp6awNj8nb43DkcjLTPEhIIrUalwHE9+9wiqvMMzt/mwwu/iTyvWSAEchATZf5Xbx+/rIkrar2Q0PJNGgzhFIVGh1wyVBTqbbeoLyQlZ+tRZVweCHFSLW8d7Ky8U+V/6tTmlW//9fXl7//xj8/Pfsbd3t7ZzNzd+glXa7snLKzMrCwxOwvn33hMHzdxkpPb066jp/1m4pgpE92nTJg7c9b8Z+a89PsXfY97qTr7YVCm5glkvXxKjQhovVsLQLuo40Ji/oeeMv/ryEZDr/vWKXFxZkWTX4wupSJ39xm6oBH4Cgp0Ei1OKTUgJrXXyoq2nLj5kacspQTEJAzIyuNSK2NS2ToedMt7Y7JyjwXpqrvQmQAokyayflaQeFX7za/PsN9WQcVA1YGg3ss3EeBKPfnOV7b4Xs3Z5q0pbQKxEnSgpJBDioZEHsGgoVuvZWd7BScd9S8Ii1M2dhWnpH+1fedfP1j326enuXm4Y8PMMUsLhyeHz5wz+53339u2bduhnXuO7d1/+PDhY14nPL8+8OnHW99YueK5FxY8YWNrb2E1YcSo8U+OXDhjzoZV73M/b/1h6RnP481FFf2F1Xk+oeStWmhFWQehrq/cLxI5ujRI+N9klZ8Mh5IOaJFWnAzvuJoBvRKQqoDR0QxDoKShAHd4xUeDW0NTEHMNgB6tG1S2hCS3+8cPBt0oPxBIFzTuXb9lxIgRmAWG2ZmbOdh+sOHDDl6PmkTjvTdn71pw/PIIaE6VT5JkUFDQxIkTFy5cePDgwSVLlri7ux87dqyvr8/ANRsMl7nFZsNdAFcw/vY3Lj+Sqz3HqtM0rVKpKioqtm3bxnmJODg4vP766+np6QYDsUfSvf/YqE6nUygUdXV1GzduHDFixGuvvXblypUNGzZw/oTZ2dmcHYrxqv9/rNO0gwkBEwImBB4yAiYC+iEDbmrOhMDPDwGBQODv729hYfHss8+2t7cHBQU5OjpOnTq1rKzMQDPdF3EaRz/GEafhfvu/ReHQoUP29vYHDhzQaDT3ffYnqf++Oh+Tl5yxyapVqywtLTEMW79+vckD+jE5NL+8btw3N3Nyct5//31bW1s7OztnZ2d7e/t/+MCEhIR89NFHDg4OXCafdevW1dfXEwQybzU8AGGY+xxExtPzlweaaUQmBH4cAgYCS0+f/hPvTOsJaBxYNTBq0DGIidbhFKKS2+obfT2PTXtq7BinEcMwzNrcwsrKavJvp/xxxZsb/rL2g/mLF5iNWOM++52xsxfPmLd966ftTc20VHndP7TkmxRSJNMJ5TBIDl0rqjh/FbqkIKdVZU3V+y7k/PWQMq4AWWEoEHWLjCkoFnliqChoF6d9dUZ4sxR49x6071dAYXvX3pCqzV59ITeQnlqJsg4qdISaIUBDqVs600LCBQW3oUfOD71evv8cNPcDpSc4BXJJbNatv+7v8YqEKh4odcgGgWLZAamgqDZutxeb26CJK0r69DBK98cAkv3ijLS4PuWI/2BRDQg0A/G5NYFxyJeD5HxCAMSqofLG6/t8haklgAMulKJPafW+FX2K7uCk8i/9ao+GKNLK9XJpLYvjDE2qcKWuX9R3Jrbqk5OIsuyUgESDtM9ypvabm1megVA3JPBPrjgcAgMKoFg1Q6kZvfxZgTBpvph4dsWG+sBYvKqVX9d89ND++c/NdTCzcLW2c7G3c3Gyd3V2GOnsNMrB3mmYhSWGWVqYDbO1RvpfDLOysnKys7e3tLbCzNBrG0vM3sbGztbO2sZqmKWbs8vCZ+b+ff2mzzd8dHDHbs/d+3yPe126dOn6N3ExB31DN+/JOXwBKjvpXhFoaFoo42WXlx0NgaSKir0ByPVYQaEjyOp5ZBoUt6rrPjtT+Tfvu24bnZKO2MyK0AR09HkqcUpxtmcAXdqKZNE4sn9BPLtQqmjuKQuNV6RVQL2oISCu6HwU0ylAWRNVFIjw7ris7C99ddn1IKeR5QUDOoLSqPS+FgJld2JOtVd4/v7zFVeSNfVd0MzPDoruvNPI4/HKikuuJya9/867s6bPmDRuvI2FpZWZ+diR7s/9dsbzM2bPnz9/wQsLn5v77NNTp7mMcbdzdHC3dfrDlNlvP/vSmc/39RfXoESUYjz3alJWQgryBO+VZJ0LvxNzE9HHMgr65D2XUxt9o6Gihy1sytrnB0Ud0I23hiTXXoyHbgkokUs4R5USGpzoFVafj6nwvQK9MmABCdvVVENUart/PB6RU3c4VJ5d7bdj/5MWKB2oxZMOmL3Va28tF8mkDICxAlo/f42/5b4r/7grw+PzKU5cUlZWtmjRosmTJ8fExCxZssTJyengwYN9fX0cUXufAvr7NwKGeOA7XO6VHtVIOZkzZxhI0/SNGzeWLl1qZoYm40svvVReXs7ls3lU3fuP7XL48fn8rVu3Yhg2ffr0kJCQffv22dvbT58+vduqF2UAACAASURBVLi4WC6XczkVuT3/Y4WmHUwImBAwIfCQETAR0A8ZcFNzJgR+HggY2CiWZQMDA8eMGTNp0qT09PTU1NSpU6e6ubllZWUZuGAu1ZghEv1pVQ9cmLh+/Xpra2tfX1+OkzWAeC+U/e6v4V8/08J3I9FbmhAEsX37dkdHRysrq0OHDhEEYTDa/pkO0NTtxxYBztymoaHh9OnTU6ZM8fDwcHR0tLGxmTZt2r59+65+c/Wll15ycHBwdHQcNWqUr6+vTCbjPmJIQGqcdZAbpvH5/NgO3NQxEwIPGYH7CGiOdL7vN6k3CVCwlIzC1SRa5tGoVOJ+fnd984VTZ5YuXTpu/HgzMzMLS0tLOxv3UaNWvbp085KV6559daHbBDvM/ElHp0Vz5h/Zsv2bQ77quk6kJh7CBdfya89EQy0PeuTQJio4Fpy95ViHbwzIANQsKAlE3eoAcdAqGnrljefjmgLioY0PNGhxEtkv3Blo3X+p67OzfZ7h0DNEiaUMSeBaREBrKQIE0tJL33QWlQHJ0vm1FSdDdGVNoKJVMgmATltwp2jHyZLdfpDfiMTIOItoTZxV1bTfvhgLBc2QWVd2KAg5I6tZlKuQhYGqxizvYF1pG9s60HazABl0NA6ADtQKJcoTSIGspKHwdHjHlZuICtfoTbQZPfssoCG/veXroLJtPpLYbMRRarVDhIJgkGG0rK27PjKleNtJlJOwWYCo5wEZKHXK/IZa/zgo6FBE5lV8dQHKu0DFMFpGzSAFNMofKKPaI1KvrN+Vcfhchn/otvUbnIY7YBg2zHqYm529PYa5uDjNfm7WuvWrD361e/lrf1g4b57zk05Ors6Ori7OriNcnJ3d3UZOmThp7ty5M2bMmP3s3Jm/mztp+jTbJ+zMzMysLa2esLEdhpk9YWFliWHDMGy4la2dpbWFhYUVZuaMYb/BbH5jZv/S1Nnvr3j7xKHDIV6nz3+2r+TEpXqfyIbT0dCvARWBLNHUJHIa4SnLDwTe3nyCDM0CKQtymv9tScmpcGVuLQgoKG0v94vUVrQjI2k5QUiR2JxS4xRPWBl9vTU2Awap3m8yC/0jiS4+WmKUa2AIV+TUJH5+TJpWjvJYqihGjZYc0IFAEmKazqqtPxbe5B2JiN02PgwqbgdcrY9OBQWBoNPQHaXVgUd98pJSyzNzM2OTzu713PDaW3+c/tyiqXPmTJ0+derUF55fsGLFii3bPj1y4FBO8NWoXcfzQ2OhRwwCHHqk1VdTa65lKJp7QKQqCY1vT8pBGRQFSuDL6xMyavyioZwHxa35J0Kk8fnQrpQm6k+YPuS8QWhwLTqz0Yb3Cnm5FTneIWgisIDgGtLw0kuqfSM7/eLuHA8XXSsI3n9i0qjRbk7OaLXVxvL3SxbdaW2idKyGJpl78meDCJpBK7D3b1xbP9/fOp2Oz+d/+umn48eP//jjj9etWzd27NitW7e2trbi+u1fKqC/z0Hfj8u9148EGa5xrmmdTsc9tcnn8w8cODB+/Hg7O7vXXnuttraWI98NCptH0tX/v1HOIe3cuXNjxowZP378If02evTokSNHRkdH4zhuoP7//3pM/zUhYELAhMDDR8BEQD98zE0tmhD4GSDA6RlJkoyMjJw8efLIkSOjoqKSkpKmTJkybdq0uLg4qVSKxDL6KMcQcXJB209LQHOPAW7ZssXGxuaLL74Qi8VchpN7QSx6/tFQNvDmPwOI/1UXuYEY8ORM3/bv38/xgImJidzY/9VHTe+ZEPivETDMF07FLJFIcnNz16xZM3LkSEtLSxsbm5EjR27YsCE6Onrt2rXj9WwXhmHLly/PzMxUKBSGE9XAO/+0c/+/Ho/pAyYEflYI3COw7iqgDRYcXMFIHI0sA+5OLoalNYRKrmhtbb1y5cpHH300euwYRxdnzBwbPtLV3d39mQlT1r++csPSlQvdJrw9Ye6aqQveefr5Txa/neETUhuWlLbfD8o7gE9Al6Jub2Dh3453hd5AGlINraNQcjxE+3Jbj7zqZMSd01egoRcRvko5ECR0CWq8Qpu+uth1KBTKOgCncQaRvnJWTZAqeWd3/pnQxrBrIFRqW3tzzgQLc8pArgQCB4kcmnrLdp7O/OiQ8FY5coJG7A4gArpbVOYfrYgvgKym+mPhUNSK9Kp6qrD/TvOt4GhJbjW0iZXZNWUBV5VFDaBEPWRoGqQENPanf+13JyAW+CTKp6citTipEElABXCrbeCrsDs7/HuDr8MAzhkckwASLQ4aWhydXbXjXKV3OHRJ8EG9uFtISNOr7nhFQnINJFTc8Qyj8xpQvj6C0ScOpFGHZTgvt+LytoOH3lz37jMvzHoKLQBgVhg20gFzsZkybcqnH310LSGuprYKWKa1uXHliuVzZj3z0UcffX3wQEh4WOrNm7GxsWlpaZWVle3t7a2trY2NjSVlpampqa+++ur2bZ9HXA6PvRpz6tSp7du3r1j+5u/mPuuif/qES/RqgWHWGOZobuVi5zD2KY+RT46wxcymPum+ZNLsv8x+KeGIH3QKAdeBmkYpBFuFglPxhesO8c4mgIAFCShza7894KcrbweeQlveVnchbiirEtGvOkDpK3Fkr6Hk8UsvJzRF3IDKnv6E3FsnQ1CdGooQy0BCMqWt6bt9xTdKQKSkVUjSjrxBGB0ioIcIXVFz064LbbuDmi8mMvU86JdVxqRWB8UjklcgBxXNz6lM8TzXm1UGQr1cWqwZTCkoOhLUHXEzesfRnIj4gfaujq7Orl6eXCxheKK6C3H90Zl4Qw8IldAt7bqWk3cxmqzphFZhVXB8cUA0csFW6aBfdueb1BvHA9C/umVVpyMHw9OhXkRl1ty+GIuk9CqK1TIyCtcAq9Ev5HSnFuScDkPJKlV6UxEK+MkFLb5X8cvZ5QcCO1PyLnv7zZ40VS9Qx8zNzafPnFFUXqpQKWmGQTPxnlWOYZ4arycZytw0+vn+xnE8OTl55MiRS5cu3bp1q6ur69q1a9vb242/943LxnH4Dyk/EmS4jhk3zVlX4zielJQ0Z84cKyurJUuWZGZmcgqb7+9v/NlHVTbArlKpYmNjJ02aZGNjs379+lOnTrm5uY0cOTIwMJC7deLujx5VP03tmhAwIWBC4F8iYCKg/yUspjdNCPxKEeAMW2maZllWqVRmZGSMHj0aw7CkpKTExMQxY8a4ublFRERIJBIuLKMoyhAJ3Vf4dwHof4ssR7keP37c0dHx+eef5/F4KpXqPuLbuK3/tv7Han8Of4OWnKMFd+3aZWVlxflfIxHc90xIHqshmDrzs0OAo6EHBgaCgoLc3d1tbGxs9duECRNOnDjR2Nj49p/e5lLGm5ub7927d2BgQKFQKJXK+6a84aXxfDQu/+yQMXXYhMADRcDAVRkXDPrKf9c09zWBbJpJsrOz09vbe+PmTbPnz0NOtRhmb2//lJ3TyxNmfPLyii9fWrnIbsysYS6zzZ1XOE06tuj9xF1eUN0D/WSTT1T+h558v0SUfY5icZZW6/QcNEnjag3I8IFvsmLX72FLmkGsBpQETwsKIu/0pcrDQZVfnYfsO9AnA5LAdbiSUeuABpky52L4DU8/aBNCpyArMKIxKQ0GhIivU+HQwEv+7HDi6p2Q16Aflw5ZG8s1wBN/eyxgICIdbtbmbPOWx+VDv97WWUUNNraHefp0phVBtwwa+blHAnkJOTAgB6Ve5KvVQa/s+j7fPK8Q4CmQnlpO6jToB/lK1/Aq1h/t/Niv/dRVZBCsoBHTCiBTKtQDIt6NgpwNng17AqGhnxXKEYWqIqBhoML7CqTWQUJF3aEwKOwAvgbUDBC0lqQQJgQ9UNN0bMsXr42fOdXK2RHDbDAzzMoCc3HwWDh7zznv9t4ulUKGhN4UgTSyLCOTDaGXLEszDKWlcYpU4zjnlYwyNlIUd+3VkhRK9sgi0l2tQNdVSkurcVyhUg7w+QnXEtetWzd58mRnZ2dLS0t7O7sJvxm/8s0Vby57feXry19+dr4LZuVubjfR1vmVKbMKY1KobgFIifrIG2lr9vV6XoHqXpCwVHZdyYlLghvFiJqv6rl58Fxr1E3gq0AHuFZvLcIAK5TXXMvIPXkJ6gV4elW2VzDV0ofobIUGJEpoERQcC+6NydI29qLBAShUStRtHcrrB1VdjUfCZMdiqz71VRfUAwmNqbnpZ8MQE90pQgLzQUWOX7ggvQxZk8sYGKKgpqdgt58yLLP2WFh/Qi70ywCnNSTBaBmQE/Vx6Rl7Tmtv1SGfFgXdHJeR5xNKl7eBgCo8EVLqEw5tIpCzMKjszSrL8w2Dyk4QaLLOhddfSoJ2OVTyMg8HoOyRgzIgaRVNynUUBTqdXCOqaLx16hIvvQQpvpUaoEFS1tBwKooIzeo4HtkWlBTtGzBu9Jhh5uYOT9hjGDZ27NiioiIUiN5jn38lBLREItmzZ4+FhcUHH3wwadKkefPmFRQUGKtMDN/4XMH4u/6HlP/d9e2Bvs917PtNsCwrlUozMjKmTZuGYdjcuXMrKytRSk69wOX7+z+qd7j+G5DnelhQUDBp0iQHB4dNmzbl5+fPmDHDysrq4MGDhgdGDVKDR9VtU7smBEwImBAwRsBEQBujYSqbEPi1I8BoGYJANwA6na6goGDcuHFOTk7BwcHZ2dnz588fM2bMpUuXBAKB4cbpvmDoAQWdLMtGR0ePGDHC1tY2KCiIC6oMEdgvTAFt7Gei0+lUKtXs2bMxDAsODuYWBn7t56hp/D8pAizL9vb2pqSkbNq0ycPDw83NzcHBwcPD4913342NjT106NCECRPMzc3NzMxmzJgRExNDUZThrobrCEeHPaC5/5OO1VSZCYHHCwED72zoluEdPV9qePu7gsFs3fCWQL8VlhSf8PZ6+eWX3V1cncysHDDMGcN+5zJ288vL/zr/tUXDx3/41Jy3rMe9aDXq45mvpq3Zl/be7ttHL0EzHwidXC5XAC0DGmcRB60TK1qSshM+3i+Oz0HOyBQDWlbT1dccff32qdAq37DeqzdBrAGJXKuUakklUIS2s2cwOas26CrV0s3yBu9cTc4OCFM0d6EsiCQwlW3lu/3TNhzsjclChglaFuUqlBHQJWkIiGv1i4VvazrOJ7Rcvo5sNPpk0CdTlzeneQc1JGYS1R3QrSj2Du0IT4UOsU6JHv5H/enmV15KKPCLILuQPQjyklaRKIGekqRrOtv8Yls2n+rYdp4sbLxrEEGzlBpne0RMXEnBBwfzPvWCii5dn4SSKRHv2dZXF5w8dCUbslrazyWK0m4jHlzFIGE4QWlJSq1QluUXvf/6iskj3N0sbC31YuSxT3msfPvtoMjwPplYqFHQLKUXdeuPjJ5NxnE1rSVpBnGX2nvmWegQsyxN00ql0kAMMTRN4sTdRHZcBQBalmX0/DVFUQRBVFRUhIaG/m3T5sWLFo0c4WplZj71NxOX/f6VLz78yGf3gS1vr37WY+JYK8ftf/nw2oWwi7s8kcVETS8M4qqC+qbAhK7LqUgJ3iys841CSRd5UpBpNCoVCucICiSqgcyycr9IKGxlMmubAuIVhfWczBmxzx2CgnNXGr65yQ5I0c76DVdraA2BGP82/tD569qzqUWfeEtickGAo/SA564MZleAkmClKrqBl3kmtDTmOjqd5AQINVDTW34gUBmUxvdLbAiIg3YhOkw0ij+1Co2yuq3mUiJaKcEBJGTPrbIMnxCUgrKPGLpWlLHnNNzpRx4gg0q8rLnEP0qaUw0dEmlGRXFAtKqqjW3qSzsR2BmXhYw7hnCgGDWOk8CirlZ1ZR290JZdqhkUoxObBqqlr/RclDgsXXDhev7+8xk+IS/OmPuEDbLkxjDMycnJx8eHJEkUGOu1z9wMve9hBcNL4/lrXOYQ+3n9rq+vnzp1qoeHx9SpUydPnhwcHMydt8axt3H5h8QAxvs8bmhw6ftiY2PHjBmDYdirr75aXFzMDfDx6SoHoAF27qYAx/Gqqqply5a5uLi8+eabZ84ggyZ7e/tPPvmkubnZkKXj8RmFqScmBEwI/MoRMBHQv/ITwDR8EwJ3vesMQHDy28rKyueffx7DsHPnzmVlZb322mujRo0KCgri7pdwHCdJkisb1Fj3EcHGgaZx2dDQDy+wLJuXlzdq1Cg7O7t58+Y1NDTcp8L4H+v/4T150HsayAXuKBAEERYW5uLi4u7unpGRwbXOue4+6J6Y6v8lIcBNEAD4/skjEAh8fX2nTZvm5uY2fPhwS0vLOXPm+Pr63rx5c8OGDRMmTLCwsHBwcFi7dm1xcbFGo6EoylDJQ5j7v6SjYBqLCYH7EOAoKuM3/yNpxfkycY9Xcx/kFoxZLTMkEHU3t10JuvTJ+o2T3DxsMMzN0s4ew2Y9Ofq10U9vmbN4w9QXFrlOWuY44dQzK7xmLj+xanNxUppMIMIpEmdpgqGRr4WaZqs607/260/MBr4SWWcAgEBWHXGt4Xx0wcGzjRHXkKMC8vyV42I+KBUgU/enZOV6noGWQSB1dem3qq4mQZ+YHBCirIZ1vN6LSTdX7+0+EwcDSlauTyOsBbjD6wpOqT8cCumNvQFJtWevIicQKYkI6E7xneCEhuBElBuwXdQadbPhcgoyrVYiNwzUtFDZfbMo0zuYqO3kQEB6ag1in0FCtgQnVe4+37TdH7LbkMGxGpk+U0MKUNKDSfmlqw9WrD4EJZ0ou6CKQvRoryj3YnTX5ZuQ1157MqojKgPpqZUUEIh9ZkhEQGdnZf3hpVeesLBCGnNL67FPeaxfvfZqdHRPTw/Lsmq9FxlJovSGSMisA8Swo9SsDK1FBSRUBCBpiqQp5p4TMfc++q1DP4RGn6cRgNEitvo79llLEwSh0WjEYmQVwmqZrvaOtG9v+pzwWjB33oSnRo9/cuQbC1/x/HxXiNfprX/+wM3CdpbHhINbt6saukAD0NhfdTGuLfImdMihRVwfGN8WmAhtEuTxDaAlKdQziQqvaq8+EwW3GqCoo/5cjCClCAQqSqtHW0KUX4rPCYxCmQ/1KTEpLaLLUc8JFrpFtRfixMdj+ndfUkbnQqdcc7v1m0O+spIGkBDAgKiDVx19oy0lF/ldkAwzKIWGvrZTV8V+SaLzKQ2noqBVALiOlMiRDYgM17T0FgRdleXXwhANQ3R/TkWqd6A8uxrapIK4XNTJ2j6Q6kBC9aQVl56LIrJroUuhyalF7HmzADqFBZGJjdeykH0K0svToCYRaU7ryJa+8pPhbeE37jpvaEHV1JN5ImjwSoY0MrvlXFy6V9Bbc19wtXUY5epmgZk9YWN78OBBgUDAHSku3yA3Qw2Ms3HBePLeV/7uWP98StHR0fb29mZmZjY2Nlu2bFEokEu48Ze+gQblCsZx+A8pP25IcBdSqVT62Wefubq62travvnmmwUFBfdWjlB/DStGj6rzHLAG5Bktw+mBGC3T3Ny8bt06Z2fnefPm7d69e/ny5cOHD3/99ddzc3NNHPSjOl6mdk0ImBD4lwiYCOh/CYvpTRMCvyIEjCMq7rZ2YGBg3rx5/8irc/To0fLy8ldffdXW1vb06dMKhQI9HanX7xjTzcZl49p+QhC7uromT56MYciPb+vWrVKplOvJ96Nh48D3J+zAw6nKIH/maL7s7OxZs2aZm5svXLiwq6uL68MDQvjhDNDUyqNCgDttlEql4fEFHMfz8vLeeOMNJycnFxcXa2trDMNWrlyZkpKSmJhobW39j7yXGIbZ2toGBAQolUpGy8hkMoM/jGER6Gc94x7V4TC1a0LgxyHAfeUZPsvNPkR6sjq9G68OZRHU6sqLSj7928e/nTTZztJ6GDKLwMY5jlg049lNf3znoxde3/bM4hVOkyaaOUx3H/fh+2uSY+MR/YeyDkq0BfUlX5xqPxuj6xdpFHJkvjEo6YlL6wxOUMRl3z4dBt2DQFK4bAhH/hIAQ2pVZvmtQ37aO22A65R51Umep7Vdgyg3nQoHkabXP756h1+bXyzU9YOc0spUyHljQN5zJa3pcBiU8QdOx98+HgpCEuQ4Yga7JOVno/J8QqFVDCKmPvJGWWi8urEHCIbEEQ8LNEiTi+M371fdbr7r7MwySDCu1QFPXu93tfbroJIv9O4NA2hnvTiaAhIEKUXpnxwr/8QHkiuR1FqkAhlBdQyknw2rD0+B273lJ6+U+UXT9X1AAaVngWmGIUnySnjEcAdHDMO4i+SKd96+lZtzl40yII+skFlOwsyyrJakUFm/MaC38DbKXGc4fP+ucI/lvGvf8U9XXS3D6sMw0IFogJ+XkfXX91ZPcHN/ArNws3N8748rXprznJOF9byJ0xqzimCIEVzNbr6QAJ1iGMAFF2+UfRUAIgrR6zgi1vVHUAMtotzdZ7TJ5VDWW/Dlmb6oDFCwWokCaAZItuGbmw3f3JR293O9ZQEIhgYW2VmAjKnwvdLmHTVwMnbgdDwM6KC6t/pCbPv1PAS7DkDJloTG516MRhQzSaplCuhXdFxIJAPStBcz6s5EI4W7ggCaRewzBVDdk3nofNO3eRRPCCTgdV25F6KI0mbgqaTXS7IO+Kvy61B+RYGCrGzP8wlV59ZCh5xOrazwCkPWHyKKf70oxy+c7RGBggScAUqHzisZCRTknwpDuS6Ves8QBtgeUU1YUtfFZMhqqPAKK/GPemn8dA8HZycbu39oL550Gr7j8+0c8hzfxy0JfP9oGnPNxgf0371vvM/jWea89fbu3evq6mpmZvbCCy80NjbePfoG7vN7BeNI4IeUH5+xG3rLaBkcx6urq2fOnGlra4th2LvvvqtS6S3L9eyzYc9HGIcb+nDfEdBoNEKh8KuvvvrHc6vu7u779+/ftGmTvb39iy++mJ+fTxCESqXi7pseH+RNPTEhYELg14mAiYD+dR5306hNCNyPgCEu6ejoWLly5fjx4w8ePFhWVvbOO+9YWVl98sknEomEEwLc57/MxUCGkOgnD8sMxNmOHTtsbNBDkWPHjvX29hYKhdwYjO8QHgIVfj9wP/VriqI4mq+iomLp0qUoAzuGbdy4USaTcc8//tQNmur7tSDAGbtzvEl1dfXRo0dnzpzp7OxsY2NjYWExffp0f3///Pz8Tz/9dOTIkRiGOTo6Pvvss2lpaZz+zrDkY6CeH/Tc/7UcGNM4TQj8YATu+4Y1fPN+x0EzejIaYGBg4Ma3qcvfWjF//nxXlxEWGObm5Dz1qbG/GzN59ZyXF3tM+63zqCfMLIeZm08aN3798nfyQ2LkSYXpHx0s//wU5DdSAgmiTPnihivX2s59Q18rrDwVqrvTAUq1llCj/hIaEMnIqubCU8FQ3QF8qaqmOd/3Ej+tGORqUOMwKOuPv1Xwd+9Wrwho6Ae+AlkqMwD9MnF6eb33FUhrwC9nt56OgYYBoIGWKkFFtSVkFfuEQYcUumT9KQVZfmGCikbEdXKbmpYW1pUfCZFdK0IJ95BtA4NTJLo6qVl5TF77wbDa3QHk9XKUk1BJIE5TrAIKtOVtGTt88r48rbhWDN0KxD6rGZBSRUExlYGxUNVTE5hQciEWsc9SJNRVEqQIV4rVijNn/SaOn8AtxS145aWgyPB+sZBm0Eo8YsONCGgD+4ziEEb/oz8836cs/+PR/v8JaJT6796GLFMIqqKwxOfI8fmz57o6Dh/tOnKEg5ODmeX2tRurr6bWnomGFinwcX5G2R2vCKjlgwx5blAUIqApgVTb3FdyLGQoPJNOLG33j+8MuwHdUnSY1BTIiMqY1NLz0eLiOhzH5cBItDjO2WnTOhATLRE3OnxjBk7H3zkeDk1S6CHr/a62RNwAEQEKnBbKKiNTSi7G6DoEoGG1OKkTK5ouJXd4RYm948q/OMNWdYKKkg1J0VM1Kkrb2Fvhe0V2oxT5ZtBAtfVXRKV0JOcCT8XmNpR6heoqOpBziEhBdvFLz0cLE/NBQFO59UXHQ0TXCqBDKswozz8drihrQvQ3so5B5uSgZEFEtwSjDJzquk5ETAOASNF1Laf1QgL5Tf7t/YGJe7z/Mn/RCCs7Z3vHYebmw8zN1/xlNa+7xzi8NMjSjb04jFnm746K/ugY/+ve4foZ/OWew1MoFO+99x6GYf94LurYsWNcv+9jPO97abgW/cDC44MF12FuODRN4zi+c+dOLgTy8PAICAjgnvrCcdx4aI+q/4Y+3Ic/F9oxWiYwMNDDw8PGxmb79u2bNm2ys7NbvHhxTg5aM6MoynCv96j6b2rXhIAJARMCJgLadA6YEDAhgBDgaOXGxsZVq1ZxgUtxcfH7779vZWW1ZcsWkQg9eom8F/XPh94X9xho358cSi7S4uKqioqKGTNmYBhmZmb2Dz9ob2/vjo6O72dBNARnxjfqxm8av/+Td/h/r1CnQ0KhjIyMRYsWjRgxgiPco6KiDFrv/70JUw2/ZgTkcnlmZubq1avHjx9vZWXl5OTk4eGxYcOGlJSU69evL1u2zEK/OTk57dy5k8fjGWOl0WiM577xtDLezVQ2IWBC4OEgYJiDHMtp+E3TtFwub2xsjImPyyrM8/f3/2D529PdxyF+DTObONxtutuYl+c89/sFC5+aPB4bZjbyCac/jJpyeuGqiCUbmi7EQjtfL2EmWiOTey4mQHFHg8/ljqRMoFlCISVIvSRQKlPXNN86H9pZVAYKDbTw7lxJ7EjNBYkaNAQMDkFG9Y31ewsPnYfWQSRtJhjkCCEgJKmlDWdjILORiCmoPRWJ2GcxyoYHYmXN9azsC5FQ1wtyoEqQDfRgaR2r1iemQ6YfNOQ1Fu4P6EvOBwEyBJADI0W5GEngiZn0mo6dgT27goeuZEG/EiiG0iElMmIzqwc6TkYn/f1o/40i5B+iJACnGJ6gP62oNjAGSjs0ObW3w1Oodj4QABoGCB1N0C383j3eR51GuAwzN3/Cxvb91avzayqGGAIJnHHyrgxZr4vkYDccCxRj6Ilp7p3/rAZmqwAAIABJREFUhYDmPKD/6arLsAxN0wTJ0LSOQW7apAqx84QGT0lKfnvlyt/Nfdba0srBymb8kyM/XvFnZX4dCBlpRkW+XwTU94IaQIV8RXCt3vp5iKq6GFcXkggVPa3n49vCbxAdA0DrkCNzv1RwLb/MO2wwr0orkGlIYogh+kk9fcvodF3CpsCEqgNBHV5RdSci4E4v9Ch6A5IqDgVDjxQkOPTJq6NvpJ8NQ+yzUIWAlZCtUTerDgRJA1MLdvtpS5pBQVNKDUlTMoEIusRlAVdrI68j1xQKpE1dmWdCe67lIq16RWe9TySZVoVcNQhQV7eXno8WJORBhwIKm7O9grsyS2BAid+qKTkVLr7dqO4TAo0SmSCqXEUDT9PqF5u200dRWK9VaNApIdV0fVtQuM8fMpqa9ofk7z23buGSEVZ2TjZ2Dk/YWw2zXLL4teaGRh3DGq+2GibXL5uA5shWHo/34osvYhj29NNPZ2VlGR58ND4VDZG/8Zn/w8sP5wr5Q1rh+mwYGk3TcXFxjo6O06ZNc3V1ffXVV42dlA0D/CE1P4h9DB0wLtA0zd0NkSRJUVRWVtaMGTMcHR3Xr1+/Z8+e0aNHT5gwISIior+/38RBP4iDYqrThIAJgf8KARMB/V/BZdrZhMAvDQEDG4vjuEql4lbL16xZ097e/uc//9nW1nbVqlUikYggkGDG4CFrCNQMBS4S+snRMQRYXMYezhDZ2trawsLC1dV1586d/84P2rgnhkoMBeP/Pqqysa+ccR9IkkxJSZk+fbqVlZWdnZ2FhcXSpUs7OztJkuQ+wgX9xh8xlU0I/EAEent7vb29Z82ahWGYs7OznZ3d2LFjjx492tzcfPr0aU74bGFhMXnyZE74zPl1cFcJlmUN6z2GqWQo/MAOmHYzIWBC4CdEgJuAHDWmBR0FOi1n+MAiOSafz1fjuEApIwiiOb/sy/UfrVj5lvNTbtbmFg5mltYYNnH02AWvvLT49aUTnhz5ztT53gveXu/w21WT5/p9uouXVShKL6o5GQq36mThN+vOR4NQBhoNo1EBqwWlWlrb9M3Xx1pTMkEsA6mqMz6tO+YmIi4JHeJwmwcKPj9Zsc8fGnigRNEFGrWYoAsab+06DdcrIae18OAForwVpSUkdSBRtqYV5F6Iwms6QKaDRn7R+Sj+7QZObosiDaEcWvi3tvt0XEiEbhFoWSUwYiBVNAkKUv1tRcu+4N7tgY3bzkHdAMhJiUSCWtTQ0COv3R2Qv+V4dUgCcjFmdEAgc4au9MKbnmehrB1yGpL3nurMKgc5CSRDqUmdmgYtfH388LDh9hiGuTg7/23T5o6uTgXQamDuOlfoj6IBeQ525m5OjQdLQOsYltUbcTA0rSUpzjxaJpNJJBKpVNrf379z586J4yc42di9OGNuV245XtX+7bEAUX4NEICMNTSIemZIClRUU2Rqhe8VqOFVhMRXhyQgX2ySlg1J8R6BJL+m7HCwPKkYsckUAyw6tQjOwFqikaVXNHqGKgNv1hy+BJU86FW0xmagI1vRi5YZZHR3Uu63xwLwhh4YQk7QoAB5alnxV+fh2/rGI2HI01mmX5NA3tgMklpfSsg8HACDGhhU6PokN4Mim2LTkRC+vj/D83zrhQSo4yNTaaHy1unQwUQ9+9yhKDkZ1nw1TdvBh355kW+4OL0cpBqNRoOMtnX6o8+TyS5n3vhwP1XUBDJSKpWyWkZU0Zhx0B+SK3gnYxqPR+x56W0XzNLF2dnO2sbO2uY3Y8Y21NWjc0dvWWCIcv8jAf39eW0QQX//X4/tO1yo39jY+MILL2AYtn79eu7xOwMOxgVDAPAjCo8PAlznDeNitEx5efns2bPnz5+/aNEiDw+PuLg4HMc5k2jDSB9V/w0dMC5w9n00TaPHMvSrYrW1ta+88oq9vf2CBQsOHjzo5ubm4uISEBBg4qAf1YEztWtCwISAAQETAW2AwlQwIfArQsDYR5LTNbe2tm7evNnGxmbt2rXt7e1ffPGFm5vbkiVLSktLOe0DR0Jx4gjjuMe4/IAQNLDkEonk+PHj48aNwzDM0tLSwcHhhRdeuPrN1a6uLi4XB6NF2iCapjndCjdMg3b4X+o1HlCf/2O1XCxLUZRUKuUyhID+oelTp05Nnz6dS/xiY2Mzd+7c0tJSznyDg/q+UfzHhkw7/DoRYFmkDCQIgpuzQqEwKSnpvffeGz16tIuLi42Njb29/dt/ejs5OTkvL+/DDz/k/G3MzMw2b95cV1dnuBkzLHjcd/dlmPi/TnhNozYh8FghoM+QhvwGGM5rmEUGxHrKDNQMJRKJ8uOvNxdVVNbXxqZd3/LJ1md/O90ds3kKs3bALMY6uCyeMHPl5Gf/Mm3+slFTJmEWs8ztd/z+j0eX/LnmVFhncEK5byhZ0aTrFyFvDSUBvSKo7S46c7k2OgXl6+tTSm4UlftehtoeEOMgZ6BBUHLgfM6eM4j10+ex49LZqWraC7wvQVotJFfeOR7eG58DUg2jJtgBad+t8upLcVRxA0hZaOirOhvZdSNXrZQzyHGYBFILXaKyM+FdV9OgqRcILYBOA6ySIpDEtbqnZqd/6zb/rgNhUMZDthsKnFargWThTl/1vvP5Gw81+0ai/mu1uExG9wsHbxYVngzBb1VB/UDt2atD6eUwqEAeIOijGkbLxMXETpw8ycnJabiD446/fw40cl6mdCylu3tpvAcvB/J3vw0XRkPc8r+cJ8a13XdNNmSMMLyvZVmVRqNlWZlSceT4MQ8PDxd7x/UrVoUdP11/Mw8pwVkgRTLloAg5VAzhnWlF2ceDmLyG7risW/4ReI9ApyFpDQFKUlnSmH3kAj82B+V+JPSu0wSD1glUlK5LyOY3dnpHkxe+rd9zXn2zHAQEmVPbdDmJKGtE4EsoeXZlaUCkrKQONFqQ4dApgmZRq3cUfjm7/utgIrUC7UYyKG8kDSDE2/+Pve+Aq+JK2x9BaqiR4mJhrWtdS1yNcU2MfzVxk5jsmuIXs2Y1Jj/TNm3XaIwlib2BIiAICIgiTQSRIlKlSq+X3uECt5dp9869738PJ5nvLpYvW5Kgzvz84blz586c85wzM+8885znjcu4HRiNfFo6VCDhSiIS6q9n60Wdxqq2Eq+wOr8oaBkEGQudsrKLV2suJiIpd31/qXd4TWg8tMugrDnn1Pm+9GJDxyCnpRkDp+VYtHMJSycUpb6xo/tULMgpzRA3J23sKA2IphOKxOev5+w5vX3NqxNHWduOGkUMLb+ZNiXlehJNk0Yjh/8ZDHpcwAQ0zynzhX/q36F8koj7RvYwD95iNBoxAV1cXLxo0SIrKysvLy880vhhhgumI/PBa+fdaoxbhAMesVj85ptvuri4bNiwwdHR8cyZMzgF6N1+90uuM63zsCcdnU5XXl7+5ptv2traPvfcc5988smcOXOsrKx27tyJU6eimSM/6Fp+yTYIxxYQEBB49BAQCOhHr8+FFgsIDL0e5xW4nJ5TKpXbt2+3sbFZu3ZtZWXlrl277O3tV65c2dTUdCelaxp3Div/1NAajUapVBoREbF27VrroQVLod95553c3FxMOuMJaNi5z5SMvjNoxpX/qet8n/2zLIvjP4qiaJpOS0tbv369vb09Tnbk6Oi4cOHCgoICrGgwjf5NYb/P/oWvHnEE8JMkSZJ1dXU7d+5cvHixm5sbzqM1f/78AwcO9Pb2+vn5zZw5E6+cMmVKYGBgV1fXMJ930zPlXuVHHGqh+QICvywCmIDmfiCg+XsE8v00GiQSSUNxOTUgpzmdhNa0dXXm3MgIPnDijwuXjyFGuRBmUy0c3QhiscektXMWvTz7iXVT5m6du2yV9di/TF30zR82ROz8TlPXBBoaCZwlWmjpLzkT0XQhCVoHQAva1NsJnx9gc6tBBcgkoUPZdOzCrc+PMZnVIKEMBoOWYzktLatrzQ2IlCUVwu2u23sD2sNToJ9CCeJobjC/OumIP1PWCGItNA0WHA/uiEmHjn4OAPn16vWgYZsvJVf4RRobuhCniXyuOfTiVstCWVuHd0znntDaL85wKeWIMJVTSPhMG6B5oM8ruvi9A3lfHIW6bnWP2MgyIFUpi2oq/CJViflQ01vuewnx4F0qoI2kSq3RMWKNorimYtkzTxMEMXaM61/e+nN9VQ1Kx6fjkPTYYDD1AjZVxeIyj/xPR0DjQ2CmjH8viM06sDk1ANTU15057WNrYTV2jOvnH35MShRDts4MULohEbRRdasmc78/l1kjScjP9L1AtvZqpAparQHKIM6vzDoe3HYpDbo1QCGbbbRblkPC9gESbrdW7/TX+6VWfHZSGZYGjYPQNFB0+JwquRDZZ9NA51bfOhkszrwNckrfPYCI74qOol0+Ut/Exv1h0stZ0IlIbeRkrUMDpj8hr9IvGpoHQExBu7rUOyIv4DJT1QZidc6ZsIYLidAmBykLou5bPmFlITHQKAYZ1xOXUe4fiYjpms68E8HNsWlIF6+mDXoOdYSeQ+828kUJW/e0HL0IIinINXqG7W9oTT0V0htxg44vjH5/96HX3lnwuMfjo1G6XQtri7FuLtcS4nn2+YdXOY8WAY3fWBcXFz/xxBMTJ06MjY1lGOSxbhqCPpQyCNPTSiqVfvLJJ05OTs8+++yoUaMOHjxI0/R/5Yz+794mTOvMl/ELA/wuYWBgYPfu3fb29jNmzPj4449xSvkNGzZ0d3fjeaX4+eK/WythbwICAgICAvdHQCCg74+P8K2AwMOMgEajYRhGpVLt3r3b1tZ20qRJzc3NBw4csLKyWrVqVVFREc5ZgWksPKsLhzj3+vsTgYVf7GONM1Z01tXVffjhh25ubtbW1mZmZubm5uPHj3/33XeLioooisIKaIqiGIbBZcxH8zG0af1/ojrff7c4QMTbGAyGurq6Tz/9FDcHy3AcHBxeffXVwsJCkiRxK3hZ90MZ+t8fLuHbfw8BtVqtUqlSUlJeeukle3t7CwsLZ2dnKyurtWvXXr58uaura9u2bRYWFgRB2NnZLV68uKamBj9q4pOdf+DE58u/VwfhVwICAgI/DwKmkkz+HseyLMnQaBqTnsPzg+Qqpd5gACOwMpW4pin0sPeiidPGjLYZTRAOBDGGMJ83dtyT4yc9P2XmU07uL0/97SJH90kWtq+vWu1z9Fh3XQP0yrLPXigMi4H2AZDS5G3RjaNnVQXVyFtZSkKHvOLUhZufH4HsOuTeq6A0HKtiKFrUlXMytCIwFqp7mwLiEec7QIKShQ65Jrfm+gHfnuxSnUIJctVAUl76tz7G1j6gkesXIgElqoqIq7ne55EzNTXEPrMcEkFrdPrKtuKdZwaOxZR/7S+OyUKJBw2ASG0SoL6v62x8zRenKr/00RfXI+02w4KKhvrepM++E1/LhvruOv/IrkupIOoF0gh6o1qrocDYJOldv3UTYWNhY2Oz5tmVjXX1eoq5k4DW/+B2wnPQGP+frq/5PjUt3DUe4PTIJ6SzoXnxnPkEQcxburi4poIy6EiNZsiJm5MU1mTv9dVcyoYbNQWnLkibOw16TjUoRYxwuyL1O9+Cs5dRuj8Wwa/jOBI4LSAO2lDdWbo3gD16VbLnwsD5ZGiSQp34xtcnu84nQbMMpAxV1ph5MmgwqwQ40EvkICN1RaLyg0GiA+c7Tka3BlwFMaoDxTJII9ylUsTm5uw+AxVdSDivNracS8j62ocrb4U+TVNoQmtUKgyqQUlDu6z4dPj1705DfS8Msh1XMvL9I6C+GzoUlSFxxUFR0C1FnctywBmNNMuIpWRNW9aeM8WHQ9iaDtQuBaOtbs33vVh7NpZOKMr7xt/v7U9mjrJzJUbZEoStpYWTs8OZM6eH7n1I+zykYUZd+r9SaExI3/H3n3r8wVdA8wT00qVLp06dmpiYyEcCpoWHLyowPa1Ikjx+/Litre3kyZPt7OzCw8PxifZPfT1iPpjWnJ/6hnzhaVqtVkulUj8/Pw8Pj4kTJ27fvn3JkiXOzs5/+uOfenp6cAt4NdKIaZBQEQEBAYGHHAGBgH7IO1honoDAnQjgJMhKpRIA5HJ5cHAwtnrIy8s7cuTItGnTZsyYkZmZicW5Op0Oc1KmIc69ynce67+yhieg+RBQo9FIpdLU1NRNmzbNmDHD0dGRIAhLS8sZM2Zs3LjR39+/vr5eIpH8qwQ0Dq9x6/6lmuMa/kv6CJpGuYyqq6u9vLyeeeYZJycngiDMzc3d3d1ffvnliIgIqVSKe0qn05nG/Xd94PyXaits/JAhcK/nh8bGxkOHDi1dutTV1dXFxcXJyekf7i7ffPNNY2Pj5cuXFy1aZG5uThDE1KlTT58+3dXVxek5iqLUajVW1fGj7t84Ix4yhIXmCAg8WAh8f87iVHicgdXrGANykAADGFl0Q0EMIICRRprQwGPehw8fXr9+/bzpv3E0t7AkiF899thcN/dVM2avmjF3jutYZ3NzS4L4tavb6//vuePvfnphx351VRMoWWNFS2XolZbUXFCzSJjcJm4MT8zcfYrOKAeZHvrVtEShUKv0KrI4KKY9LBmqxSVnIsuC4xC5qUL2C9rrJQX7/BU3SqFLAQp15Y2s9CNnoa4blCRQNDJrJtnSiPjUI/6qvCpQ0EPJ/YbYZ7VeX9lWdyZ64FhM4UfH+iIzgAQ9xajVakSbtkp6/OMz/rK78ksfKGwBmQZUatAw+uq2iuMhfSGJUNtdHx5fFxQDjb0wqERp94ygpik9QNSNJJdpnoSl2W8XzL+Rkgp65KY9Yglo02CMD5Awh0jLVR+9u40gCEc3l8NeJ5SkRqPRGOQaRtSVfSxYHJ4mi8i4fTxsILscGE6rGsKtaeD2qYjMI+e0ok7ggJargDOiVxf6IRE0xd32udjjHdvyN/+Bw1FQ2Aid8nzv0KqzUSDqBzHFlTdXRiaWRiVCv4LTaBF0fequ80ndXlG1+wKrvS5C0wDCkkZjD+TkQHxu1k5vfW4diGnolFdHpVT7RUNRG4gGO2MzCw4FgkiMHDyk2vrwhNqz0Yh97tOKr2YXnA6TFlRBj6IvOS/TOxg6BxHFTHOgR+yzQapWlIhunQwtOx4OJa1DcngddMurg+PFISmQ21J4MMj3L58/5eL5a/PHHAjicSvrX7m6eHmfADCqVIoh9tnwIwno4ZeFh4iAXr58uZOTU1hY2F0zED58UQEO4HG7dDpdWFiYlZWVra3tvHnzamtr8bSw4d09Mj7feRHAjySYgzYY0AyYkJCQmTNnTpgwYdu2ba+88srYsWOfe+65/Px8AEDXTJPFdG8mq4WigICAgIDAfw0BgYD+r0Ep7EhAYIQjgCdk8VEUVtT6+/tPmDBh7ty5iYmJAQEBHh4eTz31VHFx8T9k0Zh+4i04hvGepjEKX/4ZEEDGi0OTAbGoWS6Xp6WlHThw4OmnnzY3Nx81tDg4OMyZM+e11147fvx4QUGBSqXCeZ/57M94J7ws2rSNd23m/9kuvlZ4Sz744z/iQ/Bez3K5vKSk5JNPPnn66adHjRplb29vbm4+duzYrVu3xsXF1dTU0DSNSUDegJsHeVjh/6ybsMFDj4BOp9NoNNjMHc8AGBgYiIuLe+ONN6ZMmWJraztq1CisqU9JSamurj506JCrqyvW2j/11FOxsbEobROJnE/5fzz7POyMeOjBFBooIPDwIGAckmsagdXrSOCQPFiPpL4ooeiQnTEAcGqqvqJazdJdA+LkpMS/f/HZ3Pmzx4xxNCMIJ4KY6uIya+LEWbOnT5rgYU8Qvx87ed2k374wbub+je8XBkRVnoqs9Is2dEmQvcOARp5Z7r/+A0lsDgxSQHG0XEVLFIZeeWV0StOFZLjd0R+dVRd+DXoViH2mQV/SXLsviL2Yg3wexKQxr674xHlNQQ1oOW2P2KhUA2Xozy/P87tAFtaiXHZyLQAo+vsR392lbDufNBic0rA3uO1UDHSj3HpKHU1zOn2vtPVCSvn7Rxo/Ow25daDiQEuBloYeRblvRHf8TWgQG64X1/tchNY+kClQdxuQzbHRaOyXSV5c/8poJzt7d5evvt4ll8uRBcgPCmhMxWILjjuNOH7xYYNjAxwzAICWokJCQuxHWz1GjHpx+crO2kYkD5eoW0KTugITB+Jyrh/wJWvaQKIBioMBNYgGa7wj43cck9+uZ7UUqWOMrA75aMuGjDhaBzquZDWciGw7frniSBjkNUKHsvf6rfzgyzCoRb3T2n/zeGBl9HVmUEarVaBjYUDRfD5BdOC80udq7ufHjKIeZJFBDbHPAypZYe21XSeZ/Hr0Wwp6ruUVeV9AFHOnxphc3n4mDlmK96qhTVp7Pr7IKxRqe2GQom+Lbnzno84sgx6F5HZN+ulgaVE1qClQaZHynTHqFRpjpyTv4LmMv59A1PaQBbleobkdk1zhGwURuVU7/M68/dlTE6bbEISzGZoB5GA2+vSxY10d7RRL6QysAQzoRc0d/0xX/VNfm5LO9yr/0w9G9Ad8x+/t7V27du0/vLn27dt3HwKaH3Ijukn/SuV4GtrLy8ve3t7R0fGrr74aHBxEl8qhSwQfgf8re/05th1WMaxL0Ol0+GlCrVYnJycvWbLEyspq5cqVmzZtcnFxmTFjRnJyMp7kOizS4/fGF36ONgjHEBAQEHg0EBAI6Eejn4VWCggMIaBSqTASBoNBpVLFx8d7eno6OztHXooMDAycPHmyp6dncXExkqjodDjsuKttBR+RDCv8bDDzx8VHVKvVra2tly9ffvPNN93d3ceMGWNpaWlvb+/q6jpz5sz169fv3bs3ISFBJBIplUqGGXr+Gfql0WjE+uK71nzYUfht8HrM0JmqnvF6fjMctet0Ouz1TNN0f39/RUXFsWPHVq5cOW/ePDMzM0tLy7Fjxy5atOirr74qKyujh5ZhVeKrcdeC6eGE8iOLAEmS/OsNsVjs4+Mza9YsJycnKysrFxeX8ePHHzx4sKOjo6Sk5LnnnsO2G87Ozhs3bmxubpZKpRg3/OLkzoxDpgPvkUVYaLiAwIOHACKgjWAw6g2G7wlonQFYdO9ijQbaOKSJBqAoygiIqdMb9WpSlVmc8+W3Xy1aOMfB2tzRxnK0GWFmN3rSNM//N3vB+vlLV3hMnUiYTyQsNy1Yse/Z13OPBClrWnVdg3R5y7U93m0RqdAiBVJHqzUaqQI0bFNCVlVgLNxqGozMzD58Dhp6jRIVyDTGJnHWgQA2Oh/aWehSawpqbh8IVMbfQh7T5JD2Wa5ma9oSDp7uySxGPgwMgIZBsmjOCJ2yjojkusPhYv/ExjMxXGEjqFiVFDlcgxG6bxQl/fVgybZDEFMAcg56B0BDgVhe7htR5x+JfBtKG28fCjDkVcOgDPQ0h+jzocUA12Lj5/92ntlo88XLlpZVlKObuJ5DPOxQEkL8fm7kE9DoSg6gYqgrCVd/7TLWmRi1bPz02sRMGNQUh8Q2H4+EuKJc77DmrCJkW0HqQMOBRNd48nLBTh/yVi2o0Lw3yqBDNs0Uh5ydu9RVvlGF3wSI/RNvfxMIpa3QpVCml5QFRhlaekFOwqA6PSA8JzjS0D0ADMMxNFBc85X0m18eV4WnV+4/B+XtoCB1Oh16UcqBrr4r5ZC/OKUQWiUgITtzSm+dCkdGHIOs/GZZwT5/MrEAWYSrjV0xN2+fDIWyNmiTcVVtt3zDBxJvQWO/vrot6fQ5cUm1oV8GOr1OqUJOHXKGqu3IOxMRu3U3ZNYjYbWUhgG1KDU31SuYTq9o/DY04rVPfzdmohVBjDYj7B+zfWz06K1vbuxrb9fTmH02co82AY3DAJVKtXnzZgcHhw0bNojF4js56IcsKsAWf3w8r1ard+zYQRDEihUrqqur+Zh8JLfatG582bRdFEWJRKK1a9fa2tquWbNm+/btdnZ2Y8eOjY6O5p2g+Sc+/gGH39WDd/sTaiwgICAwUhEQCOiR2jNCvQQEfhoEcCYNmqaLioqmT58+derUmJiYiIiIyZMnu7u7h4eHq1QqnLsPH58XQvJRyH0KP02V77JXHCLzwSKeaMaybHd3d35+/pkzZ1577bUnnnjC1dV11FByczs7Ozc3tylTpjz//PNffPFFQEBAXFxcXl5eY2OjXC6nKIqXG+ODDWvjXWowtMpgMGCLEpxFkKZpbFfC6Tm1Wt3d3S0SibKzsy9cuLB79+7Nmzc//fTTs2bNwoYhbm5ub7755vvvv5+amlpTUyORSIxGI/bluOvhhlWJ/3jXjYWVjxQCeMI1DBFJCQkJ69evHzNmzJQpU5ydna2trVeuXBkXF1dbW3vo0CFsu2FlZTVr1ixfX1+NRoNtXjBc/Ml+Hy3MIwWs0FgBgQcegSECmpc8I0pRj050zKIyBo4Cw5BIFDGtBjAoaTUH0CnvLako9Pf1emvjGzPn/oYwJ0bbmDsQhKeV/W8mes7w/PWyKbOfnTBziZX7a5Of+OCpFzJOBKd8eybfPxIlglPSRjUFrEEnltcmZZWci4GsOsPl/Ipvg8jSBuR3IZYZWnqLzlxovZQMgzRIkC9zVVBMfXgCdMsB3UUpYBh5Y9vNU8EN8ekgVyMvDg0DjBG0DEi1/ddulR04134iKm+vH1XdBmoGJUikdZxcKSmsyt5xMvuvh8QRqdApQ6pYtRbEstYrKeX+F6GmGyrab58KrY29DlKFVikzAKc36lEvayhpbdPOze+Ps3JwsLHds2cPJmUYCvl+GDkDzkCI3s+B8a7/RtpQIRm6uLj4qd8ufJww+w1hd9vnYlvwtbrD4cz5jLJ9gQ3xGUAZSBmyYoNupSg4IffvXmRsPmgBlAxipXUGg55FTtyD1MDlmy1ekcb4wmqvC1DZCR0K8lZ11ne+2qxy6FeBiqmJSS68EEf1D+ooEnVWr8xwo7zt+CVNbG7eieC+wkokQh/KkKnWaiTt3amnQhoup0KPHCig08uKvEKZ6hbolCmTCnLaOdaUAAAgAElEQVS+80UW0jIaBqmepNxC3wtQ3gJKjqtqK/a/1B2fCU2DXKEoyzu47UYeerWg13Mcq9NqdT0SEFN9wcnxb3+FUh12qJB9h1ovScqr8ArXpt6uDYw5uX7r//x2mS1BWNhZEY9ZEKOJV//0x/aGBgNFGfSsYcjX+67yZ0Cs9P+Kou/Z16YK6HtuNNK/wAHAvn37rK2t3d3dU1JShrlyDYsQRnp7flz9NBoN3lAikSQnJ3t6etrY2Jw8eXLYr0ds7M1XbFgBdxZuBcuy/f39H374obOz84IFC958880FCxaMGTPm8OHDpvokPhQ03dUwHISPAgICAgIC/zYCAgH9b0Mn/FBA4IFBANO1eAYZNvzKzc319PR0cXEJCwsrLS318PBwcXGJi4szjVT4rIM4FjENRO5V/tkQ4T00hh0RM8IURUml0ry8vICAgA8++GD27Nn/mEiITaKx6a21tbWHh8e8efOWL1/+8ssvv/vuu/v37w8KCrpx40ZjYyMvQ+Yn3A07iulHo9Eol8s7OjrKysrS0tJCQ0OPHTv2xRdfbN68ee3atU8++eTs2bM9PT3t7e0JgjAzMyMIYuHChXv37o2Li+vt7cWqVUw988keTffPl39xzPmaCIWRhgAeOXV1dXv37l28eLGbmxsebJMnT963b19RUZFIJNq2bZuVlZW1tTVBEC+88EJdXR2n57ARPN8cfKG4//nObywUBAQEBEY+Aug1rQF5bmDGmWcWcAEroylErCGjCZZjkHLWSNJDzgUSqbiyqjQy+uLG9zaNneD+uJX1aIIwsxg1cdKEOb+e+tTkWQtcJ3oQxCLC8Z3fLPto6QveH+1oKC5X9A8ippiGipiUknMxhpw69lpJ/q4zxowa5M6soEBGV0cm1YTFQd+QrlmiqQmLKzsXCT0y9C5ZrQKDwdAvuxl4Adk7aJE8mSa1yJGDA6BAmVF6a9+ZHv/4ot1+yrRSIHVIoUzq0Fe3Km98dSL+f/42GHwd2sXIuFlLQp+k9UpKqV84NIqhS1l6KrQnKRs0JMeQJKNBpCjHgc6ormrKDYrcsHTV44T5pLHjbqbdwJ37/T36QSOgDQBahm5saX7+2VWPE2a/sx3r9cq7Nd8G6yNyGo5dHIjPRaJyDQ0aFnqVTReSA17/qP1cIkgBVDrdgAJoA7JUZlnQsrLkgkavS4bI7PJ9fsqUfOhTGyqb8nxDe65mgVQPbQMFodEFAZcU5SKMmL57gMqpqt3pq/aOv/nl8d6s23qaoo0setmpM3AydV5UYklEAtT3gIKR36osOx4KObUgpRSFlSlfH+uLz0CH5qApKbMkOBpqO5GMXUyWBUa1X05FqQ4rurIP+DdFo/yEOq1Wo1WxWi1QLPST8pTiS//zRadPHPQxIEUm49A+UPTdWS4uX3ElO+iD7etmzHfA5lNDf3/37LKa+hpUbR0LYBQIaNyDOBKIjY11dXW1trbevHlzV1fXMBG0aUSKf/Ug/sUqFuxPiOtPUVRFRcWaNWtsbGymTp2ak5MzMICMy00nhuK245Uj569pj9xZxvXEc1u7urqOHTs2atSoqVOnbtmyZebMmY6Ojp988gl6DafR8PeIYTsZOS0VaiIgICDwoCMgENAPeg8K9RcQ+L8RwHQtv11JScmqVavGjBnj7e2dkJBgZ2fn5OQUGBg4LJXZsODjx3zkD/FTF3im7K4Hwh4CeOoZwzAtLS2xsbFfffXVM888M2bMGBsbG4IgsFs0fhIxMzP7BwIeHh6TJk2aO3fu4sWLn3jiiZUrV7766qtvv/32li1btm7dum3bto8//vijjz7aunXrn//85zfeeGPdunUrVqxYtmzZ4sWLZ8+ePXXq1EmTJrkNLVh5am5ujhlnCwsLKysrV1fXVatWHT9+vLGxEdv1Ykh5Lcld2yKsFBC4KwI41/n3yaZoOiUlZdOmTc7OzjY2Ns7Ozq6urmvXro2Li+vq6goLCxs7diyeCjBu3LidO3eyQwue6IBnXPKTCe56mt+1AsJKAQEBgQcCgbue1Pw9FBPTeBsOOBb0LOh1Bpbj0D8AYHV0S1tzfGL8Xz9438PN1c7OliAIe2ubMXYO08ZN/P3UOW9MXbxh0hMTCCtnwuKZxUu//WJHQ3KOJrcGGW7kiOBWa+2py+LMUmSG0KeC5oGGsPgiv3DQ6kChhkGqMyatyC9cV98Gek6vVgJJQs9Aqe+lqsBoeWUDLZFpFMiIGZlvSFR0RnnZvrOq4JSqA0HIV1rOIhZVB6A0QGln++ELuVu/bT0aBq1StB8wgorsunEr8/hZZLgh0Zf6hN0KCAcVynCoYygjy6BEeSoWBqjawLj4r45//fb7owji9wsX93V2o8wNHMfqkR0Zf5vm4J/gHLEDgANQckyPbPD1P65/nDCfStgceGGTLr7o9sHg7pQCYAB5kdE6IEERm3v9nb3tp2OhWQJKllNTHMMaSQZx0yqaLKwt3u+vi8qu2evfExgL7VJo788LulgRcw06+oAGRVphuW+E/FYl6gWG4eRKVUF15vbj6hNxPfvD28KToF+h0aqQsbJUDb2qUv+o7ivZ0C6BHuVgxu2bRwP6knNhgISC+qJTwR2pOei4EuVgSVXM0VPQ2gtiJXRIxRGpFUfPQzcJ1X01ewN6/ONR9kidAXl96PUoh+QgyaSVR723+/bZKGjuBxmFXK0bum9859PuHyOPuhn15XcbfvfUOEsbB3MzazPCztbyicXzM27dHOrB78XNBjDcy39jmAL6R6mhR+zg+HEVKykpWbJkCaYpr127xqsleIKSPynwKfHj9jqCtuLPa07P4aTrLMtWV1f/6Y9/winBN27cKBKJ+NbxkhR+zQhqzD2qYlpVXMZPRmq1OiIiwt3d3d7efuvWrU8++aSzs/Obb77Z2NiIVUq4cx+avr4HPMJqAQEBgV8GAYGA/mVwF44qIPDzIIADDt6/DAAw++zh4eHj45OdnT1v3jx7e/sjR45IJBJsZGFaMfzzH//X9Lc/aZmv0v2Pwuk5jUaDs3DI5fLOzs709PSTJ09u3rx5yZIljo6OmCM2Nze3t7efMWPGokWLli5d+vTQ8uSTT86cOXPKlCmzZs2aPXv2jBkzpk2bNnXq1OnTp8+ePXv+/PlLlixZvnz50qVLn3nmmXXr1m3cuPG9997bvHnziy++uHjxYk9PT6w2dXFxWbNmzY4dO1JTU3t6ejD1jNXlWK/9I9ty/5YK3z5qCGDrDJIkRSLR7t27FyxYYG5u7uCA1F1z587dtWtXWVlZeXn59u3b3dzcrIaWlStX3riBZH13EtAYPTwUTcumax41hIX2Cgg8HAjwtxj0KnrIPgKvuZNc4Ib8KAwo197/EtBDIBhIUt3S0pSTm7Vv357ly5c5ODjg16uO5lZLnCYse9xzgp2z++Muo83MHEdZbnpytdcbH9zc4aWKyqk9eqEvKhMkJEhJqGwXnYurOR8LDZ0gkYGGFidk5hz278ssREkCOQ7kCugaKPILR54MxSIgGeQCAaBTKEFNSguqKo+FDvjGt52M7I1Mgw4psv3V0MhTOL2y+UB43afecu8rUNYOGj0yd2Y1fUXlN70C6FuV0CJt8I2sC4pRVomAphiGYnRD3CVjgA5pw4XEgqMhTFHj7vc/tTIzf+n5tUbOgAloXjmO6Cqc09EE0BE7QgwAaj3TK0UEtBNhPomwPbX5M1FgfGlANMo6yAHHsKDWsTcqkrbubToeCXUDoGR1GgrnaiYlCpBTivyqrAP+zLX8hpPhsqg0EPVA60BddFJxRCx0ikFBMpWNNWcj9XnVoGBApgKKUde1VJ651H0quuWb4IHARERY03pE9DMstPRXnb/aEp4M1T0gpnUVrQU+4e3xGaDWQUNnoXfQwPVs6BkApVZbWpcffElSXgMqCkSd9cGxFcdC4XY7dGnbQhL6/OOhsAVkJOiROh5J4xV6KGjI3H6y3jcGWgdAThkGlMZOSXlgVGvwVdnl9Evbdr7z+5XOBPEYQViNImxHEauWL8vNvqnRKnR6yoi4c9S390o/+MO3/2vB8SgQ0IODg1999RV622Rvv3r16tLSUjza77xuPLhxAlbn4BfwFEWVlZWtWbPGzs7O2traxsbG39+fnwlqctJ/Xxyx575pxUy7BhPufBZ3hUJx9erVp59+2traesWKFc8884ybm9vrr7/O5wFi2aF0AT/0tykCpocQygICAgICAv8qAgIB/a8iJmwvIPAgIcDnE9PpdBqNprq6evny5TY2Nnv27Onp6Vm2bJmNjc3OnTt7e3txaMLnMcONNA04fkx5BELDezTz+m6WZQcHB0UiUXx8/DfffPPKK6/8w6mAIAgHB4eJEyfOnj179erVmzZt2rNnT0hISFpaWsYPS1ZWVnZ2dlZWVk5OTkFBQVlZWX19fWNjY2FhYXx8/IkTJ95666158+aNHz8ex69PPPHEZ599lpKS0t3djW2msQsKTdMUhR7zeNkpjnFHIHpClUYsAmq1WqVSxcbGvvjiixMnTsTUs5ub2wsvvHDt2jW1Wp2VlTV//nys8bezs9u+fXt3dzcAqFQqlmV1Oh1OqIV1LiO2mULFBAQEBP5DBO517/6BWED//7ANh706OA5RD0N3KAPSEQMYjRy2+hGLxZWVldHR0evWrUMTiQjCliCcCAtPT89fz5ruMm7sxF+NWzvvyZWuUzd5LNj1u5cu/HWfrqIV1AB9VO/F1OITwcraRpDJQMPKMgvzvM+JM/JBLgeFDPQADZ1t5+JyvvMZLKnRKVWII8YLyYGoq8IvUhdf0HgqMvtkkLKiAdGBGhooA1R1Vu70K3rnQP/pOKjpQYQmxwHDiMsqbp45p79dC6IeJqO0+nAwFIhARuooUqNHphBoD0paUlgTuef44K1K0Bq+3b3XztHhpZdeQhNEOI4xoDyN+iHfZ2RTcucyMj1/h2qlZ1hZ/+DGl9c7ExbjzWz3vLWt7NI1UOhQq1UsSFk2pzZnu1fBPn9DbRewQJMUpWd1HAcsBwbQljfnHglUJ97qj89oiEyAPil0D/SlZOecPgdN7Uj+XNWe8c0pSVo+2puWRrvtVxQHRLaejqo7eL721CVoEoNczcoUQLIwqG27lFbkc1HXKoYeJZR05e/27UnKBQVlbO4ujIwpib6C2GcN3ZtdkH3El8otA6UWVJQsPrvgGx9FVhl0yduj06rPxYCoFwZJUNOg41i1GrR6uN1e/U1g7jf+0DgAJHIRAQXbEJfedSkVbtUlfv7dh0tWuhEE8kEjCHsb85mTJmQmJ6IXG3pKrZHzBLSJybMpw/x9+S6r7vuDOwfLg7VGpVKlpaWNGzeOIAhbW9u33nqrp6fH1Ijjh4vG9/8/WK3DUTcWNXN6jiRJrM5xdHQcN26cm5vbqlWr/mFr9qAT0Kadgp/y+Mu+SqWiKKq4uHjhwoUWFhaLFi3auXMnVjBgDtq0r03uEai7TXcrlAUEBAQEBP5VBAQC+l9FTNheQOABQICPC/m6ajSa5ubmV1991dbWdtu2bUVFRc8//7yzs/OuXbvUajXOoXdnVMHv50cW+MONhIJpc3DudbwGtwWzbzqdrre3t7CwMDw8fPv27WvXrp01a9a4cePGjx8/ceLEyZMnz50799lnn92wYcMHH3ywa9euQ4cOHTly5ODBg/v27duxY8eWLVtWr149a9asCRMmuLm5OTs7z5gx48UXX9y7d29sbGxTUxPWO2OfBLVaTdP0MN6ZB8q0tvxKoSAgcC8EWlpaTp48+eSTT9rb22MPmYkTJ37++ee1tbUSicTX13fSpEn4ufEfxFBoaCgeeLzthmmuc2Hs3QtkYb2AwEOAwL1u3zwTYUIu/BMBPbQBUgAbjRzK8zb01gozMgzD9PT0XEm4+vrrr0+fNMXW1tbaxYkgiDEThpysxk+eaeb4h8cmvewwdbG1+xsLno7ZfaIl6kb28XPq0jpZT7dOIYV2cWXgxa7rmSCRA6kBtQb61aprt27+7bAs6RawnFpHKnUkovg40Fe21J6NllxMZxMKcw4HMI2diJ1EjtIMtErrzkRnvbu/8dtQyBMhMatCDjoG5KqSC9Hi1BzoletLRJnHz0KhCLoVQOmNnJ7S00ZODwzIyhtjjvo23cgHsQJY8D52wtHRcfny5a3tbYzhewKaNaLEgzz/+E9DYsQS0AYAilX3Db61br0TYTHt8bF+3x3RtvUiT20VC50KKOqo/jY45ZNDUNVlVFNajtVwLG3kDHoOaI6sabvy9Yka74j+iymZx/309S0gkXflFsQfOEEVV0GX2FDTnLbPqyfmBgwoYUCK2GeZtuVySvWJcGTP/d1ZaBtEGSBJGlRakFN9yXk5h87B7RbQGlWVzTm7z8gvZkJTP7CQG3zhZkAIDMqgb1BeUhm6fY/4WibKbagk23MKc48MdVw/KcmvTDzqK75VBowBUeQ6DjgjKEmo7y7628mCT4/JUotBwSE3Dy2IYm+k7feDW3UJX3z37rynJhLE4wTh9pi19WjCfYzDxaCznEYNYDAi847v5c/3JZNR5/MD4EcW/mmcPIAfGIbp6OhYv369paWlubm5u7v7PxKc8B7BdzKzD0QTMQmL/7Isi4xoAEiSLC4uXrZs2bhx4zZu3Lh27drx48f7+fnhFt3r+vlAtNe0ksMIaPxCkSTJnp6eDRs2jBo1as6cOZs3b3Z0dJw1a1ZUVBS2JTG9TZjcKRAqpjsXygICAgICAj8eAYGA/vFYCVsKCDwYCOBoaVjQIBKJ3n77bUdHxy1bthQVFW3ZsmXUqFHvv//+MEUDlgnfK976P9c/GAAhMdf3C0YJk9Esyw4MDJSXl8fExJw8efLzzz/ftGnTc889t2TJklmzZk2ePNnNzc3JycnR0dF5aHF3d58+ffqSJUvWrVuHFdNRUVE1NTXNzc2Dg4M4rsUx+rC+wMd+ULAS6vnLIsAwDJ4Iiauh0+l6enqSkpJef/31iRMnuru7W1paWlhYrFmzJjo6WiKRFBcXv/DCCwRBWFlZmZubb9q0qaamhn/w+GHg/6+lqTAaf9n+FY4uIPBLIcBfDYYV7nrD4q8h+Fuj0ag3GFQUKWpvuZqS9OZ7W+Y/u4xwtjOzsXrM2sbjMaeZNi4vus981mrcLMJ2IkFsnLrk05V/2r99R8yVaPFgr1GprL14pTooElp6QK4GmobegebzCdFbd7ZFpoCMBpImGVLLkgCgrW7OORrY6X8FUlGOQWlOGco4pyZRbroqcdfxqFsfHM79xn/wZikMKtGuWFbT2Z3mG1wSFAkNvVDXkXk2tD2nEOU/VFN6muI41khSoNXTeXU3DwVUXL0Bgyrk5kFx4vqWpXMXPGZt893BA4yB65MM6MGoZWhsXYKZx3v218gho41DbCrFStq7/+elP9mPslg0a66orBLRxBoGJBTUD7btPFf+0QmusJHuGaQMSGrOAqgoklWooU+RdSqsKSRx4EJqhVfoYEYRtPXpyuuz/YL78kuA4qCpO+1UYF1cMkjUCA25Aga1soRbdXsD6aDUnoCrxpImtBmAQaUGJdl8PSv54BlZRhm0K6G6J987vCosATpVMMhUhsQUB0UaKpugUwLVLflnw0svXYFBBSg0A0UVyT6BA7crQaKhsipT9/s0ZReAwYitydFxJUqobC8/GJT+/ne667cRnS2lYYAeSCu+dTxEkpB/2+fCh0tXz7NyciKIsbYoAa+Fxaijh/dLOtqH3J45o/H7f//cp3dnmO++9t689T/v88H7hGOPyEuRnp6ebm5ukydPnjlzZnBwMLb/ujO4Nb2MjNjWGgwG3lkCeezodAAQFRU1d+5ce3v79957Dz8offDBB52dndiW0PR6+EC08T7gm17GeRUC5qA/+ugjKyurKVOmPPnkkx4eHtOnT/fy8sJTSPHjzMOEw30gEr4SEBAQ+BkQEAjonwFk4RACAj8rAjjCwKQqnl/W3d39xhtvEATxxhtviESiLVu22Nrabt26VaFQ3D/AMg22fkz5Z23nf+Ngw7DCr/fxjlmWlcvlbW1tNTU1xcXF+fn5GRkZqampaWlpN4aWjIyM/Pz8srKylpYWiURCkiQWFJjWyzTa46M3UyRNNxbKAgJ3IsC74mA1fV1d3YEDBxYsWIDTZrq4uIwdO3bnzp1Ybh8YGOjq6oodn/+REtPPz0+hUJAoGRfwtBE/DwAfC4/GO48rrBEQEBB4uBEwvROZlvlb1TC9m+l6A7bqACMFBg0YujTym2WFJwJ8f/fkknEubrYEMe0xl8mE7QJrtxW/mv7HGYv/Mn/FbDs3CzsrhwmuH72z2X/Xvgyfc9DWC7QeSVnVdFvCzQt/+XvJiVBoE4OGMmhJSqFA7g2DyuKgqJ5LqZBeU3UgSJ1ZBr1yJIDVA7Sp2w9frPzwRP5fjw+xzyqgWZSSblB2K/xy9tkwaOyBDlnMniP5MfEGlVLHDFk/MxRin2Vq6JKnf+tbE3LV2C1F5KseoEfecbNo0zNrXewdp8+YcTMni+Z0co0KeWcNeWfzDtp3HxgjjYBmdE01daufXjGaILb8eZNGrtTRDNL7Ng4UfnUm5eXPmeB06FFxDMsAMq5ASQQ1JLCQ4XehPiSBu1GZ/62//GoOtEl0RXUlvqGdcakoK+CgIjf4Yn3iDa6rD0gKAd4nEcdk5H16VHPySss3wYYhnxMkTwYABSnOL8/wC6NKGqBXAzU9laciRYHxSILdq+5OyCo4fZ4pqYd+DdR2pB/wrr6cCH0yGJRLqutjDnnVXE1BGSNlmtu+EV3Xc0FLsaBXGWmaY9AYaJc2nopM/3B/54VkaJOCFkBtUOdUl3pHUKllNQGx21/YMMXMxoMY/biZuRlBWNmafb33q35xt1GtBpYFg0BA330g47XM0CKVSjds2ODg4LB27drp06dPnDgx8lIkwzB4PoTpNcH0GnK//f6i3+GYHMfqRqNRLBZfvHhxypQpzs7OO3fu3LhxI0EQ69atKykpwZESz1abRlAPbtQ07JGE56CxGDwsLMzNzW3SpEmvvPLKzJkznZyc/va3v0ml0rvOnOPvDr9ofwoHFxAQEHggERAI6Aey24RKCwjcB4FhpCpJkl988YWDg8OaNWvS09M//PBDBweH9957T6lUajQavJ97BZGmAeWPKd+nViPzK9woPrLkLbP5yWU4TyAOv1iWpWkaB+U4UQ+Gmm+aKUR8cGa68s4y/1uhICBwHwQYhpFKpf/wE3/nnXdcXV3Nzc1dXFzc3d1XrVoVFxfX0tLS2dm5bds2W1tbS0tL/ARVVFTED2OchpQffvc5kPCVgICAwCOCAH9B+LcLHBhZMCqBIwEGSJVco+poafX65uDaxctnuU9wHGXpNNp6rI3DRPsxiybNcBptPdrB2trGctX4aZ8se/6bP797Leh8j0ikbm4js0pTtx/O+s7XWN9pUKlJjYojSaNEAVK6OjiuLigOCpu6zsZ3nU8COQskBwoSuhVy/6TKD0/cfPdbMqUUBtRAc4hD7ZN1xKZVBV7WVoigs7/24tXss2HagX65RqbmKFI3xD4rKWgfSDseUBl6FfkU65D0F5Sc+HpB8YGg+pCEp2bOI8yIP6x7qbGtRU1TKoo0JaCxHcddBsnIIaCHKkcydGR01OTJk8ePHx8XHYNeQ1IM1z7Qejom+c2dbSejoKoHKAC9kTFwWgZZKoOSrruaURoQzWZU534X0BOXAV1qqB9oOBle5RUCHTJoGcj2PV98KU7X2QvU9+yzJCWv5O/e0kORJZ8e59LLQariGBo4AygppliUfzpMnF+OcgZ2KCqC4vK8wqBhEHopZXblzaMBhvJGUNKqkpqMI2d6rt0EUgdKra6iMdMrsORyPNBGqO/IOhNSGpOE+giA5hgZeuvBQdOA9mJG9kcHpVEZoGL1EjkoaGgSV/tFSy9liiNuHH3tvTmP/4ogCJehe+Joa+Ldv27tliAXY9ChzJYCAX2XMfzDKj540Gg0WVlZM2fOnD59+tq1az08PBYuXJicnMwwDE3T93p2+GE3I+5/HOTjaikUioCAgElDy5dffvnOO++4u7u/9tpr2dnZWBn9gKq87wP6nZd6zEEDADW0xMbGzpkzZ8yYMa+88sr8+fPHjBnzwQcfiMVinK2RJ6z5hyZ+nNznoMJXAgICAgICwxAQCOhhgAgfBQQeeASGEdB79+51cnJ6/vnns7OzP/zwQzc3t9WrV9fV1WEJAM+T8nHknQHKj1/zwGGHm2YaS3F6DgfW/DRDrB7lAy/8E76lfPSGZ/aZKgV+DG78foSCgABGYFhAjyc/NjU1HTlyZMmSJZMmTXJ0dLSzs5s9e/bHH39cWlqqUCiioqIWLlxIEISZmdnkyZMPHDjQ0dGBH7Swbprf87DRK2AuICAg8Mgi8GPuUP/nNnowDjIaDRj0AJi16aptrM0pTI6M3fj6GwsWLLCxsbGysHSwsXV1dbUZYz/V0/P1mYuW27i5EMQMV/fXn1l5/u97kj/65va+M9DcD0ZQKGQ6AwscQJ9SdC6u3vsSFLd1nE9sCIyD2i6Qk0NSZQWbVpr//uGMzfv6Y7NBg4hJ0BugXyG7VZp75Kw+twoGNaKkdKSD7u7vF3fL9WqZERHQyJhYQhUEXLodFoccGzQ60LCgZDqv5d7c4wM366Gs+8SOvbNmzbJzdtzw1kZRcxP3g2sXpqH1fEbjYUNnxBDQ2CxCrlJ++eWXlpaWL/7hBY1ciSBSsDUhV5O27JH4X4N+HfQPGWigEMdopFlQMS0peZknQ9ic2tunIqoCo6FPCwpOHpMxEJoEJc3QJK49F1V6Porr6jMqlQaFAjQUmVdZe+y87GhU3d99mOu3oU/JarUMQ4FMxdS2pR0403M1CyQkDKpLLybWR6dBhwIGWU1uTfbJIGNxI0hpqrIhzTe4MSEVOahwwDV25Pucb7p0DToGoL2/KvBy7ukQRdVpsgIAACAASURBVFM7ALBaLcqjq1GCmtYnFBZ9fFR5IR3tkGKA4zS1bXlnIhQJBQOXMrxee//3bpOshrIO2lqaW5gTq9b+v8qGKspIARj0tBZlLxQU0MMGsMlHPIcSM7A0TQcHB+Mc3c8///y4ceOWLVt29epVPirGzxF445EZY5iesnhiqEKhOHz4sLu7+5QpUzZt2rR8+XJXV9f169fX1NTw0hz+6nfX5yMTtB6YIt8i0wJuHVbYcHruxo0bK1eutLW1Xbp06bJly1xcXF5++eWKigo8JHgo+IfHB6bxQkUFBAQERgwCAgE9YrpCqIiAwH8VAZIkOT23f/9+Z2fn+fPn5+bmnj592snJaeHChU1NTXzwwccQ/BrTwn+1RiN0Zz9de033bFoeoUAI1RoBCOC3R9h3D6vs5XJ5bGzsG2+84eDgMGbMGHd3dw8Pj9WrV1++fLmrq6u/v//jjz+2skIP2vhMLy8vl8vlAMC7kPPNGkZt8+uFgoCAgICAAI/Ave5Wpuv5MgdGDceyyKQCAFsP64fsLDiQ9Q8WFRVt37593rx5NpZWKF2qxShHW9tJto5zHN08LKwnm9ussZvw3ZJ1J5b8KfGjbzuKy6WyQVQNjoNeVU1AbNbXPlDUSV0pSP/6tLq0ERgAhgMNB5l1Fbv8r723R3o9H6QqWU8vctVgDYrSuhSvQEVxFaj1krT8bJ8QdV0TK5eRDEmCXouMiPTQo64PunrtoK+hY9CgpTktDVqDobqz4Hgodb0EKnqLfC4WXUlJiI797RMLLOxsNv4F2egzGpJWoxljrF53TwKaR/CnKfwYD2Kk7uU4VEODoTA7d6rHhJkTJp3z8uHUFJDQez6l8uuA3sBrUNEFUoQYp6WNLLLBNUpUPWn5yV+fgDpxT1xGzpkwaB+Ehm5tiSj2u+PKnFLoVpNpxTcOn4G2Xj2tNRpYUGihV12621fpc7V+11lp5E22pVs3xBEDzUDHYO7pUFHCTeiRg5SpiUm+eT7S2DMIak5X1XLT57w4rQBaZdBLFpw+XxN3nZPKQKmGHkWRV0jlhSuGmlYYZFQZpSVeYYayZtDSiH2mUco4UFDq3MrrW3f3+1+Fum6QaXUKJchU+b4Xyn0i4HZT4Ec7l42fiqYCWY4irM1tHW1efOUPKlqpYrUM6FlAWShBj/4OeUCjsXy3HrsT77tt9ZCuw4pX3Dh8sh8/ftzBwWHhwoUvvfTShAkTFixYkJaWRtO0TqfDUmj+mjCsMBIQ4hXNmIkWiURHjhyxsLAYP378+vXrJ06c6ODg8PHHHzc3N2MtMB4S/N9hLcIfR0K7/pM68I3CYgXetpEkyZKSkhdffNHW1nbu3LmrV6+2sLBYsmRJWVkZSZIUReEXD/zP/5M6CL8VEBAQeDQREAjoR7PfhVY/5AjgF/i+vr6urq7Tp09PSEjw8/MbM2bMggULqqur1Wo1y7J89HCfwkMO01DzcPOxduO/2957AfvfPYqwt4cVAbVa3dTUtH///kWLFpmbm7u5udnY2Dg7O3/66adFRUUAkJeXt27duiGNF+Hk5LRt27aOjg7+kUkgoB/WgSG0S0DgJ0XA9M5leiDT9Xx5SBSM2GcDT0D/QNwxFK1VqaVSaUFBgbe391NPPeXgYIfyoxKEm4X1byd6znd23+i54NvFL71m/eslhPPvfzv/8x1/u5GRpmjvGkwpavWPh/xWuFlb4x0JNT1AGkBDg5bT5NZU7/TPfnd/9+U0rq0PuT0YOFBTbEPntcNnJNmloNUP3CpJPXhaWVSll8loRqM36vVGPUUh/Wx7fFb6fj9JYQ0oKE6nA1pHljbVBMSqrhZAjqjI+0JZRCLXJ6eV6pDQUM9Jk8b9yuOpJxanxScyKg0YEb2LGV5TZH6e8g+4Iqjv9Q/XhNXrKioqfr9kqQ1htnja7PbCCpBQstTiW5+dKP3yDGKfBymgDWAAI6uj5SqgDY0pufnHgri0ss6LKdkng9iaNtAYtCWidO+g9hu50DGgzizJOOInyy8HqYJhtWDQQUN39Ylw7ZnE9r3B8ks3QdSl02qRep1mQKLOPR1afymJbekGytBxPbcwMJIUtUO/QlfbnnUmtPdGAXTIoUVWevpCWUiUsbVHL5OBTFEVeLnW7xK09YOUbL6ckr7/DFR2QKcMaNZI08gPWkpqblUlf3W8+kQ4lLeDmgGK0bZ0ia6kVZ+JhPzGq996vzh/iRm+L1qbE49ZPL3m6eyCbGQbjRIt6hkj+wODhj2g0Vi+Ww/eifHdtnp41/HnuNFoZFlWqVTu2bNn/Pjxbm5unp6eVlZWCxYsSE9Px9wupi9Nf8KXRwJCuAk6nc5oNBYVFX300UeWQ8v48eMdHR1nz54dGBgokUiMRiNOvYgdrvkm3LUwEtr1n9SBbxQWNfMENJYvtLW1bdmyZezYsTNnznzqqafGjRv39NNPp6Sk8Fkc+Z//J3UQfisgICDwaCIgENCPZr8LrX7IEaBpOiIiYsqUKTNnzoyPjz927JiDg8P06dOTk5N1Oh1FUTxLxccQdy085DAJzRMQGKkIKBSKyEuR69ev9/T0nDZtmoODg52d3YoVK2JjY1taWrq6ug4cODB9+nSCIMzNzWfNmhUREcEwjKm/4UhtmVAvAQEBgYcKAUzUfd+ku9lQqFQqkiSbmppOnDj2P6+9OtbewdnMwtXmMVczywmE+ZP2v1pg+fhEwtKeGGVFELMmTd759nvB73zJXSuF3ObiwyHqnGpgwUgyoOUgq65+h3/JOwcHzyRAlxzkQ3bDAMaqtsLjweLEXGTIUNmaevB0d3oe19vP0BoWWKR4pfUgo5oSM9JOhfQX1YCaBkYHBlBUtxR5X5BFZkFxhyg4oeVqlrKuDYxILE1pyZyUG+ufWTOGsJzqNm73377saGlF6dc4jtXrTCf1/zzdeScheucavcGgIcnC4qLn/7DW1sGeIIgP334H+kljcvmVt3ZkfOVNFdSDbIh9ZgA0rLZfCrSBqmjJPhYsj8lqD7qa8u1pWV4lqFjolhX5RbRdTIY2mTw1/9o3JxWFlUj1rNaCnpXWNVSfilD5JSpOxIj94qGh26jWcsABg7TP+d6hpSEx0NoPMrLyWvpNn/OGihaQ0kxZY/bJoJbLKUj73CJrCoirPR9PtnUaJTLok7UkpFeHxEBpI0hZZU7pjYO+8psliH1W0cAOJascUJH5NXkHAzK+8aErmkCqQrJokpGnFFYeDFJeyqjyjXz5t0vGOTqbWYwirMzHjhs7fuK4pLRrg8oBANCyJGNk9UY9xo1DSnsO26rcrQfvRPduWz286/iHAk7PYZZ5YGAgPDx8+vTp1tbW6E2SldX8+fMvXryoVqt597k7Z1WOBIRwLkGapisqKl555RUzMzNLS0tHR0cHB4dXX3312rVrFEXxZzSeiMY3/16FkdCu/6QOpu3ijTXwsyH+2Nvbe/jwYTc3t8mTJ69YsWLKlCnLli0LDg5WKpU/vMJB+/hP6iD8VkBAQODRREAgoB/Nfhda/ZAjEHkp0tnZefr06RkZGfHx8W5ublZWVikpKXi6nGmYZRqC3Fl+yGESmicgMCIR0Gg0Bw8enDNnjoeHh6urq729PRY+19fXA0Btbe3q1auxwAvnpu/s7KRpGot3KIpiGAa7HI7IxgmVEhAQEHhUEMA5FXBrsR99V0d7aX7+nr9v/9Xjj1sThANhbkMQY60fm+7u8fhoS0RrEYQbYf6805S9S1+58Jcv806EQo8S7UGrg9puxD6/vV/qkwDNSpBrgaJBS0O/qjE4vsY7AkT90KG8fTKkPe4GdPcDTeoR4cgCowe1XnOzNOdoYFd2KShI5LxB60CiqYhIrDgZAUWdjeeuph8JhF4lkDrkswFG5E2h0fVllPxx+iIngnjc3PoPq59rbW9TadSsHhFufCj183TnnYTonWtkSkXqjbSly56ysLYizEeNcXZODb3M3KrLenf/9U27ZBlliMRnkfYZOV/LKehXqcubso8FqxILIaO66GiQtrgOBrWgNtRcTKwMiILqXihoyNjn3Z+WB2odkCzCTarID75Ud+JC/+k40aFQaBhAxLQOa59V+d6h7WFJ0NgPYm3XzYKbZ8OlBVXQq4IWae6xc9XBcVDbC11khVd4U1A8tElBoQZW35dZmOkVCE09IFYab4vSDvl0pxeAkkFHVFOgZYAyQKv09vHzaTuOKzNKQamllUpg9bKS2vTtx5hLWV2BV1/1nOdEEBbmowgbc8J29IQJ427eSMXqfOTsgqTyiHT+gYA28rkl79aDd6J7t60e3nX8EwHOg6LRaDg9J5fLa2tr3377bWdnZxsbGzMzM3t7+08//bSnp0epVGLrP1M286cgKPmK4cKPmb9I07RGowkLC5s8eTKOnQiCmDNnTmhoKE3TAKBWf++Hzp/Uw45y58cHvedNW8R3GZ87hCRJ7EYSEhLi4uLi6Oi4cuVKZ2fnKVOmnDhxAssdePwfdCiE+gsICAj8zAgIBPTPDLhwOAGBnwoB/IZfKpXGxsbOnDnT1dXVz88vMTHR3d192rRpUVFR2LoLM1M4buBjDtNAxLT8U9VV2K+AwCOPAP9gZjQa+YcfuVweExOzYcMGNzc3e3v7adOmeXh4rFmz5sKFC4ODg729vefOnVu6dKmVlZW5ufmkSZO+/fbbrq4u/pzFZzSfGgivf+SRFgAQEBAQGEEI0CSlVagCTp/e+PprK1ascP/VWHNzc2c7B/fHHKe4evzaZez40XbzCaf1v5qzedbyzYtXXzjp25BdRBc3Vh0Oa/rcV3YiDio6QEXrGAq1SkJ3X07L+O4MVHVDp7bW93JnZCryL9Yb1KRKTaoMWhIGlFRBbdH+c6rrxSCjgeb0Cg1ouebE7OJTEZDb1HEuMc8rzNDYi0w2SJrSs2jPLAdSujs4KfmjA2vHzpxiO+YxaxsrB7tde/dU1dYMSiXYcJlD1tfImoO/pP9EWPOEKAdGVq+jWIbVI/tmHceptRqSodu7Oo8cOzbBc+JoK0sbG5txv/I48NkOfYHo5mfHMj85wqSUgZJhNCRD0XqKAZ0RKIAOZdmpi92R6VDZW3I0WJ5WjCrfr+yKuVl0+BzUi6G0LWufT3d0OmiMiLBWs9CvqgiPzzkaWO4TkX/yvL6yBZQ0I5UjUrtbXhEcU+57CQqboJcZuHwzaddxZU45dEmhX9sellR4MBBqOqBPK4282ROUCA2IpAbS2J1bkhsUKS2qBokKJNrGiKSW+Jv0gJRiKWScoiGRY7Wov+H4hdztJ3Q51UigzbJIc13a1BaSQKbc1qQU71zxx9nmSFw/2saCsCQsnB/z9TmN8DGwWPisN+p5xvn7xJIGMA79+4m67KHZLR9jGI1GiqIkEklmZub7778/f/58R0dHgiA8PT1feeWVQ4cOBQYGpqamVldXd3d3q9VqiqLooQVTlpgsHvbyxmAw8GuMRiNN0xRF4RwYPB2MkTStxjCpNWZO8Uq8MTaLoGlapVKJRKIdO3Z4eHgQBIHdCPft2ycSiXjhNh818Uc0PdZdyw9Z5/LPg/itIXbkwBx0UlLSggULXF1d165d6+np6eHhsXv37q6uLqlU+tCAIDREQEBA4OdEQCCgf060hWMJCPyECCgUCgDIzc2dN2+es7NzUFAQDhrc3NyCgoKw7zNv8mUabA0L40wjrZ+wusKuBQQEBADwZE+UV0mhaG5u9vb2nj59uqurq6enp729vYeHx86dO/Py8kiSrKur27Rpk9XQQhDEunXrcnJyxGIxfqLDp61AQAtjSkBAQGCEI0CxjNFo7GhpbmlqzCkq8AkO/ONrr3qOn2BJEI+NsrC3tHYcZTmVsHvSbtwCW/fxhI3HY07PzVsSsnVH1FvbS3f7Q1Er8oPmjIg7VFKalOKKo+chXwRVnf3RyIQBqttBw3BgUBmH7KFpA1lYm7L7pCapGNqVKIehioZeRXtyXtbRIENWbbXXxcJjoca6bhArwAgsy5IMjdjnAVVlSLxoX3Dd3qDKkPjQAycXzJg9atSoxxzsFy99ct+335SUlxkAVBq1jhtKwTh0Ff6PwOcNTO62F56AxgfFBDTJ0Kxep9KoE5OuvfzHVx53dbGysXYeM8bdacxbq17sSsor2heQtHWvJDYH+lASRQ3HSqVSg5YGUqcXdZedutjiFwcFzYVe4R1XMhAdLKfbrmeXHjsPFb1Q0lIeFN0Wmw6DNDLukJIgVlWdv1J2KEh0OrLE75KspBZY/VB6QBb6lQNJecXHgpE1swLU0dm3dp1i0kqhWQqdivrwhOKDgVDUDH3ajsSsusAYqOhEsmi1oTUuPdM7mKxqhj451yHOCY8uu3jV2DVA6iilccipmjVAt7rdPy7uz9t1129DnxrJt5VauqHj9qFzdFwenVu960//n73zgI+iTv//hJBKKqmSkAgBDhBEhUORv41TT3964lnvr6Kn3v93KqIidwqohA6hJCEhhDRISAIhCYSQEBLSe++9l81ma7ZP253Z53/fjLfuBb2znEqZee0rr+9udma+3/eUfeYzz3yeDauc7piFYQ5WVijF1dF6V/ABjVYFLGMuQBtY1sCynAzNSc9fC9Ac+W/Dzn9mHmNwkQZn5SeTyRoaGuLi4h566CFHR0cLC4sZM2bY29v7+/svW7Zs9erVf/jDH9577719+/ZFRUVlZGSUlpZ2d3fLZDKNBlnDKxQKU0EaE2RTJMP5fnB/9Xo9TdPfKhZzurP5vR9Od6YoSiaTqdXqgYGBrVu3Ll261NbWdsaMGffdd9/+/fu7u7sJgsBx/Pplch34Pn9Nfb7ZGybm5hq0iTxjYORyeVNT07PPPmtlZbVy5cp58+Z5enq+9tprY2NjNCpAy088AZ4AT+CHEeAF6B/Gi/82T+CGJaDRaGpqaubOnWtpaXnkyJHa2to1a9Y4OTmFh4fL5XKuBIcpvPg3orN54HXDDpbvGE/gZidgfskEAFlZWc8995ytra2np6ezs7OLi8v9998fEREhEolomk5PT1+7du2MGTNsbW2dnJx27drFGJDkAQD/KA1kfsxyx7j5Jzc7KL7/PAGewC1DwMCyJKNHFQsNLOgZCljSyAhHxioLird89MniKV97F0cnN8zad6aDr52zh42Dq439MnffTx94duPKJ3e890l+ZjYxIQPCCCNidRVyjWCvNUGfVHa1qvRgFNvYD1qKoAk5qoVnRLYLzQPFO8IG4i6BhETqM87ChFqb11i3N5bMrpell+bvjoAOAYhUrAoH1mhkWL1KSw2JBlOuNe+NGw9K6Q9OgQk1LVbUXLz69MoHPVxcZ9pYu7q5LVl2V+ypuEmVclKl5FR1oxG5OqDRfe/pmy8bzWoL/tNYlROduYWZC9A6Yir7G0CpUTe3tny0+RM3T4+ZNtazPdz97vS3sJzx/EOPK7OqWwNjrr23dyQuC6nPOK1maS1MPXCD66nWoc74yw2hSVDV33oyrTwiCR8SgIqEzomKwOO6zErolfclZrclZQJpBBWhHxSCkpZfqaz8KpyJL+zcFSPNrQI1rjNSWgMBCnwip6JobwS0CUAHiqvVlV+F4xfKYUwNQwooaGveGwONIyDQCVLzy0JPa5p6QEOzo2JlVVvBjmPGsg4Yn4RxeX3M+SsHjiNTDjAq9Drk0g0AEypFWvGl//1KeLEIJlSgpUBHg5Qo23+y48gZOq9h1+v/u8x9jj2Guc6wsrOa6eTi+Mnnn04okO8zQROU8ZsM6H8RoE0/k99sg++92W6zL5pQmTc4Y2iSJAcGBjZt2uTk5IRhmJ2d3fz58/39/b29vTkDMVtbW2trayvuxgCG2draLlmy5Nlnn/3ggw9279597uy5ioqK7u7uwcFBgUAgkUiUSqVWq+WkYe4vd8Fiun6ZFjuhg87AcM5jAECS5Pj4eHd3d3Z29iuvvOLu7o5hmLW19YIFC7gnxlBSvB49OsAZhnzPdBzzgXPtW2kXMB+dibMJPmNgCIKQy+Uvv/yytbX13LlzfXx8MAx74Y8vSKXS6+td30pk+LHwBHgCPwcBXoD+Oajyy+QJ/AoEent7n376aUdHxy1btlRVVa1du/YfZmc7d+4UiURcsGWKMK6XqEz/mtb4FYbBr5IncOsSMOU7c0PkDsyOjo7g4OA1a9b4+/tzuc/e3t7vvfdec3OzWCwWCAQ7d+50dHS0tLTEMGz16tVZWVnchYFGo+EeFzU/bK8/um9dnPzIeAI8gZuSwNf6KmtEVstIjDYaSXpCMJ6Tn/e3HdtXPXD/XE9vN3tHJzt7T1c3Byubx+5e9cJvVt9t72lla7N41T3/7/9uKEvOUJS3XNkZqsupBSHJNvbnh8XJy5uQhAqgIjWT9JSp67Ck9FA0siTuEICGQf+dUEOnqPtQEptWrc9pLAqKgR4hqPXAgFarRaYWLIBIbajq7gpK7Nt3pu1AgvJaAxCowB6MKoTXat76/fpFvv7WM63s7OycnJzWrFkTHR3d1dWlU2uMRjQiAxgZk/Hwf9o+30jM5gI0C8jYYwqTSXdGVrzIyBi9xkTC3oH+8+fPf/T+xrsWLJpt68A5287ELPzn+G798JOe7JLeA4kV/7u/+UA8tI2BEcltUkKD8hVZAKFi+EJR2Z4oaBYKkvKqwpOMfSKQqpg+QeORePZSNTQLhpJzelJyDL1joCOQCYaGVhY3dgQn6hILOnfFqNNKYEjM6nCBbAIApMX1jccSoXEIJJSioL7kSIw6pxrGcZBRkpzKxn0xkNsCY7rxS8WVwVMFCQFYqWKkov7ygXDFpXIYVIJYM1xYlRsUqe8YptRqmVaho3Fk1zyhoktaM/76leBMDrp/YJjqv4zoPJ7SeiAOynsSPvxyhYePs5W1gxVSn61nWm7522a1FvmGq3A1AFBGWs+i2oPoZZ4BbfbD+Z+20u3+fzNU3zQ5KJz+q1Qq09PTX3zxRS8vL1dX1w0bNgQHB6ekpMTExBw9ejQwMPCDDz547bXXnnvuud///vf3339/QECAm5ubk5OT89T0j6c2fX19ly1b9tBDD73wxxfeeeedTz/9NDAw8MiRI1FRUefPn8/JySksLCwqKiopKSktLa2oqKisrKyemsrKynJzc8+dPRcbG3v48OFPPvnkqaeeWrZsGYZhFhYWjo6O69atCwkJaW5u5uIlzowePeiA49xToSbJ9Xum5nAIbqV94puNajSa0zDPg+ZSobdu3erh4TF37tzFixf7+fk9++yzVVVV36pBm8O8lVjxY+EJ8AR+OgFegP7pDPkl8AR+NQIsy1IUeppVoVC89dZb1tbWn3766bVr1x5//HHu4X2RSGQKJky9NA81br1AyjRMvsETuNEImA437rlFlUqVn5//0ksveU9NLi4uNjY2Dz/88JkzZ3p7ezUaTXp6+n333efo6MgZF+7bt29kZIR7dPRbh8Yt3zzun5Yr9K1z8R/yBHgCPIFfjAAnoXIC69dmCFNnLuS6DMYRqSinpDAs4vgzzzxj+c+syVkWVnOsHf2d3GfZ2Nra2rpY2y318P3yxbfiN36hLWiAHlF+ZEJ9dh4xqZBIRJop2RFIhu0T1EaebYpNhRE5UFN6roqBhpGG3THa0/nSuKtFQTHajiFKrmJZVsfQSpqYxDUGqQqqB1q3nhDuPFP20WFFZTshUTAABjUOPdLK3VHVIWei/r7r3oVLZju7ONnYzbK0drS1++099/190yf5uXkjQoGSJig0lqn03SkRmTszI6lOr2f0ek5ZniqLh9yckdpsNOpJSjOplAvFsnGRXChWSWSTYql4QiSVSkeEgpa2tpbGpvr6+uikhHc++uCe+1etWLFirqe3HYY5Ypg/Zr/U3mOxo+eG/3m+NO0y9InE6SXX3t3ZGhijLG0BOTLfYA0M6BkgaINQ3nbxWv2JFCjuksTmdBxL0TX1g1gDfaKBpCttx89BTX/vybScwFBNax8tlhsZA6lQ6pp6m48lquOudh+I70/PAyWhlUiBolipQlnT3ngk3pDbAEKdtry1aG+EpqgR2TSrKbZtuPxYPFPdDeO45EJxwYFIaRlXCBHontGs/eFjGUUgpUDJqosbi04kqHqGgKTRi2YQPj1A1UDu/wYOxWTAyCQhlSPrFYFalVLUF3RGe7Yo7cPA5xbd6zLTGsMw21k2M6ws3njzdZlCyhUbZIDhdGc9S7OswWhk/vVl2ixf3xD5xQ6BW2ZF3xCcupEkEAhiY2Ofeuopd3d3b2/vtWvXfvbZZ8XFxWNjYwRBKBQKkUgkEAj6+vqamprKysquXr2akpJy4sSJrVu3btiw4bHHHlu+fPn8+fPnzp3r4eHh7Ozs5OTk6uo6Z84cX19fLkzy8/MLCAhYtGjRwoULAwIC5s2b5z81ubi4cEnWVlMThmGurq4PPPBATExMb28v18/rsZuuj6ZFTebj+q729Uu7BT7hBsth4RImTBo9SZIsywqFwqioKDc3NxcXlwcffNDV1XXNmjUXLlzgZjE9mWcCez29W4ASPwSeAE/gJxLgBeifCJCfnSfwaxIgSZKrYPbUU09hGLZ58+bm5ub169fb2dlt3LiRu89viiRMcQDXY9NbXqL6NTchv+7bkgCyQB0ZCQoKWrFihbu7u5ubm7Ozs5+f34YNGwoLC5VKpUajCQkJmTdvnp2dnY2NTUBAQGZmJk3TFEXhOP5dvnumiwf+6L4tdyt+0DyBG52AKYeX6yiX3svlC7OA0lvpKZ9iA8CQUJByIe3NP7+FzpDOLg5WNrYWlj7unr4eXp7OrnfN8V/nt/ghZ98/LV792TN/yotNNGp0Gj2uZUmGoVGFveFJQUpeRchpGJECaQCCBp0ReiU1u6MnY67C5ca8rcHS8hZQkzhF6oDRGL6u6aer7y39+DAdmdv++Qk6twkmkS+HWqkiRsR9URnDR89DcVdR8Kn2ytqD+/YvD1g0393bBbNyxiz9ndz9wvbuwgAAIABJREFUPbwf/D9rw2Kj6no7eoWjCq2ayw/lBstJORqNRigU9vf3t7e31zU2ZGZdDos4vmPXzi1btrzzzjuvvvTys0/8ft0Da+9btDTAy8fd0dnJwXGGnQ26B+ngZGtphc3AsBmYlaWlh52j3yzXO62cfmPl8ueHnz4VGKRo7gOpFgak4vSSgs2Hm3bFUHlNINGCjmINDK1BWcygYvqzS3MPRkFlH365pjPkHDSMgkgDKv3QuavI+rlPPng2pzI0Xl3bAVIl6AhGrtR2DFzbEy6IyWzbEyNJKQABkp6BZVilmqjvqToQjaeVwQgODf05ByNUhQ0g1oGGUA6MpAQensguh1GVKr8+70AE1diLsphJgDF5bmhMc9IlkBCgAWgZzt59TFbZQiqURsaABGgDgFjNVHZWbDlS+/kxaBkBmZolCNCzZH5j1944XWJBx5EzL/mvWGI/29bS0srBBrPEHn/6iRHhKK5H+ercS89+nf78r9Izp0R/8zt5ox82N2r/OIKm3nGXG1KpNCUl5amnngoICOBE4YCAgNdff/0fT3rl5eU1NzcPDAwIBALOo5l7Dsy0BHQXiqaFQmFNTc2lS5ciIyP37dv38ccfv/XWWy+++OLvf//7NWvWLFmyxMfHx9PT02tqcnNzs7W1tbCw4B4CmDFjho+Pz+rVq0+dOkWSJGcfMa2fptVxGuv1V0nf7Bnf3TIt5FZqcMM1AeEanEsJTdPc1aJQKMzNzV20aJGtre2TTz45Y8YMLy+vCxcucHGpWo0eO0B31wwMN/s0cf9WwsWPhSfAE/hxBHgB+sdx4+fiCdwQBFiWlUgk7777rrW19Z/+9Kfa2tq33nrLw8Pj3XffVSqVRqMRx3FTJMELzTfENuM7cdsTGB8fz8jIePPNN93d3e3s7BYtWjRnzpw1a9YcP35coVBQFFVfX//MM884ODjY2to6ODh88MEH7e3t3NOjpgST76Jofrn0Xd/hP+cJ8AR4Ar8WAZOnhKnB2VbQRpazhNYxtI6h1RRBG9nB4aH09PQvP9/20G8f8HJxm23v6GRj52hte4e9892udyyxdHzI/c4/rXr4xTWP7Pr751n5OSPCUXpSCTJCeia3YvsxUVHdVAk1hlKroV86Gp/TvDdu7GRm54k0vLrLKFFpJpUEsFqGpggcNBR0TnTuPy0Lu9i6O7rtzGWkWesBZU8r6fHMsoGjKXCxofNo8sDFIiD1CrWqqrh0/5Ztzy5F9iC+mI2PjZPNDEsre1vP+X5r/+eJz3d8cTrxTGZOdnlVZWVlZXZ29vGoyO27Al/b8Ma6deuWLl3q7u5uZWVlbW1tY2c7y8XJ9Q5P9zu8nJycHGfauGCWbpjVbAsba4sZSHSeOcN1hs1cZ/e1jzy8cdOHEbsPBm54P/CVv0Ru3qHsGASCQXUFFVoYROpzx774psBovKgFWT8raeQfomeQb/KQnChobgo7p7tSD5UDrRHnNRUdIKdAQQ9erSg5EgOV3URxS1XU2d7CCjAYkY02hVT77qOJVFLRYGhK96kM6BWi3GQdBQSNdw83HU2Qxl2BXiWUdOTtCBXnVrECCSEQqfpHUo6Et6XlQKcQv1Beuuv4eGUjkAzIdDCuak3IaE/LQW7OYhVU9rUdihfkVhglCjAiE25gGfSvLlHjvpjK3ZEwokTeKRqcnVSNVzaWBUVTl6slZ/O//N1LSywcfGfa21jNtHKwefh3j9S3NBAG0iRAc+qzee4zWvI/X2aSNJ8B/SNPBqZ4g1MbTUshSVImk1VUVAQHB7/99tsPPvigp6enra2tjY2Np6fnsmXLHn/88VdeeeXtt9/++OOPt2/fvn///pCQkOjo6Li4uJipKSEhITk5OSUlJTExMSYm5sSJE6GhoQcPHty2bdumTZvefPPN9evXP/jgg5wYzZlC3Hvvva+++mpgYGBubq5EItHr9VzSrkkGNXXPvGEawg9tmC/kVmqbczCh44o9clEoV+axoqJiw4YNzs7O8+fPt7a2njdv3oEDBwYGBkzf0ev15pefpsXeSqz4sfAEeAI/jgAvQP84bvxcPIFflMC0X26TlEyS5JYtW6ytrVeuXFlTU/P222/b29u/8cYbvb29XJ0NU/TALeEX7TS/Mp7AbUbAdJxyx923jn5sbOzw4cN33XWXr6+vv7+/hYWFl5fX+++/f/XqVaVSSZJkeHj4woULOfX5vvvuy8zMJAiCpmkurAcAjWbK2/Rblz71KLepG9/xFf5jngBPgCfwKxMwqc8MGJH0zDLcX8JAa2hSReIqXEsyei2OA4BcIq2vrjm8Z/9Tjz0+297RwcrG08F5ntPs+bZOqzzmLrGffecsZ2cr60V3/ebjjzdVpF5qOXWhaHMQlPeAmtSqlcgMQ64SphR2H0oaibxUsjdKUdIMEyqdVKFQq0gjqmCGFM+hyYmQVMXh1PavTnZGp6mHxiktjvwr5PRkTk3LoTNQ3N/wVeR4Yh4MysAI6JyM60HFKAoaA//njftd5vrNdLzD2W2mjTVmZ21hb2NjZ2tnZ+fh5XnPPff8dvk9Pu6eto4OlrNsLS0tZ2CYzQzLOZ5e99y9Yu3atf/nkYfvXnmvl5+v42wXZ3sHT1tHH8zOB7Oba++yYK7/w0898d7HH2Ymn6/Ovjbc2cvI1NA1nrc/8sqBE1T3GOiBoZC3M6hIxdXa2h2R5VuCUeFBkRbUFFKfAUBLg4YhCppLtocZc5uhZqhiT5SuuIXuG0f/bOy7tDN0MqdKdLksc++xieoWSq020CRoSZDTXbtjlYdT2/4eVr/rJPSLQKRAWeF6gB5BQ8RZeUIuVI9A/UjBjmNjaQUwrgQ9aMcmChPPt1/K09V3iy6XIRG5cRhwBs01ruo4ndGakAG9AsANxsGJrrBz/ScvgFQDBnaqnBwJBlbX1l++72TdgRhoG55anRHkal1T77WDkRMXitRXaw+8/O4CzGYOZu2EWdrZ28z2csstzEO/j5SOMtIMMCbf5ynb56/9N0zqM7D/YsfxKx8MN+3qTRnEXHa/6a9pQDRNK5XKwcHB2tra3NzcqKiobdu2rV+/fvny5XPmzPHy8vL09HR3d/f458S1uexmDw8P7q2Xl5e7uzu6MePo6Orq6ubm5unpuWDBggcffHD9+vWfffbZqVOnysrKuru7FQoFl2+LT503KIqiaZogiH9zBWSKl35owzTGW6xhzsF0Cck1GAND0zRJkhRFKZXKxsbGl156yXZq8vPzW7BgwebNm6du+Bm1Wq0pDOZ2EtNibzFc/HB4AjyBH0GAF6B/BDR+Fp7AL0qA+9nmfss56dloNMpkMrFYHBUV5ezs/Oijj/b29v6jovSMGTOeeOKJ9vZ2zprDPHQw/fabxOtfdAz8yngCtzQB8+OLSxW5PlVZIpFkZGS8/vrr3OUTd9111113hYeHSyQSlUo1Nja2efNmGxv0tLWjo+Orr74qEAhuaWz84HgCPIHblIBJgDY1OD9o5LYMRoplCAOtIwgdQVAUZaBolMNrYOura44dCX507UMeLq4WGOaAYbMxi9kY5oxZOFhZWdrOnDVz5h8Xr/rydy/l7w6HXoEGV7NIwFZJrlWXbD4iCEkr3xc9WdYCKsqIU3qKoCgCydNqHQyIB46nCnfGTx5M6QpJIlv7kd8RRYKCMlR0VWwPh6ttbUFn6o4kQJ8UJlQsQaEcYQpgVINfrqkJOhX54fbwrbs++ct7D61du3Dhwvl3zvvN3Hk+zm6+Hl6/8fH3t3H2srB1dXCysrJytrSZbYFeLjNtMQyztrZ2cHZy8/S4w9NryZ0Bq+YtfmTB8rW+i7Zv+N/KzNyRnn79lH81ocORmqwDaBU0Hkq49LeDht5xQBo4hfYhNcU2Drbviy/9+HBDaBLVOoSSl9HgUY1HGJayNX3lgScUyUVQO1p/KH4sJR8G5UCCpme0LjpVcC5fl1ObdyCit7hSr9OJ1HK5VAzjqq6ghPGv4oTbYgb3xkPTKMh1rFSBsphbRoYj0iYiLkKTEKoHhmIyxJllIMdBScCotD4poyz2HNsxoi1vvbIvnGzuA4kGFU8clEhSCmoOxSJfFACQEJVhCXXRKSBQIJdqHQ4GAyjUMK5qi0k798lOVFWSZo0a3ZTeLew4ckaRlK+8UvXVS39eOsvN39HVy9HJyWHWvAXzUtJSlBqlnqVphjL5PnMNLtPZXHr+lvYUJ/7PjyNgukgxuS5Mi4hMFyPmnxMEMT4+Xl9fn5eXl5qaeurUqeDg4F27dm3duvXzzz/fOjVt27btq6++2rlz5/79+yMjI1NTU4uKipqamsbGxq6/E2++cJMybrp0Mv33x43x9pyLg2bafKbglrODIwhCIpF8+umnzs7OnOO2i4vLa6+9JhKJKIoiSVQPltOjTfD5K9Dbc0fiR80TmEaAF6CnAeHf8gRuOAJcIGXKLCBJUq/Xy2Syo0ePWltbP/roo8XFxR988IGbm9vTTz/d0dHB3e03jxh4B64bbqPyHbq1CJiH6aZrMO4JRACgKGpgYCA0NHTlypUuLi7e3t5cXs+WLVtKSkpkMpler09MTFy5ciWXS7JixYoTJ04IhcJvrS1+a5HjR8MT4AncjgRMuvO0BleikJOh9Qyjn6raZ2RYpKVOyal6nBwZGjqXnPz075+4d+lSDxt795norp0lhsyRbS0snl/62/+Zs/iB2b5vPrM++nRMfX2turZjKOqiKDh94GCSoaqbk48pCgnQyFbYwICGJnLre/edhjMlvXvioKEfpCpKT9M6gmkd6Y9I150pat8XP5B0FYZkoGGANKJCgiyAFqC4q31ffPp7gd2ZRZN9o0DQRpIe7RsYbO4oS70c+lngtaS0uozcjL3hB/68KWJv0KEdu2N3H968/vV3f/fctr9s3LX9q8jIyISkxLSzKfVXizpySyviUuM/35cTdkrU0KlXaPQkxQDQxqnBq0gYUk/EZJd+EU5VdqG8ZgANSeAyJdXQX/RFWOnHh3tDz6tqu0BD6tQa2qBH+5YB8LreuuAz6rQyaBwfSsgZSSuEtjGQUTBJtabkDCXkQFlvR3SasKAaFGpcqwZgWfGk6kLZeNBZKvxy/85Y9loTDMuRqK2lQIK3HT83HnERulVQ0lF79PRQcg6MKECqBiUxnFNWEhwL9X2KvNrSY6eFxXWg0IGKgEGxMKusKTwJ6vpArAaBvOXUhdrIs7ruYXQDgJnK1CYNoDYMnckuDAybLGsCoRxtIC0Ow5L+05mCY6mQ3RC36YuVnnNnYZiTwyxsJmbn6pCYfGaa+sxJz7wA/cucWUzxj0n2NRcc/03bvHucWzo63g0MF0RxjeslS+6KZtq816/F/CLI/L/mM/Ltf0+A42ZO0nQpqtfrORl6bGxsx44d3t7e8+bNu+eee+zs7NatW1dRUTFtyaZNMO1z/i1PgCdwGxLgBejbcKPzQ77JCEwToImpKTo62sfHhytNFhgY6OjouGrVqo6ODi5Wm6Y4m374ucZNNn6+uzyBG56AeZjOGKZEEwPDHbkkSWZnZ7/22muenp5z5szx8fFxcXFZsWJFTEzM4OAgQRB9fX2bNm1ycnLiUuFefvnl7u5urjKPXC7n8kdueAB8B3kCPAGewA8gME13Nr01CdBcZUIU0hinEoC5ZF4WKIJkWVat1fQN9lVXV4YEBT12/wOOM62sLTDM2sLF1WmZj/8dM21tMcwew3xdZr+w+qGwl/567X93Vrx3AMoGQIQDridoiqApI06AhgAlISuqr9sRrorOyvlwlzSnHOQqMLCgN2o6hyoOxioT8iWxOeUHYvCesW9GSBlBwUDDeMu2E3n/b9dg7GVQUKBnwcAyOhIYkDV15xyMHM+qADFubBmp2hdjLOviHCqgR1wUFFMbm4Yyf43AoBECUCwoWMXlqur9sUV7IxV1XaDQsgYGp0hChyMzEFIPE2rV2eL6L04Ir1SCAUnPNBiRsfKYsjf0fOXfQlqPJmlrulDWMIBKT1Is8obWDYyXRJ2T5dRAl3zwVFZ7crZxQAxyAkbloitVNQfitCml17aF9GcVgYYEeioHWaxTXiyThKbJg9MadkcZKjpQ/rJSBzINKA0TGcUDCZehQ0hXdpSGxPVfzIchCYjUMKHqzyqqPZVKlLZC1UDjodMD2cUgmgQaeTp3ZxaURSXh3cMoS1qsGc2rqEu4QPeNAWVQq5VqWocgyIjJzPJr248OnbsKwkm0IWgGcEacWdYddg5KOtO37H1y4d2etrOsrWdaOdu7zp9zODrcAIxGqzLlPhuMBlMRQga+ttr4lqznf5pBo3/x008gMO0S4/u85TRNc7n5+vWblvMfoyDTN79P4/oV8Z98FwFznt8lQ6vVaq1Wm56e7u/v7+LiMnfuXHd393vuuaekpIRTqDUaDZdLwS3tu9bFf84T4AncPgR4Afr22db8SG9WAtcL0IWFhR4eHgsWLLh69eo/CndwTmo5OTmmjEtegL5ZNzbf75uTABdYcwE6J0Bz6SHNzc1hYWH33nuvr6+vu7u7r6+vo6Pju+++W1xcrNFoSJIsLCx84IEHLC0traysvL29jxw5IpFIuMstbgl8yH5z7hF8r3kCPIF/R8CkOE9rTBOgOdn563Rjs+XhFMmCEadwRk8N9vSEHT784h/Xz/aYjU1NMzHsDi8PDMNcMezl5Q/87d4n9qx6NvqFD0SXyvA+gV5L4HokQIOOABWhbOhM/miHLjm/9quwnnNZzIgQZeMajTAsqQtP7jyarEzIr9oTjWyjdZSeYQxgRP4bQhV0SWs+CCp7Z/fA8XQYVoCW1OI4RZBAs9resYv7wjvjL8OgCgYUDVGpY2evgdQIKoAu4dW9EUWHY2FUCYRRq1KrcC2tI0BBQosw+y+BVz8+gOoHEqBXaXEcRzcjST0ymyZhNLcq86N94nOFoKT1OKnCtaBnmD5hR0Rq09aI6r+HGpuGUL0+AKVh6vl31qgfFJVFJjefyoC6AfWV2uJDsbq2QeR3MSaTVbblbQ2m06u6gs91xmToB4WIs1wFGsaQ29Dw2TFZUErf3tNkWRvoGFatQdr0hHLkYmFndBq0C43NA/lhcV2X8mFQBAoCCFDl1ZXtP6nJr4fWsZq9UdKMEhiVoqRpgh0tqc0NjdE294IaMVeUt5RHnBmqqCdlk3oCJ0n0MkgmieKWjA93NsWmgmASdYZm6eGJifxq5CJd1FF/NP5Pi1cHzHL1cHJycHW0nu3wxZG9JKCqhXoDct5ggOGynnkB2uxY+dmb5jLl92yzLKvX66dlN5sq3XELMd3Lvz7ledqQvudKua9Nm5d/+28ImIP9VgGaMUwZ6E/VJqmurl65cuWMGTN8fX0tLS19fX3T0tJYlqUoiiAIrorJtC3+b1bN/4snwBO4hQnwAvQtvHH5od06BEyFNQiCSEpKWrZsmZ+f3/nz52NiYgICAu67777s7GzTY2umiIEbPx9y3Tr7AT+SG5uA0WjkCq9rtVqVSpWXl/fGG294eHjY29t7Tk0rVqxITEwcGRmhaVooFO7cudPPz49TTF744wv5+fk4jptc9riLLvObSTf26Pne8QR4AjyBH0NgmgY97S1aIpcEzbleGAE9rQ9GA1IejUjXMAKu1nR3dB47Hv7Cqy/ftXyZrb0dZoHOrB6Y1QPOc//gtugPbosWWjiuWbTs7xs/vnblqkAgUCqVyL9iWFB8/FR/fEZ7eFJb7HlqSAC4DlgWxsQTCTntgVHK+NyGoDhDfS/K2zUYcAqnCBxwGrpEfXtP1/7pS9nh89ArRBnMwE7iGuQWIteUnExuiEqFISVImbqT55uTLsOEChlGtwhH4rJyDkZqekaBZIwMq6FJSk+jcn/9kuq/h+b/ZRdxrQnEWiD1egY9RoOGryRABxP5tYVH49pTc9GiWEB51kYAnbEn5lLNZ2E1m45AbguMK1gDo8VxNYFrCQ0uFLeevjh66jLUDSszKwoPnqRa+oFgQawkmvvKj8TqUorHwtM6Yy+ASAM6A6oTOKEeTytoCjw5FpTU82UUnVmN7DJ0BOqGjmw+n90enwHVPVDT23E6ozs9F0RK0FCgY/R1Pe1B8ZBaCVeaWo4mCHIrUF1BFiU1q3KqS/ZFCnLK0aJESl1T75UdwdLCOjAwBpRZzQJBgs4gLa7P23qkLz4TNCSuUFByBahJZWlT7pfB0nMFo6cuf3zv4wGY5VIvn3lzfZ2cHD75++bh8RHDlOiMKg0CyiXnXqYwmBe8fswB+RPm+Z5XHL/AduH3gZ+wGf9lVnOS5jK0qc1dfur1+oaGhrVr12IY5uTk5O/vHxAQEB8fzwXG/zGN/V9Wyb/hCfAEbmkCvAB9S29efnC3FgGKoqqqqpYuXWptbR0ZGRkSEuLm5rZ48eLc3NxpopV5CGjevrV48KPhCdxYBEzXVKOjowcPHly8eLGTk1NAQAAnQG/evDkvL497TKGjo+P555/n6g26u7uHhIQIhUjCAAAu8dlkJM0L0DfWNuZ7wxPgCfy3CUxTnKe9/XptJiOOKQGa06CRDD2lgjB6PYkTSo26s683tzD/oy2b7155r4ujkxM2wwezXYDZB1g6zcAwK3tbZ1cXHx+fP7+xITM1fWJ4uCA5tS/p8kTilfa4NKqtDyhSr1aCVDmWfq1p+3E4V1765TG8vA1l+KJuIanUKFFAl6BlZ1TLJ8Hi/UlQ3gta0oCclr+2Yy49n1kRlwpjGpgge85eLQs7g9yTdXoQaybO5NXtjYVhGSVVMgZGx9BaPWWk9aBhW6PTizYf1qZVgFALOj1r4EyRQS2UgJykGwcKj8YNXq1gJSpSoSYVamQATYHkcmXF9vDKv4XAlSYYUICa0DMMSZK0jqDkioYLV3rjMqBVDHmtNQdjmNYhmMRBx8CguPRgVMvh+Ja9Me2hSTAqR87OChy5iJR2VG8PGw9NzfvrTjK7FoQa0BFysQi0pLi6pSE2FRqGoG6gOvj0QGoujE6CmkLCep+wIzoNLlRBfk/nnli2tB0mUEo4yHFlcWPt0dNkYRNIcCSdNw9Vh8YLMopApEKWG5QaWGYK6VjxvsjhxCswKKXUagYYdlJFtA9UhSVAeedATMbf1zxzL+Zwj6PnHbMcHextX3rphaHhAaORYVkDV2aQk545GdpcMvtv76388v4dgRvnioPfB/7ddvoh/zMnaRKdr28wBkalUg0ODr799ts2NjZeXl4LFiyYM2fOrl275HK5QoEKjfITT4AnwBMAAF6A5ncDnsBNQ6Crq+uxxx7z9PT84osvzp09t2zZMm9v7wsXLqhUKI43ZUD/x6fVbpoB8x3lCdxUBHAcJwiiqKjo9ddf9/Ly8vb2DggIcHFxWbhwYURExOAgevBZJBLFxcXNnz8fwzB7e/sHH3ywsLDQNEqNRsP80zzaPL6/cS7qTF3lGzwBngBP4L9CYJriPO3t16swJUH/U4DmzopfP7ZvYAD5HiOVmDbolRp1RXXVrj271z6wxtfL2wabYWtrO9PFAXOyxSyxmTbWjta2/i4e76x/8eqxmJGT6XU7wrUVjUBQRo0GtDhZ1FC5NXgiIj3/syBRYTUQeuQ+wbDI4llFQdtY9fawpo+ODO1LMNb3gVxNEbiepY0My2iI7tKazMh4ZlwOAiXU9FcfTcAb+lBGs4xsPZvdFHYOWsZARbM60siwODWV/qwiNVk11YGRgkul6JtaPbJ1njIf0REEaEhj/UD5obimC7m0TGVkWJ1SjXw2xAQUdDR/EVn+Wag4tRgmaSRJs8AaGCNJG8TK3ivFrQkZTGUn1A/1haXoC5pAhqPyiT3CkTNXxoJT+vfFV+yJROnbWhxVYlSQbHlHyYf7ZUdTm7aGE1dqYWLSQE7lPhOkqKC2MDBMf60Ryrtr9kYpr1SBUInU5zE5jKu64y9NJF6FPk1f6LnhlFwYEKHCgwQruVZdEXJ6srYdCd9aGroFg2HnpWemkriNoAejktaBFjf0jhUdOIlyn4floAdSowaG1TR0N0Wfl+XXCrPKjr74l4ft7lhiP/tuv3l3zJ79yCMPdXa2MwyNEp//+ULp8FM7wNe2Lf+VXZNfCE+AJzBF4PvI0CSJDPpHR0c3b948Z84cPz8/b29vZ2fn999/f3x8nCRJxsD7rfP7E0+AJ8AL0Pw+wBO4SQg0Nzc/+eSTLi4uO3fuzMrKWrJkiZeXV2xsLI7j3Ah4Afom2ZJ8N28FApwz+7SRDAwM7N69+5577nFzc/P39/edmp555pnKykq1Ws0YmNra2vfff9/Z2RnDsLlz5wYGBnZ0dHCKM03T6CFuiqJpmqvMwwvQ0/Dyb3kCPIFbkoBJN/zWxtdD/m4B2vToiflpGadIuUpZ3dRw6ETYky+td1/oj9nPwGxQoUK7WfYzMcwRw+bbOj3u85tdv3sx4S9/68nKo4ZHQEOwLX3124/17jhZsu2ILK8SNDiwBj2y3SCR+iymJiIu1n14qGNbhCG3AdS4jsaRFTWFCg92FVWlhkaRA0Jgge4RVB9NgJoBEOMg1vZcyL+yL0Ja0AAaI5CoUKGRpI04Bbh+srazISh+ND4HxGpWRwLFcL4USINmQNE+UBkUV300gZWo1FMT+q+MhDZR65bwyr/s6z2eBuMaIPQGdkp6NRhBq5eUNefvPY7n1UOHsDL49GjyVRhSgFQHIvVkRtloWKos9MJ4xEXoEiA7EQBU66+xv2F31MihpI4dUb3HzyMtmGEIA8lQpKC2pWBnGHupms2qKwsMF2eWwcg/c5/HVT0JmY1H4uFaS/3B2OGzV5meMRDKQU0R7QN5ByIUJY0ot5oBGBE3xKbKzxVAhwgIrsYkWjMrkFTHppSFnoYeISh1BpUafSrX1R9P6ovNGL5QcPSdjx71mPeA153r7v2tp7Pzow8/1NhYP7VXsCb1mWUNpgxoXoCegsP/4Qn8Nwn8RwHa3GRDLpdHRUUtWrRoxowZXI2568TQAAAgAElEQVSTDRs2NDY2arXa/2af+GXxBHgCNycBPgP65txufK9vGwIsy+I43tfX9/zzz1taWm7cuDE/P3/hwoWenp5xcXGmgAAF8VOT6RPTJdltg4ofKE/glyPApd1x68NxnKbp0tLS9evXu7i4LFu2zNPT097efvny5UFBQePj49wXEhMTFy5ciGGYjY3N6tWr8/PzzY9WrkKLyUvHZMFh/p1fbnj8mngCPAGewI1NwHRu/KabyCTaCCwyhjawLA1GEkAFbId8PKk4592v/uZ99yLMCnlD22IWDhg219L+Ad+Ae7185tk7Prpk6ZGNn8iyy/qDkyQHkvp3RA0lZ8OoCGjaQOqApJA/cq+4fX9c36fhfVsjtVlVoKRUikk1rUOW1Bp8oqwpLzx+vKED6dTD8ks7Q0dTC2FYDThIypov74+QlDSBnAA9UnuNJI3qCkq10CtpPJk6crHY0DvO6KYyBPUs0CxSnwkGhuW5eyLKD8XBoAwovVylpNRawI3QKqjefrz1w+D+wFPQKQQFQSjVcrmcNujRvF3jDaFJKFt5UNUSltSZcAnlKSspmFBrr9aOHTknO5raFZQADf3oy0ZgRHLoF/UfSRKFpLYdiu89cxl9n2KAolBs2TWatzvMmN8CJd1dQQnSjBJ6eAIoA8I+rhRnllXti4LSzs4T52sjz8LYJMhUU8nOwrLQ0yMFVSCQonxtobLrdMZYSp6xaxRIVjs5SWk1aAlKoiP5cmlIHNU9AozRAAyjp0CqaT6ZUrLruOZyZdLGL5+au2SJ55w19903z/uONffdd+1qLkGgvGzufoO5SxUf935zLPAtnsDPRsB07p3WMF2KsiyrVquTk5NXrlxpZ2dnZWVla2v70EMPtbS0MAaGpmlTWcKfrY/8gnkCPIEblwAvQN+424bvGU9Aq0U10EdHRzds2ODl5fXOO+/k5eXdf//9np6ewcHBKpXK/LefF6D5HYYn8AsQ4A46Ti/mou3+/v6DBw+uXr3a2dnZy8vLz8/P09PzlVdeKSoq4uxxWlpa3n//fUdHRwzDvLy83n///a6uLhzHrz9+TVnPvAD9C2xKfhU8AZ7AzUvA/PxpVqXwGwGaNDI6YDTA6gDkwHRIxtILrn6+a8fiu5be4eruhFlZY5g9hjnZIk3aFsOW2zvv+91LsU++de2NzzsPxMGEEvRTMitFGselMDI5HHmhfevx3s1hcKkexDpUOg9gUjVpUKlHqxvzDseMZpYCCSBQ9qTk1oUng1gPI2pVYVPClt3D+dVIAmaQRYaBopHJBg0gZQRJeYX7o4h+pD7rGYYBo1ahAooFCoi2odrQxOKdEZriFpgkjUZkeI3U7aaRzqPJbV9Fo8KDBR2g0gONlqlHOdoE3TlaeyjekFkNraKW0MS2uAswKEYFBpUEXtLSsj924uDZ+i3B0DQMU+4aoNLBqHw86erAntOCoym1YWdgTIrSvQ0M6EimT1B5OFZ+vhDqhir2RIrOF0C/CFijXqcDtYEsbGoPTVKcLxo5cwXJ3CMSVJBQpIBxRdeZTGQYLZQDbgChaiQtvzfmInRNgGHKYQOMpEQO45MDGQUFh6ImK1rQFgRQ4WogqZFLRb0nUqGkI2f7kT94L74Ts1mxeLGfv+/dv/lNdloaif+L+swL0DfvIcz3/CYlYH7uNW+bIlguQqZp+tq1aw888IC1tbWbm5uLi8tjjz1WWlrKqc/cbaSblADfbZ4AT+CnEOAF6J9Cj5+XJ/AzEmAMjF6vl0gkGzZscHBweOedd+rr69etW+fj4xMcHCyVSrkEENNvPy9A/4wbg180T+BfCWg0KHuLJMn09PRXX3117ty5fn5+AQEBvr6+S5YsOXr0KGd4R5Lk1atXH3vsMWtrazs7u8cff/z8+fPUVFqZWq02HbymTC7z8J0/ov8VOf+OJ8AT4Al8Q8D8/Gn6lPuQO3nSBj2q8sfQBLA6o55g9WoCH58QlpSUHNp34P/+8SV/T09bCwtUnBDDnGdaLHZwfsXnrvfn/fb936zZ88Kb+efThnu6gKJBQ4KUHo680LQltHZjkC4hHwYmwWCkGUpH6sAIxsGJihOJ3al50C+HYY0wrbjlZBqMaGBMoytrL94ZIb1SDTINsEaKZQgDjYxQNTQMqrUppRc/3E00D+goUgmMAS0LdGoNcmpuGukKTcl8f5c2px5EGk6fRcPsFI2FX2j9+/HKj47I04thkgKSnrI+BtAR0IlMluXR2VDapzhbULg/UtXcA5QRmTX3TpR9FVbzWWjDVxFQ1QsaA8qwVpIgVE+k5A9HpI2HpbUGnzEOi5D6DKCbEMOwpCfx8kBiNlXQVBMSP5xRCCKVUaZEHs0ags5vHDycpEkuHInL7EzMhBGJQaZAwnrrSGd0Wl10CgjklFDCjoqHE680HYwzVHRwkrdCLkUZ5SKF6EpFyZEYZUMnUAxF4DqNCtT4UG55Y3iS/HxhSWD4S/4r7nb2Xu57p89st8Xz5mUmn6MnlXzus2lv5xs8gV+FgPm517xtHsFSFMUZblRVVW3YsAHDMG9vbzc3t+XLl6enp3Nh8K/SeX6lPAGewK9OgBegf/VNwHeAJ/CdBAiC+PDDD62srNatW1dSUrJgwQI7O7tdu3aNjIyYVyozv+IyDwW+c7n8P3gCPIGfQICiKIIgRCLRvn37FixY4OTktGjRIh8fHxcXlxdffDExMZG7PyQUCjdu3Oji4mJjY4Nh2IcffjgyMkJRlFwupyiKyxAxHbDmgbt52/QF/uHin7DF+Fl5AjyBW43At54buQ9NWbGmEnV6Bt3R5+4aGhnkEtzf25ecmPDu23/2cnOxt7a0wLA7Zlovs5i1xsZtEWbtjVks8pnz/O+fSAk/QbcPiM4XVH4WXL8lmDpbDD1iEMiNGh16AkaHg0LTlHJ58FIhjKqgX0YVtNQEnVLm1sM4Aa2C0qBYXX4TSCjQoxRfHUPrGQZ0NEgpPLkk/eVPRWnFINOqgJGBEfWPc94YkgpisnL+slN6rgjG1KCjSY0W6cijSlViYdOWsNy/7JSnlYJMB3qGNUyZOOtpGBX1nTyvjbsCTROQ21S9P1pZ2QoaAuU4q9mG0DPV28OubtqrLWhA1Qg1JMjUMEHgaWWSiAxxVOZAwmWmfRjZQStVYGBhQtEVd3Ek5hLUDbWePC+5Vg1DYuSIzRhBoaHqe9oDo7QRl3tDzlaFJcD4JCueZCdV9ICg89TFluNnDd2jaIeTqmSVLfmBx4xlHaBjgWb0FEFrNKAgxLlVOYGhqvIWRq5kDbRCIUdVENoGSg9Fs8VtbSdS3lj6wJ2Y9SKPO9wdHR2srCKDg1GvECK0kblfyW/dB261HZ0fD0/gBiNgftyZt81jV85QjiTR3SyRSPT222+7uLi4u7tbW1t7e3sfOHDg+jGZL4qPeK/nw3/CE7hlCPAC9C2zKfmB3AoEuOJjAKDRaCiK2rlz55w5c1asWJGdnf3kk09aWVm9++67+qnJvOSg+U8+/5t9K+wH/BhuVAJcMC2TyS5duvTyyy+7u7t7eXkFBAS4urr+4/5QUFBQR0cHTdMqlaqysvK5555DbqMY9uijj164cIGiKK5EuOmAnRZt/8e3NyoVvl88AZ4AT+BGIXD9iZQ75XL20OZ/SVzX09VxJSvzk482LZo/z2e22+wZVu4WVm5WNm6W1vYY5oZZLvfy/esTzx1/bWPmxp2tRxKQiQROG0kS1ARM4qCka5Mz8mITQaoGLUCf5OqByJ6UXBCR0DLWHnpOeDYfBEqkHRvByLDIlIligQRjTlPz38IHg5KhV6ITy0mACQZXElogWRDikpSi4k+PKJKLQIgDBRqSAD0DYxo6tXLgi9iKTYdH04v04zI9SxOouh8ATcOgqDP6XH9UGlT1QUl388EYRXEdspkmCBBPatLLKjcfLtxyaOxCIUhREjGqPTim1MXlSr48rdpztnNPrKqjH0nDBIX8OsaUfbEZXUEJ1Nni2sAIaVoRjCnQKNC6jNAu7As6owy5MHIwsSnyHNE3alRpQEvAoLj/Yn5ZZCJSn2n0ZaqqoyHirLauE7QUjmvkOqVMLgGxAoraKr8IE2QWg0Q5qZqkwACMkR0Q1kUkSTNK+uIz3175aMAs17sDFiyaP8/e1nrPzl2C0bFpe5iRBfPXtP/yb3kCPIFfmID5udcU6HK3A0Ui0d69e319fe3t7W1sbDw9PQMDA8ViMXdTkOun6cah+XJ+4SHwq+MJ8AR+AQK8AP0LQOZXwRP4vgQ4eQtF7RQVEhIyZ86c1atXX7p06ZVXXnFycnrttdfEYrG5AD1NhubV5+8Lmv8eT+CHE+B8mUdHRw8fPrxq1SovL6+77rrLx8dnzpw5L730UlZWllwu12q1Y2Nje/fu9fPzs7a29vT03L59e19fH47j3I2laUG5eZz9H9s/vMv8HDwBngBP4PYiYH4i5eRmI8OirOep+oQogXeqgeIllgEW5eROyiRVFeVffbHt0YcfusPLA5WKnXKF9sAs5jnNXjVn3l/uf3z7ky/Hbv6qs7BcKpeotSqQqmBA3JFwqSQigRqZQIglRG1sWn9GEYhJ6ByvizgnTStBFQKnpFjUAUqPNNxJGsp7m7+Katl2AupGgQWKIBUUrqYIpE2LcUnitYtvbus4loLmRVnDLKWnQU1CQUf/1ujGD44MhqUZR2V6htECo0Mp0yyodAMpWZ0RSdAwBIXNFbvCtddqkemHXAkqXFXaULxpf+2nR+UXS1DuMwAwDKipvlOXFEHnIeTy4NaTUNqpFkwQNAEGI4zK+xMuN+2P1SQW9AQlKM4XQfsYKAlkzYGTbJ9AEHJ+cOvJzu2RNXuj8O5hUOtAjcOYVJJdURkaT/aMoKqGWkrb2NN0NIHKawCxUk/gCkpDgUGvUk/WttfviVIk5SNrEZLWUDqKwDWtfaVHY4cTspVZlZ8//cqdlrO8HJ3mz78Tw7A//d9XBgcHvzW+5QXo2+vY5kd7YxMwP/eax7rcA3/j4+NRUVFubm5WVlaurq4ODg4bN27s6+vjxjTtetYkRt/YI+Z7xxPgCfwYArwA/WOo8fPwBH4+AlzVsoyMDE9PT29v7+Tk5Oeff97e3v61114bHx+nKIr7keb+cj/23M/8t0bnP18/+SXzBG4rAlzZ7oqKiieffNLd3d3T03PBggUeHh5z5szZvn17f38/juMURRUXFz/66KMWFhZ2dnbz588vKiriDlJiauJCalNcbh6sf5/2bQWcHyxPgCfAE/gRBL7rXGqe+/zPNhKgDTRpZFCxQYogx0ZGszMyN7z4iiNmeccMmztm2HjMsPaYYb3Kd37ALFcfZ9ffrrx345aPyspLQKwYK6jK2h/OdowwQikoieGM4ra4DBiQw5Cy9WRax+lMGJaCFvljUMDSBj1KOpYQdHF7/e6YvI8OSC+WweSUKwijR2apBAsjGsPFmvK/7q/aFq5p6gMtTctUrBzVG4BeSU9g3NC2mIYvTkCPBEiGBCMJLK3HQUd3pWcVRsZB5yC0C9qPxXenZMLYBEpJJhhoGqrZEZbz10DJ2XwQqVHCNEGDlhpMy+sKSZoMQcbWUN0PE2pUFZBhYWKy80Ju4f5IIre+8MtQxeUKGFaAHDfSFLJ+FkjbI8/3bAnv+zS87kAM2TWskklRqcY+sfpSRfGOMLaxH+nULEDnWNWB6LHT2dArAdxgJElUtxAnQaxM3xNcH3MeRiZBawAdhayrJaqSAyd7j51TpRQFPvHKQltnl5nWixcEODk5PP0/vxeJhDQ9ZZz9I/YGfhaeAE/glyJgfu41BbqcFwdn+kwQRGFhYUBAgK2t7fLly21tbZ977jkuD5oXoH+prcSvhyfw6xPgBehffxvwPeAJcDVVuMRnACgqKlq+fLmfn9+JEyc+++wzKyurJ598sru7W6PRKBQK8x918x97rs3D5AnwBH4OAp2dnQcOHLj33nt9fHz8/f25qoPr1q1LT0+XSCQAMD4+HhQU5O/vj2GYn5/fe++9Nzo6yhgYgiC0Wi13f2hahH398fvvP/k5xsUvkyfAE+AJ3EoEvuss+k/R+esM6Km3jJEx6CmC0GkMFK0nKSPDMhQtHxNmnEp6Zc2j93v6z8YwLwvrOfaOVhhmZWuFYZiz1+w196/++LW3EnYGjeZVgEQHGqq/oCJ7d7ixohvahe2nLuXtPQEDUsD1eoahgCVYvYGiQUVB3WDr/vj4Vz9pCE2CYTmQRplMRtM0yn0W4eyFmtbNYVUfBEHdCCiIrzcKzsKYejgqs+XTsNa/H4emMaCQD7IegNKTBplcWlhVHX5KWt0AQmlD+Onmk0kgkqHR0Sz0CvqOninduGco6uJUfxiQq0Ciak661BKaKDuV0/BVhCG3AUakSDImDaAmR/MqcnYdm8yuLNgXISqohUERqoioI5H6rNKNXy7p2BfXvOnI+OFz0DEGSLcHUiIfTS9oPHQa6vpBpAOc1o+Ju+Mv9UdfhD4JKjyo0IBSAwRLtw9l7w27cihS2zsCpAHVOSQMMK4QZpU1HonXpJelfLhj9SxvKwwLmHenrZ31suVLW1qbuIf0ESV+4gnwBG5gAubnXtO1Khf96vV6giBUKhVjYGpqatavX29ra8uVJXziiSdaWlqmhcd8BvQNvJ35rvEEfioBXoD+qQT5+XkC/xUCjIHhwutr164tXLjQ29s7Kytr//79Pj4+a9eubWtr455g4qRq8994PvH5v8KfXwhPwETAaDRyRT4ZA0OSJEEQWVlZb775pp+f37x58xYtWuTs7Lx06dLPP/+8pqaG89YoLS19/PHHuWKDa9asSU1NNQXfXPYHF1tPi7CnHcj/8a2ph3yDJ8AT4AnwBH4YASPA9S/WaGRY1sBwL0avZ/R6WkcIO/quHIpM+3z/poeeee3+Rx0wbCbn6I9htrNs7K2t5to7PTx/yaZnXsoOi2nPLkg7FK4oaoJeec/xtIqDscr6bqCRTEyxKLka/UwocLyut/tIct3W47mfH0WVDBlgKFqPk6gmoZLBrza0/e147qtbqcu1MCgHFWkkaWCNrEgpSy2p2HS4/cto5moTTFIAoFarCR1uVGmE1Q25e48ZKtpgRFQSd6b4VDIzIgSZAmVby3XDKTl5G3cJItKgVwwSDUzqQDhZH5faEHpGc66o7eBp6aUyUDPIQ4Om6QnpSEFV8c7w8ahL9QdjhzMK9ZJJ5PmsJ5HHtFipKKjvCzrTsS2ieXc01PSCSIWMQcTK4ZLaktizupY+hFdGQJ+4JCiqISwRuoWsVIHLJ1EuNm6EltGavVHVB2Oge0xP4HJCRTOUUaacyChuD01SX62N/fjLVR5zZ2KYr4eHlZWlu/vs5LOJtJ7U6tSmn04UA09ZP3/LpvxhewP/bZ4AT+BnJDAtoDXFwKiMKMu2t7e/9dZb1tbWDg4OGIatWrUqOTkZWdPjOGd2Z5r9Z+wiv2ieAE/gVyLAC9C/Enh+tTyBKQLcTyyndmm12oqKirlz59rb2yckJOzatcvOzu7RRx81V5+nYeNmn/Yh/5YnwBP4KQRMd4MoihofHz969OjChQttbGwWTk3Ozs6PPPJISkoKF09rtdqQkBCusgqGYZs3b+ac3L9LgDb/3BRhf8/GTxkUPy9PgCfAE7itCVyvPhuRRny9AM3o9aAm+rOKcvcfH7lURLQPxIcdf+rpJ2fazMQsMMdZ9k42Ns4WM+dY2Tth2DJHjx1v/TVu2x6iqqvrVGbul6HQNAIkEru5p86Rg7PeCD3ChsMJrYExddsjFHn1ICOMJK1VqJBHhw7Y8q7CLUcq3jugSSyCITlo9cgrg2KBhqFrVbVfnqjYGERk1YJADQajEUCn1gDJqlp7845EkuUt0DsxUVBecOqMpKsHcBylG8u08ivlmR/v6g5LhtYRUJJIEB+WDKTmNoWcUZwvqtsZKUkpALUBjICrVUBSmqaea3vCR6MyWvbHqnOqYVBEUYRCr9MSGtAQZFlby96Yjm0R1VuOQtsoSKZcsA2AN/Sk7QsdrGsCmgGZCsbkPacvVR+Jg34J4CjBHNmbqCkQqJsPx9fujSLL2ridcEIjpzWavvzy6iNx+OWqS7uC73H3mYVZeN/h6TjbCbO2SDqXSFEoDdxcgDYajVPG3d8mQ9/WOzc/eJ7AjUXAFNZyQa9JgFapVJyjnUAg2Lx5s5ubm6WlpZ2dnYuLS1xcHHfONKU/8ylWN9ZG5XvDE/gvEeAF6P8SSH4xPIEfRYD7YeZmrampeeSRR1xcXPZNTS4uLg8++GBZWZlpwSjyZlnTW77BE+AJ/EwEjEajWq0uLi5++eWXPTw8Fi5cuGLFCl9f3yVLlnz22WddXV2cYU5ZWdnrr79uZ2fn6Oi4cuXKM2fO4DjOsiznuTEt/uYOdtOHP6LxMw2WXyxP4AcRuH7X/UGz81/mCfw6BL5bgOaqFHJKNJcEDaS+LD2z+XIejEoMQimwTNdQ76mzCS++8uLSxb/xcnWdOZUT7YRhXpjVIwFLV7nM2fPHd469vbnpfA41IgYlbsQpVHXQYETuFgJ51Y4TIweS+w8kipPzYVwNSvzr3OcxNZR05m7c17Evvvd4GgzIWB35NR+plqjqqt0XW74leCw2C0bkjI7UAqsDhpapYEhaFX5mNC0PeoV4fee12NOTPT2g0wJJghpXFNfVfHmsbudxuqkHSBqMRpAqJzPLu/edxpMKGwIjh2MvwfAkqHU6jYolCHZUPBh1ceDo2ZbD8ZLL5SBWA81oCY1YJgYNrqlsGzyc1Lw5uHV3NLSOwqQa5URr8MmWnuzgqOGSWmAZnUalF8k7M/MrTiTCkATkagBQTsrRWPrkw9EZ5YdixMX1MIksrbmsam1dZ9nhmIGUqxm7gle7z3XDZjrOsrd3d3L9zdz3vvhUx3AcjChB3cB8o0lNZUB/Sx70r7NX8WvlCfAEvoWAeZzARb/cX+6ravXU+UGpPHr0qJ+fH4Zhtra28+bN279/v0Qi4a52uSWYL5rXo81p8G2ewM1LgBegb95tx/f85iYwTUru7Oxct26dvb19cHBwSEiIp6fn8uXLq6urORMAbqh6vZ7Llb65R873nidwIxGYFtHq9agqVF9fX3R09KpVq9zd3RcvXuzv7+/i4rJu3bqUlBSRSMSyLEmSR44cWbx4MYZhjo6OW7Zs4VzaObdKHMe/K/g2//yHtm8kbHxfbl8C1++3ty8LfuQ3EYHvJ0CzBobR6420XjY6ZtToQIcMKCgwKA04AYbh8ZErWZmfffzxfXfd5T7LYRaGeVrZumMzPTDsMZ/F6/yWPnz3yi8//awkJ085IUEmG5MaakRcH5M2Fpw6uDuhIziZaRgAHQN6FjlskADFndVbQho/P167I5JtHAQaCANNAQuTWkN9f8PumNJNQQPH02FIyUxqlP+fvTcBi+JY+757ZjIzDBm2sIb1UcCDoi8Cvm4c18clfjG7Ro9L8mjUx/XVxByNGo0xrkeNBtyXBLcoRiMiLogoKigKIgEFWURW2YbZe53uru80Zfq0uMQkahCrLy+s7umurvp1V1f1v++6b5rQcaSVIEAdnvLNhtp9SeCO0ZCckbL5B11BAWdsJOvqgIUEZbrUxd+dmbUMXL4F6vSAwAHN3k66eHvVHv3qg8XLYnX7z4DbjUIxBPfTFF1ec2bNtrwl24uWx1YfSgH1gh9nQFK02SxozbfrctbuSpu+omT5LnC5ENwVzKUBAExZzZE1G4uSLgATyRA4T5LF5y4lb4zlSqoBwVpMBsCxgpPoW9W12xNOz1xuzMgDehNttTIEDlje+Eth6tcb6uNSTq7bNjSiuxbDHF5RKlQKtZvDP2ZOKjHWGEmzxWrieRbeYkiAfoGaGioqIiAdJ0gFaDGgqBB5FQCdTrf/x/1BQUFOTk6enp7+/v5z5syRfnASmz98AiCwiAAi0AoIIAG6FVxEVIUXjwDP8wzD4DhOURTDMDdv3uzTpw+GYbNmzVqzZo2jo2NgYOC5c+egFgarB/3SIgH6xbvYqMQtmwBsjAzDQCWaJMm0tLQxY8aoVCpvb++IiAhfX193d/dx48ZlZWXBqpSUlLz/3vtKpVKhULi5uR09evTB+EjSwfej0i0bDCodIvAQAvBm/o8YJLm5H7I32oQItHgC0NpOKpGIs8UBENw00zRt5Rkzz1h5huJYiqKMesP1rGvbN23u3a2HBpM7KdSvKezsMUyNYSpMpsBkwW0DZ0yddjH1vKWi9uq2g/nrD4D4rKRPVxku3QDGJsNejgdmCtwxZH+x8fYX2zI+X0+n5AIjTZksFhy3GSygqP72+oM3Zm+4MutbMjUP6Emr2WiwGgHgQK3+l5gfC1bEguwacOHWmUXrqk+nAb1BMH+2kKDaXLp6d8r/Lr57+KzgdsNAAAtLXLpxfv56sP8K911ixcbDoMwg+IO2cULAwOLK1DXbCzfE5S/dqf/xDJNfxjUa6QY9MONCtMNbdwtW704ct0A4/Fop0JPcXR3QWcHt2nOrt93ccxQ04k1qNavPLTy1eovpUi7QmRirleRpwHJAx5as/fHYmLmm+DTAAYqnBdckVgLc1Z9atTlndeytbYcHhoarMMxBpfL1fl2hUPQfNLCkstxMk3C6n/iFGJo8i39b/G2FCogIIAICAXHMAJ+x0JRKigbH8ezs7J49e0J7DkdHx+HDhxsMBgCA2SxMmBCewzaWYRjpwEOaA0ojAojAi0UACdAv1vVCpW0NBDiOkyrLVVVV06dPd3Bw+OCDD1avXu3h4eHv73/48GHoSVassNiFi8Nx8SeUQAQQgT9DwGw2w1ZZUVGxYsWKyMhIPz+/Dh06BAcHu7m5DR48ePfu3eXl5QzDmM3m7du3R0REYBjm6+s7ZcqUmzdvQn92zQog0eUemWx2CFpFBFo+AWlP1OzObvmFRyVEBB4kIBWgbRxn4ziGZRmWJVmGZBmKoXLeNeMAACAASURBVAmbIEBbeYbgGMIm6NHQdECv1xfdKozbu++jf4zuENxOhmGvyIVFpVIplUq1Wh0YGDhn4rSd0xeSiZkF38Xd+TEJ1FsAQdNWAtiAraCycMvh8sW7rkxagcdfBlVmYAOC8bWZAAam+oeTV2Z9mztnI3f8GtA3uYQGwNhQz1fVF8adLI9NBFfLwflbmSt36I5fBGU1gvqM46ABL/8+Pul/5rOHL4KyRkF9LrpbfjA585ut+A9J1KbjtdGHQV6FoD5bcAFFaV32xh/Tvt54bcUO/eFUkF8tOA8xWwFBgepGUKovjok78T8Lrs6LFtTnWpMgcFMcqDZlfLcra+OPIK8M6K0AAGtOUdrWHytPpYFak+FujY1uEtnv1BZ/d+DER/Mqtx8Fxfc2knoDuNt45fuDhbsTyvae+KRLf0cMUyoV/gG+9q/a9ejRIycnB4b2bXalROn5nvONZj+jVUQAEWiRBMQxg/Qjn2jODKf5UhR14cKFQYMGyWQyGO112LBhly9fFl+WoaUIEqBb5BVGhUIEfjcBJED/bmToAETgzxMQh9e1tbWffPKJl5fXiBEj1q1b16lTp8DAwAMHDphMJoqiRK1ZfM9v5rjjz5cE5YAIIAImk8loNJ4+fXr48OH+/v4hISEREREuLi5t2rSZPHnylStX4GSFrKyssWPHOjk5qVSqLl26HD161Gw2w+mEDMNQFMXa7k0WRkgRgdZKAKp1cIas+D4Je6jWWmVUr9ZNQBxf8TwvFaAFY2fungxN8izJC6s4Q+EUiVMkbRMmsQnelliuoqz85PETcz7/vGfPnmq1WiaTKZVKu6blb35tOjl7z39n7M6pC+qSM4Hg4QkIRtClDcVbjpT+a/8v/9xg3JMC7uLATPEsJ/iMrjbhSdcyPl+fNXfD3f0poBYHfNNRLAvqjbpjabnf7eWuFYOyxovf7izcfwLUGYDJIkTla9DXHklJ+nwFnnRF8MJcYwANOHEq8+qijeSelKqNP+duOgDK6wEPSBIHHA8qdGWbDud+ufncl99VJaSCSh0gWUDYgJkEejOoteI/XYgf9c/0L9aDzFJQZRAKT3NceW3tz+dubvvJkJEHCBY0msy37hTsSyzYf5yrbbSRRKOxUXB7XVhXtfHnk+O+vLFmN7hTy1qsNprkCMH2Of+nk1k7DlaeuDjzrQ+9VPavv/aaxl6tUr0SFNQ2Pj5etL0QB8Ct+/ZDtUMEWj0B6TNWHDZAo2Y4bOZ5niCI3NzcyZMnOzs7w0doaGjoqVOnxAeCaEyNxhut/oZBFWz1BJAA3eovMapgSyQABWiz2bxkyRIMw958883vv/++Q4cOnp6eGzduFCK00DRJks0mHKFOtyVeS1SmF59AQ0PDunXrunbt6urqGh4eHhoa6unpGRoaunPnzrq6OjgNMCEhISoqCsMwuVw+ffp0vV4P4xByHAejqcDB8YsPA9UAEXgcgYcK0PAA1EM9Dhz6raUSkIojjxKgoRhN8xzFCcbRtI2hbQx7TxgWKkbTdE1NTX5+/rZt23r16qVuWpRK5atqwTXHf4dGDmoXPjpq0IEN2+9cyQGVxuqfzuUt2Vnyza6azQmglgUsoK0EabYAEwWu3r48f0Pmgk156/eD4lpgA4S1yVqZ5HTnr2Wt2gmu3gFljRe+P5B9MNFWeheYm2yfdXrqRsmBzxZbTl4WlGILAxrx+nOZV77aCI5l18X8nLd+L3mrjLFaGcCxLA2MZPn+U2mz/nVqwqLGU5dBVVO0QKEmLDDToAE3J2fGj5uXMWc9yCoFNSbBmwduA7WmsuMXMtbFglId0BkBD9jq+sRvt/7yw89c7h2AkzhuBhwHGqzm2KTEYZ/dXP4DKKnnrDjF0/qaGkCwuvPXUtdsN6ZkfTlyvPMrKqVSoVK9gmGYk7NDdPR6KDrDWL4t9X5B5UIEEIHfR0D6jIUCdLMt0IYDytALFy50dnaGph6+vr6JiYmiBi0e9ftOj/ZGBBCBFkYACdAt7IKg4rwcBKAAvWTJEi8vr6ioqG+//TYsLEylUm3cuBHG/4VmleJso5eDCqolIvCcCFBUUwwlhiEI4ujRo6NGjQoMDPT39w8PD/f09PTw8Jg+ffqxY8eg+7mcnJypU6e6u7tjGNatW7dTp04xkgV6C4VDaqRBP6frh07zHAmI027gZFiLxXL79u3r16/v2LFj9uzZX3zxRXx8PJyyI06qfbB08L1RavHUbB/xxRKZPTYjg1afJwEW8Cy4zw4auuOAwjT8Fe7AsCx7z7sptE8GHMcRBFFbW5uVlbV58+ZRo0a5u7trVGoXtb2TQu0gU7qo7X09vfp2ivzpi1XHpy/LXLDp6sLN4Jdq0EhzBGU0GoGR4HLL85bFnpj0deamA6CBFGRfHph0emCmbJmFF5ZvMaZkgaK6st3HMzbtrS8opq2CBwxgwvGrBcmrthTGnwHlOmCgQZ217Myl1G93cPGXjduO31qzx3blFqBowkYyNgqYSOuRtKSJXx2ftexu4kVgxAHPWUkrzTS5zsA5Pu3myZnLspfvsCZngTqjcAqcAgRo+Ons9dWxjReyBb/PgCMa9TcPnri+8ydQ0QgoHjAssFKgTGc8cvHMhK+KlseC3DJgxI1G/d26uwCna9Ozf563qmTv8UXvjg118XJ0dsDsBfXZ2dl55cqVRqOxeX8K/UA/zzsAnQsRQASeJYFmfb34SZu1sYJ7I5pmGObbb79t06aNSqVycnLy9/fftWsXAMIDVnQJjQbbz/ISobwRgWdOAAnQzxwxOgEiAAnAsTVMGwyG6OhoR0fHsLCwvXv3RkVFaTSaVatWQfVZaviMell0/yACT4sAz/MURZEkCR0IWCyWjRs3RkZGurm59enTp3379g4ODl27dt26dWtxcTGchXDq1KnevXsrFAp7e/vJkyeXlpZaLBaJ/sxIX5jhwPpplRblgwg8ZwIcx4n3M3wthC+EUFmrrKw8d+5cdHT0+PHjg4OD7e3tnZyc7OzsevbsmZmZCT/qPHmBYf7N9kctqBkQtPqcCTy5AG3juGYCNBytwcZCEERdXd2pU6c+/vhjX19fjUotw7BXFSoZhgW5eE7t9saXvT/48r8/PLVsk+BhwybUkidpUGnM3RCX9L9LCjf8RBRWCgbWFEM2GICB4AqrLyzfYk5IB/nVhftP3NwUB/KrbY0Gwa9FvZ7Mv5OxYU/+3gSuvBZYbaDGWn7oTNKKjfjZ7Pz1P2Z8s4U4cw3U3QvnBSxEfcrVrDnfnfp4QV3CRaq0GnAsDWwmi5EymQAAzPXiswvWX1wUY0u7AUw0i+Ok2QQslP5iTs7qWHA2FxgpYOPMtXWXjp7I3R0PcssF9ZkHQkUq9I0HUs5O/ubq7G/BlVLBmNom5EyaTfrcwiNLvys/dGb9RzM6veLkjGEKu1fkTnYYhk2cONFiscCHj+jeB/l6fs43PzodIvAcCEgFaJgWba3gCISmaZPJFBsbGxQUBP1Bu7i4LFmyhCAIKEOTJCl+F38OBUanQAQQgadOAAnQTx0pyhAReDgBnU6Y4chxnMFgOHz4sKOjY2ho6K5duwYOHGhnZzdr1iySJHmeh7bPD88CbUUEEIE/SkAa/JO1sZcvX542bZqrq2tISEjPnj2Dg4N9fX3feeedpKQkhmF4nrdYLIsXL1apVBiGdenS5dChQ6LrdiRA/9GLgI5r0QTg2yCcDAv929I0XVVVlZqaGh0dPWLECE9PT41GA98J1Wq1QqGQyWR+fn6JiYkAAEvTYjaboVN1Q9NiNBpNJpPZbIa/WiwW6FEdfgqiaVokAs/+GAvox/wkZoISiMCfISAVoKHVs9T2mQNA3AEm4E3b7IzwRuV5HsfxlAupP548OvvLeX3Cu3rL7Z0xhSumDJQ5tNe4dfRpE+DuNf7DUUlHEjiCArUm/U/nT09emvbVJjarBABAAI4QvCkDUGrI/FfsnT3HQV619Wj6xWVbLOdzAAEEM2QjAarxnOi9SSs2ckWVQoRAA0GczrodHWc8fEGfkHYpehf7SyloxAUHGrzgRsOWWXhi9orjkxZZj6SBelzwuQF4IfiiFQe1BlBmKNp6+Myi78i0PKATNGsWcIDnTZk3D85ZZjyfDfQUX6fn6/RFJ1NTN+4Cd3TAQAnOo20A1FitR9KyZq65OnWV7ehlUIMDgqIZ0mIy1BWXntmyu/hQ0sGF/+ryqoc/pvax09qrlE6vOQ4cOLCirJwhKc7G3jc9nxP8WqMFEUAEWhMBsaN/VAKKywzDHD58uG3btnC8gWHYpEmTysvLoWmIVIBGA4PWdHugurwkBJAA/ZJcaFTNv54AdGKF43hCQkKHDh06duy4du3aQYMGqdXq2bNnl5eXMwwD1WfUm/71VwuVoPUSKCoq2rBhQ+/evf39/du3b9+pUyc3N7eOHTtGR0eXlpZCPwOHDh2C8xKcnJxmz55dVFQE4w3CeQxIgG69dweqmeBWQK/Xl5aWnjx5cuHChQMHDgwODoa6MwwNpGhaMAzTaDRqtdrd3X369OlLliyZ27TMmTNn9uzZn3766cyZM2fNmvXpp5/Onj37888/nzt37vz581euXLl58+a4uLiTJ09evnw5Nzf39u3b9fX1NE2Lr6OPugaPcfHxqEPQdkTgdxEQ9WWp+gyNndkmOVTc4TECtOASw2SCXYnBam7kKSNLleTc+G7e1//duVt7d18Nhjm8orZ3dFBqNVp7+47BIZ+MGH1o5Ybjk5ekTF7WeCIDVBug8kzQFNDjhqOXyjfHg4JaU0rWheVb+CuFwGzj7uqA2QZqcN0PJwtW7+avlwArByrqC39Ovv6vH2xHLlXsOn78m2jTtQLQ2OSmg7SBWiMoqE6csyrly/UNiWmgTCcI1jTNszbB0wdpA9XGqr0nz36xVn8mU/DvjONm3GSyGO/8kndp+/6ig6cEi2aSA3f1d5LTL27ZK+TQYAUsAGYKVOgt8Wl5C7fkfLbeuisZlJtAdSOL44Bj9WUVFw8cydx7ZN/85X/3aOOPqV0xmTOmsMOwbp07Xzp/AXA8yzD8Pf2Zu/coQAL077p30c6IwItAQOzoH5OA9bBYLNnZ2R9++KG9vb1Go7Gzs5s0aVJ+fr60lnAqFcxKuh2lEQFEoCUTQAJ0S746qGytigAMKnj+/Png4GBXV9e9e/d+8sknzs7OkyZNMplMPM/DWUXiXCRp39yqQKDKIALPlwB0LcdxnE6ny8jImDBhgo+PT2ho6BtvvBEUFOTj4/Puu++mpKTgOE6SZENDw5QpU9q3b69Wqzt06HDgwAFYWDFyt+imQHRW0KzNPt/KobMhAn+cAE3TFEVBk2eSJM1mc3Fx8b/Nmb/66qvevXu7u7vb2QkT5MVFLpcrmxZo+yyTyRQKhUqlsrOzg++HarVapVJBhVoulysUCvmvC9xNq9U6Ojq6uLg4OTm5u7u3a9eub9++H3zwwaeffrpjx460tLT8/PyGhoZmDj1YG0tRFJybj3rGP3690ZG/hwCUmOFfDgiCMPz3m3eg1Kspw7KETTDzpyx4fNxPp44eO3boyJefz+3apYuTi/O/fa9pMPmrmMxL4/hO554rB4w+NPkr8y8lgkExD4CJBDZgycjPWr0L/FJLpeWdWLu19PwVYLQCnqNrdUBnu7sj4fQni8DJbFBtBlVGy+nMC1/FgIuF5XtOHP/XZn3OLUEdxmlA20CdAVy/k7Fye+yEOQ2pWYAFLCV4fGYoguNsPE6ABnPRwVMJny0T/HVYhQLwPGujSVZvTNkTV3LqAqg1co1GgNv4y7cy1sXSJZWAoO553tCRpvi063OiE/7xT33cWaBngYEANk7wEEIQF/b8dGLt1hMbd3Zy9PDCFJ7YK+6YWoNhoX5tc69kWXQGwLC8DfA2ILg1adKdn8D2WbwgYuL3XF20LyKACLRIAvABKw65q6qqRo8eDT+Ba7XaAQMGZGZmQn9HUqc9yHKrRV5MVChE4OEEkAD9cC5oKyLwLAhcuHDBw8PDy8tr8eLFo0aN8vb2HjFiRENDA8/zBoMBTvwXO93ffMl5FiVEeSICrYmAOCTleb6mpmb79u2hoaHOzs7t27fv1q2bu7u7v7//pk2bKioqoFuA5OTkqKgohULh6Og4bNgwo9HI87zZbMZxXGyYSIBuTXfIy1kX0WgIVt9isdTV1Z09e3blypUjRoxwcXHRarVKpVLUnZVKpUqlUiqVUHeGyjJMQwFa3bQolUqoNstkMrlcDv/+qj/f+1/WtMAVKE8rFAqYv0wmc3Nz69mz58SJE1evXn3q1KmioiKTyUQQBGx04t+X86qhWj9nAk9FgIYSieDIwsYWFxfDjsZkMl27dm3ZsmVDBw4O0LoGaJxdMJU3ZtdT7RWpcv+g/xub18cUXMpibteA4rrji6PJ5OugoP7chtjClDRAkJyNZggcMKA+LiVlyjeVGw6DMhwU1t49mnpp8UaQcoM/de1qzB5BfW40AZIGVkIIIVhjzInemzxn9d2jqaCyngY2nc1qg6IvAMBMVp+7eujLf5lSsgS7ZpMVMDRgbIY7Fce/33Pt6CkhFKGZBlYbl19+YfmWyiNngdGKW0zAZgMsIJOv/bJ466XP1hR+tx9UG4GFAmZcqLXeeOHQ0fQf4q7uOvxuZJSP6lVnDHsNk3lrnF63d9q5boO1VgcoVnADIhGgn+xCi7qzmHiy49BeiAAi0IIJNBOgAQBGo/Gzzz7TaDQwGPigQYMyMzOh/y5e+EomTJ1owRVCRUMEEIHmBJAA3ZwIWkcEnhGBrKysvn37wnArw4cPd3R0HDduXGFhoRjbV7TwglIXEqCf0YVA2b5UBCiKIggiKSlp4sSJgYGB0PC5Y8eOAQEBH3744ZEjR6DKXF1dPX/+fOhqIDw8PDY2try8HJphUk0LEqBfqtvmZais2WwuKipKS0uLiYkZPny4n58f9HiuUCgwDJPJZFCAFh1uwI1S1Vhq4AwVZ1GzlgrNotwMtWbRPhoeIp4ImlfDHDQaTVBQUK9evSZPnrxp06bs7Oy6ujrYRb4MlwbVsSUQ+JMCNOwyxJB6JEmaTCbWxsLPooQVNzboyvMKEmJ2juo+wP9VFxdM5SUXPKyrMFmwf5uhvfp/+/nCHxasKDiYRJzPS9uw98rBBKA3Ce4yGJqvqjemZF2Ys/bm8h9AIw/KjYXbf76+Otby80V93NlL32yxnMkCNAAkbTUaGKMJNOJ5e44mL1xPnM4CdTgg6Eba3MBaWYYS9N9GwpJxIzUmtuzkRVBZD2gWNxkBY+OKKgt/Tj65JdZWWSfkVqkHlwrTl26pP5cJahoZq5W2Wvk6PZtdnPfV1oLF2y+s2gbK6gSrakEfZ9nq+pqkSxeiY8/u/PHNLj3aObv72GmdMMwew163c/xi6ky6UYh5KKjPvwrQgj01/5sXX1Scbb9apYtbxMRvZoJ2QAQQgZZIoJkADWMj1dbWLl++3MPDA8MwlUoVFha2b98+aL/VEuuAyoQIIAKPJYAE6MfiQT8iAk+PwNtvv+3g4PD111/Pnj3b2dl5yJAhZWVlPM8zDAPdQ8MpRWIgdSRAPz32KKeXl0BdXd2/p/YPGDDA1dX1nXfe6dSpk7u7e2Bg4KJFiwoKCoimJT8///333lcoFPb29tOmTcvPz28WG00UEURNQTr1D7ngeHlvr5ZXc9hxwO+ajyodwzD5+fnff//98OHDQ0JCHBwcMAxTKBTQgQaGYWq1GurCcrlcrVY7Ozu3bds2MjJywIAB/fv3DwwMFO2aRflYlJ5h4kEBupncDO2jHzyq2RYMw5ycnMLDw2fMmJGYmFhYWMja2IfWC/WYD8WCNv5hAk9LgGZtLIzwAT3eQIt+G0UDGwdIzlZQeWjlhj3RmxfOm98lPMLZ2fkVuVyGYV4ax/8b0G7A38KX/s/0H+YszdifYC6vBjabsa4O6K385Vsps/91ZV40SCsC9XTRvuPpSzaDC7cED85LNzYmXwU1ZmAVbJ8F9VlnKv45+fL6WOrSDUF9NgmeN2gALBwJKBtoJMG14vT1sYU/nQJ3DcBKsBTJUiRXr68/dSn92x+ogjKBYUU9uFGRtyq28eBZUN0IABBEapzCrxZcXbE976utVxdvJvJKAE2zgGM4GpiJ/IQzP32+9Mau+HEDh3qq7Ht2DFNjmLva3gGTjX1vOKUzAhsv/BMEaB664Pg9ArQNCHEPRcW5WeIPX3Z0ICKACPyVBJoJ0HByMM/zOp1u69atHh4e0PeXn5/fhg0b9Hq9tKzN/HRJf0JpRAARaDkEkADdcq4FKknrIdBMVq6vrx8yZIibm9ubb745depUJyenIUOGGI1G6HO2WbWlb9Fiutk+aBURQAQeRQC6izUajSaT6dKlS2PGjPH19e3QoUOvXr0CAgL8/f3ffvvthIQEs9lssVhqampiYmJ8fX0xDHN1dd25c6fY6JolpCqz1BpautujioS2IwLPjYDoXoO1sQRBQLkW2g7jOH779u0jR47MnDmzffv2MISgXdMCZV9o+4xhmFarVavV3t7ew4YNmz9//u7du9PS0oqKivR6vU6nW7x4ca9evQYMGDBmzJjJkydPmTJl6tSp06ZNmzFjBgw8+Nlnn82aNWvKlCkfffTRsGHDBg8e3KtXr/Dw8Hbt2vn6+rq5udnb20Nf0oIPXI1GPK9KpdJqtfb29nK5XNTE4a9ardbZ2blHjx4rVqxITU3995xcs9kM7Umhuidtoc+NNjoRIvBQArAZij0FjFsLleh7aYYBFAMIFjSQDVlCWC0zSVzKzV6zKWbo0KE+bh7uGgefV51fV9i3UTkNDImY/T+TEk8mVlSUmW/d4S7eyJi5OmvmGnCxEGTdubMjvnJnAsgqtxy7dPXbWPPlPMHpM2MDLAdsvK30bs6e+NSvN7DpNwV/0KwwV51lKIPVCGgacIC9XJCxLrZo33FQawYWijKZBN/QelPlhcyLa3bY0m4APSnIvJWmzHW7dD+nAp0NUDwgKUDSuozcnOU78r7aenruasGvNGnjeZYGLG216q/eSFm7PXd/4tQh7/vbOfz9/3R2e9VRq1R7Oru+88abuVevCdUXBGgO0DwUoH+P+txMbn5w9aGXBW1EBBCBF4CAOK5uZvMBAEhOTu7Vq5fo+2vu3LlGo1GsEsMwcFQg5iAmxH1QAhFABP5yAkiA/ssvASpAKyQgCtAwptnEiRMxDBs1atTo0aPt7Oz69et3/vx5aOks+qiFFMSeslmiFTJCVUIEnioBOE2PoijoDK6urm7dunV9+/b19/fv06dPZGSku7t7eHj44sWLc3NzYQvNyMgYM2aMl5eXq6vrzJkzCwsLzWZzs6b30FVRVpBqXs3a8lOtHMoMEfh9BESLSxjbVqfTpaWlrVmzZuTIkf7+/lDzlcvlGo1GjBkINWh7e/s2bdoMGjRo9erVSUlJJSUloqdFaL/JcRyO40VFRYWFhZWVlXq93ty0WCwWHMfhlAKSJAmCMJlMdXV1FRUVRUVFeXl5WVlZly5dOn36dFxc3Pr16xcsWPDRRx/17du3Y8eOHTp08Pf3V6vVovmzSqWyt7cXXXzA7dDaWqVSdenSZcqUKYcOHWpoaGAYBpp7wwYobbC/DxnaGxF4egSaCdDijBkxwdlYQYHFGWBhgZ7AcbyBtNRTlhqTvrKyMm733v8dOy74db8AZ/fX7Rxfk6lfs9P6BQaMHz06Zd2O83PWJv1jLjiRB87l3dwUd3dHAsjXUwmXkxZ/Z7mUB8y0zWjiSVLQc2uMBfuPH/rnMmPSVdBIAQAacSPBUSSJC+qzlQW5FZeWbS3cmwhqrVxlneC4mSABaTNn3zq+YgN5tQA0kMBAgypD4d7Em9//DGqsQIcDvRVYadO1gpzNB8pX/5i7aIvuXBYwWAHLkrgV0LS+sDQpZueV2J++GPNJREBg13btnV9RuTk4qWTyv3frcflCGk8zgG1Sn5l75s/3PG/8hv+NB4XmR215etcS5YQIIALPl4DYjz8oQJMkmZaW9v5772s0Gq1Wq1KpJkyYUFFRIXo3guMBeKCYDxqfP98LiM6GCPwGASRA/wYg9DMi8AcIiAI0AGDx4sXu7u4DBw6cOnWqh4eHt7d3WlqaEBKdEl4Gmi3SzlKabrYbWkUEEAEpARidDG7hOC4zM3PGjBleXl4hISGDBw8ODQ11dHSMjIw8fPiw0Wisra01GAy7du1q3769SqVq27btwYMHoQ3Fo0wnpI3xMWlpkVAaEfhLCMD3LnhqnucrKyvPnj07c+ZMHx8fDMOg6wypvbPoQ8PJyalr164LFy7MysrS6/U4jvM8D02nCYIQndJwHAc7r998oxO/0zzIgaZpHMeNRqNery8qKjp9+nRMTMysWbPefPPNyMhIPz8/Ozs7UYyGxYar0DeISqWSy+Vubm7Dhw+H1tDwyxNJkrDAsJE+eF60BRF4PgSadRNiW5AK0IIISzZp0DRLAc7MM1zTyJClBMNkwmC6cu7Cki8WdO3YGcMwJYb5OLl4Y8r/FzFg3YDRiZO/shw4l75ksy4uBZQT+rizZ+attZ7LBrigPgMzCQwUqDBdXfPD0c+WVSWk/up2w1aHG+pJI2ejgZHkMm6lzl79y6ofrNmFrM5gaWwU1GcTCW6W39p22HjiMndXJ+Aqbczf+XNqTCyoMYJ6A99gAAQHcssKv9tf/d1Phf/abTl5BVhtgGU5G83qDKDKtOfTry7uPfzl9Jlur2pD2rTxc3VzeEXpYKcJ8PU7ffKUxWgCHA84nmc5zsbytie/Jo+Smx/c/uR5oj0RAUSgZRGQPj+lD08AgMVi4Xk+MzNz7NixarUaztZ6++236+vreZ63WCzi/shApGVdVFQaREBCAAnQEhgoiQg8JQKiAL1o0SJ/f//evXsvW7bMw8OjY8eOKSkpFEWJL/PNTijtdKXpZruhVUQAEXgogYqKCjx0AQAAIABJREFUioMHD0ZFRfn6+rZv375Hjx5BQUEhISGzZs0qKSlhbSyO4zdu3Jg+fbqTk5Orq+u4ceMqKirgByHou+PPaNAPLRLaiAg8TwLwYwzP80VFRbt37x4/frybm5tKpXJxcWkm6To7O9vb2wcEBPTt23fatGkHDx4sLS2FEwhEcZkgCFh40Q26uAql3mbveNDwU3Q1AF8F4bEPhQD1OLgbfLfMyck5cuRITEzMpEmT+vTp4+/v7+joCP11SMsvSHJKJYZhjo6OEyZM2LdvX319PWy80MUBLNhDT4o2IgLPmoB0/NbMGvo/+oiN5WmGp4U541bA6pmmzzxMk2U0w5FGM2BY3GQuuHFz84aNQ/r0D3Jy88GwbpjjEI3vwFd9v+j9zp7/nWc4lk6dzcna+KM5NRs04ICxCbbPRgqU1Gcu335w/Bc3tv0ELBxgOcEzBuBwQAsOmmnWduVW7r9i0z9fC66WCvLxvciBHKgy5Gw+cHtnPKgwAoIGZvzGrvicrXG2kmoBGk0D0gZuVNyKOVC59kDJyt1k8jXBc7RNsH22NRpAed2F1dvPrd62YuY/PZycggIC/hbY9rVXX8UwzN3Vbc2aNeJECpEDLzgFecLlQaH5UVueMEO0GyKACLQ4AtLnp/igEAcScKxeUVExa9Ys6ElMq9X269fv3LlzcMqXeIg0nxZXSVQgROAlJoAE6Jf44qOqPxsCsOejKGrJkiUwetLMmTOdnJyCg4N/+uknjuPglOFnc3KUKyLwEhEQ3W4ITi1t7OXLlz/99FM4o79///6RkZGenp49e/Zcv359ZWUlwzB6vX779u2dO3d2cXGJjIyMjY2VOo+D4ETp7TEc0aD2MXDQT8+fAMdxUCmGeu6NGzc2b978xhtv+Pj4qFQqtVoNXSpDAVcul6tUKuiR5tNPP42Pjy8sLGxoaHj+xX7MGTmO0+l0t2/fTklJiYmJGTt2bM+ePQMCAsTqwCCHSqVSo9EolUpPT8+hQ4cmJSXBkERGo5HjOGgQDSV10efVkzTwxxQM/YQI/C4C0s6iuRJtY7mm+IQ2jsMBa2EoITIhzQKm6Z+NYxnGJpgr0AaDoaL49tLpnw8JDv+7a5t2mCZM5dYOs+/h4Dutz9trJ3yWGL2TqdELnppZntNbQH5V2sodx2Ysu7xyJyjTCY4+OOHHJq8cgKpuAIV1OYu3nxr/FZ+cC6pxgDOclQRWBpTrb2w5dHl1rO1mBcB5oLNkJ6Yc/Hpd3eU8QDGNRoNJp6+7ciN3xa66tYeuL9xa/MMxc5HwBVdYrBSoMN768eSJtdt/WLy6S5uQ8MCQN/7e9zU7rYtS46S0W71iZU21oGILUcU4wLGC/2eWFwomzJpv+teUfOgfJDQ/FAvaiAi0ZgLw+fkoQbm2tnblypWenp4qlQrDsJCQkD179lgsFtjdS31xNPtS3pqRobohAi8CASRAvwhXCZXxhSLA8zxBEDt27HB1dfXw8FiyZIm3t7dSqUxMTIQaAbLMeqGuJypsCyUAXQHgOA7d3e7bty8sLMzFxaVLly7du3cPCgpycXGZOXNmcXExrACO4xMnTlQoFBqN5uOPPy4tLTUYDFDChoHanryeUk3hyY9CeyICT5EA/JYp3rrQ6NhgMMTFxfXs2dPBwQHG7lOpVDKZDHrekMlkarU6NDR0+PDhsbGxlZWV0Fy6ZUq0sJXBb0tms7m2tjY5OXn27Nk9evTw9/eHHqJFm2j4/qlWq0eOHHn06FGDwSC+gorMxWYrbkEJROBZExDvumYJ4bxNbig4jrNxHM1zFCfo0ffUZ0ZIswxD0zRrYy0WS11V9U9bvj+wdlNaXMLGBUu7eAf6yu21GOb/isPf7N06ePrN+n8zz5w/Z2jUA4o/9PW6+HlrMtbvoa7fBhSwERTggfCZiqaAhQK36rKWbD/+0QLDrmRBfSZ4ITghA4CRKzp4OmH+WvZqsRCQEOfKL12PW7OJulUJLCxL0Ua9wVZriJuzomH9kbvf7M1du5fOK7sHkOFAveXOweQr3+09sHrj63aOf/PyG/XmuxpM9iqmwDDsH+98UFdVzZAU2+S0Xai9RIAW1eVfLwcP7vmE/nXDPYFa3FFMiDugBCKACLQ2AvCxCQXoZo9Q+C3ZbDYnJCT4+flhGGZnZ+fr6/v9999DCvX19aJyjQTo1nZnoPq84ASQAP2CX0BU/JZHoK6uLj4+vm3btv7+/nPmzPH29m7Xrt2+ffvgV9mWV15UIkTgRSVANi3Q8DkkJCQ4OLh79+4RERFeXl4DBgzYsWNHRUWFwWDAcXzfvn2RkZHQDc6mTZtomhYNIeEI9UVFgMr9shLgeZ61sTRNEwRhsViMRmNGRsbYsWPbtm2rUCi0Wi2GYQqFAkb2s7OzCwkJGTFixKpVq9LT06E+K87Feeh73V/FFVqJis3zwWJUVVUdOnRo4cKFo0ePDg0NdXJywjBMpVI5ODhAPdrFxWX69Ol79+5taGggSRIAAP1Zi9V8ME+0BRF4PgTEm1C4wyUqKwt4Fgg/Cqo02/SvyUWyINfygGc5q8lsqK2vvVMBbDzRaCzNzd++LuatfgP/y8XD8xV7dVMT8A7wmzljxpnDCVf2HU3dsu/O5euCrMxwuMXCA0AxNFVvAL+U6zYmpIxaULIuDpQ0GUfDmhtI4nze2RXb6q7cAA0WUGkoO3tl/7821OcUAgsDaAAIniuuuRSzt2FPsm17cvHXsdYLeUDf5KKH5oCBKT96/vg3G3766tt3e/YL9PSZ/PF4n9fcVRjm8Ip6cN/+lSWlwjchmhEFaL7J/BlaQD/ghEOC5pHSM9Sgn891Q2dBBBCBv4aA9JkpTUPXeQzD1NXVpaSkhIeHy+VyZ2dnNze3FStWQBMTJED/NdcMnRUR+C0CSID+LULod0TgdxI4duxYWFhYmzZtPvroI39//4CAgJ07d8JZhzAn2IP+zlzR7ogAIiD42ZBSIAji6NGjH374oaenZ2BgYFhYmJ+fX1BQ0CeffHLlyhW9Xs9xXEFBweeffx4QEKDRaKZMmZKRkcHaWLPZLObzGKlL3AclEIEWRUBsCDzP19fXl5SULF26tH379hiG2dvbQx0W+kYMDg7u0aPHvHnzkpKSysvLeZ4nSRLHcajMQgkbOu5o9mr3l9cXKuxwfgNspOJfgiD0en15eXlqauratWsHDhzo7e0N4xbKZDKNRoNhWFBQ0MSJE/fs2VNZWSn1v4Ha+19+ZVEB7hGQqqxSKHyTN4om3VmwiW5aWBtrNBppmiZJ0mKxsAxDWPGa6uqD+/ZPHz+xW+cIO3vhttfa23f8r6CJb7y/9cvlFYUlwqEkQ+pNQsJMguK66h9Opn70VcXSvaBIB4wkTpHCCcykObvo8upYMjVP0KytTF1KVvyS6LKL1wAFACVo5bbcsvOrdpRsOITvOVe6bA+4WAxowBtxok4PGiw1xy/d3H7k52+i3+rcM9Sv7czJUwP9Axw19q+q7f5v54izZ1KEqQy/2j4L4QdtgOeEf0iAhtcX/UUEEIGHEpCOTMS0uCcc0hAEcfny5UGDBgnPQK3W09Nz7ty5DQ0NUgFaagQtHo4SiAAi8JcQQAL0X4IdnbS1EYBzJAEAxcXFUVFRSqVy8uTJHTp0UKvVGzduxHEcTvaHfScMlNTaEKD6IALPhoBUMGJtLPTrCgAoLy9fvXq1u7t7cHDw0KFDu3btqtVqg4ODt23bZjabYSDQEydOeHh42NvbBwUFQQ/s0jGoNOdnU3aUKyLw9AnwPE9RFHyz4nn++vXr77zzDvRBIZPJoA7r6Ojo7+//zjvvrFu3Dvp3lloBw2PFuIJiVi2tRYgBFWHXKb5MQsUcBhuEvt0PHz48btw46JdDqVSK1tCOjo5jxoxJT08XffW0tDo+/fsD5fiiE4DCNC9YRIvucQT3zk1W0izgRZcdFMcyLEtRVHFx8aJvvg4MDlIqFBpM7oop/+bi9UbvfpvWrBM8PnMA1FtAubFkXVzKhCXZ8zeBaxXAytgAX363CpAMKNPHz1l164cEUGoARoYrrL68dhd7uZCvMwosSY66VZm6cvv1FbG2ny5dnb/R9HM6MACAc4K/aR1BZpec+HLd8cXRfduE/peLx8J583v16gU/htnb22/duhUAIIyBf7Vz5ljB/wYUoMWN9180iED0s/HQxP1HoDVEABF4WQnAbj0nJ+fdd9+FPsecnZ3ff+/90tJS+LUexkx+UL9+WYGheiMCfzEBJED/xRcAnb41EcjJyfl3xDNnZ+dx48ZFRkYGBQWtWbOmtra2mfkVegFuTRcd1eX5EBBbDU3TFotl7969w4YNc3Nz69y581tvveXh4REYGDhhwoRLly7BN/br16/PmjXLzs7OxcVl6tSpJSUlonoljkHFPJ9PFdBZEIE/TwDGGGAYhrWxFRUV69evDwoKUiqVMMygXC53dHTs0KHDtGnTjh49WlRUZDI1GT/ef2LYFlq+AC2WWtpmxYYsJsQJRjt27Hj77bc9PDygEbToIdrOzm7RokWpqakEQYiKnpg5SiACLZOAMAlA0Gkf4oSCFfToe/9Inq016Cpra67/krN5w8Z33njTXa193c4RwzBfZ7eh3ftsmrek/mLOza2Hc+ZuPDbqC3D5NjBxjUaDmWeEiuvJ69sOFW6PB7cNoMzIXL99fsMe9nKh4B66wQwsFF5UmfTd98Xb4sHJnFtr9xuPpINyIzBQwEwJJbhRmbJ8a+KSmKHBEV5K7T9nfTZ8+HDNq/ZaJ0fn11y+/mYJbWNoG0PQlKg4N0s8DD4SoB9GBW1DBBCBhxFgGMZkMhEEUVZWNmPGDC8vLzgV7J133klPT4dHQNsvOJZ4WB5oGyKACDw/AkiAfn6s0ZlaN4H8/PwBAwZotdoPP/wwJCTE29t73bp1JpNJKnKJb9GtGwWqHSLwjAhQFJWfn79o0aKgpqVXr17dunVzc3Pr2rVrTExMUVERRVEmk2nfvn3h4eEKhWLQoEGJiYn19fUURcEiIQvoZ3RpULbPgQAMvEnTNAAgPz9/9OjR7u7uSqVSJpPBkIPt27efPn362bNnS0pKYFhC6CexWdmgZaUo4Lb8VzKx62yWgCbSrI0lCAJiqaioiI6ODgoKgu+farUa2oYrlcpOnTrt3LmztLRU2ik3I4NWEYGWQEAUnR9ZmF+tpDkg+GduoHEKCMEMKYLMy8reHr1xxJvv+Di5uto7KDEswNFtaGD42vcmHvl4Pnk0A5TWAwDqjHoW8IABd1MyU9buBLfqQD0Dsm6nf7vr9qEUcNfYpD5zfFFNdmx85ob9IKsiPzqu4IcEUCmYRfM0w9UZ+ZuV2Stj05dsHdNz0Ov2Tsu/XjJvwXyf//KXqZRaF6fx/zuRtjFmq4W2NSnd4J53a5b/j/nzAxbQv1ZM8JAtYnhM4pGE0A+IACLwshEgSbKurm758uXOzs4ymQy+HSQlJZEkCUO/tPzRzst2yVB9X04CSIB+Oa87qvVTJlBfXw8nQffp06dr164Yhi1durShoQHOEYYmV9I356d8epQdItAaCUCdCDYiqKNdu3ZtyJAhHh4e0O1Gu3bttFrt+PHjz58/bzabTSYTSZIjR46EEckmTpx4+/ZtqdgEFTfUElvjzdJq6ySdhg8AgJJrfn7+8OHDRUcTMP77+++9Hx8fr9frIQuO4xiG4TgOunumaVpqASSqz+InmZZMUNpmm6Whzg4DKtI0DauTlJTUo0cPuVwOZ+NCDRr6BFixYgVBNEVOa6qwNLeWTACV7eUhIFVb76v1Q7VZAEjAG1nKwlAUI3yaYika2LjiG/mn44+NGzXG1dXVyc7eB7MLV7j20/h+PeyTa6fOsVZSaDI23vxLSfySaENaHmjkwI3q9PW7yw+mgCqzIP9aKVBUk7Y29vrGOHC9uuC7uNSvNzE3ygHFE1ZcKJiFSd9x8Ois5bO6DvFRO86ZM+fsxfPuvt5w5sF/Dx50q7gIWnDDWsB6wQiLUiPo++p4LzLjk1hAw/zuPxqtIQKIwEtJAE4LE6u+detWe3t7rVbr4uISEBCwb98+aawLOE4Qd0YJRAAReM4EkAD9nIGj07UeAiRJwinMRUVFY8eO9fT0fPPNNwcNGuTh4TF9+nQY/QDuIH3FhenWQwHVBBF4ZgSgr1sAAE3TBQUFMTEx3bt39/T07NatW8+ePZ2cnPr167d+/fqSkhKKohoaGr7//vsePXpotdpevXrFxcURBNGs6Ylam1SVfmbFRxkjAk+BABSgoR9D+C3z0qVLvXv3hj437OzsZDJZZGTknj17bt68Cc8HX7TEzy1iIUTvE7BdiM1B3OGFSDzYqMWQjKLRN2tjz58/P3LkSOiLQ61WKyXLuHHjSktLoTovze2FqD4qZCsmIJWe2fsNgO+rtVSJ5gXf0Pe0XcFrNM+zHM9ynI3lWa72bk18fPykTyZEtu/o6+jqhCkCtK4hr3lPfndk4vf7ck9f2Ld8feXZTFBjAVXm7A0H8nfEg3IDsLA2E26+U50Rs690SzzIq2dPZt9cuRtklgGzoHEDmrfVGq4lpny/dO274VHecvuJH407kZwU3LGDzE6FvSJr0y7o9Jlk0fuc+OQRtjTFHrz3t6m8v1YNVkJaNykPafrXI9D/iAAigAg8jIBerz9w4EBgYKBarcYwLDQ0dPfu3Q0NDTRNQ6la1KDRGOBh/NA2RODZEkAC9LPli3Jv3QRwHNfpdKNGjZLJZF26dBkwYICHh8fcuXMNBgM0OhPf8KU9HBK/WvddgWr3FAmQJGmxWJKTk0eMGOHn5xcZGRkVFdWuXTs/P7/333s/MTERxwVTrLy8vI8++sjd3d3Dw2PmzJnXr183GAxC8CSSbNb0xNWnWEiUFSLwrAnAEIKsjc3Ozu7fv79Wq1UqlRiGyWSyYcOGXbhwgaIoi8UCi/EoAVosJGwFYvckbn8hEmITFhOivCWIbzYW9rAcx5WXl3/00UfOzs4Yhkn0Z6W9vf2UKVPKysqgRbnIAWb4QkBAhWyVBKQiK3TxLN1yX5WlOi1MNwnWUPMV5zeQJInjeE1NTUZGxoIFC0JDQzVypSMm88CUbZVOb/6f7l9+PKX4XIa1oPzMlr0Zmw+AW7VARwArS1bUnd1x4Mr6PSC9pOFgasaKneBmA6hn6AbB/wZXVp918MS3cxaNHPxWgKvnuFFjEhIS/r+335Jr1EqtxrdNwPFTJ2EzFBupkJBKzzDd9POv9YJ1lVZMWntp+tcj0P+IACKACDyCgMViOXv2bN++feGcDH9//xkzZkANWjzivgcUz4vbUQIRQASeKQEkQD9TvCjz1kyAtbE0TS9YsMDR0TEkJGTQoEFarXbYsGEEQZBk0/TGpto3697gamvmguqGCDwlAhaLpbKycs2aNT4+Pq6urr169YqKinJ3dw8ICFi6dGlRURFJkgRB7Ny5s23bthiGBQcHHzt2DMpwFEWRJNlMWpI2xqdURpQNIvDMCbA21mw2G43G2traIUOGwLcpuVzu7Oz85ptv3r59m6Zpo1EQhqCnmt8UoEXLxNbXH4ltHIrLRqPx448/1mg0UgEaeixZtWoVEqCf+b2LTvB7CECRVYwuKCYeKb5K1dr7TwQHqHByAGtjTSaTyWAszi/YsHZdRFD7Ng5uSgzzwFSemLqLd+Dktz6Mnr+k9tZtQLBAT4AGMnXl9qLvE0BeleVC3ullmw3nroM6CyAFc2tAgrqUrF1zlk17b5QWk783+M0b13MWLlz4mrub0LLsNUuWLoVlYUgKcLzk33+Muu+3gBbrZwNP5ILj/qqiNUQAEUAEmghIhzRw9lheXt6gQYNgNAiNRjNixIjCwkKRljhRTHqg+CtKIAKIwDMigAToZwQWZdv6CRAEsXTpUk9Pzy5dugwdOtTOzm748OEVFRUcx+E4ThCExWKR+twUX4yRBXTrvzlQDf80AbPZfOnSJWj4HBwc3L9//w4dOvj7+7/77rtHjhwxmUwAgIyMjPHjx3t6erq4uIwbN66goICmadEOFPruYBhG2vTE9J8uIMoAEXhOBKAvGpPJNG7cOJlMBm2fVSrVyJEja2treZ6naRp+cYEFepkFaKitQ/XNYDBAO+iRI0dKBWgYnzA0NPTatWvo/fM53cToNE9A4CkK0PBs8NFhNpsBAIIczLDmBv2NjKxFsz7/e2h4qHeAEyZ3weQ+SocgD58RI0bs2bOnMrfg3JZ9d3aftJ3JJS7lJ0fH5v58Gtw10g1GokYHGkndxZy4Basn9X2rjYPbe4PfTD+b+uOuPZ6enhiGyeXyiRMn1tTUUASJWyy0lZCoz7w0puDDBGgbAEiAfoK7BO2CCCACjyYg+iuD8TBwHK+vr58+fTr8Dq3VaocPH15QUAAzgIMlwXW+jYVb0DvCo9GiXxCBp0YACdBPDSXK6GUgIE71JUly7969bdq06dSpU0REhJ2d3QcffHD79u1mU/6RAP0y3BWojn+GAGxTUESD32bMZnNlZeWGDRsiIiLc3d0HDhzYo0cPPz+/du3aLV++vKioyGKxmM3m6Ohof39/DMMiIiJOnDih0+nEgaOYgINLcVWa+DNlRsciAs+TAGwj0dHRarUaun7GMGzChAklJSWwGOKMe2ni5bzbYa1hqEaapqELArPZ/MYbbzg6OkJ3kNCE3NnZ+auvvoLOsqDvjud5TdG5EIEHCYiWwI9J3HeU1AL6V0cc9+3QtAItATkby9lYwLCk0bxry/aj++L2bN7eN6Kbm8pehWGvNLUKL2/vod37fPbemMLj56nrt3Ni47P2HAUG3Gow2Uw44IDuTNaJr2NmDBne1tG9e3jk1csZ51LO/pefvwKTqZWq7pFd7hSV4CYzYcVJnLBR9O8RoGGlpVWSYniwWmgLIoAIIAL3EYDPOvgXxoSgf13mz58PBwCOjo5du3ZNT0+HIysYwVh8uxcHTvfli1YQAUTgqRJAAvRTxYkya+0EYNgiAMDhw4fbtGkTEBAwaNAgjUbTo0cPGAlN7Loen2jtnFD9EIEnJUDTNEEQNN0U2qgp3mBubu7o0aP9/Px8fHx69+7dsWNHDw+Pt95668SJExRF/VtLysjIGDJkiEajsbOzmzRpUllZmdFofHyLe/DXJy0f2g8RaAEEbt++3aNHD6icqlSqiIiIyspKWC6O48SgOkiAbtbSIRySJBMSElxdXWUymZ2dnYODg0KhwDAsLCwMCtDi86cFXGpUhJeXgFRwfVT6PjpStfbRAvR/DoH7sHz+L3n6u3W66tr4/QfjYvf8z4ej3J1dVK9q1Gq1M6b4m9b9b06e/xw5/uT6naDaaGzQUYzQQZsKyjI27v/67Y/baFyGDhyckZFRWlY2ZMgQrb09hmHhHTsV594ENp4247SVEMTu+/xv/KYFNBKg/3OhUAoRQAT+AAE4AJAOhMR0TU3Npk2bPD09xd7/9OnTOp1OmB3CMNAImrWxzRz3/YEyoEMQAUTgNwkgAfo3EaEdEIH7CBiNxgsXLkRGRvr7+/ft21elUvXu3TstLU2n0z04hafZy7C4el+OaAURQASahoDl5eXbtm3r3bu3l5dX586dw8PDg4KCwsPD58yZU1hYSNN0VVXV6tWrQ0JCtFptz5494+PjKYqC8JqNGsW29qgEQo4IvCgE/h2BcNGiRXK5XKPRYBjWtm3ba9euibc9RVHwy+ijbvWXyunTQyFwHPfvb1SLFi1SKBQqlQrq+BiGOTo6ZmVlvSi3ASpnqyfwKNFZuv0+CL9XgIYHczyJEyzD6HU6i95IWfCSgsJjP8f/74SJPSK6aDG5I4Y5YVigxiUiIHjiP8b+uGtPZWlZdeHtxO/3TRn8QXevwL4R3ZJPnNLp9RMmTXRyEYJ8vu7hGbtlO2O0cFaSsRCAeVB9RgL0fZcOrSACiMBTJ/DQAQA0iIZC865du0JDQzEMc3BwCA4O3rp1q9FoNJlMUIMWDajFfJ56CVGGiAAiAABAAjS6DRCB30fg7Nmz3t7erq6u/fr1c3Z2bt++fU5Ojhh1EH5rFbuuRyV+3ynR3ohA6yUA3VNaLJbr169PmDAhMDDQx8dnwIAB0LPNG2+8kZiYWF1dzfN8SkpKt27doP/WadOmwSCEPM/jOA7xPKq5PXR76yWKatZKCIjeCXU6Hbzt5XK5i4vLxo0bRaMemqYf5eVcetu3EiJPUA1praVpHMdramrCwsK0Wq0oQKvV6nXr1sFc4YPoCc6AdkEEnhUBqdD8qPR95/79AjTP83DCxD3BheVInAAA1NfWmXT69LOpi/75RXhgiKfMzg1TqzCZUqFwe8213997fzx85IQPR4f7B3UNDv35xzjCii/6erFaa4/JMJlM9uW8+RzR9DGYBYBmASuNPSimfzMIIffoIIT31RutIAKIACLwIAFppy9NcxxH0zSO4xRFpaenh4eHw1jE/v7+CxcuhDGc4Yd8aMsiWrQ8eAq0BRFABP48ASRA/3mGKIfWTAC6hoSunAEAWVlZnTp1cnFx6dGjh5ubW/v27ZOSkmDUI2hl1mz+TmtGg+qGCPw5AhzHQftlvV4fGxsbGRnp7u4eFRXVr18/Jycnd3f3mTNn3rx502KxGAyGdevWubq6Ojo6RkVF7f9xvzTSIGyAf64s6GhEoMURIEmStbEkSU6dOhX6LpTL5f379zcYDNKYOWK5pa9bL5XVs0jgMQno4fHEiROurq4qlcquaVEoFGPGjIFHQV8cj8kB/YQIPB8CD0rPT/G80qcE/I4FP3QJE/g4nmUYY4Pu6oX0FYuXdAwOcdQ63HP784ryNSfnVzBZsH+bDevWE1Y8MTHR+TUX+Ovw4cPLSm7fKyQPBPX5VwFaerrfqgWs92/thX5HBBABROCxBKSPHWkavnSQJFlRUfHWW28plUo4Hpg0aVJ9fT38JgcHV9Kj0GjqsbDRj4jAHyGABOg/Qg0d8xIS4Dju+vV9F1XDAAAgAElEQVTrAwcO1Gg0vXv39vb2hqHPaJoWv5TCHku6+hKCQlVGBJ6EAEEQOI5zHJednT1v3ry2bdtGREQMHjw4KCjI3t6+T58+8fHxNTU1er0+JSVl8ODBMpnMz89v2rRp2dnZ0GsbTdOi05snOSPaBxF4sQjA27uqqqpt27bQWsfe3n7Dhg0EQYhvStIaoVcmKY1mafgV2WKxDBkyRKFQKJVKlUolk8k++OADuKfozKfZgWgVEXjOBJ6pAC0aTMDJ5jBcp2hjwfO8jaJJnNDr9Tk5OWvWrOnbt6+XlxcMf+rk5IRhWPv27UeOHBkRESGoz6/I23cMLSgouIcISs9IgH7Odww6HSKACEgINBsLSRVk+NwjCKK8vHz8+PEYhsnlcpVKNWbMmIKCAtbGEk0LzEzMR5I3SiICiMBTIIAE6KcAEWXRugnAKEa5ubmdO3d2cHDo3bu3j49PUFBQfHw8TdOiJabYUUkTrZsMqh0i8GcIVFRUHDhwoGvXrl5eXuHh4T179vT39/f19V20aNHNmzdxHDeZTLNnz/b09MQwLDAw8OTJkzDwGoxtDeU56cjyzxQGHYsItBwC0rs6Li5OrVbLZDIYOQc2AbHfaTllfiFKYjabDx8+DP2ZyGQyDMMGDhwIvyI/VNN/ISqFCtnKCDw3AVrUoEWXPjBBURR8BOn1+ps3b27fvr1Xr15eXl5KpdLOzk6tVsMwnvJXFN5+vqfPJN9rO79aPUtjD/6e8TCygG5lNzKqDiLQognU19cvXLgQjgccHR379++fk5MjPgx/z7OrRVcTFQ4RaIEEkADdAi8KKlKLI1BVVTVs2DC1Wt2mTRs3NzcPD48DBw7AUoo+N6SGz2K/1eJqggqECLQAAhRF5eTkLFiwoEOHDj4+Pr169YqIiPDx8enZs2dsbGx5eblerz9y5EiHDh1kMpmnp+ekSZMKCgosFgv8GgRrAFtcC6gNKgIi8PQJQJcRBoNhypQpMplMLpcrFAoXFxdowEiSJNzh6Z+49eYIP1mVl5d3795dJpMplUoMw6KioiwWi+huu/XWHtXshSHw/AVoeP8zTQvdtIhpODPg0qVLUVFR0OGGomnRaDSer3t9tyHG0jSTCYrOcOiLBOgX5lZDBUUEXj4C8MMb/GxmMpl27Njh5+cHP/CHhYUlJCSQJPnvyM/oRf7luzVQjZ8fASRAPz/W6EwvEAGe581mM3QAzTDMrFmz5HJ59+7d/f39AwMD9+zZA7UwKIGJGrTYXYmJF6jKqKiIwLMjwNpYmqYBADiO19fX7969u1+/fm3btu3atWtUVJSnp2f79u1nzZqVlZXF83xhYeHo0aP9/PwwDAsJCdm5c6fYoB5MPLsyo5wRgb+QANR9KioqoqKioAAtl8sDAwMBADCcjjhr/i8s5ItyavGFEwptb7zxBhTRMAx7/733oaYvxjJ9USqFyokI/EkCsD8VLf6g6AxX4U8wf57n6+rqVq1adc8ftEoll8udnJy27th+t64WNq4HBWjUWf/Jq4MORwQQgWdBoNlzz2g07t69Ozw8XK1W29vbh4aG7tixg7Wx4pAATgcRH2jPokgoT0TgZSOABOiX7Yqj+j4RAXPTAqc5z5kzx9HRcejQoV5eXgEBAYcPH4Y6mjhqf6jts3T4/kSnRDshAq2LALRWlrppZm1sZWXlvHnzgpuWt956q0uXLhqNJjIycu/evbW1tSaTKTY2Fnq8xTBs3LhxFRUVUGgTB3/NEq2LGaoNInAfgZs3bwYEBIi6T+fOnXmeF3UiqaeO+w5DK/cTgBqZGGxtxowZGo0GwzClUtm3b1/k/fl+WmjtZSEAO1NxKAsbyEMFaBzHT58+HRYWhmGYqkmA9vLyqqyu4ppQCbMxOB5w9zpnaVraX78sWFE9EQFEoAUTaPbcAwAQBHHs2LEuXboolUq5XO7l5TV37lyGYWia5nkexpsRH2UtuGaoaIjAC0MACdAvzKVCBX3WBKQv8zzPWyyW+vr6mJgYjUYTFhbWoUMHZ2fnlStXip4ixVE7EqCf9aVB+b+IBOAEApqmCYKwWCzV1dUJCQnvv/e+n59fWFjYoEGDApqW0aNHJycnUxSVmZk5cuRIGBKkc+fOhw8fJggCVlwc+TVLvIhYUJkRgSckwPN8enq6nZ2dVICGkwlg43rCfNBuSIBG9wAi8FACzbQYcVgLt0sPaWhoGDdunFarhQJ0UFAQjIYKfQE165ofuirNDaURAUQAEfhLCEgfenBAheM4a2PPnj3bvXt3rVar0WjUavWsWbNqamrEYDPiM+0vKTM6KSLQygggAbqVXVBUnT9IQHxBhcfDLicmJsbHxwd63vDw8FizZk1NTc29+YZN+zUbrIv9k5j4g6VBhyECLzIB6bccjuPq6uqKiooWL14cFRXVtm3bDh06tGvXztXVNSIiIiYmpr6+3mg0Lly4sEuXLiqVytvbe/78+dnZ2SaTibWxJEnCCfJim5ImXmRIqOyIwOMIcBxHkmRKSgqGYQqFQt60+Pn5AQAYhoFdz+OOR79JCMAnkmgBDV1wyOVy0QUHx3HifFvJcSiJCLRyArA/FYeyYgJul1aeJMno6Gh3d3c7Ozu5XN6xY0eDwQCFG7ibtGt+aFqaG0ojAogAIvCXEHjwocfaWIqiWBubl5c3duxYlUqlUCicnZ0nT56cl5fHMIz4QIMFbrb6l9QCnRQReKEJIAH6hb58qPBPh4CoPsOJNgAAkiT37dvn6+sbFhbm4ODg5OS0du3aB4MSiJ3QoxJPp3woF0TghSIAvQTwPE9RFEmSmZmZQ4cOdXV1bdeu3eDBg9u0aePt7T127Njs7Gye50+fPt2tWzc4I75Lly4nTpwAAOh0OvFNGM0weKEuPirs0yHA8zxJksnJydBThEKhkMlkGo3GYrFAAVr6mefpnLK15wKfSyUlJTCcGhSg586dCwBgbazZbG7tAFD9EIHHEZCOYx/cj+O49PT0nj172tvbK5XKsLCw+vp6s9mMoqE+yAptQQQQgZZMQPqsa/auUV9fv3DhQkdHRzhCCAwMTE1NZW0slKGRQUxLvqyobC8QASRAv0AXCxX1GRJo1rvs2LHD19dXq9W6ublhGPbpp59WVFRAb1DSfus308+wxChrRKDlERBFMRjGs6ys7Ntvv+3QoYO7u3unTp0iIiIcHBy6d+++YsUKnU5XUFCwaNEiV1dXlUrl7+//2WeflZaWkiQJvdw0GxQ+tK21PACoRIjAUyPA2tj09HSNRgPNn+Hfa9euQUvep3aalyMj0Rl9amqq6Fb73w5tly9fLv70cpBAtUQEHk5A2sk+dI/y8vKRI0dCLxwRERE6nY4gCLHTf+ghaCMigAggAi2NgPRZJ33XgDPMqqqqVqxY4ebmZm9v7+TkFBYWdvLkSQAAtFF70Fc+zK2l1RGVBxFoyQSQAN2Srw4q23MlAN9CTSZTcnJyUFCQVqt1dnZ2cHAYNmxYVVUVAOAxlpjSzkyafq4VQCdDBP5qAnAkB02Yz549O2bMmMDAwJCQkD59+rRr1y4gIGDixIkXLlwoKyvbt29f9+7dFQqFSqUaPHjwqVOnoENJOP8ATkoQx4XSNiVN/9XVRedHBJ4VASjr3Lhxo02bNlIBet26dcgB9B+ADj1sUBQ1e/Zs6FMb/v3/2fsSmKaW7//bNt1IFwgtENawRhDCGhYJCAYUI4LPPeLTKGKeC3GNCsY1ihrXKGpc4/p1QfNEjYpERaMiUdQIYkAhgBIWCUubrtL2/7znx/zHFhAVpcB8Qsp0OnfmzOfeO3PmzJmZ69evo3MdfiJbcglhYNAw8N2+VafTbd261cLCgsvlhoeHt7a2qtVqYoAeNA8AqQhhYIgwgLd1aKABY3ywQcvl8hMnTnh4eMAhHEFBQWfOnNHpdBqNxig9ymqIUEeqSRjoEwaIAbpPaCSZDBIG9Hp9aWlpYGAgh8NxdHRks9lz5syB0SnqY34oMEh4IdUgDPwIAzKZ7NixY+DvHBMTExYWJhKJAgMDd+3aVVNT8/nz56lTp7JYLIqinJyc9u3bB69Ye3s7FAJTQd0pefgL+CNCkbSEgYHEACxs//TpU2BgICwFBYPpnDlzYMuIgVQZM5BVLpd3fOmorq728PDADdBVVVXEgmYG94eI0P8M9KZvPXv2LJ9GZGRkW1sbbAfU/6ITCQgDhAHCQK8ZwNs6NNaAq9VqNViiwR3Ny8uLz+fzeDxHR8f169crFAqU3sgprdeFk4SEAcKAgRigyUMwpBnAd6/T6/WPHz8ODg6mKEogEDCZzJSUlOLi4u46G7wD6y48pMkllR9KDGg0GthEtays7J9//rG3t3d1dQ0ICHBzc5NKpRMmTLjwvwulpaVHjx4NDAykKMra2joxMTE/P7/L5Ww97LOGv2tDiWBS16HFAGxYrFQqt27dKhKJkM00JCTk48ePeM81tHj5hdoqlcpdu3YhJrlcblBQEDrm9BcyJpcSBoYKA/fu3fP09OTz+SEhIS0tLWQybKjceFJPwsAgZQCNKaB+aLNN0LKKioqSk5Ph5FWBQJCenv7p0yetVqtWqyG90eWDlCRSLcJAHzNADNB9TCjJzvwZwN2d5HI5CNzxpaO+vj45OdnKysrOzs7KyioxMbG8vBx23kA2aNTT9DJg/mwQCQkDfcKAVqv9/PnzwYMHo6KipFJpIA3Yf2PdunXl5eX37t1LSkqytbWlKMrX13f//v0fP36EzQQ6vnTAKwavFcjTm1esTyQnmRAGzJABnU6n1Wo7vnTk5+eLxWI4ipDJZIrF4osXL3Z86cA7MjOUvx9FQk0HLoNSqSwuLra1teVyuUAjj8fbsGEDnoaECQOEgZ4ZeP78eUREBIfD8fLyam5uRvuiotXrPV9OfiUMEAYIA2bFAFIY8ABI2PGlo7W1tbKycsmSJbDyQygUTpgwoby8XKPRQBp0FfjNmFXViDCEAbNlgBigzfbWEMF+FwP4uB3mMEF1/vvvv0Gr5nK5o0ePbmhoMLI+Gy23Qb1OD4HfVQeSL2HAnBhoa2t7/fr10qVLra2t7e3tw8LC4ODBsWPH3r59u6mpae/evUKhEHwPJ02aVFVVpVQqoQamHtAQ38NrhX4yJw6ILISBvmQA+qmOLx1yuXzevHkCgYDBYHA4HIqiVq5c2djYiHdkfVnwQM4LtQwQwKvS0tIy8a+JDAaDoijY/8fDw6OyshJPQ8KEAcJAzwxUV1dPmzaNwWBYW1t/+PAB9kuFfVF7vpD8ShggDBAGzJABI7UBfe340qFWq2FLwObm5pkzZzKZTIlEYmlpGRkZWVpaCsun0HpNFEA5mOohZlh9IhJhoF8YIAbofqGdFNpvDMDhZmBZBiHa29vr6upSU1N5PJ6vr69UKo2JiSktLYXD0Ixs0Eb9yne/9ls9ScGEgd/AQHc2r3///TchIcHe3t7f3z8oKMjFxcXT0zMzM7O8vDw/Pz85OZmiKC6X6+vre+TIEZVKpdVq4RM0NuIB/RvuFclyADOAxi0w/nn37l1ERASDwYDNoL29vauqquBUvQFcyd8gOvCGVizhJezevVsikVAUBSc6slis5cuXo1W0eEoSJgwQBrpjoLW1NT09HRZk3L17F7lldJeexBMGCAOEAXNmoMuBvEajQdZnnU6nUqmam5s3btxoaWlJURSPxxsxYkRBQQGsAkGmZ9Qe4nmac92JbISB/mKAGKD7i3lSbr8xAB0DeJap1er29vbVq1cLBAJfX1+RSBQVFfXixQs4sAh2gEKj2S67FrybMQ33WyVJwYSBvmYAnn+YkpHJZCqVSqFQVFRUZGRkeHh4ODs7BwcHDx8+3NnZOTk5OS8v7/nz52lpaa6urrDmfd68ea9fv+740qFSqYzeFKM3q68FJ/kRBgYYA/CCwP6qer1eqVRevHjRwcEB1hAwmczU1NSWlhb4CS0mGGCV/A3iwgQz6rJVKlXHl46WlpZ79+45OjpyuVwWiyUWi4VCoZubW0FBgVFD9BskIlkSBgYVA1qtNisrC9YQbNmyBbYJAlUZvU2DqsKkMoQBwsAQYwCaMtjoDJQKcL6pq6s7fPiwlZUVnBTl5ua2d+9e2AofthNEugcEUJOIAkOMSFJdwkC3DBADdLfUkB8GMQOwpgZ2r9u+fbulpaW7uzuHwwkNDX3z5o1CoQCXTOgz8B4F9SK9DAxiDknVhiYDarVaoVCoVCq5XF5QUADbpvv7+4eFhTk6Ojo4OKSnp5eUlOTl5YWEhPB4PIqivL29z58/Dzum4Voa/n7hL9TQJJbUmjCAGMBfB71er1ar29raVq9eDS8U7CNx/PhxdIYBunCIB2CsCLv6dHzpaG5ulsvl165dk0gkFhYWLBrgBH3gwAFwf8apHuLskeoTBr7LgE6nO336NI/HYzAYiYmJsFU9OrYL3qbvZkISEAYIA4QBs2UA1wqgiVOr1WCDbm1tvXPnjoeHB6hhVlZWmZmZ4Cut0WjQak5igDbbm0sEMxMGiAHaTG4EEeMPMYB6BZ1O19DQkJWVxWazwbMsICDg5s2bIAe4ZOKmZ3Qh3jN9N/yHakWKIQz8ZgbwR12hUDQ2Nh44cCA4ONjR0XH48OF+fn6WlpZBQUGXL1++fft2eno67BXg7u6+ePHi0tJS3Img40uHVqtFGZq+Wb+5KiR7wsAAYAC9IGjfm48fP8bGxrJYLCaTyWKxbG1tjx492tjYOAAq86dE1Ol0yPrc8aVDoVDcunUrNDQUeY6D52ZaWlpNTY1Go8EbIsTznxKWlEMYGJAMPHnyRCgUMhgMV1fX2tpaWBRl2l4NyLoRoQkDhIEhzwDemsHyDqAE1pzpdLpbt27FxsZSFMXhcCQSyYIFC6qrq8EAjWsgZHQz5B8lQkC3DBADdLfUkB8GJQM6nU4mkxkMBplMduDAASsrK6FQyOPxHBwcCgoKtFot1BrsZcQAPSifAVKp3jMAehhKD4dy5OfnL1q0yNbW1tvb28fHx9HRUSwWL1++PD8/Pzs729XVlcPhiESimJiYvLy89vZ2hUIBjs9wZAcyRkPmREVD9JIAYQAxgIZAsL0g7LNRVlbm5eUFRxFSFGVnZ7dnz56GhgZiPAXewACt7cSZM2cCAwPZbDZFUSKRiM1mM5nMuLi4169fa7VapVKJSDZq6NBdIAHCAGHAiIGPHz9aW1tTFCUWi/Py8uBX/FUySk++EgYIA4SBAcQA3pqhHQJBfr1eDwOZoqKisLAwLpcrFAptbGzmz5/f3t5uZIMmo5sBdNOJqH+YAWKA/sOEk+L6mQHY1Emj0dy+fdvV1ZXNZnM4HFdX1/v376MuB50ngGJQoJ+lJ8UTBv4gA/DYg00HvADev39/8uTJgIAAkUgUGhrq4eHB5XLd3d0PHjyYl5eXnJwsEol4PJ6jo+PChQuVSiW+lY1er4cJHvQ2mQb+YOVIUYSBAcOATqdTq9VarVatVufk5Dg6OjIYDHCFZrPZixYtqq2tbW9vRwfnDpiK9amgwI/BYFCr1RUVFRs2bIDmCJbKghO0v7//tWvXWltbYaBo1AT1qTgkM8LAIGQAfAAdHBwYDAaXy927d+8grCSpEmGAMDDkGUDqAfJFw2O0Wm1bW9uECRPgkBsmkxkfH//s2TOVSqVUKvEzool/wJB/lAgBXTBADNBdkEKiBisDsDTGYDAUFBT4+vpaWFhQFOXs7Hz8+HE40An1Lt0FBiszpF6EgS4ZQAcPtrW1FRQULF26NCAgQCqVBgcHu7u7u7i4zJo168SJE+vWrfPw8BAKhUwmMykpKTc3F+xlpu9RD7M7REvr8haQSMIAYkCv1zc1NaWlpUHnBUZVDocze/bs/Pz81tZWOLcQpR8KAbzd0Ov17e3td+/eTUpKAuszh8NhsVgMGj4+PpcuXdJqtV1an/F8hgJvpI6EgZ9jQKlUurq6MhgMPp8/Z84cuVyOr1L/uTzJVYQBwgBhwKwYMB2/GMXodLq6urrZs2dLpVKKorhcbkBAwL///gvHS0BdtFotaR7N6rYSYcyEAWKANpMbQcT4EwxoNBqdTldcXOzv789ms+FIorNnz8JRTkZdS5df/4SUpAzCgDkxoFKpWlpaTp8+PXLkSD6f7+XlNWzYMCsrq6CgoI0bNx4/fjw+Pp7H4/H5fCcnp40bN75//x5MOeDy3OV71F2kOdWbyEIYMEcG9Hp9bW1tdHQ07CwBNmiKojw9Pbdv315bW6tUKrsb8AxWGyssiVUoFB8+fFi/fr2rqytszgh+4lwul8/nDxs27NKlS+AfjU63N2qIzPF+E5kIA2bGQFtb27Bhw+AVCwgIKC0tNTMBiTiEAcIAYeBXGTBSD7r8ajAYWltb9+zZI5VKuVwuRVE+Pj5nz57VarVyubytre1XhSDXEwYGKQPEAD1IbyyplgkDcPRZdXV1SEgIk8m0srLi8/nZ2dlKpfK7OwOgjsckVxJBGBjkDNTW1m7evNnf39/W1jYoKMjb29vKymrChAm5ubmLFy+WSCRsGp6enkVFRbAJmlqtBh9D0x3Q0KvUZWCQU0mqRxjoCwa0Wm1JSUlISAhFURYWFrAC1MLCgsViTZ48+enTp58/f+7SBo0WNPSFFH8oD7yh6KHIT58+HT58OCEhQSwWW1tbczgcMNCDn6ZIJDpw4ABsRo9naBTuIX/yE2GAMAAMNDc3+/n5wdSXg4NDbm4uYYYwQBggDAwyBozUgy6/QpXlcvmpU6dcXFz4fL5QKLS3t9+5c2dzczOs+IQ0oJJBJoOMKFIdwsBPMEAM0D9BGrlkgDEAB6AZDIaSkpLY2Fgej2dpacnn87ds2VJVVaXVarvsV7qMHGA1J+ISBn6cAa1W2/GlA/aTvXPnzuTJkx0cHIYNG+bv729nZ/ff6oGtW7cuWbJkxIgRMOHv7u5++PDhyspK8AUwPQO692boHxeWXEEYGIoMyGSyW7duRUZGwgbHDAYD7K1MJjMyMnL9+vVFRUXw3mk0Gth0Qq1WI8/fgUIZ9MJQESQzHIXa8aVDJpMplcqSkpJjx45Nnz7d0tIS+YPDelgOh8PlckNDQ/Py8iCTntsiVAQJEAYIA10yoNPpWlpagoOD4V2ztLTcvXt3lylJJGGAMEAYGCIM6HS6W7duhYWFWVhYSCQSkUi0evXqurq69vZ2WAwKathAdAIYIneQVPMPM0AM0H+YcFLcn2ZAr9fDxOPbt28n/jURfJ8ZDMauXbtgZN6lobm7yD8tPSmPMPCnGNDr9RqNRq1Wg42msbFxx44dERERjo6O/v7+np6eHA4nOTl5165d06ZNc3BwEIvFXC530qRJT548AX9nmO2HQwvBDN0bow/+rv2pupJyCAMDngGZTJafnx8WFsbn82GbYzAJMZlMiqKCgoIOHjz48uVLhUIBS3w0NLr0jDZbLqD7hrNMUWMC0spkspqamhMnTkRHR9vY2FhYWDCZTA6HQ1EUmOMZDAaHw4mLiyssLDQYDOhydKg93vJA2Gx5IIIRBsyEAb1eL5PJwsPDWSwWRVEikSg9PV2pVJqJeEQMwgBhgDDQLwy0t7ffu3cvJiaGzWZzOByBQDBp0iTYkxANkfpFMFIoYcAMGSAGaDO8KUSkPmMAhq8KhaK5uTk1NZXL5To7O9vb2y9ZsqStra2Hgajp0JQMUPvsrpCMzI8BsBqDXLBPenp6ukQisbGxGTFihIWFhbOz88KFCzMyMv7b+pmiKCaT6enpuXPnzo8fP4K7tFwul8lkcAYacoLujdEHf9fMjxgiEWHAfBnQ6/UlJSUT/5rI4XDAFRps0Gw2WyAQMBiM8ePHnzt3rri4GHZJ1ul0MMNkJlX67p7UyACNDhBWq9XV1dUvX77cvXt3dHQ0RVF8Pp/D4YDZHXlAs9lsS0vLmTNnFhcXazQaYoA2kztOxBgEDKhUqujoaD6fD9tAjxo16tOnT4OgXqQKhAHCAGHgVxjQaDT37t2LioqC+W+KoiIiIkABA4+3X8mcXEsYGEwMEAP0YLqbpC7fMACHzyoUivr6+jlz5ljQ4PF4a9as+fjxI+zL8aM26G8KIF8IAwOcAVN3yNra2suXL48ePdrNzc3V1dXR0TEkJCQ6Onrx4sXjxo2DZf4CgWD69OmFhYWwxxlwgLIiHtAD/KEg4g8YBmBpZ1lZ2dq1a11cXBg0YE92MMUKBAKRSJSQkLBt27aCgoLGxkatVtuDDfoPrA/FJ5y+W5yRAfrVq1enTp36+++//fz8RCIR1JHP50PFkfWZyWT+t0HQtm3bwC6m0+nkcnlvJsMGzI0nghIG+o8BtVodGxsrFArBCTogICA/Px/E+e6UUv9JTUomDBAGCAO/nQGVSlVSUjJr1iyhUMjn8x0cHIKDg2/fvm3kxGb09beLRQogDJgZA8QAbWY3hIjTdwyAz5dGo9m4caOFhQVFUTweLy0tDU5Ig9lINCjFR8U9hPtOOpITYaCfGUB7PRsMBoVCYTAYPnz4sHHjRmdnZ6lU6uHhYWlpKZFIpkyZsmrVKltbWwsLC5FIFBAQcPXq1ebmZpVKBbvKogXy8OKgd+pHZ3fI2LWfHwhS/MBkABbFFxcX//PPP3Z2dsj1Bro8mDSiKMrd3X3p0qV5eXmVlZVw9C68qlDpji8d6ODQ30cD3kRA+4MmrmADH9gtBC2kgKpVVlZevnx5/vz5oaGhjo6OuLmZy+VC5w7WZzabLRKJUlJSnjx50t7ejrdFeLi7Lv73VZzkTBgYNAyoVKqxY8cKBAIej0dRlJOT0+HDh6F2+Os8aOpLKkIYIAwQBr7LAK5XqFSqpUuXOjo6wpHITk5OF/53AcZZkA8Z73yXT5JgcDNADNCD+/4O6dpB+56dne3s7AxLkmfMmNHa2gqmZxj9GtnO8P6jy/CQJpRUfiAzgJ5nqAR81el0WhpKpTI/Pz8pKcmVhlgstrKy8vPzmzFjRlxcHPhUOj/0CmoAACAASURBVDo6zpo1q6SkRKFQqNVquBDWGaDMwWMR2Xrw+N6EBzLBRHbCQH8yIJPJamtrz5w5M336dHd3d1ggb2SDpijK3t4+MTFxy5YtN2/e/PTpE1hpkdzwUv++oRHu0QytRMeXDigUdvLp+NKhVCrlcnlTU9PDhw+PHj2anp4OuwCx2WxkemaxWDwej8vlojMYoabDhw/fvHlzU1OTUqnUaDSoITIKdNcWIR5IgDBAGOiSAb1er1Qqp0yZAlvPw1ana9euVavVsNFNl1eRSMIAYYAwMLgZwPUKhULR2tq6fv16sEEzmUwPD48tW7bI5XLYE2xwU0FqRxj4LgPEAP1dikiCgcpAU1PThf9dcHR0ZLPZTCZzxowZpaWlcBATGvGCARrvNnoOD1QuiNxDmAGjR9qUierq6sOHDw8fPlxKQywWOzo6xsXFJScnu7q6UhTFYrFGjhx56dKl1tZWuFwmk5mano0K+omvprKRGMIAYaA3DIDvcMeXjrq6ups3b65evTowMBC8FKEHRLsks1gsgUDg5uaWkJCwbt26K1euvHjxorGxUa/XK2hoNJrfZIM2NUBD1fR6fVtbW2Vl5d27d48cObJy5cr/dq+GRRgw+wWL/eGAQSaTyWazcQM0n8+PiIjIyMgoKCiQy+XIzwjszr1viHrDM0lDGBjiDKjV6rS0NC6Xa2lpCRNd06ZNa2hoGOK0kOoTBggDQ5kBXNMAJarjS8eZM2c8PT15PB6Hw3F2dl62bFl1dTVYHnCu8GvxeBImDAxWBogBerDeWVIvw7Vr12CbSBaLlZSU1NTUBKNf3PeZGKDJgzLoGQDNBvkAGtX35cuXixYtsrKycnFxcXR0FAgEfn5+SUlJbm5uQqEQFrZnZGTU1NSg1bVarRa0K1xn6pOwkWzkK2GAMNBLBqB3MxgMcBaoTCZ7+/Ztdnb2mDFj3NzcwHSLdkkW0GCxWNbW1iKRSCKRLFiwICcn5+rVqx8/flSpVL/JBo0boNVqdX19/Zs3b27fvn38+PGlS5fGx8e7uLgIhUIOh8OngYzmzG+BKgJbcIDpGflggi0eNqP/oXapl1STZISBocyARqNZvnw5i8Xy9vZms9kWFhYxMTFlZWUwa/Wb5q6GMuGk7oQBwoD5M4ArG7DVZ8eXjs+fP1+5csXW1hbtEjZq1KjGxkZY8oUqhV+LIkmAMDCIGSAG6EF8c4do1eRyucFguHfvXkBAAJPJFAqF48eP7/jSgXbbgDDe3BONeYg+K0Oj2mD0QQZoZJ1pb2+/fv36mDFjrK2t2Wy2k5OTnZ1daGhoQkICWHv4fP7UqVOfPXv2Q85N+Js1NAgmtSQMmBEDuJFXr9c3NTXdvXt306ZN48eP9/T0FIlEYrGYw+Eg266FhQWfz4evXC43PDw8IyNj/fr1ly5dKi4urqysbGxsbGtrk8lksHoUdaZ4neGth0YGJdBqtSqVSi6Xt7a2NjQ0VFdXl5aW3r9///z58zt27Fi5cuWMGTPCw8OlUqlAIAABYJMNJpOJdttAtmYIMJlMPp8vlUrt7OwiIiLWrl1bVFSEGjc80MPsMi45CRMGCAM/xAAcrALromASy83N7d69e2iKmmjUP8QnSUwYIAwMMgY6vnSgoZBMJisqKoqKimKz2RKJxMrKKi4urqKiAjWYPZyXM8hoIdUhDCAGiAEaUUECg4EBaNAfPHgQEhJCURSbzY6Pj6+srERDYjRAhb4B6kzU5cFw70kdumEAN0jBrLtCoaiurl69erWHh4e9vb1EIhGLxb6+viNHjnRycgJDj6ur67Zt28rKylCuSFtCMV0GkNZFXqsu+SGRhIE/xgB4Aet0OrlcXldXV1hYeOjQodmzZ4eHhzs6OqLj+5hMJovFQjt1cLlciqKkUmlISEhsbOzYsWNTUlLWrl178ODBS5cu5eXlFRYWFhcXv3nzprS09O3bt2VlZe/evauoqPjw4UN5efnLly8LCwvz8/OvXr167NixnTt3rl69OjU1ddy4cWFhYV5eXk5OTtbW1nCCGbQ2sJUzMjGjDTdg/x+01zOTybS0tAwPD09PTz937lxxcTHaCwj17BDAWyHT8B/jnxREGBhkDOj1erVavXfvXg6HM/GviVwu18bGhs1mnz17FpYgwGmig6zWpDqEAcIAYaD3DOBaBzSJpaWlM2fO5HA4UqlULBYHBQXl5+e3t7fDoAxPj4d7XyJJSRgYWAwQA/TAul9E2u8w0PGlo7i42NfXl6IooVAYGBhYXl5uMBiQ+zMapkIT/53syM+EgYHPABihYA6m40uHWq3Oy8ubMmWKu7u7vb09l8sVi8WjRo2yt7fncDiWlpYURU2ZMqW4uNhgMMBxGXBWIRpeDnxKSA0IA0OCAY1Go1KpoKoqGmq1WqFQvH///saNGxs2bIiPj/f29hYKhWw2m8PhwE6FpkZh2MEDjNSw6F4qlXp5eQUFBYV1Ijg42MfHx8XFRSqVikQi2EODR4PL5eI2ZXw/EAaDgWzf4PXMYDDAAxrEoCiKz+fb29t7e3tPnz795MmTFRUVra2tMGzT6XRG5w2SwduQeLJJJfuJAa1Wq1arz549y+fz58+fz+PxoPXYtm1bS0sLCEXmnvvp5pBiCQOEAbNgwNTCoFKpamtrZ82axefzbWxsKIpydnY+deoULNpGpgkjb2izqAwRgjDwGxggBujfQCrJsv8YqK6ujoyMhIFreHh4ZWWlSqWCOUbUvpt2DP0nLymZMPDbGQADNBy8qdVqDx48GBgYyOPxnJycbGxspFKpi4uLSCTi8XgsFuu/g8t27dqlUqmampoUCoVGo8FXsv92WUkBhAHCQJ8yoNfrYdcdtVoNB4fC7oSwOYZMJnvx4sW5c+eysrLmzp0bExPj5uZma2sLxyfAKiI2mw02YhaLBa7K8BV3W0bGYty4DP7L4FiNEqC9NUwNzXgaHo8nkUjc3Nzi4uLS09NPnz5dWFhYX1+v1+uRSV2j0ajVaqPZZWKA7tPHh2RGGPiGAZjTys3NFQqFixYtsrCwEAgEHA5n0aJF9fX1sPD8mwvIF8IAYYAwMMQYwPUQsCmDobmlpWXZsmV2dnZSqZSiKLFYvG7duvr6emSgIAboIfakDN3qEgP00L33g6nmOp1OpVLV1NRMnjwZTuUePnz4gwcP5HK5VquFngA164Op4qQuhIEeGEDHXHR86WhsbHz27NnSpUvt7OwkEgm4KDo7O4vFYi6N//aB3bx5c3l5uUqlQu7SyLhDfJp64Jn8RBgwZwbQdoT4IAe94yC5RqNpbGx89+7do0eP8vLydu7cmZSUFBoaGhIS4u7uLhKJYF94FosFjtJoWwxkNWYymeDvjJydGQwGmwZK00OAy+VKJBIvL6/w8PBp06atXbv20qVLjx8/rqqqQmIbDeog3qh/h6/mfDuIbISBgcsALKK6f/++VCqdP38+HGdqbW09bty4iooKmOsauLUjkhMGCAOEgT5kAJ3BA5qJWq1uaGjIysoCA7RUKuXz+UuWLAGPH9isA9dz+lASkhVhwKwYIAZos7odRJifZECv17e2ts6ZMwd8tRwdHR89eoSsz5ApMUD/JLnksgHLACy6NxgMKpUqNzc3IiICNtmQSCT29vbOzs7W1tYURVlYWAQHB5eXl8MSWq1Wi4xTuAEaaUUDlg8iOGFgyDGAXls0EEL2XLxPxMPAEWxtoVQqCwoKVq1aNXXq1LFjx4aFhXl4eEgkEoFAwGazkUGZyWRyaKCzDdFPaIcNFAOGaYFAYG9vP3z48JiYmEmTJi1fvjw7O/vu3bvv379XKBTIlRIXuzd1gTRD7jaTChMG/ggDOp1Oo9E8ffrU2dl5ypQpEomEy+V6eXkFBwc/f/4c9uz6I4KQQggDhAHCwABgANdbwMTc1NR09epVcACKjo5msVhTp0799OnT58+fkc8c0WQGwK0lIv4CA8QA/QvkkUvNg4GOLx01NTUbNmz4z4WTyWTa2NjcvXu340sHtONIRtQHoBgSIAwMYgbAF0kul1dXV2dlZfn5+VnSADMQh8OBI8hcXFxWr17935mEaGF7dx7Q5A0axE8LqdpgZQC9trglF7dBQ1+JVkvAAAk26wCrNDCj1WpbW1s/fPjw7Nmzq1evHj16NCsra/Xq1WlpadOnTx83blxMTMyIESPCw8ODgoL8/f39/PwCAgKCg4NDQ0MjIyPj4uImTJiQkpKycOHCtWvX7t+//+zZs7du3Xry5ElFRUVTU5PRZhowB4bEwJ2doUZ4FfBfB+t9JPUiDJgDA/BiFhcX+/j4REdHh4aGMplMFxo3b94kHtDmcI+IDIQBwoD5MIB0MBBJqVTqdLq2trbc3Nzhw4eLRCJvb2+BQBASEvL8+XN8z0Oy8NR8biKRpM8ZIAboPqeUZPiHGEBNs0aj2bFjB2zq7+TkdObMGTCloQQgkFEf8IekJMUQBvqJAbAj5+fnp6SkwGGDcJaXpaUlbNrIYDCmTp1aWFgol8vBCIUkxc8txI078BKhZCRAGCAMmDkDqOPr0gBt9CsMfqBGarVapVIplUpkm4Zf8eURGo2mvb29oaGhurq6oqKivLy8rKzs9evXxcXFL168ePny5Zs3b0pLS8vKyioqKmpraxsaGlpaWvDFSUiALmmEspCtGSXuoS5d5kMiCQOEgT5hAOaEysrKQkJC/Pz8Zs2axeFwBAKBra3tqVOniAG6T0gmmRAGCAODhgGkt+A10ul0MpmsoKAgISHB1tbWxsaGzWYHBATk5OSgPdOMjBj45SRMGBjoDBAD9EC/g0NUfmiX1TQOHTokFothne/Vq1dlMhnsOYBTgzoA0qDjtJDwIGMAmYpkMllbW1t2drafn59IJBLTEAgE4P7MZrPd3NwOHDhgZN9By/CRxQcFyBs0yB4VUp0hyAD+FuNh8HqGaSfc69mIInQJahZ+MQAZGpWCf4X8Ubm9CeCXkzBhgDDQtwyAAbq2tjYmJsbBwWHdunVcLlcgEDg4OGzfvp0YoPuWbZIbYYAwMGgYQPYH0GTUarVery8rK0tOTmaxWLa2tnw+XyKRHDhwAMzTRsu4Bw0PpCKEAYPBQAzQ5DEYkAwolUqDwSCXyw8fPmxvb09RlJubW05ODlifDQaDWq1GFTMataJ4EiAMDEoGFArFy5cvV6xYYW9vz+fzYW9WBoMB1mculzt37ty3b9/Cmne0yzNu6zG1K+Ev0aAkjVSKMDDoGcDfYtMwmn9CwyQjQtAlpu3Dz8VAhkal4F/B0xmV25sAfjkJEwYIA33LgEaj0ev1nz9/HjdunFgs3rNnD5PJlEqlrq6uGRkZMAWOv6d9WzrJjTBAGCAMDFwG8LYRlpfp9fqCgoLk5GQ+ny+VSu3s7MRi8aZNm2pqasAnoDt9bOCSQCQnDBADNHkGBioDGo1GrVbfvn3b2dmZoihHR8c9e/Yg6zP4dUKrjTf3EB6odSZyEwa+x4BOp2tvb7/wvwsJCQkikcjBwQH2fQbfZ7FYHB0dffv27ebmZp1OZzAYiAf09xglvxMGBg8Dpr1hdzFd1hkl/jlzs+lVvemRUaG9DHQpOYkkDBAG+oQB8O2Qy+VTp04VCoUHDx7k8XhWVlb29vZz585F29+ht7VPCiWZEAYIA4SBQcAAahi1Wq1SqYQj3/V6/bt371JTU4VCoaenZ0REhL29/fz589+/fw8bJBIb9CC49aQKRgwQD2gjQshXs2YArGYGg0Gr1T548MDGxsbCwsLW1vbw4cNyuVyhUKhUKnSWEWrojQJmXUMiHGGgFwygyRW05wZc1NTUtGPHDn9/f6FQKBKJKIricDgURTGZTIlEsmbNGplMBsu+kPWZeED3gm+ShDAwGBgw6gp7+NplbVF6U1Pyz8VAhl2WhSJRob0MoAtJgDBAGOhzBkAJV6vVqampYrE4KyvLzs6Oz+eLRKKkpKTm5mbYzwe9rX0uAMmQMEAYIAwMUAZQw6jX62Elt1KphFm9+vr6bdu2CYVCW1tbPz8/NpsdGhp69+5dUxs0ngkKD1BCiNhDlgFigB6yt35AVhyOStNqtY8ePQoICGAwGA4ODrt37wbfZ7RzP76UGLXOKDAga06EJgx0MoCWpSNP/44vHc3NzQUFBbNmzbKzsxMIBDweDzbcYDKZfD5/4l8T7969azAYjF4N3GyEXpAeAp0ikP+EAcLA0GWghybip38aumySmhMGBhQDer3+P1U8MzNTJBKlp6d7eXmxWCwOhxMbG1tZWdnllDY0CwOqlkRYwgBhgDDwWxiA9hC2eIZRmEql0ul0DQ0Nx48fd3JycnBwgL044uLi7t+/r9FodDodrC8BgeAqU3Xrt4hLMiUM/AYGiAH6N5BKsvydDLS0tFRWVsbGxrJo7Nixo66uDvmBmjbHpjG/UzqSN2HgTzAAI0Dwg5bL5Vqt9sL/LowfP97Ozo7ZCRaLRVGUu7v7sWPHPn36BKcDKRQK/I0gBug/cbdIGYSBwcUA3ob0VXhwMURqQxgYtAzAFPj+/fuFQmFKSkpgYCBo41FRUaWlpcQAPWhvPKkYYYAw0BcM4FoTjMLQytSGhoZr167Z2dnxeDw3NzehUOjn55eTkwPWZ1jhDSJ02dL2hXQkD8LAn2CAGKD/BMukjD5hAJartLa2xsbGikQiPp+/ZMmSlpYWg8GgUqk0Go3R0j+8icfDfSIMyYQw0F8MIOtzx5cOhULx/v37bdu2ubq6wmH0TCaToig2my0QCObMmVNVVQXvhVqtRifUo9eBGKD76yaScgkDA5cB1ID0YWDgskEkJwwMKQbAAJ2TkyMQCMaNGxcbG8tmszkcTkhIyPPnz41WWeFNxJBiiVSWMEAYIAx0yQDeKsIoDNazwipVg8Fw5coVLy8vgUAQHh5uZ2dnb2+/a9eutrY2nU6nUCjUarVGo9FqtaYjuC6LI5GEATNkgBigzfCmEJG6ZkAul5eXl48fP57FYonF4i1btsBZatBwo/038Ja9y3DXuZNYwsAAYQBO4DQYDAqFoqioKCUlxcbGhqIoFovF4/GYTCabzY6Njb148SJsyGgwGGCLMagf/lKYqi/4r6bhAcIQEZMwQBj4jQyYtgy/HvMbxSVZEwYIA33EAFifO750PHnyRCAQjBo1auzYsRwOh81m+/r6PnjwgBig+4hpkg1hgDAwOBnA9SU0Cuv40qHRaFQqVVtbm1wuv337dmxsrEAgCA0NDQ4Otra2zszMBI8idIQPuha1uoOTL1KrwcgAMUAPxrs6SOukVCrnzp0rlUr/29x248aNNTU1cBohrEOBBn2QVp1UizBgwJ9wtVpdX19/+fLl8PBwgUAA2z1zuVyKoqytrTdv3vzu3TuYmEEKCjCI6z0/ESa3gTBAGBiaDPxEc/FDlwxNVkmtCQMDiAH8/Im6ujoHB4ewsLAxY8awWCw2m+3u7p6bm2v01g+g2hFRCQOEAcLAH2MAbyphpKbVatU0dDqdVqt99uzZhAkTOByOn58f7HQ0duzYly9fwnYcer1eLpejIR4E8Dz/WEVIQYSBn2CAGKB/gjRyyZ9jAHa5ValUDQ0Nixcvtra2trKySk1NrampUalUsKUAmvqDxH9OOFISYeBPMQADP1BKVCpVZWVlVlaWjY0Nm81Ghw1yOJzw8PCHDx9qaBgZoPHXBNdRfij8p6pLyiEMEAbMi4Efaih+IrF51ZZIQxggDHTDAGwCptPpIiMjXV1do6KiYNcvR0fHC/+7YLQVXjd5kGjCAGGAMDCkGTBSk8CCDB51wItWq62srJz410SRSOTj4xMcHGxlZRUeHl5aWgoJGhoaYNcOZIbG8xzS5JLKmz0DxABt9rdoyAuo1+vr6upWrFhhaWnJZDLnzJlTXV0Nvs9ggCYN7pB/RoYEAQqFQqfTyeXyFy9ezJs3Dw6pAOszRVERERF79uxpbW0FLmCbji4PqcDflx8NDwmiSSUJA4QBmoEfbR9+JT2hnDBAGBgoDMCM+KpVqywsLKKjoymK4vF4Uqn05MmTA6UKRE7CAGGAMNCPDHSnLyGRwKmusrJyxYoVNjY2w4YNi4qK8vT0DAsLO3LkiEwmMxgMRk7QeJ4oHxIgDJghA8QAbYY3hYj0lQFoedVqtUql2r59u0gkYrFYs2bNampqAusz0GTk10m4IwwMdAZ6UCCam5tPnDgRFRXFZrMZDAZsvMjhcDIzMz98+NDe3g5112g0Op2OeEAP9CeByE8Y6F8G8Lbod4f7t6akdMIAYeCHGNDr9bm5uUwmMyEhwcLCgsfjCYXC/fv3/1AmJDFhgDBAGBiaDJjqVDgPer0ejhns+NLR2tq6adMmHo9nY2OTmpoqFArt7Ow2bNigooHcn1EAzxnPk4QJA+bDADFAm8+9IJJ8wwCs8tNoNOfOnbO0tKQoKi4uDi08+SYp+UIYGCwMgN6A1IiOLx1aGmq1uq6ubsOGDU5OTgwGw8LCgsViURQVGRmZl5cH+6EbLX1FmRhN0uCqyY+GBwvNpB6EAcLA9xn40fbhV9J/XxqSgjBAGDAnBqqqqgQCQVxcnEgk4vP5HA5n06ZNRnqIOclLZCEMEAYIA+bIAK47Iflg7Aa+RBqNZv/+/SKRyNPTc/Xq1V5eXlKpNDU1taGhAfZmhKu6G/ehPEmAMGAmDBADtJncCCLG/zEAK/tg3k8mk50+fdrW1pbD4cycObOiokKpVBKmCAODmAF4/kHhQHuBKZXKx48fp6Sk2NjYoD033Nzc9u3b959VGtiA2fKOLx1Ij+lOEUEJfiIwiJknVSMMEAaMGPiJJuKnLzEqmnwlDBAGzJyB5uZmPz8/f39/8IBmMpmZmZlGE95mXgUiHmGAMEAY6HcGcMXJSBg0KlSr1cePH3dwcLC2tp41a9bIkSMtLCxmzpxZVFQE035qtbq7la9GeZKvhIF+Z4AYoPv9FhABvmGg40uHSqUCO9qjR4/c3d0pioqJiXn79q3BYGhsbJTJZHK5/JtryBfCwGBhAKkaoEbI5XKZTPbvv/8GBASwWCwGgyEUCimKmjRp0suXL+H0CXCR1mq1cPYgTN5APsgGjSs3vxIeLDSTehAGCAPfZ+BX2oofvfb70pAUhAHCgDkxIJfLZ8+ebWlpyWazeTweg8HIzMzEZ8HJweDmdLuILIQBwoCZMoDrS12KqNfrlUqlXC6/fPmyg4ODRCKZPn361KlTmUxmaGhoUVEROviny7N/usyTRBIG+pEBYoDuR/JJ0d8wAMYyg8EAprcXL16Eh4dTFOXr65ufn48UWY1G881l5AthYIAzgJ5tcB1C2zd3fOkoKSnJzMx0cnKiKMrCwkIgEISFhR0/fry5ufnTp08KhcJgMKjVarBBG5mb0VcjjyRc0fnRcF8x3Ztye1OWaT69ucoozXeN9fiaYqNrf/GrqfzoYfjFnMnlv8hAl7emN5G/WO4PXd6dPD+RCWoufugJ7E6An4j/IZlJYsIAYaDfGVCr1du3b6coisPh8Pl8NpudkZFBDNB9cl9604R2VxC6trsEvxiP8jcK/GK25PKBy0APaoPRQ4I0DQjArwO34n0lOc5SD3lqNJrW1tY3b96EhYUJBILExMRZs2bZ2tq6u7sfO3asra2NeED3wB75yawYIAZos7odQ12Yji8dBoOhvb392bNno0ePBt/n58+f63S6oU4Nqf/gZQCpbvD86/V6lUolk8lu3ryZlJTEZrMpimKxWPb29itWrCgsLNRoNKBkGH0ifc5IwzM3AzRoWqZCohikivVwz1GaXw9AueA1gHIDozNuekY/fTfQg9joJzwTVHF0p1CyngN4JngY1Qj2EEc7iSPv+J6zHbi/orkE9GoAFegVg6oZfTWtL5CJ35fehPFbgArCI3sIm8rQZcx3BcOL6DIHo0iUoRFjkAx+NbrE9Csq1OgnFN+bgNG15CthgDBg5gzodLqrV69yuVyRSCQQCPh8/qpVq0x7UjOvhRmKBw1md51Oz/0XuhYCprXrTWuMp4EcUG4Q6FI2dBWoHKCpglaDi4GS4QGUwGgVIHLnNK01Lgnqv0wDpgKgslDVjGL666tp3VH1TQmH6n9XVJwl00x+VOc0LQ6/iUb3CP8JFW10g/C7g6c3LWgox+DMAJNFRUWTJ09mMBixsbHLli2ztLR0d3ffs2fP58+fYSCp1WrxucChzB6pu3kyQAzQ5nlfhpZUyL6sVqv1ev379+9HjRrFYrH8/PwePHgAre3QYoTUdigxACom1FilUhkMhrq6ujVr1lhbW8OOz0wmMzY29tWrV+3t7QaDQS6XG+lw6CtS8owCuPryK+E+uS1IycZVT9OcwRMcbTCCB6C+UEeozs9Zio3UZVMZ8BgkNmK7uwBOvhHbuHu7kfx4Wb0MG2WOvnZ3OUoAAdNkRgm++9U0h/6KwUXF+YfjWWBxokajAaUc9Th9Lq3RQ9vdE2Iaj8uM1wUP43VRqVRqtRpqBJWCPH/ioYIi4ELYyQdyhi19UBH4CwhhvOHCmYQMUQxehR7CKD0JEAYIAwOCAZ1O9/Tp02HDhsEhhDweb+nSpSqVClm1fqiHHRBV/jNCImWjZx0JqT2o30G9QA/MGzXC0PKbdklGMajNh2a/y/yNWn5TrlC98My/W0fTfCAGVQTvPU3DKJmpzEge/Co8/R8Oo3vRS3lw3wJ0X0yr2R2BKB7xgJ4fXAD8de45c8inyxuKF4Fnjko0ohrJRgLoNQeKgD2tVltTU5OammplZRUWFpabmxsQEODg4LB48eLm5mYgjRigycNjzgwQA7Q5352hIhsoTxqNRqVSvX//Pjk5mc1me3t75+fnwy63MBIeKnSQeg4xBjq+dCho6PV6uVx+69at+Ph4cHy2trb28vLauXNnQ0ODWq1WKpXISxrX4FEYV+zwsJFu99Nf++TO4JooKM24qL0Jg/xGwhhlizjpOQDFGWnVSI1G13apUhsJYPrVlOfez/dk1AAAIABJREFUGKDhqp55QB5GyEqIB3ozVjSVdtDHoCcE2VLh/uJU47fsJwgxur9Gz9VPZNjDJag6RqNQ9E7hdekubJQ/yrM7TvB8kNUD7PtqtVpFQ00D3N8gf/yq7sJGkpCvhAHCgJkzoNVqa2trJ/41kcPhMBgMiqL++eef1tZW3GJl5lUwT/FQO2zaQyGNxahzgUugdTWtFMTDtUirwXsK00vwGFN58NJR5tAToc/uJnqNugC8IAhDcXgfhMuMZklVKhXMj+LCmObWQwyqF16WkXh/7GsPcvb8E7qt6CQY6ILRFDVum+6yOkifRDP0OKVwCSrFSN/AdWPEJ36/UHrcAwDlb3qvobieqzzUfsXvGtwIg8HQ3NxcX1+/YMECS0vL4cOHb9y4MSgoiM/nT5069c2bN3K5HLglfA61p2Wg1JcYoAfKnRr8coLv8+TJkymKCgwMLCws1Gq1BoMBNroFu9vgZ4HUsE8ZQFpOn+ba95mBnG/evJk7d66Hh4elpSVFUVwud9GiRUVFRaBnGwwGrVarVqvRPulGSh4aTuDKNIRx9eVXwn1Sc6SkwpyTQqGQyWRtGFpaWj5//tzY2FhfX/+pK3ykUUujpqamurr6w4cPFRUV7969K/txlJaWlpSUvHnz5vXr169evXr58mVxcfFzGkU0nj17Vkjjae/w5MmTx48fP3r06OHDhwXf4sGDB/fv38+ncZdGHo07nbh9+/atW7du3rx548aN693jP3+Ha9eu/dsNrtK4QiOHxiUaFy9evPC/C+fPnz937tzZs2fPmOD0D8Ikg/6JOEvj3Llz58+fv/C/Cxf+d+FiJ6Dily9fzsnJAVrg8xqNXBo4zTdu3Lh58+atW7du377deU96+x9u5d27d+/du/fgwYOCgoJHjx49fvz4yZMn331wCjE86wbPnz9/8eLFq1evXr9+XYrhLYYyGu9olPcCFRUV79+///DhQ2VlZTWNmpqa2traTxjqukE9jQYaTTQ+02hubm5paWlvb1cqlWjXl+82O33StpBMCAOEgT/GgEajUSqVS5cuhaVaFEUtWLCgqamJGKB/8Rb0rCO1tra2tLQ0Nzd//vy5qakJNKW6ujpos2tra0Epqqqqqqys/PDhw/v376ErgH4B+gj4LC0tff369YsXL/7b9vBpN3jy5MmjR48KCgru379/7969u3fv5uXl3cGAlJbr16+DZnLlypWcnJzLly9funQJVA7QN06fPn3q1KmT3+LEiRPHjh07fPjwwYMHs7OzDxw4sH///n0Y9tLYs2fP7t27d9HYsWPH9u3bt23blpWVtXXr1s2bN2/atGljN9iwYcP69evXrVu3du3azG+RkZGxZs2a1atXr8GQ0U/IzMxcu3btunXr1q9fj1dlUzfYTGPLli1bt27dhmE7hp07d+7atWvPnj179+7d3w0O0MjOzj548OCRI0eOHj16/PjxEydOnOrEmTNnzp07d+F/Fy5fvnzlypV///0XFKfc3FzQl0BZyqdx79490HxA7Xn27BkoLSUlJaWlpeXl5RUVFUjf+PjxY3Nzs0qlAvWAtBuGboCrTzoaMB7UaDTl5eUbNmzg8Xi+vr6ZmZmzZ8+2srIKDw/Py8uDoaJWq9Xr9d1kTKIJA/3GADFA9xv1pGDEANjRPn/+PGnSJEtLSzc3t4cPH7a3txu1uSg9CRAGesMAen4MBgOEv3sV6P3Qwf9Qn91lYp1OB16BGo0GT6DX6zu+dMDgDdQIg8Fw7NgxJycnDocDYzlHR8ebN2/CGYNgdO6uChqNRi6Xw7GEVVVVaLxRVlYGo4vi4uKioqKnT5+CVfT+/ft37ty5fv361atXL1++fP78+ZMnTx49ehRUTwgcOXIExgMHDhzYt2/f7t27Qd3funXrli1bNmzYsHbt2oyMjNWrV69cuXLVqlUrV65cvnz5okWL/vnnnwU05s+fn5aWlpqaOnfu3NmzZ/9NYyaNFBozZsyYNm3alClTJk2alJycnJiYOI7G2LFjExISRo8eHR8fH0djFI1YGjE0Ro4cCQH4hJ9QspiYmJEjR0ZHR0dFRUXSiKARTiOMRui3COlEcHBwUFBQ4LcICAjw9/f38/Pz9fUd3g18MAwbNszT09Pd3d21E2403DFADHy6uro6Ozs7OTk5dgMHGvY07GjY0JBKpRCw7YSNjY1UKrW2traysrK0tBSLxSIaQqFQgEHYCQsLCz6fz+sE9wfRed13/vNpWNAAKTrL/6X/UDX4FNPAw5aWllZWVtY0JBggBv+USqW2trYODg5OTk4uNJy7AfzaeVe//nczAdxkDxqeNLwwDMPgQ2P48OG+vr5+NHxN4O/vHxgYGBISEhYWFmECeKQhesSIEZGRkVG9QHR0NLxBsbGxo0aNQu8LHhlHA94p/BPi4+PjR48ePaYTCQkJ48aNS0xMHD9+fFJS0oROJHdiwoQJE/+aOKkTkydPnjp16rRp06ZPnz5jxoyZM2f+/fffs2jMmTNn7ty5aWlp8+fPX7hw4aJFixYvXpyenr4Uw/Lly1esWAEtzxoaGRkZmZmZMHTfsGHD5s2bYUy+Y8cOGH7v27dv//79Bw4cOHjw4KFDhw4fPnzkyNeR9pFOHDt2DEbdJ0+ePHPmzNmzZ8+dO3f+/PmLFy9eunQJJjD+/fffa9eu5ebm3rx5886dO0YzDY9oPH369NmzZ8XFxa9evSql8fbt27Kysnfv3sHYG8z9VVVV1dXVNTU1nz59qqura2xsbGpqamlpaW1tbWtra29vl9NQ0FBh262gvklPA3Zl0Wq1uHMZpNHpdGiGEr/KYAKUFbrQKD2eAM9Tr+92WItnBZfgMZAh9IMgPCzg0GJAMch9z0Tw/4tAvTYuG7JlmF4F6ZFfHvTRSqVSRUNNAwQxlRxqgeJNGYAY03hTMUxjEC0QME3Q+5geBEC0496O3y0aJTCV4eTJk1wul6IoJpP536FYVVVVpmkgBmWCAl2mRHsNqVQqpVIJ89OttNUVZqbr6uo+fvxYU1NTVVX1/v37t2/fvnnz5uXLl8iQ+vDhQ7CW5ufng7X01q1bN27cyM3NBbUHn4g9derU8ePHjxw5cujQIVB49uzZs2vXru3bt2dlZW3evBkUnszMzDVr1oDOs2zZsqVLly5ZsmTx4sULFiyYN2/enDlzZs6cOWPGjKlTp06aNGnChAnJyclJSUnjx49PTEwcO3bsmDFjRo8eDe1tdHR0ZGRkWFhYSEhIYGCgn5/f8OHDfXx8vL29oX/wpOHh4QEBLxqgV3h4eLi7u0P/gj7d3NycnZ0dHR0dHBzs7e3t7OxsbW1pTcGO1hrsIR5+gl9taUAalBICNjSkNKDntLa2hoDRJ1IzxDQsuwL8BF2zQCAAlYP/LXg0kPbB6QSbBqsT8BV+hMRwIfrkcDhsNpvFYjExMGigCFCw/8AnKrdT/P+TCuLRr0gwlAwF0E9dBlgsFpvN5nA4iDcIdJLX9X/gEP+EHPh8PpxzLhAIQC1D2hToURIaUhoSiQSUTGsa6CekeVrRgF9tbGxsbW3t7b8+hE40nDvhSmtQzs7Orq6uHh4ew4YNGz58eFBQUFhYWFRU1KhRo8aOHTt+/PgJEyZMmTJl5syZqampixYtSu/EsmXLMjIytm7dCh39/v37T5w4ce7cuUuXLuXk5Fy7du327dsFBQWPaRQWFr5586aioqK6uvrTp09NTU2tra1KpRL300ftEgRQn4U3p6aRWq1WLpe3t7erVCpoVI16IrgEz9zwPaDEqDi8Q4fuCbpIWH924sQJPp/v5uaWnZ29detWBwcHR0fHK1eugBf890ojvxMG+oEBYoDuB9JJkbCxBszL6fV6mUymUCgyMjJsbW1dXV2vXbuGrHKoFcY7AEIgYaBnBmCIhTyCYagJ+2GZXoiGr6bPGDx+ppfAxLKR4gIjXoPBoNfrwSjc2tra2NhYW1tbWVlZXl5eUlICY6Tnz58/fPjwzJkzGzZsWLVq1Zw5c0JDQymKYjAYMIoTiUTjxo2bPn3633//DeOZlJSUBAxRnQBbUlRUVERERGhoaEhICJhQ/f39hw8fjsYz3p0YNmyYFw1PT08IwCeMatw64d4JV1dXl0640oAkEO/cCRcXF7Cfgpbp6Ojo5OQEP8LVoGh2Zu8G2XvQAEmGDRvm7e3t4+MznIbvt/DD4E8jAEMgjaBOwNeAgIDAwMCgoKDg4ODQ0NCwsLBwGshaNwIDigQTHrA6shOxsbFxcXGjR48GQ9u47pFIIykpKTk5GYxuU2hMpTGtE9NpzJgxIyUlBVnfZs+ePYe2vs01QSqNeTTANrdgwQIwz6XTWEIDhsRLlixJT09HMUuXLgWD3apVq1avXr2GRgaNTBrI6Qa8hNb9CNb3DpDlWhpQKAjwi59gDoD5jxU0lncCqAByEBvACYpEgcWLFy9cuHDBggUwa5KWlgZUo89Ueh5lzpw5s2fPnjVrFhgapk+fPm3aNLiz+CeKnDJlyuTJkyfRmPjXRPgzNUwkJCSM6cRoE8THx48aNSo2NhbmVKK/RVQnRowYEREREd47wNOOnvnw8PCwsLBQGqgBgZcpsCugyRj8HYXXFj59fHy8aUBrY9S2uNFwxeBCA0XAV2dnZwjgv8K10HrAp4eHh5ubGzRHKAfU2qCUqL3C83RzcwNTDlh50Gd3eaISjQxDXt0ANWi+vr4BGIIwQHMNk14oGm+yIiIi8HmFmJiYWHraIC4uLiEhAcbnSUlJ6AGb+NfEyZMnT5kyZerUryZ+aGT+/vurfX/u3Lmpqanz5s2bP38+akAWL168ZMmS5cuXr1q1as2aNfB6wicy6G/atCkrK2vbtm3bt2/fsWPH7t2793RiH4Zs2ofu0KFDR44cwQ36p06dOkP70CGDfk5ODnjSgU3/+vXrsOzg1q2vKw/u3r17//79hw8fPn78uBBDEYYXNIppvKSBwq9evXrz5k1JyVeHu9LS0rcYIKasrKy8vPz9+/eVlZU1NGpraz9+/PiJRh2GehPAVMHnz5+bm5vBJNrSiVYabW1f5w9kMpmchgqbPNBjMHQPZB/X0YCLukyO8kO/QgxuqkB2drCJIC0FXdJDAOUGGZrKA4sUS0tLXVxcwAbN4/GCg4NjYmIiIyNRoxQaGgrPeWBgYEBAAG5v9fLy8vT0hCYCTcTa29vb2tra0JBKpRKJxIqGpaUlBOBTYgJrGmAVhflXmIIV0vOvQgxiDKZ5SqVSGxsbu06AMdeWhg1tTUMGNUcMznSTBY2P+7eAFsPLyws3IhtpPj6dgMYTvg2n4UvD398/ICAAqTShncBbfWjV4XMEjcjIyOjoaGg3UNMR3wm8wxlDA1qVcePGJdIYP3480mcmTJgwadIkNH2YQmsvs2bNAtUFaS/z5s1LS0v7559/FixYsHjxYpg+XLZs2YoVK1auXAlKSAaGzMzMtWvXrl+/HuYOwaU3Kytrx44d4MCLGpy9NPbR2E/jAIZsGgcPHkTzi9AKHT9+/MSJEydpnKJx+vRpmGU8S+PcuXPn6bVTMN14iQZaLnb+F3D27NkzZ86A3zdy/T6B4fjx48eOHYOp0MMmONQjUPJDhw4dPHgwOzsbnMf37t27pxN79+5Fk6/45MpODNu3b9+6deumTZtMJ1pWrFixbNkymGhZtGgRqElpaWlz584FRWj69OlTp06dQvuRQB80adKkiX9NBD0HZl8SEhJAjYmJiYmm/UKQawi0EiH0/HpoaCgMW0B/QG0C9O/Q9UMYxhoODg7QUIDLBdi+xWKxlZUVWMnh3QfrOfwKYRubr14a8I7b29uDWdzNzc3b29vX19fI/J2cnDx16tQZM2b8/fffc+bMmT9//tKlS9etW7eJxpYtW/bs2XPkyJFz585dvXoVejF8cvrx48dPnjx59uxZUVHRy5cvX79+XVJS8vbt23IaFTTKy8vBW+jNmzew+BKWIzx+/PgRjYeduIkBnmT43Lp1a0ZGxoQJEywtLS0sLCb+NTEuLo7JZDo4OGzYsEGv73ae2EBAGOg/BogBuv+4H5Il6zsBtQf9tb29fePGjZaWlt7e3teuXYPmEpmnO68gbeiQfGJ6UWl4QnSdgIEWPFpwNYzoUE4oPTJMdzcq0+v1SqVSLpe3tbXV19eXlZW9fPmysLDw/v37V69ePX/+/KlTpw4dOpSVlbV27dpVq1YtWbJk3rx5KSkpkydPTk5OHjduXHx8fHR0dEREREhISEBAgLe3t5ubm52dnVQqFQgEFEWBFwNyx2DR4HA41tbWUqkUVCixWCyRSJCq5Ez7C7i5ucGoxsfHJyAgIDg4OCwsDLwgR44cOWrUqPj4+DFjxiQmJoIHwcS/Jk6dOnX69OkzZ86cM2fOggULFi1atGTJEnAiWL9+/aZNm7Zs2bJt2/9ZGXbu3Lmbxp49e/bv33/w4MFDhw4dPXr02LFjJ0+eRBr8ORpnz549f/78ZXqjgys0/sWQm5t7/fr1Gzdu3Lx58za9s8Hdu3fz8/Pvd+LBgwePsM0KioqKXrx4UVxcDBrbmzf/Z03AHQk/YKikUUWj+ltU0atQYSFqz8mQTyJujPjUO9TRqK+vb2hoaOxEQ0MDxKDIpk5AEkhQV1dXX18PnyhlZx7/9x+u+0yjmV54+7lz7S2kgATNGFpptNFob29vpd3H0O8tNFAasJjIZLL2H4Ssd4BcQRgoFAT4xc/W1ta2tm/MPUictrY2qDJe056LRuQghoFwRDW6X13ebnTLYE10Y2Mjnh49R/iNbmpqwtPUda6hRolR4GM3qO1EdXU1etQrewF4e97TKC8vf/fuXRmNt2/fwo40JTTedIVXr169fPmyGMOLFy+eP39eROPZs2eFhYVPaMAIqqCg4MGDB/cx3Lt3Lz8//y6NvLy8O3fuQLMAAfBVvH79em5u7jUaV69ezcnJuXz58qVLly5evHj+/PmzNM7QgIH9CRrHaRw7duwojSM0Dh8+fLBzfH7gwIH9NPbt2wcD9d27d+/cuXP79u3baGRlZcFofOPGjRtorKexbt06cIGE1R5LaKTTWIxh0aJFMJMxb948WPwBA/UZGKbTUxfTpk2DofvkyZPRiD2JRmJi4rhx48aOHZuQkDBmzJjRo0fH0cCnIiIjvxr4wMYXERERjgGfiQz6FrCYYzjmbulFA0b7bt8CGQRhqI/cJ+3svvpX2mImQrAS0oN6qQ09vIdPcJSDT2sakAY+IRM7u69Omo4YcPsCKhTWKDg6Orq4uLi5uXnS8KABdj1YSRCAITg4OCQkJDQ0NDw8PCoqKjo6euTIkTExMWg2cezYsYk0wMoGTvqTJ08GiwPY1/6mbfezOzG304iflpa2cOHCRbQ7HprkAxPbKmyqD03vbdiwYevWrWBW27Vr114M+/b9n3t+dnb24cOHjx49euLEiVOnTsFDfu7cN9axy9gq+OvXr9+69dVkf+fOnby8vPxO3Lt37wG2BRB45RcVFT1//vzly5evXr0qKSnBl8NXVVXV1NSgjq++vr6xsRGM7G0YZDTkNBQ0dDqdTCZrbm6eOnUqj8eDfcNcXFzCw8NjO4FPmcTHx6N53ERaM0nunKmdNGkSTJlMnz49JSUFzJrAdlpa2vxOLFiwYOHChUZmTUR4RkYGWDPXdWLjxo2bN2/Oysravn37rl27du/evXfv170IsunJEtBqYL4EbJSnMZw9exZ2HrjUuQYiJyfnCo2rnbhGL4lAug1qx/Iw3Lt3DyZUHj169JRGYWEh2KTgpjx//vwFBrhHoPa8pUG3zWXvMJRjwBdVoJtYV1fXQKOxsbGpqelzN2jGYNqfyjEoOiGXy7tTFeAJgV+hC4YOWi6XKxQKZTdQKBQoT5i5gcQqlUqpVKJf0aQOCAKZqTCoaWhowLoKdCyBUqmEhCgN7qmqpQEXogN40cIL/S8AhhhGZyTgNKiwCSoYueCfIFgPn5Az4gBqZ/qJOEFZGZUCu+EhwZBUcCH6xHNGhcJtgmvRzQKVDz7b2tpasB1jGmjF+NOnT7CI4f3792CTLSsrAx+d58+fFxYWPn369BG98QtoC3fu3EGKwXUaubm5OTk5586dO378+NGjRw8fPpydnb179+6srKyNGzeuW7duzZo1K1euXLFixXIaYEnHO+jU1FRYuDBlypSkpCS08nLUqFFRUVFhYWEBAQE+Pj4eHh6urq5OTk729vYSiUQoFLLZbCaTCWM3DofDxcDj8SwsLEQikaWlpbW1tb29vZOTk7u7u5eXl5+fXwA9gRQSEgLddQSN8PBwmKILDAz09fX18fGBaSpUqK2tLfSYPBp8Pt/CwkJAO6qLaHC5XBhOgiAsFsuShkQicXFxkcvlOp0Of4oNBIQBM2CAGKDN4CYMJRFMG8GSkpLMzExoYS/870Jtba1GowHfUoVCYZp+KLFF6tpbBpBeZRRQq9VtbW11dXUVFRXFxcVPnjx58ODBnTt3rly5curUqb1794KysmbNmvnz58+cOXPChAnx8fEhISHe3t6urq52dnZCoZDFYiEDsVGAyWSy2WwulwtnBjKZTD6fL6YhEAi4XC6TyWQwGCwWi8fjWVlZubu7BwUFxcTEJCYmRkZGisViUGXYbDaM35AftFAohGu5XK5YLEbT+5C5UyfA19jNzc3Hxwd5Jvr7+4OiExwcHB4ejnzokBNlbGzsmDFjwLoxduzY5OTkKVOmzJgxIyUlBcbbc+bMmTt3LjjKLV68eNmyZch1JTMzc/369WhQt3PnTnBU2b17d3Z29pEjR44fP37y5FcLNQzeLl++/O+//yIft7u06RmGx0+fPi0qKiouLn7z5s1beqE6mJgrKr5uEgcW4U/0EvUG2rDb0tLS2toK1lKkK3c3tIA2BB4gvf7r9BU0JjoauP6NfMSMBi24ho0r2XjREEb6Ohq06Oj172iQA4X20Jrp9Xq4xEgw+ApPNT5AQiMB+AmSQTWhyugT1R3FGAWg6C5p6VIYPBKu+u4nVNyo3N/xta8Kwu8UHkYyQ2SXFe8rGVBZEMDFQGEQ4OdKRI8cGsQanVnU5QOJSjQSz+griIT46fLJNLrE9CuSEB45VDTKHD2KaHyF3ju8I0AXQhFG2eKZ42EkM0qPv2uoaqhoXCpEKRhQwC7T3t6O5kXwWQ0YkMMsFAzLa2trq2lU0fhA7+JaUVGBpgre0vMEaKrgNQ00MWA0PQDj+Sffbkz/8FvADEF+56zA3U6g6YFbGG7cuHG9c3rg6tWrV65cgemB8+fPnzlz5sSJE2AOOIzh4MGD+/fv37t3L5j7t23btnXr1i1btmzatGnjxo3r169fu3ZtZmZmRkYGWA2WLVu2dOnS9PT0RZ1ud//888/8+fPT0tLm0dsdzKa3dUpJSQEXPLTpwfjx48eNGzdmzJj4+HhYNxAZGRkeHh4SEhJMIygoyN/f38fHx8vLC3ZJcnZ2Rst3bG1tJRKJWCwWCAR8Pp/H43HoRf3Mb8HAAN00g/F19ZIpIKFpvGkMWDS4XC6YMAQCAW1bEInFYrBlSCQSGxsbW1tbO7uvJnsHGrDSyNXVFYzyXl5ew4YN8/b29qExnIafn5+/v39gYGBQUFAojbCwMFAMIiIiYNI6KioqutNPdtSoUXFxcfE0Ro8eDaqCkbF+Ao1JkyZNnjx5+vTpjo6OMJsOphA+n8/hcKAiQqEQFBhra2sJDZiuQNMSVjQsLS0hAKoOfFpZWeHxEokEDDE2GGxp2NGwpwFKkbOzs4uLiysNFwwQA5/4hIs7DS8vL1ClcK6AJUQRLD5ITExMSkoCBqZMmQKTFrgShZY0paamzps3Ly3tqxl94cKFixcvhhmLVTRWr16dgdnN169fv7HTaL5t27adNHbRANP5wYMHDx8+fAzDcRonaJw6der06dNnadP5RRqXLl26cuXKv/S+vUgNu9OJPAxgKIctCwoLC8E4jvsBvHnzpqTk69QFaGsVtJ5WXV2Nzgyoo1HfORMPhu8mGo2NX6c0WlpaYH8hJQYVDVBpNDTwMMSYtr3Q3hr1Gqj9h5YcPnU0IL2e3v4OND3IGTYvMlLV4BI8k58Io3KRkCADxKNPyBnvsFAYSdhlAMzr6AyVVhrI1PuZRmNjY319/adPn2pra6uqqiorK1FvUtEJ8MAtKSl5/fo16kRevHhRVFQEc8kFBQX37t27e/duXl7e7du3b968ee3atatXr+bk5Fy8ePHcuXOnT58+Se/jd+jQof3796Pta6CF37BhA7Ttq1evXoG5VC9cuBCGXeglSk5OTkhIgHY7hnaXBuMsrNBC7baXl5cnDXd3dzc3NxcXF3jZnZ2dHR0dwS3a3t4eIiEG5jghpa2trY2NDUxtWllZCWmI6WZWLBYLhUILemM6sPNa0ODz+dAyc2nAqI3BYECjzaKBugC8r2CxWCgeb/MhDVzIpjeNYXXuG4O6DAjgKfGcURiyRaWAWZzNZru5uUVFRf03nr1586aRloIeSBIgDPQjA8QA3Y/kD62iUfcPwzloEJVK5dixY4VCIYcGj8fjcrkQtrKysrOzc3d39/Pzi4yMjI+PR1tBzZgxIzU1deHChcuWLVuzZs3GjRu3bdu2Z8+e7OzsY8eOnT59+uLFizmdrgrXrl0DrSsvL+/BgwcPHz589OjRkydPXrx4gcxeoEjV1NR8/PixvhOwRVQbDZlMplKpjA5CRBUBpQcpKEh7QDqNqYaBK1WQHl2OAqbxSGX5bgAygWRoIG30wCGx4V4Y/Yq+Ip0J8jQ6OA7UHeTKh6a1cV0H6TdoA4pnz57h4+F79+6BZnPjxo1/O/fZzMnJAf9icFXbu3fvrl27Nm7cuHLlygULFsDE9fTp0ydNmjRu3LiRI0eGhYWhsaWrq6u1tTWMgthsNurIUScNfTaTyYTxklAoFIlEtra2sAmsl5cXjNbQIARmwt3d3Z2dncEdzMbGRiKRwKZkzIjpAAAgAElEQVQx/v7+I0aMGD169Lhx48aPH5+cnDxmzJjw8HA3NzcrKysYxIKqwWKxOBwOn88XiUSwUgyEdHBwSExMXLt27d69ew8cOLB79+5du3btpLFjx46srKxNmzatW7cuIyNjxYoV6enp//zzT2pq6ix6N4CUlJQpU6ZMmDBh/PjxiYn/t9tgXFzcqFGjYujdkGG924gRI0CZCwoKCggI8KUBA1T8E6bfvby8wCfO3d3dgwYofF6d8PT0hAQwhIPBG6RBF0IkfBotgccHzDBaxmXw9fWFMTN4doMXW1jY1zEzOPeFhn51ahsxYkRUVNTIkSNhQIjIT6b3XkxKSoJNMCZPnjxlypTpNGbQ+Pvvv2fPnp2ampqWlraAxkIasFfD8uXLkbV9zZo1GRkZa9euBQ9xMLtnZWVt27YN96jat29fNoZDNA7TOHbs2PHjx0+cOHHy5P/fW/bC/y6AU9WVK1euXr0KbdSNGzfAQxx5Ud2lAa7iYLIvKCiAFuzx48dPaDx9+hQCjx8/fvr0aWFh4XMaxcXFL168eP78OQwj4fP58+cwnnz16tXr118XA8J4stQEMMJ89+5dBY33ND50g0oM1dXVNTU1yA/rUyc+YoBTkmpqaqq/RZcXQpOCrv5ET0igIW7j/2vv2mOqOra3YMoPGhWJCkZ8BL0SQJrWR1RKxEcUNWprLbYGUFPABlGDCimoqaIRrbGCuYoG6zVXi7fV1qiVUK+ND4wPjFWJFI0VjK0aRYwiRERugd896+teLvZhH6F6FHPX9wfMmT2v/c3s2TPfrJndEmA+fO/evfu0kvFAYcHAfcI9Agwh8deet3tkj3/XGuUEcM5z47v04azmV90dAku0skkY7cv2H/LHLcOQ/MaNG/Yt7TeB3w3A77qwIrdo6SVXr1799ddfr1y5Qo/Fn3+u0je+Ll++fOnSpWKShouKii42Bp6wYgPQji9evFgowDEKCwtxCXKASVDm5/qMNQoKCmBEdsohTgqcIBwno7OjR4/C7uynpnDo0KGDBw/m5ub+YIf9ZLS+Z88eqNIQpncZHyLLycnZsWPH9u3b2Wj9K7JV30zYtGlTVlbWRsIGA5Ctv/zyS7wHoWgsXboUisYiEqyhayxcuHDBggXz589PTEycN2/eXDpXJ55ka1i6QbOOjo6Oior62DA/h3L93nvvTZw4ESuysDcfOXLkCAJWbUMJsDeHGjJw4EC8SXndN9gAH37l7+8vX5RsUd69MXx9fbt27erj49OFjpvoLOBFCiyU6PYEnKKLcTI0C6lr2LtdBPiq8HOBkCF9EAw+LHNAanF1dcUgSl6FyOLq6grtxs3Nzd/fPz4+fuHChXPnzo2Pj59FiCPExsZi//706dOjoqIiIyOnEbhGIiIiUCmT6Rhlfpu/R5hEg5wJEyaMp/0B4wjYJUCC+RiMfLj6IGNhCBQaGhpCewUwihhIGDBgQH86GOQdAtdmv6ZAqr7NPlHWrBznsLu3gJ+fXy9CT0J346RmSGCoem9CF4Ko/0ZOXEUj4abSieDp6dmhQwe0EP4rFzC8CAgMcb9jx46eJLp17NgRV728vJAO2hisLNnQEoERsqMAx/Xy8uL0n+mQN4Z79zFWVpgWLCrAH4su3brZ1l2wwNCDAEpf2l9k2v2FAvfr85cgmw03Cclt586dUReoJtSvfcNAP+NpAAHQorgxyPaAGROaBLe9Dh06wAfbN+2rFdWHGuzevTvXWq9evTDR8CcEEAIDAwMCAoKCgvr168fTAbatGUSndgwdOjRELKENI4SGhg4bNiwsLAwHzowZMyY8PHw8YQJhEgH9CU6swllVWDGKi4uLj4+fM2fO3LlzE+lwquTk5EWLFmEKsHr16i+//HL9+vUbNmzIzs7GbpUdO3Z8++23u+jgaZw9feDAgR9//JE1h5MnT/KKTlFRUWlpaVlZ2Z07d7A2cOPGjZKSksLCwoKCguPHjx8+fDgvL+/777/fvn17dnb2xo0bMzMz16xZk5aWlpSUlEiYO3dubGzstGnTJk2aFE4YO3ZsaGgobKjffvvtHj16tGnTpn379r17916xYgXOn6xvCg0KZeAVMaAC9Csi/n8vW9n11REqKytzc3N79rQtWq5duxY2FG3atGnXrh0PrCERtm/fvnPnzhime3p68ofaeDwNu1E5Mm7bti3LfHgfY80TI4eePXvyFw9wPuMAOisWb7XBgwcPGTIkJCRkOAFvtZEjR4aHh48bNw6nLk6ePDkiIuLjjz+GxSheXbPo4DOcbLBw4cIkQnJycmpq6pIlS5YtW4azFCFdQTGHLQPEqR0G2HQUlgt7xHTuO8Juwi7aj/zNv77BB1V2EjDH27Zt29atW7/66qvs7GxsTdpAX5PLzMxct27dmjVr8OXotLS0xYsXY/42f/78hISE+Pj4uLi4mTNnYm7w0UcfTZ06dcoHU96jGRrG/TzcHz169MiRI8PogyohApihDSKbo/79+2NMD2WzLwGr1j169ECddunSBWPf9u3be9BS8xtvvME7m9zIBOkNO7i5uXXo0MHX17dPnz6BgYH9+/cfPnw4Dp2Y8sGUyMjImJiY2bNnz5s3LykpCfeYkJAQHR095YMpfDjGu+++C+U6MDCwV69eGPL27NkTB1wEBAQEEvzJWgptFZuw2rZt60IL4Gh1aIqurq6enp6sSo8ePfrDDz+MjY3972fi09LSNm7cuHv37ry8vMOHD+fn53///fdhYWF9+/ZNSko6derUb7/9hs8SVtOhH1VVVZWEh4QHDx5AvoEqdN9AOR3FIKUZCDFSfGlyMUAaOxQUFJw4ceLo0aM//fQTdrrl5uYeIDO3ffv27d27l3WEb7/9Fo1tx44daGPZ2dlZWVnr16+HaA7dfE1jrFq1asWKFVANUlJSko1tcbBx41YXZyAmJmbmzJnRxid9ImiL+vvvvz+JrNvGjx8fHh4+ZsyYUaSwh4WFDRs2jLeioxkONcBiwUDSCzDV5JPm5IGMvXv35ominGb4Engu5GPIBDysx1yMZ1/obTDu9zKAwDyBZAcHZgdPw3Ayna+vr5yPdSNICy8M3Pv27evvb7N9wwgeP+H2J5MuHsQPEEBHx1J+WFjYcNqijoH7KEJ4ePjYsWPHjx8PfX+SNTCgf19gsoDwtjmxNgDLlwgDUw189NFHH3/88bRp0yIjI6MI0QamC8xoIWYKfKKwZiCGEEvAQwnZyBSDg8XFxc2yhoyLGmhhvdmCi2qfbrQF23+8p6ZNmwYB6yMDRlOy/Tfal+3/h+KESrRY/J0kMNECEyZMGDfOdibG6NGjR42yHcw9YsQIPDLywRlJwCW8HN81EEpgOczw/vM/1DHZZQ0kDBDg9ymO0QhqCoGBgRDI+vTp07sp+BF69erVs6fN+JePvEBf90xBpGtj+PjYDMogf3QS6Ezgvo71EQSRHaYMw8Hso/sY4OxYN2HtQ/rAcLiLcZ4vlxPRvb29fXx8ugnIztbX15e7WT+yLwZpoLMPoS/B398/MDAwKCion/E1UagkWMPGe2cAqZwDCHwwyGADQwgspnCr4NbCrQs982gyTw4njCOgf+Zmi7aMho3O9sMPP5w6dSr6VXSt0wygj42Ojp5OmDFjBpvuxsTExArEx8fPnj0bukwSIZnw2WefLVmyJCUlJSoq6p133omNjT158uSjR4/++M8fDx7Ydiw9JtQQnhD4w4/V1dWPCFUEHvNUEB4Q7jcGhkDlAmWk5mDlCWtOGPOUEnjR6ApBLhQ1uQ50gYBVn59//vns2bNnzpw5TThFOEmbCU4YJ7Qet0N+fv7Ro0ePHDlymM4agnXFjz/+mGcg18ABwg8//LCfsI+w1wJ7jInArl27du7cmZOT8/XXX/OKzvbG5xp/TcBizz/+8Y+tNB3YsmULZgRY6dlA5xGtX78+MzMzIyNj3bp12NC2evXqVatWpaenr1y5csWKFcuXL1+2bNnSpUs/N7CEsHjx4tTUVAytFyxotPYzxyESCLNnz8b60KeffirfEfjWwkwD3PlHE9Dho7c39e0RTgY/QRiZRL4IRBHw9M1oIfg5jYuzHeuPxzMhIWEOiadzCTCqmD9//oIFC/iZTUlJSU1NXbRo0eLFi5csWfL5558vW7YsLS1t+fLlKwjLCStWrFi5cmV6ejos8b+kE2wyMjI20Ld8sw35ddu2bf/8p83uPicnZ+fOndBhYUi0jw6o+eGHH9DODxw4kJeXB2X2EG2FPHTo0EE6PujQoUOHDx+GmcXx48dPnLAZWJw4YfsGAD7qe/78+YsXbeu1Fy9eLCoqKi4uvky4cuXKr4SrBn799derV6+WGHsof/vNZg9xk4Al6rIy26E0WBTHuS7V1bYTWmpqatAdoRfiS9gZxvvDamtrscOJD3ipqanhvY/1hDpjByT1duY/JtO0P/7zB6L/8Z8/kAu+UY9iYEd4bW0tdZ9P/1RXVz98+JA/MnTt2rXLly8zPydPnpwzZ05kZOR3331XWlpaXV2Ngtn/bVAoA6+IARWgXxHx/3vZcr9cZ6CkpCQgIMDPz2/r1q11dXUpKSkhISF9+vTp1KmTp6cnpg1eXl44yqBtY/CmFZfGYEnaxcWlffv2//0ObHBwcEhICGaDQ4cO7d+/f1BQkJ+fn7e3t5eXV4cOHdq1a+fu7u4mVE4pKSJ5V1dXd3d31kY5d5zAAKnU3d39Tdq54+5us+N2F/Dw8ICnGwHRXR1CloFvqqUOq0T4pni3Dth9g4Db8fDweJPQrl279gbYjfmep+efZhftaL+qhwHcuvHLdu9vvvmml5cXH4aFShk+fPioUaPGjRsXERERFRUVExOTkJCQkpKydOnSlStXfvHFF+vXr8/Ozt5OOwq//vrr7du3b9q0afXq1QsXLpw1a9b06dOnTp06bty40NDQ4OBgPz+/zp0780EWWJNwdXW1Is3FxYVv39XVtW3btljVR0XDQrlTp07e3t49evQICgoaOnTo+PHjp06dGhMTk5SUtHbt2i1btuTk5Ozfv//06dO//PLLtWvXbt++XVVVBUt52eDr6+vlE19XV1dfX3/nzh3Iu3fu3GloaIAn/srADQ0NSMrkKX86yAvB6uvr8dhh8PTkyRMeMJnSQTAHOZruRUZ37Eaa9WILJM9CsYuQh30VFRX3799ns/rbAjdv3sTJcdev2w69xTzTZIFYTEaImFsWFhZeuHCBp5EwDIRt4EkCppH5+fnHjh3DjBFjYp4u5ubmHjhwYP/+/Xv37t1DM8Ddu3dj7WcXgX9CmucNiZj1ZWdnb9q0Ccs/mOPxNO+LL77gad5yQlpa2rJlyz7//PMlS5YsIuO+zz77LDk5eSFhAWH+/PmJiYlz5sxJoOWiWbQnHfO3mTNnziCj+MjISMzQIkhxg3U8y2fhhDFjxmABacSIEcOGDQsNDYWIP5QwmDBo0KCBAwdC8woODu5nAawtyU+39SJtq6dADwEWenx8bNKVRBdCJwJrSehnOhhAb9TuLwF9mofCIQNgCQQz23i7yXgcDD2nUT/m/zCh4hcKx2pRBaIY+Csz8PT07NixI9TMzgJoSPgrG5iPjw+M6XxJYexuoIeAaLaNnBAi//a3vznQHAcKYIEnJCQEezWGDRsWRhghMFJgFB19EG4s+Yw3MEFg0qRJ74m9HRFNQa7fRDeF6bQF5JNPPomJiYmljSCffvrpLEJ8fHxCQgK+G7bQAklJSbxHhCWMpXR0QFpaGlQMKBfp6emrVq1avXr1FwbWCqwjZGRkZGZm/l1gg8DGjRuzsrI2b96cnZ3NW0kwJMgh7BRfD9tN5yN/b2APwfhl+/8dAT579uzZa3EuATSRf//73wcJ0EpYHMHLAj+xJSU/P//48ePSH1fz8/NPCJwiQFI5I/Dzzz+fO3dO7kopIvxCgNTSpM4iPUtKSkoN0Ivx2nUC6y+3b9++c+dOGeGugGlzQ0VFBQ65qiI8EngsUEN4QoBwU1VV9fDhw6KioocPH2KQUF1dDT0FwWoJrLZgpFFHSg1/jQNX+S+iILpMRCaFkQwGTk0OTpAFiz4yR9aS+M5wX/iLKJxyvTGI4pLLS/VNocEALnJ4w/vpfw7AxWMS2IHoT+PQyBCe9pcQTJYZWXB0XJKHFIMErjITyTx0ZPXNVCPwf/z4MS8qiLbTyFlNeEySHxLhoSAuydBVjU0x0D65icqQznajJHyS0oMXgQoC3w4eumb+raysRGFMicjjth89esTFfkiorKzkI7ZR12jtqDU8s7W1tdyuuBmY2hg3LdNDx0+Hqb2ZGl6TyXKaLMjy+XjcuvjZxOMp/+JJsX9sTSXElKqurg5lMIVH+fmhw13U19cjcF1dHd8I0uGZFHLh8ByMpzxNhuTsTCljSsglBPnymQUzeHD4i0eQsB8+fNjQ0FBeXl5WVoZioFSmqrGqIC65OpQBpzKgArRT6dXEnzJg6gHr6uru3r27Zs2a7OzsJ0+e8FV09Pjm27Vr14qKik6fPn3o0KH9+/d/869vtm7dmpGRkZ6eDmvK5OTkefPmzZo1a8aMGTiNYeLEieHh4fgG95AhQwYNGjRgwIC33nrL39+/V69e3bp18/b2hsDt7u7OZrZubm5scw29ki2vvby8fHx8unfv3rt374CAgLfoMwL44FtoaCgk1FFkDAV7qDCyxwwJCRk8eDDkG5wLAXslWFzCLgkaTXexHa+bga5du3p720yKeCsTn2DVi+Dn5wfLR39//4CAP7cp9SMEBQUF0t4lfwMIEBwczPuYYJszgACjb8yQ2b5m7NixMHh8//33p3wwBScYREdHT58+PSYmBnuUME1NTExcQJg/f35iYuLcuXPnzJkza9asTz75BBtdI8h8dcKECaNGjcIpECEhIUOHDsWhFn379sVRy126dOnYsWO7du1wmLKVatymTRs3NzdUSrdu3Xx9ff38/GDMHhwc3L9/f3z9Bucaw0Q9ij5ogzNbEhMTk5OTFy9enJ6evm7duqysrC1btmzbtu2bf32zb9++3NzcgwcPHj58uKCgoLi4+NatW/fu3auoqKiqqsIKOYZlaNOmUQXGK2jG8hKPn/jdzwM7DEcwrLcffGBwwwMyOfzCoXW8qYrFa1NePOriUYscn/FgSGbEoy4ea9pP3qyKahohcVLIiK8+7RGES44F5XBQBGnkZJ6tHMy2/S1L/pGXqYSOi9qoHMYPZgm1yX9N6aOCUJVyosUTiQcPHsDOvZwM28sJ9wzAs6zMtncP1l43bty4SbhFuH37NhzwvEli/Q0C7MKuk2pfWlpaUlJy1ThM4PLly5cuNfrAEXyKSccvKiq6SIYnF6xRSGYpOBrSFKvQgFVs47rt/4ULF86fP3/u3LmfG+OcgP1awulm49SpUzCrOU5qUb7CgoFjhKOEI0eOHCVrPtbUZCRcOmyNIwQW72DZdIrOiml2vdlsoAoKCs6cOXP27Fk0DdEi/mwtZwU4zHn65BqkvUIDaIrnBeCDZkzSn+2cU3sUEy7Zobi4mB+TixcvFhXZohcXF1+iEznwRMi40A1hpVXaGCUCpaWlOAf/+vXrvxn4nXCDwI+5yXGLcJtwpymUEfhEGtiC3RMobwY4OMJyavcJ6MrQm7FPRUUFm5VBfpJaFV6y0BdYc6wVQGde1xRqDas0fjlyP4/OWUbiF7QpF7wIjE796X+8QJEFunR+t7KWId9EeCOjt7dPE6mZyiMTfJqxoTCCA5bq8BM3yAVozguXCymzsHcjmL2/Ax/cFEbvqIKGhgZ8/ApsoBaYE/lmlO9ovinkhZKYuHJQDKtLXLwmA8gasaoIWR7HYUxZIHGuQbQH+xTkncqqNLn5aZCDlibbgAyA7GQW8nlBfWFwKwc/HB4O030xIVyznKOsLyu36b5MtCDH5hSgyVK9dp6yBVoxZu8vWeLqkJ5NNjNOx/6q5M1xOqaQsg3g0ZYNSQZmN1euLI/05GdWJmVVZukv3cjO3of9kaMsFSYjGKXz24Q7f0x/JDmmLsuUsgwpa9mUL7+kuCRw/NcyD8tCfAuIyHM9nlPYR4SZEToHPG72VHOypuj6Uxl4CQyoAP0SSNYsnjKA3hP9IOvOsl/mLhIOU/dt+oleu7a29vHjx5WVlRVkOFleXn779m0ILiUlJVeuXMGEEbNEmEPizIFjx44dPHiQv6WbnZ2dkZGxcuXKRYsWLViwIDExMSEhIS4uLjo6GgcNjxVfthkyZEhwcHBAQAC+kNu9e/euXbvCpNrDw8Okorq4PP1AjSvBxcUFVrdsTM3WuGxP/X8Ed3d3Dw8PmB6z5ZcnoSPBi9BJwN5yELZmbKDNFt+Q3WXxoPzCOlganTsIg1tgs25OAYcd46RjfBEiICCgX79+b7/99pAhQ9j8eeLEiZMnT8aJGTiTd968eampqenp6X//+983b968devWnJycvLy8Y8eOHSfgOK1zZDQE7ezq1aulpaXYaXXr1q2ysjL+1ElNTY1sS0/b4kt0cbuVJYFnc0rB0Z/pcJAax21ywOQgIkYwHJ0dMgp78rMMHxnGyi3jWoWxKoOMa+WWXUpzSmWVTkv9Zb72bpmag7s2XZKxXke36Xb0pzKgDCgDyoCTGJDvCCdlYZUsZ/3MABzy+R1WebU2f3mnr6pssgz24xP4yDDS7YwyOzt9Z5T5dU9Tct5St9W9tzSd5wkvy2CVjgzTUrdVmlb+Mn2rMDxFMgnreOJkCg7cSJwfW5kXe0qHaXFIhneQi15SBpzKgArQTqVXEzczIPtN2Qn+ZTc6We5ekY4pVw5jfxUvgydPnvDuMzbN4DQR3ZQmInIYLj9r4k+ePHn06NHdu3d///33kpKSS5cuFRYWnj179sSJE0eOHMnLy9u3b9+uXbt27Njx1Vdfbd68OSsra+PGjTiULTMzMyMjYx1h7dq12Kq/kj4Zv5ywbNmypUv//HB8amoqztVNJqSmpi5atAinemEb7KpVq3Dq9Lp16zIzM9evX79p0yZsaN22bZs8b3ofYf/+/bAF5mO5cBQXrM9gTQY7L4i/sOcqoSO3bt68WV5eXllZWVNTw4ur8o0LfuR6LGuLuAQmsQrNy7xNWt2aasTqJ1eNVYCX4M9lQFvin0yR4zLI8I7dDtLhiCpAO2CJWyPT5SSH4zLoVWVAGVAGlAFlQBlQBpQBZcAZDDhpcKvJmua8LSXkmXWNBDGdZCHb5MlX7R2yPM/MSwMoA05iQAVoJxGryTbNgOz4nt/NeUDIY1EYKfNVOOCJvhgCKLRmjovzsOxjQZNi5ZQ3wbGQx/lysghjOp4Jm3pQDOwz5bz4DSE5YU/TC8YqDMLLq1wwbCAybThFIVFmqQg3qYoiWb5lLjn2VyJ9lonr6up47xKLyPJYMaTDdSEdnLJp8xG/0bm+WLDmKHAgALPX5O2Yojj7J1eKfR01J2uO/kyHg9RMcR2EtL9kioufMpgMIO9RhrFyy7hWYZ5HF+aWwM+Rg1yeJyN5I890Oy6DXlUGlAFlQBlQBpQBZUAZUAacwcAzh6ka4JUw0Jy6tiqYnO9YuWXc5uSlYZQBZzCgArQzWNU0LRmQHd/zuy2zaXwBGUnRE/0yn+uE4JBNYdRspVrKMjfO5M9ffLwg69Q1NTWszyI61F7+7AYOQ+TwbIJt7yPFYsdu3KB9ae19mrwLe09EbFKANgn0pjBMCCRpqPC4Ry6kfXb2aTYZxuTJgjtL4aYAr+on0863zD7NKRIHfqbDQWqmuA5C2l8yxcVPGUwGkPcow1i5ZVyrMM+jC6M8zS+VLI/z3A7uVC8pA8qAMqAMKAPKgDKgDCgDTmLAeeNbTfl5GGhOdVulL+c7Vm4Ztzl5aRhlwBkMqADtDFY1zVbHgOxw4UbXjC+5OSguB5YpNCe8FLwQt8lYDtJvTo4yTEvdTZbHpPTJMEhf+li5TSHxk+1PTVetEjH5m5YE7H+yiTSYN0VvJT9x73+NgRd1CybqXlSynE5ruEcujKk9t7ayyXKqWxlQBpQBZUAZUAaUAWVAGVAGlAEHDPB0RoZhz2Y6ZFx1KwMvkwEVoF8m25rXq2HA1BGjEPB8ZoEQrPniKYdXAZq5ZU7gwF+++tcc9nbWMnGur7+WuPNiyUI6LxfHKasA/UJaoGOS9aoyoAwoA8qAMqAMKAPKgDKgDCgDL5YBnk7KZNmzmQ4ZV93KwMtkQAXol8m25vX6MYBOnAVN/HRwGxxeBWhmiTmB45kcckQHDpOKKlOWbgcpvJJLrblsL4qQ1naPsjzS/aLuV9NRBpQBZUAZUAaUAWVAGVAGlAFl4FUxIOc4zXG/qnJqvsqACtDaBpQBRwygB1cBmo8ycESWcQ2kGb8aWsohR3TgUAHaATmv9pIc9LzakiB3WR7pbg1l0zIoA8qAMqAMKAPKgDKgDCgDyoAy8DwMyDlOc9zPk5fGVQaehwEVoJ+HPY37P8GAVSdudfPPE94qTSt/q7ya42+VpjP8ZXmckb6mqQwoA8qAMqAMKAPKgDKgDCgDyoAyoAwoA8qAMtA6GVABunXWi5aqFTEgxVPptiqiDCPdzQlvFcbKX6bfUrdVms7wl2VzRvqapjKgDCgDyoAyoAwoA8qAMqAMKAPKgDKgDCgDykDrZEAF6NZZL1qqVsSAFE+l26qIMox0Nye8VRgrf5l+S91WaTrDX5bNGelrmsqAMqAMKAPKgDKgDCgDyoAyoAwoA8qAMqAMKAOtkwEVoFtnvWipWhEDUjyVbqsiyjDS3ZzwVmGs/GX6LXVbpekMf1k2Z6SvaSoDyoAyoAwoA8qAMqAMKAPKgDKgDCgDyoAyoAy0TgZUgG6d9aKlUgaUAWVAGVAGlAFlQBlQBpQBZUAZUAaUAWVAGVAGlAFl4LVnQAXo174K9QaUAWVAGVAGlAFlQBlQBpQBZUAZUAaUAWVAGVAGlAFlQBlonQyoAN0660VLpQwoA8qAMqAMKAPKgBQhmR8AAAD4SURBVDKgDCgDyoAyoAwoA8qAMqAMKAPKwGvPgArQr30V6g0oA8qAMqAMKAPKgDKgDCgDyoAyoAwoA8qAMqAMKAPKgDLQOhlQAbp11ouWShlQBpQBZUAZUAaUAWVAGVAGlAFlQBlQBpQBZUAZUAaUgdeeARWgX/sq1BtQBpQBZUAZUAaUAWVAGVAGlAFlQBlQBpQBZUAZUAaUAWWgdTKgAnTrrBctlTKgDCgDyoAyoAwoA8qAMqAMKAPKgDKgDCgDyoAyoAwoA689AypAv/ZVqDegDCgDyoAyoAwoA8qAMqAMKAPKgDKgDCgDyoAyoAwoA8pA62Tg/wG4Vhn1RX00+gAAAABJRU5ErkJggg==" width="296.755905511811" height="166.9251968503937" preserveAspectRatio="none"/>
</g>
<g transform="translate(59.127952755905525 179.9251968503937)">
<g class="typst-group">
<g>
<g transform="translate(0 13.160000000000002)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="0" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE68C39294AA7FBA9B91EA2F8E9CC3997" x="9.7" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gFB54B84572F46C3C9CB2B1A90182D6B2" x="15.12" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gD8CB364949770E6EB9E57283C62D30EB" x="25.119999999999997" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB9C04FB79CAD4691AB5EC7F01BE2AD7F" x="35.739999999999995" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g7FBC39AA6D9FB89D8B638A3651405A80" x="43.019999999999996" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g13CAD87D675A42FC6A129543D89F948C" x="56.959999999999994" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g616EA0B06482AD9EB82F211B94D5D49E" x="66.25999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8C7315D77A5D71E18736DE61553C419F" x="75.55999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8934F85724FE2A1B73A1C811C5B32995" x="85.27999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gC3F91E6BB9F8304E319658F9D45F8B38" x="91.69999999999999" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g8D44D9C01F9AF6C3B1D634FDF54DE6FB" x="104.74" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gE8171CD7697771DDE124968BDB3EF0D7" x="114.44" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#gB8789F2F5F06048D4163694E4C0F3B6C" x="121.2" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g560AC22EF992EFD90E66808483D7B3BA" x="135.8" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g3BBBD96D467CC564123619D79E97B4D6" x="149.78" fill="#000000" fill-rule="nonzero"/>
<use xlink:href="#g87DD77732F07A5C65A64D31E4C3C918D" x="159.48" fill="#000000" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<g transform="translate(0 433.56299212598424)">
<g class="typst-group">
<g>
<g transform="translate(8 18.5)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#gAA14E57E2DCC57A3F7809273EECD3C51" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="9.344000000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="12.812800000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="18.5344" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="23.296000000000003" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="29.1456" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="33.8048" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="39.2832" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="46.1696" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g68DDE7C8FDC8A226B6C32EAD39AF7364" x="49.638400000000004" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="55.116800000000005" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="60.96640000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g1CB3EC9D05726EBFDE8ADABEC8504FCD" x="67.54560000000001" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="76.4928" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD62975B7DE3250BE5F195D0E8335F60D" x="82.3424" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF5F8064101DBF0FCB4BCFDA7012527FE" x="88.704" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="92.1728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="98.5728" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gD5EEFB9760BC9A91B84F628EDDA52971" x="104.4224" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="110.7328" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g3976D55F213F07C6469FD06EC16139AA" x="114.112" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g83A6AA7A836EACB3652229F4716CDAF" x="123.03359999999999" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gDB4862E33098F259EEBBA99A57E5AFA" x="129.2416" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="139.3536" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="145.2032" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="148.5824" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g793DBE65A5AEC1A16A65955B6C0E046" x="155.1616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gA11612CECC8CBEF18835767DAB11B2F7" x="166.3104" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="172.7616" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g9662C1D9A80FEB5040A57FD9DFCA7985" x="177.52319999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gCEFEF3D67F35C6E83CC3757B1DD21B13" x="180.90239999999997" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gEFCBD5CCFA072E8B49E2065B449FDBBF" x="190.57919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gB7BB853387AAC07ADB7DDEF96856059B" x="196.97919999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#gF8EC31AC53CF59E01ED9143906F6DA7B" x="201.74079999999995" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g645CA8FA3D9155E2CBD9F8EED3C1540D" x="207.59039999999996" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g570B752173035444311A253BD2376AD" x="214.23359999999997" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(790.9617637795276 8)">
<g class="typst-group">
<g>
<g transform="translate(0 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="7.44" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" x="18.880000000000003" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
<g transform="translate(28.048000000000005 24)">
<g class="typst-text" transform="scale(1, -1)">
<use xlink:href="#g18211A4637362A458F3F8DC5AA4C67BF" x="0" fill="#a38acb" fill-rule="nonzero"/>
<use xlink:href="#g6271973D35E483E673220139289FB3C5" x="7.44" fill="#a38acb" fill-rule="nonzero"/>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
</g>
<defs id="glyph">
<symbol id="g5396A27CA60B9808846A090320835A9F" overflow="visible">
<path d="M 1.91 1.22 L 1.91 5.23 C 1.91 6.06 2.08 6.1099997 2.78 6.14 C 2.84 6.2 2.84 6.41 2.78 6.47 C 2.34 6.46 1.87 6.45 1.48 6.45 C 1.15 6.45 0.65999997 6.46 0.19 6.47 C 0.13 6.41 0.13 6.2 0.19 6.14 C 0.89 6.1099997 1.06 6.06 1.06 5.23 L 1.06 1.22 C 1.06 0.39 0.89 0.34 0.19 0.31 C 0.13 0.25 0.13 0.04 0.19 -0.02 C 0.64 -0.01 1.13 0 1.49 0 C 1.8499999 0 2.33 -0.01 2.78 -0.02 C 2.84 0.04 2.84 0.25 2.78 0.31 C 2.08 0.34 1.91 0.39 1.91 1.22 Z "/>
</symbol>
<symbol id="gEEE4EC0F13100E99C1017169F912BE3E" overflow="visible">
<path d="M 1.55 1.22 L 1.55 3.12 C 1.55 3.61 1.68 3.52 1.91 3.23 L 4.2599998 0.099999994 C 4.41 -0.06 4.5699997 -0.12 4.72 -0.12 C 4.8399997 -0.12 4.94 -0.049999997 4.94 0.14999999 L 4.94 3.3799999 C 4.94 4.21 5.0499997 4.24 5.66 4.29 C 5.72 4.35 5.72 4.56 5.66 4.62 C 5.3599997 4.61 5 4.6 4.7 4.6 C 4.4 4.6 4.0499997 4.61 3.75 4.62 C 3.6899998 4.56 3.6899998 4.35 3.75 4.29 C 4.36 4.25 4.47 4.21 4.47 3.3799999 L 4.47 1.51 C 4.47 1.24 4.44 1.0699999 4.13 1.49 L 1.8399999 4.6 L 0.42 4.62 L 0.39999998 4.5899997 L 0.39999998 4.35 C 0.39999998 4.31 0.45999998 4.29 0.48999998 4.29 C 0.87 4.2599998 0.97999996 4.14 1.0799999 3.9599998 L 1.0799999 1.22 C 1.0799999 0.39 0.96999997 0.35 0.35999998 0.31 C 0.29999998 0.25 0.29999998 0.04 0.35999998 -0.02 C 0.65999997 -0.01 1.01 0 1.31 0 C 1.61 0 1.9699999 -0.01 2.27 -0.02 C 2.33 0.04 2.33 0.25 2.27 0.31 C 1.66 0.35999998 1.55 0.39 1.55 1.22 Z "/>
</symbol>
<symbol id="gA419F36517085793EDBF3FE4736A2E59" overflow="visible">
<path d="M 3.04 1.22 L 3.04 3.74 C 3.04 4.11 3.1399999 4.2599998 3.46 4.2599998 L 3.72 4.2599998 C 4.35 4.2599998 4.48 4.06 4.68 3.34 C 4.7799997 3.32 4.87 3.32 4.95 3.37 C 4.9 3.86 4.89 4.23 4.87 4.7 C 4.52 4.66 3.8799999 4.6 3.04 4.6 L 2.25 4.6 C 1.27 4.6 0.69 4.65 0.42 4.7 C 0.42 4.23 0.41 3.84 0.35 3.37 C 0.44 3.34 0.53 3.33 0.62 3.34 C 0.82 4.06 0.93 4.2599998 1.5799999 4.2599998 L 1.8199999 4.2599998 C 2.1299999 4.2599998 2.25 4.14 2.25 3.75 L 2.25 1.22 C 2.25 0.39 2.1399999 0.35999998 1.53 0.31 C 1.4699999 0.25 1.4699999 0.04 1.53 -0.02 C 1.9 -0.01 2.31 0 2.6499999 0 C 3 0 3.3899999 -0.01 3.76 -0.02 C 3.82 0.04 3.82 0.25 3.76 0.31 C 3.1499999 0.35 3.04 0.39 3.04 1.22 Z "/>
</symbol>
<symbol id="gFAD9169AC3141E7FC4EA568E3BBD2E9B" overflow="visible">
<path d="M 1.91 1.22 L 1.91 2.09 L 2.46 2.09 C 2.84 2.09 2.98 1.76 3.11 1.39 L 3.33 0.78999996 C 3.56 0.17 3.8999999 -0.07 4.33 -0.07 C 4.48 -0.07 4.79 -0.04 4.96 0 C 4.99 0.099999994 4.97 0.19999999 4.9 0.28 C 4.54 0.28 4.35 0.34 4.15 0.85999995 L 3.86 1.61 C 3.74 1.92 3.62 2.09 3.49 2.22 L 3.49 2.24 C 3.83 2.36 4.3399997 2.77 4.3399997 3.46 C 4.3399997 4.29 3.82 4.64 2.6299999 4.64 C 2.3799999 4.64 1.81 4.6 1.51 4.6 C 1.22 4.6 0.79999995 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.01 0.35999998 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.78 -0.01 1.1899999 0 1.52 0 C 1.8299999 0 2.1599998 -0.01 2.48 -0.02 C 2.54 0.04 2.54 0.25 2.48 0.31 C 2.01 0.34 1.91 0.39 1.91 1.22 Z M 3.47 3.46 C 3.47 2.6699998 3.24 2.3799999 2.35 2.3799999 L 1.91 2.3799999 L 1.91 3.6799998 C 1.91 4.21 2.01 4.31 2.57 4.31 C 3.27 4.31 3.47 4.06 3.47 3.46 Z "/>
</symbol>
<symbol id="g7FD6A8241485CEBC032BD9E4CE659816" overflow="visible">
<path d="M 5.27 2.35 C 5.27 3.77 4.13 4.7 2.83 4.7 C 1.4399999 4.7 0.37 3.6899998 0.37 2.22 C 0.37 0.85999995 1.4 -0.099999994 2.75 -0.099999994 C 4.39 -0.099999994 5.27 1.05 5.27 2.35 Z M 2.74 4.37 C 3.6299999 4.37 4.4 3.55 4.4 2.21 C 4.4 0.97999996 3.79 0.22999999 2.8999999 0.22999999 C 1.93 0.22999999 1.24 1.11 1.24 2.34 C 1.24 3.6899998 1.99 4.37 2.74 4.37 Z "/>
</symbol>
<symbol id="gBFFDA84A1400D9E1136DF0DD93EA19F5" overflow="visible">
<path d="M 1.48 4.6 C 1.2099999 4.6 0.76 4.61 0.37 4.62 C 0.31 4.56 0.31 4.35 0.37 4.29 C 0.97999996 4.25 1.09 4.21 1.09 3.3799999 L 1.09 1.22 C 1.09 0.39 0.97999996 0.35999998 0.37 0.31 C 0.31 0.25 0.31 0.04 0.37 -0.02 C 0.75 -0.01 1.1999999 0 1.49 0 C 1.75 0 2.1499999 -0.02 2.95 -0.02 C 4.06 -0.02 5.2999997 0.5 5.2999997 2.25 C 5.2999997 3.58 4.48 4.62 2.81 4.62 C 2.1299999 4.62 1.77 4.6 1.48 4.6 Z M 1.88 0.76 L 1.88 3.98 C 1.88 4.23 2.1299999 4.29 2.52 4.29 C 4.2 4.29 4.43 3.12 4.43 2.08 C 4.43 0.68 3.81 0.31 2.71 0.31 C 1.9499999 0.31 1.88 0.48 1.88 0.76 Z "/>
</symbol>
<symbol id="gEC3CC7DEE79E0AA801DFAAEF4B6C0B50" overflow="visible">
<path d="M 4.35 3.3799999 L 4.35 2.11 C 4.35 1.25 4.35 0.31 3.03 0.31 C 2.04 0.31 1.8299999 1.09 1.8299999 2.02 L 1.8299999 3.3799999 C 1.8299999 4.21 1.9399999 4.24 2.55 4.29 C 2.61 4.35 2.61 4.56 2.55 4.62 C 2.1599998 4.61 1.76 4.6 1.43 4.6 C 1.0699999 4.6 0.68 4.61 0.32 4.62 C 0.26 4.56 0.26 4.35 0.32 4.29 C 0.93 4.25 1.04 4.21 1.04 3.3799999 L 1.04 1.81 C 1.04 0.31 1.77 -0.099999994 2.86 -0.099999994 C 4.41 -0.099999994 4.8199997 0.78 4.8199997 2.24 L 4.8199997 3.3799999 C 4.8199997 4.21 4.93 4.24 5.54 4.29 C 5.6 4.35 5.6 4.56 5.54 4.62 C 5.24 4.61 4.88 4.6 4.58 4.6 C 4.2799997 4.6 3.9299998 4.61 3.6299999 4.62 C 3.57 4.56 3.57 4.35 3.6299999 4.29 C 4.24 4.25 4.35 4.21 4.35 3.3799999 Z "/>
</symbol>
<symbol id="g202CCBD46865F83C12D50E1B4FF9BBEA" overflow="visible">
<path d="M 2.76 -0.099999994 C 3.54 -0.099999994 4.02 0.19 4.49 0.82 C 4.47 0.89 4.37 1 4.29 1.02 C 3.83 0.48 3.48 0.28 2.81 0.28 C 1.8199999 0.28 1.24 1.35 1.24 2.34 C 1.24 4.02 2.02 4.37 2.77 4.37 C 3.57 4.37 4.04 3.9299998 4.16 3.23 C 4.2599998 3.1999998 4.36 3.1999998 4.46 3.26 C 4.46 3.6699998 4.44 4.0899997 4.3399997 4.54 C 3.9599998 4.54 3.51 4.7 2.71 4.7 C 1.39 4.7 0.37 3.6999998 0.37 2.24 C 0.37 1.61 0.57 0.91999996 1.06 0.47 C 1.4599999 0.099999994 2.02 -0.099999994 2.76 -0.099999994 Z "/>
</symbol>
<symbol id="g5503E15E5E4E70E9E217A15BD1ECD752" overflow="visible">
<path d="M 1.9499999 3.3799999 C 1.9499999 4.21 2.06 4.24 2.6699998 4.29 C 2.73 4.35 2.73 4.56 2.6699998 4.62 C 2.29 4.61 1.86 4.6 1.55 4.6 C 1.25 4.6 0.83 4.61 0.44 4.62 C 0.38 4.56 0.38 4.35 0.44 4.29 C 1.05 4.25 1.16 4.21 1.16 3.3799999 L 1.16 1.22 C 1.16 0.39 1.05 0.35999998 0.44 0.31 C 0.38 0.25 0.38 0.04 0.44 -0.02 C 0.81 -0.01 1.22 0 1.56 0 C 1.88 0 2.32 -0.01 2.6699998 -0.02 C 2.73 0.04 2.73 0.25 2.6699998 0.31 C 2.06 0.35 1.9499999 0.39 1.9499999 1.22 Z "/>
</symbol>
<symbol id="g1E8994F5C297EC73FA26D93D22635023" overflow="visible">
<path d="M 2.82 -0.14999999 C 4.11 -0.14999999 5.16 0.9 5.16 2.19 C 5.16 3.48 4.11 4.52 2.82 4.52 C 1.53 4.52 0.48999998 3.48 0.48999998 2.19 C 0.48999998 0.9 1.53 -0.14999999 2.82 -0.14999999 Z M 2.82 4.2599998 C 3.97 4.2599998 4.9 3.34 4.9 2.19 C 4.9 1.04 3.9599998 0.11 2.82 0.11 C 1.67 0.11 0.75 1.04 0.75 2.19 C 0.75 3.33 1.67 4.2599998 2.82 4.2599998 Z "/>
</symbol>
<symbol id="g6F0940D406D545443F0C3F5AB20F1452" overflow="visible">
<path d="M 1.55 0.78999996 L 2.1 2.24 C 2.1499999 2.37 2.21 2.4099998 2.45 2.4099998 L 4.56 2.4099998 L 5.14 0.71999997 C 5.2599998 0.38 4.88 0.34 4.4 0.31 C 4.3399997 0.25 4.3399997 0.04 4.4 -0.02 C 4.77 -0.01 5.3199997 0 5.71 0 C 6.12 0 6.5 -0.01 6.85 -0.02 C 6.91 0.04 6.91 0.25 6.85 0.31 C 6.46 0.35 6.12 0.38 5.95 0.85999995 L 3.8899999 6.58 C 3.74 6.49 3.47 6.3799996 3.34 6.3799996 L 1.0699999 1.02 C 0.81 0.39999998 0.51 0.34 0.07 0.31 C 0.01 0.25 0.01 0.04 0.07 -0.02 C 0.32999998 -0.01 0.65999997 0 0.96 0 C 1.37 0 1.87 -0.01 2.24 -0.02 C 2.3 0.04 2.3 0.25 2.24 0.31 C 1.86 0.34 1.39 0.38 1.55 0.78999996 Z M 2.6299999 2.83 C 2.4099998 2.83 2.34 2.86 2.3799999 2.96 L 3.3999999 5.5499997 L 3.46 5.5499997 L 4.4 2.83 Z "/>
</symbol>
<symbol id="g6D72A0AB4EFB019D977FFECF4A1600A9" overflow="visible">
<path d="M 3.79 0 C 3.79 0 4.02 0.96 4.0899997 1.38 C 4 1.43 3.9199998 1.4499999 3.81 1.42 C 3.6499999 0.83 3.36 0.34 2.73 0.34 L 2.28 0.34 C 2.05 0.34 1.91 0.5 1.91 0.69 L 1.91 3.3799999 C 1.91 4.21 2.02 4.24 2.6299999 4.29 C 2.69 4.35 2.69 4.56 2.6299999 4.62 C 2.26 4.61 1.8499999 4.6 1.51 4.6 C 1.1999999 4.6 0.77 4.61 0.39999998 4.62 C 0.34 4.56 0.34 4.35 0.39999998 4.29 C 1.01 4.25 1.12 4.21 1.12 3.3799999 L 1.12 1.22 C 1.12 0.39 1.1 0.34 0.39999998 0.31 C 0.34 0.25 0.34 0.04 0.39999998 -0.02 C 0.89 -0.01 1.55 0 1.55 0 Z "/>
</symbol>
<symbol id="g7035BD9A81EA6DB089327941BB80DFF8" overflow="visible">
<path d="M 4.72 0.90999997 C 4.72 1.74 4.7799997 1.77 5.0899997 1.8199999 C 5.15 1.88 5.15 2.09 5.0899997 2.1499999 C 4.91 2.1399999 4.63 2.1299999 4.3199997 2.1299999 C 4.02 2.1299999 3.56 2.1399999 3.27 2.1499999 C 3.21 2.09 3.21 1.88 3.27 1.8199999 C 3.8799999 1.78 3.9299998 1.74 3.9299998 0.90999997 L 3.9299998 0.37 C 3.61 0.28 3.28 0.22999999 2.9299998 0.22999999 C 1.68 0.22999999 1.27 1.51 1.27 2.33 C 1.27 3.54 1.8499999 4.37 2.81 4.37 C 3.8 4.37 4.22 3.87 4.37 3.23 C 4.47 3.1999998 4.5699997 3.1999998 4.67 3.26 C 4.66 3.6699998 4.63 4.0899997 4.54 4.54 C 4.24 4.54 3.5 4.7 2.9399998 4.7 C 1.51 4.7 0.37 3.78 0.37 2.2 C 0.37 0.93 1.3199999 -0.099999994 2.75 -0.099999994 C 3.4299998 -0.099999994 4.17 0 4.83 0.35999998 C 4.7599998 0.42999998 4.72 0.52 4.72 0.59 Z "/>
</symbol>
<symbol id="gFF65128B49BB3276E17D04989ECB7ACE" overflow="visible">
<path d="M 5 3.3799999 C 5 4.21 5.1099997 4.24 5.72 4.29 C 5.7799997 4.35 5.7799997 4.56 5.72 4.62 C 5.37 4.6 4.93 4.6 4.6 4.6 C 4.3199997 4.6 3.8799999 4.61 3.49 4.62 C 3.4299998 4.56 3.4299998 4.35 3.49 4.29 C 4.1 4.25 4.21 4.21 4.21 3.3799999 L 4.21 2.52 L 1.9 2.52 L 1.9 3.3799999 C 1.9 4.21 2.01 4.24 2.62 4.29 C 2.6799998 4.35 2.6799998 4.56 2.62 4.62 C 2.24 4.61 1.8199999 4.6 1.5 4.6 C 1.1999999 4.6 0.78999996 4.61 0.39 4.62 C 0.32999998 4.56 0.32999998 4.35 0.39 4.29 C 1 4.25 1.11 4.21 1.11 3.3799999 L 1.11 1.22 C 1.11 0.39 1 0.35999998 0.39 0.31 C 0.32999998 0.25 0.32999998 0.04 0.39 -0.02 C 0.78999996 -0.01 1.1899999 0 1.51 0 C 1.8299999 0 2.23 -0.01 2.62 -0.02 C 2.6799998 0.04 2.6799998 0.25 2.62 0.31 C 2.01 0.35 1.9 0.39 1.9 1.22 L 1.9 2.19 L 4.21 2.19 L 4.21 1.22 C 4.21 0.39 4.1 0.35999998 3.49 0.31 C 3.4299998 0.25 3.4299998 0.04 3.49 -0.02 C 3.86 -0.01 4.2599998 0 4.61 0 C 4.91 0 5.33 -0.01 5.72 -0.02 C 5.7799997 0.04 5.7799997 0.25 5.72 0.31 C 5.1099997 0.35 5 0.39 5 1.22 Z "/>
</symbol>
<symbol id="gEDADDD9BA25BBB833C1F4B684DC50419" overflow="visible">
<path d="M 4.83 3.82 L 4.9 3.82 L 5.0299997 1.23 C 5.0699997 0.39999998 5.06 0.35999998 4.52 0.31 C 4.46 0.25 4.46 0.04 4.52 -0.02 C 4.87 -0.01 5.24 0 5.52 0 C 5.8199997 0 6.1099997 -0.01 6.3799996 -0.02 C 6.44 0.04 6.44 0.25 6.3799996 0.31 C 5.87 0.35999998 5.8599997 0.42 5.7999997 1.23 L 5.6 3.81 C 5.5699997 4.21 5.66 4.25 6.16 4.29 C 6.22 4.35 6.22 4.56 6.16 4.62 L 4.81 4.6 L 3.31 1.02 L 2.03 4.6 L 0.64 4.62 C 0.58 4.56 0.58 4.35 0.64 4.29 C 1.13 4.2599998 1.22 4.21 1.1999999 4.02 L 0.88 1.2099999 C 0.78999996 0.38 0.65999997 0.34 0.28 0.31 C 0.22 0.25 0.22 0.04 0.28 -0.02 C 0.48 -0.01 0.78 0 0.94 0 C 1.14 0 1.51 -0.01 1.7099999 -0.02 C 1.77 0.04 1.77 0.25 1.7099999 0.31 C 1.14 0.35 1.15 0.47 1.23 1.2099999 L 1.52 3.75 L 1.54 3.75 L 2.96 -0.04 C 2.98 -0.089999996 3.03 -0.12 3.08 -0.12 C 3.12 -0.12 3.1699998 -0.089999996 3.1899998 -0.04 Z "/>
</symbol>
<symbol id="gF74D1E4498220F56E34936C81B24ED2C" overflow="visible">
<path d="M 2.292 1.464 L 2.292 6.276 C 2.292 7.272 2.496 7.3320003 3.336 7.368 C 3.408 7.44 3.408 7.692 3.336 7.764 C 2.808 7.752 2.244 7.7400002 1.776 7.7400002 C 1.38 7.7400002 0.792 7.752 0.228 7.764 C 0.156 7.692 0.156 7.44 0.228 7.368 C 1.068 7.3320003 1.272 7.272 1.272 6.276 L 1.272 1.464 C 1.272 0.468 1.068 0.408 0.228 0.372 C 0.156 0.3 0.156 0.048 0.228 -0.024 C 0.768 -0.012 1.3560001 0 1.788 0 C 2.22 0 2.796 -0.012 3.336 -0.024 C 3.408 0.048 3.408 0.3 3.336 0.372 C 2.496 0.408 2.292 0.468 2.292 1.464 Z "/>
</symbol>
<symbol id="gFF269982F0E4C510F3A3BFF016D72390" overflow="visible">
<path d="M 5.796 4.584 L 5.88 4.584 L 6.0360003 1.4760001 C 6.084 0.48000002 6.072 0.432 5.4240003 0.372 C 5.352 0.3 5.352 0.048 5.4240003 -0.024 C 5.844 -0.012 6.288 0 6.624 0 C 6.984 0 7.3320003 -0.012 7.656 -0.024 C 7.728 0.048 7.728 0.3 7.656 0.372 C 7.044 0.432 7.032 0.504 6.96 1.4760001 L 6.7200003 4.572 C 6.684 5.052 6.7920003 5.1 7.392 5.1480002 C 7.464 5.2200003 7.464 5.472 7.392 5.544 L 5.772 5.52 L 3.9720001 1.224 L 2.436 5.52 L 0.768 5.544 C 0.696 5.472 0.696 5.2200003 0.768 5.1480002 C 1.3560001 5.112 1.464 5.052 1.44 4.824 L 1.056 1.452 C 0.948 0.456 0.792 0.408 0.336 0.372 C 0.264 0.3 0.264 0.048 0.336 -0.024 C 0.576 -0.012 0.936 0 1.128 0 C 1.368 0 1.812 -0.012 2.052 -0.024 C 2.124 0.048 2.124 0.3 2.052 0.372 C 1.368 0.42000002 1.38 0.564 1.4760001 1.452 L 1.824 4.5 L 1.848 4.5 L 3.552 -0.048 C 3.576 -0.108 3.636 -0.144 3.696 -0.144 C 3.744 -0.144 3.8040001 -0.108 3.828 -0.048 Z "/>
</symbol>
<symbol id="gD17E61D06C745FD691E5D7AFE136D0C0" overflow="visible">
<path d="M 2.2680001 1.464 L 2.2680001 2.352 C 2.484 2.256 2.724 2.208 3.024 2.208 C 4.632 2.208 5.124 3.3600001 5.124 4.08 C 5.124 4.704 4.764 5.544 3.06 5.544 C 2.616 5.544 2.112 5.52 1.788 5.52 C 1.44 5.52 0.936 5.532 0.456 5.544 C 0.384 5.472 0.384 5.2200003 0.456 5.1480002 C 1.188 5.1 1.32 5.052 1.32 4.056 L 1.32 1.464 C 1.32 0.468 1.188 0.432 0.456 0.372 C 0.384 0.3 0.384 0.048 0.456 -0.024 C 0.852 -0.012 1.272 0 1.8000001 0 C 2.316 0 2.736 -0.012 3.132 -0.024 C 3.204 0.048 3.204 0.3 3.132 0.372 C 2.4 0.42000002 2.2680001 0.468 2.2680001 1.464 Z M 2.2680001 4.608 C 2.2680001 4.992 2.412 5.1480002 2.988 5.1480002 C 3.696 5.1480002 4.08 4.776 4.08 3.936 C 4.08 3.072 3.7680001 2.604 3.048 2.604 C 2.808 2.604 2.5080001 2.64 2.2680001 2.736 Z "/>
</symbol>
<symbol id="g48BCA4F06942DA5990D42018985FC781" overflow="visible">
<path d="M 2.292 1.464 L 2.292 2.5080001 L 2.9520001 2.5080001 C 3.408 2.5080001 3.576 2.112 3.732 1.668 L 3.996 0.948 C 4.272 0.204 4.68 -0.084 5.196 -0.084 C 5.376 -0.084 5.748 -0.048 5.952 0 C 5.988 0.120000005 5.964 0.24000001 5.88 0.336 C 5.448 0.336 5.2200003 0.408 4.98 1.0320001 L 4.632 1.932 C 4.488 2.304 4.344 2.5080001 4.188 2.664 L 4.188 2.688 C 4.596 2.832 5.208 3.3240001 5.208 4.152 C 5.208 5.1480002 4.584 5.568 3.1560001 5.568 C 2.856 5.568 2.172 5.52 1.812 5.52 C 1.464 5.52 0.96000004 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.212 0.432 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 0.936 -0.012 1.428 0 1.824 0 C 2.196 0 2.592 -0.012 2.976 -0.024 C 3.048 0.048 3.048 0.3 2.976 0.372 C 2.412 0.408 2.292 0.468 2.292 1.464 Z M 4.164 4.152 C 4.164 3.204 3.888 2.856 2.82 2.856 L 2.292 2.856 L 2.292 4.416 C 2.292 5.052 2.412 5.172 3.084 5.172 C 3.924 5.172 4.164 4.872 4.164 4.152 Z "/>
</symbol>
<symbol id="g4C6038BE04CA3E1481E54A97A0E34303" overflow="visible">
<path d="M 6.324 2.82 C 6.324 4.524 4.956 5.64 3.3960001 5.64 C 1.728 5.64 0.444 4.428 0.444 2.664 C 0.444 1.0320001 1.6800001 -0.120000005 3.3 -0.120000005 C 5.268 -0.120000005 6.324 1.26 6.324 2.82 Z M 3.288 5.244 C 4.356 5.244 5.28 4.26 5.28 2.652 C 5.28 1.176 4.548 0.276 3.48 0.276 C 2.316 0.276 1.488 1.332 1.488 2.808 C 1.488 4.428 2.388 5.244 3.288 5.244 Z "/>
</symbol>
<symbol id="g5490A23BDA1B2697F526AA72E92A878C" overflow="visible">
<path d="M 2.196 4.344 C 1.908 5.028 1.9200001 5.088 2.568 5.1480002 C 2.64 5.2200003 2.64 5.472 2.568 5.544 C 2.196 5.532 1.788 5.52 1.296 5.52 C 0.912 5.52 0.552 5.532 0.24000001 5.544 C 0.168 5.472 0.168 5.2200003 0.24000001 5.1480002 C 0.828 5.088 0.912 4.956 1.2 4.272 L 2.904 0.336 C 3.06 -0.012 3.1200001 -0.144 3.252 -0.144 C 3.336 -0.144 3.384 -0.048 3.552 0.336 L 5.304 4.26 C 5.556 4.8120003 5.688 5.1 6.336 5.1480002 C 6.408 5.2200003 6.408 5.472 6.336 5.544 C 6.072 5.532 5.784 5.52 5.472 5.52 C 5.028 5.52 4.692 5.532 4.368 5.544 C 4.296 5.472 4.296 5.2200003 4.368 5.1480002 C 5.0160003 5.1 5.076 4.956 4.836 4.344 L 3.528 1.3560001 C 3.492 1.32 3.48 1.32 3.444 1.3560001 Z "/>
</symbol>
<symbol id="gD36D2D678ADE356EA3610170EDF710ED" overflow="visible">
<path d="M 2.976 2.7 C 3.7680001 2.7 3.78 2.4720001 3.8040001 2.028 C 3.864 1.968 4.08 1.968 4.14 2.028 C 4.1280003 2.304 4.116 2.7120001 4.116 2.904 C 4.116 3.072 4.1280003 3.456 4.14 3.756 C 4.08 3.816 3.864 3.816 3.8040001 3.756 C 3.78 3.216 3.756 3.084 2.976 3.084 L 2.292 3.084 L 2.292 4.788 C 2.292 4.992 2.448 5.124 2.676 5.124 L 3.3600001 5.124 C 4.344 5.124 4.5 4.728 4.716 4.044 C 4.836 4.032 4.9440002 4.056 5.04 4.104 C 4.992 4.512 4.848 5.448 4.824 5.532 C 4.824 5.556 4.8120003 5.568 4.788 5.568 C 4.62 5.532 4.5 5.52 4.296 5.52 L 1.812 5.52 C 1.464 5.52 0.912 5.532 0.48000002 5.544 C 0.408 5.472 0.408 5.2200003 0.48000002 5.1480002 C 1.212 5.1 1.344 5.052 1.344 4.056 L 1.344 1.464 C 1.344 0.468 1.212 0.432 0.48000002 0.372 C 0.408 0.3 0.408 0.048 0.48000002 -0.024 C 0.912 -0.012 1.44 0 1.824 0 L 3.672 0 C 4.152 0 4.9440002 -0.024 4.9440002 -0.024 C 5.088 0.468 5.2200003 1.128 5.304 1.632 C 5.196 1.692 5.1 1.716 4.968 1.6800001 C 4.776 0.972 4.428 0.372 3.432 0.372 L 2.9160001 0.372 C 2.412 0.372 2.292 0.504 2.292 0.90000004 L 2.292 2.7 Z "/>
</symbol>
<symbol id="g46E28FC12585DA626130081849FE40B4" overflow="visible">
<path d="M 1.86 1.464 L 1.86 3.744 C 1.86 4.3320003 2.016 4.224 2.292 3.876 L 5.112 0.120000005 C 5.292 -0.072 5.484 -0.144 5.664 -0.144 C 5.808 -0.144 5.928 -0.060000002 5.928 0.18 L 5.928 4.056 C 5.928 5.052 6.06 5.088 6.7920003 5.1480002 C 6.864 5.2200003 6.864 5.472 6.7920003 5.544 C 6.432 5.532 6 5.52 5.64 5.52 C 5.28 5.52 4.86 5.532 4.5 5.544 C 4.428 5.472 4.428 5.2200003 4.5 5.1480002 C 5.232 5.1 5.364 5.052 5.364 4.056 L 5.364 1.812 C 5.364 1.488 5.328 1.284 4.956 1.788 L 2.208 5.52 L 0.504 5.544 L 0.48000002 5.508 L 0.48000002 5.2200003 C 0.48000002 5.172 0.552 5.1480002 0.588 5.1480002 C 1.044 5.112 1.176 4.968 1.296 4.752 L 1.296 1.464 C 1.296 0.468 1.164 0.42000002 0.432 0.372 C 0.36 0.3 0.36 0.048 0.432 -0.024 C 0.792 -0.012 1.212 0 1.572 0 C 1.932 0 2.364 -0.012 2.724 -0.024 C 2.796 0.048 2.796 0.3 2.724 0.372 C 1.992 0.432 1.86 0.468 1.86 1.464 Z "/>
</symbol>
<symbol id="gA2769E14ED9B16297025579DD26D23A1" overflow="visible">
<path d="M 3.648 1.464 L 3.648 4.488 C 3.648 4.932 3.7680001 5.112 4.152 5.112 L 4.464 5.112 C 5.2200003 5.112 5.376 4.872 5.616 4.008 C 5.736 3.984 5.844 3.984 5.94 4.044 C 5.88 4.632 5.868 5.076 5.844 5.64 C 5.4240003 5.592 4.656 5.52 3.648 5.52 L 2.7 5.52 C 1.524 5.52 0.828 5.58 0.504 5.64 C 0.504 5.076 0.492 4.608 0.42000002 4.044 C 0.528 4.008 0.636 3.996 0.744 4.008 C 0.984 4.872 1.116 5.112 1.896 5.112 L 2.184 5.112 C 2.556 5.112 2.7 4.968 2.7 4.5 L 2.7 1.464 C 2.7 0.468 2.568 0.432 1.836 0.372 C 1.764 0.3 1.764 0.048 1.836 -0.024 C 2.28 -0.012 2.772 0 3.18 0 C 3.6000001 0 4.068 -0.012 4.512 -0.024 C 4.584 0.048 4.584 0.3 4.512 0.372 C 3.78 0.42000002 3.648 0.468 3.648 1.464 Z "/>
</symbol>
<symbol id="g5ABA589ED074A65FC8C929AB4EB2344C" overflow="visible">
<path d="M 3.384 -0.18 C 4.932 -0.18 6.192 1.08 6.192 2.628 C 6.192 4.176 4.932 5.4240003 3.384 5.4240003 C 1.836 5.4240003 0.588 4.176 0.588 2.628 C 0.588 1.08 1.836 -0.18 3.384 -0.18 Z "/>
</symbol>
<symbol id="g1BED8054A02AECF3BF3EC56A671C1672" overflow="visible">
<path d="M 9.528 -0.24000001 C 11.856 -0.24000001 13.992001 0.864 15.624001 3 C 15.504 3.216 15.096 3.504 14.832 3.504 C 13.128 1.632 11.184 1.008 9.504 1.008 C 6.7200003 1.008 4.512 4.272 4.512 8.016 C 4.512 11.736 6.432 14.808001 9.288 14.808001 C 12.6 14.808001 13.68 12.936 14.304 10.872 C 14.592 10.776 15.0720005 10.848001 15.336 10.992 C 15.216001 12.24 15.024 13.392 14.808001 14.712 C 13.584001 14.832 12.504 15.792 9.552 15.792 C 4.848 15.792 0.888 12.84 0.888 7.56 C 0.888 5.304 1.872 2.664 3.792 1.272 C 5.328 0.168 7.2000003 -0.24000001 9.528 -0.24000001 Z "/>
</symbol>
<symbol id="g841363B3896A8C79F18618DF16186242" overflow="visible">
<path d="M 0.888 4.968 C 0.888 1.824 3.384 -0.24000001 6.6 -0.24000001 C 8.304 -0.24000001 9.72 0.24000001 10.704 1.128 C 11.928 2.208 12.336 3.8400002 12.336 5.184 C 12.336 8.328 10.2 10.656 6.624 10.656 C 4.632 10.656 3.144 9.96 2.208 8.88 C 1.296 7.824 0.888 6.384 0.888 4.968 Z M 6.2400002 9.648 C 7.872 9.648 8.976 7.704 8.976 4.416 C 8.976 1.536 7.848 0.768 6.984 0.768 C 5.0160003 0.768 4.248 3.72 4.248 5.496 C 4.248 7.704 4.632 9.648 6.2400002 9.648 Z "/>
</symbol>
<symbol id="gC0E7F247CAD2177580FB7ED865B072E5" overflow="visible">
<path d="M 5.472 2.928 L 5.472 7.704 C 5.472 7.824 5.472 7.9440002 5.472 8.064 C 6.408 8.64 7.248 8.88 7.656 8.88 C 8.616 8.88 9.336 8.448 9.336 7.08 L 9.336 3.072 C 9.336 1.056 8.952 0.84000003 7.968 0.768 C 7.824 0.624 7.824 0.096 7.968 -0.048 C 8.976 -0.024 9.744 0 10.896 0 C 12.048 0 12.792 -0.024 13.824 -0.048 C 13.968 0.096 13.968 0.624 13.824 0.768 C 12.864 0.84000003 12.456 1.056 12.456 3.072 L 12.456 6.816 C 12.456 7.416 12.432 7.896 12.36 8.136 C 13.272 8.592 14.304 8.88 14.688 8.88 C 15.648 8.88 16.32 8.448 16.32 7.08 L 16.32 3.072 C 16.32 1.056 15.936 0.84000003 14.952 0.768 C 14.808001 0.624 14.808001 0.096 14.952 -0.048 C 15.96 -0.024 16.728 0 17.880001 0 C 19.2 0 20.256 -0.024 21.288 -0.048 C 21.432001 0.096 21.432001 0.624 21.288 0.768 C 19.824 0.84000003 19.44 1.056 19.44 3.072 L 19.44 6.816 C 19.44 9.456 18.48 10.656 16.416 10.656 C 15.528 10.656 13.512 9.696 12.12 8.928 C 11.76 9.96 10.8 10.656 9.384 10.656 C 8.52 10.656 6.7920003 9.744 5.4240003 8.976 C 5.352 9.696 5.28 10.248 5.28 10.248 C 5.256 10.536 5.064 10.656 4.728 10.656 C 3.8400002 10.416 2.4 10.08 0.744 9.864 C 0.696 9.72 0.744 9.24 0.792 9.096 C 2.112 8.976 2.352 8.784 2.352 7.416 L 2.352 2.928 C 2.352 0.936 2.088 0.888 0.624 0.768 C 0.48000002 0.624 0.48000002 0.096 0.624 -0.048 C 1.632 -0.024 2.64 0 3.912 0 C 5.0160003 0 5.688 -0.024 6.7200003 -0.048 C 6.864 0.096 6.864 0.624 6.7200003 0.768 C 5.712 0.864 5.472 0.936 5.472 2.928 Z "/>
</symbol>
<symbol id="g79601DAFF2C13DD0AF25B87F7A83C884" overflow="visible">
<path d="M 1.776 3.048 C 1.776 1.056 1.728 0.768 1.632 -0.144 C 1.9200001 -0.24000001 2.184 -0.312 2.448 -0.312 C 2.76 -0.048 3 0.288 3.216 0.72 C 4.152 0 5.616 -0.24000001 6.7200003 -0.24000001 C 9.384 -0.24000001 12.192 2.4 12.192 5.8320003 C 12.192 7.2000003 11.6640005 8.544 10.896 9.432 C 10.032001 10.416 8.88 10.656 7.6080003 10.656 C 6.864 10.656 5.592 9.816 4.896 9.312 L 4.896 13.992001 C 4.896 15.552 4.968 16.44 4.968 16.44 C 4.968 16.656 4.8 16.752 4.584 16.752 C 3.696 16.464 1.776 16.2 0.072 16.128 C 0 15.84 0.024 15.576 0.144 15.360001 C 1.656 15.24 1.776 15.216001 1.776 13.56 Z M 4.896 8.352 C 5.688 8.88 6.216 8.952 6.768 8.952 C 7.9440002 8.952 8.832 7.872 8.832 5.52 C 8.832 3.552 8.496 0.768 6.6 0.768 C 5.9040003 0.768 5.352 1.056 4.896 1.608 Z "/>
</symbol>
<symbol id="g24FA36D774E663C81AD78F0ED3820373" overflow="visible">
<path d="M 5.568 2.928 L 5.568 7.704 C 5.568 8.904 5.664 10.248 5.664 10.248 C 5.664 10.512 5.448 10.656 5.112 10.656 C 4.44 10.392 2.496 10.2 0.84000003 9.984 C 0.792 9.84 0.84000003 9.36 0.888 9.216 C 2.208 9.096 2.448 8.904 2.448 7.5360003 L 2.448 2.928 C 2.448 0.936 2.184 0.888 0.72 0.768 C 0.576 0.624 0.576 0.096 0.72 -0.048 C 1.728 -0.024 2.736 0 4.008 0 C 5.28 0 6.264 -0.024 7.296 -0.048 C 7.44 0.096 7.44 0.624 7.296 0.768 C 5.8320003 0.864 5.568 0.936 5.568 2.928 Z M 2.328 14.304 C 2.328 13.512 2.904 12.72 3.864 12.72 C 4.9440002 12.72 5.568 13.584001 5.568 14.208 C 5.568 14.928 5.0160003 15.792 4.008 15.792 C 2.88 15.792 2.328 15.024 2.328 14.304 Z "/>
</symbol>
<symbol id="g42F794F2554BA43C69EE8F3AA6FD9BAC" overflow="visible">
<path d="M 5.472 2.928 L 5.472 7.752 C 6.432 8.4 7.392 8.88 7.824 8.88 C 8.784 8.88 9.504 8.448 9.504 7.08 L 9.504 3.072 C 9.504 1.056 9.12 0.84000003 8.136 0.768 C 7.992 0.624 7.992 0.096 8.136 -0.048 C 9.144 -0.024 9.912 0 11.064 0 C 12.384 0 13.440001 -0.024 14.472 -0.048 C 14.616 0.096 14.616 0.624 14.472 0.768 C 13.008 0.84000003 12.624001 1.056 12.624001 3.072 L 12.624001 6.816 C 12.624001 9.456 11.496 10.656 9.432 10.656 C 8.472 10.656 6.768 9.6 5.448 8.688 C 5.376 9.528 5.28 10.248 5.28 10.248 C 5.256 10.536 5.064 10.656 4.728 10.656 C 3.8400002 10.416 2.4 10.08 0.744 9.864 C 0.696 9.72 0.744 9.24 0.792 9.096 C 2.112 8.976 2.352 8.784 2.352 7.416 L 2.352 2.928 C 2.352 0.936 2.088 0.888 0.624 0.768 C 0.48000002 0.624 0.48000002 0.096 0.624 -0.048 C 1.632 -0.024 2.64 0 3.912 0 C 5.0160003 0 5.688 -0.024 6.7200003 -0.048 C 6.864 0.096 6.864 0.624 6.7200003 0.768 C 5.712 0.864 5.472 0.936 5.472 2.928 Z "/>
</symbol>
<symbol id="gB6675D993E92546012E46240B36958EC" overflow="visible">
<path d="M 10.344 3.096 C 9.36 2.088 8.064 1.824 7.152 1.824 C 5.28 1.824 4.1280003 2.904 4.1280003 5.256 C 4.1280003 5.4240003 4.152 5.52 4.152 5.64 L 9.912 5.64 C 10.488 5.64 10.608 6.048 10.608 6.384 C 10.608 8.424 9.816 10.656 6.288 10.656 C 3.7680001 10.656 0.888 8.424 0.888 4.752 C 0.888 3.3600001 1.392 1.896 2.424 0.96000004 C 3.336 0.144 4.512 -0.24000001 6.216 -0.24000001 C 7.872 -0.24000001 9.504 0.6 10.704 2.352 C 10.704 2.664 10.584 3.096 10.344 3.096 Z M 4.248 6.6 C 4.272 7.44 4.392 8.352 4.728 8.832 C 5.112 9.408 5.76 9.648 6.024 9.648 C 6.672 9.648 7.56 9.024 7.56 7.104 C 7.56 6.96 7.56 6.6480002 7.512 6.6 Z "/>
</symbol>
<symbol id="gC80183FE843BD5B521235E3B107ADB69" overflow="visible">
<path d="M 8.52 1.152 C 8.568 0.576 8.616 0.168 8.616 0.168 C 8.64 -0.120000005 8.832 -0.24000001 9.168 -0.24000001 C 10.056 0 11.496 0.336 13.152 0.552 C 13.2 0.696 13.152 1.176 13.104 1.32 C 11.808001 1.44 11.544 1.824 11.544 3.192 L 11.544 13.992001 C 11.544 15.552 11.616 16.44 11.616 16.44 C 11.616 16.656 11.448 16.752 11.232 16.752 C 10.344 16.464 8.424 16.2 6.7200003 16.128 C 6.6480002 15.84 6.672 15.528 6.7920003 15.312 C 8.304 15.192 8.424 15.168 8.424 13.512 L 8.424 10.392 C 7.968 10.536 7.392 10.656 6.696 10.656 C 3.6000001 10.656 0.888 7.9440002 0.888 4.752 C 0.888 3.336 1.392 1.6800001 2.568 0.768 C 3.432 0.096 4.032 -0.24000001 5.376 -0.24000001 C 6.024 -0.24000001 7.8 0.816 8.304 1.152 Z M 8.448 2.28 C 7.9440002 1.872 6.672 1.344 6.384 1.344 C 5.184 1.344 4.248 2.688 4.248 5.496 C 4.248 6.768 4.392 7.872 4.848 8.616 C 5.256 9.264 5.9040003 9.648 6.624 9.648 C 7.248 9.648 7.848 9.576 8.424 8.784 L 8.424 2.88 C 8.424 2.688 8.424 2.4720001 8.448 2.28 Z "/>
</symbol>
<symbol id="g5CE84699333B5C2123530E7EB1AB2F63" overflow="visible">
<path d="M 11.568 7.9440002 C 11.112 9.096 10.824 10.152 10.824 10.152 C 10.392 10.128 9.936 10.128 9.4800005 10.176 L 7.2000003 3.8400002 C 7.1280003 3.672 7.032 3.624 6.936 3.864 L 5.568 7.9440002 C 5.544 8.016 5.52 8.064 5.496 8.136 C 5.16 9.144 5.0160003 9.528 6.432 9.648 C 6.576 9.792 6.576 10.32 6.432 10.464 C 5.544 10.440001 4.512 10.416 3.288 10.416 C 2.448 10.416 1.224 10.440001 0.336 10.464 C 0.192 10.32 0.192 9.792 0.336 9.648 C 1.728 9.4800005 1.8000001 9.024 2.256 7.8 L 5.184 0.216 C 5.352 -0.24000001 5.664 -0.288 5.976 -0.288 C 6.216 -0.288 6.672 -0.24000001 6.864 0.264 L 9.12 6.192 L 11.424 0.216 C 11.592 -0.216 12.048 -0.288 12.36 -0.288 C 12.6 -0.288 13.008 -0.216 13.2 0.264 L 16.152 7.584 C 16.56 8.616 16.968 9.528 18.312 9.648 C 18.456 9.792 18.456 10.32 18.312 10.464 C 17.784 10.440001 17.352 10.416 16.728 10.416 C 15.84 10.416 14.808001 10.440001 13.92 10.464 C 13.776 10.32 13.776 9.792 13.92 9.648 C 15.216001 9.552 15.336 8.928 14.88 7.752 L 13.488 3.96 C 13.392 3.672 13.248 3.696 13.152 3.936 Z "/>
</symbol>
<symbol id="g10AC66E6714D96E9762627FFB6E156C6" overflow="visible">
<path d="M 1.512 10.416 C 1.176 10.416 0.816 10.32 0.504 10.056 L 0.504 9.36 C 0.504 9.24 0.528 9.216 0.624 9.216 L 2.184 9.216 C 2.136 6.7920003 2.112 3.72 2.112 2.52 C 2.112 1.6800001 2.328 0.864 2.832 0.432 C 3.384 -0.024 4.248 -0.24000001 4.824 -0.24000001 C 6.144 -0.24000001 7.6080003 0.432 8.088 1.104 C 8.088 1.392 7.9440002 1.536 7.656 1.776 C 7.344 1.536 6.744 1.44 6.288 1.44 C 5.76 1.44 5.232 1.848 5.232 3.048 C 5.232 4.248 5.208 6.816 5.208 9.216 L 7.632 9.216 C 7.872 9.216 8.208 9.312 8.208 9.528 L 8.208 10.272 C 8.208 10.368 8.136 10.416 8.016 10.416 L 5.208 10.416 L 5.232 11.232 C 5.28 12.84 5.352 13.944 5.352 13.944 C 5.352 14.088 5.28 14.16 5.16 14.16 C 4.992 14.16 4.104 13.896 3.72 13.728 C 3.312 13.56 2.616 13.416 2.448 13.2 C 2.28 12.984 2.184 12.336 2.184 10.416 Z "/>
</symbol>
<symbol id="g2825DE3DACAF761B898A0442866AE569" overflow="visible">
<path d="M 12.672 3.072 L 12.672 6.816 C 12.672 9.456 11.544 10.656 9.4800005 10.656 C 8.592 10.656 6.888 9.768 5.52 8.928 L 5.52 13.992001 C 5.52 15.552 5.592 16.44 5.592 16.44 C 5.592 16.656 5.4240003 16.752 5.208 16.752 C 4.32 16.464 2.4 16.2 0.696 16.128 C 0.624 15.84 0.648 15.576 0.768 15.360001 C 2.28 15.24 2.4 15.216001 2.4 13.56 L 2.4 3.048 C 2.4 1.056 2.016 0.84000003 0.552 0.768 C 0.408 0.624 0.408 0.096 0.552 -0.048 C 1.5600001 -0.024 2.64 0 3.96 0 C 5.112 0 5.856 -0.024 6.888 -0.048 C 7.032 0.096 7.032 0.624 6.888 0.768 C 5.88 0.84000003 5.52 1.056 5.52 3.048 L 5.52 7.968 C 6.528 8.592 7.32 8.88 7.752 8.88 C 8.712 8.88 9.552 8.448 9.552 7.08 L 9.552 3.072 C 9.552 1.056 9.168 0.84000003 8.184 0.768 C 8.04 0.624 8.04 0.096 8.184 -0.048 C 9.192 -0.024 9.96 0 11.112 0 C 12.432 0 13.488 -0.024 14.52 -0.048 C 14.6640005 0.096 14.6640005 0.624 14.52 0.768 C 13.056 0.84000003 12.672 1.056 12.672 3.072 Z "/>
</symbol>
<symbol id="gF2A450DA789E2AF150390BAEDFF9DA86" overflow="visible">
<path d="M 2.736 12.552 L 2.736 2.928 C 2.736 0.936 2.0640001 0.84000003 0.744 0.768 C 0.504 0.624 0.504 0.096 0.744 -0.048 C 1.704 -0.024 3.48 0 4.44 0 C 5.4 0 7.1280003 -0.024 8.088 -0.048 C 8.328 0.096 8.328 0.624 8.088 0.768 C 6.768 0.84000003 6.096 0.936 6.096 2.928 L 6.096 12.552 C 6.096 14.544 6.768 14.64 8.088 14.712 C 8.328 14.856 8.328 15.384 8.088 15.528 C 7.1280003 15.504 5.4 15.4800005 4.44 15.4800005 C 3.48 15.4800005 1.704 15.504 0.744 15.528 C 0.504 15.384 0.504 14.856 0.744 14.712 C 2.0640001 14.64 2.736 14.544 2.736 12.552 Z "/>
</symbol>
<symbol id="g3005F72D4AFC838AB38DA6C1497F98C5" overflow="visible">
<path d="M 14.2560005 13.032001 C 14.832 14.472 15.6 14.64 16.656 14.712 C 16.8 14.856 16.8 15.384 16.656 15.528 C 15.936 15.504 15.168 15.4800005 14.400001 15.4800005 C 13.416 15.4800005 12.096 15.504 11.208 15.528 C 11.064 15.384 11.064 14.856 11.208 14.712 C 12.12 14.64 13.224 14.496 12.864 13.584001 L 9.552 5.04 L 9.168 4.104 L 8.784 5.184 L 5.808 13.752 C 5.544 14.544 6.432 14.64 7.584 14.712 C 7.728 14.856 7.728 15.384 7.584 15.528 C 6.696 15.504 4.296 15.4800005 3.3600001 15.4800005 C 2.376 15.4800005 1.0320001 15.504 0.144 15.528 C 0 15.384 0 14.856 0.144 14.712 C 1.08 14.616 1.872 14.496 2.304 13.416 L 7.5360003 0.264 C 7.704 -0.144 7.992 -0.288 8.328 -0.288 C 8.6640005 -0.288 8.976 -0.168 9.144 0.264 Z "/>
</symbol>
<symbol id="g63CC3E63B28F8D9D90BA6C1A685A1E05" overflow="visible">
<path d="M 5.808 2.928 L 5.808 7.176 L 7.752 7.176 C 9.408 7.176 9.864 6.7200003 9.936 5.64 C 10.08 5.496 10.824 5.496 10.968 5.64 C 10.92 6.48 10.92 7.2000003 10.92 7.752 C 10.92 8.304 10.944 9.12 10.968 9.816 C 10.824 9.96 10.08 9.96 9.936 9.816 C 9.864 8.496 9.36 8.28 7.752 8.28 L 5.808 8.28 L 5.808 13.2960005 C 5.808 13.872 6.216 14.472 6.7920003 14.472 L 8.952 14.472 C 10.752 14.472 11.376 13.440001 11.904 11.784 C 12.192 11.736 12.504 11.784 12.744 11.904 C 12.672 12.96 12.4800005 15.312 12.456 15.504 C 12.456 15.552 12.432 15.576 12.36 15.576 C 11.952 15.504 11.76 15.4800005 11.184 15.4800005 L 4.056 15.4800005 C 4.056 15.4800005 1.5600001 15.504 0.36 15.528 C 0.216 15.384 0.216 14.856 0.36 14.712 C 2.04 14.64 2.448 14.52 2.448 12.528 L 2.448 2.928 C 2.448 0.936 1.776 0.84000003 0.456 0.768 C 0.216 0.624 0.216 0.096 0.456 -0.048 C 1.416 -0.024 3.192 0 4.152 0 C 5.112 0 7.08 -0.024 8.04 -0.048 C 8.28 0.096 8.28 0.624 8.04 0.768 C 6.7200003 0.84000003 5.808 0.936 5.808 2.928 Z "/>
</symbol>
<symbol id="gA335A20E4C1D7F39210005AFF7F1A0EF" overflow="visible">
<path d="M 7.14 -0.19999999 C 9.08 -0.19999999 10.86 0.71999997 12.219999 2.5 C 12.12 2.6799998 11.98 2.8 11.759999 2.8 C 10.34 1.24 8.98 0.62 7.12 0.62 C 4.42 0.62 2.56 3.6599998 2.56 6.58 C 2.56 8.3 3.02 9.74 3.74 10.639999 C 4.74 11.86 5.9 12.42 6.94 12.42 C 9.7 12.42 10.8 10.78 11.32 9.059999 C 11.559999 8.98 11.759999 9.04 11.98 9.16 C 11.88 10.2 11.74 11.16 11.54 12.259999 C 10.5199995 12.36 9.62 13.16 7.16 13.16 C 5.46 13.16 4.04 12.54 2.86 11.46 C 1.54 10.24 0.74 8.28 0.74 6.2 C 0.74 2.72 2.84 -0.19999999 7.14 -0.19999999 Z "/>
</symbol>
<symbol id="gFB78EB03C35D4F852337F4EC6AC104AC" overflow="visible">
<path d="M 0.82 4.1 C 0.82 2.06 2.18 -0.19999999 5.02 -0.19999999 C 6.2999997 -0.19999999 7.2799997 0.26 7.96 0.91999996 C 8.86 1.8 9.26 3.06 9.26 4.2799997 C 9.26 6.3599997 8.12 8.78 5.06 8.78 C 3.74 8.78 2.6599998 8.24 1.92 7.3799996 C 1.1999999 6.52 0.82 5.3599997 0.82 4.1 Z M 4.7599998 8.08 C 6.48 8.08 7.54 6.52 7.54 3.6399999 C 7.54 1.12 6.24 0.5 5.2999997 0.5 C 3.22 0.5 2.54 3.02 2.54 4.56 C 2.54 6.2999997 2.96 8.08 4.7599998 8.08 Z "/>
</symbol>
<symbol id="gD3761FB0B01B207797C607CDFB6E3A0B" overflow="visible">
<path d="M 3.3999999 7.16 C 3.3799999 7.7599998 3.34 8.48 3.24 8.679999 C 3.1999998 8.78 3.1599998 8.84 3 8.84 C 2.44 8.62 1.92 8.44 0.53999996 8.26 C 0.5 8.139999 0.53999996 7.8199997 0.58 7.7 C 1.66 7.6 1.88 7.5 1.88 6.3399997 L 1.88 2.44 C 1.88 0.79999995 1.62 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.88 0 2.6799998 0 C 3.48 0 4.1 -0.02 4.7 -0.04 C 4.8199997 0.08 4.8199997 0.5 4.7 0.62 C 3.6799998 0.71999997 3.46 0.79999995 3.46 2.44 L 3.46 5.72 C 3.46 6.14 3.6399999 6.3799996 3.8 6.56 C 4.6 7.3399997 5.3399997 7.74 5.96 7.74 C 6.72 7.74 7.2799997 7.2599998 7.2799997 5.92 L 7.2799997 2.44 C 7.2799997 0.79999995 7.12 0.7 6.04 0.62 C 5.94 0.5 5.94 0.08 6.04 -0.04 C 6.54 -0.02 7.2799997 0 8.08 0 C 8.88 0 9.54 -0.02 10.04 -0.04 C 10.139999 0.08 10.139999 0.5 10.04 0.62 C 9.04 0.7 8.86 0.79999995 8.86 2.44 L 8.86 5.62 C 8.86 5.9 8.86 6.18 8.84 6.42 C 9.8 7.48 10.7 7.74 11.48 7.74 C 12.24 7.74 12.679999 7.2999997 12.679999 5.96 L 12.679999 2.44 C 12.679999 0.79999995 12.48 0.7 11.44 0.62 C 11.34 0.5 11.34 0.08 11.44 -0.04 C 11.94 -0.02 12.679999 0 13.48 0 C 14.28 0 14.98 -0.02 15.54 -0.04 C 15.639999 0.08 15.639999 0.5 15.54 0.62 C 14.44 0.7 14.259999 0.79999995 14.259999 2.44 L 14.259999 5.6 C 14.259999 7.3799996 13.96 8.78 12.2 8.78 C 11.179999 8.78 9.94 8.4 8.9 7.2999997 C 8.84 7.24 8.72 7.14 8.679999 7.3199997 C 8.5 8.139999 7.72 8.78 6.68 8.78 C 5.52 8.78 4.48 8.099999 3.6399999 7.16 C 3.54 7.06 3.4199998 6.92 3.3999999 7.16 Z "/>
</symbol>
<symbol id="g733371913480EE84B3609C9E9CD62F8C" overflow="visible">
<path d="M 3.34 7.8799996 C 3.22 7.7599998 3.1399999 7.7999997 3.1399999 7.98 L 3.1399999 11.66 C 3.1399999 12.96 3.22 13.759999 3.22 13.759999 C 3.22 13.9 3.1399999 13.96 2.96 13.96 C 2.46 13.759999 0.96 13.48 0.16 13.42 C 0.12 13.259999 0.16 12.94 0.28 12.82 C 0.34 12.82 0.39999998 12.82 0.45999998 12.82 C 1.3399999 12.759999 1.56 12.759999 1.56 11.179999 L 1.56 1.42 C 1.56 0.64 1.54 0.28 1.48 0 C 1.5799999 -0.16 1.68 -0.24 1.92 -0.24 C 2.04 -0.12 2.24 0.06 2.3999999 0.24 C 2.6 0.48 2.72 0.48 2.9399998 0.29999998 C 3.3999999 -0.08 4 -0.19999999 4.7 -0.19999999 C 6.74 -0.19999999 9.12 1.66 9.12 4.8399997 C 9.12 7.2799997 7.3199997 8.78 5.58 8.78 C 4.72 8.78 3.9599998 8.44 3.34 7.8799996 Z M 3.48 7.2599998 C 4 7.72 4.6 7.8999996 5.18 7.8999996 C 6.3999996 7.8999996 7.3999996 6.42 7.3999996 4.48 C 7.3999996 2.2 6.48 0.48 4.58 0.48 C 3.9599998 0.48 3.54 0.91999996 3.1399999 1.42 L 3.1399999 6.42 C 3.1399999 6.8399997 3.22 7.04 3.48 7.2599998 Z "/>
</symbol>
<symbol id="gE68C39294AA7FBA9B91EA2F8E9CC3997" overflow="visible">
<path d="M 3.62 2.44 L 3.62 6.42 C 3.62 7.4199996 3.6999998 8.7 3.6999998 8.7 C 3.6999998 8.78 3.6 8.84 3.4399998 8.84 C 2.8799999 8.62 2.08 8.44 0.7 8.26 C 0.65999997 8.139999 0.7 7.8199997 0.74 7.7 C 1.8399999 7.6 2.04 7.48 2.04 6.3399997 L 2.04 2.44 C 2.04 0.78 1.8199999 0.71999997 0.59999996 0.62 C 0.48 0.5 0.48 0.08 0.59999996 -0.04 C 1.26 -0.02 2.04 0 2.84 0 C 3.6399999 0 4.4 -0.02 5.06 -0.04 C 5.18 0.08 5.18 0.5 5.06 0.62 C 3.84 0.7 3.62 0.78 3.62 2.44 Z M 1.8 11.98 C 1.8 11.46 2.28 10.94 2.76 10.94 C 3.32 10.94 3.8 11.48 3.8 11.9 C 3.8 12.38 3.3799999 12.94 2.84 12.94 C 2.36 12.94 1.8 12.46 1.8 11.98 Z "/>
</symbol>
<symbol id="g35631D62198EF939061DC90C9391724A" overflow="visible">
<path d="M 3.6799998 7.16 C 3.56 7.02 3.4399998 6.98 3.4399998 7.16 C 3.4199998 7.7 3.3799999 8.48 3.28 8.679999 C 3.24 8.78 3.1999998 8.84 3.04 8.84 C 2.48 8.62 1.9599999 8.44 0.58 8.26 C 0.53999996 8.139999 0.58 7.8199997 0.62 7.7 C 1.6999999 7.6 1.92 7.5 1.92 6.3399997 L 1.92 2.44 C 1.92 0.79999995 1.7199999 0.71999997 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.12 -0.02 1.92 0 2.72 0 C 3.52 0 4.12 -0.02 4.72 -0.04 C 4.8399997 0.08 4.8399997 0.5 4.72 0.62 C 3.6999998 0.71999997 3.5 0.79999995 3.5 2.44 L 3.5 5.72 C 3.5 6.14 3.6799998 6.3799996 3.84 6.56 C 4.6 7.2999997 5.5 7.74 6.2799997 7.74 C 6.68 7.74 7.1 7.48 7.3399997 7.02 C 7.54 6.62 7.58 6.08 7.58 5.48 L 7.58 2.44 C 7.58 0.79999995 7.3799996 0.71999997 6.3399997 0.62 C 6.24 0.5 6.24 0.08 6.3399997 -0.04 C 6.94 -0.02 7.58 0 8.38 0 C 9.179999 0 9.9 -0.02 10.5 -0.04 C 10.599999 0.08 10.599999 0.5 10.5 0.62 C 9.38 0.71999997 9.16 0.79999995 9.16 2.44 L 9.16 5.42 C 9.16 6.52 9.08 7.48 8.62 8.099999 C 8.28 8.54 7.66 8.78 6.96 8.78 C 5.98 8.78 4.8599997 8.5199995 3.6799998 7.16 Z "/>
</symbol>
<symbol id="g7FBC39AA6D9FB89D8B638A3651405A80" overflow="visible">
<path d="M 7.72 1.86 C 6.98 1.1 6.3999996 0.78 5.24 0.78 C 4.52 0.78 3.6799998 1.1999999 3.06 2.22 C 2.6599998 2.8799999 2.4199998 3.8 2.4199998 4.96 L 7.74 4.92 C 7.98 4.92 8.12 5.04 8.12 5.2599998 C 8.12 6.94 7.52 8.74 4.74 8.74 C 3 8.74 0.74 7.08 0.74 4.04 C 0.74 2.9199998 1.02 1.8399999 1.68 1.0799999 C 2.36 0.28 3.3 -0.19999999 4.74 -0.19999999 C 6.2599998 -0.19999999 7.3399997 0.5 8.139999 1.54 C 8.08 1.74 7.96 1.8399999 7.72 1.86 Z M 2.48 5.64 C 2.86 7.8999996 4.2599998 8.08 4.74 8.08 C 5.5 8.08 6.3999996 7.66 6.3999996 5.98 C 6.3999996 5.7999997 6.3199997 5.7 6.1 5.7 Z "/>
</symbol>
<symbol id="g67483374C2628B9150A7D3585AC4A61B" overflow="visible">
<path d="M 0.96 2.76 C 1.04 1.78 1.1 0.84 1.1 0 C 1.3 0.04 1.5 0.06 1.5999999 0.06 C 1.74 0.06 1.86 0.06 2 0.02 C 2.54 -0.12 3.08 -0.19999999 3.82 -0.19999999 C 4.94 -0.19999999 7 0.34 7 2.32 C 7 3.6799998 6.02 4.48 4.66 4.98 C 3.46 5.44 2.6599998 5.74 2.6599998 6.8399997 C 2.6599998 7.66 3.3799999 8.12 4.06 8.12 C 4.5 8.12 5.66 7.96 5.92 6.2599998 C 6.04 6.14 6.44 6.16 6.56 6.2799997 C 6.62 7 6.66 7.74 6.68 8.4 C 6.06 8.5 5.1 8.78 4.06 8.78 C 2.58 8.78 1.24 7.8199997 1.24 6.54 C 1.24 5.08 1.9 4.46 3.4399998 3.82 C 5.1 3.1399999 5.48 2.72 5.48 1.86 C 5.48 0.88 4.52 0.45999998 3.78 0.45999998 C 3 0.45999998 2.56 0.71999997 2.36 0.94 C 1.92 1.4 1.6999999 2.28 1.5799999 2.78 C 1.4599999 2.8999999 1.0799999 2.8799999 0.96 2.76 Z "/>
</symbol>
<symbol id="g713198A7DA4F5CD7D462D4529B1D64BD" overflow="visible">
<path d="M 7.96 1.8199999 C 7.8799996 2 7.72 2.08 7.54 2.1 C 6.8599997 1.22 6 0.78 5.14 0.78 C 3.6799998 0.78 2.46 2.26 2.46 4.6 C 2.46 6.7999997 3.4199998 8.12 4.74 8.12 C 5.92 8.12 6.08 7.4199996 6.16 6.72 C 6.22 6.18 6.5 6 6.92 6 C 7.3399997 6 7.8999996 6.2599998 7.8999996 6.8799996 C 7.8999996 7.98 6.7599998 8.78 4.8399997 8.78 C 2.86 8.78 0.74 7 0.74 4.16 C 0.74 1.5799999 2.18 -0.19999999 4.7 -0.19999999 C 5.9 -0.19999999 6.96 0.17999999 7.96 1.8199999 Z "/>
</symbol>
<symbol id="g1788914935A6D7BFA016214155630E72" overflow="visible">
<path d="M 1.9 2.44 C 1.9 0.78 1.68 0.68 0.45999998 0.62 C 0.34 0.5 0.34 0.08 0.45999998 -0.04 C 1.16 -0.02 1.9 0 2.7 0 C 3.5 0 4.2599998 -0.02 4.92 -0.04 C 5.04 0.08 5.04 0.5 4.92 0.62 C 3.6999998 0.68 3.48 0.78 3.48 2.44 L 3.48 11.66 C 3.48 12.96 3.56 13.759999 3.56 13.759999 C 3.56 13.9 3.48 13.96 3.3 13.96 C 2.8 13.759999 1.3 13.48 0.5 13.42 C 0.45999998 13.259999 0.5 12.94 0.62 12.82 C 1.78 12.74 1.9 12.679999 1.9 11.179999 Z "/>
</symbol>
<symbol id="gD8CB364949770E6EB9E57283C62D30EB" overflow="visible">
<path d="M 4.3399997 -0.19999999 C 5.12 -0.19999999 6.06 0.19999999 7.04 1 C 7.14 1.0799999 7.3199997 1.12 7.3399997 0.97999996 C 7.3999996 0.48 7.56 -0.19999999 7.56 -0.19999999 C 7.72 -0.26 7.8199997 -0.24 7.94 -0.19999999 C 8.38 0.16 9.08 0.45999998 10.3 0.59999996 C 10.42 0.71999997 10.42 1.02 10.3 1.14 C 9.0199995 1.24 8.84 1.62 8.84 2.6 L 8.84 6.44 C 8.84 7.04 8.92 8.5 8.92 8.5 C 8.92 8.559999 8.86 8.62 8.76 8.62 C 8.66 8.599999 8.36 8.58 8.059999 8.58 C 7.4199996 8.58 6.7 8.599999 6.02 8.62 C 5.9 8.5 5.9 8.08 6.02 7.96 C 7 7.8999996 7.2599998 7.66 7.2599998 6.3399997 L 7.2599998 2.48 C 7.2599998 2.1 7.22 1.9399999 6.94 1.6999999 C 6.2 1.06 5.44 0.74 4.94 0.74 C 4.3399997 0.74 3.34 1.02 3.34 2.8 L 3.34 6.44 C 3.34 7.04 3.4199998 8.5 3.4199998 8.5 C 3.4199998 8.559999 3.36 8.62 3.26 8.62 C 3.1599998 8.599999 2.86 8.58 2.56 8.58 C 1.92 8.58 1.1999999 8.599999 0.52 8.62 C 0.39999998 8.5 0.39999998 8.08 0.52 7.96 C 1.48 7.8799996 1.76 7.66 1.76 6.3599997 L 1.76 2.52 C 1.76 1.14 2.36 -0.19999999 4.3399997 -0.19999999 Z "/>
</symbol>
<symbol id="g22D858CFD6AD86697C1391C74FD687D1" overflow="visible">
<path d="M 0.85999995 8.58 C 0.58 8.58 0.5 8.34 0.5 8.179999 L 0.5 7.9199996 C 0.5 7.8199997 0.52 7.7999997 0.59999996 7.7999997 L 1.78 7.7999997 L 1.78 1.78 C 1.78 0.35999998 2.3999999 -0.19999999 3.32 -0.19999999 C 4.24 -0.19999999 5.24 0.24 6.02 1.12 C 5.98 1.3199999 5.8599997 1.4399999 5.66 1.4599999 C 5.14 1.06 4.54 0.9 4.02 0.9 C 3.48 0.9 3.36 1.5 3.36 2.74 L 3.36 7.7999997 L 5.44 7.7999997 C 5.64 7.7999997 5.92 7.8799996 5.92 8.059999 L 5.92 8.46 C 5.92 8.54 5.8599997 8.58 5.7599998 8.58 L 3.36 8.58 L 3.36 9.36 C 3.36 10.66 3.4399998 11.46 3.4399998 11.46 C 3.4399998 11.58 3.3799999 11.639999 3.28 11.639999 C 3.1999998 11.639999 3.02 11.559999 2.84 11.46 C 2.62 11.34 2.4199998 11.24 2.1599998 11.179999 C 1.92 11.099999 1.7199999 11.04 1.7199999 10.9 C 1.7199999 10.66 1.78 10.8 1.78 8.58 Z "/>
</symbol>
<symbol id="gB9C04FB79CAD4691AB5EC7F01BE2AD7F" overflow="visible">
<path d="M 3.52 7.16 C 3.48 7.96 3.46 8.48 3.36 8.679999 C 3.32 8.78 3.28 8.84 3.12 8.84 C 2.56 8.62 2.04 8.44 0.65999997 8.26 C 0.62 8.139999 0.65999997 7.8199997 0.7 7.7 C 1.78 7.6 2 7.5 2 6.3399997 L 2 2.44 C 2 0.78 1.76 0.7 0.52 0.62 C 0.39999998 0.5 0.39999998 0.08 0.52 -0.04 C 1.22 -0.02 2 0 2.8 0 C 3.6 0 4.52 -0.02 5.22 -0.04 C 5.3399997 0.08 5.3399997 0.5 5.22 0.62 C 3.82 0.71999997 3.58 0.78 3.58 2.44 L 3.58 5.22 C 3.58 5.74 3.82 6.2 4.06 6.56 C 4.2799997 6.8799996 4.74 7.54 4.98 7.54 C 5.16 7.54 5.3399997 7.5 5.5 7.2799997 C 5.64 7.08 5.8799996 6.8199997 6.22 6.8199997 C 6.7 6.8199997 7.16 7.3199997 7.16 7.8199997 C 7.16 8.2 6.7999997 8.78 5.96 8.78 C 5.02 8.78 4.2 7.8999996 3.74 7.12 C 3.62 6.8999996 3.52 7.06 3.52 7.16 Z "/>
</symbol>
<symbol id="gE8171CD7697771DDE124968BDB3EF0D7" overflow="visible">
<path d="M 5.42 4.46 C 5.68 4.46 5.96 5.02 5.96 5.2599998 C 5.96 5.46 5.8799996 5.66 5.68 5.66 L 1.3 5.66 C 1.06 5.66 0.79999995 5.2 0.79999995 4.8399997 C 0.79999995 4.64 0.91999996 4.46 1.1 4.46 Z "/>
</symbol>
<symbol id="gAA212A9DBB5FA7333A767E41B2F6A3B3" overflow="visible">
<path d="M 5.8599997 0.96 C 5.98 0.34 6.2 -0.19999999 7.2 -0.19999999 C 7.96 -0.19999999 8.679999 0.14 9.099999 0.53999996 C 9.059999 0.78 8.98 0.96 8.76 1.0799999 C 8.62 0.96 8.28 0.76 8.0199995 0.76 C 7.44 0.76 7.4199996 1.54 7.4199996 2.46 L 7.4199996 5.4 C 7.4199996 8.24 5.8599997 8.78 4.4 8.78 C 2.76 8.78 1.1 7.7 1.1 6.56 C 1.1 6.08 1.3399999 5.8399997 1.8 5.8399997 C 2.3799999 5.8399997 2.74 6.2599998 2.74 6.52 C 2.74 6.66 2.72 6.7999997 2.6799998 6.8799996 C 2.6599998 6.94 2.6399999 7.06 2.6399999 7.2799997 C 2.6399999 7.8999996 3.48 8.12 4.24 8.12 C 4.92 8.12 5.8599997 7.7799997 5.8599997 5.52 C 5.8599997 5.38 5.7999997 5.2999997 5.74 5.2799997 L 4.02 4.8599997 C 2.1 4.38 0.71999997 3.32 0.71999997 1.9599999 C 0.71999997 0.32 1.8399999 -0.19999999 3.24 -0.19999999 C 3.9399998 -0.19999999 4.54 -0.04 5.42 0.64 L 5.8199997 0.96 Z M 5.8599997 4.66 L 5.8599997 2.02 C 5.8599997 1.76 5.74 1.62 5.58 1.5 C 5.06 1.0799999 4.38 0.62 3.82 0.62 C 2.82 0.62 2.3799999 1.42 2.3799999 2.04 C 2.3799999 2.9399998 2.8 3.86 4.2799997 4.24 Z "/>
</symbol>
<symbol id="g42587C4E387B2C5F870DA01C2914651F" overflow="visible">
<path d="M 6.68 1 C 6.7799997 1.0799999 6.96 1.12 6.98 0.97999996 C 7.04 0.5 7.2 -0.19999999 7.2 -0.19999999 C 7.3599997 -0.26 7.46 -0.24 7.58 -0.19999999 C 8.0199995 0.16 8.72 0.45999998 9.94 0.59999996 C 10.059999 0.71999997 10.059999 1.02 9.94 1.14 C 8.66 1.24 8.48 1.62 8.48 2.6 L 8.48 11.66 C 8.48 12.96 8.559999 13.759999 8.559999 13.759999 C 8.559999 13.9 8.48 13.96 8.3 13.96 C 7.7999997 13.759999 6.2999997 13.48 5.5 13.42 C 5.46 13.259999 5.5 12.94 5.62 12.82 C 5.68 12.82 5.74 12.82 5.7999997 12.82 C 6.68 12.759999 6.8999996 12.759999 6.8999996 11.179999 L 6.8999996 8.62 C 6.8999996 8.48 6.8599997 8.44 6.72 8.44 C 6.64 8.44 5.8199997 8.78 5.16 8.78 C 3.84 8.78 2.96 8.34 2.1599998 7.58 C 1.3 6.72 0.78 5.54 0.78 4.06 C 0.78 1.5999999 2.02 -0.19999999 4.18 -0.19999999 C 4.96 -0.19999999 5.7 0.19999999 6.68 1 Z M 6.8999996 2.48 C 6.8999996 2.1 6.8599997 1.9399999 6.58 1.6999999 C 5.8399997 1.06 5.2 0.74 4.7 0.74 C 3.62 0.74 2.5 1.92 2.5 4.42 C 2.5 5.8599997 2.78 6.66 3.08 7.08 C 3.6999998 8.0199995 4.54 8.08 4.94 8.08 C 5.66 8.08 6.16 7.8199997 6.56 7.3599997 C 6.8399997 7.04 6.8999996 6.8999996 6.8999996 6.2799997 Z "/>
</symbol>
<symbol id="gFB54B84572F46C3C9CB2B1A90182D6B2" overflow="visible">
<path d="M 8.88 7.74 C 9.26 7.74 9.62 8.099999 9.62 8.5 C 9.62 8.92 9.24 9.24 8.7 9.24 C 8.179999 9.24 7.22 8.9 6.7 8.22 C 6.46 8.38 5.7999997 8.78 4.62 8.78 C 2.84 8.78 1.1999999 7.58 1.1999999 5.74 C 1.1999999 4.66 1.68 4.04 2.24 3.5 C 1.68 3.02 1.36 2.1599998 1.36 1.48 C 1.36 0.76 1.76 0.19999999 2.28 -0.06 C 1.1999999 -0.7 0.64 -1.62 0.64 -2.48 C 0.64 -4.22 2.28 -4.7599998 3.82 -4.7599998 C 6.52 -4.7599998 9.44 -3.46 9.44 -1.3 C 9.44 -0.65999997 9.139999 -0.16 8.559999 0.32 C 7.7799997 0.96 6.3799996 0.97999996 5.64 0.97999996 C 5.2799997 0.97999996 4.7799997 0.94 4.2999997 0.88 C 4 0.85999995 3.8 0.84 3.6999998 0.84 C 3.12 0.84 2.4199998 1.12 2.4199998 1.9799999 C 2.4199998 2.3799999 2.54 2.8 2.78 3.1399999 C 3.26 2.86 3.82 2.72 4.6 2.72 C 6.3599997 2.72 7.98 3.82 7.98 5.7799997 C 7.98 6.72 7.7 7.2599998 7.12 7.8599997 C 7.2599998 8.059999 7.66 8.34 7.9199996 8.34 C 8.059999 8.34 8.2 8.28 8.32 8.099999 C 8.4 7.94 8.66 7.74 8.88 7.74 Z M 2.6399999 -0.19999999 C 2.86 -0.26 3.1799998 -0.29999998 3.4399998 -0.29999998 C 4.06 -0.29999998 4.62 -0.24 4.9 -0.24 C 5.9 -0.24 6.74 -0.26 7.3199997 -0.58 C 8.099999 -1.02 8.34 -1.3 8.34 -1.8199999 C 8.34 -3.26 6.22 -4.02 4.42 -4.02 C 3.6999998 -4.02 2.02 -3.4399998 2.02 -2.08 C 2.02 -1.4 2.06 -0.9 2.6399999 -0.19999999 Z M 6.3799996 5.58 C 6.3799996 3.72 5.44 3.34 4.7 3.34 C 3.02 3.34 2.84 4.7599998 2.84 6.04 C 2.84 7.44 3.34 8.16 4.44 8.16 C 5.7 8.16 6.3799996 7.24 6.3799996 5.58 Z "/>
</symbol>
<symbol id="gAC7FD886AB12F72ED3B61B0327264BE7" overflow="visible">
<path d="M 3.12 7.3599997 C 3.1 7.96 3.06 8.48 2.96 8.679999 C 2.9199998 8.78 2.8799999 8.84 2.72 8.84 C 2.1599998 8.62 1.64 8.44 0.26 8.26 C 0.22 8.139999 0.26 7.8199997 0.29999998 7.7 C 1.38 7.6 1.5999999 7.5 1.5999999 6.3399997 L 1.5999999 -2.2 C 1.5999999 -3.86 1.38 -3.9599998 0.16 -4.02 C 0.04 -4.14 0.04 -4.56 0.16 -4.68 C 0.85999995 -4.66 1.5999999 -4.64 2.3999999 -4.64 C 3.1999998 -4.64 4.16 -4.66 4.8199997 -4.68 C 4.94 -4.56 4.94 -4.14 4.8199997 -4.02 C 3.3999999 -3.9399998 3.1799998 -3.86 3.1799998 -2.2 L 3.1799998 -0.04 C 3.1799998 0.22 3.26 0.19999999 3.46 0.12 C 3.9599998 -0.08 4.56 -0.19999999 5.2 -0.19999999 C 6.3199997 -0.19999999 7.3199997 0.14 8.139999 0.91999996 C 9.08 1.8399999 9.62 3.08 9.62 4.7 C 9.62 6.8199997 8.12 8.78 6.08 8.78 C 5.16 8.78 4.14 8.179999 3.34 7.2799997 C 3.22 7.16 3.1399999 7.16 3.12 7.3599997 Z M 3.5 6.62 C 4.02 7.2599998 4.94 7.8599997 5.52 7.8599997 C 6.7999997 7.8599997 7.8999996 6.42 7.8999996 4.16 C 7.8999996 2.52 7.3199997 0.48 5.08 0.48 C 4.72 0.48 4.02 0.58 3.6599998 0.9 C 3.26 1.26 3.1799998 1.38 3.1799998 2.1 L 3.1799998 5.74 C 3.1799998 6.16 3.26 6.3399997 3.5 6.62 Z "/>
</symbol>
<symbol id="g3C2FFF86BC828E66F78F8A687CE12C70" overflow="visible">
<path d="M 3.34 5.72 C 3.34 6.14 3.52 6.3799996 3.6799998 6.56 C 4.44 7.2999997 5.46 7.74 6.24 7.74 C 6.64 7.74 7.06 7.48 7.2999997 7.02 C 7.5 6.62 7.54 6.08 7.54 5.48 L 7.54 2.44 C 7.54 0.79999995 7.3399997 0.71999997 6.2999997 0.62 C 6.2 0.5 6.2 0.08 6.2999997 -0.04 C 6.8599997 -0.02 7.54 0 8.34 0 C 9.139999 0 9.8 -0.02 10.46 -0.04 C 10.559999 0.08 10.559999 0.5 10.46 0.62 C 9.34 0.71999997 9.12 0.79999995 9.12 2.44 L 9.12 5.42 C 9.12 6.52 9.04 7.5 8.58 8.099999 C 8.24 8.54 7.62 8.78 6.92 8.78 C 5.94 8.78 4.74 8.5199995 3.52 7.16 C 3.52 7.14 3.5 7.14 3.48 7.12 C 3.4199998 7.04 3.32 6.92 3.32 7.16 L 3.34 11.66 C 3.34 12.96 3.4199998 13.759999 3.4199998 13.759999 C 3.4199998 13.9 3.34 13.96 3.1599998 13.96 C 2.6599998 13.759999 1.16 13.48 0.35999998 13.42 C 0.32 13.259999 0.35999998 12.94 0.48 12.82 C 0.53999996 12.82 0.59999996 12.82 0.65999997 12.82 C 1.54 12.759999 1.76 12.759999 1.76 11.179999 L 1.76 2.44 C 1.76 0.78 1.52 0.7 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.02 -0.02 1.76 0 2.56 0 C 3.32 0 3.98 -0.02 4.54 -0.04 C 4.66 0.08 4.66 0.5 4.54 0.62 C 3.52 0.7 3.34 0.78 3.34 2.44 Z "/>
</symbol>
<symbol id="g5925E4E4FE8F59A76637BD462660B390" overflow="visible">
<path d="M 3.6399999 7.16 C 3.1799998 7.8399997 3.32 7.8599997 4.22 7.96 C 4.3399997 8.08 4.3399997 8.5 4.22 8.62 C 3.6799998 8.599999 2.8 8.58 2.2 8.58 C 1.5999999 8.58 1 8.599999 0.48 8.62 C 0.35999998 8.5 0.35999998 8.08 0.48 7.96 C 1.16 7.8999996 1.7199999 7.56 2.28 6.74 L 4.02 4.2 C 4.12 4.06 4.12 4 4.04 3.8999999 L 2.36 1.74 C 1.56 0.71999997 1.12 0.65999997 0.42 0.62 C 0.29999998 0.5 0.29999998 0.08 0.42 -0.04 C 0.82 -0.02 1.26 0 1.86 0 C 2.46 0 3.02 -0.02 3.54 -0.04 C 3.6599998 0.08 3.6599998 0.5 3.54 0.62 C 2.82 0.7 2.6599998 0.78 3.1 1.42 L 4.36 3.24 C 4.52 3.48 4.6 3.46 4.72 3.28 L 5.8799996 1.68 C 6.58 0.71999997 6.2599998 0.68 5.62 0.62 C 5.5 0.5 5.5 0.08 5.62 -0.04 C 6.22 -0.02 6.8799996 0 7.6 0 C 8.36 0 8.9 -0.02 9.38 -0.04 C 9.5 0.08 9.5 0.5 9.38 0.62 C 8.48 0.68 8.179999 0.74 7.3799996 1.88 L 5.58 4.42 C 5.5 4.54 5.48 4.6 5.58 4.72 L 7.2599998 6.8599997 C 8 7.7999997 8.48 7.8999996 9.2 7.96 C 9.32 8.08 9.32 8.5 9.2 8.62 C 8.8 8.599999 8.34 8.58 7.74 8.58 C 7.14 8.58 6.58 8.599999 6.06 8.62 C 5.94 8.5 5.94 8.08 6.06 7.96 C 6.7999997 7.8799996 7.02 7.8199997 6.54 7.14 L 5.24 5.3199997 C 5.1 5.12 5.02 5.14 4.8599997 5.3599997 Z "/>
</symbol>
<symbol id="gC1513612DA0E34F2B247DB2830CD7DFD" overflow="visible">
<path d="M 1.24 4.6 C 1.24 3.34 2.26 2.32 3.52 2.32 C 4.7799997 2.32 5.7999997 3.34 5.7999997 4.6 C 5.7999997 5.8599997 4.7799997 6.8799996 3.52 6.8799996 C 2.26 6.8799996 1.24 5.8599997 1.24 4.6 Z "/>
</symbol>
<symbol id="g8934F85724FE2A1B73A1C811C5B32995" overflow="visible">
<path d="M 3.82 2.44 L 3.82 10.46 C 3.82 12.12 4.16 12.219999 5.56 12.28 C 5.68 12.4 5.68 12.82 5.56 12.94 C 4.68 12.92 3.74 12.9 2.96 12.9 C 2.3 12.9 1.3199999 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.28 -0.02 2.26 0 2.98 0 C 3.6999998 0 4.66 -0.02 5.56 -0.04 C 5.68 0.08 5.68 0.5 5.56 0.62 C 4.16 0.68 3.82 0.78 3.82 2.44 Z "/>
</symbol>
<symbol id="gC3F91E6BB9F8304E319658F9D45F8B38" overflow="visible">
<path d="M 8.96 12.28 C 10.44 12.179999 10.44 11.639999 10.0199995 10.559999 L 6.8599997 2.54 L 6.7799997 2.54 L 3.58 10.679999 C 3.12 11.88 3.24 12.139999 4.6 12.28 C 4.72 12.4 4.72 12.82 4.6 12.94 C 3.8 12.92 2.8999999 12.9 2.18 12.9 C 1.4599999 12.9 0.76 12.92 0.099999994 12.94 C -0.02 12.82 0 12.4 0.12 12.28 C 1.22 12.179999 1.38 11.84 1.92 10.46 L 5.8599997 0.22 C 5.98 -0.099999994 6.12 -0.24 6.3199997 -0.24 C 6.54 -0.24 6.68 -0.06 6.7999997 0.22 L 10.94 10.42 C 11.32 11.36 11.639999 12.139999 12.9 12.28 C 13.0199995 12.4 13.0199995 12.82 12.9 12.94 C 12.3 12.92 11.599999 12.9 11.139999 12.9 C 10.679999 12.9 9.78 12.92 8.96 12.94 C 8.84 12.82 8.84 12.4 8.96 12.28 Z "/>
</symbol>
<symbol id="g8D44D9C01F9AF6C3B1D634FDF54DE6FB" overflow="visible">
<path d="M 5.66 6.46 C 7.3599997 6.46 7.4199996 6 7.48 5.1 C 7.6 4.98 8.0199995 4.98 8.139999 5.1 C 8.12 5.6 8.099999 6.18 8.099999 6.8599997 C 8.099999 7.54 8.12 8.059999 8.139999 8.58 C 8.0199995 8.7 7.6 8.7 7.48 8.58 C 7.4199996 7.48 7.3599997 7.22 5.66 7.22 L 3.8 7.22 L 3.8 10.82 C 3.8 11.9 4.04 12.099999 4.92 12.099999 L 5.8199997 12.099999 C 7.94 12.099999 8.44 11.3 8.88 9.92 C 9.12 9.92 9.34 9.96 9.5 10.0199995 C 9.4 10.84 9.099999 12.759999 9.059999 12.92 C 9.059999 12.96 9.04 12.98 8.98 12.98 C 8.639999 12.92 8.54 12.9 8.04 12.9 L 2.9399998 12.9 C 2.3 12.9 1.16 12.92 0.35999998 12.94 C 0.24 12.82 0.24 12.4 0.35999998 12.28 C 1.76 12.219999 2.1 12.12 2.1 10.46 L 2.1 2.44 C 2.1 0.78 1.76 0.68 0.35999998 0.62 C 0.24 0.5 0.24 0.08 0.35999998 -0.04 C 1.06 -0.02 2.06 0 2.96 0 C 3.86 0 4.8399997 -0.02 5.54 -0.04 C 5.66 0.08 5.66 0.5 5.54 0.62 C 4.14 0.68 3.8 0.78 3.8 2.44 L 3.8 6.46 Z "/>
</symbol>
<symbol id="gFE29E79896646B3825DA2D41961151C9" overflow="visible">
<path d="M 2.96 12.9 C 2.24 12.9 1.16 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.16 -0.02 2.24 0 2.98 0 C 3.6999998 0 4.22 -0.04 5.9 -0.04 C 9.88 -0.04 10.94 1.9599999 10.94 3.6799998 C 10.94 5.6 9.599999 6.7 7.8599997 7.2 L 7.8599997 7.24 C 8.86 7.74 9.76 8.78 9.76 9.86 C 9.76 11.2 9.179999 12.94 5.46 12.94 C 4.7599998 12.94 3.6799998 12.9 2.96 12.9 Z M 3.82 6.64 L 5.2 6.64 C 7.94 6.64 9.08 5.1 9.08 3.3 C 9.08 1.8399999 8.5199995 0.62 5.48 0.62 C 4.08 0.62 3.82 1.14 3.82 2.36 Z M 3.82 11 C 3.82 12.059999 3.82 12.259999 5.56 12.259999 C 6.68 12.259999 8.139999 11.66 8.139999 9.62 C 8.139999 7.9199996 6.96 7.3199997 5.2999997 7.3199997 L 3.82 7.3199997 Z "/>
</symbol>
<symbol id="gB8789F2F5F06048D4163694E4C0F3B6C" overflow="visible">
<path d="M 12.36 2.44 L 12.36 10.46 C 12.36 12.12 12.7 12.219999 14.099999 12.28 C 14.219999 12.4 14.219999 12.82 14.099999 12.94 C 13.28 12.92 12.259999 12.9 11.5 12.9 C 10.76 12.9 9.8 12.92 8.92 12.94 C 8.8 12.82 8.8 12.4 8.92 12.28 C 10.32 12.219999 10.66 12.12 10.66 10.46 L 10.66 7.2599998 L 3.82 7.2599998 L 3.82 10.46 C 3.82 12.12 4.16 12.219999 5.56 12.28 C 5.68 12.4 5.68 12.82 5.56 12.94 C 4.7999997 12.92 3.98 12.9 2.96 12.9 C 1.9599999 12.9 1.14 12.92 0.38 12.94 C 0.26 12.82 0.26 12.4 0.38 12.28 C 1.78 12.219999 2.12 12.12 2.12 10.46 L 2.12 2.44 C 2.12 0.78 1.78 0.68 0.38 0.62 C 0.26 0.5 0.26 0.08 0.38 -0.04 C 1.26 -0.02 2.22 0 2.98 0 C 3.6999998 0 4.68 -0.02 5.56 -0.04 C 5.68 0.08 5.68 0.5 5.56 0.62 C 4.16 0.68 3.82 0.78 3.82 2.44 L 3.82 6.42 L 10.66 6.42 L 10.66 2.44 C 10.66 0.78 10.32 0.68 8.92 0.62 C 8.8 0.5 8.8 0.08 8.92 -0.04 C 9.82 -0.02 10.78 0 11.5199995 0 C 12.259999 0 13.219999 -0.02 14.099999 -0.04 C 14.219999 0.08 14.219999 0.5 14.099999 0.62 C 12.7 0.68 12.36 0.78 12.36 2.44 Z "/>
</symbol>
<symbol id="g560AC22EF992EFD90E66808483D7B3BA" overflow="visible">
<path d="M 11.12 10.24 L 11.12 3.6999998 C 11.12 3.32 11.12 3.1 10.98 3.1 C 10.9 3.1 10.599999 3.46 10.0199995 4.2 L 3.1599998 12.9 L 0.45999998 12.94 C 0.34 12.82 0.34 12.4 0.45999998 12.28 C 1.3199999 12.219999 1.92 11.5199995 2.04 11 L 2.04 2.6599998 C 2.04 0.88 1.6999999 0.76 0.29999998 0.62 C 0.17999999 0.5 0.17999999 0.08 0.29999998 -0.04 C 1.16 -0.02 2.06 0 2.54 0 C 3 0 3.9199998 -0.02 4.7599998 -0.04 C 4.88 0.08 4.88 0.5 4.7599998 0.62 C 3.36 0.76 3.02 0.84 3.02 2.6599998 L 3.02 8.78 C 3.02 9.46 3.02 9.76 3.1799998 9.76 C 3.3 9.76 3.52 9.54 3.86 9.099999 L 10.84 0.28 C 11.059999 -0.02 11.32 -0.19999999 11.639999 -0.19999999 C 11.92 -0.19999999 12.099999 0.04 12.099999 0.42 L 12.099999 10.24 C 12.099999 12.0199995 12.44 12.139999 13.84 12.28 C 13.96 12.4 13.96 12.82 13.84 12.94 C 13.0199995 12.92 12.08 12.9 11.599999 12.9 C 11.179999 12.9 10.26 12.92 9.38 12.94 C 9.26 12.82 9.26 12.4 9.38 12.28 C 10.78 12.139999 11.12 12.059999 11.12 10.24 Z "/>
</symbol>
<symbol id="g3BBBD96D467CC564123619D79E97B4D6" overflow="visible">
<path d="M 7.8999996 12.62 C 6.74 12.78 6.7799997 13.16 4.8199997 13.16 C 2.8 13.16 1.02 11.82 1.02 9.7 C 1.02 7.6 2.76 6.64 4.52 5.96 C 5.72 5.5 7.2 4.94 7.2 2.98 C 7.2 1.36 6.2999997 0.52 4.7 0.52 C 2.84 0.52 1.64 1.38 1.1999999 3.36 C 0.94 3.4399998 0.74 3.3999999 0.53999996 3.3 C 0.62 1.76 0.7 1.24 0.94 0.26 C 2.2 0.26 2.76 -0.19999999 4.54 -0.19999999 C 5.44 -0.19999999 6.2999997 0.02 7 0.45999998 C 8.16 1.18 8.88 2.3999999 8.88 3.6799998 C 8.88 5.7999997 7.2799997 6.74 5.64 7.3599997 C 4.44 7.7999997 2.44 8.559999 2.44 10.24 C 2.44 11.36 3.46 12.48 4.64 12.48 C 6.58 12.48 7.2 11.24 7.6 9.92 C 7.8199997 9.88 8.08 9.9 8.26 10.04 C 8.179999 11 8.099999 11.559999 7.8999996 12.62 Z "/>
</symbol>
<symbol id="g87DD77732F07A5C65A64D31E4C3C918D" overflow="visible">
<path d="M 16.199999 11.3 L 13.08 2.62 L 13.0199995 2.6399999 L 10.26 11.08 C 9.92 12.16 10.62 12.219999 11.3 12.28 C 11.42 12.4 11.42 12.82 11.3 12.94 C 10.48 12.92 9.599999 12.9 8.8 12.9 C 8.139999 12.9 7.44 12.92 6.7999997 12.94 C 6.68 12.82 6.68 12.4 6.7999997 12.28 C 7.8599997 12.219999 8.3 11.599999 8.48 11.08 L 8.94 9.76 C 9.0199995 9.5199995 9.08 9.32 9.08 9.139999 C 9.08 8.94 9.059999 8.78 8.9 8.44 L 6.3199997 2.58 L 6.22 2.6 L 3.3 11.44 C 3.06 12.139999 3.6 12.24 4.2999997 12.28 C 4.42 12.4 4.42 12.82 4.2999997 12.94 C 3.6399999 12.92 2.76 12.9 1.9799999 12.9 C 1.28 12.9 0.7 12.92 0.12 12.94 C 0 12.82 0 12.4 0.12 12.28 C 1.02 12.219999 1.16 12.2 1.54 11.12 L 5.2999997 0.29999998 C 5.4 -0.02 5.52 -0.24 5.74 -0.24 C 6 -0.24 6.12 -0.04 6.2599998 0.29999998 L 9.24 7 C 9.42 7.3999996 9.48 7.5 9.58 7.5 C 9.66 7.5 9.74 7.2799997 9.86 6.94 L 12.16 0.29999998 C 12.28 -0.04 12.38 -0.24 12.62 -0.24 C 12.84 -0.24 12.98 -0.02 13.08 0.28 L 17.1 11.059999 C 17.359999 11.759999 17.72 12.219999 18.82 12.28 C 18.939999 12.4 18.939999 12.82 18.82 12.94 C 18.24 12.92 17.6 12.9 17.08 12.9 C 16.56 12.9 15.679999 12.92 14.88 12.94 C 14.759999 12.82 14.759999 12.4 14.88 12.28 C 15.7 12.219999 16.5 12.16 16.199999 11.3 Z "/>
</symbol>
<symbol id="gA1481BA28623480CC7E6165783E2A864" overflow="visible">
<path d="M 4.06 7.96 C 4.18 8.08 4.18 8.5 4.06 8.62 C 3.46 8.599999 2.76 8.58 2.04 8.58 C 1.28 8.58 0.74 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.16 7.8599997 1.38 7.66 1.8 6.62 L 4.42 0.16 C 4.54 -0.12 4.7 -0.24 4.9 -0.24 C 5.08 -0.24 5.24 -0.12 5.38 0.19999999 L 7.3999996 5.12 L 9.46 0.16 C 9.58 -0.12 9.74 -0.24 9.94 -0.24 C 10.12 -0.24 10.28 -0.12 10.4 0.17999999 L 13.0199995 6.52 C 13.34 7.3399997 13.679999 7.8999996 14.7 7.96 C 14.82 8.08 14.82 8.5 14.7 8.62 C 14.299999 8.599999 13.86 8.58 13.259999 8.58 C 12.66 8.58 11.82 8.599999 11.219999 8.62 C 11.099999 8.5 11.099999 8.08 11.219999 7.96 C 12.719999 7.8799996 12.5199995 7.2999997 12.24 6.6 L 10.559999 2.44 C 10.36 1.9399999 10.28 1.9399999 10.12 2.36 L 8.4 6.74 C 8.0199995 7.68 8.059999 7.8799996 9.12 7.96 C 9.24 8.08 9.24 8.5 9.12 8.62 C 8.5199995 8.599999 7.72 8.58 7.12 8.58 C 6.62 8.58 5.96 8.599999 5.3599997 8.62 C 5.24 8.5 5.24 8.08 5.3599997 7.96 C 6.2999997 7.8799996 6.54 7.2999997 6.8999996 6.3999996 L 7.02 6.08 L 5.62 2.54 C 5.3599997 1.88 5.3199997 1.86 5.06 2.5 L 3.46 6.62 C 3.08 7.58 3.1 7.8999996 4.06 7.96 Z "/>
</symbol>
<symbol id="g17AD34DB90B05275C6F1422A9B4B5274" overflow="visible">
<path d="M 6.5 7.96 C 7.58 7.8799996 7.7 7.64 7.2799997 6.62 L 5.66 2.7 C 5.3399997 1.92 5.24 1.92 4.92 2.76 L 3.48 6.62 C 3.12 7.58 3.04 7.8199997 4.1 7.96 C 4.22 8.08 4.22 8.5 4.1 8.62 C 3.4399998 8.599999 2.74 8.58 2.08 8.58 C 1.42 8.58 0.82 8.599999 0.22 8.62 C 0.099999994 8.5 0.099999994 8.08 0.22 7.96 C 1.28 7.8399997 1.42 7.52 1.8199999 6.5 L 4.38 0.17999999 C 4.5 -0.12 4.62 -0.24 4.88 -0.24 C 5.08 -0.24 5.22 -0.12 5.3599997 0.22 L 8.0199995 6.48 C 8.4 7.3599997 8.62 7.8599997 9.74 7.96 C 9.86 8.08 9.86 8.5 9.74 8.62 C 9.34 8.599999 8.86 8.58 8.34 8.58 C 7.68 8.58 7 8.599999 6.5 8.62 C 6.3799996 8.5 6.3799996 8.08 6.5 7.96 Z "/>
</symbol>
<symbol id="gF1C3ABAD267D886F542252ABBAAA32" overflow="visible">
<path d="M 3.5 7.7999997 L 7.3799996 7.7999997 L 7.3799996 1.78 C 7.3799996 0.35999998 8 -0.19999999 8.92 -0.19999999 C 9.84 -0.19999999 10.84 0.24 11.62 1.12 C 11.58 1.3199999 11.46 1.4399999 11.259999 1.4599999 C 10.74 1.06 10.139999 0.9 9.62 0.9 C 9.08 0.9 8.96 1.5 8.96 2.74 L 8.96 7.7999997 L 11.04 7.7999997 C 11.24 7.7999997 11.5199995 7.8799996 11.5199995 8.059999 L 11.5199995 8.46 C 11.5199995 8.54 11.46 8.58 11.36 8.58 L 8.96 8.58 L 8.96 9.36 C 8.96 10.66 9.04 11.46 9.04 11.46 C 9.04 11.599999 8.96 11.66 8.78 11.66 L 7.62 11.139999 C 7.6 11.12 7.56 11.099999 7.52 11.08 C 7.4199996 11.04 7.3399997 10.98 7.3399997 10.88 C 7.3799996 10.44 7.3799996 10.26 7.3799996 8.8 C 7.3799996 8.72 7.3799996 8.66 7.3799996 8.58 L 3.5 8.58 L 3.5 9.719999 C 3.5 10.059999 3.5 10.4 3.5 10.7 C 3.48 11.54 3.46 12.179999 3.58 12.5199995 C 3.74 13 4.18 13.28 4.48 13.28 C 5.04 13.28 5.3199997 12.94 5.56 12.36 C 5.7 12.0199995 5.94 11.8 6.3399997 11.8 C 6.72 11.8 7 12.099999 7 12.5199995 C 7 12.84 6.8199997 13.179999 6.42 13.48 C 6.02 13.78 5.42 13.96 4.66 13.96 C 4.08 13.96 3.1599998 13.639999 2.6799998 13 C 2.08 12.2 1.92 11.139999 1.92 9.38 L 1.92 8.58 L 0.9 8.58 C 0.53999996 8.58 0.44 8.34 0.44 8.179999 L 0.44 7.9199996 C 0.44 7.8199997 0.45999998 7.7999997 0.53999996 7.7999997 L 1.92 7.7999997 L 1.92 2.44 C 1.92 0.78 1.6999999 0.7 0.62 0.62 C 0.5 0.5 0.5 0.08 0.62 -0.04 C 1.3 -0.02 2.02 0 2.72 0 C 3.4199998 0 4.2799997 -0.02 5.08 -0.04 C 5.2 0.08 5.2 0.5 5.08 0.62 C 3.72 0.7 3.5 0.78 3.5 2.44 Z "/>
</symbol>
<symbol id="g13CAD87D675A42FC6A129543D89F948C" overflow="visible">
<path d="M 5.7599998 2.44 L 5.7599998 9.38 C 5.7599998 10.58 5.7799997 11.8 5.8199997 12.059999 C 5.8199997 12.16 5.7799997 12.16 5.7 12.16 C 4.6 11.48 3.54 10.98 1.78 10.16 C 1.8199999 9.94 1.9 9.74 2.08 9.62 C 3 10 3.4399998 10.12 3.82 10.12 C 4.16 10.12 4.22 9.639999 4.22 8.96 L 4.22 2.44 C 4.22 0.78 3.6799998 0.68 2.28 0.62 C 2.1599998 0.5 2.1599998 0.08 2.28 -0.04 C 3.26 -0.02 3.98 0 5.06 0 C 6.02 0 6.5 -0.02 7.5 -0.04 C 7.62 0.08 7.62 0.5 7.5 0.62 C 6.1 0.68 5.7599998 0.78 5.7599998 2.44 Z "/>
</symbol>
<symbol id="g616EA0B06482AD9EB82F211B94D5D49E" overflow="visible">
<path d="M 4.56 -0.19999999 C 6.1 -0.19999999 8.44 1.36 8.44 6.06 C 8.44 8.04 7.96 9.74 7.08 10.9 C 6.56 11.599999 5.72 12.2 4.64 12.2 C 2.6599998 12.2 0.78 9.84 0.78 5.8799996 C 0.78 3.74 1.4399999 1.74 2.54 0.64 C 3.1 0.08 3.78 -0.19999999 4.56 -0.19999999 Z M 4.64 11.5 C 4.98 11.5 5.2999997 11.38 5.54 11.16 C 6.16 10.639999 6.7 9.12 6.7 6.44 C 6.7 4.6 6.64 3.34 6.3599997 2.32 C 5.92 0.68 4.94 0.5 4.58 0.5 C 2.72 0.5 2.52 3.9199998 2.52 5.66 C 2.52 10.58 3.74 11.5 4.64 11.5 Z "/>
</symbol>
<symbol id="g8C7315D77A5D71E18736DE61553C419F" overflow="visible">
<path d="M 1.4 1.1999999 C 1.4 0.62 1.88 0.14 2.46 0.14 C 3.04 0.14 3.52 0.62 3.52 1.1999999 C 3.52 1.78 3.04 2.26 2.46 2.26 C 1.88 2.26 1.4 1.78 1.4 1.1999999 Z M 1.4 7.16 C 1.4 6.58 1.88 6.1 2.46 6.1 C 3.04 6.1 3.52 6.58 3.52 7.16 C 3.52 7.74 3.04 8.22 2.46 8.22 C 1.88 8.22 1.4 7.74 1.4 7.16 Z "/>
</symbol>
<symbol id="gAA14E57E2DCC57A3F7809273EECD3C51" overflow="visible">
<path d="M 7.9104 1.5616 L 7.9104 6.6944 C 7.9104 7.7567997 8.128 7.8208 9.024 7.8592 C 9.1008 7.936 9.1008 8.2048 9.024 8.2816 C 8.4992 8.2688 7.8464 8.256 7.3599997 8.256 C 6.8863997 8.256 6.272 8.2688 5.7088 8.2816 C 5.632 8.2048 5.632 7.936 5.7088 7.8592 C 6.6047997 7.8208 6.8223996 7.7567997 6.8223996 6.6944 L 6.8223996 4.6464 L 2.4448 4.6464 L 2.4448 6.6944 C 2.4448 7.7567997 2.6624 7.8208 3.5584 7.8592 C 3.6352 7.936 3.6352 8.2048 3.5584 8.2816 C 3.072 8.2688 2.5472 8.256 1.8944 8.256 C 1.2544 8.256 0.72959995 8.2688 0.24319999 8.2816 C 0.1664 8.2048 0.1664 7.936 0.24319999 7.8592 C 1.1392 7.8208 1.3568 7.7567997 1.3568 6.6944 L 1.3568 1.5616 C 1.3568 0.4992 1.1392 0.43519998 0.24319999 0.39679998 C 0.1664 0.32 0.1664 0.0512 0.24319999 -0.0256 C 0.8064 -0.0128 1.4208 0 1.9072 0 C 2.368 0 2.9952 -0.0128 3.5584 -0.0256 C 3.6352 0.0512 3.6352 0.32 3.5584 0.39679998 C 2.6624 0.43519998 2.4448 0.4992 2.4448 1.5616 L 2.4448 4.1088 L 6.8223996 4.1088 L 6.8223996 1.5616 C 6.8223996 0.4992 6.6047997 0.43519998 5.7088 0.39679998 C 5.632 0.32 5.632 0.0512 5.7088 -0.0256 C 6.2848 -0.0128 6.8992 0 7.3728 0 C 7.8464 0 8.4608 -0.0128 9.024 -0.0256 C 9.1008 0.0512 9.1008 0.32 9.024 0.39679998 C 8.128 0.43519998 7.9104 0.4992 7.9104 1.5616 Z "/>
</symbol>
<symbol id="gF5F8064101DBF0FCB4BCFDA7012527FE" overflow="visible">
<path d="M 2.3167999 1.5616 L 2.3167999 4.1088 C 2.3167999 4.7488 2.368 5.568 2.368 5.568 C 2.368 5.6191998 2.304 5.6576 2.2015998 5.6576 C 1.8432 5.5168 1.3312 5.4016 0.44799998 5.2864 C 0.4224 5.2096 0.44799998 5.0048 0.4736 4.928 C 1.1776 4.864 1.3055999 4.7872 1.3055999 4.0576 L 1.3055999 1.5616 C 1.3055999 0.4992 1.1647999 0.4608 0.384 0.39679998 C 0.30719998 0.32 0.30719998 0.0512 0.384 -0.0256 C 0.8064 -0.0128 1.3055999 0 1.8176 0 C 2.3295999 0 2.816 -0.0128 3.2384 -0.0256 C 3.3151999 0.0512 3.3151999 0.32 3.2384 0.39679998 C 2.4575999 0.44799998 2.3167999 0.4992 2.3167999 1.5616 Z M 1.152 7.6671996 C 1.152 7.3343997 1.4591999 7.0016 1.7664 7.0016 C 2.1248 7.0016 2.432 7.3472 2.432 7.6159997 C 2.432 7.9231997 2.1632 8.2816 1.8176 8.2816 C 1.5103999 8.2816 1.152 7.9743996 1.152 7.6671996 Z "/>
</symbol>
<symbol id="g3976D55F213F07C6469FD06EC16139AA" overflow="visible">
<path d="M 4.9407997 1.1904 C 4.4672 0.704 4.0959997 0.4992 3.3536 0.4992 C 2.8927999 0.4992 2.3552 0.768 1.9583999 1.4208 C 1.7024 1.8432 1.5488 2.432 1.5488 3.1743999 L 4.9536 3.1488 C 5.1071997 3.1488 5.1967998 3.2256 5.1967998 3.3664 C 5.1967998 4.4416 4.8128 5.5936 3.0335999 5.5936 C 1.92 5.5936 0.4736 4.5312 0.4736 2.5856 C 0.4736 1.8687999 0.65279996 1.1776 1.0752 0.69119996 C 1.5103999 0.1792 2.112 -0.12799999 3.0335999 -0.12799999 C 4.0064 -0.12799999 4.6976 0.32 5.2096 0.9856 C 5.1712 1.1136 5.0944 1.1776 4.9407997 1.1904 Z M 1.5871999 3.6095998 C 1.8304 5.0559998 2.7264 5.1712 3.0335999 5.1712 C 3.52 5.1712 4.0959997 4.9024 4.0959997 3.8272 C 4.0959997 3.712 4.0448 3.648 3.9039998 3.648 Z "/>
</symbol>
<symbol id="gB7BB853387AAC07ADB7DDEF96856059B" overflow="visible">
<path d="M 2.2528 4.5824 C 2.2272 5.0944 2.2144 5.4272 2.1504 5.5551996 C 2.1248 5.6191998 2.0992 5.6576 1.9968 5.6576 C 1.6384 5.5168 1.3055999 5.4016 0.4224 5.2864 C 0.39679998 5.2096 0.4224 5.0048 0.44799998 4.928 C 1.1392 4.864 1.28 4.7999997 1.28 4.0576 L 1.28 1.5616 C 1.28 0.4992 1.1264 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7808 -0.0128 1.28 0 1.7919999 0 C 2.304 0 2.8927999 -0.0128 3.3407998 -0.0256 C 3.4176 0.0512 3.4176 0.32 3.3407998 0.39679998 C 2.4448 0.4608 2.2912 0.4992 2.2912 1.5616 L 2.2912 3.3407998 C 2.2912 3.6736 2.4448 3.968 2.5983999 4.1984 C 2.7391999 4.4031997 3.0335999 4.8255997 3.1871998 4.8255997 C 3.3023999 4.8255997 3.4176 4.7999997 3.52 4.6591997 C 3.6095998 4.5312 3.7631998 4.3648 3.9808 4.3648 C 4.288 4.3648 4.5824 4.6847997 4.5824 5.0048 C 4.5824 5.2479997 4.3519998 5.6191998 3.8144 5.6191998 C 3.2128 5.6191998 2.688 5.0559998 2.3936 4.5568 C 2.3167999 4.416 2.2528 4.5183997 2.2528 4.5824 Z "/>
</symbol>
<symbol id="gF8EC31AC53CF59E01ED9143906F6DA7B" overflow="visible">
<path d="M 3.7503998 0.61439997 C 3.8272 0.21759999 3.968 -0.12799999 4.608 -0.12799999 C 5.0944 -0.12799999 5.5551996 0.0896 5.824 0.34559998 C 5.7984 0.4992 5.7472 0.61439997 5.6064 0.69119996 C 5.5168 0.61439997 5.2992 0.48639998 5.1328 0.48639998 C 4.7616 0.48639998 4.7488 0.9856 4.7488 1.5744 L 4.7488 3.4559999 C 4.7488 5.2736 3.7503998 5.6191998 2.816 5.6191998 C 1.7664 5.6191998 0.704 4.928 0.704 4.1984 C 0.704 3.8911998 0.8576 3.7375998 1.152 3.7375998 C 1.5231999 3.7375998 1.7536 4.0064 1.7536 4.1728 C 1.7536 4.2623997 1.7407999 4.3519998 1.7152 4.4031997 C 1.7024 4.4416 1.6896 4.5183997 1.6896 4.6591997 C 1.6896 5.0559998 2.2272 5.1967998 2.7136 5.1967998 C 3.1488 5.1967998 3.7503998 4.9792 3.7503998 3.5328 C 3.7503998 3.4431999 3.712 3.392 3.6736 3.3792 L 2.5728 3.1104 C 1.344 2.8032 0.4608 2.1248 0.4608 1.2544 C 0.4608 0.2048 1.1776 -0.12799999 2.0736 -0.12799999 C 2.5216 -0.12799999 2.9055998 -0.0256 3.4687998 0.4096 L 3.7247999 0.61439997 Z M 3.7503998 2.9824 L 3.7503998 1.2928 C 3.7503998 1.1264 3.6736 1.0368 3.5712 0.96 C 3.2384 0.69119996 2.8032 0.39679998 2.4448 0.39679998 C 1.8047999 0.39679998 1.5231999 0.9088 1.5231999 1.3055999 C 1.5231999 1.8815999 1.7919999 2.4703999 2.7391999 2.7136 Z "/>
</symbol>
<symbol id="g68DDE7C8FDC8A226B6C32EAD39AF7364" overflow="visible">
<path d="M 5.0944 1.1647999 C 5.0432 1.28 4.9407997 1.3312 4.8255997 1.344 C 4.3904 0.7808 3.84 0.4992 3.2896 0.4992 C 2.3552 0.4992 1.5744 1.4463999 1.5744 2.944 C 1.5744 4.3519998 2.1887999 5.1967998 3.0335999 5.1967998 C 3.7888 5.1967998 3.8911998 4.7488 3.9424 4.3008 C 3.9808 3.9552 4.16 3.84 4.4288 3.84 C 4.6976 3.84 5.0559998 4.0064 5.0559998 4.4031997 C 5.0559998 5.1071997 4.3264 5.6191998 3.0976 5.6191998 C 1.8304 5.6191998 0.4736 4.48 0.4736 2.6624 C 0.4736 1.0112 1.3952 -0.12799999 3.008 -0.12799999 C 3.776 -0.12799999 4.4544 0.1152 5.0944 1.1647999 Z "/>
</symbol>
<symbol id="g570B752173035444311A253BD2376AD" overflow="visible">
<path d="M 2.1376 3.6608 C 2.1376 3.9296 2.2528 4.0832 2.3552 4.1984 C 2.8416 4.672 3.4944 4.9536 3.9936 4.9536 C 4.2496 4.9536 4.5183997 4.7872 4.672 4.4927998 C 4.7999997 4.2367997 4.8255997 3.8911998 4.8255997 3.5072 L 4.8255997 1.5616 C 4.8255997 0.51199996 4.6976 0.4608 4.032 0.39679998 C 3.968 0.32 3.968 0.0512 4.032 -0.0256 C 4.3904 -0.0128 4.8255997 0 5.3375998 0 C 5.8496 0 6.272 -0.0128 6.6944 -0.0256 C 6.7584 0.0512 6.7584 0.32 6.6944 0.39679998 C 5.9775996 0.4608 5.8367996 0.51199996 5.8367996 1.5616 L 5.8367996 3.4687998 C 5.8367996 4.1728 5.7855997 4.7999997 5.4912 5.184 C 5.2736 5.4656 4.8768 5.6191998 4.4288 5.6191998 C 3.8016 5.6191998 3.0335999 5.4528 2.2528 4.5824 C 2.2528 4.5696 2.24 4.5696 2.2272 4.5568 C 2.1887999 4.5056 2.1248 4.4288 2.1248 4.5824 L 2.1376 7.4624 C 2.1376 8.2944 2.1887999 8.806399 2.1887999 8.806399 C 2.1887999 8.896 2.1376 8.9344 2.0224 8.9344 C 1.7024 8.806399 0.7424 8.6272 0.2304 8.588799 C 0.2048 8.4864 0.2304 8.2816 0.30719998 8.2048 C 0.34559998 8.2048 0.384 8.2048 0.4224 8.2048 C 0.9856 8.1664 1.1264 8.1664 1.1264 7.1552 L 1.1264 1.5616 C 1.1264 0.4992 0.97279996 0.44799998 0.2304 0.39679998 C 0.15359999 0.32 0.15359999 0.0512 0.2304 -0.0256 C 0.65279996 -0.0128 1.1264 0 1.6384 0 C 2.1248 0 2.5472 -0.0128 2.9055998 -0.0256 C 2.9824 0.0512 2.9824 0.32 2.9055998 0.39679998 C 2.2528 0.44799998 2.1376 0.4992 2.1376 1.5616 Z "/>
</symbol>
<symbol id="g9662C1D9A80FEB5040A57FD9DFCA7985" overflow="visible">
<path d="M 1.216 1.5616 C 1.216 0.4992 1.0752 0.43519998 0.2944 0.39679998 C 0.21759999 0.32 0.21759999 0.0512 0.2944 -0.0256 C 0.7424 -0.0128 1.216 0 1.7279999 0 C 2.24 0 2.7264 -0.0128 3.1488 -0.0256 C 3.2256 0.0512 3.2256 0.32 3.1488 0.39679998 C 2.368 0.43519998 2.2272 0.4992 2.2272 1.5616 L 2.2272 7.4624 C 2.2272 8.2944 2.2784 8.806399 2.2784 8.806399 C 2.2784 8.896 2.2272 8.9344 2.112 8.9344 C 1.7919999 8.806399 0.83199996 8.6272 0.32 8.588799 C 0.2944 8.4864 0.32 8.2816 0.39679998 8.2048 C 1.1392 8.1536 1.216 8.1152 1.216 7.1552 Z "/>
</symbol>
<symbol id="g1CB3EC9D05726EBFDE8ADABEC8504FCD" overflow="visible">
<path d="M 7.1168 6.5536 L 7.1168 2.368 C 7.1168 2.1248 7.1168 1.984 7.0271997 1.984 C 6.976 1.984 6.784 2.2144 6.4128 2.688 L 2.0224 8.256 L 0.2944 8.2816 C 0.21759999 8.2048 0.21759999 7.936 0.2944 7.8592 C 0.8448 7.8208 1.2287999 7.3728 1.3055999 7.04 L 1.3055999 1.7024 C 1.3055999 0.5632 1.0879999 0.48639998 0.192 0.39679998 C 0.1152 0.32 0.1152 0.0512 0.192 -0.0256 C 0.7424 -0.0128 1.3184 0 1.6256 0 C 1.92 0 2.5088 -0.0128 3.0463998 -0.0256 C 3.1232 0.0512 3.1232 0.32 3.0463998 0.39679998 C 2.1504 0.48639998 1.9327999 0.5376 1.9327999 1.7024 L 1.9327999 5.6191998 C 1.9327999 6.0544 1.9327999 6.2464 2.0351999 6.2464 C 2.112 6.2464 2.2528 6.1056 2.4703999 5.824 L 6.9375997 0.1792 C 7.0783997 -0.0128 7.2447996 -0.12799999 7.4495997 -0.12799999 C 7.6288 -0.12799999 7.744 0.0256 7.744 0.2688 L 7.744 6.5536 C 7.744 7.6927996 7.9616 7.7696 8.8576 7.8592 C 8.9344 7.936 8.9344 8.2048 8.8576 8.2816 C 8.3328 8.2688 7.7311997 8.256 7.424 8.256 C 7.1552 8.256 6.5664 8.2688 6.0032 8.2816 C 5.9263997 8.2048 5.9263997 7.936 6.0032 7.8592 C 6.8992 7.7696 7.1168 7.7184 7.1168 6.5536 Z "/>
</symbol>
<symbol id="gD62975B7DE3250BE5F195D0E8335F60D" overflow="visible">
<path d="M 4.16 5.0944 C 4.8512 5.0432 4.928 4.8896 4.6591997 4.2367997 L 3.6223998 1.7279999 C 3.4176 1.2287999 3.3536 1.2287999 3.1488 1.7664 L 2.2272 4.2367997 C 1.9968 4.8512 1.9455999 5.0048 2.6239998 5.0944 C 2.7008 5.1712 2.7008 5.44 2.6239998 5.5168 C 2.2015998 5.5039997 1.7536 5.4912 1.3312 5.4912 C 0.9088 5.4912 0.5248 5.5039997 0.1408 5.5168 C 0.063999996 5.44 0.063999996 5.1712 0.1408 5.0944 C 0.8192 5.0176 0.9088 4.8128 1.1647999 4.16 L 2.8032 0.1152 C 2.8799999 -0.076799996 2.9568 -0.15359999 3.1232 -0.15359999 C 3.2512 -0.15359999 3.3407998 -0.076799996 3.4304 0.1408 L 5.1328 4.1472 C 5.376 4.7104 5.5168 5.0304 6.2335997 5.0944 C 6.3104 5.1712 6.3104 5.44 6.2335997 5.5168 C 5.9775996 5.5039997 5.6703997 5.4912 5.3375998 5.4912 C 4.9151998 5.4912 4.48 5.5039997 4.16 5.5168 C 4.0832 5.44 4.0832 5.1712 4.16 5.0944 Z "/>
</symbol>
<symbol id="gEFCBD5CCFA072E8B49E2065B449FDBBF" overflow="visible">
<path d="M 5.6832 4.9536 C 5.9263997 4.9536 6.1568 5.184 6.1568 5.44 C 6.1568 5.7088 5.9136 5.9136 5.568 5.9136 C 5.2352 5.9136 4.6208 5.6959996 4.288 5.2608 C 4.1344 5.3631997 3.712 5.6191998 2.9568 5.6191998 C 1.8176 5.6191998 0.768 4.8512 0.768 3.6736 C 0.768 2.9824 1.0752 2.5856 1.4336 2.24 C 1.0752 1.9327999 0.87039995 1.3823999 0.87039995 0.9472 C 0.87039995 0.48639998 1.1264 0.12799999 1.4591999 -0.038399998 C 0.768 -0.44799998 0.4096 -1.0368 0.4096 -1.5871999 C 0.4096 -2.7008 1.4591999 -3.0463998 2.4448 -3.0463998 C 4.1728 -3.0463998 6.0415998 -2.2144 6.0415998 -0.83199996 C 6.0415998 -0.4224 5.8496 -0.1024 5.4783998 0.2048 C 4.9792 0.61439997 4.0832 0.6272 3.6095998 0.6272 C 3.3792 0.6272 3.0591998 0.6016 2.7519999 0.5632 C 2.56 0.55039996 2.432 0.5376 2.368 0.5376 C 1.9968 0.5376 1.5488 0.7168 1.5488 1.2672 C 1.5488 1.5231999 1.6256 1.7919999 1.7792 2.0096 C 2.0864 1.8304 2.4448 1.7407999 2.944 1.7407999 C 4.0703998 1.7407999 5.1071997 2.4448 5.1071997 3.6992 C 5.1071997 4.3008 4.928 4.6464 4.5568 5.0304 C 4.6464 5.1584 4.9024 5.3375998 5.0688 5.3375998 C 5.1584 5.3375998 5.2479997 5.2992 5.3248 5.184 C 5.376 5.0815997 5.5424 4.9536 5.6832 4.9536 Z M 1.6896 -0.12799999 C 1.8304 -0.1664 2.0351999 -0.192 2.2015998 -0.192 C 2.5983999 -0.192 2.9568 -0.15359999 3.136 -0.15359999 C 3.776 -0.15359999 4.3136 -0.1664 4.6847997 -0.3712 C 5.184 -0.65279996 5.3375998 -0.83199996 5.3375998 -1.1647999 C 5.3375998 -2.0864 3.9808 -2.5728 2.8288 -2.5728 C 2.368 -2.5728 1.2928 -2.2015998 1.2928 -1.3312 C 1.2928 -0.89599997 1.3184 -0.576 1.6896 -0.12799999 Z M 4.0832 3.5712 C 4.0832 2.3808 3.4815998 2.1376 3.008 2.1376 C 1.9327999 2.1376 1.8176 3.0463998 1.8176 3.8655999 C 1.8176 4.7616 2.1376 5.2223997 2.8416 5.2223997 C 3.648 5.2223997 4.0832 4.6335998 4.0832 3.5712 Z "/>
</symbol>
<symbol id="gD5EEFB9760BC9A91B84F628EDDA52971" overflow="visible">
<path d="M 2.1376 5.0432 C 2.0607998 4.9663997 2.0096 4.992 2.0096 5.1071997 L 2.0096 7.4624 C 2.0096 8.2944 2.0607998 8.806399 2.0607998 8.806399 C 2.0607998 8.896 2.0096 8.9344 1.8944 8.9344 C 1.5744 8.806399 0.61439997 8.6272 0.1024 8.588799 C 0.076799996 8.4864 0.1024 8.2816 0.1792 8.2048 C 0.21759999 8.2048 0.25599998 8.2048 0.2944 8.2048 C 0.8576 8.1664 0.9984 8.1664 0.9984 7.1552 L 0.9984 0.9088 C 0.9984 0.4096 0.9856 0.1792 0.9472 0 C 1.0112 -0.1024 1.0752 -0.15359999 1.2287999 -0.15359999 C 1.3055999 -0.076799996 1.4336 0.038399998 1.536 0.15359999 C 1.6639999 0.30719998 1.7407999 0.30719998 1.8815999 0.192 C 2.1759999 -0.0512 2.56 -0.12799999 3.008 -0.12799999 C 4.3136 -0.12799999 5.8367996 1.0624 5.8367996 3.0976 C 5.8367996 4.6591997 4.6847997 5.6191998 3.5712 5.6191998 C 3.0207999 5.6191998 2.5344 5.4016 2.1376 5.0432 Z M 2.2272 4.6464 C 2.56 4.9407997 2.944 5.0559998 3.3151999 5.0559998 C 4.0959997 5.0559998 4.736 4.1088 4.736 2.8672 C 4.736 1.408 4.1472 0.30719998 2.9312 0.30719998 C 2.5344 0.30719998 2.2656 0.5888 2.0096 0.9088 L 2.0096 4.1088 C 2.0096 4.3775997 2.0607998 4.5056 2.2272 4.6464 Z "/>
</symbol>
<symbol id="g83A6AA7A836EACB3652229F4716CDAF" overflow="visible">
<path d="M 5.0559998 8.076799 C 4.3136 8.1792 4.3392 8.4223995 3.0848 8.4223995 C 1.7919999 8.4223995 0.65279996 7.5648 0.65279996 6.2079997 C 0.65279996 4.864 1.7664 4.2496 2.8927999 3.8144 C 3.6608 3.52 4.608 3.1615999 4.608 1.9072 C 4.608 0.87039995 4.032 0.3328 3.008 0.3328 C 1.8176 0.3328 1.0496 0.8832 0.768 2.1504 C 0.6016 2.2015998 0.4736 2.1759999 0.34559998 2.112 C 0.39679998 1.1264 0.44799998 0.79359996 0.6016 0.1664 C 1.408 0.1664 1.7664 -0.12799999 2.9055998 -0.12799999 C 3.4815998 -0.12799999 4.032 0.0128 4.48 0.2944 C 5.2223997 0.75519997 5.6832 1.536 5.6832 2.3552 C 5.6832 3.712 4.6591997 4.3136 3.6095998 4.7104 C 2.8416 4.992 1.5616 5.4783998 1.5616 6.5536 C 1.5616 7.2704 2.2144 7.9872 2.9696 7.9872 C 4.2111998 7.9872 4.608 7.1935997 4.864 6.3487997 C 5.0048 6.3231997 5.1712 6.336 5.2864 6.4256 C 5.2352 7.04 5.184 7.3984 5.0559998 8.076799 Z "/>
</symbol>
<symbol id="gDB4862E33098F259EEBBA99A57E5AFA" overflow="visible">
<path d="M 2.1759999 4.5824 C 2.1632 4.9663997 2.1376 5.4272 2.0736 5.5551996 C 2.0479999 5.6191998 2.0224 5.6576 1.92 5.6576 C 1.5616 5.5168 1.2287999 5.4016 0.34559998 5.2864 C 0.32 5.2096 0.34559998 5.0048 0.3712 4.928 C 1.0624 4.864 1.2032 4.7999997 1.2032 4.0576 L 1.2032 1.5616 C 1.2032 0.51199996 1.0368 0.44799998 0.3328 0.39679998 C 0.25599998 0.32 0.25599998 0.0512 0.3328 -0.0256 C 0.7168 -0.0128 1.2032 0 1.7152 0 C 2.2272 0 2.6239998 -0.0128 3.008 -0.0256 C 3.0848 0.0512 3.0848 0.32 3.008 0.39679998 C 2.3552 0.4608 2.2144 0.51199996 2.2144 1.5616 L 2.2144 3.6608 C 2.2144 3.9296 2.3295999 4.0832 2.432 4.1984 C 2.944 4.6976 3.4176 4.9536 3.8144 4.9536 C 4.3008 4.9536 4.6591997 4.6464 4.6591997 3.7888 L 4.6591997 1.5616 C 4.6591997 0.51199996 4.5568 0.44799998 3.8655999 0.39679998 C 3.8016 0.32 3.8016 0.0512 3.8655999 -0.0256 C 4.1856 -0.0128 4.6591997 0 5.1712 0 C 5.6832 0 6.1056 -0.0128 6.4256 -0.0256 C 6.4895997 0.0512 6.4895997 0.32 6.4256 0.39679998 C 5.7855997 0.44799998 5.6703997 0.51199996 5.6703997 1.5616 L 5.6703997 3.5967999 C 5.6703997 3.776 5.6703997 3.9552 5.6576 4.1088 C 6.272 4.7872 6.848 4.9536 7.3472 4.9536 C 7.8335996 4.9536 8.1152 4.672 8.1152 3.8144 L 8.1152 1.5616 C 8.1152 0.51199996 7.9872 0.44799998 7.3216 0.39679998 C 7.2576 0.32 7.2576 0.0512 7.3216 -0.0256 C 7.6415997 -0.0128 8.1152 0 8.6272 0 C 9.1392 0 9.5872 -0.0128 9.9456 -0.0256 C 10.0096 0.0512 10.0096 0.32 9.9456 0.39679998 C 9.2416 0.44799998 9.1264 0.51199996 9.1264 1.5616 L 9.1264 3.5839999 C 9.1264 4.7232 8.9344 5.6191998 7.8079996 5.6191998 C 7.1552 5.6191998 6.3616 5.376 5.6959996 4.672 C 5.6576 4.6335998 5.5808 4.5696 5.5551996 4.6847997 C 5.44 5.2096 4.9407997 5.6191998 4.2752 5.6191998 C 3.5328 5.6191998 2.8672 5.184 2.3295999 4.5824 C 2.2656 4.5183997 2.1887999 4.4288 2.1759999 4.5824 Z "/>
</symbol>
<symbol id="g793DBE65A5AEC1A16A65955B6C0E046" overflow="visible">
<path d="M 10.368 7.232 L 8.3712 1.6768 L 8.3328 1.6896 L 6.5664 7.0912 C 6.3487997 7.7823997 6.7967997 7.8208 7.232 7.8592 C 7.3087997 7.936 7.3087997 8.2048 7.232 8.2816 C 6.7072 8.2688 6.144 8.256 5.632 8.256 C 5.2096 8.256 4.7616 8.2688 4.3519998 8.2816 C 4.2752 8.2048 4.2752 7.936 4.3519998 7.8592 C 5.0304 7.8208 5.312 7.424 5.4272 7.0912 L 5.7216 6.2464 C 5.7728 6.0927997 5.8111997 5.9648 5.8111997 5.8496 C 5.8111997 5.7216 5.7984 5.6191998 5.6959996 5.4016 L 4.0448 1.6511999 L 3.9808 1.6639999 L 2.112 7.3216 C 1.9583999 7.7696 2.304 7.8335996 2.7519999 7.8592 C 2.8288 7.936 2.8288 8.2048 2.7519999 8.2816 C 2.3295999 8.2688 1.7664 8.256 1.2672 8.256 C 0.8192 8.256 0.44799998 8.2688 0.076799996 8.2816 C 0 8.2048 0 7.936 0.076799996 7.8592 C 0.65279996 7.8208 0.7424 7.8079996 0.9856 7.1168 L 3.392 0.192 C 3.4559999 -0.0128 3.5328 -0.15359999 3.6736 -0.15359999 C 3.84 -0.15359999 3.9167998 -0.0256 4.0064 0.192 L 5.9136 4.48 C 6.0288 4.736 6.0671997 4.7999997 6.1312 4.7999997 C 6.1823997 4.7999997 6.2335997 4.6591997 6.3104 4.4416 L 7.7823997 0.192 C 7.8592 -0.0256 7.9231997 -0.15359999 8.076799 -0.15359999 C 8.2176 -0.15359999 8.3071995 -0.0128 8.3712 0.1792 L 10.943999 7.0783997 C 11.110399 7.5263996 11.340799 7.8208 12.0448 7.8592 C 12.1216 7.936 12.1216 8.2048 12.0448 8.2816 C 11.673599 8.2688 11.264 8.256 10.9312 8.256 C 10.5984 8.256 10.0352 8.2688 9.5232 8.2816 C 9.4464 8.2048 9.4464 7.936 9.5232 7.8592 C 10.047999 7.8208 10.559999 7.7823997 10.368 7.232 Z "/>
</symbol>
<symbol id="gA11612CECC8CBEF18835767DAB11B2F7" overflow="visible">
<path d="M 0.5248 2.6239998 C 0.5248 1.3184 1.3952 -0.12799999 3.2128 -0.12799999 C 4.032 -0.12799999 4.6591997 0.1664 5.0944 0.5888 C 5.6703997 1.152 5.9263997 1.9583999 5.9263997 2.7391999 C 5.9263997 4.0703998 5.1967998 5.6191998 3.2384 5.6191998 C 2.3936 5.6191998 1.7024 5.2736 1.2287999 4.7232 C 0.768 4.1728 0.5248 3.4304 0.5248 2.6239998 Z M 3.0463998 5.1712 C 4.1472 5.1712 4.8255997 4.1728 4.8255997 2.3295999 C 4.8255997 0.7168 3.9936 0.32 3.392 0.32 C 2.0607998 0.32 1.6256 1.9327999 1.6256 2.9183998 C 1.6256 4.032 1.8944 5.1712 3.0463998 5.1712 Z "/>
</symbol>
<symbol id="gCEFEF3D67F35C6E83CC3757B1DD21B13" overflow="visible">
<path d="M 4.2752 0.64 C 4.3392 0.69119996 4.4544 0.7168 4.4672 0.6272 C 4.5056 0.32 4.608 -0.12799999 4.608 -0.12799999 C 4.7104 -0.1664 4.7743998 -0.15359999 4.8512 -0.12799999 C 5.1328 0.1024 5.5808 0.2944 6.3616 0.384 C 6.4384 0.4608 6.4384 0.65279996 6.3616 0.72959995 C 5.5424 0.79359996 5.4272 1.0368 5.4272 1.6639999 L 5.4272 7.4624 C 5.4272 8.2944 5.4783998 8.806399 5.4783998 8.806399 C 5.4783998 8.896 5.4272 8.9344 5.312 8.9344 C 4.992 8.806399 4.032 8.6272 3.52 8.588799 C 3.4944 8.4864 3.52 8.2816 3.5967999 8.2048 C 3.6352 8.2048 3.6736 8.2048 3.712 8.2048 C 4.2752 8.1664 4.416 8.1664 4.416 7.1552 L 4.416 5.5168 C 4.416 5.4272 4.3904 5.4016 4.3008 5.4016 C 4.2496 5.4016 3.7247999 5.6191998 3.3023999 5.6191998 C 2.4575999 5.6191998 1.8944 5.3375998 1.3823999 4.8512 C 0.83199996 4.3008 0.4992 3.5456 0.4992 2.5983999 C 0.4992 1.0239999 1.2928 -0.12799999 2.6752 -0.12799999 C 3.1743999 -0.12799999 3.648 0.12799999 4.2752 0.64 Z M 4.416 1.5871999 C 4.416 1.344 4.3904 1.2415999 4.2111998 1.0879999 C 3.7375998 0.6784 3.3279998 0.4736 3.008 0.4736 C 2.3167999 0.4736 1.5999999 1.2287999 1.5999999 2.8288 C 1.5999999 3.7503998 1.7792 4.2623997 1.9712 4.5312 C 2.368 5.1328 2.9055998 5.1712 3.1615999 5.1712 C 3.6223998 5.1712 3.9424 5.0048 4.1984 4.7104 C 4.3775997 4.5056 4.416 4.416 4.416 4.0192 Z "/>
</symbol>
<symbol id="g645CA8FA3D9155E2CBD9F8EED3C1540D" overflow="visible">
<path d="M 1.9968 4.7104 C 1.984 5.0944 1.9583999 5.4272 1.8944 5.5551996 C 1.8687999 5.6191998 1.8432 5.6576 1.7407999 5.6576 C 1.3823999 5.5168 1.0496 5.4016 0.1664 5.2864 C 0.1408 5.2096 0.1664 5.0048 0.192 4.928 C 0.8832 4.864 1.0239999 4.7999997 1.0239999 4.0576 L 1.0239999 -1.408 C 1.0239999 -2.4703999 0.8832 -2.5344 0.1024 -2.5728 C 0.0256 -2.6496 0.0256 -2.9183998 0.1024 -2.9952 C 0.55039996 -2.9824 1.0239999 -2.9696 1.536 -2.9696 C 2.0479999 -2.9696 2.6624 -2.9824 3.0848 -2.9952 C 3.1615999 -2.9183998 3.1615999 -2.6496 3.0848 -2.5728 C 2.1759999 -2.5216 2.0351999 -2.4703999 2.0351999 -1.408 L 2.0351999 -0.0256 C 2.0351999 0.1408 2.0864 0.12799999 2.2144 0.076799996 C 2.5344 -0.0512 2.9183998 -0.12799999 3.3279998 -0.12799999 C 4.0448 -0.12799999 4.6847997 0.0896 5.2096 0.5888 C 5.8111997 1.1776 6.1568 1.9712 6.1568 3.008 C 6.1568 4.3648 5.1967998 5.6191998 3.8911998 5.6191998 C 3.3023999 5.6191998 2.6496 5.2352 2.1376 4.6591997 C 2.0607998 4.5824 2.0096 4.5824 1.9968 4.7104 Z M 2.24 4.2367997 C 2.5728 4.6464 3.1615999 5.0304 3.5328 5.0304 C 4.3519998 5.0304 5.0559998 4.1088 5.0559998 2.6624 C 5.0559998 1.6128 4.6847997 0.30719998 3.2512 0.30719998 C 3.0207999 0.30719998 2.5728 0.3712 2.3423998 0.576 C 2.0864 0.8064 2.0351999 0.8832 2.0351999 1.344 L 2.0351999 3.6736 C 2.0351999 3.9424 2.0864 4.0576 2.24 4.2367997 Z "/>
</symbol>
<symbol id="g18211A4637362A458F3F8DC5AA4C67BF" overflow="visible">
<path d="M 4.6080003 1.9520001 L 4.6080003 7.504 C 4.6080003 8.464001 4.624 9.440001 4.656 9.648001 C 4.656 9.728001 4.624 9.728001 4.5600004 9.728001 C 3.68 9.184 2.832 8.784 1.424 8.128 C 1.4560001 7.952 1.5200001 7.7920003 1.664 7.6960006 C 2.4 8 2.752 8.096001 3.0560002 8.096001 C 3.328 8.096001 3.3760002 7.7120004 3.3760002 7.168 L 3.3760002 1.9520001 C 3.3760002 0.624 2.9440002 0.544 1.8240001 0.49600002 C 1.728 0.4 1.728 0.064 1.8240001 -0.032 C 2.608 -0.016 3.1840003 0 4.0480003 0 C 4.8160005 0 5.2000003 -0.016 6.0000005 -0.032 C 6.096 0.064 6.096 0.4 6.0000005 0.49600002 C 4.88 0.544 4.6080003 0.624 4.6080003 1.9520001 Z "/>
</symbol>
<symbol id="g6271973D35E483E673220139289FB3C5" overflow="visible">
<path d="M 0.9760001 7.4880004 C 0.9760001 7.1520004 1.2800001 6.8640003 1.616 6.8640003 C 1.8880001 6.8640003 2.368 7.1520004 2.368 7.504 C 2.368 7.6320004 2.3360002 7.728 2.3040001 7.84 C 2.272 7.952 2.176 8.096001 2.176 8.224 C 2.176 8.624001 2.592 9.200001 3.7600002 9.200001 C 4.3360004 9.200001 5.1520004 8.8 5.1520004 7.2640004 C 5.1520004 6.2400002 4.7840004 5.4080005 3.8400002 4.4480004 L 2.6560001 3.2800002 C 1.088 1.6800001 0.832 0.91200006 0.832 -0.032 C 0.832 -0.032 1.6480001 0 2.16 0 L 4.96 0 C 5.472 0 6.208 -0.032 6.208 -0.032 C 6.4160004 0.81600004 6.576 2.016 6.5920005 2.496 C 6.4960003 2.5760002 6.288 2.608 6.1280003 2.5760002 C 5.8560004 1.44 5.584 1.0400001 5.0080004 1.0400001 L 2.16 1.0400001 C 2.16 1.8080001 3.2640002 2.8960001 3.344 2.976 L 4.96 4.5280004 C 5.872 5.4080005 6.5600004 6.1120005 6.5600004 7.3280005 C 6.5600004 9.056001 5.1520004 9.76 3.8560002 9.76 C 2.0800002 9.76 0.9760001 8.448 0.9760001 7.4880004 Z "/>
</symbol>
<symbol id="g6AD8B6A1EC3B7A5AED163A4B2FEB1C10" overflow="visible">
<path d="M 4.688 10.336 L 4.032 10.336 L 0.24000001 -0.94400007 L 0.896 -0.94400007 Z "/>
</symbol>
</defs>
</div>
Setup
本书使用mdbook构建,托管于github.io,以WSL环境为例,记录一下构建过程。
安装
安装WSL
略
打开WSL
安装Rust
curl --proto '=https' --tlsv1.2 -sSf https://sh.rustup.rs | sh
验证安装是否成功:
rustc --version
安装mdbook
cargo install mdbook
构建并运行
创建mdbook项目
mdbook init paper
- 是否需要
.gitignore文件:y - 输入项目名称:
paper_reading(后续可在book.toml中更改)
构建mdbook
在/paper目录下执行:
- 构建项目:
mdbook build
- 或是在浏览器中实时预览:
mdbook serve
部署
- 新建Github仓库,将项目上传至仓库。
- 在顶栏目录中找到
Actions,搜索mdbook,点击Configure,自动生成.yml文件。点击Commit Changes提交。 - 在顶栏目录中找到
Settings,在侧边栏中找到Pages,在Build and deployment下找到Source,选择Github Actions。 - 第二步会在
/paper下创建./.github/workflows/mdbook.yml文件,在本地pull更改。 - 之后本地修改内容后push到仓库,Github Actions会自动构建并部署。访问
https://<username>.github.io/<reponame>/即可查看。