Hierarchical Navigable Small World Graphs

Introduction

important

HNSW是ANNS最佳索引之一。

note

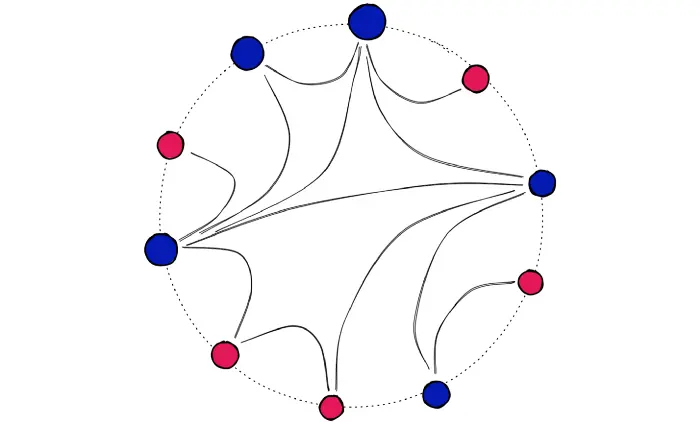
NSW 是一种所有顶点都与最近的一些邻居相连的图。

一张可视化的NSW图。（但是不清楚“所有顶点都与最近的一些邻居相连”如何理解） NSW

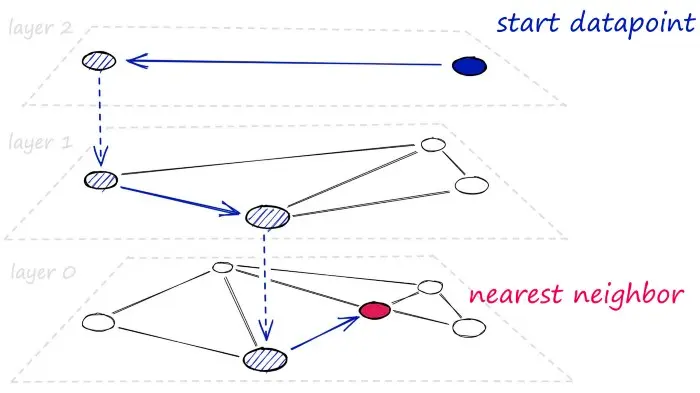
HNSW将NSW分解成多层来构建，每个新增的层都消除了一些顶点到顶点的中间连接。

HNSW

Probability Skip List

跳表能像排序数组一样快速进行搜索，同时也能使用链表结构快速插入新元素。

跳表的实现方式是构建多层次的链表，在第一层找到跳过很多中间节点的连接，随着向下移动层，每个链接跳过的节点会减少。

搜索时，从具有最长跳跃长度的最高层开始，沿着边朝右（下）方移动，如果下一跳的值大于我们要搜索的值，那么就向下移动一层再进行搜索。

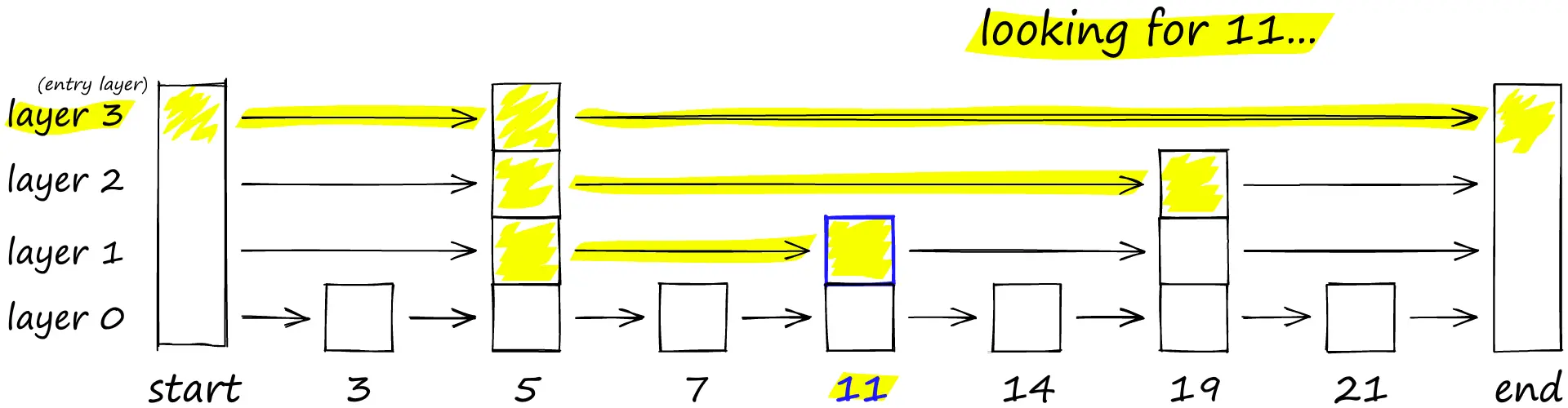
SkipList

HNSW 继承了相同的分层设计格式，高层的边较长（用于快速搜索），低层的边较短（用于准确搜索）。

Navigable Small World Graphs

可导航的小世界(NSW)图的向量搜索理念是：采用邻近图，但同时为其构建短距离和长距离连接，则搜索时间将缩短至（多/poly）对数/logarithmic复杂度。

在搜索NSW图时，我们从预定义的入口点开始，每次搜索时寻找最接近查询点的向量，并移动到该点。

最终，我们将找不到比当前顶点更接近查询点的点——这是一个局部最小值，作为结束查询的条件。

nswsearch

当一个具有大量节点的网络中存在图不可导航时，这种贪心搜搜的策略有效性大大降低。

路由（通过图的路线）由两阶段组成：

首先是缩小（zoom-out）阶段，通过低度节点。
然后是放大（zoom-in）阶段，通过高度节点。

zoom

因为缩小的条件是找不到下一跳的节点更接近查询点，所以我们在zoom-out阶段更有可能因为到达局部最小值而过早停止。

为了尽量减少提前结束搜索的概率（并提高召回率），我们可以增加节点的平均度数，但同时这会增加网络的复杂性（显著增加内存占用）和搜索时间。

另一个方法是从高度节点开始搜索（先zoom-in），这样确实能增加低维数据上的性能，这也是HNSW结构中一个重要因素。

HNSW是NSW的自然演进，为NSW添加层次结构生成的图结构其中的链接分散在不同层上

在顶层，有最长的链接
在底层，有最短的链接

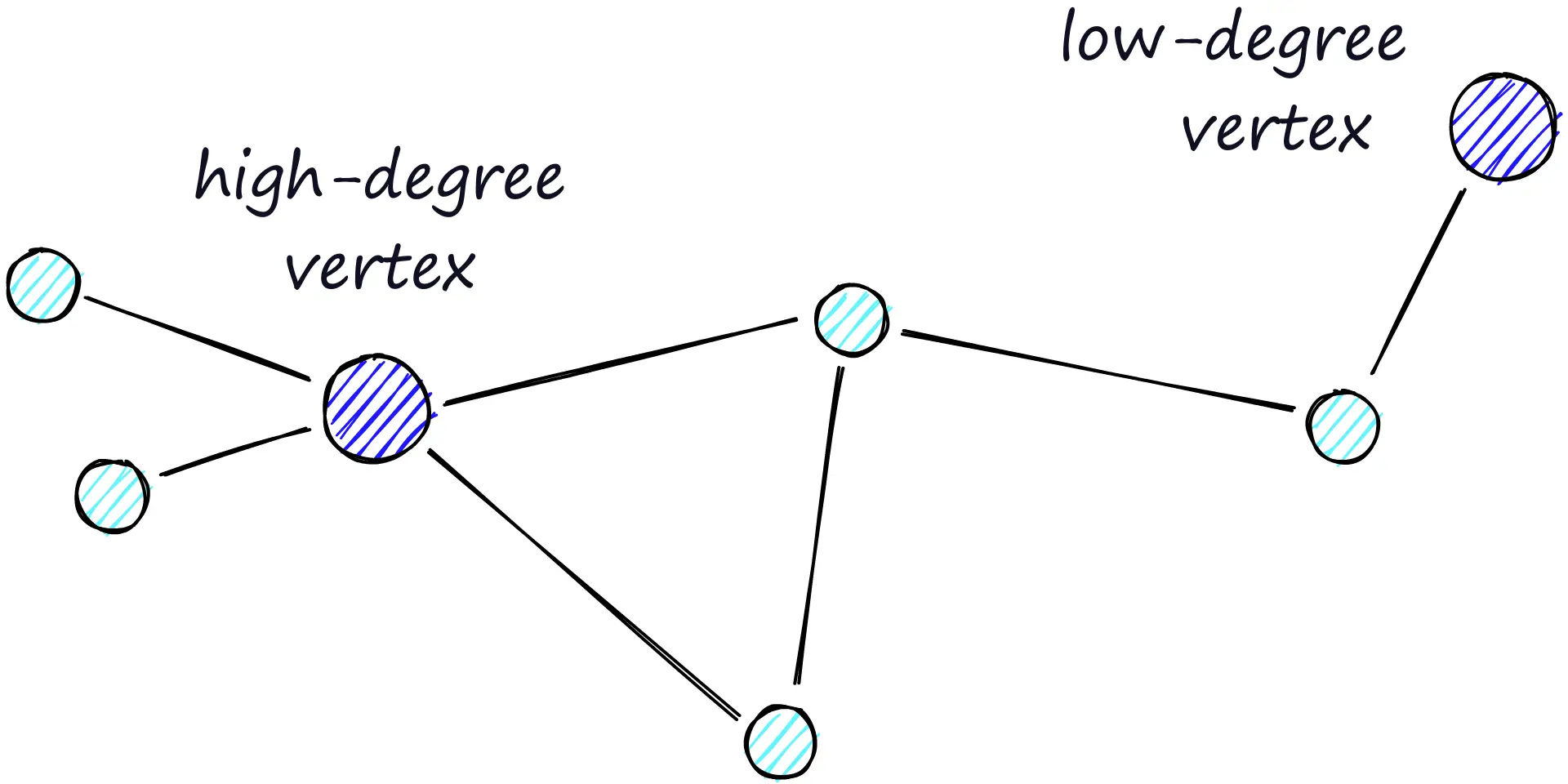
搜索时总是从顶层出发，这里链接最长，而且这些顶点往往是高度数的顶点（链接分散在每一层上），这意味着HNSW默认从NSW描述中的zoom-in阶段开始。

Algorithm

Construction

在构建图的过程中，向量会逐个插入。层数由参数L表示。

向量插入到哪一层是由m_L（level mutilplier）决定的，当m_L为0时表示向量仅插入到第0层，向量会被插入到该层及其以下所有层。

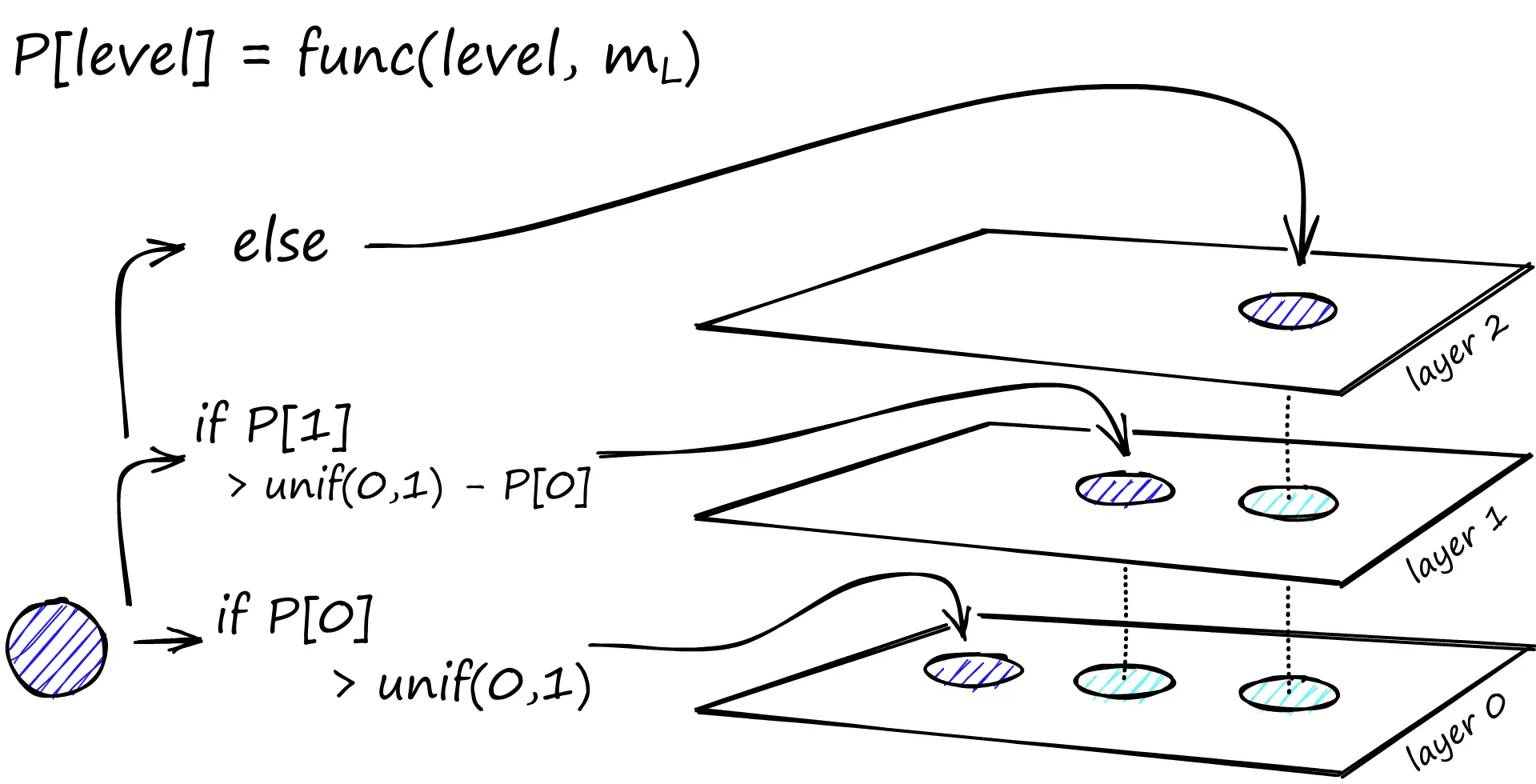
HNSWConstruction

note

当最小化重复跨层共享的邻居（每一个顶点都会出现在下面的层，但是边（邻居关系）不是，这条规则的目的是减少跨层重复的边），可以获得最佳性能。

减少m_L可以帮助最小化重叠（将更多的向量推送到0层），但这会增加搜索期间遍历的次数。

因此需要权衡m_L的值。一个经验值是 $\frac{1}{l n ( M )}$

第一阶段：在待插入的层级之上：
1. 从顶层开始，找到距待插入向量q最近的点（W，ef = 1），作为下一层的入口点
第二阶段：在待插入的层级及以下：
1. 将上一层的候选列表作为这一层的入口点。（入口点即预先放入这一层候选列表中的点）
2. 搜索据插入点q最近的ef=ef_construction个点，产生候选列表W
3. 从W中为插入点q选择M个邻居（最近 or 启发式）
4. 为q和邻居添加双向边，检查邻居的连接数是否超过Mmax（第0层则为Mmax0），若超过则重新选择Mmax个邻居
如果为插入点分配的层级大于当前顶层，则将HNSW图的入口点设置为q

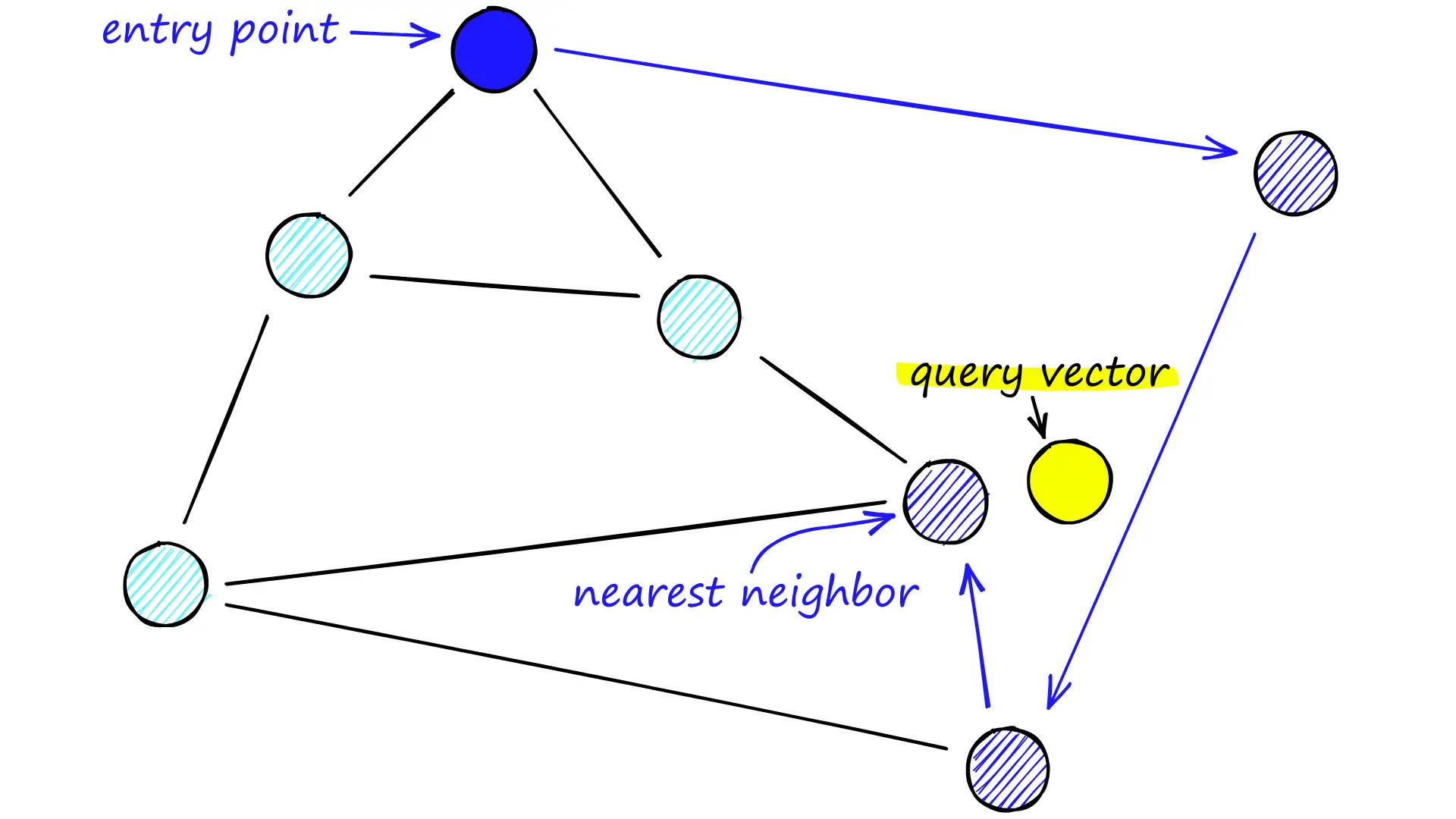
Search nearest neighbors

将已访问集合v，候选集合C，最近邻集合W初始化为入口点ep
当候选集不为空时：
1. 若候选集C中距插入点q最近的元素c的距离大于最近邻集中距插入点最远的元素f的距离，则停止。
2. 对于候选集C中的每一个点，访问它们的邻居e，如果邻居e未被访问：
  1. 添加到已访问集v
  2. 若e距q的距离比最近邻集中最远的点f还要近，或者最近邻集W未满（ef）则将e添加到候选集和最近邻集中。
  3. 保持最近邻集元素不超过ef个

Implementation

# set HNSW index parameters
M = 64  # number of connections each vertex will have
ef_search = 32  # depth of layers explored during search
ef_construction = 64  # depth of layers explored during index construction

# initialize index (d == 128)
index = faiss.IndexHNSWFlat(d, M)
# set efConstruction and efSearch parameters
index.hnsw.efConstruction = ef_construction
index.hnsw.efSearch = ef_search
# add data to index
index.add(wb)

# search as usual
D, I = index.search(wb, k)

	M	efSearch	efConstruction
含义	每个顶点的连接数	搜索时队列的长度	构建时队列的长度

分析

初始化HNSW

# setup our HNSW parameters
d = 128  # vector size
M = 32

index = faiss.IndexHNSWFlat(d, M)
print(index.hnsw) #<faiss.swigfaiss.HNSW; proxy of <Swig Object of type 'faiss::HNSW *' at 0x7f91183ef120> >

M_max 值默认设置为M ， M_max0设置为M*2

在使用index.add(xb)构建index之前，我们会发现层数（或 Faiss 中的级别）尚未设置：

# the HNSW index starts with no levels
index.hnsw.max_level # -1

# and levels (or layers) are empty too
levels = faiss.vector_to_array(index.hnsw.levels)
np.bincount(levels) # array([], dtype=int64)

如果我们继续建立索引，我们会发现这两个参数现在都已设置。

index.add(xb)

# after adding our data we will find that the level
# has been set automatically
index.hnsw.max_level # 4

# and levels (or layers) are now populated
levels = faiss.vector_to_array(index.hnsw.levels)
np.bincount(levels) # array([     0, 968746,  30276,    951,     26,      1], dtype=int64)

甚至可以找到哪个向量是我们的入口点：

index.hnsw.entry_point # 118295

HNSW不同参数下性能表现部分将放在Comparison中讨论。

锟斤拷烫烫烫